Análisis de Complete Works de William Shakespeare
Índice
Información General
| Título: | Complete Works |
|---|
| Autor: | William Shakespeare |
|---|
| Idioma: | Inglés |
|---|
| #Palabras total: | 910657 |
|---|
| #Palabras distintas: | 23514 |
|---|
| Type-Token ratio: | 2.58% |
|---|
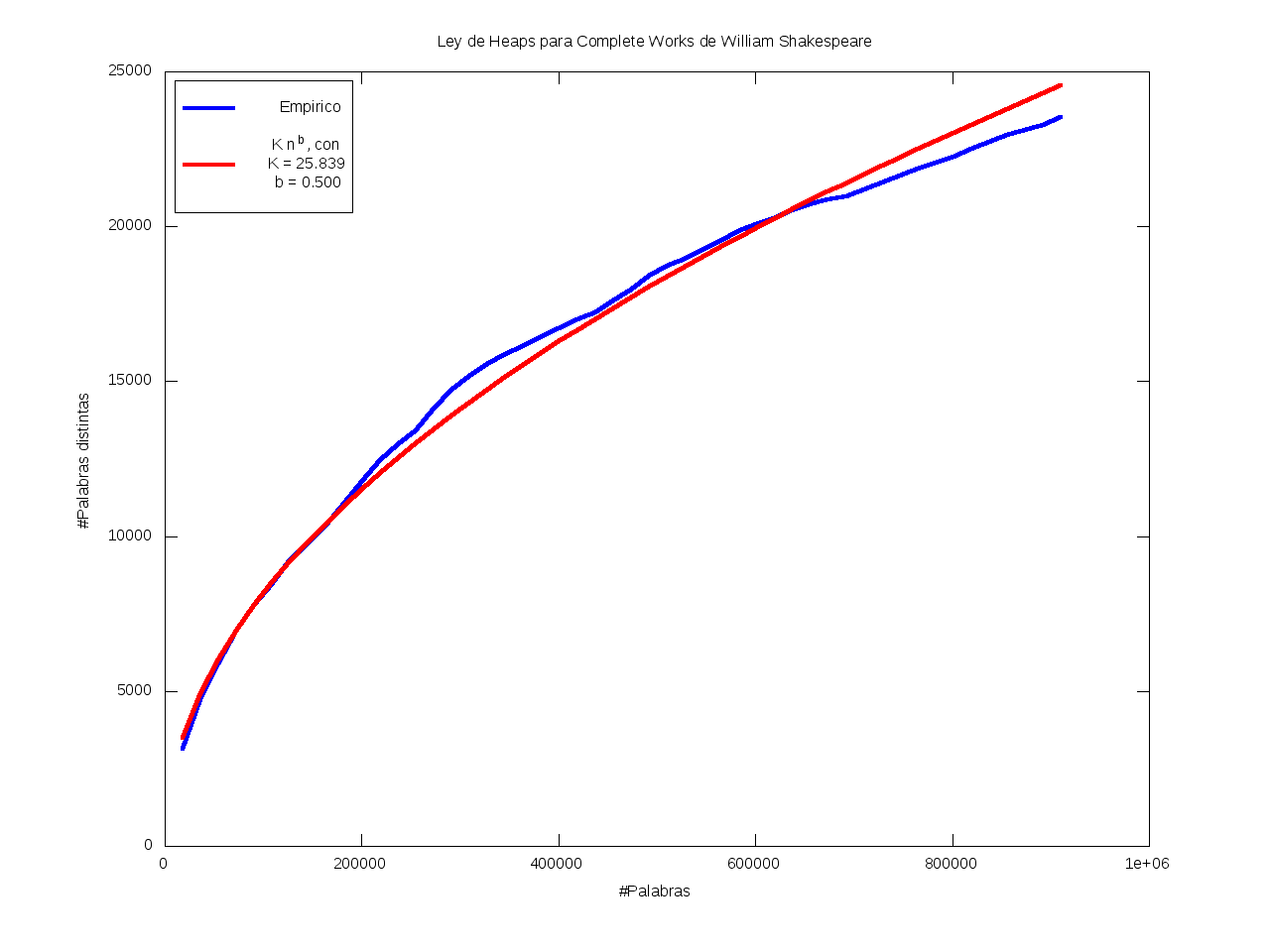
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| #Palabras: | #Palabras distintas: |
|---|
| 18213 | 3132 |
| 36426 | 4740 |
| 54639 | 5898 |
| 72852 | 6940 |
| 91065 | 7779 |
| 109278 | 8464 |
| 127491 | 9207 |
| 145704 | 9792 |
| 163917 | 10373 |
| 182130 | 11067 |
| 200343 | 11770 |
| 218556 | 12454 |
| 236769 | 12952 |
| 254982 | 13425 |
| 273195 | 14118 |
| 291408 | 14738 |
| 309621 | 15177 |
| 327834 | 15559 |
| 346047 | 15883 |
| 364260 | 16133 |
| 382473 | 16427 |
| 400686 | 16710 |
| 418899 | 16994 |
| 437112 | 17222 |
| 455325 | 17597 |
| 473538 | 17963 |
| 491751 | 18393 |
| 509964 | 18717 |
| 528177 | 18960 |
| 546390 | 19233 |
| 564603 | 19512 |
| 582816 | 19841 |
| 601029 | 20057 |
| 619242 | 20259 |
| 637455 | 20525 |
| 655668 | 20705 |
| 673881 | 20868 |
| 692094 | 20981 |
| 710307 | 21198 |
| 728520 | 21408 |
| 746733 | 21643 |
| 764946 | 21866 |
| 783159 | 22061 |
| 801372 | 22254 |
| 819585 | 22492 |
| 837798 | 22735 |
| 856011 | 22961 |
| 874224 | 23108 |
| 892437 | 23273 |
| 910650 | 23514 |
| 910657 | 23514 |
|
Ajuste por mínimos cuadrados de los datos a K*n^b:
|
| K = 25.839 |
|
b = 0.500 |
|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Rank | Palabra | Frec |
|---|
| 1 | the | 27377 |
| 2 | and | 26084 |
| 3 | i | 22538 |
| 4 | to | 19771 |
| 5 | of | 17481 |
| 6 | a | 14725 |
| 7 | you | 13826 |
| 8 | my | 12489 |
| 9 | that | 11318 |
| 10 | in | 11112 |
| 11 | is | 9319 |
| 12 | d | 8960 |
| 13 | not | 8512 |
| 14 | with | 7791 |
| 15 | me | 7777 |
| 16 | it | 7725 |
| 17 | s | 7721 |
| 18 | for | 7655 |
| 19 | be | 6897 |
| 20 | his | 6859 |
| 21 | he | 6679 |
| 22 | your | 6657 |
| 23 | this | 6608 |
| 24 | but | 6277 |
| 25 | have | 5902 |
| 26 | as | 5749 |
| 27 | thou | 5549 |
| 28 | him | 5205 |
| 29 | so | 5058 |
| 30 | will | 5008 |
| 31 | what | 4808 |
| 32 | thy | 4034 |
| 33 | all | 3960 |
| 34 | her | 3850 |
| 35 | do | 3828 |
| 36 | no | 3797 |
| 37 | by | 3793 |
| 38 | we | 3614 |
| 39 | shall | 3600 |
| 40 | if | 3511 |
| 41 | are | 3446 |
| 42 | on | 3188 |
| 43 | thee | 3181 |
| 44 | lord | 3094 |
| 45 | our | 3061 |
| 46 | o | 3053 |
| 47 | king | 3042 |
| 48 | good | 2834 |
| 49 | now | 2792 |
| 50 | sir | 2764 |
| 51 | from | 2647 |
| 52 | they | 2531 |
| 53 | come | 2519 |
| 54 | at | 2516 |
| 55 | or | 2429 |
| 56 | she | 2410 |
| 57 | ll | 2409 |
| 58 | let | 2369 |
| 59 | enter | 2357 |
| 60 | here | 2331 |
| 61 | which | 2321 |
| 62 | would | 2299 |
| 63 | more | 2292 |
| 64 | was | 2249 |
| 65 | well | 2241 |
| 66 | then | 2223 |
| 67 | there | 2210 |
| 68 | love | 2198 |
| 69 | am | 2168 |
| 70 | how | 2167 |
| 71 | their | 2075 |
| 72 | when | 2054 |
| 73 | man | 2034 |
| 74 | them | 1980 |
| 75 | hath | 1942 |
| 76 | an | 1890 |
| 77 | than | 1881 |
| 78 | one | 1806 |
| 79 | like | 1786 |
| 80 | upon | 1759 |
| 81 | say | 1758 |
| 82 | know | 1741 |
| 83 | go | 1741 |
| 84 | us | 1677 |
| 85 | may | 1644 |
| 86 | make | 1637 |
| 87 | did | 1629 |
| 88 | were | 1593 |
| 89 | yet | 1577 |
| 90 | should | 1576 |
| 91 | must | 1491 |
| 92 | why | 1476 |
| 93 | see | 1460 |
| 94 | had | 1428 |
| 95 | out | 1415 |
| 96 | tis | 1408 |
| 97 | such | 1397 |
| 98 | where | 1347 |
| 99 | give | 1345 |
| 100 | some | 1338 |
| 101 | these | 1323 |
| 102 | who | 1296 |
| 103 | too | 1235 |
| 104 | t | 1212 |
| 105 | can | 1212 |
| 106 | take | 1211 |
| 107 | speak | 1206 |
| 108 | most | 1182 |
| 109 | th | 1177 |
| 110 | mine | 1170 |
| 111 | first | 1170 |
| 112 | duke | 1127 |
| 113 | time | 1106 |
| 114 | up | 1092 |
| 115 | tell | 1083 |
| 116 | father | 1076 |
| 117 | think | 1073 |
| 118 | st | 1065 |
| 119 | heart | 1061 |
| 120 | much | 1037 |
| 121 | exeunt | 1035 |
| 122 | never | 1020 |
| 123 | exit | 984 |
| 124 | queen | 979 |
| 125 | nor | 970 |
| 126 | men | 958 |
| 127 | doth | 940 |
| 128 | look | 938 |
| 129 | art | 936 |
| 130 | day | 931 |
| 131 | lady | 927 |
| 132 | god | 925 |
| 133 | great | 921 |
| 134 | death | 900 |
| 135 | hear | 883 |
| 136 | life | 862 |
| 137 | away | 860 |
| 138 | hand | 854 |
| 139 | master | 844 |
| 140 | before | 839 |
| 141 | made | 834 |
| 142 | true | 818 |
| 143 | night | 816 |
| 144 | very | 813 |
| 145 | sweet | 807 |
| 146 | scene | 799 |
| 147 | thus | 781 |
| 148 | prince | 772 |
| 149 | own | 772 |
| 150 | fair | 770 |
| 151 | ay | 769 |
| 152 | again | 769 |
| 153 | cannot | 761 |
| 154 | pray | 757 |
| 155 | call | 753 |
| 156 | son | 721 |
| 157 | old | 714 |
| 158 | two | 713 |
| 159 | any | 707 |
| 160 | other | 703 |
| 161 | been | 698 |
| 162 | eyes | 685 |
| 163 | world | 679 |
| 164 | fear | 676 |
| 165 | blood | 667 |
| 166 | name | 666 |
| 167 | being | 664 |
| 168 | down | 663 |
| 169 | done | 663 |
| 170 | leave | 657 |
| 171 | heaven | 654 |
| 172 | brother | 645 |
| 173 | both | 644 |
| 174 | into | 643 |
| 175 | nothing | 636 |
| 176 | though | 634 |
| 177 | honour | 632 |
| 178 | poor | 631 |
| 179 | therefore | 627 |
| 180 | could | 627 |
| 181 | er | 625 |
| 182 | till | 619 |
| 183 | whose | 618 |
| 184 | comes | 617 |
| 185 | noble | 616 |
| 186 | henry | 612 |
| 187 | gloucester | 608 |
| 188 | ever | 608 |
| 189 | caesar | 608 |
| 190 | grace | 597 |
| 191 | better | 595 |
| 192 | against | 595 |
| 193 | nay | 589 |
| 194 | stand | 586 |
| 195 | hast | 585 |
| 196 | many | 578 |
| 197 | second | 571 |
| 198 | even | 571 |
| 199 | house | 569 |
| 200 | way | 568 |
| 201 | myself | 567 |
| 202 | still | 564 |
| 203 | bear | 553 |
| 204 | john | 551 |
| 205 | those | 545 |
| 206 | wife | 542 |
| 207 | peace | 539 |
| 208 | head | 537 |
| 209 | dead | 533 |
| 210 | find | 531 |
| 211 | france | 528 |
| 212 | gentleman | 523 |
| 213 | richard | 520 |
| 214 | antony | 520 |
| 215 | live | 514 |
| 216 | part | 509 |
| 217 | madam | 509 |
| 218 | word | 501 |
| 219 | off | 501 |
| 220 | put | 500 |
| 221 | might | 500 |
| 222 | york | 495 |
| 223 | show | 493 |
| 224 | within | 492 |
| 225 | every | 492 |
| 226 | keep | 487 |
| 227 | fool | 486 |
| 228 | little | 483 |
| 229 | brutus | 483 |
| 230 | long | 481 |
| 231 | die | 475 |
| 232 | friends | 474 |
| 233 | none | 469 |
| 234 | young | 467 |
| 235 | hold | 467 |
| 236 | lords | 466 |
| 237 | gone | 466 |
| 238 | aside | 466 |
| 239 | set | 465 |
| 240 | stay | 464 |
| 241 | soul | 464 |
| 242 | dear | 459 |
| 243 | thine | 457 |
| 244 | place | 457 |
| 245 | another | 455 |
| 246 | mistress | 453 |
| 247 | himself | 452 |
| 248 | falstaff | 452 |
| 249 | best | 450 |
| 250 | bring | 449 |
| 251 | friend | 446 |
| 252 | since | 445 |
| 253 | page | 438 |
| 254 | indeed | 438 |
| 255 | daughter | 438 |
| 256 | boy | 438 |
| 257 | mother | 437 |
| 258 | eye | 435 |
| 259 | unto | 430 |
| 260 | full | 430 |
| 261 | servant | 429 |
| 262 | dost | 429 |
| 263 | answer | 426 |
| 264 | whom | 424 |
| 265 | warwick | 424 |
| 266 | face | 423 |
| 267 | words | 421 |
| 268 | once | 421 |
| 269 | tongue | 420 |
| 270 | after | 420 |
| 271 | woman | 419 |
| 272 | else | 416 |
| 273 | three | 411 |
| 274 | faith | 408 |
| 275 | about | 400 |
| 276 | please | 391 |
| 277 | nature | 385 |
| 278 | has | 385 |
| 279 | said | 383 |
| 280 | act | 378 |
| 281 | thought | 377 |
| 282 | edward | 373 |
| 283 | gentle | 372 |
| 284 | forth | 372 |
| 285 | without | 368 |
| 286 | hence | 368 |
| 287 | mind | 366 |
| 288 | marry | 366 |
| 289 | ere | 366 |
| 290 | welcome | 365 |
| 291 | iago | 362 |
| 292 | fortune | 362 |
| 293 | turn | 360 |
| 294 | thing | 359 |
| 295 | rest | 358 |
| 296 | ham | 358 |
| 297 | matter | 357 |
| 298 | hope | 357 |
| 299 | play | 356 |
| 300 | makes | 356 |
| 301 | fall | 356 |
| 302 | sword | 355 |
| 303 | end | 355 |
| 304 | back | 355 |
| 305 | farewell | 353 |
| 306 | rome | 350 |
| 307 | right | 350 |
| 308 | clown | 350 |
| 309 | heard | 349 |
| 310 | timon | 348 |
| 311 | home | 342 |
| 312 | bid | 342 |
| 313 | truth | 338 |
| 314 | cause | 337 |
| 315 | came | 337 |
| 316 | follow | 336 |
| 317 | othello | 335 |
| 318 | things | 332 |
| 319 | england | 330 |
| 320 | meet | 327 |
| 321 | lie | 327 |
| 322 | husband | 327 |
| 323 | use | 326 |
| 324 | morrow | 326 |
| 325 | thousand | 325 |
| 326 | fellow | 325 |
| 327 | does | 325 |
| 328 | help | 324 |
| 329 | rather | 322 |
| 330 | kill | 322 |
| 331 | hands | 319 |
| 332 | news | 318 |
| 333 | earth | 317 |
| 334 | hour | 313 |
| 335 | enough | 313 |
| 336 | only | 312 |
| 337 | ring | 311 |
| 338 | state | 310 |
| 339 | pardon | 310 |
| 340 | bed | 308 |
| 341 | wilt | 307 |
| 342 | shame | 307 |
| 343 | power | 307 |
| 344 | get | 306 |
| 345 | re | 303 |
| 346 | crown | 302 |
| 347 | messenger | 300 |
| 348 | false | 299 |
| 349 | red | 297 |
| 350 | under | 296 |
| 351 | mean | 296 |
| 352 | shalt | 295 |
| 353 | thank | 294 |
| 354 | hither | 293 |
| 355 | ye | 292 |
| 356 | sure | 292 |
| 357 | macbeth | 291 |
| 358 | ford | 291 |
| 359 | honest | 289 |
| 360 | reason | 288 |
| 361 | gods | 287 |
| 362 | far | 286 |
| 363 | tears | 284 |
| 364 | youth | 283 |
| 365 | lay | 283 |
| 366 | fight | 283 |
| 367 | kind | 281 |
| 368 | yourself | 280 |
| 369 | cleopatra | 280 |
| 370 | body | 280 |
| 371 | ill | 279 |
| 372 | saw | 277 |
| 373 | wrong | 276 |
| 374 | war | 272 |
| 375 | soldier | 272 |
| 376 | cousin | 272 |
| 377 | new | 271 |
| 378 | majesty | 270 |
| 379 | light | 270 |
| 380 | wit | 269 |
| 381 | near | 269 |
| 382 | seen | 268 |
| 383 | last | 268 |
| 384 | fire | 268 |
| 385 | sent | 267 |
| 386 | swear | 265 |
| 387 | spirit | 265 |
| 388 | court | 265 |
| 389 | sleep | 264 |
| 390 | rosalind | 264 |
| 391 | means | 264 |
| 392 | through | 263 |
| 393 | mad | 263 |
| 394 | antonio | 263 |
| 395 | high | 262 |
| 396 | break | 262 |
| 397 | lucius | 261 |
| 398 | hot | 261 |
| 399 | send | 260 |
| 400 | suffolk | 259 |
| 401 | shallow | 258 |
| 402 | mark | 258 |
| 403 | buckingham | 258 |
| 404 | arms | 258 |
| 405 | together | 257 |
| 406 | lost | 257 |
| 407 | yours | 256 |
| 408 | villain | 253 |
| 409 | cassio | 253 |
| 410 | wish | 252 |
| 411 | strange | 252 |
| 412 | prove | 252 |
| 413 | troilus | 251 |
| 414 | while | 247 |
| 415 | thoughts | 247 |
| 416 | sea | 247 |
| 417 | return | 246 |
| 418 | present | 246 |
| 419 | letter | 246 |
| 420 | left | 246 |
| 421 | lies | 245 |
| 422 | fly | 245 |
| 423 | third | 244 |
| 424 | horse | 243 |
| 425 | child | 242 |
| 426 | between | 241 |
| 427 | speed | 240 |
| 428 | itself | 240 |
| 429 | believe | 240 |
| 430 | justice | 239 |
| 431 | devil | 239 |
| 432 | syracuse | 238 |
| 433 | says | 238 |
| 434 | hang | 238 |
| 435 | each | 238 |
| 436 | sun | 237 |
| 437 | same | 237 |
| 438 | beat | 237 |
| 439 | alone | 237 |
| 440 | talk | 236 |
| 441 | seek | 235 |
| 442 | half | 234 |
| 443 | valentine | 233 |
| 444 | told | 233 |
| 445 | lear | 233 |
| 446 | beauty | 233 |
| 447 | gave | 232 |
| 448 | business | 232 |
| 449 | titus | 230 |
| 450 | ha | 230 |
| 451 | breath | 230 |
| 452 | worthy | 229 |
| 453 | found | 229 |
| 454 | desdemona | 229 |
| 455 | cassius | 229 |
| 456 | bloody | 229 |
| 457 | foul | 227 |
| 458 | ne | 226 |
| 459 | alas | 226 |
| 460 | french | 225 |
| 461 | beseech | 225 |
| 462 | service | 223 |
| 463 | less | 223 |
| 464 | dromio | 223 |
| 465 | hector | 222 |
| 466 | gold | 222 |
| 467 | proteus | 221 |
| 468 | pity | 221 |
| 469 | people | 220 |
| 470 | law | 220 |
| 471 | antipholus | 220 |
| 472 | desire | 219 |
| 473 | sound | 218 |
| 474 | prithee | 218 |
| 475 | grief | 217 |
| 476 | care | 217 |
| 477 | seem | 216 |
| 478 | petruchio | 216 |
| 479 | mrs | 216 |
| 480 | land | 216 |
| 481 | angelo | 216 |
| 482 | general | 215 |
| 483 | cry | 215 |
| 484 | coriolanus | 215 |
| 485 | sit | 214 |
| 486 | looks | 214 |
| 487 | save | 213 |
| 488 | royal | 213 |
| 489 | knows | 213 |
| 490 | kiss | 213 |
| 491 | self | 212 |
| 492 | proud | 212 |
| 493 | gentlemen | 212 |
| 494 | uncle | 211 |
| 495 | soldiers | 211 |
| 496 | pompey | 211 |
| 497 | over | 211 |
| 498 | clarence | 211 |
| 499 | margaret | 210 |
| 500 | draw | 210 |
| 501 | nurse | 209 |
| 502 | ho | 209 |
| 503 | times | 208 |
| 504 | lose | 208 |
| 505 | days | 208 |
| 506 | dare | 208 |
| 507 | bastard | 208 |
| 508 | watch | 207 |
| 509 | toby | 207 |
| 510 | purpose | 207 |
| 511 | dog | 207 |
| 512 | company | 206 |
| 513 | yes | 205 |
| 514 | worth | 205 |
| 515 | wear | 205 |
| 516 | read | 205 |
| 517 | lives | 205 |
| 518 | sister | 204 |
| 519 | happy | 204 |
| 520 | music | 203 |
| 521 | age | 203 |
| 522 | cold | 202 |
| 523 | charge | 202 |
| 524 | sight | 201 |
| 525 | run | 201 |
| 526 | others | 199 |
| 527 | ear | 199 |
| 528 | quickly | 198 |
| 529 | loves | 198 |
| 530 | holy | 198 |
| 531 | gracious | 198 |
| 532 | thyself | 197 |
| 533 | born | 197 |
| 534 | berowne | 197 |
| 535 | strong | 196 |
| 536 | menenius | 196 |
| 537 | late | 196 |
| 538 | joy | 196 |
| 539 | brought | 196 |
| 540 | work | 195 |
| 541 | virtue | 195 |
| 542 | helena | 194 |
| 543 | sorrow | 193 |
| 544 | bardolph | 193 |
| 545 | yea | 192 |
| 546 | kent | 192 |
| 547 | field | 192 |
| 548 | ask | 192 |
| 549 | remember | 191 |
| 550 | given | 191 |
| 551 | patience | 190 |
| 552 | maid | 190 |
| 553 | highness | 189 |
| 554 | free | 189 |
| 555 | air | 189 |
| 556 | pass | 188 |
| 557 | pandarus | 188 |
| 558 | known | 188 |
| 559 | further | 188 |
| 560 | comfort | 188 |
| 561 | arm | 188 |
| 562 | years | 187 |
| 563 | serve | 187 |
| 564 | pistol | 187 |
| 565 | because | 187 |
| 566 | friar | 186 |
| 567 | citizen | 186 |
| 568 | portia | 185 |
| 569 | neither | 185 |
| 570 | wind | 184 |
| 571 | need | 184 |
| 572 | grave | 184 |
| 573 | something | 183 |
| 574 | money | 183 |
| 575 | hard | 183 |
| 576 | didst | 183 |
| 577 | country | 183 |
| 578 | ah | 183 |
| 579 | side | 182 |
| 580 | praise | 182 |
| 581 | mercy | 182 |
| 582 | foot | 182 |
| 583 | women | 181 |
| 584 | pleasure | 180 |
| 585 | cressida | 180 |
| 586 | claudio | 180 |
| 587 | bolingbroke | 180 |
| 588 | hate | 179 |
| 589 | sons | 178 |
| 590 | bound | 178 |
| 591 | anne | 178 |
| 592 | cut | 177 |
| 593 | captain | 177 |
| 594 | warrant | 176 |
| 595 | trust | 176 |
| 596 | sick | 176 |
| 597 | parolles | 175 |
| 598 | hell | 175 |
| 599 | certain | 175 |
| 600 | knave | 174 |
| 601 | hearts | 174 |
| 602 | goes | 174 |
| 603 | sake | 173 |
| 604 | princess | 173 |
| 605 | doubt | 173 |
| 606 | command | 173 |
| 607 | black | 173 |
| 608 | truly | 172 |
| 609 | talbot | 172 |
| 610 | em | 172 |
| 611 | canst | 172 |
| 612 | weep | 171 |
| 613 | thanks | 171 |
| 614 | ii | 171 |
| 615 | either | 171 |
| 616 | rich | 170 |
| 617 | merry | 170 |
| 618 | fault | 170 |
| 619 | heavy | 169 |
| 620 | host | 168 |
| 621 | ephesus | 167 |
| 622 | enemy | 167 |
| 623 | achilles | 167 |
| 624 | next | 166 |
| 625 | imogen | 166 |
| 626 | english | 166 |
| 627 | demetrius | 166 |
| 628 | sad | 165 |
| 629 | lov | 165 |
| 630 | knew | 165 |
| 631 | ground | 165 |
| 632 | wise | 164 |
| 633 | touch | 164 |
| 634 | took | 164 |
| 635 | orlando | 164 |
| 636 | cardinal | 164 |
| 637 | rom | 163 |
| 638 | haste | 163 |
| 639 | behold | 163 |
| 640 | twenty | 162 |
| 641 | fit | 162 |
| 642 | worse | 161 |
| 643 | twas | 161 |
| 644 | open | 161 |
| 645 | olivia | 161 |
| 646 | almost | 161 |
| 647 | palace | 160 |
| 648 | brave | 160 |
| 649 | themselves | 159 |
| 650 | sin | 159 |
| 651 | n | 159 |
| 652 | isabella | 159 |
| 653 | base | 159 |
| 654 | voice | 158 |
| 655 | content | 158 |
| 656 | coming | 158 |
| 657 | ears | 157 |
| 658 | drink | 157 |
| 659 | course | 157 |
| 660 | valiant | 156 |
| 661 | romeo | 156 |
| 662 | question | 156 |
| 663 | having | 156 |
| 664 | change | 156 |
| 665 | ten | 155 |
| 666 | stands | 155 |
| 667 | revenge | 155 |
| 668 | pedro | 155 |
| 669 | earl | 155 |
| 670 | strike | 154 |
| 671 | sovereign | 154 |
| 672 | fie | 154 |
| 673 | enobarbus | 154 |
| 674 | common | 154 |
| 675 | unless | 153 |
| 676 | straight | 153 |
| 677 | julia | 153 |
| 678 | northumberland | 152 |
| 679 | methinks | 152 |
| 680 | married | 152 |
| 681 | duty | 152 |
| 682 | door | 152 |
| 683 | past | 151 |
| 684 | four | 151 |
| 685 | fal | 151 |
| 686 | deed | 151 |
| 687 | oft | 150 |
| 688 | note | 150 |
| 689 | leontes | 150 |
| 690 | deep | 150 |
| 691 | appear | 150 |
| 692 | water | 149 |
| 693 | tender | 149 |
| 694 | person | 149 |
| 695 | lead | 149 |
| 696 | hastings | 149 |
| 697 | emilia | 149 |
| 698 | spoke | 148 |
| 699 | sirrah | 148 |
| 700 | report | 148 |
| 701 | hark | 148 |
| 702 | already | 148 |
| 703 | somerset | 147 |
| 704 | oath | 147 |
| 705 | needs | 147 |
| 706 | en | 147 |
| 707 | white | 146 |
| 708 | salisbury | 146 |
| 709 | point | 146 |
| 710 | lest | 146 |
| 711 | confess | 146 |
| 712 | above | 146 |
| 713 | suit | 145 |
| 714 | prospero | 145 |
| 715 | mouth | 145 |
| 716 | ladies | 145 |
| 717 | iii | 145 |
| 718 | gives | 145 |
| 719 | soon | 144 |
| 720 | sing | 144 |
| 721 | heavens | 144 |
| 722 | yield | 143 |
| 723 | ready | 143 |
| 724 | marcius | 143 |
| 725 | eat | 143 |
| 726 | withal | 142 |
| 727 | want | 142 |
| 728 | viola | 142 |
| 729 | london | 142 |
| 730 | become | 142 |
| 731 | wherefore | 141 |
| 732 | walk | 141 |
| 733 | presently | 141 |
| 734 | liege | 141 |
| 735 | duchess | 141 |
| 736 | deliver | 141 |
| 737 | city | 141 |
| 738 | attendants | 141 |
| 739 | sebastian | 140 |
| 740 | pay | 140 |
| 741 | just | 140 |
| 742 | hours | 140 |
| 743 | grow | 140 |
| 744 | five | 140 |
| 745 | fast | 140 |
| 746 | tranio | 139 |
| 747 | pluck | 139 |
| 748 | moon | 139 |
| 749 | clifford | 139 |
| 750 | bold | 139 |
| 751 | sicinius | 138 |
| 752 | paris | 138 |
| 753 | marcus | 138 |
| 754 | flesh | 138 |
| 755 | met | 137 |
| 756 | lips | 137 |
| 757 | flourish | 137 |
| 758 | favour | 137 |
| 759 | fare | 137 |
| 760 | deny | 137 |
| 761 | knight | 136 |
| 762 | bertram | 136 |
| 763 | wars | 135 |
| 764 | signior | 135 |
| 765 | pale | 135 |
| 766 | counsel | 135 |
| 767 | bene | 135 |
| 768 | traitor | 134 |
| 769 | lucio | 134 |
| 770 | sworn | 133 |
| 771 | march | 133 |
| 772 | dream | 133 |
| 773 | caius | 133 |
| 774 | apemantus | 133 |
| 775 | woe | 132 |
| 776 | wherein | 132 |
| 777 | slave | 132 |
| 778 | silvia | 132 |
| 779 | morning | 132 |
| 780 | count | 132 |
| 781 | wouldst | 131 |
| 782 | lucentio | 131 |
| 783 | fell | 131 |
| 784 | bosom | 131 |
| 785 | norfolk | 130 |
| 786 | letters | 130 |
| 787 | saint | 129 |
| 788 | posthumus | 129 |
| 789 | malvolio | 129 |
| 790 | guard | 129 |
| 791 | got | 129 |
| 792 | de | 129 |
| 793 | witness | 128 |
| 794 | town | 128 |
| 795 | spirits | 128 |
| 796 | speech | 128 |
| 797 | speaks | 128 |
| 798 | office | 128 |
| 799 | anon | 128 |
| 800 | ajax | 128 |
| 801 | slain | 127 |
| 802 | bassanio | 127 |
| 803 | banish | 127 |
| 804 | shepherd | 126 |
| 805 | chamber | 126 |
| 806 | celia | 126 |
| 807 | camillo | 126 |
| 808 | bad | 126 |
| 809 | thersites | 125 |
| 810 | sense | 125 |
| 811 | hero | 125 |
| 812 | glad | 125 |
| 813 | claud | 125 |
| 814 | charles | 125 |
| 815 | write | 124 |
| 816 | strength | 124 |
| 817 | soft | 124 |
| 818 | roman | 124 |
| 819 | lordship | 124 |
| 820 | fetch | 124 |
| 821 | armado | 124 |
| 822 | william | 123 |
| 823 | widow | 123 |
| 824 | twere | 123 |
| 825 | sport | 123 |
| 826 | children | 123 |
| 827 | often | 122 |
| 828 | conscience | 122 |
| 829 | wonder | 121 |
| 830 | whole | 121 |
| 831 | rage | 121 |
| 832 | mock | 121 |
| 833 | living | 121 |
| 834 | iv | 121 |
| 835 | cymbeline | 121 |
| 836 | countess | 121 |
| 837 | leon | 120 |
| 838 | learn | 120 |
| 839 | costard | 120 |
| 840 | behind | 120 |
| 841 | marriage | 119 |
| 842 | lion | 119 |
| 843 | lack | 119 |
| 844 | excellent | 119 |
| 845 | elizabeth | 119 |
| 846 | e | 119 |
| 847 | bless | 119 |
| 848 | attend | 119 |
| 849 | plain | 118 |
| 850 | loving | 118 |
| 851 | loss | 118 |
| 852 | lafeu | 118 |
| 853 | hortensio | 118 |
| 854 | hair | 118 |
| 855 | glou | 118 |
| 856 | deeds | 118 |
| 857 | baptista | 118 |
| 858 | vile | 117 |
| 859 | simple | 117 |
| 860 | pretty | 117 |
| 861 | kings | 117 |
| 862 | jul | 117 |
| 863 | hamlet | 117 |
| 864 | bianca | 117 |
| 865 | battle | 117 |
| 866 | seems | 116 |
| 867 | provost | 116 |
| 868 | action | 116 |
| 869 | win | 115 |
| 870 | whilst | 115 |
| 871 | ourselves | 115 |
| 872 | maria | 115 |
| 873 | harry | 115 |
| 874 | ulysses | 114 |
| 875 | souls | 114 |
| 876 | green | 114 |
| 877 | tale | 113 |
| 878 | laugh | 113 |
| 879 | hundred | 113 |
| 880 | dull | 113 |
| 881 | doctor | 113 |
| 882 | dauphin | 113 |
| 883 | begin | 113 |
| 884 | silence | 112 |
| 885 | longer | 112 |
| 886 | hostess | 112 |
| 887 | form | 112 |
| 888 | fashion | 112 |
| 889 | emperor | 112 |
| 890 | along | 112 |
| 891 | slender | 111 |
| 892 | quick | 111 |
| 893 | pride | 111 |
| 894 | parts | 111 |
| 895 | katherina | 111 |
| 896 | issue | 111 |
| 897 | grant | 111 |
| 898 | entreat | 111 |
| 899 | enemies | 111 |
| 900 | drum | 111 |
| 901 | shylock | 110 |
| 902 | servants | 110 |
| 903 | noise | 110 |
| 904 | mighty | 110 |
| 905 | macduff | 110 |
| 906 | hide | 110 |
| 907 | heads | 110 |
| 908 | cloten | 110 |
| 909 | case | 110 |
| 910 | cap | 110 |
| 911 | takes | 109 |
| 912 | katharine | 109 |
| 913 | hor | 109 |
| 914 | heir | 109 |
| 915 | going | 109 |
| 916 | fortunes | 109 |
| 917 | besides | 109 |
| 918 | woo | 108 |
| 919 | weak | 108 |
| 920 | scorn | 108 |
| 921 | promise | 108 |
| 922 | passion | 108 |
| 923 | offer | 108 |
| 924 | kate | 108 |
| 925 | feel | 108 |
| 926 | chief | 108 |
| 927 | suffer | 107 |
| 928 | roderigo | 107 |
| 929 | force | 107 |
| 930 | evans | 107 |
| 931 | castle | 107 |
| 932 | book | 107 |
| 933 | bears | 107 |
| 934 | throw | 106 |
| 935 | short | 106 |
| 936 | presence | 106 |
| 937 | low | 106 |
| 938 | bottom | 106 |
| 939 | worst | 105 |
| 940 | paper | 105 |
| 941 | masters | 105 |
| 942 | close | 105 |
| 943 | anything | 105 |
| 944 | worship | 104 |
| 945 | teach | 104 |
| 946 | subject | 104 |
| 947 | pisanio | 104 |
| 948 | judgment | 104 |
| 949 | jest | 104 |
| 950 | hermia | 104 |
| 951 | fools | 104 |
| 952 | died | 104 |
| 953 | cominius | 104 |
| 954 | charmian | 104 |
| 955 | chance | 104 |
| 956 | toward | 103 |
| 957 | shows | 103 |
| 958 | princes | 103 |
| 959 | poins | 103 |
| 960 | officer | 103 |
| 961 | lysander | 103 |
| 962 | health | 103 |
| 963 | dies | 103 |
| 964 | choose | 103 |
| 965 | went | 102 |
| 966 | troth | 102 |
| 967 | shake | 102 |
| 968 | moth | 102 |
| 969 | kingdom | 102 |
| 970 | honourable | 102 |
| 971 | awhile | 102 |
| 972 | wolsey | 101 |
| 973 | valour | 101 |
| 974 | respect | 101 |
| 975 | hadst | 101 |
| 976 | gates | 101 |
| 977 | gainst | 101 |
| 978 | feast | 101 |
| 979 | danger | 101 |
| 980 | cross | 101 |
| 981 | cast | 101 |
| 982 | buy | 101 |
| 983 | boyet | 101 |
| 984 | adieu | 101 |
| 985 | writ | 100 |
| 986 | least | 100 |
| 987 | gratiano | 100 |
| 988 | dangerous | 100 |
| 989 | curse | 100 |
| 990 | agamemnon | 100 |
| 991 | year | 99 |
| 992 | match | 99 |
| 993 | faults | 99 |
| 994 | edg | 99 |
| 995 | v | 98 |
| 996 | understand | 98 |
| 997 | quarrel | 98 |
| 998 | move | 98 |
| 999 | mortal | 98 |
| 1000 | kept | 98 |
| 1001 | herself | 98 |
| 1002 | harm | 98 |
| 1003 | exeter | 98 |
| 1004 | escalus | 98 |
| 1005 | cade | 98 |
| 1006 | breast | 98 |
| 1007 | won | 97 |
| 1008 | wisdom | 97 |
| 1009 | whether | 97 |
| 1010 | vow | 97 |
| 1011 | virtuous | 97 |
| 1012 | foolish | 97 |
| 1013 | aufidius | 97 |
| 1014 | army | 97 |
| 1015 | aaron | 97 |
| 1016 | wert | 96 |
| 1017 | tent | 96 |
| 1018 | ta | 96 |
| 1019 | seal | 96 |
| 1020 | offence | 96 |
| 1021 | laid | 96 |
| 1022 | iachimo | 96 |
| 1023 | hubert | 96 |
| 1024 | grumio | 96 |
| 1025 | fine | 96 |
| 1026 | fill | 96 |
| 1027 | beg | 96 |
| 1028 | beard | 96 |
| 1029 | stop | 95 |
| 1030 | receive | 95 |
| 1031 | poison | 95 |
| 1032 | murderer | 95 |
| 1033 | measure | 95 |
| 1034 | labour | 95 |
| 1035 | forget | 95 |
| 1036 | dinner | 95 |
| 1037 | brain | 95 |
| 1038 | witch | 94 |
| 1039 | westmoreland | 94 |
| 1040 | taken | 94 |
| 1041 | small | 94 |
| 1042 | rosaline | 94 |
| 1043 | plague | 94 |
| 1044 | order | 94 |
| 1045 | hearing | 94 |
| 1046 | consent | 94 |
| 1047 | ass | 94 |
| 1048 | angry | 94 |
| 1049 | among | 94 |
| 1050 | troy | 93 |
| 1051 | stood | 93 |
| 1052 | lend | 93 |
| 1053 | ariel | 93 |
| 1054 | aguecheek | 93 |
| 1055 | treason | 92 |
| 1056 | thither | 92 |
| 1057 | sorry | 92 |
| 1058 | r | 92 |
| 1059 | prison | 92 |
| 1060 | perceive | 92 |
| 1061 | judge | 92 |
| 1062 | gremio | 92 |
| 1063 | dispatch | 92 |
| 1064 | calls | 92 |
| 1065 | wild | 91 |
| 1066 | try | 91 |
| 1067 | title | 91 |
| 1068 | sings | 91 |
| 1069 | senator | 91 |
| 1070 | pains | 91 |
| 1071 | jack | 91 |
| 1072 | golden | 91 |
| 1073 | brief | 91 |
| 1074 | adriana | 91 |
| 1075 | trumpet | 90 |
| 1076 | thence | 90 |
| 1077 | tamora | 90 |
| 1078 | stephano | 90 |
| 1079 | reads | 90 |
| 1080 | piece | 90 |
| 1081 | patient | 90 |
| 1082 | hurt | 90 |
| 1083 | humour | 90 |
| 1084 | grey | 90 |
| 1085 | fresh | 90 |
| 1086 | forward | 90 |
| 1087 | fearful | 90 |
| 1088 | drawn | 90 |
| 1089 | double | 90 |
| 1090 | commend | 90 |
| 1091 | colour | 90 |
| 1092 | alive | 90 |
| 1093 | summer | 89 |
| 1094 | join | 89 |
| 1095 | forgot | 89 |
| 1096 | fluellen | 89 |
| 1097 | fled | 89 |
| 1098 | carry | 89 |
| 1099 | burn | 89 |
| 1100 | whither | 88 |
| 1101 | touchstone | 88 |
| 1102 | purse | 88 |
| 1103 | ours | 88 |
| 1104 | lewis | 88 |
| 1105 | jove | 88 |
| 1106 | jaques | 88 |
| 1107 | glory | 88 |
| 1108 | drown | 88 |
| 1109 | corn | 88 |
| 1110 | alarum | 88 |
| 1111 | song | 87 |
| 1112 | shape | 87 |
| 1113 | percy | 87 |
| 1114 | officers | 87 |
| 1115 | moor | 87 |
| 1116 | honesty | 87 |
| 1117 | diomedes | 87 |
| 1118 | constable | 87 |
| 1119 | broke | 87 |
| 1120 | boys | 87 |
| 1121 | birth | 87 |
| 1122 | venice | 86 |
| 1123 | trumpets | 86 |
| 1124 | thrice | 86 |
| 1125 | quite | 86 |
| 1126 | pol | 86 |
| 1127 | paulina | 86 |
| 1128 | greater | 86 |
| 1129 | ghost | 86 |
| 1130 | coward | 86 |
| 1131 | clock | 86 |
| 1132 | wine | 85 |
| 1133 | walls | 85 |
| 1134 | train | 85 |
| 1135 | prayers | 85 |
| 1136 | helen | 85 |
| 1137 | held | 85 |
| 1138 | damn | 85 |
| 1139 | blow | 85 |
| 1140 | blind | 85 |
| 1141 | wounds | 84 |
| 1142 | steal | 84 |
| 1143 | polixenes | 84 |
| 1144 | opinion | 84 |
| 1145 | obey | 84 |
| 1146 | brook | 84 |
| 1147 | amen | 84 |
| 1148 | street | 83 |
| 1149 | prisoner | 83 |
| 1150 | monster | 83 |
| 1151 | making | 83 |
| 1152 | knock | 83 |
| 1153 | juliet | 83 |
| 1154 | feed | 83 |
| 1155 | dark | 83 |
| 1156 | borne | 83 |
| 1157 | blame | 83 |
| 1158 | aeneas | 83 |
| 1159 | whereof | 82 |
| 1160 | view | 82 |
| 1161 | tear | 82 |
| 1162 | stir | 82 |
| 1163 | safe | 82 |
| 1164 | proof | 82 |
| 1165 | launcelot | 82 |
| 1166 | launce | 82 |
| 1167 | holds | 82 |
| 1168 | citizens | 82 |
| 1169 | belarius | 82 |
| 1170 | vain | 81 |
| 1171 | tower | 81 |
| 1172 | shadow | 81 |
| 1173 | rogue | 81 |
| 1174 | motion | 81 |
| 1175 | manner | 81 |
| 1176 | lorenzo | 81 |
| 1177 | lancaster | 81 |
| 1178 | falls | 81 |
| 1179 | cheer | 81 |
| 1180 | wast | 80 |
| 1181 | taste | 80 |
| 1182 | pucelle | 80 |
| 1183 | peter | 80 |
| 1184 | folly | 80 |
| 1185 | wits | 79 |
| 1186 | whiles | 79 |
| 1187 | wall | 79 |
| 1188 | sudden | 79 |
| 1189 | several | 79 |
| 1190 | rise | 79 |
| 1191 | edm | 79 |
| 1192 | cheek | 79 |
| 1193 | camp | 79 |
| 1194 | burgundy | 79 |
| 1195 | brothers | 79 |
| 1196 | blessed | 79 |
| 1197 | ancient | 79 |
| 1198 | weary | 78 |
| 1199 | princely | 78 |
| 1200 | precious | 78 |
| 1201 | lieutenant | 78 |
| 1202 | la | 78 |
| 1203 | knowledge | 78 |
| 1204 | jew | 78 |
| 1205 | excuse | 78 |
| 1206 | desires | 78 |
| 1207 | awake | 78 |
| 1208 | although | 78 |
| 1209 | alack | 78 |
| 1210 | trouble | 77 |
| 1211 | sometime | 77 |
| 1212 | smile | 77 |
| 1213 | quiet | 77 |
| 1214 | plantagenet | 77 |
| 1215 | liv | 77 |
| 1216 | grows | 77 |
| 1217 | greatness | 77 |
| 1218 | fears | 77 |
| 1219 | due | 77 |
| 1220 | beggar | 77 |
| 1221 | approach | 77 |
| 1222 | wash | 76 |
| 1223 | wales | 76 |
| 1224 | until | 76 |
| 1225 | tongues | 76 |
| 1226 | struck | 76 |
| 1227 | serv | 76 |
| 1228 | murder | 76 |
| 1229 | keeps | 76 |
| 1230 | guiderius | 76 |
| 1231 | fellows | 76 |
| 1232 | endure | 76 |
| 1233 | dumain | 76 |
| 1234 | drop | 76 |
| 1235 | cunning | 76 |
| 1236 | catch | 76 |
| 1237 | bones | 76 |
| 1238 | aught | 76 |
| 1239 | affection | 76 |
| 1240 | whence | 75 |
| 1241 | thomas | 75 |
| 1242 | terms | 75 |
| 1243 | round | 75 |
| 1244 | perform | 75 |
| 1245 | lavinia | 75 |
| 1246 | goodly | 75 |
| 1247 | doing | 75 |
| 1248 | banquo | 75 |
| 1249 | autolycus | 75 |
| 1250 | yonder | 74 |
| 1251 | twixt | 74 |
| 1252 | safety | 74 |
| 1253 | room | 74 |
| 1254 | occasion | 74 |
| 1255 | neck | 74 |
| 1256 | lo | 74 |
| 1257 | forgive | 74 |
| 1258 | forbid | 74 |
| 1259 | fabian | 74 |
| 1260 | bond | 74 |
| 1261 | bitter | 74 |
| 1262 | arthur | 74 |
| 1263 | yourselves | 73 |
| 1264 | wrongs | 73 |
| 1265 | wound | 73 |
| 1266 | winter | 73 |
| 1267 | shouldst | 73 |
| 1268 | scarce | 73 |
| 1269 | rude | 73 |
| 1270 | reg | 73 |
| 1271 | patroclus | 73 |
| 1272 | owe | 73 |
| 1273 | montague | 73 |
| 1274 | liberty | 73 |
| 1275 | heels | 73 |
| 1276 | foes | 73 |
| 1277 | casca | 73 |
| 1278 | brow | 73 |
| 1279 | biondello | 73 |
| 1280 | beast | 73 |
| 1281 | bearing | 73 |
| 1282 | archbishop | 73 |
| 1283 | wealth | 72 |
| 1284 | twice | 72 |
| 1285 | thurio | 72 |
| 1286 | seven | 72 |
| 1287 | rough | 72 |
| 1288 | ross | 72 |
| 1289 | proceed | 72 |
| 1290 | priest | 72 |
| 1291 | post | 72 |
| 1292 | orleans | 72 |
| 1293 | manners | 72 |
| 1294 | malice | 72 |
| 1295 | leaves | 72 |
| 1296 | large | 72 |
| 1297 | kneel | 72 |
| 1298 | humble | 72 |
| 1299 | george | 72 |
| 1300 | gaunt | 72 |
| 1301 | fat | 72 |
| 1302 | edmund | 72 |
| 1303 | dance | 72 |
| 1304 | cruel | 72 |
| 1305 | creature | 72 |
| 1306 | christian | 72 |
| 1307 | catesby | 72 |
| 1308 | caliban | 72 |
| 1309 | bright | 72 |
| 1310 | athens | 72 |
| 1311 | advantage | 72 |
| 1312 | wretched | 71 |
| 1313 | thunder | 71 |
| 1314 | stars | 71 |
| 1315 | sharp | 71 |
| 1316 | richmond | 71 |
| 1317 | philip | 71 |
| 1318 | humphrey | 71 |
| 1319 | hail | 71 |
| 1320 | guilty | 71 |
| 1321 | forest | 71 |
| 1322 | effect | 71 |
| 1323 | cheeks | 71 |
| 1324 | blows | 71 |
| 1325 | aumerle | 71 |
| 1326 | towards | 70 |
| 1327 | swift | 70 |
| 1328 | steel | 70 |
| 1329 | melancholy | 70 |
| 1330 | meat | 70 |
| 1331 | lepidus | 70 |
| 1332 | legs | 70 |
| 1333 | led | 70 |
| 1334 | gentlewoman | 70 |
| 1335 | fame | 70 |
| 1336 | drunk | 70 |
| 1337 | choice | 70 |
| 1338 | theseus | 69 |
| 1339 | swords | 69 |
| 1340 | spent | 69 |
| 1341 | sort | 69 |
| 1342 | silver | 69 |
| 1343 | possess | 69 |
| 1344 | pleas | 69 |
| 1345 | oaths | 69 |
| 1346 | honours | 69 |
| 1347 | dry | 69 |
| 1348 | diana | 69 |
| 1349 | cried | 69 |
| 1350 | benedick | 69 |
| 1351 | ways | 68 |
| 1352 | volumnia | 68 |
| 1353 | thief | 68 |
| 1354 | spend | 68 |
| 1355 | rose | 68 |
| 1356 | pure | 68 |
| 1357 | nose | 68 |
| 1358 | nestor | 68 |
| 1359 | mayst | 68 |
| 1360 | madness | 68 |
| 1361 | loud | 68 |
| 1362 | gonzalo | 68 |
| 1363 | glass | 68 |
| 1364 | follows | 68 |
| 1365 | flow | 68 |
| 1366 | embrace | 68 |
| 1367 | chamberlain | 68 |
| 1368 | bow | 68 |
| 1369 | blunt | 68 |
| 1370 | ben | 68 |
| 1371 | affairs | 68 |
| 1372 | wood | 67 |
| 1373 | vows | 67 |
| 1374 | tribunes | 67 |
| 1375 | throne | 67 |
| 1376 | story | 67 |
| 1377 | stone | 67 |
| 1378 | stain | 67 |
| 1379 | rain | 67 |
| 1380 | pain | 67 |
| 1381 | merchant | 67 |
| 1382 | katherine | 67 |
| 1383 | idle | 67 |
| 1384 | heat | 67 |
| 1385 | fiend | 67 |
| 1386 | fail | 67 |
| 1387 | courage | 67 |
| 1388 | chain | 67 |
| 1389 | bestow | 67 |
| 1390 | argument | 67 |
| 1391 | winchester | 66 |
| 1392 | request | 66 |
| 1393 | remain | 66 |
| 1394 | quoth | 66 |
| 1395 | private | 66 |
| 1396 | nerissa | 66 |
| 1397 | mowbray | 66 |
| 1398 | knee | 66 |
| 1399 | gift | 66 |
| 1400 | fury | 66 |
| 1401 | fought | 66 |
| 1402 | finger | 66 |
| 1403 | fain | 66 |
| 1404 | depart | 66 |
| 1405 | defend | 66 |
| 1406 | clear | 66 |
| 1407 | church | 66 |
| 1408 | becomes | 66 |
| 1409 | tybalt | 65 |
| 1410 | study | 65 |
| 1411 | secret | 65 |
| 1412 | saturninus | 65 |
| 1413 | proper | 65 |
| 1414 | prepare | 65 |
| 1415 | pow | 65 |
| 1416 | mortimer | 65 |
| 1417 | miranda | 65 |
| 1418 | lover | 65 |
| 1419 | food | 65 |
| 1420 | few | 65 |
| 1421 | easy | 65 |
| 1422 | deserve | 65 |
| 1423 | courtesy | 65 |
| 1424 | wicked | 64 |
| 1425 | stuff | 64 |
| 1426 | reasons | 64 |
| 1427 | poet | 64 |
| 1428 | paid | 64 |
| 1429 | niece | 64 |
| 1430 | monstrous | 64 |
| 1431 | lucetta | 64 |
| 1432 | keeper | 64 |
| 1433 | gate | 64 |
| 1434 | eros | 64 |
| 1435 | colours | 64 |
| 1436 | claim | 64 |
| 1437 | breathe | 64 |
| 1438 | abroad | 64 |
| 1439 | twill | 63 |
| 1440 | remembrance | 63 |
| 1441 | nym | 63 |
| 1442 | leonato | 63 |
| 1443 | leisure | 63 |
| 1444 | hermione | 63 |
| 1445 | gain | 63 |
| 1446 | forsworn | 63 |
| 1447 | former | 63 |
| 1448 | foe | 63 |
| 1449 | evil | 63 |
| 1450 | cries | 63 |
| 1451 | bare | 63 |
| 1452 | arviragus | 63 |
| 1453 | always | 63 |
| 1454 | wives | 62 |
| 1455 | wench | 62 |
| 1456 | wait | 62 |
| 1457 | tune | 62 |
| 1458 | trinculo | 62 |
| 1459 | supper | 62 |
| 1460 | spring | 62 |
| 1461 | sooner | 62 |
| 1462 | six | 62 |
| 1463 | seeming | 62 |
| 1464 | mer | 62 |
| 1465 | laer | 62 |
| 1466 | horses | 62 |
| 1467 | holofernes | 62 |
| 1468 | flavius | 62 |
| 1469 | doors | 62 |
| 1470 | wanton | 61 |
| 1471 | tree | 61 |
| 1472 | stones | 61 |
| 1473 | spare | 61 |
| 1474 | sometimes | 61 |
| 1475 | sigh | 61 |
| 1476 | rascal | 61 |
| 1477 | proclaim | 61 |
| 1478 | nine | 61 |
| 1479 | lovers | 61 |
| 1480 | lawful | 61 |
| 1481 | instant | 61 |
| 1482 | humbly | 61 |
| 1483 | grown | 61 |
| 1484 | broken | 61 |
| 1485 | alcibiades | 61 |
| 1486 | weeping | 60 |
| 1487 | tyrant | 60 |
| 1488 | trial | 60 |
| 1489 | top | 60 |
| 1490 | table | 60 |
| 1491 | subjects | 60 |
| 1492 | stol | 60 |
| 1493 | ry | 60 |
| 1494 | receiv | 60 |
| 1495 | pyramus | 60 |
| 1496 | offend | 60 |
| 1497 | ned | 60 |
| 1498 | mend | 60 |
| 1499 | meaning | 60 |
| 1500 | mayor | 60 |
| 1501 | malcolm | 60 |
| 1502 | longaville | 60 |
| 1503 | list | 60 |
| 1504 | le | 60 |
| 1505 | jewel | 60 |
| 1506 | herald | 60 |
| 1507 | giving | 60 |
| 1508 | florizel | 60 |
| 1509 | discourse | 60 |
| 1510 | demand | 60 |
| 1511 | crowns | 60 |
| 1512 | beyond | 60 |
| 1513 | asleep | 60 |
| 1514 | anger | 60 |
| 1515 | wretch | 59 |
| 1516 | wide | 59 |
| 1517 | weigh | 59 |
| 1518 | thinks | 59 |
| 1519 | storm | 59 |
| 1520 | stanley | 59 |
| 1521 | spite | 59 |
| 1522 | sits | 59 |
| 1523 | single | 59 |
| 1524 | shut | 59 |
| 1525 | ship | 59 |
| 1526 | senators | 59 |
| 1527 | seat | 59 |
| 1528 | rs | 59 |
| 1529 | repent | 59 |
| 1530 | remedy | 59 |
| 1531 | ransom | 59 |
| 1532 | powers | 59 |
| 1533 | ones | 59 |
| 1534 | murther | 59 |
| 1535 | mar | 59 |
| 1536 | jessica | 59 |
| 1537 | hit | 59 |
| 1538 | elbow | 59 |
| 1539 | dust | 59 |
| 1540 | dreadful | 59 |
| 1541 | condition | 59 |
| 1542 | clouds | 59 |
| 1543 | andronicus | 59 |
| 1544 | able | 59 |
| 1545 | warlike | 58 |
| 1546 | traitors | 58 |
| 1547 | spoken | 58 |
| 1548 | sack | 58 |
| 1549 | rivers | 58 |
| 1550 | possible | 58 |
| 1551 | oph | 58 |
| 1552 | nought | 58 |
| 1553 | neighbour | 58 |
| 1554 | natural | 58 |
| 1555 | mere | 58 |
| 1556 | memory | 58 |
| 1557 | forbear | 58 |
| 1558 | fond | 58 |
| 1559 | flies | 58 |
| 1560 | feet | 58 |
| 1561 | fairy | 58 |
| 1562 | cupid | 58 |
| 1563 | consider | 58 |
| 1564 | alb | 58 |
| 1565 | aid | 58 |
| 1566 | wrath | 57 |
| 1567 | shore | 57 |
| 1568 | sheep | 57 |
| 1569 | ride | 57 |
| 1570 | rare | 57 |
| 1571 | oliver | 57 |
| 1572 | luciana | 57 |
| 1573 | horns | 57 |
| 1574 | happiness | 57 |
| 1575 | fancy | 57 |
| 1576 | buried | 57 |
| 1577 | bids | 57 |
| 1578 | betray | 57 |
| 1579 | beatrice | 57 |
| 1580 | agrippa | 57 |
| 1581 | thrive | 56 |
| 1582 | therein | 56 |
| 1583 | teeth | 56 |
| 1584 | sum | 56 |
| 1585 | saying | 56 |
| 1586 | rank | 56 |
| 1587 | protector | 56 |
| 1588 | oxford | 56 |
| 1589 | minds | 56 |
| 1590 | hopes | 56 |
| 1591 | gross | 56 |
| 1592 | griefs | 56 |
| 1593 | goodness | 56 |
| 1594 | delight | 56 |
| 1595 | dearest | 56 |
| 1596 | daughters | 56 |
| 1597 | cure | 56 |
| 1598 | countenance | 56 |
| 1599 | blush | 56 |
| 1600 | betwixt | 56 |
| 1601 | womb | 55 |
| 1602 | wings | 55 |
| 1603 | voices | 55 |
| 1604 | visit | 55 |
| 1605 | undone | 55 |
| 1606 | turns | 55 |
| 1607 | slow | 55 |
| 1608 | romans | 55 |
| 1609 | reverend | 55 |
| 1610 | quince | 55 |
| 1611 | quality | 55 |
| 1612 | puck | 55 |
| 1613 | perfect | 55 |
| 1614 | particular | 55 |
| 1615 | knife | 55 |
| 1616 | heavenly | 55 |
| 1617 | gallant | 55 |
| 1618 | envy | 55 |
| 1619 | entertain | 55 |
| 1620 | doom | 55 |
| 1621 | denied | 55 |
| 1622 | counterfeit | 55 |
| 1623 | charity | 55 |
| 1624 | begins | 55 |
| 1625 | authority | 55 |
| 1626 | angel | 55 |
| 1627 | absence | 55 |
| 1628 | tomb | 54 |
| 1629 | thrust | 54 |
| 1630 | thisby | 54 |
| 1631 | sign | 54 |
| 1632 | sickness | 54 |
| 1633 | pound | 54 |
| 1634 | plot | 54 |
| 1635 | lands | 54 |
| 1636 | intend | 54 |
| 1637 | freely | 54 |
| 1638 | flatter | 54 |
| 1639 | enjoy | 54 |
| 1640 | ease | 54 |
| 1641 | despair | 54 |
| 1642 | blest | 54 |
| 1643 | vice | 53 |
| 1644 | trick | 53 |
| 1645 | treasure | 53 |
| 1646 | slander | 53 |
| 1647 | seeing | 53 |
| 1648 | realm | 53 |
| 1649 | puts | 53 |
| 1650 | public | 53 |
| 1651 | protest | 53 |
| 1652 | promis | 53 |
| 1653 | painted | 53 |
| 1654 | menas | 53 |
| 1655 | meeting | 53 |
| 1656 | meant | 53 |
| 1657 | maintain | 53 |
| 1658 | lovely | 53 |
| 1659 | heed | 53 |
| 1660 | guess | 53 |
| 1661 | gower | 53 |
| 1662 | gon | 53 |
| 1663 | flight | 53 |
| 1664 | ferdinand | 53 |
| 1665 | faces | 53 |
| 1666 | encounter | 53 |
| 1667 | ducats | 53 |
| 1668 | drops | 53 |
| 1669 | deal | 53 |
| 1670 | britain | 53 |
| 1671 | brings | 53 |
| 1672 | wake | 52 |
| 1673 | vouchsafe | 52 |
| 1674 | vengeance | 52 |
| 1675 | tidings | 52 |
| 1676 | tide | 52 |
| 1677 | skill | 52 |
| 1678 | obedience | 52 |
| 1679 | number | 52 |
| 1680 | naked | 52 |
| 1681 | mirth | 52 |
| 1682 | kindness | 52 |
| 1683 | innocent | 52 |
| 1684 | hers | 52 |
| 1685 | frown | 52 |
| 1686 | followers | 52 |
| 1687 | despite | 52 |
| 1688 | chiron | 52 |
| 1689 | below | 52 |
| 1690 | y | 51 |
| 1691 | warm | 51 |
| 1692 | throat | 51 |
| 1693 | tailor | 51 |
| 1694 | swore | 51 |
| 1695 | smell | 51 |
| 1696 | sleeping | 51 |
| 1697 | shed | 51 |
| 1698 | sail | 51 |
| 1699 | north | 51 |
| 1700 | merit | 51 |
| 1701 | knees | 51 |
| 1702 | greatest | 51 |
| 1703 | gown | 51 |
| 1704 | girl | 51 |
| 1705 | francis | 51 |
| 1706 | fourth | 51 |
| 1707 | following | 51 |
| 1708 | empty | 51 |
| 1709 | durst | 51 |
| 1710 | doll | 51 |
| 1711 | deadly | 51 |
| 1712 | dar | 51 |
| 1713 | credit | 51 |
| 1714 | council | 51 |
| 1715 | civil | 51 |
| 1716 | burning | 51 |
| 1717 | bought | 51 |
| 1718 | window | 50 |
| 1719 | taught | 50 |
| 1720 | surrey | 50 |
| 1721 | suddenly | 50 |
| 1722 | streets | 50 |
| 1723 | sighs | 50 |
| 1724 | seest | 50 |
| 1725 | search | 50 |
| 1726 | rule | 50 |
| 1727 | party | 50 |
| 1728 | outward | 50 |
| 1729 | modesty | 50 |
| 1730 | maiden | 50 |
| 1731 | loose | 50 |
| 1732 | learned | 50 |
| 1733 | jealous | 50 |
| 1734 | intent | 50 |
| 1735 | flower | 50 |
| 1736 | early | 50 |
| 1737 | dishonour | 50 |
| 1738 | devise | 50 |
| 1739 | desperate | 50 |
| 1740 | breed | 50 |
| 1741 | beaten | 50 |
| 1742 | assure | 50 |
| 1743 | appears | 50 |
| 1744 | alonso | 50 |
| 1745 | alencon | 50 |
| 1746 | winds | 49 |
| 1747 | virtues | 49 |
| 1748 | vincentio | 49 |
| 1749 | tonight | 49 |
| 1750 | stranger | 49 |
| 1751 | star | 49 |
| 1752 | spake | 49 |
| 1753 | shot | 49 |
| 1754 | salt | 49 |
| 1755 | reignier | 49 |
| 1756 | perchance | 49 |
| 1757 | names | 49 |
| 1758 | main | 49 |
| 1759 | lust | 49 |
| 1760 | kinsman | 49 |
| 1761 | hollow | 49 |
| 1762 | fish | 49 |
| 1763 | fiery | 49 |
| 1764 | estate | 49 |
| 1765 | ends | 49 |
| 1766 | employ | 49 |
| 1767 | egypt | 49 |
| 1768 | dread | 49 |
| 1769 | dogs | 49 |
| 1770 | divine | 49 |
| 1771 | disgrace | 49 |
| 1772 | convey | 49 |
| 1773 | constant | 49 |
| 1774 | chide | 49 |
| 1775 | bred | 49 |
| 1776 | bedford | 49 |
| 1777 | bark | 49 |
| 1778 | wont | 48 |
| 1779 | whore | 48 |
| 1780 | triumph | 48 |
| 1781 | thinking | 48 |
| 1782 | thieves | 48 |
| 1783 | success | 48 |
| 1784 | speaking | 48 |
| 1785 | satisfied | 48 |
| 1786 | salerio | 48 |
| 1787 | ruin | 48 |
| 1788 | reign | 48 |
| 1789 | prick | 48 |
| 1790 | plead | 48 |
| 1791 | mariana | 48 |
| 1792 | ignorant | 48 |
| 1793 | hereafter | 48 |
| 1794 | graces | 48 |
| 1795 | gifts | 48 |
| 1796 | garments | 48 |
| 1797 | forsooth | 48 |
| 1798 | execution | 48 |
| 1799 | dying | 48 |
| 1800 | draws | 48 |
| 1801 | don | 48 |
| 1802 | cup | 48 |
| 1803 | crack | 48 |
| 1804 | constance | 48 |
| 1805 | conduct | 48 |
| 1806 | condemn | 48 |
| 1807 | commission | 48 |
| 1808 | challenge | 48 |
| 1809 | burden | 48 |
| 1810 | bishop | 48 |
| 1811 | villains | 47 |
| 1812 | victory | 47 |
| 1813 | strikes | 47 |
| 1814 | steward | 47 |
| 1815 | sounds | 47 |
| 1816 | season | 47 |
| 1817 | sacred | 47 |
| 1818 | raise | 47 |
| 1819 | prize | 47 |
| 1820 | phebe | 47 |
| 1821 | perforce | 47 |
| 1822 | parted | 47 |
| 1823 | octavius | 47 |
| 1824 | mov | 47 |
| 1825 | messala | 47 |
| 1826 | loved | 47 |
| 1827 | lock | 47 |
| 1828 | limbs | 47 |
| 1829 | lean | 47 |
| 1830 | laertes | 47 |
| 1831 | knowing | 47 |
| 1832 | horatio | 47 |
| 1833 | garden | 47 |
| 1834 | flood | 47 |
| 1835 | degree | 47 |
| 1836 | contrary | 47 |
| 1837 | contempt | 47 |
| 1838 | cease | 47 |
| 1839 | blessing | 47 |
| 1840 | big | 47 |
| 1841 | ambition | 47 |
| 1842 | allow | 47 |
| 1843 | abuse | 47 |
| 1844 | twelve | 46 |
| 1845 | temper | 46 |
| 1846 | sides | 46 |
| 1847 | shortly | 46 |
| 1848 | sees | 46 |
| 1849 | ros | 46 |
| 1850 | reputation | 46 |
| 1851 | repair | 46 |
| 1852 | render | 46 |
| 1853 | ratcliff | 46 |
| 1854 | quit | 46 |
| 1855 | press | 46 |
| 1856 | kisses | 46 |
| 1857 | iron | 46 |
| 1858 | image | 46 |
| 1859 | honey | 46 |
| 1860 | hie | 46 |
| 1861 | frame | 46 |
| 1862 | flowers | 46 |
| 1863 | fenton | 46 |
| 1864 | fairly | 46 |
| 1865 | faint | 46 |
| 1866 | express | 46 |
| 1867 | dreams | 46 |
| 1868 | davy | 46 |
| 1869 | dares | 46 |
| 1870 | cost | 46 |
| 1871 | brabantio | 46 |
| 1872 | bird | 46 |
| 1873 | aim | 46 |
| 1874 | account | 46 |
| 1875 | undertake | 45 |
| 1876 | tedious | 45 |
| 1877 | tarry | 45 |
| 1878 | taking | 45 |
| 1879 | sway | 45 |
| 1880 | smooth | 45 |
| 1881 | shine | 45 |
| 1882 | priam | 45 |
| 1883 | porter | 45 |
| 1884 | policy | 45 |
| 1885 | perhaps | 45 |
| 1886 | painter | 45 |
| 1887 | octavia | 45 |
| 1888 | oberon | 45 |
| 1889 | mars | 45 |
| 1890 | line | 45 |
| 1891 | liest | 45 |
| 1892 | hid | 45 |
| 1893 | haply | 45 |
| 1894 | hal | 45 |
| 1895 | fathers | 45 |
| 1896 | equal | 45 |
| 1897 | empress | 45 |
| 1898 | damned | 45 |
| 1899 | custom | 45 |
| 1900 | cur | 45 |
| 1901 | capulet | 45 |
| 1902 | brows | 45 |
| 1903 | brains | 45 |
| 1904 | bend | 45 |
| 1905 | behalf | 45 |
| 1906 | bassianus | 45 |
| 1907 | attended | 45 |
| 1908 | according | 45 |
| 1909 | yond | 44 |
| 1910 | west | 44 |
| 1911 | weight | 44 |
| 1912 | weeds | 44 |
| 1913 | waste | 44 |
| 1914 | unknown | 44 |
| 1915 | tempest | 44 |
| 1916 | stomach | 44 |
| 1917 | sore | 44 |
| 1918 | sooth | 44 |
| 1919 | smiles | 44 |
| 1920 | sleeps | 44 |
| 1921 | silvius | 44 |
| 1922 | runs | 44 |
| 1923 | root | 44 |
| 1924 | robert | 44 |
| 1925 | reverence | 44 |
| 1926 | prisoners | 44 |
| 1927 | prevail | 44 |
| 1928 | pinch | 44 |
| 1929 | offended | 44 |
| 1930 | maids | 44 |
| 1931 | lodovico | 44 |
| 1932 | ladyship | 44 |
| 1933 | knaves | 44 |
| 1934 | horn | 44 |
| 1935 | fore | 44 |
| 1936 | forces | 44 |
| 1937 | fate | 44 |
| 1938 | fatal | 44 |
| 1939 | fac | 44 |
| 1940 | disposition | 44 |
| 1941 | desert | 44 |
| 1942 | dagger | 44 |
| 1943 | cromwell | 44 |
| 1944 | bodies | 44 |
| 1945 | bind | 44 |
| 1946 | bade | 44 |
| 1947 | wrought | 43 |
| 1948 | utter | 43 |
| 1949 | tread | 43 |
| 1950 | soothsayer | 43 |
| 1951 | slaughter | 43 |
| 1952 | ripe | 43 |
| 1953 | regard | 43 |
| 1954 | pour | 43 |
| 1955 | picture | 43 |
| 1956 | peril | 43 |
| 1957 | odds | 43 |
| 1958 | numbers | 43 |
| 1959 | native | 43 |
| 1960 | methought | 43 |
| 1961 | iras | 43 |
| 1962 | greet | 43 |
| 1963 | govern | 43 |
| 1964 | gent | 43 |
| 1965 | friendship | 43 |
| 1966 | fingers | 43 |
| 1967 | farther | 43 |
| 1968 | elder | 43 |
| 1969 | dumb | 43 |
| 1970 | device | 43 |
| 1971 | courtier | 43 |
| 1972 | capitol | 43 |
| 1973 | attending | 43 |
| 1974 | advice | 43 |
| 1975 | woes | 42 |
| 1976 | weapons | 42 |
| 1977 | tells | 42 |
| 1978 | sorrows | 42 |
| 1979 | sly | 42 |
| 1980 | sirs | 42 |
| 1981 | senate | 42 |
| 1982 | seas | 42 |
| 1983 | revolt | 42 |
| 1984 | perdita | 42 |
| 1985 | ning | 42 |
| 1986 | mischief | 42 |
| 1987 | midnight | 42 |
| 1988 | hugh | 42 |
| 1989 | hill | 42 |
| 1990 | firm | 42 |
| 1991 | finds | 42 |
| 1992 | fairest | 42 |
| 1993 | everything | 42 |
| 1994 | edge | 42 |
| 1995 | discover | 42 |
| 1996 | deserv | 42 |
| 1997 | debt | 42 |
| 1998 | dearly | 42 |
| 1999 | crave | 42 |
| 2000 | cover | 42 |
| 2001 | conceit | 42 |
| 2002 | bury | 42 |
| 2003 | bounty | 42 |
| 2004 | bell | 42 |
| 2005 | belike | 42 |
| 2006 | apt | 42 |
| 2007 | alike | 42 |
| 2008 | adam | 42 |
| 2009 | violent | 41 |
| 2010 | titania | 41 |
| 2011 | tied | 41 |
| 2012 | substance | 41 |
| 2013 | staff | 41 |
| 2014 | solemn | 41 |
| 2015 | sold | 41 |
| 2016 | sky | 41 |
| 2017 | prey | 41 |
| 2018 | practice | 41 |
| 2019 | pembroke | 41 |
| 2020 | pair | 41 |
| 2021 | padua | 41 |
| 2022 | nobles | 41 |
| 2023 | murtherer | 41 |
| 2024 | month | 41 |
| 2025 | monsieur | 41 |
| 2026 | moe | 41 |
| 2027 | milan | 41 |
| 2028 | lovell | 41 |
| 2029 | looking | 41 |
| 2030 | lartius | 41 |
| 2031 | honor | 41 |
| 2032 | hazard | 41 |
| 2033 | hanging | 41 |
| 2034 | glorious | 41 |
| 2035 | gaoler | 41 |
| 2036 | fits | 41 |
| 2037 | figure | 41 |
| 2038 | favours | 41 |
| 2039 | fairies | 41 |
| 2040 | east | 41 |
| 2041 | dwell | 41 |
| 2042 | drums | 41 |
| 2043 | douglas | 41 |
| 2044 | displeasure | 41 |
| 2045 | dew | 41 |
| 2046 | deceiv | 41 |
| 2047 | countrymen | 41 |
| 2048 | canterbury | 41 |
| 2049 | belly | 41 |
| 2050 | barren | 41 |
| 2051 | armour | 41 |
| 2052 | afraid | 41 |
| 2053 | wounded | 40 |
| 2054 | wing | 40 |
| 2055 | willing | 40 |
| 2056 | whoreson | 40 |
| 2057 | wants | 40 |
| 2058 | villainy | 40 |
| 2059 | vantage | 40 |
| 2060 | thick | 40 |
| 2061 | surely | 40 |
| 2062 | stroke | 40 |
| 2063 | store | 40 |
| 2064 | sends | 40 |
| 2065 | rous | 40 |
| 2066 | roar | 40 |
| 2067 | rate | 40 |
| 2068 | purposes | 40 |
| 2069 | prologue | 40 |
| 2070 | pen | 40 |
| 2071 | mountain | 40 |
| 2072 | mistake | 40 |
| 2073 | isle | 40 |
| 2074 | inform | 40 |
| 2075 | ignorance | 40 |
| 2076 | henceforth | 40 |
| 2077 | grieve | 40 |
| 2078 | garter | 40 |
| 2079 | followed | 40 |
| 2080 | fierce | 40 |
| 2081 | duncan | 40 |
| 2082 | devils | 40 |
| 2083 | confirm | 40 |
| 2084 | complexion | 40 |
| 2085 | commit | 40 |
| 2086 | commanded | 40 |
| 2087 | clothes | 40 |
| 2088 | cinna | 40 |
| 2089 | chair | 40 |
| 2090 | cave | 40 |
| 2091 | blown | 40 |
| 2092 | bite | 40 |
| 2093 | banishment | 40 |
| 2094 | apparel | 40 |
| 2095 | apart | 40 |
| 2096 | also | 40 |
| 2097 | affections | 40 |
| 2098 | acquainted | 40 |
| 2099 | wreck | 39 |
| 2100 | worn | 39 |
| 2101 | windsor | 39 |
| 2102 | wears | 39 |
| 2103 | varro | 39 |
| 2104 | unhappy | 39 |
| 2105 | thereof | 39 |
| 2106 | sweat | 39 |
| 2107 | stoop | 39 |
| 2108 | snow | 39 |
| 2109 | sentence | 39 |
| 2110 | sell | 39 |
| 2111 | school | 39 |
| 2112 | remains | 39 |
| 2113 | profit | 39 |
| 2114 | places | 39 |
| 2115 | pieces | 39 |
| 2116 | object | 39 |
| 2117 | misery | 39 |
| 2118 | impossible | 39 |
| 2119 | hateful | 39 |
| 2120 | hardly | 39 |
| 2121 | habit | 39 |
| 2122 | furnish | 39 |
| 2123 | eternal | 39 |
| 2124 | eight | 39 |
| 2125 | dolabella | 39 |
| 2126 | disdain | 39 |
| 2127 | deer | 39 |
| 2128 | darkness | 39 |
| 2129 | cock | 39 |
| 2130 | chaste | 39 |
| 2131 | charm | 39 |
| 2132 | cell | 39 |
| 2133 | cat | 39 |
| 2134 | car | 39 |
| 2135 | benefit | 39 |
| 2136 | beauteous | 39 |
| 2137 | bawd | 39 |
| 2138 | babe | 39 |
| 2139 | advise | 39 |
| 2140 | add | 39 |
| 2141 | worm | 38 |
| 2142 | virgin | 38 |
| 2143 | virgilia | 38 |
| 2144 | unnatural | 38 |
| 2145 | twain | 38 |
| 2146 | tut | 38 |
| 2147 | trade | 38 |
| 2148 | suspect | 38 |
| 2149 | stronger | 38 |
| 2150 | special | 38 |
| 2151 | slew | 38 |
| 2152 | rotten | 38 |
| 2153 | rock | 38 |
| 2154 | robin | 38 |
| 2155 | retire | 38 |
| 2156 | punish | 38 |
| 2157 | prayer | 38 |
| 2158 | pick | 38 |
| 2159 | peers | 38 |
| 2160 | pause | 38 |
| 2161 | osw | 38 |
| 2162 | nights | 38 |
| 2163 | months | 38 |
| 2164 | modest | 38 |
| 2165 | minute | 38 |
| 2166 | minister | 38 |
| 2167 | length | 38 |
| 2168 | laws | 38 |
| 2169 | infinite | 38 |
| 2170 | hereford | 38 |
| 2171 | hearted | 38 |
| 2172 | fairer | 38 |
| 2173 | except | 38 |
| 2174 | esteem | 38 |
| 2175 | earnest | 38 |
| 2176 | deserves | 38 |
| 2177 | delay | 38 |
| 2178 | cressid | 38 |
| 2179 | creatures | 38 |
| 2180 | compass | 38 |
| 2181 | bent | 38 |
| 2182 | avoid | 38 |
| 2183 | athenian | 38 |
| 2184 | appetite | 38 |
| 2185 | afterwards | 38 |
| 2186 | accuse | 38 |
| 2187 | whip | 37 |
| 2188 | verona | 37 |
| 2189 | titinius | 37 |
| 2190 | threat | 37 |
| 2191 | tame | 37 |
| 2192 | stays | 37 |
| 2193 | stage | 37 |
| 2194 | sought | 37 |
| 2195 | slept | 37 |
| 2196 | shakespeare | 37 |
| 2197 | senior | 37 |
| 2198 | scape | 37 |
| 2199 | rail | 37 |
| 2200 | park | 37 |
| 2201 | nobility | 37 |
| 2202 | necessity | 37 |
| 2203 | nathaniel | 37 |
| 2204 | morn | 37 |
| 2205 | monument | 37 |
| 2206 | mess | 37 |
| 2207 | marks | 37 |
| 2208 | lip | 37 |
| 2209 | leg | 37 |
| 2210 | instrument | 37 |
| 2211 | heartily | 37 |
| 2212 | hangs | 37 |
| 2213 | guest | 37 |
| 2214 | groan | 37 |
| 2215 | gall | 37 |
| 2216 | fruit | 37 |
| 2217 | feeble | 37 |
| 2218 | familiar | 37 |
| 2219 | edgar | 37 |
| 2220 | dish | 37 |
| 2221 | dignity | 37 |
| 2222 | difference | 37 |
| 2223 | defence | 37 |
| 2224 | companion | 37 |
| 2225 | calm | 37 |
| 2226 | bora | 37 |
| 2227 | books | 37 |
| 2228 | bar | 37 |
| 2229 | banished | 37 |
| 2230 | attendant | 37 |
| 2231 | assur | 37 |
| 2232 | arise | 37 |
| 2233 | angels | 37 |
| 2234 | amongst | 37 |
| 2235 | amiss | 37 |
| 2236 | ambitious | 37 |
| 2237 | abide | 37 |
| 2238 | wor | 36 |
| 2239 | withdraw | 36 |
| 2240 | unworthy | 36 |
| 2241 | tall | 36 |
| 2242 | suck | 36 |
| 2243 | standing | 36 |
| 2244 | sour | 36 |
| 2245 | slaves | 36 |
| 2246 | sins | 36 |
| 2247 | silent | 36 |
| 2248 | senses | 36 |
| 2249 | scotland | 36 |
| 2250 | rob | 36 |
| 2251 | polonius | 36 |
| 2252 | pitch | 36 |
| 2253 | personae | 36 |
| 2254 | pedant | 36 |
| 2255 | passing | 36 |
| 2256 | otherwise | 36 |
| 2257 | nobly | 36 |
| 2258 | nephew | 36 |
| 2259 | mouths | 36 |
| 2260 | montano | 36 |
| 2261 | lusty | 36 |
| 2262 | language | 36 |
| 2263 | lamb | 36 |
| 2264 | jupiter | 36 |
| 2265 | hercules | 36 |
| 2266 | hat | 36 |
| 2267 | handkerchief | 36 |
| 2268 | groans | 36 |
| 2269 | goths | 36 |
| 2270 | glove | 36 |
| 2271 | friendly | 36 |
| 2272 | fox | 36 |
| 2273 | felt | 36 |
| 2274 | entertainment | 36 |
| 2275 | dst | 36 |
| 2276 | dramatis | 36 |
| 2277 | diomed | 36 |
| 2278 | cranmer | 36 |
| 2279 | coz | 36 |
| 2280 | committed | 36 |
| 2281 | cares | 36 |
| 2282 | bride | 36 |
| 2283 | bravely | 36 |
| 2284 | bleed | 36 |
| 2285 | basket | 36 |
| 2286 | acquaintance | 36 |
| 2287 | wolf | 35 |
| 2288 | willingly | 35 |
| 2289 | whisper | 35 |
| 2290 | tyranny | 35 |
| 2291 | troyan | 35 |
| 2292 | sink | 35 |
| 2293 | serves | 35 |
| 2294 | saucy | 35 |
| 2295 | reward | 35 |
| 2296 | recover | 35 |
| 2297 | pocket | 35 |
| 2298 | pleasures | 35 |
| 2299 | pleasant | 35 |
| 2300 | plays | 35 |
| 2301 | players | 35 |
| 2302 | pawn | 35 |
| 2303 | passage | 35 |
| 2304 | partly | 35 |
| 2305 | marvel | 35 |
| 2306 | lucilius | 35 |
| 2307 | lennox | 35 |
| 2308 | knit | 35 |
| 2309 | kindly | 35 |
| 2310 | jealousy | 35 |
| 2311 | italy | 35 |
| 2312 | huge | 35 |
| 2313 | height | 35 |
| 2314 | frederick | 35 |
| 2315 | fee | 35 |
| 2316 | envious | 35 |
| 2317 | drew | 35 |
| 2318 | dress | 35 |
| 2319 | cuckold | 35 |
| 2320 | corin | 35 |
| 2321 | cool | 35 |
| 2322 | confound | 35 |
| 2323 | birds | 35 |
| 2324 | began | 35 |
| 2325 | befall | 35 |
| 2326 | written | 34 |
| 2327 | wondrous | 34 |
| 2328 | wither | 34 |
| 2329 | wedding | 34 |
| 2330 | weather | 34 |
| 2331 | visage | 34 |
| 2332 | usurp | 34 |
| 2333 | urge | 34 |
| 2334 | tremble | 34 |
| 2335 | travel | 34 |
| 2336 | strain | 34 |
| 2337 | start | 34 |
| 2338 | services | 34 |
| 2339 | score | 34 |
| 2340 | sc | 34 |
| 2341 | savage | 34 |
| 2342 | rhyme | 34 |
| 2343 | reveng | 34 |
| 2344 | rememb | 34 |
| 2345 | rash | 34 |
| 2346 | ran | 34 |
| 2347 | perish | 34 |
| 2348 | odd | 34 |
| 2349 | observe | 34 |
| 2350 | moved | 34 |
| 2351 | miss | 34 |
| 2352 | miserable | 34 |
| 2353 | messengers | 34 |
| 2354 | lines | 34 |
| 2355 | league | 34 |
| 2356 | kin | 34 |
| 2357 | island | 34 |
| 2358 | hunt | 34 |
| 2359 | hall | 34 |
| 2360 | grew | 34 |
| 2361 | gardiner | 34 |
| 2362 | feeling | 34 |
| 2363 | falsehood | 34 |
| 2364 | enforce | 34 |
| 2365 | drive | 34 |
| 2366 | direct | 34 |
| 2367 | dick | 34 |
| 2368 | crying | 34 |
| 2369 | circumstance | 34 |
| 2370 | check | 34 |
| 2371 | chase | 34 |
| 2372 | chang | 34 |
| 2373 | breach | 34 |
| 2374 | bohemia | 34 |
| 2375 | boast | 34 |
| 2376 | beside | 34 |
| 2377 | beasts | 34 |
| 2378 | attempt | 34 |
| 2379 | armed | 34 |
| 2380 | appointed | 34 |
| 2381 | alexas | 34 |
| 2382 | alexander | 34 |
| 2383 | absent | 34 |
| 2384 | zeal | 33 |
| 2385 | younger | 33 |
| 2386 | yoke | 33 |
| 2387 | weeps | 33 |
| 2388 | wed | 33 |
| 2389 | vex | 33 |
| 2390 | task | 33 |
| 2391 | strive | 33 |
| 2392 | stretch | 33 |
| 2393 | step | 33 |
| 2394 | spur | 33 |
| 2395 | spoil | 33 |
| 2396 | skin | 33 |
| 2397 | satisfaction | 33 |
| 2398 | rugby | 33 |
| 2399 | resolv | 33 |
| 2400 | renowned | 33 |
| 2401 | reading | 33 |
| 2402 | pursue | 33 |
| 2403 | possession | 33 |
| 2404 | pomp | 33 |
| 2405 | physic | 33 |
| 2406 | parley | 33 |
| 2407 | outlaw | 33 |
| 2408 | naples | 33 |
| 2409 | mount | 33 |
| 2410 | mile | 33 |
| 2411 | menelaus | 33 |
| 2412 | marshal | 33 |
| 2413 | market | 33 |
| 2414 | loath | 33 |
| 2415 | knocking | 33 |
| 2416 | isabel | 33 |
| 2417 | humours | 33 |
| 2418 | guarded | 33 |
| 2419 | greek | 33 |
| 2420 | grecian | 33 |
| 2421 | gait | 33 |
| 2422 | freedom | 33 |
| 2423 | fed | 33 |
| 2424 | faithful | 33 |
| 2425 | exchange | 33 |
| 2426 | et | 33 |
| 2427 | dozen | 33 |
| 2428 | commons | 33 |
| 2429 | carried | 33 |
| 2430 | bleeding | 33 |
| 2431 | wishes | 32 |
| 2432 | wisely | 32 |
| 2433 | wink | 32 |
| 2434 | williams | 32 |
| 2435 | wholesome | 32 |
| 2436 | vessel | 32 |
| 2437 | verse | 32 |
| 2438 | vernon | 32 |
| 2439 | tricks | 32 |
| 2440 | torment | 32 |
| 2441 | toil | 32 |
| 2442 | tend | 32 |
| 2443 | suspicion | 32 |
| 2444 | suits | 32 |
| 2445 | subtle | 32 |
| 2446 | strife | 32 |
| 2447 | stick | 32 |
| 2448 | stern | 32 |
| 2449 | stamp | 32 |
| 2450 | smiling | 32 |
| 2451 | slight | 32 |
| 2452 | sixth | 32 |
| 2453 | signs | 32 |
| 2454 | shoulders | 32 |
| 2455 | serpent | 32 |
| 2456 | sceptre | 32 |
| 2457 | roses | 32 |
| 2458 | regan | 32 |
| 2459 | rebels | 32 |
| 2460 | rebellion | 32 |
| 2461 | publius | 32 |
| 2462 | profess | 32 |
| 2463 | pate | 32 |
| 2464 | pack | 32 |
| 2465 | pace | 32 |
| 2466 | orchard | 32 |
| 2467 | mourn | 32 |
| 2468 | moment | 32 |
| 2469 | learning | 32 |
| 2470 | leads | 32 |
| 2471 | knights | 32 |
| 2472 | graves | 32 |
| 2473 | goose | 32 |
| 2474 | goneril | 32 |
| 2475 | fright | 32 |
| 2476 | fifty | 32 |
| 2477 | fifth | 32 |
| 2478 | example | 32 |
| 2479 | earthly | 32 |
| 2480 | dorset | 32 |
| 2481 | discretion | 32 |
| 2482 | directly | 32 |
| 2483 | derby | 32 |
| 2484 | cursed | 32 |
| 2485 | crow | 32 |
| 2486 | cor | 32 |
| 2487 | continue | 32 |
| 2488 | consul | 32 |
| 2489 | confusion | 32 |
| 2490 | conference | 32 |
| 2491 | coat | 32 |
| 2492 | bore | 32 |
| 2493 | boot | 32 |
| 2494 | beshrew | 32 |
| 2495 | audrey | 32 |
| 2496 | audience | 32 |
| 2497 | antigonus | 32 |
| 2498 | youthful | 31 |
| 2499 | wot | 31 |
| 2500 | troubled | 31 |
| 2501 | trees | 31 |
| 2502 | torture | 31 |
| 2503 | thrown | 31 |
| 2504 | theirs | 31 |
| 2505 | tempt | 31 |
| 2506 | stream | 31 |
| 2507 | singing | 31 |
| 2508 | siege | 31 |
| 2509 | shown | 31 |
| 2510 | shapes | 31 |
| 2511 | seize | 31 |
| 2512 | secure | 31 |
| 2513 | scroop | 31 |
| 2514 | rid | 31 |
| 2515 | remove | 31 |
| 2516 | refuse | 31 |
| 2517 | redeem | 31 |
| 2518 | provided | 31 |
| 2519 | privilege | 31 |
| 2520 | points | 31 |
| 2521 | pitiful | 31 |
| 2522 | persuade | 31 |
| 2523 | offices | 31 |
| 2524 | nice | 31 |
| 2525 | muse | 31 |
| 2526 | milk | 31 |
| 2527 | message | 31 |
| 2528 | mass | 31 |
| 2529 | loyal | 31 |
| 2530 | lent | 31 |
| 2531 | leap | 31 |
| 2532 | lately | 31 |
| 2533 | key | 31 |
| 2534 | joyful | 31 |
| 2535 | item | 31 |
| 2536 | ireland | 31 |
| 2537 | higher | 31 |
| 2538 | growing | 31 |
| 2539 | gently | 31 |
| 2540 | gar | 31 |
| 2541 | fields | 31 |
| 2542 | expect | 31 |
| 2543 | error | 31 |
| 2544 | enterprise | 31 |
| 2545 | dismiss | 31 |
| 2546 | discharge | 31 |
| 2547 | daily | 31 |
| 2548 | county | 31 |
| 2549 | cordelia | 31 |
| 2550 | conquest | 31 |
| 2551 | beloved | 31 |
| 2552 | belov | 31 |
| 2553 | banquet | 31 |
| 2554 | band | 31 |
| 2555 | wills | 30 |
| 2556 | whereon | 30 |
| 2557 | weapon | 30 |
| 2558 | wax | 30 |
| 2559 | unfold | 30 |
| 2560 | troops | 30 |
| 2561 | tom | 30 |
| 2562 | terror | 30 |
| 2563 | term | 30 |
| 2564 | suppose | 30 |
| 2565 | stock | 30 |
| 2566 | steps | 30 |
| 2567 | soil | 30 |
| 2568 | shoulder | 30 |
| 2569 | shook | 30 |
| 2570 | serving | 30 |
| 2571 | running | 30 |
| 2572 | rescue | 30 |
| 2573 | provide | 30 |
| 2574 | pronounce | 30 |
| 2575 | price | 30 |
| 2576 | prepar | 30 |
| 2577 | pandulph | 30 |
| 2578 | ophelia | 30 |
| 2579 | notice | 30 |
| 2580 | newly | 30 |
| 2581 | nation | 30 |
| 2582 | meantime | 30 |
| 2583 | m | 30 |
| 2584 | lying | 30 |
| 2585 | kissing | 30 |
| 2586 | kindred | 30 |
| 2587 | jaquenetta | 30 |
| 2588 | invisible | 30 |
| 2589 | invention | 30 |
| 2590 | injury | 30 |
| 2591 | hole | 30 |
| 2592 | hairs | 30 |
| 2593 | guildenstern | 30 |
| 2594 | granted | 30 |
| 2595 | grandam | 30 |
| 2596 | gobbo | 30 |
| 2597 | giddy | 30 |
| 2598 | forty | 30 |
| 2599 | forswear | 30 |
| 2600 | famous | 30 |
| 2601 | falling | 30 |
| 2602 | ended | 30 |
| 2603 | disease | 30 |
| 2604 | delivered | 30 |
| 2605 | dam | 30 |
| 2606 | curses | 30 |
| 2607 | curs | 30 |
| 2608 | corse | 30 |
| 2609 | commands | 30 |
| 2610 | caught | 30 |
| 2611 | calf | 30 |
| 2612 | breeding | 30 |
| 2613 | beats | 30 |
| 2614 | bay | 30 |
| 2615 | alice | 30 |
| 2616 | ago | 30 |
| 2617 | afeard | 30 |
| 2618 | advance | 30 |
| 2619 | accept | 30 |
| 2620 | absolute | 30 |
| 2621 | vi | 29 |
| 2622 | troop | 29 |
| 2623 | towns | 29 |
| 2624 | thirty | 29 |
| 2625 | temple | 29 |
| 2626 | telling | 29 |
| 2627 | strongly | 29 |
| 2628 | space | 29 |
| 2629 | shoot | 29 |
| 2630 | shines | 29 |
| 2631 | seldom | 29 |
| 2632 | scope | 29 |
| 2633 | sat | 29 |
| 2634 | rouse | 29 |
| 2635 | resolution | 29 |
| 2636 | redress | 29 |
| 2637 | rapier | 29 |
| 2638 | quench | 29 |
| 2639 | quarter | 29 |
| 2640 | purchase | 29 |
| 2641 | petty | 29 |
| 2642 | ocean | 29 |
| 2643 | needful | 29 |
| 2644 | musicians | 29 |
| 2645 | murd | 29 |
| 2646 | mild | 29 |
| 2647 | liberal | 29 |
| 2648 | lays | 29 |
| 2649 | laughter | 29 |
| 2650 | knot | 29 |
| 2651 | kills | 29 |
| 2652 | journey | 29 |
| 2653 | je | 29 |
| 2654 | interest | 29 |
| 2655 | ink | 29 |
| 2656 | hated | 29 |
| 2657 | harsh | 29 |
| 2658 | happily | 29 |
| 2659 | guil | 29 |
| 2660 | greeks | 29 |
| 2661 | forfeit | 29 |
| 2662 | fares | 29 |
| 2663 | ely | 29 |
| 2664 | drinking | 29 |
| 2665 | dote | 29 |
| 2666 | destroy | 29 |
| 2667 | delicate | 29 |
| 2668 | dame | 29 |
| 2669 | curtis | 29 |
| 2670 | cowards | 29 |
| 2671 | corrupt | 29 |
| 2672 | contented | 29 |
| 2673 | con | 29 |
| 2674 | cam | 29 |
| 2675 | breaks | 29 |
| 2676 | breaking | 29 |
| 2677 | borrow | 29 |
| 2678 | beware | 29 |
| 2679 | begun | 29 |
| 2680 | assurance | 29 |
| 2681 | andrew | 29 |
| 2682 | amaz | 29 |
| 2683 | alter | 29 |
| 2684 | advis | 29 |
| 2685 | abus | 29 |
| 2686 | yellow | 28 |
| 2687 | worcester | 28 |
| 2688 | wept | 28 |
| 2689 | welsh | 28 |
| 2690 | week | 28 |
| 2691 | waters | 28 |
| 2692 | walks | 28 |
| 2693 | venture | 28 |
| 2694 | undo | 28 |
| 2695 | torch | 28 |
| 2696 | token | 28 |
| 2697 | theme | 28 |
| 2698 | thane | 28 |
| 2699 | supply | 28 |
| 2700 | strumpet | 28 |
| 2701 | stafford | 28 |
| 2702 | spleen | 28 |
| 2703 | spit | 28 |
| 2704 | solanio | 28 |
| 2705 | sisters | 28 |
| 2706 | sicilia | 28 |
| 2707 | shadows | 28 |
| 2708 | sets | 28 |
| 2709 | rul | 28 |
| 2710 | rousillon | 28 |
| 2711 | resolve | 28 |
| 2712 | remorse | 28 |
| 2713 | reach | 28 |
| 2714 | preparation | 28 |
| 2715 | praises | 28 |
| 2716 | pierce | 28 |
| 2717 | phrase | 28 |
| 2718 | peevish | 28 |
| 2719 | parting | 28 |
| 2720 | par | 28 |
| 2721 | palm | 28 |
| 2722 | obedient | 28 |
| 2723 | nails | 28 |
| 2724 | mettle | 28 |
| 2725 | merely | 28 |
| 2726 | maecenas | 28 |
| 2727 | liking | 28 |
| 2728 | lesser | 28 |
| 2729 | lad | 28 |
| 2730 | kneels | 28 |
| 2731 | inward | 28 |
| 2732 | increase | 28 |
| 2733 | houses | 28 |
| 2734 | hotspur | 28 |
| 2735 | herein | 28 |
| 2736 | hears | 28 |
| 2737 | guilt | 28 |
| 2738 | goddess | 28 |
| 2739 | foreign | 28 |
| 2740 | fix | 28 |
| 2741 | ev | 28 |
| 2742 | ent | 28 |
| 2743 | elinor | 28 |
| 2744 | easily | 28 |
| 2745 | drinks | 28 |
| 2746 | destruction | 28 |
| 2747 | defy | 28 |
| 2748 | deceive | 28 |
| 2749 | cyprus | 28 |
| 2750 | conquer | 28 |
| 2751 | conjure | 28 |
| 2752 | conclusion | 28 |
| 2753 | conclude | 28 |
| 2754 | commonwealth | 28 |
| 2755 | cloak | 28 |
| 2756 | clerk | 28 |
| 2757 | ceremony | 28 |
| 2758 | censure | 28 |
| 2759 | bushy | 28 |
| 2760 | burst | 28 |
| 2761 | boar | 28 |
| 2762 | beholding | 28 |
| 2763 | beheld | 28 |
| 2764 | ambassador | 28 |
| 2765 | addition | 28 |
| 2766 | aboard | 28 |
| 2767 | writes | 27 |
| 2768 | woeful | 27 |
| 2769 | vous | 27 |
| 2770 | veins | 27 |
| 2771 | touching | 27 |
| 2772 | throats | 27 |
| 2773 | threw | 27 |
| 2774 | terrible | 27 |
| 2775 | sweetly | 27 |
| 2776 | sue | 27 |
| 2777 | strangely | 27 |
| 2778 | stale | 27 |
| 2779 | spy | 27 |
| 2780 | spurn | 27 |
| 2781 | south | 27 |
| 2782 | sitting | 27 |
| 2783 | share | 27 |
| 2784 | shade | 27 |
| 2785 | scurvy | 27 |
| 2786 | satisfy | 27 |
| 2787 | rush | 27 |
| 2788 | retreat | 27 |
| 2789 | rend | 27 |
| 2790 | recompense | 27 |
| 2791 | prov | 27 |
| 2792 | proportion | 27 |
| 2793 | physician | 27 |
| 2794 | oracle | 27 |
| 2795 | ope | 27 |
| 2796 | oak | 27 |
| 2797 | mightst | 27 |
| 2798 | melt | 27 |
| 2799 | likes | 27 |
| 2800 | lights | 27 |
| 2801 | keeping | 27 |
| 2802 | joys | 27 |
| 2803 | joan | 27 |
| 2804 | jewels | 27 |
| 2805 | intelligence | 27 |
| 2806 | instruments | 27 |
| 2807 | husbands | 27 |
| 2808 | hue | 27 |
| 2809 | hap | 27 |
| 2810 | grandsire | 27 |
| 2811 | gaze | 27 |
| 2812 | forc | 27 |
| 2813 | extremity | 27 |
| 2814 | exceeding | 27 |
| 2815 | eldest | 27 |
| 2816 | effects | 27 |
| 2817 | eagle | 27 |
| 2818 | divide | 27 |
| 2819 | distance | 27 |
| 2820 | couldst | 27 |
| 2821 | contract | 27 |
| 2822 | contents | 27 |
| 2823 | conceive | 27 |
| 2824 | cloud | 27 |
| 2825 | closet | 27 |
| 2826 | captains | 27 |
| 2827 | butcher | 27 |
| 2828 | busy | 27 |
| 2829 | bush | 27 |
| 2830 | burns | 27 |
| 2831 | bottle | 27 |
| 2832 | bosoms | 27 |
| 2833 | behaviour | 27 |
| 2834 | arrest | 27 |
| 2835 | approve | 27 |
| 2836 | apace | 27 |
| 2837 | aloud | 27 |
| 2838 | afternoon | 27 |
| 2839 | working | 26 |
| 2840 | whate | 26 |
| 2841 | weakness | 26 |
| 2842 | walter | 26 |
| 2843 | waking | 26 |
| 2844 | value | 26 |
| 2845 | urg | 26 |
| 2846 | unkind | 26 |
| 2847 | turning | 26 |
| 2848 | treacherous | 26 |
| 2849 | touches | 26 |
| 2850 | tooth | 26 |
| 2851 | thereby | 26 |
| 2852 | swell | 26 |
| 2853 | swears | 26 |
| 2854 | stubborn | 26 |
| 2855 | stocks | 26 |
| 2856 | sting | 26 |
| 2857 | spread | 26 |
| 2858 | sole | 26 |
| 2859 | society | 26 |
| 2860 | slay | 26 |
| 2861 | shrewd | 26 |
| 2862 | shift | 26 |
| 2863 | senseless | 26 |
| 2864 | rutland | 26 |
| 2865 | rosencrantz | 26 |
| 2866 | renown | 26 |
| 2867 | prevent | 26 |
| 2868 | prais | 26 |
| 2869 | pearl | 26 |
| 2870 | pays | 26 |
| 2871 | owes | 26 |
| 2872 | overdone | 26 |
| 2873 | opposite | 26 |
| 2874 | nimble | 26 |
| 2875 | natures | 26 |
| 2876 | miracle | 26 |
| 2877 | metal | 26 |
| 2878 | mercutio | 26 |
| 2879 | matters | 26 |
| 2880 | marg | 26 |
| 2881 | manhood | 26 |
| 2882 | luck | 26 |
| 2883 | likewise | 26 |
| 2884 | lightning | 26 |
| 2885 | knocks | 26 |
| 2886 | kingly | 26 |
| 2887 | killing | 26 |
| 2888 | justly | 26 |
| 2889 | imagination | 26 |
| 2890 | hungry | 26 |
| 2891 | hippolyta | 26 |
| 2892 | grievous | 26 |
| 2893 | glendower | 26 |
| 2894 | gather | 26 |
| 2895 | froth | 26 |
| 2896 | fleet | 26 |
| 2897 | feather | 26 |
| 2898 | fearing | 26 |
| 2899 | event | 26 |
| 2900 | desir | 26 |
| 2901 | denmark | 26 |
| 2902 | decius | 26 |
| 2903 | decay | 26 |
| 2904 | deaf | 26 |
| 2905 | curst | 26 |
| 2906 | creep | 26 |
| 2907 | corioli | 26 |
| 2908 | conditions | 26 |
| 2909 | climb | 26 |
| 2910 | choler | 26 |
| 2911 | cherish | 26 |
| 2912 | charg | 26 |
| 2913 | box | 26 |
| 2914 | boots | 26 |
| 2915 | bidding | 26 |
| 2916 | begot | 26 |
| 2917 | begg | 26 |
| 2918 | barnardine | 26 |
| 2919 | austria | 26 |
| 2920 | aunt | 26 |
| 2921 | aspect | 26 |
| 2922 | asham | 26 |
| 2923 | apparent | 26 |
| 2924 | apollo | 26 |
| 2925 | allegiance | 26 |
| 2926 | aegeon | 26 |
| 2927 | yesterday | 25 |
| 2928 | wore | 25 |
| 2929 | wooing | 25 |
| 2930 | wipe | 25 |
| 2931 | willow | 25 |
| 2932 | whereto | 25 |
| 2933 | wail | 25 |
| 2934 | virginity | 25 |
| 2935 | ventidius | 25 |
| 2936 | ugly | 25 |
| 2937 | trunk | 25 |
| 2938 | trifle | 25 |
| 2939 | tribute | 25 |
| 2940 | thin | 25 |
| 2941 | talking | 25 |
| 2942 | sweetest | 25 |
| 2943 | suitor | 25 |
| 2944 | stopp | 25 |
| 2945 | stabs | 25 |
| 2946 | sovereignty | 25 |
| 2947 | siward | 25 |
| 2948 | signify | 25 |
| 2949 | sheriff | 25 |
| 2950 | sex | 25 |
| 2951 | setting | 25 |
| 2952 | sandys | 25 |
| 2953 | safely | 25 |
| 2954 | royalty | 25 |
| 2955 | roaring | 25 |
| 2956 | rightly | 25 |
| 2957 | repose | 25 |
| 2958 | rejoice | 25 |
| 2959 | received | 25 |
| 2960 | rebel | 25 |
| 2961 | proceeding | 25 |
| 2962 | plebeians | 25 |
| 2963 | perfection | 25 |
| 2964 | parliament | 25 |
| 2965 | osr | 25 |
| 2966 | michael | 25 |
| 2967 | mantua | 25 |
| 2968 | madman | 25 |
| 2969 | level | 25 |
| 2970 | leaving | 25 |
| 2971 | kingdoms | 25 |
| 2972 | instruct | 25 |
| 2973 | instance | 25 |
| 2974 | imperial | 25 |
| 2975 | immortal | 25 |
| 2976 | hung | 25 |
| 2977 | human | 25 |
| 2978 | horrible | 25 |
| 2979 | hey | 25 |
| 2980 | government | 25 |
| 2981 | garland | 25 |
| 2982 | game | 25 |
| 2983 | forsake | 25 |
| 2984 | forms | 25 |
| 2985 | florence | 25 |
| 2986 | flat | 25 |
| 2987 | flame | 25 |
| 2988 | expedition | 25 |
| 2989 | exile | 25 |
| 2990 | evils | 25 |
| 2991 | evermore | 25 |
| 2992 | doublet | 25 |
| 2993 | dine | 25 |
| 2994 | determine | 25 |
| 2995 | deputy | 25 |
| 2996 | current | 25 |
| 2997 | compare | 25 |
| 2998 | combat | 25 |
| 2999 | certainly | 25 |
| 3000 | blue | 25 |
| 3001 | beds | 25 |
| 3002 | beams | 25 |
| 3003 | alexandria | 25 |
| 3004 | aged | 25 |
| 3005 | abbess | 25 |
| 3006 | zounds | 24 |
| 3007 | yielded | 24 |
| 3008 | wonderful | 24 |
| 3009 | vulgar | 24 |
| 3010 | treachery | 24 |
| 3011 | today | 24 |
| 3012 | swallow | 24 |
| 3013 | swain | 24 |
| 3014 | strew | 24 |
| 3015 | sounded | 24 |
| 3016 | severally | 24 |
| 3017 | servingman | 24 |
| 3018 | seeks | 24 |
| 3019 | seeking | 24 |
| 3020 | secrets | 24 |
| 3021 | river | 24 |
| 3022 | resign | 24 |
| 3023 | requite | 24 |
| 3024 | reply | 24 |
| 3025 | rais | 24 |
| 3026 | ragged | 24 |
| 3027 | qualities | 24 |
| 3028 | push | 24 |
| 3029 | prosper | 24 |
| 3030 | preserve | 24 |
| 3031 | pit | 24 |
| 3032 | owl | 24 |
| 3033 | ourself | 24 |
| 3034 | offences | 24 |
| 3035 | noted | 24 |
| 3036 | nobleman | 24 |
| 3037 | nest | 24 |
| 3038 | neglect | 24 |
| 3039 | moral | 24 |
| 3040 | manage | 24 |
| 3041 | loyalty | 24 |
| 3042 | lower | 24 |
| 3043 | lodging | 24 |
| 3044 | liver | 24 |
| 3045 | lions | 24 |
| 3046 | likely | 24 |
| 3047 | lift | 24 |
| 3048 | lark | 24 |
| 3049 | lament | 24 |
| 3050 | knowest | 24 |
| 3051 | keen | 24 |
| 3052 | juno | 24 |
| 3053 | joint | 24 |
| 3054 | instantly | 24 |
| 3055 | heirs | 24 |
| 3056 | guide | 24 |
| 3057 | griffith | 24 |
| 3058 | glend | 24 |
| 3059 | fever | 24 |
| 3060 | expectation | 24 |
| 3061 | eaten | 24 |
| 3062 | dukes | 24 |
| 3063 | dukedom | 24 |
| 3064 | dove | 24 |
| 3065 | den | 24 |
| 3066 | dat | 24 |
| 3067 | comforts | 24 |
| 3068 | coin | 24 |
| 3069 | clean | 24 |
| 3070 | chin | 24 |
| 3071 | cassandra | 24 |
| 3072 | carries | 24 |
| 3073 | c | 24 |
| 3074 | breathing | 24 |
| 3075 | bread | 24 |
| 3076 | blanch | 24 |
| 3077 | betimes | 24 |
| 3078 | beguile | 24 |
| 3079 | beggars | 24 |
| 3080 | became | 24 |
| 3081 | ant | 24 |
| 3082 | answers | 24 |
| 3083 | amends | 24 |
| 3084 | altogether | 24 |
| 3085 | alarums | 24 |
| 3086 | admit | 24 |
| 3087 | youngest | 23 |
| 3088 | writing | 23 |
| 3089 | worms | 23 |
| 3090 | works | 23 |
| 3091 | whit | 23 |
| 3092 | whipt | 23 |
| 3093 | wand | 23 |
| 3094 | wak | 23 |
| 3095 | wager | 23 |
| 3096 | venom | 23 |
| 3097 | varlet | 23 |
| 3098 | valeria | 23 |
| 3099 | unkindness | 23 |
| 3100 | twould | 23 |
| 3101 | tomorrow | 23 |
| 3102 | tales | 23 |
| 3103 | swearing | 23 |
| 3104 | sufferance | 23 |
| 3105 | strokes | 23 |
| 3106 | steep | 23 |
| 3107 | softly | 23 |
| 3108 | slip | 23 |
| 3109 | simpcox | 23 |
| 3110 | shout | 23 |
| 3111 | serious | 23 |
| 3112 | scruple | 23 |
| 3113 | scratch | 23 |
| 3114 | sadness | 23 |
| 3115 | robb | 23 |
| 3116 | record | 23 |
| 3117 | raven | 23 |
| 3118 | putting | 23 |
| 3119 | promises | 23 |
| 3120 | promised | 23 |
| 3121 | poverty | 23 |
| 3122 | plant | 23 |
| 3123 | pin | 23 |
| 3124 | philario | 23 |
| 3125 | perjur | 23 |
| 3126 | penny | 23 |
| 3127 | peasant | 23 |
| 3128 | mutiny | 23 |
| 3129 | moves | 23 |
| 3130 | ministers | 23 |
| 3131 | merrily | 23 |
| 3132 | mask | 23 |
| 3133 | lodge | 23 |
| 3134 | likeness | 23 |
| 3135 | lads | 23 |
| 3136 | l | 23 |
| 3137 | injuries | 23 |
| 3138 | hounds | 23 |
| 3139 | hose | 23 |
| 3140 | holding | 23 |
| 3141 | groom | 23 |
| 3142 | greeting | 23 |
| 3143 | grass | 23 |
| 3144 | governor | 23 |
| 3145 | goods | 23 |
| 3146 | front | 23 |
| 3147 | forthwith | 23 |
| 3148 | forehead | 23 |
| 3149 | flaminius | 23 |
| 3150 | ey | 23 |
| 3151 | elsinore | 23 |
| 3152 | elements | 23 |
| 3153 | dowry | 23 |
| 3154 | doubtful | 23 |
| 3155 | divers | 23 |
| 3156 | dispose | 23 |
| 3157 | disguised | 23 |
| 3158 | direction | 23 |
| 3159 | din | 23 |
| 3160 | descend | 23 |
| 3161 | deaths | 23 |
| 3162 | dearer | 23 |
| 3163 | crowned | 23 |
| 3164 | craves | 23 |
| 3165 | couch | 23 |
| 3166 | cornwall | 23 |
| 3167 | converse | 23 |
| 3168 | conqueror | 23 |
| 3169 | careful | 23 |
| 3170 | called | 23 |
| 3171 | build | 23 |
| 3172 | bonds | 23 |
| 3173 | bona | 23 |
| 3174 | axe | 23 |
| 3175 | ape | 23 |
| 3176 | amorous | 23 |
| 3177 | amity | 23 |
| 3178 | afoot | 23 |
| 3179 | affect | 23 |
| 3180 | acts | 23 |
| 3181 | actions | 23 |
| 3182 | accident | 23 |
| 3183 | wheel | 22 |
| 3184 | wenches | 22 |
| 3185 | wanting | 22 |
| 3186 | wander | 22 |
| 3187 | waiting | 22 |
| 3188 | wag | 22 |
| 3189 | volsces | 22 |
| 3190 | upright | 22 |
| 3191 | tush | 22 |
| 3192 | throws | 22 |
| 3193 | surety | 22 |
| 3194 | stole | 22 |
| 3195 | speeches | 22 |
| 3196 | soundly | 22 |
| 3197 | sleeve | 22 |
| 3198 | sinews | 22 |
| 3199 | shrewsbury | 22 |
| 3200 | ships | 22 |
| 3201 | sergeant | 22 |
| 3202 | sensible | 22 |
| 3203 | rights | 22 |
| 3204 | prodigal | 22 |
| 3205 | presume | 22 |
| 3206 | pox | 22 |
| 3207 | pleasing | 22 |
| 3208 | piteous | 22 |
| 3209 | peto | 22 |
| 3210 | perpetual | 22 |
| 3211 | patricians | 22 |
| 3212 | panthino | 22 |
| 3213 | painting | 22 |
| 3214 | notwithstanding | 22 |
| 3215 | notes | 22 |
| 3216 | nightly | 22 |
| 3217 | neighbours | 22 |
| 3218 | naught | 22 |
| 3219 | moving | 22 |
| 3220 | marching | 22 |
| 3221 | mak | 22 |
| 3222 | lucy | 22 |
| 3223 | losing | 22 |
| 3224 | laurence | 22 |
| 3225 | innocence | 22 |
| 3226 | infant | 22 |
| 3227 | imagine | 22 |
| 3228 | hourly | 22 |
| 3229 | history | 22 |
| 3230 | hideous | 22 |
| 3231 | gallows | 22 |
| 3232 | funeral | 22 |
| 3233 | frenchman | 22 |
| 3234 | fran | 22 |
| 3235 | fourteen | 22 |
| 3236 | fold | 22 |
| 3237 | flattery | 22 |
| 3238 | faulconbridge | 22 |
| 3239 | faction | 22 |
| 3240 | est | 22 |
| 3241 | eglamour | 22 |
| 3242 | diseases | 22 |
| 3243 | diest | 22 |
| 3244 | cuckoo | 22 |
| 3245 | crest | 22 |
| 3246 | create | 22 |
| 3247 | corporal | 22 |
| 3248 | cornelius | 22 |
| 3249 | coats | 22 |
| 3250 | chorus | 22 |
| 3251 | charms | 22 |
| 3252 | changes | 22 |
| 3253 | cawdor | 22 |
| 3254 | carriage | 22 |
| 3255 | campeius | 22 |
| 3256 | burnt | 22 |
| 3257 | breeds | 22 |
| 3258 | bowels | 22 |
| 3259 | blot | 22 |
| 3260 | beget | 22 |
| 3261 | beaufort | 22 |
| 3262 | beau | 22 |
| 3263 | backs | 22 |
| 3264 | babes | 22 |
| 3265 | aloft | 22 |
| 3266 | adventure | 22 |
| 3267 | acquaint | 22 |
| 3268 | access | 22 |
| 3269 | voyage | 21 |
| 3270 | verses | 21 |
| 3271 | venus | 21 |
| 3272 | vanity | 21 |
| 3273 | vanish | 21 |
| 3274 | unjust | 21 |
| 3275 | tyrrel | 21 |
| 3276 | tutor | 21 |
| 3277 | stuck | 21 |
| 3278 | stirring | 21 |
| 3279 | shield | 21 |
| 3280 | servilius | 21 |
| 3281 | scorns | 21 |
| 3282 | sacrifice | 21 |
| 3283 | rumour | 21 |
| 3284 | rt | 21 |
| 3285 | rogues | 21 |
| 3286 | rites | 21 |
| 3287 | riches | 21 |
| 3288 | religious | 21 |
| 3289 | rack | 21 |
| 3290 | punishment | 21 |
| 3291 | pull | 21 |
| 3292 | prosperous | 21 |
| 3293 | proculeius | 21 |
| 3294 | proclamation | 21 |
| 3295 | playing | 21 |
| 3296 | petition | 21 |
| 3297 | pernicious | 21 |
| 3298 | patch | 21 |
| 3299 | ought | 21 |
| 3300 | nuptial | 21 |
| 3301 | nobler | 21 |
| 3302 | muster | 21 |
| 3303 | mourning | 21 |
| 3304 | mouldy | 21 |
| 3305 | moonshine | 21 |
| 3306 | montjoy | 21 |
| 3307 | mongst | 21 |
| 3308 | miseries | 21 |
| 3309 | mischance | 21 |
| 3310 | miles | 21 |
| 3311 | middle | 21 |
| 3312 | mamillius | 21 |
| 3313 | livery | 21 |
| 3314 | lets | 21 |
| 3315 | les | 21 |
| 3316 | lap | 21 |
| 3317 | jot | 21 |
| 3318 | jesu | 21 |
| 3319 | intents | 21 |
| 3320 | inn | 21 |
| 3321 | ingratitude | 21 |
| 3322 | infected | 21 |
| 3323 | inch | 21 |
| 3324 | hume | 21 |
| 3325 | hasty | 21 |
| 3326 | hare | 21 |
| 3327 | guests | 21 |
| 3328 | grieves | 21 |
| 3329 | gilded | 21 |
| 3330 | flout | 21 |
| 3331 | flint | 21 |
| 3332 | filthy | 21 |
| 3333 | execute | 21 |
| 3334 | excursions | 21 |
| 3335 | everlasting | 21 |
| 3336 | estimation | 21 |
| 3337 | employment | 21 |
| 3338 | eleven | 21 |
| 3339 | election | 21 |
| 3340 | divorce | 21 |
| 3341 | division | 21 |
| 3342 | dispos | 21 |
| 3343 | dismal | 21 |
| 3344 | deserts | 21 |
| 3345 | dainty | 21 |
| 3346 | cruelty | 21 |
| 3347 | courteous | 21 |
| 3348 | correction | 21 |
| 3349 | coronation | 21 |
| 3350 | corner | 21 |
| 3351 | concerns | 21 |
| 3352 | com | 21 |
| 3353 | chosen | 21 |
| 3354 | chastity | 21 |
| 3355 | candle | 21 |
| 3356 | bull | 21 |
| 3357 | brown | 21 |
| 3358 | brakenbury | 21 |
| 3359 | bounds | 21 |
| 3360 | bone | 21 |
| 3361 | bondage | 21 |
| 3362 | bliss | 21 |
| 3363 | bethink | 21 |
| 3364 | beating | 21 |
| 3365 | beastly | 21 |
| 3366 | bargain | 21 |
| 3367 | afford | 21 |
| 3368 | accus | 21 |
| 3369 | abhorson | 21 |
| 3370 | ward | 20 |
| 3371 | vii | 20 |
| 3372 | used | 20 |
| 3373 | unseen | 20 |
| 3374 | trim | 20 |
| 3375 | treasons | 20 |
| 3376 | titles | 20 |
| 3377 | tie | 20 |
| 3378 | thyreus | 20 |
| 3379 | tail | 20 |
| 3380 | sup | 20 |
| 3381 | strangers | 20 |
| 3382 | sober | 20 |
| 3383 | smoke | 20 |
| 3384 | sith | 20 |
| 3385 | sights | 20 |
| 3386 | shun | 20 |
| 3387 | shoes | 20 |
| 3388 | scarus | 20 |
| 3389 | saved | 20 |
| 3390 | samp | 20 |
| 3391 | salute | 20 |
| 3392 | robes | 20 |
| 3393 | robe | 20 |
| 3394 | rising | 20 |
| 3395 | rings | 20 |
| 3396 | richer | 20 |
| 3397 | restore | 20 |
| 3398 | require | 20 |
| 3399 | reproach | 20 |
| 3400 | rear | 20 |
| 3401 | ravish | 20 |
| 3402 | quintus | 20 |
| 3403 | purge | 20 |
| 3404 | process | 20 |
| 3405 | prefer | 20 |
| 3406 | pope | 20 |
| 3407 | pole | 20 |
| 3408 | plainly | 20 |
| 3409 | pitied | 20 |
| 3410 | pindarus | 20 |
| 3411 | persuaded | 20 |
| 3412 | perjury | 20 |
| 3413 | peep | 20 |
| 3414 | offers | 20 |
| 3415 | nobody | 20 |
| 3416 | necessary | 20 |
| 3417 | nearer | 20 |
| 3418 | narrow | 20 |
| 3419 | mountains | 20 |
| 3420 | mood | 20 |
| 3421 | monarch | 20 |
| 3422 | mocks | 20 |
| 3423 | moan | 20 |
| 3424 | mistook | 20 |
| 3425 | meddle | 20 |
| 3426 | load | 20 |
| 3427 | lived | 20 |
| 3428 | leonatus | 20 |
| 3429 | legions | 20 |
| 3430 | ld | 20 |
| 3431 | infection | 20 |
| 3432 | import | 20 |
| 3433 | immediately | 20 |
| 3434 | hack | 20 |
| 3435 | guiltless | 20 |
| 3436 | fires | 20 |
| 3437 | experience | 20 |
| 3438 | excellence | 20 |
| 3439 | escape | 20 |
| 3440 | epilogue | 20 |
| 3441 | eats | 20 |
| 3442 | duties | 20 |
| 3443 | divided | 20 |
| 3444 | dian | 20 |
| 3445 | destiny | 20 |
| 3446 | design | 20 |
| 3447 | deserved | 20 |
| 3448 | departure | 20 |
| 3449 | delights | 20 |
| 3450 | date | 20 |
| 3451 | craft | 20 |
| 3452 | convenient | 20 |
| 3453 | coast | 20 |
| 3454 | character | 20 |
| 3455 | cannon | 20 |
| 3456 | canker | 20 |
| 3457 | cambridge | 20 |
| 3458 | burial | 20 |
| 3459 | bully | 20 |
| 3460 | borrowed | 20 |
| 3461 | bootless | 20 |
| 3462 | boatswain | 20 |
| 3463 | blushing | 20 |
| 3464 | blessings | 20 |
| 3465 | ber | 20 |
| 3466 | beneath | 20 |
| 3467 | barbarous | 20 |
| 3468 | bald | 20 |
| 3469 | backward | 20 |
| 3470 | assist | 20 |
| 3471 | arch | 20 |
| 3472 | anointed | 20 |
| 3473 | ancestors | 20 |
| 3474 | ambassadors | 20 |
| 3475 | albany | 20 |
| 3476 | agree | 20 |
| 3477 | affliction | 20 |
| 3478 | afar | 20 |
| 3479 | abbey | 20 |
| 3480 | windows | 19 |
| 3481 | wet | 19 |
| 3482 | westminster | 19 |
| 3483 | wearing | 19 |
| 3484 | utmost | 19 |
| 3485 | urs | 19 |
| 3486 | untimely | 19 |
| 3487 | tubal | 19 |
| 3488 | tried | 19 |
| 3489 | tribune | 19 |
| 3490 | tragedy | 19 |
| 3491 | thread | 19 |
| 3492 | thankful | 19 |
| 3493 | tents | 19 |
| 3494 | surpris | 19 |
| 3495 | suitors | 19 |
| 3496 | style | 19 |
| 3497 | stout | 19 |
| 3498 | stabb | 19 |
| 3499 | speedy | 19 |
| 3500 | silk | 19 |
| 3501 | sickly | 19 |
| 3502 | sheets | 19 |
| 3503 | semblance | 19 |
| 3504 | scholar | 19 |
| 3505 | sav | 19 |
| 3506 | rot | 19 |
| 3507 | rocks | 19 |
| 3508 | rises | 19 |
| 3509 | removed | 19 |
| 3510 | relish | 19 |
| 3511 | regent | 19 |
| 3512 | reasonable | 19 |
| 3513 | raging | 19 |
| 3514 | prophesy | 19 |
| 3515 | procure | 19 |
| 3516 | prevented | 19 |
| 3517 | precedent | 19 |
| 3518 | practise | 19 |
| 3519 | potent | 19 |
| 3520 | pledge | 19 |
| 3521 | pine | 19 |
| 3522 | persons | 19 |
| 3523 | penance | 19 |
| 3524 | parson | 19 |
| 3525 | nod | 19 |
| 3526 | noblest | 19 |
| 3527 | nigh | 19 |
| 3528 | neptune | 19 |
| 3529 | musician | 19 |
| 3530 | multitude | 19 |
| 3531 | mothers | 19 |
| 3532 | moreover | 19 |
| 3533 | milford | 19 |
| 3534 | metellus | 19 |
| 3535 | merciful | 19 |
| 3536 | medicine | 19 |
| 3537 | martius | 19 |
| 3538 | mardian | 19 |
| 3539 | mankind | 19 |
| 3540 | maine | 19 |
| 3541 | lungs | 19 |
| 3542 | liquor | 19 |
| 3543 | ladder | 19 |
| 3544 | kinsmen | 19 |
| 3545 | judas | 19 |
| 3546 | invite | 19 |
| 3547 | integrity | 19 |
| 3548 | infect | 19 |
| 3549 | impatient | 19 |
| 3550 | hush | 19 |
| 3551 | honorable | 19 |
| 3552 | holp | 19 |
| 3553 | hides | 19 |
| 3554 | harvest | 19 |
| 3555 | harbour | 19 |
| 3556 | hangman | 19 |
| 3557 | grossly | 19 |
| 3558 | greece | 19 |
| 3559 | frowns | 19 |
| 3560 | fortunate | 19 |
| 3561 | flute | 19 |
| 3562 | flock | 19 |
| 3563 | flattering | 19 |
| 3564 | fixed | 19 |
| 3565 | fighting | 19 |
| 3566 | executed | 19 |
| 3567 | evening | 19 |
| 3568 | entrance | 19 |
| 3569 | enmity | 19 |
| 3570 | drunken | 19 |
| 3571 | drift | 19 |
| 3572 | dreamt | 19 |
| 3573 | doug | 19 |
| 3574 | distress | 19 |
| 3575 | devotion | 19 |
| 3576 | deserving | 19 |
| 3577 | depos | 19 |
| 3578 | demands | 19 |
| 3579 | deck | 19 |
| 3580 | deceit | 19 |
| 3581 | dancing | 19 |
| 3582 | coxcomb | 19 |
| 3583 | courtezan | 19 |
| 3584 | countryman | 19 |
| 3585 | cook | 19 |
| 3586 | consequence | 19 |
| 3587 | confident | 19 |
| 3588 | conceal | 19 |
| 3589 | complete | 19 |
| 3590 | chid | 19 |
| 3591 | caps | 19 |
| 3592 | caphis | 19 |
| 3593 | canidius | 19 |
| 3594 | buck | 19 |
| 3595 | broad | 19 |
| 3596 | briefly | 19 |
| 3597 | brethren | 19 |
| 3598 | bending | 19 |
| 3599 | belong | 19 |
| 3600 | balthasar | 19 |
| 3601 | ballad | 19 |
| 3602 | bagot | 19 |
| 3603 | attends | 19 |
| 3604 | ashes | 19 |
| 3605 | articles | 19 |
| 3606 | appeal | 19 |
| 3607 | aloof | 19 |
| 3608 | ale | 19 |
| 3609 | albans | 19 |
| 3610 | affected | 19 |
| 3611 | ado | 19 |
| 3612 | acknowledge | 19 |
| 3613 | abhor | 19 |
| 3614 | witchcraft | 18 |
| 3615 | weed | 18 |
| 3616 | wart | 18 |
| 3617 | violence | 18 |
| 3618 | verg | 18 |
| 3619 | vent | 18 |
| 3620 | velvet | 18 |
| 3621 | vassal | 18 |
| 3622 | understanding | 18 |
| 3623 | turk | 18 |
| 3624 | trusty | 18 |
| 3625 | trespass | 18 |
| 3626 | torches | 18 |
| 3627 | toad | 18 |
| 3628 | tiger | 18 |
| 3629 | throng | 18 |
| 3630 | thousands | 18 |
| 3631 | swelling | 18 |
| 3632 | sullen | 18 |
| 3633 | sufficient | 18 |
| 3634 | straw | 18 |
| 3635 | stops | 18 |
| 3636 | stool | 18 |
| 3637 | statue | 18 |
| 3638 | stake | 18 |
| 3639 | stab | 18 |
| 3640 | sire | 18 |
| 3641 | shames | 18 |
| 3642 | sennet | 18 |
| 3643 | scandal | 18 |
| 3644 | safer | 18 |
| 3645 | sadly | 18 |
| 3646 | rue | 18 |
| 3647 | roof | 18 |
| 3648 | road | 18 |
| 3649 | revenue | 18 |
| 3650 | returns | 18 |
| 3651 | respects | 18 |
| 3652 | reports | 18 |
| 3653 | rebuke | 18 |
| 3654 | rascals | 18 |
| 3655 | quarrels | 18 |
| 3656 | profane | 18 |
| 3657 | priests | 18 |
| 3658 | pomfret | 18 |
| 3659 | pleases | 18 |
| 3660 | persuasion | 18 |
| 3661 | oswald | 18 |
| 3662 | ornament | 18 |
| 3663 | oppose | 18 |
| 3664 | neat | 18 |
| 3665 | mort | 18 |
| 3666 | mopsa | 18 |
| 3667 | minion | 18 |
| 3668 | minded | 18 |
| 3669 | marvellous | 18 |
| 3670 | mart | 18 |
| 3671 | mantle | 18 |
| 3672 | manly | 18 |
| 3673 | lofty | 18 |
| 3674 | locks | 18 |
| 3675 | linen | 18 |
| 3676 | limit | 18 |
| 3677 | limb | 18 |
| 3678 | lechery | 18 |
| 3679 | leading | 18 |
| 3680 | julius | 18 |
| 3681 | joints | 18 |
| 3682 | intended | 18 |
| 3683 | impatience | 18 |
| 3684 | il | 18 |
| 3685 | iden | 18 |
| 3686 | ice | 18 |
| 3687 | hunting | 18 |
| 3688 | household | 18 |
| 3689 | hire | 18 |
| 3690 | helm | 18 |
| 3691 | hedge | 18 |
| 3692 | heap | 18 |
| 3693 | hates | 18 |
| 3694 | hatch | 18 |
| 3695 | harmony | 18 |
| 3696 | grandfather | 18 |
| 3697 | grain | 18 |
| 3698 | ghosts | 18 |
| 3699 | garment | 18 |
| 3700 | fulvia | 18 |
| 3701 | frenchmen | 18 |
| 3702 | fray | 18 |
| 3703 | frail | 18 |
| 3704 | forlorn | 18 |
| 3705 | fellowship | 18 |
| 3706 | famish | 18 |
| 3707 | falsely | 18 |
| 3708 | exercise | 18 |
| 3709 | etc | 18 |
| 3710 | especially | 18 |
| 3711 | errand | 18 |
| 3712 | enrich | 18 |
| 3713 | dwells | 18 |
| 3714 | during | 18 |
| 3715 | disguise | 18 |
| 3716 | dire | 18 |
| 3717 | diet | 18 |
| 3718 | despise | 18 |
| 3719 | description | 18 |
| 3720 | degrees | 18 |
| 3721 | dangers | 18 |
| 3722 | created | 18 |
| 3723 | cozen | 18 |
| 3724 | counsels | 18 |
| 3725 | contain | 18 |
| 3726 | confession | 18 |
| 3727 | compound | 18 |
| 3728 | commodity | 18 |
| 3729 | commends | 18 |
| 3730 | chose | 18 |
| 3731 | cesario | 18 |
| 3732 | bringing | 18 |
| 3733 | brass | 18 |
| 3734 | bounteous | 18 |
| 3735 | board | 18 |
| 3736 | bill | 18 |
| 3737 | belongs | 18 |
| 3738 | battles | 18 |
| 3739 | bait | 18 |
| 3740 | bachelor | 18 |
| 3741 | awe | 18 |
| 3742 | assay | 18 |
| 3743 | article | 18 |
| 3744 | arriv | 18 |
| 3745 | april | 18 |
| 3746 | apprehend | 18 |
| 3747 | anjou | 18 |
| 3748 | angiers | 18 |
| 3749 | amend | 18 |
| 3750 | address | 18 |
| 3751 | added | 18 |
| 3752 | accursed | 18 |
| 3753 | yielding | 17 |
| 3754 | worthless | 17 |
| 3755 | worser | 17 |
| 3756 | wonders | 17 |
| 3757 | wolves | 17 |
| 3758 | whispers | 17 |
| 3759 | whipp | 17 |
| 3760 | welkin | 17 |
| 3761 | wedded | 17 |
| 3762 | waves | 17 |
| 3763 | watchman | 17 |
| 3764 | walking | 17 |
| 3765 | vouch | 17 |
| 3766 | visitation | 17 |
| 3767 | uses | 17 |
| 3768 | undergo | 17 |
| 3769 | tyb | 17 |
| 3770 | trembling | 17 |
| 3771 | trebonius | 17 |
| 3772 | topas | 17 |
| 3773 | thursday | 17 |
| 3774 | thereto | 17 |
| 3775 | tavern | 17 |
| 3776 | sustain | 17 |
| 3777 | survey | 17 |
| 3778 | supposed | 17 |
| 3779 | sung | 17 |
| 3780 | sums | 17 |
| 3781 | summon | 17 |
| 3782 | succession | 17 |
| 3783 | steed | 17 |
| 3784 | split | 17 |
| 3785 | snout | 17 |
| 3786 | smallest | 17 |
| 3787 | slumber | 17 |
| 3788 | silly | 17 |
| 3789 | silken | 17 |
| 3790 | shores | 17 |
| 3791 | shoe | 17 |
| 3792 | settled | 17 |
| 3793 | scourge | 17 |
| 3794 | scot | 17 |
| 3795 | scarcely | 17 |
| 3796 | saturnine | 17 |
| 3797 | sands | 17 |
| 3798 | sails | 17 |
| 3799 | rope | 17 |
| 3800 | rode | 17 |
| 3801 | ribs | 17 |
| 3802 | retires | 17 |
| 3803 | reproof | 17 |
| 3804 | religion | 17 |
| 3805 | relent | 17 |
| 3806 | reap | 17 |
| 3807 | rated | 17 |
| 3808 | race | 17 |
| 3809 | que | 17 |
| 3810 | pursuit | 17 |
| 3811 | proves | 17 |
| 3812 | prophet | 17 |
| 3813 | profession | 17 |
| 3814 | produce | 17 |
| 3815 | prime | 17 |
| 3816 | prays | 17 |
| 3817 | pounds | 17 |
| 3818 | pot | 17 |
| 3819 | plac | 17 |
| 3820 | pipe | 17 |
| 3821 | performance | 17 |
| 3822 | peer | 17 |
| 3823 | patiently | 17 |
| 3824 | partner | 17 |
| 3825 | parents | 17 |
| 3826 | outlive | 17 |
| 3827 | orsino | 17 |
| 3828 | oppos | 17 |
| 3829 | occasions | 17 |
| 3830 | nuncle | 17 |
| 3831 | noon | 17 |
| 3832 | nam | 17 |
| 3833 | mystery | 17 |
| 3834 | murderers | 17 |
| 3835 | monmouth | 17 |
| 3836 | mocking | 17 |
| 3837 | marble | 17 |
| 3838 | maker | 17 |
| 3839 | lute | 17 |
| 3840 | longing | 17 |
| 3841 | lily | 17 |
| 3842 | lief | 17 |
| 3843 | latter | 17 |
| 3844 | knavery | 17 |
| 3845 | jests | 17 |
| 3846 | intends | 17 |
| 3847 | idly | 17 |
| 3848 | humility | 17 |
| 3849 | howl | 17 |
| 3850 | homage | 17 |
| 3851 | hind | 17 |
| 3852 | herd | 17 |
| 3853 | heinous | 17 |
| 3854 | heel | 17 |
| 3855 | heav | 17 |
| 3856 | headed | 17 |
| 3857 | haven | 17 |
| 3858 | haunt | 17 |
| 3859 | hatred | 17 |
| 3860 | happier | 17 |
| 3861 | grim | 17 |
| 3862 | gloves | 17 |
| 3863 | gilt | 17 |
| 3864 | giant | 17 |
| 3865 | gentleness | 17 |
| 3866 | gads | 17 |
| 3867 | function | 17 |
| 3868 | flying | 17 |
| 3869 | female | 17 |
| 3870 | feasts | 17 |
| 3871 | fan | 17 |
| 3872 | extend | 17 |
| 3873 | exploit | 17 |
| 3874 | endeavour | 17 |
| 3875 | encount | 17 |
| 3876 | empire | 17 |
| 3877 | egg | 17 |
| 3878 | egeus | 17 |
| 3879 | ebb | 17 |
| 3880 | drowsy | 17 |
| 3881 | dover | 17 |
| 3882 | disturb | 17 |
| 3883 | discord | 17 |
| 3884 | debts | 17 |
| 3885 | dealing | 17 |
| 3886 | dash | 17 |
| 3887 | curtain | 17 |
| 3888 | crows | 17 |
| 3889 | crimes | 17 |
| 3890 | cowardly | 17 |
| 3891 | couple | 17 |
| 3892 | corruption | 17 |
| 3893 | corrupted | 17 |
| 3894 | constancy | 17 |
| 3895 | confine | 17 |
| 3896 | concluded | 17 |
| 3897 | complain | 17 |
| 3898 | cloth | 17 |
| 3899 | cleomenes | 17 |
| 3900 | christendom | 17 |
| 3901 | cheerful | 17 |
| 3902 | charitable | 17 |
| 3903 | calpurnia | 17 |
| 3904 | calling | 17 |
| 3905 | calchas | 17 |
| 3906 | butt | 17 |
| 3907 | buds | 17 |
| 3908 | britaine | 17 |
| 3909 | boldly | 17 |
| 3910 | bereft | 17 |
| 3911 | benvolio | 17 |
| 3912 | beginning | 17 |
| 3913 | baseness | 17 |
| 3914 | bard | 17 |
| 3915 | baby | 17 |
| 3916 | antenor | 17 |
| 3917 | answered | 17 |
| 3918 | agreed | 17 |
| 3919 | aedile | 17 |
| 3920 | abused | 17 |
| 3921 | worthiness | 16 |
| 3922 | wasted | 16 |
| 3923 | warriors | 16 |
| 3924 | vision | 16 |
| 3925 | villainous | 16 |
| 3926 | vein | 16 |
| 3927 | vault | 16 |
| 3928 | usurping | 16 |
| 3929 | ursula | 16 |
| 3930 | truer | 16 |
| 3931 | tokens | 16 |
| 3932 | toe | 16 |
| 3933 | tax | 16 |
| 3934 | talents | 16 |
| 3935 | tainted | 16 |
| 3936 | sweets | 16 |
| 3937 | sweeter | 16 |
| 3938 | surveyor | 16 |
| 3939 | surfeit | 16 |
| 3940 | suppos | 16 |
| 3941 | sugar | 16 |
| 3942 | strict | 16 |
| 3943 | storms | 16 |
| 3944 | stirs | 16 |
| 3945 | stealing | 16 |
| 3946 | starve | 16 |
| 3947 | squire | 16 |
| 3948 | spurs | 16 |
| 3949 | sow | 16 |
| 3950 | snatch | 16 |
| 3951 | slanders | 16 |
| 3952 | skull | 16 |
| 3953 | showing | 16 |
| 3954 | security | 16 |
| 3955 | scars | 16 |
| 3956 | scar | 16 |
| 3957 | saving | 16 |
| 3958 | sans | 16 |
| 3959 | sailors | 16 |
| 3960 | ruffian | 16 |
| 3961 | revels | 16 |
| 3962 | revel | 16 |
| 3963 | requires | 16 |
| 3964 | ranks | 16 |
| 3965 | rags | 16 |
| 3966 | provoke | 16 |
| 3967 | prosperity | 16 |
| 3968 | proceedings | 16 |
| 3969 | privy | 16 |
| 3970 | presented | 16 |
| 3971 | praised | 16 |
| 3972 | port | 16 |
| 3973 | politic | 16 |
| 3974 | plight | 16 |
| 3975 | pleaseth | 16 |
| 3976 | plains | 16 |
| 3977 | pillow | 16 |
| 3978 | pilgrimage | 16 |
| 3979 | phoebus | 16 |
| 3980 | philippi | 16 |
| 3981 | passions | 16 |
| 3982 | passes | 16 |
| 3983 | papers | 16 |
| 3984 | paint | 16 |
| 3985 | overthrow | 16 |
| 3986 | motive | 16 |
| 3987 | moiety | 16 |
| 3988 | minutes | 16 |
| 3989 | melted | 16 |
| 3990 | meed | 16 |
| 3991 | mate | 16 |
| 3992 | lucullus | 16 |
| 3993 | luce | 16 |
| 3994 | lt | 16 |
| 3995 | loathsome | 16 |
| 3996 | leaden | 16 |
| 3997 | latest | 16 |
| 3998 | lacks | 16 |
| 3999 | kneeling | 16 |
| 4000 | judgement | 16 |
| 4001 | italian | 16 |
| 4002 | instinct | 16 |
| 4003 | instead | 16 |
| 4004 | inherit | 16 |
| 4005 | infirmity | 16 |
| 4006 | inclin | 16 |
| 4007 | imprisonment | 16 |
| 4008 | huntsman | 16 |
| 4009 | hum | 16 |
| 4010 | horror | 16 |
| 4011 | horrid | 16 |
| 4012 | hop | 16 |
| 4013 | highest | 16 |
| 4014 | heaviness | 16 |
| 4015 | heal | 16 |
| 4016 | harms | 16 |
| 4017 | growth | 16 |
| 4018 | gladly | 16 |
| 4019 | gazing | 16 |
| 4020 | gage | 16 |
| 4021 | foil | 16 |
| 4022 | fleance | 16 |
| 4023 | flatterer | 16 |
| 4024 | finding | 16 |
| 4025 | file | 16 |
| 4026 | figures | 16 |
| 4027 | fifteen | 16 |
| 4028 | fertile | 16 |
| 4029 | feeds | 16 |
| 4030 | feeding | 16 |
| 4031 | faster | 16 |
| 4032 | extreme | 16 |
| 4033 | expense | 16 |
| 4034 | everywhere | 16 |
| 4035 | err | 16 |
| 4036 | envoy | 16 |
| 4037 | enters | 16 |
| 4038 | dried | 16 |
| 4039 | drawer | 16 |
| 4040 | dram | 16 |
| 4041 | donalbain | 16 |
| 4042 | distemper | 16 |
| 4043 | disguis | 16 |
| 4044 | devis | 16 |
| 4045 | detested | 16 |
| 4046 | determin | 16 |
| 4047 | descent | 16 |
| 4048 | deeply | 16 |
| 4049 | deceived | 16 |
| 4050 | curtsy | 16 |
| 4051 | cudgel | 16 |
| 4052 | crush | 16 |
| 4053 | crept | 16 |
| 4054 | cradle | 16 |
| 4055 | cowardice | 16 |
| 4056 | courses | 16 |
| 4057 | control | 16 |
| 4058 | confin | 16 |
| 4059 | confidence | 16 |
| 4060 | composition | 16 |
| 4061 | compell | 16 |
| 4062 | companions | 16 |
| 4063 | colville | 16 |
| 4064 | coffin | 16 |
| 4065 | clay | 16 |
| 4066 | clapp | 16 |
| 4067 | cicero | 16 |
| 4068 | churlish | 16 |
| 4069 | choke | 16 |
| 4070 | chatillon | 16 |
| 4071 | celestial | 16 |
| 4072 | capable | 16 |
| 4073 | built | 16 |
| 4074 | bridegroom | 16 |
| 4075 | brawl | 16 |
| 4076 | branches | 16 |
| 4077 | brace | 16 |
| 4078 | boldness | 16 |
| 4079 | block | 16 |
| 4080 | bigot | 16 |
| 4081 | bide | 16 |
| 4082 | belmont | 16 |
| 4083 | beguil | 16 |
| 4084 | beautiful | 16 |
| 4085 | bate | 16 |
| 4086 | bastards | 16 |
| 4087 | bands | 16 |
| 4088 | balm | 16 |
| 4089 | bail | 16 |
| 4090 | attach | 16 |
| 4091 | assured | 16 |
| 4092 | assault | 16 |
| 4093 | arrant | 16 |
| 4094 | approaches | 16 |
| 4095 | ample | 16 |
| 4096 | amiens | 16 |
| 4097 | alms | 16 |
| 4098 | alliance | 16 |
| 4099 | albeit | 16 |
| 4100 | adrian | 16 |
| 4101 | accent | 16 |
| 4102 | yon | 15 |
| 4103 | yields | 15 |
| 4104 | wronged | 15 |
| 4105 | worthies | 15 |
| 4106 | worldly | 15 |
| 4107 | woods | 15 |
| 4108 | wond | 15 |
| 4109 | witty | 15 |
| 4110 | wiser | 15 |
| 4111 | winged | 15 |
| 4112 | willoughby | 15 |
| 4113 | wilful | 15 |
| 4114 | whatsoever | 15 |
| 4115 | wednesday | 15 |
| 4116 | weal | 15 |
| 4117 | warning | 15 |
| 4118 | wakes | 15 |
| 4119 | vilely | 15 |
| 4120 | victorious | 15 |
| 4121 | ver | 15 |
| 4122 | unlike | 15 |
| 4123 | tween | 15 |
| 4124 | trifles | 15 |
| 4125 | traveller | 15 |
| 4126 | toys | 15 |
| 4127 | torn | 15 |
| 4128 | tired | 15 |
| 4129 | tire | 15 |
| 4130 | thorns | 15 |
| 4131 | theft | 15 |
| 4132 | tempted | 15 |
| 4133 | taint | 15 |
| 4134 | superfluous | 15 |
| 4135 | suff | 15 |
| 4136 | studied | 15 |
| 4137 | stomachs | 15 |
| 4138 | steals | 15 |
| 4139 | somewhat | 15 |
| 4140 | smith | 15 |
| 4141 | shrew | 15 |
| 4142 | shirt | 15 |
| 4143 | shameful | 15 |
| 4144 | sham | 15 |
| 4145 | shakes | 15 |
| 4146 | seiz | 15 |
| 4147 | sauce | 15 |
| 4148 | rouen | 15 |
| 4149 | rod | 15 |
| 4150 | ridiculous | 15 |
| 4151 | richly | 15 |
| 4152 | revenges | 15 |
| 4153 | reported | 15 |
| 4154 | renew | 15 |
| 4155 | reigns | 15 |
| 4156 | region | 15 |
| 4157 | reckoning | 15 |
| 4158 | readiness | 15 |
| 4159 | rape | 15 |
| 4160 | purpos | 15 |
| 4161 | purple | 15 |
| 4162 | property | 15 |
| 4163 | profound | 15 |
| 4164 | print | 15 |
| 4165 | presents | 15 |
| 4166 | pregnant | 15 |
| 4167 | prate | 15 |
| 4168 | pisa | 15 |
| 4169 | period | 15 |
| 4170 | peradventure | 15 |
| 4171 | pattern | 15 |
| 4172 | parties | 15 |
| 4173 | parcel | 15 |
| 4174 | oppression | 15 |
| 4175 | opportunity | 15 |
| 4176 | oil | 15 |
| 4177 | offender | 15 |
| 4178 | obtain | 15 |
| 4179 | observance | 15 |
| 4180 | oblivion | 15 |
| 4181 | norway | 15 |
| 4182 | nobleness | 15 |
| 4183 | nell | 15 |
| 4184 | naughty | 15 |
| 4185 | mutual | 15 |
| 4186 | mus | 15 |
| 4187 | mouse | 15 |
| 4188 | mounted | 15 |
| 4189 | mon | 15 |
| 4190 | mistrust | 15 |
| 4191 | mightily | 15 |
| 4192 | mercury | 15 |
| 4193 | mates | 15 |
| 4194 | madly | 15 |
| 4195 | losses | 15 |
| 4196 | lists | 15 |
| 4197 | listen | 15 |
| 4198 | ligarius | 15 |
| 4199 | leaf | 15 |
| 4200 | laying | 15 |
| 4201 | laughing | 15 |
| 4202 | lascivious | 15 |
| 4203 | landed | 15 |
| 4204 | lamentable | 15 |
| 4205 | lame | 15 |
| 4206 | labouring | 15 |
| 4207 | keys | 15 |
| 4208 | instruction | 15 |
| 4209 | inquire | 15 |
| 4210 | injurious | 15 |
| 4211 | indifferent | 15 |
| 4212 | impediment | 15 |
| 4213 | immediate | 15 |
| 4214 | idleness | 15 |
| 4215 | hunger | 15 |
| 4216 | homely | 15 |
| 4217 | highly | 15 |
| 4218 | heigh | 15 |
| 4219 | harmless | 15 |
| 4220 | guts | 15 |
| 4221 | grove | 15 |
| 4222 | greg | 15 |
| 4223 | gentry | 15 |
| 4224 | furious | 15 |
| 4225 | fruitful | 15 |
| 4226 | frowning | 15 |
| 4227 | frantic | 15 |
| 4228 | fountain | 15 |
| 4229 | fortinbras | 15 |
| 4230 | forgotten | 15 |
| 4231 | fiends | 15 |
| 4232 | feature | 15 |
| 4233 | fantastical | 15 |
| 4234 | fang | 15 |
| 4235 | executioner | 15 |
| 4236 | enforc | 15 |
| 4237 | eastcheap | 15 |
| 4238 | dunsinane | 15 |
| 4239 | driven | 15 |
| 4240 | drawing | 15 |
| 4241 | dorcas | 15 |
| 4242 | distracted | 15 |
| 4243 | dismay | 15 |
| 4244 | dislike | 15 |
| 4245 | discontent | 15 |
| 4246 | discipline | 15 |
| 4247 | devour | 15 |
| 4248 | daring | 15 |
| 4249 | crooked | 15 |
| 4250 | cousins | 15 |
| 4251 | contend | 15 |
| 4252 | conspirator | 15 |
| 4253 | confer | 15 |
| 4254 | complaint | 15 |
| 4255 | commandment | 15 |
| 4256 | coldly | 15 |
| 4257 | coal | 15 |
| 4258 | clitus | 15 |
| 4259 | clap | 15 |
| 4260 | clamour | 15 |
| 4261 | cheap | 15 |
| 4262 | changing | 15 |
| 4263 | causes | 15 |
| 4264 | cato | 15 |
| 4265 | carlisle | 15 |
| 4266 | careless | 15 |
| 4267 | bullcalf | 15 |
| 4268 | bulk | 15 |
| 4269 | breakfast | 15 |
| 4270 | branch | 15 |
| 4271 | bills | 15 |
| 4272 | bigger | 15 |
| 4273 | beadle | 15 |
| 4274 | bank | 15 |
| 4275 | bag | 15 |
| 4276 | aye | 15 |
| 4277 | awak | 15 |
| 4278 | avaunt | 15 |
| 4279 | author | 15 |
| 4280 | asunder | 15 |
| 4281 | assembly | 15 |
| 4282 | array | 15 |
| 4283 | apply | 15 |
| 4284 | apes | 15 |
| 4285 | antique | 15 |
| 4286 | airy | 15 |
| 4287 | admirable | 15 |
| 4288 | wrinkles | 14 |
| 4289 | worthier | 14 |
| 4290 | witches | 14 |
| 4291 | whitmore | 14 |
| 4292 | whereupon | 14 |
| 4293 | wat | 14 |
| 4294 | warrior | 14 |
| 4295 | waist | 14 |
| 4296 | upward | 14 |
| 4297 | unruly | 14 |
| 4298 | universal | 14 |
| 4299 | underneath | 14 |
| 4300 | unarm | 14 |
| 4301 | truce | 14 |
| 4302 | truant | 14 |
| 4303 | trow | 14 |
| 4304 | troubles | 14 |
| 4305 | triumphant | 14 |
| 4306 | throwing | 14 |
| 4307 | threats | 14 |
| 4308 | threaten | 14 |
| 4309 | tawny | 14 |
| 4310 | tardy | 14 |
| 4311 | tapster | 14 |
| 4312 | talks | 14 |
| 4313 | tables | 14 |
| 4314 | swoon | 14 |
| 4315 | surgeon | 14 |
| 4316 | suffice | 14 |
| 4317 | subscribe | 14 |
| 4318 | subdu | 14 |
| 4319 | stockings | 14 |
| 4320 | stiff | 14 |
| 4321 | stead | 14 |
| 4322 | states | 14 |
| 4323 | starveling | 14 |
| 4324 | starts | 14 |
| 4325 | springs | 14 |
| 4326 | spotted | 14 |
| 4327 | songs | 14 |
| 4328 | shining | 14 |
| 4329 | sheet | 14 |
| 4330 | secrecy | 14 |
| 4331 | schoolmaster | 14 |
| 4332 | scale | 14 |
| 4333 | saints | 14 |
| 4334 | riot | 14 |
| 4335 | rheum | 14 |
| 4336 | rests | 14 |
| 4337 | requests | 14 |
| 4338 | repeal | 14 |
| 4339 | remov | 14 |
| 4340 | rehearse | 14 |
| 4341 | receives | 14 |
| 4342 | provok | 14 |
| 4343 | proverb | 14 |
| 4344 | proved | 14 |
| 4345 | proudest | 14 |
| 4346 | proofs | 14 |
| 4347 | powerful | 14 |
| 4348 | plucks | 14 |
| 4349 | plots | 14 |
| 4350 | plagues | 14 |
| 4351 | piercing | 14 |
| 4352 | phoenix | 14 |
| 4353 | philostrate | 14 |
| 4354 | philosophy | 14 |
| 4355 | peruse | 14 |
| 4356 | penitent | 14 |
| 4357 | payment | 14 |
| 4358 | pastime | 14 |
| 4359 | pangs | 14 |
| 4360 | owner | 14 |
| 4361 | outside | 14 |
| 4362 | nourish | 14 |
| 4363 | notorious | 14 |
| 4364 | notable | 14 |
| 4365 | noses | 14 |
| 4366 | non | 14 |
| 4367 | negligence | 14 |
| 4368 | neglected | 14 |
| 4369 | nearest | 14 |
| 4370 | nativity | 14 |
| 4371 | napkin | 14 |
| 4372 | mutius | 14 |
| 4373 | mute | 14 |
| 4374 | mustardseed | 14 |
| 4375 | mortality | 14 |
| 4376 | million | 14 |
| 4377 | mended | 14 |
| 4378 | meanest | 14 |
| 4379 | mast | 14 |
| 4380 | marquis | 14 |
| 4381 | ling | 14 |
| 4382 | lime | 14 |
| 4383 | levied | 14 |
| 4384 | leader | 14 |
| 4385 | lasting | 14 |
| 4386 | lance | 14 |
| 4387 | insolence | 14 |
| 4388 | imperious | 14 |
| 4389 | husbandry | 14 |
| 4390 | hurts | 14 |
| 4391 | hound | 14 |
| 4392 | hook | 14 |
| 4393 | holiday | 14 |
| 4394 | hinder | 14 |
| 4395 | helps | 14 |
| 4396 | hecate | 14 |
| 4397 | heavier | 14 |
| 4398 | haughty | 14 |
| 4399 | habits | 14 |
| 4400 | guards | 14 |
| 4401 | gravity | 14 |
| 4402 | goodman | 14 |
| 4403 | goest | 14 |
| 4404 | gertrude | 14 |
| 4405 | gav | 14 |
| 4406 | frighted | 14 |
| 4407 | fram | 14 |
| 4408 | forever | 14 |
| 4409 | forced | 14 |
| 4410 | footing | 14 |
| 4411 | fitted | 14 |
| 4412 | finish | 14 |
| 4413 | fife | 14 |
| 4414 | fawn | 14 |
| 4415 | fates | 14 |
| 4416 | farthest | 14 |
| 4417 | fantasy | 14 |
| 4418 | extremes | 14 |
| 4419 | exton | 14 |
| 4420 | excess | 14 |
| 4421 | exceed | 14 |
| 4422 | eunuch | 14 |
| 4423 | epitaph | 14 |
| 4424 | engag | 14 |
| 4425 | enforced | 14 |
| 4426 | endur | 14 |
| 4427 | embassy | 14 |
| 4428 | eleanor | 14 |
| 4429 | egyptian | 14 |
| 4430 | eating | 14 |
| 4431 | dropp | 14 |
| 4432 | drives | 14 |
| 4433 | dissembling | 14 |
| 4434 | dim | 14 |
| 4435 | dignities | 14 |
| 4436 | digest | 14 |
| 4437 | diamond | 14 |
| 4438 | devilish | 14 |
| 4439 | despised | 14 |
| 4440 | deformed | 14 |
| 4441 | defeat | 14 |
| 4442 | debate | 14 |
| 4443 | damnation | 14 |
| 4444 | cuts | 14 |
| 4445 | crab | 14 |
| 4446 | cornets | 14 |
| 4447 | copy | 14 |
| 4448 | compact | 14 |
| 4449 | cities | 14 |
| 4450 | circle | 14 |
| 4451 | chiefest | 14 |
| 4452 | cheese | 14 |
| 4453 | charges | 14 |
| 4454 | captive | 14 |
| 4455 | capital | 14 |
| 4456 | cambio | 14 |
| 4457 | bud | 14 |
| 4458 | bridge | 14 |
| 4459 | bowl | 14 |
| 4460 | bloods | 14 |
| 4461 | bestowed | 14 |
| 4462 | berkeley | 14 |
| 4463 | believ | 14 |
| 4464 | beards | 14 |
| 4465 | bars | 14 |
| 4466 | banks | 14 |
| 4467 | balls | 14 |
| 4468 | badge | 14 |
| 4469 | attain | 14 |
| 4470 | assistance | 14 |
| 4471 | arts | 14 |
| 4472 | arras | 14 |
| 4473 | apprehension | 14 |
| 4474 | amain | 14 |
| 4475 | allay | 14 |
| 4476 | affords | 14 |
| 4477 | aemilius | 14 |
| 4478 | advanc | 14 |
| 4479 | adore | 14 |
| 4480 | admitted | 14 |
| 4481 | adder | 14 |
| 4482 | ad | 14 |
| 4483 | achieve | 14 |
| 4484 | ache | 14 |
| 4485 | accidents | 14 |
| 4486 | abominable | 14 |
| 4487 | abate | 14 |
| 4488 | wretches | 13 |
| 4489 | wrathful | 13 |
| 4490 | worthiest | 13 |
| 4491 | wisest | 13 |
| 4492 | whoever | 13 |
| 4493 | weighty | 13 |
| 4494 | vices | 13 |
| 4495 | verily | 13 |
| 4496 | vast | 13 |
| 4497 | vanquish | 13 |
| 4498 | unmannerly | 13 |
| 4499 | twelvemonth | 13 |
| 4500 | tullus | 13 |
| 4501 | transform | 13 |
| 4502 | toy | 13 |
| 4503 | thumb | 13 |
| 4504 | thorough | 13 |
| 4505 | testimony | 13 |
| 4506 | tenour | 13 |
| 4507 | tenderness | 13 |
| 4508 | temples | 13 |
| 4509 | taper | 13 |
| 4510 | swifter | 13 |
| 4511 | sweep | 13 |
| 4512 | succour | 13 |
| 4513 | succeed | 13 |
| 4514 | studies | 13 |
| 4515 | strings | 13 |
| 4516 | stray | 13 |
| 4517 | strato | 13 |
| 4518 | stirr | 13 |
| 4519 | steeds | 13 |
| 4520 | square | 13 |
| 4521 | speechless | 13 |
| 4522 | spain | 13 |
| 4523 | sorts | 13 |
| 4524 | snare | 13 |
| 4525 | smother | 13 |
| 4526 | simplicity | 13 |
| 4527 | shroud | 13 |
| 4528 | shop | 13 |
| 4529 | shelter | 13 |
| 4530 | seyton | 13 |
| 4531 | scroll | 13 |
| 4532 | scarlet | 13 |
| 4533 | scales | 13 |
| 4534 | sayest | 13 |
| 4535 | sap | 13 |
| 4536 | sanctuary | 13 |
| 4537 | rightful | 13 |
| 4538 | rey | 13 |
| 4539 | restraint | 13 |
| 4540 | resort | 13 |
| 4541 | resolved | 13 |
| 4542 | repeat | 13 |
| 4543 | relief | 13 |
| 4544 | recreant | 13 |
| 4545 | reckon | 13 |
| 4546 | raw | 13 |
| 4547 | rabble | 13 |
| 4548 | quantity | 13 |
| 4549 | quake | 13 |
| 4550 | puff | 13 |
| 4551 | publish | 13 |
| 4552 | protection | 13 |
| 4553 | prophecy | 13 |
| 4554 | prompt | 13 |
| 4555 | progress | 13 |
| 4556 | proceeded | 13 |
| 4557 | practices | 13 |
| 4558 | ports | 13 |
| 4559 | plants | 13 |
| 4560 | pigeons | 13 |
| 4561 | pestilence | 13 |
| 4562 | personal | 13 |
| 4563 | permit | 13 |
| 4564 | perilous | 13 |
| 4565 | ox | 13 |
| 4566 | outrage | 13 |
| 4567 | ordinary | 13 |
| 4568 | opinions | 13 |
| 4569 | opens | 13 |
| 4570 | omit | 13 |
| 4571 | nicholas | 13 |
| 4572 | nail | 13 |
| 4573 | motley | 13 |
| 4574 | motions | 13 |
| 4575 | morton | 13 |
| 4576 | moody | 13 |
| 4577 | model | 13 |
| 4578 | miscarry | 13 |
| 4579 | mingled | 13 |
| 4580 | messina | 13 |
| 4581 | merriment | 13 |
| 4582 | meets | 13 |
| 4583 | meaner | 13 |
| 4584 | marcellus | 13 |
| 4585 | mansion | 13 |
| 4586 | manifest | 13 |
| 4587 | mangled | 13 |
| 4588 | male | 13 |
| 4589 | magic | 13 |
| 4590 | lustre | 13 |
| 4591 | lowly | 13 |
| 4592 | longs | 13 |
| 4593 | linger | 13 |
| 4594 | likelihood | 13 |
| 4595 | liar | 13 |
| 4596 | lends | 13 |
| 4597 | leek | 13 |
| 4598 | lane | 13 |
| 4599 | lambs | 13 |
| 4600 | justices | 13 |
| 4601 | jump | 13 |
| 4602 | judgments | 13 |
| 4603 | jade | 13 |
| 4604 | ingrateful | 13 |
| 4605 | imprison | 13 |
| 4606 | importune | 13 |
| 4607 | illyria | 13 |
| 4608 | hymen | 13 |
| 4609 | howling | 13 |
| 4610 | holiness | 13 |
| 4611 | helenus | 13 |
| 4612 | hecuba | 13 |
| 4613 | heavily | 13 |
| 4614 | hautboys | 13 |
| 4615 | handsome | 13 |
| 4616 | grand | 13 |
| 4617 | girls | 13 |
| 4618 | gild | 13 |
| 4619 | gallia | 13 |
| 4620 | gadshill | 13 |
| 4621 | future | 13 |
| 4622 | fully | 13 |
| 4623 | frank | 13 |
| 4624 | fowl | 13 |
| 4625 | fourscore | 13 |
| 4626 | foolery | 13 |
| 4627 | follower | 13 |
| 4628 | follies | 13 |
| 4629 | florentine | 13 |
| 4630 | fills | 13 |
| 4631 | fights | 13 |
| 4632 | fence | 13 |
| 4633 | feats | 13 |
| 4634 | feathers | 13 |
| 4635 | fasting | 13 |
| 4636 | fancies | 13 |
| 4637 | eyelids | 13 |
| 4638 | events | 13 |
| 4639 | eve | 13 |
| 4640 | errors | 13 |
| 4641 | ensue | 13 |
| 4642 | ending | 13 |
| 4643 | ecstasy | 13 |
| 4644 | earn | 13 |
| 4645 | dwelling | 13 |
| 4646 | drunkard | 13 |
| 4647 | dragon | 13 |
| 4648 | doting | 13 |
| 4649 | disorder | 13 |
| 4650 | dishes | 13 |
| 4651 | disgrac | 13 |
| 4652 | discontented | 13 |
| 4653 | discharg | 13 |
| 4654 | directed | 13 |
| 4655 | dido | 13 |
| 4656 | diadem | 13 |
| 4657 | despis | 13 |
| 4658 | descended | 13 |
| 4659 | deriv | 13 |
| 4660 | depend | 13 |
| 4661 | daggers | 13 |
| 4662 | curious | 13 |
| 4663 | curio | 13 |
| 4664 | curb | 13 |
| 4665 | crystal | 13 |
| 4666 | coventry | 13 |
| 4667 | counsellor | 13 |
| 4668 | contemplation | 13 |
| 4669 | conspiracy | 13 |
| 4670 | comment | 13 |
| 4671 | commendations | 13 |
| 4672 | cobweb | 13 |
| 4673 | churchyard | 13 |
| 4674 | cheerly | 13 |
| 4675 | chances | 13 |
| 4676 | chancellor | 13 |
| 4677 | champion | 13 |
| 4678 | chambers | 13 |
| 4679 | ceres | 13 |
| 4680 | centre | 13 |
| 4681 | casket | 13 |
| 4682 | carrion | 13 |
| 4683 | caitiff | 13 |
| 4684 | brazen | 13 |
| 4685 | brandon | 13 |
| 4686 | brag | 13 |
| 4687 | bows | 13 |
| 4688 | blank | 13 |
| 4689 | bells | 13 |
| 4690 | beef | 13 |
| 4691 | beauties | 13 |
| 4692 | bearer | 13 |
| 4693 | bawdy | 13 |
| 4694 | basest | 13 |
| 4695 | attire | 13 |
| 4696 | assume | 13 |
| 4697 | arrows | 13 |
| 4698 | approved | 13 |
| 4699 | approbation | 13 |
| 4700 | apple | 13 |
| 4701 | applause | 13 |
| 4702 | appearance | 13 |
| 4703 | ages | 13 |
| 4704 | afore | 13 |
| 4705 | afflict | 13 |
| 4706 | actor | 13 |
| 4707 | accusation | 13 |
| 4708 | accurs | 13 |
| 4709 | abundance | 13 |
| 4710 | yesternight | 12 |
| 4711 | yard | 12 |
| 4712 | wrinkled | 12 |
| 4713 | wring | 12 |
| 4714 | worthily | 12 |
| 4715 | wi | 12 |
| 4716 | whereby | 12 |
| 4717 | wave | 12 |
| 4718 | voluntary | 12 |
| 4719 | volumnius | 12 |
| 4720 | volsce | 12 |
| 4721 | veil | 12 |
| 4722 | vaughan | 12 |
| 4723 | vat | 12 |
| 4724 | understood | 12 |
| 4725 | tyrannous | 12 |
| 4726 | turned | 12 |
| 4727 | trod | 12 |
| 4728 | trip | 12 |
| 4729 | treble | 12 |
| 4730 | traffic | 12 |
| 4731 | tickle | 12 |
| 4732 | throughly | 12 |
| 4733 | thrift | 12 |
| 4734 | teaching | 12 |
| 4735 | tak | 12 |
| 4736 | swim | 12 |
| 4737 | support | 12 |
| 4738 | suffers | 12 |
| 4739 | spies | 12 |
| 4740 | speedily | 12 |
| 4741 | spacious | 12 |
| 4742 | smil | 12 |
| 4743 | smells | 12 |
| 4744 | size | 12 |
| 4745 | sixteen | 12 |
| 4746 | sixpence | 12 |
| 4747 | sinful | 12 |
| 4748 | simply | 12 |
| 4749 | shouts | 12 |
| 4750 | shaking | 12 |
| 4751 | shaft | 12 |
| 4752 | sever | 12 |
| 4753 | sepulchre | 12 |
| 4754 | seed | 12 |
| 4755 | secretly | 12 |
| 4756 | seated | 12 |
| 4757 | seasons | 12 |
| 4758 | rub | 12 |
| 4759 | rowland | 12 |
| 4760 | revolted | 12 |
| 4761 | restrain | 12 |
| 4762 | respected | 12 |
| 4763 | resolute | 12 |
| 4764 | reserv | 12 |
| 4765 | remuneration | 12 |
| 4766 | relieve | 12 |
| 4767 | rein | 12 |
| 4768 | regal | 12 |
| 4769 | receipt | 12 |
| 4770 | rages | 12 |
| 4771 | questions | 12 |
| 4772 | pursu | 12 |
| 4773 | purses | 12 |
| 4774 | purchas | 12 |
| 4775 | pupil | 12 |
| 4776 | protect | 12 |
| 4777 | project | 12 |
| 4778 | praising | 12 |
| 4779 | posts | 12 |
| 4780 | plenty | 12 |
| 4781 | player | 12 |
| 4782 | plainness | 12 |
| 4783 | pig | 12 |
| 4784 | philosopher | 12 |
| 4785 | peremptory | 12 |
| 4786 | penalty | 12 |
| 4787 | peck | 12 |
| 4788 | peaseblossom | 12 |
| 4789 | pasture | 12 |
| 4790 | parle | 12 |
| 4791 | paradise | 12 |
| 4792 | oppress | 12 |
| 4793 | offense | 12 |
| 4794 | nymphs | 12 |
| 4795 | numb | 12 |
| 4796 | necessities | 12 |
| 4797 | navarre | 12 |
| 4798 | mum | 12 |
| 4799 | muddy | 12 |
| 4800 | mounsieur | 12 |
| 4801 | morocco | 12 |
| 4802 | monsters | 12 |
| 4803 | mingle | 12 |
| 4804 | merits | 12 |
| 4805 | meal | 12 |
| 4806 | marr | 12 |
| 4807 | malicious | 12 |
| 4808 | macmorris | 12 |
| 4809 | lunatic | 12 |
| 4810 | loins | 12 |
| 4811 | lively | 12 |
| 4812 | lik | 12 |
| 4813 | lightly | 12 |
| 4814 | lewd | 12 |
| 4815 | leather | 12 |
| 4816 | latin | 12 |
| 4817 | jeweller | 12 |
| 4818 | jerkin | 12 |
| 4819 | james | 12 |
| 4820 | jades | 12 |
| 4821 | inheritance | 12 |
| 4822 | infamy | 12 |
| 4823 | incens | 12 |
| 4824 | impart | 12 |
| 4825 | hurl | 12 |
| 4826 | hunter | 12 |
| 4827 | humorous | 12 |
| 4828 | however | 12 |
| 4829 | howe | 12 |
| 4830 | holla | 12 |
| 4831 | hic | 12 |
| 4832 | heralds | 12 |
| 4833 | harfleur | 12 |
| 4834 | handle | 12 |
| 4835 | greatly | 12 |
| 4836 | grac | 12 |
| 4837 | gloss | 12 |
| 4838 | glories | 12 |
| 4839 | gets | 12 |
| 4840 | generally | 12 |
| 4841 | gallants | 12 |
| 4842 | frost | 12 |
| 4843 | fret | 12 |
| 4844 | frenzy | 12 |
| 4845 | frailty | 12 |
| 4846 | forester | 12 |
| 4847 | folks | 12 |
| 4848 | flatterers | 12 |
| 4849 | flames | 12 |
| 4850 | fitzwater | 12 |
| 4851 | feign | 12 |
| 4852 | famine | 12 |
| 4853 | fact | 12 |
| 4854 | exquisite | 12 |
| 4855 | exclaim | 12 |
| 4856 | examine | 12 |
| 4857 | erpingham | 12 |
| 4858 | entreaty | 12 |
| 4859 | entreated | 12 |
| 4860 | element | 12 |
| 4861 | dower | 12 |
| 4862 | distraction | 12 |
| 4863 | disloyal | 12 |
| 4864 | dishonoured | 12 |
| 4865 | discovery | 12 |
| 4866 | dion | 12 |
| 4867 | different | 12 |
| 4868 | dieu | 12 |
| 4869 | dial | 12 |
| 4870 | detain | 12 |
| 4871 | denies | 12 |
| 4872 | defiance | 12 |
| 4873 | defect | 12 |
| 4874 | deeper | 12 |
| 4875 | deem | 12 |
| 4876 | decrees | 12 |
| 4877 | daylight | 12 |
| 4878 | cull | 12 |
| 4879 | cue | 12 |
| 4880 | crimson | 12 |
| 4881 | crime | 12 |
| 4882 | crafty | 12 |
| 4883 | cords | 12 |
| 4884 | continual | 12 |
| 4885 | continent | 12 |
| 4886 | contains | 12 |
| 4887 | consort | 12 |
| 4888 | concerning | 12 |
| 4889 | concern | 12 |
| 4890 | commander | 12 |
| 4891 | comedy | 12 |
| 4892 | coil | 12 |
| 4893 | coffers | 12 |
| 4894 | cimber | 12 |
| 4895 | chiefly | 12 |
| 4896 | chat | 12 |
| 4897 | chains | 12 |
| 4898 | capt | 12 |
| 4899 | calais | 12 |
| 4900 | butter | 12 |
| 4901 | broils | 12 |
| 4902 | broach | 12 |
| 4903 | breathless | 12 |
| 4904 | borachio | 12 |
| 4905 | bolt | 12 |
| 4906 | blushes | 12 |
| 4907 | blemish | 12 |
| 4908 | blast | 12 |
| 4909 | bishops | 12 |
| 4910 | bias | 12 |
| 4911 | betters | 12 |
| 4912 | belief | 12 |
| 4913 | beggary | 12 |
| 4914 | beest | 12 |
| 4915 | bath | 12 |
| 4916 | bankrupt | 12 |
| 4917 | bandit | 12 |
| 4918 | balthazar | 12 |
| 4919 | asking | 12 |
| 4920 | ascend | 12 |
| 4921 | arrested | 12 |
| 4922 | armies | 12 |
| 4923 | appoint | 12 |
| 4924 | apparition | 12 |
| 4925 | angus | 12 |
| 4926 | andromache | 12 |
| 4927 | amazement | 12 |
| 4928 | ague | 12 |
| 4929 | affair | 12 |
| 4930 | adverse | 12 |
| 4931 | admiration | 12 |
| 4932 | accomplish | 12 |
| 4933 | abhorr | 12 |
| 4934 | wildly | 11 |
| 4935 | whistle | 11 |
| 4936 | whe | 11 |
| 4937 | web | 11 |
| 4938 | weaker | 11 |
| 4939 | watchful | 11 |
| 4940 | wary | 11 |
| 4941 | wages | 11 |
| 4942 | void | 11 |
| 4943 | visor | 11 |
| 4944 | villany | 11 |
| 4945 | villanous | 11 |
| 4946 | vigour | 11 |
| 4947 | vienna | 11 |
| 4948 | venetian | 11 |
| 4949 | valued | 11 |
| 4950 | usurer | 11 |
| 4951 | usage | 11 |
| 4952 | unlawful | 11 |
| 4953 | ungentle | 11 |
| 4954 | unfortunate | 11 |
| 4955 | uncertain | 11 |
| 4956 | trusted | 11 |
| 4957 | truest | 11 |
| 4958 | troyans | 11 |
| 4959 | trot | 11 |
| 4960 | trimm | 11 |
| 4961 | tow | 11 |
| 4962 | torments | 11 |
| 4963 | timandra | 11 |
| 4964 | thorn | 11 |
| 4965 | text | 11 |
| 4966 | territories | 11 |
| 4967 | tapers | 11 |
| 4968 | sweetheart | 11 |
| 4969 | swallowed | 11 |
| 4970 | surly | 11 |
| 4971 | suffering | 11 |
| 4972 | submit | 11 |
| 4973 | submission | 11 |
| 4974 | streams | 11 |
| 4975 | stinking | 11 |
| 4976 | sticks | 11 |
| 4977 | staying | 11 |
| 4978 | statutes | 11 |
| 4979 | stare | 11 |
| 4980 | spot | 11 |
| 4981 | spoils | 11 |
| 4982 | spider | 11 |
| 4983 | spell | 11 |
| 4984 | solicit | 11 |
| 4985 | solemnity | 11 |
| 4986 | snake | 11 |
| 4987 | slipp | 11 |
| 4988 | signal | 11 |
| 4989 | shrink | 11 |
| 4990 | shriek | 11 |
| 4991 | sexton | 11 |
| 4992 | sending | 11 |
| 4993 | seleucus | 11 |
| 4994 | scarf | 11 |
| 4995 | sblood | 11 |
| 4996 | salve | 11 |
| 4997 | sailor | 11 |
| 4998 | ruthless | 11 |
| 4999 | rushes | 11 |
| 5000 | rosalinde | 11 |
| 5001 | restor | 11 |
| 5002 | reputed | 11 |
| 5003 | remainder | 11 |
| 5004 | recount | 11 |
| 5005 | rambures | 11 |
| 5006 | quaint | 11 |
| 5007 | pyrrhus | 11 |
| 5008 | puissant | 11 |
| 5009 | proudly | 11 |
| 5010 | pronounc | 11 |
| 5011 | pricks | 11 |
| 5012 | preferr | 11 |
| 5013 | preferment | 11 |
| 5014 | prating | 11 |
| 5015 | practis | 11 |
| 5016 | posterity | 11 |
| 5017 | poisonous | 11 |
| 5018 | plenteous | 11 |
| 5019 | plate | 11 |
| 5020 | planted | 11 |
| 5021 | perfume | 11 |
| 5022 | pent | 11 |
| 5023 | pence | 11 |
| 5024 | pearls | 11 |
| 5025 | peaceful | 11 |
| 5026 | particulars | 11 |
| 5027 | paltry | 11 |
| 5028 | palate | 11 |
| 5029 | overthrown | 11 |
| 5030 | ornaments | 11 |
| 5031 | orator | 11 |
| 5032 | opposed | 11 |
| 5033 | opening | 11 |
| 5034 | oman | 11 |
| 5035 | offenders | 11 |
| 5036 | observation | 11 |
| 5037 | obscure | 11 |
| 5038 | objects | 11 |
| 5039 | needless | 11 |
| 5040 | necks | 11 |
| 5041 | nan | 11 |
| 5042 | mutton | 11 |
| 5043 | moist | 11 |
| 5044 | mockery | 11 |
| 5045 | midwife | 11 |
| 5046 | midst | 11 |
| 5047 | mew | 11 |
| 5048 | member | 11 |
| 5049 | melun | 11 |
| 5050 | med | 11 |
| 5051 | marrying | 11 |
| 5052 | map | 11 |
| 5053 | malady | 11 |
| 5054 | madmen | 11 |
| 5055 | lovel | 11 |
| 5056 | legate | 11 |
| 5057 | leagues | 11 |
| 5058 | lazy | 11 |
| 5059 | lawyer | 11 |
| 5060 | knell | 11 |
| 5061 | jerusalem | 11 |
| 5062 | jealousies | 11 |
| 5063 | jaws | 11 |
| 5064 | its | 11 |
| 5065 | interim | 11 |
| 5066 | infancy | 11 |
| 5067 | indignation | 11 |
| 5068 | inconstant | 11 |
| 5069 | inclination | 11 |
| 5070 | inches | 11 |
| 5071 | impeach | 11 |
| 5072 | imitate | 11 |
| 5073 | images | 11 |
| 5074 | horsemen | 11 |
| 5075 | horner | 11 |
| 5076 | honors | 11 |
| 5077 | hiss | 11 |
| 5078 | hew | 11 |
| 5079 | herbs | 11 |
| 5080 | heave | 11 |
| 5081 | heath | 11 |
| 5082 | harder | 11 |
| 5083 | hag | 11 |
| 5084 | griev | 11 |
| 5085 | greets | 11 |
| 5086 | goth | 11 |
| 5087 | gossip | 11 |
| 5088 | goldsmith | 11 |
| 5089 | gloucestershire | 11 |
| 5090 | glance | 11 |
| 5091 | getting | 11 |
| 5092 | german | 11 |
| 5093 | gentlewomen | 11 |
| 5094 | geese | 11 |
| 5095 | gape | 11 |
| 5096 | gap | 11 |
| 5097 | frozen | 11 |
| 5098 | froward | 11 |
| 5099 | fort | 11 |
| 5100 | formal | 11 |
| 5101 | footed | 11 |
| 5102 | floods | 11 |
| 5103 | fickle | 11 |
| 5104 | favor | 11 |
| 5105 | faithfully | 11 |
| 5106 | euphronius | 11 |
| 5107 | entreats | 11 |
| 5108 | entreaties | 11 |
| 5109 | entrails | 11 |
| 5110 | enrag | 11 |
| 5111 | embrac | 11 |
| 5112 | eloquence | 11 |
| 5113 | earls | 11 |
| 5114 | duteous | 11 |
| 5115 | drugs | 11 |
| 5116 | downright | 11 |
| 5117 | doubts | 11 |
| 5118 | doomsday | 11 |
| 5119 | dissemble | 11 |
| 5120 | disperse | 11 |
| 5121 | dispers | 11 |
| 5122 | dishonest | 11 |
| 5123 | dirt | 11 |
| 5124 | dig | 11 |
| 5125 | desp | 11 |
| 5126 | designs | 11 |
| 5127 | derive | 11 |
| 5128 | depends | 11 |
| 5129 | degenerate | 11 |
| 5130 | decree | 11 |
| 5131 | debtor | 11 |
| 5132 | damnable | 11 |
| 5133 | dally | 11 |
| 5134 | crutch | 11 |
| 5135 | cow | 11 |
| 5136 | costly | 11 |
| 5137 | controversy | 11 |
| 5138 | contracted | 11 |
| 5139 | contagious | 11 |
| 5140 | construe | 11 |
| 5141 | conspirators | 11 |
| 5142 | confounds | 11 |
| 5143 | compliment | 11 |
| 5144 | companies | 11 |
| 5145 | comfortable | 11 |
| 5146 | cloudy | 11 |
| 5147 | cleave | 11 |
| 5148 | clamorous | 11 |
| 5149 | circumstances | 11 |
| 5150 | christ | 11 |
| 5151 | chooseth | 11 |
| 5152 | chivalry | 11 |
| 5153 | chiding | 11 |
| 5154 | charged | 11 |
| 5155 | channel | 11 |
| 5156 | catching | 11 |
| 5157 | cases | 11 |
| 5158 | capacity | 11 |
| 5159 | buzz | 11 |
| 5160 | butts | 11 |
| 5161 | budge | 11 |
| 5162 | britons | 11 |
| 5163 | british | 11 |
| 5164 | breathes | 11 |
| 5165 | boon | 11 |
| 5166 | bitterness | 11 |
| 5167 | biting | 11 |
| 5168 | birnam | 11 |
| 5169 | beseeming | 11 |
| 5170 | bequeath | 11 |
| 5171 | bench | 11 |
| 5172 | bee | 11 |
| 5173 | beam | 11 |
| 5174 | bates | 11 |
| 5175 | basset | 11 |
| 5176 | baser | 11 |
| 5177 | barr | 11 |
| 5178 | barbary | 11 |
| 5179 | balance | 11 |
| 5180 | avouch | 11 |
| 5181 | ashore | 11 |
| 5182 | arguments | 11 |
| 5183 | argues | 11 |
| 5184 | applaud | 11 |
| 5185 | antic | 11 |
| 5186 | amazed | 11 |
| 5187 | altar | 11 |
| 5188 | agent | 11 |
| 5189 | affects | 11 |
| 5190 | adversaries | 11 |
| 5191 | abuses | 11 |
| 5192 | abject | 11 |
| 5193 | yeoman | 10 |
| 5194 | yare | 10 |
| 5195 | wrestling | 10 |
| 5196 | worships | 10 |
| 5197 | wonted | 10 |
| 5198 | witted | 10 |
| 5199 | witnesses | 10 |
| 5200 | withered | 10 |
| 5201 | winters | 10 |
| 5202 | wins | 10 |
| 5203 | winking | 10 |
| 5204 | wickedness | 10 |
| 5205 | whoe | 10 |
| 5206 | whet | 10 |
| 5207 | wherewith | 10 |
| 5208 | whelp | 10 |
| 5209 | wheels | 10 |
| 5210 | western | 10 |
| 5211 | wedlock | 10 |
| 5212 | wealthy | 10 |
| 5213 | wayward | 10 |
| 5214 | watching | 10 |
| 5215 | ware | 10 |
| 5216 | waits | 10 |
| 5217 | volume | 10 |
| 5218 | volscian | 10 |
| 5219 | visited | 10 |
| 5220 | viii | 10 |
| 5221 | vexation | 10 |
| 5222 | verity | 10 |
| 5223 | verges | 10 |
| 5224 | unfit | 10 |
| 5225 | tyrants | 10 |
| 5226 | tucket | 10 |
| 5227 | tribe | 10 |
| 5228 | trencher | 10 |
| 5229 | trash | 10 |
| 5230 | transported | 10 |
| 5231 | trace | 10 |
| 5232 | toss | 10 |
| 5233 | tops | 10 |
| 5234 | testament | 10 |
| 5235 | tenth | 10 |
| 5236 | tearsheet | 10 |
| 5237 | tabor | 10 |
| 5238 | sympathy | 10 |
| 5239 | syllable | 10 |
| 5240 | swine | 10 |
| 5241 | swan | 10 |
| 5242 | suns | 10 |
| 5243 | suited | 10 |
| 5244 | substitute | 10 |
| 5245 | subdue | 10 |
| 5246 | strives | 10 |
| 5247 | striking | 10 |
| 5248 | stratagem | 10 |
| 5249 | strangeness | 10 |
| 5250 | stings | 10 |
| 5251 | stew | 10 |
| 5252 | stealth | 10 |
| 5253 | staves | 10 |
| 5254 | stately | 10 |
| 5255 | stark | 10 |
| 5256 | stairs | 10 |
| 5257 | sprung | 10 |
| 5258 | sports | 10 |
| 5259 | sphere | 10 |
| 5260 | speaker | 10 |
| 5261 | sparrow | 10 |
| 5262 | sonnet | 10 |
| 5263 | solus | 10 |
| 5264 | sola | 10 |
| 5265 | snug | 10 |
| 5266 | snail | 10 |
| 5267 | sleepy | 10 |
| 5268 | slaught | 10 |
| 5269 | slack | 10 |
| 5270 | sighing | 10 |
| 5271 | sicilius | 10 |
| 5272 | shrill | 10 |
| 5273 | shrift | 10 |
| 5274 | shrewdly | 10 |
| 5275 | shillings | 10 |
| 5276 | shepherds | 10 |
| 5277 | seventh | 10 |
| 5278 | served | 10 |
| 5279 | sequel | 10 |
| 5280 | sempronius | 10 |
| 5281 | secretary | 10 |
| 5282 | seals | 10 |
| 5283 | scatter | 10 |
| 5284 | scald | 10 |
| 5285 | sand | 10 |
| 5286 | saddle | 10 |
| 5287 | rout | 10 |
| 5288 | roundly | 10 |
| 5289 | roots | 10 |
| 5290 | rite | 10 |
| 5291 | riotous | 10 |
| 5292 | rewards | 10 |
| 5293 | revive | 10 |
| 5294 | repute | 10 |
| 5295 | rent | 10 |
| 5296 | rats | 10 |
| 5297 | rat | 10 |
| 5298 | rashness | 10 |
| 5299 | rascally | 10 |
| 5300 | quicken | 10 |
| 5301 | quest | 10 |
| 5302 | purity | 10 |
| 5303 | publicly | 10 |
| 5304 | provokes | 10 |
| 5305 | propose | 10 |
| 5306 | probable | 10 |
| 5307 | prepared | 10 |
| 5308 | powder | 10 |
| 5309 | plough | 10 |
| 5310 | plotted | 10 |
| 5311 | pleased | 10 |
| 5312 | placed | 10 |
| 5313 | pious | 10 |
| 5314 | pins | 10 |
| 5315 | pilgrim | 10 |
| 5316 | pile | 10 |
| 5317 | petitioner | 10 |
| 5318 | pet | 10 |
| 5319 | perdition | 10 |
| 5320 | perceiv | 10 |
| 5321 | paul | 10 |
| 5322 | path | 10 |
| 5323 | pages | 10 |
| 5324 | pageant | 10 |
| 5325 | owen | 10 |
| 5326 | overcame | 10 |
| 5327 | orb | 10 |
| 5328 | ominous | 10 |
| 5329 | odious | 10 |
| 5330 | occupation | 10 |
| 5331 | observ | 10 |
| 5332 | northern | 10 |
| 5333 | nightingale | 10 |
| 5334 | navy | 10 |
| 5335 | murtherers | 10 |
| 5336 | murdered | 10 |
| 5337 | mould | 10 |
| 5338 | montgomery | 10 |
| 5339 | modern | 10 |
| 5340 | mistaking | 10 |
| 5341 | miscarried | 10 |
| 5342 | mirror | 10 |
| 5343 | merchants | 10 |
| 5344 | members | 10 |
| 5345 | melting | 10 |
| 5346 | measures | 10 |
| 5347 | maskers | 10 |
| 5348 | mary | 10 |
| 5349 | martial | 10 |
| 5350 | mariners | 10 |
| 5351 | maidenhead | 10 |
| 5352 | madonna | 10 |
| 5353 | madame | 10 |
| 5354 | lodg | 10 |
| 5355 | loathed | 10 |
| 5356 | litter | 10 |
| 5357 | link | 10 |
| 5358 | lighted | 10 |
| 5359 | levy | 10 |
| 5360 | lamp | 10 |
| 5361 | lamentation | 10 |
| 5362 | labours | 10 |
| 5363 | labor | 10 |
| 5364 | knives | 10 |
| 5365 | knighthood | 10 |
| 5366 | irish | 10 |
| 5367 | iris | 10 |
| 5368 | invited | 10 |
| 5369 | inhabit | 10 |
| 5370 | ingenious | 10 |
| 5371 | influence | 10 |
| 5372 | inferior | 10 |
| 5373 | infants | 10 |
| 5374 | incensed | 10 |
| 5375 | incense | 10 |
| 5376 | impression | 10 |
| 5377 | impose | 10 |
| 5378 | humor | 10 |
| 5379 | humanity | 10 |
| 5380 | hood | 10 |
| 5381 | holes | 10 |
| 5382 | hills | 10 |
| 5383 | hiding | 10 |
| 5384 | hem | 10 |
| 5385 | hearers | 10 |
| 5386 | healthful | 10 |
| 5387 | headstrong | 10 |
| 5388 | hay | 10 |
| 5389 | happen | 10 |
| 5390 | hanged | 10 |
| 5391 | gull | 10 |
| 5392 | grudge | 10 |
| 5393 | gregory | 10 |
| 5394 | greasy | 10 |
| 5395 | gorgeous | 10 |
| 5396 | gnaw | 10 |
| 5397 | globe | 10 |
| 5398 | glasses | 10 |
| 5399 | girdle | 10 |
| 5400 | generous | 10 |
| 5401 | generation | 10 |
| 5402 | geffrey | 10 |
| 5403 | gear | 10 |
| 5404 | fraught | 10 |
| 5405 | frankly | 10 |
| 5406 | francisco | 10 |
| 5407 | forfend | 10 |
| 5408 | fooling | 10 |
| 5409 | flinty | 10 |
| 5410 | fist | 10 |
| 5411 | fishes | 10 |
| 5412 | finely | 10 |
| 5413 | fidele | 10 |
| 5414 | fastolfe | 10 |
| 5415 | farm | 10 |
| 5416 | falcon | 10 |
| 5417 | faintly | 10 |
| 5418 | fails | 10 |
| 5419 | factious | 10 |
| 5420 | extremest | 10 |
| 5421 | expressly | 10 |
| 5422 | expected | 10 |
| 5423 | excus | 10 |
| 5424 | exceeds | 10 |
| 5425 | ewes | 10 |
| 5426 | evidence | 10 |
| 5427 | europe | 10 |
| 5428 | eternity | 10 |
| 5429 | enow | 10 |
| 5430 | englishman | 10 |
| 5431 | emulation | 10 |
| 5432 | elsewhere | 10 |
| 5433 | eke | 10 |
| 5434 | echo | 10 |
| 5435 | dunghill | 10 |
| 5436 | duck | 10 |
| 5437 | drooping | 10 |
| 5438 | drag | 10 |
| 5439 | dotage | 10 |
| 5440 | ditch | 10 |
| 5441 | distract | 10 |
| 5442 | distinguish | 10 |
| 5443 | distinction | 10 |
| 5444 | dispraise | 10 |
| 5445 | display | 10 |
| 5446 | dice | 10 |
| 5447 | desolation | 10 |
| 5448 | desired | 10 |
| 5449 | descends | 10 |
| 5450 | dercetas | 10 |
| 5451 | depose | 10 |
| 5452 | demi | 10 |
| 5453 | delivers | 10 |
| 5454 | deiphobus | 10 |
| 5455 | dearth | 10 |
| 5456 | dames | 10 |
| 5457 | crop | 10 |
| 5458 | crew | 10 |
| 5459 | creation | 10 |
| 5460 | cramm | 10 |
| 5461 | courtiers | 10 |
| 5462 | courageous | 10 |
| 5463 | coronet | 10 |
| 5464 | confines | 10 |
| 5465 | confessor | 10 |
| 5466 | confederates | 10 |
| 5467 | condemned | 10 |
| 5468 | compulsion | 10 |
| 5469 | compounded | 10 |
| 5470 | complaints | 10 |
| 5471 | compassion | 10 |
| 5472 | commonweal | 10 |
| 5473 | commended | 10 |
| 5474 | commanding | 10 |
| 5475 | collected | 10 |
| 5476 | clubs | 10 |
| 5477 | chok | 10 |
| 5478 | chimney | 10 |
| 5479 | characters | 10 |
| 5480 | chapel | 10 |
| 5481 | challeng | 10 |
| 5482 | ceremonies | 10 |
| 5483 | cedar | 10 |
| 5484 | caus | 10 |
| 5485 | carve | 10 |
| 5486 | carrying | 10 |
| 5487 | capon | 10 |
| 5488 | canopy | 10 |
| 5489 | calamity | 10 |
| 5490 | cabin | 10 |
| 5491 | bullen | 10 |
| 5492 | breasts | 10 |
| 5493 | brand | 10 |
| 5494 | bout | 10 |
| 5495 | boughs | 10 |
| 5496 | bordeaux | 10 |
| 5497 | bondman | 10 |
| 5498 | boist | 10 |
| 5499 | boil | 10 |
| 5500 | boat | 10 |
| 5501 | blowing | 10 |
| 5502 | blossom | 10 |
| 5503 | blade | 10 |
| 5504 | bites | 10 |
| 5505 | besiege | 10 |
| 5506 | belie | 10 |
| 5507 | beggarly | 10 |
| 5508 | bees | 10 |
| 5509 | bedfellow | 10 |
| 5510 | beads | 10 |
| 5511 | balth | 10 |
| 5512 | bags | 10 |
| 5513 | b | 10 |
| 5514 | assembled | 10 |
| 5515 | arragon | 10 |
| 5516 | appointment | 10 |
| 5517 | antium | 10 |
| 5518 | allowance | 10 |
| 5519 | advised | 10 |
| 5520 | advantages | 10 |
| 5521 | admittance | 10 |
| 5522 | actors | 10 |
| 5523 | accordingly | 10 |
| 5524 | accord | 10 |
| 5525 | ability | 10 |
| 5526 | abhorred | 10 |
| 5527 | abandon | 10 |
| 5528 | wrote | 9 |
| 5529 | wretchedness | 9 |
| 5530 | wooer | 9 |
| 5531 | wishing | 9 |
| 5532 | wip | 9 |
| 5533 | wildness | 9 |
| 5534 | widows | 9 |
| 5535 | whipping | 9 |
| 5536 | whatever | 9 |
| 5537 | weighs | 9 |
| 5538 | weaver | 9 |
| 5539 | wearied | 9 |
| 5540 | wasteful | 9 |
| 5541 | warn | 9 |
| 5542 | votre | 9 |
| 5543 | virgins | 9 |
| 5544 | vicious | 9 |
| 5545 | vaux | 9 |
| 5546 | varrius | 9 |
| 5547 | vale | 9 |
| 5548 | vainly | 9 |
| 5549 | utt | 9 |
| 5550 | usurper | 9 |
| 5551 | usher | 9 |
| 5552 | urging | 9 |
| 5553 | upbraid | 9 |
| 5554 | uncles | 9 |
| 5555 | turkish | 9 |
| 5556 | tunis | 9 |
| 5557 | tun | 9 |
| 5558 | tu | 9 |
| 5559 | triumphs | 9 |
| 5560 | travail | 9 |
| 5561 | translate | 9 |
| 5562 | transgression | 9 |
| 5563 | transformed | 9 |
| 5564 | tides | 9 |
| 5565 | thunders | 9 |
| 5566 | thigh | 9 |
| 5567 | therewithal | 9 |
| 5568 | temperate | 9 |
| 5569 | temperance | 9 |
| 5570 | taurus | 9 |
| 5571 | tartar | 9 |
| 5572 | swoons | 9 |
| 5573 | swells | 9 |
| 5574 | survive | 9 |
| 5575 | surge | 9 |
| 5576 | supplied | 9 |
| 5577 | sunday | 9 |
| 5578 | summons | 9 |
| 5579 | suggestion | 9 |
| 5580 | stumble | 9 |
| 5581 | strait | 9 |
| 5582 | stony | 9 |
| 5583 | starv | 9 |
| 5584 | sprites | 9 |
| 5585 | spots | 9 |
| 5586 | spheres | 9 |
| 5587 | sped | 9 |
| 5588 | spectacle | 9 |
| 5589 | spear | 9 |
| 5590 | sparks | 9 |
| 5591 | spark | 9 |
| 5592 | spaniel | 9 |
| 5593 | solely | 9 |
| 5594 | sojourn | 9 |
| 5595 | snuff | 9 |
| 5596 | smart | 9 |
| 5597 | smack | 9 |
| 5598 | slightly | 9 |
| 5599 | shunn | 9 |
| 5600 | showers | 9 |
| 5601 | shin | 9 |
| 5602 | sheathe | 9 |
| 5603 | sequent | 9 |
| 5604 | seemeth | 9 |
| 5605 | scap | 9 |
| 5606 | scant | 9 |
| 5607 | savour | 9 |
| 5608 | salique | 9 |
| 5609 | sale | 9 |
| 5610 | rust | 9 |
| 5611 | rules | 9 |
| 5612 | royally | 9 |
| 5613 | roll | 9 |
| 5614 | riding | 9 |
| 5615 | riddle | 9 |
| 5616 | rhymes | 9 |
| 5617 | retir | 9 |
| 5618 | retain | 9 |
| 5619 | residence | 9 |
| 5620 | reserve | 9 |
| 5621 | replete | 9 |
| 5622 | relate | 9 |
| 5623 | redemption | 9 |
| 5624 | reck | 9 |
| 5625 | rebellious | 9 |
| 5626 | ravenspurgh | 9 |
| 5627 | rarely | 9 |
| 5628 | rance | 9 |
| 5629 | quietly | 9 |
| 5630 | queens | 9 |
| 5631 | puppet | 9 |
| 5632 | pulse | 9 |
| 5633 | puissance | 9 |
| 5634 | proffer | 9 |
| 5635 | proclaims | 9 |
| 5636 | proclaimed | 9 |
| 5637 | priz | 9 |
| 5638 | prettiest | 9 |
| 5639 | preserv | 9 |
| 5640 | prelate | 9 |
| 5641 | pranks | 9 |
| 5642 | polydore | 9 |
| 5643 | poisons | 9 |
| 5644 | pointing | 9 |
| 5645 | poetry | 9 |
| 5646 | plea | 9 |
| 5647 | planet | 9 |
| 5648 | pilot | 9 |
| 5649 | pie | 9 |
| 5650 | philotus | 9 |
| 5651 | philomel | 9 |
| 5652 | pedlar | 9 |
| 5653 | patron | 9 |
| 5654 | passionate | 9 |
| 5655 | passages | 9 |
| 5656 | parentage | 9 |
| 5657 | parcels | 9 |
| 5658 | paragon | 9 |
| 5659 | pander | 9 |
| 5660 | p | 9 |
| 5661 | ow | 9 |
| 5662 | overcome | 9 |
| 5663 | ordinance | 9 |
| 5664 | ordain | 9 |
| 5665 | oration | 9 |
| 5666 | offered | 9 |
| 5667 | offending | 9 |
| 5668 | nymph | 9 |
| 5669 | nightgown | 9 |
| 5670 | nick | 9 |
| 5671 | neigh | 9 |
| 5672 | nations | 9 |
| 5673 | mustard | 9 |
| 5674 | mole | 9 |
| 5675 | moi | 9 |
| 5676 | mistaken | 9 |
| 5677 | misled | 9 |
| 5678 | misfortune | 9 |
| 5679 | mire | 9 |
| 5680 | mines | 9 |
| 5681 | mildly | 9 |
| 5682 | menteith | 9 |
| 5683 | measur | 9 |
| 5684 | masque | 9 |
| 5685 | marullus | 9 |
| 5686 | margery | 9 |
| 5687 | louder | 9 |
| 5688 | loses | 9 |
| 5689 | livers | 9 |
| 5690 | liquid | 9 |
| 5691 | limits | 9 |
| 5692 | lick | 9 |
| 5693 | licio | 9 |
| 5694 | lesson | 9 |
| 5695 | lease | 9 |
| 5696 | kites | 9 |
| 5697 | juice | 9 |
| 5698 | judges | 9 |
| 5699 | jolly | 9 |
| 5700 | jet | 9 |
| 5701 | jamy | 9 |
| 5702 | issues | 9 |
| 5703 | isidore | 9 |
| 5704 | irons | 9 |
| 5705 | intolerable | 9 |
| 5706 | interpreter | 9 |
| 5707 | insulting | 9 |
| 5708 | insolent | 9 |
| 5709 | indian | 9 |
| 5710 | incorporate | 9 |
| 5711 | incline | 9 |
| 5712 | impudent | 9 |
| 5713 | impress | 9 |
| 5714 | imports | 9 |
| 5715 | ills | 9 |
| 5716 | ignoble | 9 |
| 5717 | idiot | 9 |
| 5718 | humbled | 9 |
| 5719 | howsoever | 9 |
| 5720 | hortensius | 9 |
| 5721 | hopeful | 9 |
| 5722 | hits | 9 |
| 5723 | hitherto | 9 |
| 5724 | hearty | 9 |
| 5725 | havoc | 9 |
| 5726 | haunts | 9 |
| 5727 | hart | 9 |
| 5728 | harp | 9 |
| 5729 | harness | 9 |
| 5730 | harmful | 9 |
| 5731 | harlot | 9 |
| 5732 | halt | 9 |
| 5733 | hale | 9 |
| 5734 | gulf | 9 |
| 5735 | guiltiness | 9 |
| 5736 | guides | 9 |
| 5737 | grounds | 9 |
| 5738 | grooms | 9 |
| 5739 | groaning | 9 |
| 5740 | grieved | 9 |
| 5741 | greetings | 9 |
| 5742 | greekish | 9 |
| 5743 | gratis | 9 |
| 5744 | grapple | 9 |
| 5745 | gore | 9 |
| 5746 | goats | 9 |
| 5747 | glow | 9 |
| 5748 | glamis | 9 |
| 5749 | gentler | 9 |
| 5750 | gay | 9 |
| 5751 | gaping | 9 |
| 5752 | ganymede | 9 |
| 5753 | fruits | 9 |
| 5754 | frosty | 9 |
| 5755 | fresher | 9 |
| 5756 | freeze | 9 |
| 5757 | fortnight | 9 |
| 5758 | forswore | 9 |
| 5759 | forgiveness | 9 |
| 5760 | fondly | 9 |
| 5761 | foils | 9 |
| 5762 | fleece | 9 |
| 5763 | flaw | 9 |
| 5764 | fitter | 9 |
| 5765 | fitness | 9 |
| 5766 | filling | 9 |
| 5767 | feasting | 9 |
| 5768 | fam | 9 |
| 5769 | eyne | 9 |
| 5770 | exempt | 9 |
| 5771 | entirely | 9 |
| 5772 | ensuing | 9 |
| 5773 | enjoin | 9 |
| 5774 | endeavours | 9 |
| 5775 | effected | 9 |
| 5776 | easier | 9 |
| 5777 | earnestly | 9 |
| 5778 | eagles | 9 |
| 5779 | eager | 9 |
| 5780 | drowning | 9 |
| 5781 | drench | 9 |
| 5782 | draught | 9 |
| 5783 | doves | 9 |
| 5784 | doubtless | 9 |
| 5785 | dole | 9 |
| 5786 | divinity | 9 |
| 5787 | dissension | 9 |
| 5788 | disdainful | 9 |
| 5789 | diligence | 9 |
| 5790 | detest | 9 |
| 5791 | denny | 9 |
| 5792 | denial | 9 |
| 5793 | deliverance | 9 |
| 5794 | decline | 9 |
| 5795 | deceas | 9 |
| 5796 | dane | 9 |
| 5797 | dances | 9 |
| 5798 | curtains | 9 |
| 5799 | cups | 9 |
| 5800 | credulous | 9 |
| 5801 | covetous | 9 |
| 5802 | courtesies | 9 |
| 5803 | counted | 9 |
| 5804 | corpse | 9 |
| 5805 | cordial | 9 |
| 5806 | cord | 9 |
| 5807 | cope | 9 |
| 5808 | convert | 9 |
| 5809 | continuance | 9 |
| 5810 | construction | 9 |
| 5811 | constrain | 9 |
| 5812 | consecrate | 9 |
| 5813 | conrade | 9 |
| 5814 | conjunction | 9 |
| 5815 | confounded | 9 |
| 5816 | conflict | 9 |
| 5817 | concord | 9 |
| 5818 | conceited | 9 |
| 5819 | compos | 9 |
| 5820 | compel | 9 |
| 5821 | comparisons | 9 |
| 5822 | commoner | 9 |
| 5823 | commendation | 9 |
| 5824 | commendable | 9 |
| 5825 | comest | 9 |
| 5826 | climate | 9 |
| 5827 | cleft | 9 |
| 5828 | churl | 9 |
| 5829 | chronicle | 9 |
| 5830 | christians | 9 |
| 5831 | chop | 9 |
| 5832 | choleric | 9 |
| 5833 | childish | 9 |
| 5834 | chides | 9 |
| 5835 | chest | 9 |
| 5836 | cheerfully | 9 |
| 5837 | chastisement | 9 |
| 5838 | charter | 9 |
| 5839 | chaff | 9 |
| 5840 | casement | 9 |
| 5841 | cars | 9 |
| 5842 | captives | 9 |
| 5843 | buys | 9 |
| 5844 | building | 9 |
| 5845 | buckram | 9 |
| 5846 | brine | 9 |
| 5847 | breadth | 9 |
| 5848 | braver | 9 |
| 5849 | brat | 9 |
| 5850 | brake | 9 |
| 5851 | braggart | 9 |
| 5852 | bourbon | 9 |
| 5853 | bon | 9 |
| 5854 | blaze | 9 |
| 5855 | blasted | 9 |
| 5856 | bitterly | 9 |
| 5857 | bestride | 9 |
| 5858 | bernardo | 9 |
| 5859 | bellario | 9 |
| 5860 | befits | 9 |
| 5861 | batt | 9 |
| 5862 | bated | 9 |
| 5863 | basely | 9 |
| 5864 | barber | 9 |
| 5865 | bal | 9 |
| 5866 | aweary | 9 |
| 5867 | autumn | 9 |
| 5868 | audit | 9 |
| 5869 | asses | 9 |
| 5870 | aright | 9 |
| 5871 | archidamus | 9 |
| 5872 | apprehended | 9 |
| 5873 | appearing | 9 |
| 5874 | annoy | 9 |
| 5875 | anchor | 9 |
| 5876 | amaze | 9 |
| 5877 | alteration | 9 |
| 5878 | alehouse | 9 |
| 5879 | affright | 9 |
| 5880 | advocate | 9 |
| 5881 | adversary | 9 |
| 5882 | advancement | 9 |
| 5883 | adding | 9 |
| 5884 | accompanied | 9 |
| 5885 | abode | 9 |
| 5886 | abbot | 9 |
| 5887 | wrongfully | 8 |
| 5888 | wrestler | 8 |
| 5889 | wrangling | 8 |
| 5890 | wounding | 8 |
| 5891 | worshipp | 8 |
| 5892 | wooden | 8 |
| 5893 | woful | 8 |
| 5894 | withhold | 8 |
| 5895 | wisdoms | 8 |
| 5896 | wiltshire | 8 |
| 5897 | wilderness | 8 |
| 5898 | whores | 8 |
| 5899 | whips | 8 |
| 5900 | wheat | 8 |
| 5901 | waxen | 8 |
| 5902 | waving | 8 |
| 5903 | wantonness | 8 |
| 5904 | wanted | 8 |
| 5905 | violet | 8 |
| 5906 | vill | 8 |
| 5907 | verge | 8 |
| 5908 | verdict | 8 |
| 5909 | valor | 8 |
| 5910 | utterly | 8 |
| 5911 | utterance | 8 |
| 5912 | using | 8 |
| 5913 | unwilling | 8 |
| 5914 | unlook | 8 |
| 5915 | ungracious | 8 |
| 5916 | uncivil | 8 |
| 5917 | unborn | 8 |
| 5918 | tunes | 8 |
| 5919 | tuesday | 8 |
| 5920 | troublesome | 8 |
| 5921 | trenches | 8 |
| 5922 | trembles | 8 |
| 5923 | treads | 8 |
| 5924 | traitorous | 8 |
| 5925 | trail | 8 |
| 5926 | tragic | 8 |
| 5927 | tough | 8 |
| 5928 | toads | 8 |
| 5929 | tinker | 8 |
| 5930 | timeless | 8 |
| 5931 | tigers | 8 |
| 5932 | tiber | 8 |
| 5933 | thump | 8 |
| 5934 | threefold | 8 |
| 5935 | thirst | 8 |
| 5936 | thereupon | 8 |
| 5937 | tewksbury | 8 |
| 5938 | tearing | 8 |
| 5939 | te | 8 |
| 5940 | tarquin | 8 |
| 5941 | swing | 8 |
| 5942 | sweeten | 8 |
| 5943 | sways | 8 |
| 5944 | surprise | 8 |
| 5945 | suppress | 8 |
| 5946 | sunshine | 8 |
| 5947 | sunder | 8 |
| 5948 | suffered | 8 |
| 5949 | succeeding | 8 |
| 5950 | suburbs | 8 |
| 5951 | suborn | 8 |
| 5952 | strucken | 8 |
| 5953 | striving | 8 |
| 5954 | string | 8 |
| 5955 | strengthen | 8 |
| 5956 | strains | 8 |
| 5957 | starved | 8 |
| 5958 | starting | 8 |
| 5959 | stained | 8 |
| 5960 | spectacles | 8 |
| 5961 | sparkling | 8 |
| 5962 | spade | 8 |
| 5963 | sounding | 8 |
| 5964 | somebody | 8 |
| 5965 | soldiership | 8 |
| 5966 | smock | 8 |
| 5967 | slips | 8 |
| 5968 | slippery | 8 |
| 5969 | sleeves | 8 |
| 5970 | skins | 8 |
| 5971 | silius | 8 |
| 5972 | sicken | 8 |
| 5973 | shrunk | 8 |
| 5974 | shipp | 8 |
| 5975 | shak | 8 |
| 5976 | sew | 8 |
| 5977 | servile | 8 |
| 5978 | seigneur | 8 |
| 5979 | seats | 8 |
| 5980 | scout | 8 |
| 5981 | scour | 8 |
| 5982 | scots | 8 |
| 5983 | scold | 8 |
| 5984 | savours | 8 |
| 5985 | satan | 8 |
| 5986 | safest | 8 |
| 5987 | sacrament | 8 |
| 5988 | ruminate | 8 |
| 5989 | rooted | 8 |
| 5990 | robs | 8 |
| 5991 | robbery | 8 |
| 5992 | roasted | 8 |
| 5993 | rivals | 8 |
| 5994 | rigour | 8 |
| 5995 | rides | 8 |
| 5996 | rider | 8 |
| 5997 | rhetoric | 8 |
| 5998 | reverent | 8 |
| 5999 | revengeful | 8 |
| 6000 | revenged | 8 |
| 6001 | reveal | 8 |
| 6002 | resist | 8 |
| 6003 | resemble | 8 |
| 6004 | requir | 8 |
| 6005 | replied | 8 |
| 6006 | repentance | 8 |
| 6007 | remote | 8 |
| 6008 | remedies | 8 |
| 6009 | reliev | 8 |
| 6010 | relation | 8 |
| 6011 | regarded | 8 |
| 6012 | recreation | 8 |
| 6013 | recovery | 8 |
| 6014 | recovered | 8 |
| 6015 | reconcile | 8 |
| 6016 | rarest | 8 |
| 6017 | rapt | 8 |
| 6018 | range | 8 |
| 6019 | ram | 8 |
| 6020 | raised | 8 |
| 6021 | raiment | 8 |
| 6022 | railing | 8 |
| 6023 | radiant | 8 |
| 6024 | qualify | 8 |
| 6025 | pursuivant | 8 |
| 6026 | purg | 8 |
| 6027 | pry | 8 |
| 6028 | prouder | 8 |
| 6029 | prophecies | 8 |
| 6030 | profits | 8 |
| 6031 | principal | 8 |
| 6032 | pretence | 8 |
| 6033 | prerogative | 8 |
| 6034 | precise | 8 |
| 6035 | precepts | 8 |
| 6036 | praying | 8 |
| 6037 | prattle | 8 |
| 6038 | porridge | 8 |
| 6039 | porpentine | 8 |
| 6040 | popilius | 8 |
| 6041 | poorest | 8 |
| 6042 | pluto | 8 |
| 6043 | pless | 8 |
| 6044 | pikes | 8 |
| 6045 | pictures | 8 |
| 6046 | physicians | 8 |
| 6047 | persever | 8 |
| 6048 | perils | 8 |
| 6049 | pavilion | 8 |
| 6050 | partial | 8 |
| 6051 | partake | 8 |
| 6052 | parish | 8 |
| 6053 | parchment | 8 |
| 6054 | painful | 8 |
| 6055 | packing | 8 |
| 6056 | packet | 8 |
| 6057 | oyster | 8 |
| 6058 | oxen | 8 |
| 6059 | overheard | 8 |
| 6060 | outrun | 8 |
| 6061 | ostentation | 8 |
| 6062 | orphans | 8 |
| 6063 | organ | 8 |
| 6064 | orderly | 8 |
| 6065 | opposition | 8 |
| 6066 | openly | 8 |
| 6067 | oh | 8 |
| 6068 | obsequious | 8 |
| 6069 | nut | 8 |
| 6070 | niggard | 8 |
| 6071 | nicely | 8 |
| 6072 | negligent | 8 |
| 6073 | needle | 8 |
| 6074 | mutinous | 8 |
| 6075 | musty | 8 |
| 6076 | murders | 8 |
| 6077 | muffled | 8 |
| 6078 | mud | 8 |
| 6079 | mow | 8 |
| 6080 | moulded | 8 |
| 6081 | morsel | 8 |
| 6082 | moonlight | 8 |
| 6083 | monkey | 8 |
| 6084 | moderate | 8 |
| 6085 | misuse | 8 |
| 6086 | mischiefs | 8 |
| 6087 | millions | 8 |
| 6088 | military | 8 |
| 6089 | method | 8 |
| 6090 | melody | 8 |
| 6091 | martext | 8 |
| 6092 | majestical | 8 |
| 6093 | maim | 8 |
| 6094 | maidens | 8 |
| 6095 | mace | 8 |
| 6096 | luxury | 8 |
| 6097 | lovest | 8 |
| 6098 | lousy | 8 |
| 6099 | lopp | 8 |
| 6100 | lineal | 8 |
| 6101 | lightness | 8 |
| 6102 | lieu | 8 |
| 6103 | lenity | 8 |
| 6104 | legitimate | 8 |
| 6105 | learnt | 8 |
| 6106 | laughs | 8 |
| 6107 | lastly | 8 |
| 6108 | lass | 8 |
| 6109 | lanthorn | 8 |
| 6110 | lantern | 8 |
| 6111 | lances | 8 |
| 6112 | lamenting | 8 |
| 6113 | lackey | 8 |
| 6114 | knots | 8 |
| 6115 | kite | 8 |
| 6116 | kitchen | 8 |
| 6117 | kindle | 8 |
| 6118 | killed | 8 |
| 6119 | keepers | 8 |
| 6120 | justify | 8 |
| 6121 | jocund | 8 |
| 6122 | jig | 8 |
| 6123 | jester | 8 |
| 6124 | jars | 8 |
| 6125 | jacob | 8 |
| 6126 | itch | 8 |
| 6127 | isis | 8 |
| 6128 | invest | 8 |
| 6129 | inter | 8 |
| 6130 | instructions | 8 |
| 6131 | injustice | 8 |
| 6132 | iniquity | 8 |
| 6133 | inhuman | 8 |
| 6134 | industry | 8 |
| 6135 | indirectly | 8 |
| 6136 | indirect | 8 |
| 6137 | importing | 8 |
| 6138 | important | 8 |
| 6139 | imaginary | 8 |
| 6140 | imagin | 8 |
| 6141 | idol | 8 |
| 6142 | huswife | 8 |
| 6143 | hovel | 8 |
| 6144 | hoop | 8 |
| 6145 | honoured | 8 |
| 6146 | hip | 8 |
| 6147 | hint | 8 |
| 6148 | hinds | 8 |
| 6149 | hidden | 8 |
| 6150 | herod | 8 |
| 6151 | heretic | 8 |
| 6152 | hereditary | 8 |
| 6153 | herb | 8 |
| 6154 | hen | 8 |
| 6155 | hellish | 8 |
| 6156 | hats | 8 |
| 6157 | hasten | 8 |
| 6158 | handed | 8 |
| 6159 | halter | 8 |
| 6160 | gripe | 8 |
| 6161 | greyhound | 8 |
| 6162 | gratify | 8 |
| 6163 | grapes | 8 |
| 6164 | gorge | 8 |
| 6165 | ginger | 8 |
| 6166 | gesture | 8 |
| 6167 | gentles | 8 |
| 6168 | generals | 8 |
| 6169 | gasp | 8 |
| 6170 | garlands | 8 |
| 6171 | gardener | 8 |
| 6172 | functions | 8 |
| 6173 | fun | 8 |
| 6174 | fulfill | 8 |
| 6175 | freshly | 8 |
| 6176 | fouler | 8 |
| 6177 | forsook | 8 |
| 6178 | forg | 8 |
| 6179 | forfeiture | 8 |
| 6180 | foh | 8 |
| 6181 | fitting | 8 |
| 6182 | firmly | 8 |
| 6183 | fin | 8 |
| 6184 | filth | 8 |
| 6185 | feels | 8 |
| 6186 | fathom | 8 |
| 6187 | fashions | 8 |
| 6188 | family | 8 |
| 6189 | fainting | 8 |
| 6190 | expedient | 8 |
| 6191 | exact | 8 |
| 6192 | esteemed | 8 |
| 6193 | estates | 8 |
| 6194 | establish | 8 |
| 6195 | ertake | 8 |
| 6196 | erlook | 8 |
| 6197 | equally | 8 |
| 6198 | entire | 8 |
| 6199 | enquire | 8 |
| 6200 | enlarge | 8 |
| 6201 | engine | 8 |
| 6202 | endless | 8 |
| 6203 | emperess | 8 |
| 6204 | elves | 8 |
| 6205 | education | 8 |
| 6206 | dungeon | 8 |
| 6207 | duly | 8 |
| 6208 | dukedoms | 8 |
| 6209 | drudge | 8 |
| 6210 | dreaming | 8 |
| 6211 | drab | 8 |
| 6212 | doubted | 8 |
| 6213 | doubly | 8 |
| 6214 | dotes | 8 |
| 6215 | domestic | 8 |
| 6216 | dolphin | 8 |
| 6217 | doit | 8 |
| 6218 | dogberry | 8 |
| 6219 | doctrine | 8 |
| 6220 | doct | 8 |
| 6221 | distressed | 8 |
| 6222 | distill | 8 |
| 6223 | dissolve | 8 |
| 6224 | displeas | 8 |
| 6225 | dispense | 8 |
| 6226 | disobedience | 8 |
| 6227 | discovered | 8 |
| 6228 | discomfort | 8 |
| 6229 | discern | 8 |
| 6230 | digg | 8 |
| 6231 | devout | 8 |
| 6232 | depending | 8 |
| 6233 | demanded | 8 |
| 6234 | dedicate | 8 |
| 6235 | darkly | 8 |
| 6236 | dardanius | 8 |
| 6237 | cutting | 8 |
| 6238 | cures | 8 |
| 6239 | crosses | 8 |
| 6240 | creeping | 8 |
| 6241 | creditors | 8 |
| 6242 | covert | 8 |
| 6243 | courtship | 8 |
| 6244 | courts | 8 |
| 6245 | counter | 8 |
| 6246 | correct | 8 |
| 6247 | corners | 8 |
| 6248 | conversation | 8 |
| 6249 | contrive | 8 |
| 6250 | continues | 8 |
| 6251 | contention | 8 |
| 6252 | consume | 8 |
| 6253 | conspire | 8 |
| 6254 | considered | 8 |
| 6255 | consideration | 8 |
| 6256 | consented | 8 |
| 6257 | confederate | 8 |
| 6258 | conception | 8 |
| 6259 | comparison | 8 |
| 6260 | commotion | 8 |
| 6261 | commanders | 8 |
| 6262 | coals | 8 |
| 6263 | club | 8 |
| 6264 | cloy | 8 |
| 6265 | closely | 8 |
| 6266 | clip | 8 |
| 6267 | claims | 8 |
| 6268 | christopher | 8 |
| 6269 | cherry | 8 |
| 6270 | checks | 8 |
| 6271 | chas | 8 |
| 6272 | chariot | 8 |
| 6273 | chanced | 8 |
| 6274 | certainty | 8 |
| 6275 | cauldron | 8 |
| 6276 | castles | 8 |
| 6277 | carrier | 8 |
| 6278 | carefully | 8 |
| 6279 | capucius | 8 |
| 6280 | calendar | 8 |
| 6281 | cadwal | 8 |
| 6282 | burdens | 8 |
| 6283 | bullets | 8 |
| 6284 | bubble | 8 |
| 6285 | bruise | 8 |
| 6286 | brood | 8 |
| 6287 | broker | 8 |
| 6288 | broil | 8 |
| 6289 | briers | 8 |
| 6290 | bridal | 8 |
| 6291 | brew | 8 |
| 6292 | breaths | 8 |
| 6293 | brav | 8 |
| 6294 | brands | 8 |
| 6295 | bragging | 8 |
| 6296 | bower | 8 |
| 6297 | blots | 8 |
| 6298 | blasts | 8 |
| 6299 | bit | 8 |
| 6300 | betroth | 8 |
| 6301 | betrayed | 8 |
| 6302 | betide | 8 |
| 6303 | belch | 8 |
| 6304 | begging | 8 |
| 6305 | bedlam | 8 |
| 6306 | bedchamber | 8 |
| 6307 | becoming | 8 |
| 6308 | bauble | 8 |
| 6309 | battlements | 8 |
| 6310 | bastardy | 8 |
| 6311 | banners | 8 |
| 6312 | ban | 8 |
| 6313 | avoided | 8 |
| 6314 | aunchient | 8 |
| 6315 | attorney | 8 |
| 6316 | attendance | 8 |
| 6317 | athwart | 8 |
| 6318 | assail | 8 |
| 6319 | arrow | 8 |
| 6320 | armourer | 8 |
| 6321 | aquitaine | 8 |
| 6322 | answering | 8 |
| 6323 | angle | 8 |
| 6324 | anew | 8 |
| 6325 | ambush | 8 |
| 6326 | afterward | 8 |
| 6327 | afflicted | 8 |
| 6328 | aediles | 8 |
| 6329 | adversity | 8 |
| 6330 | advancing | 8 |
| 6331 | admired | 8 |
| 6332 | acting | 8 |
| 6333 | acquit | 8 |
| 6334 | achiev | 8 |
| 6335 | accompany | 8 |
| 6336 | acceptance | 8 |
| 6337 | abound | 8 |
| 6338 | abides | 8 |
| 6339 | abergavenny | 8 |
| 6340 | abed | 8 |
| 6341 | writers | 7 |
| 6342 | wrestle | 7 |
| 6343 | wren | 7 |
| 6344 | wrangle | 7 |
| 6345 | wooers | 7 |
| 6346 | woodville | 7 |
| 6347 | woodcock | 7 |
| 6348 | womanish | 7 |
| 6349 | windy | 7 |
| 6350 | wight | 7 |
| 6351 | whereat | 7 |
| 6352 | welcomes | 7 |
| 6353 | weeks | 7 |
| 6354 | warp | 7 |
| 6355 | wage | 7 |
| 6356 | volscians | 7 |
| 6357 | vizards | 7 |
| 6358 | violets | 7 |
| 6359 | vine | 7 |
| 6360 | victor | 7 |
| 6361 | via | 7 |
| 6362 | venge | 7 |
| 6363 | vapours | 7 |
| 6364 | vapour | 7 |
| 6365 | uttermost | 7 |
| 6366 | upper | 7 |
| 6367 | unwholesome | 7 |
| 6368 | untrue | 7 |
| 6369 | untie | 7 |
| 6370 | unrest | 7 |
| 6371 | unquiet | 7 |
| 6372 | unluckily | 7 |
| 6373 | unjustly | 7 |
| 6374 | unity | 7 |
| 6375 | uneven | 7 |
| 6376 | unable | 7 |
| 6377 | twin | 7 |
| 6378 | turks | 7 |
| 6379 | tumult | 7 |
| 6380 | tumble | 7 |
| 6381 | truths | 7 |
| 6382 | trodden | 7 |
| 6383 | trivial | 7 |
| 6384 | tripping | 7 |
| 6385 | travers | 7 |
| 6386 | travellers | 7 |
| 6387 | travell | 7 |
| 6388 | trains | 7 |
| 6389 | tragical | 7 |
| 6390 | tithe | 7 |
| 6391 | tir | 7 |
| 6392 | throughout | 7 |
| 6393 | thorny | 7 |
| 6394 | thirsty | 7 |
| 6395 | thereon | 7 |
| 6396 | thaw | 7 |
| 6397 | thankfully | 7 |
| 6398 | thames | 7 |
| 6399 | tends | 7 |
| 6400 | temporal | 7 |
| 6401 | teaches | 7 |
| 6402 | taunts | 7 |
| 6403 | taunt | 7 |
| 6404 | tasted | 7 |
| 6405 | tam | 7 |
| 6406 | tallow | 7 |
| 6407 | tailors | 7 |
| 6408 | syracusian | 7 |
| 6409 | sycorax | 7 |
| 6410 | swiftly | 7 |
| 6411 | sweetness | 7 |
| 6412 | suspected | 7 |
| 6413 | surmise | 7 |
| 6414 | supreme | 7 |
| 6415 | supp | 7 |
| 6416 | summers | 7 |
| 6417 | suggest | 7 |
| 6418 | sufficeth | 7 |
| 6419 | sucking | 7 |
| 6420 | strengths | 7 |
| 6421 | strangle | 7 |
| 6422 | straightway | 7 |
| 6423 | stepp | 7 |
| 6424 | station | 7 |
| 6425 | staring | 7 |
| 6426 | stalk | 7 |
| 6427 | stable | 7 |
| 6428 | spotless | 7 |
| 6429 | spill | 7 |
| 6430 | spied | 7 |
| 6431 | spaniard | 7 |
| 6432 | southwell | 7 |
| 6433 | sot | 7 |
| 6434 | sores | 7 |
| 6435 | solemnly | 7 |
| 6436 | solace | 7 |
| 6437 | soar | 7 |
| 6438 | smelt | 7 |
| 6439 | skirmish | 7 |
| 6440 | skies | 7 |
| 6441 | singular | 7 |
| 6442 | shifts | 7 |
| 6443 | sheath | 7 |
| 6444 | shameless | 7 |
| 6445 | severe | 7 |
| 6446 | session | 7 |
| 6447 | servingmen | 7 |
| 6448 | selfsame | 7 |
| 6449 | sear | 7 |
| 6450 | sealed | 7 |
| 6451 | scythe | 7 |
| 6452 | scornful | 7 |
| 6453 | sconce | 7 |
| 6454 | scattered | 7 |
| 6455 | sandy | 7 |
| 6456 | sanctified | 7 |
| 6457 | samson | 7 |
| 6458 | salutation | 7 |
| 6459 | saith | 7 |
| 6460 | safeguard | 7 |
| 6461 | rival | 7 |
| 6462 | richest | 7 |
| 6463 | revenues | 7 |
| 6464 | returned | 7 |
| 6465 | requital | 7 |
| 6466 | repetition | 7 |
| 6467 | religiously | 7 |
| 6468 | release | 7 |
| 6469 | regions | 7 |
| 6470 | regiment | 7 |
| 6471 | regards | 7 |
| 6472 | refus | 7 |
| 6473 | reform | 7 |
| 6474 | recorded | 7 |
| 6475 | receiving | 7 |
| 6476 | realms | 7 |
| 6477 | rancour | 7 |
| 6478 | rag | 7 |
| 6479 | quietness | 7 |
| 6480 | quarters | 7 |
| 6481 | quarrelling | 7 |
| 6482 | qualified | 7 |
| 6483 | pursues | 7 |
| 6484 | purposed | 7 |
| 6485 | puppy | 7 |
| 6486 | puny | 7 |
| 6487 | pulpit | 7 |
| 6488 | prunes | 7 |
| 6489 | provision | 7 |
| 6490 | professes | 7 |
| 6491 | prodigious | 7 |
| 6492 | proceeds | 7 |
| 6493 | probation | 7 |
| 6494 | presenting | 7 |
| 6495 | presage | 7 |
| 6496 | portion | 7 |
| 6497 | poorly | 7 |
| 6498 | poisoned | 7 |
| 6499 | poise | 7 |
| 6500 | pockets | 7 |
| 6501 | plume | 7 |
| 6502 | plucking | 7 |
| 6503 | pleading | 7 |
| 6504 | played | 7 |
| 6505 | planets | 7 |
| 6506 | pith | 7 |
| 6507 | pirate | 7 |
| 6508 | pipes | 7 |
| 6509 | phrynia | 7 |
| 6510 | petticoat | 7 |
| 6511 | pestilent | 7 |
| 6512 | perfumes | 7 |
| 6513 | perfections | 7 |
| 6514 | penury | 7 |
| 6515 | pennyworth | 7 |
| 6516 | peerless | 7 |
| 6517 | peculiar | 7 |
| 6518 | peasants | 7 |
| 6519 | peal | 7 |
| 6520 | paying | 7 |
| 6521 | parthia | 7 |
| 6522 | parrot | 7 |
| 6523 | parallel | 7 |
| 6524 | pandar | 7 |
| 6525 | palaces | 7 |
| 6526 | paces | 7 |
| 6527 | overtake | 7 |
| 6528 | outlaws | 7 |
| 6529 | ostler | 7 |
| 6530 | osric | 7 |
| 6531 | organs | 7 |
| 6532 | ordnance | 7 |
| 6533 | oppressed | 7 |
| 6534 | olympus | 7 |
| 6535 | oftentimes | 7 |
| 6536 | offends | 7 |
| 6537 | od | 7 |
| 6538 | obsequies | 7 |
| 6539 | obscur | 7 |
| 6540 | obdurate | 7 |
| 6541 | nun | 7 |
| 6542 | normandy | 7 |
| 6543 | ninth | 7 |
| 6544 | nether | 7 |
| 6545 | nerves | 7 |
| 6546 | neighbourhood | 7 |
| 6547 | musical | 7 |
| 6548 | murderous | 7 |
| 6549 | multitudes | 7 |
| 6550 | mournful | 7 |
| 6551 | mounting | 7 |
| 6552 | mortals | 7 |
| 6553 | moons | 7 |
| 6554 | moneys | 7 |
| 6555 | monday | 7 |
| 6556 | mix | 7 |
| 6557 | mistresses | 7 |
| 6558 | missing | 7 |
| 6559 | misprision | 7 |
| 6560 | miracles | 7 |
| 6561 | minola | 7 |
| 6562 | mildness | 7 |
| 6563 | mightiest | 7 |
| 6564 | mightier | 7 |
| 6565 | mid | 7 |
| 6566 | merrier | 7 |
| 6567 | merited | 7 |
| 6568 | merchandise | 7 |
| 6569 | mellow | 7 |
| 6570 | meek | 7 |
| 6571 | meditation | 7 |
| 6572 | meals | 7 |
| 6573 | mature | 7 |
| 6574 | masks | 7 |
| 6575 | martyr | 7 |
| 6576 | mannerly | 7 |
| 6577 | manifold | 7 |
| 6578 | malignant | 7 |
| 6579 | magnanimous | 7 |
| 6580 | ma | 7 |
| 6581 | lurk | 7 |
| 6582 | lullaby | 7 |
| 6583 | lowest | 7 |
| 6584 | logs | 7 |
| 6585 | loaden | 7 |
| 6586 | lioness | 7 |
| 6587 | lightens | 7 |
| 6588 | license | 7 |
| 6589 | liars | 7 |
| 6590 | letting | 7 |
| 6591 | lethe | 7 |
| 6592 | leaps | 7 |
| 6593 | lawless | 7 |
| 6594 | languish | 7 |
| 6595 | lacking | 7 |
| 6596 | lace | 7 |
| 6597 | knavish | 7 |
| 6598 | kindled | 7 |
| 6599 | kerns | 7 |
| 6600 | juvenal | 7 |
| 6601 | judg | 7 |
| 6602 | jewry | 7 |
| 6603 | jar | 7 |
| 6604 | jacks | 7 |
| 6605 | ish | 7 |
| 6606 | invent | 7 |
| 6607 | instances | 7 |
| 6608 | india | 7 |
| 6609 | increasing | 7 |
| 6610 | inclining | 7 |
| 6611 | imputation | 7 |
| 6612 | imposition | 7 |
| 6613 | importun | 7 |
| 6614 | impediments | 7 |
| 6615 | imminent | 7 |
| 6616 | ides | 7 |
| 6617 | hypocrite | 7 |
| 6618 | humbleness | 7 |
| 6619 | housewife | 7 |
| 6620 | horribly | 7 |
| 6621 | hopeless | 7 |
| 6622 | hoo | 7 |
| 6623 | honestly | 7 |
| 6624 | hog | 7 |
| 6625 | hobby | 7 |
| 6626 | hoar | 7 |
| 6627 | hilts | 7 |
| 6628 | heme | 7 |
| 6629 | helping | 7 |
| 6630 | heaps | 7 |
| 6631 | hawk | 7 |
| 6632 | haunted | 7 |
| 6633 | hatches | 7 |
| 6634 | hardy | 7 |
| 6635 | hapless | 7 |
| 6636 | gusts | 7 |
| 6637 | gunner | 7 |
| 6638 | gun | 7 |
| 6639 | grievances | 7 |
| 6640 | greedy | 7 |
| 6641 | grecians | 7 |
| 6642 | graze | 7 |
| 6643 | gossips | 7 |
| 6644 | goat | 7 |
| 6645 | giv | 7 |
| 6646 | ghostly | 7 |
| 6647 | genius | 7 |
| 6648 | gargrave | 7 |
| 6649 | gaolers | 7 |
| 6650 | gan | 7 |
| 6651 | gamester | 7 |
| 6652 | gallus | 7 |
| 6653 | galls | 7 |
| 6654 | gains | 7 |
| 6655 | frights | 7 |
| 6656 | fortify | 7 |
| 6657 | formerly | 7 |
| 6658 | forgo | 7 |
| 6659 | forestall | 7 |
| 6660 | folded | 7 |
| 6661 | fog | 7 |
| 6662 | flows | 7 |
| 6663 | flown | 7 |
| 6664 | flowing | 7 |
| 6665 | flew | 7 |
| 6666 | flag | 7 |
| 6667 | fig | 7 |
| 6668 | feat | 7 |
| 6669 | fearfully | 7 |
| 6670 | favourites | 7 |
| 6671 | fasten | 7 |
| 6672 | fardel | 7 |
| 6673 | faints | 7 |
| 6674 | faculties | 7 |
| 6675 | factions | 7 |
| 6676 | eyesight | 7 |
| 6677 | external | 7 |
| 6678 | exchequer | 7 |
| 6679 | excels | 7 |
| 6680 | examples | 7 |
| 6681 | evident | 7 |
| 6682 | esquire | 7 |
| 6683 | escap | 7 |
| 6684 | ergo | 7 |
| 6685 | epidamnum | 7 |
| 6686 | enjoys | 7 |
| 6687 | enforcement | 7 |
| 6688 | encounters | 7 |
| 6689 | eminence | 7 |
| 6690 | embark | 7 |
| 6691 | eggs | 7 |
| 6692 | effeminate | 7 |
| 6693 | edict | 7 |
| 6694 | durance | 7 |
| 6695 | drove | 7 |
| 6696 | droop | 7 |
| 6697 | driving | 7 |
| 6698 | dregs | 7 |
| 6699 | downfall | 7 |
| 6700 | dow | 7 |
| 6701 | doubting | 7 |
| 6702 | dominions | 7 |
| 6703 | doe | 7 |
| 6704 | doctors | 7 |
| 6705 | dive | 7 |
| 6706 | distinctly | 7 |
| 6707 | dissuade | 7 |
| 6708 | discreet | 7 |
| 6709 | discontents | 7 |
| 6710 | disciplines | 7 |
| 6711 | dirty | 7 |
| 6712 | direful | 7 |
| 6713 | directions | 7 |
| 6714 | ding | 7 |
| 6715 | differences | 7 |
| 6716 | dialogue | 7 |
| 6717 | devouring | 7 |
| 6718 | devoted | 7 |
| 6719 | despiteful | 7 |
| 6720 | desolate | 7 |
| 6721 | depth | 7 |
| 6722 | departed | 7 |
| 6723 | dennis | 7 |
| 6724 | delays | 7 |
| 6725 | deity | 7 |
| 6726 | decreed | 7 |
| 6727 | declining | 7 |
| 6728 | declare | 7 |
| 6729 | december | 7 |
| 6730 | deceitful | 7 |
| 6731 | dealt | 7 |
| 6732 | darts | 7 |
| 6733 | dart | 7 |
| 6734 | dalliance | 7 |
| 6735 | dale | 7 |
| 6736 | cushions | 7 |
| 6737 | cushion | 7 |
| 6738 | cursing | 7 |
| 6739 | cropp | 7 |
| 6740 | crook | 7 |
| 6741 | crier | 7 |
| 6742 | courtly | 7 |
| 6743 | coupled | 7 |
| 6744 | counts | 7 |
| 6745 | countries | 7 |
| 6746 | corinth | 7 |
| 6747 | copper | 7 |
| 6748 | convoy | 7 |
| 6749 | conveyance | 7 |
| 6750 | converted | 7 |
| 6751 | contagion | 7 |
| 6752 | consum | 7 |
| 6753 | consorted | 7 |
| 6754 | conquered | 7 |
| 6755 | conclusions | 7 |
| 6756 | combine | 7 |
| 6757 | coloured | 7 |
| 6758 | cog | 7 |
| 6759 | coffer | 7 |
| 6760 | codpiece | 7 |
| 6761 | coach | 7 |
| 6762 | clout | 7 |
| 6763 | clothe | 7 |
| 6764 | cloister | 7 |
| 6765 | clime | 7 |
| 6766 | climbing | 7 |
| 6767 | clamours | 7 |
| 6768 | citadel | 7 |
| 6769 | cine | 7 |
| 6770 | churchmen | 7 |
| 6771 | churchman | 7 |
| 6772 | chuck | 7 |
| 6773 | chaps | 7 |
| 6774 | changeling | 7 |
| 6775 | changed | 7 |
| 6776 | cham | 7 |
| 6777 | ceremonious | 7 |
| 6778 | centaur | 7 |
| 6779 | caskets | 7 |
| 6780 | carthage | 7 |
| 6781 | carriages | 7 |
| 6782 | carpenter | 7 |
| 6783 | cargo | 7 |
| 6784 | cardinals | 7 |
| 6785 | card | 7 |
| 6786 | candles | 7 |
| 6787 | camps | 7 |
| 6788 | cain | 7 |
| 6789 | cage | 7 |
| 6790 | butchers | 7 |
| 6791 | buckle | 7 |
| 6792 | brooks | 7 |
| 6793 | briton | 7 |
| 6794 | brim | 7 |
| 6795 | breeches | 7 |
| 6796 | brawling | 7 |
| 6797 | brandish | 7 |
| 6798 | bran | 7 |
| 6799 | brags | 7 |
| 6800 | bracelet | 7 |
| 6801 | bourn | 7 |
| 6802 | bountiful | 7 |
| 6803 | boundless | 7 |
| 6804 | bonny | 7 |
| 6805 | bode | 7 |
| 6806 | boarded | 7 |
| 6807 | blister | 7 |
| 6808 | bleeds | 7 |
| 6809 | blazon | 7 |
| 6810 | bewray | 7 |
| 6811 | bewitch | 7 |
| 6812 | benefits | 7 |
| 6813 | bended | 7 |
| 6814 | belied | 7 |
| 6815 | begs | 7 |
| 6816 | beetle | 7 |
| 6817 | beck | 7 |
| 6818 | bearded | 7 |
| 6819 | battery | 7 |
| 6820 | bat | 7 |
| 6821 | bandy | 7 |
| 6822 | baleful | 7 |
| 6823 | bak | 7 |
| 6824 | baggage | 7 |
| 6825 | awry | 7 |
| 6826 | awful | 7 |
| 6827 | audacious | 7 |
| 6828 | attempts | 7 |
| 6829 | attaint | 7 |
| 6830 | atone | 7 |
| 6831 | assign | 7 |
| 6832 | assemble | 7 |
| 6833 | aspiring | 7 |
| 6834 | ashamed | 7 |
| 6835 | artemidorus | 7 |
| 6836 | arrived | 7 |
| 6837 | arden | 7 |
| 6838 | aptly | 7 |
| 6839 | apparell | 7 |
| 6840 | apothecary | 7 |
| 6841 | antiquity | 7 |
| 6842 | amount | 7 |
| 6843 | amiable | 7 |
| 6844 | amber | 7 |
| 6845 | almighty | 7 |
| 6846 | aliena | 7 |
| 6847 | aldermen | 7 |
| 6848 | alcides | 7 |
| 6849 | affrighted | 7 |
| 6850 | adultery | 7 |
| 6851 | admits | 7 |
| 6852 | admiring | 7 |
| 6853 | admire | 7 |
| 6854 | admir | 7 |
| 6855 | active | 7 |
| 6856 | acted | 7 |
| 6857 | accounted | 7 |
| 6858 | accommodated | 7 |
| 6859 | accents | 7 |
| 6860 | zealous | 6 |
| 6861 | yorkshire | 6 |
| 6862 | yew | 6 |
| 6863 | yawn | 6 |
| 6864 | wrest | 6 |
| 6865 | wrench | 6 |
| 6866 | wrapp | 6 |
| 6867 | worshipful | 6 |
| 6868 | wooed | 6 |
| 6869 | womanhood | 6 |
| 6870 | wive | 6 |
| 6871 | wished | 6 |
| 6872 | winding | 6 |
| 6873 | wilfully | 6 |
| 6874 | widower | 6 |
| 6875 | wholly | 6 |
| 6876 | wherever | 6 |
| 6877 | wheresoe | 6 |
| 6878 | whale | 6 |
| 6879 | welshmen | 6 |
| 6880 | welshman | 6 |
| 6881 | weird | 6 |
| 6882 | weighing | 6 |
| 6883 | weasel | 6 |
| 6884 | watery | 6 |
| 6885 | watchmen | 6 |
| 6886 | washing | 6 |
| 6887 | washes | 6 |
| 6888 | wards | 6 |
| 6889 | warder | 6 |
| 6890 | waning | 6 |
| 6891 | waken | 6 |
| 6892 | waited | 6 |
| 6893 | wailing | 6 |
| 6894 | waft | 6 |
| 6895 | vulcan | 6 |
| 6896 | voltemand | 6 |
| 6897 | village | 6 |
| 6898 | victors | 6 |
| 6899 | viands | 6 |
| 6900 | verified | 6 |
| 6901 | ventures | 6 |
| 6902 | venison | 6 |
| 6903 | varnish | 6 |
| 6904 | variable | 6 |
| 6905 | vanities | 6 |
| 6906 | values | 6 |
| 6907 | vail | 6 |
| 6908 | vacant | 6 |
| 6909 | uttered | 6 |
| 6910 | usual | 6 |
| 6911 | unwillingly | 6 |
| 6912 | unusual | 6 |
| 6913 | unsure | 6 |
| 6914 | unsettled | 6 |
| 6915 | unsatisfied | 6 |
| 6916 | unprovided | 6 |
| 6917 | unpleasing | 6 |
| 6918 | unkindly | 6 |
| 6919 | united | 6 |
| 6920 | unite | 6 |
| 6921 | unhallowed | 6 |
| 6922 | ungrateful | 6 |
| 6923 | unfurnish | 6 |
| 6924 | un | 6 |
| 6925 | twigs | 6 |
| 6926 | turf | 6 |
| 6927 | tuned | 6 |
| 6928 | trusting | 6 |
| 6929 | truncheon | 6 |
| 6930 | trump | 6 |
| 6931 | trudge | 6 |
| 6932 | trophies | 6 |
| 6933 | treaty | 6 |
| 6934 | treasury | 6 |
| 6935 | travels | 6 |
| 6936 | transport | 6 |
| 6937 | transformation | 6 |
| 6938 | towers | 6 |
| 6939 | tongu | 6 |
| 6940 | titan | 6 |
| 6941 | tires | 6 |
| 6942 | timorous | 6 |
| 6943 | timber | 6 |
| 6944 | tickling | 6 |
| 6945 | thrusts | 6 |
| 6946 | throngs | 6 |
| 6947 | threescore | 6 |
| 6948 | threatens | 6 |
| 6949 | thrall | 6 |
| 6950 | thinkest | 6 |
| 6951 | theatre | 6 |
| 6952 | thanked | 6 |
| 6953 | thanes | 6 |
| 6954 | testy | 6 |
| 6955 | testify | 6 |
| 6956 | terrors | 6 |
| 6957 | tending | 6 |
| 6958 | tenderly | 6 |
| 6959 | temp | 6 |
| 6960 | syria | 6 |
| 6961 | swiftest | 6 |
| 6962 | sweating | 6 |
| 6963 | swarm | 6 |
| 6964 | swallowing | 6 |
| 6965 | swaggering | 6 |
| 6966 | swagger | 6 |
| 6967 | swagg | 6 |
| 6968 | supple | 6 |
| 6969 | supplant | 6 |
| 6970 | successful | 6 |
| 6971 | subscrib | 6 |
| 6972 | subdued | 6 |
| 6973 | stung | 6 |
| 6974 | stumbling | 6 |
| 6975 | strongest | 6 |
| 6976 | strip | 6 |
| 6977 | stride | 6 |
| 6978 | strangled | 6 |
| 6979 | stooping | 6 |
| 6980 | stephen | 6 |
| 6981 | steeled | 6 |
| 6982 | stamps | 6 |
| 6983 | stains | 6 |
| 6984 | spurns | 6 |
| 6985 | spits | 6 |
| 6986 | spiritual | 6 |
| 6987 | spirited | 6 |
| 6988 | spices | 6 |
| 6989 | spar | 6 |
| 6990 | source | 6 |
| 6991 | sorely | 6 |
| 6992 | soonest | 6 |
| 6993 | somerville | 6 |
| 6994 | soften | 6 |
| 6995 | soe | 6 |
| 6996 | sociable | 6 |
| 6997 | snatches | 6 |
| 6998 | snakes | 6 |
| 6999 | smithfield | 6 |
| 7000 | smelling | 6 |
| 7001 | sloth | 6 |
| 7002 | slily | 6 |
| 7003 | slaughtered | 6 |
| 7004 | slanderous | 6 |
| 7005 | sland | 6 |
| 7006 | skirts | 6 |
| 7007 | skip | 6 |
| 7008 | skilful | 6 |
| 7009 | sinks | 6 |
| 7010 | sinister | 6 |
| 7011 | sincerity | 6 |
| 7012 | sicily | 6 |
| 7013 | shuts | 6 |
| 7014 | shrine | 6 |
| 7015 | shorter | 6 |
| 7016 | shoots | 6 |
| 7017 | shock | 6 |
| 7018 | shirts | 6 |
| 7019 | shepherdess | 6 |
| 7020 | shell | 6 |
| 7021 | shearing | 6 |
| 7022 | sharper | 6 |
| 7023 | shaken | 6 |
| 7024 | severn | 6 |
| 7025 | seventeen | 6 |
| 7026 | serpents | 6 |
| 7027 | sentinels | 6 |
| 7028 | sentences | 6 |
| 7029 | sentenc | 6 |
| 7030 | selves | 6 |
| 7031 | securely | 6 |
| 7032 | seconds | 6 |
| 7033 | searching | 6 |
| 7034 | scolding | 6 |
| 7035 | saves | 6 |
| 7036 | sauciness | 6 |
| 7037 | saturn | 6 |
| 7038 | salvation | 6 |
| 7039 | sallet | 6 |
| 7040 | sall | 6 |
| 7041 | sacrifices | 6 |
| 7042 | sa | 6 |
| 7043 | rusty | 6 |
| 7044 | rushing | 6 |
| 7045 | rung | 6 |
| 7046 | ruler | 6 |
| 7047 | ruinous | 6 |
| 7048 | rudeness | 6 |
| 7049 | rudely | 6 |
| 7050 | royalties | 6 |
| 7051 | roughly | 6 |
| 7052 | rosemary | 6 |
| 7053 | rood | 6 |
| 7054 | roger | 6 |
| 7055 | robbing | 6 |
| 7056 | robbers | 6 |
| 7057 | roars | 6 |
| 7058 | rive | 6 |
| 7059 | riots | 6 |
| 7060 | righteous | 6 |
| 7061 | rhodes | 6 |
| 7062 | reynaldo | 6 |
| 7063 | revolts | 6 |
| 7064 | reviv | 6 |
| 7065 | returning | 6 |
| 7066 | retort | 6 |
| 7067 | restored | 6 |
| 7068 | rested | 6 |
| 7069 | resides | 6 |
| 7070 | rescu | 6 |
| 7071 | reprove | 6 |
| 7072 | reprieve | 6 |
| 7073 | rejoicing | 6 |
| 7074 | refuge | 6 |
| 7075 | reformation | 6 |
| 7076 | reflection | 6 |
| 7077 | reek | 6 |
| 7078 | recoil | 6 |
| 7079 | reckless | 6 |
| 7080 | raze | 6 |
| 7081 | ravenous | 6 |
| 7082 | raising | 6 |
| 7083 | rails | 6 |
| 7084 | quondam | 6 |
| 7085 | quittance | 6 |
| 7086 | quillets | 6 |
| 7087 | qui | 6 |
| 7088 | quell | 6 |
| 7089 | putter | 6 |
| 7090 | puritan | 6 |
| 7091 | purgation | 6 |
| 7092 | purest | 6 |
| 7093 | pudding | 6 |
| 7094 | provinces | 6 |
| 7095 | providence | 6 |
| 7096 | protestation | 6 |
| 7097 | prostrate | 6 |
| 7098 | prospect | 6 |
| 7099 | proportions | 6 |
| 7100 | prophetic | 6 |
| 7101 | promontory | 6 |
| 7102 | promising | 6 |
| 7103 | prolong | 6 |
| 7104 | privately | 6 |
| 7105 | pricket | 6 |
| 7106 | prevention | 6 |
| 7107 | pretend | 6 |
| 7108 | presumption | 6 |
| 7109 | preservation | 6 |
| 7110 | preposterous | 6 |
| 7111 | precisely | 6 |
| 7112 | pre | 6 |
| 7113 | pottle | 6 |
| 7114 | potion | 6 |
| 7115 | potency | 6 |
| 7116 | posted | 6 |
| 7117 | portly | 6 |
| 7118 | popular | 6 |
| 7119 | poll | 6 |
| 7120 | pointed | 6 |
| 7121 | poets | 6 |
| 7122 | ply | 6 |
| 7123 | playfellow | 6 |
| 7124 | pities | 6 |
| 7125 | pirates | 6 |
| 7126 | pil | 6 |
| 7127 | piety | 6 |
| 7128 | pierc | 6 |
| 7129 | petitions | 6 |
| 7130 | perus | 6 |
| 7131 | persuades | 6 |
| 7132 | perplex | 6 |
| 7133 | pense | 6 |
| 7134 | penitence | 6 |
| 7135 | pelting | 6 |
| 7136 | pauca | 6 |
| 7137 | paths | 6 |
| 7138 | pated | 6 |
| 7139 | pat | 6 |
| 7140 | partners | 6 |
| 7141 | pardons | 6 |
| 7142 | paramour | 6 |
| 7143 | palpable | 6 |
| 7144 | pageants | 6 |
| 7145 | pagan | 6 |
| 7146 | owls | 6 |
| 7147 | owed | 6 |
| 7148 | overture | 6 |
| 7149 | overborne | 6 |
| 7150 | outrageous | 6 |
| 7151 | outface | 6 |
| 7152 | ounce | 6 |
| 7153 | oui | 6 |
| 7154 | operation | 6 |
| 7155 | olive | 6 |
| 7156 | offspring | 6 |
| 7157 | officious | 6 |
| 7158 | obstinate | 6 |
| 7159 | obligation | 6 |
| 7160 | nunnery | 6 |
| 7161 | nilus | 6 |
| 7162 | nile | 6 |
| 7163 | newer | 6 |
| 7164 | nettles | 6 |
| 7165 | nettle | 6 |
| 7166 | net | 6 |
| 7167 | needy | 6 |
| 7168 | necessaries | 6 |
| 7169 | nearly | 6 |
| 7170 | neapolitan | 6 |
| 7171 | nance | 6 |
| 7172 | namely | 6 |
| 7173 | myrmidons | 6 |
| 7174 | murtherous | 6 |
| 7175 | murmur | 6 |
| 7176 | mounts | 6 |
| 7177 | motives | 6 |
| 7178 | mote | 6 |
| 7179 | monuments | 6 |
| 7180 | monk | 6 |
| 7181 | monarchy | 6 |
| 7182 | monarchs | 6 |
| 7183 | momentary | 6 |
| 7184 | misdoubt | 6 |
| 7185 | minist | 6 |
| 7186 | mill | 6 |
| 7187 | mi | 6 |
| 7188 | meteors | 6 |
| 7189 | mermaid | 6 |
| 7190 | merciless | 6 |
| 7191 | melodious | 6 |
| 7192 | mell | 6 |
| 7193 | medlar | 6 |
| 7194 | maw | 6 |
| 7195 | mated | 6 |
| 7196 | massacre | 6 |
| 7197 | marian | 6 |
| 7198 | margent | 6 |
| 7199 | margarelon | 6 |
| 7200 | mare | 6 |
| 7201 | marches | 6 |
| 7202 | marcade | 6 |
| 7203 | mann | 6 |
| 7204 | magistrates | 6 |
| 7205 | lurking | 6 |
| 7206 | lump | 6 |
| 7207 | lucrece | 6 |
| 7208 | lucky | 6 |
| 7209 | lucifer | 6 |
| 7210 | lordly | 6 |
| 7211 | loo | 6 |
| 7212 | lodges | 6 |
| 7213 | liveries | 6 |
| 7214 | lineaments | 6 |
| 7215 | lincoln | 6 |
| 7216 | lim | 6 |
| 7217 | liberties | 6 |
| 7218 | liable | 6 |
| 7219 | levity | 6 |
| 7220 | legg | 6 |
| 7221 | leapt | 6 |
| 7222 | leaning | 6 |
| 7223 | lash | 6 |
| 7224 | laments | 6 |
| 7225 | lamented | 6 |
| 7226 | lag | 6 |
| 7227 | kinds | 6 |
| 7228 | kinder | 6 |
| 7229 | kennel | 6 |
| 7230 | ken | 6 |
| 7231 | jourdain | 6 |
| 7232 | jollity | 6 |
| 7233 | ix | 6 |
| 7234 | invites | 6 |
| 7235 | inventory | 6 |
| 7236 | interpret | 6 |
| 7237 | interchange | 6 |
| 7238 | intercession | 6 |
| 7239 | instructed | 6 |
| 7240 | inside | 6 |
| 7241 | infer | 6 |
| 7242 | infectious | 6 |
| 7243 | induction | 6 |
| 7244 | indignity | 6 |
| 7245 | incur | 6 |
| 7246 | incontinent | 6 |
| 7247 | incision | 6 |
| 7248 | incertain | 6 |
| 7249 | incapable | 6 |
| 7250 | importunate | 6 |
| 7251 | implore | 6 |
| 7252 | impious | 6 |
| 7253 | impiety | 6 |
| 7254 | imperfect | 6 |
| 7255 | immaculate | 6 |
| 7256 | ilion | 6 |
| 7257 | idolatry | 6 |
| 7258 | icy | 6 |
| 7259 | hyperion | 6 |
| 7260 | hymn | 6 |
| 7261 | hunted | 6 |
| 7262 | humane | 6 |
| 7263 | hug | 6 |
| 7264 | howsoe | 6 |
| 7265 | horseback | 6 |
| 7266 | hoping | 6 |
| 7267 | hoodwink | 6 |
| 7268 | honourably | 6 |
| 7269 | hive | 6 |
| 7270 | herring | 6 |
| 7271 | hermit | 6 |
| 7272 | heresy | 6 |
| 7273 | henceforward | 6 |
| 7274 | helmet | 6 |
| 7275 | heaviest | 6 |
| 7276 | hearken | 6 |
| 7277 | hearer | 6 |
| 7278 | headlong | 6 |
| 7279 | hawthorn | 6 |
| 7280 | haviour | 6 |
| 7281 | hardness | 6 |
| 7282 | hammer | 6 |
| 7283 | halting | 6 |
| 7284 | hallow | 6 |
| 7285 | halfpenny | 6 |
| 7286 | gust | 6 |
| 7287 | gud | 6 |
| 7288 | guardsman | 6 |
| 7289 | grossness | 6 |
| 7290 | groat | 6 |
| 7291 | grind | 6 |
| 7292 | grin | 6 |
| 7293 | grievously | 6 |
| 7294 | grievance | 6 |
| 7295 | grease | 6 |
| 7296 | graver | 6 |
| 7297 | grandpre | 6 |
| 7298 | gowns | 6 |
| 7299 | gout | 6 |
| 7300 | goot | 6 |
| 7301 | glittering | 6 |
| 7302 | glean | 6 |
| 7303 | ghastly | 6 |
| 7304 | germany | 6 |
| 7305 | gaudy | 6 |
| 7306 | gathered | 6 |
| 7307 | gaol | 6 |
| 7308 | gallop | 6 |
| 7309 | galleys | 6 |
| 7310 | galled | 6 |
| 7311 | fry | 6 |
| 7312 | frets | 6 |
| 7313 | framed | 6 |
| 7314 | foundation | 6 |
| 7315 | forsaken | 6 |
| 7316 | forked | 6 |
| 7317 | forgetfulness | 6 |
| 7318 | foresee | 6 |
| 7319 | foresaid | 6 |
| 7320 | forbids | 6 |
| 7321 | forbearance | 6 |
| 7322 | fling | 6 |
| 7323 | flea | 6 |
| 7324 | flay | 6 |
| 7325 | flatteries | 6 |
| 7326 | firmament | 6 |
| 7327 | finer | 6 |
| 7328 | fetter | 6 |
| 7329 | festival | 6 |
| 7330 | fery | 6 |
| 7331 | feigned | 6 |
| 7332 | fealty | 6 |
| 7333 | fawning | 6 |
| 7334 | fantastic | 6 |
| 7335 | faiths | 6 |
| 7336 | failing | 6 |
| 7337 | fading | 6 |
| 7338 | fade | 6 |
| 7339 | fa | 6 |
| 7340 | eyeless | 6 |
| 7341 | extended | 6 |
| 7342 | expos | 6 |
| 7343 | exploits | 6 |
| 7344 | expire | 6 |
| 7345 | exil | 6 |
| 7346 | exhibition | 6 |
| 7347 | executioners | 6 |
| 7348 | exclaims | 6 |
| 7349 | exceptions | 6 |
| 7350 | excepted | 6 |
| 7351 | excellently | 6 |
| 7352 | excel | 6 |
| 7353 | exactly | 6 |
| 7354 | estimate | 6 |
| 7355 | erwhelm | 6 |
| 7356 | erthrown | 6 |
| 7357 | erst | 6 |
| 7358 | environ | 6 |
| 7359 | ensign | 6 |
| 7360 | enrolled | 6 |
| 7361 | englishmen | 6 |
| 7362 | engenders | 6 |
| 7363 | enfranchisement | 6 |
| 7364 | enchanting | 6 |
| 7365 | empery | 6 |
| 7366 | embracing | 6 |
| 7367 | embassage | 6 |
| 7368 | elysium | 6 |
| 7369 | elephant | 6 |
| 7370 | eighth | 6 |
| 7371 | eighteen | 6 |
| 7372 | eel | 6 |
| 7373 | eastern | 6 |
| 7374 | earthy | 6 |
| 7375 | earthquake | 6 |
| 7376 | dusky | 6 |
| 7377 | dulcet | 6 |
| 7378 | dug | 6 |
| 7379 | dues | 6 |
| 7380 | ducat | 6 |
| 7381 | drunkards | 6 |
| 7382 | drug | 6 |
| 7383 | drowned | 6 |
| 7384 | dropping | 6 |
| 7385 | dressed | 6 |
| 7386 | dreaded | 6 |
| 7387 | drawers | 6 |
| 7388 | dragons | 6 |
| 7389 | dowager | 6 |
| 7390 | doubled | 6 |
| 7391 | doff | 6 |
| 7392 | distrust | 6 |
| 7393 | dispositions | 6 |
| 7394 | disposed | 6 |
| 7395 | disdains | 6 |
| 7396 | discuss | 6 |
| 7397 | discovers | 6 |
| 7398 | disclos | 6 |
| 7399 | discarded | 6 |
| 7400 | dimm | 6 |
| 7401 | diligent | 6 |
| 7402 | digestion | 6 |
| 7403 | digested | 6 |
| 7404 | dieted | 6 |
| 7405 | dews | 6 |
| 7406 | devised | 6 |
| 7407 | devices | 6 |
| 7408 | detestable | 6 |
| 7409 | determination | 6 |
| 7410 | despairing | 6 |
| 7411 | desirous | 6 |
| 7412 | desiring | 6 |
| 7413 | deservings | 6 |
| 7414 | derived | 6 |
| 7415 | depriv | 6 |
| 7416 | denying | 6 |
| 7417 | delighted | 6 |
| 7418 | deliberate | 6 |
| 7419 | deign | 6 |
| 7420 | defil | 6 |
| 7421 | defended | 6 |
| 7422 | defects | 6 |
| 7423 | deepest | 6 |
| 7424 | deceased | 6 |
| 7425 | decease | 6 |
| 7426 | daws | 6 |
| 7427 | dawning | 6 |
| 7428 | dastard | 6 |
| 7429 | darling | 6 |
| 7430 | darest | 6 |
| 7431 | danish | 6 |
| 7432 | daniel | 6 |
| 7433 | danc | 6 |
| 7434 | damsel | 6 |
| 7435 | cypress | 6 |
| 7436 | customary | 6 |
| 7437 | currents | 6 |
| 7438 | creditor | 6 |
| 7439 | cream | 6 |
| 7440 | cram | 6 |
| 7441 | coy | 6 |
| 7442 | counties | 6 |
| 7443 | counsellors | 6 |
| 7444 | cottage | 6 |
| 7445 | cools | 6 |
| 7446 | cooling | 6 |
| 7447 | contriv | 6 |
| 7448 | contemn | 6 |
| 7449 | containing | 6 |
| 7450 | consuming | 6 |
| 7451 | consuls | 6 |
| 7452 | constraint | 6 |
| 7453 | constantly | 6 |
| 7454 | consents | 6 |
| 7455 | conquerors | 6 |
| 7456 | conquering | 6 |
| 7457 | conjurer | 6 |
| 7458 | confused | 6 |
| 7459 | confirmation | 6 |
| 7460 | concludes | 6 |
| 7461 | conceiving | 6 |
| 7462 | conceiv | 6 |
| 7463 | compounds | 6 |
| 7464 | complexions | 6 |
| 7465 | complaining | 6 |
| 7466 | commoners | 6 |
| 7467 | comforted | 6 |
| 7468 | comely | 6 |
| 7469 | comb | 6 |
| 7470 | colors | 6 |
| 7471 | colder | 6 |
| 7472 | coeur | 6 |
| 7473 | co | 6 |
| 7474 | cloven | 6 |
| 7475 | clog | 6 |
| 7476 | clement | 6 |
| 7477 | claw | 6 |
| 7478 | clapper | 6 |
| 7479 | clad | 6 |
| 7480 | civility | 6 |
| 7481 | chronicles | 6 |
| 7482 | chrish | 6 |
| 7483 | childhood | 6 |
| 7484 | chests | 6 |
| 7485 | cheater | 6 |
| 7486 | charming | 6 |
| 7487 | charmed | 6 |
| 7488 | challenger | 6 |
| 7489 | chairs | 6 |
| 7490 | centurion | 6 |
| 7491 | celerity | 6 |
| 7492 | caves | 6 |
| 7493 | caution | 6 |
| 7494 | cats | 6 |
| 7495 | carved | 6 |
| 7496 | cart | 6 |
| 7497 | career | 6 |
| 7498 | capulets | 6 |
| 7499 | captivity | 6 |
| 7500 | caper | 6 |
| 7501 | canon | 6 |
| 7502 | cank | 6 |
| 7503 | canary | 6 |
| 7504 | caithness | 6 |
| 7505 | burthen | 6 |
| 7506 | builds | 6 |
| 7507 | buckler | 6 |
| 7508 | buckled | 6 |
| 7509 | brutish | 6 |
| 7510 | brotherhood | 6 |
| 7511 | brooch | 6 |
| 7512 | brier | 6 |
| 7513 | bribe | 6 |
| 7514 | breeder | 6 |
| 7515 | breaker | 6 |
| 7516 | brawls | 6 |
| 7517 | bravery | 6 |
| 7518 | brainford | 6 |
| 7519 | brach | 6 |
| 7520 | bonnet | 6 |
| 7521 | bolts | 6 |
| 7522 | bolder | 6 |
| 7523 | boding | 6 |
| 7524 | bodes | 6 |
| 7525 | boats | 6 |
| 7526 | blossoms | 6 |
| 7527 | bloodless | 6 |
| 7528 | blanket | 6 |
| 7529 | bits | 6 |
| 7530 | bier | 6 |
| 7531 | betake | 6 |
| 7532 | bestrid | 6 |
| 7533 | bespeak | 6 |
| 7534 | beset | 6 |
| 7535 | beseem | 6 |
| 7536 | berries | 6 |
| 7537 | benediction | 6 |
| 7538 | believing | 6 |
| 7539 | believed | 6 |
| 7540 | beheaded | 6 |
| 7541 | behaviours | 6 |
| 7542 | begotten | 6 |
| 7543 | beer | 6 |
| 7544 | beaver | 6 |
| 7545 | bawds | 6 |
| 7546 | bathe | 6 |
| 7547 | bass | 6 |
| 7548 | basis | 6 |
| 7549 | bashful | 6 |
| 7550 | barons | 6 |
| 7551 | barks | 6 |
| 7552 | barefoot | 6 |
| 7553 | bane | 6 |
| 7554 | baited | 6 |
| 7555 | babbling | 6 |
| 7556 | awaking | 6 |
| 7557 | auspicious | 6 |
| 7558 | augustus | 6 |
| 7559 | astonish | 6 |
| 7560 | artificial | 6 |
| 7561 | arrogance | 6 |
| 7562 | arrival | 6 |
| 7563 | arraign | 6 |
| 7564 | arithmetic | 6 |
| 7565 | arbour | 6 |
| 7566 | arbitrement | 6 |
| 7567 | aqua | 6 |
| 7568 | applied | 6 |
| 7569 | appeared | 6 |
| 7570 | anywhere | 6 |
| 7571 | anguish | 6 |
| 7572 | alt | 6 |
| 7573 | allies | 6 |
| 7574 | alisander | 6 |
| 7575 | albion | 6 |
| 7576 | agony | 6 |
| 7577 | agincourt | 6 |
| 7578 | affable | 6 |
| 7579 | adopted | 6 |
| 7580 | admiral | 6 |
| 7581 | across | 6 |
| 7582 | aches | 6 |
| 7583 | accusers | 6 |
| 7584 | accusations | 6 |
| 7585 | accost | 6 |
| 7586 | abstract | 6 |
| 7587 | yearly | 5 |
| 7588 | yards | 5 |
| 7589 | wrung | 5 |
| 7590 | wrinkle | 5 |
| 7591 | wringing | 5 |
| 7592 | wrap | 5 |
| 7593 | wrack | 5 |
| 7594 | wormwood | 5 |
| 7595 | workman | 5 |
| 7596 | woos | 5 |
| 7597 | winner | 5 |
| 7598 | whoop | 5 |
| 7599 | whiteness | 5 |
| 7600 | whispering | 5 |
| 7601 | whatsoe | 5 |
| 7602 | westward | 5 |
| 7603 | welfare | 5 |
| 7604 | weakest | 5 |
| 7605 | watches | 5 |
| 7606 | wasp | 5 |
| 7607 | warranted | 5 |
| 7608 | warmth | 5 |
| 7609 | wardrobe | 5 |
| 7610 | walked | 5 |
| 7611 | vowed | 5 |
| 7612 | vizard | 5 |
| 7613 | vitae | 5 |
| 7614 | visiting | 5 |
| 7615 | visible | 5 |
| 7616 | virtuously | 5 |
| 7617 | violently | 5 |
| 7618 | violate | 5 |
| 7619 | vineyard | 5 |
| 7620 | vilest | 5 |
| 7621 | viewing | 5 |
| 7622 | victories | 5 |
| 7623 | vicar | 5 |
| 7624 | vial | 5 |
| 7625 | vesture | 5 |
| 7626 | vestal | 5 |
| 7627 | venturous | 5 |
| 7628 | ventur | 5 |
| 7629 | venomous | 5 |
| 7630 | vehement | 5 |
| 7631 | vaward | 5 |
| 7632 | vasty | 5 |
| 7633 | vassals | 5 |
| 7634 | varying | 5 |
| 7635 | vantages | 5 |
| 7636 | vanquished | 5 |
| 7637 | vanished | 5 |
| 7638 | validity | 5 |
| 7639 | valiantly | 5 |
| 7640 | utters | 5 |
| 7641 | usurers | 5 |
| 7642 | usest | 5 |
| 7643 | uphold | 5 |
| 7644 | upbraided | 5 |
| 7645 | unworthiness | 5 |
| 7646 | unwelcome | 5 |
| 7647 | unused | 5 |
| 7648 | unthrifty | 5 |
| 7649 | untaught | 5 |
| 7650 | untainted | 5 |
| 7651 | unspeakable | 5 |
| 7652 | unseal | 5 |
| 7653 | unmeet | 5 |
| 7654 | unloose | 5 |
| 7655 | unlock | 5 |
| 7656 | union | 5 |
| 7657 | unhappily | 5 |
| 7658 | ungovern | 5 |
| 7659 | unequal | 5 |
| 7660 | undoubted | 5 |
| 7661 | undoing | 5 |
| 7662 | undertook | 5 |
| 7663 | understands | 5 |
| 7664 | uncleanly | 5 |
| 7665 | unclean | 5 |
| 7666 | unclasp | 5 |
| 7667 | unawares | 5 |
| 7668 | unaccustom | 5 |
| 7669 | twofold | 5 |
| 7670 | tutors | 5 |
| 7671 | turtles | 5 |
| 7672 | turtle | 5 |
| 7673 | trophy | 5 |
| 7674 | tripp | 5 |
| 7675 | triple | 5 |
| 7676 | trifling | 5 |
| 7677 | tributary | 5 |
| 7678 | transparent | 5 |
| 7679 | translated | 5 |
| 7680 | tractable | 5 |
| 7681 | touraine | 5 |
| 7682 | toucheth | 5 |
| 7683 | tortures | 5 |
| 7684 | tore | 5 |
| 7685 | toothache | 5 |
| 7686 | tiring | 5 |
| 7687 | tip | 5 |
| 7688 | timely | 5 |
| 7689 | tickled | 5 |
| 7690 | thunderbolt | 5 |
| 7691 | thrusting | 5 |
| 7692 | thrifty | 5 |
| 7693 | threshold | 5 |
| 7694 | thracian | 5 |
| 7695 | thoroughly | 5 |
| 7696 | thirteen | 5 |
| 7697 | thighs | 5 |
| 7698 | thievish | 5 |
| 7699 | thicket | 5 |
| 7700 | thatch | 5 |
| 7701 | thankfulness | 5 |
| 7702 | tennis | 5 |
| 7703 | tenants | 5 |
| 7704 | tempts | 5 |
| 7705 | temptation | 5 |
| 7706 | tempests | 5 |
| 7707 | teen | 5 |
| 7708 | teeming | 5 |
| 7709 | team | 5 |
| 7710 | teachest | 5 |
| 7711 | taxation | 5 |
| 7712 | tarpeian | 5 |
| 7713 | target | 5 |
| 7714 | tapestry | 5 |
| 7715 | taints | 5 |
| 7716 | taffeta | 5 |
| 7717 | tackle | 5 |
| 7718 | synod | 5 |
| 7719 | swol | 5 |
| 7720 | sweeting | 5 |
| 7721 | sweats | 5 |
| 7722 | swallows | 5 |
| 7723 | suspicious | 5 |
| 7724 | suspects | 5 |
| 7725 | surrender | 5 |
| 7726 | surgery | 5 |
| 7727 | surfeited | 5 |
| 7728 | sups | 5 |
| 7729 | supplication | 5 |
| 7730 | suppliant | 5 |
| 7731 | sues | 5 |
| 7732 | sued | 5 |
| 7733 | sucks | 5 |
| 7734 | successive | 5 |
| 7735 | substantial | 5 |
| 7736 | subjection | 5 |
| 7737 | subdues | 5 |
| 7738 | stumps | 5 |
| 7739 | straws | 5 |
| 7740 | stratagems | 5 |
| 7741 | strangest | 5 |
| 7742 | stories | 5 |
| 7743 | stools | 5 |
| 7744 | stolen | 5 |
| 7745 | stillness | 5 |
| 7746 | sterile | 5 |
| 7747 | stem | 5 |
| 7748 | steer | 5 |
| 7749 | statute | 5 |
| 7750 | started | 5 |
| 7751 | standers | 5 |
| 7752 | standard | 5 |
| 7753 | stall | 5 |
| 7754 | stag | 5 |
| 7755 | stabbing | 5 |
| 7756 | sprite | 5 |
| 7757 | sprightly | 5 |
| 7758 | spout | 5 |
| 7759 | spoon | 5 |
| 7760 | spongy | 5 |
| 7761 | spells | 5 |
| 7762 | speeds | 5 |
| 7763 | sparing | 5 |
| 7764 | span | 5 |
| 7765 | southampton | 5 |
| 7766 | sourest | 5 |
| 7767 | sorted | 5 |
| 7768 | sorrowful | 5 |
| 7769 | sol | 5 |
| 7770 | soever | 5 |
| 7771 | snares | 5 |
| 7772 | smote | 5 |
| 7773 | smoky | 5 |
| 7774 | smear | 5 |
| 7775 | slumbers | 5 |
| 7776 | slowly | 5 |
| 7777 | slough | 5 |
| 7778 | slime | 5 |
| 7779 | slide | 5 |
| 7780 | sleepers | 5 |
| 7781 | slavish | 5 |
| 7782 | slavery | 5 |
| 7783 | skipping | 5 |
| 7784 | sisterhood | 5 |
| 7785 | sinn | 5 |
| 7786 | sinking | 5 |
| 7787 | singly | 5 |
| 7788 | sinew | 5 |
| 7789 | simples | 5 |
| 7790 | simpleness | 5 |
| 7791 | similes | 5 |
| 7792 | signieur | 5 |
| 7793 | sightless | 5 |
| 7794 | showed | 5 |
| 7795 | shouting | 5 |
| 7796 | shorten | 5 |
| 7797 | shooting | 5 |
| 7798 | shone | 5 |
| 7799 | shipping | 5 |
| 7800 | shilling | 5 |
| 7801 | sherris | 5 |
| 7802 | sher | 5 |
| 7803 | shent | 5 |
| 7804 | shap | 5 |
| 7805 | shamefully | 5 |
| 7806 | serviceable | 5 |
| 7807 | seriously | 5 |
| 7808 | separation | 5 |
| 7809 | semblable | 5 |
| 7810 | seemed | 5 |
| 7811 | seeds | 5 |
| 7812 | se | 5 |
| 7813 | screech | 5 |
| 7814 | scouts | 5 |
| 7815 | schools | 5 |
| 7816 | schedule | 5 |
| 7817 | sceptres | 5 |
| 7818 | scatt | 5 |
| 7819 | scarfs | 5 |
| 7820 | scapes | 5 |
| 7821 | scaped | 5 |
| 7822 | scanted | 5 |
| 7823 | sayings | 5 |
| 7824 | sauf | 5 |
| 7825 | sanctity | 5 |
| 7826 | sampson | 5 |
| 7827 | sainted | 5 |
| 7828 | russian | 5 |
| 7829 | ruled | 5 |
| 7830 | ruins | 5 |
| 7831 | rugged | 5 |
| 7832 | ruffle | 5 |
| 7833 | rubs | 5 |
| 7834 | rubies | 5 |
| 7835 | rounds | 5 |
| 7836 | rook | 5 |
| 7837 | rolling | 5 |
| 7838 | rocky | 5 |
| 7839 | riseth | 5 |
| 7840 | rialto | 5 |
| 7841 | rful | 5 |
| 7842 | reverse | 5 |
| 7843 | retirement | 5 |
| 7844 | resting | 5 |
| 7845 | respite | 5 |
| 7846 | resisted | 5 |
| 7847 | reservation | 5 |
| 7848 | requited | 5 |
| 7849 | repulse | 5 |
| 7850 | replies | 5 |
| 7851 | repay | 5 |
| 7852 | repaid | 5 |
| 7853 | rents | 5 |
| 7854 | renounce | 5 |
| 7855 | remnant | 5 |
| 7856 | remiss | 5 |
| 7857 | remembrances | 5 |
| 7858 | remembered | 5 |
| 7859 | remaining | 5 |
| 7860 | rely | 5 |
| 7861 | register | 5 |
| 7862 | refresh | 5 |
| 7863 | refrain | 5 |
| 7864 | reference | 5 |
| 7865 | reeking | 5 |
| 7866 | redoubted | 5 |
| 7867 | reconcil | 5 |
| 7868 | reckonings | 5 |
| 7869 | recall | 5 |
| 7870 | rearward | 5 |
| 7871 | raz | 5 |
| 7872 | rays | 5 |
| 7873 | ravens | 5 |
| 7874 | raught | 5 |
| 7875 | rattling | 5 |
| 7876 | rates | 5 |
| 7877 | rancorous | 5 |
| 7878 | rams | 5 |
| 7879 | raineth | 5 |
| 7880 | quoted | 5 |
| 7881 | quote | 5 |
| 7882 | quill | 5 |
| 7883 | quean | 5 |
| 7884 | quaintly | 5 |
| 7885 | purblind | 5 |
| 7886 | pulls | 5 |
| 7887 | proverbs | 5 |
| 7888 | provender | 5 |
| 7889 | propos | 5 |
| 7890 | prophetess | 5 |
| 7891 | prophesied | 5 |
| 7892 | properties | 5 |
| 7893 | properly | 5 |
| 7894 | prop | 5 |
| 7895 | prone | 5 |
| 7896 | prompts | 5 |
| 7897 | progeny | 5 |
| 7898 | procession | 5 |
| 7899 | prizes | 5 |
| 7900 | primrose | 5 |
| 7901 | pridge | 5 |
| 7902 | prettily | 5 |
| 7903 | presumptuous | 5 |
| 7904 | prentice | 5 |
| 7905 | predominant | 5 |
| 7906 | preach | 5 |
| 7907 | prat | 5 |
| 7908 | pours | 5 |
| 7909 | potions | 5 |
| 7910 | posture | 5 |
| 7911 | possessions | 5 |
| 7912 | possessed | 5 |
| 7913 | populous | 5 |
| 7914 | poland | 5 |
| 7915 | poictiers | 5 |
| 7916 | poesy | 5 |
| 7917 | plunge | 5 |
| 7918 | plumes | 5 |
| 7919 | platform | 5 |
| 7920 | plantain | 5 |
| 7921 | pitying | 5 |
| 7922 | pinion | 5 |
| 7923 | pinches | 5 |
| 7924 | pillars | 5 |
| 7925 | pillage | 5 |
| 7926 | pike | 5 |
| 7927 | pied | 5 |
| 7928 | picking | 5 |
| 7929 | phrases | 5 |
| 7930 | perpend | 5 |
| 7931 | perjured | 5 |
| 7932 | perfum | 5 |
| 7933 | perceived | 5 |
| 7934 | pepper | 5 |
| 7935 | pepin | 5 |
| 7936 | penn | 5 |
| 7937 | penetrate | 5 |
| 7938 | pell | 5 |
| 7939 | peering | 5 |
| 7940 | peascod | 5 |
| 7941 | pear | 5 |
| 7942 | patches | 5 |
| 7943 | paste | 5 |
| 7944 | passed | 5 |
| 7945 | pang | 5 |
| 7946 | owners | 5 |
| 7947 | outwardly | 5 |
| 7948 | outright | 5 |
| 7949 | outrages | 5 |
| 7950 | orisons | 5 |
| 7951 | orient | 5 |
| 7952 | orders | 5 |
| 7953 | orbs | 5 |
| 7954 | orange | 5 |
| 7955 | ooze | 5 |
| 7956 | older | 5 |
| 7957 | offering | 5 |
| 7958 | ofephesus | 5 |
| 7959 | odours | 5 |
| 7960 | odour | 5 |
| 7961 | observing | 5 |
| 7962 | obeying | 5 |
| 7963 | oats | 5 |
| 7964 | oaks | 5 |
| 7965 | nursery | 5 |
| 7966 | nurs | 5 |
| 7967 | nous | 5 |
| 7968 | nonpareil | 5 |
| 7969 | noisome | 5 |
| 7970 | nods | 5 |
| 7971 | noblemen | 5 |
| 7972 | newest | 5 |
| 7973 | nevils | 5 |
| 7974 | nephews | 5 |
| 7975 | neighing | 5 |
| 7976 | napkins | 5 |
| 7977 | naming | 5 |
| 7978 | mutually | 5 |
| 7979 | mutinies | 5 |
| 7980 | musters | 5 |
| 7981 | musk | 5 |
| 7982 | murthers | 5 |
| 7983 | mots | 5 |
| 7984 | mortified | 5 |
| 7985 | moods | 5 |
| 7986 | montagues | 5 |
| 7987 | monkeys | 5 |
| 7988 | mongrel | 5 |
| 7989 | modestly | 5 |
| 7990 | moans | 5 |
| 7991 | misshapen | 5 |
| 7992 | minions | 5 |
| 7993 | mince | 5 |
| 7994 | mightiness | 5 |
| 7995 | mickle | 5 |
| 7996 | mice | 5 |
| 7997 | methoughts | 5 |
| 7998 | menecrates | 5 |
| 7999 | meg | 5 |
| 8000 | meditating | 5 |
| 8001 | meagre | 5 |
| 8002 | meads | 5 |
| 8003 | mead | 5 |
| 8004 | mayest | 5 |
| 8005 | matron | 5 |
| 8006 | material | 5 |
| 8007 | massy | 5 |
| 8008 | masked | 5 |
| 8009 | marseilles | 5 |
| 8010 | marketplace | 5 |
| 8011 | mariner | 5 |
| 8012 | manent | 5 |
| 8013 | makers | 5 |
| 8014 | majesties | 5 |
| 8015 | magician | 5 |
| 8016 | madcap | 5 |
| 8017 | macedon | 5 |
| 8018 | maccabaeus | 5 |
| 8019 | luxurious | 5 |
| 8020 | lunacy | 5 |
| 8021 | luggage | 5 |
| 8022 | lubber | 5 |
| 8023 | lowliness | 5 |
| 8024 | lout | 5 |
| 8025 | longest | 5 |
| 8026 | lodowick | 5 |
| 8027 | lodged | 5 |
| 8028 | loathes | 5 |
| 8029 | loathe | 5 |
| 8030 | loam | 5 |
| 8031 | lionel | 5 |
| 8032 | lin | 5 |
| 8033 | lifts | 5 |
| 8034 | libertine | 5 |
| 8035 | lethargy | 5 |
| 8036 | leonardo | 5 |
| 8037 | legacy | 5 |
| 8038 | leer | 5 |
| 8039 | leeks | 5 |
| 8040 | lecture | 5 |
| 8041 | leathern | 5 |
| 8042 | leans | 5 |
| 8043 | lawyers | 5 |
| 8044 | lavish | 5 |
| 8045 | laud | 5 |
| 8046 | lath | 5 |
| 8047 | lasts | 5 |
| 8048 | largess | 5 |
| 8049 | larger | 5 |
| 8050 | lamps | 5 |
| 8051 | lake | 5 |
| 8052 | lac | 5 |
| 8053 | knightly | 5 |
| 8054 | knighted | 5 |
| 8055 | kick | 5 |
| 8056 | jumps | 5 |
| 8057 | juggling | 5 |
| 8058 | judicious | 5 |
| 8059 | jointure | 5 |
| 8060 | joiner | 5 |
| 8061 | jesting | 5 |
| 8062 | issued | 5 |
| 8063 | islanders | 5 |
| 8064 | inviting | 5 |
| 8065 | interview | 5 |
| 8066 | interr | 5 |
| 8067 | interpretation | 5 |
| 8068 | insurrection | 5 |
| 8069 | instructs | 5 |
| 8070 | inspir | 5 |
| 8071 | insinuate | 5 |
| 8072 | innocency | 5 |
| 8073 | inland | 5 |
| 8074 | ingrate | 5 |
| 8075 | infringe | 5 |
| 8076 | infinitely | 5 |
| 8077 | infects | 5 |
| 8078 | infallible | 5 |
| 8079 | indifferently | 5 |
| 8080 | indies | 5 |
| 8081 | inconstancy | 5 |
| 8082 | incite | 5 |
| 8083 | incestuous | 5 |
| 8084 | incessant | 5 |
| 8085 | imprisoned | 5 |
| 8086 | impossibility | 5 |
| 8087 | importance | 5 |
| 8088 | imp | 5 |
| 8089 | immodest | 5 |
| 8090 | illustrious | 5 |
| 8091 | ilium | 5 |
| 8092 | hypocrisy | 5 |
| 8093 | hydra | 5 |
| 8094 | husks | 5 |
| 8095 | hurried | 5 |
| 8096 | huntsmen | 5 |
| 8097 | humh | 5 |
| 8098 | hover | 5 |
| 8099 | hotter | 5 |
| 8100 | honneur | 5 |
| 8101 | honester | 5 |
| 8102 | homeward | 5 |
| 8103 | holmedon | 5 |
| 8104 | hoist | 5 |
| 8105 | hoarse | 5 |
| 8106 | hoa | 5 |
| 8107 | hitherward | 5 |
| 8108 | hir | 5 |
| 8109 | hips | 5 |
| 8110 | hilding | 5 |
| 8111 | highway | 5 |
| 8112 | hereof | 5 |
| 8113 | herbert | 5 |
| 8114 | heraldry | 5 |
| 8115 | heedful | 5 |
| 8116 | hedges | 5 |
| 8117 | heathen | 5 |
| 8118 | headless | 5 |
| 8119 | hawks | 5 |
| 8120 | hastily | 5 |
| 8121 | happiest | 5 |
| 8122 | hallowed | 5 |
| 8123 | halberds | 5 |
| 8124 | hairy | 5 |
| 8125 | habited | 5 |
| 8126 | habitation | 5 |
| 8127 | haberdasher | 5 |
| 8128 | gyves | 5 |
| 8129 | gurney | 5 |
| 8130 | guise | 5 |
| 8131 | guildford | 5 |
| 8132 | guided | 5 |
| 8133 | guardian | 5 |
| 8134 | groves | 5 |
| 8135 | grounded | 5 |
| 8136 | grosser | 5 |
| 8137 | groats | 5 |
| 8138 | grieving | 5 |
| 8139 | greyhounds | 5 |
| 8140 | greed | 5 |
| 8141 | grate | 5 |
| 8142 | grasp | 5 |
| 8143 | gramercy | 5 |
| 8144 | grafted | 5 |
| 8145 | graciously | 5 |
| 8146 | graceless | 5 |
| 8147 | graceful | 5 |
| 8148 | graced | 5 |
| 8149 | gotten | 5 |
| 8150 | gor | 5 |
| 8151 | goblins | 5 |
| 8152 | gnats | 5 |
| 8153 | giver | 5 |
| 8154 | gins | 5 |
| 8155 | gibes | 5 |
| 8156 | germans | 5 |
| 8157 | genoa | 5 |
| 8158 | gem | 5 |
| 8159 | gashes | 5 |
| 8160 | gash | 5 |
| 8161 | garlic | 5 |
| 8162 | garb | 5 |
| 8163 | gamut | 5 |
| 8164 | gallops | 5 |
| 8165 | galen | 5 |
| 8166 | furr | 5 |
| 8167 | furniture | 5 |
| 8168 | furies | 5 |
| 8169 | fulsome | 5 |
| 8170 | fulness | 5 |
| 8171 | fulfil | 5 |
| 8172 | fuel | 5 |
| 8173 | frustrate | 5 |
| 8174 | fretted | 5 |
| 8175 | freer | 5 |
| 8176 | francisca | 5 |
| 8177 | fragrant | 5 |
| 8178 | foulness | 5 |
| 8179 | foster | 5 |
| 8180 | forwardness | 5 |
| 8181 | fortitude | 5 |
| 8182 | fortified | 5 |
| 8183 | forres | 5 |
| 8184 | fork | 5 |
| 8185 | forgiven | 5 |
| 8186 | forgetting | 5 |
| 8187 | forgetful | 5 |
| 8188 | forged | 5 |
| 8189 | forge | 5 |
| 8190 | forfeited | 5 |
| 8191 | foremost | 5 |
| 8192 | forbidden | 5 |
| 8193 | footman | 5 |
| 8194 | foolishly | 5 |
| 8195 | foison | 5 |
| 8196 | foaming | 5 |
| 8197 | flung | 5 |
| 8198 | flax | 5 |
| 8199 | flatt | 5 |
| 8200 | flats | 5 |
| 8201 | flap | 5 |
| 8202 | flaming | 5 |
| 8203 | fitly | 5 |
| 8204 | fines | 5 |
| 8205 | files | 5 |
| 8206 | fer | 5 |
| 8207 | feigning | 5 |
| 8208 | feelingly | 5 |
| 8209 | feeder | 5 |
| 8210 | feasted | 5 |
| 8211 | fated | 5 |
| 8212 | falconbridge | 5 |
| 8213 | fairs | 5 |
| 8214 | factor | 5 |
| 8215 | eyeballs | 5 |
| 8216 | extremities | 5 |
| 8217 | extremely | 5 |
| 8218 | extort | 5 |
| 8219 | extenuate | 5 |
| 8220 | extent | 5 |
| 8221 | extempore | 5 |
| 8222 | extant | 5 |
| 8223 | expostulate | 5 |
| 8224 | expose | 5 |
| 8225 | expel | 5 |
| 8226 | expecting | 5 |
| 8227 | exercises | 5 |
| 8228 | excrement | 5 |
| 8229 | exception | 5 |
| 8230 | exceedingly | 5 |
| 8231 | examination | 5 |
| 8232 | everyone | 5 |
| 8233 | ethiope | 5 |
| 8234 | esteems | 5 |
| 8235 | escapes | 5 |
| 8236 | erring | 5 |
| 8237 | enlargement | 5 |
| 8238 | enjoying | 5 |
| 8239 | engage | 5 |
| 8240 | encompass | 5 |
| 8241 | enclosed | 5 |
| 8242 | enchanted | 5 |
| 8243 | encamp | 5 |
| 8244 | eminent | 5 |
| 8245 | embracements | 5 |
| 8246 | elected | 5 |
| 8247 | edified | 5 |
| 8248 | eclipses | 5 |
| 8249 | eclipse | 5 |
| 8250 | earldom | 5 |
| 8251 | dye | 5 |
| 8252 | dy | 5 |
| 8253 | dwarfish | 5 |
| 8254 | dwarf | 5 |
| 8255 | dutchman | 5 |
| 8256 | dun | 5 |
| 8257 | dumbness | 5 |
| 8258 | duller | 5 |
| 8259 | drowns | 5 |
| 8260 | dross | 5 |
| 8261 | downward | 5 |
| 8262 | dolour | 5 |
| 8263 | doleful | 5 |
| 8264 | doings | 5 |
| 8265 | doigts | 5 |
| 8266 | dogg | 5 |
| 8267 | dit | 5 |
| 8268 | distilled | 5 |
| 8269 | dispute | 5 |
| 8270 | dispossess | 5 |
| 8271 | disposing | 5 |
| 8272 | dishonourable | 5 |
| 8273 | disgraces | 5 |
| 8274 | disfigure | 5 |
| 8275 | diseas | 5 |
| 8276 | discredit | 5 |
| 8277 | discords | 5 |
| 8278 | disaster | 5 |
| 8279 | dis | 5 |
| 8280 | dignified | 5 |
| 8281 | diamonds | 5 |
| 8282 | dexterity | 5 |
| 8283 | determinate | 5 |
| 8284 | descry | 5 |
| 8285 | derives | 5 |
| 8286 | derision | 5 |
| 8287 | deputation | 5 |
| 8288 | denote | 5 |
| 8289 | demonstrate | 5 |
| 8290 | demean | 5 |
| 8291 | dejected | 5 |
| 8292 | deformity | 5 |
| 8293 | deform | 5 |
| 8294 | define | 5 |
| 8295 | defile | 5 |
| 8296 | defendant | 5 |
| 8297 | defective | 5 |
| 8298 | declin | 5 |
| 8299 | deceiving | 5 |
| 8300 | debating | 5 |
| 8301 | daub | 5 |
| 8302 | dates | 5 |
| 8303 | dank | 5 |
| 8304 | damask | 5 |
| 8305 | curtsies | 5 |
| 8306 | currish | 5 |
| 8307 | curl | 5 |
| 8308 | curer | 5 |
| 8309 | curate | 5 |
| 8310 | cuff | 5 |
| 8311 | cudgell | 5 |
| 8312 | crowd | 5 |
| 8313 | crossing | 5 |
| 8314 | crocodile | 5 |
| 8315 | crispian | 5 |
| 8316 | cripple | 5 |
| 8317 | crete | 5 |
| 8318 | creeps | 5 |
| 8319 | creating | 5 |
| 8320 | craven | 5 |
| 8321 | cracking | 5 |
| 8322 | cowslip | 5 |
| 8323 | covering | 5 |
| 8324 | covered | 5 |
| 8325 | couples | 5 |
| 8326 | counterpoise | 5 |
| 8327 | counterfeiting | 5 |
| 8328 | counterfeited | 5 |
| 8329 | cough | 5 |
| 8330 | couched | 5 |
| 8331 | cote | 5 |
| 8332 | cop | 5 |
| 8333 | cony | 5 |
| 8334 | convince | 5 |
| 8335 | convenience | 5 |
| 8336 | controlling | 5 |
| 8337 | contrived | 5 |
| 8338 | contradiction | 5 |
| 8339 | contradict | 5 |
| 8340 | continued | 5 |
| 8341 | contending | 5 |
| 8342 | contaminated | 5 |
| 8343 | consciences | 5 |
| 8344 | conn | 5 |
| 8345 | conjuration | 5 |
| 8346 | conjoin | 5 |
| 8347 | conjecture | 5 |
| 8348 | congeal | 5 |
| 8349 | confiscate | 5 |
| 8350 | confederacy | 5 |
| 8351 | conceits | 5 |
| 8352 | complices | 5 |
| 8353 | competitors | 5 |
| 8354 | commonly | 5 |
| 8355 | commits | 5 |
| 8356 | commence | 5 |
| 8357 | comfortless | 5 |
| 8358 | combined | 5 |
| 8359 | colt | 5 |
| 8360 | clutch | 5 |
| 8361 | closing | 5 |
| 8362 | closes | 5 |
| 8363 | clos | 5 |
| 8364 | clocks | 5 |
| 8365 | cloaks | 5 |
| 8366 | clears | 5 |
| 8367 | clearly | 5 |
| 8368 | clearer | 5 |
| 8369 | claps | 5 |
| 8370 | cited | 5 |
| 8371 | cinque | 5 |
| 8372 | churches | 5 |
| 8373 | christen | 5 |
| 8374 | choughs | 5 |
| 8375 | chink | 5 |
| 8376 | chill | 5 |
| 8377 | cherubin | 5 |
| 8378 | chastise | 5 |
| 8379 | chafed | 5 |
| 8380 | chafe | 5 |
| 8381 | chaf | 5 |
| 8382 | certes | 5 |
| 8383 | celebration | 5 |
| 8384 | celebrate | 5 |
| 8385 | cavil | 5 |
| 8386 | cattle | 5 |
| 8387 | caterpillars | 5 |
| 8388 | cashier | 5 |
| 8389 | carelessly | 5 |
| 8390 | carcass | 5 |
| 8391 | carbonado | 5 |
| 8392 | cape | 5 |
| 8393 | caparison | 5 |
| 8394 | cannons | 5 |
| 8395 | cancel | 5 |
| 8396 | camel | 5 |
| 8397 | calumny | 5 |
| 8398 | cakes | 5 |
| 8399 | cake | 5 |
| 8400 | buzzing | 5 |
| 8401 | button | 5 |
| 8402 | buttock | 5 |
| 8403 | butler | 5 |
| 8404 | burned | 5 |
| 8405 | bur | 5 |
| 8406 | buffets | 5 |
| 8407 | bucklers | 5 |
| 8408 | bruis | 5 |
| 8409 | brothel | 5 |
| 8410 | bridle | 5 |
| 8411 | breathed | 5 |
| 8412 | brawn | 5 |
| 8413 | braving | 5 |
| 8414 | brabant | 5 |
| 8415 | bough | 5 |
| 8416 | bonfires | 5 |
| 8417 | boasting | 5 |
| 8418 | blooded | 5 |
| 8419 | blocks | 5 |
| 8420 | blindness | 5 |
| 8421 | blench | 5 |
| 8422 | bleak | 5 |
| 8423 | blasting | 5 |
| 8424 | blanks | 5 |
| 8425 | births | 5 |
| 8426 | birding | 5 |
| 8427 | billows | 5 |
| 8428 | bestows | 5 |
| 8429 | bestowing | 5 |
| 8430 | bespoke | 5 |
| 8431 | besmear | 5 |
| 8432 | belonging | 5 |
| 8433 | beholders | 5 |
| 8434 | beguiles | 5 |
| 8435 | befriend | 5 |
| 8436 | beckons | 5 |
| 8437 | bearest | 5 |
| 8438 | bearers | 5 |
| 8439 | beach | 5 |
| 8440 | basin | 5 |
| 8441 | barge | 5 |
| 8442 | bareheaded | 5 |
| 8443 | banditti | 5 |
| 8444 | ballads | 5 |
| 8445 | ball | 5 |
| 8446 | authors | 5 |
| 8447 | authorities | 5 |
| 8448 | attentive | 5 |
| 8449 | attention | 5 |
| 8450 | ascension | 5 |
| 8451 | ascends | 5 |
| 8452 | artillery | 5 |
| 8453 | arrive | 5 |
| 8454 | arming | 5 |
| 8455 | argue | 5 |
| 8456 | argosy | 5 |
| 8457 | arbitrate | 5 |
| 8458 | arabia | 5 |
| 8459 | aprons | 5 |
| 8460 | approves | 5 |
| 8461 | approv | 5 |
| 8462 | approaching | 5 |
| 8463 | appellant | 5 |
| 8464 | apology | 5 |
| 8465 | apish | 5 |
| 8466 | antipodes | 5 |
| 8467 | anthony | 5 |
| 8468 | annoyance | 5 |
| 8469 | animals | 5 |
| 8470 | anglais | 5 |
| 8471 | ang | 5 |
| 8472 | anchors | 5 |
| 8473 | ancestor | 5 |
| 8474 | allied | 5 |
| 8475 | alarbus | 5 |
| 8476 | airs | 5 |
| 8477 | agrees | 5 |
| 8478 | aggravate | 5 |
| 8479 | agate | 5 |
| 8480 | afresh | 5 |
| 8481 | affrights | 5 |
| 8482 | afflictions | 5 |
| 8483 | adulterate | 5 |
| 8484 | adds | 5 |
| 8485 | additions | 5 |
| 8486 | adders | 5 |
| 8487 | acorn | 5 |
| 8488 | acold | 5 |
| 8489 | achieved | 5 |
| 8490 | ace | 5 |
| 8491 | abram | 5 |
| 8492 | abr | 5 |
| 8493 | abilities | 5 |
| 8494 | youths | 4 |
| 8495 | yeomen | 4 |
| 8496 | x | 4 |
| 8497 | wrings | 4 |
| 8498 | wrested | 4 |
| 8499 | wreath | 4 |
| 8500 | wreak | 4 |
| 8501 | wooes | 4 |
| 8502 | wittenberg | 4 |
| 8503 | withholds | 4 |
| 8504 | withheld | 4 |
| 8505 | withering | 4 |
| 8506 | winning | 4 |
| 8507 | winded | 4 |
| 8508 | wildest | 4 |
| 8509 | wield | 4 |
| 8510 | whoso | 4 |
| 8511 | whoremaster | 4 |
| 8512 | whiter | 4 |
| 8513 | whistling | 4 |
| 8514 | whirl | 4 |
| 8515 | whining | 4 |
| 8516 | whetstone | 4 |
| 8517 | whereas | 4 |
| 8518 | wether | 4 |
| 8519 | weening | 4 |
| 8520 | wean | 4 |
| 8521 | wavering | 4 |
| 8522 | wastes | 4 |
| 8523 | waspish | 4 |
| 8524 | warwickshire | 4 |
| 8525 | warr | 4 |
| 8526 | warmed | 4 |
| 8527 | warkworth | 4 |
| 8528 | wandering | 4 |
| 8529 | wan | 4 |
| 8530 | waggon | 4 |
| 8531 | wagging | 4 |
| 8532 | vulture | 4 |
| 8533 | votary | 4 |
| 8534 | vomit | 4 |
| 8535 | volumes | 4 |
| 8536 | volley | 4 |
| 8537 | vocation | 4 |
| 8538 | vital | 4 |
| 8539 | visages | 4 |
| 8540 | visag | 4 |
| 8541 | violation | 4 |
| 8542 | vines | 4 |
| 8543 | villainies | 4 |
| 8544 | villages | 4 |
| 8545 | vie | 4 |
| 8546 | videlicet | 4 |
| 8547 | vessels | 4 |
| 8548 | veriest | 4 |
| 8549 | vere | 4 |
| 8550 | venerable | 4 |
| 8551 | vaulting | 4 |
| 8552 | vary | 4 |
| 8553 | varlets | 4 |
| 8554 | varied | 4 |
| 8555 | valorous | 4 |
| 8556 | valley | 4 |
| 8557 | vagabond | 4 |
| 8558 | vacancy | 4 |
| 8559 | usury | 4 |
| 8560 | usurps | 4 |
| 8561 | useth | 4 |
| 8562 | uplifted | 4 |
| 8563 | upholds | 4 |
| 8564 | unspotted | 4 |
| 8565 | unsay | 4 |
| 8566 | unsafe | 4 |
| 8567 | unreasonable | 4 |
| 8568 | unprofitable | 4 |
| 8569 | unpitied | 4 |
| 8570 | unpeople | 4 |
| 8571 | unpaid | 4 |
| 8572 | unmatchable | 4 |
| 8573 | unmanly | 4 |
| 8574 | unlucky | 4 |
| 8575 | unknit | 4 |
| 8576 | unkindest | 4 |
| 8577 | unhandsome | 4 |
| 8578 | unfolded | 4 |
| 8579 | unfirm | 4 |
| 8580 | uneasy | 4 |
| 8581 | undeserved | 4 |
| 8582 | undertaking | 4 |
| 8583 | undaunted | 4 |
| 8584 | uncover | 4 |
| 8585 | unconstant | 4 |
| 8586 | unchaste | 4 |
| 8587 | unavoided | 4 |
| 8588 | unapt | 4 |
| 8589 | unadvis | 4 |
| 8590 | tying | 4 |
| 8591 | twins | 4 |
| 8592 | twinn | 4 |
| 8593 | turkey | 4 |
| 8594 | tumultuous | 4 |
| 8595 | tumbling | 4 |
| 8596 | tumbled | 4 |
| 8597 | tug | 4 |
| 8598 | tub | 4 |
| 8599 | trusts | 4 |
| 8600 | trunks | 4 |
| 8601 | trull | 4 |
| 8602 | troublous | 4 |
| 8603 | trice | 4 |
| 8604 | trib | 4 |
| 8605 | tres | 4 |
| 8606 | trent | 4 |
| 8607 | trembled | 4 |
| 8608 | traverse | 4 |
| 8609 | travelling | 4 |
| 8610 | trap | 4 |
| 8611 | traitorously | 4 |
| 8612 | traduc | 4 |
| 8613 | trades | 4 |
| 8614 | traders | 4 |
| 8615 | tract | 4 |
| 8616 | tortur | 4 |
| 8617 | tongueless | 4 |
| 8618 | tombs | 4 |
| 8619 | toll | 4 |
| 8620 | tish | 4 |
| 8621 | tiny | 4 |
| 8622 | tinct | 4 |
| 8623 | tilt | 4 |
| 8624 | thwarted | 4 |
| 8625 | thwack | 4 |
| 8626 | throned | 4 |
| 8627 | thron | 4 |
| 8628 | throes | 4 |
| 8629 | thrives | 4 |
| 8630 | thriftless | 4 |
| 8631 | threes | 4 |
| 8632 | thickest | 4 |
| 8633 | thetis | 4 |
| 8634 | thereabouts | 4 |
| 8635 | test | 4 |
| 8636 | terribly | 4 |
| 8637 | tereus | 4 |
| 8638 | tenders | 4 |
| 8639 | tended | 4 |
| 8640 | tendance | 4 |
| 8641 | tempting | 4 |
| 8642 | tellus | 4 |
| 8643 | tediousness | 4 |
| 8644 | teacher | 4 |
| 8645 | tastes | 4 |
| 8646 | tarrying | 4 |
| 8647 | tarried | 4 |
| 8648 | tangle | 4 |
| 8649 | taming | 4 |
| 8650 | talent | 4 |
| 8651 | swinstead | 4 |
| 8652 | swiftness | 4 |
| 8653 | swerve | 4 |
| 8654 | swart | 4 |
| 8655 | surnamed | 4 |
| 8656 | surmises | 4 |
| 8657 | surges | 4 |
| 8658 | surfeits | 4 |
| 8659 | surfeiting | 4 |
| 8660 | sur | 4 |
| 8661 | supremacy | 4 |
| 8662 | supposition | 4 |
| 8663 | supposing | 4 |
| 8664 | supplies | 4 |
| 8665 | superstitious | 4 |
| 8666 | superfluity | 4 |
| 8667 | sunset | 4 |
| 8668 | sunk | 4 |
| 8669 | sundry | 4 |
| 8670 | sumptuous | 4 |
| 8671 | sulphur | 4 |
| 8672 | suis | 4 |
| 8673 | suggested | 4 |
| 8674 | sug | 4 |
| 8675 | sufficiency | 4 |
| 8676 | substitutes | 4 |
| 8677 | submissive | 4 |
| 8678 | sty | 4 |
| 8679 | stumbled | 4 |
| 8680 | student | 4 |
| 8681 | strut | 4 |
| 8682 | stripp | 4 |
| 8683 | stripes | 4 |
| 8684 | straying | 4 |
| 8685 | straining | 4 |
| 8686 | stormy | 4 |
| 8687 | stor | 4 |
| 8688 | stirrup | 4 |
| 8689 | stint | 4 |
| 8690 | stink | 4 |
| 8691 | sticking | 4 |
| 8692 | steads | 4 |
| 8693 | stature | 4 |
| 8694 | statues | 4 |
| 8695 | stalls | 4 |
| 8696 | staggers | 4 |
| 8697 | squires | 4 |
| 8698 | spurring | 4 |
| 8699 | spurr | 4 |
| 8700 | spritely | 4 |
| 8701 | spreading | 4 |
| 8702 | spouse | 4 |
| 8703 | sportive | 4 |
| 8704 | sportful | 4 |
| 8705 | sponge | 4 |
| 8706 | splitting | 4 |
| 8707 | splitted | 4 |
| 8708 | spin | 4 |
| 8709 | spilt | 4 |
| 8710 | spiders | 4 |
| 8711 | spends | 4 |
| 8712 | spectators | 4 |
| 8713 | specify | 4 |
| 8714 | speakest | 4 |
| 8715 | sparrows | 4 |
| 8716 | sparkle | 4 |
| 8717 | spanish | 4 |
| 8718 | southern | 4 |
| 8719 | soud | 4 |
| 8720 | sop | 4 |
| 8721 | soothe | 4 |
| 8722 | sonnets | 4 |
| 8723 | solid | 4 |
| 8724 | soliciting | 4 |
| 8725 | solemniz | 4 |
| 8726 | societies | 4 |
| 8727 | sobs | 4 |
| 8728 | snores | 4 |
| 8729 | sneak | 4 |
| 8730 | snatching | 4 |
| 8731 | smoking | 4 |
| 8732 | smaller | 4 |
| 8733 | sluttish | 4 |
| 8734 | sliver | 4 |
| 8735 | slipper | 4 |
| 8736 | sleek | 4 |
| 8737 | slaughters | 4 |
| 8738 | slanderer | 4 |
| 8739 | skulls | 4 |
| 8740 | skilless | 4 |
| 8741 | sixty | 4 |
| 8742 | sinners | 4 |
| 8743 | sinner | 4 |
| 8744 | singer | 4 |
| 8745 | sinewy | 4 |
| 8746 | sincere | 4 |
| 8747 | silks | 4 |
| 8748 | signifies | 4 |
| 8749 | sieve | 4 |
| 8750 | shuns | 4 |
| 8751 | shrug | 4 |
| 8752 | shrieking | 4 |
| 8753 | shortness | 4 |
| 8754 | shins | 4 |
| 8755 | shifted | 4 |
| 8756 | shedding | 4 |
| 8757 | shears | 4 |
| 8758 | sharply | 4 |
| 8759 | shares | 4 |
| 8760 | shapeless | 4 |
| 8761 | shamed | 4 |
| 8762 | sextus | 4 |
| 8763 | severity | 4 |
| 8764 | setter | 4 |
| 8765 | servitor | 4 |
| 8766 | sequence | 4 |
| 8767 | separated | 4 |
| 8768 | separate | 4 |
| 8769 | sentinel | 4 |
| 8770 | sensual | 4 |
| 8771 | sensibly | 4 |
| 8772 | sender | 4 |
| 8773 | seduced | 4 |
| 8774 | seduc | 4 |
| 8775 | sect | 4 |
| 8776 | scum | 4 |
| 8777 | scruples | 4 |
| 8778 | scrivener | 4 |
| 8779 | scripture | 4 |
| 8780 | scribes | 4 |
| 8781 | scribe | 4 |
| 8782 | scraps | 4 |
| 8783 | scottish | 4 |
| 8784 | scotch | 4 |
| 8785 | scholars | 4 |
| 8786 | scatters | 4 |
| 8787 | scathe | 4 |
| 8788 | scare | 4 |
| 8789 | scabbard | 4 |
| 8790 | scab | 4 |
| 8791 | saws | 4 |
| 8792 | savages | 4 |
| 8793 | satire | 4 |
| 8794 | sardis | 4 |
| 8795 | sanguine | 4 |
| 8796 | sandal | 4 |
| 8797 | sanctify | 4 |
| 8798 | salutes | 4 |
| 8799 | sage | 4 |
| 8800 | saffron | 4 |
| 8801 | sable | 4 |
| 8802 | ruth | 4 |
| 8803 | russians | 4 |
| 8804 | row | 4 |
| 8805 | rounded | 4 |
| 8806 | rote | 4 |
| 8807 | roofs | 4 |
| 8808 | rolls | 4 |
| 8809 | rods | 4 |
| 8810 | roast | 4 |
| 8811 | roan | 4 |
| 8812 | risen | 4 |
| 8813 | ripened | 4 |
| 8814 | ripen | 4 |
| 8815 | riddles | 4 |
| 8816 | rheumatic | 4 |
| 8817 | rhenish | 4 |
| 8818 | revolve | 4 |
| 8819 | revolution | 4 |
| 8820 | revolting | 4 |
| 8821 | revoke | 4 |
| 8822 | reversion | 4 |
| 8823 | retention | 4 |
| 8824 | restless | 4 |
| 8825 | restitution | 4 |
| 8826 | respective | 4 |
| 8827 | respecting | 4 |
| 8828 | resembling | 4 |
| 8829 | resembles | 4 |
| 8830 | rescued | 4 |
| 8831 | required | 4 |
| 8832 | repossess | 4 |
| 8833 | replication | 4 |
| 8834 | repented | 4 |
| 8835 | repast | 4 |
| 8836 | rendezvous | 4 |
| 8837 | renders | 4 |
| 8838 | remorseful | 4 |
| 8839 | remit | 4 |
| 8840 | remission | 4 |
| 8841 | remembers | 4 |
| 8842 | relics | 4 |
| 8843 | reins | 4 |
| 8844 | regreet | 4 |
| 8845 | refused | 4 |
| 8846 | reft | 4 |
| 8847 | recourse | 4 |
| 8848 | records | 4 |
| 8849 | reconciled | 4 |
| 8850 | rebukes | 4 |
| 8851 | readiest | 4 |
| 8852 | ravin | 4 |
| 8853 | ravel | 4 |
| 8854 | ratify | 4 |
| 8855 | ratified | 4 |
| 8856 | rashly | 4 |
| 8857 | rarity | 4 |
| 8858 | rarer | 4 |
| 8859 | ransack | 4 |
| 8860 | random | 4 |
| 8861 | rake | 4 |
| 8862 | rainy | 4 |
| 8863 | rabbit | 4 |
| 8864 | quiver | 4 |
| 8865 | quips | 4 |
| 8866 | quart | 4 |
| 8867 | qualm | 4 |
| 8868 | quail | 4 |
| 8869 | pythagoras | 4 |
| 8870 | pursuing | 4 |
| 8871 | pursued | 4 |
| 8872 | purposely | 4 |
| 8873 | puppies | 4 |
| 8874 | punk | 4 |
| 8875 | pulling | 4 |
| 8876 | puling | 4 |
| 8877 | prudent | 4 |
| 8878 | provoked | 4 |
| 8879 | prosecute | 4 |
| 8880 | proposed | 4 |
| 8881 | prompted | 4 |
| 8882 | promotion | 4 |
| 8883 | profitable | 4 |
| 8884 | professions | 4 |
| 8885 | profan | 4 |
| 8886 | prodigy | 4 |
| 8887 | prodigies | 4 |
| 8888 | privily | 4 |
| 8889 | privileg | 4 |
| 8890 | prisons | 4 |
| 8891 | pricking | 4 |
| 8892 | preys | 4 |
| 8893 | prevails | 4 |
| 8894 | presses | 4 |
| 8895 | preserved | 4 |
| 8896 | presenteth | 4 |
| 8897 | prescription | 4 |
| 8898 | prescribe | 4 |
| 8899 | presages | 4 |
| 8900 | preposterously | 4 |
| 8901 | predecessors | 4 |
| 8902 | prave | 4 |
| 8903 | prabbles | 4 |
| 8904 | posting | 4 |
| 8905 | possesses | 4 |
| 8906 | position | 4 |
| 8907 | portents | 4 |
| 8908 | portend | 4 |
| 8909 | porch | 4 |
| 8910 | poorer | 4 |
| 8911 | pool | 4 |
| 8912 | pond | 4 |
| 8913 | pompeius | 4 |
| 8914 | politician | 4 |
| 8915 | polack | 4 |
| 8916 | poetical | 4 |
| 8917 | plum | 4 |
| 8918 | plod | 4 |
| 8919 | plies | 4 |
| 8920 | plentiful | 4 |
| 8921 | pledges | 4 |
| 8922 | plaster | 4 |
| 8923 | plainer | 4 |
| 8924 | pitiless | 4 |
| 8925 | pish | 4 |
| 8926 | pink | 4 |
| 8927 | pines | 4 |
| 8928 | pill | 4 |
| 8929 | pickle | 4 |
| 8930 | phrygian | 4 |
| 8931 | philo | 4 |
| 8932 | phaethon | 4 |
| 8933 | petter | 4 |
| 8934 | petitioners | 4 |
| 8935 | perturbation | 4 |
| 8936 | pertains | 4 |
| 8937 | permission | 4 |
| 8938 | perfumed | 4 |
| 8939 | performed | 4 |
| 8940 | perfidious | 4 |
| 8941 | perfectly | 4 |
| 8942 | perdy | 4 |
| 8943 | perceives | 4 |
| 8944 | peopled | 4 |
| 8945 | pencil | 4 |
| 8946 | pedigree | 4 |
| 8947 | pebble | 4 |
| 8948 | peacock | 4 |
| 8949 | paved | 4 |
| 8950 | patrimony | 4 |
| 8951 | patrick | 4 |
| 8952 | pates | 4 |
| 8953 | patent | 4 |
| 8954 | pastoral | 4 |
| 8955 | passengers | 4 |
| 8956 | partition | 4 |
| 8957 | partisans | 4 |
| 8958 | parthian | 4 |
| 8959 | pare | 4 |
| 8960 | pard | 4 |
| 8961 | panting | 4 |
| 8962 | palter | 4 |
| 8963 | pales | 4 |
| 8964 | palates | 4 |
| 8965 | painfully | 4 |
| 8966 | pac | 4 |
| 8967 | owest | 4 |
| 8968 | overwhelm | 4 |
| 8969 | overlook | 4 |
| 8970 | oublie | 4 |
| 8971 | origin | 4 |
| 8972 | ordered | 4 |
| 8973 | ord | 4 |
| 8974 | oratory | 4 |
| 8975 | orators | 4 |
| 8976 | opposites | 4 |
| 8977 | op | 4 |
| 8978 | onset | 4 |
| 8979 | oily | 4 |
| 8980 | oddly | 4 |
| 8981 | obstruction | 4 |
| 8982 | observed | 4 |
| 8983 | nuts | 4 |
| 8984 | nursing | 4 |
| 8985 | nowhere | 4 |
| 8986 | noting | 4 |
| 8987 | nothings | 4 |
| 8988 | noontide | 4 |
| 8989 | nook | 4 |
| 8990 | nonino | 4 |
| 8991 | noises | 4 |
| 8992 | ninny | 4 |
| 8993 | nimbly | 4 |
| 8994 | niggardly | 4 |
| 8995 | nero | 4 |
| 8996 | ner | 4 |
| 8997 | neighbouring | 4 |
| 8998 | neglecting | 4 |
| 8999 | needed | 4 |
| 9000 | naturally | 4 |
| 9001 | nap | 4 |
| 9002 | named | 4 |
| 9003 | nakedness | 4 |
| 9004 | mysteries | 4 |
| 9005 | mutter | 4 |
| 9006 | musing | 4 |
| 9007 | murmuring | 4 |
| 9008 | multiplying | 4 |
| 9009 | mules | 4 |
| 9010 | mule | 4 |
| 9011 | muffler | 4 |
| 9012 | moss | 4 |
| 9013 | morrows | 4 |
| 9014 | morris | 4 |
| 9015 | morgan | 4 |
| 9016 | mordake | 4 |
| 9017 | mong | 4 |
| 9018 | monastery | 4 |
| 9019 | mocker | 4 |
| 9020 | misus | 4 |
| 9021 | misty | 4 |
| 9022 | mislike | 4 |
| 9023 | miser | 4 |
| 9024 | miscreant | 4 |
| 9025 | misbegotten | 4 |
| 9026 | mint | 4 |
| 9027 | minstrels | 4 |
| 9028 | minority | 4 |
| 9029 | mincing | 4 |
| 9030 | milder | 4 |
| 9031 | midsummer | 4 |
| 9032 | meteor | 4 |
| 9033 | metaphor | 4 |
| 9034 | mention | 4 |
| 9035 | mender | 4 |
| 9036 | memorable | 4 |
| 9037 | melts | 4 |
| 9038 | meekness | 4 |
| 9039 | meditations | 4 |
| 9040 | medicines | 4 |
| 9041 | meddling | 4 |
| 9042 | mechanical | 4 |
| 9043 | meanwhile | 4 |
| 9044 | meanly | 4 |
| 9045 | meanings | 4 |
| 9046 | mattock | 4 |
| 9047 | matrons | 4 |
| 9048 | matching | 4 |
| 9049 | matches | 4 |
| 9050 | masterly | 4 |
| 9051 | masham | 4 |
| 9052 | marrow | 4 |
| 9053 | marring | 4 |
| 9054 | marking | 4 |
| 9055 | marjoram | 4 |
| 9056 | marchioness | 4 |
| 9057 | manifested | 4 |
| 9058 | mandate | 4 |
| 9059 | manacles | 4 |
| 9060 | malt | 4 |
| 9061 | malmsey | 4 |
| 9062 | makest | 4 |
| 9063 | major | 4 |
| 9064 | mainly | 4 |
| 9065 | mail | 4 |
| 9066 | maidenheads | 4 |
| 9067 | magnificoes | 4 |
| 9068 | madding | 4 |
| 9069 | lusts | 4 |
| 9070 | lustful | 4 |
| 9071 | lulla | 4 |
| 9072 | lud | 4 |
| 9073 | lour | 4 |
| 9074 | lott | 4 |
| 9075 | lot | 4 |
| 9076 | losers | 4 |
| 9077 | loser | 4 |
| 9078 | los | 4 |
| 9079 | lordships | 4 |
| 9080 | looker | 4 |
| 9081 | looked | 4 |
| 9082 | lolling | 4 |
| 9083 | log | 4 |
| 9084 | lobby | 4 |
| 9085 | lingers | 4 |
| 9086 | limp | 4 |
| 9087 | limited | 4 |
| 9088 | limbo | 4 |
| 9089 | likelihoods | 4 |
| 9090 | lifeless | 4 |
| 9091 | lied | 4 |
| 9092 | lids | 4 |
| 9093 | licence | 4 |
| 9094 | libya | 4 |
| 9095 | lessen | 4 |
| 9096 | leprosy | 4 |
| 9097 | lecherous | 4 |
| 9098 | lecher | 4 |
| 9099 | leash | 4 |
| 9100 | leas | 4 |
| 9101 | leanness | 4 |
| 9102 | leander | 4 |
| 9103 | leak | 4 |
| 9104 | laur | 4 |
| 9105 | laughed | 4 |
| 9106 | lattice | 4 |
| 9107 | larded | 4 |
| 9108 | lapwing | 4 |
| 9109 | lank | 4 |
| 9110 | languages | 4 |
| 9111 | langley | 4 |
| 9112 | lamely | 4 |
| 9113 | lackeys | 4 |
| 9114 | laboured | 4 |
| 9115 | knits | 4 |
| 9116 | knaveries | 4 |
| 9117 | kindnesses | 4 |
| 9118 | justified | 4 |
| 9119 | junius | 4 |
| 9120 | jovial | 4 |
| 9121 | jointly | 4 |
| 9122 | jesus | 4 |
| 9123 | jay | 4 |
| 9124 | jarring | 4 |
| 9125 | j | 4 |
| 9126 | ivy | 4 |
| 9127 | issuing | 4 |
| 9128 | irregular | 4 |
| 9129 | ireful | 4 |
| 9130 | ire | 4 |
| 9131 | invocation | 4 |
| 9132 | invincible | 4 |
| 9133 | inveterate | 4 |
| 9134 | invested | 4 |
| 9135 | inundation | 4 |
| 9136 | intrusion | 4 |
| 9137 | interrupt | 4 |
| 9138 | intermission | 4 |
| 9139 | interlude | 4 |
| 9140 | interchangeably | 4 |
| 9141 | intercepted | 4 |
| 9142 | intercept | 4 |
| 9143 | intelligent | 4 |
| 9144 | intellect | 4 |
| 9145 | int | 4 |
| 9146 | insult | 4 |
| 9147 | install | 4 |
| 9148 | inspired | 4 |
| 9149 | insinuating | 4 |
| 9150 | insatiate | 4 |
| 9151 | innocents | 4 |
| 9152 | inly | 4 |
| 9153 | injur | 4 |
| 9154 | inheritor | 4 |
| 9155 | inhabits | 4 |
| 9156 | inflame | 4 |
| 9157 | infirmities | 4 |
| 9158 | infirm | 4 |
| 9159 | inevitable | 4 |
| 9160 | industrious | 4 |
| 9161 | induce | 4 |
| 9162 | indignities | 4 |
| 9163 | indictment | 4 |
| 9164 | index | 4 |
| 9165 | indentures | 4 |
| 9166 | incurable | 4 |
| 9167 | incomparable | 4 |
| 9168 | impute | 4 |
| 9169 | impregnable | 4 |
| 9170 | impotent | 4 |
| 9171 | importunes | 4 |
| 9172 | imperfections | 4 |
| 9173 | impartial | 4 |
| 9174 | immured | 4 |
| 9175 | imitation | 4 |
| 9176 | imaginations | 4 |
| 9177 | ignobly | 4 |
| 9178 | hymns | 4 |
| 9179 | husbanded | 4 |
| 9180 | hurly | 4 |
| 9181 | hunters | 4 |
| 9182 | hous | 4 |
| 9183 | hotly | 4 |
| 9184 | hostility | 4 |
| 9185 | hostile | 4 |
| 9186 | hostages | 4 |
| 9187 | horrors | 4 |
| 9188 | horned | 4 |
| 9189 | hoofs | 4 |
| 9190 | homicide | 4 |
| 9191 | holland | 4 |
| 9192 | hogshead | 4 |
| 9193 | hoard | 4 |
| 9194 | hired | 4 |
| 9195 | hilt | 4 |
| 9196 | hies | 4 |
| 9197 | heroical | 4 |
| 9198 | herne | 4 |
| 9199 | hereabout | 4 |
| 9200 | helpful | 4 |
| 9201 | helms | 4 |
| 9202 | helmets | 4 |
| 9203 | hellespont | 4 |
| 9204 | heated | 4 |
| 9205 | hearse | 4 |
| 9206 | healths | 4 |
| 9207 | heady | 4 |
| 9208 | hazards | 4 |
| 9209 | hawking | 4 |
| 9210 | haud | 4 |
| 9211 | hating | 4 |
| 9212 | hateth | 4 |
| 9213 | harlotry | 4 |
| 9214 | hares | 4 |
| 9215 | haps | 4 |
| 9216 | hannibal | 4 |
| 9217 | hangers | 4 |
| 9218 | handmaid | 4 |
| 9219 | handling | 4 |
| 9220 | handled | 4 |
| 9221 | hallowmas | 4 |
| 9222 | hags | 4 |
| 9223 | haggard | 4 |
| 9224 | habiliments | 4 |
| 9225 | guns | 4 |
| 9226 | gum | 4 |
| 9227 | guerdon | 4 |
| 9228 | greediness | 4 |
| 9229 | gravel | 4 |
| 9230 | gratulate | 4 |
| 9231 | gratitude | 4 |
| 9232 | grateful | 4 |
| 9233 | grape | 4 |
| 9234 | grange | 4 |
| 9235 | grandmother | 4 |
| 9236 | grained | 4 |
| 9237 | gorg | 4 |
| 9238 | gonzago | 4 |
| 9239 | godly | 4 |
| 9240 | goddesses | 4 |
| 9241 | gnat | 4 |
| 9242 | glutton | 4 |
| 9243 | glowing | 4 |
| 9244 | glib | 4 |
| 9245 | glansdale | 4 |
| 9246 | gird | 4 |
| 9247 | gin | 4 |
| 9248 | gibbet | 4 |
| 9249 | gender | 4 |
| 9250 | gems | 4 |
| 9251 | gelding | 4 |
| 9252 | gazes | 4 |
| 9253 | gawds | 4 |
| 9254 | gavest | 4 |
| 9255 | gauntlet | 4 |
| 9256 | garnish | 4 |
| 9257 | gardon | 4 |
| 9258 | gardeners | 4 |
| 9259 | galliard | 4 |
| 9260 | gallery | 4 |
| 9261 | gainsay | 4 |
| 9262 | g | 4 |
| 9263 | fustian | 4 |
| 9264 | fume | 4 |
| 9265 | fubb | 4 |
| 9266 | fruitless | 4 |
| 9267 | frosts | 4 |
| 9268 | fronts | 4 |
| 9269 | frontiers | 4 |
| 9270 | frogmore | 4 |
| 9271 | fro | 4 |
| 9272 | fretting | 4 |
| 9273 | fretful | 4 |
| 9274 | fraud | 4 |
| 9275 | frailties | 4 |
| 9276 | fragments | 4 |
| 9277 | fountains | 4 |
| 9278 | founder | 4 |
| 9279 | foully | 4 |
| 9280 | fornication | 4 |
| 9281 | forges | 4 |
| 9282 | forfeits | 4 |
| 9283 | foretold | 4 |
| 9284 | foretell | 4 |
| 9285 | foresters | 4 |
| 9286 | forerun | 4 |
| 9287 | forcibly | 4 |
| 9288 | folk | 4 |
| 9289 | foam | 4 |
| 9290 | fo | 4 |
| 9291 | flouted | 4 |
| 9292 | flourishes | 4 |
| 9293 | floor | 4 |
| 9294 | flocks | 4 |
| 9295 | fliers | 4 |
| 9296 | fleeting | 4 |
| 9297 | flaws | 4 |
| 9298 | flattered | 4 |
| 9299 | flatly | 4 |
| 9300 | flash | 4 |
| 9301 | fittest | 4 |
| 9302 | fishermen | 4 |
| 9303 | fingres | 4 |
| 9304 | finder | 4 |
| 9305 | filled | 4 |
| 9306 | filial | 4 |
| 9307 | filed | 4 |
| 9308 | figur | 4 |
| 9309 | figs | 4 |
| 9310 | fighter | 4 |
| 9311 | fewer | 4 |
| 9312 | feverous | 4 |
| 9313 | fetches | 4 |
| 9314 | fet | 4 |
| 9315 | fen | 4 |
| 9316 | fees | 4 |
| 9317 | feared | 4 |
| 9318 | fe | 4 |
| 9319 | favouredly | 4 |
| 9320 | favourable | 4 |
| 9321 | fasts | 4 |
| 9322 | fantasies | 4 |
| 9323 | fangs | 4 |
| 9324 | fangled | 4 |
| 9325 | familiarly | 4 |
| 9326 | familiarity | 4 |
| 9327 | fallen | 4 |
| 9328 | falchion | 4 |
| 9329 | faithless | 4 |
| 9330 | fairness | 4 |
| 9331 | faded | 4 |
| 9332 | fabric | 4 |
| 9333 | fable | 4 |
| 9334 | extraordinary | 4 |
| 9335 | extol | 4 |
| 9336 | exterior | 4 |
| 9337 | expressed | 4 |
| 9338 | expound | 4 |
| 9339 | exposition | 4 |
| 9340 | expert | 4 |
| 9341 | experienc | 4 |
| 9342 | expedience | 4 |
| 9343 | expects | 4 |
| 9344 | exhibit | 4 |
| 9345 | excuses | 4 |
| 9346 | exclamation | 4 |
| 9347 | excepting | 4 |
| 9348 | ewe | 4 |
| 9349 | everlastingly | 4 |
| 9350 | evasion | 4 |
| 9351 | euriphile | 4 |
| 9352 | eton | 4 |
| 9353 | established | 4 |
| 9354 | essex | 4 |
| 9355 | espouse | 4 |
| 9356 | esperance | 4 |
| 9357 | erewhile | 4 |
| 9358 | erect | 4 |
| 9359 | equity | 4 |
| 9360 | equals | 4 |
| 9361 | envied | 4 |
| 9362 | envenom | 4 |
| 9363 | entrap | 4 |
| 9364 | entomb | 4 |
| 9365 | ensues | 4 |
| 9366 | enkindled | 4 |
| 9367 | enjoyed | 4 |
| 9368 | engross | 4 |
| 9369 | engines | 4 |
| 9370 | engender | 4 |
| 9371 | engaged | 4 |
| 9372 | enfranchise | 4 |
| 9373 | enfranchis | 4 |
| 9374 | endured | 4 |
| 9375 | endow | 4 |
| 9376 | endeared | 4 |
| 9377 | encourage | 4 |
| 9378 | enchant | 4 |
| 9379 | enacted | 4 |
| 9380 | emulous | 4 |
| 9381 | embraces | 4 |
| 9382 | embracement | 4 |
| 9383 | embowell | 4 |
| 9384 | emboss | 4 |
| 9385 | eloquent | 4 |
| 9386 | elect | 4 |
| 9387 | elders | 4 |
| 9388 | eld | 4 |
| 9389 | egregious | 4 |
| 9390 | effusion | 4 |
| 9391 | effectual | 4 |
| 9392 | eaves | 4 |
| 9393 | eas | 4 |
| 9394 | earnestness | 4 |
| 9395 | dumps | 4 |
| 9396 | dullness | 4 |
| 9397 | ducdame | 4 |
| 9398 | dubb | 4 |
| 9399 | drunkenness | 4 |
| 9400 | drave | 4 |
| 9401 | drain | 4 |
| 9402 | downy | 4 |
| 9403 | doubtfully | 4 |
| 9404 | doublets | 4 |
| 9405 | doricles | 4 |
| 9406 | dong | 4 |
| 9407 | donation | 4 |
| 9408 | dolours | 4 |
| 9409 | doers | 4 |
| 9410 | divorc | 4 |
| 9411 | divisions | 4 |
| 9412 | divining | 4 |
| 9413 | divines | 4 |
| 9414 | ditty | 4 |
| 9415 | distressful | 4 |
| 9416 | distil | 4 |
| 9417 | distempered | 4 |
| 9418 | distemp | 4 |
| 9419 | distaste | 4 |
| 9420 | distant | 4 |
| 9421 | distaff | 4 |
| 9422 | dissolv | 4 |
| 9423 | dissolute | 4 |
| 9424 | dissentious | 4 |
| 9425 | disprove | 4 |
| 9426 | displease | 4 |
| 9427 | disobedient | 4 |
| 9428 | dishonesty | 4 |
| 9429 | diseased | 4 |
| 9430 | disdaining | 4 |
| 9431 | discourses | 4 |
| 9432 | discomfited | 4 |
| 9433 | disclose | 4 |
| 9434 | disclaim | 4 |
| 9435 | discharged | 4 |
| 9436 | disasters | 4 |
| 9437 | differs | 4 |
| 9438 | diable | 4 |
| 9439 | determined | 4 |
| 9440 | detect | 4 |
| 9441 | destinies | 4 |
| 9442 | destin | 4 |
| 9443 | desperation | 4 |
| 9444 | desperately | 4 |
| 9445 | desk | 4 |
| 9446 | descried | 4 |
| 9447 | departing | 4 |
| 9448 | denis | 4 |
| 9449 | delivery | 4 |
| 9450 | delivering | 4 |
| 9451 | delightful | 4 |
| 9452 | deities | 4 |
| 9453 | defied | 4 |
| 9454 | defense | 4 |
| 9455 | defences | 4 |
| 9456 | defeated | 4 |
| 9457 | default | 4 |
| 9458 | deface | 4 |
| 9459 | defac | 4 |
| 9460 | declines | 4 |
| 9461 | decays | 4 |
| 9462 | decayed | 4 |
| 9463 | dauntless | 4 |
| 9464 | daunted | 4 |
| 9465 | dateless | 4 |
| 9466 | datchet | 4 |
| 9467 | daff | 4 |
| 9468 | customs | 4 |
| 9469 | curls | 4 |
| 9470 | curiously | 4 |
| 9471 | curiosity | 4 |
| 9472 | curfew | 4 |
| 9473 | cured | 4 |
| 9474 | curbs | 4 |
| 9475 | cunningly | 4 |
| 9476 | cumberland | 4 |
| 9477 | cuckolds | 4 |
| 9478 | cuckoldly | 4 |
| 9479 | crutches | 4 |
| 9480 | crust | 4 |
| 9481 | cruelly | 4 |
| 9482 | crotchets | 4 |
| 9483 | crickets | 4 |
| 9484 | crests | 4 |
| 9485 | crescent | 4 |
| 9486 | credo | 4 |
| 9487 | credent | 4 |
| 9488 | craving | 4 |
| 9489 | cracks | 4 |
| 9490 | cozening | 4 |
| 9491 | coxcombs | 4 |
| 9492 | covetousness | 4 |
| 9493 | covenants | 4 |
| 9494 | courser | 4 |
| 9495 | counters | 4 |
| 9496 | councils | 4 |
| 9497 | cormorant | 4 |
| 9498 | core | 4 |
| 9499 | convers | 4 |
| 9500 | conveniently | 4 |
| 9501 | controlment | 4 |
| 9502 | contriver | 4 |
| 9503 | contraries | 4 |
| 9504 | consumption | 4 |
| 9505 | consummate | 4 |
| 9506 | consult | 4 |
| 9507 | conspir | 4 |
| 9508 | consistory | 4 |
| 9509 | consist | 4 |
| 9510 | consign | 4 |
| 9511 | considering | 4 |
| 9512 | consenting | 4 |
| 9513 | consecrated | 4 |
| 9514 | conjured | 4 |
| 9515 | conjur | 4 |
| 9516 | conjectures | 4 |
| 9517 | confus | 4 |
| 9518 | confronted | 4 |
| 9519 | confounding | 4 |
| 9520 | confirms | 4 |
| 9521 | confined | 4 |
| 9522 | conduit | 4 |
| 9523 | conceived | 4 |
| 9524 | concealment | 4 |
| 9525 | concealed | 4 |
| 9526 | compt | 4 |
| 9527 | complot | 4 |
| 9528 | competitor | 4 |
| 9529 | commune | 4 |
| 9530 | committing | 4 |
| 9531 | commerce | 4 |
| 9532 | comments | 4 |
| 9533 | comforting | 4 |
| 9534 | comforter | 4 |
| 9535 | cometh | 4 |
| 9536 | combatants | 4 |
| 9537 | color | 4 |
| 9538 | coldest | 4 |
| 9539 | cocks | 4 |
| 9540 | cockle | 4 |
| 9541 | cobham | 4 |
| 9542 | clouded | 4 |
| 9543 | closed | 4 |
| 9544 | clipp | 4 |
| 9545 | clink | 4 |
| 9546 | cliff | 4 |
| 9547 | clerks | 4 |
| 9548 | clerkly | 4 |
| 9549 | clergy | 4 |
| 9550 | cleanly | 4 |
| 9551 | claribel | 4 |
| 9552 | civet | 4 |
| 9553 | circled | 4 |
| 9554 | cipher | 4 |
| 9555 | cinders | 4 |
| 9556 | cinable | 4 |
| 9557 | christening | 4 |
| 9558 | choosing | 4 |
| 9559 | chooses | 4 |
| 9560 | chins | 4 |
| 9561 | chidden | 4 |
| 9562 | chickens | 4 |
| 9563 | cherubins | 4 |
| 9564 | cheers | 4 |
| 9565 | cheat | 4 |
| 9566 | chaplain | 4 |
| 9567 | chaos | 4 |
| 9568 | changeable | 4 |
| 9569 | champions | 4 |
| 9570 | chameleon | 4 |
| 9571 | chafes | 4 |
| 9572 | cerberus | 4 |
| 9573 | censures | 4 |
| 9574 | ceases | 4 |
| 9575 | cavaleiro | 4 |
| 9576 | catches | 4 |
| 9577 | catastrophe | 4 |
| 9578 | catalogue | 4 |
| 9579 | cassibelan | 4 |
| 9580 | carriers | 4 |
| 9581 | carp | 4 |
| 9582 | cannibals | 4 |
| 9583 | cankers | 4 |
| 9584 | caesars | 4 |
| 9585 | cable | 4 |
| 9586 | butterflies | 4 |
| 9587 | bustle | 4 |
| 9588 | businesses | 4 |
| 9589 | busines | 4 |
| 9590 | busied | 4 |
| 9591 | burs | 4 |
| 9592 | burgonet | 4 |
| 9593 | bunch | 4 |
| 9594 | bum | 4 |
| 9595 | bulwarks | 4 |
| 9596 | bulwark | 4 |
| 9597 | bulls | 4 |
| 9598 | buildings | 4 |
| 9599 | buffet | 4 |
| 9600 | buff | 4 |
| 9601 | budget | 4 |
| 9602 | buckles | 4 |
| 9603 | brush | 4 |
| 9604 | bruit | 4 |
| 9605 | bruising | 4 |
| 9606 | bruised | 4 |
| 9607 | broth | 4 |
| 9608 | brittle | 4 |
| 9609 | brittany | 4 |
| 9610 | bristow | 4 |
| 9611 | bristle | 4 |
| 9612 | brisk | 4 |
| 9613 | brightest | 4 |
| 9614 | brevity | 4 |
| 9615 | bravest | 4 |
| 9616 | braves | 4 |
| 9617 | bowls | 4 |
| 9618 | bove | 4 |
| 9619 | bounties | 4 |
| 9620 | botch | 4 |
| 9621 | borrows | 4 |
| 9622 | borrowing | 4 |
| 9623 | booty | 4 |
| 9624 | bondmen | 4 |
| 9625 | bolted | 4 |
| 9626 | boisterous | 4 |
| 9627 | boiling | 4 |
| 9628 | bodily | 4 |
| 9629 | bodied | 4 |
| 9630 | bloodily | 4 |
| 9631 | blinded | 4 |
| 9632 | blew | 4 |
| 9633 | bleat | 4 |
| 9634 | blamed | 4 |
| 9635 | blackheath | 4 |
| 9636 | blacker | 4 |
| 9637 | birthright | 4 |
| 9638 | binds | 4 |
| 9639 | bides | 4 |
| 9640 | beweep | 4 |
| 9641 | bevis | 4 |
| 9642 | betrothed | 4 |
| 9643 | betime | 4 |
| 9644 | bethought | 4 |
| 9645 | besieg | 4 |
| 9646 | beseems | 4 |
| 9647 | bequeathed | 4 |
| 9648 | benefactors | 4 |
| 9649 | benedictus | 4 |
| 9650 | bellows | 4 |
| 9651 | bellied | 4 |
| 9652 | believes | 4 |
| 9653 | beguiled | 4 |
| 9654 | begone | 4 |
| 9655 | begets | 4 |
| 9656 | beetles | 4 |
| 9657 | becom | 4 |
| 9658 | beadles | 4 |
| 9659 | beacon | 4 |
| 9660 | bawcock | 4 |
| 9661 | basilisks | 4 |
| 9662 | basilisk | 4 |
| 9663 | bareness | 4 |
| 9664 | barely | 4 |
| 9665 | barbarism | 4 |
| 9666 | banner | 4 |
| 9667 | baiting | 4 |
| 9668 | bagpipe | 4 |
| 9669 | badness | 4 |
| 9670 | badges | 4 |
| 9671 | baboon | 4 |
| 9672 | awakes | 4 |
| 9673 | avez | 4 |
| 9674 | avail | 4 |
| 9675 | authentic | 4 |
| 9676 | austere | 4 |
| 9677 | augment | 4 |
| 9678 | attribute | 4 |
| 9679 | attest | 4 |
| 9680 | attainted | 4 |
| 9681 | attainder | 4 |
| 9682 | athenians | 4 |
| 9683 | assuredly | 4 |
| 9684 | assistant | 4 |
| 9685 | assailed | 4 |
| 9686 | aspire | 4 |
| 9687 | aspects | 4 |
| 9688 | asked | 4 |
| 9689 | asia | 4 |
| 9690 | arrogant | 4 |
| 9691 | approof | 4 |
| 9692 | approacheth | 4 |
| 9693 | appetites | 4 |
| 9694 | appelez | 4 |
| 9695 | appease | 4 |
| 9696 | appeas | 4 |
| 9697 | apoth | 4 |
| 9698 | apoplexy | 4 |
| 9699 | apiece | 4 |
| 9700 | anybody | 4 |
| 9701 | antonius | 4 |
| 9702 | antiates | 4 |
| 9703 | annual | 4 |
| 9704 | angleterre | 4 |
| 9705 | angers | 4 |
| 9706 | andronici | 4 |
| 9707 | ancestry | 4 |
| 9708 | anatomy | 4 |
| 9709 | amendment | 4 |
| 9710 | amended | 4 |
| 9711 | ambles | 4 |
| 9712 | amazons | 4 |
| 9713 | amazon | 4 |
| 9714 | amazedly | 4 |
| 9715 | alters | 4 |
| 9716 | alps | 4 |
| 9717 | allows | 4 |
| 9718 | allowed | 4 |
| 9719 | allons | 4 |
| 9720 | alias | 4 |
| 9721 | alban | 4 |
| 9722 | alarm | 4 |
| 9723 | alacrity | 4 |
| 9724 | aims | 4 |
| 9725 | agreement | 4 |
| 9726 | afric | 4 |
| 9727 | affront | 4 |
| 9728 | affirm | 4 |
| 9729 | aery | 4 |
| 9730 | aemilia | 4 |
| 9731 | advertisement | 4 |
| 9732 | advances | 4 |
| 9733 | advanced | 4 |
| 9734 | adultress | 4 |
| 9735 | adriano | 4 |
| 9736 | adoption | 4 |
| 9737 | adjunct | 4 |
| 9738 | adjudg | 4 |
| 9739 | acres | 4 |
| 9740 | acquire | 4 |
| 9741 | achievements | 4 |
| 9742 | accustom | 4 |
| 9743 | accurst | 4 |
| 9744 | accompt | 4 |
| 9745 | abundant | 4 |
| 9746 | absurd | 4 |
| 9747 | abstinence | 4 |
| 9748 | abridgment | 4 |
| 9749 | abraham | 4 |
| 9750 | abortive | 4 |
| 9751 | abjure | 4 |
| 9752 | abhors | 4 |
| 9753 | younker | 3 |
| 9754 | yoked | 3 |
| 9755 | yell | 3 |
| 9756 | yawning | 3 |
| 9757 | xi | 3 |
| 9758 | wye | 3 |
| 9759 | wronger | 3 |
| 9760 | wrestled | 3 |
| 9761 | wrenching | 3 |
| 9762 | woven | 3 |
| 9763 | worlds | 3 |
| 9764 | workmen | 3 |
| 9765 | workings | 3 |
| 9766 | woollen | 3 |
| 9767 | wool | 3 |
| 9768 | woodstock | 3 |
| 9769 | woodman | 3 |
| 9770 | woodbine | 3 |
| 9771 | wombs | 3 |
| 9772 | womanly | 3 |
| 9773 | wolvish | 3 |
| 9774 | wizard | 3 |
| 9775 | wittingly | 3 |
| 9776 | witless | 3 |
| 9777 | withdrew | 3 |
| 9778 | winnowed | 3 |
| 9779 | widowed | 3 |
| 9780 | wider | 3 |
| 9781 | whisp | 3 |
| 9782 | whirlwind | 3 |
| 9783 | whey | 3 |
| 9784 | whereso | 3 |
| 9785 | whelps | 3 |
| 9786 | wend | 3 |
| 9787 | weightier | 3 |
| 9788 | weathercock | 3 |
| 9789 | wearisome | 3 |
| 9790 | weariness | 3 |
| 9791 | wearer | 3 |
| 9792 | weakly | 3 |
| 9793 | waxes | 3 |
| 9794 | wav | 3 |
| 9795 | wasting | 3 |
| 9796 | wassail | 3 |
| 9797 | wasps | 3 |
| 9798 | warranty | 3 |
| 9799 | warrants | 3 |
| 9800 | warms | 3 |
| 9801 | wares | 3 |
| 9802 | warders | 3 |
| 9803 | wantons | 3 |
| 9804 | wanteth | 3 |
| 9805 | walled | 3 |
| 9806 | wakefield | 3 |
| 9807 | wags | 3 |
| 9808 | wade | 3 |
| 9809 | vowing | 3 |
| 9810 | voluble | 3 |
| 9811 | voic | 3 |
| 9812 | visits | 3 |
| 9813 | visions | 3 |
| 9814 | vipers | 3 |
| 9815 | viperous | 3 |
| 9816 | viper | 3 |
| 9817 | viol | 3 |
| 9818 | vintner | 3 |
| 9819 | vinegar | 3 |
| 9820 | vigilant | 3 |
| 9821 | vigilance | 3 |
| 9822 | victuals | 3 |
| 9823 | vials | 3 |
| 9824 | vexed | 3 |
| 9825 | verbal | 3 |
| 9826 | venuto | 3 |
| 9827 | vengeful | 3 |
| 9828 | velutus | 3 |
| 9829 | veiled | 3 |
| 9830 | vehemency | 3 |
| 9831 | vaunting | 3 |
| 9832 | vaunt | 3 |
| 9833 | vaulty | 3 |
| 9834 | variation | 3 |
| 9835 | variance | 3 |
| 9836 | vane | 3 |
| 9837 | valu | 3 |
| 9838 | valleys | 3 |
| 9839 | valentinus | 3 |
| 9840 | uttering | 3 |
| 9841 | usurped | 3 |
| 9842 | usurpation | 3 |
| 9843 | urine | 3 |
| 9844 | urged | 3 |
| 9845 | urchins | 3 |
| 9846 | uproar | 3 |
| 9847 | uprear | 3 |
| 9848 | upbraids | 3 |
| 9849 | unworthiest | 3 |
| 9850 | unwise | 3 |
| 9851 | unwillingness | 3 |
| 9852 | unwieldy | 3 |
| 9853 | unwash | 3 |
| 9854 | untun | 3 |
| 9855 | untruths | 3 |
| 9856 | unthrift | 3 |
| 9857 | unthought | 3 |
| 9858 | unthankfulness | 3 |
| 9859 | untender | 3 |
| 9860 | unswept | 3 |
| 9861 | unstained | 3 |
| 9862 | unstaid | 3 |
| 9863 | unsought | 3 |
| 9864 | unskilful | 3 |
| 9865 | unsheathe | 3 |
| 9866 | unseasonable | 3 |
| 9867 | unsavoury | 3 |
| 9868 | unsanctified | 3 |
| 9869 | unreverent | 3 |
| 9870 | unreverend | 3 |
| 9871 | unrelenting | 3 |
| 9872 | unready | 3 |
| 9873 | unprepared | 3 |
| 9874 | unpeopled | 3 |
| 9875 | unparallel | 3 |
| 9876 | unnecessary | 3 |
| 9877 | unmasks | 3 |
| 9878 | unmask | 3 |
| 9879 | unlikely | 3 |
| 9880 | unlettered | 3 |
| 9881 | unlearned | 3 |
| 9882 | unlawfully | 3 |
| 9883 | unholy | 3 |
| 9884 | unheard | 3 |
| 9885 | unguarded | 3 |
| 9886 | ungently | 3 |
| 9887 | unfolds | 3 |
| 9888 | unfolding | 3 |
| 9889 | unfledg | 3 |
| 9890 | unfix | 3 |
| 9891 | unfinish | 3 |
| 9892 | unfelt | 3 |
| 9893 | unfeignedly | 3 |
| 9894 | unfeigned | 3 |
| 9895 | unfeeling | 3 |
| 9896 | une | 3 |
| 9897 | undiscover | 3 |
| 9898 | undertakings | 3 |
| 9899 | undertakes | 3 |
| 9900 | undermine | 3 |
| 9901 | uncurrent | 3 |
| 9902 | uncertainty | 3 |
| 9903 | unbruis | 3 |
| 9904 | unbound | 3 |
| 9905 | unbated | 3 |
| 9906 | unacquainted | 3 |
| 9907 | umpire | 3 |
| 9908 | ulcerous | 3 |
| 9909 | u | 3 |
| 9910 | tyrannize | 3 |
| 9911 | twisted | 3 |
| 9912 | twinkling | 3 |
| 9913 | tuft | 3 |
| 9914 | trumpeter | 3 |
| 9915 | trowest | 3 |
| 9916 | trots | 3 |
| 9917 | trojan | 3 |
| 9918 | triumphing | 3 |
| 9919 | triumphantly | 3 |
| 9920 | tripolis | 3 |
| 9921 | tribes | 3 |
| 9922 | trials | 3 |
| 9923 | tresses | 3 |
| 9924 | tressel | 3 |
| 9925 | trespasses | 3 |
| 9926 | tremblest | 3 |
| 9927 | treats | 3 |
| 9928 | treasures | 3 |
| 9929 | treasonous | 3 |
| 9930 | treading | 3 |
| 9931 | tradition | 3 |
| 9932 | townsman | 3 |
| 9933 | tout | 3 |
| 9934 | tours | 3 |
| 9935 | touched | 3 |
| 9936 | tott | 3 |
| 9937 | torrent | 3 |
| 9938 | tools | 3 |
| 9939 | tongued | 3 |
| 9940 | ton | 3 |
| 9941 | tolling | 3 |
| 9942 | toes | 3 |
| 9943 | toasted | 3 |
| 9944 | toast | 3 |
| 9945 | tisick | 3 |
| 9946 | tinkers | 3 |
| 9947 | tinder | 3 |
| 9948 | tincture | 3 |
| 9949 | tilting | 3 |
| 9950 | tight | 3 |
| 9951 | ties | 3 |
| 9952 | thwart | 3 |
| 9953 | thrill | 3 |
| 9954 | threepence | 3 |
| 9955 | thistle | 3 |
| 9956 | thinly | 3 |
| 9957 | thinkings | 3 |
| 9958 | thievery | 3 |
| 9959 | thicker | 3 |
| 9960 | thews | 3 |
| 9961 | thereunto | 3 |
| 9962 | thereat | 3 |
| 9963 | theoric | 3 |
| 9964 | thankless | 3 |
| 9965 | thankings | 3 |
| 9966 | tetter | 3 |
| 9967 | tetchy | 3 |
| 9968 | tenure | 3 |
| 9969 | tenant | 3 |
| 9970 | temporize | 3 |
| 9971 | tempestuous | 3 |
| 9972 | teems | 3 |
| 9973 | teem | 3 |
| 9974 | teacheth | 3 |
| 9975 | taverns | 3 |
| 9976 | tattling | 3 |
| 9977 | tattered | 3 |
| 9978 | tasks | 3 |
| 9979 | tarre | 3 |
| 9980 | tar | 3 |
| 9981 | tapsters | 3 |
| 9982 | tap | 3 |
| 9983 | tang | 3 |
| 9984 | tamely | 3 |
| 9985 | talkest | 3 |
| 9986 | taker | 3 |
| 9987 | tainting | 3 |
| 9988 | sympathise | 3 |
| 9989 | sycamore | 3 |
| 9990 | swor | 3 |
| 9991 | swinge | 3 |
| 9992 | swims | 3 |
| 9993 | swerving | 3 |
| 9994 | sweeps | 3 |
| 9995 | swaggerers | 3 |
| 9996 | susan | 3 |
| 9997 | surprised | 3 |
| 9998 | surname | 3 |
| 9999 | surer | 3 |
| 10000 | surcease | 3 |
| 10001 | supposes | 3 |
| 10002 | supplications | 3 |
| 10003 | superscription | 3 |
| 10004 | sunny | 3 |
| 10005 | sunken | 3 |
| 10006 | sund | 3 |
| 10007 | summit | 3 |
| 10008 | sulphurous | 3 |
| 10009 | sully | 3 |
| 10010 | suggestions | 3 |
| 10011 | suffocate | 3 |
| 10012 | succours | 3 |
| 10013 | successively | 3 |
| 10014 | successfully | 3 |
| 10015 | succeeds | 3 |
| 10016 | subscribes | 3 |
| 10017 | subornation | 3 |
| 10018 | stuffs | 3 |
| 10019 | studying | 3 |
| 10020 | stubbornness | 3 |
| 10021 | strove | 3 |
| 10022 | strides | 3 |
| 10023 | stretches | 3 |
| 10024 | streaks | 3 |
| 10025 | streak | 3 |
| 10026 | strays | 3 |
| 10027 | strawberries | 3 |
| 10028 | strand | 3 |
| 10029 | stoutly | 3 |
| 10030 | stoup | 3 |
| 10031 | storehouse | 3 |
| 10032 | stopping | 3 |
| 10033 | stoops | 3 |
| 10034 | stocking | 3 |
| 10035 | stinging | 3 |
| 10036 | stile | 3 |
| 10037 | stifled | 3 |
| 10038 | stifle | 3 |
| 10039 | steterat | 3 |
| 10040 | sterling | 3 |
| 10041 | stench | 3 |
| 10042 | stealer | 3 |
| 10043 | statesman | 3 |
| 10044 | startles | 3 |
| 10045 | standeth | 3 |
| 10046 | standards | 3 |
| 10047 | stamped | 3 |
| 10048 | stalks | 3 |
| 10049 | stakes | 3 |
| 10050 | stair | 3 |
| 10051 | stagger | 3 |
| 10052 | stables | 3 |
| 10053 | squirrel | 3 |
| 10054 | squash | 3 |
| 10055 | squar | 3 |
| 10056 | squadrons | 3 |
| 10057 | spruce | 3 |
| 10058 | sprinkle | 3 |
| 10059 | sprays | 3 |
| 10060 | spouts | 3 |
| 10061 | spoons | 3 |
| 10062 | spokes | 3 |
| 10063 | spok | 3 |
| 10064 | splits | 3 |
| 10065 | splinter | 3 |
| 10066 | splendour | 3 |
| 10067 | spites | 3 |
| 10068 | spiteful | 3 |
| 10069 | spital | 3 |
| 10070 | spice | 3 |
| 10071 | spherical | 3 |
| 10072 | spending | 3 |
| 10073 | speeding | 3 |
| 10074 | speediest | 3 |
| 10075 | speculation | 3 |
| 10076 | spartan | 3 |
| 10077 | sparta | 3 |
| 10078 | southwark | 3 |
| 10079 | sourly | 3 |
| 10080 | sounder | 3 |
| 10081 | sorel | 3 |
| 10082 | sorceress | 3 |
| 10083 | sorcerers | 3 |
| 10084 | sophy | 3 |
| 10085 | sont | 3 |
| 10086 | somewhere | 3 |
| 10087 | solicits | 3 |
| 10088 | solicited | 3 |
| 10089 | soles | 3 |
| 10090 | softest | 3 |
| 10091 | softer | 3 |
| 10092 | sodden | 3 |
| 10093 | soaring | 3 |
| 10094 | snore | 3 |
| 10095 | snip | 3 |
| 10096 | sneaking | 3 |
| 10097 | snap | 3 |
| 10098 | smug | 3 |
| 10099 | smokes | 3 |
| 10100 | smocks | 3 |
| 10101 | smirch | 3 |
| 10102 | slug | 3 |
| 10103 | slower | 3 |
| 10104 | slink | 3 |
| 10105 | slightest | 3 |
| 10106 | slighted | 3 |
| 10107 | slandered | 3 |
| 10108 | skittish | 3 |
| 10109 | skills | 3 |
| 10110 | siz | 3 |
| 10111 | siren | 3 |
| 10112 | sip | 3 |
| 10113 | sinon | 3 |
| 10114 | singularity | 3 |
| 10115 | singled | 3 |
| 10116 | sincerely | 3 |
| 10117 | simon | 3 |
| 10118 | simois | 3 |
| 10119 | silenc | 3 |
| 10120 | signories | 3 |
| 10121 | signiors | 3 |
| 10122 | signified | 3 |
| 10123 | signet | 3 |
| 10124 | sighted | 3 |
| 10125 | sighed | 3 |
| 10126 | sigeia | 3 |
| 10127 | sift | 3 |
| 10128 | sicyon | 3 |
| 10129 | sibyl | 3 |
| 10130 | si | 3 |
| 10131 | shuffling | 3 |
| 10132 | shuffle | 3 |
| 10133 | shrouds | 3 |
| 10134 | shrouded | 3 |
| 10135 | shrinks | 3 |
| 10136 | shrinking | 3 |
| 10137 | shrieks | 3 |
| 10138 | shower | 3 |
| 10139 | shovel | 3 |
| 10140 | shotten | 3 |
| 10141 | shortens | 3 |
| 10142 | shops | 3 |
| 10143 | shooter | 3 |
| 10144 | shocks | 3 |
| 10145 | shipwreck | 3 |
| 10146 | shipmaster | 3 |
| 10147 | sheds | 3 |
| 10148 | sheathing | 3 |
| 10149 | shave | 3 |
| 10150 | sharpness | 3 |
| 10151 | sharing | 3 |
| 10152 | shanks | 3 |
| 10153 | shamest | 3 |
| 10154 | shady | 3 |
| 10155 | shades | 3 |
| 10156 | seward | 3 |
| 10157 | severals | 3 |
| 10158 | seventy | 3 |
| 10159 | settle | 3 |
| 10160 | sessions | 3 |
| 10161 | sessa | 3 |
| 10162 | servitude | 3 |
| 10163 | servitors | 3 |
| 10164 | sere | 3 |
| 10165 | sequestration | 3 |
| 10166 | sequest | 3 |
| 10167 | sepulchres | 3 |
| 10168 | sententious | 3 |
| 10169 | senis | 3 |
| 10170 | semiramis | 3 |
| 10171 | selling | 3 |
| 10172 | seizure | 3 |
| 10173 | seel | 3 |
| 10174 | seduce | 3 |
| 10175 | sedition | 3 |
| 10176 | sedges | 3 |
| 10177 | sects | 3 |
| 10178 | seconded | 3 |
| 10179 | seasoned | 3 |
| 10180 | sealing | 3 |
| 10181 | seacoal | 3 |
| 10182 | scratching | 3 |
| 10183 | scrape | 3 |
| 10184 | scrap | 3 |
| 10185 | scouring | 3 |
| 10186 | scorning | 3 |
| 10187 | scornfully | 3 |
| 10188 | scorned | 3 |
| 10189 | scorch | 3 |
| 10190 | scone | 3 |
| 10191 | scoffs | 3 |
| 10192 | scimitar | 3 |
| 10193 | schoolmasters | 3 |
| 10194 | scent | 3 |
| 10195 | scenes | 3 |
| 10196 | scarr | 3 |
| 10197 | scarcity | 3 |
| 10198 | scann | 3 |
| 10199 | scambling | 3 |
| 10200 | scaling | 3 |
| 10201 | savageness | 3 |
| 10202 | saunder | 3 |
| 10203 | sauc | 3 |
| 10204 | satyr | 3 |
| 10205 | satisfying | 3 |
| 10206 | satin | 3 |
| 10207 | satiety | 3 |
| 10208 | sanctimony | 3 |
| 10209 | salutations | 3 |
| 10210 | sally | 3 |
| 10211 | sallets | 3 |
| 10212 | sala | 3 |
| 10213 | sakes | 3 |
| 10214 | sailing | 3 |
| 10215 | sagittary | 3 |
| 10216 | sadder | 3 |
| 10217 | sacks | 3 |
| 10218 | rye | 3 |
| 10219 | ruthful | 3 |
| 10220 | rustic | 3 |
| 10221 | russia | 3 |
| 10222 | russet | 3 |
| 10223 | runaways | 3 |
| 10224 | runaway | 3 |
| 10225 | runagate | 3 |
| 10226 | rumours | 3 |
| 10227 | rumor | 3 |
| 10228 | ruffians | 3 |
| 10229 | ruff | 3 |
| 10230 | rubb | 3 |
| 10231 | rosy | 3 |
| 10232 | rooms | 3 |
| 10233 | roi | 3 |
| 10234 | roe | 3 |
| 10235 | rochester | 3 |
| 10236 | robber | 3 |
| 10237 | roaming | 3 |
| 10238 | riveted | 3 |
| 10239 | ripp | 3 |
| 10240 | riper | 3 |
| 10241 | ripens | 3 |
| 10242 | rigorous | 3 |
| 10243 | rigg | 3 |
| 10244 | rift | 3 |
| 10245 | riddling | 3 |
| 10246 | rice | 3 |
| 10247 | ribbons | 3 |
| 10248 | ribb | 3 |
| 10249 | rib | 3 |
| 10250 | rheims | 3 |
| 10251 | revives | 3 |
| 10252 | reverently | 3 |
| 10253 | revelling | 3 |
| 10254 | revell | 3 |
| 10255 | retiring | 3 |
| 10256 | retired | 3 |
| 10257 | retainers | 3 |
| 10258 | retail | 3 |
| 10259 | resume | 3 |
| 10260 | resty | 3 |
| 10261 | restrained | 3 |
| 10262 | resteth | 3 |
| 10263 | resolutely | 3 |
| 10264 | resistance | 3 |
| 10265 | residing | 3 |
| 10266 | reside | 3 |
| 10267 | reserved | 3 |
| 10268 | resembled | 3 |
| 10269 | resemblance | 3 |
| 10270 | rer | 3 |
| 10271 | requiring | 3 |
| 10272 | requested | 3 |
| 10273 | represent | 3 |
| 10274 | reprehended | 3 |
| 10275 | reprehend | 3 |
| 10276 | reposing | 3 |
| 10277 | repents | 3 |
| 10278 | repeals | 3 |
| 10279 | repays | 3 |
| 10280 | repairs | 3 |
| 10281 | removing | 3 |
| 10282 | removes | 3 |
| 10283 | remorseless | 3 |
| 10284 | remnants | 3 |
| 10285 | releas | 3 |
| 10286 | rel | 3 |
| 10287 | rehears | 3 |
| 10288 | regist | 3 |
| 10289 | regia | 3 |
| 10290 | refusing | 3 |
| 10291 | reflect | 3 |
| 10292 | refined | 3 |
| 10293 | refer | 3 |
| 10294 | reels | 3 |
| 10295 | reeling | 3 |
| 10296 | reel | 3 |
| 10297 | reeds | 3 |
| 10298 | reed | 3 |
| 10299 | reechy | 3 |
| 10300 | reduce | 3 |
| 10301 | redoubled | 3 |
| 10302 | redeems | 3 |
| 10303 | redeeming | 3 |
| 10304 | rectify | 3 |
| 10305 | recovers | 3 |
| 10306 | recorders | 3 |
| 10307 | recompens | 3 |
| 10308 | receptacle | 3 |
| 10309 | reapers | 3 |
| 10310 | real | 3 |
| 10311 | reaching | 3 |
| 10312 | reaches | 3 |
| 10313 | razed | 3 |
| 10314 | ravished | 3 |
| 10315 | rave | 3 |
| 10316 | rav | 3 |
| 10317 | rature | 3 |
| 10318 | ratsbane | 3 |
| 10319 | rately | 3 |
| 10320 | rareness | 3 |
| 10321 | rapine | 3 |
| 10322 | rapiers | 3 |
| 10323 | rapes | 3 |
| 10324 | rap | 3 |
| 10325 | rankness | 3 |
| 10326 | ranker | 3 |
| 10327 | ranges | 3 |
| 10328 | rang | 3 |
| 10329 | ramping | 3 |
| 10330 | ralph | 3 |
| 10331 | rainbow | 3 |
| 10332 | ragozine | 3 |
| 10333 | radiance | 3 |
| 10334 | quod | 3 |
| 10335 | quits | 3 |
| 10336 | quis | 3 |
| 10337 | quirks | 3 |
| 10338 | questioned | 3 |
| 10339 | quenching | 3 |
| 10340 | queller | 3 |
| 10341 | queasy | 3 |
| 10342 | quarry | 3 |
| 10343 | quarrelsome | 3 |
| 10344 | quaff | 3 |
| 10345 | qu | 3 |
| 10346 | pushes | 3 |
| 10347 | purging | 3 |
| 10348 | purged | 3 |
| 10349 | purchasing | 3 |
| 10350 | purchased | 3 |
| 10351 | ptolemy | 3 |
| 10352 | prowess | 3 |
| 10353 | province | 3 |
| 10354 | protests | 3 |
| 10355 | protects | 3 |
| 10356 | protectorship | 3 |
| 10357 | protected | 3 |
| 10358 | proscription | 3 |
| 10359 | prophets | 3 |
| 10360 | propertied | 3 |
| 10361 | properer | 3 |
| 10362 | propagate | 3 |
| 10363 | pronouncing | 3 |
| 10364 | promotions | 3 |
| 10365 | promiseth | 3 |
| 10366 | promethean | 3 |
| 10367 | prologues | 3 |
| 10368 | progenitors | 3 |
| 10369 | profitless | 3 |
| 10370 | professors | 3 |
| 10371 | professed | 3 |
| 10372 | profaned | 3 |
| 10373 | profanation | 3 |
| 10374 | privacy | 3 |
| 10375 | priory | 3 |
| 10376 | priami | 3 |
| 10377 | prevents | 3 |
| 10378 | prevailing | 3 |
| 10379 | preserving | 3 |
| 10380 | preserver | 3 |
| 10381 | prescriptions | 3 |
| 10382 | prescience | 3 |
| 10383 | presageth | 3 |
| 10384 | preparations | 3 |
| 10385 | prentices | 3 |
| 10386 | premises | 3 |
| 10387 | premeditated | 3 |
| 10388 | prejudice | 3 |
| 10389 | prefix | 3 |
| 10390 | prediction | 3 |
| 10391 | predicament | 3 |
| 10392 | preceding | 3 |
| 10393 | prains | 3 |
| 10394 | pouch | 3 |
| 10395 | pots | 3 |
| 10396 | potential | 3 |
| 10397 | potentates | 3 |
| 10398 | posy | 3 |
| 10399 | posterns | 3 |
| 10400 | postern | 3 |
| 10401 | possibly | 3 |
| 10402 | possibility | 3 |
| 10403 | posset | 3 |
| 10404 | positive | 3 |
| 10405 | portentous | 3 |
| 10406 | portends | 3 |
| 10407 | portable | 3 |
| 10408 | porn | 3 |
| 10409 | pork | 3 |
| 10410 | poniards | 3 |
| 10411 | ponderous | 3 |
| 10412 | poisoner | 3 |
| 10413 | pois | 3 |
| 10414 | plutus | 3 |
| 10415 | plus | 3 |
| 10416 | plummet | 3 |
| 10417 | plumed | 3 |
| 10418 | ploughman | 3 |
| 10419 | plighted | 3 |
| 10420 | plentifully | 3 |
| 10421 | pleads | 3 |
| 10422 | pleaded | 3 |
| 10423 | plausive | 3 |
| 10424 | plashy | 3 |
| 10425 | plaints | 3 |
| 10426 | placket | 3 |
| 10427 | placing | 3 |
| 10428 | pitifully | 3 |
| 10429 | pitchy | 3 |
| 10430 | pint | 3 |
| 10431 | pinnace | 3 |
| 10432 | pined | 3 |
| 10433 | pillows | 3 |
| 10434 | pillar | 3 |
| 10435 | pilgrims | 3 |
| 10436 | pight | 3 |
| 10437 | pigeon | 3 |
| 10438 | pies | 3 |
| 10439 | pierced | 3 |
| 10440 | piec | 3 |
| 10441 | picked | 3 |
| 10442 | picardy | 3 |
| 10443 | pia | 3 |
| 10444 | phrygia | 3 |
| 10445 | phoebe | 3 |
| 10446 | pharamond | 3 |
| 10447 | pest | 3 |
| 10448 | pervert | 3 |
| 10449 | perverse | 3 |
| 10450 | persuading | 3 |
| 10451 | perspective | 3 |
| 10452 | personally | 3 |
| 10453 | personage | 3 |
| 10454 | perseus | 3 |
| 10455 | perplexity | 3 |
| 10456 | perpetuity | 3 |
| 10457 | periwig | 3 |
| 10458 | perfected | 3 |
| 10459 | perdu | 3 |
| 10460 | perch | 3 |
| 10461 | per | 3 |
| 10462 | penthouse | 3 |
| 10463 | pentecost | 3 |
| 10464 | pension | 3 |
| 10465 | pens | 3 |
| 10466 | pendent | 3 |
| 10467 | pelican | 3 |
| 10468 | pegasus | 3 |
| 10469 | peeps | 3 |
| 10470 | pebbles | 3 |
| 10471 | peat | 3 |
| 10472 | peach | 3 |
| 10473 | paws | 3 |
| 10474 | paw | 3 |
| 10475 | paunch | 3 |
| 10476 | patterns | 3 |
| 10477 | pathetical | 3 |
| 10478 | patents | 3 |
| 10479 | passado | 3 |
| 10480 | partaker | 3 |
| 10481 | parlous | 3 |
| 10482 | parings | 3 |
| 10483 | paring | 3 |
| 10484 | parent | 3 |
| 10485 | parching | 3 |
| 10486 | parasite | 3 |
| 10487 | parallels | 3 |
| 10488 | paradox | 3 |
| 10489 | pap | 3 |
| 10490 | pants | 3 |
| 10491 | pantler | 3 |
| 10492 | panther | 3 |
| 10493 | pantaloon | 3 |
| 10494 | pant | 3 |
| 10495 | paly | 3 |
| 10496 | palsy | 3 |
| 10497 | palmers | 3 |
| 10498 | pallas | 3 |
| 10499 | pall | 3 |
| 10500 | paler | 3 |
| 10501 | pah | 3 |
| 10502 | pagans | 3 |
| 10503 | ovid | 3 |
| 10504 | overweening | 3 |
| 10505 | overrul | 3 |
| 10506 | overpeer | 3 |
| 10507 | overflow | 3 |
| 10508 | overcharged | 3 |
| 10509 | overblown | 3 |
| 10510 | outstrip | 3 |
| 10511 | outstretch | 3 |
| 10512 | outlives | 3 |
| 10513 | outcast | 3 |
| 10514 | ottomites | 3 |
| 10515 | otter | 3 |
| 10516 | orpheus | 3 |
| 10517 | orphan | 3 |
| 10518 | orld | 3 |
| 10519 | ordering | 3 |
| 10520 | orbed | 3 |
| 10521 | oracles | 3 |
| 10522 | opposing | 3 |
| 10523 | opportunities | 3 |
| 10524 | onward | 3 |
| 10525 | onion | 3 |
| 10526 | omnipotent | 3 |
| 10527 | omnes | 3 |
| 10528 | omitted | 3 |
| 10529 | oldest | 3 |
| 10530 | offal | 3 |
| 10531 | odorous | 3 |
| 10532 | obtaining | 3 |
| 10533 | obscured | 3 |
| 10534 | obscene | 3 |
| 10535 | obloquy | 3 |
| 10536 | objections | 3 |
| 10537 | obeys | 3 |
| 10538 | oars | 3 |
| 10539 | nuns | 3 |
| 10540 | ns | 3 |
| 10541 | novice | 3 |
| 10542 | notion | 3 |
| 10543 | nostrils | 3 |
| 10544 | nostril | 3 |
| 10545 | norweyan | 3 |
| 10546 | northward | 3 |
| 10547 | northampton | 3 |
| 10548 | normans | 3 |
| 10549 | norman | 3 |
| 10550 | nony | 3 |
| 10551 | nonny | 3 |
| 10552 | nonce | 3 |
| 10553 | nomination | 3 |
| 10554 | nominated | 3 |
| 10555 | nominate | 3 |
| 10556 | noddy | 3 |
| 10557 | nodding | 3 |
| 10558 | nip | 3 |
| 10559 | nineteen | 3 |
| 10560 | nightwork | 3 |
| 10561 | nickname | 3 |
| 10562 | nicanor | 3 |
| 10563 | newt | 3 |
| 10564 | newness | 3 |
| 10565 | nevil | 3 |
| 10566 | nev | 3 |
| 10567 | neutral | 3 |
| 10568 | neer | 3 |
| 10569 | needles | 3 |
| 10570 | nave | 3 |
| 10571 | narbon | 3 |
| 10572 | nameless | 3 |
| 10573 | muzzle | 3 |
| 10574 | murrain | 3 |
| 10575 | mummy | 3 |
| 10576 | multiplied | 3 |
| 10577 | muffle | 3 |
| 10578 | muddied | 3 |
| 10579 | mows | 3 |
| 10580 | movables | 3 |
| 10581 | mourners | 3 |
| 10582 | mourner | 3 |
| 10583 | mountebank | 3 |
| 10584 | mountaineers | 3 |
| 10585 | mounch | 3 |
| 10586 | moralize | 3 |
| 10587 | monumental | 3 |
| 10588 | mongers | 3 |
| 10589 | molten | 3 |
| 10590 | molehill | 3 |
| 10591 | mobled | 3 |
| 10592 | mixture | 3 |
| 10593 | mitigation | 3 |
| 10594 | mitigate | 3 |
| 10595 | mistrusted | 3 |
| 10596 | mistakes | 3 |
| 10597 | mist | 3 |
| 10598 | misprizing | 3 |
| 10599 | misgives | 3 |
| 10600 | misfortunes | 3 |
| 10601 | misenum | 3 |
| 10602 | miraculous | 3 |
| 10603 | minx | 3 |
| 10604 | mineral | 3 |
| 10605 | millstones | 3 |
| 10606 | milky | 3 |
| 10607 | milch | 3 |
| 10608 | metre | 3 |
| 10609 | messes | 3 |
| 10610 | merriest | 3 |
| 10611 | meritorious | 3 |
| 10612 | mercies | 3 |
| 10613 | mercer | 3 |
| 10614 | mercenary | 3 |
| 10615 | mental | 3 |
| 10616 | mending | 3 |
| 10617 | menace | 3 |
| 10618 | memories | 3 |
| 10619 | memorial | 3 |
| 10620 | meetings | 3 |
| 10621 | mechanic | 3 |
| 10622 | meats | 3 |
| 10623 | measuring | 3 |
| 10624 | measured | 3 |
| 10625 | meadows | 3 |
| 10626 | maze | 3 |
| 10627 | maugre | 3 |
| 10628 | matthew | 3 |
| 10629 | mathematics | 3 |
| 10630 | mater | 3 |
| 10631 | mastiffs | 3 |
| 10632 | mastership | 3 |
| 10633 | masques | 3 |
| 10634 | masculine | 3 |
| 10635 | marvell | 3 |
| 10636 | marries | 3 |
| 10637 | marriages | 3 |
| 10638 | markets | 3 |
| 10639 | marked | 3 |
| 10640 | marcheth | 3 |
| 10641 | mantuan | 3 |
| 10642 | manors | 3 |
| 10643 | manor | 3 |
| 10644 | mannish | 3 |
| 10645 | manes | 3 |
| 10646 | mandrake | 3 |
| 10647 | manacle | 3 |
| 10648 | mall | 3 |
| 10649 | maliciously | 3 |
| 10650 | malcontent | 3 |
| 10651 | malapert | 3 |
| 10652 | maladies | 3 |
| 10653 | maketh | 3 |
| 10654 | majestic | 3 |
| 10655 | maintenance | 3 |
| 10656 | maintains | 3 |
| 10657 | magistrate | 3 |
| 10658 | madded | 3 |
| 10659 | machiavel | 3 |
| 10660 | mab | 3 |
| 10661 | lustily | 3 |
| 10662 | lustier | 3 |
| 10663 | lurks | 3 |
| 10664 | lunes | 3 |
| 10665 | luke | 3 |
| 10666 | ludlow | 3 |
| 10667 | luces | 3 |
| 10668 | lowness | 3 |
| 10669 | loveth | 3 |
| 10670 | lottery | 3 |
| 10671 | lots | 3 |
| 10672 | losest | 3 |
| 10673 | lop | 3 |
| 10674 | loos | 3 |
| 10675 | loop | 3 |
| 10676 | lonely | 3 |
| 10677 | locking | 3 |
| 10678 | loathness | 3 |
| 10679 | loathly | 3 |
| 10680 | loan | 3 |
| 10681 | loads | 3 |
| 10682 | liveth | 3 |
| 10683 | livest | 3 |
| 10684 | livelong | 3 |
| 10685 | lisping | 3 |
| 10686 | lisp | 3 |
| 10687 | lipp | 3 |
| 10688 | limping | 3 |
| 10689 | limed | 3 |
| 10690 | lilies | 3 |
| 10691 | liker | 3 |
| 10692 | lighter | 3 |
| 10693 | lighten | 3 |
| 10694 | lifted | 3 |
| 10695 | lictors | 3 |
| 10696 | licentious | 3 |
| 10697 | library | 3 |
| 10698 | liberality | 3 |
| 10699 | levies | 3 |
| 10700 | leven | 3 |
| 10701 | levell | 3 |
| 10702 | leopard | 3 |
| 10703 | leonati | 3 |
| 10704 | lenten | 3 |
| 10705 | lengthens | 3 |
| 10706 | lengthen | 3 |
| 10707 | lending | 3 |
| 10708 | lender | 3 |
| 10709 | lena | 3 |
| 10710 | leman | 3 |
| 10711 | leisures | 3 |
| 10712 | leicester | 3 |
| 10713 | legion | 3 |
| 10714 | lectures | 3 |
| 10715 | leaven | 3 |
| 10716 | learns | 3 |
| 10717 | learnedly | 3 |
| 10718 | leaping | 3 |
| 10719 | ldst | 3 |
| 10720 | lazar | 3 |
| 10721 | layest | 3 |
| 10722 | lawn | 3 |
| 10723 | lave | 3 |
| 10724 | laurel | 3 |
| 10725 | later | 3 |
| 10726 | latch | 3 |
| 10727 | larum | 3 |
| 10728 | larks | 3 |
| 10729 | largely | 3 |
| 10730 | laps | 3 |
| 10731 | lapp | 3 |
| 10732 | lapis | 3 |
| 10733 | landlord | 3 |
| 10734 | laissez | 3 |
| 10735 | lain | 3 |
| 10736 | laden | 3 |
| 10737 | ladders | 3 |
| 10738 | lacked | 3 |
| 10739 | knotty | 3 |
| 10740 | knotted | 3 |
| 10741 | knoll | 3 |
| 10742 | knog | 3 |
| 10743 | kissed | 3 |
| 10744 | kinswoman | 3 |
| 10745 | kine | 3 |
| 10746 | kindling | 3 |
| 10747 | kindest | 3 |
| 10748 | kimbolton | 3 |
| 10749 | kiln | 3 |
| 10750 | kersey | 3 |
| 10751 | kernel | 3 |
| 10752 | kerchief | 3 |
| 10753 | kentish | 3 |
| 10754 | keepest | 3 |
| 10755 | keel | 3 |
| 10756 | justicer | 3 |
| 10757 | june | 3 |
| 10758 | july | 3 |
| 10759 | jule | 3 |
| 10760 | juggler | 3 |
| 10761 | joyfully | 3 |
| 10762 | journeys | 3 |
| 10763 | jour | 3 |
| 10764 | jointed | 3 |
| 10765 | johns | 3 |
| 10766 | jephthah | 3 |
| 10767 | jelly | 3 |
| 10768 | jarteer | 3 |
| 10769 | jail | 3 |
| 10770 | jaded | 3 |
| 10771 | iwis | 3 |
| 10772 | ivory | 3 |
| 10773 | iteration | 3 |
| 10774 | islands | 3 |
| 10775 | isbel | 3 |
| 10776 | irrevocable | 3 |
| 10777 | irreligious | 3 |
| 10778 | irksome | 3 |
| 10779 | irks | 3 |
| 10780 | inwardly | 3 |
| 10781 | invulnerable | 3 |
| 10782 | invocate | 3 |
| 10783 | inviolable | 3 |
| 10784 | inverness | 3 |
| 10785 | intimate | 3 |
| 10786 | interruption | 3 |
| 10787 | interrupted | 3 |
| 10788 | interred | 3 |
| 10789 | interior | 3 |
| 10790 | intendment | 3 |
| 10791 | insupportable | 3 |
| 10792 | instigation | 3 |
| 10793 | inspiration | 3 |
| 10794 | insinuation | 3 |
| 10795 | insensible | 3 |
| 10796 | inns | 3 |
| 10797 | innovation | 3 |
| 10798 | inky | 3 |
| 10799 | inkhorn | 3 |
| 10800 | injunction | 3 |
| 10801 | inherited | 3 |
| 10802 | infused | 3 |
| 10803 | infuse | 3 |
| 10804 | informed | 3 |
| 10805 | infold | 3 |
| 10806 | inflaming | 3 |
| 10807 | inflam | 3 |
| 10808 | infidel | 3 |
| 10809 | inferr | 3 |
| 10810 | infernal | 3 |
| 10811 | indued | 3 |
| 10812 | inducement | 3 |
| 10813 | induc | 3 |
| 10814 | indigest | 3 |
| 10815 | incurr | 3 |
| 10816 | incontinency | 3 |
| 10817 | incident | 3 |
| 10818 | impudence | 3 |
| 10819 | imprimis | 3 |
| 10820 | impressure | 3 |
| 10821 | impostor | 3 |
| 10822 | importunity | 3 |
| 10823 | impawn | 3 |
| 10824 | impatiently | 3 |
| 10825 | impair | 3 |
| 10826 | illusion | 3 |
| 10827 | ignominy | 3 |
| 10828 | ignominious | 3 |
| 10829 | icicles | 3 |
| 10830 | icarus | 3 |
| 10831 | ibat | 3 |
| 10832 | hurry | 3 |
| 10833 | hunts | 3 |
| 10834 | hungerly | 3 |
| 10835 | hundreds | 3 |
| 10836 | humbler | 3 |
| 10837 | hulk | 3 |
| 10838 | howbeit | 3 |
| 10839 | hospitable | 3 |
| 10840 | horum | 3 |
| 10841 | hors | 3 |
| 10842 | horace | 3 |
| 10843 | hooks | 3 |
| 10844 | hollowness | 3 |
| 10845 | holily | 3 |
| 10846 | hogs | 3 |
| 10847 | hobgoblin | 3 |
| 10848 | historical | 3 |
| 10849 | hindmost | 3 |
| 10850 | hight | 3 |
| 10851 | hest | 3 |
| 10852 | hermits | 3 |
| 10853 | hereby | 3 |
| 10854 | hent | 3 |
| 10855 | hempen | 3 |
| 10856 | hemp | 3 |
| 10857 | hemm | 3 |
| 10858 | hemlock | 3 |
| 10859 | helpless | 3 |
| 10860 | heifer | 3 |
| 10861 | heedfully | 3 |
| 10862 | hebrew | 3 |
| 10863 | hearth | 3 |
| 10864 | headsman | 3 |
| 10865 | hazel | 3 |
| 10866 | haunting | 3 |
| 10867 | haught | 3 |
| 10868 | harshness | 3 |
| 10869 | harshly | 3 |
| 10870 | harpy | 3 |
| 10871 | harlots | 3 |
| 10872 | hardiness | 3 |
| 10873 | hardiment | 3 |
| 10874 | hardest | 3 |
| 10875 | harcourt | 3 |
| 10876 | harbours | 3 |
| 10877 | harbinger | 3 |
| 10878 | hangings | 3 |
| 10879 | handsomely | 3 |
| 10880 | handkercher | 3 |
| 10881 | handiwork | 3 |
| 10882 | hammers | 3 |
| 10883 | hammering | 3 |
| 10884 | halts | 3 |
| 10885 | halters | 3 |
| 10886 | halfpence | 3 |
| 10887 | hales | 3 |
| 10888 | gunpowder | 3 |
| 10889 | gules | 3 |
| 10890 | guile | 3 |
| 10891 | guiding | 3 |
| 10892 | grumbling | 3 |
| 10893 | grudging | 3 |
| 10894 | grub | 3 |
| 10895 | gripes | 3 |
| 10896 | grinning | 3 |
| 10897 | gray | 3 |
| 10898 | grants | 3 |
| 10899 | granting | 3 |
| 10900 | gramercies | 3 |
| 10901 | grains | 3 |
| 10902 | graft | 3 |
| 10903 | governs | 3 |
| 10904 | gouty | 3 |
| 10905 | gory | 3 |
| 10906 | goodliest | 3 |
| 10907 | goffe | 3 |
| 10908 | goers | 3 |
| 10909 | godlike | 3 |
| 10910 | godhead | 3 |
| 10911 | godfather | 3 |
| 10912 | goal | 3 |
| 10913 | gnawing | 3 |
| 10914 | glorify | 3 |
| 10915 | glist | 3 |
| 10916 | glimmering | 3 |
| 10917 | glide | 3 |
| 10918 | glazed | 3 |
| 10919 | glassy | 3 |
| 10920 | glances | 3 |
| 10921 | gladness | 3 |
| 10922 | givest | 3 |
| 10923 | girt | 3 |
| 10924 | girdles | 3 |
| 10925 | gilbert | 3 |
| 10926 | gig | 3 |
| 10927 | gibbets | 3 |
| 10928 | gerard | 3 |
| 10929 | genitive | 3 |
| 10930 | gelded | 3 |
| 10931 | geld | 3 |
| 10932 | gathering | 3 |
| 10933 | gasping | 3 |
| 10934 | garters | 3 |
| 10935 | garrison | 3 |
| 10936 | gardens | 3 |
| 10937 | gaming | 3 |
| 10938 | gamesome | 3 |
| 10939 | games | 3 |
| 10940 | gambols | 3 |
| 10941 | gambol | 3 |
| 10942 | gallantly | 3 |
| 10943 | gale | 3 |
| 10944 | gaited | 3 |
| 10945 | gaberdine | 3 |
| 10946 | gabble | 3 |
| 10947 | fusty | 3 |
| 10948 | furrow | 3 |
| 10949 | furnace | 3 |
| 10950 | funerals | 3 |
| 10951 | fugitive | 3 |
| 10952 | froze | 3 |
| 10953 | frog | 3 |
| 10954 | frivolous | 3 |
| 10955 | frighting | 3 |
| 10956 | frieze | 3 |
| 10957 | friended | 3 |
| 10958 | friday | 3 |
| 10959 | freshest | 3 |
| 10960 | frequent | 3 |
| 10961 | freed | 3 |
| 10962 | franciscan | 3 |
| 10963 | frames | 3 |
| 10964 | fragment | 3 |
| 10965 | foxes | 3 |
| 10966 | fowls | 3 |
| 10967 | fount | 3 |
| 10968 | foundations | 3 |
| 10969 | foulest | 3 |
| 10970 | forum | 3 |
| 10971 | fortunately | 3 |
| 10972 | fortress | 3 |
| 10973 | forthcoming | 3 |
| 10974 | forrest | 3 |
| 10975 | forgets | 3 |
| 10976 | foretells | 3 |
| 10977 | forests | 3 |
| 10978 | forerunner | 3 |
| 10979 | forehand | 3 |
| 10980 | foregone | 3 |
| 10981 | forefathers | 3 |
| 10982 | forcing | 3 |
| 10983 | forcible | 3 |
| 10984 | forage | 3 |
| 10985 | foppery | 3 |
| 10986 | fondness | 3 |
| 10987 | foi | 3 |
| 10988 | fogs | 3 |
| 10989 | foggy | 3 |
| 10990 | foemen | 3 |
| 10991 | foams | 3 |
| 10992 | flush | 3 |
| 10993 | flouting | 3 |
| 10994 | flourishing | 3 |
| 10995 | fleer | 3 |
| 10996 | flatters | 3 |
| 10997 | flashes | 3 |
| 10998 | fixture | 3 |
| 10999 | fixing | 3 |
| 11000 | fitteth | 3 |
| 11001 | fitchew | 3 |
| 11002 | firstlings | 3 |
| 11003 | firebrand | 3 |
| 11004 | finished | 3 |
| 11005 | fingre | 3 |
| 11006 | fingering | 3 |
| 11007 | finest | 3 |
| 11008 | fineness | 3 |
| 11009 | fillip | 3 |
| 11010 | filching | 3 |
| 11011 | fil | 3 |
| 11012 | fike | 3 |
| 11013 | figuring | 3 |
| 11014 | fierceness | 3 |
| 11015 | fiddler | 3 |
| 11016 | fiction | 3 |
| 11017 | fester | 3 |
| 11018 | feste | 3 |
| 11019 | fest | 3 |
| 11020 | fervour | 3 |
| 11021 | ferret | 3 |
| 11022 | fencing | 3 |
| 11023 | females | 3 |
| 11024 | feeders | 3 |
| 11025 | features | 3 |
| 11026 | fearless | 3 |
| 11027 | fay | 3 |
| 11028 | favoured | 3 |
| 11029 | faulty | 3 |
| 11030 | faultless | 3 |
| 11031 | fathoms | 3 |
| 11032 | fatherly | 3 |
| 11033 | farthings | 3 |
| 11034 | farthingale | 3 |
| 11035 | farthing | 3 |
| 11036 | farmer | 3 |
| 11037 | fantastically | 3 |
| 11038 | fanning | 3 |
| 11039 | fann | 3 |
| 11040 | fallow | 3 |
| 11041 | falconers | 3 |
| 11042 | fadom | 3 |
| 11043 | facility | 3 |
| 11044 | extravagant | 3 |
| 11045 | extemporal | 3 |
| 11046 | expressure | 3 |
| 11047 | expressing | 3 |
| 11048 | expiration | 3 |
| 11049 | expend | 3 |
| 11050 | exigent | 3 |
| 11051 | executors | 3 |
| 11052 | executing | 3 |
| 11053 | excellency | 3 |
| 11054 | exceeded | 3 |
| 11055 | exasperate | 3 |
| 11056 | examined | 3 |
| 11057 | exalted | 3 |
| 11058 | exactions | 3 |
| 11059 | exaction | 3 |
| 11060 | ewer | 3 |
| 11061 | evenly | 3 |
| 11062 | europa | 3 |
| 11063 | etes | 3 |
| 11064 | essentially | 3 |
| 11065 | essence | 3 |
| 11066 | espy | 3 |
| 11067 | espous | 3 |
| 11068 | espied | 3 |
| 11069 | espials | 3 |
| 11070 | especial | 3 |
| 11071 | eruptions | 3 |
| 11072 | erthrow | 3 |
| 11073 | erswell | 3 |
| 11074 | errule | 3 |
| 11075 | errs | 3 |
| 11076 | ernight | 3 |
| 11077 | erheard | 3 |
| 11078 | ergrown | 3 |
| 11079 | erflows | 3 |
| 11080 | erection | 3 |
| 11081 | erected | 3 |
| 11082 | erebus | 3 |
| 11083 | erbear | 3 |
| 11084 | equivocator | 3 |
| 11085 | epithet | 3 |
| 11086 | environed | 3 |
| 11087 | entitle | 3 |
| 11088 | enthron | 3 |
| 11089 | enthrall | 3 |
| 11090 | entertained | 3 |
| 11091 | enterprises | 3 |
| 11092 | entail | 3 |
| 11093 | ensconce | 3 |
| 11094 | enraged | 3 |
| 11095 | engend | 3 |
| 11096 | enfeebled | 3 |
| 11097 | enamour | 3 |
| 11098 | enact | 3 |
| 11099 | emptying | 3 |
| 11100 | emptiness | 3 |
| 11101 | embraced | 3 |
| 11102 | embossed | 3 |
| 11103 | eltham | 3 |
| 11104 | elm | 3 |
| 11105 | ell | 3 |
| 11106 | elf | 3 |
| 11107 | elbows | 3 |
| 11108 | egyptians | 3 |
| 11109 | edmundsbury | 3 |
| 11110 | edges | 3 |
| 11111 | ecoutez | 3 |
| 11112 | ebony | 3 |
| 11113 | ebbs | 3 |
| 11114 | easiness | 3 |
| 11115 | earliest | 3 |
| 11116 | eagerly | 3 |
| 11117 | dyed | 3 |
| 11118 | dutch | 3 |
| 11119 | dump | 3 |
| 11120 | dully | 3 |
| 11121 | dullest | 3 |
| 11122 | dugs | 3 |
| 11123 | ducks | 3 |
| 11124 | dub | 3 |
| 11125 | du | 3 |
| 11126 | droops | 3 |
| 11127 | drone | 3 |
| 11128 | dries | 3 |
| 11129 | dreamer | 3 |
| 11130 | dreading | 3 |
| 11131 | draughts | 3 |
| 11132 | dout | 3 |
| 11133 | dotard | 3 |
| 11134 | dorothy | 3 |
| 11135 | domitius | 3 |
| 11136 | dominator | 3 |
| 11137 | dogged | 3 |
| 11138 | doer | 3 |
| 11139 | dizzy | 3 |
| 11140 | divination | 3 |
| 11141 | divides | 3 |
| 11142 | diverted | 3 |
| 11143 | divert | 3 |
| 11144 | disturbed | 3 |
| 11145 | distinct | 3 |
| 11146 | dissolution | 3 |
| 11147 | dissolutely | 3 |
| 11148 | dissever | 3 |
| 11149 | disrobe | 3 |
| 11150 | disquiet | 3 |
| 11151 | disproportion | 3 |
| 11152 | disprais | 3 |
| 11153 | disposer | 3 |
| 11154 | disorders | 3 |
| 11155 | disobey | 3 |
| 11156 | dismount | 3 |
| 11157 | dislikes | 3 |
| 11158 | disinherited | 3 |
| 11159 | disinherit | 3 |
| 11160 | disgraced | 3 |
| 11161 | disgorge | 3 |
| 11162 | discretions | 3 |
| 11163 | discoveries | 3 |
| 11164 | discard | 3 |
| 11165 | disarms | 3 |
| 11166 | disarm | 3 |
| 11167 | disabled | 3 |
| 11168 | dip | 3 |
| 11169 | dimpled | 3 |
| 11170 | diminish | 3 |
| 11171 | dimensions | 3 |
| 11172 | dilated | 3 |
| 11173 | dignifies | 3 |
| 11174 | dighton | 3 |
| 11175 | digging | 3 |
| 11176 | difficulty | 3 |
| 11177 | diff | 3 |
| 11178 | dictynna | 3 |
| 11179 | dialect | 3 |
| 11180 | devoutly | 3 |
| 11181 | detraction | 3 |
| 11182 | determines | 3 |
| 11183 | destroying | 3 |
| 11184 | despising | 3 |
| 11185 | desdemon | 3 |
| 11186 | descant | 3 |
| 11187 | des | 3 |
| 11188 | derogate | 3 |
| 11189 | dere | 3 |
| 11190 | deposing | 3 |
| 11191 | deposed | 3 |
| 11192 | dependency | 3 |
| 11193 | dependants | 3 |
| 11194 | deniest | 3 |
| 11195 | denier | 3 |
| 11196 | demure | 3 |
| 11197 | demesnes | 3 |
| 11198 | demerits | 3 |
| 11199 | demeanour | 3 |
| 11200 | delphos | 3 |
| 11201 | delicious | 3 |
| 11202 | deject | 3 |
| 11203 | defunct | 3 |
| 11204 | deflower | 3 |
| 11205 | defiles | 3 |
| 11206 | defending | 3 |
| 11207 | dedication | 3 |
| 11208 | dedicated | 3 |
| 11209 | decrepit | 3 |
| 11210 | decorum | 3 |
| 11211 | declined | 3 |
| 11212 | decision | 3 |
| 11213 | decipher | 3 |
| 11214 | deceives | 3 |
| 11215 | deceits | 3 |
| 11216 | debated | 3 |
| 11217 | debase | 3 |
| 11218 | deathbed | 3 |
| 11219 | dealings | 3 |
| 11220 | dealer | 3 |
| 11221 | dazzle | 3 |
| 11222 | darted | 3 |
| 11223 | darnel | 3 |
| 11224 | darkling | 3 |
| 11225 | darken | 3 |
| 11226 | daphne | 3 |
| 11227 | dangerously | 3 |
| 11228 | damage | 3 |
| 11229 | dainties | 3 |
| 11230 | dad | 3 |
| 11231 | cytherea | 3 |
| 11232 | cydnus | 3 |
| 11233 | cutpurse | 3 |
| 11234 | customers | 3 |
| 11235 | custody | 3 |
| 11236 | curtal | 3 |
| 11237 | cursy | 3 |
| 11238 | curled | 3 |
| 11239 | curds | 3 |
| 11240 | curan | 3 |
| 11241 | cum | 3 |
| 11242 | crupper | 3 |
| 11243 | crowner | 3 |
| 11244 | crouch | 3 |
| 11245 | crosby | 3 |
| 11246 | critic | 3 |
| 11247 | crispin | 3 |
| 11248 | crisp | 3 |
| 11249 | criminal | 3 |
| 11250 | cricket | 3 |
| 11251 | credence | 3 |
| 11252 | craz | 3 |
| 11253 | crawl | 3 |
| 11254 | crassus | 3 |
| 11255 | cramps | 3 |
| 11256 | cramp | 3 |
| 11257 | crafts | 3 |
| 11258 | crabbed | 3 |
| 11259 | cozeners | 3 |
| 11260 | cozened | 3 |
| 11261 | cozenage | 3 |
| 11262 | covers | 3 |
| 11263 | covenant | 3 |
| 11264 | coursers | 3 |
| 11265 | counting | 3 |
| 11266 | counterpois | 3 |
| 11267 | countermand | 3 |
| 11268 | counterfeits | 3 |
| 11269 | countercheck | 3 |
| 11270 | countenanc | 3 |
| 11271 | councillor | 3 |
| 11272 | couching | 3 |
| 11273 | costs | 3 |
| 11274 | corrupting | 3 |
| 11275 | coronets | 3 |
| 11276 | coral | 3 |
| 11277 | coragio | 3 |
| 11278 | copied | 3 |
| 11279 | cophetua | 3 |
| 11280 | cooks | 3 |
| 11281 | converting | 3 |
| 11282 | convented | 3 |
| 11283 | contumelious | 3 |
| 11284 | controll | 3 |
| 11285 | contriving | 3 |
| 11286 | continually | 3 |
| 11287 | continents | 3 |
| 11288 | contempts | 3 |
| 11289 | contemplative | 3 |
| 11290 | contemning | 3 |
| 11291 | consumed | 3 |
| 11292 | constrains | 3 |
| 11293 | constrained | 3 |
| 11294 | constables | 3 |
| 11295 | consists | 3 |
| 11296 | conserves | 3 |
| 11297 | consequently | 3 |
| 11298 | conquers | 3 |
| 11299 | congregation | 3 |
| 11300 | congealed | 3 |
| 11301 | confront | 3 |
| 11302 | confessions | 3 |
| 11303 | confessing | 3 |
| 11304 | conferr | 3 |
| 11305 | conducted | 3 |
| 11306 | condole | 3 |
| 11307 | condemns | 3 |
| 11308 | condemnation | 3 |
| 11309 | conceives | 3 |
| 11310 | concealing | 3 |
| 11311 | concave | 3 |
| 11312 | compromise | 3 |
| 11313 | composure | 3 |
| 11314 | composed | 3 |
| 11315 | comply | 3 |
| 11316 | complots | 3 |
| 11317 | complement | 3 |
| 11318 | compared | 3 |
| 11319 | comparative | 3 |
| 11320 | communicate | 3 |
| 11321 | commodities | 3 |
| 11322 | commissions | 3 |
| 11323 | commiseration | 3 |
| 11324 | commenting | 3 |
| 11325 | comet | 3 |
| 11326 | combination | 3 |
| 11327 | combating | 3 |
| 11328 | colts | 3 |
| 11329 | colossus | 3 |
| 11330 | college | 3 |
| 11331 | collection | 3 |
| 11332 | collect | 3 |
| 11333 | collars | 3 |
| 11334 | colic | 3 |
| 11335 | cognizance | 3 |
| 11336 | cogging | 3 |
| 11337 | coated | 3 |
| 11338 | clust | 3 |
| 11339 | clowns | 3 |
| 11340 | clouts | 3 |
| 11341 | closure | 3 |
| 11342 | clod | 3 |
| 11343 | clifton | 3 |
| 11344 | clergymen | 3 |
| 11345 | cleaving | 3 |
| 11346 | clearness | 3 |
| 11347 | claws | 3 |
| 11348 | clasp | 3 |
| 11349 | clamor | 3 |
| 11350 | cite | 3 |
| 11351 | circumstantial | 3 |
| 11352 | circumference | 3 |
| 11353 | cicatrice | 3 |
| 11354 | chronicled | 3 |
| 11355 | christmas | 3 |
| 11356 | chopt | 3 |
| 11357 | chopp | 3 |
| 11358 | choir | 3 |
| 11359 | childishness | 3 |
| 11360 | chew | 3 |
| 11361 | cheshu | 3 |
| 11362 | chertsey | 3 |
| 11363 | cheering | 3 |
| 11364 | cheated | 3 |
| 11365 | chatter | 3 |
| 11366 | chatham | 3 |
| 11367 | chastis | 3 |
| 11368 | chastely | 3 |
| 11369 | charters | 3 |
| 11370 | chariots | 3 |
| 11371 | chants | 3 |
| 11372 | chalky | 3 |
| 11373 | certainties | 3 |
| 11374 | centaurs | 3 |
| 11375 | censured | 3 |
| 11376 | censur | 3 |
| 11377 | cement | 3 |
| 11378 | celsa | 3 |
| 11379 | ceas | 3 |
| 11380 | ce | 3 |
| 11381 | causer | 3 |
| 11382 | causeless | 3 |
| 11383 | caudle | 3 |
| 11384 | cates | 3 |
| 11385 | catechize | 3 |
| 11386 | casts | 3 |
| 11387 | casting | 3 |
| 11388 | casque | 3 |
| 11389 | casements | 3 |
| 11390 | carv | 3 |
| 11391 | carters | 3 |
| 11392 | carping | 3 |
| 11393 | carpet | 3 |
| 11394 | carouses | 3 |
| 11395 | carnal | 3 |
| 11396 | carbuncle | 3 |
| 11397 | capilet | 3 |
| 11398 | capet | 3 |
| 11399 | capers | 3 |
| 11400 | canopied | 3 |
| 11401 | candy | 3 |
| 11402 | candied | 3 |
| 11403 | calumnious | 3 |
| 11404 | calmly | 3 |
| 11405 | callet | 3 |
| 11406 | caliver | 3 |
| 11407 | buzzard | 3 |
| 11408 | butterfly | 3 |
| 11409 | butchery | 3 |
| 11410 | butchered | 3 |
| 11411 | bushes | 3 |
| 11412 | bunting | 3 |
| 11413 | bullet | 3 |
| 11414 | buildeth | 3 |
| 11415 | builded | 3 |
| 11416 | bugs | 3 |
| 11417 | bugle | 3 |
| 11418 | budding | 3 |
| 11419 | bucket | 3 |
| 11420 | bubbles | 3 |
| 11421 | brute | 3 |
| 11422 | bruited | 3 |
| 11423 | browner | 3 |
| 11424 | brotherly | 3 |
| 11425 | broom | 3 |
| 11426 | brokers | 3 |
| 11427 | broached | 3 |
| 11428 | brinish | 3 |
| 11429 | bringer | 3 |
| 11430 | brimstone | 3 |
| 11431 | brightness | 3 |
| 11432 | bridget | 3 |
| 11433 | brick | 3 |
| 11434 | bribes | 3 |
| 11435 | brib | 3 |
| 11436 | breech | 3 |
| 11437 | breather | 3 |
| 11438 | bray | 3 |
| 11439 | brats | 3 |
| 11440 | branded | 3 |
| 11441 | brainsick | 3 |
| 11442 | bounded | 3 |
| 11443 | botcher | 3 |
| 11444 | boskos | 3 |
| 11445 | borrower | 3 |
| 11446 | borough | 3 |
| 11447 | bores | 3 |
| 11448 | bor | 3 |
| 11449 | bookish | 3 |
| 11450 | bolting | 3 |
| 11451 | boils | 3 |
| 11452 | bogs | 3 |
| 11453 | bodkin | 3 |
| 11454 | bobb | 3 |
| 11455 | bob | 3 |
| 11456 | bluntly | 3 |
| 11457 | blotted | 3 |
| 11458 | bloom | 3 |
| 11459 | blithe | 3 |
| 11460 | blessedness | 3 |
| 11461 | blemishes | 3 |
| 11462 | bled | 3 |
| 11463 | blasphemy | 3 |
| 11464 | blaspheme | 3 |
| 11465 | blameful | 3 |
| 11466 | blam | 3 |
| 11467 | blades | 3 |
| 11468 | bladders | 3 |
| 11469 | blackness | 3 |
| 11470 | bitten | 3 |
| 11471 | bitch | 3 |
| 11472 | bin | 3 |
| 11473 | bien | 3 |
| 11474 | bewitched | 3 |
| 11475 | bewept | 3 |
| 11476 | bettered | 3 |
| 11477 | bett | 3 |
| 11478 | betid | 3 |
| 11479 | bestrew | 3 |
| 11480 | bestial | 3 |
| 11481 | beseeching | 3 |
| 11482 | berwick | 3 |
| 11483 | berri | 3 |
| 11484 | bereave | 3 |
| 11485 | benison | 3 |
| 11486 | beneficial | 3 |
| 11487 | bends | 3 |
| 11488 | belzebub | 3 |
| 11489 | behoves | 3 |
| 11490 | behove | 3 |
| 11491 | beguiling | 3 |
| 11492 | begetting | 3 |
| 11493 | befell | 3 |
| 11494 | bedew | 3 |
| 11495 | bedded | 3 |
| 11496 | beautify | 3 |
| 11497 | beautified | 3 |
| 11498 | beamed | 3 |
| 11499 | beak | 3 |
| 11500 | baynard | 3 |
| 11501 | bawdry | 3 |
| 11502 | batters | 3 |
| 11503 | batter | 3 |
| 11504 | bats | 3 |
| 11505 | bastinado | 3 |
| 11506 | bartholomew | 3 |
| 11507 | barnet | 3 |
| 11508 | barley | 3 |
| 11509 | bargains | 3 |
| 11510 | baptism | 3 |
| 11511 | bans | 3 |
| 11512 | banqueting | 3 |
| 11513 | bang | 3 |
| 11514 | balmy | 3 |
| 11515 | baits | 3 |
| 11516 | bacon | 3 |
| 11517 | backing | 3 |
| 11518 | bachelors | 3 |
| 11519 | babies | 3 |
| 11520 | babble | 3 |
| 11521 | awkward | 3 |
| 11522 | awards | 3 |
| 11523 | avis | 3 |
| 11524 | aveng | 3 |
| 11525 | ave | 3 |
| 11526 | auvergne | 3 |
| 11527 | austerity | 3 |
| 11528 | augurers | 3 |
| 11529 | augmented | 3 |
| 11530 | attorneys | 3 |
| 11531 | attires | 3 |
| 11532 | attired | 3 |
| 11533 | attir | 3 |
| 11534 | atomies | 3 |
| 11535 | athversary | 3 |
| 11536 | ate | 3 |
| 11537 | assisted | 3 |
| 11538 | assays | 3 |
| 11539 | assaults | 3 |
| 11540 | aspic | 3 |
| 11541 | asp | 3 |
| 11542 | ascribe | 3 |
| 11543 | arose | 3 |
| 11544 | aroint | 3 |
| 11545 | arn | 3 |
| 11546 | armoury | 3 |
| 11547 | armours | 3 |
| 11548 | armor | 3 |
| 11549 | armagnac | 3 |
| 11550 | argus | 3 |
| 11551 | arguing | 3 |
| 11552 | argosies | 3 |
| 11553 | argal | 3 |
| 11554 | archers | 3 |
| 11555 | arc | 3 |
| 11556 | arabian | 3 |
| 11557 | aptness | 3 |
| 11558 | apron | 3 |
| 11559 | apprehensive | 3 |
| 11560 | apprehensions | 3 |
| 11561 | apprehends | 3 |
| 11562 | appointments | 3 |
| 11563 | applying | 3 |
| 11564 | applies | 3 |
| 11565 | appliance | 3 |
| 11566 | apples | 3 |
| 11567 | appertaining | 3 |
| 11568 | appeareth | 3 |
| 11569 | appeach | 3 |
| 11570 | apparitions | 3 |
| 11571 | answerable | 3 |
| 11572 | animal | 3 |
| 11573 | angling | 3 |
| 11574 | anchises | 3 |
| 11575 | anatomize | 3 |
| 11576 | amply | 3 |
| 11577 | amplify | 3 |
| 11578 | amounts | 3 |
| 11579 | ambling | 3 |
| 11580 | altitude | 3 |
| 11581 | althaea | 3 |
| 11582 | altars | 3 |
| 11583 | allowing | 3 |
| 11584 | alighted | 3 |
| 11585 | alien | 3 |
| 11586 | alchemy | 3 |
| 11587 | alabaster | 3 |
| 11588 | aiming | 3 |
| 11589 | ail | 3 |
| 11590 | ai | 3 |
| 11591 | agues | 3 |
| 11592 | agreeing | 3 |
| 11593 | agents | 3 |
| 11594 | ag | 3 |
| 11595 | aforesaid | 3 |
| 11596 | afire | 3 |
| 11597 | affiance | 3 |
| 11598 | affecting | 3 |
| 11599 | affability | 3 |
| 11600 | afear | 3 |
| 11601 | advertised | 3 |
| 11602 | advertis | 3 |
| 11603 | adventures | 3 |
| 11604 | adorn | 3 |
| 11605 | ador | 3 |
| 11606 | adopt | 3 |
| 11607 | adonis | 3 |
| 11608 | adheres | 3 |
| 11609 | addle | 3 |
| 11610 | adamant | 3 |
| 11611 | activity | 3 |
| 11612 | actium | 3 |
| 11613 | actaeon | 3 |
| 11614 | acre | 3 |
| 11615 | acquitted | 3 |
| 11616 | acquittance | 3 |
| 11617 | acknowledg | 3 |
| 11618 | aching | 3 |
| 11619 | achievement | 3 |
| 11620 | acheron | 3 |
| 11621 | accusing | 3 |
| 11622 | accuser | 3 |
| 11623 | accused | 3 |
| 11624 | accords | 3 |
| 11625 | accomplished | 3 |
| 11626 | accidentally | 3 |
| 11627 | accidental | 3 |
| 11628 | accessary | 3 |
| 11629 | accepted | 3 |
| 11630 | abysm | 3 |
| 11631 | abusing | 3 |
| 11632 | absolv | 3 |
| 11633 | abroach | 3 |
| 11634 | abreast | 3 |
| 11635 | abatement | 3 |
| 11636 | abated | 3 |
| 11637 | zir | 2 |
| 11638 | youngly | 2 |
| 11639 | youngling | 2 |
| 11640 | yorkists | 2 |
| 11641 | yorick | 2 |
| 11642 | yokes | 2 |
| 11643 | yok | 2 |
| 11644 | yielder | 2 |
| 11645 | yesty | 2 |
| 11646 | yerk | 2 |
| 11647 | yeas | 2 |
| 11648 | yearns | 2 |
| 11649 | yarn | 2 |
| 11650 | yarely | 2 |
| 11651 | xiii | 2 |
| 11652 | xii | 2 |
| 11653 | wrongful | 2 |
| 11654 | writings | 2 |
| 11655 | writer | 2 |
| 11656 | wrist | 2 |
| 11657 | wrecked | 2 |
| 11658 | wreaths | 2 |
| 11659 | wreathed | 2 |
| 11660 | wreakful | 2 |
| 11661 | wraths | 2 |
| 11662 | wow | 2 |
| 11663 | wots | 2 |
| 11664 | worts | 2 |
| 11665 | worths | 2 |
| 11666 | wort | 2 |
| 11667 | worshippers | 2 |
| 11668 | worldlings | 2 |
| 11669 | woolly | 2 |
| 11670 | woodcocks | 2 |
| 11671 | woefull | 2 |
| 11672 | wizards | 2 |
| 11673 | wiving | 2 |
| 11674 | wiv | 2 |
| 11675 | witnessing | 2 |
| 11676 | witnesseth | 2 |
| 11677 | withstand | 2 |
| 11678 | withers | 2 |
| 11679 | withdrawn | 2 |
| 11680 | witb | 2 |
| 11681 | wishest | 2 |
| 11682 | wiry | 2 |
| 11683 | wires | 2 |
| 11684 | wiped | 2 |
| 11685 | winnow | 2 |
| 11686 | winners | 2 |
| 11687 | winks | 2 |
| 11688 | windpipe | 2 |
| 11689 | windmill | 2 |
| 11690 | willingness | 2 |
| 11691 | willed | 2 |
| 11692 | wilfull | 2 |
| 11693 | wiles | 2 |
| 11694 | wilder | 2 |
| 11695 | wights | 2 |
| 11696 | whosoever | 2 |
| 11697 | whosoe | 2 |
| 11698 | whoa | 2 |
| 11699 | whitsun | 2 |
| 11700 | whites | 2 |
| 11701 | whisperings | 2 |
| 11702 | whirlwinds | 2 |
| 11703 | whirls | 2 |
| 11704 | whirling | 2 |
| 11705 | whine | 2 |
| 11706 | whetted | 2 |
| 11707 | wherewithal | 2 |
| 11708 | whereunto | 2 |
| 11709 | whereuntil | 2 |
| 11710 | wheresoever | 2 |
| 11711 | whereabout | 2 |
| 11712 | whensoever | 2 |
| 11713 | whenever | 2 |
| 11714 | whene | 2 |
| 11715 | weraday | 2 |
| 11716 | wells | 2 |
| 11717 | welcom | 2 |
| 11718 | weights | 2 |
| 11719 | ween | 2 |
| 11720 | weeke | 2 |
| 11721 | wedges | 2 |
| 11722 | wedg | 2 |
| 11723 | weaves | 2 |
| 11724 | weav | 2 |
| 11725 | wearies | 2 |
| 11726 | wealthily | 2 |
| 11727 | weakens | 2 |
| 11728 | weaken | 2 |
| 11729 | waxed | 2 |
| 11730 | watchers | 2 |
| 11731 | watched | 2 |
| 11732 | wassails | 2 |
| 11733 | warnings | 2 |
| 11734 | warming | 2 |
| 11735 | warmer | 2 |
| 11736 | warily | 2 |
| 11737 | warbling | 2 |
| 11738 | warble | 2 |
| 11739 | wane | 2 |
| 11740 | wands | 2 |
| 11741 | wanderers | 2 |
| 11742 | wanderer | 2 |
| 11743 | walnut | 2 |
| 11744 | wallow | 2 |
| 11745 | wakened | 2 |
| 11746 | waked | 2 |
| 11747 | wails | 2 |
| 11748 | wagoner | 2 |
| 11749 | waggish | 2 |
| 11750 | wagers | 2 |
| 11751 | wafts | 2 |
| 11752 | waftage | 2 |
| 11753 | waded | 2 |
| 11754 | w | 2 |
| 11755 | vultures | 2 |
| 11756 | vraiment | 2 |
| 11757 | voyages | 2 |
| 11758 | vouchsafed | 2 |
| 11759 | vouchsaf | 2 |
| 11760 | vouches | 2 |
| 11761 | vouchers | 2 |
| 11762 | votarist | 2 |
| 11763 | votaries | 2 |
| 11764 | vot | 2 |
| 11765 | vor | 2 |
| 11766 | voluptuousness | 2 |
| 11767 | volubility | 2 |
| 11768 | volt | 2 |
| 11769 | vlouting | 2 |
| 11770 | vizarded | 2 |
| 11771 | visitors | 2 |
| 11772 | virginius | 2 |
| 11773 | virginal | 2 |
| 11774 | violenta | 2 |
| 11775 | vineyards | 2 |
| 11776 | villian | 2 |
| 11777 | villanies | 2 |
| 11778 | villainously | 2 |
| 11779 | views | 2 |
| 11780 | viewest | 2 |
| 11781 | vied | 2 |
| 11782 | victual | 2 |
| 11783 | viceroy | 2 |
| 11784 | vicentio | 2 |
| 11785 | vexing | 2 |
| 11786 | vexations | 2 |
| 11787 | vestments | 2 |
| 11788 | verify | 2 |
| 11789 | verier | 2 |
| 11790 | verdure | 2 |
| 11791 | verba | 2 |
| 11792 | vents | 2 |
| 11793 | vented | 2 |
| 11794 | venetia | 2 |
| 11795 | vendible | 2 |
| 11796 | vell | 2 |
| 11797 | veal | 2 |
| 11798 | vaunts | 2 |
| 11799 | vaults | 2 |
| 11800 | vaulted | 2 |
| 11801 | vaudemont | 2 |
| 11802 | vassalage | 2 |
| 11803 | vaporous | 2 |
| 11804 | vanquisher | 2 |
| 11805 | vanishest | 2 |
| 11806 | vanishes | 2 |
| 11807 | valuation | 2 |
| 11808 | vainness | 2 |
| 11809 | vailing | 2 |
| 11810 | ut | 2 |
| 11811 | usurpers | 2 |
| 11812 | usuring | 2 |
| 11813 | usuries | 2 |
| 11814 | usually | 2 |
| 11815 | ushers | 2 |
| 11816 | user | 2 |
| 11817 | useful | 2 |
| 11818 | usance | 2 |
| 11819 | urswick | 2 |
| 11820 | urn | 2 |
| 11821 | urinals | 2 |
| 11822 | urinal | 2 |
| 11823 | urgest | 2 |
| 11824 | urgent | 2 |
| 11825 | upstart | 2 |
| 11826 | upshot | 2 |
| 11827 | uproars | 2 |
| 11828 | uprise | 2 |
| 11829 | uplift | 2 |
| 11830 | upbraidings | 2 |
| 11831 | unyoke | 2 |
| 11832 | unyok | 2 |
| 11833 | unworthily | 2 |
| 11834 | unwonted | 2 |
| 11835 | unwittingly | 2 |
| 11836 | unwind | 2 |
| 11837 | unveiling | 2 |
| 11838 | unvalued | 2 |
| 11839 | unurg | 2 |
| 11840 | untwine | 2 |
| 11841 | untutor | 2 |
| 11842 | untuneable | 2 |
| 11843 | untrimmed | 2 |
| 11844 | untread | 2 |
| 11845 | untoward | 2 |
| 11846 | untouch | 2 |
| 11847 | unthrifts | 2 |
| 11848 | unswear | 2 |
| 11849 | unsuspected | 2 |
| 11850 | unsuitable | 2 |
| 11851 | unsubstantial | 2 |
| 11852 | unstate | 2 |
| 11853 | unstanched | 2 |
| 11854 | unstain | 2 |
| 11855 | unsounded | 2 |
| 11856 | unsolicited | 2 |
| 11857 | unshaken | 2 |
| 11858 | unseeing | 2 |
| 11859 | unseason | 2 |
| 11860 | unschool | 2 |
| 11861 | unscarr | 2 |
| 11862 | unroll | 2 |
| 11863 | unreveng | 2 |
| 11864 | unrespective | 2 |
| 11865 | unrespected | 2 |
| 11866 | unreal | 2 |
| 11867 | unquietness | 2 |
| 11868 | unquestion | 2 |
| 11869 | unpruned | 2 |
| 11870 | unprizable | 2 |
| 11871 | unprepar | 2 |
| 11872 | unpregnant | 2 |
| 11873 | unpractis | 2 |
| 11874 | unpolish | 2 |
| 11875 | unpin | 2 |
| 11876 | unparagon | 2 |
| 11877 | unnoted | 2 |
| 11878 | unmuffling | 2 |
| 11879 | unmingled | 2 |
| 11880 | unmeritable | 2 |
| 11881 | unmeasurable | 2 |
| 11882 | unmatched | 2 |
| 11883 | unmatch | 2 |
| 11884 | unmann | 2 |
| 11885 | unmake | 2 |
| 11886 | unlov | 2 |
| 11887 | unlooked | 2 |
| 11888 | unload | 2 |
| 11889 | unlearn | 2 |
| 11890 | unkiss | 2 |
| 11891 | unking | 2 |
| 11892 | unkennel | 2 |
| 11893 | university | 2 |
| 11894 | universe | 2 |
| 11895 | unicorns | 2 |
| 11896 | unhoused | 2 |
| 11897 | unheedful | 2 |
| 11898 | unhatch | 2 |
| 11899 | unhappiness | 2 |
| 11900 | unhandled | 2 |
| 11901 | unhallow | 2 |
| 11902 | unhair | 2 |
| 11903 | unhack | 2 |
| 11904 | unguided | 2 |
| 11905 | ungarter | 2 |
| 11906 | ungalled | 2 |
| 11907 | ungain | 2 |
| 11908 | unfriended | 2 |
| 11909 | unfrequented | 2 |
| 11910 | unfill | 2 |
| 11911 | unfathered | 2 |
| 11912 | unexpected | 2 |
| 11913 | undrown | 2 |
| 11914 | undoes | 2 |
| 11915 | undivulged | 2 |
| 11916 | undistinguishable | 2 |
| 11917 | undid | 2 |
| 11918 | undeserving | 2 |
| 11919 | undeserver | 2 |
| 11920 | undertaker | 2 |
| 11921 | underprop | 2 |
| 11922 | underhand | 2 |
| 11923 | undergoes | 2 |
| 11924 | uncurable | 2 |
| 11925 | unction | 2 |
| 11926 | uncrown | 2 |
| 11927 | uncovered | 2 |
| 11928 | uncouth | 2 |
| 11929 | uncouple | 2 |
| 11930 | unconstrained | 2 |
| 11931 | unconsidered | 2 |
| 11932 | uncheck | 2 |
| 11933 | uncaught | 2 |
| 11934 | uncapable | 2 |
| 11935 | unbutton | 2 |
| 11936 | unburied | 2 |
| 11937 | unbuckle | 2 |
| 11938 | unbruised | 2 |
| 11939 | unbridled | 2 |
| 11940 | unbraced | 2 |
| 11941 | unbonneted | 2 |
| 11942 | unbolt | 2 |
| 11943 | unblest | 2 |
| 11944 | unbind | 2 |
| 11945 | unbar | 2 |
| 11946 | unadvised | 2 |
| 11947 | umber | 2 |
| 11948 | ulcer | 2 |
| 11949 | uglier | 2 |
| 11950 | tyrannical | 2 |
| 11951 | typhon | 2 |
| 11952 | type | 2 |
| 11953 | twos | 2 |
| 11954 | twit | 2 |
| 11955 | twist | 2 |
| 11956 | twink | 2 |
| 11957 | twine | 2 |
| 11958 | twentieth | 2 |
| 11959 | twelfth | 2 |
| 11960 | twangling | 2 |
| 11961 | tuscan | 2 |
| 11962 | turret | 2 |
| 11963 | turpitude | 2 |
| 11964 | turbulent | 2 |
| 11965 | tuns | 2 |
| 11966 | tuneable | 2 |
| 11967 | tully | 2 |
| 11968 | tugging | 2 |
| 11969 | tugg | 2 |
| 11970 | tuck | 2 |
| 11971 | trumpeters | 2 |
| 11972 | trumpery | 2 |
| 11973 | truckle | 2 |
| 11974 | trotting | 2 |
| 11975 | troll | 2 |
| 11976 | triumvirate | 2 |
| 11977 | triumvir | 2 |
| 11978 | tristful | 2 |
| 11979 | trippingly | 2 |
| 11980 | tripe | 2 |
| 11981 | trinkets | 2 |
| 11982 | trimming | 2 |
| 11983 | trident | 2 |
| 11984 | tricksy | 2 |
| 11985 | tributaries | 2 |
| 11986 | tribunal | 2 |
| 11987 | trenched | 2 |
| 11988 | trebles | 2 |
| 11989 | treatise | 2 |
| 11990 | tray | 2 |
| 11991 | traps | 2 |
| 11992 | trappings | 2 |
| 11993 | trapp | 2 |
| 11994 | transpose | 2 |
| 11995 | transporting | 2 |
| 11996 | transgressing | 2 |
| 11997 | transgress | 2 |
| 11998 | trance | 2 |
| 11999 | trample | 2 |
| 12000 | tragedians | 2 |
| 12001 | tradesmen | 2 |
| 12002 | traded | 2 |
| 12003 | townsmen | 2 |
| 12004 | total | 2 |
| 12005 | tot | 2 |
| 12006 | tossing | 2 |
| 12007 | toryne | 2 |
| 12008 | torturing | 2 |
| 12009 | torturer | 2 |
| 12010 | tortoise | 2 |
| 12011 | tormenting | 2 |
| 12012 | torchbearers | 2 |
| 12013 | topples | 2 |
| 12014 | topple | 2 |
| 12015 | topping | 2 |
| 12016 | topp | 2 |
| 12017 | topmast | 2 |
| 12018 | toothpick | 2 |
| 12019 | tool | 2 |
| 12020 | tolerable | 2 |
| 12021 | toils | 2 |
| 12022 | tofore | 2 |
| 12023 | toasts | 2 |
| 12024 | titled | 2 |
| 12025 | tithing | 2 |
| 12026 | tilts | 2 |
| 12027 | tilth | 2 |
| 12028 | tilter | 2 |
| 12029 | tilly | 2 |
| 12030 | tightly | 2 |
| 12031 | tickles | 2 |
| 12032 | tick | 2 |
| 12033 | ti | 2 |
| 12034 | thyme | 2 |
| 12035 | thwarting | 2 |
| 12036 | thunderbolts | 2 |
| 12037 | thund | 2 |
| 12038 | thumbs | 2 |
| 12039 | throstle | 2 |
| 12040 | thronging | 2 |
| 12041 | thrones | 2 |
| 12042 | thriving | 2 |
| 12043 | threatening | 2 |
| 12044 | threaden | 2 |
| 12045 | threadbare | 2 |
| 12046 | thrasonical | 2 |
| 12047 | thrash | 2 |
| 12048 | thisne | 2 |
| 12049 | thirdly | 2 |
| 12050 | thimble | 2 |
| 12051 | thickens | 2 |
| 12052 | thessaly | 2 |
| 12053 | therewith | 2 |
| 12054 | themes | 2 |
| 12055 | thefts | 2 |
| 12056 | thanksgiving | 2 |
| 12057 | testimonies | 2 |
| 12058 | tester | 2 |
| 12059 | territory | 2 |
| 12060 | terrestrial | 2 |
| 12061 | terra | 2 |
| 12062 | termed | 2 |
| 12063 | termagant | 2 |
| 12064 | tenfold | 2 |
| 12065 | tench | 2 |
| 12066 | tenantless | 2 |
| 12067 | tenantius | 2 |
| 12068 | tempters | 2 |
| 12069 | tempter | 2 |
| 12070 | tempers | 2 |
| 12071 | temperately | 2 |
| 12072 | teller | 2 |
| 12073 | tediously | 2 |
| 12074 | teat | 2 |
| 12075 | teachers | 2 |
| 12076 | taxing | 2 |
| 12077 | taxations | 2 |
| 12078 | tasting | 2 |
| 12079 | tassel | 2 |
| 12080 | tasking | 2 |
| 12081 | tartness | 2 |
| 12082 | tart | 2 |
| 12083 | tarries | 2 |
| 12084 | targets | 2 |
| 12085 | targes | 2 |
| 12086 | tape | 2 |
| 12087 | tanner | 2 |
| 12088 | tangled | 2 |
| 12089 | tamworth | 2 |
| 12090 | tameness | 2 |
| 12091 | talons | 2 |
| 12092 | tallest | 2 |
| 12093 | taller | 2 |
| 12094 | talker | 2 |
| 12095 | talbots | 2 |
| 12096 | tah | 2 |
| 12097 | tack | 2 |
| 12098 | syrups | 2 |
| 12099 | synagogue | 2 |
| 12100 | sympathized | 2 |
| 12101 | sympathize | 2 |
| 12102 | syllables | 2 |
| 12103 | sy | 2 |
| 12104 | swum | 2 |
| 12105 | swounds | 2 |
| 12106 | swounded | 2 |
| 12107 | sworder | 2 |
| 12108 | swooning | 2 |
| 12109 | swooned | 2 |
| 12110 | swoln | 2 |
| 12111 | swits | 2 |
| 12112 | swinish | 2 |
| 12113 | swimming | 2 |
| 12114 | swept | 2 |
| 12115 | sweetmeats | 2 |
| 12116 | sweepers | 2 |
| 12117 | sweaty | 2 |
| 12118 | swearings | 2 |
| 12119 | swearers | 2 |
| 12120 | swath | 2 |
| 12121 | swashing | 2 |
| 12122 | swarming | 2 |
| 12123 | sware | 2 |
| 12124 | swam | 2 |
| 12125 | swains | 2 |
| 12126 | swabber | 2 |
| 12127 | suum | 2 |
| 12128 | sustaining | 2 |
| 12129 | suspire | 2 |
| 12130 | suspend | 2 |
| 12131 | survivor | 2 |
| 12132 | survives | 2 |
| 12133 | surplus | 2 |
| 12134 | surnam | 2 |
| 12135 | surmount | 2 |
| 12136 | surest | 2 |
| 12137 | supporter | 2 |
| 12138 | supported | 2 |
| 12139 | supportance | 2 |
| 12140 | supplie | 2 |
| 12141 | suppler | 2 |
| 12142 | supervise | 2 |
| 12143 | supernatural | 2 |
| 12144 | superficially | 2 |
| 12145 | superficial | 2 |
| 12146 | sundays | 2 |
| 12147 | sunburnt | 2 |
| 12148 | summary | 2 |
| 12149 | sultry | 2 |
| 12150 | sulph | 2 |
| 12151 | sullied | 2 |
| 12152 | suggests | 2 |
| 12153 | suffrages | 2 |
| 12154 | sufficiently | 2 |
| 12155 | suffic | 2 |
| 12156 | suckle | 2 |
| 12157 | sucker | 2 |
| 12158 | successors | 2 |
| 12159 | successes | 2 |
| 12160 | succeeders | 2 |
| 12161 | subtly | 2 |
| 12162 | subtleties | 2 |
| 12163 | substituted | 2 |
| 12164 | substances | 2 |
| 12165 | suborned | 2 |
| 12166 | subjected | 2 |
| 12167 | su | 2 |
| 12168 | styx | 2 |
| 12169 | stuffing | 2 |
| 12170 | studious | 2 |
| 12171 | stubble | 2 |
| 12172 | strutting | 2 |
| 12173 | strung | 2 |
| 12174 | strumpeted | 2 |
| 12175 | struggling | 2 |
| 12176 | struggle | 2 |
| 12177 | stripling | 2 |
| 12178 | strikest | 2 |
| 12179 | strik | 2 |
| 12180 | strifes | 2 |
| 12181 | strewing | 2 |
| 12182 | stretched | 2 |
| 12183 | strengthless | 2 |
| 12184 | strengthened | 2 |
| 12185 | strangling | 2 |
| 12186 | strangles | 2 |
| 12187 | strained | 2 |
| 12188 | stow | 2 |
| 12189 | stoutness | 2 |
| 12190 | stopped | 2 |
| 12191 | ston | 2 |
| 12192 | stomachers | 2 |
| 12193 | stockfish | 2 |
| 12194 | stitches | 2 |
| 12195 | stinted | 2 |
| 12196 | stigmatic | 2 |
| 12197 | stews | 2 |
| 12198 | stewardship | 2 |
| 12199 | sterner | 2 |
| 12200 | steers | 2 |
| 12201 | steepy | 2 |
| 12202 | steeples | 2 |
| 12203 | steely | 2 |
| 12204 | stayed | 2 |
| 12205 | startle | 2 |
| 12206 | starr | 2 |
| 12207 | starlight | 2 |
| 12208 | stares | 2 |
| 12209 | stared | 2 |
| 12210 | standest | 2 |
| 12211 | stanch | 2 |
| 12212 | stainless | 2 |
| 12213 | stags | 2 |
| 12214 | staffords | 2 |
| 12215 | stabbed | 2 |
| 12216 | squier | 2 |
| 12217 | squeezing | 2 |
| 12218 | squeak | 2 |
| 12219 | squares | 2 |
| 12220 | squand | 2 |
| 12221 | spying | 2 |
| 12222 | spurio | 2 |
| 12223 | spun | 2 |
| 12224 | springing | 2 |
| 12225 | springe | 2 |
| 12226 | spreads | 2 |
| 12227 | sprawl | 2 |
| 12228 | sprang | 2 |
| 12229 | spousal | 2 |
| 12230 | spleens | 2 |
| 12231 | spleenful | 2 |
| 12232 | spinsters | 2 |
| 12233 | spinners | 2 |
| 12234 | spills | 2 |
| 12235 | spendthrift | 2 |
| 12236 | speedier | 2 |
| 12237 | speeded | 2 |
| 12238 | speculative | 2 |
| 12239 | speciously | 2 |
| 12240 | specially | 2 |
| 12241 | spawn | 2 |
| 12242 | sparingly | 2 |
| 12243 | spares | 2 |
| 12244 | spangled | 2 |
| 12245 | spak | 2 |
| 12246 | sov | 2 |
| 12247 | southward | 2 |
| 12248 | southam | 2 |
| 12249 | soundless | 2 |
| 12250 | soundest | 2 |
| 12251 | sorrowed | 2 |
| 12252 | sorcery | 2 |
| 12253 | sops | 2 |
| 12254 | soothing | 2 |
| 12255 | solomon | 2 |
| 12256 | solitary | 2 |
| 12257 | solinus | 2 |
| 12258 | solicitor | 2 |
| 12259 | solemnized | 2 |
| 12260 | solemnize | 2 |
| 12261 | sobriety | 2 |
| 12262 | sob | 2 |
| 12263 | soaking | 2 |
| 12264 | snorting | 2 |
| 12265 | sneaping | 2 |
| 12266 | snar | 2 |
| 12267 | snapper | 2 |
| 12268 | smothered | 2 |
| 12269 | smoothness | 2 |
| 12270 | smoothly | 2 |
| 12271 | smoothing | 2 |
| 12272 | smoothed | 2 |
| 12273 | smites | 2 |
| 12274 | smite | 2 |
| 12275 | smilingly | 2 |
| 12276 | smiled | 2 |
| 12277 | smarting | 2 |
| 12278 | smacks | 2 |
| 12279 | sluttery | 2 |
| 12280 | sluts | 2 |
| 12281 | slut | 2 |
| 12282 | sluic | 2 |
| 12283 | slubber | 2 |
| 12284 | slowness | 2 |
| 12285 | slops | 2 |
| 12286 | slop | 2 |
| 12287 | slippers | 2 |
| 12288 | slings | 2 |
| 12289 | slimy | 2 |
| 12290 | slides | 2 |
| 12291 | slid | 2 |
| 12292 | slice | 2 |
| 12293 | sleepest | 2 |
| 12294 | sleeper | 2 |
| 12295 | slays | 2 |
| 12296 | slaughtermen | 2 |
| 12297 | slaughterman | 2 |
| 12298 | slash | 2 |
| 12299 | slandering | 2 |
| 12300 | slanderers | 2 |
| 12301 | slackness | 2 |
| 12302 | slackly | 2 |
| 12303 | skirted | 2 |
| 12304 | skirr | 2 |
| 12305 | skim | 2 |
| 12306 | skein | 2 |
| 12307 | sizes | 2 |
| 12308 | situation | 2 |
| 12309 | situate | 2 |
| 12310 | sithence | 2 |
| 12311 | singleness | 2 |
| 12312 | singe | 2 |
| 12313 | sinfully | 2 |
| 12314 | simular | 2 |
| 12315 | simpler | 2 |
| 12316 | simp | 2 |
| 12317 | silenced | 2 |
| 12318 | sickens | 2 |
| 12319 | sicils | 2 |
| 12320 | shy | 2 |
| 12321 | shunning | 2 |
| 12322 | shrubs | 2 |
| 12323 | shrub | 2 |
| 12324 | shrove | 2 |
| 12325 | shriving | 2 |
| 12326 | shrive | 2 |
| 12327 | shrimp | 2 |
| 12328 | shrilly | 2 |
| 12329 | shrieve | 2 |
| 12330 | shreds | 2 |
| 12331 | showest | 2 |
| 12332 | shove | 2 |
| 12333 | shov | 2 |
| 12334 | shouted | 2 |
| 12335 | shorn | 2 |
| 12336 | shoon | 2 |
| 12337 | shog | 2 |
| 12338 | shoeing | 2 |
| 12339 | shivers | 2 |
| 12340 | shivering | 2 |
| 12341 | shiver | 2 |
| 12342 | shipwright | 2 |
| 12343 | shipboard | 2 |
| 12344 | shifting | 2 |
| 12345 | shields | 2 |
| 12346 | shielded | 2 |
| 12347 | shes | 2 |
| 12348 | shepherdesses | 2 |
| 12349 | shelves | 2 |
| 12350 | sheer | 2 |
| 12351 | sheen | 2 |
| 12352 | sheathes | 2 |
| 12353 | shearers | 2 |
| 12354 | shear | 2 |
| 12355 | sheaf | 2 |
| 12356 | sharpest | 2 |
| 12357 | shark | 2 |
| 12358 | shards | 2 |
| 12359 | shar | 2 |
| 12360 | shambles | 2 |
| 12361 | shallows | 2 |
| 12362 | shallowest | 2 |
| 12363 | shag | 2 |
| 12364 | shafalus | 2 |
| 12365 | shadowy | 2 |
| 12366 | shadowing | 2 |
| 12367 | shadowed | 2 |
| 12368 | shackles | 2 |
| 12369 | sewing | 2 |
| 12370 | sewer | 2 |
| 12371 | severing | 2 |
| 12372 | severely | 2 |
| 12373 | sevenfold | 2 |
| 12374 | sev | 2 |
| 12375 | setebos | 2 |
| 12376 | serviteur | 2 |
| 12377 | serpigo | 2 |
| 12378 | sermon | 2 |
| 12379 | sensuality | 2 |
| 12380 | semblances | 2 |
| 12381 | seller | 2 |
| 12382 | select | 2 |
| 12383 | seld | 2 |
| 12384 | seizing | 2 |
| 12385 | seizes | 2 |
| 12386 | seese | 2 |
| 12387 | seemly | 2 |
| 12388 | seducing | 2 |
| 12389 | seditious | 2 |
| 12390 | sectary | 2 |
| 12391 | secretaries | 2 |
| 12392 | secondary | 2 |
| 12393 | seaside | 2 |
| 12394 | scythian | 2 |
| 12395 | scythia | 2 |
| 12396 | scutcheon | 2 |
| 12397 | scuse | 2 |
| 12398 | scurrilous | 2 |
| 12399 | scurrility | 2 |
| 12400 | scullion | 2 |
| 12401 | scrupulous | 2 |
| 12402 | scrubbed | 2 |
| 12403 | scrip | 2 |
| 12404 | screw | 2 |
| 12405 | screen | 2 |
| 12406 | scowl | 2 |
| 12407 | scourg | 2 |
| 12408 | scoured | 2 |
| 12409 | scorpion | 2 |
| 12410 | scores | 2 |
| 12411 | scolds | 2 |
| 12412 | scoff | 2 |
| 12413 | scion | 2 |
| 12414 | sciences | 2 |
| 12415 | science | 2 |
| 12416 | sciatica | 2 |
| 12417 | schoolboys | 2 |
| 12418 | schedules | 2 |
| 12419 | scept | 2 |
| 12420 | scarecrow | 2 |
| 12421 | scandalous | 2 |
| 12422 | scandaliz | 2 |
| 12423 | scalp | 2 |
| 12424 | scaled | 2 |
| 12425 | scalding | 2 |
| 12426 | scaffold | 2 |
| 12427 | saxons | 2 |
| 12428 | sawest | 2 |
| 12429 | savoury | 2 |
| 12430 | savagery | 2 |
| 12431 | saucily | 2 |
| 12432 | sate | 2 |
| 12433 | sarcenet | 2 |
| 12434 | sapphire | 2 |
| 12435 | sapling | 2 |
| 12436 | sapless | 2 |
| 12437 | sanctimonious | 2 |
| 12438 | sampler | 2 |
| 12439 | saluteth | 2 |
| 12440 | saidst | 2 |
| 12441 | saddler | 2 |
| 12442 | saddest | 2 |
| 12443 | sacrilegious | 2 |
| 12444 | sacrificing | 2 |
| 12445 | sacrific | 2 |
| 12446 | sables | 2 |
| 12447 | sabbath | 2 |
| 12448 | rustling | 2 |
| 12449 | rural | 2 |
| 12450 | runagates | 2 |
| 12451 | rump | 2 |
| 12452 | ruminated | 2 |
| 12453 | ruined | 2 |
| 12454 | ruinate | 2 |
| 12455 | rudiments | 2 |
| 12456 | rudesby | 2 |
| 12457 | ruder | 2 |
| 12458 | rudder | 2 |
| 12459 | rud | 2 |
| 12460 | ruby | 2 |
| 12461 | rubbish | 2 |
| 12462 | rubbing | 2 |
| 12463 | roy | 2 |
| 12464 | rowel | 2 |
| 12465 | routs | 2 |
| 12466 | roussi | 2 |
| 12467 | roughest | 2 |
| 12468 | rougher | 2 |
| 12469 | rottenness | 2 |
| 12470 | rotted | 2 |
| 12471 | roscius | 2 |
| 12472 | roping | 2 |
| 12473 | ropes | 2 |
| 12474 | rooks | 2 |
| 12475 | ronyon | 2 |
| 12476 | roguery | 2 |
| 12477 | robustious | 2 |
| 12478 | robbed | 2 |
| 12479 | roared | 2 |
| 12480 | roam | 2 |
| 12481 | roads | 2 |
| 12482 | rivets | 2 |
| 12483 | rivet | 2 |
| 12484 | rived | 2 |
| 12485 | rivall | 2 |
| 12486 | ripest | 2 |
| 12487 | ripening | 2 |
| 12488 | ripeness | 2 |
| 12489 | rip | 2 |
| 12490 | ringlets | 2 |
| 12491 | rind | 2 |
| 12492 | rinaldo | 2 |
| 12493 | rim | 2 |
| 12494 | rig | 2 |
| 12495 | rids | 2 |
| 12496 | ridges | 2 |
| 12497 | ridden | 2 |
| 12498 | riddance | 2 |
| 12499 | ribbon | 2 |
| 12500 | riband | 2 |
| 12501 | rhyming | 2 |
| 12502 | rhymers | 2 |
| 12503 | rfull | 2 |
| 12504 | rex | 2 |
| 12505 | rewarded | 2 |
| 12506 | revolving | 2 |
| 12507 | reviving | 2 |
| 12508 | revil | 2 |
| 12509 | reverted | 2 |
| 12510 | reverenc | 2 |
| 12511 | reverberate | 2 |
| 12512 | revenging | 2 |
| 12513 | revellers | 2 |
| 12514 | returneth | 2 |
| 12515 | retrograde | 2 |
| 12516 | retorts | 2 |
| 12517 | retold | 2 |
| 12518 | retinue | 2 |
| 12519 | retentive | 2 |
| 12520 | restraining | 2 |
| 12521 | restful | 2 |
| 12522 | ress | 2 |
| 12523 | resolves | 2 |
| 12524 | resists | 2 |
| 12525 | resident | 2 |
| 12526 | rescues | 2 |
| 12527 | rers | 2 |
| 12528 | requites | 2 |
| 12529 | reputes | 2 |
| 12530 | reproving | 2 |
| 12531 | reprobate | 2 |
| 12532 | reproachful | 2 |
| 12533 | reproaches | 2 |
| 12534 | reprieves | 2 |
| 12535 | replying | 2 |
| 12536 | replenished | 2 |
| 12537 | repentant | 2 |
| 12538 | repeated | 2 |
| 12539 | repairing | 2 |
| 12540 | renewed | 2 |
| 12541 | rendered | 2 |
| 12542 | rence | 2 |
| 12543 | remotion | 2 |
| 12544 | remembrancer | 2 |
| 12545 | remarkable | 2 |
| 12546 | remaineth | 2 |
| 12547 | remained | 2 |
| 12548 | remainders | 2 |
| 12549 | relieved | 2 |
| 12550 | relenting | 2 |
| 12551 | released | 2 |
| 12552 | rejoices | 2 |
| 12553 | reigning | 2 |
| 12554 | reigned | 2 |
| 12555 | rehearsal | 2 |
| 12556 | reguerdon | 2 |
| 12557 | reformed | 2 |
| 12558 | reflex | 2 |
| 12559 | redresses | 2 |
| 12560 | redeliver | 2 |
| 12561 | redeemer | 2 |
| 12562 | redbreast | 2 |
| 12563 | recreants | 2 |
| 12564 | recoveries | 2 |
| 12565 | recounting | 2 |
| 12566 | recorder | 2 |
| 12567 | recordation | 2 |
| 12568 | reconciles | 2 |
| 12569 | recommends | 2 |
| 12570 | reclaim | 2 |
| 12571 | recks | 2 |
| 12572 | reciterai | 2 |
| 12573 | receivest | 2 |
| 12574 | recanting | 2 |
| 12575 | recantation | 2 |
| 12576 | rebuked | 2 |
| 12577 | rebell | 2 |
| 12578 | reave | 2 |
| 12579 | reasonless | 2 |
| 12580 | reasoning | 2 |
| 12581 | ray | 2 |
| 12582 | ravishing | 2 |
| 12583 | ravisher | 2 |
| 12584 | raves | 2 |
| 12585 | ravening | 2 |
| 12586 | rational | 2 |
| 12587 | rarities | 2 |
| 12588 | rapture | 2 |
| 12589 | ransoms | 2 |
| 12590 | ransomless | 2 |
| 12591 | ransomed | 2 |
| 12592 | rankle | 2 |
| 12593 | rankest | 2 |
| 12594 | ranging | 2 |
| 12595 | ramm | 2 |
| 12596 | rald | 2 |
| 12597 | ral | 2 |
| 12598 | raises | 2 |
| 12599 | railest | 2 |
| 12600 | radish | 2 |
| 12601 | racks | 2 |
| 12602 | rabblement | 2 |
| 12603 | quotidian | 2 |
| 12604 | quire | 2 |
| 12605 | quip | 2 |
| 12606 | quintessence | 2 |
| 12607 | quietus | 2 |
| 12608 | quicker | 2 |
| 12609 | quickens | 2 |
| 12610 | quenched | 2 |
| 12611 | quand | 2 |
| 12612 | quak | 2 |
| 12613 | quails | 2 |
| 12614 | quailing | 2 |
| 12615 | quagmire | 2 |
| 12616 | quae | 2 |
| 12617 | pyramids | 2 |
| 12618 | puttock | 2 |
| 12619 | pursy | 2 |
| 12620 | pursuivants | 2 |
| 12621 | pursuest | 2 |
| 12622 | purposeth | 2 |
| 12623 | purpled | 2 |
| 12624 | purgatory | 2 |
| 12625 | purer | 2 |
| 12626 | puppets | 2 |
| 12627 | punto | 2 |
| 12628 | punished | 2 |
| 12629 | pumps | 2 |
| 12630 | pump | 2 |
| 12631 | puffing | 2 |
| 12632 | puddled | 2 |
| 12633 | puddle | 2 |
| 12634 | puddings | 2 |
| 12635 | publicola | 2 |
| 12636 | ptolemies | 2 |
| 12637 | psalms | 2 |
| 12638 | pruning | 2 |
| 12639 | prune | 2 |
| 12640 | prudence | 2 |
| 12641 | provoking | 2 |
| 12642 | provocation | 2 |
| 12643 | provincial | 2 |
| 12644 | provident | 2 |
| 12645 | proveth | 2 |
| 12646 | protract | 2 |
| 12647 | protestations | 2 |
| 12648 | protectors | 2 |
| 12649 | prosperously | 2 |
| 12650 | prosp | 2 |
| 12651 | proserpina | 2 |
| 12652 | prose | 2 |
| 12653 | prorogue | 2 |
| 12654 | props | 2 |
| 12655 | propriety | 2 |
| 12656 | prophetically | 2 |
| 12657 | prophesying | 2 |
| 12658 | pronounced | 2 |
| 12659 | prompting | 2 |
| 12660 | prompter | 2 |
| 12661 | prolixity | 2 |
| 12662 | prognostication | 2 |
| 12663 | profiting | 2 |
| 12664 | profited | 2 |
| 12665 | profitably | 2 |
| 12666 | proffers | 2 |
| 12667 | producing | 2 |
| 12668 | produc | 2 |
| 12669 | procures | 2 |
| 12670 | procured | 2 |
| 12671 | procur | 2 |
| 12672 | procrus | 2 |
| 12673 | proclamations | 2 |
| 12674 | prizer | 2 |
| 12675 | privilegio | 2 |
| 12676 | privileged | 2 |
| 12677 | privates | 2 |
| 12678 | pristine | 2 |
| 12679 | priority | 2 |
| 12680 | printing | 2 |
| 12681 | printed | 2 |
| 12682 | prings | 2 |
| 12683 | principle | 2 |
| 12684 | primroses | 2 |
| 12685 | primero | 2 |
| 12686 | primal | 2 |
| 12687 | prig | 2 |
| 12688 | priesthood | 2 |
| 12689 | pribbles | 2 |
| 12690 | priamus | 2 |
| 12691 | pretending | 2 |
| 12692 | presuming | 2 |
| 12693 | prest | 2 |
| 12694 | pressing | 2 |
| 12695 | presentment | 2 |
| 12696 | presentation | 2 |
| 12697 | prescript | 2 |
| 12698 | prepost | 2 |
| 12699 | preparing | 2 |
| 12700 | prenominate | 2 |
| 12701 | preferments | 2 |
| 12702 | predominate | 2 |
| 12703 | predominance | 2 |
| 12704 | precipitation | 2 |
| 12705 | precedence | 2 |
| 12706 | prattling | 2 |
| 12707 | prank | 2 |
| 12708 | prain | 2 |
| 12709 | practising | 2 |
| 12710 | pout | 2 |
| 12711 | pourquoi | 2 |
| 12712 | pouring | 2 |
| 12713 | pourest | 2 |
| 12714 | potpan | 2 |
| 12715 | potently | 2 |
| 12716 | potations | 2 |
| 12717 | postures | 2 |
| 12718 | postscript | 2 |
| 12719 | postmaster | 2 |
| 12720 | posterior | 2 |
| 12721 | possessor | 2 |
| 12722 | possessing | 2 |
| 12723 | possesseth | 2 |
| 12724 | positively | 2 |
| 12725 | posies | 2 |
| 12726 | porters | 2 |
| 12727 | portance | 2 |
| 12728 | portal | 2 |
| 12729 | porringer | 2 |
| 12730 | pore | 2 |
| 12731 | popularity | 2 |
| 12732 | popp | 2 |
| 12733 | poop | 2 |
| 12734 | poole | 2 |
| 12735 | pompous | 2 |
| 12736 | pomegranate | 2 |
| 12737 | pollution | 2 |
| 12738 | polluted | 2 |
| 12739 | politicly | 2 |
| 12740 | polecats | 2 |
| 12741 | poem | 2 |
| 12742 | pody | 2 |
| 12743 | plural | 2 |
| 12744 | plung | 2 |
| 12745 | plucked | 2 |
| 12746 | plodded | 2 |
| 12747 | pleasest | 2 |
| 12748 | pleached | 2 |
| 12749 | pleach | 2 |
| 12750 | playfellows | 2 |
| 12751 | plated | 2 |
| 12752 | plantagenets | 2 |
| 12753 | planks | 2 |
| 12754 | planetary | 2 |
| 12755 | plaintiff | 2 |
| 12756 | plainest | 2 |
| 12757 | plagued | 2 |
| 12758 | plagu | 2 |
| 12759 | plackets | 2 |
| 12760 | placeth | 2 |
| 12761 | piteously | 2 |
| 12762 | pitchers | 2 |
| 12763 | pitched | 2 |
| 12764 | pissing | 2 |
| 12765 | piss | 2 |
| 12766 | piping | 2 |
| 12767 | pining | 2 |
| 12768 | pinfold | 2 |
| 12769 | pinching | 2 |
| 12770 | pills | 2 |
| 12771 | pillory | 2 |
| 12772 | pillicock | 2 |
| 12773 | piles | 2 |
| 12774 | pilate | 2 |
| 12775 | pickaxes | 2 |
| 12776 | physics | 2 |
| 12777 | physical | 2 |
| 12778 | philippe | 2 |
| 12779 | pheeze | 2 |
| 12780 | pheasant | 2 |
| 12781 | pharaoh | 2 |
| 12782 | pewter | 2 |
| 12783 | pew | 2 |
| 12784 | peu | 2 |
| 12785 | petticoats | 2 |
| 12786 | petitionary | 2 |
| 12787 | pestiferous | 2 |
| 12788 | pester | 2 |
| 12789 | perused | 2 |
| 12790 | perusal | 2 |
| 12791 | pertly | 2 |
| 12792 | pertinent | 2 |
| 12793 | pertain | 2 |
| 12794 | pert | 2 |
| 12795 | persuasions | 2 |
| 12796 | personages | 2 |
| 12797 | persian | 2 |
| 12798 | perseverance | 2 |
| 12799 | perpetually | 2 |
| 12800 | permitted | 2 |
| 12801 | perjure | 2 |
| 12802 | perishing | 2 |
| 12803 | periods | 2 |
| 12804 | perge | 2 |
| 12805 | performs | 2 |
| 12806 | performing | 2 |
| 12807 | performers | 2 |
| 12808 | performances | 2 |
| 12809 | perfectness | 2 |
| 12810 | perfectest | 2 |
| 12811 | perdurable | 2 |
| 12812 | pensive | 2 |
| 12813 | pensioners | 2 |
| 12814 | pennyworths | 2 |
| 12815 | penetrable | 2 |
| 12816 | pendant | 2 |
| 12817 | penalties | 2 |
| 12818 | pelt | 2 |
| 12819 | pelleted | 2 |
| 12820 | pelion | 2 |
| 12821 | peg | 2 |
| 12822 | peeping | 2 |
| 12823 | pease | 2 |
| 12824 | peas | 2 |
| 12825 | peard | 2 |
| 12826 | peak | 2 |
| 12827 | peaceably | 2 |
| 12828 | pe | 2 |
| 12829 | pax | 2 |
| 12830 | pavement | 2 |
| 12831 | patroness | 2 |
| 12832 | patronage | 2 |
| 12833 | patrician | 2 |
| 12834 | patchery | 2 |
| 12835 | pasty | 2 |
| 12836 | pastimes | 2 |
| 12837 | passport | 2 |
| 12838 | passeth | 2 |
| 12839 | passenger | 2 |
| 12840 | passable | 2 |
| 12841 | pash | 2 |
| 12842 | pas | 2 |
| 12843 | partridge | 2 |
| 12844 | partlet | 2 |
| 12845 | particularly | 2 |
| 12846 | particularities | 2 |
| 12847 | particle | 2 |
| 12848 | participation | 2 |
| 12849 | participate | 2 |
| 12850 | parti | 2 |
| 12851 | parrots | 2 |
| 12852 | parlour | 2 |
| 12853 | parks | 2 |
| 12854 | parishioners | 2 |
| 12855 | pardonnez | 2 |
| 12856 | pardonner | 2 |
| 12857 | pardoning | 2 |
| 12858 | pardoned | 2 |
| 12859 | parch | 2 |
| 12860 | paradoxes | 2 |
| 12861 | pantheon | 2 |
| 12862 | pannonians | 2 |
| 12863 | panders | 2 |
| 12864 | pandars | 2 |
| 12865 | pancakes | 2 |
| 12866 | pamper | 2 |
| 12867 | palsied | 2 |
| 12868 | palms | 2 |
| 12869 | palmer | 2 |
| 12870 | palfreys | 2 |
| 12871 | palfrey | 2 |
| 12872 | palestine | 2 |
| 12873 | paleness | 2 |
| 12874 | palatine | 2 |
| 12875 | paintings | 2 |
| 12876 | pail | 2 |
| 12877 | paddock | 2 |
| 12878 | paddling | 2 |
| 12879 | pacorus | 2 |
| 12880 | packets | 2 |
| 12881 | pacing | 2 |
| 12882 | pacified | 2 |
| 12883 | oyes | 2 |
| 12884 | oxlips | 2 |
| 12885 | owing | 2 |
| 12886 | overturn | 2 |
| 12887 | overta | 2 |
| 12888 | overshine | 2 |
| 12889 | overplus | 2 |
| 12890 | overlooks | 2 |
| 12891 | overjoyed | 2 |
| 12892 | overhear | 2 |
| 12893 | overboard | 2 |
| 12894 | overbear | 2 |
| 12895 | oven | 2 |
| 12896 | outworn | 2 |
| 12897 | outweighs | 2 |
| 12898 | outwear | 2 |
| 12899 | outwards | 2 |
| 12900 | outstare | 2 |
| 12901 | outfacing | 2 |
| 12902 | outfac | 2 |
| 12903 | ousel | 2 |
| 12904 | ouphes | 2 |
| 12905 | otherwhere | 2 |
| 12906 | ostent | 2 |
| 12907 | osiers | 2 |
| 12908 | orthography | 2 |
| 12909 | ort | 2 |
| 12910 | ork | 2 |
| 12911 | original | 2 |
| 12912 | ore | 2 |
| 12913 | ordained | 2 |
| 12914 | orchards | 2 |
| 12915 | opulent | 2 |
| 12916 | oppressing | 2 |
| 12917 | opposers | 2 |
| 12918 | opposer | 2 |
| 12919 | opportune | 2 |
| 12920 | opes | 2 |
| 12921 | operate | 2 |
| 12922 | operant | 2 |
| 12923 | opal | 2 |
| 12924 | onions | 2 |
| 12925 | ongles | 2 |
| 12926 | omne | 2 |
| 12927 | omitting | 2 |
| 12928 | olympian | 2 |
| 12929 | olives | 2 |
| 12930 | oftener | 2 |
| 12931 | official | 2 |
| 12932 | offic | 2 |
| 12933 | offerings | 2 |
| 12934 | offensive | 2 |
| 12935 | odoriferous | 2 |
| 12936 | oceans | 2 |
| 12937 | occupy | 2 |
| 12938 | occident | 2 |
| 12939 | obtained | 2 |
| 12940 | obstinacy | 2 |
| 12941 | obstacles | 2 |
| 12942 | obstacle | 2 |
| 12943 | observer | 2 |
| 12944 | observant | 2 |
| 12945 | observances | 2 |
| 12946 | obscenely | 2 |
| 12947 | oblivious | 2 |
| 12948 | oblique | 2 |
| 12949 | obeyed | 2 |
| 12950 | oaken | 2 |
| 12951 | ny | 2 |
| 12952 | nutshell | 2 |
| 12953 | nutmeg | 2 |
| 12954 | nurture | 2 |
| 12955 | numberless | 2 |
| 12956 | novices | 2 |
| 12957 | novelty | 2 |
| 12958 | nourishment | 2 |
| 12959 | nourisheth | 2 |
| 12960 | nourished | 2 |
| 12961 | nouns | 2 |
| 12962 | notre | 2 |
| 12963 | notoriously | 2 |
| 12964 | notify | 2 |
| 12965 | notary | 2 |
| 12966 | nosegays | 2 |
| 12967 | northgate | 2 |
| 12968 | nominativo | 2 |
| 12969 | noiseless | 2 |
| 12970 | nois | 2 |
| 12971 | nointed | 2 |
| 12972 | nodded | 2 |
| 12973 | nob | 2 |
| 12974 | noah | 2 |
| 12975 | nnight | 2 |
| 12976 | nit | 2 |
| 12977 | nips | 2 |
| 12978 | nipple | 2 |
| 12979 | nipping | 2 |
| 12980 | ninus | 2 |
| 12981 | nill | 2 |
| 12982 | nightingales | 2 |
| 12983 | nighted | 2 |
| 12984 | nibbling | 2 |
| 12985 | nettled | 2 |
| 12986 | nets | 2 |
| 12987 | nests | 2 |
| 12988 | nessus | 2 |
| 12989 | nerve | 2 |
| 12990 | nemean | 2 |
| 12991 | neighs | 2 |
| 12992 | neighbourly | 2 |
| 12993 | negotiate | 2 |
| 12994 | neglection | 2 |
| 12995 | nedar | 2 |
| 12996 | nectar | 2 |
| 12997 | nearness | 2 |
| 12998 | neaf | 2 |
| 12999 | natur | 2 |
| 13000 | nasty | 2 |
| 13001 | naso | 2 |
| 13002 | narrowly | 2 |
| 13003 | napping | 2 |
| 13004 | nape | 2 |
| 13005 | nag | 2 |
| 13006 | myrtle | 2 |
| 13007 | myrmidon | 2 |
| 13008 | muttons | 2 |
| 13009 | mutes | 2 |
| 13010 | mutability | 2 |
| 13011 | mustachio | 2 |
| 13012 | musics | 2 |
| 13013 | muses | 2 |
| 13014 | muscovites | 2 |
| 13015 | murdering | 2 |
| 13016 | munition | 2 |
| 13017 | mumbling | 2 |
| 13018 | multitudinous | 2 |
| 13019 | mulmutius | 2 |
| 13020 | mulier | 2 |
| 13021 | muleteers | 2 |
| 13022 | mulberry | 2 |
| 13023 | mudded | 2 |
| 13024 | moys | 2 |
| 13025 | moy | 2 |
| 13026 | mowing | 2 |
| 13027 | movers | 2 |
| 13028 | moveables | 2 |
| 13029 | moveable | 2 |
| 13030 | mouthed | 2 |
| 13031 | mousing | 2 |
| 13032 | mourns | 2 |
| 13033 | mountebanks | 2 |
| 13034 | mountainous | 2 |
| 13035 | mountaineer | 2 |
| 13036 | mortifying | 2 |
| 13037 | mortar | 2 |
| 13038 | mornings | 2 |
| 13039 | mope | 2 |
| 13040 | monthly | 2 |
| 13041 | monger | 2 |
| 13042 | monde | 2 |
| 13043 | monachum | 2 |
| 13044 | mollis | 2 |
| 13045 | molest | 2 |
| 13046 | moles | 2 |
| 13047 | moisture | 2 |
| 13048 | module | 2 |
| 13049 | modo | 2 |
| 13050 | modesties | 2 |
| 13051 | moderately | 2 |
| 13052 | mockwater | 2 |
| 13053 | mockers | 2 |
| 13054 | moated | 2 |
| 13055 | mistak | 2 |
| 13056 | mista | 2 |
| 13057 | misprised | 2 |
| 13058 | misplaced | 2 |
| 13059 | misplac | 2 |
| 13060 | misleader | 2 |
| 13061 | mislead | 2 |
| 13062 | mishaps | 2 |
| 13063 | mishap | 2 |
| 13064 | misdoubts | 2 |
| 13065 | misconstrued | 2 |
| 13066 | misconster | 2 |
| 13067 | mischievous | 2 |
| 13068 | miscall | 2 |
| 13069 | misadventure | 2 |
| 13070 | miry | 2 |
| 13071 | mirrors | 2 |
| 13072 | minstrelsy | 2 |
| 13073 | minstrel | 2 |
| 13074 | mingling | 2 |
| 13075 | minerva | 2 |
| 13076 | mindless | 2 |
| 13077 | minding | 2 |
| 13078 | mills | 2 |
| 13079 | milliner | 2 |
| 13080 | miller | 2 |
| 13081 | milks | 2 |
| 13082 | milkmaid | 2 |
| 13083 | mildest | 2 |
| 13084 | midway | 2 |
| 13085 | michaelmas | 2 |
| 13086 | mexico | 2 |
| 13087 | mettled | 2 |
| 13088 | mete | 2 |
| 13089 | metamorphis | 2 |
| 13090 | metals | 2 |
| 13091 | messaline | 2 |
| 13092 | messages | 2 |
| 13093 | mesh | 2 |
| 13094 | merlin | 2 |
| 13095 | menton | 2 |
| 13096 | mends | 2 |
| 13097 | menac | 2 |
| 13098 | melteth | 2 |
| 13099 | meiny | 2 |
| 13100 | meetest | 2 |
| 13101 | meeter | 2 |
| 13102 | medlars | 2 |
| 13103 | meditate | 2 |
| 13104 | medicinal | 2 |
| 13105 | mediation | 2 |
| 13106 | media | 2 |
| 13107 | medea | 2 |
| 13108 | meddler | 2 |
| 13109 | measureless | 2 |
| 13110 | mazzard | 2 |
| 13111 | maz | 2 |
| 13112 | maws | 2 |
| 13113 | maul | 2 |
| 13114 | maturity | 2 |
| 13115 | matchless | 2 |
| 13116 | masterless | 2 |
| 13117 | massacres | 2 |
| 13118 | masquing | 2 |
| 13119 | masquers | 2 |
| 13120 | masonry | 2 |
| 13121 | mason | 2 |
| 13122 | marvellously | 2 |
| 13123 | marv | 2 |
| 13124 | martlet | 2 |
| 13125 | marrows | 2 |
| 13126 | marquess | 2 |
| 13127 | marketable | 2 |
| 13128 | marigold | 2 |
| 13129 | maries | 2 |
| 13130 | mares | 2 |
| 13131 | maps | 2 |
| 13132 | mapp | 2 |
| 13133 | manured | 2 |
| 13134 | mantled | 2 |
| 13135 | mans | 2 |
| 13136 | manifests | 2 |
| 13137 | manhoods | 2 |
| 13138 | mangle | 2 |
| 13139 | manfully | 2 |
| 13140 | mane | 2 |
| 13141 | mandragora | 2 |
| 13142 | managing | 2 |
| 13143 | manager | 2 |
| 13144 | managed | 2 |
| 13145 | males | 2 |
| 13146 | malefactors | 2 |
| 13147 | malcontents | 2 |
| 13148 | majestee | 2 |
| 13149 | maintained | 2 |
| 13150 | maidhood | 2 |
| 13151 | maidenly | 2 |
| 13152 | maidenhood | 2 |
| 13153 | mahu | 2 |
| 13154 | magnificent | 2 |
| 13155 | maggots | 2 |
| 13156 | maggot | 2 |
| 13157 | mads | 2 |
| 13158 | madrigals | 2 |
| 13159 | madams | 2 |
| 13160 | lymoges | 2 |
| 13161 | lydia | 2 |
| 13162 | ly | 2 |
| 13163 | lutes | 2 |
| 13164 | lustrous | 2 |
| 13165 | lustihood | 2 |
| 13166 | luscious | 2 |
| 13167 | lure | 2 |
| 13168 | lurch | 2 |
| 13169 | lupercal | 2 |
| 13170 | lunatics | 2 |
| 13171 | lulls | 2 |
| 13172 | lull | 2 |
| 13173 | lukewarm | 2 |
| 13174 | lugg | 2 |
| 13175 | lug | 2 |
| 13176 | lucre | 2 |
| 13177 | luckless | 2 |
| 13178 | lucianus | 2 |
| 13179 | lowing | 2 |
| 13180 | lovingly | 2 |
| 13181 | loveliness | 2 |
| 13182 | lovelier | 2 |
| 13183 | lovedst | 2 |
| 13184 | louvre | 2 |
| 13185 | louse | 2 |
| 13186 | louring | 2 |
| 13187 | loseth | 2 |
| 13188 | lorraine | 2 |
| 13189 | lordings | 2 |
| 13190 | loosely | 2 |
| 13191 | loosed | 2 |
| 13192 | longeth | 2 |
| 13193 | loneliness | 2 |
| 13194 | lone | 2 |
| 13195 | loggerhead | 2 |
| 13196 | lodgers | 2 |
| 13197 | locked | 2 |
| 13198 | local | 2 |
| 13199 | lob | 2 |
| 13200 | loathing | 2 |
| 13201 | llous | 2 |
| 13202 | lizards | 2 |
| 13203 | lizard | 2 |
| 13204 | livia | 2 |
| 13205 | livelihood | 2 |
| 13206 | listening | 2 |
| 13207 | liquors | 2 |
| 13208 | linstock | 2 |
| 13209 | links | 2 |
| 13210 | lining | 2 |
| 13211 | linguist | 2 |
| 13212 | lineament | 2 |
| 13213 | limitation | 2 |
| 13214 | likings | 2 |
| 13215 | likest | 2 |
| 13216 | liked | 2 |
| 13217 | lightest | 2 |
| 13218 | lifting | 2 |
| 13219 | lieve | 2 |
| 13220 | lieutenantry | 2 |
| 13221 | lieth | 2 |
| 13222 | liegemen | 2 |
| 13223 | liegeman | 2 |
| 13224 | liefest | 2 |
| 13225 | lid | 2 |
| 13226 | lichas | 2 |
| 13227 | lewdness | 2 |
| 13228 | lewdly | 2 |
| 13229 | levying | 2 |
| 13230 | leviathan | 2 |
| 13231 | levelled | 2 |
| 13232 | lestrake | 2 |
| 13233 | lessons | 2 |
| 13234 | lessens | 2 |
| 13235 | lentus | 2 |
| 13236 | lengths | 2 |
| 13237 | lendings | 2 |
| 13238 | leisurely | 2 |
| 13239 | lees | 2 |
| 13240 | leda | 2 |
| 13241 | leavy | 2 |
| 13242 | leavening | 2 |
| 13243 | leasing | 2 |
| 13244 | leases | 2 |
| 13245 | leaky | 2 |
| 13246 | leaders | 2 |
| 13247 | lazars | 2 |
| 13248 | lawrence | 2 |
| 13249 | lawfully | 2 |
| 13250 | lavache | 2 |
| 13251 | laundress | 2 |
| 13252 | laund | 2 |
| 13253 | laugher | 2 |
| 13254 | laudable | 2 |
| 13255 | lated | 2 |
| 13256 | lasted | 2 |
| 13257 | larums | 2 |
| 13258 | largeness | 2 |
| 13259 | lards | 2 |
| 13260 | lapse | 2 |
| 13261 | languishes | 2 |
| 13262 | lanes | 2 |
| 13263 | lammas | 2 |
| 13264 | lamentably | 2 |
| 13265 | lameness | 2 |
| 13266 | lam | 2 |
| 13267 | lakin | 2 |
| 13268 | lading | 2 |
| 13269 | lacedaemon | 2 |
| 13270 | labyrinth | 2 |
| 13271 | laboursome | 2 |
| 13272 | labourer | 2 |
| 13273 | laboring | 2 |
| 13274 | label | 2 |
| 13275 | laban | 2 |
| 13276 | knowingly | 2 |
| 13277 | knower | 2 |
| 13278 | kneading | 2 |
| 13279 | knapp | 2 |
| 13280 | knacks | 2 |
| 13281 | knack | 2 |
| 13282 | kitten | 2 |
| 13283 | kitchens | 2 |
| 13284 | killingworth | 2 |
| 13285 | killeth | 2 |
| 13286 | killer | 2 |
| 13287 | kidney | 2 |
| 13288 | kibes | 2 |
| 13289 | kibe | 2 |
| 13290 | kernels | 2 |
| 13291 | kern | 2 |
| 13292 | kendal | 2 |
| 13293 | keech | 2 |
| 13294 | kates | 2 |
| 13295 | jutty | 2 |
| 13296 | justle | 2 |
| 13297 | jury | 2 |
| 13298 | jurisdiction | 2 |
| 13299 | julietta | 2 |
| 13300 | judging | 2 |
| 13301 | judgest | 2 |
| 13302 | jude | 2 |
| 13303 | joyous | 2 |
| 13304 | joyless | 2 |
| 13305 | jowl | 2 |
| 13306 | journal | 2 |
| 13307 | joseph | 2 |
| 13308 | jordan | 2 |
| 13309 | joined | 2 |
| 13310 | jog | 2 |
| 13311 | job | 2 |
| 13312 | jill | 2 |
| 13313 | jewish | 2 |
| 13314 | jesters | 2 |
| 13315 | jerkins | 2 |
| 13316 | jauncing | 2 |
| 13317 | jasons | 2 |
| 13318 | janus | 2 |
| 13319 | january | 2 |
| 13320 | jangling | 2 |
| 13321 | jane | 2 |
| 13322 | ithaca | 2 |
| 13323 | itching | 2 |
| 13324 | itches | 2 |
| 13325 | issueless | 2 |
| 13326 | isles | 2 |
| 13327 | isbels | 2 |
| 13328 | irishman | 2 |
| 13329 | ipswich | 2 |
| 13330 | ipse | 2 |
| 13331 | inwards | 2 |
| 13332 | investments | 2 |
| 13333 | invert | 2 |
| 13334 | inventions | 2 |
| 13335 | invented | 2 |
| 13336 | invades | 2 |
| 13337 | invade | 2 |
| 13338 | intruder | 2 |
| 13339 | intrude | 2 |
| 13340 | intestine | 2 |
| 13341 | interrogatories | 2 |
| 13342 | interprets | 2 |
| 13343 | interpreters | 2 |
| 13344 | interpreted | 2 |
| 13345 | interpose | 2 |
| 13346 | intermingle | 2 |
| 13347 | interchanging | 2 |
| 13348 | intention | 2 |
| 13349 | intending | 2 |
| 13350 | intemperate | 2 |
| 13351 | intemperance | 2 |
| 13352 | intelligencer | 2 |
| 13353 | intellectual | 2 |
| 13354 | insufficiency | 2 |
| 13355 | institute | 2 |
| 13356 | instalment | 2 |
| 13357 | inspire | 2 |
| 13358 | insociable | 2 |
| 13359 | insert | 2 |
| 13360 | inseparable | 2 |
| 13361 | inquisitive | 2 |
| 13362 | inquisition | 2 |
| 13363 | inquiry | 2 |
| 13364 | inquir | 2 |
| 13365 | inprimis | 2 |
| 13366 | inordinate | 2 |
| 13367 | inmost | 2 |
| 13368 | inkling | 2 |
| 13369 | injunctions | 2 |
| 13370 | inhibited | 2 |
| 13371 | inherits | 2 |
| 13372 | inheritors | 2 |
| 13373 | inhabitants | 2 |
| 13374 | ingredients | 2 |
| 13375 | ingredient | 2 |
| 13376 | infusion | 2 |
| 13377 | infus | 2 |
| 13378 | infortunate | 2 |
| 13379 | information | 2 |
| 13380 | influences | 2 |
| 13381 | infidels | 2 |
| 13382 | infamous | 2 |
| 13383 | infallibly | 2 |
| 13384 | inexorable | 2 |
| 13385 | inestimable | 2 |
| 13386 | indulgence | 2 |
| 13387 | induced | 2 |
| 13388 | indited | 2 |
| 13389 | indistinct | 2 |
| 13390 | indiscretion | 2 |
| 13391 | indiscreet | 2 |
| 13392 | indirection | 2 |
| 13393 | indifferency | 2 |
| 13394 | indenture | 2 |
| 13395 | indent | 2 |
| 13396 | indebted | 2 |
| 13397 | inde | 2 |
| 13398 | incursions | 2 |
| 13399 | incredulous | 2 |
| 13400 | increaseth | 2 |
| 13401 | incony | 2 |
| 13402 | inconsiderate | 2 |
| 13403 | inclusive | 2 |
| 13404 | includes | 2 |
| 13405 | incest | 2 |
| 13406 | incertainties | 2 |
| 13407 | incarnate | 2 |
| 13408 | incaged | 2 |
| 13409 | inaccessible | 2 |
| 13410 | improvident | 2 |
| 13411 | impressed | 2 |
| 13412 | imposthume | 2 |
| 13413 | impossibilities | 2 |
| 13414 | imposed | 2 |
| 13415 | impos | 2 |
| 13416 | importunacy | 2 |
| 13417 | importeth | 2 |
| 13418 | impon | 2 |
| 13419 | implements | 2 |
| 13420 | impetuous | 2 |
| 13421 | impertinent | 2 |
| 13422 | imperfection | 2 |
| 13423 | impeachment | 2 |
| 13424 | immur | 2 |
| 13425 | imitated | 2 |
| 13426 | imbrue | 2 |
| 13427 | ils | 2 |
| 13428 | illustrate | 2 |
| 13429 | illusions | 2 |
| 13430 | illegitimate | 2 |
| 13431 | idiots | 2 |
| 13432 | idea | 2 |
| 13433 | icicle | 2 |
| 13434 | iceland | 2 |
| 13435 | hyrcanian | 2 |
| 13436 | hyperbolical | 2 |
| 13437 | hyperboles | 2 |
| 13438 | hybla | 2 |
| 13439 | hurries | 2 |
| 13440 | hurlyburly | 2 |
| 13441 | hungerford | 2 |
| 13442 | hungary | 2 |
| 13443 | hums | 2 |
| 13444 | humors | 2 |
| 13445 | humidity | 2 |
| 13446 | humblest | 2 |
| 13447 | humanely | 2 |
| 13448 | hull | 2 |
| 13449 | hugg | 2 |
| 13450 | hugely | 2 |
| 13451 | hued | 2 |
| 13452 | howsome | 2 |
| 13453 | housewives | 2 |
| 13454 | housewifery | 2 |
| 13455 | houseless | 2 |
| 13456 | housekeeping | 2 |
| 13457 | housekeeper | 2 |
| 13458 | households | 2 |
| 13459 | hottest | 2 |
| 13460 | hosts | 2 |
| 13461 | hostilius | 2 |
| 13462 | hostage | 2 |
| 13463 | horsemanship | 2 |
| 13464 | horseman | 2 |
| 13465 | horridly | 2 |
| 13466 | hopkins | 2 |
| 13467 | hooting | 2 |
| 13468 | hooted | 2 |
| 13469 | hoops | 2 |
| 13470 | hoof | 2 |
| 13471 | hoodman | 2 |
| 13472 | hooded | 2 |
| 13473 | honeysuckle | 2 |
| 13474 | homes | 2 |
| 13475 | holly | 2 |
| 13476 | hollowly | 2 |
| 13477 | hollander | 2 |
| 13478 | holier | 2 |
| 13479 | holidame | 2 |
| 13480 | holdeth | 2 |
| 13481 | hoisted | 2 |
| 13482 | hoc | 2 |
| 13483 | hobnails | 2 |
| 13484 | hob | 2 |
| 13485 | hoarding | 2 |
| 13486 | hoarded | 2 |
| 13487 | hitting | 2 |
| 13488 | hitherwards | 2 |
| 13489 | hist | 2 |
| 13490 | hissing | 2 |
| 13491 | hiren | 2 |
| 13492 | hipp | 2 |
| 13493 | hinges | 2 |
| 13494 | hinge | 2 |
| 13495 | highways | 2 |
| 13496 | highmost | 2 |
| 13497 | hiems | 2 |
| 13498 | hews | 2 |
| 13499 | hewn | 2 |
| 13500 | hests | 2 |
| 13501 | herrings | 2 |
| 13502 | heroes | 2 |
| 13503 | hermitage | 2 |
| 13504 | heretics | 2 |
| 13505 | heresies | 2 |
| 13506 | herefordshire | 2 |
| 13507 | herdsmen | 2 |
| 13508 | herds | 2 |
| 13509 | henton | 2 |
| 13510 | hems | 2 |
| 13511 | helper | 2 |
| 13512 | heedless | 2 |
| 13513 | hedgehogs | 2 |
| 13514 | hedg | 2 |
| 13515 | hectors | 2 |
| 13516 | heaving | 2 |
| 13517 | heaves | 2 |
| 13518 | heaved | 2 |
| 13519 | heats | 2 |
| 13520 | heartstrings | 2 |
| 13521 | heartly | 2 |
| 13522 | hearsay | 2 |
| 13523 | hearkens | 2 |
| 13524 | heark | 2 |
| 13525 | heaping | 2 |
| 13526 | healthy | 2 |
| 13527 | healing | 2 |
| 13528 | headborough | 2 |
| 13529 | hazarded | 2 |
| 13530 | havings | 2 |
| 13531 | haunch | 2 |
| 13532 | hatfield | 2 |
| 13533 | hasting | 2 |
| 13534 | harts | 2 |
| 13535 | harrow | 2 |
| 13536 | harping | 2 |
| 13537 | harmonious | 2 |
| 13538 | harming | 2 |
| 13539 | harbor | 2 |
| 13540 | harbingers | 2 |
| 13541 | happened | 2 |
| 13542 | happ | 2 |
| 13543 | hangmen | 2 |
| 13544 | hangeth | 2 |
| 13545 | handsaw | 2 |
| 13546 | handless | 2 |
| 13547 | handkerchers | 2 |
| 13548 | handful | 2 |
| 13549 | hams | 2 |
| 13550 | hampton | 2 |
| 13551 | halloo | 2 |
| 13552 | halloing | 2 |
| 13553 | halloa | 2 |
| 13554 | halfway | 2 |
| 13555 | halcyon | 2 |
| 13556 | hacks | 2 |
| 13557 | hackney | 2 |
| 13558 | hacket | 2 |
| 13559 | h | 2 |
| 13560 | gypsy | 2 |
| 13561 | gulls | 2 |
| 13562 | guiltier | 2 |
| 13563 | guileful | 2 |
| 13564 | guildhall | 2 |
| 13565 | guilders | 2 |
| 13566 | guardant | 2 |
| 13567 | gualtier | 2 |
| 13568 | grunt | 2 |
| 13569 | grumble | 2 |
| 13570 | grovelling | 2 |
| 13571 | grovel | 2 |
| 13572 | gros | 2 |
| 13573 | grizzled | 2 |
| 13574 | grisly | 2 |
| 13575 | grise | 2 |
| 13576 | griping | 2 |
| 13577 | grip | 2 |
| 13578 | grinding | 2 |
| 13579 | grimly | 2 |
| 13580 | grime | 2 |
| 13581 | griffin | 2 |
| 13582 | greybeards | 2 |
| 13583 | greybeard | 2 |
| 13584 | greensleeves | 2 |
| 13585 | greenly | 2 |
| 13586 | grazing | 2 |
| 13587 | gravy | 2 |
| 13588 | gravestone | 2 |
| 13589 | grav | 2 |
| 13590 | grating | 2 |
| 13591 | grated | 2 |
| 13592 | grasps | 2 |
| 13593 | grapples | 2 |
| 13594 | grandsires | 2 |
| 13595 | grammar | 2 |
| 13596 | graff | 2 |
| 13597 | gradation | 2 |
| 13598 | governed | 2 |
| 13599 | gossiping | 2 |
| 13600 | gossamer | 2 |
| 13601 | gorgon | 2 |
| 13602 | gored | 2 |
| 13603 | gordian | 2 |
| 13604 | goodwin | 2 |
| 13605 | goodlier | 2 |
| 13606 | goodfellow | 2 |
| 13607 | gondola | 2 |
| 13608 | golgotha | 2 |
| 13609 | godmother | 2 |
| 13610 | godliness | 2 |
| 13611 | godfathers | 2 |
| 13612 | goblin | 2 |
| 13613 | goblet | 2 |
| 13614 | gobbets | 2 |
| 13615 | goaded | 2 |
| 13616 | gnaws | 2 |
| 13617 | gnawn | 2 |
| 13618 | gnarling | 2 |
| 13619 | gluttony | 2 |
| 13620 | gloze | 2 |
| 13621 | gloomy | 2 |
| 13622 | glisters | 2 |
| 13623 | glistering | 2 |
| 13624 | glimpse | 2 |
| 13625 | glimmer | 2 |
| 13626 | glides | 2 |
| 13627 | gleek | 2 |
| 13628 | gleaned | 2 |
| 13629 | glares | 2 |
| 13630 | glanced | 2 |
| 13631 | giveth | 2 |
| 13632 | girdling | 2 |
| 13633 | girdled | 2 |
| 13634 | girded | 2 |
| 13635 | gillyvors | 2 |
| 13636 | gilding | 2 |
| 13637 | giglot | 2 |
| 13638 | giddily | 2 |
| 13639 | gibing | 2 |
| 13640 | gib | 2 |
| 13641 | gestures | 2 |
| 13642 | germane | 2 |
| 13643 | gentility | 2 |
| 13644 | gentilhomme | 2 |
| 13645 | gens | 2 |
| 13646 | geck | 2 |
| 13647 | gazers | 2 |
| 13648 | gaz | 2 |
| 13649 | gawsey | 2 |
| 13650 | gauntlets | 2 |
| 13651 | gaultree | 2 |
| 13652 | gatories | 2 |
| 13653 | gascony | 2 |
| 13654 | garish | 2 |
| 13655 | gard | 2 |
| 13656 | garboils | 2 |
| 13657 | garbage | 2 |
| 13658 | gapes | 2 |
| 13659 | gallowglasses | 2 |
| 13660 | galling | 2 |
| 13661 | gallimaufry | 2 |
| 13662 | gallian | 2 |
| 13663 | galley | 2 |
| 13664 | gainer | 2 |
| 13665 | gained | 2 |
| 13666 | gagg | 2 |
| 13667 | gad | 2 |
| 13668 | furthest | 2 |
| 13669 | furthermore | 2 |
| 13670 | furnished | 2 |
| 13671 | furlongs | 2 |
| 13672 | furbish | 2 |
| 13673 | fur | 2 |
| 13674 | fundamental | 2 |
| 13675 | fumes | 2 |
| 13676 | fumble | 2 |
| 13677 | fuller | 2 |
| 13678 | fruitfully | 2 |
| 13679 | frugal | 2 |
| 13680 | fronting | 2 |
| 13681 | frontier | 2 |
| 13682 | fronted | 2 |
| 13683 | frolic | 2 |
| 13684 | frightful | 2 |
| 13685 | fridays | 2 |
| 13686 | friars | 2 |
| 13687 | freshness | 2 |
| 13688 | frenchwoman | 2 |
| 13689 | freezes | 2 |
| 13690 | fraughtage | 2 |
| 13691 | franklin | 2 |
| 13692 | fractions | 2 |
| 13693 | fracted | 2 |
| 13694 | foutra | 2 |
| 13695 | founded | 2 |
| 13696 | fostered | 2 |
| 13697 | fortuna | 2 |
| 13698 | forts | 2 |
| 13699 | forswearing | 2 |
| 13700 | forspent | 2 |
| 13701 | formless | 2 |
| 13702 | formally | 2 |
| 13703 | forgery | 2 |
| 13704 | forgeries | 2 |
| 13705 | forgave | 2 |
| 13706 | forfeiting | 2 |
| 13707 | forewarn | 2 |
| 13708 | forespent | 2 |
| 13709 | forenoon | 2 |
| 13710 | foreknowing | 2 |
| 13711 | forefinger | 2 |
| 13712 | fordone | 2 |
| 13713 | fordoes | 2 |
| 13714 | forbade | 2 |
| 13715 | footpath | 2 |
| 13716 | footboy | 2 |
| 13717 | football | 2 |
| 13718 | foolhardy | 2 |
| 13719 | font | 2 |
| 13720 | folds | 2 |
| 13721 | foix | 2 |
| 13722 | fois | 2 |
| 13723 | foining | 2 |
| 13724 | foin | 2 |
| 13725 | foeman | 2 |
| 13726 | focative | 2 |
| 13727 | flux | 2 |
| 13728 | flutes | 2 |
| 13729 | flowed | 2 |
| 13730 | flouts | 2 |
| 13731 | florentines | 2 |
| 13732 | floating | 2 |
| 13733 | float | 2 |
| 13734 | flinch | 2 |
| 13735 | flights | 2 |
| 13736 | flieth | 2 |
| 13737 | flibbertigibbet | 2 |
| 13738 | flexure | 2 |
| 13739 | flexible | 2 |
| 13740 | fleeter | 2 |
| 13741 | flee | 2 |
| 13742 | fleas | 2 |
| 13743 | flaying | 2 |
| 13744 | flask | 2 |
| 13745 | flanders | 2 |
| 13746 | flags | 2 |
| 13747 | fishmonger | 2 |
| 13748 | firmness | 2 |
| 13749 | firk | 2 |
| 13750 | fired | 2 |
| 13751 | fir | 2 |
| 13752 | fins | 2 |
| 13753 | finch | 2 |
| 13754 | filths | 2 |
| 13755 | film | 2 |
| 13756 | fillet | 2 |
| 13757 | filch | 2 |
| 13758 | figo | 2 |
| 13759 | fighteth | 2 |
| 13760 | fidelicet | 2 |
| 13761 | fiddlestick | 2 |
| 13762 | fiddle | 2 |
| 13763 | fewest | 2 |
| 13764 | feu | 2 |
| 13765 | fetters | 2 |
| 13766 | fett | 2 |
| 13767 | fertility | 2 |
| 13768 | fernseed | 2 |
| 13769 | fens | 2 |
| 13770 | fennel | 2 |
| 13771 | fencer | 2 |
| 13772 | felony | 2 |
| 13773 | felon | 2 |
| 13774 | fells | 2 |
| 13775 | fellest | 2 |
| 13776 | felicity | 2 |
| 13777 | fedary | 2 |
| 13778 | featly | 2 |
| 13779 | feathered | 2 |
| 13780 | fawns | 2 |
| 13781 | favourite | 2 |
| 13782 | favouring | 2 |
| 13783 | favourer | 2 |
| 13784 | fauconbridge | 2 |
| 13785 | fattest | 2 |
| 13786 | fatted | 2 |
| 13787 | fatherless | 2 |
| 13788 | fastest | 2 |
| 13789 | fastened | 2 |
| 13790 | fashioning | 2 |
| 13791 | fashionable | 2 |
| 13792 | faring | 2 |
| 13793 | farewells | 2 |
| 13794 | fans | 2 |
| 13795 | famously | 2 |
| 13796 | familiars | 2 |
| 13797 | famed | 2 |
| 13798 | falter | 2 |
| 13799 | falstaffs | 2 |
| 13800 | falser | 2 |
| 13801 | falseness | 2 |
| 13802 | faintness | 2 |
| 13803 | fainted | 2 |
| 13804 | fadge | 2 |
| 13805 | faculty | 2 |
| 13806 | facit | 2 |
| 13807 | faced | 2 |
| 13808 | fabulous | 2 |
| 13809 | fables | 2 |
| 13810 | eyed | 2 |
| 13811 | eyebrows | 2 |
| 13812 | exult | 2 |
| 13813 | extraordinarily | 2 |
| 13814 | extracting | 2 |
| 13815 | extorted | 2 |
| 13816 | extinct | 2 |
| 13817 | extern | 2 |
| 13818 | expulsion | 2 |
| 13819 | exposure | 2 |
| 13820 | exposing | 2 |
| 13821 | explication | 2 |
| 13822 | expir | 2 |
| 13823 | expiate | 2 |
| 13824 | expertness | 2 |
| 13825 | experiments | 2 |
| 13826 | experiment | 2 |
| 13827 | expenses | 2 |
| 13828 | expectancy | 2 |
| 13829 | exorcist | 2 |
| 13830 | exist | 2 |
| 13831 | exhort | 2 |
| 13832 | exhales | 2 |
| 13833 | exhale | 2 |
| 13834 | exhalations | 2 |
| 13835 | exhalation | 2 |
| 13836 | exhal | 2 |
| 13837 | executor | 2 |
| 13838 | execrations | 2 |
| 13839 | excusing | 2 |
| 13840 | excusez | 2 |
| 13841 | excused | 2 |
| 13842 | excommunicate | 2 |
| 13843 | excitements | 2 |
| 13844 | excite | 2 |
| 13845 | exchang | 2 |
| 13846 | excelling | 2 |
| 13847 | exampled | 2 |
| 13848 | examin | 2 |
| 13849 | evilly | 2 |
| 13850 | eunuchs | 2 |
| 13851 | ethiopian | 2 |
| 13852 | eterne | 2 |
| 13853 | estranged | 2 |
| 13854 | estimable | 2 |
| 13855 | esses | 2 |
| 13856 | esquires | 2 |
| 13857 | espies | 2 |
| 13858 | escaped | 2 |
| 13859 | erwatch | 2 |
| 13860 | erturn | 2 |
| 13861 | ertop | 2 |
| 13862 | ertook | 2 |
| 13863 | ersways | 2 |
| 13864 | ersway | 2 |
| 13865 | ershot | 2 |
| 13866 | ershades | 2 |
| 13867 | errun | 2 |
| 13868 | erroneous | 2 |
| 13869 | erraught | 2 |
| 13870 | errant | 2 |
| 13871 | errands | 2 |
| 13872 | erpow | 2 |
| 13873 | erpast | 2 |
| 13874 | erleap | 2 |
| 13875 | erflow | 2 |
| 13876 | ercome | 2 |
| 13877 | ercles | 2 |
| 13878 | ercharg | 2 |
| 13879 | ercast | 2 |
| 13880 | erborne | 2 |
| 13881 | erboard | 2 |
| 13882 | erbears | 2 |
| 13883 | erbearing | 2 |
| 13884 | equivocation | 2 |
| 13885 | equivocal | 2 |
| 13886 | equipage | 2 |
| 13887 | equall | 2 |
| 13888 | equality | 2 |
| 13889 | epithets | 2 |
| 13890 | epitaphs | 2 |
| 13891 | epistles | 2 |
| 13892 | epicurean | 2 |
| 13893 | envying | 2 |
| 13894 | envenomed | 2 |
| 13895 | envelop | 2 |
| 13896 | enticing | 2 |
| 13897 | entice | 2 |
| 13898 | enthroned | 2 |
| 13899 | enthralled | 2 |
| 13900 | entering | 2 |
| 13901 | entered | 2 |
| 13902 | entangled | 2 |
| 13903 | ensigns | 2 |
| 13904 | enroll | 2 |
| 13905 | enriched | 2 |
| 13906 | enrage | 2 |
| 13907 | enquired | 2 |
| 13908 | enlarged | 2 |
| 13909 | enlarg | 2 |
| 13910 | enkindle | 2 |
| 13911 | enigma | 2 |
| 13912 | engrossed | 2 |
| 13913 | engrav | 2 |
| 13914 | englutted | 2 |
| 13915 | engirt | 2 |
| 13916 | enforces | 2 |
| 13917 | endue | 2 |
| 13918 | endowments | 2 |
| 13919 | endowed | 2 |
| 13920 | endings | 2 |
| 13921 | endear | 2 |
| 13922 | endanger | 2 |
| 13923 | endamage | 2 |
| 13924 | encouragement | 2 |
| 13925 | enchants | 2 |
| 13926 | enchantment | 2 |
| 13927 | enamoured | 2 |
| 13928 | enamell | 2 |
| 13929 | enacts | 2 |
| 13930 | emulate | 2 |
| 13931 | empties | 2 |
| 13932 | emptier | 2 |
| 13933 | emptied | 2 |
| 13934 | empoison | 2 |
| 13935 | employments | 2 |
| 13936 | emphasis | 2 |
| 13937 | emnity | 2 |
| 13938 | embattl | 2 |
| 13939 | embassies | 2 |
| 13940 | eleventh | 2 |
| 13941 | elegies | 2 |
| 13942 | elbe | 2 |
| 13943 | eglantine | 2 |
| 13944 | effectually | 2 |
| 13945 | edmunds | 2 |
| 13946 | edifice | 2 |
| 13947 | edicts | 2 |
| 13948 | edgeless | 2 |
| 13949 | edged | 2 |
| 13950 | ecus | 2 |
| 13951 | eclips | 2 |
| 13952 | echoes | 2 |
| 13953 | ebon | 2 |
| 13954 | ebbing | 2 |
| 13955 | eaters | 2 |
| 13956 | eater | 2 |
| 13957 | easing | 2 |
| 13958 | eased | 2 |
| 13959 | earned | 2 |
| 13960 | dwindle | 2 |
| 13961 | dwelt | 2 |
| 13962 | dutiful | 2 |
| 13963 | dusty | 2 |
| 13964 | dungy | 2 |
| 13965 | dunghills | 2 |
| 13966 | dungeons | 2 |
| 13967 | dumbly | 2 |
| 13968 | dulness | 2 |
| 13969 | dulling | 2 |
| 13970 | dullard | 2 |
| 13971 | duello | 2 |
| 13972 | duellist | 2 |
| 13973 | ducking | 2 |
| 13974 | duchy | 2 |
| 13975 | drunkenly | 2 |
| 13976 | drones | 2 |
| 13977 | drollery | 2 |
| 13978 | drizzled | 2 |
| 13979 | driveth | 2 |
| 13980 | drinkings | 2 |
| 13981 | drinketh | 2 |
| 13982 | drier | 2 |
| 13983 | dressings | 2 |
| 13984 | dreads | 2 |
| 13985 | dreadfully | 2 |
| 13986 | draweth | 2 |
| 13987 | drank | 2 |
| 13988 | drained | 2 |
| 13989 | dragging | 2 |
| 13990 | dragg | 2 |
| 13991 | draff | 2 |
| 13992 | drachmas | 2 |
| 13993 | dowlas | 2 |
| 13994 | dowers | 2 |
| 13995 | dovehouse | 2 |
| 13996 | dough | 2 |
| 13997 | doubling | 2 |
| 13998 | donn | 2 |
| 13999 | doncaster | 2 |
| 14000 | domine | 2 |
| 14001 | docks | 2 |
| 14002 | dobbin | 2 |
| 14003 | divulged | 2 |
| 14004 | divorced | 2 |
| 14005 | divinest | 2 |
| 14006 | divinely | 2 |
| 14007 | divest | 2 |
| 14008 | dives | 2 |
| 14009 | ditties | 2 |
| 14010 | dites | 2 |
| 14011 | ditches | 2 |
| 14012 | disturbers | 2 |
| 14013 | distribution | 2 |
| 14014 | distribute | 2 |
| 14015 | distresses | 2 |
| 14016 | distraught | 2 |
| 14017 | distrain | 2 |
| 14018 | distractions | 2 |
| 14019 | distractedly | 2 |
| 14020 | distillation | 2 |
| 14021 | dissuaded | 2 |
| 14022 | dissolves | 2 |
| 14023 | dissolved | 2 |
| 14024 | dissembler | 2 |
| 14025 | dissembled | 2 |
| 14026 | disputes | 2 |
| 14027 | dispraising | 2 |
| 14028 | disport | 2 |
| 14029 | displeasures | 2 |
| 14030 | displeasing | 2 |
| 14031 | displace | 2 |
| 14032 | displac | 2 |
| 14033 | dispersedly | 2 |
| 14034 | dispensation | 2 |
| 14035 | disparagement | 2 |
| 14036 | disparage | 2 |
| 14037 | disordered | 2 |
| 14038 | dismounted | 2 |
| 14039 | dismission | 2 |
| 14040 | dismember | 2 |
| 14041 | dismantle | 2 |
| 14042 | disloyalty | 2 |
| 14043 | dislik | 2 |
| 14044 | disjoint | 2 |
| 14045 | disjoin | 2 |
| 14046 | dishonours | 2 |
| 14047 | dishonestly | 2 |
| 14048 | dishclout | 2 |
| 14049 | disguising | 2 |
| 14050 | disguises | 2 |
| 14051 | disgracious | 2 |
| 14052 | disfurnish | 2 |
| 14053 | disfigured | 2 |
| 14054 | disembark | 2 |
| 14055 | disdaineth | 2 |
| 14056 | discreetly | 2 |
| 14057 | discredited | 2 |
| 14058 | discovering | 2 |
| 14059 | discoursed | 2 |
| 14060 | discoloured | 2 |
| 14061 | discolour | 2 |
| 14062 | disclosed | 2 |
| 14063 | disclaiming | 2 |
| 14064 | disciplin | 2 |
| 14065 | discase | 2 |
| 14066 | disbursed | 2 |
| 14067 | disadvantage | 2 |
| 14068 | disable | 2 |
| 14069 | directitude | 2 |
| 14070 | dint | 2 |
| 14071 | dinners | 2 |
| 14072 | dining | 2 |
| 14073 | dines | 2 |
| 14074 | dined | 2 |
| 14075 | diminutives | 2 |
| 14076 | diminutive | 2 |
| 14077 | diminution | 2 |
| 14078 | dimension | 2 |
| 14079 | dilatory | 2 |
| 14080 | dilate | 2 |
| 14081 | digression | 2 |
| 14082 | digressing | 2 |
| 14083 | digress | 2 |
| 14084 | dignify | 2 |
| 14085 | digestions | 2 |
| 14086 | diffus | 2 |
| 14087 | diffidence | 2 |
| 14088 | difficulties | 2 |
| 14089 | differing | 2 |
| 14090 | differ | 2 |
| 14091 | dials | 2 |
| 14092 | devours | 2 |
| 14093 | devoured | 2 |
| 14094 | devant | 2 |
| 14095 | deux | 2 |
| 14096 | deum | 2 |
| 14097 | deucalion | 2 |
| 14098 | detract | 2 |
| 14099 | detests | 2 |
| 14100 | detected | 2 |
| 14101 | destroys | 2 |
| 14102 | destroyed | 2 |
| 14103 | despiseth | 2 |
| 14104 | despairs | 2 |
| 14105 | desist | 2 |
| 14106 | desirest | 2 |
| 14107 | deserver | 2 |
| 14108 | describes | 2 |
| 14109 | describe | 2 |
| 14110 | descending | 2 |
| 14111 | deracinate | 2 |
| 14112 | deprive | 2 |
| 14113 | dens | 2 |
| 14114 | denounc | 2 |
| 14115 | denials | 2 |
| 14116 | denay | 2 |
| 14117 | demurely | 2 |
| 14118 | demonstration | 2 |
| 14119 | demigod | 2 |
| 14120 | demanding | 2 |
| 14121 | delve | 2 |
| 14122 | deluge | 2 |
| 14123 | deluding | 2 |
| 14124 | delectable | 2 |
| 14125 | delaying | 2 |
| 14126 | delabreth | 2 |
| 14127 | degraded | 2 |
| 14128 | deflowered | 2 |
| 14129 | deficient | 2 |
| 14130 | defer | 2 |
| 14131 | defensive | 2 |
| 14132 | defensible | 2 |
| 14133 | defends | 2 |
| 14134 | defender | 2 |
| 14135 | defeatures | 2 |
| 14136 | deeps | 2 |
| 14137 | deemed | 2 |
| 14138 | dedicates | 2 |
| 14139 | decrease | 2 |
| 14140 | declension | 2 |
| 14141 | decide | 2 |
| 14142 | deceivable | 2 |
| 14143 | debtors | 2 |
| 14144 | debosh | 2 |
| 14145 | debitor | 2 |
| 14146 | debile | 2 |
| 14147 | debauch | 2 |
| 14148 | debatement | 2 |
| 14149 | deathsman | 2 |
| 14150 | dean | 2 |
| 14151 | deafness | 2 |
| 14152 | dazzled | 2 |
| 14153 | dawn | 2 |
| 14154 | daw | 2 |
| 14155 | daunt | 2 |
| 14156 | dastards | 2 |
| 14157 | dashing | 2 |
| 14158 | dashes | 2 |
| 14159 | darting | 2 |
| 14160 | darkest | 2 |
| 14161 | darker | 2 |
| 14162 | dardan | 2 |
| 14163 | dandle | 2 |
| 14164 | dancer | 2 |
| 14165 | damp | 2 |
| 14166 | damm | 2 |
| 14167 | dalmatians | 2 |
| 14168 | dallying | 2 |
| 14169 | dallies | 2 |
| 14170 | daisies | 2 |
| 14171 | daintily | 2 |
| 14172 | daintiest | 2 |
| 14173 | daffodils | 2 |
| 14174 | cygnet | 2 |
| 14175 | cyclops | 2 |
| 14176 | cutter | 2 |
| 14177 | customer | 2 |
| 14178 | custard | 2 |
| 14179 | curtle | 2 |
| 14180 | curtail | 2 |
| 14181 | cursies | 2 |
| 14182 | curing | 2 |
| 14183 | cureless | 2 |
| 14184 | curd | 2 |
| 14185 | cupids | 2 |
| 14186 | cupbearer | 2 |
| 14187 | cumber | 2 |
| 14188 | cullions | 2 |
| 14189 | culling | 2 |
| 14190 | cuffs | 2 |
| 14191 | cudgels | 2 |
| 14192 | cucullus | 2 |
| 14193 | cub | 2 |
| 14194 | crowning | 2 |
| 14195 | crownets | 2 |
| 14196 | crowing | 2 |
| 14197 | crowding | 2 |
| 14198 | croak | 2 |
| 14199 | critical | 2 |
| 14200 | criest | 2 |
| 14201 | criedst | 2 |
| 14202 | crestfall | 2 |
| 14203 | creator | 2 |
| 14204 | creaking | 2 |
| 14205 | crazed | 2 |
| 14206 | crawling | 2 |
| 14207 | crav | 2 |
| 14208 | cranny | 2 |
| 14209 | craftily | 2 |
| 14210 | cradles | 2 |
| 14211 | crabs | 2 |
| 14212 | cox | 2 |
| 14213 | cowslips | 2 |
| 14214 | covet | 2 |
| 14215 | coverture | 2 |
| 14216 | covent | 2 |
| 14217 | courtezans | 2 |
| 14218 | courteously | 2 |
| 14219 | coursing | 2 |
| 14220 | couriers | 2 |
| 14221 | courageously | 2 |
| 14222 | couplement | 2 |
| 14223 | countesses | 2 |
| 14224 | counsell | 2 |
| 14225 | coughing | 2 |
| 14226 | cotus | 2 |
| 14227 | cottages | 2 |
| 14228 | corses | 2 |
| 14229 | corrupter | 2 |
| 14230 | corrosive | 2 |
| 14231 | corrigible | 2 |
| 14232 | corrects | 2 |
| 14233 | corrected | 2 |
| 14234 | corporate | 2 |
| 14235 | coronal | 2 |
| 14236 | corns | 2 |
| 14237 | cornish | 2 |
| 14238 | cornelia | 2 |
| 14239 | cork | 2 |
| 14240 | corded | 2 |
| 14241 | coranto | 2 |
| 14242 | copulation | 2 |
| 14243 | copies | 2 |
| 14244 | cooled | 2 |
| 14245 | cookery | 2 |
| 14246 | convocation | 2 |
| 14247 | conveyances | 2 |
| 14248 | converts | 2 |
| 14249 | conversion | 2 |
| 14250 | conversing | 2 |
| 14251 | converses | 2 |
| 14252 | conversant | 2 |
| 14253 | conveniency | 2 |
| 14254 | conveniences | 2 |
| 14255 | controller | 2 |
| 14256 | contrives | 2 |
| 14257 | contribution | 2 |
| 14258 | contrarious | 2 |
| 14259 | continuate | 2 |
| 14260 | continency | 2 |
| 14261 | contentious | 2 |
| 14262 | contemptuous | 2 |
| 14263 | contemptible | 2 |
| 14264 | contaminate | 2 |
| 14265 | consummation | 2 |
| 14266 | constitution | 2 |
| 14267 | conspired | 2 |
| 14268 | consonancy | 2 |
| 14269 | consolation | 2 |
| 14270 | consisting | 2 |
| 14271 | considerations | 2 |
| 14272 | considerate | 2 |
| 14273 | conjures | 2 |
| 14274 | conjurers | 2 |
| 14275 | conjunctive | 2 |
| 14276 | conjunct | 2 |
| 14277 | conjointly | 2 |
| 14278 | conjectural | 2 |
| 14279 | congruent | 2 |
| 14280 | congregated | 2 |
| 14281 | conger | 2 |
| 14282 | confutes | 2 |
| 14283 | confusions | 2 |
| 14284 | conformable | 2 |
| 14285 | conflicting | 2 |
| 14286 | confirmations | 2 |
| 14287 | confining | 2 |
| 14288 | confidently | 2 |
| 14289 | confesses | 2 |
| 14290 | confessed | 2 |
| 14291 | conferring | 2 |
| 14292 | conduits | 2 |
| 14293 | conduce | 2 |
| 14294 | condign | 2 |
| 14295 | condescend | 2 |
| 14296 | condemning | 2 |
| 14297 | concernings | 2 |
| 14298 | comrade | 2 |
| 14299 | computation | 2 |
| 14300 | compulsive | 2 |
| 14301 | comprehends | 2 |
| 14302 | comprehend | 2 |
| 14303 | compose | 2 |
| 14304 | compliments | 2 |
| 14305 | complements | 2 |
| 14306 | compiled | 2 |
| 14307 | compile | 2 |
| 14308 | competent | 2 |
| 14309 | competency | 2 |
| 14310 | compeers | 2 |
| 14311 | compassionate | 2 |
| 14312 | compassing | 2 |
| 14313 | companionship | 2 |
| 14314 | communication | 2 |
| 14315 | commonalty | 2 |
| 14316 | commixture | 2 |
| 14317 | commencement | 2 |
| 14318 | commenc | 2 |
| 14319 | commandments | 2 |
| 14320 | comma | 2 |
| 14321 | comical | 2 |
| 14322 | comic | 2 |
| 14323 | comets | 2 |
| 14324 | combustion | 2 |
| 14325 | combin | 2 |
| 14326 | colted | 2 |
| 14327 | collop | 2 |
| 14328 | colliers | 2 |
| 14329 | collied | 2 |
| 14330 | collateral | 2 |
| 14331 | coldness | 2 |
| 14332 | colbrand | 2 |
| 14333 | col | 2 |
| 14334 | coins | 2 |
| 14335 | coinage | 2 |
| 14336 | coign | 2 |
| 14337 | coffins | 2 |
| 14338 | cockney | 2 |
| 14339 | cockatrice | 2 |
| 14340 | cobwebs | 2 |
| 14341 | cobbler | 2 |
| 14342 | coasts | 2 |
| 14343 | coasting | 2 |
| 14344 | coaches | 2 |
| 14345 | clusters | 2 |
| 14346 | cloyed | 2 |
| 14347 | clownish | 2 |
| 14348 | clouted | 2 |
| 14349 | clotpoll | 2 |
| 14350 | clothier | 2 |
| 14351 | closer | 2 |
| 14352 | clogs | 2 |
| 14353 | clipt | 2 |
| 14354 | cling | 2 |
| 14355 | climbs | 2 |
| 14356 | cliffs | 2 |
| 14357 | cleitus | 2 |
| 14358 | cleanse | 2 |
| 14359 | claudius | 2 |
| 14360 | clasps | 2 |
| 14361 | clapping | 2 |
| 14362 | clangor | 2 |
| 14363 | clamors | 2 |
| 14364 | clamb | 2 |
| 14365 | cites | 2 |
| 14366 | cistern | 2 |
| 14367 | circumvention | 2 |
| 14368 | circumspect | 2 |
| 14369 | circuit | 2 |
| 14370 | circling | 2 |
| 14371 | circe | 2 |
| 14372 | cicely | 2 |
| 14373 | churls | 2 |
| 14374 | churchyards | 2 |
| 14375 | chough | 2 |
| 14376 | chor | 2 |
| 14377 | chops | 2 |
| 14378 | choking | 2 |
| 14379 | choked | 2 |
| 14380 | chirrah | 2 |
| 14381 | chipp | 2 |
| 14382 | chine | 2 |
| 14383 | chimneys | 2 |
| 14384 | childlike | 2 |
| 14385 | chicken | 2 |
| 14386 | chick | 2 |
| 14387 | cheveril | 2 |
| 14388 | chevalier | 2 |
| 14389 | cheval | 2 |
| 14390 | chestnut | 2 |
| 14391 | cherishing | 2 |
| 14392 | cher | 2 |
| 14393 | cheered | 2 |
| 14394 | checked | 2 |
| 14395 | cheaters | 2 |
| 14396 | cheapside | 2 |
| 14397 | chattels | 2 |
| 14398 | chastised | 2 |
| 14399 | chased | 2 |
| 14400 | chartreux | 2 |
| 14401 | charnel | 2 |
| 14402 | charlemain | 2 |
| 14403 | charactery | 2 |
| 14404 | chapmen | 2 |
| 14405 | chapless | 2 |
| 14406 | chanticleer | 2 |
| 14407 | chant | 2 |
| 14408 | channels | 2 |
| 14409 | chanc | 2 |
| 14410 | chambermaids | 2 |
| 14411 | chalice | 2 |
| 14412 | cetera | 2 |
| 14413 | cesse | 2 |
| 14414 | certified | 2 |
| 14415 | century | 2 |
| 14416 | censer | 2 |
| 14417 | celebrated | 2 |
| 14418 | cedars | 2 |
| 14419 | cavern | 2 |
| 14420 | cautelous | 2 |
| 14421 | caucasus | 2 |
| 14422 | caterwauling | 2 |
| 14423 | catechism | 2 |
| 14424 | cataian | 2 |
| 14425 | casual | 2 |
| 14426 | cas | 2 |
| 14427 | carving | 2 |
| 14428 | carver | 2 |
| 14429 | carrions | 2 |
| 14430 | carousing | 2 |
| 14431 | carouse | 2 |
| 14432 | carous | 2 |
| 14433 | carol | 2 |
| 14434 | carnation | 2 |
| 14435 | caret | 2 |
| 14436 | careers | 2 |
| 14437 | cards | 2 |
| 14438 | cardecue | 2 |
| 14439 | carcasses | 2 |
| 14440 | carcanet | 2 |
| 14441 | carbuncles | 2 |
| 14442 | carat | 2 |
| 14443 | captivate | 2 |
| 14444 | captainship | 2 |
| 14445 | capp | 2 |
| 14446 | capons | 2 |
| 14447 | capitulate | 2 |
| 14448 | canvass | 2 |
| 14449 | cantle | 2 |
| 14450 | canopies | 2 |
| 14451 | canonized | 2 |
| 14452 | canoniz | 2 |
| 14453 | cannoneer | 2 |
| 14454 | cancell | 2 |
| 14455 | canaries | 2 |
| 14456 | canakin | 2 |
| 14457 | camest | 2 |
| 14458 | cambria | 2 |
| 14459 | calves | 2 |
| 14460 | calculate | 2 |
| 14461 | caged | 2 |
| 14462 | caesarion | 2 |
| 14463 | cackling | 2 |
| 14464 | ca | 2 |
| 14465 | bye | 2 |
| 14466 | buyer | 2 |
| 14467 | buttons | 2 |
| 14468 | buttocks | 2 |
| 14469 | butcheries | 2 |
| 14470 | buss | 2 |
| 14471 | busily | 2 |
| 14472 | burying | 2 |
| 14473 | burton | 2 |
| 14474 | burr | 2 |
| 14475 | burnish | 2 |
| 14476 | burneth | 2 |
| 14477 | burly | 2 |
| 14478 | burghers | 2 |
| 14479 | buoy | 2 |
| 14480 | bundle | 2 |
| 14481 | bunches | 2 |
| 14482 | bullocks | 2 |
| 14483 | bullens | 2 |
| 14484 | bug | 2 |
| 14485 | buckets | 2 |
| 14486 | brushes | 2 |
| 14487 | broader | 2 |
| 14488 | britaines | 2 |
| 14489 | bristol | 2 |
| 14490 | bristled | 2 |
| 14491 | brink | 2 |
| 14492 | bringeth | 2 |
| 14493 | brightly | 2 |
| 14494 | briefness | 2 |
| 14495 | bridled | 2 |
| 14496 | bridges | 2 |
| 14497 | bridgenorth | 2 |
| 14498 | brides | 2 |
| 14499 | bricklayer | 2 |
| 14500 | brewing | 2 |
| 14501 | brewer | 2 |
| 14502 | bretheren | 2 |
| 14503 | breeders | 2 |
| 14504 | breasted | 2 |
| 14505 | breaches | 2 |
| 14506 | braz | 2 |
| 14507 | braved | 2 |
| 14508 | bras | 2 |
| 14509 | brained | 2 |
| 14510 | braggarts | 2 |
| 14511 | bragg | 2 |
| 14512 | bracelets | 2 |
| 14513 | brabbler | 2 |
| 14514 | brabble | 2 |
| 14515 | boyish | 2 |
| 14516 | bowing | 2 |
| 14517 | bowed | 2 |
| 14518 | bourchier | 2 |
| 14519 | bounding | 2 |
| 14520 | bounden | 2 |
| 14521 | bounce | 2 |
| 14522 | bouciqualt | 2 |
| 14523 | bottoms | 2 |
| 14524 | bottomless | 2 |
| 14525 | bottles | 2 |
| 14526 | bottled | 2 |
| 14527 | bots | 2 |
| 14528 | bosworth | 2 |
| 14529 | bonne | 2 |
| 14530 | bonfire | 2 |
| 14531 | bombast | 2 |
| 14532 | bombard | 2 |
| 14533 | bolster | 2 |
| 14534 | boldest | 2 |
| 14535 | bohemian | 2 |
| 14536 | bog | 2 |
| 14537 | bodykins | 2 |
| 14538 | bodements | 2 |
| 14539 | boded | 2 |
| 14540 | boasts | 2 |
| 14541 | boards | 2 |
| 14542 | blust | 2 |
| 14543 | blunts | 2 |
| 14544 | blunting | 2 |
| 14545 | blunted | 2 |
| 14546 | blossoming | 2 |
| 14547 | bloodshed | 2 |
| 14548 | bloodied | 2 |
| 14549 | blisters | 2 |
| 14550 | blinking | 2 |
| 14551 | blinding | 2 |
| 14552 | blindfold | 2 |
| 14553 | blesses | 2 |
| 14554 | blessedly | 2 |
| 14555 | blent | 2 |
| 14556 | blended | 2 |
| 14557 | bleared | 2 |
| 14558 | bleaching | 2 |
| 14559 | blazoning | 2 |
| 14560 | blazing | 2 |
| 14561 | blaz | 2 |
| 14562 | blaspheming | 2 |
| 14563 | blames | 2 |
| 14564 | blameless | 2 |
| 14565 | bladed | 2 |
| 14566 | blackfriars | 2 |
| 14567 | blackest | 2 |
| 14568 | blackberries | 2 |
| 14569 | blackamoors | 2 |
| 14570 | blackamoor | 2 |
| 14571 | blabb | 2 |
| 14572 | blab | 2 |
| 14573 | bitterest | 2 |
| 14574 | bitt | 2 |
| 14575 | bisson | 2 |
| 14576 | biscuit | 2 |
| 14577 | birthday | 2 |
| 14578 | billow | 2 |
| 14579 | billeted | 2 |
| 14580 | bilbo | 2 |
| 14581 | biding | 2 |
| 14582 | bewail | 2 |
| 14583 | bevy | 2 |
| 14584 | betting | 2 |
| 14585 | bettering | 2 |
| 14586 | betraying | 2 |
| 14587 | betideth | 2 |
| 14588 | beteem | 2 |
| 14589 | bestirr | 2 |
| 14590 | bestir | 2 |
| 14591 | bespake | 2 |
| 14592 | besort | 2 |
| 14593 | besmirch | 2 |
| 14594 | bergomask | 2 |
| 14595 | bereaved | 2 |
| 14596 | berard | 2 |
| 14597 | bequeathing | 2 |
| 14598 | bennet | 2 |
| 14599 | benedicite | 2 |
| 14600 | benches | 2 |
| 14601 | bemock | 2 |
| 14602 | belt | 2 |
| 14603 | bellyful | 2 |
| 14604 | bellowing | 2 |
| 14605 | bellowed | 2 |
| 14606 | bellow | 2 |
| 14607 | bellies | 2 |
| 14608 | belgia | 2 |
| 14609 | beldams | 2 |
| 14610 | behoof | 2 |
| 14611 | behaved | 2 |
| 14612 | beginners | 2 |
| 14613 | befriends | 2 |
| 14614 | befriended | 2 |
| 14615 | beeves | 2 |
| 14616 | bedtime | 2 |
| 14617 | bedrid | 2 |
| 14618 | becks | 2 |
| 14619 | beaumont | 2 |
| 14620 | beardless | 2 |
| 14621 | bean | 2 |
| 14622 | beached | 2 |
| 14623 | bays | 2 |
| 14624 | battering | 2 |
| 14625 | batten | 2 |
| 14626 | bathed | 2 |
| 14627 | basting | 2 |
| 14628 | baskets | 2 |
| 14629 | bases | 2 |
| 14630 | bas | 2 |
| 14631 | barricado | 2 |
| 14632 | barns | 2 |
| 14633 | barnes | 2 |
| 14634 | barne | 2 |
| 14635 | barn | 2 |
| 14636 | barking | 2 |
| 14637 | barbed | 2 |
| 14638 | barbason | 2 |
| 14639 | barbarian | 2 |
| 14640 | banquets | 2 |
| 14641 | banns | 2 |
| 14642 | banes | 2 |
| 14643 | bandying | 2 |
| 14644 | balk | 2 |
| 14645 | bake | 2 |
| 14646 | baffle | 2 |
| 14647 | baffl | 2 |
| 14648 | baes | 2 |
| 14649 | bacchus | 2 |
| 14650 | bacchanals | 2 |
| 14651 | babylon | 2 |
| 14652 | ba | 2 |
| 14653 | azur | 2 |
| 14654 | awork | 2 |
| 14655 | awl | 2 |
| 14656 | aweless | 2 |
| 14657 | awaked | 2 |
| 14658 | await | 2 |
| 14659 | avow | 2 |
| 14660 | avouches | 2 |
| 14661 | avenged | 2 |
| 14662 | avarice | 2 |
| 14663 | avails | 2 |
| 14664 | authorized | 2 |
| 14665 | austerely | 2 |
| 14666 | aussi | 2 |
| 14667 | aurora | 2 |
| 14668 | august | 2 |
| 14669 | augury | 2 |
| 14670 | augurer | 2 |
| 14671 | augmenting | 2 |
| 14672 | auger | 2 |
| 14673 | auditor | 2 |
| 14674 | audible | 2 |
| 14675 | audacity | 2 |
| 14676 | au | 2 |
| 14677 | atwain | 2 |
| 14678 | attributes | 2 |
| 14679 | attracts | 2 |
| 14680 | attractive | 2 |
| 14681 | attraction | 2 |
| 14682 | attendents | 2 |
| 14683 | attempting | 2 |
| 14684 | attempted | 2 |
| 14685 | atonement | 2 |
| 14686 | atlas | 2 |
| 14687 | ates | 2 |
| 14688 | atalanta | 2 |
| 14689 | astray | 2 |
| 14690 | assyrian | 2 |
| 14691 | assumes | 2 |
| 14692 | assuage | 2 |
| 14693 | assistants | 2 |
| 14694 | assigns | 2 |
| 14695 | assent | 2 |
| 14696 | assemblies | 2 |
| 14697 | assaulted | 2 |
| 14698 | assails | 2 |
| 14699 | assailing | 2 |
| 14700 | aspir | 2 |
| 14701 | aspen | 2 |
| 14702 | asks | 2 |
| 14703 | asketh | 2 |
| 14704 | askance | 2 |
| 14705 | ashford | 2 |
| 14706 | ash | 2 |
| 14707 | ascended | 2 |
| 14708 | articulate | 2 |
| 14709 | arrives | 2 |
| 14710 | arrests | 2 |
| 14711 | armourers | 2 |
| 14712 | armipotent | 2 |
| 14713 | armigero | 2 |
| 14714 | armenia | 2 |
| 14715 | arme | 2 |
| 14716 | ariseth | 2 |
| 14717 | ariadne | 2 |
| 14718 | argued | 2 |
| 14719 | argier | 2 |
| 14720 | ardour | 2 |
| 14721 | archibald | 2 |
| 14722 | archery | 2 |
| 14723 | archer | 2 |
| 14724 | arched | 2 |
| 14725 | archdeacon | 2 |
| 14726 | arbitrator | 2 |
| 14727 | apter | 2 |
| 14728 | apricocks | 2 |
| 14729 | appliances | 2 |
| 14730 | applauding | 2 |
| 14731 | appertinent | 2 |
| 14732 | appertainings | 2 |
| 14733 | appertain | 2 |
| 14734 | appals | 2 |
| 14735 | appal | 2 |
| 14736 | apartments | 2 |
| 14737 | anvil | 2 |
| 14738 | antics | 2 |
| 14739 | ante | 2 |
| 14740 | anoint | 2 |
| 14741 | angerly | 2 |
| 14742 | ancientry | 2 |
| 14743 | anchoring | 2 |
| 14744 | anatomiz | 2 |
| 14745 | amurath | 2 |
| 14746 | amplest | 2 |
| 14747 | amort | 2 |
| 14748 | amities | 2 |
| 14749 | amis | 2 |
| 14750 | ambitiously | 2 |
| 14751 | ambitions | 2 |
| 14752 | amazonian | 2 |
| 14753 | amazedness | 2 |
| 14754 | altered | 2 |
| 14755 | almanac | 2 |
| 14756 | allusion | 2 |
| 14757 | allure | 2 |
| 14758 | alleys | 2 |
| 14759 | alley | 2 |
| 14760 | alleged | 2 |
| 14761 | allege | 2 |
| 14762 | allaying | 2 |
| 14763 | alla | 2 |
| 14764 | alexandrian | 2 |
| 14765 | ales | 2 |
| 14766 | aleppo | 2 |
| 14767 | alderman | 2 |
| 14768 | alchemist | 2 |
| 14769 | ainsi | 2 |
| 14770 | aids | 2 |
| 14771 | aiding | 2 |
| 14772 | aha | 2 |
| 14773 | agone | 2 |
| 14774 | agitation | 2 |
| 14775 | afloat | 2 |
| 14776 | afield | 2 |
| 14777 | affy | 2 |
| 14778 | afflicts | 2 |
| 14779 | affined | 2 |
| 14780 | affectation | 2 |
| 14781 | aer | 2 |
| 14782 | advises | 2 |
| 14783 | advisedly | 2 |
| 14784 | advertise | 2 |
| 14785 | adventurous | 2 |
| 14786 | advantageous | 2 |
| 14787 | adulterous | 2 |
| 14788 | adramadio | 2 |
| 14789 | adornment | 2 |
| 14790 | adorned | 2 |
| 14791 | adores | 2 |
| 14792 | adoration | 2 |
| 14793 | admonition | 2 |
| 14794 | admiringly | 2 |
| 14795 | adjourn | 2 |
| 14796 | adjoining | 2 |
| 14797 | adjacent | 2 |
| 14798 | adieus | 2 |
| 14799 | adhere | 2 |
| 14800 | addrest | 2 |
| 14801 | addiction | 2 |
| 14802 | addicted | 2 |
| 14803 | adage | 2 |
| 14804 | acute | 2 |
| 14805 | actual | 2 |
| 14806 | acquir | 2 |
| 14807 | accustomed | 2 |
| 14808 | accuses | 2 |
| 14809 | accusativo | 2 |
| 14810 | accumulate | 2 |
| 14811 | accoutrements | 2 |
| 14812 | accoutrement | 2 |
| 14813 | accoutred | 2 |
| 14814 | accounts | 2 |
| 14815 | accountant | 2 |
| 14816 | accepts | 2 |
| 14817 | academes | 2 |
| 14818 | aby | 2 |
| 14819 | absolutely | 2 |
| 14820 | abridge | 2 |
| 14821 | abjur | 2 |
| 14822 | abjects | 2 |
| 14823 | abhorring | 2 |
| 14824 | aberga | 2 |
| 14825 | abel | 2 |
| 14826 | abase | 2 |
| 14827 | abandoned | 2 |
| 14828 | zwagger | 1 |
| 14829 | zone | 1 |
| 14830 | zodiacs | 1 |
| 14831 | zodiac | 1 |
| 14832 | zo | 1 |
| 14833 | zephyrs | 1 |
| 14834 | zenith | 1 |
| 14835 | zenelophon | 1 |
| 14836 | zed | 1 |
| 14837 | zeals | 1 |
| 14838 | zany | 1 |
| 14839 | zanies | 1 |
| 14840 | youtli | 1 |
| 14841 | younglings | 1 |
| 14842 | yorks | 1 |
| 14843 | yore | 1 |
| 14844 | yongrey | 1 |
| 14845 | yoketh | 1 |
| 14846 | yokefellow | 1 |
| 14847 | yielders | 1 |
| 14848 | yicld | 1 |
| 14849 | yesterdays | 1 |
| 14850 | yelping | 1 |
| 14851 | yells | 1 |
| 14852 | yellows | 1 |
| 14853 | yellowness | 1 |
| 14854 | yellowing | 1 |
| 14855 | yellowed | 1 |
| 14856 | yedward | 1 |
| 14857 | yeast | 1 |
| 14858 | yearn | 1 |
| 14859 | yead | 1 |
| 14860 | ycliped | 1 |
| 14861 | ycleped | 1 |
| 14862 | yaw | 1 |
| 14863 | yaughan | 1 |
| 14864 | xv | 1 |
| 14865 | xiv | 1 |
| 14866 | xanthippe | 1 |
| 14867 | wul | 1 |
| 14868 | wrying | 1 |
| 14869 | wry | 1 |
| 14870 | wroth | 1 |
| 14871 | wronk | 1 |
| 14872 | wrongly | 1 |
| 14873 | wronging | 1 |
| 14874 | writs | 1 |
| 14875 | writhled | 1 |
| 14876 | wrists | 1 |
| 14877 | wringer | 1 |
| 14878 | wretchcd | 1 |
| 14879 | wresting | 1 |
| 14880 | wrens | 1 |
| 14881 | wrecks | 1 |
| 14882 | wreathen | 1 |
| 14883 | wreaks | 1 |
| 14884 | wrathfully | 1 |
| 14885 | wrapt | 1 |
| 14886 | wraps | 1 |
| 14887 | wranglers | 1 |
| 14888 | wrangler | 1 |
| 14889 | wrackful | 1 |
| 14890 | wouns | 1 |
| 14891 | woundless | 1 |
| 14892 | woundings | 1 |
| 14893 | wouldest | 1 |
| 14894 | wouid | 1 |
| 14895 | wotting | 1 |
| 14896 | worthied | 1 |
| 14897 | worsted | 1 |
| 14898 | worshippest | 1 |
| 14899 | worshipper | 1 |
| 14900 | worshipfully | 1 |
| 14901 | worrying | 1 |
| 14902 | worry | 1 |
| 14903 | worries | 1 |
| 14904 | worried | 1 |
| 14905 | wormy | 1 |
| 14906 | worky | 1 |
| 14907 | workmanship | 1 |
| 14908 | workmanly | 1 |
| 14909 | workers | 1 |
| 14910 | worins | 1 |
| 14911 | woolward | 1 |
| 14912 | woolsey | 1 |
| 14913 | woolsack | 1 |
| 14914 | wooingly | 1 |
| 14915 | woof | 1 |
| 14916 | woodmonger | 1 |
| 14917 | woodland | 1 |
| 14918 | wondrously | 1 |
| 14919 | wondering | 1 |
| 14920 | wonderfully | 1 |
| 14921 | wondered | 1 |
| 14922 | woncot | 1 |
| 14923 | womby | 1 |
| 14924 | womankind | 1 |
| 14925 | wolfish | 1 |
| 14926 | woefullest | 1 |
| 14927 | wo | 1 |
| 14928 | wived | 1 |
| 14929 | wittolly | 1 |
| 14930 | wittol | 1 |
| 14931 | witting | 1 |
| 14932 | wittily | 1 |
| 14933 | wittiest | 1 |
| 14934 | withstood | 1 |
| 14935 | withstanding | 1 |
| 14936 | withold | 1 |
| 14937 | withdrawing | 1 |
| 14938 | witching | 1 |
| 14939 | wist | 1 |
| 14940 | wisp | 1 |
| 14941 | wishtly | 1 |
| 14942 | wishful | 1 |
| 14943 | wisheth | 1 |
| 14944 | wishers | 1 |
| 14945 | wisher | 1 |
| 14946 | wiselier | 1 |
| 14947 | wire | 1 |
| 14948 | wiping | 1 |
| 14949 | wipes | 1 |
| 14950 | winterly | 1 |
| 14951 | winnows | 1 |
| 14952 | wingham | 1 |
| 14953 | wingfield | 1 |
| 14954 | windlasses | 1 |
| 14955 | windgalls | 1 |
| 14956 | wincot | 1 |
| 14957 | winch | 1 |
| 14958 | wince | 1 |
| 14959 | wimpled | 1 |
| 14960 | willeth | 1 |
| 14961 | willers | 1 |
| 14962 | wilfulness | 1 |
| 14963 | wilfulnes | 1 |
| 14964 | wilds | 1 |
| 14965 | wildfire | 1 |
| 14966 | wildcats | 1 |
| 14967 | widowhood | 1 |
| 14968 | widens | 1 |
| 14969 | wid | 1 |
| 14970 | wicky | 1 |
| 14971 | wicket | 1 |
| 14972 | wickednes | 1 |
| 14973 | wick | 1 |
| 14974 | whorish | 1 |
| 14975 | whoring | 1 |
| 14976 | whoresons | 1 |
| 14977 | whoremonger | 1 |
| 14978 | whoremasterly | 1 |
| 14979 | whor | 1 |
| 14980 | whooping | 1 |
| 14981 | whoobub | 1 |
| 14982 | wholesom | 1 |
| 14983 | whizzing | 1 |
| 14984 | whittle | 1 |
| 14985 | whitsters | 1 |
| 14986 | whiting | 1 |
| 14987 | whitest | 1 |
| 14988 | whitely | 1 |
| 14989 | whitehall | 1 |
| 14990 | whistles | 1 |
| 14991 | whist | 1 |
| 14992 | whirlpool | 1 |
| 14993 | whirligig | 1 |
| 14994 | whirled | 1 |
| 14995 | whipstock | 1 |
| 14996 | whipster | 1 |
| 14997 | whippers | 1 |
| 14998 | whinid | 1 |
| 14999 | whined | 1 |
| 15000 | whin | 1 |
| 15001 | whiffler | 1 |
| 15002 | whiff | 1 |
| 15003 | whew | 1 |
| 15004 | wheresome | 1 |
| 15005 | whereout | 1 |
| 15006 | whereinto | 1 |
| 15007 | whencesoever | 1 |
| 15008 | whenas | 1 |
| 15009 | whelped | 1 |
| 15010 | whelm | 1 |
| 15011 | whelks | 1 |
| 15012 | whelk | 1 |
| 15013 | wheezing | 1 |
| 15014 | wheeson | 1 |
| 15015 | wheer | 1 |
| 15016 | wheeling | 1 |
| 15017 | wheaten | 1 |
| 15018 | whatsome | 1 |
| 15019 | wharfs | 1 |
| 15020 | wharf | 1 |
| 15021 | whales | 1 |
| 15022 | wezand | 1 |
| 15023 | wetting | 1 |
| 15024 | wenching | 1 |
| 15025 | welshwomen | 1 |
| 15026 | welcomest | 1 |
| 15027 | welcomer | 1 |
| 15028 | weightless | 1 |
| 15029 | weighed | 1 |
| 15030 | weet | 1 |
| 15031 | weepings | 1 |
| 15032 | weepingly | 1 |
| 15033 | weeper | 1 |
| 15034 | weekly | 1 |
| 15035 | weedy | 1 |
| 15036 | weeding | 1 |
| 15037 | weeder | 1 |
| 15038 | weeded | 1 |
| 15039 | wedged | 1 |
| 15040 | weaving | 1 |
| 15041 | weavers | 1 |
| 15042 | weave | 1 |
| 15043 | weathers | 1 |
| 15044 | wearily | 1 |
| 15045 | weariest | 1 |
| 15046 | wearers | 1 |
| 15047 | wealtlly | 1 |
| 15048 | wealthiest | 1 |
| 15049 | wealsmen | 1 |
| 15050 | weakling | 1 |
| 15051 | waywardness | 1 |
| 15052 | waywarder | 1 |
| 15053 | waylay | 1 |
| 15054 | waylaid | 1 |
| 15055 | waxing | 1 |
| 15056 | wawl | 1 |
| 15057 | waw | 1 |
| 15058 | waverer | 1 |
| 15059 | waver | 1 |
| 15060 | waved | 1 |
| 15061 | waterton | 1 |
| 15062 | waterrugs | 1 |
| 15063 | waterpots | 1 |
| 15064 | waterish | 1 |
| 15065 | watering | 1 |
| 15066 | waterford | 1 |
| 15067 | waterfly | 1 |
| 15068 | watered | 1 |
| 15069 | waterdrops | 1 |
| 15070 | watchword | 1 |
| 15071 | watchings | 1 |
| 15072 | wasters | 1 |
| 15073 | washford | 1 |
| 15074 | washer | 1 |
| 15075 | washed | 1 |
| 15076 | warring | 1 |
| 15077 | warrener | 1 |
| 15078 | warren | 1 |
| 15079 | warrantize | 1 |
| 15080 | warrantise | 1 |
| 15081 | warranteth | 1 |
| 15082 | warped | 1 |
| 15083 | warns | 1 |
| 15084 | warned | 1 |
| 15085 | wardrop | 1 |
| 15086 | warden | 1 |
| 15087 | warded | 1 |
| 15088 | wappen | 1 |
| 15089 | wantonly | 1 |
| 15090 | wann | 1 |
| 15091 | wanes | 1 |
| 15092 | waned | 1 |
| 15093 | wanders | 1 |
| 15094 | walloon | 1 |
| 15095 | wallon | 1 |
| 15096 | wallets | 1 |
| 15097 | wallet | 1 |
| 15098 | wakest | 1 |
| 15099 | waiteth | 1 |
| 15100 | waiter | 1 |
| 15101 | wainscot | 1 |
| 15102 | wainropes | 1 |
| 15103 | wain | 1 |
| 15104 | wailful | 1 |
| 15105 | wagtail | 1 |
| 15106 | wagon | 1 |
| 15107 | waggoner | 1 |
| 15108 | waggling | 1 |
| 15109 | wafting | 1 |
| 15110 | wafer | 1 |
| 15111 | waddled | 1 |
| 15112 | wad | 1 |
| 15113 | vurther | 1 |
| 15114 | vulnerable | 1 |
| 15115 | vulgo | 1 |
| 15116 | vulgars | 1 |
| 15117 | vulgarly | 1 |
| 15118 | vox | 1 |
| 15119 | vowels | 1 |
| 15120 | vowel | 1 |
| 15121 | voutsafe | 1 |
| 15122 | vour | 1 |
| 15123 | voudrais | 1 |
| 15124 | vouchsafing | 1 |
| 15125 | vouchsafes | 1 |
| 15126 | vouching | 1 |
| 15127 | voucher | 1 |
| 15128 | votarists | 1 |
| 15129 | vortnight | 1 |
| 15130 | vore | 1 |
| 15131 | vomits | 1 |
| 15132 | vomissement | 1 |
| 15133 | voluptuously | 1 |
| 15134 | voluntaries | 1 |
| 15135 | volquessen | 1 |
| 15136 | volivorco | 1 |
| 15137 | volant | 1 |
| 15138 | volable | 1 |
| 15139 | voke | 1 |
| 15140 | voiding | 1 |
| 15141 | voided | 1 |
| 15142 | voce | 1 |
| 15143 | vocatur | 1 |
| 15144 | vocativo | 1 |
| 15145 | vizor | 1 |
| 15146 | vizaments | 1 |
| 15147 | viz | 1 |
| 15148 | vixen | 1 |
| 15149 | vive | 1 |
| 15150 | vivant | 1 |
| 15151 | viva | 1 |
| 15152 | vitx | 1 |
| 15153 | vitruvio | 1 |
| 15154 | vitement | 1 |
| 15155 | vita | 1 |
| 15156 | visitor | 1 |
| 15157 | visitings | 1 |
| 15158 | visitations | 1 |
| 15159 | visibly | 1 |
| 15160 | viscount | 1 |
| 15161 | visard | 1 |
| 15162 | virgo | 1 |
| 15163 | virginalling | 1 |
| 15164 | vir | 1 |
| 15165 | violenteth | 1 |
| 15166 | violator | 1 |
| 15167 | violates | 1 |
| 15168 | violated | 1 |
| 15169 | vint | 1 |
| 15170 | vindicative | 1 |
| 15171 | vincere | 1 |
| 15172 | vinaigre | 1 |
| 15173 | villians | 1 |
| 15174 | villianda | 1 |
| 15175 | villiago | 1 |
| 15176 | villagery | 1 |
| 15177 | villager | 1 |
| 15178 | viler | 1 |
| 15179 | vileness | 1 |
| 15180 | vigitant | 1 |
| 15181 | vigil | 1 |
| 15182 | viewless | 1 |
| 15183 | vieweth | 1 |
| 15184 | vidi | 1 |
| 15185 | videsne | 1 |
| 15186 | vides | 1 |
| 15187 | video | 1 |
| 15188 | victuall | 1 |
| 15189 | victoress | 1 |
| 15190 | victims | 1 |
| 15191 | vict | 1 |
| 15192 | viciousness | 1 |
| 15193 | vici | 1 |
| 15194 | viceroys | 1 |
| 15195 | vicegerent | 1 |
| 15196 | vic | 1 |
| 15197 | viand | 1 |
| 15198 | vexeth | 1 |
| 15199 | vexest | 1 |
| 15200 | vexes | 1 |
| 15201 | veux | 1 |
| 15202 | vetches | 1 |
| 15203 | vetch | 1 |
| 15204 | vesper | 1 |
| 15205 | vert | 1 |
| 15206 | versing | 1 |
| 15207 | versal | 1 |
| 15208 | veronesa | 1 |
| 15209 | vermin | 1 |
| 15210 | vermilion | 1 |
| 15211 | verities | 1 |
| 15212 | verite | 1 |
| 15213 | veritable | 1 |
| 15214 | vergers | 1 |
| 15215 | verefore | 1 |
| 15216 | verdun | 1 |
| 15217 | verbosity | 1 |
| 15218 | verbatim | 1 |
| 15219 | verb | 1 |
| 15220 | venue | 1 |
| 15221 | venturing | 1 |
| 15222 | ventured | 1 |
| 15223 | ventricle | 1 |
| 15224 | ventages | 1 |
| 15225 | venomously | 1 |
| 15226 | venit | 1 |
| 15227 | venial | 1 |
| 15228 | veni | 1 |
| 15229 | vengeances | 1 |
| 15230 | veneys | 1 |
| 15231 | venetians | 1 |
| 15232 | venereal | 1 |
| 15233 | velure | 1 |
| 15234 | veiling | 1 |
| 15235 | vehor | 1 |
| 15236 | vehemence | 1 |
| 15237 | vede | 1 |
| 15238 | ve | 1 |
| 15239 | vauvado | 1 |
| 15240 | vauntingly | 1 |
| 15241 | vaunter | 1 |
| 15242 | vaunted | 1 |
| 15243 | vaumond | 1 |
| 15244 | vaultages | 1 |
| 15245 | vater | 1 |
| 15246 | vastidity | 1 |
| 15247 | varletto | 1 |
| 15248 | varletry | 1 |
| 15249 | varld | 1 |
| 15250 | variety | 1 |
| 15251 | variest | 1 |
| 15252 | variations | 1 |
| 15253 | vara | 1 |
| 15254 | vapor | 1 |
| 15255 | vapians | 1 |
| 15256 | vantbrace | 1 |
| 15257 | vant | 1 |
| 15258 | vanquisheth | 1 |
| 15259 | vanquishest | 1 |
| 15260 | vanishing | 1 |
| 15261 | valuing | 1 |
| 15262 | valueless | 1 |
| 15263 | valorously | 1 |
| 15264 | vally | 1 |
| 15265 | vallant | 1 |
| 15266 | valiantness | 1 |
| 15267 | vales | 1 |
| 15268 | valerius | 1 |
| 15269 | valentio | 1 |
| 15270 | valence | 1 |
| 15271 | valance | 1 |
| 15272 | valanc | 1 |
| 15273 | vais | 1 |
| 15274 | vainglory | 1 |
| 15275 | vainer | 1 |
| 15276 | vaillant | 1 |
| 15277 | vailed | 1 |
| 15278 | vagrom | 1 |
| 15279 | vagram | 1 |
| 15280 | vagabonds | 1 |
| 15281 | vade | 1 |
| 15282 | vacation | 1 |
| 15283 | va | 1 |
| 15284 | uy | 1 |
| 15285 | uttereth | 1 |
| 15286 | utility | 1 |
| 15287 | utensils | 1 |
| 15288 | utensil | 1 |
| 15289 | usurpingly | 1 |
| 15290 | ushering | 1 |
| 15291 | ushered | 1 |
| 15292 | useless | 1 |
| 15293 | usances | 1 |
| 15294 | ursley | 1 |
| 15295 | ursa | 1 |
| 15296 | urns | 1 |
| 15297 | urges | 1 |
| 15298 | urchinfield | 1 |
| 15299 | urchin | 1 |
| 15300 | upwards | 1 |
| 15301 | upturned | 1 |
| 15302 | upstairs | 1 |
| 15303 | upspring | 1 |
| 15304 | upside | 1 |
| 15305 | upshoot | 1 |
| 15306 | uprous | 1 |
| 15307 | uprising | 1 |
| 15308 | uprightness | 1 |
| 15309 | uprighteously | 1 |
| 15310 | upreared | 1 |
| 15311 | upmost | 1 |
| 15312 | upholding | 1 |
| 15313 | upholdeth | 1 |
| 15314 | uphoarded | 1 |
| 15315 | unwrung | 1 |
| 15316 | unworthier | 1 |
| 15317 | unwooed | 1 |
| 15318 | unwitted | 1 |
| 15319 | unwished | 1 |
| 15320 | unwish | 1 |
| 15321 | unwisely | 1 |
| 15322 | unwiped | 1 |
| 15323 | unwhipp | 1 |
| 15324 | unwept | 1 |
| 15325 | unweighing | 1 |
| 15326 | unweighed | 1 |
| 15327 | unweeded | 1 |
| 15328 | unwedgeable | 1 |
| 15329 | unwed | 1 |
| 15330 | unwearied | 1 |
| 15331 | unwatch | 1 |
| 15332 | unwarily | 1 |
| 15333 | unwares | 1 |
| 15334 | unvulnerable | 1 |
| 15335 | unvisited | 1 |
| 15336 | unvirtuous | 1 |
| 15337 | unviolated | 1 |
| 15338 | unvex | 1 |
| 15339 | unvenerable | 1 |
| 15340 | unveil | 1 |
| 15341 | unvarnish | 1 |
| 15342 | unvanquish | 1 |
| 15343 | unus | 1 |
| 15344 | untutored | 1 |
| 15345 | untune | 1 |
| 15346 | untucked | 1 |
| 15347 | untruth | 1 |
| 15348 | untrussing | 1 |
| 15349 | untroubled | 1 |
| 15350 | untrodden | 1 |
| 15351 | untrod | 1 |
| 15352 | untried | 1 |
| 15353 | untreasur | 1 |
| 15354 | untrained | 1 |
| 15355 | untrain | 1 |
| 15356 | untraded | 1 |
| 15357 | untowardly | 1 |
| 15358 | untold | 1 |
| 15359 | untitled | 1 |
| 15360 | untired | 1 |
| 15361 | untirable | 1 |
| 15362 | untir | 1 |
| 15363 | untimber | 1 |
| 15364 | untied | 1 |
| 15365 | unthread | 1 |
| 15366 | unthink | 1 |
| 15367 | unthankful | 1 |
| 15368 | untented | 1 |
| 15369 | untent | 1 |
| 15370 | untempering | 1 |
| 15371 | untasted | 1 |
| 15372 | untangled | 1 |
| 15373 | untangle | 1 |
| 15374 | untalk | 1 |
| 15375 | unsworn | 1 |
| 15376 | unswayed | 1 |
| 15377 | unswayable | 1 |
| 15378 | unsway | 1 |
| 15379 | unsur | 1 |
| 15380 | unsunn | 1 |
| 15381 | unsullied | 1 |
| 15382 | unsuiting | 1 |
| 15383 | unstuff | 1 |
| 15384 | unstringed | 1 |
| 15385 | unstooping | 1 |
| 15386 | unsteadfast | 1 |
| 15387 | unstable | 1 |
| 15388 | unsquar | 1 |
| 15389 | unspoken | 1 |
| 15390 | unspoke | 1 |
| 15391 | unsphere | 1 |
| 15392 | unspeaking | 1 |
| 15393 | unspeak | 1 |
| 15394 | unsound | 1 |
| 15395 | unsorted | 1 |
| 15396 | unsoil | 1 |
| 15397 | unsmirched | 1 |
| 15398 | unslipping | 1 |
| 15399 | unskillful | 1 |
| 15400 | unskilfully | 1 |
| 15401 | unsisting | 1 |
| 15402 | unsinew | 1 |
| 15403 | unsightly | 1 |
| 15404 | unsifted | 1 |
| 15405 | unshunnable | 1 |
| 15406 | unshunn | 1 |
| 15407 | unshrubb | 1 |
| 15408 | unshrinking | 1 |
| 15409 | unshown | 1 |
| 15410 | unshout | 1 |
| 15411 | unshorn | 1 |
| 15412 | unsheath | 1 |
| 15413 | unshapes | 1 |
| 15414 | unshaped | 1 |
| 15415 | unshaked | 1 |
| 15416 | unshak | 1 |
| 15417 | unsex | 1 |
| 15418 | unsever | 1 |
| 15419 | unsettle | 1 |
| 15420 | unset | 1 |
| 15421 | unserviceable | 1 |
| 15422 | unseparable | 1 |
| 15423 | unseminar | 1 |
| 15424 | unseemly | 1 |
| 15425 | unseeming | 1 |
| 15426 | unseduc | 1 |
| 15427 | unsecret | 1 |
| 15428 | unseconded | 1 |
| 15429 | unseasoned | 1 |
| 15430 | unseasonably | 1 |
| 15431 | unsearch | 1 |
| 15432 | unseam | 1 |
| 15433 | unscratch | 1 |
| 15434 | unscour | 1 |
| 15435 | unscorch | 1 |
| 15436 | unscann | 1 |
| 15437 | unscalable | 1 |
| 15438 | unsaluted | 1 |
| 15439 | unrough | 1 |
| 15440 | unroot | 1 |
| 15441 | unroosted | 1 |
| 15442 | unroof | 1 |
| 15443 | unrivall | 1 |
| 15444 | unripp | 1 |
| 15445 | unripe | 1 |
| 15446 | unrightful | 1 |
| 15447 | unrighteous | 1 |
| 15448 | unrewarded | 1 |
| 15449 | unrevers | 1 |
| 15450 | unrestrained | 1 |
| 15451 | unrestor | 1 |
| 15452 | unresolv | 1 |
| 15453 | unreprievable | 1 |
| 15454 | unremovably | 1 |
| 15455 | unremovable | 1 |
| 15456 | unregist | 1 |
| 15457 | unregarded | 1 |
| 15458 | unrecuring | 1 |
| 15459 | unrecounted | 1 |
| 15460 | unreconciliable | 1 |
| 15461 | unreconciled | 1 |
| 15462 | unreclaimed | 1 |
| 15463 | unreasonably | 1 |
| 15464 | unread | 1 |
| 15465 | unrak | 1 |
| 15466 | unraised | 1 |
| 15467 | unquietly | 1 |
| 15468 | unquestionable | 1 |
| 15469 | unqueen | 1 |
| 15470 | unqualitied | 1 |
| 15471 | unpurpos | 1 |
| 15472 | unpurged | 1 |
| 15473 | unpublish | 1 |
| 15474 | unprun | 1 |
| 15475 | unprovokes | 1 |
| 15476 | unprovident | 1 |
| 15477 | unprovide | 1 |
| 15478 | unproportion | 1 |
| 15479 | unproperly | 1 |
| 15480 | unproper | 1 |
| 15481 | unprofited | 1 |
| 15482 | unpriz | 1 |
| 15483 | unprevented | 1 |
| 15484 | unprevailing | 1 |
| 15485 | unpress | 1 |
| 15486 | unpremeditated | 1 |
| 15487 | unpossible | 1 |
| 15488 | unpossessing | 1 |
| 15489 | unpossess | 1 |
| 15490 | unpolluted | 1 |
| 15491 | unpolished | 1 |
| 15492 | unpolicied | 1 |
| 15493 | unpleasant | 1 |
| 15494 | unpleas | 1 |
| 15495 | unplausive | 1 |
| 15496 | unplagu | 1 |
| 15497 | unpitifully | 1 |
| 15498 | unpink | 1 |
| 15499 | unpick | 1 |
| 15500 | unperfectness | 1 |
| 15501 | unperfect | 1 |
| 15502 | unpeg | 1 |
| 15503 | unpeaceable | 1 |
| 15504 | unpay | 1 |
| 15505 | unpaved | 1 |
| 15506 | unpath | 1 |
| 15507 | unpartial | 1 |
| 15508 | unpack | 1 |
| 15509 | unowed | 1 |
| 15510 | unnumber | 1 |
| 15511 | unnumb | 1 |
| 15512 | unnoble | 1 |
| 15513 | unnerved | 1 |
| 15514 | unneighbourly | 1 |
| 15515 | unnecessarily | 1 |
| 15516 | unnaturalness | 1 |
| 15517 | unnaturally | 1 |
| 15518 | unmuzzled | 1 |
| 15519 | unmuzzle | 1 |
| 15520 | unmusical | 1 |
| 15521 | unmuffles | 1 |
| 15522 | unmoving | 1 |
| 15523 | unmoved | 1 |
| 15524 | unmov | 1 |
| 15525 | unmoan | 1 |
| 15526 | unmix | 1 |
| 15527 | unmitigated | 1 |
| 15528 | unmitigable | 1 |
| 15529 | unmindfull | 1 |
| 15530 | unminded | 1 |
| 15531 | unmeriting | 1 |
| 15532 | unmerciful | 1 |
| 15533 | unmellowed | 1 |
| 15534 | unmast | 1 |
| 15535 | unmasking | 1 |
| 15536 | unmasked | 1 |
| 15537 | unmarried | 1 |
| 15538 | unmannerd | 1 |
| 15539 | unmanner | 1 |
| 15540 | unmade | 1 |
| 15541 | unloving | 1 |
| 15542 | unloos | 1 |
| 15543 | unlocks | 1 |
| 15544 | unloads | 1 |
| 15545 | unloading | 1 |
| 15546 | unloaded | 1 |
| 15547 | unlink | 1 |
| 15548 | unlineal | 1 |
| 15549 | unlimited | 1 |
| 15550 | unlick | 1 |
| 15551 | unletter | 1 |
| 15552 | unlesson | 1 |
| 15553 | unlaid | 1 |
| 15554 | unlace | 1 |
| 15555 | unknowing | 1 |
| 15556 | unkinglike | 1 |
| 15557 | unkept | 1 |
| 15558 | unjustice | 1 |
| 15559 | unjointed | 1 |
| 15560 | universities | 1 |
| 15561 | unions | 1 |
| 15562 | unintelligent | 1 |
| 15563 | uninhabited | 1 |
| 15564 | uninhabitable | 1 |
| 15565 | unimproved | 1 |
| 15566 | unicorn | 1 |
| 15567 | unhurtful | 1 |
| 15568 | unhous | 1 |
| 15569 | unhospitable | 1 |
| 15570 | unhorse | 1 |
| 15571 | unhopefullest | 1 |
| 15572 | unhop | 1 |
| 15573 | unhidden | 1 |
| 15574 | unhelpful | 1 |
| 15575 | unheedy | 1 |
| 15576 | unheedfully | 1 |
| 15577 | unhearts | 1 |
| 15578 | unharm | 1 |
| 15579 | unhardened | 1 |
| 15580 | unhappied | 1 |
| 15581 | unhang | 1 |
| 15582 | unhand | 1 |
| 15583 | unguem | 1 |
| 15584 | ungrown | 1 |
| 15585 | ungravely | 1 |
| 15586 | ungotten | 1 |
| 15587 | ungot | 1 |
| 15588 | ungor | 1 |
| 15589 | ungodly | 1 |
| 15590 | ungird | 1 |
| 15591 | ungentleness | 1 |
| 15592 | ungenitur | 1 |
| 15593 | ungart | 1 |
| 15594 | unfought | 1 |
| 15595 | unfortified | 1 |
| 15596 | unforfeited | 1 |
| 15597 | unforced | 1 |
| 15598 | unforc | 1 |
| 15599 | unfool | 1 |
| 15600 | unfoldeth | 1 |
| 15601 | unfitness | 1 |
| 15602 | unfilial | 1 |
| 15603 | unfenced | 1 |
| 15604 | unfellowed | 1 |
| 15605 | unfeed | 1 |
| 15606 | unfed | 1 |
| 15607 | unfather | 1 |
| 15608 | unfasten | 1 |
| 15609 | unfashionable | 1 |
| 15610 | unfam | 1 |
| 15611 | unfallible | 1 |
| 15612 | unfaithful | 1 |
| 15613 | unfair | 1 |
| 15614 | unexpressive | 1 |
| 15615 | unexperient | 1 |
| 15616 | unexperienc | 1 |
| 15617 | unexecuted | 1 |
| 15618 | unexamin | 1 |
| 15619 | unelected | 1 |
| 15620 | uneffectual | 1 |
| 15621 | uneducated | 1 |
| 15622 | uneath | 1 |
| 15623 | uneasines | 1 |
| 15624 | unearthly | 1 |
| 15625 | unearned | 1 |
| 15626 | uneared | 1 |
| 15627 | undutiful | 1 |
| 15628 | unduteous | 1 |
| 15629 | undressed | 1 |
| 15630 | undress | 1 |
| 15631 | undream | 1 |
| 15632 | undoubtedly | 1 |
| 15633 | undivided | 1 |
| 15634 | undividable | 1 |
| 15635 | undistinguished | 1 |
| 15636 | undispos | 1 |
| 15637 | undishonoured | 1 |
| 15638 | undiscernible | 1 |
| 15639 | undinted | 1 |
| 15640 | undetermin | 1 |
| 15641 | undeservers | 1 |
| 15642 | undescried | 1 |
| 15643 | underwrite | 1 |
| 15644 | underwrit | 1 |
| 15645 | underwent | 1 |
| 15646 | undervalued | 1 |
| 15647 | undervalu | 1 |
| 15648 | undertakeing | 1 |
| 15649 | underta | 1 |
| 15650 | understandings | 1 |
| 15651 | understandeth | 1 |
| 15652 | underprizing | 1 |
| 15653 | underminers | 1 |
| 15654 | underlings | 1 |
| 15655 | underground | 1 |
| 15656 | undergone | 1 |
| 15657 | undergoing | 1 |
| 15658 | underfoot | 1 |
| 15659 | undercrest | 1 |
| 15660 | underborne | 1 |
| 15661 | underbearing | 1 |
| 15662 | undeeded | 1 |
| 15663 | undeck | 1 |
| 15664 | undeaf | 1 |
| 15665 | uncurse | 1 |
| 15666 | uncurls | 1 |
| 15667 | uncurbed | 1 |
| 15668 | uncurbable | 1 |
| 15669 | uncuckolded | 1 |
| 15670 | unctuous | 1 |
| 15671 | uncross | 1 |
| 15672 | uncropped | 1 |
| 15673 | uncourteous | 1 |
| 15674 | uncounted | 1 |
| 15675 | uncorrected | 1 |
| 15676 | uncontroll | 1 |
| 15677 | uncontemn | 1 |
| 15678 | unconstrain | 1 |
| 15679 | unconquered | 1 |
| 15680 | unconquer | 1 |
| 15681 | unconfirmed | 1 |
| 15682 | unconfirm | 1 |
| 15683 | unconfinable | 1 |
| 15684 | uncomprehensive | 1 |
| 15685 | uncompassionate | 1 |
| 15686 | uncomfortable | 1 |
| 15687 | uncomeliness | 1 |
| 15688 | uncolted | 1 |
| 15689 | uncoined | 1 |
| 15690 | unclog | 1 |
| 15691 | unclew | 1 |
| 15692 | uncleanness | 1 |
| 15693 | uncleanliness | 1 |
| 15694 | unclaim | 1 |
| 15695 | unchilded | 1 |
| 15696 | unchary | 1 |
| 15697 | uncharitably | 1 |
| 15698 | uncharged | 1 |
| 15699 | uncharge | 1 |
| 15700 | unchanging | 1 |
| 15701 | unchain | 1 |
| 15702 | uncasing | 1 |
| 15703 | uncase | 1 |
| 15704 | uncape | 1 |
| 15705 | unbuttoning | 1 |
| 15706 | unburthen | 1 |
| 15707 | unburnt | 1 |
| 15708 | unburdens | 1 |
| 15709 | unburden | 1 |
| 15710 | unbuild | 1 |
| 15711 | unbuckling | 1 |
| 15712 | unbuckles | 1 |
| 15713 | unbroke | 1 |
| 15714 | unbreech | 1 |
| 15715 | unbred | 1 |
| 15716 | unbreathed | 1 |
| 15717 | unbraided | 1 |
| 15718 | unbrac | 1 |
| 15719 | unbowed | 1 |
| 15720 | unbow | 1 |
| 15721 | unbounded | 1 |
| 15722 | unbosom | 1 |
| 15723 | unbookish | 1 |
| 15724 | unbolted | 1 |
| 15725 | unbodied | 1 |
| 15726 | unblown | 1 |
| 15727 | unbloodied | 1 |
| 15728 | unbless | 1 |
| 15729 | unbitted | 1 |
| 15730 | unbinds | 1 |
| 15731 | unbidden | 1 |
| 15732 | unbid | 1 |
| 15733 | unbewail | 1 |
| 15734 | unbent | 1 |
| 15735 | unbend | 1 |
| 15736 | unbelieved | 1 |
| 15737 | unbegotten | 1 |
| 15738 | unbegot | 1 |
| 15739 | unbefitting | 1 |
| 15740 | unbecoming | 1 |
| 15741 | unbatter | 1 |
| 15742 | unbashful | 1 |
| 15743 | unbarb | 1 |
| 15744 | unbanded | 1 |
| 15745 | unbak | 1 |
| 15746 | unback | 1 |
| 15747 | unauthorized | 1 |
| 15748 | unauspicious | 1 |
| 15749 | unattended | 1 |
| 15750 | unattempted | 1 |
| 15751 | unattainted | 1 |
| 15752 | unassailable | 1 |
| 15753 | unassail | 1 |
| 15754 | unarms | 1 |
| 15755 | unarmed | 1 |
| 15756 | unaptness | 1 |
| 15757 | unapproved | 1 |
| 15758 | unappeas | 1 |
| 15759 | unanswer | 1 |
| 15760 | unanel | 1 |
| 15761 | unagreeable | 1 |
| 15762 | unadvisedly | 1 |
| 15763 | unactive | 1 |
| 15764 | unaching | 1 |
| 15765 | unaccompanied | 1 |
| 15766 | unaccommodated | 1 |
| 15767 | umpires | 1 |
| 15768 | umfrevile | 1 |
| 15769 | umbrage | 1 |
| 15770 | umbra | 1 |
| 15771 | um | 1 |
| 15772 | ugliest | 1 |
| 15773 | uds | 1 |
| 15774 | udge | 1 |
| 15775 | udders | 1 |
| 15776 | ubique | 1 |
| 15777 | tyrian | 1 |
| 15778 | tyrannically | 1 |
| 15779 | types | 1 |
| 15780 | tymbria | 1 |
| 15781 | tyke | 1 |
| 15782 | tyburn | 1 |
| 15783 | tybalts | 1 |
| 15784 | twopences | 1 |
| 15785 | twopence | 1 |
| 15786 | twitting | 1 |
| 15787 | twits | 1 |
| 15788 | twire | 1 |
| 15789 | twinkled | 1 |
| 15790 | twinkle | 1 |
| 15791 | twilled | 1 |
| 15792 | twilight | 1 |
| 15793 | twiggen | 1 |
| 15794 | twig | 1 |
| 15795 | tweaks | 1 |
| 15796 | tway | 1 |
| 15797 | twang | 1 |
| 15798 | tutto | 1 |
| 15799 | tutored | 1 |
| 15800 | turvy | 1 |
| 15801 | turrets | 1 |
| 15802 | turquoise | 1 |
| 15803 | turph | 1 |
| 15804 | turnips | 1 |
| 15805 | turneth | 1 |
| 15806 | turncoats | 1 |
| 15807 | turncoat | 1 |
| 15808 | turnbull | 1 |
| 15809 | turmoiled | 1 |
| 15810 | turmoil | 1 |
| 15811 | turlygod | 1 |
| 15812 | turkeys | 1 |
| 15813 | turfy | 1 |
| 15814 | turd | 1 |
| 15815 | turbulence | 1 |
| 15816 | turbans | 1 |
| 15817 | turban | 1 |
| 15818 | tupping | 1 |
| 15819 | tuners | 1 |
| 15820 | tumbler | 1 |
| 15821 | tuition | 1 |
| 15822 | tufts | 1 |
| 15823 | tubs | 1 |
| 15824 | tuae | 1 |
| 15825 | trusters | 1 |
| 15826 | truster | 1 |
| 15827 | trundle | 1 |
| 15828 | truncheoners | 1 |
| 15829 | trulls | 1 |
| 15830 | truie | 1 |
| 15831 | truepenny | 1 |
| 15832 | trueborn | 1 |
| 15833 | trowel | 1 |
| 15834 | trovato | 1 |
| 15835 | trouts | 1 |
| 15836 | trout | 1 |
| 15837 | trough | 1 |
| 15838 | troublest | 1 |
| 15839 | troubler | 1 |
| 15840 | troths | 1 |
| 15841 | trothed | 1 |
| 15842 | tropically | 1 |
| 15843 | trop | 1 |
| 15844 | trooping | 1 |
| 15845 | trompet | 1 |
| 15846 | tromperies | 1 |
| 15847 | trojans | 1 |
| 15848 | troiluses | 1 |
| 15849 | troien | 1 |
| 15850 | troiant | 1 |
| 15851 | troat | 1 |
| 15852 | triumviry | 1 |
| 15853 | triumvirs | 1 |
| 15854 | triumphers | 1 |
| 15855 | triumpher | 1 |
| 15856 | triton | 1 |
| 15857 | trips | 1 |
| 15858 | tripoli | 1 |
| 15859 | triplex | 1 |
| 15860 | tripartite | 1 |
| 15861 | trinculos | 1 |
| 15862 | trims | 1 |
| 15863 | trimmed | 1 |
| 15864 | trimly | 1 |
| 15865 | trill | 1 |
| 15866 | trigon | 1 |
| 15867 | trifler | 1 |
| 15868 | trifled | 1 |
| 15869 | trier | 1 |
| 15870 | trickling | 1 |
| 15871 | tricking | 1 |
| 15872 | tributes | 1 |
| 15873 | tribulation | 1 |
| 15874 | treys | 1 |
| 15875 | trenching | 1 |
| 15876 | trenchers | 1 |
| 15877 | trencherman | 1 |
| 15878 | trenchering | 1 |
| 15879 | trenchant | 1 |
| 15880 | trench | 1 |
| 15881 | trempling | 1 |
| 15882 | tremor | 1 |
| 15883 | tremblingly | 1 |
| 15884 | trebled | 1 |
| 15885 | treaties | 1 |
| 15886 | treat | 1 |
| 15887 | treasuries | 1 |
| 15888 | treasurer | 1 |
| 15889 | treasonable | 1 |
| 15890 | treachers | 1 |
| 15891 | treacherously | 1 |
| 15892 | travellest | 1 |
| 15893 | travelled | 1 |
| 15894 | traveling | 1 |
| 15895 | traveler | 1 |
| 15896 | travails | 1 |
| 15897 | transshape | 1 |
| 15898 | transports | 1 |
| 15899 | transportance | 1 |
| 15900 | transmutation | 1 |
| 15901 | transmigrates | 1 |
| 15902 | translation | 1 |
| 15903 | translates | 1 |
| 15904 | transgresses | 1 |
| 15905 | transformations | 1 |
| 15906 | transfix | 1 |
| 15907 | transfigur | 1 |
| 15908 | transferred | 1 |
| 15909 | transcends | 1 |
| 15910 | transcendence | 1 |
| 15911 | tranquillity | 1 |
| 15912 | tranquil | 1 |
| 15913 | tranc | 1 |
| 15914 | trampling | 1 |
| 15915 | trampled | 1 |
| 15916 | trammel | 1 |
| 15917 | traject | 1 |
| 15918 | traitress | 1 |
| 15919 | traitorly | 1 |
| 15920 | trait | 1 |
| 15921 | training | 1 |
| 15922 | trained | 1 |
| 15923 | tragedies | 1 |
| 15924 | tragedian | 1 |
| 15925 | traffics | 1 |
| 15926 | traffickers | 1 |
| 15927 | traducement | 1 |
| 15928 | traduced | 1 |
| 15929 | traditional | 1 |
| 15930 | trading | 1 |
| 15931 | tradesman | 1 |
| 15932 | track | 1 |
| 15933 | traces | 1 |
| 15934 | towton | 1 |
| 15935 | township | 1 |
| 15936 | towering | 1 |
| 15937 | towardly | 1 |
| 15938 | touze | 1 |
| 15939 | tous | 1 |
| 15940 | tournaments | 1 |
| 15941 | toughness | 1 |
| 15942 | tougher | 1 |
| 15943 | tou | 1 |
| 15944 | totters | 1 |
| 15945 | tottered | 1 |
| 15946 | totally | 1 |
| 15947 | tosseth | 1 |
| 15948 | tossed | 1 |
| 15949 | torturest | 1 |
| 15950 | torturers | 1 |
| 15951 | tortured | 1 |
| 15952 | tortive | 1 |
| 15953 | tormentors | 1 |
| 15954 | tormented | 1 |
| 15955 | tormente | 1 |
| 15956 | tormenta | 1 |
| 15957 | torchlight | 1 |
| 15958 | torcher | 1 |
| 15959 | torchbearer | 1 |
| 15960 | topsy | 1 |
| 15961 | topsail | 1 |
| 15962 | topless | 1 |
| 15963 | topgallant | 1 |
| 15964 | topful | 1 |
| 15965 | toothpicker | 1 |
| 15966 | tongs | 1 |
| 15967 | tomyris | 1 |
| 15968 | tomboys | 1 |
| 15969 | tombless | 1 |
| 15970 | tombed | 1 |
| 15971 | tombe | 1 |
| 15972 | toledo | 1 |
| 15973 | toiling | 1 |
| 15974 | toiled | 1 |
| 15975 | toged | 1 |
| 15976 | toge | 1 |
| 15977 | tods | 1 |
| 15978 | todpole | 1 |
| 15979 | tod | 1 |
| 15980 | tock | 1 |
| 15981 | toaze | 1 |
| 15982 | toasting | 1 |
| 15983 | toadstool | 1 |
| 15984 | titular | 1 |
| 15985 | tittles | 1 |
| 15986 | tittle | 1 |
| 15987 | titleless | 1 |
| 15988 | tithed | 1 |
| 15989 | tissue | 1 |
| 15990 | tirrits | 1 |
| 15991 | tirra | 1 |
| 15992 | tirest | 1 |
| 15993 | tiptoe | 1 |
| 15994 | tipsy | 1 |
| 15995 | tips | 1 |
| 15996 | tippling | 1 |
| 15997 | tipp | 1 |
| 15998 | tinsel | 1 |
| 15999 | tingling | 1 |
| 16000 | tinctures | 1 |
| 16001 | timorously | 1 |
| 16002 | timor | 1 |
| 16003 | timelier | 1 |
| 16004 | tim | 1 |
| 16005 | tiltyard | 1 |
| 16006 | tillage | 1 |
| 16007 | tile | 1 |
| 16008 | til | 1 |
| 16009 | tike | 1 |
| 16010 | tiff | 1 |
| 16011 | tidy | 1 |
| 16012 | tiddle | 1 |
| 16013 | ticklish | 1 |
| 16014 | tickl | 1 |
| 16015 | ticed | 1 |
| 16016 | tibey | 1 |
| 16017 | tiberio | 1 |
| 16018 | tib | 1 |
| 16019 | thymus | 1 |
| 16020 | thwartings | 1 |
| 16021 | thunderstroke | 1 |
| 16022 | thunderstone | 1 |
| 16023 | thunderer | 1 |
| 16024 | thrusteth | 1 |
| 16025 | thrush | 1 |
| 16026 | thrumm | 1 |
| 16027 | thrum | 1 |
| 16028 | throwest | 1 |
| 16029 | thrower | 1 |
| 16030 | throughfares | 1 |
| 16031 | throughfare | 1 |
| 16032 | throttle | 1 |
| 16033 | thromuldo | 1 |
| 16034 | throe | 1 |
| 16035 | throca | 1 |
| 16036 | throbs | 1 |
| 16037 | throbbing | 1 |
| 16038 | thrivers | 1 |
| 16039 | thrived | 1 |
| 16040 | thrills | 1 |
| 16041 | thrilling | 1 |
| 16042 | thrifts | 1 |
| 16043 | thresher | 1 |
| 16044 | threepile | 1 |
| 16045 | threatest | 1 |
| 16046 | threading | 1 |
| 16047 | thralls | 1 |
| 16048 | thralled | 1 |
| 16049 | thraldom | 1 |
| 16050 | thoughtful | 1 |
| 16051 | thoas | 1 |
| 16052 | thitherward | 1 |
| 16053 | thistles | 1 |
| 16054 | thirtieth | 1 |
| 16055 | thirties | 1 |
| 16056 | thirsts | 1 |
| 16057 | thirsting | 1 |
| 16058 | thirds | 1 |
| 16059 | thinkst | 1 |
| 16060 | thimbles | 1 |
| 16061 | thickskin | 1 |
| 16062 | thicken | 1 |
| 16063 | thessalian | 1 |
| 16064 | thereafter | 1 |
| 16065 | thereabout | 1 |
| 16066 | thenceforth | 1 |
| 16067 | theise | 1 |
| 16068 | thein | 1 |
| 16069 | thebes | 1 |
| 16070 | theban | 1 |
| 16071 | thaws | 1 |
| 16072 | thawing | 1 |
| 16073 | thasos | 1 |
| 16074 | thanking | 1 |
| 16075 | thaes | 1 |
| 16076 | tevil | 1 |
| 16077 | tether | 1 |
| 16078 | testril | 1 |
| 16079 | testiness | 1 |
| 16080 | testimonied | 1 |
| 16081 | testern | 1 |
| 16082 | tested | 1 |
| 16083 | tertio | 1 |
| 16084 | tertian | 1 |
| 16085 | terrene | 1 |
| 16086 | terre | 1 |
| 16087 | terras | 1 |
| 16088 | terram | 1 |
| 16089 | terrace | 1 |
| 16090 | termless | 1 |
| 16091 | terminations | 1 |
| 16092 | tercel | 1 |
| 16093 | tenures | 1 |
| 16094 | tenths | 1 |
| 16095 | tented | 1 |
| 16096 | tens | 1 |
| 16097 | tenours | 1 |
| 16098 | tenements | 1 |
| 16099 | tenement | 1 |
| 16100 | tenedos | 1 |
| 16101 | tendered | 1 |
| 16102 | tenable | 1 |
| 16103 | tempteth | 1 |
| 16104 | temptations | 1 |
| 16105 | temps | 1 |
| 16106 | temporizer | 1 |
| 16107 | temporiz | 1 |
| 16108 | temporary | 1 |
| 16109 | temperality | 1 |
| 16110 | telamonius | 1 |
| 16111 | telamon | 1 |
| 16112 | teipsum | 1 |
| 16113 | tearful | 1 |
| 16114 | taxes | 1 |
| 16115 | tawdry | 1 |
| 16116 | tavy | 1 |
| 16117 | tauntingly | 1 |
| 16118 | taunting | 1 |
| 16119 | taunted | 1 |
| 16120 | tattlings | 1 |
| 16121 | tattle | 1 |
| 16122 | tatters | 1 |
| 16123 | tatter | 1 |
| 16124 | tatt | 1 |
| 16125 | tasker | 1 |
| 16126 | tartly | 1 |
| 16127 | tartars | 1 |
| 16128 | tarriance | 1 |
| 16129 | tarr | 1 |
| 16130 | tarquins | 1 |
| 16131 | targe | 1 |
| 16132 | tarentum | 1 |
| 16133 | tardiness | 1 |
| 16134 | tardily | 1 |
| 16135 | tardied | 1 |
| 16136 | tapp | 1 |
| 16137 | taphouse | 1 |
| 16138 | tapestries | 1 |
| 16139 | tantaene | 1 |
| 16140 | tanta | 1 |
| 16141 | tanquam | 1 |
| 16142 | tanned | 1 |
| 16143 | tann | 1 |
| 16144 | tanlings | 1 |
| 16145 | tank | 1 |
| 16146 | tan | 1 |
| 16147 | tames | 1 |
| 16148 | tamer | 1 |
| 16149 | tamed | 1 |
| 16150 | tambourines | 1 |
| 16151 | tally | 1 |
| 16152 | tallies | 1 |
| 16153 | talkers | 1 |
| 16154 | talked | 1 |
| 16155 | taleporter | 1 |
| 16156 | talbotites | 1 |
| 16157 | tal | 1 |
| 16158 | taketh | 1 |
| 16159 | takest | 1 |
| 16160 | tainture | 1 |
| 16161 | tails | 1 |
| 16162 | tagrag | 1 |
| 16163 | tag | 1 |
| 16164 | taffety | 1 |
| 16165 | tadpole | 1 |
| 16166 | taddle | 1 |
| 16167 | tacklings | 1 |
| 16168 | tackling | 1 |
| 16169 | tackles | 1 |
| 16170 | tackled | 1 |
| 16171 | taciturnity | 1 |
| 16172 | tabourines | 1 |
| 16173 | tabors | 1 |
| 16174 | taborer | 1 |
| 16175 | tablet | 1 |
| 16176 | tabled | 1 |
| 16177 | taber | 1 |
| 16178 | syracusians | 1 |
| 16179 | synods | 1 |
| 16180 | sympathiz | 1 |
| 16181 | symbols | 1 |
| 16182 | syllogism | 1 |
| 16183 | sylla | 1 |
| 16184 | swung | 1 |
| 16185 | swoopstake | 1 |
| 16186 | swoop | 1 |
| 16187 | swoll | 1 |
| 16188 | switzers | 1 |
| 16189 | switches | 1 |
| 16190 | swineherds | 1 |
| 16191 | swimmers | 1 |
| 16192 | swimmer | 1 |
| 16193 | swills | 1 |
| 16194 | swill | 1 |
| 16195 | swerver | 1 |
| 16196 | sweno | 1 |
| 16197 | swelter | 1 |
| 16198 | swellings | 1 |
| 16199 | sweetens | 1 |
| 16200 | sweaten | 1 |
| 16201 | swearest | 1 |
| 16202 | swearer | 1 |
| 16203 | swaying | 1 |
| 16204 | swathling | 1 |
| 16205 | swathing | 1 |
| 16206 | swashers | 1 |
| 16207 | swarthy | 1 |
| 16208 | swarths | 1 |
| 16209 | swarth | 1 |
| 16210 | sward | 1 |
| 16211 | swans | 1 |
| 16212 | swaggerer | 1 |
| 16213 | swag | 1 |
| 16214 | swaddling | 1 |
| 16215 | sutton | 1 |
| 16216 | sutler | 1 |
| 16217 | sust | 1 |
| 16218 | suspiration | 1 |
| 16219 | suspicions | 1 |
| 16220 | suspense | 1 |
| 16221 | suspecting | 1 |
| 16222 | surveys | 1 |
| 16223 | surveyors | 1 |
| 16224 | surveying | 1 |
| 16225 | surveyest | 1 |
| 16226 | surreys | 1 |
| 16227 | surplice | 1 |
| 16228 | surpassing | 1 |
| 16229 | surpasseth | 1 |
| 16230 | surmounts | 1 |
| 16231 | surmounted | 1 |
| 16232 | surmised | 1 |
| 16233 | surmis | 1 |
| 16234 | surgere | 1 |
| 16235 | surgeons | 1 |
| 16236 | surfeiter | 1 |
| 16237 | sureties | 1 |
| 16238 | surecard | 1 |
| 16239 | surd | 1 |
| 16240 | surance | 1 |
| 16241 | suppresseth | 1 |
| 16242 | suppressed | 1 |
| 16243 | supposest | 1 |
| 16244 | supposal | 1 |
| 16245 | supportor | 1 |
| 16246 | supporting | 1 |
| 16247 | supporters | 1 |
| 16248 | supportable | 1 |
| 16249 | supplyment | 1 |
| 16250 | supplying | 1 |
| 16251 | supplyant | 1 |
| 16252 | suppliest | 1 |
| 16253 | supplicant | 1 |
| 16254 | suppliants | 1 |
| 16255 | suppliance | 1 |
| 16256 | supping | 1 |
| 16257 | suppertime | 1 |
| 16258 | suppers | 1 |
| 16259 | supervisor | 1 |
| 16260 | supersubtle | 1 |
| 16261 | superstitiously | 1 |
| 16262 | superstition | 1 |
| 16263 | superserviceable | 1 |
| 16264 | superscript | 1 |
| 16265 | superpraise | 1 |
| 16266 | supernal | 1 |
| 16267 | superior | 1 |
| 16268 | superflux | 1 |
| 16269 | superfluously | 1 |
| 16270 | super | 1 |
| 16271 | sunrising | 1 |
| 16272 | sunders | 1 |
| 16273 | sunburning | 1 |
| 16274 | sunbeams | 1 |
| 16275 | sumptuously | 1 |
| 16276 | sumpter | 1 |
| 16277 | summoners | 1 |
| 16278 | summa | 1 |
| 16279 | summ | 1 |
| 16280 | sumless | 1 |
| 16281 | sultan | 1 |
| 16282 | sulpherous | 1 |
| 16283 | sullies | 1 |
| 16284 | sullens | 1 |
| 16285 | suivez | 1 |
| 16286 | suiting | 1 |
| 16287 | suitable | 1 |
| 16288 | suggesting | 1 |
| 16289 | sugarsop | 1 |
| 16290 | suffrage | 1 |
| 16291 | suffocation | 1 |
| 16292 | suffocating | 1 |
| 16293 | suffigance | 1 |
| 16294 | sufficit | 1 |
| 16295 | sufficing | 1 |
| 16296 | suffices | 1 |
| 16297 | sufficed | 1 |
| 16298 | sufferances | 1 |
| 16299 | sueth | 1 |
| 16300 | suerly | 1 |
| 16301 | suckers | 1 |
| 16302 | successor | 1 |
| 16303 | successantly | 1 |
| 16304 | succeeded | 1 |
| 16305 | succedant | 1 |
| 16306 | subverts | 1 |
| 16307 | subversion | 1 |
| 16308 | subtractors | 1 |
| 16309 | subtlety | 1 |
| 16310 | subtilly | 1 |
| 16311 | subtile | 1 |
| 16312 | substitution | 1 |
| 16313 | subsisting | 1 |
| 16314 | subsist | 1 |
| 16315 | subsidy | 1 |
| 16316 | subsidies | 1 |
| 16317 | subsequent | 1 |
| 16318 | subscription | 1 |
| 16319 | subscribed | 1 |
| 16320 | submitting | 1 |
| 16321 | submits | 1 |
| 16322 | submerg | 1 |
| 16323 | subduing | 1 |
| 16324 | subduements | 1 |
| 16325 | subcontracted | 1 |
| 16326 | sub | 1 |
| 16327 | styl | 1 |
| 16328 | stygian | 1 |
| 16329 | styga | 1 |
| 16330 | sturdy | 1 |
| 16331 | stuprum | 1 |
| 16332 | stupified | 1 |
| 16333 | stupid | 1 |
| 16334 | stupefy | 1 |
| 16335 | stump | 1 |
| 16336 | stumblest | 1 |
| 16337 | studs | 1 |
| 16338 | studiously | 1 |
| 16339 | students | 1 |
| 16340 | studded | 1 |
| 16341 | stubbornly | 1 |
| 16342 | stubbornest | 1 |
| 16343 | strutted | 1 |
| 16344 | struts | 1 |
| 16345 | strumpets | 1 |
| 16346 | struggles | 1 |
| 16347 | stroy | 1 |
| 16348 | strown | 1 |
| 16349 | strossers | 1 |
| 16350 | strooke | 1 |
| 16351 | stronds | 1 |
| 16352 | strond | 1 |
| 16353 | strok | 1 |
| 16354 | striv | 1 |
| 16355 | stripping | 1 |
| 16356 | striplings | 1 |
| 16357 | stringless | 1 |
| 16358 | strikers | 1 |
| 16359 | striding | 1 |
| 16360 | stricture | 1 |
| 16361 | strictly | 1 |
| 16362 | strictest | 1 |
| 16363 | stricter | 1 |
| 16364 | stricken | 1 |
| 16365 | strewments | 1 |
| 16366 | strewings | 1 |
| 16367 | stretching | 1 |
| 16368 | streching | 1 |
| 16369 | streaming | 1 |
| 16370 | streamers | 1 |
| 16371 | strawy | 1 |
| 16372 | strawberry | 1 |
| 16373 | stratford | 1 |
| 16374 | straps | 1 |
| 16375 | strappado | 1 |
| 16376 | strangler | 1 |
| 16377 | straits | 1 |
| 16378 | straitness | 1 |
| 16379 | straitly | 1 |
| 16380 | straiter | 1 |
| 16381 | straited | 1 |
| 16382 | straightest | 1 |
| 16383 | straggling | 1 |
| 16384 | stragglers | 1 |
| 16385 | strachy | 1 |
| 16386 | stowed | 1 |
| 16387 | stowage | 1 |
| 16388 | stover | 1 |
| 16389 | stouter | 1 |
| 16390 | stoups | 1 |
| 16391 | storming | 1 |
| 16392 | stormed | 1 |
| 16393 | stores | 1 |
| 16394 | storehouses | 1 |
| 16395 | stope | 1 |
| 16396 | stonish | 1 |
| 16397 | stonecutter | 1 |
| 16398 | stomaching | 1 |
| 16399 | stolest | 1 |
| 16400 | stokesly | 1 |
| 16401 | stoics | 1 |
| 16402 | stogs | 1 |
| 16403 | stog | 1 |
| 16404 | stockish | 1 |
| 16405 | stoccata | 1 |
| 16406 | stoccadoes | 1 |
| 16407 | stithy | 1 |
| 16408 | stithied | 1 |
| 16409 | stitchery | 1 |
| 16410 | stirrups | 1 |
| 16411 | stirreth | 1 |
| 16412 | stirrers | 1 |
| 16413 | stirrer | 1 |
| 16414 | stirred | 1 |
| 16415 | stints | 1 |
| 16416 | stinks | 1 |
| 16417 | stinkingly | 1 |
| 16418 | stingless | 1 |
| 16419 | stilly | 1 |
| 16420 | stillest | 1 |
| 16421 | stiller | 1 |
| 16422 | stigmatical | 1 |
| 16423 | stifles | 1 |
| 16424 | stiffly | 1 |
| 16425 | stiffen | 1 |
| 16426 | stickler | 1 |
| 16427 | stewed | 1 |
| 16428 | stewards | 1 |
| 16429 | sternness | 1 |
| 16430 | sternest | 1 |
| 16431 | sternage | 1 |
| 16432 | sterility | 1 |
| 16433 | stepping | 1 |
| 16434 | stepmothers | 1 |
| 16435 | stepdame | 1 |
| 16436 | stemming | 1 |
| 16437 | stelled | 1 |
| 16438 | steering | 1 |
| 16439 | steerage | 1 |
| 16440 | steeps | 1 |
| 16441 | steeple | 1 |
| 16442 | steeped | 1 |
| 16443 | stealthy | 1 |
| 16444 | stealers | 1 |
| 16445 | steadier | 1 |
| 16446 | steadfast | 1 |
| 16447 | steaded | 1 |
| 16448 | stayest | 1 |
| 16449 | stave | 1 |
| 16450 | statures | 1 |
| 16451 | statists | 1 |
| 16452 | statist | 1 |
| 16453 | statilius | 1 |
| 16454 | statesmen | 1 |
| 16455 | statelier | 1 |
| 16456 | starving | 1 |
| 16457 | starveth | 1 |
| 16458 | starvelackey | 1 |
| 16459 | startingly | 1 |
| 16460 | starry | 1 |
| 16461 | starling | 1 |
| 16462 | starkly | 1 |
| 16463 | starings | 1 |
| 16464 | staples | 1 |
| 16465 | staple | 1 |
| 16466 | stanzos | 1 |
| 16467 | stanzo | 1 |
| 16468 | stanze | 1 |
| 16469 | staniel | 1 |
| 16470 | stander | 1 |
| 16471 | stanchless | 1 |
| 16472 | stammer | 1 |
| 16473 | stamford | 1 |
| 16474 | stalling | 1 |
| 16475 | stalking | 1 |
| 16476 | staled | 1 |
| 16477 | staining | 1 |
| 16478 | staineth | 1 |
| 16479 | staines | 1 |
| 16480 | staider | 1 |
| 16481 | staid | 1 |
| 16482 | staggering | 1 |
| 16483 | stages | 1 |
| 16484 | staffordshire | 1 |
| 16485 | stacks | 1 |
| 16486 | stablishment | 1 |
| 16487 | stablish | 1 |
| 16488 | stableness | 1 |
| 16489 | squiny | 1 |
| 16490 | squints | 1 |
| 16491 | squele | 1 |
| 16492 | squeezes | 1 |
| 16493 | squealing | 1 |
| 16494 | squeal | 1 |
| 16495 | squeaking | 1 |
| 16496 | squarer | 1 |
| 16497 | squadron | 1 |
| 16498 | squabble | 1 |
| 16499 | spurrer | 1 |
| 16500 | sprout | 1 |
| 16501 | spriting | 1 |
| 16502 | sprited | 1 |
| 16503 | sprinkles | 1 |
| 16504 | springtime | 1 |
| 16505 | springhalt | 1 |
| 16506 | springeth | 1 |
| 16507 | springes | 1 |
| 16508 | sprigs | 1 |
| 16509 | sprightful | 1 |
| 16510 | sprighted | 1 |
| 16511 | spray | 1 |
| 16512 | sprat | 1 |
| 16513 | sprag | 1 |
| 16514 | spouting | 1 |
| 16515 | sporting | 1 |
| 16516 | spokesman | 1 |
| 16517 | splinters | 1 |
| 16518 | splenitive | 1 |
| 16519 | spleeny | 1 |
| 16520 | splay | 1 |
| 16521 | spitting | 1 |
| 16522 | spitted | 1 |
| 16523 | spited | 1 |
| 16524 | spirt | 1 |
| 16525 | spiritualty | 1 |
| 16526 | spiritless | 1 |
| 16527 | spire | 1 |
| 16528 | spinster | 1 |
| 16529 | spinii | 1 |
| 16530 | spilth | 1 |
| 16531 | spilling | 1 |
| 16532 | spigot | 1 |
| 16533 | spightfully | 1 |
| 16534 | spieth | 1 |
| 16535 | spicery | 1 |
| 16536 | spiced | 1 |
| 16537 | sphinx | 1 |
| 16538 | sphery | 1 |
| 16539 | sphered | 1 |
| 16540 | spher | 1 |
| 16541 | sperr | 1 |
| 16542 | spero | 1 |
| 16543 | sperm | 1 |
| 16544 | sperato | 1 |
| 16545 | spendest | 1 |
| 16546 | spencer | 1 |
| 16547 | spelt | 1 |
| 16548 | spelling | 1 |
| 16549 | speens | 1 |
| 16550 | speediness | 1 |
| 16551 | speculations | 1 |
| 16552 | spectatorship | 1 |
| 16553 | spectacled | 1 |
| 16554 | specialty | 1 |
| 16555 | specialties | 1 |
| 16556 | specialities | 1 |
| 16557 | spears | 1 |
| 16558 | speargrass | 1 |
| 16559 | speaketh | 1 |
| 16560 | speakers | 1 |
| 16561 | spavins | 1 |
| 16562 | spavin | 1 |
| 16563 | sparkles | 1 |
| 16564 | spans | 1 |
| 16565 | spann | 1 |
| 16566 | spaniels | 1 |
| 16567 | spangle | 1 |
| 16568 | spakest | 1 |
| 16569 | spades | 1 |
| 16570 | spaces | 1 |
| 16571 | sowter | 1 |
| 16572 | sowl | 1 |
| 16573 | sowing | 1 |
| 16574 | sovereignvours | 1 |
| 16575 | sovereignly | 1 |
| 16576 | sovereignest | 1 |
| 16577 | souviendrai | 1 |
| 16578 | southerly | 1 |
| 16579 | souse | 1 |
| 16580 | sous | 1 |
| 16581 | sours | 1 |
| 16582 | sources | 1 |
| 16583 | soundpost | 1 |
| 16584 | soundness | 1 |
| 16585 | soulless | 1 |
| 16586 | sould | 1 |
| 16587 | sottish | 1 |
| 16588 | sots | 1 |
| 16589 | soto | 1 |
| 16590 | sossius | 1 |
| 16591 | sorting | 1 |
| 16592 | sortance | 1 |
| 16593 | sorrowing | 1 |
| 16594 | sorrowest | 1 |
| 16595 | sorriest | 1 |
| 16596 | sorrier | 1 |
| 16597 | sorer | 1 |
| 16598 | sorceries | 1 |
| 16599 | sorcerer | 1 |
| 16600 | sophisticated | 1 |
| 16601 | sophister | 1 |
| 16602 | sooty | 1 |
| 16603 | soothsay | 1 |
| 16604 | soothers | 1 |
| 16605 | sonties | 1 |
| 16606 | sonneting | 1 |
| 16607 | sonance | 1 |
| 16608 | somme | 1 |
| 16609 | somewhither | 1 |
| 16610 | somever | 1 |
| 16611 | someone | 1 |
| 16612 | solyman | 1 |
| 16613 | solum | 1 |
| 16614 | solon | 1 |
| 16615 | solidity | 1 |
| 16616 | solidares | 1 |
| 16617 | solicitings | 1 |
| 16618 | solicitation | 1 |
| 16619 | solemnities | 1 |
| 16620 | solemness | 1 |
| 16621 | solem | 1 |
| 16622 | soldest | 1 |
| 16623 | solder | 1 |
| 16624 | soldat | 1 |
| 16625 | soit | 1 |
| 16626 | soilure | 1 |
| 16627 | soiled | 1 |
| 16628 | softness | 1 |
| 16629 | softens | 1 |
| 16630 | sod | 1 |
| 16631 | socrates | 1 |
| 16632 | socks | 1 |
| 16633 | soberly | 1 |
| 16634 | sobbing | 1 |
| 16635 | soars | 1 |
| 16636 | soaks | 1 |
| 16637 | soak | 1 |
| 16638 | snuffs | 1 |
| 16639 | snowy | 1 |
| 16640 | snowed | 1 |
| 16641 | snowballs | 1 |
| 16642 | snoring | 1 |
| 16643 | snipt | 1 |
| 16644 | snipe | 1 |
| 16645 | sneck | 1 |
| 16646 | sneap | 1 |
| 16647 | snatchers | 1 |
| 16648 | snarling | 1 |
| 16649 | snarleth | 1 |
| 16650 | snarl | 1 |
| 16651 | snapp | 1 |
| 16652 | snaky | 1 |
| 16653 | snails | 1 |
| 16654 | snaffle | 1 |
| 16655 | smutch | 1 |
| 16656 | smulkin | 1 |
| 16657 | smothering | 1 |
| 16658 | smoth | 1 |
| 16659 | smooths | 1 |
| 16660 | smoked | 1 |
| 16661 | smok | 1 |
| 16662 | smit | 1 |
| 16663 | smirched | 1 |
| 16664 | smilets | 1 |
| 16665 | smilest | 1 |
| 16666 | smatter | 1 |
| 16667 | smatch | 1 |
| 16668 | smartly | 1 |
| 16669 | smalus | 1 |
| 16670 | smallness | 1 |
| 16671 | smacking | 1 |
| 16672 | slys | 1 |
| 16673 | sluttishness | 1 |
| 16674 | slunk | 1 |
| 16675 | slumbery | 1 |
| 16676 | slumb | 1 |
| 16677 | sluggish | 1 |
| 16678 | sluggardiz | 1 |
| 16679 | sluggard | 1 |
| 16680 | slovenry | 1 |
| 16681 | slovenly | 1 |
| 16682 | slothful | 1 |
| 16683 | slope | 1 |
| 16684 | slomber | 1 |
| 16685 | slobb | 1 |
| 16686 | slit | 1 |
| 16687 | slish | 1 |
| 16688 | slights | 1 |
| 16689 | slightness | 1 |
| 16690 | sliding | 1 |
| 16691 | slewest | 1 |
| 16692 | slenderly | 1 |
| 16693 | slenderer | 1 |
| 16694 | sleights | 1 |
| 16695 | sleight | 1 |
| 16696 | sleided | 1 |
| 16697 | sleid | 1 |
| 16698 | sleekly | 1 |
| 16699 | sledded | 1 |
| 16700 | sleave | 1 |
| 16701 | slaying | 1 |
| 16702 | slayeth | 1 |
| 16703 | slaver | 1 |
| 16704 | slaughterous | 1 |
| 16705 | slaughterer | 1 |
| 16706 | slake | 1 |
| 16707 | slab | 1 |
| 16708 | skyish | 1 |
| 16709 | skyey | 1 |
| 16710 | skulking | 1 |
| 16711 | skirmishes | 1 |
| 16712 | skipper | 1 |
| 16713 | skipp | 1 |
| 16714 | skinny | 1 |
| 16715 | skinker | 1 |
| 16716 | skimble | 1 |
| 16717 | skillful | 1 |
| 16718 | skillet | 1 |
| 16719 | skilfully | 1 |
| 16720 | skelter | 1 |
| 16721 | skamble | 1 |
| 16722 | skains | 1 |
| 16723 | sizzle | 1 |
| 16724 | sixpenny | 1 |
| 16725 | sixpences | 1 |
| 16726 | situations | 1 |
| 16727 | sisterly | 1 |
| 16728 | sist | 1 |
| 16729 | sipping | 1 |
| 16730 | sinning | 1 |
| 16731 | singuled | 1 |
| 16732 | singularities | 1 |
| 16733 | singulariter | 1 |
| 16734 | singeth | 1 |
| 16735 | singes | 1 |
| 16736 | singeing | 1 |
| 16737 | sinewed | 1 |
| 16738 | sinel | 1 |
| 16739 | simulation | 1 |
| 16740 | simony | 1 |
| 16741 | simile | 1 |
| 16742 | sima | 1 |
| 16743 | silverly | 1 |
| 16744 | silvered | 1 |
| 16745 | silva | 1 |
| 16746 | silling | 1 |
| 16747 | silliness | 1 |
| 16748 | silliest | 1 |
| 16749 | silkman | 1 |
| 16750 | silently | 1 |
| 16751 | silencing | 1 |
| 16752 | signum | 1 |
| 16753 | signor | 1 |
| 16754 | signiory | 1 |
| 16755 | signiories | 1 |
| 16756 | signifying | 1 |
| 16757 | significants | 1 |
| 16758 | significant | 1 |
| 16759 | sightly | 1 |
| 16760 | sifted | 1 |
| 16761 | sies | 1 |
| 16762 | sienna | 1 |
| 16763 | sieges | 1 |
| 16764 | sided | 1 |
| 16765 | sicles | 1 |
| 16766 | sickliness | 1 |
| 16767 | sicklied | 1 |
| 16768 | sicklemen | 1 |
| 16769 | sickle | 1 |
| 16770 | sicker | 1 |
| 16771 | sicilian | 1 |
| 16772 | sicil | 1 |
| 16773 | sibyls | 1 |
| 16774 | sibylla | 1 |
| 16775 | shuttle | 1 |
| 16776 | shunned | 1 |
| 16777 | shunless | 1 |
| 16778 | shuffled | 1 |
| 16779 | shuffl | 1 |
| 16780 | shudders | 1 |
| 16781 | shudd | 1 |
| 16782 | shrugs | 1 |
| 16783 | shrows | 1 |
| 16784 | shrow | 1 |
| 16785 | shrouding | 1 |
| 16786 | shrives | 1 |
| 16787 | shriver | 1 |
| 16788 | shriv | 1 |
| 16789 | shrills | 1 |
| 16790 | shriller | 1 |
| 16791 | shrews | 1 |
| 16792 | shrewishness | 1 |
| 16793 | shrewishly | 1 |
| 16794 | shrewish | 1 |
| 16795 | shrewdness | 1 |
| 16796 | shovels | 1 |
| 16797 | shouldering | 1 |
| 16798 | shoughs | 1 |
| 16799 | shortened | 1 |
| 16800 | shortcake | 1 |
| 16801 | shootie | 1 |
| 16802 | shoemaker | 1 |
| 16803 | shod | 1 |
| 16804 | shoals | 1 |
| 16805 | shoal | 1 |
| 16806 | shive | 1 |
| 16807 | shirley | 1 |
| 16808 | shire | 1 |
| 16809 | shipwrights | 1 |
| 16810 | shipwrecking | 1 |
| 16811 | shipt | 1 |
| 16812 | shipped | 1 |
| 16813 | shipmen | 1 |
| 16814 | shipman | 1 |
| 16815 | shiny | 1 |
| 16816 | shineth | 1 |
| 16817 | sheweth | 1 |
| 16818 | shepherdes | 1 |
| 16819 | shelvy | 1 |
| 16820 | shelving | 1 |
| 16821 | shelters | 1 |
| 16822 | shelt | 1 |
| 16823 | shells | 1 |
| 16824 | shelf | 1 |
| 16825 | sheffield | 1 |
| 16826 | sheeted | 1 |
| 16827 | sheepskins | 1 |
| 16828 | sheeps | 1 |
| 16829 | sheepcotes | 1 |
| 16830 | sheepcote | 1 |
| 16831 | sheaves | 1 |
| 16832 | sheaved | 1 |
| 16833 | sheathed | 1 |
| 16834 | shearman | 1 |
| 16835 | sheal | 1 |
| 16836 | shaw | 1 |
| 16837 | shaven | 1 |
| 16838 | shav | 1 |
| 16839 | shatter | 1 |
| 16840 | sharps | 1 |
| 16841 | sharpens | 1 |
| 16842 | sharpened | 1 |
| 16843 | sharpen | 1 |
| 16844 | sharers | 1 |
| 16845 | shared | 1 |
| 16846 | sharded | 1 |
| 16847 | shard | 1 |
| 16848 | shaping | 1 |
| 16849 | shapen | 1 |
| 16850 | shaped | 1 |
| 16851 | shank | 1 |
| 16852 | shaming | 1 |
| 16853 | shallowly | 1 |
| 16854 | shallenge | 1 |
| 16855 | shales | 1 |
| 16856 | shaked | 1 |
| 16857 | shafts | 1 |
| 16858 | shackle | 1 |
| 16859 | sh | 1 |
| 16860 | sfoot | 1 |
| 16861 | seymour | 1 |
| 16862 | sexes | 1 |
| 16863 | severs | 1 |
| 16864 | severest | 1 |
| 16865 | severed | 1 |
| 16866 | sevennight | 1 |
| 16867 | settling | 1 |
| 16868 | settlest | 1 |
| 16869 | sestos | 1 |
| 16870 | servility | 1 |
| 16871 | serveth | 1 |
| 16872 | server | 1 |
| 16873 | servanted | 1 |
| 16874 | serpentine | 1 |
| 16875 | sermons | 1 |
| 16876 | serge | 1 |
| 16877 | serenis | 1 |
| 16878 | sequester | 1 |
| 16879 | sepulchring | 1 |
| 16880 | septentrion | 1 |
| 16881 | separates | 1 |
| 16882 | separable | 1 |
| 16883 | senoys | 1 |
| 16884 | seniory | 1 |
| 16885 | seneca | 1 |
| 16886 | sendeth | 1 |
| 16887 | semper | 1 |
| 16888 | semicircle | 1 |
| 16889 | semi | 1 |
| 16890 | semblative | 1 |
| 16891 | semblably | 1 |
| 16892 | sells | 1 |
| 16893 | seizeth | 1 |
| 16894 | seized | 1 |
| 16895 | seigneurs | 1 |
| 16896 | segregation | 1 |
| 16897 | seeting | 1 |
| 16898 | seething | 1 |
| 16899 | seethes | 1 |
| 16900 | seethe | 1 |
| 16901 | seer | 1 |
| 16902 | seemingly | 1 |
| 16903 | seemest | 1 |
| 16904 | seemers | 1 |
| 16905 | seely | 1 |
| 16906 | seeling | 1 |
| 16907 | seein | 1 |
| 16908 | seedsman | 1 |
| 16909 | seedness | 1 |
| 16910 | seeded | 1 |
| 16911 | seducer | 1 |
| 16912 | sedgy | 1 |
| 16913 | sedge | 1 |
| 16914 | sedg | 1 |
| 16915 | securing | 1 |
| 16916 | secundo | 1 |
| 16917 | secondarily | 1 |
| 16918 | seasick | 1 |
| 16919 | seared | 1 |
| 16920 | searcheth | 1 |
| 16921 | searches | 1 |
| 16922 | searchers | 1 |
| 16923 | searce | 1 |
| 16924 | seaport | 1 |
| 16925 | seamy | 1 |
| 16926 | seamen | 1 |
| 16927 | seam | 1 |
| 16928 | seafaring | 1 |
| 16929 | sdeath | 1 |
| 16930 | scythed | 1 |
| 16931 | scylla | 1 |
| 16932 | scutcheons | 1 |
| 16933 | scut | 1 |
| 16934 | scurril | 1 |
| 16935 | sculls | 1 |
| 16936 | scuffling | 1 |
| 16937 | scuffles | 1 |
| 16938 | scroyles | 1 |
| 16939 | scrowl | 1 |
| 16940 | scrolls | 1 |
| 16941 | scriptures | 1 |
| 16942 | scrippage | 1 |
| 16943 | scrimers | 1 |
| 16944 | scribbled | 1 |
| 16945 | scribbl | 1 |
| 16946 | screws | 1 |
| 16947 | screens | 1 |
| 16948 | screeching | 1 |
| 16949 | screams | 1 |
| 16950 | scream | 1 |
| 16951 | scratches | 1 |
| 16952 | scraping | 1 |
| 16953 | scoundrels | 1 |
| 16954 | scotches | 1 |
| 16955 | scorpions | 1 |
| 16956 | scoring | 1 |
| 16957 | scored | 1 |
| 16958 | scorched | 1 |
| 16959 | scopes | 1 |
| 16960 | scoggin | 1 |
| 16961 | scoffing | 1 |
| 16962 | scoffer | 1 |
| 16963 | scissors | 1 |
| 16964 | scions | 1 |
| 16965 | sciaticas | 1 |
| 16966 | schooling | 1 |
| 16967 | schoolfellows | 1 |
| 16968 | schoolboy | 1 |
| 16969 | scholarly | 1 |
| 16970 | sceptred | 1 |
| 16971 | scepter | 1 |
| 16972 | scented | 1 |
| 16973 | scelerisque | 1 |
| 16974 | scelera | 1 |
| 16975 | scattering | 1 |
| 16976 | scathful | 1 |
| 16977 | scath | 1 |
| 16978 | scarre | 1 |
| 16979 | scaring | 1 |
| 16980 | scarfed | 1 |
| 16981 | scarecrows | 1 |
| 16982 | scapeth | 1 |
| 16983 | scants | 1 |
| 16984 | scantling | 1 |
| 16985 | scanting | 1 |
| 16986 | scanter | 1 |
| 16987 | scandy | 1 |
| 16988 | scan | 1 |
| 16989 | scamels | 1 |
| 16990 | scamble | 1 |
| 16991 | scaly | 1 |
| 16992 | scalps | 1 |
| 16993 | scall | 1 |
| 16994 | scalded | 1 |
| 16995 | scal | 1 |
| 16996 | scaffoldage | 1 |
| 16997 | scabs | 1 |
| 16998 | sayst | 1 |
| 16999 | saxton | 1 |
| 17000 | saxony | 1 |
| 17001 | sawyer | 1 |
| 17002 | sawpit | 1 |
| 17003 | sawn | 1 |
| 17004 | sawed | 1 |
| 17005 | savoy | 1 |
| 17006 | savouring | 1 |
| 17007 | savory | 1 |
| 17008 | saviour | 1 |
| 17009 | savagely | 1 |
| 17010 | sauces | 1 |
| 17011 | saucers | 1 |
| 17012 | sauced | 1 |
| 17013 | satyrs | 1 |
| 17014 | saturdays | 1 |
| 17015 | saturday | 1 |
| 17016 | satisfies | 1 |
| 17017 | satis | 1 |
| 17018 | satirical | 1 |
| 17019 | satiate | 1 |
| 17020 | sated | 1 |
| 17021 | satchel | 1 |
| 17022 | sarum | 1 |
| 17023 | sardinia | 1 |
| 17024 | sardians | 1 |
| 17025 | sard | 1 |
| 17026 | saracens | 1 |
| 17027 | sapphires | 1 |
| 17028 | sapit | 1 |
| 17029 | sapient | 1 |
| 17030 | santrailles | 1 |
| 17031 | sanity | 1 |
| 17032 | sanguis | 1 |
| 17033 | sang | 1 |
| 17034 | sanded | 1 |
| 17035 | sandbag | 1 |
| 17036 | sanctuarize | 1 |
| 17037 | sanctities | 1 |
| 17038 | sanctimonies | 1 |
| 17039 | sanctifies | 1 |
| 17040 | sancta | 1 |
| 17041 | samsons | 1 |
| 17042 | sample | 1 |
| 17043 | sampire | 1 |
| 17044 | samingo | 1 |
| 17045 | salving | 1 |
| 17046 | salv | 1 |
| 17047 | saluted | 1 |
| 17048 | saltpetre | 1 |
| 17049 | saltness | 1 |
| 17050 | saltiers | 1 |
| 17051 | salter | 1 |
| 17052 | salmons | 1 |
| 17053 | salmon | 1 |
| 17054 | sallow | 1 |
| 17055 | sallies | 1 |
| 17056 | salicam | 1 |
| 17057 | salary | 1 |
| 17058 | salamander | 1 |
| 17059 | salad | 1 |
| 17060 | saintlike | 1 |
| 17061 | sain | 1 |
| 17062 | sailmaker | 1 |
| 17063 | sag | 1 |
| 17064 | safeties | 1 |
| 17065 | saf | 1 |
| 17066 | saddles | 1 |
| 17067 | sacring | 1 |
| 17068 | sacrificial | 1 |
| 17069 | sacrificers | 1 |
| 17070 | sackerson | 1 |
| 17071 | sacked | 1 |
| 17072 | sackcloth | 1 |
| 17073 | sackbuts | 1 |
| 17074 | saba | 1 |
| 17075 | rything | 1 |
| 17076 | ruttish | 1 |
| 17077 | rut | 1 |
| 17078 | rusts | 1 |
| 17079 | rustle | 1 |
| 17080 | rustics | 1 |
| 17081 | rustically | 1 |
| 17082 | rusted | 1 |
| 17083 | rushy | 1 |
| 17084 | rushling | 1 |
| 17085 | ruptures | 1 |
| 17086 | rupture | 1 |
| 17087 | runners | 1 |
| 17088 | runner | 1 |
| 17089 | runn | 1 |
| 17090 | rumourer | 1 |
| 17091 | rumination | 1 |
| 17092 | ruminates | 1 |
| 17093 | ruminat | 1 |
| 17094 | ruminaies | 1 |
| 17095 | rumble | 1 |
| 17096 | ruling | 1 |
| 17097 | rulers | 1 |
| 17098 | ruining | 1 |
| 17099 | rugemount | 1 |
| 17100 | rug | 1 |
| 17101 | ruffs | 1 |
| 17102 | ruffling | 1 |
| 17103 | rued | 1 |
| 17104 | rudest | 1 |
| 17105 | ruddy | 1 |
| 17106 | ruddock | 1 |
| 17107 | ruddiness | 1 |
| 17108 | rudand | 1 |
| 17109 | rubious | 1 |
| 17110 | roynish | 1 |
| 17111 | royalize | 1 |
| 17112 | rowlands | 1 |
| 17113 | rover | 1 |
| 17114 | rove | 1 |
| 17115 | routed | 1 |
| 17116 | rously | 1 |
| 17117 | roused | 1 |
| 17118 | roundure | 1 |
| 17119 | rounding | 1 |
| 17120 | roundest | 1 |
| 17121 | rounder | 1 |
| 17122 | roundel | 1 |
| 17123 | roughness | 1 |
| 17124 | rotundity | 1 |
| 17125 | rotting | 1 |
| 17126 | rots | 1 |
| 17127 | rotherham | 1 |
| 17128 | rother | 1 |
| 17129 | roted | 1 |
| 17130 | rosed | 1 |
| 17131 | rosalinda | 1 |
| 17132 | ropery | 1 |
| 17133 | rooting | 1 |
| 17134 | rooteth | 1 |
| 17135 | rootedly | 1 |
| 17136 | rooky | 1 |
| 17137 | rondure | 1 |
| 17138 | romish | 1 |
| 17139 | romanos | 1 |
| 17140 | romano | 1 |
| 17141 | romage | 1 |
| 17142 | rolled | 1 |
| 17143 | roisting | 1 |
| 17144 | roguish | 1 |
| 17145 | rogero | 1 |
| 17146 | roes | 1 |
| 17147 | rochford | 1 |
| 17148 | robed | 1 |
| 17149 | robas | 1 |
| 17150 | roba | 1 |
| 17151 | roarers | 1 |
| 17152 | rless | 1 |
| 17153 | rivo | 1 |
| 17154 | rivelled | 1 |
| 17155 | rivality | 1 |
| 17156 | rivage | 1 |
| 17157 | rish | 1 |
| 17158 | ripping | 1 |
| 17159 | riping | 1 |
| 17160 | ripely | 1 |
| 17161 | rioting | 1 |
| 17162 | rioter | 1 |
| 17163 | ringwood | 1 |
| 17164 | ringleader | 1 |
| 17165 | ringing | 1 |
| 17166 | rin | 1 |
| 17167 | ril | 1 |
| 17168 | rigorously | 1 |
| 17169 | rigol | 1 |
| 17170 | rightfully | 1 |
| 17171 | righteously | 1 |
| 17172 | riggish | 1 |
| 17173 | rifted | 1 |
| 17174 | rifle | 1 |
| 17175 | ries | 1 |
| 17176 | rien | 1 |
| 17177 | ridge | 1 |
| 17178 | rideth | 1 |
| 17179 | ridest | 1 |
| 17180 | riders | 1 |
| 17181 | richmonds | 1 |
| 17182 | ribbed | 1 |
| 17183 | ribaudred | 1 |
| 17184 | ribands | 1 |
| 17185 | ribald | 1 |
| 17186 | rhym | 1 |
| 17187 | rhubarb | 1 |
| 17188 | rhodope | 1 |
| 17189 | rhinoceros | 1 |
| 17190 | rheumy | 1 |
| 17191 | rheums | 1 |
| 17192 | rhesus | 1 |
| 17193 | rhapsody | 1 |
| 17194 | rford | 1 |
| 17195 | reworded | 1 |
| 17196 | reword | 1 |
| 17197 | rewarding | 1 |
| 17198 | rewarder | 1 |
| 17199 | revolutions | 1 |
| 17200 | revokement | 1 |
| 17201 | revok | 1 |
| 17202 | revisits | 1 |
| 17203 | revile | 1 |
| 17204 | reviewest | 1 |
| 17205 | review | 1 |
| 17206 | revers | 1 |
| 17207 | reverbs | 1 |
| 17208 | reverb | 1 |
| 17209 | revengingly | 1 |
| 17210 | revengers | 1 |
| 17211 | revenger | 1 |
| 17212 | revengement | 1 |
| 17213 | revelry | 1 |
| 17214 | reveller | 1 |
| 17215 | reveler | 1 |
| 17216 | reveals | 1 |
| 17217 | revania | 1 |
| 17218 | returnest | 1 |
| 17219 | rets | 1 |
| 17220 | retract | 1 |
| 17221 | retourne | 1 |
| 17222 | retell | 1 |
| 17223 | retaining | 1 |
| 17224 | retails | 1 |
| 17225 | resurrections | 1 |
| 17226 | resumes | 1 |
| 17227 | resum | 1 |
| 17228 | restrains | 1 |
| 17229 | restoring | 1 |
| 17230 | restores | 1 |
| 17231 | restorative | 1 |
| 17232 | restoration | 1 |
| 17233 | respose | 1 |
| 17234 | responsive | 1 |
| 17235 | respites | 1 |
| 17236 | respice | 1 |
| 17237 | respectively | 1 |
| 17238 | respeaking | 1 |
| 17239 | resounds | 1 |
| 17240 | resounding | 1 |
| 17241 | resorted | 1 |
| 17242 | resolveth | 1 |
| 17243 | resolvedly | 1 |
| 17244 | resolutes | 1 |
| 17245 | resisting | 1 |
| 17246 | resignation | 1 |
| 17247 | residue | 1 |
| 17248 | reserves | 1 |
| 17249 | resembleth | 1 |
| 17250 | rescuing | 1 |
| 17251 | rere | 1 |
| 17252 | requit | 1 |
| 17253 | requisites | 1 |
| 17254 | requisite | 1 |
| 17255 | requireth | 1 |
| 17256 | requiem | 1 |
| 17257 | requesting | 1 |
| 17258 | reputing | 1 |
| 17259 | reputeless | 1 |
| 17260 | repured | 1 |
| 17261 | repurchas | 1 |
| 17262 | repulsed | 1 |
| 17263 | repugnant | 1 |
| 17264 | repugnancy | 1 |
| 17265 | repugn | 1 |
| 17266 | reproves | 1 |
| 17267 | reproveable | 1 |
| 17268 | reprov | 1 |
| 17269 | reprobation | 1 |
| 17270 | reproachfully | 1 |
| 17271 | reprisal | 1 |
| 17272 | representing | 1 |
| 17273 | reprehending | 1 |
| 17274 | reposeth | 1 |
| 17275 | reposal | 1 |
| 17276 | reportingly | 1 |
| 17277 | reporting | 1 |
| 17278 | reportest | 1 |
| 17279 | reporter | 1 |
| 17280 | repliest | 1 |
| 17281 | replenish | 1 |
| 17282 | replant | 1 |
| 17283 | repining | 1 |
| 17284 | repine | 1 |
| 17285 | repin | 1 |
| 17286 | repetitions | 1 |
| 17287 | repenting | 1 |
| 17288 | repel | 1 |
| 17289 | repeats | 1 |
| 17290 | repeating | 1 |
| 17291 | repealing | 1 |
| 17292 | repaying | 1 |
| 17293 | repasture | 1 |
| 17294 | repass | 1 |
| 17295 | repaired | 1 |
| 17296 | renowmed | 1 |
| 17297 | renouncing | 1 |
| 17298 | renouncement | 1 |
| 17299 | renewest | 1 |
| 17300 | reneges | 1 |
| 17301 | renege | 1 |
| 17302 | renegado | 1 |
| 17303 | remunerate | 1 |
| 17304 | remover | 1 |
| 17305 | removedness | 1 |
| 17306 | remonstrance | 1 |
| 17307 | remissness | 1 |
| 17308 | remercimens | 1 |
| 17309 | remedied | 1 |
| 17310 | remediate | 1 |
| 17311 | remark | 1 |
| 17312 | relying | 1 |
| 17313 | relume | 1 |
| 17314 | reliquit | 1 |
| 17315 | reliques | 1 |
| 17316 | relinquish | 1 |
| 17317 | religions | 1 |
| 17318 | relieving | 1 |
| 17319 | relieves | 1 |
| 17320 | reliances | 1 |
| 17321 | relents | 1 |
| 17322 | releasing | 1 |
| 17323 | relative | 1 |
| 17324 | relations | 1 |
| 17325 | relates | 1 |
| 17326 | relapse | 1 |
| 17327 | rejourn | 1 |
| 17328 | rejoindure | 1 |
| 17329 | rejoicingly | 1 |
| 17330 | rejoiceth | 1 |
| 17331 | rejoic | 1 |
| 17332 | rejected | 1 |
| 17333 | reject | 1 |
| 17334 | reiterate | 1 |
| 17335 | reinforcement | 1 |
| 17336 | reinforce | 1 |
| 17337 | reinforc | 1 |
| 17338 | regular | 1 |
| 17339 | regress | 1 |
| 17340 | regreets | 1 |
| 17341 | registers | 1 |
| 17342 | regina | 1 |
| 17343 | regiments | 1 |
| 17344 | regentship | 1 |
| 17345 | regenerate | 1 |
| 17346 | regarding | 1 |
| 17347 | regardfully | 1 |
| 17348 | regardance | 1 |
| 17349 | regalia | 1 |
| 17350 | refusest | 1 |
| 17351 | refusal | 1 |
| 17352 | refts | 1 |
| 17353 | refreshing | 1 |
| 17354 | refractory | 1 |
| 17355 | reflecting | 1 |
| 17356 | refin | 1 |
| 17357 | refigured | 1 |
| 17358 | referred | 1 |
| 17359 | referr | 1 |
| 17360 | refell | 1 |
| 17361 | reeleth | 1 |
| 17362 | reeky | 1 |
| 17363 | reeks | 1 |
| 17364 | redressed | 1 |
| 17365 | redound | 1 |
| 17366 | redness | 1 |
| 17367 | redime | 1 |
| 17368 | redeemed | 1 |
| 17369 | rede | 1 |
| 17370 | reddest | 1 |
| 17371 | redder | 1 |
| 17372 | recured | 1 |
| 17373 | recure | 1 |
| 17374 | rectorship | 1 |
| 17375 | rector | 1 |
| 17376 | recreate | 1 |
| 17377 | recoverable | 1 |
| 17378 | recov | 1 |
| 17379 | recounts | 1 |
| 17380 | recountments | 1 |
| 17381 | recounted | 1 |
| 17382 | reconciliation | 1 |
| 17383 | reconciler | 1 |
| 17384 | reconcilement | 1 |
| 17385 | recommended | 1 |
| 17386 | recommend | 1 |
| 17387 | recomforture | 1 |
| 17388 | recomforted | 1 |
| 17389 | recollected | 1 |
| 17390 | recoiling | 1 |
| 17391 | recognizances | 1 |
| 17392 | recognizance | 1 |
| 17393 | reclusive | 1 |
| 17394 | reclaims | 1 |
| 17395 | reckoned | 1 |
| 17396 | recking | 1 |
| 17397 | recited | 1 |
| 17398 | recite | 1 |
| 17399 | reciprocally | 1 |
| 17400 | reciprocal | 1 |
| 17401 | rechate | 1 |
| 17402 | receiveth | 1 |
| 17403 | receiver | 1 |
| 17404 | receipts | 1 |
| 17405 | recanter | 1 |
| 17406 | recant | 1 |
| 17407 | rebus | 1 |
| 17408 | rebukeable | 1 |
| 17409 | rebuk | 1 |
| 17410 | rebound | 1 |
| 17411 | rebelling | 1 |
| 17412 | rebeck | 1 |
| 17413 | rebato | 1 |
| 17414 | rebate | 1 |
| 17415 | reasoned | 1 |
| 17416 | reasonably | 1 |
| 17417 | rears | 1 |
| 17418 | reaps | 1 |
| 17419 | reaping | 1 |
| 17420 | really | 1 |
| 17421 | readins | 1 |
| 17422 | readily | 1 |
| 17423 | reader | 1 |
| 17424 | reacheth | 1 |
| 17425 | razure | 1 |
| 17426 | razors | 1 |
| 17427 | razorable | 1 |
| 17428 | razor | 1 |
| 17429 | razing | 1 |
| 17430 | razeth | 1 |
| 17431 | razes | 1 |
| 17432 | rayed | 1 |
| 17433 | rawness | 1 |
| 17434 | rawly | 1 |
| 17435 | rawer | 1 |
| 17436 | ravishments | 1 |
| 17437 | raving | 1 |
| 17438 | rattles | 1 |
| 17439 | rattle | 1 |
| 17440 | ratolorum | 1 |
| 17441 | rating | 1 |
| 17442 | ratifiers | 1 |
| 17443 | ratherest | 1 |
| 17444 | ratcatcher | 1 |
| 17445 | rasher | 1 |
| 17446 | rased | 1 |
| 17447 | rascalliest | 1 |
| 17448 | rar | 1 |
| 17449 | raptures | 1 |
| 17450 | raps | 1 |
| 17451 | ranting | 1 |
| 17452 | rant | 1 |
| 17453 | ransoming | 1 |
| 17454 | ransacking | 1 |
| 17455 | rankly | 1 |
| 17456 | ranking | 1 |
| 17457 | rangers | 1 |
| 17458 | ranged | 1 |
| 17459 | rancors | 1 |
| 17460 | ramston | 1 |
| 17461 | ramsey | 1 |
| 17462 | ramps | 1 |
| 17463 | rampir | 1 |
| 17464 | rampant | 1 |
| 17465 | rampallian | 1 |
| 17466 | rakes | 1 |
| 17467 | rakers | 1 |
| 17468 | rak | 1 |
| 17469 | raisins | 1 |
| 17470 | rains | 1 |
| 17471 | rainold | 1 |
| 17472 | raining | 1 |
| 17473 | raileth | 1 |
| 17474 | railer | 1 |
| 17475 | railed | 1 |
| 17476 | rah | 1 |
| 17477 | raggedness | 1 |
| 17478 | ragg | 1 |
| 17479 | rageth | 1 |
| 17480 | raft | 1 |
| 17481 | rafe | 1 |
| 17482 | racking | 1 |
| 17483 | rackets | 1 |
| 17484 | racket | 1 |
| 17485 | rackers | 1 |
| 17486 | quotes | 1 |
| 17487 | quoniam | 1 |
| 17488 | quoits | 1 |
| 17489 | quoit | 1 |
| 17490 | quoint | 1 |
| 17491 | quoifs | 1 |
| 17492 | quo | 1 |
| 17493 | quivers | 1 |
| 17494 | quivering | 1 |
| 17495 | quitting | 1 |
| 17496 | quitted | 1 |
| 17497 | quirk | 1 |
| 17498 | quiring | 1 |
| 17499 | quintain | 1 |
| 17500 | quinces | 1 |
| 17501 | quinapalus | 1 |
| 17502 | quilt | 1 |
| 17503 | quills | 1 |
| 17504 | quieter | 1 |
| 17505 | quier | 1 |
| 17506 | quiddits | 1 |
| 17507 | quiddities | 1 |
| 17508 | quid | 1 |
| 17509 | quicksilverr | 1 |
| 17510 | quicksands | 1 |
| 17511 | quicksand | 1 |
| 17512 | quickness | 1 |
| 17513 | quicklier | 1 |
| 17514 | queubus | 1 |
| 17515 | quests | 1 |
| 17516 | questrists | 1 |
| 17517 | questionless | 1 |
| 17518 | questioning | 1 |
| 17519 | questionable | 1 |
| 17520 | questant | 1 |
| 17521 | quern | 1 |
| 17522 | quenchless | 1 |
| 17523 | queasiness | 1 |
| 17524 | queas | 1 |
| 17525 | quay | 1 |
| 17526 | quatch | 1 |
| 17527 | quat | 1 |
| 17528 | quasi | 1 |
| 17529 | quarts | 1 |
| 17530 | quartering | 1 |
| 17531 | quartered | 1 |
| 17532 | quarries | 1 |
| 17533 | quarrelous | 1 |
| 17534 | quarreller | 1 |
| 17535 | quarrell | 1 |
| 17536 | quare | 1 |
| 17537 | quantities | 1 |
| 17538 | quando | 1 |
| 17539 | quam | 1 |
| 17540 | qualmish | 1 |
| 17541 | qualite | 1 |
| 17542 | qualifying | 1 |
| 17543 | qualifies | 1 |
| 17544 | qualification | 1 |
| 17545 | quakes | 1 |
| 17546 | quaffing | 1 |
| 17547 | quadrangle | 1 |
| 17548 | pyrenean | 1 |
| 17549 | pyramises | 1 |
| 17550 | pyramis | 1 |
| 17551 | pyramides | 1 |
| 17552 | pyramid | 1 |
| 17553 | pygmy | 1 |
| 17554 | pygmies | 1 |
| 17555 | pygmalion | 1 |
| 17556 | py | 1 |
| 17557 | puzzles | 1 |
| 17558 | puzzled | 1 |
| 17559 | puzzle | 1 |
| 17560 | puzzel | 1 |
| 17561 | putrified | 1 |
| 17562 | putrefy | 1 |
| 17563 | pusillanimity | 1 |
| 17564 | purveyor | 1 |
| 17565 | purus | 1 |
| 17566 | pursueth | 1 |
| 17567 | pursuers | 1 |
| 17568 | pursents | 1 |
| 17569 | purs | 1 |
| 17570 | purr | 1 |
| 17571 | purposing | 1 |
| 17572 | purport | 1 |
| 17573 | purples | 1 |
| 17574 | purlieus | 1 |
| 17575 | purifying | 1 |
| 17576 | purifies | 1 |
| 17577 | purgers | 1 |
| 17578 | purgative | 1 |
| 17579 | purely | 1 |
| 17580 | purchaseth | 1 |
| 17581 | purchases | 1 |
| 17582 | pur | 1 |
| 17583 | pupils | 1 |
| 17584 | punishments | 1 |
| 17585 | punishes | 1 |
| 17586 | punched | 1 |
| 17587 | pun | 1 |
| 17588 | pumpion | 1 |
| 17589 | pulsidge | 1 |
| 17590 | pulpits | 1 |
| 17591 | pulpiter | 1 |
| 17592 | pullet | 1 |
| 17593 | puller | 1 |
| 17594 | pulcher | 1 |
| 17595 | puking | 1 |
| 17596 | puke | 1 |
| 17597 | puis | 1 |
| 17598 | pugging | 1 |
| 17599 | puffs | 1 |
| 17600 | pueritia | 1 |
| 17601 | pudency | 1 |
| 17602 | pudder | 1 |
| 17603 | publishing | 1 |
| 17604 | publisher | 1 |
| 17605 | published | 1 |
| 17606 | publication | 1 |
| 17607 | publican | 1 |
| 17608 | psalteries | 1 |
| 17609 | psalmist | 1 |
| 17610 | psalm | 1 |
| 17611 | prying | 1 |
| 17612 | prun | 1 |
| 17613 | provoketh | 1 |
| 17614 | provoker | 1 |
| 17615 | proviso | 1 |
| 17616 | proving | 1 |
| 17617 | provides | 1 |
| 17618 | provider | 1 |
| 17619 | providently | 1 |
| 17620 | provand | 1 |
| 17621 | prouds | 1 |
| 17622 | proudlier | 1 |
| 17623 | protractive | 1 |
| 17624 | protheus | 1 |
| 17625 | protesting | 1 |
| 17626 | protester | 1 |
| 17627 | protested | 1 |
| 17628 | protectress | 1 |
| 17629 | prostitute | 1 |
| 17630 | prospers | 1 |
| 17631 | proselytes | 1 |
| 17632 | prosecution | 1 |
| 17633 | proscriptions | 1 |
| 17634 | prorogued | 1 |
| 17635 | propugnation | 1 |
| 17636 | propre | 1 |
| 17637 | propp | 1 |
| 17638 | propounded | 1 |
| 17639 | propositions | 1 |
| 17640 | proposition | 1 |
| 17641 | proposing | 1 |
| 17642 | proposes | 1 |
| 17643 | proposer | 1 |
| 17644 | proportionable | 1 |
| 17645 | propontic | 1 |
| 17646 | propinquity | 1 |
| 17647 | prophesier | 1 |
| 17648 | propension | 1 |
| 17649 | propend | 1 |
| 17650 | propagation | 1 |
| 17651 | pronouns | 1 |
| 17652 | pronoun | 1 |
| 17653 | prononcez | 1 |
| 17654 | prononcer | 1 |
| 17655 | promulgate | 1 |
| 17656 | prompture | 1 |
| 17657 | promptement | 1 |
| 17658 | prometheus | 1 |
| 17659 | prolongs | 1 |
| 17660 | prolixious | 1 |
| 17661 | projects | 1 |
| 17662 | projection | 1 |
| 17663 | prohibition | 1 |
| 17664 | prohibit | 1 |
| 17665 | progression | 1 |
| 17666 | prognosticate | 1 |
| 17667 | progne | 1 |
| 17668 | profoundly | 1 |
| 17669 | profoundest | 1 |
| 17670 | proficient | 1 |
| 17671 | profferer | 1 |
| 17672 | proffered | 1 |
| 17673 | profaning | 1 |
| 17674 | profaners | 1 |
| 17675 | profaneness | 1 |
| 17676 | profanely | 1 |
| 17677 | proface | 1 |
| 17678 | produces | 1 |
| 17679 | produced | 1 |
| 17680 | proditor | 1 |
| 17681 | prodigiously | 1 |
| 17682 | prodigals | 1 |
| 17683 | prodigally | 1 |
| 17684 | prodigality | 1 |
| 17685 | procuring | 1 |
| 17686 | procurator | 1 |
| 17687 | procreation | 1 |
| 17688 | procreants | 1 |
| 17689 | procreant | 1 |
| 17690 | procrastinate | 1 |
| 17691 | proconsul | 1 |
| 17692 | proclaimeth | 1 |
| 17693 | proceeders | 1 |
| 17694 | probal | 1 |
| 17695 | pro | 1 |
| 17696 | prizing | 1 |
| 17697 | prizest | 1 |
| 17698 | prized | 1 |
| 17699 | privity | 1 |
| 17700 | privileges | 1 |
| 17701 | privilage | 1 |
| 17702 | prithe | 1 |
| 17703 | prisonnier | 1 |
| 17704 | prisonment | 1 |
| 17705 | priscian | 1 |
| 17706 | priories | 1 |
| 17707 | prioress | 1 |
| 17708 | prints | 1 |
| 17709 | printless | 1 |
| 17710 | princox | 1 |
| 17711 | principles | 1 |
| 17712 | principality | 1 |
| 17713 | principalities | 1 |
| 17714 | primy | 1 |
| 17715 | primogenity | 1 |
| 17716 | primo | 1 |
| 17717 | primitive | 1 |
| 17718 | primest | 1 |
| 17719 | primer | 1 |
| 17720 | pries | 1 |
| 17721 | prief | 1 |
| 17722 | pried | 1 |
| 17723 | prie | 1 |
| 17724 | prides | 1 |
| 17725 | pricksong | 1 |
| 17726 | pricked | 1 |
| 17727 | preyful | 1 |
| 17728 | preventions | 1 |
| 17729 | prevailment | 1 |
| 17730 | prevaileth | 1 |
| 17731 | prevailed | 1 |
| 17732 | prettiness | 1 |
| 17733 | prettier | 1 |
| 17734 | pretia | 1 |
| 17735 | pretext | 1 |
| 17736 | pretense | 1 |
| 17737 | pretended | 1 |
| 17738 | pretences | 1 |
| 17739 | pret | 1 |
| 17740 | presuppos | 1 |
| 17741 | presumes | 1 |
| 17742 | prester | 1 |
| 17743 | pressures | 1 |
| 17744 | pressure | 1 |
| 17745 | presser | 1 |
| 17746 | pressed | 1 |
| 17747 | president | 1 |
| 17748 | preservers | 1 |
| 17749 | preservative | 1 |
| 17750 | presenters | 1 |
| 17751 | presenter | 1 |
| 17752 | presences | 1 |
| 17753 | prescripts | 1 |
| 17754 | presaging | 1 |
| 17755 | presagers | 1 |
| 17756 | prerogatived | 1 |
| 17757 | prerogatifes | 1 |
| 17758 | prepares | 1 |
| 17759 | preparedly | 1 |
| 17760 | preordinance | 1 |
| 17761 | prenez | 1 |
| 17762 | premised | 1 |
| 17763 | premeditation | 1 |
| 17764 | prejudicial | 1 |
| 17765 | prejudicates | 1 |
| 17766 | pregnantly | 1 |
| 17767 | pregnancy | 1 |
| 17768 | preformed | 1 |
| 17769 | prefixed | 1 |
| 17770 | prefiguring | 1 |
| 17771 | prefers | 1 |
| 17772 | preferring | 1 |
| 17773 | preferreth | 1 |
| 17774 | preface | 1 |
| 17775 | preeminence | 1 |
| 17776 | preeches | 1 |
| 17777 | predictions | 1 |
| 17778 | predict | 1 |
| 17779 | predestinate | 1 |
| 17780 | predecessor | 1 |
| 17781 | predeceased | 1 |
| 17782 | precursors | 1 |
| 17783 | precurse | 1 |
| 17784 | precor | 1 |
| 17785 | precisian | 1 |
| 17786 | preciseness | 1 |
| 17787 | precipitating | 1 |
| 17788 | precipice | 1 |
| 17789 | preciously | 1 |
| 17790 | precinct | 1 |
| 17791 | preceptial | 1 |
| 17792 | precept | 1 |
| 17793 | preambulate | 1 |
| 17794 | pread | 1 |
| 17795 | preachment | 1 |
| 17796 | preaching | 1 |
| 17797 | preaches | 1 |
| 17798 | preachers | 1 |
| 17799 | preached | 1 |
| 17800 | prawns | 1 |
| 17801 | prawls | 1 |
| 17802 | prattler | 1 |
| 17803 | prater | 1 |
| 17804 | prated | 1 |
| 17805 | prancing | 1 |
| 17806 | praiseworthy | 1 |
| 17807 | praisest | 1 |
| 17808 | prague | 1 |
| 17809 | pragging | 1 |
| 17810 | praetors | 1 |
| 17811 | praetor | 1 |
| 17812 | praemunire | 1 |
| 17813 | praeclarissimus | 1 |
| 17814 | practises | 1 |
| 17815 | practisers | 1 |
| 17816 | practiser | 1 |
| 17817 | practisants | 1 |
| 17818 | practicing | 1 |
| 17819 | practicer | 1 |
| 17820 | practiced | 1 |
| 17821 | practic | 1 |
| 17822 | poysam | 1 |
| 17823 | poys | 1 |
| 17824 | powerless | 1 |
| 17825 | powerfully | 1 |
| 17826 | powd | 1 |
| 17827 | pouncet | 1 |
| 17828 | poultney | 1 |
| 17829 | poultice | 1 |
| 17830 | poulter | 1 |
| 17831 | potting | 1 |
| 17832 | potter | 1 |
| 17833 | pother | 1 |
| 17834 | pothecary | 1 |
| 17835 | potents | 1 |
| 17836 | potch | 1 |
| 17837 | potatoes | 1 |
| 17838 | potato | 1 |
| 17839 | potable | 1 |
| 17840 | posthorses | 1 |
| 17841 | posthorse | 1 |
| 17842 | posters | 1 |
| 17843 | posteriors | 1 |
| 17844 | poste | 1 |
| 17845 | possitable | 1 |
| 17846 | possibilities | 1 |
| 17847 | possets | 1 |
| 17848 | posse | 1 |
| 17849 | posied | 1 |
| 17850 | pose | 1 |
| 17851 | portugal | 1 |
| 17852 | portraiture | 1 |
| 17853 | portrait | 1 |
| 17854 | portotartarossa | 1 |
| 17855 | portent | 1 |
| 17856 | portcullis | 1 |
| 17857 | portage | 1 |
| 17858 | poring | 1 |
| 17859 | porches | 1 |
| 17860 | pops | 1 |
| 17861 | poppy | 1 |
| 17862 | popish | 1 |
| 17863 | popingay | 1 |
| 17864 | popedom | 1 |
| 17865 | pop | 1 |
| 17866 | pooh | 1 |
| 17867 | ponton | 1 |
| 17868 | pontifical | 1 |
| 17869 | pontic | 1 |
| 17870 | pont | 1 |
| 17871 | poniard | 1 |
| 17872 | ponds | 1 |
| 17873 | ponder | 1 |
| 17874 | pomps | 1 |
| 17875 | pompion | 1 |
| 17876 | pommel | 1 |
| 17877 | pomgarnet | 1 |
| 17878 | pomewater | 1 |
| 17879 | pomander | 1 |
| 17880 | polyxena | 1 |
| 17881 | polydamus | 1 |
| 17882 | polusion | 1 |
| 17883 | poltroons | 1 |
| 17884 | politicians | 1 |
| 17885 | polished | 1 |
| 17886 | polish | 1 |
| 17887 | policies | 1 |
| 17888 | poli | 1 |
| 17889 | poles | 1 |
| 17890 | polemon | 1 |
| 17891 | polecat | 1 |
| 17892 | poleaxe | 1 |
| 17893 | pold | 1 |
| 17894 | polacks | 1 |
| 17895 | poking | 1 |
| 17896 | poke | 1 |
| 17897 | poisoning | 1 |
| 17898 | poising | 1 |
| 17899 | pointblank | 1 |
| 17900 | poinards | 1 |
| 17901 | pocky | 1 |
| 17902 | pocketing | 1 |
| 17903 | po | 1 |
| 17904 | plurisy | 1 |
| 17905 | plunged | 1 |
| 17906 | plums | 1 |
| 17907 | plumpy | 1 |
| 17908 | plump | 1 |
| 17909 | plue | 1 |
| 17910 | plucker | 1 |
| 17911 | plows | 1 |
| 17912 | plow | 1 |
| 17913 | ploughmen | 1 |
| 17914 | ploughed | 1 |
| 17915 | plotter | 1 |
| 17916 | ploody | 1 |
| 17917 | plood | 1 |
| 17918 | plods | 1 |
| 17919 | plodding | 1 |
| 17920 | plodders | 1 |
| 17921 | plighter | 1 |
| 17922 | plied | 1 |
| 17923 | pliant | 1 |
| 17924 | plessing | 1 |
| 17925 | plessed | 1 |
| 17926 | plenties | 1 |
| 17927 | plenteously | 1 |
| 17928 | plenitude | 1 |
| 17929 | pleines | 1 |
| 17930 | plebs | 1 |
| 17931 | plebeii | 1 |
| 17932 | pleasers | 1 |
| 17933 | pleaser | 1 |
| 17934 | pleasantly | 1 |
| 17935 | pleasance | 1 |
| 17936 | pleaders | 1 |
| 17937 | pleader | 1 |
| 17938 | playhouse | 1 |
| 17939 | playeth | 1 |
| 17940 | plautus | 1 |
| 17941 | plausible | 1 |
| 17942 | platted | 1 |
| 17943 | plats | 1 |
| 17944 | platforms | 1 |
| 17945 | plates | 1 |
| 17946 | plat | 1 |
| 17947 | plasterer | 1 |
| 17948 | plast | 1 |
| 17949 | plash | 1 |
| 17950 | planteth | 1 |
| 17951 | plantation | 1 |
| 17952 | plantage | 1 |
| 17953 | planched | 1 |
| 17954 | plaintiffs | 1 |
| 17955 | plaintful | 1 |
| 17956 | plainsong | 1 |
| 17957 | plainings | 1 |
| 17958 | plaining | 1 |
| 17959 | plaguy | 1 |
| 17960 | plaguing | 1 |
| 17961 | plack | 1 |
| 17962 | placid | 1 |
| 17963 | placentio | 1 |
| 17964 | pius | 1 |
| 17965 | pittikins | 1 |
| 17966 | pittie | 1 |
| 17967 | pittance | 1 |
| 17968 | pits | 1 |
| 17969 | pitie | 1 |
| 17970 | pithy | 1 |
| 17971 | pithless | 1 |
| 17972 | pitfall | 1 |
| 17973 | pitcher | 1 |
| 17974 | pistols | 1 |
| 17975 | pismires | 1 |
| 17976 | pippins | 1 |
| 17977 | pippin | 1 |
| 17978 | pipers | 1 |
| 17979 | piper | 1 |
| 17980 | pip | 1 |
| 17981 | pioners | 1 |
| 17982 | pioner | 1 |
| 17983 | pioneers | 1 |
| 17984 | pioned | 1 |
| 17985 | pintpot | 1 |
| 17986 | pinse | 1 |
| 17987 | pinn | 1 |
| 17988 | pinched | 1 |
| 17989 | pimpernell | 1 |
| 17990 | pilots | 1 |
| 17991 | pillagers | 1 |
| 17992 | pilfering | 1 |
| 17993 | pilf | 1 |
| 17994 | pilchers | 1 |
| 17995 | pilates | 1 |
| 17996 | pigrogromitus | 1 |
| 17997 | pigmy | 1 |
| 17998 | piers | 1 |
| 17999 | piercy | 1 |
| 18000 | pierceth | 1 |
| 18001 | pierces | 1 |
| 18002 | pier | 1 |
| 18003 | piedness | 1 |
| 18004 | piecing | 1 |
| 18005 | pid | 1 |
| 18006 | pictured | 1 |
| 18007 | pictur | 1 |
| 18008 | pickthanks | 1 |
| 18009 | pickt | 1 |
| 18010 | picks | 1 |
| 18011 | pickpurse | 1 |
| 18012 | picklock | 1 |
| 18013 | pickers | 1 |
| 18014 | pickbone | 1 |
| 18015 | pickaxe | 1 |
| 18016 | pible | 1 |
| 18017 | pibble | 1 |
| 18018 | phraseless | 1 |
| 18019 | photinus | 1 |
| 18020 | phorbus | 1 |
| 18021 | phoenicians | 1 |
| 18022 | phoenicia | 1 |
| 18023 | phlegmatic | 1 |
| 18024 | philosophical | 1 |
| 18025 | philosophers | 1 |
| 18026 | philomela | 1 |
| 18027 | phillida | 1 |
| 18028 | philippan | 1 |
| 18029 | philemon | 1 |
| 18030 | philarmonus | 1 |
| 18031 | philadelphos | 1 |
| 18032 | phibbus | 1 |
| 18033 | pheebus | 1 |
| 18034 | phebes | 1 |
| 18035 | pheazar | 1 |
| 18036 | pharsalia | 1 |
| 18037 | phantasma | 1 |
| 18038 | phantasimes | 1 |
| 18039 | phantasime | 1 |
| 18040 | phaeton | 1 |
| 18041 | pewterer | 1 |
| 18042 | pettitoes | 1 |
| 18043 | pettish | 1 |
| 18044 | pettiness | 1 |
| 18045 | petrarch | 1 |
| 18046 | petit | 1 |
| 18047 | petar | 1 |
| 18048 | peseech | 1 |
| 18049 | perverted | 1 |
| 18050 | perverseness | 1 |
| 18051 | perversely | 1 |
| 18052 | perusing | 1 |
| 18053 | perturbed | 1 |
| 18054 | perturbations | 1 |
| 18055 | perturb | 1 |
| 18056 | pertaunt | 1 |
| 18057 | pertaining | 1 |
| 18058 | perspicuous | 1 |
| 18059 | perspectives | 1 |
| 18060 | perspectively | 1 |
| 18061 | personating | 1 |
| 18062 | personates | 1 |
| 18063 | personated | 1 |
| 18064 | personate | 1 |
| 18065 | persists | 1 |
| 18066 | persistive | 1 |
| 18067 | persistency | 1 |
| 18068 | persisted | 1 |
| 18069 | persist | 1 |
| 18070 | persia | 1 |
| 18071 | persevers | 1 |
| 18072 | persecutor | 1 |
| 18073 | persecutions | 1 |
| 18074 | persecuted | 1 |
| 18075 | pers | 1 |
| 18076 | perplexed | 1 |
| 18077 | perpendicularly | 1 |
| 18078 | perpendicular | 1 |
| 18079 | peroration | 1 |
| 18080 | perniciously | 1 |
| 18081 | permissive | 1 |
| 18082 | permanent | 1 |
| 18083 | permafoy | 1 |
| 18084 | perkes | 1 |
| 18085 | perk | 1 |
| 18086 | perjuries | 1 |
| 18087 | perisheth | 1 |
| 18088 | perishest | 1 |
| 18089 | perished | 1 |
| 18090 | perigouna | 1 |
| 18091 | perigort | 1 |
| 18092 | periapts | 1 |
| 18093 | perfumer | 1 |
| 18094 | performer | 1 |
| 18095 | perfidiously | 1 |
| 18096 | perfecter | 1 |
| 18097 | peremptorily | 1 |
| 18098 | peregrinate | 1 |
| 18099 | pere | 1 |
| 18100 | perdurably | 1 |
| 18101 | perdonato | 1 |
| 18102 | perdie | 1 |
| 18103 | percussion | 1 |
| 18104 | percies | 1 |
| 18105 | perceiveth | 1 |
| 18106 | peradventures | 1 |
| 18107 | peppered | 1 |
| 18108 | peppercorn | 1 |
| 18109 | peoples | 1 |
| 18110 | peopl | 1 |
| 18111 | penurious | 1 |
| 18112 | penthesilea | 1 |
| 18113 | pensively | 1 |
| 18114 | pensived | 1 |
| 18115 | pennons | 1 |
| 18116 | penning | 1 |
| 18117 | penned | 1 |
| 18118 | penknife | 1 |
| 18119 | penker | 1 |
| 18120 | penitents | 1 |
| 18121 | penitently | 1 |
| 18122 | penitential | 1 |
| 18123 | penetrative | 1 |
| 18124 | penelope | 1 |
| 18125 | pendulous | 1 |
| 18126 | pendragon | 1 |
| 18127 | pencils | 1 |
| 18128 | pencill | 1 |
| 18129 | peloponnesus | 1 |
| 18130 | pella | 1 |
| 18131 | pelf | 1 |
| 18132 | peize | 1 |
| 18133 | peised | 1 |
| 18134 | peise | 1 |
| 18135 | pegs | 1 |
| 18136 | peflur | 1 |
| 18137 | peevishly | 1 |
| 18138 | peesel | 1 |
| 18139 | peereth | 1 |
| 18140 | peeped | 1 |
| 18141 | peel | 1 |
| 18142 | peds | 1 |
| 18143 | pedlars | 1 |
| 18144 | pedestal | 1 |
| 18145 | pede | 1 |
| 18146 | pedascule | 1 |
| 18147 | pedantical | 1 |
| 18148 | pecus | 1 |
| 18149 | pecks | 1 |
| 18150 | pebbled | 1 |
| 18151 | peating | 1 |
| 18152 | peaten | 1 |
| 18153 | peasantry | 1 |
| 18154 | pears | 1 |
| 18155 | peals | 1 |
| 18156 | peaking | 1 |
| 18157 | peacocks | 1 |
| 18158 | peaches | 1 |
| 18159 | peaces | 1 |
| 18160 | peacemakers | 1 |
| 18161 | peaceable | 1 |
| 18162 | paysans | 1 |
| 18163 | paysan | 1 |
| 18164 | payments | 1 |
| 18165 | payest | 1 |
| 18166 | pawns | 1 |
| 18167 | pavin | 1 |
| 18168 | pavilions | 1 |
| 18169 | pav | 1 |
| 18170 | pauvres | 1 |
| 18171 | pausingly | 1 |
| 18172 | pauses | 1 |
| 18173 | pauser | 1 |
| 18174 | paunches | 1 |
| 18175 | paucas | 1 |
| 18176 | pattle | 1 |
| 18177 | patter | 1 |
| 18178 | patrum | 1 |
| 18179 | patrons | 1 |
| 18180 | patines | 1 |
| 18181 | patients | 1 |
| 18182 | pathways | 1 |
| 18183 | pathway | 1 |
| 18184 | paternal | 1 |
| 18185 | patay | 1 |
| 18186 | pastures | 1 |
| 18187 | pastry | 1 |
| 18188 | pastors | 1 |
| 18189 | pastorals | 1 |
| 18190 | pasties | 1 |
| 18191 | pasterns | 1 |
| 18192 | passy | 1 |
| 18193 | passive | 1 |
| 18194 | passioning | 1 |
| 18195 | passio | 1 |
| 18196 | passant | 1 |
| 18197 | pashful | 1 |
| 18198 | pashed | 1 |
| 18199 | partizan | 1 |
| 18200 | partisan | 1 |
| 18201 | particularize | 1 |
| 18202 | partially | 1 |
| 18203 | partialize | 1 |
| 18204 | parthians | 1 |
| 18205 | partakers | 1 |
| 18206 | partaken | 1 |
| 18207 | parsley | 1 |
| 18208 | parricides | 1 |
| 18209 | parricide | 1 |
| 18210 | parmacity | 1 |
| 18211 | parlors | 1 |
| 18212 | parlez | 1 |
| 18213 | parles | 1 |
| 18214 | parler | 1 |
| 18215 | paritors | 1 |
| 18216 | parisians | 1 |
| 18217 | parfect | 1 |
| 18218 | parel | 1 |
| 18219 | pared | 1 |
| 18220 | pardonne | 1 |
| 18221 | pardoner | 1 |
| 18222 | pardona | 1 |
| 18223 | parched | 1 |
| 18224 | parcell | 1 |
| 18225 | parca | 1 |
| 18226 | parasites | 1 |
| 18227 | paraquito | 1 |
| 18228 | parapets | 1 |
| 18229 | paramours | 1 |
| 18230 | paragons | 1 |
| 18231 | paracelsus | 1 |
| 18232 | parable | 1 |
| 18233 | paps | 1 |
| 18234 | papist | 1 |
| 18235 | paphos | 1 |
| 18236 | paphlagonia | 1 |
| 18237 | papal | 1 |
| 18238 | pantry | 1 |
| 18239 | pantingly | 1 |
| 18240 | panted | 1 |
| 18241 | pansies | 1 |
| 18242 | pansa | 1 |
| 18243 | pannier | 1 |
| 18244 | panging | 1 |
| 18245 | panel | 1 |
| 18246 | panderly | 1 |
| 18247 | pancake | 1 |
| 18248 | pancackes | 1 |
| 18249 | pan | 1 |
| 18250 | pamphlets | 1 |
| 18251 | pamp | 1 |
| 18252 | palt | 1 |
| 18253 | palsies | 1 |
| 18254 | palmy | 1 |
| 18255 | pallets | 1 |
| 18256 | pallabris | 1 |
| 18257 | palisadoes | 1 |
| 18258 | paled | 1 |
| 18259 | palating | 1 |
| 18260 | palamedes | 1 |
| 18261 | palabras | 1 |
| 18262 | pal | 1 |
| 18263 | pajock | 1 |
| 18264 | pairs | 1 |
| 18265 | paired | 1 |
| 18266 | paints | 1 |
| 18267 | pained | 1 |
| 18268 | pails | 1 |
| 18269 | pailfuls | 1 |
| 18270 | paddle | 1 |
| 18271 | pad | 1 |
| 18272 | paction | 1 |
| 18273 | packthread | 1 |
| 18274 | packs | 1 |
| 18275 | packings | 1 |
| 18276 | packhorses | 1 |
| 18277 | pacify | 1 |
| 18278 | paced | 1 |
| 18279 | pabylon | 1 |
| 18280 | pabble | 1 |
| 18281 | oxfordshire | 1 |
| 18282 | owy | 1 |
| 18283 | owns | 1 |
| 18284 | owning | 1 |
| 18285 | oweth | 1 |
| 18286 | owedst | 1 |
| 18287 | ovidius | 1 |
| 18288 | overworn | 1 |
| 18289 | overwhelming | 1 |
| 18290 | overweigh | 1 |
| 18291 | overween | 1 |
| 18292 | overwatch | 1 |
| 18293 | overtopp | 1 |
| 18294 | overtook | 1 |
| 18295 | overthrows | 1 |
| 18296 | overtaketh | 1 |
| 18297 | overt | 1 |
| 18298 | overswear | 1 |
| 18299 | overstain | 1 |
| 18300 | overspread | 1 |
| 18301 | oversights | 1 |
| 18302 | overshot | 1 |
| 18303 | overshines | 1 |
| 18304 | overshades | 1 |
| 18305 | overset | 1 |
| 18306 | overscutch | 1 |
| 18307 | overrun | 1 |
| 18308 | overpeering | 1 |
| 18309 | overpass | 1 |
| 18310 | overmuch | 1 |
| 18311 | overmounting | 1 |
| 18312 | overmaster | 1 |
| 18313 | overlooking | 1 |
| 18314 | overlive | 1 |
| 18315 | overleather | 1 |
| 18316 | overland | 1 |
| 18317 | overkind | 1 |
| 18318 | overhold | 1 |
| 18319 | overhead | 1 |
| 18320 | overgrown | 1 |
| 18321 | overgorg | 1 |
| 18322 | overgone | 1 |
| 18323 | overgo | 1 |
| 18324 | overglance | 1 |
| 18325 | overflown | 1 |
| 18326 | overfar | 1 |
| 18327 | overearnest | 1 |
| 18328 | overcomes | 1 |
| 18329 | overcharg | 1 |
| 18330 | overcast | 1 |
| 18331 | overbuys | 1 |
| 18332 | overbulk | 1 |
| 18333 | overbold | 1 |
| 18334 | overawe | 1 |
| 18335 | outworths | 1 |
| 18336 | outwent | 1 |
| 18337 | outvenoms | 1 |
| 18338 | outswear | 1 |
| 18339 | outstripped | 1 |
| 18340 | outstrike | 1 |
| 18341 | outstretched | 1 |
| 18342 | outstood | 1 |
| 18343 | outstay | 1 |
| 18344 | outsport | 1 |
| 18345 | outspeaks | 1 |
| 18346 | outsides | 1 |
| 18347 | outsells | 1 |
| 18348 | outsell | 1 |
| 18349 | outscorn | 1 |
| 18350 | outscold | 1 |
| 18351 | outruns | 1 |
| 18352 | outrunning | 1 |
| 18353 | outroar | 1 |
| 18354 | outran | 1 |
| 18355 | outpriz | 1 |
| 18356 | outlustres | 1 |
| 18357 | outlook | 1 |
| 18358 | outliving | 1 |
| 18359 | outliv | 1 |
| 18360 | outlawry | 1 |
| 18361 | outjest | 1 |
| 18362 | outgrown | 1 |
| 18363 | outgoes | 1 |
| 18364 | outgo | 1 |
| 18365 | outfrown | 1 |
| 18366 | outfly | 1 |
| 18367 | outfaced | 1 |
| 18368 | outdone | 1 |
| 18369 | outdares | 1 |
| 18370 | outdare | 1 |
| 18371 | outdar | 1 |
| 18372 | outcry | 1 |
| 18373 | outcries | 1 |
| 18374 | outbreak | 1 |
| 18375 | outbraves | 1 |
| 18376 | outbrave | 1 |
| 18377 | outbids | 1 |
| 18378 | ounces | 1 |
| 18379 | ouches | 1 |
| 18380 | ottoman | 1 |
| 18381 | otherwhiles | 1 |
| 18382 | othergates | 1 |
| 18383 | ostrich | 1 |
| 18384 | ostlers | 1 |
| 18385 | ostents | 1 |
| 18386 | ostentare | 1 |
| 18387 | ost | 1 |
| 18388 | ossa | 1 |
| 18389 | osprey | 1 |
| 18390 | osier | 1 |
| 18391 | oscorbidulchos | 1 |
| 18392 | orts | 1 |
| 18393 | orodes | 1 |
| 18394 | orifex | 1 |
| 18395 | orgillous | 1 |
| 18396 | ordure | 1 |
| 18397 | ords | 1 |
| 18398 | ordinaries | 1 |
| 18399 | ordinant | 1 |
| 18400 | orderless | 1 |
| 18401 | ordaining | 1 |
| 18402 | opulency | 1 |
| 18403 | oppugnancy | 1 |
| 18404 | opprobriously | 1 |
| 18405 | opprest | 1 |
| 18406 | oppressor | 1 |
| 18407 | oppresseth | 1 |
| 18408 | oppresses | 1 |
| 18409 | oppositions | 1 |
| 18410 | opposes | 1 |
| 18411 | opposeless | 1 |
| 18412 | operative | 1 |
| 18413 | operations | 1 |
| 18414 | openness | 1 |
| 18415 | opener | 1 |
| 18416 | oozy | 1 |
| 18417 | oozes | 1 |
| 18418 | oo | 1 |
| 18419 | onwards | 1 |
| 18420 | oneyers | 1 |
| 18421 | omittance | 1 |
| 18422 | omission | 1 |
| 18423 | omen | 1 |
| 18424 | omans | 1 |
| 18425 | olivers | 1 |
| 18426 | oldness | 1 |
| 18427 | olden | 1 |
| 18428 | oldcastle | 1 |
| 18429 | oils | 1 |
| 18430 | officed | 1 |
| 18431 | offert | 1 |
| 18432 | offenses | 1 |
| 18433 | offenseless | 1 |
| 18434 | offendress | 1 |
| 18435 | offendeth | 1 |
| 18436 | offendendo | 1 |
| 18437 | offenceful | 1 |
| 18438 | oeuvres | 1 |
| 18439 | oes | 1 |
| 18440 | oeillades | 1 |
| 18441 | ods | 1 |
| 18442 | odes | 1 |
| 18443 | ode | 1 |
| 18444 | oddest | 1 |
| 18445 | ocular | 1 |
| 18446 | occurrents | 1 |
| 18447 | occurrences | 1 |
| 18448 | occurrence | 1 |
| 18449 | occupies | 1 |
| 18450 | occupied | 1 |
| 18451 | occupations | 1 |
| 18452 | occupat | 1 |
| 18453 | occulted | 1 |
| 18454 | occidental | 1 |
| 18455 | obstructions | 1 |
| 18456 | obstruct | 1 |
| 18457 | obstinately | 1 |
| 18458 | obsque | 1 |
| 18459 | observingly | 1 |
| 18460 | observers | 1 |
| 18461 | observants | 1 |
| 18462 | observancy | 1 |
| 18463 | obsequiously | 1 |
| 18464 | obscurity | 1 |
| 18465 | obscuring | 1 |
| 18466 | obscures | 1 |
| 18467 | obscurely | 1 |
| 18468 | obliged | 1 |
| 18469 | obligations | 1 |
| 18470 | oblations | 1 |
| 18471 | oblation | 1 |
| 18472 | objected | 1 |
| 18473 | obidicut | 1 |
| 18474 | obeisance | 1 |
| 18475 | obduracy | 1 |
| 18476 | ob | 1 |
| 18477 | oathable | 1 |
| 18478 | oaten | 1 |
| 18479 | oatcake | 1 |
| 18480 | oared | 1 |
| 18481 | nutriment | 1 |
| 18482 | nutmegs | 1 |
| 18483 | nuthook | 1 |
| 18484 | nurtur | 1 |
| 18485 | nursh | 1 |
| 18486 | nurseth | 1 |
| 18487 | nurses | 1 |
| 18488 | nurser | 1 |
| 18489 | nursed | 1 |
| 18490 | nuntius | 1 |
| 18491 | nuncio | 1 |
| 18492 | numbness | 1 |
| 18493 | numbering | 1 |
| 18494 | numbered | 1 |
| 18495 | numa | 1 |
| 18496 | nubibus | 1 |
| 18497 | nt | 1 |
| 18498 | noyance | 1 |
| 18499 | novum | 1 |
| 18500 | novi | 1 |
| 18501 | noverbs | 1 |
| 18502 | novelties | 1 |
| 18503 | novel | 1 |
| 18504 | nourishing | 1 |
| 18505 | nourishes | 1 |
| 18506 | nourisher | 1 |
| 18507 | noun | 1 |
| 18508 | noteworthy | 1 |
| 18509 | notest | 1 |
| 18510 | notedly | 1 |
| 18511 | notebook | 1 |
| 18512 | notch | 1 |
| 18513 | notably | 1 |
| 18514 | nostra | 1 |
| 18515 | noster | 1 |
| 18516 | noseless | 1 |
| 18517 | nos | 1 |
| 18518 | norwegian | 1 |
| 18519 | norways | 1 |
| 18520 | northumberlands | 1 |
| 18521 | northerly | 1 |
| 18522 | northamptonshire | 1 |
| 18523 | norbery | 1 |
| 18524 | noonday | 1 |
| 18525 | nooks | 1 |
| 18526 | nonsuits | 1 |
| 18527 | nonage | 1 |
| 18528 | nole | 1 |
| 18529 | noisemaker | 1 |
| 18530 | noes | 1 |
| 18531 | noddles | 1 |
| 18532 | noddle | 1 |
| 18533 | noces | 1 |
| 18534 | noblesse | 1 |
| 18535 | nobis | 1 |
| 18536 | nnights | 1 |
| 18537 | nly | 1 |
| 18538 | nipp | 1 |
| 18539 | niobes | 1 |
| 18540 | niobe | 1 |
| 18541 | ningly | 1 |
| 18542 | nimbler | 1 |
| 18543 | nimbleness | 1 |
| 18544 | nihil | 1 |
| 18545 | nightmare | 1 |
| 18546 | nightcaps | 1 |
| 18547 | nightcap | 1 |
| 18548 | niggarding | 1 |
| 18549 | nieces | 1 |
| 18550 | nicks | 1 |
| 18551 | nicety | 1 |
| 18552 | nicer | 1 |
| 18553 | niceness | 1 |
| 18554 | newts | 1 |
| 18555 | newsmongers | 1 |
| 18556 | newgate | 1 |
| 18557 | newborn | 1 |
| 18558 | neuter | 1 |
| 18559 | netherlands | 1 |
| 18560 | nervy | 1 |
| 18561 | nervii | 1 |
| 18562 | ners | 1 |
| 18563 | neroes | 1 |
| 18564 | nereides | 1 |
| 18565 | neoptolemus | 1 |
| 18566 | nemesis | 1 |
| 18567 | neighbors | 1 |
| 18568 | negro | 1 |
| 18569 | negotiations | 1 |
| 18570 | neglectingly | 1 |
| 18571 | negatives | 1 |
| 18572 | negative | 1 |
| 18573 | negation | 1 |
| 18574 | nefas | 1 |
| 18575 | neeze | 1 |
| 18576 | needly | 1 |
| 18577 | needing | 1 |
| 18578 | needfull | 1 |
| 18579 | needer | 1 |
| 18580 | necklace | 1 |
| 18581 | necessitied | 1 |
| 18582 | necessarily | 1 |
| 18583 | nec | 1 |
| 18584 | nebuchadnezzar | 1 |
| 18585 | nebour | 1 |
| 18586 | neb | 1 |
| 18587 | neatly | 1 |
| 18588 | neapolitans | 1 |
| 18589 | neanmoins | 1 |
| 18590 | neamnoins | 1 |
| 18591 | nazarite | 1 |
| 18592 | nayword | 1 |
| 18593 | nayward | 1 |
| 18594 | navigation | 1 |
| 18595 | navel | 1 |
| 18596 | naughtily | 1 |
| 18597 | natus | 1 |
| 18598 | natured | 1 |
| 18599 | naturalize | 1 |
| 18600 | natifs | 1 |
| 18601 | narines | 1 |
| 18602 | narcissus | 1 |
| 18603 | naps | 1 |
| 18604 | napless | 1 |
| 18605 | napes | 1 |
| 18606 | namest | 1 |
| 18607 | nal | 1 |
| 18608 | nak | 1 |
| 18609 | naiads | 1 |
| 18610 | nags | 1 |
| 18611 | nage | 1 |
| 18612 | myst | 1 |
| 18613 | mynheers | 1 |
| 18614 | muzzled | 1 |
| 18615 | muzzl | 1 |
| 18616 | mutualities | 1 |
| 18617 | muttered | 1 |
| 18618 | mutines | 1 |
| 18619 | mutineers | 1 |
| 18620 | mutineer | 1 |
| 18621 | mutine | 1 |
| 18622 | mutest | 1 |
| 18623 | mutations | 1 |
| 18624 | mutation | 1 |
| 18625 | mutable | 1 |
| 18626 | mustering | 1 |
| 18627 | mussels | 1 |
| 18628 | mussel | 1 |
| 18629 | muss | 1 |
| 18630 | muskos | 1 |
| 18631 | muskets | 1 |
| 18632 | musket | 1 |
| 18633 | musings | 1 |
| 18634 | mushrooms | 1 |
| 18635 | mush | 1 |
| 18636 | muscovy | 1 |
| 18637 | muscovits | 1 |
| 18638 | muscadel | 1 |
| 18639 | murthering | 1 |
| 18640 | murrion | 1 |
| 18641 | murray | 1 |
| 18642 | murmurers | 1 |
| 18643 | murky | 1 |
| 18644 | murkiest | 1 |
| 18645 | murk | 1 |
| 18646 | mure | 1 |
| 18647 | muniments | 1 |
| 18648 | munch | 1 |
| 18649 | mun | 1 |
| 18650 | mummers | 1 |
| 18651 | mumble | 1 |
| 18652 | multipotent | 1 |
| 18653 | multiply | 1 |
| 18654 | mull | 1 |
| 18655 | muliteus | 1 |
| 18656 | mulieres | 1 |
| 18657 | mulberries | 1 |
| 18658 | mugs | 1 |
| 18659 | mugger | 1 |
| 18660 | muffling | 1 |
| 18661 | muffl | 1 |
| 18662 | muffins | 1 |
| 18663 | muck | 1 |
| 18664 | moyses | 1 |
| 18665 | mower | 1 |
| 18666 | movousus | 1 |
| 18667 | movingly | 1 |
| 18668 | moveth | 1 |
| 18669 | mover | 1 |
| 18670 | mousetrap | 1 |
| 18671 | mous | 1 |
| 18672 | mournings | 1 |
| 18673 | mourningly | 1 |
| 18674 | mournfully | 1 |
| 18675 | mourned | 1 |
| 18676 | mounteth | 1 |
| 18677 | mountanto | 1 |
| 18678 | mountant | 1 |
| 18679 | mounseur | 1 |
| 18680 | moulten | 1 |
| 18681 | moult | 1 |
| 18682 | moulds | 1 |
| 18683 | mouldeth | 1 |
| 18684 | mought | 1 |
| 18685 | motionless | 1 |
| 18686 | moths | 1 |
| 18687 | mossgrown | 1 |
| 18688 | mose | 1 |
| 18689 | mortise | 1 |
| 18690 | mortis | 1 |
| 18691 | mortimers | 1 |
| 18692 | mortgaged | 1 |
| 18693 | mortally | 1 |
| 18694 | morsels | 1 |
| 18695 | morisco | 1 |
| 18696 | mori | 1 |
| 18697 | mores | 1 |
| 18698 | morality | 1 |
| 18699 | moraler | 1 |
| 18700 | mopping | 1 |
| 18701 | moping | 1 |
| 18702 | mop | 1 |
| 18703 | moorship | 1 |
| 18704 | moors | 1 |
| 18705 | moorfields | 1 |
| 18706 | moonshines | 1 |
| 18707 | moonish | 1 |
| 18708 | moonbeams | 1 |
| 18709 | montferrat | 1 |
| 18710 | montez | 1 |
| 18711 | montant | 1 |
| 18712 | montage | 1 |
| 18713 | montacute | 1 |
| 18714 | monstruosity | 1 |
| 18715 | monstrousness | 1 |
| 18716 | monstrously | 1 |
| 18717 | monsieurs | 1 |
| 18718 | mons | 1 |
| 18719 | monopoly | 1 |
| 18720 | monks | 1 |
| 18721 | mongrels | 1 |
| 18722 | monging | 1 |
| 18723 | monastic | 1 |
| 18724 | monast | 1 |
| 18725 | monarcho | 1 |
| 18726 | monarchize | 1 |
| 18727 | monarchies | 1 |
| 18728 | moming | 1 |
| 18729 | mome | 1 |
| 18730 | molto | 1 |
| 18731 | mollification | 1 |
| 18732 | molestation | 1 |
| 18733 | moldwarp | 1 |
| 18734 | moisten | 1 |
| 18735 | modicums | 1 |
| 18736 | moderation | 1 |
| 18737 | modena | 1 |
| 18738 | mockvater | 1 |
| 18739 | mockeries | 1 |
| 18740 | mockable | 1 |
| 18741 | moat | 1 |
| 18742 | mixtures | 1 |
| 18743 | mixed | 1 |
| 18744 | mithridates | 1 |
| 18745 | mites | 1 |
| 18746 | misuses | 1 |
| 18747 | misused | 1 |
| 18748 | mists | 1 |
| 18749 | mistrusting | 1 |
| 18750 | mistrustful | 1 |
| 18751 | mistriship | 1 |
| 18752 | mistresss | 1 |
| 18753 | mistreadings | 1 |
| 18754 | mistletoe | 1 |
| 18755 | misthought | 1 |
| 18756 | misthink | 1 |
| 18757 | mistful | 1 |
| 18758 | misterm | 1 |
| 18759 | mistempered | 1 |
| 18760 | mistemp | 1 |
| 18761 | mistakings | 1 |
| 18762 | mistaketh | 1 |
| 18763 | misspoke | 1 |
| 18764 | missives | 1 |
| 18765 | missive | 1 |
| 18766 | missions | 1 |
| 18767 | missingly | 1 |
| 18768 | missheathed | 1 |
| 18769 | misshap | 1 |
| 18770 | misses | 1 |
| 18771 | missed | 1 |
| 18772 | misreport | 1 |
| 18773 | misquote | 1 |
| 18774 | misproud | 1 |
| 18775 | mispris | 1 |
| 18776 | misplaces | 1 |
| 18777 | misord | 1 |
| 18778 | misleading | 1 |
| 18779 | misleaders | 1 |
| 18780 | misinterpret | 1 |
| 18781 | misheard | 1 |
| 18782 | misguide | 1 |
| 18783 | misgraffed | 1 |
| 18784 | misgovernment | 1 |
| 18785 | misgoverned | 1 |
| 18786 | misgiving | 1 |
| 18787 | misgive | 1 |
| 18788 | misers | 1 |
| 18789 | misericorde | 1 |
| 18790 | miserably | 1 |
| 18791 | misdoubteth | 1 |
| 18792 | misdemeanours | 1 |
| 18793 | misdemean | 1 |
| 18794 | misdeeds | 1 |
| 18795 | misdeed | 1 |
| 18796 | miscreate | 1 |
| 18797 | misconstrues | 1 |
| 18798 | misconstruction | 1 |
| 18799 | misconst | 1 |
| 18800 | misconceived | 1 |
| 18801 | mischances | 1 |
| 18802 | miscarrying | 1 |
| 18803 | miscarries | 1 |
| 18804 | miscalled | 1 |
| 18805 | misbhav | 1 |
| 18806 | misbelieving | 1 |
| 18807 | misbeliever | 1 |
| 18808 | misbegot | 1 |
| 18809 | misbecome | 1 |
| 18810 | misbecom | 1 |
| 18811 | misbecame | 1 |
| 18812 | misapplied | 1 |
| 18813 | misanthropos | 1 |
| 18814 | misadventur | 1 |
| 18815 | mis | 1 |
| 18816 | mirthful | 1 |
| 18817 | mirable | 1 |
| 18818 | mir | 1 |
| 18819 | mio | 1 |
| 18820 | minutely | 1 |
| 18821 | mints | 1 |
| 18822 | minotaurs | 1 |
| 18823 | minos | 1 |
| 18824 | minnows | 1 |
| 18825 | minnow | 1 |
| 18826 | ministration | 1 |
| 18827 | mining | 1 |
| 18828 | minimus | 1 |
| 18829 | minimo | 1 |
| 18830 | minime | 1 |
| 18831 | minim | 1 |
| 18832 | minikin | 1 |
| 18833 | minerals | 1 |
| 18834 | minces | 1 |
| 18835 | minc | 1 |
| 18836 | mimic | 1 |
| 18837 | milo | 1 |
| 18838 | millioned | 1 |
| 18839 | mille | 1 |
| 18840 | milksops | 1 |
| 18841 | milking | 1 |
| 18842 | militarist | 1 |
| 18843 | mildews | 1 |
| 18844 | mildew | 1 |
| 18845 | mightful | 1 |
| 18846 | mienne | 1 |
| 18847 | midwives | 1 |
| 18848 | midriff | 1 |
| 18849 | middleham | 1 |
| 18850 | middest | 1 |
| 18851 | midas | 1 |
| 18852 | microcosm | 1 |
| 18853 | miching | 1 |
| 18854 | micher | 1 |
| 18855 | mewling | 1 |
| 18856 | mewed | 1 |
| 18857 | meus | 1 |
| 18858 | mette | 1 |
| 18859 | metropolis | 1 |
| 18860 | metres | 1 |
| 18861 | methods | 1 |
| 18862 | methink | 1 |
| 18863 | metheglins | 1 |
| 18864 | metheglin | 1 |
| 18865 | meteyard | 1 |
| 18866 | metaphysics | 1 |
| 18867 | metaphysical | 1 |
| 18868 | metamorphoses | 1 |
| 18869 | mesopotamia | 1 |
| 18870 | meshes | 1 |
| 18871 | mes | 1 |
| 18872 | mervailous | 1 |
| 18873 | merriness | 1 |
| 18874 | merriments | 1 |
| 18875 | merriman | 1 |
| 18876 | merops | 1 |
| 18877 | mermaids | 1 |
| 18878 | meridian | 1 |
| 18879 | merest | 1 |
| 18880 | mered | 1 |
| 18881 | mercuries | 1 |
| 18882 | mercurial | 1 |
| 18883 | mercifully | 1 |
| 18884 | merchandized | 1 |
| 18885 | mercenaries | 1 |
| 18886 | mercatio | 1 |
| 18887 | mercatante | 1 |
| 18888 | mephostophilus | 1 |
| 18889 | mentis | 1 |
| 18890 | menaphon | 1 |
| 18891 | menaces | 1 |
| 18892 | memphis | 1 |
| 18893 | memorize | 1 |
| 18894 | memoriz | 1 |
| 18895 | memorials | 1 |
| 18896 | memorandums | 1 |
| 18897 | memento | 1 |
| 18898 | mellowing | 1 |
| 18899 | mellifluous | 1 |
| 18900 | melford | 1 |
| 18901 | melancholies | 1 |
| 18902 | meisen | 1 |
| 18903 | meilleur | 1 |
| 18904 | mehercle | 1 |
| 18905 | meetness | 1 |
| 18906 | meetly | 1 |
| 18907 | meekly | 1 |
| 18908 | meeds | 1 |
| 18909 | mediterraneum | 1 |
| 18910 | mediterranean | 1 |
| 18911 | meditates | 1 |
| 18912 | medice | 1 |
| 18913 | mediators | 1 |
| 18914 | mede | 1 |
| 18915 | medal | 1 |
| 18916 | mechante | 1 |
| 18917 | mechanics | 1 |
| 18918 | mechanicals | 1 |
| 18919 | measurable | 1 |
| 18920 | measles | 1 |
| 18921 | meaneth | 1 |
| 18922 | meanders | 1 |
| 18923 | mealy | 1 |
| 18924 | meadow | 1 |
| 18925 | meacock | 1 |
| 18926 | mazes | 1 |
| 18927 | mazed | 1 |
| 18928 | maypole | 1 |
| 18929 | mayday | 1 |
| 18930 | maxim | 1 |
| 18931 | mauvais | 1 |
| 18932 | mauritania | 1 |
| 18933 | mauri | 1 |
| 18934 | maund | 1 |
| 18935 | maudlin | 1 |
| 18936 | maud | 1 |
| 18937 | mattress | 1 |
| 18938 | matin | 1 |
| 18939 | matcheth | 1 |
| 18940 | masts | 1 |
| 18941 | mastiff | 1 |
| 18942 | mastic | 1 |
| 18943 | masterpiece | 1 |
| 18944 | masterest | 1 |
| 18945 | masterdom | 1 |
| 18946 | mastcr | 1 |
| 18947 | masses | 1 |
| 18948 | masons | 1 |
| 18949 | masking | 1 |
| 18950 | masker | 1 |
| 18951 | mas | 1 |
| 18952 | marvels | 1 |
| 18953 | martyrs | 1 |
| 18954 | marts | 1 |
| 18955 | martlemas | 1 |
| 18956 | martino | 1 |
| 18957 | martin | 1 |
| 18958 | martem | 1 |
| 18959 | marted | 1 |
| 18960 | marshalship | 1 |
| 18961 | marshalsea | 1 |
| 18962 | marsh | 1 |
| 18963 | marrowless | 1 |
| 18964 | marmoset | 1 |
| 18965 | marle | 1 |
| 18966 | marl | 1 |
| 18967 | markman | 1 |
| 18968 | maritime | 1 |
| 18969 | marge | 1 |
| 18970 | marcians | 1 |
| 18971 | marchpane | 1 |
| 18972 | marbled | 1 |
| 18973 | manus | 1 |
| 18974 | manure | 1 |
| 18975 | manual | 1 |
| 18976 | mantles | 1 |
| 18977 | manslaughter | 1 |
| 18978 | mansions | 1 |
| 18979 | mansionry | 1 |
| 18980 | manningtree | 1 |
| 18981 | manna | 1 |
| 18982 | manlike | 1 |
| 18983 | manka | 1 |
| 18984 | manifoldly | 1 |
| 18985 | mangy | 1 |
| 18986 | mangling | 1 |
| 18987 | mangles | 1 |
| 18988 | manet | 1 |
| 18989 | mandrakes | 1 |
| 18990 | manchus | 1 |
| 18991 | manakin | 1 |
| 18992 | mammock | 1 |
| 18993 | mammets | 1 |
| 18994 | mammet | 1 |
| 18995 | mammering | 1 |
| 18996 | maltworms | 1 |
| 18997 | mallows | 1 |
| 18998 | mallet | 1 |
| 18999 | mallard | 1 |
| 19000 | malkin | 1 |
| 19001 | malignantly | 1 |
| 19002 | malignancy | 1 |
| 19003 | malign | 1 |
| 19004 | malhecho | 1 |
| 19005 | malevolent | 1 |
| 19006 | malevolence | 1 |
| 19007 | malefactor | 1 |
| 19008 | malefactions | 1 |
| 19009 | maledictions | 1 |
| 19010 | mala | 1 |
| 19011 | mal | 1 |
| 19012 | makings | 1 |
| 19013 | makeless | 1 |
| 19014 | majority | 1 |
| 19015 | majestically | 1 |
| 19016 | majestas | 1 |
| 19017 | maison | 1 |
| 19018 | mais | 1 |
| 19019 | mains | 1 |
| 19020 | mainmast | 1 |
| 19021 | maincourse | 1 |
| 19022 | maims | 1 |
| 19023 | maimed | 1 |
| 19024 | mails | 1 |
| 19025 | mailed | 1 |
| 19026 | maidenliest | 1 |
| 19027 | maidenhoods | 1 |
| 19028 | mahomet | 1 |
| 19029 | magnus | 1 |
| 19030 | magnifico | 1 |
| 19031 | magnificence | 1 |
| 19032 | magnifi | 1 |
| 19033 | magni | 1 |
| 19034 | magnanimity | 1 |
| 19035 | magical | 1 |
| 19036 | madeira | 1 |
| 19037 | maculation | 1 |
| 19038 | maculate | 1 |
| 19039 | mack | 1 |
| 19040 | machine | 1 |
| 19041 | machinations | 1 |
| 19042 | machination | 1 |
| 19043 | maces | 1 |
| 19044 | macdonwald | 1 |
| 19045 | lynn | 1 |
| 19046 | lym | 1 |
| 19047 | lyen | 1 |
| 19048 | lye | 1 |
| 19049 | lycurguses | 1 |
| 19050 | lycaonia | 1 |
| 19051 | luxuriously | 1 |
| 19052 | lutheran | 1 |
| 19053 | lutestring | 1 |
| 19054 | lustig | 1 |
| 19055 | lustiest | 1 |
| 19056 | luster | 1 |
| 19057 | lusted | 1 |
| 19058 | lush | 1 |
| 19059 | lurketh | 1 |
| 19060 | lunacies | 1 |
| 19061 | luna | 1 |
| 19062 | lumpish | 1 |
| 19063 | lumbert | 1 |
| 19064 | lucullius | 1 |
| 19065 | lucretia | 1 |
| 19066 | luckily | 1 |
| 19067 | luckiest | 1 |
| 19068 | luckier | 1 |
| 19069 | lucina | 1 |
| 19070 | lucifier | 1 |
| 19071 | luccicos | 1 |
| 19072 | luc | 1 |
| 19073 | lubberly | 1 |
| 19074 | lozel | 1 |
| 19075 | loyalties | 1 |
| 19076 | loyally | 1 |
| 19077 | lown | 1 |
| 19078 | lowe | 1 |
| 19079 | lovered | 1 |
| 19080 | louts | 1 |
| 19081 | louted | 1 |
| 19082 | louses | 1 |
| 19083 | loureth | 1 |
| 19084 | loudly | 1 |
| 19085 | lorship | 1 |
| 19086 | lorn | 1 |
| 19087 | lordliness | 1 |
| 19088 | lording | 1 |
| 19089 | lorded | 1 |
| 19090 | loquitur | 1 |
| 19091 | loosing | 1 |
| 19092 | loosen | 1 |
| 19093 | loon | 1 |
| 19094 | lookest | 1 |
| 19095 | lookers | 1 |
| 19096 | loof | 1 |
| 19097 | longtail | 1 |
| 19098 | longly | 1 |
| 19099 | longings | 1 |
| 19100 | longed | 1 |
| 19101 | longboat | 1 |
| 19102 | londoners | 1 |
| 19103 | lombardy | 1 |
| 19104 | lolls | 1 |
| 19105 | loitering | 1 |
| 19106 | loiterers | 1 |
| 19107 | loiterer | 1 |
| 19108 | loiter | 1 |
| 19109 | logic | 1 |
| 19110 | loggets | 1 |
| 19111 | loggerheads | 1 |
| 19112 | logger | 1 |
| 19113 | lodgings | 1 |
| 19114 | lode | 1 |
| 19115 | locusts | 1 |
| 19116 | lockram | 1 |
| 19117 | lochaber | 1 |
| 19118 | lobbies | 1 |
| 19119 | loaves | 1 |
| 19120 | loathsomest | 1 |
| 19121 | loathsomeness | 1 |
| 19122 | loather | 1 |
| 19123 | loaf | 1 |
| 19124 | loading | 1 |
| 19125 | loach | 1 |
| 19126 | loa | 1 |
| 19127 | lnd | 1 |
| 19128 | livings | 1 |
| 19129 | livelier | 1 |
| 19130 | littlest | 1 |
| 19131 | lither | 1 |
| 19132 | literatured | 1 |
| 19133 | lisbon | 1 |
| 19134 | lirra | 1 |
| 19135 | liquorish | 1 |
| 19136 | lipsbury | 1 |
| 19137 | linta | 1 |
| 19138 | linsey | 1 |
| 19139 | lingered | 1 |
| 19140 | lingare | 1 |
| 19141 | linens | 1 |
| 19142 | lined | 1 |
| 19143 | lineally | 1 |
| 19144 | lincolnshire | 1 |
| 19145 | limps | 1 |
| 19146 | limn | 1 |
| 19147 | limekilns | 1 |
| 19148 | limehouse | 1 |
| 19149 | limber | 1 |
| 19150 | limbecks | 1 |
| 19151 | limbeck | 1 |
| 19152 | limander | 1 |
| 19153 | likeliest | 1 |
| 19154 | lightnings | 1 |
| 19155 | liggens | 1 |
| 19156 | lig | 1 |
| 19157 | lifteth | 1 |
| 19158 | lifter | 1 |
| 19159 | lifelings | 1 |
| 19160 | lifeblood | 1 |
| 19161 | lieutenants | 1 |
| 19162 | lien | 1 |
| 19163 | licker | 1 |
| 19164 | licked | 1 |
| 19165 | licens | 1 |
| 19166 | libertines | 1 |
| 19167 | liberte | 1 |
| 19168 | libels | 1 |
| 19169 | libelling | 1 |
| 19170 | libbard | 1 |
| 19171 | lewdsters | 1 |
| 19172 | leviathans | 1 |
| 19173 | levers | 1 |
| 19174 | levels | 1 |
| 19175 | leve | 1 |
| 19176 | leur | 1 |
| 19177 | lettuce | 1 |
| 19178 | lett | 1 |
| 19179 | lethargies | 1 |
| 19180 | lethargied | 1 |
| 19181 | lessoned | 1 |
| 19182 | lers | 1 |
| 19183 | lequel | 1 |
| 19184 | leperous | 1 |
| 19185 | leper | 1 |
| 19186 | leopards | 1 |
| 19187 | leo | 1 |
| 19188 | lemon | 1 |
| 19189 | leigers | 1 |
| 19190 | leiger | 1 |
| 19191 | leicestershire | 1 |
| 19192 | legitimation | 1 |
| 19193 | leges | 1 |
| 19194 | legerity | 1 |
| 19195 | lege | 1 |
| 19196 | legatine | 1 |
| 19197 | legacies | 1 |
| 19198 | leets | 1 |
| 19199 | leet | 1 |
| 19200 | leese | 1 |
| 19201 | leers | 1 |
| 19202 | leeches | 1 |
| 19203 | leech | 1 |
| 19204 | lecon | 1 |
| 19205 | lechers | 1 |
| 19206 | leaver | 1 |
| 19207 | leav | 1 |
| 19208 | learnings | 1 |
| 19209 | leaped | 1 |
| 19210 | leaner | 1 |
| 19211 | leah | 1 |
| 19212 | leaguer | 1 |
| 19213 | leagued | 1 |
| 19214 | leagu | 1 |
| 19215 | leadest | 1 |
| 19216 | lazarus | 1 |
| 19217 | layer | 1 |
| 19218 | lawns | 1 |
| 19219 | lawlessly | 1 |
| 19220 | lavoltas | 1 |
| 19221 | lavolt | 1 |
| 19222 | lavishly | 1 |
| 19223 | lavina | 1 |
| 19224 | lavender | 1 |
| 19225 | lavee | 1 |
| 19226 | laus | 1 |
| 19227 | laurels | 1 |
| 19228 | laura | 1 |
| 19229 | laundry | 1 |
| 19230 | launch | 1 |
| 19231 | launces | 1 |
| 19232 | laughest | 1 |
| 19233 | laughable | 1 |
| 19234 | laudis | 1 |
| 19235 | latten | 1 |
| 19236 | latches | 1 |
| 19237 | lasses | 1 |
| 19238 | las | 1 |
| 19239 | larron | 1 |
| 19240 | largest | 1 |
| 19241 | larding | 1 |
| 19242 | larder | 1 |
| 19243 | laquais | 1 |
| 19244 | lapsing | 1 |
| 19245 | lapsed | 1 |
| 19246 | lapland | 1 |
| 19247 | lanterns | 1 |
| 19248 | languor | 1 |
| 19249 | languishment | 1 |
| 19250 | languishings | 1 |
| 19251 | languishing | 1 |
| 19252 | languished | 1 |
| 19253 | langues | 1 |
| 19254 | languageless | 1 |
| 19255 | langton | 1 |
| 19256 | langage | 1 |
| 19257 | landmen | 1 |
| 19258 | landless | 1 |
| 19259 | landing | 1 |
| 19260 | lanch | 1 |
| 19261 | lanceth | 1 |
| 19262 | lanc | 1 |
| 19263 | lampass | 1 |
| 19264 | lamound | 1 |
| 19265 | lammastide | 1 |
| 19266 | laming | 1 |
| 19267 | lames | 1 |
| 19268 | lamentings | 1 |
| 19269 | lamentations | 1 |
| 19270 | lambkins | 1 |
| 19271 | lambkin | 1 |
| 19272 | lambert | 1 |
| 19273 | lakes | 1 |
| 19274 | lagging | 1 |
| 19275 | ladyships | 1 |
| 19276 | ladybird | 1 |
| 19277 | lade | 1 |
| 19278 | lackeying | 1 |
| 19279 | lackbeard | 1 |
| 19280 | lacies | 1 |
| 19281 | laces | 1 |
| 19282 | laced | 1 |
| 19283 | labras | 1 |
| 19284 | labourers | 1 |
| 19285 | labors | 1 |
| 19286 | labio | 1 |
| 19287 | labienus | 1 |
| 19288 | labell | 1 |
| 19289 | knowings | 1 |
| 19290 | knobs | 1 |
| 19291 | knitteth | 1 |
| 19292 | knitters | 1 |
| 19293 | knighthoods | 1 |
| 19294 | knewest | 1 |
| 19295 | kneaded | 1 |
| 19296 | knead | 1 |
| 19297 | knav | 1 |
| 19298 | klll | 1 |
| 19299 | kirtles | 1 |
| 19300 | kirtle | 1 |
| 19301 | kins | 1 |
| 19302 | kinred | 1 |
| 19303 | kindreds | 1 |
| 19304 | kindlier | 1 |
| 19305 | kindless | 1 |
| 19306 | kildare | 1 |
| 19307 | kikely | 1 |
| 19308 | kid | 1 |
| 19309 | kicky | 1 |
| 19310 | kickshawses | 1 |
| 19311 | kickshaws | 1 |
| 19312 | kicked | 1 |
| 19313 | kettledrums | 1 |
| 19314 | kettledrum | 1 |
| 19315 | kettle | 1 |
| 19316 | kernal | 1 |
| 19317 | kerely | 1 |
| 19318 | kentishmen | 1 |
| 19319 | kentishman | 1 |
| 19320 | keiser | 1 |
| 19321 | keepdown | 1 |
| 19322 | keenness | 1 |
| 19323 | keels | 1 |
| 19324 | kecksies | 1 |
| 19325 | kated | 1 |
| 19326 | kam | 1 |
| 19327 | jutting | 1 |
| 19328 | justs | 1 |
| 19329 | justness | 1 |
| 19330 | justling | 1 |
| 19331 | justles | 1 |
| 19332 | justled | 1 |
| 19333 | justification | 1 |
| 19334 | justicers | 1 |
| 19335 | justest | 1 |
| 19336 | justeius | 1 |
| 19337 | jurymen | 1 |
| 19338 | jurors | 1 |
| 19339 | juror | 1 |
| 19340 | jurement | 1 |
| 19341 | jure | 1 |
| 19342 | junkets | 1 |
| 19343 | junior | 1 |
| 19344 | junes | 1 |
| 19345 | jumping | 1 |
| 19346 | jumpeth | 1 |
| 19347 | julio | 1 |
| 19348 | juiced | 1 |
| 19349 | jugs | 1 |
| 19350 | jugglers | 1 |
| 19351 | juggled | 1 |
| 19352 | juggle | 1 |
| 19353 | jug | 1 |
| 19354 | judged | 1 |
| 19355 | judases | 1 |
| 19356 | jud | 1 |
| 19357 | juan | 1 |
| 19358 | joyed | 1 |
| 19359 | jowls | 1 |
| 19360 | jovem | 1 |
| 19361 | journeymen | 1 |
| 19362 | journeyman | 1 |
| 19363 | journeying | 1 |
| 19364 | joshua | 1 |
| 19365 | joltheads | 1 |
| 19366 | jolt | 1 |
| 19367 | jointress | 1 |
| 19368 | jointing | 1 |
| 19369 | joins | 1 |
| 19370 | joineth | 1 |
| 19371 | joinder | 1 |
| 19372 | jogging | 1 |
| 19373 | jockey | 1 |
| 19374 | jingling | 1 |
| 19375 | jills | 1 |
| 19376 | jigging | 1 |
| 19377 | jezebel | 1 |
| 19378 | jews | 1 |
| 19379 | jewess | 1 |
| 19380 | jets | 1 |
| 19381 | jested | 1 |
| 19382 | jesses | 1 |
| 19383 | jeshu | 1 |
| 19384 | jeronimy | 1 |
| 19385 | jerks | 1 |
| 19386 | jephtha | 1 |
| 19387 | jeopardy | 1 |
| 19388 | jenny | 1 |
| 19389 | jeering | 1 |
| 19390 | jeer | 1 |
| 19391 | jays | 1 |
| 19392 | jawbone | 1 |
| 19393 | jaw | 1 |
| 19394 | jaundies | 1 |
| 19395 | jaundice | 1 |
| 19396 | jaunce | 1 |
| 19397 | japhet | 1 |
| 19398 | jangled | 1 |
| 19399 | jamany | 1 |
| 19400 | jakes | 1 |
| 19401 | jackslave | 1 |
| 19402 | jacksauce | 1 |
| 19403 | jackanapes | 1 |
| 19404 | jacet | 1 |
| 19405 | itshall | 1 |
| 19406 | items | 1 |
| 19407 | ista | 1 |
| 19408 | ist | 1 |
| 19409 | issu | 1 |
| 19410 | israel | 1 |
| 19411 | islander | 1 |
| 19412 | ise | 1 |
| 19413 | iscariot | 1 |
| 19414 | irresolute | 1 |
| 19415 | irreparable | 1 |
| 19416 | irremovable | 1 |
| 19417 | irregulous | 1 |
| 19418 | irrecoverable | 1 |
| 19419 | irreconcil | 1 |
| 19420 | irishmen | 1 |
| 19421 | irae | 1 |
| 19422 | ira | 1 |
| 19423 | ionian | 1 |
| 19424 | ionia | 1 |
| 19425 | inwardness | 1 |
| 19426 | invoked | 1 |
| 19427 | invoke | 1 |
| 19428 | invitis | 1 |
| 19429 | invitation | 1 |
| 19430 | invised | 1 |
| 19431 | investing | 1 |
| 19432 | inventors | 1 |
| 19433 | inventoried | 1 |
| 19434 | inventorially | 1 |
| 19435 | inventor | 1 |
| 19436 | inveigled | 1 |
| 19437 | invectives | 1 |
| 19438 | invectively | 1 |
| 19439 | invasive | 1 |
| 19440 | invasion | 1 |
| 19441 | inurn | 1 |
| 19442 | inure | 1 |
| 19443 | intruding | 1 |
| 19444 | intrinsicate | 1 |
| 19445 | intrinse | 1 |
| 19446 | intricate | 1 |
| 19447 | intrenchant | 1 |
| 19448 | intrench | 1 |
| 19449 | intreat | 1 |
| 19450 | intreasured | 1 |
| 19451 | intoxicates | 1 |
| 19452 | intituled | 1 |
| 19453 | intitled | 1 |
| 19454 | intimation | 1 |
| 19455 | intil | 1 |
| 19456 | intestate | 1 |
| 19457 | intervallums | 1 |
| 19458 | intertissued | 1 |
| 19459 | interrupts | 1 |
| 19460 | interruptest | 1 |
| 19461 | interrupter | 1 |
| 19462 | interposes | 1 |
| 19463 | interposer | 1 |
| 19464 | intermixed | 1 |
| 19465 | intermix | 1 |
| 19466 | intermit | 1 |
| 19467 | intermissive | 1 |
| 19468 | interjoin | 1 |
| 19469 | interjections | 1 |
| 19470 | interims | 1 |
| 19471 | interdiction | 1 |
| 19472 | interchangement | 1 |
| 19473 | interchang | 1 |
| 19474 | interchained | 1 |
| 19475 | intercessors | 1 |
| 19476 | intercepts | 1 |
| 19477 | interception | 1 |
| 19478 | intercepter | 1 |
| 19479 | intentively | 1 |
| 19480 | intenible | 1 |
| 19481 | intendeth | 1 |
| 19482 | intelligo | 1 |
| 19483 | intelligis | 1 |
| 19484 | intelligencing | 1 |
| 19485 | intellects | 1 |
| 19486 | integritas | 1 |
| 19487 | integer | 1 |
| 19488 | insurrections | 1 |
| 19489 | insuppressive | 1 |
| 19490 | insults | 1 |
| 19491 | insultment | 1 |
| 19492 | insulted | 1 |
| 19493 | insufficience | 1 |
| 19494 | insubstantial | 1 |
| 19495 | instrumental | 1 |
| 19496 | institutions | 1 |
| 19497 | instinctively | 1 |
| 19498 | instigator | 1 |
| 19499 | instigations | 1 |
| 19500 | instigated | 1 |
| 19501 | instigate | 1 |
| 19502 | insteeped | 1 |
| 19503 | instate | 1 |
| 19504 | installed | 1 |
| 19505 | inspirations | 1 |
| 19506 | insomuch | 1 |
| 19507 | insisture | 1 |
| 19508 | insisting | 1 |
| 19509 | insisted | 1 |
| 19510 | insinuateth | 1 |
| 19511 | insinewed | 1 |
| 19512 | inshipp | 1 |
| 19513 | inshell | 1 |
| 19514 | inset | 1 |
| 19515 | inserted | 1 |
| 19516 | inseparate | 1 |
| 19517 | insculpture | 1 |
| 19518 | insculp | 1 |
| 19519 | inscrutable | 1 |
| 19520 | inscroll | 1 |
| 19521 | inscriptions | 1 |
| 19522 | inscription | 1 |
| 19523 | inscrib | 1 |
| 19524 | insconce | 1 |
| 19525 | insanie | 1 |
| 19526 | insane | 1 |
| 19527 | inroads | 1 |
| 19528 | inoculate | 1 |
| 19529 | innumerable | 1 |
| 19530 | innovator | 1 |
| 19531 | innkeeper | 1 |
| 19532 | inner | 1 |
| 19533 | inlay | 1 |
| 19534 | inlaid | 1 |
| 19535 | inkles | 1 |
| 19536 | inkle | 1 |
| 19537 | injurer | 1 |
| 19538 | injure | 1 |
| 19539 | injointed | 1 |
| 19540 | initiate | 1 |
| 19541 | iniquities | 1 |
| 19542 | inhoop | 1 |
| 19543 | inhibition | 1 |
| 19544 | inheritrix | 1 |
| 19545 | inheriting | 1 |
| 19546 | inherent | 1 |
| 19547 | inhearsed | 1 |
| 19548 | inhearse | 1 |
| 19549 | inhabited | 1 |
| 19550 | inhabitable | 1 |
| 19551 | ingross | 1 |
| 19552 | ingratitudes | 1 |
| 19553 | ingrated | 1 |
| 19554 | ingraft | 1 |
| 19555 | ingraffed | 1 |
| 19556 | ingots | 1 |
| 19557 | inglorious | 1 |
| 19558 | ingeniously | 1 |
| 19559 | ingener | 1 |
| 19560 | infusing | 1 |
| 19561 | infringed | 1 |
| 19562 | infring | 1 |
| 19563 | informs | 1 |
| 19564 | informer | 1 |
| 19565 | informations | 1 |
| 19566 | informal | 1 |
| 19567 | infliction | 1 |
| 19568 | inflict | 1 |
| 19569 | inflammation | 1 |
| 19570 | infixing | 1 |
| 19571 | infixed | 1 |
| 19572 | infinitive | 1 |
| 19573 | infest | 1 |
| 19574 | inferring | 1 |
| 19575 | inferreth | 1 |
| 19576 | inferiors | 1 |
| 19577 | inference | 1 |
| 19578 | infectiously | 1 |
| 19579 | infections | 1 |
| 19580 | infecting | 1 |
| 19581 | infamonize | 1 |
| 19582 | inexplicable | 1 |
| 19583 | inexecrable | 1 |
| 19584 | inequality | 1 |
| 19585 | industriously | 1 |
| 19586 | indurance | 1 |
| 19587 | indulgent | 1 |
| 19588 | indulgences | 1 |
| 19589 | indues | 1 |
| 19590 | indue | 1 |
| 19591 | inductions | 1 |
| 19592 | indubitate | 1 |
| 19593 | indu | 1 |
| 19594 | indrench | 1 |
| 19595 | individable | 1 |
| 19596 | indistinguishable | 1 |
| 19597 | indistinguish | 1 |
| 19598 | indissoluble | 1 |
| 19599 | indisposition | 1 |
| 19600 | indispos | 1 |
| 19601 | indirections | 1 |
| 19602 | indigne | 1 |
| 19603 | indignations | 1 |
| 19604 | indign | 1 |
| 19605 | indigested | 1 |
| 19606 | indigent | 1 |
| 19607 | indicted | 1 |
| 19608 | indict | 1 |
| 19609 | indexes | 1 |
| 19610 | indented | 1 |
| 19611 | ind | 1 |
| 19612 | incurred | 1 |
| 19613 | incredible | 1 |
| 19614 | increases | 1 |
| 19615 | increas | 1 |
| 19616 | incorrect | 1 |
| 19617 | incorps | 1 |
| 19618 | inconvenient | 1 |
| 19619 | inconveniences | 1 |
| 19620 | inconvenience | 1 |
| 19621 | incontinently | 1 |
| 19622 | incomprehensible | 1 |
| 19623 | included | 1 |
| 19624 | include | 1 |
| 19625 | inclips | 1 |
| 19626 | inclines | 1 |
| 19627 | inclined | 1 |
| 19628 | inclinable | 1 |
| 19629 | incivility | 1 |
| 19630 | incivil | 1 |
| 19631 | incites | 1 |
| 19632 | incidency | 1 |
| 19633 | incharitable | 1 |
| 19634 | incessantly | 1 |
| 19635 | incertainty | 1 |
| 19636 | incensing | 1 |
| 19637 | incenses | 1 |
| 19638 | incensement | 1 |
| 19639 | incarnation | 1 |
| 19640 | incarnadine | 1 |
| 19641 | incardinate | 1 |
| 19642 | incantations | 1 |
| 19643 | inauspicious | 1 |
| 19644 | inaudible | 1 |
| 19645 | inaidable | 1 |
| 19646 | impure | 1 |
| 19647 | impugns | 1 |
| 19648 | impugn | 1 |
| 19649 | impudique | 1 |
| 19650 | impudently | 1 |
| 19651 | impudency | 1 |
| 19652 | improve | 1 |
| 19653 | improper | 1 |
| 19654 | improbable | 1 |
| 19655 | imprisoning | 1 |
| 19656 | imprinted | 1 |
| 19657 | imprint | 1 |
| 19658 | imprimendum | 1 |
| 19659 | impressest | 1 |
| 19660 | imprese | 1 |
| 19661 | impounded | 1 |
| 19662 | impotence | 1 |
| 19663 | impostors | 1 |
| 19664 | impositions | 1 |
| 19665 | importless | 1 |
| 19666 | imported | 1 |
| 19667 | importantly | 1 |
| 19668 | importancy | 1 |
| 19669 | imploring | 1 |
| 19670 | implored | 1 |
| 19671 | implorators | 1 |
| 19672 | implor | 1 |
| 19673 | implies | 1 |
| 19674 | implacable | 1 |
| 19675 | impieties | 1 |
| 19676 | impetuosity | 1 |
| 19677 | impeticos | 1 |
| 19678 | impertinency | 1 |
| 19679 | imperiously | 1 |
| 19680 | imperfectly | 1 |
| 19681 | imperceiverant | 1 |
| 19682 | imperator | 1 |
| 19683 | impenetrable | 1 |
| 19684 | impedes | 1 |
| 19685 | impeachments | 1 |
| 19686 | impeached | 1 |
| 19687 | impasted | 1 |
| 19688 | imparts | 1 |
| 19689 | impartment | 1 |
| 19690 | imparted | 1 |
| 19691 | impanelled | 1 |
| 19692 | impaled | 1 |
| 19693 | impale | 1 |
| 19694 | impairing | 1 |
| 19695 | impaint | 1 |
| 19696 | immures | 1 |
| 19697 | immortally | 1 |
| 19698 | immortaliz | 1 |
| 19699 | immoment | 1 |
| 19700 | immoderately | 1 |
| 19701 | immoderate | 1 |
| 19702 | imminence | 1 |
| 19703 | immediacy | 1 |
| 19704 | immaterial | 1 |
| 19705 | immask | 1 |
| 19706 | immanity | 1 |
| 19707 | imitations | 1 |
| 19708 | imitari | 1 |
| 19709 | imbecility | 1 |
| 19710 | imbar | 1 |
| 19711 | imaginings | 1 |
| 19712 | imagining | 1 |
| 19713 | imagery | 1 |
| 19714 | im | 1 |
| 19715 | illyrian | 1 |
| 19716 | illustrated | 1 |
| 19717 | illumineth | 1 |
| 19718 | illuminate | 1 |
| 19719 | illumin | 1 |
| 19720 | illume | 1 |
| 19721 | illo | 1 |
| 19722 | illness | 1 |
| 19723 | illiterate | 1 |
| 19724 | ild | 1 |
| 19725 | ilbow | 1 |
| 19726 | iiii | 1 |
| 19727 | ignomy | 1 |
| 19728 | ignis | 1 |
| 19729 | ifs | 1 |
| 19730 | ield | 1 |
| 19731 | idolatrous | 1 |
| 19732 | idles | 1 |
| 19733 | idem | 1 |
| 19734 | ideas | 1 |
| 19735 | ici | 1 |
| 19736 | iament | 1 |
| 19737 | iaculis | 1 |
| 19738 | hysterica | 1 |
| 19739 | hyssop | 1 |
| 19740 | hyrcania | 1 |
| 19741 | hyrcan | 1 |
| 19742 | hypocrites | 1 |
| 19743 | hymenaeus | 1 |
| 19744 | hyen | 1 |
| 19745 | hutch | 1 |
| 19746 | huswifes | 1 |
| 19747 | husht | 1 |
| 19748 | hushes | 1 |
| 19749 | husbandless | 1 |
| 19750 | hurtling | 1 |
| 19751 | hurtless | 1 |
| 19752 | hurtled | 1 |
| 19753 | hurting | 1 |
| 19754 | hurricanoes | 1 |
| 19755 | hurricano | 1 |
| 19756 | hurls | 1 |
| 19757 | hurling | 1 |
| 19758 | hurdle | 1 |
| 19759 | huntress | 1 |
| 19760 | huntington | 1 |
| 19761 | hunteth | 1 |
| 19762 | hungarian | 1 |
| 19763 | hundredth | 1 |
| 19764 | humphry | 1 |
| 19765 | humourists | 1 |
| 19766 | humming | 1 |
| 19767 | humbling | 1 |
| 19768 | humbles | 1 |
| 19769 | hullo | 1 |
| 19770 | hulling | 1 |
| 19771 | hulks | 1 |
| 19772 | hujus | 1 |
| 19773 | hugs | 1 |
| 19774 | hugger | 1 |
| 19775 | hugeness | 1 |
| 19776 | hues | 1 |
| 19777 | huddling | 1 |
| 19778 | huddled | 1 |
| 19779 | hoyday | 1 |
| 19780 | hoy | 1 |
| 19781 | hoxes | 1 |
| 19782 | howls | 1 |
| 19783 | howlet | 1 |
| 19784 | howled | 1 |
| 19785 | howeer | 1 |
| 19786 | hovers | 1 |
| 19787 | hovering | 1 |
| 19788 | hovered | 1 |
| 19789 | housekeepers | 1 |
| 19790 | householders | 1 |
| 19791 | householder | 1 |
| 19792 | hospitality | 1 |
| 19793 | hospital | 1 |
| 19794 | horsing | 1 |
| 19795 | horseway | 1 |
| 19796 | horsehairs | 1 |
| 19797 | horsed | 1 |
| 19798 | horrider | 1 |
| 19799 | horologe | 1 |
| 19800 | hornpipes | 1 |
| 19801 | horning | 1 |
| 19802 | hornbook | 1 |
| 19803 | horizon | 1 |
| 19804 | hoppedance | 1 |
| 19805 | hopest | 1 |
| 19806 | hoots | 1 |
| 19807 | hoot | 1 |
| 19808 | hooking | 1 |
| 19809 | hoods | 1 |
| 19810 | honouring | 1 |
| 19811 | honourible | 1 |
| 19812 | honourest | 1 |
| 19813 | honorificabilitudinitatibus | 1 |
| 19814 | honorato | 1 |
| 19815 | honorably | 1 |
| 19816 | honi | 1 |
| 19817 | honeysuckles | 1 |
| 19818 | honeyless | 1 |
| 19819 | honeying | 1 |
| 19820 | honeycomb | 1 |
| 19821 | honestest | 1 |
| 19822 | homo | 1 |
| 19823 | hommes | 1 |
| 19824 | hominem | 1 |
| 19825 | homily | 1 |
| 19826 | homicides | 1 |
| 19827 | homewards | 1 |
| 19828 | homespuns | 1 |
| 19829 | homager | 1 |
| 19830 | holloaing | 1 |
| 19831 | holloa | 1 |
| 19832 | hollanders | 1 |
| 19833 | holiest | 1 |
| 19834 | holidays | 1 |
| 19835 | holidam | 1 |
| 19836 | holdfast | 1 |
| 19837 | holder | 1 |
| 19838 | holden | 1 |
| 19839 | holborn | 1 |
| 19840 | hoists | 1 |
| 19841 | hoise | 1 |
| 19842 | hois | 1 |
| 19843 | hogsheads | 1 |
| 19844 | hodge | 1 |
| 19845 | hod | 1 |
| 19846 | hobbyhorse | 1 |
| 19847 | hobbididence | 1 |
| 19848 | hoary | 1 |
| 19849 | hoars | 1 |
| 19850 | hizzing | 1 |
| 19851 | hives | 1 |
| 19852 | hisses | 1 |
| 19853 | hisperia | 1 |
| 19854 | hirtius | 1 |
| 19855 | hipparchus | 1 |
| 19856 | hing | 1 |
| 19857 | hinders | 1 |
| 19858 | hindered | 1 |
| 19859 | hinckley | 1 |
| 19860 | hinc | 1 |
| 19861 | hily | 1 |
| 19862 | hilloa | 1 |
| 19863 | hillo | 1 |
| 19864 | hildings | 1 |
| 19865 | hig | 1 |
| 19866 | hied | 1 |
| 19867 | hidest | 1 |
| 19868 | hideousness | 1 |
| 19869 | hideously | 1 |
| 19870 | hick | 1 |
| 19871 | hiccups | 1 |
| 19872 | hibocrates | 1 |
| 19873 | heyday | 1 |
| 19874 | hewing | 1 |
| 19875 | hewgh | 1 |
| 19876 | heureux | 1 |
| 19877 | heure | 1 |
| 19878 | hesperus | 1 |
| 19879 | hesperides | 1 |
| 19880 | heroic | 1 |
| 19881 | herods | 1 |
| 19882 | hermes | 1 |
| 19883 | heritier | 1 |
| 19884 | heritage | 1 |
| 19885 | hereupon | 1 |
| 19886 | hereto | 1 |
| 19887 | hereabouts | 1 |
| 19888 | herdsman | 1 |
| 19889 | herculean | 1 |
| 19890 | herblets | 1 |
| 19891 | hens | 1 |
| 19892 | henricus | 1 |
| 19893 | henri | 1 |
| 19894 | henchman | 1 |
| 19895 | helter | 1 |
| 19896 | helpers | 1 |
| 19897 | helmed | 1 |
| 19898 | hellfire | 1 |
| 19899 | helicons | 1 |
| 19900 | helias | 1 |
| 19901 | heirless | 1 |
| 19902 | heiress | 1 |
| 19903 | heinously | 1 |
| 19904 | heighten | 1 |
| 19905 | heifers | 1 |
| 19906 | hefts | 1 |
| 19907 | hefted | 1 |
| 19908 | heedfull | 1 |
| 19909 | heeded | 1 |
| 19910 | hedgehog | 1 |
| 19911 | hectic | 1 |
| 19912 | hebona | 1 |
| 19913 | heavings | 1 |
| 19914 | heauties | 1 |
| 19915 | heating | 1 |
| 19916 | heathenish | 1 |
| 19917 | heartsick | 1 |
| 19918 | heartlings | 1 |
| 19919 | heartless | 1 |
| 19920 | heartiness | 1 |
| 19921 | hearths | 1 |
| 19922 | hearten | 1 |
| 19923 | heartbreaking | 1 |
| 19924 | heartbreak | 1 |
| 19925 | heartache | 1 |
| 19926 | hearst | 1 |
| 19927 | hearsed | 1 |
| 19928 | hearings | 1 |
| 19929 | heareth | 1 |
| 19930 | hearest | 1 |
| 19931 | healthsome | 1 |
| 19932 | heals | 1 |
| 19933 | healed | 1 |
| 19934 | headland | 1 |
| 19935 | heading | 1 |
| 19936 | headier | 1 |
| 19937 | hazelnut | 1 |
| 19938 | hawthorns | 1 |
| 19939 | havior | 1 |
| 19940 | haver | 1 |
| 19941 | havens | 1 |
| 19942 | hautboy | 1 |
| 19943 | haunches | 1 |
| 19944 | haughtiness | 1 |
| 19945 | hauf | 1 |
| 19946 | haters | 1 |
| 19947 | hater | 1 |
| 19948 | hatchment | 1 |
| 19949 | hatching | 1 |
| 19950 | hatchet | 1 |
| 19951 | hastes | 1 |
| 19952 | hasted | 1 |
| 19953 | harum | 1 |
| 19954 | harrows | 1 |
| 19955 | harried | 1 |
| 19956 | harpier | 1 |
| 19957 | harper | 1 |
| 19958 | harmed | 1 |
| 19959 | harelip | 1 |
| 19960 | hardocks | 1 |
| 19961 | hardiest | 1 |
| 19962 | harbouring | 1 |
| 19963 | harbourage | 1 |
| 19964 | happies | 1 |
| 19965 | handy | 1 |
| 19966 | handwriting | 1 |
| 19967 | handsomeness | 1 |
| 19968 | handmaids | 1 |
| 19969 | handlest | 1 |
| 19970 | handles | 1 |
| 19971 | handing | 1 |
| 19972 | handicraftsmen | 1 |
| 19973 | handicraft | 1 |
| 19974 | hamstring | 1 |
| 19975 | hamper | 1 |
| 19976 | hammered | 1 |
| 19977 | hames | 1 |
| 19978 | halves | 1 |
| 19979 | hals | 1 |
| 19980 | hallown | 1 |
| 19981 | hallooing | 1 |
| 19982 | hallond | 1 |
| 19983 | halidom | 1 |
| 19984 | halfpennyworth | 1 |
| 19985 | halfcan | 1 |
| 19986 | haled | 1 |
| 19987 | halberd | 1 |
| 19988 | hairless | 1 |
| 19989 | hailstones | 1 |
| 19990 | hailstone | 1 |
| 19991 | hailed | 1 |
| 19992 | haggled | 1 |
| 19993 | haggish | 1 |
| 19994 | haggards | 1 |
| 19995 | hagar | 1 |
| 19996 | haeres | 1 |
| 19997 | haec | 1 |
| 19998 | habitude | 1 |
| 19999 | habiliment | 1 |
| 20000 | gyved | 1 |
| 20001 | gyve | 1 |
| 20002 | guysors | 1 |
| 20003 | guynes | 1 |
| 20004 | guy | 1 |
| 20005 | gutter | 1 |
| 20006 | gusty | 1 |
| 20007 | gurnet | 1 |
| 20008 | gums | 1 |
| 20009 | gumm | 1 |
| 20010 | gulfs | 1 |
| 20011 | gul | 1 |
| 20012 | guinever | 1 |
| 20013 | guinea | 1 |
| 20014 | guilts | 1 |
| 20015 | guiltily | 1 |
| 20016 | guiltian | 1 |
| 20017 | guilfords | 1 |
| 20018 | guiled | 1 |
| 20019 | guienne | 1 |
| 20020 | guidon | 1 |
| 20021 | guider | 1 |
| 20022 | guichard | 1 |
| 20023 | guiana | 1 |
| 20024 | guessingly | 1 |
| 20025 | guesses | 1 |
| 20026 | guerra | 1 |
| 20027 | gudgeon | 1 |
| 20028 | guardians | 1 |
| 20029 | guardage | 1 |
| 20030 | grund | 1 |
| 20031 | grumblings | 1 |
| 20032 | grumblest | 1 |
| 20033 | gruel | 1 |
| 20034 | grudges | 1 |
| 20035 | grudged | 1 |
| 20036 | grubs | 1 |
| 20037 | grubb | 1 |
| 20038 | groweth | 1 |
| 20039 | groundlings | 1 |
| 20040 | groping | 1 |
| 20041 | grop | 1 |
| 20042 | groin | 1 |
| 20043 | grizzle | 1 |
| 20044 | grize | 1 |
| 20045 | grissel | 1 |
| 20046 | grindstone | 1 |
| 20047 | grievingly | 1 |
| 20048 | grievest | 1 |
| 20049 | greeted | 1 |
| 20050 | greenwood | 1 |
| 20051 | greenwich | 1 |
| 20052 | greens | 1 |
| 20053 | greener | 1 |
| 20054 | greeing | 1 |
| 20055 | greedily | 1 |
| 20056 | gree | 1 |
| 20057 | greasily | 1 |
| 20058 | greases | 1 |
| 20059 | grazed | 1 |
| 20060 | graz | 1 |
| 20061 | graymalkin | 1 |
| 20062 | gravities | 1 |
| 20063 | gravest | 1 |
| 20064 | graveness | 1 |
| 20065 | graven | 1 |
| 20066 | gravely | 1 |
| 20067 | gravell | 1 |
| 20068 | graveless | 1 |
| 20069 | gravediggers | 1 |
| 20070 | gratillity | 1 |
| 20071 | gratii | 1 |
| 20072 | grates | 1 |
| 20073 | grassy | 1 |
| 20074 | grasshoppers | 1 |
| 20075 | grasped | 1 |
| 20076 | grappling | 1 |
| 20077 | grandsir | 1 |
| 20078 | grandjurors | 1 |
| 20079 | grandeur | 1 |
| 20080 | grande | 1 |
| 20081 | grandchild | 1 |
| 20082 | grandame | 1 |
| 20083 | grafters | 1 |
| 20084 | graffing | 1 |
| 20085 | gracing | 1 |
| 20086 | gracefully | 1 |
| 20087 | governors | 1 |
| 20088 | governess | 1 |
| 20089 | governance | 1 |
| 20090 | gouts | 1 |
| 20091 | gourd | 1 |
| 20092 | gossiplike | 1 |
| 20093 | goss | 1 |
| 20094 | gospels | 1 |
| 20095 | gospel | 1 |
| 20096 | gosling | 1 |
| 20097 | gormandizing | 1 |
| 20098 | gormandize | 1 |
| 20099 | gorging | 1 |
| 20100 | gorget | 1 |
| 20101 | gorboduc | 1 |
| 20102 | gorbellied | 1 |
| 20103 | goosequills | 1 |
| 20104 | gooseberry | 1 |
| 20105 | goodyears | 1 |
| 20106 | goodyear | 1 |
| 20107 | goodwins | 1 |
| 20108 | goodwill | 1 |
| 20109 | goodwife | 1 |
| 20110 | goodrig | 1 |
| 20111 | goodnight | 1 |
| 20112 | gong | 1 |
| 20113 | gondolier | 1 |
| 20114 | goliath | 1 |
| 20115 | goliases | 1 |
| 20116 | goldsmiths | 1 |
| 20117 | goldenly | 1 |
| 20118 | gogs | 1 |
| 20119 | goeth | 1 |
| 20120 | goer | 1 |
| 20121 | godson | 1 |
| 20122 | goddild | 1 |
| 20123 | godden | 1 |
| 20124 | godded | 1 |
| 20125 | goblets | 1 |
| 20126 | goatish | 1 |
| 20127 | goads | 1 |
| 20128 | goad | 1 |
| 20129 | gnarled | 1 |
| 20130 | gluttoning | 1 |
| 20131 | glutted | 1 |
| 20132 | glutt | 1 |
| 20133 | glut | 1 |
| 20134 | glues | 1 |
| 20135 | glued | 1 |
| 20136 | glue | 1 |
| 20137 | glu | 1 |
| 20138 | glozes | 1 |
| 20139 | gloz | 1 |
| 20140 | glowworm | 1 |
| 20141 | glowed | 1 |
| 20142 | glover | 1 |
| 20143 | glouceste | 1 |
| 20144 | glosses | 1 |
| 20145 | glose | 1 |
| 20146 | gloriously | 1 |
| 20147 | glorified | 1 |
| 20148 | glooming | 1 |
| 20149 | globes | 1 |
| 20150 | glitt | 1 |
| 20151 | glister | 1 |
| 20152 | glistening | 1 |
| 20153 | glimpses | 1 |
| 20154 | glimmers | 1 |
| 20155 | gliding | 1 |
| 20156 | glideth | 1 |
| 20157 | glided | 1 |
| 20158 | gleeks | 1 |
| 20159 | gleeking | 1 |
| 20160 | gleeful | 1 |
| 20161 | gleaning | 1 |
| 20162 | gleams | 1 |
| 20163 | glaz | 1 |
| 20164 | glare | 1 |
| 20165 | glanders | 1 |
| 20166 | glancing | 1 |
| 20167 | glanc | 1 |
| 20168 | gladding | 1 |
| 20169 | gladded | 1 |
| 20170 | givings | 1 |
| 20171 | givers | 1 |
| 20172 | gis | 1 |
| 20173 | girth | 1 |
| 20174 | gipsy | 1 |
| 20175 | gipsies | 1 |
| 20176 | gipes | 1 |
| 20177 | gioucestershire | 1 |
| 20178 | ginn | 1 |
| 20179 | gingerly | 1 |
| 20180 | gingerbread | 1 |
| 20181 | ging | 1 |
| 20182 | gimmers | 1 |
| 20183 | gimmal | 1 |
| 20184 | gills | 1 |
| 20185 | gillian | 1 |
| 20186 | gilliams | 1 |
| 20187 | giglets | 1 |
| 20188 | giddiness | 1 |
| 20189 | gibingly | 1 |
| 20190 | giber | 1 |
| 20191 | gibe | 1 |
| 20192 | gibber | 1 |
| 20193 | giants | 1 |
| 20194 | giantlike | 1 |
| 20195 | giantess | 1 |
| 20196 | gi | 1 |
| 20197 | ghosted | 1 |
| 20198 | getter | 1 |
| 20199 | getrude | 1 |
| 20200 | gests | 1 |
| 20201 | gest | 1 |
| 20202 | germains | 1 |
| 20203 | germaines | 1 |
| 20204 | gentlest | 1 |
| 20205 | gentlemanlike | 1 |
| 20206 | gentlefolks | 1 |
| 20207 | genoux | 1 |
| 20208 | gennets | 1 |
| 20209 | genitivo | 1 |
| 20210 | generosity | 1 |
| 20211 | generative | 1 |
| 20212 | generations | 1 |
| 20213 | genders | 1 |
| 20214 | gen | 1 |
| 20215 | geminy | 1 |
| 20216 | gelt | 1 |
| 20217 | gelidus | 1 |
| 20218 | gelida | 1 |
| 20219 | gazeth | 1 |
| 20220 | gazer | 1 |
| 20221 | gazed | 1 |
| 20222 | gayness | 1 |
| 20223 | gawded | 1 |
| 20224 | gaul | 1 |
| 20225 | gauge | 1 |
| 20226 | gaudeo | 1 |
| 20227 | gaud | 1 |
| 20228 | gatory | 1 |
| 20229 | gathers | 1 |
| 20230 | gath | 1 |
| 20231 | gated | 1 |
| 20232 | gat | 1 |
| 20233 | gastness | 1 |
| 20234 | gasted | 1 |
| 20235 | gaskins | 1 |
| 20236 | gartering | 1 |
| 20237 | garterd | 1 |
| 20238 | gart | 1 |
| 20239 | garrisons | 1 |
| 20240 | garret | 1 |
| 20241 | garnished | 1 |
| 20242 | garners | 1 |
| 20243 | garner | 1 |
| 20244 | garmet | 1 |
| 20245 | gargantua | 1 |
| 20246 | gardez | 1 |
| 20247 | garde | 1 |
| 20248 | garcon | 1 |
| 20249 | gaols | 1 |
| 20250 | gangren | 1 |
| 20251 | gammon | 1 |
| 20252 | gamers | 1 |
| 20253 | gamboys | 1 |
| 20254 | gambold | 1 |
| 20255 | gam | 1 |
| 20256 | gallowses | 1 |
| 20257 | galloway | 1 |
| 20258 | gallow | 1 |
| 20259 | galloping | 1 |
| 20260 | gallons | 1 |
| 20261 | galliasses | 1 |
| 20262 | gallantry | 1 |
| 20263 | gales | 1 |
| 20264 | galathe | 1 |
| 20265 | gainsays | 1 |
| 20266 | gainsaying | 1 |
| 20267 | gainsaid | 1 |
| 20268 | gaingiving | 1 |
| 20269 | gagne | 1 |
| 20270 | gaging | 1 |
| 20271 | gaged | 1 |
| 20272 | gag | 1 |
| 20273 | gadding | 1 |
| 20274 | gabriel | 1 |
| 20275 | futurity | 1 |
| 20276 | fut | 1 |
| 20277 | fustilarian | 1 |
| 20278 | fust | 1 |
| 20279 | furzes | 1 |
| 20280 | furze | 1 |
| 20281 | furtherer | 1 |
| 20282 | furtherance | 1 |
| 20283 | furth | 1 |
| 20284 | furrows | 1 |
| 20285 | furrowed | 1 |
| 20286 | furor | 1 |
| 20287 | furnival | 1 |
| 20288 | furnishings | 1 |
| 20289 | furnaces | 1 |
| 20290 | fumitory | 1 |
| 20291 | fumiter | 1 |
| 20292 | fuming | 1 |
| 20293 | fumbling | 1 |
| 20294 | fumblest | 1 |
| 20295 | fumbles | 1 |
| 20296 | fum | 1 |
| 20297 | fullness | 1 |
| 20298 | fullest | 1 |
| 20299 | fullers | 1 |
| 20300 | fullam | 1 |
| 20301 | fulfils | 1 |
| 20302 | fulfilling | 1 |
| 20303 | frutify | 1 |
| 20304 | frush | 1 |
| 20305 | fruition | 1 |
| 20306 | fruitfulness | 1 |
| 20307 | fruiterer | 1 |
| 20308 | fructify | 1 |
| 20309 | frowningly | 1 |
| 20310 | frontlet | 1 |
| 20311 | froissart | 1 |
| 20312 | frock | 1 |
| 20313 | fritters | 1 |
| 20314 | frisk | 1 |
| 20315 | frippery | 1 |
| 20316 | fringed | 1 |
| 20317 | fringe | 1 |
| 20318 | frightened | 1 |
| 20319 | friendships | 1 |
| 20320 | friendliness | 1 |
| 20321 | friendless | 1 |
| 20322 | friending | 1 |
| 20323 | fretten | 1 |
| 20324 | freshes | 1 |
| 20325 | frequents | 1 |
| 20326 | freezings | 1 |
| 20327 | freezing | 1 |
| 20328 | freetown | 1 |
| 20329 | freestone | 1 |
| 20330 | frees | 1 |
| 20331 | freeness | 1 |
| 20332 | freemen | 1 |
| 20333 | freeman | 1 |
| 20334 | freelier | 1 |
| 20335 | freehearted | 1 |
| 20336 | freedoms | 1 |
| 20337 | freckles | 1 |
| 20338 | freckled | 1 |
| 20339 | freckl | 1 |
| 20340 | frays | 1 |
| 20341 | fraughting | 1 |
| 20342 | fraudful | 1 |
| 20343 | fratrum | 1 |
| 20344 | frateretto | 1 |
| 20345 | franticly | 1 |
| 20346 | frankness | 1 |
| 20347 | franklins | 1 |
| 20348 | frankfort | 1 |
| 20349 | franker | 1 |
| 20350 | franciae | 1 |
| 20351 | franchises | 1 |
| 20352 | franchisement | 1 |
| 20353 | franchised | 1 |
| 20354 | franchise | 1 |
| 20355 | frances | 1 |
| 20356 | francais | 1 |
| 20357 | frampold | 1 |
| 20358 | frailer | 1 |
| 20359 | fragile | 1 |
| 20360 | fraction | 1 |
| 20361 | foxship | 1 |
| 20362 | fowling | 1 |
| 20363 | fowler | 1 |
| 20364 | founts | 1 |
| 20365 | foughten | 1 |
| 20366 | fost | 1 |
| 20367 | fosset | 1 |
| 20368 | forwearied | 1 |
| 20369 | forwards | 1 |
| 20370 | forwarding | 1 |
| 20371 | fortward | 1 |
| 20372 | fortuned | 1 |
| 20373 | fortun | 1 |
| 20374 | fortresses | 1 |
| 20375 | fortifies | 1 |
| 20376 | fortifications | 1 |
| 20377 | fortification | 1 |
| 20378 | forthright | 1 |
| 20379 | forthlight | 1 |
| 20380 | forted | 1 |
| 20381 | forspoke | 1 |
| 20382 | forslow | 1 |
| 20383 | forsaketh | 1 |
| 20384 | fornicatress | 1 |
| 20385 | fornications | 1 |
| 20386 | formed | 1 |
| 20387 | forks | 1 |
| 20388 | forgone | 1 |
| 20389 | forgoing | 1 |
| 20390 | forgetive | 1 |
| 20391 | forfended | 1 |
| 20392 | forfeitures | 1 |
| 20393 | forfeiters | 1 |
| 20394 | forewarning | 1 |
| 20395 | forewarned | 1 |
| 20396 | foreward | 1 |
| 20397 | forethought | 1 |
| 20398 | forethink | 1 |
| 20399 | foretelling | 1 |
| 20400 | forestalled | 1 |
| 20401 | foreskirt | 1 |
| 20402 | foreshow | 1 |
| 20403 | foresees | 1 |
| 20404 | foreseeing | 1 |
| 20405 | foresay | 1 |
| 20406 | foresaw | 1 |
| 20407 | foreruns | 1 |
| 20408 | forerunning | 1 |
| 20409 | forenamed | 1 |
| 20410 | foreknowledge | 1 |
| 20411 | foreigners | 1 |
| 20412 | foreigner | 1 |
| 20413 | forehorse | 1 |
| 20414 | foreheads | 1 |
| 20415 | forego | 1 |
| 20416 | forefather | 1 |
| 20417 | forecast | 1 |
| 20418 | fordo | 1 |
| 20419 | fordid | 1 |
| 20420 | forceless | 1 |
| 20421 | forceful | 1 |
| 20422 | forborne | 1 |
| 20423 | forbod | 1 |
| 20424 | forbiddenly | 1 |
| 20425 | forbears | 1 |
| 20426 | foragers | 1 |
| 20427 | fops | 1 |
| 20428 | foppish | 1 |
| 20429 | fopped | 1 |
| 20430 | fopp | 1 |
| 20431 | footstool | 1 |
| 20432 | footsteps | 1 |
| 20433 | footmen | 1 |
| 20434 | footfall | 1 |
| 20435 | footboys | 1 |
| 20436 | foolishness | 1 |
| 20437 | fooleries | 1 |
| 20438 | fontibell | 1 |
| 20439 | fonder | 1 |
| 20440 | followest | 1 |
| 20441 | folio | 1 |
| 20442 | foist | 1 |
| 20443 | foisons | 1 |
| 20444 | foins | 1 |
| 20445 | foiled | 1 |
| 20446 | fodder | 1 |
| 20447 | fob | 1 |
| 20448 | foamy | 1 |
| 20449 | foamed | 1 |
| 20450 | foals | 1 |
| 20451 | foal | 1 |
| 20452 | fluxive | 1 |
| 20453 | flutter | 1 |
| 20454 | fluster | 1 |
| 20455 | flushing | 1 |
| 20456 | fluent | 1 |
| 20457 | flowerets | 1 |
| 20458 | flourisheth | 1 |
| 20459 | flour | 1 |
| 20460 | floulish | 1 |
| 20461 | flote | 1 |
| 20462 | florentius | 1 |
| 20463 | flora | 1 |
| 20464 | floodgates | 1 |
| 20465 | floated | 1 |
| 20466 | flirt | 1 |
| 20467 | flints | 1 |
| 20468 | flighty | 1 |
| 20469 | flidge | 1 |
| 20470 | flickering | 1 |
| 20471 | fleshmonger | 1 |
| 20472 | fleshment | 1 |
| 20473 | fleshly | 1 |
| 20474 | fleshes | 1 |
| 20475 | flemish | 1 |
| 20476 | fleming | 1 |
| 20477 | fleers | 1 |
| 20478 | fleering | 1 |
| 20479 | fleeces | 1 |
| 20480 | fleec | 1 |
| 20481 | fledge | 1 |
| 20482 | flecked | 1 |
| 20483 | flaxen | 1 |
| 20484 | flavio | 1 |
| 20485 | flaunts | 1 |
| 20486 | flatterest | 1 |
| 20487 | flatness | 1 |
| 20488 | flashing | 1 |
| 20489 | flaring | 1 |
| 20490 | flannel | 1 |
| 20491 | flamens | 1 |
| 20492 | flamen | 1 |
| 20493 | flam | 1 |
| 20494 | flaky | 1 |
| 20495 | flakes | 1 |
| 20496 | flail | 1 |
| 20497 | flagons | 1 |
| 20498 | flagon | 1 |
| 20499 | flagging | 1 |
| 20500 | fl | 1 |
| 20501 | fixeth | 1 |
| 20502 | fixes | 1 |
| 20503 | fives | 1 |
| 20504 | fivepence | 1 |
| 20505 | fitment | 1 |
| 20506 | fitful | 1 |
| 20507 | fistula | 1 |
| 20508 | fists | 1 |
| 20509 | fisting | 1 |
| 20510 | fisnomy | 1 |
| 20511 | fishpond | 1 |
| 20512 | fishified | 1 |
| 20513 | fishers | 1 |
| 20514 | fisher | 1 |
| 20515 | firing | 1 |
| 20516 | fireworks | 1 |
| 20517 | firework | 1 |
| 20518 | firebrands | 1 |
| 20519 | firago | 1 |
| 20520 | finsbury | 1 |
| 20521 | finn | 1 |
| 20522 | finless | 1 |
| 20523 | finisher | 1 |
| 20524 | finical | 1 |
| 20525 | fing | 1 |
| 20526 | finem | 1 |
| 20527 | fineless | 1 |
| 20528 | findings | 1 |
| 20529 | findeth | 1 |
| 20530 | finally | 1 |
| 20531 | fils | 1 |
| 20532 | filly | 1 |
| 20533 | filius | 1 |
| 20534 | filches | 1 |
| 20535 | filberts | 1 |
| 20536 | figured | 1 |
| 20537 | fightest | 1 |
| 20538 | fiftyfold | 1 |
| 20539 | fifteenth | 1 |
| 20540 | fifteens | 1 |
| 20541 | fifes | 1 |
| 20542 | fiercely | 1 |
| 20543 | fielded | 1 |
| 20544 | fidius | 1 |
| 20545 | fidelity | 1 |
| 20546 | fico | 1 |
| 20547 | fickleness | 1 |
| 20548 | fewness | 1 |
| 20549 | fevers | 1 |
| 20550 | feud | 1 |
| 20551 | fettle | 1 |
| 20552 | fettering | 1 |
| 20553 | fetlocks | 1 |
| 20554 | fetlock | 1 |
| 20555 | fetching | 1 |
| 20556 | festivals | 1 |
| 20557 | festinately | 1 |
| 20558 | festinate | 1 |
| 20559 | fervency | 1 |
| 20560 | ferryman | 1 |
| 20561 | ferry | 1 |
| 20562 | ferrers | 1 |
| 20563 | ferrara | 1 |
| 20564 | fere | 1 |
| 20565 | fenny | 1 |
| 20566 | fends | 1 |
| 20567 | fenc | 1 |
| 20568 | feminine | 1 |
| 20569 | felonious | 1 |
| 20570 | fellowships | 1 |
| 20571 | fellowly | 1 |
| 20572 | fellies | 1 |
| 20573 | felicitate | 1 |
| 20574 | feith | 1 |
| 20575 | feil | 1 |
| 20576 | fehemently | 1 |
| 20577 | feeler | 1 |
| 20578 | feedeth | 1 |
| 20579 | feebly | 1 |
| 20580 | feebling | 1 |
| 20581 | feebleness | 1 |
| 20582 | feebled | 1 |
| 20583 | federary | 1 |
| 20584 | fecks | 1 |
| 20585 | february | 1 |
| 20586 | featureless | 1 |
| 20587 | featured | 1 |
| 20588 | featur | 1 |
| 20589 | feater | 1 |
| 20590 | feated | 1 |
| 20591 | fearfulness | 1 |
| 20592 | fearfull | 1 |
| 20593 | fearest | 1 |
| 20594 | fawneth | 1 |
| 20595 | favout | 1 |
| 20596 | favourers | 1 |
| 20597 | favors | 1 |
| 20598 | favorably | 1 |
| 20599 | favorable | 1 |
| 20600 | faut | 1 |
| 20601 | faustuses | 1 |
| 20602 | fauste | 1 |
| 20603 | fausse | 1 |
| 20604 | faultiness | 1 |
| 20605 | fatuus | 1 |
| 20606 | fatting | 1 |
| 20607 | fatter | 1 |
| 20608 | fats | 1 |
| 20609 | fatness | 1 |
| 20610 | fatigate | 1 |
| 20611 | fathomless | 1 |
| 20612 | fathered | 1 |
| 20613 | fatally | 1 |
| 20614 | fastly | 1 |
| 20615 | fasted | 1 |
| 20616 | fas | 1 |
| 20617 | fartuous | 1 |
| 20618 | farthingales | 1 |
| 20619 | farrow | 1 |
| 20620 | farre | 1 |
| 20621 | farms | 1 |
| 20622 | farmhouse | 1 |
| 20623 | fariner | 1 |
| 20624 | fardels | 1 |
| 20625 | farced | 1 |
| 20626 | farborough | 1 |
| 20627 | fap | 1 |
| 20628 | fantasticoes | 1 |
| 20629 | fantasied | 1 |
| 20630 | fangless | 1 |
| 20631 | fanes | 1 |
| 20632 | fane | 1 |
| 20633 | fanatical | 1 |
| 20634 | famoused | 1 |
| 20635 | famished | 1 |
| 20636 | falsing | 1 |
| 20637 | falsify | 1 |
| 20638 | falorous | 1 |
| 20639 | fally | 1 |
| 20640 | fallows | 1 |
| 20641 | fallible | 1 |
| 20642 | falliable | 1 |
| 20643 | falleth | 1 |
| 20644 | fallacy | 1 |
| 20645 | falconer | 1 |
| 20646 | faitors | 1 |
| 20647 | faithfull | 1 |
| 20648 | faites | 1 |
| 20649 | fait | 1 |
| 20650 | fais | 1 |
| 20651 | fairwell | 1 |
| 20652 | fairings | 1 |
| 20653 | fairing | 1 |
| 20654 | fainter | 1 |
| 20655 | fagots | 1 |
| 20656 | fagot | 1 |
| 20657 | fadoms | 1 |
| 20658 | fadings | 1 |
| 20659 | fadeth | 1 |
| 20660 | factors | 1 |
| 20661 | factionary | 1 |
| 20662 | facing | 1 |
| 20663 | facinerious | 1 |
| 20664 | facile | 1 |
| 20665 | faciant | 1 |
| 20666 | facere | 1 |
| 20667 | eyrie | 1 |
| 20668 | eying | 1 |
| 20669 | eyestrings | 1 |
| 20670 | eyelid | 1 |
| 20671 | eyebrow | 1 |
| 20672 | eyeball | 1 |
| 20673 | eyases | 1 |
| 20674 | eyas | 1 |
| 20675 | exultation | 1 |
| 20676 | exuent | 1 |
| 20677 | extravagancy | 1 |
| 20678 | extraught | 1 |
| 20679 | extracted | 1 |
| 20680 | extract | 1 |
| 20681 | extra | 1 |
| 20682 | extortions | 1 |
| 20683 | extortion | 1 |
| 20684 | extolment | 1 |
| 20685 | extoll | 1 |
| 20686 | extirped | 1 |
| 20687 | extirpate | 1 |
| 20688 | extirp | 1 |
| 20689 | extinguish | 1 |
| 20690 | extincture | 1 |
| 20691 | extincted | 1 |
| 20692 | extermin | 1 |
| 20693 | exteriors | 1 |
| 20694 | exteriorly | 1 |
| 20695 | extenuation | 1 |
| 20696 | extenuates | 1 |
| 20697 | extenuated | 1 |
| 20698 | extends | 1 |
| 20699 | extemporally | 1 |
| 20700 | exsufflicate | 1 |
| 20701 | expuls | 1 |
| 20702 | expressive | 1 |
| 20703 | expresseth | 1 |
| 20704 | expounded | 1 |
| 20705 | exposture | 1 |
| 20706 | expostulation | 1 |
| 20707 | expositor | 1 |
| 20708 | expiring | 1 |
| 20709 | expires | 1 |
| 20710 | expired | 1 |
| 20711 | expiation | 1 |
| 20712 | experimental | 1 |
| 20713 | experiences | 1 |
| 20714 | expels | 1 |
| 20715 | expelling | 1 |
| 20716 | expell | 1 |
| 20717 | expeditious | 1 |
| 20718 | expediently | 1 |
| 20719 | expecters | 1 |
| 20720 | expectations | 1 |
| 20721 | expectance | 1 |
| 20722 | exorcisms | 1 |
| 20723 | exorciser | 1 |
| 20724 | exits | 1 |
| 20725 | exists | 1 |
| 20726 | exion | 1 |
| 20727 | exiled | 1 |
| 20728 | exhortation | 1 |
| 20729 | exhibiters | 1 |
| 20730 | exhaust | 1 |
| 20731 | exequies | 1 |
| 20732 | exempted | 1 |
| 20733 | execrable | 1 |
| 20734 | excusable | 1 |
| 20735 | excursion | 1 |
| 20736 | excrements | 1 |
| 20737 | excommunication | 1 |
| 20738 | excludes | 1 |
| 20739 | exclamations | 1 |
| 20740 | excites | 1 |
| 20741 | excited | 1 |
| 20742 | exchequers | 1 |
| 20743 | exchanged | 1 |
| 20744 | excessive | 1 |
| 20745 | exceptless | 1 |
| 20746 | excellencies | 1 |
| 20747 | excelled | 1 |
| 20748 | exceedeth | 1 |
| 20749 | exasperates | 1 |
| 20750 | exampl | 1 |
| 20751 | examines | 1 |
| 20752 | examinations | 1 |
| 20753 | exalt | 1 |
| 20754 | exacts | 1 |
| 20755 | exacting | 1 |
| 20756 | exactest | 1 |
| 20757 | exacted | 1 |
| 20758 | ewers | 1 |
| 20759 | evitate | 1 |
| 20760 | evidences | 1 |
| 20761 | eventful | 1 |
| 20762 | evasions | 1 |
| 20763 | evades | 1 |
| 20764 | evade | 1 |
| 20765 | euphrates | 1 |
| 20766 | etre | 1 |
| 20767 | etna | 1 |
| 20768 | ethiopes | 1 |
| 20769 | ethiop | 1 |
| 20770 | eterniz | 1 |
| 20771 | eternally | 1 |
| 20772 | ete | 1 |
| 20773 | etceteras | 1 |
| 20774 | estridges | 1 |
| 20775 | estridge | 1 |
| 20776 | estime | 1 |
| 20777 | estimations | 1 |
| 20778 | esteeming | 1 |
| 20779 | esteemeth | 1 |
| 20780 | essential | 1 |
| 20781 | essays | 1 |
| 20782 | essay | 1 |
| 20783 | esill | 1 |
| 20784 | escoted | 1 |
| 20785 | eschew | 1 |
| 20786 | es | 1 |
| 20787 | erworn | 1 |
| 20788 | erwhelmed | 1 |
| 20789 | erweighs | 1 |
| 20790 | erweigh | 1 |
| 20791 | erweens | 1 |
| 20792 | erween | 1 |
| 20793 | erwalk | 1 |
| 20794 | ervalues | 1 |
| 20795 | eruption | 1 |
| 20796 | erudition | 1 |
| 20797 | ertrip | 1 |
| 20798 | ertopping | 1 |
| 20799 | erthrows | 1 |
| 20800 | erteemed | 1 |
| 20801 | erta | 1 |
| 20802 | erstunk | 1 |
| 20803 | erstep | 1 |
| 20804 | erstare | 1 |
| 20805 | erspreads | 1 |
| 20806 | erslips | 1 |
| 20807 | erskip | 1 |
| 20808 | ersized | 1 |
| 20809 | ershine | 1 |
| 20810 | ershade | 1 |
| 20811 | erset | 1 |
| 20812 | errest | 1 |
| 20813 | erred | 1 |
| 20814 | erreaches | 1 |
| 20815 | errate | 1 |
| 20816 | erpressed | 1 |
| 20817 | erpress | 1 |
| 20818 | erposting | 1 |
| 20819 | erpicturing | 1 |
| 20820 | erperch | 1 |
| 20821 | erpeer | 1 |
| 20822 | erpays | 1 |
| 20823 | erparted | 1 |
| 20824 | erpaid | 1 |
| 20825 | ern | 1 |
| 20826 | ermount | 1 |
| 20827 | ermengare | 1 |
| 20828 | ermaster | 1 |
| 20829 | erlooking | 1 |
| 20830 | erleavens | 1 |
| 20831 | erleaps | 1 |
| 20832 | erjoy | 1 |
| 20833 | eringoes | 1 |
| 20834 | erhear | 1 |
| 20835 | erhasty | 1 |
| 20836 | erhanging | 1 |
| 20837 | erhang | 1 |
| 20838 | ergrowth | 1 |
| 20839 | ergrow | 1 |
| 20840 | ergone | 1 |
| 20841 | erglanced | 1 |
| 20842 | ergalled | 1 |
| 20843 | erga | 1 |
| 20844 | erfraught | 1 |
| 20845 | erflowing | 1 |
| 20846 | erflourish | 1 |
| 20847 | erects | 1 |
| 20848 | erecting | 1 |
| 20849 | erdoing | 1 |
| 20850 | ercrows | 1 |
| 20851 | ercover | 1 |
| 20852 | ercharging | 1 |
| 20853 | ercharged | 1 |
| 20854 | ercame | 1 |
| 20855 | erblows | 1 |
| 20856 | erbeat | 1 |
| 20857 | equivocates | 1 |
| 20858 | equivocate | 1 |
| 20859 | equinox | 1 |
| 20860 | equinoctial | 1 |
| 20861 | equalness | 1 |
| 20862 | equalities | 1 |
| 20863 | epitome | 1 |
| 20864 | epitheton | 1 |
| 20865 | epistrophus | 1 |
| 20866 | epilogues | 1 |
| 20867 | epileptic | 1 |
| 20868 | epilepsy | 1 |
| 20869 | epigram | 1 |
| 20870 | epidaurus | 1 |
| 20871 | epicurus | 1 |
| 20872 | epicurism | 1 |
| 20873 | epicures | 1 |
| 20874 | epicure | 1 |
| 20875 | ephesians | 1 |
| 20876 | ephesian | 1 |
| 20877 | enwraps | 1 |
| 20878 | enwombed | 1 |
| 20879 | enwheel | 1 |
| 20880 | enviously | 1 |
| 20881 | envies | 1 |
| 20882 | envenoms | 1 |
| 20883 | entwist | 1 |
| 20884 | entry | 1 |
| 20885 | entrench | 1 |
| 20886 | entreatments | 1 |
| 20887 | entreating | 1 |
| 20888 | entre | 1 |
| 20889 | entrapp | 1 |
| 20890 | entrances | 1 |
| 20891 | entombed | 1 |
| 20892 | entitling | 1 |
| 20893 | entitled | 1 |
| 20894 | enticements | 1 |
| 20895 | entertainments | 1 |
| 20896 | entertaining | 1 |
| 20897 | entertainer | 1 |
| 20898 | entendre | 1 |
| 20899 | entangles | 1 |
| 20900 | entame | 1 |
| 20901 | enswathed | 1 |
| 20902 | ensued | 1 |
| 20903 | ensu | 1 |
| 20904 | ensteep | 1 |
| 20905 | ensnareth | 1 |
| 20906 | ensnared | 1 |
| 20907 | ensnare | 1 |
| 20908 | ensman | 1 |
| 20909 | enskied | 1 |
| 20910 | enshrines | 1 |
| 20911 | enshielded | 1 |
| 20912 | enshelter | 1 |
| 20913 | ensemble | 1 |
| 20914 | enseignez | 1 |
| 20915 | enseigne | 1 |
| 20916 | ensear | 1 |
| 20917 | enseamed | 1 |
| 20918 | ensconcing | 1 |
| 20919 | enschedul | 1 |
| 20920 | enrounded | 1 |
| 20921 | enrooted | 1 |
| 20922 | enrobe | 1 |
| 20923 | enrob | 1 |
| 20924 | enrings | 1 |
| 20925 | enridged | 1 |
| 20926 | enriches | 1 |
| 20927 | enrapt | 1 |
| 20928 | enrank | 1 |
| 20929 | enrages | 1 |
| 20930 | enquir | 1 |
| 20931 | enpierced | 1 |
| 20932 | enpatron | 1 |
| 20933 | enormous | 1 |
| 20934 | enormity | 1 |
| 20935 | enon | 1 |
| 20936 | enobarb | 1 |
| 20937 | ennobled | 1 |
| 20938 | ennoble | 1 |
| 20939 | enmities | 1 |
| 20940 | enmesh | 1 |
| 20941 | enlink | 1 |
| 20942 | enlighten | 1 |
| 20943 | enlargeth | 1 |
| 20944 | enlard | 1 |
| 20945 | enjoyer | 1 |
| 20946 | enjoined | 1 |
| 20947 | enigmatical | 1 |
| 20948 | enguard | 1 |
| 20949 | engrossments | 1 |
| 20950 | engrossing | 1 |
| 20951 | engrossest | 1 |
| 20952 | engrave | 1 |
| 20953 | engrafted | 1 |
| 20954 | engraft | 1 |
| 20955 | engraffed | 1 |
| 20956 | engluts | 1 |
| 20957 | enginer | 1 |
| 20958 | engineer | 1 |
| 20959 | engilds | 1 |
| 20960 | engaol | 1 |
| 20961 | engaging | 1 |
| 20962 | engagements | 1 |
| 20963 | enfreedoming | 1 |
| 20964 | enfreed | 1 |
| 20965 | enfranchised | 1 |
| 20966 | enfranched | 1 |
| 20967 | enforcest | 1 |
| 20968 | enforcedly | 1 |
| 20969 | enfoldings | 1 |
| 20970 | enfetter | 1 |
| 20971 | enfeoff | 1 |
| 20972 | enfeebles | 1 |
| 20973 | enew | 1 |
| 20974 | enernies | 1 |
| 20975 | eneas | 1 |
| 20976 | endymion | 1 |
| 20977 | enduring | 1 |
| 20978 | endures | 1 |
| 20979 | endurance | 1 |
| 20980 | endu | 1 |
| 20981 | endows | 1 |
| 20982 | endite | 1 |
| 20983 | ender | 1 |
| 20984 | endart | 1 |
| 20985 | endamagement | 1 |
| 20986 | encumb | 1 |
| 20987 | encroaching | 1 |
| 20988 | encrimsoned | 1 |
| 20989 | encouraged | 1 |
| 20990 | encountered | 1 |
| 20991 | encorporal | 1 |
| 20992 | encore | 1 |
| 20993 | encompassment | 1 |
| 20994 | encompasseth | 1 |
| 20995 | encompassed | 1 |
| 20996 | enclouded | 1 |
| 20997 | enclosing | 1 |
| 20998 | encloseth | 1 |
| 20999 | encloses | 1 |
| 21000 | enclose | 1 |
| 21001 | enclos | 1 |
| 21002 | encircled | 1 |
| 21003 | encircle | 1 |
| 21004 | enchas | 1 |
| 21005 | enchantress | 1 |
| 21006 | enchantingly | 1 |
| 21007 | enchafed | 1 |
| 21008 | enchaf | 1 |
| 21009 | enceladus | 1 |
| 21010 | encave | 1 |
| 21011 | encamped | 1 |
| 21012 | enanmour | 1 |
| 21013 | enamelled | 1 |
| 21014 | enactures | 1 |
| 21015 | emulator | 1 |
| 21016 | emulations | 1 |
| 21017 | employer | 1 |
| 21018 | employed | 1 |
| 21019 | empleached | 1 |
| 21020 | empiricutic | 1 |
| 21021 | empirics | 1 |
| 21022 | emperial | 1 |
| 21023 | emperal | 1 |
| 21024 | empale | 1 |
| 21025 | emmanuel | 1 |
| 21026 | eminently | 1 |
| 21027 | emhracing | 1 |
| 21028 | embroidery | 1 |
| 21029 | embroider | 1 |
| 21030 | embrasures | 1 |
| 21031 | embowel | 1 |
| 21032 | embounded | 1 |
| 21033 | emboldens | 1 |
| 21034 | embold | 1 |
| 21035 | embodied | 1 |
| 21036 | emblems | 1 |
| 21037 | emblem | 1 |
| 21038 | emblaze | 1 |
| 21039 | embers | 1 |
| 21040 | embellished | 1 |
| 21041 | embay | 1 |
| 21042 | embattle | 1 |
| 21043 | embattailed | 1 |
| 21044 | embassade | 1 |
| 21045 | embarquements | 1 |
| 21046 | embarked | 1 |
| 21047 | embalms | 1 |
| 21048 | embalm | 1 |
| 21049 | emballing | 1 |
| 21050 | elvish | 1 |
| 21051 | ellen | 1 |
| 21052 | elle | 1 |
| 21053 | eliads | 1 |
| 21054 | elflocks | 1 |
| 21055 | elevated | 1 |
| 21056 | elephants | 1 |
| 21057 | elegancy | 1 |
| 21058 | el | 1 |
| 21059 | eject | 1 |
| 21060 | eisel | 1 |
| 21061 | eighty | 1 |
| 21062 | eightpenny | 1 |
| 21063 | eie | 1 |
| 21064 | egress | 1 |
| 21065 | egregiously | 1 |
| 21066 | ego | 1 |
| 21067 | egma | 1 |
| 21068 | eggshell | 1 |
| 21069 | eget | 1 |
| 21070 | egally | 1 |
| 21071 | egal | 1 |
| 21072 | eftest | 1 |
| 21073 | effuse | 1 |
| 21074 | effus | 1 |
| 21075 | effigies | 1 |
| 21076 | effectless | 1 |
| 21077 | eels | 1 |
| 21078 | educated | 1 |
| 21079 | educate | 1 |
| 21080 | edition | 1 |
| 21081 | edifies | 1 |
| 21082 | edifices | 1 |
| 21083 | eden | 1 |
| 21084 | ecstasies | 1 |
| 21085 | ecstacy | 1 |
| 21086 | ecolier | 1 |
| 21087 | echapper | 1 |
| 21088 | ecce | 1 |
| 21089 | ebrew | 1 |
| 21090 | eaux | 1 |
| 21091 | eastward | 1 |
| 21092 | easter | 1 |
| 21093 | easiliest | 1 |
| 21094 | easiest | 1 |
| 21095 | eases | 1 |
| 21096 | easeful | 1 |
| 21097 | earthquakes | 1 |
| 21098 | earthlier | 1 |
| 21099 | earthen | 1 |
| 21100 | earns | 1 |
| 21101 | earliness | 1 |
| 21102 | earlier | 1 |
| 21103 | earing | 1 |
| 21104 | eanlings | 1 |
| 21105 | eaning | 1 |
| 21106 | eagerness | 1 |
| 21107 | dyer | 1 |
| 21108 | dwellers | 1 |
| 21109 | dusted | 1 |
| 21110 | dupp | 1 |
| 21111 | dunstable | 1 |
| 21112 | dunsmore | 1 |
| 21113 | dunnest | 1 |
| 21114 | dung | 1 |
| 21115 | dumbe | 1 |
| 21116 | dulls | 1 |
| 21117 | dulche | 1 |
| 21118 | duff | 1 |
| 21119 | duer | 1 |
| 21120 | dudgeon | 1 |
| 21121 | duchies | 1 |
| 21122 | dryness | 1 |
| 21123 | drumming | 1 |
| 21124 | drummer | 1 |
| 21125 | drumble | 1 |
| 21126 | drugg | 1 |
| 21127 | drudges | 1 |
| 21128 | drudgery | 1 |
| 21129 | drowsiness | 1 |
| 21130 | drowsily | 1 |
| 21131 | drowse | 1 |
| 21132 | drows | 1 |
| 21133 | drovier | 1 |
| 21134 | droven | 1 |
| 21135 | drought | 1 |
| 21136 | drossy | 1 |
| 21137 | dropt | 1 |
| 21138 | dropsy | 1 |
| 21139 | dropsies | 1 |
| 21140 | dropsied | 1 |
| 21141 | droppings | 1 |
| 21142 | droppeth | 1 |
| 21143 | dropper | 1 |
| 21144 | droplets | 1 |
| 21145 | dropheir | 1 |
| 21146 | droopeth | 1 |
| 21147 | dromios | 1 |
| 21148 | droit | 1 |
| 21149 | drizzles | 1 |
| 21150 | drizzle | 1 |
| 21151 | drivelling | 1 |
| 21152 | driv | 1 |
| 21153 | drily | 1 |
| 21154 | dribbling | 1 |
| 21155 | drest | 1 |
| 21156 | dressing | 1 |
| 21157 | dresser | 1 |
| 21158 | drenched | 1 |
| 21159 | dreg | 1 |
| 21160 | dreary | 1 |
| 21161 | drearning | 1 |
| 21162 | dreamers | 1 |
| 21163 | draymen | 1 |
| 21164 | drayman | 1 |
| 21165 | drawling | 1 |
| 21166 | drawbridge | 1 |
| 21167 | drake | 1 |
| 21168 | drains | 1 |
| 21169 | dragonish | 1 |
| 21170 | dragged | 1 |
| 21171 | drachma | 1 |
| 21172 | drabs | 1 |
| 21173 | drabbing | 1 |
| 21174 | dozy | 1 |
| 21175 | dozens | 1 |
| 21176 | dozed | 1 |
| 21177 | doxy | 1 |
| 21178 | dowsabel | 1 |
| 21179 | dowries | 1 |
| 21180 | downwards | 1 |
| 21181 | downtrod | 1 |
| 21182 | downstairs | 1 |
| 21183 | downs | 1 |
| 21184 | dowle | 1 |
| 21185 | dowerless | 1 |
| 21186 | dowdy | 1 |
| 21187 | douts | 1 |
| 21188 | doute | 1 |
| 21189 | doughy | 1 |
| 21190 | doughty | 1 |
| 21191 | doubler | 1 |
| 21192 | doubleness | 1 |
| 21193 | doteth | 1 |
| 21194 | doters | 1 |
| 21195 | doted | 1 |
| 21196 | dotards | 1 |
| 21197 | dotant | 1 |
| 21198 | dorsetshire | 1 |
| 21199 | dormouse | 1 |
| 21200 | doreus | 1 |
| 21201 | doorkeeper | 1 |
| 21202 | donnerai | 1 |
| 21203 | donner | 1 |
| 21204 | donne | 1 |
| 21205 | donc | 1 |
| 21206 | dommelton | 1 |
| 21207 | dominion | 1 |
| 21208 | dominical | 1 |
| 21209 | domineering | 1 |
| 21210 | domineer | 1 |
| 21211 | dominations | 1 |
| 21212 | dominance | 1 |
| 21213 | domestics | 1 |
| 21214 | dolts | 1 |
| 21215 | dolt | 1 |
| 21216 | dolorous | 1 |
| 21217 | dolor | 1 |
| 21218 | dollars | 1 |
| 21219 | dollar | 1 |
| 21220 | doits | 1 |
| 21221 | dogfish | 1 |
| 21222 | doest | 1 |
| 21223 | dodge | 1 |
| 21224 | document | 1 |
| 21225 | dock | 1 |
| 21226 | doating | 1 |
| 21227 | dizy | 1 |
| 21228 | divulging | 1 |
| 21229 | divulge | 1 |
| 21230 | divulg | 1 |
| 21231 | divorcing | 1 |
| 21232 | divorcement | 1 |
| 21233 | diviner | 1 |
| 21234 | divineness | 1 |
| 21235 | divin | 1 |
| 21236 | divideth | 1 |
| 21237 | dividant | 1 |
| 21238 | dividable | 1 |
| 21239 | diverts | 1 |
| 21240 | diversity | 1 |
| 21241 | diversely | 1 |
| 21242 | diver | 1 |
| 21243 | div | 1 |
| 21244 | diurnal | 1 |
| 21245 | ditchers | 1 |
| 21246 | disvouch | 1 |
| 21247 | disvalued | 1 |
| 21248 | disunite | 1 |
| 21249 | disturbing | 1 |
| 21250 | distrustful | 1 |
| 21251 | distributed | 1 |
| 21252 | distracts | 1 |
| 21253 | distinguishment | 1 |
| 21254 | distinguishes | 1 |
| 21255 | distingue | 1 |
| 21256 | distilment | 1 |
| 21257 | distills | 1 |
| 21258 | distempering | 1 |
| 21259 | distemperatures | 1 |
| 21260 | distemperature | 1 |
| 21261 | distasteful | 1 |
| 21262 | distasted | 1 |
| 21263 | distains | 1 |
| 21264 | distain | 1 |
| 21265 | distaffs | 1 |
| 21266 | dissolutions | 1 |
| 21267 | dissipation | 1 |
| 21268 | dissensions | 1 |
| 21269 | dissembly | 1 |
| 21270 | dissemblers | 1 |
| 21271 | disseat | 1 |
| 21272 | disrelish | 1 |
| 21273 | disquietly | 1 |
| 21274 | disquantity | 1 |
| 21275 | disputing | 1 |
| 21276 | disputed | 1 |
| 21277 | disputations | 1 |
| 21278 | disputation | 1 |
| 21279 | disputable | 1 |
| 21280 | dispursed | 1 |
| 21281 | disproved | 1 |
| 21282 | disprov | 1 |
| 21283 | disproportioned | 1 |
| 21284 | dispropertied | 1 |
| 21285 | dispraisingly | 1 |
| 21286 | dispossessing | 1 |
| 21287 | disports | 1 |
| 21288 | disponge | 1 |
| 21289 | displeased | 1 |
| 21290 | displayed | 1 |
| 21291 | displanting | 1 |
| 21292 | displant | 1 |
| 21293 | displaced | 1 |
| 21294 | dispiteous | 1 |
| 21295 | dispersing | 1 |
| 21296 | dispersed | 1 |
| 21297 | dispenses | 1 |
| 21298 | dispark | 1 |
| 21299 | disparagements | 1 |
| 21300 | disorderly | 1 |
| 21301 | disorb | 1 |
| 21302 | disobeys | 1 |
| 21303 | disnatur | 1 |
| 21304 | dismissing | 1 |
| 21305 | dismissed | 1 |
| 21306 | dismes | 1 |
| 21307 | dismemb | 1 |
| 21308 | dismayed | 1 |
| 21309 | dismask | 1 |
| 21310 | dismantled | 1 |
| 21311 | dislodg | 1 |
| 21312 | dislocate | 1 |
| 21313 | dislimns | 1 |
| 21314 | disliken | 1 |
| 21315 | disjunction | 1 |
| 21316 | disjoins | 1 |
| 21317 | disjoining | 1 |
| 21318 | dishonors | 1 |
| 21319 | dishonorable | 1 |
| 21320 | dishonor | 1 |
| 21321 | disheartens | 1 |
| 21322 | dishearten | 1 |
| 21323 | dishabited | 1 |
| 21324 | disguiser | 1 |
| 21325 | disgracing | 1 |
| 21326 | disgraceful | 1 |
| 21327 | disedg | 1 |
| 21328 | disdnguish | 1 |
| 21329 | disdainfully | 1 |
| 21330 | disdained | 1 |
| 21331 | discredits | 1 |
| 21332 | discoverers | 1 |
| 21333 | discov | 1 |
| 21334 | discourtesy | 1 |
| 21335 | discoursive | 1 |
| 21336 | discourser | 1 |
| 21337 | discordant | 1 |
| 21338 | discontinued | 1 |
| 21339 | discontinue | 1 |
| 21340 | discontenting | 1 |
| 21341 | discontentedly | 1 |
| 21342 | disconsolate | 1 |
| 21343 | discommend | 1 |
| 21344 | discomfortable | 1 |
| 21345 | discomfiture | 1 |
| 21346 | discomfit | 1 |
| 21347 | discolours | 1 |
| 21348 | discloses | 1 |
| 21349 | disclaims | 1 |
| 21350 | disciplined | 1 |
| 21351 | disciples | 1 |
| 21352 | discipled | 1 |
| 21353 | discharging | 1 |
| 21354 | discerns | 1 |
| 21355 | discernings | 1 |
| 21356 | discerning | 1 |
| 21357 | discerner | 1 |
| 21358 | discased | 1 |
| 21359 | discandying | 1 |
| 21360 | discandy | 1 |
| 21361 | disburse | 1 |
| 21362 | disburs | 1 |
| 21363 | disburdened | 1 |
| 21364 | disbranch | 1 |
| 21365 | disbench | 1 |
| 21366 | disastrous | 1 |
| 21367 | disarmeth | 1 |
| 21368 | disarmed | 1 |
| 21369 | disappointed | 1 |
| 21370 | disannuls | 1 |
| 21371 | disannul | 1 |
| 21372 | disanimates | 1 |
| 21373 | disallow | 1 |
| 21374 | disagree | 1 |
| 21375 | disabling | 1 |
| 21376 | disability | 1 |
| 21377 | dirges | 1 |
| 21378 | dirge | 1 |
| 21379 | direst | 1 |
| 21380 | direness | 1 |
| 21381 | directs | 1 |
| 21382 | directive | 1 |
| 21383 | directing | 1 |
| 21384 | dir | 1 |
| 21385 | dips | 1 |
| 21386 | dipping | 1 |
| 21387 | dipp | 1 |
| 21388 | diomede | 1 |
| 21389 | dinnertime | 1 |
| 21390 | diner | 1 |
| 21391 | dims | 1 |
| 21392 | dimples | 1 |
| 21393 | dimming | 1 |
| 21394 | dimmed | 1 |
| 21395 | diminishing | 1 |
| 21396 | diluculo | 1 |
| 21397 | dilemmas | 1 |
| 21398 | dilemma | 1 |
| 21399 | dildos | 1 |
| 21400 | dild | 1 |
| 21401 | dilations | 1 |
| 21402 | digt | 1 |
| 21403 | digs | 1 |
| 21404 | diffusest | 1 |
| 21405 | diffused | 1 |
| 21406 | diffidences | 1 |
| 21407 | difficult | 1 |
| 21408 | difficile | 1 |
| 21409 | differency | 1 |
| 21410 | dieter | 1 |
| 21411 | diedst | 1 |
| 21412 | didest | 1 |
| 21413 | diddle | 1 |
| 21414 | diction | 1 |
| 21415 | dictator | 1 |
| 21416 | dicky | 1 |
| 21417 | dickon | 1 |
| 21418 | dickens | 1 |
| 21419 | dich | 1 |
| 21420 | dicers | 1 |
| 21421 | dic | 1 |
| 21422 | dibble | 1 |
| 21423 | diaper | 1 |
| 21424 | diameter | 1 |
| 21425 | dialogued | 1 |
| 21426 | diablo | 1 |
| 21427 | di | 1 |
| 21428 | dexteriously | 1 |
| 21429 | dexter | 1 |
| 21430 | dewy | 1 |
| 21431 | dewlapp | 1 |
| 21432 | dewlap | 1 |
| 21433 | dewdrops | 1 |
| 21434 | dewberries | 1 |
| 21435 | devourers | 1 |
| 21436 | devote | 1 |
| 21437 | devonshire | 1 |
| 21438 | devoid | 1 |
| 21439 | devising | 1 |
| 21440 | devises | 1 |
| 21441 | devesting | 1 |
| 21442 | deuce | 1 |
| 21443 | detractions | 1 |
| 21444 | detesting | 1 |
| 21445 | determinations | 1 |
| 21446 | detention | 1 |
| 21447 | detects | 1 |
| 21448 | detector | 1 |
| 21449 | detection | 1 |
| 21450 | detecting | 1 |
| 21451 | detains | 1 |
| 21452 | det | 1 |
| 21453 | destructions | 1 |
| 21454 | destroyers | 1 |
| 21455 | destroyer | 1 |
| 21456 | destitute | 1 |
| 21457 | destined | 1 |
| 21458 | dest | 1 |
| 21459 | despoiled | 1 |
| 21460 | despiser | 1 |
| 21461 | despatch | 1 |
| 21462 | desirers | 1 |
| 21463 | designments | 1 |
| 21464 | designment | 1 |
| 21465 | deservest | 1 |
| 21466 | deservers | 1 |
| 21467 | deservedly | 1 |
| 21468 | descriptions | 1 |
| 21469 | described | 1 |
| 21470 | descents | 1 |
| 21471 | descension | 1 |
| 21472 | desartless | 1 |
| 21473 | derogation | 1 |
| 21474 | derogately | 1 |
| 21475 | derivative | 1 |
| 21476 | derivation | 1 |
| 21477 | derides | 1 |
| 21478 | deputing | 1 |
| 21479 | deputies | 1 |
| 21480 | deputed | 1 |
| 21481 | depute | 1 |
| 21482 | depths | 1 |
| 21483 | depress | 1 |
| 21484 | depraves | 1 |
| 21485 | depraved | 1 |
| 21486 | deprave | 1 |
| 21487 | depravation | 1 |
| 21488 | deprav | 1 |
| 21489 | depositaries | 1 |
| 21490 | depopulate | 1 |
| 21491 | deploring | 1 |
| 21492 | deplore | 1 |
| 21493 | depender | 1 |
| 21494 | dependents | 1 |
| 21495 | dependent | 1 |
| 21496 | dependences | 1 |
| 21497 | dependence | 1 |
| 21498 | depended | 1 |
| 21499 | dependant | 1 |
| 21500 | depeche | 1 |
| 21501 | departest | 1 |
| 21502 | deo | 1 |
| 21503 | denunciation | 1 |
| 21504 | denouncing | 1 |
| 21505 | denounce | 1 |
| 21506 | denotement | 1 |
| 21507 | denoted | 1 |
| 21508 | deni | 1 |
| 21509 | demuring | 1 |
| 21510 | demonstrative | 1 |
| 21511 | demonstrating | 1 |
| 21512 | demonstrated | 1 |
| 21513 | demonstrable | 1 |
| 21514 | demon | 1 |
| 21515 | demoiselles | 1 |
| 21516 | demise | 1 |
| 21517 | demeanor | 1 |
| 21518 | delves | 1 |
| 21519 | delver | 1 |
| 21520 | deluded | 1 |
| 21521 | deliv | 1 |
| 21522 | delinquents | 1 |
| 21523 | deliciousness | 1 |
| 21524 | delicates | 1 |
| 21525 | delayed | 1 |
| 21526 | deja | 1 |
| 21527 | deigned | 1 |
| 21528 | deifying | 1 |
| 21529 | deified | 1 |
| 21530 | defying | 1 |
| 21531 | defuse | 1 |
| 21532 | defunction | 1 |
| 21533 | deftly | 1 |
| 21534 | deformities | 1 |
| 21535 | deflow | 1 |
| 21536 | definitively | 1 |
| 21537 | definitive | 1 |
| 21538 | definite | 1 |
| 21539 | definement | 1 |
| 21540 | defiling | 1 |
| 21541 | defiler | 1 |
| 21542 | defies | 1 |
| 21543 | deferr | 1 |
| 21544 | defenders | 1 |
| 21545 | defeats | 1 |
| 21546 | defam | 1 |
| 21547 | defacing | 1 |
| 21548 | defacers | 1 |
| 21549 | defacer | 1 |
| 21550 | defaced | 1 |
| 21551 | deesse | 1 |
| 21552 | deepvow | 1 |
| 21553 | deedless | 1 |
| 21554 | decreasing | 1 |
| 21555 | decreas | 1 |
| 21556 | decoct | 1 |
| 21557 | declensions | 1 |
| 21558 | declares | 1 |
| 21559 | deckt | 1 |
| 21560 | decks | 1 |
| 21561 | decking | 1 |
| 21562 | deciphers | 1 |
| 21563 | decimation | 1 |
| 21564 | decides | 1 |
| 21565 | decerns | 1 |
| 21566 | deceptious | 1 |
| 21567 | decent | 1 |
| 21568 | deceiveth | 1 |
| 21569 | deceivest | 1 |
| 21570 | deceivers | 1 |
| 21571 | deceiver | 1 |
| 21572 | decaying | 1 |
| 21573 | decayer | 1 |
| 21574 | debuty | 1 |
| 21575 | debted | 1 |
| 21576 | deborah | 1 |
| 21577 | debonair | 1 |
| 21578 | debility | 1 |
| 21579 | debateth | 1 |
| 21580 | debarred | 1 |
| 21581 | deathsmen | 1 |
| 21582 | deathful | 1 |
| 21583 | dearths | 1 |
| 21584 | dears | 1 |
| 21585 | dearness | 1 |
| 21586 | deanery | 1 |
| 21587 | deals | 1 |
| 21588 | dealest | 1 |
| 21589 | dealers | 1 |
| 21590 | deafs | 1 |
| 21591 | deafing | 1 |
| 21592 | dazzling | 1 |
| 21593 | daventry | 1 |
| 21594 | dated | 1 |
| 21595 | dartford | 1 |
| 21596 | darter | 1 |
| 21597 | darraign | 1 |
| 21598 | darlings | 1 |
| 21599 | darkens | 1 |
| 21600 | darkening | 1 |
| 21601 | darius | 1 |
| 21602 | dareful | 1 |
| 21603 | dared | 1 |
| 21604 | dardanian | 1 |
| 21605 | dapples | 1 |
| 21606 | dappled | 1 |
| 21607 | danskers | 1 |
| 21608 | dankish | 1 |
| 21609 | dangling | 1 |
| 21610 | dang | 1 |
| 21611 | dandy | 1 |
| 21612 | dan | 1 |
| 21613 | damsons | 1 |
| 21614 | dams | 1 |
| 21615 | damosella | 1 |
| 21616 | damon | 1 |
| 21617 | damoiselle | 1 |
| 21618 | damns | 1 |
| 21619 | damnably | 1 |
| 21620 | damasked | 1 |
| 21621 | damascus | 1 |
| 21622 | dallied | 1 |
| 21623 | daisy | 1 |
| 21624 | daisied | 1 |
| 21625 | daintry | 1 |
| 21626 | daintiness | 1 |
| 21627 | daintier | 1 |
| 21628 | dagonet | 1 |
| 21629 | daffest | 1 |
| 21630 | daffed | 1 |
| 21631 | daemon | 1 |
| 21632 | daedalus | 1 |
| 21633 | dace | 1 |
| 21634 | dabbled | 1 |
| 21635 | cyrus | 1 |
| 21636 | cypriot | 1 |
| 21637 | cynthia | 1 |
| 21638 | cynic | 1 |
| 21639 | cyme | 1 |
| 21640 | cymbals | 1 |
| 21641 | cygnets | 1 |
| 21642 | cxsar | 1 |
| 21643 | cuttle | 1 |
| 21644 | cutpurses | 1 |
| 21645 | cutler | 1 |
| 21646 | custure | 1 |
| 21647 | customed | 1 |
| 21648 | custalorum | 1 |
| 21649 | cushes | 1 |
| 21650 | curvets | 1 |
| 21651 | curvet | 1 |
| 21652 | curtsied | 1 |
| 21653 | curstness | 1 |
| 21654 | curstest | 1 |
| 21655 | curster | 1 |
| 21656 | cursorary | 1 |
| 21657 | curry | 1 |
| 21658 | currants | 1 |
| 21659 | currance | 1 |
| 21660 | curling | 1 |
| 21661 | curdied | 1 |
| 21662 | curbing | 1 |
| 21663 | curbed | 1 |
| 21664 | cuppele | 1 |
| 21665 | cupboarding | 1 |
| 21666 | cuore | 1 |
| 21667 | cunnings | 1 |
| 21668 | culverin | 1 |
| 21669 | culpable | 1 |
| 21670 | cullionly | 1 |
| 21671 | cullion | 1 |
| 21672 | cuique | 1 |
| 21673 | cues | 1 |
| 21674 | cudgelling | 1 |
| 21675 | cudgeled | 1 |
| 21676 | cubs | 1 |
| 21677 | cubit | 1 |
| 21678 | cubiculo | 1 |
| 21679 | cubbert | 1 |
| 21680 | crystals | 1 |
| 21681 | crystalline | 1 |
| 21682 | crusty | 1 |
| 21683 | crusts | 1 |
| 21684 | crushing | 1 |
| 21685 | crushest | 1 |
| 21686 | crushed | 1 |
| 21687 | crusadoes | 1 |
| 21688 | crumbs | 1 |
| 21689 | crumble | 1 |
| 21690 | crum | 1 |
| 21691 | cruels | 1 |
| 21692 | crueller | 1 |
| 21693 | cruell | 1 |
| 21694 | crudy | 1 |
| 21695 | crownet | 1 |
| 21696 | crowkeeper | 1 |
| 21697 | crowflowers | 1 |
| 21698 | crowds | 1 |
| 21699 | crowded | 1 |
| 21700 | crouching | 1 |
| 21701 | crost | 1 |
| 21702 | crossness | 1 |
| 21703 | crossly | 1 |
| 21704 | crossings | 1 |
| 21705 | crossest | 1 |
| 21706 | crossed | 1 |
| 21707 | crooking | 1 |
| 21708 | crookback | 1 |
| 21709 | crone | 1 |
| 21710 | cromer | 1 |
| 21711 | croaks | 1 |
| 21712 | croaking | 1 |
| 21713 | critics | 1 |
| 21714 | crispianus | 1 |
| 21715 | crisped | 1 |
| 21716 | cringe | 1 |
| 21717 | crimeless | 1 |
| 21718 | crimeful | 1 |
| 21719 | crieth | 1 |
| 21720 | cribs | 1 |
| 21721 | cribb | 1 |
| 21722 | crib | 1 |
| 21723 | crews | 1 |
| 21724 | crevice | 1 |
| 21725 | cretan | 1 |
| 21726 | crestless | 1 |
| 21727 | crested | 1 |
| 21728 | cressy | 1 |
| 21729 | cressids | 1 |
| 21730 | cressets | 1 |
| 21731 | crescive | 1 |
| 21732 | creeks | 1 |
| 21733 | creek | 1 |
| 21734 | creed | 1 |
| 21735 | credulity | 1 |
| 21736 | credible | 1 |
| 21737 | creates | 1 |
| 21738 | crazy | 1 |
| 21739 | crawls | 1 |
| 21740 | craveth | 1 |
| 21741 | cravens | 1 |
| 21742 | craved | 1 |
| 21743 | crash | 1 |
| 21744 | crare | 1 |
| 21745 | crants | 1 |
| 21746 | crannies | 1 |
| 21747 | crannied | 1 |
| 21748 | cranks | 1 |
| 21749 | cranking | 1 |
| 21750 | crams | 1 |
| 21751 | craftsmen | 1 |
| 21752 | craftier | 1 |
| 21753 | craftied | 1 |
| 21754 | crafted | 1 |
| 21755 | cradled | 1 |
| 21756 | crackers | 1 |
| 21757 | cracker | 1 |
| 21758 | cracked | 1 |
| 21759 | coziers | 1 |
| 21760 | cozener | 1 |
| 21761 | coystrill | 1 |
| 21762 | cowl | 1 |
| 21763 | cowish | 1 |
| 21764 | cowardship | 1 |
| 21765 | cowarded | 1 |
| 21766 | covets | 1 |
| 21767 | covetously | 1 |
| 21768 | covetings | 1 |
| 21769 | coveting | 1 |
| 21770 | coveted | 1 |
| 21771 | covertly | 1 |
| 21772 | coverlet | 1 |
| 21773 | coutume | 1 |
| 21774 | couterfeit | 1 |
| 21775 | courtney | 1 |
| 21776 | courtlike | 1 |
| 21777 | courtesan | 1 |
| 21778 | courted | 1 |
| 21779 | coursed | 1 |
| 21780 | cours | 1 |
| 21781 | couronne | 1 |
| 21782 | courier | 1 |
| 21783 | courages | 1 |
| 21784 | cour | 1 |
| 21785 | couplets | 1 |
| 21786 | couplet | 1 |
| 21787 | couper | 1 |
| 21788 | countrv | 1 |
| 21789 | countless | 1 |
| 21790 | countervail | 1 |
| 21791 | counterpoints | 1 |
| 21792 | counterpart | 1 |
| 21793 | countermines | 1 |
| 21794 | countermands | 1 |
| 21795 | counterfeitly | 1 |
| 21796 | counterchange | 1 |
| 21797 | countenances | 1 |
| 21798 | counselors | 1 |
| 21799 | counselor | 1 |
| 21800 | coulter | 1 |
| 21801 | coude | 1 |
| 21802 | couchings | 1 |
| 21803 | cotswold | 1 |
| 21804 | cotsole | 1 |
| 21805 | cotsall | 1 |
| 21806 | coted | 1 |
| 21807 | cot | 1 |
| 21808 | costlier | 1 |
| 21809 | costermongers | 1 |
| 21810 | cosmo | 1 |
| 21811 | corslet | 1 |
| 21812 | corrupts | 1 |
| 21813 | corruptly | 1 |
| 21814 | corruptibly | 1 |
| 21815 | corruptible | 1 |
| 21816 | corrupters | 1 |
| 21817 | corroborate | 1 |
| 21818 | corrivals | 1 |
| 21819 | corrival | 1 |
| 21820 | corresponsive | 1 |
| 21821 | corresponding | 1 |
| 21822 | correspondent | 1 |
| 21823 | correspondence | 1 |
| 21824 | correctioner | 1 |
| 21825 | correcting | 1 |
| 21826 | corpulent | 1 |
| 21827 | corporals | 1 |
| 21828 | corollary | 1 |
| 21829 | cornuto | 1 |
| 21830 | cornerstone | 1 |
| 21831 | corky | 1 |
| 21832 | corinthian | 1 |
| 21833 | cordis | 1 |
| 21834 | corbo | 1 |
| 21835 | corantos | 1 |
| 21836 | corambus | 1 |
| 21837 | coram | 1 |
| 21838 | copulatives | 1 |
| 21839 | coppice | 1 |
| 21840 | copperspur | 1 |
| 21841 | copious | 1 |
| 21842 | copatain | 1 |
| 21843 | coops | 1 |
| 21844 | coop | 1 |
| 21845 | convulsions | 1 |
| 21846 | convive | 1 |
| 21847 | convinces | 1 |
| 21848 | convinced | 1 |
| 21849 | convicted | 1 |
| 21850 | convict | 1 |
| 21851 | conveying | 1 |
| 21852 | conveyers | 1 |
| 21853 | convertites | 1 |
| 21854 | convertite | 1 |
| 21855 | convertest | 1 |
| 21856 | conversed | 1 |
| 21857 | conversations | 1 |
| 21858 | convents | 1 |
| 21859 | conventicles | 1 |
| 21860 | contusions | 1 |
| 21861 | contumely | 1 |
| 21862 | contumeliously | 1 |
| 21863 | controls | 1 |
| 21864 | contrite | 1 |
| 21865 | contributors | 1 |
| 21866 | contre | 1 |
| 21867 | contrariously | 1 |
| 21868 | contrariety | 1 |
| 21869 | contrarieties | 1 |
| 21870 | contradicts | 1 |
| 21871 | contradicted | 1 |
| 21872 | contraction | 1 |
| 21873 | contracting | 1 |
| 21874 | continuing | 1 |
| 21875 | continuer | 1 |
| 21876 | continuantly | 1 |
| 21877 | continu | 1 |
| 21878 | continence | 1 |
| 21879 | contestation | 1 |
| 21880 | contest | 1 |
| 21881 | contento | 1 |
| 21882 | contentless | 1 |
| 21883 | contenteth | 1 |
| 21884 | contenta | 1 |
| 21885 | contendon | 1 |
| 21886 | contended | 1 |
| 21887 | contemptuously | 1 |
| 21888 | contemplate | 1 |
| 21889 | contemns | 1 |
| 21890 | contemned | 1 |
| 21891 | consumptions | 1 |
| 21892 | consumes | 1 |
| 21893 | consults | 1 |
| 21894 | consulting | 1 |
| 21895 | consulships | 1 |
| 21896 | consulship | 1 |
| 21897 | constring | 1 |
| 21898 | constraineth | 1 |
| 21899 | constellation | 1 |
| 21900 | constantinople | 1 |
| 21901 | constantine | 1 |
| 21902 | constancies | 1 |
| 21903 | conspiring | 1 |
| 21904 | conspires | 1 |
| 21905 | conspirers | 1 |
| 21906 | conspirant | 1 |
| 21907 | conspectuities | 1 |
| 21908 | consortest | 1 |
| 21909 | consonant | 1 |
| 21910 | consolate | 1 |
| 21911 | consisteth | 1 |
| 21912 | consigning | 1 |
| 21913 | considers | 1 |
| 21914 | considerings | 1 |
| 21915 | considerance | 1 |
| 21916 | conserved | 1 |
| 21917 | conserve | 1 |
| 21918 | consequences | 1 |
| 21919 | consecrations | 1 |
| 21920 | conscionable | 1 |
| 21921 | conscienc | 1 |
| 21922 | consanguinity | 1 |
| 21923 | consanguineous | 1 |
| 21924 | cons | 1 |
| 21925 | conquring | 1 |
| 21926 | conquests | 1 |
| 21927 | conqu | 1 |
| 21928 | connive | 1 |
| 21929 | connected | 1 |
| 21930 | conjuro | 1 |
| 21931 | conjuring | 1 |
| 21932 | conjurations | 1 |
| 21933 | conjoins | 1 |
| 21934 | conjoined | 1 |
| 21935 | conies | 1 |
| 21936 | congruing | 1 |
| 21937 | congregations | 1 |
| 21938 | congregate | 1 |
| 21939 | congreeted | 1 |
| 21940 | congreeing | 1 |
| 21941 | congratulate | 1 |
| 21942 | congied | 1 |
| 21943 | congest | 1 |
| 21944 | congee | 1 |
| 21945 | congealment | 1 |
| 21946 | confutation | 1 |
| 21947 | confusedly | 1 |
| 21948 | conform | 1 |
| 21949 | conflux | 1 |
| 21950 | confluence | 1 |
| 21951 | conflicts | 1 |
| 21952 | confixed | 1 |
| 21953 | confiscation | 1 |
| 21954 | confiscated | 1 |
| 21955 | confirmities | 1 |
| 21956 | confirming | 1 |
| 21957 | confirmers | 1 |
| 21958 | confirmer | 1 |
| 21959 | confirmed | 1 |
| 21960 | confiners | 1 |
| 21961 | confineless | 1 |
| 21962 | confesseth | 1 |
| 21963 | confections | 1 |
| 21964 | confectionary | 1 |
| 21965 | confection | 1 |
| 21966 | coney | 1 |
| 21967 | conected | 1 |
| 21968 | conductor | 1 |
| 21969 | conducting | 1 |
| 21970 | condoling | 1 |
| 21971 | condolement | 1 |
| 21972 | conditionally | 1 |
| 21973 | concurs | 1 |
| 21974 | concurring | 1 |
| 21975 | concur | 1 |
| 21976 | concupy | 1 |
| 21977 | concupiscible | 1 |
| 21978 | concubine | 1 |
| 21979 | concolinel | 1 |
| 21980 | concluding | 1 |
| 21981 | conclud | 1 |
| 21982 | conclave | 1 |
| 21983 | concerneth | 1 |
| 21984 | concernancy | 1 |
| 21985 | conceptious | 1 |
| 21986 | conceptions | 1 |
| 21987 | conceitless | 1 |
| 21988 | conceals | 1 |
| 21989 | concealments | 1 |
| 21990 | concavities | 1 |
| 21991 | comutual | 1 |
| 21992 | comrades | 1 |
| 21993 | compunctious | 1 |
| 21994 | compulsatory | 1 |
| 21995 | comptrollers | 1 |
| 21996 | comptible | 1 |
| 21997 | compromis | 1 |
| 21998 | comprising | 1 |
| 21999 | compris | 1 |
| 22000 | compremises | 1 |
| 22001 | comprehended | 1 |
| 22002 | composture | 1 |
| 22003 | compost | 1 |
| 22004 | complotted | 1 |
| 22005 | complimental | 1 |
| 22006 | complies | 1 |
| 22007 | complexioned | 1 |
| 22008 | complains | 1 |
| 22009 | complainings | 1 |
| 22010 | complainest | 1 |
| 22011 | complainer | 1 |
| 22012 | compil | 1 |
| 22013 | competence | 1 |
| 22014 | compensation | 1 |
| 22015 | compels | 1 |
| 22016 | compelling | 1 |
| 22017 | compelled | 1 |
| 22018 | compasses | 1 |
| 22019 | compartner | 1 |
| 22020 | comparing | 1 |
| 22021 | compar | 1 |
| 22022 | comonty | 1 |
| 22023 | community | 1 |
| 22024 | communities | 1 |
| 22025 | communicat | 1 |
| 22026 | commotions | 1 |
| 22027 | commodious | 1 |
| 22028 | commixtion | 1 |
| 22029 | commixed | 1 |
| 22030 | commix | 1 |
| 22031 | committ | 1 |
| 22032 | commissioners | 1 |
| 22033 | commingled | 1 |
| 22034 | commentaries | 1 |
| 22035 | commending | 1 |
| 22036 | commencing | 1 |
| 22037 | commences | 1 |
| 22038 | commenced | 1 |
| 22039 | comme | 1 |
| 22040 | commande | 1 |
| 22041 | comings | 1 |
| 22042 | comfits | 1 |
| 22043 | comfit | 1 |
| 22044 | comfect | 1 |
| 22045 | comers | 1 |
| 22046 | comer | 1 |
| 22047 | comeliness | 1 |
| 22048 | comedians | 1 |
| 22049 | comedian | 1 |
| 22050 | combless | 1 |
| 22051 | combinate | 1 |
| 22052 | combated | 1 |
| 22053 | combatant | 1 |
| 22054 | comart | 1 |
| 22055 | comagene | 1 |
| 22056 | columbines | 1 |
| 22057 | columbine | 1 |
| 22058 | colouring | 1 |
| 22059 | colourable | 1 |
| 22060 | coloquintida | 1 |
| 22061 | colmekill | 1 |
| 22062 | colme | 1 |
| 22063 | collusion | 1 |
| 22064 | collier | 1 |
| 22065 | colleges | 1 |
| 22066 | colleagued | 1 |
| 22067 | collar | 1 |
| 22068 | colebrook | 1 |
| 22069 | coldspur | 1 |
| 22070 | colchos | 1 |
| 22071 | coining | 1 |
| 22072 | coiner | 1 |
| 22073 | coif | 1 |
| 22074 | cohorts | 1 |
| 22075 | coherent | 1 |
| 22076 | coherence | 1 |
| 22077 | cohere | 1 |
| 22078 | coher | 1 |
| 22079 | cohabitants | 1 |
| 22080 | cogscomb | 1 |
| 22081 | cognition | 1 |
| 22082 | cogitations | 1 |
| 22083 | cogitation | 1 |
| 22084 | coesar | 1 |
| 22085 | coelestibus | 1 |
| 22086 | cods | 1 |
| 22087 | codpieces | 1 |
| 22088 | codling | 1 |
| 22089 | codding | 1 |
| 22090 | cod | 1 |
| 22091 | cocytus | 1 |
| 22092 | coctus | 1 |
| 22093 | cocksure | 1 |
| 22094 | cockpit | 1 |
| 22095 | cockled | 1 |
| 22096 | cockatrices | 1 |
| 22097 | cobloaf | 1 |
| 22098 | cobbled | 1 |
| 22099 | cobble | 1 |
| 22100 | coarsely | 1 |
| 22101 | coarse | 1 |
| 22102 | coagulate | 1 |
| 22103 | coactive | 1 |
| 22104 | coact | 1 |
| 22105 | coachmakers | 1 |
| 22106 | cnemies | 1 |
| 22107 | cneius | 1 |
| 22108 | clyster | 1 |
| 22109 | clung | 1 |
| 22110 | cluck | 1 |
| 22111 | cloys | 1 |
| 22112 | cloyment | 1 |
| 22113 | cloyless | 1 |
| 22114 | cloying | 1 |
| 22115 | clowder | 1 |
| 22116 | clovest | 1 |
| 22117 | cloves | 1 |
| 22118 | clover | 1 |
| 22119 | cloudiness | 1 |
| 22120 | clotpoles | 1 |
| 22121 | cloths | 1 |
| 22122 | clothing | 1 |
| 22123 | clothiers | 1 |
| 22124 | clotharius | 1 |
| 22125 | clothair | 1 |
| 22126 | clotens | 1 |
| 22127 | closest | 1 |
| 22128 | closeness | 1 |
| 22129 | cloquence | 1 |
| 22130 | cloistress | 1 |
| 22131 | clogging | 1 |
| 22132 | clodpole | 1 |
| 22133 | cloddy | 1 |
| 22134 | cloakbag | 1 |
| 22135 | clo | 1 |
| 22136 | clipping | 1 |
| 22137 | clippeth | 1 |
| 22138 | clipper | 1 |
| 22139 | clinquant | 1 |
| 22140 | clinking | 1 |
| 22141 | climbeth | 1 |
| 22142 | climber | 1 |
| 22143 | climbed | 1 |
| 22144 | climature | 1 |
| 22145 | cliffords | 1 |
| 22146 | clients | 1 |
| 22147 | client | 1 |
| 22148 | clew | 1 |
| 22149 | clergyman | 1 |
| 22150 | clerestories | 1 |
| 22151 | clept | 1 |
| 22152 | clepeth | 1 |
| 22153 | cleopatpa | 1 |
| 22154 | clemency | 1 |
| 22155 | clef | 1 |
| 22156 | clearest | 1 |
| 22157 | cleansing | 1 |
| 22158 | cleans | 1 |
| 22159 | cleanliest | 1 |
| 22160 | clays | 1 |
| 22161 | clawing | 1 |
| 22162 | clawed | 1 |
| 22163 | clause | 1 |
| 22164 | clatter | 1 |
| 22165 | claret | 1 |
| 22166 | clare | 1 |
| 22167 | clapped | 1 |
| 22168 | clang | 1 |
| 22169 | clammer | 1 |
| 22170 | clamber | 1 |
| 22171 | claiming | 1 |
| 22172 | clack | 1 |
| 22173 | civilly | 1 |
| 22174 | cittern | 1 |
| 22175 | citing | 1 |
| 22176 | cital | 1 |
| 22177 | circumvent | 1 |
| 22178 | circumstanced | 1 |
| 22179 | circumscription | 1 |
| 22180 | circumscribed | 1 |
| 22181 | circumscrib | 1 |
| 22182 | circummur | 1 |
| 22183 | circumcised | 1 |
| 22184 | circum | 1 |
| 22185 | circlets | 1 |
| 22186 | circa | 1 |
| 22187 | ciphers | 1 |
| 22188 | cincture | 1 |
| 22189 | cimmerian | 1 |
| 22190 | cilicia | 1 |
| 22191 | ciitzens | 1 |
| 22192 | ciel | 1 |
| 22193 | ciceter | 1 |
| 22194 | cicatrices | 1 |
| 22195 | chus | 1 |
| 22196 | churn | 1 |
| 22197 | churlishly | 1 |
| 22198 | chuffs | 1 |
| 22199 | chud | 1 |
| 22200 | chucks | 1 |
| 22201 | chrysolite | 1 |
| 22202 | chroniclers | 1 |
| 22203 | chronicler | 1 |
| 22204 | christophero | 1 |
| 22205 | christom | 1 |
| 22206 | christianlike | 1 |
| 22207 | christenings | 1 |
| 22208 | christendoms | 1 |
| 22209 | choristers | 1 |
| 22210 | choppy | 1 |
| 22211 | chopping | 1 |
| 22212 | chopped | 1 |
| 22213 | choplogic | 1 |
| 22214 | chopine | 1 |
| 22215 | chooser | 1 |
| 22216 | chollors | 1 |
| 22217 | cholers | 1 |
| 22218 | chokes | 1 |
| 22219 | choirs | 1 |
| 22220 | choicest | 1 |
| 22221 | choicely | 1 |
| 22222 | chivalrous | 1 |
| 22223 | chitopher | 1 |
| 22224 | chisel | 1 |
| 22225 | chirurgeonly | 1 |
| 22226 | chirping | 1 |
| 22227 | chips | 1 |
| 22228 | chipper | 1 |
| 22229 | chinks | 1 |
| 22230 | chines | 1 |
| 22231 | china | 1 |
| 22232 | chimurcho | 1 |
| 22233 | chimneypiece | 1 |
| 22234 | chimes | 1 |
| 22235 | chime | 1 |
| 22236 | chilling | 1 |
| 22237 | childness | 1 |
| 22238 | childing | 1 |
| 22239 | childhoods | 1 |
| 22240 | childeric | 1 |
| 22241 | childed | 1 |
| 22242 | chien | 1 |
| 22243 | chiders | 1 |
| 22244 | chicurmurco | 1 |
| 22245 | chi | 1 |
| 22246 | chez | 1 |
| 22247 | chewing | 1 |
| 22248 | chewet | 1 |
| 22249 | chewed | 1 |
| 22250 | chevaliers | 1 |
| 22251 | chev | 1 |
| 22252 | chetas | 1 |
| 22253 | chestnuts | 1 |
| 22254 | chester | 1 |
| 22255 | chess | 1 |
| 22256 | cherubims | 1 |
| 22257 | cherub | 1 |
| 22258 | cherrypit | 1 |
| 22259 | cherries | 1 |
| 22260 | cherishes | 1 |
| 22261 | cherisher | 1 |
| 22262 | cherished | 1 |
| 22263 | chequer | 1 |
| 22264 | cheerless | 1 |
| 22265 | cheerer | 1 |
| 22266 | checking | 1 |
| 22267 | checker | 1 |
| 22268 | cheats | 1 |
| 22269 | cheating | 1 |
| 22270 | cheaply | 1 |
| 22271 | cheapest | 1 |
| 22272 | cheaper | 1 |
| 22273 | cheapen | 1 |
| 22274 | che | 1 |
| 22275 | chawdron | 1 |
| 22276 | chaw | 1 |
| 22277 | chaunted | 1 |
| 22278 | chaud | 1 |
| 22279 | chattles | 1 |
| 22280 | chattering | 1 |
| 22281 | chatt | 1 |
| 22282 | chats | 1 |
| 22283 | chasing | 1 |
| 22284 | chaseth | 1 |
| 22285 | chaser | 1 |
| 22286 | charybdis | 1 |
| 22287 | chary | 1 |
| 22288 | charon | 1 |
| 22289 | charolois | 1 |
| 22290 | charneco | 1 |
| 22291 | charmingly | 1 |
| 22292 | charmeth | 1 |
| 22293 | charmer | 1 |
| 22294 | charities | 1 |
| 22295 | charitably | 1 |
| 22296 | charing | 1 |
| 22297 | chariness | 1 |
| 22298 | chariest | 1 |
| 22299 | charging | 1 |
| 22300 | chargeth | 1 |
| 22301 | chargeful | 1 |
| 22302 | chares | 1 |
| 22303 | chare | 1 |
| 22304 | charbon | 1 |
| 22305 | characts | 1 |
| 22306 | characterless | 1 |
| 22307 | charactered | 1 |
| 22308 | chapter | 1 |
| 22309 | chaplet | 1 |
| 22310 | chaplains | 1 |
| 22311 | chapels | 1 |
| 22312 | chapeless | 1 |
| 22313 | chape | 1 |
| 22314 | chap | 1 |
| 22315 | chantry | 1 |
| 22316 | chantries | 1 |
| 22317 | chanting | 1 |
| 22318 | chanson | 1 |
| 22319 | changest | 1 |
| 22320 | changer | 1 |
| 22321 | changelings | 1 |
| 22322 | changeful | 1 |
| 22323 | chandler | 1 |
| 22324 | champains | 1 |
| 22325 | champain | 1 |
| 22326 | champagne | 1 |
| 22327 | champ | 1 |
| 22328 | chambermaid | 1 |
| 22329 | chamberlains | 1 |
| 22330 | chamberers | 1 |
| 22331 | challenges | 1 |
| 22332 | challengers | 1 |
| 22333 | challenged | 1 |
| 22334 | chalks | 1 |
| 22335 | chalk | 1 |
| 22336 | chalices | 1 |
| 22337 | chalic | 1 |
| 22338 | chafing | 1 |
| 22339 | chaffless | 1 |
| 22340 | chaces | 1 |
| 22341 | cette | 1 |
| 22342 | cestern | 1 |
| 22343 | cess | 1 |
| 22344 | ces | 1 |
| 22345 | certify | 1 |
| 22346 | certifies | 1 |
| 22347 | certificate | 1 |
| 22348 | certainer | 1 |
| 22349 | cerns | 1 |
| 22350 | ceremoniously | 1 |
| 22351 | ceremonial | 1 |
| 22352 | cerements | 1 |
| 22353 | cerecloth | 1 |
| 22354 | centurions | 1 |
| 22355 | centuries | 1 |
| 22356 | cents | 1 |
| 22357 | censuring | 1 |
| 22358 | censurers | 1 |
| 22359 | censorinus | 1 |
| 22360 | censor | 1 |
| 22361 | cellarage | 1 |
| 22362 | cellar | 1 |
| 22363 | celebrates | 1 |
| 22364 | cedius | 1 |
| 22365 | ceaseth | 1 |
| 22366 | cawing | 1 |
| 22367 | cawdron | 1 |
| 22368 | cavilling | 1 |
| 22369 | caviary | 1 |
| 22370 | caveto | 1 |
| 22371 | caverns | 1 |
| 22372 | cavaliers | 1 |
| 22373 | cavalery | 1 |
| 22374 | cautions | 1 |
| 22375 | cauterizing | 1 |
| 22376 | cautels | 1 |
| 22377 | cautel | 1 |
| 22378 | causeth | 1 |
| 22379 | causest | 1 |
| 22380 | caused | 1 |
| 22381 | cauf | 1 |
| 22382 | catlings | 1 |
| 22383 | catling | 1 |
| 22384 | catlike | 1 |
| 22385 | cathedral | 1 |
| 22386 | caters | 1 |
| 22387 | cater | 1 |
| 22388 | catechising | 1 |
| 22389 | cate | 1 |
| 22390 | catcher | 1 |
| 22391 | catarrhs | 1 |
| 22392 | cataracts | 1 |
| 22393 | cataplasm | 1 |
| 22394 | casualty | 1 |
| 22395 | casualties | 1 |
| 22396 | casually | 1 |
| 22397 | castiliano | 1 |
| 22398 | castile | 1 |
| 22399 | castigation | 1 |
| 22400 | castigate | 1 |
| 22401 | caster | 1 |
| 22402 | casted | 1 |
| 22403 | castaways | 1 |
| 22404 | castaway | 1 |
| 22405 | castalion | 1 |
| 22406 | cassocks | 1 |
| 22407 | cassado | 1 |
| 22408 | casques | 1 |
| 22409 | casketed | 1 |
| 22410 | cask | 1 |
| 22411 | casing | 1 |
| 22412 | cash | 1 |
| 22413 | casaer | 1 |
| 22414 | casa | 1 |
| 22415 | carves | 1 |
| 22416 | carts | 1 |
| 22417 | carpets | 1 |
| 22418 | carper | 1 |
| 22419 | caroused | 1 |
| 22420 | carnations | 1 |
| 22421 | carnarvonshire | 1 |
| 22422 | carnally | 1 |
| 22423 | carmen | 1 |
| 22424 | carman | 1 |
| 22425 | carlot | 1 |
| 22426 | carl | 1 |
| 22427 | carelessness | 1 |
| 22428 | cared | 1 |
| 22429 | carduus | 1 |
| 22430 | cardmaker | 1 |
| 22431 | cardinally | 1 |
| 22432 | carders | 1 |
| 22433 | carded | 1 |
| 22434 | carcases | 1 |
| 22435 | carcase | 1 |
| 22436 | carbuncled | 1 |
| 22437 | caraways | 1 |
| 22438 | caracks | 1 |
| 22439 | carack | 1 |
| 22440 | captum | 1 |
| 22441 | captivates | 1 |
| 22442 | captivated | 1 |
| 22443 | captious | 1 |
| 22444 | capricious | 1 |
| 22445 | capriccio | 1 |
| 22446 | cappadocia | 1 |
| 22447 | capocchia | 1 |
| 22448 | capite | 1 |
| 22449 | capitaine | 1 |
| 22450 | capels | 1 |
| 22451 | capel | 1 |
| 22452 | capdv | 1 |
| 22453 | capacities | 1 |
| 22454 | capability | 1 |
| 22455 | canzonet | 1 |
| 22456 | canvas | 1 |
| 22457 | canus | 1 |
| 22458 | cantons | 1 |
| 22459 | canstick | 1 |
| 22460 | canons | 1 |
| 22461 | canonize | 1 |
| 22462 | cannibally | 1 |
| 22463 | cankerblossom | 1 |
| 22464 | candlesticks | 1 |
| 22465 | candidatus | 1 |
| 22466 | cancer | 1 |
| 22467 | cancels | 1 |
| 22468 | cancelling | 1 |
| 22469 | cancelled | 1 |
| 22470 | camping | 1 |
| 22471 | camomile | 1 |
| 22472 | camlet | 1 |
| 22473 | camels | 1 |
| 22474 | camelot | 1 |
| 22475 | cambyses | 1 |
| 22476 | cambrics | 1 |
| 22477 | cambric | 1 |
| 22478 | calydon | 1 |
| 22479 | calveskins | 1 |
| 22480 | calved | 1 |
| 22481 | calve | 1 |
| 22482 | calumniating | 1 |
| 22483 | calumniate | 1 |
| 22484 | calms | 1 |
| 22485 | calmness | 1 |
| 22486 | calmest | 1 |
| 22487 | callat | 1 |
| 22488 | cality | 1 |
| 22489 | calipolis | 1 |
| 22490 | calibans | 1 |
| 22491 | calendars | 1 |
| 22492 | calen | 1 |
| 22493 | calamities | 1 |
| 22494 | calaber | 1 |
| 22495 | cak | 1 |
| 22496 | caitiffs | 1 |
| 22497 | cagion | 1 |
| 22498 | caelo | 1 |
| 22499 | caelius | 1 |
| 22500 | cadwallader | 1 |
| 22501 | caduceus | 1 |
| 22502 | cadmus | 1 |
| 22503 | cades | 1 |
| 22504 | cadent | 1 |
| 22505 | cadence | 1 |
| 22506 | caddisses | 1 |
| 22507 | caddis | 1 |
| 22508 | cacodemon | 1 |
| 22509 | cables | 1 |
| 22510 | cabins | 1 |
| 22511 | cabileros | 1 |
| 22512 | cabbage | 1 |
| 22513 | byzantium | 1 |
| 22514 | buzzers | 1 |
| 22515 | buzzards | 1 |
| 22516 | buying | 1 |
| 22517 | buxom | 1 |
| 22518 | buttry | 1 |
| 22519 | buttress | 1 |
| 22520 | buttonhole | 1 |
| 22521 | buttery | 1 |
| 22522 | butterwoman | 1 |
| 22523 | buttered | 1 |
| 22524 | butcherly | 1 |
| 22525 | butcheed | 1 |
| 22526 | bustling | 1 |
| 22527 | bussing | 1 |
| 22528 | busses | 1 |
| 22529 | busky | 1 |
| 22530 | buskin | 1 |
| 22531 | bushels | 1 |
| 22532 | burthens | 1 |
| 22533 | bursts | 1 |
| 22534 | bursting | 1 |
| 22535 | burrows | 1 |
| 22536 | burnet | 1 |
| 22537 | buriest | 1 |
| 22538 | burier | 1 |
| 22539 | burgomasters | 1 |
| 22540 | burglary | 1 |
| 22541 | burgher | 1 |
| 22542 | burgh | 1 |
| 22543 | burdenous | 1 |
| 22544 | burdening | 1 |
| 22545 | burdened | 1 |
| 22546 | burd | 1 |
| 22547 | burbolt | 1 |
| 22548 | bungle | 1 |
| 22549 | bunghole | 1 |
| 22550 | bung | 1 |
| 22551 | bums | 1 |
| 22552 | bumper | 1 |
| 22553 | bump | 1 |
| 22554 | bumbast | 1 |
| 22555 | bulmer | 1 |
| 22556 | bulks | 1 |
| 22557 | bugbear | 1 |
| 22558 | buffeting | 1 |
| 22559 | budger | 1 |
| 22560 | budded | 1 |
| 22561 | bucks | 1 |
| 22562 | bucklersbury | 1 |
| 22563 | bucking | 1 |
| 22564 | bubukles | 1 |
| 22565 | bubbling | 1 |
| 22566 | brunt | 1 |
| 22567 | brundusium | 1 |
| 22568 | bruises | 1 |
| 22569 | browsing | 1 |
| 22570 | browse | 1 |
| 22571 | browny | 1 |
| 22572 | brownist | 1 |
| 22573 | broths | 1 |
| 22574 | brotherhoods | 1 |
| 22575 | broomstaff | 1 |
| 22576 | brooding | 1 |
| 22577 | brooded | 1 |
| 22578 | brooches | 1 |
| 22579 | broking | 1 |
| 22580 | brokes | 1 |
| 22581 | brokenly | 1 |
| 22582 | broiling | 1 |
| 22583 | brogues | 1 |
| 22584 | brock | 1 |
| 22585 | brocas | 1 |
| 22586 | broadsides | 1 |
| 22587 | bristly | 1 |
| 22588 | brisky | 1 |
| 22589 | bringings | 1 |
| 22590 | brinded | 1 |
| 22591 | brims | 1 |
| 22592 | brimful | 1 |
| 22593 | brighten | 1 |
| 22594 | brigandine | 1 |
| 22595 | briefest | 1 |
| 22596 | briefer | 1 |
| 22597 | bridegrooms | 1 |
| 22598 | bricks | 1 |
| 22599 | briber | 1 |
| 22600 | briars | 1 |
| 22601 | briareus | 1 |
| 22602 | brews | 1 |
| 22603 | brewers | 1 |
| 22604 | brewage | 1 |
| 22605 | brevis | 1 |
| 22606 | brethen | 1 |
| 22607 | bretagne | 1 |
| 22608 | breff | 1 |
| 22609 | breeze | 1 |
| 22610 | breese | 1 |
| 22611 | breeching | 1 |
| 22612 | brecknock | 1 |
| 22613 | breathest | 1 |
| 22614 | breathers | 1 |
| 22615 | breastplate | 1 |
| 22616 | breasting | 1 |
| 22617 | brazier | 1 |
| 22618 | braying | 1 |
| 22619 | brawns | 1 |
| 22620 | brawler | 1 |
| 22621 | brassy | 1 |
| 22622 | branchless | 1 |
| 22623 | brambles | 1 |
| 22624 | brakes | 1 |
| 22625 | brainsickly | 1 |
| 22626 | brainless | 1 |
| 22627 | brainish | 1 |
| 22628 | braided | 1 |
| 22629 | braid | 1 |
| 22630 | bragless | 1 |
| 22631 | bragged | 1 |
| 22632 | braggards | 1 |
| 22633 | braggardism | 1 |
| 22634 | bracy | 1 |
| 22635 | brac | 1 |
| 22636 | boxes | 1 |
| 22637 | bowstring | 1 |
| 22638 | bowsprit | 1 |
| 22639 | bowling | 1 |
| 22640 | bowler | 1 |
| 22641 | bowcase | 1 |
| 22642 | bouts | 1 |
| 22643 | bourdeaux | 1 |
| 22644 | bourbier | 1 |
| 22645 | bountifully | 1 |
| 22646 | bounteously | 1 |
| 22647 | boundeth | 1 |
| 22648 | bouncing | 1 |
| 22649 | bouge | 1 |
| 22650 | botchy | 1 |
| 22651 | botches | 1 |
| 22652 | boss | 1 |
| 22653 | boson | 1 |
| 22654 | bosky | 1 |
| 22655 | bosko | 1 |
| 22656 | boroughs | 1 |
| 22657 | boring | 1 |
| 22658 | boreas | 1 |
| 22659 | borders | 1 |
| 22660 | borderers | 1 |
| 22661 | bordered | 1 |
| 22662 | border | 1 |
| 22663 | booties | 1 |
| 22664 | booted | 1 |
| 22665 | boors | 1 |
| 22666 | boorish | 1 |
| 22667 | boor | 1 |
| 22668 | bood | 1 |
| 22669 | bonville | 1 |
| 22670 | bonto | 1 |
| 22671 | bonos | 1 |
| 22672 | bonneted | 1 |
| 22673 | bonjour | 1 |
| 22674 | boneless | 1 |
| 22675 | bondslave | 1 |
| 22676 | bondmaid | 1 |
| 22677 | bonded | 1 |
| 22678 | bombards | 1 |
| 22679 | bolters | 1 |
| 22680 | bolter | 1 |
| 22681 | bolds | 1 |
| 22682 | bolden | 1 |
| 22683 | boitier | 1 |
| 22684 | boisterously | 1 |
| 22685 | bohun | 1 |
| 22686 | boggler | 1 |
| 22687 | boggle | 1 |
| 22688 | bodiless | 1 |
| 22689 | bodg | 1 |
| 22690 | bocchus | 1 |
| 22691 | bobtail | 1 |
| 22692 | boblibindo | 1 |
| 22693 | boastful | 1 |
| 22694 | boasted | 1 |
| 22695 | boars | 1 |
| 22696 | boarish | 1 |
| 22697 | boarding | 1 |
| 22698 | bo | 1 |
| 22699 | blusters | 1 |
| 22700 | blusterer | 1 |
| 22701 | bluster | 1 |
| 22702 | blushest | 1 |
| 22703 | blurs | 1 |
| 22704 | blurr | 1 |
| 22705 | blur | 1 |
| 22706 | bluntness | 1 |
| 22707 | bluntest | 1 |
| 22708 | blunter | 1 |
| 22709 | bluest | 1 |
| 22710 | bluecaps | 1 |
| 22711 | blubbering | 1 |
| 22712 | blubber | 1 |
| 22713 | blubb | 1 |
| 22714 | blowse | 1 |
| 22715 | blowest | 1 |
| 22716 | blowers | 1 |
| 22717 | blowed | 1 |
| 22718 | blount | 1 |
| 22719 | blotting | 1 |
| 22720 | blooms | 1 |
| 22721 | bloodstained | 1 |
| 22722 | bloodshedding | 1 |
| 22723 | bloodiest | 1 |
| 22724 | bloodier | 1 |
| 22725 | bloodhound | 1 |
| 22726 | blois | 1 |
| 22727 | blockish | 1 |
| 22728 | bloat | 1 |
| 22729 | blithild | 1 |
| 22730 | blist | 1 |
| 22731 | blink | 1 |
| 22732 | blinds | 1 |
| 22733 | blindly | 1 |
| 22734 | blesseth | 1 |
| 22735 | blend | 1 |
| 22736 | blenches | 1 |
| 22737 | bleedeth | 1 |
| 22738 | bleedest | 1 |
| 22739 | bleats | 1 |
| 22740 | bleated | 1 |
| 22741 | blear | 1 |
| 22742 | bleach | 1 |
| 22743 | blazoned | 1 |
| 22744 | blazes | 1 |
| 22745 | blastments | 1 |
| 22746 | blasphemous | 1 |
| 22747 | blanca | 1 |
| 22748 | blanc | 1 |
| 22749 | blains | 1 |
| 22750 | bladder | 1 |
| 22751 | blacks | 1 |
| 22752 | blackmere | 1 |
| 22753 | blackberry | 1 |
| 22754 | blabs | 1 |
| 22755 | blabbing | 1 |
| 22756 | biter | 1 |
| 22757 | bis | 1 |
| 22758 | birthrights | 1 |
| 22759 | birthplace | 1 |
| 22760 | birthdom | 1 |
| 22761 | birdlime | 1 |
| 22762 | birch | 1 |
| 22763 | binding | 1 |
| 22764 | bindeth | 1 |
| 22765 | billing | 1 |
| 22766 | billiards | 1 |
| 22767 | billets | 1 |
| 22768 | bilbow | 1 |
| 22769 | bilboes | 1 |
| 22770 | bilberry | 1 |
| 22771 | bigness | 1 |
| 22772 | biggen | 1 |
| 22773 | bigamy | 1 |
| 22774 | bifold | 1 |
| 22775 | biddy | 1 |
| 22776 | biddings | 1 |
| 22777 | bidden | 1 |
| 22778 | bickerings | 1 |
| 22779 | bibble | 1 |
| 22780 | bianco | 1 |
| 22781 | bezonians | 1 |
| 22782 | bezonian | 1 |
| 22783 | bewitchment | 1 |
| 22784 | bewhored | 1 |
| 22785 | bewet | 1 |
| 22786 | bewasted | 1 |
| 22787 | bewails | 1 |
| 22788 | bewailing | 1 |
| 22789 | bewailed | 1 |
| 22790 | beverage | 1 |
| 22791 | bevel | 1 |
| 22792 | bettre | 1 |
| 22793 | betted | 1 |
| 22794 | betroths | 1 |
| 22795 | betrims | 1 |
| 22796 | betrays | 1 |
| 22797 | betossed | 1 |
| 22798 | betook | 1 |
| 22799 | betoken | 1 |
| 22800 | bethump | 1 |
| 22801 | bethrothed | 1 |
| 22802 | bet | 1 |
| 22803 | bestrides | 1 |
| 22804 | bestraught | 1 |
| 22805 | bested | 1 |
| 22806 | bestained | 1 |
| 22807 | bessy | 1 |
| 22808 | bess | 1 |
| 22809 | bespotted | 1 |
| 22810 | bespice | 1 |
| 22811 | besotted | 1 |
| 22812 | besom | 1 |
| 22813 | besmeared | 1 |
| 22814 | beslubber | 1 |
| 22815 | besieged | 1 |
| 22816 | beseemeth | 1 |
| 22817 | beseek | 1 |
| 22818 | beseechers | 1 |
| 22819 | beseeched | 1 |
| 22820 | bescreen | 1 |
| 22821 | berry | 1 |
| 22822 | berrord | 1 |
| 22823 | berod | 1 |
| 22824 | bermoothes | 1 |
| 22825 | berhyme | 1 |
| 22826 | berhym | 1 |
| 22827 | bergamo | 1 |
| 22828 | bereaves | 1 |
| 22829 | bere | 1 |
| 22830 | beray | 1 |
| 22831 | berattle | 1 |
| 22832 | bequest | 1 |
| 22833 | bepray | 1 |
| 22834 | bepaint | 1 |
| 22835 | benumbed | 1 |
| 22836 | bents | 1 |
| 22837 | bentivolii | 1 |
| 22838 | bentii | 1 |
| 22839 | benied | 1 |
| 22840 | benevolences | 1 |
| 22841 | benevolence | 1 |
| 22842 | benetted | 1 |
| 22843 | benefited | 1 |
| 22844 | benefice | 1 |
| 22845 | bencher | 1 |
| 22846 | bemonster | 1 |
| 22847 | bemoil | 1 |
| 22848 | bemoaned | 1 |
| 22849 | bemoan | 1 |
| 22850 | bemete | 1 |
| 22851 | bemet | 1 |
| 22852 | bemadding | 1 |
| 22853 | beloving | 1 |
| 22854 | belongings | 1 |
| 22855 | belock | 1 |
| 22856 | belman | 1 |
| 22857 | bellona | 1 |
| 22858 | bellman | 1 |
| 22859 | belle | 1 |
| 22860 | believest | 1 |
| 22861 | beliest | 1 |
| 22862 | belee | 1 |
| 22863 | beldame | 1 |
| 22864 | beldam | 1 |
| 22865 | belching | 1 |
| 22866 | bel | 1 |
| 22867 | behowls | 1 |
| 22868 | behooves | 1 |
| 22869 | behooffull | 1 |
| 22870 | beholds | 1 |
| 22871 | beholdest | 1 |
| 22872 | beholder | 1 |
| 22873 | behests | 1 |
| 22874 | behest | 1 |
| 22875 | behead | 1 |
| 22876 | behaviors | 1 |
| 22877 | behavior | 1 |
| 22878 | behavedst | 1 |
| 22879 | behav | 1 |
| 22880 | behalfs | 1 |
| 22881 | begrimed | 1 |
| 22882 | begnawn | 1 |
| 22883 | beginnings | 1 |
| 22884 | beggarman | 1 |
| 22885 | beggared | 1 |
| 22886 | befortune | 1 |
| 22887 | beforehand | 1 |
| 22888 | befor | 1 |
| 22889 | befitting | 1 |
| 22890 | befitted | 1 |
| 22891 | befalls | 1 |
| 22892 | befallen | 1 |
| 22893 | beehives | 1 |
| 22894 | beefs | 1 |
| 22895 | bedward | 1 |
| 22896 | bedrench | 1 |
| 22897 | bedfellows | 1 |
| 22898 | bedecking | 1 |
| 22899 | bedeck | 1 |
| 22900 | bedclothes | 1 |
| 22901 | bedazzled | 1 |
| 22902 | bedaub | 1 |
| 22903 | bedash | 1 |
| 22904 | bedabbled | 1 |
| 22905 | becomings | 1 |
| 22906 | becomed | 1 |
| 22907 | beckon | 1 |
| 22908 | bechanced | 1 |
| 22909 | bechance | 1 |
| 22910 | bechanc | 1 |
| 22911 | beavers | 1 |
| 22912 | beautied | 1 |
| 22913 | beaumond | 1 |
| 22914 | beated | 1 |
| 22915 | beastliness | 1 |
| 22916 | beastliest | 1 |
| 22917 | beareth | 1 |
| 22918 | beans | 1 |
| 22919 | beaks | 1 |
| 22920 | beagles | 1 |
| 22921 | beagle | 1 |
| 22922 | beadsmen | 1 |
| 22923 | beaded | 1 |
| 22924 | bead | 1 |
| 22925 | beachy | 1 |
| 22926 | bayonne | 1 |
| 22927 | baying | 1 |
| 22928 | bawling | 1 |
| 22929 | bawl | 1 |
| 22930 | bavin | 1 |
| 22931 | baulk | 1 |
| 22932 | baubling | 1 |
| 22933 | baubles | 1 |
| 22934 | batty | 1 |
| 22935 | battlefield | 1 |
| 22936 | battled | 1 |
| 22937 | battalions | 1 |
| 22938 | battalia | 1 |
| 22939 | batler | 1 |
| 22940 | bating | 1 |
| 22941 | baths | 1 |
| 22942 | bathing | 1 |
| 22943 | batch | 1 |
| 22944 | batailles | 1 |
| 22945 | bastes | 1 |
| 22946 | basted | 1 |
| 22947 | bastardly | 1 |
| 22948 | bastardizing | 1 |
| 22949 | basta | 1 |
| 22950 | bask | 1 |
| 22951 | basins | 1 |
| 22952 | basingstoke | 1 |
| 22953 | basimecu | 1 |
| 22954 | basilisco | 1 |
| 22955 | bashfulness | 1 |
| 22956 | baseless | 1 |
| 22957 | basan | 1 |
| 22958 | barter | 1 |
| 22959 | barson | 1 |
| 22960 | barrow | 1 |
| 22961 | barricadoes | 1 |
| 22962 | barrenness | 1 |
| 22963 | barrenly | 1 |
| 22964 | barrels | 1 |
| 22965 | barrel | 1 |
| 22966 | barrabas | 1 |
| 22967 | barony | 1 |
| 22968 | baron | 1 |
| 22969 | barnacles | 1 |
| 22970 | barm | 1 |
| 22971 | barky | 1 |
| 22972 | barkloughly | 1 |
| 22973 | baring | 1 |
| 22974 | bargulus | 1 |
| 22975 | barful | 1 |
| 22976 | barefaced | 1 |
| 22977 | barefac | 1 |
| 22978 | bared | 1 |
| 22979 | bards | 1 |
| 22980 | barbermonger | 1 |
| 22981 | barbarians | 1 |
| 22982 | baptiz | 1 |
| 22983 | banqueted | 1 |
| 22984 | banning | 1 |
| 22985 | bannerets | 1 |
| 22986 | bankrupts | 1 |
| 22987 | bankrout | 1 |
| 22988 | banister | 1 |
| 22989 | banishers | 1 |
| 22990 | bangor | 1 |
| 22991 | banditto | 1 |
| 22992 | banding | 1 |
| 22993 | bandied | 1 |
| 22994 | banbury | 1 |
| 22995 | bames | 1 |
| 22996 | balsamum | 1 |
| 22997 | balsam | 1 |
| 22998 | balms | 1 |
| 22999 | ballow | 1 |
| 23000 | ballet | 1 |
| 23001 | ballasting | 1 |
| 23002 | ballast | 1 |
| 23003 | bale | 1 |
| 23004 | baldrick | 1 |
| 23005 | balcony | 1 |
| 23006 | balanc | 1 |
| 23007 | baking | 1 |
| 23008 | bakes | 1 |
| 23009 | bakers | 1 |
| 23010 | baker | 1 |
| 23011 | baked | 1 |
| 23012 | bajazet | 1 |
| 23013 | baitings | 1 |
| 23014 | baiser | 1 |
| 23015 | baisees | 1 |
| 23016 | baisant | 1 |
| 23017 | baily | 1 |
| 23018 | baillez | 1 |
| 23019 | bailiff | 1 |
| 23020 | baffled | 1 |
| 23021 | badly | 1 |
| 23022 | badged | 1 |
| 23023 | bacons | 1 |
| 23024 | backwards | 1 |
| 23025 | backwardly | 1 |
| 23026 | backbitten | 1 |
| 23027 | backbite | 1 |
| 23028 | bach | 1 |
| 23029 | bacare | 1 |
| 23030 | baboons | 1 |
| 23031 | babbl | 1 |
| 23032 | baa | 1 |
| 23033 | azure | 1 |
| 23034 | ayez | 1 |
| 23035 | axletree | 1 |
| 23036 | axle | 1 |
| 23037 | awooing | 1 |
| 23038 | awasy | 1 |
| 23039 | award | 1 |
| 23040 | awakens | 1 |
| 23041 | awakened | 1 |
| 23042 | awaken | 1 |
| 23043 | awaits | 1 |
| 23044 | aw | 1 |
| 23045 | avouchment | 1 |
| 23046 | avouched | 1 |
| 23047 | avoirdupois | 1 |
| 23048 | avoids | 1 |
| 23049 | avoiding | 1 |
| 23050 | aves | 1 |
| 23051 | avert | 1 |
| 23052 | averring | 1 |
| 23053 | avenge | 1 |
| 23054 | avaricious | 1 |
| 23055 | autre | 1 |
| 23056 | authorizing | 1 |
| 23057 | aut | 1 |
| 23058 | austereness | 1 |
| 23059 | auricular | 1 |
| 23060 | aunts | 1 |
| 23061 | auld | 1 |
| 23062 | augurs | 1 |
| 23063 | auguring | 1 |
| 23064 | augures | 1 |
| 23065 | augmentation | 1 |
| 23066 | aufidiuses | 1 |
| 23067 | audre | 1 |
| 23068 | auditory | 1 |
| 23069 | auditors | 1 |
| 23070 | audis | 1 |
| 23071 | audaciously | 1 |
| 23072 | aucun | 1 |
| 23073 | auburn | 1 |
| 23074 | aubrey | 1 |
| 23075 | attributive | 1 |
| 23076 | attribution | 1 |
| 23077 | attributed | 1 |
| 23078 | attract | 1 |
| 23079 | attorneyship | 1 |
| 23080 | attorneyed | 1 |
| 23081 | attested | 1 |
| 23082 | attentivenes | 1 |
| 23083 | attent | 1 |
| 23084 | attendeth | 1 |
| 23085 | attemptable | 1 |
| 23086 | attainture | 1 |
| 23087 | attains | 1 |
| 23088 | attachment | 1 |
| 23089 | attached | 1 |
| 23090 | atropos | 1 |
| 23091 | atonements | 1 |
| 23092 | atomy | 1 |
| 23093 | athol | 1 |
| 23094 | astronomy | 1 |
| 23095 | astronomical | 1 |
| 23096 | astronomers | 1 |
| 23097 | astronomer | 1 |
| 23098 | astrea | 1 |
| 23099 | astraea | 1 |
| 23100 | astonished | 1 |
| 23101 | assures | 1 |
| 23102 | assumption | 1 |
| 23103 | assum | 1 |
| 23104 | assubjugate | 1 |
| 23105 | associates | 1 |
| 23106 | associated | 1 |
| 23107 | associate | 1 |
| 23108 | assisting | 1 |
| 23109 | assistances | 1 |
| 23110 | assinico | 1 |
| 23111 | assigned | 1 |
| 23112 | assez | 1 |
| 23113 | assemblance | 1 |
| 23114 | assaying | 1 |
| 23115 | assassination | 1 |
| 23116 | assaileth | 1 |
| 23117 | assailants | 1 |
| 23118 | assailant | 1 |
| 23119 | assailable | 1 |
| 23120 | asquint | 1 |
| 23121 | aspiration | 1 |
| 23122 | aspics | 1 |
| 23123 | aspicious | 1 |
| 23124 | aspersion | 1 |
| 23125 | asmath | 1 |
| 23126 | aslant | 1 |
| 23127 | asker | 1 |
| 23128 | ashy | 1 |
| 23129 | ashouting | 1 |
| 23130 | asher | 1 |
| 23131 | ascribes | 1 |
| 23132 | ascent | 1 |
| 23133 | ascendeth | 1 |
| 23134 | ascanius | 1 |
| 23135 | asaph | 1 |
| 23136 | artus | 1 |
| 23137 | artois | 1 |
| 23138 | artless | 1 |
| 23139 | artists | 1 |
| 23140 | artist | 1 |
| 23141 | artire | 1 |
| 23142 | artificer | 1 |
| 23143 | arteries | 1 |
| 23144 | arrogancy | 1 |
| 23145 | arriving | 1 |
| 23146 | arrivance | 1 |
| 23147 | arrearages | 1 |
| 23148 | arraignment | 1 |
| 23149 | arraigning | 1 |
| 23150 | arraigned | 1 |
| 23151 | aroused | 1 |
| 23152 | arouse | 1 |
| 23153 | armadoes | 1 |
| 23154 | arma | 1 |
| 23155 | ark | 1 |
| 23156 | arithmetician | 1 |
| 23157 | aristotle | 1 |
| 23158 | aristode | 1 |
| 23159 | arising | 1 |
| 23160 | arises | 1 |
| 23161 | arion | 1 |
| 23162 | arinies | 1 |
| 23163 | arinado | 1 |
| 23164 | aries | 1 |
| 23165 | ariachne | 1 |
| 23166 | argu | 1 |
| 23167 | argo | 1 |
| 23168 | ardent | 1 |
| 23169 | arde | 1 |
| 23170 | arcu | 1 |
| 23171 | architect | 1 |
| 23172 | archelaus | 1 |
| 23173 | archbishopric | 1 |
| 23174 | arbors | 1 |
| 23175 | arbitrating | 1 |
| 23176 | araise | 1 |
| 23177 | aquilon | 1 |
| 23178 | aptest | 1 |
| 23179 | appurtenances | 1 |
| 23180 | appurtenance | 1 |
| 23181 | approvers | 1 |
| 23182 | appropriation | 1 |
| 23183 | approachers | 1 |
| 23184 | appris | 1 |
| 23185 | apprenticehood | 1 |
| 23186 | apprenne | 1 |
| 23187 | apprendre | 1 |
| 23188 | appoints | 1 |
| 23189 | applications | 1 |
| 23190 | appletart | 1 |
| 23191 | applauses | 1 |
| 23192 | applauded | 1 |
| 23193 | appertinents | 1 |
| 23194 | appertains | 1 |
| 23195 | apperil | 1 |
| 23196 | appendix | 1 |
| 23197 | appelons | 1 |
| 23198 | appellants | 1 |
| 23199 | appeles | 1 |
| 23200 | appelee | 1 |
| 23201 | appele | 1 |
| 23202 | appelant | 1 |
| 23203 | appeased | 1 |
| 23204 | appeals | 1 |
| 23205 | apparently | 1 |
| 23206 | apparelled | 1 |
| 23207 | appalled | 1 |
| 23208 | appall | 1 |
| 23209 | apostrophas | 1 |
| 23210 | apostles | 1 |
| 23211 | apostle | 1 |
| 23212 | apoplex | 1 |
| 23213 | apollodorus | 1 |
| 23214 | apollinem | 1 |
| 23215 | apennines | 1 |
| 23216 | apartment | 1 |
| 23217 | ap | 1 |
| 23218 | anyone | 1 |
| 23219 | antres | 1 |
| 23220 | antoniad | 1 |
| 23221 | antiquary | 1 |
| 23222 | antipholuses | 1 |
| 23223 | antipathy | 1 |
| 23224 | antiopa | 1 |
| 23225 | antidotes | 1 |
| 23226 | antidote | 1 |
| 23227 | anticly | 1 |
| 23228 | antick | 1 |
| 23229 | anticipation | 1 |
| 23230 | anticipating | 1 |
| 23231 | anticipatest | 1 |
| 23232 | anticipates | 1 |
| 23233 | anticipate | 1 |
| 23234 | anthropophaginian | 1 |
| 23235 | anthropophagi | 1 |
| 23236 | anthems | 1 |
| 23237 | anthem | 1 |
| 23238 | anteroom | 1 |
| 23239 | antenorides | 1 |
| 23240 | answerest | 1 |
| 23241 | anselmo | 1 |
| 23242 | annoying | 1 |
| 23243 | announces | 1 |
| 23244 | annothanize | 1 |
| 23245 | annexment | 1 |
| 23246 | annexions | 1 |
| 23247 | annexed | 1 |
| 23248 | annex | 1 |
| 23249 | annals | 1 |
| 23250 | anna | 1 |
| 23251 | ankle | 1 |
| 23252 | animis | 1 |
| 23253 | angrily | 1 |
| 23254 | anglish | 1 |
| 23255 | angliae | 1 |
| 23256 | angler | 1 |
| 23257 | angl | 1 |
| 23258 | anges | 1 |
| 23259 | angelical | 1 |
| 23260 | angelica | 1 |
| 23261 | andren | 1 |
| 23262 | andpholus | 1 |
| 23263 | andirons | 1 |
| 23264 | ancus | 1 |
| 23265 | ancients | 1 |
| 23266 | anchovies | 1 |
| 23267 | anchored | 1 |
| 23268 | anchorage | 1 |
| 23269 | amyntas | 1 |
| 23270 | ampthill | 1 |
| 23271 | amplified | 1 |
| 23272 | ampler | 1 |
| 23273 | amphimacus | 1 |
| 23274 | amour | 1 |
| 23275 | amorously | 1 |
| 23276 | amnipotent | 1 |
| 23277 | amidst | 1 |
| 23278 | amid | 1 |
| 23279 | ames | 1 |
| 23280 | america | 1 |
| 23281 | amerce | 1 |
| 23282 | ambuscadoes | 1 |
| 23283 | ambo | 1 |
| 23284 | ambled | 1 |
| 23285 | amble | 1 |
| 23286 | ambiguous | 1 |
| 23287 | ambiguities | 1 |
| 23288 | ambiguides | 1 |
| 23289 | amazing | 1 |
| 23290 | amazeth | 1 |
| 23291 | amazes | 1 |
| 23292 | amamon | 1 |
| 23293 | amaking | 1 |
| 23294 | amaimon | 1 |
| 23295 | alway | 1 |
| 23296 | alton | 1 |
| 23297 | alphonso | 1 |
| 23298 | alphabetical | 1 |
| 23299 | alphabet | 1 |
| 23300 | aloes | 1 |
| 23301 | almsman | 1 |
| 23302 | almond | 1 |
| 23303 | almanacs | 1 |
| 23304 | almanack | 1 |
| 23305 | almain | 1 |
| 23306 | allycholly | 1 |
| 23307 | ally | 1 |
| 23308 | alluring | 1 |
| 23309 | allurement | 1 |
| 23310 | allur | 1 |
| 23311 | alls | 1 |
| 23312 | allottery | 1 |
| 23313 | allotted | 1 |
| 23314 | allots | 1 |
| 23315 | allot | 1 |
| 23316 | alligator | 1 |
| 23317 | alligant | 1 |
| 23318 | allicholy | 1 |
| 23319 | allhallowmas | 1 |
| 23320 | allegiant | 1 |
| 23321 | allegations | 1 |
| 23322 | allegation | 1 |
| 23323 | allays | 1 |
| 23324 | allayments | 1 |
| 23325 | allayment | 1 |
| 23326 | allayed | 1 |
| 23327 | aliis | 1 |
| 23328 | alights | 1 |
| 23329 | alight | 1 |
| 23330 | alexanders | 1 |
| 23331 | alewife | 1 |
| 23332 | alengon | 1 |
| 23333 | alehouses | 1 |
| 23334 | alecto | 1 |
| 23335 | alder | 1 |
| 23336 | alarms | 1 |
| 23337 | al | 1 |
| 23338 | akilling | 1 |
| 23339 | airless | 1 |
| 23340 | aired | 1 |
| 23341 | aio | 1 |
| 23342 | aimest | 1 |
| 23343 | aimed | 1 |
| 23344 | aidless | 1 |
| 23345 | aided | 1 |
| 23346 | aidant | 1 |
| 23347 | aidance | 1 |
| 23348 | aiaria | 1 |
| 23349 | aialvolio | 1 |
| 23350 | ahungry | 1 |
| 23351 | agueface | 1 |
| 23352 | agued | 1 |
| 23353 | aground | 1 |
| 23354 | agnize | 1 |
| 23355 | aglet | 1 |
| 23356 | agile | 1 |
| 23357 | aggrief | 1 |
| 23358 | agenor | 1 |
| 23359 | agaz | 1 |
| 23360 | agamemmon | 1 |
| 23361 | afront | 1 |
| 23362 | african | 1 |
| 23363 | africa | 1 |
| 23364 | aforehand | 1 |
| 23365 | affronted | 1 |
| 23366 | affray | 1 |
| 23367 | affordeth | 1 |
| 23368 | affirmatives | 1 |
| 23369 | affirmation | 1 |
| 23370 | affinity | 1 |
| 23371 | affin | 1 |
| 23372 | affied | 1 |
| 23373 | affianced | 1 |
| 23374 | affianc | 1 |
| 23375 | affeer | 1 |
| 23376 | affectionately | 1 |
| 23377 | affectionate | 1 |
| 23378 | affecteth | 1 |
| 23379 | affectedly | 1 |
| 23380 | affectations | 1 |
| 23381 | affaire | 1 |
| 23382 | aetna | 1 |
| 23383 | aesop | 1 |
| 23384 | aeson | 1 |
| 23385 | aesculapius | 1 |
| 23386 | aerial | 1 |
| 23387 | aeolus | 1 |
| 23388 | aemelia | 1 |
| 23389 | aegles | 1 |
| 23390 | aegion | 1 |
| 23391 | aeacides | 1 |
| 23392 | aeacida | 1 |
| 23393 | advocation | 1 |
| 23394 | advisings | 1 |
| 23395 | advertising | 1 |
| 23396 | adversities | 1 |
| 23397 | adversely | 1 |
| 23398 | adventurously | 1 |
| 23399 | adventuring | 1 |
| 23400 | adventur | 1 |
| 23401 | advent | 1 |
| 23402 | advantaging | 1 |
| 23403 | advantaged | 1 |
| 23404 | advantageable | 1 |
| 23405 | advancements | 1 |
| 23406 | adulteries | 1 |
| 23407 | adulteress | 1 |
| 23408 | adulterers | 1 |
| 23409 | adulterates | 1 |
| 23410 | adulation | 1 |
| 23411 | adsum | 1 |
| 23412 | adriatic | 1 |
| 23413 | adown | 1 |
| 23414 | adorns | 1 |
| 23415 | adornings | 1 |
| 23416 | adoring | 1 |
| 23417 | adoreth | 1 |
| 23418 | adorest | 1 |
| 23419 | adorer | 1 |
| 23420 | adorations | 1 |
| 23421 | adopts | 1 |
| 23422 | adoptious | 1 |
| 23423 | adoptedly | 1 |
| 23424 | admonishments | 1 |
| 23425 | admonishment | 1 |
| 23426 | admonishing | 1 |
| 23427 | admonish | 1 |
| 23428 | admitting | 1 |
| 23429 | admission | 1 |
| 23430 | admirer | 1 |
| 23431 | administration | 1 |
| 23432 | administer | 1 |
| 23433 | adjudged | 1 |
| 23434 | adjoin | 1 |
| 23435 | addressing | 1 |
| 23436 | addict | 1 |
| 23437 | addeth | 1 |
| 23438 | adallas | 1 |
| 23439 | acutely | 1 |
| 23440 | acture | 1 |
| 23441 | actively | 1 |
| 23442 | acquittances | 1 |
| 23443 | acquisition | 1 |
| 23444 | acquaints | 1 |
| 23445 | acordo | 1 |
| 23446 | aconitum | 1 |
| 23447 | acknown | 1 |
| 23448 | acknowledgment | 1 |
| 23449 | acknowledged | 1 |
| 23450 | achitophel | 1 |
| 23451 | achieving | 1 |
| 23452 | achieves | 1 |
| 23453 | achiever | 1 |
| 23454 | acerb | 1 |
| 23455 | accuseth | 1 |
| 23456 | accusative | 1 |
| 23457 | accumulation | 1 |
| 23458 | accumulated | 1 |
| 23459 | accrue | 1 |
| 23460 | accosted | 1 |
| 23461 | accordeth | 1 |
| 23462 | accorded | 1 |
| 23463 | accordant | 1 |
| 23464 | accomplishment | 1 |
| 23465 | accomplishing | 1 |
| 23466 | accomplices | 1 |
| 23467 | accompanying | 1 |
| 23468 | accommodo | 1 |
| 23469 | accommodations | 1 |
| 23470 | accommodation | 1 |
| 23471 | accommodate | 1 |
| 23472 | acclamations | 1 |
| 23473 | accites | 1 |
| 23474 | accited | 1 |
| 23475 | accite | 1 |
| 23476 | accidence | 1 |
| 23477 | accessible | 1 |
| 23478 | acceptable | 1 |
| 23479 | academe | 1 |
| 23480 | abutting | 1 |
| 23481 | abuser | 1 |
| 23482 | abundantly | 1 |
| 23483 | absyrtus | 1 |
| 23484 | abstemious | 1 |
| 23485 | abstains | 1 |
| 23486 | absolver | 1 |
| 23487 | absey | 1 |
| 23488 | abruptly | 1 |
| 23489 | abruption | 1 |
| 23490 | abrupt | 1 |
| 23491 | abrook | 1 |
| 23492 | abrogate | 1 |
| 23493 | abridged | 1 |
| 23494 | abridg | 1 |
| 23495 | abounding | 1 |
| 23496 | abortives | 1 |
| 23497 | abominations | 1 |
| 23498 | abominably | 1 |
| 23499 | aboding | 1 |
| 23500 | abodements | 1 |
| 23501 | aboded | 1 |
| 23502 | abler | 1 |
| 23503 | abjectly | 1 |
| 23504 | abhominable | 1 |
| 23505 | abetting | 1 |
| 23506 | abet | 1 |
| 23507 | abbreviated | 1 |
| 23508 | abbots | 1 |
| 23509 | abbominable | 1 |
| 23510 | abbeys | 1 |
| 23511 | abates | 1 |
| 23512 | abatements | 1 |
| 23513 | abash | 1 |
| 23514 | abaissiez | 1 |
|
Ilustración del principio de mínimo esfuerzo: |
|
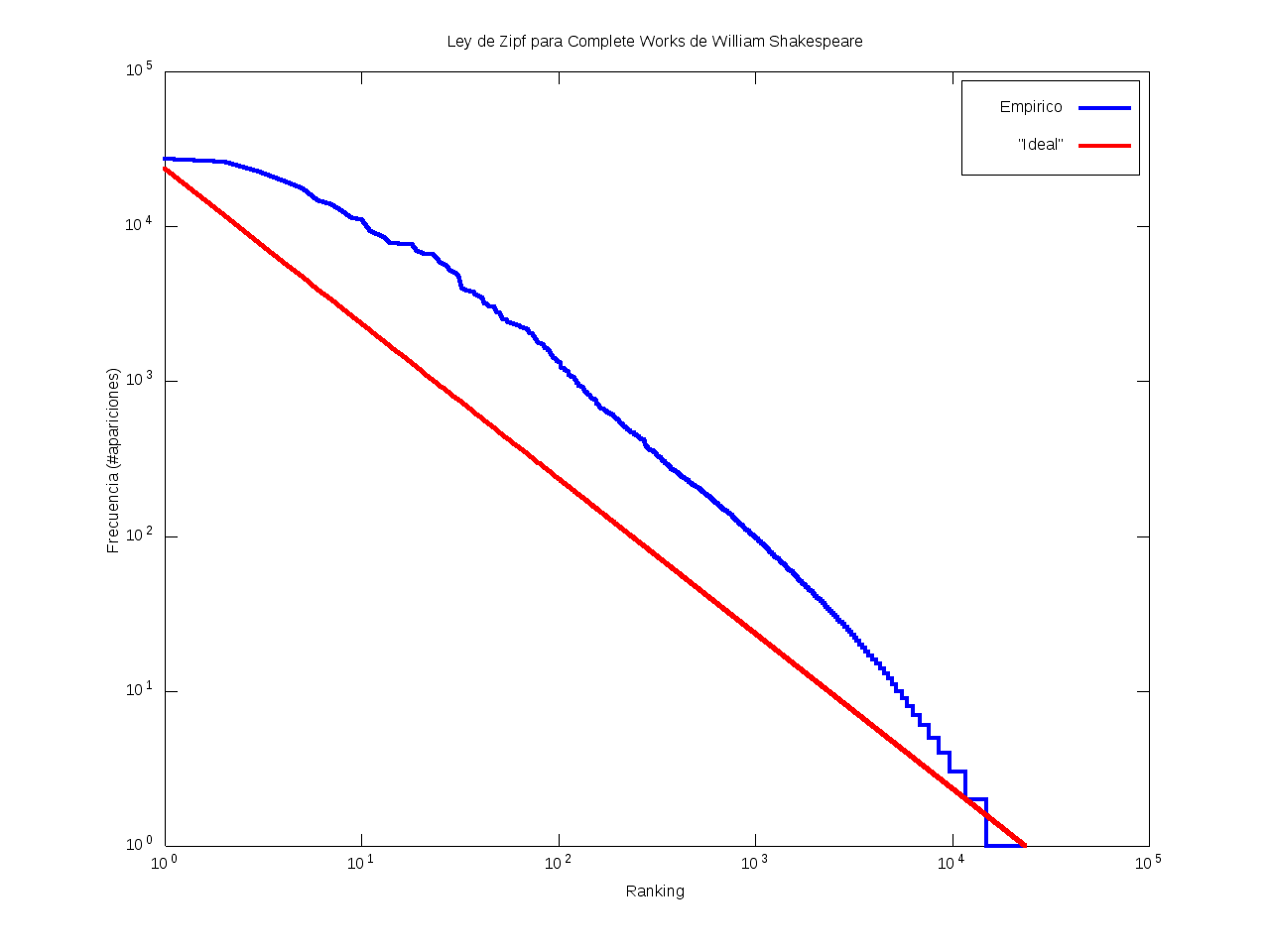
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará el texto actual (Complete Works de William Shakespeare) (conjunto 1)
contra el resto de textos en el mismo idioma (Inglés) (conjunto 2).
A continuación se muestra una lista de las palabras presentes en el texto actual,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
Mostrar todo
Recoger

