Análisis de la obra de Lope de Vega
Índice
Información General
| Escritor: | Lope de Vega |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 38483 |
|---|
| #Palabras distintas: | 6110 |
|---|
| Type-Token ratio: | 15.88% |
|---|
Relación de obras consideradas:
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| #Palabras: | #Palabras distintas: |
|---|
| 1000 | 458 |
| 2000 | 807 |
| 3000 | 1069 |
| 4000 | 1276 |
| 5000 | 1438 |
| 6000 | 1620 |
| 7000 | 1785 |
| 8000 | 1945 |
| 9000 | 2129 |
| 10000 | 2303 |
| 11000 | 2440 |
| 12000 | 2627 |
| 13000 | 2770 |
| 14000 | 2906 |
| 15000 | 3018 |
| 16000 | 3101 |
| 17000 | 3241 |
| 18000 | 3389 |
| 19000 | 3502 |
| 20000 | 3603 |
| 21000 | 3700 |
| 22000 | 3806 |
| 23000 | 3931 |
| 24000 | 4046 |
| 25000 | 4177 |
| 26000 | 4270 |
| 27000 | 4358 |
| 28000 | 4432 |
| 29000 | 4534 |
| 30000 | 4614 |
| 31000 | 4805 |
| 32000 | 4994 |
| 33000 | 5219 |
| 34000 | 5367 |
| 35000 | 5536 |
| 36000 | 5703 |
| 37000 | 5868 |
| 38000 | 6045 |
| 38483 | 6110 |
|
Ajuste por mínimos cuadrados de los datos a K*n^b:
|
| K = 4.493 |
|
b = 0.677 |

|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Rank | Palabra | Frec |
|---|
| 1 | que | 1749 |
| 2 | de | 1422 |
| 3 | y | 1188 |
| 4 | la | 934 |
| 5 | a | 835 |
| 6 | el | 802 |
| 7 | en | 777 |
| 8 | no | 669 |
| 9 | es | 399 |
| 10 | por | 350 |
| 11 | me | 340 |
| 12 | mi | 331 |
| 13 | los | 331 |
| 14 | con | 316 |
| 15 | nuño | 308 |
| 16 | su | 259 |
| 17 | sancho | 253 |
| 18 | si | 242 |
| 19 | yo | 223 |
| 20 | del | 199 |
| 21 | te | 198 |
| 22 | lo | 198 |
| 23 | qué | 195 |
| 24 | se | 194 |
| 25 | narv | 193 |
| 26 | señor | 183 |
| 27 | las | 183 |
| 28 | al | 174 |
| 29 | pelayo | 171 |
| 30 | tu | 170 |
| 31 | rey | 170 |
| 32 | un | 167 |
| 33 | pues | 164 |
| 34 | más | 161 |
| 35 | jarifa | 160 |
| 36 | le | 152 |
| 37 | ha | 152 |
| 38 | bien | 146 |
| 39 | ya | 145 |
| 40 | abind | 145 |
| 41 | como | 137 |
| 42 | d | 133 |
| 43 | tan | 131 |
| 44 | elvira | 124 |
| 45 | amor | 124 |
| 46 | tell | 122 |
| 47 | aquí | 114 |
| 48 | o | 110 |
| 49 | ser | 109 |
| 50 | os | 107 |
| 51 | para | 104 |
| 52 | una | 100 |
| 53 | porque | 93 |
| 54 | soy | 91 |
| 55 | pero | 91 |
| 56 | he | 90 |
| 57 | esta | 86 |
| 58 | mí | 84 |
| 59 | quien | 81 |
| 60 | e | 78 |
| 61 | parte | 77 |
| 62 | don | 76 |
| 63 | vida | 75 |
| 64 | dios | 75 |
| 65 | aunque | 74 |
| 66 | sus | 73 |
| 67 | vos | 71 |
| 68 | este | 70 |
| 69 | celio | 69 |
| 70 | hay | 68 |
| 71 | dos | 65 |
| 72 | alma | 64 |
| 73 | sin | 63 |
| 74 | ni | 63 |
| 75 | está | 62 |
| 76 | cuando | 62 |
| 77 | tú | 61 |
| 78 | mis | 61 |
| 79 | mas | 61 |
| 80 | tello | 60 |
| 81 | lope | 57 |
| 82 | sí | 56 |
| 83 | fué | 56 |
| 84 | todo | 54 |
| 85 | narváez | 54 |
| 86 | alara | 54 |
| 87 | casa | 53 |
| 88 | sale | 51 |
| 89 | mujer | 51 |
| 90 | hombre | 51 |
| 91 | quién | 50 |
| 92 | moro | 50 |
| 93 | cómo | 50 |
| 94 | cielo | 49 |
| 95 | tiene | 48 |
| 96 | quiero | 47 |
| 97 | has | 47 |
| 98 | él | 47 |
| 99 | ay | 47 |
| 100 | padre | 46 |
| 101 | tengo | 45 |
| 102 | abindarráez | 45 |
| 103 | luego | 44 |
| 104 | hermano | 44 |
| 105 | v | 43 |
| 106 | son | 43 |
| 107 | mal | 43 |
| 108 | esto | 43 |
| 109 | era | 43 |
| 110 | tus | 42 |
| 111 | arr | 42 |
| 112 | ti | 41 |
| 113 | felic | 41 |
| 114 | todos | 40 |
| 115 | tanto | 40 |
| 116 | entre | 39 |
| 117 | ella | 39 |
| 118 | valor | 38 |
| 119 | también | 38 |
| 120 | fin | 38 |
| 121 | donde | 38 |
| 122 | así | 38 |
| 123 | alcaide | 38 |
| 124 | sólo | 37 |
| 125 | mano | 37 |
| 126 | di | 37 |
| 127 | tal | 36 |
| 128 | señora | 36 |
| 129 | páez | 36 |
| 130 | ansí | 36 |
| 131 | puede | 35 |
| 132 | nota | 35 |
| 133 | hacer | 35 |
| 134 | fuera | 35 |
| 135 | conde | 35 |
| 136 | aquel | 35 |
| 137 | sino | 34 |
| 138 | salen | 34 |
| 139 | oh | 34 |
| 140 | estoy | 34 |
| 141 | ver | 33 |
| 142 | tierra | 33 |
| 143 | ojos | 33 |
| 144 | nos | 33 |
| 145 | eres | 33 |
| 146 | vase | 32 |
| 147 | nombre | 32 |
| 148 | noche | 32 |
| 149 | muy | 32 |
| 150 | mil | 32 |
| 151 | mejor | 32 |
| 152 | mayor | 32 |
| 153 | agora | 32 |
| 154 | vuestro | 30 |
| 155 | vuestra | 30 |
| 156 | mía | 30 |
| 157 | hasta | 30 |
| 158 | celos | 30 |
| 159 | buen | 30 |
| 160 | véase | 29 |
| 161 | sé | 29 |
| 162 | poco | 29 |
| 163 | gran | 29 |
| 164 | esposo | 29 |
| 165 | dice | 29 |
| 166 | viene | 28 |
| 167 | vanse | 28 |
| 168 | quiere | 28 |
| 169 | pies | 28 |
| 170 | parece | 28 |
| 171 | han | 28 |
| 172 | dar | 28 |
| 173 | sol | 27 |
| 174 | justo | 27 |
| 175 | juana | 27 |
| 176 | gusto | 27 |
| 177 | esa | 27 |
| 178 | b | 27 |
| 179 | alora | 27 |
| 180 | sido | 26 |
| 181 | puedo | 26 |
| 182 | hermana | 26 |
| 183 | después | 26 |
| 184 | dame | 26 |
| 185 | cosa | 26 |
| 186 | coín | 26 |
| 187 | carta | 26 |
| 188 | tiempo | 25 |
| 189 | remedio | 25 |
| 190 | otra | 25 |
| 191 | marido | 25 |
| 192 | labrador | 25 |
| 193 | dulce | 25 |
| 194 | digo | 25 |
| 195 | desde | 25 |
| 196 | visto | 24 |
| 197 | siempre | 24 |
| 198 | muerte | 24 |
| 199 | mira | 24 |
| 200 | manos | 24 |
| 201 | hermosa | 24 |
| 202 | hablar | 24 |
| 203 | eso | 24 |
| 204 | día | 24 |
| 205 | xxi | 23 |
| 206 | vez | 23 |
| 207 | será | 23 |
| 208 | historia | 23 |
| 209 | haber | 23 |
| 210 | vive | 22 |
| 211 | verdad | 22 |
| 212 | toda | 22 |
| 213 | tanta | 22 |
| 214 | posible | 22 |
| 215 | noble | 22 |
| 216 | mundo | 22 |
| 217 | mucho | 22 |
| 218 | hoy | 22 |
| 219 | honor | 22 |
| 220 | granada | 22 |
| 221 | decir | 22 |
| 222 | villano | 21 |
| 223 | triste | 21 |
| 224 | suelta | 21 |
| 225 | puesto | 21 |
| 226 | piedad | 21 |
| 227 | estás | 21 |
| 228 | esperanza | 21 |
| 229 | espada | 21 |
| 230 | emperador | 21 |
| 231 | dijo | 21 |
| 232 | años | 21 |
| 233 | sabe | 20 |
| 234 | presto | 20 |
| 235 | hermosura | 20 |
| 236 | favor | 20 |
| 237 | dió | 20 |
| 238 | dado | 20 |
| 239 | cuanto | 20 |
| 240 | antes | 20 |
| 241 | allá | 20 |
| 242 | alfonso | 20 |
| 243 | xiii | 19 |
| 244 | vengo | 19 |
| 245 | veces | 19 |
| 246 | sois | 19 |
| 247 | siendo | 19 |
| 248 | primero | 19 |
| 249 | mío | 19 |
| 250 | libertad | 19 |
| 251 | ii | 19 |
| 252 | hombres | 19 |
| 253 | hijo | 19 |
| 254 | estos | 19 |
| 255 | ese | 19 |
| 256 | ellos | 19 |
| 257 | dónde | 19 |
| 258 | da | 19 |
| 259 | conmigo | 19 |
| 260 | amores | 19 |
| 261 | sea | 18 |
| 262 | razón | 18 |
| 263 | pobre | 18 |
| 264 | pág | 18 |
| 265 | otro | 18 |
| 266 | justicia | 18 |
| 267 | estar | 18 |
| 268 | diana | 18 |
| 269 | caballero | 18 |
| 270 | aquella | 18 |
| 271 | alvar | 18 |
| 272 | allí | 18 |
| 273 | alguna | 18 |
| 274 | algún | 18 |
| 275 | veo | 17 |
| 276 | rodrigo | 17 |
| 277 | reyes | 17 |
| 278 | ir | 17 |
| 279 | i | 17 |
| 280 | fortuna | 17 |
| 281 | famoso | 17 |
| 282 | esos | 17 |
| 283 | deste | 17 |
| 284 | deseo | 17 |
| 285 | desdicha | 17 |
| 286 | dentro | 17 |
| 287 | cuerpo | 17 |
| 288 | castilla | 17 |
| 289 | armas | 17 |
| 290 | abencerraje | 17 |
| 291 | zoraid | 16 |
| 292 | voy | 16 |
| 293 | vamos | 16 |
| 294 | tuya | 16 |
| 295 | tres | 16 |
| 296 | tienes | 16 |
| 297 | sobre | 16 |
| 298 | rigor | 16 |
| 299 | querer | 16 |
| 300 | pienso | 16 |
| 301 | palabra | 16 |
| 302 | otras | 16 |
| 303 | mismo | 16 |
| 304 | matar | 16 |
| 305 | galicia | 16 |
| 306 | estaba | 16 |
| 307 | esposa | 16 |
| 308 | dices | 16 |
| 309 | desta | 16 |
| 310 | celind | 16 |
| 311 | cartama | 16 |
| 312 | boca | 16 |
| 313 | basta | 16 |
| 314 | aun | 16 |
| 315 | arráez | 16 |
| 316 | villanos | 15 |
| 317 | sabes | 15 |
| 318 | ninguno | 15 |
| 319 | mora | 15 |
| 320 | menéndez | 15 |
| 321 | llama | 15 |
| 322 | lengua | 15 |
| 323 | hija | 15 |
| 324 | hecho | 15 |
| 325 | haré | 15 |
| 326 | hace | 15 |
| 327 | gente | 15 |
| 328 | fuerza | 15 |
| 329 | fuerte | 15 |
| 330 | fe | 15 |
| 331 | fama | 15 |
| 332 | doy | 15 |
| 333 | dime | 15 |
| 334 | dan | 15 |
| 335 | cuidado | 15 |
| 336 | comedia | 15 |
| 337 | celindo | 15 |
| 338 | causa | 15 |
| 339 | brazos | 15 |
| 340 | verso | 14 |
| 341 | venido | 14 |
| 342 | suerte | 14 |
| 343 | quijote | 14 |
| 344 | quieres | 14 |
| 345 | porfía | 14 |
| 346 | poderoso | 14 |
| 347 | pensamiento | 14 |
| 348 | pena | 14 |
| 349 | nunca | 14 |
| 350 | miedo | 14 |
| 351 | merced | 14 |
| 352 | menos | 14 |
| 353 | mar | 14 |
| 354 | madre | 14 |
| 355 | licencia | 14 |
| 356 | julio | 14 |
| 357 | ilustre | 14 |
| 358 | igual | 14 |
| 359 | haya | 14 |
| 360 | guerra | 14 |
| 361 | gloria | 14 |
| 362 | feliciana | 14 |
| 363 | están | 14 |
| 364 | espera | 14 |
| 365 | cuenta | 14 |
| 366 | criado | 14 |
| 367 | castro | 14 |
| 368 | campo | 14 |
| 369 | amigo | 14 |
| 370 | ahora | 14 |
| 371 | vi | 13 |
| 372 | secreto | 13 |
| 373 | punto | 13 |
| 374 | puerta | 13 |
| 375 | per | 13 |
| 376 | pecho | 13 |
| 377 | pasa | 13 |
| 378 | muero | 13 |
| 379 | morir | 13 |
| 380 | lugar | 13 |
| 381 | llaman | 13 |
| 382 | hora | 13 |
| 383 | hermanos | 13 |
| 384 | flores | 13 |
| 385 | fernando | 13 |
| 386 | entiendo | 13 |
| 387 | efeto | 13 |
| 388 | diez | 13 |
| 389 | debe | 13 |
| 390 | cuatro | 13 |
| 391 | caso | 13 |
| 392 | camino | 13 |
| 393 | buena | 13 |
| 394 | aquellos | 13 |
| 395 | antiguo | 13 |
| 396 | vv | 12 |
| 397 | voluntad | 12 |
| 398 | versos | 12 |
| 399 | ventura | 12 |
| 400 | ven | 12 |
| 401 | vega | 12 |
| 402 | uno | 12 |
| 403 | tienen | 12 |
| 404 | solo | 12 |
| 405 | soldados | 12 |
| 406 | según | 12 |
| 407 | sangre | 12 |
| 408 | salir | 12 |
| 409 | podré | 12 |
| 410 | persona | 12 |
| 411 | pedro | 12 |
| 412 | ortuñ | 12 |
| 413 | ocasión | 12 |
| 414 | grande | 12 |
| 415 | fuentes | 12 |
| 416 | espin | 12 |
| 417 | españa | 12 |
| 418 | enemigo | 12 |
| 419 | días | 12 |
| 420 | deja | 12 |
| 421 | cura | 12 |
| 422 | creo | 12 |
| 423 | consejo | 12 |
| 424 | cierto | 12 |
| 425 | caballo | 12 |
| 426 | c | 12 |
| 427 | bueno | 12 |
| 428 | ardin | 12 |
| 429 | aquesta | 12 |
| 430 | alvarado | 12 |
| 431 | zor | 11 |
| 432 | xxiv | 11 |
| 433 | ve | 11 |
| 434 | tantas | 11 |
| 435 | suelo | 11 |
| 436 | pueda | 11 |
| 437 | pudiera | 11 |
| 438 | preso | 11 |
| 439 | podrá | 11 |
| 440 | poder | 11 |
| 441 | nobleza | 11 |
| 442 | necio | 11 |
| 443 | moros | 11 |
| 444 | mend | 11 |
| 445 | llegar | 11 |
| 446 | libre | 11 |
| 447 | león | 11 |
| 448 | infançon | 11 |
| 449 | iii | 11 |
| 450 | honra | 11 |
| 451 | gallardo | 11 |
| 452 | estas | 11 |
| 453 | ésta | 11 |
| 454 | espinosa | 11 |
| 455 | esp | 11 |
| 456 | escucha | 11 |
| 457 | esas | 11 |
| 458 | dicha | 11 |
| 459 | daré | 11 |
| 460 | cual | 11 |
| 461 | cristiano | 11 |
| 462 | corrección | 11 |
| 463 | contra | 11 |
| 464 | contento | 11 |
| 465 | cielos | 11 |
| 466 | cautivo | 11 |
| 467 | cada | 11 |
| 468 | caballeros | 11 |
| 469 | ayer | 11 |
| 470 | ausencia | 11 |
| 471 | año | 11 |
| 472 | albor | 11 |
| 473 | ah | 11 |
| 474 | advierte | 11 |
| 475 | acto | 11 |
| 476 | viva | 10 |
| 477 | viento | 10 |
| 478 | vienes | 10 |
| 479 | vencido | 10 |
| 480 | vano | 10 |
| 481 | va | 10 |
| 482 | unos | 10 |
| 483 | toma | 10 |
| 484 | tener | 10 |
| 485 | suceso | 10 |
| 486 | soldado | 10 |
| 487 | rico | 10 |
| 488 | real | 10 |
| 489 | quiso | 10 |
| 490 | quisiera | 10 |
| 491 | primera | 10 |
| 492 | paz | 10 |
| 493 | nueva | 10 |
| 494 | nuestros | 10 |
| 495 | nuestro | 10 |
| 496 | mañana | 10 |
| 497 | manda | 10 |
| 498 | justa | 10 |
| 499 | intento | 10 |
| 500 | había | 10 |
| 501 | habéis | 10 |
| 502 | fuí | 10 |
| 503 | fiero | 10 |
| 504 | entra | 10 |
| 505 | enrique | 10 |
| 506 | edad | 10 |
| 507 | discreto | 10 |
| 508 | dichosa | 10 |
| 509 | cosas | 10 |
| 510 | césar | 10 |
| 511 | castigo | 10 |
| 512 | cara | 10 |
| 513 | bello | 10 |
| 514 | antequera | 10 |
| 515 | amar | 10 |
| 516 | alto | 10 |
| 517 | alejandro | 10 |
| 518 | alcalde | 10 |
| 519 | zaro | 9 |
| 520 | zara | 9 |
| 521 | volver | 9 |
| 522 | vino | 9 |
| 523 | vil | 9 |
| 524 | viendo | 9 |
| 525 | venga | 9 |
| 526 | toledo | 9 |
| 527 | tercero | 9 |
| 528 | tenga | 9 |
| 529 | temo | 9 |
| 530 | teatro | 9 |
| 531 | tarde | 9 |
| 532 | siento | 9 |
| 533 | señores | 9 |
| 534 | san | 9 |
| 535 | saber | 9 |
| 536 | queda | 9 |
| 537 | presencia | 9 |
| 538 | pasaje | 9 |
| 539 | otros | 9 |
| 540 | non | 9 |
| 541 | nada | 9 |
| 542 | manil | 9 |
| 543 | mandó | 9 |
| 544 | lejos | 9 |
| 545 | lágrimas | 9 |
| 546 | juro | 9 |
| 547 | hidalgo | 9 |
| 548 | hartzenbusch | 9 |
| 549 | habla | 9 |
| 550 | gozar | 9 |
| 551 | falta | 9 |
| 552 | español | 9 |
| 553 | eran | 9 |
| 554 | envidia | 9 |
| 555 | enojos | 9 |
| 556 | engaño | 9 |
| 557 | dueño | 9 |
| 558 | doña | 9 |
| 559 | dicen | 9 |
| 560 | derecho | 9 |
| 561 | dama | 9 |
| 562 | criados | 9 |
| 563 | corte | 9 |
| 564 | comer | 9 |
| 565 | claro | 9 |
| 566 | casado | 9 |
| 567 | calla | 9 |
| 568 | brito | 9 |
| 569 | árboles | 9 |
| 570 | alguno | 9 |
| 571 | albricias | 9 |
| 572 | agravio | 9 |
| 573 | zoraide | 8 |
| 574 | vivir | 8 |
| 575 | virtud | 8 |
| 576 | vete | 8 |
| 577 | ves | 8 |
| 578 | verdes | 8 |
| 579 | venus | 8 |
| 580 | tuviera | 8 |
| 581 | torre | 8 |
| 582 | todas | 8 |
| 583 | tierno | 8 |
| 584 | tenía | 8 |
| 585 | temor | 8 |
| 586 | tales | 8 |
| 587 | solos | 8 |
| 588 | sentido | 8 |
| 589 | sabido | 8 |
| 590 | rescate | 8 |
| 591 | quitar | 8 |
| 592 | quejas | 8 |
| 593 | prisión | 8 |
| 594 | presente | 8 |
| 595 | presa | 8 |
| 596 | poner | 8 |
| 597 | plata | 8 |
| 598 | perder | 8 |
| 599 | paso | 8 |
| 600 | palacio | 8 |
| 601 | oro | 8 |
| 602 | obras | 8 |
| 603 | mujeres | 8 |
| 604 | muchos | 8 |
| 605 | mucha | 8 |
| 606 | mozo | 8 |
| 607 | misma | 8 |
| 608 | manera | 8 |
| 609 | loco | 8 |
| 610 | llanto | 8 |
| 611 | letra | 8 |
| 612 | les | 8 |
| 613 | lanza | 8 |
| 614 | juego | 8 |
| 615 | importa | 8 |
| 616 | ido | 8 |
| 617 | id | 8 |
| 618 | humilde | 8 |
| 619 | honrar | 8 |
| 620 | gracias | 8 |
| 621 | galán | 8 |
| 622 | fuego | 8 |
| 623 | famosa | 8 |
| 624 | éste | 8 |
| 625 | escribe | 8 |
| 626 | entendimiento | 8 |
| 627 | enr | 8 |
| 628 | edición | 8 |
| 629 | dirá | 8 |
| 630 | dije | 8 |
| 631 | dicc | 8 |
| 632 | des | 8 |
| 633 | dél | 8 |
| 634 | das | 8 |
| 635 | crueldad | 8 |
| 636 | contigo | 8 |
| 637 | cit | 8 |
| 638 | capitán | 8 |
| 639 | cabeza | 8 |
| 640 | boda | 8 |
| 641 | batalla | 8 |
| 642 | apenas | 8 |
| 643 | alá | 8 |
| 644 | agua | 8 |
| 645 | acaba | 8 |
| 646 | vivo | 7 |
| 647 | vió | 7 |
| 648 | vii | 7 |
| 649 | viera | 7 |
| 650 | venir | 7 |
| 651 | urraca | 7 |
| 652 | tuvo | 7 |
| 653 | tristeza | 7 |
| 654 | traigo | 7 |
| 655 | tormento | 7 |
| 656 | tenido | 7 |
| 657 | tenéis | 7 |
| 658 | suelen | 7 |
| 659 | suele | 7 |
| 660 | siglo | 7 |
| 661 | seguro | 7 |
| 662 | rostro | 7 |
| 663 | responde | 7 |
| 664 | rara | 7 |
| 665 | r | 7 |
| 666 | puertas | 7 |
| 667 | prenda | 7 |
| 668 | pierdo | 7 |
| 669 | pierde | 7 |
| 670 | pie | 7 |
| 671 | pide | 7 |
| 672 | pidal | 7 |
| 673 | pida | 7 |
| 674 | personas | 7 |
| 675 | peralta | 7 |
| 676 | pedir | 7 |
| 677 | partida | 7 |
| 678 | palas | 7 |
| 679 | obliga | 7 |
| 680 | ob | 7 |
| 681 | nuestra | 7 |
| 682 | novia | 7 |
| 683 | ningún | 7 |
| 684 | nadie | 7 |
| 685 | muestra | 7 |
| 686 | moza | 7 |
| 687 | montemayor | 7 |
| 688 | madrid | 7 |
| 689 | luz | 7 |
| 690 | llamar | 7 |
| 691 | leyes | 7 |
| 692 | lanzas | 7 |
| 693 | labradora | 7 |
| 694 | juez | 7 |
| 695 | imposible | 7 |
| 696 | humano | 7 |
| 697 | hubiera | 7 |
| 698 | hizo | 7 |
| 699 | haga | 7 |
| 700 | hacienda | 7 |
| 701 | habrá | 7 |
| 702 | habiendo | 7 |
| 703 | guarde | 7 |
| 704 | guarda | 7 |
| 705 | gramática | 7 |
| 706 | fue | 7 |
| 707 | estremo | 7 |
| 708 | estraño | 7 |
| 709 | espero | 7 |
| 710 | entrar | 7 |
| 711 | dinero | 7 |
| 712 | diga | 7 |
| 713 | dicho | 7 |
| 714 | desto | 7 |
| 715 | demás | 7 |
| 716 | dellos | 7 |
| 717 | dé | 7 |
| 718 | culpa | 7 |
| 719 | cuál | 7 |
| 720 | crónica | 7 |
| 721 | cristianos | 7 |
| 722 | covarrubias | 7 |
| 723 | coronado | 7 |
| 724 | cinco | 7 |
| 725 | cerca | 7 |
| 726 | casas | 7 |
| 727 | bencerraje | 7 |
| 728 | belleza | 7 |
| 729 | bella | 7 |
| 730 | aún | 7 |
| 731 | atrevimiento | 7 |
| 732 | aparece | 7 |
| 733 | algo | 7 |
| 734 | alborán | 7 |
| 735 | airado | 7 |
| 736 | adoro | 7 |
| 737 | adónde | 7 |
| 738 | acaso | 7 |
| 739 | xvi | 6 |
| 740 | vuelve | 6 |
| 741 | vienen | 6 |
| 742 | verás | 6 |
| 743 | vencer | 6 |
| 744 | veinte | 6 |
| 745 | tuyo | 6 |
| 746 | trato | 6 |
| 747 | tratado | 6 |
| 748 | trata | 6 |
| 749 | tomo | 6 |
| 750 | toca | 6 |
| 751 | tiernos | 6 |
| 752 | tantos | 6 |
| 753 | suya | 6 |
| 754 | sufrir | 6 |
| 755 | somos | 6 |
| 756 | solía | 6 |
| 757 | sola | 6 |
| 758 | siente | 6 |
| 759 | seso | 6 |
| 760 | seis | 6 |
| 761 | santo | 6 |
| 762 | sabio | 6 |
| 763 | ruego | 6 |
| 764 | rouanet | 6 |
| 765 | ropa | 6 |
| 766 | ríos | 6 |
| 767 | río | 6 |
| 768 | reino | 6 |
| 769 | quitarme | 6 |
| 770 | quita | 6 |
| 771 | querida | 6 |
| 772 | quando | 6 |
| 773 | puercos | 6 |
| 774 | pude | 6 |
| 775 | propia | 6 |
| 776 | prometo | 6 |
| 777 | podía | 6 |
| 778 | plumas | 6 |
| 779 | pido | 6 |
| 780 | perro | 6 |
| 781 | perdí | 6 |
| 782 | peligro | 6 |
| 783 | palos | 6 |
| 784 | págs | 6 |
| 785 | oficio | 6 |
| 786 | nuevas | 6 |
| 787 | novela | 6 |
| 788 | montes | 6 |
| 789 | mientras | 6 |
| 790 | mendoza | 6 |
| 791 | medio | 6 |
| 792 | marte | 6 |
| 793 | maniloro | 6 |
| 794 | males | 6 |
| 795 | m | 6 |
| 796 | luna | 6 |
| 797 | llego | 6 |
| 798 | juntos | 6 |
| 799 | jamás | 6 |
| 800 | ingenio | 6 |
| 801 | honrado | 6 |
| 802 | hijos | 6 |
| 803 | hermoso | 6 |
| 804 | guirnalda | 6 |
| 805 | guardar | 6 |
| 806 | fueron | 6 |
| 807 | forzoso | 6 |
| 808 | forma | 6 |
| 809 | fieras | 6 |
| 810 | fiera | 6 |
| 811 | estimo | 6 |
| 812 | esté | 6 |
| 813 | escrito | 6 |
| 814 | esclavo | 6 |
| 815 | esclava | 6 |
| 816 | entonces | 6 |
| 817 | entiende | 6 |
| 818 | enamorado | 6 |
| 819 | ellas | 6 |
| 820 | ejemplos | 6 |
| 821 | ejemplo | 6 |
| 822 | dolor | 6 |
| 823 | diera | 6 |
| 824 | deshonra | 6 |
| 825 | desdén | 6 |
| 826 | dedos | 6 |
| 827 | decid | 6 |
| 828 | debo | 6 |
| 829 | darín | 6 |
| 830 | corta | 6 |
| 831 | corazón | 6 |
| 832 | conoces | 6 |
| 833 | clara | 6 |
| 834 | cervantes | 6 |
| 835 | castellano | 6 |
| 836 | cartas | 6 |
| 837 | carpio | 6 |
| 838 | cap | 6 |
| 839 | canten | 6 |
| 840 | cabello | 6 |
| 841 | caballos | 6 |
| 842 | buenas | 6 |
| 843 | bajeza | 6 |
| 844 | bajamed | 6 |
| 845 | aut | 6 |
| 846 | ausente | 6 |
| 847 | andar | 6 |
| 848 | aliento | 6 |
| 849 | alcanza | 6 |
| 850 | aguas | 6 |
| 851 | advertid | 6 |
| 852 | adiós | 6 |
| 853 | acad | 6 |
| 854 | acá | 6 |
| 855 | xvii | 5 |
| 856 | weigert | 5 |
| 857 | vuelvo | 5 |
| 858 | voz | 5 |
| 859 | voto | 5 |
| 860 | volvió | 5 |
| 861 | vista | 5 |
| 862 | villa | 5 |
| 863 | viejo | 5 |
| 864 | verdadero | 5 |
| 865 | venció | 5 |
| 866 | unas | 5 |
| 867 | triunfo | 5 |
| 868 | tente | 5 |
| 869 | suyo | 5 |
| 870 | sujeto | 5 |
| 871 | sospecho | 5 |
| 872 | soneto | 5 |
| 873 | sirve | 5 |
| 874 | siguiente | 5 |
| 875 | siglos | 5 |
| 876 | serlo | 5 |
| 877 | sandoval | 5 |
| 878 | robles | 5 |
| 879 | respondió | 5 |
| 880 | respeto | 5 |
| 881 | quitado | 5 |
| 882 | quise | 5 |
| 883 | quiera | 5 |
| 884 | puesta | 5 |
| 885 | puedan | 5 |
| 886 | propio | 5 |
| 887 | procura | 5 |
| 888 | pregunta | 5 |
| 889 | pocas | 5 |
| 890 | piensa | 5 |
| 891 | piedras | 5 |
| 892 | pesquisidor | 5 |
| 893 | pesar | 5 |
| 894 | perra | 5 |
| 895 | pequeño | 5 |
| 896 | pasado | 5 |
| 897 | partes | 5 |
| 898 | paga | 5 |
| 899 | padres | 5 |
| 900 | paciencia | 5 |
| 901 | oye | 5 |
| 902 | opinión | 5 |
| 903 | olvido | 5 |
| 904 | obligado | 5 |
| 905 | núm | 5 |
| 906 | nuevo | 5 |
| 907 | nueve | 5 |
| 908 | nombres | 5 |
| 909 | ninguna | 5 |
| 910 | nacido | 5 |
| 911 | nací | 5 |
| 912 | muchas | 5 |
| 913 | mirad | 5 |
| 914 | míos | 5 |
| 915 | merece | 5 |
| 916 | mala | 5 |
| 917 | mahoma | 5 |
| 918 | lloro | 5 |
| 919 | llorar | 5 |
| 920 | llevó | 5 |
| 921 | llegó | 5 |
| 922 | llegado | 5 |
| 923 | llegad | 5 |
| 924 | leonor | 5 |
| 925 | labios | 5 |
| 926 | juramento | 5 |
| 927 | junto | 5 |
| 928 | juan | 5 |
| 929 | jardín | 5 |
| 930 | iré | 5 |
| 931 | ira | 5 |
| 932 | infante | 5 |
| 933 | hola | 5 |
| 934 | hice | 5 |
| 935 | hermosos | 5 |
| 936 | hermosas | 5 |
| 937 | herido | 5 |
| 938 | heridas | 5 |
| 939 | herida | 5 |
| 940 | hábito | 5 |
| 941 | grandes | 5 |
| 942 | generoso | 5 |
| 943 | ganados | 5 |
| 944 | ganado | 5 |
| 945 | galas | 5 |
| 946 | fuesse | 5 |
| 947 | fuerzas | 5 |
| 948 | firma | 5 |
| 949 | fileno | 5 |
| 950 | fiesta | 5 |
| 951 | fácil | 5 |
| 952 | estamos | 5 |
| 953 | estáis | 5 |
| 954 | estado | 5 |
| 955 | esperar | 5 |
| 956 | especialmente | 5 |
| 957 | escribir | 5 |
| 958 | escena | 5 |
| 959 | entró | 5 |
| 960 | enseñado | 5 |
| 961 | engañado | 5 |
| 962 | engaña | 5 |
| 963 | empresa | 5 |
| 964 | dura | 5 |
| 965 | dorotea | 5 |
| 966 | disgusto | 5 |
| 967 | dichoso | 5 |
| 968 | desdichado | 5 |
| 969 | dejo | 5 |
| 970 | dejar | 5 |
| 971 | déjame | 5 |
| 972 | dario | 5 |
| 973 | dadme | 5 |
| 974 | daba | 5 |
| 975 | cuya | 5 |
| 976 | cuánto | 5 |
| 977 | cruel | 5 |
| 978 | corresponde | 5 |
| 979 | corre | 5 |
| 980 | corona | 5 |
| 981 | consuelo | 5 |
| 982 | condición | 5 |
| 983 | comedias | 5 |
| 984 | come | 5 |
| 985 | colores | 5 |
| 986 | cobarde | 5 |
| 987 | ciego | 5 |
| 988 | cfr | 5 |
| 989 | castellanos | 5 |
| 990 | casamiento | 5 |
| 991 | cama | 5 |
| 992 | calle | 5 |
| 993 | cabr | 5 |
| 994 | cabellos | 5 |
| 995 | buscar | 5 |
| 996 | buenos | 5 |
| 997 | breve | 5 |
| 998 | blanco | 5 |
| 999 | bestia | 5 |
| 1000 | beso | 5 |
| 1001 | bajo | 5 |
| 1002 | autor | 5 |
| 1003 | atrevido | 5 |
| 1004 | armada | 5 |
| 1005 | aquestos | 5 |
| 1006 | aparte | 5 |
| 1007 | antonio | 5 |
| 1008 | ante | 5 |
| 1009 | anda | 5 |
| 1010 | amante | 5 |
| 1011 | ama | 5 |
| 1012 | alta | 5 |
| 1013 | algunas | 5 |
| 1014 | alegría | 5 |
| 1015 | álamo | 5 |
| 1016 | aguarda | 5 |
| 1017 | agrada | 5 |
| 1018 | adonde | 5 |
| 1019 | adarga | 5 |
| 1020 | acero | 5 |
| 1021 | x | 4 |
| 1022 | vuelto | 4 |
| 1023 | vosotros | 4 |
| 1024 | viuda | 4 |
| 1025 | viste | 4 |
| 1026 | vestidos | 4 |
| 1027 | verte | 4 |
| 1028 | versión | 4 |
| 1029 | verme | 4 |
| 1030 | verdugo | 4 |
| 1031 | verdadera | 4 |
| 1032 | vélez | 4 |
| 1033 | veas | 4 |
| 1034 | vea | 4 |
| 1035 | varones | 4 |
| 1036 | vara | 4 |
| 1037 | van | 4 |
| 1038 | valle | 4 |
| 1039 | valladolid | 4 |
| 1040 | valiente | 4 |
| 1041 | vacas | 4 |
| 1042 | tuviesen | 4 |
| 1043 | trate | 4 |
| 1044 | trae | 4 |
| 1045 | tomar | 4 |
| 1046 | tomado | 4 |
| 1047 | tomad | 4 |
| 1048 | tirano | 4 |
| 1049 | tío | 4 |
| 1050 | tierna | 4 |
| 1051 | tendrán | 4 |
| 1052 | ten | 4 |
| 1053 | tema | 4 |
| 1054 | suspiros | 4 |
| 1055 | sueño | 4 |
| 1056 | solicita | 4 |
| 1057 | soberano | 4 |
| 1058 | sigs | 4 |
| 1059 | sevilla | 4 |
| 1060 | servicio | 4 |
| 1061 | seréis | 4 |
| 1062 | serás | 4 |
| 1063 | sepa | 4 |
| 1064 | sentidos | 4 |
| 1065 | sentaos | 4 |
| 1066 | segundo | 4 |
| 1067 | segunda | 4 |
| 1068 | sargento | 4 |
| 1069 | salga | 4 |
| 1070 | sabrás | 4 |
| 1071 | sabéis | 4 |
| 1072 | sabed | 4 |
| 1073 | romance | 4 |
| 1074 | rodríguez | 4 |
| 1075 | ricos | 4 |
| 1076 | respuesta | 4 |
| 1077 | renacimiento | 4 |
| 1078 | rejas | 4 |
| 1079 | reina | 4 |
| 1080 | recibo | 4 |
| 1081 | recado | 4 |
| 1082 | razones | 4 |
| 1083 | rayos | 4 |
| 1084 | ramas | 4 |
| 1085 | querido | 4 |
| 1086 | queréis | 4 |
| 1087 | quedar | 4 |
| 1088 | quedado | 4 |
| 1089 | puedes | 4 |
| 1090 | pudo | 4 |
| 1091 | pretende | 4 |
| 1092 | posesión | 4 |
| 1093 | pone | 4 |
| 1094 | podréis | 4 |
| 1095 | podéis | 4 |
| 1096 | poca | 4 |
| 1097 | pobres | 4 |
| 1098 | plega | 4 |
| 1099 | plantas | 4 |
| 1100 | piensas | 4 |
| 1101 | piadoso | 4 |
| 1102 | pésame | 4 |
| 1103 | peregrino | 4 |
| 1104 | perdona | 4 |
| 1105 | perdido | 4 |
| 1106 | penas | 4 |
| 1107 | partir | 4 |
| 1108 | palabras | 4 |
| 1109 | ovejas | 4 |
| 1110 | ortuño | 4 |
| 1111 | olvidéme | 4 |
| 1112 | oigo | 4 |
| 1113 | ofensa | 4 |
| 1114 | ofendido | 4 |
| 1115 | ofende | 4 |
| 1116 | ocampo | 4 |
| 1117 | obligue | 4 |
| 1118 | obligación | 4 |
| 1119 | nobles | 4 |
| 1120 | niño | 4 |
| 1121 | nieve | 4 |
| 1122 | neira | 4 |
| 1123 | negras | 4 |
| 1124 | murió | 4 |
| 1125 | modo | 4 |
| 1126 | mías | 4 |
| 1127 | menester | 4 |
| 1128 | matrimonio | 4 |
| 1129 | matarme | 4 |
| 1130 | marín | 4 |
| 1131 | marcela | 4 |
| 1132 | manga | 4 |
| 1133 | mandas | 4 |
| 1134 | lleve | 4 |
| 1135 | llevar | 4 |
| 1136 | lleva | 4 |
| 1137 | lleno | 4 |
| 1138 | llegue | 4 |
| 1139 | llega | 4 |
| 1140 | llano | 4 |
| 1141 | linaje | 4 |
| 1142 | libro | 4 |
| 1143 | ley | 4 |
| 1144 | lara | 4 |
| 1145 | labradores | 4 |
| 1146 | l | 4 |
| 1147 | juicio | 4 |
| 1148 | joyas | 4 |
| 1149 | invicto | 4 |
| 1150 | inventario | 4 |
| 1151 | injusto | 4 |
| 1152 | inhumano | 4 |
| 1153 | infame | 4 |
| 1154 | imaginación | 4 |
| 1155 | iban | 4 |
| 1156 | iba | 4 |
| 1157 | huerta | 4 |
| 1158 | hojas | 4 |
| 1159 | hijas | 4 |
| 1160 | heredad | 4 |
| 1161 | hércules | 4 |
| 1162 | hechos | 4 |
| 1163 | haz | 4 |
| 1164 | hallo | 4 |
| 1165 | hacia | 4 |
| 1166 | haces | 4 |
| 1167 | haced | 4 |
| 1168 | hablarte | 4 |
| 1169 | habemos | 4 |
| 1170 | grave | 4 |
| 1171 | grandeza | 4 |
| 1172 | gracia | 4 |
| 1173 | gobierno | 4 |
| 1174 | gallego | 4 |
| 1175 | galizia | 4 |
| 1176 | fuente | 4 |
| 1177 | freno | 4 |
| 1178 | frase | 4 |
| 1179 | fío | 4 |
| 1180 | fea | 4 |
| 1181 | faltar | 4 |
| 1182 | facilidad | 4 |
| 1183 | eterna | 4 |
| 1184 | estraña | 4 |
| 1185 | estando | 4 |
| 1186 | estaban | 4 |
| 1187 | esperanzas | 4 |
| 1188 | espanto | 4 |
| 1189 | escuchar | 4 |
| 1190 | escribió | 4 |
| 1191 | entrañas | 4 |
| 1192 | entienda | 4 |
| 1193 | entender | 4 |
| 1194 | efecto | 4 |
| 1195 | ea | 4 |
| 1196 | durán | 4 |
| 1197 | duda | 4 |
| 1198 | dote | 4 |
| 1199 | doce | 4 |
| 1200 | doble | 4 |
| 1201 | dixo | 4 |
| 1202 | dixe | 4 |
| 1203 | divina | 4 |
| 1204 | diré | 4 |
| 1205 | digan | 4 |
| 1206 | diferencia | 4 |
| 1207 | dieron | 4 |
| 1208 | desvelos | 4 |
| 1209 | destos | 4 |
| 1210 | desnuda | 4 |
| 1211 | desdichada | 4 |
| 1212 | den | 4 |
| 1213 | dellas | 4 |
| 1214 | delante | 4 |
| 1215 | dejas | 4 |
| 1216 | defensa | 4 |
| 1217 | decía | 4 |
| 1218 | deben | 4 |
| 1219 | date | 4 |
| 1220 | darte | 4 |
| 1221 | dafne | 4 |
| 1222 | dad | 4 |
| 1223 | cueto | 4 |
| 1224 | cuento | 4 |
| 1225 | cuello | 4 |
| 1226 | cuán | 4 |
| 1227 | cualquiera | 4 |
| 1228 | cristiana | 4 |
| 1229 | creer | 4 |
| 1230 | contrario | 4 |
| 1231 | considera | 4 |
| 1232 | consejos | 4 |
| 1233 | conocido | 4 |
| 1234 | conjunción | 4 |
| 1235 | color | 4 |
| 1236 | cochinos | 4 |
| 1237 | clemencia | 4 |
| 1238 | cf | 4 |
| 1239 | caza | 4 |
| 1240 | casi | 4 |
| 1241 | casarme | 4 |
| 1242 | casados | 4 |
| 1243 | canta | 4 |
| 1244 | campos | 4 |
| 1245 | camina | 4 |
| 1246 | cámara | 4 |
| 1247 | calma | 4 |
| 1248 | cabrera | 4 |
| 1249 | cabe | 4 |
| 1250 | bravo | 4 |
| 1251 | blancas | 4 |
| 1252 | blanca | 4 |
| 1253 | bibl | 4 |
| 1254 | besar | 4 |
| 1255 | bellos | 4 |
| 1256 | bastante | 4 |
| 1257 | baja | 4 |
| 1258 | aves | 4 |
| 1259 | ardino | 4 |
| 1260 | aquesto | 4 |
| 1261 | aquélla | 4 |
| 1262 | apolo | 4 |
| 1263 | ánimo | 4 |
| 1264 | ángel | 4 |
| 1265 | amo | 4 |
| 1266 | almas | 4 |
| 1267 | alcayde | 4 |
| 1268 | alcanzar | 4 |
| 1269 | alabanza | 4 |
| 1270 | afuera | 4 |
| 1271 | adora | 4 |
| 1272 | acude | 4 |
| 1273 | abraso | 4 |
| 1274 | zaragoza | 3 |
| 1275 | xxx | 3 |
| 1276 | xv | 3 |
| 1277 | vuestros | 3 |
| 1278 | vuelta | 3 |
| 1279 | vto | 3 |
| 1280 | volviendo | 3 |
| 1281 | voces | 3 |
| 1282 | viviré | 3 |
| 1283 | vitorias | 3 |
| 1284 | vine | 3 |
| 1285 | villegas | 3 |
| 1286 | villana | 3 |
| 1287 | viles | 3 |
| 1288 | vestido | 3 |
| 1289 | vergüenza | 3 |
| 1290 | veréis | 3 |
| 1291 | venganza | 3 |
| 1292 | vencedor | 3 |
| 1293 | vasallos | 3 |
| 1294 | vale | 3 |
| 1295 | vais | 3 |
| 1296 | vaina | 3 |
| 1297 | usó | 3 |
| 1298 | tristes | 3 |
| 1299 | treguas | 3 |
| 1300 | tras | 3 |
| 1301 | traidores | 3 |
| 1302 | traidor | 3 |
| 1303 | traer | 3 |
| 1304 | traemos | 3 |
| 1305 | tomó | 3 |
| 1306 | tomé | 3 |
| 1307 | tome | 3 |
| 1308 | tomamos | 3 |
| 1309 | tocado | 3 |
| 1310 | títulos | 3 |
| 1311 | título | 3 |
| 1312 | texto | 3 |
| 1313 | testigos | 3 |
| 1314 | testigo | 3 |
| 1315 | tesoro | 3 |
| 1316 | término | 3 |
| 1317 | tenemos | 3 |
| 1318 | tendré | 3 |
| 1319 | tendrá | 3 |
| 1320 | temido | 3 |
| 1321 | temer | 3 |
| 1322 | teme | 3 |
| 1323 | temblando | 3 |
| 1324 | talle | 3 |
| 1325 | suspirar | 3 |
| 1326 | suma | 3 |
| 1327 | suegro | 3 |
| 1328 | sucesión | 3 |
| 1329 | sospecha | 3 |
| 1330 | solas | 3 |
| 1331 | solamente | 3 |
| 1332 | sobrino | 3 |
| 1333 | soberbia | 3 |
| 1334 | so | 3 |
| 1335 | siguientes | 3 |
| 1336 | servir | 3 |
| 1337 | serán | 3 |
| 1338 | serafín | 3 |
| 1339 | semejantes | 3 |
| 1340 | semejante | 3 |
| 1341 | seguimos | 3 |
| 1342 | seas | 3 |
| 1343 | santa | 3 |
| 1344 | sacas | 3 |
| 1345 | saben | 3 |
| 1346 | s | 3 |
| 1347 | rojas | 3 |
| 1348 | rindo | 3 |
| 1349 | rica | 3 |
| 1350 | reyna | 3 |
| 1351 | representa | 3 |
| 1352 | remedialla | 3 |
| 1353 | reinos | 3 |
| 1354 | regalo | 3 |
| 1355 | quitándome | 3 |
| 1356 | quijera | 3 |
| 1357 | quieren | 3 |
| 1358 | querella | 3 |
| 1359 | quejo | 3 |
| 1360 | queja | 3 |
| 1361 | quedó | 3 |
| 1362 | quedo | 3 |
| 1363 | quede | 3 |
| 1364 | qual | 3 |
| 1365 | puso | 3 |
| 1366 | puerco | 3 |
| 1367 | pueden | 3 |
| 1368 | pudieran | 3 |
| 1369 | publicada | 3 |
| 1370 | prosa | 3 |
| 1371 | proponemos | 3 |
| 1372 | pronombre | 3 |
| 1373 | probar | 3 |
| 1374 | principal | 3 |
| 1375 | primer | 3 |
| 1376 | primavera | 3 |
| 1377 | presumo | 3 |
| 1378 | preposición | 3 |
| 1379 | premio | 3 |
| 1380 | prados | 3 |
| 1381 | poned | 3 |
| 1382 | podrás | 3 |
| 1383 | poderosos | 3 |
| 1384 | plural | 3 |
| 1385 | plaza | 3 |
| 1386 | piezas | 3 |
| 1387 | pidió | 3 |
| 1388 | picazo | 3 |
| 1389 | pesado | 3 |
| 1390 | pesa | 3 |
| 1391 | perros | 3 |
| 1392 | perlas | 3 |
| 1393 | perfeto | 3 |
| 1394 | perfeta | 3 |
| 1395 | pensaba | 3 |
| 1396 | penar | 3 |
| 1397 | patria | 3 |
| 1398 | pasos | 3 |
| 1399 | pasó | 3 |
| 1400 | pasados | 3 |
| 1401 | parecido | 3 |
| 1402 | parecer | 3 |
| 1403 | paréceme | 3 |
| 1404 | papel | 3 |
| 1405 | paje | 3 |
| 1406 | pago | 3 |
| 1407 | padrino | 3 |
| 1408 | p | 3 |
| 1409 | oyendo | 3 |
| 1410 | orilla | 3 |
| 1411 | omes | 3 |
| 1412 | olvidado | 3 |
| 1413 | olivares | 3 |
| 1414 | olas | 3 |
| 1415 | ojalá | 3 |
| 1416 | oído | 3 |
| 1417 | oí | 3 |
| 1418 | obligar | 3 |
| 1419 | nubes | 3 |
| 1420 | notable | 3 |
| 1421 | niña | 3 |
| 1422 | nido | 3 |
| 1423 | necia | 3 |
| 1424 | necesidad | 3 |
| 1425 | nace | 3 |
| 1426 | muestras | 3 |
| 1427 | muerto | 3 |
| 1428 | muere | 3 |
| 1429 | mudanzas | 3 |
| 1430 | mudable | 3 |
| 1431 | mos | 3 |
| 1432 | mortal | 3 |
| 1433 | momento | 3 |
| 1434 | mitad | 3 |
| 1435 | mismos | 3 |
| 1436 | mirase | 3 |
| 1437 | mirando | 3 |
| 1438 | miran | 3 |
| 1439 | miraba | 3 |
| 1440 | militar | 3 |
| 1441 | metido | 3 |
| 1442 | merino | 3 |
| 1443 | media | 3 |
| 1444 | mayores | 3 |
| 1445 | matalla | 3 |
| 1446 | matadlos | 3 |
| 1447 | mata | 3 |
| 1448 | máscaras | 3 |
| 1449 | maravilla | 3 |
| 1450 | mandando | 3 |
| 1451 | mancebo | 3 |
| 1452 | magnánimo | 3 |
| 1453 | logar | 3 |
| 1454 | llora | 3 |
| 1455 | llevo | 3 |
| 1456 | llevaron | 3 |
| 1457 | llevan | 3 |
| 1458 | llevado | 3 |
| 1459 | llevaba | 3 |
| 1460 | llena | 3 |
| 1461 | llegué | 3 |
| 1462 | llanos | 3 |
| 1463 | llaneza | 3 |
| 1464 | llamáis | 3 |
| 1465 | llamado | 3 |
| 1466 | llamad | 3 |
| 1467 | limpio | 3 |
| 1468 | libres | 3 |
| 1469 | lenguaje | 3 |
| 1470 | lectura | 3 |
| 1471 | laurel | 3 |
| 1472 | largo | 3 |
| 1473 | kohler | 3 |
| 1474 | joven | 3 |
| 1475 | jornada | 3 |
| 1476 | jardines | 3 |
| 1477 | irá | 3 |
| 1478 | intención | 3 |
| 1479 | injustos | 3 |
| 1480 | ingrato | 3 |
| 1481 | importancia | 3 |
| 1482 | iguales | 3 |
| 1483 | ignorancia | 3 |
| 1484 | idea | 3 |
| 1485 | ibas | 3 |
| 1486 | huyendo | 3 |
| 1487 | hubo | 3 |
| 1488 | honrada | 3 |
| 1489 | historias | 3 |
| 1490 | hidalgos | 3 |
| 1491 | hicieron | 3 |
| 1492 | herreruelos | 3 |
| 1493 | hemos | 3 |
| 1494 | harás | 3 |
| 1495 | haciendo | 3 |
| 1496 | hablando | 3 |
| 1497 | hablado | 3 |
| 1498 | haberle | 3 |
| 1499 | guardo | 3 |
| 1500 | guarden | 3 |
| 1501 | grosero | 3 |
| 1502 | gozaros | 3 |
| 1503 | gozado | 3 |
| 1504 | goces | 3 |
| 1505 | gentileza | 3 |
| 1506 | gentil | 3 |
| 1507 | general | 3 |
| 1508 | gallarda | 3 |
| 1509 | furor | 3 |
| 1510 | fuiste | 3 |
| 1511 | fuése | 3 |
| 1512 | fuese | 3 |
| 1513 | fueras | 3 |
| 1514 | frontero | 3 |
| 1515 | fol | 3 |
| 1516 | flaqueza | 3 |
| 1517 | firme | 3 |
| 1518 | finalmente | 3 |
| 1519 | fijo | 3 |
| 1520 | figura | 3 |
| 1521 | fieros | 3 |
| 1522 | feo | 3 |
| 1523 | félix | 3 |
| 1524 | fecho | 3 |
| 1525 | falte | 3 |
| 1526 | experiencia | 3 |
| 1527 | estrellas | 3 |
| 1528 | estima | 3 |
| 1529 | esperé | 3 |
| 1530 | española | 3 |
| 1531 | espaldas | 3 |
| 1532 | espadas | 3 |
| 1533 | ése | 3 |
| 1534 | escuras | 3 |
| 1535 | escudero | 3 |
| 1536 | envía | 3 |
| 1537 | entretenida | 3 |
| 1538 | entré | 3 |
| 1539 | entran | 3 |
| 1540 | engaños | 3 |
| 1541 | enfermedad | 3 |
| 1542 | encuentro | 3 |
| 1543 | enamora | 3 |
| 1544 | ello | 3 |
| 1545 | edic | 3 |
| 1546 | dureza | 3 |
| 1547 | durante | 3 |
| 1548 | ducados | 3 |
| 1549 | discreta | 3 |
| 1550 | dijiste | 3 |
| 1551 | dijera | 3 |
| 1552 | digna | 3 |
| 1553 | dificultoso | 3 |
| 1554 | diese | 3 |
| 1555 | dichosos | 3 |
| 1556 | desvarío | 3 |
| 1557 | desprecio | 3 |
| 1558 | deseos | 3 |
| 1559 | desdichas | 3 |
| 1560 | descansar | 3 |
| 1561 | descansa | 3 |
| 1562 | della | 3 |
| 1563 | deje | 3 |
| 1564 | decís | 3 |
| 1565 | deciros | 3 |
| 1566 | decirlo | 3 |
| 1567 | debió | 3 |
| 1568 | debes | 3 |
| 1569 | david | 3 |
| 1570 | darme | 3 |
| 1571 | darás | 3 |
| 1572 | dará | 3 |
| 1573 | dando | 3 |
| 1574 | dais | 3 |
| 1575 | cuyas | 3 |
| 1576 | curso | 3 |
| 1577 | cuidados | 3 |
| 1578 | cueva | 3 |
| 1579 | cuervo | 3 |
| 1580 | cuerdo | 3 |
| 1581 | cuándo | 3 |
| 1582 | cualquier | 3 |
| 1583 | crióse | 3 |
| 1584 | cortesano | 3 |
| 1585 | corriente | 3 |
| 1586 | cordel | 3 |
| 1587 | conveniente | 3 |
| 1588 | consta | 3 |
| 1589 | conquistada | 3 |
| 1590 | conoce | 3 |
| 1591 | condenado | 3 |
| 1592 | compone | 3 |
| 1593 | comp | 3 |
| 1594 | cocina | 3 |
| 1595 | cobras | 3 |
| 1596 | clásicos | 3 |
| 1597 | clás | 3 |
| 1598 | claros | 3 |
| 1599 | claras | 3 |
| 1600 | ciudad | 3 |
| 1601 | citadas | 3 |
| 1602 | citada | 3 |
| 1603 | cita | 3 |
| 1604 | cipión | 3 |
| 1605 | ciento | 3 |
| 1606 | celoso | 3 |
| 1607 | cautiverio | 3 |
| 1608 | cause | 3 |
| 1609 | castigar | 3 |
| 1610 | cast | 3 |
| 1611 | casos | 3 |
| 1612 | casarse | 3 |
| 1613 | casar | 3 |
| 1614 | capitanes | 3 |
| 1615 | cañas | 3 |
| 1616 | cantar | 3 |
| 1617 | canamor | 3 |
| 1618 | cabeça | 3 |
| 1619 | busca | 3 |
| 1620 | biblioteca | 3 |
| 1621 | bellas | 3 |
| 1622 | barbechos | 3 |
| 1623 | bárbaro | 3 |
| 1624 | bajam | 3 |
| 1625 | azules | 3 |
| 1626 | ayuda | 3 |
| 1627 | aurora | 3 |
| 1628 | aumente | 3 |
| 1629 | atento | 3 |
| 1630 | arroyuelo | 3 |
| 1631 | arrogante | 3 |
| 1632 | arnés | 3 |
| 1633 | árbol | 3 |
| 1634 | aragón | 3 |
| 1635 | aquestas | 3 |
| 1636 | aquellas | 3 |
| 1637 | aposento | 3 |
| 1638 | antología | 3 |
| 1639 | angélica | 3 |
| 1640 | andan | 3 |
| 1641 | amigos | 3 |
| 1642 | amartelado | 3 |
| 1643 | amaltea | 3 |
| 1644 | amada | 3 |
| 1645 | alude | 3 |
| 1646 | altos | 3 |
| 1647 | algunos | 3 |
| 1648 | alegre | 3 |
| 1649 | alcides | 3 |
| 1650 | alabo | 3 |
| 1651 | alaba | 3 |
| 1652 | aguardo | 3 |
| 1653 | afición | 3 |
| 1654 | adelante | 3 |
| 1655 | adargas | 3 |
| 1656 | achaques | 3 |
| 1657 | acción | 3 |
| 1658 | academia | 3 |
| 1659 | abierta | 3 |
| 1660 | abencerrajes | 3 |
| 1661 | zeugma | 2 |
| 1662 | zegríes | 2 |
| 1663 | zagales | 2 |
| 1664 | yerro | 2 |
| 1665 | yerbas | 2 |
| 1666 | yeguas | 2 |
| 1667 | yedras | 2 |
| 1668 | xli | 2 |
| 1669 | xi | 2 |
| 1670 | xarifa | 2 |
| 1671 | vulgo | 2 |
| 1672 | vuestras | 2 |
| 1673 | vuelva | 2 |
| 1674 | voluntades | 2 |
| 1675 | vivid | 2 |
| 1676 | vivas | 2 |
| 1677 | vitoria | 2 |
| 1678 | virtudes | 2 |
| 1679 | viniese | 2 |
| 1680 | viniendo | 2 |
| 1681 | viii | 2 |
| 1682 | viejos | 2 |
| 1683 | vidas | 2 |
| 1684 | víctima | 2 |
| 1685 | vestida | 2 |
| 1686 | versificar | 2 |
| 1687 | verse | 2 |
| 1688 | verle | 2 |
| 1689 | verla | 2 |
| 1690 | ventana | 2 |
| 1691 | venme | 2 |
| 1692 | venís | 2 |
| 1693 | venimos | 2 |
| 1694 | venid | 2 |
| 1695 | vengan | 2 |
| 1696 | vendrán | 2 |
| 1697 | vendrá | 2 |
| 1698 | venda | 2 |
| 1699 | vencerme | 2 |
| 1700 | vence | 2 |
| 1701 | veloz | 2 |
| 1702 | veis | 2 |
| 1703 | vean | 2 |
| 1704 | vayas | 2 |
| 1705 | vayan | 2 |
| 1706 | vas | 2 |
| 1707 | varias | 2 |
| 1708 | vanas | 2 |
| 1709 | vana | 2 |
| 1710 | valenciana | 2 |
| 1711 | untersuchungen | 2 |
| 1712 | universalmente | 2 |
| 1713 | últimos | 2 |
| 1714 | u | 2 |
| 1715 | tuviese | 2 |
| 1716 | tuve | 2 |
| 1717 | turbado | 2 |
| 1718 | turbada | 2 |
| 1719 | tuerto | 2 |
| 1720 | trujo | 2 |
| 1721 | truecan | 2 |
| 1722 | tropelías | 2 |
| 1723 | trompeta | 2 |
| 1724 | treinta | 2 |
| 1725 | trebejos | 2 |
| 1726 | trazada | 2 |
| 1727 | trava | 2 |
| 1728 | traten | 2 |
| 1729 | tratar | 2 |
| 1730 | trajo | 2 |
| 1731 | traje | 2 |
| 1732 | traído | 2 |
| 1733 | traición | 2 |
| 1734 | traes | 2 |
| 1735 | torres | 2 |
| 1736 | torpe | 2 |
| 1737 | tormentos | 2 |
| 1738 | todavía | 2 |
| 1739 | tirso | 2 |
| 1740 | tiró | 2 |
| 1741 | tierras | 2 |
| 1742 | tiernas | 2 |
| 1743 | tiernamente | 2 |
| 1744 | tien | 2 |
| 1745 | tiempos | 2 |
| 1746 | tiemblo | 2 |
| 1747 | the | 2 |
| 1748 | testimonio | 2 |
| 1749 | tercer | 2 |
| 1750 | teniendo | 2 |
| 1751 | tenías | 2 |
| 1752 | tengas | 2 |
| 1753 | ténganse | 2 |
| 1754 | tengan | 2 |
| 1755 | teneos | 2 |
| 1756 | tened | 2 |
| 1757 | tendrás | 2 |
| 1758 | temí | 2 |
| 1759 | temeroso | 2 |
| 1760 | techos | 2 |
| 1761 | tebas | 2 |
| 1762 | tarquino | 2 |
| 1763 | tamar | 2 |
| 1764 | talega | 2 |
| 1765 | tajos | 2 |
| 1766 | tabla | 2 |
| 1767 | t | 2 |
| 1768 | sutil | 2 |
| 1769 | sustento | 2 |
| 1770 | sustantivo | 2 |
| 1771 | surto | 2 |
| 1772 | sur | 2 |
| 1773 | supuesto | 2 |
| 1774 | supone | 2 |
| 1775 | sufrimiento | 2 |
| 1776 | sufrido | 2 |
| 1777 | sueltas | 2 |
| 1778 | sueles | 2 |
| 1779 | sudor | 2 |
| 1780 | suciedad | 2 |
| 1781 | sucesos | 2 |
| 1782 | sucedido | 2 |
| 1783 | sucederá | 2 |
| 1784 | subir | 2 |
| 1785 | spanischen | 2 |
| 1786 | sosiega | 2 |
| 1787 | sombrero | 2 |
| 1788 | sombra | 2 |
| 1789 | soledad | 2 |
| 1790 | sobrentendido | 2 |
| 1791 | sobra | 2 |
| 1792 | sirves | 2 |
| 1793 | sinónimo | 2 |
| 1794 | simplemente | 2 |
| 1795 | símbolo | 2 |
| 1796 | sillas | 2 |
| 1797 | silla | 2 |
| 1798 | sil | 2 |
| 1799 | sigue | 2 |
| 1800 | significar | 2 |
| 1801 | significa | 2 |
| 1802 | siete | 2 |
| 1803 | serrana | 2 |
| 1804 | sería | 2 |
| 1805 | seré | 2 |
| 1806 | sepas | 2 |
| 1807 | señorías | 2 |
| 1808 | señas | 2 |
| 1809 | señal | 2 |
| 1810 | sentir | 2 |
| 1811 | sentimiento | 2 |
| 1812 | sentí | 2 |
| 1813 | sentencia | 2 |
| 1814 | sencilla | 2 |
| 1815 | segura | 2 |
| 1816 | scipión | 2 |
| 1817 | saúl | 2 |
| 1818 | saqué | 2 |
| 1819 | sanz | 2 |
| 1820 | sangriento | 2 |
| 1821 | samos | 2 |
| 1822 | salud | 2 |
| 1823 | salíos | 2 |
| 1824 | salimos | 2 |
| 1825 | salid | 2 |
| 1826 | salí | 2 |
| 1827 | salgo | 2 |
| 1828 | salgan | 2 |
| 1829 | salario | 2 |
| 1830 | sal | 2 |
| 1831 | said | 2 |
| 1832 | sagrado | 2 |
| 1833 | sacan | 2 |
| 1834 | saca | 2 |
| 1835 | sabré | 2 |
| 1836 | sabrá | 2 |
| 1837 | sabiendo | 2 |
| 1838 | ruiseñor | 2 |
| 1839 | rompió | 2 |
| 1840 | rompieron | 2 |
| 1841 | rompella | 2 |
| 1842 | rompe | 2 |
| 1843 | romances | 2 |
| 1844 | romancero | 2 |
| 1845 | romana | 2 |
| 1846 | rogar | 2 |
| 1847 | rocines | 2 |
| 1848 | rocín | 2 |
| 1849 | robo | 2 |
| 1850 | rinde | 2 |
| 1851 | rimas | 2 |
| 1852 | riguroso | 2 |
| 1853 | rigores | 2 |
| 1854 | ribera | 2 |
| 1855 | revista | 2 |
| 1856 | revés | 2 |
| 1857 | reto | 2 |
| 1858 | resulta | 2 |
| 1859 | restori | 2 |
| 1860 | responder | 2 |
| 1861 | responda | 2 |
| 1862 | resiste | 2 |
| 1863 | reside | 2 |
| 1864 | resfría | 2 |
| 1865 | requiebros | 2 |
| 1866 | requiebro | 2 |
| 1867 | representóla | 2 |
| 1868 | representante | 2 |
| 1869 | repostero | 2 |
| 1870 | replicó | 2 |
| 1871 | reparan | 2 |
| 1872 | reñir | 2 |
| 1873 | remediar | 2 |
| 1874 | remate | 2 |
| 1875 | relinchos | 2 |
| 1876 | relación | 2 |
| 1877 | reja | 2 |
| 1878 | regalos | 2 |
| 1879 | refresco | 2 |
| 1880 | referirte | 2 |
| 1881 | recuerda | 2 |
| 1882 | recordado | 2 |
| 1883 | rayo | 2 |
| 1884 | quitarte | 2 |
| 1885 | quisiste | 2 |
| 1886 | quisiere | 2 |
| 1887 | quiñones | 2 |
| 1888 | quinta | 2 |
| 1889 | quince | 2 |
| 1890 | quiéreme | 2 |
| 1891 | quemado | 2 |
| 1892 | quejosa | 2 |
| 1893 | quejarse | 2 |
| 1894 | queden | 2 |
| 1895 | quédate | 2 |
| 1896 | quedas | 2 |
| 1897 | quedaré | 2 |
| 1898 | quatro | 2 |
| 1899 | pusiste | 2 |
| 1900 | puro | 2 |
| 1901 | puras | 2 |
| 1902 | puño | 2 |
| 1903 | puerto | 2 |
| 1904 | puédese | 2 |
| 1905 | pueblo | 2 |
| 1906 | pudieron | 2 |
| 1907 | pudieras | 2 |
| 1908 | público | 2 |
| 1909 | publica | 2 |
| 1910 | prueba | 2 |
| 1911 | proverbio | 2 |
| 1912 | protección | 2 |
| 1913 | protagonista | 2 |
| 1914 | prosistas | 2 |
| 1915 | prosigue | 2 |
| 1916 | propósito | 2 |
| 1917 | propios | 2 |
| 1918 | propias | 2 |
| 1919 | prometes | 2 |
| 1920 | prometer | 2 |
| 1921 | promesa | 2 |
| 1922 | profundo | 2 |
| 1923 | procuran | 2 |
| 1924 | procurado | 2 |
| 1925 | procede | 2 |
| 1926 | privados | 2 |
| 1927 | prisiones | 2 |
| 1928 | prisionero | 2 |
| 1929 | principio | 2 |
| 1930 | príncipe | 2 |
| 1931 | principales | 2 |
| 1932 | priesa | 2 |
| 1933 | prevenir | 2 |
| 1934 | presentalle | 2 |
| 1935 | prendió | 2 |
| 1936 | preguntar | 2 |
| 1937 | preguntado | 2 |
| 1938 | porfías | 2 |
| 1939 | ponle | 2 |
| 1940 | ponía | 2 |
| 1941 | pongo | 2 |
| 1942 | pongas | 2 |
| 1943 | pon | 2 |
| 1944 | poetas | 2 |
| 1945 | poeta | 2 |
| 1946 | poesía | 2 |
| 1947 | podría | 2 |
| 1948 | podie | 2 |
| 1949 | pleito | 2 |
| 1950 | pintan | 2 |
| 1951 | pierdes | 2 |
| 1952 | pierdas | 2 |
| 1953 | piedra | 2 |
| 1954 | phenix | 2 |
| 1955 | pesia | 2 |
| 1956 | pescuda | 2 |
| 1957 | pesadumbre | 2 |
| 1958 | personaje | 2 |
| 1959 | permitir | 2 |
| 1960 | perfecto | 2 |
| 1961 | perfección | 2 |
| 1962 | perdones | 2 |
| 1963 | pensé | 2 |
| 1964 | pensar | 2 |
| 1965 | pensado | 2 |
| 1966 | pelear | 2 |
| 1967 | pegar | 2 |
| 1968 | pedirla | 2 |
| 1969 | pecados | 2 |
| 1970 | pasiones | 2 |
| 1971 | pasión | 2 |
| 1972 | pase | 2 |
| 1973 | pasan | 2 |
| 1974 | pasadas | 2 |
| 1975 | pasaba | 2 |
| 1976 | partido | 2 |
| 1977 | parque | 2 |
| 1978 | pareció | 2 |
| 1979 | parecen | 2 |
| 1980 | pare | 2 |
| 1981 | parar | 2 |
| 1982 | pára | 2 |
| 1983 | palo | 2 |
| 1984 | página | 2 |
| 1985 | pagas | 2 |
| 1986 | pagar | 2 |
| 1987 | padrinos | 2 |
| 1988 | oyó | 2 |
| 1989 | ovo | 2 |
| 1990 | ovidio | 2 |
| 1991 | overo | 2 |
| 1992 | osara | 2 |
| 1993 | osadía | 2 |
| 1994 | origen | 2 |
| 1995 | olvidar | 2 |
| 1996 | olvidada | 2 |
| 1997 | oiga | 2 |
| 1998 | oídos | 2 |
| 1999 | oíd | 2 |
| 2000 | ofrezco | 2 |
| 2001 | ofendo | 2 |
| 2002 | ocho | 2 |
| 2003 | observación | 2 |
| 2004 | observa | 2 |
| 2005 | obra | 2 |
| 2006 | obligaciones | 2 |
| 2007 | numerosos | 2 |
| 2008 | nuestras | 2 |
| 2009 | notas | 2 |
| 2010 | nosotros | 2 |
| 2011 | niños | 2 |
| 2012 | nin | 2 |
| 2013 | nicolás | 2 |
| 2014 | negro | 2 |
| 2015 | necedad | 2 |
| 2016 | naturalmente | 2 |
| 2017 | natural | 2 |
| 2018 | narbaez | 2 |
| 2019 | naipes | 2 |
| 2020 | nació | 2 |
| 2021 | naciendo | 2 |
| 2022 | murmuran | 2 |
| 2023 | mulas | 2 |
| 2024 | muerta | 2 |
| 2025 | muelas | 2 |
| 2026 | mude | 2 |
| 2027 | mozos | 2 |
| 2028 | moysen | 2 |
| 2029 | movimiento | 2 |
| 2030 | movido | 2 |
| 2031 | mover | 2 |
| 2032 | mostró | 2 |
| 2033 | morisco | 2 |
| 2034 | morisca | 2 |
| 2035 | morirás | 2 |
| 2036 | monte | 2 |
| 2037 | mocedad | 2 |
| 2038 | mismas | 2 |
| 2039 | miré | 2 |
| 2040 | milagro | 2 |
| 2041 | mieses | 2 |
| 2042 | miente | 2 |
| 2043 | miedos | 2 |
| 2044 | mesmo | 2 |
| 2045 | mes | 2 |
| 2046 | merezco | 2 |
| 2047 | merezca | 2 |
| 2048 | mercedes | 2 |
| 2049 | mentira | 2 |
| 2050 | mensajero | 2 |
| 2051 | memoria | 2 |
| 2052 | melancolía | 2 |
| 2053 | mejillas | 2 |
| 2054 | maten | 2 |
| 2055 | mate | 2 |
| 2056 | matarte | 2 |
| 2057 | matara | 2 |
| 2058 | mascarillas | 2 |
| 2059 | marqués | 2 |
| 2060 | maridada | 2 |
| 2061 | maría | 2 |
| 2062 | margen | 2 |
| 2063 | mandól | 2 |
| 2064 | mando | 2 |
| 2065 | mandava | 2 |
| 2066 | mandaste | 2 |
| 2067 | mandáis | 2 |
| 2068 | manchas | 2 |
| 2069 | malo | 2 |
| 2070 | malas | 2 |
| 2071 | madera | 2 |
| 2072 | luchar | 2 |
| 2073 | lobo | 2 |
| 2074 | llevamos | 2 |
| 2075 | llenas | 2 |
| 2076 | llegan | 2 |
| 2077 | llegada | 2 |
| 2078 | llana | 2 |
| 2079 | llamó | 2 |
| 2080 | llame | 2 |
| 2081 | llamase | 2 |
| 2082 | llamarte | 2 |
| 2083 | llamarse | 2 |
| 2084 | llamaran | 2 |
| 2085 | llamando | 2 |
| 2086 | llamaban | 2 |
| 2087 | literalmente | 2 |
| 2088 | libros | 2 |
| 2089 | libremente | 2 |
| 2090 | liberal | 2 |
| 2091 | letras | 2 |
| 2092 | leon | 2 |
| 2093 | lenguas | 2 |
| 2094 | leer | 2 |
| 2095 | lee | 2 |
| 2096 | lea | 2 |
| 2097 | lazo | 2 |
| 2098 | laureles | 2 |
| 2099 | lastimoso | 2 |
| 2100 | laso | 2 |
| 2101 | larga | 2 |
| 2102 | lado | 2 |
| 2103 | labor | 2 |
| 2104 | juzgo | 2 |
| 2105 | justiciero | 2 |
| 2106 | jura | 2 |
| 2107 | juntamente | 2 |
| 2108 | jugar | 2 |
| 2109 | jugando | 2 |
| 2110 | jazmines | 2 |
| 2111 | jaco | 2 |
| 2112 | iv | 2 |
| 2113 | italia | 2 |
| 2114 | isabel | 2 |
| 2115 | invierno | 2 |
| 2116 | invención | 2 |
| 2117 | interés | 2 |
| 2118 | intenta | 2 |
| 2119 | instante | 2 |
| 2120 | inorme | 2 |
| 2121 | inocencia | 2 |
| 2122 | inmortal | 2 |
| 2123 | ingrata | 2 |
| 2124 | ingenios | 2 |
| 2125 | información | 2 |
| 2126 | infinitivo | 2 |
| 2127 | infinitas | 2 |
| 2128 | infierno | 2 |
| 2129 | inferior | 2 |
| 2130 | indignos | 2 |
| 2131 | indicios | 2 |
| 2132 | indicio | 2 |
| 2133 | inclina | 2 |
| 2134 | importuno | 2 |
| 2135 | impedir | 2 |
| 2136 | impedimento | 2 |
| 2137 | ilustres | 2 |
| 2138 | igualé | 2 |
| 2139 | ignores | 2 |
| 2140 | huye | 2 |
| 2141 | hurto | 2 |
| 2142 | humo | 2 |
| 2143 | humildad | 2 |
| 2144 | huéspedes | 2 |
| 2145 | huésped | 2 |
| 2146 | huerte | 2 |
| 2147 | huélgome | 2 |
| 2148 | honras | 2 |
| 2149 | honesto | 2 |
| 2150 | honestidad | 2 |
| 2151 | homenaje | 2 |
| 2152 | hombros | 2 |
| 2153 | históricos | 2 |
| 2154 | hirió | 2 |
| 2155 | hiciste | 2 |
| 2156 | herreruelo | 2 |
| 2157 | heroico | 2 |
| 2158 | hermandad | 2 |
| 2159 | heredado | 2 |
| 2160 | héctor | 2 |
| 2161 | hazañas | 2 |
| 2162 | hazaña | 2 |
| 2163 | harto | 2 |
| 2164 | harán | 2 |
| 2165 | hará | 2 |
| 2166 | hambre | 2 |
| 2167 | halló | 2 |
| 2168 | hallé | 2 |
| 2169 | hallaros | 2 |
| 2170 | hallar | 2 |
| 2171 | hallado | 2 |
| 2172 | hago | 2 |
| 2173 | hacerme | 2 |
| 2174 | hacerle | 2 |
| 2175 | hacen | 2 |
| 2176 | hacello | 2 |
| 2177 | habremos | 2 |
| 2178 | habré | 2 |
| 2179 | habraba | 2 |
| 2180 | habló | 2 |
| 2181 | hablo | 2 |
| 2182 | hablaros | 2 |
| 2183 | hâblar | 2 |
| 2184 | habladme | 2 |
| 2185 | habiéndome | 2 |
| 2186 | haberme | 2 |
| 2187 | haberlo | 2 |
| 2188 | guillén | 2 |
| 2189 | guevara | 2 |
| 2190 | guerras | 2 |
| 2191 | guardarte | 2 |
| 2192 | grecia | 2 |
| 2193 | graves | 2 |
| 2194 | gravemente | 2 |
| 2195 | gracioso | 2 |
| 2196 | gozarla | 2 |
| 2197 | goza | 2 |
| 2198 | goyri | 2 |
| 2199 | gordos | 2 |
| 2200 | golpe | 2 |
| 2201 | glorias | 2 |
| 2202 | gigante | 2 |
| 2203 | gentes | 2 |
| 2204 | genio | 2 |
| 2205 | generosos | 2 |
| 2206 | género | 2 |
| 2207 | ganó | 2 |
| 2208 | gana | 2 |
| 2209 | galga | 2 |
| 2210 | furia | 2 |
| 2211 | funda | 2 |
| 2212 | fuertes | 2 |
| 2213 | fuerça | 2 |
| 2214 | fruto | 2 |
| 2215 | fronterizos | 2 |
| 2216 | frío | 2 |
| 2217 | frescos | 2 |
| 2218 | fregona | 2 |
| 2219 | forzalla | 2 |
| 2220 | fondo | 2 |
| 2221 | fols | 2 |
| 2222 | fizo | 2 |
| 2223 | firmeza | 2 |
| 2224 | firmes | 2 |
| 2225 | fingido | 2 |
| 2226 | fines | 2 |
| 2227 | fil | 2 |
| 2228 | fija | 2 |
| 2229 | fiestas | 2 |
| 2230 | feroz | 2 |
| 2231 | fernán | 2 |
| 2232 | fénix | 2 |
| 2233 | febrero | 2 |
| 2234 | febeo | 2 |
| 2235 | fazie | 2 |
| 2236 | fazer | 2 |
| 2237 | favores | 2 |
| 2238 | favoreced | 2 |
| 2239 | famosos | 2 |
| 2240 | familia | 2 |
| 2241 | faltan | 2 |
| 2242 | fábula | 2 |
| 2243 | f | 2 |
| 2244 | exige | 2 |
| 2245 | eterno | 2 |
| 2246 | eternamente | 2 |
| 2247 | estuvo | 2 |
| 2248 | estuviera | 2 |
| 2249 | estudiante | 2 |
| 2250 | estremos | 2 |
| 2251 | éstos | 2 |
| 2252 | estó | 2 |
| 2253 | estimado | 2 |
| 2254 | estilo | 2 |
| 2255 | estén | 2 |
| 2256 | estéis | 2 |
| 2257 | estad | 2 |
| 2258 | esse | 2 |
| 2259 | espere | 2 |
| 2260 | esperas | 2 |
| 2261 | esperara | 2 |
| 2262 | esperan | 2 |
| 2263 | espanta | 2 |
| 2264 | espacio | 2 |
| 2265 | esfuerzo | 2 |
| 2266 | escusa | 2 |
| 2267 | escuadrón | 2 |
| 2268 | escritores | 2 |
| 2269 | escrita | 2 |
| 2270 | escribas | 2 |
| 2271 | escondida | 2 |
| 2272 | escóndese | 2 |
| 2273 | escapar | 2 |
| 2274 | época | 2 |
| 2275 | episodio | 2 |
| 2276 | envío | 2 |
| 2277 | enviarte | 2 |
| 2278 | enviaré | 2 |
| 2279 | entretenido | 2 |
| 2280 | entrego | 2 |
| 2281 | éntre | 2 |
| 2282 | entrara | 2 |
| 2283 | entrambos | 2 |
| 2284 | entrad | 2 |
| 2285 | entiendas | 2 |
| 2286 | entendido | 2 |
| 2287 | ensillar | 2 |
| 2288 | ensilla | 2 |
| 2289 | enojo | 2 |
| 2290 | enoje | 2 |
| 2291 | engañar | 2 |
| 2292 | enfermo | 2 |
| 2293 | enero | 2 |
| 2294 | encuentra | 2 |
| 2295 | encina | 2 |
| 2296 | encierra | 2 |
| 2297 | encendido | 2 |
| 2298 | encendida | 2 |
| 2299 | enamorada | 2 |
| 2300 | empuño | 2 |
| 2301 | empleos | 2 |
| 2302 | empleo | 2 |
| 2303 | empleado | 2 |
| 2304 | emplea | 2 |
| 2305 | empida | 2 |
| 2306 | embustes | 2 |
| 2307 | embió | 2 |
| 2308 | elementos | 2 |
| 2309 | ed | 2 |
| 2310 | echar | 2 |
| 2311 | durmiendo | 2 |
| 2312 | duerme | 2 |
| 2313 | duele | 2 |
| 2314 | dudosa | 2 |
| 2315 | dormir | 2 |
| 2316 | doradas | 2 |
| 2317 | donoso | 2 |
| 2318 | doncella | 2 |
| 2319 | doblones | 2 |
| 2320 | dó | 2 |
| 2321 | do | 2 |
| 2322 | divino | 2 |
| 2323 | disimules | 2 |
| 2324 | discreción | 2 |
| 2325 | diría | 2 |
| 2326 | dirás | 2 |
| 2327 | dirán | 2 |
| 2328 | diosa | 2 |
| 2329 | dióme | 2 |
| 2330 | dile | 2 |
| 2331 | digno | 2 |
| 2332 | digas | 2 |
| 2333 | difiere | 2 |
| 2334 | dificultad | 2 |
| 2335 | diferentes | 2 |
| 2336 | diego | 2 |
| 2337 | diccionarios | 2 |
| 2338 | diccionario | 2 |
| 2339 | diablo | 2 |
| 2340 | deudos | 2 |
| 2341 | deuda | 2 |
| 2342 | detrás | 2 |
| 2343 | detente | 2 |
| 2344 | desvergüenza | 2 |
| 2345 | desventuras | 2 |
| 2346 | desvaríos | 2 |
| 2347 | destas | 2 |
| 2348 | despecho | 2 |
| 2349 | desmayado | 2 |
| 2350 | deshonre | 2 |
| 2351 | desgracia | 2 |
| 2352 | desespero | 2 |
| 2353 | desea | 2 |
| 2354 | dése | 2 |
| 2355 | desdenes | 2 |
| 2356 | descuido | 2 |
| 2357 | descontento | 2 |
| 2358 | descanso | 2 |
| 2359 | descansad | 2 |
| 2360 | desatino | 2 |
| 2361 | desafío | 2 |
| 2362 | demanda | 2 |
| 2363 | dello | 2 |
| 2364 | delito | 2 |
| 2365 | dejó | 2 |
| 2366 | dejarme | 2 |
| 2367 | dejan | 2 |
| 2368 | déjala | 2 |
| 2369 | dejáis | 2 |
| 2370 | defender | 2 |
| 2371 | decoro | 2 |
| 2372 | declararte | 2 |
| 2373 | decirle | 2 |
| 2374 | darlos | 2 |
| 2375 | darle | 2 |
| 2376 | darla | 2 |
| 2377 | daños | 2 |
| 2378 | daño | 2 |
| 2379 | damos | 2 |
| 2380 | dale | 2 |
| 2381 | dadivoso | 2 |
| 2382 | dádivas | 2 |
| 2383 | cuyos | 2 |
| 2384 | cuyo | 2 |
| 2385 | cúya | 2 |
| 2386 | cupiera | 2 |
| 2387 | culpados | 2 |
| 2388 | cuentan | 2 |
| 2389 | cuarto | 2 |
| 2390 | cuántos | 2 |
| 2391 | cuáles | 2 |
| 2392 | crueles | 2 |
| 2393 | crónicas | 2 |
| 2394 | crítica | 2 |
| 2395 | crié | 2 |
| 2396 | crecer | 2 |
| 2397 | coyuntura | 2 |
| 2398 | costumbres | 2 |
| 2399 | corteza | 2 |
| 2400 | cortesía | 2 |
| 2401 | corrigió | 2 |
| 2402 | corrige | 2 |
| 2403 | correspondiente | 2 |
| 2404 | correr | 2 |
| 2405 | corren | 2 |
| 2406 | corregido | 2 |
| 2407 | coronica | 2 |
| 2408 | coro | 2 |
| 2409 | copia | 2 |
| 2410 | continuos | 2 |
| 2411 | contemporáneo | 2 |
| 2412 | contaros | 2 |
| 2413 | consuene | 2 |
| 2414 | consolara | 2 |
| 2415 | conquistar | 2 |
| 2416 | conozco | 2 |
| 2417 | conocidas | 2 |
| 2418 | conocida | 2 |
| 2419 | conocí | 2 |
| 2420 | confiscalles | 2 |
| 2421 | confirma | 2 |
| 2422 | confieso | 2 |
| 2423 | confiésame | 2 |
| 2424 | confianza | 2 |
| 2425 | confiado | 2 |
| 2426 | concejo | 2 |
| 2427 | concede | 2 |
| 2428 | compuesta | 2 |
| 2429 | complemento | 2 |
| 2430 | comienza | 2 |
| 2431 | comerán | 2 |
| 2432 | començó | 2 |
| 2433 | collera | 2 |
| 2434 | cólera | 2 |
| 2435 | coincide | 2 |
| 2436 | codicia | 2 |
| 2437 | cobre | 2 |
| 2438 | clérigo | 2 |
| 2439 | citado | 2 |
| 2440 | ciertos | 2 |
| 2441 | cien | 2 |
| 2442 | ciega | 2 |
| 2443 | cerros | 2 |
| 2444 | celestial | 2 |
| 2445 | celebrados | 2 |
| 2446 | celebra | 2 |
| 2447 | celauro | 2 |
| 2448 | celadas | 2 |
| 2449 | celada | 2 |
| 2450 | cazador | 2 |
| 2451 | cautiva | 2 |
| 2452 | causas | 2 |
| 2453 | causarme | 2 |
| 2454 | castillo | 2 |
| 2455 | castidad | 2 |
| 2456 | castellana | 2 |
| 2457 | castaños | 2 |
| 2458 | casta | 2 |
| 2459 | casó | 2 |
| 2460 | casería | 2 |
| 2461 | casaréis | 2 |
| 2462 | casamientos | 2 |
| 2463 | casada | 2 |
| 2464 | carrera | 2 |
| 2465 | caros | 2 |
| 2466 | canse | 2 |
| 2467 | cansarte | 2 |
| 2468 | cansado | 2 |
| 2469 | canas | 2 |
| 2470 | canalla | 2 |
| 2471 | campaña | 2 |
| 2472 | camisas | 2 |
| 2473 | camisa | 2 |
| 2474 | calidad | 2 |
| 2475 | caída | 2 |
| 2476 | cabezas | 2 |
| 2477 | buscado | 2 |
| 2478 | burlo | 2 |
| 2479 | brujas | 2 |
| 2480 | bronce | 2 |
| 2481 | brocado | 2 |
| 2482 | brazo | 2 |
| 2483 | bol | 2 |
| 2484 | bodas | 2 |
| 2485 | blancos | 2 |
| 2486 | bienes | 2 |
| 2487 | besos | 2 |
| 2488 | besan | 2 |
| 2489 | besa | 2 |
| 2490 | bencerrajes | 2 |
| 2491 | bellaquerías | 2 |
| 2492 | beldad | 2 |
| 2493 | baúl | 2 |
| 2494 | batallador | 2 |
| 2495 | basilisco | 2 |
| 2496 | barquero | 2 |
| 2497 | barca | 2 |
| 2498 | bañaba | 2 |
| 2499 | balde | 2 |
| 2500 | balcones | 2 |
| 2501 | azul | 2 |
| 2502 | ayudarme | 2 |
| 2503 | ayo | 2 |
| 2504 | avisar | 2 |
| 2505 | aver | 2 |
| 2506 | aventuras | 2 |
| 2507 | avenencia | 2 |
| 2508 | avara | 2 |
| 2509 | atroz | 2 |
| 2510 | atributo | 2 |
| 2511 | atenta | 2 |
| 2512 | asunto | 2 |
| 2513 | astrólogo | 2 |
| 2514 | asiento | 2 |
| 2515 | asegurar | 2 |
| 2516 | arroyuelos | 2 |
| 2517 | arrima | 2 |
| 2518 | armesto | 2 |
| 2519 | armados | 2 |
| 2520 | armado | 2 |
| 2521 | argumento | 2 |
| 2522 | arenas | 2 |
| 2523 | arcaísmo | 2 |
| 2524 | aqueste | 2 |
| 2525 | aquese | 2 |
| 2526 | aquello | 2 |
| 2527 | aprieta | 2 |
| 2528 | aplica | 2 |
| 2529 | apercibe | 2 |
| 2530 | apedrear | 2 |
| 2531 | apartamiento | 2 |
| 2532 | aparezca | 2 |
| 2533 | antigüedad | 2 |
| 2534 | anterior | 2 |
| 2535 | ant | 2 |
| 2536 | anoche | 2 |
| 2537 | andrada | 2 |
| 2538 | andaluz | 2 |
| 2539 | análoga | 2 |
| 2540 | amoroso | 2 |
| 2541 | amora | 2 |
| 2542 | amistades | 2 |
| 2543 | amistad | 2 |
| 2544 | amiga | 2 |
| 2545 | amiclas | 2 |
| 2546 | amén | 2 |
| 2547 | amantes | 2 |
| 2548 | alusiones | 2 |
| 2549 | alternando | 2 |
| 2550 | alonso | 2 |
| 2551 | almanzor | 2 |
| 2552 | aljófar | 2 |
| 2553 | alhambra | 2 |
| 2554 | alfaquí | 2 |
| 2555 | alexandre | 2 |
| 2556 | aldea | 2 |
| 2557 | alas | 2 |
| 2558 | álamos | 2 |
| 2559 | alabes | 2 |
| 2560 | alabanzas | 2 |
| 2561 | aibar | 2 |
| 2562 | ahí | 2 |
| 2563 | aguarde | 2 |
| 2564 | agravios | 2 |
| 2565 | agraviado | 2 |
| 2566 | agradezco | 2 |
| 2567 | africa | 2 |
| 2568 | adoptamos | 2 |
| 2569 | admitir | 2 |
| 2570 | admira | 2 |
| 2571 | acuerdo | 2 |
| 2572 | acompañamiento | 2 |
| 2573 | acompaña | 2 |
| 2574 | acicates | 2 |
| 2575 | acepción | 2 |
| 2576 | abrir | 2 |
| 2577 | abrazos | 2 |
| 2578 | abad | 2 |
| 2579 | zur | 1 |
| 2580 | zeitschrift | 1 |
| 2581 | zegrí | 1 |
| 2582 | zaros | 1 |
| 2583 | zarabanda | 1 |
| 2584 | zancarrón | 1 |
| 2585 | zaides | 1 |
| 2586 | zagalas | 1 |
| 2587 | zagala | 1 |
| 2588 | zagal | 1 |
| 2589 | zafir | 1 |
| 2590 | yva | 1 |
| 2591 | yrien | 1 |
| 2592 | yerros | 1 |
| 2593 | yerra | 1 |
| 2594 | yerno | 1 |
| 2595 | yermo | 1 |
| 2596 | yendo | 1 |
| 2597 | yelmo | 1 |
| 2598 | xxxviii | 1 |
| 2599 | xxxv | 1 |
| 2600 | xxxix | 1 |
| 2601 | xxxiv | 1 |
| 2602 | xxvii | 1 |
| 2603 | xxvi | 1 |
| 2604 | xxii | 1 |
| 2605 | xviii | 1 |
| 2606 | xlvii | 1 |
| 2607 | xlv | 1 |
| 2608 | xiv | 1 |
| 2609 | xii | 1 |
| 2610 | werke | 1 |
| 2611 | vueseñoría | 1 |
| 2612 | vuesa | 1 |
| 2613 | vuélvete | 1 |
| 2614 | vuelvas | 1 |
| 2615 | voyme | 1 |
| 2616 | volviste | 1 |
| 2617 | volvióla | 1 |
| 2618 | volviéndome | 1 |
| 2619 | volvías | 1 |
| 2620 | volverte | 1 |
| 2621 | volverme | 1 |
| 2622 | volvería | 1 |
| 2623 | volveréme | 1 |
| 2624 | volveréis | 1 |
| 2625 | volvedme | 1 |
| 2626 | volvámonos | 1 |
| 2627 | volváis | 1 |
| 2628 | volumen | 1 |
| 2629 | volarán | 1 |
| 2630 | vivís | 1 |
| 2631 | vivió | 1 |
| 2632 | vivimos | 1 |
| 2633 | viviese | 1 |
| 2634 | viviendo | 1 |
| 2635 | vivíe | 1 |
| 2636 | vivían | 1 |
| 2637 | vivía | 1 |
| 2638 | vivan | 1 |
| 2639 | vistes | 1 |
| 2640 | vísperas | 1 |
| 2641 | visitar | 1 |
| 2642 | vióme | 1 |
| 2643 | violó | 1 |
| 2644 | violeta | 1 |
| 2645 | violentamente | 1 |
| 2646 | violenta | 1 |
| 2647 | violencia | 1 |
| 2648 | vióla | 1 |
| 2649 | viña | 1 |
| 2650 | vinagre | 1 |
| 2651 | vimos | 1 |
| 2652 | villanesco | 1 |
| 2653 | villanas | 1 |
| 2654 | viesse | 1 |
| 2655 | viese | 1 |
| 2656 | vieron | 1 |
| 2657 | viernes | 1 |
| 2658 | viere | 1 |
| 2659 | viéndote | 1 |
| 2660 | viéndolos | 1 |
| 2661 | viéndola | 1 |
| 2662 | vieja | 1 |
| 2663 | vides | 1 |
| 2664 | victoria | 1 |
| 2665 | viciado | 1 |
| 2666 | viaje | 1 |
| 2667 | vía | 1 |
| 2668 | vezes | 1 |
| 2669 | veys | 1 |
| 2670 | vestir | 1 |
| 2671 | vestíme | 1 |
| 2672 | vesla | 1 |
| 2673 | versificado | 1 |
| 2674 | veros | 1 |
| 2675 | vero | 1 |
| 2676 | verlos | 1 |
| 2677 | verlas | 1 |
| 2678 | verisímiles | 1 |
| 2679 | vergonzoso | 1 |
| 2680 | vergonzosa | 1 |
| 2681 | veremos | 1 |
| 2682 | veré | 1 |
| 2683 | verde | 1 |
| 2684 | verdades | 1 |
| 2685 | verdaderas | 1 |
| 2686 | verbos | 1 |
| 2687 | vera | 1 |
| 2688 | véome | 1 |
| 2689 | venza | 1 |
| 2690 | venturosos | 1 |
| 2691 | veniste | 1 |
| 2692 | veniessen | 1 |
| 2693 | venidos | 1 |
| 2694 | venida | 1 |
| 2695 | venías | 1 |
| 2696 | venía | 1 |
| 2697 | vengas | 1 |
| 2698 | vengarme | 1 |
| 2699 | venganzas | 1 |
| 2700 | véngante | 1 |
| 2701 | vengáis | 1 |
| 2702 | vengador | 1 |
| 2703 | venerables | 1 |
| 2704 | veneno | 1 |
| 2705 | vendría | 1 |
| 2706 | vendido | 1 |
| 2707 | venderte | 1 |
| 2708 | vendaval | 1 |
| 2709 | vencimiento | 1 |
| 2710 | venciese | 1 |
| 2711 | vencerla | 1 |
| 2712 | vencería | 1 |
| 2713 | vençer | 1 |
| 2714 | vencéis | 1 |
| 2715 | vencedora | 1 |
| 2716 | venablo | 1 |
| 2717 | vemos | 1 |
| 2718 | velo | 1 |
| 2719 | vela | 1 |
| 2720 | vejez | 1 |
| 2721 | vedava | 1 |
| 2722 | ved | 1 |
| 2723 | vecindades | 1 |
| 2724 | vecindad | 1 |
| 2725 | véanse | 1 |
| 2726 | veamos | 1 |
| 2727 | vé | 1 |
| 2728 | váyase | 1 |
| 2729 | vayáis | 1 |
| 2730 | vaya | 1 |
| 2731 | vassallos | 1 |
| 2732 | vasallo | 1 |
| 2733 | varraco | 1 |
| 2734 | varios | 1 |
| 2735 | variedades | 1 |
| 2736 | variedad | 1 |
| 2737 | variantes | 1 |
| 2738 | variación | 1 |
| 2739 | varia | 1 |
| 2740 | varas | 1 |
| 2741 | vanegas | 1 |
| 2742 | valles | 1 |
| 2743 | valientes | 1 |
| 2744 | valgo | 1 |
| 2745 | válgame | 1 |
| 2746 | valetudinario | 1 |
| 2747 | valerte | 1 |
| 2748 | valerosos | 1 |
| 2749 | valeroso | 1 |
| 2750 | valerme | 1 |
| 2751 | valentía | 1 |
| 2752 | valencia | 1 |
| 2753 | valdré | 1 |
| 2754 | válate | 1 |
| 2755 | valança | 1 |
| 2756 | uso | 1 |
| 2757 | usarse | 1 |
| 2758 | usar | 1 |
| 2759 | usanza | 1 |
| 2760 | usan | 1 |
| 2761 | usado | 1 |
| 2762 | usada | 1 |
| 2763 | usaban | 1 |
| 2764 | urdemalas | 1 |
| 2765 | universal | 1 |
| 2766 | unión | 1 |
| 2767 | único | 1 |
| 2768 | única | 1 |
| 2769 | umbrales | 1 |
| 2770 | último | 1 |
| 2771 | última | 1 |
| 2772 | ufano | 1 |
| 2773 | tuyos | 1 |
| 2774 | tuvistes | 1 |
| 2775 | tuviste | 1 |
| 2776 | tuviere | 1 |
| 2777 | turquí | 1 |
| 2778 | turián | 1 |
| 2779 | turco | 1 |
| 2780 | turbulenta | 1 |
| 2781 | túrbase | 1 |
| 2782 | túnica | 1 |
| 2783 | túnez | 1 |
| 2784 | tuerza | 1 |
| 2785 | tuertos | 1 |
| 2786 | tudesco | 1 |
| 2787 | trujese | 1 |
| 2788 | trueno | 1 |
| 2789 | trueco | 1 |
| 2790 | truécale | 1 |
| 2791 | trozo | 1 |
| 2792 | troya | 1 |
| 2793 | tropezar | 1 |
| 2794 | troncos | 1 |
| 2795 | trocar | 1 |
| 2796 | trobada | 1 |
| 2797 | triunmphe | 1 |
| 2798 | triunfar | 1 |
| 2799 | triunfado | 1 |
| 2800 | triunfa | 1 |
| 2801 | tristemente | 1 |
| 2802 | trinitarias | 1 |
| 2803 | tributo | 1 |
| 2804 | tribunal | 1 |
| 2805 | tretas | 1 |
| 2806 | trestaurar | 1 |
| 2807 | trecho | 1 |
| 2808 | trazó | 1 |
| 2809 | trazado | 1 |
| 2810 | traza | 1 |
| 2811 | tratos | 1 |
| 2812 | trátase | 1 |
| 2813 | tratas | 1 |
| 2814 | tratarse | 1 |
| 2815 | trataron | 1 |
| 2816 | tratarme | 1 |
| 2817 | trataréis | 1 |
| 2818 | tratare | 1 |
| 2819 | tratan | 1 |
| 2820 | trátalos | 1 |
| 2821 | tratáis | 1 |
| 2822 | traspuesto | 1 |
| 2823 | transición | 1 |
| 2824 | tranquilo | 1 |
| 2825 | trajes | 1 |
| 2826 | trajano | 1 |
| 2827 | traigamos | 1 |
| 2828 | traigáis | 1 |
| 2829 | traiga | 1 |
| 2830 | traido | 1 |
| 2831 | traida | 1 |
| 2832 | traiciones | 1 |
| 2833 | traías | 1 |
| 2834 | traía | 1 |
| 2835 | trai | 1 |
| 2836 | trague | 1 |
| 2837 | tragos | 1 |
| 2838 | trágica | 1 |
| 2839 | traerte | 1 |
| 2840 | traerme | 1 |
| 2841 | traeré | 1 |
| 2842 | traerá | 1 |
| 2843 | traen | 1 |
| 2844 | traéis | 1 |
| 2845 | traedle | 1 |
| 2846 | traducción | 1 |
| 2847 | tradición | 1 |
| 2848 | tracemos | 1 |
| 2849 | trabajos | 1 |
| 2850 | toviera | 1 |
| 2851 | tórtola | 1 |
| 2852 | torreznos | 1 |
| 2853 | torrezno | 1 |
| 2854 | toros | 1 |
| 2855 | tornose | 1 |
| 2856 | tornes | 1 |
| 2857 | tornasse | 1 |
| 2858 | tormenta | 1 |
| 2859 | torcer | 1 |
| 2860 | topemos | 1 |
| 2861 | tomes | 1 |
| 2862 | tomeras | 1 |
| 2863 | tomemos | 1 |
| 2864 | tomélos | 1 |
| 2865 | tomastes | 1 |
| 2866 | tomasse | 1 |
| 2867 | tomarla | 1 |
| 2868 | tomaré | 1 |
| 2869 | toman | 1 |
| 2870 | tomados | 1 |
| 2871 | tomadlos | 1 |
| 2872 | tomadle | 1 |
| 2873 | toledos | 1 |
| 2874 | tocó | 1 |
| 2875 | tocas | 1 |
| 2876 | tocaros | 1 |
| 2877 | tocar | 1 |
| 2878 | tiros | 1 |
| 2879 | tiranos | 1 |
| 2880 | tiranía | 1 |
| 2881 | tipografía | 1 |
| 2882 | tipo | 1 |
| 2883 | tiñe | 1 |
| 2884 | tintos | 1 |
| 2885 | tinta | 1 |
| 2886 | tinieblas | 1 |
| 2887 | tigre | 1 |
| 2888 | tiento | 1 |
| 2889 | tiembla | 1 |
| 2890 | tías | 1 |
| 2891 | textos | 1 |
| 2892 | textes | 1 |
| 2893 | terrible | 1 |
| 2894 | tercio | 1 |
| 2895 | tercetos | 1 |
| 2896 | tentar | 1 |
| 2897 | tentado | 1 |
| 2898 | tenreiro | 1 |
| 2899 | teníe | 1 |
| 2900 | tenían | 1 |
| 2901 | téngase | 1 |
| 2902 | tengamos | 1 |
| 2903 | tengáis | 1 |
| 2904 | teneys | 1 |
| 2905 | teneros | 1 |
| 2906 | tenerlos | 1 |
| 2907 | tenella | 1 |
| 2908 | tenéisla | 1 |
| 2909 | tenedme | 1 |
| 2910 | tendrásla | 1 |
| 2911 | temores | 1 |
| 2912 | temiendo | 1 |
| 2913 | temía | 1 |
| 2914 | temblar | 1 |
| 2915 | temas | 1 |
| 2916 | tela | 1 |
| 2917 | tejos | 1 |
| 2918 | tejido | 1 |
| 2919 | teatral | 1 |
| 2920 | tascando | 1 |
| 2921 | tasajo | 1 |
| 2922 | tardía | 1 |
| 2923 | tardanza | 1 |
| 2924 | tardado | 1 |
| 2925 | tarda | 1 |
| 2926 | tapiz | 1 |
| 2927 | tápala | 1 |
| 2928 | tañer | 1 |
| 2929 | tamaño | 1 |
| 2930 | talis | 1 |
| 2931 | talento | 1 |
| 2932 | talas | 1 |
| 2933 | tálamo | 1 |
| 2934 | tafetán | 1 |
| 2935 | syntax | 1 |
| 2936 | suyos | 1 |
| 2937 | susto | 1 |
| 2938 | sustitución | 1 |
| 2939 | suspiras | 1 |
| 2940 | suspira | 1 |
| 2941 | suprimido | 1 |
| 2942 | suprime | 1 |
| 2943 | supremo | 1 |
| 2944 | súpolo | 1 |
| 2945 | supo | 1 |
| 2946 | supliendo | 1 |
| 2947 | suplícote | 1 |
| 2948 | supiste | 1 |
| 2949 | supe | 1 |
| 2950 | sujetas | 1 |
| 2951 | sujetarme | 1 |
| 2952 | sujetáis | 1 |
| 2953 | sujeta | 1 |
| 2954 | sujeción | 1 |
| 2955 | sugerida | 1 |
| 2956 | sufrirás | 1 |
| 2957 | sufriendo | 1 |
| 2958 | sufra | 1 |
| 2959 | suficiencia | 1 |
| 2960 | sueños | 1 |
| 2961 | sueltos | 1 |
| 2962 | sucias | 1 |
| 2963 | sucesores | 1 |
| 2964 | sucediese | 1 |
| 2965 | sucede | 1 |
| 2966 | subieron | 1 |
| 2967 | subes | 1 |
| 2968 | suave | 1 |
| 2969 | suárez | 1 |
| 2970 | stage | 1 |
| 2971 | sr | 1 |
| 2972 | spanish | 1 |
| 2973 | spain | 1 |
| 2974 | soys | 1 |
| 2975 | soto | 1 |
| 2976 | sostenerse | 1 |
| 2977 | sospechosa | 1 |
| 2978 | sospechas | 1 |
| 2979 | sosiego | 1 |
| 2980 | sosegado | 1 |
| 2981 | sordas | 1 |
| 2982 | sor | 1 |
| 2983 | sopo | 1 |
| 2984 | sopalandas | 1 |
| 2985 | sonetos | 1 |
| 2986 | sonaban | 1 |
| 2987 | són | 1 |
| 2988 | sombras | 1 |
| 2989 | solicitas | 1 |
| 2990 | solían | 1 |
| 2991 | soles | 1 |
| 2992 | soler | 1 |
| 2993 | solenniza | 1 |
| 2994 | soldadesco | 1 |
| 2995 | solar | 1 |
| 2996 | sofisterías | 1 |
| 2997 | socorro | 1 |
| 2998 | socorre | 1 |
| 2999 | société | 1 |
| 3000 | sobrevivido | 1 |
| 3001 | sobrenombre | 1 |
| 3002 | sobreescribidla | 1 |
| 3003 | soberbios | 1 |
| 3004 | soberbio | 1 |
| 3005 | sitio | 1 |
| 3006 | sirvió | 1 |
| 3007 | sirviéndoles | 1 |
| 3008 | sirviendo | 1 |
| 3009 | siquiera | 1 |
| 3010 | sintieras | 1 |
| 3011 | sintáctica | 1 |
| 3012 | sinrazones | 1 |
| 3013 | singular | 1 |
| 3014 | simple | 1 |
| 3015 | símiles | 1 |
| 3016 | silos | 1 |
| 3017 | silencio | 1 |
| 3018 | silbo | 1 |
| 3019 | siguen | 1 |
| 3020 | sigts | 1 |
| 3021 | sigo | 1 |
| 3022 | significativo | 1 |
| 3023 | significación | 1 |
| 3024 | siesta | 1 |
| 3025 | sierra | 1 |
| 3026 | siéntense | 1 |
| 3027 | sienten | 1 |
| 3028 | siéntase | 1 |
| 3029 | sientas | 1 |
| 3030 | sientan | 1 |
| 3031 | sienta | 1 |
| 3032 | sienes | 1 |
| 3033 | sieben | 1 |
| 3034 | sexto | 1 |
| 3035 | servís | 1 |
| 3036 | servirle | 1 |
| 3037 | servíos | 1 |
| 3038 | servía | 1 |
| 3039 | serrano | 1 |
| 3040 | sereno | 1 |
| 3041 | serenissimo | 1 |
| 3042 | seremos | 1 |
| 3043 | serafines | 1 |
| 3044 | sepultura | 1 |
| 3045 | separadas | 1 |
| 3046 | sepan | 1 |
| 3047 | sepamos | 1 |
| 3048 | señorío | 1 |
| 3049 | señoría | 1 |
| 3050 | señales | 1 |
| 3051 | sentís | 1 |
| 3052 | sentirse | 1 |
| 3053 | sentía | 1 |
| 3054 | sentencias | 1 |
| 3055 | sentenciado | 1 |
| 3056 | sentarme | 1 |
| 3057 | sentar | 1 |
| 3058 | sentad | 1 |
| 3059 | seno | 1 |
| 3060 | senderos | 1 |
| 3061 | sendas | 1 |
| 3062 | senado | 1 |
| 3063 | sembró | 1 |
| 3064 | selva | 1 |
| 3065 | selimo | 1 |
| 3066 | seiás | 1 |
| 3067 | seguramente | 1 |
| 3068 | segundar | 1 |
| 3069 | seguirte | 1 |
| 3070 | seguían | 1 |
| 3071 | seda | 1 |
| 3072 | sed | 1 |
| 3073 | secretamente | 1 |
| 3074 | sebastián | 1 |
| 3075 | sean | 1 |
| 3076 | seamos | 1 |
| 3077 | seáis | 1 |
| 3078 | scipion | 1 |
| 3079 | schevill | 1 |
| 3080 | sayo | 1 |
| 3081 | sayal | 1 |
| 3082 | satisfice | 1 |
| 3083 | satisfecho | 1 |
| 3084 | satisfago | 1 |
| 3085 | satisfagas | 1 |
| 3086 | satisfaciones | 1 |
| 3087 | satisfación | 1 |
| 3088 | satisfaces | 1 |
| 3089 | satisfacerte | 1 |
| 3090 | satisfacer | 1 |
| 3091 | saque | 1 |
| 3092 | sañudo | 1 |
| 3093 | santas | 1 |
| 3094 | sangrienta | 1 |
| 3095 | sangría | 1 |
| 3096 | sangren | 1 |
| 3097 | sancha | 1 |
| 3098 | sanar | 1 |
| 3099 | samuel | 1 |
| 3100 | salvo | 1 |
| 3101 | salvaje | 1 |
| 3102 | salutífero | 1 |
| 3103 | saludables | 1 |
| 3104 | salte | 1 |
| 3105 | salmón | 1 |
| 3106 | salió | 1 |
| 3107 | saliesse | 1 |
| 3108 | salieron | 1 |
| 3109 | salido | 1 |
| 3110 | salida | 1 |
| 3111 | sales | 1 |
| 3112 | saldré | 1 |
| 3113 | saldrán | 1 |
| 3114 | saldrá | 1 |
| 3115 | salas | 1 |
| 3116 | sala | 1 |
| 3117 | sacristán | 1 |
| 3118 | saco | 1 |
| 3119 | sacaron | 1 |
| 3120 | sacar | 1 |
| 3121 | sacadas | 1 |
| 3122 | sabueso | 1 |
| 3123 | sabráslo | 1 |
| 3124 | sabor | 1 |
| 3125 | sabios | 1 |
| 3126 | sabías | 1 |
| 3127 | sabían | 1 |
| 3128 | sabía | 1 |
| 3129 | sabello | 1 |
| 3130 | sabedme | 1 |
| 3131 | rústicos | 1 |
| 3132 | rústico | 1 |
| 3133 | ruiz | 1 |
| 3134 | ruines | 1 |
| 3135 | ruído | 1 |
| 3136 | ruegos | 1 |
| 3137 | ruedas | 1 |
| 3138 | rueda | 1 |
| 3139 | rudo | 1 |
| 3140 | rudeza | 1 |
| 3141 | rubia | 1 |
| 3142 | rubí | 1 |
| 3143 | rrazonó | 1 |
| 3144 | rotas | 1 |
| 3145 | rota | 1 |
| 3146 | rostros | 1 |
| 3147 | rosas | 1 |
| 3148 | rosa | 1 |
| 3149 | roques | 1 |
| 3150 | ropas | 1 |
| 3151 | rompiendo | 1 |
| 3152 | rompáis | 1 |
| 3153 | romano | 1 |
| 3154 | romanische | 1 |
| 3155 | roma | 1 |
| 3156 | roelas | 1 |
| 3157 | rodilla | 1 |
| 3158 | rodamontes | 1 |
| 3159 | robos | 1 |
| 3160 | robes | 1 |
| 3161 | robase | 1 |
| 3162 | robaron | 1 |
| 3163 | robara | 1 |
| 3164 | robándome | 1 |
| 3165 | roban | 1 |
| 3166 | robado | 1 |
| 3167 | roba | 1 |
| 3168 | rizos | 1 |
| 3169 | rivalidad | 1 |
| 3170 | riquezas | 1 |
| 3171 | riqueza | 1 |
| 3172 | riman | 1 |
| 3173 | rima | 1 |
| 3174 | rifa | 1 |
| 3175 | riendo | 1 |
| 3176 | rienda | 1 |
| 3177 | reyno | 1 |
| 3178 | reynar | 1 |
| 3179 | revilla | 1 |
| 3180 | reviente | 1 |
| 3181 | reveses | 1 |
| 3182 | rev | 1 |
| 3183 | reunidos | 1 |
| 3184 | retrocede | 1 |
| 3185 | retrate | 1 |
| 3186 | retóricamente | 1 |
| 3187 | retoque | 1 |
| 3188 | retocó | 1 |
| 3189 | retocarla | 1 |
| 3190 | retírese | 1 |
| 3191 | retara | 1 |
| 3192 | retamas | 1 |
| 3193 | resultó | 1 |
| 3194 | restaurar | 1 |
| 3195 | restablecer | 1 |
| 3196 | restablece | 1 |
| 3197 | resquiebro | 1 |
| 3198 | resquiebra | 1 |
| 3199 | respondistes | 1 |
| 3200 | respondiste | 1 |
| 3201 | respondióme | 1 |
| 3202 | respondieron | 1 |
| 3203 | respondiéndola | 1 |
| 3204 | respondido | 1 |
| 3205 | respondía | 1 |
| 3206 | responderte | 1 |
| 3207 | responderé | 1 |
| 3208 | respondéis | 1 |
| 3209 | resplandeciente | 1 |
| 3210 | resplandece | 1 |
| 3211 | respira | 1 |
| 3212 | respetos | 1 |
| 3213 | respete | 1 |
| 3214 | respetar | 1 |
| 3215 | respetando | 1 |
| 3216 | respetado | 1 |
| 3217 | respetada | 1 |
| 3218 | respeta | 1 |
| 3219 | respecto | 1 |
| 3220 | resolución | 1 |
| 3221 | resisto | 1 |
| 3222 | resistir | 1 |
| 3223 | resistencias | 1 |
| 3224 | residencia | 1 |
| 3225 | reseña | 1 |
| 3226 | rescataré | 1 |
| 3227 | rescatar | 1 |
| 3228 | requebrando | 1 |
| 3229 | repugnancia | 1 |
| 3230 | reproducción | 1 |
| 3231 | representó | 1 |
| 3232 | representamos | 1 |
| 3233 | reprehender | 1 |
| 3234 | reposo | 1 |
| 3235 | repórtola | 1 |
| 3236 | repliques | 1 |
| 3237 | repliquéis | 1 |
| 3238 | replique | 1 |
| 3239 | replicar | 1 |
| 3240 | replicáis | 1 |
| 3241 | réplica | 1 |
| 3242 | repiten | 1 |
| 3243 | repite | 1 |
| 3244 | repetidas | 1 |
| 3245 | repentimiento | 1 |
| 3246 | reparte | 1 |
| 3247 | repares | 1 |
| 3248 | reparas | 1 |
| 3249 | renueves | 1 |
| 3250 | renta | 1 |
| 3251 | renovar | 1 |
| 3252 | rennert | 1 |
| 3253 | rendir | 1 |
| 3254 | rendido | 1 |
| 3255 | rendida | 1 |
| 3256 | renascence | 1 |
| 3257 | remonta | 1 |
| 3258 | remón | 1 |
| 3259 | remítome | 1 |
| 3260 | reminiscencias | 1 |
| 3261 | remienda | 1 |
| 3262 | remedie | 1 |
| 3263 | remediarlo | 1 |
| 3264 | remediadlo | 1 |
| 3265 | remedia | 1 |
| 3266 | reliquia | 1 |
| 3267 | relincharán | 1 |
| 3268 | religiosos | 1 |
| 3269 | relato | 1 |
| 3270 | relativo | 1 |
| 3271 | reír | 1 |
| 3272 | reinar | 1 |
| 3273 | reinado | 1 |
| 3274 | reimprimirlo | 1 |
| 3275 | reimpresiones | 1 |
| 3276 | regocijad | 1 |
| 3277 | reglas | 1 |
| 3278 | registran | 1 |
| 3279 | régimen | 1 |
| 3280 | regido | 1 |
| 3281 | regales | 1 |
| 3282 | regalarte | 1 |
| 3283 | regalaré | 1 |
| 3284 | regalalle | 1 |
| 3285 | regalalla | 1 |
| 3286 | regalado | 1 |
| 3287 | regalada | 1 |
| 3288 | regala | 1 |
| 3289 | refrán | 1 |
| 3290 | reforzar | 1 |
| 3291 | refirieran | 1 |
| 3292 | refiriera | 1 |
| 3293 | refieren | 1 |
| 3294 | refiérela | 1 |
| 3295 | redondillas | 1 |
| 3296 | redactándolo | 1 |
| 3297 | redacción | 1 |
| 3298 | recuesta | 1 |
| 3299 | recto | 1 |
| 3300 | recta | 1 |
| 3301 | recordar | 1 |
| 3302 | recordando | 1 |
| 3303 | recordamos | 1 |
| 3304 | reconocer | 1 |
| 3305 | reconcilia | 1 |
| 3306 | recogido | 1 |
| 3307 | reclamar | 1 |
| 3308 | recio | 1 |
| 3309 | recién | 1 |
| 3310 | recibir | 1 |
| 3311 | recibiendo | 1 |
| 3312 | reciben | 1 |
| 3313 | recibe | 1 |
| 3314 | recibas | 1 |
| 3315 | reciba | 1 |
| 3316 | rechazado | 1 |
| 3317 | recelos | 1 |
| 3318 | recelo | 1 |
| 3319 | recebido | 1 |
| 3320 | recebida | 1 |
| 3321 | recato | 1 |
| 3322 | rebozo | 1 |
| 3323 | rebozada | 1 |
| 3324 | rebaños | 1 |
| 3325 | reales | 1 |
| 3326 | razon | 1 |
| 3327 | rayas | 1 |
| 3328 | rayados | 1 |
| 3329 | rato | 1 |
| 3330 | raso | 1 |
| 3331 | rasguño | 1 |
| 3332 | rasgo | 1 |
| 3333 | raros | 1 |
| 3334 | rápida | 1 |
| 3335 | rapaz | 1 |
| 3336 | rapaces | 1 |
| 3337 | rapacejos | 1 |
| 3338 | ramón | 1 |
| 3339 | ramiro | 1 |
| 3340 | ración | 1 |
| 3341 | rabiando | 1 |
| 3342 | rabia | 1 |
| 3343 | quizá | 1 |
| 3344 | quixera | 1 |
| 3345 | quite | 1 |
| 3346 | quitaste | 1 |
| 3347 | quitas | 1 |
| 3348 | quitara | 1 |
| 3349 | quitándole | 1 |
| 3350 | quitan | 1 |
| 3351 | quitalle | 1 |
| 3352 | quitadle | 1 |
| 3353 | quisiesse | 1 |
| 3354 | quisiese | 1 |
| 3355 | quisiéronse | 1 |
| 3356 | quisieron | 1 |
| 3357 | quisieres | 1 |
| 3358 | quisieras | 1 |
| 3359 | quisierais | 1 |
| 3360 | quisierades | 1 |
| 3361 | quinientos | 1 |
| 3362 | quilate | 1 |
| 3363 | quijo | 1 |
| 3364 | quij | 1 |
| 3365 | quietud | 1 |
| 3366 | quiérole | 1 |
| 3367 | quiéreslo | 1 |
| 3368 | quiérelo | 1 |
| 3369 | quieras | 1 |
| 3370 | quieran | 1 |
| 3371 | quiebre | 1 |
| 3372 | quiebra | 1 |
| 3373 | querría | 1 |
| 3374 | queriendo | 1 |
| 3375 | queridos | 1 |
| 3376 | querías | 1 |
| 3377 | quería | 1 |
| 3378 | quererte | 1 |
| 3379 | quereros | 1 |
| 3380 | quererme | 1 |
| 3381 | querémoslas | 1 |
| 3382 | querelloso | 1 |
| 3383 | querellas | 1 |
| 3384 | querellar | 1 |
| 3385 | querellado | 1 |
| 3386 | queredme | 1 |
| 3387 | quepa | 1 |
| 3388 | quemas | 1 |
| 3389 | quemarse | 1 |
| 3390 | quemaría | 1 |
| 3391 | quemar | 1 |
| 3392 | quel | 1 |
| 3393 | quejarte | 1 |
| 3394 | quejarme | 1 |
| 3395 | quejara | 1 |
| 3396 | quedos | 1 |
| 3397 | quedaros | 1 |
| 3398 | quedaron | 1 |
| 3399 | quedaráse | 1 |
| 3400 | quedará | 1 |
| 3401 | quedaos | 1 |
| 3402 | quedando | 1 |
| 3403 | quedaba | 1 |
| 3404 | quebraste | 1 |
| 3405 | quebrarla | 1 |
| 3406 | quebrar | 1 |
| 3407 | qualis | 1 |
| 3408 | quales | 1 |
| 3409 | pusilánimo | 1 |
| 3410 | pusiéronlos | 1 |
| 3411 | puse | 1 |
| 3412 | puros | 1 |
| 3413 | pura | 1 |
| 3414 | puntuación | 1 |
| 3415 | puntas | 1 |
| 3416 | puntadas | 1 |
| 3417 | pulgar | 1 |
| 3418 | puente | 1 |
| 3419 | puebro | 1 |
| 3420 | pudiese | 1 |
| 3421 | pudiere | 1 |
| 3422 | pudiérades | 1 |
| 3423 | pucheros | 1 |
| 3424 | publique | 1 |
| 3425 | publicación | 1 |
| 3426 | pruebo | 1 |
| 3427 | pruebe | 1 |
| 3428 | pruebas | 1 |
| 3429 | prudencio | 1 |
| 3430 | provisionalmente | 1 |
| 3431 | protejo | 1 |
| 3432 | protector | 1 |
| 3433 | próspera | 1 |
| 3434 | propuso | 1 |
| 3435 | proposiciones | 1 |
| 3436 | proporcionado | 1 |
| 3437 | propone | 1 |
| 3438 | propicia | 1 |
| 3439 | pronunciar | 1 |
| 3440 | pronuncia | 1 |
| 3441 | prometistes | 1 |
| 3442 | prometió | 1 |
| 3443 | prometida | 1 |
| 3444 | prométela | 1 |
| 3445 | prometéisme | 1 |
| 3446 | promesas | 1 |
| 3447 | prólogo | 1 |
| 3448 | prolijos | 1 |
| 3449 | profunda | 1 |
| 3450 | profesando | 1 |
| 3451 | pródigo | 1 |
| 3452 | prodigiosa | 1 |
| 3453 | procuro | 1 |
| 3454 | procuras | 1 |
| 3455 | procurador | 1 |
| 3456 | proclamado | 1 |
| 3457 | proclamaba | 1 |
| 3458 | proceso | 1 |
| 3459 | procedió | 1 |
| 3460 | proceder | 1 |
| 3461 | probreza | 1 |
| 3462 | probó | 1 |
| 3463 | probaré | 1 |
| 3464 | probado | 1 |
| 3465 | privilegios | 1 |
| 3466 | privilegio | 1 |
| 3467 | principios | 1 |
| 3468 | príncipes | 1 |
| 3469 | primorosa | 1 |
| 3470 | primitiva | 1 |
| 3471 | primeros | 1 |
| 3472 | primeras | 1 |
| 3473 | preyto | 1 |
| 3474 | previene | 1 |
| 3475 | prevenirme | 1 |
| 3476 | prevenid | 1 |
| 3477 | prevengamos | 1 |
| 3478 | prevención | 1 |
| 3479 | preux | 1 |
| 3480 | pretensión | 1 |
| 3481 | pretendo | 1 |
| 3482 | pretendientes | 1 |
| 3483 | pretendido | 1 |
| 3484 | pretendía | 1 |
| 3485 | pretenden | 1 |
| 3486 | pretenda | 1 |
| 3487 | presuroso | 1 |
| 3488 | presunciones | 1 |
| 3489 | presumís | 1 |
| 3490 | presumirá | 1 |
| 3491 | presumir | 1 |
| 3492 | presumas | 1 |
| 3493 | prestó | 1 |
| 3494 | prestigio | 1 |
| 3495 | prestada | 1 |
| 3496 | presso | 1 |
| 3497 | presidio | 1 |
| 3498 | presentes | 1 |
| 3499 | preséntase | 1 |
| 3500 | presentaron | 1 |
| 3501 | presentar | 1 |
| 3502 | presentan | 1 |
| 3503 | presenta | 1 |
| 3504 | prenderme | 1 |
| 3505 | prenderlo | 1 |
| 3506 | prendas | 1 |
| 3507 | prendada | 1 |
| 3508 | preliminares | 1 |
| 3509 | pregunto | 1 |
| 3510 | preguntéle | 1 |
| 3511 | preguntas | 1 |
| 3512 | preguntaré | 1 |
| 3513 | pregonarlos | 1 |
| 3514 | predicaba | 1 |
| 3515 | preciosa | 1 |
| 3516 | precio | 1 |
| 3517 | preciados | 1 |
| 3518 | precia | 1 |
| 3519 | preceptos | 1 |
| 3520 | precediera | 1 |
| 3521 | prado | 1 |
| 3522 | potro | 1 |
| 3523 | postrero | 1 |
| 3524 | postrer | 1 |
| 3525 | posteriori | 1 |
| 3526 | posteriores | 1 |
| 3527 | postas | 1 |
| 3528 | posta | 1 |
| 3529 | posee | 1 |
| 3530 | posada | 1 |
| 3531 | porto | 1 |
| 3532 | portillo | 1 |
| 3533 | porteros | 1 |
| 3534 | portero | 1 |
| 3535 | porte | 1 |
| 3536 | portal | 1 |
| 3537 | porras | 1 |
| 3538 | porquerizo | 1 |
| 3539 | poridad | 1 |
| 3540 | porfiar | 1 |
| 3541 | popular | 1 |
| 3542 | poniente | 1 |
| 3543 | poniéndomela | 1 |
| 3544 | poniendo | 1 |
| 3545 | ponías | 1 |
| 3546 | póngome | 1 |
| 3547 | póngase | 1 |
| 3548 | pongan | 1 |
| 3549 | ponga | 1 |
| 3550 | pónese | 1 |
| 3551 | pones | 1 |
| 3552 | ponerte | 1 |
| 3553 | ponello | 1 |
| 3554 | pondría | 1 |
| 3555 | pondrémela | 1 |
| 3556 | pondréme | 1 |
| 3557 | pondréla | 1 |
| 3558 | pondré | 1 |
| 3559 | pondrán | 1 |
| 3560 | ponce | 1 |
| 3561 | polvo | 1 |
| 3562 | poético | 1 |
| 3563 | poema | 1 |
| 3564 | podremos | 1 |
| 3565 | podrásme | 1 |
| 3566 | podrán | 1 |
| 3567 | podíen | 1 |
| 3568 | poderlas | 1 |
| 3569 | pocos | 1 |
| 3570 | poblado | 1 |
| 3571 | plutarco | 1 |
| 3572 | pluma | 1 |
| 3573 | pluguiera | 1 |
| 3574 | plena | 1 |
| 3575 | pleitos | 1 |
| 3576 | plazuela | 1 |
| 3577 | plazas | 1 |
| 3578 | plática | 1 |
| 3579 | planta | 1 |
| 3580 | plano | 1 |
| 3581 | placer | 1 |
| 3582 | pisar | 1 |
| 3583 | pintamos | 1 |
| 3584 | pintada | 1 |
| 3585 | pimenteles | 1 |
| 3586 | pierna | 1 |
| 3587 | pierda | 1 |
| 3588 | piensos | 1 |
| 3589 | piensan | 1 |
| 3590 | pidiendole | 1 |
| 3591 | pides | 1 |
| 3592 | píctima | 1 |
| 3593 | picazos | 1 |
| 3594 | picaza | 1 |
| 3595 | pícaros | 1 |
| 3596 | pica | 1 |
| 3597 | piadosa | 1 |
| 3598 | philologie | 1 |
| 3599 | pessó | 1 |
| 3600 | peso | 1 |
| 3601 | pesebre | 1 |
| 3602 | pese | 1 |
| 3603 | pescuezo | 1 |
| 3604 | pescudar | 1 |
| 3605 | pesares | 1 |
| 3606 | pertinaz | 1 |
| 3607 | persuades | 1 |
| 3608 | persigue | 1 |
| 3609 | perseguirlas | 1 |
| 3610 | perno | 1 |
| 3611 | permitirá | 1 |
| 3612 | permíteme | 1 |
| 3613 | permite | 1 |
| 3614 | permitas | 1 |
| 3615 | permitáis | 1 |
| 3616 | perjuro | 1 |
| 3617 | perfeción | 1 |
| 3618 | peregrinos | 1 |
| 3619 | peregrina | 1 |
| 3620 | perdurado | 1 |
| 3621 | perdonéis | 1 |
| 3622 | perdonar | 1 |
| 3623 | perdonadme | 1 |
| 3624 | perdonad | 1 |
| 3625 | perdón | 1 |
| 3626 | perdistes | 1 |
| 3627 | perdiste | 1 |
| 3628 | perdió | 1 |
| 3629 | perdieras | 1 |
| 3630 | perdierades | 1 |
| 3631 | perdiendo | 1 |
| 3632 | perdidos | 1 |
| 3633 | pérdida | 1 |
| 3634 | perdida | 1 |
| 3635 | perderte | 1 |
| 3636 | perderos | 1 |
| 3637 | perdéis | 1 |
| 3638 | percibir | 1 |
| 3639 | pequeños | 1 |
| 3640 | pequeña | 1 |
| 3641 | peor | 1 |
| 3642 | peones | 1 |
| 3643 | peñasco | 1 |
| 3644 | peña | 1 |
| 3645 | pensaría | 1 |
| 3646 | pensaré | 1 |
| 3647 | pensando | 1 |
| 3648 | pensamientos | 1 |
| 3649 | pensallo | 1 |
| 3650 | peno | 1 |
| 3651 | penetra | 1 |
| 3652 | penes | 1 |
| 3653 | pelota | 1 |
| 3654 | peligrosas | 1 |
| 3655 | peligrosa | 1 |
| 3656 | pelean | 1 |
| 3657 | pelado | 1 |
| 3658 | pegó | 1 |
| 3659 | pediros | 1 |
| 3660 | pedirles | 1 |
| 3661 | pediréte | 1 |
| 3662 | pediré | 1 |
| 3663 | pedirás | 1 |
| 3664 | pedido | 1 |
| 3665 | pedí | 1 |
| 3666 | pedazos | 1 |
| 3667 | pecilga | 1 |
| 3668 | pechos | 1 |
| 3669 | pecheros | 1 |
| 3670 | peces | 1 |
| 3671 | pecador | 1 |
| 3672 | pavillo | 1 |
| 3673 | paveses | 1 |
| 3674 | paternidad | 1 |
| 3675 | pater | 1 |
| 3676 | pastores | 1 |
| 3677 | passara | 1 |
| 3678 | pasea | 1 |
| 3679 | pasas | 1 |
| 3680 | pasarla | 1 |
| 3681 | pasaréte | 1 |
| 3682 | pasará | 1 |
| 3683 | pasajes | 1 |
| 3684 | pasada | 1 |
| 3685 | pasabas | 1 |
| 3686 | pasábamos | 1 |
| 3687 | parto | 1 |
| 3688 | partiste | 1 |
| 3689 | partirme | 1 |
| 3690 | partiremos | 1 |
| 3691 | partiese | 1 |
| 3692 | partiendo | 1 |
| 3693 | partid | 1 |
| 3694 | particularidad | 1 |
| 3695 | partas | 1 |
| 3696 | partan | 1 |
| 3697 | partamos | 1 |
| 3698 | parta | 1 |
| 3699 | párrafos | 1 |
| 3700 | paróse | 1 |
| 3701 | parieran | 1 |
| 3702 | parientes | 1 |
| 3703 | pariente | 1 |
| 3704 | parezca | 1 |
| 3705 | parésçeme | 1 |
| 3706 | paresce | 1 |
| 3707 | pares | 1 |
| 3708 | paréis | 1 |
| 3709 | pared | 1 |
| 3710 | pareciera | 1 |
| 3711 | parecía | 1 |
| 3712 | pareceré | 1 |
| 3713 | pareçeme | 1 |
| 3714 | pareçe | 1 |
| 3715 | pardo | 1 |
| 3716 | paralelo | 1 |
| 3717 | parado | 1 |
| 3718 | parabién | 1 |
| 3719 | paños | 1 |
| 3720 | paño | 1 |
| 3721 | pámpanos | 1 |
| 3722 | paloma | 1 |
| 3723 | palmas | 1 |
| 3724 | palma | 1 |
| 3725 | pálidas | 1 |
| 3726 | paladión | 1 |
| 3727 | paladines | 1 |
| 3728 | pajizo | 1 |
| 3729 | pajes | 1 |
| 3730 | pagues | 1 |
| 3731 | pagúele | 1 |
| 3732 | pagos | 1 |
| 3733 | páginas | 1 |
| 3734 | pagan | 1 |
| 3735 | pagados | 1 |
| 3736 | pagada | 1 |
| 3737 | padecer | 1 |
| 3738 | pachecos | 1 |
| 3739 | paces | 1 |
| 3740 | pablo | 1 |
| 3741 | oyete | 1 |
| 3742 | oyeron | 1 |
| 3743 | óyeme | 1 |
| 3744 | oyeme | 1 |
| 3745 | oviesse | 1 |
| 3746 | ovieron | 1 |
| 3747 | ovid | 1 |
| 3748 | otrosí | 1 |
| 3749 | ostende | 1 |
| 3750 | oso | 1 |
| 3751 | osaré | 1 |
| 3752 | osará | 1 |
| 3753 | osar | 1 |
| 3754 | osado | 1 |
| 3755 | oropéndola | 1 |
| 3756 | orillas | 1 |
| 3757 | originales | 1 |
| 3758 | orgulloso | 1 |
| 3759 | ordinaria | 1 |
| 3760 | ordenes | 1 |
| 3761 | orden | 1 |
| 3762 | oráculo | 1 |
| 3763 | oración | 1 |
| 3764 | opúsculo | 1 |
| 3765 | optativa | 1 |
| 3766 | oprimido | 1 |
| 3767 | oprimida | 1 |
| 3768 | oponerse | 1 |
| 3769 | opina | 1 |
| 3770 | oocampo | 1 |
| 3771 | onceno | 1 |
| 3772 | omiten | 1 |
| 3773 | olvidos | 1 |
| 3774 | olvides | 1 |
| 3775 | olvida | 1 |
| 3776 | olorosas | 1 |
| 3777 | olorosa | 1 |
| 3778 | olor | 1 |
| 3779 | olmo | 1 |
| 3780 | olla | 1 |
| 3781 | olía | 1 |
| 3782 | olalla | 1 |
| 3783 | oíste | 1 |
| 3784 | oirán | 1 |
| 3785 | oídme | 1 |
| 3786 | ofrecí | 1 |
| 3787 | oficios | 1 |
| 3788 | ofensas | 1 |
| 3789 | ofendí | 1 |
| 3790 | ofenderte | 1 |
| 3791 | ofender | 1 |
| 3792 | odio | 1 |
| 3793 | ocurrido | 1 |
| 3794 | ocuparála | 1 |
| 3795 | ocupada | 1 |
| 3796 | octavas | 1 |
| 3797 | octava | 1 |
| 3798 | ochenta | 1 |
| 3799 | ocerin | 1 |
| 3800 | océano | 1 |
| 3801 | oceano | 1 |
| 3802 | ocasiones | 1 |
| 3803 | obstáculo | 1 |
| 3804 | observó | 1 |
| 3805 | observada | 1 |
| 3806 | observaciones | 1 |
| 3807 | obrita | 1 |
| 3808 | obligó | 1 |
| 3809 | obligo | 1 |
| 3810 | obligaron | 1 |
| 3811 | obligando | 1 |
| 3812 | obligados | 1 |
| 3813 | obligada | 1 |
| 3814 | obligaba | 1 |
| 3815 | obispo | 1 |
| 3816 | obedezco | 1 |
| 3817 | obedezca | 1 |
| 3818 | obedecer | 1 |
| 3819 | obedecelle | 1 |
| 3820 | núñez | 1 |
| 3821 | numerosísimos | 1 |
| 3822 | numerales | 1 |
| 3823 | nuevos | 1 |
| 3824 | nuevam | 1 |
| 3825 | novios | 1 |
| 3826 | novio | 1 |
| 3827 | noviazgo | 1 |
| 3828 | novedades | 1 |
| 3829 | notó | 1 |
| 3830 | noticia | 1 |
| 3831 | nótese | 1 |
| 3832 | note | 1 |
| 3833 | norte | 1 |
| 3834 | nombradía | 1 |
| 3835 | noches | 1 |
| 3836 | nobre | 1 |
| 3837 | nobiliario | 1 |
| 3838 | nietos | 1 |
| 3839 | nieto | 1 |
| 3840 | nevado | 1 |
| 3841 | neuf | 1 |
| 3842 | negros | 1 |
| 3843 | negocio | 1 |
| 3844 | negociara | 1 |
| 3845 | negociar | 1 |
| 3846 | negocia | 1 |
| 3847 | negativa | 1 |
| 3848 | negará | 1 |
| 3849 | negar | 1 |
| 3850 | negándose | 1 |
| 3851 | negamos | 1 |
| 3852 | negaba | 1 |
| 3853 | necios | 1 |
| 3854 | necesario | 1 |
| 3855 | naves | 1 |
| 3856 | naturaleza | 1 |
| 3857 | narices | 1 |
| 3858 | narbáez | 1 |
| 3859 | nado | 1 |
| 3860 | naciones | 1 |
| 3861 | nacional | 1 |
| 3862 | nacer | 1 |
| 3863 | nacen | 1 |
| 3864 | nabos | 1 |
| 3865 | n | 1 |
| 3866 | myrrha | 1 |
| 3867 | muzas | 1 |
| 3868 | muslo | 1 |
| 3869 | músicos | 1 |
| 3870 | música | 1 |
| 3871 | muros | 1 |
| 3872 | murmuró | 1 |
| 3873 | müller | 1 |
| 3874 | mula | 1 |
| 3875 | mueven | 1 |
| 3876 | mueve | 1 |
| 3877 | muévaos | 1 |
| 3878 | mueva | 1 |
| 3879 | muertes | 1 |
| 3880 | muerde | 1 |
| 3881 | mueran | 1 |
| 3882 | muera | 1 |
| 3883 | mudas | 1 |
| 3884 | mudarse | 1 |
| 3885 | mudar | 1 |
| 3886 | mudanza | 1 |
| 3887 | muda | 1 |
| 3888 | moverte | 1 |
| 3889 | moveros | 1 |
| 3890 | motivos | 1 |
| 3891 | motes | 1 |
| 3892 | mostrase | 1 |
| 3893 | mostrar | 1 |
| 3894 | mostrando | 1 |
| 3895 | mostráis | 1 |
| 3896 | mostraba | 1 |
| 3897 | mortífero | 1 |
| 3898 | moriscas | 1 |
| 3899 | morillo | 1 |
| 3900 | morganero | 1 |
| 3901 | morava | 1 |
| 3902 | moras | 1 |
| 3903 | montañas | 1 |
| 3904 | montaña | 1 |
| 3905 | monopolizadores | 1 |
| 3906 | monje | 1 |
| 3907 | monesterio | 1 |
| 3908 | moneda | 1 |
| 3909 | monarquía | 1 |
| 3910 | monarca | 1 |
| 3911 | mollera | 1 |
| 3912 | molins | 1 |
| 3913 | molido | 1 |
| 3914 | molestar | 1 |
| 3915 | moisén | 1 |
| 3916 | mohosa | 1 |
| 3917 | mohíno | 1 |
| 3918 | modificación | 1 |
| 3919 | moderno | 1 |
| 3920 | moderna | 1 |
| 3921 | modelos | 1 |
| 3922 | mochilas | 1 |
| 3923 | mochila | 1 |
| 3924 | mocedades | 1 |
| 3925 | mito | 1 |
| 3926 | miserable | 1 |
| 3927 | miscelánea | 1 |
| 3928 | miró | 1 |
| 3929 | miro | 1 |
| 3930 | miren | 1 |
| 3931 | miréla | 1 |
| 3932 | miralla | 1 |
| 3933 | miráis | 1 |
| 3934 | miraban | 1 |
| 3935 | mio | 1 |
| 3936 | minoría | 1 |
| 3937 | milicia | 1 |
| 3938 | milán | 1 |
| 3939 | mijor | 1 |
| 3940 | miguel | 1 |
| 3941 | mies | 1 |
| 3942 | miento | 1 |
| 3943 | mientes | 1 |
| 3944 | mido | 1 |
| 3945 | mides | 1 |
| 3946 | micaela | 1 |
| 3947 | mezcla | 1 |
| 3948 | meyer | 1 |
| 3949 | mexía | 1 |
| 3950 | métrica | 1 |
| 3951 | metieron | 1 |
| 3952 | meter | 1 |
| 3953 | mete | 1 |
| 3954 | metamorfosis | 1 |
| 3955 | mesón | 1 |
| 3956 | meses | 1 |
| 3957 | mesas | 1 |
| 3958 | mesa | 1 |
| 3959 | méritos | 1 |
| 3960 | mereces | 1 |
| 3961 | merecer | 1 |
| 3962 | merecéis | 1 |
| 3963 | mercaderes | 1 |
| 3964 | mercader | 1 |
| 3965 | menudencias | 1 |
| 3966 | mentecato | 1 |
| 3967 | menosprecio | 1 |
| 3968 | menor | 1 |
| 3969 | mengua | 1 |
| 3970 | mendozas | 1 |
| 3971 | mención | 1 |
| 3972 | memorias | 1 |
| 3973 | memoriales | 1 |
| 3974 | melindres | 1 |
| 3975 | melancólico | 1 |
| 3976 | mejores | 1 |
| 3977 | mejorada | 1 |
| 3978 | mediodía | 1 |
| 3979 | medinaceli | 1 |
| 3980 | medina | 1 |
| 3981 | medievales | 1 |
| 3982 | medida | 1 |
| 3983 | médico | 1 |
| 3984 | medicina | 1 |
| 3985 | mediados | 1 |
| 3986 | mdccxcii | 1 |
| 3987 | mcmxx | 1 |
| 3988 | mazas | 1 |
| 3989 | mayo | 1 |
| 3990 | mayer | 1 |
| 3991 | mató | 1 |
| 3992 | materia | 1 |
| 3993 | matarse | 1 |
| 3994 | mataron | 1 |
| 3995 | matarnos | 1 |
| 3996 | matarla | 1 |
| 3997 | mataríe | 1 |
| 3998 | mataréme | 1 |
| 3999 | mataré | 1 |
| 4000 | matarás | 1 |
| 4001 | matan | 1 |
| 4002 | matadora | 1 |
| 4003 | matadme | 1 |
| 4004 | matad | 1 |
| 4005 | masalanca | 1 |
| 4006 | martín | 1 |
| 4007 | martin | 1 |
| 4008 | martillos | 1 |
| 4009 | martes | 1 |
| 4010 | martelo | 1 |
| 4011 | marsilios | 1 |
| 4012 | marruecos | 1 |
| 4013 | marranos | 1 |
| 4014 | mármol | 1 |
| 4015 | marlota | 1 |
| 4016 | maridos | 1 |
| 4017 | mariana | 1 |
| 4018 | marfuz | 1 |
| 4019 | mares | 1 |
| 4020 | marcelino | 1 |
| 4021 | marcelica | 1 |
| 4022 | máquina | 1 |
| 4023 | mañas | 1 |
| 4024 | manuscrito | 1 |
| 4025 | manuel | 1 |
| 4026 | mantua | 1 |
| 4027 | mantiene | 1 |
| 4028 | manifiestas | 1 |
| 4029 | mandóme | 1 |
| 4030 | mandoles | 1 |
| 4031 | mandóle | 1 |
| 4032 | mandes | 1 |
| 4033 | mandéis | 1 |
| 4034 | mandato | 1 |
| 4035 | mandan | 1 |
| 4036 | mandado | 1 |
| 4037 | mandadlos | 1 |
| 4038 | mandadero | 1 |
| 4039 | manche | 1 |
| 4040 | manchar | 1 |
| 4041 | mancha | 1 |
| 4042 | mançanedo | 1 |
| 4043 | maltratas | 1 |
| 4044 | maltratada | 1 |
| 4045 | maltrata | 1 |
| 4046 | malos | 1 |
| 4047 | malogrados | 1 |
| 4048 | malla | 1 |
| 4049 | malilla | 1 |
| 4050 | malicioso | 1 |
| 4051 | malicias | 1 |
| 4052 | malicia | 1 |
| 4053 | maletas | 1 |
| 4054 | maleta | 1 |
| 4055 | maldonado | 1 |
| 4056 | maldito | 1 |
| 4057 | maldiciente | 1 |
| 4058 | maldad | 1 |
| 4059 | majadero | 1 |
| 4060 | mahométicos | 1 |
| 4061 | magno | 1 |
| 4062 | mágica | 1 |
| 4063 | maestros | 1 |
| 4064 | maestro | 1 |
| 4065 | maeso | 1 |
| 4066 | madrina | 1 |
| 4067 | madrastra | 1 |
| 4068 | macedón | 1 |
| 4069 | macario | 1 |
| 4070 | macabeo | 1 |
| 4071 | lxxvi | 1 |
| 4072 | lxviii | 1 |
| 4073 | luzgan | 1 |
| 4074 | lupercio | 1 |
| 4075 | lumpia | 1 |
| 4076 | lumbre | 1 |
| 4077 | lujanes | 1 |
| 4078 | luján | 1 |
| 4079 | ludovico | 1 |
| 4080 | lucrecia | 1 |
| 4081 | lucinda | 1 |
| 4082 | lucero | 1 |
| 4083 | lora | 1 |
| 4084 | loores | 1 |
| 4085 | logroño | 1 |
| 4086 | logre | 1 |
| 4087 | lograrán | 1 |
| 4088 | logrado | 1 |
| 4089 | lograda | 1 |
| 4090 | locos | 1 |
| 4091 | loca | 1 |
| 4092 | lloroso | 1 |
| 4093 | lloró | 1 |
| 4094 | llores | 1 |
| 4095 | lloré | 1 |
| 4096 | llorava | 1 |
| 4097 | lloras | 1 |
| 4098 | llorando | 1 |
| 4099 | lloramos | 1 |
| 4100 | llorado | 1 |
| 4101 | lloraba | 1 |
| 4102 | llevóme | 1 |
| 4103 | lleves | 1 |
| 4104 | llevéis | 1 |
| 4105 | llevé | 1 |
| 4106 | llevase | 1 |
| 4107 | llevas | 1 |
| 4108 | llevarse | 1 |
| 4109 | llevarássela | 1 |
| 4110 | llevará | 1 |
| 4111 | llevara | 1 |
| 4112 | llévanla | 1 |
| 4113 | llévame | 1 |
| 4114 | llevallos | 1 |
| 4115 | llévala | 1 |
| 4116 | llegastes | 1 |
| 4117 | llegaste | 1 |
| 4118 | llegarte | 1 |
| 4119 | llegare | 1 |
| 4120 | llegando | 1 |
| 4121 | llegadme | 1 |
| 4122 | llave | 1 |
| 4123 | llantos | 1 |
| 4124 | llamo | 1 |
| 4125 | llamen | 1 |
| 4126 | llamemos | 1 |
| 4127 | llamava | 1 |
| 4128 | llamas | 1 |
| 4129 | llamaron | 1 |
| 4130 | llamarme | 1 |
| 4131 | llamaremos | 1 |
| 4132 | llamarásme | 1 |
| 4133 | llamados | 1 |
| 4134 | llamada | 1 |
| 4135 | llamábase | 1 |
| 4136 | ll | 1 |
| 4137 | liviandad | 1 |
| 4138 | literatura | 1 |
| 4139 | literario | 1 |
| 4140 | literaria | 1 |
| 4141 | lista | 1 |
| 4142 | liríope | 1 |
| 4143 | lirio | 1 |
| 4144 | linterna | 1 |
| 4145 | líneas | 1 |
| 4146 | lindos | 1 |
| 4147 | linda | 1 |
| 4148 | linaloel | 1 |
| 4149 | linajes | 1 |
| 4150 | limpia | 1 |
| 4151 | ligeros | 1 |
| 4152 | ligera | 1 |
| 4153 | lienzo | 1 |
| 4154 | liebre | 1 |
| 4155 | lición | 1 |
| 4156 | librería | 1 |
| 4157 | libranza | 1 |
| 4158 | libralla | 1 |
| 4159 | liberalidad | 1 |
| 4160 | liberales | 1 |
| 4161 | lib | 1 |
| 4162 | leyóla | 1 |
| 4163 | leyenda | 1 |
| 4164 | levantó | 1 |
| 4165 | levántese | 1 |
| 4166 | levantaron | 1 |
| 4167 | levanta | 1 |
| 4168 | leonesismos | 1 |
| 4169 | lemos | 1 |
| 4170 | leivas | 1 |
| 4171 | leíla | 1 |
| 4172 | leído | 1 |
| 4173 | leída | 1 |
| 4174 | leguas | 1 |
| 4175 | legua | 1 |
| 4176 | legítimo | 1 |
| 4177 | legítima | 1 |
| 4178 | leerla | 1 |
| 4179 | leella | 1 |
| 4180 | leed | 1 |
| 4181 | lección | 1 |
| 4182 | lebrel | 1 |
| 4183 | lealtad | 1 |
| 4184 | lazos | 1 |
| 4185 | laves | 1 |
| 4186 | lavaste | 1 |
| 4187 | lavar | 1 |
| 4188 | lauro | 1 |
| 4189 | laurea | 1 |
| 4190 | lastimado | 1 |
| 4191 | lasos | 1 |
| 4192 | lascivas | 1 |
| 4193 | lasciva | 1 |
| 4194 | largamente | 1 |
| 4195 | laras | 1 |
| 4196 | lánzate | 1 |
| 4197 | lance | 1 |
| 4198 | lamentarme | 1 |
| 4199 | lamenta | 1 |
| 4200 | laguna | 1 |
| 4201 | lagrimas | 1 |
| 4202 | lágrima | 1 |
| 4203 | ladra | 1 |
| 4204 | labrar | 1 |
| 4205 | labradoras | 1 |
| 4206 | labradas | 1 |
| 4207 | labrada | 1 |
| 4208 | labra | 1 |
| 4209 | labio | 1 |
| 4210 | kyries | 1 |
| 4211 | juzgué | 1 |
| 4212 | juzgó | 1 |
| 4213 | juzgamos | 1 |
| 4214 | juventud | 1 |
| 4215 | juveniles | 1 |
| 4216 | justos | 1 |
| 4217 | justizia | 1 |
| 4218 | justifica | 1 |
| 4219 | justamente | 1 |
| 4220 | juró | 1 |
| 4221 | jures | 1 |
| 4222 | juras | 1 |
| 4223 | jurara | 1 |
| 4224 | jurar | 1 |
| 4225 | juráis | 1 |
| 4226 | juntó | 1 |
| 4227 | juntase | 1 |
| 4228 | juntas | 1 |
| 4229 | juntar | 1 |
| 4230 | juntan | 1 |
| 4231 | junta | 1 |
| 4232 | julián | 1 |
| 4233 | jugado | 1 |
| 4234 | jugada | 1 |
| 4235 | jueguen | 1 |
| 4236 | juegue | 1 |
| 4237 | juegos | 1 |
| 4238 | juegan | 1 |
| 4239 | jueces | 1 |
| 4240 | judas | 1 |
| 4241 | joya | 1 |
| 4242 | josué | 1 |
| 4243 | jorge | 1 |
| 4244 | jazmín | 1 |
| 4245 | jaspe | 1 |
| 4246 | jaén | 1 |
| 4247 | jabalí | 1 |
| 4248 | j | 1 |
| 4249 | iuan | 1 |
| 4250 | iremos | 1 |
| 4251 | irás | 1 |
| 4252 | invito | 1 |
| 4253 | inviolabilidad | 1 |
| 4254 | invictísimo | 1 |
| 4255 | inventores | 1 |
| 4256 | invenciones | 1 |
| 4257 | invencible | 1 |
| 4258 | introducida | 1 |
| 4259 | introduce | 1 |
| 4260 | intitulaba | 1 |
| 4261 | interrogativa | 1 |
| 4262 | interrogaciones | 1 |
| 4263 | interpretación | 1 |
| 4264 | interpreta | 1 |
| 4265 | interpolador | 1 |
| 4266 | interceder | 1 |
| 4267 | intercalada | 1 |
| 4268 | intercala | 1 |
| 4269 | intentos | 1 |
| 4270 | intentes | 1 |
| 4271 | intente | 1 |
| 4272 | intentas | 1 |
| 4273 | intentar | 1 |
| 4274 | intentalla | 1 |
| 4275 | instrumento | 1 |
| 4276 | institución | 1 |
| 4277 | inquisición | 1 |
| 4278 | inquietes | 1 |
| 4279 | inoportunamente | 1 |
| 4280 | inmortales | 1 |
| 4281 | inmenso | 1 |
| 4282 | inifica | 1 |
| 4283 | iniciándose | 1 |
| 4284 | inicial | 1 |
| 4285 | informaros | 1 |
| 4286 | informarásle | 1 |
| 4287 | informado | 1 |
| 4288 | influjo | 1 |
| 4289 | infinitos | 1 |
| 4290 | infinito | 1 |
| 4291 | infiel | 1 |
| 4292 | inferiores | 1 |
| 4293 | infélices | 1 |
| 4294 | infanzones | 1 |
| 4295 | infanta | 1 |
| 4296 | infamia | 1 |
| 4297 | infames | 1 |
| 4298 | inexperiencia | 1 |
| 4299 | industria | 1 |
| 4300 | induce | 1 |
| 4301 | indispuesta | 1 |
| 4302 | indio | 1 |
| 4303 | indinos | 1 |
| 4304 | indigne | 1 |
| 4305 | indicó | 1 |
| 4306 | indicación | 1 |
| 4307 | indias | 1 |
| 4308 | incorporó | 1 |
| 4309 | incorporarse | 1 |
| 4310 | inconstancia | 1 |
| 4311 | incluírla | 1 |
| 4312 | inclito | 1 |
| 4313 | inclinas | 1 |
| 4314 | inclinado | 1 |
| 4315 | inclinaban | 1 |
| 4316 | inclinaba | 1 |
| 4317 | inclemencia | 1 |
| 4318 | in | 1 |
| 4319 | imprimir | 1 |
| 4320 | imprimen | 1 |
| 4321 | impression | 1 |
| 4322 | impresión | 1 |
| 4323 | impresas | 1 |
| 4324 | impotente | 1 |
| 4325 | imposibles | 1 |
| 4326 | importunado | 1 |
| 4327 | importuna | 1 |
| 4328 | importante | 1 |
| 4329 | imperfecto | 1 |
| 4330 | imperfección | 1 |
| 4331 | impaciente | 1 |
| 4332 | imitáis | 1 |
| 4333 | imitadores | 1 |
| 4334 | imita | 1 |
| 4335 | imaginó | 1 |
| 4336 | imagino | 1 |
| 4337 | imaginé | 1 |
| 4338 | imaginara | 1 |
| 4339 | imaginando | 1 |
| 4340 | imaginallas | 1 |
| 4341 | imaginabas | 1 |
| 4342 | imaginaba | 1 |
| 4343 | imagen | 1 |
| 4344 | ilustrísimo | 1 |
| 4345 | illescas | 1 |
| 4346 | igualen | 1 |
| 4347 | iguale | 1 |
| 4348 | igualar | 1 |
| 4349 | iguala | 1 |
| 4350 | igreja | 1 |
| 4351 | ignoras | 1 |
| 4352 | ignorar | 1 |
| 4353 | ignorantes | 1 |
| 4354 | ignorante | 1 |
| 4355 | ignorado | 1 |
| 4356 | ignoradas | 1 |
| 4357 | iglesia | 1 |
| 4358 | idos | 1 |
| 4359 | idéntico | 1 |
| 4360 | idem | 1 |
| 4361 | íd | 1 |
| 4362 | huyera | 1 |
| 4363 | huyamos | 1 |
| 4364 | huya | 1 |
| 4365 | huviesse | 1 |
| 4366 | huvieron | 1 |
| 4367 | hurtábades | 1 |
| 4368 | humor | 1 |
| 4369 | humillar | 1 |
| 4370 | humillan | 1 |
| 4371 | humillado | 1 |
| 4372 | humilla | 1 |
| 4373 | humildes | 1 |
| 4374 | humanas | 1 |
| 4375 | humana | 1 |
| 4376 | huevos | 1 |
| 4377 | huesca | 1 |
| 4378 | huerza | 1 |
| 4379 | huente | 1 |
| 4380 | huelgo | 1 |
| 4381 | huelga | 1 |
| 4382 | huego | 1 |
| 4383 | hue | 1 |
| 4384 | hornachuelos | 1 |
| 4385 | hormiga | 1 |
| 4386 | horas | 1 |
| 4387 | honren | 1 |
| 4388 | honraste | 1 |
| 4389 | honraros | 1 |
| 4390 | honraremos | 1 |
| 4391 | honrara | 1 |
| 4392 | honores | 1 |
| 4393 | honesta | 1 |
| 4394 | homicida | 1 |
| 4395 | hollín | 1 |
| 4396 | holgárame | 1 |
| 4397 | hoguera | 1 |
| 4398 | hize | 1 |
| 4399 | histórico | 1 |
| 4400 | hipótesis | 1 |
| 4401 | hinchadas | 1 |
| 4402 | hinca | 1 |
| 4403 | hierros | 1 |
| 4404 | hidalguía | 1 |
| 4405 | hidalga | 1 |
| 4406 | hicieras | 1 |
| 4407 | hiciera | 1 |
| 4408 | hétor | 1 |
| 4409 | hesperia | 1 |
| 4410 | heroica | 1 |
| 4411 | héroe | 1 |
| 4412 | hernando | 1 |
| 4413 | hermosísimas | 1 |
| 4414 | hermosea | 1 |
| 4415 | herías | 1 |
| 4416 | herencia | 1 |
| 4417 | heredamiento | 1 |
| 4418 | heredáis | 1 |
| 4419 | heredades | 1 |
| 4420 | hérauts | 1 |
| 4421 | heme | 1 |
| 4422 | helado | 1 |
| 4423 | hebrero | 1 |
| 4424 | hebras | 1 |
| 4425 | hebilla | 1 |
| 4426 | hazme | 1 |
| 4427 | hazértela | 1 |
| 4428 | hazer | 1 |
| 4429 | hazén | 1 |
| 4430 | hazen | 1 |
| 4431 | hayáis | 1 |
| 4432 | harta | 1 |
| 4433 | harriero | 1 |
| 4434 | haremos | 1 |
| 4435 | harélo | 1 |
| 4436 | halles | 1 |
| 4437 | hallen | 1 |
| 4438 | hálleme | 1 |
| 4439 | halle | 1 |
| 4440 | hallaste | 1 |
| 4441 | hallase | 1 |
| 4442 | hallaron | 1 |
| 4443 | hallarme | 1 |
| 4444 | hallares | 1 |
| 4445 | hallaré | 1 |
| 4446 | hallaráse | 1 |
| 4447 | hallarán | 1 |
| 4448 | hallará | 1 |
| 4449 | hallara | 1 |
| 4450 | hallando | 1 |
| 4451 | hallamos | 1 |
| 4452 | hallados | 1 |
| 4453 | hagas | 1 |
| 4454 | hagan | 1 |
| 4455 | hado | 1 |
| 4456 | haceros | 1 |
| 4457 | hacenes | 1 |
| 4458 | hacémoslas | 1 |
| 4459 | hacellas | 1 |
| 4460 | hacella | 1 |
| 4461 | hacéis | 1 |
| 4462 | hacedles | 1 |
| 4463 | habro | 1 |
| 4464 | habréis | 1 |
| 4465 | habraré | 1 |
| 4466 | habrán | 1 |
| 4467 | habra | 1 |
| 4468 | hablóle | 1 |
| 4469 | hables | 1 |
| 4470 | hablé | 1 |
| 4471 | hable | 1 |
| 4472 | hablas | 1 |
| 4473 | hablarme | 1 |
| 4474 | hablarle | 1 |
| 4475 | hablarla | 1 |
| 4476 | hablaremos | 1 |
| 4477 | hablaréis | 1 |
| 4478 | hablare | 1 |
| 4479 | hablará | 1 |
| 4480 | hablan | 1 |
| 4481 | hablamos | 1 |
| 4482 | hablalle | 1 |
| 4483 | hablalla | 1 |
| 4484 | habláis | 1 |
| 4485 | habitualmente | 1 |
| 4486 | hábitos | 1 |
| 4487 | habilita | 1 |
| 4488 | habiéndole | 1 |
| 4489 | habiéndola | 1 |
| 4490 | habíais | 1 |
| 4491 | haberos | 1 |
| 4492 | haberla | 1 |
| 4493 | h | 1 |
| 4494 | guzmanes | 1 |
| 4495 | gutierre | 1 |
| 4496 | gutier | 1 |
| 4497 | gustos | 1 |
| 4498 | gustas | 1 |
| 4499 | gustáis | 1 |
| 4500 | gustado | 1 |
| 4501 | guissasen | 1 |
| 4502 | guijarros | 1 |
| 4503 | guíete | 1 |
| 4504 | guerrero | 1 |
| 4505 | guardemos | 1 |
| 4506 | guardaste | 1 |
| 4507 | guardamos | 1 |
| 4508 | guardalla | 1 |
| 4509 | guardada | 1 |
| 4510 | guardaba | 1 |
| 4511 | grund | 1 |
| 4512 | grosera | 1 |
| 4513 | griegos | 1 |
| 4514 | griego | 1 |
| 4515 | grebas | 1 |
| 4516 | grandioso | 1 |
| 4517 | grandezas | 1 |
| 4518 | grand | 1 |
| 4519 | grana | 1 |
| 4520 | gram | 1 |
| 4521 | grado | 1 |
| 4522 | graciosamente | 1 |
| 4523 | gozoso | 1 |
| 4524 | gozarse | 1 |
| 4525 | gozarme | 1 |
| 4526 | gozaras | 1 |
| 4527 | gózala | 1 |
| 4528 | gozada | 1 |
| 4529 | gozaban | 1 |
| 4530 | gótico | 1 |
| 4531 | gonzález | 1 |
| 4532 | gómez | 1 |
| 4533 | gomez | 1 |
| 4534 | gomeles | 1 |
| 4535 | gomel | 1 |
| 4536 | golías | 1 |
| 4537 | gola | 1 |
| 4538 | godofredo | 1 |
| 4539 | gobiernas | 1 |
| 4540 | gobierna | 1 |
| 4541 | gobernar | 1 |
| 4542 | girones | 1 |
| 4543 | gime | 1 |
| 4544 | germen | 1 |
| 4545 | george | 1 |
| 4546 | gentilhombre | 1 |
| 4547 | gentiles | 1 |
| 4548 | genoveses | 1 |
| 4549 | generosidad | 1 |
| 4550 | generosa | 1 |
| 4551 | generos | 1 |
| 4552 | gelo | 1 |
| 4553 | gazul | 1 |
| 4554 | gaste | 1 |
| 4555 | gasta | 1 |
| 4556 | garzón | 1 |
| 4557 | garrucha | 1 |
| 4558 | ganáronsela | 1 |
| 4559 | ganaron | 1 |
| 4560 | gallo | 1 |
| 4561 | gallinas | 1 |
| 4562 | gallina | 1 |
| 4563 | gallardos | 1 |
| 4564 | gallardía | 1 |
| 4565 | galgos | 1 |
| 4566 | galgo | 1 |
| 4567 | galgamentos | 1 |
| 4568 | gala | 1 |
| 4569 | gaitero | 1 |
| 4570 | gabriel | 1 |
| 4571 | fuy | 1 |
| 4572 | futuro | 1 |
| 4573 | furiosa | 1 |
| 4574 | für | 1 |
| 4575 | funestas | 1 |
| 4576 | fundo | 1 |
| 4577 | fundido | 1 |
| 4578 | fundada | 1 |
| 4579 | fulgores | 1 |
| 4580 | fuistes | 1 |
| 4581 | fuilo | 1 |
| 4582 | fuessen | 1 |
| 4583 | fuertemente | 1 |
| 4584 | fuere | 1 |
| 4585 | fueran | 1 |
| 4586 | fuéramos | 1 |
| 4587 | fuerais | 1 |
| 4588 | frutos | 1 |
| 4589 | frores | 1 |
| 4590 | fronterizo | 1 |
| 4591 | fronteras | 1 |
| 4592 | frontera | 1 |
| 4593 | frojaz | 1 |
| 4594 | fríos | 1 |
| 4595 | fría | 1 |
| 4596 | frey | 1 |
| 4597 | fresca | 1 |
| 4598 | frentes | 1 |
| 4599 | frenos | 1 |
| 4600 | frei | 1 |
| 4601 | fray | 1 |
| 4602 | franco | 1 |
| 4603 | francisco | 1 |
| 4604 | francia | 1 |
| 4605 | francesilla | 1 |
| 4606 | francés | 1 |
| 4607 | francas | 1 |
| 4608 | français | 1 |
| 4609 | franca | 1 |
| 4610 | fraco | 1 |
| 4611 | foyr | 1 |
| 4612 | forzosas | 1 |
| 4613 | forzosa | 1 |
| 4614 | forzarán | 1 |
| 4615 | forzara | 1 |
| 4616 | forzador | 1 |
| 4617 | fortaleza | 1 |
| 4618 | forméis | 1 |
| 4619 | formarla | 1 |
| 4620 | formados | 1 |
| 4621 | forasteros | 1 |
| 4622 | follaje | 1 |
| 4623 | folios | 1 |
| 4624 | folio | 1 |
| 4625 | fogoso | 1 |
| 4626 | florisel | 1 |
| 4627 | florian | 1 |
| 4628 | flor | 1 |
| 4629 | flébiles | 1 |
| 4630 | flandes | 1 |
| 4631 | flamencos | 1 |
| 4632 | flacas | 1 |
| 4633 | fiziesse | 1 |
| 4634 | fisgando | 1 |
| 4635 | fiscalización | 1 |
| 4636 | fiscal | 1 |
| 4637 | firmezas | 1 |
| 4638 | firmas | 1 |
| 4639 | fingiendo | 1 |
| 4640 | fingida | 1 |
| 4641 | finge | 1 |
| 4642 | finas | 1 |
| 4643 | final | 1 |
| 4644 | filos | 1 |
| 4645 | filológica | 1 |
| 4646 | filología | 1 |
| 4647 | filius | 1 |
| 4648 | filatería | 1 |
| 4649 | figurado | 1 |
| 4650 | figueroa | 1 |
| 4651 | fielmente | 1 |
| 4652 | fidelidad | 1 |
| 4653 | fías | 1 |
| 4654 | fiarse | 1 |
| 4655 | fiador | 1 |
| 4656 | fiad | 1 |
| 4657 | fía | 1 |
| 4658 | feziera | 1 |
| 4659 | feudal | 1 |
| 4660 | fertilidad | 1 |
| 4661 | fértil | 1 |
| 4662 | ferrant | 1 |
| 4663 | ferrando | 1 |
| 4664 | ferrandez | 1 |
| 4665 | ferrada | 1 |
| 4666 | fernández | 1 |
| 4667 | felicísimos | 1 |
| 4668 | felicísimo | 1 |
| 4669 | félices | 1 |
| 4670 | felice | 1 |
| 4671 | fecha | 1 |
| 4672 | febo | 1 |
| 4673 | fazíe | 1 |
| 4674 | farsalia | 1 |
| 4675 | farsa | 1 |
| 4676 | faro | 1 |
| 4677 | far | 1 |
| 4678 | famosas | 1 |
| 4679 | familiar | 1 |
| 4680 | famas | 1 |
| 4681 | faltóles | 1 |
| 4682 | faltó | 1 |
| 4683 | faltará | 1 |
| 4684 | faltara | 1 |
| 4685 | faltado | 1 |
| 4686 | fallece | 1 |
| 4687 | falda | 1 |
| 4688 | fácilmente | 1 |
| 4689 | extremo | 1 |
| 4690 | extremadura | 1 |
| 4691 | extremada | 1 |
| 4692 | extranjeros | 1 |
| 4693 | expreso | 1 |
| 4694 | expresión | 1 |
| 4695 | expresar | 1 |
| 4696 | explica | 1 |
| 4697 | exhala | 1 |
| 4698 | exemplos | 1 |
| 4699 | executar | 1 |
| 4700 | exclusión | 1 |
| 4701 | exclamaciones | 1 |
| 4702 | excesiva | 1 |
| 4703 | exceder | 1 |
| 4704 | excede | 1 |
| 4705 | exactitud | 1 |
| 4706 | europa | 1 |
| 4707 | eugenia | 1 |
| 4708 | etíope | 1 |
| 4709 | eterniza | 1 |
| 4710 | etc | 1 |
| 4711 | et | 1 |
| 4712 | estuvieras | 1 |
| 4713 | estuvieran | 1 |
| 4714 | estuve | 1 |
| 4715 | estribos | 1 |
| 4716 | estribo | 1 |
| 4717 | estremada | 1 |
| 4718 | estrecho | 1 |
| 4719 | estraños | 1 |
| 4720 | estrañas | 1 |
| 4721 | estranjero | 1 |
| 4722 | estrago | 1 |
| 4723 | estotro | 1 |
| 4724 | estoria | 1 |
| 4725 | estorbar | 1 |
| 4726 | estorbaba | 1 |
| 4727 | estopa | 1 |
| 4728 | estimen | 1 |
| 4729 | estimarme | 1 |
| 4730 | estimadas | 1 |
| 4731 | estilos | 1 |
| 4732 | estés | 1 |
| 4733 | estériles | 1 |
| 4734 | estemos | 1 |
| 4735 | éstas | 1 |
| 4736 | estaréis | 1 |
| 4737 | estaré | 1 |
| 4738 | estarán | 1 |
| 4739 | estampa | 1 |
| 4740 | estados | 1 |
| 4741 | establos | 1 |
| 4742 | establecer | 1 |
| 4743 | estabas | 1 |
| 4744 | esso | 1 |
| 4745 | esquivo | 1 |
| 4746 | esquiva | 1 |
| 4747 | esquilmos | 1 |
| 4748 | espuma | 1 |
| 4749 | espuelas | 1 |
| 4750 | espirar | 1 |
| 4751 | espirando | 1 |
| 4752 | espesos | 1 |
| 4753 | espesa | 1 |
| 4754 | esperaréis | 1 |
| 4755 | esperarás | 1 |
| 4756 | esperándote | 1 |
| 4757 | esperándole | 1 |
| 4758 | españoles | 1 |
| 4759 | españolas | 1 |
| 4760 | españas | 1 |
| 4761 | espantes | 1 |
| 4762 | espante | 1 |
| 4763 | espantado | 1 |
| 4764 | espalda | 1 |
| 4765 | espadilla | 1 |
| 4766 | esmeralda | 1 |
| 4767 | esfuérzate | 1 |
| 4768 | esfuerzas | 1 |
| 4769 | esfuerza | 1 |
| 4770 | esforzar | 1 |
| 4771 | esforzado | 1 |
| 4772 | escuso | 1 |
| 4773 | escusara | 1 |
| 4774 | escusar | 1 |
| 4775 | escusados | 1 |
| 4776 | escusado | 1 |
| 4777 | escuelas | 1 |
| 4778 | escudos | 1 |
| 4779 | escuderos | 1 |
| 4780 | escucho | 1 |
| 4781 | escuchemos | 1 |
| 4782 | escuchéis | 1 |
| 4783 | escucharte | 1 |
| 4784 | escucharme | 1 |
| 4785 | escuchan | 1 |
| 4786 | escúchame | 1 |
| 4787 | escuchados | 1 |
| 4788 | escuchad | 1 |
| 4789 | escritura | 1 |
| 4790 | escritos | 1 |
| 4791 | escritoras | 1 |
| 4792 | escritas | 1 |
| 4793 | escribo | 1 |
| 4794 | escribiste | 1 |
| 4795 | escribiré | 1 |
| 4796 | escribirá | 1 |
| 4797 | escribióme | 1 |
| 4798 | escribiera | 1 |
| 4799 | escribano | 1 |
| 4800 | escondiste | 1 |
| 4801 | escóndete | 1 |
| 4802 | esconde | 1 |
| 4803 | escondas | 1 |
| 4804 | esconda | 1 |
| 4805 | esclavina | 1 |
| 4806 | escenas | 1 |
| 4807 | escaso | 1 |
| 4808 | escapes | 1 |
| 4809 | escaparse | 1 |
| 4810 | escalaron | 1 |
| 4811 | errática | 1 |
| 4812 | errado | 1 |
| 4813 | ermita | 1 |
| 4814 | erais | 1 |
| 4815 | equivocada | 1 |
| 4816 | epístola | 1 |
| 4817 | epiro | 1 |
| 4818 | epigramas | 1 |
| 4819 | épico | 1 |
| 4820 | épica | 1 |
| 4821 | envio | 1 |
| 4822 | enviéle | 1 |
| 4823 | envidiado | 1 |
| 4824 | enviasen | 1 |
| 4825 | envías | 1 |
| 4826 | enviara | 1 |
| 4827 | enviar | 1 |
| 4828 | enviádselo | 1 |
| 4829 | enviado | 1 |
| 4830 | enviad | 1 |
| 4831 | envainen | 1 |
| 4832 | envainar | 1 |
| 4833 | envainada | 1 |
| 4834 | enunciada | 1 |
| 4835 | enumeración | 1 |
| 4836 | entretiene | 1 |
| 4837 | entretengo | 1 |
| 4838 | entren | 1 |
| 4839 | entrase | 1 |
| 4840 | entraré | 1 |
| 4841 | entrado | 1 |
| 4842 | enternézcaos | 1 |
| 4843 | enternecen | 1 |
| 4844 | enternece | 1 |
| 4845 | enternazcaos | 1 |
| 4846 | enteras | 1 |
| 4847 | enteramente | 1 |
| 4848 | entera | 1 |
| 4849 | entendiese | 1 |
| 4850 | entenderte | 1 |
| 4851 | entenderse | 1 |
| 4852 | ensillen | 1 |
| 4853 | ensillarásme | 1 |
| 4854 | ensíllame | 1 |
| 4855 | enseñarte | 1 |
| 4856 | enseñarme | 1 |
| 4857 | enseñanza | 1 |
| 4858 | enséñame | 1 |
| 4859 | ensangrentada | 1 |
| 4860 | ensancho | 1 |
| 4861 | ensanchara | 1 |
| 4862 | enríquez | 1 |
| 4863 | enredos | 1 |
| 4864 | enorme | 1 |
| 4865 | enojé | 1 |
| 4866 | enojártela | 1 |
| 4867 | enojara | 1 |
| 4868 | enojados | 1 |
| 4869 | enojado | 1 |
| 4870 | enojada | 1 |
| 4871 | ennobleza | 1 |
| 4872 | enmienda | 1 |
| 4873 | enmendaré | 1 |
| 4874 | enjugan | 1 |
| 4875 | enhorabuena | 1 |
| 4876 | engañó | 1 |
| 4877 | engañé | 1 |
| 4878 | engáñaste | 1 |
| 4879 | engañara | 1 |
| 4880 | engañan | 1 |
| 4881 | engañalle | 1 |
| 4882 | engañados | 1 |
| 4883 | engañador | 1 |
| 4884 | engañada | 1 |
| 4885 | enfrente | 1 |
| 4886 | enfreno | 1 |
| 4887 | enforcar | 1 |
| 4888 | énfasis | 1 |
| 4889 | enemigos | 1 |
| 4890 | endurecida | 1 |
| 4891 | endechas | 1 |
| 4892 | endecasílabos | 1 |
| 4893 | encuéntrase | 1 |
| 4894 | encubiertos | 1 |
| 4895 | encubierto | 1 |
| 4896 | encubiertamente | 1 |
| 4897 | encubierta | 1 |
| 4898 | encontró | 1 |
| 4899 | encontrarse | 1 |
| 4900 | encontrado | 1 |
| 4901 | encogido | 1 |
| 4902 | encinas | 1 |
| 4903 | enciende | 1 |
| 4904 | encerró | 1 |
| 4905 | encerrada | 1 |
| 4906 | encarnado | 1 |
| 4907 | encarnaciones | 1 |
| 4908 | encargo | 1 |
| 4909 | encarecer | 1 |
| 4910 | encaprichado | 1 |
| 4911 | empos | 1 |
| 4912 | empobrecer | 1 |
| 4913 | empiézate | 1 |
| 4914 | empiedran | 1 |
| 4915 | emperadora | 1 |
| 4916 | emparentarme | 1 |
| 4917 | emendada | 1 |
| 4918 | embiasse | 1 |
| 4919 | embiaría | 1 |
| 4920 | embargo | 1 |
| 4921 | élices | 1 |
| 4922 | elegido | 1 |
| 4923 | elección | 1 |
| 4924 | eklogen | 1 |
| 4925 | ejercitados | 1 |
| 4926 | ejercita | 1 |
| 4927 | ejercicio | 1 |
| 4928 | efectos | 1 |
| 4929 | editor | 1 |
| 4930 | edificios | 1 |
| 4931 | ediciones | 1 |
| 4932 | eco | 1 |
| 4933 | eclipsan | 1 |
| 4934 | echase | 1 |
| 4935 | echaremos | 1 |
| 4936 | echanlos | 1 |
| 4937 | echame | 1 |
| 4938 | echado | 1 |
| 4939 | echaba | 1 |
| 4940 | echa | 1 |
| 4941 | duro | 1 |
| 4942 | durando | 1 |
| 4943 | durable | 1 |
| 4944 | dulcísimo | 1 |
| 4945 | dulces | 1 |
| 4946 | duermo | 1 |
| 4947 | duerma | 1 |
| 4948 | dudoso | 1 |
| 4949 | dudas | 1 |
| 4950 | ducientos | 1 |
| 4951 | dramatiza | 1 |
| 4952 | dramatische | 1 |
| 4953 | drama | 1 |
| 4954 | doyla | 1 |
| 4955 | dora | 1 |
| 4956 | dones | 1 |
| 4957 | doncellas | 1 |
| 4958 | doncel | 1 |
| 4959 | donaire | 1 |
| 4960 | domingo | 1 |
| 4961 | dominarse | 1 |
| 4962 | doliente | 1 |
| 4963 | doleos | 1 |
| 4964 | doite | 1 |
| 4965 | doile | 1 |
| 4966 | documento | 1 |
| 4967 | doctor | 1 |
| 4968 | docientos | 1 |
| 4969 | docampo | 1 |
| 4970 | dixol | 1 |
| 4971 | dixogelo | 1 |
| 4972 | dixessen | 1 |
| 4973 | dixesse | 1 |
| 4974 | divisas | 1 |
| 4975 | divinas | 1 |
| 4976 | divididos | 1 |
| 4977 | divides | 1 |
| 4978 | divertido | 1 |
| 4979 | distilar | 1 |
| 4980 | diste | 1 |
| 4981 | dispuesto | 1 |
| 4982 | disposición | 1 |
| 4983 | dispónese | 1 |
| 4984 | dispone | 1 |
| 4985 | disimulado | 1 |
| 4986 | disfrázate | 1 |
| 4987 | disfrazado | 1 |
| 4988 | disculpado | 1 |
| 4989 | disculpa | 1 |
| 4990 | disciplina | 1 |
| 4991 | disc | 1 |
| 4992 | dirigida | 1 |
| 4993 | dirige | 1 |
| 4994 | diréte | 1 |
| 4995 | diremos | 1 |
| 4996 | diréle | 1 |
| 4997 | diréis | 1 |
| 4998 | directo | 1 |
| 4999 | directas | 1 |
| 5000 | dioses | 1 |
| 5001 | dineros | 1 |
| 5002 | dímela | 1 |
| 5003 | diligencias | 1 |
| 5004 | diles | 1 |
| 5005 | dilates | 1 |
| 5006 | dilatar | 1 |
| 5007 | dilación | 1 |
| 5008 | díjole | 1 |
| 5009 | díjele | 1 |
| 5010 | dignamente | 1 |
| 5011 | digáis | 1 |
| 5012 | difinición | 1 |
| 5013 | dificulto | 1 |
| 5014 | difícil | 1 |
| 5015 | diferente | 1 |
| 5016 | diferencio | 1 |
| 5017 | diestro | 1 |
| 5018 | diestra | 1 |
| 5019 | diéronse | 1 |
| 5020 | diere | 1 |
| 5021 | diente | 1 |
| 5022 | diciendo | 1 |
| 5023 | dichosas | 1 |
| 5024 | dichosamente | 1 |
| 5025 | dícenme | 1 |
| 5026 | díaz | 1 |
| 5027 | diálogos | 1 |
| 5028 | diabro | 1 |
| 5029 | diablos | 1 |
| 5030 | dia | 1 |
| 5031 | dí | 1 |
| 5032 | dezirme | 1 |
| 5033 | dezir | 1 |
| 5034 | dezidme | 1 |
| 5035 | dezían | 1 |
| 5036 | dexassen | 1 |
| 5037 | dexarme | 1 |
| 5038 | dexarían | 1 |
| 5039 | dexan | 1 |
| 5040 | dexa | 1 |
| 5041 | devotos | 1 |
| 5042 | devaneos | 1 |
| 5043 | determinó | 1 |
| 5044 | determinaron | 1 |
| 5045 | determinar | 1 |
| 5046 | deteniéndolos | 1 |
| 5047 | deteniéndole | 1 |
| 5048 | deteniendo | 1 |
| 5049 | detenerme | 1 |
| 5050 | detén | 1 |
| 5051 | déte | 1 |
| 5052 | detalle | 1 |
| 5053 | desvíate | 1 |
| 5054 | desventura | 1 |
| 5055 | desvelo | 1 |
| 5056 | desvelada | 1 |
| 5057 | desueles | 1 |
| 5058 | destruya | 1 |
| 5059 | déstos | 1 |
| 5060 | destorvo | 1 |
| 5061 | desterrados | 1 |
| 5062 | déste | 1 |
| 5063 | despues | 1 |
| 5064 | desprecies | 1 |
| 5065 | despreciéis | 1 |
| 5066 | despreciara | 1 |
| 5067 | despreciado | 1 |
| 5068 | despreciada | 1 |
| 5069 | desprecia | 1 |
| 5070 | desposarte | 1 |
| 5071 | desposarme | 1 |
| 5072 | desposado | 1 |
| 5073 | despojos | 1 |
| 5074 | despierto | 1 |
| 5075 | despedíme | 1 |
| 5076 | despachar | 1 |
| 5077 | despachados | 1 |
| 5078 | despachado | 1 |
| 5079 | deso | 1 |
| 5080 | desnudo | 1 |
| 5081 | desnudas | 1 |
| 5082 | desmintió | 1 |
| 5083 | desmentido | 1 |
| 5084 | desmayo | 1 |
| 5085 | desmaya | 1 |
| 5086 | desinios | 1 |
| 5087 | designación | 1 |
| 5088 | designa | 1 |
| 5089 | desiertos | 1 |
| 5090 | deshonrar | 1 |
| 5091 | deshonrada | 1 |
| 5092 | deshonor | 1 |
| 5093 | deshizo | 1 |
| 5094 | deshecho | 1 |
| 5095 | deshacer | 1 |
| 5096 | desgraciado | 1 |
| 5097 | desesperado | 1 |
| 5098 | desenvuelto | 1 |
| 5099 | desentonar | 1 |
| 5100 | desentonada | 1 |
| 5101 | desengañónos | 1 |
| 5102 | desengaño | 1 |
| 5103 | desengañar | 1 |
| 5104 | desemejanza | 1 |
| 5105 | desechóme | 1 |
| 5106 | desechéis | 1 |
| 5107 | desecha | 1 |
| 5108 | deseaste | 1 |
| 5109 | deseas | 1 |
| 5110 | desear | 1 |
| 5111 | deseaban | 1 |
| 5112 | desdeñosas | 1 |
| 5113 | desdeñosa | 1 |
| 5114 | descuidados | 1 |
| 5115 | descubre | 1 |
| 5116 | descripción | 1 |
| 5117 | describe | 1 |
| 5118 | desconoces | 1 |
| 5119 | desconfías | 1 |
| 5120 | desconfianzas | 1 |
| 5121 | desconfiado | 1 |
| 5122 | desconfía | 1 |
| 5123 | descompuesto | 1 |
| 5124 | descolorido | 1 |
| 5125 | descogidos | 1 |
| 5126 | descogido | 1 |
| 5127 | descobiertamente | 1 |
| 5128 | descendientes | 1 |
| 5129 | descansen | 1 |
| 5130 | descansemos | 1 |
| 5131 | descanséis | 1 |
| 5132 | descansare | 1 |
| 5133 | descansado | 1 |
| 5134 | descansada | 1 |
| 5135 | descalzas | 1 |
| 5136 | descalabrar | 1 |
| 5137 | desbaratado | 1 |
| 5138 | desatinos | 1 |
| 5139 | desasosiego | 1 |
| 5140 | desarmado | 1 |
| 5141 | desaparecería | 1 |
| 5142 | desamparo | 1 |
| 5143 | desagraviada | 1 |
| 5144 | desafíos | 1 |
| 5145 | desafióme | 1 |
| 5146 | derribó | 1 |
| 5147 | derribáronles | 1 |
| 5148 | derribaron | 1 |
| 5149 | derribar | 1 |
| 5150 | derriballes | 1 |
| 5151 | derribado | 1 |
| 5152 | derrame | 1 |
| 5153 | deriva | 1 |
| 5154 | der | 1 |
| 5155 | depósito | 1 |
| 5156 | démosle | 1 |
| 5157 | demonio | 1 |
| 5158 | demandol | 1 |
| 5159 | demandar | 1 |
| 5160 | delicadeza | 1 |
| 5161 | deliberadamente | 1 |
| 5162 | dejes | 1 |
| 5163 | dejen | 1 |
| 5164 | dejé | 1 |
| 5165 | déjase | 1 |
| 5166 | dejase | 1 |
| 5167 | dejarte | 1 |
| 5168 | dejarnos | 1 |
| 5169 | dejaréis | 1 |
| 5170 | dejaré | 1 |
| 5171 | dejara | 1 |
| 5172 | dejando | 1 |
| 5173 | déjale | 1 |
| 5174 | dejado | 1 |
| 5175 | dejadlos | 1 |
| 5176 | dejad | 1 |
| 5177 | dejaba | 1 |
| 5178 | deis | 1 |
| 5179 | defienden | 1 |
| 5180 | defiende | 1 |
| 5181 | defienda | 1 |
| 5182 | defensas | 1 |
| 5183 | defendiendo | 1 |
| 5184 | defenderme | 1 |
| 5185 | defenderá | 1 |
| 5186 | defectos | 1 |
| 5187 | dedicóle | 1 |
| 5188 | dedicado | 1 |
| 5189 | declaran | 1 |
| 5190 | declarada | 1 |
| 5191 | declara | 1 |
| 5192 | decirte | 1 |
| 5193 | deciendo | 1 |
| 5194 | decídselo | 1 |
| 5195 | decidme | 1 |
| 5196 | decendiente | 1 |
| 5197 | débiles | 1 |
| 5198 | debía | 1 |
| 5199 | debéis | 1 |
| 5200 | debaxo | 1 |
| 5201 | débat | 1 |
| 5202 | deba | 1 |
| 5203 | dcc | 1 |
| 5204 | dasme | 1 |
| 5205 | daros | 1 |
| 5206 | darles | 1 |
| 5207 | darlas | 1 |
| 5208 | darío | 1 |
| 5209 | daréte | 1 |
| 5210 | daréle | 1 |
| 5211 | daréis | 1 |
| 5212 | daráte | 1 |
| 5213 | darán | 1 |
| 5214 | daña | 1 |
| 5215 | danos | 1 |
| 5216 | danle | 1 |
| 5217 | dándome | 1 |
| 5218 | dámela | 1 |
| 5219 | damas | 1 |
| 5220 | dalle | 1 |
| 5221 | daga | 1 |
| 5222 | dador | 1 |
| 5223 | dadnos | 1 |
| 5224 | dadle | 1 |
| 5225 | dádiva | 1 |
| 5226 | dada | 1 |
| 5227 | cxxxix | 1 |
| 5228 | curarme | 1 |
| 5229 | curadas | 1 |
| 5230 | cupo | 1 |
| 5231 | cunde | 1 |
| 5232 | cuna | 1 |
| 5233 | cumplo | 1 |
| 5234 | cumplirás | 1 |
| 5235 | cumplióse | 1 |
| 5236 | cumplió | 1 |
| 5237 | cumplidos | 1 |
| 5238 | cumplido | 1 |
| 5239 | cumplí | 1 |
| 5240 | cumples | 1 |
| 5241 | cumpláis | 1 |
| 5242 | cumpla | 1 |
| 5243 | culpo | 1 |
| 5244 | culparte | 1 |
| 5245 | culparles | 1 |
| 5246 | culpada | 1 |
| 5247 | cuistión | 1 |
| 5248 | cueza | 1 |
| 5249 | cuestas | 1 |
| 5250 | cuesta | 1 |
| 5251 | cuerno | 1 |
| 5252 | cuerda | 1 |
| 5253 | cuentos | 1 |
| 5254 | cuente | 1 |
| 5255 | cuéntaste | 1 |
| 5256 | cuéntase | 1 |
| 5257 | cuenca | 1 |
| 5258 | cuellos | 1 |
| 5259 | cuelgo | 1 |
| 5260 | cuelga | 1 |
| 5261 | cuchillas | 1 |
| 5262 | cucharón | 1 |
| 5263 | cubrieron | 1 |
| 5264 | cubriendo | 1 |
| 5265 | cuatrines | 1 |
| 5266 | cuartana | 1 |
| 5267 | cuarta | 1 |
| 5268 | cuantos | 1 |
| 5269 | cuántas | 1 |
| 5270 | cuantas | 1 |
| 5271 | cuan | 1 |
| 5272 | cuadre | 1 |
| 5273 | cruzada | 1 |
| 5274 | cristianas | 1 |
| 5275 | cristalinas | 1 |
| 5276 | cristales | 1 |
| 5277 | cristal | 1 |
| 5278 | crió | 1 |
| 5279 | crines | 1 |
| 5280 | criava | 1 |
| 5281 | criasen | 1 |
| 5282 | criarme | 1 |
| 5283 | criar | 1 |
| 5284 | crianza | 1 |
| 5285 | criada | 1 |
| 5286 | cria | 1 |
| 5287 | creyera | 1 |
| 5288 | cresta | 1 |
| 5289 | crespa | 1 |
| 5290 | creimos | 1 |
| 5291 | creerá | 1 |
| 5292 | creedme | 1 |
| 5293 | creed | 1 |
| 5294 | crédito | 1 |
| 5295 | creció | 1 |
| 5296 | creciera | 1 |
| 5297 | creciente | 1 |
| 5298 | creciendo | 1 |
| 5299 | crece | 1 |
| 5300 | creas | 1 |
| 5301 | crear | 1 |
| 5302 | crea | 1 |
| 5303 | coxín | 1 |
| 5304 | covarde | 1 |
| 5305 | cota | 1 |
| 5306 | costar | 1 |
| 5307 | costa | 1 |
| 5308 | coruña | 1 |
| 5309 | corto | 1 |
| 5310 | cortimos | 1 |
| 5311 | cortijo | 1 |
| 5312 | cortezas | 1 |
| 5313 | cortés | 1 |
| 5314 | corten | 1 |
| 5315 | cortedad | 1 |
| 5316 | cortase | 1 |
| 5317 | cortáronles | 1 |
| 5318 | cortándole | 1 |
| 5319 | cortando | 1 |
| 5320 | córtame | 1 |
| 5321 | corrimos | 1 |
| 5322 | corrido | 1 |
| 5323 | corrida | 1 |
| 5324 | correspondencia | 1 |
| 5325 | correrías | 1 |
| 5326 | corregimos | 1 |
| 5327 | corredor | 1 |
| 5328 | coronista | 1 |
| 5329 | corónicas | 1 |
| 5330 | corónica | 1 |
| 5331 | coronarán | 1 |
| 5332 | coronan | 1 |
| 5333 | coronados | 1 |
| 5334 | corneta | 1 |
| 5335 | cordones | 1 |
| 5336 | córdoba | 1 |
| 5337 | cordera | 1 |
| 5338 | cordeles | 1 |
| 5339 | corales | 1 |
| 5340 | copilla | 1 |
| 5341 | copiamos | 1 |
| 5342 | copiado | 1 |
| 5343 | copa | 1 |
| 5344 | convienen | 1 |
| 5345 | convertida | 1 |
| 5346 | convertían | 1 |
| 5347 | conversación | 1 |
| 5348 | convento | 1 |
| 5349 | convenía | 1 |
| 5350 | convencional | 1 |
| 5351 | contraria | 1 |
| 5352 | contrallavalo | 1 |
| 5353 | contradixo | 1 |
| 5354 | contradice | 1 |
| 5355 | continencia | 1 |
| 5356 | contexto | 1 |
| 5357 | contemporáneos | 1 |
| 5358 | contarla | 1 |
| 5359 | contaré | 1 |
| 5360 | contar | 1 |
| 5361 | contándole | 1 |
| 5362 | contaban | 1 |
| 5363 | contaba | 1 |
| 5364 | consumo | 1 |
| 5365 | consuelos | 1 |
| 5366 | construcción | 1 |
| 5367 | constituyéndolos | 1 |
| 5368 | consolarme | 1 |
| 5369 | consiste | 1 |
| 5370 | consintiera | 1 |
| 5371 | considero | 1 |
| 5372 | consideraste | 1 |
| 5373 | considerar | 1 |
| 5374 | considerados | 1 |
| 5375 | consejeros | 1 |
| 5376 | consagre | 1 |
| 5377 | consagrado | 1 |
| 5378 | conquistas | 1 |
| 5379 | conquistado | 1 |
| 5380 | conocidos | 1 |
| 5381 | conocían | 1 |
| 5382 | conócesme | 1 |
| 5383 | conocernos | 1 |
| 5384 | conocerme | 1 |
| 5385 | conocerlos | 1 |
| 5386 | conoceréis | 1 |
| 5387 | conocen | 1 |
| 5388 | conocemos | 1 |
| 5389 | conocedor | 1 |
| 5390 | confusión | 1 |
| 5391 | conformes | 1 |
| 5392 | conforme | 1 |
| 5393 | confiesas | 1 |
| 5394 | confiados | 1 |
| 5395 | confiada | 1 |
| 5396 | conejo | 1 |
| 5397 | conduzca | 1 |
| 5398 | conduces | 1 |
| 5399 | conduce | 1 |
| 5400 | condiciones | 1 |
| 5401 | condicional | 1 |
| 5402 | condesa | 1 |
| 5403 | conciertos | 1 |
| 5404 | concierta | 1 |
| 5405 | conciencia | 1 |
| 5406 | concertaremos | 1 |
| 5407 | concertamos | 1 |
| 5408 | concertados | 1 |
| 5409 | concertado | 1 |
| 5410 | concedió | 1 |
| 5411 | concedida | 1 |
| 5412 | concedemos | 1 |
| 5413 | conceda | 1 |
| 5414 | común | 1 |
| 5415 | compuesto | 1 |
| 5416 | compre | 1 |
| 5417 | comprado | 1 |
| 5418 | compostura | 1 |
| 5419 | componiendo | 1 |
| 5420 | componer | 1 |
| 5421 | completado | 1 |
| 5422 | compassion | 1 |
| 5423 | compasiva | 1 |
| 5424 | comparaciones | 1 |
| 5425 | compañía | 1 |
| 5426 | comienzos | 1 |
| 5427 | comido | 1 |
| 5428 | cómico | 1 |
| 5429 | cometido | 1 |
| 5430 | cometían | 1 |
| 5431 | comercio | 1 |
| 5432 | comerá | 1 |
| 5433 | comenzamos | 1 |
| 5434 | comendador | 1 |
| 5435 | combates | 1 |
| 5436 | combate | 1 |
| 5437 | comas | 1 |
| 5438 | coma | 1 |
| 5439 | colocar | 1 |
| 5440 | colige | 1 |
| 5441 | colguemos | 1 |
| 5442 | colgados | 1 |
| 5443 | colgado | 1 |
| 5444 | colgaba | 1 |
| 5445 | colera | 1 |
| 5446 | colección | 1 |
| 5447 | coin | 1 |
| 5448 | cohechos | 1 |
| 5449 | cogines | 1 |
| 5450 | cogieron | 1 |
| 5451 | codicióme | 1 |
| 5452 | cochino | 1 |
| 5453 | coches | 1 |
| 5454 | cochero | 1 |
| 5455 | cochera | 1 |
| 5456 | cobardía | 1 |
| 5457 | cnde | 1 |
| 5458 | clemencín | 1 |
| 5459 | clavos | 1 |
| 5460 | clavo | 1 |
| 5461 | clavadas | 1 |
| 5462 | classense | 1 |
| 5463 | class | 1 |
| 5464 | clásica | 1 |
| 5465 | civiles | 1 |
| 5466 | citan | 1 |
| 5467 | cisne | 1 |
| 5468 | círculo | 1 |
| 5469 | circe | 1 |
| 5470 | cipiones | 1 |
| 5471 | ciña | 1 |
| 5472 | cintura | 1 |
| 5473 | cincuenta | 1 |
| 5474 | cinammomo | 1 |
| 5475 | cifra | 1 |
| 5476 | cierta | 1 |
| 5477 | cierre | 1 |
| 5478 | cierra | 1 |
| 5479 | ciencias | 1 |
| 5480 | ciencia | 1 |
| 5481 | cid | 1 |
| 5482 | chulos | 1 |
| 5483 | chulesco | 1 |
| 5484 | chozas | 1 |
| 5485 | chiste | 1 |
| 5486 | chiquito | 1 |
| 5487 | chipre | 1 |
| 5488 | chico | 1 |
| 5489 | chanson | 1 |
| 5490 | cetera | 1 |
| 5491 | cesó | 1 |
| 5492 | cese | 1 |
| 5493 | cesado | 1 |
| 5494 | cesaban | 1 |
| 5495 | cesa | 1 |
| 5496 | cerrados | 1 |
| 5497 | cerrada | 1 |
| 5498 | cerrad | 1 |
| 5499 | ceremonia | 1 |
| 5500 | cercanos | 1 |
| 5501 | centro | 1 |
| 5502 | cenizas | 1 |
| 5503 | ceniza | 1 |
| 5504 | cenado | 1 |
| 5505 | cena | 1 |
| 5506 | celosos | 1 |
| 5507 | celosías | 1 |
| 5508 | celosa | 1 |
| 5509 | celo | 1 |
| 5510 | celebre | 1 |
| 5511 | celebrarles | 1 |
| 5512 | celebran | 1 |
| 5513 | celebralo | 1 |
| 5514 | celebrado | 1 |
| 5515 | celebrada | 1 |
| 5516 | cebreros | 1 |
| 5517 | cayeron | 1 |
| 5518 | cavallos | 1 |
| 5519 | cavalleros | 1 |
| 5520 | cautivé | 1 |
| 5521 | causóle | 1 |
| 5522 | causado | 1 |
| 5523 | causaban | 1 |
| 5524 | caudillo | 1 |
| 5525 | caudalosas | 1 |
| 5526 | católicos | 1 |
| 5527 | católica | 1 |
| 5528 | castros | 1 |
| 5529 | casto | 1 |
| 5530 | castillos | 1 |
| 5531 | castiglione | 1 |
| 5532 | castaño | 1 |
| 5533 | casilla | 1 |
| 5534 | casémonos | 1 |
| 5535 | casarte | 1 |
| 5536 | casaron | 1 |
| 5537 | casarnos | 1 |
| 5538 | casara | 1 |
| 5539 | casámonos | 1 |
| 5540 | casaba | 1 |
| 5541 | cártama | 1 |
| 5542 | cartago | 1 |
| 5543 | carroza | 1 |
| 5544 | carneros | 1 |
| 5545 | carmesí | 1 |
| 5546 | carlomagno | 1 |
| 5547 | carlanca | 1 |
| 5548 | cargo | 1 |
| 5549 | cargar | 1 |
| 5550 | carga | 1 |
| 5551 | careció | 1 |
| 5552 | carecer | 1 |
| 5553 | cárcel | 1 |
| 5554 | carbón | 1 |
| 5555 | caras | 1 |
| 5556 | caracterizar | 1 |
| 5557 | caracteriza | 1 |
| 5558 | caps | 1 |
| 5559 | caprichosamente | 1 |
| 5560 | capítulos | 1 |
| 5561 | capilla | 1 |
| 5562 | capellar | 1 |
| 5563 | capaz | 1 |
| 5564 | capa | 1 |
| 5565 | caña | 1 |
| 5566 | cantidad | 1 |
| 5567 | cantéis | 1 |
| 5568 | cantarte | 1 |
| 5569 | cantarranas | 1 |
| 5570 | cantando | 1 |
| 5571 | cantáis | 1 |
| 5572 | cansaros | 1 |
| 5573 | cansarme | 1 |
| 5574 | cansara | 1 |
| 5575 | cansan | 1 |
| 5576 | cansada | 1 |
| 5577 | cansa | 1 |
| 5578 | canela | 1 |
| 5579 | cándida | 1 |
| 5580 | cancionero | 1 |
| 5581 | canc | 1 |
| 5582 | can | 1 |
| 5583 | campanillas | 1 |
| 5584 | campana | 1 |
| 5585 | caminad | 1 |
| 5586 | cambiar | 1 |
| 5587 | camara | 1 |
| 5588 | calzare | 1 |
| 5589 | calza | 1 |
| 5590 | calor | 1 |
| 5591 | calles | 1 |
| 5592 | callas | 1 |
| 5593 | callara | 1 |
| 5594 | callar | 1 |
| 5595 | callando | 1 |
| 5596 | callamos | 1 |
| 5597 | callado | 1 |
| 5598 | calíope | 1 |
| 5599 | calificaron | 1 |
| 5600 | caliente | 1 |
| 5601 | calambuco | 1 |
| 5602 | cajas | 1 |
| 5603 | caja | 1 |
| 5604 | caen | 1 |
| 5605 | caducos | 1 |
| 5606 | caduco | 1 |
| 5607 | cadena | 1 |
| 5608 | cabrito | 1 |
| 5609 | cabreros | 1 |
| 5610 | cabrán | 1 |
| 5611 | caber | 1 |
| 5612 | caben | 1 |
| 5613 | cabeceras | 1 |
| 5614 | caballeriza | 1 |
| 5615 | caballerías | 1 |
| 5616 | caballería | 1 |
| 5617 | buscas | 1 |
| 5618 | buscando | 1 |
| 5619 | buscan | 1 |
| 5620 | burro | 1 |
| 5621 | burlan | 1 |
| 5622 | burladora | 1 |
| 5623 | burlado | 1 |
| 5624 | burguillos | 1 |
| 5625 | bulto | 1 |
| 5626 | bullón | 1 |
| 5627 | bufones | 1 |
| 5628 | bufete | 1 |
| 5629 | bríos | 1 |
| 5630 | brío | 1 |
| 5631 | brillar | 1 |
| 5632 | breves | 1 |
| 5633 | brevemente | 1 |
| 5634 | brama | 1 |
| 5635 | botas | 1 |
| 5636 | bostezar | 1 |
| 5637 | bosque | 1 |
| 5638 | borradas | 1 |
| 5639 | bordado | 1 |
| 5640 | bordada | 1 |
| 5641 | borceguí | 1 |
| 5642 | bonete | 1 |
| 5643 | bolvieron | 1 |
| 5644 | bolví | 1 |
| 5645 | bolvérmela | 1 |
| 5646 | bolsillo | 1 |
| 5647 | boletín | 1 |
| 5648 | bodega | 1 |
| 5649 | boba | 1 |
| 5650 | blasfemia | 1 |
| 5651 | blas | 1 |
| 5652 | blandura | 1 |
| 5653 | blando | 1 |
| 5654 | bizarro | 1 |
| 5655 | bésoos | 1 |
| 5656 | beséla | 1 |
| 5657 | besarle | 1 |
| 5658 | besando | 1 |
| 5659 | besadle | 1 |
| 5660 | berlín | 1 |
| 5661 | benito | 1 |
| 5662 | bengalas | 1 |
| 5663 | bendito | 1 |
| 5664 | bendigo | 1 |
| 5665 | bendición | 1 |
| 5666 | benavente | 1 |
| 5667 | belona | 1 |
| 5668 | bellísimo | 1 |
| 5669 | bellaca | 1 |
| 5670 | belífero | 1 |
| 5671 | bélica | 1 |
| 5672 | beber | 1 |
| 5673 | bebe | 1 |
| 5674 | bazanes | 1 |
| 5675 | baxar | 1 |
| 5676 | bautismal | 1 |
| 5677 | batiendo | 1 |
| 5678 | batallen | 1 |
| 5679 | bastan | 1 |
| 5680 | bastamos | 1 |
| 5681 | barcelona | 1 |
| 5682 | barbuquejo | 1 |
| 5683 | barbirrubio | 1 |
| 5684 | barbinegro | 1 |
| 5685 | bárbaras | 1 |
| 5686 | bárbara | 1 |
| 5687 | barajara | 1 |
| 5688 | barajar | 1 |
| 5689 | barajando | 1 |
| 5690 | bañas | 1 |
| 5691 | bandera | 1 |
| 5692 | banda | 1 |
| 5693 | balcón | 1 |
| 5694 | bálago | 1 |
| 5695 | bajos | 1 |
| 5696 | bajes | 1 |
| 5697 | bájense | 1 |
| 5698 | bajen | 1 |
| 5699 | bajé | 1 |
| 5700 | bajas | 1 |
| 5701 | bajando | 1 |
| 5702 | bajaba | 1 |
| 5703 | baile | 1 |
| 5704 | bailad | 1 |
| 5705 | badil | 1 |
| 5706 | báculo | 1 |
| 5707 | azucenas | 1 |
| 5708 | azotes | 1 |
| 5709 | azotar | 1 |
| 5710 | azero | 1 |
| 5711 | azagayas | 1 |
| 5712 | ayunarle | 1 |
| 5713 | ayude | 1 |
| 5714 | ayudaron | 1 |
| 5715 | ayudarla | 1 |
| 5716 | ayudandola | 1 |
| 5717 | ayre | 1 |
| 5718 | avisad | 1 |
| 5719 | avisa | 1 |
| 5720 | avindarraez | 1 |
| 5721 | avíe | 1 |
| 5722 | avie | 1 |
| 5723 | avían | 1 |
| 5724 | aventuran | 1 |
| 5725 | aventuralla | 1 |
| 5726 | aventura | 1 |
| 5727 | ave | 1 |
| 5728 | auxiliar | 1 |
| 5729 | autos | 1 |
| 5730 | autoridades | 1 |
| 5731 | autoridad | 1 |
| 5732 | autorices | 1 |
| 5733 | ausonio | 1 |
| 5734 | aunq | 1 |
| 5735 | aumento | 1 |
| 5736 | aumentas | 1 |
| 5737 | aumentar | 1 |
| 5738 | auf | 1 |
| 5739 | aturde | 1 |
| 5740 | atribuye | 1 |
| 5741 | atribuyan | 1 |
| 5742 | atribuídos | 1 |
| 5743 | atribución | 1 |
| 5744 | atrevimientos | 1 |
| 5745 | atrevas | 1 |
| 5746 | atrevan | 1 |
| 5747 | atraviese | 1 |
| 5748 | atrás | 1 |
| 5749 | atracción | 1 |
| 5750 | atormentarme | 1 |
| 5751 | atormentar | 1 |
| 5752 | atordidos | 1 |
| 5753 | atiende | 1 |
| 5754 | atesora | 1 |
| 5755 | ate | 1 |
| 5756 | ataos | 1 |
| 5757 | atambor | 1 |
| 5758 | atajalla | 1 |
| 5759 | ataja | 1 |
| 5760 | atados | 1 |
| 5761 | atado | 1 |
| 5762 | asseverar | 1 |
| 5763 | assegurar | 1 |
| 5764 | assegura | 1 |
| 5765 | áspera | 1 |
| 5766 | asombres | 1 |
| 5767 | asombre | 1 |
| 5768 | asiste | 1 |
| 5769 | asilla | 1 |
| 5770 | asidas | 1 |
| 5771 | asida | 1 |
| 5772 | asia | 1 |
| 5773 | asestando | 1 |
| 5774 | asentó | 1 |
| 5775 | aseguro | 1 |
| 5776 | asegurado | 1 |
| 5777 | asegunda | 1 |
| 5778 | ase | 1 |
| 5779 | asarás | 1 |
| 5780 | arzones | 1 |
| 5781 | arzón | 1 |
| 5782 | artús | 1 |
| 5783 | artes | 1 |
| 5784 | arte | 1 |
| 5785 | ars | 1 |
| 5786 | arroja | 1 |
| 5787 | arriesgue | 1 |
| 5788 | arriba | 1 |
| 5789 | arrepentido | 1 |
| 5790 | arpa | 1 |
| 5791 | aromática | 1 |
| 5792 | aromas | 1 |
| 5793 | aroma | 1 |
| 5794 | armen | 1 |
| 5795 | ármate | 1 |
| 5796 | armar | 1 |
| 5797 | argumentos | 1 |
| 5798 | argolla | 1 |
| 5799 | argólico | 1 |
| 5800 | argel | 1 |
| 5801 | arena | 1 |
| 5802 | ardor | 1 |
| 5803 | ardo | 1 |
| 5804 | ardiente | 1 |
| 5805 | ardiendo | 1 |
| 5806 | ardía | 1 |
| 5807 | arder | 1 |
| 5808 | arco | 1 |
| 5809 | arcas | 1 |
| 5810 | arcaísmos | 1 |
| 5811 | arboleda | 1 |
| 5812 | arbitrio | 1 |
| 5813 | araucana | 1 |
| 5814 | arábigo | 1 |
| 5815 | arabia | 1 |
| 5816 | aquiles | 1 |
| 5817 | aqui | 1 |
| 5818 | aquesas | 1 |
| 5819 | aquél | 1 |
| 5820 | aprovechado | 1 |
| 5821 | aprieto | 1 |
| 5822 | aprietes | 1 |
| 5823 | aprietas | 1 |
| 5824 | apretar | 1 |
| 5825 | apretados | 1 |
| 5826 | apresta | 1 |
| 5827 | aprendidos | 1 |
| 5828 | aprendí | 1 |
| 5829 | aprender | 1 |
| 5830 | apregonallos | 1 |
| 5831 | apoyó | 1 |
| 5832 | apoya | 1 |
| 5833 | apostolica | 1 |
| 5834 | apostaré | 1 |
| 5835 | apostará | 1 |
| 5836 | apólogo | 1 |
| 5837 | apódosis | 1 |
| 5838 | aplacan | 1 |
| 5839 | apetitos | 1 |
| 5840 | apetito | 1 |
| 5841 | apercibo | 1 |
| 5842 | aperciban | 1 |
| 5843 | apercebidas | 1 |
| 5844 | apercebida | 1 |
| 5845 | apelo | 1 |
| 5846 | apellidos | 1 |
| 5847 | apellido | 1 |
| 5848 | apellida | 1 |
| 5849 | apelación | 1 |
| 5850 | apean | 1 |
| 5851 | apaziguó | 1 |
| 5852 | apartó | 1 |
| 5853 | apartes | 1 |
| 5854 | apartaos | 1 |
| 5855 | apartándose | 1 |
| 5856 | apareció | 1 |
| 5857 | apacible | 1 |
| 5858 | añade | 1 |
| 5859 | antona | 1 |
| 5860 | antojen | 1 |
| 5861 | antoje | 1 |
| 5862 | antipatía | 1 |
| 5863 | antiguos | 1 |
| 5864 | antigua | 1 |
| 5865 | ansias | 1 |
| 5866 | anónimo | 1 |
| 5867 | anocheciese | 1 |
| 5868 | animoso | 1 |
| 5869 | animo | 1 |
| 5870 | animal | 1 |
| 5871 | anima | 1 |
| 5872 | ángeles | 1 |
| 5873 | anega | 1 |
| 5874 | anduvo | 1 |
| 5875 | andrade | 1 |
| 5876 | ando | 1 |
| 5877 | andáis | 1 |
| 5878 | andad | 1 |
| 5879 | and | 1 |
| 5880 | anciens | 1 |
| 5881 | anca | 1 |
| 5882 | análogo | 1 |
| 5883 | analiza | 1 |
| 5884 | anacrónico | 1 |
| 5885 | anacoluto | 1 |
| 5886 | an | 1 |
| 5887 | amorosas | 1 |
| 5888 | amnón | 1 |
| 5889 | amenazas | 1 |
| 5890 | amenazado | 1 |
| 5891 | amenaza | 1 |
| 5892 | amenaçar | 1 |
| 5893 | amen | 1 |
| 5894 | amartelar | 1 |
| 5895 | amarnos | 1 |
| 5896 | amanezca | 1 |
| 5897 | amandi | 1 |
| 5898 | amala | 1 |
| 5899 | amáis | 1 |
| 5900 | amábalos | 1 |
| 5901 | amaba | 1 |
| 5902 | am | 1 |
| 5903 | alzo | 1 |
| 5904 | alzarse | 1 |
| 5905 | alzado | 1 |
| 5906 | alza | 1 |
| 5907 | alva | 1 |
| 5908 | alteres | 1 |
| 5909 | alteras | 1 |
| 5910 | altera | 1 |
| 5911 | altamente | 1 |
| 5912 | alrededor | 1 |
| 5913 | alquila | 1 |
| 5914 | alquicel | 1 |
| 5915 | álora | 1 |
| 5916 | almuerzo | 1 |
| 5917 | almorcemos | 1 |
| 5918 | almoradíes | 1 |
| 5919 | almohada | 1 |
| 5920 | almirante | 1 |
| 5921 | almenas | 1 |
| 5922 | almena | 1 |
| 5923 | almatea | 1 |
| 5924 | almaizales | 1 |
| 5925 | allegando | 1 |
| 5926 | aljófares | 1 |
| 5927 | aljaba | 1 |
| 5928 | alivio | 1 |
| 5929 | aliscans | 1 |
| 5930 | alhombras | 1 |
| 5931 | alhelí | 1 |
| 5932 | alguacil | 1 |
| 5933 | algodón | 1 |
| 5934 | algazaras | 1 |
| 5935 | algarabía | 1 |
| 5936 | alfombra | 1 |
| 5937 | alfiles | 1 |
| 5938 | alfaquíes | 1 |
| 5939 | alfanjes | 1 |
| 5940 | aleve | 1 |
| 5941 | alemán | 1 |
| 5942 | alejéme | 1 |
| 5943 | alejarse | 1 |
| 5944 | alejandros | 1 |
| 5945 | alejandrías | 1 |
| 5946 | alegres | 1 |
| 5947 | alegra | 1 |
| 5948 | aldeana | 1 |
| 5949 | aldas | 1 |
| 5950 | alcatifa | 1 |
| 5951 | alcanzo | 1 |
| 5952 | alcanzase | 1 |
| 5953 | alcances | 1 |
| 5954 | alcance | 1 |
| 5955 | alcaidía | 1 |
| 5956 | alcagüete | 1 |
| 5957 | alboroto | 1 |
| 5958 | alborote | 1 |
| 5959 | alba | 1 |
| 5960 | alargue | 1 |
| 5961 | alarga | 1 |
| 5962 | alarcón | 1 |
| 5963 | alameda | 1 |
| 5964 | alaben | 1 |
| 5965 | alabas | 1 |
| 5966 | alabarda | 1 |
| 5967 | alabar | 1 |
| 5968 | ala | 1 |
| 5969 | ajena | 1 |
| 5970 | ajedrez | 1 |
| 5971 | aibenzaides | 1 |
| 5972 | ahorque | 1 |
| 5973 | agustín | 1 |
| 5974 | agujero | 1 |
| 5975 | águila | 1 |
| 5976 | agüelo | 1 |
| 5977 | aguárdate | 1 |
| 5978 | aguardaras | 1 |
| 5979 | aguardándome | 1 |
| 5980 | aguardan | 1 |
| 5981 | aguardad | 1 |
| 5982 | agregan | 1 |
| 5983 | agradecerles | 1 |
| 5984 | afrontar | 1 |
| 5985 | africano | 1 |
| 5986 | africanas | 1 |
| 5987 | afrentara | 1 |
| 5988 | afrenta | 1 |
| 5989 | aflojarse | 1 |
| 5990 | aflijas | 1 |
| 5991 | afligen | 1 |
| 5992 | afirmes | 1 |
| 5993 | afirmación | 1 |
| 5994 | afirma | 1 |
| 5995 | aficionado | 1 |
| 5996 | afeminas | 1 |
| 5997 | afeminada | 1 |
| 5998 | afeites | 1 |
| 5999 | afecto | 1 |
| 6000 | advierta | 1 |
| 6001 | advertencia | 1 |
| 6002 | adverbio | 1 |
| 6003 | adverbializada | 1 |
| 6004 | aduxeronle | 1 |
| 6005 | adúlteros | 1 |
| 6006 | adulterio | 1 |
| 6007 | aduce | 1 |
| 6008 | aduares | 1 |
| 6009 | adquiriendo | 1 |
| 6010 | adornes | 1 |
| 6011 | adorna | 1 |
| 6012 | adoras | 1 |
| 6013 | adoran | 1 |
| 6014 | adonis | 1 |
| 6015 | adolescente | 1 |
| 6016 | adolescencia | 1 |
| 6017 | admitiendo | 1 |
| 6018 | admite | 1 |
| 6019 | admiraba | 1 |
| 6020 | adjetivo | 1 |
| 6021 | adherentes | 1 |
| 6022 | adereza | 1 |
| 6023 | aderecéme | 1 |
| 6024 | acusativo | 1 |
| 6025 | acusaban | 1 |
| 6026 | acumula | 1 |
| 6027 | acuérdome | 1 |
| 6028 | acuerde | 1 |
| 6029 | acudir | 1 |
| 6030 | acudid | 1 |
| 6031 | acuda | 1 |
| 6032 | actos | 1 |
| 6033 | actores | 1 |
| 6034 | acrecientas | 1 |
| 6035 | acotación | 1 |
| 6036 | acostara | 1 |
| 6037 | acórtola | 1 |
| 6038 | acordó | 1 |
| 6039 | acordaos | 1 |
| 6040 | acordáisos | 1 |
| 6041 | aconsejes | 1 |
| 6042 | aconsejaste | 1 |
| 6043 | aconsejarte | 1 |
| 6044 | aconséjame | 1 |
| 6045 | acompañarme | 1 |
| 6046 | acompañan | 1 |
| 6047 | acompañado | 1 |
| 6048 | acompañada | 1 |
| 6049 | acompañaba | 1 |
| 6050 | acomodáronme | 1 |
| 6051 | acomete | 1 |
| 6052 | acometáis | 1 |
| 6053 | acobarda | 1 |
| 6054 | acierto | 1 |
| 6055 | aciertas | 1 |
| 6056 | acierta | 1 |
| 6057 | acidalia | 1 |
| 6058 | acicate | 1 |
| 6059 | aciago | 1 |
| 6060 | achares | 1 |
| 6061 | acetéle | 1 |
| 6062 | aceros | 1 |
| 6063 | acerada | 1 |
| 6064 | aceptar | 1 |
| 6065 | aceptamos | 1 |
| 6066 | acento | 1 |
| 6067 | aceite | 1 |
| 6068 | accidente | 1 |
| 6069 | accesorio | 1 |
| 6070 | acaecido | 1 |
| 6071 | académica | 1 |
| 6072 | acabó | 1 |
| 6073 | acabo | 1 |
| 6074 | acabes | 1 |
| 6075 | acabe | 1 |
| 6076 | acabáys | 1 |
| 6077 | acabarse | 1 |
| 6078 | acabarme | 1 |
| 6079 | acabara | 1 |
| 6080 | acabar | 1 |
| 6081 | acabáis | 1 |
| 6082 | acabadas | 1 |
| 6083 | acabad | 1 |
| 6084 | abundancia | 1 |
| 6085 | abundan | 1 |
| 6086 | abrirme | 1 |
| 6087 | abril | 1 |
| 6088 | abrieron | 1 |
| 6089 | abrid | 1 |
| 6090 | abren | 1 |
| 6091 | abrazaros | 1 |
| 6092 | abrazar | 1 |
| 6093 | abrasarme | 1 |
| 6094 | abrásame | 1 |
| 6095 | abrasado | 1 |
| 6096 | abrasa | 1 |
| 6097 | abona | 1 |
| 6098 | ablandaros | 1 |
| 6099 | ablandar | 1 |
| 6100 | ablanda | 1 |
| 6101 | abito | 1 |
| 6102 | abin | 1 |
| 6103 | abigarrara | 1 |
| 6104 | abigarrada | 1 |
| 6105 | abiertas | 1 |
| 6106 | abendarraxe | 1 |
| 6107 | abenabos | 1 |
| 6108 | abenabo | 1 |
| 6109 | abbeville | 1 |
| 6110 | abandonan | 1 |
|
Ilustración del principio de mínimo esfuerzo: |
|
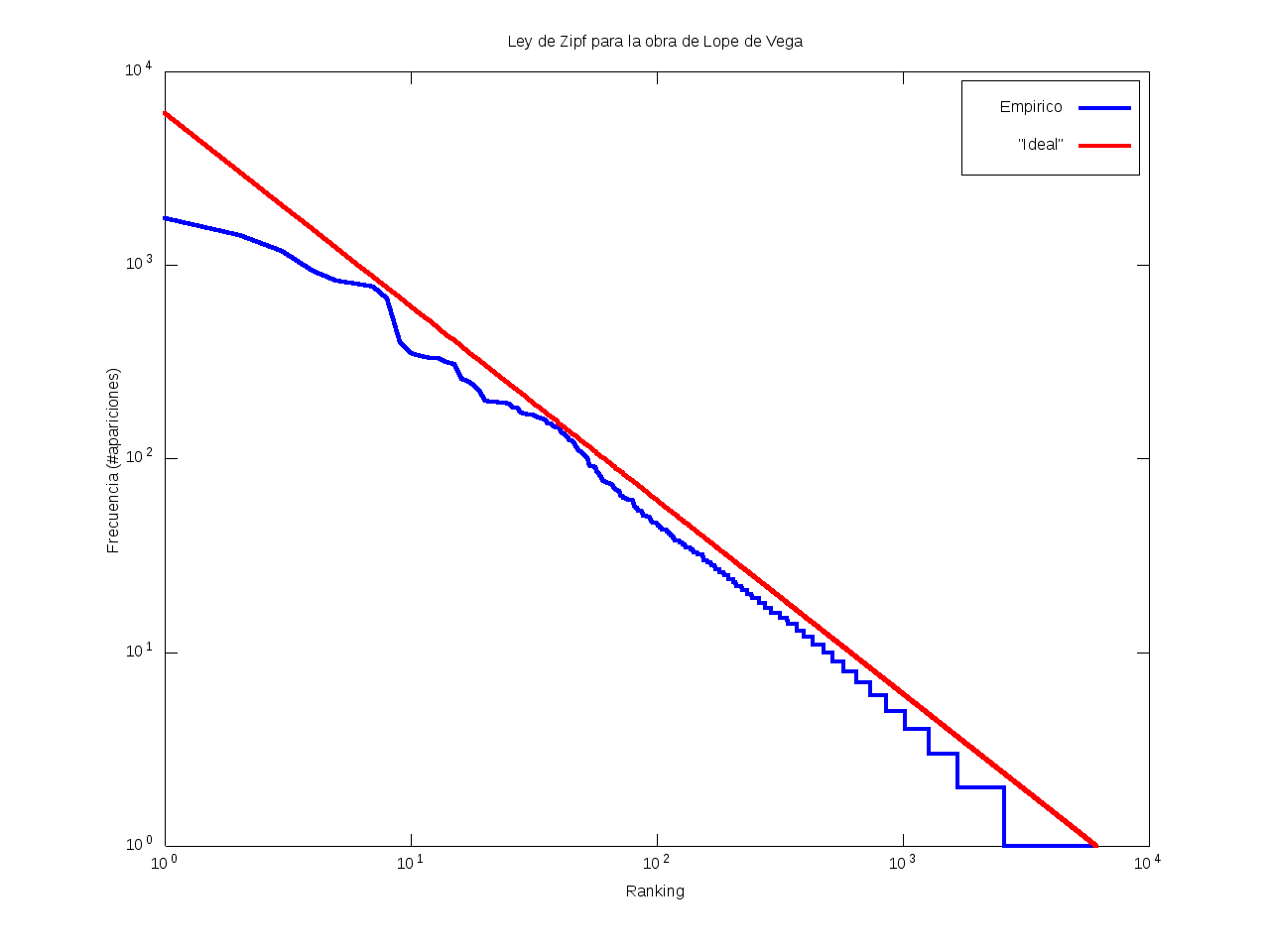
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará el texto actual (la obra de Lope de Vega) (conjunto 1)
contra el resto de textos en el mismo idioma (Castellano) (conjunto 2).
A continuación se muestra una lista de las palabras presentes en el texto actual,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
Mostrar todo
Recoger

