Comparativa: Traducción del Quijote
Índice
Información General
| Título: | Don Quijote de la Mancha |
|---|
| Autor: | Miguel de Cervantes |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 381216 |
|---|
| #Palabras distintas: | 22935 |
|---|
| Type-Token ratio: | 6.02% |
|---|
|
| Título: | Don Quixote |
|---|
| Autor: | Miguel de Cervantes |
|---|
| Idioma: | Inglés |
|---|
| #Palabras total: | 413057 |
|---|
| #Palabras distintas: | 14810 |
|---|
| Type-Token ratio: | 3.59% |
|---|
|
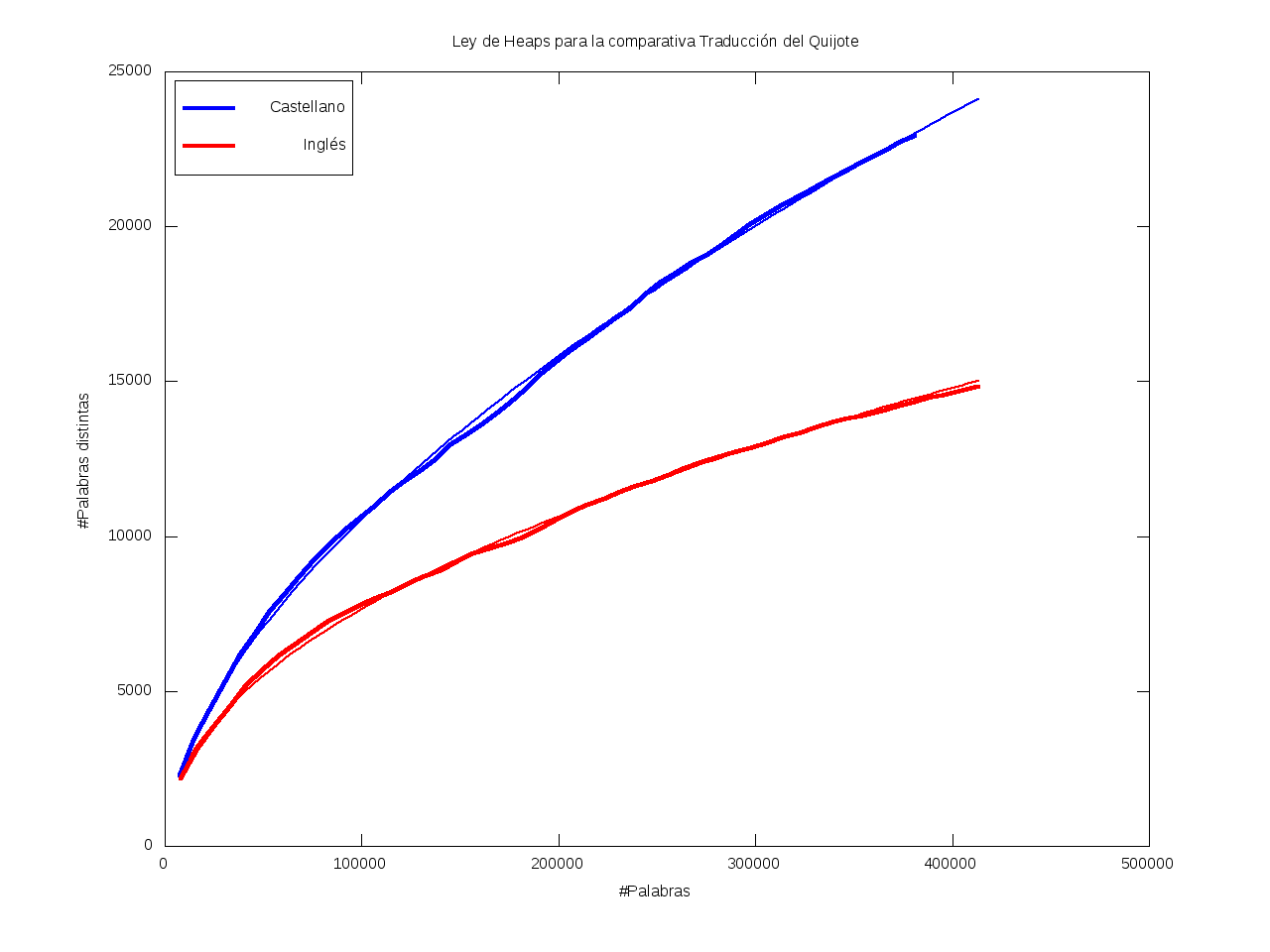
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| Castellano | Inglés |
|---|
| #Palabras: | #Palabras distintas: |
|---|
| 7624 | 2284 |
| 15248 | 3484 |
| 22872 | 4380 |
| 30496 | 5317 |
| 38120 | 6187 |
| 45744 | 6860 |
| 53368 | 7577 |
| 60992 | 8125 |
| 68616 | 8700 |
| 76240 | 9236 |
| 83864 | 9726 |
| 91488 | 10210 |
| 99112 | 10584 |
| 106736 | 10988 |
| 114360 | 11415 |
| 121984 | 11765 |
| 129608 | 12093 |
| 137232 | 12464 |
| 144856 | 12932 |
| 152480 | 13263 |
| 160104 | 13572 |
| 167728 | 13909 |
| 175352 | 14296 |
| 182976 | 14723 |
| 190600 | 15199 |
| 198224 | 15575 |
| 205848 | 15961 |
| 213472 | 16323 |
| 221096 | 16671 |
| 228720 | 17022 |
| 236344 | 17360 |
| 243968 | 17809 |
| 251592 | 18169 |
| 259216 | 18475 |
| 266840 | 18801 |
| 274464 | 19043 |
| 282088 | 19353 |
| 289712 | 19714 |
| 297336 | 20059 |
| 304960 | 20372 |
| 312584 | 20658 |
| 320208 | 20906 |
| 327832 | 21160 |
| 335456 | 21444 |
| 343080 | 21711 |
| 350704 | 21962 |
| 358328 | 22215 |
| 365952 | 22426 |
| 373576 | 22714 |
| 381200 | 22935 |
| 381216 | 22935 |
|
| #Palabras: | #Palabras distintas: |
|---|
| 8261 | 2188 |
| 16522 | 3135 |
| 24783 | 3840 |
| 33044 | 4525 |
| 41305 | 5188 |
| 49566 | 5664 |
| 57827 | 6154 |
| 66088 | 6498 |
| 74349 | 6880 |
| 82610 | 7233 |
| 90871 | 7505 |
| 99132 | 7790 |
| 107393 | 8001 |
| 115654 | 8210 |
| 123915 | 8480 |
| 132176 | 8718 |
| 140437 | 8910 |
| 148698 | 9176 |
| 156959 | 9442 |
| 165220 | 9598 |
| 173481 | 9757 |
| 181742 | 9956 |
| 190003 | 10199 |
| 198264 | 10497 |
| 206525 | 10789 |
| 214786 | 11006 |
| 223047 | 11212 |
| 231308 | 11416 |
| 239569 | 11606 |
| 247830 | 11786 |
| 256091 | 11973 |
| 264352 | 12209 |
| 272613 | 12372 |
| 280874 | 12540 |
| 289135 | 12698 |
| 297396 | 12844 |
| 305657 | 13009 |
| 313918 | 13182 |
| 322179 | 13305 |
| 330440 | 13498 |
| 338701 | 13667 |
| 346962 | 13791 |
| 355223 | 13904 |
| 363484 | 14030 |
| 371745 | 14171 |
| 380006 | 14309 |
| 388267 | 14458 |
| 396528 | 14551 |
| 404789 | 14694 |
| 413050 | 14810 |
| 413057 | 14810 |
|
|
Ajuste por mínimos cuadrados de los datos a K*n^b: |
| Castellano |
|
Inglés |
| K = 12.991 |
|
K = 32.002 |
| b = 0.582 |
|
b = 0.476 |
|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Castellano | Inglés |
Ilustración del principio de mínimo esfuerzo: |
| Rank | Palabra | Frec |
|---|
| 1 | que | 20628 |
| 2 | de | 18213 |
| 3 | y | 18189 |
| 4 | la | 10363 |
| 5 | a | 9824 |
| 6 | en | 8242 |
| 7 | el | 8210 |
| 8 | no | 6335 |
| 9 | los | 4748 |
| 10 | se | 4691 |
| 11 | con | 4202 |
| 12 | por | 3940 |
| 13 | las | 3468 |
| 14 | lo | 3461 |
| 15 | le | 3398 |
| 16 | su | 3352 |
| 17 | don | 2647 |
| 18 | del | 2491 |
| 19 | me | 2345 |
| 20 | como | 2264 |
| 21 | quijote | 2175 |
| 22 | sancho | 2148 |
| 23 | es | 2142 |
| 24 | yo | 2077 |
| 25 | más | 2044 |
| 26 | si | 1966 |
| 27 | un | 1938 |
| 28 | dijo | 1808 |
| 29 | al | 1737 |
| 30 | mi | 1705 |
| 31 | para | 1463 |
| 32 | porque | 1395 |
| 33 | ni | 1376 |
| 34 | una | 1329 |
| 35 | él | 1278 |
| 36 | tan | 1243 |
| 37 | o | 1213 |
| 38 | todo | 1180 |
| 39 | sin | 1156 |
| 40 | así | 1065 |
| 41 | señor | 1063 |
| 42 | respondió | 1063 |
| 43 | ser | 1056 |
| 44 | ha | 1052 |
| 45 | bien | 1050 |
| 46 | sus | 1049 |
| 47 | había | 1034 |
| 48 | pero | 1014 |
| 49 | merced | 900 |
| 50 | esto | 886 |
| 51 | pues | 865 |
| 52 | vuestra | 852 |
| 53 | qué | 849 |
| 54 | todos | 817 |
| 55 | ya | 785 |
| 56 | cuando | 757 |
| 57 | era | 754 |
| 58 | te | 726 |
| 59 | cual | 704 |
| 60 | sino | 694 |
| 61 | dos | 684 |
| 62 | donde | 674 |
| 63 | caballero | 661 |
| 64 | fue | 651 |
| 65 | este | 642 |
| 66 | esta | 624 |
| 67 | quien | 618 |
| 68 | ella | 604 |
| 69 | decir | 578 |
| 70 | he | 537 |
| 71 | muy | 535 |
| 72 | hacer | 535 |
| 73 | dios | 531 |
| 74 | aunque | 531 |
| 75 | otra | 517 |
| 76 | señora | 516 |
| 77 | aquí | 516 |
| 78 | otro | 511 |
| 79 | mí | 502 |
| 80 | aquel | 487 |
| 81 | son | 485 |
| 82 | estaba | 478 |
| 83 | hay | 471 |
| 84 | os | 463 |
| 85 | mal | 459 |
| 86 | sobre | 454 |
| 87 | nos | 450 |
| 88 | cosa | 447 |
| 89 | buen | 442 |
| 90 | está | 441 |
| 91 | verdad | 432 |
| 92 | tal | 428 |
| 93 | allí | 421 |
| 94 | tanto | 420 |
| 95 | ver | 408 |
| 96 | tengo | 402 |
| 97 | mundo | 394 |
| 98 | luego | 390 |
| 99 | tiene | 389 |
| 100 | sé | 388 |
| 101 | mis | 388 |
| 102 | hasta | 386 |
| 103 | alguna | 385 |
| 104 | poco | 380 |
| 105 | todas | 374 |
| 106 | entre | 374 |
| 107 | dicho | 373 |
| 108 | dar | 368 |
| 109 | ahora | 366 |
| 110 | parte | 363 |
| 111 | buena | 363 |
| 112 | vida | 356 |
| 113 | uno | 350 |
| 114 | tenía | 350 |
| 115 | han | 349 |
| 116 | menos | 347 |
| 117 | les | 347 |
| 118 | cosas | 347 |
| 119 | sí | 346 |
| 120 | lugar | 345 |
| 121 | gran | 340 |
| 122 | soy | 336 |
| 123 | eso | 335 |
| 124 | tu | 334 |
| 125 | casa | 334 |
| 126 | aquella | 333 |
| 127 | panza | 329 |
| 128 | manera | 328 |
| 129 | tiempo | 327 |
| 130 | digo | 323 |
| 131 | toda | 320 |
| 132 | cura | 313 |
| 133 | puesto | 307 |
| 134 | mano | 304 |
| 135 | amo | 297 |
| 136 | ellos | 295 |
| 137 | mucho | 294 |
| 138 | dio | 294 |
| 139 | mejor | 293 |
| 140 | caballeros | 293 |
| 141 | antes | 291 |
| 142 | fuera | 288 |
| 143 | visto | 285 |
| 144 | puede | 285 |
| 145 | ojos | 285 |
| 146 | sea | 284 |
| 147 | algún | 283 |
| 148 | dulcinea | 282 |
| 149 | cómo | 275 |
| 150 | tierra | 274 |
| 151 | día | 274 |
| 152 | otras | 273 |
| 153 | hecho | 272 |
| 154 | quién | 270 |
| 155 | tú | 265 |
| 156 | otros | 265 |
| 157 | quiero | 261 |
| 158 | padre | 259 |
| 159 | hombre | 259 |
| 160 | aun | 259 |
| 161 | haber | 254 |
| 162 | cielo | 252 |
| 163 | habían | 251 |
| 164 | historia | 249 |
| 165 | amigo | 249 |
| 166 | vio | 248 |
| 167 | saber | 247 |
| 168 | parece | 245 |
| 169 | camino | 245 |
| 170 | estas | 244 |
| 171 | hizo | 243 |
| 172 | tener | 242 |
| 173 | muchas | 242 |
| 174 | escudero | 242 |
| 175 | mas | 240 |
| 176 | días | 240 |
| 177 | manos | 239 |
| 178 | cuanto | 238 |
| 179 | tres | 234 |
| 180 | también | 234 |
| 181 | fin | 234 |
| 182 | desta | 234 |
| 183 | mujer | 226 |
| 184 | dice | 225 |
| 185 | será | 222 |
| 186 | cada | 221 |
| 187 | mesmo | 219 |
| 188 | cabeza | 215 |
| 189 | cuenta | 214 |
| 190 | nuestro | 213 |
| 191 | vos | 212 |
| 192 | punto | 211 |
| 193 | noche | 211 |
| 194 | replicó | 208 |
| 195 | veces | 207 |
| 196 | fuese | 207 |
| 197 | rocinante | 206 |
| 198 | vuesa | 203 |
| 199 | parecer | 202 |
| 200 | estos | 201 |
| 201 | razones | 200 |
| 202 | muchos | 200 |
| 203 | duque | 200 |
| 204 | diciendo | 198 |
| 205 | sólo | 197 |
| 206 | caballo | 197 |
| 207 | andante | 197 |
| 208 | grande | 196 |
| 209 | después | 196 |
| 210 | debe | 196 |
| 211 | podía | 193 |
| 212 | pie | 193 |
| 213 | gusto | 193 |
| 214 | vez | 191 |
| 215 | mil | 191 |
| 216 | eran | 191 |
| 217 | primero | 190 |
| 218 | decía | 190 |
| 219 | mío | 189 |
| 220 | duquesa | 189 |
| 221 | oh | 188 |
| 222 | llegó | 185 |
| 223 | nombre | 180 |
| 224 | mucha | 180 |
| 225 | voz | 179 |
| 226 | mismo | 178 |
| 227 | duda | 177 |
| 228 | adelante | 176 |
| 229 | mancha | 175 |
| 230 | estaban | 175 |
| 231 | gobernador | 174 |
| 232 | modo | 170 |
| 233 | desde | 169 |
| 234 | barbero | 167 |
| 235 | nada | 166 |
| 236 | según | 164 |
| 237 | toboso | 163 |
| 238 | vuestro | 162 |
| 239 | sido | 162 |
| 240 | hija | 162 |
| 241 | estar | 162 |
| 242 | dado | 162 |
| 243 | andantes | 162 |
| 244 | iba | 161 |
| 245 | voluntad | 160 |
| 246 | cuatro | 160 |
| 247 | deseo | 159 |
| 248 | quiso | 158 |
| 249 | aquellos | 158 |
| 250 | gente | 157 |
| 251 | has | 156 |
| 252 | hace | 156 |
| 253 | armas | 156 |
| 254 | ventura | 155 |
| 255 | tales | 154 |
| 256 | nunca | 154 |
| 257 | rostro | 153 |
| 258 | capítulo | 153 |
| 259 | alma | 153 |
| 260 | razón | 152 |
| 261 | viendo | 151 |
| 262 | venía | 151 |
| 263 | señores | 151 |
| 264 | entender | 151 |
| 265 | va | 150 |
| 266 | tanta | 150 |
| 267 | siempre | 150 |
| 268 | muerte | 150 |
| 269 | fueron | 149 |
| 270 | agora | 149 |
| 271 | menester | 148 |
| 272 | deste | 148 |
| 273 | cuerpo | 148 |
| 274 | camila | 148 |
| 275 | tienen | 147 |
| 276 | palabra | 147 |
| 277 | libros | 147 |
| 278 | doncella | 147 |
| 279 | mía | 146 |
| 280 | nuestra | 145 |
| 281 | quiere | 144 |
| 282 | entonces | 144 |
| 283 | puso | 143 |
| 284 | cuales | 143 |
| 285 | caballería | 143 |
| 286 | alguno | 143 |
| 287 | nadie | 142 |
| 288 | lotario | 142 |
| 289 | suerte | 141 |
| 290 | suelo | 141 |
| 291 | ninguna | 141 |
| 292 | hermosa | 141 |
| 293 | venta | 140 |
| 294 | jamás | 140 |
| 295 | ir | 140 |
| 296 | dicen | 140 |
| 297 | corazón | 140 |
| 298 | castillo | 140 |
| 299 | preguntó | 139 |
| 300 | anselmo | 138 |
| 301 | vino | 137 |
| 302 | rey | 137 |
| 303 | pies | 137 |
| 304 | años | 137 |
| 305 | persona | 136 |
| 306 | fernando | 135 |
| 307 | unos | 133 |
| 308 | tus | 133 |
| 309 | finalmente | 133 |
| 310 | voces | 132 |
| 311 | quedó | 132 |
| 312 | mayor | 132 |
| 313 | mala | 132 |
| 314 | dél | 132 |
| 315 | comenzó | 132 |
| 316 | poner | 131 |
| 317 | caso | 130 |
| 318 | fuerza | 129 |
| 319 | salir | 128 |
| 320 | éste | 128 |
| 321 | aventura | 128 |
| 322 | oído | 127 |
| 323 | memoria | 127 |
| 324 | ellas | 127 |
| 325 | contra | 127 |
| 326 | algo | 127 |
| 327 | grandes | 126 |
| 328 | palabras | 125 |
| 329 | mitad | 125 |
| 330 | delante | 125 |
| 331 | amor | 125 |
| 332 | fama | 124 |
| 333 | causa | 124 |
| 334 | tuvo | 123 |
| 335 | posible | 123 |
| 336 | hermosura | 123 |
| 337 | libro | 122 |
| 338 | cierto | 122 |
| 339 | volvió | 121 |
| 340 | algunos | 121 |
| 341 | contento | 120 |
| 342 | sabe | 119 |
| 343 | rucio | 119 |
| 344 | ventero | 118 |
| 345 | demás | 117 |
| 346 | sería | 116 |
| 347 | pasar | 116 |
| 348 | ínsula | 116 |
| 349 | hacía | 116 |
| 350 | están | 116 |
| 351 | ese | 116 |
| 352 | casi | 115 |
| 353 | venir | 114 |
| 354 | haya | 114 |
| 355 | nuevo | 113 |
| 356 | gobierno | 113 |
| 357 | figura | 113 |
| 358 | espada | 112 |
| 359 | ello | 112 |
| 360 | dejar | 112 |
| 361 | debía | 112 |
| 362 | nosotros | 111 |
| 363 | loco | 111 |
| 364 | habéis | 111 |
| 365 | dorotea | 111 |
| 366 | tantas | 110 |
| 367 | siendo | 110 |
| 368 | pena | 109 |
| 369 | bueno | 109 |
| 370 | bachiller | 109 |
| 371 | junto | 108 |
| 372 | hora | 108 |
| 373 | volver | 107 |
| 374 | triste | 107 |
| 375 | muerto | 107 |
| 376 | da | 107 |
| 377 | tomar | 106 |
| 378 | intención | 106 |
| 379 | hermano | 106 |
| 380 | daba | 106 |
| 381 | boca | 106 |
| 382 | poder | 105 |
| 383 | ocasión | 105 |
| 384 | buscar | 105 |
| 385 | aquello | 105 |
| 386 | pueblo | 104 |
| 387 | della | 104 |
| 388 | apenas | 104 |
| 389 | pedro | 103 |
| 390 | hombres | 103 |
| 391 | pensamientos | 102 |
| 392 | partes | 102 |
| 393 | lengua | 102 |
| 394 | ciudad | 102 |
| 395 | unas | 101 |
| 396 | estoy | 101 |
| 397 | cardenio | 101 |
| 398 | buenos | 101 |
| 399 | solo | 100 |
| 400 | pareció | 100 |
| 401 | ninguno | 100 |
| 402 | medio | 100 |
| 403 | llevar | 100 |
| 404 | hijo | 100 |
| 405 | estado | 100 |
| 406 | tantos | 99 |
| 407 | pudo | 99 |
| 408 | paso | 99 |
| 409 | luscinda | 99 |
| 410 | lágrimas | 99 |
| 411 | comer | 99 |
| 412 | pobre | 98 |
| 413 | dellos | 98 |
| 414 | quería | 97 |
| 415 | puedo | 97 |
| 416 | pienso | 97 |
| 417 | hablar | 97 |
| 418 | esa | 97 |
| 419 | carta | 97 |
| 420 | adonde | 97 |
| 421 | vista | 96 |
| 422 | creo | 96 |
| 423 | aquellas | 96 |
| 424 | parecía | 95 |
| 425 | orden | 95 |
| 426 | traía | 94 |
| 427 | oro | 94 |
| 428 | buenas | 94 |
| 429 | viene | 93 |
| 430 | primera | 93 |
| 431 | hubo | 93 |
| 432 | famoso | 93 |
| 433 | diablo | 93 |
| 434 | aposento | 93 |
| 435 | podría | 92 |
| 436 | fe | 92 |
| 437 | estando | 92 |
| 438 | ésta | 92 |
| 439 | aventuras | 92 |
| 440 | suyo | 91 |
| 441 | conmigo | 91 |
| 442 | brazos | 91 |
| 443 | dando | 90 |
| 444 | cabo | 90 |
| 445 | sabía | 89 |
| 446 | pudiera | 89 |
| 447 | pensar | 89 |
| 448 | mira | 89 |
| 449 | entrar | 89 |
| 450 | quisiera | 88 |
| 451 | cuento | 88 |
| 452 | asno | 88 |
| 453 | teresa | 87 |
| 454 | suele | 87 |
| 455 | salió | 87 |
| 456 | dieron | 87 |
| 457 | vuestras | 86 |
| 458 | trabajo | 86 |
| 459 | puerta | 86 |
| 460 | mozo | 86 |
| 461 | mañana | 86 |
| 462 | habiendo | 86 |
| 463 | algunas | 86 |
| 464 | pecho | 85 |
| 465 | mesma | 85 |
| 466 | campo | 85 |
| 467 | valor | 84 |
| 468 | juicio | 84 |
| 469 | gana | 84 |
| 470 | dé | 84 |
| 471 | autor | 84 |
| 472 | aún | 84 |
| 473 | tras | 83 |
| 474 | pueden | 83 |
| 475 | nuevas | 83 |
| 476 | ti | 82 |
| 477 | sazón | 82 |
| 478 | dejó | 82 |
| 479 | cuya | 82 |
| 480 | cuantos | 82 |
| 481 | llaman | 81 |
| 482 | libertad | 81 |
| 483 | entendimiento | 81 |
| 484 | batalla | 81 |
| 485 | tenga | 80 |
| 486 | sean | 80 |
| 487 | quizá | 80 |
| 488 | pueda | 80 |
| 489 | natural | 80 |
| 490 | madre | 80 |
| 491 | falta | 79 |
| 492 | desgracia | 79 |
| 493 | caballerías | 79 |
| 494 | zoraida | 78 |
| 495 | sol | 78 |
| 496 | pensamiento | 78 |
| 497 | peligro | 78 |
| 498 | pasó | 78 |
| 499 | marido | 78 |
| 500 | locura | 78 |
| 501 | honra | 78 |
| 502 | cerca | 78 |
| 503 | allá | 78 |
| 504 | seis | 77 |
| 505 | misma | 77 |
| 506 | eres | 77 |
| 507 | brazo | 77 |
| 508 | rico | 76 |
| 509 | mercedes | 76 |
| 510 | hoy | 76 |
| 511 | debajo | 76 |
| 512 | criado | 76 |
| 513 | agua | 76 |
| 514 | silencio | 75 |
| 515 | sansón | 75 |
| 516 | remedio | 75 |
| 517 | presto | 75 |
| 518 | podrá | 75 |
| 519 | nuestros | 75 |
| 520 | hubiera | 75 |
| 521 | haga | 75 |
| 522 | hacen | 75 |
| 523 | fortuna | 75 |
| 524 | españa | 75 |
| 525 | doña | 75 |
| 526 | sucedió | 74 |
| 527 | semejantes | 74 |
| 528 | licencia | 74 |
| 529 | jumento | 74 |
| 530 | dueña | 74 |
| 531 | ama | 74 |
| 532 | valeroso | 73 |
| 533 | priesa | 73 |
| 534 | discreto | 73 |
| 535 | deseos | 73 |
| 536 | venían | 72 |
| 537 | reino | 72 |
| 538 | fuere | 72 |
| 539 | espacio | 72 |
| 540 | entró | 72 |
| 541 | e | 72 |
| 542 | cuán | 72 |
| 543 | cristiano | 72 |
| 544 | labrador | 71 |
| 545 | hidalgo | 71 |
| 546 | doncellas | 71 |
| 547 | condición | 71 |
| 548 | padres | 70 |
| 549 | luz | 70 |
| 550 | llegar | 70 |
| 551 | hicieron | 70 |
| 552 | halló | 70 |
| 553 | gracias | 70 |
| 554 | cristianos | 70 |
| 555 | vestido | 69 |
| 556 | quisiere | 69 |
| 557 | pensaba | 69 |
| 558 | llegaron | 69 |
| 559 | leído | 69 |
| 560 | haré | 69 |
| 561 | suceso | 68 |
| 562 | par | 68 |
| 563 | mandó | 68 |
| 564 | hazañas | 68 |
| 565 | tomó | 67 |
| 566 | suya | 67 |
| 567 | querría | 67 |
| 568 | pasado | 67 |
| 569 | mayores | 67 |
| 570 | creer | 67 |
| 571 | amigos | 67 |
| 572 | virtud | 66 |
| 573 | tenido | 66 |
| 574 | tenían | 66 |
| 575 | hago | 66 |
| 576 | espaldas | 66 |
| 577 | bosque | 66 |
| 578 | andar | 66 |
| 579 | silla | 65 |
| 580 | sangre | 65 |
| 581 | pan | 65 |
| 582 | oír | 65 |
| 583 | muestras | 65 |
| 584 | leer | 65 |
| 585 | hemos | 65 |
| 586 | esperar | 65 |
| 587 | dije | 65 |
| 588 | barbas | 65 |
| 589 | antonio | 65 |
| 590 | ánimo | 65 |
| 591 | señal | 64 |
| 592 | querer | 64 |
| 593 | principio | 64 |
| 594 | noticia | 64 |
| 595 | llamaba | 64 |
| 596 | lanza | 64 |
| 597 | grandeza | 64 |
| 598 | escuderos | 64 |
| 599 | discurso | 64 |
| 600 | culpa | 64 |
| 601 | criados | 64 |
| 602 | verde | 63 |
| 603 | maese | 63 |
| 604 | enemigo | 63 |
| 605 | encantadores | 63 |
| 606 | edad | 63 |
| 607 | ansí | 63 |
| 608 | temor | 62 |
| 609 | oyendo | 62 |
| 610 | hijos | 62 |
| 611 | dormir | 62 |
| 612 | dónde | 62 |
| 613 | altisidora | 62 |
| 614 | ahí | 62 |
| 615 | vea | 61 |
| 616 | sucesos | 61 |
| 617 | sola | 61 |
| 618 | queda | 61 |
| 619 | obras | 61 |
| 620 | obra | 61 |
| 621 | ningún | 61 |
| 622 | diez | 61 |
| 623 | daño | 61 |
| 624 | consigo | 61 |
| 625 | consejo | 61 |
| 626 | compañía | 61 |
| 627 | azotes | 61 |
| 628 | valiente | 60 |
| 629 | tuviese | 60 |
| 630 | tienes | 60 |
| 631 | resolución | 60 |
| 632 | renegado | 60 |
| 633 | provecho | 60 |
| 634 | hallado | 60 |
| 635 | haciendo | 60 |
| 636 | enamorado | 60 |
| 637 | dolor | 60 |
| 638 | diese | 60 |
| 639 | carrasco | 60 |
| 640 | vi | 59 |
| 641 | veo | 59 |
| 642 | suelen | 59 |
| 643 | quedaron | 59 |
| 644 | presente | 59 |
| 645 | paz | 59 |
| 646 | mar | 59 |
| 647 | libre | 59 |
| 648 | hubiese | 59 |
| 649 | hambre | 59 |
| 650 | dineros | 59 |
| 651 | cuyo | 59 |
| 652 | vieron | 58 |
| 653 | venga | 58 |
| 654 | sobrina | 58 |
| 655 | principal | 58 |
| 656 | pastor | 58 |
| 657 | oídos | 58 |
| 658 | necesidad | 58 |
| 659 | mirar | 58 |
| 660 | media | 58 |
| 661 | llama | 58 |
| 662 | hallar | 58 |
| 663 | diga | 58 |
| 664 | acabó | 58 |
| 665 | sois | 57 |
| 666 | poeta | 57 |
| 667 | pasaba | 57 |
| 668 | nueva | 57 |
| 669 | licenciado | 57 |
| 670 | letras | 57 |
| 671 | estuvo | 57 |
| 672 | esposo | 57 |
| 673 | dijese | 57 |
| 674 | destos | 57 |
| 675 | caer | 57 |
| 676 | ante | 57 |
| 677 | veinte | 56 |
| 678 | reina | 56 |
| 679 | quitar | 56 |
| 680 | oficio | 56 |
| 681 | lado | 56 |
| 682 | gigante | 56 |
| 683 | encantado | 56 |
| 684 | alta | 56 |
| 685 | aldea | 56 |
| 686 | vencido | 55 |
| 687 | responder | 55 |
| 688 | reales | 55 |
| 689 | princesa | 55 |
| 690 | lleno | 55 |
| 691 | lejos | 55 |
| 692 | habrá | 55 |
| 693 | encima | 55 |
| 694 | dueñas | 55 |
| 695 | doy | 55 |
| 696 | discreción | 55 |
| 697 | risa | 54 |
| 698 | plática | 54 |
| 699 | mirando | 54 |
| 700 | llamar | 54 |
| 701 | esperando | 54 |
| 702 | ejercicio | 54 |
| 703 | darle | 54 |
| 704 | aire | 54 |
| 705 | acaso | 54 |
| 706 | servir | 53 |
| 707 | sacar | 53 |
| 708 | quieres | 53 |
| 709 | prosiguió | 53 |
| 710 | poca | 53 |
| 711 | oyó | 53 |
| 712 | mujeres | 53 |
| 713 | miedo | 53 |
| 714 | hacienda | 53 |
| 715 | fuego | 53 |
| 716 | destas | 53 |
| 717 | dentro | 53 |
| 718 | dejando | 53 |
| 719 | cuidado | 53 |
| 720 | carro | 53 |
| 721 | blanca | 53 |
| 722 | versos | 52 |
| 723 | verdadera | 52 |
| 724 | roque | 52 |
| 725 | moros | 52 |
| 726 | iban | 52 |
| 727 | diciéndole | 52 |
| 728 | decís | 52 |
| 729 | daré | 52 |
| 730 | contar | 52 |
| 731 | claro | 52 |
| 732 | basilio | 52 |
| 733 | asimismo | 52 |
| 734 | acuerdo | 52 |
| 735 | acabar | 52 |
| 736 | voy | 51 |
| 737 | sucedido | 51 |
| 738 | servido | 51 |
| 739 | sepa | 51 |
| 740 | segunda | 51 |
| 741 | presencia | 51 |
| 742 | negocio | 51 |
| 743 | montesinos | 51 |
| 744 | llegando | 51 |
| 745 | historias | 51 |
| 746 | esposa | 51 |
| 747 | escrito | 51 |
| 748 | contó | 51 |
| 749 | burla | 51 |
| 750 | verdadero | 50 |
| 751 | supo | 50 |
| 752 | señoras | 50 |
| 753 | ruido | 50 |
| 754 | puesta | 50 |
| 755 | presentes | 50 |
| 756 | justicia | 50 |
| 757 | fuerzas | 50 |
| 758 | efecto | 50 |
| 759 | trae | 49 |
| 760 | santa | 49 |
| 761 | salud | 49 |
| 762 | sacó | 49 |
| 763 | pesar | 49 |
| 764 | personas | 49 |
| 765 | moro | 49 |
| 766 | huésped | 49 |
| 767 | enemigos | 49 |
| 768 | disparates | 49 |
| 769 | diré | 49 |
| 770 | dejado | 49 |
| 771 | deben | 49 |
| 772 | dan | 49 |
| 773 | bondad | 49 |
| 774 | andaba | 49 |
| 775 | acá | 49 |
| 776 | vestidos | 48 |
| 777 | verdaderamente | 48 |
| 778 | van | 48 |
| 779 | toca | 48 |
| 780 | término | 48 |
| 781 | sabes | 48 |
| 782 | respuesta | 48 |
| 783 | real | 48 |
| 784 | pusieron | 48 |
| 785 | paje | 48 |
| 786 | nuestras | 48 |
| 787 | hacia | 48 |
| 788 | género | 48 |
| 789 | especialmente | 48 |
| 790 | emperador | 48 |
| 791 | dices | 48 |
| 792 | conocido | 48 |
| 793 | blanco | 48 |
| 794 | vuelto | 47 |
| 795 | propósito | 47 |
| 796 | pocos | 47 |
| 797 | pidió | 47 |
| 798 | pesadumbre | 47 |
| 799 | perder | 47 |
| 800 | opinión | 47 |
| 801 | muestra | 47 |
| 802 | esté | 47 |
| 803 | esas | 47 |
| 804 | efeto | 47 |
| 805 | cólera | 47 |
| 806 | cinco | 47 |
| 807 | cargo | 47 |
| 808 | aquél | 47 |
| 809 | venido | 46 |
| 810 | todavía | 46 |
| 811 | tarde | 46 |
| 812 | sabio | 46 |
| 813 | quieren | 46 |
| 814 | primo | 46 |
| 815 | mirad | 46 |
| 816 | llegado | 46 |
| 817 | ingenio | 46 |
| 818 | imaginación | 46 |
| 819 | fueran | 46 |
| 820 | entiendo | 46 |
| 821 | darme | 46 |
| 822 | cueva | 46 |
| 823 | cortesía | 46 |
| 824 | conocer | 46 |
| 825 | cabrero | 46 |
| 826 | cabellos | 46 |
| 827 | año | 46 |
| 828 | amadís | 46 |
| 829 | viento | 45 |
| 830 | sueño | 45 |
| 831 | pudiese | 45 |
| 832 | peor | 45 |
| 833 | mesa | 45 |
| 834 | instante | 45 |
| 835 | horas | 45 |
| 836 | gloria | 45 |
| 837 | general | 45 |
| 838 | favor | 45 |
| 839 | estremo | 45 |
| 840 | esperanza | 45 |
| 841 | escudos | 45 |
| 842 | dueño | 45 |
| 843 | cuál | 45 |
| 844 | árboles | 45 |
| 845 | amores | 45 |
| 846 | albarda | 45 |
| 847 | vivo | 44 |
| 848 | vamos | 44 |
| 849 | tuvieron | 44 |
| 850 | llevaba | 44 |
| 851 | leonela | 44 |
| 852 | largo | 44 |
| 853 | honestidad | 44 |
| 854 | hechos | 44 |
| 855 | guerra | 44 |
| 856 | fuesen | 44 |
| 857 | desdichado | 44 |
| 858 | corte | 44 |
| 859 | capitán | 44 |
| 860 | buscando | 44 |
| 861 | belleza | 44 |
| 862 | basta | 44 |
| 863 | arriba | 44 |
| 864 | anda | 44 |
| 865 | vaya | 43 |
| 866 | tiempos | 43 |
| 867 | subir | 43 |
| 868 | quedar | 43 |
| 869 | primer | 43 |
| 870 | diego | 43 |
| 871 | di | 43 |
| 872 | contado | 43 |
| 873 | clara | 43 |
| 874 | cautivo | 43 |
| 875 | adónde | 43 |
| 876 | vuestros | 42 |
| 877 | venganza | 42 |
| 878 | rodríguez | 42 |
| 879 | oyeron | 42 |
| 880 | mono | 42 |
| 881 | mejores | 42 |
| 882 | llamado | 42 |
| 883 | linaje | 42 |
| 884 | jardín | 42 |
| 885 | imposible | 42 |
| 886 | fuerte | 42 |
| 887 | éstos | 42 |
| 888 | doce | 42 |
| 889 | alto | 42 |
| 890 | viaje | 41 |
| 891 | verá | 41 |
| 892 | traje | 41 |
| 893 | tornó | 41 |
| 894 | siglos | 41 |
| 895 | señas | 41 |
| 896 | seguro | 41 |
| 897 | pedir | 41 |
| 898 | pastores | 41 |
| 899 | mías | 41 |
| 900 | malos | 41 |
| 901 | llevó | 41 |
| 902 | lleva | 41 |
| 903 | escribir | 41 |
| 904 | duques | 41 |
| 905 | armado | 41 |
| 906 | amistad | 41 |
| 907 | alcanzar | 41 |
| 908 | agravio | 41 |
| 909 | abajo | 41 |
| 910 | vienen | 40 |
| 911 | verse | 40 |
| 912 | veras | 40 |
| 913 | quiteria | 40 |
| 914 | pasaron | 40 |
| 915 | papel | 40 |
| 916 | oidor | 40 |
| 917 | luna | 40 |
| 918 | leyes | 40 |
| 919 | hiciese | 40 |
| 920 | hallaron | 40 |
| 921 | fui | 40 |
| 922 | esos | 40 |
| 923 | deja | 40 |
| 924 | costumbre | 40 |
| 925 | contrario | 40 |
| 926 | cama | 40 |
| 927 | alzó | 40 |
| 928 | alegre | 40 |
| 929 | admiración | 40 |
| 930 | uso | 39 |
| 931 | señales | 39 |
| 932 | rodillas | 39 |
| 933 | podían | 39 |
| 934 | pide | 39 |
| 935 | míos | 39 |
| 936 | mentira | 39 |
| 937 | leguas | 39 |
| 938 | dientes | 39 |
| 939 | dama | 39 |
| 940 | conciencia | 39 |
| 941 | yelmo | 38 |
| 942 | volvieron | 38 |
| 943 | viejo | 38 |
| 944 | trata | 38 |
| 945 | salido | 38 |
| 946 | perlas | 38 |
| 947 | parar | 38 |
| 948 | paciencia | 38 |
| 949 | mire | 38 |
| 950 | mayordomo | 38 |
| 951 | luis | 38 |
| 952 | levantó | 38 |
| 953 | juan | 38 |
| 954 | hará | 38 |
| 955 | donaire | 38 |
| 956 | discreta | 38 |
| 957 | dinero | 38 |
| 958 | dime | 38 |
| 959 | diligencia | 38 |
| 960 | díjole | 38 |
| 961 | dicha | 38 |
| 962 | conozco | 38 |
| 963 | cide | 38 |
| 964 | canónigo | 38 |
| 965 | caminos | 38 |
| 966 | barba | 38 |
| 967 | vivir | 37 |
| 968 | viese | 37 |
| 969 | tuviera | 37 |
| 970 | sala | 37 |
| 971 | reyes | 37 |
| 972 | mostraba | 37 |
| 973 | molido | 37 |
| 974 | justo | 37 |
| 975 | juntos | 37 |
| 976 | iglesia | 37 |
| 977 | hecha | 37 |
| 978 | hamete | 37 |
| 979 | hacían | 37 |
| 980 | grado | 37 |
| 981 | gentil | 37 |
| 982 | entrambos | 37 |
| 983 | cualquiera | 37 |
| 984 | correr | 37 |
| 985 | caído | 37 |
| 986 | viniese | 36 |
| 987 | trabajos | 36 |
| 988 | título | 36 |
| 989 | tenemos | 36 |
| 990 | serlo | 36 |
| 991 | sepultura | 36 |
| 992 | pasos | 36 |
| 993 | palos | 36 |
| 994 | obligado | 36 |
| 995 | morir | 36 |
| 996 | labradora | 36 |
| 997 | haría | 36 |
| 998 | grandísimo | 36 |
| 999 | gentes | 36 |
| 1000 | galeras | 36 |
| 1001 | experiencia | 36 |
| 1002 | echar | 36 |
| 1003 | desto | 36 |
| 1004 | baja | 36 |
| 1005 | vale | 35 |
| 1006 | soldado | 35 |
| 1007 | ricote | 35 |
| 1008 | querido | 35 |
| 1009 | queréis | 35 |
| 1010 | quedaba | 35 |
| 1011 | profesión | 35 |
| 1012 | presteza | 35 |
| 1013 | pedazos | 35 |
| 1014 | pasados | 35 |
| 1015 | locuras | 35 |
| 1016 | imagino | 35 |
| 1017 | guardar | 35 |
| 1018 | estamos | 35 |
| 1019 | entrañas | 35 |
| 1020 | encantador | 35 |
| 1021 | dígame | 35 |
| 1022 | decían | 35 |
| 1023 | cumplir | 35 |
| 1024 | cristiana | 35 |
| 1025 | creyendo | 35 |
| 1026 | cien | 35 |
| 1027 | celada | 35 |
| 1028 | ausencia | 35 |
| 1029 | asimesmo | 35 |
| 1030 | sale | 34 |
| 1031 | punta | 34 |
| 1032 | parecen | 34 |
| 1033 | pagar | 34 |
| 1034 | ocho | 34 |
| 1035 | moza | 34 |
| 1036 | llevado | 34 |
| 1037 | lecho | 34 |
| 1038 | industria | 34 |
| 1039 | hice | 34 |
| 1040 | facilidad | 34 |
| 1041 | estás | 34 |
| 1042 | éstas | 34 |
| 1043 | entraron | 34 |
| 1044 | engaño | 34 |
| 1045 | dellas | 34 |
| 1046 | damas | 34 |
| 1047 | costa | 34 |
| 1048 | coche | 34 |
| 1049 | camacho | 34 |
| 1050 | acudió | 34 |
| 1051 | vive | 33 |
| 1052 | tuve | 33 |
| 1053 | sombra | 33 |
| 1054 | solos | 33 |
| 1055 | segundo | 33 |
| 1056 | refranes | 33 |
| 1057 | ponerse | 33 |
| 1058 | podré | 33 |
| 1059 | pláticas | 33 |
| 1060 | número | 33 |
| 1061 | naturaleza | 33 |
| 1062 | leones | 33 |
| 1063 | juro | 33 |
| 1064 | jaula | 33 |
| 1065 | hacerse | 33 |
| 1066 | encantamento | 33 |
| 1067 | dolorida | 33 |
| 1068 | deseaba | 33 |
| 1069 | dejaba | 33 |
| 1070 | decirse | 33 |
| 1071 | cuello | 33 |
| 1072 | cualquier | 33 |
| 1073 | calle | 33 |
| 1074 | barca | 33 |
| 1075 | andado | 33 |
| 1076 | alforjas | 33 |
| 1077 | viéndose | 32 |
| 1078 | temeroso | 32 |
| 1079 | somos | 32 |
| 1080 | siquiera | 32 |
| 1081 | seguir | 32 |
| 1082 | san | 32 |
| 1083 | riendas | 32 |
| 1084 | revés | 32 |
| 1085 | recibió | 32 |
| 1086 | recebir | 32 |
| 1087 | puedes | 32 |
| 1088 | principales | 32 |
| 1089 | pone | 32 |
| 1090 | merece | 32 |
| 1091 | mandado | 32 |
| 1092 | mancebo | 32 |
| 1093 | llevaban | 32 |
| 1094 | hablando | 32 |
| 1095 | esperaba | 32 |
| 1096 | diera | 32 |
| 1097 | deje | 32 |
| 1098 | daban | 32 |
| 1099 | carne | 32 |
| 1100 | burlas | 32 |
| 1101 | bacía | 32 |
| 1102 | ayuda | 32 |
| 1103 | ay | 32 |
| 1104 | ancas | 32 |
| 1105 | admirado | 32 |
| 1106 | vuelta | 31 |
| 1107 | volviéndose | 31 |
| 1108 | verle | 31 |
| 1109 | verás | 31 |
| 1110 | ventana | 31 |
| 1111 | valentía | 31 |
| 1112 | suspiros | 31 |
| 1113 | sosiego | 31 |
| 1114 | sierra | 31 |
| 1115 | salieron | 31 |
| 1116 | rogó | 31 |
| 1117 | respeto | 31 |
| 1118 | quisiese | 31 |
| 1119 | quedo | 31 |
| 1120 | príncipes | 31 |
| 1121 | momento | 31 |
| 1122 | maritornes | 31 |
| 1123 | llegaba | 31 |
| 1124 | hallo | 31 |
| 1125 | haberle | 31 |
| 1126 | gracia | 31 |
| 1127 | golpe | 31 |
| 1128 | gigantes | 31 |
| 1129 | ganado | 31 |
| 1130 | francia | 31 |
| 1131 | echó | 31 |
| 1132 | doctor | 31 |
| 1133 | dirá | 31 |
| 1134 | derecho | 31 |
| 1135 | dejase | 31 |
| 1136 | dejaron | 31 |
| 1137 | debió | 31 |
| 1138 | cruel | 31 |
| 1139 | crédito | 31 |
| 1140 | conoció | 31 |
| 1141 | condesa | 31 |
| 1142 | caminar | 31 |
| 1143 | vosotros | 30 |
| 1144 | volviese | 30 |
| 1145 | viva | 30 |
| 1146 | verdaderas | 30 |
| 1147 | ventera | 30 |
| 1148 | tomado | 30 |
| 1149 | suspenso | 30 |
| 1150 | soldados | 30 |
| 1151 | solas | 30 |
| 1152 | sobresalto | 30 |
| 1153 | servicio | 30 |
| 1154 | quitó | 30 |
| 1155 | puestos | 30 |
| 1156 | prometido | 30 |
| 1157 | ponga | 30 |
| 1158 | majestad | 30 |
| 1159 | lorenzo | 30 |
| 1160 | llorar | 30 |
| 1161 | letra | 30 |
| 1162 | harto | 30 |
| 1163 | hacerle | 30 |
| 1164 | hábito | 30 |
| 1165 | guarda | 30 |
| 1166 | forzoso | 30 |
| 1167 | excelencia | 30 |
| 1168 | encantada | 30 |
| 1169 | diferentes | 30 |
| 1170 | determinado | 30 |
| 1171 | descubierto | 30 |
| 1172 | casas | 30 |
| 1173 | acudir | 30 |
| 1174 | acometer | 30 |
| 1175 | vuelve | 29 |
| 1176 | volviendo | 29 |
| 1177 | vizcaíno | 29 |
| 1178 | villano | 29 |
| 1179 | términos | 29 |
| 1180 | tampoco | 29 |
| 1181 | suplico | 29 |
| 1182 | soneto | 29 |
| 1183 | solamente | 29 |
| 1184 | puertas | 29 |
| 1185 | poetas | 29 |
| 1186 | pensó | 29 |
| 1187 | particular | 29 |
| 1188 | parecido | 29 |
| 1189 | negro | 29 |
| 1190 | mulas | 29 |
| 1191 | mula | 29 |
| 1192 | muchacho | 29 |
| 1193 | mostró | 29 |
| 1194 | mesmos | 29 |
| 1195 | malas | 29 |
| 1196 | levantar | 29 |
| 1197 | infierno | 29 |
| 1198 | hombros | 29 |
| 1199 | grisóstomo | 29 |
| 1200 | famosos | 29 |
| 1201 | estraño | 29 |
| 1202 | espejos | 29 |
| 1203 | enojo | 29 |
| 1204 | determinación | 29 |
| 1205 | decirle | 29 |
| 1206 | debo | 29 |
| 1207 | confuso | 29 |
| 1208 | comenzaron | 29 |
| 1209 | acabado | 29 |
| 1210 | usar | 28 |
| 1211 | trifaldi | 28 |
| 1212 | treinta | 28 |
| 1213 | señoría | 28 |
| 1214 | secreto | 28 |
| 1215 | sano | 28 |
| 1216 | salida | 28 |
| 1217 | rostros | 28 |
| 1218 | retablo | 28 |
| 1219 | quisieres | 28 |
| 1220 | quiera | 28 |
| 1221 | promesas | 28 |
| 1222 | plaza | 28 |
| 1223 | pequeño | 28 |
| 1224 | pensativo | 28 |
| 1225 | partida | 28 |
| 1226 | pareciéndole | 28 |
| 1227 | ofreció | 28 |
| 1228 | nuevos | 28 |
| 1229 | nombres | 28 |
| 1230 | narices | 28 |
| 1231 | nacido | 28 |
| 1232 | malo | 28 |
| 1233 | ínsulas | 28 |
| 1234 | hallé | 28 |
| 1235 | hablado | 28 |
| 1236 | gaula | 28 |
| 1237 | firme | 28 |
| 1238 | derecha | 28 |
| 1239 | cuyas | 28 |
| 1240 | compadre | 28 |
| 1241 | calidad | 28 |
| 1242 | artificio | 28 |
| 1243 | ánima | 28 |
| 1244 | admirados | 28 |
| 1245 | voto | 27 |
| 1246 | último | 27 |
| 1247 | tratar | 27 |
| 1248 | traído | 27 |
| 1249 | tosilos | 27 |
| 1250 | tío | 27 |
| 1251 | siete | 27 |
| 1252 | semejante | 27 |
| 1253 | respondía | 27 |
| 1254 | reinos | 27 |
| 1255 | pendencia | 27 |
| 1256 | pedía | 27 |
| 1257 | pasada | 27 |
| 1258 | mes | 27 |
| 1259 | marcela | 27 |
| 1260 | lugares | 27 |
| 1261 | ladrón | 27 |
| 1262 | infanta | 27 |
| 1263 | imaginar | 27 |
| 1264 | hiciera | 27 |
| 1265 | hallaba | 27 |
| 1266 | fácil | 27 |
| 1267 | estuviese | 27 |
| 1268 | estómago | 27 |
| 1269 | escudo | 27 |
| 1270 | empresa | 27 |
| 1271 | determinó | 27 |
| 1272 | despecho | 27 |
| 1273 | desnudo | 27 |
| 1274 | cuerdo | 27 |
| 1275 | cuentan | 27 |
| 1276 | conviene | 27 |
| 1277 | color | 27 |
| 1278 | cartas | 27 |
| 1279 | carnes | 27 |
| 1280 | barco | 27 |
| 1281 | árbol | 27 |
| 1282 | andaban | 27 |
| 1283 | aliento | 27 |
| 1284 | aguas | 27 |
| 1285 | acerca | 27 |
| 1286 | yendo | 26 |
| 1287 | viéndole | 26 |
| 1288 | valientes | 26 |
| 1289 | traza | 26 |
| 1290 | traían | 26 |
| 1291 | traer | 26 |
| 1292 | tonto | 26 |
| 1293 | tomé | 26 |
| 1294 | tercera | 26 |
| 1295 | subió | 26 |
| 1296 | simple | 26 |
| 1297 | ricos | 26 |
| 1298 | quedan | 26 |
| 1299 | pocas | 26 |
| 1300 | piernas | 26 |
| 1301 | pequeña | 26 |
| 1302 | ordenó | 26 |
| 1303 | mover | 26 |
| 1304 | milagro | 26 |
| 1305 | merlín | 26 |
| 1306 | médico | 26 |
| 1307 | matar | 26 |
| 1308 | malicia | 26 |
| 1309 | llevan | 26 |
| 1310 | ley | 26 |
| 1311 | honesta | 26 |
| 1312 | hermoso | 26 |
| 1313 | hacerme | 26 |
| 1314 | gracioso | 26 |
| 1315 | gobernar | 26 |
| 1316 | estudiante | 26 |
| 1317 | estraña | 26 |
| 1318 | esperanzas | 26 |
| 1319 | duro | 26 |
| 1320 | dulce | 26 |
| 1321 | diablos | 26 |
| 1322 | desa | 26 |
| 1323 | comodidad | 26 |
| 1324 | busca | 26 |
| 1325 | atrevido | 26 |
| 1326 | asió | 26 |
| 1327 | altos | 26 |
| 1328 | altas | 26 |
| 1329 | agradable | 26 |
| 1330 | vuelva | 25 |
| 1331 | verme | 25 |
| 1332 | turcos | 25 |
| 1333 | tomando | 25 |
| 1334 | toma | 25 |
| 1335 | tendré | 25 |
| 1336 | tendido | 25 |
| 1337 | sentido | 25 |
| 1338 | rigor | 25 |
| 1339 | recebido | 25 |
| 1340 | quitado | 25 |
| 1341 | quise | 25 |
| 1342 | puro | 25 |
| 1343 | pobres | 25 |
| 1344 | piensa | 25 |
| 1345 | piedra | 25 |
| 1346 | pecador | 25 |
| 1347 | pecado | 25 |
| 1348 | pasa | 25 |
| 1349 | necesario | 25 |
| 1350 | mostrar | 25 |
| 1351 | miró | 25 |
| 1352 | manda | 25 |
| 1353 | maestresala | 25 |
| 1354 | llega | 25 |
| 1355 | limpio | 25 |
| 1356 | legua | 25 |
| 1357 | lacayo | 25 |
| 1358 | jurar | 25 |
| 1359 | juramento | 25 |
| 1360 | irse | 25 |
| 1361 | furia | 25 |
| 1362 | famosa | 25 |
| 1363 | espero | 25 |
| 1364 | entrado | 25 |
| 1365 | digna | 25 |
| 1366 | desventura | 25 |
| 1367 | den | 25 |
| 1368 | dejé | 25 |
| 1369 | cuantas | 25 |
| 1370 | conforme | 25 |
| 1371 | cierta | 25 |
| 1372 | castellano | 25 |
| 1373 | caña | 25 |
| 1374 | caída | 25 |
| 1375 | caballos | 25 |
| 1376 | bajel | 25 |
| 1377 | aquélla | 25 |
| 1378 | añadió | 25 |
| 1379 | amiga | 25 |
| 1380 | abrió | 25 |
| 1381 | volvía | 24 |
| 1382 | veía | 24 |
| 1383 | vecino | 24 |
| 1384 | trecho | 24 |
| 1385 | traigo | 24 |
| 1386 | tenéis | 24 |
| 1387 | talante | 24 |
| 1388 | sintió | 24 |
| 1389 | serán | 24 |
| 1390 | sentado | 24 |
| 1391 | satisfecho | 24 |
| 1392 | quince | 24 |
| 1393 | pude | 24 |
| 1394 | propio | 24 |
| 1395 | preguntar | 24 |
| 1396 | ponía | 24 |
| 1397 | ponerme | 24 |
| 1398 | perdido | 24 |
| 1399 | penitencia | 24 |
| 1400 | pechos | 24 |
| 1401 | patria | 24 |
| 1402 | paño | 24 |
| 1403 | mentecato | 24 |
| 1404 | llegándose | 24 |
| 1405 | ligereza | 24 |
| 1406 | larga | 24 |
| 1407 | juntamente | 24 |
| 1408 | invención | 24 |
| 1409 | infinitos | 24 |
| 1410 | importancia | 24 |
| 1411 | importa | 24 |
| 1412 | honrado | 24 |
| 1413 | honrada | 24 |
| 1414 | gregorio | 24 |
| 1415 | gobernadores | 24 |
| 1416 | estancia | 24 |
| 1417 | estáis | 24 |
| 1418 | entrada | 24 |
| 1419 | encantados | 24 |
| 1420 | ejemplo | 24 |
| 1421 | echado | 24 |
| 1422 | discretos | 24 |
| 1423 | dijeron | 24 |
| 1424 | desgracias | 24 |
| 1425 | dará | 24 |
| 1426 | compañeros | 24 |
| 1427 | cielos | 24 |
| 1428 | caza | 24 |
| 1429 | carga | 24 |
| 1430 | breves | 24 |
| 1431 | bastante | 24 |
| 1432 | ayer | 24 |
| 1433 | aviso | 24 |
| 1434 | apriesa | 24 |
| 1435 | aparte | 24 |
| 1436 | alcanza | 24 |
| 1437 | alabanzas | 24 |
| 1438 | además | 24 |
| 1439 | visorrey | 23 |
| 1440 | vinieron | 23 |
| 1441 | vergüenza | 23 |
| 1442 | venida | 23 |
| 1443 | vee | 23 |
| 1444 | usan | 23 |
| 1445 | tocar | 23 |
| 1446 | teniendo | 23 |
| 1447 | sitio | 23 |
| 1448 | saliese | 23 |
| 1449 | romance | 23 |
| 1450 | recio | 23 |
| 1451 | prosigue | 23 |
| 1452 | pobreza | 23 |
| 1453 | parecían | 23 |
| 1454 | muerta | 23 |
| 1455 | liberal | 23 |
| 1456 | león | 23 |
| 1457 | intento | 23 |
| 1458 | ingenioso | 23 |
| 1459 | impertinente | 23 |
| 1460 | ido | 23 |
| 1461 | hízolo | 23 |
| 1462 | haz | 23 |
| 1463 | habido | 23 |
| 1464 | golpes | 23 |
| 1465 | fecho | 23 |
| 1466 | entendió | 23 |
| 1467 | dura | 23 |
| 1468 | detrás | 23 |
| 1469 | desencanto | 23 |
| 1470 | cuadrilleros | 23 |
| 1471 | corral | 23 |
| 1472 | convenía | 23 |
| 1473 | consejos | 23 |
| 1474 | conocimiento | 23 |
| 1475 | conde | 23 |
| 1476 | celos | 23 |
| 1477 | cantidad | 23 |
| 1478 | blancas | 23 |
| 1479 | atención | 23 |
| 1480 | arte | 23 |
| 1481 | arremetió | 23 |
| 1482 | acertado | 23 |
| 1483 | yerbas | 22 |
| 1484 | vestida | 22 |
| 1485 | vencimiento | 22 |
| 1486 | vela | 22 |
| 1487 | vas | 22 |
| 1488 | traidor | 22 |
| 1489 | talle | 22 |
| 1490 | suyos | 22 |
| 1491 | salvo | 22 |
| 1492 | sacado | 22 |
| 1493 | roto | 22 |
| 1494 | roldán | 22 |
| 1495 | riquezas | 22 |
| 1496 | río | 22 |
| 1497 | refrán | 22 |
| 1498 | pusiese | 22 |
| 1499 | puestas | 22 |
| 1500 | prado | 22 |
| 1501 | ponerle | 22 |
| 1502 | podéis | 22 |
| 1503 | pintado | 22 |
| 1504 | pelo | 22 |
| 1505 | paréceme | 22 |
| 1506 | papeles | 22 |
| 1507 | ordinario | 22 |
| 1508 | mostrado | 22 |
| 1509 | miraba | 22 |
| 1510 | meses | 22 |
| 1511 | llevo | 22 |
| 1512 | llegue | 22 |
| 1513 | llamó | 22 |
| 1514 | lenguas | 22 |
| 1515 | humilde | 22 |
| 1516 | haberse | 22 |
| 1517 | grave | 22 |
| 1518 | faltar | 22 |
| 1519 | escuchando | 22 |
| 1520 | ejecución | 22 |
| 1521 | diversas | 22 |
| 1522 | desenvoltura | 22 |
| 1523 | desdichada | 22 |
| 1524 | corona | 22 |
| 1525 | cayó | 22 |
| 1526 | cabras | 22 |
| 1527 | atento | 22 |
| 1528 | alegría | 22 |
| 1529 | acaba | 22 |
| 1530 | zaragoza | 21 |
| 1531 | vendrá | 21 |
| 1532 | ven | 21 |
| 1533 | trigo | 21 |
| 1534 | tome | 21 |
| 1535 | temiendo | 21 |
| 1536 | temerosa | 21 |
| 1537 | suspensos | 21 |
| 1538 | soledad | 21 |
| 1539 | sentimiento | 21 |
| 1540 | sentencias | 21 |
| 1541 | sanchica | 21 |
| 1542 | sabían | 21 |
| 1543 | rica | 21 |
| 1544 | prueba | 21 |
| 1545 | prudente | 21 |
| 1546 | pregunta | 21 |
| 1547 | poesía | 21 |
| 1548 | peso | 21 |
| 1549 | perjuicio | 21 |
| 1550 | pagado | 21 |
| 1551 | ofrecimientos | 21 |
| 1552 | nací | 21 |
| 1553 | música | 21 |
| 1554 | mora | 21 |
| 1555 | monte | 21 |
| 1556 | misericordia | 21 |
| 1557 | miserable | 21 |
| 1558 | menor | 21 |
| 1559 | maravilla | 21 |
| 1560 | máquina | 21 |
| 1561 | mandar | 21 |
| 1562 | llena | 21 |
| 1563 | liberalidad | 21 |
| 1564 | lástima | 21 |
| 1565 | labios | 21 |
| 1566 | justas | 21 |
| 1567 | jaez | 21 |
| 1568 | hermandad | 21 |
| 1569 | hechas | 21 |
| 1570 | hayan | 21 |
| 1571 | halla | 21 |
| 1572 | habla | 21 |
| 1573 | galeotes | 21 |
| 1574 | figuras | 21 |
| 1575 | estilo | 21 |
| 1576 | escritos | 21 |
| 1577 | entiende | 21 |
| 1578 | dijera | 21 |
| 1579 | diferencia | 21 |
| 1580 | descuido | 21 |
| 1581 | demonio | 21 |
| 1582 | debían | 21 |
| 1583 | dándole | 21 |
| 1584 | daga | 21 |
| 1585 | confusión | 21 |
| 1586 | cola | 21 |
| 1587 | campos | 21 |
| 1588 | calles | 21 |
| 1589 | bellaco | 21 |
| 1590 | atrevimiento | 21 |
| 1591 | acabe | 21 |
| 1592 | vulgo | 20 |
| 1593 | viniere | 20 |
| 1594 | vimos | 20 |
| 1595 | verla | 20 |
| 1596 | vencedor | 20 |
| 1597 | veis | 20 |
| 1598 | válame | 20 |
| 1599 | vais | 20 |
| 1600 | tuyo | 20 |
| 1601 | trecientos | 20 |
| 1602 | suyas | 20 |
| 1603 | sujeto | 20 |
| 1604 | suceder | 20 |
| 1605 | segura | 20 |
| 1606 | ruego | 20 |
| 1607 | ropa | 20 |
| 1608 | recato | 20 |
| 1609 | quede | 20 |
| 1610 | quedará | 20 |
| 1611 | quedado | 20 |
| 1612 | puerto | 20 |
| 1613 | prudencia | 20 |
| 1614 | precio | 20 |
| 1615 | poderoso | 20 |
| 1616 | persiguen | 20 |
| 1617 | peña | 20 |
| 1618 | patio | 20 |
| 1619 | pastora | 20 |
| 1620 | mozos | 20 |
| 1621 | movido | 20 |
| 1622 | montaña | 20 |
| 1623 | miraban | 20 |
| 1624 | mientras | 20 |
| 1625 | maravillas | 20 |
| 1626 | lienzo | 20 |
| 1627 | ignorante | 20 |
| 1628 | hierro | 20 |
| 1629 | guía | 20 |
| 1630 | flor | 20 |
| 1631 | felice | 20 |
| 1632 | fee | 20 |
| 1633 | faltaba | 20 |
| 1634 | estuviera | 20 |
| 1635 | estrellas | 20 |
| 1636 | escribió | 20 |
| 1637 | entendido | 20 |
| 1638 | encierra | 20 |
| 1639 | enamorados | 20 |
| 1640 | duerme | 20 |
| 1641 | do | 20 |
| 1642 | diesen | 20 |
| 1643 | descubrió | 20 |
| 1644 | defensa | 20 |
| 1645 | dedo | 20 |
| 1646 | debes | 20 |
| 1647 | daría | 20 |
| 1648 | cubierto | 20 |
| 1649 | cuántas | 20 |
| 1650 | cuándo | 20 |
| 1651 | costillas | 20 |
| 1652 | contigo | 20 |
| 1653 | comido | 20 |
| 1654 | comedia | 20 |
| 1655 | ciencia | 20 |
| 1656 | canto | 20 |
| 1657 | caballeriza | 20 |
| 1658 | bronce | 20 |
| 1659 | brevedad | 20 |
| 1660 | batallas | 20 |
| 1661 | autores | 20 |
| 1662 | arrojó | 20 |
| 1663 | arriero | 20 |
| 1664 | argel | 20 |
| 1665 | andan | 20 |
| 1666 | álvaro | 20 |
| 1667 | acudieron | 20 |
| 1668 | yerba | 19 |
| 1669 | virtudes | 19 |
| 1670 | veréis | 19 |
| 1671 | verdaderos | 19 |
| 1672 | vengo | 19 |
| 1673 | trance | 19 |
| 1674 | tocaba | 19 |
| 1675 | tengan | 19 |
| 1676 | sufrir | 19 |
| 1677 | sirva | 19 |
| 1678 | sevilla | 19 |
| 1679 | secretario | 19 |
| 1680 | sabré | 19 |
| 1681 | sabéis | 19 |
| 1682 | responde | 19 |
| 1683 | pudiere | 19 |
| 1684 | pudieran | 19 |
| 1685 | primeros | 19 |
| 1686 | preguntóle | 19 |
| 1687 | poniendo | 19 |
| 1688 | plata | 19 |
| 1689 | piedras | 19 |
| 1690 | peligros | 19 |
| 1691 | paga | 19 |
| 1692 | olvido | 19 |
| 1693 | ojo | 19 |
| 1694 | nación | 19 |
| 1695 | muelas | 19 |
| 1696 | montañas | 19 |
| 1697 | mirado | 19 |
| 1698 | menudo | 19 |
| 1699 | melisendra | 19 |
| 1700 | llenas | 19 |
| 1701 | llegóse | 19 |
| 1702 | llano | 19 |
| 1703 | improviso | 19 |
| 1704 | humor | 19 |
| 1705 | humano | 19 |
| 1706 | humana | 19 |
| 1707 | hubieran | 19 |
| 1708 | hermanos | 19 |
| 1709 | gallardo | 19 |
| 1710 | fortaleza | 19 |
| 1711 | estrecheza | 19 |
| 1712 | espíritu | 19 |
| 1713 | espanto | 19 |
| 1714 | espadas | 19 |
| 1715 | escondido | 19 |
| 1716 | entra | 19 |
| 1717 | engañado | 19 |
| 1718 | durmiendo | 19 |
| 1719 | docientos | 19 |
| 1720 | discretas | 19 |
| 1721 | digas | 19 |
| 1722 | desventuras | 19 |
| 1723 | despertó | 19 |
| 1724 | desmayada | 19 |
| 1725 | dejan | 19 |
| 1726 | defender | 19 |
| 1727 | dedos | 19 |
| 1728 | cortés | 19 |
| 1729 | corta | 19 |
| 1730 | compañero | 19 |
| 1731 | comida | 19 |
| 1732 | claudia | 19 |
| 1733 | circunstantes | 19 |
| 1734 | ceremonias | 19 |
| 1735 | cautivos | 19 |
| 1736 | casado | 19 |
| 1737 | carrera | 19 |
| 1738 | cara | 19 |
| 1739 | camisa | 19 |
| 1740 | calla | 19 |
| 1741 | blanda | 19 |
| 1742 | bestias | 19 |
| 1743 | bendición | 19 |
| 1744 | bella | 19 |
| 1745 | andrés | 19 |
| 1746 | ah | 19 |
| 1747 | adarga | 19 |
| 1748 | acciones | 19 |
| 1749 | veas | 18 |
| 1750 | usa | 18 |
| 1751 | turco | 18 |
| 1752 | testamento | 18 |
| 1753 | servicios | 18 |
| 1754 | saque | 18 |
| 1755 | salario | 18 |
| 1756 | sabido | 18 |
| 1757 | saben | 18 |
| 1758 | ruegos | 18 |
| 1759 | roma | 18 |
| 1760 | reposo | 18 |
| 1761 | redonda | 18 |
| 1762 | rayos | 18 |
| 1763 | queso | 18 |
| 1764 | querían | 18 |
| 1765 | proseguir | 18 |
| 1766 | prometió | 18 |
| 1767 | prometida | 18 |
| 1768 | profundo | 18 |
| 1769 | probar | 18 |
| 1770 | premio | 18 |
| 1771 | posesión | 18 |
| 1772 | persuadir | 18 |
| 1773 | perro | 18 |
| 1774 | pensado | 18 |
| 1775 | pecados | 18 |
| 1776 | parientes | 18 |
| 1777 | nicolás | 18 |
| 1778 | necedades | 18 |
| 1779 | morena | 18 |
| 1780 | miguel | 18 |
| 1781 | manteles | 18 |
| 1782 | malambruno | 18 |
| 1783 | llenos | 18 |
| 1784 | levantándose | 18 |
| 1785 | leandra | 18 |
| 1786 | lanzón | 18 |
| 1787 | interés | 18 |
| 1788 | imaginaba | 18 |
| 1789 | huir | 18 |
| 1790 | huesos | 18 |
| 1791 | hubiere | 18 |
| 1792 | honesto | 18 |
| 1793 | hilo | 18 |
| 1794 | herida | 18 |
| 1795 | gozar | 18 |
| 1796 | frío | 18 |
| 1797 | freno | 18 |
| 1798 | espejo | 18 |
| 1799 | escuadrón | 18 |
| 1800 | escribano | 18 |
| 1801 | ducados | 18 |
| 1802 | despojos | 18 |
| 1803 | desear | 18 |
| 1804 | desdichas | 18 |
| 1805 | cuerpos | 18 |
| 1806 | cueros | 18 |
| 1807 | corría | 18 |
| 1808 | corre | 18 |
| 1809 | contenta | 18 |
| 1810 | común | 18 |
| 1811 | come | 18 |
| 1812 | clavileño | 18 |
| 1813 | casos | 18 |
| 1814 | carreta | 18 |
| 1815 | canta | 18 |
| 1816 | campaña | 18 |
| 1817 | breve | 18 |
| 1818 | bienes | 18 |
| 1819 | benengeli | 18 |
| 1820 | bálsamo | 18 |
| 1821 | bajo | 18 |
| 1822 | atado | 18 |
| 1823 | aquéllos | 18 |
| 1824 | alegres | 18 |
| 1825 | aires | 18 |
| 1826 | agravios | 18 |
| 1827 | vuesas | 17 |
| 1828 | vuelvo | 17 |
| 1829 | vicente | 17 |
| 1830 | vía | 17 |
| 1831 | usanza | 17 |
| 1832 | tesoro | 17 |
| 1833 | terrible | 17 |
| 1834 | tendría | 17 |
| 1835 | supiese | 17 |
| 1836 | sospecha | 17 |
| 1837 | solía | 17 |
| 1838 | siguiente | 17 |
| 1839 | sentidos | 17 |
| 1840 | seiscientos | 17 |
| 1841 | seguridad | 17 |
| 1842 | seda | 17 |
| 1843 | sed | 17 |
| 1844 | seas | 17 |
| 1845 | santos | 17 |
| 1846 | salga | 17 |
| 1847 | remo | 17 |
| 1848 | regalo | 17 |
| 1849 | recado | 17 |
| 1850 | quedase | 17 |
| 1851 | puntualidad | 17 |
| 1852 | prometo | 17 |
| 1853 | promesa | 17 |
| 1854 | procura | 17 |
| 1855 | podido | 17 |
| 1856 | pluma | 17 |
| 1857 | perdón | 17 |
| 1858 | pasase | 17 |
| 1859 | parecerle | 17 |
| 1860 | palo | 17 |
| 1861 | ora | 17 |
| 1862 | oí | 17 |
| 1863 | ofrecía | 17 |
| 1864 | mortal | 17 |
| 1865 | menesterosos | 17 |
| 1866 | mármol | 17 |
| 1867 | maravedís | 17 |
| 1868 | mandamiento | 17 |
| 1869 | malandrines | 17 |
| 1870 | llevaron | 17 |
| 1871 | llegase | 17 |
| 1872 | llamada | 17 |
| 1873 | levantaron | 17 |
| 1874 | justa | 17 |
| 1875 | infinitas | 17 |
| 1876 | iguales | 17 |
| 1877 | huyendo | 17 |
| 1878 | heridas | 17 |
| 1879 | hallarse | 17 |
| 1880 | ginés | 17 |
| 1881 | garganta | 17 |
| 1882 | fuente | 17 |
| 1883 | flores | 17 |
| 1884 | favorecer | 17 |
| 1885 | estuvieron | 17 |
| 1886 | estruendo | 17 |
| 1887 | ése | 17 |
| 1888 | escribe | 17 |
| 1889 | entera | 17 |
| 1890 | encina | 17 |
| 1891 | encantamentos | 17 |
| 1892 | discursos | 17 |
| 1893 | diere | 17 |
| 1894 | detuvo | 17 |
| 1895 | desmayo | 17 |
| 1896 | deshora | 17 |
| 1897 | descubrieron | 17 |
| 1898 | darte | 17 |
| 1899 | curioso | 17 |
| 1900 | curiosidad | 17 |
| 1901 | continente | 17 |
| 1902 | consideración | 17 |
| 1903 | compuesto | 17 |
| 1904 | compasión | 17 |
| 1905 | comenzado | 17 |
| 1906 | castigo | 17 |
| 1907 | casar | 17 |
| 1908 | cadena | 17 |
| 1909 | cabreros | 17 |
| 1910 | bueyes | 17 |
| 1911 | berbería | 17 |
| 1912 | ausente | 17 |
| 1913 | arzobispo | 17 |
| 1914 | antigua | 17 |
| 1915 | amantes | 17 |
| 1916 | ajena | 17 |
| 1917 | acordó | 17 |
| 1918 | acabada | 17 |
| 1919 | abundancia | 17 |
| 1920 | volverse | 16 |
| 1921 | vivía | 16 |
| 1922 | viven | 16 |
| 1923 | vitoria | 16 |
| 1924 | verdades | 16 |
| 1925 | verano | 16 |
| 1926 | ventaja | 16 |
| 1927 | vano | 16 |
| 1928 | tristeza | 16 |
| 1929 | trato | 16 |
| 1930 | tiento | 16 |
| 1931 | temer | 16 |
| 1932 | subieron | 16 |
| 1933 | sosegado | 16 |
| 1934 | soga | 16 |
| 1935 | sirve | 16 |
| 1936 | siguió | 16 |
| 1937 | seco | 16 |
| 1938 | salí | 16 |
| 1939 | sabrá | 16 |
| 1940 | rogar | 16 |
| 1941 | rocín | 16 |
| 1942 | respondiese | 16 |
| 1943 | respondido | 16 |
| 1944 | rato | 16 |
| 1945 | quisieren | 16 |
| 1946 | quisiéredes | 16 |
| 1947 | quienquiera | 16 |
| 1948 | quejas | 16 |
| 1949 | pudieron | 16 |
| 1950 | príncipe | 16 |
| 1951 | principalmente | 16 |
| 1952 | pondré | 16 |
| 1953 | placer | 16 |
| 1954 | pensando | 16 |
| 1955 | penas | 16 |
| 1956 | pase | 16 |
| 1957 | pasaban | 16 |
| 1958 | parezca | 16 |
| 1959 | paredes | 16 |
| 1960 | orbe | 16 |
| 1961 | novela | 16 |
| 1962 | noble | 16 |
| 1963 | naturales | 16 |
| 1964 | muchachos | 16 |
| 1965 | molde | 16 |
| 1966 | micomicona | 16 |
| 1967 | marqués | 16 |
| 1968 | marién | 16 |
| 1969 | mandaba | 16 |
| 1970 | maleta | 16 |
| 1971 | llevando | 16 |
| 1972 | límites | 16 |
| 1973 | labradores | 16 |
| 1974 | joyas | 16 |
| 1975 | imprimir | 16 |
| 1976 | igual | 16 |
| 1977 | habrán | 16 |
| 1978 | habló | 16 |
| 1979 | hablaba | 16 |
| 1980 | habilidad | 16 |
| 1981 | ganar | 16 |
| 1982 | gaiferos | 16 |
| 1983 | fermosa | 16 |
| 1984 | falto | 16 |
| 1985 | estacas | 16 |
| 1986 | espuelas | 16 |
| 1987 | escritura | 16 |
| 1988 | envidia | 16 |
| 1989 | envía | 16 |
| 1990 | entrambas | 16 |
| 1991 | entero | 16 |
| 1992 | enfermedad | 16 |
| 1993 | enamorada | 16 |
| 1994 | ejercicios | 16 |
| 1995 | ea | 16 |
| 1996 | dondequiera | 16 |
| 1997 | disparate | 16 |
| 1998 | dijere | 16 |
| 1999 | dígolo | 16 |
| 2000 | digan | 16 |
| 2001 | deso | 16 |
| 2002 | demasiadamente | 16 |
| 2003 | dello | 16 |
| 2004 | dejaré | 16 |
| 2005 | cuesta | 16 |
| 2006 | cuánto | 16 |
| 2007 | creyó | 16 |
| 2008 | costumbres | 16 |
| 2009 | contentos | 16 |
| 2010 | contando | 16 |
| 2011 | consintió | 16 |
| 2012 | conocía | 16 |
| 2013 | confieso | 16 |
| 2014 | concierto | 16 |
| 2015 | comedias | 16 |
| 2016 | colores | 16 |
| 2017 | cincuenta | 16 |
| 2018 | ciento | 16 |
| 2019 | cena | 16 |
| 2020 | cantar | 16 |
| 2021 | bodas | 16 |
| 2022 | bendito | 16 |
| 2023 | beber | 16 |
| 2024 | atrás | 16 |
| 2025 | atentamente | 16 |
| 2026 | apostaré | 16 |
| 2027 | antiguos | 16 |
| 2028 | ansimesmo | 16 |
| 2029 | ana | 16 |
| 2030 | ambrosio | 16 |
| 2031 | alas | 16 |
| 2032 | adorno | 16 |
| 2033 | abrazó | 16 |
| 2034 | vuelven | 15 |
| 2035 | vivos | 15 |
| 2036 | virrey | 15 |
| 2037 | viesen | 15 |
| 2038 | ves | 15 |
| 2039 | vasallos | 15 |
| 2040 | varón | 15 |
| 2041 | valle | 15 |
| 2042 | tuya | 15 |
| 2043 | tuertos | 15 |
| 2044 | traen | 15 |
| 2045 | toque | 15 |
| 2046 | sustentar | 15 |
| 2047 | so | 15 |
| 2048 | sirven | 15 |
| 2049 | simplicidad | 15 |
| 2050 | sigue | 15 |
| 2051 | serían | 15 |
| 2052 | seré | 15 |
| 2053 | satisfación | 15 |
| 2054 | santo | 15 |
| 2055 | saltó | 15 |
| 2056 | salamanca | 15 |
| 2057 | sacaron | 15 |
| 2058 | sabiendo | 15 |
| 2059 | rescate | 15 |
| 2060 | remediar | 15 |
| 2061 | reír | 15 |
| 2062 | quédese | 15 |
| 2063 | púsose | 15 |
| 2064 | puntos | 15 |
| 2065 | puntas | 15 |
| 2066 | propuso | 15 |
| 2067 | prendas | 15 |
| 2068 | pido | 15 |
| 2069 | piden | 15 |
| 2070 | perdición | 15 |
| 2071 | pedido | 15 |
| 2072 | pares | 15 |
| 2073 | palacios | 15 |
| 2074 | pago | 15 |
| 2075 | noches | 15 |
| 2076 | negros | 15 |
| 2077 | negra | 15 |
| 2078 | murió | 15 |
| 2079 | montes | 15 |
| 2080 | mirase | 15 |
| 2081 | milagros | 15 |
| 2082 | mentiras | 15 |
| 2083 | mentir | 15 |
| 2084 | mambrino | 15 |
| 2085 | males | 15 |
| 2086 | llegan | 15 |
| 2087 | libres | 15 |
| 2088 | levantado | 15 |
| 2089 | leonero | 15 |
| 2090 | juez | 15 |
| 2091 | jornada | 15 |
| 2092 | ingrata | 15 |
| 2093 | imagen | 15 |
| 2094 | humildad | 15 |
| 2095 | huéspedes | 15 |
| 2096 | hermosas | 15 |
| 2097 | grandezas | 15 |
| 2098 | gentileza | 15 |
| 2099 | gato | 15 |
| 2100 | frente | 15 |
| 2101 | fermosura | 15 |
| 2102 | félix | 15 |
| 2103 | falte | 15 |
| 2104 | estima | 15 |
| 2105 | escuchaba | 15 |
| 2106 | escrúpulo | 15 |
| 2107 | entretenimiento | 15 |
| 2108 | entré | 15 |
| 2109 | entrando | 15 |
| 2110 | diole | 15 |
| 2111 | deshonra | 15 |
| 2112 | descubrir | 15 |
| 2113 | dejasen | 15 |
| 2114 | dejará | 15 |
| 2115 | decoro | 15 |
| 2116 | dádivas | 15 |
| 2117 | cuchilladas | 15 |
| 2118 | cuántos | 15 |
| 2119 | cuadrillero | 15 |
| 2120 | contornos | 15 |
| 2121 | consuelo | 15 |
| 2122 | confesar | 15 |
| 2123 | condado | 15 |
| 2124 | cobrar | 15 |
| 2125 | ciertos | 15 |
| 2126 | cerrar | 15 |
| 2127 | cerrada | 15 |
| 2128 | castigar | 15 |
| 2129 | cae | 15 |
| 2130 | cabestro | 15 |
| 2131 | buscarle | 15 |
| 2132 | brío | 15 |
| 2133 | bolsa | 15 |
| 2134 | bellotas | 15 |
| 2135 | barcelona | 15 |
| 2136 | azote | 15 |
| 2137 | autoridad | 15 |
| 2138 | asiento | 15 |
| 2139 | asiéndole | 15 |
| 2140 | antiguo | 15 |
| 2141 | amparo | 15 |
| 2142 | amante | 15 |
| 2143 | alteza | 15 |
| 2144 | alabanza | 15 |
| 2145 | ajenas | 15 |
| 2146 | zapatos | 14 |
| 2147 | viniesen | 14 |
| 2148 | vidas | 14 |
| 2149 | vender | 14 |
| 2150 | veen | 14 |
| 2151 | vara | 14 |
| 2152 | tuviere | 14 |
| 2153 | trujo | 14 |
| 2154 | tristes | 14 |
| 2155 | tomase | 14 |
| 2156 | testigos | 14 |
| 2157 | testigo | 14 |
| 2158 | suave | 14 |
| 2159 | sima | 14 |
| 2160 | siguieron | 14 |
| 2161 | sesenta | 14 |
| 2162 | sentir | 14 |
| 2163 | sentencia | 14 |
| 2164 | seno | 14 |
| 2165 | saco | 14 |
| 2166 | riqueza | 14 |
| 2167 | rienda | 14 |
| 2168 | república | 14 |
| 2169 | reja | 14 |
| 2170 | referido | 14 |
| 2171 | razonable | 14 |
| 2172 | quedé | 14 |
| 2173 | quedaré | 14 |
| 2174 | puse | 14 |
| 2175 | puñadas | 14 |
| 2176 | pudiesen | 14 |
| 2177 | procuraba | 14 |
| 2178 | procesión | 14 |
| 2179 | pro | 14 |
| 2180 | prisión | 14 |
| 2181 | pieza | 14 |
| 2182 | pierna | 14 |
| 2183 | pidiese | 14 |
| 2184 | pendencias | 14 |
| 2185 | pelear | 14 |
| 2186 | pasamonte | 14 |
| 2187 | pasadas | 14 |
| 2188 | partió | 14 |
| 2189 | parió | 14 |
| 2190 | paraba | 14 |
| 2191 | palma | 14 |
| 2192 | palacio | 14 |
| 2193 | ovejas | 14 |
| 2194 | original | 14 |
| 2195 | olvidado | 14 |
| 2196 | olor | 14 |
| 2197 | oía | 14 |
| 2198 | niñerías | 14 |
| 2199 | negar | 14 |
| 2200 | músico | 14 |
| 2201 | muera | 14 |
| 2202 | muchacha | 14 |
| 2203 | mismos | 14 |
| 2204 | mismas | 14 |
| 2205 | medias | 14 |
| 2206 | mata | 14 |
| 2207 | manta | 14 |
| 2208 | maestro | 14 |
| 2209 | madrid | 14 |
| 2210 | lleve | 14 |
| 2211 | llamo | 14 |
| 2212 | limpia | 14 |
| 2213 | ligero | 14 |
| 2214 | leyó | 14 |
| 2215 | lela | 14 |
| 2216 | lana | 14 |
| 2217 | juzgar | 14 |
| 2218 | izquierdo | 14 |
| 2219 | iré | 14 |
| 2220 | hojas | 14 |
| 2221 | harán | 14 |
| 2222 | hallará | 14 |
| 2223 | hagan | 14 |
| 2224 | guarde | 14 |
| 2225 | fuentes | 14 |
| 2226 | fiestas | 14 |
| 2227 | fiesta | 14 |
| 2228 | faltan | 14 |
| 2229 | faldas | 14 |
| 2230 | estrella | 14 |
| 2231 | ésa | 14 |
| 2232 | error | 14 |
| 2233 | entretener | 14 |
| 2234 | enfermo | 14 |
| 2235 | encanto | 14 |
| 2236 | docena | 14 |
| 2237 | digno | 14 |
| 2238 | dichoso | 14 |
| 2239 | dese | 14 |
| 2240 | dejo | 14 |
| 2241 | dejaban | 14 |
| 2242 | decirte | 14 |
| 2243 | dalle | 14 |
| 2244 | cruz | 14 |
| 2245 | corrido | 14 |
| 2246 | contiene | 14 |
| 2247 | conocidos | 14 |
| 2248 | comedido | 14 |
| 2249 | cobarde | 14 |
| 2250 | claridad | 14 |
| 2251 | cervantes | 14 |
| 2252 | cenar | 14 |
| 2253 | cecial | 14 |
| 2254 | castellana | 14 |
| 2255 | cárcel | 14 |
| 2256 | canalla | 14 |
| 2257 | caminante | 14 |
| 2258 | cabra | 14 |
| 2259 | blando | 14 |
| 2260 | báculo | 14 |
| 2261 | averiguar | 14 |
| 2262 | arroyo | 14 |
| 2263 | arrogante | 14 |
| 2264 | arma | 14 |
| 2265 | apearse | 14 |
| 2266 | apartó | 14 |
| 2267 | añadidura | 14 |
| 2268 | animal | 14 |
| 2269 | alzando | 14 |
| 2270 | almas | 14 |
| 2271 | alcanzó | 14 |
| 2272 | ahínco | 14 |
| 2273 | afrenta | 14 |
| 2274 | advierta | 14 |
| 2275 | acomodó | 14 |
| 2276 | acertó | 14 |
| 2277 | acabando | 14 |
| 2278 | abrir | 14 |
| 2279 | visera | 13 |
| 2280 | verdes | 13 |
| 2281 | venturoso | 13 |
| 2282 | venideros | 13 |
| 2283 | vees | 13 |
| 2284 | valer | 13 |
| 2285 | uñas | 13 |
| 2286 | testimonio | 13 |
| 2287 | tardanza | 13 |
| 2288 | suspiro | 13 |
| 2289 | socarrón | 13 |
| 2290 | simples | 13 |
| 2291 | siglo | 13 |
| 2292 | siento | 13 |
| 2293 | sentía | 13 |
| 2294 | sandeces | 13 |
| 2295 | salía | 13 |
| 2296 | sacando | 13 |
| 2297 | romper | 13 |
| 2298 | reverencia | 13 |
| 2299 | respondí | 13 |
| 2300 | remos | 13 |
| 2301 | relación | 13 |
| 2302 | región | 13 |
| 2303 | quisieron | 13 |
| 2304 | quedara | 13 |
| 2305 | puedan | 13 |
| 2306 | público | 13 |
| 2307 | propia | 13 |
| 2308 | principios | 13 |
| 2309 | preguntado | 13 |
| 2310 | prados | 13 |
| 2311 | podrán | 13 |
| 2312 | pliego | 13 |
| 2313 | playa | 13 |
| 2314 | place | 13 |
| 2315 | pierda | 13 |
| 2316 | piense | 13 |
| 2317 | peñas | 13 |
| 2318 | pelea | 13 |
| 2319 | pasan | 13 |
| 2320 | ollas | 13 |
| 2321 | norte | 13 |
| 2322 | nombrar | 13 |
| 2323 | niña | 13 |
| 2324 | movió | 13 |
| 2325 | moreno | 13 |
| 2326 | miente | 13 |
| 2327 | miembros | 13 |
| 2328 | manifiesto | 13 |
| 2329 | mando | 13 |
| 2330 | maldiciones | 13 |
| 2331 | luengos | 13 |
| 2332 | llevase | 13 |
| 2333 | llamando | 13 |
| 2334 | ligera | 13 |
| 2335 | leyese | 13 |
| 2336 | leyendo | 13 |
| 2337 | lanzas | 13 |
| 2338 | juntas | 13 |
| 2339 | jueces | 13 |
| 2340 | instrumentos | 13 |
| 2341 | imitar | 13 |
| 2342 | hueso | 13 |
| 2343 | hueco | 13 |
| 2344 | historiador | 13 |
| 2345 | hideputa | 13 |
| 2346 | herido | 13 |
| 2347 | halle | 13 |
| 2348 | habría | 13 |
| 2349 | habemos | 13 |
| 2350 | gritos | 13 |
| 2351 | graves | 13 |
| 2352 | gravedad | 13 |
| 2353 | grandísima | 13 |
| 2354 | gabán | 13 |
| 2355 | fuertemente | 13 |
| 2356 | frailes | 13 |
| 2357 | fondo | 13 |
| 2358 | fea | 13 |
| 2359 | fatiga | 13 |
| 2360 | fantasmas | 13 |
| 2361 | falso | 13 |
| 2362 | falsa | 13 |
| 2363 | estimar | 13 |
| 2364 | estará | 13 |
| 2365 | español | 13 |
| 2366 | escusar | 13 |
| 2367 | escuchar | 13 |
| 2368 | escritas | 13 |
| 2369 | entereza | 13 |
| 2370 | encerrado | 13 |
| 2371 | emperadores | 13 |
| 2372 | echando | 13 |
| 2373 | dormía | 13 |
| 2374 | diligencias | 13 |
| 2375 | desesperado | 13 |
| 2376 | desengaño | 13 |
| 2377 | descubre | 13 |
| 2378 | denuedo | 13 |
| 2379 | dejemos | 13 |
| 2380 | déjeme | 13 |
| 2381 | decirme | 13 |
| 2382 | decidme | 13 |
| 2383 | darles | 13 |
| 2384 | cumplido | 13 |
| 2385 | criadas | 13 |
| 2386 | corto | 13 |
| 2387 | corriendo | 13 |
| 2388 | corales | 13 |
| 2389 | conversación | 13 |
| 2390 | considerando | 13 |
| 2391 | conocida | 13 |
| 2392 | condiciones | 13 |
| 2393 | compuso | 13 |
| 2394 | coces | 13 |
| 2395 | claras | 13 |
| 2396 | cima | 13 |
| 2397 | cebada | 13 |
| 2398 | católico | 13 |
| 2399 | capellán | 13 |
| 2400 | cantando | 13 |
| 2401 | cansado | 13 |
| 2402 | calor | 13 |
| 2403 | callando | 13 |
| 2404 | buscaba | 13 |
| 2405 | bardas | 13 |
| 2406 | bajó | 13 |
| 2407 | atónito | 13 |
| 2408 | apeándose | 13 |
| 2409 | añadir | 13 |
| 2410 | anoche | 13 |
| 2411 | anduvo | 13 |
| 2412 | ancho | 13 |
| 2413 | amenazas | 13 |
| 2414 | alcornoque | 13 |
| 2415 | agradecido | 13 |
| 2416 | advierte | 13 |
| 2417 | acullá | 13 |
| 2418 | acomodado | 13 |
| 2419 | abismo | 13 |
| 2420 | abierto | 13 |
| 2421 | viera | 12 |
| 2422 | vicio | 12 |
| 2423 | verso | 12 |
| 2424 | venid | 12 |
| 2425 | vecinos | 12 |
| 2426 | valerosos | 12 |
| 2427 | único | 12 |
| 2428 | tratan | 12 |
| 2429 | torre | 12 |
| 2430 | tierna | 12 |
| 2431 | tendrá | 12 |
| 2432 | tela | 12 |
| 2433 | tasa | 12 |
| 2434 | tablas | 12 |
| 2435 | tabla | 12 |
| 2436 | supiera | 12 |
| 2437 | sucediese | 12 |
| 2438 | suceden | 12 |
| 2439 | socorro | 12 |
| 2440 | sirvió | 12 |
| 2441 | sierras | 12 |
| 2442 | serviros | 12 |
| 2443 | selvas | 12 |
| 2444 | sayo | 12 |
| 2445 | saliendo | 12 |
| 2446 | salían | 12 |
| 2447 | respondieron | 12 |
| 2448 | repuesto | 12 |
| 2449 | religión | 12 |
| 2450 | referidas | 12 |
| 2451 | recibieron | 12 |
| 2452 | raso | 12 |
| 2453 | rabia | 12 |
| 2454 | quedos | 12 |
| 2455 | quedamos | 12 |
| 2456 | puente | 12 |
| 2457 | procurar | 12 |
| 2458 | presa | 12 |
| 2459 | posada | 12 |
| 2460 | ponen | 12 |
| 2461 | pintada | 12 |
| 2462 | pesa | 12 |
| 2463 | perros | 12 |
| 2464 | perdió | 12 |
| 2465 | pedían | 12 |
| 2466 | pasara | 12 |
| 2467 | parecióle | 12 |
| 2468 | palmo | 12 |
| 2469 | pagó | 12 |
| 2470 | osaré | 12 |
| 2471 | obligados | 12 |
| 2472 | nubes | 12 |
| 2473 | notó | 12 |
| 2474 | nace | 12 |
| 2475 | muriendo | 12 |
| 2476 | mostrarse | 12 |
| 2477 | molinos | 12 |
| 2478 | mezcla | 12 |
| 2479 | maría | 12 |
| 2480 | locos | 12 |
| 2481 | llanto | 12 |
| 2482 | llana | 12 |
| 2483 | linajes | 12 |
| 2484 | levantarse | 12 |
| 2485 | lastimada | 12 |
| 2486 | largas | 12 |
| 2487 | ladrones | 12 |
| 2488 | juró | 12 |
| 2489 | juego | 12 |
| 2490 | instrumento | 12 |
| 2491 | indicio | 12 |
| 2492 | imitación | 12 |
| 2493 | imaginarse | 12 |
| 2494 | imaginaciones | 12 |
| 2495 | ignorancia | 12 |
| 2496 | honrados | 12 |
| 2497 | hombro | 12 |
| 2498 | hidalgos | 12 |
| 2499 | hiciere | 12 |
| 2500 | habilidades | 12 |
| 2501 | habiéndose | 12 |
| 2502 | haberme | 12 |
| 2503 | guardado | 12 |
| 2504 | goleta | 12 |
| 2505 | gobiernos | 12 |
| 2506 | flaqueza | 12 |
| 2507 | faltas | 12 |
| 2508 | estrecha | 12 |
| 2509 | estraños | 12 |
| 2510 | españoles | 12 |
| 2511 | escura | 12 |
| 2512 | enviado | 12 |
| 2513 | entienda | 12 |
| 2514 | enemiga | 12 |
| 2515 | encubrir | 12 |
| 2516 | encantos | 12 |
| 2517 | despacio | 12 |
| 2518 | desdicha | 12 |
| 2519 | desdeñado | 12 |
| 2520 | desdenes | 12 |
| 2521 | descubriese | 12 |
| 2522 | des | 12 |
| 2523 | demanda | 12 |
| 2524 | dejarse | 12 |
| 2525 | cuita | 12 |
| 2526 | cuentos | 12 |
| 2527 | cubierta | 12 |
| 2528 | cuáles | 12 |
| 2529 | crueldad | 12 |
| 2530 | costal | 12 |
| 2531 | corteses | 12 |
| 2532 | correo | 12 |
| 2533 | conocían | 12 |
| 2534 | concertado | 12 |
| 2535 | comenzar | 12 |
| 2536 | coloquio | 12 |
| 2537 | ciudades | 12 |
| 2538 | cerró | 12 |
| 2539 | cédula | 12 |
| 2540 | casarse | 12 |
| 2541 | casamiento | 12 |
| 2542 | calló | 12 |
| 2543 | callar | 12 |
| 2544 | bestia | 12 |
| 2545 | barataria | 12 |
| 2546 | ayudar | 12 |
| 2547 | asido | 12 |
| 2548 | armados | 12 |
| 2549 | armada | 12 |
| 2550 | apartado | 12 |
| 2551 | apacible | 12 |
| 2552 | ángel | 12 |
| 2553 | andando | 12 |
| 2554 | andad | 12 |
| 2555 | amorosa | 12 |
| 2556 | amada | 12 |
| 2557 | almohada | 12 |
| 2558 | alcalde | 12 |
| 2559 | alá | 12 |
| 2560 | ajeno | 12 |
| 2561 | agujero | 12 |
| 2562 | agudo | 12 |
| 2563 | aguardar | 12 |
| 2564 | agradezco | 12 |
| 2565 | advertir | 12 |
| 2566 | advertido | 12 |
| 2567 | admiró | 12 |
| 2568 | acabase | 12 |
| 2569 | acabaron | 12 |
| 2570 | abrazar | 12 |
| 2571 | abierta | 12 |
| 2572 | volverme | 11 |
| 2573 | volveré | 11 |
| 2574 | vivaldo | 11 |
| 2575 | vistas | 11 |
| 2576 | viejos | 11 |
| 2577 | vendría | 11 |
| 2578 | váyase | 11 |
| 2579 | usado | 11 |
| 2580 | última | 11 |
| 2581 | trujeron | 11 |
| 2582 | trueco | 11 |
| 2583 | través | 11 |
| 2584 | traición | 11 |
| 2585 | torres | 11 |
| 2586 | toros | 11 |
| 2587 | tomad | 11 |
| 2588 | toledo | 11 |
| 2589 | tiro | 11 |
| 2590 | tierras | 11 |
| 2591 | terciopelo | 11 |
| 2592 | temo | 11 |
| 2593 | sustento | 11 |
| 2594 | supe | 11 |
| 2595 | sujetos | 11 |
| 2596 | solicitud | 11 |
| 2597 | servida | 11 |
| 2598 | servían | 11 |
| 2599 | sentaron | 11 |
| 2600 | senda | 11 |
| 2601 | secas | 11 |
| 2602 | seáis | 11 |
| 2603 | saldrá | 11 |
| 2604 | saca | 11 |
| 2605 | sabor | 11 |
| 2606 | sabed | 11 |
| 2607 | rueda | 11 |
| 2608 | rodela | 11 |
| 2609 | rióse | 11 |
| 2610 | respuestas | 11 |
| 2611 | reposar | 11 |
| 2612 | rendido | 11 |
| 2613 | recibe | 11 |
| 2614 | rebuzno | 11 |
| 2615 | raya | 11 |
| 2616 | rara | 11 |
| 2617 | quite | 11 |
| 2618 | quitarme | 11 |
| 2619 | quieras | 11 |
| 2620 | queriendo | 11 |
| 2621 | querida | 11 |
| 2622 | quejarse | 11 |
| 2623 | queja | 11 |
| 2624 | pusiera | 11 |
| 2625 | puercos | 11 |
| 2626 | pudiendo | 11 |
| 2627 | prosiguiendo | 11 |
| 2628 | propias | 11 |
| 2629 | promete | 11 |
| 2630 | preguntas | 11 |
| 2631 | pongo | 11 |
| 2632 | podemos | 11 |
| 2633 | plega | 11 |
| 2634 | pique | 11 |
| 2635 | pesada | 11 |
| 2636 | pérdida | 11 |
| 2637 | pensáis | 11 |
| 2638 | peligrosa | 11 |
| 2639 | pareciese | 11 |
| 2640 | parado | 11 |
| 2641 | oreja | 11 |
| 2642 | órdenes | 11 |
| 2643 | ordenado | 11 |
| 2644 | oficios | 11 |
| 2645 | ocasiones | 11 |
| 2646 | obligación | 11 |
| 2647 | nieve | 11 |
| 2648 | negocios | 11 |
| 2649 | necio | 11 |
| 2650 | necedad | 11 |
| 2651 | nacidos | 11 |
| 2652 | muertos | 11 |
| 2653 | monesterio | 11 |
| 2654 | moneda | 11 |
| 2655 | molino | 11 |
| 2656 | miren | 11 |
| 2657 | metido | 11 |
| 2658 | mesón | 11 |
| 2659 | mesmas | 11 |
| 2660 | merecía | 11 |
| 2661 | merecen | 11 |
| 2662 | matrimonio | 11 |
| 2663 | materia | 11 |
| 2664 | macho | 11 |
| 2665 | llover | 11 |
| 2666 | llegué | 11 |
| 2667 | llegasen | 11 |
| 2668 | llegaban | 11 |
| 2669 | llamarse | 11 |
| 2670 | línea | 11 |
| 2671 | linda | 11 |
| 2672 | limpieza | 11 |
| 2673 | levantóse | 11 |
| 2674 | leal | 11 |
| 2675 | lados | 11 |
| 2676 | laberinto | 11 |
| 2677 | joya | 11 |
| 2678 | ira | 11 |
| 2679 | invierno | 11 |
| 2680 | invidia | 11 |
| 2681 | ingenios | 11 |
| 2682 | inconveniente | 11 |
| 2683 | imposibles | 11 |
| 2684 | imaginó | 11 |
| 2685 | humanas | 11 |
| 2686 | hito | 11 |
| 2687 | hermana | 11 |
| 2688 | hacerla | 11 |
| 2689 | hablo | 11 |
| 2690 | hablase | 11 |
| 2691 | guinart | 11 |
| 2692 | guardas | 11 |
| 2693 | gallarda | 11 |
| 2694 | flaco | 11 |
| 2695 | ferido | 11 |
| 2696 | feo | 11 |
| 2697 | faltó | 11 |
| 2698 | estrecho | 11 |
| 2699 | estrañas | 11 |
| 2700 | estimación | 11 |
| 2701 | esperaban | 11 |
| 2702 | espera | 11 |
| 2703 | escuridad | 11 |
| 2704 | escoger | 11 |
| 2705 | encuentro | 11 |
| 2706 | ejército | 11 |
| 2707 | ejemplos | 11 |
| 2708 | durandarte | 11 |
| 2709 | dormido | 11 |
| 2710 | dirán | 11 |
| 2711 | dignas | 11 |
| 2712 | dificultades | 11 |
| 2713 | dieren | 11 |
| 2714 | determinaron | 11 |
| 2715 | detener | 11 |
| 2716 | deshacer | 11 |
| 2717 | desaguisado | 11 |
| 2718 | desafío | 11 |
| 2719 | derribado | 11 |
| 2720 | dejarle | 11 |
| 2721 | dejara | 11 |
| 2722 | dejamos | 11 |
| 2723 | das | 11 |
| 2724 | darse | 11 |
| 2725 | cuestas | 11 |
| 2726 | cuarta | 11 |
| 2727 | criatura | 11 |
| 2728 | cortesanos | 11 |
| 2729 | corriente | 11 |
| 2730 | contraria | 11 |
| 2731 | consiste | 11 |
| 2732 | conocieron | 11 |
| 2733 | conoce | 11 |
| 2734 | compuesta | 11 |
| 2735 | componer | 11 |
| 2736 | comparación | 11 |
| 2737 | comisario | 11 |
| 2738 | cometido | 11 |
| 2739 | comen | 11 |
| 2740 | colgado | 11 |
| 2741 | clavija | 11 |
| 2742 | claramente | 11 |
| 2743 | ciertas | 11 |
| 2744 | ciego | 11 |
| 2745 | chusma | 11 |
| 2746 | cayeron | 11 |
| 2747 | caterva | 11 |
| 2748 | case | 11 |
| 2749 | cascos | 11 |
| 2750 | carretero | 11 |
| 2751 | caridad | 11 |
| 2752 | capitanes | 11 |
| 2753 | cansancio | 11 |
| 2754 | camisas | 11 |
| 2755 | camaradas | 11 |
| 2756 | cabezas | 11 |
| 2757 | caber | 11 |
| 2758 | cabecera | 11 |
| 2759 | batanes | 11 |
| 2760 | baño | 11 |
| 2761 | ayude | 11 |
| 2762 | aventurero | 11 |
| 2763 | asaz | 11 |
| 2764 | arzón | 11 |
| 2765 | artillería | 11 |
| 2766 | arábigo | 11 |
| 2767 | antonomasia | 11 |
| 2768 | animales | 11 |
| 2769 | andas | 11 |
| 2770 | ambas | 11 |
| 2771 | alivio | 11 |
| 2772 | alejandro | 11 |
| 2773 | alcázar | 11 |
| 2774 | alba | 11 |
| 2775 | agraviado | 11 |
| 2776 | advertid | 11 |
| 2777 | admirar | 11 |
| 2778 | ademán | 11 |
| 2779 | acontecido | 11 |
| 2780 | acompañar | 11 |
| 2781 | acogimiento | 11 |
| 2782 | acababa | 11 |
| 2783 | abiertos | 11 |
| 2784 | yegua | 10 |
| 2785 | volvióse | 10 |
| 2786 | viuda | 10 |
| 2787 | viniendo | 10 |
| 2788 | vine | 10 |
| 2789 | viernes | 10 |
| 2790 | venís | 10 |
| 2791 | venimos | 10 |
| 2792 | vengan | 10 |
| 2793 | vencer | 10 |
| 2794 | vean | 10 |
| 2795 | veamos | 10 |
| 2796 | ve | 10 |
| 2797 | varas | 10 |
| 2798 | uña | 10 |
| 2799 | turbada | 10 |
| 2800 | tropel | 10 |
| 2801 | tronco | 10 |
| 2802 | tormento | 10 |
| 2803 | tocantes | 10 |
| 2804 | tengas | 10 |
| 2805 | tendrás | 10 |
| 2806 | tendió | 10 |
| 2807 | temeridad | 10 |
| 2808 | sospechas | 10 |
| 2809 | sonetos | 10 |
| 2810 | soltó | 10 |
| 2811 | soltar | 10 |
| 2812 | soledades | 10 |
| 2813 | soberbia | 10 |
| 2814 | singular | 10 |
| 2815 | siguiendo | 10 |
| 2816 | sentar | 10 |
| 2817 | saya | 10 |
| 2818 | satisfacer | 10 |
| 2819 | satanás | 10 |
| 2820 | sandez | 10 |
| 2821 | salen | 10 |
| 2822 | sal | 10 |
| 2823 | ruin | 10 |
| 2824 | rodrigo | 10 |
| 2825 | responderé | 10 |
| 2826 | requesones | 10 |
| 2827 | reliquias | 10 |
| 2828 | reinas | 10 |
| 2829 | referida | 10 |
| 2830 | realmente | 10 |
| 2831 | razonamiento | 10 |
| 2832 | quitaron | 10 |
| 2833 | quitan | 10 |
| 2834 | quinto | 10 |
| 2835 | quietud | 10 |
| 2836 | puta | 10 |
| 2837 | pura | 10 |
| 2838 | pulso | 10 |
| 2839 | prometer | 10 |
| 2840 | profeso | 10 |
| 2841 | primeras | 10 |
| 2842 | prenda | 10 |
| 2843 | pregunté | 10 |
| 2844 | poniéndose | 10 |
| 2845 | pondría | 10 |
| 2846 | podrás | 10 |
| 2847 | poderosa | 10 |
| 2848 | pintor | 10 |
| 2849 | pierres | 10 |
| 2850 | pierde | 10 |
| 2851 | pida | 10 |
| 2852 | pese | 10 |
| 2853 | perfeción | 10 |
| 2854 | peregrino | 10 |
| 2855 | pensé | 10 |
| 2856 | pendiente | 10 |
| 2857 | pelota | 10 |
| 2858 | pedazo | 10 |
| 2859 | pasatiempo | 10 |
| 2860 | parto | 10 |
| 2861 | pardo | 10 |
| 2862 | osaba | 10 |
| 2863 | oían | 10 |
| 2864 | ofrezco | 10 |
| 2865 | ofrece | 10 |
| 2866 | nosotras | 10 |
| 2867 | non | 10 |
| 2868 | nombrado | 10 |
| 2869 | nobleza | 10 |
| 2870 | muestre | 10 |
| 2871 | movimientos | 10 |
| 2872 | morisco | 10 |
| 2873 | morisca | 10 |
| 2874 | mohíno | 10 |
| 2875 | miseria | 10 |
| 2876 | miserables | 10 |
| 2877 | mientes | 10 |
| 2878 | miel | 10 |
| 2879 | menoscabo | 10 |
| 2880 | mató | 10 |
| 2881 | manchego | 10 |
| 2882 | llevas | 10 |
| 2883 | llevarle | 10 |
| 2884 | limpias | 10 |
| 2885 | licor | 10 |
| 2886 | lenguaje | 10 |
| 2887 | lealtad | 10 |
| 2888 | infinita | 10 |
| 2889 | imágines | 10 |
| 2890 | ilustre | 10 |
| 2891 | huye | 10 |
| 2892 | hurto | 10 |
| 2893 | hijas | 10 |
| 2894 | hermosos | 10 |
| 2895 | harta | 10 |
| 2896 | hallazgo | 10 |
| 2897 | hallase | 10 |
| 2898 | hagas | 10 |
| 2899 | hachas | 10 |
| 2900 | haced | 10 |
| 2901 | hable | 10 |
| 2902 | habiéndole | 10 |
| 2903 | guíe | 10 |
| 2904 | grecia | 10 |
| 2905 | gordo | 10 |
| 2906 | gentilhombre | 10 |
| 2907 | gallo | 10 |
| 2908 | gallardía | 10 |
| 2909 | galera | 10 |
| 2910 | galán | 10 |
| 2911 | gala | 10 |
| 2912 | fuele | 10 |
| 2913 | fruto | 10 |
| 2914 | forma | 10 |
| 2915 | felicísimo | 10 |
| 2916 | faltado | 10 |
| 2917 | estribos | 10 |
| 2918 | espíritus | 10 |
| 2919 | escusado | 10 |
| 2920 | escucha | 10 |
| 2921 | éramos | 10 |
| 2922 | enviar | 10 |
| 2923 | eneas | 10 |
| 2924 | encomendándose | 10 |
| 2925 | embajada | 10 |
| 2926 | ejércitos | 10 |
| 2927 | echaron | 10 |
| 2928 | donaires | 10 |
| 2929 | divina | 10 |
| 2930 | disposición | 10 |
| 2931 | disculpa | 10 |
| 2932 | díjome | 10 |
| 2933 | digáis | 10 |
| 2934 | déstos | 10 |
| 2935 | despierto | 10 |
| 2936 | despidió | 10 |
| 2937 | despedirse | 10 |
| 2938 | desgraciado | 10 |
| 2939 | deseosos | 10 |
| 2940 | desea | 10 |
| 2941 | demonios | 10 |
| 2942 | dejes | 10 |
| 2943 | dejen | 10 |
| 2944 | dejarme | 10 |
| 2945 | decid | 10 |
| 2946 | debida | 10 |
| 2947 | dada | 10 |
| 2948 | cuyos | 10 |
| 2949 | curar | 10 |
| 2950 | cumplimiento | 10 |
| 2951 | cuerno | 10 |
| 2952 | cuentas | 10 |
| 2953 | cubrir | 10 |
| 2954 | cuarto | 10 |
| 2955 | criada | 10 |
| 2956 | creído | 10 |
| 2957 | creía | 10 |
| 2958 | coyuntura | 10 |
| 2959 | corren | 10 |
| 2960 | corredores | 10 |
| 2961 | corchuelo | 10 |
| 2962 | continua | 10 |
| 2963 | considerar | 10 |
| 2964 | consentir | 10 |
| 2965 | comúnmente | 10 |
| 2966 | componen | 10 |
| 2967 | compás | 10 |
| 2968 | comiendo | 10 |
| 2969 | comenzaba | 10 |
| 2970 | cera | 10 |
| 2971 | cautiva | 10 |
| 2972 | causas | 10 |
| 2973 | causado | 10 |
| 2974 | catorce | 10 |
| 2975 | cántaro | 10 |
| 2976 | candaya | 10 |
| 2977 | caminantes | 10 |
| 2978 | caminando | 10 |
| 2979 | camina | 10 |
| 2980 | bulto | 10 |
| 2981 | besar | 10 |
| 2982 | beneficio | 10 |
| 2983 | belerma | 10 |
| 2984 | bastantes | 10 |
| 2985 | asperezas | 10 |
| 2986 | arrobas | 10 |
| 2987 | aragón | 10 |
| 2988 | aprobación | 10 |
| 2989 | apartar | 10 |
| 2990 | andalucía | 10 |
| 2991 | amorosos | 10 |
| 2992 | amorosas | 10 |
| 2993 | alrededor | 10 |
| 2994 | alonso | 10 |
| 2995 | alcaide | 10 |
| 2996 | alabado | 10 |
| 2997 | ajenos | 10 |
| 2998 | agüero | 10 |
| 2999 | aficionado | 10 |
| 3000 | acompañe | 10 |
| 3001 | acertar | 10 |
| 3002 | aceite | 10 |
| 3003 | accidente | 10 |
| 3004 | zaga | 9 |
| 3005 | yace | 9 |
| 3006 | volviesen | 9 |
| 3007 | volverá | 9 |
| 3008 | viudas | 9 |
| 3009 | vituperios | 9 |
| 3010 | visión | 9 |
| 3011 | virgilio | 9 |
| 3012 | villana | 9 |
| 3013 | viéndola | 9 |
| 3014 | vieja | 9 |
| 3015 | vestir | 9 |
| 3016 | veremos | 9 |
| 3017 | venerable | 9 |
| 3018 | tuviesen | 9 |
| 3019 | turbado | 9 |
| 3020 | trompetas | 9 |
| 3021 | tratado | 9 |
| 3022 | trataba | 9 |
| 3023 | trasluce | 9 |
| 3024 | traes | 9 |
| 3025 | tornaron | 9 |
| 3026 | tomo | 9 |
| 3027 | tocan | 9 |
| 3028 | tocado | 9 |
| 3029 | tirteafuera | 9 |
| 3030 | tercero | 9 |
| 3031 | ten | 9 |
| 3032 | suelta | 9 |
| 3033 | sudor | 9 |
| 3034 | suceda | 9 |
| 3035 | subido | 9 |
| 3036 | suba | 9 |
| 3037 | sollozos | 9 |
| 3038 | siéndolo | 9 |
| 3039 | seso | 9 |
| 3040 | servía | 9 |
| 3041 | sepan | 9 |
| 3042 | sepáis | 9 |
| 3043 | sentóse | 9 |
| 3044 | sentimientos | 9 |
| 3045 | saltando | 9 |
| 3046 | salgo | 9 |
| 3047 | sacarle | 9 |
| 3048 | sabios | 9 |
| 3049 | sabemos | 9 |
| 3050 | saavedra | 9 |
| 3051 | rústico | 9 |
| 3052 | roncesvalles | 9 |
| 3053 | rincón | 9 |
| 3054 | riguroso | 9 |
| 3055 | riberas | 9 |
| 3056 | retor | 9 |
| 3057 | resucitar | 9 |
| 3058 | reprehensión | 9 |
| 3059 | reposada | 9 |
| 3060 | reinaldos | 9 |
| 3061 | rayo | 9 |
| 3062 | ratos | 9 |
| 3063 | quedóse | 9 |
| 3064 | quedándose | 9 |
| 3065 | quedaban | 9 |
| 3066 | puño | 9 |
| 3067 | prosupuesto | 9 |
| 3068 | profunda | 9 |
| 3069 | preguntase | 9 |
| 3070 | preguntáronle | 9 |
| 3071 | porfía | 9 |
| 3072 | poniéndole | 9 |
| 3073 | ponían | 9 |
| 3074 | pongan | 9 |
| 3075 | pon | 9 |
| 3076 | podrían | 9 |
| 3077 | plazas | 9 |
| 3078 | plato | 9 |
| 3079 | pintar | 9 |
| 3080 | pinta | 9 |
| 3081 | piensas | 9 |
| 3082 | peregrinos | 9 |
| 3083 | peores | 9 |
| 3084 | pedirle | 9 |
| 3085 | pastoral | 9 |
| 3086 | partirse | 9 |
| 3087 | partir | 9 |
| 3088 | partido | 9 |
| 3089 | parecerme | 9 |
| 3090 | palafrén | 9 |
| 3091 | padece | 9 |
| 3092 | ordinaria | 9 |
| 3093 | olvide | 9 |
| 3094 | olla | 9 |
| 3095 | ojeriza | 9 |
| 3096 | oigo | 9 |
| 3097 | obligaciones | 9 |
| 3098 | nueve | 9 |
| 3099 | notado | 9 |
| 3100 | niños | 9 |
| 3101 | nacimiento | 9 |
| 3102 | nacida | 9 |
| 3103 | mueve | 9 |
| 3104 | mudar | 9 |
| 3105 | mudado | 9 |
| 3106 | moverse | 9 |
| 3107 | mostraron | 9 |
| 3108 | merecido | 9 |
| 3109 | mercader | 9 |
| 3110 | melancolía | 9 |
| 3111 | medroso | 9 |
| 3112 | medios | 9 |
| 3113 | maten | 9 |
| 3114 | mantua | 9 |
| 3115 | maneras | 9 |
| 3116 | maltrecho | 9 |
| 3117 | malezas | 9 |
| 3118 | lobos | 9 |
| 3119 | lloraba | 9 |
| 3120 | lleven | 9 |
| 3121 | ligas | 9 |
| 3122 | liebre | 9 |
| 3123 | levantando | 9 |
| 3124 | levantada | 9 |
| 3125 | letrados | 9 |
| 3126 | lector | 9 |
| 3127 | lastimado | 9 |
| 3128 | lanzarote | 9 |
| 3129 | lago | 9 |
| 3130 | labor | 9 |
| 3131 | juramentos | 9 |
| 3132 | inútil | 9 |
| 3133 | intrépido | 9 |
| 3134 | indias | 9 |
| 3135 | incomparable | 9 |
| 3136 | impreso | 9 |
| 3137 | impresión | 9 |
| 3138 | imperio | 9 |
| 3139 | iguala | 9 |
| 3140 | humo | 9 |
| 3141 | humildes | 9 |
| 3142 | hubiesen | 9 |
| 3143 | hubieron | 9 |
| 3144 | honor | 9 |
| 3145 | hermosísima | 9 |
| 3146 | hayas | 9 |
| 3147 | hallara | 9 |
| 3148 | hacha | 9 |
| 3149 | haces | 9 |
| 3150 | hacerlo | 9 |
| 3151 | haberla | 9 |
| 3152 | guisa | 9 |
| 3153 | guardando | 9 |
| 3154 | guardaba | 9 |
| 3155 | glosa | 9 |
| 3156 | géneros | 9 |
| 3157 | ganancia | 9 |
| 3158 | gallinas | 9 |
| 3159 | furioso | 9 |
| 3160 | frontero | 9 |
| 3161 | fresca | 9 |
| 3162 | franceses | 9 |
| 3163 | firmeza | 9 |
| 3164 | fiel | 9 |
| 3165 | fácilmente | 9 |
| 3166 | eterna | 9 |
| 3167 | estremos | 9 |
| 3168 | estampa | 9 |
| 3169 | espuma | 9 |
| 3170 | espacioso | 9 |
| 3171 | esfuerzo | 9 |
| 3172 | escrita | 9 |
| 3173 | ermita | 9 |
| 3174 | entretenía | 9 |
| 3175 | entraba | 9 |
| 3176 | entendía | 9 |
| 3177 | encontrar | 9 |
| 3178 | enamoró | 9 |
| 3179 | eche | 9 |
| 3180 | echa | 9 |
| 3181 | duelen | 9 |
| 3182 | doliente | 9 |
| 3183 | docenas | 9 |
| 3184 | diría | 9 |
| 3185 | dignos | 9 |
| 3186 | difunto | 9 |
| 3187 | dificultoso | 9 |
| 3188 | dichas | 9 |
| 3189 | desventurado | 9 |
| 3190 | desatino | 9 |
| 3191 | demasiado | 9 |
| 3192 | dejaremos | 9 |
| 3193 | déjame | 9 |
| 3194 | deciros | 9 |
| 3195 | cumbre | 9 |
| 3196 | cuero | 9 |
| 3197 | creció | 9 |
| 3198 | cortésmente | 9 |
| 3199 | córdoba | 9 |
| 3200 | cordel | 9 |
| 3201 | contino | 9 |
| 3202 | contenía | 9 |
| 3203 | conocen | 9 |
| 3204 | conocemos | 9 |
| 3205 | confirmación | 9 |
| 3206 | comprar | 9 |
| 3207 | comedimiento | 9 |
| 3208 | cojín | 9 |
| 3209 | circunstancias | 9 |
| 3210 | cintura | 9 |
| 3211 | chirimías | 9 |
| 3212 | césar | 9 |
| 3213 | cerrado | 9 |
| 3214 | cejas | 9 |
| 3215 | cazadores | 9 |
| 3216 | católica | 9 |
| 3217 | castillos | 9 |
| 3218 | casildea | 9 |
| 3219 | casarme | 9 |
| 3220 | caro | 9 |
| 3221 | carlomagno | 9 |
| 3222 | caritativo | 9 |
| 3223 | capitana | 9 |
| 3224 | capa | 9 |
| 3225 | cantó | 9 |
| 3226 | calzas | 9 |
| 3227 | callaba | 9 |
| 3228 | caen | 9 |
| 3229 | cadenas | 9 |
| 3230 | cabe | 9 |
| 3231 | bravo | 9 |
| 3232 | bocado | 9 |
| 3233 | bergantín | 9 |
| 3234 | avino | 9 |
| 3235 | atrevidos | 9 |
| 3236 | asida | 9 |
| 3237 | ardite | 9 |
| 3238 | aprieta | 9 |
| 3239 | angélica | 9 |
| 3240 | amos | 9 |
| 3241 | amigas | 9 |
| 3242 | amén | 9 |
| 3243 | amar | 9 |
| 3244 | amado | 9 |
| 3245 | alzar | 9 |
| 3246 | alcanzan | 9 |
| 3247 | alcanzado | 9 |
| 3248 | agradecimiento | 9 |
| 3249 | afición | 9 |
| 3250 | admiraron | 9 |
| 3251 | admirada | 9 |
| 3252 | admiraba | 9 |
| 3253 | acostumbrado | 9 |
| 3254 | acostumbrada | 9 |
| 3255 | acompañaban | 9 |
| 3256 | achaque | 9 |
| 3257 | acero | 9 |
| 3258 | acabóse | 9 |
| 3259 | abriendo | 9 |
| 3260 | zapato | 8 |
| 3261 | yerra | 8 |
| 3262 | yeguas | 8 |
| 3263 | volar | 8 |
| 3264 | viere | 8 |
| 3265 | verte | 8 |
| 3266 | ventanas | 8 |
| 3267 | vengarse | 8 |
| 3268 | vengar | 8 |
| 3269 | vencidos | 8 |
| 3270 | vencida | 8 |
| 3271 | velar | 8 |
| 3272 | vayan | 8 |
| 3273 | vaca | 8 |
| 3274 | turba | 8 |
| 3275 | túmulo | 8 |
| 3276 | tuerto | 8 |
| 3277 | tripas | 8 |
| 3278 | trifaldín | 8 |
| 3279 | trataban | 8 |
| 3280 | trajes | 8 |
| 3281 | traerle | 8 |
| 3282 | torno | 8 |
| 3283 | tono | 8 |
| 3284 | tomaron | 8 |
| 3285 | toman | 8 |
| 3286 | tomaba | 8 |
| 3287 | tocadores | 8 |
| 3288 | títulos | 8 |
| 3289 | tinieblas | 8 |
| 3290 | tienda | 8 |
| 3291 | tenerle | 8 |
| 3292 | tenerla | 8 |
| 3293 | tendida | 8 |
| 3294 | tarfe | 8 |
| 3295 | tajo | 8 |
| 3296 | socorrer | 8 |
| 3297 | soberbio | 8 |
| 3298 | siente | 8 |
| 3299 | servirle | 8 |
| 3300 | servidos | 8 |
| 3301 | sepas | 8 |
| 3302 | sepamos | 8 |
| 3303 | seguramente | 8 |
| 3304 | seguía | 8 |
| 3305 | sastre | 8 |
| 3306 | sarta | 8 |
| 3307 | saqué | 8 |
| 3308 | sancha | 8 |
| 3309 | sana | 8 |
| 3310 | salimos | 8 |
| 3311 | sagacidad | 8 |
| 3312 | sacaré | 8 |
| 3313 | sacaba | 8 |
| 3314 | sábanas | 8 |
| 3315 | ruidera | 8 |
| 3316 | ruedas | 8 |
| 3317 | rompió | 8 |
| 3318 | rogando | 8 |
| 3319 | riscos | 8 |
| 3320 | riesgo | 8 |
| 3321 | ricas | 8 |
| 3322 | repúblicas | 8 |
| 3323 | reñir | 8 |
| 3324 | regocijo | 8 |
| 3325 | redes | 8 |
| 3326 | recogió | 8 |
| 3327 | recién | 8 |
| 3328 | recebirle | 8 |
| 3329 | recebida | 8 |
| 3330 | rebuznar | 8 |
| 3331 | raras | 8 |
| 3332 | quitarle | 8 |
| 3333 | quemar | 8 |
| 3334 | quedarse | 8 |
| 3335 | quebrantado | 8 |
| 3336 | quebrada | 8 |
| 3337 | pusiesen | 8 |
| 3338 | purgatorio | 8 |
| 3339 | procurando | 8 |
| 3340 | proceder | 8 |
| 3341 | preso | 8 |
| 3342 | pozo | 8 |
| 3343 | polvo | 8 |
| 3344 | pollinos | 8 |
| 3345 | poblado | 8 |
| 3346 | pidiendo | 8 |
| 3347 | piadoso | 8 |
| 3348 | pesaba | 8 |
| 3349 | personaje | 8 |
| 3350 | perezoso | 8 |
| 3351 | pérez | 8 |
| 3352 | perdone | 8 |
| 3353 | perdonar | 8 |
| 3354 | pensase | 8 |
| 3355 | pensaban | 8 |
| 3356 | pasamos | 8 |
| 3357 | particulares | 8 |
| 3358 | parecieron | 8 |
| 3359 | paradero | 8 |
| 3360 | pajes | 8 |
| 3361 | oye | 8 |
| 3362 | orejas | 8 |
| 3363 | ordenanzas | 8 |
| 3364 | ordena | 8 |
| 3365 | oler | 8 |
| 3366 | oírle | 8 |
| 3367 | ofrecido | 8 |
| 3368 | ociosidad | 8 |
| 3369 | obligada | 8 |
| 3370 | notable | 8 |
| 3371 | niño | 8 |
| 3372 | niñas | 8 |
| 3373 | ninfas | 8 |
| 3374 | necesarias | 8 |
| 3375 | necesaria | 8 |
| 3376 | naturalmente | 8 |
| 3377 | nápoles | 8 |
| 3378 | naciones | 8 |
| 3379 | mueva | 8 |
| 3380 | mudanza | 8 |
| 3381 | movía | 8 |
| 3382 | montalbán | 8 |
| 3383 | momentos | 8 |
| 3384 | molineros | 8 |
| 3385 | modos | 8 |
| 3386 | miranda | 8 |
| 3387 | micomicón | 8 |
| 3388 | mesas | 8 |
| 3389 | memorias | 8 |
| 3390 | médicos | 8 |
| 3391 | medicina | 8 |
| 3392 | mate | 8 |
| 3393 | margen | 8 |
| 3394 | maravillado | 8 |
| 3395 | manso | 8 |
| 3396 | manjares | 8 |
| 3397 | mandase | 8 |
| 3398 | maldito | 8 |
| 3399 | luces | 8 |
| 3400 | lloró | 8 |
| 3401 | llegamos | 8 |
| 3402 | llamaron | 8 |
| 3403 | llamaban | 8 |
| 3404 | lícito | 8 |
| 3405 | libreas | 8 |
| 3406 | leyenda | 8 |
| 3407 | legítima | 8 |
| 3408 | lee | 8 |
| 3409 | latín | 8 |
| 3410 | labradoras | 8 |
| 3411 | juzgó | 8 |
| 3412 | juzgado | 8 |
| 3413 | jurado | 8 |
| 3414 | irá | 8 |
| 3415 | intenciones | 8 |
| 3416 | intencionado | 8 |
| 3417 | infinito | 8 |
| 3418 | infame | 8 |
| 3419 | impresa | 8 |
| 3420 | imposibilidad | 8 |
| 3421 | imaginando | 8 |
| 3422 | ignorantes | 8 |
| 3423 | huevos | 8 |
| 3424 | honroso | 8 |
| 3425 | holgara | 8 |
| 3426 | hízose | 8 |
| 3427 | historiadores | 8 |
| 3428 | hallan | 8 |
| 3429 | hacerte | 8 |
| 3430 | habréis | 8 |
| 3431 | habrás | 8 |
| 3432 | hablador | 8 |
| 3433 | habíamos | 8 |
| 3434 | gusta | 8 |
| 3435 | guardada | 8 |
| 3436 | greguescos | 8 |
| 3437 | granada | 8 |
| 3438 | graciosa | 8 |
| 3439 | generoso | 8 |
| 3440 | gemidos | 8 |
| 3441 | gatos | 8 |
| 3442 | ganadero | 8 |
| 3443 | galeote | 8 |
| 3444 | galas | 8 |
| 3445 | fuertes | 8 |
| 3446 | fueren | 8 |
| 3447 | follones | 8 |
| 3448 | firmes | 8 |
| 3449 | firma | 8 |
| 3450 | fino | 8 |
| 3451 | finísimo | 8 |
| 3452 | fiera | 8 |
| 3453 | fidelidad | 8 |
| 3454 | feridas | 8 |
| 3455 | fecha | 8 |
| 3456 | fatigaba | 8 |
| 3457 | fantasma | 8 |
| 3458 | faltarán | 8 |
| 3459 | faltaban | 8 |
| 3460 | falsas | 8 |
| 3461 | falda | 8 |
| 3462 | eterno | 8 |
| 3463 | estuviere | 8 |
| 3464 | estarse | 8 |
| 3465 | estaría | 8 |
| 3466 | estábamos | 8 |
| 3467 | esperiencia | 8 |
| 3468 | espantado | 8 |
| 3469 | escuchado | 8 |
| 3470 | escondida | 8 |
| 3471 | escogido | 8 |
| 3472 | entretanto | 8 |
| 3473 | entierro | 8 |
| 3474 | engañar | 8 |
| 3475 | encomendarse | 8 |
| 3476 | encerramiento | 8 |
| 3477 | encaje | 8 |
| 3478 | embustes | 8 |
| 3479 | embuste | 8 |
| 3480 | embestir | 8 |
| 3481 | edificio | 8 |
| 3482 | durmió | 8 |
| 3483 | duras | 8 |
| 3484 | duermen | 8 |
| 3485 | duela | 8 |
| 3486 | dudas | 8 |
| 3487 | dudar | 8 |
| 3488 | divino | 8 |
| 3489 | diversos | 8 |
| 3490 | distintamente | 8 |
| 3491 | discreciones | 8 |
| 3492 | dimos | 8 |
| 3493 | dijesen | 8 |
| 3494 | dificultad | 8 |
| 3495 | diferente | 8 |
| 3496 | diciplinantes | 8 |
| 3497 | diciéndoles | 8 |
| 3498 | dichosa | 8 |
| 3499 | despoblados | 8 |
| 3500 | desigual | 8 |
| 3501 | desdén | 8 |
| 3502 | descubriendo | 8 |
| 3503 | descubría | 8 |
| 3504 | descomunal | 8 |
| 3505 | descanso | 8 |
| 3506 | desafíos | 8 |
| 3507 | derrota | 8 |
| 3508 | derribó | 8 |
| 3509 | demasía | 8 |
| 3510 | dejaría | 8 |
| 3511 | dejadme | 8 |
| 3512 | declaraba | 8 |
| 3513 | debieron | 8 |
| 3514 | debéis | 8 |
| 3515 | dándome | 8 |
| 3516 | dadme | 8 |
| 3517 | dadas | 8 |
| 3518 | cumpla | 8 |
| 3519 | cuchillada | 8 |
| 3520 | cuatrocientos | 8 |
| 3521 | cuarenta | 8 |
| 3522 | cristal | 8 |
| 3523 | créame | 8 |
| 3524 | cortesías | 8 |
| 3525 | cortesano | 8 |
| 3526 | cordura | 8 |
| 3527 | coplas | 8 |
| 3528 | contentó | 8 |
| 3529 | contaba | 8 |
| 3530 | consiente | 8 |
| 3531 | considera | 8 |
| 3532 | conozca | 8 |
| 3533 | conocí | 8 |
| 3534 | conoces | 8 |
| 3535 | conocerle | 8 |
| 3536 | confianza | 8 |
| 3537 | concertadas | 8 |
| 3538 | comoquiera | 8 |
| 3539 | coma | 8 |
| 3540 | cogido | 8 |
| 3541 | coger | 8 |
| 3542 | cobre | 8 |
| 3543 | clori | 8 |
| 3544 | cinchas | 8 |
| 3545 | ciencias | 8 |
| 3546 | cesó | 8 |
| 3547 | causó | 8 |
| 3548 | castilla | 8 |
| 3549 | casta | 8 |
| 3550 | carneros | 8 |
| 3551 | capaz | 8 |
| 3552 | cantaba | 8 |
| 3553 | caminaban | 8 |
| 3554 | caliente | 8 |
| 3555 | caldero | 8 |
| 3556 | brevemente | 8 |
| 3557 | bonitamente | 8 |
| 3558 | blancos | 8 |
| 3559 | bebe | 8 |
| 3560 | bastaba | 8 |
| 3561 | barruntos | 8 |
| 3562 | balde | 8 |
| 3563 | bajar | 8 |
| 3564 | b | 8 |
| 3565 | atentos | 8 |
| 3566 | atadas | 8 |
| 3567 | áspero | 8 |
| 3568 | asiendo | 8 |
| 3569 | arrieros | 8 |
| 3570 | arráez | 8 |
| 3571 | armar | 8 |
| 3572 | arena | 8 |
| 3573 | aprovecharse | 8 |
| 3574 | apartaron | 8 |
| 3575 | apartándose | 8 |
| 3576 | anochecer | 8 |
| 3577 | ando | 8 |
| 3578 | amenaza | 8 |
| 3579 | ámbar | 8 |
| 3580 | amarillo | 8 |
| 3581 | alfanje | 8 |
| 3582 | alcuza | 8 |
| 3583 | alboroto | 8 |
| 3584 | afuera | 8 |
| 3585 | acompañamiento | 8 |
| 3586 | aceñas | 8 |
| 3587 | zagal | 7 |
| 3588 | voluntades | 7 |
| 3589 | volando | 7 |
| 3590 | vivas | 7 |
| 3591 | viste | 7 |
| 3592 | villa | 7 |
| 3593 | vieres | 7 |
| 3594 | vientre | 7 |
| 3595 | vienes | 7 |
| 3596 | viéndome | 7 |
| 3597 | vete | 7 |
| 3598 | vestiglos | 7 |
| 3599 | venturas | 7 |
| 3600 | ventajas | 7 |
| 3601 | velo | 7 |
| 3602 | velas | 7 |
| 3603 | vayas | 7 |
| 3604 | valles | 7 |
| 3605 | valencia | 7 |
| 3606 | valen | 7 |
| 3607 | universal | 7 |
| 3608 | única | 7 |
| 3609 | tuvieran | 7 |
| 3610 | turbó | 7 |
| 3611 | trujese | 7 |
| 3612 | troya | 7 |
| 3613 | tragedia | 7 |
| 3614 | torralba | 7 |
| 3615 | tontos | 7 |
| 3616 | tocas | 7 |
| 3617 | tiraba | 7 |
| 3618 | tinto | 7 |
| 3619 | tiernos | 7 |
| 3620 | tierno | 7 |
| 3621 | ternera | 7 |
| 3622 | tened | 7 |
| 3623 | tendrían | 7 |
| 3624 | tendrán | 7 |
| 3625 | temió | 7 |
| 3626 | temerario | 7 |
| 3627 | telas | 7 |
| 3628 | tambores | 7 |
| 3629 | tamaño | 7 |
| 3630 | sustenta | 7 |
| 3631 | sustancia | 7 |
| 3632 | suspensión | 7 |
| 3633 | suspender | 7 |
| 3634 | suma | 7 |
| 3635 | suelto | 7 |
| 3636 | sostenía | 7 |
| 3637 | sosegados | 7 |
| 3638 | sosegada | 7 |
| 3639 | sobrino | 7 |
| 3640 | sobremanera | 7 |
| 3641 | sobra | 7 |
| 3642 | siguiese | 7 |
| 3643 | sigo | 7 |
| 3644 | setenta | 7 |
| 3645 | sepultado | 7 |
| 3646 | señalado | 7 |
| 3647 | sentada | 7 |
| 3648 | selva | 7 |
| 3649 | segovia | 7 |
| 3650 | secretos | 7 |
| 3651 | salgan | 7 |
| 3652 | sacase | 7 |
| 3653 | rústica | 7 |
| 3654 | rumor | 7 |
| 3655 | rubios | 7 |
| 3656 | rosario | 7 |
| 3657 | romano | 7 |
| 3658 | rigurosa | 7 |
| 3659 | revuelto | 7 |
| 3660 | respondióle | 7 |
| 3661 | responda | 7 |
| 3662 | requieren | 7 |
| 3663 | requiebros | 7 |
| 3664 | representó | 7 |
| 3665 | representan | 7 |
| 3666 | religioso | 7 |
| 3667 | regidor | 7 |
| 3668 | regalos | 7 |
| 3669 | referidos | 7 |
| 3670 | reducir | 7 |
| 3671 | recogimiento | 7 |
| 3672 | recogiendo | 7 |
| 3673 | recibo | 7 |
| 3674 | reciben | 7 |
| 3675 | rasa | 7 |
| 3676 | ralea | 7 |
| 3677 | quitaba | 7 |
| 3678 | quita | 7 |
| 3679 | quisiesen | 7 |
| 3680 | quejar | 7 |
| 3681 | pública | 7 |
| 3682 | prudentes | 7 |
| 3683 | prosiga | 7 |
| 3684 | proprio | 7 |
| 3685 | prometen | 7 |
| 3686 | prólogo | 7 |
| 3687 | profundos | 7 |
| 3688 | profesa | 7 |
| 3689 | procuraré | 7 |
| 3690 | prevenciones | 7 |
| 3691 | pretende | 7 |
| 3692 | presos | 7 |
| 3693 | pregunto | 7 |
| 3694 | preguntándole | 7 |
| 3695 | predicar | 7 |
| 3696 | pompa | 7 |
| 3697 | podremos | 7 |
| 3698 | podréis | 7 |
| 3699 | plumas | 7 |
| 3700 | pleito | 7 |
| 3701 | personajes | 7 |
| 3702 | perpetuo | 7 |
| 3703 | pereza | 7 |
| 3704 | perdóneme | 7 |
| 3705 | perdiese | 7 |
| 3706 | pastoras | 7 |
| 3707 | pasando | 7 |
| 3708 | parezcan | 7 |
| 3709 | pardiez | 7 |
| 3710 | pajas | 7 |
| 3711 | paja | 7 |
| 3712 | oyera | 7 |
| 3713 | osuna | 7 |
| 3714 | orlando | 7 |
| 3715 | orientales | 7 |
| 3716 | oración | 7 |
| 3717 | once | 7 |
| 3718 | oídas | 7 |
| 3719 | ofrecimiento | 7 |
| 3720 | ofrecer | 7 |
| 3721 | ofrecen | 7 |
| 3722 | ofender | 7 |
| 3723 | ocupado | 7 |
| 3724 | nudo | 7 |
| 3725 | nube | 7 |
| 3726 | ningunas | 7 |
| 3727 | nata | 7 |
| 3728 | narración | 7 |
| 3729 | nació | 7 |
| 3730 | muere | 7 |
| 3731 | mozas | 7 |
| 3732 | movimiento | 7 |
| 3733 | morato | 7 |
| 3734 | montera | 7 |
| 3735 | monta | 7 |
| 3736 | mochachos | 7 |
| 3737 | mirara | 7 |
| 3738 | mirándole | 7 |
| 3739 | miran | 7 |
| 3740 | ministros | 7 |
| 3741 | mínima | 7 |
| 3742 | metió | 7 |
| 3743 | meter | 7 |
| 3744 | merecían | 7 |
| 3745 | menudencias | 7 |
| 3746 | mentirosos | 7 |
| 3747 | menguado | 7 |
| 3748 | menesterosa | 7 |
| 3749 | menear | 7 |
| 3750 | medida | 7 |
| 3751 | medicinas | 7 |
| 3752 | mediano | 7 |
| 3753 | marsilio | 7 |
| 3754 | maravilloso | 7 |
| 3755 | maravillo | 7 |
| 3756 | manjar | 7 |
| 3757 | manadas | 7 |
| 3758 | mamonas | 7 |
| 3759 | malicias | 7 |
| 3760 | luto | 7 |
| 3761 | llorando | 7 |
| 3762 | llevasen | 7 |
| 3763 | lleváis | 7 |
| 3764 | llegará | 7 |
| 3765 | llave | 7 |
| 3766 | llamas | 7 |
| 3767 | limosna | 7 |
| 3768 | librillo | 7 |
| 3769 | libremente | 7 |
| 3770 | levantase | 7 |
| 3771 | levantados | 7 |
| 3772 | levanta | 7 |
| 3773 | leche | 7 |
| 3774 | lea | 7 |
| 3775 | lagunas | 7 |
| 3776 | justos | 7 |
| 3777 | juridición | 7 |
| 3778 | julio | 7 |
| 3779 | jubón | 7 |
| 3780 | jornadas | 7 |
| 3781 | irme | 7 |
| 3782 | invenciones | 7 |
| 3783 | invencible | 7 |
| 3784 | insulanos | 7 |
| 3785 | indicios | 7 |
| 3786 | inconvenientes | 7 |
| 3787 | inclinado | 7 |
| 3788 | imprimiere | 7 |
| 3789 | imposibilitado | 7 |
| 3790 | igualar | 7 |
| 3791 | huérfanos | 7 |
| 3792 | horca | 7 |
| 3793 | homero | 7 |
| 3794 | hircania | 7 |
| 3795 | hincar | 7 |
| 3796 | hilas | 7 |
| 3797 | hiciesen | 7 |
| 3798 | herreruelo | 7 |
| 3799 | heredera | 7 |
| 3800 | hembra | 7 |
| 3801 | hazaña | 7 |
| 3802 | hato | 7 |
| 3803 | haremos | 7 |
| 3804 | hallóle | 7 |
| 3805 | hallarle | 7 |
| 3806 | hagáis | 7 |
| 3807 | haciéndole | 7 |
| 3808 | hacerlas | 7 |
| 3809 | hablara | 7 |
| 3810 | guiaba | 7 |
| 3811 | guardarse | 7 |
| 3812 | guardan | 7 |
| 3813 | guadiana | 7 |
| 3814 | griego | 7 |
| 3815 | gentiles | 7 |
| 3816 | gastar | 7 |
| 3817 | garras | 7 |
| 3818 | galope | 7 |
| 3819 | fuimos | 7 |
| 3820 | fría | 7 |
| 3821 | fingidas | 7 |
| 3822 | fiero | 7 |
| 3823 | felixmarte | 7 |
| 3824 | febo | 7 |
| 3825 | fazañas | 7 |
| 3826 | favorezca | 7 |
| 3827 | favorable | 7 |
| 3828 | fantasía | 7 |
| 3829 | famosas | 7 |
| 3830 | estuviesen | 7 |
| 3831 | estuve | 7 |
| 3832 | estudio | 7 |
| 3833 | estudiar | 7 |
| 3834 | estrechamente | 7 |
| 3835 | estranjeros | 7 |
| 3836 | estimaba | 7 |
| 3837 | estés | 7 |
| 3838 | estéril | 7 |
| 3839 | estén | 7 |
| 3840 | estaré | 7 |
| 3841 | estados | 7 |
| 3842 | esperan | 7 |
| 3843 | esperad | 7 |
| 3844 | espantosa | 7 |
| 3845 | espantable | 7 |
| 3846 | escuela | 7 |
| 3847 | escopetas | 7 |
| 3848 | ésas | 7 |
| 3849 | ermitaño | 7 |
| 3850 | envuelto | 7 |
| 3851 | enviase | 7 |
| 3852 | entregó | 7 |
| 3853 | entrase | 7 |
| 3854 | engendró | 7 |
| 3855 | encontrado | 7 |
| 3856 | encierran | 7 |
| 3857 | encendidas | 7 |
| 3858 | encarecidamente | 7 |
| 3859 | encaminó | 7 |
| 3860 | encaminaban | 7 |
| 3861 | empero | 7 |
| 3862 | eclesiástico | 7 |
| 3863 | dueños | 7 |
| 3864 | duele | 7 |
| 3865 | doloroso | 7 |
| 3866 | disparatados | 7 |
| 3867 | dijésemos | 7 |
| 3868 | diente | 7 |
| 3869 | diciplina | 7 |
| 3870 | diana | 7 |
| 3871 | diamantes | 7 |
| 3872 | diamante | 7 |
| 3873 | detenía | 7 |
| 3874 | deteneos | 7 |
| 3875 | destreza | 7 |
| 3876 | despechado | 7 |
| 3877 | desmán | 7 |
| 3878 | desiertos | 7 |
| 3879 | desencantada | 7 |
| 3880 | desean | 7 |
| 3881 | deseado | 7 |
| 3882 | deseaban | 7 |
| 3883 | denme | 7 |
| 3884 | demostraciones | 7 |
| 3885 | demasiada | 7 |
| 3886 | dejándole | 7 |
| 3887 | defenderse | 7 |
| 3888 | declarado | 7 |
| 3889 | decencia | 7 |
| 3890 | darían | 7 |
| 3891 | daremos | 7 |
| 3892 | dame | 7 |
| 3893 | dádiva | 7 |
| 3894 | curso | 7 |
| 3895 | curado | 7 |
| 3896 | cuitas | 7 |
| 3897 | cubrió | 7 |
| 3898 | cubre | 7 |
| 3899 | cubiertos | 7 |
| 3900 | cuánta | 7 |
| 3901 | cuan | 7 |
| 3902 | cruces | 7 |
| 3903 | crianza | 7 |
| 3904 | creyese | 7 |
| 3905 | creyeron | 7 |
| 3906 | cree | 7 |
| 3907 | crea | 7 |
| 3908 | costó | 7 |
| 3909 | cortes | 7 |
| 3910 | coronas | 7 |
| 3911 | corazones | 7 |
| 3912 | conveniente | 7 |
| 3913 | contravenir | 7 |
| 3914 | contrarios | 7 |
| 3915 | contase | 7 |
| 3916 | constantinopla | 7 |
| 3917 | consolar | 7 |
| 3918 | confusa | 7 |
| 3919 | confirmó | 7 |
| 3920 | confirmar | 7 |
| 3921 | confesó | 7 |
| 3922 | compuestas | 7 |
| 3923 | compostura | 7 |
| 3924 | compasivo | 7 |
| 3925 | comieron | 7 |
| 3926 | comienzan | 7 |
| 3927 | comenzando | 7 |
| 3928 | colérico | 7 |
| 3929 | codicioso | 7 |
| 3930 | cid | 7 |
| 3931 | cerrados | 7 |
| 3932 | cenaron | 7 |
| 3933 | celoso | 7 |
| 3934 | celebro | 7 |
| 3935 | cava | 7 |
| 3936 | causar | 7 |
| 3937 | carreras | 7 |
| 3938 | caperuzas | 7 |
| 3939 | cansados | 7 |
| 3940 | candil | 7 |
| 3941 | campanas | 7 |
| 3942 | cámara | 7 |
| 3943 | calzones | 7 |
| 3944 | caía | 7 |
| 3945 | bota | 7 |
| 3946 | borrasca | 7 |
| 3947 | blandas | 7 |
| 3948 | bizarría | 7 |
| 3949 | billete | 7 |
| 3950 | besó | 7 |
| 3951 | bernardo | 7 |
| 3952 | beneplácito | 7 |
| 3953 | bellaquería | 7 |
| 3954 | belianís | 7 |
| 3955 | bastan | 7 |
| 3956 | banderas | 7 |
| 3957 | ballesta | 7 |
| 3958 | averiguada | 7 |
| 3959 | aventaja | 7 |
| 3960 | aurora | 7 |
| 3961 | atrevió | 7 |
| 3962 | atados | 7 |
| 3963 | asumpto | 7 |
| 3964 | asturiana | 7 |
| 3965 | aspereza | 7 |
| 3966 | áspera | 7 |
| 3967 | asalto | 7 |
| 3968 | arrimado | 7 |
| 3969 | arcabuces | 7 |
| 3970 | aprovechar | 7 |
| 3971 | apolo | 7 |
| 3972 | aplauso | 7 |
| 3973 | apeó | 7 |
| 3974 | aparejos | 7 |
| 3975 | antojadiza | 7 |
| 3976 | ánimos | 7 |
| 3977 | ande | 7 |
| 3978 | amoroso | 7 |
| 3979 | alzaron | 7 |
| 3980 | alerta | 7 |
| 3981 | alegrar | 7 |
| 3982 | aldonza | 7 |
| 3983 | aldeana | 7 |
| 3984 | albricias | 7 |
| 3985 | alborotado | 7 |
| 3986 | albedrío | 7 |
| 3987 | aguarda | 7 |
| 3988 | agradeció | 7 |
| 3989 | agradecida | 7 |
| 3990 | agi | 7 |
| 3991 | afirmar | 7 |
| 3992 | adornada | 7 |
| 3993 | aderezada | 7 |
| 3994 | acuerda | 7 |
| 3995 | acordaba | 7 |
| 3996 | acomodarse | 7 |
| 3997 | acomodados | 7 |
| 3998 | acémila | 7 |
| 3999 | académico | 7 |
| 4000 | zagalas | 6 |
| 4001 | vuelvan | 6 |
| 4002 | vueltas | 6 |
| 4003 | vuelo | 6 |
| 4004 | vomitar | 6 |
| 4005 | volvamos | 6 |
| 4006 | visitar | 6 |
| 4007 | virtuosos | 6 |
| 4008 | vinieren | 6 |
| 4009 | viniera | 6 |
| 4010 | vicios | 6 |
| 4011 | vestidas | 6 |
| 4012 | veros | 6 |
| 4013 | verlas | 6 |
| 4014 | vería | 6 |
| 4015 | verdugo | 6 |
| 4016 | verán | 6 |
| 4017 | venturosa | 6 |
| 4018 | ventas | 6 |
| 4019 | venganzas | 6 |
| 4020 | vengamos | 6 |
| 4021 | vengado | 6 |
| 4022 | venda | 6 |
| 4023 | venció | 6 |
| 4024 | vence | 6 |
| 4025 | vemos | 6 |
| 4026 | vejigas | 6 |
| 4027 | veían | 6 |
| 4028 | vandalia | 6 |
| 4029 | vámonos | 6 |
| 4030 | válate | 6 |
| 4031 | vacío | 6 |
| 4032 | usando | 6 |
| 4033 | usaban | 6 |
| 4034 | uchalí | 6 |
| 4035 | úbeda | 6 |
| 4036 | tuyos | 6 |
| 4037 | trompeta | 6 |
| 4038 | trofeo | 6 |
| 4039 | trocara | 6 |
| 4040 | triunfo | 6 |
| 4041 | tratando | 6 |
| 4042 | trasladar | 6 |
| 4043 | transformado | 6 |
| 4044 | transformada | 6 |
| 4045 | transformaciones | 6 |
| 4046 | tragos | 6 |
| 4047 | traerme | 6 |
| 4048 | tortas | 6 |
| 4049 | topó | 6 |
| 4050 | tomara | 6 |
| 4051 | tirar | 6 |
| 4052 | tiendas | 6 |
| 4053 | tercia | 6 |
| 4054 | tentar | 6 |
| 4055 | tengamos | 6 |
| 4056 | tengáis | 6 |
| 4057 | tenerme | 6 |
| 4058 | templo | 6 |
| 4059 | temes | 6 |
| 4060 | temerosos | 6 |
| 4061 | tardó | 6 |
| 4062 | ta | 6 |
| 4063 | sutil | 6 |
| 4064 | suplicándole | 6 |
| 4065 | sumo | 6 |
| 4066 | sufrimiento | 6 |
| 4067 | suertes | 6 |
| 4068 | sueltos | 6 |
| 4069 | subiendo | 6 |
| 4070 | sordo | 6 |
| 4071 | sonaban | 6 |
| 4072 | sonaba | 6 |
| 4073 | sombrero | 6 |
| 4074 | soez | 6 |
| 4075 | sobras | 6 |
| 4076 | soberbios | 6 |
| 4077 | sirvo | 6 |
| 4078 | sirvieron | 6 |
| 4079 | sintieron | 6 |
| 4080 | simplicidades | 6 |
| 4081 | siesta | 6 |
| 4082 | serpiente | 6 |
| 4083 | sentó | 6 |
| 4084 | sendas | 6 |
| 4085 | seguido | 6 |
| 4086 | secreta | 6 |
| 4087 | seca | 6 |
| 4088 | seamos | 6 |
| 4089 | satisfechos | 6 |
| 4090 | satisfaré | 6 |
| 4091 | salto | 6 |
| 4092 | salteador | 6 |
| 4093 | saliera | 6 |
| 4094 | saldré | 6 |
| 4095 | saldrán | 6 |
| 4096 | saetas | 6 |
| 4097 | sacerdote | 6 |
| 4098 | sabrosa | 6 |
| 4099 | sabiduría | 6 |
| 4100 | sabidor | 6 |
| 4101 | sábete | 6 |
| 4102 | saberse | 6 |
| 4103 | ronda | 6 |
| 4104 | rogaron | 6 |
| 4105 | rodeos | 6 |
| 4106 | rodearon | 6 |
| 4107 | ricardo | 6 |
| 4108 | retrato | 6 |
| 4109 | retiró | 6 |
| 4110 | retirada | 6 |
| 4111 | respetos | 6 |
| 4112 | requiere | 6 |
| 4113 | representar | 6 |
| 4114 | representa | 6 |
| 4115 | replicar | 6 |
| 4116 | renta | 6 |
| 4117 | renombre | 6 |
| 4118 | reglas | 6 |
| 4119 | redundar | 6 |
| 4120 | redondo | 6 |
| 4121 | recta | 6 |
| 4122 | recebían | 6 |
| 4123 | recebí | 6 |
| 4124 | rebuznos | 6 |
| 4125 | razonamientos | 6 |
| 4126 | ramos | 6 |
| 4127 | radamanto | 6 |
| 4128 | r | 6 |
| 4129 | quito | 6 |
| 4130 | quitasen | 6 |
| 4131 | quitársela | 6 |
| 4132 | quisieran | 6 |
| 4133 | quinientos | 6 |
| 4134 | queden | 6 |
| 4135 | puntualmente | 6 |
| 4136 | provincia | 6 |
| 4137 | provechoso | 6 |
| 4138 | propios | 6 |
| 4139 | propiedad | 6 |
| 4140 | profesan | 6 |
| 4141 | profesamos | 6 |
| 4142 | procure | 6 |
| 4143 | procurase | 6 |
| 4144 | privilegio | 6 |
| 4145 | princesas | 6 |
| 4146 | prestado | 6 |
| 4147 | preguntéle | 6 |
| 4148 | portugal | 6 |
| 4149 | porfiar | 6 |
| 4150 | porfiaba | 6 |
| 4151 | pondrá | 6 |
| 4152 | pollina | 6 |
| 4153 | plegarias | 6 |
| 4154 | pierdo | 6 |
| 4155 | pienses | 6 |
| 4156 | piensan | 6 |
| 4157 | pidieron | 6 |
| 4158 | pides | 6 |
| 4159 | picó | 6 |
| 4160 | pescadores | 6 |
| 4161 | pesaroso | 6 |
| 4162 | permite | 6 |
| 4163 | permita | 6 |
| 4164 | pergamino | 6 |
| 4165 | perdóname | 6 |
| 4166 | perdida | 6 |
| 4167 | perdices | 6 |
| 4168 | peras | 6 |
| 4169 | pequeños | 6 |
| 4170 | peligroso | 6 |
| 4171 | peine | 6 |
| 4172 | pasmado | 6 |
| 4173 | pasatiempos | 6 |
| 4174 | partí | 6 |
| 4175 | parecerles | 6 |
| 4176 | panzas | 6 |
| 4177 | pájaros | 6 |
| 4178 | pajarillos | 6 |
| 4179 | pacífico | 6 |
| 4180 | oyólo | 6 |
| 4181 | oyese | 6 |
| 4182 | ovidio | 6 |
| 4183 | osar | 6 |
| 4184 | ordinarios | 6 |
| 4185 | ocupar | 6 |
| 4186 | ocupada | 6 |
| 4187 | ociosos | 6 |
| 4188 | ociosas | 6 |
| 4189 | ochenta | 6 |
| 4190 | obligó | 6 |
| 4191 | novelas | 6 |
| 4192 | niega | 6 |
| 4193 | negras | 6 |
| 4194 | necesidades | 6 |
| 4195 | necesarios | 6 |
| 4196 | nariz | 6 |
| 4197 | músicas | 6 |
| 4198 | murmurando | 6 |
| 4199 | muñeca | 6 |
| 4200 | muertas | 6 |
| 4201 | muero | 6 |
| 4202 | mudo | 6 |
| 4203 | mudan | 6 |
| 4204 | muchedumbre | 6 |
| 4205 | movieron | 6 |
| 4206 | mostrase | 6 |
| 4207 | morrión | 6 |
| 4208 | monarca | 6 |
| 4209 | molimiento | 6 |
| 4210 | moderno | 6 |
| 4211 | mochacho | 6 |
| 4212 | mocedad | 6 |
| 4213 | misterio | 6 |
| 4214 | misa | 6 |
| 4215 | miróle | 6 |
| 4216 | millas | 6 |
| 4217 | miembro | 6 |
| 4218 | mentís | 6 |
| 4219 | mentiroso | 6 |
| 4220 | mase | 6 |
| 4221 | mari | 6 |
| 4222 | maravillosa | 6 |
| 4223 | maña | 6 |
| 4224 | manto | 6 |
| 4225 | manteado | 6 |
| 4226 | manifiesta | 6 |
| 4227 | malferido | 6 |
| 4228 | maldita | 6 |
| 4229 | maldecía | 6 |
| 4230 | maldades | 6 |
| 4231 | malandrín | 6 |
| 4232 | majadero | 6 |
| 4233 | magnificencia | 6 |
| 4234 | magalona | 6 |
| 4235 | madera | 6 |
| 4236 | lunar | 6 |
| 4237 | lumbre | 6 |
| 4238 | luciente | 6 |
| 4239 | llevaría | 6 |
| 4240 | llegara | 6 |
| 4241 | llaneza | 6 |
| 4242 | levante | 6 |
| 4243 | levantadas | 6 |
| 4244 | letura | 6 |
| 4245 | letrado | 6 |
| 4246 | leía | 6 |
| 4247 | legítimo | 6 |
| 4248 | leerla | 6 |
| 4249 | lavar | 6 |
| 4250 | largos | 6 |
| 4251 | juzgo | 6 |
| 4252 | justamente | 6 |
| 4253 | jorge | 6 |
| 4254 | jineta | 6 |
| 4255 | jerónimo | 6 |
| 4256 | izquierda | 6 |
| 4257 | italia | 6 |
| 4258 | isla | 6 |
| 4259 | iría | 6 |
| 4260 | innumerables | 6 |
| 4261 | ingalaterra | 6 |
| 4262 | inclinación | 6 |
| 4263 | inclemencias | 6 |
| 4264 | impresas | 6 |
| 4265 | importaba | 6 |
| 4266 | imitando | 6 |
| 4267 | igualmente | 6 |
| 4268 | idos | 6 |
| 4269 | ida | 6 |
| 4270 | honrosa | 6 |
| 4271 | hinojos | 6 |
| 4272 | hincó | 6 |
| 4273 | hierros | 6 |
| 4274 | hiciéronlo | 6 |
| 4275 | heredero | 6 |
| 4276 | hércules | 6 |
| 4277 | hechura | 6 |
| 4278 | hechicero | 6 |
| 4279 | hase | 6 |
| 4280 | harían | 6 |
| 4281 | haréis | 6 |
| 4282 | hallas | 6 |
| 4283 | hallamos | 6 |
| 4284 | hallaban | 6 |
| 4285 | hados | 6 |
| 4286 | hacernos | 6 |
| 4287 | hacéis | 6 |
| 4288 | habré | 6 |
| 4289 | hablé | 6 |
| 4290 | hablaban | 6 |
| 4291 | habérsela | 6 |
| 4292 | haberos | 6 |
| 4293 | habedes | 6 |
| 4294 | gustoso | 6 |
| 4295 | gustos | 6 |
| 4296 | guarden | 6 |
| 4297 | gremio | 6 |
| 4298 | graduado | 6 |
| 4299 | gota | 6 |
| 4300 | golfo | 6 |
| 4301 | gobiernan | 6 |
| 4302 | garcía | 6 |
| 4303 | gano | 6 |
| 4304 | gallegos | 6 |
| 4305 | galgos | 6 |
| 4306 | frutas | 6 |
| 4307 | fruta | 6 |
| 4308 | fresco | 6 |
| 4309 | formar | 6 |
| 4310 | follón | 6 |
| 4311 | flema | 6 |
| 4312 | flandes | 6 |
| 4313 | flaca | 6 |
| 4314 | firmar | 6 |
| 4315 | fingiendo | 6 |
| 4316 | fingidos | 6 |
| 4317 | fingido | 6 |
| 4318 | fineza | 6 |
| 4319 | fechos | 6 |
| 4320 | fealdad | 6 |
| 4321 | faz | 6 |
| 4322 | fasta | 6 |
| 4323 | faltase | 6 |
| 4324 | faltará | 6 |
| 4325 | fábula | 6 |
| 4326 | etc | 6 |
| 4327 | estuvimos | 6 |
| 4328 | estudiantes | 6 |
| 4329 | estribo | 6 |
| 4330 | estrañeza | 6 |
| 4331 | estorbar | 6 |
| 4332 | estiende | 6 |
| 4333 | estender | 6 |
| 4334 | estandarte | 6 |
| 4335 | estancias | 6 |
| 4336 | espías | 6 |
| 4337 | espesas | 6 |
| 4338 | escuchan | 6 |
| 4339 | escopeta | 6 |
| 4340 | erutar | 6 |
| 4341 | envíe | 6 |
| 4342 | entremeto | 6 |
| 4343 | entienden | 6 |
| 4344 | encerró | 6 |
| 4345 | encerrar | 6 |
| 4346 | encerrada | 6 |
| 4347 | encendida | 6 |
| 4348 | encarecer | 6 |
| 4349 | encantadas | 6 |
| 4350 | encamisados | 6 |
| 4351 | enano | 6 |
| 4352 | empleada | 6 |
| 4353 | empacho | 6 |
| 4354 | embustero | 6 |
| 4355 | embrazó | 6 |
| 4356 | elegante | 6 |
| 4357 | edades | 6 |
| 4358 | echándole | 6 |
| 4359 | echaba | 6 |
| 4360 | duró | 6 |
| 4361 | duelo | 6 |
| 4362 | dudoso | 6 |
| 4363 | dudo | 6 |
| 4364 | dote | 6 |
| 4365 | dones | 6 |
| 4366 | doctrina | 6 |
| 4367 | divinas | 6 |
| 4368 | disparatado | 6 |
| 4369 | diremos | 6 |
| 4370 | díjele | 6 |
| 4371 | dignidad | 6 |
| 4372 | dieran | 6 |
| 4373 | dichos | 6 |
| 4374 | detuvieron | 6 |
| 4375 | determiné | 6 |
| 4376 | destruir | 6 |
| 4377 | despierta | 6 |
| 4378 | despidieron | 6 |
| 4379 | despertar | 6 |
| 4380 | despachó | 6 |
| 4381 | desnudez | 6 |
| 4382 | desnuda | 6 |
| 4383 | deshizo | 6 |
| 4384 | deshecho | 6 |
| 4385 | desesperaba | 6 |
| 4386 | deseada | 6 |
| 4387 | desdichados | 6 |
| 4388 | descuidos | 6 |
| 4389 | descuidado | 6 |
| 4390 | descubrirse | 6 |
| 4391 | descubierta | 6 |
| 4392 | desconocida | 6 |
| 4393 | descargar | 6 |
| 4394 | desagradecido | 6 |
| 4395 | desaforado | 6 |
| 4396 | derechos | 6 |
| 4397 | derechas | 6 |
| 4398 | derechamente | 6 |
| 4399 | déjenme | 6 |
| 4400 | deis | 6 |
| 4401 | declarar | 6 |
| 4402 | declaración | 6 |
| 4403 | declara | 6 |
| 4404 | decille | 6 |
| 4405 | debemos | 6 |
| 4406 | dársela | 6 |
| 4407 | darnos | 6 |
| 4408 | danza | 6 |
| 4409 | cure | 6 |
| 4410 | cupo | 6 |
| 4411 | cumplirá | 6 |
| 4412 | cumplió | 6 |
| 4413 | cumple | 6 |
| 4414 | culebras | 6 |
| 4415 | cuerda | 6 |
| 4416 | cuente | 6 |
| 4417 | cuchillo | 6 |
| 4418 | cubrían | 6 |
| 4419 | cubiertas | 6 |
| 4420 | cuartos | 6 |
| 4421 | cuartillo | 6 |
| 4422 | cristiandad | 6 |
| 4423 | cristianas | 6 |
| 4424 | cortar | 6 |
| 4425 | cortada | 6 |
| 4426 | corso | 6 |
| 4427 | corrió | 6 |
| 4428 | convidó | 6 |
| 4429 | convertida | 6 |
| 4430 | contrahecha | 6 |
| 4431 | continuas | 6 |
| 4432 | contienen | 6 |
| 4433 | consoló | 6 |
| 4434 | consentiré | 6 |
| 4435 | consentimiento | 6 |
| 4436 | conseguir | 6 |
| 4437 | conociera | 6 |
| 4438 | confusos | 6 |
| 4439 | concluir | 6 |
| 4440 | conceptos | 6 |
| 4441 | comunicar | 6 |
| 4442 | compra | 6 |
| 4443 | comía | 6 |
| 4444 | comedimientos | 6 |
| 4445 | coloquios | 6 |
| 4446 | colas | 6 |
| 4447 | cogiendo | 6 |
| 4448 | clavijo | 6 |
| 4449 | cierra | 6 |
| 4450 | chozas | 6 |
| 4451 | cetro | 6 |
| 4452 | cesaba | 6 |
| 4453 | cautiverio | 6 |
| 4454 | casada | 6 |
| 4455 | campea | 6 |
| 4456 | caletre | 6 |
| 4457 | caí | 6 |
| 4458 | cabalgadura | 6 |
| 4459 | buscase | 6 |
| 4460 | buscalle | 6 |
| 4461 | buey | 6 |
| 4462 | buenamente | 6 |
| 4463 | brocado | 6 |
| 4464 | bravos | 6 |
| 4465 | boticario | 6 |
| 4466 | botas | 6 |
| 4467 | borrica | 6 |
| 4468 | borracho | 6 |
| 4469 | blandura | 6 |
| 4470 | bigotes | 6 |
| 4471 | bellacos | 6 |
| 4472 | barrabás | 6 |
| 4473 | barra | 6 |
| 4474 | barato | 6 |
| 4475 | bajos | 6 |
| 4476 | ayudó | 6 |
| 4477 | averiguado | 6 |
| 4478 | aventureros | 6 |
| 4479 | atravesado | 6 |
| 4480 | atenta | 6 |
| 4481 | atengo | 6 |
| 4482 | atendiendo | 6 |
| 4483 | asidos | 6 |
| 4484 | artes | 6 |
| 4485 | arroyos | 6 |
| 4486 | arpa | 6 |
| 4487 | argamasilla | 6 |
| 4488 | ardiendo | 6 |
| 4489 | archivo | 6 |
| 4490 | aprovechó | 6 |
| 4491 | aprieto | 6 |
| 4492 | apeáronse | 6 |
| 4493 | apear | 6 |
| 4494 | apartarse | 6 |
| 4495 | apariencia | 6 |
| 4496 | apaleado | 6 |
| 4497 | antojos | 6 |
| 4498 | antoja | 6 |
| 4499 | ansimismo | 6 |
| 4500 | ángeles | 6 |
| 4501 | anejas | 6 |
| 4502 | andurriales | 6 |
| 4503 | andamos | 6 |
| 4504 | amarga | 6 |
| 4505 | amaneció | 6 |
| 4506 | amanecer | 6 |
| 4507 | algodón | 6 |
| 4508 | aldeas | 6 |
| 4509 | alcurnia | 6 |
| 4510 | alcanzaba | 6 |
| 4511 | alcance | 6 |
| 4512 | alcaldes | 6 |
| 4513 | alborotada | 6 |
| 4514 | albogues | 6 |
| 4515 | ahorrar | 6 |
| 4516 | agramante | 6 |
| 4517 | advirtiese | 6 |
| 4518 | advertida | 6 |
| 4519 | adulación | 6 |
| 4520 | adivino | 6 |
| 4521 | adelantó | 6 |
| 4522 | acto | 6 |
| 4523 | acrecentar | 6 |
| 4524 | acosado | 6 |
| 4525 | aconteció | 6 |
| 4526 | acontecimiento | 6 |
| 4527 | acompañados | 6 |
| 4528 | acompañado | 6 |
| 4529 | acomodar | 6 |
| 4530 | acierto | 6 |
| 4531 | acaeció | 6 |
| 4532 | acabo | 6 |
| 4533 | acaban | 6 |
| 4534 | abrid | 6 |
| 4535 | abrazada | 6 |
| 4536 | abra | 6 |
| 4537 | abismos | 6 |
| 4538 | yerro | 5 |
| 4539 | yangüeses | 5 |
| 4540 | vuelvas | 5 |
| 4541 | volvían | 5 |
| 4542 | volvería | 5 |
| 4543 | volved | 5 |
| 4544 | volváis | 5 |
| 4545 | vocablos | 5 |
| 4546 | vistió | 5 |
| 4547 | visita | 5 |
| 4548 | visiones | 5 |
| 4549 | virtuoso | 5 |
| 4550 | vientos | 5 |
| 4551 | vicioso | 5 |
| 4552 | vicario | 5 |
| 4553 | vías | 5 |
| 4554 | veré | 5 |
| 4555 | verdugos | 5 |
| 4556 | vengas | 5 |
| 4557 | vendrán | 5 |
| 4558 | vencedora | 5 |
| 4559 | vejez | 5 |
| 4560 | veáis | 5 |
| 4561 | varilla | 5 |
| 4562 | vana | 5 |
| 4563 | valían | 5 |
| 4564 | valía | 5 |
| 4565 | valga | 5 |
| 4566 | valerosa | 5 |
| 4567 | valdovinos | 5 |
| 4568 | universo | 5 |
| 4569 | últimamente | 5 |
| 4570 | tuvimos | 5 |
| 4571 | turbar | 5 |
| 4572 | trujesen | 5 |
| 4573 | truje | 5 |
| 4574 | tristezas | 5 |
| 4575 | trazas | 5 |
| 4576 | trayendo | 5 |
| 4577 | transformación | 5 |
| 4578 | trances | 5 |
| 4579 | traducir | 5 |
| 4580 | tracia | 5 |
| 4581 | toscano | 5 |
| 4582 | torpes | 5 |
| 4583 | toro | 5 |
| 4584 | topé | 5 |
| 4585 | topar | 5 |
| 4586 | tomóle | 5 |
| 4587 | tomarla | 5 |
| 4588 | tocinos | 5 |
| 4589 | tocino | 5 |
| 4590 | tocare | 5 |
| 4591 | tocando | 5 |
| 4592 | titerero | 5 |
| 4593 | tiró | 5 |
| 4594 | tirante | 5 |
| 4595 | tinajas | 5 |
| 4596 | tesoros | 5 |
| 4597 | tercio | 5 |
| 4598 | teniéndole | 5 |
| 4599 | tendieron | 5 |
| 4600 | tendidas | 5 |
| 4601 | temía | 5 |
| 4602 | tema | 5 |
| 4603 | teatro | 5 |
| 4604 | tarda | 5 |
| 4605 | tapices | 5 |
| 4606 | tafetán | 5 |
| 4607 | sutiles | 5 |
| 4608 | sustentado | 5 |
| 4609 | suspirar | 5 |
| 4610 | suspenden | 5 |
| 4611 | suplir | 5 |
| 4612 | suplicó | 5 |
| 4613 | suplicaba | 5 |
| 4614 | sufre | 5 |
| 4615 | suficiente | 5 |
| 4616 | sucedióle | 5 |
| 4617 | sucedieron | 5 |
| 4618 | sucediere | 5 |
| 4619 | sucedidas | 5 |
| 4620 | subiese | 5 |
| 4621 | sube | 5 |
| 4622 | suaves | 5 |
| 4623 | sosegar | 5 |
| 4624 | sosegadamente | 5 |
| 4625 | sonaron | 5 |
| 4626 | socorriese | 5 |
| 4627 | sobrenombre | 5 |
| 4628 | sirviendo | 5 |
| 4629 | sinrazones | 5 |
| 4630 | sinrazón | 5 |
| 4631 | siguen | 5 |
| 4632 | sienta | 5 |
| 4633 | serás | 5 |
| 4634 | señorío | 5 |
| 4635 | señalando | 5 |
| 4636 | sentí | 5 |
| 4637 | sentarse | 5 |
| 4638 | sentándose | 5 |
| 4639 | semana | 5 |
| 4640 | seguros | 5 |
| 4641 | seguían | 5 |
| 4642 | seguíale | 5 |
| 4643 | santiguada | 5 |
| 4644 | santiago | 5 |
| 4645 | santas | 5 |
| 4646 | sandio | 5 |
| 4647 | salta | 5 |
| 4648 | saliesen | 5 |
| 4649 | saldría | 5 |
| 4650 | sacristán | 5 |
| 4651 | sacarán | 5 |
| 4652 | sabrosas | 5 |
| 4653 | sabida | 5 |
| 4654 | sabia | 5 |
| 4655 | saberlo | 5 |
| 4656 | rústicos | 5 |
| 4657 | ropilla | 5 |
| 4658 | romero | 5 |
| 4659 | romana | 5 |
| 4660 | rogué | 5 |
| 4661 | rogóle | 5 |
| 4662 | rogado | 5 |
| 4663 | rogaba | 5 |
| 4664 | reventar | 5 |
| 4665 | retiróse | 5 |
| 4666 | resquicios | 5 |
| 4667 | respondelle | 5 |
| 4668 | resplandecientes | 5 |
| 4669 | rescatado | 5 |
| 4670 | reprehendido | 5 |
| 4671 | repostería | 5 |
| 4672 | reposado | 5 |
| 4673 | renovó | 5 |
| 4674 | renovaron | 5 |
| 4675 | renovar | 5 |
| 4676 | rendida | 5 |
| 4677 | remedios | 5 |
| 4678 | remedie | 5 |
| 4679 | remate | 5 |
| 4680 | religiosos | 5 |
| 4681 | reírse | 5 |
| 4682 | regla | 5 |
| 4683 | regidores | 5 |
| 4684 | redondez | 5 |
| 4685 | redoma | 5 |
| 4686 | recuesto | 5 |
| 4687 | recua | 5 |
| 4688 | recompensa | 5 |
| 4689 | recogida | 5 |
| 4690 | recelo | 5 |
| 4691 | recebidos | 5 |
| 4692 | recebía | 5 |
| 4693 | recatada | 5 |
| 4694 | recámara | 5 |
| 4695 | randas | 5 |
| 4696 | raíces | 5 |
| 4697 | quitarte | 5 |
| 4698 | quitarse | 5 |
| 4699 | quitármela | 5 |
| 4700 | quitarles | 5 |
| 4701 | quitándole | 5 |
| 4702 | quintañona | 5 |
| 4703 | quimeras | 5 |
| 4704 | quijano | 5 |
| 4705 | quijadas | 5 |
| 4706 | quejaba | 5 |
| 4707 | quedando | 5 |
| 4708 | pusimos | 5 |
| 4709 | pupilos | 5 |
| 4710 | puñada | 5 |
| 4711 | púlpito | 5 |
| 4712 | pugnaba | 5 |
| 4713 | pueblos | 5 |
| 4714 | pudieres | 5 |
| 4715 | provincias | 5 |
| 4716 | providencia | 5 |
| 4717 | proveído | 5 |
| 4718 | proveídas | 5 |
| 4719 | prosa | 5 |
| 4720 | propuesto | 5 |
| 4721 | propria | 5 |
| 4722 | prometía | 5 |
| 4723 | procuro | 5 |
| 4724 | presunción | 5 |
| 4725 | presentados | 5 |
| 4726 | prender | 5 |
| 4727 | premiar | 5 |
| 4728 | pregunte | 5 |
| 4729 | preguntarle | 5 |
| 4730 | preguntare | 5 |
| 4731 | preguntan | 5 |
| 4732 | precia | 5 |
| 4733 | posibles | 5 |
| 4734 | posaderas | 5 |
| 4735 | porro | 5 |
| 4736 | porqué | 5 |
| 4737 | popa | 5 |
| 4738 | pongáis | 5 |
| 4739 | polo | 5 |
| 4740 | podrido | 5 |
| 4741 | podridas | 5 |
| 4742 | poderlo | 5 |
| 4743 | plomo | 5 |
| 4744 | platos | 5 |
| 4745 | pisando | 5 |
| 4746 | pintura | 5 |
| 4747 | pintó | 5 |
| 4748 | pintadas | 5 |
| 4749 | pintaba | 5 |
| 4750 | pila | 5 |
| 4751 | pífaro | 5 |
| 4752 | picando | 5 |
| 4753 | pesado | 5 |
| 4754 | pertrechos | 5 |
| 4755 | persuasión | 5 |
| 4756 | persuadió | 5 |
| 4757 | perseguida | 5 |
| 4758 | perezosos | 5 |
| 4759 | perdono | 5 |
| 4760 | perdidos | 5 |
| 4761 | perdí | 5 |
| 4762 | perderse | 5 |
| 4763 | pensaron | 5 |
| 4764 | pensarlo | 5 |
| 4765 | pendientes | 5 |
| 4766 | pellizcos | 5 |
| 4767 | pegar | 5 |
| 4768 | pedís | 5 |
| 4769 | pecadores | 5 |
| 4770 | pasear | 5 |
| 4771 | paró | 5 |
| 4772 | pariente | 5 |
| 4773 | parentela | 5 |
| 4774 | pared | 5 |
| 4775 | pareciere | 5 |
| 4776 | pareciéndoles | 5 |
| 4777 | pararon | 5 |
| 4778 | papa | 5 |
| 4779 | pañuelo | 5 |
| 4780 | pague | 5 |
| 4781 | pagaría | 5 |
| 4782 | pagano | 5 |
| 4783 | pagados | 5 |
| 4784 | pagador | 5 |
| 4785 | pacífica | 5 |
| 4786 | paces | 5 |
| 4787 | oyentes | 5 |
| 4788 | oyéndole | 5 |
| 4789 | oveja | 5 |
| 4790 | osó | 5 |
| 4791 | ordenaron | 5 |
| 4792 | ordenaba | 5 |
| 4793 | oraciones | 5 |
| 4794 | olvidada | 5 |
| 4795 | olmo | 5 |
| 4796 | ofreciese | 5 |
| 4797 | ofrecieron | 5 |
| 4798 | ofreciere | 5 |
| 4799 | ofreciéndole | 5 |
| 4800 | ofrecían | 5 |
| 4801 | ocio | 5 |
| 4802 | obliga | 5 |
| 4803 | obediencia | 5 |
| 4804 | nueces | 5 |
| 4805 | novedad | 5 |
| 4806 | notorio | 5 |
| 4807 | nones | 5 |
| 4808 | nombró | 5 |
| 4809 | ninfa | 5 |
| 4810 | negociante | 5 |
| 4811 | necios | 5 |
| 4812 | narváez | 5 |
| 4813 | nacer | 5 |
| 4814 | musas | 5 |
| 4815 | muestran | 5 |
| 4816 | mudanzas | 5 |
| 4817 | mudando | 5 |
| 4818 | mostrara | 5 |
| 4819 | mortales | 5 |
| 4820 | monstruo | 5 |
| 4821 | monja | 5 |
| 4822 | molidos | 5 |
| 4823 | miserias | 5 |
| 4824 | miré | 5 |
| 4825 | miraron | 5 |
| 4826 | mirarle | 5 |
| 4827 | mirábanle | 5 |
| 4828 | mentirosas | 5 |
| 4829 | menguada | 5 |
| 4830 | mención | 5 |
| 4831 | memorable | 5 |
| 4832 | melindroso | 5 |
| 4833 | melindrosa | 5 |
| 4834 | melindre | 5 |
| 4835 | medianamente | 5 |
| 4836 | mazos | 5 |
| 4837 | mayorazgo | 5 |
| 4838 | matarme | 5 |
| 4839 | matan | 5 |
| 4840 | mascar | 5 |
| 4841 | martirios | 5 |
| 4842 | marras | 5 |
| 4843 | marina | 5 |
| 4844 | mangas | 5 |
| 4845 | mande | 5 |
| 4846 | malparado | 5 |
| 4847 | maldad | 5 |
| 4848 | málaga | 5 |
| 4849 | mahoma | 5 |
| 4850 | maguer | 5 |
| 4851 | madura | 5 |
| 4852 | lomos | 5 |
| 4853 | llevamos | 5 |
| 4854 | llegada | 5 |
| 4855 | llaves | 5 |
| 4856 | llamarla | 5 |
| 4857 | llamándose | 5 |
| 4858 | litera | 5 |
| 4859 | lista | 5 |
| 4860 | lío | 5 |
| 4861 | ligeras | 5 |
| 4862 | librea | 5 |
| 4863 | libras | 5 |
| 4864 | libertador | 5 |
| 4865 | leyere | 5 |
| 4866 | leonado | 5 |
| 4867 | lascivo | 5 |
| 4868 | lamentable | 5 |
| 4869 | juzga | 5 |
| 4870 | júpiter | 5 |
| 4871 | juntarse | 5 |
| 4872 | jaulas | 5 |
| 4873 | jaspe | 5 |
| 4874 | islas | 5 |
| 4875 | invidiosos | 5 |
| 4876 | inumerables | 5 |
| 4877 | intitulado | 5 |
| 4878 | intérprete | 5 |
| 4879 | ingratitud | 5 |
| 4880 | informado | 5 |
| 4881 | infinidad | 5 |
| 4882 | inferir | 5 |
| 4883 | infantería | 5 |
| 4884 | indigno | 5 |
| 4885 | incomodidades | 5 |
| 4886 | inclinó | 5 |
| 4887 | inclinada | 5 |
| 4888 | inaudito | 5 |
| 4889 | impresos | 5 |
| 4890 | impiden | 5 |
| 4891 | impertinentes | 5 |
| 4892 | impertinencias | 5 |
| 4893 | ilustres | 5 |
| 4894 | igualarse | 5 |
| 4895 | íbamos | 5 |
| 4896 | huele | 5 |
| 4897 | honestos | 5 |
| 4898 | honestas | 5 |
| 4899 | honda | 5 |
| 4900 | holanda | 5 |
| 4901 | hoja | 5 |
| 4902 | hicieran | 5 |
| 4903 | heridos | 5 |
| 4904 | hallarme | 5 |
| 4905 | hallándose | 5 |
| 4906 | hallando | 5 |
| 4907 | haciéndose | 5 |
| 4908 | haceros | 5 |
| 4909 | habremos | 5 |
| 4910 | hablas | 5 |
| 4911 | hábitos | 5 |
| 4912 | guirnaldas | 5 |
| 4913 | guardó | 5 |
| 4914 | grita | 5 |
| 4915 | grano | 5 |
| 4916 | graciosos | 5 |
| 4917 | gonzalo | 5 |
| 4918 | gobierna | 5 |
| 4919 | ginesillo | 5 |
| 4920 | ginebra | 5 |
| 4921 | generosos | 5 |
| 4922 | gasto | 5 |
| 4923 | gaspar | 5 |
| 4924 | gansos | 5 |
| 4925 | ganó | 5 |
| 4926 | gane | 5 |
| 4927 | gallina | 5 |
| 4928 | galaor | 5 |
| 4929 | fulano | 5 |
| 4930 | fugitivo | 5 |
| 4931 | fuésemos | 5 |
| 4932 | fueras | 5 |
| 4933 | franco | 5 |
| 4934 | fraile | 5 |
| 4935 | forzosamente | 5 |
| 4936 | forzado | 5 |
| 4937 | forzada | 5 |
| 4938 | formaban | 5 |
| 4939 | florestas | 5 |
| 4940 | flechas | 5 |
| 4941 | fingir | 5 |
| 4942 | fingida | 5 |
| 4943 | fines | 5 |
| 4944 | filos | 5 |
| 4945 | fiar | 5 |
| 4946 | felicísima | 5 |
| 4947 | felicidad | 5 |
| 4948 | fatigaban | 5 |
| 4949 | fantástico | 5 |
| 4950 | faltare | 5 |
| 4951 | faltando | 5 |
| 4952 | facultad | 5 |
| 4953 | facilitar | 5 |
| 4954 | fábulas | 5 |
| 4955 | fabricada | 5 |
| 4956 | experiencias | 5 |
| 4957 | excepto | 5 |
| 4958 | eternamente | 5 |
| 4959 | estudios | 5 |
| 4960 | estremadura | 5 |
| 4961 | estremado | 5 |
| 4962 | estrema | 5 |
| 4963 | estrechas | 5 |
| 4964 | estrado | 5 |
| 4965 | estimada | 5 |
| 4966 | estendió | 5 |
| 4967 | estemos | 5 |
| 4968 | estatua | 5 |
| 4969 | estacada | 5 |
| 4970 | esquife | 5 |
| 4971 | espantoso | 5 |
| 4972 | espaciosa | 5 |
| 4973 | escuderil | 5 |
| 4974 | escuchó | 5 |
| 4975 | escribía | 5 |
| 4976 | escrebir | 5 |
| 4977 | escogió | 5 |
| 4978 | escaparse | 5 |
| 4979 | erratas | 5 |
| 4980 | errar | 5 |
| 4981 | epitafio | 5 |
| 4982 | enviarle | 5 |
| 4983 | enviaba | 5 |
| 4984 | entretiene | 5 |
| 4985 | entretenimientos | 5 |
| 4986 | entretenidos | 5 |
| 4987 | entramos | 5 |
| 4988 | enterrar | 5 |
| 4989 | enteros | 5 |
| 4990 | enterado | 5 |
| 4991 | entendieron | 5 |
| 4992 | entendiendo | 5 |
| 4993 | entendí | 5 |
| 4994 | entena | 5 |
| 4995 | enseñar | 5 |
| 4996 | enseñan | 5 |
| 4997 | enseñado | 5 |
| 4998 | enramada | 5 |
| 4999 | enoja | 5 |
| 5000 | enmienda | 5 |
| 5001 | enjaulado | 5 |
| 5002 | enhoramala | 5 |
| 5003 | engañaba | 5 |
| 5004 | enferma | 5 |
| 5005 | enfado | 5 |
| 5006 | enderezar | 5 |
| 5007 | encuentros | 5 |
| 5008 | encubre | 5 |
| 5009 | encrucijadas | 5 |
| 5010 | encontró | 5 |
| 5011 | encoger | 5 |
| 5012 | encerrados | 5 |
| 5013 | encerraba | 5 |
| 5014 | encender | 5 |
| 5015 | encaminar | 5 |
| 5016 | encaminando | 5 |
| 5017 | encaminadas | 5 |
| 5018 | encaja | 5 |
| 5019 | empresas | 5 |
| 5020 | emperatriz | 5 |
| 5021 | emperatrices | 5 |
| 5022 | embrazando | 5 |
| 5023 | embajador | 5 |
| 5024 | elena | 5 |
| 5025 | dure | 5 |
| 5026 | dulces | 5 |
| 5027 | duelos | 5 |
| 5028 | dudosos | 5 |
| 5029 | dorado | 5 |
| 5030 | doradas | 5 |
| 5031 | doquiera | 5 |
| 5032 | diversidad | 5 |
| 5033 | disimular | 5 |
| 5034 | disignio | 5 |
| 5035 | disgusto | 5 |
| 5036 | disculpas | 5 |
| 5037 | dirás | 5 |
| 5038 | dilatado | 5 |
| 5039 | dijes | 5 |
| 5040 | dijeren | 5 |
| 5041 | dígote | 5 |
| 5042 | díganme | 5 |
| 5043 | dígalo | 5 |
| 5044 | dificultosas | 5 |
| 5045 | difícil | 5 |
| 5046 | devoción | 5 |
| 5047 | deuda | 5 |
| 5048 | detuviese | 5 |
| 5049 | determinaba | 5 |
| 5050 | detenga | 5 |
| 5051 | detenerse | 5 |
| 5052 | detenerme | 5 |
| 5053 | desviados | 5 |
| 5054 | destierro | 5 |
| 5055 | desposorios | 5 |
| 5056 | desposado | 5 |
| 5057 | desnudar | 5 |
| 5058 | desmesurado | 5 |
| 5059 | desmayado | 5 |
| 5060 | desierto | 5 |
| 5061 | desierta | 5 |
| 5062 | deshechas | 5 |
| 5063 | deshaciendo | 5 |
| 5064 | desenvuelta | 5 |
| 5065 | desengaños | 5 |
| 5066 | desembarazado | 5 |
| 5067 | descubrirme | 5 |
| 5068 | descortés | 5 |
| 5069 | descontenta | 5 |
| 5070 | descargó | 5 |
| 5071 | descalzos | 5 |
| 5072 | desalmados | 5 |
| 5073 | desalmado | 5 |
| 5074 | desagradecida | 5 |
| 5075 | desaforados | 5 |
| 5076 | derribar | 5 |
| 5077 | derramar | 5 |
| 5078 | derramando | 5 |
| 5079 | denantes | 5 |
| 5080 | delitos | 5 |
| 5081 | delicado | 5 |
| 5082 | delgado | 5 |
| 5083 | deleitar | 5 |
| 5084 | dejéis | 5 |
| 5085 | dejas | 5 |
| 5086 | dejarte | 5 |
| 5087 | dejalle | 5 |
| 5088 | dejad | 5 |
| 5089 | declarase | 5 |
| 5090 | decirlo | 5 |
| 5091 | debiera | 5 |
| 5092 | danzas | 5 |
| 5093 | dándose | 5 |
| 5094 | dados | 5 |
| 5095 | dad | 5 |
| 5096 | curó | 5 |
| 5097 | curiosos | 5 |
| 5098 | cupido | 5 |
| 5099 | cumplan | 5 |
| 5100 | cuidados | 5 |
| 5101 | cuerdos | 5 |
| 5102 | cubría | 5 |
| 5103 | cualesquiera | 5 |
| 5104 | cuadrilla | 5 |
| 5105 | cuadra | 5 |
| 5106 | crujía | 5 |
| 5107 | crió | 5 |
| 5108 | criar | 5 |
| 5109 | creyera | 5 |
| 5110 | creciendo | 5 |
| 5111 | crecer | 5 |
| 5112 | costas | 5 |
| 5113 | cortado | 5 |
| 5114 | corresponder | 5 |
| 5115 | correspondencia | 5 |
| 5116 | coroza | 5 |
| 5117 | coronista | 5 |
| 5118 | convertido | 5 |
| 5119 | contienda | 5 |
| 5120 | contentísimo | 5 |
| 5121 | contentar | 5 |
| 5122 | contarse | 5 |
| 5123 | contarle | 5 |
| 5124 | contaré | 5 |
| 5125 | consiguiente | 5 |
| 5126 | considerado | 5 |
| 5127 | conservar | 5 |
| 5128 | confío | 5 |
| 5129 | conducido | 5 |
| 5130 | concertó | 5 |
| 5131 | concertada | 5 |
| 5132 | concedido | 5 |
| 5133 | comunique | 5 |
| 5134 | competir | 5 |
| 5135 | compañera | 5 |
| 5136 | comisión | 5 |
| 5137 | comencé | 5 |
| 5138 | coman | 5 |
| 5139 | colcha | 5 |
| 5140 | cohecho | 5 |
| 5141 | cogió | 5 |
| 5142 | coge | 5 |
| 5143 | codicia | 5 |
| 5144 | cocinero | 5 |
| 5145 | cirongilio | 5 |
| 5146 | cerdas | 5 |
| 5147 | celo | 5 |
| 5148 | celebrar | 5 |
| 5149 | cebolla | 5 |
| 5150 | cayese | 5 |
| 5151 | cayera | 5 |
| 5152 | causaba | 5 |
| 5153 | catón | 5 |
| 5154 | católicas | 5 |
| 5155 | catadura | 5 |
| 5156 | cata | 5 |
| 5157 | castigados | 5 |
| 5158 | casó | 5 |
| 5159 | cásese | 5 |
| 5160 | carpio | 5 |
| 5161 | cariño | 5 |
| 5162 | capilla | 5 |
| 5163 | cantor | 5 |
| 5164 | canséis | 5 |
| 5165 | canción | 5 |
| 5166 | canas | 5 |
| 5167 | caminado | 5 |
| 5168 | caminaba | 5 |
| 5169 | camarada | 5 |
| 5170 | callaré | 5 |
| 5171 | caja | 5 |
| 5172 | caídos | 5 |
| 5173 | caían | 5 |
| 5174 | cabal | 5 |
| 5175 | burlado | 5 |
| 5176 | buitre | 5 |
| 5177 | brinco | 5 |
| 5178 | bretaña | 5 |
| 5179 | brebaje | 5 |
| 5180 | bonísima | 5 |
| 5181 | bogar | 5 |
| 5182 | boda | 5 |
| 5183 | bocací | 5 |
| 5184 | besa | 5 |
| 5185 | bastón | 5 |
| 5186 | barriga | 5 |
| 5187 | barbado | 5 |
| 5188 | bañó | 5 |
| 5189 | bando | 5 |
| 5190 | banco | 5 |
| 5191 | balcón | 5 |
| 5192 | bajaba | 5 |
| 5193 | azul | 5 |
| 5194 | ayudase | 5 |
| 5195 | avisar | 5 |
| 5196 | avisado | 5 |
| 5197 | avínole | 5 |
| 5198 | averiguación | 5 |
| 5199 | avemarías | 5 |
| 5200 | avellanas | 5 |
| 5201 | aumento | 5 |
| 5202 | atrevo | 5 |
| 5203 | atrevida | 5 |
| 5204 | atreva | 5 |
| 5205 | atónitos | 5 |
| 5206 | ató | 5 |
| 5207 | atentado | 5 |
| 5208 | atendía | 5 |
| 5209 | atender | 5 |
| 5210 | atambores | 5 |
| 5211 | atabales | 5 |
| 5212 | asendereado | 5 |
| 5213 | ascuras | 5 |
| 5214 | asaltos | 5 |
| 5215 | arrimó | 5 |
| 5216 | arrimo | 5 |
| 5217 | arrimada | 5 |
| 5218 | arrepentimiento | 5 |
| 5219 | arrepentido | 5 |
| 5220 | aristóteles | 5 |
| 5221 | arenga | 5 |
| 5222 | ardor | 5 |
| 5223 | ardiente | 5 |
| 5224 | arco | 5 |
| 5225 | aquéllas | 5 |
| 5226 | apuesta | 5 |
| 5227 | apretó | 5 |
| 5228 | apretar | 5 |
| 5229 | aprendido | 5 |
| 5230 | apostura | 5 |
| 5231 | aporreado | 5 |
| 5232 | apetito | 5 |
| 5233 | apeóse | 5 |
| 5234 | apellido | 5 |
| 5235 | aparato | 5 |
| 5236 | ansias | 5 |
| 5237 | ansia | 5 |
| 5238 | anillo | 5 |
| 5239 | angustia | 5 |
| 5240 | anduviesen | 5 |
| 5241 | andará | 5 |
| 5242 | andanza | 5 |
| 5243 | ancha | 5 |
| 5244 | ambición | 5 |
| 5245 | amargo | 5 |
| 5246 | amadises | 5 |
| 5247 | alzaba | 5 |
| 5248 | altamente | 5 |
| 5249 | aljófar | 5 |
| 5250 | alguaciles | 5 |
| 5251 | alfilerazos | 5 |
| 5252 | alemania | 5 |
| 5253 | alegró | 5 |
| 5254 | alegraron | 5 |
| 5255 | alcázares | 5 |
| 5256 | alcanzaron | 5 |
| 5257 | alcanzara | 5 |
| 5258 | alcahuete | 5 |
| 5259 | alameda | 5 |
| 5260 | alabardas | 5 |
| 5261 | ala | 5 |
| 5262 | ajos | 5 |
| 5263 | ahorcar | 5 |
| 5264 | ahorcado | 5 |
| 5265 | ahechando | 5 |
| 5266 | aguijón | 5 |
| 5267 | agüeros | 5 |
| 5268 | agudeza | 5 |
| 5269 | aguardando | 5 |
| 5270 | agradables | 5 |
| 5271 | afrentado | 5 |
| 5272 | afligidos | 5 |
| 5273 | afligida | 5 |
| 5274 | advertimiento | 5 |
| 5275 | adornan | 5 |
| 5276 | adondequiera | 5 |
| 5277 | admirarse | 5 |
| 5278 | admirables | 5 |
| 5279 | aderezado | 5 |
| 5280 | adentro | 5 |
| 5281 | ademanes | 5 |
| 5282 | acreditar | 5 |
| 5283 | acostumbrados | 5 |
| 5284 | acostumbradas | 5 |
| 5285 | acorrer | 5 |
| 5286 | acordarse | 5 |
| 5287 | acordado | 5 |
| 5288 | acontecimientos | 5 |
| 5289 | acontecer | 5 |
| 5290 | acontece | 5 |
| 5291 | aconsejaba | 5 |
| 5292 | acompañada | 5 |
| 5293 | acomodaron | 5 |
| 5294 | acomete | 5 |
| 5295 | acertare | 5 |
| 5296 | acertara | 5 |
| 5297 | abundante | 5 |
| 5298 | abrazándole | 5 |
| 5299 | abrasó | 5 |
| 5300 | aborrecido | 5 |
| 5301 | abad | 5 |
| 5302 | zarandajas | 4 |
| 5303 | zagales | 4 |
| 5304 | yelo | 4 |
| 5305 | yedra | 4 |
| 5306 | vuelves | 4 |
| 5307 | votos | 4 |
| 5308 | vosotras | 4 |
| 5309 | volviera | 4 |
| 5310 | volvernos | 4 |
| 5311 | volvámonos | 4 |
| 5312 | vituperio | 4 |
| 5313 | vistos | 4 |
| 5314 | vistióse | 4 |
| 5315 | vislumbres | 4 |
| 5316 | vireno | 4 |
| 5317 | viole | 4 |
| 5318 | viejas | 4 |
| 5319 | viedma | 4 |
| 5320 | viajes | 4 |
| 5321 | vestirse | 4 |
| 5322 | vestiglo | 4 |
| 5323 | verjas | 4 |
| 5324 | vente | 4 |
| 5325 | venidero | 4 |
| 5326 | vengarme | 4 |
| 5327 | vengada | 4 |
| 5328 | velando | 4 |
| 5329 | vehemencia | 4 |
| 5330 | varones | 4 |
| 5331 | varias | 4 |
| 5332 | vaquilla | 4 |
| 5333 | valerosas | 4 |
| 5334 | valentísimo | 4 |
| 5335 | valenciano | 4 |
| 5336 | vaina | 4 |
| 5337 | vado | 4 |
| 5338 | útil | 4 |
| 5339 | usaba | 4 |
| 5340 | urganda | 4 |
| 5341 | umbrales | 4 |
| 5342 | últimas | 4 |
| 5343 | ufano | 4 |
| 5344 | turra | 4 |
| 5345 | turquesca | 4 |
| 5346 | turpín | 4 |
| 5347 | turbio | 4 |
| 5348 | turbes | 4 |
| 5349 | turbe | 4 |
| 5350 | turbación | 4 |
| 5351 | tropezando | 4 |
| 5352 | trono | 4 |
| 5353 | tratasen | 4 |
| 5354 | tratáredes | 4 |
| 5355 | tratamos | 4 |
| 5356 | trasudando | 4 |
| 5357 | traspasado | 4 |
| 5358 | transparente | 4 |
| 5359 | transformaron | 4 |
| 5360 | traigáis | 4 |
| 5361 | traeré | 4 |
| 5362 | traéis | 4 |
| 5363 | tradición | 4 |
| 5364 | torpe | 4 |
| 5365 | tordesillas | 4 |
| 5366 | torcido | 4 |
| 5367 | torcer | 4 |
| 5368 | topase | 4 |
| 5369 | topado | 4 |
| 5370 | topaba | 4 |
| 5371 | toméis | 4 |
| 5372 | tomasen | 4 |
| 5373 | tomaré | 4 |
| 5374 | tomándola | 4 |
| 5375 | toledano | 4 |
| 5376 | tocase | 4 |
| 5377 | tocarle | 4 |
| 5378 | toallas | 4 |
| 5379 | tirones | 4 |
| 5380 | tira | 4 |
| 5381 | tíos | 4 |
| 5382 | tintero | 4 |
| 5383 | tiernas | 4 |
| 5384 | tiernamente | 4 |
| 5385 | tibia | 4 |
| 5386 | tez | 4 |
| 5387 | tente | 4 |
| 5388 | tenor | 4 |
| 5389 | teníamos | 4 |
| 5390 | ténganse | 4 |
| 5391 | tendremos | 4 |
| 5392 | temple | 4 |
| 5393 | temores | 4 |
| 5394 | temiera | 4 |
| 5395 | temblando | 4 |
| 5396 | techado | 4 |
| 5397 | tardado | 4 |
| 5398 | tardaba | 4 |
| 5399 | tanda | 4 |
| 5400 | tamaña | 4 |
| 5401 | tálamo | 4 |
| 5402 | tahalí | 4 |
| 5403 | tachas | 4 |
| 5404 | supieron | 4 |
| 5405 | sufrido | 4 |
| 5406 | sueños | 4 |
| 5407 | suena | 4 |
| 5408 | sudar | 4 |
| 5409 | sudaba | 4 |
| 5410 | sucedía | 4 |
| 5411 | sucede | 4 |
| 5412 | subjeto | 4 |
| 5413 | subía | 4 |
| 5414 | suben | 4 |
| 5415 | suavidad | 4 |
| 5416 | sospiros | 4 |
| 5417 | soplar | 4 |
| 5418 | soñadas | 4 |
| 5419 | sonar | 4 |
| 5420 | soguilla | 4 |
| 5421 | socorrerle | 4 |
| 5422 | socorra | 4 |
| 5423 | sobresaltos | 4 |
| 5424 | sintiendo | 4 |
| 5425 | sillón | 4 |
| 5426 | sillas | 4 |
| 5427 | siguióle | 4 |
| 5428 | siguientes | 4 |
| 5429 | siguiéndole | 4 |
| 5430 | siga | 4 |
| 5431 | siestas | 4 |
| 5432 | sierpe | 4 |
| 5433 | servirla | 4 |
| 5434 | servirá | 4 |
| 5435 | sereno | 4 |
| 5436 | seréis | 4 |
| 5437 | sepulturas | 4 |
| 5438 | sepulcro | 4 |
| 5439 | señoríos | 4 |
| 5440 | sentase | 4 |
| 5441 | semblante | 4 |
| 5442 | sello | 4 |
| 5443 | seguirle | 4 |
| 5444 | satisfecha | 4 |
| 5445 | satisfaga | 4 |
| 5446 | sarna | 4 |
| 5447 | santidad | 4 |
| 5448 | sanos | 4 |
| 5449 | salvajes | 4 |
| 5450 | salva | 4 |
| 5451 | saludó | 4 |
| 5452 | saltos | 4 |
| 5453 | salteadores | 4 |
| 5454 | saliere | 4 |
| 5455 | salidas | 4 |
| 5456 | salgamos | 4 |
| 5457 | salarios | 4 |
| 5458 | sacudiendo | 4 |
| 5459 | sacripante | 4 |
| 5460 | sacra | 4 |
| 5461 | sacasen | 4 |
| 5462 | sacara | 4 |
| 5463 | sacadas | 4 |
| 5464 | sabroso | 4 |
| 5465 | sabría | 4 |
| 5466 | sabrás | 4 |
| 5467 | sabidores | 4 |
| 5468 | sábana | 4 |
| 5469 | ruy | 4 |
| 5470 | rústicas | 4 |
| 5471 | ruines | 4 |
| 5472 | rota | 4 |
| 5473 | rosas | 4 |
| 5474 | ropas | 4 |
| 5475 | ronca | 4 |
| 5476 | rompiendo | 4 |
| 5477 | rompe | 4 |
| 5478 | romances | 4 |
| 5479 | rollizo | 4 |
| 5480 | rodear | 4 |
| 5481 | rodeados | 4 |
| 5482 | rocino | 4 |
| 5483 | robó | 4 |
| 5484 | robar | 4 |
| 5485 | robador | 4 |
| 5486 | robada | 4 |
| 5487 | riquísimo | 4 |
| 5488 | riquísimas | 4 |
| 5489 | ríos | 4 |
| 5490 | rindiese | 4 |
| 5491 | rindieron | 4 |
| 5492 | riendo | 4 |
| 5493 | ricamente | 4 |
| 5494 | ribera | 4 |
| 5495 | rétulo | 4 |
| 5496 | retórica | 4 |
| 5497 | retírate | 4 |
| 5498 | resto | 4 |
| 5499 | resta | 4 |
| 5500 | respondióme | 4 |
| 5501 | respondiendo | 4 |
| 5502 | respondían | 4 |
| 5503 | resplandor | 4 |
| 5504 | resplandeciente | 4 |
| 5505 | resistir | 4 |
| 5506 | residen | 4 |
| 5507 | representantes | 4 |
| 5508 | representadas | 4 |
| 5509 | representaban | 4 |
| 5510 | representaba | 4 |
| 5511 | repliques | 4 |
| 5512 | réplica | 4 |
| 5513 | repente | 4 |
| 5514 | renegados | 4 |
| 5515 | rendir | 4 |
| 5516 | remisión | 4 |
| 5517 | rematado | 4 |
| 5518 | relinchos | 4 |
| 5519 | regoldar | 4 |
| 5520 | regiones | 4 |
| 5521 | regalar | 4 |
| 5522 | regalados | 4 |
| 5523 | refriega | 4 |
| 5524 | recogiese | 4 |
| 5525 | recogieron | 4 |
| 5526 | recoger | 4 |
| 5527 | recitantes | 4 |
| 5528 | reciba | 4 |
| 5529 | recebirla | 4 |
| 5530 | rebuznaron | 4 |
| 5531 | rebaño | 4 |
| 5532 | rata | 4 |
| 5533 | raro | 4 |
| 5534 | rancor | 4 |
| 5535 | rajas | 4 |
| 5536 | rabel | 4 |
| 5537 | quité | 4 |
| 5538 | quitase | 4 |
| 5539 | quitara | 4 |
| 5540 | quitalle | 4 |
| 5541 | quiñones | 4 |
| 5542 | quilates | 4 |
| 5543 | quijotes | 4 |
| 5544 | quijana | 4 |
| 5545 | quijada | 4 |
| 5546 | quiénes | 4 |
| 5547 | quiebra | 4 |
| 5548 | quicios | 4 |
| 5549 | querrá | 4 |
| 5550 | queremos | 4 |
| 5551 | quemado | 4 |
| 5552 | quejo | 4 |
| 5553 | quedéis | 4 |
| 5554 | quédate | 4 |
| 5555 | quedasen | 4 |
| 5556 | quedarme | 4 |
| 5557 | quedaría | 4 |
| 5558 | puto | 4 |
| 5559 | pusiéronle | 4 |
| 5560 | purísimo | 4 |
| 5561 | puños | 4 |
| 5562 | puñal | 4 |
| 5563 | puntual | 4 |
| 5564 | pugnando | 4 |
| 5565 | pudieras | 4 |
| 5566 | públicas | 4 |
| 5567 | pruebas | 4 |
| 5568 | prósperos | 4 |
| 5569 | próspero | 4 |
| 5570 | prosiguieron | 4 |
| 5571 | prosiguen | 4 |
| 5572 | progreso | 4 |
| 5573 | profundidad | 4 |
| 5574 | profecía | 4 |
| 5575 | proezas | 4 |
| 5576 | pródigo | 4 |
| 5577 | procuran | 4 |
| 5578 | procurado | 4 |
| 5579 | probado | 4 |
| 5580 | prevención | 4 |
| 5581 | presupuesto | 4 |
| 5582 | presté | 4 |
| 5583 | presta | 4 |
| 5584 | presentar | 4 |
| 5585 | premios | 4 |
| 5586 | preguntaron | 4 |
| 5587 | preguntaban | 4 |
| 5588 | pregón | 4 |
| 5589 | precisas | 4 |
| 5590 | precioso | 4 |
| 5591 | pradecillo | 4 |
| 5592 | postura | 4 |
| 5593 | posta | 4 |
| 5594 | portal | 4 |
| 5595 | poniéndome | 4 |
| 5596 | pongas | 4 |
| 5597 | ponerla | 4 |
| 5598 | pondrás | 4 |
| 5599 | polvareda | 4 |
| 5600 | poderse | 4 |
| 5601 | poderosas | 4 |
| 5602 | podenco | 4 |
| 5603 | podáis | 4 |
| 5604 | pliegos | 4 |
| 5605 | plazo | 4 |
| 5606 | plantas | 4 |
| 5607 | pirámide | 4 |
| 5608 | pintando | 4 |
| 5609 | pintados | 4 |
| 5610 | pierden | 4 |
| 5611 | piedad | 4 |
| 5612 | pidiéronle | 4 |
| 5613 | pico | 4 |
| 5614 | petición | 4 |
| 5615 | pesia | 4 |
| 5616 | pescador | 4 |
| 5617 | persuasiones | 4 |
| 5618 | persigue | 4 |
| 5619 | perseverar | 4 |
| 5620 | perpetua | 4 |
| 5621 | permitía | 4 |
| 5622 | peregrina | 4 |
| 5623 | perdióse | 4 |
| 5624 | pequeñas | 4 |
| 5625 | pentapolín | 4 |
| 5626 | pensamos | 4 |
| 5627 | pensábamos | 4 |
| 5628 | peleando | 4 |
| 5629 | pelean | 4 |
| 5630 | pedrada | 4 |
| 5631 | pedirme | 4 |
| 5632 | pavor | 4 |
| 5633 | paveses | 4 |
| 5634 | patrón | 4 |
| 5635 | patente | 4 |
| 5636 | pasmóse | 4 |
| 5637 | pasión | 4 |
| 5638 | paseó | 4 |
| 5639 | paseo | 4 |
| 5640 | pasearse | 4 |
| 5641 | paseándose | 4 |
| 5642 | pasaremos | 4 |
| 5643 | pasajero | 4 |
| 5644 | partieron | 4 |
| 5645 | parís | 4 |
| 5646 | parezco | 4 |
| 5647 | pareciéndome | 4 |
| 5648 | parda | 4 |
| 5649 | parasismo | 4 |
| 5650 | parapilla | 4 |
| 5651 | paraban | 4 |
| 5652 | pañizuelo | 4 |
| 5653 | palmerín | 4 |
| 5654 | paletas | 4 |
| 5655 | pajar | 4 |
| 5656 | pagase | 4 |
| 5657 | pagaba | 4 |
| 5658 | pacíficamente | 4 |
| 5659 | pacer | 4 |
| 5660 | ovillo | 4 |
| 5661 | osado | 4 |
| 5662 | oriente | 4 |
| 5663 | oriana | 4 |
| 5664 | ordenare | 4 |
| 5665 | orán | 4 |
| 5666 | opiniones | 4 |
| 5667 | oírme | 4 |
| 5668 | oiga | 4 |
| 5669 | oída | 4 |
| 5670 | ocupación | 4 |
| 5671 | ocupa | 4 |
| 5672 | ocioso | 4 |
| 5673 | obrar | 4 |
| 5674 | obligar | 4 |
| 5675 | obispos | 4 |
| 5676 | novel | 4 |
| 5677 | note | 4 |
| 5678 | notar | 4 |
| 5679 | norabuena | 4 |
| 5680 | nombraba | 4 |
| 5681 | nobles | 4 |
| 5682 | nietos | 4 |
| 5683 | niego | 4 |
| 5684 | neptuno | 4 |
| 5685 | negociar | 4 |
| 5686 | necesitados | 4 |
| 5687 | navaja | 4 |
| 5688 | naipes | 4 |
| 5689 | nacieron | 4 |
| 5690 | muslo | 4 |
| 5691 | músicos | 4 |
| 5692 | muro | 4 |
| 5693 | murmurar | 4 |
| 5694 | murcia | 4 |
| 5695 | murallas | 4 |
| 5696 | mundos | 4 |
| 5697 | muestren | 4 |
| 5698 | muertes | 4 |
| 5699 | mueren | 4 |
| 5700 | mudas | 4 |
| 5701 | muda | 4 |
| 5702 | mostrenco | 4 |
| 5703 | mostrando | 4 |
| 5704 | mostráis | 4 |
| 5705 | mostraban | 4 |
| 5706 | moscas | 4 |
| 5707 | moras | 4 |
| 5708 | morada | 4 |
| 5709 | montón | 4 |
| 5710 | montiel | 4 |
| 5711 | molió | 4 |
| 5712 | mojicones | 4 |
| 5713 | modernos | 4 |
| 5714 | mísero | 4 |
| 5715 | ministro | 4 |
| 5716 | millón | 4 |
| 5717 | millares | 4 |
| 5718 | migas | 4 |
| 5719 | mienten | 4 |
| 5720 | mezquino | 4 |
| 5721 | mezclar | 4 |
| 5722 | mezclando | 4 |
| 5723 | mezcladas | 4 |
| 5724 | meterse | 4 |
| 5725 | metas | 4 |
| 5726 | merezcan | 4 |
| 5727 | mercancía | 4 |
| 5728 | menudas | 4 |
| 5729 | menuda | 4 |
| 5730 | mentirosa | 4 |
| 5731 | menosprecio | 4 |
| 5732 | menores | 4 |
| 5733 | mengua | 4 |
| 5734 | mejoría | 4 |
| 5735 | mejillas | 4 |
| 5736 | mejilla | 4 |
| 5737 | medidas | 4 |
| 5738 | medianera | 4 |
| 5739 | mazo | 4 |
| 5740 | matando | 4 |
| 5741 | marte | 4 |
| 5742 | mármoles | 4 |
| 5743 | maridos | 4 |
| 5744 | maravillosamente | 4 |
| 5745 | maravedí | 4 |
| 5746 | manteamiento | 4 |
| 5747 | mansedumbre | 4 |
| 5748 | mandare | 4 |
| 5749 | manchada | 4 |
| 5750 | manada | 4 |
| 5751 | mallorca | 4 |
| 5752 | maligno | 4 |
| 5753 | malicioso | 4 |
| 5754 | maliciosa | 4 |
| 5755 | malditos | 4 |
| 5756 | maldiciendo | 4 |
| 5757 | majada | 4 |
| 5758 | maguncia | 4 |
| 5759 | magno | 4 |
| 5760 | magnífico | 4 |
| 5761 | magín | 4 |
| 5762 | maduro | 4 |
| 5763 | madásima | 4 |
| 5764 | lunares | 4 |
| 5765 | luenga | 4 |
| 5766 | losa | 4 |
| 5767 | lope | 4 |
| 5768 | loma | 4 |
| 5769 | logrado | 4 |
| 5770 | lodo | 4 |
| 5771 | lobo | 4 |
| 5772 | loba | 4 |
| 5773 | llevarme | 4 |
| 5774 | llevaré | 4 |
| 5775 | llevará | 4 |
| 5776 | llevándole | 4 |
| 5777 | llevados | 4 |
| 5778 | lléguese | 4 |
| 5779 | llegáronse | 4 |
| 5780 | llegaos | 4 |
| 5781 | llame | 4 |
| 5782 | llamase | 4 |
| 5783 | llamábase | 4 |
| 5784 | lisura | 4 |
| 5785 | liso | 4 |
| 5786 | lisas | 4 |
| 5787 | líquidos | 4 |
| 5788 | lindezas | 4 |
| 5789 | limpiar | 4 |
| 5790 | liga | 4 |
| 5791 | lícita | 4 |
| 5792 | librase | 4 |
| 5793 | librar | 4 |
| 5794 | libranza | 4 |
| 5795 | leyeren | 4 |
| 5796 | levántese | 4 |
| 5797 | levántate | 4 |
| 5798 | levantarle | 4 |
| 5799 | levantaos | 4 |
| 5800 | levantaban | 4 |
| 5801 | leales | 4 |
| 5802 | lazos | 4 |
| 5803 | lazo | 4 |
| 5804 | lavó | 4 |
| 5805 | lavatorio | 4 |
| 5806 | laúd | 4 |
| 5807 | latina | 4 |
| 5808 | lata | 4 |
| 5809 | lascivos | 4 |
| 5810 | largamente | 4 |
| 5811 | lanzada | 4 |
| 5812 | lamentaciones | 4 |
| 5813 | lagartos | 4 |
| 5814 | juzgada | 4 |
| 5815 | jura | 4 |
| 5816 | jugar | 4 |
| 5817 | jugando | 4 |
| 5818 | juana | 4 |
| 5819 | jarro | 4 |
| 5820 | jardines | 4 |
| 5821 | ítem | 4 |
| 5822 | inventor | 4 |
| 5823 | interese | 4 |
| 5824 | intentar | 4 |
| 5825 | insolentes | 4 |
| 5826 | insolencias | 4 |
| 5827 | insolencia | 4 |
| 5828 | insigne | 4 |
| 5829 | inmortalidad | 4 |
| 5830 | injuria | 4 |
| 5831 | infiere | 4 |
| 5832 | incomodidad | 4 |
| 5833 | inauditas | 4 |
| 5834 | impresor | 4 |
| 5835 | importunidades | 4 |
| 5836 | impida | 4 |
| 5837 | ímpetu | 4 |
| 5838 | impedimento | 4 |
| 5839 | impedido | 4 |
| 5840 | imaginados | 4 |
| 5841 | ijadas | 4 |
| 5842 | hurtó | 4 |
| 5843 | humanos | 4 |
| 5844 | huida | 4 |
| 5845 | huéspeda | 4 |
| 5846 | huelen | 4 |
| 5847 | hubiéredes | 4 |
| 5848 | hube | 4 |
| 5849 | horrendo | 4 |
| 5850 | horacio | 4 |
| 5851 | honre | 4 |
| 5852 | honras | 4 |
| 5853 | honrar | 4 |
| 5854 | hondo | 4 |
| 5855 | holgó | 4 |
| 5856 | hileras | 4 |
| 5857 | hiciste | 4 |
| 5858 | hermosuras | 4 |
| 5859 | hermosísimas | 4 |
| 5860 | hermanas | 4 |
| 5861 | herir | 4 |
| 5862 | heno | 4 |
| 5863 | hallen | 4 |
| 5864 | hallastes | 4 |
| 5865 | hallaros | 4 |
| 5866 | hallarla | 4 |
| 5867 | hallares | 4 |
| 5868 | hallaréis | 4 |
| 5869 | hallados | 4 |
| 5870 | hagamos | 4 |
| 5871 | habrían | 4 |
| 5872 | hablarle | 4 |
| 5873 | hablarla | 4 |
| 5874 | habitación | 4 |
| 5875 | habiéndome | 4 |
| 5876 | habiéndola | 4 |
| 5877 | haberlo | 4 |
| 5878 | haberles | 4 |
| 5879 | gutiérrez | 4 |
| 5880 | gustosa | 4 |
| 5881 | gustar | 4 |
| 5882 | gustáis | 4 |
| 5883 | gustaba | 4 |
| 5884 | gurapas | 4 |
| 5885 | guijarro | 4 |
| 5886 | guiando | 4 |
| 5887 | guerrero | 4 |
| 5888 | guárdese | 4 |
| 5889 | guardase | 4 |
| 5890 | guardarme | 4 |
| 5891 | grillos | 4 |
| 5892 | griegos | 4 |
| 5893 | griega | 4 |
| 5894 | granos | 4 |
| 5895 | grandísimos | 4 |
| 5896 | grados | 4 |
| 5897 | golpear | 4 |
| 5898 | goce | 4 |
| 5899 | gobernado | 4 |
| 5900 | gasté | 4 |
| 5901 | gasta | 4 |
| 5902 | ganase | 4 |
| 5903 | gamo | 4 |
| 5904 | gallardos | 4 |
| 5905 | gaeta | 4 |
| 5906 | fuga | 4 |
| 5907 | frutos | 4 |
| 5908 | francisco | 4 |
| 5909 | francés | 4 |
| 5910 | forzó | 4 |
| 5911 | forzar | 4 |
| 5912 | formó | 4 |
| 5913 | formado | 4 |
| 5914 | floresta | 4 |
| 5915 | fío | 4 |
| 5916 | finísima | 4 |
| 5917 | fingió | 4 |
| 5918 | fingía | 4 |
| 5919 | filósofos | 4 |
| 5920 | filósofo | 4 |
| 5921 | fieros | 4 |
| 5922 | ficción | 4 |
| 5923 | fermosas | 4 |
| 5924 | feos | 4 |
| 5925 | fénix | 4 |
| 5926 | fementido | 4 |
| 5927 | felicemente | 4 |
| 5928 | feas | 4 |
| 5929 | favores | 4 |
| 5930 | favorece | 4 |
| 5931 | fatigado | 4 |
| 5932 | faltaron | 4 |
| 5933 | falsos | 4 |
| 5934 | faldellín | 4 |
| 5935 | fáciles | 4 |
| 5936 | extraordinario | 4 |
| 5937 | excede | 4 |
| 5938 | etcétera | 4 |
| 5939 | estudiado | 4 |
| 5940 | estremada | 4 |
| 5941 | estratagemas | 4 |
| 5942 | estotro | 4 |
| 5943 | estorbó | 4 |
| 5944 | estorbase | 4 |
| 5945 | estorbarlo | 4 |
| 5946 | estoque | 4 |
| 5947 | estimo | 4 |
| 5948 | estimado | 4 |
| 5949 | estimadas | 4 |
| 5950 | estera | 4 |
| 5951 | espinazo | 4 |
| 5952 | espere | 4 |
| 5953 | esperamos | 4 |
| 5954 | esperado | 4 |
| 5955 | especial | 4 |
| 5956 | esparto | 4 |
| 5957 | espanta | 4 |
| 5958 | esotro | 4 |
| 5959 | ésos | 4 |
| 5960 | escuelas | 4 |
| 5961 | escuderiles | 4 |
| 5962 | escuadras | 4 |
| 5963 | escrutinio | 4 |
| 5964 | escribiese | 4 |
| 5965 | escribiendo | 4 |
| 5966 | escribí | 4 |
| 5967 | escriben | 4 |
| 5968 | escriban | 4 |
| 5969 | escriba | 4 |
| 5970 | escote | 4 |
| 5971 | escondidos | 4 |
| 5972 | escondidas | 4 |
| 5973 | esconderse | 4 |
| 5974 | escarlata | 4 |
| 5975 | erudición | 4 |
| 5976 | eras | 4 |
| 5977 | equivalente | 4 |
| 5978 | envió | 4 |
| 5979 | envié | 4 |
| 5980 | enviaron | 4 |
| 5981 | entretenerse | 4 |
| 5982 | entrega | 4 |
| 5983 | entonada | 4 |
| 5984 | entiendan | 4 |
| 5985 | entendiese | 4 |
| 5986 | entendidos | 4 |
| 5987 | entendían | 4 |
| 5988 | ensartando | 4 |
| 5989 | ensalada | 4 |
| 5990 | enriquecer | 4 |
| 5991 | enojado | 4 |
| 5992 | enjuto | 4 |
| 5993 | enjalmas | 4 |
| 5994 | engañarme | 4 |
| 5995 | engañan | 4 |
| 5996 | engañados | 4 |
| 5997 | endriagos | 4 |
| 5998 | endiablada | 4 |
| 5999 | enderezando | 4 |
| 6000 | endereza | 4 |
| 6001 | encubría | 4 |
| 6002 | encubierta | 4 |
| 6003 | encomendarme | 4 |
| 6004 | encinas | 4 |
| 6005 | encendido | 4 |
| 6006 | encarecimiento | 4 |
| 6007 | encamine | 4 |
| 6008 | encaminase | 4 |
| 6009 | enamorar | 4 |
| 6010 | eminente | 4 |
| 6011 | embozo | 4 |
| 6012 | elíseos | 4 |
| 6013 | elisabat | 4 |
| 6014 | elegantemente | 4 |
| 6015 | elección | 4 |
| 6016 | ejercitar | 4 |
| 6017 | ejercitan | 4 |
| 6018 | ejecutar | 4 |
| 6019 | egipto | 4 |
| 6020 | echase | 4 |
| 6021 | echarle | 4 |
| 6022 | echará | 4 |
| 6023 | duros | 4 |
| 6024 | dureza | 4 |
| 6025 | dulcísima | 4 |
| 6026 | duermo | 4 |
| 6027 | duermes | 4 |
| 6028 | dorada | 4 |
| 6029 | doloridas | 4 |
| 6030 | dolía | 4 |
| 6031 | dolencia | 4 |
| 6032 | documentos | 4 |
| 6033 | docto | 4 |
| 6034 | docientas | 4 |
| 6035 | dobló | 4 |
| 6036 | dividía | 4 |
| 6037 | divide | 4 |
| 6038 | diste | 4 |
| 6039 | dispuesto | 4 |
| 6040 | dispone | 4 |
| 6041 | disparatadas | 4 |
| 6042 | disparaba | 4 |
| 6043 | discordia | 4 |
| 6044 | diose | 4 |
| 6045 | dile | 4 |
| 6046 | dilatar | 4 |
| 6047 | dijiste | 4 |
| 6048 | dijeres | 4 |
| 6049 | dificultosa | 4 |
| 6050 | diestro | 4 |
| 6051 | diéronse | 4 |
| 6052 | diciplinas | 4 |
| 6053 | devota | 4 |
| 6054 | detenerle | 4 |
| 6055 | desviado | 4 |
| 6056 | déste | 4 |
| 6057 | déstas | 4 |
| 6058 | désta | 4 |
| 6059 | desposorio | 4 |
| 6060 | despojaron | 4 |
| 6061 | despoblado | 4 |
| 6062 | despertase | 4 |
| 6063 | despertado | 4 |
| 6064 | despertaba | 4 |
| 6065 | despensa | 4 |
| 6066 | despedir | 4 |
| 6067 | despacho | 4 |
| 6068 | desinteresada | 4 |
| 6069 | desiguales | 4 |
| 6070 | designio | 4 |
| 6071 | deshonrado | 4 |
| 6072 | deshonesta | 4 |
| 6073 | desfacedor | 4 |
| 6074 | desesperados | 4 |
| 6075 | desesperada | 4 |
| 6076 | deseoso | 4 |
| 6077 | desencantar | 4 |
| 6078 | desechar | 4 |
| 6079 | desearse | 4 |
| 6080 | deseamos | 4 |
| 6081 | deseáis | 4 |
| 6082 | descubro | 4 |
| 6083 | descubrimos | 4 |
| 6084 | descubrí | 4 |
| 6085 | descubra | 4 |
| 6086 | descubiertos | 4 |
| 6087 | describe | 4 |
| 6088 | descomedidos | 4 |
| 6089 | desayunado | 4 |
| 6090 | desatinos | 4 |
| 6091 | desatinada | 4 |
| 6092 | desagradecimiento | 4 |
| 6093 | desaforadas | 4 |
| 6094 | deparase | 4 |
| 6095 | demos | 4 |
| 6096 | déme | 4 |
| 6097 | demandas | 4 |
| 6098 | delito | 4 |
| 6099 | delincuente | 4 |
| 6100 | delicados | 4 |
| 6101 | delicadas | 4 |
| 6102 | delicada | 4 |
| 6103 | déjese | 4 |
| 6104 | dejémonos | 4 |
| 6105 | déjate | 4 |
| 6106 | dejaran | 4 |
| 6107 | defendía | 4 |
| 6108 | defenderme | 4 |
| 6109 | declaró | 4 |
| 6110 | decírselo | 4 |
| 6111 | decirles | 4 |
| 6112 | decirlas | 4 |
| 6113 | debíamos | 4 |
| 6114 | darla | 4 |
| 6115 | darás | 4 |
| 6116 | darán | 4 |
| 6117 | damos | 4 |
| 6118 | curarse | 4 |
| 6119 | curarle | 4 |
| 6120 | cumpliría | 4 |
| 6121 | cumpliese | 4 |
| 6122 | culpas | 4 |
| 6123 | cueste | 4 |
| 6124 | cuervos | 4 |
| 6125 | cuernos | 4 |
| 6126 | cuenten | 4 |
| 6127 | cuellos | 4 |
| 6128 | cubrirse | 4 |
| 6129 | cuba | 4 |
| 6130 | crueles | 4 |
| 6131 | cristales | 4 |
| 6132 | creí | 4 |
| 6133 | creen | 4 |
| 6134 | costilla | 4 |
| 6135 | costantinopla | 4 |
| 6136 | cosmógrafo | 4 |
| 6137 | cosarios | 4 |
| 6138 | cortó | 4 |
| 6139 | cortezas | 4 |
| 6140 | cortesana | 4 |
| 6141 | corridos | 4 |
| 6142 | corrida | 4 |
| 6143 | corresponda | 4 |
| 6144 | correrse | 4 |
| 6145 | corran | 4 |
| 6146 | corra | 4 |
| 6147 | coronado | 4 |
| 6148 | coronada | 4 |
| 6149 | cordobán | 4 |
| 6150 | continuos | 4 |
| 6151 | continencia | 4 |
| 6152 | contente | 4 |
| 6153 | contentado | 4 |
| 6154 | contenían | 4 |
| 6155 | contarla | 4 |
| 6156 | consistía | 4 |
| 6157 | consintiera | 4 |
| 6158 | consigue | 4 |
| 6159 | conservan | 4 |
| 6160 | conserva | 4 |
| 6161 | consejero | 4 |
| 6162 | conjeturas | 4 |
| 6163 | congoja | 4 |
| 6164 | confusiones | 4 |
| 6165 | confusas | 4 |
| 6166 | confirmo | 4 |
| 6167 | confiado | 4 |
| 6168 | confesión | 4 |
| 6169 | condena | 4 |
| 6170 | conceder | 4 |
| 6171 | concede | 4 |
| 6172 | concavidad | 4 |
| 6173 | compone | 4 |
| 6174 | complexión | 4 |
| 6175 | complacer | 4 |
| 6176 | compañeras | 4 |
| 6177 | compaña | 4 |
| 6178 | cómodo | 4 |
| 6179 | comió | 4 |
| 6180 | comiese | 4 |
| 6181 | comienza | 4 |
| 6182 | comían | 4 |
| 6183 | comenzamos | 4 |
| 6184 | comedidamente | 4 |
| 6185 | combatientes | 4 |
| 6186 | comamos | 4 |
| 6187 | collar | 4 |
| 6188 | coligió | 4 |
| 6189 | colgada | 4 |
| 6190 | colchones | 4 |
| 6191 | colada | 4 |
| 6192 | cojo | 4 |
| 6193 | cobrado | 4 |
| 6194 | cobardía | 4 |
| 6195 | clérigos | 4 |
| 6196 | clarines | 4 |
| 6197 | circustantes | 4 |
| 6198 | circunvecinas | 4 |
| 6199 | cinchado | 4 |
| 6200 | cifra | 4 |
| 6201 | ciega | 4 |
| 6202 | chata | 4 |
| 6203 | cerradas | 4 |
| 6204 | ceremonia | 4 |
| 6205 | cerco | 4 |
| 6206 | centro | 4 |
| 6207 | centinelas | 4 |
| 6208 | cencerros | 4 |
| 6209 | celosa | 4 |
| 6210 | cautivaron | 4 |
| 6211 | cause | 4 |
| 6212 | castigado | 4 |
| 6213 | cascajo | 4 |
| 6214 | cascabeles | 4 |
| 6215 | casadas | 4 |
| 6216 | cartapacios | 4 |
| 6217 | carrillos | 4 |
| 6218 | cargaron | 4 |
| 6219 | cargado | 4 |
| 6220 | carecen | 4 |
| 6221 | captivo | 4 |
| 6222 | cañón | 4 |
| 6223 | cañas | 4 |
| 6224 | cansarse | 4 |
| 6225 | cansada | 4 |
| 6226 | camuza | 4 |
| 6227 | campana | 4 |
| 6228 | camas | 4 |
| 6229 | callejuelas | 4 |
| 6230 | callado | 4 |
| 6231 | calamidades | 4 |
| 6232 | calabazadas | 4 |
| 6233 | caco | 4 |
| 6234 | cabello | 4 |
| 6235 | caballerescas | 4 |
| 6236 | caballeresca | 4 |
| 6237 | buscándole | 4 |
| 6238 | buscan | 4 |
| 6239 | burlados | 4 |
| 6240 | burladores | 4 |
| 6241 | bronces | 4 |
| 6242 | bríos | 4 |
| 6243 | boyero | 4 |
| 6244 | bosques | 4 |
| 6245 | bogaban | 4 |
| 6246 | bocados | 4 |
| 6247 | boba | 4 |
| 6248 | blasfemias | 4 |
| 6249 | blasfemia | 4 |
| 6250 | blancura | 4 |
| 6251 | beso | 4 |
| 6252 | beneficios | 4 |
| 6253 | beneficiado | 4 |
| 6254 | bellaquerías | 4 |
| 6255 | bebiendo | 4 |
| 6256 | bebido | 4 |
| 6257 | bebida | 4 |
| 6258 | bebas | 4 |
| 6259 | bayeta | 4 |
| 6260 | bautismo | 4 |
| 6261 | batán | 4 |
| 6262 | bástame | 4 |
| 6263 | barras | 4 |
| 6264 | bárbaros | 4 |
| 6265 | barata | 4 |
| 6266 | banquete | 4 |
| 6267 | bandoleros | 4 |
| 6268 | banda | 4 |
| 6269 | bancos | 4 |
| 6270 | balcones | 4 |
| 6271 | bala | 4 |
| 6272 | bajeza | 4 |
| 6273 | bajeles | 4 |
| 6274 | babieca | 4 |
| 6275 | azules | 4 |
| 6276 | azotarse | 4 |
| 6277 | azotarme | 4 |
| 6278 | azotar | 4 |
| 6279 | ayudasen | 4 |
| 6280 | ayudarme | 4 |
| 6281 | ayudan | 4 |
| 6282 | avisó | 4 |
| 6283 | avisase | 4 |
| 6284 | aves | 4 |
| 6285 | avengas | 4 |
| 6286 | audiencia | 4 |
| 6287 | atrevimientos | 4 |
| 6288 | átomos | 4 |
| 6289 | atinar | 4 |
| 6290 | atienda | 4 |
| 6291 | atar | 4 |
| 6292 | atañe | 4 |
| 6293 | atalaya | 4 |
| 6294 | atada | 4 |
| 6295 | ata | 4 |
| 6296 | asnos | 4 |
| 6297 | asistir | 4 |
| 6298 | asentar | 4 |
| 6299 | aseguro | 4 |
| 6300 | asegurar | 4 |
| 6301 | arrojarse | 4 |
| 6302 | arrojaron | 4 |
| 6303 | arrojando | 4 |
| 6304 | arrancaba | 4 |
| 6305 | arnés | 4 |
| 6306 | arminio | 4 |
| 6307 | arguye | 4 |
| 6308 | arenas | 4 |
| 6309 | ardía | 4 |
| 6310 | archivos | 4 |
| 6311 | arcadia | 4 |
| 6312 | aragonés | 4 |
| 6313 | arabia | 4 |
| 6314 | aprovecha | 4 |
| 6315 | apretaba | 4 |
| 6316 | aprendí | 4 |
| 6317 | apócrifo | 4 |
| 6318 | apartóse | 4 |
| 6319 | aparta | 4 |
| 6320 | apariencias | 4 |
| 6321 | apaciguó | 4 |
| 6322 | añadiduras | 4 |
| 6323 | antiguas | 4 |
| 6324 | antifaces | 4 |
| 6325 | antaño | 4 |
| 6326 | anotación | 4 |
| 6327 | anochecía | 4 |
| 6328 | andes | 4 |
| 6329 | andemos | 4 |
| 6330 | andarse | 4 |
| 6331 | ancianos | 4 |
| 6332 | anciano | 4 |
| 6333 | ámexi | 4 |
| 6334 | amenazaba | 4 |
| 6335 | amargamente | 4 |
| 6336 | amaneciese | 4 |
| 6337 | amanecerá | 4 |
| 6338 | amador | 4 |
| 6339 | alumbra | 4 |
| 6340 | altura | 4 |
| 6341 | alquiler | 4 |
| 6342 | almohadas | 4 |
| 6343 | almodóvar | 4 |
| 6344 | alhajas | 4 |
| 6345 | alfiler | 4 |
| 6346 | alevosía | 4 |
| 6347 | alegran | 4 |
| 6348 | alegraba | 4 |
| 6349 | alegra | 4 |
| 6350 | aldeanas | 4 |
| 6351 | alcanzo | 4 |
| 6352 | alcanzase | 4 |
| 6353 | alborotóse | 4 |
| 6354 | alabó | 4 |
| 6355 | alabar | 4 |
| 6356 | ahogó | 4 |
| 6357 | agujeros | 4 |
| 6358 | aguardase | 4 |
| 6359 | aguardaban | 4 |
| 6360 | aguardaba | 4 |
| 6361 | aguamanil | 4 |
| 6362 | agradecidos | 4 |
| 6363 | agradecía | 4 |
| 6364 | agradecer | 4 |
| 6365 | afrentados | 4 |
| 6366 | afligido | 4 |
| 6367 | afirma | 4 |
| 6368 | advirtieron | 4 |
| 6369 | advirtiendo | 4 |
| 6370 | advertimientos | 4 |
| 6371 | advertencia | 4 |
| 6372 | adoro | 4 |
| 6373 | adornado | 4 |
| 6374 | adornadas | 4 |
| 6375 | adora | 4 |
| 6376 | admiróse | 4 |
| 6377 | admiráronse | 4 |
| 6378 | admirable | 4 |
| 6379 | admira | 4 |
| 6380 | adherentes | 4 |
| 6381 | aderezo | 4 |
| 6382 | adelantado | 4 |
| 6383 | adán | 4 |
| 6384 | acuerde | 4 |
| 6385 | acreciente | 4 |
| 6386 | acordamos | 4 |
| 6387 | aconsejado | 4 |
| 6388 | acompañase | 4 |
| 6389 | acompañaron | 4 |
| 6390 | acentos | 4 |
| 6391 | accidentes | 4 |
| 6392 | acaecimientos | 4 |
| 6393 | acabasen | 4 |
| 6394 | acabarás | 4 |
| 6395 | acabadas | 4 |
| 6396 | abundantes | 4 |
| 6397 | absorto | 4 |
| 6398 | abriese | 4 |
| 6399 | abrían | 4 |
| 6400 | abreviar | 4 |
| 6401 | abre | 4 |
| 6402 | abrazaron | 4 |
| 6403 | abrazando | 4 |
| 6404 | abrazado | 4 |
| 6405 | abrasar | 4 |
| 6406 | abran | 4 |
| 6407 | zarzas | 3 |
| 6408 | zaque | 3 |
| 6409 | zapatero | 3 |
| 6410 | zancas | 3 |
| 6411 | zalemas | 3 |
| 6412 | yugo | 3 |
| 6413 | yerros | 3 |
| 6414 | yago | 3 |
| 6415 | x | 3 |
| 6416 | vuela | 3 |
| 6417 | volví | 3 |
| 6418 | volverle | 3 |
| 6419 | volverla | 3 |
| 6420 | volveremos | 3 |
| 6421 | volverán | 3 |
| 6422 | volumen | 3 |
| 6423 | volteador | 3 |
| 6424 | volandas | 3 |
| 6425 | vobis | 3 |
| 6426 | vivirás | 3 |
| 6427 | vivimos | 3 |
| 6428 | viviera | 3 |
| 6429 | vivientes | 3 |
| 6430 | viviendo | 3 |
| 6431 | vivían | 3 |
| 6432 | viváis | 3 |
| 6433 | viudo | 3 |
| 6434 | vistosos | 3 |
| 6435 | vistoso | 3 |
| 6436 | vistosa | 3 |
| 6437 | vistiese | 3 |
| 6438 | vistes | 3 |
| 6439 | virtuosa | 3 |
| 6440 | virgen | 3 |
| 6441 | viose | 3 |
| 6442 | viniésemos | 3 |
| 6443 | villas | 3 |
| 6444 | villanos | 3 |
| 6445 | viles | 3 |
| 6446 | vil | 3 |
| 6447 | viga | 3 |
| 6448 | vieren | 3 |
| 6449 | vieras | 3 |
| 6450 | vidrio | 3 |
| 6451 | vido | 3 |
| 6452 | vestía | 3 |
| 6453 | verlo | 3 |
| 6454 | verisímiles | 3 |
| 6455 | veredes | 3 |
| 6456 | verdugado | 3 |
| 6457 | venirnos | 3 |
| 6458 | vengativo | 3 |
| 6459 | véngase | 3 |
| 6460 | veneno | 3 |
| 6461 | venecia | 3 |
| 6462 | vendré | 3 |
| 6463 | vendas | 3 |
| 6464 | vencerle | 3 |
| 6465 | vencedores | 3 |
| 6466 | vello | 3 |
| 6467 | vellido | 3 |
| 6468 | vélez | 3 |
| 6469 | ved | 3 |
| 6470 | véase | 3 |
| 6471 | vaso | 3 |
| 6472 | vasallo | 3 |
| 6473 | vasalla | 3 |
| 6474 | vargas | 3 |
| 6475 | vanidad | 3 |
| 6476 | vanas | 3 |
| 6477 | vallejo | 3 |
| 6478 | valladolid | 3 |
| 6479 | valgan | 3 |
| 6480 | vales | 3 |
| 6481 | valerse | 3 |
| 6482 | valentías | 3 |
| 6483 | valedera | 3 |
| 6484 | váguidos | 3 |
| 6485 | vaciedades | 3 |
| 6486 | uvas | 3 |
| 6487 | usurpado | 3 |
| 6488 | usó | 3 |
| 6489 | use | 3 |
| 6490 | usara | 3 |
| 6491 | universidad | 3 |
| 6492 | ungüentos | 3 |
| 6493 | ungüento | 3 |
| 6494 | últimos | 3 |
| 6495 | túvole | 3 |
| 6496 | tuvieren | 3 |
| 6497 | turquesco | 3 |
| 6498 | túnez | 3 |
| 6499 | tumba | 3 |
| 6500 | tuerta | 3 |
| 6501 | trote | 3 |
| 6502 | tropiece | 3 |
| 6503 | tropa | 3 |
| 6504 | troche | 3 |
| 6505 | trocaron | 3 |
| 6506 | trocar | 3 |
| 6507 | trocado | 3 |
| 6508 | trocada | 3 |
| 6509 | triunfar | 3 |
| 6510 | triunfa | 3 |
| 6511 | tristísimo | 3 |
| 6512 | trincheas | 3 |
| 6513 | trecientas | 3 |
| 6514 | trece | 3 |
| 6515 | trayo | 3 |
| 6516 | tratándole | 3 |
| 6517 | tratamiento | 3 |
| 6518 | trasladó | 3 |
| 6519 | trapobana | 3 |
| 6520 | trapisonda | 3 |
| 6521 | traiga | 3 |
| 6522 | traidores | 3 |
| 6523 | trago | 3 |
| 6524 | trágico | 3 |
| 6525 | traemos | 3 |
| 6526 | tradujo | 3 |
| 6527 | traductor | 3 |
| 6528 | tradución | 3 |
| 6529 | trabó | 3 |
| 6530 | trabando | 3 |
| 6531 | trabajar | 3 |
| 6532 | trabados | 3 |
| 6533 | trabada | 3 |
| 6534 | total | 3 |
| 6535 | torrellas | 3 |
| 6536 | tornóle | 3 |
| 6537 | torne | 3 |
| 6538 | tornase | 3 |
| 6539 | tornar | 3 |
| 6540 | torna | 3 |
| 6541 | tormentos | 3 |
| 6542 | tormenta | 3 |
| 6543 | torcida | 3 |
| 6544 | toquen | 3 |
| 6545 | toparemos | 3 |
| 6546 | tonta | 3 |
| 6547 | tomóla | 3 |
| 6548 | tomen | 3 |
| 6549 | tomarse | 3 |
| 6550 | tomarle | 3 |
| 6551 | tomaría | 3 |
| 6552 | tomándole | 3 |
| 6553 | tomada | 3 |
| 6554 | toledanos | 3 |
| 6555 | todopoderoso | 3 |
| 6556 | toco | 3 |
| 6557 | tocaron | 3 |
| 6558 | tocarme | 3 |
| 6559 | toalla | 3 |
| 6560 | titubear | 3 |
| 6561 | tisbe | 3 |
| 6562 | tiros | 3 |
| 6563 | tiras | 3 |
| 6564 | tirando | 3 |
| 6565 | tirado | 3 |
| 6566 | tiraban | 3 |
| 6567 | timón | 3 |
| 6568 | tijeras | 3 |
| 6569 | tigre | 3 |
| 6570 | tetuán | 3 |
| 6571 | teólogos | 3 |
| 6572 | tentóse | 3 |
| 6573 | tentó | 3 |
| 6574 | teniéndola | 3 |
| 6575 | tenida | 3 |
| 6576 | tenías | 3 |
| 6577 | tenerse | 3 |
| 6578 | tenerlas | 3 |
| 6579 | tendidos | 3 |
| 6580 | temprano | 3 |
| 6581 | templos | 3 |
| 6582 | templado | 3 |
| 6583 | tempestad | 3 |
| 6584 | temieron | 3 |
| 6585 | temen | 3 |
| 6586 | tememos | 3 |
| 6587 | tembló | 3 |
| 6588 | tejida | 3 |
| 6589 | techo | 3 |
| 6590 | tarea | 3 |
| 6591 | tardo | 3 |
| 6592 | tardare | 3 |
| 6593 | tamborinos | 3 |
| 6594 | talego | 3 |
| 6595 | talegas | 3 |
| 6596 | tajado | 3 |
| 6597 | tahelí | 3 |
| 6598 | tagarino | 3 |
| 6599 | tácito | 3 |
| 6600 | taberna | 3 |
| 6601 | sustentaba | 3 |
| 6602 | sustanciales | 3 |
| 6603 | suspirando | 3 |
| 6604 | suspensa | 3 |
| 6605 | suspendió | 3 |
| 6606 | suspendan | 3 |
| 6607 | suplicar | 3 |
| 6608 | supimos | 3 |
| 6609 | supiesen | 3 |
| 6610 | supiere | 3 |
| 6611 | superchería | 3 |
| 6612 | suntuosos | 3 |
| 6613 | sujeta | 3 |
| 6614 | sufridor | 3 |
| 6615 | sufra | 3 |
| 6616 | suero | 3 |
| 6617 | sueles | 3 |
| 6618 | suela | 3 |
| 6619 | suegro | 3 |
| 6620 | sudo | 3 |
| 6621 | sudando | 3 |
| 6622 | sucedidos | 3 |
| 6623 | sucederles | 3 |
| 6624 | sospechaba | 3 |
| 6625 | sosegóse | 3 |
| 6626 | sosegó | 3 |
| 6627 | sosegarse | 3 |
| 6628 | sortija | 3 |
| 6629 | sopla | 3 |
| 6630 | soñar | 3 |
| 6631 | sonido | 3 |
| 6632 | soltura | 3 |
| 6633 | soltarse | 3 |
| 6634 | soltaron | 3 |
| 6635 | solicitudes | 3 |
| 6636 | solícitos | 3 |
| 6637 | solícito | 3 |
| 6638 | solicito | 3 |
| 6639 | solicitar | 3 |
| 6640 | solicitan | 3 |
| 6641 | solicitado | 3 |
| 6642 | solicitada | 3 |
| 6643 | solían | 3 |
| 6644 | soles | 3 |
| 6645 | sogas | 3 |
| 6646 | socorriendo | 3 |
| 6647 | socorre | 3 |
| 6648 | sobrinas | 3 |
| 6649 | sobrescrito | 3 |
| 6650 | sobresaltada | 3 |
| 6651 | sobremodo | 3 |
| 6652 | sobreescrito | 3 |
| 6653 | sobran | 3 |
| 6654 | soberana | 3 |
| 6655 | sobajada | 3 |
| 6656 | sirviese | 3 |
| 6657 | sirvientes | 3 |
| 6658 | sirvan | 3 |
| 6659 | sirgo | 3 |
| 6660 | siniestra | 3 |
| 6661 | signum | 3 |
| 6662 | significativo | 3 |
| 6663 | sienten | 3 |
| 6664 | siega | 3 |
| 6665 | sicilia | 3 |
| 6666 | sestear | 3 |
| 6667 | sesos | 3 |
| 6668 | servirte | 3 |
| 6669 | servirse | 3 |
| 6670 | serviré | 3 |
| 6671 | servirán | 3 |
| 6672 | servidores | 3 |
| 6673 | sequedad | 3 |
| 6674 | señorías | 3 |
| 6675 | señale | 3 |
| 6676 | sentida | 3 |
| 6677 | sentenciado | 3 |
| 6678 | sentáronse | 3 |
| 6679 | sentados | 3 |
| 6680 | sencillez | 3 |
| 6681 | semejas | 3 |
| 6682 | semejanza | 3 |
| 6683 | seguille | 3 |
| 6684 | seguidillas | 3 |
| 6685 | seguid | 3 |
| 6686 | secretamente | 3 |
| 6687 | satisfizo | 3 |
| 6688 | sátiras | 3 |
| 6689 | sátira | 3 |
| 6690 | satanases | 3 |
| 6691 | sarra | 3 |
| 6692 | sargel | 3 |
| 6693 | sarao | 3 |
| 6694 | sapos | 3 |
| 6695 | santiguaron | 3 |
| 6696 | sansueña | 3 |
| 6697 | sangrientas | 3 |
| 6698 | sanas | 3 |
| 6699 | salvoconduto | 3 |
| 6700 | salve | 3 |
| 6701 | saludado | 3 |
| 6702 | saltear | 3 |
| 6703 | saltar | 3 |
| 6704 | salirse | 3 |
| 6705 | saldremos | 3 |
| 6706 | salas | 3 |
| 6707 | sacrificio | 3 |
| 6708 | sacarte | 3 |
| 6709 | sacaros | 3 |
| 6710 | sacarme | 3 |
| 6711 | sacan | 3 |
| 6712 | sacamos | 3 |
| 6713 | sabidora | 3 |
| 6714 | ruina | 3 |
| 6715 | ruégote | 3 |
| 6716 | rubión | 3 |
| 6717 | rotos | 3 |
| 6718 | rosa | 3 |
| 6719 | romanos | 3 |
| 6720 | rolliza | 3 |
| 6721 | rogarle | 3 |
| 6722 | rodilla | 3 |
| 6723 | rodeo | 3 |
| 6724 | rodeado | 3 |
| 6725 | rodado | 3 |
| 6726 | rocío | 3 |
| 6727 | roca | 3 |
| 6728 | robusto | 3 |
| 6729 | robo | 3 |
| 6730 | robado | 3 |
| 6731 | risueño | 3 |
| 6732 | risueña | 3 |
| 6733 | ristre | 3 |
| 6734 | risco | 3 |
| 6735 | riñas | 3 |
| 6736 | rindió | 3 |
| 6737 | rinda | 3 |
| 6738 | rigurosos | 3 |
| 6739 | rigurosas | 3 |
| 6740 | rige | 3 |
| 6741 | rieron | 3 |
| 6742 | ricota | 3 |
| 6743 | rezar | 3 |
| 6744 | rezando | 3 |
| 6745 | revueltas | 3 |
| 6746 | revuelta | 3 |
| 6747 | reveses | 3 |
| 6748 | retorno | 3 |
| 6749 | retóricas | 3 |
| 6750 | retiraron | 3 |
| 6751 | retirar | 3 |
| 6752 | retencio | 3 |
| 6753 | respondiéronle | 3 |
| 6754 | respondiera | 3 |
| 6755 | responderme | 3 |
| 6756 | responderle | 3 |
| 6757 | respóndeme | 3 |
| 6758 | resplandece | 3 |
| 6759 | resoluta | 3 |
| 6760 | residencia | 3 |
| 6761 | reservada | 3 |
| 6762 | represente | 3 |
| 6763 | representado | 3 |
| 6764 | reposaba | 3 |
| 6765 | replicarle | 3 |
| 6766 | repitiendo | 3 |
| 6767 | repite | 3 |
| 6768 | repica | 3 |
| 6769 | repartidas | 3 |
| 6770 | reparar | 3 |
| 6771 | reparaba | 3 |
| 6772 | reñida | 3 |
| 6773 | renuncio | 3 |
| 6774 | rencuentros | 3 |
| 6775 | remota | 3 |
| 6776 | remediarlos | 3 |
| 6777 | reliquia | 3 |
| 6778 | rejas | 3 |
| 6779 | reiterar | 3 |
| 6780 | rehusaba | 3 |
| 6781 | regir | 3 |
| 6782 | regenta | 3 |
| 6783 | regalaron | 3 |
| 6784 | regaladas | 3 |
| 6785 | refugio | 3 |
| 6786 | reforzar | 3 |
| 6787 | referir | 3 |
| 6788 | redunde | 3 |
| 6789 | redundase | 3 |
| 6790 | reducirse | 3 |
| 6791 | recreación | 3 |
| 6792 | recordación | 3 |
| 6793 | recogiesen | 3 |
| 6794 | recogido | 3 |
| 6795 | recogidas | 3 |
| 6796 | recibían | 3 |
| 6797 | reciamente | 3 |
| 6798 | recia | 3 |
| 6799 | receta | 3 |
| 6800 | recebidas | 3 |
| 6801 | recatos | 3 |
| 6802 | rebuznaba | 3 |
| 6803 | rasas | 3 |
| 6804 | rancho | 3 |
| 6805 | ramo | 3 |
| 6806 | ramas | 3 |
| 6807 | raíz | 3 |
| 6808 | rabo | 3 |
| 6809 | quitárselo | 3 |
| 6810 | quitársele | 3 |
| 6811 | quitaran | 3 |
| 6812 | quitándose | 3 |
| 6813 | quinta | 3 |
| 6814 | quieto | 3 |
| 6815 | quiérote | 3 |
| 6816 | quiebras | 3 |
| 6817 | querrás | 3 |
| 6818 | querencia | 3 |
| 6819 | querella | 3 |
| 6820 | queráis | 3 |
| 6821 | queme | 3 |
| 6822 | quédense | 3 |
| 6823 | quedaran | 3 |
| 6824 | quebrar | 3 |
| 6825 | púsosela | 3 |
| 6826 | púsole | 3 |
| 6827 | pusiere | 3 |
| 6828 | puñaladas | 3 |
| 6829 | puntada | 3 |
| 6830 | puertos | 3 |
| 6831 | pudiésemos | 3 |
| 6832 | públicamente | 3 |
| 6833 | prudentísimo | 3 |
| 6834 | proveyó | 3 |
| 6835 | proveídos | 3 |
| 6836 | proveída | 3 |
| 6837 | proveer | 3 |
| 6838 | provechosas | 3 |
| 6839 | prosopopeya | 3 |
| 6840 | prosiguiese | 3 |
| 6841 | proseguía | 3 |
| 6842 | proprios | 3 |
| 6843 | propriedad | 3 |
| 6844 | propincua | 3 |
| 6845 | prometióselo | 3 |
| 6846 | prometidas | 3 |
| 6847 | prometían | 3 |
| 6848 | prometí | 3 |
| 6849 | profesaron | 3 |
| 6850 | profesar | 3 |
| 6851 | procuras | 3 |
| 6852 | procuraría | 3 |
| 6853 | procuraban | 3 |
| 6854 | procede | 3 |
| 6855 | probó | 3 |
| 6856 | probase | 3 |
| 6857 | prístino | 3 |
| 6858 | prisiones | 3 |
| 6859 | primeramente | 3 |
| 6860 | prevenir | 3 |
| 6861 | pretensión | 3 |
| 6862 | pretendo | 3 |
| 6863 | pretenden | 3 |
| 6864 | preste | 3 |
| 6865 | presentado | 3 |
| 6866 | prerrogativa | 3 |
| 6867 | preñado | 3 |
| 6868 | preñada | 3 |
| 6869 | premiados | 3 |
| 6870 | premiado | 3 |
| 6871 | premática | 3 |
| 6872 | preguntóme | 3 |
| 6873 | preguntara | 3 |
| 6874 | preguntante | 3 |
| 6875 | preguntando | 3 |
| 6876 | preguntaba | 3 |
| 6877 | preeminencias | 3 |
| 6878 | predicador | 3 |
| 6879 | precisa | 3 |
| 6880 | preciosa | 3 |
| 6881 | preceptos | 3 |
| 6882 | pragmáticas | 3 |
| 6883 | poyo | 3 |
| 6884 | poso | 3 |
| 6885 | posas | 3 |
| 6886 | portador | 3 |
| 6887 | porrazos | 3 |
| 6888 | porfió | 3 |
| 6889 | pongamos | 3 |
| 6890 | pones | 3 |
| 6891 | ponerte | 3 |
| 6892 | poneros | 3 |
| 6893 | ponerlos | 3 |
| 6894 | ponerlas | 3 |
| 6895 | ponello | 3 |
| 6896 | pondremos | 3 |
| 6897 | pondrán | 3 |
| 6898 | pólvora | 3 |
| 6899 | pollinas | 3 |
| 6900 | polidoro | 3 |
| 6901 | podridos | 3 |
| 6902 | podíamos | 3 |
| 6903 | poderío | 3 |
| 6904 | podamos | 3 |
| 6905 | poblados | 3 |
| 6906 | pluguiera | 3 |
| 6907 | platónicos | 3 |
| 6908 | píramo | 3 |
| 6909 | pinto | 3 |
| 6910 | pintiparada | 3 |
| 6911 | pintarse | 3 |
| 6912 | piezas | 3 |
| 6913 | pierdas | 3 |
| 6914 | piensos | 3 |
| 6915 | pidióle | 3 |
| 6916 | pidiesen | 3 |
| 6917 | pidiéndole | 3 |
| 6918 | pícaro | 3 |
| 6919 | piadosas | 3 |
| 6920 | pestaña | 3 |
| 6921 | pesos | 3 |
| 6922 | pescado | 3 |
| 6923 | persuadirme | 3 |
| 6924 | persuadiendo | 3 |
| 6925 | persuadido | 3 |
| 6926 | persuadía | 3 |
| 6927 | persiles | 3 |
| 6928 | perseguir | 3 |
| 6929 | perseguido | 3 |
| 6930 | permitiese | 3 |
| 6931 | permitido | 3 |
| 6932 | permitas | 3 |
| 6933 | perlerines | 3 |
| 6934 | perjudicial | 3 |
| 6935 | perfecto | 3 |
| 6936 | perfecta | 3 |
| 6937 | perdonadme | 3 |
| 6938 | perdona | 3 |
| 6939 | perdieron | 3 |
| 6940 | perdidoso | 3 |
| 6941 | perdía | 3 |
| 6942 | perderá | 3 |
| 6943 | pensemos | 3 |
| 6944 | penséis | 3 |
| 6945 | pensasen | 3 |
| 6946 | pensará | 3 |
| 6947 | pensara | 3 |
| 6948 | penitencias | 3 |
| 6949 | pendía | 3 |
| 6950 | pelos | 3 |
| 6951 | pellizcaron | 3 |
| 6952 | pellicos | 3 |
| 6953 | peligrosas | 3 |
| 6954 | pegue | 3 |
| 6955 | pecadora | 3 |
| 6956 | pasto | 3 |
| 6957 | pasta | 3 |
| 6958 | pasito | 3 |
| 6959 | pasen | 3 |
| 6960 | paseaba | 3 |
| 6961 | pasé | 3 |
| 6962 | pasásemos | 3 |
| 6963 | pasarse | 3 |
| 6964 | pasarle | 3 |
| 6965 | pasaran | 3 |
| 6966 | pasamanos | 3 |
| 6967 | pasajeros | 3 |
| 6968 | partióse | 3 |
| 6969 | partiesen | 3 |
| 6970 | partiendo | 3 |
| 6971 | partidas | 3 |
| 6972 | particularmente | 3 |
| 6973 | paróse | 3 |
| 6974 | parido | 3 |
| 6975 | parejas | 3 |
| 6976 | parecióme | 3 |
| 6977 | parecíale | 3 |
| 6978 | pareceres | 3 |
| 6979 | paréceos | 3 |
| 6980 | parecéis | 3 |
| 6981 | páramos | 3 |
| 6982 | pandafilando | 3 |
| 6983 | palmos | 3 |
| 6984 | palmas | 3 |
| 6985 | palmadas | 3 |
| 6986 | palmada | 3 |
| 6987 | palillos | 3 |
| 6988 | palas | 3 |
| 6989 | pájaro | 3 |
| 6990 | paguen | 3 |
| 6991 | pagaré | 3 |
| 6992 | pagará | 3 |
| 6993 | padrastro | 3 |
| 6994 | padezco | 3 |
| 6995 | padecer | 3 |
| 6996 | pacíficos | 3 |
| 6997 | paciendo | 3 |
| 6998 | oyes | 3 |
| 6999 | oyere | 3 |
| 7000 | otubre | 3 |
| 7001 | otorgo | 3 |
| 7002 | otomana | 3 |
| 7003 | ostentación | 3 |
| 7004 | osa | 3 |
| 7005 | orilla | 3 |
| 7006 | onza | 3 |
| 7007 | olvidó | 3 |
| 7008 | olvidábaseme | 3 |
| 7009 | olvida | 3 |
| 7010 | olores | 3 |
| 7011 | olfato | 3 |
| 7012 | oístes | 3 |
| 7013 | oíslo | 3 |
| 7014 | oirán | 3 |
| 7015 | oirá | 3 |
| 7016 | oímos | 3 |
| 7017 | oílla | 3 |
| 7018 | ofreciósele | 3 |
| 7019 | ofreciendo | 3 |
| 7020 | ofrecí | 3 |
| 7021 | oficial | 3 |
| 7022 | ofensivas | 3 |
| 7023 | ofensa | 3 |
| 7024 | ofendidos | 3 |
| 7025 | ofendido | 3 |
| 7026 | ofendía | 3 |
| 7027 | ofenden | 3 |
| 7028 | ociosa | 3 |
| 7029 | obligue | 3 |
| 7030 | obligan | 3 |
| 7031 | obediente | 3 |
| 7032 | obedeció | 3 |
| 7033 | obedecido | 3 |
| 7034 | obedecer | 3 |
| 7035 | nuevamente | 3 |
| 7036 | nublado | 3 |
| 7037 | novios | 3 |
| 7038 | noventa | 3 |
| 7039 | notomía | 3 |
| 7040 | notaba | 3 |
| 7041 | nora | 3 |
| 7042 | nonada | 3 |
| 7043 | nombran | 3 |
| 7044 | nigromante | 3 |
| 7045 | negociantes | 3 |
| 7046 | negarme | 3 |
| 7047 | negándome | 3 |
| 7048 | navío | 3 |
| 7049 | nave | 3 |
| 7050 | nadar | 3 |
| 7051 | naciste | 3 |
| 7052 | naces | 3 |
| 7053 | nacen | 3 |
| 7054 | muslos | 3 |
| 7055 | murmuran | 3 |
| 7056 | murmurador | 3 |
| 7057 | murmura | 3 |
| 7058 | muñecas | 3 |
| 7059 | multitud | 3 |
| 7060 | muestres | 3 |
| 7061 | muela | 3 |
| 7062 | mudase | 3 |
| 7063 | mudarse | 3 |
| 7064 | moviesen | 3 |
| 7065 | moviese | 3 |
| 7066 | movidos | 3 |
| 7067 | movían | 3 |
| 7068 | mostrarme | 3 |
| 7069 | mostaza | 3 |
| 7070 | mosén | 3 |
| 7071 | mosca | 3 |
| 7072 | mortajas | 3 |
| 7073 | morisma | 3 |
| 7074 | moriscos | 3 |
| 7075 | morirse | 3 |
| 7076 | morirás | 3 |
| 7077 | moría | 3 |
| 7078 | morgante | 3 |
| 7079 | montemayor | 3 |
| 7080 | montas | 3 |
| 7081 | mondos | 3 |
| 7082 | monasterio | 3 |
| 7083 | momia | 3 |
| 7084 | molieron | 3 |
| 7085 | moler | 3 |
| 7086 | mojones | 3 |
| 7087 | moho | 3 |
| 7088 | mohína | 3 |
| 7089 | moderna | 3 |
| 7090 | moche | 3 |
| 7091 | mochacha | 3 |
| 7092 | misericordias | 3 |
| 7093 | mirándola | 3 |
| 7094 | mínimas | 3 |
| 7095 | mingo | 3 |
| 7096 | mina | 3 |
| 7097 | mezclado | 3 |
| 7098 | meto | 3 |
| 7099 | meterme | 3 |
| 7100 | mete | 3 |
| 7101 | metal | 3 |
| 7102 | meta | 3 |
| 7103 | merecimientos | 3 |
| 7104 | merecimiento | 3 |
| 7105 | merecerlo | 3 |
| 7106 | merecéis | 3 |
| 7107 | merecedora | 3 |
| 7108 | mercaderes | 3 |
| 7109 | mensajero | 3 |
| 7110 | menguar | 3 |
| 7111 | menearse | 3 |
| 7112 | meneallo | 3 |
| 7113 | memorables | 3 |
| 7114 | melancólicos | 3 |
| 7115 | mejorar | 3 |
| 7116 | medraremos | 3 |
| 7117 | medoro | 3 |
| 7118 | medir | 3 |
| 7119 | mediodía | 3 |
| 7120 | mediana | 3 |
| 7121 | matemáticas | 3 |
| 7122 | matas | 3 |
| 7123 | matará | 3 |
| 7124 | matara | 3 |
| 7125 | matadores | 3 |
| 7126 | masa | 3 |
| 7127 | marinero | 3 |
| 7128 | márgenes | 3 |
| 7129 | mares | 3 |
| 7130 | marca | 3 |
| 7131 | maravillarse | 3 |
| 7132 | mantón | 3 |
| 7133 | manteaban | 3 |
| 7134 | manosearme | 3 |
| 7135 | manifiestas | 3 |
| 7136 | mandóle | 3 |
| 7137 | manden | 3 |
| 7138 | mandé | 3 |
| 7139 | mandaron | 3 |
| 7140 | mandando | 3 |
| 7141 | mandamientos | 3 |
| 7142 | manchega | 3 |
| 7143 | mancebos | 3 |
| 7144 | mana | 3 |
| 7145 | maltratan | 3 |
| 7146 | malta | 3 |
| 7147 | malignos | 3 |
| 7148 | malencólico | 3 |
| 7149 | maldicientes | 3 |
| 7150 | maldiciente | 3 |
| 7151 | maldecir | 3 |
| 7152 | malaventurado | 3 |
| 7153 | malandantes | 3 |
| 7154 | magos | 3 |
| 7155 | magnífica | 3 |
| 7156 | magnánimo | 3 |
| 7157 | maestros | 3 |
| 7158 | madruga | 3 |
| 7159 | madeja | 3 |
| 7160 | ma | 3 |
| 7161 | lunas | 3 |
| 7162 | luminarias | 3 |
| 7163 | lumbres | 3 |
| 7164 | lueñes | 3 |
| 7165 | luengo | 3 |
| 7166 | luengas | 3 |
| 7167 | lucero | 3 |
| 7168 | lópez | 3 |
| 7169 | llovía | 3 |
| 7170 | llorosa | 3 |
| 7171 | llorón | 3 |
| 7172 | lloro | 3 |
| 7173 | llorarla | 3 |
| 7174 | llorado | 3 |
| 7175 | lloraban | 3 |
| 7176 | lleves | 3 |
| 7177 | llevéis | 3 |
| 7178 | llevaste | 3 |
| 7179 | llevare | 3 |
| 7180 | llevarán | 3 |
| 7181 | llevada | 3 |
| 7182 | lleguen | 3 |
| 7183 | llegaren | 3 |
| 7184 | llegarán | 3 |
| 7185 | llantos | 3 |
| 7186 | llámase | 3 |
| 7187 | llamarte | 3 |
| 7188 | llamarle | 3 |
| 7189 | llamamos | 3 |
| 7190 | llamáis | 3 |
| 7191 | llaga | 3 |
| 7192 | liviandad | 3 |
| 7193 | livianas | 3 |
| 7194 | literaria | 3 |
| 7195 | listos | 3 |
| 7196 | lindos | 3 |
| 7197 | limpios | 3 |
| 7198 | limpió | 3 |
| 7199 | limpiado | 3 |
| 7200 | límite | 3 |
| 7201 | ligeros | 3 |
| 7202 | lienzos | 3 |
| 7203 | liebres | 3 |
| 7204 | libra | 3 |
| 7205 | liberalmente | 3 |
| 7206 | levantarla | 3 |
| 7207 | levantaré | 3 |
| 7208 | leño | 3 |
| 7209 | leña | 3 |
| 7210 | lemos | 3 |
| 7211 | lejía | 3 |
| 7212 | leí | 3 |
| 7213 | legislador | 3 |
| 7214 | legal | 3 |
| 7215 | lavando | 3 |
| 7216 | lápice | 3 |
| 7217 | lámparas | 3 |
| 7218 | lamentos | 3 |
| 7219 | lamentarse | 3 |
| 7220 | lamentación | 3 |
| 7221 | lamentables | 3 |
| 7222 | labrar | 3 |
| 7223 | labio | 3 |
| 7224 | laberintos | 3 |
| 7225 | juzgué | 3 |
| 7226 | juzgue | 3 |
| 7227 | juzgaron | 3 |
| 7228 | juzgaba | 3 |
| 7229 | justicias | 3 |
| 7230 | jurare | 3 |
| 7231 | jurara | 3 |
| 7232 | juraba | 3 |
| 7233 | juntando | 3 |
| 7234 | junta | 3 |
| 7235 | jumentos | 3 |
| 7236 | juicios | 3 |
| 7237 | judas | 3 |
| 7238 | jerónima | 3 |
| 7239 | jayanes | 3 |
| 7240 | jarcias | 3 |
| 7241 | jáquima | 3 |
| 7242 | jaeces | 3 |
| 7243 | jabón | 3 |
| 7244 | jabalí | 3 |
| 7245 | iremos | 3 |
| 7246 | iras | 3 |
| 7247 | irán | 3 |
| 7248 | inventaron | 3 |
| 7249 | inútiles | 3 |
| 7250 | intricados | 3 |
| 7251 | intricado | 3 |
| 7252 | intencionada | 3 |
| 7253 | ínsulos | 3 |
| 7254 | inquieto | 3 |
| 7255 | inmenso | 3 |
| 7256 | injurias | 3 |
| 7257 | infundió | 3 |
| 7258 | información | 3 |
| 7259 | infalible | 3 |
| 7260 | indómito | 3 |
| 7261 | indignado | 3 |
| 7262 | indigna | 3 |
| 7263 | increíble | 3 |
| 7264 | incapaz | 3 |
| 7265 | inaudita | 3 |
| 7266 | in | 3 |
| 7267 | imperios | 3 |
| 7268 | imitado | 3 |
| 7269 | imagine | 3 |
| 7270 | imaginaron | 3 |
| 7271 | imaginamos | 3 |
| 7272 | imaginado | 3 |
| 7273 | imaginada | 3 |
| 7274 | imágenes | 3 |
| 7275 | ii | 3 |
| 7276 | igualó | 3 |
| 7277 | igualdad | 3 |
| 7278 | ignorar | 3 |
| 7279 | idiota | 3 |
| 7280 | id | 3 |
| 7281 | íbase | 3 |
| 7282 | huyó | 3 |
| 7283 | huirse | 3 |
| 7284 | huían | 3 |
| 7285 | hubiérades | 3 |
| 7286 | hu | 3 |
| 7287 | hoz | 3 |
| 7288 | hospital | 3 |
| 7289 | hormiga | 3 |
| 7290 | horcajadas | 3 |
| 7291 | honran | 3 |
| 7292 | honradas | 3 |
| 7293 | honraba | 3 |
| 7294 | homicida | 3 |
| 7295 | holgarse | 3 |
| 7296 | holgaron | 3 |
| 7297 | holgaría | 3 |
| 7298 | hola | 3 |
| 7299 | hoguera | 3 |
| 7300 | hogaza | 3 |
| 7301 | hipócrita | 3 |
| 7302 | hincando | 3 |
| 7303 | hilaza | 3 |
| 7304 | hiere | 3 |
| 7305 | hidalguía | 3 |
| 7306 | hidalgas | 3 |
| 7307 | hiciéronse | 3 |
| 7308 | hernando | 3 |
| 7309 | hernández | 3 |
| 7310 | henares | 3 |
| 7311 | hele | 3 |
| 7312 | héctor | 3 |
| 7313 | heciste | 3 |
| 7314 | hecimos | 3 |
| 7315 | hechiceros | 3 |
| 7316 | hebras | 3 |
| 7317 | hayáis | 3 |
| 7318 | hasme | 3 |
| 7319 | hásele | 3 |
| 7320 | hanse | 3 |
| 7321 | hallóse | 3 |
| 7322 | hallemos | 3 |
| 7323 | halléme | 3 |
| 7324 | hallaste | 3 |
| 7325 | halláronle | 3 |
| 7326 | hallaría | 3 |
| 7327 | hallaran | 3 |
| 7328 | hallándola | 3 |
| 7329 | halláis | 3 |
| 7330 | hágote | 3 |
| 7331 | haciéndoles | 3 |
| 7332 | hacerles | 3 |
| 7333 | hacemos | 3 |
| 7334 | hacelle | 3 |
| 7335 | hacaneas | 3 |
| 7336 | hacanea | 3 |
| 7337 | hablará | 3 |
| 7338 | habláis | 3 |
| 7339 | habitar | 3 |
| 7340 | hábil | 3 |
| 7341 | habiéndolos | 3 |
| 7342 | haberte | 3 |
| 7343 | haberlos | 3 |
| 7344 | habas | 3 |
| 7345 | gutierre | 3 |
| 7346 | gustosos | 3 |
| 7347 | gustase | 3 |
| 7348 | guitarra | 3 |
| 7349 | guisando | 3 |
| 7350 | guisados | 3 |
| 7351 | guillermo | 3 |
| 7352 | guijarros | 3 |
| 7353 | guiase | 3 |
| 7354 | guiar | 3 |
| 7355 | güevos | 3 |
| 7356 | guardarla | 3 |
| 7357 | guardaré | 3 |
| 7358 | guardadas | 3 |
| 7359 | guardaban | 3 |
| 7360 | grueso | 3 |
| 7361 | gruesa | 3 |
| 7362 | grosera | 3 |
| 7363 | grito | 3 |
| 7364 | granjerías | 3 |
| 7365 | granjear | 3 |
| 7366 | granjeado | 3 |
| 7367 | granjeada | 3 |
| 7368 | gozó | 3 |
| 7369 | gozo | 3 |
| 7370 | gozando | 3 |
| 7371 | gozan | 3 |
| 7372 | gorra | 3 |
| 7373 | gordura | 3 |
| 7374 | gordas | 3 |
| 7375 | golías | 3 |
| 7376 | gobernaré | 3 |
| 7377 | glotón | 3 |
| 7378 | glorias | 3 |
| 7379 | giralda | 3 |
| 7380 | génova | 3 |
| 7381 | generales | 3 |
| 7382 | generación | 3 |
| 7383 | gata | 3 |
| 7384 | gastado | 3 |
| 7385 | garrotazos | 3 |
| 7386 | garcilaso | 3 |
| 7387 | ganados | 3 |
| 7388 | ganaderos | 3 |
| 7389 | galgo | 3 |
| 7390 | galería | 3 |
| 7391 | galeota | 3 |
| 7392 | galatea | 3 |
| 7393 | galalón | 3 |
| 7394 | furibundos | 3 |
| 7395 | fundándose | 3 |
| 7396 | fulleros | 3 |
| 7397 | fugitiva | 3 |
| 7398 | fueses | 3 |
| 7399 | fueros | 3 |
| 7400 | fuero | 3 |
| 7401 | fueres | 3 |
| 7402 | frontera | 3 |
| 7403 | frestón | 3 |
| 7404 | fraude | 3 |
| 7405 | forastero | 3 |
| 7406 | fócil | 3 |
| 7407 | floridos | 3 |
| 7408 | florencia | 3 |
| 7409 | flojo | 3 |
| 7410 | flojedad | 3 |
| 7411 | flecha | 3 |
| 7412 | flautas | 3 |
| 7413 | flamante | 3 |
| 7414 | flacas | 3 |
| 7415 | firmas | 3 |
| 7416 | firmado | 3 |
| 7417 | finos | 3 |
| 7418 | filosofía | 3 |
| 7419 | fieras | 3 |
| 7420 | fierabrás | 3 |
| 7421 | fielmente | 3 |
| 7422 | ficieron | 3 |
| 7423 | fiambre | 3 |
| 7424 | fértil | 3 |
| 7425 | favoreciese | 3 |
| 7426 | fantástica | 3 |
| 7427 | fanegas | 3 |
| 7428 | familiar | 3 |
| 7429 | familia | 3 |
| 7430 | faltarme | 3 |
| 7431 | faltaran | 3 |
| 7432 | faltara | 3 |
| 7433 | faldriquera | 3 |
| 7434 | faciones | 3 |
| 7435 | fabricado | 3 |
| 7436 | extraordinarios | 3 |
| 7437 | extraordinaria | 3 |
| 7438 | excelencias | 3 |
| 7439 | exceden | 3 |
| 7440 | examinase | 3 |
| 7441 | evitar | 3 |
| 7442 | et | 3 |
| 7443 | estricote | 3 |
| 7444 | estrechos | 3 |
| 7445 | estrechezas | 3 |
| 7446 | estorbaran | 3 |
| 7447 | estopas | 3 |
| 7448 | estómagos | 3 |
| 7449 | estocadas | 3 |
| 7450 | estiman | 3 |
| 7451 | estienden | 3 |
| 7452 | estése | 3 |
| 7453 | esténme | 3 |
| 7454 | estendido | 3 |
| 7455 | estendía | 3 |
| 7456 | estéis | 3 |
| 7457 | estaño | 3 |
| 7458 | estadme | 3 |
| 7459 | estábase | 3 |
| 7460 | esposas | 3 |
| 7461 | esplandián | 3 |
| 7462 | espinas | 3 |
| 7463 | esperase | 3 |
| 7464 | esperaré | 3 |
| 7465 | española | 3 |
| 7466 | españas | 3 |
| 7467 | espantóse | 3 |
| 7468 | espantó | 3 |
| 7469 | espante | 3 |
| 7470 | espantajo | 3 |
| 7471 | espantada | 3 |
| 7472 | espaldar | 3 |
| 7473 | esmeraldas | 3 |
| 7474 | esforzado | 3 |
| 7475 | escusa | 3 |
| 7476 | escuros | 3 |
| 7477 | escurecer | 3 |
| 7478 | escuras | 3 |
| 7479 | escuches | 3 |
| 7480 | escuche | 3 |
| 7481 | escuchad | 3 |
| 7482 | escuadrones | 3 |
| 7483 | escrituras | 3 |
| 7484 | escribirme | 3 |
| 7485 | escribirle | 3 |
| 7486 | escribieron | 3 |
| 7487 | escribiere | 3 |
| 7488 | escoja | 3 |
| 7489 | escogidos | 3 |
| 7490 | escogí | 3 |
| 7491 | esclavos | 3 |
| 7492 | esclavo | 3 |
| 7493 | esclava | 3 |
| 7494 | escasa | 3 |
| 7495 | escapó | 3 |
| 7496 | errado | 3 |
| 7497 | epitafios | 3 |
| 7498 | episodios | 3 |
| 7499 | envío | 3 |
| 7500 | envidiosos | 3 |
| 7501 | enviarme | 3 |
| 7502 | enviaré | 3 |
| 7503 | envían | 3 |
| 7504 | entretienen | 3 |
| 7505 | entretenido | 3 |
| 7506 | entretengan | 3 |
| 7507 | entren | 3 |
| 7508 | entrego | 3 |
| 7509 | entregar | 3 |
| 7510 | entregado | 3 |
| 7511 | éntrate | 3 |
| 7512 | entrasen | 3 |
| 7513 | entrarse | 3 |
| 7514 | entrara | 3 |
| 7515 | entran | 3 |
| 7516 | entradas | 3 |
| 7517 | entono | 3 |
| 7518 | entiendes | 3 |
| 7519 | enterrado | 3 |
| 7520 | entendióle | 3 |
| 7521 | entendimientos | 3 |
| 7522 | entendiera | 3 |
| 7523 | entendida | 3 |
| 7524 | entendemos | 3 |
| 7525 | ensuciar | 3 |
| 7526 | ensillase | 3 |
| 7527 | ensillar | 3 |
| 7528 | enseñóle | 3 |
| 7529 | enseñó | 3 |
| 7530 | enseñase | 3 |
| 7531 | ensartados | 3 |
| 7532 | ensalza | 3 |
| 7533 | enristró | 3 |
| 7534 | enredos | 3 |
| 7535 | enojar | 3 |
| 7536 | enmudeció | 3 |
| 7537 | enlutados | 3 |
| 7538 | engendraron | 3 |
| 7539 | engendrar | 3 |
| 7540 | engendra | 3 |
| 7541 | engaños | 3 |
| 7542 | engañe | 3 |
| 7543 | engáñaste | 3 |
| 7544 | engañas | 3 |
| 7545 | engañada | 3 |
| 7546 | enfadosa | 3 |
| 7547 | enfadan | 3 |
| 7548 | enfada | 3 |
| 7549 | encuentran | 3 |
| 7550 | encubren | 3 |
| 7551 | encubra | 3 |
| 7552 | encubiertos | 3 |
| 7553 | encubierto | 3 |
| 7554 | encomendaba | 3 |
| 7555 | encogió | 3 |
| 7556 | encerrase | 3 |
| 7557 | encerraron | 3 |
| 7558 | encerradas | 3 |
| 7559 | encendía | 3 |
| 7560 | encargó | 3 |
| 7561 | encantan | 3 |
| 7562 | encaminaron | 3 |
| 7563 | encajó | 3 |
| 7564 | encajar | 3 |
| 7565 | encadenados | 3 |
| 7566 | enamoradas | 3 |
| 7567 | emprenta | 3 |
| 7568 | empleado | 3 |
| 7569 | emboscó | 3 |
| 7570 | emboscar | 3 |
| 7571 | embelesamiento | 3 |
| 7572 | embelecos | 3 |
| 7573 | embeleco | 3 |
| 7574 | embarcarse | 3 |
| 7575 | embarcar | 3 |
| 7576 | elogios | 3 |
| 7577 | elocuencia | 3 |
| 7578 | églogas | 3 |
| 7579 | eficaces | 3 |
| 7580 | edificios | 3 |
| 7581 | échese | 3 |
| 7582 | echen | 3 |
| 7583 | echásemos | 3 |
| 7584 | echaban | 3 |
| 7585 | ebro | 3 |
| 7586 | durar | 3 |
| 7587 | durante | 3 |
| 7588 | duraba | 3 |
| 7589 | duerma | 3 |
| 7590 | dueñesco | 3 |
| 7591 | dude | 3 |
| 7592 | dromedarios | 3 |
| 7593 | dormidos | 3 |
| 7594 | dormían | 3 |
| 7595 | domingo | 3 |
| 7596 | dolorosos | 3 |
| 7597 | doliera | 3 |
| 7598 | dolerse | 3 |
| 7599 | doblando | 3 |
| 7600 | dó | 3 |
| 7601 | distrito | 3 |
| 7602 | distributiva | 3 |
| 7603 | distinguir | 3 |
| 7604 | distancia | 3 |
| 7605 | disputar | 3 |
| 7606 | discretamente | 3 |
| 7607 | diligentes | 3 |
| 7608 | díjoles | 3 |
| 7609 | dijímosle | 3 |
| 7610 | dijeran | 3 |
| 7611 | digresiones | 3 |
| 7612 | digamos | 3 |
| 7613 | diéronle | 3 |
| 7614 | dido | 3 |
| 7615 | díaz | 3 |
| 7616 | devoto | 3 |
| 7617 | deudas | 3 |
| 7618 | detúvose | 3 |
| 7619 | determinarse | 3 |
| 7620 | determinamos | 3 |
| 7621 | determinada | 3 |
| 7622 | detenido | 3 |
| 7623 | desventurada | 3 |
| 7624 | desvariado | 3 |
| 7625 | desvalidos | 3 |
| 7626 | desuellacaras | 3 |
| 7627 | destraído | 3 |
| 7628 | desprecie | 3 |
| 7629 | despojado | 3 |
| 7630 | despierte | 3 |
| 7631 | despidiéndose | 3 |
| 7632 | despertara | 3 |
| 7633 | despertador | 3 |
| 7634 | despedirme | 3 |
| 7635 | despedido | 3 |
| 7636 | despedían | 3 |
| 7637 | despedí | 3 |
| 7638 | despavorido | 3 |
| 7639 | desos | 3 |
| 7640 | desocupado | 3 |
| 7641 | desmesurada | 3 |
| 7642 | desmayos | 3 |
| 7643 | desmayarse | 3 |
| 7644 | desmayados | 3 |
| 7645 | desmayaba | 3 |
| 7646 | desigualdad | 3 |
| 7647 | designios | 3 |
| 7648 | deshonrar | 3 |
| 7649 | deshiciese | 3 |
| 7650 | deshace | 3 |
| 7651 | desgobernado | 3 |
| 7652 | desgajó | 3 |
| 7653 | desfaga | 3 |
| 7654 | desfacer | 3 |
| 7655 | desesperarse | 3 |
| 7656 | desesperábase | 3 |
| 7657 | desenvainada | 3 |
| 7658 | desengañar | 3 |
| 7659 | desengañado | 3 |
| 7660 | desenfado | 3 |
| 7661 | desencantarla | 3 |
| 7662 | desembarcó | 3 |
| 7663 | desembarcar | 3 |
| 7664 | deseando | 3 |
| 7665 | descuidados | 3 |
| 7666 | descuidada | 3 |
| 7667 | descubrirle | 3 |
| 7668 | descubridor | 3 |
| 7669 | descubren | 3 |
| 7670 | descoser | 3 |
| 7671 | desconsolada | 3 |
| 7672 | descompuestos | 3 |
| 7673 | descansado | 3 |
| 7674 | descaminado | 3 |
| 7675 | desató | 3 |
| 7676 | desatar | 3 |
| 7677 | desastrado | 3 |
| 7678 | desasosiego | 3 |
| 7679 | desarmarle | 3 |
| 7680 | desarmado | 3 |
| 7681 | desamparó | 3 |
| 7682 | desamparar | 3 |
| 7683 | desamparado | 3 |
| 7684 | desamorado | 3 |
| 7685 | desaforada | 3 |
| 7686 | desafiar | 3 |
| 7687 | desafiado | 3 |
| 7688 | derribando | 3 |
| 7689 | derribada | 3 |
| 7690 | depósito | 3 |
| 7691 | deparó | 3 |
| 7692 | depare | 3 |
| 7693 | demostina | 3 |
| 7694 | delincuentes | 3 |
| 7695 | delicadezas | 3 |
| 7696 | deleite | 3 |
| 7697 | delantero | 3 |
| 7698 | delantera | 3 |
| 7699 | déjenmos | 3 |
| 7700 | dejarla | 3 |
| 7701 | dejarán | 3 |
| 7702 | defensivas | 3 |
| 7703 | defendían | 3 |
| 7704 | declaro | 3 |
| 7705 | debilitada | 3 |
| 7706 | debiendo | 3 |
| 7707 | debido | 3 |
| 7708 | deber | 3 |
| 7709 | date | 3 |
| 7710 | data | 3 |
| 7711 | dártela | 3 |
| 7712 | dársele | 3 |
| 7713 | dármele | 3 |
| 7714 | daños | 3 |
| 7715 | dándoles | 3 |
| 7716 | damasco | 3 |
| 7717 | dale | 3 |
| 7718 | daca | 3 |
| 7719 | dábanle | 3 |
| 7720 | curiosa | 3 |
| 7721 | curase | 3 |
| 7722 | curan | 3 |
| 7723 | cuñado | 3 |
| 7724 | cumplirlo | 3 |
| 7725 | cumpláis | 3 |
| 7726 | cuitado | 3 |
| 7727 | cuervo | 3 |
| 7728 | cuéntase | 3 |
| 7729 | cuelga | 3 |
| 7730 | cuchilla | 3 |
| 7731 | cubra | 3 |
| 7732 | cuatralbo | 3 |
| 7733 | cuartillos | 3 |
| 7734 | cuanta | 3 |
| 7735 | cristo | 3 |
| 7736 | crías | 3 |
| 7737 | cría | 3 |
| 7738 | crees | 3 |
| 7739 | credos | 3 |
| 7740 | crecen | 3 |
| 7741 | crece | 3 |
| 7742 | cotufas | 3 |
| 7743 | costosa | 3 |
| 7744 | costar | 3 |
| 7745 | costado | 3 |
| 7746 | cosquillas | 3 |
| 7747 | coser | 3 |
| 7748 | cosecha | 3 |
| 7749 | corva | 3 |
| 7750 | cortos | 3 |
| 7751 | corteza | 3 |
| 7752 | cortesanas | 3 |
| 7753 | cortando | 3 |
| 7754 | corro | 3 |
| 7755 | corrieron | 3 |
| 7756 | corrían | 3 |
| 7757 | correspondía | 3 |
| 7758 | correspondencias | 3 |
| 7759 | corredor | 3 |
| 7760 | correción | 3 |
| 7761 | coro | 3 |
| 7762 | cordales | 3 |
| 7763 | corcovos | 3 |
| 7764 | corbacho | 3 |
| 7765 | coraje | 3 |
| 7766 | copos | 3 |
| 7767 | convidaba | 3 |
| 7768 | contravenido | 3 |
| 7769 | contrahechas | 3 |
| 7770 | contorno | 3 |
| 7771 | contentase | 3 |
| 7772 | contentaron | 3 |
| 7773 | contentaba | 3 |
| 7774 | contenido | 3 |
| 7775 | contarlo | 3 |
| 7776 | contados | 3 |
| 7777 | contadme | 3 |
| 7778 | consuma | 3 |
| 7779 | consorte | 3 |
| 7780 | consolado | 3 |
| 7781 | consiento | 3 |
| 7782 | considere | 3 |
| 7783 | considerase | 3 |
| 7784 | considerada | 3 |
| 7785 | consideraba | 3 |
| 7786 | conserve | 3 |
| 7787 | consentía | 3 |
| 7788 | consejas | 3 |
| 7789 | conociendo | 3 |
| 7790 | conjúrote | 3 |
| 7791 | conjuro | 3 |
| 7792 | conduce | 3 |
| 7793 | condesas | 3 |
| 7794 | condes | 3 |
| 7795 | concluye | 3 |
| 7796 | conchas | 3 |
| 7797 | concertaron | 3 |
| 7798 | concertados | 3 |
| 7799 | concejo | 3 |
| 7800 | concedía | 3 |
| 7801 | conceda | 3 |
| 7802 | comunicó | 3 |
| 7803 | comunicado | 3 |
| 7804 | compró | 3 |
| 7805 | compre | 3 |
| 7806 | composición | 3 |
| 7807 | componerle | 3 |
| 7808 | competencia | 3 |
| 7809 | compatrioto | 3 |
| 7810 | comparar | 3 |
| 7811 | comparaciones | 3 |
| 7812 | compaño | 3 |
| 7813 | compañías | 3 |
| 7814 | comilón | 3 |
| 7815 | comete | 3 |
| 7816 | comeré | 3 |
| 7817 | comemos | 3 |
| 7818 | comedor | 3 |
| 7819 | comedidas | 3 |
| 7820 | coluna | 3 |
| 7821 | colgó | 3 |
| 7822 | colgados | 3 |
| 7823 | colegir | 3 |
| 7824 | colegio | 3 |
| 7825 | cofradía | 3 |
| 7826 | codiciosos | 3 |
| 7827 | codicilo | 3 |
| 7828 | cocido | 3 |
| 7829 | cocía | 3 |
| 7830 | cobró | 3 |
| 7831 | cobro | 3 |
| 7832 | cobraron | 3 |
| 7833 | cobardes | 3 |
| 7834 | clavados | 3 |
| 7835 | claustro | 3 |
| 7836 | claros | 3 |
| 7837 | clarísimo | 3 |
| 7838 | claraboya | 3 |
| 7839 | ciudadano | 3 |
| 7840 | cita | 3 |
| 7841 | circunvecinos | 3 |
| 7842 | ciprés | 3 |
| 7843 | cintas | 3 |
| 7844 | cimiento | 3 |
| 7845 | cierre | 3 |
| 7846 | cieno | 3 |
| 7847 | ciegos | 3 |
| 7848 | cicerón | 3 |
| 7849 | cibera | 3 |
| 7850 | choza | 3 |
| 7851 | chipre | 3 |
| 7852 | china | 3 |
| 7853 | chimenea | 3 |
| 7854 | cesaban | 3 |
| 7855 | certidumbre | 3 |
| 7856 | cerros | 3 |
| 7857 | cerraron | 3 |
| 7858 | cercen | 3 |
| 7859 | cercana | 3 |
| 7860 | ceptro | 3 |
| 7861 | centinela | 3 |
| 7862 | cenó | 3 |
| 7863 | cenizas | 3 |
| 7864 | cendal | 3 |
| 7865 | celeridad | 3 |
| 7866 | celebran | 3 |
| 7867 | celebrada | 3 |
| 7868 | cebra | 3 |
| 7869 | cebollas | 3 |
| 7870 | cayendo | 3 |
| 7871 | cautela | 3 |
| 7872 | caudal | 3 |
| 7873 | católicos | 3 |
| 7874 | casto | 3 |
| 7875 | castellanas | 3 |
| 7876 | casase | 3 |
| 7877 | casarla | 3 |
| 7878 | casados | 3 |
| 7879 | casaca | 3 |
| 7880 | carros | 3 |
| 7881 | carrascón | 3 |
| 7882 | carnero | 3 |
| 7883 | carmesí | 3 |
| 7884 | cargos | 3 |
| 7885 | cargar | 3 |
| 7886 | cargan | 3 |
| 7887 | cargada | 3 |
| 7888 | cardenal | 3 |
| 7889 | caras | 3 |
| 7890 | capítulos | 3 |
| 7891 | caperuza | 3 |
| 7892 | cañones | 3 |
| 7893 | cañaheja | 3 |
| 7894 | cante | 3 |
| 7895 | cantase | 3 |
| 7896 | cantaban | 3 |
| 7897 | canses | 3 |
| 7898 | cansa | 3 |
| 7899 | canes | 3 |
| 7900 | candeal | 3 |
| 7901 | canciones | 3 |
| 7902 | caminaron | 3 |
| 7903 | camaranchón | 3 |
| 7904 | callase | 3 |
| 7905 | callaron | 3 |
| 7906 | callad | 3 |
| 7907 | calderas | 3 |
| 7908 | caigo | 3 |
| 7909 | caiga | 3 |
| 7910 | cabrón | 3 |
| 7911 | cabrito | 3 |
| 7912 | cabrillas | 3 |
| 7913 | cabrerizo | 3 |
| 7914 | cabizbajo | 3 |
| 7915 | cabido | 3 |
| 7916 | cabía | 3 |
| 7917 | cabalgaduras | 3 |
| 7918 | busque | 3 |
| 7919 | buscas | 3 |
| 7920 | buscarte | 3 |
| 7921 | buscarme | 3 |
| 7922 | buscara | 3 |
| 7923 | buscaban | 3 |
| 7924 | burlo | 3 |
| 7925 | burlar | 3 |
| 7926 | brincar | 3 |
| 7927 | brincando | 3 |
| 7928 | brazas | 3 |
| 7929 | brava | 3 |
| 7930 | botones | 3 |
| 7931 | borró | 3 |
| 7932 | borricos | 3 |
| 7933 | borrador | 3 |
| 7934 | borra | 3 |
| 7935 | borgoña | 3 |
| 7936 | bordones | 3 |
| 7937 | borceguíes | 3 |
| 7938 | bonete | 3 |
| 7939 | bon | 3 |
| 7940 | bofetadas | 3 |
| 7941 | bocas | 3 |
| 7942 | bobo | 3 |
| 7943 | blandamente | 3 |
| 7944 | bizmas | 3 |
| 7945 | bizarra | 3 |
| 7946 | billetes | 3 |
| 7947 | besos | 3 |
| 7948 | besóle | 3 |
| 7949 | besarle | 3 |
| 7950 | besaba | 3 |
| 7951 | benito | 3 |
| 7952 | bendita | 3 |
| 7953 | bendiga | 3 |
| 7954 | beltenebros | 3 |
| 7955 | bellos | 3 |
| 7956 | bellísima | 3 |
| 7957 | bellezas | 3 |
| 7958 | belianises | 3 |
| 7959 | bebió | 3 |
| 7960 | beben | 3 |
| 7961 | basilisco | 3 |
| 7962 | bartolomé | 3 |
| 7963 | barranco | 3 |
| 7964 | bárbaro | 3 |
| 7965 | bandera | 3 |
| 7966 | ballestas | 3 |
| 7967 | baje | 3 |
| 7968 | bajase | 3 |
| 7969 | bajaban | 3 |
| 7970 | bagatele | 3 |
| 7971 | bacallao | 3 |
| 7972 | azotado | 3 |
| 7973 | azogue | 3 |
| 7974 | azófar | 3 |
| 7975 | ayudaré | 3 |
| 7976 | ayudara | 3 |
| 7977 | ayo | 3 |
| 7978 | ayes | 3 |
| 7979 | avisarme | 3 |
| 7980 | avestruz | 3 |
| 7981 | autorizar | 3 |
| 7982 | auto | 3 |
| 7983 | austria | 3 |
| 7984 | ausentarse | 3 |
| 7985 | ausencias | 3 |
| 7986 | aumentan | 3 |
| 7987 | atropellando | 3 |
| 7988 | atributos | 3 |
| 7989 | atreven | 3 |
| 7990 | atrevan | 3 |
| 7991 | atravesada | 3 |
| 7992 | atravesaba | 3 |
| 7993 | átomo | 3 |
| 7994 | atienden | 3 |
| 7995 | atiende | 3 |
| 7996 | atentas | 3 |
| 7997 | atenido | 3 |
| 7998 | atendiese | 3 |
| 7999 | atañen | 3 |
| 8000 | asunto | 3 |
| 8001 | astucias | 3 |
| 8002 | astrólogo | 3 |
| 8003 | astrología | 3 |
| 8004 | asomos | 3 |
| 8005 | asombro | 3 |
| 8006 | asombrado | 3 |
| 8007 | asoma | 3 |
| 8008 | asir | 3 |
| 8009 | asientos | 3 |
| 8010 | asentó | 3 |
| 8011 | asegurándole | 3 |
| 8012 | asco | 3 |
| 8013 | asalariado | 3 |
| 8014 | artificiosa | 3 |
| 8015 | arroje | 3 |
| 8016 | arrojar | 3 |
| 8017 | arrojado | 3 |
| 8018 | arrojaba | 3 |
| 8019 | arroja | 3 |
| 8020 | arrogancia | 3 |
| 8021 | arrendador | 3 |
| 8022 | arremetieron | 3 |
| 8023 | arremetida | 3 |
| 8024 | arremeter | 3 |
| 8025 | arrastraba | 3 |
| 8026 | arrancó | 3 |
| 8027 | arpillera | 3 |
| 8028 | arnaúte | 3 |
| 8029 | armonía | 3 |
| 8030 | armería | 3 |
| 8031 | ariosto | 3 |
| 8032 | ardites | 3 |
| 8033 | ardían | 3 |
| 8034 | arcos | 3 |
| 8035 | arcabuz | 3 |
| 8036 | arado | 3 |
| 8037 | aquiles | 3 |
| 8038 | aquestos | 3 |
| 8039 | aquéste | 3 |
| 8040 | aprovechaba | 3 |
| 8041 | apretando | 3 |
| 8042 | apretada | 3 |
| 8043 | aprendan | 3 |
| 8044 | aposta | 3 |
| 8045 | apolonia | 3 |
| 8046 | apearon | 3 |
| 8047 | apeaos | 3 |
| 8048 | apasionado | 3 |
| 8049 | apártense | 3 |
| 8050 | aparté | 3 |
| 8051 | apartáronse | 3 |
| 8052 | apartarme | 3 |
| 8053 | apartando | 3 |
| 8054 | aparentes | 3 |
| 8055 | añadiéndose | 3 |
| 8056 | añadiendo | 3 |
| 8057 | antojase | 3 |
| 8058 | antojare | 3 |
| 8059 | antigüedad | 3 |
| 8060 | antifaz | 3 |
| 8061 | antequera | 3 |
| 8062 | antecogiendo | 3 |
| 8063 | antecedente | 3 |
| 8064 | anotaciones | 3 |
| 8065 | aniquilar | 3 |
| 8066 | animoso | 3 |
| 8067 | angustiada | 3 |
| 8068 | anduviese | 3 |
| 8069 | anduviera | 3 |
| 8070 | anduve | 3 |
| 8071 | andrada | 3 |
| 8072 | ándeme | 3 |
| 8073 | andarme | 3 |
| 8074 | andantesca | 3 |
| 8075 | andáis | 3 |
| 8076 | ampare | 3 |
| 8077 | amparar | 3 |
| 8078 | amorosamente | 3 |
| 8079 | amojamado | 3 |
| 8080 | amenazando | 3 |
| 8081 | ambos | 3 |
| 8082 | amarillez | 3 |
| 8083 | amarillas | 3 |
| 8084 | amanece | 3 |
| 8085 | amable | 3 |
| 8086 | alzarse | 3 |
| 8087 | alzándose | 3 |
| 8088 | alzado | 3 |
| 8089 | alzada | 3 |
| 8090 | altanería | 3 |
| 8091 | alongado | 3 |
| 8092 | alojar | 3 |
| 8093 | alojado | 3 |
| 8094 | alojaba | 3 |
| 8095 | almenas | 3 |
| 8096 | almalafa | 3 |
| 8097 | aljaba | 3 |
| 8098 | aliviado | 3 |
| 8099 | alhombra | 3 |
| 8100 | alheña | 3 |
| 8101 | alguacil | 3 |
| 8102 | alférez | 3 |
| 8103 | alcornoques | 3 |
| 8104 | alcanzarle | 3 |
| 8105 | alcances | 3 |
| 8106 | alcancé | 3 |
| 8107 | alcabalas | 3 |
| 8108 | albraca | 3 |
| 8109 | alborozado | 3 |
| 8110 | alborotó | 3 |
| 8111 | albaceas | 3 |
| 8112 | alargaba | 3 |
| 8113 | alárabes | 3 |
| 8114 | alabóle | 3 |
| 8115 | alabo | 3 |
| 8116 | alabastro | 3 |
| 8117 | alabados | 3 |
| 8118 | ál | 3 |
| 8119 | aína | 3 |
| 8120 | ahorquen | 3 |
| 8121 | aguja | 3 |
| 8122 | aguileña | 3 |
| 8123 | aguilar | 3 |
| 8124 | agüela | 3 |
| 8125 | agudos | 3 |
| 8126 | agudezas | 3 |
| 8127 | aguda | 3 |
| 8128 | aguardó | 3 |
| 8129 | agradecieron | 3 |
| 8130 | agradare | 3 |
| 8131 | agosto | 3 |
| 8132 | agorero | 3 |
| 8133 | agobiado | 3 |
| 8134 | ágil | 3 |
| 8135 | áfrica | 3 |
| 8136 | africa | 3 |
| 8137 | afrentas | 3 |
| 8138 | afrentar | 3 |
| 8139 | afortunada | 3 |
| 8140 | afirmó | 3 |
| 8141 | afirmo | 3 |
| 8142 | afirmaba | 3 |
| 8143 | afincamiento | 3 |
| 8144 | afeó | 3 |
| 8145 | afectación | 3 |
| 8146 | afable | 3 |
| 8147 | advertidos | 3 |
| 8148 | adversos | 3 |
| 8149 | adornos | 3 |
| 8150 | adornar | 3 |
| 8151 | adobo | 3 |
| 8152 | admitir | 3 |
| 8153 | admiren | 3 |
| 8154 | admiran | 3 |
| 8155 | admirábase | 3 |
| 8156 | admirábanse | 3 |
| 8157 | admiraban | 3 |
| 8158 | adivinanzas | 3 |
| 8159 | adevinaba | 3 |
| 8160 | aderezados | 3 |
| 8161 | acuerdan | 3 |
| 8162 | acudid | 3 |
| 8163 | acudí | 3 |
| 8164 | acude | 3 |
| 8165 | acuda | 3 |
| 8166 | actos | 3 |
| 8167 | acrecentó | 3 |
| 8168 | acotaciones | 3 |
| 8169 | acostó | 3 |
| 8170 | acortar | 3 |
| 8171 | acordaron | 3 |
| 8172 | acordarme | 3 |
| 8173 | acordar | 3 |
| 8174 | acordándose | 3 |
| 8175 | aconsejarte | 3 |
| 8176 | aconsejar | 3 |
| 8177 | acompañando | 3 |
| 8178 | acompañan | 3 |
| 8179 | acompañamos | 3 |
| 8180 | acompañaba | 3 |
| 8181 | acompaña | 3 |
| 8182 | acomodándose | 3 |
| 8183 | acomodaba | 3 |
| 8184 | acometimientos | 3 |
| 8185 | acometido | 3 |
| 8186 | acometía | 3 |
| 8187 | acometen | 3 |
| 8188 | acometa | 3 |
| 8189 | acogió | 3 |
| 8190 | acogida | 3 |
| 8191 | acierta | 3 |
| 8192 | acidente | 3 |
| 8193 | aciago | 3 |
| 8194 | acertada | 3 |
| 8195 | acertaba | 3 |
| 8196 | acercando | 3 |
| 8197 | acatamiento | 3 |
| 8198 | acaben | 3 |
| 8199 | acabarse | 3 |
| 8200 | acabaré | 3 |
| 8201 | acabará | 3 |
| 8202 | acabara | 3 |
| 8203 | acabamiento | 3 |
| 8204 | acababan | 3 |
| 8205 | abundoso | 3 |
| 8206 | abrióle | 3 |
| 8207 | abriera | 3 |
| 8208 | abrazóle | 3 |
| 8209 | abrasa | 3 |
| 8210 | aborrezco | 3 |
| 8211 | aborrecimiento | 3 |
| 8212 | aborrece | 3 |
| 8213 | abindarráez | 3 |
| 8214 | abejas | 3 |
| 8215 | abc | 3 |
| 8216 | zurdo | 2 |
| 8217 | zocodover | 2 |
| 8218 | zaques | 2 |
| 8219 | zapatillas | 2 |
| 8220 | zapatetas | 2 |
| 8221 | zancadilla | 2 |
| 8222 | zalá | 2 |
| 8223 | zafio | 2 |
| 8224 | zafia | 2 |
| 8225 | z | 2 |
| 8226 | yerno | 2 |
| 8227 | yéndose | 2 |
| 8228 | yéndoles | 2 |
| 8229 | yéndole | 2 |
| 8230 | yelos | 2 |
| 8231 | yantar | 2 |
| 8232 | yanta | 2 |
| 8233 | xxxviii | 2 |
| 8234 | xxxvii | 2 |
| 8235 | xxxvi | 2 |
| 8236 | xxxv | 2 |
| 8237 | xxxix | 2 |
| 8238 | xxxiv | 2 |
| 8239 | xxxiii | 2 |
| 8240 | xxxii | 2 |
| 8241 | xxxi | 2 |
| 8242 | xxx | 2 |
| 8243 | xxviii | 2 |
| 8244 | xxvii | 2 |
| 8245 | xxvi | 2 |
| 8246 | xxv | 2 |
| 8247 | xxix | 2 |
| 8248 | xxiv | 2 |
| 8249 | xxiii | 2 |
| 8250 | xxii | 2 |
| 8251 | xxi | 2 |
| 8252 | xx | 2 |
| 8253 | xviii | 2 |
| 8254 | xvii | 2 |
| 8255 | xvi | 2 |
| 8256 | xv | 2 |
| 8257 | xlviii | 2 |
| 8258 | xlvii | 2 |
| 8259 | xlvi | 2 |
| 8260 | xlv | 2 |
| 8261 | xlix | 2 |
| 8262 | xliv | 2 |
| 8263 | xliii | 2 |
| 8264 | xlii | 2 |
| 8265 | xli | 2 |
| 8266 | xl | 2 |
| 8267 | xix | 2 |
| 8268 | xiv | 2 |
| 8269 | xiii | 2 |
| 8270 | xii | 2 |
| 8271 | xi | 2 |
| 8272 | wamba | 2 |
| 8273 | vuélvete | 2 |
| 8274 | vuélvase | 2 |
| 8275 | vómito | 2 |
| 8276 | volvíme | 2 |
| 8277 | volviéronse | 2 |
| 8278 | volvíame | 2 |
| 8279 | volvérselos | 2 |
| 8280 | volvérsela | 2 |
| 8281 | volveros | 2 |
| 8282 | volverlos | 2 |
| 8283 | volverás | 2 |
| 8284 | volveos | 2 |
| 8285 | volteando | 2 |
| 8286 | volatería | 2 |
| 8287 | vocablo | 2 |
| 8288 | voacé | 2 |
| 8289 | vizcaína | 2 |
| 8290 | vivió | 2 |
| 8291 | viviese | 2 |
| 8292 | vivido | 2 |
| 8293 | vivid | 2 |
| 8294 | vives | 2 |
| 8295 | vivan | 2 |
| 8296 | vivamos | 2 |
| 8297 | vitupera | 2 |
| 8298 | visten | 2 |
| 8299 | vísperas | 2 |
| 8300 | visitas | 2 |
| 8301 | visitado | 2 |
| 8302 | virote | 2 |
| 8303 | viola | 2 |
| 8304 | viñas | 2 |
| 8305 | vínosele | 2 |
| 8306 | vinos | 2 |
| 8307 | viniéndosele | 2 |
| 8308 | víneme | 2 |
| 8309 | vileza | 2 |
| 8310 | viii | 2 |
| 8311 | vii | 2 |
| 8312 | vihuela | 2 |
| 8313 | vigor | 2 |
| 8314 | vigilias | 2 |
| 8315 | vigilia | 2 |
| 8316 | vigilancia | 2 |
| 8317 | vieses | 2 |
| 8318 | viéredes | 2 |
| 8319 | vieran | 2 |
| 8320 | vidro | 2 |
| 8321 | viciosos | 2 |
| 8322 | versado | 2 |
| 8323 | verrugas | 2 |
| 8324 | verlos | 2 |
| 8325 | verían | 2 |
| 8326 | vergonzosa | 2 |
| 8327 | verbis | 2 |
| 8328 | venzo | 2 |
| 8329 | venza | 2 |
| 8330 | venus | 2 |
| 8331 | venturosos | 2 |
| 8332 | ventrera | 2 |
| 8333 | veniste | 2 |
| 8334 | veniere | 2 |
| 8335 | veníamos | 2 |
| 8336 | vengaros | 2 |
| 8337 | vengarle | 2 |
| 8338 | vengara | 2 |
| 8339 | venerables | 2 |
| 8340 | venenos | 2 |
| 8341 | veneciano | 2 |
| 8342 | vendió | 2 |
| 8343 | vendiere | 2 |
| 8344 | vendido | 2 |
| 8345 | vendible | 2 |
| 8346 | vendía | 2 |
| 8347 | vendados | 2 |
| 8348 | vendado | 2 |
| 8349 | venciste | 2 |
| 8350 | venciese | 2 |
| 8351 | vencí | 2 |
| 8352 | vencerlos | 2 |
| 8353 | venablo | 2 |
| 8354 | velos | 2 |
| 8355 | velludo | 2 |
| 8356 | vella | 2 |
| 8357 | velasco | 2 |
| 8358 | veíamos | 2 |
| 8359 | vehemente | 2 |
| 8360 | vegadas | 2 |
| 8361 | vecindad | 2 |
| 8362 | vecinas | 2 |
| 8363 | vaste | 2 |
| 8364 | vasos | 2 |
| 8365 | vase | 2 |
| 8366 | varios | 2 |
| 8367 | varapalo | 2 |
| 8368 | vaqueros | 2 |
| 8369 | vápulo | 2 |
| 8370 | vapulamiento | 2 |
| 8371 | vanos | 2 |
| 8372 | valona | 2 |
| 8373 | valiese | 2 |
| 8374 | validos | 2 |
| 8375 | válgate | 2 |
| 8376 | válgame | 2 |
| 8377 | valentísima | 2 |
| 8378 | valedores | 2 |
| 8379 | valedero | 2 |
| 8380 | vagar | 2 |
| 8381 | vagando | 2 |
| 8382 | vagamundo | 2 |
| 8383 | vacíos | 2 |
| 8384 | v | 2 |
| 8385 | usurpar | 2 |
| 8386 | usos | 2 |
| 8387 | usaran | 2 |
| 8388 | usará | 2 |
| 8389 | usadas | 2 |
| 8390 | usada | 2 |
| 8391 | urgente | 2 |
| 8392 | unció | 2 |
| 8393 | ulises | 2 |
| 8394 | tuyas | 2 |
| 8395 | tuvímoslo | 2 |
| 8396 | tuviéramos | 2 |
| 8397 | turquesa | 2 |
| 8398 | turbéme | 2 |
| 8399 | turbamulta | 2 |
| 8400 | túnica | 2 |
| 8401 | tumbas | 2 |
| 8402 | tulio | 2 |
| 8403 | tufo | 2 |
| 8404 | trújole | 2 |
| 8405 | trujiste | 2 |
| 8406 | trujéronle | 2 |
| 8407 | trujeres | 2 |
| 8408 | trujere | 2 |
| 8409 | truhanes | 2 |
| 8410 | truhán | 2 |
| 8411 | trueque | 2 |
| 8412 | truecan | 2 |
| 8413 | trueca | 2 |
| 8414 | truchuelas | 2 |
| 8415 | truchuela | 2 |
| 8416 | truchas | 2 |
| 8417 | troyas | 2 |
| 8418 | trovas | 2 |
| 8419 | trovadores | 2 |
| 8420 | trova | 2 |
| 8421 | tropiezo | 2 |
| 8422 | tropieza | 2 |
| 8423 | tropezó | 2 |
| 8424 | tropezar | 2 |
| 8425 | tropas | 2 |
| 8426 | troncos | 2 |
| 8427 | tronchón | 2 |
| 8428 | trómpogelas | 2 |
| 8429 | trocó | 2 |
| 8430 | trocaría | 2 |
| 8431 | triunfos | 2 |
| 8432 | triunfó | 2 |
| 8433 | triunfante | 2 |
| 8434 | triquete | 2 |
| 8435 | trinidad | 2 |
| 8436 | tretas | 2 |
| 8437 | trayéndole | 2 |
| 8438 | travieso | 2 |
| 8439 | tratos | 2 |
| 8440 | tratase | 2 |
| 8441 | tratarme | 2 |
| 8442 | tratare | 2 |
| 8443 | tratará | 2 |
| 8444 | trasudar | 2 |
| 8445 | trasudaba | 2 |
| 8446 | trastrigo | 2 |
| 8447 | trastornado | 2 |
| 8448 | traslada | 2 |
| 8449 | trasero | 2 |
| 8450 | trapo | 2 |
| 8451 | trapa | 2 |
| 8452 | transportado | 2 |
| 8453 | tranquilo | 2 |
| 8454 | tranquila | 2 |
| 8455 | trampas | 2 |
| 8456 | traigan | 2 |
| 8457 | traídos | 2 |
| 8458 | traidora | 2 |
| 8459 | traiciones | 2 |
| 8460 | tragedias | 2 |
| 8461 | tragaba | 2 |
| 8462 | traerte | 2 |
| 8463 | traerse | 2 |
| 8464 | traerlos | 2 |
| 8465 | traerlas | 2 |
| 8466 | traed | 2 |
| 8467 | tradutor | 2 |
| 8468 | trabajoso | 2 |
| 8469 | trabaje | 2 |
| 8470 | trabajando | 2 |
| 8471 | trabaja | 2 |
| 8472 | trabadas | 2 |
| 8473 | tostado | 2 |
| 8474 | toser | 2 |
| 8475 | toscana | 2 |
| 8476 | tosca | 2 |
| 8477 | torneo | 2 |
| 8478 | torné | 2 |
| 8479 | tornándose | 2 |
| 8480 | tornando | 2 |
| 8481 | tormentas | 2 |
| 8482 | tordilla | 2 |
| 8483 | torció | 2 |
| 8484 | torciendo | 2 |
| 8485 | torcidas | 2 |
| 8486 | toparon | 2 |
| 8487 | toparéis | 2 |
| 8488 | topare | 2 |
| 8489 | topamos | 2 |
| 8490 | tomes | 2 |
| 8491 | tomases | 2 |
| 8492 | tomaros | 2 |
| 8493 | tomáronse | 2 |
| 8494 | tomarme | 2 |
| 8495 | tomares | 2 |
| 8496 | tomaréis | 2 |
| 8497 | tomándome | 2 |
| 8498 | tomados | 2 |
| 8499 | tomadme | 2 |
| 8500 | tomaban | 2 |
| 8501 | tomá | 2 |
| 8502 | tolosa | 2 |
| 8503 | toldo | 2 |
| 8504 | tocó | 2 |
| 8505 | tocho | 2 |
| 8506 | tocasen | 2 |
| 8507 | tocarlas | 2 |
| 8508 | tocará | 2 |
| 8509 | tocándole | 2 |
| 8510 | tocaban | 2 |
| 8511 | tirase | 2 |
| 8512 | tirarle | 2 |
| 8513 | tiranía | 2 |
| 8514 | tirador | 2 |
| 8515 | tiñoso | 2 |
| 8516 | tinelo | 2 |
| 8517 | tinacrio | 2 |
| 8518 | tigres | 2 |
| 8519 | tiesas | 2 |
| 8520 | tiemblo | 2 |
| 8521 | testimonios | 2 |
| 8522 | teseo | 2 |
| 8523 | tesalia | 2 |
| 8524 | terrones | 2 |
| 8525 | terrenal | 2 |
| 8526 | terrado | 2 |
| 8527 | terradillo | 2 |
| 8528 | ternura | 2 |
| 8529 | teodora | 2 |
| 8530 | tentación | 2 |
| 8531 | teniéndose | 2 |
| 8532 | teniéndolo | 2 |
| 8533 | tenidos | 2 |
| 8534 | tenidas | 2 |
| 8535 | teníades | 2 |
| 8536 | tenérsele | 2 |
| 8537 | teneros | 2 |
| 8538 | tenerlos | 2 |
| 8539 | teneos | 2 |
| 8540 | tendimos | 2 |
| 8541 | tendiendo | 2 |
| 8542 | tenderse | 2 |
| 8543 | tenazas | 2 |
| 8544 | templó | 2 |
| 8545 | templar | 2 |
| 8546 | templando | 2 |
| 8547 | templa | 2 |
| 8548 | temido | 2 |
| 8549 | temían | 2 |
| 8550 | temíamos | 2 |
| 8551 | temerarios | 2 |
| 8552 | teme | 2 |
| 8553 | tembleque | 2 |
| 8554 | temblar | 2 |
| 8555 | tejidas | 2 |
| 8556 | tejados | 2 |
| 8557 | tejado | 2 |
| 8558 | tate | 2 |
| 8559 | tasaron | 2 |
| 8560 | tasado | 2 |
| 8561 | tartesios | 2 |
| 8562 | tardase | 2 |
| 8563 | tardaría | 2 |
| 8564 | tardará | 2 |
| 8565 | tapiz | 2 |
| 8566 | tápenme | 2 |
| 8567 | tapaboca | 2 |
| 8568 | tapa | 2 |
| 8569 | tañendo | 2 |
| 8570 | tantico | 2 |
| 8571 | tanteando | 2 |
| 8572 | tanteado | 2 |
| 8573 | tamaños | 2 |
| 8574 | tajada | 2 |
| 8575 | tacto | 2 |
| 8576 | tacha | 2 |
| 8577 | tabique | 2 |
| 8578 | susurro | 2 |
| 8579 | sustentase | 2 |
| 8580 | sustentarse | 2 |
| 8581 | sustentaré | 2 |
| 8582 | sustentan | 2 |
| 8583 | sustentaban | 2 |
| 8584 | suspendieron | 2 |
| 8585 | sur | 2 |
| 8586 | suplícoos | 2 |
| 8587 | suplicio | 2 |
| 8588 | suplicastes | 2 |
| 8589 | suplica | 2 |
| 8590 | suplemento | 2 |
| 8591 | suple | 2 |
| 8592 | supieres | 2 |
| 8593 | supieras | 2 |
| 8594 | supieran | 2 |
| 8595 | superficie | 2 |
| 8596 | suntuoso | 2 |
| 8597 | sujetarme | 2 |
| 8598 | sufrida | 2 |
| 8599 | sufría | 2 |
| 8600 | suficiencia | 2 |
| 8601 | suenan | 2 |
| 8602 | sueltas | 2 |
| 8603 | sucio | 2 |
| 8604 | sucintamente | 2 |
| 8605 | sucedernos | 2 |
| 8606 | sucederme | 2 |
| 8607 | sucederle | 2 |
| 8608 | sucedería | 2 |
| 8609 | súbito | 2 |
| 8610 | subirse | 2 |
| 8611 | subida | 2 |
| 8612 | subid | 2 |
| 8613 | subí | 2 |
| 8614 | subamos | 2 |
| 8615 | sotana | 2 |
| 8616 | sostenerme | 2 |
| 8617 | sospiro | 2 |
| 8618 | sospira | 2 |
| 8619 | sospechar | 2 |
| 8620 | sosiéguese | 2 |
| 8621 | sosiegue | 2 |
| 8622 | sosiégate | 2 |
| 8623 | sosegase | 2 |
| 8624 | sosegaron | 2 |
| 8625 | sosegaos | 2 |
| 8626 | sosegadas | 2 |
| 8627 | sortijas | 2 |
| 8628 | sordos | 2 |
| 8629 | sorda | 2 |
| 8630 | sopa | 2 |
| 8631 | sonoro | 2 |
| 8632 | sonora | 2 |
| 8633 | sonó | 2 |
| 8634 | sonidos | 2 |
| 8635 | sonajas | 2 |
| 8636 | sonadas | 2 |
| 8637 | sombras | 2 |
| 8638 | solteros | 2 |
| 8639 | soltalle | 2 |
| 8640 | soliloquio | 2 |
| 8641 | solicitó | 2 |
| 8642 | solicite | 2 |
| 8643 | solenes | 2 |
| 8644 | solemos | 2 |
| 8645 | soldadesca | 2 |
| 8646 | soldada | 2 |
| 8647 | solazando | 2 |
| 8648 | solapa | 2 |
| 8649 | soeces | 2 |
| 8650 | socorros | 2 |
| 8651 | socorrido | 2 |
| 8652 | socorrida | 2 |
| 8653 | socorred | 2 |
| 8654 | socapa | 2 |
| 8655 | socaliñas | 2 |
| 8656 | sobrevino | 2 |
| 8657 | sobresaltóse | 2 |
| 8658 | sobresaltó | 2 |
| 8659 | sobresalte | 2 |
| 8660 | sobresaltaron | 2 |
| 8661 | sobresaltan | 2 |
| 8662 | sobrenombres | 2 |
| 8663 | sobrehumana | 2 |
| 8664 | sirviesen | 2 |
| 8665 | sintieses | 2 |
| 8666 | sintiese | 2 |
| 8667 | sinsabores | 2 |
| 8668 | siniestro | 2 |
| 8669 | sincero | 2 |
| 8670 | sincera | 2 |
| 8671 | simpleza | 2 |
| 8672 | silbo | 2 |
| 8673 | siguiesen | 2 |
| 8674 | síguese | 2 |
| 8675 | sigues | 2 |
| 8676 | signos | 2 |
| 8677 | significantes | 2 |
| 8678 | significado | 2 |
| 8679 | sierpes | 2 |
| 8680 | sientes | 2 |
| 8681 | sienes | 2 |
| 8682 | sicut | 2 |
| 8683 | setenas | 2 |
| 8684 | setecientos | 2 |
| 8685 | setecientas | 2 |
| 8686 | séte | 2 |
| 8687 | sesga | 2 |
| 8688 | servirían | 2 |
| 8689 | servimos | 2 |
| 8690 | servilla | 2 |
| 8691 | servidor | 2 |
| 8692 | serpientes | 2 |
| 8693 | serenidad | 2 |
| 8694 | sepultó | 2 |
| 8695 | sepultados | 2 |
| 8696 | sepulcros | 2 |
| 8697 | señuelo | 2 |
| 8698 | señaladas | 2 |
| 8699 | señalada | 2 |
| 8700 | señalaba | 2 |
| 8701 | señala | 2 |
| 8702 | sentís | 2 |
| 8703 | sentirlo | 2 |
| 8704 | sentimos | 2 |
| 8705 | sentenciare | 2 |
| 8706 | sentaos | 2 |
| 8707 | senos | 2 |
| 8708 | sendos | 2 |
| 8709 | sendero | 2 |
| 8710 | sencillamente | 2 |
| 8711 | senado | 2 |
| 8712 | semejan | 2 |
| 8713 | semejaban | 2 |
| 8714 | semejaba | 2 |
| 8715 | semeja | 2 |
| 8716 | sembrar | 2 |
| 8717 | seguras | 2 |
| 8718 | segundos | 2 |
| 8719 | segundas | 2 |
| 8720 | segundar | 2 |
| 8721 | seguistes | 2 |
| 8722 | seguirla | 2 |
| 8723 | seguida | 2 |
| 8724 | segadores | 2 |
| 8725 | sedero | 2 |
| 8726 | secuaces | 2 |
| 8727 | secta | 2 |
| 8728 | secó | 2 |
| 8729 | séase | 2 |
| 8730 | sazonadas | 2 |
| 8731 | sayas | 2 |
| 8732 | sauces | 2 |
| 8733 | satisfechas | 2 |
| 8734 | satisfará | 2 |
| 8735 | satisfagas | 2 |
| 8736 | satisfaceros | 2 |
| 8737 | satisfacerme | 2 |
| 8738 | sartén | 2 |
| 8739 | sargas | 2 |
| 8740 | sardinas | 2 |
| 8741 | saña | 2 |
| 8742 | santísimo | 2 |
| 8743 | santísima | 2 |
| 8744 | santiguarse | 2 |
| 8745 | sanlúcar | 2 |
| 8746 | sanidad | 2 |
| 8747 | sangrienta | 2 |
| 8748 | sangrías | 2 |
| 8749 | sane | 2 |
| 8750 | sandoval | 2 |
| 8751 | sanchos | 2 |
| 8752 | sanase | 2 |
| 8753 | sanar | 2 |
| 8754 | sanaba | 2 |
| 8755 | salvaje | 2 |
| 8756 | salvación | 2 |
| 8757 | saludes | 2 |
| 8758 | saludaban | 2 |
| 8759 | salteó | 2 |
| 8760 | saltaembarca | 2 |
| 8761 | saltaban | 2 |
| 8762 | salsa | 2 |
| 8763 | salpicón | 2 |
| 8764 | salmantino | 2 |
| 8765 | salióse | 2 |
| 8766 | saliéronse | 2 |
| 8767 | saliéndose | 2 |
| 8768 | salid | 2 |
| 8769 | sales | 2 |
| 8770 | sahumados | 2 |
| 8771 | sagrada | 2 |
| 8772 | sagaz | 2 |
| 8773 | saeta | 2 |
| 8774 | sacudiéndose | 2 |
| 8775 | sacramento | 2 |
| 8776 | sacos | 2 |
| 8777 | sacerdotes | 2 |
| 8778 | sacarlas | 2 |
| 8779 | sacarían | 2 |
| 8780 | sacaría | 2 |
| 8781 | sacará | 2 |
| 8782 | sacándole | 2 |
| 8783 | sabrosamente | 2 |
| 8784 | sabrían | 2 |
| 8785 | sabremos | 2 |
| 8786 | sabrán | 2 |
| 8787 | sabíamos | 2 |
| 8788 | rusticidad | 2 |
| 8789 | rumía | 2 |
| 8790 | ruiz | 2 |
| 8791 | ruinas | 2 |
| 8792 | rugero | 2 |
| 8793 | rufianes | 2 |
| 8794 | rufián | 2 |
| 8795 | ruegan | 2 |
| 8796 | rueca | 2 |
| 8797 | rubricado | 2 |
| 8798 | rubíes | 2 |
| 8799 | rubias | 2 |
| 8800 | rotolando | 2 |
| 8801 | rondón | 2 |
| 8802 | roncos | 2 |
| 8803 | ronco | 2 |
| 8804 | rompiese | 2 |
| 8805 | rompieron | 2 |
| 8806 | rompa | 2 |
| 8807 | romancistas | 2 |
| 8808 | rojo | 2 |
| 8809 | rojas | 2 |
| 8810 | roja | 2 |
| 8811 | rogase | 2 |
| 8812 | rogarte | 2 |
| 8813 | rogaré | 2 |
| 8814 | rogamos | 2 |
| 8815 | rodease | 2 |
| 8816 | rodeando | 2 |
| 8817 | rodeada | 2 |
| 8818 | rodeaban | 2 |
| 8819 | rodar | 2 |
| 8820 | rodando | 2 |
| 8821 | rocines | 2 |
| 8822 | roballa | 2 |
| 8823 | riquísima | 2 |
| 8824 | rió | 2 |
| 8825 | riñen | 2 |
| 8826 | rindo | 2 |
| 8827 | rindióse | 2 |
| 8828 | rindiesen | 2 |
| 8829 | rinde | 2 |
| 8830 | rincones | 2 |
| 8831 | rimero | 2 |
| 8832 | rijoso | 2 |
| 8833 | riguridad | 2 |
| 8834 | riera | 2 |
| 8835 | ridículos | 2 |
| 8836 | ribetes | 2 |
| 8837 | rezaba | 2 |
| 8838 | revolviéndose | 2 |
| 8839 | revolvía | 2 |
| 8840 | revolverse | 2 |
| 8841 | revolcar | 2 |
| 8842 | reverenda | 2 |
| 8843 | reverencias | 2 |
| 8844 | reventaban | 2 |
| 8845 | revalidar | 2 |
| 8846 | retumbaron | 2 |
| 8847 | retóricos | 2 |
| 8848 | retó | 2 |
| 8849 | reto | 2 |
| 8850 | retirémonos | 2 |
| 8851 | retirarnos | 2 |
| 8852 | retira | 2 |
| 8853 | resurreción | 2 |
| 8854 | resultare | 2 |
| 8855 | resuelto | 2 |
| 8856 | resuelta | 2 |
| 8857 | resucitase | 2 |
| 8858 | resucitado | 2 |
| 8859 | resucita | 2 |
| 8860 | restituya | 2 |
| 8861 | restaba | 2 |
| 8862 | respondona | 2 |
| 8863 | respondo | 2 |
| 8864 | respondíle | 2 |
| 8865 | responderles | 2 |
| 8866 | responderla | 2 |
| 8867 | responderá | 2 |
| 8868 | responden | 2 |
| 8869 | respondéis | 2 |
| 8870 | respiro | 2 |
| 8871 | respectos | 2 |
| 8872 | respecto | 2 |
| 8873 | resolvió | 2 |
| 8874 | resiste | 2 |
| 8875 | resista | 2 |
| 8876 | resintió | 2 |
| 8877 | reservado | 2 |
| 8878 | rescaté | 2 |
| 8879 | rescatar | 2 |
| 8880 | requiriendo | 2 |
| 8881 | requerir | 2 |
| 8882 | requebrando | 2 |
| 8883 | repugna | 2 |
| 8884 | representaron | 2 |
| 8885 | representando | 2 |
| 8886 | reportes | 2 |
| 8887 | repliqué | 2 |
| 8888 | replique | 2 |
| 8889 | replico | 2 |
| 8890 | repitió | 2 |
| 8891 | repentino | 2 |
| 8892 | repentina | 2 |
| 8893 | repartir | 2 |
| 8894 | repartieron | 2 |
| 8895 | reparó | 2 |
| 8896 | reparando | 2 |
| 8897 | repara | 2 |
| 8898 | reñían | 2 |
| 8899 | renovóse | 2 |
| 8900 | reniego | 2 |
| 8901 | renglones | 2 |
| 8902 | renegada | 2 |
| 8903 | rendirme | 2 |
| 8904 | rendidos | 2 |
| 8905 | rencuentro | 2 |
| 8906 | remotos | 2 |
| 8907 | remitieron | 2 |
| 8908 | remeros | 2 |
| 8909 | remediarlas | 2 |
| 8910 | remediara | 2 |
| 8911 | remedialla | 2 |
| 8912 | rematadamente | 2 |
| 8913 | remanece | 2 |
| 8914 | relumbraba | 2 |
| 8915 | relucida | 2 |
| 8916 | reluce | 2 |
| 8917 | relinchar | 2 |
| 8918 | relieves | 2 |
| 8919 | relente | 2 |
| 8920 | rejo | 2 |
| 8921 | reinar | 2 |
| 8922 | reían | 2 |
| 8923 | reía | 2 |
| 8924 | regocijos | 2 |
| 8925 | regocijados | 2 |
| 8926 | regocijado | 2 |
| 8927 | regocijada | 2 |
| 8928 | regirle | 2 |
| 8929 | regida | 2 |
| 8930 | regía | 2 |
| 8931 | regalase | 2 |
| 8932 | regalarse | 2 |
| 8933 | regalado | 2 |
| 8934 | regala | 2 |
| 8935 | refrigerio | 2 |
| 8936 | refriegas | 2 |
| 8937 | refiero | 2 |
| 8938 | referirlas | 2 |
| 8939 | referían | 2 |
| 8940 | redundará | 2 |
| 8941 | redundaba | 2 |
| 8942 | redunda | 2 |
| 8943 | reducido | 2 |
| 8944 | reducida | 2 |
| 8945 | red | 2 |
| 8946 | recrear | 2 |
| 8947 | recostado | 2 |
| 8948 | reconocióle | 2 |
| 8949 | recogerse | 2 |
| 8950 | recogen | 2 |
| 8951 | reclusión | 2 |
| 8952 | recibiría | 2 |
| 8953 | recibiré | 2 |
| 8954 | recibir | 2 |
| 8955 | recibiera | 2 |
| 8956 | recibiendo | 2 |
| 8957 | recatado | 2 |
| 8958 | rebuznando | 2 |
| 8959 | rebién | 2 |
| 8960 | razonada | 2 |
| 8961 | razonables | 2 |
| 8962 | raza | 2 |
| 8963 | raudal | 2 |
| 8964 | rastrojos | 2 |
| 8965 | rastro | 2 |
| 8966 | rastrillando | 2 |
| 8967 | rasgó | 2 |
| 8968 | rasgado | 2 |
| 8969 | rapista | 2 |
| 8970 | rapes | 2 |
| 8971 | rape | 2 |
| 8972 | rapaza | 2 |
| 8973 | rapamiento | 2 |
| 8974 | ramón | 2 |
| 8975 | rameras | 2 |
| 8976 | rama | 2 |
| 8977 | raja | 2 |
| 8978 | racimos | 2 |
| 8979 | racimo | 2 |
| 8980 | rabiosa | 2 |
| 8981 | rabiaba | 2 |
| 8982 | quitóse | 2 |
| 8983 | quiten | 2 |
| 8984 | quítate | 2 |
| 8985 | quitasoles | 2 |
| 8986 | quitárselos | 2 |
| 8987 | quitármele | 2 |
| 8988 | quitarían | 2 |
| 8989 | quitarán | 2 |
| 8990 | quitará | 2 |
| 8991 | quitando | 2 |
| 8992 | quitamos | 2 |
| 8993 | quítame | 2 |
| 8994 | quitadas | 2 |
| 8995 | quistión | 2 |
| 8996 | quisiste | 2 |
| 8997 | quisieses | 2 |
| 8998 | quisiéremos | 2 |
| 8999 | quisieras | 2 |
| 9000 | quis | 2 |
| 9001 | quiriendo | 2 |
| 9002 | quintanar | 2 |
| 9003 | quimera | 2 |
| 9004 | quijotiz | 2 |
| 9005 | quijo | 2 |
| 9006 | quietó | 2 |
| 9007 | quieta | 2 |
| 9008 | quiérole | 2 |
| 9009 | quiéranme | 2 |
| 9010 | quiebre | 2 |
| 9011 | quesada | 2 |
| 9012 | querrían | 2 |
| 9013 | querríamos | 2 |
| 9014 | querré | 2 |
| 9015 | querrán | 2 |
| 9016 | queríamos | 2 |
| 9017 | quererlo | 2 |
| 9018 | quererla | 2 |
| 9019 | quemasen | 2 |
| 9020 | quemaran | 2 |
| 9021 | quemados | 2 |
| 9022 | quejarme | 2 |
| 9023 | quejara | 2 |
| 9024 | quedito | 2 |
| 9025 | quedes | 2 |
| 9026 | quedaremos | 2 |
| 9027 | quedada | 2 |
| 9028 | quedad | 2 |
| 9029 | quebré | 2 |
| 9030 | quebrantamiento | 2 |
| 9031 | quebrantada | 2 |
| 9032 | quebranta | 2 |
| 9033 | quebrado | 2 |
| 9034 | quebradas | 2 |
| 9035 | pusiéronse | 2 |
| 9036 | pusieran | 2 |
| 9037 | puros | 2 |
| 9038 | puntuales | 2 |
| 9039 | puntería | 2 |
| 9040 | puncen | 2 |
| 9041 | pulsos | 2 |
| 9042 | pulir | 2 |
| 9043 | pulgas | 2 |
| 9044 | pulgares | 2 |
| 9045 | puerco | 2 |
| 9046 | puedas | 2 |
| 9047 | púdolo | 2 |
| 9048 | pudiéremos | 2 |
| 9049 | pudiéramos | 2 |
| 9050 | ptolomeo | 2 |
| 9051 | proveeré | 2 |
| 9052 | proveedor | 2 |
| 9053 | provechosos | 2 |
| 9054 | prosperidades | 2 |
| 9055 | prosperidad | 2 |
| 9056 | prospere | 2 |
| 9057 | próspera | 2 |
| 9058 | proseguid | 2 |
| 9059 | proporcionada | 2 |
| 9060 | proporción | 2 |
| 9061 | proponía | 2 |
| 9062 | pronunciada | 2 |
| 9063 | prontos | 2 |
| 9064 | pronto | 2 |
| 9065 | prometióle | 2 |
| 9066 | prometiéndome | 2 |
| 9067 | prometiendo | 2 |
| 9068 | prometerse | 2 |
| 9069 | prometa | 2 |
| 9070 | profundamente | 2 |
| 9071 | profetizado | 2 |
| 9072 | profetizadas | 2 |
| 9073 | profeta | 2 |
| 9074 | profesado | 2 |
| 9075 | profesaba | 2 |
| 9076 | profanos | 2 |
| 9077 | prodigiosa | 2 |
| 9078 | procuró | 2 |
| 9079 | procures | 2 |
| 9080 | procuremos | 2 |
| 9081 | procuréis | 2 |
| 9082 | procuré | 2 |
| 9083 | procurarían | 2 |
| 9084 | procurad | 2 |
| 9085 | proceloso | 2 |
| 9086 | procedido | 2 |
| 9087 | procedía | 2 |
| 9088 | proceden | 2 |
| 9089 | probarla | 2 |
| 9090 | probará | 2 |
| 9091 | privarse | 2 |
| 9092 | privanza | 2 |
| 9093 | prístina | 2 |
| 9094 | prisa | 2 |
| 9095 | prioste | 2 |
| 9096 | priora | 2 |
| 9097 | principalidad | 2 |
| 9098 | primor | 2 |
| 9099 | primavera | 2 |
| 9100 | primas | 2 |
| 9101 | prez | 2 |
| 9102 | previlegios | 2 |
| 9103 | previene | 2 |
| 9104 | prevenirse | 2 |
| 9105 | prevenido | 2 |
| 9106 | prevaricador | 2 |
| 9107 | pretina | 2 |
| 9108 | pretendientes | 2 |
| 9109 | pretendes | 2 |
| 9110 | presurosa | 2 |
| 9111 | presupone | 2 |
| 9112 | presumir | 2 |
| 9113 | presumía | 2 |
| 9114 | presumen | 2 |
| 9115 | prestó | 2 |
| 9116 | prestasen | 2 |
| 9117 | prestarme | 2 |
| 9118 | prestará | 2 |
| 9119 | prestar | 2 |
| 9120 | prestada | 2 |
| 9121 | prestaba | 2 |
| 9122 | presonajes | 2 |
| 9123 | presentéis | 2 |
| 9124 | presentarse | 2 |
| 9125 | presentaron | 2 |
| 9126 | preseas | 2 |
| 9127 | preparada | 2 |
| 9128 | preñados | 2 |
| 9129 | premian | 2 |
| 9130 | premáticas | 2 |
| 9131 | preguntóles | 2 |
| 9132 | preguntasen | 2 |
| 9133 | preguntarte | 2 |
| 9134 | preguntarnos | 2 |
| 9135 | preguntarme | 2 |
| 9136 | preguntándoles | 2 |
| 9137 | predicando | 2 |
| 9138 | preciosísimas | 2 |
| 9139 | preciosas | 2 |
| 9140 | precias | 2 |
| 9141 | preciaba | 2 |
| 9142 | precedido | 2 |
| 9143 | preámbulo | 2 |
| 9144 | potro | 2 |
| 9145 | potosí | 2 |
| 9146 | potencia | 2 |
| 9147 | postrero | 2 |
| 9148 | postizos | 2 |
| 9149 | posibilidad | 2 |
| 9150 | posesor | 2 |
| 9151 | poseía | 2 |
| 9152 | portamanteo | 2 |
| 9153 | porfiando | 2 |
| 9154 | porfían | 2 |
| 9155 | poquito | 2 |
| 9156 | pontífices | 2 |
| 9157 | ponte | 2 |
| 9158 | poniente | 2 |
| 9159 | ponérselas | 2 |
| 9160 | ponernos | 2 |
| 9161 | ponella | 2 |
| 9162 | pomposo | 2 |
| 9163 | pomposas | 2 |
| 9164 | polvos | 2 |
| 9165 | polvorosa | 2 |
| 9166 | polos | 2 |
| 9167 | pollos | 2 |
| 9168 | pollas | 2 |
| 9169 | polla | 2 |
| 9170 | polido | 2 |
| 9171 | polainas | 2 |
| 9172 | poética | 2 |
| 9173 | podrida | 2 |
| 9174 | podimos | 2 |
| 9175 | poderosos | 2 |
| 9176 | poderosísimo | 2 |
| 9177 | poderosamente | 2 |
| 9178 | poderle | 2 |
| 9179 | pobretes | 2 |
| 9180 | pleitos | 2 |
| 9181 | plectro | 2 |
| 9182 | plebeyo | 2 |
| 9183 | plebeya | 2 |
| 9184 | platón | 2 |
| 9185 | platir | 2 |
| 9186 | platica | 2 |
| 9187 | planta | 2 |
| 9188 | placeras | 2 |
| 9189 | pisuerga | 2 |
| 9190 | pistolas | 2 |
| 9191 | pisar | 2 |
| 9192 | pisan | 2 |
| 9193 | pisado | 2 |
| 9194 | piojos | 2 |
| 9195 | pinturas | 2 |
| 9196 | pintarnos | 2 |
| 9197 | pintan | 2 |
| 9198 | pintaban | 2 |
| 9199 | pieles | 2 |
| 9200 | piélago | 2 |
| 9201 | piel | 2 |
| 9202 | pidieran | 2 |
| 9203 | pidiera | 2 |
| 9204 | pidiéndome | 2 |
| 9205 | pidas | 2 |
| 9206 | picota | 2 |
| 9207 | picos | 2 |
| 9208 | picaron | 2 |
| 9209 | picado | 2 |
| 9210 | picada | 2 |
| 9211 | piara | 2 |
| 9212 | piadosos | 2 |
| 9213 | piadosa | 2 |
| 9214 | piache | 2 |
| 9215 | pez | 2 |
| 9216 | peto | 2 |
| 9217 | pestilencia | 2 |
| 9218 | pesó | 2 |
| 9219 | pesebre | 2 |
| 9220 | pescar | 2 |
| 9221 | pescados | 2 |
| 9222 | pesase | 2 |
| 9223 | pésame | 2 |
| 9224 | pesadumbres | 2 |
| 9225 | pesadas | 2 |
| 9226 | perverso | 2 |
| 9227 | pertinaz | 2 |
| 9228 | pertinacia | 2 |
| 9229 | pertenecientes | 2 |
| 9230 | persuadirles | 2 |
| 9231 | persuadiese | 2 |
| 9232 | persia | 2 |
| 9233 | persas | 2 |
| 9234 | perra | 2 |
| 9235 | perpleja | 2 |
| 9236 | permitir | 2 |
| 9237 | permitiendo | 2 |
| 9238 | perjudiciales | 2 |
| 9239 | pergaminos | 2 |
| 9240 | perfección | 2 |
| 9241 | peregrinación | 2 |
| 9242 | perecer | 2 |
| 9243 | perece | 2 |
| 9244 | perdigón | 2 |
| 9245 | perdiesen | 2 |
| 9246 | perdiera | 2 |
| 9247 | perdiendo | 2 |
| 9248 | perdidas | 2 |
| 9249 | perderle | 2 |
| 9250 | perderla | 2 |
| 9251 | perdería | 2 |
| 9252 | pepita | 2 |
| 9253 | peñasco | 2 |
| 9254 | pensares | 2 |
| 9255 | pensaré | 2 |
| 9256 | pensarán | 2 |
| 9257 | pensados | 2 |
| 9258 | pensada | 2 |
| 9259 | penetrado | 2 |
| 9260 | pellizcado | 2 |
| 9261 | pellejo | 2 |
| 9262 | pelearon | 2 |
| 9263 | peleantes | 2 |
| 9264 | pelaría | 2 |
| 9265 | peladas | 2 |
| 9266 | peje | 2 |
| 9267 | pegaso | 2 |
| 9268 | pegan | 2 |
| 9269 | pegada | 2 |
| 9270 | pedreñales | 2 |
| 9271 | pedradas | 2 |
| 9272 | pedírsela | 2 |
| 9273 | pedilla | 2 |
| 9274 | pedí | 2 |
| 9275 | pecadoras | 2 |
| 9276 | peana | 2 |
| 9277 | pausas | 2 |
| 9278 | patochadas | 2 |
| 9279 | patios | 2 |
| 9280 | paternostres | 2 |
| 9281 | patas | 2 |
| 9282 | pastoriles | 2 |
| 9283 | pastorales | 2 |
| 9284 | pasmáronse | 2 |
| 9285 | pasiones | 2 |
| 9286 | paseando | 2 |
| 9287 | pasean | 2 |
| 9288 | paseado | 2 |
| 9289 | pascuas | 2 |
| 9290 | pascua | 2 |
| 9291 | pasases | 2 |
| 9292 | pasarían | 2 |
| 9293 | pasare | 2 |
| 9294 | pasará | 2 |
| 9295 | pasaje | 2 |
| 9296 | partos | 2 |
| 9297 | partirme | 2 |
| 9298 | partiré | 2 |
| 9299 | partirás | 2 |
| 9300 | partimos | 2 |
| 9301 | partía | 2 |
| 9302 | pariría | 2 |
| 9303 | parienta | 2 |
| 9304 | parí | 2 |
| 9305 | pargamino | 2 |
| 9306 | parezcas | 2 |
| 9307 | pareja | 2 |
| 9308 | paréis | 2 |
| 9309 | parecióles | 2 |
| 9310 | pareciesen | 2 |
| 9311 | pareciera | 2 |
| 9312 | pareces | 2 |
| 9313 | parecerá | 2 |
| 9314 | pardas | 2 |
| 9315 | parcialidad | 2 |
| 9316 | parche | 2 |
| 9317 | parase | 2 |
| 9318 | paranzas | 2 |
| 9319 | paralelos | 2 |
| 9320 | paraje | 2 |
| 9321 | paraíso | 2 |
| 9322 | parada | 2 |
| 9323 | pandero | 2 |
| 9324 | pancino | 2 |
| 9325 | paloma | 2 |
| 9326 | palmilla | 2 |
| 9327 | palamenta | 2 |
| 9328 | palaciega | 2 |
| 9329 | pagaros | 2 |
| 9330 | pagarle | 2 |
| 9331 | pagaos | 2 |
| 9332 | pagan | 2 |
| 9333 | pagalle | 2 |
| 9334 | padrón | 2 |
| 9335 | padrino | 2 |
| 9336 | padecen | 2 |
| 9337 | pacto | 2 |
| 9338 | pablo | 2 |
| 9339 | oyesen | 2 |
| 9340 | oyente | 2 |
| 9341 | oyéndose | 2 |
| 9342 | oyen | 2 |
| 9343 | oyas | 2 |
| 9344 | otorgue | 2 |
| 9345 | otorgado | 2 |
| 9346 | otoño | 2 |
| 9347 | otero | 2 |
| 9348 | ostugo | 2 |
| 9349 | osos | 2 |
| 9350 | oropel | 2 |
| 9351 | orondas | 2 |
| 9352 | orín | 2 |
| 9353 | origen | 2 |
| 9354 | oria | 2 |
| 9355 | orfandad | 2 |
| 9356 | orégano | 2 |
| 9357 | ordené | 2 |
| 9358 | ordene | 2 |
| 9359 | ordenadas | 2 |
| 9360 | ordenada | 2 |
| 9361 | orbaneja | 2 |
| 9362 | oráculo | 2 |
| 9363 | oprobrio | 2 |
| 9364 | oprime | 2 |
| 9365 | opresos | 2 |
| 9366 | opone | 2 |
| 9367 | operibus | 2 |
| 9368 | olvidase | 2 |
| 9369 | olvidar | 2 |
| 9370 | olvidándose | 2 |
| 9371 | olvidaba | 2 |
| 9372 | olorosas | 2 |
| 9373 | olorosa | 2 |
| 9374 | oliva | 2 |
| 9375 | olía | 2 |
| 9376 | olalla | 2 |
| 9377 | ojeras | 2 |
| 9378 | oíste | 2 |
| 9379 | oís | 2 |
| 9380 | oírse | 2 |
| 9381 | oiré | 2 |
| 9382 | oirás | 2 |
| 9383 | oíllo | 2 |
| 9384 | oílle | 2 |
| 9385 | ofrezcan | 2 |
| 9386 | ofrecida | 2 |
| 9387 | ofrecerle | 2 |
| 9388 | oficina | 2 |
| 9389 | oficiales | 2 |
| 9390 | ofendida | 2 |
| 9391 | ofenderle | 2 |
| 9392 | ofende | 2 |
| 9393 | odiosas | 2 |
| 9394 | ocupó | 2 |
| 9395 | ocupe | 2 |
| 9396 | ocupase | 2 |
| 9397 | ocupados | 2 |
| 9398 | ocultas | 2 |
| 9399 | ochocientos | 2 |
| 9400 | obligo | 2 |
| 9401 | obligase | 2 |
| 9402 | obligaban | 2 |
| 9403 | objeto | 2 |
| 9404 | objeción | 2 |
| 9405 | obedientes | 2 |
| 9406 | obedecerle | 2 |
| 9407 | obedecelle | 2 |
| 9408 | ñudos | 2 |
| 9409 | novillo | 2 |
| 9410 | novia | 2 |
| 9411 | novedades | 2 |
| 9412 | novecientos | 2 |
| 9413 | notoria | 2 |
| 9414 | noté | 2 |
| 9415 | nota | 2 |
| 9416 | nombrando | 2 |
| 9417 | nombra | 2 |
| 9418 | niñería | 2 |
| 9419 | ningunos | 2 |
| 9420 | nieto | 2 |
| 9421 | niegues | 2 |
| 9422 | niegue | 2 |
| 9423 | nidos | 2 |
| 9424 | negase | 2 |
| 9425 | negaría | 2 |
| 9426 | negado | 2 |
| 9427 | necesitada | 2 |
| 9428 | navíos | 2 |
| 9429 | navego | 2 |
| 9430 | navegar | 2 |
| 9431 | navarino | 2 |
| 9432 | nadando | 2 |
| 9433 | nacimos | 2 |
| 9434 | naciese | 2 |
| 9435 | nacidas | 2 |
| 9436 | nacía | 2 |
| 9437 | muros | 2 |
| 9438 | murmure | 2 |
| 9439 | muriese | 2 |
| 9440 | murieron | 2 |
| 9441 | muriere | 2 |
| 9442 | muralla | 2 |
| 9443 | muñidor | 2 |
| 9444 | mulos | 2 |
| 9445 | muley | 2 |
| 9446 | muletas | 2 |
| 9447 | muladar | 2 |
| 9448 | mujeriegas | 2 |
| 9449 | mujercillas | 2 |
| 9450 | muéveme | 2 |
| 9451 | muévale | 2 |
| 9452 | muérese | 2 |
| 9453 | mudó | 2 |
| 9454 | mudéjares | 2 |
| 9455 | mude | 2 |
| 9456 | mudaron | 2 |
| 9457 | mudada | 2 |
| 9458 | mudable | 2 |
| 9459 | mudaban | 2 |
| 9460 | movible | 2 |
| 9461 | moví | 2 |
| 9462 | moverme | 2 |
| 9463 | moverle | 2 |
| 9464 | movemos | 2 |
| 9465 | motivo | 2 |
| 9466 | motes | 2 |
| 9467 | mostréis | 2 |
| 9468 | mostré | 2 |
| 9469 | mostrasen | 2 |
| 9470 | mostradme | 2 |
| 9471 | mosquitos | 2 |
| 9472 | mortaja | 2 |
| 9473 | morillo | 2 |
| 9474 | mordiera | 2 |
| 9475 | morderse | 2 |
| 9476 | mordaza | 2 |
| 9477 | morales | 2 |
| 9478 | moral | 2 |
| 9479 | montones | 2 |
| 9480 | montiña | 2 |
| 9481 | monteros | 2 |
| 9482 | montería | 2 |
| 9483 | monstro | 2 |
| 9484 | monos | 2 |
| 9485 | monjil | 2 |
| 9486 | mondas | 2 |
| 9487 | monarcas | 2 |
| 9488 | monacillo | 2 |
| 9489 | mona | 2 |
| 9490 | mollera | 2 |
| 9491 | molinera | 2 |
| 9492 | molida | 2 |
| 9493 | moldes | 2 |
| 9494 | moharracho | 2 |
| 9495 | modestia | 2 |
| 9496 | mocosa | 2 |
| 9497 | mitras | 2 |
| 9498 | mitra | 2 |
| 9499 | mirarla | 2 |
| 9500 | mirará | 2 |
| 9501 | mírala | 2 |
| 9502 | mirados | 2 |
| 9503 | mirábase | 2 |
| 9504 | mirábale | 2 |
| 9505 | mirá | 2 |
| 9506 | mintió | 2 |
| 9507 | minos | 2 |
| 9508 | ministerio | 2 |
| 9509 | milicia | 2 |
| 9510 | milanos | 2 |
| 9511 | milán | 2 |
| 9512 | milagrosos | 2 |
| 9513 | milagroso | 2 |
| 9514 | milagrosa | 2 |
| 9515 | migaja | 2 |
| 9516 | miento | 2 |
| 9517 | miedos | 2 |
| 9518 | mezclaron | 2 |
| 9519 | mezclados | 2 |
| 9520 | metros | 2 |
| 9521 | metieron | 2 |
| 9522 | metiendo | 2 |
| 9523 | metida | 2 |
| 9524 | metía | 2 |
| 9525 | meten | 2 |
| 9526 | metamorfóseos | 2 |
| 9527 | metáis | 2 |
| 9528 | metad | 2 |
| 9529 | mesura | 2 |
| 9530 | merezco | 2 |
| 9531 | merendaron | 2 |
| 9532 | mereció | 2 |
| 9533 | mereces | 2 |
| 9534 | meollo | 2 |
| 9535 | menudear | 2 |
| 9536 | menudeaban | 2 |
| 9537 | mentirás | 2 |
| 9538 | mentía | 2 |
| 9539 | mentecatos | 2 |
| 9540 | mentar | 2 |
| 9541 | menjurjes | 2 |
| 9542 | menesteroso | 2 |
| 9543 | menesterosas | 2 |
| 9544 | menesteres | 2 |
| 9545 | meneo | 2 |
| 9546 | meneando | 2 |
| 9547 | meneaba | 2 |
| 9548 | mendrugos | 2 |
| 9549 | mendigo | 2 |
| 9550 | mendigando | 2 |
| 9551 | melancólico | 2 |
| 9552 | melancolías | 2 |
| 9553 | mejorará | 2 |
| 9554 | mejorado | 2 |
| 9555 | medrados | 2 |
| 9556 | medos | 2 |
| 9557 | medido | 2 |
| 9558 | medianeros | 2 |
| 9559 | medalla | 2 |
| 9560 | meaja | 2 |
| 9561 | mazmorras | 2 |
| 9562 | mazmorra | 2 |
| 9563 | mayorales | 2 |
| 9564 | mayo | 2 |
| 9565 | matusalén | 2 |
| 9566 | mato | 2 |
| 9567 | mates | 2 |
| 9568 | materias | 2 |
| 9569 | matase | 2 |
| 9570 | mataron | 2 |
| 9571 | mataría | 2 |
| 9572 | matamoros | 2 |
| 9573 | matador | 2 |
| 9574 | máscara | 2 |
| 9575 | masca | 2 |
| 9576 | marzo | 2 |
| 9577 | martín | 2 |
| 9578 | martillo | 2 |
| 9579 | martas | 2 |
| 9580 | marruecos | 2 |
| 9581 | marinos | 2 |
| 9582 | marica | 2 |
| 9583 | marfil | 2 |
| 9584 | marcó | 2 |
| 9585 | marco | 2 |
| 9586 | marcial | 2 |
| 9587 | maravillaría | 2 |
| 9588 | maravillar | 2 |
| 9589 | maravillaba | 2 |
| 9590 | máquinas | 2 |
| 9591 | mapa | 2 |
| 9592 | mañero | 2 |
| 9593 | mañas | 2 |
| 9594 | manuel | 2 |
| 9595 | manual | 2 |
| 9596 | mantillas | 2 |
| 9597 | mantiene | 2 |
| 9598 | mantenimiento | 2 |
| 9599 | mantellina | 2 |
| 9600 | mantearon | 2 |
| 9601 | manteamientos | 2 |
| 9602 | manteadores | 2 |
| 9603 | mantas | 2 |
| 9604 | manquedad | 2 |
| 9605 | manosear | 2 |
| 9606 | manifiestamente | 2 |
| 9607 | manifestarse | 2 |
| 9608 | manida | 2 |
| 9609 | mándote | 2 |
| 9610 | mandóme | 2 |
| 9611 | mándoles | 2 |
| 9612 | mandobles | 2 |
| 9613 | manderecha | 2 |
| 9614 | mandato | 2 |
| 9615 | mandásemos | 2 |
| 9616 | mandas | 2 |
| 9617 | mandarle | 2 |
| 9618 | mandará | 2 |
| 9619 | mandándome | 2 |
| 9620 | mandándoles | 2 |
| 9621 | mandándole | 2 |
| 9622 | mandan | 2 |
| 9623 | mandamos | 2 |
| 9624 | mandáis | 2 |
| 9625 | mancilla | 2 |
| 9626 | manchegos | 2 |
| 9627 | manchas | 2 |
| 9628 | manca | 2 |
| 9629 | manantiales | 2 |
| 9630 | mamí | 2 |
| 9631 | malum | 2 |
| 9632 | maltrate | 2 |
| 9633 | maltratase | 2 |
| 9634 | malquisto | 2 |
| 9635 | malísima | 2 |
| 9636 | malintencionado | 2 |
| 9637 | maliciosos | 2 |
| 9638 | malhechores | 2 |
| 9639 | maletilla | 2 |
| 9640 | malencónico | 2 |
| 9641 | malenconía | 2 |
| 9642 | maleficio | 2 |
| 9643 | maleante | 2 |
| 9644 | maldijo | 2 |
| 9645 | maldiga | 2 |
| 9646 | malaventurados | 2 |
| 9647 | malandanzas | 2 |
| 9648 | malandante | 2 |
| 9649 | malamente | 2 |
| 9650 | maguera | 2 |
| 9651 | mágica | 2 |
| 9652 | maestría | 2 |
| 9653 | madrugó | 2 |
| 9654 | madrugar | 2 |
| 9655 | madrugado | 2 |
| 9656 | machuca | 2 |
| 9657 | machos | 2 |
| 9658 | lunes | 2 |
| 9659 | lucrecia | 2 |
| 9660 | lucios | 2 |
| 9661 | lucientes | 2 |
| 9662 | lúcidos | 2 |
| 9663 | lucida | 2 |
| 9664 | lucía | 2 |
| 9665 | longincuos | 2 |
| 9666 | londres | 2 |
| 9667 | lomo | 2 |
| 9668 | loca | 2 |
| 9669 | lobuna | 2 |
| 9670 | lóbregas | 2 |
| 9671 | loado | 2 |
| 9672 | loables | 2 |
| 9673 | loable | 2 |
| 9674 | lluvia | 2 |
| 9675 | lluevan | 2 |
| 9676 | lloviese | 2 |
| 9677 | llovidos | 2 |
| 9678 | llovido | 2 |
| 9679 | lloveré | 2 |
| 9680 | llorosos | 2 |
| 9681 | lloroso | 2 |
| 9682 | lloros | 2 |
| 9683 | llore | 2 |
| 9684 | llora | 2 |
| 9685 | lléveme | 2 |
| 9686 | llévelo | 2 |
| 9687 | llevé | 2 |
| 9688 | llévaste | 2 |
| 9689 | llevársele | 2 |
| 9690 | llevarse | 2 |
| 9691 | llevarla | 2 |
| 9692 | llevarían | 2 |
| 9693 | llevaran | 2 |
| 9694 | llevara | 2 |
| 9695 | llevándose | 2 |
| 9696 | llevándome | 2 |
| 9697 | llevándola | 2 |
| 9698 | llevadme | 2 |
| 9699 | llevadle | 2 |
| 9700 | llevadas | 2 |
| 9701 | llenó | 2 |
| 9702 | llenar | 2 |
| 9703 | lleguemos | 2 |
| 9704 | llego | 2 |
| 9705 | llegé | 2 |
| 9706 | llegaste | 2 |
| 9707 | llegásemos | 2 |
| 9708 | llegas | 2 |
| 9709 | llegaría | 2 |
| 9710 | llegaré | 2 |
| 9711 | llegare | 2 |
| 9712 | llegándole | 2 |
| 9713 | llegábase | 2 |
| 9714 | llanos | 2 |
| 9715 | llamen | 2 |
| 9716 | llamaría | 2 |
| 9717 | llamare | 2 |
| 9718 | llamaran | 2 |
| 9719 | llamándome | 2 |
| 9720 | llamándole | 2 |
| 9721 | llámame | 2 |
| 9722 | llámale | 2 |
| 9723 | llamados | 2 |
| 9724 | llamadas | 2 |
| 9725 | llagas | 2 |
| 9726 | liviano | 2 |
| 9727 | liviana | 2 |
| 9728 | litado | 2 |
| 9729 | lisa | 2 |
| 9730 | lirgandeo | 2 |
| 9731 | líquidas | 2 |
| 9732 | lino | 2 |
| 9733 | lindas | 2 |
| 9734 | lince | 2 |
| 9735 | limpióse | 2 |
| 9736 | limpie | 2 |
| 9737 | limpiárselos | 2 |
| 9738 | limpiarse | 2 |
| 9739 | limpiarme | 2 |
| 9740 | limitados | 2 |
| 9741 | limitada | 2 |
| 9742 | lililíes | 2 |
| 9743 | lii | 2 |
| 9744 | ligítima | 2 |
| 9745 | ligeramente | 2 |
| 9746 | ligadura | 2 |
| 9747 | licurgo | 2 |
| 9748 | lícitos | 2 |
| 9749 | licencias | 2 |
| 9750 | libró | 2 |
| 9751 | librero | 2 |
| 9752 | liberales | 2 |
| 9753 | li | 2 |
| 9754 | leyera | 2 |
| 9755 | leyentes | 2 |
| 9756 | leyéndola | 2 |
| 9757 | levantándome | 2 |
| 9758 | levantador | 2 |
| 9759 | levadiza | 2 |
| 9760 | letu | 2 |
| 9761 | leoncitos | 2 |
| 9762 | leo | 2 |
| 9763 | leídos | 2 |
| 9764 | leella | 2 |
| 9765 | lechos | 2 |
| 9766 | leamos | 2 |
| 9767 | lazadas | 2 |
| 9768 | lazada | 2 |
| 9769 | laven | 2 |
| 9770 | lavarse | 2 |
| 9771 | lavarme | 2 |
| 9772 | lavaba | 2 |
| 9773 | laurel | 2 |
| 9774 | laureado | 2 |
| 9775 | latino | 2 |
| 9776 | latines | 2 |
| 9777 | lastimosa | 2 |
| 9778 | lastimero | 2 |
| 9779 | lastimeras | 2 |
| 9780 | lástimas | 2 |
| 9781 | lastimados | 2 |
| 9782 | lascivia | 2 |
| 9783 | lanzando | 2 |
| 9784 | lanternas | 2 |
| 9785 | lanterna | 2 |
| 9786 | lance | 2 |
| 9787 | lámpara | 2 |
| 9788 | lamentaba | 2 |
| 9789 | laguna | 2 |
| 9790 | ladridos | 2 |
| 9791 | ladito | 2 |
| 9792 | lacedemonios | 2 |
| 9793 | lacayos | 2 |
| 9794 | labranza | 2 |
| 9795 | labrando | 2 |
| 9796 | l | 2 |
| 9797 | juzgas | 2 |
| 9798 | juzgara | 2 |
| 9799 | jurisperito | 2 |
| 9800 | juré | 2 |
| 9801 | juraré | 2 |
| 9802 | jurando | 2 |
| 9803 | junten | 2 |
| 9804 | juntáronse | 2 |
| 9805 | juntar | 2 |
| 9806 | juntándose | 2 |
| 9807 | juntaba | 2 |
| 9808 | juncos | 2 |
| 9809 | jumentiles | 2 |
| 9810 | jumá | 2 |
| 9811 | jueguen | 2 |
| 9812 | judiciario | 2 |
| 9813 | jironado | 2 |
| 9814 | jirón | 2 |
| 9815 | jinete | 2 |
| 9816 | jimia | 2 |
| 9817 | jesús | 2 |
| 9818 | jesucristo | 2 |
| 9819 | jerigonza | 2 |
| 9820 | jarama | 2 |
| 9821 | jadeando | 2 |
| 9822 | jabonaduras | 2 |
| 9823 | jabonado | 2 |
| 9824 | ix | 2 |
| 9825 | iv | 2 |
| 9826 | italiano | 2 |
| 9827 | irte | 2 |
| 9828 | irritase | 2 |
| 9829 | irritar | 2 |
| 9830 | iréis | 2 |
| 9831 | irás | 2 |
| 9832 | invito | 2 |
| 9833 | invisibles | 2 |
| 9834 | invidioso | 2 |
| 9835 | invidiado | 2 |
| 9836 | invicto | 2 |
| 9837 | inventores | 2 |
| 9838 | inventó | 2 |
| 9839 | inventado | 2 |
| 9840 | invencibles | 2 |
| 9841 | intricadas | 2 |
| 9842 | intricada | 2 |
| 9843 | intitulada | 2 |
| 9844 | intitulaba | 2 |
| 9845 | intitula | 2 |
| 9846 | íntimo | 2 |
| 9847 | intervalos | 2 |
| 9848 | interrumpáis | 2 |
| 9849 | interromper | 2 |
| 9850 | intereses | 2 |
| 9851 | intentos | 2 |
| 9852 | intentarlas | 2 |
| 9853 | intentan | 2 |
| 9854 | intenta | 2 |
| 9855 | intensa | 2 |
| 9856 | intencionadas | 2 |
| 9857 | inteligente | 2 |
| 9858 | instigado | 2 |
| 9859 | instabilidad | 2 |
| 9860 | insignias | 2 |
| 9861 | insignia | 2 |
| 9862 | inreparable | 2 |
| 9863 | inquietud | 2 |
| 9864 | inquieta | 2 |
| 9865 | inmundos | 2 |
| 9866 | inmundicia | 2 |
| 9867 | injusta | 2 |
| 9868 | inhabitable | 2 |
| 9869 | inglaterra | 2 |
| 9870 | infundan | 2 |
| 9871 | informó | 2 |
| 9872 | informarse | 2 |
| 9873 | informándose | 2 |
| 9874 | influjo | 2 |
| 9875 | infernal | 2 |
| 9876 | infante | 2 |
| 9877 | infamia | 2 |
| 9878 | infames | 2 |
| 9879 | inexpugnable | 2 |
| 9880 | inexcusables | 2 |
| 9881 | industrias | 2 |
| 9882 | industriado | 2 |
| 9883 | indubitables | 2 |
| 9884 | indubitablemente | 2 |
| 9885 | indignación | 2 |
| 9886 | indecente | 2 |
| 9887 | incurrir | 2 |
| 9888 | incurra | 2 |
| 9889 | inconvinientes | 2 |
| 9890 | inconsiderada | 2 |
| 9891 | ínclito | 2 |
| 9892 | inclinarme | 2 |
| 9893 | inclinando | 2 |
| 9894 | inclina | 2 |
| 9895 | incitan | 2 |
| 9896 | incitado | 2 |
| 9897 | incita | 2 |
| 9898 | incendio | 2 |
| 9899 | incansable | 2 |
| 9900 | improvisamente | 2 |
| 9901 | impropiedades | 2 |
| 9902 | imprimo | 2 |
| 9903 | imprimió | 2 |
| 9904 | imprime | 2 |
| 9905 | imprima | 2 |
| 9906 | impresores | 2 |
| 9907 | imposibilita | 2 |
| 9908 | importunó | 2 |
| 9909 | importunado | 2 |
| 9910 | importunaciones | 2 |
| 9911 | importara | 2 |
| 9912 | importantes | 2 |
| 9913 | impide | 2 |
| 9914 | ímpetus | 2 |
| 9915 | impertinencia | 2 |
| 9916 | impenetrables | 2 |
| 9917 | impelió | 2 |
| 9918 | impaciente | 2 |
| 9919 | imitarlos | 2 |
| 9920 | imaginé | 2 |
| 9921 | imaginadas | 2 |
| 9922 | imagina | 2 |
| 9923 | ilustrísimo | 2 |
| 9924 | ilustrísima | 2 |
| 9925 | iii | 2 |
| 9926 | igualen | 2 |
| 9927 | igualará | 2 |
| 9928 | igualara | 2 |
| 9929 | igualan | 2 |
| 9930 | igualaban | 2 |
| 9931 | ignoraban | 2 |
| 9932 | ignoraba | 2 |
| 9933 | idioma | 2 |
| 9934 | idea | 2 |
| 9935 | íbanse | 2 |
| 9936 | i | 2 |
| 9937 | huyen | 2 |
| 9938 | huyan | 2 |
| 9939 | huso | 2 |
| 9940 | hurtar | 2 |
| 9941 | hurón | 2 |
| 9942 | hundía | 2 |
| 9943 | humores | 2 |
| 9944 | humilla | 2 |
| 9945 | humedecer | 2 |
| 9946 | huido | 2 |
| 9947 | huía | 2 |
| 9948 | huevo | 2 |
| 9949 | huérfana | 2 |
| 9950 | huellas | 2 |
| 9951 | huelgo | 2 |
| 9952 | hubieras | 2 |
| 9953 | hoyos | 2 |
| 9954 | hoyo | 2 |
| 9955 | horror | 2 |
| 9956 | horrenda | 2 |
| 9957 | horizonte | 2 |
| 9958 | horadados | 2 |
| 9959 | honralle | 2 |
| 9960 | hondas | 2 |
| 9961 | holgazanes | 2 |
| 9962 | holgaré | 2 |
| 9963 | holgándose | 2 |
| 9964 | holandas | 2 |
| 9965 | hogaño | 2 |
| 9966 | hoces | 2 |
| 9967 | hirviendo | 2 |
| 9968 | hirió | 2 |
| 9969 | hipogrifo | 2 |
| 9970 | hipocresía | 2 |
| 9971 | hipócrates | 2 |
| 9972 | hipérboles | 2 |
| 9973 | hinque | 2 |
| 9974 | hilos | 2 |
| 9975 | hilar | 2 |
| 9976 | hijodalgo | 2 |
| 9977 | higa | 2 |
| 9978 | hieren | 2 |
| 9979 | hiera | 2 |
| 9980 | hidalga | 2 |
| 9981 | hiciésemos | 2 |
| 9982 | hicieres | 2 |
| 9983 | hicieren | 2 |
| 9984 | hiciérades | 2 |
| 9985 | herrero | 2 |
| 9986 | herrar | 2 |
| 9987 | herraduras | 2 |
| 9988 | heroica | 2 |
| 9989 | hermosísimo | 2 |
| 9990 | hermosean | 2 |
| 9991 | herejes | 2 |
| 9992 | herederos | 2 |
| 9993 | heredado | 2 |
| 9994 | hereda | 2 |
| 9995 | hémosle | 2 |
| 9996 | hechuras | 2 |
| 9997 | hechiceras | 2 |
| 9998 | hartarme | 2 |
| 9999 | hartar | 2 |
| 10000 | hartaba | 2 |
| 10001 | harbar | 2 |
| 10002 | harás | 2 |
| 10003 | hanegas | 2 |
| 10004 | hambrientos | 2 |
| 10005 | hambriento | 2 |
| 10006 | halo | 2 |
| 10007 | hallasen | 2 |
| 10008 | hallarían | 2 |
| 10009 | hallaren | 2 |
| 10010 | hallaremos | 2 |
| 10011 | hallaré | 2 |
| 10012 | hallare | 2 |
| 10013 | hallarán | 2 |
| 10014 | hallándole | 2 |
| 10015 | haldas | 2 |
| 10016 | halcón | 2 |
| 10017 | haciéndote | 2 |
| 10018 | haciendas | 2 |
| 10019 | hacíase | 2 |
| 10020 | hacíamos | 2 |
| 10021 | hacerlos | 2 |
| 10022 | haceos | 2 |
| 10023 | hacello | 2 |
| 10024 | hablaron | 2 |
| 10025 | hablaré | 2 |
| 10026 | hablaran | 2 |
| 10027 | hablándole | 2 |
| 10028 | hablan | 2 |
| 10029 | hablamos | 2 |
| 10030 | habitadores | 2 |
| 10031 | habiéndosele | 2 |
| 10032 | habíase | 2 |
| 10033 | habíales | 2 |
| 10034 | habíades | 2 |
| 10035 | habérsele | 2 |
| 10036 | habernos | 2 |
| 10037 | habérmelo | 2 |
| 10038 | haberlas | 2 |
| 10039 | haberes | 2 |
| 10040 | habéisla | 2 |
| 10041 | gustó | 2 |
| 10042 | gustas | 2 |
| 10043 | gustáredes | 2 |
| 10044 | gustare | 2 |
| 10045 | gustara | 2 |
| 10046 | gustando | 2 |
| 10047 | gula | 2 |
| 10048 | guirnalda | 2 |
| 10049 | guiomar | 2 |
| 10050 | guió | 2 |
| 10051 | guinea | 2 |
| 10052 | guiados | 2 |
| 10053 | guelte | 2 |
| 10054 | guarniciones | 2 |
| 10055 | guardia | 2 |
| 10056 | guardasen | 2 |
| 10057 | guardarlos | 2 |
| 10058 | guardará | 2 |
| 10059 | guardados | 2 |
| 10060 | guardábala | 2 |
| 10061 | guante | 2 |
| 10062 | guadalajara | 2 |
| 10063 | gruta | 2 |
| 10064 | gruñir | 2 |
| 10065 | gruñían | 2 |
| 10066 | grosero | 2 |
| 10067 | gritando | 2 |
| 10068 | gritaba | 2 |
| 10069 | grifo | 2 |
| 10070 | grata | 2 |
| 10071 | granjería | 2 |
| 10072 | granjearme | 2 |
| 10073 | granizo | 2 |
| 10074 | grandor | 2 |
| 10075 | gramática | 2 |
| 10076 | grajos | 2 |
| 10077 | gradas | 2 |
| 10078 | graciosas | 2 |
| 10079 | grabada | 2 |
| 10080 | gozasen | 2 |
| 10081 | gozase | 2 |
| 10082 | gozaré | 2 |
| 10083 | gozara | 2 |
| 10084 | góticas | 2 |
| 10085 | gotas | 2 |
| 10086 | gordiano | 2 |
| 10087 | gonzález | 2 |
| 10088 | goloso | 2 |
| 10089 | golosina | 2 |
| 10090 | gola | 2 |
| 10091 | godo | 2 |
| 10092 | gocen | 2 |
| 10093 | gobierne | 2 |
| 10094 | gobiernas | 2 |
| 10095 | gobernadora | 2 |
| 10096 | gobernaba | 2 |
| 10097 | gitano | 2 |
| 10098 | girifaltes | 2 |
| 10099 | girifalte | 2 |
| 10100 | gil | 2 |
| 10101 | gigantazo | 2 |
| 10102 | giganta | 2 |
| 10103 | gentilidad | 2 |
| 10104 | generosidad | 2 |
| 10105 | generosa | 2 |
| 10106 | gatas | 2 |
| 10107 | gastó | 2 |
| 10108 | gastarlas | 2 |
| 10109 | gastados | 2 |
| 10110 | gastador | 2 |
| 10111 | gascona | 2 |
| 10112 | garrote | 2 |
| 10113 | garbanzos | 2 |
| 10114 | gangoso | 2 |
| 10115 | ganen | 2 |
| 10116 | gandalín | 2 |
| 10117 | ganarla | 2 |
| 10118 | ganapanes | 2 |
| 10119 | ganapán | 2 |
| 10120 | ganando | 2 |
| 10121 | gananciosos | 2 |
| 10122 | ganan | 2 |
| 10123 | ganaba | 2 |
| 10124 | galocha | 2 |
| 10125 | galateas | 2 |
| 10126 | galanas | 2 |
| 10127 | gaita | 2 |
| 10128 | furto | 2 |
| 10129 | furiosa | 2 |
| 10130 | fundo | 2 |
| 10131 | fundamentos | 2 |
| 10132 | fundado | 2 |
| 10133 | funda | 2 |
| 10134 | fuéronse | 2 |
| 10135 | fuéramos | 2 |
| 10136 | fuérades | 2 |
| 10137 | fuelles | 2 |
| 10138 | frontino | 2 |
| 10139 | friscal | 2 |
| 10140 | frisar | 2 |
| 10141 | frescas | 2 |
| 10142 | freír | 2 |
| 10143 | francisca | 2 |
| 10144 | fragua | 2 |
| 10145 | fosca | 2 |
| 10146 | forzados | 2 |
| 10147 | forzadas | 2 |
| 10148 | forzaba | 2 |
| 10149 | fortu | 2 |
| 10150 | forjó | 2 |
| 10151 | fonseca | 2 |
| 10152 | folgar | 2 |
| 10153 | florimorte | 2 |
| 10154 | flo | 2 |
| 10155 | flemáticos | 2 |
| 10156 | flacos | 2 |
| 10157 | fisonomía | 2 |
| 10158 | fírmela | 2 |
| 10159 | firmada | 2 |
| 10160 | fió | 2 |
| 10161 | fingidamente | 2 |
| 10162 | fingen | 2 |
| 10163 | finge | 2 |
| 10164 | filosofías | 2 |
| 10165 | filo | 2 |
| 10166 | filis | 2 |
| 10167 | fili | 2 |
| 10168 | figurósele | 2 |
| 10169 | fiarse | 2 |
| 10170 | fiarme | 2 |
| 10171 | fiada | 2 |
| 10172 | fía | 2 |
| 10173 | festivo | 2 |
| 10174 | ferro | 2 |
| 10175 | fernández | 2 |
| 10176 | ferida | 2 |
| 10177 | fenecer | 2 |
| 10178 | felicísimos | 2 |
| 10179 | felicísimamente | 2 |
| 10180 | felices | 2 |
| 10181 | fechurías | 2 |
| 10182 | fechorías | 2 |
| 10183 | febrero | 2 |
| 10184 | favorecida | 2 |
| 10185 | favorecerme | 2 |
| 10186 | favorecerle | 2 |
| 10187 | fatigue | 2 |
| 10188 | fatigar | 2 |
| 10189 | farsantes | 2 |
| 10190 | farol | 2 |
| 10191 | faltarle | 2 |
| 10192 | falsamente | 2 |
| 10193 | faldamentos | 2 |
| 10194 | fajas | 2 |
| 10195 | faga | 2 |
| 10196 | facinoroso | 2 |
| 10197 | facilitaba | 2 |
| 10198 | facilita | 2 |
| 10199 | facienda | 2 |
| 10200 | facción | 2 |
| 10201 | fabulosos | 2 |
| 10202 | fabricar | 2 |
| 10203 | fabricador | 2 |
| 10204 | extraordinarias | 2 |
| 10205 | expulsión | 2 |
| 10206 | expiriencia | 2 |
| 10207 | exequias | 2 |
| 10208 | excepción | 2 |
| 10209 | excelentes | 2 |
| 10210 | excelente | 2 |
| 10211 | examen | 2 |
| 10212 | exagerando | 2 |
| 10213 | exageración | 2 |
| 10214 | europa | 2 |
| 10215 | eugenio | 2 |
| 10216 | etiopía | 2 |
| 10217 | eternos | 2 |
| 10218 | estúvose | 2 |
| 10219 | estuvieras | 2 |
| 10220 | estupenda | 2 |
| 10221 | estudia | 2 |
| 10222 | estuche | 2 |
| 10223 | estropeados | 2 |
| 10224 | estropeado | 2 |
| 10225 | estremadas | 2 |
| 10226 | estrellado | 2 |
| 10227 | estraordinario | 2 |
| 10228 | estrañezas | 2 |
| 10229 | estranjero | 2 |
| 10230 | estorbo | 2 |
| 10231 | estorbara | 2 |
| 10232 | estorba | 2 |
| 10233 | estopa | 2 |
| 10234 | estirpe | 2 |
| 10235 | estirarse | 2 |
| 10236 | estirado | 2 |
| 10237 | estío | 2 |
| 10238 | estimas | 2 |
| 10239 | estimaré | 2 |
| 10240 | estimara | 2 |
| 10241 | estil | 2 |
| 10242 | estiércol | 2 |
| 10243 | estériles | 2 |
| 10244 | estenso | 2 |
| 10245 | estendiendo | 2 |
| 10246 | estenderse | 2 |
| 10247 | estarlo | 2 |
| 10248 | estarían | 2 |
| 10249 | estaos | 2 |
| 10250 | estanterol | 2 |
| 10251 | estándola | 2 |
| 10252 | estáme | 2 |
| 10253 | estada | 2 |
| 10254 | estaciones | 2 |
| 10255 | establo | 2 |
| 10256 | estabas | 2 |
| 10257 | estábale | 2 |
| 10258 | est | 2 |
| 10259 | esquiva | 2 |
| 10260 | esquila | 2 |
| 10261 | espuela | 2 |
| 10262 | espolear | 2 |
| 10263 | esplendor | 2 |
| 10264 | espirar | 2 |
| 10265 | espesura | 2 |
| 10266 | espeso | 2 |
| 10267 | espesa | 2 |
| 10268 | esperó | 2 |
| 10269 | esperes | 2 |
| 10270 | espérenme | 2 |
| 10271 | espérate | 2 |
| 10272 | esperasen | 2 |
| 10273 | esperaría | 2 |
| 10274 | esperara | 2 |
| 10275 | esperándole | 2 |
| 10276 | espérame | 2 |
| 10277 | esperados | 2 |
| 10278 | especulación | 2 |
| 10279 | esparcieron | 2 |
| 10280 | esparciendo | 2 |
| 10281 | espanten | 2 |
| 10282 | espantas | 2 |
| 10283 | espantar | 2 |
| 10284 | espantados | 2 |
| 10285 | eslabón | 2 |
| 10286 | esgrimir | 2 |
| 10287 | esgrima | 2 |
| 10288 | esfuerza | 2 |
| 10289 | esfuércese | 2 |
| 10290 | esforzados | 2 |
| 10291 | esforcé | 2 |
| 10292 | esfera | 2 |
| 10293 | eses | 2 |
| 10294 | esencia | 2 |
| 10295 | escusó | 2 |
| 10296 | escusarás | 2 |
| 10297 | escusara | 2 |
| 10298 | escuro | 2 |
| 10299 | escureció | 2 |
| 10300 | escurecerse | 2 |
| 10301 | escurecerlos | 2 |
| 10302 | escurecen | 2 |
| 10303 | escudriñador | 2 |
| 10304 | escucho | 2 |
| 10305 | escuchen | 2 |
| 10306 | escuchas | 2 |
| 10307 | escucharte | 2 |
| 10308 | escuchare | 2 |
| 10309 | escuchándole | 2 |
| 10310 | escuchada | 2 |
| 10311 | escuchaban | 2 |
| 10312 | escuadra | 2 |
| 10313 | escrupulosos | 2 |
| 10314 | escrupuloso | 2 |
| 10315 | escritor | 2 |
| 10316 | escribirse | 2 |
| 10317 | escribirla | 2 |
| 10318 | escribanos | 2 |
| 10319 | escondiese | 2 |
| 10320 | esconde | 2 |
| 10321 | escojo | 2 |
| 10322 | escogiese | 2 |
| 10323 | escogieron | 2 |
| 10324 | escogerme | 2 |
| 10325 | escoge | 2 |
| 10326 | esclavinas | 2 |
| 10327 | escarpines | 2 |
| 10328 | escaramuza | 2 |
| 10329 | escape | 2 |
| 10330 | escapase | 2 |
| 10331 | escapado | 2 |
| 10332 | escalera | 2 |
| 10333 | erudito | 2 |
| 10334 | errada | 2 |
| 10335 | eris | 2 |
| 10336 | erat | 2 |
| 10337 | érades | 2 |
| 10338 | equinocial | 2 |
| 10339 | equidad | 2 |
| 10340 | epigramas | 2 |
| 10341 | envueltos | 2 |
| 10342 | envuelta | 2 |
| 10343 | envoltorio | 2 |
| 10344 | envite | 2 |
| 10345 | envíeme | 2 |
| 10346 | envidioso | 2 |
| 10347 | envidio | 2 |
| 10348 | envidiara | 2 |
| 10349 | envidiado | 2 |
| 10350 | enviando | 2 |
| 10351 | envasó | 2 |
| 10352 | entróse | 2 |
| 10353 | entronizado | 2 |
| 10354 | entristezca | 2 |
| 10355 | entristecióse | 2 |
| 10356 | entristecía | 2 |
| 10357 | entristecerse | 2 |
| 10358 | entristece | 2 |
| 10359 | entreverado | 2 |
| 10360 | entretuviesen | 2 |
| 10361 | entretuviese | 2 |
| 10362 | entretuviera | 2 |
| 10363 | entretenida | 2 |
| 10364 | entretenerme | 2 |
| 10365 | entretenerle | 2 |
| 10366 | entreoído | 2 |
| 10367 | entremos | 2 |
| 10368 | entremeterse | 2 |
| 10369 | entremeter | 2 |
| 10370 | entregue | 2 |
| 10371 | entregase | 2 |
| 10372 | entregaron | 2 |
| 10373 | entregara | 2 |
| 10374 | entregándose | 2 |
| 10375 | entrarnos | 2 |
| 10376 | entraré | 2 |
| 10377 | entrará | 2 |
| 10378 | entraban | 2 |
| 10379 | entierren | 2 |
| 10380 | enterrasen | 2 |
| 10381 | enterrarte | 2 |
| 10382 | enterramos | 2 |
| 10383 | enterrada | 2 |
| 10384 | enterneció | 2 |
| 10385 | enternecer | 2 |
| 10386 | enterados | 2 |
| 10387 | entendidas | 2 |
| 10388 | entenderla | 2 |
| 10389 | entenderemos | 2 |
| 10390 | entendedor | 2 |
| 10391 | ensilló | 2 |
| 10392 | ensillando | 2 |
| 10393 | ensilla | 2 |
| 10394 | ensayarse | 2 |
| 10395 | ensartar | 2 |
| 10396 | ensarta | 2 |
| 10397 | ensanche | 2 |
| 10398 | ensancha | 2 |
| 10399 | ensalmo | 2 |
| 10400 | enrizados | 2 |
| 10401 | enriquecen | 2 |
| 10402 | enrejados | 2 |
| 10403 | enoje | 2 |
| 10404 | enmendar | 2 |
| 10405 | enlutada | 2 |
| 10406 | engrandecer | 2 |
| 10407 | engrandecen | 2 |
| 10408 | engendré | 2 |
| 10409 | engendran | 2 |
| 10410 | engañóse | 2 |
| 10411 | engañó | 2 |
| 10412 | engañes | 2 |
| 10413 | engañáis | 2 |
| 10414 | enfriase | 2 |
| 10415 | enfermedades | 2 |
| 10416 | enemistad | 2 |
| 10417 | enea | 2 |
| 10418 | endiablados | 2 |
| 10419 | enderécese | 2 |
| 10420 | endechas | 2 |
| 10421 | encumbrada | 2 |
| 10422 | encuentra | 2 |
| 10423 | encubrirlo | 2 |
| 10424 | encubrió | 2 |
| 10425 | encubriera | 2 |
| 10426 | encubriendo | 2 |
| 10427 | encontrarse | 2 |
| 10428 | encontrándose | 2 |
| 10429 | encomiende | 2 |
| 10430 | encomiendan | 2 |
| 10431 | encomienda | 2 |
| 10432 | encomendó | 2 |
| 10433 | encomendarnos | 2 |
| 10434 | encomendándonos | 2 |
| 10435 | encogida | 2 |
| 10436 | encierro | 2 |
| 10437 | enciende | 2 |
| 10438 | encerrarse | 2 |
| 10439 | encerrarme | 2 |
| 10440 | encerrándose | 2 |
| 10441 | encerraban | 2 |
| 10442 | encendió | 2 |
| 10443 | encarnado | 2 |
| 10444 | encargo | 2 |
| 10445 | encargándole | 2 |
| 10446 | encarecimientos | 2 |
| 10447 | encarecida | 2 |
| 10448 | encarecerlos | 2 |
| 10449 | encarecerlo | 2 |
| 10450 | encantó | 2 |
| 10451 | encantadora | 2 |
| 10452 | encanta | 2 |
| 10453 | encaminan | 2 |
| 10454 | encaminado | 2 |
| 10455 | encaminaba | 2 |
| 10456 | encamina | 2 |
| 10457 | encajaron | 2 |
| 10458 | encajado | 2 |
| 10459 | enarboló | 2 |
| 10460 | enanos | 2 |
| 10461 | enamora | 2 |
| 10462 | enalbardase | 2 |
| 10463 | enalbardado | 2 |
| 10464 | émulo | 2 |
| 10465 | empuñó | 2 |
| 10466 | empuñadura | 2 |
| 10467 | empreñaría | 2 |
| 10468 | emprentas | 2 |
| 10469 | emprendido | 2 |
| 10470 | empinadas | 2 |
| 10471 | empedernido | 2 |
| 10472 | empanada | 2 |
| 10473 | emienda | 2 |
| 10474 | emerencia | 2 |
| 10475 | embusteros | 2 |
| 10476 | embozada | 2 |
| 10477 | embosque | 2 |
| 10478 | embobados | 2 |
| 10479 | embobado | 2 |
| 10480 | embisten | 2 |
| 10481 | embista | 2 |
| 10482 | embestirse | 2 |
| 10483 | embestido | 2 |
| 10484 | embelesado | 2 |
| 10485 | embebido | 2 |
| 10486 | embebecido | 2 |
| 10487 | embaular | 2 |
| 10488 | embarcarnos | 2 |
| 10489 | embarazos | 2 |
| 10490 | embajadas | 2 |
| 10491 | elogio | 2 |
| 10492 | elocuentes | 2 |
| 10493 | elocución | 2 |
| 10494 | elevado | 2 |
| 10495 | elegir | 2 |
| 10496 | elegantes | 2 |
| 10497 | eleción | 2 |
| 10498 | ejercitando | 2 |
| 10499 | ejercitada | 2 |
| 10500 | ejecutase | 2 |
| 10501 | ejecutan | 2 |
| 10502 | efectos | 2 |
| 10503 | ecos | 2 |
| 10504 | eco | 2 |
| 10505 | eclesiásticos | 2 |
| 10506 | echóse | 2 |
| 10507 | echo | 2 |
| 10508 | écheme | 2 |
| 10509 | eché | 2 |
| 10510 | echasen | 2 |
| 10511 | échase | 2 |
| 10512 | echarse | 2 |
| 10513 | echaría | 2 |
| 10514 | echaremos | 2 |
| 10515 | echaré | 2 |
| 10516 | echándose | 2 |
| 10517 | echándolos | 2 |
| 10518 | echan | 2 |
| 10519 | eceto | 2 |
| 10520 | durmiese | 2 |
| 10521 | durmamos | 2 |
| 10522 | durísimos | 2 |
| 10523 | duran | 2 |
| 10524 | duradera | 2 |
| 10525 | duquesas | 2 |
| 10526 | dulzainas | 2 |
| 10527 | dulcísimos | 2 |
| 10528 | dulcísimo | 2 |
| 10529 | dulcineas | 2 |
| 10530 | duendes | 2 |
| 10531 | dudes | 2 |
| 10532 | dudaban | 2 |
| 10533 | dotado | 2 |
| 10534 | dormiré | 2 |
| 10535 | dormíos | 2 |
| 10536 | dormimos | 2 |
| 10537 | dormí | 2 |
| 10538 | dorados | 2 |
| 10539 | donoso | 2 |
| 10540 | donosa | 2 |
| 10541 | donas | 2 |
| 10542 | domingos | 2 |
| 10543 | domeñar | 2 |
| 10544 | dolorosa | 2 |
| 10545 | dolo | 2 |
| 10546 | doliendo | 2 |
| 10547 | dolerme | 2 |
| 10548 | doblones | 2 |
| 10549 | doblo | 2 |
| 10550 | doblas | 2 |
| 10551 | doblar | 2 |
| 10552 | dobla | 2 |
| 10553 | divulgóse | 2 |
| 10554 | divisó | 2 |
| 10555 | divisar | 2 |
| 10556 | divididos | 2 |
| 10557 | dividido | 2 |
| 10558 | distinto | 2 |
| 10559 | distantes | 2 |
| 10560 | disputa | 2 |
| 10561 | dispusiese | 2 |
| 10562 | dispuesta | 2 |
| 10563 | disponer | 2 |
| 10564 | disparó | 2 |
| 10565 | disparatada | 2 |
| 10566 | dispararon | 2 |
| 10567 | disparar | 2 |
| 10568 | disparando | 2 |
| 10569 | disparaban | 2 |
| 10570 | disimules | 2 |
| 10571 | disimule | 2 |
| 10572 | disimulando | 2 |
| 10573 | disimulación | 2 |
| 10574 | disignios | 2 |
| 10575 | disfrazaron | 2 |
| 10576 | disfrazado | 2 |
| 10577 | disfrazada | 2 |
| 10578 | discurrir | 2 |
| 10579 | discurriendo | 2 |
| 10580 | discurría | 2 |
| 10581 | discurra | 2 |
| 10582 | dirigirlos | 2 |
| 10583 | dirían | 2 |
| 10584 | diretes | 2 |
| 10585 | diréisle | 2 |
| 10586 | diputó | 2 |
| 10587 | dioses | 2 |
| 10588 | diosa | 2 |
| 10589 | diome | 2 |
| 10590 | dímosle | 2 |
| 10591 | dimes | 2 |
| 10592 | dímelo | 2 |
| 10593 | dilo | 2 |
| 10594 | diligente | 2 |
| 10595 | dilate | 2 |
| 10596 | dilatando | 2 |
| 10597 | dilata | 2 |
| 10598 | díjose | 2 |
| 10599 | dijistes | 2 |
| 10600 | díganlo | 2 |
| 10601 | dígale | 2 |
| 10602 | dieta | 2 |
| 10603 | diestros | 2 |
| 10604 | dieses | 2 |
| 10605 | diésemos | 2 |
| 10606 | diéronselos | 2 |
| 10607 | diéronsela | 2 |
| 10608 | dieras | 2 |
| 10609 | diciéndoselo | 2 |
| 10610 | dichosos | 2 |
| 10611 | dichosas | 2 |
| 10612 | dícenme | 2 |
| 10613 | dibujos | 2 |
| 10614 | dianas | 2 |
| 10615 | diabólica | 2 |
| 10616 | devaneos | 2 |
| 10617 | deudor | 2 |
| 10618 | detúvole | 2 |
| 10619 | detuviesen | 2 |
| 10620 | detestables | 2 |
| 10621 | detestable | 2 |
| 10622 | determino | 2 |
| 10623 | determinar | 2 |
| 10624 | deteniéndose | 2 |
| 10625 | detenida | 2 |
| 10626 | detenernos | 2 |
| 10627 | desvióse | 2 |
| 10628 | desviarse | 2 |
| 10629 | desviada | 2 |
| 10630 | desvarío | 2 |
| 10631 | desvariados | 2 |
| 10632 | desvariadas | 2 |
| 10633 | desvanecidos | 2 |
| 10634 | desvalijando | 2 |
| 10635 | desuso | 2 |
| 10636 | desusados | 2 |
| 10637 | desunció | 2 |
| 10638 | destruyó | 2 |
| 10639 | destruye | 2 |
| 10640 | destruirme | 2 |
| 10641 | destrozo | 2 |
| 10642 | destroza | 2 |
| 10643 | destino | 2 |
| 10644 | desterrar | 2 |
| 10645 | desterrados | 2 |
| 10646 | destaja | 2 |
| 10647 | despuntan | 2 |
| 10648 | desprecio | 2 |
| 10649 | desposados | 2 |
| 10650 | despojo | 2 |
| 10651 | despojar | 2 |
| 10652 | despiertos | 2 |
| 10653 | despiertas | 2 |
| 10654 | despiadado | 2 |
| 10655 | despertalle | 2 |
| 10656 | despeñar | 2 |
| 10657 | despensero | 2 |
| 10658 | despejar | 2 |
| 10659 | despedimos | 2 |
| 10660 | despechéis | 2 |
| 10661 | despachar | 2 |
| 10662 | despachado | 2 |
| 10663 | desollar | 2 |
| 10664 | desnudó | 2 |
| 10665 | desnudas | 2 |
| 10666 | desnudarse | 2 |
| 10667 | desnudaron | 2 |
| 10668 | desnudándose | 2 |
| 10669 | desmiento | 2 |
| 10670 | desmazalado | 2 |
| 10671 | desmaye | 2 |
| 10672 | desmande | 2 |
| 10673 | deslocado | 2 |
| 10674 | deslizaba | 2 |
| 10675 | desliáronle | 2 |
| 10676 | desleal | 2 |
| 10677 | deshoras | 2 |
| 10678 | deshonrada | 2 |
| 10679 | deshonestidades | 2 |
| 10680 | deshonestidad | 2 |
| 10681 | desgreñada | 2 |
| 10682 | desgraciada | 2 |
| 10683 | desfaciendo | 2 |
| 10684 | desface | 2 |
| 10685 | desesperó | 2 |
| 10686 | desespérese | 2 |
| 10687 | desenvolturas | 2 |
| 10688 | desenvainó | 2 |
| 10689 | desenvainando | 2 |
| 10690 | desengañó | 2 |
| 10691 | desenfadado | 2 |
| 10692 | desenfadada | 2 |
| 10693 | desencante | 2 |
| 10694 | desencantase | 2 |
| 10695 | desencantados | 2 |
| 10696 | desencajó | 2 |
| 10697 | desembolsó | 2 |
| 10698 | desembolsase | 2 |
| 10699 | desembarcado | 2 |
| 10700 | desembarcadero | 2 |
| 10701 | deseas | 2 |
| 10702 | desearme | 2 |
| 10703 | desearle | 2 |
| 10704 | desdichadas | 2 |
| 10705 | desdeñar | 2 |
| 10706 | descuida | 2 |
| 10707 | descubriría | 2 |
| 10708 | descubrían | 2 |
| 10709 | descubiertas | 2 |
| 10710 | descosiese | 2 |
| 10711 | descortesía | 2 |
| 10712 | descontento | 2 |
| 10713 | desconsolados | 2 |
| 10714 | descomunales | 2 |
| 10715 | descomulgados | 2 |
| 10716 | descomulgado | 2 |
| 10717 | descompuesto | 2 |
| 10718 | descompuestas | 2 |
| 10719 | descompostura | 2 |
| 10720 | descomedimiento | 2 |
| 10721 | descolorido | 2 |
| 10722 | descolgó | 2 |
| 10723 | descolgarse | 2 |
| 10724 | descendientes | 2 |
| 10725 | descarnada | 2 |
| 10726 | descargo | 2 |
| 10727 | descansará | 2 |
| 10728 | descansar | 2 |
| 10729 | descansando | 2 |
| 10730 | descalza | 2 |
| 10731 | descaecimiento | 2 |
| 10732 | descabezar | 2 |
| 10733 | desbaratado | 2 |
| 10734 | desbaratada | 2 |
| 10735 | desayunarse | 2 |
| 10736 | desaté | 2 |
| 10737 | desatada | 2 |
| 10738 | desasosiegos | 2 |
| 10739 | desasirse | 2 |
| 10740 | desas | 2 |
| 10741 | desarmando | 2 |
| 10742 | desapercebido | 2 |
| 10743 | desalmada | 2 |
| 10744 | desagradecidos | 2 |
| 10745 | desafiador | 2 |
| 10746 | derrumbadero | 2 |
| 10747 | derribaron | 2 |
| 10748 | derriba | 2 |
| 10749 | derredor | 2 |
| 10750 | derrame | 2 |
| 10751 | derrámasele | 2 |
| 10752 | derramado | 2 |
| 10753 | derramada | 2 |
| 10754 | depravada | 2 |
| 10755 | depositario | 2 |
| 10756 | depositar | 2 |
| 10757 | departa | 2 |
| 10758 | depararme | 2 |
| 10759 | deo | 2 |
| 10760 | denuestos | 2 |
| 10761 | démonos | 2 |
| 10762 | delgada | 2 |
| 10763 | deleites | 2 |
| 10764 | deleitan | 2 |
| 10765 | deleitable | 2 |
| 10766 | dejóle | 2 |
| 10767 | déjenle | 2 |
| 10768 | dejémosle | 2 |
| 10769 | dejáronle | 2 |
| 10770 | dejarnos | 2 |
| 10771 | dejarlo | 2 |
| 10772 | dejarlas | 2 |
| 10773 | dejárame | 2 |
| 10774 | déjanse | 2 |
| 10775 | dejándose | 2 |
| 10776 | dejándonos | 2 |
| 10777 | dejándome | 2 |
| 10778 | dejándolos | 2 |
| 10779 | dejada | 2 |
| 10780 | defraudar | 2 |
| 10781 | defensor | 2 |
| 10782 | dedicaron | 2 |
| 10783 | decreto | 2 |
| 10784 | declarasen | 2 |
| 10785 | declararnos | 2 |
| 10786 | declararme | 2 |
| 10787 | declararle | 2 |
| 10788 | declarándole | 2 |
| 10789 | declaran | 2 |
| 10790 | declarados | 2 |
| 10791 | declarador | 2 |
| 10792 | declarada | 2 |
| 10793 | decirlos | 2 |
| 10794 | decirla | 2 |
| 10795 | decillas | 2 |
| 10796 | decilla | 2 |
| 10797 | deciendo | 2 |
| 10798 | decienden | 2 |
| 10799 | decíase | 2 |
| 10800 | decendió | 2 |
| 10801 | decendientes | 2 |
| 10802 | decendencia | 2 |
| 10803 | decantado | 2 |
| 10804 | debistes | 2 |
| 10805 | debilitado | 2 |
| 10806 | debidas | 2 |
| 10807 | debí | 2 |
| 10808 | deba | 2 |
| 10809 | datilados | 2 |
| 10810 | dárselos | 2 |
| 10811 | dárosla | 2 |
| 10812 | daros | 2 |
| 10813 | darinel | 2 |
| 10814 | dares | 2 |
| 10815 | dardos | 2 |
| 10816 | dañan | 2 |
| 10817 | dañadores | 2 |
| 10818 | danzar | 2 |
| 10819 | dándoselos | 2 |
| 10820 | damascos | 2 |
| 10821 | dais | 2 |
| 10822 | dador | 2 |
| 10823 | dádmele | 2 |
| 10824 | dadivoso | 2 |
| 10825 | dábale | 2 |
| 10826 | cursado | 2 |
| 10827 | curiosas | 2 |
| 10828 | curiambro | 2 |
| 10829 | curarme | 2 |
| 10830 | curara | 2 |
| 10831 | curaban | 2 |
| 10832 | curaba | 2 |
| 10833 | cupiese | 2 |
| 10834 | cuna | 2 |
| 10835 | cumplirla | 2 |
| 10836 | cumplirás | 2 |
| 10837 | cumpliera | 2 |
| 10838 | cumpliendo | 2 |
| 10839 | cumplidos | 2 |
| 10840 | cumplían | 2 |
| 10841 | cumplía | 2 |
| 10842 | cumplen | 2 |
| 10843 | culpado | 2 |
| 10844 | cuitada | 2 |
| 10845 | cuestión | 2 |
| 10846 | cuerdas | 2 |
| 10847 | cuentes | 2 |
| 10848 | cuenca | 2 |
| 10849 | cuece | 2 |
| 10850 | cuchillos | 2 |
| 10851 | cubriese | 2 |
| 10852 | cubrieron | 2 |
| 10853 | cubriendo | 2 |
| 10854 | cúbrete | 2 |
| 10855 | cuarteles | 2 |
| 10856 | cuartana | 2 |
| 10857 | cuajada | 2 |
| 10858 | cruzar | 2 |
| 10859 | cruzando | 2 |
| 10860 | cruzadas | 2 |
| 10861 | crueldades | 2 |
| 10862 | cristóbal | 2 |
| 10863 | cristina | 2 |
| 10864 | cris | 2 |
| 10865 | crines | 2 |
| 10866 | criba | 2 |
| 10867 | crían | 2 |
| 10868 | criaban | 2 |
| 10869 | creyente | 2 |
| 10870 | creídas | 2 |
| 10871 | creerla | 2 |
| 10872 | creeré | 2 |
| 10873 | creéis | 2 |
| 10874 | creedme | 2 |
| 10875 | credo | 2 |
| 10876 | credite | 2 |
| 10877 | crecido | 2 |
| 10878 | crecidas | 2 |
| 10879 | creas | 2 |
| 10880 | creáis | 2 |
| 10881 | coyundas | 2 |
| 10882 | coto | 2 |
| 10883 | costase | 2 |
| 10884 | costará | 2 |
| 10885 | cosario | 2 |
| 10886 | cortedad | 2 |
| 10887 | corté | 2 |
| 10888 | cortaron | 2 |
| 10889 | cortarme | 2 |
| 10890 | cortadoras | 2 |
| 10891 | corrillos | 2 |
| 10892 | corrigió | 2 |
| 10893 | corrigiendo | 2 |
| 10894 | corriesen | 2 |
| 10895 | corrientes | 2 |
| 10896 | corretor | 2 |
| 10897 | correspondió | 2 |
| 10898 | corresponde | 2 |
| 10899 | corregir | 2 |
| 10900 | corregido | 2 |
| 10901 | corrediza | 2 |
| 10902 | corred | 2 |
| 10903 | correa | 2 |
| 10904 | corporales | 2 |
| 10905 | corpezuelo | 2 |
| 10906 | coronados | 2 |
| 10907 | cornetas | 2 |
| 10908 | corneta | 2 |
| 10909 | cordobés | 2 |
| 10910 | cordero | 2 |
| 10911 | corchetes | 2 |
| 10912 | copo | 2 |
| 10913 | copla | 2 |
| 10914 | copiosísimo | 2 |
| 10915 | convirtió | 2 |
| 10916 | convino | 2 |
| 10917 | convido | 2 |
| 10918 | convidando | 2 |
| 10919 | convida | 2 |
| 10920 | conversión | 2 |
| 10921 | convengan | 2 |
| 10922 | convenga | 2 |
| 10923 | convendrá | 2 |
| 10924 | contrecho | 2 |
| 10925 | contraste | 2 |
| 10926 | contrapunto | 2 |
| 10927 | contrapuestos | 2 |
| 10928 | contoneo | 2 |
| 10929 | contóles | 2 |
| 10930 | continuo | 2 |
| 10931 | continuado | 2 |
| 10932 | contina | 2 |
| 10933 | contiendas | 2 |
| 10934 | contentóse | 2 |
| 10935 | conténtate | 2 |
| 10936 | contentas | 2 |
| 10937 | contentarse | 2 |
| 10938 | contentara | 2 |
| 10939 | conteniéndose | 2 |
| 10940 | contenidas | 2 |
| 10941 | contendor | 2 |
| 10942 | contender | 2 |
| 10943 | contemplar | 2 |
| 10944 | contaron | 2 |
| 10945 | contaría | 2 |
| 10946 | contará | 2 |
| 10947 | contándose | 2 |
| 10948 | contad | 2 |
| 10949 | contaban | 2 |
| 10950 | consumida | 2 |
| 10951 | consumía | 2 |
| 10952 | consume | 2 |
| 10953 | consuela | 2 |
| 10954 | constituidas | 2 |
| 10955 | consta | 2 |
| 10956 | consolóse | 2 |
| 10957 | consolarse | 2 |
| 10958 | consolaba | 2 |
| 10959 | consiguiese | 2 |
| 10960 | consienten | 2 |
| 10961 | considero | 2 |
| 10962 | consideres | 2 |
| 10963 | consideradas | 2 |
| 10964 | consideraciones | 2 |
| 10965 | conseja | 2 |
| 10966 | conseguiría | 2 |
| 10967 | conquista | 2 |
| 10968 | conozcas | 2 |
| 10969 | conozcan | 2 |
| 10970 | conocíla | 2 |
| 10971 | conociese | 2 |
| 10972 | conocidas | 2 |
| 10973 | conocerte | 2 |
| 10974 | conocelle | 2 |
| 10975 | conllevar | 2 |
| 10976 | conjeturar | 2 |
| 10977 | congojó | 2 |
| 10978 | congojado | 2 |
| 10979 | confundiese | 2 |
| 10980 | conformes | 2 |
| 10981 | confirmaron | 2 |
| 10982 | confirmándose | 2 |
| 10983 | confirman | 2 |
| 10984 | confirmado | 2 |
| 10985 | confirmaba | 2 |
| 10986 | confiese | 2 |
| 10987 | confiesas | 2 |
| 10988 | confiesa | 2 |
| 10989 | confiada | 2 |
| 10990 | confesor | 2 |
| 10991 | confesáis | 2 |
| 10992 | confesado | 2 |
| 10993 | conejos | 2 |
| 10994 | conejo | 2 |
| 10995 | condenar | 2 |
| 10996 | condenados | 2 |
| 10997 | condenado | 2 |
| 10998 | concordia | 2 |
| 10999 | concluyese | 2 |
| 11000 | concluya | 2 |
| 11001 | conclusión | 2 |
| 11002 | concluido | 2 |
| 11003 | concierta | 2 |
| 11004 | concetos | 2 |
| 11005 | concertamos | 2 |
| 11006 | concertaba | 2 |
| 11007 | concernientes | 2 |
| 11008 | concerniente | 2 |
| 11009 | concedió | 2 |
| 11010 | concediese | 2 |
| 11011 | comunico | 2 |
| 11012 | cómputo | 2 |
| 11013 | compuse | 2 |
| 11014 | compuestos | 2 |
| 11015 | compré | 2 |
| 11016 | comprado | 2 |
| 11017 | comprada | 2 |
| 11018 | componiendo | 2 |
| 11019 | componía | 2 |
| 11020 | componerse | 2 |
| 11021 | competidor | 2 |
| 11022 | compasivas | 2 |
| 11023 | compasiva | 2 |
| 11024 | comparados | 2 |
| 11025 | comparado | 2 |
| 11026 | cómitre | 2 |
| 11027 | comiesen | 2 |
| 11028 | comienzo | 2 |
| 11029 | comienzas | 2 |
| 11030 | comiences | 2 |
| 11031 | comidas | 2 |
| 11032 | cometió | 2 |
| 11033 | cometer | 2 |
| 11034 | comeros | 2 |
| 11035 | comería | 2 |
| 11036 | comenzóse | 2 |
| 11037 | comenzase | 2 |
| 11038 | comenzaría | 2 |
| 11039 | coméme | 2 |
| 11040 | comedidos | 2 |
| 11041 | comedida | 2 |
| 11042 | comediantes | 2 |
| 11043 | combatió | 2 |
| 11044 | combatido | 2 |
| 11045 | comas | 2 |
| 11046 | cómalos | 2 |
| 11047 | colunas | 2 |
| 11048 | colorados | 2 |
| 11049 | colorado | 2 |
| 11050 | colodrillo | 2 |
| 11051 | colocados | 2 |
| 11052 | colocado | 2 |
| 11053 | colocadas | 2 |
| 11054 | colmo | 2 |
| 11055 | colmenas | 2 |
| 11056 | coligiendo | 2 |
| 11057 | colgando | 2 |
| 11058 | colgadas | 2 |
| 11059 | coleto | 2 |
| 11060 | colegios | 2 |
| 11061 | cojea | 2 |
| 11062 | coja | 2 |
| 11063 | cogote | 2 |
| 11064 | cogiéndola | 2 |
| 11065 | cogía | 2 |
| 11066 | cogen | 2 |
| 11067 | cofres | 2 |
| 11068 | cofrecillo | 2 |
| 11069 | cofre | 2 |
| 11070 | codos | 2 |
| 11071 | codo | 2 |
| 11072 | coco | 2 |
| 11073 | cocineros | 2 |
| 11074 | cocina | 2 |
| 11075 | cocidas | 2 |
| 11076 | cochero | 2 |
| 11077 | cobrase | 2 |
| 11078 | cobrarán | 2 |
| 11079 | clérigo | 2 |
| 11080 | clavó | 2 |
| 11081 | citar | 2 |
| 11082 | circunstancia | 2 |
| 11083 | ciñóse | 2 |
| 11084 | cinta | 2 |
| 11085 | ciegan | 2 |
| 11086 | ciceroniana | 2 |
| 11087 | cianíis | 2 |
| 11088 | chicos | 2 |
| 11089 | chapa | 2 |
| 11090 | cetros | 2 |
| 11091 | cetina | 2 |
| 11092 | cesen | 2 |
| 11093 | cesar | 2 |
| 11094 | certifico | 2 |
| 11095 | cerrojo | 2 |
| 11096 | cerro | 2 |
| 11097 | cerrera | 2 |
| 11098 | cernido | 2 |
| 11099 | cernadero | 2 |
| 11100 | cercanos | 2 |
| 11101 | cercan | 2 |
| 11102 | cercada | 2 |
| 11103 | cerbelo | 2 |
| 11104 | ceptros | 2 |
| 11105 | ceñido | 2 |
| 11106 | ceñida | 2 |
| 11107 | ceñían | 2 |
| 11108 | cenando | 2 |
| 11109 | cenado | 2 |
| 11110 | celosías | 2 |
| 11111 | celosía | 2 |
| 11112 | celestes | 2 |
| 11113 | celemín | 2 |
| 11114 | celebrado | 2 |
| 11115 | celebérrimo | 2 |
| 11116 | ceguezuelo | 2 |
| 11117 | cegase | 2 |
| 11118 | cebollinas | 2 |
| 11119 | cebo | 2 |
| 11120 | cazadora | 2 |
| 11121 | cayesen | 2 |
| 11122 | cayere | 2 |
| 11123 | cavernas | 2 |
| 11124 | cavando | 2 |
| 11125 | causaban | 2 |
| 11126 | cato | 2 |
| 11127 | catedrático | 2 |
| 11128 | cate | 2 |
| 11129 | catay | 2 |
| 11130 | cataratas | 2 |
| 11131 | catálogo | 2 |
| 11132 | catalana | 2 |
| 11133 | castos | 2 |
| 11134 | castíguele | 2 |
| 11135 | castigaros | 2 |
| 11136 | castigarme | 2 |
| 11137 | castígame | 2 |
| 11138 | castigalle | 2 |
| 11139 | castellanos | 2 |
| 11140 | castas | 2 |
| 11141 | castaños | 2 |
| 11142 | casillas | 2 |
| 11143 | casilda | 2 |
| 11144 | cásense | 2 |
| 11145 | casare | 2 |
| 11146 | casara | 2 |
| 11147 | casamientos | 2 |
| 11148 | casaba | 2 |
| 11149 | cartujos | 2 |
| 11150 | cartel | 2 |
| 11151 | cartapacio | 2 |
| 11152 | cartago | 2 |
| 11153 | cartagena | 2 |
| 11154 | carrozas | 2 |
| 11155 | carniceros | 2 |
| 11156 | caritativa | 2 |
| 11157 | carísimos | 2 |
| 11158 | carísimo | 2 |
| 11159 | cargó | 2 |
| 11160 | cargaba | 2 |
| 11161 | carestía | 2 |
| 11162 | carecieron | 2 |
| 11163 | carecer | 2 |
| 11164 | carece | 2 |
| 11165 | cardenales | 2 |
| 11166 | cardado | 2 |
| 11167 | carcaños | 2 |
| 11168 | carcajes | 2 |
| 11169 | caramanchón | 2 |
| 11170 | caracuel | 2 |
| 11171 | caracol | 2 |
| 11172 | capotillo | 2 |
| 11173 | capitales | 2 |
| 11174 | capillas | 2 |
| 11175 | capellina | 2 |
| 11176 | caos | 2 |
| 11177 | cañuto | 2 |
| 11178 | caño | 2 |
| 11179 | cantillo | 2 |
| 11180 | cantía | 2 |
| 11181 | canten | 2 |
| 11182 | cansóse | 2 |
| 11183 | canse | 2 |
| 11184 | canónigos | 2 |
| 11185 | cánones | 2 |
| 11186 | candeleros | 2 |
| 11187 | candado | 2 |
| 11188 | canasta | 2 |
| 11189 | cananeas | 2 |
| 11190 | canal | 2 |
| 11191 | campanario | 2 |
| 11192 | caminemos | 2 |
| 11193 | caminé | 2 |
| 11194 | camine | 2 |
| 11195 | caminasen | 2 |
| 11196 | caminase | 2 |
| 11197 | caminan | 2 |
| 11198 | camilia | 2 |
| 11199 | cambio | 2 |
| 11200 | calzó | 2 |
| 11201 | calzarse | 2 |
| 11202 | calzado | 2 |
| 11203 | callejuela | 2 |
| 11204 | callasen | 2 |
| 11205 | callaban | 2 |
| 11206 | calidades | 2 |
| 11207 | calentura | 2 |
| 11208 | calderos | 2 |
| 11209 | caldera | 2 |
| 11210 | calar | 2 |
| 11211 | calandria | 2 |
| 11212 | calamitosos | 2 |
| 11213 | calamidad | 2 |
| 11214 | calada | 2 |
| 11215 | calabozo | 2 |
| 11216 | calabaza | 2 |
| 11217 | cala | 2 |
| 11218 | cajón | 2 |
| 11219 | caigas | 2 |
| 11220 | caigan | 2 |
| 11221 | caídas | 2 |
| 11222 | caería | 2 |
| 11223 | caerá | 2 |
| 11224 | cadáver | 2 |
| 11225 | cachorros | 2 |
| 11226 | cabriolas | 2 |
| 11227 | cabriola | 2 |
| 11228 | cabida | 2 |
| 11229 | caben | 2 |
| 11230 | cabelleras | 2 |
| 11231 | cabañas | 2 |
| 11232 | caballerizos | 2 |
| 11233 | caballerizo | 2 |
| 11234 | caballerescos | 2 |
| 11235 | c | 2 |
| 11236 | busilis | 2 |
| 11237 | busco | 2 |
| 11238 | buscaron | 2 |
| 11239 | buscamos | 2 |
| 11240 | buscábamos | 2 |
| 11241 | burra | 2 |
| 11242 | burlón | 2 |
| 11243 | burló | 2 |
| 11244 | burlesco | 2 |
| 11245 | burlé | 2 |
| 11246 | burlarse | 2 |
| 11247 | burlador | 2 |
| 11248 | burlada | 2 |
| 11249 | bureo | 2 |
| 11250 | bultos | 2 |
| 11251 | bullía | 2 |
| 11252 | bufete | 2 |
| 11253 | bucéfalo | 2 |
| 11254 | bruto | 2 |
| 11255 | brunelo | 2 |
| 11256 | brumado | 2 |
| 11257 | brumadas | 2 |
| 11258 | brujo | 2 |
| 11259 | broches | 2 |
| 11260 | brocados | 2 |
| 11261 | brioso | 2 |
| 11262 | brincadora | 2 |
| 11263 | brilladoro | 2 |
| 11264 | breñas | 2 |
| 11265 | bosquejo | 2 |
| 11266 | borricas | 2 |
| 11267 | borracha | 2 |
| 11268 | bordón | 2 |
| 11269 | bonita | 2 |
| 11270 | bonísimo | 2 |
| 11271 | bonísimas | 2 |
| 11272 | bonico | 2 |
| 11273 | bonetillo | 2 |
| 11274 | bolos | 2 |
| 11275 | bogasen | 2 |
| 11276 | bogando | 2 |
| 11277 | bocinas | 2 |
| 11278 | bóbilis | 2 |
| 11279 | bobas | 2 |
| 11280 | bo | 2 |
| 11281 | blanquísimo | 2 |
| 11282 | blanquísimas | 2 |
| 11283 | blanquísima | 2 |
| 11284 | bizmar | 2 |
| 11285 | bizcocho | 2 |
| 11286 | bizarro | 2 |
| 11287 | bizarramente | 2 |
| 11288 | bigote | 2 |
| 11289 | bienaventurado | 2 |
| 11290 | betis | 2 |
| 11291 | bestión | 2 |
| 11292 | bestezuela | 2 |
| 11293 | besárselas | 2 |
| 11294 | besará | 2 |
| 11295 | besándole | 2 |
| 11296 | besando | 2 |
| 11297 | besan | 2 |
| 11298 | besamanos | 2 |
| 11299 | besaban | 2 |
| 11300 | bernardino | 2 |
| 11301 | bermejo | 2 |
| 11302 | berenjena | 2 |
| 11303 | benignos | 2 |
| 11304 | benevolencia | 2 |
| 11305 | bene | 2 |
| 11306 | benditos | 2 |
| 11307 | bendiciones | 2 |
| 11308 | bellas | 2 |
| 11309 | bellaca | 2 |
| 11310 | bélico | 2 |
| 11311 | beldad | 2 |
| 11312 | béjar | 2 |
| 11313 | bebieron | 2 |
| 11314 | bebamos | 2 |
| 11315 | bastó | 2 |
| 11316 | bastimentos | 2 |
| 11317 | bastase | 2 |
| 11318 | bastardo | 2 |
| 11319 | bastará | 2 |
| 11320 | basa | 2 |
| 11321 | barro | 2 |
| 11322 | barriendo | 2 |
| 11323 | barniz | 2 |
| 11324 | barberos | 2 |
| 11325 | barbarroja | 2 |
| 11326 | barbada | 2 |
| 11327 | baratijas | 2 |
| 11328 | barajar | 2 |
| 11329 | baraja | 2 |
| 11330 | bañada | 2 |
| 11331 | banquetes | 2 |
| 11332 | bandolero | 2 |
| 11333 | ballena | 2 |
| 11334 | baldía | 2 |
| 11335 | balanza | 2 |
| 11336 | balandrán | 2 |
| 11337 | bajé | 2 |
| 11338 | bajaron | 2 |
| 11339 | baile | 2 |
| 11340 | bailar | 2 |
| 11341 | bailando | 2 |
| 11342 | bailador | 2 |
| 11343 | bailado | 2 |
| 11344 | bagarinos | 2 |
| 11345 | baeza | 2 |
| 11346 | bacín | 2 |
| 11347 | babador | 2 |
| 11348 | azufre | 2 |
| 11349 | azotaba | 2 |
| 11350 | azoróse | 2 |
| 11351 | azor | 2 |
| 11352 | azogado | 2 |
| 11353 | azada | 2 |
| 11354 | azabache | 2 |
| 11355 | ayunos | 2 |
| 11356 | ayunas | 2 |
| 11357 | ayuden | 2 |
| 11358 | ayudarle | 2 |
| 11359 | ayudándole | 2 |
| 11360 | ayúdame | 2 |
| 11361 | ayudado | 2 |
| 11362 | avivar | 2 |
| 11363 | avisos | 2 |
| 11364 | avisé | 2 |
| 11365 | avisarle | 2 |
| 11366 | avísame | 2 |
| 11367 | averiguarlo | 2 |
| 11368 | avergüenza | 2 |
| 11369 | aventurarse | 2 |
| 11370 | aventajarme | 2 |
| 11371 | aventajaba | 2 |
| 11372 | avenid | 2 |
| 11373 | avenía | 2 |
| 11374 | avellanado | 2 |
| 11375 | avellana | 2 |
| 11376 | ave | 2 |
| 11377 | avaro | 2 |
| 11378 | auténticas | 2 |
| 11379 | autem | 2 |
| 11380 | ausentó | 2 |
| 11381 | ausentes | 2 |
| 11382 | ausentar | 2 |
| 11383 | ausentado | 2 |
| 11384 | aumentarla | 2 |
| 11385 | aullido | 2 |
| 11386 | auditorio | 2 |
| 11387 | audiencias | 2 |
| 11388 | aturdido | 2 |
| 11389 | atropellar | 2 |
| 11390 | atropellados | 2 |
| 11391 | atribuyeron | 2 |
| 11392 | atribuyas | 2 |
| 11393 | atreviera | 2 |
| 11394 | atreverse | 2 |
| 11395 | atrevería | 2 |
| 11396 | atreverá | 2 |
| 11397 | atraviesan | 2 |
| 11398 | atraviesa | 2 |
| 11399 | atravesó | 2 |
| 11400 | atraer | 2 |
| 11401 | atrae | 2 |
| 11402 | atormentaban | 2 |
| 11403 | atónitas | 2 |
| 11404 | atienen | 2 |
| 11405 | atenuada | 2 |
| 11406 | atentísimo | 2 |
| 11407 | atentísimamente | 2 |
| 11408 | atenía | 2 |
| 11409 | atener | 2 |
| 11410 | atendió | 2 |
| 11411 | atended | 2 |
| 11412 | atavíos | 2 |
| 11413 | ataron | 2 |
| 11414 | ataduras | 2 |
| 11415 | atacadas | 2 |
| 11416 | asustado | 2 |
| 11417 | astillero | 2 |
| 11418 | astillas | 2 |
| 11419 | ásperos | 2 |
| 11420 | aspas | 2 |
| 11421 | asomándose | 2 |
| 11422 | asolviese | 2 |
| 11423 | asistentes | 2 |
| 11424 | asistencia | 2 |
| 11425 | asisten | 2 |
| 11426 | asirle | 2 |
| 11427 | asientan | 2 |
| 11428 | asienta | 2 |
| 11429 | asiéndola | 2 |
| 11430 | asían | 2 |
| 11431 | asia | 2 |
| 11432 | asentaré | 2 |
| 11433 | asentado | 2 |
| 11434 | asentaba | 2 |
| 11435 | asendereados | 2 |
| 11436 | asegúrote | 2 |
| 11437 | asegurarse | 2 |
| 11438 | asegurara | 2 |
| 11439 | asegura | 2 |
| 11440 | ascua | 2 |
| 11441 | asar | 2 |
| 11442 | asada | 2 |
| 11443 | arzobispos | 2 |
| 11444 | aruños | 2 |
| 11445 | artús | 2 |
| 11446 | artífice | 2 |
| 11447 | artículos | 2 |
| 11448 | artesillas | 2 |
| 11449 | arroyuelos | 2 |
| 11450 | arroyuelo | 2 |
| 11451 | arrostre | 2 |
| 11452 | arrojóle | 2 |
| 11453 | arrojan | 2 |
| 11454 | arrogancias | 2 |
| 11455 | arrodillada | 2 |
| 11456 | arrimarse | 2 |
| 11457 | arreos | 2 |
| 11458 | arremetiendo | 2 |
| 11459 | arremangado | 2 |
| 11460 | arrancarse | 2 |
| 11461 | arrancar | 2 |
| 11462 | arrancado | 2 |
| 11463 | armóse | 2 |
| 11464 | armó | 2 |
| 11465 | ármese | 2 |
| 11466 | argumentos | 2 |
| 11467 | argumento | 2 |
| 11468 | argamasa | 2 |
| 11469 | argado | 2 |
| 11470 | arengas | 2 |
| 11471 | arcaláus | 2 |
| 11472 | árbitros | 2 |
| 11473 | arañaron | 2 |
| 11474 | arábigos | 2 |
| 11475 | aqueste | 2 |
| 11476 | aquésta | 2 |
| 11477 | aquéllo | 2 |
| 11478 | apuntamiento | 2 |
| 11479 | apuntadas | 2 |
| 11480 | apunta | 2 |
| 11481 | aprovechase | 2 |
| 11482 | aprovechamiento | 2 |
| 11483 | aprovechado | 2 |
| 11484 | aprobé | 2 |
| 11485 | aprisco | 2 |
| 11486 | apriete | 2 |
| 11487 | apretado | 2 |
| 11488 | apresurados | 2 |
| 11489 | aprendió | 2 |
| 11490 | apremio | 2 |
| 11491 | aprehensión | 2 |
| 11492 | apoyar | 2 |
| 11493 | aposentos | 2 |
| 11494 | aporrear | 2 |
| 11495 | apócrifa | 2 |
| 11496 | aplicación | 2 |
| 11497 | apero | 2 |
| 11498 | apellidos | 2 |
| 11499 | apeles | 2 |
| 11500 | apelativo | 2 |
| 11501 | apéate | 2 |
| 11502 | apease | 2 |
| 11503 | apearme | 2 |
| 11504 | apasionados | 2 |
| 11505 | aparto | 2 |
| 11506 | apartémonos | 2 |
| 11507 | apártate | 2 |
| 11508 | apartarle | 2 |
| 11509 | apartados | 2 |
| 11510 | apartadas | 2 |
| 11511 | apartaba | 2 |
| 11512 | aparéjese | 2 |
| 11513 | apareja | 2 |
| 11514 | añasca | 2 |
| 11515 | añado | 2 |
| 11516 | añadióse | 2 |
| 11517 | añadido | 2 |
| 11518 | anzuelo | 2 |
| 11519 | antonia | 2 |
| 11520 | antojósele | 2 |
| 11521 | antojó | 2 |
| 11522 | antojo | 2 |
| 11523 | antípodas | 2 |
| 11524 | anteón | 2 |
| 11525 | anocheció | 2 |
| 11526 | anjeo | 2 |
| 11527 | aniquilado | 2 |
| 11528 | animase | 2 |
| 11529 | anillos | 2 |
| 11530 | anibal | 2 |
| 11531 | ángulos | 2 |
| 11532 | anexas | 2 |
| 11533 | anejo | 2 |
| 11534 | anduvieron | 2 |
| 11535 | andrea | 2 |
| 11536 | ándese | 2 |
| 11537 | ándense | 2 |
| 11538 | anden | 2 |
| 11539 | andariega | 2 |
| 11540 | andarán | 2 |
| 11541 | andaluz | 2 |
| 11542 | anchuras | 2 |
| 11543 | anascote | 2 |
| 11544 | anales | 2 |
| 11545 | ampara | 2 |
| 11546 | amistades | 2 |
| 11547 | amenidad | 2 |
| 11548 | amenazar | 2 |
| 11549 | amenazándole | 2 |
| 11550 | amenazan | 2 |
| 11551 | amenazadora | 2 |
| 11552 | amenazaban | 2 |
| 11553 | ambicioso | 2 |
| 11554 | amas | 2 |
| 11555 | amaranto | 2 |
| 11556 | amanecía | 2 |
| 11557 | amancebados | 2 |
| 11558 | amáis | 2 |
| 11559 | amainar | 2 |
| 11560 | alzados | 2 |
| 11561 | altivez | 2 |
| 11562 | altísimo | 2 |
| 11563 | altibajos | 2 |
| 11564 | alterar | 2 |
| 11565 | alterado | 2 |
| 11566 | alteración | 2 |
| 11567 | altares | 2 |
| 11568 | alquimia | 2 |
| 11569 | alquife | 2 |
| 11570 | alongó | 2 |
| 11571 | almorzaron | 2 |
| 11572 | almorzar | 2 |
| 11573 | almidón | 2 |
| 11574 | almete | 2 |
| 11575 | almacén | 2 |
| 11576 | allegados | 2 |
| 11577 | alientos | 2 |
| 11578 | alicante | 2 |
| 11579 | algazara | 2 |
| 11580 | algalia | 2 |
| 11581 | alfombras | 2 |
| 11582 | alfenique | 2 |
| 11583 | alfana | 2 |
| 11584 | alentar | 2 |
| 11585 | alemán | 2 |
| 11586 | alejandros | 2 |
| 11587 | alegrías | 2 |
| 11588 | alegrasen | 2 |
| 11589 | alegrase | 2 |
| 11590 | alegrarse | 2 |
| 11591 | alefanfarón | 2 |
| 11592 | alcé | 2 |
| 11593 | alce | 2 |
| 11594 | alcanzaren | 2 |
| 11595 | alcanzare | 2 |
| 11596 | alcanzará | 2 |
| 11597 | alcanzada | 2 |
| 11598 | alcancías | 2 |
| 11599 | alcancía | 2 |
| 11600 | alborozo | 2 |
| 11601 | alborotasen | 2 |
| 11602 | alborotáronse | 2 |
| 11603 | alborotara | 2 |
| 11604 | alborotar | 2 |
| 11605 | alborotados | 2 |
| 11606 | álamo | 2 |
| 11607 | alaben | 2 |
| 11608 | alabarla | 2 |
| 11609 | alabando | 2 |
| 11610 | alaban | 2 |
| 11611 | alababa | 2 |
| 11612 | ajusto | 2 |
| 11613 | ajorcas | 2 |
| 11614 | ajedrez | 2 |
| 11615 | airado | 2 |
| 11616 | ahorrarse | 2 |
| 11617 | ahorraréis | 2 |
| 11618 | águila | 2 |
| 11619 | aguija | 2 |
| 11620 | agüelo | 2 |
| 11621 | aguamanos | 2 |
| 11622 | agravias | 2 |
| 11623 | agraviar | 2 |
| 11624 | agravian | 2 |
| 11625 | agrado | 2 |
| 11626 | agradecióselo | 2 |
| 11627 | agradeciéndole | 2 |
| 11628 | agradeciendo | 2 |
| 11629 | agradar | 2 |
| 11630 | agraciado | 2 |
| 11631 | agraciada | 2 |
| 11632 | agasajar | 2 |
| 11633 | agarenos | 2 |
| 11634 | agallas | 2 |
| 11635 | aforrado | 2 |
| 11636 | aforismos | 2 |
| 11637 | afligirse | 2 |
| 11638 | afligióse | 2 |
| 11639 | aflición | 2 |
| 11640 | afirmándose | 2 |
| 11641 | afirman | 2 |
| 11642 | aficionados | 2 |
| 11643 | aficionada | 2 |
| 11644 | afectos | 2 |
| 11645 | adviertes | 2 |
| 11646 | aduló | 2 |
| 11647 | adquirir | 2 |
| 11648 | adquiriendo | 2 |
| 11649 | adornó | 2 |
| 11650 | adorar | 2 |
| 11651 | adoran | 2 |
| 11652 | adoraba | 2 |
| 11653 | adoban | 2 |
| 11654 | admitido | 2 |
| 11655 | admitidas | 2 |
| 11656 | admite | 2 |
| 11657 | admiróle | 2 |
| 11658 | admire | 2 |
| 11659 | admirándose | 2 |
| 11660 | adivinar | 2 |
| 11661 | aderezó | 2 |
| 11662 | aderezasen | 2 |
| 11663 | aderezaron | 2 |
| 11664 | aderezar | 2 |
| 11665 | adeliñado | 2 |
| 11666 | adelantados | 2 |
| 11667 | adargas | 2 |
| 11668 | acuerdas | 2 |
| 11669 | acudimos | 2 |
| 11670 | acudiendo | 2 |
| 11671 | acudido | 2 |
| 11672 | acudían | 2 |
| 11673 | acuchillador | 2 |
| 11674 | acuchillado | 2 |
| 11675 | actores | 2 |
| 11676 | acreditó | 2 |
| 11677 | acreditaba | 2 |
| 11678 | acrecientan | 2 |
| 11679 | acostado | 2 |
| 11680 | acosa | 2 |
| 11681 | acorrucó | 2 |
| 11682 | acordase | 2 |
| 11683 | acordará | 2 |
| 11684 | acordara | 2 |
| 11685 | acordáis | 2 |
| 11686 | acontecieron | 2 |
| 11687 | acontecía | 2 |
| 11688 | acontecerle | 2 |
| 11689 | acontecen | 2 |
| 11690 | aconsejóle | 2 |
| 11691 | aconsejó | 2 |
| 11692 | aconsejo | 2 |
| 11693 | aconseje | 2 |
| 11694 | aconsejas | 2 |
| 11695 | aconsejarme | 2 |
| 11696 | aconsejada | 2 |
| 11697 | aconseja | 2 |
| 11698 | acondicionado | 2 |
| 11699 | acompañasen | 2 |
| 11700 | acompañarle | 2 |
| 11701 | acompañarla | 2 |
| 11702 | acompañadas | 2 |
| 11703 | acomodóse | 2 |
| 11704 | acomode | 2 |
| 11705 | acomodasen | 2 |
| 11706 | acomodada | 2 |
| 11707 | acometió | 2 |
| 11708 | acometieron | 2 |
| 11709 | acometiendo | 2 |
| 11710 | acometedor | 2 |
| 11711 | acogiese | 2 |
| 11712 | acoger | 2 |
| 11713 | acobardado | 2 |
| 11714 | acierte | 2 |
| 11715 | aciertan | 2 |
| 11716 | aciagos | 2 |
| 11717 | acertaron | 2 |
| 11718 | acertaré | 2 |
| 11719 | acerada | 2 |
| 11720 | acepto | 2 |
| 11721 | acento | 2 |
| 11722 | acelerada | 2 |
| 11723 | aceitunas | 2 |
| 11724 | acción | 2 |
| 11725 | acanaladas | 2 |
| 11726 | acamuzado | 2 |
| 11727 | acabaste | 2 |
| 11728 | acabarla | 2 |
| 11729 | acabaremos | 2 |
| 11730 | acabándose | 2 |
| 11731 | acabándola | 2 |
| 11732 | acabamos | 2 |
| 11733 | abuso | 2 |
| 11734 | abundosa | 2 |
| 11735 | abrirse | 2 |
| 11736 | abrirla | 2 |
| 11737 | abrigo | 2 |
| 11738 | abrieron | 2 |
| 11739 | abriéndole | 2 |
| 11740 | abriéndola | 2 |
| 11741 | abrazos | 2 |
| 11742 | abrazo | 2 |
| 11743 | abrazáronse | 2 |
| 11744 | abrazarme | 2 |
| 11745 | abrazara | 2 |
| 11746 | abrazándose | 2 |
| 11747 | abrasados | 2 |
| 11748 | abrasada | 2 |
| 11749 | aborrecía | 2 |
| 11750 | abono | 2 |
| 11751 | abominado | 2 |
| 11752 | abernuncio | 2 |
| 11753 | abatieron | 2 |
| 11754 | abatido | 2 |
| 11755 | abaten | 2 |
| 11756 | abajó | 2 |
| 11757 | abajarse | 2 |
| 11758 | abadesa | 2 |
| 11759 | abadejo | 2 |
| 11760 | zuzaban | 1 |
| 11761 | zurrón | 1 |
| 11762 | zumban | 1 |
| 11763 | zulema | 1 |
| 11764 | zuecos | 1 |
| 11765 | zorruna | 1 |
| 11766 | zorras | 1 |
| 11767 | zorra | 1 |
| 11768 | zoroástrica | 1 |
| 11769 | zoroastes | 1 |
| 11770 | zopiro | 1 |
| 11771 | zonzorino | 1 |
| 11772 | zoltanís | 1 |
| 11773 | zoílo | 1 |
| 11774 | zodíacos | 1 |
| 11775 | zoca | 1 |
| 11776 | zeuxis | 1 |
| 11777 | zelador | 1 |
| 11778 | zas | 1 |
| 11779 | zarzo | 1 |
| 11780 | zarpasen | 1 |
| 11781 | zaquizamí | 1 |
| 11782 | zapatilla | 1 |
| 11783 | zapaticos | 1 |
| 11784 | zapateo | 1 |
| 11785 | zapatear | 1 |
| 11786 | zapateadores | 1 |
| 11787 | zanoguera | 1 |
| 11788 | zanja | 1 |
| 11789 | zánganos | 1 |
| 11790 | zancajos | 1 |
| 11791 | zanahorias | 1 |
| 11792 | zampoñas | 1 |
| 11793 | zamorano | 1 |
| 11794 | zamoranas | 1 |
| 11795 | zamorana | 1 |
| 11796 | zamora | 1 |
| 11797 | zamarro | 1 |
| 11798 | zaleas | 1 |
| 11799 | zahúrda | 1 |
| 11800 | zahorí | 1 |
| 11801 | zaheriendo | 1 |
| 11802 | zahareña | 1 |
| 11803 | zagalejas | 1 |
| 11804 | zagala | 1 |
| 11805 | zabullían | 1 |
| 11806 | yugadas | 1 |
| 11807 | yoguieren | 1 |
| 11808 | yogásemos | 1 |
| 11809 | yogase | 1 |
| 11810 | yogar | 1 |
| 11811 | yeso | 1 |
| 11812 | yerres | 1 |
| 11813 | yerran | 1 |
| 11814 | yernos | 1 |
| 11815 | yermos | 1 |
| 11816 | yéndonos | 1 |
| 11817 | yéndome | 1 |
| 11818 | yema | 1 |
| 11819 | yele | 1 |
| 11820 | yelan | 1 |
| 11821 | yantaría | 1 |
| 11822 | yacía | 1 |
| 11823 | yacer | 1 |
| 11824 | yacen | 1 |
| 11825 | xenofonte | 1 |
| 11826 | vulgar | 1 |
| 11827 | vueso | 1 |
| 11828 | vuélvese | 1 |
| 11829 | vuélveme | 1 |
| 11830 | vuélvele | 1 |
| 11831 | vuélvate | 1 |
| 11832 | vuélvanse | 1 |
| 11833 | vueltos | 1 |
| 11834 | vuelos | 1 |
| 11835 | votaba | 1 |
| 11836 | voquibles | 1 |
| 11837 | vomitó | 1 |
| 11838 | vomitase | 1 |
| 11839 | vomitan | 1 |
| 11840 | vomita | 1 |
| 11841 | volviósela | 1 |
| 11842 | volvímosle | 1 |
| 11843 | volvimos | 1 |
| 11844 | volvíle | 1 |
| 11845 | volviéronla | 1 |
| 11846 | volviéredes | 1 |
| 11847 | volviere | 1 |
| 11848 | volvieras | 1 |
| 11849 | volviéndoselo | 1 |
| 11850 | volviéndome | 1 |
| 11851 | volviéndola | 1 |
| 11852 | volverte | 1 |
| 11853 | volvérsele | 1 |
| 11854 | volvérmelos | 1 |
| 11855 | volverían | 1 |
| 11856 | volvedle | 1 |
| 11857 | voluntarios | 1 |
| 11858 | voluntario | 1 |
| 11859 | volúmenes | 1 |
| 11860 | volume | 1 |
| 11861 | voltearle | 1 |
| 11862 | volteadas | 1 |
| 11863 | volteaban | 1 |
| 11864 | voltaria | 1 |
| 11865 | voló | 1 |
| 11866 | voleo | 1 |
| 11867 | volente | 1 |
| 11868 | volcar | 1 |
| 11869 | volátiles | 1 |
| 11870 | volaterías | 1 |
| 11871 | volante | 1 |
| 11872 | volandillas | 1 |
| 11873 | volador | 1 |
| 11874 | volado | 1 |
| 11875 | volábanle | 1 |
| 11876 | volaban | 1 |
| 11877 | volábamos | 1 |
| 11878 | volaba | 1 |
| 11879 | vocería | 1 |
| 11880 | voceando | 1 |
| 11881 | vocación | 1 |
| 11882 | vizconde | 1 |
| 11883 | vizcaya | 1 |
| 11884 | viviría | 1 |
| 11885 | viviré | 1 |
| 11886 | vivieron | 1 |
| 11887 | viviere | 1 |
| 11888 | vivieran | 1 |
| 11889 | vivienda | 1 |
| 11890 | vivar | 1 |
| 11891 | vivamente | 1 |
| 11892 | vívame | 1 |
| 11893 | vituperoso | 1 |
| 11894 | vituperóme | 1 |
| 11895 | vituperado | 1 |
| 11896 | vituperaba | 1 |
| 11897 | vitoriosos | 1 |
| 11898 | vitorias | 1 |
| 11899 | vistosas | 1 |
| 11900 | vistosamente | 1 |
| 11901 | vistiré | 1 |
| 11902 | vistióle | 1 |
| 11903 | vistieron | 1 |
| 11904 | vistieren | 1 |
| 11905 | vistiere | 1 |
| 11906 | vistiéndonos | 1 |
| 11907 | vístete | 1 |
| 11908 | vístesos | 1 |
| 11909 | vístele | 1 |
| 11910 | vístase | 1 |
| 11911 | vístanme | 1 |
| 11912 | víspera | 1 |
| 11913 | viso | 1 |
| 11914 | visito | 1 |
| 11915 | visiten | 1 |
| 11916 | visitáronle | 1 |
| 11917 | visitarle | 1 |
| 11918 | visitando | 1 |
| 11919 | visitaba | 1 |
| 11920 | visibles | 1 |
| 11921 | visiblemente | 1 |
| 11922 | visajes | 1 |
| 11923 | visaje | 1 |
| 11924 | virués | 1 |
| 11925 | viruelas | 1 |
| 11926 | virtuosas | 1 |
| 11927 | virtualmente | 1 |
| 11928 | virreyes | 1 |
| 11929 | viriato | 1 |
| 11930 | virginidad | 1 |
| 11931 | vira | 1 |
| 11932 | viperina | 1 |
| 11933 | viome | 1 |
| 11934 | violo | 1 |
| 11935 | violentamente | 1 |
| 11936 | violencia | 1 |
| 11937 | violadas | 1 |
| 11938 | viña | 1 |
| 11939 | vínose | 1 |
| 11940 | vínole | 1 |
| 11941 | viniérale | 1 |
| 11942 | viniéndole | 1 |
| 11943 | vinagrillo | 1 |
| 11944 | vinagre | 1 |
| 11945 | villanovas | 1 |
| 11946 | villanías | 1 |
| 11947 | villanería | 1 |
| 11948 | villancicos | 1 |
| 11949 | villalpando | 1 |
| 11950 | villadiego | 1 |
| 11951 | villadie | 1 |
| 11952 | vilezas | 1 |
| 11953 | vile | 1 |
| 11954 | vila | 1 |
| 11955 | vigüela | 1 |
| 11956 | vigilantes | 1 |
| 11957 | vierten | 1 |
| 11958 | viertan | 1 |
| 11959 | viéronle | 1 |
| 11960 | viénenseme | 1 |
| 11961 | viéndoos | 1 |
| 11962 | viéndolas | 1 |
| 11963 | vie | 1 |
| 11964 | victoria | 1 |
| 11965 | viciosa | 1 |
| 11966 | vicaría | 1 |
| 11967 | víbora | 1 |
| 11968 | viandas | 1 |
| 11969 | viandantes | 1 |
| 11970 | vían | 1 |
| 11971 | víamos | 1 |
| 11972 | víame | 1 |
| 11973 | vetas | 1 |
| 11974 | vestros | 1 |
| 11975 | vestirte | 1 |
| 11976 | vestirme | 1 |
| 11977 | vestirlo | 1 |
| 11978 | vestirle | 1 |
| 11979 | vestiría | 1 |
| 11980 | vestíle | 1 |
| 11981 | vestiéndose | 1 |
| 11982 | vestiduras | 1 |
| 11983 | vestidura | 1 |
| 11984 | vestían | 1 |
| 11985 | verterlas | 1 |
| 11986 | verter | 1 |
| 11987 | versados | 1 |
| 11988 | verosímiles | 1 |
| 11989 | vernos | 1 |
| 11990 | verles | 1 |
| 11991 | veritas | 1 |
| 11992 | verisimilitud | 1 |
| 11993 | verino | 1 |
| 11994 | verificó | 1 |
| 11995 | verídico | 1 |
| 11996 | vericuetos | 1 |
| 11997 | veríades | 1 |
| 11998 | vergonzoso | 1 |
| 11999 | verémonos | 1 |
| 12000 | veréisos | 1 |
| 12001 | veréislo | 1 |
| 12002 | veredas | 1 |
| 12003 | verdura | 1 |
| 12004 | verbos | 1 |
| 12005 | verásme | 1 |
| 12006 | veráslos | 1 |
| 12007 | veráslo | 1 |
| 12008 | véome | 1 |
| 12009 | venzan | 1 |
| 12010 | venturosas | 1 |
| 12011 | ventillas | 1 |
| 12012 | venteriles | 1 |
| 12013 | venteril | 1 |
| 12014 | ventanillas | 1 |
| 12015 | ventanilla | 1 |
| 12016 | vense | 1 |
| 12017 | venirse | 1 |
| 12018 | veniros | 1 |
| 12019 | venirme | 1 |
| 12020 | venidos | 1 |
| 12021 | venideras | 1 |
| 12022 | veníades | 1 |
| 12023 | venia | 1 |
| 12024 | venguéis | 1 |
| 12025 | vengué | 1 |
| 12026 | vengue | 1 |
| 12027 | véngote | 1 |
| 12028 | vengó | 1 |
| 12029 | vengasen | 1 |
| 12030 | vengarnos | 1 |
| 12031 | vénganse | 1 |
| 12032 | vengáis | 1 |
| 12033 | veneranda | 1 |
| 12034 | veneración | 1 |
| 12035 | venenosos | 1 |
| 12036 | venenosa | 1 |
| 12037 | venecianos | 1 |
| 12038 | vendrían | 1 |
| 12039 | vendremos | 1 |
| 12040 | vendrás | 1 |
| 12041 | vendó | 1 |
| 12042 | venditur | 1 |
| 12043 | vendióse | 1 |
| 12044 | vendiendo | 1 |
| 12045 | vendibles | 1 |
| 12046 | vendían | 1 |
| 12047 | venderme | 1 |
| 12048 | venderle | 1 |
| 12049 | venden | 1 |
| 12050 | vendar | 1 |
| 12051 | vendáis | 1 |
| 12052 | vencistes | 1 |
| 12053 | vencíla | 1 |
| 12054 | vencieron | 1 |
| 12055 | vencieres | 1 |
| 12056 | venciere | 1 |
| 12057 | venciéndose | 1 |
| 12058 | venciendo | 1 |
| 12059 | vencía | 1 |
| 12060 | venceros | 1 |
| 12061 | vencejos | 1 |
| 12062 | vencéis | 1 |
| 12063 | venas | 1 |
| 12064 | venablos | 1 |
| 12065 | velocidad | 1 |
| 12066 | velloso | 1 |
| 12067 | vellorí | 1 |
| 12068 | velle | 1 |
| 12069 | vellas | 1 |
| 12070 | veleta | 1 |
| 12071 | veldo | 1 |
| 12072 | velase | 1 |
| 12073 | velarte | 1 |
| 12074 | velaré | 1 |
| 12075 | velamos | 1 |
| 12076 | vejote | 1 |
| 12077 | vejación | 1 |
| 12078 | veíase | 1 |
| 12079 | veías | 1 |
| 12080 | véese | 1 |
| 12081 | veemos | 1 |
| 12082 | veedores | 1 |
| 12083 | veedor | 1 |
| 12084 | veduño | 1 |
| 12085 | vedo | 1 |
| 12086 | vedija | 1 |
| 12087 | vedado | 1 |
| 12088 | vecinguerra | 1 |
| 12089 | vecina | 1 |
| 12090 | veci | 1 |
| 12091 | veámosla | 1 |
| 12092 | veámonos | 1 |
| 12093 | vates | 1 |
| 12094 | vasijas | 1 |
| 12095 | váselo | 1 |
| 12096 | varonil | 1 |
| 12097 | variar | 1 |
| 12098 | variado | 1 |
| 12099 | variada | 1 |
| 12100 | varia | 1 |
| 12101 | vareó | 1 |
| 12102 | varazos | 1 |
| 12103 | varapalos | 1 |
| 12104 | vaqueta | 1 |
| 12105 | vaquero | 1 |
| 12106 | vapularon | 1 |
| 12107 | vapularme | 1 |
| 12108 | vapulaba | 1 |
| 12109 | vapores | 1 |
| 12110 | vanle | 1 |
| 12111 | vanidades | 1 |
| 12112 | vanagloriosos | 1 |
| 12113 | vanaglorioso | 1 |
| 12114 | vanagloria | 1 |
| 12115 | vame | 1 |
| 12116 | valores | 1 |
| 12117 | valones | 1 |
| 12118 | valonas | 1 |
| 12119 | valme | 1 |
| 12120 | valió | 1 |
| 12121 | valija | 1 |
| 12122 | valiesen | 1 |
| 12123 | valieron | 1 |
| 12124 | valiéndose | 1 |
| 12125 | valgo | 1 |
| 12126 | valerosísimos | 1 |
| 12127 | valerosamente | 1 |
| 12128 | valerme | 1 |
| 12129 | valerle | 1 |
| 12130 | valentón | 1 |
| 12131 | valentísimamente | 1 |
| 12132 | váleme | 1 |
| 12133 | valederas | 1 |
| 12134 | valdrá | 1 |
| 12135 | valdivielso | 1 |
| 12136 | val | 1 |
| 12137 | vainillas | 1 |
| 12138 | vahando | 1 |
| 12139 | vago | 1 |
| 12140 | vagaren | 1 |
| 12141 | vagan | 1 |
| 12142 | vagamundos | 1 |
| 12143 | vagamunda | 1 |
| 12144 | vagabundos | 1 |
| 12145 | vació | 1 |
| 12146 | vacile | 1 |
| 12147 | vacilando | 1 |
| 12148 | vacías | 1 |
| 12149 | vacía | 1 |
| 12150 | vacase | 1 |
| 12151 | vacada | 1 |
| 12152 | uva | 1 |
| 12153 | utrique | 1 |
| 12154 | utilidad | 1 |
| 12155 | útiles | 1 |
| 12156 | usque | 1 |
| 12157 | uses | 1 |
| 12158 | usemos | 1 |
| 12159 | úsase | 1 |
| 12160 | usase | 1 |
| 12161 | usarlo | 1 |
| 12162 | usaréis | 1 |
| 12163 | usanzas | 1 |
| 12164 | usadla | 1 |
| 12165 | usad | 1 |
| 12166 | ursinos | 1 |
| 12167 | urreas | 1 |
| 12168 | urraca | 1 |
| 12169 | urbina | 1 |
| 12170 | untarle | 1 |
| 12171 | untar | 1 |
| 12172 | untaos | 1 |
| 12173 | untado | 1 |
| 12174 | universidades | 1 |
| 12175 | únicos | 1 |
| 12176 | unicornio | 1 |
| 12177 | undoso | 1 |
| 12178 | uncir | 1 |
| 12179 | unciones | 1 |
| 12180 | ultramarino | 1 |
| 12181 | ultraja | 1 |
| 12182 | ultimadamente | 1 |
| 12183 | ulixes | 1 |
| 12184 | ufanidad | 1 |
| 12185 | ufánese | 1 |
| 12186 | ufane | 1 |
| 12187 | ufanarte | 1 |
| 12188 | túvose | 1 |
| 12189 | túvolos | 1 |
| 12190 | túvola | 1 |
| 12191 | tuviste | 1 |
| 12192 | tuvieses | 1 |
| 12193 | tuviésemos | 1 |
| 12194 | tuviésedes | 1 |
| 12195 | tuviéralo | 1 |
| 12196 | tuviérades | 1 |
| 12197 | tutor | 1 |
| 12198 | tuto | 1 |
| 12199 | tutela | 1 |
| 12200 | turres | 1 |
| 12201 | turbóse | 1 |
| 12202 | turbasen | 1 |
| 12203 | turbas | 1 |
| 12204 | turbarte | 1 |
| 12205 | turbarme | 1 |
| 12206 | turbara | 1 |
| 12207 | turbantes | 1 |
| 12208 | turbante | 1 |
| 12209 | turbando | 1 |
| 12210 | turban | 1 |
| 12211 | turbaban | 1 |
| 12212 | tunicela | 1 |
| 12213 | túnicas | 1 |
| 12214 | tundido | 1 |
| 12215 | tundas | 1 |
| 12216 | tunda | 1 |
| 12217 | tullida | 1 |
| 12218 | tuis | 1 |
| 12219 | tuho | 1 |
| 12220 | tuerza | 1 |
| 12221 | tueras | 1 |
| 12222 | tudesqui | 1 |
| 12223 | tudesco | 1 |
| 12224 | trujillo | 1 |
| 12225 | trujéronsele | 1 |
| 12226 | trujéronla | 1 |
| 12227 | trujera | 1 |
| 12228 | trujamán | 1 |
| 12229 | trueques | 1 |
| 12230 | truenos | 1 |
| 12231 | truculento | 1 |
| 12232 | trucos | 1 |
| 12233 | trucha | 1 |
| 12234 | trozos | 1 |
| 12235 | troyanos | 1 |
| 12236 | troyano | 1 |
| 12237 | trotico | 1 |
| 12238 | trotes | 1 |
| 12239 | tropiezos | 1 |
| 12240 | tropezones | 1 |
| 12241 | tropezón | 1 |
| 12242 | tropezase | 1 |
| 12243 | tropezara | 1 |
| 12244 | tropezado | 1 |
| 12245 | tropezaban | 1 |
| 12246 | tropezaba | 1 |
| 12247 | tronque | 1 |
| 12248 | tronadores | 1 |
| 12249 | trogloditas | 1 |
| 12250 | trofeos | 1 |
| 12251 | trocaste | 1 |
| 12252 | trocasen | 1 |
| 12253 | trocáreme | 1 |
| 12254 | trocando | 1 |
| 12255 | trocalle | 1 |
| 12256 | trocados | 1 |
| 12257 | triunfe | 1 |
| 12258 | triunfan | 1 |
| 12259 | triunfales | 1 |
| 12260 | tristísima | 1 |
| 12261 | tristemente | 1 |
| 12262 | tristán | 1 |
| 12263 | tris | 1 |
| 12264 | trinchéense | 1 |
| 12265 | trillando | 1 |
| 12266 | trillada | 1 |
| 12267 | tributo | 1 |
| 12268 | tributarios | 1 |
| 12269 | tribus | 1 |
| 12270 | tribunales | 1 |
| 12271 | tribulación | 1 |
| 12272 | treta | 1 |
| 12273 | tresquilen | 1 |
| 12274 | tresquilados | 1 |
| 12275 | tresquilado | 1 |
| 12276 | trenza | 1 |
| 12277 | tremolaban | 1 |
| 12278 | tremola | 1 |
| 12279 | tremente | 1 |
| 12280 | treguas | 1 |
| 12281 | tregua | 1 |
| 12282 | trechos | 1 |
| 12283 | trechel | 1 |
| 12284 | trazaré | 1 |
| 12285 | trazando | 1 |
| 12286 | trazador | 1 |
| 12287 | trazado | 1 |
| 12288 | trazada | 1 |
| 12289 | trayéndome | 1 |
| 12290 | traya | 1 |
| 12291 | traviesos | 1 |
| 12292 | tratóse | 1 |
| 12293 | trató | 1 |
| 12294 | trates | 1 |
| 12295 | tratéis | 1 |
| 12296 | tratásemos | 1 |
| 12297 | tratas | 1 |
| 12298 | trataron | 1 |
| 12299 | tratarle | 1 |
| 12300 | trataré | 1 |
| 12301 | tratarán | 1 |
| 12302 | tratante | 1 |
| 12303 | tratamientos | 1 |
| 12304 | tratalle | 1 |
| 12305 | tratados | 1 |
| 12306 | tratábamos | 1 |
| 12307 | trasudores | 1 |
| 12308 | trasudor | 1 |
| 12309 | trastulo | 1 |
| 12310 | trastruecan | 1 |
| 12311 | trastrocada | 1 |
| 12312 | trastornaron | 1 |
| 12313 | trastornar | 1 |
| 12314 | trastes | 1 |
| 12315 | traste | 1 |
| 12316 | trasquiló | 1 |
| 12317 | trasquilen | 1 |
| 12318 | trasquilar | 1 |
| 12319 | trasquilados | 1 |
| 12320 | trasquilada | 1 |
| 12321 | traspuso | 1 |
| 12322 | traspuesto | 1 |
| 12323 | traspuesta | 1 |
| 12324 | trasportado | 1 |
| 12325 | trasponella | 1 |
| 12326 | traspiés | 1 |
| 12327 | traspásenme | 1 |
| 12328 | traspásasele | 1 |
| 12329 | traspasarla | 1 |
| 12330 | traspasada | 1 |
| 12331 | traspasa | 1 |
| 12332 | trasparentes | 1 |
| 12333 | trasparente | 1 |
| 12334 | trasnochar | 1 |
| 12335 | trasnochados | 1 |
| 12336 | trasnochada | 1 |
| 12337 | trasmutación | 1 |
| 12338 | traslucido | 1 |
| 12339 | traslucían | 1 |
| 12340 | traslados | 1 |
| 12341 | traslado | 1 |
| 12342 | trasladen | 1 |
| 12343 | trasladarlos | 1 |
| 12344 | trasladaría | 1 |
| 12345 | trasladaremos | 1 |
| 12346 | trasladará | 1 |
| 12347 | trasladalla | 1 |
| 12348 | trasladado | 1 |
| 12349 | trasladaba | 1 |
| 12350 | trasijadas | 1 |
| 12351 | trasformación | 1 |
| 12352 | traseros | 1 |
| 12353 | traseras | 1 |
| 12354 | trasegando | 1 |
| 12355 | tranzados | 1 |
| 12356 | tranzado | 1 |
| 12357 | transversales | 1 |
| 12358 | transparentes | 1 |
| 12359 | translaciones | 1 |
| 12360 | tránsito | 1 |
| 12361 | transforma | 1 |
| 12362 | transferido | 1 |
| 12363 | tranquen | 1 |
| 12364 | trampa | 1 |
| 12365 | tramontana | 1 |
| 12366 | trama | 1 |
| 12367 | trajo | 1 |
| 12368 | trajano | 1 |
| 12369 | traigas | 1 |
| 12370 | traíganme | 1 |
| 12371 | tráiganme | 1 |
| 12372 | traídole | 1 |
| 12373 | traídola | 1 |
| 12374 | traídas | 1 |
| 12375 | traída | 1 |
| 12376 | traíamos | 1 |
| 12377 | traguito | 1 |
| 12378 | tragón | 1 |
| 12379 | tragarme | 1 |
| 12380 | tragara | 1 |
| 12381 | tragantón | 1 |
| 12382 | tragaderos | 1 |
| 12383 | traga | 1 |
| 12384 | tráeslos | 1 |
| 12385 | traés | 1 |
| 12386 | traérosle | 1 |
| 12387 | traérosla | 1 |
| 12388 | traerán | 1 |
| 12389 | traerá | 1 |
| 12390 | traelle | 1 |
| 12391 | traella | 1 |
| 12392 | tráele | 1 |
| 12393 | traédmelos | 1 |
| 12394 | traedme | 1 |
| 12395 | traduzga | 1 |
| 12396 | traductores | 1 |
| 12397 | traducirlos | 1 |
| 12398 | traducirlo | 1 |
| 12399 | traduciendo | 1 |
| 12400 | traducido | 1 |
| 12401 | traduce | 1 |
| 12402 | tracista | 1 |
| 12403 | trabuco | 1 |
| 12404 | trabe | 1 |
| 12405 | trabazón | 1 |
| 12406 | trabase | 1 |
| 12407 | trabándole | 1 |
| 12408 | traban | 1 |
| 12409 | trabajosa | 1 |
| 12410 | trabajó | 1 |
| 12411 | trabajemos | 1 |
| 12412 | trabajaste | 1 |
| 12413 | trabajase | 1 |
| 12414 | trabajan | 1 |
| 12415 | trabajadoras | 1 |
| 12416 | trabajador | 1 |
| 12417 | trabajado | 1 |
| 12418 | trabajaba | 1 |
| 12419 | trabacuentas | 1 |
| 12420 | trababa | 1 |
| 12421 | toto | 1 |
| 12422 | totalmente | 1 |
| 12423 | tosió | 1 |
| 12424 | toscas | 1 |
| 12425 | tortuoso | 1 |
| 12426 | tortolitas | 1 |
| 12427 | tortolilla | 1 |
| 12428 | torreznos | 1 |
| 12429 | torrezno | 1 |
| 12430 | tórnote | 1 |
| 12431 | tornóla | 1 |
| 12432 | torniscones | 1 |
| 12433 | tornes | 1 |
| 12434 | torneos | 1 |
| 12435 | tornémonos | 1 |
| 12436 | tornásemos | 1 |
| 12437 | tornarse | 1 |
| 12438 | tornáronla | 1 |
| 12439 | tornarle | 1 |
| 12440 | tornaremos | 1 |
| 12441 | tornaré | 1 |
| 12442 | tornándole | 1 |
| 12443 | tórnale | 1 |
| 12444 | tornaba | 1 |
| 12445 | tormes | 1 |
| 12446 | tordillo | 1 |
| 12447 | tordesillesco | 1 |
| 12448 | torcidos | 1 |
| 12449 | toraquís | 1 |
| 12450 | toquiblanca | 1 |
| 12451 | toques | 1 |
| 12452 | toquéis | 1 |
| 12453 | toqué | 1 |
| 12454 | topasen | 1 |
| 12455 | topásemos | 1 |
| 12456 | topares | 1 |
| 12457 | toparen | 1 |
| 12458 | topando | 1 |
| 12459 | topacios | 1 |
| 12460 | tontería | 1 |
| 12461 | tontas | 1 |
| 12462 | tonel | 1 |
| 12463 | tonante | 1 |
| 12464 | tón | 1 |
| 12465 | tomóse | 1 |
| 12466 | tomólo | 1 |
| 12467 | tomillos | 1 |
| 12468 | tomillas | 1 |
| 12469 | tómese | 1 |
| 12470 | tómense | 1 |
| 12471 | tomemos | 1 |
| 12472 | tomasillo | 1 |
| 12473 | tomás | 1 |
| 12474 | tomas | 1 |
| 12475 | tomáronle | 1 |
| 12476 | tomarlos | 1 |
| 12477 | tomarlo | 1 |
| 12478 | tomarles | 1 |
| 12479 | tomarlas | 1 |
| 12480 | tomarían | 1 |
| 12481 | tomaríamos | 1 |
| 12482 | tomaréle | 1 |
| 12483 | tomare | 1 |
| 12484 | tomárase | 1 |
| 12485 | tomarás | 1 |
| 12486 | tomará | 1 |
| 12487 | tomaos | 1 |
| 12488 | tomándolas | 1 |
| 12489 | tomadas | 1 |
| 12490 | tolomeos | 1 |
| 12491 | tolomeo | 1 |
| 12492 | tólogo | 1 |
| 12493 | tologías | 1 |
| 12494 | togados | 1 |
| 12495 | tocastes | 1 |
| 12496 | tocarse | 1 |
| 12497 | tocarla | 1 |
| 12498 | tocaré | 1 |
| 12499 | tocárades | 1 |
| 12500 | tocara | 1 |
| 12501 | tocante | 1 |
| 12502 | tocamos | 1 |
| 12503 | tócalos | 1 |
| 12504 | tocados | 1 |
| 12505 | tocadas | 1 |
| 12506 | tocada | 1 |
| 12507 | tobosina | 1 |
| 12508 | tobosescas | 1 |
| 12509 | tobosa | 1 |
| 12510 | tobo | 1 |
| 12511 | tobillos | 1 |
| 12512 | tobillo | 1 |
| 12513 | tizona | 1 |
| 12514 | titulillos | 1 |
| 12515 | titerera | 1 |
| 12516 | tirón | 1 |
| 12517 | tirios | 1 |
| 12518 | tire | 1 |
| 12519 | tiraron | 1 |
| 12520 | tiraré | 1 |
| 12521 | tirantes | 1 |
| 12522 | tiranos | 1 |
| 12523 | tirándoles | 1 |
| 12524 | tirándola | 1 |
| 12525 | tirámosla | 1 |
| 12526 | tiramira | 1 |
| 12527 | tiradas | 1 |
| 12528 | tirada | 1 |
| 12529 | tirad | 1 |
| 12530 | tirábanle | 1 |
| 12531 | tiquitoc | 1 |
| 12532 | tiopieyo | 1 |
| 12533 | tinte | 1 |
| 12534 | tinta | 1 |
| 12535 | timonel | 1 |
| 12536 | tímido | 1 |
| 12537 | timbrio | 1 |
| 12538 | timantes | 1 |
| 12539 | tiesa | 1 |
| 12540 | tientes | 1 |
| 12541 | tientas | 1 |
| 12542 | tiénesla | 1 |
| 12543 | tiénese | 1 |
| 12544 | tiénenlo | 1 |
| 12545 | tiénele | 1 |
| 12546 | tiemblan | 1 |
| 12547 | ticio | 1 |
| 12548 | tica | 1 |
| 12549 | tibulo | 1 |
| 12550 | tibre | 1 |
| 12551 | tibio | 1 |
| 12552 | tíbar | 1 |
| 12553 | tía | 1 |
| 12554 | texto | 1 |
| 12555 | testas | 1 |
| 12556 | testarudos | 1 |
| 12557 | tesón | 1 |
| 12558 | terso | 1 |
| 12559 | tersas | 1 |
| 12560 | tersan | 1 |
| 12561 | tersa | 1 |
| 12562 | terror | 1 |
| 12563 | terribles | 1 |
| 12564 | terrestre | 1 |
| 12565 | terrero | 1 |
| 12566 | ternísimamente | 1 |
| 12567 | termodonte | 1 |
| 12568 | teresona | 1 |
| 12569 | teresaina | 1 |
| 12570 | terencio | 1 |
| 12571 | terebinto | 1 |
| 12572 | terco | 1 |
| 12573 | tercios | 1 |
| 12574 | terció | 1 |
| 12575 | terciando | 1 |
| 12576 | terciado | 1 |
| 12577 | terceros | 1 |
| 12578 | tercería | 1 |
| 12579 | terceras | 1 |
| 12580 | tercas | 1 |
| 12581 | teórica | 1 |
| 12582 | teólogo | 1 |
| 12583 | teología | 1 |
| 12584 | teologales | 1 |
| 12585 | teñido | 1 |
| 12586 | tentólos | 1 |
| 12587 | tentóle | 1 |
| 12588 | tenté | 1 |
| 12589 | tentarme | 1 |
| 12590 | tentando | 1 |
| 12591 | tentaciones | 1 |
| 12592 | tentábala | 1 |
| 12593 | tenorio | 1 |
| 12594 | teniéndomela | 1 |
| 12595 | teniéndolos | 1 |
| 12596 | teníala | 1 |
| 12597 | téngolo | 1 |
| 12598 | téngase | 1 |
| 12599 | ténganos | 1 |
| 12600 | téngame | 1 |
| 12601 | téngale | 1 |
| 12602 | tenerte | 1 |
| 12603 | tenerles | 1 |
| 12604 | tenerías | 1 |
| 12605 | tenelle | 1 |
| 12606 | tenella | 1 |
| 12607 | tenedor | 1 |
| 12608 | tenedlos | 1 |
| 12609 | tenedle | 1 |
| 12610 | tenebras | 1 |
| 12611 | tendillas | 1 |
| 12612 | tendiéronse | 1 |
| 12613 | tendiéronle | 1 |
| 12614 | tendero | 1 |
| 12615 | tenderme | 1 |
| 12616 | tendera | 1 |
| 12617 | tender | 1 |
| 12618 | tendeos | 1 |
| 12619 | tendemos | 1 |
| 12620 | tempora | 1 |
| 12621 | templóse | 1 |
| 12622 | templóla | 1 |
| 12623 | templase | 1 |
| 12624 | templarles | 1 |
| 12625 | templarle | 1 |
| 12626 | templaréis | 1 |
| 12627 | templanza | 1 |
| 12628 | templados | 1 |
| 12629 | templadas | 1 |
| 12630 | templad | 1 |
| 12631 | temperet | 1 |
| 12632 | temorosos | 1 |
| 12633 | témome | 1 |
| 12634 | temiese | 1 |
| 12635 | temidas | 1 |
| 12636 | temíase | 1 |
| 12637 | temíades | 1 |
| 12638 | temerosas | 1 |
| 12639 | temerlo | 1 |
| 12640 | temerle | 1 |
| 12641 | teméis | 1 |
| 12642 | temblor | 1 |
| 12643 | temblándome | 1 |
| 12644 | tembladora | 1 |
| 12645 | temblaba | 1 |
| 12646 | temas | 1 |
| 12647 | teman | 1 |
| 12648 | telilla | 1 |
| 12649 | tejo | 1 |
| 12650 | tejió | 1 |
| 12651 | tejieron | 1 |
| 12652 | tejiendo | 1 |
| 12653 | tejido | 1 |
| 12654 | tejes | 1 |
| 12655 | tejedor | 1 |
| 12656 | teja | 1 |
| 12657 | techos | 1 |
| 12658 | teatros | 1 |
| 12659 | tazas | 1 |
| 12660 | taza | 1 |
| 12661 | tase | 1 |
| 12662 | tasaran | 1 |
| 12663 | tasajos | 1 |
| 12664 | tasajo | 1 |
| 12665 | tartamuda | 1 |
| 12666 | tártagos | 1 |
| 12667 | tarragona | 1 |
| 12668 | tarquino | 1 |
| 12669 | tarpeya | 1 |
| 12670 | tareas | 1 |
| 12671 | tardíos | 1 |
| 12672 | tardes | 1 |
| 12673 | tardaremos | 1 |
| 12674 | tardaré | 1 |
| 12675 | tardárades | 1 |
| 12676 | tardara | 1 |
| 12677 | tardar | 1 |
| 12678 | tardaban | 1 |
| 12679 | taraza | 1 |
| 12680 | tapó | 1 |
| 12681 | tapiasen | 1 |
| 12682 | tapetes | 1 |
| 12683 | tapete | 1 |
| 12684 | tápese | 1 |
| 12685 | tapaos | 1 |
| 12686 | tapaba | 1 |
| 12687 | tañida | 1 |
| 12688 | tañía | 1 |
| 12689 | tañer | 1 |
| 12690 | tañedores | 1 |
| 12691 | tañe | 1 |
| 12692 | tantum | 1 |
| 12693 | tantica | 1 |
| 12694 | tanteó | 1 |
| 12695 | tanteo | 1 |
| 12696 | tantearemos | 1 |
| 12697 | tántalo | 1 |
| 12698 | tansilo | 1 |
| 12699 | tamborines | 1 |
| 12700 | tamborín | 1 |
| 12701 | tamboril | 1 |
| 12702 | tambor | 1 |
| 12703 | talia | 1 |
| 12704 | talento | 1 |
| 12705 | talente | 1 |
| 12706 | talegazos | 1 |
| 12707 | taladrar | 1 |
| 12708 | tajos | 1 |
| 12709 | tajar | 1 |
| 12710 | tajantes | 1 |
| 12711 | tajadora | 1 |
| 12712 | tajadicas | 1 |
| 12713 | tajadas | 1 |
| 12714 | tagarninas | 1 |
| 12715 | tagarinos | 1 |
| 12716 | tácitos | 1 |
| 12717 | tácitas | 1 |
| 12718 | tacharle | 1 |
| 12719 | tablitas | 1 |
| 12720 | tablero | 1 |
| 12721 | tablantes | 1 |
| 12722 | tablante | 1 |
| 12723 | tabí | 1 |
| 12724 | tabernas | 1 |
| 12725 | tabarca | 1 |
| 12726 | tabaque | 1 |
| 12727 | sutilezas | 1 |
| 12728 | sutileza | 1 |
| 12729 | sustos | 1 |
| 12730 | susto | 1 |
| 12731 | sustentó | 1 |
| 12732 | sustente | 1 |
| 12733 | sustentarme | 1 |
| 12734 | sustentarlos | 1 |
| 12735 | sustentarla | 1 |
| 12736 | sustentaría | 1 |
| 12737 | sustentaran | 1 |
| 12738 | sustentará | 1 |
| 12739 | sustentándome | 1 |
| 12740 | sustentándola | 1 |
| 12741 | sustentadas | 1 |
| 12742 | sustentada | 1 |
| 12743 | sustancial | 1 |
| 12744 | suspiró | 1 |
| 12745 | suspiraba | 1 |
| 12746 | suspensas | 1 |
| 12747 | suspendióse | 1 |
| 12748 | suspendióme | 1 |
| 12749 | suspendióles | 1 |
| 12750 | suspendiendo | 1 |
| 12751 | suspenderse | 1 |
| 12752 | suspenderme | 1 |
| 12753 | suspended | 1 |
| 12754 | susodicha | 1 |
| 12755 | surcos | 1 |
| 12756 | súpose | 1 |
| 12757 | súpolo | 1 |
| 12758 | suplirla | 1 |
| 12759 | supliquémosle | 1 |
| 12760 | suplió | 1 |
| 12761 | supliera | 1 |
| 12762 | suplícote | 1 |
| 12763 | suplicóle | 1 |
| 12764 | suplicase | 1 |
| 12765 | suplicarte | 1 |
| 12766 | suplicáronle | 1 |
| 12767 | suplicándome | 1 |
| 12768 | suplicando | 1 |
| 12769 | suplicamos | 1 |
| 12770 | suplicado | 1 |
| 12771 | suplicad | 1 |
| 12772 | suplicaciones | 1 |
| 12773 | suplicación | 1 |
| 12774 | suplía | 1 |
| 12775 | supla | 1 |
| 12776 | supistes | 1 |
| 12777 | supina | 1 |
| 12778 | supiésemos | 1 |
| 12779 | supiésedes | 1 |
| 12780 | supiérades | 1 |
| 12781 | superstición | 1 |
| 12782 | supeditar | 1 |
| 12783 | súmulas | 1 |
| 12784 | sumptuosa | 1 |
| 12785 | summa | 1 |
| 12786 | sumiso | 1 |
| 12787 | sumisión | 1 |
| 12788 | sumisa | 1 |
| 12789 | sumiese | 1 |
| 12790 | sumergió | 1 |
| 12791 | sujetas | 1 |
| 12792 | sujetar | 1 |
| 12793 | sujeción | 1 |
| 12794 | sufrirle | 1 |
| 12795 | sufriré | 1 |
| 12796 | sufriere | 1 |
| 12797 | sufrían | 1 |
| 12798 | sufran | 1 |
| 12799 | súfrala | 1 |
| 12800 | sufragios | 1 |
| 12801 | suficientes | 1 |
| 12802 | sueñan | 1 |
| 12803 | sueña | 1 |
| 12804 | suenen | 1 |
| 12805 | suelte | 1 |
| 12806 | suelos | 1 |
| 12807 | suélenles | 1 |
| 12808 | sueldos | 1 |
| 12809 | suelas | 1 |
| 12810 | suegros | 1 |
| 12811 | suegra | 1 |
| 12812 | sudase | 1 |
| 12813 | sudada | 1 |
| 12814 | sucinta | 1 |
| 12815 | sucias | 1 |
| 12816 | sucesivamente | 1 |
| 12817 | sucedióme | 1 |
| 12818 | sucedióles | 1 |
| 12819 | sucedieren | 1 |
| 12820 | sucedida | 1 |
| 12821 | sucederá | 1 |
| 12822 | subtiles | 1 |
| 12823 | subo | 1 |
| 12824 | sublimidad | 1 |
| 12825 | sublimado | 1 |
| 12826 | sublimada | 1 |
| 12827 | súbita | 1 |
| 12828 | subiste | 1 |
| 12829 | subirme | 1 |
| 12830 | subirá | 1 |
| 12831 | subimos | 1 |
| 12832 | subímonos | 1 |
| 12833 | subieres | 1 |
| 12834 | subiéndole | 1 |
| 12835 | subían | 1 |
| 12836 | subas | 1 |
| 12837 | subáis | 1 |
| 12838 | suavísimamente | 1 |
| 12839 | suavísima | 1 |
| 12840 | suavemente | 1 |
| 12841 | suadente | 1 |
| 12842 | stupendo | 1 |
| 12843 | stultorum | 1 |
| 12844 | spero | 1 |
| 12845 | sotilmente | 1 |
| 12846 | sotilezas | 1 |
| 12847 | sotileza | 1 |
| 12848 | sotiles | 1 |
| 12849 | sotil | 1 |
| 12850 | sotavento | 1 |
| 12851 | sotanilla | 1 |
| 12852 | sotaermitaño | 1 |
| 12853 | sota | 1 |
| 12854 | sostuvo | 1 |
| 12855 | sostenido | 1 |
| 12856 | sostenían | 1 |
| 12857 | sostengo | 1 |
| 12858 | sostener | 1 |
| 12859 | sospiró | 1 |
| 12860 | sospirará | 1 |
| 12861 | sospirar | 1 |
| 12862 | sospirando | 1 |
| 12863 | sospechosos | 1 |
| 12864 | sospechoso | 1 |
| 12865 | sospechosa | 1 |
| 12866 | sospechaste | 1 |
| 12867 | soslayo | 1 |
| 12868 | sosieguen | 1 |
| 12869 | soseguéis | 1 |
| 12870 | sosegasen | 1 |
| 12871 | sosegáronse | 1 |
| 12872 | sosegándole | 1 |
| 12873 | sosegad | 1 |
| 12874 | sorrento | 1 |
| 12875 | sorbiese | 1 |
| 12876 | soplo | 1 |
| 12877 | soplaron | 1 |
| 12878 | soplándole | 1 |
| 12879 | soplando | 1 |
| 12880 | soplaba | 1 |
| 12881 | soñolientos | 1 |
| 12882 | soñoliento | 1 |
| 12883 | soñolienta | 1 |
| 12884 | soñando | 1 |
| 12885 | soñado | 1 |
| 12886 | soñaba | 1 |
| 12887 | sonsacarles | 1 |
| 12888 | sonsacado | 1 |
| 12889 | sonsaca | 1 |
| 12890 | sonrieron | 1 |
| 12891 | sonriéndose | 1 |
| 12892 | sonreía | 1 |
| 12893 | sones | 1 |
| 12894 | sonda | 1 |
| 12895 | sonarse | 1 |
| 12896 | sonara | 1 |
| 12897 | sonante | 1 |
| 12898 | sonando | 1 |
| 12899 | sombrosos | 1 |
| 12900 | sombríos | 1 |
| 12901 | solus | 1 |
| 12902 | soltero | 1 |
| 12903 | solté | 1 |
| 12904 | soltasen | 1 |
| 12905 | soltarte | 1 |
| 12906 | soltarlos | 1 |
| 12907 | soltara | 1 |
| 12908 | soltando | 1 |
| 12909 | soltaban | 1 |
| 12910 | soltaba | 1 |
| 12911 | solsticios | 1 |
| 12912 | solón | 1 |
| 12913 | sólito | 1 |
| 12914 | solitarios | 1 |
| 12915 | solisdán | 1 |
| 12916 | solicitaste | 1 |
| 12917 | solícitas | 1 |
| 12918 | solicitarle | 1 |
| 12919 | solicitares | 1 |
| 12920 | solicitaré | 1 |
| 12921 | solicitallo | 1 |
| 12922 | solicitalla | 1 |
| 12923 | solícita | 1 |
| 12924 | solicita | 1 |
| 12925 | solías | 1 |
| 12926 | solíamos | 1 |
| 12927 | soliadisa | 1 |
| 12928 | solíades | 1 |
| 12929 | solenizar | 1 |
| 12930 | solenizalle | 1 |
| 12931 | solenizados | 1 |
| 12932 | solenizadas | 1 |
| 12933 | solenísimas | 1 |
| 12934 | solene | 1 |
| 12935 | soldarse | 1 |
| 12936 | soldar | 1 |
| 12937 | solazasen | 1 |
| 12938 | solazarse | 1 |
| 12939 | solazaron | 1 |
| 12940 | solazándose | 1 |
| 12941 | solaz | 1 |
| 12942 | solar | 1 |
| 12943 | solapar | 1 |
| 12944 | solapada | 1 |
| 12945 | sofístico | 1 |
| 12946 | sofistería | 1 |
| 12947 | soficiente | 1 |
| 12948 | socorrió | 1 |
| 12949 | socorría | 1 |
| 12950 | socorreros | 1 |
| 12951 | socorren | 1 |
| 12952 | socorrelle | 1 |
| 12953 | socorrella | 1 |
| 12954 | socorredor | 1 |
| 12955 | socarronería | 1 |
| 12956 | socarronamente | 1 |
| 12957 | socaliñado | 1 |
| 12958 | sobró | 1 |
| 12959 | sobrevista | 1 |
| 12960 | sobreviniese | 1 |
| 12961 | sobrevinieron | 1 |
| 12962 | sobrevenido | 1 |
| 12963 | sobresaltes | 1 |
| 12964 | sobresaltase | 1 |
| 12965 | sobresaltarse | 1 |
| 12966 | sobresaltar | 1 |
| 12967 | sobresaltado | 1 |
| 12968 | sobresaltadas | 1 |
| 12969 | sobresalta | 1 |
| 12970 | sobrerropa | 1 |
| 12971 | sobrepujar | 1 |
| 12972 | sobrepujaban | 1 |
| 12973 | sobrepuja | 1 |
| 12974 | sobrepellices | 1 |
| 12975 | sobrenaturales | 1 |
| 12976 | sobrelleve | 1 |
| 12977 | sobredicho | 1 |
| 12978 | sobrecarga | 1 |
| 12979 | sobrebarbero | 1 |
| 12980 | sobrase | 1 |
| 12981 | sobrare | 1 |
| 12982 | sobrará | 1 |
| 12983 | sobrara | 1 |
| 12984 | sobrar | 1 |
| 12985 | sobrados | 1 |
| 12986 | sobraba | 1 |
| 12987 | sobornó | 1 |
| 12988 | soberano | 1 |
| 12989 | sitios | 1 |
| 12990 | sitiada | 1 |
| 12991 | sísifo | 1 |
| 12992 | sirviéremos | 1 |
| 12993 | sirviere | 1 |
| 12994 | sirviéndole | 1 |
| 12995 | sirviéndola | 1 |
| 12996 | sirves | 1 |
| 12997 | sírvate | 1 |
| 12998 | sirvas | 1 |
| 12999 | sírvale | 1 |
| 13000 | sirtes | 1 |
| 13001 | siríaca | 1 |
| 13002 | sintióse | 1 |
| 13003 | sintiólo | 1 |
| 13004 | sintiéndose | 1 |
| 13005 | sinsabor | 1 |
| 13006 | sinón | 1 |
| 13007 | sinificativo | 1 |
| 13008 | singulares | 1 |
| 13009 | sinabafas | 1 |
| 13010 | simulacro | 1 |
| 13011 | simplicísimo | 1 |
| 13012 | simón | 1 |
| 13013 | similitud | 1 |
| 13014 | simiente | 1 |
| 13015 | silvoso | 1 |
| 13016 | silvias | 1 |
| 13017 | silvestres | 1 |
| 13018 | silvato | 1 |
| 13019 | silvanos | 1 |
| 13020 | silva | 1 |
| 13021 | silo | 1 |
| 13022 | silguero | 1 |
| 13023 | sileno | 1 |
| 13024 | silbos | 1 |
| 13025 | silbato | 1 |
| 13026 | silbando | 1 |
| 13027 | sila | 1 |
| 13028 | siguiólas | 1 |
| 13029 | siguimiento | 1 |
| 13030 | siguiéronle | 1 |
| 13031 | sigüenza | 1 |
| 13032 | sígueme | 1 |
| 13033 | síguelos | 1 |
| 13034 | signis | 1 |
| 13035 | significó | 1 |
| 13036 | significarme | 1 |
| 13037 | significar | 1 |
| 13038 | significáis | 1 |
| 13039 | significación | 1 |
| 13040 | significaban | 1 |
| 13041 | significaba | 1 |
| 13042 | significa | 1 |
| 13043 | sigismunda | 1 |
| 13044 | sigas | 1 |
| 13045 | sigan | 1 |
| 13046 | sigamos | 1 |
| 13047 | sígame | 1 |
| 13048 | sigáis | 1 |
| 13049 | sietes | 1 |
| 13050 | síes | 1 |
| 13051 | siéntate | 1 |
| 13052 | sientas | 1 |
| 13053 | siéndole | 1 |
| 13054 | sevillano | 1 |
| 13055 | severo | 1 |
| 13056 | severa | 1 |
| 13057 | setiembre | 1 |
| 13058 | sesto | 1 |
| 13059 | sesteando | 1 |
| 13060 | sesgo | 1 |
| 13061 | servirme | 1 |
| 13062 | servirles | 1 |
| 13063 | serviría | 1 |
| 13064 | servillas | 1 |
| 13065 | servíle | 1 |
| 13066 | servil | 1 |
| 13067 | servidumbre | 1 |
| 13068 | servidorísimos | 1 |
| 13069 | servidas | 1 |
| 13070 | servíanos | 1 |
| 13071 | serví | 1 |
| 13072 | serte | 1 |
| 13073 | serrezuela | 1 |
| 13074 | serrallo | 1 |
| 13075 | seros | 1 |
| 13076 | sernos | 1 |
| 13077 | sermones | 1 |
| 13078 | sermoncico | 1 |
| 13079 | sermón | 1 |
| 13080 | serles | 1 |
| 13081 | sergas | 1 |
| 13082 | serenos | 1 |
| 13083 | serenísimo | 1 |
| 13084 | serenísima | 1 |
| 13085 | serenar | 1 |
| 13086 | serena | 1 |
| 13087 | seremos | 1 |
| 13088 | sepultarlas | 1 |
| 13089 | sepultar | 1 |
| 13090 | sepultan | 1 |
| 13091 | séptima | 1 |
| 13092 | separar | 1 |
| 13093 | separadas | 1 |
| 13094 | sepades | 1 |
| 13095 | séos | 1 |
| 13096 | señoritos | 1 |
| 13097 | señorísimas | 1 |
| 13098 | señoril | 1 |
| 13099 | señoreaba | 1 |
| 13100 | señorea | 1 |
| 13101 | señorazos | 1 |
| 13102 | señaló | 1 |
| 13103 | señalo | 1 |
| 13104 | señálensele | 1 |
| 13105 | señalé | 1 |
| 13106 | señalas | 1 |
| 13107 | señalaría | 1 |
| 13108 | señalaré | 1 |
| 13109 | señalaran | 1 |
| 13110 | señalar | 1 |
| 13111 | señalamos | 1 |
| 13112 | señalados | 1 |
| 13113 | señaladísima | 1 |
| 13114 | seña | 1 |
| 13115 | sentiste | 1 |
| 13116 | sentirse | 1 |
| 13117 | sentirme | 1 |
| 13118 | sentirle | 1 |
| 13119 | sentiríades | 1 |
| 13120 | sentiría | 1 |
| 13121 | sentiré | 1 |
| 13122 | sentirán | 1 |
| 13123 | sentidas | 1 |
| 13124 | sentible | 1 |
| 13125 | sentenció | 1 |
| 13126 | sentenciéla | 1 |
| 13127 | sentenciáronme | 1 |
| 13128 | sentencian | 1 |
| 13129 | senté | 1 |
| 13130 | sentábase | 1 |
| 13131 | senderos | 1 |
| 13132 | sencillos | 1 |
| 13133 | sencillo | 1 |
| 13134 | sencilla | 1 |
| 13135 | semínimas | 1 |
| 13136 | semidoncellas | 1 |
| 13137 | semejábades | 1 |
| 13138 | sembradura | 1 |
| 13139 | sembradas | 1 |
| 13140 | sembrada | 1 |
| 13141 | sembrad | 1 |
| 13142 | sembraba | 1 |
| 13143 | semblantes | 1 |
| 13144 | semanas | 1 |
| 13145 | sélo | 1 |
| 13146 | sellaron | 1 |
| 13147 | sellar | 1 |
| 13148 | selladas | 1 |
| 13149 | sellada | 1 |
| 13150 | sellad | 1 |
| 13151 | selim | 1 |
| 13152 | segundara | 1 |
| 13153 | seguís | 1 |
| 13154 | seguiría | 1 |
| 13155 | seguiréis | 1 |
| 13156 | seguiré | 1 |
| 13157 | seguirá | 1 |
| 13158 | seguimiento | 1 |
| 13159 | seguidor | 1 |
| 13160 | seguidme | 1 |
| 13161 | seguidamente | 1 |
| 13162 | seguí | 1 |
| 13163 | seglar | 1 |
| 13164 | segarme | 1 |
| 13165 | segar | 1 |
| 13166 | segador | 1 |
| 13167 | sediento | 1 |
| 13168 | sedienta | 1 |
| 13169 | secutoria | 1 |
| 13170 | sectas | 1 |
| 13171 | secretas | 1 |
| 13172 | secos | 1 |
| 13173 | séanme | 1 |
| 13174 | séalo | 1 |
| 13175 | séale | 1 |
| 13176 | scripserunt | 1 |
| 13177 | scitas | 1 |
| 13178 | scilas | 1 |
| 13179 | sazones | 1 |
| 13180 | sazonados | 1 |
| 13181 | sazonado | 1 |
| 13182 | sazonada | 1 |
| 13183 | sayagués | 1 |
| 13184 | sayago | 1 |
| 13185 | sauce | 1 |
| 13186 | saturninos | 1 |
| 13187 | saturatio | 1 |
| 13188 | satisficieron | 1 |
| 13189 | satisficiera | 1 |
| 13190 | satisfice | 1 |
| 13191 | satisfaría | 1 |
| 13192 | satisfarás | 1 |
| 13193 | satisfago | 1 |
| 13194 | satisfagáis | 1 |
| 13195 | satisfaciendo | 1 |
| 13196 | satisfacían | 1 |
| 13197 | satisfacerse | 1 |
| 13198 | satisfacerles | 1 |
| 13199 | satisfacerle | 1 |
| 13200 | satisfacerlas | 1 |
| 13201 | satisfacelle | 1 |
| 13202 | satisfacéis | 1 |
| 13203 | satisface | 1 |
| 13204 | sátiros | 1 |
| 13205 | satírico | 1 |
| 13206 | satíricas | 1 |
| 13207 | sastres | 1 |
| 13208 | sartenes | 1 |
| 13209 | sartas | 1 |
| 13210 | sardo | 1 |
| 13211 | sardesco | 1 |
| 13212 | saques | 1 |
| 13213 | saquen | 1 |
| 13214 | santuarios | 1 |
| 13215 | santiguarnos | 1 |
| 13216 | santángel | 1 |
| 13217 | sansonino | 1 |
| 13218 | sanó | 1 |
| 13219 | sanguinolenta | 1 |
| 13220 | sanguínea | 1 |
| 13221 | sangrarse | 1 |
| 13222 | sangran | 1 |
| 13223 | sanen | 1 |
| 13224 | sanchuelo | 1 |
| 13225 | sanchico | 1 |
| 13226 | sanazaro | 1 |
| 13227 | sanarlas | 1 |
| 13228 | sanaremos | 1 |
| 13229 | sanarás | 1 |
| 13230 | sanado | 1 |
| 13231 | sambenito | 1 |
| 13232 | salvó | 1 |
| 13233 | salves | 1 |
| 13234 | salvas | 1 |
| 13235 | salvar | 1 |
| 13236 | salvando | 1 |
| 13237 | salvamento | 1 |
| 13238 | salvamano | 1 |
| 13239 | salutífero | 1 |
| 13240 | salutación | 1 |
| 13241 | saludónos | 1 |
| 13242 | saludóles | 1 |
| 13243 | saludáronse | 1 |
| 13244 | saludaron | 1 |
| 13245 | saludarla | 1 |
| 13246 | saludándolos | 1 |
| 13247 | saludalle | 1 |
| 13248 | saludables | 1 |
| 13249 | saludable | 1 |
| 13250 | salterios | 1 |
| 13251 | saltee | 1 |
| 13252 | saltearon | 1 |
| 13253 | salteándosele | 1 |
| 13254 | salteándole | 1 |
| 13255 | salté | 1 |
| 13256 | saltase | 1 |
| 13257 | saltados | 1 |
| 13258 | saltado | 1 |
| 13259 | saltaba | 1 |
| 13260 | salomón | 1 |
| 13261 | salobre | 1 |
| 13262 | salmanticenses | 1 |
| 13263 | saliva | 1 |
| 13264 | salistes | 1 |
| 13265 | salirme | 1 |
| 13266 | salíos | 1 |
| 13267 | saliónos | 1 |
| 13268 | salióle | 1 |
| 13269 | salieses | 1 |
| 13270 | saliésemos | 1 |
| 13271 | saliéronle | 1 |
| 13272 | salieran | 1 |
| 13273 | salidad | 1 |
| 13274 | salíale | 1 |
| 13275 | salgas | 1 |
| 13276 | salgáis | 1 |
| 13277 | sálese | 1 |
| 13278 | saldrían | 1 |
| 13279 | salazar | 1 |
| 13280 | salar | 1 |
| 13281 | salamanquesa | 1 |
| 13282 | sahumerio | 1 |
| 13283 | sagrado | 1 |
| 13284 | sagitario | 1 |
| 13285 | sacudir | 1 |
| 13286 | sacudieron | 1 |
| 13287 | sacudiéndole | 1 |
| 13288 | sacudido | 1 |
| 13289 | sacuda | 1 |
| 13290 | sacristanía | 1 |
| 13291 | sacristanes | 1 |
| 13292 | sacrilegio | 1 |
| 13293 | sacre | 1 |
| 13294 | sacramentos | 1 |
| 13295 | sacólos | 1 |
| 13296 | sacaste | 1 |
| 13297 | sacas | 1 |
| 13298 | sacársele | 1 |
| 13299 | sacármela | 1 |
| 13300 | sacarlos | 1 |
| 13301 | sacarlo | 1 |
| 13302 | sacarla | 1 |
| 13303 | sacares | 1 |
| 13304 | sacaren | 1 |
| 13305 | sacaremos | 1 |
| 13306 | sacaréis | 1 |
| 13307 | sacáredes | 1 |
| 13308 | sacaran | 1 |
| 13309 | sacáramos | 1 |
| 13310 | sacapotras | 1 |
| 13311 | sacándomele | 1 |
| 13312 | sácame | 1 |
| 13313 | sacallos | 1 |
| 13314 | sacáis | 1 |
| 13315 | sacádole | 1 |
| 13316 | sacada | 1 |
| 13317 | sacabuches | 1 |
| 13318 | sacaban | 1 |
| 13319 | sabrosos | 1 |
| 13320 | sabrosísimo | 1 |
| 13321 | sabríame | 1 |
| 13322 | sabréisme | 1 |
| 13323 | sabréis | 1 |
| 13324 | saboyanas | 1 |
| 13325 | saboyana | 1 |
| 13326 | sabores | 1 |
| 13327 | saboreándose | 1 |
| 13328 | sabogas | 1 |
| 13329 | sabiendas | 1 |
| 13330 | sabidas | 1 |
| 13331 | sábese | 1 |
| 13332 | saberlos | 1 |
| 13333 | saberlas | 1 |
| 13334 | saberla | 1 |
| 13335 | sabeo | 1 |
| 13336 | sabandijas | 1 |
| 13337 | sábados | 1 |
| 13338 | sábado | 1 |
| 13339 | rutilantes | 1 |
| 13340 | rus | 1 |
| 13341 | rumpantes | 1 |
| 13342 | rumia | 1 |
| 13343 | rumbos | 1 |
| 13344 | rüina | 1 |
| 13345 | ruidos | 1 |
| 13346 | rüido | 1 |
| 13347 | ruibarbo | 1 |
| 13348 | rugir | 1 |
| 13349 | rugidos | 1 |
| 13350 | rugel | 1 |
| 13351 | rufo | 1 |
| 13352 | ruégole | 1 |
| 13353 | ruégale | 1 |
| 13354 | rudeza | 1 |
| 13355 | rucia | 1 |
| 13356 | rúbrica | 1 |
| 13357 | rubio | 1 |
| 13358 | rubicundo | 1 |
| 13359 | rubicón | 1 |
| 13360 | rúa | 1 |
| 13361 | roznar | 1 |
| 13362 | rozagantes | 1 |
| 13363 | roturas | 1 |
| 13364 | rotunda | 1 |
| 13365 | rotas | 1 |
| 13366 | rosca | 1 |
| 13367 | rosadas | 1 |
| 13368 | rosada | 1 |
| 13369 | ropón | 1 |
| 13370 | ropillas | 1 |
| 13371 | ronquilla | 1 |
| 13372 | rondilla | 1 |
| 13373 | rondar | 1 |
| 13374 | rondando | 1 |
| 13375 | roncando | 1 |
| 13376 | roncaba | 1 |
| 13377 | rompiera | 1 |
| 13378 | rompiéndolos | 1 |
| 13379 | rompidos | 1 |
| 13380 | rompido | 1 |
| 13381 | rompidas | 1 |
| 13382 | rompida | 1 |
| 13383 | rompía | 1 |
| 13384 | rompí | 1 |
| 13385 | romperse | 1 |
| 13386 | romperme | 1 |
| 13387 | romperlo | 1 |
| 13388 | romperlas | 1 |
| 13389 | romperla | 1 |
| 13390 | rompelle | 1 |
| 13391 | rómpaselas | 1 |
| 13392 | rompáis | 1 |
| 13393 | rombos | 1 |
| 13394 | romadizado | 1 |
| 13395 | roldanes | 1 |
| 13396 | roído | 1 |
| 13397 | roía | 1 |
| 13398 | roguéle | 1 |
| 13399 | rogativas | 1 |
| 13400 | rogaste | 1 |
| 13401 | rogaremos | 1 |
| 13402 | rogarán | 1 |
| 13403 | rogarále | 1 |
| 13404 | rogara | 1 |
| 13405 | rogándome | 1 |
| 13406 | rogándole | 1 |
| 13407 | rogámosle | 1 |
| 13408 | rogada | 1 |
| 13409 | rogad | 1 |
| 13410 | rogaciones | 1 |
| 13411 | roerá | 1 |
| 13412 | roen | 1 |
| 13413 | roe | 1 |
| 13414 | rodeó | 1 |
| 13415 | rodelas | 1 |
| 13416 | rodeen | 1 |
| 13417 | rodeemos | 1 |
| 13418 | rodeé | 1 |
| 13419 | rodearemos | 1 |
| 13420 | rodeándola | 1 |
| 13421 | rodean | 1 |
| 13422 | rodeámonos | 1 |
| 13423 | rodeaba | 1 |
| 13424 | rodea | 1 |
| 13425 | rodamonte | 1 |
| 13426 | rodajas | 1 |
| 13427 | rodaja | 1 |
| 13428 | rocíe | 1 |
| 13429 | rochela | 1 |
| 13430 | rocabertis | 1 |
| 13431 | robustos | 1 |
| 13432 | robustas | 1 |
| 13433 | robusta | 1 |
| 13434 | roble | 1 |
| 13435 | roben | 1 |
| 13436 | robastes | 1 |
| 13437 | robaron | 1 |
| 13438 | robarla | 1 |
| 13439 | robando | 1 |
| 13440 | robadores | 1 |
| 13441 | riyó | 1 |
| 13442 | rival | 1 |
| 13443 | riquísimos | 1 |
| 13444 | ripio | 1 |
| 13445 | ríome | 1 |
| 13446 | riñones | 1 |
| 13447 | riñó | 1 |
| 13448 | riño | 1 |
| 13449 | riñiremos | 1 |
| 13450 | riñese | 1 |
| 13451 | riñeren | 1 |
| 13452 | riñendo | 1 |
| 13453 | riñe | 1 |
| 13454 | riña | 1 |
| 13455 | rindiera | 1 |
| 13456 | rinden | 1 |
| 13457 | rindan | 1 |
| 13458 | rinconete | 1 |
| 13459 | rimeros | 1 |
| 13460 | rigurosamente | 1 |
| 13461 | rígida | 1 |
| 13462 | rifeas | 1 |
| 13463 | rieto | 1 |
| 13464 | riesen | 1 |
| 13465 | riese | 1 |
| 13466 | ríes | 1 |
| 13467 | riéronse | 1 |
| 13468 | rieres | 1 |
| 13469 | ridículo | 1 |
| 13470 | ridículas | 1 |
| 13471 | ricamonte | 1 |
| 13472 | ribete | 1 |
| 13473 | ribazo | 1 |
| 13474 | ríase | 1 |
| 13475 | riarán | 1 |
| 13476 | ría | 1 |
| 13477 | rezó | 1 |
| 13478 | rezan | 1 |
| 13479 | revulgo | 1 |
| 13480 | revuelve | 1 |
| 13481 | revueltos | 1 |
| 13482 | revolvieron | 1 |
| 13483 | revolviéndosele | 1 |
| 13484 | revolviendo | 1 |
| 13485 | revolví | 1 |
| 13486 | revolver | 1 |
| 13487 | revoltillos | 1 |
| 13488 | revocarle | 1 |
| 13489 | revocar | 1 |
| 13490 | revivió | 1 |
| 13491 | revienten | 1 |
| 13492 | reviente | 1 |
| 13493 | revientan | 1 |
| 13494 | reverendísimas | 1 |
| 13495 | reverendísima | 1 |
| 13496 | reverendas | 1 |
| 13497 | reverencio | 1 |
| 13498 | reverencien | 1 |
| 13499 | reverenciar | 1 |
| 13500 | reventó | 1 |
| 13501 | reventasen | 1 |
| 13502 | reventaran | 1 |
| 13503 | reventara | 1 |
| 13504 | reventando | 1 |
| 13505 | reventaba | 1 |
| 13506 | revellín | 1 |
| 13507 | reuma | 1 |
| 13508 | retumban | 1 |
| 13509 | retumbaba | 1 |
| 13510 | rétulos | 1 |
| 13511 | retule | 1 |
| 13512 | retretes | 1 |
| 13513 | retrató | 1 |
| 13514 | retráteme | 1 |
| 13515 | retratarle | 1 |
| 13516 | retratado | 1 |
| 13517 | retratada | 1 |
| 13518 | retraer | 1 |
| 13519 | retozar | 1 |
| 13520 | retozaba | 1 |
| 13521 | retores | 1 |
| 13522 | retiro | 1 |
| 13523 | retires | 1 |
| 13524 | retiréis | 1 |
| 13525 | retiré | 1 |
| 13526 | retire | 1 |
| 13527 | retirases | 1 |
| 13528 | retirasen | 1 |
| 13529 | retirásemos | 1 |
| 13530 | retirarse | 1 |
| 13531 | retiráronse | 1 |
| 13532 | retirarme | 1 |
| 13533 | retirándose | 1 |
| 13534 | retirado | 1 |
| 13535 | retintín | 1 |
| 13536 | retazos | 1 |
| 13537 | retar | 1 |
| 13538 | retándole | 1 |
| 13539 | retamas | 1 |
| 13540 | retama | 1 |
| 13541 | reta | 1 |
| 13542 | resumirse | 1 |
| 13543 | resulución | 1 |
| 13544 | resultó | 1 |
| 13545 | resultaba | 1 |
| 13546 | resuenan | 1 |
| 13547 | resuena | 1 |
| 13548 | resuelven | 1 |
| 13549 | resuelve | 1 |
| 13550 | resucites | 1 |
| 13551 | resucite | 1 |
| 13552 | resucitara | 1 |
| 13553 | resucitando | 1 |
| 13554 | resucitador | 1 |
| 13555 | restituye | 1 |
| 13556 | restituir | 1 |
| 13557 | restituido | 1 |
| 13558 | restituida | 1 |
| 13559 | restaurarse | 1 |
| 13560 | restauración | 1 |
| 13561 | restante | 1 |
| 13562 | resquicio | 1 |
| 13563 | resquebrajos | 1 |
| 13564 | respondistes | 1 |
| 13565 | respondiste | 1 |
| 13566 | respondióles | 1 |
| 13567 | respondiesen | 1 |
| 13568 | respondiéronme | 1 |
| 13569 | respondiente | 1 |
| 13570 | respondes | 1 |
| 13571 | respondería | 1 |
| 13572 | responderás | 1 |
| 13573 | respondemos | 1 |
| 13574 | respondelles | 1 |
| 13575 | responded | 1 |
| 13576 | respondas | 1 |
| 13577 | respondan | 1 |
| 13578 | respondáis | 1 |
| 13579 | resplandecieron | 1 |
| 13580 | resplandecía | 1 |
| 13581 | resplandecen | 1 |
| 13582 | respetó | 1 |
| 13583 | respetar | 1 |
| 13584 | respetado | 1 |
| 13585 | resonaron | 1 |
| 13586 | resonar | 1 |
| 13587 | resolvióse | 1 |
| 13588 | resolviéronse | 1 |
| 13589 | resolví | 1 |
| 13590 | resolverse | 1 |
| 13591 | resolverlas | 1 |
| 13592 | resolvámonos | 1 |
| 13593 | resistirle | 1 |
| 13594 | resistiese | 1 |
| 13595 | resistido | 1 |
| 13596 | resistencia | 1 |
| 13597 | resina | 1 |
| 13598 | resfriaron | 1 |
| 13599 | resfriarme | 1 |
| 13600 | resfriado | 1 |
| 13601 | reses | 1 |
| 13602 | reservadas | 1 |
| 13603 | resentirse | 1 |
| 13604 | rescibió | 1 |
| 13605 | rescebido | 1 |
| 13606 | rescató | 1 |
| 13607 | rescátate | 1 |
| 13608 | rescatasen | 1 |
| 13609 | rescatase | 1 |
| 13610 | rescatarlos | 1 |
| 13611 | rescataos | 1 |
| 13612 | rescatando | 1 |
| 13613 | rescatados | 1 |
| 13614 | rescataba | 1 |
| 13615 | resbaloso | 1 |
| 13616 | resbalando | 1 |
| 13617 | requisitos | 1 |
| 13618 | requisito | 1 |
| 13619 | requirió | 1 |
| 13620 | requirimientos | 1 |
| 13621 | requiriese | 1 |
| 13622 | requiriera | 1 |
| 13623 | requirido | 1 |
| 13624 | requiría | 1 |
| 13625 | requiebro | 1 |
| 13626 | requiébranse | 1 |
| 13627 | requesenes | 1 |
| 13628 | requerido | 1 |
| 13629 | requerida | 1 |
| 13630 | requerid | 1 |
| 13631 | requebróme | 1 |
| 13632 | requebrar | 1 |
| 13633 | requebrábanle | 1 |
| 13634 | reputado | 1 |
| 13635 | repulgadas | 1 |
| 13636 | repulgada | 1 |
| 13637 | repuesta | 1 |
| 13638 | repto | 1 |
| 13639 | repruebas | 1 |
| 13640 | reproches | 1 |
| 13641 | reprocharme | 1 |
| 13642 | reprochándole | 1 |
| 13643 | reprochador | 1 |
| 13644 | reprochado | 1 |
| 13645 | reprimiré | 1 |
| 13646 | represento | 1 |
| 13647 | representes | 1 |
| 13648 | representasen | 1 |
| 13649 | representarnos | 1 |
| 13650 | representarme | 1 |
| 13651 | representaría | 1 |
| 13652 | representante | 1 |
| 13653 | representamos | 1 |
| 13654 | representallas | 1 |
| 13655 | representaciones | 1 |
| 13656 | reprehensores | 1 |
| 13657 | reprehensor | 1 |
| 13658 | reprehensiones | 1 |
| 13659 | reprehendiendo | 1 |
| 13660 | reprehendidas | 1 |
| 13661 | reprehendida | 1 |
| 13662 | reprehender | 1 |
| 13663 | reprehende | 1 |
| 13664 | reprehendáis | 1 |
| 13665 | reprehenda | 1 |
| 13666 | repostero | 1 |
| 13667 | reposterías | 1 |
| 13668 | reposemos | 1 |
| 13669 | reposaría | 1 |
| 13670 | reposando | 1 |
| 13671 | reposadamente | 1 |
| 13672 | reposaban | 1 |
| 13673 | reposa | 1 |
| 13674 | reportóse | 1 |
| 13675 | reporte | 1 |
| 13676 | reportaré | 1 |
| 13677 | repliquéis | 1 |
| 13678 | replicóme | 1 |
| 13679 | replicase | 1 |
| 13680 | réplicas | 1 |
| 13681 | replicaré | 1 |
| 13682 | replicalle | 1 |
| 13683 | repitiéndole | 1 |
| 13684 | repique | 1 |
| 13685 | repetidme | 1 |
| 13686 | repelón | 1 |
| 13687 | repasándola | 1 |
| 13688 | repasa | 1 |
| 13689 | reparto | 1 |
| 13690 | repartió | 1 |
| 13691 | repartiendo | 1 |
| 13692 | repartido | 1 |
| 13693 | repartida | 1 |
| 13694 | repartición | 1 |
| 13695 | repartible | 1 |
| 13696 | repártela | 1 |
| 13697 | reparo | 1 |
| 13698 | repares | 1 |
| 13699 | repare | 1 |
| 13700 | reparas | 1 |
| 13701 | repararon | 1 |
| 13702 | repararé | 1 |
| 13703 | reparáis | 1 |
| 13704 | reparábamos | 1 |
| 13705 | renueva | 1 |
| 13706 | rentas | 1 |
| 13707 | rentada | 1 |
| 13708 | renqueando | 1 |
| 13709 | renovarse | 1 |
| 13710 | renovarle | 1 |
| 13711 | renovando | 1 |
| 13712 | renovaban | 1 |
| 13713 | renovaba | 1 |
| 13714 | reniegos | 1 |
| 13715 | reniega | 1 |
| 13716 | renglón | 1 |
| 13717 | renegó | 1 |
| 13718 | renegad | 1 |
| 13719 | rendiros | 1 |
| 13720 | rendirnos | 1 |
| 13721 | rendirle | 1 |
| 13722 | rendirla | 1 |
| 13723 | rendí | 1 |
| 13724 | rencor | 1 |
| 13725 | rencillas | 1 |
| 13726 | renca | 1 |
| 13727 | renacuajos | 1 |
| 13728 | renacer | 1 |
| 13729 | remunerar | 1 |
| 13730 | remunerado | 1 |
| 13731 | remoto | 1 |
| 13732 | remotas | 1 |
| 13733 | remordiéndole | 1 |
| 13734 | remonte | 1 |
| 13735 | remondóse | 1 |
| 13736 | remolino | 1 |
| 13737 | remojado | 1 |
| 13738 | remitiéndome | 1 |
| 13739 | remisos | 1 |
| 13740 | remirólos | 1 |
| 13741 | remirarle | 1 |
| 13742 | remirado | 1 |
| 13743 | remira | 1 |
| 13744 | remiente | 1 |
| 13745 | remiendos | 1 |
| 13746 | remiendo | 1 |
| 13747 | remestán | 1 |
| 13748 | remendón | 1 |
| 13749 | remendar | 1 |
| 13750 | remendado | 1 |
| 13751 | remendadas | 1 |
| 13752 | remedien | 1 |
| 13753 | remediase | 1 |
| 13754 | remediaron | 1 |
| 13755 | remediarme | 1 |
| 13756 | remediarlo | 1 |
| 13757 | remediaran | 1 |
| 13758 | remediárades | 1 |
| 13759 | remediará | 1 |
| 13760 | remediando | 1 |
| 13761 | remedian | 1 |
| 13762 | remediallo | 1 |
| 13763 | remediados | 1 |
| 13764 | remediador | 1 |
| 13765 | remediadas | 1 |
| 13766 | remedia | 1 |
| 13767 | remató | 1 |
| 13768 | remates | 1 |
| 13769 | rematar | 1 |
| 13770 | rematan | 1 |
| 13771 | remanso | 1 |
| 13772 | remaneció | 1 |
| 13773 | remachó | 1 |
| 13774 | relumbra | 1 |
| 13775 | reloja | 1 |
| 13776 | reloj | 1 |
| 13777 | relinche | 1 |
| 13778 | relieve | 1 |
| 13779 | relatares | 1 |
| 13780 | relatando | 1 |
| 13781 | relasos | 1 |
| 13782 | relámpagos | 1 |
| 13783 | reiteráronse | 1 |
| 13784 | reiteraban | 1 |
| 13785 | reírme | 1 |
| 13786 | reincorporóse | 1 |
| 13787 | reinase | 1 |
| 13788 | reinado | 1 |
| 13789 | reídas | 1 |
| 13790 | reíase | 1 |
| 13791 | reíanse | 1 |
| 13792 | rehúya | 1 |
| 13793 | rehusólo | 1 |
| 13794 | rehusó | 1 |
| 13795 | rehú | 1 |
| 13796 | rehacerse | 1 |
| 13797 | regumque | 1 |
| 13798 | regüeldos | 1 |
| 13799 | regostóse | 1 |
| 13800 | regodeo | 1 |
| 13801 | regocijó | 1 |
| 13802 | regocijarse | 1 |
| 13803 | regocijar | 1 |
| 13804 | regocijalle | 1 |
| 13805 | regocijadores | 1 |
| 13806 | regocijador | 1 |
| 13807 | regocijadas | 1 |
| 13808 | regocijadamente | 1 |
| 13809 | regocijaba | 1 |
| 13810 | registro | 1 |
| 13811 | registrar | 1 |
| 13812 | registran | 1 |
| 13813 | regimiento | 1 |
| 13814 | regente | 1 |
| 13815 | regazo | 1 |
| 13816 | regatones | 1 |
| 13817 | regañaban | 1 |
| 13818 | regalen | 1 |
| 13819 | regale | 1 |
| 13820 | regalastes | 1 |
| 13821 | regalasen | 1 |
| 13822 | regalarle | 1 |
| 13823 | regaladísimo | 1 |
| 13824 | regaladamente | 1 |
| 13825 | regalada | 1 |
| 13826 | regalaba | 1 |
| 13827 | refrigerios | 1 |
| 13828 | refrancico | 1 |
| 13829 | reforzó | 1 |
| 13830 | reformando | 1 |
| 13831 | refociló | 1 |
| 13832 | refocilarse | 1 |
| 13833 | refocilarían | 1 |
| 13834 | refiriese | 1 |
| 13835 | refiriéndola | 1 |
| 13836 | refiere | 1 |
| 13837 | refacción | 1 |
| 13838 | redúzgase | 1 |
| 13839 | redundó | 1 |
| 13840 | redundara | 1 |
| 13841 | redundan | 1 |
| 13842 | redújose | 1 |
| 13843 | redujeron | 1 |
| 13844 | reducirte | 1 |
| 13845 | reducirme | 1 |
| 13846 | reducirle | 1 |
| 13847 | reducille | 1 |
| 13848 | reduciéndolo | 1 |
| 13849 | reduciendo | 1 |
| 13850 | reducíansele | 1 |
| 13851 | redropelo | 1 |
| 13852 | redondillas | 1 |
| 13853 | redención | 1 |
| 13854 | redemir | 1 |
| 13855 | redecilla | 1 |
| 13856 | recuéstate | 1 |
| 13857 | recuestando | 1 |
| 13858 | recuestaban | 1 |
| 13859 | recuerda | 1 |
| 13860 | rectórico | 1 |
| 13861 | rectorías | 1 |
| 13862 | rector | 1 |
| 13863 | rectitud | 1 |
| 13864 | recrearse | 1 |
| 13865 | recreando | 1 |
| 13866 | recreaba | 1 |
| 13867 | recostó | 1 |
| 13868 | recostarme | 1 |
| 13869 | recorriendo | 1 |
| 13870 | recorrido | 1 |
| 13871 | recorrida | 1 |
| 13872 | recorred | 1 |
| 13873 | reconoció | 1 |
| 13874 | reconociéndole | 1 |
| 13875 | reconociendo | 1 |
| 13876 | reconocíamos | 1 |
| 13877 | reconocer | 1 |
| 13878 | reconciliar | 1 |
| 13879 | reconcilian | 1 |
| 13880 | reconciliado | 1 |
| 13881 | recompensas | 1 |
| 13882 | recompensara | 1 |
| 13883 | recompensallas | 1 |
| 13884 | recomendación | 1 |
| 13885 | recojas | 1 |
| 13886 | recogióse | 1 |
| 13887 | recogiéronse | 1 |
| 13888 | recogiera | 1 |
| 13889 | recogiéndolas | 1 |
| 13890 | recogidos | 1 |
| 13891 | recogían | 1 |
| 13892 | recogía | 1 |
| 13893 | recogernos | 1 |
| 13894 | recogeos | 1 |
| 13895 | recogella | 1 |
| 13896 | recobrar | 1 |
| 13897 | recluso | 1 |
| 13898 | recitante | 1 |
| 13899 | recíproca | 1 |
| 13900 | recibirá | 1 |
| 13901 | recibiólo | 1 |
| 13902 | recibióle | 1 |
| 13903 | recibióla | 1 |
| 13904 | recibiéronse | 1 |
| 13905 | recibiéronle | 1 |
| 13906 | recibiere | 1 |
| 13907 | recibía | 1 |
| 13908 | recibí | 1 |
| 13909 | recíbeme | 1 |
| 13910 | recibas | 1 |
| 13911 | rechinantes | 1 |
| 13912 | recetes | 1 |
| 13913 | recetas | 1 |
| 13914 | recetada | 1 |
| 13915 | receloso | 1 |
| 13916 | receló | 1 |
| 13917 | recelarme | 1 |
| 13918 | recebiros | 1 |
| 13919 | recebidme | 1 |
| 13920 | recebid | 1 |
| 13921 | recebíale | 1 |
| 13922 | rece | 1 |
| 13923 | recatarse | 1 |
| 13924 | recatadas | 1 |
| 13925 | recapacite | 1 |
| 13926 | recambio | 1 |
| 13927 | rebuznó | 1 |
| 13928 | rebuznasen | 1 |
| 13929 | rebuznase | 1 |
| 13930 | rebuznaréis | 1 |
| 13931 | rebuznaré | 1 |
| 13932 | rebuznara | 1 |
| 13933 | rebuznadores | 1 |
| 13934 | rebuznador | 1 |
| 13935 | rebuznado | 1 |
| 13936 | rebuznaban | 1 |
| 13937 | rebuzna | 1 |
| 13938 | rebullir | 1 |
| 13939 | rebullen | 1 |
| 13940 | rebenque | 1 |
| 13941 | rebellas | 1 |
| 13942 | rebaños | 1 |
| 13943 | reata | 1 |
| 13944 | realzarla | 1 |
| 13945 | realidad | 1 |
| 13946 | razonar | 1 |
| 13947 | razonando | 1 |
| 13948 | rayaba | 1 |
| 13949 | rávena | 1 |
| 13950 | ratón | 1 |
| 13951 | rateras | 1 |
| 13952 | rastrillos | 1 |
| 13953 | rastrillado | 1 |
| 13954 | rastrear | 1 |
| 13955 | rastreando | 1 |
| 13956 | rastrea | 1 |
| 13957 | rasguño | 1 |
| 13958 | rasgarla | 1 |
| 13959 | rasgará | 1 |
| 13960 | rasgar | 1 |
| 13961 | rasgándome | 1 |
| 13962 | rasgados | 1 |
| 13963 | rasgaba | 1 |
| 13964 | rascó | 1 |
| 13965 | rascarse | 1 |
| 13966 | rascarme | 1 |
| 13967 | rascaría | 1 |
| 13968 | rascar | 1 |
| 13969 | rascándote | 1 |
| 13970 | ras | 1 |
| 13971 | raros | 1 |
| 13972 | raridad | 1 |
| 13973 | raposa | 1 |
| 13974 | rapiña | 1 |
| 13975 | rápido | 1 |
| 13976 | rapaz | 1 |
| 13977 | rapasen | 1 |
| 13978 | rapase | 1 |
| 13979 | rapas | 1 |
| 13980 | raparía | 1 |
| 13981 | rapar | 1 |
| 13982 | rapador | 1 |
| 13983 | rapadas | 1 |
| 13984 | rapacería | 1 |
| 13985 | rapacejos | 1 |
| 13986 | randera | 1 |
| 13987 | randado | 1 |
| 13988 | rancores | 1 |
| 13989 | ranciosos | 1 |
| 13990 | ranchos | 1 |
| 13991 | ranas | 1 |
| 13992 | rana | 1 |
| 13993 | ramal | 1 |
| 13994 | ralos | 1 |
| 13995 | ralla | 1 |
| 13996 | rajitas | 1 |
| 13997 | raigones | 1 |
| 13998 | raídos | 1 |
| 13999 | raheces | 1 |
| 14000 | rafigurarle | 1 |
| 14001 | radical | 1 |
| 14002 | raciones | 1 |
| 14003 | ración | 1 |
| 14004 | rabultados | 1 |
| 14005 | rabias | 1 |
| 14006 | rabeles | 1 |
| 14007 | quitóle | 1 |
| 14008 | quíteseme | 1 |
| 14009 | quítesele | 1 |
| 14010 | quítese | 1 |
| 14011 | quítenseme | 1 |
| 14012 | quitasol | 1 |
| 14013 | quitases | 1 |
| 14014 | quitas | 1 |
| 14015 | quitárosle | 1 |
| 14016 | quitaros | 1 |
| 14017 | quitáronsela | 1 |
| 14018 | quitáronse | 1 |
| 14019 | quitáronle | 1 |
| 14020 | quitarnos | 1 |
| 14021 | quitarlos | 1 |
| 14022 | quitarlo | 1 |
| 14023 | quitaríase | 1 |
| 14024 | quitaría | 1 |
| 14025 | quitaren | 1 |
| 14026 | quitaré | 1 |
| 14027 | quitáramos | 1 |
| 14028 | quitándosela | 1 |
| 14029 | quitándome | 1 |
| 14030 | quitándola | 1 |
| 14031 | quitámossele | 1 |
| 14032 | quítalas | 1 |
| 14033 | quitádmele | 1 |
| 14034 | quitadle | 1 |
| 14035 | quitada | 1 |
| 14036 | quitación | 1 |
| 14037 | quitábale | 1 |
| 14038 | quísome | 1 |
| 14039 | quisístelo | 1 |
| 14040 | quisimos | 1 |
| 14041 | quisiésemos | 1 |
| 14042 | quisiésedes | 1 |
| 14043 | quisiéronle | 1 |
| 14044 | quisieridísimis | 1 |
| 14045 | quisierdes | 1 |
| 14046 | quisiéramos | 1 |
| 14047 | quísele | 1 |
| 14048 | quirocia | 1 |
| 14049 | quirieleisón | 1 |
| 14050 | quintaesencia | 1 |
| 14051 | quínola | 1 |
| 14052 | quinientas | 1 |
| 14053 | quimeristas | 1 |
| 14054 | quiméricos | 1 |
| 14055 | quilate | 1 |
| 14056 | quilata | 1 |
| 14057 | quijotísimo | 1 |
| 14058 | quijotadas | 1 |
| 14059 | quietos | 1 |
| 14060 | quietarse | 1 |
| 14061 | quiéroos | 1 |
| 14062 | quiérola | 1 |
| 14063 | quiéreste | 1 |
| 14064 | quierénse | 1 |
| 14065 | quiéreme | 1 |
| 14066 | quiéralo | 1 |
| 14067 | quier | 1 |
| 14068 | quiébrome | 1 |
| 14069 | quiebren | 1 |
| 14070 | quidem | 1 |
| 14071 | quicio | 1 |
| 14072 | quesos | 1 |
| 14073 | querrías | 1 |
| 14074 | queriéndose | 1 |
| 14075 | queriéndolo | 1 |
| 14076 | queríale | 1 |
| 14077 | querérselas | 1 |
| 14078 | quererse | 1 |
| 14079 | quererlos | 1 |
| 14080 | querencias | 1 |
| 14081 | querellas | 1 |
| 14082 | querellante | 1 |
| 14083 | queréislo | 1 |
| 14084 | queredes | 1 |
| 14085 | quepa | 1 |
| 14086 | quemó | 1 |
| 14087 | quémate | 1 |
| 14088 | quemaré | 1 |
| 14089 | quemallos | 1 |
| 14090 | quemaban | 1 |
| 14091 | quema | 1 |
| 14092 | quejosos | 1 |
| 14093 | quejóse | 1 |
| 14094 | quejó | 1 |
| 14095 | quéjese | 1 |
| 14096 | quejes | 1 |
| 14097 | quejéis | 1 |
| 14098 | queje | 1 |
| 14099 | quejaré | 1 |
| 14100 | quejaos | 1 |
| 14101 | quejándose | 1 |
| 14102 | quejana | 1 |
| 14103 | quejado | 1 |
| 14104 | quédome | 1 |
| 14105 | quédesele | 1 |
| 14106 | quédente | 1 |
| 14107 | quedemos | 1 |
| 14108 | quedásedes | 1 |
| 14109 | quedarte | 1 |
| 14110 | quedáronse | 1 |
| 14111 | quedarlo | 1 |
| 14112 | quedarías | 1 |
| 14113 | quedaréme | 1 |
| 14114 | quedare | 1 |
| 14115 | quedarás | 1 |
| 14116 | quedarán | 1 |
| 14117 | quedáramos | 1 |
| 14118 | quedárades | 1 |
| 14119 | quedaos | 1 |
| 14120 | quedáis | 1 |
| 14121 | quedábase | 1 |
| 14122 | quedábamos | 1 |
| 14123 | quebró | 1 |
| 14124 | quebréis | 1 |
| 14125 | quebrarse | 1 |
| 14126 | quebrantos | 1 |
| 14127 | quebranto | 1 |
| 14128 | quebrantáredes | 1 |
| 14129 | quebrantan | 1 |
| 14130 | quebrantamientos | 1 |
| 14131 | quebrando | 1 |
| 14132 | quebrados | 1 |
| 14133 | quebradiza | 1 |
| 14134 | quebraba | 1 |
| 14135 | quantioso | 1 |
| 14136 | quando | 1 |
| 14137 | putería | 1 |
| 14138 | putativo | 1 |
| 14139 | púsoseme | 1 |
| 14140 | púsosele | 1 |
| 14141 | púsola | 1 |
| 14142 | pusistes | 1 |
| 14143 | pusilanimidad | 1 |
| 14144 | pusieses | 1 |
| 14145 | pusierónse | 1 |
| 14146 | pusiéronme | 1 |
| 14147 | pusiéronlos | 1 |
| 14148 | pusieren | 1 |
| 14149 | pusiéredes | 1 |
| 14150 | púrpura | 1 |
| 14151 | puridad | 1 |
| 14152 | purgó | 1 |
| 14153 | purgar | 1 |
| 14154 | puras | 1 |
| 14155 | pupilaje | 1 |
| 14156 | puñalero | 1 |
| 14157 | puñados | 1 |
| 14158 | punzón | 1 |
| 14159 | punzamiento | 1 |
| 14160 | punzaban | 1 |
| 14161 | punzaba | 1 |
| 14162 | puntuosas | 1 |
| 14163 | puntualísimo | 1 |
| 14164 | puntualísima | 1 |
| 14165 | puntualidades | 1 |
| 14166 | puntoso | 1 |
| 14167 | puntillos | 1 |
| 14168 | puntillazos | 1 |
| 14169 | puntiagudo | 1 |
| 14170 | puntiaguda | 1 |
| 14171 | puntapié | 1 |
| 14172 | pulsat | 1 |
| 14173 | pulpo | 1 |
| 14174 | púlpitos | 1 |
| 14175 | pullas | 1 |
| 14176 | pulirte | 1 |
| 14177 | pulgar | 1 |
| 14178 | pulga | 1 |
| 14179 | pulen | 1 |
| 14180 | pulcela | 1 |
| 14181 | pula | 1 |
| 14182 | pugnó | 1 |
| 14183 | pugnaré | 1 |
| 14184 | puéstoos | 1 |
| 14185 | puéstome | 1 |
| 14186 | puertocarrero | 1 |
| 14187 | puédeslo | 1 |
| 14188 | puédesele | 1 |
| 14189 | puédese | 1 |
| 14190 | puédense | 1 |
| 14191 | puédela | 1 |
| 14192 | puebla | 1 |
| 14193 | pudriesen | 1 |
| 14194 | pudre | 1 |
| 14195 | pudimos | 1 |
| 14196 | pudieren | 1 |
| 14197 | pudiéredes | 1 |
| 14198 | pudiérate | 1 |
| 14199 | pudiérase | 1 |
| 14200 | pudiéndose | 1 |
| 14201 | pucheros | 1 |
| 14202 | puchero | 1 |
| 14203 | pucheritos | 1 |
| 14204 | publique | 1 |
| 14205 | publico | 1 |
| 14206 | publicase | 1 |
| 14207 | publicar | 1 |
| 14208 | publicando | 1 |
| 14209 | publicador | 1 |
| 14210 | publicado | 1 |
| 14211 | publicada | 1 |
| 14212 | publica | 1 |
| 14213 | pruebo | 1 |
| 14214 | pruébensela | 1 |
| 14215 | prueben | 1 |
| 14216 | provocó | 1 |
| 14217 | provocaron | 1 |
| 14218 | provocados | 1 |
| 14219 | provisión | 1 |
| 14220 | proveyóse | 1 |
| 14221 | proverse | 1 |
| 14222 | proverbio | 1 |
| 14223 | proveernos | 1 |
| 14224 | provee | 1 |
| 14225 | provechosa | 1 |
| 14226 | protoencantador | 1 |
| 14227 | protesto | 1 |
| 14228 | protestaba | 1 |
| 14229 | proteción | 1 |
| 14230 | protección | 1 |
| 14231 | prosupuesta | 1 |
| 14232 | prosuponga | 1 |
| 14233 | prósperas | 1 |
| 14234 | prosigamos | 1 |
| 14235 | proseguido | 1 |
| 14236 | proseguían | 1 |
| 14237 | proseguí | 1 |
| 14238 | prosapia | 1 |
| 14239 | propusieran | 1 |
| 14240 | proprias | 1 |
| 14241 | propósitos | 1 |
| 14242 | proponiendo | 1 |
| 14243 | propongan | 1 |
| 14244 | propone | 1 |
| 14245 | propincuas | 1 |
| 14246 | propiamente | 1 |
| 14247 | pronunció | 1 |
| 14248 | pronunciarle | 1 |
| 14249 | pronunciaba | 1 |
| 14250 | pronosticado | 1 |
| 14251 | prompta | 1 |
| 14252 | promovido | 1 |
| 14253 | promontorio | 1 |
| 14254 | prometímosselo | 1 |
| 14255 | prometímosle | 1 |
| 14256 | prometimos | 1 |
| 14257 | prometimientos | 1 |
| 14258 | prometieron | 1 |
| 14259 | prometidos | 1 |
| 14260 | prometías | 1 |
| 14261 | prometes | 1 |
| 14262 | prometérselo | 1 |
| 14263 | prolongada | 1 |
| 14264 | prolijo | 1 |
| 14265 | prolijidad | 1 |
| 14266 | prolija | 1 |
| 14267 | prójimos | 1 |
| 14268 | prójimo | 1 |
| 14269 | prohíbe | 1 |
| 14270 | profundísimos | 1 |
| 14271 | profundísimo | 1 |
| 14272 | profundidades | 1 |
| 14273 | profesor | 1 |
| 14274 | profesiones | 1 |
| 14275 | profesen | 1 |
| 14276 | profanas | 1 |
| 14277 | profanarte | 1 |
| 14278 | profanaba | 1 |
| 14279 | producido | 1 |
| 14280 | prodigioso | 1 |
| 14281 | prodigalidad | 1 |
| 14282 | pródiga | 1 |
| 14283 | procuraron | 1 |
| 14284 | procurarlo | 1 |
| 14285 | procurarles | 1 |
| 14286 | procuraran | 1 |
| 14287 | procurárades | 1 |
| 14288 | procurara | 1 |
| 14289 | procuramos | 1 |
| 14290 | procuralle | 1 |
| 14291 | procuradores | 1 |
| 14292 | procurador | 1 |
| 14293 | procrearon | 1 |
| 14294 | proceso | 1 |
| 14295 | procesiones | 1 |
| 14296 | procesada | 1 |
| 14297 | procedió | 1 |
| 14298 | probóseme | 1 |
| 14299 | probásemos | 1 |
| 14300 | probarme | 1 |
| 14301 | probarlo | 1 |
| 14302 | probarle | 1 |
| 14303 | probare | 1 |
| 14304 | probanzas | 1 |
| 14305 | probándola | 1 |
| 14306 | probáis | 1 |
| 14307 | proas | 1 |
| 14308 | proa | 1 |
| 14309 | privar | 1 |
| 14310 | privados | 1 |
| 14311 | privado | 1 |
| 14312 | primores | 1 |
| 14313 | priesas | 1 |
| 14314 | prevista | 1 |
| 14315 | previnieron | 1 |
| 14316 | previniera | 1 |
| 14317 | previniendo | 1 |
| 14318 | previlegio | 1 |
| 14319 | prevenirlas | 1 |
| 14320 | prevenídose | 1 |
| 14321 | prevenidos | 1 |
| 14322 | prevenida | 1 |
| 14323 | prevenía | 1 |
| 14324 | prevengamos | 1 |
| 14325 | pretéritas | 1 |
| 14326 | pretensiones | 1 |
| 14327 | pretendieron | 1 |
| 14328 | pretendía | 1 |
| 14329 | pretender | 1 |
| 14330 | pretendemos | 1 |
| 14331 | presurosas | 1 |
| 14332 | presupuesta | 1 |
| 14333 | presupongamos | 1 |
| 14334 | presuntuosos | 1 |
| 14335 | presunciones | 1 |
| 14336 | presumíamos | 1 |
| 14337 | presuma | 1 |
| 14338 | prestósele | 1 |
| 14339 | prestos | 1 |
| 14340 | prestaron | 1 |
| 14341 | prestarle | 1 |
| 14342 | prestaban | 1 |
| 14343 | presonas | 1 |
| 14344 | presona | 1 |
| 14345 | presidentes | 1 |
| 14346 | preside | 1 |
| 14347 | presentósela | 1 |
| 14348 | presentó | 1 |
| 14349 | presentase | 1 |
| 14350 | presentaros | 1 |
| 14351 | presentaría | 1 |
| 14352 | presentaren | 1 |
| 14353 | presentándome | 1 |
| 14354 | presentan | 1 |
| 14355 | presentación | 1 |
| 14356 | presencias | 1 |
| 14357 | prerrogativas | 1 |
| 14358 | prepararse | 1 |
| 14359 | preñez | 1 |
| 14360 | prendió | 1 |
| 14361 | prendiesen | 1 |
| 14362 | prenderte | 1 |
| 14363 | prenderla | 1 |
| 14364 | prendéis | 1 |
| 14365 | prendan | 1 |
| 14366 | premien | 1 |
| 14367 | preguntónos | 1 |
| 14368 | preguntes | 1 |
| 14369 | pregúntenme | 1 |
| 14370 | pregunten | 1 |
| 14371 | pregúntemelo | 1 |
| 14372 | pregúntele | 1 |
| 14373 | preguntaste | 1 |
| 14374 | pregúntaselo | 1 |
| 14375 | preguntarse | 1 |
| 14376 | preguntáronme | 1 |
| 14377 | preguntarles | 1 |
| 14378 | preguntaren | 1 |
| 14379 | preguntaremos | 1 |
| 14380 | preguntáredes | 1 |
| 14381 | preguntantes | 1 |
| 14382 | preguntanta | 1 |
| 14383 | preguntándoselo | 1 |
| 14384 | preguntándose | 1 |
| 14385 | preguntalle | 1 |
| 14386 | preguntáis | 1 |
| 14387 | preguntador | 1 |
| 14388 | preguntad | 1 |
| 14389 | pregones | 1 |
| 14390 | pregonando | 1 |
| 14391 | pregonaba | 1 |
| 14392 | pregona | 1 |
| 14393 | prefación | 1 |
| 14394 | prefacio | 1 |
| 14395 | preeminencia | 1 |
| 14396 | predicó | 1 |
| 14397 | predican | 1 |
| 14398 | predicamento | 1 |
| 14399 | predica | 1 |
| 14400 | precisos | 1 |
| 14401 | precipitosamente | 1 |
| 14402 | precipitase | 1 |
| 14403 | precipitaba | 1 |
| 14404 | preciosos | 1 |
| 14405 | preciosísima | 1 |
| 14406 | preció | 1 |
| 14407 | préciate | 1 |
| 14408 | preciarte | 1 |
| 14409 | preciarse | 1 |
| 14410 | preciados | 1 |
| 14411 | preciada | 1 |
| 14412 | preciaban | 1 |
| 14413 | preceto | 1 |
| 14414 | precepto | 1 |
| 14415 | precedió | 1 |
| 14416 | precedencia | 1 |
| 14417 | preámbulos | 1 |
| 14418 | prazga | 1 |
| 14419 | pradillo | 1 |
| 14420 | práctica | 1 |
| 14421 | pozos | 1 |
| 14422 | potestades | 1 |
| 14423 | potestad | 1 |
| 14424 | postrera | 1 |
| 14425 | postre | 1 |
| 14426 | postrar | 1 |
| 14427 | postrada | 1 |
| 14428 | postizas | 1 |
| 14429 | postillón | 1 |
| 14430 | postigo | 1 |
| 14431 | posteridad | 1 |
| 14432 | postemas | 1 |
| 14433 | post | 1 |
| 14434 | pospuesto | 1 |
| 14435 | posibilitado | 1 |
| 14436 | posesivo | 1 |
| 14437 | poseo | 1 |
| 14438 | poseían | 1 |
| 14439 | posees | 1 |
| 14440 | poseerme | 1 |
| 14441 | poseerlo | 1 |
| 14442 | poseello | 1 |
| 14443 | poseedor | 1 |
| 14444 | posee | 1 |
| 14445 | posea | 1 |
| 14446 | posar | 1 |
| 14447 | posado | 1 |
| 14448 | posadas | 1 |
| 14449 | pos | 1 |
| 14450 | porvenir | 1 |
| 14451 | portuguesa | 1 |
| 14452 | portogal | 1 |
| 14453 | portó | 1 |
| 14454 | portillo | 1 |
| 14455 | portezuelo | 1 |
| 14456 | portero | 1 |
| 14457 | portería | 1 |
| 14458 | porte | 1 |
| 14459 | portazgo | 1 |
| 14460 | portar | 1 |
| 14461 | portantes | 1 |
| 14462 | portante | 1 |
| 14463 | portales | 1 |
| 14464 | portaba | 1 |
| 14465 | porta | 1 |
| 14466 | porros | 1 |
| 14467 | porras | 1 |
| 14468 | porquero | 1 |
| 14469 | poros | 1 |
| 14470 | porfíes | 1 |
| 14471 | porfías | 1 |
| 14472 | porfiarle | 1 |
| 14473 | porfiaré | 1 |
| 14474 | porfiare | 1 |
| 14475 | porfiados | 1 |
| 14476 | porción | 1 |
| 14477 | porcia | 1 |
| 14478 | popen | 1 |
| 14479 | ponzoña | 1 |
| 14480 | ponto | 1 |
| 14481 | pontificia | 1 |
| 14482 | ponme | 1 |
| 14483 | ponlas | 1 |
| 14484 | poniéndote | 1 |
| 14485 | poniéndosele | 1 |
| 14486 | poniéndonos | 1 |
| 14487 | poniéndolas | 1 |
| 14488 | póngolo | 1 |
| 14489 | póngasele | 1 |
| 14490 | póngase | 1 |
| 14491 | pónganos | 1 |
| 14492 | pónganme | 1 |
| 14493 | pongámonos | 1 |
| 14494 | póngame | 1 |
| 14495 | ponérselo | 1 |
| 14496 | ponérsele | 1 |
| 14497 | ponérsela | 1 |
| 14498 | ponérmela | 1 |
| 14499 | ponerlo | 1 |
| 14500 | ponerles | 1 |
| 14501 | ponemos | 1 |
| 14502 | ponelle | 1 |
| 14503 | ponedme | 1 |
| 14504 | ponedla | 1 |
| 14505 | poned | 1 |
| 14506 | pondríala | 1 |
| 14507 | pondréis | 1 |
| 14508 | ponderemos | 1 |
| 14509 | ponderan | 1 |
| 14510 | ponderaba | 1 |
| 14511 | pomposidad | 1 |
| 14512 | pomos | 1 |
| 14513 | polvoroso | 1 |
| 14514 | polvoro | 1 |
| 14515 | pólux | 1 |
| 14516 | poltrón | 1 |
| 14517 | pollinesca | 1 |
| 14518 | políticas | 1 |
| 14519 | polilla | 1 |
| 14520 | polifemos | 1 |
| 14521 | polidas | 1 |
| 14522 | policía | 1 |
| 14523 | polaco | 1 |
| 14524 | poesías | 1 |
| 14525 | poemas | 1 |
| 14526 | podrir | 1 |
| 14527 | podrías | 1 |
| 14528 | podríamos | 1 |
| 14529 | podréislo | 1 |
| 14530 | podíades | 1 |
| 14531 | poderla | 1 |
| 14532 | poderíos | 1 |
| 14533 | podencos | 1 |
| 14534 | podar | 1 |
| 14535 | podadera | 1 |
| 14536 | pobrísima | 1 |
| 14537 | pobrezas | 1 |
| 14538 | pobrecito | 1 |
| 14539 | pobrecilla | 1 |
| 14540 | poblada | 1 |
| 14541 | pluvias | 1 |
| 14542 | plutarco | 1 |
| 14543 | plumajes | 1 |
| 14544 | plumaje | 1 |
| 14545 | pluguiese | 1 |
| 14546 | pluguieron | 1 |
| 14547 | plu | 1 |
| 14548 | plo | 1 |
| 14549 | plegaria | 1 |
| 14550 | plegar | 1 |
| 14551 | plégaos | 1 |
| 14552 | plectio | 1 |
| 14553 | plebeyos | 1 |
| 14554 | playas | 1 |
| 14555 | platonazo | 1 |
| 14556 | platires | 1 |
| 14557 | platican | 1 |
| 14558 | plasmador | 1 |
| 14559 | plañirla | 1 |
| 14560 | plañendo | 1 |
| 14561 | plantadas | 1 |
| 14562 | plano | 1 |
| 14563 | planetas | 1 |
| 14564 | planeta | 1 |
| 14565 | plancha | 1 |
| 14566 | plana | 1 |
| 14567 | plácido | 1 |
| 14568 | placerdemivida | 1 |
| 14569 | pizmiento | 1 |
| 14570 | pizmienta | 1 |
| 14571 | più | 1 |
| 14572 | pito | 1 |
| 14573 | pistos | 1 |
| 14574 | pistoletes | 1 |
| 14575 | pisó | 1 |
| 14576 | pisen | 1 |
| 14577 | pise | 1 |
| 14578 | pisaron | 1 |
| 14579 | pisamos | 1 |
| 14580 | pisadas | 1 |
| 14581 | pisacorto | 1 |
| 14582 | pisaba | 1 |
| 14583 | piruétanos | 1 |
| 14584 | pirú | 1 |
| 14585 | pirineo | 1 |
| 14586 | piquen | 1 |
| 14587 | pipote | 1 |
| 14588 | piojoso | 1 |
| 14589 | piojo | 1 |
| 14590 | pío | 1 |
| 14591 | piñata | 1 |
| 14592 | pintores | 1 |
| 14593 | píntola | 1 |
| 14594 | pintiquiniestra | 1 |
| 14595 | pintiparados | 1 |
| 14596 | pinté | 1 |
| 14597 | pintaste | 1 |
| 14598 | pintasen | 1 |
| 14599 | pintase | 1 |
| 14600 | pintarla | 1 |
| 14601 | píntaos | 1 |
| 14602 | pintándonos | 1 |
| 14603 | pintándolo | 1 |
| 14604 | pintad | 1 |
| 14605 | pinos | 1 |
| 14606 | pino | 1 |
| 14607 | pinganitos | 1 |
| 14608 | pinceles | 1 |
| 14609 | pincel | 1 |
| 14610 | piloto | 1 |
| 14611 | pillamo | 1 |
| 14612 | pílades | 1 |
| 14613 | pífaros | 1 |
| 14614 | piedrahíta | 1 |
| 14615 | piedeamigo | 1 |
| 14616 | pidiría | 1 |
| 14617 | pidióles | 1 |
| 14618 | pidiésemos | 1 |
| 14619 | pidiésedes | 1 |
| 14620 | pidiere | 1 |
| 14621 | pidiéndoos | 1 |
| 14622 | pidiéndoles | 1 |
| 14623 | pidiéndola | 1 |
| 14624 | pídeselo | 1 |
| 14625 | pídese | 1 |
| 14626 | pídanmelo | 1 |
| 14627 | pidan | 1 |
| 14628 | píctima | 1 |
| 14629 | picote | 1 |
| 14630 | pícome | 1 |
| 14631 | pichones | 1 |
| 14632 | picase | 1 |
| 14633 | picas | 1 |
| 14634 | pícaros | 1 |
| 14635 | picáredes | 1 |
| 14636 | picar | 1 |
| 14637 | picante | 1 |
| 14638 | picáis | 1 |
| 14639 | picados | 1 |
| 14640 | picadillo | 1 |
| 14641 | picaban | 1 |
| 14642 | pías | 1 |
| 14643 | piamonte | 1 |
| 14644 | petrales | 1 |
| 14645 | pestilentes | 1 |
| 14646 | pestíferos | 1 |
| 14647 | pestífera | 1 |
| 14648 | pestañas | 1 |
| 14649 | pessima | 1 |
| 14650 | pesques | 1 |
| 14651 | pesquería | 1 |
| 14652 | pespetiva | 1 |
| 14653 | pesóle | 1 |
| 14654 | pésimos | 1 |
| 14655 | pésima | 1 |
| 14656 | pésetes | 1 |
| 14657 | pesen | 1 |
| 14658 | pesé | 1 |
| 14659 | pescuezo | 1 |
| 14660 | pescozada | 1 |
| 14661 | pescando | 1 |
| 14662 | pescan | 1 |
| 14663 | pesca | 1 |
| 14664 | pesarosos | 1 |
| 14665 | pesarosa | 1 |
| 14666 | pesarme | 1 |
| 14667 | pesarle | 1 |
| 14668 | pesaría | 1 |
| 14669 | pesare | 1 |
| 14670 | pesará | 1 |
| 14671 | pesan | 1 |
| 14672 | pesados | 1 |
| 14673 | pesadilla | 1 |
| 14674 | perturben | 1 |
| 14675 | pertrechando | 1 |
| 14676 | pertinaces | 1 |
| 14677 | perteneciente | 1 |
| 14678 | pertenecían | 1 |
| 14679 | pertenecen | 1 |
| 14680 | persuadirle | 1 |
| 14681 | persuadille | 1 |
| 14682 | persuadieron | 1 |
| 14683 | persuadieran | 1 |
| 14684 | persuadiéndome | 1 |
| 14685 | persuadiéndole | 1 |
| 14686 | persuadida | 1 |
| 14687 | persuadían | 1 |
| 14688 | persuades | 1 |
| 14689 | persuádeles | 1 |
| 14690 | persuada | 1 |
| 14691 | personilla | 1 |
| 14692 | persio | 1 |
| 14693 | persiguirán | 1 |
| 14694 | persiguiese | 1 |
| 14695 | persiguiéronle | 1 |
| 14696 | persigáis | 1 |
| 14697 | persevero | 1 |
| 14698 | perseguís | 1 |
| 14699 | perseguirme | 1 |
| 14700 | perseguirá | 1 |
| 14701 | perseguimiento | 1 |
| 14702 | perseguían | 1 |
| 14703 | perseguíale | 1 |
| 14704 | perroquia | 1 |
| 14705 | perritas | 1 |
| 14706 | perrillo | 1 |
| 14707 | perrilla | 1 |
| 14708 | perricos | 1 |
| 14709 | perrica | 1 |
| 14710 | perplejo | 1 |
| 14711 | perpetuos | 1 |
| 14712 | perpetuas | 1 |
| 14713 | perpe | 1 |
| 14714 | perogrullo | 1 |
| 14715 | permitió | 1 |
| 14716 | permítesele | 1 |
| 14717 | permiten | 1 |
| 14718 | perlerino | 1 |
| 14719 | perlerina | 1 |
| 14720 | perláticos | 1 |
| 14721 | perla | 1 |
| 14722 | perjudiquen | 1 |
| 14723 | peritos | 1 |
| 14724 | peritoa | 1 |
| 14725 | perito | 1 |
| 14726 | periquillo | 1 |
| 14727 | perión | 1 |
| 14728 | período | 1 |
| 14729 | perictos | 1 |
| 14730 | pergenio | 1 |
| 14731 | perfumada | 1 |
| 14732 | perficiónala | 1 |
| 14733 | perfetísimo | 1 |
| 14734 | perfeta | 1 |
| 14735 | perfectos | 1 |
| 14736 | perfeciones | 1 |
| 14737 | perezosamente | 1 |
| 14738 | perezosa | 1 |
| 14739 | perezcan | 1 |
| 14740 | perendenga | 1 |
| 14741 | peregrinas | 1 |
| 14742 | peregrinamos | 1 |
| 14743 | peregrinaciones | 1 |
| 14744 | perecido | 1 |
| 14745 | perecida | 1 |
| 14746 | perecían | 1 |
| 14747 | perecía | 1 |
| 14748 | perdones | 1 |
| 14749 | perdónenme | 1 |
| 14750 | perdonéis | 1 |
| 14751 | perdoné | 1 |
| 14752 | perdonaros | 1 |
| 14753 | perdonáramos | 1 |
| 14754 | perdonara | 1 |
| 14755 | perdonalle | 1 |
| 14756 | perdonado | 1 |
| 14757 | perdonad | 1 |
| 14758 | perdonaba | 1 |
| 14759 | perdiste | 1 |
| 14760 | perdimos | 1 |
| 14761 | perdían | 1 |
| 14762 | perderte | 1 |
| 14763 | perderme | 1 |
| 14764 | perderlos | 1 |
| 14765 | perderíamos | 1 |
| 14766 | perderás | 1 |
| 14767 | perdemos | 1 |
| 14768 | perdella | 1 |
| 14769 | perded | 1 |
| 14770 | percibieron | 1 |
| 14771 | percheles | 1 |
| 14772 | percebir | 1 |
| 14773 | peralvillo | 1 |
| 14774 | perailes | 1 |
| 14775 | per | 1 |
| 14776 | pequeñez | 1 |
| 14777 | pepino | 1 |
| 14778 | peones | 1 |
| 14779 | peñón | 1 |
| 14780 | péñola | 1 |
| 14781 | penuria | 1 |
| 14782 | pentapolén | 1 |
| 14783 | pensativa | 1 |
| 14784 | pensarse | 1 |
| 14785 | pensaría | 1 |
| 14786 | pensaren | 1 |
| 14787 | pensadas | 1 |
| 14788 | pensabas | 1 |
| 14789 | pensábanlo | 1 |
| 14790 | penosamente | 1 |
| 14791 | penitenciados | 1 |
| 14792 | peneo | 1 |
| 14793 | penélope | 1 |
| 14794 | penéis | 1 |
| 14795 | péndola | 1 |
| 14796 | pendían | 1 |
| 14797 | pende | 1 |
| 14798 | penase | 1 |
| 14799 | penantes | 1 |
| 14800 | penando | 1 |
| 14801 | penado | 1 |
| 14802 | peluda | 1 |
| 14803 | pelras | 1 |
| 14804 | peloteando | 1 |
| 14805 | pelotas | 1 |
| 14806 | pelón | 1 |
| 14807 | peló | 1 |
| 14808 | pellis | 1 |
| 14809 | pellico | 1 |
| 14810 | pella | 1 |
| 14811 | pelillos | 1 |
| 14812 | peligrosos | 1 |
| 14813 | peligrosísima | 1 |
| 14814 | peliagudo | 1 |
| 14815 | peleo | 1 |
| 14816 | peleen | 1 |
| 14817 | peleé | 1 |
| 14818 | peleares | 1 |
| 14819 | peleante | 1 |
| 14820 | peleamos | 1 |
| 14821 | peleado | 1 |
| 14822 | peleaba | 1 |
| 14823 | pele | 1 |
| 14824 | pelaza | 1 |
| 14825 | pelarruecas | 1 |
| 14826 | pelando | 1 |
| 14827 | pelaje | 1 |
| 14828 | pelados | 1 |
| 14829 | peladilla | 1 |
| 14830 | pelada | 1 |
| 14831 | peinarse | 1 |
| 14832 | peinadas | 1 |
| 14833 | pegujares | 1 |
| 14834 | pegotes | 1 |
| 14835 | pegóseme | 1 |
| 14836 | pégate | 1 |
| 14837 | pegaron | 1 |
| 14838 | pegarles | 1 |
| 14839 | pegajosos | 1 |
| 14840 | pegajosa | 1 |
| 14841 | pegados | 1 |
| 14842 | pegado | 1 |
| 14843 | pegadizas | 1 |
| 14844 | pegadiza | 1 |
| 14845 | pedrisco | 1 |
| 14846 | pedrezuelas | 1 |
| 14847 | pedorreras | 1 |
| 14848 | pedistes | 1 |
| 14849 | pedirte | 1 |
| 14850 | pedírselos | 1 |
| 14851 | pedírsele | 1 |
| 14852 | pedirlo | 1 |
| 14853 | pediría | 1 |
| 14854 | pediré | 1 |
| 14855 | pedímosle | 1 |
| 14856 | pedimiento | 1 |
| 14857 | pedillo | 1 |
| 14858 | pedilde | 1 |
| 14859 | pedídole | 1 |
| 14860 | pedídmela | 1 |
| 14861 | pedida | 1 |
| 14862 | pedid | 1 |
| 14863 | pedíale | 1 |
| 14864 | pedestre | 1 |
| 14865 | pedernalinas | 1 |
| 14866 | pedernal | 1 |
| 14867 | pede | 1 |
| 14868 | pedantes | 1 |
| 14869 | pedagogo | 1 |
| 14870 | pechero | 1 |
| 14871 | peces | 1 |
| 14872 | pecaron | 1 |
| 14873 | pecará | 1 |
| 14874 | pecar | 1 |
| 14875 | pecaba | 1 |
| 14876 | pazpuerca | 1 |
| 14877 | pavés | 1 |
| 14878 | pausanias | 1 |
| 14879 | pauperum | 1 |
| 14880 | patriarca | 1 |
| 14881 | patraña | 1 |
| 14882 | paternidad | 1 |
| 14883 | patentes | 1 |
| 14884 | patentemente | 1 |
| 14885 | patenas | 1 |
| 14886 | pateado | 1 |
| 14887 | patán | 1 |
| 14888 | patada | 1 |
| 14889 | pata | 1 |
| 14890 | pastraña | 1 |
| 14891 | pastos | 1 |
| 14892 | pastoril | 1 |
| 14893 | pastorcillo | 1 |
| 14894 | pastorcico | 1 |
| 14895 | pasóse | 1 |
| 14896 | pasmo | 1 |
| 14897 | pasmados | 1 |
| 14898 | pasmada | 1 |
| 14899 | pasma | 1 |
| 14900 | pasitamente | 1 |
| 14901 | pases | 1 |
| 14902 | paseóse | 1 |
| 14903 | pasemos | 1 |
| 14904 | paséis | 1 |
| 14905 | pasees | 1 |
| 14906 | pasee | 1 |
| 14907 | pasaste | 1 |
| 14908 | pasasen | 1 |
| 14909 | pasas | 1 |
| 14910 | pasaros | 1 |
| 14911 | pasáronse | 1 |
| 14912 | pasarlas | 1 |
| 14913 | pasarla | 1 |
| 14914 | pasaré | 1 |
| 14915 | pasarás | 1 |
| 14916 | pasaras | 1 |
| 14917 | pasándoseme | 1 |
| 14918 | pasándole | 1 |
| 14919 | pasamiento | 1 |
| 14920 | pasamaques | 1 |
| 14921 | pásalas | 1 |
| 14922 | pasajera | 1 |
| 14923 | pasáis | 1 |
| 14924 | pasagonzalo | 1 |
| 14925 | pasá | 1 |
| 14926 | parva | 1 |
| 14927 | pártome | 1 |
| 14928 | partióles | 1 |
| 14929 | partieses | 1 |
| 14930 | partiésemos | 1 |
| 14931 | partiéronse | 1 |
| 14932 | partidos | 1 |
| 14933 | particularidad | 1 |
| 14934 | participar | 1 |
| 14935 | participantes | 1 |
| 14936 | participante | 1 |
| 14937 | partesanas | 1 |
| 14938 | partámonos | 1 |
| 14939 | parta | 1 |
| 14940 | parsimonia | 1 |
| 14941 | parrasio | 1 |
| 14942 | párpados | 1 |
| 14943 | paropillo | 1 |
| 14944 | paro | 1 |
| 14945 | paris | 1 |
| 14946 | parir | 1 |
| 14947 | pariese | 1 |
| 14948 | pariera | 1 |
| 14949 | parida | 1 |
| 14950 | paréntesis | 1 |
| 14951 | pareciónos | 1 |
| 14952 | pareciéronle | 1 |
| 14953 | parecieran | 1 |
| 14954 | pareciendo | 1 |
| 14955 | parecidos | 1 |
| 14956 | parecíame | 1 |
| 14957 | parecíales | 1 |
| 14958 | parécete | 1 |
| 14959 | parecerse | 1 |
| 14960 | parecerlo | 1 |
| 14961 | parecerás | 1 |
| 14962 | parécelo | 1 |
| 14963 | pardos | 1 |
| 14964 | parches | 1 |
| 14965 | parcas | 1 |
| 14966 | parasismos | 1 |
| 14967 | pararse | 1 |
| 14968 | paráronse | 1 |
| 14969 | pararía | 1 |
| 14970 | pararé | 1 |
| 14971 | parará | 1 |
| 14972 | parara | 1 |
| 14973 | parándose | 1 |
| 14974 | parando | 1 |
| 14975 | paran | 1 |
| 14976 | paramentos | 1 |
| 14977 | paramento | 1 |
| 14978 | paralipomenón | 1 |
| 14979 | paraderos | 1 |
| 14980 | parabienes | 1 |
| 14981 | parabién | 1 |
| 14982 | papirotazo | 1 |
| 14983 | papín | 1 |
| 14984 | papilla | 1 |
| 14985 | papesa | 1 |
| 14986 | papen | 1 |
| 14987 | papelón | 1 |
| 14988 | pape | 1 |
| 14989 | paparos | 1 |
| 14990 | papando | 1 |
| 14991 | papahígo | 1 |
| 14992 | paños | 1 |
| 14993 | pañales | 1 |
| 14994 | pantuflos | 1 |
| 14995 | pantalia | 1 |
| 14996 | paniaguados | 1 |
| 14997 | paniaguado | 1 |
| 14998 | panes | 1 |
| 14999 | panegírico | 1 |
| 15000 | panecillo | 1 |
| 15001 | pane | 1 |
| 15002 | panderos | 1 |
| 15003 | pandahilado | 1 |
| 15004 | pancaya | 1 |
| 15005 | palpar | 1 |
| 15006 | pálpalos | 1 |
| 15007 | palpables | 1 |
| 15008 | palominos | 1 |
| 15009 | palomino | 1 |
| 15010 | palomeque | 1 |
| 15011 | palomas | 1 |
| 15012 | palomar | 1 |
| 15013 | palmito | 1 |
| 15014 | palmease | 1 |
| 15015 | palmaditas | 1 |
| 15016 | palmadicas | 1 |
| 15017 | pallida | 1 |
| 15018 | pallas | 1 |
| 15019 | palla | 1 |
| 15020 | paliza | 1 |
| 15021 | palinuro | 1 |
| 15022 | palillo | 1 |
| 15023 | paleta | 1 |
| 15024 | palafrenes | 1 |
| 15025 | palafreneros | 1 |
| 15026 | palafoxes | 1 |
| 15027 | paladión | 1 |
| 15028 | paladino | 1 |
| 15029 | paladar | 1 |
| 15030 | pala | 1 |
| 15031 | pajecillos | 1 |
| 15032 | pajecillo | 1 |
| 15033 | pajaricas | 1 |
| 15034 | págueseme | 1 |
| 15035 | paguéle | 1 |
| 15036 | págate | 1 |
| 15037 | pagastes | 1 |
| 15038 | pagarte | 1 |
| 15039 | pagárselo | 1 |
| 15040 | pagarse | 1 |
| 15041 | pagároslo | 1 |
| 15042 | pagaron | 1 |
| 15043 | pagárnoslo | 1 |
| 15044 | pagarme | 1 |
| 15045 | pagarla | 1 |
| 15046 | pagaréis | 1 |
| 15047 | pagare | 1 |
| 15048 | pagarás | 1 |
| 15049 | pagarán | 1 |
| 15050 | pagara | 1 |
| 15051 | paganos | 1 |
| 15052 | pagán | 1 |
| 15053 | pagadle | 1 |
| 15054 | pagada | 1 |
| 15055 | pagad | 1 |
| 15056 | padrinos | 1 |
| 15057 | padezca | 1 |
| 15058 | padecía | 1 |
| 15059 | padécense | 1 |
| 15060 | pactolo | 1 |
| 15061 | paciente | 1 |
| 15062 | pa | 1 |
| 15063 | oyóse | 1 |
| 15064 | oyóle | 1 |
| 15065 | oyo | 1 |
| 15066 | oyéronse | 1 |
| 15067 | oyeres | 1 |
| 15068 | oyeren | 1 |
| 15069 | oyeran | 1 |
| 15070 | oyéndolos | 1 |
| 15071 | oyéndolo | 1 |
| 15072 | oyan | 1 |
| 15073 | oya | 1 |
| 15074 | oxte | 1 |
| 15075 | oviedo | 1 |
| 15076 | ovejuno | 1 |
| 15077 | otorgase | 1 |
| 15078 | otorgar | 1 |
| 15079 | otorgaba | 1 |
| 15080 | otorga | 1 |
| 15081 | otaviano | 1 |
| 15082 | ossa | 1 |
| 15083 | oso | 1 |
| 15084 | osiris | 1 |
| 15085 | osé | 1 |
| 15086 | ose | 1 |
| 15087 | osaste | 1 |
| 15088 | osasen | 1 |
| 15089 | osase | 1 |
| 15090 | osas | 1 |
| 15091 | osarse | 1 |
| 15092 | osaron | 1 |
| 15093 | osaría | 1 |
| 15094 | osara | 1 |
| 15095 | osamos | 1 |
| 15096 | orza | 1 |
| 15097 | ornato | 1 |
| 15098 | ornamentos | 1 |
| 15099 | ornamento | 1 |
| 15100 | orina | 1 |
| 15101 | originales | 1 |
| 15102 | oriental | 1 |
| 15103 | orianas | 1 |
| 15104 | orgulloso | 1 |
| 15105 | orgullo | 1 |
| 15106 | órgano | 1 |
| 15107 | orestes | 1 |
| 15108 | orelia | 1 |
| 15109 | orearme | 1 |
| 15110 | ore | 1 |
| 15111 | ordóñez | 1 |
| 15112 | ordinaro | 1 |
| 15113 | ordeñando | 1 |
| 15114 | ordenase | 1 |
| 15115 | ordenas | 1 |
| 15116 | ordenarse | 1 |
| 15117 | ordenaría | 1 |
| 15118 | ordenara | 1 |
| 15119 | ordenar | 1 |
| 15120 | ordenanza | 1 |
| 15121 | ordenando | 1 |
| 15122 | oratorios | 1 |
| 15123 | oratorio | 1 |
| 15124 | oratoria | 1 |
| 15125 | orador | 1 |
| 15126 | opuso | 1 |
| 15127 | opusiesen | 1 |
| 15128 | opuestos | 1 |
| 15129 | opuesto | 1 |
| 15130 | oprimo | 1 |
| 15131 | oprimir | 1 |
| 15132 | oprimió | 1 |
| 15133 | oprimido | 1 |
| 15134 | oprimidas | 1 |
| 15135 | oprimida | 1 |
| 15136 | opresión | 1 |
| 15137 | oposición | 1 |
| 15138 | oponiéndose | 1 |
| 15139 | oponérsele | 1 |
| 15140 | oponer | 1 |
| 15141 | oponen | 1 |
| 15142 | operación | 1 |
| 15143 | onzas | 1 |
| 15144 | onesto | 1 |
| 15145 | omnis | 1 |
| 15146 | omnipotente | 1 |
| 15147 | omecillos | 1 |
| 15148 | omecillo | 1 |
| 15149 | olvidósele | 1 |
| 15150 | olvidos | 1 |
| 15151 | olvides | 1 |
| 15152 | olviden | 1 |
| 15153 | olvidéis | 1 |
| 15154 | olvidasen | 1 |
| 15155 | olvídaseme | 1 |
| 15156 | olvidas | 1 |
| 15157 | olvidársele | 1 |
| 15158 | olvidaron | 1 |
| 15159 | olvidarme | 1 |
| 15160 | olvidándome | 1 |
| 15161 | olvidalla | 1 |
| 15162 | olvidados | 1 |
| 15163 | olvidadas | 1 |
| 15164 | olorosos | 1 |
| 15165 | olorcillo | 1 |
| 15166 | olivífero | 1 |
| 15167 | olivera | 1 |
| 15168 | olivas | 1 |
| 15169 | olivantes | 1 |
| 15170 | olivante | 1 |
| 15171 | oliscan | 1 |
| 15172 | olió | 1 |
| 15173 | oliese | 1 |
| 15174 | oliéndolas | 1 |
| 15175 | oliendo | 1 |
| 15176 | olido | 1 |
| 15177 | olas | 1 |
| 15178 | ojinegra | 1 |
| 15179 | ojeo | 1 |
| 15180 | ojeándole | 1 |
| 15181 | ojeados | 1 |
| 15182 | ojalá | 1 |
| 15183 | oírte | 1 |
| 15184 | oíros | 1 |
| 15185 | oírlo | 1 |
| 15186 | oírla | 1 |
| 15187 | oiréis | 1 |
| 15188 | óiganme | 1 |
| 15189 | oigamos | 1 |
| 15190 | oidores | 1 |
| 15191 | oíd | 1 |
| 15192 | ofuscan | 1 |
| 15193 | ofrezcáis | 1 |
| 15194 | ofrezca | 1 |
| 15195 | ofrendas | 1 |
| 15196 | ofrecióseme | 1 |
| 15197 | ofreciósela | 1 |
| 15198 | ofrecióse | 1 |
| 15199 | ofrecióle | 1 |
| 15200 | ofrecímele | 1 |
| 15201 | ofreciéronsele | 1 |
| 15202 | ofreciéndosele | 1 |
| 15203 | ofreciéndose | 1 |
| 15204 | ofrécesele | 1 |
| 15205 | ofreces | 1 |
| 15206 | ofrecérseles | 1 |
| 15207 | ofrecerla | 1 |
| 15208 | ofreceré | 1 |
| 15209 | ofrecerán | 1 |
| 15210 | ofrecerá | 1 |
| 15211 | ofrecelle | 1 |
| 15212 | ofre | 1 |
| 15213 | oficioso | 1 |
| 15214 | ofendo | 1 |
| 15215 | ofenderte | 1 |
| 15216 | ofenderos | 1 |
| 15217 | ofenderá | 1 |
| 15218 | ofendellos | 1 |
| 15219 | ofendelle | 1 |
| 15220 | ofendedme | 1 |
| 15221 | ofenda | 1 |
| 15222 | odoríferas | 1 |
| 15223 | odiosos | 1 |
| 15224 | odiosa | 1 |
| 15225 | odio | 1 |
| 15226 | ocurrieron | 1 |
| 15227 | ocurrieren | 1 |
| 15228 | ocurrían | 1 |
| 15229 | ocuparse | 1 |
| 15230 | ocuparme | 1 |
| 15231 | ocuparle | 1 |
| 15232 | ocuparía | 1 |
| 15233 | ocupare | 1 |
| 15234 | ocuparan | 1 |
| 15235 | ocupaos | 1 |
| 15236 | ocupando | 1 |
| 15237 | ocupadas | 1 |
| 15238 | ocupaciones | 1 |
| 15239 | ocupaban | 1 |
| 15240 | ocupaba | 1 |
| 15241 | oculte | 1 |
| 15242 | ocultarlos | 1 |
| 15243 | ocultaba | 1 |
| 15244 | oculta | 1 |
| 15245 | octavo | 1 |
| 15246 | octava | 1 |
| 15247 | ochocientas | 1 |
| 15248 | océano | 1 |
| 15249 | occidit | 1 |
| 15250 | ocasionado | 1 |
| 15251 | obstante | 1 |
| 15252 | observó | 1 |
| 15253 | observancia | 1 |
| 15254 | observaciones | 1 |
| 15255 | obsequias | 1 |
| 15256 | obscenas | 1 |
| 15257 | obrastes | 1 |
| 15258 | obrallo | 1 |
| 15259 | obrado | 1 |
| 15260 | obliguen | 1 |
| 15261 | obligué | 1 |
| 15262 | obligaste | 1 |
| 15263 | obligasen | 1 |
| 15264 | obligas | 1 |
| 15265 | obligarse | 1 |
| 15266 | obligaron | 1 |
| 15267 | obligarnos | 1 |
| 15268 | obligarlos | 1 |
| 15269 | obligara | 1 |
| 15270 | obligadísimo | 1 |
| 15271 | obligaba | 1 |
| 15272 | objeciones | 1 |
| 15273 | obispo | 1 |
| 15274 | obedicido | 1 |
| 15275 | obedezcan | 1 |
| 15276 | obedezca | 1 |
| 15277 | obedeciéronle | 1 |
| 15278 | obedeciendo | 1 |
| 15279 | obedecidas | 1 |
| 15280 | obedecían | 1 |
| 15281 | obedecí | 1 |
| 15282 | obedecerte | 1 |
| 15283 | obedecerlos | 1 |
| 15284 | obedecería | 1 |
| 15285 | obedeceré | 1 |
| 15286 | obedecella | 1 |
| 15287 | nuzas | 1 |
| 15288 | nuncio | 1 |
| 15289 | númidas | 1 |
| 15290 | numerus | 1 |
| 15291 | numeroso | 1 |
| 15292 | numerabis | 1 |
| 15293 | numancia | 1 |
| 15294 | nula | 1 |
| 15295 | nuez | 1 |
| 15296 | nuestramo | 1 |
| 15297 | nueso | 1 |
| 15298 | nudos | 1 |
| 15299 | nuca | 1 |
| 15300 | nublados | 1 |
| 15301 | nubila | 1 |
| 15302 | noviembre | 1 |
| 15303 | noviciado | 1 |
| 15304 | novias | 1 |
| 15305 | noturnas | 1 |
| 15306 | notorias | 1 |
| 15307 | notifiqué | 1 |
| 15308 | notes | 1 |
| 15309 | notaste | 1 |
| 15310 | notase | 1 |
| 15311 | notas | 1 |
| 15312 | notando | 1 |
| 15313 | notadas | 1 |
| 15314 | notada | 1 |
| 15315 | notad | 1 |
| 15316 | notables | 1 |
| 15317 | nortes | 1 |
| 15318 | noriz | 1 |
| 15319 | noria | 1 |
| 15320 | noramala | 1 |
| 15321 | nona | 1 |
| 15322 | nombro | 1 |
| 15323 | nombrastes | 1 |
| 15324 | nombrase | 1 |
| 15325 | nombrarle | 1 |
| 15326 | nombráredes | 1 |
| 15327 | nombráis | 1 |
| 15328 | nombraban | 1 |
| 15329 | nogales | 1 |
| 15330 | nocivo | 1 |
| 15331 | nobis | 1 |
| 15332 | nizarani | 1 |
| 15333 | nivelado | 1 |
| 15334 | nísperos | 1 |
| 15335 | niso | 1 |
| 15336 | niñez | 1 |
| 15337 | nigromancia | 1 |
| 15338 | nieves | 1 |
| 15339 | nieta | 1 |
| 15340 | niéguenme | 1 |
| 15341 | niegas | 1 |
| 15342 | niegan | 1 |
| 15343 | nicolao | 1 |
| 15344 | niarros | 1 |
| 15345 | netezuelos | 1 |
| 15346 | néstor | 1 |
| 15347 | nervuda | 1 |
| 15348 | nervosa | 1 |
| 15349 | nervios | 1 |
| 15350 | nerón | 1 |
| 15351 | nero | 1 |
| 15352 | nerbia | 1 |
| 15353 | nemoroso | 1 |
| 15354 | nembrot | 1 |
| 15355 | neguijón | 1 |
| 15356 | negrura | 1 |
| 15357 | negrísima | 1 |
| 15358 | negregura | 1 |
| 15359 | negósela | 1 |
| 15360 | negociarlo | 1 |
| 15361 | negligencia | 1 |
| 15362 | negároslo | 1 |
| 15363 | negarás | 1 |
| 15364 | negando | 1 |
| 15365 | negación | 1 |
| 15366 | negaba | 1 |
| 15367 | necias | 1 |
| 15368 | neciamente | 1 |
| 15369 | necia | 1 |
| 15370 | necesitar | 1 |
| 15371 | necesitado | 1 |
| 15372 | necesita | 1 |
| 15373 | necesarísimo | 1 |
| 15374 | neceda | 1 |
| 15375 | neblí | 1 |
| 15376 | nazcan | 1 |
| 15377 | navegue | 1 |
| 15378 | navegando | 1 |
| 15379 | navegamos | 1 |
| 15380 | navegado | 1 |
| 15381 | navegación | 1 |
| 15382 | navegaban | 1 |
| 15383 | navegábamos | 1 |
| 15384 | navegaba | 1 |
| 15385 | navega | 1 |
| 15386 | navarra | 1 |
| 15387 | naval | 1 |
| 15388 | náusea | 1 |
| 15389 | naufragios | 1 |
| 15390 | natas | 1 |
| 15391 | narigudo | 1 |
| 15392 | narigante | 1 |
| 15393 | naranjos | 1 |
| 15394 | naranja | 1 |
| 15395 | napolitano | 1 |
| 15396 | napeas | 1 |
| 15397 | nadaba | 1 |
| 15398 | nacistes | 1 |
| 15399 | nacían | 1 |
| 15400 | nacemos | 1 |
| 15401 | nabos | 1 |
| 15402 | nabo | 1 |
| 15403 | muzaraque | 1 |
| 15404 | mutatio | 1 |
| 15405 | mutaciones | 1 |
| 15406 | mutación | 1 |
| 15407 | mustia | 1 |
| 15408 | músculos | 1 |
| 15409 | musarañas | 1 |
| 15410 | musa | 1 |
| 15411 | murmuro | 1 |
| 15412 | murmuren | 1 |
| 15413 | murmurase | 1 |
| 15414 | murmuras | 1 |
| 15415 | murmuradores | 1 |
| 15416 | murmurado | 1 |
| 15417 | murmuración | 1 |
| 15418 | murmuraban | 1 |
| 15419 | murmuraba | 1 |
| 15420 | muriésemos | 1 |
| 15421 | muriérase | 1 |
| 15422 | murciélagos | 1 |
| 15423 | murasen | 1 |
| 15424 | muramos | 1 |
| 15425 | mur | 1 |
| 15426 | muñidos | 1 |
| 15427 | muñatón | 1 |
| 15428 | municiones | 1 |
| 15429 | multos | 1 |
| 15430 | mujeriego | 1 |
| 15431 | mujeriega | 1 |
| 15432 | mujercilla | 1 |
| 15433 | mugriento | 1 |
| 15434 | mugre | 1 |
| 15435 | muévenos | 1 |
| 15436 | mueven | 1 |
| 15437 | muévate | 1 |
| 15438 | muevan | 1 |
| 15439 | muestro | 1 |
| 15440 | muéstrese | 1 |
| 15441 | muéstrateles | 1 |
| 15442 | muéstratele | 1 |
| 15443 | muérome | 1 |
| 15444 | mueres | 1 |
| 15445 | muerdan | 1 |
| 15446 | muérame | 1 |
| 15447 | muelle | 1 |
| 15448 | muele | 1 |
| 15449 | mueca | 1 |
| 15450 | muebles | 1 |
| 15451 | mudos | 1 |
| 15452 | muden | 1 |
| 15453 | mudé | 1 |
| 15454 | mudarme | 1 |
| 15455 | mudarán | 1 |
| 15456 | mudándose | 1 |
| 15457 | mudamiento | 1 |
| 15458 | mudad | 1 |
| 15459 | mudables | 1 |
| 15460 | mudaba | 1 |
| 15461 | mucio | 1 |
| 15462 | muchísimos | 1 |
| 15463 | muchísima | 1 |
| 15464 | muchacherías | 1 |
| 15465 | muchachas | 1 |
| 15466 | mucetas | 1 |
| 15467 | mozuela | 1 |
| 15468 | moviste | 1 |
| 15469 | moviéndose | 1 |
| 15470 | moviéndola | 1 |
| 15471 | movidas | 1 |
| 15472 | movida | 1 |
| 15473 | movibles | 1 |
| 15474 | moverte | 1 |
| 15475 | moverlos | 1 |
| 15476 | moverán | 1 |
| 15477 | mováis | 1 |
| 15478 | motilón | 1 |
| 15479 | mota | 1 |
| 15480 | mostrósela | 1 |
| 15481 | mostróse | 1 |
| 15482 | mostróle | 1 |
| 15483 | mostredes | 1 |
| 15484 | mostraste | 1 |
| 15485 | mostraros | 1 |
| 15486 | mostrarnos | 1 |
| 15487 | mostrarle | 1 |
| 15488 | mostraré | 1 |
| 15489 | mostrarás | 1 |
| 15490 | mostraras | 1 |
| 15491 | mostrárades | 1 |
| 15492 | mostrará | 1 |
| 15493 | mostrándose | 1 |
| 15494 | mostrándonos | 1 |
| 15495 | mostrámosle | 1 |
| 15496 | mostrádnosla | 1 |
| 15497 | mostrad | 1 |
| 15498 | mosqueo | 1 |
| 15499 | mosquearme | 1 |
| 15500 | mosquear | 1 |
| 15501 | mortíferos | 1 |
| 15502 | mortero | 1 |
| 15503 | mors | 1 |
| 15504 | morón | 1 |
| 15505 | moriscas | 1 |
| 15506 | morirme | 1 |
| 15507 | moriré | 1 |
| 15508 | morirá | 1 |
| 15509 | morimos | 1 |
| 15510 | morillos | 1 |
| 15511 | morían | 1 |
| 15512 | more | 1 |
| 15513 | morbo | 1 |
| 15514 | morbidez | 1 |
| 15515 | moralmente | 1 |
| 15516 | moráis | 1 |
| 15517 | morado | 1 |
| 15518 | moradas | 1 |
| 15519 | moraban | 1 |
| 15520 | montuosos | 1 |
| 15521 | montoncillo | 1 |
| 15522 | montïel | 1 |
| 15523 | montazgo | 1 |
| 15524 | montare | 1 |
| 15525 | montaraz | 1 |
| 15526 | montaraces | 1 |
| 15527 | montañuelas | 1 |
| 15528 | montañuela | 1 |
| 15529 | montañés | 1 |
| 15530 | montante | 1 |
| 15531 | montan | 1 |
| 15532 | montaban | 1 |
| 15533 | monstruos | 1 |
| 15534 | monstros | 1 |
| 15535 | monsiur | 1 |
| 15536 | monserrato | 1 |
| 15537 | monjuí | 1 |
| 15538 | monjío | 1 |
| 15539 | monjiles | 1 |
| 15540 | monjas | 1 |
| 15541 | monísimo | 1 |
| 15542 | monicongo | 1 |
| 15543 | monedas | 1 |
| 15544 | mondoñedo | 1 |
| 15545 | mondo | 1 |
| 15546 | monde | 1 |
| 15547 | mondarnos | 1 |
| 15548 | mondándose | 1 |
| 15549 | monda | 1 |
| 15550 | moncadas | 1 |
| 15551 | monas | 1 |
| 15552 | monarquías | 1 |
| 15553 | monarquía | 1 |
| 15554 | molinero | 1 |
| 15555 | molimientos | 1 |
| 15556 | molificar | 1 |
| 15557 | molifica | 1 |
| 15558 | moliesen | 1 |
| 15559 | moliente | 1 |
| 15560 | moliendo | 1 |
| 15561 | molía | 1 |
| 15562 | molesto | 1 |
| 15563 | molestia | 1 |
| 15564 | moles | 1 |
| 15565 | molerle | 1 |
| 15566 | molerá | 1 |
| 15567 | moledor | 1 |
| 15568 | mojón | 1 |
| 15569 | mojicón | 1 |
| 15570 | mojar | 1 |
| 15571 | mojados | 1 |
| 15572 | mojado | 1 |
| 15573 | mohínos | 1 |
| 15574 | mohinísimo | 1 |
| 15575 | mohatra | 1 |
| 15576 | mofante | 1 |
| 15577 | modón | 1 |
| 15578 | moderó | 1 |
| 15579 | moderaron | 1 |
| 15580 | moderaré | 1 |
| 15581 | moderado | 1 |
| 15582 | mocho | 1 |
| 15583 | mo | 1 |
| 15584 | mixto | 1 |
| 15585 | miulina | 1 |
| 15586 | mitigar | 1 |
| 15587 | mitades | 1 |
| 15588 | misturas | 1 |
| 15589 | misterios | 1 |
| 15590 | mismísimos | 1 |
| 15591 | misiva | 1 |
| 15592 | misericordiosos | 1 |
| 15593 | míseras | 1 |
| 15594 | mísera | 1 |
| 15595 | mirto | 1 |
| 15596 | mirones | 1 |
| 15597 | mirólos | 1 |
| 15598 | miróla | 1 |
| 15599 | miro | 1 |
| 15600 | mírese | 1 |
| 15601 | mires | 1 |
| 15602 | mírenlo | 1 |
| 15603 | míreme | 1 |
| 15604 | miréis | 1 |
| 15605 | mírate | 1 |
| 15606 | miraste | 1 |
| 15607 | mirasen | 1 |
| 15608 | miras | 1 |
| 15609 | mirarse | 1 |
| 15610 | miráronse | 1 |
| 15611 | miráronla | 1 |
| 15612 | mirarme | 1 |
| 15613 | mirarlos | 1 |
| 15614 | mirarlo | 1 |
| 15615 | mirarían | 1 |
| 15616 | miraren | 1 |
| 15617 | mirante | 1 |
| 15618 | mirándome | 1 |
| 15619 | mirándolos | 1 |
| 15620 | mirándolas | 1 |
| 15621 | miramos | 1 |
| 15622 | mirallos | 1 |
| 15623 | miralle | 1 |
| 15624 | miralla | 1 |
| 15625 | miraldo | 1 |
| 15626 | miraguarda | 1 |
| 15627 | miraflores | 1 |
| 15628 | miradores | 1 |
| 15629 | miradlo | 1 |
| 15630 | miradas | 1 |
| 15631 | mirada | 1 |
| 15632 | mirábanse | 1 |
| 15633 | mirábalo | 1 |
| 15634 | mirábalas | 1 |
| 15635 | mirábala | 1 |
| 15636 | mintiese | 1 |
| 15637 | minó | 1 |
| 15638 | mínimos | 1 |
| 15639 | mínimo | 1 |
| 15640 | minguilla | 1 |
| 15641 | minas | 1 |
| 15642 | minaron | 1 |
| 15643 | minando | 1 |
| 15644 | millones | 1 |
| 15645 | milla | 1 |
| 15646 | mílite | 1 |
| 15647 | militares | 1 |
| 15648 | militar | 1 |
| 15649 | militamos | 1 |
| 15650 | militáis | 1 |
| 15651 | milesias | 1 |
| 15652 | milanesa | 1 |
| 15653 | milanés | 1 |
| 15654 | milagrosas | 1 |
| 15655 | milagrosamente | 1 |
| 15656 | miglior | 1 |
| 15657 | migajas | 1 |
| 15658 | mientas | 1 |
| 15659 | mientan | 1 |
| 15660 | miémbresele | 1 |
| 15661 | mieles | 1 |
| 15662 | midiesen | 1 |
| 15663 | midiere | 1 |
| 15664 | midiéndolos | 1 |
| 15665 | midiéndole | 1 |
| 15666 | mide | 1 |
| 15667 | mida | 1 |
| 15668 | miculoso | 1 |
| 15669 | micocolembo | 1 |
| 15670 | micer | 1 |
| 15671 | micael | 1 |
| 15672 | miau | 1 |
| 15673 | mezquitas | 1 |
| 15674 | mezquina | 1 |
| 15675 | mezclóse | 1 |
| 15676 | mezcló | 1 |
| 15677 | mezclarle | 1 |
| 15678 | mezclarla | 1 |
| 15679 | mezclaras | 1 |
| 15680 | mezclándolos | 1 |
| 15681 | mezclan | 1 |
| 15682 | mezcládose | 1 |
| 15683 | mezclada | 1 |
| 15684 | metimos | 1 |
| 15685 | metiese | 1 |
| 15686 | metiéndose | 1 |
| 15687 | metiéndole | 1 |
| 15688 | metídome | 1 |
| 15689 | meternos | 1 |
| 15690 | mételo | 1 |
| 15691 | métele | 1 |
| 15692 | metedle | 1 |
| 15693 | metan | 1 |
| 15694 | metáforas | 1 |
| 15695 | metafísico | 1 |
| 15696 | mesurado | 1 |
| 15697 | mesones | 1 |
| 15698 | mesnada | 1 |
| 15699 | mesarse | 1 |
| 15700 | mesaron | 1 |
| 15701 | meros | 1 |
| 15702 | mero | 1 |
| 15703 | merlo | 1 |
| 15704 | méritos | 1 |
| 15705 | mérito | 1 |
| 15706 | méritamente | 1 |
| 15707 | merezca | 1 |
| 15708 | merendado | 1 |
| 15709 | mereciesen | 1 |
| 15710 | mereciese | 1 |
| 15711 | merecidas | 1 |
| 15712 | merecida | 1 |
| 15713 | merecerla | 1 |
| 15714 | merecer | 1 |
| 15715 | merecedores | 1 |
| 15716 | merecedor | 1 |
| 15717 | mercancías | 1 |
| 15718 | mercaduría | 1 |
| 15719 | mercadería | 1 |
| 15720 | meramente | 1 |
| 15721 | mera | 1 |
| 15722 | meótides | 1 |
| 15723 | meona | 1 |
| 15724 | meón | 1 |
| 15725 | meo | 1 |
| 15726 | menudearon | 1 |
| 15727 | menudeando | 1 |
| 15728 | menudamente | 1 |
| 15729 | mentirosamente | 1 |
| 15730 | mentironiana | 1 |
| 15731 | mentiré | 1 |
| 15732 | mentirán | 1 |
| 15733 | mentille | 1 |
| 15734 | mentéis | 1 |
| 15735 | mentecaterías | 1 |
| 15736 | mentecata | 1 |
| 15737 | mensil | 1 |
| 15738 | mensajerías | 1 |
| 15739 | menospreciaron | 1 |
| 15740 | menospreciando | 1 |
| 15741 | menospreciado | 1 |
| 15742 | menospreciadas | 1 |
| 15743 | menoscabasen | 1 |
| 15744 | menoscábase | 1 |
| 15745 | menoscabaron | 1 |
| 15746 | menoscabar | 1 |
| 15747 | menoscaban | 1 |
| 15748 | menoscabado | 1 |
| 15749 | menoscabadas | 1 |
| 15750 | menoscaba | 1 |
| 15751 | mengüe | 1 |
| 15752 | menguadas | 1 |
| 15753 | meneses | 1 |
| 15754 | menéese | 1 |
| 15755 | menease | 1 |
| 15756 | menearon | 1 |
| 15757 | menearán | 1 |
| 15758 | mendrugo | 1 |
| 15759 | mendozas | 1 |
| 15760 | mendoza | 1 |
| 15761 | mencía | 1 |
| 15762 | menalao | 1 |
| 15763 | memos | 1 |
| 15764 | memorioso | 1 |
| 15765 | memoriales | 1 |
| 15766 | memorial | 1 |
| 15767 | membrudo | 1 |
| 15768 | membrillo | 1 |
| 15769 | membraros | 1 |
| 15770 | melón | 1 |
| 15771 | melindrosos | 1 |
| 15772 | melindres | 1 |
| 15773 | meliflua | 1 |
| 15774 | melificada | 1 |
| 15775 | melena | 1 |
| 15776 | melecinas | 1 |
| 15777 | melanconía | 1 |
| 15778 | melancólica | 1 |
| 15779 | mejorasen | 1 |
| 15780 | mejorarse | 1 |
| 15781 | mejorarla | 1 |
| 15782 | mejorares | 1 |
| 15783 | mejorándose | 1 |
| 15784 | mejoran | 1 |
| 15785 | mejorados | 1 |
| 15786 | mejorada | 1 |
| 15787 | mejora | 1 |
| 15788 | méjico | 1 |
| 15789 | mejicano | 1 |
| 15790 | medusa | 1 |
| 15791 | medrosos | 1 |
| 15792 | medrosica | 1 |
| 15793 | medrosa | 1 |
| 15794 | medre | 1 |
| 15795 | medrar | 1 |
| 15796 | medradas | 1 |
| 15797 | mediterráneo | 1 |
| 15798 | medíos | 1 |
| 15799 | medina | 1 |
| 15800 | medimos | 1 |
| 15801 | medíme | 1 |
| 15802 | médiese | 1 |
| 15803 | mediaron | 1 |
| 15804 | medianos | 1 |
| 15805 | medianas | 1 |
| 15806 | medecinas | 1 |
| 15807 | medea | 1 |
| 15808 | mecina | 1 |
| 15809 | meca | 1 |
| 15810 | mazorcas | 1 |
| 15811 | mazorca | 1 |
| 15812 | mazapán | 1 |
| 15813 | maza | 1 |
| 15814 | mayormente | 1 |
| 15815 | mayordoma | 1 |
| 15816 | mayorazgos | 1 |
| 15817 | mayar | 1 |
| 15818 | mayaban | 1 |
| 15819 | mausoleo | 1 |
| 15820 | mauleón | 1 |
| 15821 | matrona | 1 |
| 15822 | matrimoñesco | 1 |
| 15823 | matorrales | 1 |
| 15824 | matizar | 1 |
| 15825 | matizadas | 1 |
| 15826 | mateo | 1 |
| 15827 | matemática | 1 |
| 15828 | matasen | 1 |
| 15829 | matarse | 1 |
| 15830 | matarle | 1 |
| 15831 | mataré | 1 |
| 15832 | mataras | 1 |
| 15833 | matándote | 1 |
| 15834 | matalote | 1 |
| 15835 | matalotaje | 1 |
| 15836 | mástil | 1 |
| 15837 | masílicos | 1 |
| 15838 | mascó | 1 |
| 15839 | máscaras | 1 |
| 15840 | mascando | 1 |
| 15841 | martos | 1 |
| 15842 | martirizado | 1 |
| 15843 | martirizada | 1 |
| 15844 | martirio | 1 |
| 15845 | martino | 1 |
| 15846 | martínez | 1 |
| 15847 | martillos | 1 |
| 15848 | marta | 1 |
| 15849 | marrido | 1 |
| 15850 | márquez | 1 |
| 15851 | marqueses | 1 |
| 15852 | marquesas | 1 |
| 15853 | maromas | 1 |
| 15854 | mármores | 1 |
| 15855 | marmol | 1 |
| 15856 | mario | 1 |
| 15857 | margarita | 1 |
| 15858 | marfuces | 1 |
| 15859 | mare | 1 |
| 15860 | marchitos | 1 |
| 15861 | marchito | 1 |
| 15862 | marchitan | 1 |
| 15863 | marchita | 1 |
| 15864 | marchena | 1 |
| 15865 | marchando | 1 |
| 15866 | marcha | 1 |
| 15867 | marcaron | 1 |
| 15868 | maravillosos | 1 |
| 15869 | maravilles | 1 |
| 15870 | maraville | 1 |
| 15871 | maravillásemos | 1 |
| 15872 | maravillase | 1 |
| 15873 | maravillaron | 1 |
| 15874 | maravillarme | 1 |
| 15875 | maravillarán | 1 |
| 15876 | maravillárame | 1 |
| 15877 | maravillándose | 1 |
| 15878 | maravillan | 1 |
| 15879 | maravillados | 1 |
| 15880 | marañón | 1 |
| 15881 | marañas | 1 |
| 15882 | maraña | 1 |
| 15883 | maquinase | 1 |
| 15884 | mañoso | 1 |
| 15885 | mañosamente | 1 |
| 15886 | mañeruelas | 1 |
| 15887 | manzanares | 1 |
| 15888 | manzana | 1 |
| 15889 | manuales | 1 |
| 15890 | mantuve | 1 |
| 15891 | mantuano | 1 |
| 15892 | mantos | 1 |
| 15893 | mantienen | 1 |
| 15894 | mantible | 1 |
| 15895 | mantequillas | 1 |
| 15896 | mantenimientos | 1 |
| 15897 | mantenidos | 1 |
| 15898 | mantengo | 1 |
| 15899 | mantenga | 1 |
| 15900 | mantener | 1 |
| 15901 | mantenedor | 1 |
| 15902 | manteca | 1 |
| 15903 | mansos | 1 |
| 15904 | mansedumbres | 1 |
| 15905 | mansamente | 1 |
| 15906 | mansa | 1 |
| 15907 | manriques | 1 |
| 15908 | manotadas | 1 |
| 15909 | manoseóse | 1 |
| 15910 | manoseó | 1 |
| 15911 | manosee | 1 |
| 15912 | manosean | 1 |
| 15913 | manoseada | 1 |
| 15914 | manojos | 1 |
| 15915 | manillas | 1 |
| 15916 | manifiestos | 1 |
| 15917 | manifieste | 1 |
| 15918 | manifiestan | 1 |
| 15919 | manifestaran | 1 |
| 15920 | manifestar | 1 |
| 15921 | manifatura | 1 |
| 15922 | maniatar | 1 |
| 15923 | manga | 1 |
| 15924 | manejaré | 1 |
| 15925 | manejar | 1 |
| 15926 | manejan | 1 |
| 15927 | mandóselos | 1 |
| 15928 | mandos | 1 |
| 15929 | mandólo | 1 |
| 15930 | mandóles | 1 |
| 15931 | mándole | 1 |
| 15932 | mandóla | 1 |
| 15933 | mandastes | 1 |
| 15934 | mandárselo | 1 |
| 15935 | mandáronles | 1 |
| 15936 | mandárnoslo | 1 |
| 15937 | mandarme | 1 |
| 15938 | mandaren | 1 |
| 15939 | mandaran | 1 |
| 15940 | mandara | 1 |
| 15941 | mandallas | 1 |
| 15942 | mandadería | 1 |
| 15943 | mandad | 1 |
| 15944 | mancos | 1 |
| 15945 | manco | 1 |
| 15946 | manchísima | 1 |
| 15947 | manche | 1 |
| 15948 | manchase | 1 |
| 15949 | manchado | 1 |
| 15950 | mancebito | 1 |
| 15951 | mancebas | 1 |
| 15952 | manceba | 1 |
| 15953 | manar | 1 |
| 15954 | maná | 1 |
| 15955 | mamonado | 1 |
| 15956 | mamona | 1 |
| 15957 | mamo | 1 |
| 15958 | mameluco | 1 |
| 15959 | mamé | 1 |
| 15960 | mamaron | 1 |
| 15961 | malvas | 1 |
| 15962 | malvada | 1 |
| 15963 | maltrechos | 1 |
| 15964 | maltrecha | 1 |
| 15965 | maltrató | 1 |
| 15966 | maltraten | 1 |
| 15967 | maltratar | 1 |
| 15968 | maltratando | 1 |
| 15969 | maltratado | 1 |
| 15970 | maltrataban | 1 |
| 15971 | malsonantes | 1 |
| 15972 | malparados | 1 |
| 15973 | malparada | 1 |
| 15974 | malnacida | 1 |
| 15975 | malla | 1 |
| 15976 | malintencionados | 1 |
| 15977 | malino | 1 |
| 15978 | malindrania | 1 |
| 15979 | malignidad | 1 |
| 15980 | maligna | 1 |
| 15981 | maliciosas | 1 |
| 15982 | malheridos | 1 |
| 15983 | malherido | 1 |
| 15984 | malhadada | 1 |
| 15985 | malferida | 1 |
| 15986 | malévolo | 1 |
| 15987 | malencónicos | 1 |
| 15988 | malencónicas | 1 |
| 15989 | malencolía | 1 |
| 15990 | maleador | 1 |
| 15991 | maldonado | 1 |
| 15992 | maldíjose | 1 |
| 15993 | maldíjome | 1 |
| 15994 | maldigo | 1 |
| 15995 | maldicen | 1 |
| 15996 | maldice | 1 |
| 15997 | maldecirte | 1 |
| 15998 | maldecían | 1 |
| 15999 | maldecíamos | 1 |
| 16000 | malcriado | 1 |
| 16001 | malbaratándolas | 1 |
| 16002 | malaventura | 1 |
| 16003 | malandrino | 1 |
| 16004 | malandrina | 1 |
| 16005 | malandanza | 1 |
| 16006 | malae | 1 |
| 16007 | majar | 1 |
| 16008 | majalahonda | 1 |
| 16009 | majagranzas | 1 |
| 16010 | majadería | 1 |
| 16011 | majadas | 1 |
| 16012 | mahomético | 1 |
| 16013 | maheridas | 1 |
| 16014 | mahamate | 1 |
| 16015 | magra | 1 |
| 16016 | magnum | 1 |
| 16017 | magnitudes | 1 |
| 16018 | magníficos | 1 |
| 16019 | magníficamente | 1 |
| 16020 | magnánima | 1 |
| 16021 | magis | 1 |
| 16022 | magimasa | 1 |
| 16023 | mágicos | 1 |
| 16024 | magia | 1 |
| 16025 | magallanes | 1 |
| 16026 | maga | 1 |
| 16027 | maestre | 1 |
| 16028 | maestra | 1 |
| 16029 | maesecoral | 1 |
| 16030 | maduras | 1 |
| 16031 | madurado | 1 |
| 16032 | madrugan | 1 |
| 16033 | madrugador | 1 |
| 16034 | madrugada | 1 |
| 16035 | madrina | 1 |
| 16036 | madrigalete | 1 |
| 16037 | madreselva | 1 |
| 16038 | madésima | 1 |
| 16039 | maderos | 1 |
| 16040 | madásimas | 1 |
| 16041 | madama | 1 |
| 16042 | madalena | 1 |
| 16043 | macizo | 1 |
| 16044 | macizas | 1 |
| 16045 | macilenta | 1 |
| 16046 | machuelo | 1 |
| 16047 | machucándole | 1 |
| 16048 | machacó | 1 |
| 16049 | machacaron | 1 |
| 16050 | machacan | 1 |
| 16051 | macange | 1 |
| 16052 | macabeos | 1 |
| 16053 | lxxiv | 1 |
| 16054 | lxxiii | 1 |
| 16055 | lxxii | 1 |
| 16056 | lxxi | 1 |
| 16057 | lxx | 1 |
| 16058 | lxviii | 1 |
| 16059 | lxvii | 1 |
| 16060 | lxvi | 1 |
| 16061 | lxv | 1 |
| 16062 | lxix | 1 |
| 16063 | lxiv | 1 |
| 16064 | lxiii | 1 |
| 16065 | lxii | 1 |
| 16066 | lxi | 1 |
| 16067 | lx | 1 |
| 16068 | lviii | 1 |
| 16069 | lvii | 1 |
| 16070 | lvi | 1 |
| 16071 | lv | 1 |
| 16072 | lustre | 1 |
| 16073 | lusitano | 1 |
| 16074 | lusitania | 1 |
| 16075 | luminaria | 1 |
| 16076 | luminares | 1 |
| 16077 | lujuria | 1 |
| 16078 | lueñas | 1 |
| 16079 | ludovico | 1 |
| 16080 | lucrando | 1 |
| 16081 | lucinda | 1 |
| 16082 | lucifer | 1 |
| 16083 | lucidísimo | 1 |
| 16084 | luchar | 1 |
| 16085 | luchador | 1 |
| 16086 | lucem | 1 |
| 16087 | luce | 1 |
| 16088 | lu | 1 |
| 16089 | lozanías | 1 |
| 16090 | lot | 1 |
| 16091 | loriga | 1 |
| 16092 | loores | 1 |
| 16093 | loor | 1 |
| 16094 | lonjas | 1 |
| 16095 | lonja | 1 |
| 16096 | longura | 1 |
| 16097 | longísima | 1 |
| 16098 | lombardía | 1 |
| 16099 | loja | 1 |
| 16100 | lograse | 1 |
| 16101 | lograda | 1 |
| 16102 | logicuos | 1 |
| 16103 | lofraso | 1 |
| 16104 | lodos | 1 |
| 16105 | lobas | 1 |
| 16106 | loa | 1 |
| 16107 | llueve | 1 |
| 16108 | llueva | 1 |
| 16109 | llovió | 1 |
| 16110 | lloviere | 1 |
| 16111 | llovidas | 1 |
| 16112 | llovida | 1 |
| 16113 | llovían | 1 |
| 16114 | llorosas | 1 |
| 16115 | llores | 1 |
| 16116 | lloréis | 1 |
| 16117 | lloras | 1 |
| 16118 | lloraron | 1 |
| 16119 | lloraran | 1 |
| 16120 | lloráralas | 1 |
| 16121 | llorara | 1 |
| 16122 | lloramos | 1 |
| 16123 | lloramicos | 1 |
| 16124 | llorados | 1 |
| 16125 | llevóse | 1 |
| 16126 | llevóle | 1 |
| 16127 | llévola | 1 |
| 16128 | llévete | 1 |
| 16129 | llévese | 1 |
| 16130 | llévense | 1 |
| 16131 | llévenme | 1 |
| 16132 | llevemos | 1 |
| 16133 | llévele | 1 |
| 16134 | llevastes | 1 |
| 16135 | llevaros | 1 |
| 16136 | llevarónse | 1 |
| 16137 | lleváronse | 1 |
| 16138 | lleváronme | 1 |
| 16139 | lleváronle | 1 |
| 16140 | llevárnosle | 1 |
| 16141 | llevarnos | 1 |
| 16142 | llevarlos | 1 |
| 16143 | llevarlo | 1 |
| 16144 | llevarles | 1 |
| 16145 | llevarlas | 1 |
| 16146 | llevaríamos | 1 |
| 16147 | llevárades | 1 |
| 16148 | llevaos | 1 |
| 16149 | llevantan | 1 |
| 16150 | llevándoos | 1 |
| 16151 | llevándonos | 1 |
| 16152 | llevándolo | 1 |
| 16153 | llevándolas | 1 |
| 16154 | llevámoslas | 1 |
| 16155 | llevallos | 1 |
| 16156 | llevalle | 1 |
| 16157 | llevalla | 1 |
| 16158 | llevalde | 1 |
| 16159 | llevádolos | 1 |
| 16160 | llevádole | 1 |
| 16161 | llevaderos | 1 |
| 16162 | llevad | 1 |
| 16163 | llevábase | 1 |
| 16164 | llevábamos | 1 |
| 16165 | llenósele | 1 |
| 16166 | llene | 1 |
| 16167 | llenaros | 1 |
| 16168 | llenáronse | 1 |
| 16169 | llenaron | 1 |
| 16170 | llenaran | 1 |
| 16171 | llenándosele | 1 |
| 16172 | llenaban | 1 |
| 16173 | llenaba | 1 |
| 16174 | llegues | 1 |
| 16175 | lléguense | 1 |
| 16176 | lleguéis | 1 |
| 16177 | llégate | 1 |
| 16178 | llegarte | 1 |
| 16179 | llegarse | 1 |
| 16180 | llegáronle | 1 |
| 16181 | llegarlo | 1 |
| 16182 | llegarla | 1 |
| 16183 | llegares | 1 |
| 16184 | llegaremos | 1 |
| 16185 | llegándosele | 1 |
| 16186 | llegadas | 1 |
| 16187 | llegad | 1 |
| 16188 | llanura | 1 |
| 16189 | llanas | 1 |
| 16190 | llamóse | 1 |
| 16191 | llamóme | 1 |
| 16192 | llámome | 1 |
| 16193 | llámola | 1 |
| 16194 | llámese | 1 |
| 16195 | llaméis | 1 |
| 16196 | llamé | 1 |
| 16197 | llamativo | 1 |
| 16198 | llamaste | 1 |
| 16199 | llamases | 1 |
| 16200 | llamasen | 1 |
| 16201 | llamarme | 1 |
| 16202 | llamáremos | 1 |
| 16203 | llamaremos | 1 |
| 16204 | llamaré | 1 |
| 16205 | llamarán | 1 |
| 16206 | llamara | 1 |
| 16207 | llamándonos | 1 |
| 16208 | llamándolos | 1 |
| 16209 | llamándola | 1 |
| 16210 | llamadme | 1 |
| 16211 | llamad | 1 |
| 16212 | llamabas | 1 |
| 16213 | llagar | 1 |
| 16214 | llagado | 1 |
| 16215 | llagada | 1 |
| 16216 | lladres | 1 |
| 16217 | lizos | 1 |
| 16218 | lix | 1 |
| 16219 | liv | 1 |
| 16220 | literas | 1 |
| 16221 | lite | 1 |
| 16222 | lita | 1 |
| 16223 | lisuarte | 1 |
| 16224 | lisonjero | 1 |
| 16225 | lisonjee | 1 |
| 16226 | lisonjea | 1 |
| 16227 | lisonja | 1 |
| 16228 | lisipo | 1 |
| 16229 | lisión | 1 |
| 16230 | lisboa | 1 |
| 16231 | lirón | 1 |
| 16232 | lirios | 1 |
| 16233 | lirio | 1 |
| 16234 | lírico | 1 |
| 16235 | líquido | 1 |
| 16236 | liólas | 1 |
| 16237 | líneas | 1 |
| 16238 | linces | 1 |
| 16239 | limpísima | 1 |
| 16240 | limpiólas | 1 |
| 16241 | limpiémelos | 1 |
| 16242 | limpié | 1 |
| 16243 | limpiáronle | 1 |
| 16244 | limpiarlas | 1 |
| 16245 | limpiándose | 1 |
| 16246 | limpiando | 1 |
| 16247 | límpiale | 1 |
| 16248 | limiten | 1 |
| 16249 | limitado | 1 |
| 16250 | limitadamente | 1 |
| 16251 | límiste | 1 |
| 16252 | lima | 1 |
| 16253 | liii | 1 |
| 16254 | ligítimo | 1 |
| 16255 | ligítimamente | 1 |
| 16256 | ligamiento | 1 |
| 16257 | ligados | 1 |
| 16258 | ligaba | 1 |
| 16259 | lides | 1 |
| 16260 | lícitamente | 1 |
| 16261 | lición | 1 |
| 16262 | licenciosa | 1 |
| 16263 | licenciadillo | 1 |
| 16264 | librería | 1 |
| 16265 | libré | 1 |
| 16266 | libraros | 1 |
| 16267 | librarme | 1 |
| 16268 | librarle | 1 |
| 16269 | libraría | 1 |
| 16270 | libraré | 1 |
| 16271 | librara | 1 |
| 16272 | librados | 1 |
| 16273 | librado | 1 |
| 16274 | librada | 1 |
| 16275 | libio | 1 |
| 16276 | libia | 1 |
| 16277 | libertó | 1 |
| 16278 | libertas | 1 |
| 16279 | libertados | 1 |
| 16280 | libertades | 1 |
| 16281 | libertada | 1 |
| 16282 | liberalidades | 1 |
| 16283 | libelos | 1 |
| 16284 | liaron | 1 |
| 16285 | liar | 1 |
| 16286 | liaba | 1 |
| 16287 | lezna | 1 |
| 16288 | leyóle | 1 |
| 16289 | leyólas | 1 |
| 16290 | leyéndolos | 1 |
| 16291 | leyéndolo | 1 |
| 16292 | leyéndole | 1 |
| 16293 | leventes | 1 |
| 16294 | leve | 1 |
| 16295 | levar | 1 |
| 16296 | levántose | 1 |
| 16297 | levántenme | 1 |
| 16298 | levanten | 1 |
| 16299 | levantéis | 1 |
| 16300 | levanté | 1 |
| 16301 | levantastes | 1 |
| 16302 | levántase | 1 |
| 16303 | levantáronse | 1 |
| 16304 | levantarme | 1 |
| 16305 | levantarlas | 1 |
| 16306 | levantares | 1 |
| 16307 | levantaran | 1 |
| 16308 | levantara | 1 |
| 16309 | levantándole | 1 |
| 16310 | levantándola | 1 |
| 16311 | levantan | 1 |
| 16312 | levantalla | 1 |
| 16313 | levantadores | 1 |
| 16314 | levantaba | 1 |
| 16315 | levadas | 1 |
| 16316 | letores | 1 |
| 16317 | letor | 1 |
| 16318 | letanía | 1 |
| 16319 | lesa | 1 |
| 16320 | lercha | 1 |
| 16321 | lepanto | 1 |
| 16322 | leonora | 1 |
| 16323 | leoneses | 1 |
| 16324 | leños | 1 |
| 16325 | lentamente | 1 |
| 16326 | lenitivas | 1 |
| 16327 | lencería | 1 |
| 16328 | lelilíes | 1 |
| 16329 | leímos | 1 |
| 16330 | leídas | 1 |
| 16331 | leída | 1 |
| 16332 | leían | 1 |
| 16333 | lego | 1 |
| 16334 | legítimas | 1 |
| 16335 | legítimamente | 1 |
| 16336 | legión | 1 |
| 16337 | legibus | 1 |
| 16338 | leganitos | 1 |
| 16339 | legalmente | 1 |
| 16340 | legalidad | 1 |
| 16341 | leerlos | 1 |
| 16342 | leerle | 1 |
| 16343 | leería | 1 |
| 16344 | leeré | 1 |
| 16345 | leen | 1 |
| 16346 | leemos | 1 |
| 16347 | leellos | 1 |
| 16348 | leelle | 1 |
| 16349 | leellas | 1 |
| 16350 | leelde | 1 |
| 16351 | leedle | 1 |
| 16352 | ledanías | 1 |
| 16353 | leción | 1 |
| 16354 | lechones | 1 |
| 16355 | léase | 1 |
| 16356 | léamela | 1 |
| 16357 | léalos | 1 |
| 16358 | lazarillo | 1 |
| 16359 | lazari | 1 |
| 16360 | lavóse | 1 |
| 16361 | lavaron | 1 |
| 16362 | lavaran | 1 |
| 16363 | lavapiés | 1 |
| 16364 | lavajos | 1 |
| 16365 | lavado | 1 |
| 16366 | lavadme | 1 |
| 16367 | lavadas | 1 |
| 16368 | lautrec | 1 |
| 16369 | lauros | 1 |
| 16370 | lauro | 1 |
| 16371 | laureles | 1 |
| 16372 | laurcalco | 1 |
| 16373 | laura | 1 |
| 16374 | laúdes | 1 |
| 16375 | laudem | 1 |
| 16376 | latrocinio | 1 |
| 16377 | latinicos | 1 |
| 16378 | látigo | 1 |
| 16379 | lati | 1 |
| 16380 | lastimosas | 1 |
| 16381 | lastimeros | 1 |
| 16382 | lastimera | 1 |
| 16383 | lastimen | 1 |
| 16384 | lastime | 1 |
| 16385 | lastimadas | 1 |
| 16386 | lastima | 1 |
| 16387 | lastamos | 1 |
| 16388 | largarse | 1 |
| 16389 | laredo | 1 |
| 16390 | lara | 1 |
| 16391 | lapidarios | 1 |
| 16392 | lanzones | 1 |
| 16393 | lanzarse | 1 |
| 16394 | lanzadas | 1 |
| 16395 | lantejas | 1 |
| 16396 | lances | 1 |
| 16397 | lanceros | 1 |
| 16398 | lanas | 1 |
| 16399 | lampiñas | 1 |
| 16400 | lampazos | 1 |
| 16401 | láminas | 1 |
| 16402 | lamieron | 1 |
| 16403 | lamia | 1 |
| 16404 | lamentes | 1 |
| 16405 | lamente | 1 |
| 16406 | lamentar | 1 |
| 16407 | lamentador | 1 |
| 16408 | lamentaban | 1 |
| 16409 | lamenta | 1 |
| 16410 | lame | 1 |
| 16411 | lambicando | 1 |
| 16412 | laida | 1 |
| 16413 | lágrima | 1 |
| 16414 | lagarto | 1 |
| 16415 | lagartijero | 1 |
| 16416 | lagartija | 1 |
| 16417 | lagares | 1 |
| 16418 | lagañoso | 1 |
| 16419 | lagañas | 1 |
| 16420 | ladrillos | 1 |
| 16421 | ladrillazos | 1 |
| 16422 | ladrido | 1 |
| 16423 | ladino | 1 |
| 16424 | ladi | 1 |
| 16425 | ladearme | 1 |
| 16426 | lachrymis | 1 |
| 16427 | lacayuna | 1 |
| 16428 | labró | 1 |
| 16429 | labre | 1 |
| 16430 | labrandera | 1 |
| 16431 | labrados | 1 |
| 16432 | labradorescas | 1 |
| 16433 | labrado | 1 |
| 16434 | labores | 1 |
| 16435 | júzguenlo | 1 |
| 16436 | juzgarlo | 1 |
| 16437 | juzgarle | 1 |
| 16438 | juzgaran | 1 |
| 16439 | juzgando | 1 |
| 16440 | juzgáis | 1 |
| 16441 | juzgad | 1 |
| 16442 | juzgaban | 1 |
| 16443 | juxta | 1 |
| 16444 | juvenal | 1 |
| 16445 | justísimas | 1 |
| 16446 | jurisdición | 1 |
| 16447 | jurisconsultos | 1 |
| 16448 | jurídicamente | 1 |
| 16449 | jure | 1 |
| 16450 | juraste | 1 |
| 16451 | juraban | 1 |
| 16452 | juntura | 1 |
| 16453 | juntó | 1 |
| 16454 | juntillas | 1 |
| 16455 | juntéme | 1 |
| 16456 | júntate | 1 |
| 16457 | juntase | 1 |
| 16458 | juntaron | 1 |
| 16459 | juntan | 1 |
| 16460 | juntado | 1 |
| 16461 | juntábansele | 1 |
| 16462 | juntaban | 1 |
| 16463 | jumenta | 1 |
| 16464 | julios | 1 |
| 16465 | julián | 1 |
| 16466 | jüicio | 1 |
| 16467 | jui | 1 |
| 16468 | juguetona | 1 |
| 16469 | juguetes | 1 |
| 16470 | juglar | 1 |
| 16471 | jugares | 1 |
| 16472 | jugadores | 1 |
| 16473 | jugador | 1 |
| 16474 | jugaban | 1 |
| 16475 | jueves | 1 |
| 16476 | juegue | 1 |
| 16477 | juegos | 1 |
| 16478 | juega | 1 |
| 16479 | judíos | 1 |
| 16480 | judiciarias | 1 |
| 16481 | judiciaria | 1 |
| 16482 | judicial | 1 |
| 16483 | jubilarle | 1 |
| 16484 | jubilaba | 1 |
| 16485 | joviales | 1 |
| 16486 | joventud | 1 |
| 16487 | joven | 1 |
| 16488 | josef | 1 |
| 16489 | jornaleros | 1 |
| 16490 | jornalero | 1 |
| 16491 | joeces | 1 |
| 16492 | jocunda | 1 |
| 16493 | jo | 1 |
| 16494 | jira | 1 |
| 16495 | jinetes | 1 |
| 16496 | jimio | 1 |
| 16497 | jerusalén | 1 |
| 16498 | jeringas | 1 |
| 16499 | jerezanos | 1 |
| 16500 | jerez | 1 |
| 16501 | jenízaros | 1 |
| 16502 | jazmines | 1 |
| 16503 | jáurigui | 1 |
| 16504 | jaspeados | 1 |
| 16505 | jaspeada | 1 |
| 16506 | jaspeaban | 1 |
| 16507 | jasón | 1 |
| 16508 | jarifa | 1 |
| 16509 | jarcia | 1 |
| 16510 | jaramilla | 1 |
| 16511 | jarales | 1 |
| 16512 | jara | 1 |
| 16513 | jáquimas | 1 |
| 16514 | janto | 1 |
| 16515 | jamón | 1 |
| 16516 | jaldes | 1 |
| 16517 | jacintos | 1 |
| 16518 | jaca | 1 |
| 16519 | jaboneros | 1 |
| 16520 | jabonaron | 1 |
| 16521 | jabonadura | 1 |
| 16522 | jabalíes | 1 |
| 16523 | izquierdeaba | 1 |
| 16524 | izó | 1 |
| 16525 | iten | 1 |
| 16526 | italias | 1 |
| 16527 | israel | 1 |
| 16528 | islilla | 1 |
| 16529 | iseo | 1 |
| 16530 | isabela | 1 |
| 16531 | irritado | 1 |
| 16532 | irnos | 1 |
| 16533 | irían | 1 |
| 16534 | invocó | 1 |
| 16535 | invocar | 1 |
| 16536 | invocando | 1 |
| 16537 | invocan | 1 |
| 16538 | invisible | 1 |
| 16539 | invidio | 1 |
| 16540 | invidiara | 1 |
| 16541 | invidiada | 1 |
| 16542 | invictísimo | 1 |
| 16543 | inventarla | 1 |
| 16544 | inventar | 1 |
| 16545 | inventando | 1 |
| 16546 | inventa | 1 |
| 16547 | invenerable | 1 |
| 16548 | invectiva | 1 |
| 16549 | inusitadas | 1 |
| 16550 | inumerable | 1 |
| 16551 | inumerabilidad | 1 |
| 16552 | intrumentos | 1 |
| 16553 | introducir | 1 |
| 16554 | introduciendo | 1 |
| 16555 | introducen | 1 |
| 16556 | intricarlos | 1 |
| 16557 | intricadamente | 1 |
| 16558 | intricable | 1 |
| 16559 | intrépidamente | 1 |
| 16560 | intrépida | 1 |
| 16561 | intonsos | 1 |
| 16562 | intolerables | 1 |
| 16563 | intolerable | 1 |
| 16564 | intimo | 1 |
| 16565 | intimase | 1 |
| 16566 | intimar | 1 |
| 16567 | intimado | 1 |
| 16568 | intimaciones | 1 |
| 16569 | interviniesen | 1 |
| 16570 | interviene | 1 |
| 16571 | intervenga | 1 |
| 16572 | intervención | 1 |
| 16573 | interrumpiese | 1 |
| 16574 | interrumpidas | 1 |
| 16575 | interrotos | 1 |
| 16576 | interrompiendo | 1 |
| 16577 | interromperéis | 1 |
| 16578 | interrogantes | 1 |
| 16579 | interpretación | 1 |
| 16580 | interpone | 1 |
| 16581 | interior | 1 |
| 16582 | ínterin | 1 |
| 16583 | interesal | 1 |
| 16584 | interesado | 1 |
| 16585 | interdum | 1 |
| 16586 | intercesor | 1 |
| 16587 | intentó | 1 |
| 16588 | intentas | 1 |
| 16589 | intentarse | 1 |
| 16590 | intentarla | 1 |
| 16591 | intentare | 1 |
| 16592 | intentado | 1 |
| 16593 | intensamente | 1 |
| 16594 | intencionados | 1 |
| 16595 | inteligibles | 1 |
| 16596 | inteligencia | 1 |
| 16597 | intelegibles | 1 |
| 16598 | integridad | 1 |
| 16599 | intactas | 1 |
| 16600 | ínsulo | 1 |
| 16601 | insulano | 1 |
| 16602 | insufribles | 1 |
| 16603 | insufrible | 1 |
| 16604 | insuficiencia | 1 |
| 16605 | instituyó | 1 |
| 16606 | instituido | 1 |
| 16607 | instituida | 1 |
| 16608 | instinto | 1 |
| 16609 | instigo | 1 |
| 16610 | instigados | 1 |
| 16611 | instable | 1 |
| 16612 | inspiración | 1 |
| 16613 | insignes | 1 |
| 16614 | insidias | 1 |
| 16615 | inserto | 1 |
| 16616 | inseparable | 1 |
| 16617 | inresolutas | 1 |
| 16618 | inremediables | 1 |
| 16619 | inremediable | 1 |
| 16620 | inquisidores | 1 |
| 16621 | inquisición | 1 |
| 16622 | inquirir | 1 |
| 16623 | inquiriese | 1 |
| 16624 | inquiriendo | 1 |
| 16625 | inquerir | 1 |
| 16626 | inormes | 1 |
| 16627 | inominia | 1 |
| 16628 | inocentes | 1 |
| 16629 | inocencia | 1 |
| 16630 | innumerable | 1 |
| 16631 | inmundicias | 1 |
| 16632 | inmortal | 1 |
| 16633 | inmensidad | 1 |
| 16634 | inmemoriales | 1 |
| 16635 | injustos | 1 |
| 16636 | injustamente | 1 |
| 16637 | inimicos | 1 |
| 16638 | inhumanidad | 1 |
| 16639 | inhumana | 1 |
| 16640 | inhabilitado | 1 |
| 16641 | ingrato | 1 |
| 16642 | inglés | 1 |
| 16643 | ingerir | 1 |
| 16644 | ingeniosa | 1 |
| 16645 | ingeniero | 1 |
| 16646 | infundir | 1 |
| 16647 | infundiendo | 1 |
| 16648 | infunde | 1 |
| 16649 | infunda | 1 |
| 16650 | infortunios | 1 |
| 16651 | infortunio | 1 |
| 16652 | informase | 1 |
| 16653 | informaremos | 1 |
| 16654 | informando | 1 |
| 16655 | informalle | 1 |
| 16656 | informada | 1 |
| 16657 | informaciones | 1 |
| 16658 | informaba | 1 |
| 16659 | influencia | 1 |
| 16660 | infiráis | 1 |
| 16661 | infinitus | 1 |
| 16662 | infinitamente | 1 |
| 16663 | ínfima | 1 |
| 16664 | infiernos | 1 |
| 16665 | infiera | 1 |
| 16666 | infernales | 1 |
| 16667 | inferiores | 1 |
| 16668 | inferior | 1 |
| 16669 | infelice | 1 |
| 16670 | infantes | 1 |
| 16671 | infamatorio | 1 |
| 16672 | infacundo | 1 |
| 16673 | inevitable | 1 |
| 16674 | inestimable | 1 |
| 16675 | inescrutables | 1 |
| 16676 | inescrutable | 1 |
| 16677 | inefable | 1 |
| 16678 | industriosos | 1 |
| 16679 | industriándole | 1 |
| 16680 | industriadas | 1 |
| 16681 | indubitadamente | 1 |
| 16682 | indomable | 1 |
| 16683 | indisposición | 1 |
| 16684 | indiscretos | 1 |
| 16685 | indiscreto | 1 |
| 16686 | indigestiones | 1 |
| 16687 | indiferente | 1 |
| 16688 | índice | 1 |
| 16689 | india | 1 |
| 16690 | indecible | 1 |
| 16691 | indecencia | 1 |
| 16692 | incurrido | 1 |
| 16693 | incurable | 1 |
| 16694 | inculto | 1 |
| 16695 | increíbles | 1 |
| 16696 | incredulidad | 1 |
| 16697 | incontrastable | 1 |
| 16698 | inconstancia | 1 |
| 16699 | incomportable | 1 |
| 16700 | incomparables | 1 |
| 16701 | incómodos | 1 |
| 16702 | incluyese | 1 |
| 16703 | ínclitas | 1 |
| 16704 | inclinósele | 1 |
| 16705 | inclinóse | 1 |
| 16706 | inclino | 1 |
| 16707 | incliné | 1 |
| 16708 | inclinar | 1 |
| 16709 | inclinaciones | 1 |
| 16710 | inclinaba | 1 |
| 16711 | inclemencia | 1 |
| 16712 | incitó | 1 |
| 16713 | incite | 1 |
| 16714 | incitativo | 1 |
| 16715 | incitativas | 1 |
| 16716 | inciertos | 1 |
| 16717 | incesable | 1 |
| 16718 | incentivos | 1 |
| 16719 | inauditos | 1 |
| 16720 | inadvertidos | 1 |
| 16721 | inadvertidamente | 1 |
| 16722 | inacesible | 1 |
| 16723 | inacabables | 1 |
| 16724 | inacabable | 1 |
| 16725 | impusiere | 1 |
| 16726 | impuse | 1 |
| 16727 | impura | 1 |
| 16728 | impulso | 1 |
| 16729 | impuesta | 1 |
| 16730 | imprudentemente | 1 |
| 16731 | imprudente | 1 |
| 16732 | imprudencia | 1 |
| 16733 | improvisa | 1 |
| 16734 | impropio | 1 |
| 16735 | imprimirse | 1 |
| 16736 | imprimirle | 1 |
| 16737 | imprimieron | 1 |
| 16738 | imprimiendo | 1 |
| 16739 | imprimid | 1 |
| 16740 | imprímese | 1 |
| 16741 | imprimen | 1 |
| 16742 | impriman | 1 |
| 16743 | imposibilitó | 1 |
| 16744 | imposibilitar | 1 |
| 16745 | imposibilitada | 1 |
| 16746 | importunos | 1 |
| 16747 | importunarle | 1 |
| 16748 | importunarla | 1 |
| 16749 | importunan | 1 |
| 16750 | importunaban | 1 |
| 16751 | importunaba | 1 |
| 16752 | importuna | 1 |
| 16753 | importe | 1 |
| 16754 | importare | 1 |
| 16755 | importar | 1 |
| 16756 | importante | 1 |
| 16757 | importan | 1 |
| 16758 | imponerse | 1 |
| 16759 | implicaría | 1 |
| 16760 | implacables | 1 |
| 16761 | implacable | 1 |
| 16762 | impíreas | 1 |
| 16763 | impío | 1 |
| 16764 | impidió | 1 |
| 16765 | impidiese | 1 |
| 16766 | impidiera | 1 |
| 16767 | impidía | 1 |
| 16768 | impidan | 1 |
| 16769 | imperiosos | 1 |
| 16770 | imperfeto | 1 |
| 16771 | imperfecto | 1 |
| 16772 | imperfecta | 1 |
| 16773 | imperatoria | 1 |
| 16774 | impensado | 1 |
| 16775 | impensada | 1 |
| 16776 | impeliendo | 1 |
| 16777 | impedirlo | 1 |
| 16778 | impedirles | 1 |
| 16779 | impedimiento | 1 |
| 16780 | impedidos | 1 |
| 16781 | impaciencia | 1 |
| 16782 | imito | 1 |
| 16783 | imitaste | 1 |
| 16784 | imitaros | 1 |
| 16785 | imitarle | 1 |
| 16786 | imitare | 1 |
| 16787 | imitarán | 1 |
| 16788 | imitalle | 1 |
| 16789 | imitáis | 1 |
| 16790 | imitados | 1 |
| 16791 | imitador | 1 |
| 16792 | imediatamente | 1 |
| 16793 | imaginativo | 1 |
| 16794 | imaginase | 1 |
| 16795 | imaginarla | 1 |
| 16796 | imaginaren | 1 |
| 16797 | imaginaremos | 1 |
| 16798 | imaginándose | 1 |
| 16799 | imaginaldo | 1 |
| 16800 | imaginábase | 1 |
| 16801 | ilustrado | 1 |
| 16802 | illud | 1 |
| 16803 | ilíada | 1 |
| 16804 | ijas | 1 |
| 16805 | ijadeando | 1 |
| 16806 | iguale | 1 |
| 16807 | igualasen | 1 |
| 16808 | igualarían | 1 |
| 16809 | igualaran | 1 |
| 16810 | ignoró | 1 |
| 16811 | ignoraste | 1 |
| 16812 | ignoras | 1 |
| 16813 | ignorando | 1 |
| 16814 | ignorancias | 1 |
| 16815 | ignoran | 1 |
| 16816 | ignoráis | 1 |
| 16817 | ignorados | 1 |
| 16818 | ignorado | 1 |
| 16819 | ignorada | 1 |
| 16820 | ignora | 1 |
| 16821 | idóneo | 1 |
| 16822 | ídolo | 1 |
| 16823 | idio | 1 |
| 16824 | ides | 1 |
| 16825 | idas | 1 |
| 16826 | iberia | 1 |
| 16827 | ibas | 1 |
| 16828 | íbades | 1 |
| 16829 | huyóse | 1 |
| 16830 | huyeron | 1 |
| 16831 | huyere | 1 |
| 16832 | huyas | 1 |
| 16833 | huya | 1 |
| 16834 | hurtos | 1 |
| 16835 | hurtes | 1 |
| 16836 | hurte | 1 |
| 16837 | hurtaron | 1 |
| 16838 | hurtada | 1 |
| 16839 | hurtacordel | 1 |
| 16840 | hurgada | 1 |
| 16841 | huraño | 1 |
| 16842 | hundirme | 1 |
| 16843 | hundió | 1 |
| 16844 | hundiéndola | 1 |
| 16845 | hundidos | 1 |
| 16846 | hunde | 1 |
| 16847 | humos | 1 |
| 16848 | humíllome | 1 |
| 16849 | humilló | 1 |
| 16850 | humíllate | 1 |
| 16851 | humillan | 1 |
| 16852 | humilladas | 1 |
| 16853 | humillación | 1 |
| 16854 | humilísima | 1 |
| 16855 | humildemente | 1 |
| 16856 | húmida | 1 |
| 16857 | humi | 1 |
| 16858 | húmedo | 1 |
| 16859 | humedece | 1 |
| 16860 | humedad | 1 |
| 16861 | húmeda | 1 |
| 16862 | humanista | 1 |
| 16863 | humanidad | 1 |
| 16864 | huma | 1 |
| 16865 | huirme | 1 |
| 16866 | huilla | 1 |
| 16867 | huidos | 1 |
| 16868 | huías | 1 |
| 16869 | huérfanas | 1 |
| 16870 | huella | 1 |
| 16871 | huelga | 1 |
| 16872 | hueles | 1 |
| 16873 | huelan | 1 |
| 16874 | huecos | 1 |
| 16875 | hueca | 1 |
| 16876 | húbolo | 1 |
| 16877 | hubistes | 1 |
| 16878 | hubieses | 1 |
| 16879 | hubieren | 1 |
| 16880 | hubiérale | 1 |
| 16881 | hoto | 1 |
| 16882 | hostalero | 1 |
| 16883 | horros | 1 |
| 16884 | horrísono | 1 |
| 16885 | horrísona | 1 |
| 16886 | horquilla | 1 |
| 16887 | hornos | 1 |
| 16888 | horno | 1 |
| 16889 | hormigas | 1 |
| 16890 | horma | 1 |
| 16891 | horcajadura | 1 |
| 16892 | horadó | 1 |
| 16893 | horadara | 1 |
| 16894 | horadado | 1 |
| 16895 | horadación | 1 |
| 16896 | hopo | 1 |
| 16897 | honrarte | 1 |
| 16898 | honrarse | 1 |
| 16899 | honraron | 1 |
| 16900 | honrarme | 1 |
| 16901 | honrarle | 1 |
| 16902 | honraré | 1 |
| 16903 | honrándola | 1 |
| 16904 | honrando | 1 |
| 16905 | honradísimos | 1 |
| 16906 | honradísima | 1 |
| 16907 | honestísimos | 1 |
| 16908 | honestísima | 1 |
| 16909 | honestamente | 1 |
| 16910 | hondura | 1 |
| 16911 | hondos | 1 |
| 16912 | hondonada | 1 |
| 16913 | homicidios | 1 |
| 16914 | homerus | 1 |
| 16915 | home | 1 |
| 16916 | hombruno | 1 |
| 16917 | hombruna | 1 |
| 16918 | hombrón | 1 |
| 16919 | hombrecito | 1 |
| 16920 | hombrecillo | 1 |
| 16921 | hollen | 1 |
| 16922 | hollar | 1 |
| 16923 | holgué | 1 |
| 16924 | holgóse | 1 |
| 16925 | holgase | 1 |
| 16926 | holgaréme | 1 |
| 16927 | holgáredes | 1 |
| 16928 | holgaran | 1 |
| 16929 | holgáramos | 1 |
| 16930 | holgar | 1 |
| 16931 | holgando | 1 |
| 16932 | holgáis | 1 |
| 16933 | holgados | 1 |
| 16934 | holgadamente | 1 |
| 16935 | holgaba | 1 |
| 16936 | hojuelas | 1 |
| 16937 | hojeo | 1 |
| 16938 | hojeé | 1 |
| 16939 | hojearle | 1 |
| 16940 | hojeando | 1 |
| 16941 | hogueras | 1 |
| 16942 | hogazas | 1 |
| 16943 | hocicos | 1 |
| 16944 | hocicando | 1 |
| 16945 | hoc | 1 |
| 16946 | hobiese | 1 |
| 16947 | hobiere | 1 |
| 16948 | hízome | 1 |
| 16949 | hízole | 1 |
| 16950 | historiado | 1 |
| 16951 | hisopo | 1 |
| 16952 | hirióle | 1 |
| 16953 | hipólito | 1 |
| 16954 | hipócritas | 1 |
| 16955 | hipérbole | 1 |
| 16956 | hinchó | 1 |
| 16957 | hinche | 1 |
| 16958 | hinchazón | 1 |
| 16959 | hincharte | 1 |
| 16960 | hinchar | 1 |
| 16961 | hinchados | 1 |
| 16962 | hinchadas | 1 |
| 16963 | hincha | 1 |
| 16964 | híncate | 1 |
| 16965 | hincarse | 1 |
| 16966 | hincapié | 1 |
| 16967 | hincándose | 1 |
| 16968 | hincados | 1 |
| 16969 | hincado | 1 |
| 16970 | hincada | 1 |
| 16971 | hilera | 1 |
| 16972 | hile | 1 |
| 16973 | hilando | 1 |
| 16974 | hilachas | 1 |
| 16975 | hijitos | 1 |
| 16976 | higos | 1 |
| 16977 | higo | 1 |
| 16978 | higas | 1 |
| 16979 | hígados | 1 |
| 16980 | hígado | 1 |
| 16981 | hieroglí | 1 |
| 16982 | hidrópica | 1 |
| 16983 | hidiondas | 1 |
| 16984 | hideperro | 1 |
| 16985 | hicistes | 1 |
| 16986 | hicimos | 1 |
| 16987 | hiciésedes | 1 |
| 16988 | hiciéronle | 1 |
| 16989 | hiciéremos | 1 |
| 16990 | hicieras | 1 |
| 16991 | hiciéramos | 1 |
| 16992 | hícelo | 1 |
| 16993 | hícela | 1 |
| 16994 | hía | 1 |
| 16995 | hétores | 1 |
| 16996 | hético | 1 |
| 16997 | hételo | 1 |
| 16998 | hete | 1 |
| 16999 | herreruelos | 1 |
| 17000 | herreros | 1 |
| 17001 | herrerías | 1 |
| 17002 | herradura | 1 |
| 17003 | herrados | 1 |
| 17004 | herradas | 1 |
| 17005 | heroicos | 1 |
| 17006 | heroico | 1 |
| 17007 | heroicas | 1 |
| 17008 | hermandades | 1 |
| 17009 | herirse | 1 |
| 17010 | herirnos | 1 |
| 17011 | herirles | 1 |
| 17012 | herirle | 1 |
| 17013 | heria | 1 |
| 17014 | herencia | 1 |
| 17015 | hereje | 1 |
| 17016 | hereden | 1 |
| 17017 | heredase | 1 |
| 17018 | heredar | 1 |
| 17019 | herboso | 1 |
| 17020 | herbolario | 1 |
| 17021 | heraclio | 1 |
| 17022 | hepila | 1 |
| 17023 | hender | 1 |
| 17024 | henchir | 1 |
| 17025 | helase | 1 |
| 17026 | helárseme | 1 |
| 17027 | helado | 1 |
| 17028 | helada | 1 |
| 17029 | heis | 1 |
| 17030 | hediondo | 1 |
| 17031 | héchoos | 1 |
| 17032 | héchole | 1 |
| 17033 | hechizos | 1 |
| 17034 | hechiceresca | 1 |
| 17035 | hebreo | 1 |
| 17036 | hazlo | 1 |
| 17037 | hazañosos | 1 |
| 17038 | hayades | 1 |
| 17039 | haste | 1 |
| 17040 | háselo | 1 |
| 17041 | háseles | 1 |
| 17042 | hartura | 1 |
| 17043 | hartos | 1 |
| 17044 | hártome | 1 |
| 17045 | hartó | 1 |
| 17046 | hartazga | 1 |
| 17047 | hártate | 1 |
| 17048 | hartamos | 1 |
| 17049 | hartaban | 1 |
| 17050 | harpillera | 1 |
| 17051 | harón | 1 |
| 17052 | harina | 1 |
| 17053 | haríamos | 1 |
| 17054 | haríale | 1 |
| 17055 | harásme | 1 |
| 17056 | harásela | 1 |
| 17057 | háosla | 1 |
| 17058 | hanos | 1 |
| 17059 | hanme | 1 |
| 17060 | hanla | 1 |
| 17061 | hanega | 1 |
| 17062 | hamida | 1 |
| 17063 | hamet | 1 |
| 17064 | hámela | 1 |
| 17065 | hame | 1 |
| 17066 | hambrientas | 1 |
| 17067 | hámago | 1 |
| 17068 | hallóla | 1 |
| 17069 | halles | 1 |
| 17070 | halléle | 1 |
| 17071 | halléla | 1 |
| 17072 | hallástete | 1 |
| 17073 | hallásemos | 1 |
| 17074 | hallarte | 1 |
| 17075 | halláronse | 1 |
| 17076 | hallarlo | 1 |
| 17077 | hallaríamos | 1 |
| 17078 | halláredes | 1 |
| 17079 | hallándome | 1 |
| 17080 | hallámonos | 1 |
| 17081 | hallador | 1 |
| 17082 | halladas | 1 |
| 17083 | hallada | 1 |
| 17084 | hale | 1 |
| 17085 | haldudos | 1 |
| 17086 | haldudo | 1 |
| 17087 | halda | 1 |
| 17088 | halagarme | 1 |
| 17089 | hala | 1 |
| 17090 | hágole | 1 |
| 17091 | hágase | 1 |
| 17092 | háganle | 1 |
| 17093 | hágame | 1 |
| 17094 | hágalo | 1 |
| 17095 | hágale | 1 |
| 17096 | hágalas | 1 |
| 17097 | hadriani | 1 |
| 17098 | haciéndonos | 1 |
| 17099 | haciéndome | 1 |
| 17100 | haciéndolo | 1 |
| 17101 | haciéndola | 1 |
| 17102 | hacíanles | 1 |
| 17103 | hacíales | 1 |
| 17104 | hacíale | 1 |
| 17105 | hacíades | 1 |
| 17106 | hácense | 1 |
| 17107 | hacendosa | 1 |
| 17108 | háceme | 1 |
| 17109 | hacellas | 1 |
| 17110 | hacella | 1 |
| 17111 | hacelde | 1 |
| 17112 | hacednos | 1 |
| 17113 | hacedme | 1 |
| 17114 | hacedero | 1 |
| 17115 | hacedera | 1 |
| 17116 | hacas | 1 |
| 17117 | habríamos | 1 |
| 17118 | habríades | 1 |
| 17119 | habréla | 1 |
| 17120 | háblese | 1 |
| 17121 | hablen | 1 |
| 17122 | hablemos | 1 |
| 17123 | habléla | 1 |
| 17124 | habléis | 1 |
| 17125 | hablarse | 1 |
| 17126 | hablaros | 1 |
| 17127 | hablarnos | 1 |
| 17128 | hablarlo | 1 |
| 17129 | hablarles | 1 |
| 17130 | hablaríamos | 1 |
| 17131 | hablaremos | 1 |
| 17132 | hablantes | 1 |
| 17133 | hablándolos | 1 |
| 17134 | hablalle | 1 |
| 17135 | háblale | 1 |
| 17136 | hablados | 1 |
| 17137 | habladores | 1 |
| 17138 | habladora | 1 |
| 17139 | habladas | 1 |
| 17140 | hablada | 1 |
| 17141 | hablad | 1 |
| 17142 | hablábamos | 1 |
| 17143 | habitadoras | 1 |
| 17144 | habilitándole | 1 |
| 17145 | habilitado | 1 |
| 17146 | hábiles | 1 |
| 17147 | habiéndoselos | 1 |
| 17148 | habiéndoos | 1 |
| 17149 | habiéndonos | 1 |
| 17150 | habiéndolas | 1 |
| 17151 | habías | 1 |
| 17152 | habíanse | 1 |
| 17153 | habíale | 1 |
| 17154 | habérselas | 1 |
| 17155 | habérosla | 1 |
| 17156 | habérmelos | 1 |
| 17157 | habérmelas | 1 |
| 17158 | habérmela | 1 |
| 17159 | habello | 1 |
| 17160 | habelle | 1 |
| 17161 | habéisme | 1 |
| 17162 | guzmanes | 1 |
| 17163 | guzmán | 1 |
| 17164 | guy | 1 |
| 17165 | gustosas | 1 |
| 17166 | gustosamente | 1 |
| 17167 | gustes | 1 |
| 17168 | guste | 1 |
| 17169 | gustaron | 1 |
| 17170 | gustaría | 1 |
| 17171 | gustares | 1 |
| 17172 | gustarán | 1 |
| 17173 | gustará | 1 |
| 17174 | gustan | 1 |
| 17175 | gustado | 1 |
| 17176 | gusanos | 1 |
| 17177 | gusanillos | 1 |
| 17178 | gurreas | 1 |
| 17179 | gullurías | 1 |
| 17180 | guitarristas | 1 |
| 17181 | guisopete | 1 |
| 17182 | guío | 1 |
| 17183 | guindas | 1 |
| 17184 | guilla | 1 |
| 17185 | guijeñas | 1 |
| 17186 | guijas | 1 |
| 17187 | guíete | 1 |
| 17188 | guíes | 1 |
| 17189 | guías | 1 |
| 17190 | guiarse | 1 |
| 17191 | guiándolos | 1 |
| 17192 | guiándole | 1 |
| 17193 | guían | 1 |
| 17194 | guiadas | 1 |
| 17195 | guiada | 1 |
| 17196 | guiábanle | 1 |
| 17197 | guiaban | 1 |
| 17198 | guiábalas | 1 |
| 17199 | güevo | 1 |
| 17200 | guevara | 1 |
| 17201 | güéspedes | 1 |
| 17202 | güéspeda | 1 |
| 17203 | güesos | 1 |
| 17204 | güero | 1 |
| 17205 | guedejas | 1 |
| 17206 | guedeja | 1 |
| 17207 | guay | 1 |
| 17208 | guarnición | 1 |
| 17209 | guarnecidos | 1 |
| 17210 | guarnecido | 1 |
| 17211 | guarnecidas | 1 |
| 17212 | guarnecida | 1 |
| 17213 | guarismo | 1 |
| 17214 | guarino | 1 |
| 17215 | guardo | 1 |
| 17216 | guardianes | 1 |
| 17217 | guárdense | 1 |
| 17218 | guardé | 1 |
| 17219 | guárdate | 1 |
| 17220 | guardarropas | 1 |
| 17221 | guardarnos | 1 |
| 17222 | guardarlo | 1 |
| 17223 | guardándose | 1 |
| 17224 | guardamos | 1 |
| 17225 | guardalle | 1 |
| 17226 | guardalla | 1 |
| 17227 | guárdale | 1 |
| 17228 | guardáis | 1 |
| 17229 | guardad | 1 |
| 17230 | guardábase | 1 |
| 17231 | guardaamigo | 1 |
| 17232 | guantero | 1 |
| 17233 | gualá | 1 |
| 17234 | guadarrama | 1 |
| 17235 | guadaña | 1 |
| 17236 | guadameciles | 1 |
| 17237 | gruñidora | 1 |
| 17238 | gruñía | 1 |
| 17239 | gruñen | 1 |
| 17240 | grumete | 1 |
| 17241 | grullas | 1 |
| 17242 | gruesos | 1 |
| 17243 | groseras | 1 |
| 17244 | gritó | 1 |
| 17245 | grijalba | 1 |
| 17246 | griegas | 1 |
| 17247 | grial | 1 |
| 17248 | grebas | 1 |
| 17249 | graznar | 1 |
| 17250 | gravísimas | 1 |
| 17251 | gravísima | 1 |
| 17252 | gratis | 1 |
| 17253 | gratificallas | 1 |
| 17254 | gratificado | 1 |
| 17255 | grasiento | 1 |
| 17256 | granjeen | 1 |
| 17257 | granjee | 1 |
| 17258 | granjeadas | 1 |
| 17259 | granjea | 1 |
| 17260 | grandísimas | 1 |
| 17261 | grandiosidad | 1 |
| 17262 | grandiosas | 1 |
| 17263 | grandílocua | 1 |
| 17264 | grandemente | 1 |
| 17265 | grana | 1 |
| 17266 | gramático | 1 |
| 17267 | grama | 1 |
| 17268 | graduarse | 1 |
| 17269 | graduaron | 1 |
| 17270 | graciosísimos | 1 |
| 17271 | graciosísimo | 1 |
| 17272 | graciosico | 1 |
| 17273 | grace | 1 |
| 17274 | grabó | 1 |
| 17275 | grabe | 1 |
| 17276 | grabarla | 1 |
| 17277 | grabaremos | 1 |
| 17278 | grabar | 1 |
| 17279 | grabando | 1 |
| 17280 | grabado | 1 |
| 17281 | gozques | 1 |
| 17282 | gozosos | 1 |
| 17283 | gozaron | 1 |
| 17284 | gozarás | 1 |
| 17285 | gozamos | 1 |
| 17286 | gozado | 1 |
| 17287 | gozaba | 1 |
| 17288 | goza | 1 |
| 17289 | gorjear | 1 |
| 17290 | gordos | 1 |
| 17291 | gonela | 1 |
| 17292 | gomia | 1 |
| 17293 | golosazo | 1 |
| 17294 | golondrina | 1 |
| 17295 | goliat | 1 |
| 17296 | godos | 1 |
| 17297 | godofre | 1 |
| 17298 | goda | 1 |
| 17299 | goces | 1 |
| 17300 | gobiernito | 1 |
| 17301 | goberné | 1 |
| 17302 | gobernases | 1 |
| 17303 | gobernase | 1 |
| 17304 | gobernarse | 1 |
| 17305 | gobernarlos | 1 |
| 17306 | gobernarle | 1 |
| 17307 | gobernarla | 1 |
| 17308 | gobernares | 1 |
| 17309 | gobernare | 1 |
| 17310 | gobernarás | 1 |
| 17311 | gobernando | 1 |
| 17312 | gobernamos | 1 |
| 17313 | gobernadoresco | 1 |
| 17314 | glosas | 1 |
| 17315 | glosar | 1 |
| 17316 | glosan | 1 |
| 17317 | glosados | 1 |
| 17318 | glosaba | 1 |
| 17319 | gloriosa | 1 |
| 17320 | globo | 1 |
| 17321 | giù | 1 |
| 17322 | ginoveses | 1 |
| 17323 | ginovesa | 1 |
| 17324 | ginosofistas | 1 |
| 17325 | ginasios | 1 |
| 17326 | gimió | 1 |
| 17327 | gimiendo | 1 |
| 17328 | gilecuelco | 1 |
| 17329 | gigote | 1 |
| 17330 | gigantillo | 1 |
| 17331 | giganteos | 1 |
| 17332 | gigantea | 1 |
| 17333 | gibraltar | 1 |
| 17334 | gibraleón | 1 |
| 17335 | gerifalte | 1 |
| 17336 | geraya | 1 |
| 17337 | geométricas | 1 |
| 17338 | geometría | 1 |
| 17339 | gentileshombres | 1 |
| 17340 | genil | 1 |
| 17341 | generosas | 1 |
| 17342 | generalmente | 1 |
| 17343 | gemir | 1 |
| 17344 | gemidicos | 1 |
| 17345 | gemía | 1 |
| 17346 | gazpachos | 1 |
| 17347 | gaznatico | 1 |
| 17348 | gayos | 1 |
| 17349 | gayado | 1 |
| 17350 | gayadas | 1 |
| 17351 | gaudia | 1 |
| 17352 | gaudeamus | 1 |
| 17353 | gatuno | 1 |
| 17354 | gatescas | 1 |
| 17355 | gatesca | 1 |
| 17356 | gatéenme | 1 |
| 17357 | gateamiento | 1 |
| 17358 | gateado | 1 |
| 17359 | gastos | 1 |
| 17360 | gastes | 1 |
| 17361 | gaste | 1 |
| 17362 | gastase | 1 |
| 17363 | gastarías | 1 |
| 17364 | gastara | 1 |
| 17365 | gastan | 1 |
| 17366 | gastalla | 1 |
| 17367 | gastadores | 1 |
| 17368 | gastadora | 1 |
| 17369 | gastaban | 1 |
| 17370 | gastaba | 1 |
| 17371 | gascones | 1 |
| 17372 | gascón | 1 |
| 17373 | gasajos | 1 |
| 17374 | gasaje | 1 |
| 17375 | gasabal | 1 |
| 17376 | garzones | 1 |
| 17377 | garza | 1 |
| 17378 | garrucha | 1 |
| 17379 | garrotazo | 1 |
| 17380 | garrida | 1 |
| 17381 | garrancho | 1 |
| 17382 | garra | 1 |
| 17383 | garnachas | 1 |
| 17384 | garitos | 1 |
| 17385 | gargantas | 1 |
| 17386 | garci | 1 |
| 17387 | garbeare | 1 |
| 17388 | garbanzo | 1 |
| 17389 | garamantas | 1 |
| 17390 | garamanta | 1 |
| 17391 | garabato | 1 |
| 17392 | gañir | 1 |
| 17393 | gañán | 1 |
| 17394 | gante | 1 |
| 17395 | ganso | 1 |
| 17396 | gancho | 1 |
| 17397 | ganare | 1 |
| 17398 | ganándola | 1 |
| 17399 | ganancioso | 1 |
| 17400 | ganada | 1 |
| 17401 | ganaban | 1 |
| 17402 | gamella | 1 |
| 17403 | gallipavos | 1 |
| 17404 | gallarín | 1 |
| 17405 | gallardetes | 1 |
| 17406 | gallardeó | 1 |
| 17407 | gálico | 1 |
| 17408 | galicianas | 1 |
| 17409 | galiana | 1 |
| 17410 | galerías | 1 |
| 17411 | galardón | 1 |
| 17412 | galápago | 1 |
| 17413 | galaores | 1 |
| 17414 | galante | 1 |
| 17415 | galanos | 1 |
| 17416 | gaitas | 1 |
| 17417 | gafo | 1 |
| 17418 | gachas | 1 |
| 17419 | gabrio | 1 |
| 17420 | fuyan | 1 |
| 17421 | fuyáis | 1 |
| 17422 | fuyades | 1 |
| 17423 | futuros | 1 |
| 17424 | futuro | 1 |
| 17425 | futuras | 1 |
| 17426 | fustán | 1 |
| 17427 | furor | 1 |
| 17428 | furio | 1 |
| 17429 | furibundo | 1 |
| 17430 | funesto | 1 |
| 17431 | funesta | 1 |
| 17432 | fundir | 1 |
| 17433 | fundar | 1 |
| 17434 | fundan | 1 |
| 17435 | fundamento | 1 |
| 17436 | fundadores | 1 |
| 17437 | fundadas | 1 |
| 17438 | fundada | 1 |
| 17439 | fullero | 1 |
| 17440 | fulana | 1 |
| 17441 | fuit | 1 |
| 17442 | fuiste | 1 |
| 17443 | fuime | 1 |
| 17444 | fugite | 1 |
| 17445 | fuésele | 1 |
| 17446 | fuesa | 1 |
| 17447 | fuerzan | 1 |
| 17448 | fuérzame | 1 |
| 17449 | fuéronselo | 1 |
| 17450 | fuéronle | 1 |
| 17451 | fuerint | 1 |
| 17452 | fuerce | 1 |
| 17453 | fuérale | 1 |
| 17454 | fuenos | 1 |
| 17455 | fueles | 1 |
| 17456 | fúcar | 1 |
| 17457 | fruncida | 1 |
| 17458 | fru | 1 |
| 17459 | frondosos | 1 |
| 17460 | fritón | 1 |
| 17461 | fritas | 1 |
| 17462 | frisón | 1 |
| 17463 | frisada | 1 |
| 17464 | frisaba | 1 |
| 17465 | fríos | 1 |
| 17466 | frión | 1 |
| 17467 | frías | 1 |
| 17468 | frialdad | 1 |
| 17469 | fresquísima | 1 |
| 17470 | fresno | 1 |
| 17471 | frescura | 1 |
| 17472 | frescos | 1 |
| 17473 | frescor | 1 |
| 17474 | frenos | 1 |
| 17475 | frenillados | 1 |
| 17476 | frenético | 1 |
| 17477 | fregona | 1 |
| 17478 | fregar | 1 |
| 17479 | frecuencia | 1 |
| 17480 | frazada | 1 |
| 17481 | fraudes | 1 |
| 17482 | fratín | 1 |
| 17483 | fraternal | 1 |
| 17484 | frasis | 1 |
| 17485 | frasco | 1 |
| 17486 | franjas | 1 |
| 17487 | francolines | 1 |
| 17488 | franchote | 1 |
| 17489 | francesas | 1 |
| 17490 | francesa | 1 |
| 17491 | francenia | 1 |
| 17492 | franca | 1 |
| 17493 | frailecitos | 1 |
| 17494 | frailecito | 1 |
| 17495 | frailecicos | 1 |
| 17496 | fragrancia | 1 |
| 17497 | fragatas | 1 |
| 17498 | fragata | 1 |
| 17499 | fragante | 1 |
| 17500 | fragancia | 1 |
| 17501 | frade | 1 |
| 17502 | fracaso | 1 |
| 17503 | fracasar | 1 |
| 17504 | forzudo | 1 |
| 17505 | forzosas | 1 |
| 17506 | forzosa | 1 |
| 17507 | forzasen | 1 |
| 17508 | forzaron | 1 |
| 17509 | forzarles | 1 |
| 17510 | forzarle | 1 |
| 17511 | forzándose | 1 |
| 17512 | forzando | 1 |
| 17513 | forzábame | 1 |
| 17514 | fortunas | 1 |
| 17515 | fortísimo | 1 |
| 17516 | fortísimamente | 1 |
| 17517 | fortificó | 1 |
| 17518 | fortificase | 1 |
| 17519 | fortifican | 1 |
| 17520 | fortificación | 1 |
| 17521 | fortificaba | 1 |
| 17522 | fortifica | 1 |
| 17523 | forte | 1 |
| 17524 | fortalezas | 1 |
| 17525 | fortalecerá | 1 |
| 17526 | fortalecer | 1 |
| 17527 | fortalecen | 1 |
| 17528 | fortalece | 1 |
| 17529 | forsi | 1 |
| 17530 | formarse | 1 |
| 17531 | formaría | 1 |
| 17532 | formando | 1 |
| 17533 | forman | 1 |
| 17534 | formalmente | 1 |
| 17535 | formales | 1 |
| 17536 | formados | 1 |
| 17537 | formadas | 1 |
| 17538 | formaba | 1 |
| 17539 | forjaron | 1 |
| 17540 | forjar | 1 |
| 17541 | foribundo | 1 |
| 17542 | forera | 1 |
| 17543 | forcejaba | 1 |
| 17544 | forcé | 1 |
| 17545 | forasteros | 1 |
| 17546 | forasteras | 1 |
| 17547 | forajidos | 1 |
| 17548 | fontecilla | 1 |
| 17549 | fontana | 1 |
| 17550 | folloncicos | 1 |
| 17551 | foces | 1 |
| 17552 | flota | 1 |
| 17553 | floripes | 1 |
| 17554 | florido | 1 |
| 17555 | florida | 1 |
| 17556 | florentibus | 1 |
| 17557 | floreció | 1 |
| 17558 | florecillas | 1 |
| 17559 | floreciente | 1 |
| 17560 | flora | 1 |
| 17561 | flojamente | 1 |
| 17562 | floja | 1 |
| 17563 | flexible | 1 |
| 17564 | fléridas | 1 |
| 17565 | flemático | 1 |
| 17566 | flechaba | 1 |
| 17567 | flauta | 1 |
| 17568 | flaque | 1 |
| 17569 | flámulas | 1 |
| 17570 | flamencos | 1 |
| 17571 | flamenco | 1 |
| 17572 | flamencas | 1 |
| 17573 | flamantes | 1 |
| 17574 | fizo | 1 |
| 17575 | físicos | 1 |
| 17576 | fisga | 1 |
| 17577 | fiscal | 1 |
| 17578 | firmó | 1 |
| 17579 | firmezas | 1 |
| 17580 | firmemente | 1 |
| 17581 | firmarla | 1 |
| 17582 | firman | 1 |
| 17583 | firmados | 1 |
| 17584 | fióle | 1 |
| 17585 | finta | 1 |
| 17586 | finojos | 1 |
| 17587 | fínisimo | 1 |
| 17588 | finísimas | 1 |
| 17589 | finis | 1 |
| 17590 | fingiré | 1 |
| 17591 | fingimientos | 1 |
| 17592 | fingimiento | 1 |
| 17593 | fingían | 1 |
| 17594 | fingí | 1 |
| 17595 | finges | 1 |
| 17596 | finezas | 1 |
| 17597 | finas | 1 |
| 17598 | fina | 1 |
| 17599 | filó | 1 |
| 17600 | filisteo | 1 |
| 17601 | filisteazo | 1 |
| 17602 | filipo | 1 |
| 17603 | fílidas | 1 |
| 17604 | fílida | 1 |
| 17605 | fil | 1 |
| 17606 | fijó | 1 |
| 17607 | fijo | 1 |
| 17608 | fija | 1 |
| 17609 | figuró | 1 |
| 17610 | figuro | 1 |
| 17611 | figurillas | 1 |
| 17612 | figureros | 1 |
| 17613 | figuraba | 1 |
| 17614 | figueroa | 1 |
| 17615 | figu | 1 |
| 17616 | fíese | 1 |
| 17617 | fíes | 1 |
| 17618 | fierro | 1 |
| 17619 | fiereza | 1 |
| 17620 | fieltro | 1 |
| 17621 | fïel | 1 |
| 17622 | fiéis | 1 |
| 17623 | fido | 1 |
| 17624 | fidelísima | 1 |
| 17625 | fidedigno | 1 |
| 17626 | ficticio | 1 |
| 17627 | ficiesen | 1 |
| 17628 | fiásemos | 1 |
| 17629 | fías | 1 |
| 17630 | fianzas | 1 |
| 17631 | fianza | 1 |
| 17632 | fiambreras | 1 |
| 17633 | fiambrera | 1 |
| 17634 | fiadores | 1 |
| 17635 | fiador | 1 |
| 17636 | fiado | 1 |
| 17637 | fiaba | 1 |
| 17638 | fez | 1 |
| 17639 | festejalle | 1 |
| 17640 | ferviente | 1 |
| 17641 | fertiliza | 1 |
| 17642 | fertilidad | 1 |
| 17643 | ferreruelo | 1 |
| 17644 | ferrara | 1 |
| 17645 | ferradas | 1 |
| 17646 | feroz | 1 |
| 17647 | ferocidad | 1 |
| 17648 | feroces | 1 |
| 17649 | fernán | 1 |
| 17650 | fermosuras | 1 |
| 17651 | ferir | 1 |
| 17652 | feriar | 1 |
| 17653 | feria | 1 |
| 17654 | fenestras | 1 |
| 17655 | feneció | 1 |
| 17656 | fendientes | 1 |
| 17657 | fenderían | 1 |
| 17658 | fementida | 1 |
| 17659 | felizmente | 1 |
| 17660 | feliz | 1 |
| 17661 | felix | 1 |
| 17662 | felipe | 1 |
| 17663 | feligreses | 1 |
| 17664 | feliciano | 1 |
| 17665 | felicia | 1 |
| 17666 | fees | 1 |
| 17667 | fecundas | 1 |
| 17668 | fecistes | 1 |
| 17669 | fechuría | 1 |
| 17670 | fechas | 1 |
| 17671 | febos | 1 |
| 17672 | fazaña | 1 |
| 17673 | favoridos | 1 |
| 17674 | favorézcate | 1 |
| 17675 | favorezcas | 1 |
| 17676 | favorezcan | 1 |
| 17677 | favoreció | 1 |
| 17678 | favoreciesen | 1 |
| 17679 | favoreciéndome | 1 |
| 17680 | favoreciendo | 1 |
| 17681 | favorecidos | 1 |
| 17682 | favorecían | 1 |
| 17683 | favoreces | 1 |
| 17684 | favorecerse | 1 |
| 17685 | favorecernos | 1 |
| 17686 | favorecen | 1 |
| 17687 | favila | 1 |
| 17688 | faunos | 1 |
| 17689 | fatigues | 1 |
| 17690 | fatigóse | 1 |
| 17691 | fatigó | 1 |
| 17692 | fatigo | 1 |
| 17693 | fatigaron | 1 |
| 17694 | fatigarnos | 1 |
| 17695 | fatigalles | 1 |
| 17696 | fatigados | 1 |
| 17697 | fatigábase | 1 |
| 17698 | fatal | 1 |
| 17699 | fastidio | 1 |
| 17700 | fartax | 1 |
| 17701 | farseto | 1 |
| 17702 | farsante | 1 |
| 17703 | fardo | 1 |
| 17704 | faraones | 1 |
| 17705 | farándula | 1 |
| 17706 | fará | 1 |
| 17707 | faquín | 1 |
| 17708 | fantásticos | 1 |
| 17709 | fantásticas | 1 |
| 17710 | fantasiosa | 1 |
| 17711 | fantasías | 1 |
| 17712 | fanfarrón | 1 |
| 17713 | fando | 1 |
| 17714 | fanales | 1 |
| 17715 | famosísimos | 1 |
| 17716 | famo | 1 |
| 17717 | familias | 1 |
| 17718 | faltriquera | 1 |
| 17719 | faltóles | 1 |
| 17720 | faltarte | 1 |
| 17721 | faltaría | 1 |
| 17722 | faltaren | 1 |
| 17723 | falsías | 1 |
| 17724 | falsedades | 1 |
| 17725 | falsarios | 1 |
| 17726 | fallar | 1 |
| 17727 | faldellines | 1 |
| 17728 | falces | 1 |
| 17729 | fajaban | 1 |
| 17730 | faisanes | 1 |
| 17731 | fadas | 1 |
| 17732 | facinorosa | 1 |
| 17733 | facilitó | 1 |
| 17734 | facilitarlo | 1 |
| 17735 | facilitaría | 1 |
| 17736 | facilitaran | 1 |
| 17737 | facilitando | 1 |
| 17738 | facilitado | 1 |
| 17739 | facilísima | 1 |
| 17740 | faceto | 1 |
| 17741 | faceros | 1 |
| 17742 | facerle | 1 |
| 17743 | facer | 1 |
| 17744 | face | 1 |
| 17745 | facciones | 1 |
| 17746 | facas | 1 |
| 17747 | fabulosas | 1 |
| 17748 | fabricase | 1 |
| 17749 | fabricarla | 1 |
| 17750 | fabricados | 1 |
| 17751 | fabricaba | 1 |
| 17752 | fábrica | 1 |
| 17753 | fabló | 1 |
| 17754 | fablar | 1 |
| 17755 | fablado | 1 |
| 17756 | fa | 1 |
| 17757 | extravagantes | 1 |
| 17758 | extraordinariamente | 1 |
| 17759 | extrañas | 1 |
| 17760 | extirpar | 1 |
| 17761 | exteriores | 1 |
| 17762 | exprimieron | 1 |
| 17763 | expreso | 1 |
| 17764 | expresas | 1 |
| 17765 | expresadas | 1 |
| 17766 | expresa | 1 |
| 17767 | experimento | 1 |
| 17768 | experimentado | 1 |
| 17769 | exorbitancia | 1 |
| 17770 | exhalaciones | 1 |
| 17771 | exeunt | 1 |
| 17772 | exclamó | 1 |
| 17773 | exclamación | 1 |
| 17774 | exclama | 1 |
| 17775 | exceto | 1 |
| 17776 | excetado | 1 |
| 17777 | excelentísimo | 1 |
| 17778 | excediese | 1 |
| 17779 | exceder | 1 |
| 17780 | exceda | 1 |
| 17781 | examinar | 1 |
| 17782 | examinador | 1 |
| 17783 | examinádole | 1 |
| 17784 | examinado | 1 |
| 17785 | examinadas | 1 |
| 17786 | exagerar | 1 |
| 17787 | exagerado | 1 |
| 17788 | exageraba | 1 |
| 17789 | evidentes | 1 |
| 17790 | evidentemente | 1 |
| 17791 | evidencia | 1 |
| 17792 | evangelios | 1 |
| 17793 | evangelio | 1 |
| 17794 | eva | 1 |
| 17795 | euríalo | 1 |
| 17796 | eurialio | 1 |
| 17797 | etiopes | 1 |
| 17798 | eternizarlos | 1 |
| 17799 | eternizar | 1 |
| 17800 | eternice | 1 |
| 17801 | eternas | 1 |
| 17802 | etéreas | 1 |
| 17803 | estuviésemos | 1 |
| 17804 | estuviésedes | 1 |
| 17805 | estuvieres | 1 |
| 17806 | estuvieren | 1 |
| 17807 | estuvieran | 1 |
| 17808 | estupendo | 1 |
| 17809 | estudien | 1 |
| 17810 | estudie | 1 |
| 17811 | estudiaré | 1 |
| 17812 | estudiara | 1 |
| 17813 | estudiantil | 1 |
| 17814 | estudiantado | 1 |
| 17815 | estudiando | 1 |
| 17816 | estudiadas | 1 |
| 17817 | estudiada | 1 |
| 17818 | estropeando | 1 |
| 17819 | estropeada | 1 |
| 17820 | estropajos | 1 |
| 17821 | estripaterrones | 1 |
| 17822 | estribando | 1 |
| 17823 | estrépito | 1 |
| 17824 | estrenado | 1 |
| 17825 | estremeció | 1 |
| 17826 | estremecido | 1 |
| 17827 | estremarme | 1 |
| 17828 | estremadamente | 1 |
| 17829 | estrellarte | 1 |
| 17830 | estrellaré | 1 |
| 17831 | estrego | 1 |
| 17832 | estrechísimamente | 1 |
| 17833 | estrechísima | 1 |
| 17834 | estrechar | 1 |
| 17835 | estre | 1 |
| 17836 | estraordinarios | 1 |
| 17837 | estraordinariamente | 1 |
| 17838 | estranjeras | 1 |
| 17839 | estrambotes | 1 |
| 17840 | estrago | 1 |
| 17841 | estoyte | 1 |
| 17842 | estoyle | 1 |
| 17843 | estotra | 1 |
| 17844 | estornudo | 1 |
| 17845 | estornudar | 1 |
| 17846 | estorbóselo | 1 |
| 17847 | estorbos | 1 |
| 17848 | estorben | 1 |
| 17849 | estorbasen | 1 |
| 17850 | estorbársela | 1 |
| 17851 | estorbáronlo | 1 |
| 17852 | estorbarme | 1 |
| 17853 | estorbarle | 1 |
| 17854 | estorbaren | 1 |
| 17855 | estorban | 1 |
| 17856 | estorbado | 1 |
| 17857 | estorbábanselo | 1 |
| 17858 | estorbaba | 1 |
| 17859 | estobarlo | 1 |
| 17860 | estiren | 1 |
| 17861 | estirar | 1 |
| 17862 | estirándose | 1 |
| 17863 | estirados | 1 |
| 17864 | estiradas | 1 |
| 17865 | estirábase | 1 |
| 17866 | estimen | 1 |
| 17867 | estime | 1 |
| 17868 | estimase | 1 |
| 17869 | estimarse | 1 |
| 17870 | estimaron | 1 |
| 17871 | estimarme | 1 |
| 17872 | estimaran | 1 |
| 17873 | estimándole | 1 |
| 17874 | estímalos | 1 |
| 17875 | estimáis | 1 |
| 17876 | estimados | 1 |
| 17877 | estigio | 1 |
| 17878 | estiendes | 1 |
| 17879 | estiendan | 1 |
| 17880 | estevado | 1 |
| 17881 | esterilidad | 1 |
| 17882 | estercolándolas | 1 |
| 17883 | estendiese | 1 |
| 17884 | estendiéndose | 1 |
| 17885 | estendidos | 1 |
| 17886 | estendidas | 1 |
| 17887 | estendida | 1 |
| 17888 | estendería | 1 |
| 17889 | estenderá | 1 |
| 17890 | estéme | 1 |
| 17891 | estatutos | 1 |
| 17892 | estaturas | 1 |
| 17893 | estatura | 1 |
| 17894 | estatuido | 1 |
| 17895 | estatuas | 1 |
| 17896 | estarme | 1 |
| 17897 | estarle | 1 |
| 17898 | estaréis | 1 |
| 17899 | estante | 1 |
| 17900 | estándose | 1 |
| 17901 | estándome | 1 |
| 17902 | estándole | 1 |
| 17903 | estanco | 1 |
| 17904 | estampes | 1 |
| 17905 | estampero | 1 |
| 17906 | estampado | 1 |
| 17907 | estampadas | 1 |
| 17908 | estampada | 1 |
| 17909 | estámosle | 1 |
| 17910 | estambre | 1 |
| 17911 | estad | 1 |
| 17912 | estacazos | 1 |
| 17913 | establecida | 1 |
| 17914 | estable | 1 |
| 17915 | estábaselo | 1 |
| 17916 | estábanle | 1 |
| 17917 | esquivo | 1 |
| 17918 | esquiveza | 1 |
| 17919 | esquivas | 1 |
| 17920 | esquivarse | 1 |
| 17921 | esquivan | 1 |
| 17922 | esquisitos | 1 |
| 17923 | esquinen | 1 |
| 17924 | esquinas | 1 |
| 17925 | esquinado | 1 |
| 17926 | esquina | 1 |
| 17927 | esquilón | 1 |
| 17928 | esqueros | 1 |
| 17929 | espumas | 1 |
| 17930 | espumad | 1 |
| 17931 | espulgar | 1 |
| 17932 | espreso | 1 |
| 17933 | espresa | 1 |
| 17934 | esponja | 1 |
| 17935 | espolón | 1 |
| 17936 | espléndido | 1 |
| 17937 | espléndidamente | 1 |
| 17938 | espléndida | 1 |
| 17939 | esplandianes | 1 |
| 17940 | espirado | 1 |
| 17941 | espina | 1 |
| 17942 | espilorchería | 1 |
| 17943 | espigas | 1 |
| 17944 | espiaba | 1 |
| 17945 | espía | 1 |
| 17946 | espetera | 1 |
| 17947 | espetado | 1 |
| 17948 | espetáculo | 1 |
| 17949 | espesuras | 1 |
| 17950 | espesos | 1 |
| 17951 | esperezóse | 1 |
| 17952 | esperen | 1 |
| 17953 | esperemos | 1 |
| 17954 | espéreme | 1 |
| 17955 | esperé | 1 |
| 17956 | esperásemos | 1 |
| 17957 | esperaros | 1 |
| 17958 | esperaron | 1 |
| 17959 | esperarle | 1 |
| 17960 | esperaremos | 1 |
| 17961 | esperaos | 1 |
| 17962 | esperante | 1 |
| 17963 | esperándote | 1 |
| 17964 | esperándola | 1 |
| 17965 | esperadas | 1 |
| 17966 | esperada | 1 |
| 17967 | esperábamos | 1 |
| 17968 | espediente | 1 |
| 17969 | especule | 1 |
| 17970 | espectáculo | 1 |
| 17971 | especies | 1 |
| 17972 | especie | 1 |
| 17973 | especias | 1 |
| 17974 | espartafilardo | 1 |
| 17975 | esparraguera | 1 |
| 17976 | esparcirán | 1 |
| 17977 | esparcir | 1 |
| 17978 | esparció | 1 |
| 17979 | esparcidas | 1 |
| 17980 | españolas | 1 |
| 17981 | espantáronse | 1 |
| 17982 | espantaron | 1 |
| 17983 | espantaría | 1 |
| 17984 | espantaran | 1 |
| 17985 | espantan | 1 |
| 17986 | espantadizo | 1 |
| 17987 | espantadiza | 1 |
| 17988 | espantables | 1 |
| 17989 | espantaba | 1 |
| 17990 | espalder | 1 |
| 17991 | espaldazaro | 1 |
| 17992 | espaldarazo | 1 |
| 17993 | espalda | 1 |
| 17994 | espadachín | 1 |
| 17995 | espaciosísimo | 1 |
| 17996 | espaciosidad | 1 |
| 17997 | espaciarse | 1 |
| 17998 | espaciar | 1 |
| 17999 | espa | 1 |
| 18000 | esotros | 1 |
| 18001 | esotras | 1 |
| 18002 | esotra | 1 |
| 18003 | esorbitante | 1 |
| 18004 | esme | 1 |
| 18005 | eslabonando | 1 |
| 18006 | eslabonado | 1 |
| 18007 | esgrimirla | 1 |
| 18008 | esgremir | 1 |
| 18009 | esforzó | 1 |
| 18010 | esforzaré | 1 |
| 18011 | esforzar | 1 |
| 18012 | esforzándose | 1 |
| 18013 | esforzada | 1 |
| 18014 | esfogue | 1 |
| 18015 | esferas | 1 |
| 18016 | esentos | 1 |
| 18017 | esentas | 1 |
| 18018 | esenta | 1 |
| 18019 | esenciones | 1 |
| 18020 | esencias | 1 |
| 18021 | esenciales | 1 |
| 18022 | escuses | 1 |
| 18023 | escuse | 1 |
| 18024 | escusas | 1 |
| 18025 | escusarla | 1 |
| 18026 | escusarían | 1 |
| 18027 | escusaré | 1 |
| 18028 | escusare | 1 |
| 18029 | escusaran | 1 |
| 18030 | escusará | 1 |
| 18031 | escusados | 1 |
| 18032 | escusadas | 1 |
| 18033 | escurriésedes | 1 |
| 18034 | escurriendo | 1 |
| 18035 | escurísima | 1 |
| 18036 | escurezcan | 1 |
| 18037 | escureciesen | 1 |
| 18038 | escurecieron | 1 |
| 18039 | escurecida | 1 |
| 18040 | escurecía | 1 |
| 18041 | escurecerla | 1 |
| 18042 | escupir | 1 |
| 18043 | escupió | 1 |
| 18044 | escupía | 1 |
| 18045 | escupe | 1 |
| 18046 | esculpirse | 1 |
| 18047 | esculpido | 1 |
| 18048 | escuezan | 1 |
| 18049 | escueto | 1 |
| 18050 | escudriño | 1 |
| 18051 | escudriñase | 1 |
| 18052 | escudriñáronse | 1 |
| 18053 | escudriñando | 1 |
| 18054 | escudriñan | 1 |
| 18055 | escudó | 1 |
| 18056 | escudillar | 1 |
| 18057 | escudilla | 1 |
| 18058 | escuderísimo | 1 |
| 18059 | escuderilmente | 1 |
| 18060 | escuderías | 1 |
| 18061 | escudera | 1 |
| 18062 | escude | 1 |
| 18063 | escudar | 1 |
| 18064 | escuchóla | 1 |
| 18065 | escuchémosle | 1 |
| 18066 | escuchemos | 1 |
| 18067 | escuchéle | 1 |
| 18068 | escuchéis | 1 |
| 18069 | escuchastes | 1 |
| 18070 | escuchasen | 1 |
| 18071 | escuchase | 1 |
| 18072 | escucharon | 1 |
| 18073 | escucharlo | 1 |
| 18074 | escucharle | 1 |
| 18075 | escucharían | 1 |
| 18076 | escucharemos | 1 |
| 18077 | escuchara | 1 |
| 18078 | escuchantes | 1 |
| 18079 | escúchame | 1 |
| 18080 | escuchalle | 1 |
| 18081 | escuchábamos | 1 |
| 18082 | escu | 1 |
| 18083 | escrutiñador | 1 |
| 18084 | escrupulosa | 1 |
| 18085 | escritorios | 1 |
| 18086 | escribo | 1 |
| 18087 | escribístesla | 1 |
| 18088 | escribistes | 1 |
| 18089 | escribirlos | 1 |
| 18090 | escribirlo | 1 |
| 18091 | escribirlas | 1 |
| 18092 | escribiría | 1 |
| 18093 | escribióme | 1 |
| 18094 | escribillos | 1 |
| 18095 | escribille | 1 |
| 18096 | escribilla | 1 |
| 18097 | escribiésemos | 1 |
| 18098 | escribieren | 1 |
| 18099 | escribiera | 1 |
| 18100 | escribiéndose | 1 |
| 18101 | escribían | 1 |
| 18102 | escríbame | 1 |
| 18103 | escríbala | 1 |
| 18104 | escrementos | 1 |
| 18105 | escremento | 1 |
| 18106 | escrebirse | 1 |
| 18107 | escotillo | 1 |
| 18108 | escoplos | 1 |
| 18109 | escopeteros | 1 |
| 18110 | escondrijos | 1 |
| 18111 | escondió | 1 |
| 18112 | escondimiento | 1 |
| 18113 | escondiesen | 1 |
| 18114 | escondieron | 1 |
| 18115 | esconderme | 1 |
| 18116 | esconderla | 1 |
| 18117 | esconder | 1 |
| 18118 | escondáis | 1 |
| 18119 | escolares | 1 |
| 18120 | escolar | 1 |
| 18121 | escojan | 1 |
| 18122 | escogiendo | 1 |
| 18123 | escogella | 1 |
| 18124 | esclavas | 1 |
| 18125 | escasos | 1 |
| 18126 | escaseza | 1 |
| 18127 | escarolados | 1 |
| 18128 | escarnidos | 1 |
| 18129 | escarnida | 1 |
| 18130 | escarnecido | 1 |
| 18131 | escarnecen | 1 |
| 18132 | escarmentó | 1 |
| 18133 | escarmentará | 1 |
| 18134 | escarmentar | 1 |
| 18135 | escarmentando | 1 |
| 18136 | escarmentados | 1 |
| 18137 | escarmenase | 1 |
| 18138 | escarde | 1 |
| 18139 | escardaré | 1 |
| 18140 | escardara | 1 |
| 18141 | escarba | 1 |
| 18142 | escaparte | 1 |
| 18143 | escaparnos | 1 |
| 18144 | escaparme | 1 |
| 18145 | escaparía | 1 |
| 18146 | escapara | 1 |
| 18147 | escapar | 1 |
| 18148 | escapan | 1 |
| 18149 | escapaba | 1 |
| 18150 | escaño | 1 |
| 18151 | escandalizase | 1 |
| 18152 | escancie | 1 |
| 18153 | escanciando | 1 |
| 18154 | escanciadora | 1 |
| 18155 | escamosas | 1 |
| 18156 | escamosa | 1 |
| 18157 | escamonde | 1 |
| 18158 | escalones | 1 |
| 18159 | escalón | 1 |
| 18160 | escalas | 1 |
| 18161 | escala | 1 |
| 18162 | escabroso | 1 |
| 18163 | esaminadores | 1 |
| 18164 | erutaciones | 1 |
| 18165 | eruditos | 1 |
| 18166 | errores | 1 |
| 18167 | errarte | 1 |
| 18168 | errarse | 1 |
| 18169 | erraría | 1 |
| 18170 | erraren | 1 |
| 18171 | errare | 1 |
| 18172 | errando | 1 |
| 18173 | errados | 1 |
| 18174 | eróstrato | 1 |
| 18175 | ermitaños | 1 |
| 18176 | erizarse | 1 |
| 18177 | erizaron | 1 |
| 18178 | erizados | 1 |
| 18179 | erguido | 1 |
| 18180 | erguían | 1 |
| 18181 | ercilla | 1 |
| 18182 | érase | 1 |
| 18183 | erario | 1 |
| 18184 | equivalentes | 1 |
| 18185 | equis | 1 |
| 18186 | equinocios | 1 |
| 18187 | epístola | 1 |
| 18188 | epigrama | 1 |
| 18189 | épico | 1 |
| 18190 | épica | 1 |
| 18191 | envolver | 1 |
| 18192 | enviudó | 1 |
| 18193 | enviudares | 1 |
| 18194 | envilecen | 1 |
| 18195 | envilece | 1 |
| 18196 | envidiar | 1 |
| 18197 | envidiados | 1 |
| 18198 | envidiada | 1 |
| 18199 | envidar | 1 |
| 18200 | envidado | 1 |
| 18201 | enviaste | 1 |
| 18202 | enviarte | 1 |
| 18203 | enviaría | 1 |
| 18204 | envíanos | 1 |
| 18205 | enviándole | 1 |
| 18206 | envíame | 1 |
| 18207 | enviallo | 1 |
| 18208 | enviádole | 1 |
| 18209 | enviad | 1 |
| 18210 | enviábades | 1 |
| 18211 | envi | 1 |
| 18212 | envasar | 1 |
| 18213 | envásala | 1 |
| 18214 | envaramiento | 1 |
| 18215 | envainen | 1 |
| 18216 | enturbió | 1 |
| 18217 | enturbiar | 1 |
| 18218 | entristecieron | 1 |
| 18219 | entriégame | 1 |
| 18220 | entricadas | 1 |
| 18221 | entretuvo | 1 |
| 18222 | entretuviésemos | 1 |
| 18223 | entretuvieron | 1 |
| 18224 | entretuve | 1 |
| 18225 | entretenidas | 1 |
| 18226 | entretengo | 1 |
| 18227 | entretengamos | 1 |
| 18228 | entretenga | 1 |
| 18229 | entreteneros | 1 |
| 18230 | entretenerlas | 1 |
| 18231 | entretenerla | 1 |
| 18232 | entretenellos | 1 |
| 18233 | entretenelle | 1 |
| 18234 | entretendré | 1 |
| 18235 | entretejióse | 1 |
| 18236 | entretejidas | 1 |
| 18237 | entresemana | 1 |
| 18238 | éntrese | 1 |
| 18239 | entresaque | 1 |
| 18240 | entreparecía | 1 |
| 18241 | entreoyóle | 1 |
| 18242 | entremetiera | 1 |
| 18243 | entremetidas | 1 |
| 18244 | entremétete | 1 |
| 18245 | entremeterme | 1 |
| 18246 | entremeten | 1 |
| 18247 | entremés | 1 |
| 18248 | entreguéme | 1 |
| 18249 | entregué | 1 |
| 18250 | entregóse | 1 |
| 18251 | entregaste | 1 |
| 18252 | entregas | 1 |
| 18253 | entregarlos | 1 |
| 18254 | entregarle | 1 |
| 18255 | entregarla | 1 |
| 18256 | entregaría | 1 |
| 18257 | entregaran | 1 |
| 18258 | entregará | 1 |
| 18259 | entregándolos | 1 |
| 18260 | entregando | 1 |
| 18261 | entregan | 1 |
| 18262 | entregalle | 1 |
| 18263 | entregadas | 1 |
| 18264 | entregada | 1 |
| 18265 | entredicho | 1 |
| 18266 | entreclara | 1 |
| 18267 | entrecano | 1 |
| 18268 | entraros | 1 |
| 18269 | entrarme | 1 |
| 18270 | entrarle | 1 |
| 18271 | entraría | 1 |
| 18272 | entraréis | 1 |
| 18273 | entrarán | 1 |
| 18274 | entraran | 1 |
| 18275 | entrándose | 1 |
| 18276 | éntrale | 1 |
| 18277 | entráis | 1 |
| 18278 | entrados | 1 |
| 18279 | entorpecen | 1 |
| 18280 | entorpece | 1 |
| 18281 | entonos | 1 |
| 18282 | entonaos | 1 |
| 18283 | entonado | 1 |
| 18284 | entomecen | 1 |
| 18285 | entomece | 1 |
| 18286 | entierre | 1 |
| 18287 | entierran | 1 |
| 18288 | entiéndese | 1 |
| 18289 | entiéndase | 1 |
| 18290 | entiendas | 1 |
| 18291 | entibie | 1 |
| 18292 | entibia | 1 |
| 18293 | enterrarse | 1 |
| 18294 | enterrarme | 1 |
| 18295 | enterrarle | 1 |
| 18296 | enterrándonos | 1 |
| 18297 | enterrados | 1 |
| 18298 | enterradas | 1 |
| 18299 | enternezca | 1 |
| 18300 | enternecióse | 1 |
| 18301 | enterneciera | 1 |
| 18302 | enternecido | 1 |
| 18303 | enternecida | 1 |
| 18304 | enternecerme | 1 |
| 18305 | enternecerle | 1 |
| 18306 | enternece | 1 |
| 18307 | enteras | 1 |
| 18308 | enterarse | 1 |
| 18309 | enteraros | 1 |
| 18310 | enterarme | 1 |
| 18311 | enterándose | 1 |
| 18312 | enteramente | 1 |
| 18313 | enteradas | 1 |
| 18314 | entendimos | 1 |
| 18315 | entendiere | 1 |
| 18316 | entendiérades | 1 |
| 18317 | entenderos | 1 |
| 18318 | entenderlo | 1 |
| 18319 | entenderlas | 1 |
| 18320 | entenderás | 1 |
| 18321 | entenderá | 1 |
| 18322 | entended | 1 |
| 18323 | entendáis | 1 |
| 18324 | entallarse | 1 |
| 18325 | entallad | 1 |
| 18326 | entablarle | 1 |
| 18327 | entabladura | 1 |
| 18328 | entablado | 1 |
| 18329 | ensucio | 1 |
| 18330 | ensordecieron | 1 |
| 18331 | ensille | 1 |
| 18332 | ensillaron | 1 |
| 18333 | ensillada | 1 |
| 18334 | ensillaba | 1 |
| 18335 | enseñéis | 1 |
| 18336 | enseñarte | 1 |
| 18337 | enseñársele | 1 |
| 18338 | enseñaron | 1 |
| 18339 | enseñármele | 1 |
| 18340 | enseñarle | 1 |
| 18341 | enseñaría | 1 |
| 18342 | enseñaré | 1 |
| 18343 | enseñare | 1 |
| 18344 | enseñándosela | 1 |
| 18345 | enseñando | 1 |
| 18346 | enséñala | 1 |
| 18347 | enseñadme | 1 |
| 18348 | enseñábale | 1 |
| 18349 | enseña | 1 |
| 18350 | ense | 1 |
| 18351 | ensayados | 1 |
| 18352 | ensártalos | 1 |
| 18353 | ensartado | 1 |
| 18354 | ensarmentar | 1 |
| 18355 | ensangrentada | 1 |
| 18356 | ensanchar | 1 |
| 18357 | ensalzamiento | 1 |
| 18358 | ensabanados | 1 |
| 18359 | enroscada | 1 |
| 18360 | enristrando | 1 |
| 18361 | enriqueciendo | 1 |
| 18362 | enriquecido | 1 |
| 18363 | enriquecíanse | 1 |
| 18364 | enriquece | 1 |
| 18365 | enrique | 1 |
| 18366 | enrejada | 1 |
| 18367 | enredó | 1 |
| 18368 | enredo | 1 |
| 18369 | enredarse | 1 |
| 18370 | enredarme | 1 |
| 18371 | enredado | 1 |
| 18372 | enramar | 1 |
| 18373 | enojóse | 1 |
| 18374 | enojó | 1 |
| 18375 | enojes | 1 |
| 18376 | enojarse | 1 |
| 18377 | enojaré | 1 |
| 18378 | enojalla | 1 |
| 18379 | enojados | 1 |
| 18380 | enojadas | 1 |
| 18381 | enojada | 1 |
| 18382 | enojaban | 1 |
| 18383 | enoblecer | 1 |
| 18384 | enmudecióse | 1 |
| 18385 | enmudecí | 1 |
| 18386 | enmudece | 1 |
| 18387 | enmiende | 1 |
| 18388 | enmendarse | 1 |
| 18389 | enmendarme | 1 |
| 18390 | enmendarla | 1 |
| 18391 | enmendaren | 1 |
| 18392 | enmendaré | 1 |
| 18393 | enmendando | 1 |
| 18394 | enmendado | 1 |
| 18395 | enmantaban | 1 |
| 18396 | enlutadas | 1 |
| 18397 | enlazados | 1 |
| 18398 | enlazaba | 1 |
| 18399 | enjutos | 1 |
| 18400 | enjutas | 1 |
| 18401 | enjuta | 1 |
| 18402 | enjundia | 1 |
| 18403 | enjugue | 1 |
| 18404 | enjugó | 1 |
| 18405 | enjugase | 1 |
| 18406 | enjugadlas | 1 |
| 18407 | enjuagóse | 1 |
| 18408 | enjaulasen | 1 |
| 18409 | enjaularme | 1 |
| 18410 | enjaulados | 1 |
| 18411 | enjambres | 1 |
| 18412 | enjaezada | 1 |
| 18413 | enhilas | 1 |
| 18414 | enhilar | 1 |
| 18415 | enhila | 1 |
| 18416 | enharinados | 1 |
| 18417 | engullía | 1 |
| 18418 | engulle | 1 |
| 18419 | engrandecerlas | 1 |
| 18420 | engolfarte | 1 |
| 18421 | engolfados | 1 |
| 18422 | engendraren | 1 |
| 18423 | engendrando | 1 |
| 18424 | engendrado | 1 |
| 18425 | engendrada | 1 |
| 18426 | engastados | 1 |
| 18427 | engastado | 1 |
| 18428 | engañoso | 1 |
| 18429 | engañosa | 1 |
| 18430 | engañifas | 1 |
| 18431 | engañarte | 1 |
| 18432 | engañarnos | 1 |
| 18433 | engañándonos | 1 |
| 18434 | engañando | 1 |
| 18435 | engañador | 1 |
| 18436 | engañaban | 1 |
| 18437 | engaña | 1 |
| 18438 | enfriar | 1 |
| 18439 | enfriaba | 1 |
| 18440 | enfría | 1 |
| 18441 | enfrenó | 1 |
| 18442 | enfrenase | 1 |
| 18443 | enfrenada | 1 |
| 18444 | enfrena | 1 |
| 18445 | enfrascó | 1 |
| 18446 | enflaquece | 1 |
| 18447 | enfermos | 1 |
| 18448 | enfermiza | 1 |
| 18449 | enfadoso | 1 |
| 18450 | enfadosas | 1 |
| 18451 | enfaden | 1 |
| 18452 | enfade | 1 |
| 18453 | enfadase | 1 |
| 18454 | enfadaros | 1 |
| 18455 | enfadará | 1 |
| 18456 | enfadar | 1 |
| 18457 | enfadáis | 1 |
| 18458 | enemigas | 1 |
| 18459 | endurecidos | 1 |
| 18460 | endurecido | 1 |
| 18461 | endurecidas | 1 |
| 18462 | endurecida | 1 |
| 18463 | endurecía | 1 |
| 18464 | endrigos | 1 |
| 18465 | endriago | 1 |
| 18466 | endiabladas | 1 |
| 18467 | enderezo | 1 |
| 18468 | enderezase | 1 |
| 18469 | enderezarse | 1 |
| 18470 | enderezándole | 1 |
| 18471 | enderezador | 1 |
| 18472 | enderezado | 1 |
| 18473 | enderece | 1 |
| 18474 | endemoniados | 1 |
| 18475 | endemoniado | 1 |
| 18476 | endemoniada | 1 |
| 18477 | endechando | 1 |
| 18478 | endechaderas | 1 |
| 18479 | endeble | 1 |
| 18480 | encumbres | 1 |
| 18481 | encuentren | 1 |
| 18482 | encuéntrase | 1 |
| 18483 | encubrís | 1 |
| 18484 | encubrirte | 1 |
| 18485 | encubrírsela | 1 |
| 18486 | encubrirse | 1 |
| 18487 | encubrirme | 1 |
| 18488 | encubrirles | 1 |
| 18489 | encubrirle | 1 |
| 18490 | encubriéndosela | 1 |
| 18491 | encubras | 1 |
| 18492 | encubiertas | 1 |
| 18493 | encubertadas | 1 |
| 18494 | encuadernados | 1 |
| 18495 | encuadernado | 1 |
| 18496 | encrucejadas | 1 |
| 18497 | encorvamiento | 1 |
| 18498 | encorporados | 1 |
| 18499 | encontré | 1 |
| 18500 | encontrasen | 1 |
| 18501 | encontrase | 1 |
| 18502 | encontrare | 1 |
| 18503 | encontrara | 1 |
| 18504 | encontramos | 1 |
| 18505 | encontraba | 1 |
| 18506 | encontinente | 1 |
| 18507 | enconar | 1 |
| 18508 | encomiéndole | 1 |
| 18509 | encomiendo | 1 |
| 18510 | encomiéndenme | 1 |
| 18511 | encomiéndeme | 1 |
| 18512 | encomiéndate | 1 |
| 18513 | encomiéndalo | 1 |
| 18514 | encomendémoslo | 1 |
| 18515 | encomendasen | 1 |
| 18516 | encomendaros | 1 |
| 18517 | encomendarle | 1 |
| 18518 | encomendar | 1 |
| 18519 | encomendados | 1 |
| 18520 | encomendado | 1 |
| 18521 | encomendadlo | 1 |
| 18522 | encolerizado | 1 |
| 18523 | encojan | 1 |
| 18524 | encogiera | 1 |
| 18525 | encogido | 1 |
| 18526 | encogía | 1 |
| 18527 | encogemos | 1 |
| 18528 | encoge | 1 |
| 18529 | enclavijadas | 1 |
| 18530 | enclavársela | 1 |
| 18531 | encinta | 1 |
| 18532 | encinar | 1 |
| 18533 | encierren | 1 |
| 18534 | encierre | 1 |
| 18535 | enciérrate | 1 |
| 18536 | encerróse | 1 |
| 18537 | encerré | 1 |
| 18538 | encerrasen | 1 |
| 18539 | encerráronse | 1 |
| 18540 | encerrarlo | 1 |
| 18541 | encerrarle | 1 |
| 18542 | encerrándole | 1 |
| 18543 | encerrando | 1 |
| 18544 | encerados | 1 |
| 18545 | enceradas | 1 |
| 18546 | encendiósele | 1 |
| 18547 | encendiendo | 1 |
| 18548 | encendidos | 1 |
| 18549 | encenderse | 1 |
| 18550 | encenderme | 1 |
| 18551 | encenderle | 1 |
| 18552 | encastilladas | 1 |
| 18553 | encasquetóse | 1 |
| 18554 | encarnizados | 1 |
| 18555 | encarnadas | 1 |
| 18556 | encarnada | 1 |
| 18557 | encarguemos | 1 |
| 18558 | encargóse | 1 |
| 18559 | encargóles | 1 |
| 18560 | encargase | 1 |
| 18561 | encargármelo | 1 |
| 18562 | encargaría | 1 |
| 18563 | encargándonos | 1 |
| 18564 | encargándolas | 1 |
| 18565 | encargando | 1 |
| 18566 | encargado | 1 |
| 18567 | encargaban | 1 |
| 18568 | encargaba | 1 |
| 18569 | encareció | 1 |
| 18570 | encareciendo | 1 |
| 18571 | encarecerte | 1 |
| 18572 | encarecerlas | 1 |
| 18573 | encarecen | 1 |
| 18574 | encarecella | 1 |
| 18575 | encarece | 1 |
| 18576 | encaramar | 1 |
| 18577 | encaradas | 1 |
| 18578 | encantorio | 1 |
| 18579 | encanten | 1 |
| 18580 | encanté | 1 |
| 18581 | encantáronla | 1 |
| 18582 | encantaron | 1 |
| 18583 | encantar | 1 |
| 18584 | encamisado | 1 |
| 18585 | encaminóse | 1 |
| 18586 | encamino | 1 |
| 18587 | encaminen | 1 |
| 18588 | encaminéis | 1 |
| 18589 | encaminé | 1 |
| 18590 | encaminarlos | 1 |
| 18591 | encaminare | 1 |
| 18592 | encaminara | 1 |
| 18593 | encaminados | 1 |
| 18594 | encambronado | 1 |
| 18595 | encalabrinó | 1 |
| 18596 | encájenme | 1 |
| 18597 | encajársela | 1 |
| 18598 | encajarse | 1 |
| 18599 | encajándole | 1 |
| 18600 | encajallo | 1 |
| 18601 | encajados | 1 |
| 18602 | encajador | 1 |
| 18603 | encajada | 1 |
| 18604 | encajaba | 1 |
| 18605 | enarcó | 1 |
| 18606 | enarcar | 1 |
| 18607 | enarcando | 1 |
| 18608 | enarbolando | 1 |
| 18609 | enamoróla | 1 |
| 18610 | enamoréme | 1 |
| 18611 | enamoré | 1 |
| 18612 | enamore | 1 |
| 18613 | enamorasen | 1 |
| 18614 | enamorarse | 1 |
| 18615 | enamoraron | 1 |
| 18616 | enamoran | 1 |
| 18617 | enalbardó | 1 |
| 18618 | enalbardando | 1 |
| 18619 | enajenado | 1 |
| 18620 | émula | 1 |
| 18621 | empuñará | 1 |
| 18622 | empuñar | 1 |
| 18623 | empuñando | 1 |
| 18624 | empujón | 1 |
| 18625 | empujaba | 1 |
| 18626 | emprincipio | 1 |
| 18627 | empreñastes | 1 |
| 18628 | empreñar | 1 |
| 18629 | emprender | 1 |
| 18630 | emprendella | 1 |
| 18631 | empozarme | 1 |
| 18632 | empobrecieron | 1 |
| 18633 | emplearán | 1 |
| 18634 | emplear | 1 |
| 18635 | empleando | 1 |
| 18636 | empleados | 1 |
| 18637 | empleadísima | 1 |
| 18638 | empleadas | 1 |
| 18639 | emplastos | 1 |
| 18640 | emplastaron | 1 |
| 18641 | emplastado | 1 |
| 18642 | empinándola | 1 |
| 18643 | empinaba | 1 |
| 18644 | empezca | 1 |
| 18645 | emperante | 1 |
| 18646 | empeñé | 1 |
| 18647 | empeñando | 1 |
| 18648 | empeñado | 1 |
| 18649 | empedrarle | 1 |
| 18650 | empedrados | 1 |
| 18651 | emparedado | 1 |
| 18652 | empapado | 1 |
| 18653 | empañarse | 1 |
| 18654 | empalado | 1 |
| 18655 | empalaba | 1 |
| 18656 | empache | 1 |
| 18657 | empachados | 1 |
| 18658 | emiendes | 1 |
| 18659 | emiende | 1 |
| 18660 | emendarme | 1 |
| 18661 | emendar | 1 |
| 18662 | embutirse | 1 |
| 18663 | embrazado | 1 |
| 18664 | embozarse | 1 |
| 18665 | embozado | 1 |
| 18666 | embotó | 1 |
| 18667 | embotan | 1 |
| 18668 | embota | 1 |
| 18669 | emboscasen | 1 |
| 18670 | emboscarse | 1 |
| 18671 | embolsó | 1 |
| 18672 | embocar | 1 |
| 18673 | embistió | 1 |
| 18674 | embistiera | 1 |
| 18675 | embestirle | 1 |
| 18676 | embestimos | 1 |
| 18677 | embelesada | 1 |
| 18678 | embelecadores | 1 |
| 18679 | embebían | 1 |
| 18680 | embeber | 1 |
| 18681 | embazó | 1 |
| 18682 | embaulando | 1 |
| 18683 | embaulaban | 1 |
| 18684 | embarquéme | 1 |
| 18685 | embarcó | 1 |
| 18686 | embarcarme | 1 |
| 18687 | embarcarlos | 1 |
| 18688 | embarcan | 1 |
| 18689 | embarcadero | 1 |
| 18690 | embarazoso | 1 |
| 18691 | embarazo | 1 |
| 18692 | embarazara | 1 |
| 18693 | embarazado | 1 |
| 18694 | embaidora | 1 |
| 18695 | embaído | 1 |
| 18696 | elocuente | 1 |
| 18697 | eligrosas | 1 |
| 18698 | elevamiento | 1 |
| 18699 | elegancia | 1 |
| 18700 | elefantes | 1 |
| 18701 | electo | 1 |
| 18702 | elches | 1 |
| 18703 | ejercitastes | 1 |
| 18704 | ejercitarse | 1 |
| 18705 | ejercitándose | 1 |
| 18706 | ejercitado | 1 |
| 18707 | ejercitaban | 1 |
| 18708 | ejercer | 1 |
| 18709 | ejemplares | 1 |
| 18710 | ejecute | 1 |
| 18711 | ejecutarme | 1 |
| 18712 | ejecutallos | 1 |
| 18713 | ejecutado | 1 |
| 18714 | ejecutaba | 1 |
| 18715 | ejecuta | 1 |
| 18716 | eguemón | 1 |
| 18717 | ego | 1 |
| 18718 | egïón | 1 |
| 18719 | efusión | 1 |
| 18720 | efigie | 1 |
| 18721 | eficacísimas | 1 |
| 18722 | eficacia | 1 |
| 18723 | efetuase | 1 |
| 18724 | efetuar | 1 |
| 18725 | efetos | 1 |
| 18726 | efectivo | 1 |
| 18727 | edificar | 1 |
| 18728 | edificados | 1 |
| 18729 | écloga | 1 |
| 18730 | eclipse | 1 |
| 18731 | eclipsado | 1 |
| 18732 | eclesiástica | 1 |
| 18733 | echóles | 1 |
| 18734 | echemos | 1 |
| 18735 | echaros | 1 |
| 18736 | echáronse | 1 |
| 18737 | echarme | 1 |
| 18738 | echarlos | 1 |
| 18739 | echarlo | 1 |
| 18740 | echarles | 1 |
| 18741 | echarla | 1 |
| 18742 | echarían | 1 |
| 18743 | echaréis | 1 |
| 18744 | echaras | 1 |
| 18745 | echarán | 1 |
| 18746 | echaran | 1 |
| 18747 | echara | 1 |
| 18748 | echándonos | 1 |
| 18749 | echándome | 1 |
| 18750 | echándola | 1 |
| 18751 | echallo | 1 |
| 18752 | echalle | 1 |
| 18753 | echáis | 1 |
| 18754 | echados | 1 |
| 18755 | echádmelos | 1 |
| 18756 | echadme | 1 |
| 18757 | echadle | 1 |
| 18758 | echadas | 1 |
| 18759 | echad | 1 |
| 18760 | echacuervos | 1 |
| 18761 | ecetuando | 1 |
| 18762 | eceptar | 1 |
| 18763 | ecclesiae | 1 |
| 18764 | ébano | 1 |
| 18765 | duróle | 1 |
| 18766 | durmiesen | 1 |
| 18767 | durmiéronse | 1 |
| 18768 | durmieron | 1 |
| 18769 | durísima | 1 |
| 18770 | durindana | 1 |
| 18771 | duraron | 1 |
| 18772 | durare | 1 |
| 18773 | durará | 1 |
| 18774 | durara | 1 |
| 18775 | durado | 1 |
| 18776 | duración | 1 |
| 18777 | durables | 1 |
| 18778 | dulzura | 1 |
| 18779 | dulcísimas | 1 |
| 18780 | dulcineae | 1 |
| 18781 | dulcina | 1 |
| 18782 | dueñísima | 1 |
| 18783 | dueñesca | 1 |
| 18784 | duélase | 1 |
| 18785 | duecho | 1 |
| 18786 | dudosas | 1 |
| 18787 | dudosa | 1 |
| 18788 | dudaron | 1 |
| 18789 | dudare | 1 |
| 18790 | dudara | 1 |
| 18791 | dudamos | 1 |
| 18792 | dudaba | 1 |
| 18793 | ducal | 1 |
| 18794 | dubitat | 1 |
| 18795 | du | 1 |
| 18796 | dríadas | 1 |
| 18797 | doyme | 1 |
| 18798 | dotos | 1 |
| 18799 | dotó | 1 |
| 18800 | dotes | 1 |
| 18801 | doseles | 1 |
| 18802 | dosel | 1 |
| 18803 | dornajos | 1 |
| 18804 | dornajo | 1 |
| 18805 | dormitat | 1 |
| 18806 | dormitando | 1 |
| 18807 | dormirla | 1 |
| 18808 | dormida | 1 |
| 18809 | donosas | 1 |
| 18810 | donec | 1 |
| 18811 | doncellez | 1 |
| 18812 | donce | 1 |
| 18813 | donairoso | 1 |
| 18814 | donación | 1 |
| 18815 | domó | 1 |
| 18816 | dominio | 1 |
| 18817 | domas | 1 |
| 18818 | dolorosísima | 1 |
| 18819 | dolorosamente | 1 |
| 18820 | dolorido | 1 |
| 18821 | dolores | 1 |
| 18822 | doliese | 1 |
| 18823 | dolieran | 1 |
| 18824 | dolientes | 1 |
| 18825 | dolían | 1 |
| 18826 | dolfos | 1 |
| 18827 | dolet | 1 |
| 18828 | dolerá | 1 |
| 18829 | doler | 1 |
| 18830 | dogmatizador | 1 |
| 18831 | doctrínala | 1 |
| 18832 | doctores | 1 |
| 18833 | dócil | 1 |
| 18834 | doblega | 1 |
| 18835 | doble | 1 |
| 18836 | doblaron | 1 |
| 18837 | doblares | 1 |
| 18838 | doblará | 1 |
| 18839 | doblados | 1 |
| 18840 | doblado | 1 |
| 18841 | dobladle | 1 |
| 18842 | divulgándose | 1 |
| 18843 | diviso | 1 |
| 18844 | divisaron | 1 |
| 18845 | divisaban | 1 |
| 18846 | divinidad | 1 |
| 18847 | divinamente | 1 |
| 18848 | divierto | 1 |
| 18849 | dividirían | 1 |
| 18850 | dividir | 1 |
| 18851 | dividiesen | 1 |
| 18852 | dividieron | 1 |
| 18853 | dividiéndose | 1 |
| 18854 | dividiéndolas | 1 |
| 18855 | divididas | 1 |
| 18856 | dividida | 1 |
| 18857 | divida | 1 |
| 18858 | divi | 1 |
| 18859 | divertirme | 1 |
| 18860 | divertirla | 1 |
| 18861 | divertimiento | 1 |
| 18862 | divertille | 1 |
| 18863 | divertiesen | 1 |
| 18864 | divertiéndose | 1 |
| 18865 | divertidos | 1 |
| 18866 | dite | 1 |
| 18867 | ditado | 1 |
| 18868 | disuene | 1 |
| 18869 | disuadiendo | 1 |
| 18870 | distribuir | 1 |
| 18871 | distinta | 1 |
| 18872 | distingue | 1 |
| 18873 | distilada | 1 |
| 18874 | dístico | 1 |
| 18875 | distes | 1 |
| 18876 | distante | 1 |
| 18877 | distan | 1 |
| 18878 | dista | 1 |
| 18879 | disputen | 1 |
| 18880 | dispuso | 1 |
| 18881 | dispusición | 1 |
| 18882 | dispuestas | 1 |
| 18883 | disponiéndola | 1 |
| 18884 | dispongas | 1 |
| 18885 | disponga | 1 |
| 18886 | disponerme | 1 |
| 18887 | disponen | 1 |
| 18888 | disponed | 1 |
| 18889 | dispón | 1 |
| 18890 | dispensaciones | 1 |
| 18891 | disparé | 1 |
| 18892 | dispararse | 1 |
| 18893 | disparalla | 1 |
| 18894 | disparada | 1 |
| 18895 | disoluble | 1 |
| 18896 | disminuya | 1 |
| 18897 | disimularon | 1 |
| 18898 | disimuladamente | 1 |
| 18899 | disimulada | 1 |
| 18900 | disimilar | 1 |
| 18901 | disgustos | 1 |
| 18902 | disgustado | 1 |
| 18903 | disgusta | 1 |
| 18904 | disfrazadas | 1 |
| 18905 | disfraz | 1 |
| 18906 | disformísima | 1 |
| 18907 | disforme | 1 |
| 18908 | disfigurado | 1 |
| 18909 | discurrimientos | 1 |
| 18910 | discurrido | 1 |
| 18911 | discurren | 1 |
| 18912 | discurre | 1 |
| 18913 | disculpo | 1 |
| 18914 | disculparan | 1 |
| 18915 | disculpar | 1 |
| 18916 | disculpándose | 1 |
| 18917 | discretísimos | 1 |
| 18918 | discretísimo | 1 |
| 18919 | discre | 1 |
| 18920 | discorde | 1 |
| 18921 | discernir | 1 |
| 18922 | discantaba | 1 |
| 18923 | dirlos | 1 |
| 18924 | dirigirse | 1 |
| 18925 | direte | 1 |
| 18926 | diréis | 1 |
| 18927 | dirección | 1 |
| 18928 | dirásle | 1 |
| 18929 | diráles | 1 |
| 18930 | diputo | 1 |
| 18931 | diputado | 1 |
| 18932 | dióselos | 1 |
| 18933 | dióselo | 1 |
| 18934 | diósela | 1 |
| 18935 | dioscórides | 1 |
| 18936 | dioles | 1 |
| 18937 | diógenes | 1 |
| 18938 | dinos | 1 |
| 18939 | dinerillo | 1 |
| 18940 | dinamarca | 1 |
| 18941 | dímosles | 1 |
| 18942 | diminuyóla | 1 |
| 18943 | diminuirse | 1 |
| 18944 | diminuirla | 1 |
| 18945 | diminuido | 1 |
| 18946 | diligite | 1 |
| 18947 | dilicada | 1 |
| 18948 | dilatemos | 1 |
| 18949 | dilátelo | 1 |
| 18950 | dilatase | 1 |
| 18951 | dilatas | 1 |
| 18952 | dilatarme | 1 |
| 18953 | dilatarlo | 1 |
| 18954 | dilatándose | 1 |
| 18955 | dilatados | 1 |
| 18956 | dilatadas | 1 |
| 18957 | dilatada | 1 |
| 18958 | dilataba | 1 |
| 18959 | dilas | 1 |
| 18960 | dilaciones | 1 |
| 18961 | dilación | 1 |
| 18962 | dila | 1 |
| 18963 | dijéronme | 1 |
| 18964 | dijéronle | 1 |
| 18965 | dijeras | 1 |
| 18966 | dígoos | 1 |
| 18967 | dígole | 1 |
| 18968 | dignísima | 1 |
| 18969 | dignase | 1 |
| 18970 | dignamente | 1 |
| 18971 | digestión | 1 |
| 18972 | díganos | 1 |
| 18973 | dígamela | 1 |
| 18974 | dígalos | 1 |
| 18975 | dígalas | 1 |
| 18976 | difunta | 1 |
| 18977 | difinitiva | 1 |
| 18978 | difinición | 1 |
| 18979 | dificultar | 1 |
| 18980 | difícilmente | 1 |
| 18981 | diferentemente | 1 |
| 18982 | diferencias | 1 |
| 18983 | diferenciar | 1 |
| 18984 | diferenciados | 1 |
| 18985 | diferenciaban | 1 |
| 18986 | diestramente | 1 |
| 18987 | diestra | 1 |
| 18988 | diéronles | 1 |
| 18989 | dieres | 1 |
| 18990 | diéramos | 1 |
| 18991 | dieces | 1 |
| 18992 | dictado | 1 |
| 18993 | dictaba | 1 |
| 18994 | dicta | 1 |
| 18995 | dico | 1 |
| 18996 | dicípulo | 1 |
| 18997 | dicipline | 1 |
| 18998 | diciplinante | 1 |
| 18999 | diciéndoos | 1 |
| 19000 | diciéndonos | 1 |
| 19001 | diciembre | 1 |
| 19002 | díchoselo | 1 |
| 19003 | dícese | 1 |
| 19004 | dícenle | 1 |
| 19005 | dibu | 1 |
| 19006 | dïana | 1 |
| 19007 | diamantino | 1 |
| 19008 | diálogo | 1 |
| 19009 | diabolo | 1 |
| 19010 | dezmar | 1 |
| 19011 | devotos | 1 |
| 19012 | devotas | 1 |
| 19013 | devotamente | 1 |
| 19014 | devorador | 1 |
| 19015 | devidirse | 1 |
| 19016 | devengar | 1 |
| 19017 | deus | 1 |
| 19018 | deum | 1 |
| 19019 | detuviéronse | 1 |
| 19020 | detuve | 1 |
| 19021 | detrimento | 1 |
| 19022 | detienen | 1 |
| 19023 | detestación | 1 |
| 19024 | determinase | 1 |
| 19025 | determinándose | 1 |
| 19026 | determinados | 1 |
| 19027 | determinadas | 1 |
| 19028 | determinaciones | 1 |
| 19029 | deteniendo | 1 |
| 19030 | detenían | 1 |
| 19031 | deteníamos | 1 |
| 19032 | deténgome | 1 |
| 19033 | deténgase | 1 |
| 19034 | detengamos | 1 |
| 19035 | detenerlos | 1 |
| 19036 | detenerles | 1 |
| 19037 | detenelle | 1 |
| 19038 | detenéis | 1 |
| 19039 | detened | 1 |
| 19040 | detén | 1 |
| 19041 | desvíos | 1 |
| 19042 | desvió | 1 |
| 19043 | desvíe | 1 |
| 19044 | desvíate | 1 |
| 19045 | desviases | 1 |
| 19046 | desviase | 1 |
| 19047 | desviaron | 1 |
| 19048 | desviarnos | 1 |
| 19049 | desviaos | 1 |
| 19050 | desviándose | 1 |
| 19051 | desviadas | 1 |
| 19052 | desviaban | 1 |
| 19053 | desviaba | 1 |
| 19054 | desvía | 1 |
| 19055 | desvergüenzas | 1 |
| 19056 | desvergüenza | 1 |
| 19057 | desvergonzadas | 1 |
| 19058 | desvergonzada | 1 |
| 19059 | desventurados | 1 |
| 19060 | desventuradas | 1 |
| 19061 | desvelen | 1 |
| 19062 | desvelaron | 1 |
| 19063 | desvelado | 1 |
| 19064 | desvelábase | 1 |
| 19065 | desvelaban | 1 |
| 19066 | desvaríos | 1 |
| 19067 | desvariada | 1 |
| 19068 | desvaría | 1 |
| 19069 | desvanecimientos | 1 |
| 19070 | desvanecido | 1 |
| 19071 | desvanecerse | 1 |
| 19072 | desusado | 1 |
| 19073 | desuncir | 1 |
| 19074 | desunce | 1 |
| 19075 | desuelle | 1 |
| 19076 | desuellan | 1 |
| 19077 | destruyese | 1 |
| 19078 | destruyendo | 1 |
| 19079 | destruyen | 1 |
| 19080 | destruirnos | 1 |
| 19081 | destruille | 1 |
| 19082 | destruida | 1 |
| 19083 | destruición | 1 |
| 19084 | destrozando | 1 |
| 19085 | destrozadas | 1 |
| 19086 | destroncaron | 1 |
| 19087 | destroncada | 1 |
| 19088 | destripaterrones | 1 |
| 19089 | destraídas | 1 |
| 19090 | destraída | 1 |
| 19091 | destrae | 1 |
| 19092 | destotro | 1 |
| 19093 | destinguir | 1 |
| 19094 | destilaban | 1 |
| 19095 | destierren | 1 |
| 19096 | destierran | 1 |
| 19097 | destierra | 1 |
| 19098 | destetan | 1 |
| 19099 | desterrarme | 1 |
| 19100 | desterrando | 1 |
| 19101 | desterrado | 1 |
| 19102 | desterraban | 1 |
| 19103 | destemplanza | 1 |
| 19104 | destemplado | 1 |
| 19105 | despuntes | 1 |
| 19106 | despuntas | 1 |
| 19107 | despreció | 1 |
| 19108 | desprecies | 1 |
| 19109 | desprecié | 1 |
| 19110 | desprecias | 1 |
| 19111 | despreciar | 1 |
| 19112 | despreciando | 1 |
| 19113 | despreciada | 1 |
| 19114 | desprecia | 1 |
| 19115 | despotrique | 1 |
| 19116 | desposó | 1 |
| 19117 | desposarte | 1 |
| 19118 | desposarse | 1 |
| 19119 | desposara | 1 |
| 19120 | desposar | 1 |
| 19121 | desposada | 1 |
| 19122 | despolvoreó | 1 |
| 19123 | despolvorearnos | 1 |
| 19124 | despojarse | 1 |
| 19125 | despliegue | 1 |
| 19126 | desplegó | 1 |
| 19127 | desplegarás | 1 |
| 19128 | desplegar | 1 |
| 19129 | desplegado | 1 |
| 19130 | desplace | 1 |
| 19131 | despierten | 1 |
| 19132 | despiertan | 1 |
| 19133 | despido | 1 |
| 19134 | despidióse | 1 |
| 19135 | despidiéronse | 1 |
| 19136 | despidiendo | 1 |
| 19137 | despídese | 1 |
| 19138 | despides | 1 |
| 19139 | despidámonos | 1 |
| 19140 | desperté | 1 |
| 19141 | despertastes | 1 |
| 19142 | despertáronlos | 1 |
| 19143 | despertaron | 1 |
| 19144 | despertarme | 1 |
| 19145 | despertarle | 1 |
| 19146 | despertará | 1 |
| 19147 | despertadores | 1 |
| 19148 | desperezarse | 1 |
| 19149 | desperezándose | 1 |
| 19150 | despeñéme | 1 |
| 19151 | despeñas | 1 |
| 19152 | despeñarse | 1 |
| 19153 | despeñarme | 1 |
| 19154 | despeñándose | 1 |
| 19155 | despeñándome | 1 |
| 19156 | despeñaderos | 1 |
| 19157 | despeñaba | 1 |
| 19158 | despeña | 1 |
| 19159 | despensas | 1 |
| 19160 | despenar | 1 |
| 19161 | despejan | 1 |
| 19162 | despejalle | 1 |
| 19163 | despegador | 1 |
| 19164 | despedirte | 1 |
| 19165 | despedirá | 1 |
| 19166 | despedió | 1 |
| 19167 | despedimientos | 1 |
| 19168 | despedille | 1 |
| 19169 | despediéndose | 1 |
| 19170 | despedida | 1 |
| 19171 | despedía | 1 |
| 19172 | despeado | 1 |
| 19173 | despavorida | 1 |
| 19174 | despartirla | 1 |
| 19175 | despartir | 1 |
| 19176 | despartió | 1 |
| 19177 | despareció | 1 |
| 19178 | desparecido | 1 |
| 19179 | desparecían | 1 |
| 19180 | desparecer | 1 |
| 19181 | desparcir | 1 |
| 19182 | desparatado | 1 |
| 19183 | despaldado | 1 |
| 19184 | despáchenme | 1 |
| 19185 | despachen | 1 |
| 19186 | despácheme | 1 |
| 19187 | despacharme | 1 |
| 19188 | despacharle | 1 |
| 19189 | despachará | 1 |
| 19190 | despacha | 1 |
| 19191 | despabilé | 1 |
| 19192 | despabile | 1 |
| 19193 | despabilaron | 1 |
| 19194 | despabilarme | 1 |
| 19195 | despabilaré | 1 |
| 19196 | despabilar | 1 |
| 19197 | desotros | 1 |
| 19198 | desorejaba | 1 |
| 19199 | desordenado | 1 |
| 19200 | desordenada | 1 |
| 19201 | desoluto | 1 |
| 19202 | desollaros | 1 |
| 19203 | desollado | 1 |
| 19204 | desolado | 1 |
| 19205 | desocupados | 1 |
| 19206 | desobligaba | 1 |
| 19207 | desnudóse | 1 |
| 19208 | desnúdese | 1 |
| 19209 | desnude | 1 |
| 19210 | desnudase | 1 |
| 19211 | desnudarnos | 1 |
| 19212 | desnudarme | 1 |
| 19213 | desnudaba | 1 |
| 19214 | desnatan | 1 |
| 19215 | desnarigado | 1 |
| 19216 | desnarigada | 1 |
| 19217 | desmoronar | 1 |
| 19218 | desmochada | 1 |
| 19219 | desmenuzadas | 1 |
| 19220 | desmentir | 1 |
| 19221 | desmentille | 1 |
| 19222 | desmentíla | 1 |
| 19223 | desmedrado | 1 |
| 19224 | desmayóse | 1 |
| 19225 | desmayó | 1 |
| 19226 | desmayes | 1 |
| 19227 | desmayasen | 1 |
| 19228 | desmayaráse | 1 |
| 19229 | desmayar | 1 |
| 19230 | desmayadas | 1 |
| 19231 | desmayábase | 1 |
| 19232 | desmantelar | 1 |
| 19233 | desmandó | 1 |
| 19234 | desmandas | 1 |
| 19235 | desmandada | 1 |
| 19236 | deslumbrar | 1 |
| 19237 | deslumbrada | 1 |
| 19238 | deslizó | 1 |
| 19239 | deslizarme | 1 |
| 19240 | desliza | 1 |
| 19241 | deslindase | 1 |
| 19242 | deslindar | 1 |
| 19243 | deslindan | 1 |
| 19244 | desligó | 1 |
| 19245 | deslicen | 1 |
| 19246 | deslenguados | 1 |
| 19247 | deslenguado | 1 |
| 19248 | desleído | 1 |
| 19249 | desjarrete | 1 |
| 19250 | desistiré | 1 |
| 19251 | desistir | 1 |
| 19252 | desistiese | 1 |
| 19253 | designo | 1 |
| 19254 | deshonró | 1 |
| 19255 | deshonras | 1 |
| 19256 | deshonran | 1 |
| 19257 | deshonraba | 1 |
| 19258 | deshonestos | 1 |
| 19259 | deshonesto | 1 |
| 19260 | deshogar | 1 |
| 19261 | deshiciéronse | 1 |
| 19262 | deshice | 1 |
| 19263 | desheredada | 1 |
| 19264 | deshechos | 1 |
| 19265 | deshecha | 1 |
| 19266 | desharé | 1 |
| 19267 | deshacía | 1 |
| 19268 | deshacerte | 1 |
| 19269 | deshacerse | 1 |
| 19270 | deshacerlos | 1 |
| 19271 | deshacen | 1 |
| 19272 | deshacedor | 1 |
| 19273 | desgobernada | 1 |
| 19274 | desgarrase | 1 |
| 19275 | desgarrarse | 1 |
| 19276 | desgarrado | 1 |
| 19277 | desgajar | 1 |
| 19278 | desfogaré | 1 |
| 19279 | desfloren | 1 |
| 19280 | desfigurar | 1 |
| 19281 | desfigurado | 1 |
| 19282 | desfiguraban | 1 |
| 19283 | desfecho | 1 |
| 19284 | desfavorecido | 1 |
| 19285 | desfavorecer | 1 |
| 19286 | desfallezca | 1 |
| 19287 | desfalcaré | 1 |
| 19288 | desfagan | 1 |
| 19289 | desfacelle | 1 |
| 19290 | desestimase | 1 |
| 19291 | desesperaron | 1 |
| 19292 | desesperar | 1 |
| 19293 | desesperadas | 1 |
| 19294 | desesperaban | 1 |
| 19295 | deservicios | 1 |
| 19296 | deservicio | 1 |
| 19297 | deseosas | 1 |
| 19298 | deseosa | 1 |
| 19299 | desenvueltamente | 1 |
| 19300 | desenvolviéndole | 1 |
| 19301 | desenvainen | 1 |
| 19302 | desenvaine | 1 |
| 19303 | desenvainaron | 1 |
| 19304 | desenvainar | 1 |
| 19305 | desenvainadas | 1 |
| 19306 | desentrañarles | 1 |
| 19307 | desentonada | 1 |
| 19308 | desenterrar | 1 |
| 19309 | desenterrándonos | 1 |
| 19310 | desensillado | 1 |
| 19311 | desenredarle | 1 |
| 19312 | desenlazarle | 1 |
| 19313 | desenlazando | 1 |
| 19314 | desenjaularon | 1 |
| 19315 | desengañes | 1 |
| 19316 | desengañarse | 1 |
| 19317 | desengañarle | 1 |
| 19318 | desengañara | 1 |
| 19319 | desengañados | 1 |
| 19320 | desengañada | 1 |
| 19321 | desengañaban | 1 |
| 19322 | desenfadadamente | 1 |
| 19323 | desenclavijó | 1 |
| 19324 | desencinta | 1 |
| 19325 | desencantos | 1 |
| 19326 | desencantó | 1 |
| 19327 | desencantes | 1 |
| 19328 | desencantado | 1 |
| 19329 | desencajaron | 1 |
| 19330 | desencajarle | 1 |
| 19331 | desencajados | 1 |
| 19332 | desencajaba | 1 |
| 19333 | desenamorado | 1 |
| 19334 | desenalbardar | 1 |
| 19335 | desemejable | 1 |
| 19336 | desembolsar | 1 |
| 19337 | desembolsado | 1 |
| 19338 | desembaúle | 1 |
| 19339 | desembarcásemos | 1 |
| 19340 | desembarazaron | 1 |
| 19341 | desembarazar | 1 |
| 19342 | desembarazadamente | 1 |
| 19343 | desembarazada | 1 |
| 19344 | desembaraza | 1 |
| 19345 | desembanastasen | 1 |
| 19346 | deseen | 1 |
| 19347 | deseches | 1 |
| 19348 | deseche | 1 |
| 19349 | desechásteme | 1 |
| 19350 | desechase | 1 |
| 19351 | desechado | 1 |
| 19352 | desechaba | 1 |
| 19353 | desease | 1 |
| 19354 | desearon | 1 |
| 19355 | desearen | 1 |
| 19356 | deseábamos | 1 |
| 19357 | dése | 1 |
| 19358 | desdijese | 1 |
| 19359 | desdigan | 1 |
| 19360 | desdiga | 1 |
| 19361 | desdichadísimas | 1 |
| 19362 | desdichadísima | 1 |
| 19363 | desdeñosa | 1 |
| 19364 | desdeñé | 1 |
| 19365 | desdeñase | 1 |
| 19366 | desdeñará | 1 |
| 19367 | desdeñados | 1 |
| 19368 | desdeñada | 1 |
| 19369 | desdeñaba | 1 |
| 19370 | desculpó | 1 |
| 19371 | desculpaba | 1 |
| 19372 | desculpa | 1 |
| 19373 | descuide | 1 |
| 19374 | descuidasen | 1 |
| 19375 | descuidase | 1 |
| 19376 | descuidarse | 1 |
| 19377 | descuidaba | 1 |
| 19378 | descuentos | 1 |
| 19379 | descuente | 1 |
| 19380 | descuelgan | 1 |
| 19381 | descuelga | 1 |
| 19382 | descubrirte | 1 |
| 19383 | descubrirnos | 1 |
| 19384 | descubrióla | 1 |
| 19385 | descubrille | 1 |
| 19386 | descubriésemos | 1 |
| 19387 | descubriéronle | 1 |
| 19388 | descubrieres | 1 |
| 19389 | descubrieras | 1 |
| 19390 | descubrieran | 1 |
| 19391 | descubriera | 1 |
| 19392 | descubriéndome | 1 |
| 19393 | descubriéndolo | 1 |
| 19394 | descubres | 1 |
| 19395 | descubras | 1 |
| 19396 | descubran | 1 |
| 19397 | descubráis | 1 |
| 19398 | descrito | 1 |
| 19399 | descripción | 1 |
| 19400 | descríe | 1 |
| 19401 | describirla | 1 |
| 19402 | describir | 1 |
| 19403 | describió | 1 |
| 19404 | describiese | 1 |
| 19405 | describía | 1 |
| 19406 | describen | 1 |
| 19407 | describa | 1 |
| 19408 | descreer | 1 |
| 19409 | descrédito | 1 |
| 19410 | descosido | 1 |
| 19411 | descoserse | 1 |
| 19412 | descorazonado | 1 |
| 19413 | descontente | 1 |
| 19414 | descontentar | 1 |
| 19415 | descontar | 1 |
| 19416 | desconsolóle | 1 |
| 19417 | desconsolado | 1 |
| 19418 | desconocido | 1 |
| 19419 | desconfianzas | 1 |
| 19420 | desconfianza | 1 |
| 19421 | desconcierta | 1 |
| 19422 | desconcertados | 1 |
| 19423 | descomunión | 1 |
| 19424 | descomulgó | 1 |
| 19425 | descolorida | 1 |
| 19426 | descollaban | 1 |
| 19427 | descolgásedes | 1 |
| 19428 | descolgaron | 1 |
| 19429 | descolgar | 1 |
| 19430 | descolgándose | 1 |
| 19431 | descolgado | 1 |
| 19432 | descolgadas | 1 |
| 19433 | descoger | 1 |
| 19434 | desciñéronse | 1 |
| 19435 | desceñido | 1 |
| 19436 | descarne | 1 |
| 19437 | descargaré | 1 |
| 19438 | descargado | 1 |
| 19439 | descansadamente | 1 |
| 19440 | descansaba | 1 |
| 19441 | descaminadas | 1 |
| 19442 | descaminada | 1 |
| 19443 | descalzo | 1 |
| 19444 | descalzarse | 1 |
| 19445 | descalzándose | 1 |
| 19446 | descalabrar | 1 |
| 19447 | descalabrado | 1 |
| 19448 | descabezando | 1 |
| 19449 | descabezado | 1 |
| 19450 | descabalar | 1 |
| 19451 | descabalado | 1 |
| 19452 | desbuchase | 1 |
| 19453 | desbuchar | 1 |
| 19454 | desbocado | 1 |
| 19455 | desbástala | 1 |
| 19456 | desbarató | 1 |
| 19457 | desbaratarlos | 1 |
| 19458 | desbaratar | 1 |
| 19459 | desbaratados | 1 |
| 19460 | desbarataba | 1 |
| 19461 | desayunarnos | 1 |
| 19462 | desayunar | 1 |
| 19463 | desayunaos | 1 |
| 19464 | desavenidos | 1 |
| 19465 | desatinar | 1 |
| 19466 | desatinado | 1 |
| 19467 | desatinaba | 1 |
| 19468 | desati | 1 |
| 19469 | desatentado | 1 |
| 19470 | desatarse | 1 |
| 19471 | desataros | 1 |
| 19472 | desatarlos | 1 |
| 19473 | desatarle | 1 |
| 19474 | desatamos | 1 |
| 19475 | desatados | 1 |
| 19476 | desatadlo | 1 |
| 19477 | desatácate | 1 |
| 19478 | desataban | 1 |
| 19479 | desataba | 1 |
| 19480 | desata | 1 |
| 19481 | desastres | 1 |
| 19482 | desastre | 1 |
| 19483 | desasosiega | 1 |
| 19484 | desasosegarles | 1 |
| 19485 | desasosegar | 1 |
| 19486 | desasosegado | 1 |
| 19487 | desasir | 1 |
| 19488 | desarraigó | 1 |
| 19489 | desarraigar | 1 |
| 19490 | desarmóle | 1 |
| 19491 | desarmaron | 1 |
| 19492 | desarmar | 1 |
| 19493 | desarmaban | 1 |
| 19494 | desarma | 1 |
| 19495 | desapasionado | 1 |
| 19496 | desaparecido | 1 |
| 19497 | desamparo | 1 |
| 19498 | desampare | 1 |
| 19499 | desampararos | 1 |
| 19500 | desampararme | 1 |
| 19501 | desamparando | 1 |
| 19502 | desamparados | 1 |
| 19503 | desamparada | 1 |
| 19504 | desamor | 1 |
| 19505 | desalumbrados | 1 |
| 19506 | desalumbradamente | 1 |
| 19507 | desalmadas | 1 |
| 19508 | desaliñase | 1 |
| 19509 | desaliñando | 1 |
| 19510 | desalforjó | 1 |
| 19511 | desalentados | 1 |
| 19512 | desalentado | 1 |
| 19513 | desalbardara | 1 |
| 19514 | desairado | 1 |
| 19515 | desagüe | 1 |
| 19516 | desaguarse | 1 |
| 19517 | desaguaderos | 1 |
| 19518 | desagua | 1 |
| 19519 | desagrade | 1 |
| 19520 | desafióme | 1 |
| 19521 | desafió | 1 |
| 19522 | desafiásedes | 1 |
| 19523 | desafiarle | 1 |
| 19524 | desafiaré | 1 |
| 19525 | desafialle | 1 |
| 19526 | desafiaba | 1 |
| 19527 | desacreditasen | 1 |
| 19528 | desacreditaban | 1 |
| 19529 | desaconsejaban | 1 |
| 19530 | desabrocharle | 1 |
| 19531 | desabrochar | 1 |
| 19532 | desabrochándole | 1 |
| 19533 | desabrimientos | 1 |
| 19534 | desabridos | 1 |
| 19535 | desabrido | 1 |
| 19536 | desabridamente | 1 |
| 19537 | derrumbado | 1 |
| 19538 | derrumba | 1 |
| 19539 | derriten | 1 |
| 19540 | derribóle | 1 |
| 19541 | derribo | 1 |
| 19542 | derribé | 1 |
| 19543 | derribas | 1 |
| 19544 | derribarte | 1 |
| 19545 | derribarse | 1 |
| 19546 | derribáronme | 1 |
| 19547 | derriban | 1 |
| 19548 | derribados | 1 |
| 19549 | derretirle | 1 |
| 19550 | derrengado | 1 |
| 19551 | derramaron | 1 |
| 19552 | derramarme | 1 |
| 19553 | derramaban | 1 |
| 19554 | derramaba | 1 |
| 19555 | derivativo | 1 |
| 19556 | deputado | 1 |
| 19557 | depusiese | 1 |
| 19558 | depriesa | 1 |
| 19559 | deprecaciones | 1 |
| 19560 | depositó | 1 |
| 19561 | depositen | 1 |
| 19562 | depositasen | 1 |
| 19563 | depositarlos | 1 |
| 19564 | depositando | 1 |
| 19565 | depositado | 1 |
| 19566 | depositaban | 1 |
| 19567 | deponer | 1 |
| 19568 | dependen | 1 |
| 19569 | departiremos | 1 |
| 19570 | departiré | 1 |
| 19571 | departir | 1 |
| 19572 | departiese | 1 |
| 19573 | departiera | 1 |
| 19574 | departido | 1 |
| 19575 | deparare | 1 |
| 19576 | deparará | 1 |
| 19577 | deparara | 1 |
| 19578 | deparan | 1 |
| 19579 | deparado | 1 |
| 19580 | depara | 1 |
| 19581 | déosle | 1 |
| 19582 | denunciare | 1 |
| 19583 | dentellear | 1 |
| 19584 | dénsele | 1 |
| 19585 | dense | 1 |
| 19586 | denostar | 1 |
| 19587 | dénoslo | 1 |
| 19588 | denominación | 1 |
| 19589 | demuestran | 1 |
| 19590 | demostrativas | 1 |
| 19591 | demóstenes | 1 |
| 19592 | démosle | 1 |
| 19593 | demonstrativos | 1 |
| 19594 | démelos | 1 |
| 19595 | démele | 1 |
| 19596 | demasías | 1 |
| 19597 | demandase | 1 |
| 19598 | demandantes | 1 |
| 19599 | demandante | 1 |
| 19600 | deliñada | 1 |
| 19601 | delinease | 1 |
| 19602 | delinear | 1 |
| 19603 | delineado | 1 |
| 19604 | delineadas | 1 |
| 19605 | delicadamente | 1 |
| 19606 | deliberado | 1 |
| 19607 | deliberada | 1 |
| 19608 | delgadísimo | 1 |
| 19609 | deleitoso | 1 |
| 19610 | deleiten | 1 |
| 19611 | deleitables | 1 |
| 19612 | deleita | 1 |
| 19613 | déla | 1 |
| 19614 | dejóse | 1 |
| 19615 | dejos | 1 |
| 19616 | dejólos | 1 |
| 19617 | dejóla | 1 |
| 19618 | déjola | 1 |
| 19619 | déjeseme | 1 |
| 19620 | déjense | 1 |
| 19621 | déjennos | 1 |
| 19622 | dejémoslos | 1 |
| 19623 | dejastes | 1 |
| 19624 | dejaste | 1 |
| 19625 | dejársele | 1 |
| 19626 | dejaros | 1 |
| 19627 | dejáronla | 1 |
| 19628 | dejarlos | 1 |
| 19629 | dejarles | 1 |
| 19630 | dejarían | 1 |
| 19631 | dejares | 1 |
| 19632 | dejaren | 1 |
| 19633 | dejarémosle | 1 |
| 19634 | dejaréis | 1 |
| 19635 | dejare | 1 |
| 19636 | dejarás | 1 |
| 19637 | dejaras | 1 |
| 19638 | dejáramos | 1 |
| 19639 | dejaos | 1 |
| 19640 | dejándolas | 1 |
| 19641 | dejándola | 1 |
| 19642 | déjamela | 1 |
| 19643 | déjalos | 1 |
| 19644 | déjalo | 1 |
| 19645 | dejallos | 1 |
| 19646 | dejáis | 1 |
| 19647 | dejadnos | 1 |
| 19648 | dejadlo | 1 |
| 19649 | dejadas | 1 |
| 19650 | deidad | 1 |
| 19651 | dehesas | 1 |
| 19652 | dehesa | 1 |
| 19653 | degollado | 1 |
| 19654 | degollada | 1 |
| 19655 | defuera | 1 |
| 19656 | defraudó | 1 |
| 19657 | defraude | 1 |
| 19658 | defraudaros | 1 |
| 19659 | defraudarme | 1 |
| 19660 | defraudarle | 1 |
| 19661 | defraudando | 1 |
| 19662 | defraudados | 1 |
| 19663 | defraudadas | 1 |
| 19664 | defraudada | 1 |
| 19665 | defrauda | 1 |
| 19666 | defiéndete | 1 |
| 19667 | defienden | 1 |
| 19668 | defiendas | 1 |
| 19669 | defiendan | 1 |
| 19670 | defienda | 1 |
| 19671 | defensores | 1 |
| 19672 | defensiva | 1 |
| 19673 | defendiéndolo | 1 |
| 19674 | defendiéndola | 1 |
| 19675 | defendiendo | 1 |
| 19676 | defendido | 1 |
| 19677 | defenderte | 1 |
| 19678 | defenderla | 1 |
| 19679 | defendedor | 1 |
| 19680 | defectos | 1 |
| 19681 | deditos | 1 |
| 19682 | dedicatoria | 1 |
| 19683 | dedicado | 1 |
| 19684 | decretado | 1 |
| 19685 | decreta | 1 |
| 19686 | decoraban | 1 |
| 19687 | declinar | 1 |
| 19688 | declinación | 1 |
| 19689 | declina | 1 |
| 19690 | declare | 1 |
| 19691 | declararte | 1 |
| 19692 | declararlos | 1 |
| 19693 | declararé | 1 |
| 19694 | declarare | 1 |
| 19695 | declarará | 1 |
| 19696 | declarara | 1 |
| 19697 | declaraos | 1 |
| 19698 | declarando | 1 |
| 19699 | decláralo | 1 |
| 19700 | declarad | 1 |
| 19701 | decírosla | 1 |
| 19702 | decirnos | 1 |
| 19703 | décimas | 1 |
| 19704 | decillo | 1 |
| 19705 | decilles | 1 |
| 19706 | decildo | 1 |
| 19707 | deciembre | 1 |
| 19708 | decidle | 1 |
| 19709 | decías | 1 |
| 19710 | decíanme | 1 |
| 19711 | decíale | 1 |
| 19712 | dechado | 1 |
| 19713 | deceplinantes | 1 |
| 19714 | decentes | 1 |
| 19715 | decente | 1 |
| 19716 | decendiendo | 1 |
| 19717 | decendían | 1 |
| 19718 | decender | 1 |
| 19719 | decendencias | 1 |
| 19720 | decantase | 1 |
| 19721 | decantada | 1 |
| 19722 | debiste | 1 |
| 19723 | debióse | 1 |
| 19724 | debilidad | 1 |
| 19725 | débiles | 1 |
| 19726 | débil | 1 |
| 19727 | debiere | 1 |
| 19728 | debiérase | 1 |
| 19729 | debieras | 1 |
| 19730 | debías | 1 |
| 19731 | débelo | 1 |
| 19732 | debas | 1 |
| 19733 | deban | 1 |
| 19734 | david | 1 |
| 19735 | dátiles | 1 |
| 19736 | dátil | 1 |
| 19737 | dáselos | 1 |
| 19738 | dásela | 1 |
| 19739 | dase | 1 |
| 19740 | dárseme | 1 |
| 19741 | dárselas | 1 |
| 19742 | dármelos | 1 |
| 19743 | dármela | 1 |
| 19744 | darlas | 1 |
| 19745 | dario | 1 |
| 19746 | darémosles | 1 |
| 19747 | daréis | 1 |
| 19748 | darásme | 1 |
| 19749 | darásela | 1 |
| 19750 | daránnos | 1 |
| 19751 | daraida | 1 |
| 19752 | dañoso | 1 |
| 19753 | dañosa | 1 |
| 19754 | dañó | 1 |
| 19755 | dañar | 1 |
| 19756 | dañador | 1 |
| 19757 | dañado | 1 |
| 19758 | dañada | 1 |
| 19759 | dañaba | 1 |
| 19760 | danzantes | 1 |
| 19761 | danzando | 1 |
| 19762 | danzadores | 1 |
| 19763 | dándoselo | 1 |
| 19764 | dándosele | 1 |
| 19765 | dándosela | 1 |
| 19766 | dándonos | 1 |
| 19767 | dándomela | 1 |
| 19768 | dándolos | 1 |
| 19769 | dándola | 1 |
| 19770 | dánaes | 1 |
| 19771 | damiselas | 1 |
| 19772 | dámela | 1 |
| 19773 | damasquino | 1 |
| 19774 | dalo | 1 |
| 19775 | dallas | 1 |
| 19776 | dalas | 1 |
| 19777 | dagas | 1 |
| 19778 | dádselos | 1 |
| 19779 | dádole | 1 |
| 19780 | dácame | 1 |
| 19781 | dábanse | 1 |
| 19782 | dábanlas | 1 |
| 19783 | dábamos | 1 |
| 19784 | cúyos | 1 |
| 19785 | cutiré | 1 |
| 19786 | curvas | 1 |
| 19787 | curtidos | 1 |
| 19788 | cursos | 1 |
| 19789 | curo | 1 |
| 19790 | curis | 1 |
| 19791 | curio | 1 |
| 19792 | curiel | 1 |
| 19793 | cures | 1 |
| 19794 | curen | 1 |
| 19795 | curémonos | 1 |
| 19796 | curéis | 1 |
| 19797 | curcios | 1 |
| 19798 | curcio | 1 |
| 19799 | curaron | 1 |
| 19800 | curaría | 1 |
| 19801 | curaremos | 1 |
| 19802 | curándose | 1 |
| 19803 | curándome | 1 |
| 19804 | curambro | 1 |
| 19805 | curadillo | 1 |
| 19806 | curad | 1 |
| 19807 | cupe | 1 |
| 19808 | cuñada | 1 |
| 19809 | cundiendo | 1 |
| 19810 | cundido | 1 |
| 19811 | cumplo | 1 |
| 19812 | cumplíselos | 1 |
| 19813 | cumplís | 1 |
| 19814 | cumplirle | 1 |
| 19815 | cumpliólo | 1 |
| 19816 | cumplillos | 1 |
| 19817 | cumplille | 1 |
| 19818 | cumplilla | 1 |
| 19819 | cumpliere | 1 |
| 19820 | cumpliéndosela | 1 |
| 19821 | cumplidle | 1 |
| 19822 | cumplidas | 1 |
| 19823 | cumplida | 1 |
| 19824 | cumplid | 1 |
| 19825 | cultivándolas | 1 |
| 19826 | cultivado | 1 |
| 19827 | cultivación | 1 |
| 19828 | culpo | 1 |
| 19829 | culparle | 1 |
| 19830 | culpar | 1 |
| 19831 | culpante | 1 |
| 19832 | culpando | 1 |
| 19833 | culpan | 1 |
| 19834 | culpados | 1 |
| 19835 | culpada | 1 |
| 19836 | culpábase | 1 |
| 19837 | cuitísima | 1 |
| 19838 | cuitadas | 1 |
| 19839 | cuidadosa | 1 |
| 19840 | cuesten | 1 |
| 19841 | cuesco | 1 |
| 19842 | cuerdamente | 1 |
| 19843 | cuéntenosla | 1 |
| 19844 | cuéntamelo | 1 |
| 19845 | cuéntalo | 1 |
| 19846 | cuélguense | 1 |
| 19847 | cuecen | 1 |
| 19848 | cue | 1 |
| 19849 | cudicia | 1 |
| 19850 | cuchillas | 1 |
| 19851 | cucharón | 1 |
| 19852 | cuchares | 1 |
| 19853 | cucharada | 1 |
| 19854 | cuchara | 1 |
| 19855 | cubrirá | 1 |
| 19856 | cubrióse | 1 |
| 19857 | cubrimos | 1 |
| 19858 | cubriéronse | 1 |
| 19859 | cubriéndose | 1 |
| 19860 | cubriéndole | 1 |
| 19861 | cubríale | 1 |
| 19862 | cubramos | 1 |
| 19863 | cuatrín | 1 |
| 19864 | cuatrero | 1 |
| 19865 | cuasi | 1 |
| 19866 | cuartal | 1 |
| 19867 | cuaresma | 1 |
| 19868 | cualque | 1 |
| 19869 | cualificada | 1 |
| 19870 | cualidad | 1 |
| 19871 | cualesquier | 1 |
| 19872 | cuajo | 1 |
| 19873 | cuadros | 1 |
| 19874 | cuadrillas | 1 |
| 19875 | cuadren | 1 |
| 19876 | cuadre | 1 |
| 19877 | cuadraren | 1 |
| 19878 | cuadrare | 1 |
| 19879 | cuadran | 1 |
| 19880 | cuadrados | 1 |
| 19881 | cuadrado | 1 |
| 19882 | cuadrada | 1 |
| 19883 | cuadraba | 1 |
| 19884 | cruzados | 1 |
| 19885 | cruzaba | 1 |
| 19886 | crujir | 1 |
| 19887 | crujieron | 1 |
| 19888 | crujiéndole | 1 |
| 19889 | crujiendo | 1 |
| 19890 | crujen | 1 |
| 19891 | crudos | 1 |
| 19892 | crudeza | 1 |
| 19893 | cruda | 1 |
| 19894 | crucis | 1 |
| 19895 | crucifijo | 1 |
| 19896 | cruce | 1 |
| 19897 | crítico | 1 |
| 19898 | cristianesca | 1 |
| 19899 | cristianamente | 1 |
| 19900 | cristel | 1 |
| 19901 | cristalino | 1 |
| 19902 | cristalinas | 1 |
| 19903 | crióme | 1 |
| 19904 | crío | 1 |
| 19905 | criéme | 1 |
| 19906 | cribando | 1 |
| 19907 | criban | 1 |
| 19908 | criaturas | 1 |
| 19909 | criaste | 1 |
| 19910 | criaron | 1 |
| 19911 | criarlos | 1 |
| 19912 | criador | 1 |
| 19913 | criad | 1 |
| 19914 | creyóle | 1 |
| 19915 | creyeses | 1 |
| 19916 | creyeran | 1 |
| 19917 | creyéndolo | 1 |
| 19918 | creyéndola | 1 |
| 19919 | creta | 1 |
| 19920 | crepúsculo | 1 |
| 19921 | creó | 1 |
| 19922 | creída | 1 |
| 19923 | creíble | 1 |
| 19924 | creían | 1 |
| 19925 | creerlos | 1 |
| 19926 | creerlo | 1 |
| 19927 | creerá | 1 |
| 19928 | creencia | 1 |
| 19929 | creemos | 1 |
| 19930 | creéme | 1 |
| 19931 | créeme | 1 |
| 19932 | créelo | 1 |
| 19933 | creed | 1 |
| 19934 | crédulo | 1 |
| 19935 | crecidos | 1 |
| 19936 | crecida | 1 |
| 19937 | crecía | 1 |
| 19938 | créanme | 1 |
| 19939 | créalo | 1 |
| 19940 | coz | 1 |
| 19941 | cotonía | 1 |
| 19942 | cotejando | 1 |
| 19943 | cota | 1 |
| 19944 | costura | 1 |
| 19945 | costosas | 1 |
| 19946 | costo | 1 |
| 19947 | costezuela | 1 |
| 19948 | costaron | 1 |
| 19949 | costarme | 1 |
| 19950 | costarles | 1 |
| 19951 | costaría | 1 |
| 19952 | costarán | 1 |
| 19953 | cosqueamos | 1 |
| 19954 | cosmografía | 1 |
| 19955 | cosió | 1 |
| 19956 | cosillas | 1 |
| 19957 | cosieron | 1 |
| 19958 | cosidos | 1 |
| 19959 | cosido | 1 |
| 19960 | cosidas | 1 |
| 19961 | cosida | 1 |
| 19962 | coserse | 1 |
| 19963 | coselete | 1 |
| 19964 | cosechas | 1 |
| 19965 | cose | 1 |
| 19966 | coscorrones | 1 |
| 19967 | corvo | 1 |
| 19968 | corvetas | 1 |
| 19969 | cortesísimo | 1 |
| 19970 | cortesísimamente | 1 |
| 19971 | cortesanía | 1 |
| 19972 | corten | 1 |
| 19973 | cortarlas | 1 |
| 19974 | cortaría | 1 |
| 19975 | cortares | 1 |
| 19976 | cortaré | 1 |
| 19977 | cortapisas | 1 |
| 19978 | cortamente | 1 |
| 19979 | cortadillo | 1 |
| 19980 | cortaban | 1 |
| 19981 | cortaba | 1 |
| 19982 | corroborarla | 1 |
| 19983 | corrobóranse | 1 |
| 19984 | corriste | 1 |
| 19985 | corrillo | 1 |
| 19986 | corrija | 1 |
| 19987 | corrige | 1 |
| 19988 | corriere | 1 |
| 19989 | corriera | 1 |
| 19990 | corridísimo | 1 |
| 19991 | corridica | 1 |
| 19992 | corrí | 1 |
| 19993 | correspondiesen | 1 |
| 19994 | correspondiese | 1 |
| 19995 | correspondiente | 1 |
| 19996 | correspondiéndoles | 1 |
| 19997 | correspondiendo | 1 |
| 19998 | correspondían | 1 |
| 19999 | correspondes | 1 |
| 20000 | corresponderos | 1 |
| 20001 | corresponderás | 1 |
| 20002 | corresponden | 1 |
| 20003 | correspondéis | 1 |
| 20004 | correspondas | 1 |
| 20005 | correspondan | 1 |
| 20006 | corres | 1 |
| 20007 | correrte | 1 |
| 20008 | correrían | 1 |
| 20009 | correosa | 1 |
| 20010 | correos | 1 |
| 20011 | correcto | 1 |
| 20012 | correas | 1 |
| 20013 | corras | 1 |
| 20014 | corrales | 1 |
| 20015 | corpus | 1 |
| 20016 | corpiños | 1 |
| 20017 | corónicas | 1 |
| 20018 | coronarte | 1 |
| 20019 | coronaron | 1 |
| 20020 | coronan | 1 |
| 20021 | coronadas | 1 |
| 20022 | coronaban | 1 |
| 20023 | corneja | 1 |
| 20024 | cornado | 1 |
| 20025 | cormano | 1 |
| 20026 | cormana | 1 |
| 20027 | corma | 1 |
| 20028 | corellas | 1 |
| 20029 | cordu | 1 |
| 20030 | cordones | 1 |
| 20031 | corderilla | 1 |
| 20032 | cordellate | 1 |
| 20033 | cordeles | 1 |
| 20034 | cordelejo | 1 |
| 20035 | corde | 1 |
| 20036 | cordal | 1 |
| 20037 | corcovada | 1 |
| 20038 | corchete | 1 |
| 20039 | corazoncillo | 1 |
| 20040 | coral | 1 |
| 20041 | coplitas | 1 |
| 20042 | copleros | 1 |
| 20043 | coplee | 1 |
| 20044 | copioso | 1 |
| 20045 | copia | 1 |
| 20046 | copete | 1 |
| 20047 | copa | 1 |
| 20048 | convites | 1 |
| 20049 | convite | 1 |
| 20050 | convirtiésemos | 1 |
| 20051 | convirtieron | 1 |
| 20052 | convirtiéndoseles | 1 |
| 20053 | conviértalas | 1 |
| 20054 | convierta | 1 |
| 20055 | convienen | 1 |
| 20056 | convidase | 1 |
| 20057 | convidaron | 1 |
| 20058 | convidándonos | 1 |
| 20059 | convidados | 1 |
| 20060 | convidador | 1 |
| 20061 | convidado | 1 |
| 20062 | conversaciones | 1 |
| 20063 | conversaba | 1 |
| 20064 | convenirles | 1 |
| 20065 | convenirle | 1 |
| 20066 | convenimos | 1 |
| 20067 | convenientes | 1 |
| 20068 | convenible | 1 |
| 20069 | convenencia | 1 |
| 20070 | convencido | 1 |
| 20071 | contumaz | 1 |
| 20072 | contreras | 1 |
| 20073 | contrato | 1 |
| 20074 | contratación | 1 |
| 20075 | contrastando | 1 |
| 20076 | contrastado | 1 |
| 20077 | contraseño | 1 |
| 20078 | contrarias | 1 |
| 20079 | contrapuntos | 1 |
| 20080 | contrapuestas | 1 |
| 20081 | contrapeso | 1 |
| 20082 | contramina | 1 |
| 20083 | contrahecho | 1 |
| 20084 | contrahacer | 1 |
| 20085 | contradiga | 1 |
| 20086 | contradición | 1 |
| 20087 | contradecirme | 1 |
| 20088 | contradecirlo | 1 |
| 20089 | contradecirle | 1 |
| 20090 | contradecirla | 1 |
| 20091 | contradecir | 1 |
| 20092 | contradecía | 1 |
| 20093 | contóselo | 1 |
| 20094 | contóle | 1 |
| 20095 | contóla | 1 |
| 20096 | continuó | 1 |
| 20097 | continuar | 1 |
| 20098 | continuamente | 1 |
| 20099 | continuación | 1 |
| 20100 | continos | 1 |
| 20101 | continiéndose | 1 |
| 20102 | contingibles | 1 |
| 20103 | contingente | 1 |
| 20104 | contingencia | 1 |
| 20105 | continentes | 1 |
| 20106 | contestura | 1 |
| 20107 | contesto | 1 |
| 20108 | contestas | 1 |
| 20109 | contentísimas | 1 |
| 20110 | contentísima | 1 |
| 20111 | contentasen | 1 |
| 20112 | contentarme | 1 |
| 20113 | contentarle | 1 |
| 20114 | contentare | 1 |
| 20115 | contentándose | 1 |
| 20116 | contentan | 1 |
| 20117 | contentamos | 1 |
| 20118 | contentalle | 1 |
| 20119 | conteniéndome | 1 |
| 20120 | contengo | 1 |
| 20121 | contenga | 1 |
| 20122 | contenerse | 1 |
| 20123 | contener | 1 |
| 20124 | contendré | 1 |
| 20125 | contendiesen | 1 |
| 20126 | contendieron | 1 |
| 20127 | contempló | 1 |
| 20128 | contemplo | 1 |
| 20129 | contemplábase | 1 |
| 20130 | contemplaba | 1 |
| 20131 | contempla | 1 |
| 20132 | contéle | 1 |
| 20133 | contéis | 1 |
| 20134 | contaste | 1 |
| 20135 | contártela | 1 |
| 20136 | contarte | 1 |
| 20137 | contároslo | 1 |
| 20138 | contaros | 1 |
| 20139 | contáronle | 1 |
| 20140 | contarnos | 1 |
| 20141 | contármelo | 1 |
| 20142 | contarlos | 1 |
| 20143 | contarlas | 1 |
| 20144 | contarás | 1 |
| 20145 | contaran | 1 |
| 20146 | contándoseles | 1 |
| 20147 | contándonos | 1 |
| 20148 | contándolos | 1 |
| 20149 | contándole | 1 |
| 20150 | contaminado | 1 |
| 20151 | contalle | 1 |
| 20152 | contalla | 1 |
| 20153 | contáis | 1 |
| 20154 | contagiosa | 1 |
| 20155 | contagio | 1 |
| 20156 | contador | 1 |
| 20157 | contadnos | 1 |
| 20158 | contadas | 1 |
| 20159 | contábamos | 1 |
| 20160 | consumió | 1 |
| 20161 | consumiendo | 1 |
| 20162 | consumidos | 1 |
| 20163 | consumidor | 1 |
| 20164 | consumido | 1 |
| 20165 | consumían | 1 |
| 20166 | consuman | 1 |
| 20167 | consumado | 1 |
| 20168 | consumadamente | 1 |
| 20169 | consulta | 1 |
| 20170 | consuélome | 1 |
| 20171 | consuele | 1 |
| 20172 | consuélase | 1 |
| 20173 | consuegro | 1 |
| 20174 | construyéndole | 1 |
| 20175 | constituidos | 1 |
| 20176 | constituciones | 1 |
| 20177 | conste | 1 |
| 20178 | consorcio | 1 |
| 20179 | consolóle | 1 |
| 20180 | consolasen | 1 |
| 20181 | consolase | 1 |
| 20182 | consolarme | 1 |
| 20183 | consolarla | 1 |
| 20184 | consolaré | 1 |
| 20185 | consolando | 1 |
| 20186 | consolación | 1 |
| 20187 | consolábale | 1 |
| 20188 | consistir | 1 |
| 20189 | consistiese | 1 |
| 20190 | consistan | 1 |
| 20191 | consintiría | 1 |
| 20192 | consintiese | 1 |
| 20193 | consintieron | 1 |
| 20194 | consiga | 1 |
| 20195 | consienta | 1 |
| 20196 | consideró | 1 |
| 20197 | consideren | 1 |
| 20198 | considerasen | 1 |
| 20199 | considerándole | 1 |
| 20200 | considérame | 1 |
| 20201 | considérale | 1 |
| 20202 | consideráis | 1 |
| 20203 | conservo | 1 |
| 20204 | conservarla | 1 |
| 20205 | conservándome | 1 |
| 20206 | conservando | 1 |
| 20207 | consentirlo | 1 |
| 20208 | consentiría | 1 |
| 20209 | consentirán | 1 |
| 20210 | consentirá | 1 |
| 20211 | consentimos | 1 |
| 20212 | consentían | 1 |
| 20213 | consentí | 1 |
| 20214 | consejeros | 1 |
| 20215 | conseguirse | 1 |
| 20216 | conseguirle | 1 |
| 20217 | conseguido | 1 |
| 20218 | consecuencias | 1 |
| 20219 | consagro | 1 |
| 20220 | consabidores | 1 |
| 20221 | conquisto | 1 |
| 20222 | conquistaron | 1 |
| 20223 | conquistar | 1 |
| 20224 | conquistados | 1 |
| 20225 | conozcamos | 1 |
| 20226 | conozan | 1 |
| 20227 | conorte | 1 |
| 20228 | conocístela | 1 |
| 20229 | conocióme | 1 |
| 20230 | conociólos | 1 |
| 20231 | conocióle | 1 |
| 20232 | conocimos | 1 |
| 20233 | conocíle | 1 |
| 20234 | conociésemos | 1 |
| 20235 | conociésedes | 1 |
| 20236 | conociéronle | 1 |
| 20237 | conocieran | 1 |
| 20238 | conociéndole | 1 |
| 20239 | conocíamos | 1 |
| 20240 | conocerse | 1 |
| 20241 | conocerme | 1 |
| 20242 | conocerlos | 1 |
| 20243 | conocerla | 1 |
| 20244 | conocerán | 1 |
| 20245 | conocerá | 1 |
| 20246 | conmovió | 1 |
| 20247 | conmovido | 1 |
| 20248 | conllevador | 1 |
| 20249 | conjurarte | 1 |
| 20250 | conjurarse | 1 |
| 20251 | conjurarme | 1 |
| 20252 | conjeturo | 1 |
| 20253 | conjeturaron | 1 |
| 20254 | conjeturando | 1 |
| 20255 | conjeturamos | 1 |
| 20256 | congratulándose | 1 |
| 20257 | congojóse | 1 |
| 20258 | congojosa | 1 |
| 20259 | congoje | 1 |
| 20260 | congojarte | 1 |
| 20261 | congojadísima | 1 |
| 20262 | congojaban | 1 |
| 20263 | confutación | 1 |
| 20264 | confundo | 1 |
| 20265 | confundir | 1 |
| 20266 | confundidas | 1 |
| 20267 | confundan | 1 |
| 20268 | confunda | 1 |
| 20269 | confortativo | 1 |
| 20270 | confortativas | 1 |
| 20271 | conformidad | 1 |
| 20272 | conformaba | 1 |
| 20273 | conflito | 1 |
| 20274 | confiscación | 1 |
| 20275 | confirmóse | 1 |
| 20276 | confirmólo | 1 |
| 20277 | confirmóle | 1 |
| 20278 | confírmole | 1 |
| 20279 | confirme | 1 |
| 20280 | confirmase | 1 |
| 20281 | confirmará | 1 |
| 20282 | confirmada | 1 |
| 20283 | confirma | 1 |
| 20284 | confinantes | 1 |
| 20285 | confieses | 1 |
| 20286 | confiesen | 1 |
| 20287 | confíese | 1 |
| 20288 | confiar | 1 |
| 20289 | confiados | 1 |
| 20290 | confiad | 1 |
| 20291 | confía | 1 |
| 20292 | confesóle | 1 |
| 20293 | confesase | 1 |
| 20294 | confesarse | 1 |
| 20295 | confesarme | 1 |
| 20296 | confesarle | 1 |
| 20297 | confesaría | 1 |
| 20298 | confesaremos | 1 |
| 20299 | confesando | 1 |
| 20300 | confesad | 1 |
| 20301 | condutor | 1 |
| 20302 | condumio | 1 |
| 20303 | conducís | 1 |
| 20304 | conducirle | 1 |
| 20305 | conducidas | 1 |
| 20306 | conducida | 1 |
| 20307 | condolíme | 1 |
| 20308 | condoliéndose | 1 |
| 20309 | condolidos | 1 |
| 20310 | condolido | 1 |
| 20311 | condesil | 1 |
| 20312 | condescender | 1 |
| 20313 | condenaron | 1 |
| 20314 | condenarme | 1 |
| 20315 | condenarlos | 1 |
| 20316 | condenarle | 1 |
| 20317 | condenando | 1 |
| 20318 | condenan | 1 |
| 20319 | condenada | 1 |
| 20320 | condecendió | 1 |
| 20321 | condecender | 1 |
| 20322 | condecenció | 1 |
| 20323 | condazo | 1 |
| 20324 | condados | 1 |
| 20325 | concordarnos | 1 |
| 20326 | concordancia | 1 |
| 20327 | concluyóse | 1 |
| 20328 | concluyó | 1 |
| 20329 | concluyo | 1 |
| 20330 | concluyesen | 1 |
| 20331 | concluyente | 1 |
| 20332 | concluyas | 1 |
| 20333 | concluyamos | 1 |
| 20334 | concluida | 1 |
| 20335 | concluían | 1 |
| 20336 | concilio | 1 |
| 20337 | concierte | 1 |
| 20338 | conciértase | 1 |
| 20339 | conciencias | 1 |
| 20340 | concibe | 1 |
| 20341 | concertáronse | 1 |
| 20342 | concertar | 1 |
| 20343 | concertadamente | 1 |
| 20344 | concertaban | 1 |
| 20345 | concejil | 1 |
| 20346 | concedo | 1 |
| 20347 | concedióselo | 1 |
| 20348 | concedieron | 1 |
| 20349 | concediera | 1 |
| 20350 | concedían | 1 |
| 20351 | concedérsele | 1 |
| 20352 | concederle | 1 |
| 20353 | concebido | 1 |
| 20354 | concebía | 1 |
| 20355 | concebí | 1 |
| 20356 | concavidades | 1 |
| 20357 | comutativa | 1 |
| 20358 | comuniquemos | 1 |
| 20359 | comunidades | 1 |
| 20360 | comunidad | 1 |
| 20361 | comunicase | 1 |
| 20362 | comunicaré | 1 |
| 20363 | comunicándolo | 1 |
| 20364 | comunicando | 1 |
| 20365 | comunican | 1 |
| 20366 | comunicamos | 1 |
| 20367 | comunicallo | 1 |
| 20368 | comunicalle | 1 |
| 20369 | comunicada | 1 |
| 20370 | comunicación | 1 |
| 20371 | comunes | 1 |
| 20372 | compusiesen | 1 |
| 20373 | compusiese | 1 |
| 20374 | compusieron | 1 |
| 20375 | compungióse | 1 |
| 20376 | compuertas | 1 |
| 20377 | compres | 1 |
| 20378 | compréis | 1 |
| 20379 | comprehendo | 1 |
| 20380 | compraron | 1 |
| 20381 | comprarían | 1 |
| 20382 | compraría | 1 |
| 20383 | compraré | 1 |
| 20384 | comprara | 1 |
| 20385 | comprando | 1 |
| 20386 | compran | 1 |
| 20387 | comprados | 1 |
| 20388 | compradas | 1 |
| 20389 | componerla | 1 |
| 20390 | compondré | 1 |
| 20391 | compondrá | 1 |
| 20392 | compo | 1 |
| 20393 | compluto | 1 |
| 20394 | complacerte | 1 |
| 20395 | complacéis | 1 |
| 20396 | competientes | 1 |
| 20397 | competencias | 1 |
| 20398 | compelidos | 1 |
| 20399 | compelía | 1 |
| 20400 | compatriotos | 1 |
| 20401 | compatriote | 1 |
| 20402 | compasiones | 1 |
| 20403 | comparéis | 1 |
| 20404 | compararse | 1 |
| 20405 | compararlas | 1 |
| 20406 | compararla | 1 |
| 20407 | comparándolos | 1 |
| 20408 | comparan | 1 |
| 20409 | comparaban | 1 |
| 20410 | compadres | 1 |
| 20411 | comorín | 1 |
| 20412 | cómodamente | 1 |
| 20413 | comimos | 1 |
| 20414 | comieras | 1 |
| 20415 | comiéramos | 1 |
| 20416 | comiera | 1 |
| 20417 | comidos | 1 |
| 20418 | cómico | 1 |
| 20419 | comíamos | 1 |
| 20420 | comí | 1 |
| 20421 | cometieron | 1 |
| 20422 | cometida | 1 |
| 20423 | cometerá | 1 |
| 20424 | cometen | 1 |
| 20425 | comerse | 1 |
| 20426 | comerás | 1 |
| 20427 | comerá | 1 |
| 20428 | comenzóle | 1 |
| 20429 | comenzaremos | 1 |
| 20430 | comenzará | 1 |
| 20431 | comenzara | 1 |
| 20432 | comenzáis | 1 |
| 20433 | comenzados | 1 |
| 20434 | comenzada | 1 |
| 20435 | comenzad | 1 |
| 20436 | comenzaban | 1 |
| 20437 | comento | 1 |
| 20438 | comentarios | 1 |
| 20439 | comendador | 1 |
| 20440 | comencemos | 1 |
| 20441 | comed | 1 |
| 20442 | combatistes | 1 |
| 20443 | combatir | 1 |
| 20444 | combatiente | 1 |
| 20445 | combatiéndose | 1 |
| 20446 | combatidos | 1 |
| 20447 | combatían | 1 |
| 20448 | combaten | 1 |
| 20449 | combate | 1 |
| 20450 | comarca | 1 |
| 20451 | comáis | 1 |
| 20452 | coluros | 1 |
| 20453 | columbró | 1 |
| 20454 | columbro | 1 |
| 20455 | colorastes | 1 |
| 20456 | colorada | 1 |
| 20457 | colonas | 1 |
| 20458 | colodra | 1 |
| 20459 | colocar | 1 |
| 20460 | colmó | 1 |
| 20461 | colmilludo | 1 |
| 20462 | colmillos | 1 |
| 20463 | colmillo | 1 |
| 20464 | cólmese | 1 |
| 20465 | colmen | 1 |
| 20466 | colmados | 1 |
| 20467 | colmado | 1 |
| 20468 | colmadas | 1 |
| 20469 | colmada | 1 |
| 20470 | collares | 1 |
| 20471 | colijo | 1 |
| 20472 | coligieron | 1 |
| 20473 | colige | 1 |
| 20474 | colgarle | 1 |
| 20475 | colgar | 1 |
| 20476 | colgándoos | 1 |
| 20477 | colgaban | 1 |
| 20478 | colérica | 1 |
| 20479 | colegirse | 1 |
| 20480 | colegido | 1 |
| 20481 | colegial | 1 |
| 20482 | colegí | 1 |
| 20483 | colchón | 1 |
| 20484 | colchas | 1 |
| 20485 | colchado | 1 |
| 20486 | colar | 1 |
| 20487 | colambre | 1 |
| 20488 | cojos | 1 |
| 20489 | cojeéis | 1 |
| 20490 | cojear | 1 |
| 20491 | cojeaba | 1 |
| 20492 | coima | 1 |
| 20493 | cohonda | 1 |
| 20494 | cohetes | 1 |
| 20495 | cohechos | 1 |
| 20496 | cohecharme | 1 |
| 20497 | cohechan | 1 |
| 20498 | cogitationes | 1 |
| 20499 | cogióle | 1 |
| 20500 | cogióla | 1 |
| 20501 | cogiese | 1 |
| 20502 | cogiéronlos | 1 |
| 20503 | cogiéronle | 1 |
| 20504 | cogieron | 1 |
| 20505 | cogiera | 1 |
| 20506 | cogiéndole | 1 |
| 20507 | cogidos | 1 |
| 20508 | cogerla | 1 |
| 20509 | cogeré | 1 |
| 20510 | cogerá | 1 |
| 20511 | cógele | 1 |
| 20512 | cofias | 1 |
| 20513 | cofadría | 1 |
| 20514 | codiciosa | 1 |
| 20515 | codicio | 1 |
| 20516 | codiciada | 1 |
| 20517 | cocos | 1 |
| 20518 | cocodrilo | 1 |
| 20519 | cocineras | 1 |
| 20520 | cociéndolos | 1 |
| 20521 | coches | 1 |
| 20522 | cobres | 1 |
| 20523 | cobraría | 1 |
| 20524 | cobraremos | 1 |
| 20525 | cobraré | 1 |
| 20526 | cobraba | 1 |
| 20527 | cobija | 1 |
| 20528 | cobi | 1 |
| 20529 | clíticas | 1 |
| 20530 | climas | 1 |
| 20531 | clima | 1 |
| 20532 | clerical | 1 |
| 20533 | clenardo | 1 |
| 20534 | clemente | 1 |
| 20535 | clemencia | 1 |
| 20536 | clavósele | 1 |
| 20537 | clavos | 1 |
| 20538 | clavo | 1 |
| 20539 | claves | 1 |
| 20540 | claven | 1 |
| 20541 | clavásedes | 1 |
| 20542 | clavaron | 1 |
| 20543 | clavado | 1 |
| 20544 | clavadas | 1 |
| 20545 | clava | 1 |
| 20546 | clauquel | 1 |
| 20547 | claroescuro | 1 |
| 20548 | clarísimos | 1 |
| 20549 | clarísima | 1 |
| 20550 | claridiana | 1 |
| 20551 | cla | 1 |
| 20552 | civil | 1 |
| 20553 | citas | 1 |
| 20554 | citan | 1 |
| 20555 | citación | 1 |
| 20556 | cismáticos | 1 |
| 20557 | cirujano | 1 |
| 20558 | cirimonias | 1 |
| 20559 | ciriales | 1 |
| 20560 | circustancias | 1 |
| 20561 | circunspecto | 1 |
| 20562 | círculos | 1 |
| 20563 | círculo | 1 |
| 20564 | circuito | 1 |
| 20565 | circe | 1 |
| 20566 | cipiones | 1 |
| 20567 | cipión | 1 |
| 20568 | ciñó | 1 |
| 20569 | ciñiéndole | 1 |
| 20570 | ciñese | 1 |
| 20571 | ciñen | 1 |
| 20572 | ciñe | 1 |
| 20573 | cinto | 1 |
| 20574 | cínico | 1 |
| 20575 | cinchar | 1 |
| 20576 | cincha | 1 |
| 20577 | cimitarra | 1 |
| 20578 | cimientos | 1 |
| 20579 | cimenterios | 1 |
| 20580 | cigüeñas | 1 |
| 20581 | cifró | 1 |
| 20582 | cifras | 1 |
| 20583 | cifrado | 1 |
| 20584 | cifradas | 1 |
| 20585 | ciérrese | 1 |
| 20586 | cientos | 1 |
| 20587 | ciegue | 1 |
| 20588 | cides | 1 |
| 20589 | cicatrices | 1 |
| 20590 | chuzo | 1 |
| 20591 | churumbelas | 1 |
| 20592 | churrillera | 1 |
| 20593 | chupados | 1 |
| 20594 | chufeta | 1 |
| 20595 | christus | 1 |
| 20596 | choquezuelas | 1 |
| 20597 | chocarrero | 1 |
| 20598 | chismosas | 1 |
| 20599 | chirrío | 1 |
| 20600 | chinesca | 1 |
| 20601 | chinelas | 1 |
| 20602 | chinela | 1 |
| 20603 | chinche | 1 |
| 20604 | chilladores | 1 |
| 20605 | chicoria | 1 |
| 20606 | chico | 1 |
| 20607 | chichones | 1 |
| 20608 | chica | 1 |
| 20609 | charní | 1 |
| 20610 | chapiteles | 1 |
| 20611 | chapines | 1 |
| 20612 | chapín | 1 |
| 20613 | chapas | 1 |
| 20614 | chapada | 1 |
| 20615 | chanto | 1 |
| 20616 | chancillerías | 1 |
| 20617 | chamuscados | 1 |
| 20618 | chamuscado | 1 |
| 20619 | chamelote | 1 |
| 20620 | cevil | 1 |
| 20621 | cesarían | 1 |
| 20622 | cesaría | 1 |
| 20623 | césares | 1 |
| 20624 | cesara | 1 |
| 20625 | cesan | 1 |
| 20626 | cesado | 1 |
| 20627 | cervino | 1 |
| 20628 | cervices | 1 |
| 20629 | cervellón | 1 |
| 20630 | certísimos | 1 |
| 20631 | certísimo | 1 |
| 20632 | certísima | 1 |
| 20633 | certificarse | 1 |
| 20634 | certificaron | 1 |
| 20635 | certificarme | 1 |
| 20636 | certificándose | 1 |
| 20637 | certificándoles | 1 |
| 20638 | certificado | 1 |
| 20639 | certeza | 1 |
| 20640 | cerróse | 1 |
| 20641 | cerremos | 1 |
| 20642 | cerrasen | 1 |
| 20643 | cerrase | 1 |
| 20644 | cerras | 1 |
| 20645 | cerrarlos | 1 |
| 20646 | cerrarla | 1 |
| 20647 | cerrarán | 1 |
| 20648 | cerrara | 1 |
| 20649 | cerraduras | 1 |
| 20650 | cerradura | 1 |
| 20651 | cerraban | 1 |
| 20652 | cerraba | 1 |
| 20653 | cernícalo | 1 |
| 20654 | cerimonia | 1 |
| 20655 | ceremonial | 1 |
| 20656 | cerdosa | 1 |
| 20657 | cerda | 1 |
| 20658 | cercenara | 1 |
| 20659 | cercano | 1 |
| 20660 | cercado | 1 |
| 20661 | cerbatana | 1 |
| 20662 | cepos | 1 |
| 20663 | cepas | 1 |
| 20664 | ceñirle | 1 |
| 20665 | ceñíale | 1 |
| 20666 | ceñía | 1 |
| 20667 | censurar | 1 |
| 20668 | censurando | 1 |
| 20669 | censuradores | 1 |
| 20670 | censura | 1 |
| 20671 | censos | 1 |
| 20672 | censo | 1 |
| 20673 | cenóse | 1 |
| 20674 | ceniza | 1 |
| 20675 | cenemos | 1 |
| 20676 | cencerruna | 1 |
| 20677 | cencerro | 1 |
| 20678 | cencerril | 1 |
| 20679 | cenase | 1 |
| 20680 | cenas | 1 |
| 20681 | cenaréis | 1 |
| 20682 | cenará | 1 |
| 20683 | cenamos | 1 |
| 20684 | cenaban | 1 |
| 20685 | celsitud | 1 |
| 20686 | celillos | 1 |
| 20687 | celestiales | 1 |
| 20688 | celesti | 1 |
| 20689 | celeste | 1 |
| 20690 | celebros | 1 |
| 20691 | celebrarse | 1 |
| 20692 | celebraron | 1 |
| 20693 | celebrarla | 1 |
| 20694 | celebraré | 1 |
| 20695 | celebrarán | 1 |
| 20696 | celebrándote | 1 |
| 20697 | celebrándola | 1 |
| 20698 | celebrados | 1 |
| 20699 | celebraba | 1 |
| 20700 | celebra | 1 |
| 20701 | celebérrimos | 1 |
| 20702 | celadas | 1 |
| 20703 | celaba | 1 |
| 20704 | cejijunta | 1 |
| 20705 | ceguera | 1 |
| 20706 | ceguedad | 1 |
| 20707 | cegaron | 1 |
| 20708 | cegara | 1 |
| 20709 | cedulilla | 1 |
| 20710 | cedazo | 1 |
| 20711 | cecina | 1 |
| 20712 | cecear | 1 |
| 20713 | ceca | 1 |
| 20714 | cebolluda | 1 |
| 20715 | cebarla | 1 |
| 20716 | cebar | 1 |
| 20717 | cebado | 1 |
| 20718 | ceba | 1 |
| 20719 | ce | 1 |
| 20720 | cazos | 1 |
| 20721 | cazoleros | 1 |
| 20722 | cazas | 1 |
| 20723 | cazarle | 1 |
| 20724 | cazando | 1 |
| 20725 | cazador | 1 |
| 20726 | cayo | 1 |
| 20727 | cayeran | 1 |
| 20728 | cayas | 1 |
| 20729 | cayan | 1 |
| 20730 | cayado | 1 |
| 20731 | caya | 1 |
| 20732 | caviloso | 1 |
| 20733 | cavial | 1 |
| 20734 | caverna | 1 |
| 20735 | cavase | 1 |
| 20736 | cavar | 1 |
| 20737 | cavaba | 1 |
| 20738 | cauto | 1 |
| 20739 | cautivó | 1 |
| 20740 | cautivarla | 1 |
| 20741 | cautivar | 1 |
| 20742 | cautivan | 1 |
| 20743 | cautivado | 1 |
| 20744 | cauterios | 1 |
| 20745 | cauterio | 1 |
| 20746 | causóme | 1 |
| 20747 | causarme | 1 |
| 20748 | causarán | 1 |
| 20749 | causara | 1 |
| 20750 | causan | 1 |
| 20751 | causadora | 1 |
| 20752 | causábanle | 1 |
| 20753 | caudalosos | 1 |
| 20754 | caudaloso | 1 |
| 20755 | catorceno | 1 |
| 20756 | catonianas | 1 |
| 20757 | catilina | 1 |
| 20758 | cátedras | 1 |
| 20759 | caté | 1 |
| 20760 | cátate | 1 |
| 20761 | catarros | 1 |
| 20762 | catarro | 1 |
| 20763 | catarriberas | 1 |
| 20764 | catarle | 1 |
| 20765 | catándole | 1 |
| 20766 | cataluña | 1 |
| 20767 | cátalo | 1 |
| 20768 | cataduras | 1 |
| 20769 | castrador | 1 |
| 20770 | cástor | 1 |
| 20771 | castor | 1 |
| 20772 | castizo | 1 |
| 20773 | castiza | 1 |
| 20774 | castíguese | 1 |
| 20775 | castiguen | 1 |
| 20776 | castigue | 1 |
| 20777 | castigó | 1 |
| 20778 | castigarnos | 1 |
| 20779 | castigarle | 1 |
| 20780 | castigaré | 1 |
| 20781 | castigándome | 1 |
| 20782 | castigando | 1 |
| 20783 | castígalos | 1 |
| 20784 | castigallos | 1 |
| 20785 | castiga | 1 |
| 20786 | castidad | 1 |
| 20787 | castamente | 1 |
| 20788 | caspa | 1 |
| 20789 | caseros | 1 |
| 20790 | casero | 1 |
| 20791 | casen | 1 |
| 20792 | casco | 1 |
| 20793 | cascabel | 1 |
| 20794 | casarnos | 1 |
| 20795 | casármela | 1 |
| 20796 | casarían | 1 |
| 20797 | casaría | 1 |
| 20798 | casárase | 1 |
| 20799 | casarás | 1 |
| 20800 | casaos | 1 |
| 20801 | casan | 1 |
| 20802 | casamos | 1 |
| 20803 | casamentero | 1 |
| 20804 | casadla | 1 |
| 20805 | cartones | 1 |
| 20806 | cartero | 1 |
| 20807 | carriola | 1 |
| 20808 | carrillo | 1 |
| 20809 | carril | 1 |
| 20810 | carricoche | 1 |
| 20811 | carreteros | 1 |
| 20812 | carpían | 1 |
| 20813 | caros | 1 |
| 20814 | carón | 1 |
| 20815 | carolea | 1 |
| 20816 | carnicerías | 1 |
| 20817 | carnestolendas | 1 |
| 20818 | carnazas | 1 |
| 20819 | carnal | 1 |
| 20820 | carmín | 1 |
| 20821 | carloto | 1 |
| 20822 | carlos | 1 |
| 20823 | carlo | 1 |
| 20824 | caritativas | 1 |
| 20825 | carirredondo | 1 |
| 20826 | carirredonda | 1 |
| 20827 | caricias | 1 |
| 20828 | caribdis | 1 |
| 20829 | cargues | 1 |
| 20830 | cargas | 1 |
| 20831 | cargarse | 1 |
| 20832 | cargando | 1 |
| 20833 | cargados | 1 |
| 20834 | cargaban | 1 |
| 20835 | careciere | 1 |
| 20836 | carecieran | 1 |
| 20837 | careciera | 1 |
| 20838 | careciendo | 1 |
| 20839 | carecería | 1 |
| 20840 | cardinales | 1 |
| 20841 | carcomida | 1 |
| 20842 | carcomen | 1 |
| 20843 | carcoma | 1 |
| 20844 | cárceles | 1 |
| 20845 | carcajona | 1 |
| 20846 | carcaj | 1 |
| 20847 | carbuncos | 1 |
| 20848 | carbón | 1 |
| 20849 | carátula | 1 |
| 20850 | caráteres | 1 |
| 20851 | caramillos | 1 |
| 20852 | caraculiambro | 1 |
| 20853 | carácteres | 1 |
| 20854 | caracteres | 1 |
| 20855 | capuz | 1 |
| 20856 | caput | 1 |
| 20857 | capullos | 1 |
| 20858 | capuchino | 1 |
| 20859 | captiva | 1 |
| 20860 | captar | 1 |
| 20861 | caprichoso | 1 |
| 20862 | capones | 1 |
| 20863 | capitanas | 1 |
| 20864 | capital | 1 |
| 20865 | capirotes | 1 |
| 20866 | caperu | 1 |
| 20867 | capellanes | 1 |
| 20868 | capataces | 1 |
| 20869 | capas | 1 |
| 20870 | caparum | 1 |
| 20871 | capacidad | 1 |
| 20872 | capachos | 1 |
| 20873 | cap | 1 |
| 20874 | cañutos | 1 |
| 20875 | cañutillos | 1 |
| 20876 | cañutillo | 1 |
| 20877 | cáñamo | 1 |
| 20878 | cantusado | 1 |
| 20879 | cantueso | 1 |
| 20880 | cantos | 1 |
| 20881 | cantores | 1 |
| 20882 | cantimploras | 1 |
| 20883 | cantillana | 1 |
| 20884 | cantes | 1 |
| 20885 | canterà | 1 |
| 20886 | cantasen | 1 |
| 20887 | cantas | 1 |
| 20888 | cantaron | 1 |
| 20889 | cantarillo | 1 |
| 20890 | cantares | 1 |
| 20891 | cantaré | 1 |
| 20892 | cantará | 1 |
| 20893 | cantara | 1 |
| 20894 | cantan | 1 |
| 20895 | cantados | 1 |
| 20896 | cantado | 1 |
| 20897 | cantadas | 1 |
| 20898 | cansóle | 1 |
| 20899 | cansé | 1 |
| 20900 | cansase | 1 |
| 20901 | cansas | 1 |
| 20902 | cansaros | 1 |
| 20903 | cansarme | 1 |
| 20904 | cansaran | 1 |
| 20905 | cansar | 1 |
| 20906 | cansan | 1 |
| 20907 | cansábanse | 1 |
| 20908 | cansaban | 1 |
| 20909 | cansaba | 1 |
| 20910 | canonizaron | 1 |
| 20911 | canonizar | 1 |
| 20912 | canonizan | 1 |
| 20913 | canonicato | 1 |
| 20914 | canísima | 1 |
| 20915 | canina | 1 |
| 20916 | canillas | 1 |
| 20917 | canequí | 1 |
| 20918 | canelones | 1 |
| 20919 | candiles | 1 |
| 20920 | candilazos | 1 |
| 20921 | candilazo | 1 |
| 20922 | candelillas | 1 |
| 20923 | candayesca | 1 |
| 20924 | candados | 1 |
| 20925 | cancionero | 1 |
| 20926 | canario | 1 |
| 20927 | cananea | 1 |
| 20928 | canales | 1 |
| 20929 | campeó | 1 |
| 20930 | campear | 1 |
| 20931 | campeador | 1 |
| 20932 | campeaba | 1 |
| 20933 | campañas | 1 |
| 20934 | camoes | 1 |
| 20935 | caminó | 1 |
| 20936 | caminen | 1 |
| 20937 | caminallas | 1 |
| 20938 | caminad | 1 |
| 20939 | caminábamos | 1 |
| 20940 | camellos | 1 |
| 20941 | cambroneras | 1 |
| 20942 | cambie | 1 |
| 20943 | cambiasen | 1 |
| 20944 | cambiado | 1 |
| 20945 | cambia | 1 |
| 20946 | camaranchones | 1 |
| 20947 | calzo | 1 |
| 20948 | calzarme | 1 |
| 20949 | calzándose | 1 |
| 20950 | calzadas | 1 |
| 20951 | calza | 1 |
| 20952 | calvatrueno | 1 |
| 20953 | calva | 1 |
| 20954 | calurosos | 1 |
| 20955 | calunien | 1 |
| 20956 | calumnias | 1 |
| 20957 | calumniado | 1 |
| 20958 | calores | 1 |
| 20959 | calóñenme | 1 |
| 20960 | caloñas | 1 |
| 20961 | calonjía | 1 |
| 20962 | caló | 1 |
| 20963 | calo | 1 |
| 20964 | callos | 1 |
| 20965 | callenta | 1 |
| 20966 | callen | 1 |
| 20967 | callarlos | 1 |
| 20968 | callarlo | 1 |
| 20969 | callandico | 1 |
| 20970 | callados | 1 |
| 20971 | calipso | 1 |
| 20972 | caliginosas | 1 |
| 20973 | calificados | 1 |
| 20974 | calificadas | 1 |
| 20975 | calientes | 1 |
| 20976 | calientan | 1 |
| 20977 | calienta | 1 |
| 20978 | caleta | 1 |
| 20979 | calenturas | 1 |
| 20980 | calentar | 1 |
| 20981 | calentaban | 1 |
| 20982 | calderadas | 1 |
| 20983 | caldeos | 1 |
| 20984 | caldeas | 1 |
| 20985 | calatrava | 1 |
| 20986 | calándose | 1 |
| 20987 | calaínos | 1 |
| 20988 | calado | 1 |
| 20989 | calabrés | 1 |
| 20990 | calabozos | 1 |
| 20991 | cajita | 1 |
| 20992 | caíste | 1 |
| 20993 | caerse | 1 |
| 20994 | caerán | 1 |
| 20995 | cádiz | 1 |
| 20996 | cadenilla | 1 |
| 20997 | cadells | 1 |
| 20998 | cadahalso | 1 |
| 20999 | cacique | 1 |
| 21000 | cachopines | 1 |
| 21001 | cachidiablo | 1 |
| 21002 | cabría | 1 |
| 21003 | cabrahígos | 1 |
| 21004 | cabrahígo | 1 |
| 21005 | cabos | 1 |
| 21006 | cabizbaja | 1 |
| 21007 | cabestros | 1 |
| 21008 | caballerote | 1 |
| 21009 | caballerizas | 1 |
| 21010 | caballeresco | 1 |
| 21011 | caballera | 1 |
| 21012 | caballe | 1 |
| 21013 | cabalgaba | 1 |
| 21014 | cabales | 1 |
| 21015 | caba | 1 |
| 21016 | ca | 1 |
| 21017 | buzcorona | 1 |
| 21018 | butrón | 1 |
| 21019 | bustamante | 1 |
| 21020 | busquemos | 1 |
| 21021 | buscó | 1 |
| 21022 | buscases | 1 |
| 21023 | buscasen | 1 |
| 21024 | buscásemos | 1 |
| 21025 | buscarse | 1 |
| 21026 | buscaros | 1 |
| 21027 | buscarnos | 1 |
| 21028 | buscarlos | 1 |
| 21029 | buscaremos | 1 |
| 21030 | buscaré | 1 |
| 21031 | buscará | 1 |
| 21032 | buscándoos | 1 |
| 21033 | buscándola | 1 |
| 21034 | buscallos | 1 |
| 21035 | buscador | 1 |
| 21036 | buscado | 1 |
| 21037 | buscadas | 1 |
| 21038 | buscada | 1 |
| 21039 | burlonas | 1 |
| 21040 | burlería | 1 |
| 21041 | burléis | 1 |
| 21042 | burle | 1 |
| 21043 | burlaron | 1 |
| 21044 | burlando | 1 |
| 21045 | burláis | 1 |
| 21046 | burladora | 1 |
| 21047 | burladas | 1 |
| 21048 | burlaban | 1 |
| 21049 | buriles | 1 |
| 21050 | burguillos | 1 |
| 21051 | burdos | 1 |
| 21052 | buñuelos | 1 |
| 21053 | bullón | 1 |
| 21054 | bullente | 1 |
| 21055 | bullendo | 1 |
| 21056 | buido | 1 |
| 21057 | buidas | 1 |
| 21058 | búho | 1 |
| 21059 | bufar | 1 |
| 21060 | bue | 1 |
| 21061 | bucólicas | 1 |
| 21062 | bucólica | 1 |
| 21063 | búcaros | 1 |
| 21064 | brutesco | 1 |
| 21065 | bruñidas | 1 |
| 21066 | brumó | 1 |
| 21067 | brumada | 1 |
| 21068 | bruja | 1 |
| 21069 | brotar | 1 |
| 21070 | brotaban | 1 |
| 21071 | bronco | 1 |
| 21072 | broncínea | 1 |
| 21073 | bronca | 1 |
| 21074 | brocabruno | 1 |
| 21075 | briznas | 1 |
| 21076 | brindis | 1 |
| 21077 | brindaba | 1 |
| 21078 | brincos | 1 |
| 21079 | brillando | 1 |
| 21080 | brida | 1 |
| 21081 | briareos | 1 |
| 21082 | briareo | 1 |
| 21083 | breva | 1 |
| 21084 | bretones | 1 |
| 21085 | bravatas | 1 |
| 21086 | bravamente | 1 |
| 21087 | brasero | 1 |
| 21088 | brasas | 1 |
| 21089 | brandabarbarán | 1 |
| 21090 | bramidos | 1 |
| 21091 | bramido | 1 |
| 21092 | bramando | 1 |
| 21093 | bramaba | 1 |
| 21094 | bragas | 1 |
| 21095 | bradamante | 1 |
| 21096 | bracmanes | 1 |
| 21097 | bra | 1 |
| 21098 | boyardo | 1 |
| 21099 | boto | 1 |
| 21100 | botillerías | 1 |
| 21101 | boticarios | 1 |
| 21102 | botica | 1 |
| 21103 | botecillo | 1 |
| 21104 | botanas | 1 |
| 21105 | bostezó | 1 |
| 21106 | bosqueril | 1 |
| 21107 | bosio | 1 |
| 21108 | boscán | 1 |
| 21109 | borrico | 1 |
| 21110 | borrega | 1 |
| 21111 | borrascas | 1 |
| 21112 | borraron | 1 |
| 21113 | borrarle | 1 |
| 21114 | borrarla | 1 |
| 21115 | borrarán | 1 |
| 21116 | borran | 1 |
| 21117 | borrado | 1 |
| 21118 | borrachos | 1 |
| 21119 | borracherías | 1 |
| 21120 | borraba | 1 |
| 21121 | borla | 1 |
| 21122 | bordo | 1 |
| 21123 | bordando | 1 |
| 21124 | borceguí | 1 |
| 21125 | borbón | 1 |
| 21126 | borbollones | 1 |
| 21127 | boquirru | 1 |
| 21128 | boquear | 1 |
| 21129 | bootes | 1 |
| 21130 | bonus | 1 |
| 21131 | bonitos | 1 |
| 21132 | bonísimos | 1 |
| 21133 | bonetero | 1 |
| 21134 | bolsón | 1 |
| 21135 | bolsilla | 1 |
| 21136 | bolsico | 1 |
| 21137 | bolsas | 1 |
| 21138 | bolonia | 1 |
| 21139 | bollo | 1 |
| 21140 | boliche | 1 |
| 21141 | bola | 1 |
| 21142 | bojiganga | 1 |
| 21143 | bogó | 1 |
| 21144 | bogase | 1 |
| 21145 | bogado | 1 |
| 21146 | bofetones | 1 |
| 21147 | bofetón | 1 |
| 21148 | bodoques | 1 |
| 21149 | bodegonero | 1 |
| 21150 | bodegón | 1 |
| 21151 | bodega | 1 |
| 21152 | bocina | 1 |
| 21153 | boberías | 1 |
| 21154 | bledos | 1 |
| 21155 | blasón | 1 |
| 21156 | blasfemo | 1 |
| 21157 | blas | 1 |
| 21158 | blandos | 1 |
| 21159 | blandones | 1 |
| 21160 | blandió | 1 |
| 21161 | blandiendo | 1 |
| 21162 | blandeando | 1 |
| 21163 | bizmarse | 1 |
| 21164 | bizmarle | 1 |
| 21165 | bizmalle | 1 |
| 21166 | bizmado | 1 |
| 21167 | bizco | 1 |
| 21168 | bizarras | 1 |
| 21169 | bisunto | 1 |
| 21170 | bisnieto | 1 |
| 21171 | bisabuelos | 1 |
| 21172 | birretillo | 1 |
| 21173 | birla | 1 |
| 21174 | bienvenida | 1 |
| 21175 | bienllegada | 1 |
| 21176 | bienintencionadamente | 1 |
| 21177 | bienhechor | 1 |
| 21178 | bienestar | 1 |
| 21179 | bienaya | 1 |
| 21180 | bienaventurada | 1 |
| 21181 | bién | 1 |
| 21182 | besugo | 1 |
| 21183 | besóla | 1 |
| 21184 | bésele | 1 |
| 21185 | beséis | 1 |
| 21186 | besé | 1 |
| 21187 | besárselos | 1 |
| 21188 | besársela | 1 |
| 21189 | besarse | 1 |
| 21190 | besarlas | 1 |
| 21191 | besándoselas | 1 |
| 21192 | besándola | 1 |
| 21193 | besamos | 1 |
| 21194 | besado | 1 |
| 21195 | besad | 1 |
| 21196 | berzas | 1 |
| 21197 | berrueca | 1 |
| 21198 | berrocal | 1 |
| 21199 | bermellón | 1 |
| 21200 | bermeja | 1 |
| 21201 | bergante | 1 |
| 21202 | berenjeneros | 1 |
| 21203 | berenjenas | 1 |
| 21204 | benitos | 1 |
| 21205 | benigno | 1 |
| 21206 | benevolencias | 1 |
| 21207 | benditísimo | 1 |
| 21208 | benditísima | 1 |
| 21209 | benditas | 1 |
| 21210 | bendijo | 1 |
| 21211 | bendigo | 1 |
| 21212 | bendeciré | 1 |
| 21213 | bendecía | 1 |
| 21214 | benalcázar | 1 |
| 21215 | belorofonte | 1 |
| 21216 | belona | 1 |
| 21217 | bello | 1 |
| 21218 | bellacuelo | 1 |
| 21219 | bellaconazo | 1 |
| 21220 | bellacón | 1 |
| 21221 | belitre | 1 |
| 21222 | belisardas | 1 |
| 21223 | belicosos | 1 |
| 21224 | bélicos | 1 |
| 21225 | becoquín | 1 |
| 21226 | beca | 1 |
| 21227 | bebo | 1 |
| 21228 | bebiere | 1 |
| 21229 | bebidos | 1 |
| 21230 | bebidas | 1 |
| 21231 | bebíase | 1 |
| 21232 | bebían | 1 |
| 21233 | bebí | 1 |
| 21234 | beberé | 1 |
| 21235 | bebedor | 1 |
| 21236 | bebed | 1 |
| 21237 | beatificaron | 1 |
| 21238 | bazán | 1 |
| 21239 | baza | 1 |
| 21240 | bayarte | 1 |
| 21241 | bayardo | 1 |
| 21242 | bautizar | 1 |
| 21243 | bautista | 1 |
| 21244 | bautice | 1 |
| 21245 | bausanes | 1 |
| 21246 | batir | 1 |
| 21247 | batido | 1 |
| 21248 | batería | 1 |
| 21249 | batel | 1 |
| 21250 | bate | 1 |
| 21251 | batanee | 1 |
| 21252 | batanado | 1 |
| 21253 | batallar | 1 |
| 21254 | basura | 1 |
| 21255 | basto | 1 |
| 21256 | bastimento | 1 |
| 21257 | bastecida | 1 |
| 21258 | baste | 1 |
| 21259 | bastaros | 1 |
| 21260 | bastare | 1 |
| 21261 | bastarda | 1 |
| 21262 | bastaran | 1 |
| 21263 | bastaráme | 1 |
| 21264 | bastar | 1 |
| 21265 | bastantísima | 1 |
| 21266 | bastantemente | 1 |
| 21267 | bástale | 1 |
| 21268 | bastaban | 1 |
| 21269 | basilea | 1 |
| 21270 | bascas | 1 |
| 21271 | basas | 1 |
| 21272 | barroso | 1 |
| 21273 | barriles | 1 |
| 21274 | barrían | 1 |
| 21275 | barrer | 1 |
| 21276 | barrenó | 1 |
| 21277 | barraganía | 1 |
| 21278 | baronías | 1 |
| 21279 | barnizada | 1 |
| 21280 | barcino | 1 |
| 21281 | barcadas | 1 |
| 21282 | barbudo | 1 |
| 21283 | barbitaheño | 1 |
| 21284 | barbiponiente | 1 |
| 21285 | barbilucio | 1 |
| 21286 | barbería | 1 |
| 21287 | barbera | 1 |
| 21288 | barbecho | 1 |
| 21289 | barbarlas | 1 |
| 21290 | bárbara | 1 |
| 21291 | barbadas | 1 |
| 21292 | báratro | 1 |
| 21293 | baratario | 1 |
| 21294 | barajan | 1 |
| 21295 | baptizalla | 1 |
| 21296 | baptizada | 1 |
| 21297 | baños | 1 |
| 21298 | bañarse | 1 |
| 21299 | bañaron | 1 |
| 21300 | bañarle | 1 |
| 21301 | bañares | 1 |
| 21302 | bañará | 1 |
| 21303 | bañándose | 1 |
| 21304 | bañan | 1 |
| 21305 | bañados | 1 |
| 21306 | bañado | 1 |
| 21307 | bañadas | 1 |
| 21308 | bandos | 1 |
| 21309 | bandines | 1 |
| 21310 | bamboleas | 1 |
| 21311 | balvastro | 1 |
| 21312 | ballenatos | 1 |
| 21313 | balidos | 1 |
| 21314 | baldovinos | 1 |
| 21315 | baldones | 1 |
| 21316 | balbastro | 1 |
| 21317 | balazo | 1 |
| 21318 | balas | 1 |
| 21319 | baladros | 1 |
| 21320 | baladro | 1 |
| 21321 | bajezas | 1 |
| 21322 | bajas | 1 |
| 21323 | bajarla | 1 |
| 21324 | bajara | 1 |
| 21325 | bajándose | 1 |
| 21326 | bajando | 1 |
| 21327 | bajan | 1 |
| 21328 | bajado | 1 |
| 21329 | bajada | 1 |
| 21330 | bajábale | 1 |
| 21331 | bailarines | 1 |
| 21332 | bailarín | 1 |
| 21333 | bailaré | 1 |
| 21334 | bailadores | 1 |
| 21335 | bailadoras | 1 |
| 21336 | baila | 1 |
| 21337 | bagajes | 1 |
| 21338 | badulaques | 1 |
| 21339 | badeas | 1 |
| 21340 | baciyelmo | 1 |
| 21341 | bachilleres | 1 |
| 21342 | bachillerada | 1 |
| 21343 | bachillear | 1 |
| 21344 | babie | 1 |
| 21345 | babera | 1 |
| 21346 | babazón | 1 |
| 21347 | azumbres | 1 |
| 21348 | azumbre | 1 |
| 21349 | azpetia | 1 |
| 21350 | azotesca | 1 |
| 21351 | azótate | 1 |
| 21352 | azotase | 1 |
| 21353 | azotarte | 1 |
| 21354 | azotaron | 1 |
| 21355 | azotarle | 1 |
| 21356 | azótanme | 1 |
| 21357 | azotan | 1 |
| 21358 | azotaina | 1 |
| 21359 | azota | 1 |
| 21360 | azoguejo | 1 |
| 21361 | azcona | 1 |
| 21362 | azar | 1 |
| 21363 | azán | 1 |
| 21364 | azadón | 1 |
| 21365 | azacán | 1 |
| 21366 | ayuso | 1 |
| 21367 | ayuntamiento | 1 |
| 21368 | ayuntados | 1 |
| 21369 | ayunque | 1 |
| 21370 | ayuno | 1 |
| 21371 | ayunase | 1 |
| 21372 | ayúdome | 1 |
| 21373 | ayudóle | 1 |
| 21374 | ayudes | 1 |
| 21375 | ayudéis | 1 |
| 21376 | ayudarte | 1 |
| 21377 | ayudarse | 1 |
| 21378 | ayudaros | 1 |
| 21379 | ayudáronle | 1 |
| 21380 | ayudaron | 1 |
| 21381 | ayudarles | 1 |
| 21382 | ayudaría | 1 |
| 21383 | ayudaremos | 1 |
| 21384 | ayudare | 1 |
| 21385 | ayudaran | 1 |
| 21386 | ayudándoos | 1 |
| 21387 | ayudador | 1 |
| 21388 | ayudábala | 1 |
| 21389 | avivo | 1 |
| 21390 | avives | 1 |
| 21391 | avive | 1 |
| 21392 | avivado | 1 |
| 21393 | avivaban | 1 |
| 21394 | avispas | 1 |
| 21395 | avísote | 1 |
| 21396 | avísenme | 1 |
| 21397 | avise | 1 |
| 21398 | avisasen | 1 |
| 21399 | avisásemos | 1 |
| 21400 | avisarte | 1 |
| 21401 | avisaría | 1 |
| 21402 | avisaréte | 1 |
| 21403 | avisándome | 1 |
| 21404 | avisando | 1 |
| 21405 | avisadas | 1 |
| 21406 | avisada | 1 |
| 21407 | ávila | 1 |
| 21408 | avieso | 1 |
| 21409 | aviesas | 1 |
| 21410 | averiguo | 1 |
| 21411 | averigüen | 1 |
| 21412 | averigüéle | 1 |
| 21413 | averiguase | 1 |
| 21414 | averiguarse | 1 |
| 21415 | averiguare | 1 |
| 21416 | averiguallo | 1 |
| 21417 | averiguadas | 1 |
| 21418 | averiguaciones | 1 |
| 21419 | avergonzados | 1 |
| 21420 | avergonzada | 1 |
| 21421 | aventureras | 1 |
| 21422 | aventurera | 1 |
| 21423 | aventuréis | 1 |
| 21424 | aventuré | 1 |
| 21425 | aventure | 1 |
| 21426 | aventurarlo | 1 |
| 21427 | aventuraría | 1 |
| 21428 | aventurar | 1 |
| 21429 | aventurándote | 1 |
| 21430 | aventurando | 1 |
| 21431 | aventurado | 1 |
| 21432 | aventuraba | 1 |
| 21433 | aventu | 1 |
| 21434 | aventajase | 1 |
| 21435 | aventajaron | 1 |
| 21436 | aventajarán | 1 |
| 21437 | aventajará | 1 |
| 21438 | aventajado | 1 |
| 21439 | aventajada | 1 |
| 21440 | aventajaban | 1 |
| 21441 | avenir | 1 |
| 21442 | avenga | 1 |
| 21443 | avendría | 1 |
| 21444 | avendremos | 1 |
| 21445 | avendré | 1 |
| 21446 | avellaneda | 1 |
| 21447 | avellanadas | 1 |
| 21448 | avellanada | 1 |
| 21449 | avecitas | 1 |
| 21450 | avasallen | 1 |
| 21451 | avasallase | 1 |
| 21452 | avasallara | 1 |
| 21453 | avasallado | 1 |
| 21454 | avariento | 1 |
| 21455 | autos | 1 |
| 21456 | autorizo | 1 |
| 21457 | autorizada | 1 |
| 21458 | autorice | 1 |
| 21459 | auténtico | 1 |
| 21460 | auténticamente | 1 |
| 21461 | austríada | 1 |
| 21462 | ausentasen | 1 |
| 21463 | ausentase | 1 |
| 21464 | ausentas | 1 |
| 21465 | ausentádose | 1 |
| 21466 | auro | 1 |
| 21467 | aumentó | 1 |
| 21468 | aumentaron | 1 |
| 21469 | aumentármela | 1 |
| 21470 | aumentarán | 1 |
| 21471 | aumentáis | 1 |
| 21472 | aumentaban | 1 |
| 21473 | aumenta | 1 |
| 21474 | aullidos | 1 |
| 21475 | aula | 1 |
| 21476 | augusto | 1 |
| 21477 | augustinus | 1 |
| 21478 | augusta | 1 |
| 21479 | augmenta | 1 |
| 21480 | audacísimo | 1 |
| 21481 | atusándole | 1 |
| 21482 | atrozmente | 1 |
| 21483 | atroz | 1 |
| 21484 | atropellaron | 1 |
| 21485 | atropellan | 1 |
| 21486 | atropellado | 1 |
| 21487 | atropellada | 1 |
| 21488 | atronaron | 1 |
| 21489 | atronaban | 1 |
| 21490 | atronaba | 1 |
| 21491 | atribuyéndolos | 1 |
| 21492 | atribuyendo | 1 |
| 21493 | atribuyen | 1 |
| 21494 | atribuyan | 1 |
| 21495 | atribuya | 1 |
| 21496 | atribularon | 1 |
| 21497 | atribuirme | 1 |
| 21498 | atribuirlo | 1 |
| 21499 | atribuirle | 1 |
| 21500 | atribuían | 1 |
| 21501 | atribuía | 1 |
| 21502 | atribuí | 1 |
| 21503 | atrevióse | 1 |
| 21504 | atrevíme | 1 |
| 21505 | atrevieres | 1 |
| 21506 | atreviere | 1 |
| 21507 | atrevidillo | 1 |
| 21508 | atrevidas | 1 |
| 21509 | atrevía | 1 |
| 21510 | atreví | 1 |
| 21511 | atreves | 1 |
| 21512 | atreveré | 1 |
| 21513 | atreverán | 1 |
| 21514 | atrever | 1 |
| 21515 | atreve | 1 |
| 21516 | atraviesen | 1 |
| 21517 | atravesé | 1 |
| 21518 | atravesaron | 1 |
| 21519 | atravesarla | 1 |
| 21520 | atravesar | 1 |
| 21521 | atravesando | 1 |
| 21522 | atravesados | 1 |
| 21523 | atrancar | 1 |
| 21524 | atraillado | 1 |
| 21525 | atraerle | 1 |
| 21526 | atraerán | 1 |
| 21527 | atosigó | 1 |
| 21528 | atormenten | 1 |
| 21529 | atontada | 1 |
| 21530 | atónita | 1 |
| 21531 | atilde | 1 |
| 21532 | atildadura | 1 |
| 21533 | atierra | 1 |
| 21534 | atiéntame | 1 |
| 21535 | atiene | 1 |
| 21536 | atestados | 1 |
| 21537 | atestada | 1 |
| 21538 | atenuado | 1 |
| 21539 | atentísimos | 1 |
| 21540 | atentados | 1 |
| 21541 | atentadamente | 1 |
| 21542 | ateniéndose | 1 |
| 21543 | ateniéndome | 1 |
| 21544 | atenida | 1 |
| 21545 | atenga | 1 |
| 21546 | atenerse | 1 |
| 21547 | atendióle | 1 |
| 21548 | atendimos | 1 |
| 21549 | atendían | 1 |
| 21550 | atenas | 1 |
| 21551 | atenácenme | 1 |
| 21552 | atemorizan | 1 |
| 21553 | atemoricen | 1 |
| 21554 | até | 1 |
| 21555 | ate | 1 |
| 21556 | atase | 1 |
| 21557 | atarse | 1 |
| 21558 | atármela | 1 |
| 21559 | atarles | 1 |
| 21560 | atañederas | 1 |
| 21561 | atan | 1 |
| 21562 | atalegar | 1 |
| 21563 | atajos | 1 |
| 21564 | atajase | 1 |
| 21565 | atajar | 1 |
| 21566 | atajan | 1 |
| 21567 | atadura | 1 |
| 21568 | atadillo | 1 |
| 21569 | ataba | 1 |
| 21570 | asuramos | 1 |
| 21571 | asuela | 1 |
| 21572 | astuto | 1 |
| 21573 | asturias | 1 |
| 21574 | astroso | 1 |
| 21575 | astros | 1 |
| 21576 | astrolabio | 1 |
| 21577 | astolfo | 1 |
| 21578 | astas | 1 |
| 21579 | asqueroso | 1 |
| 21580 | asquerosas | 1 |
| 21581 | asquerosa | 1 |
| 21582 | aspirar | 1 |
| 21583 | aspiran | 1 |
| 21584 | aspetatores | 1 |
| 21585 | asperísima | 1 |
| 21586 | ásperamente | 1 |
| 21587 | aspecto | 1 |
| 21588 | aspar | 1 |
| 21589 | aspado | 1 |
| 21590 | aspa | 1 |
| 21591 | asomó | 1 |
| 21592 | asombren | 1 |
| 21593 | asombraran | 1 |
| 21594 | asombrara | 1 |
| 21595 | asombradiza | 1 |
| 21596 | asomaron | 1 |
| 21597 | asomar | 1 |
| 21598 | asolverle | 1 |
| 21599 | asolase | 1 |
| 21600 | asolados | 1 |
| 21601 | asnalmente | 1 |
| 21602 | asnales | 1 |
| 21603 | asistían | 1 |
| 21604 | asiste | 1 |
| 21605 | asirse | 1 |
| 21606 | asirios | 1 |
| 21607 | asilde | 1 |
| 21608 | asiesten | 1 |
| 21609 | asieron | 1 |
| 21610 | asiera | 1 |
| 21611 | asienten | 1 |
| 21612 | asiéndome | 1 |
| 21613 | asidero | 1 |
| 21614 | asidas | 1 |
| 21615 | asestan | 1 |
| 21616 | asesor | 1 |
| 21617 | ases | 1 |
| 21618 | asentósele | 1 |
| 21619 | asentóme | 1 |
| 21620 | asentarse | 1 |
| 21621 | asentaría | 1 |
| 21622 | asentada | 1 |
| 21623 | asendereada | 1 |
| 21624 | asenderado | 1 |
| 21625 | asen | 1 |
| 21626 | aseguró | 1 |
| 21627 | asegúrate | 1 |
| 21628 | asegurarte | 1 |
| 21629 | aseguraríamos | 1 |
| 21630 | aseguraría | 1 |
| 21631 | aseguraré | 1 |
| 21632 | asegurándose | 1 |
| 21633 | aseguran | 1 |
| 21634 | asegúrala | 1 |
| 21635 | aseguraba | 1 |
| 21636 | aseados | 1 |
| 21637 | ase | 1 |
| 21638 | asconderme | 1 |
| 21639 | ascondéis | 1 |
| 21640 | asconde | 1 |
| 21641 | asaltó | 1 |
| 21642 | asalten | 1 |
| 21643 | asaltásemos | 1 |
| 21644 | asalta | 1 |
| 21645 | asaetee | 1 |
| 21646 | asaetearan | 1 |
| 21647 | asaduras | 1 |
| 21648 | asados | 1 |
| 21649 | asador | 1 |
| 21650 | asado | 1 |
| 21651 | asadas | 1 |
| 21652 | arzones | 1 |
| 21653 | arzobispales | 1 |
| 21654 | arturo | 1 |
| 21655 | artificiosos | 1 |
| 21656 | artificioso | 1 |
| 21657 | artificiosas | 1 |
| 21658 | articuladas | 1 |
| 21659 | artesoncillo | 1 |
| 21660 | artesas | 1 |
| 21661 | artesa | 1 |
| 21662 | artemisa | 1 |
| 21663 | arrumbadas | 1 |
| 21664 | arrullar | 1 |
| 21665 | arrullador | 1 |
| 21666 | arrugado | 1 |
| 21667 | arroz | 1 |
| 21668 | arrostrar | 1 |
| 21669 | arropasen | 1 |
| 21670 | arroparon | 1 |
| 21671 | arroparme | 1 |
| 21672 | arropándole | 1 |
| 21673 | arrojóse | 1 |
| 21674 | arrojóla | 1 |
| 21675 | arrojo | 1 |
| 21676 | arrojemos | 1 |
| 21677 | arrójate | 1 |
| 21678 | arrojasen | 1 |
| 21679 | arrojas | 1 |
| 21680 | arrojáronse | 1 |
| 21681 | arrojarme | 1 |
| 21682 | arrojarlos | 1 |
| 21683 | arrojaría | 1 |
| 21684 | arrojaras | 1 |
| 21685 | arrojara | 1 |
| 21686 | arrojándose | 1 |
| 21687 | arrojándole | 1 |
| 21688 | arrojada | 1 |
| 21689 | arrodillamiento | 1 |
| 21690 | arrodillado | 1 |
| 21691 | arrocadas | 1 |
| 21692 | arrobamiento | 1 |
| 21693 | arroba | 1 |
| 21694 | arrinconados | 1 |
| 21695 | arrimos | 1 |
| 21696 | arrima | 1 |
| 21697 | arri | 1 |
| 21698 | arrequives | 1 |
| 21699 | arrepintió | 1 |
| 21700 | arrepiento | 1 |
| 21701 | arrepienta | 1 |
| 21702 | arrepentidos | 1 |
| 21703 | arrepentida | 1 |
| 21704 | arreo | 1 |
| 21705 | arrendara | 1 |
| 21706 | arrendar | 1 |
| 21707 | arrendamiento | 1 |
| 21708 | arrendada | 1 |
| 21709 | arremeto | 1 |
| 21710 | arremetido | 1 |
| 21711 | arremetía | 1 |
| 21712 | arremangadas | 1 |
| 21713 | arrebató | 1 |
| 21714 | arrebatándola | 1 |
| 21715 | arrebatando | 1 |
| 21716 | arrebatan | 1 |
| 21717 | arrebatadamente | 1 |
| 21718 | arrear | 1 |
| 21719 | arrastró | 1 |
| 21720 | arrastras | 1 |
| 21721 | arrastrarse | 1 |
| 21722 | arrastran | 1 |
| 21723 | arrastradas | 1 |
| 21724 | arrasó | 1 |
| 21725 | arrasan | 1 |
| 21726 | arranquen | 1 |
| 21727 | arrancaré | 1 |
| 21728 | arrancarán | 1 |
| 21729 | arrancándosele | 1 |
| 21730 | arrancada | 1 |
| 21731 | arrancábase | 1 |
| 21732 | arranca | 1 |
| 21733 | arraigó | 1 |
| 21734 | arraigado | 1 |
| 21735 | arquitetura | 1 |
| 21736 | arqueta | 1 |
| 21737 | arpas | 1 |
| 21738 | arpadas | 1 |
| 21739 | aros | 1 |
| 21740 | aromático | 1 |
| 21741 | aromática | 1 |
| 21742 | armónico | 1 |
| 21743 | armiño | 1 |
| 21744 | ármenme | 1 |
| 21745 | armenia | 1 |
| 21746 | armazón | 1 |
| 21747 | armase | 1 |
| 21748 | armarse | 1 |
| 21749 | arman | 1 |
| 21750 | armalle | 1 |
| 21751 | armadura | 1 |
| 21752 | armadas | 1 |
| 21753 | arlanza | 1 |
| 21754 | aristas | 1 |
| 21755 | aridiana | 1 |
| 21756 | arguyo | 1 |
| 21757 | argüir | 1 |
| 21758 | argos | 1 |
| 21759 | argollas | 1 |
| 21760 | argentería | 1 |
| 21761 | argentada | 1 |
| 21762 | argamasillesco | 1 |
| 21763 | arévalo | 1 |
| 21764 | arenques | 1 |
| 21765 | arenoso | 1 |
| 21766 | arduo | 1 |
| 21767 | ardua | 1 |
| 21768 | ardo | 1 |
| 21769 | ardimiento | 1 |
| 21770 | ardientes | 1 |
| 21771 | ardides | 1 |
| 21772 | ardid | 1 |
| 21773 | arder | 1 |
| 21774 | arden | 1 |
| 21775 | archipiela | 1 |
| 21776 | archiduque | 1 |
| 21777 | archidignísimo | 1 |
| 21778 | arcaduz | 1 |
| 21779 | arcaduces | 1 |
| 21780 | arcabuzazos | 1 |
| 21781 | arcabucería | 1 |
| 21782 | arca | 1 |
| 21783 | arboleda | 1 |
| 21784 | arbolando | 1 |
| 21785 | arbitrios | 1 |
| 21786 | arbitrio | 1 |
| 21787 | arbitrante | 1 |
| 21788 | araucana | 1 |
| 21789 | aras | 1 |
| 21790 | arar | 1 |
| 21791 | aranjüez | 1 |
| 21792 | aranjuez | 1 |
| 21793 | aranceles | 1 |
| 21794 | arambeles | 1 |
| 21795 | aragoneses | 1 |
| 21796 | arados | 1 |
| 21797 | arábiga | 1 |
| 21798 | arabias | 1 |
| 21799 | árabes | 1 |
| 21800 | aquista | 1 |
| 21801 | aquéstos | 1 |
| 21802 | aquéstas | 1 |
| 21803 | aquesta | 1 |
| 21804 | aquesos | 1 |
| 21805 | aquesa | 1 |
| 21806 | apuróla | 1 |
| 21807 | apuro | 1 |
| 21808 | apurado | 1 |
| 21809 | apurada | 1 |
| 21810 | apuraba | 1 |
| 21811 | apuñeado | 1 |
| 21812 | apunté | 1 |
| 21813 | apunte | 1 |
| 21814 | apuntarme | 1 |
| 21815 | apuntándome | 1 |
| 21816 | apuntando | 1 |
| 21817 | apuntado | 1 |
| 21818 | aptitud | 1 |
| 21819 | aprueba | 1 |
| 21820 | aproveche | 1 |
| 21821 | aprovecharos | 1 |
| 21822 | aprovecharnos | 1 |
| 21823 | aprovechará | 1 |
| 21824 | aprovechándose | 1 |
| 21825 | aprovechaban | 1 |
| 21826 | apropiado | 1 |
| 21827 | apropiadas | 1 |
| 21828 | aprobó | 1 |
| 21829 | aprobaron | 1 |
| 21830 | aprobará | 1 |
| 21831 | aprobara | 1 |
| 21832 | aprobaciones | 1 |
| 21833 | aprisionado | 1 |
| 21834 | apriscos | 1 |
| 21835 | aprisa | 1 |
| 21836 | aprietos | 1 |
| 21837 | aprietes | 1 |
| 21838 | apretósele | 1 |
| 21839 | apretóme | 1 |
| 21840 | apretóle | 1 |
| 21841 | apretarse | 1 |
| 21842 | apretáronle | 1 |
| 21843 | apretaron | 1 |
| 21844 | apretándose | 1 |
| 21845 | apretándole | 1 |
| 21846 | apretándolas | 1 |
| 21847 | apretados | 1 |
| 21848 | apretadas | 1 |
| 21849 | apresures | 1 |
| 21850 | apresurarte | 1 |
| 21851 | apresuraron | 1 |
| 21852 | apresurando | 1 |
| 21853 | apresurado | 1 |
| 21854 | aprendieses | 1 |
| 21855 | aprendiendo | 1 |
| 21856 | aprendida | 1 |
| 21857 | aprender | 1 |
| 21858 | aprende | 1 |
| 21859 | aprecie | 1 |
| 21860 | apreciadores | 1 |
| 21861 | apostar | 1 |
| 21862 | aportares | 1 |
| 21863 | aporrearon | 1 |
| 21864 | aporreantes | 1 |
| 21865 | aporreaba | 1 |
| 21866 | aporrea | 1 |
| 21867 | apoques | 1 |
| 21868 | apólogas | 1 |
| 21869 | apoderan | 1 |
| 21870 | apócrifos | 1 |
| 21871 | apócrifas | 1 |
| 21872 | apocado | 1 |
| 21873 | apocábase | 1 |
| 21874 | apoca | 1 |
| 21875 | apliquélas | 1 |
| 21876 | aplicas | 1 |
| 21877 | aplicarle | 1 |
| 21878 | aplicará | 1 |
| 21879 | aplicándoselas | 1 |
| 21880 | aplicándolos | 1 |
| 21881 | aplicando | 1 |
| 21882 | aplicados | 1 |
| 21883 | aplicaba | 1 |
| 21884 | aplazada | 1 |
| 21885 | aplace | 1 |
| 21886 | aplacaron | 1 |
| 21887 | aplacara | 1 |
| 21888 | aplacar | 1 |
| 21889 | aplacado | 1 |
| 21890 | apiñados | 1 |
| 21891 | apicarados | 1 |
| 21892 | apetites | 1 |
| 21893 | apetezco | 1 |
| 21894 | apetecerlo | 1 |
| 21895 | apesarado | 1 |
| 21896 | apersonado | 1 |
| 21897 | aperciba | 1 |
| 21898 | apercebidos | 1 |
| 21899 | apercebido | 1 |
| 21900 | apercebida | 1 |
| 21901 | apenino | 1 |
| 21902 | apellidarían | 1 |
| 21903 | apellidado | 1 |
| 21904 | apeé | 1 |
| 21905 | apedernaladas | 1 |
| 21906 | apearla | 1 |
| 21907 | apeándole | 1 |
| 21908 | apeamiento | 1 |
| 21909 | apeados | 1 |
| 21910 | apeado | 1 |
| 21911 | apártese | 1 |
| 21912 | aparten | 1 |
| 21913 | apartéme | 1 |
| 21914 | apartándome | 1 |
| 21915 | apartándoles | 1 |
| 21916 | apartan | 1 |
| 21917 | apartamiento | 1 |
| 21918 | apartáis | 1 |
| 21919 | apartaban | 1 |
| 21920 | aparicio | 1 |
| 21921 | aparejó | 1 |
| 21922 | aparejo | 1 |
| 21923 | apareje | 1 |
| 21924 | aparejaos | 1 |
| 21925 | aparejadísimos | 1 |
| 21926 | aparejada | 1 |
| 21927 | apareció | 1 |
| 21928 | aparecido | 1 |
| 21929 | aparatos | 1 |
| 21930 | aparadores | 1 |
| 21931 | apaleó | 1 |
| 21932 | apaleen | 1 |
| 21933 | apalee | 1 |
| 21934 | apalear | 1 |
| 21935 | apagó | 1 |
| 21936 | apagarse | 1 |
| 21937 | apagaron | 1 |
| 21938 | apagando | 1 |
| 21939 | apaciguarse | 1 |
| 21940 | apacientan | 1 |
| 21941 | apacibles | 1 |
| 21942 | apacibilidad | 1 |
| 21943 | apacentando | 1 |
| 21944 | añudemos | 1 |
| 21945 | añudadas | 1 |
| 21946 | añudada | 1 |
| 21947 | añejo | 1 |
| 21948 | añadís | 1 |
| 21949 | añadirles | 1 |
| 21950 | añadiría | 1 |
| 21951 | añadiósele | 1 |
| 21952 | añadiesen | 1 |
| 21953 | añadiese | 1 |
| 21954 | añadieron | 1 |
| 21955 | añadía | 1 |
| 21956 | añadí | 1 |
| 21957 | añade | 1 |
| 21958 | añadas | 1 |
| 21959 | anulo | 1 |
| 21960 | anudando | 1 |
| 21961 | anubló | 1 |
| 21962 | anublar | 1 |
| 21963 | antropófagos | 1 |
| 21964 | antorchas | 1 |
| 21965 | antojuna | 1 |
| 21966 | antojaron | 1 |
| 21967 | antojado | 1 |
| 21968 | antojadizo | 1 |
| 21969 | antojaba | 1 |
| 21970 | antiquísimo | 1 |
| 21971 | antigüedades | 1 |
| 21972 | antídoto | 1 |
| 21973 | anteviendo | 1 |
| 21974 | antesalas | 1 |
| 21975 | antesala | 1 |
| 21976 | anteo | 1 |
| 21977 | antecogió | 1 |
| 21978 | antecogidos | 1 |
| 21979 | antecoger | 1 |
| 21980 | antecedentes | 1 |
| 21981 | antecámara | 1 |
| 21982 | ansioso | 1 |
| 21983 | anque | 1 |
| 21984 | anotar | 1 |
| 21985 | anocheciese | 1 |
| 21986 | anochecido | 1 |
| 21987 | anochecen | 1 |
| 21988 | anochece | 1 |
| 21989 | annis | 1 |
| 21990 | aniquiló | 1 |
| 21991 | aniquile | 1 |
| 21992 | aniquilarlas | 1 |
| 21993 | aniquilan | 1 |
| 21994 | aniquilada | 1 |
| 21995 | animosísimo | 1 |
| 21996 | animóle | 1 |
| 21997 | animes | 1 |
| 21998 | animé | 1 |
| 21999 | ánimas | 1 |
| 22000 | animará | 1 |
| 22001 | animándose | 1 |
| 22002 | animalia | 1 |
| 22003 | animalejo | 1 |
| 22004 | anima | 1 |
| 22005 | angustiados | 1 |
| 22006 | angustiado | 1 |
| 22007 | angustiadas | 1 |
| 22008 | angulo | 1 |
| 22009 | anguila | 1 |
| 22010 | angosto | 1 |
| 22011 | angosta | 1 |
| 22012 | anexo | 1 |
| 22013 | anejos | 1 |
| 22014 | anegue | 1 |
| 22015 | anegase | 1 |
| 22016 | anegaron | 1 |
| 22017 | anegábamos | 1 |
| 22018 | anduvistes | 1 |
| 22019 | anduvimos | 1 |
| 22020 | anduviéremos | 1 |
| 22021 | anduviere | 1 |
| 22022 | andradilla | 1 |
| 22023 | andéis | 1 |
| 22024 | ándase | 1 |
| 22025 | andaros | 1 |
| 22026 | andarlas | 1 |
| 22027 | andaría | 1 |
| 22028 | andaremos | 1 |
| 22029 | andantescas | 1 |
| 22030 | ándanla | 1 |
| 22031 | andandona | 1 |
| 22032 | andamios | 1 |
| 22033 | andamio | 1 |
| 22034 | andadura | 1 |
| 22035 | andados | 1 |
| 22036 | andadas | 1 |
| 22037 | andábanse | 1 |
| 22038 | andábamos | 1 |
| 22039 | andá | 1 |
| 22040 | áncoras | 1 |
| 22041 | ancianidad | 1 |
| 22042 | anciana | 1 |
| 22043 | anchura | 1 |
| 22044 | anchos | 1 |
| 22045 | anchísima | 1 |
| 22046 | anchas | 1 |
| 22047 | anarda | 1 |
| 22048 | ampo | 1 |
| 22049 | amparase | 1 |
| 22050 | amparando | 1 |
| 22051 | amparan | 1 |
| 22052 | amparador | 1 |
| 22053 | amortiguados | 1 |
| 22054 | amorosísimos | 1 |
| 22055 | amoríos | 1 |
| 22056 | amoratado | 1 |
| 22057 | amondongado | 1 |
| 22058 | amohinóse | 1 |
| 22059 | amohinábase | 1 |
| 22060 | aminta | 1 |
| 22061 | amiguita | 1 |
| 22062 | amigablemente | 1 |
| 22063 | amicus | 1 |
| 22064 | amicos | 1 |
| 22065 | amica | 1 |
| 22066 | amezqueta | 1 |
| 22067 | américa | 1 |
| 22068 | amenos | 1 |
| 22069 | ameno | 1 |
| 22070 | amenísimos | 1 |
| 22071 | amenazóle | 1 |
| 22072 | amemos | 1 |
| 22073 | améla | 1 |
| 22074 | améis | 1 |
| 22075 | amé | 1 |
| 22076 | ame | 1 |
| 22077 | amberes | 1 |
| 22078 | ámbares | 1 |
| 22079 | amasa | 1 |
| 22080 | amarraros | 1 |
| 22081 | amarrará | 1 |
| 22082 | amarra | 1 |
| 22083 | amaros | 1 |
| 22084 | amarla | 1 |
| 22085 | amarillos | 1 |
| 22086 | amarilla | 1 |
| 22087 | amarilis | 1 |
| 22088 | amariles | 1 |
| 22089 | amargura | 1 |
| 22090 | amarguen | 1 |
| 22091 | amaño | 1 |
| 22092 | amañar | 1 |
| 22093 | amantado | 1 |
| 22094 | amansar | 1 |
| 22095 | amanezca | 1 |
| 22096 | amanecido | 1 |
| 22097 | amanecían | 1 |
| 22098 | amanecen | 1 |
| 22099 | amancebar | 1 |
| 22100 | amancebado | 1 |
| 22101 | amancebada | 1 |
| 22102 | amainaron | 1 |
| 22103 | amainado | 1 |
| 22104 | amadas | 1 |
| 22105 | amaban | 1 |
| 22106 | amábades | 1 |
| 22107 | alzóse | 1 |
| 22108 | alzaste | 1 |
| 22109 | alzase | 1 |
| 22110 | alzaros | 1 |
| 22111 | alzarme | 1 |
| 22112 | alzándote | 1 |
| 22113 | alzan | 1 |
| 22114 | alzamiento | 1 |
| 22115 | alzádole | 1 |
| 22116 | alzadas | 1 |
| 22117 | alzaban | 1 |
| 22118 | alumbres | 1 |
| 22119 | alumbrará | 1 |
| 22120 | alumbrándoles | 1 |
| 22121 | alude | 1 |
| 22122 | alturas | 1 |
| 22123 | altro | 1 |
| 22124 | altitud | 1 |
| 22125 | altisonante | 1 |
| 22126 | altísimas | 1 |
| 22127 | altisidorilla | 1 |
| 22128 | altillo | 1 |
| 22129 | altibajo | 1 |
| 22130 | alteró | 1 |
| 22131 | alternativos | 1 |
| 22132 | alternativamente | 1 |
| 22133 | altercar | 1 |
| 22134 | altercaciones | 1 |
| 22135 | alterarse | 1 |
| 22136 | alterando | 1 |
| 22137 | alteran | 1 |
| 22138 | alterada | 1 |
| 22139 | altera | 1 |
| 22140 | altar | 1 |
| 22141 | altaneros | 1 |
| 22142 | altanerías | 1 |
| 22143 | alrededores | 1 |
| 22144 | alpargatas | 1 |
| 22145 | alongados | 1 |
| 22146 | along | 1 |
| 22147 | alojó | 1 |
| 22148 | alojemos | 1 |
| 22149 | alojáronle | 1 |
| 22150 | alojarnos | 1 |
| 22151 | alojando | 1 |
| 22152 | alojan | 1 |
| 22153 | alojamiento | 1 |
| 22154 | alojados | 1 |
| 22155 | alojaban | 1 |
| 22156 | almohaza | 1 |
| 22157 | almohadillas | 1 |
| 22158 | almohadilla | 1 |
| 22159 | almohácenme | 1 |
| 22160 | almirez | 1 |
| 22161 | almilla | 1 |
| 22162 | almidonar | 1 |
| 22163 | almíbar | 1 |
| 22164 | almendras | 1 |
| 22165 | almendra | 1 |
| 22166 | almena | 1 |
| 22167 | almejas | 1 |
| 22168 | almario | 1 |
| 22169 | almagre | 1 |
| 22170 | allombre | 1 |
| 22171 | allento | 1 |
| 22172 | allende | 1 |
| 22173 | allegaba | 1 |
| 22174 | allano | 1 |
| 22175 | allane | 1 |
| 22176 | allanando | 1 |
| 22177 | aljamiado | 1 |
| 22178 | aljafería | 1 |
| 22179 | alivios | 1 |
| 22180 | alivió | 1 |
| 22181 | aliviaría | 1 |
| 22182 | aliviar | 1 |
| 22183 | aliviadísimo | 1 |
| 22184 | alivia | 1 |
| 22185 | alistaba | 1 |
| 22186 | alisarse | 1 |
| 22187 | aliquando | 1 |
| 22188 | alinda | 1 |
| 22189 | alimpiando | 1 |
| 22190 | alimentado | 1 |
| 22191 | alimenta | 1 |
| 22192 | alimañas | 1 |
| 22193 | alimaña | 1 |
| 22194 | alígero | 1 |
| 22195 | aligera | 1 |
| 22196 | alifanfuón | 1 |
| 22197 | alifanfarón | 1 |
| 22198 | alientes | 1 |
| 22199 | alidas | 1 |
| 22200 | alias | 1 |
| 22201 | aliagas | 1 |
| 22202 | alhucema | 1 |
| 22203 | alhelíes | 1 |
| 22204 | alhelí | 1 |
| 22205 | alhaja | 1 |
| 22206 | alguien | 1 |
| 22207 | algu | 1 |
| 22208 | algos | 1 |
| 22209 | algodones | 1 |
| 22210 | algebrista | 1 |
| 22211 | algarrobas | 1 |
| 22212 | algarbe | 1 |
| 22213 | alforja | 1 |
| 22214 | alfileres | 1 |
| 22215 | alferecía | 1 |
| 22216 | alfeñiquén | 1 |
| 22217 | alfeñique | 1 |
| 22218 | alfaquí | 1 |
| 22219 | alevosos | 1 |
| 22220 | alevosías | 1 |
| 22221 | alerto | 1 |
| 22222 | alentando | 1 |
| 22223 | alencastros | 1 |
| 22224 | alemañas | 1 |
| 22225 | alemaña | 1 |
| 22226 | alemanes | 1 |
| 22227 | alemanas | 1 |
| 22228 | alejase | 1 |
| 22229 | alejandría | 1 |
| 22230 | alejandra | 1 |
| 22231 | alejándose | 1 |
| 22232 | alegues | 1 |
| 22233 | alegróse | 1 |
| 22234 | alegróles | 1 |
| 22235 | alegrísimo | 1 |
| 22236 | alégrese | 1 |
| 22237 | alegren | 1 |
| 22238 | alegréme | 1 |
| 22239 | alégrate | 1 |
| 22240 | alegrarle | 1 |
| 22241 | alegrarán | 1 |
| 22242 | alegrándose | 1 |
| 22243 | alegrando | 1 |
| 22244 | alegrábanse | 1 |
| 22245 | alegorías | 1 |
| 22246 | alegando | 1 |
| 22247 | alegado | 1 |
| 22248 | alega | 1 |
| 22249 | aldegüela | 1 |
| 22250 | aldeano | 1 |
| 22251 | aldabazos | 1 |
| 22252 | alcornoqueñas | 1 |
| 22253 | alcocer | 1 |
| 22254 | alcobendas | 1 |
| 22255 | álcense | 1 |
| 22256 | alcéis | 1 |
| 22257 | alcatifa | 1 |
| 22258 | alcarria | 1 |
| 22259 | alcanzólo | 1 |
| 22260 | alcanzásedes | 1 |
| 22261 | alcanzas | 1 |
| 22262 | alcanzarlos | 1 |
| 22263 | alcanzarlo | 1 |
| 22264 | alcanzaremos | 1 |
| 22265 | alcanzáredes | 1 |
| 22266 | alcanzaré | 1 |
| 22267 | alcanzándoles | 1 |
| 22268 | alcanzando | 1 |
| 22269 | alcanzados | 1 |
| 22270 | alcanzadas | 1 |
| 22271 | alcántara | 1 |
| 22272 | alcancen | 1 |
| 22273 | alcaná | 1 |
| 22274 | alcaller | 1 |
| 22275 | alcalá | 1 |
| 22276 | alcaidía | 1 |
| 22277 | alcagüete | 1 |
| 22278 | alcacel | 1 |
| 22279 | alcabalero | 1 |
| 22280 | alcabala | 1 |
| 22281 | albos | 1 |
| 22282 | alborozados | 1 |
| 22283 | alborotes | 1 |
| 22284 | alborote | 1 |
| 22285 | alborotarse | 1 |
| 22286 | alborotarían | 1 |
| 22287 | alborotaba | 1 |
| 22288 | alborocen | 1 |
| 22289 | albondiguillas | 1 |
| 22290 | albergue | 1 |
| 22291 | albergase | 1 |
| 22292 | albergaron | 1 |
| 22293 | albergan | 1 |
| 22294 | albarrazadas | 1 |
| 22295 | albarde | 1 |
| 22296 | albardas | 1 |
| 22297 | albar | 1 |
| 22298 | albañir | 1 |
| 22299 | albañil | 1 |
| 22300 | albanega | 1 |
| 22301 | alastrajareas | 1 |
| 22302 | alaridos | 1 |
| 22303 | alargó | 1 |
| 22304 | alargase | 1 |
| 22305 | alargarme | 1 |
| 22306 | alargar | 1 |
| 22307 | alargan | 1 |
| 22308 | alarde | 1 |
| 22309 | alanos | 1 |
| 22310 | alano | 1 |
| 22311 | alanceara | 1 |
| 22312 | alanceallas | 1 |
| 22313 | álamos | 1 |
| 22314 | alambre | 1 |
| 22315 | alagones | 1 |
| 22316 | alabéle | 1 |
| 22317 | alábele | 1 |
| 22318 | alabe | 1 |
| 22319 | alabase | 1 |
| 22320 | alabáronsela | 1 |
| 22321 | alabaron | 1 |
| 22322 | alabarle | 1 |
| 22323 | alabarás | 1 |
| 22324 | alabándote | 1 |
| 22325 | alabada | 1 |
| 22326 | alababan | 1 |
| 22327 | ajustará | 1 |
| 22328 | ajustara | 1 |
| 22329 | ajustar | 1 |
| 22330 | ajustándola | 1 |
| 22331 | ajustan | 1 |
| 22332 | ajustamos | 1 |
| 22333 | ajuar | 1 |
| 22334 | aje | 1 |
| 22335 | aislados | 1 |
| 22336 | airarse | 1 |
| 22337 | airada | 1 |
| 22338 | ahuyentado | 1 |
| 22339 | ahuyenta | 1 |
| 22340 | ahorró | 1 |
| 22341 | ahorro | 1 |
| 22342 | ahorrativo | 1 |
| 22343 | ahorraran | 1 |
| 22344 | ahorrara | 1 |
| 22345 | ahorran | 1 |
| 22346 | ahorrado | 1 |
| 22347 | ahorrad | 1 |
| 22348 | ahorcase | 1 |
| 22349 | ahorcarse | 1 |
| 22350 | ahorcarme | 1 |
| 22351 | ahorcan | 1 |
| 22352 | ahorcamos | 1 |
| 22353 | ahorcados | 1 |
| 22354 | ahorcaba | 1 |
| 22355 | ahondar | 1 |
| 22356 | ahoguen | 1 |
| 22357 | ahogaros | 1 |
| 22358 | ahogara | 1 |
| 22359 | ahogando | 1 |
| 22360 | ahogalle | 1 |
| 22361 | ahogado | 1 |
| 22362 | ahoga | 1 |
| 22363 | ahitarse | 1 |
| 22364 | ahíta | 1 |
| 22365 | ahíncos | 1 |
| 22366 | ahincadas | 1 |
| 22367 | ahincadamente | 1 |
| 22368 | ahijársele | 1 |
| 22369 | ahijándolos | 1 |
| 22370 | ahijados | 1 |
| 22371 | ahijado | 1 |
| 22372 | ahecho | 1 |
| 22373 | ahechar | 1 |
| 22374 | ahechándole | 1 |
| 22375 | ahechado | 1 |
| 22376 | ahechaba | 1 |
| 22377 | aguzan | 1 |
| 22378 | aguó | 1 |
| 22379 | agujereado | 1 |
| 22380 | agujas | 1 |
| 22381 | aguileño | 1 |
| 22382 | águilas | 1 |
| 22383 | aguijó | 1 |
| 22384 | aguije | 1 |
| 22385 | aguijar | 1 |
| 22386 | agüelos | 1 |
| 22387 | agudas | 1 |
| 22388 | aguase | 1 |
| 22389 | aguardo | 1 |
| 22390 | aguardes | 1 |
| 22391 | aguarden | 1 |
| 22392 | aguardé | 1 |
| 22393 | aguarde | 1 |
| 22394 | aguardasen | 1 |
| 22395 | aguardaron | 1 |
| 22396 | aguardarle | 1 |
| 22397 | aguardaré | 1 |
| 22398 | aguardándonos | 1 |
| 22399 | aguardándome | 1 |
| 22400 | aguardándolos | 1 |
| 22401 | aguardan | 1 |
| 22402 | aguardador | 1 |
| 22403 | aguardábades | 1 |
| 22404 | aguamaniles | 1 |
| 22405 | aguachirle | 1 |
| 22406 | agu | 1 |
| 22407 | agregar | 1 |
| 22408 | agraz | 1 |
| 22409 | agraviarle | 1 |
| 22410 | agraviada | 1 |
| 22411 | agraviaba | 1 |
| 22412 | agrajes | 1 |
| 22413 | agradézcoos | 1 |
| 22414 | agradezcas | 1 |
| 22415 | agradezca | 1 |
| 22416 | agradeciólo | 1 |
| 22417 | agradecióle | 1 |
| 22418 | agradeciéronselo | 1 |
| 22419 | agradeciera | 1 |
| 22420 | agradeciéndoselo | 1 |
| 22421 | agradecidísimo | 1 |
| 22422 | agradecidas | 1 |
| 22423 | agradecíamos | 1 |
| 22424 | agradecí | 1 |
| 22425 | agradecérselo | 1 |
| 22426 | agradecéroslo | 1 |
| 22427 | agradecéroslas | 1 |
| 22428 | agradeceros | 1 |
| 22429 | agradecerlo | 1 |
| 22430 | agradeceré | 1 |
| 22431 | agradecemos | 1 |
| 22432 | agradablemente | 1 |
| 22433 | agradaba | 1 |
| 22434 | agrada | 1 |
| 22435 | agostos | 1 |
| 22436 | agostado | 1 |
| 22437 | agoreros | 1 |
| 22438 | agonía | 1 |
| 22439 | agobiándola | 1 |
| 22440 | agobiada | 1 |
| 22441 | agobiaba | 1 |
| 22442 | agitación | 1 |
| 22443 | agilítanse | 1 |
| 22444 | agigantado | 1 |
| 22445 | agible | 1 |
| 22446 | agazapó | 1 |
| 22447 | agazapasen | 1 |
| 22448 | agazapar | 1 |
| 22449 | agazapándose | 1 |
| 22450 | agazapa | 1 |
| 22451 | agasajamos | 1 |
| 22452 | agasajado | 1 |
| 22453 | agárrale | 1 |
| 22454 | agalla | 1 |
| 22455 | agá | 1 |
| 22456 | afrontara | 1 |
| 22457 | africanas | 1 |
| 22458 | afrentes | 1 |
| 22459 | afrente | 1 |
| 22460 | afrentarse | 1 |
| 22461 | afrentan | 1 |
| 22462 | afrentaba | 1 |
| 22463 | afortunado | 1 |
| 22464 | aforro | 1 |
| 22465 | aforismo | 1 |
| 22466 | afligirte | 1 |
| 22467 | afligiósele | 1 |
| 22468 | afligidas | 1 |
| 22469 | afligía | 1 |
| 22470 | aflige | 1 |
| 22471 | afliciones | 1 |
| 22472 | afirmativamente | 1 |
| 22473 | afirmaron | 1 |
| 22474 | afirmarla | 1 |
| 22475 | afinándola | 1 |
| 22476 | afinada | 1 |
| 22477 | aficionó | 1 |
| 22478 | aficionaron | 1 |
| 22479 | aficionando | 1 |
| 22480 | aficionadas | 1 |
| 22481 | aficionaba | 1 |
| 22482 | aférrate | 1 |
| 22483 | aferrados | 1 |
| 22484 | afeminado | 1 |
| 22485 | afectuosa | 1 |
| 22486 | afecto | 1 |
| 22487 | afectadas | 1 |
| 22488 | afeado | 1 |
| 22489 | afeaban | 1 |
| 22490 | afeaba | 1 |
| 22491 | afanando | 1 |
| 22492 | afán | 1 |
| 22493 | afamado | 1 |
| 22494 | afabilidad | 1 |
| 22495 | aequo | 1 |
| 22496 | advirtióle | 1 |
| 22497 | advirtió | 1 |
| 22498 | advirtiéndole | 1 |
| 22499 | adviértase | 1 |
| 22500 | adviertas | 1 |
| 22501 | adviertan | 1 |
| 22502 | advertirte | 1 |
| 22503 | advertirme | 1 |
| 22504 | advertirle | 1 |
| 22505 | advertirás | 1 |
| 22506 | advertimento | 1 |
| 22507 | advertidas | 1 |
| 22508 | advertía | 1 |
| 22509 | adversidades | 1 |
| 22510 | adversas | 1 |
| 22511 | adversae | 1 |
| 22512 | advenediza | 1 |
| 22513 | adunia | 1 |
| 22514 | adulterado | 1 |
| 22515 | adúltera | 1 |
| 22516 | adulador | 1 |
| 22517 | adriano | 1 |
| 22518 | adquirida | 1 |
| 22519 | adquiere | 1 |
| 22520 | adoró | 1 |
| 22521 | adornes | 1 |
| 22522 | adornen | 1 |
| 22523 | adorne | 1 |
| 22524 | adornarte | 1 |
| 22525 | adornarse | 1 |
| 22526 | adornaron | 1 |
| 22527 | adornaren | 1 |
| 22528 | adornara | 1 |
| 22529 | adornados | 1 |
| 22530 | adorna | 1 |
| 22531 | adoré | 1 |
| 22532 | adorase | 1 |
| 22533 | adoras | 1 |
| 22534 | adorarte | 1 |
| 22535 | adorarlas | 1 |
| 22536 | adorada | 1 |
| 22537 | adoquiera | 1 |
| 22538 | adobarlo | 1 |
| 22539 | adobarla | 1 |
| 22540 | adobaría | 1 |
| 22541 | adobándoseme | 1 |
| 22542 | adóbame | 1 |
| 22543 | admito | 1 |
| 22544 | admitirlos | 1 |
| 22545 | admitirlas | 1 |
| 22546 | admitieron | 1 |
| 22547 | admitiere | 1 |
| 22548 | admitidos | 1 |
| 22549 | admíteme | 1 |
| 22550 | admita | 1 |
| 22551 | admiróme | 1 |
| 22552 | admiro | 1 |
| 22553 | admiréme | 1 |
| 22554 | admirativa | 1 |
| 22555 | admirasen | 1 |
| 22556 | admiraros | 1 |
| 22557 | admirarla | 1 |
| 22558 | admirarás | 1 |
| 22559 | admiraran | 1 |
| 22560 | admirara | 1 |
| 22561 | admiradas | 1 |
| 22562 | admirablemente | 1 |
| 22563 | admirábame | 1 |
| 22564 | administrar | 1 |
| 22565 | administrando | 1 |
| 22566 | administración | 1 |
| 22567 | adminícula | 1 |
| 22568 | adjunto | 1 |
| 22569 | adivinos | 1 |
| 22570 | adivinen | 1 |
| 22571 | adivinéle | 1 |
| 22572 | adivinase | 1 |
| 22573 | adivinando | 1 |
| 22574 | adivinaba | 1 |
| 22575 | adivina | 1 |
| 22576 | adivas | 1 |
| 22577 | aditamentos | 1 |
| 22578 | aditamento | 1 |
| 22579 | adiós | 1 |
| 22580 | adherente | 1 |
| 22581 | aderezólas | 1 |
| 22582 | aderezaste | 1 |
| 22583 | aderezas | 1 |
| 22584 | aderezáronse | 1 |
| 22585 | aderezarles | 1 |
| 22586 | aderezarla | 1 |
| 22587 | aderezaré | 1 |
| 22588 | aderezando | 1 |
| 22589 | aderézame | 1 |
| 22590 | aderezaban | 1 |
| 22591 | aderece | 1 |
| 22592 | adeliño | 1 |
| 22593 | adeliñase | 1 |
| 22594 | adelgaza | 1 |
| 22595 | adelfas | 1 |
| 22596 | adelfa | 1 |
| 22597 | adelantóse | 1 |
| 22598 | adelantasen | 1 |
| 22599 | adelantaron | 1 |
| 22600 | adelantara | 1 |
| 22601 | adelantándose | 1 |
| 22602 | adelantaba | 1 |
| 22603 | adelanta | 1 |
| 22604 | adarva | 1 |
| 22605 | adarme | 1 |
| 22606 | adamo | 1 |
| 22607 | adamar | 1 |
| 22608 | adamada | 1 |
| 22609 | adamaba | 1 |
| 22610 | adalid | 1 |
| 22611 | adahala | 1 |
| 22612 | ad | 1 |
| 22613 | acutos | 1 |
| 22614 | acuso | 1 |
| 22615 | acusare | 1 |
| 22616 | acusar | 1 |
| 22617 | acusado | 1 |
| 22618 | acurrucó | 1 |
| 22619 | acuitéis | 1 |
| 22620 | acuitedes | 1 |
| 22621 | acuitaráse | 1 |
| 22622 | acuitar | 1 |
| 22623 | acuestan | 1 |
| 22624 | acuesta | 1 |
| 22625 | acuerdos | 1 |
| 22626 | acuérdome | 1 |
| 22627 | acuerdes | 1 |
| 22628 | acuérdate | 1 |
| 22629 | acudiría | 1 |
| 22630 | acudirás | 1 |
| 22631 | acudiesen | 1 |
| 22632 | acudiéronme | 1 |
| 22633 | acudieren | 1 |
| 22634 | acudas | 1 |
| 22635 | acucies | 1 |
| 22636 | acuciéis | 1 |
| 22637 | acuchilladas | 1 |
| 22638 | activo | 1 |
| 22639 | acrisole | 1 |
| 22640 | acribarme | 1 |
| 22641 | acribar | 1 |
| 22642 | acribado | 1 |
| 22643 | acreedor | 1 |
| 22644 | acredite | 1 |
| 22645 | acreditasen | 1 |
| 22646 | acreditarte | 1 |
| 22647 | acreditarse | 1 |
| 22648 | acreditaré | 1 |
| 22649 | acreditan | 1 |
| 22650 | acreditado | 1 |
| 22651 | acreditaban | 1 |
| 22652 | acreditábamos | 1 |
| 22653 | acrecentóseles | 1 |
| 22654 | acrecentase | 1 |
| 22655 | acrecentarse | 1 |
| 22656 | acrecentará | 1 |
| 22657 | acrecentamiento | 1 |
| 22658 | acrecentaba | 1 |
| 22659 | acrebillaron | 1 |
| 22660 | acrebillado | 1 |
| 22661 | acote | 1 |
| 22662 | acotar | 1 |
| 22663 | acotán | 1 |
| 22664 | acostumbro | 1 |
| 22665 | acostumbrar | 1 |
| 22666 | acostóse | 1 |
| 22667 | acostasen | 1 |
| 22668 | acostarme | 1 |
| 22669 | acostaráse | 1 |
| 22670 | acostar | 1 |
| 22671 | acosáis | 1 |
| 22672 | acosados | 1 |
| 22673 | acortes | 1 |
| 22674 | acortando | 1 |
| 22675 | acorta | 1 |
| 22676 | acorrió | 1 |
| 22677 | acorriesen | 1 |
| 22678 | acorrerme | 1 |
| 22679 | acorredme | 1 |
| 22680 | acordarte | 1 |
| 22681 | acordaran | 1 |
| 22682 | acontencido | 1 |
| 22683 | acontecieran | 1 |
| 22684 | acontecerles | 1 |
| 22685 | aconséjoos | 1 |
| 22686 | aconsejéis | 1 |
| 22687 | aconsejaron | 1 |
| 22688 | aconsejarle | 1 |
| 22689 | aconsejarla | 1 |
| 22690 | aconsejaríale | 1 |
| 22691 | aconsejaría | 1 |
| 22692 | aconsejaremos | 1 |
| 22693 | aconsejárale | 1 |
| 22694 | aconsejara | 1 |
| 22695 | aconsejando | 1 |
| 22696 | acompañen | 1 |
| 22697 | acompañarse | 1 |
| 22698 | acompañaros | 1 |
| 22699 | acompañarme | 1 |
| 22700 | acompañarles | 1 |
| 22701 | acompañaremos | 1 |
| 22702 | acompañáramos | 1 |
| 22703 | acompañámosla | 1 |
| 22704 | acompañador | 1 |
| 22705 | acomodóle | 1 |
| 22706 | acomodé | 1 |
| 22707 | acomódate | 1 |
| 22708 | acomodase | 1 |
| 22709 | acomodársele | 1 |
| 22710 | acomodáronme | 1 |
| 22711 | acomodarme | 1 |
| 22712 | acomodarle | 1 |
| 22713 | acomodaría | 1 |
| 22714 | acomodáremos | 1 |
| 22715 | acomodarán | 1 |
| 22716 | acomodándoos | 1 |
| 22717 | acomodándome | 1 |
| 22718 | acomodándole | 1 |
| 22719 | acomodando | 1 |
| 22720 | acomodan | 1 |
| 22721 | acomódale | 1 |
| 22722 | acomodádose | 1 |
| 22723 | acomodádolas | 1 |
| 22724 | acometiese | 1 |
| 22725 | acometiéronnos | 1 |
| 22726 | acometieran | 1 |
| 22727 | acometiera | 1 |
| 22728 | acometiéndoos | 1 |
| 22729 | acometidos | 1 |
| 22730 | acometida | 1 |
| 22731 | acometían | 1 |
| 22732 | acometí | 1 |
| 22733 | acometerlas | 1 |
| 22734 | acometerla | 1 |
| 22735 | acometería | 1 |
| 22736 | acometemos | 1 |
| 22737 | acometellas | 1 |
| 22738 | acometella | 1 |
| 22739 | acometedores | 1 |
| 22740 | acólitos | 1 |
| 22741 | acoja | 1 |
| 22742 | acogistes | 1 |
| 22743 | acogimientos | 1 |
| 22744 | acogiesen | 1 |
| 22745 | acogidos | 1 |
| 22746 | acogido | 1 |
| 22747 | acogía | 1 |
| 22748 | acogerse | 1 |
| 22749 | acogen | 1 |
| 22750 | acocear | 1 |
| 22751 | acoceado | 1 |
| 22752 | acobardóse | 1 |
| 22753 | acobarde | 1 |
| 22754 | acobardan | 1 |
| 22755 | acobardaban | 1 |
| 22756 | aclare | 1 |
| 22757 | aclárate | 1 |
| 22758 | aclarase | 1 |
| 22759 | aclaraba | 1 |
| 22760 | aclara | 1 |
| 22761 | aclamaron | 1 |
| 22762 | aclamaban | 1 |
| 22763 | aciones | 1 |
| 22764 | aciertes | 1 |
| 22765 | acicalada | 1 |
| 22766 | acíbar | 1 |
| 22767 | aceto | 1 |
| 22768 | acete | 1 |
| 22769 | acetaros | 1 |
| 22770 | acetaron | 1 |
| 22771 | acetarlos | 1 |
| 22772 | acetar | 1 |
| 22773 | acetación | 1 |
| 22774 | acetaban | 1 |
| 22775 | acetaba | 1 |
| 22776 | acerté | 1 |
| 22777 | acertastes | 1 |
| 22778 | acertasen | 1 |
| 22779 | acertase | 1 |
| 22780 | acertarle | 1 |
| 22781 | acertares | 1 |
| 22782 | acertaréis | 1 |
| 22783 | acertáramos | 1 |
| 22784 | acertándole | 1 |
| 22785 | acertáis | 1 |
| 22786 | acertados | 1 |
| 22787 | acertadísimo | 1 |
| 22788 | acertadas | 1 |
| 22789 | acertaban | 1 |
| 22790 | aceros | 1 |
| 22791 | acercóse | 1 |
| 22792 | acercó | 1 |
| 22793 | acercado | 1 |
| 22794 | acerado | 1 |
| 22795 | aceptólo | 1 |
| 22796 | aceptó | 1 |
| 22797 | aceptar | 1 |
| 22798 | acendradísimo | 1 |
| 22799 | acelerando | 1 |
| 22800 | acelerado | 1 |
| 22801 | aceitera | 1 |
| 22802 | aceda | 1 |
| 22803 | acebo | 1 |
| 22804 | acarrean | 1 |
| 22805 | acarrea | 1 |
| 22806 | acariciase | 1 |
| 22807 | acariciar | 1 |
| 22808 | acardenalarme | 1 |
| 22809 | acardenalado | 1 |
| 22810 | acaecimiento | 1 |
| 22811 | acaecido | 1 |
| 22812 | acaecen | 1 |
| 22813 | acaece | 1 |
| 22814 | académicos | 1 |
| 22815 | academias | 1 |
| 22816 | acábese | 1 |
| 22817 | acabéis | 1 |
| 22818 | acabas | 1 |
| 22819 | acabárseme | 1 |
| 22820 | acabársele | 1 |
| 22821 | acabarle | 1 |
| 22822 | acabare | 1 |
| 22823 | acabándonoslas | 1 |
| 22824 | acabándolos | 1 |
| 22825 | acaballe | 1 |
| 22826 | acaballa | 1 |
| 22827 | acabados | 1 |
| 22828 | acabadme | 1 |
| 22829 | acabad | 1 |
| 22830 | acabable | 1 |
| 22831 | acabábamos | 1 |
| 22832 | abusos | 1 |
| 22833 | abundantísimo | 1 |
| 22834 | abundantísima | 1 |
| 22835 | abundantemente | 1 |
| 22836 | abundan | 1 |
| 22837 | abundaban | 1 |
| 22838 | abundaba | 1 |
| 22839 | abunda | 1 |
| 22840 | absurdos | 1 |
| 22841 | absuelve | 1 |
| 22842 | absteniéndote | 1 |
| 22843 | abstengas | 1 |
| 22844 | absortar | 1 |
| 22845 | absolutamente | 1 |
| 22846 | absoluta | 1 |
| 22847 | absit | 1 |
| 22848 | abrojos | 1 |
| 22849 | abro | 1 |
| 22850 | abriste | 1 |
| 22851 | abrís | 1 |
| 22852 | abrirle | 1 |
| 22853 | abrirían | 1 |
| 22854 | abriría | 1 |
| 22855 | abriré | 1 |
| 22856 | abrirá | 1 |
| 22857 | abrióse | 1 |
| 22858 | abríla | 1 |
| 22859 | abril | 1 |
| 22860 | abrigó | 1 |
| 22861 | abriesen | 1 |
| 22862 | abrieran | 1 |
| 22863 | abriéndose | 1 |
| 22864 | abriéndolos | 1 |
| 22865 | abría | 1 |
| 22866 | abrí | 1 |
| 22867 | abrevió | 1 |
| 22868 | abrevies | 1 |
| 22869 | abrevian | 1 |
| 22870 | abrenuncio | 1 |
| 22871 | abrazólos | 1 |
| 22872 | abrazóla | 1 |
| 22873 | abrazase | 1 |
| 22874 | abrazárselos | 1 |
| 22875 | abrazarse | 1 |
| 22876 | abrazáronle | 1 |
| 22877 | abrazarle | 1 |
| 22878 | abrazará | 1 |
| 22879 | abrazándonos | 1 |
| 22880 | abrazamiento | 1 |
| 22881 | abrazaba | 1 |
| 22882 | abrasemos | 1 |
| 22883 | abrasasen | 1 |
| 22884 | abrasarnos | 1 |
| 22885 | abrasarla | 1 |
| 22886 | abrasan | 1 |
| 22887 | abrasadores | 1 |
| 22888 | abrasadas | 1 |
| 22889 | abráis | 1 |
| 22890 | abracé | 1 |
| 22891 | aborreció | 1 |
| 22892 | aborrecidos | 1 |
| 22893 | aborrecida | 1 |
| 22894 | aborrecible | 1 |
| 22895 | aborrecí | 1 |
| 22896 | aborrecen | 1 |
| 22897 | aborrascadas | 1 |
| 22898 | abonasen | 1 |
| 22899 | abomino | 1 |
| 22900 | abominable | 1 |
| 22901 | abominábamos | 1 |
| 22902 | abollé | 1 |
| 22903 | abollado | 1 |
| 22904 | abollada | 1 |
| 22905 | abolengo | 1 |
| 22906 | abobado | 1 |
| 22907 | ablandó | 1 |
| 22908 | ablande | 1 |
| 22909 | ablándate | 1 |
| 22910 | ablandarte | 1 |
| 22911 | ablandaron | 1 |
| 22912 | ablandarme | 1 |
| 22913 | ablandara | 1 |
| 22914 | ablandar | 1 |
| 22915 | ablandan | 1 |
| 22916 | ablandáis | 1 |
| 22917 | ablandado | 1 |
| 22918 | ablandaban | 1 |
| 22919 | ablandaba | 1 |
| 22920 | abiertas | 1 |
| 22921 | abertura | 1 |
| 22922 | aberenjenado | 1 |
| 22923 | abencerraje | 1 |
| 22924 | abecedario | 1 |
| 22925 | abatieres | 1 |
| 22926 | abatiendo | 1 |
| 22927 | abatanar | 1 |
| 22928 | abarraganados | 1 |
| 22929 | abarraganada | 1 |
| 22930 | abandonarme | 1 |
| 22931 | abalánzase | 1 |
| 22932 | abajen | 1 |
| 22933 | abajan | 1 |
| 22934 | abaja | 1 |
| 22935 | abades | 1 |
|
| Rank | Palabra | Frec |
|---|
| 1 | the | 21069 |
| 2 | and | 17110 |
| 3 | to | 13412 |
| 4 | of | 12521 |
| 5 | that | 7705 |
| 6 | in | 6863 |
| 7 | a | 6744 |
| 8 | i | 6636 |
| 9 | he | 5881 |
| 10 | it | 5394 |
| 11 | for | 4992 |
| 12 | his | 4378 |
| 13 | as | 4294 |
| 14 | is | 3621 |
| 15 | with | 3593 |
| 16 | not | 3519 |
| 17 | him | 3428 |
| 18 | was | 3390 |
| 19 | be | 3212 |
| 20 | don | 2874 |
| 21 | my | 2803 |
| 22 | they | 2675 |
| 23 | this | 2671 |
| 24 | all | 2638 |
| 25 | said | 2615 |
| 26 | have | 2505 |
| 27 | me | 2496 |
| 28 | so | 2366 |
| 29 | on | 2323 |
| 30 | you | 2303 |
| 31 | quixote | 2193 |
| 32 | sancho | 2169 |
| 33 | had | 2153 |
| 34 | but | 2153 |
| 35 | her | 2117 |
| 36 | or | 2104 |
| 37 | by | 2098 |
| 38 | at | 1972 |
| 39 | what | 1918 |
| 40 | which | 1898 |
| 41 | who | 1897 |
| 42 | if | 1780 |
| 43 | them | 1717 |
| 44 | will | 1641 |
| 45 | s | 1641 |
| 46 | one | 1591 |
| 47 | from | 1506 |
| 48 | your | 1358 |
| 49 | are | 1336 |
| 50 | there | 1310 |
| 51 | were | 1294 |
| 52 | no | 1239 |
| 53 | thou | 1229 |
| 54 | she | 1222 |
| 55 | would | 1208 |
| 56 | more | 1080 |
| 57 | their | 971 |
| 58 | when | 966 |
| 59 | out | 965 |
| 60 | we | 940 |
| 61 | than | 935 |
| 62 | has | 900 |
| 63 | say | 894 |
| 64 | good | 872 |
| 65 | do | 859 |
| 66 | any | 845 |
| 67 | been | 823 |
| 68 | up | 821 |
| 69 | some | 805 |
| 70 | may | 802 |
| 71 | such | 797 |
| 72 | himself | 792 |
| 73 | an | 790 |
| 74 | thee | 764 |
| 75 | see | 759 |
| 76 | now | 757 |
| 77 | am | 742 |
| 78 | know | 708 |
| 79 | well | 700 |
| 80 | without | 699 |
| 81 | then | 671 |
| 82 | made | 660 |
| 83 | those | 659 |
| 84 | let | 651 |
| 85 | could | 650 |
| 86 | upon | 649 |
| 87 | us | 644 |
| 88 | come | 643 |
| 89 | time | 640 |
| 90 | other | 640 |
| 91 | great | 635 |
| 92 | should | 627 |
| 93 | knight | 624 |
| 94 | did | 609 |
| 95 | these | 602 |
| 96 | master | 599 |
| 97 | very | 594 |
| 98 | make | 580 |
| 99 | into | 564 |
| 100 | can | 562 |
| 101 | about | 562 |
| 102 | though | 561 |
| 103 | like | 560 |
| 104 | give | 560 |
| 105 | take | 553 |
| 106 | go | 543 |
| 107 | thy | 537 |
| 108 | where | 529 |
| 109 | our | 528 |
| 110 | god | 528 |
| 111 | how | 524 |
| 112 | worship | 522 |
| 113 | senor | 510 |
| 114 | two | 504 |
| 115 | must | 496 |
| 116 | came | 490 |
| 117 | way | 477 |
| 118 | being | 471 |
| 119 | here | 470 |
| 120 | tell | 467 |
| 121 | man | 458 |
| 122 | own | 445 |
| 123 | lady | 437 |
| 124 | before | 433 |
| 125 | nor | 429 |
| 126 | much | 429 |
| 127 | shall | 424 |
| 128 | same | 419 |
| 129 | replied | 416 |
| 130 | over | 403 |
| 131 | might | 400 |
| 132 | only | 398 |
| 133 | world | 384 |
| 134 | off | 376 |
| 135 | life | 374 |
| 136 | t | 371 |
| 137 | many | 366 |
| 138 | never | 357 |
| 139 | myself | 354 |
| 140 | another | 338 |
| 141 | saw | 336 |
| 142 | little | 330 |
| 143 | having | 330 |
| 144 | even | 328 |
| 145 | day | 328 |
| 146 | love | 325 |
| 147 | once | 323 |
| 148 | most | 322 |
| 149 | whom | 314 |
| 150 | heart | 314 |
| 151 | hand | 314 |
| 152 | told | 311 |
| 153 | heard | 310 |
| 154 | left | 305 |
| 155 | put | 304 |
| 156 | found | 304 |
| 157 | curate | 303 |
| 158 | took | 302 |
| 159 | because | 302 |
| 160 | down | 299 |
| 161 | first | 298 |
| 162 | head | 297 |
| 163 | after | 294 |
| 164 | errant | 292 |
| 165 | eyes | 291 |
| 166 | nothing | 287 |
| 167 | going | 285 |
| 168 | dulcinea | 285 |
| 169 | gave | 282 |
| 170 | went | 281 |
| 171 | while | 280 |
| 172 | panza | 278 |
| 173 | name | 277 |
| 174 | seen | 275 |
| 175 | asked | 272 |
| 176 | truth | 265 |
| 177 | father | 265 |
| 178 | art | 263 |
| 179 | its | 260 |
| 180 | end | 257 |
| 181 | saying | 255 |
| 182 | words | 254 |
| 183 | three | 254 |
| 184 | knights | 253 |
| 185 | mind | 250 |
| 186 | house | 249 |
| 187 | things | 248 |
| 188 | called | 248 |
| 189 | back | 248 |
| 190 | friend | 247 |
| 191 | duke | 247 |
| 192 | find | 245 |
| 193 | leave | 244 |
| 194 | long | 241 |
| 195 | squire | 240 |
| 196 | seeing | 238 |
| 197 | heaven | 236 |
| 198 | ever | 234 |
| 199 | mine | 233 |
| 200 | night | 231 |
| 201 | duchess | 227 |
| 202 | chapter | 226 |
| 203 | true | 225 |
| 204 | still | 225 |
| 205 | better | 224 |
| 206 | done | 219 |
| 207 | just | 218 |
| 208 | does | 217 |
| 209 | however | 216 |
| 210 | place | 213 |
| 211 | cannot | 212 |
| 212 | away | 211 |
| 213 | rocinante | 210 |
| 214 | too | 209 |
| 215 | set | 208 |
| 216 | days | 208 |
| 217 | look | 206 |
| 218 | given | 202 |
| 219 | arms | 202 |
| 220 | themselves | 201 |
| 221 | right | 201 |
| 222 | answer | 201 |
| 223 | think | 200 |
| 224 | anything | 200 |
| 225 | beauty | 199 |
| 226 | whole | 198 |
| 227 | against | 197 |
| 228 | already | 196 |
| 229 | through | 195 |
| 230 | present | 194 |
| 231 | hands | 193 |
| 232 | enough | 193 |
| 233 | again | 192 |
| 234 | until | 191 |
| 235 | ll | 189 |
| 236 | thought | 188 |
| 237 | soon | 188 |
| 238 | read | 188 |
| 239 | brought | 188 |
| 240 | governor | 186 |
| 241 | between | 186 |
| 242 | ass | 186 |
| 243 | village | 185 |
| 244 | fair | 184 |
| 245 | word | 183 |
| 246 | whether | 181 |
| 247 | thing | 179 |
| 248 | returned | 179 |
| 249 | under | 178 |
| 250 | doubt | 178 |
| 251 | men | 177 |
| 252 | began | 177 |
| 253 | history | 176 |
| 254 | taken | 175 |
| 255 | gentleman | 175 |
| 256 | part | 174 |
| 257 | every | 173 |
| 258 | wife | 172 |
| 259 | la | 172 |
| 260 | barber | 172 |
| 261 | full | 171 |
| 262 | keep | 170 |
| 263 | far | 169 |
| 264 | show | 167 |
| 265 | reason | 167 |
| 266 | got | 167 |
| 267 | others | 166 |
| 268 | daughter | 166 |
| 269 | adventure | 165 |
| 270 | seemed | 163 |
| 271 | death | 163 |
| 272 | short | 162 |
| 273 | story | 161 |
| 274 | people | 161 |
| 275 | best | 159 |
| 276 | voice | 157 |
| 277 | mean | 157 |
| 278 | ground | 157 |
| 279 | believe | 157 |
| 280 | among | 157 |
| 281 | want | 156 |
| 282 | toboso | 156 |
| 283 | mancha | 155 |
| 284 | order | 154 |
| 285 | hast | 154 |
| 286 | hold | 153 |
| 287 | help | 153 |
| 288 | four | 153 |
| 289 | taking | 152 |
| 290 | get | 152 |
| 291 | side | 151 |
| 292 | call | 151 |
| 293 | coming | 150 |
| 294 | always | 150 |
| 295 | alone | 149 |
| 296 | together | 148 |
| 297 | less | 148 |
| 298 | castle | 148 |
| 299 | sort | 147 |
| 300 | fortune | 147 |
| 301 | return | 145 |
| 302 | moment | 145 |
| 303 | making | 145 |
| 304 | inn | 144 |
| 305 | ill | 144 |
| 306 | matter | 143 |
| 307 | books | 143 |
| 308 | answered | 142 |
| 309 | says | 140 |
| 310 | rather | 140 |
| 311 | lord | 140 |
| 312 | half | 140 |
| 313 | camilla | 140 |
| 314 | thousand | 139 |
| 315 | stood | 139 |
| 316 | something | 139 |
| 317 | poor | 138 |
| 318 | lothario | 137 |
| 319 | knew | 136 |
| 320 | king | 136 |
| 321 | anselmo | 136 |
| 322 | road | 135 |
| 323 | famous | 135 |
| 324 | face | 135 |
| 325 | earth | 135 |
| 326 | chivalry | 135 |
| 327 | fear | 134 |
| 328 | case | 134 |
| 329 | point | 133 |
| 330 | fernando | 133 |
| 331 | herself | 132 |
| 332 | foot | 132 |
| 333 | carried | 132 |
| 334 | care | 132 |
| 335 | o | 130 |
| 336 | lay | 130 |
| 337 | husband | 129 |
| 338 | devil | 128 |
| 339 | ask | 128 |
| 340 | turned | 127 |
| 341 | tears | 127 |
| 342 | neither | 127 |
| 343 | happened | 127 |
| 344 | bring | 127 |
| 345 | whose | 126 |
| 346 | since | 126 |
| 347 | passed | 126 |
| 348 | last | 126 |
| 349 | island | 126 |
| 350 | honour | 126 |
| 351 | christian | 126 |
| 352 | body | 126 |
| 353 | pass | 125 |
| 354 | both | 125 |
| 355 | worthy | 124 |
| 356 | turn | 124 |
| 357 | least | 124 |
| 358 | rest | 123 |
| 359 | horse | 123 |
| 360 | round | 122 |
| 361 | hear | 122 |
| 362 | everything | 122 |
| 363 | comes | 122 |
| 364 | sword | 121 |
| 365 | dapple | 121 |
| 366 | wilt | 120 |
| 367 | itself | 120 |
| 368 | hundred | 120 |
| 369 | feet | 120 |
| 370 | del | 120 |
| 371 | account | 120 |
| 372 | each | 119 |
| 373 | government | 118 |
| 374 | fell | 118 |
| 375 | de | 117 |
| 376 | bachelor | 117 |
| 377 | saddle | 116 |
| 378 | room | 116 |
| 379 | fall | 115 |
| 380 | enchanted | 115 |
| 381 | thus | 114 |
| 382 | need | 114 |
| 383 | valiant | 113 |
| 384 | open | 113 |
| 385 | known | 113 |
| 386 | indeed | 113 |
| 387 | high | 113 |
| 388 | felt | 113 |
| 389 | course | 113 |
| 390 | adventures | 113 |
| 391 | soul | 112 |
| 392 | seems | 112 |
| 393 | means | 112 |
| 394 | instant | 112 |
| 395 | why | 111 |
| 396 | held | 111 |
| 397 | dorothea | 111 |
| 398 | desire | 111 |
| 399 | carry | 111 |
| 400 | brother | 111 |
| 401 | woman | 110 |
| 402 | else | 110 |
| 403 | speak | 109 |
| 404 | money | 109 |
| 405 | book | 109 |
| 406 | rich | 108 |
| 407 | ought | 108 |
| 408 | letter | 108 |
| 409 | home | 108 |
| 410 | ye | 107 |
| 411 | either | 107 |
| 412 | anyone | 107 |
| 413 | above | 107 |
| 414 | pleasure | 106 |
| 415 | kind | 106 |
| 416 | feel | 106 |
| 417 | years | 105 |
| 418 | old | 105 |
| 419 | certain | 105 |
| 420 | bad | 105 |
| 421 | arm | 105 |
| 422 | able | 105 |
| 423 | yet | 104 |
| 424 | dead | 104 |
| 425 | sleep | 103 |
| 426 | giving | 103 |
| 427 | times | 102 |
| 428 | city | 102 |
| 429 | dost | 101 |
| 430 | thyself | 100 |
| 431 | son | 100 |
| 432 | light | 100 |
| 433 | hard | 100 |
| 434 | close | 100 |
| 435 | cardenio | 100 |
| 436 | gone | 99 |
| 437 | exclaimed | 99 |
| 438 | also | 99 |
| 439 | sir | 98 |
| 440 | perhaps | 98 |
| 441 | whatever | 97 |
| 442 | new | 97 |
| 443 | won | 96 |
| 444 | reached | 96 |
| 445 | eat | 96 |
| 446 | next | 95 |
| 447 | luscinda | 95 |
| 448 | looking | 95 |
| 449 | live | 95 |
| 450 | finding | 95 |
| 451 | calling | 95 |
| 452 | bound | 95 |
| 453 | senora | 94 |
| 454 | landlord | 94 |
| 455 | wish | 93 |
| 456 | white | 93 |
| 457 | virtue | 93 |
| 458 | perceived | 93 |
| 459 | pedro | 93 |
| 460 | knows | 93 |
| 461 | yourself | 92 |
| 462 | purpose | 92 |
| 463 | peace | 92 |
| 464 | looked | 92 |
| 465 | doing | 92 |
| 466 | armour | 92 |
| 467 | town | 91 |
| 468 | teresa | 91 |
| 469 | promise | 91 |
| 470 | person | 91 |
| 471 | free | 91 |
| 472 | faith | 91 |
| 473 | waiting | 90 |
| 474 | hearing | 90 |
| 475 | greater | 90 |
| 476 | gold | 90 |
| 477 | damsel | 90 |
| 478 | country | 90 |
| 479 | write | 89 |
| 480 | behind | 89 |
| 481 | observed | 88 |
| 482 | become | 88 |
| 483 | sure | 87 |
| 484 | reply | 87 |
| 485 | received | 87 |
| 486 | mounted | 87 |
| 487 | except | 87 |
| 488 | therefore | 86 |
| 489 | m | 86 |
| 490 | bear | 86 |
| 491 | strange | 85 |
| 492 | bed | 85 |
| 493 | author | 85 |
| 494 | thine | 84 |
| 495 | servants | 84 |
| 496 | plain | 84 |
| 497 | countenance | 84 |
| 498 | unless | 83 |
| 499 | sight | 83 |
| 500 | power | 83 |
| 501 | ladies | 83 |
| 502 | young | 82 |
| 503 | second | 82 |
| 504 | mouth | 82 |
| 505 | lost | 82 |
| 506 | dress | 82 |
| 507 | appearance | 82 |
| 508 | wonder | 81 |
| 509 | trouble | 81 |
| 510 | sound | 81 |
| 511 | princess | 81 |
| 512 | pay | 81 |
| 513 | kept | 81 |
| 514 | forth | 81 |
| 515 | blood | 81 |
| 516 | wrong | 80 |
| 517 | serve | 80 |
| 518 | remember | 80 |
| 519 | mother | 80 |
| 520 | happy | 80 |
| 521 | air | 80 |
| 522 | samson | 79 |
| 523 | near | 79 |
| 524 | few | 79 |
| 525 | fancy | 79 |
| 526 | enemy | 79 |
| 527 | unable | 78 |
| 528 | thoughts | 78 |
| 529 | silence | 78 |
| 530 | letters | 78 |
| 531 | service | 77 |
| 532 | memory | 77 |
| 533 | laid | 77 |
| 534 | along | 77 |
| 535 | zoraida | 76 |
| 536 | work | 76 |
| 537 | understand | 76 |
| 538 | six | 76 |
| 539 | resolved | 76 |
| 540 | leaving | 76 |
| 541 | follow | 76 |
| 542 | bade | 76 |
| 543 | try | 75 |
| 544 | spot | 75 |
| 545 | ready | 75 |
| 546 | pleased | 75 |
| 547 | misfortune | 75 |
| 548 | lance | 75 |
| 549 | evil | 75 |
| 550 | cause | 75 |
| 551 | beyond | 75 |
| 552 | battle | 75 |
| 553 | water | 74 |
| 554 | wait | 74 |
| 555 | used | 74 |
| 556 | object | 74 |
| 557 | makes | 74 |
| 558 | senses | 73 |
| 559 | ran | 73 |
| 560 | promised | 73 |
| 561 | luck | 73 |
| 562 | helmet | 73 |
| 563 | force | 73 |
| 564 | favour | 73 |
| 565 | dona | 73 |
| 566 | almost | 73 |
| 567 | youth | 72 |
| 568 | tongue | 72 |
| 569 | spain | 72 |
| 570 | opportunity | 72 |
| 571 | kingdom | 72 |
| 572 | goes | 72 |
| 573 | conversation | 72 |
| 574 | begged | 72 |
| 575 | beautiful | 72 |
| 576 | beard | 72 |
| 577 | small | 71 |
| 578 | send | 71 |
| 579 | placed | 71 |
| 580 | pain | 71 |
| 581 | mighty | 71 |
| 582 | matters | 71 |
| 583 | judge | 71 |
| 584 | impossible | 71 |
| 585 | hope | 71 |
| 586 | green | 71 |
| 587 | fame | 71 |
| 588 | easy | 71 |
| 589 | duenna | 71 |
| 590 | door | 71 |
| 591 | deeds | 71 |
| 592 | beginning | 71 |
| 593 | written | 70 |
| 594 | telling | 70 |
| 595 | talk | 70 |
| 596 | possible | 70 |
| 597 | none | 70 |
| 598 | large | 70 |
| 599 | filled | 70 |
| 600 | die | 70 |
| 601 | company | 70 |
| 602 | business | 70 |
| 603 | born | 70 |
| 604 | allow | 70 |
| 605 | spite | 69 |
| 606 | gentlemen | 69 |
| 607 | cut | 69 |
| 608 | continued | 69 |
| 609 | towards | 68 |
| 610 | sent | 68 |
| 611 | raised | 68 |
| 612 | putting | 68 |
| 613 | opinion | 68 |
| 614 | mad | 68 |
| 615 | friends | 68 |
| 616 | fit | 68 |
| 617 | swear | 67 |
| 618 | rate | 67 |
| 619 | question | 67 |
| 620 | nature | 67 |
| 621 | madness | 67 |
| 622 | housekeeper | 67 |
| 623 | holy | 67 |
| 624 | court | 67 |
| 625 | aid | 67 |
| 626 | worth | 66 |
| 627 | worse | 66 |
| 628 | turning | 66 |
| 629 | squires | 66 |
| 630 | lie | 66 |
| 631 | language | 66 |
| 632 | journey | 66 |
| 633 | greatest | 66 |
| 634 | distressed | 66 |
| 635 | advice | 66 |
| 636 | please | 65 |
| 637 | nay | 65 |
| 638 | knowing | 65 |
| 639 | fine | 65 |
| 640 | clear | 65 |
| 641 | chance | 65 |
| 642 | wine | 64 |
| 643 | thanks | 64 |
| 644 | sun | 64 |
| 645 | stand | 64 |
| 646 | showed | 64 |
| 647 | shepherd | 64 |
| 648 | length | 64 |
| 649 | hour | 64 |
| 650 | grant | 64 |
| 651 | entered | 64 |
| 652 | besides | 64 |
| 653 | antonio | 64 |
| 654 | altisidora | 64 |
| 655 | seek | 63 |
| 656 | persons | 63 |
| 657 | offered | 63 |
| 658 | lies | 63 |
| 659 | further | 63 |
| 660 | followed | 63 |
| 661 | errantry | 63 |
| 662 | carrasco | 63 |
| 663 | wherein | 62 |
| 664 | seem | 62 |
| 665 | renegade | 62 |
| 666 | enchanters | 62 |
| 667 | use | 61 |
| 668 | speaking | 61 |
| 669 | run | 61 |
| 670 | remained | 61 |
| 671 | niece | 61 |
| 672 | fixed | 61 |
| 673 | deep | 61 |
| 674 | women | 60 |
| 675 | sea | 60 |
| 676 | lest | 60 |
| 677 | following | 60 |
| 678 | covered | 60 |
| 679 | bread | 60 |
| 680 | age | 60 |
| 681 | vanquished | 59 |
| 682 | parents | 59 |
| 683 | paid | 59 |
| 684 | often | 59 |
| 685 | moor | 59 |
| 686 | meant | 59 |
| 687 | giant | 59 |
| 688 | fashion | 59 |
| 689 | fact | 59 |
| 690 | talking | 58 |
| 691 | save | 58 |
| 692 | queen | 58 |
| 693 | poet | 58 |
| 694 | pack | 58 |
| 695 | offer | 58 |
| 696 | number | 58 |
| 697 | haste | 58 |
| 698 | forward | 58 |
| 699 | escape | 58 |
| 700 | deal | 58 |
| 701 | cloth | 58 |
| 702 | afterwards | 58 |
| 703 | according | 58 |
| 704 | servant | 57 |
| 705 | quite | 57 |
| 706 | prove | 57 |
| 707 | orders | 57 |
| 708 | mistress | 57 |
| 709 | madman | 57 |
| 710 | especially | 57 |
| 711 | el | 57 |
| 712 | contrary | 57 |
| 713 | children | 57 |
| 714 | cart | 57 |
| 715 | shut | 56 |
| 716 | reach | 56 |
| 717 | moreover | 56 |
| 718 | marry | 56 |
| 719 | licentiate | 56 |
| 720 | led | 56 |
| 721 | learned | 56 |
| 722 | hair | 56 |
| 723 | ears | 56 |
| 724 | condition | 56 |
| 725 | wise | 55 |
| 726 | middle | 55 |
| 727 | effect | 55 |
| 728 | duennas | 55 |
| 729 | damsels | 55 |
| 730 | crowns | 55 |
| 731 | attention | 55 |
| 732 | table | 54 |
| 733 | somewhat | 54 |
| 734 | shoulders | 54 |
| 735 | proper | 54 |
| 736 | easily | 54 |
| 737 | broken | 54 |
| 738 | black | 54 |
| 739 | state | 53 |
| 740 | satisfaction | 53 |
| 741 | sake | 53 |
| 742 | montesinos | 53 |
| 743 | listening | 53 |
| 744 | fallen | 53 |
| 745 | couple | 53 |
| 746 | consider | 53 |
| 747 | captive | 53 |
| 748 | basilio | 53 |
| 749 | trees | 52 |
| 750 | sense | 52 |
| 751 | satisfied | 52 |
| 752 | ones | 52 |
| 753 | morning | 52 |
| 754 | low | 52 |
| 755 | girl | 52 |
| 756 | d | 52 |
| 757 | common | 52 |
| 758 | aside | 52 |
| 759 | verses | 51 |
| 760 | twenty | 51 |
| 761 | sage | 51 |
| 762 | rise | 51 |
| 763 | remain | 51 |
| 764 | ordered | 51 |
| 765 | mentioned | 51 |
| 766 | lead | 51 |
| 767 | justice | 51 |
| 768 | instead | 51 |
| 769 | grove | 51 |
| 770 | glory | 51 |
| 771 | fool | 51 |
| 772 | fate | 51 |
| 773 | described | 51 |
| 774 | christians | 51 |
| 775 | birth | 51 |
| 776 | wanted | 50 |
| 777 | stretched | 50 |
| 778 | served | 50 |
| 779 | rueful | 50 |
| 780 | carrying | 50 |
| 781 | wouldst | 49 |
| 782 | vessel | 49 |
| 783 | till | 49 |
| 784 | teeth | 49 |
| 785 | standing | 49 |
| 786 | sirs | 49 |
| 787 | receive | 49 |
| 788 | page | 49 |
| 789 | occasion | 49 |
| 790 | noise | 49 |
| 791 | natural | 49 |
| 792 | loud | 49 |
| 793 | hunger | 49 |
| 794 | five | 49 |
| 795 | figure | 49 |
| 796 | emperor | 49 |
| 797 | different | 49 |
| 798 | achievements | 49 |
| 799 | year | 48 |
| 800 | sign | 48 |
| 801 | plainly | 48 |
| 802 | past | 48 |
| 803 | gives | 48 |
| 804 | field | 48 |
| 805 | enchantment | 48 |
| 806 | count | 48 |
| 807 | ape | 48 |
| 808 | added | 48 |
| 809 | wit | 47 |
| 810 | style | 47 |
| 811 | struck | 47 |
| 812 | stay | 47 |
| 813 | reals | 47 |
| 814 | nonsense | 47 |
| 815 | longer | 47 |
| 816 | horseback | 47 |
| 817 | goatherd | 47 |
| 818 | flesh | 47 |
| 819 | fire | 47 |
| 820 | distance | 47 |
| 821 | departure | 47 |
| 822 | danger | 47 |
| 823 | cave | 47 |
| 824 | affair | 47 |
| 825 | yours | 46 |
| 826 | wits | 46 |
| 827 | tree | 46 |
| 828 | sweet | 46 |
| 829 | shown | 46 |
| 830 | safe | 46 |
| 831 | roque | 46 |
| 832 | quest | 46 |
| 833 | mule | 46 |
| 834 | moors | 46 |
| 835 | law | 46 |
| 836 | knowest | 46 |
| 837 | galley | 46 |
| 838 | amazed | 46 |
| 839 | amadis | 46 |
| 840 | advanced | 46 |
| 841 | within | 45 |
| 842 | unlucky | 45 |
| 843 | unhappy | 45 |
| 844 | step | 45 |
| 845 | several | 45 |
| 846 | search | 45 |
| 847 | rodriguez | 45 |
| 848 | recognised | 45 |
| 849 | reading | 45 |
| 850 | presence | 45 |
| 851 | morrow | 45 |
| 852 | fresh | 45 |
| 853 | cousin | 45 |
| 854 | courtesy | 45 |
| 855 | captain | 45 |
| 856 | thinking | 44 |
| 857 | strength | 44 |
| 858 | signs | 44 |
| 859 | related | 44 |
| 860 | play | 44 |
| 861 | pair | 44 |
| 862 | news | 44 |
| 863 | leonela | 44 |
| 864 | lashes | 44 |
| 865 | glad | 44 |
| 866 | drew | 44 |
| 867 | agreed | 44 |
| 868 | valour | 43 |
| 869 | stop | 43 |
| 870 | spoke | 43 |
| 871 | shalt | 43 |
| 872 | seated | 43 |
| 873 | rank | 43 |
| 874 | promises | 43 |
| 875 | ourselves | 43 |
| 876 | oh | 43 |
| 877 | nobody | 43 |
| 878 | necessary | 43 |
| 879 | mount | 43 |
| 880 | happiness | 43 |
| 881 | gentle | 43 |
| 882 | expected | 43 |
| 883 | doctor | 43 |
| 884 | changed | 43 |
| 885 | canst | 43 |
| 886 | believed | 43 |
| 887 | alive | 43 |
| 888 | virtuous | 42 |
| 889 | sometimes | 42 |
| 890 | secret | 42 |
| 891 | removed | 42 |
| 892 | real | 42 |
| 893 | presented | 42 |
| 894 | peasant | 42 |
| 895 | meet | 42 |
| 896 | lover | 42 |
| 897 | lose | 42 |
| 898 | joke | 42 |
| 899 | human | 42 |
| 900 | hardly | 42 |
| 901 | grave | 42 |
| 902 | equal | 42 |
| 903 | dread | 42 |
| 904 | chamber | 42 |
| 905 | breast | 42 |
| 906 | stone | 41 |
| 907 | provided | 41 |
| 908 | praise | 41 |
| 909 | mountains | 41 |
| 910 | misfortunes | 41 |
| 911 | land | 41 |
| 912 | gallant | 41 |
| 913 | fellow | 41 |
| 914 | fail | 41 |
| 915 | entreat | 41 |
| 916 | enemies | 41 |
| 917 | diego | 41 |
| 918 | beast | 41 |
| 919 | bearing | 41 |
| 920 | asleep | 41 |
| 921 | wished | 40 |
| 922 | support | 40 |
| 923 | remedy | 40 |
| 924 | persuaded | 40 |
| 925 | noble | 40 |
| 926 | keeping | 40 |
| 927 | garden | 40 |
| 928 | finished | 40 |
| 929 | feeling | 40 |
| 930 | entirely | 40 |
| 931 | engaged | 40 |
| 932 | dressed | 40 |
| 933 | deserve | 40 |
| 934 | dear | 40 |
| 935 | content | 40 |
| 936 | conscience | 40 |
| 937 | combat | 40 |
| 938 | canon | 40 |
| 939 | bore | 40 |
| 940 | wounded | 39 |
| 941 | wealth | 39 |
| 942 | viceroy | 39 |
| 943 | touch | 39 |
| 944 | sorrow | 39 |
| 945 | shepherds | 39 |
| 946 | quiteria | 39 |
| 947 | quarters | 39 |
| 948 | pure | 39 |
| 949 | perceive | 39 |
| 950 | measure | 39 |
| 951 | marriage | 39 |
| 952 | lying | 39 |
| 953 | looks | 39 |
| 954 | intention | 39 |
| 955 | happen | 39 |
| 956 | hamete | 39 |
| 957 | friendship | 39 |
| 958 | fault | 39 |
| 959 | farmer | 39 |
| 960 | enter | 39 |
| 961 | cried | 39 |
| 962 | cide | 39 |
| 963 | bosom | 39 |
| 964 | across | 39 |
| 965 | wicked | 38 |
| 966 | uttered | 38 |
| 967 | understanding | 38 |
| 968 | soldier | 38 |
| 969 | single | 38 |
| 970 | sighs | 38 |
| 971 | sad | 38 |
| 972 | respect | 38 |
| 973 | regard | 38 |
| 974 | quiet | 38 |
| 975 | plan | 38 |
| 976 | passion | 38 |
| 977 | observe | 38 |
| 978 | neck | 38 |
| 979 | moved | 38 |
| 980 | likely | 38 |
| 981 | laws | 38 |
| 982 | distress | 38 |
| 983 | delight | 38 |
| 984 | cross | 38 |
| 985 | cold | 38 |
| 986 | basin | 38 |
| 987 | anger | 38 |
| 988 | amazement | 38 |
| 989 | allowed | 38 |
| 990 | addressed | 38 |
| 991 | tied | 37 |
| 992 | suit | 37 |
| 993 | settled | 37 |
| 994 | required | 37 |
| 995 | proved | 37 |
| 996 | profession | 37 |
| 997 | proceed | 37 |
| 998 | paper | 37 |
| 999 | otherwise | 37 |
| 1000 | moon | 37 |
| 1001 | majordomo | 37 |
| 1002 | listen | 37 |
| 1003 | liberty | 37 |
| 1004 | leagues | 37 |
| 1005 | laughter | 37 |
| 1006 | host | 37 |
| 1007 | hers | 37 |
| 1008 | grace | 37 |
| 1009 | galleys | 37 |
| 1010 | eye | 37 |
| 1011 | expect | 37 |
| 1012 | church | 37 |
| 1013 | bringing | 37 |
| 1014 | attempt | 37 |
| 1015 | appeared | 37 |
| 1016 | yes | 36 |
| 1017 | window | 36 |
| 1018 | usual | 36 |
| 1019 | unfortunate | 36 |
| 1020 | title | 36 |
| 1021 | ten | 36 |
| 1022 | spanish | 36 |
| 1023 | relief | 36 |
| 1024 | proceeded | 36 |
| 1025 | pieces | 36 |
| 1026 | opened | 36 |
| 1027 | mayest | 36 |
| 1028 | kiss | 36 |
| 1029 | intelligence | 36 |
| 1030 | hide | 36 |
| 1031 | general | 36 |
| 1032 | war | 35 |
| 1033 | utter | 35 |
| 1034 | twelve | 35 |
| 1035 | tender | 35 |
| 1036 | subject | 35 |
| 1037 | spoken | 35 |
| 1038 | spirit | 35 |
| 1039 | speed | 35 |
| 1040 | ricote | 35 |
| 1041 | possession | 35 |
| 1042 | peerless | 35 |
| 1043 | pace | 35 |
| 1044 | office | 35 |
| 1045 | married | 35 |
| 1046 | luis | 35 |
| 1047 | listened | 35 |
| 1048 | lips | 35 |
| 1049 | lions | 35 |
| 1050 | kill | 35 |
| 1051 | histories | 35 |
| 1052 | highness | 35 |
| 1053 | hell | 35 |
| 1054 | harm | 35 |
| 1055 | fully | 35 |
| 1056 | folly | 35 |
| 1057 | experience | 35 |
| 1058 | due | 35 |
| 1059 | dinner | 35 |
| 1060 | didst | 35 |
| 1061 | delivered | 35 |
| 1062 | cure | 35 |
| 1063 | cruel | 35 |
| 1064 | courage | 35 |
| 1065 | change | 35 |
| 1066 | camacho | 35 |
| 1067 | buried | 35 |
| 1068 | bred | 35 |
| 1069 | although | 35 |
| 1070 | yard | 34 |
| 1071 | third | 34 |
| 1072 | share | 34 |
| 1073 | quality | 34 |
| 1074 | proverbs | 34 |
| 1075 | position | 34 |
| 1076 | pearls | 34 |
| 1077 | merely | 34 |
| 1078 | marvellous | 34 |
| 1079 | living | 34 |
| 1080 | lives | 34 |
| 1081 | knees | 34 |
| 1082 | idea | 34 |
| 1083 | hours | 34 |
| 1084 | giants | 34 |
| 1085 | ease | 34 |
| 1086 | ear | 34 |
| 1087 | droll | 34 |
| 1088 | discovered | 34 |
| 1089 | determined | 34 |
| 1090 | deliver | 34 |
| 1091 | countess | 34 |
| 1092 | brotherhood | 34 |
| 1093 | break | 34 |
| 1094 | attack | 34 |
| 1095 | anybody | 34 |
| 1096 | wood | 33 |
| 1097 | wishes | 33 |
| 1098 | understood | 33 |
| 1099 | supper | 33 |
| 1100 | strong | 33 |
| 1101 | stir | 33 |
| 1102 | stick | 33 |
| 1103 | sorts | 33 |
| 1104 | showing | 33 |
| 1105 | resolution | 33 |
| 1106 | questions | 33 |
| 1107 | quarter | 33 |
| 1108 | piece | 33 |
| 1109 | permission | 33 |
| 1110 | patience | 33 |
| 1111 | parts | 33 |
| 1112 | observing | 33 |
| 1113 | nose | 33 |
| 1114 | modesty | 33 |
| 1115 | met | 33 |
| 1116 | loves | 33 |
| 1117 | line | 33 |
| 1118 | likewise | 33 |
| 1119 | importance | 33 |
| 1120 | immediately | 33 |
| 1121 | govern | 33 |
| 1122 | getting | 33 |
| 1123 | fly | 33 |
| 1124 | falling | 33 |
| 1125 | died | 33 |
| 1126 | countless | 33 |
| 1127 | commonly | 33 |
| 1128 | coach | 33 |
| 1129 | cage | 33 |
| 1130 | befell | 33 |
| 1131 | advantage | 33 |
| 1132 | writing | 32 |
| 1133 | wants | 32 |
| 1134 | wanting | 32 |
| 1135 | venture | 32 |
| 1136 | touched | 32 |
| 1137 | tale | 32 |
| 1138 | takes | 32 |
| 1139 | suffering | 32 |
| 1140 | simple | 32 |
| 1141 | seat | 32 |
| 1142 | reward | 32 |
| 1143 | rare | 32 |
| 1144 | raise | 32 |
| 1145 | places | 32 |
| 1146 | persuade | 32 |
| 1147 | owner | 32 |
| 1148 | oath | 32 |
| 1149 | move | 32 |
| 1150 | mischief | 32 |
| 1151 | leaves | 32 |
| 1152 | health | 32 |
| 1153 | gate | 32 |
| 1154 | drink | 32 |
| 1155 | dozen | 32 |
| 1156 | delay | 32 |
| 1157 | cost | 32 |
| 1158 | charge | 32 |
| 1159 | buckler | 32 |
| 1160 | board | 32 |
| 1161 | begin | 32 |
| 1162 | beg | 32 |
| 1163 | accompany | 32 |
| 1164 | wind | 31 |
| 1165 | win | 31 |
| 1166 | waited | 31 |
| 1167 | trust | 31 |
| 1168 | top | 31 |
| 1169 | suppose | 31 |
| 1170 | suffer | 31 |
| 1171 | shows | 31 |
| 1172 | seeking | 31 |
| 1173 | release | 31 |
| 1174 | quickly | 31 |
| 1175 | punishment | 31 |
| 1176 | proof | 31 |
| 1177 | opposite | 31 |
| 1178 | offence | 31 |
| 1179 | nevertheless | 31 |
| 1180 | knowledge | 31 |
| 1181 | islands | 31 |
| 1182 | hopes | 31 |
| 1183 | highest | 31 |
| 1184 | grief | 31 |
| 1185 | greatly | 31 |
| 1186 | false | 31 |
| 1187 | deserves | 31 |
| 1188 | command | 31 |
| 1189 | choose | 31 |
| 1190 | child | 31 |
| 1191 | caught | 31 |
| 1192 | bit | 31 |
| 1193 | became | 31 |
| 1194 | approached | 31 |
| 1195 | ah | 31 |
| 1196 | act | 31 |
| 1197 | yield | 30 |
| 1198 | wounds | 30 |
| 1199 | wound | 30 |
| 1200 | welcome | 30 |
| 1201 | trifaldi | 30 |
| 1202 | taste | 30 |
| 1203 | shame | 30 |
| 1204 | rose | 30 |
| 1205 | raising | 30 |
| 1206 | property | 30 |
| 1207 | particularly | 30 |
| 1208 | officers | 30 |
| 1209 | names | 30 |
| 1210 | miserable | 30 |
| 1211 | mirrors | 30 |
| 1212 | midst | 30 |
| 1213 | maritornes | 30 |
| 1214 | lovers | 30 |
| 1215 | lorenzo | 30 |
| 1216 | illustrious | 30 |
| 1217 | honourable | 30 |
| 1218 | holding | 30 |
| 1219 | grand | 30 |
| 1220 | generous | 30 |
| 1221 | form | 30 |
| 1222 | dying | 30 |
| 1223 | duty | 30 |
| 1224 | drawing | 30 |
| 1225 | desires | 30 |
| 1226 | dare | 30 |
| 1227 | custom | 30 |
| 1228 | courteous | 30 |
| 1229 | confess | 30 |
| 1230 | clown | 30 |
| 1231 | calls | 30 |
| 1232 | big | 30 |
| 1233 | bestowed | 30 |
| 1234 | becoming | 30 |
| 1235 | alforjas | 30 |
| 1236 | whence | 29 |
| 1237 | vengeance | 29 |
| 1238 | treated | 29 |
| 1239 | throw | 29 |
| 1240 | suspect | 29 |
| 1241 | simplicity | 29 |
| 1242 | sierra | 29 |
| 1243 | seized | 29 |
| 1244 | running | 29 |
| 1245 | remove | 29 |
| 1246 | poverty | 29 |
| 1247 | poets | 29 |
| 1248 | pleasant | 29 |
| 1249 | perfection | 29 |
| 1250 | perceiving | 29 |
| 1251 | penance | 29 |
| 1252 | obeyed | 29 |
| 1253 | naked | 29 |
| 1254 | manner | 29 |
| 1255 | league | 29 |
| 1256 | leading | 29 |
| 1257 | late | 29 |
| 1258 | imagine | 29 |
| 1259 | ignorant | 29 |
| 1260 | idle | 29 |
| 1261 | houses | 29 |
| 1262 | honest | 29 |
| 1263 | hearts | 29 |
| 1264 | hath | 29 |
| 1265 | gossip | 29 |
| 1266 | forget | 29 |
| 1267 | exalted | 29 |
| 1268 | everybody | 29 |
| 1269 | enjoy | 29 |
| 1270 | embraced | 29 |
| 1271 | eight | 29 |
| 1272 | directed | 29 |
| 1273 | difficulty | 29 |
| 1274 | declared | 29 |
| 1275 | considered | 29 |
| 1276 | conclusion | 29 |
| 1277 | comfort | 29 |
| 1278 | clean | 29 |
| 1279 | chrysostom | 29 |
| 1280 | boy | 29 |
| 1281 | blows | 29 |
| 1282 | blow | 29 |
| 1283 | biscayan | 29 |
| 1284 | belonging | 29 |
| 1285 | arranged | 29 |
| 1286 | approaching | 29 |
| 1287 | aloud | 29 |
| 1288 | acted | 29 |
| 1289 | wore | 28 |
| 1290 | wert | 28 |
| 1291 | uncle | 28 |
| 1292 | tosilos | 28 |
| 1293 | tail | 28 |
| 1294 | suspicion | 28 |
| 1295 | sonnet | 28 |
| 1296 | slaves | 28 |
| 1297 | shield | 28 |
| 1298 | seven | 28 |
| 1299 | saint | 28 |
| 1300 | risk | 28 |
| 1301 | quitted | 28 |
| 1302 | public | 28 |
| 1303 | prevent | 28 |
| 1304 | particular | 28 |
| 1305 | mountain | 28 |
| 1306 | moorish | 28 |
| 1307 | legs | 28 |
| 1308 | kings | 28 |
| 1309 | innkeeper | 28 |
| 1310 | hastened | 28 |
| 1311 | gaul | 28 |
| 1312 | front | 28 |
| 1313 | forgive | 28 |
| 1314 | flung | 28 |
| 1315 | figures | 28 |
| 1316 | fast | 28 |
| 1317 | exactly | 28 |
| 1318 | everyone | 28 |
| 1319 | engage | 28 |
| 1320 | enchantments | 28 |
| 1321 | desired | 28 |
| 1322 | declare | 28 |
| 1323 | convinced | 28 |
| 1324 | clothes | 28 |
| 1325 | clearly | 28 |
| 1326 | wrote | 27 |
| 1327 | weep | 27 |
| 1328 | ways | 27 |
| 1329 | watching | 27 |
| 1330 | wall | 27 |
| 1331 | treats | 27 |
| 1332 | thief | 27 |
| 1333 | staff | 27 |
| 1334 | sorry | 27 |
| 1335 | sore | 27 |
| 1336 | sinner | 27 |
| 1337 | shape | 27 |
| 1338 | returning | 27 |
| 1339 | reasonable | 27 |
| 1340 | rage | 27 |
| 1341 | loved | 27 |
| 1342 | loose | 27 |
| 1343 | lived | 27 |
| 1344 | lawful | 27 |
| 1345 | incidents | 27 |
| 1346 | imagined | 27 |
| 1347 | hung | 27 |
| 1348 | humble | 27 |
| 1349 | future | 27 |
| 1350 | freedom | 27 |
| 1351 | forced | 27 |
| 1352 | follows | 27 |
| 1353 | farther | 27 |
| 1354 | fancied | 27 |
| 1355 | envy | 27 |
| 1356 | earnest | 27 |
| 1357 | eager | 27 |
| 1358 | dignity | 27 |
| 1359 | describe | 27 |
| 1360 | demand | 27 |
| 1361 | degree | 27 |
| 1362 | consent | 27 |
| 1363 | bright | 27 |
| 1364 | beside | 27 |
| 1365 | beheld | 27 |
| 1366 | aware | 27 |
| 1367 | astonishment | 27 |
| 1368 | asking | 27 |
| 1369 | anxious | 27 |
| 1370 | ages | 27 |
| 1371 | works | 26 |
| 1372 | wide | 26 |
| 1373 | whoever | 26 |
| 1374 | truly | 26 |
| 1375 | strove | 26 |
| 1376 | sleeping | 26 |
| 1377 | sing | 26 |
| 1378 | silent | 26 |
| 1379 | retired | 26 |
| 1380 | restore | 26 |
| 1381 | regarded | 26 |
| 1382 | red | 26 |
| 1383 | portion | 26 |
| 1384 | permit | 26 |
| 1385 | ours | 26 |
| 1386 | obey | 26 |
| 1387 | merlin | 26 |
| 1388 | mention | 26 |
| 1389 | melancholy | 26 |
| 1390 | marcela | 26 |
| 1391 | majesty | 26 |
| 1392 | lot | 26 |
| 1393 | loss | 26 |
| 1394 | landlady | 26 |
| 1395 | lacquey | 26 |
| 1396 | labour | 26 |
| 1397 | helped | 26 |
| 1398 | goodness | 26 |
| 1399 | gifts | 26 |
| 1400 | fight | 26 |
| 1401 | family | 26 |
| 1402 | excellence | 26 |
| 1403 | enjoyment | 26 |
| 1404 | ended | 26 |
| 1405 | enchanter | 26 |
| 1406 | drove | 26 |
| 1407 | draw | 26 |
| 1408 | difference | 26 |
| 1409 | dark | 26 |
| 1410 | curiosity | 26 |
| 1411 | choice | 26 |
| 1412 | catholic | 26 |
| 1413 | blind | 26 |
| 1414 | blessing | 26 |
| 1415 | badly | 26 |
| 1416 | awake | 26 |
| 1417 | arrived | 26 |
| 1418 | ancient | 26 |
| 1419 | woe | 25 |
| 1420 | willing | 25 |
| 1421 | watch | 25 |
| 1422 | uttering | 25 |
| 1423 | treasure | 25 |
| 1424 | sought | 25 |
| 1425 | soldiers | 25 |
| 1426 | silk | 25 |
| 1427 | shouldst | 25 |
| 1428 | really | 25 |
| 1429 | pressed | 25 |
| 1430 | palace | 25 |
| 1431 | occurred | 25 |
| 1432 | music | 25 |
| 1433 | lofty | 25 |
| 1434 | liked | 25 |
| 1435 | lifted | 25 |
| 1436 | kindness | 25 |
| 1437 | governors | 25 |
| 1438 | france | 25 |
| 1439 | former | 25 |
| 1440 | fingers | 25 |
| 1441 | fields | 25 |
| 1442 | favours | 25 |
| 1443 | disposed | 25 |
| 1444 | disenchantment | 25 |
| 1445 | daylight | 25 |
| 1446 | crown | 25 |
| 1447 | cries | 25 |
| 1448 | completely | 25 |
| 1449 | carefully | 25 |
| 1450 | brings | 25 |
| 1451 | bold | 25 |
| 1452 | belief | 25 |
| 1453 | beasts | 25 |
| 1454 | astonished | 25 |
| 1455 | afraid | 25 |
| 1456 | affairs | 25 |
| 1457 | yesterday | 24 |
| 1458 | worships | 24 |
| 1459 | witness | 24 |
| 1460 | weight | 24 |
| 1461 | weary | 24 |
| 1462 | wear | 24 |
| 1463 | wages | 24 |
| 1464 | victory | 24 |
| 1465 | trying | 24 |
| 1466 | stripped | 24 |
| 1467 | spent | 24 |
| 1468 | singing | 24 |
| 1469 | sayest | 24 |
| 1470 | satisfy | 24 |
| 1471 | safely | 24 |
| 1472 | reputation | 24 |
| 1473 | recognise | 24 |
| 1474 | pray | 24 |
| 1475 | passing | 24 |
| 1476 | pardon | 24 |
| 1477 | mistake | 24 |
| 1478 | mercy | 24 |
| 1479 | maiden | 24 |
| 1480 | judgment | 24 |
| 1481 | joy | 24 |
| 1482 | jealousy | 24 |
| 1483 | issue | 24 |
| 1484 | intentions | 24 |
| 1485 | humour | 24 |
| 1486 | higher | 24 |
| 1487 | hanging | 24 |
| 1488 | handed | 24 |
| 1489 | goats | 24 |
| 1490 | firmly | 24 |
| 1491 | falsehood | 24 |
| 1492 | extraordinary | 24 |
| 1493 | exclaiming | 24 |
| 1494 | excellent | 24 |
| 1495 | during | 24 |
| 1496 | dry | 24 |
| 1497 | drop | 24 |
| 1498 | disposition | 24 |
| 1499 | dagger | 24 |
| 1500 | crazy | 24 |
| 1501 | confusion | 24 |
| 1502 | comrades | 24 |
| 1503 | compassion | 24 |
| 1504 | burned | 24 |
| 1505 | broad | 24 |
| 1506 | bridle | 24 |
| 1507 | brass | 24 |
| 1508 | bowels | 24 |
| 1509 | bent | 24 |
| 1510 | bears | 24 |
| 1511 | base | 24 |
| 1512 | attacked | 24 |
| 1513 | amusement | 24 |
| 1514 | advised | 24 |
| 1515 | add | 24 |
| 1516 | wild | 23 |
| 1517 | wench | 23 |
| 1518 | ungrateful | 23 |
| 1519 | uneasy | 23 |
| 1520 | sufferings | 23 |
| 1521 | suddenly | 23 |
| 1522 | stopped | 23 |
| 1523 | stones | 23 |
| 1524 | stomach | 23 |
| 1525 | slowly | 23 |
| 1526 | shouting | 23 |
| 1527 | scarcely | 23 |
| 1528 | robbed | 23 |
| 1529 | revenge | 23 |
| 1530 | result | 23 |
| 1531 | requisite | 23 |
| 1532 | princes | 23 |
| 1533 | pressing | 23 |
| 1534 | plenty | 23 |
| 1535 | pity | 23 |
| 1536 | painted | 23 |
| 1537 | pains | 23 |
| 1538 | oak | 23 |
| 1539 | meaning | 23 |
| 1540 | horses | 23 |
| 1541 | hit | 23 |
| 1542 | guide | 23 |
| 1543 | grey | 23 |
| 1544 | gregorio | 23 |
| 1545 | grass | 23 |
| 1546 | forgotten | 23 |
| 1547 | fond | 23 |
| 1548 | folk | 23 |
| 1549 | flying | 23 |
| 1550 | features | 23 |
| 1551 | entreated | 23 |
| 1552 | eating | 23 |
| 1553 | dog | 23 |
| 1554 | divine | 23 |
| 1555 | devils | 23 |
| 1556 | defend | 23 |
| 1557 | cover | 23 |
| 1558 | consequence | 23 |
| 1559 | concluded | 23 |
| 1560 | chair | 23 |
| 1561 | burst | 23 |
| 1562 | brave | 23 |
| 1563 | blessed | 23 |
| 1564 | befallen | 23 |
| 1565 | avoid | 23 |
| 1566 | attend | 23 |
| 1567 | arguments | 23 |
| 1568 | anxiety | 23 |
| 1569 | whenever | 22 |
| 1570 | wheat | 22 |
| 1571 | weeping | 22 |
| 1572 | value | 22 |
| 1573 | turks | 22 |
| 1574 | tried | 22 |
| 1575 | travelling | 22 |
| 1576 | threw | 22 |
| 1577 | thirty | 22 |
| 1578 | task | 22 |
| 1579 | student | 22 |
| 1580 | stout | 22 |
| 1581 | steps | 22 |
| 1582 | star | 22 |
| 1583 | stable | 22 |
| 1584 | shepherdess | 22 |
| 1585 | sanchica | 22 |
| 1586 | roland | 22 |
| 1587 | rob | 22 |
| 1588 | request | 22 |
| 1589 | released | 22 |
| 1590 | quit | 22 |
| 1591 | proverb | 22 |
| 1592 | protection | 22 |
| 1593 | precious | 22 |
| 1594 | plays | 22 |
| 1595 | minute | 22 |
| 1596 | meadow | 22 |
| 1597 | marble | 22 |
| 1598 | losing | 22 |
| 1599 | laughing | 22 |
| 1600 | laughed | 22 |
| 1601 | killed | 22 |
| 1602 | interest | 22 |
| 1603 | insult | 22 |
| 1604 | gathered | 22 |
| 1605 | gain | 22 |
| 1606 | food | 22 |
| 1607 | embrace | 22 |
| 1608 | device | 22 |
| 1609 | despair | 22 |
| 1610 | depths | 22 |
| 1611 | cured | 22 |
| 1612 | conduct | 22 |
| 1613 | complete | 22 |
| 1614 | colour | 22 |
| 1615 | clad | 22 |
| 1616 | certainly | 22 |
| 1617 | caused | 22 |
| 1618 | cat | 22 |
| 1619 | boys | 22 |
| 1620 | attentively | 22 |
| 1621 | appear | 22 |
| 1622 | ago | 22 |
| 1623 | accompanied | 22 |
| 1624 | absurdities | 22 |
| 1625 | absence | 22 |
| 1626 | wrongs | 21 |
| 1627 | wisdom | 21 |
| 1628 | wherever | 21 |
| 1629 | weak | 21 |
| 1630 | wandering | 21 |
| 1631 | view | 21 |
| 1632 | trick | 21 |
| 1633 | surprised | 21 |
| 1634 | streets | 21 |
| 1635 | stars | 21 |
| 1636 | spare | 21 |
| 1637 | soft | 21 |
| 1638 | sit | 21 |
| 1639 | sin | 21 |
| 1640 | shrewd | 21 |
| 1641 | shortly | 21 |
| 1642 | shoes | 21 |
| 1643 | seest | 21 |
| 1644 | saragossa | 21 |
| 1645 | sally | 21 |
| 1646 | rode | 21 |
| 1647 | roads | 21 |
| 1648 | retire | 21 |
| 1649 | repeated | 21 |
| 1650 | relieve | 21 |
| 1651 | protect | 21 |
| 1652 | prize | 21 |
| 1653 | printed | 21 |
| 1654 | preserve | 21 |
| 1655 | peril | 21 |
| 1656 | party | 21 |
| 1657 | novel | 21 |
| 1658 | needed | 21 |
| 1659 | nearly | 21 |
| 1660 | mules | 21 |
| 1661 | modest | 21 |
| 1662 | miracle | 21 |
| 1663 | mills | 21 |
| 1664 | mere | 21 |
| 1665 | masters | 21 |
| 1666 | inclined | 21 |
| 1667 | image | 21 |
| 1668 | height | 21 |
| 1669 | heavy | 21 |
| 1670 | hearted | 21 |
| 1671 | guest | 21 |
| 1672 | gladly | 21 |
| 1673 | gines | 21 |
| 1674 | finish | 21 |
| 1675 | example | 21 |
| 1676 | ere | 21 |
| 1677 | enjoyed | 21 |
| 1678 | dismounted | 21 |
| 1679 | defence | 21 |
| 1680 | cruelty | 21 |
| 1681 | commanded | 21 |
| 1682 | clara | 21 |
| 1683 | chain | 21 |
| 1684 | carver | 21 |
| 1685 | burning | 21 |
| 1686 | breaking | 21 |
| 1687 | boat | 21 |
| 1688 | bestow | 21 |
| 1689 | authority | 21 |
| 1690 | apparently | 21 |
| 1691 | affection | 21 |
| 1692 | adopted | 21 |
| 1693 | wrath | 20 |
| 1694 | wont | 20 |
| 1695 | verily | 20 |
| 1696 | vain | 20 |
| 1697 | troubled | 20 |
| 1698 | treat | 20 |
| 1699 | touching | 20 |
| 1700 | terror | 20 |
| 1701 | sweat | 20 |
| 1702 | supposed | 20 |
| 1703 | street | 20 |
| 1704 | spread | 20 |
| 1705 | special | 20 |
| 1706 | smell | 20 |
| 1707 | sins | 20 |
| 1708 | sheep | 20 |
| 1709 | services | 20 |
| 1710 | sensible | 20 |
| 1711 | rope | 20 |
| 1712 | rocks | 20 |
| 1713 | river | 20 |
| 1714 | repeat | 20 |
| 1715 | relieved | 20 |
| 1716 | properly | 20 |
| 1717 | print | 20 |
| 1718 | presents | 20 |
| 1719 | prepared | 20 |
| 1720 | points | 20 |
| 1721 | pit | 20 |
| 1722 | penalty | 20 |
| 1723 | original | 20 |
| 1724 | note | 20 |
| 1725 | months | 20 |
| 1726 | month | 20 |
| 1727 | mistaken | 20 |
| 1728 | mark | 20 |
| 1729 | ladyship | 20 |
| 1730 | important | 20 |
| 1731 | heat | 20 |
| 1732 | halter | 20 |
| 1733 | hack | 20 |
| 1734 | grew | 20 |
| 1735 | girls | 20 |
| 1736 | gained | 20 |
| 1737 | fruit | 20 |
| 1738 | flower | 20 |
| 1739 | flight | 20 |
| 1740 | finger | 20 |
| 1741 | finally | 20 |
| 1742 | fill | 20 |
| 1743 | favoured | 20 |
| 1744 | fairly | 20 |
| 1745 | entreaties | 20 |
| 1746 | entrance | 20 |
| 1747 | dubbed | 20 |
| 1748 | drawn | 20 |
| 1749 | discourse | 20 |
| 1750 | direct | 20 |
| 1751 | decided | 20 |
| 1752 | compel | 20 |
| 1753 | commend | 20 |
| 1754 | charms | 20 |
| 1755 | castilian | 20 |
| 1756 | carrier | 20 |
| 1757 | calm | 20 |
| 1758 | breeches | 20 |
| 1759 | braying | 20 |
| 1760 | behalf | 20 |
| 1761 | beards | 20 |
| 1762 | bark | 20 |
| 1763 | arrival | 20 |
| 1764 | alvaro | 20 |
| 1765 | yonder | 19 |
| 1766 | whither | 19 |
| 1767 | vast | 19 |
| 1768 | valise | 19 |
| 1769 | travel | 19 |
| 1770 | throat | 19 |
| 1771 | thoroughly | 19 |
| 1772 | thick | 19 |
| 1773 | thanked | 19 |
| 1774 | terrible | 19 |
| 1775 | swords | 19 |
| 1776 | stories | 19 |
| 1777 | steed | 19 |
| 1778 | speaks | 19 |
| 1779 | sooner | 19 |
| 1780 | sole | 19 |
| 1781 | smooth | 19 |
| 1782 | silver | 19 |
| 1783 | sides | 19 |
| 1784 | shed | 19 |
| 1785 | seville | 19 |
| 1786 | sees | 19 |
| 1787 | scheme | 19 |
| 1788 | safety | 19 |
| 1789 | rock | 19 |
| 1790 | render | 19 |
| 1791 | remains | 19 |
| 1792 | reed | 19 |
| 1793 | reduced | 19 |
| 1794 | reckon | 19 |
| 1795 | quietly | 19 |
| 1796 | prudent | 19 |
| 1797 | priest | 19 |
| 1798 | prevented | 19 |
| 1799 | press | 19 |
| 1800 | possess | 19 |
| 1801 | poetry | 19 |
| 1802 | payment | 19 |
| 1803 | path | 19 |
| 1804 | owe | 19 |
| 1805 | obtain | 19 |
| 1806 | morisco | 19 |
| 1807 | mishap | 19 |
| 1808 | maybe | 19 |
| 1809 | manage | 19 |
| 1810 | maid | 19 |
| 1811 | learn | 19 |
| 1812 | hidden | 19 |
| 1813 | hence | 19 |
| 1814 | granted | 19 |
| 1815 | generosity | 19 |
| 1816 | gay | 19 |
| 1817 | foul | 19 |
| 1818 | foolish | 19 |
| 1819 | fling | 19 |
| 1820 | fetch | 19 |
| 1821 | feeble | 19 |
| 1822 | faces | 19 |
| 1823 | ducats | 19 |
| 1824 | distinction | 19 |
| 1825 | crossed | 19 |
| 1826 | complain | 19 |
| 1827 | companion | 19 |
| 1828 | closely | 19 |
| 1829 | closed | 19 |
| 1830 | clavileno | 19 |
| 1831 | claudia | 19 |
| 1832 | charged | 19 |
| 1833 | bow | 19 |
| 1834 | blame | 19 |
| 1835 | below | 19 |
| 1836 | bare | 19 |
| 1837 | balsam | 19 |
| 1838 | ballad | 19 |
| 1839 | avenge | 19 |
| 1840 | algiers | 19 |
| 1841 | afternoon | 19 |
| 1842 | abundance | 19 |
| 1843 | yourselves | 18 |
| 1844 | wretched | 18 |
| 1845 | wondering | 18 |
| 1846 | withdrew | 18 |
| 1847 | whip | 18 |
| 1848 | vicente | 18 |
| 1849 | unwilling | 18 |
| 1850 | tall | 18 |
| 1851 | strip | 18 |
| 1852 | straight | 18 |
| 1853 | spoils | 18 |
| 1854 | sorely | 18 |
| 1855 | sigh | 18 |
| 1856 | shoulder | 18 |
| 1857 | shore | 18 |
| 1858 | setting | 18 |
| 1859 | sends | 18 |
| 1860 | seizing | 18 |
| 1861 | secretary | 18 |
| 1862 | ruin | 18 |
| 1863 | ribs | 18 |
| 1864 | report | 18 |
| 1865 | relate | 18 |
| 1866 | recollect | 18 |
| 1867 | ransom | 18 |
| 1868 | quarrel | 18 |
| 1869 | purse | 18 |
| 1870 | proposed | 18 |
| 1871 | prince | 18 |
| 1872 | practice | 18 |
| 1873 | polished | 18 |
| 1874 | persecute | 18 |
| 1875 | perplexity | 18 |
| 1876 | paying | 18 |
| 1877 | notice | 18 |
| 1878 | nicholas | 18 |
| 1879 | melisendra | 18 |
| 1880 | match | 18 |
| 1881 | malambruno | 18 |
| 1882 | maidens | 18 |
| 1883 | lovely | 18 |
| 1884 | longing | 18 |
| 1885 | leandra | 18 |
| 1886 | kissed | 18 |
| 1887 | kindly | 18 |
| 1888 | juan | 18 |
| 1889 | joined | 18 |
| 1890 | iron | 18 |
| 1891 | invention | 18 |
| 1892 | imagination | 18 |
| 1893 | heads | 18 |
| 1894 | guard | 18 |
| 1895 | grateful | 18 |
| 1896 | goat | 18 |
| 1897 | gift | 18 |
| 1898 | finest | 18 |
| 1899 | faint | 18 |
| 1900 | explain | 18 |
| 1901 | endure | 18 |
| 1902 | displayed | 18 |
| 1903 | dismounting | 18 |
| 1904 | discover | 18 |
| 1905 | demanded | 18 |
| 1906 | delightful | 18 |
| 1907 | composed | 18 |
| 1908 | companions | 18 |
| 1909 | commending | 18 |
| 1910 | cloak | 18 |
| 1911 | chief | 18 |
| 1912 | cheese | 18 |
| 1913 | cast | 18 |
| 1914 | cap | 18 |
| 1915 | broke | 18 |
| 1916 | breath | 18 |
| 1917 | borne | 18 |
| 1918 | boon | 18 |
| 1919 | bones | 18 |
| 1920 | bless | 18 |
| 1921 | astonish | 18 |
| 1922 | answering | 18 |
| 1923 | andres | 18 |
| 1924 | addressing | 18 |
| 1925 | accomplished | 18 |
| 1926 | woods | 17 |
| 1927 | wings | 17 |
| 1928 | wedding | 17 |
| 1929 | waters | 17 |
| 1930 | vile | 17 |
| 1931 | various | 17 |
| 1932 | turk | 17 |
| 1933 | traveller | 17 |
| 1934 | transformed | 17 |
| 1935 | thrust | 17 |
| 1936 | thank | 17 |
| 1937 | swore | 17 |
| 1938 | strive | 17 |
| 1939 | stirred | 17 |
| 1940 | spring | 17 |
| 1941 | slave | 17 |
| 1942 | silly | 17 |
| 1943 | shirt | 17 |
| 1944 | scorn | 17 |
| 1945 | rule | 17 |
| 1946 | ring | 17 |
| 1947 | recorded | 17 |
| 1948 | recio | 17 |
| 1949 | reality | 17 |
| 1950 | re | 17 |
| 1951 | pursued | 17 |
| 1952 | punish | 17 |
| 1953 | produced | 17 |
| 1954 | played | 17 |
| 1955 | perilous | 17 |
| 1956 | pasamonte | 17 |
| 1957 | paces | 17 |
| 1958 | opening | 17 |
| 1959 | offers | 17 |
| 1960 | neighbours | 17 |
| 1961 | neighbourhood | 17 |
| 1962 | neighbour | 17 |
| 1963 | needful | 17 |
| 1964 | missing | 17 |
| 1965 | misery | 17 |
| 1966 | mirror | 17 |
| 1967 | marrying | 17 |
| 1968 | lion | 17 |
| 1969 | lines | 17 |
| 1970 | learning | 17 |
| 1971 | leaning | 17 |
| 1972 | lass | 17 |
| 1973 | knocked | 17 |
| 1974 | knighthood | 17 |
| 1975 | injury | 17 |
| 1976 | ingenious | 17 |
| 1977 | honoured | 17 |
| 1978 | hole | 17 |
| 1979 | holds | 17 |
| 1980 | highly | 17 |
| 1981 | gratitude | 17 |
| 1982 | gratify | 17 |
| 1983 | goatherds | 17 |
| 1984 | furious | 17 |
| 1985 | flowers | 17 |
| 1986 | felix | 17 |
| 1987 | faithful | 17 |
| 1988 | execution | 17 |
| 1989 | escaped | 17 |
| 1990 | error | 17 |
| 1991 | empty | 17 |
| 1992 | deception | 17 |
| 1993 | darkness | 17 |
| 1994 | daring | 17 |
| 1995 | counsel | 17 |
| 1996 | cool | 17 |
| 1997 | compared | 17 |
| 1998 | character | 17 |
| 1999 | ceased | 17 |
| 2000 | brothers | 17 |
| 2001 | blockhead | 17 |
| 2002 | bitter | 17 |
| 2003 | belong | 17 |
| 2004 | bells | 17 |
| 2005 | battles | 17 |
| 2006 | barcelona | 17 |
| 2007 | barbary | 17 |
| 2008 | awoke | 17 |
| 2009 | avail | 17 |
| 2010 | assured | 17 |
| 2011 | armed | 17 |
| 2012 | archbishop | 17 |
| 2013 | anywhere | 17 |
| 2014 | aim | 17 |
| 2015 | afford | 17 |
| 2016 | admiration | 17 |
| 2017 | address | 17 |
| 2018 | accordance | 17 |
| 2019 | accept | 17 |
| 2020 | worst | 16 |
| 2021 | wool | 16 |
| 2022 | wherewith | 16 |
| 2023 | trifling | 16 |
| 2024 | travellers | 16 |
| 2025 | tone | 16 |
| 2026 | tom | 16 |
| 2027 | thirst | 16 |
| 2028 | thence | 16 |
| 2029 | talked | 16 |
| 2030 | sufficient | 16 |
| 2031 | strokes | 16 |
| 2032 | stretch | 16 |
| 2033 | spirits | 16 |
| 2034 | space | 16 |
| 2035 | sons | 16 |
| 2036 | slept | 16 |
| 2037 | slain | 16 |
| 2038 | sky | 16 |
| 2039 | skins | 16 |
| 2040 | skin | 16 |
| 2041 | sixty | 16 |
| 2042 | sharp | 16 |
| 2043 | shade | 16 |
| 2044 | settle | 16 |
| 2045 | sat | 16 |
| 2046 | royal | 16 |
| 2047 | rough | 16 |
| 2048 | rome | 16 |
| 2049 | rising | 16 |
| 2050 | reserved | 16 |
| 2051 | require | 16 |
| 2052 | renown | 16 |
| 2053 | rejected | 16 |
| 2054 | reaching | 16 |
| 2055 | rash | 16 |
| 2056 | profound | 16 |
| 2057 | produce | 16 |
| 2058 | pride | 16 |
| 2059 | preserved | 16 |
| 2060 | presently | 16 |
| 2061 | prayers | 16 |
| 2062 | praises | 16 |
| 2063 | possessed | 16 |
| 2064 | pleases | 16 |
| 2065 | perfectly | 16 |
| 2066 | perchance | 16 |
| 2067 | papers | 16 |
| 2068 | ox | 16 |
| 2069 | nine | 16 |
| 2070 | mortal | 16 |
| 2071 | morena | 16 |
| 2072 | micomicona | 16 |
| 2073 | marquis | 16 |
| 2074 | marien | 16 |
| 2075 | manifest | 16 |
| 2076 | manchegan | 16 |
| 2077 | malice | 16 |
| 2078 | maintain | 16 |
| 2079 | loyal | 16 |
| 2080 | lowly | 16 |
| 2081 | lordship | 16 |
| 2082 | lively | 16 |
| 2083 | laugh | 16 |
| 2084 | latter | 16 |
| 2085 | latin | 16 |
| 2086 | lad | 16 |
| 2087 | keeper | 16 |
| 2088 | john | 16 |
| 2089 | jewels | 16 |
| 2090 | inasmuch | 16 |
| 2091 | household | 16 |
| 2092 | heavens | 16 |
| 2093 | habit | 16 |
| 2094 | guilty | 16 |
| 2095 | greatness | 16 |
| 2096 | golden | 16 |
| 2097 | garments | 16 |
| 2098 | gaiferos | 16 |
| 2099 | fulling | 16 |
| 2100 | fortunes | 16 |
| 2101 | fortunate | 16 |
| 2102 | fort | 16 |
| 2103 | forest | 16 |
| 2104 | firm | 16 |
| 2105 | fighting | 16 |
| 2106 | farewell | 16 |
| 2107 | falls | 16 |
| 2108 | fairest | 16 |
| 2109 | failed | 16 |
| 2110 | exposed | 16 |
| 2111 | excuse | 16 |
| 2112 | esteemed | 16 |
| 2113 | ends | 16 |
| 2114 | enable | 16 |
| 2115 | earnestly | 16 |
| 2116 | drive | 16 |
| 2117 | deny | 16 |
| 2118 | declaration | 16 |
| 2119 | dame | 16 |
| 2120 | curious | 16 |
| 2121 | crying | 16 |
| 2122 | corner | 16 |
| 2123 | cork | 16 |
| 2124 | contrived | 16 |
| 2125 | concealed | 16 |
| 2126 | chosen | 16 |
| 2127 | chose | 16 |
| 2128 | challenge | 16 |
| 2129 | capable | 16 |
| 2130 | bystanders | 16 |
| 2131 | bidding | 16 |
| 2132 | benengeli | 16 |
| 2133 | beloved | 16 |
| 2134 | behold | 16 |
| 2135 | beads | 16 |
| 2136 | ball | 16 |
| 2137 | authors | 16 |
| 2138 | around | 16 |
| 2139 | approach | 16 |
| 2140 | ana | 16 |
| 2141 | altogether | 16 |
| 2142 | abuse | 16 |
| 2143 | absurd | 16 |
| 2144 | abroad | 16 |
| 2145 | whipping | 15 |
| 2146 | wheel | 15 |
| 2147 | warning | 15 |
| 2148 | waist | 15 |
| 2149 | vassals | 15 |
| 2150 | utmost | 15 |
| 2151 | turns | 15 |
| 2152 | trifle | 15 |
| 2153 | tricks | 15 |
| 2154 | trembling | 15 |
| 2155 | thrown | 15 |
| 2156 | tells | 15 |
| 2157 | surprise | 15 |
| 2158 | summer | 15 |
| 2159 | suffice | 15 |
| 2160 | striving | 15 |
| 2161 | string | 15 |
| 2162 | sick | 15 |
| 2163 | shouts | 15 |
| 2164 | sheets | 15 |
| 2165 | salamanca | 15 |
| 2166 | saints | 15 |
| 2167 | rules | 15 |
| 2168 | restrain | 15 |
| 2169 | refuse | 15 |
| 2170 | recover | 15 |
| 2171 | reasons | 15 |
| 2172 | rashness | 15 |
| 2173 | quick | 15 |
| 2174 | pursuit | 15 |
| 2175 | purity | 15 |
| 2176 | provide | 15 |
| 2177 | private | 15 |
| 2178 | prison | 15 |
| 2179 | pitch | 15 |
| 2180 | petticoat | 15 |
| 2181 | palm | 15 |
| 2182 | ordinary | 15 |
| 2183 | offering | 15 |
| 2184 | oars | 15 |
| 2185 | naturally | 15 |
| 2186 | narrow | 15 |
| 2187 | named | 15 |
| 2188 | minded | 15 |
| 2189 | mambrino | 15 |
| 2190 | letting | 15 |
| 2191 | lean | 15 |
| 2192 | lastly | 15 |
| 2193 | kingdoms | 15 |
| 2194 | intended | 15 |
| 2195 | imitate | 15 |
| 2196 | hunting | 15 |
| 2197 | herbs | 15 |
| 2198 | heed | 15 |
| 2199 | gown | 15 |
| 2200 | game | 15 |
| 2201 | fury | 15 |
| 2202 | fools | 15 |
| 2203 | fierce | 15 |
| 2204 | farthing | 15 |
| 2205 | fainting | 15 |
| 2206 | extreme | 15 |
| 2207 | excited | 15 |
| 2208 | established | 15 |
| 2209 | entertainment | 15 |
| 2210 | entertain | 15 |
| 2211 | entering | 15 |
| 2212 | dull | 15 |
| 2213 | drums | 15 |
| 2214 | distant | 15 |
| 2215 | dismount | 15 |
| 2216 | dishonour | 15 |
| 2217 | discretion | 15 |
| 2218 | discreet | 15 |
| 2219 | directions | 15 |
| 2220 | deliberately | 15 |
| 2221 | dejected | 15 |
| 2222 | deeply | 15 |
| 2223 | deceive | 15 |
| 2224 | crowned | 15 |
| 2225 | contained | 15 |
| 2226 | conquered | 15 |
| 2227 | conditions | 15 |
| 2228 | compassionate | 15 |
| 2229 | circumstances | 15 |
| 2230 | cheer | 15 |
| 2231 | captives | 15 |
| 2232 | buy | 15 |
| 2233 | burn | 15 |
| 2234 | burden | 15 |
| 2235 | breeding | 15 |
| 2236 | brains | 15 |
| 2237 | birds | 15 |
| 2238 | bell | 15 |
| 2239 | attended | 15 |
| 2240 | attained | 15 |
| 2241 | appears | 15 |
| 2242 | answers | 15 |
| 2243 | amused | 15 |
| 2244 | amuse | 15 |
| 2245 | adding | 15 |
| 2246 | acorns | 15 |
| 2247 | yielded | 14 |
| 2248 | yellow | 14 |
| 2249 | willingly | 14 |
| 2250 | wholly | 14 |
| 2251 | watched | 14 |
| 2252 | walls | 14 |
| 2253 | visor | 14 |
| 2254 | visit | 14 |
| 2255 | villages | 14 |
| 2256 | victorious | 14 |
| 2257 | verse | 14 |
| 2258 | veracious | 14 |
| 2259 | veil | 14 |
| 2260 | variety | 14 |
| 2261 | urge | 14 |
| 2262 | twice | 14 |
| 2263 | trade | 14 |
| 2264 | toledo | 14 |
| 2265 | thread | 14 |
| 2266 | therein | 14 |
| 2267 | theirs | 14 |
| 2268 | tear | 14 |
| 2269 | teach | 14 |
| 2270 | sudden | 14 |
| 2271 | succour | 14 |
| 2272 | success | 14 |
| 2273 | stockings | 14 |
| 2274 | spurs | 14 |
| 2275 | spur | 14 |
| 2276 | speech | 14 |
| 2277 | solitudes | 14 |
| 2278 | solitude | 14 |
| 2279 | smitten | 14 |
| 2280 | sleeps | 14 |
| 2281 | shelter | 14 |
| 2282 | sentence | 14 |
| 2283 | sending | 14 |
| 2284 | sell | 14 |
| 2285 | score | 14 |
| 2286 | sack | 14 |
| 2287 | roman | 14 |
| 2288 | robe | 14 |
| 2289 | rightly | 14 |
| 2290 | resist | 14 |
| 2291 | relates | 14 |
| 2292 | refused | 14 |
| 2293 | recovered | 14 |
| 2294 | recourse | 14 |
| 2295 | reckoned | 14 |
| 2296 | reception | 14 |
| 2297 | readily | 14 |
| 2298 | rain | 14 |
| 2299 | quantity | 14 |
| 2300 | prodigious | 14 |
| 2301 | posted | 14 |
| 2302 | pike | 14 |
| 2303 | pick | 14 |
| 2304 | perfect | 14 |
| 2305 | pen | 14 |
| 2306 | obligation | 14 |
| 2307 | notes | 14 |
| 2308 | necessity | 14 |
| 2309 | multitude | 14 |
| 2310 | moving | 14 |
| 2311 | mounting | 14 |
| 2312 | miracles | 14 |
| 2313 | longed | 14 |
| 2314 | likes | 14 |
| 2315 | lela | 14 |
| 2316 | later | 14 |
| 2317 | labourer | 14 |
| 2318 | informed | 14 |
| 2319 | induced | 14 |
| 2320 | ignorance | 14 |
| 2321 | hiding | 14 |
| 2322 | heels | 14 |
| 2323 | halt | 14 |
| 2324 | growing | 14 |
| 2325 | governing | 14 |
| 2326 | gaiety | 14 |
| 2327 | furnish | 14 |
| 2328 | friars | 14 |
| 2329 | freely | 14 |
| 2330 | fortress | 14 |
| 2331 | fifty | 14 |
| 2332 | fifteen | 14 |
| 2333 | feed | 14 |
| 2334 | fearing | 14 |
| 2335 | enterprise | 14 |
| 2336 | encounter | 14 |
| 2337 | enamoured | 14 |
| 2338 | emperors | 14 |
| 2339 | dropped | 14 |
| 2340 | divers | 14 |
| 2341 | display | 14 |
| 2342 | direction | 14 |
| 2343 | daybreak | 14 |
| 2344 | dared | 14 |
| 2345 | cursed | 14 |
| 2346 | crystal | 14 |
| 2347 | creature | 14 |
| 2348 | county | 14 |
| 2349 | coral | 14 |
| 2350 | compare | 14 |
| 2351 | coast | 14 |
| 2352 | cloud | 14 |
| 2353 | ceremony | 14 |
| 2354 | cecial | 14 |
| 2355 | catch | 14 |
| 2356 | carter | 14 |
| 2357 | blanket | 14 |
| 2358 | bid | 14 |
| 2359 | befall | 14 |
| 2360 | attire | 14 |
| 2361 | afflicted | 14 |
| 2362 | achieved | 14 |
| 2363 | wonderful | 13 |
| 2364 | winning | 13 |
| 2365 | whereat | 13 |
| 2366 | wept | 13 |
| 2367 | virtues | 13 |
| 2368 | villain | 13 |
| 2369 | vexed | 13 |
| 2370 | venerable | 13 |
| 2371 | velvet | 13 |
| 2372 | troubles | 13 |
| 2373 | traitor | 13 |
| 2374 | tongues | 13 |
| 2375 | tired | 13 |
| 2376 | test | 13 |
| 2377 | successful | 13 |
| 2378 | stuff | 13 |
| 2379 | stroke | 13 |
| 2380 | strikes | 13 |
| 2381 | straw | 13 |
| 2382 | strain | 13 |
| 2383 | store | 13 |
| 2384 | stopping | 13 |
| 2385 | steel | 13 |
| 2386 | st | 13 |
| 2387 | snow | 13 |
| 2388 | size | 13 |
| 2389 | shoe | 13 |
| 2390 | serious | 13 |
| 2391 | self | 13 |
| 2392 | season | 13 |
| 2393 | scoundrel | 13 |
| 2394 | science | 13 |
| 2395 | sail | 13 |
| 2396 | rogue | 13 |
| 2397 | rid | 13 |
| 2398 | rendered | 13 |
| 2399 | relating | 13 |
| 2400 | regards | 13 |
| 2401 | reflection | 13 |
| 2402 | reckoning | 13 |
| 2403 | reader | 13 |
| 2404 | rabble | 13 |
| 2405 | qualities | 13 |
| 2406 | pushed | 13 |
| 2407 | pursue | 13 |
| 2408 | procession | 13 |
| 2409 | pretended | 13 |
| 2410 | prejudice | 13 |
| 2411 | polite | 13 |
| 2412 | pointed | 13 |
| 2413 | playing | 13 |
| 2414 | pin | 13 |
| 2415 | physician | 13 |
| 2416 | phantoms | 13 |
| 2417 | perform | 13 |
| 2418 | pastoral | 13 |
| 2419 | palaces | 13 |
| 2420 | pages | 13 |
| 2421 | overcome | 13 |
| 2422 | occasions | 13 |
| 2423 | obliged | 13 |
| 2424 | notary | 13 |
| 2425 | notable | 13 |
| 2426 | mode | 13 |
| 2427 | mend | 13 |
| 2428 | meanwhile | 13 |
| 2429 | lords | 13 |
| 2430 | lighted | 13 |
| 2431 | killing | 13 |
| 2432 | keeps | 13 |
| 2433 | judges | 13 |
| 2434 | join | 13 |
| 2435 | jest | 13 |
| 2436 | instruments | 13 |
| 2437 | instrument | 13 |
| 2438 | inclination | 13 |
| 2439 | implore | 13 |
| 2440 | hurt | 13 |
| 2441 | hoped | 13 |
| 2442 | happens | 13 |
| 2443 | hang | 13 |
| 2444 | handled | 13 |
| 2445 | hall | 13 |
| 2446 | grieved | 13 |
| 2447 | graceful | 13 |
| 2448 | frightened | 13 |
| 2449 | forthwith | 13 |
| 2450 | fled | 13 |
| 2451 | fidelity | 13 |
| 2452 | fellows | 13 |
| 2453 | fancies | 13 |
| 2454 | esteem | 13 |
| 2455 | er | 13 |
| 2456 | encountered | 13 |
| 2457 | employed | 13 |
| 2458 | elegant | 13 |
| 2459 | eaten | 13 |
| 2460 | early | 13 |
| 2461 | dust | 13 |
| 2462 | driven | 13 |
| 2463 | doubts | 13 |
| 2464 | doublet | 13 |
| 2465 | doth | 13 |
| 2466 | doleful | 13 |
| 2467 | dogs | 13 |
| 2468 | distinguished | 13 |
| 2469 | difficult | 13 |
| 2470 | design | 13 |
| 2471 | desert | 13 |
| 2472 | deceived | 13 |
| 2473 | craft | 13 |
| 2474 | courier | 13 |
| 2475 | counsels | 13 |
| 2476 | correct | 13 |
| 2477 | continue | 13 |
| 2478 | contents | 13 |
| 2479 | consolation | 13 |
| 2480 | confidence | 13 |
| 2481 | comrade | 13 |
| 2482 | comply | 13 |
| 2483 | compelled | 13 |
| 2484 | committed | 13 |
| 2485 | colours | 13 |
| 2486 | cleared | 13 |
| 2487 | bride | 13 |
| 2488 | breadth | 13 |
| 2489 | bray | 13 |
| 2490 | bought | 13 |
| 2491 | bottom | 13 |
| 2492 | bodily | 13 |
| 2493 | bodies | 13 |
| 2494 | bigger | 13 |
| 2495 | belaboured | 13 |
| 2496 | beat | 13 |
| 2497 | bathed | 13 |
| 2498 | appetite | 13 |
| 2499 | animal | 13 |
| 2500 | angry | 13 |
| 2501 | angel | 13 |
| 2502 | allah | 13 |
| 2503 | agree | 13 |
| 2504 | afforded | 13 |
| 2505 | acquainted | 13 |
| 2506 | wives | 12 |
| 2507 | whereby | 12 |
| 2508 | violence | 12 |
| 2509 | victor | 12 |
| 2510 | vexation | 12 |
| 2511 | valley | 12 |
| 2512 | unexampled | 12 |
| 2513 | uneasiness | 12 |
| 2514 | troop | 12 |
| 2515 | treachery | 12 |
| 2516 | treacherous | 12 |
| 2517 | travelled | 12 |
| 2518 | tower | 12 |
| 2519 | tomb | 12 |
| 2520 | tight | 12 |
| 2521 | threats | 12 |
| 2522 | thin | 12 |
| 2523 | terms | 12 |
| 2524 | taught | 12 |
| 2525 | sworn | 12 |
| 2526 | sum | 12 |
| 2527 | stupid | 12 |
| 2528 | study | 12 |
| 2529 | strike | 12 |
| 2530 | stricken | 12 |
| 2531 | strangest | 12 |
| 2532 | strait | 12 |
| 2533 | stakes | 12 |
| 2534 | sprang | 12 |
| 2535 | spacious | 12 |
| 2536 | sorrows | 12 |
| 2537 | sobs | 12 |
| 2538 | slow | 12 |
| 2539 | skill | 12 |
| 2540 | sitting | 12 |
| 2541 | sister | 12 |
| 2542 | seclusion | 12 |
| 2543 | saving | 12 |
| 2544 | sang | 12 |
| 2545 | risen | 12 |
| 2546 | restored | 12 |
| 2547 | repose | 12 |
| 2548 | renowned | 12 |
| 2549 | remaining | 12 |
| 2550 | regarding | 12 |
| 2551 | reflections | 12 |
| 2552 | reflect | 12 |
| 2553 | rational | 12 |
| 2554 | ransomed | 12 |
| 2555 | ragged | 12 |
| 2556 | pulled | 12 |
| 2557 | proud | 12 |
| 2558 | profit | 12 |
| 2559 | profess | 12 |
| 2560 | proceeding | 12 |
| 2561 | praised | 12 |
| 2562 | powerful | 12 |
| 2563 | pluck | 12 |
| 2564 | peter | 12 |
| 2565 | peasants | 12 |
| 2566 | paint | 12 |
| 2567 | outcry | 12 |
| 2568 | opportunities | 12 |
| 2569 | oblivion | 12 |
| 2570 | musician | 12 |
| 2571 | message | 12 |
| 2572 | meeting | 12 |
| 2573 | meantime | 12 |
| 2574 | meadows | 12 |
| 2575 | mass | 12 |
| 2576 | mare | 12 |
| 2577 | maravedis | 12 |
| 2578 | magic | 12 |
| 2579 | locked | 12 |
| 2580 | linen | 12 |
| 2581 | lent | 12 |
| 2582 | leg | 12 |
| 2583 | lances | 12 |
| 2584 | lamentations | 12 |
| 2585 | jokes | 12 |
| 2586 | inside | 12 |
| 2587 | inform | 12 |
| 2588 | impudent | 12 |
| 2589 | impossibility | 12 |
| 2590 | hush | 12 |
| 2591 | hurry | 12 |
| 2592 | happier | 12 |
| 2593 | grinders | 12 |
| 2594 | greek | 12 |
| 2595 | grating | 12 |
| 2596 | governments | 12 |
| 2597 | goletta | 12 |
| 2598 | gets | 12 |
| 2599 | gates | 12 |
| 2600 | fright | 12 |
| 2601 | fourth | 12 |
| 2602 | flock | 12 |
| 2603 | fix | 12 |
| 2604 | fitting | 12 |
| 2605 | finds | 12 |
| 2606 | feared | 12 |
| 2607 | fared | 12 |
| 2608 | fare | 12 |
| 2609 | fancying | 12 |
| 2610 | extremely | 12 |
| 2611 | exploits | 12 |
| 2612 | exchanged | 12 |
| 2613 | examine | 12 |
| 2614 | events | 12 |
| 2615 | eternal | 12 |
| 2616 | enjoying | 12 |
| 2617 | embracing | 12 |
| 2618 | eagerness | 12 |
| 2619 | disenchanted | 12 |
| 2620 | disclosed | 12 |
| 2621 | difficulties | 12 |
| 2622 | devoted | 12 |
| 2623 | determination | 12 |
| 2624 | destruction | 12 |
| 2625 | delighted | 12 |
| 2626 | defiance | 12 |
| 2627 | dawn | 12 |
| 2628 | daughters | 12 |
| 2629 | dance | 12 |
| 2630 | croup | 12 |
| 2631 | credit | 12 |
| 2632 | craze | 12 |
| 2633 | costume | 12 |
| 2634 | contains | 12 |
| 2635 | constant | 12 |
| 2636 | considering | 12 |
| 2637 | consideration | 12 |
| 2638 | conclude | 12 |
| 2639 | conceal | 12 |
| 2640 | coat | 12 |
| 2641 | cities | 12 |
| 2642 | chaste | 12 |
| 2643 | charity | 12 |
| 2644 | chains | 12 |
| 2645 | caparison | 12 |
| 2646 | bruised | 12 |
| 2647 | brook | 12 |
| 2648 | briefly | 12 |
| 2649 | brief | 12 |
| 2650 | bounds | 12 |
| 2651 | bone | 12 |
| 2652 | bet | 12 |
| 2653 | belonged | 12 |
| 2654 | begun | 12 |
| 2655 | beaten | 12 |
| 2656 | bearded | 12 |
| 2657 | barley | 12 |
| 2658 | barataria | 12 |
| 2659 | attempted | 12 |
| 2660 | asses | 12 |
| 2661 | ascertain | 12 |
| 2662 | apprehension | 12 |
| 2663 | afresh | 12 |
| 2664 | advance | 12 |
| 2665 | acquired | 12 |
| 2666 | accepted | 12 |
| 2667 | yore | 11 |
| 2668 | writes | 11 |
| 2669 | witted | 11 |
| 2670 | winter | 11 |
| 2671 | whoreson | 11 |
| 2672 | weakness | 11 |
| 2673 | wax | 11 |
| 2674 | vivaldo | 11 |
| 2675 | ventured | 11 |
| 2676 | vanquish | 11 |
| 2677 | usage | 11 |
| 2678 | urged | 11 |
| 2679 | unworthy | 11 |
| 2680 | unparalleled | 11 |
| 2681 | unheard | 11 |
| 2682 | truthful | 11 |
| 2683 | trumpets | 11 |
| 2684 | trial | 11 |
| 2685 | token | 11 |
| 2686 | toil | 11 |
| 2687 | throwing | 11 |
| 2688 | terrified | 11 |
| 2689 | surely | 11 |
| 2690 | supped | 11 |
| 2691 | sumptuous | 11 |
| 2692 | summit | 11 |
| 2693 | suggested | 11 |
| 2694 | succeeded | 11 |
| 2695 | struggle | 11 |
| 2696 | started | 11 |
| 2697 | stands | 11 |
| 2698 | slay | 11 |
| 2699 | skirts | 11 |
| 2700 | singer | 11 |
| 2701 | sifting | 11 |
| 2702 | severe | 11 |
| 2703 | separated | 11 |
| 2704 | sadness | 11 |
| 2705 | rush | 11 |
| 2706 | roof | 11 |
| 2707 | richly | 11 |
| 2708 | region | 11 |
| 2709 | reflecting | 11 |
| 2710 | redress | 11 |
| 2711 | reads | 11 |
| 2712 | race | 11 |
| 2713 | propriety | 11 |
| 2714 | probably | 11 |
| 2715 | pretence | 11 |
| 2716 | post | 11 |
| 2717 | possibility | 11 |
| 2718 | politeness | 11 |
| 2719 | plight | 11 |
| 2720 | pleasing | 11 |
| 2721 | planted | 11 |
| 2722 | pigs | 11 |
| 2723 | pierced | 11 |
| 2724 | peers | 11 |
| 2725 | origin | 11 |
| 2726 | oil | 11 |
| 2727 | occupied | 11 |
| 2728 | numbers | 11 |
| 2729 | notion | 11 |
| 2730 | nights | 11 |
| 2731 | nice | 11 |
| 2732 | miss | 11 |
| 2733 | mischievous | 11 |
| 2734 | merit | 11 |
| 2735 | market | 11 |
| 2736 | march | 11 |
| 2737 | main | 11 |
| 2738 | magician | 11 |
| 2739 | lucky | 11 |
| 2740 | loyalty | 11 |
| 2741 | lower | 11 |
| 2742 | limits | 11 |
| 2743 | leisure | 11 |
| 2744 | leather | 11 |
| 2745 | knocking | 11 |
| 2746 | jewel | 11 |
| 2747 | jealous | 11 |
| 2748 | intending | 11 |
| 2749 | intelligent | 11 |
| 2750 | infinite | 11 |
| 2751 | impression | 11 |
| 2752 | horn | 11 |
| 2753 | honey | 11 |
| 2754 | hollow | 11 |
| 2755 | historian | 11 |
| 2756 | hill | 11 |
| 2757 | heartily | 11 |
| 2758 | haven | 11 |
| 2759 | hated | 11 |
| 2760 | hastily | 11 |
| 2761 | guinart | 11 |
| 2762 | guests | 11 |
| 2763 | gazed | 11 |
| 2764 | gather | 11 |
| 2765 | furnished | 11 |
| 2766 | frequently | 11 |
| 2767 | formed | 11 |
| 2768 | forgot | 11 |
| 2769 | forehead | 11 |
| 2770 | foe | 11 |
| 2771 | fleet | 11 |
| 2772 | fixing | 11 |
| 2773 | festival | 11 |
| 2774 | fat | 11 |
| 2775 | excellency | 11 |
| 2776 | examined | 11 |
| 2777 | envious | 11 |
| 2778 | efforts | 11 |
| 2779 | durandarte | 11 |
| 2780 | drinking | 11 |
| 2781 | double | 11 |
| 2782 | discharged | 11 |
| 2783 | dine | 11 |
| 2784 | despatch | 11 |
| 2785 | deserved | 11 |
| 2786 | depend | 11 |
| 2787 | depart | 11 |
| 2788 | deed | 11 |
| 2789 | decision | 11 |
| 2790 | dearly | 11 |
| 2791 | dainty | 11 |
| 2792 | cushion | 11 |
| 2793 | crew | 11 |
| 2794 | courteously | 11 |
| 2795 | corchuelo | 11 |
| 2796 | constantinople | 11 |
| 2797 | commissary | 11 |
| 2798 | commended | 11 |
| 2799 | clouds | 11 |
| 2800 | characters | 11 |
| 2801 | chaplain | 11 |
| 2802 | certainty | 11 |
| 2803 | castles | 11 |
| 2804 | captains | 11 |
| 2805 | capital | 11 |
| 2806 | burial | 11 |
| 2807 | belongs | 11 |
| 2808 | behave | 11 |
| 2809 | battered | 11 |
| 2810 | bano | 11 |
| 2811 | banks | 11 |
| 2812 | banished | 11 |
| 2813 | attain | 11 |
| 2814 | ate | 11 |
| 2815 | astray | 11 |
| 2816 | assailed | 11 |
| 2817 | arrows | 11 |
| 2818 | army | 11 |
| 2819 | argument | 11 |
| 2820 | aragon | 11 |
| 2821 | arabic | 11 |
| 2822 | ambrosio | 11 |
| 2823 | ambition | 11 |
| 2824 | alexander | 11 |
| 2825 | agitated | 11 |
| 2826 | adorned | 11 |
| 2827 | adopt | 11 |
| 2828 | accursed | 11 |
| 2829 | accomplishments | 11 |
| 2830 | writings | 10 |
| 2831 | woes | 10 |
| 2832 | witnesses | 10 |
| 2833 | windmills | 10 |
| 2834 | widow | 10 |
| 2835 | wheeled | 10 |
| 2836 | washing | 10 |
| 2837 | washed | 10 |
| 2838 | voyage | 10 |
| 2839 | voices | 10 |
| 2840 | vice | 10 |
| 2841 | usually | 10 |
| 2842 | upset | 10 |
| 2843 | undertake | 10 |
| 2844 | uncertain | 10 |
| 2845 | ugly | 10 |
| 2846 | trunk | 10 |
| 2847 | trim | 10 |
| 2848 | treasures | 10 |
| 2849 | trappings | 10 |
| 2850 | torn | 10 |
| 2851 | torches | 10 |
| 2852 | thinkest | 10 |
| 2853 | thieves | 10 |
| 2854 | temper | 10 |
| 2855 | tales | 10 |
| 2856 | tables | 10 |
| 2857 | swoon | 10 |
| 2858 | suspicions | 10 |
| 2859 | suspense | 10 |
| 2860 | supreme | 10 |
| 2861 | suffered | 10 |
| 2862 | stirrups | 10 |
| 2863 | souls | 10 |
| 2864 | sonnets | 10 |
| 2865 | song | 10 |
| 2866 | soil | 10 |
| 2867 | society | 10 |
| 2868 | simply | 10 |
| 2869 | ship | 10 |
| 2870 | shining | 10 |
| 2871 | shepherdesses | 10 |
| 2872 | shaking | 10 |
| 2873 | shadow | 10 |
| 2874 | serves | 10 |
| 2875 | separate | 10 |
| 2876 | seldom | 10 |
| 2877 | secured | 10 |
| 2878 | searching | 10 |
| 2879 | scrupulous | 10 |
| 2880 | rustic | 10 |
| 2881 | ripe | 10 |
| 2882 | retirement | 10 |
| 2883 | rescue | 10 |
| 2884 | repay | 10 |
| 2885 | remote | 10 |
| 2886 | relish | 10 |
| 2887 | recollection | 10 |
| 2888 | range | 10 |
| 2889 | queens | 10 |
| 2890 | quarrels | 10 |
| 2891 | puzzled | 10 |
| 2892 | push | 10 |
| 2893 | prudence | 10 |
| 2894 | prisoners | 10 |
| 2895 | prey | 10 |
| 2896 | prayer | 10 |
| 2897 | pots | 10 |
| 2898 | port | 10 |
| 2899 | plunged | 10 |
| 2900 | plunge | 10 |
| 2901 | plucked | 10 |
| 2902 | piteous | 10 |
| 2903 | pilgrims | 10 |
| 2904 | pilgrim | 10 |
| 2905 | pierres | 10 |
| 2906 | personage | 10 |
| 2907 | patient | 10 |
| 2908 | paths | 10 |
| 2909 | particulars | 10 |
| 2910 | parchment | 10 |
| 2911 | outside | 10 |
| 2912 | opposed | 10 |
| 2913 | odd | 10 |
| 2914 | numerous | 10 |
| 2915 | notwithstanding | 10 |
| 2916 | nobility | 10 |
| 2917 | newly | 10 |
| 2918 | needy | 10 |
| 2919 | native | 10 |
| 2920 | nation | 10 |
| 2921 | mourning | 10 |
| 2922 | monsters | 10 |
| 2923 | minds | 10 |
| 2924 | mill | 10 |
| 2925 | maxims | 10 |
| 2926 | mantle | 10 |
| 2927 | lowered | 10 |
| 2928 | lineage | 10 |
| 2929 | leads | 10 |
| 2930 | lake | 10 |
| 2931 | knock | 10 |
| 2932 | kissing | 10 |
| 2933 | kandy | 10 |
| 2934 | invincible | 10 |
| 2935 | instructed | 10 |
| 2936 | ingenuity | 10 |
| 2937 | influence | 10 |
| 2938 | increased | 10 |
| 2939 | incomparable | 10 |
| 2940 | imitation | 10 |
| 2941 | hot | 10 |
| 2942 | hideous | 10 |
| 2943 | heir | 10 |
| 2944 | haunches | 10 |
| 2945 | harmony | 10 |
| 2946 | hadst | 10 |
| 2947 | guards | 10 |
| 2948 | greece | 10 |
| 2949 | gloss | 10 |
| 2950 | gaze | 10 |
| 2951 | gaban | 10 |
| 2952 | fought | 10 |
| 2953 | forgetting | 10 |
| 2954 | forbid | 10 |
| 2955 | fiction | 10 |
| 2956 | feats | 10 |
| 2957 | fears | 10 |
| 2958 | explained | 10 |
| 2959 | expense | 10 |
| 2960 | examples | 10 |
| 2961 | evidence | 10 |
| 2962 | evening | 10 |
| 2963 | estimation | 10 |
| 2964 | entire | 10 |
| 2965 | energy | 10 |
| 2966 | eggs | 10 |
| 2967 | easier | 10 |
| 2968 | dressing | 10 |
| 2969 | dream | 10 |
| 2970 | dispute | 10 |
| 2971 | disposal | 10 |
| 2972 | disdain | 10 |
| 2973 | discussing | 10 |
| 2974 | discovery | 10 |
| 2975 | dies | 10 |
| 2976 | destroy | 10 |
| 2977 | deserving | 10 |
| 2978 | descended | 10 |
| 2979 | deals | 10 |
| 2980 | damage | 10 |
| 2981 | customary | 10 |
| 2982 | curse | 10 |
| 2983 | curds | 10 |
| 2984 | crafty | 10 |
| 2985 | covetous | 10 |
| 2986 | courtyard | 10 |
| 2987 | costs | 10 |
| 2988 | convent | 10 |
| 2989 | constancy | 10 |
| 2990 | confirmed | 10 |
| 2991 | conceived | 10 |
| 2992 | commands | 10 |
| 2993 | colts | 10 |
| 2994 | clever | 10 |
| 2995 | claws | 10 |
| 2996 | clarions | 10 |
| 2997 | charm | 10 |
| 2998 | cease | 10 |
| 2999 | cases | 10 |
| 3000 | carriers | 10 |
| 3001 | bury | 10 |
| 3002 | bundle | 10 |
| 3003 | bulls | 10 |
| 3004 | bridge | 10 |
| 3005 | brayed | 10 |
| 3006 | boldness | 10 |
| 3007 | blowing | 10 |
| 3008 | bethink | 10 |
| 3009 | believing | 10 |
| 3010 | belerma | 10 |
| 3011 | behaviour | 10 |
| 3012 | band | 10 |
| 3013 | bag | 10 |
| 3014 | avenged | 10 |
| 3015 | audacity | 10 |
| 3016 | assistance | 10 |
| 3017 | arrayed | 10 |
| 3018 | arrange | 10 |
| 3019 | armies | 10 |
| 3020 | antonomasia | 10 |
| 3021 | animals | 10 |
| 3022 | andalusia | 10 |
| 3023 | aeneas | 10 |
| 3024 | adventurers | 10 |
| 3025 | adventurer | 10 |
| 3026 | acting | 10 |
| 3027 | abundant | 10 |
| 3028 | absent | 10 |
| 3029 | yielding | 9 |
| 3030 | wooden | 9 |
| 3031 | woke | 9 |
| 3032 | wilds | 9 |
| 3033 | whipped | 9 |
| 3034 | wherefore | 9 |
| 3035 | wheels | 9 |
| 3036 | wealthy | 9 |
| 3037 | wash | 9 |
| 3038 | walking | 9 |
| 3039 | wager | 9 |
| 3040 | vulgar | 9 |
| 3041 | valued | 9 |
| 3042 | urgent | 9 |
| 3043 | unknown | 9 |
| 3044 | unexpectedly | 9 |
| 3045 | turkish | 9 |
| 3046 | trifles | 9 |
| 3047 | transformation | 9 |
| 3048 | towers | 9 |
| 3049 | tirteafuera | 9 |
| 3050 | tie | 9 |
| 3051 | tidings | 9 |
| 3052 | throughout | 9 |
| 3053 | thicket | 9 |
| 3054 | tenderness | 9 |
| 3055 | supposing | 9 |
| 3056 | supply | 9 |
| 3057 | sup | 9 |
| 3058 | sung | 9 |
| 3059 | sufficiently | 9 |
| 3060 | substance | 9 |
| 3061 | submit | 9 |
| 3062 | sturdy | 9 |
| 3063 | stock | 9 |
| 3064 | stayed | 9 |
| 3065 | stature | 9 |
| 3066 | station | 9 |
| 3067 | squadron | 9 |
| 3068 | speedily | 9 |
| 3069 | spectacle | 9 |
| 3070 | smote | 9 |
| 3071 | smoke | 9 |
| 3072 | slashing | 9 |
| 3073 | sings | 9 |
| 3074 | signed | 9 |
| 3075 | signal | 9 |
| 3076 | shower | 9 |
| 3077 | shot | 9 |
| 3078 | shirts | 9 |
| 3079 | sets | 9 |
| 3080 | seize | 9 |
| 3081 | secrets | 9 |
| 3082 | scraps | 9 |
| 3083 | scourge | 9 |
| 3084 | saved | 9 |
| 3085 | sallied | 9 |
| 3086 | roncesvalles | 9 |
| 3087 | rival | 9 |
| 3088 | riding | 9 |
| 3089 | retreat | 9 |
| 3090 | respectable | 9 |
| 3091 | remarked | 9 |
| 3092 | regions | 9 |
| 3093 | recovery | 9 |
| 3094 | record | 9 |
| 3095 | quitting | 9 |
| 3096 | puppet | 9 |
| 3097 | province | 9 |
| 3098 | prisoner | 9 |
| 3099 | price | 9 |
| 3100 | praying | 9 |
| 3101 | practise | 9 |
| 3102 | positively | 9 |
| 3103 | pledges | 9 |
| 3104 | pledge | 9 |
| 3105 | plaza | 9 |
| 3106 | pitcher | 9 |
| 3107 | permitted | 9 |
| 3108 | peaceful | 9 |
| 3109 | passes | 9 |
| 3110 | passage | 9 |
| 3111 | partly | 9 |
| 3112 | painter | 9 |
| 3113 | pad | 9 |
| 3114 | oxen | 9 |
| 3115 | officer | 9 |
| 3116 | offensive | 9 |
| 3117 | nymphs | 9 |
| 3118 | noticed | 9 |
| 3119 | nigh | 9 |
| 3120 | needs | 9 |
| 3121 | nail | 9 |
| 3122 | mystery | 9 |
| 3123 | muleteer | 9 |
| 3124 | movement | 9 |
| 3125 | mouths | 9 |
| 3126 | mostly | 9 |
| 3127 | monstrous | 9 |
| 3128 | modern | 9 |
| 3129 | mistresses | 9 |
| 3130 | mishaps | 9 |
| 3131 | merry | 9 |
| 3132 | memorable | 9 |
| 3133 | measured | 9 |
| 3134 | mantua | 9 |
| 3135 | malignant | 9 |
| 3136 | madrid | 9 |
| 3137 | locks | 9 |
| 3138 | livest | 9 |
| 3139 | lights | 9 |
| 3140 | lift | 9 |
| 3141 | leaped | 9 |
| 3142 | lasts | 9 |
| 3143 | lamp | 9 |
| 3144 | jousts | 9 |
| 3145 | irritation | 9 |
| 3146 | invented | 9 |
| 3147 | ingratitude | 9 |
| 3148 | inflicted | 9 |
| 3149 | inflict | 9 |
| 3150 | indies | 9 |
| 3151 | images | 9 |
| 3152 | humours | 9 |
| 3153 | ho | 9 |
| 3154 | hitherto | 9 |
| 3155 | hither | 9 |
| 3156 | highnesses | 9 |
| 3157 | hermitage | 9 |
| 3158 | hearers | 9 |
| 3159 | hare | 9 |
| 3160 | hanged | 9 |
| 3161 | handsome | 9 |
| 3162 | hairs | 9 |
| 3163 | grow | 9 |
| 3164 | grasp | 9 |
| 3165 | girths | 9 |
| 3166 | gazing | 9 |
| 3167 | garters | 9 |
| 3168 | fro | 9 |
| 3169 | friday | 9 |
| 3170 | french | 9 |
| 3171 | fourteen | 9 |
| 3172 | floor | 9 |
| 3173 | fig | 9 |
| 3174 | extent | 9 |
| 3175 | expedition | 9 |
| 3176 | expecting | 9 |
| 3177 | everywhere | 9 |
| 3178 | esquire | 9 |
| 3179 | entreating | 9 |
| 3180 | entitled | 9 |
| 3181 | ending | 9 |
| 3182 | embarrassment | 9 |
| 3183 | earned | 9 |
| 3184 | drolleries | 9 |
| 3185 | driving | 9 |
| 3186 | dragged | 9 |
| 3187 | doings | 9 |
| 3188 | distinctly | 9 |
| 3189 | din | 9 |
| 3190 | devices | 9 |
| 3191 | despatched | 9 |
| 3192 | deprive | 9 |
| 3193 | delicate | 9 |
| 3194 | deepest | 9 |
| 3195 | cutting | 9 |
| 3196 | cuts | 9 |
| 3197 | curses | 9 |
| 3198 | cunning | 9 |
| 3199 | cry | 9 |
| 3200 | crossing | 9 |
| 3201 | covering | 9 |
| 3202 | countenances | 9 |
| 3203 | cordova | 9 |
| 3204 | cord | 9 |
| 3205 | control | 9 |
| 3206 | constructed | 9 |
| 3207 | conducted | 9 |
| 3208 | conditioned | 9 |
| 3209 | composure | 9 |
| 3210 | complied | 9 |
| 3211 | complexion | 9 |
| 3212 | comfortable | 9 |
| 3213 | coarse | 9 |
| 3214 | claim | 9 |
| 3215 | chastise | 9 |
| 3216 | charlemagne | 9 |
| 3217 | changing | 9 |
| 3218 | cattle | 9 |
| 3219 | casildea | 9 |
| 3220 | cares | 9 |
| 3221 | car | 9 |
| 3222 | captivity | 9 |
| 3223 | candle | 9 |
| 3224 | caesar | 9 |
| 3225 | brute | 9 |
| 3226 | brooks | 9 |
| 3227 | brigantine | 9 |
| 3228 | breeze | 9 |
| 3229 | breed | 9 |
| 3230 | blanketed | 9 |
| 3231 | bitterly | 9 |
| 3232 | betook | 9 |
| 3233 | bench | 9 |
| 3234 | belly | 9 |
| 3235 | begging | 9 |
| 3236 | bargain | 9 |
| 3237 | b | 9 |
| 3238 | await | 9 |
| 3239 | avoided | 9 |
| 3240 | attendants | 9 |
| 3241 | attempting | 9 |
| 3242 | attached | 9 |
| 3243 | assigned | 9 |
| 3244 | ascertained | 9 |
| 3245 | arrangement | 9 |
| 3246 | arduous | 9 |
| 3247 | apocryphal | 9 |
| 3248 | angelica | 9 |
| 3249 | amount | 9 |
| 3250 | alcalde | 9 |
| 3251 | admitted | 9 |
| 3252 | acts | 9 |
| 3253 | accord | 9 |
| 3254 | absorbed | 9 |
| 3255 | abode | 9 |
| 3256 | aback | 9 |
| 3257 | yards | 8 |
| 3258 | yanguesans | 8 |
| 3259 | wrapped | 8 |
| 3260 | working | 8 |
| 3261 | wonders | 8 |
| 3262 | wolves | 8 |
| 3263 | wiped | 8 |
| 3264 | wipe | 8 |
| 3265 | windows | 8 |
| 3266 | widows | 8 |
| 3267 | victim | 8 |
| 3268 | veiled | 8 |
| 3269 | ve | 8 |
| 3270 | valleys | 8 |
| 3271 | vagabond | 8 |
| 3272 | useless | 8 |
| 3273 | upwards | 8 |
| 3274 | unexpected | 8 |
| 3275 | undertaken | 8 |
| 3276 | underneath | 8 |
| 3277 | twinkling | 8 |
| 3278 | trumpet | 8 |
| 3279 | troy | 8 |
| 3280 | trough | 8 |
| 3281 | trifaldin | 8 |
| 3282 | treating | 8 |
| 3283 | travels | 8 |
| 3284 | tranquil | 8 |
| 3285 | torture | 8 |
| 3286 | titles | 8 |
| 3287 | throne | 8 |
| 3288 | threatened | 8 |
| 3289 | tempted | 8 |
| 3290 | tailor | 8 |
| 3291 | tagus | 8 |
| 3292 | surrender | 8 |
| 3293 | surface | 8 |
| 3294 | studies | 8 |
| 3295 | studied | 8 |
| 3296 | storm | 8 |
| 3297 | startled | 8 |
| 3298 | stage | 8 |
| 3299 | sprightly | 8 |
| 3300 | spend | 8 |
| 3301 | skull | 8 |
| 3302 | sixteen | 8 |
| 3303 | sincerity | 8 |
| 3304 | showman | 8 |
| 3305 | shouted | 8 |
| 3306 | shout | 8 |
| 3307 | shave | 8 |
| 3308 | serving | 8 |
| 3309 | serpent | 8 |
| 3310 | sciences | 8 |
| 3311 | satin | 8 |
| 3312 | runs | 8 |
| 3313 | ruidera | 8 |
| 3314 | rude | 8 |
| 3315 | rowers | 8 |
| 3316 | rodrigo | 8 |
| 3317 | rewards | 8 |
| 3318 | revive | 8 |
| 3319 | retiring | 8 |
| 3320 | resumed | 8 |
| 3321 | respected | 8 |
| 3322 | resolve | 8 |
| 3323 | repaired | 8 |
| 3324 | reminded | 8 |
| 3325 | remainder | 8 |
| 3326 | rely | 8 |
| 3327 | religion | 8 |
| 3328 | relics | 8 |
| 3329 | relations | 8 |
| 3330 | rejoiced | 8 |
| 3331 | reinaldos | 8 |
| 3332 | rein | 8 |
| 3333 | regular | 8 |
| 3334 | refuge | 8 |
| 3335 | recall | 8 |
| 3336 | reaches | 8 |
| 3337 | rascally | 8 |
| 3338 | quote | 8 |
| 3339 | purgatory | 8 |
| 3340 | pulse | 8 |
| 3341 | provoked | 8 |
| 3342 | proportion | 8 |
| 3343 | proofs | 8 |
| 3344 | privileges | 8 |
| 3345 | pretty | 8 |
| 3346 | preface | 8 |
| 3347 | possibly | 8 |
| 3348 | plans | 8 |
| 3349 | plaintive | 8 |
| 3350 | placing | 8 |
| 3351 | pinches | 8 |
| 3352 | picture | 8 |
| 3353 | phrase | 8 |
| 3354 | performing | 8 |
| 3355 | performed | 8 |
| 3356 | perforce | 8 |
| 3357 | perez | 8 |
| 3358 | peg | 8 |
| 3359 | panzas | 8 |
| 3360 | palfrey | 8 |
| 3361 | pale | 8 |
| 3362 | painting | 8 |
| 3363 | pagan | 8 |
| 3364 | owed | 8 |
| 3365 | overheard | 8 |
| 3366 | opposition | 8 |
| 3367 | omens | 8 |
| 3368 | obtaining | 8 |
| 3369 | obeisance | 8 |
| 3370 | oaths | 8 |
| 3371 | nightfall | 8 |
| 3372 | nations | 8 |
| 3373 | naples | 8 |
| 3374 | nails | 8 |
| 3375 | muskets | 8 |
| 3376 | musket | 8 |
| 3377 | muleteers | 8 |
| 3378 | morsel | 8 |
| 3379 | monster | 8 |
| 3380 | mixed | 8 |
| 3381 | mitre | 8 |
| 3382 | miranda | 8 |
| 3383 | millers | 8 |
| 3384 | milk | 8 |
| 3385 | midnight | 8 |
| 3386 | mid | 8 |
| 3387 | micomicon | 8 |
| 3388 | meddle | 8 |
| 3389 | maria | 8 |
| 3390 | mares | 8 |
| 3391 | mankind | 8 |
| 3392 | maledictions | 8 |
| 3393 | maintained | 8 |
| 3394 | loving | 8 |
| 3395 | loaf | 8 |
| 3396 | loaded | 8 |
| 3397 | lit | 8 |
| 3398 | licence | 8 |
| 3399 | liable | 8 |
| 3400 | level | 8 |
| 3401 | lend | 8 |
| 3402 | leap | 8 |
| 3403 | lazy | 8 |
| 3404 | lately | 8 |
| 3405 | lasted | 8 |
| 3406 | lancelot | 8 |
| 3407 | lakes | 8 |
| 3408 | labyrinth | 8 |
| 3409 | labours | 8 |
| 3410 | knot | 8 |
| 3411 | kicks | 8 |
| 3412 | kerchiefs | 8 |
| 3413 | jug | 8 |
| 3414 | jacket | 8 |
| 3415 | innumerable | 8 |
| 3416 | injuries | 8 |
| 3417 | inhabitants | 8 |
| 3418 | indolence | 8 |
| 3419 | inclinations | 8 |
| 3420 | incident | 8 |
| 3421 | impulse | 8 |
| 3422 | impossibilities | 8 |
| 3423 | imploring | 8 |
| 3424 | ii | 8 |
| 3425 | ideas | 8 |
| 3426 | hurried | 8 |
| 3427 | humility | 8 |
| 3428 | huge | 8 |
| 3429 | hosts | 8 |
| 3430 | hood | 8 |
| 3431 | hoarse | 8 |
| 3432 | hermit | 8 |
| 3433 | hens | 8 |
| 3434 | henceforward | 8 |
| 3435 | heedless | 8 |
| 3436 | haughty | 8 |
| 3437 | hardships | 8 |
| 3438 | harder | 8 |
| 3439 | handkerchief | 8 |
| 3440 | guise | 8 |
| 3441 | guided | 8 |
| 3442 | guessed | 8 |
| 3443 | grown | 8 |
| 3444 | gravity | 8 |
| 3445 | grasping | 8 |
| 3446 | gracious | 8 |
| 3447 | gently | 8 |
| 3448 | gentleness | 8 |
| 3449 | gallop | 8 |
| 3450 | gaining | 8 |
| 3451 | friar | 8 |
| 3452 | founded | 8 |
| 3453 | forty | 8 |
| 3454 | flowed | 8 |
| 3455 | flies | 8 |
| 3456 | flask | 8 |
| 3457 | flames | 8 |
| 3458 | fish | 8 |
| 3459 | finishing | 8 |
| 3460 | female | 8 |
| 3461 | fatigue | 8 |
| 3462 | extolled | 8 |
| 3463 | expression | 8 |
| 3464 | expressed | 8 |
| 3465 | express | 8 |
| 3466 | expose | 8 |
| 3467 | expectation | 8 |
| 3468 | exercise | 8 |
| 3469 | exceedingly | 8 |
| 3470 | essential | 8 |
| 3471 | envied | 8 |
| 3472 | england | 8 |
| 3473 | endured | 8 |
| 3474 | endowed | 8 |
| 3475 | endless | 8 |
| 3476 | encouraged | 8 |
| 3477 | eloquence | 8 |
| 3478 | edge | 8 |
| 3479 | eats | 8 |
| 3480 | dwell | 8 |
| 3481 | dried | 8 |
| 3482 | doubtful | 8 |
| 3483 | doctors | 8 |
| 3484 | disturb | 8 |
| 3485 | disguised | 8 |
| 3486 | disclose | 8 |
| 3487 | discharge | 8 |
| 3488 | dined | 8 |
| 3489 | diana | 8 |
| 3490 | destroyed | 8 |
| 3491 | designs | 8 |
| 3492 | deprived | 8 |
| 3493 | demeanour | 8 |
| 3494 | delectable | 8 |
| 3495 | defending | 8 |
| 3496 | defeat | 8 |
| 3497 | deceiving | 8 |
| 3498 | dealt | 8 |
| 3499 | deaf | 8 |
| 3500 | dancers | 8 |
| 3501 | crushed | 8 |
| 3502 | corn | 8 |
| 3503 | convince | 8 |
| 3504 | contrive | 8 |
| 3505 | contain | 8 |
| 3506 | consists | 8 |
| 3507 | connected | 8 |
| 3508 | confused | 8 |
| 3509 | confirm | 8 |
| 3510 | confession | 8 |
| 3511 | confessed | 8 |
| 3512 | confer | 8 |
| 3513 | concern | 8 |
| 3514 | compose | 8 |
| 3515 | complaint | 8 |
| 3516 | combatants | 8 |
| 3517 | coloured | 8 |
| 3518 | cid | 8 |
| 3519 | chloris | 8 |
| 3520 | cheeks | 8 |
| 3521 | checked | 8 |
| 3522 | charitable | 8 |
| 3523 | charging | 8 |
| 3524 | ceremonies | 8 |
| 3525 | celebrated | 8 |
| 3526 | ceaseless | 8 |
| 3527 | caution | 8 |
| 3528 | catafalque | 8 |
| 3529 | castile | 8 |
| 3530 | castellan | 8 |
| 3531 | carries | 8 |
| 3532 | caring | 8 |
| 3533 | carelessness | 8 |
| 3534 | busy | 8 |
| 3535 | built | 8 |
| 3536 | briskly | 8 |
| 3537 | breaks | 8 |
| 3538 | branches | 8 |
| 3539 | boorish | 8 |
| 3540 | booby | 8 |
| 3541 | bitch | 8 |
| 3542 | bewildered | 8 |
| 3543 | betrothal | 8 |
| 3544 | beneath | 8 |
| 3545 | beings | 8 |
| 3546 | behaved | 8 |
| 3547 | becomes | 8 |
| 3548 | beating | 8 |
| 3549 | beams | 8 |
| 3550 | ay | 8 |
| 3551 | awe | 8 |
| 3552 | awaiting | 8 |
| 3553 | assure | 8 |
| 3554 | assail | 8 |
| 3555 | aspect | 8 |
| 3556 | asks | 8 |
| 3557 | ashamed | 8 |
| 3558 | apt | 8 |
| 3559 | apply | 8 |
| 3560 | apart | 8 |
| 3561 | anxiously | 8 |
| 3562 | amusing | 8 |
| 3563 | amiss | 8 |
| 3564 | alonso | 8 |
| 3565 | agitation | 8 |
| 3566 | aforesaid | 8 |
| 3567 | ado | 8 |
| 3568 | addition | 8 |
| 3569 | actors | 8 |
| 3570 | action | 8 |
| 3571 | acknowledge | 8 |
| 3572 | accident | 8 |
| 3573 | zeal | 7 |
| 3574 | wronged | 7 |
| 3575 | wrist | 7 |
| 3576 | worn | 7 |
| 3577 | winds | 7 |
| 3578 | welcomed | 7 |
| 3579 | week | 7 |
| 3580 | wears | 7 |
| 3581 | waste | 7 |
| 3582 | warned | 7 |
| 3583 | warn | 7 |
| 3584 | warm | 7 |
| 3585 | warlike | 7 |
| 3586 | wanton | 7 |
| 3587 | wander | 7 |
| 3588 | vow | 7 |
| 3589 | vent | 7 |
| 3590 | valencia | 7 |
| 3591 | vagaries | 7 |
| 3592 | urging | 7 |
| 3593 | untied | 7 |
| 3594 | unseen | 7 |
| 3595 | uncovered | 7 |
| 3596 | unceasingly | 7 |
| 3597 | troubling | 7 |
| 3598 | triumph | 7 |
| 3599 | treatment | 7 |
| 3600 | translated | 7 |
| 3601 | tranquilly | 7 |
| 3602 | tradition | 7 |
| 3603 | towns | 7 |
| 3604 | torralva | 7 |
| 3605 | tore | 7 |
| 3606 | tomorrow | 7 |
| 3607 | threads | 7 |
| 3608 | thinks | 7 |
| 3609 | termination | 7 |
| 3610 | tarfe | 7 |
| 3611 | tame | 7 |
| 3612 | tails | 7 |
| 3613 | sweating | 7 |
| 3614 | suspected | 7 |
| 3615 | surrounded | 7 |
| 3616 | surpassed | 7 |
| 3617 | supported | 7 |
| 3618 | sumpter | 7 |
| 3619 | summoned | 7 |
| 3620 | summon | 7 |
| 3621 | suits | 7 |
| 3622 | succeed | 7 |
| 3623 | stumbling | 7 |
| 3624 | struggling | 7 |
| 3625 | stronger | 7 |
| 3626 | stringing | 7 |
| 3627 | strict | 7 |
| 3628 | stranger | 7 |
| 3629 | stoutly | 7 |
| 3630 | stole | 7 |
| 3631 | stirrup | 7 |
| 3632 | sport | 7 |
| 3633 | speaker | 7 |
| 3634 | spared | 7 |
| 3635 | sounding | 7 |
| 3636 | sorrowful | 7 |
| 3637 | softly | 7 |
| 3638 | slope | 7 |
| 3639 | slip | 7 |
| 3640 | slight | 7 |
| 3641 | skirt | 7 |
| 3642 | skimmings | 7 |
| 3643 | skies | 7 |
| 3644 | sighing | 7 |
| 3645 | shift | 7 |
| 3646 | shapes | 7 |
| 3647 | separation | 7 |
| 3648 | segovia | 7 |
| 3649 | seeks | 7 |
| 3650 | security | 7 |
| 3651 | scoundrels | 7 |
| 3652 | schemes | 7 |
| 3653 | sceptre | 7 |
| 3654 | scattered | 7 |
| 3655 | scared | 7 |
| 3656 | scanty | 7 |
| 3657 | satisfactory | 7 |
| 3658 | saluted | 7 |
| 3659 | salt | 7 |
| 3660 | saddled | 7 |
| 3661 | rugged | 7 |
| 3662 | row | 7 |
| 3663 | roughly | 7 |
| 3664 | roaming | 7 |
| 3665 | roam | 7 |
| 3666 | righteous | 7 |
| 3667 | reverence | 7 |
| 3668 | restless | 7 |
| 3669 | resting | 7 |
| 3670 | respects | 7 |
| 3671 | reserve | 7 |
| 3672 | represented | 7 |
| 3673 | reported | 7 |
| 3674 | replying | 7 |
| 3675 | renewed | 7 |
| 3676 | regardless | 7 |
| 3677 | recovering | 7 |
| 3678 | recommended | 7 |
| 3679 | recognising | 7 |
| 3680 | receives | 7 |
| 3681 | rays | 7 |
| 3682 | rais | 7 |
| 3683 | quartered | 7 |
| 3684 | puts | 7 |
| 3685 | purchase | 7 |
| 3686 | prowess | 7 |
| 3687 | provocation | 7 |
| 3688 | provisions | 7 |
| 3689 | protector | 7 |
| 3690 | pronounced | 7 |
| 3691 | promising | 7 |
| 3692 | profuse | 7 |
| 3693 | princesses | 7 |
| 3694 | preferred | 7 |
| 3695 | precautions | 7 |
| 3696 | poured | 7 |
| 3697 | possesses | 7 |
| 3698 | portugal | 7 |
| 3699 | portrait | 7 |
| 3700 | pledged | 7 |
| 3701 | players | 7 |
| 3702 | plasters | 7 |
| 3703 | pierce | 7 |
| 3704 | phoebus | 7 |
| 3705 | persuasion | 7 |
| 3706 | persecuted | 7 |
| 3707 | perplexed | 7 |
| 3708 | penitents | 7 |
| 3709 | pebbles | 7 |
| 3710 | pears | 7 |
| 3711 | peacefully | 7 |
| 3712 | pat | 7 |
| 3713 | pacing | 7 |
| 3714 | pacified | 7 |
| 3715 | paced | 7 |
| 3716 | owest | 7 |
| 3717 | overwhelmed | 7 |
| 3718 | overtook | 7 |
| 3719 | osuna | 7 |
| 3720 | orphans | 7 |
| 3721 | orlando | 7 |
| 3722 | opinions | 7 |
| 3723 | omitted | 7 |
| 3724 | omen | 7 |
| 3725 | occurrence | 7 |
| 3726 | occupation | 7 |
| 3727 | observations | 7 |
| 3728 | nets | 7 |
| 3729 | neat | 7 |
| 3730 | moreno | 7 |
| 3731 | morato | 7 |
| 3732 | mood | 7 |
| 3733 | montera | 7 |
| 3734 | moisture | 7 |
| 3735 | mixture | 7 |
| 3736 | mingled | 7 |
| 3737 | messenger | 7 |
| 3738 | merchant | 7 |
| 3739 | members | 7 |
| 3740 | marsilio | 7 |
| 3741 | margin | 7 |
| 3742 | manners | 7 |
| 3743 | male | 7 |
| 3744 | liveries | 7 |
| 3745 | lint | 7 |
| 3746 | limit | 7 |
| 3747 | liberality | 7 |
| 3748 | liberal | 7 |
| 3749 | leisurely | 7 |
| 3750 | laying | 7 |
| 3751 | lace | 7 |
| 3752 | knave | 7 |
| 3753 | justly | 7 |
| 3754 | judgments | 7 |
| 3755 | italian | 7 |
| 3756 | interrupt | 7 |
| 3757 | instructions | 7 |
| 3758 | insert | 7 |
| 3759 | inscription | 7 |
| 3760 | inferred | 7 |
| 3761 | induce | 7 |
| 3762 | indignation | 7 |
| 3763 | indicate | 7 |
| 3764 | increase | 7 |
| 3765 | impelled | 7 |
| 3766 | impediment | 7 |
| 3767 | imitating | 7 |
| 3768 | imaginary | 7 |
| 3769 | idleness | 7 |
| 3770 | hunt | 7 |
| 3771 | hungry | 7 |
| 3772 | hostess | 7 |
| 3773 | horsemen | 7 |
| 3774 | horns | 7 |
| 3775 | homer | 7 |
| 3776 | holland | 7 |
| 3777 | historians | 7 |
| 3778 | hircania | 7 |
| 3779 | heroic | 7 |
| 3780 | herd | 7 |
| 3781 | hearty | 7 |
| 3782 | happily | 7 |
| 3783 | handmaid | 7 |
| 3784 | handle | 7 |
| 3785 | halted | 7 |
| 3786 | hadji | 7 |
| 3787 | guitar | 7 |
| 3788 | guadiana | 7 |
| 3789 | grasped | 7 |
| 3790 | grain | 7 |
| 3791 | graces | 7 |
| 3792 | glittering | 7 |
| 3793 | glass | 7 |
| 3794 | gipsy | 7 |
| 3795 | genuine | 7 |
| 3796 | gathering | 7 |
| 3797 | gallows | 7 |
| 3798 | gallantry | 7 |
| 3799 | foundation | 7 |
| 3800 | fooleries | 7 |
| 3801 | fold | 7 |
| 3802 | flowing | 7 |
| 3803 | flow | 7 |
| 3804 | flattery | 7 |
| 3805 | flat | 7 |
| 3806 | fitted | 7 |
| 3807 | fifth | 7 |
| 3808 | fetched | 7 |
| 3809 | feelings | 7 |
| 3810 | farm | 7 |
| 3811 | eyebrows | 7 |
| 3812 | existence | 7 |
| 3813 | exertion | 7 |
| 3814 | execute | 7 |
| 3815 | everlasting | 7 |
| 3816 | estate | 7 |
| 3817 | entrusted | 7 |
| 3818 | enormous | 7 |
| 3819 | endeavour | 7 |
| 3820 | encounters | 7 |
| 3821 | employ | 7 |
| 3822 | eleven | 7 |
| 3823 | elegance | 7 |
| 3824 | eighteen | 7 |
| 3825 | effected | 7 |
| 3826 | ecclesiastic | 7 |
| 3827 | east | 7 |
| 3828 | duties | 7 |
| 3829 | drunk | 7 |
| 3830 | drank | 7 |
| 3831 | doubtless | 7 |
| 3832 | doors | 7 |
| 3833 | divert | 7 |
| 3834 | distinguish | 7 |
| 3835 | dissuade | 7 |
| 3836 | dismay | 7 |
| 3837 | disenchant | 7 |
| 3838 | discord | 7 |
| 3839 | diligence | 7 |
| 3840 | digging | 7 |
| 3841 | diet | 7 |
| 3842 | diamond | 7 |
| 3843 | destiny | 7 |
| 3844 | desperate | 7 |
| 3845 | describing | 7 |
| 3846 | demands | 7 |
| 3847 | delayed | 7 |
| 3848 | dangers | 7 |
| 3849 | cuffs | 7 |
| 3850 | crowd | 7 |
| 3851 | cream | 7 |
| 3852 | counted | 7 |
| 3853 | couch | 7 |
| 3854 | cotton | 7 |
| 3855 | cook | 7 |
| 3856 | contrivance | 7 |
| 3857 | contented | 7 |
| 3858 | consoled | 7 |
| 3859 | console | 7 |
| 3860 | conjure | 7 |
| 3861 | condemned | 7 |
| 3862 | concerns | 7 |
| 3863 | concerned | 7 |
| 3864 | completed | 7 |
| 3865 | closer | 7 |
| 3866 | circumstance | 7 |
| 3867 | chide | 7 |
| 3868 | chanced | 7 |
| 3869 | causes | 7 |
| 3870 | cats | 7 |
| 3871 | careless | 7 |
| 3872 | careful | 7 |
| 3873 | card | 7 |
| 3874 | caps | 7 |
| 3875 | capers | 7 |
| 3876 | capering | 7 |
| 3877 | capacity | 7 |
| 3878 | campo | 7 |
| 3879 | calmness | 7 |
| 3880 | cakes | 7 |
| 3881 | building | 7 |
| 3882 | brown | 7 |
| 3883 | brain | 7 |
| 3884 | bota | 7 |
| 3885 | bind | 7 |
| 3886 | bids | 7 |
| 3887 | betide | 7 |
| 3888 | bereft | 7 |
| 3889 | benefit | 7 |
| 3890 | belianis | 7 |
| 3891 | beauteous | 7 |
| 3892 | beach | 7 |
| 3893 | banish | 7 |
| 3894 | baldric | 7 |
| 3895 | attendance | 7 |
| 3896 | asunder | 7 |
| 3897 | asturian | 7 |
| 3898 | astounded | 7 |
| 3899 | assault | 7 |
| 3900 | ashes | 7 |
| 3901 | argamasilla | 7 |
| 3902 | apothecary | 7 |
| 3903 | apollo | 7 |
| 3904 | amid | 7 |
| 3905 | alms | 7 |
| 3906 | alike | 7 |
| 3907 | aldonza | 7 |
| 3908 | alcaide | 7 |
| 3909 | alarm | 7 |
| 3910 | agreement | 7 |
| 3911 | africa | 7 |
| 3912 | affliction | 7 |
| 3913 | affections | 7 |
| 3914 | advise | 7 |
| 3915 | adversary | 7 |
| 3916 | advancing | 7 |
| 3917 | acute | 7 |
| 3918 | active | 7 |
| 3919 | accompanying | 7 |
| 3920 | accidents | 7 |
| 3921 | wretch | 6 |
| 3922 | worked | 6 |
| 3923 | wolf | 6 |
| 3924 | withdrawn | 6 |
| 3925 | withdraw | 6 |
| 3926 | wisest | 6 |
| 3927 | winding | 6 |
| 3928 | wiles | 6 |
| 3929 | whitest | 6 |
| 3930 | whereabouts | 6 |
| 3931 | weariness | 6 |
| 3932 | wearied | 6 |
| 3933 | warrant | 6 |
| 3934 | wandered | 6 |
| 3935 | walk | 6 |
| 3936 | waken | 6 |
| 3937 | volume | 6 |
| 3938 | vogue | 6 |
| 3939 | visible | 6 |
| 3940 | virgil | 6 |
| 3941 | vigour | 6 |
| 3942 | vicious | 6 |
| 3943 | vassal | 6 |
| 3944 | vandalia | 6 |
| 3945 | v | 6 |
| 3946 | uplifted | 6 |
| 3947 | universal | 6 |
| 3948 | undergo | 6 |
| 3949 | uncover | 6 |
| 3950 | uchali | 6 |
| 3951 | ubeda | 6 |
| 3952 | trophy | 6 |
| 3953 | transparent | 6 |
| 3954 | translation | 6 |
| 3955 | transformations | 6 |
| 3956 | trampling | 6 |
| 3957 | tragedy | 6 |
| 3958 | tooth | 6 |
| 3959 | toils | 6 |
| 3960 | tightly | 6 |
| 3961 | thereby | 6 |
| 3962 | territory | 6 |
| 3963 | temple | 6 |
| 3964 | tablecloth | 6 |
| 3965 | swift | 6 |
| 3966 | swept | 6 |
| 3967 | surpasses | 6 |
| 3968 | surpass | 6 |
| 3969 | surname | 6 |
| 3970 | suggest | 6 |
| 3971 | suffers | 6 |
| 3972 | submission | 6 |
| 3973 | subjects | 6 |
| 3974 | students | 6 |
| 3975 | stripping | 6 |
| 3976 | streams | 6 |
| 3977 | stream | 6 |
| 3978 | stores | 6 |
| 3979 | sticks | 6 |
| 3980 | states | 6 |
| 3981 | stated | 6 |
| 3982 | staring | 6 |
| 3983 | stanzas | 6 |
| 3984 | squirely | 6 |
| 3985 | squeezed | 6 |
| 3986 | sprightliness | 6 |
| 3987 | spreading | 6 |
| 3988 | spoil | 6 |
| 3989 | spinning | 6 |
| 3990 | spectacles | 6 |
| 3991 | speakest | 6 |
| 3992 | spaniards | 6 |
| 3993 | source | 6 |
| 3994 | sounded | 6 |
| 3995 | solid | 6 |
| 3996 | smacks | 6 |
| 3997 | slung | 6 |
| 3998 | slaps | 6 |
| 3999 | slap | 6 |
| 4000 | signature | 6 |
| 4001 | signals | 6 |
| 4002 | shop | 6 |
| 4003 | shock | 6 |
| 4004 | sheet | 6 |
| 4005 | shaved | 6 |
| 4006 | shaken | 6 |
| 4007 | settling | 6 |
| 4008 | seekest | 6 |
| 4009 | seed | 6 |
| 4010 | school | 6 |
| 4011 | sayings | 6 |
| 4012 | sawest | 6 |
| 4013 | sancha | 6 |
| 4014 | salad | 6 |
| 4015 | sails | 6 |
| 4016 | sacristan | 6 |
| 4017 | sacred | 6 |
| 4018 | rushed | 6 |
| 4019 | rowing | 6 |
| 4020 | roused | 6 |
| 4021 | rouse | 6 |
| 4022 | rosary | 6 |
| 4023 | roots | 6 |
| 4024 | roguery | 6 |
| 4025 | robber | 6 |
| 4026 | rises | 6 |
| 4027 | rings | 6 |
| 4028 | rights | 6 |
| 4029 | riches | 6 |
| 4030 | rhadamanthus | 6 |
| 4031 | retreated | 6 |
| 4032 | retain | 6 |
| 4033 | restoring | 6 |
| 4034 | requires | 6 |
| 4035 | reproach | 6 |
| 4036 | represent | 6 |
| 4037 | replies | 6 |
| 4038 | repeating | 6 |
| 4039 | repast | 6 |
| 4040 | remarks | 6 |
| 4041 | remarkable | 6 |
| 4042 | releasing | 6 |
| 4043 | rejoice | 6 |
| 4044 | reins | 6 |
| 4045 | regidors | 6 |
| 4046 | reasoning | 6 |
| 4047 | reasonably | 6 |
| 4048 | realm | 6 |
| 4049 | readiness | 6 |
| 4050 | rarest | 6 |
| 4051 | r | 6 |
| 4052 | quickness | 6 |
| 4053 | pursuits | 6 |
| 4054 | purposes | 6 |
| 4055 | purposely | 6 |
| 4056 | purest | 6 |
| 4057 | punished | 6 |
| 4058 | provoke | 6 |
| 4059 | prostrate | 6 |
| 4060 | prosperity | 6 |
| 4061 | promptly | 6 |
| 4062 | profitable | 6 |
| 4063 | printing | 6 |
| 4064 | pretending | 6 |
| 4065 | pressure | 6 |
| 4066 | practised | 6 |
| 4067 | powers | 6 |
| 4068 | pour | 6 |
| 4069 | pope | 6 |
| 4070 | pole | 6 |
| 4071 | pocket | 6 |
| 4072 | plot | 6 |
| 4073 | plentiful | 6 |
| 4074 | plates | 6 |
| 4075 | plaster | 6 |
| 4076 | plains | 6 |
| 4077 | plague | 6 |
| 4078 | picked | 6 |
| 4079 | personages | 6 |
| 4080 | perpetual | 6 |
| 4081 | pena | 6 |
| 4082 | peer | 6 |
| 4083 | pearl | 6 |
| 4084 | pause | 6 |
| 4085 | ovid | 6 |
| 4086 | overthrown | 6 |
| 4087 | overtaken | 6 |
| 4088 | opponent | 6 |
| 4089 | onions | 6 |
| 4090 | obstinate | 6 |
| 4091 | obligations | 6 |
| 4092 | objects | 6 |
| 4093 | objection | 6 |
| 4094 | nymph | 6 |
| 4095 | nowhere | 6 |
| 4096 | noontide | 6 |
| 4097 | nearer | 6 |
| 4098 | morion | 6 |
| 4099 | montalvan | 6 |
| 4100 | monarch | 6 |
| 4101 | mole | 6 |
| 4102 | moderate | 6 |
| 4103 | miles | 6 |
| 4104 | mightily | 6 |
| 4105 | merits | 6 |
| 4106 | meat | 6 |
| 4107 | measures | 6 |
| 4108 | marvelled | 6 |
| 4109 | mari | 6 |
| 4110 | marched | 6 |
| 4111 | managed | 6 |
| 4112 | maintaining | 6 |
| 4113 | magnificence | 6 |
| 4114 | magicians | 6 |
| 4115 | magalona | 6 |
| 4116 | lonely | 6 |
| 4117 | lodging | 6 |
| 4118 | loan | 6 |
| 4119 | load | 6 |
| 4120 | lists | 6 |
| 4121 | listeners | 6 |
| 4122 | liquor | 6 |
| 4123 | link | 6 |
| 4124 | lineages | 6 |
| 4125 | lightly | 6 |
| 4126 | lifting | 6 |
| 4127 | leon | 6 |
| 4128 | lank | 6 |
| 4129 | landed | 6 |
| 4130 | lamps | 6 |
| 4131 | lamentation | 6 |
| 4132 | lamb | 6 |
| 4133 | lack | 6 |
| 4134 | kneel | 6 |
| 4135 | kitchen | 6 |
| 4136 | kinds | 6 |
| 4137 | keen | 6 |
| 4138 | julius | 6 |
| 4139 | judging | 6 |
| 4140 | joyful | 6 |
| 4141 | jeronimo | 6 |
| 4142 | jaws | 6 |
| 4143 | jasper | 6 |
| 4144 | jars | 6 |
| 4145 | italy | 6 |
| 4146 | invitation | 6 |
| 4147 | invent | 6 |
| 4148 | introduced | 6 |
| 4149 | interesting | 6 |
| 4150 | intellect | 6 |
| 4151 | instruction | 6 |
| 4152 | inscribed | 6 |
| 4153 | inquire | 6 |
| 4154 | inns | 6 |
| 4155 | injustice | 6 |
| 4156 | information | 6 |
| 4157 | increasing | 6 |
| 4158 | imposed | 6 |
| 4159 | impatience | 6 |
| 4160 | illusions | 6 |
| 4161 | huts | 6 |
| 4162 | honours | 6 |
| 4163 | highwayman | 6 |
| 4164 | hesitation | 6 |
| 4165 | hercules | 6 |
| 4166 | heiress | 6 |
| 4167 | hears | 6 |
| 4168 | hate | 6 |
| 4169 | hat | 6 |
| 4170 | harsh | 6 |
| 4171 | harmless | 6 |
| 4172 | harbour | 6 |
| 4173 | harangue | 6 |
| 4174 | haply | 6 |
| 4175 | hail | 6 |
| 4176 | guess | 6 |
| 4177 | grudge | 6 |
| 4178 | greyhounds | 6 |
| 4179 | governed | 6 |
| 4180 | glutton | 6 |
| 4181 | glowing | 6 |
| 4182 | glorious | 6 |
| 4183 | glorify | 6 |
| 4184 | glance | 6 |
| 4185 | girdle | 6 |
| 4186 | ginesillo | 6 |
| 4187 | gentlefolk | 6 |
| 4188 | garcia | 6 |
| 4189 | garb | 6 |
| 4190 | gaol | 6 |
| 4191 | gangway | 6 |
| 4192 | gaily | 6 |
| 4193 | frenchmen | 6 |
| 4194 | fountain | 6 |
| 4195 | foreign | 6 |
| 4196 | followers | 6 |
| 4197 | follies | 6 |
| 4198 | flocks | 6 |
| 4199 | flavour | 6 |
| 4200 | flags | 6 |
| 4201 | fitter | 6 |
| 4202 | fits | 6 |
| 4203 | fisticuffs | 6 |
| 4204 | fist | 6 |
| 4205 | fishermen | 6 |
| 4206 | fineness | 6 |
| 4207 | fiery | 6 |
| 4208 | felixmarte | 6 |
| 4209 | fed | 6 |
| 4210 | favourable | 6 |
| 4211 | faults | 6 |
| 4212 | fathers | 6 |
| 4213 | families | 6 |
| 4214 | famed | 6 |
| 4215 | failing | 6 |
| 4216 | fables | 6 |
| 4217 | extend | 6 |
| 4218 | experiment | 6 |
| 4219 | expects | 6 |
| 4220 | exist | 6 |
| 4221 | exertions | 6 |
| 4222 | exchange | 6 |
| 4223 | examining | 6 |
| 4224 | ewes | 6 |
| 4225 | event | 6 |
| 4226 | escaping | 6 |
| 4227 | eruct | 6 |
| 4228 | enveloped | 6 |
| 4229 | entreaty | 6 |
| 4230 | ensconced | 6 |
| 4231 | endeavouring | 6 |
| 4232 | emotion | 6 |
| 4233 | embark | 6 |
| 4234 | eldest | 6 |
| 4235 | earnestness | 6 |
| 4236 | dumb | 6 |
| 4237 | drollest | 6 |
| 4238 | draught | 6 |
| 4239 | divided | 6 |
| 4240 | diverting | 6 |
| 4241 | disturbance | 6 |
| 4242 | distresses | 6 |
| 4243 | dismissed | 6 |
| 4244 | disguise | 6 |
| 4245 | discussed | 6 |
| 4246 | discuss | 6 |
| 4247 | discourteous | 6 |
| 4248 | discomfort | 6 |
| 4249 | dirty | 6 |
| 4250 | diamonds | 6 |
| 4251 | devout | 6 |
| 4252 | devotion | 6 |
| 4253 | devilish | 6 |
| 4254 | desirous | 6 |
| 4255 | deserts | 6 |
| 4256 | deserting | 6 |
| 4257 | descried | 6 |
| 4258 | descendants | 6 |
| 4259 | derived | 6 |
| 4260 | denies | 6 |
| 4261 | delusion | 6 |
| 4262 | delivering | 6 |
| 4263 | deliberate | 6 |
| 4264 | declaring | 6 |
| 4265 | decide | 6 |
| 4266 | debt | 6 |
| 4267 | dancing | 6 |
| 4268 | dances | 6 |
| 4269 | current | 6 |
| 4270 | cowardly | 6 |
| 4271 | covetousness | 6 |
| 4272 | covers | 6 |
| 4273 | copy | 6 |
| 4274 | copied | 6 |
| 4275 | contentment | 6 |
| 4276 | constraint | 6 |
| 4277 | consented | 6 |
| 4278 | confident | 6 |
| 4279 | conferred | 6 |
| 4280 | conceive | 6 |
| 4281 | composition | 6 |
| 4282 | compliments | 6 |
| 4283 | complaints | 6 |
| 4284 | complained | 6 |
| 4285 | compass | 6 |
| 4286 | comparison | 6 |
| 4287 | commit | 6 |
| 4288 | comforted | 6 |
| 4289 | comfortably | 6 |
| 4290 | comeliness | 6 |
| 4291 | comb | 6 |
| 4292 | colloquy | 6 |
| 4293 | coin | 6 |
| 4294 | cock | 6 |
| 4295 | clock | 6 |
| 4296 | clavijo | 6 |
| 4297 | clasped | 6 |
| 4298 | civilities | 6 |
| 4299 | circuit | 6 |
| 4300 | churchman | 6 |
| 4301 | chooses | 6 |
| 4302 | cheerful | 6 |
| 4303 | cheek | 6 |
| 4304 | check | 6 |
| 4305 | chase | 6 |
| 4306 | charmed | 6 |
| 4307 | changes | 6 |
| 4308 | chamois | 6 |
| 4309 | cavern | 6 |
| 4310 | catching | 6 |
| 4311 | casting | 6 |
| 4312 | cards | 6 |
| 4313 | cannon | 6 |
| 4314 | cane | 6 |
| 4315 | burying | 6 |
| 4316 | bull | 6 |
| 4317 | bucket | 6 |
| 4318 | brocade | 6 |
| 4319 | bridegroom | 6 |
| 4320 | bravest | 6 |
| 4321 | brambles | 6 |
| 4322 | braced | 6 |
| 4323 | bowed | 6 |
| 4324 | boor | 6 |
| 4325 | boast | 6 |
| 4326 | blanketing | 6 |
| 4327 | bladders | 6 |
| 4328 | bier | 6 |
| 4329 | bewail | 6 |
| 4330 | bernardo | 6 |
| 4331 | begot | 6 |
| 4332 | begone | 6 |
| 4333 | begins | 6 |
| 4334 | beggar | 6 |
| 4335 | beforehand | 6 |
| 4336 | beech | 6 |
| 4337 | beds | 6 |
| 4338 | bathing | 6 |
| 4339 | bars | 6 |
| 4340 | barabbas | 6 |
| 4341 | baldwin | 6 |
| 4342 | balcony | 6 |
| 4343 | bags | 6 |
| 4344 | bacon | 6 |
| 4345 | awful | 6 |
| 4346 | avaunt | 6 |
| 4347 | aught | 6 |
| 4348 | attentions | 6 |
| 4349 | assuring | 6 |
| 4350 | assuredly | 6 |
| 4351 | assurance | 6 |
| 4352 | arts | 6 |
| 4353 | articles | 6 |
| 4354 | arrogant | 6 |
| 4355 | arrogance | 6 |
| 4356 | approval | 6 |
| 4357 | approbation | 6 |
| 4358 | appointed | 6 |
| 4359 | appeased | 6 |
| 4360 | aphorisms | 6 |
| 4361 | anguish | 6 |
| 4362 | angrily | 6 |
| 4363 | angels | 6 |
| 4364 | amber | 6 |
| 4365 | alongside | 6 |
| 4366 | alcaldes | 6 |
| 4367 | agramante | 6 |
| 4368 | advisable | 6 |
| 4369 | adorn | 6 |
| 4370 | adore | 6 |
| 4371 | accustomed | 6 |
| 4372 | academician | 6 |
| 4373 | abyss | 6 |
| 4374 | abused | 6 |
| 4375 | youths | 5 |
| 4376 | younger | 5 |
| 4377 | yoke | 5 |
| 4378 | y | 5 |
| 4379 | x | 5 |
| 4380 | writer | 5 |
| 4381 | wouldn | 5 |
| 4382 | withhold | 5 |
| 4383 | withheld | 5 |
| 4384 | wisely | 5 |
| 4385 | wins | 5 |
| 4386 | wing | 5 |
| 4387 | widower | 5 |
| 4388 | whithersoever | 5 |
| 4389 | whisper | 5 |
| 4390 | whereof | 5 |
| 4391 | wheeling | 5 |
| 4392 | whacks | 5 |
| 4393 | weigh | 5 |
| 4394 | web | 5 |
| 4395 | wasn | 5 |
| 4396 | wars | 5 |
| 4397 | wand | 5 |
| 4398 | waits | 5 |
| 4399 | wag | 5 |
| 4400 | vomit | 5 |
| 4401 | visits | 5 |
| 4402 | visited | 5 |
| 4403 | vision | 5 |
| 4404 | virgin | 5 |
| 4405 | violent | 5 |
| 4406 | vial | 5 |
| 4407 | versed | 5 |
| 4408 | veils | 5 |
| 4409 | vanished | 5 |
| 4410 | valorous | 5 |
| 4411 | vale | 5 |
| 4412 | useful | 5 |
| 4413 | upside | 5 |
| 4414 | upright | 5 |
| 4415 | unusual | 5 |
| 4416 | untoward | 5 |
| 4417 | untie | 5 |
| 4418 | unnumbered | 5 |
| 4419 | unlike | 5 |
| 4420 | unequalled | 5 |
| 4421 | unequal | 5 |
| 4422 | undo | 5 |
| 4423 | unconquered | 5 |
| 4424 | unavailing | 5 |
| 4425 | tube | 5 |
| 4426 | trusting | 5 |
| 4427 | trot | 5 |
| 4428 | trivial | 5 |
| 4429 | trinkets | 5 |
| 4430 | trice | 5 |
| 4431 | trenchant | 5 |
| 4432 | tremendous | 5 |
| 4433 | trembled | 5 |
| 4434 | translator | 5 |
| 4435 | transferred | 5 |
| 4436 | torch | 5 |
| 4437 | tombs | 5 |
| 4438 | tokens | 5 |
| 4439 | tirante | 5 |
| 4440 | tip | 5 |
| 4441 | tin | 5 |
| 4442 | thunderstruck | 5 |
| 4443 | threatening | 5 |
| 4444 | thrashed | 5 |
| 4445 | thousands | 5 |
| 4446 | thickest | 5 |
| 4447 | testimony | 5 |
| 4448 | tend | 5 |
| 4449 | tawny | 5 |
| 4450 | tastes | 5 |
| 4451 | tapestries | 5 |
| 4452 | tapers | 5 |
| 4453 | talks | 5 |
| 4454 | tabors | 5 |
| 4455 | swiftness | 5 |
| 4456 | sweetest | 5 |
| 4457 | sweeping | 5 |
| 4458 | sway | 5 |
| 4459 | sustain | 5 |
| 4460 | suspended | 5 |
| 4461 | surnames | 5 |
| 4462 | supporting | 5 |
| 4463 | superiority | 5 |
| 4464 | superior | 5 |
| 4465 | suited | 5 |
| 4466 | studying | 5 |
| 4467 | stuck | 5 |
| 4468 | strung | 5 |
| 4469 | strongly | 5 |
| 4470 | stroll | 5 |
| 4471 | strengthened | 5 |
| 4472 | strangers | 5 |
| 4473 | strand | 5 |
| 4474 | straits | 5 |
| 4475 | stowed | 5 |
| 4476 | stolen | 5 |
| 4477 | stirring | 5 |
| 4478 | sticking | 5 |
| 4479 | steer | 5 |
| 4480 | steeds | 5 |
| 4481 | steadily | 5 |
| 4482 | standard | 5 |
| 4483 | springs | 5 |
| 4484 | split | 5 |
| 4485 | spiteful | 5 |
| 4486 | spilt | 5 |
| 4487 | spies | 5 |
| 4488 | sovereign | 5 |
| 4489 | sounder | 5 |
| 4490 | songs | 5 |
| 4491 | somewhere | 5 |
| 4492 | solemn | 5 |
| 4493 | sold | 5 |
| 4494 | soften | 5 |
| 4495 | sociably | 5 |
| 4496 | smelt | 5 |
| 4497 | smart | 5 |
| 4498 | sluggish | 5 |
| 4499 | slew | 5 |
| 4500 | sleeves | 5 |
| 4501 | silently | 5 |
| 4502 | siege | 5 |
| 4503 | shrewdness | 5 |
| 4504 | shook | 5 |
| 4505 | shone | 5 |
| 4506 | shines | 5 |
| 4507 | shares | 5 |
| 4508 | seventy | 5 |
| 4509 | seriously | 5 |
| 4510 | sentences | 5 |
| 4511 | semblance | 5 |
| 4512 | secure | 5 |
| 4513 | scratch | 5 |
| 4514 | scourging | 5 |
| 4515 | scorned | 5 |
| 4516 | scimitar | 5 |
| 4517 | sceptres | 5 |
| 4518 | scene | 5 |
| 4519 | santiago | 5 |
| 4520 | santa | 5 |
| 4521 | sand | 5 |
| 4522 | salute | 5 |
| 4523 | sages | 5 |
| 4524 | saddles | 5 |
| 4525 | rubbed | 5 |
| 4526 | rotten | 5 |
| 4527 | ropes | 5 |
| 4528 | roll | 5 |
| 4529 | robbing | 5 |
| 4530 | robbers | 5 |
| 4531 | roamed | 5 |
| 4532 | ringing | 5 |
| 4533 | righting | 5 |
| 4534 | richest | 5 |
| 4535 | ricardo | 5 |
| 4536 | revived | 5 |
| 4537 | revenged | 5 |
| 4538 | reveal | 5 |
| 4539 | returns | 5 |
| 4540 | requite | 5 |
| 4541 | requirements | 5 |
| 4542 | requested | 5 |
| 4543 | repentance | 5 |
| 4544 | repair | 5 |
| 4545 | renegades | 5 |
| 4546 | removing | 5 |
| 4547 | remind | 5 |
| 4548 | remembrance | 5 |
| 4549 | relieving | 5 |
| 4550 | regret | 5 |
| 4551 | regidor | 5 |
| 4552 | regained | 5 |
| 4553 | reflected | 5 |
| 4554 | rectitude | 5 |
| 4555 | receiving | 5 |
| 4556 | receipt | 5 |
| 4557 | rapidly | 5 |
| 4558 | rapidity | 5 |
| 4559 | random | 5 |
| 4560 | quixotes | 5 |
| 4561 | quixano | 5 |
| 4562 | quixada | 5 |
| 4563 | quintanona | 5 |
| 4564 | questioning | 5 |
| 4565 | pursuing | 5 |
| 4566 | pursues | 5 |
| 4567 | pummelled | 5 |
| 4568 | pulpit | 5 |
| 4569 | protects | 5 |
| 4570 | prosperous | 5 |
| 4571 | professions | 5 |
| 4572 | professes | 5 |
| 4573 | proclamations | 5 |
| 4574 | proceedings | 5 |
| 4575 | prized | 5 |
| 4576 | principal | 5 |
| 4577 | previously | 5 |
| 4578 | presses | 5 |
| 4579 | preserving | 5 |
| 4580 | precisely | 5 |
| 4581 | preaching | 5 |
| 4582 | praiseworthy | 5 |
| 4583 | possessing | 5 |
| 4584 | pobre | 5 |
| 4585 | plume | 5 |
| 4586 | plate | 5 |
| 4587 | plant | 5 |
| 4588 | plainer | 5 |
| 4589 | pinched | 5 |
| 4590 | pile | 5 |
| 4591 | phrases | 5 |
| 4592 | phantom | 5 |
| 4593 | persuading | 5 |
| 4594 | pentapolin | 5 |
| 4595 | pedestal | 5 |
| 4596 | payer | 5 |
| 4597 | parties | 5 |
| 4598 | paris | 5 |
| 4599 | pamphlets | 5 |
| 4600 | palms | 5 |
| 4601 | packed | 5 |
| 4602 | owned | 5 |
| 4603 | owing | 5 |
| 4604 | owes | 5 |
| 4605 | overtake | 5 |
| 4606 | outlet | 5 |
| 4607 | outburst | 5 |
| 4608 | ornament | 5 |
| 4609 | ordinances | 5 |
| 4610 | oppose | 5 |
| 4611 | oneself | 5 |
| 4612 | olla | 5 |
| 4613 | odds | 5 |
| 4614 | occurs | 5 |
| 4615 | occurrences | 5 |
| 4616 | occur | 5 |
| 4617 | obstacle | 5 |
| 4618 | oblige | 5 |
| 4619 | obedient | 5 |
| 4620 | oar | 5 |
| 4621 | nuts | 5 |
| 4622 | novice | 5 |
| 4623 | novels | 5 |
| 4624 | notions | 5 |
| 4625 | non | 5 |
| 4626 | nimbleness | 5 |
| 4627 | needst | 5 |
| 4628 | needle | 5 |
| 4629 | naught | 5 |
| 4630 | narvaez | 5 |
| 4631 | nakedness | 5 |
| 4632 | muttering | 5 |
| 4633 | musicians | 5 |
| 4634 | muses | 5 |
| 4635 | moustaches | 5 |
| 4636 | montiel | 5 |
| 4637 | moles | 5 |
| 4638 | moans | 5 |
| 4639 | missed | 5 |
| 4640 | miseries | 5 |
| 4641 | misadventure | 5 |
| 4642 | messages | 5 |
| 4643 | mercies | 5 |
| 4644 | medicines | 5 |
| 4645 | matched | 5 |
| 4646 | marvel | 5 |
| 4647 | marshal | 5 |
| 4648 | marias | 5 |
| 4649 | malaga | 5 |
| 4650 | malady | 5 |
| 4651 | maker | 5 |
| 4652 | madmen | 5 |
| 4653 | madasima | 5 |
| 4654 | lustre | 5 |
| 4655 | louder | 5 |
| 4656 | loins | 5 |
| 4657 | lodged | 5 |
| 4658 | livery | 5 |
| 4659 | litter | 5 |
| 4660 | list | 5 |
| 4661 | linked | 5 |
| 4662 | limbs | 5 |
| 4663 | limb | 5 |
| 4664 | levelled | 5 |
| 4665 | legitimate | 5 |
| 4666 | lawless | 5 |
| 4667 | lash | 5 |
| 4668 | larder | 5 |
| 4669 | languages | 5 |
| 4670 | lands | 5 |
| 4671 | lamenting | 5 |
| 4672 | lament | 5 |
| 4673 | lame | 5 |
| 4674 | ladyships | 5 |
| 4675 | knelt | 5 |
| 4676 | kneeling | 5 |
| 4677 | knee | 5 |
| 4678 | kisses | 5 |
| 4679 | kindred | 5 |
| 4680 | keys | 5 |
| 4681 | key | 5 |
| 4682 | jurisdiction | 5 |
| 4683 | jupiter | 5 |
| 4684 | jumps | 5 |
| 4685 | jumped | 5 |
| 4686 | joking | 5 |
| 4687 | jests | 5 |
| 4688 | jade | 5 |
| 4689 | item | 5 |
| 4690 | issues | 5 |
| 4691 | involved | 5 |
| 4692 | inviting | 5 |
| 4693 | invited | 5 |
| 4694 | inventor | 5 |
| 4695 | intervals | 5 |
| 4696 | interpreter | 5 |
| 4697 | intercourse | 5 |
| 4698 | instruct | 5 |
| 4699 | inspired | 5 |
| 4700 | insolence | 5 |
| 4701 | insisted | 5 |
| 4702 | inquiring | 5 |
| 4703 | innocence | 5 |
| 4704 | injurious | 5 |
| 4705 | infer | 5 |
| 4706 | infantry | 5 |
| 4707 | incapable | 5 |
| 4708 | imprudence | 5 |
| 4709 | imposing | 5 |
| 4710 | importunities | 5 |
| 4711 | immediate | 5 |
| 4712 | hospitality | 5 |
| 4713 | hoping | 5 |
| 4714 | holiday | 5 |
| 4715 | hoisted | 5 |
| 4716 | hind | 5 |
| 4717 | hills | 5 |
| 4718 | hid | 5 |
| 4719 | henceforth | 5 |
| 4720 | hen | 5 |
| 4721 | helen | 5 |
| 4722 | hazel | 5 |
| 4723 | hay | 5 |
| 4724 | hasty | 5 |
| 4725 | hasten | 5 |
| 4726 | harp | 5 |
| 4727 | harness | 5 |
| 4728 | harassed | 5 |
| 4729 | happening | 5 |
| 4730 | hammers | 5 |
| 4731 | halberds | 5 |
| 4732 | guinevere | 5 |
| 4733 | grieve | 5 |
| 4734 | graves | 5 |
| 4735 | graduate | 5 |
| 4736 | gothic | 5 |
| 4737 | gonzalo | 5 |
| 4738 | globe | 5 |
| 4739 | givest | 5 |
| 4740 | giver | 5 |
| 4741 | germany | 5 |
| 4742 | genius | 5 |
| 4743 | geese | 5 |
| 4744 | gaspar | 5 |
| 4745 | garret | 5 |
| 4746 | garlic | 5 |
| 4747 | garlands | 5 |
| 4748 | gallery | 5 |
| 4749 | galaor | 5 |
| 4750 | fulfillment | 5 |
| 4751 | fruits | 5 |
| 4752 | fray | 5 |
| 4753 | fraud | 5 |
| 4754 | fraternity | 5 |
| 4755 | fragrance | 5 |
| 4756 | formerly | 5 |
| 4757 | foretold | 5 |
| 4758 | forests | 5 |
| 4759 | forces | 5 |
| 4760 | footsteps | 5 |
| 4761 | footing | 5 |
| 4762 | flourish | 5 |
| 4763 | flew | 5 |
| 4764 | flanders | 5 |
| 4765 | final | 5 |
| 4766 | fever | 5 |
| 4767 | fertile | 5 |
| 4768 | feeding | 5 |
| 4769 | favouring | 5 |
| 4770 | fatal | 5 |
| 4771 | fasting | 5 |
| 4772 | faster | 5 |
| 4773 | fanciful | 5 |
| 4774 | falsehoods | 5 |
| 4775 | faithfully | 5 |
| 4776 | fairer | 5 |
| 4777 | fain | 5 |
| 4778 | faced | 5 |
| 4779 | fable | 5 |
| 4780 | eyed | 5 |
| 4781 | extremes | 5 |
| 4782 | expressions | 5 |
| 4783 | exploit | 5 |
| 4784 | excuses | 5 |
| 4785 | excused | 5 |
| 4786 | excite | 5 |
| 4787 | excessive | 5 |
| 4788 | exceed | 5 |
| 4789 | evident | 5 |
| 4790 | eve | 5 |
| 4791 | eulogies | 5 |
| 4792 | etc | 5 |
| 4793 | estremadura | 5 |
| 4794 | establish | 5 |
| 4795 | escapes | 5 |
| 4796 | erudition | 5 |
| 4797 | errors | 5 |
| 4798 | ermine | 5 |
| 4799 | equals | 5 |
| 4800 | entertaining | 5 |
| 4801 | entertained | 5 |
| 4802 | enslaved | 5 |
| 4803 | endeavoured | 5 |
| 4804 | encourage | 5 |
| 4805 | encountering | 5 |
| 4806 | enchant | 5 |
| 4807 | encamisados | 5 |
| 4808 | emprise | 5 |
| 4809 | empresses | 5 |
| 4810 | employment | 5 |
| 4811 | elm | 5 |
| 4812 | eighty | 5 |
| 4813 | egg | 5 |
| 4814 | effecting | 5 |
| 4815 | earn | 5 |
| 4816 | dwelling | 5 |
| 4817 | dwarf | 5 |
| 4818 | duly | 5 |
| 4819 | drowned | 5 |
| 4820 | droves | 5 |
| 4821 | drinks | 5 |
| 4822 | dreams | 5 |
| 4823 | dreaming | 5 |
| 4824 | dreaded | 5 |
| 4825 | drama | 5 |
| 4826 | downcast | 5 |
| 4827 | divining | 5 |
| 4828 | divide | 5 |
| 4829 | displeasure | 5 |
| 4830 | dish | 5 |
| 4831 | disgrace | 5 |
| 4832 | discussion | 5 |
| 4833 | disaster | 5 |
| 4834 | disappointed | 5 |
| 4835 | disappeared | 5 |
| 4836 | didn | 5 |
| 4837 | dexterity | 5 |
| 4838 | devoured | 5 |
| 4839 | devote | 5 |
| 4840 | detestable | 5 |
| 4841 | despised | 5 |
| 4842 | deserted | 5 |
| 4843 | describes | 5 |
| 4844 | demon | 5 |
| 4845 | deliverer | 5 |
| 4846 | dejection | 5 |
| 4847 | deign | 5 |
| 4848 | defensive | 5 |
| 4849 | decreed | 5 |
| 4850 | decorum | 5 |
| 4851 | declined | 5 |
| 4852 | dauntless | 5 |
| 4853 | damask | 5 |
| 4854 | dainties | 5 |
| 4855 | custody | 5 |
| 4856 | cursing | 5 |
| 4857 | cupid | 5 |
| 4858 | cuff | 5 |
| 4859 | cudgellings | 5 |
| 4860 | cudgelled | 5 |
| 4861 | crush | 5 |
| 4862 | crippled | 5 |
| 4863 | crimes | 5 |
| 4864 | crime | 5 |
| 4865 | coy | 5 |
| 4866 | cowardice | 5 |
| 4867 | coverlet | 5 |
| 4868 | courtly | 5 |
| 4869 | courtiers | 5 |
| 4870 | countries | 5 |
| 4871 | counting | 5 |
| 4872 | corners | 5 |
| 4873 | cordovan | 5 |
| 4874 | converse | 5 |
| 4875 | conveniently | 5 |
| 4876 | convenient | 5 |
| 4877 | contemplated | 5 |
| 4878 | containing | 5 |
| 4879 | constrained | 5 |
| 4880 | constantly | 5 |
| 4881 | consigned | 5 |
| 4882 | considerable | 5 |
| 4883 | consequences | 5 |
| 4884 | conjured | 5 |
| 4885 | conjecture | 5 |
| 4886 | confide | 5 |
| 4887 | confidante | 5 |
| 4888 | conducting | 5 |
| 4889 | conceits | 5 |
| 4890 | comprehend | 5 |
| 4891 | composing | 5 |
| 4892 | complicated | 5 |
| 4893 | compact | 5 |
| 4894 | commandant | 5 |
| 4895 | comest | 5 |
| 4896 | comely | 5 |
| 4897 | collecting | 5 |
| 4898 | clothed | 5 |
| 4899 | clinging | 5 |
| 4900 | cleverness | 5 |
| 4901 | clay | 5 |
| 4902 | civilly | 5 |
| 4903 | cirongilio | 5 |
| 4904 | chronicler | 5 |
| 4905 | christ | 5 |
| 4906 | choosing | 5 |
| 4907 | childish | 5 |
| 4908 | chest | 5 |
| 4909 | chatterer | 5 |
| 4910 | chastisement | 5 |
| 4911 | cervantes | 5 |
| 4912 | ceasing | 5 |
| 4913 | cavalier | 5 |
| 4914 | cautiously | 5 |
| 4915 | cato | 5 |
| 4916 | carpio | 5 |
| 4917 | career | 5 |
| 4918 | capture | 5 |
| 4919 | calmly | 5 |
| 4920 | cages | 5 |
| 4921 | buckram | 5 |
| 4922 | bruises | 5 |
| 4923 | bronze | 5 |
| 4924 | britain | 5 |
| 4925 | bribes | 5 |
| 4926 | bribe | 5 |
| 4927 | breathless | 5 |
| 4928 | breathing | 5 |
| 4929 | breathe | 5 |
| 4930 | brays | 5 |
| 4931 | branch | 5 |
| 4932 | bracing | 5 |
| 4933 | box | 5 |
| 4934 | bowshot | 5 |
| 4935 | bounty | 5 |
| 4936 | bottomless | 5 |
| 4937 | bottle | 5 |
| 4938 | bordered | 5 |
| 4939 | boards | 5 |
| 4940 | boar | 5 |
| 4941 | blue | 5 |
| 4942 | blessings | 5 |
| 4943 | blanco | 5 |
| 4944 | blamed | 5 |
| 4945 | blade | 5 |
| 4946 | bitten | 5 |
| 4947 | binding | 5 |
| 4948 | bewailing | 5 |
| 4949 | bend | 5 |
| 4950 | believes | 5 |
| 4951 | barren | 5 |
| 4952 | barely | 5 |
| 4953 | bar | 5 |
| 4954 | bands | 5 |
| 4955 | bandaged | 5 |
| 4956 | backside | 5 |
| 4957 | awaited | 5 |
| 4958 | ave | 5 |
| 4959 | authorities | 5 |
| 4960 | attribute | 5 |
| 4961 | attired | 5 |
| 4962 | attempts | 5 |
| 4963 | attach | 5 |
| 4964 | assumed | 5 |
| 4965 | assiduity | 5 |
| 4966 | assert | 5 |
| 4967 | ashore | 5 |
| 4968 | arrow | 5 |
| 4969 | aristotle | 5 |
| 4970 | ardour | 5 |
| 4971 | arcade | 5 |
| 4972 | approved | 5 |
| 4973 | approaches | 5 |
| 4974 | appearances | 5 |
| 4975 | appeal | 5 |
| 4976 | apparel | 5 |
| 4977 | anticipated | 5 |
| 4978 | anew | 5 |
| 4979 | anchor | 5 |
| 4980 | ample | 5 |
| 4981 | amour | 5 |
| 4982 | ambrosia | 5 |
| 4983 | amadises | 5 |
| 4984 | altercation | 5 |
| 4985 | alas | 5 |
| 4986 | alarmed | 5 |
| 4987 | airs | 5 |
| 4988 | ailment | 5 |
| 4989 | ahead | 5 |
| 4990 | advising | 5 |
| 4991 | adversity | 5 |
| 4992 | adverse | 5 |
| 4993 | adored | 5 |
| 4994 | admit | 5 |
| 4995 | admired | 5 |
| 4996 | administered | 5 |
| 4997 | additional | 5 |
| 4998 | actually | 5 |
| 4999 | actor | 5 |
| 5000 | actions | 5 |
| 5001 | acquaintances | 5 |
| 5002 | acquaintance | 5 |
| 5003 | acknowledged | 5 |
| 5004 | accounts | 5 |
| 5005 | accomplishment | 5 |
| 5006 | accomplish | 5 |
| 5007 | accompaniment | 5 |
| 5008 | absolutely | 5 |
| 5009 | abbot | 5 |
| 5010 | abandon | 5 |
| 5011 | zamora | 4 |
| 5012 | wretches | 4 |
| 5013 | wooed | 4 |
| 5014 | witty | 4 |
| 5015 | witnessed | 4 |
| 5016 | willed | 4 |
| 5017 | whim | 4 |
| 5018 | whelps | 4 |
| 5019 | whate | 4 |
| 5020 | wenches | 4 |
| 5021 | welfare | 4 |
| 5022 | wedded | 4 |
| 5023 | weather | 4 |
| 5024 | wearing | 4 |
| 5025 | weapons | 4 |
| 5026 | weapon | 4 |
| 5027 | wastes | 4 |
| 5028 | wasted | 4 |
| 5029 | warrior | 4 |
| 5030 | wanderings | 4 |
| 5031 | vulture | 4 |
| 5032 | volumes | 4 |
| 5033 | visionary | 4 |
| 5034 | vigorously | 4 |
| 5035 | viedma | 4 |
| 5036 | venturing | 4 |
| 5037 | vehemence | 4 |
| 5038 | veal | 4 |
| 5039 | valencian | 4 |
| 5040 | utterance | 4 |
| 5041 | using | 4 |
| 5042 | uses | 4 |
| 5043 | urganda | 4 |
| 5044 | upshot | 4 |
| 5045 | uphold | 4 |
| 5046 | unto | 4 |
| 5047 | unsheathed | 4 |
| 5048 | unnecessary | 4 |
| 5049 | universe | 4 |
| 5050 | undoubtedly | 4 |
| 5051 | undone | 4 |
| 5052 | undoer | 4 |
| 5053 | undertook | 4 |
| 5054 | undertaking | 4 |
| 5055 | undergoing | 4 |
| 5056 | undeceive | 4 |
| 5057 | uncles | 4 |
| 5058 | unbound | 4 |
| 5059 | ugliness | 4 |
| 5060 | tus | 4 |
| 5061 | turrets | 4 |
| 5062 | turpin | 4 |
| 5063 | trusty | 4 |
| 5064 | troth | 4 |
| 5065 | troops | 4 |
| 5066 | triumphs | 4 |
| 5067 | triumphant | 4 |
| 5068 | tripes | 4 |
| 5069 | trip | 4 |
| 5070 | trimming | 4 |
| 5071 | trimmed | 4 |
| 5072 | trickery | 4 |
| 5073 | tribute | 4 |
| 5074 | trepidation | 4 |
| 5075 | tremble | 4 |
| 5076 | treason | 4 |
| 5077 | traversed | 4 |
| 5078 | translate | 4 |
| 5079 | transfer | 4 |
| 5080 | trample | 4 |
| 5081 | tramping | 4 |
| 5082 | traitors | 4 |
| 5083 | tracing | 4 |
| 5084 | trace | 4 |
| 5085 | towering | 4 |
| 5086 | towels | 4 |
| 5087 | tournament | 4 |
| 5088 | tortured | 4 |
| 5089 | tormented | 4 |
| 5090 | torment | 4 |
| 5091 | tordesillas | 4 |
| 5092 | tones | 4 |
| 5093 | today | 4 |
| 5094 | thrusts | 4 |
| 5095 | threshing | 4 |
| 5096 | thrace | 4 |
| 5097 | thorns | 4 |
| 5098 | thigh | 4 |
| 5099 | thickly | 4 |
| 5100 | thanking | 4 |
| 5101 | terrace | 4 |
| 5102 | tents | 4 |
| 5103 | tends | 4 |
| 5104 | temptation | 4 |
| 5105 | temerity | 4 |
| 5106 | tearing | 4 |
| 5107 | team | 4 |
| 5108 | taxes | 4 |
| 5109 | tavern | 4 |
| 5110 | talkative | 4 |
| 5111 | swimming | 4 |
| 5112 | swell | 4 |
| 5113 | swears | 4 |
| 5114 | swearing | 4 |
| 5115 | swarm | 4 |
| 5116 | swallow | 4 |
| 5117 | surveyed | 4 |
| 5118 | surrendered | 4 |
| 5119 | surpassing | 4 |
| 5120 | sunset | 4 |
| 5121 | sunk | 4 |
| 5122 | sunday | 4 |
| 5123 | successfully | 4 |
| 5124 | submitted | 4 |
| 5125 | submissive | 4 |
| 5126 | stumbled | 4 |
| 5127 | stumble | 4 |
| 5128 | stuffed | 4 |
| 5129 | struggled | 4 |
| 5130 | stronghold | 4 |
| 5131 | stripes | 4 |
| 5132 | strife | 4 |
| 5133 | stratagem | 4 |
| 5134 | stitches | 4 |
| 5135 | sting | 4 |
| 5136 | stern | 4 |
| 5137 | steal | 4 |
| 5138 | steady | 4 |
| 5139 | statue | 4 |
| 5140 | stately | 4 |
| 5141 | stark | 4 |
| 5142 | stake | 4 |
| 5143 | square | 4 |
| 5144 | spurring | 4 |
| 5145 | spurred | 4 |
| 5146 | spoiled | 4 |
| 5147 | splendour | 4 |
| 5148 | splendid | 4 |
| 5149 | spending | 4 |
| 5150 | spell | 4 |
| 5151 | speeches | 4 |
| 5152 | specially | 4 |
| 5153 | sparing | 4 |
| 5154 | solitary | 4 |
| 5155 | solemnity | 4 |
| 5156 | softer | 4 |
| 5157 | softened | 4 |
| 5158 | soap | 4 |
| 5159 | snatch | 4 |
| 5160 | smock | 4 |
| 5161 | smiling | 4 |
| 5162 | smashed | 4 |
| 5163 | sloth | 4 |
| 5164 | slightly | 4 |
| 5165 | slightest | 4 |
| 5166 | slaying | 4 |
| 5167 | slashes | 4 |
| 5168 | skiff | 4 |
| 5169 | sized | 4 |
| 5170 | sinners | 4 |
| 5171 | sink | 4 |
| 5172 | simpleton | 4 |
| 5173 | similar | 4 |
| 5174 | signor | 4 |
| 5175 | sighted | 4 |
| 5176 | sighed | 4 |
| 5177 | shy | 4 |
| 5178 | showers | 4 |
| 5179 | shorn | 4 |
| 5180 | shod | 4 |
| 5181 | ships | 4 |
| 5182 | shields | 4 |
| 5183 | sheer | 4 |
| 5184 | sheepskins | 4 |
| 5185 | shaving | 4 |
| 5186 | shan | 4 |
| 5187 | shameless | 4 |
| 5188 | shake | 4 |
| 5189 | serpents | 4 |
| 5190 | serge | 4 |
| 5191 | senseless | 4 |
| 5192 | seneschal | 4 |
| 5193 | seizes | 4 |
| 5194 | secretly | 4 |
| 5195 | secrecy | 4 |
| 5196 | secondly | 4 |
| 5197 | seasons | 4 |
| 5198 | seas | 4 |
| 5199 | seal | 4 |
| 5200 | scrutiny | 4 |
| 5201 | scriptures | 4 |
| 5202 | scrap | 4 |
| 5203 | scholar | 4 |
| 5204 | scented | 4 |
| 5205 | scarlet | 4 |
| 5206 | savour | 4 |
| 5207 | satisfying | 4 |
| 5208 | satire | 4 |
| 5209 | satan | 4 |
| 5210 | sarna | 4 |
| 5211 | sane | 4 |
| 5212 | san | 4 |
| 5213 | salvation | 4 |
| 5214 | sagacious | 4 |
| 5215 | sacripante | 4 |
| 5216 | sackcloth | 4 |
| 5217 | ruy | 4 |
| 5218 | ruthless | 4 |
| 5219 | rushing | 4 |
| 5220 | rowed | 4 |
| 5221 | rounds | 4 |
| 5222 | roughness | 4 |
| 5223 | roses | 4 |
| 5224 | rosemary | 4 |
| 5225 | roast | 4 |
| 5226 | ride | 4 |
| 5227 | richer | 4 |
| 5228 | rib | 4 |
| 5229 | rewarded | 4 |
| 5230 | reviving | 4 |
| 5231 | reverses | 4 |
| 5232 | revenue | 4 |
| 5233 | revealed | 4 |
| 5234 | resume | 4 |
| 5235 | restraint | 4 |
| 5236 | restoration | 4 |
| 5237 | resolutions | 4 |
| 5238 | resolute | 4 |
| 5239 | research | 4 |
| 5240 | repute | 4 |
| 5241 | reproved | 4 |
| 5242 | repent | 4 |
| 5243 | repel | 4 |
| 5244 | repaid | 4 |
| 5245 | rent | 4 |
| 5246 | rend | 4 |
| 5247 | remembered | 4 |
| 5248 | relished | 4 |
| 5249 | relatives | 4 |
| 5250 | regent | 4 |
| 5251 | refusing | 4 |
| 5252 | refer | 4 |
| 5253 | recreation | 4 |
| 5254 | recompensed | 4 |
| 5255 | recommend | 4 |
| 5256 | reckless | 4 |
| 5257 | rebeck | 4 |
| 5258 | reared | 4 |
| 5259 | rear | 4 |
| 5260 | reap | 4 |
| 5261 | realms | 4 |
| 5262 | readers | 4 |
| 5263 | ray | 4 |
| 5264 | rascal | 4 |
| 5265 | rapier | 4 |
| 5266 | rap | 4 |
| 5267 | rang | 4 |
| 5268 | rained | 4 |
| 5269 | quinones | 4 |
| 5270 | questioned | 4 |
| 5271 | qualified | 4 |
| 5272 | pyramid | 4 |
| 5273 | puzzling | 4 |
| 5274 | pull | 4 |
| 5275 | published | 4 |
| 5276 | prudish | 4 |
| 5277 | provision | 4 |
| 5278 | provinces | 4 |
| 5279 | protracted | 4 |
| 5280 | protest | 4 |
| 5281 | prose | 4 |
| 5282 | prop | 4 |
| 5283 | project | 4 |
| 5284 | professed | 4 |
| 5285 | procure | 4 |
| 5286 | process | 4 |
| 5287 | privilege | 4 |
| 5288 | priests | 4 |
| 5289 | pretend | 4 |
| 5290 | prepare | 4 |
| 5291 | preach | 4 |
| 5292 | practising | 4 |
| 5293 | powerless | 4 |
| 5294 | pounded | 4 |
| 5295 | pound | 4 |
| 5296 | pot | 4 |
| 5297 | positive | 4 |
| 5298 | porter | 4 |
| 5299 | poniard | 4 |
| 5300 | pomp | 4 |
| 5301 | polo | 4 |
| 5302 | polestar | 4 |
| 5303 | poles | 4 |
| 5304 | poison | 4 |
| 5305 | pointing | 4 |
| 5306 | plots | 4 |
| 5307 | plighted | 4 |
| 5308 | pleasures | 4 |
| 5309 | pleasantest | 4 |
| 5310 | player | 4 |
| 5311 | placard | 4 |
| 5312 | pious | 4 |
| 5313 | pimp | 4 |
| 5314 | pictures | 4 |
| 5315 | phoenix | 4 |
| 5316 | philosophy | 4 |
| 5317 | philosophers | 4 |
| 5318 | personal | 4 |
| 5319 | persist | 4 |
| 5320 | persecutes | 4 |
| 5321 | pernicious | 4 |
| 5322 | perish | 4 |
| 5323 | perils | 4 |
| 5324 | perfumed | 4 |
| 5325 | perfections | 4 |
| 5326 | penances | 4 |
| 5327 | penalties | 4 |
| 5328 | pegs | 4 |
| 5329 | pedigree | 4 |
| 5330 | pathetic | 4 |
| 5331 | patch | 4 |
| 5332 | pasture | 4 |
| 5333 | pasteboard | 4 |
| 5334 | paste | 4 |
| 5335 | partridges | 4 |
| 5336 | parting | 4 |
| 5337 | paredes | 4 |
| 5338 | parched | 4 |
| 5339 | parapilla | 4 |
| 5340 | par | 4 |
| 5341 | paltry | 4 |
| 5342 | palmerin | 4 |
| 5343 | overtures | 4 |
| 5344 | overcame | 4 |
| 5345 | orphan | 4 |
| 5346 | ornaments | 4 |
| 5347 | ornamented | 4 |
| 5348 | oriental | 4 |
| 5349 | oriana | 4 |
| 5350 | ordains | 4 |
| 5351 | oran | 4 |
| 5352 | opposing | 4 |
| 5353 | openly | 4 |
| 5354 | onward | 4 |
| 5355 | omit | 4 |
| 5356 | older | 4 |
| 5357 | ointment | 4 |
| 5358 | offices | 4 |
| 5359 | odious | 4 |
| 5360 | ocean | 4 |
| 5361 | occupy | 4 |
| 5362 | obstacles | 4 |
| 5363 | obscure | 4 |
| 5364 | obedience | 4 |
| 5365 | numberless | 4 |
| 5366 | noting | 4 |
| 5367 | noticing | 4 |
| 5368 | nosed | 4 |
| 5369 | niceties | 4 |
| 5370 | neptune | 4 |
| 5371 | nephew | 4 |
| 5372 | neighing | 4 |
| 5373 | needless | 4 |
| 5374 | necessities | 4 |
| 5375 | neatly | 4 |
| 5376 | nearest | 4 |
| 5377 | murmuring | 4 |
| 5378 | movements | 4 |
| 5379 | motion | 4 |
| 5380 | mortar | 4 |
| 5381 | moody | 4 |
| 5382 | monastery | 4 |
| 5383 | modes | 4 |
| 5384 | mixing | 4 |
| 5385 | miscreants | 4 |
| 5386 | misadventures | 4 |
| 5387 | miraculous | 4 |
| 5388 | minors | 4 |
| 5389 | ministers | 4 |
| 5390 | miguelturra | 4 |
| 5391 | miguel | 4 |
| 5392 | mien | 4 |
| 5393 | mettle | 4 |
| 5394 | methinks | 4 |
| 5395 | melt | 4 |
| 5396 | meek | 4 |
| 5397 | medicine | 4 |
| 5398 | matrimony | 4 |
| 5399 | materials | 4 |
| 5400 | mate | 4 |
| 5401 | mat | 4 |
| 5402 | mars | 4 |
| 5403 | marks | 4 |
| 5404 | majorca | 4 |
| 5405 | maintains | 4 |
| 5406 | mainland | 4 |
| 5407 | maguncia | 4 |
| 5408 | madder | 4 |
| 5409 | luxury | 4 |
| 5410 | lute | 4 |
| 5411 | lure | 4 |
| 5412 | lurcher | 4 |
| 5413 | ludicrous | 4 |
| 5414 | lowering | 4 |
| 5415 | loudly | 4 |
| 5416 | lope | 4 |
| 5417 | loft | 4 |
| 5418 | lodge | 4 |
| 5419 | lock | 4 |
| 5420 | loathing | 4 |
| 5421 | lo | 4 |
| 5422 | lizards | 4 |
| 5423 | listens | 4 |
| 5424 | liquid | 4 |
| 5425 | limpid | 4 |
| 5426 | liking | 4 |
| 5427 | lightning | 4 |
| 5428 | lightness | 4 |
| 5429 | lighten | 4 |
| 5430 | lifetime | 4 |
| 5431 | lied | 4 |
| 5432 | liar | 4 |
| 5433 | lenient | 4 |
| 5434 | leaping | 4 |
| 5435 | leant | 4 |
| 5436 | lays | 4 |
| 5437 | lawfully | 4 |
| 5438 | laughable | 4 |
| 5439 | lattice | 4 |
| 5440 | lasting | 4 |
| 5441 | larger | 4 |
| 5442 | laden | 4 |
| 5443 | labouring | 4 |
| 5444 | knocks | 4 |
| 5445 | kinsmen | 4 |
| 5446 | kicked | 4 |
| 5447 | jesus | 4 |
| 5448 | jerkin | 4 |
| 5449 | jealousies | 4 |
| 5450 | ivy | 4 |
| 5451 | issuing | 4 |
| 5452 | issued | 4 |
| 5453 | isn | 4 |
| 5454 | islanders | 4 |
| 5455 | invisible | 4 |
| 5456 | introduce | 4 |
| 5457 | intricate | 4 |
| 5458 | intrepidity | 4 |
| 5459 | intrepid | 4 |
| 5460 | interview | 4 |
| 5461 | interfere | 4 |
| 5462 | intend | 4 |
| 5463 | intelligible | 4 |
| 5464 | instinct | 4 |
| 5465 | instances | 4 |
| 5466 | instance | 4 |
| 5467 | insolent | 4 |
| 5468 | inserted | 4 |
| 5469 | insensible | 4 |
| 5470 | inquisitive | 4 |
| 5471 | ink | 4 |
| 5472 | injured | 4 |
| 5473 | injunction | 4 |
| 5474 | ingrate | 4 |
| 5475 | infinity | 4 |
| 5476 | industry | 4 |
| 5477 | indignant | 4 |
| 5478 | inconvenience | 4 |
| 5479 | inconsistent | 4 |
| 5480 | included | 4 |
| 5481 | inclemency | 4 |
| 5482 | inclemencies | 4 |
| 5483 | impulses | 4 |
| 5484 | impudence | 4 |
| 5485 | impertinence | 4 |
| 5486 | immortality | 4 |
| 5487 | imminent | 4 |
| 5488 | idlers | 4 |
| 5489 | husbands | 4 |
| 5490 | huntsmen | 4 |
| 5491 | hostelry | 4 |
| 5492 | hose | 4 |
| 5493 | hopeless | 4 |
| 5494 | hook | 4 |
| 5495 | honestly | 4 |
| 5496 | holiness | 4 |
| 5497 | holidays | 4 |
| 5498 | holes | 4 |
| 5499 | hoard | 4 |
| 5500 | hint | 4 |
| 5501 | hindrance | 4 |
| 5502 | hides | 4 |
| 5503 | hidalgos | 4 |
| 5504 | hero | 4 |
| 5505 | helps | 4 |
| 5506 | heifer | 4 |
| 5507 | heartless | 4 |
| 5508 | heap | 4 |
| 5509 | headed | 4 |
| 5510 | hatred | 4 |
| 5511 | harshly | 4 |
| 5512 | hardship | 4 |
| 5513 | hammer | 4 |
| 5514 | halting | 4 |
| 5515 | gutierrez | 4 |
| 5516 | gurapas | 4 |
| 5517 | guilt | 4 |
| 5518 | guessing | 4 |
| 5519 | grounds | 4 |
| 5520 | grim | 4 |
| 5521 | grievous | 4 |
| 5522 | grieves | 4 |
| 5523 | grievance | 4 |
| 5524 | greeks | 4 |
| 5525 | greedy | 4 |
| 5526 | gratified | 4 |
| 5527 | grapes | 4 |
| 5528 | grants | 4 |
| 5529 | granting | 4 |
| 5530 | grandfather | 4 |
| 5531 | grandchildren | 4 |
| 5532 | granada | 4 |
| 5533 | goal | 4 |
| 5534 | glove | 4 |
| 5535 | gloomy | 4 |
| 5536 | gloom | 4 |
| 5537 | george | 4 |
| 5538 | gentles | 4 |
| 5539 | gambling | 4 |
| 5540 | gait | 4 |
| 5541 | gaeta | 4 |
| 5542 | furiously | 4 |
| 5543 | fulfilling | 4 |
| 5544 | fulfilled | 4 |
| 5545 | fulfil | 4 |
| 5546 | friendly | 4 |
| 5547 | frequent | 4 |
| 5548 | frame | 4 |
| 5549 | fountains | 4 |
| 5550 | fortnight | 4 |
| 5551 | fortitude | 4 |
| 5552 | forming | 4 |
| 5553 | forcible | 4 |
| 5554 | folded | 4 |
| 5555 | flogging | 4 |
| 5556 | flocked | 4 |
| 5557 | flings | 4 |
| 5558 | flinging | 4 |
| 5559 | flights | 4 |
| 5560 | flee | 4 |
| 5561 | flea | 4 |
| 5562 | flax | 4 |
| 5563 | flame | 4 |
| 5564 | fisherman | 4 |
| 5565 | fired | 4 |
| 5566 | fills | 4 |
| 5567 | fife | 4 |
| 5568 | fictitious | 4 |
| 5569 | fickle | 4 |
| 5570 | fellowship | 4 |
| 5571 | feigned | 4 |
| 5572 | feels | 4 |
| 5573 | feature | 4 |
| 5574 | feather | 4 |
| 5575 | feast | 4 |
| 5576 | fearless | 4 |
| 5577 | fathoms | 4 |
| 5578 | fates | 4 |
| 5579 | familiar | 4 |
| 5580 | falsely | 4 |
| 5581 | faculties | 4 |
| 5582 | facts | 4 |
| 5583 | extinguished | 4 |
| 5584 | extends | 4 |
| 5585 | expenses | 4 |
| 5586 | exhausted | 4 |
| 5587 | executed | 4 |
| 5588 | exclamations | 4 |
| 5589 | excitement | 4 |
| 5590 | excessively | 4 |
| 5591 | exception | 4 |
| 5592 | excellences | 4 |
| 5593 | exalt | 4 |
| 5594 | exact | 4 |
| 5595 | ewe | 4 |
| 5596 | evils | 4 |
| 5597 | evidently | 4 |
| 5598 | evermore | 4 |
| 5599 | erected | 4 |
| 5600 | equally | 4 |
| 5601 | epitaph | 4 |
| 5602 | entrust | 4 |
| 5603 | entanglement | 4 |
| 5604 | enmity | 4 |
| 5605 | engaging | 4 |
| 5606 | engagement | 4 |
| 5607 | enforced | 4 |
| 5608 | endeavours | 4 |
| 5609 | empress | 4 |
| 5610 | embroidered | 4 |
| 5611 | elysian | 4 |
| 5612 | elisabad | 4 |
| 5613 | elegantly | 4 |
| 5614 | elder | 4 |
| 5615 | egad | 4 |
| 5616 | earthly | 4 |
| 5617 | eagerly | 4 |
| 5618 | dues | 4 |
| 5619 | drunken | 4 |
| 5620 | drunkard | 4 |
| 5621 | drubbings | 4 |
| 5622 | drops | 4 |
| 5623 | dropping | 4 |
| 5624 | drooping | 4 |
| 5625 | dresses | 4 |
| 5626 | dreary | 4 |
| 5627 | draped | 4 |
| 5628 | dragons | 4 |
| 5629 | drag | 4 |
| 5630 | downwards | 4 |
| 5631 | doughty | 4 |
| 5632 | dons | 4 |
| 5633 | divinations | 4 |
| 5634 | district | 4 |
| 5635 | distinctive | 4 |
| 5636 | dispose | 4 |
| 5637 | dishes | 4 |
| 5638 | discredit | 4 |
| 5639 | disconsolate | 4 |
| 5640 | disastrous | 4 |
| 5641 | disagreeable | 4 |
| 5642 | disabused | 4 |
| 5643 | dint | 4 |
| 5644 | dimmed | 4 |
| 5645 | dictated | 4 |
| 5646 | dice | 4 |
| 5647 | devising | 4 |
| 5648 | devised | 4 |
| 5649 | devise | 4 |
| 5650 | detriment | 4 |
| 5651 | destination | 4 |
| 5652 | despite | 4 |
| 5653 | despise | 4 |
| 5654 | despairing | 4 |
| 5655 | description | 4 |
| 5656 | descent | 4 |
| 5657 | depth | 4 |
| 5658 | depriving | 4 |
| 5659 | depicted | 4 |
| 5660 | depended | 4 |
| 5661 | degrees | 4 |
| 5662 | defy | 4 |
| 5663 | deficiency | 4 |
| 5664 | defects | 4 |
| 5665 | deer | 4 |
| 5666 | dedicated | 4 |
| 5667 | declares | 4 |
| 5668 | decked | 4 |
| 5669 | deaths | 4 |
| 5670 | dealing | 4 |
| 5671 | dealer | 4 |
| 5672 | date | 4 |
| 5673 | dangerous | 4 |
| 5674 | cutlass | 4 |
| 5675 | cushions | 4 |
| 5676 | curtsey | 4 |
| 5677 | cup | 4 |
| 5678 | cudgel | 4 |
| 5679 | cuadrillero | 4 |
| 5680 | crosses | 4 |
| 5681 | crooked | 4 |
| 5682 | crimson | 4 |
| 5683 | credence | 4 |
| 5684 | craving | 4 |
| 5685 | crags | 4 |
| 5686 | cracked | 4 |
| 5687 | coward | 4 |
| 5688 | cow | 4 |
| 5689 | courts | 4 |
| 5690 | council | 4 |
| 5691 | cortes | 4 |
| 5692 | correctly | 4 |
| 5693 | correcting | 4 |
| 5694 | cords | 4 |
| 5695 | cooled | 4 |
| 5696 | continuing | 4 |
| 5697 | contest | 4 |
| 5698 | contempt | 4 |
| 5699 | contemplating | 4 |
| 5700 | construction | 4 |
| 5701 | consort | 4 |
| 5702 | consign | 4 |
| 5703 | confound | 4 |
| 5704 | confinement | 4 |
| 5705 | confined | 4 |
| 5706 | confided | 4 |
| 5707 | confessing | 4 |
| 5708 | condensed | 4 |
| 5709 | condemn | 4 |
| 5710 | concord | 4 |
| 5711 | concealing | 4 |
| 5712 | comprehension | 4 |
| 5713 | complication | 4 |
| 5714 | compliance | 4 |
| 5715 | complains | 4 |
| 5716 | committing | 4 |
| 5717 | commanding | 4 |
| 5718 | collected | 4 |
| 5719 | collar | 4 |
| 5720 | cobbler | 4 |
| 5721 | clue | 4 |
| 5722 | closet | 4 |
| 5723 | cloaks | 4 |
| 5724 | cleverest | 4 |
| 5725 | cleaving | 4 |
| 5726 | cleanly | 4 |
| 5727 | cleanliness | 4 |
| 5728 | claims | 4 |
| 5729 | civil | 4 |
| 5730 | chinks | 4 |
| 5731 | chiefly | 4 |
| 5732 | cheat | 4 |
| 5733 | cheap | 4 |
| 5734 | chastity | 4 |
| 5735 | charges | 4 |
| 5736 | chapel | 4 |
| 5737 | chances | 4 |
| 5738 | champion | 4 |
| 5739 | chairs | 4 |
| 5740 | cell | 4 |
| 5741 | cava | 4 |
| 5742 | cassock | 4 |
| 5743 | cask | 4 |
| 5744 | cascajo | 4 |
| 5745 | carved | 4 |
| 5746 | carts | 4 |
| 5747 | carpet | 4 |
| 5748 | cared | 4 |
| 5749 | candles | 4 |
| 5750 | calves | 4 |
| 5751 | calamity | 4 |
| 5752 | caged | 4 |
| 5753 | cacus | 4 |
| 5754 | caballero | 4 |
| 5755 | buttons | 4 |
| 5756 | bushes | 4 |
| 5757 | bushels | 4 |
| 5758 | bursting | 4 |
| 5759 | burnished | 4 |
| 5760 | brightness | 4 |
| 5761 | brighter | 4 |
| 5762 | bridal | 4 |
| 5763 | brand | 4 |
| 5764 | bowing | 4 |
| 5765 | bounded | 4 |
| 5766 | boughs | 4 |
| 5767 | boots | 4 |
| 5768 | bolt | 4 |
| 5769 | boldest | 4 |
| 5770 | boiling | 4 |
| 5771 | boiled | 4 |
| 5772 | bloody | 4 |
| 5773 | bliss | 4 |
| 5774 | blasphemy | 4 |
| 5775 | blasphemies | 4 |
| 5776 | bitterness | 4 |
| 5777 | bits | 4 |
| 5778 | bireno | 4 |
| 5779 | binds | 4 |
| 5780 | bewilderment | 4 |
| 5781 | betake | 4 |
| 5782 | bestowing | 4 |
| 5783 | belch | 4 |
| 5784 | befitting | 4 |
| 5785 | beef | 4 |
| 5786 | bearer | 4 |
| 5787 | basket | 4 |
| 5788 | barefoot | 4 |
| 5789 | barbarous | 4 |
| 5790 | baptism | 4 |
| 5791 | banquet | 4 |
| 5792 | bank | 4 |
| 5793 | banishment | 4 |
| 5794 | bandage | 4 |
| 5795 | ballads | 4 |
| 5796 | balconies | 4 |
| 5797 | babieca | 4 |
| 5798 | azure | 4 |
| 5799 | awaits | 4 |
| 5800 | availing | 4 |
| 5801 | austere | 4 |
| 5802 | aurora | 4 |
| 5803 | attracted | 4 |
| 5804 | attitude | 4 |
| 5805 | attaining | 4 |
| 5806 | attacks | 4 |
| 5807 | atom | 4 |
| 5808 | assails | 4 |
| 5809 | arrest | 4 |
| 5810 | array | 4 |
| 5811 | arrangements | 4 |
| 5812 | argue | 4 |
| 5813 | archives | 4 |
| 5814 | arch | 4 |
| 5815 | arcadia | 4 |
| 5816 | aragonese | 4 |
| 5817 | arabs | 4 |
| 5818 | approve | 4 |
| 5819 | apprehended | 4 |
| 5820 | applied | 4 |
| 5821 | applauded | 4 |
| 5822 | appearing | 4 |
| 5823 | apiece | 4 |
| 5824 | antagonist | 4 |
| 5825 | ant | 4 |
| 5826 | annoyance | 4 |
| 5827 | announced | 4 |
| 5828 | amorous | 4 |
| 5829 | altering | 4 |
| 5830 | altered | 4 |
| 5831 | alter | 4 |
| 5832 | almodovar | 4 |
| 5833 | almighty | 4 |
| 5834 | allows | 4 |
| 5835 | alifanfaron | 4 |
| 5836 | alguacils | 4 |
| 5837 | albogues | 4 |
| 5838 | aims | 4 |
| 5839 | ailed | 4 |
| 5840 | aided | 4 |
| 5841 | agile | 4 |
| 5842 | affect | 4 |
| 5843 | adroitly | 4 |
| 5844 | adders | 4 |
| 5845 | adam | 4 |
| 5846 | activity | 4 |
| 5847 | acknowledgment | 4 |
| 5848 | achievement | 4 |
| 5849 | ace | 4 |
| 5850 | accommodation | 4 |
| 5851 | access | 4 |
| 5852 | absurdity | 4 |
| 5853 | abindarraez | 4 |
| 5854 | ability | 4 |
| 5855 | zebra | 3 |
| 5856 | xxxviii | 3 |
| 5857 | xxxvii | 3 |
| 5858 | xxxvi | 3 |
| 5859 | xxxv | 3 |
| 5860 | xxxix | 3 |
| 5861 | xxxiv | 3 |
| 5862 | xxxiii | 3 |
| 5863 | xxxii | 3 |
| 5864 | xxxi | 3 |
| 5865 | xxx | 3 |
| 5866 | xxviii | 3 |
| 5867 | xxvii | 3 |
| 5868 | xxvi | 3 |
| 5869 | xxv | 3 |
| 5870 | xxix | 3 |
| 5871 | xxiv | 3 |
| 5872 | xxiii | 3 |
| 5873 | xxii | 3 |
| 5874 | xxi | 3 |
| 5875 | xx | 3 |
| 5876 | xviii | 3 |
| 5877 | xvii | 3 |
| 5878 | xvi | 3 |
| 5879 | xv | 3 |
| 5880 | xlviii | 3 |
| 5881 | xlvii | 3 |
| 5882 | xlvi | 3 |
| 5883 | xlv | 3 |
| 5884 | xlix | 3 |
| 5885 | xliv | 3 |
| 5886 | xliii | 3 |
| 5887 | xlii | 3 |
| 5888 | xli | 3 |
| 5889 | xl | 3 |
| 5890 | xix | 3 |
| 5891 | xiv | 3 |
| 5892 | xiii | 3 |
| 5893 | xii | 3 |
| 5894 | xi | 3 |
| 5895 | wrung | 3 |
| 5896 | wrought | 3 |
| 5897 | wronging | 3 |
| 5898 | writhing | 3 |
| 5899 | writers | 3 |
| 5900 | wrathful | 3 |
| 5901 | wrangle | 3 |
| 5902 | wounding | 3 |
| 5903 | wondrous | 3 |
| 5904 | wondered | 3 |
| 5905 | womb | 3 |
| 5906 | wizards | 3 |
| 5907 | withdrawing | 3 |
| 5908 | witch | 3 |
| 5909 | winnings | 3 |
| 5910 | wilderness | 3 |
| 5911 | wickedness | 3 |
| 5912 | whosoever | 3 |
| 5913 | whomsoever | 3 |
| 5914 | whiter | 3 |
| 5915 | whiteness | 3 |
| 5916 | whit | 3 |
| 5917 | whispered | 3 |
| 5918 | whimsical | 3 |
| 5919 | whereupon | 3 |
| 5920 | weighed | 3 |
| 5921 | wearisome | 3 |
| 5922 | watchtower | 3 |
| 5923 | watches | 3 |
| 5924 | wasting | 3 |
| 5925 | warmly | 3 |
| 5926 | walked | 3 |
| 5927 | waking | 3 |
| 5928 | vows | 3 |
| 5929 | vowed | 3 |
| 5930 | votes | 3 |
| 5931 | vomiting | 3 |
| 5932 | voluntarily | 3 |
| 5933 | virgins | 3 |
| 5934 | viper | 3 |
| 5935 | vineyard | 3 |
| 5936 | viii | 3 |
| 5937 | vii | 3 |
| 5938 | vie | 3 |
| 5939 | victuals | 3 |
| 5940 | vices | 3 |
| 5941 | vicar | 3 |
| 5942 | vi | 3 |
| 5943 | vex | 3 |
| 5944 | vessels | 3 |
| 5945 | verified | 3 |
| 5946 | vellido | 3 |
| 5947 | velez | 3 |
| 5948 | varied | 3 |
| 5949 | vargas | 3 |
| 5950 | vanity | 3 |
| 5951 | values | 3 |
| 5952 | valid | 3 |
| 5953 | utterly | 3 |
| 5954 | urges | 3 |
| 5955 | upstairs | 3 |
| 5956 | upsetting | 3 |
| 5957 | uproar | 3 |
| 5958 | upper | 3 |
| 5959 | upbraiding | 3 |
| 5960 | unwelcome | 3 |
| 5961 | untold | 3 |
| 5962 | untimely | 3 |
| 5963 | unsettle | 3 |
| 5964 | unseasonably | 3 |
| 5965 | unseasonable | 3 |
| 5966 | unreasonable | 3 |
| 5967 | unquestionably | 3 |
| 5968 | unprotected | 3 |
| 5969 | unnatural | 3 |
| 5970 | unlacing | 3 |
| 5971 | university | 3 |
| 5972 | unhurt | 3 |
| 5973 | unholy | 3 |
| 5974 | unfinished | 3 |
| 5975 | undressed | 3 |
| 5976 | undreamt | 3 |
| 5977 | understands | 3 |
| 5978 | underground | 3 |
| 5979 | undergone | 3 |
| 5980 | uncommon | 3 |
| 5981 | uncalled | 3 |
| 5982 | unattended | 3 |
| 5983 | ulysses | 3 |
| 5984 | type | 3 |
| 5985 | tying | 3 |
| 5986 | twelvemonth | 3 |
| 5987 | twas | 3 |
| 5988 | twain | 3 |
| 5989 | tunis | 3 |
| 5990 | tumult | 3 |
| 5991 | tumbler | 3 |
| 5992 | trustworthy | 3 |
| 5993 | truer | 3 |
| 5994 | truce | 3 |
| 5995 | trout | 3 |
| 5996 | troughs | 3 |
| 5997 | tries | 3 |
| 5998 | tresses | 3 |
| 5999 | trebizond | 3 |
| 6000 | treads | 3 |
| 6001 | treading | 3 |
| 6002 | tread | 3 |
| 6003 | traverse | 3 |
| 6004 | trapobana | 3 |
| 6005 | transgression | 3 |
| 6006 | transgress | 3 |
| 6007 | transcends | 3 |
| 6008 | tranquillity | 3 |
| 6009 | trampled | 3 |
| 6010 | tramp | 3 |
| 6011 | trained | 3 |
| 6012 | tragic | 3 |
| 6013 | traders | 3 |
| 6014 | trader | 3 |
| 6015 | townsman | 3 |
| 6016 | tow | 3 |
| 6017 | totally | 3 |
| 6018 | tortures | 3 |
| 6019 | torrellas | 3 |
| 6020 | toothsome | 3 |
| 6021 | toe | 3 |
| 6022 | toads | 3 |
| 6023 | tis | 3 |
| 6024 | timid | 3 |
| 6025 | tiger | 3 |
| 6026 | thwacks | 3 |
| 6027 | thunderbolt | 3 |
| 6028 | threshold | 3 |
| 6029 | threatens | 3 |
| 6030 | threaten | 3 |
| 6031 | thrashing | 3 |
| 6032 | thisbe | 3 |
| 6033 | thereupon | 3 |
| 6034 | thenceforward | 3 |
| 6035 | thankful | 3 |
| 6036 | tetuan | 3 |
| 6037 | terrific | 3 |
| 6038 | terra | 3 |
| 6039 | tending | 3 |
| 6040 | tenderly | 3 |
| 6041 | tempt | 3 |
| 6042 | tempered | 3 |
| 6043 | tearful | 3 |
| 6044 | tattling | 3 |
| 6045 | target | 3 |
| 6046 | taper | 3 |
| 6047 | tagarin | 3 |
| 6048 | tackle | 3 |
| 6049 | swooned | 3 |
| 6050 | swiftly | 3 |
| 6051 | swerve | 3 |
| 6052 | swarthy | 3 |
| 6053 | suspecting | 3 |
| 6054 | surcoat | 3 |
| 6055 | sups | 3 |
| 6056 | suppressed | 3 |
| 6057 | suns | 3 |
| 6058 | sunrise | 3 |
| 6059 | suitors | 3 |
| 6060 | suitable | 3 |
| 6061 | sugar | 3 |
| 6062 | sufficed | 3 |
| 6063 | sufferer | 3 |
| 6064 | succouring | 3 |
| 6065 | succeeds | 3 |
| 6066 | succeeding | 3 |
| 6067 | submitting | 3 |
| 6068 | subdue | 3 |
| 6069 | stupidities | 3 |
| 6070 | stupendous | 3 |
| 6071 | stupefied | 3 |
| 6072 | strumpet | 3 |
| 6073 | struggles | 3 |
| 6074 | strives | 3 |
| 6075 | strips | 3 |
| 6076 | striking | 3 |
| 6077 | strictly | 3 |
| 6078 | stretching | 3 |
| 6079 | stratagems | 3 |
| 6080 | strangled | 3 |
| 6081 | straining | 3 |
| 6082 | stockfish | 3 |
| 6083 | steward | 3 |
| 6084 | stepped | 3 |
| 6085 | stepfather | 3 |
| 6086 | stem | 3 |
| 6087 | stealing | 3 |
| 6088 | staying | 3 |
| 6089 | staves | 3 |
| 6090 | stations | 3 |
| 6091 | stationed | 3 |
| 6092 | start | 3 |
| 6093 | starred | 3 |
| 6094 | stared | 3 |
| 6095 | stare | 3 |
| 6096 | stamp | 3 |
| 6097 | stains | 3 |
| 6098 | stained | 3 |
| 6099 | stages | 3 |
| 6100 | stab | 3 |
| 6101 | squadrons | 3 |
| 6102 | springing | 3 |
| 6103 | spotty | 3 |
| 6104 | spirited | 3 |
| 6105 | speedy | 3 |
| 6106 | spectre | 3 |
| 6107 | species | 3 |
| 6108 | spear | 3 |
| 6109 | sparrow | 3 |
| 6110 | sparingly | 3 |
| 6111 | spaniard | 3 |
| 6112 | sounds | 3 |
| 6113 | soundly | 3 |
| 6114 | somehow | 3 |
| 6115 | softness | 3 |
| 6116 | softest | 3 |
| 6117 | sobrino | 3 |
| 6118 | snub | 3 |
| 6119 | snatching | 3 |
| 6120 | snatched | 3 |
| 6121 | smocks | 3 |
| 6122 | smiled | 3 |
| 6123 | smells | 3 |
| 6124 | smelling | 3 |
| 6125 | smallest | 3 |
| 6126 | smacked | 3 |
| 6127 | sly | 3 |
| 6128 | slumbers | 3 |
| 6129 | slipping | 3 |
| 6130 | slipped | 3 |
| 6131 | sleepest | 3 |
| 6132 | slays | 3 |
| 6133 | slaughter | 3 |
| 6134 | slashed | 3 |
| 6135 | slash | 3 |
| 6136 | skylight | 3 |
| 6137 | skipping | 3 |
| 6138 | skinned | 3 |
| 6139 | skilful | 3 |
| 6140 | simplicities | 3 |
| 6141 | simpletons | 3 |
| 6142 | signum | 3 |
| 6143 | significant | 3 |
| 6144 | sieve | 3 |
| 6145 | sicily | 3 |
| 6146 | si | 3 |
| 6147 | shutting | 3 |
| 6148 | showy | 3 |
| 6149 | shots | 3 |
| 6150 | shortsighted | 3 |
| 6151 | shorter | 3 |
| 6152 | shorten | 3 |
| 6153 | shortcomings | 3 |
| 6154 | shivered | 3 |
| 6155 | shershel | 3 |
| 6156 | shedding | 3 |
| 6157 | sheath | 3 |
| 6158 | shear | 3 |
| 6159 | shaver | 3 |
| 6160 | shattered | 3 |
| 6161 | sharpness | 3 |
| 6162 | sharpers | 3 |
| 6163 | shared | 3 |
| 6164 | sham | 3 |
| 6165 | seventeen | 3 |
| 6166 | separately | 3 |
| 6167 | sentinels | 3 |
| 6168 | sentinel | 3 |
| 6169 | sentenced | 3 |
| 6170 | selling | 3 |
| 6171 | select | 3 |
| 6172 | seguidillas | 3 |
| 6173 | seemly | 3 |
| 6174 | secluded | 3 |
| 6175 | seats | 3 |
| 6176 | seasonably | 3 |
| 6177 | sealed | 3 |
| 6178 | scurvy | 3 |
| 6179 | scruples | 3 |
| 6180 | scrubbing | 3 |
| 6181 | scripture | 3 |
| 6182 | screened | 3 |
| 6183 | scouring | 3 |
| 6184 | scolding | 3 |
| 6185 | schools | 3 |
| 6186 | scattering | 3 |
| 6187 | scarcity | 3 |
| 6188 | scarce | 3 |
| 6189 | scaly | 3 |
| 6190 | savoury | 3 |
| 6191 | satisfactorily | 3 |
| 6192 | satires | 3 |
| 6193 | sarra | 3 |
| 6194 | sansuena | 3 |
| 6195 | sands | 3 |
| 6196 | sallowness | 3 |
| 6197 | sallies | 3 |
| 6198 | salary | 3 |
| 6199 | salamancan | 3 |
| 6200 | salaams | 3 |
| 6201 | sailing | 3 |
| 6202 | saidst | 3 |
| 6203 | sagacity | 3 |
| 6204 | sacrifice | 3 |
| 6205 | rust | 3 |
| 6206 | ruining | 3 |
| 6207 | rudeness | 3 |
| 6208 | ruddy | 3 |
| 6209 | routed | 3 |
| 6210 | route | 3 |
| 6211 | root | 3 |
| 6212 | rolling | 3 |
| 6213 | roca | 3 |
| 6214 | robust | 3 |
| 6215 | robes | 3 |
| 6216 | robbery | 3 |
| 6217 | roasted | 3 |
| 6218 | rip | 3 |
| 6219 | ringer | 3 |
| 6220 | rigour | 3 |
| 6221 | righted | 3 |
| 6222 | ridicule | 3 |
| 6223 | rider | 3 |
| 6224 | ricota | 3 |
| 6225 | rhyme | 3 |
| 6226 | rhetoric | 3 |
| 6227 | reverse | 3 |
| 6228 | retreating | 3 |
| 6229 | retentio | 3 |
| 6230 | resuming | 3 |
| 6231 | restrained | 3 |
| 6232 | resignation | 3 |
| 6233 | resentment | 3 |
| 6234 | resembled | 3 |
| 6235 | reproof | 3 |
| 6236 | repeats | 3 |
| 6237 | rents | 3 |
| 6238 | renounce | 3 |
| 6239 | renew | 3 |
| 6240 | relying | 3 |
| 6241 | religious | 3 |
| 6242 | relic | 3 |
| 6243 | reigned | 3 |
| 6244 | reign | 3 |
| 6245 | regulated | 3 |
| 6246 | refuses | 3 |
| 6247 | refresh | 3 |
| 6248 | refrain | 3 |
| 6249 | refined | 3 |
| 6250 | referred | 3 |
| 6251 | reference | 3 |
| 6252 | reduce | 3 |
| 6253 | redound | 3 |
| 6254 | rectify | 3 |
| 6255 | recounted | 3 |
| 6256 | recount | 3 |
| 6257 | recording | 3 |
| 6258 | recompense | 3 |
| 6259 | recollecting | 3 |
| 6260 | recognition | 3 |
| 6261 | recite | 3 |
| 6262 | recesses | 3 |
| 6263 | recess | 3 |
| 6264 | reaping | 3 |
| 6265 | realities | 3 |
| 6266 | realised | 3 |
| 6267 | razor | 3 |
| 6268 | raven | 3 |
| 6269 | rationally | 3 |
| 6270 | rat | 3 |
| 6271 | rascalities | 3 |
| 6272 | rapid | 3 |
| 6273 | raiment | 3 |
| 6274 | quotations | 3 |
| 6275 | quiver | 3 |
| 6276 | quits | 3 |
| 6277 | quill | 3 |
| 6278 | quicksilver | 3 |
| 6279 | querist | 3 |
| 6280 | quench | 3 |
| 6281 | qualifications | 3 |
| 6282 | quailed | 3 |
| 6283 | pyramus | 3 |
| 6284 | pushing | 3 |
| 6285 | purge | 3 |
| 6286 | purer | 3 |
| 6287 | pummelling | 3 |
| 6288 | puffed | 3 |
| 6289 | puerto | 3 |
| 6290 | publish | 3 |
| 6291 | ptolemy | 3 |
| 6292 | proving | 3 |
| 6293 | protected | 3 |
| 6294 | propose | 3 |
| 6295 | proposal | 3 |
| 6296 | proportioned | 3 |
| 6297 | prophecy | 3 |
| 6298 | propensity | 3 |
| 6299 | prompt | 3 |
| 6300 | promotion | 3 |
| 6301 | promoted | 3 |
| 6302 | progress | 3 |
| 6303 | progeny | 3 |
| 6304 | profusion | 3 |
| 6305 | profane | 3 |
| 6306 | prodigal | 3 |
| 6307 | prodding | 3 |
| 6308 | privately | 3 |
| 6309 | prints | 3 |
| 6310 | previous | 3 |
| 6311 | prevents | 3 |
| 6312 | prevailed | 3 |
| 6313 | prevail | 3 |
| 6314 | presenting | 3 |
| 6315 | preparing | 3 |
| 6316 | preparations | 3 |
| 6317 | preference | 3 |
| 6318 | prefer | 3 |
| 6319 | precision | 3 |
| 6320 | precise | 3 |
| 6321 | precepts | 3 |
| 6322 | precaution | 3 |
| 6323 | preacher | 3 |
| 6324 | pranks | 3 |
| 6325 | praising | 3 |
| 6326 | pounds | 3 |
| 6327 | pouch | 3 |
| 6328 | posts | 3 |
| 6329 | possessor | 3 |
| 6330 | poop | 3 |
| 6331 | pomegranate | 3 |
| 6332 | polydore | 3 |
| 6333 | poll | 3 |
| 6334 | poetical | 3 |
| 6335 | poesy | 3 |
| 6336 | plying | 3 |
| 6337 | plundered | 3 |
| 6338 | plump | 3 |
| 6339 | plumes | 3 |
| 6340 | plumed | 3 |
| 6341 | plucking | 3 |
| 6342 | plough | 3 |
| 6343 | plebeian | 3 |
| 6344 | pleasantry | 3 |
| 6345 | pleasanter | 3 |
| 6346 | plead | 3 |
| 6347 | platonic | 3 |
| 6348 | plato | 3 |
| 6349 | planet | 3 |
| 6350 | plaint | 3 |
| 6351 | pitched | 3 |
| 6352 | pistols | 3 |
| 6353 | pique | 3 |
| 6354 | pipes | 3 |
| 6355 | pins | 3 |
| 6356 | pillow | 3 |
| 6357 | pillars | 3 |
| 6358 | pillar | 3 |
| 6359 | pigeons | 3 |
| 6360 | pig | 3 |
| 6361 | philosopher | 3 |
| 6362 | pervert | 3 |
| 6363 | persistence | 3 |
| 6364 | persiles | 3 |
| 6365 | perpetually | 3 |
| 6366 | perlerines | 3 |
| 6367 | performance | 3 |
| 6368 | perfidious | 3 |
| 6369 | perceives | 3 |
| 6370 | penetrates | 3 |
| 6371 | pellets | 3 |
| 6372 | peculiar | 3 |
| 6373 | pattern | 3 |
| 6374 | patiently | 3 |
| 6375 | paternosters | 3 |
| 6376 | pate | 3 |
| 6377 | pastor | 3 |
| 6378 | passages | 3 |
| 6379 | partridge | 3 |
| 6380 | particle | 3 |
| 6381 | parti | 3 |
| 6382 | parted | 3 |
| 6383 | partake | 3 |
| 6384 | pardoned | 3 |
| 6385 | paramount | 3 |
| 6386 | pandafilando | 3 |
| 6387 | pan | 3 |
| 6388 | pairs | 3 |
| 6389 | packet | 3 |
| 6390 | owners | 3 |
| 6391 | overthrew | 3 |
| 6392 | outrages | 3 |
| 6393 | ounce | 3 |
| 6394 | ottoman | 3 |
| 6395 | ostrich | 3 |
| 6396 | orators | 3 |
| 6397 | opens | 3 |
| 6398 | onslaught | 3 |
| 6399 | onset | 3 |
| 6400 | ollas | 3 |
| 6401 | olive | 3 |
| 6402 | offerings | 3 |
| 6403 | offend | 3 |
| 6404 | odour | 3 |
| 6405 | occurring | 3 |
| 6406 | obvious | 3 |
| 6407 | obscured | 3 |
| 6408 | objurgations | 3 |
| 6409 | objected | 3 |
| 6410 | obeying | 3 |
| 6411 | obdurate | 3 |
| 6412 | nut | 3 |
| 6413 | nun | 3 |
| 6414 | nourished | 3 |
| 6415 | noonday | 3 |
| 6416 | noiseless | 3 |
| 6417 | nobles | 3 |
| 6418 | nimbly | 3 |
| 6419 | nieces | 3 |
| 6420 | neglected | 3 |
| 6421 | narrative | 3 |
| 6422 | muttered | 3 |
| 6423 | mute | 3 |
| 6424 | mustard | 3 |
| 6425 | musical | 3 |
| 6426 | murmur | 3 |
| 6427 | mummy | 3 |
| 6428 | mulberry | 3 |
| 6429 | mud | 3 |
| 6430 | mournful | 3 |
| 6431 | mould | 3 |
| 6432 | mottoes | 3 |
| 6433 | motto | 3 |
| 6434 | mothers | 3 |
| 6435 | mosen | 3 |
| 6436 | mortals | 3 |
| 6437 | morgante | 3 |
| 6438 | montemayor | 3 |
| 6439 | monday | 3 |
| 6440 | moments | 3 |
| 6441 | moist | 3 |
| 6442 | moderation | 3 |
| 6443 | model | 3 |
| 6444 | mock | 3 |
| 6445 | moan | 3 |
| 6446 | mire | 3 |
| 6447 | minutely | 3 |
| 6448 | mingo | 3 |
| 6449 | mingling | 3 |
| 6450 | minding | 3 |
| 6451 | million | 3 |
| 6452 | mightiness | 3 |
| 6453 | midway | 3 |
| 6454 | midday | 3 |
| 6455 | metal | 3 |
| 6456 | merited | 3 |
| 6457 | merciful | 3 |
| 6458 | mentioning | 3 |
| 6459 | memorandum | 3 |
| 6460 | member | 3 |
| 6461 | medoro | 3 |
| 6462 | medley | 3 |
| 6463 | medium | 3 |
| 6464 | meditating | 3 |
| 6465 | meddling | 3 |
| 6466 | measuring | 3 |
| 6467 | meanest | 3 |
| 6468 | maxim | 3 |
| 6469 | material | 3 |
| 6470 | mast | 3 |
| 6471 | masses | 3 |
| 6472 | mary | 3 |
| 6473 | marvels | 3 |
| 6474 | marked | 3 |
| 6475 | maravedi | 3 |
| 6476 | mansion | 3 |
| 6477 | mandate | 3 |
| 6478 | manacles | 3 |
| 6479 | malign | 3 |
| 6480 | malevolent | 3 |
| 6481 | maids | 3 |
| 6482 | mahomet | 3 |
| 6483 | magnanimous | 3 |
| 6484 | lye | 3 |
| 6485 | lusty | 3 |
| 6486 | lukewarm | 3 |
| 6487 | lucid | 3 |
| 6488 | lovingly | 3 |
| 6489 | lore | 3 |
| 6490 | lordships | 3 |
| 6491 | lopez | 3 |
| 6492 | loftiness | 3 |
| 6493 | loftiest | 3 |
| 6494 | loftier | 3 |
| 6495 | llana | 3 |
| 6496 | lizard | 3 |
| 6497 | limited | 3 |
| 6498 | likeness | 3 |
| 6499 | lii | 3 |
| 6500 | liest | 3 |
| 6501 | liberally | 3 |
| 6502 | li | 3 |
| 6503 | lesser | 3 |
| 6504 | lemos | 3 |
| 6505 | legion | 3 |
| 6506 | leanness | 3 |
| 6507 | le | 3 |
| 6508 | laurel | 3 |
| 6509 | lasses | 3 |
| 6510 | lapice | 3 |
| 6511 | lap | 3 |
| 6512 | lanterns | 3 |
| 6513 | lantern | 3 |
| 6514 | landing | 3 |
| 6515 | laments | 3 |
| 6516 | lads | 3 |
| 6517 | laced | 3 |
| 6518 | labourers | 3 |
| 6519 | l | 3 |
| 6520 | knots | 3 |
| 6521 | knightly | 3 |
| 6522 | kills | 3 |
| 6523 | kid | 3 |
| 6524 | kick | 3 |
| 6525 | justify | 3 |
| 6526 | judicious | 3 |
| 6527 | judas | 3 |
| 6528 | jovial | 3 |
| 6529 | journeys | 3 |
| 6530 | joining | 3 |
| 6531 | jineta | 3 |
| 6532 | jeronima | 3 |
| 6533 | jackasses | 3 |
| 6534 | ix | 3 |
| 6535 | iv | 3 |
| 6536 | isle | 3 |
| 6537 | irritated | 3 |
| 6538 | irresistible | 3 |
| 6539 | irrelevant | 3 |
| 6540 | irons | 3 |
| 6541 | involving | 3 |
| 6542 | involve | 3 |
| 6543 | invested | 3 |
| 6544 | intolerable | 3 |
| 6545 | interpose | 3 |
| 6546 | interests | 3 |
| 6547 | insults | 3 |
| 6548 | instituted | 3 |
| 6549 | instantly | 3 |
| 6550 | inquired | 3 |
| 6551 | innocent | 3 |
| 6552 | injure | 3 |
| 6553 | inhuman | 3 |
| 6554 | infused | 3 |
| 6555 | inflicting | 3 |
| 6556 | inflexible | 3 |
| 6557 | infirmity | 3 |
| 6558 | infatuation | 3 |
| 6559 | infamous | 3 |
| 6560 | indulged | 3 |
| 6561 | individuals | 3 |
| 6562 | individual | 3 |
| 6563 | indisposed | 3 |
| 6564 | indignity | 3 |
| 6565 | indicates | 3 |
| 6566 | independent | 3 |
| 6567 | incredible | 3 |
| 6568 | improvement | 3 |
| 6569 | implored | 3 |
| 6570 | imperilled | 3 |
| 6571 | impatient | 3 |
| 6572 | immense | 3 |
| 6573 | ills | 3 |
| 6574 | iii | 3 |
| 6575 | idly | 3 |
| 6576 | ice | 3 |
| 6577 | hypocrite | 3 |
| 6578 | hypocrisy | 3 |
| 6579 | hut | 3 |
| 6580 | hurting | 3 |
| 6581 | hurled | 3 |
| 6582 | huntress | 3 |
| 6583 | hunters | 3 |
| 6584 | hu | 3 |
| 6585 | hostel | 3 |
| 6586 | horseman | 3 |
| 6587 | horace | 3 |
| 6588 | homely | 3 |
| 6589 | homage | 3 |
| 6590 | hobble | 3 |
| 6591 | hitting | 3 |
| 6592 | hits | 3 |
| 6593 | hired | 3 |
| 6594 | hilt | 3 |
| 6595 | highways | 3 |
| 6596 | highway | 3 |
| 6597 | highborn | 3 |
| 6598 | hesitated | 3 |
| 6599 | hernandez | 3 |
| 6600 | herdsmen | 3 |
| 6601 | herdsman | 3 |
| 6602 | hemp | 3 |
| 6603 | helpless | 3 |
| 6604 | helping | 3 |
| 6605 | heirs | 3 |
| 6606 | hector | 3 |
| 6607 | heathens | 3 |
| 6608 | heathen | 3 |
| 6609 | hearth | 3 |
| 6610 | hearsay | 3 |
| 6611 | hearer | 3 |
| 6612 | headpiece | 3 |
| 6613 | headlong | 3 |
| 6614 | hares | 3 |
| 6615 | hardness | 3 |
| 6616 | harass | 3 |
| 6617 | happiest | 3 |
| 6618 | hapless | 3 |
| 6619 | haphazard | 3 |
| 6620 | hangings | 3 |
| 6621 | handwriting | 3 |
| 6622 | handling | 3 |
| 6623 | hailed | 3 |
| 6624 | hackneys | 3 |
| 6625 | hackney | 3 |
| 6626 | habitation | 3 |
| 6627 | guns | 3 |
| 6628 | guisando | 3 |
| 6629 | guillermo | 3 |
| 6630 | guerdon | 3 |
| 6631 | grunting | 3 |
| 6632 | groans | 3 |
| 6633 | grip | 3 |
| 6634 | grind | 3 |
| 6635 | grievances | 3 |
| 6636 | greeted | 3 |
| 6637 | grated | 3 |
| 6638 | grandmother | 3 |
| 6639 | gradually | 3 |
| 6640 | gowns | 3 |
| 6641 | governs | 3 |
| 6642 | gorgeous | 3 |
| 6643 | goodly | 3 |
| 6644 | goliath | 3 |
| 6645 | goddess | 3 |
| 6646 | gnaw | 3 |
| 6647 | glimpse | 3 |
| 6648 | glee | 3 |
| 6649 | glanced | 3 |
| 6650 | girthed | 3 |
| 6651 | girt | 3 |
| 6652 | giralda | 3 |
| 6653 | gilt | 3 |
| 6654 | gigantic | 3 |
| 6655 | gifted | 3 |
| 6656 | gestures | 3 |
| 6657 | german | 3 |
| 6658 | gerfalcon | 3 |
| 6659 | genoa | 3 |
| 6660 | generally | 3 |
| 6661 | gear | 3 |
| 6662 | gavest | 3 |
| 6663 | gaunt | 3 |
| 6664 | gascon | 3 |
| 6665 | gardens | 3 |
| 6666 | gaping | 3 |
| 6667 | ganelon | 3 |
| 6668 | fuss | 3 |
| 6669 | furnishing | 3 |
| 6670 | furioso | 3 |
| 6671 | fuming | 3 |
| 6672 | fullest | 3 |
| 6673 | fugitives | 3 |
| 6674 | frying | 3 |
| 6675 | friston | 3 |
| 6676 | fried | 3 |
| 6677 | frenchman | 3 |
| 6678 | freed | 3 |
| 6679 | freebooters | 3 |
| 6680 | freaks | 3 |
| 6681 | fragments | 3 |
| 6682 | fours | 3 |
| 6683 | founders | 3 |
| 6684 | fortify | 3 |
| 6685 | formalities | 3 |
| 6686 | forlorn | 3 |
| 6687 | forged | 3 |
| 6688 | forelock | 3 |
| 6689 | forbidden | 3 |
| 6690 | footpads | 3 |
| 6691 | focile | 3 |
| 6692 | foals | 3 |
| 6693 | flutes | 3 |
| 6694 | flurried | 3 |
| 6695 | florence | 3 |
| 6696 | flogged | 3 |
| 6697 | flitches | 3 |
| 6698 | flit | 3 |
| 6699 | flighty | 3 |
| 6700 | flemish | 3 |
| 6701 | flatter | 3 |
| 6702 | flash | 3 |
| 6703 | flanks | 3 |
| 6704 | flaming | 3 |
| 6705 | flag | 3 |
| 6706 | fishing | 3 |
| 6707 | findest | 3 |
| 6708 | filthy | 3 |
| 6709 | filling | 3 |
| 6710 | fights | 3 |
| 6711 | fierceness | 3 |
| 6712 | fierabras | 3 |
| 6713 | fetching | 3 |
| 6714 | festivals | 3 |
| 6715 | fencing | 3 |
| 6716 | fence | 3 |
| 6717 | feebleness | 3 |
| 6718 | feat | 3 |
| 6719 | favourite | 3 |
| 6720 | favourably | 3 |
| 6721 | fated | 3 |
| 6722 | fascinated | 3 |
| 6723 | farthings | 3 |
| 6724 | famishing | 3 |
| 6725 | faithlessness | 3 |
| 6726 | faintness | 3 |
| 6727 | fainted | 3 |
| 6728 | failure | 3 |
| 6729 | facetious | 3 |
| 6730 | extensive | 3 |
| 6731 | explore | 3 |
| 6732 | explanations | 3 |
| 6733 | explaining | 3 |
| 6734 | experienced | 3 |
| 6735 | existed | 3 |
| 6736 | exert | 3 |
| 6737 | executors | 3 |
| 6738 | executioners | 3 |
| 6739 | exclamation | 3 |
| 6740 | exchanging | 3 |
| 6741 | excepting | 3 |
| 6742 | exactitude | 3 |
| 6743 | et | 3 |
| 6744 | estimable | 3 |
| 6745 | est | 3 |
| 6746 | essence | 3 |
| 6747 | esplandian | 3 |
| 6748 | equivalent | 3 |
| 6749 | equality | 3 |
| 6750 | epitaphs | 3 |
| 6751 | episodes | 3 |
| 6752 | enterprises | 3 |
| 6753 | ensign | 3 |
| 6754 | enrich | 3 |
| 6755 | enliven | 3 |
| 6756 | engines | 3 |
| 6757 | engendered | 3 |
| 6758 | endures | 3 |
| 6759 | eminent | 3 |
| 6760 | eminence | 3 |
| 6761 | emeralds | 3 |
| 6762 | egypt | 3 |
| 6763 | effrontery | 3 |
| 6764 | effort | 3 |
| 6765 | effects | 3 |
| 6766 | efface | 3 |
| 6767 | edict | 3 |
| 6768 | eclogues | 3 |
| 6769 | ecclesiastics | 3 |
| 6770 | ebro | 3 |
| 6771 | easter | 3 |
| 6772 | easiest | 3 |
| 6773 | earliest | 3 |
| 6774 | dwelt | 3 |
| 6775 | durance | 3 |
| 6776 | dunghill | 3 |
| 6777 | dulcet | 3 |
| 6778 | dug | 3 |
| 6779 | drubbing | 3 |
| 6780 | drubbed | 3 |
| 6781 | drown | 3 |
| 6782 | dromedaries | 3 |
| 6783 | drollery | 3 |
| 6784 | drives | 3 |
| 6785 | drift | 3 |
| 6786 | dreamt | 3 |
| 6787 | dove | 3 |
| 6788 | doubloons | 3 |
| 6789 | doubled | 3 |
| 6790 | doomed | 3 |
| 6791 | dominions | 3 |
| 6792 | dolt | 3 |
| 6793 | divined | 3 |
| 6794 | dividing | 3 |
| 6795 | diversion | 3 |
| 6796 | disturbed | 3 |
| 6797 | distributive | 3 |
| 6798 | distinct | 3 |
| 6799 | disputes | 3 |
| 6800 | displays | 3 |
| 6801 | displaying | 3 |
| 6802 | disordered | 3 |
| 6803 | disorder | 3 |
| 6804 | dismiss | 3 |
| 6805 | dismayed | 3 |
| 6806 | dismal | 3 |
| 6807 | dishonoured | 3 |
| 6808 | disgusted | 3 |
| 6809 | disgraced | 3 |
| 6810 | disfigured | 3 |
| 6811 | disenchanting | 3 |
| 6812 | disease | 3 |
| 6813 | discrimination | 3 |
| 6814 | discovering | 3 |
| 6815 | discernment | 3 |
| 6816 | discard | 3 |
| 6817 | disabled | 3 |
| 6818 | directs | 3 |
| 6819 | directing | 3 |
| 6820 | dim | 3 |
| 6821 | digressions | 3 |
| 6822 | dignified | 3 |
| 6823 | differ | 3 |
| 6824 | dido | 3 |
| 6825 | diaz | 3 |
| 6826 | devotional | 3 |
| 6827 | devoid | 3 |
| 6828 | details | 3 |
| 6829 | detail | 3 |
| 6830 | destroying | 3 |
| 6831 | desperation | 3 |
| 6832 | descending | 3 |
| 6833 | derive | 3 |
| 6834 | depict | 3 |
| 6835 | depends | 3 |
| 6836 | dependent | 3 |
| 6837 | demosthenian | 3 |
| 6838 | demonstrations | 3 |
| 6839 | delivers | 3 |
| 6840 | deliverance | 3 |
| 6841 | delicacy | 3 |
| 6842 | degrade | 3 |
| 6843 | defrauding | 3 |
| 6844 | defer | 3 |
| 6845 | defended | 3 |
| 6846 | defect | 3 |
| 6847 | deemed | 3 |
| 6848 | dedication | 3 |
| 6849 | decree | 3 |
| 6850 | deciphered | 3 |
| 6851 | deceit | 3 |
| 6852 | deceased | 3 |
| 6853 | debarred | 3 |
| 6854 | deafened | 3 |
| 6855 | deadly | 3 |
| 6856 | dazed | 3 |
| 6857 | dash | 3 |
| 6858 | dares | 3 |
| 6859 | dames | 3 |
| 6860 | damaged | 3 |
| 6861 | daily | 3 |
| 6862 | cyprus | 3 |
| 6863 | cypress | 3 |
| 6864 | cynosure | 3 |
| 6865 | customs | 3 |
| 6866 | curtly | 3 |
| 6867 | crumbs | 3 |
| 6868 | cruelly | 3 |
| 6869 | crows | 3 |
| 6870 | crowding | 3 |
| 6871 | crossbows | 3 |
| 6872 | crossbow | 3 |
| 6873 | crisis | 3 |
| 6874 | credos | 3 |
| 6875 | creditable | 3 |
| 6876 | created | 3 |
| 6877 | crazes | 3 |
| 6878 | coyness | 3 |
| 6879 | cowards | 3 |
| 6880 | courtier | 3 |
| 6881 | courbash | 3 |
| 6882 | counts | 3 |
| 6883 | countesses | 3 |
| 6884 | costumes | 3 |
| 6885 | cosmographer | 3 |
| 6886 | corsair | 3 |
| 6887 | corridors | 3 |
| 6888 | corridor | 3 |
| 6889 | core | 3 |
| 6890 | cordially | 3 |
| 6891 | copies | 3 |
| 6892 | cooked | 3 |
| 6893 | conviction | 3 |
| 6894 | conversed | 3 |
| 6895 | controversy | 3 |
| 6896 | continues | 3 |
| 6897 | continence | 3 |
| 6898 | contemptible | 3 |
| 6899 | contemplate | 3 |
| 6900 | consultation | 3 |
| 6901 | considers | 3 |
| 6902 | considerations | 3 |
| 6903 | conserve | 3 |
| 6904 | consequently | 3 |
| 6905 | consciousness | 3 |
| 6906 | conquers | 3 |
| 6907 | conjectures | 3 |
| 6908 | confirmation | 3 |
| 6909 | condemning | 3 |
| 6910 | conde | 3 |
| 6911 | concerning | 3 |
| 6912 | conceals | 3 |
| 6913 | concealment | 3 |
| 6914 | con | 3 |
| 6915 | compound | 3 |
| 6916 | complaining | 3 |
| 6917 | compensation | 3 |
| 6918 | compelling | 3 |
| 6919 | comparisons | 3 |
| 6920 | comparing | 3 |
| 6921 | companies | 3 |
| 6922 | community | 3 |
| 6923 | communication | 3 |
| 6924 | commotion | 3 |
| 6925 | commander | 3 |
| 6926 | comforts | 3 |
| 6927 | comedy | 3 |
| 6928 | combined | 3 |
| 6929 | combats | 3 |
| 6930 | colt | 3 |
| 6931 | coldness | 3 |
| 6932 | codicil | 3 |
| 6933 | coaches | 3 |
| 6934 | clumsy | 3 |
| 6935 | clownish | 3 |
| 6936 | cloths | 3 |
| 6937 | clothing | 3 |
| 6938 | clothe | 3 |
| 6939 | closing | 3 |
| 6940 | clipped | 3 |
| 6941 | cling | 3 |
| 6942 | clemency | 3 |
| 6943 | cleft | 3 |
| 6944 | class | 3 |
| 6945 | civility | 3 |
| 6946 | citizen | 3 |
| 6947 | cicero | 3 |
| 6948 | christendom | 3 |
| 6949 | chink | 3 |
| 6950 | chin | 3 |
| 6951 | chill | 3 |
| 6952 | chew | 3 |
| 6953 | cherish | 3 |
| 6954 | cheerfully | 3 |
| 6955 | cheating | 3 |
| 6956 | charming | 3 |
| 6957 | chariot | 3 |
| 6958 | chapters | 3 |
| 6959 | channel | 3 |
| 6960 | chambers | 3 |
| 6961 | challenges | 3 |
| 6962 | challenged | 3 |
| 6963 | certificates | 3 |
| 6964 | caverns | 3 |
| 6965 | cavaliers | 3 |
| 6966 | catastrophe | 3 |
| 6967 | carriest | 3 |
| 6968 | carrascon | 3 |
| 6969 | carpets | 3 |
| 6970 | cargo | 3 |
| 6971 | carded | 3 |
| 6972 | camp | 3 |
| 6973 | calmer | 3 |
| 6974 | caitiffs | 3 |
| 6975 | c | 3 |
| 6976 | butt | 3 |
| 6977 | buskins | 3 |
| 6978 | bush | 3 |
| 6979 | bursts | 3 |
| 6980 | burnt | 3 |
| 6981 | burlesque | 3 |
| 6982 | burgundy | 3 |
| 6983 | burdens | 3 |
| 6984 | bucklers | 3 |
| 6985 | brows | 3 |
| 6986 | broom | 3 |
| 6987 | brooding | 3 |
| 6988 | bristles | 3 |
| 6989 | brisk | 3 |
| 6990 | bringest | 3 |
| 6991 | brilliantly | 3 |
| 6992 | brilliant | 3 |
| 6993 | breach | 3 |
| 6994 | bravely | 3 |
| 6995 | bountiful | 3 |
| 6996 | bounden | 3 |
| 6997 | botas | 3 |
| 6998 | bosoms | 3 |
| 6999 | border | 3 |
| 7000 | boot | 3 |
| 7001 | bondage | 3 |
| 7002 | bon | 3 |
| 7003 | bolts | 3 |
| 7004 | bodice | 3 |
| 7005 | blush | 3 |
| 7006 | blunted | 3 |
| 7007 | blunders | 3 |
| 7008 | blindness | 3 |
| 7009 | blinded | 3 |
| 7010 | blew | 3 |
| 7011 | blest | 3 |
| 7012 | blemishes | 3 |
| 7013 | blaze | 3 |
| 7014 | blast | 3 |
| 7015 | blandishments | 3 |
| 7016 | blacks | 3 |
| 7017 | bite | 3 |
| 7018 | bishops | 3 |
| 7019 | beset | 3 |
| 7020 | benevolence | 3 |
| 7021 | benefits | 3 |
| 7022 | benediction | 3 |
| 7023 | benedict | 3 |
| 7024 | bending | 3 |
| 7025 | bemoaning | 3 |
| 7026 | beltenebros | 3 |
| 7027 | belianises | 3 |
| 7028 | begotten | 3 |
| 7029 | beginnings | 3 |
| 7030 | befooled | 3 |
| 7031 | befalls | 3 |
| 7032 | bees | 3 |
| 7033 | becomingly | 3 |
| 7034 | beaver | 3 |
| 7035 | beauties | 3 |
| 7036 | bearest | 3 |
| 7037 | beam | 3 |
| 7038 | beacon | 3 |
| 7039 | bastard | 3 |
| 7040 | basilisk | 3 |
| 7041 | based | 3 |
| 7042 | bartholomew | 3 |
| 7043 | bared | 3 |
| 7044 | balance | 3 |
| 7045 | bake | 3 |
| 7046 | baize | 3 |
| 7047 | bagatelle | 3 |
| 7048 | backwards | 3 |
| 7049 | backs | 3 |
| 7050 | backed | 3 |
| 7051 | backbone | 3 |
| 7052 | aye | 3 |
| 7053 | awkward | 3 |
| 7054 | awarded | 3 |
| 7055 | awakened | 3 |
| 7056 | authentic | 3 |
| 7057 | austerity | 3 |
| 7058 | august | 3 |
| 7059 | audience | 3 |
| 7060 | audacious | 3 |
| 7061 | attributes | 3 |
| 7062 | attractions | 3 |
| 7063 | attentive | 3 |
| 7064 | attendant | 3 |
| 7065 | astrology | 3 |
| 7066 | astrologer | 3 |
| 7067 | asserted | 3 |
| 7068 | assembled | 3 |
| 7069 | assailant | 3 |
| 7070 | ascended | 3 |
| 7071 | artifice | 3 |
| 7072 | article | 3 |
| 7073 | arrested | 3 |
| 7074 | arranging | 3 |
| 7075 | arose | 3 |
| 7076 | arnaut | 3 |
| 7077 | armoury | 3 |
| 7078 | arising | 3 |
| 7079 | arises | 3 |
| 7080 | ariosto | 3 |
| 7081 | arab | 3 |
| 7082 | appropriate | 3 |
| 7083 | apprehensive | 3 |
| 7084 | applying | 3 |
| 7085 | apple | 3 |
| 7086 | apparition | 3 |
| 7087 | apollonia | 3 |
| 7088 | apartment | 3 |
| 7089 | apace | 3 |
| 7090 | anxieties | 3 |
| 7091 | antonia | 3 |
| 7092 | antequera | 3 |
| 7093 | annotations | 3 |
| 7094 | annals | 3 |
| 7095 | ancients | 3 |
| 7096 | anchored | 3 |
| 7097 | ancestry | 3 |
| 7098 | amours | 3 |
| 7099 | amiable | 3 |
| 7100 | amendment | 3 |
| 7101 | ambassador | 3 |
| 7102 | amazes | 3 |
| 7103 | amaze | 3 |
| 7104 | alteration | 3 |
| 7105 | alphabet | 3 |
| 7106 | aloft | 3 |
| 7107 | almond | 3 |
| 7108 | allowable | 3 |
| 7109 | alleys | 3 |
| 7110 | alguacil | 3 |
| 7111 | alert | 3 |
| 7112 | alacrity | 3 |
| 7113 | alabaster | 3 |
| 7114 | aiming | 3 |
| 7115 | ails | 3 |
| 7116 | ailments | 3 |
| 7117 | aguilar | 3 |
| 7118 | agility | 3 |
| 7119 | aghast | 3 |
| 7120 | aggrieved | 3 |
| 7121 | afield | 3 |
| 7122 | affront | 3 |
| 7123 | afflict | 3 |
| 7124 | affected | 3 |
| 7125 | afar | 3 |
| 7126 | advancement | 3 |
| 7127 | adroitness | 3 |
| 7128 | adores | 3 |
| 7129 | adopting | 3 |
| 7130 | admits | 3 |
| 7131 | admission | 3 |
| 7132 | administer | 3 |
| 7133 | adjusted | 3 |
| 7134 | adieu | 3 |
| 7135 | additions | 3 |
| 7136 | achieve | 3 |
| 7137 | aches | 3 |
| 7138 | accurately | 3 |
| 7139 | accountable | 3 |
| 7140 | accordingly | 3 |
| 7141 | accompaniments | 3 |
| 7142 | accessories | 3 |
| 7143 | abandoned | 3 |
| 7144 | zocodover | 2 |
| 7145 | zancas | 2 |
| 7146 | z | 2 |
| 7147 | youthful | 2 |
| 7148 | yon | 2 |
| 7149 | yoked | 2 |
| 7150 | yields | 2 |
| 7151 | yell | 2 |
| 7152 | wroth | 2 |
| 7153 | wrists | 2 |
| 7154 | wreak | 2 |
| 7155 | wove | 2 |
| 7156 | worthless | 2 |
| 7157 | worthies | 2 |
| 7158 | worrying | 2 |
| 7159 | worry | 2 |
| 7160 | worm | 2 |
| 7161 | worldly | 2 |
| 7162 | workman | 2 |
| 7163 | wooing | 2 |
| 7164 | wonted | 2 |
| 7165 | wonderfully | 2 |
| 7166 | woebegone | 2 |
| 7167 | wizard | 2 |
| 7168 | wishing | 2 |
| 7169 | wiser | 2 |
| 7170 | winnowing | 2 |
| 7171 | winnowed | 2 |
| 7172 | winners | 2 |
| 7173 | winner | 2 |
| 7174 | wines | 2 |
| 7175 | winded | 2 |
| 7176 | wills | 2 |
| 7177 | willows | 2 |
| 7178 | wight | 2 |
| 7179 | wield | 2 |
| 7180 | width | 2 |
| 7181 | widowed | 2 |
| 7182 | widely | 2 |
| 7183 | whistling | 2 |
| 7184 | whey | 2 |
| 7185 | wherin | 2 |
| 7186 | wherewithal | 2 |
| 7187 | whereon | 2 |
| 7188 | wheals | 2 |
| 7189 | west | 2 |
| 7190 | weighty | 2 |
| 7191 | weights | 2 |
| 7192 | ween | 2 |
| 7193 | weddings | 2 |
| 7194 | weaving | 2 |
| 7195 | weave | 2 |
| 7196 | wearying | 2 |
| 7197 | wearisomeness | 2 |
| 7198 | weals | 2 |
| 7199 | wayward | 2 |
| 7200 | waves | 2 |
| 7201 | wavering | 2 |
| 7202 | waver | 2 |
| 7203 | watered | 2 |
| 7204 | watchful | 2 |
| 7205 | wast | 2 |
| 7206 | warts | 2 |
| 7207 | warrants | 2 |
| 7208 | warnings | 2 |
| 7209 | ward | 2 |
| 7210 | wanders | 2 |
| 7211 | wanderer | 2 |
| 7212 | wamba | 2 |
| 7213 | walnuts | 2 |
| 7214 | walloon | 2 |
| 7215 | walled | 2 |
| 7216 | wakener | 2 |
| 7217 | wake | 2 |
| 7218 | wailing | 2 |
| 7219 | voracity | 2 |
| 7220 | vomits | 2 |
| 7221 | voluntary | 2 |
| 7222 | vividly | 2 |
| 7223 | vitals | 2 |
| 7224 | visiting | 2 |
| 7225 | visions | 2 |
| 7226 | violently | 2 |
| 7227 | violated | 2 |
| 7228 | vinegar | 2 |
| 7229 | vindictive | 2 |
| 7230 | vindicate | 2 |
| 7231 | villainy | 2 |
| 7232 | villains | 2 |
| 7233 | vigorous | 2 |
| 7234 | vigils | 2 |
| 7235 | vigilance | 2 |
| 7236 | vied | 2 |
| 7237 | victors | 2 |
| 7238 | vexes | 2 |
| 7239 | veritable | 2 |
| 7240 | vergil | 2 |
| 7241 | verbis | 2 |
| 7242 | venus | 2 |
| 7243 | venice | 2 |
| 7244 | venetians | 2 |
| 7245 | venetian | 2 |
| 7246 | velasco | 2 |
| 7247 | veins | 2 |
| 7248 | vein | 2 |
| 7249 | varnished | 2 |
| 7250 | variance | 2 |
| 7251 | vanquishing | 2 |
| 7252 | vanishing | 2 |
| 7253 | valuable | 2 |
| 7254 | vair | 2 |
| 7255 | vainly | 2 |
| 7256 | vainglorious | 2 |
| 7257 | vaguely | 2 |
| 7258 | vague | 2 |
| 7259 | vagabonds | 2 |
| 7260 | utters | 2 |
| 7261 | utensils | 2 |
| 7262 | usurped | 2 |
| 7263 | usurp | 2 |
| 7264 | unyoked | 2 |
| 7265 | unyoke | 2 |
| 7266 | untying | 2 |
| 7267 | untrue | 2 |
| 7268 | untamed | 2 |
| 7269 | unstable | 2 |
| 7270 | unsatisfactory | 2 |
| 7271 | unrivalled | 2 |
| 7272 | unoccupied | 2 |
| 7273 | unnoticed | 2 |
| 7274 | unmarried | 2 |
| 7275 | unlooked | 2 |
| 7276 | unlace | 2 |
| 7277 | unjustly | 2 |
| 7278 | unjust | 2 |
| 7279 | united | 2 |
| 7280 | unintelligible | 2 |
| 7281 | uninhabited | 2 |
| 7282 | unimpeachable | 2 |
| 7283 | uniform | 2 |
| 7284 | unhindered | 2 |
| 7285 | unhappiness | 2 |
| 7286 | ungirt | 2 |
| 7287 | unfortunately | 2 |
| 7288 | unforeseen | 2 |
| 7289 | unfettered | 2 |
| 7290 | undress | 2 |
| 7291 | undisturbed | 2 |
| 7292 | undescribed | 2 |
| 7293 | undervalue | 2 |
| 7294 | undecided | 2 |
| 7295 | undeceived | 2 |
| 7296 | unconscious | 2 |
| 7297 | unconcern | 2 |
| 7298 | uncommonly | 2 |
| 7299 | unclouded | 2 |
| 7300 | unclean | 2 |
| 7301 | unchaste | 2 |
| 7302 | uncertainty | 2 |
| 7303 | unceasing | 2 |
| 7304 | unbridled | 2 |
| 7305 | unbiassed | 2 |
| 7306 | unbecoming | 2 |
| 7307 | unarmed | 2 |
| 7308 | unaffected | 2 |
| 7309 | unaccompanied | 2 |
| 7310 | tyrant | 2 |
| 7311 | tyranny | 2 |
| 7312 | twisted | 2 |
| 7313 | twere | 2 |
| 7314 | tussock | 2 |
| 7315 | tuning | 2 |
| 7316 | tuned | 2 |
| 7317 | tumbling | 2 |
| 7318 | tumbled | 2 |
| 7319 | tuft | 2 |
| 7320 | tub | 2 |
| 7321 | trusted | 2 |
| 7322 | truss | 2 |
| 7323 | trunks | 2 |
| 7324 | trumpeted | 2 |
| 7325 | troutlets | 2 |
| 7326 | troutlet | 2 |
| 7327 | troublous | 2 |
| 7328 | troubadours | 2 |
| 7329 | tronchon | 2 |
| 7330 | trod | 2 |
| 7331 | triumphing | 2 |
| 7332 | triumphal | 2 |
| 7333 | tripping | 2 |
| 7334 | trinity | 2 |
| 7335 | tribunal | 2 |
| 7336 | treasury | 2 |
| 7337 | treacherously | 2 |
| 7338 | traversing | 2 |
| 7339 | transport | 2 |
| 7340 | translating | 2 |
| 7341 | transitory | 2 |
| 7342 | transactions | 2 |
| 7343 | transact | 2 |
| 7344 | trailed | 2 |
| 7345 | tragedies | 2 |
| 7346 | trades | 2 |
| 7347 | tractable | 2 |
| 7348 | towel | 2 |
| 7349 | tourney | 2 |
| 7350 | touches | 2 |
| 7351 | tottering | 2 |
| 7352 | total | 2 |
| 7353 | tossing | 2 |
| 7354 | torments | 2 |
| 7355 | tonight | 2 |
| 7356 | tolosa | 2 |
| 7357 | tolerably | 2 |
| 7358 | tolerable | 2 |
| 7359 | toledans | 2 |
| 7360 | toilsome | 2 |
| 7361 | tocho | 2 |
| 7362 | tobosan | 2 |
| 7363 | tittle | 2 |
| 7364 | tire | 2 |
| 7365 | tipstaffs | 2 |
| 7366 | tinacrio | 2 |
| 7367 | timbrels | 2 |
| 7368 | tilting | 2 |
| 7369 | tilt | 2 |
| 7370 | tightening | 2 |
| 7371 | tighten | 2 |
| 7372 | tigers | 2 |
| 7373 | thunder | 2 |
| 7374 | throws | 2 |
| 7375 | thrice | 2 |
| 7376 | threat | 2 |
| 7377 | threadbare | 2 |
| 7378 | thoughtless | 2 |
| 7379 | thorn | 2 |
| 7380 | thither | 2 |
| 7381 | thirsty | 2 |
| 7382 | thirsting | 2 |
| 7383 | thirds | 2 |
| 7384 | thighs | 2 |
| 7385 | thickets | 2 |
| 7386 | theseus | 2 |
| 7387 | thereat | 2 |
| 7388 | theology | 2 |
| 7389 | theft | 2 |
| 7390 | thanklessly | 2 |
| 7391 | texture | 2 |
| 7392 | text | 2 |
| 7393 | testify | 2 |
| 7394 | tested | 2 |
| 7395 | terrors | 2 |
| 7396 | terrify | 2 |
| 7397 | term | 2 |
| 7398 | tennis | 2 |
| 7399 | tended | 2 |
| 7400 | tempting | 2 |
| 7401 | temptations | 2 |
| 7402 | temples | 2 |
| 7403 | tempests | 2 |
| 7404 | tempest | 2 |
| 7405 | tempers | 2 |
| 7406 | temperate | 2 |
| 7407 | temperament | 2 |
| 7408 | tembleque | 2 |
| 7409 | teaching | 2 |
| 7410 | tattle | 2 |
| 7411 | tattered | 2 |
| 7412 | tasty | 2 |
| 7413 | tasters | 2 |
| 7414 | taster | 2 |
| 7415 | tasted | 2 |
| 7416 | tapestry | 2 |
| 7417 | tameji | 2 |
| 7418 | talkest | 2 |
| 7419 | talents | 2 |
| 7420 | taffety | 2 |
| 7421 | tackling | 2 |
| 7422 | tabor | 2 |
| 7423 | tablets | 2 |
| 7424 | sympathy | 2 |
| 7425 | sympathise | 2 |
| 7426 | swoonings | 2 |
| 7427 | swim | 2 |
| 7428 | swifter | 2 |
| 7429 | sweep | 2 |
| 7430 | swashbuckler | 2 |
| 7431 | swallowing | 2 |
| 7432 | swallowed | 2 |
| 7433 | swaggering | 2 |
| 7434 | swagger | 2 |
| 7435 | swaddling | 2 |
| 7436 | sustains | 2 |
| 7437 | surround | 2 |
| 7438 | surprises | 2 |
| 7439 | surgeon | 2 |
| 7440 | surfeit | 2 |
| 7441 | surer | 2 |
| 7442 | supremely | 2 |
| 7443 | supports | 2 |
| 7444 | supporters | 2 |
| 7445 | supplied | 2 |
| 7446 | supplications | 2 |
| 7447 | supplement | 2 |
| 7448 | superhuman | 2 |
| 7449 | superabundance | 2 |
| 7450 | sunshine | 2 |
| 7451 | sunshades | 2 |
| 7452 | sundays | 2 |
| 7453 | sunbeams | 2 |
| 7454 | sunbeam | 2 |
| 7455 | sumptuously | 2 |
| 7456 | summed | 2 |
| 7457 | suiting | 2 |
| 7458 | suffices | 2 |
| 7459 | sufferers | 2 |
| 7460 | sued | 2 |
| 7461 | sucking | 2 |
| 7462 | suck | 2 |
| 7463 | succours | 2 |
| 7464 | succoured | 2 |
| 7465 | succession | 2 |
| 7466 | subtly | 2 |
| 7467 | subtle | 2 |
| 7468 | subterfuge | 2 |
| 7469 | substitute | 2 |
| 7470 | substantial | 2 |
| 7471 | subdued | 2 |
| 7472 | sturdily | 2 |
| 7473 | stupidity | 2 |
| 7474 | stunned | 2 |
| 7475 | studious | 2 |
| 7476 | structure | 2 |
| 7477 | strolling | 2 |
| 7478 | strings | 2 |
| 7479 | strenuously | 2 |
| 7480 | stray | 2 |
| 7481 | strangeness | 2 |
| 7482 | stow | 2 |
| 7483 | stove | 2 |
| 7484 | stoutness | 2 |
| 7485 | stoutest | 2 |
| 7486 | stormy | 2 |
| 7487 | storehouse | 2 |
| 7488 | stocks | 2 |
| 7489 | stocked | 2 |
| 7490 | stimulate | 2 |
| 7491 | stillness | 2 |
| 7492 | stiff | 2 |
| 7493 | stew | 2 |
| 7494 | sternly | 2 |
| 7495 | sterility | 2 |
| 7496 | stealthily | 2 |
| 7497 | steadfast | 2 |
| 7498 | starting | 2 |
| 7499 | starch | 2 |
| 7500 | stanza | 2 |
| 7501 | stanch | 2 |
| 7502 | stamped | 2 |
| 7503 | stalls | 2 |
| 7504 | stale | 2 |
| 7505 | staircase | 2 |
| 7506 | stabbed | 2 |
| 7507 | squeeze | 2 |
| 7508 | squeamish | 2 |
| 7509 | spy | 2 |
| 7510 | spun | 2 |
| 7511 | sprinkle | 2 |
| 7512 | spouse | 2 |
| 7513 | spots | 2 |
| 7514 | sportsmen | 2 |
| 7515 | sports | 2 |
| 7516 | splendidly | 2 |
| 7517 | spitting | 2 |
| 7518 | spiritless | 2 |
| 7519 | spindle | 2 |
| 7520 | spin | 2 |
| 7521 | spike | 2 |
| 7522 | spied | 2 |
| 7523 | spices | 2 |
| 7524 | spice | 2 |
| 7525 | spheres | 2 |
| 7526 | sphere | 2 |
| 7527 | sped | 2 |
| 7528 | spears | 2 |
| 7529 | speaketh | 2 |
| 7530 | spade | 2 |
| 7531 | sow | 2 |
| 7532 | soundness | 2 |
| 7533 | sorrowing | 2 |
| 7534 | sorrier | 2 |
| 7535 | soreness | 2 |
| 7536 | sorcerer | 2 |
| 7537 | soothes | 2 |
| 7538 | sonorous | 2 |
| 7539 | somersaults | 2 |
| 7540 | somebody | 2 |
| 7541 | solve | 2 |
| 7542 | soliloquy | 2 |
| 7543 | solemnly | 2 |
| 7544 | solely | 2 |
| 7545 | sojourned | 2 |
| 7546 | softening | 2 |
| 7547 | sober | 2 |
| 7548 | snoring | 2 |
| 7549 | sneeze | 2 |
| 7550 | snakes | 2 |
| 7551 | smoothness | 2 |
| 7552 | smoothly | 2 |
| 7553 | smoothed | 2 |
| 7554 | smiles | 2 |
| 7555 | smartness | 2 |
| 7556 | smaller | 2 |
| 7557 | slippers | 2 |
| 7558 | slighted | 2 |
| 7559 | sliced | 2 |
| 7560 | sleepy | 2 |
| 7561 | sleepless | 2 |
| 7562 | slanderer | 2 |
| 7563 | slackness | 2 |
| 7564 | slacken | 2 |
| 7565 | slab | 2 |
| 7566 | skirted | 2 |
| 7567 | skirmish | 2 |
| 7568 | skimming | 2 |
| 7569 | skilled | 2 |
| 7570 | skilfully | 2 |
| 7571 | sisters | 2 |
| 7572 | sinking | 2 |
| 7573 | singular | 2 |
| 7574 | singed | 2 |
| 7575 | sincere | 2 |
| 7576 | silliness | 2 |
| 7577 | signing | 2 |
| 7578 | sideways | 2 |
| 7579 | sicut | 2 |
| 7580 | sickly | 2 |
| 7581 | shun | 2 |
| 7582 | shuffle | 2 |
| 7583 | shrugged | 2 |
| 7584 | shrubs | 2 |
| 7585 | shrines | 2 |
| 7586 | shred | 2 |
| 7587 | shooting | 2 |
| 7588 | shelters | 2 |
| 7589 | sheltered | 2 |
| 7590 | shells | 2 |
| 7591 | shell | 2 |
| 7592 | sheepskin | 2 |
| 7593 | sheen | 2 |
| 7594 | shatter | 2 |
| 7595 | sharper | 2 |
| 7596 | sharpened | 2 |
| 7597 | shaping | 2 |
| 7598 | shafts | 2 |
| 7599 | shady | 2 |
| 7600 | shadows | 2 |
| 7601 | shades | 2 |
| 7602 | sewing | 2 |
| 7603 | severity | 2 |
| 7604 | severed | 2 |
| 7605 | seventh | 2 |
| 7606 | sevenfold | 2 |
| 7607 | serviceable | 2 |
| 7608 | sermons | 2 |
| 7609 | sermon | 2 |
| 7610 | serene | 2 |
| 7611 | sepulchre | 2 |
| 7612 | separating | 2 |
| 7613 | sendal | 2 |
| 7614 | seeming | 2 |
| 7615 | seeker | 2 |
| 7616 | securing | 2 |
| 7617 | secular | 2 |
| 7618 | seating | 2 |
| 7619 | searched | 2 |
| 7620 | scythians | 2 |
| 7621 | scrupulously | 2 |
| 7622 | screen | 2 |
| 7623 | scratching | 2 |
| 7624 | scratches | 2 |
| 7625 | scratched | 2 |
| 7626 | scowl | 2 |
| 7627 | scoured | 2 |
| 7628 | scour | 2 |
| 7629 | scot | 2 |
| 7630 | scorning | 2 |
| 7631 | scoffer | 2 |
| 7632 | scissors | 2 |
| 7633 | schoolmaster | 2 |
| 7634 | schooled | 2 |
| 7635 | schemers | 2 |
| 7636 | scent | 2 |
| 7637 | scarecrow | 2 |
| 7638 | scabby | 2 |
| 7639 | scabbard | 2 |
| 7640 | sayas | 2 |
| 7641 | sayago | 2 |
| 7642 | savage | 2 |
| 7643 | saucy | 2 |
| 7644 | sauce | 2 |
| 7645 | satyrs | 2 |
| 7646 | saturated | 2 |
| 7647 | sapient | 2 |
| 7648 | sanction | 2 |
| 7649 | sample | 2 |
| 7650 | salve | 2 |
| 7651 | saluting | 2 |
| 7652 | salutations | 2 |
| 7653 | salutation | 2 |
| 7654 | salted | 2 |
| 7655 | sallying | 2 |
| 7656 | sale | 2 |
| 7657 | saith | 2 |
| 7658 | sailor | 2 |
| 7659 | saddling | 2 |
| 7660 | saddest | 2 |
| 7661 | sacrament | 2 |
| 7662 | sables | 2 |
| 7663 | saavedra | 2 |
| 7664 | rumia | 2 |
| 7665 | ruler | 2 |
| 7666 | ruiz | 2 |
| 7667 | ruined | 2 |
| 7668 | ruggiero | 2 |
| 7669 | ruffs | 2 |
| 7670 | ruffian | 2 |
| 7671 | rubies | 2 |
| 7672 | rubbish | 2 |
| 7673 | rubbing | 2 |
| 7674 | roving | 2 |
| 7675 | roundly | 2 |
| 7676 | roundabout | 2 |
| 7677 | rotolando | 2 |
| 7678 | rosy | 2 |
| 7679 | rooted | 2 |
| 7680 | rooms | 2 |
| 7681 | rook | 2 |
| 7682 | roofs | 2 |
| 7683 | rolls | 2 |
| 7684 | rolled | 2 |
| 7685 | roguish | 2 |
| 7686 | roderick | 2 |
| 7687 | rod | 2 |
| 7688 | robed | 2 |
| 7689 | roadside | 2 |
| 7690 | rivers | 2 |
| 7691 | risks | 2 |
| 7692 | righter | 2 |
| 7693 | rigging | 2 |
| 7694 | rides | 2 |
| 7695 | ribbons | 2 |
| 7696 | revolved | 2 |
| 7697 | reverend | 2 |
| 7698 | revenges | 2 |
| 7699 | reveals | 2 |
| 7700 | revealing | 2 |
| 7701 | returnest | 2 |
| 7702 | retires | 2 |
| 7703 | retinue | 2 |
| 7704 | reticent | 2 |
| 7705 | resurrection | 2 |
| 7706 | rests | 2 |
| 7707 | restrictions | 2 |
| 7708 | restricted | 2 |
| 7709 | restitution | 2 |
| 7710 | rested | 2 |
| 7711 | responsible | 2 |
| 7712 | responsibilities | 2 |
| 7713 | respectfully | 2 |
| 7714 | resounded | 2 |
| 7715 | resolutely | 2 |
| 7716 | resign | 2 |
| 7717 | reserving | 2 |
| 7718 | resembling | 2 |
| 7719 | resemblance | 2 |
| 7720 | requited | 2 |
| 7721 | requisites | 2 |
| 7722 | requirest | 2 |
| 7723 | requests | 2 |
| 7724 | repulsed | 2 |
| 7725 | reproaches | 2 |
| 7726 | represents | 2 |
| 7727 | representations | 2 |
| 7728 | repletion | 2 |
| 7729 | repented | 2 |
| 7730 | repentant | 2 |
| 7731 | reparation | 2 |
| 7732 | repairing | 2 |
| 7733 | renewal | 2 |
| 7734 | remorse | 2 |
| 7735 | reminds | 2 |
| 7736 | reminding | 2 |
| 7737 | rememberest | 2 |
| 7738 | remedied | 2 |
| 7739 | remark | 2 |
| 7740 | reluctantly | 2 |
| 7741 | relishing | 2 |
| 7742 | relinquish | 2 |
| 7743 | relieves | 2 |
| 7744 | relentless | 2 |
| 7745 | relent | 2 |
| 7746 | relative | 2 |
| 7747 | relation | 2 |
| 7748 | rejoined | 2 |
| 7749 | reining | 2 |
| 7750 | regain | 2 |
| 7751 | refrained | 2 |
| 7752 | refers | 2 |
| 7753 | referring | 2 |
| 7754 | references | 2 |
| 7755 | reeds | 2 |
| 7756 | redressing | 2 |
| 7757 | redressed | 2 |
| 7758 | redoubled | 2 |
| 7759 | redemption | 2 |
| 7760 | records | 2 |
| 7761 | reconsider | 2 |
| 7762 | recommendation | 2 |
| 7763 | recollections | 2 |
| 7764 | recollected | 2 |
| 7765 | recklessly | 2 |
| 7766 | recital | 2 |
| 7767 | recalling | 2 |
| 7768 | recalled | 2 |
| 7769 | rebuked | 2 |
| 7770 | rebuilt | 2 |
| 7771 | reapers | 2 |
| 7772 | realise | 2 |
| 7773 | readiest | 2 |
| 7774 | raw | 2 |
| 7775 | ravings | 2 |
| 7776 | raving | 2 |
| 7777 | ravine | 2 |
| 7778 | rattled | 2 |
| 7779 | rating | 2 |
| 7780 | rated | 2 |
| 7781 | rashly | 2 |
| 7782 | rape | 2 |
| 7783 | ransacked | 2 |
| 7784 | ramon | 2 |
| 7785 | rambling | 2 |
| 7786 | raises | 2 |
| 7787 | raining | 2 |
| 7788 | rainbows | 2 |
| 7789 | rail | 2 |
| 7790 | raging | 2 |
| 7791 | racked | 2 |
| 7792 | rabbits | 2 |
| 7793 | rabbit | 2 |
| 7794 | quoted | 2 |
| 7795 | quixotize | 2 |
| 7796 | quixana | 2 |
| 7797 | quis | 2 |
| 7798 | quintanar | 2 |
| 7799 | quietness | 2 |
| 7800 | quickwitted | 2 |
| 7801 | quesada | 2 |
| 7802 | quarts | 2 |
| 7803 | quarrelling | 2 |
| 7804 | quail | 2 |
| 7805 | puzzle | 2 |
| 7806 | pursuance | 2 |
| 7807 | purple | 2 |
| 7808 | purchased | 2 |
| 7809 | pups | 2 |
| 7810 | pupil | 2 |
| 7811 | pup | 2 |
| 7812 | punctilious | 2 |
| 7813 | punches | 2 |
| 7814 | pullets | 2 |
| 7815 | pullet | 2 |
| 7816 | puffing | 2 |
| 7817 | prying | 2 |
| 7818 | prudery | 2 |
| 7819 | provocative | 2 |
| 7820 | providing | 2 |
| 7821 | providence | 2 |
| 7822 | proves | 2 |
| 7823 | protested | 2 |
| 7824 | protecting | 2 |
| 7825 | prosper | 2 |
| 7826 | proposes | 2 |
| 7827 | prophet | 2 |
| 7828 | promptitude | 2 |
| 7829 | prolix | 2 |
| 7830 | projects | 2 |
| 7831 | prog | 2 |
| 7832 | produces | 2 |
| 7833 | prodigality | 2 |
| 7834 | proclamation | 2 |
| 7835 | proclaiming | 2 |
| 7836 | proclaimed | 2 |
| 7837 | proclaim | 2 |
| 7838 | proceeds | 2 |
| 7839 | probable | 2 |
| 7840 | probability | 2 |
| 7841 | prizes | 2 |
| 7842 | privy | 2 |
| 7843 | pristine | 2 |
| 7844 | printers | 2 |
| 7845 | principles | 2 |
| 7846 | princely | 2 |
| 7847 | prime | 2 |
| 7848 | prided | 2 |
| 7849 | pricks | 2 |
| 7850 | pricked | 2 |
| 7851 | prick | 2 |
| 7852 | prices | 2 |
| 7853 | preventing | 2 |
| 7854 | prevails | 2 |
| 7855 | presumption | 2 |
| 7856 | prester | 2 |
| 7857 | presonages | 2 |
| 7858 | preservation | 2 |
| 7859 | prescribed | 2 |
| 7860 | preliminaries | 2 |
| 7861 | precipitating | 2 |
| 7862 | precipice | 2 |
| 7863 | prebendary | 2 |
| 7864 | preamble | 2 |
| 7865 | practices | 2 |
| 7866 | pounced | 2 |
| 7867 | potosi | 2 |
| 7868 | potion | 2 |
| 7869 | pothouse | 2 |
| 7870 | potent | 2 |
| 7871 | posterity | 2 |
| 7872 | possessions | 2 |
| 7873 | positions | 2 |
| 7874 | portrayed | 2 |
| 7875 | portray | 2 |
| 7876 | portmanteau | 2 |
| 7877 | portals | 2 |
| 7878 | poring | 2 |
| 7879 | popular | 2 |
| 7880 | poplar | 2 |
| 7881 | ponies | 2 |
| 7882 | pondering | 2 |
| 7883 | poltroon | 2 |
| 7884 | poisons | 2 |
| 7885 | poetic | 2 |
| 7886 | poems | 2 |
| 7887 | podridas | 2 |
| 7888 | podrida | 2 |
| 7889 | ply | 2 |
| 7890 | plunging | 2 |
| 7891 | plunges | 2 |
| 7892 | plunder | 2 |
| 7893 | plumage | 2 |
| 7894 | plotting | 2 |
| 7895 | plotted | 2 |
| 7896 | plied | 2 |
| 7897 | pliancy | 2 |
| 7898 | plentifully | 2 |
| 7899 | pledging | 2 |
| 7900 | pleasantly | 2 |
| 7901 | pleadings | 2 |
| 7902 | platir | 2 |
| 7903 | plastered | 2 |
| 7904 | planting | 2 |
| 7905 | planned | 2 |
| 7906 | plank | 2 |
| 7907 | planets | 2 |
| 7908 | plagues | 2 |
| 7909 | pitiless | 2 |
| 7910 | piteously | 2 |
| 7911 | pipe | 2 |
| 7912 | pip | 2 |
| 7913 | pining | 2 |
| 7914 | pines | 2 |
| 7915 | pine | 2 |
| 7916 | pincers | 2 |
| 7917 | pilot | 2 |
| 7918 | pigskin | 2 |
| 7919 | pigeon | 2 |
| 7920 | piercing | 2 |
| 7921 | pierces | 2 |
| 7922 | physiognomy | 2 |
| 7923 | phraseology | 2 |
| 7924 | philistine | 2 |
| 7925 | philip | 2 |
| 7926 | petty | 2 |
| 7927 | petitions | 2 |
| 7928 | pestiferous | 2 |
| 7929 | perverse | 2 |
| 7930 | perturbation | 2 |
| 7931 | pertinacity | 2 |
| 7932 | persuasions | 2 |
| 7933 | personable | 2 |
| 7934 | persisted | 2 |
| 7935 | persians | 2 |
| 7936 | persia | 2 |
| 7937 | persevering | 2 |
| 7938 | persevere | 2 |
| 7939 | persecuting | 2 |
| 7940 | perplex | 2 |
| 7941 | perpetrated | 2 |
| 7942 | permitting | 2 |
| 7943 | perished | 2 |
| 7944 | period | 2 |
| 7945 | performers | 2 |
| 7946 | perfidy | 2 |
| 7947 | penury | 2 |
| 7948 | pension | 2 |
| 7949 | pens | 2 |
| 7950 | penetrated | 2 |
| 7951 | pegasus | 2 |
| 7952 | peck | 2 |
| 7953 | peaceably | 2 |
| 7954 | pays | 2 |
| 7955 | pawn | 2 |
| 7956 | paw | 2 |
| 7957 | pausing | 2 |
| 7958 | paused | 2 |
| 7959 | pauper | 2 |
| 7960 | paunch | 2 |
| 7961 | paul | 2 |
| 7962 | patterns | 2 |
| 7963 | patron | 2 |
| 7964 | patio | 2 |
| 7965 | patent | 2 |
| 7966 | patches | 2 |
| 7967 | patched | 2 |
| 7968 | pasty | 2 |
| 7969 | pastures | 2 |
| 7970 | pastime | 2 |
| 7971 | passions | 2 |
| 7972 | partner | 2 |
| 7973 | partition | 2 |
| 7974 | partisans | 2 |
| 7975 | parallels | 2 |
| 7976 | paradise | 2 |
| 7977 | pantaloons | 2 |
| 7978 | pans | 2 |
| 7979 | panoply | 2 |
| 7980 | pangs | 2 |
| 7981 | pallas | 2 |
| 7982 | palfreys | 2 |
| 7983 | painstaking | 2 |
| 7984 | painful | 2 |
| 7985 | padlock | 2 |
| 7986 | owl | 2 |
| 7987 | overthrow | 2 |
| 7988 | overnight | 2 |
| 7989 | overmuch | 2 |
| 7990 | overhear | 2 |
| 7991 | overhead | 2 |
| 7992 | overflowing | 2 |
| 7993 | overawed | 2 |
| 7994 | outwardly | 2 |
| 7995 | outset | 2 |
| 7996 | outright | 2 |
| 7997 | outrage | 2 |
| 7998 | outlets | 2 |
| 7999 | originals | 2 |
| 8000 | orient | 2 |
| 8001 | ordering | 2 |
| 8002 | ordained | 2 |
| 8003 | orbaneja | 2 |
| 8004 | orb | 2 |
| 8005 | orange | 2 |
| 8006 | oracle | 2 |
| 8007 | oppressor | 2 |
| 8008 | oppressive | 2 |
| 8009 | oppressed | 2 |
| 8010 | operibus | 2 |
| 8011 | onion | 2 |
| 8012 | omitting | 2 |
| 8013 | omissions | 2 |
| 8014 | omission | 2 |
| 8015 | olives | 2 |
| 8016 | oleander | 2 |
| 8017 | olalla | 2 |
| 8018 | oft | 2 |
| 8019 | officials | 2 |
| 8020 | offhand | 2 |
| 8021 | offending | 2 |
| 8022 | offended | 2 |
| 8023 | offences | 2 |
| 8024 | ods | 2 |
| 8025 | oddest | 2 |
| 8026 | occupies | 2 |
| 8027 | obtained | 2 |
| 8028 | obstinacy | 2 |
| 8029 | observes | 2 |
| 8030 | observation | 2 |
| 8031 | observance | 2 |
| 8032 | obsequies | 2 |
| 8033 | obscurity | 2 |
| 8034 | obduracy | 2 |
| 8035 | oaks | 2 |
| 8036 | nursed | 2 |
| 8037 | nuptial | 2 |
| 8038 | nuns | 2 |
| 8039 | numskull | 2 |
| 8040 | novelty | 2 |
| 8041 | nourishment | 2 |
| 8042 | nought | 2 |
| 8043 | notorious | 2 |
| 8044 | notoriety | 2 |
| 8045 | notaries | 2 |
| 8046 | noses | 2 |
| 8047 | noose | 2 |
| 8048 | noon | 2 |
| 8049 | nook | 2 |
| 8050 | noised | 2 |
| 8051 | nobly | 2 |
| 8052 | nobleness | 2 |
| 8053 | noblemen | 2 |
| 8054 | nobleman | 2 |
| 8055 | ninety | 2 |
| 8056 | nimble | 2 |
| 8057 | niggardliness | 2 |
| 8058 | niggard | 2 |
| 8059 | nicety | 2 |
| 8060 | nicely | 2 |
| 8061 | nests | 2 |
| 8062 | nero | 2 |
| 8063 | negotiation | 2 |
| 8064 | negligence | 2 |
| 8065 | neglect | 2 |
| 8066 | needn | 2 |
| 8067 | necks | 2 |
| 8068 | necessarily | 2 |
| 8069 | neatness | 2 |
| 8070 | navarino | 2 |
| 8071 | natured | 2 |
| 8072 | naturalists | 2 |
| 8073 | napkin | 2 |
| 8074 | nap | 2 |
| 8075 | naming | 2 |
| 8076 | namely | 2 |
| 8077 | mystification | 2 |
| 8078 | mysterious | 2 |
| 8079 | muster | 2 |
| 8080 | musketry | 2 |
| 8081 | muse | 2 |
| 8082 | murderous | 2 |
| 8083 | murdered | 2 |
| 8084 | murcia | 2 |
| 8085 | municipality | 2 |
| 8086 | munching | 2 |
| 8087 | muley | 2 |
| 8088 | mudejars | 2 |
| 8089 | mouthfuls | 2 |
| 8090 | mouthed | 2 |
| 8091 | moustache | 2 |
| 8092 | mouse | 2 |
| 8093 | mourners | 2 |
| 8094 | mourned | 2 |
| 8095 | moulded | 2 |
| 8096 | mottled | 2 |
| 8097 | motley | 2 |
| 8098 | motive | 2 |
| 8099 | motions | 2 |
| 8100 | mortified | 2 |
| 8101 | mortifications | 2 |
| 8102 | morocco | 2 |
| 8103 | morn | 2 |
| 8104 | morals | 2 |
| 8105 | moral | 2 |
| 8106 | moorslayer | 2 |
| 8107 | moons | 2 |
| 8108 | monthly | 2 |
| 8109 | montalban | 2 |
| 8110 | monks | 2 |
| 8111 | monkey | 2 |
| 8112 | monk | 2 |
| 8113 | mollify | 2 |
| 8114 | molinera | 2 |
| 8115 | modestly | 2 |
| 8116 | mockeries | 2 |
| 8117 | moat | 2 |
| 8118 | moaned | 2 |
| 8119 | mix | 2 |
| 8120 | mission | 2 |
| 8121 | mislead | 2 |
| 8122 | miser | 2 |
| 8123 | misdeeds | 2 |
| 8124 | misbehaved | 2 |
| 8125 | mirth | 2 |
| 8126 | minos | 2 |
| 8127 | minor | 2 |
| 8128 | mingle | 2 |
| 8129 | mindful | 2 |
| 8130 | millstone | 2 |
| 8131 | milled | 2 |
| 8132 | military | 2 |
| 8133 | mildew | 2 |
| 8134 | mild | 2 |
| 8135 | milanese | 2 |
| 8136 | milan | 2 |
| 8137 | mightst | 2 |
| 8138 | midsummer | 2 |
| 8139 | midges | 2 |
| 8140 | mettled | 2 |
| 8141 | methuselah | 2 |
| 8142 | methodical | 2 |
| 8143 | method | 2 |
| 8144 | merriment | 2 |
| 8145 | mercury | 2 |
| 8146 | mercer | 2 |
| 8147 | mended | 2 |
| 8148 | menacing | 2 |
| 8149 | menaces | 2 |
| 8150 | melted | 2 |
| 8151 | medes | 2 |
| 8152 | meddlesome | 2 |
| 8153 | meddled | 2 |
| 8154 | meal | 2 |
| 8155 | mature | 2 |
| 8156 | mattress | 2 |
| 8157 | mathematical | 2 |
| 8158 | matchless | 2 |
| 8159 | matches | 2 |
| 8160 | mastery | 2 |
| 8161 | masquerade | 2 |
| 8162 | mask | 2 |
| 8163 | marvelling | 2 |
| 8164 | martial | 2 |
| 8165 | marica | 2 |
| 8166 | marching | 2 |
| 8167 | marches | 2 |
| 8168 | mar | 2 |
| 8169 | map | 2 |
| 8170 | manuscripts | 2 |
| 8171 | manuscript | 2 |
| 8172 | manuel | 2 |
| 8173 | mansions | 2 |
| 8174 | mannerly | 2 |
| 8175 | mannered | 2 |
| 8176 | manned | 2 |
| 8177 | manly | 2 |
| 8178 | manger | 2 |
| 8179 | mane | 2 |
| 8180 | mami | 2 |
| 8181 | malum | 2 |
| 8182 | maltreat | 2 |
| 8183 | malta | 2 |
| 8184 | malicious | 2 |
| 8185 | maketh | 2 |
| 8186 | makest | 2 |
| 8187 | maimed | 2 |
| 8188 | mail | 2 |
| 8189 | magnitude | 2 |
| 8190 | magnify | 2 |
| 8191 | magnificent | 2 |
| 8192 | magnanimity | 2 |
| 8193 | madhouse | 2 |
| 8194 | machuca | 2 |
| 8195 | machine | 2 |
| 8196 | machinations | 2 |
| 8197 | lynx | 2 |
| 8198 | lycurgus | 2 |
| 8199 | lxxiv | 2 |
| 8200 | lxxiii | 2 |
| 8201 | lxxii | 2 |
| 8202 | lxxi | 2 |
| 8203 | lxx | 2 |
| 8204 | lxviii | 2 |
| 8205 | lxvii | 2 |
| 8206 | lxvi | 2 |
| 8207 | lxv | 2 |
| 8208 | lxix | 2 |
| 8209 | lxiv | 2 |
| 8210 | lxiii | 2 |
| 8211 | lxii | 2 |
| 8212 | lxi | 2 |
| 8213 | lx | 2 |
| 8214 | lviii | 2 |
| 8215 | lvii | 2 |
| 8216 | lvi | 2 |
| 8217 | lv | 2 |
| 8218 | luxurious | 2 |
| 8219 | luxuries | 2 |
| 8220 | lustily | 2 |
| 8221 | lust | 2 |
| 8222 | lump | 2 |
| 8223 | lucretia | 2 |
| 8224 | lucia | 2 |
| 8225 | lucar | 2 |
| 8226 | lout | 2 |
| 8227 | losses | 2 |
| 8228 | loser | 2 |
| 8229 | lordly | 2 |
| 8230 | loquacity | 2 |
| 8231 | loosed | 2 |
| 8232 | longinquous | 2 |
| 8233 | longings | 2 |
| 8234 | london | 2 |
| 8235 | lobuna | 2 |
| 8236 | loathe | 2 |
| 8237 | lix | 2 |
| 8238 | liv | 2 |
| 8239 | literature | 2 |
| 8240 | litany | 2 |
| 8241 | lirgandeo | 2 |
| 8242 | lip | 2 |
| 8243 | lining | 2 |
| 8244 | lined | 2 |
| 8245 | limping | 2 |
| 8246 | limp | 2 |
| 8247 | lily | 2 |
| 8248 | liii | 2 |
| 8249 | lighting | 2 |
| 8250 | lighter | 2 |
| 8251 | lieu | 2 |
| 8252 | licked | 2 |
| 8253 | licentious | 2 |
| 8254 | lice | 2 |
| 8255 | liberties | 2 |
| 8256 | liberation | 2 |
| 8257 | lewdness | 2 |
| 8258 | lewd | 2 |
| 8259 | levels | 2 |
| 8260 | lettings | 2 |
| 8261 | lets | 2 |
| 8262 | lesson | 2 |
| 8263 | lessen | 2 |
| 8264 | lengthy | 2 |
| 8265 | lengths | 2 |
| 8266 | lends | 2 |
| 8267 | lelilies | 2 |
| 8268 | legged | 2 |
| 8269 | leaps | 2 |
| 8270 | leans | 2 |
| 8271 | leafy | 2 |
| 8272 | leader | 2 |
| 8273 | leaden | 2 |
| 8274 | laziness | 2 |
| 8275 | lawyers | 2 |
| 8276 | lawyer | 2 |
| 8277 | lavish | 2 |
| 8278 | laurels | 2 |
| 8279 | lather | 2 |
| 8280 | lark | 2 |
| 8281 | largest | 2 |
| 8282 | languishing | 2 |
| 8283 | lain | 2 |
| 8284 | lackey | 2 |
| 8285 | lachrymose | 2 |
| 8286 | laboured | 2 |
| 8287 | laborious | 2 |
| 8288 | knotty | 2 |
| 8289 | knives | 2 |
| 8290 | knife | 2 |
| 8291 | knavery | 2 |
| 8292 | kites | 2 |
| 8293 | kinsman | 2 |
| 8294 | kingly | 2 |
| 8295 | kindnesses | 2 |
| 8296 | kinder | 2 |
| 8297 | keyhole | 2 |
| 8298 | keepest | 2 |
| 8299 | keenly | 2 |
| 8300 | jurist | 2 |
| 8301 | jumping | 2 |
| 8302 | jump | 2 |
| 8303 | juma | 2 |
| 8304 | july | 2 |
| 8305 | judged | 2 |
| 8306 | joys | 2 |
| 8307 | joustings | 2 |
| 8308 | jorge | 2 |
| 8309 | jokers | 2 |
| 8310 | jogged | 2 |
| 8311 | jewellery | 2 |
| 8312 | jet | 2 |
| 8313 | jester | 2 |
| 8314 | jerk | 2 |
| 8315 | jerez | 2 |
| 8316 | jeopardy | 2 |
| 8317 | jelly | 2 |
| 8318 | javelins | 2 |
| 8319 | javelin | 2 |
| 8320 | jarama | 2 |
| 8321 | james | 2 |
| 8322 | ivory | 2 |
| 8323 | isles | 2 |
| 8324 | irreparable | 2 |
| 8325 | irremediable | 2 |
| 8326 | invulnerable | 2 |
| 8327 | involves | 2 |
| 8328 | invoked | 2 |
| 8329 | invite | 2 |
| 8330 | invariably | 2 |
| 8331 | intrigue | 2 |
| 8332 | intimation | 2 |
| 8333 | intimate | 2 |
| 8334 | interval | 2 |
| 8335 | interposing | 2 |
| 8336 | interposed | 2 |
| 8337 | interminable | 2 |
| 8338 | interested | 2 |
| 8339 | intense | 2 |
| 8340 | integrity | 2 |
| 8341 | insulting | 2 |
| 8342 | insulted | 2 |
| 8343 | insula | 2 |
| 8344 | instructor | 2 |
| 8345 | inspiring | 2 |
| 8346 | inspiration | 2 |
| 8347 | insomuch | 2 |
| 8348 | insists | 2 |
| 8349 | insides | 2 |
| 8350 | inseparable | 2 |
| 8351 | inscrutable | 2 |
| 8352 | insanities | 2 |
| 8353 | insane | 2 |
| 8354 | innocents | 2 |
| 8355 | inmost | 2 |
| 8356 | injustices | 2 |
| 8357 | injuring | 2 |
| 8358 | inheritance | 2 |
| 8359 | infuse | 2 |
| 8360 | influenced | 2 |
| 8361 | inflicts | 2 |
| 8362 | inflamed | 2 |
| 8363 | inflame | 2 |
| 8364 | inferior | 2 |
| 8365 | infanta | 2 |
| 8366 | infamy | 2 |
| 8367 | inextricable | 2 |
| 8368 | inexorable | 2 |
| 8369 | inevitable | 2 |
| 8370 | indulge | 2 |
| 8371 | inducing | 2 |
| 8372 | indistinct | 2 |
| 8373 | indispensable | 2 |
| 8374 | indignities | 2 |
| 8375 | indications | 2 |
| 8376 | independence | 2 |
| 8377 | indefatigable | 2 |
| 8378 | indecorous | 2 |
| 8379 | incurring | 2 |
| 8380 | incurred | 2 |
| 8381 | incur | 2 |
| 8382 | incumbent | 2 |
| 8383 | incomprehensible | 2 |
| 8384 | incomparably | 2 |
| 8385 | income | 2 |
| 8386 | include | 2 |
| 8387 | inch | 2 |
| 8388 | incapacitated | 2 |
| 8389 | inadvertence | 2 |
| 8390 | inaccuracies | 2 |
| 8391 | improve | 2 |
| 8392 | impropriety | 2 |
| 8393 | imprisonment | 2 |
| 8394 | impress | 2 |
| 8395 | impregnable | 2 |
| 8396 | impostors | 2 |
| 8397 | imposition | 2 |
| 8398 | impose | 2 |
| 8399 | importunity | 2 |
| 8400 | importuned | 2 |
| 8401 | import | 2 |
| 8402 | impetuosity | 2 |
| 8403 | impertinent | 2 |
| 8404 | imperilling | 2 |
| 8405 | imperative | 2 |
| 8406 | impending | 2 |
| 8407 | impediments | 2 |
| 8408 | impaled | 2 |
| 8409 | impair | 2 |
| 8410 | immured | 2 |
| 8411 | immodesty | 2 |
| 8412 | immodest | 2 |
| 8413 | imitated | 2 |
| 8414 | imbibed | 2 |
| 8415 | imagining | 2 |
| 8416 | idiot | 2 |
| 8417 | iberia | 2 |
| 8418 | hyperboles | 2 |
| 8419 | husk | 2 |
| 8420 | husbandman | 2 |
| 8421 | hurts | 2 |
| 8422 | humbly | 2 |
| 8423 | huff | 2 |
| 8424 | howling | 2 |
| 8425 | howl | 2 |
| 8426 | housings | 2 |
| 8427 | hounds | 2 |
| 8428 | hostile | 2 |
| 8429 | hostelries | 2 |
| 8430 | hospital | 2 |
| 8431 | horrible | 2 |
| 8432 | horizon | 2 |
| 8433 | hopelessly | 2 |
| 8434 | hoops | 2 |
| 8435 | hooped | 2 |
| 8436 | hooked | 2 |
| 8437 | hoodwinked | 2 |
| 8438 | hoods | 2 |
| 8439 | homicide | 2 |
| 8440 | homespun | 2 |
| 8441 | holdest | 2 |
| 8442 | hoces | 2 |
| 8443 | hitch | 2 |
| 8444 | hippogriff | 2 |
| 8445 | hippocrates | 2 |
| 8446 | hints | 2 |
| 8447 | hinting | 2 |
| 8448 | hinges | 2 |
| 8449 | hindering | 2 |
| 8450 | hinder | 2 |
| 8451 | highwaymen | 2 |
| 8452 | hight | 2 |
| 8453 | hidalgo | 2 |
| 8454 | hesitating | 2 |
| 8455 | hesitate | 2 |
| 8456 | heroes | 2 |
| 8457 | hermits | 2 |
| 8458 | hereupon | 2 |
| 8459 | heretics | 2 |
| 8460 | hereafter | 2 |
| 8461 | herds | 2 |
| 8462 | henares | 2 |
| 8463 | heights | 2 |
| 8464 | heighten | 2 |
| 8465 | heel | 2 |
| 8466 | heedlessness | 2 |
| 8467 | heeding | 2 |
| 8468 | heavier | 2 |
| 8469 | heaved | 2 |
| 8470 | hearest | 2 |
| 8471 | healing | 2 |
| 8472 | healed | 2 |
| 8473 | heal | 2 |
| 8474 | headstall | 2 |
| 8475 | hazardous | 2 |
| 8476 | hazard | 2 |
| 8477 | hawking | 2 |
| 8478 | hawk | 2 |
| 8479 | haves | 2 |
| 8480 | haunt | 2 |
| 8481 | haughtiness | 2 |
| 8482 | hateful | 2 |
| 8483 | hatchet | 2 |
| 8484 | hasn | 2 |
| 8485 | harvest | 2 |
| 8486 | harmonious | 2 |
| 8487 | harmonies | 2 |
| 8488 | hardy | 2 |
| 8489 | hardened | 2 |
| 8490 | harboured | 2 |
| 8491 | harasses | 2 |
| 8492 | hannibal | 2 |
| 8493 | hangs | 2 |
| 8494 | hangers | 2 |
| 8495 | handsomest | 2 |
| 8496 | handsomely | 2 |
| 8497 | handing | 2 |
| 8498 | handful | 2 |
| 8499 | hammering | 2 |
| 8500 | hamlets | 2 |
| 8501 | halts | 2 |
| 8502 | hairy | 2 |
| 8503 | hacks | 2 |
| 8504 | hackling | 2 |
| 8505 | ha | 2 |
| 8506 | guts | 2 |
| 8507 | gunpowder | 2 |
| 8508 | gulf | 2 |
| 8509 | guiomar | 2 |
| 8510 | guinea | 2 |
| 8511 | guile | 2 |
| 8512 | guiding | 2 |
| 8513 | guardian | 2 |
| 8514 | guadalajara | 2 |
| 8515 | growth | 2 |
| 8516 | groves | 2 |
| 8517 | grips | 2 |
| 8518 | grin | 2 |
| 8519 | griffin | 2 |
| 8520 | greyhound | 2 |
| 8521 | grazier | 2 |
| 8522 | graven | 2 |
| 8523 | gravelling | 2 |
| 8524 | graved | 2 |
| 8525 | gratifying | 2 |
| 8526 | grappling | 2 |
| 8527 | grandson | 2 |
| 8528 | grandest | 2 |
| 8529 | grandees | 2 |
| 8530 | grandee | 2 |
| 8531 | grammar | 2 |
| 8532 | grains | 2 |
| 8533 | gracefulness | 2 |
| 8534 | governest | 2 |
| 8535 | gourd | 2 |
| 8536 | gotten | 2 |
| 8537 | gossips | 2 |
| 8538 | gorging | 2 |
| 8539 | gordian | 2 |
| 8540 | goodwill | 2 |
| 8541 | goods | 2 |
| 8542 | gonzalez | 2 |
| 8543 | goest | 2 |
| 8544 | gods | 2 |
| 8545 | gnawed | 2 |
| 8546 | gluttony | 2 |
| 8547 | glow | 2 |
| 8548 | glossed | 2 |
| 8549 | glorified | 2 |
| 8550 | glitters | 2 |
| 8551 | glitter | 2 |
| 8552 | glances | 2 |
| 8553 | gladness | 2 |
| 8554 | gladden | 2 |
| 8555 | girding | 2 |
| 8556 | gilded | 2 |
| 8557 | gil | 2 |
| 8558 | giddy | 2 |
| 8559 | gibbet | 2 |
| 8560 | giantess | 2 |
| 8561 | ghost | 2 |
| 8562 | gerfalcons | 2 |
| 8563 | geometrical | 2 |
| 8564 | gentlewomen | 2 |
| 8565 | genoese | 2 |
| 8566 | genil | 2 |
| 8567 | generously | 2 |
| 8568 | generation | 2 |
| 8569 | gems | 2 |
| 8570 | geld | 2 |
| 8571 | gayest | 2 |
| 8572 | gateway | 2 |
| 8573 | garland | 2 |
| 8574 | garcilasso | 2 |
| 8575 | garcilaso | 2 |
| 8576 | gaoler | 2 |
| 8577 | gandalin | 2 |
| 8578 | games | 2 |
| 8579 | galls | 2 |
| 8580 | galloping | 2 |
| 8581 | gallons | 2 |
| 8582 | galliot | 2 |
| 8583 | galateas | 2 |
| 8584 | galatea | 2 |
| 8585 | gala | 2 |
| 8586 | gaiters | 2 |
| 8587 | gainsay | 2 |
| 8588 | gains | 2 |
| 8589 | gag | 2 |
| 8590 | gad | 2 |
| 8591 | furthest | 2 |
| 8592 | furniture | 2 |
| 8593 | furnace | 2 |
| 8594 | fuller | 2 |
| 8595 | fulfilment | 2 |
| 8596 | fulfill | 2 |
| 8597 | fugitive | 2 |
| 8598 | frustrates | 2 |
| 8599 | fruitless | 2 |
| 8600 | frosts | 2 |
| 8601 | frontino | 2 |
| 8602 | frivolity | 2 |
| 8603 | fritters | 2 |
| 8604 | frightful | 2 |
| 8605 | frighten | 2 |
| 8606 | friendships | 2 |
| 8607 | fridays | 2 |
| 8608 | frequented | 2 |
| 8609 | freak | 2 |
| 8610 | frays | 2 |
| 8611 | frankness | 2 |
| 8612 | frank | 2 |
| 8613 | francisca | 2 |
| 8614 | francis | 2 |
| 8615 | fragrant | 2 |
| 8616 | fox | 2 |
| 8617 | fowls | 2 |
| 8618 | founder | 2 |
| 8619 | foundations | 2 |
| 8620 | fortified | 2 |
| 8621 | forthcoming | 2 |
| 8622 | forsake | 2 |
| 8623 | fork | 2 |
| 8624 | forfeited | 2 |
| 8625 | forfeit | 2 |
| 8626 | forewarned | 2 |
| 8627 | forestall | 2 |
| 8628 | foresight | 2 |
| 8629 | foreseeing | 2 |
| 8630 | foresaw | 2 |
| 8631 | foremost | 2 |
| 8632 | foreigners | 2 |
| 8633 | forego | 2 |
| 8634 | forbidding | 2 |
| 8635 | fonseca | 2 |
| 8636 | fondly | 2 |
| 8637 | follower | 2 |
| 8638 | foils | 2 |
| 8639 | foeman | 2 |
| 8640 | foam | 2 |
| 8641 | foal | 2 |
| 8642 | flows | 2 |
| 8643 | flown | 2 |
| 8644 | flowery | 2 |
| 8645 | flourishing | 2 |
| 8646 | flourished | 2 |
| 8647 | florismarte | 2 |
| 8648 | flood | 2 |
| 8649 | flog | 2 |
| 8650 | flinty | 2 |
| 8651 | flint | 2 |
| 8652 | fletches | 2 |
| 8653 | fleshless | 2 |
| 8654 | fleeting | 2 |
| 8655 | fledged | 2 |
| 8656 | fleas | 2 |
| 8657 | flattering | 2 |
| 8658 | flap | 2 |
| 8659 | flagrant | 2 |
| 8660 | flagellation | 2 |
| 8661 | fixes | 2 |
| 8662 | fitly | 2 |
| 8663 | fists | 2 |
| 8664 | firmness | 2 |
| 8665 | firme | 2 |
| 8666 | finery | 2 |
| 8667 | finder | 2 |
| 8668 | filidas | 2 |
| 8669 | file | 2 |
| 8670 | filberts | 2 |
| 8671 | figs | 2 |
| 8672 | figments | 2 |
| 8673 | fiercest | 2 |
| 8674 | fictions | 2 |
| 8675 | fickleness | 2 |
| 8676 | fewer | 2 |
| 8677 | fetters | 2 |
| 8678 | fervour | 2 |
| 8679 | fervent | 2 |
| 8680 | ferry | 2 |
| 8681 | ferret | 2 |
| 8682 | fernandez | 2 |
| 8683 | felicity | 2 |
| 8684 | featured | 2 |
| 8685 | fatherland | 2 |
| 8686 | fastened | 2 |
| 8687 | farewells | 2 |
| 8688 | fantasy | 2 |
| 8689 | fantastic | 2 |
| 8690 | familiarity | 2 |
| 8691 | falsest | 2 |
| 8692 | falcon | 2 |
| 8693 | faithless | 2 |
| 8694 | fairness | 2 |
| 8695 | fails | 2 |
| 8696 | facing | 2 |
| 8697 | fabricated | 2 |
| 8698 | fabric | 2 |
| 8699 | eyelids | 2 |
| 8700 | extricate | 2 |
| 8701 | extremities | 2 |
| 8702 | extravagant | 2 |
| 8703 | extracted | 2 |
| 8704 | extra | 2 |
| 8705 | extol | 2 |
| 8706 | extending | 2 |
| 8707 | expulsion | 2 |
| 8708 | expressing | 2 |
| 8709 | exposing | 2 |
| 8710 | explanation | 2 |
| 8711 | expert | 2 |
| 8712 | experiments | 2 |
| 8713 | expenditure | 2 |
| 8714 | expeditions | 2 |
| 8715 | expedient | 2 |
| 8716 | expanse | 2 |
| 8717 | exists | 2 |
| 8718 | exhibition | 2 |
| 8719 | exhibit | 2 |
| 8720 | exerting | 2 |
| 8721 | executioner | 2 |
| 8722 | excursion | 2 |
| 8723 | excommunicated | 2 |
| 8724 | excites | 2 |
| 8725 | excess | 2 |
| 8726 | excels | 2 |
| 8727 | exceeding | 2 |
| 8728 | exceeded | 2 |
| 8729 | examination | 2 |
| 8730 | exalts | 2 |
| 8731 | exactness | 2 |
| 8732 | everyday | 2 |
| 8733 | euryalus | 2 |
| 8734 | europe | 2 |
| 8735 | eugenio | 2 |
| 8736 | ethiopia | 2 |
| 8737 | estimate | 2 |
| 8738 | estility | 2 |
| 8739 | erring | 2 |
| 8740 | errand | 2 |
| 8741 | err | 2 |
| 8742 | eris | 2 |
| 8743 | erat | 2 |
| 8744 | equipped | 2 |
| 8745 | equinoctial | 2 |
| 8746 | equerry | 2 |
| 8747 | equerries | 2 |
| 8748 | equalled | 2 |
| 8749 | epigrams | 2 |
| 8750 | epic | 2 |
| 8751 | envying | 2 |
| 8752 | entrenchments | 2 |
| 8753 | entreats | 2 |
| 8754 | entitle | 2 |
| 8755 | entice | 2 |
| 8756 | enthroned | 2 |
| 8757 | enthralled | 2 |
| 8758 | entanglements | 2 |
| 8759 | entangled | 2 |
| 8760 | enraged | 2 |
| 8761 | enlivened | 2 |
| 8762 | enlightenment | 2 |
| 8763 | enlighten | 2 |
| 8764 | enjoys | 2 |
| 8765 | enjoyments | 2 |
| 8766 | enjoined | 2 |
| 8767 | enjoin | 2 |
| 8768 | enduring | 2 |
| 8769 | encouragement | 2 |
| 8770 | enchants | 2 |
| 8771 | enacted | 2 |
| 8772 | enabling | 2 |
| 8773 | enabled | 2 |
| 8774 | employs | 2 |
| 8775 | employments | 2 |
| 8776 | employing | 2 |
| 8777 | empires | 2 |
| 8778 | empire | 2 |
| 8779 | emergency | 2 |
| 8780 | emergencies | 2 |
| 8781 | emerged | 2 |
| 8782 | emerencia | 2 |
| 8783 | embroidery | 2 |
| 8784 | embellish | 2 |
| 8785 | embarrassments | 2 |
| 8786 | embarrassed | 2 |
| 8787 | embarking | 2 |
| 8788 | embarked | 2 |
| 8789 | elsewhere | 2 |
| 8790 | eloquent | 2 |
| 8791 | elevation | 2 |
| 8792 | elegies | 2 |
| 8793 | elbows | 2 |
| 8794 | elbow | 2 |
| 8795 | elated | 2 |
| 8796 | elaborate | 2 |
| 8797 | educed | 2 |
| 8798 | eclipse | 2 |
| 8799 | echoes | 2 |
| 8800 | echo | 2 |
| 8801 | easing | 2 |
| 8802 | eagles | 2 |
| 8803 | dyes | 2 |
| 8804 | dwells | 2 |
| 8805 | dwellers | 2 |
| 8806 | dwarfs | 2 |
| 8807 | dusty | 2 |
| 8808 | dungeons | 2 |
| 8809 | dungeon | 2 |
| 8810 | dung | 2 |
| 8811 | dumbfoundered | 2 |
| 8812 | dulcineas | 2 |
| 8813 | dukes | 2 |
| 8814 | duel | 2 |
| 8815 | ducked | 2 |
| 8816 | duchesses | 2 |
| 8817 | dub | 2 |
| 8818 | drum | 2 |
| 8819 | drowsy | 2 |
| 8820 | droller | 2 |
| 8821 | dreading | 2 |
| 8822 | dreadful | 2 |
| 8823 | draws | 2 |
| 8824 | drawbridge | 2 |
| 8825 | drained | 2 |
| 8826 | dragon | 2 |
| 8827 | dragging | 2 |
| 8828 | downright | 2 |
| 8829 | dosed | 2 |
| 8830 | doria | 2 |
| 8831 | donkey | 2 |
| 8832 | donas | 2 |
| 8833 | dolefully | 2 |
| 8834 | doesn | 2 |
| 8835 | doers | 2 |
| 8836 | doer | 2 |
| 8837 | documents | 2 |
| 8838 | divinity | 2 |
| 8839 | divines | 2 |
| 8840 | divest | 2 |
| 8841 | diverted | 2 |
| 8842 | distrust | 2 |
| 8843 | distributing | 2 |
| 8844 | distributed | 2 |
| 8845 | distraction | 2 |
| 8846 | distracted | 2 |
| 8847 | distinguishes | 2 |
| 8848 | distilled | 2 |
| 8849 | dissatisfied | 2 |
| 8850 | disposes | 2 |
| 8851 | displeases | 2 |
| 8852 | displeased | 2 |
| 8853 | dispersed | 2 |
| 8854 | dispensed | 2 |
| 8855 | disparagement | 2 |
| 8856 | disparaged | 2 |
| 8857 | disown | 2 |
| 8858 | dismissing | 2 |
| 8859 | disliked | 2 |
| 8860 | dislike | 2 |
| 8861 | dishonesty | 2 |
| 8862 | disgust | 2 |
| 8863 | disguises | 2 |
| 8864 | discussions | 2 |
| 8865 | discovers | 2 |
| 8866 | discourses | 2 |
| 8867 | discordant | 2 |
| 8868 | discontentedly | 2 |
| 8869 | disconcerted | 2 |
| 8870 | discloses | 2 |
| 8871 | discharging | 2 |
| 8872 | disappearance | 2 |
| 8873 | disabuse | 2 |
| 8874 | dis | 2 |
| 8875 | directly | 2 |
| 8876 | dinted | 2 |
| 8877 | dingy | 2 |
| 8878 | diners | 2 |
| 8879 | dimensions | 2 |
| 8880 | dignities | 2 |
| 8881 | dig | 2 |
| 8882 | differently | 2 |
| 8883 | diest | 2 |
| 8884 | dianas | 2 |
| 8885 | dialogue | 2 |
| 8886 | diabolical | 2 |
| 8887 | di | 2 |
| 8888 | devoutly | 2 |
| 8889 | devours | 2 |
| 8890 | devourer | 2 |
| 8891 | devour | 2 |
| 8892 | detestation | 2 |
| 8893 | detect | 2 |
| 8894 | detach | 2 |
| 8895 | destitute | 2 |
| 8896 | despaired | 2 |
| 8897 | desist | 2 |
| 8898 | descend | 2 |
| 8899 | depravity | 2 |
| 8900 | depraved | 2 |
| 8901 | deposited | 2 |
| 8902 | deplore | 2 |
| 8903 | departing | 2 |
| 8904 | deo | 2 |
| 8905 | denying | 2 |
| 8906 | denounced | 2 |
| 8907 | denied | 2 |
| 8908 | demons | 2 |
| 8909 | demolishing | 2 |
| 8910 | demolish | 2 |
| 8911 | demandest | 2 |
| 8912 | delusive | 2 |
| 8913 | delusions | 2 |
| 8914 | deluded | 2 |
| 8915 | delude | 2 |
| 8916 | delivery | 2 |
| 8917 | deliberation | 2 |
| 8918 | delays | 2 |
| 8919 | degrading | 2 |
| 8920 | defter | 2 |
| 8921 | defied | 2 |
| 8922 | deferred | 2 |
| 8923 | deference | 2 |
| 8924 | defenders | 2 |
| 8925 | defender | 2 |
| 8926 | deem | 2 |
| 8927 | deducted | 2 |
| 8928 | decorous | 2 |
| 8929 | deceptions | 2 |
| 8930 | decent | 2 |
| 8931 | deceives | 2 |
| 8932 | deceiver | 2 |
| 8933 | debts | 2 |
| 8934 | debtor | 2 |
| 8935 | debase | 2 |
| 8936 | dealings | 2 |
| 8937 | dawning | 2 |
| 8938 | dawned | 2 |
| 8939 | daunt | 2 |
| 8940 | dashing | 2 |
| 8941 | dashed | 2 |
| 8942 | darkly | 2 |
| 8943 | darinel | 2 |
| 8944 | dareth | 2 |
| 8945 | curtains | 2 |
| 8946 | curly | 2 |
| 8947 | curing | 2 |
| 8948 | curiambro | 2 |
| 8949 | curb | 2 |
| 8950 | culprit | 2 |
| 8951 | cuenca | 2 |
| 8952 | crutches | 2 |
| 8953 | cruelest | 2 |
| 8954 | crow | 2 |
| 8955 | crouching | 2 |
| 8956 | crop | 2 |
| 8957 | crook | 2 |
| 8958 | croak | 2 |
| 8959 | critical | 2 |
| 8960 | cristiano | 2 |
| 8961 | cris | 2 |
| 8962 | crimped | 2 |
| 8963 | credo | 2 |
| 8964 | credite | 2 |
| 8965 | credible | 2 |
| 8966 | creaking | 2 |
| 8967 | crazed | 2 |
| 8968 | crash | 2 |
| 8969 | craftiness | 2 |
| 8970 | cowed | 2 |
| 8971 | cousins | 2 |
| 8972 | courtesan | 2 |
| 8973 | courted | 2 |
| 8974 | courses | 2 |
| 8975 | counterfeit | 2 |
| 8976 | couldst | 2 |
| 8977 | costing | 2 |
| 8978 | cosmography | 2 |
| 8979 | cosmetics | 2 |
| 8980 | corsairs | 2 |
| 8981 | corrupt | 2 |
| 8982 | corresponds | 2 |
| 8983 | corresponding | 2 |
| 8984 | correspondence | 2 |
| 8985 | corpus | 2 |
| 8986 | corpse | 2 |
| 8987 | cordial | 2 |
| 8988 | copyright | 2 |
| 8989 | copper | 2 |
| 8990 | coolness | 2 |
| 8991 | coolly | 2 |
| 8992 | cooks | 2 |
| 8993 | convulsions | 2 |
| 8994 | convey | 2 |
| 8995 | conversing | 2 |
| 8996 | contriving | 2 |
| 8997 | contravene | 2 |
| 8998 | consumed | 2 |
| 8999 | constitution | 2 |
| 9000 | consternation | 2 |
| 9001 | conspicuously | 2 |
| 9002 | consistent | 2 |
| 9003 | consisted | 2 |
| 9004 | conscious | 2 |
| 9005 | conqueror | 2 |
| 9006 | conquering | 2 |
| 9007 | connection | 2 |
| 9008 | congratulated | 2 |
| 9009 | congeal | 2 |
| 9010 | conformity | 2 |
| 9011 | conform | 2 |
| 9012 | conflict | 2 |
| 9013 | confiscated | 2 |
| 9014 | confines | 2 |
| 9015 | confine | 2 |
| 9016 | confiding | 2 |
| 9017 | confessor | 2 |
| 9018 | confers | 2 |
| 9019 | condolence | 2 |
| 9020 | condescend | 2 |
| 9021 | condemns | 2 |
| 9022 | concocters | 2 |
| 9023 | conclusive | 2 |
| 9024 | conciseness | 2 |
| 9025 | computed | 2 |
| 9026 | compulsion | 2 |
| 9027 | compressing | 2 |
| 9028 | comprehended | 2 |
| 9029 | comport | 2 |
| 9030 | completing | 2 |
| 9031 | compensate | 2 |
| 9032 | compels | 2 |
| 9033 | compano | 2 |
| 9034 | communicate | 2 |
| 9035 | commons | 2 |
| 9036 | commits | 2 |
| 9037 | comforting | 2 |
| 9038 | comers | 2 |
| 9039 | comedies | 2 |
| 9040 | combatant | 2 |
| 9041 | colleges | 2 |
| 9042 | college | 2 |
| 9043 | collars | 2 |
| 9044 | coins | 2 |
| 9045 | coil | 2 |
| 9046 | coherent | 2 |
| 9047 | cogitations | 2 |
| 9048 | coax | 2 |
| 9049 | coachman | 2 |
| 9050 | clyster | 2 |
| 9051 | clustered | 2 |
| 9052 | clung | 2 |
| 9053 | cloisters | 2 |
| 9054 | climbed | 2 |
| 9055 | climb | 2 |
| 9056 | cleverly | 2 |
| 9057 | clerical | 2 |
| 9058 | cleansed | 2 |
| 9059 | cleaner | 2 |
| 9060 | clatter | 2 |
| 9061 | clasps | 2 |
| 9062 | clasping | 2 |
| 9063 | civet | 2 |
| 9064 | ciudad | 2 |
| 9065 | circumspection | 2 |
| 9066 | circumspect | 2 |
| 9067 | circuitous | 2 |
| 9068 | circles | 2 |
| 9069 | circle | 2 |
| 9070 | ciceronian | 2 |
| 9071 | cianis | 2 |
| 9072 | christina | 2 |
| 9073 | christi | 2 |
| 9074 | chloe | 2 |
| 9075 | chivalrous | 2 |
| 9076 | chivalries | 2 |
| 9077 | china | 2 |
| 9078 | childhood | 2 |
| 9079 | chickens | 2 |
| 9080 | chewed | 2 |
| 9081 | chess | 2 |
| 9082 | cheers | 2 |
| 9083 | cheerfulness | 2 |
| 9084 | cheered | 2 |
| 9085 | checking | 2 |
| 9086 | cheats | 2 |
| 9087 | cheaply | 2 |
| 9088 | chatter | 2 |
| 9089 | charmingly | 2 |
| 9090 | charles | 2 |
| 9091 | charger | 2 |
| 9092 | chapels | 2 |
| 9093 | chaos | 2 |
| 9094 | chants | 2 |
| 9095 | challenger | 2 |
| 9096 | certificate | 2 |
| 9097 | ceremonial | 2 |
| 9098 | censurer | 2 |
| 9099 | censured | 2 |
| 9100 | celestial | 2 |
| 9101 | ceiling | 2 |
| 9102 | cavity | 2 |
| 9103 | cautious | 2 |
| 9104 | cautions | 2 |
| 9105 | causing | 2 |
| 9106 | cauldrons | 2 |
| 9107 | cathedral | 2 |
| 9108 | cathay | 2 |
| 9109 | caterer | 2 |
| 9110 | cataracts | 2 |
| 9111 | catalan | 2 |
| 9112 | casts | 2 |
| 9113 | casilda | 2 |
| 9114 | cash | 2 |
| 9115 | carving | 2 |
| 9116 | carve | 2 |
| 9117 | carthusian | 2 |
| 9118 | carthage | 2 |
| 9119 | caressing | 2 |
| 9120 | caracuel | 2 |
| 9121 | caper | 2 |
| 9122 | cape | 2 |
| 9123 | caparisoned | 2 |
| 9124 | capacious | 2 |
| 9125 | canvas | 2 |
| 9126 | canopy | 2 |
| 9127 | canons | 2 |
| 9128 | candour | 2 |
| 9129 | candlesticks | 2 |
| 9130 | calumnies | 2 |
| 9131 | cake | 2 |
| 9132 | cager | 2 |
| 9133 | cadiz | 2 |
| 9134 | cackneys | 2 |
| 9135 | caballeros | 2 |
| 9136 | byways | 2 |
| 9137 | buys | 2 |
| 9138 | buying | 2 |
| 9139 | buttocks | 2 |
| 9140 | butter | 2 |
| 9141 | bust | 2 |
| 9142 | bushel | 2 |
| 9143 | burns | 2 |
| 9144 | bunch | 2 |
| 9145 | bumpkin | 2 |
| 9146 | bullies | 2 |
| 9147 | bullet | 2 |
| 9148 | bulky | 2 |
| 9149 | bulk | 2 |
| 9150 | buildings | 2 |
| 9151 | bugles | 2 |
| 9152 | buffoon | 2 |
| 9153 | buffets | 2 |
| 9154 | buckets | 2 |
| 9155 | bucephalus | 2 |
| 9156 | brunello | 2 |
| 9157 | bruising | 2 |
| 9158 | broker | 2 |
| 9159 | broaches | 2 |
| 9160 | bristly | 2 |
| 9161 | brink | 2 |
| 9162 | brilliancy | 2 |
| 9163 | brightest | 2 |
| 9164 | bridles | 2 |
| 9165 | bridled | 2 |
| 9166 | brethren | 2 |
| 9167 | breeds | 2 |
| 9168 | breasts | 2 |
| 9169 | breastplate | 2 |
| 9170 | bravery | 2 |
| 9171 | bravado | 2 |
| 9172 | brakes | 2 |
| 9173 | bragging | 2 |
| 9174 | braggart | 2 |
| 9175 | bracelets | 2 |
| 9176 | bowls | 2 |
| 9177 | boundless | 2 |
| 9178 | bough | 2 |
| 9179 | borrowed | 2 |
| 9180 | borrow | 2 |
| 9181 | borders | 2 |
| 9182 | bookseller | 2 |
| 9183 | bonfire | 2 |
| 9184 | bonelace | 2 |
| 9185 | bolted | 2 |
| 9186 | bobbins | 2 |
| 9187 | boatswain | 2 |
| 9188 | blundering | 2 |
| 9189 | blunder | 2 |
| 9190 | blown | 2 |
| 9191 | blooming | 2 |
| 9192 | blocks | 2 |
| 9193 | block | 2 |
| 9194 | blindfold | 2 |
| 9195 | blemish | 2 |
| 9196 | bleeding | 2 |
| 9197 | blear | 2 |
| 9198 | blanketings | 2 |
| 9199 | blades | 2 |
| 9200 | bitterest | 2 |
| 9201 | bishop | 2 |
| 9202 | biscuit | 2 |
| 9203 | biscay | 2 |
| 9204 | biding | 2 |
| 9205 | bide | 2 |
| 9206 | bib | 2 |
| 9207 | bewitched | 2 |
| 9208 | beware | 2 |
| 9209 | betrothed | 2 |
| 9210 | betrayed | 2 |
| 9211 | betray | 2 |
| 9212 | betis | 2 |
| 9213 | betimes | 2 |
| 9214 | betakes | 2 |
| 9215 | bestows | 2 |
| 9216 | bestowal | 2 |
| 9217 | berth | 2 |
| 9218 | bernardino | 2 |
| 9219 | bequests | 2 |
| 9220 | beneficiary | 2 |
| 9221 | beneficial | 2 |
| 9222 | benefice | 2 |
| 9223 | bene | 2 |
| 9224 | benches | 2 |
| 9225 | belt | 2 |
| 9226 | belongings | 2 |
| 9227 | bellows | 2 |
| 9228 | bellowing | 2 |
| 9229 | believest | 2 |
| 9230 | belabouring | 2 |
| 9231 | bejar | 2 |
| 9232 | beholders | 2 |
| 9233 | behaving | 2 |
| 9234 | beguile | 2 |
| 9235 | begs | 2 |
| 9236 | beget | 2 |
| 9237 | bedevilled | 2 |
| 9238 | beats | 2 |
| 9239 | beatified | 2 |
| 9240 | bearers | 2 |
| 9241 | beans | 2 |
| 9242 | beadle | 2 |
| 9243 | bayard | 2 |
| 9244 | baste | 2 |
| 9245 | bashfulness | 2 |
| 9246 | barking | 2 |
| 9247 | barefooted | 2 |
| 9248 | barefaced | 2 |
| 9249 | barbers | 2 |
| 9250 | barbarossa | 2 |
| 9251 | barbarians | 2 |
| 9252 | baptised | 2 |
| 9253 | baptise | 2 |
| 9254 | banquets | 2 |
| 9255 | banner | 2 |
| 9256 | bang | 2 |
| 9257 | bandages | 2 |
| 9258 | balls | 2 |
| 9259 | balanced | 2 |
| 9260 | bail | 2 |
| 9261 | bagpipe | 2 |
| 9262 | baggage | 2 |
| 9263 | baeza | 2 |
| 9264 | backpiece | 2 |
| 9265 | backbiters | 2 |
| 9266 | awnings | 2 |
| 9267 | awning | 2 |
| 9268 | awaken | 2 |
| 9269 | avoiding | 2 |
| 9270 | avocations | 2 |
| 9271 | avenging | 2 |
| 9272 | avails | 2 |
| 9273 | availed | 2 |
| 9274 | available | 2 |
| 9275 | autumn | 2 |
| 9276 | autem | 2 |
| 9277 | austria | 2 |
| 9278 | auburn | 2 |
| 9279 | attributing | 2 |
| 9280 | attributed | 2 |
| 9281 | attracts | 2 |
| 9282 | attraction | 2 |
| 9283 | attract | 2 |
| 9284 | attending | 2 |
| 9285 | attacking | 2 |
| 9286 | attachment | 2 |
| 9287 | astronomer | 2 |
| 9288 | astride | 2 |
| 9289 | assures | 2 |
| 9290 | assume | 2 |
| 9291 | assertion | 2 |
| 9292 | assent | 2 |
| 9293 | assaulted | 2 |
| 9294 | assassins | 2 |
| 9295 | assailants | 2 |
| 9296 | askance | 2 |
| 9297 | asia | 2 |
| 9298 | ascribed | 2 |
| 9299 | ascending | 2 |
| 9300 | artistic | 2 |
| 9301 | artifices | 2 |
| 9302 | arthur | 2 |
| 9303 | arrives | 2 |
| 9304 | arrive | 2 |
| 9305 | aroused | 2 |
| 9306 | aromatic | 2 |
| 9307 | arise | 2 |
| 9308 | argues | 2 |
| 9309 | argued | 2 |
| 9310 | ardent | 2 |
| 9311 | archbishops | 2 |
| 9312 | arbitrators | 2 |
| 9313 | arbitrary | 2 |
| 9314 | aranjuez | 2 |
| 9315 | araby | 2 |
| 9316 | arabia | 2 |
| 9317 | aquiline | 2 |
| 9318 | aptly | 2 |
| 9319 | apprehensions | 2 |
| 9320 | apprehend | 2 |
| 9321 | appointment | 2 |
| 9322 | appoint | 2 |
| 9323 | applies | 2 |
| 9324 | apples | 2 |
| 9325 | applause | 2 |
| 9326 | appeals | 2 |
| 9327 | apparitions | 2 |
| 9328 | apology | 2 |
| 9329 | apelles | 2 |
| 9330 | anyhow | 2 |
| 9331 | antiquity | 2 |
| 9332 | antipodes | 2 |
| 9333 | antechamber | 2 |
| 9334 | antaeus | 2 |
| 9335 | answerest | 2 |
| 9336 | annoyed | 2 |
| 9337 | announcing | 2 |
| 9338 | anklets | 2 |
| 9339 | ankles | 2 |
| 9340 | angles | 2 |
| 9341 | angered | 2 |
| 9342 | andrea | 2 |
| 9343 | andalusian | 2 |
| 9344 | ancestors | 2 |
| 9345 | amply | 2 |
| 9346 | amends | 2 |
| 9347 | amen | 2 |
| 9348 | ameji | 2 |
| 9349 | ambitious | 2 |
| 9350 | ambergris | 2 |
| 9351 | alva | 2 |
| 9352 | altitude | 2 |
| 9353 | altars | 2 |
| 9354 | alquife | 2 |
| 9355 | alonzo | 2 |
| 9356 | almacen | 2 |
| 9357 | ally | 2 |
| 9358 | alleviate | 2 |
| 9359 | allegiance | 2 |
| 9360 | alicante | 2 |
| 9361 | alias | 2 |
| 9362 | alexanders | 2 |
| 9363 | albracca | 2 |
| 9364 | albeit | 2 |
| 9365 | al | 2 |
| 9366 | akin | 2 |
| 9367 | airily | 2 |
| 9368 | aimed | 2 |
| 9369 | aids | 2 |
| 9370 | aiding | 2 |
| 9371 | ague | 2 |
| 9372 | agrees | 2 |
| 9373 | agony | 2 |
| 9374 | aged | 2 |
| 9375 | affright | 2 |
| 9376 | affording | 2 |
| 9377 | afflictions | 2 |
| 9378 | affects | 2 |
| 9379 | affectionately | 2 |
| 9380 | affectionate | 2 |
| 9381 | affecting | 2 |
| 9382 | affectation | 2 |
| 9383 | affable | 2 |
| 9384 | affability | 2 |
| 9385 | advises | 2 |
| 9386 | advantages | 2 |
| 9387 | advantageous | 2 |
| 9388 | advances | 2 |
| 9389 | adornment | 2 |
| 9390 | admire | 2 |
| 9391 | admirably | 2 |
| 9392 | admirable | 2 |
| 9393 | addresses | 2 |
| 9394 | addled | 2 |
| 9395 | adapted | 2 |
| 9396 | adapt | 2 |
| 9397 | acquisition | 2 |
| 9398 | acquire | 2 |
| 9399 | acolyte | 2 |
| 9400 | achilles | 2 |
| 9401 | achieving | 2 |
| 9402 | accoutrements | 2 |
| 9403 | accounted | 2 |
| 9404 | accords | 2 |
| 9405 | accorded | 2 |
| 9406 | accommodate | 2 |
| 9407 | acclamations | 2 |
| 9408 | accepts | 2 |
| 9409 | accepting | 2 |
| 9410 | accents | 2 |
| 9411 | academicians | 2 |
| 9412 | abstraction | 2 |
| 9413 | absolute | 2 |
| 9414 | abruptly | 2 |
| 9415 | abounds | 2 |
| 9416 | abound | 2 |
| 9417 | abodes | 2 |
| 9418 | abject | 2 |
| 9419 | abide | 2 |
| 9420 | abhorrence | 2 |
| 9421 | abernuncio | 2 |
| 9422 | abbess | 2 |
| 9423 | abate | 2 |
| 9424 | zulema | 1 |
| 9425 | zorruna | 1 |
| 9426 | zoroastric | 1 |
| 9427 | zoroaster | 1 |
| 9428 | zopyrus | 1 |
| 9429 | zonzorino | 1 |
| 9430 | zoltanis | 1 |
| 9431 | zoilus | 1 |
| 9432 | zodiacs | 1 |
| 9433 | zeuxis | 1 |
| 9434 | zerbino | 1 |
| 9435 | zeca | 1 |
| 9436 | zealous | 1 |
| 9437 | zaquizami | 1 |
| 9438 | zanoguera | 1 |
| 9439 | zagals | 1 |
| 9440 | yseult | 1 |
| 9441 | youngest | 1 |
| 9442 | yokes | 1 |
| 9443 | yieldeth | 1 |
| 9444 | yew | 1 |
| 9445 | yearning | 1 |
| 9446 | yearn | 1 |
| 9447 | yearly | 1 |
| 9448 | yea | 1 |
| 9449 | yawned | 1 |
| 9450 | yanguesan | 1 |
| 9451 | xenophon | 1 |
| 9452 | xarifa | 1 |
| 9453 | xanthus | 1 |
| 9454 | wry | 1 |
| 9455 | wristbands | 1 |
| 9456 | wrinkled | 1 |
| 9457 | wretchedly | 1 |
| 9458 | wretcheder | 1 |
| 9459 | wrestling | 1 |
| 9460 | wrestler | 1 |
| 9461 | wrestle | 1 |
| 9462 | wrest | 1 |
| 9463 | wrecking | 1 |
| 9464 | wreathed | 1 |
| 9465 | wrapper | 1 |
| 9466 | wrap | 1 |
| 9467 | wrangling | 1 |
| 9468 | woven | 1 |
| 9469 | wot | 1 |
| 9470 | worthily | 1 |
| 9471 | worthiest | 1 |
| 9472 | worthier | 1 |
| 9473 | wort | 1 |
| 9474 | worshipped | 1 |
| 9475 | worries | 1 |
| 9476 | worms | 1 |
| 9477 | worlds | 1 |
| 9478 | workshop | 1 |
| 9479 | workmen | 1 |
| 9480 | workmanship | 1 |
| 9481 | woolcarders | 1 |
| 9482 | wooings | 1 |
| 9483 | woody | 1 |
| 9484 | wooded | 1 |
| 9485 | woo | 1 |
| 9486 | wonderstruck | 1 |
| 9487 | wolds | 1 |
| 9488 | wobble | 1 |
| 9489 | woa | 1 |
| 9490 | wittingly | 1 |
| 9491 | witticisms | 1 |
| 9492 | witnessing | 1 |
| 9493 | withouten | 1 |
| 9494 | withering | 1 |
| 9495 | withered | 1 |
| 9496 | withdrawal | 1 |
| 9497 | witches | 1 |
| 9498 | witchcraft | 1 |
| 9499 | wis | 1 |
| 9500 | wire | 1 |
| 9501 | wiping | 1 |
| 9502 | wipes | 1 |
| 9503 | winsome | 1 |
| 9504 | winks | 1 |
| 9505 | wink | 1 |
| 9506 | windpipe | 1 |
| 9507 | wily | 1 |
| 9508 | willow | 1 |
| 9509 | willissimus | 1 |
| 9510 | willingness | 1 |
| 9511 | wildfowl | 1 |
| 9512 | wig | 1 |
| 9513 | widest | 1 |
| 9514 | widespread | 1 |
| 9515 | widened | 1 |
| 9516 | wickeder | 1 |
| 9517 | whoso | 1 |
| 9518 | whored | 1 |
| 9519 | whoe | 1 |
| 9520 | whites | 1 |
| 9521 | whistle | 1 |
| 9522 | whispering | 1 |
| 9523 | whirling | 1 |
| 9524 | whirled | 1 |
| 9525 | whirl | 1 |
| 9526 | whippings | 1 |
| 9527 | whilst | 1 |
| 9528 | whiff | 1 |
| 9529 | whichever | 1 |
| 9530 | wheresoever | 1 |
| 9531 | wherefrom | 1 |
| 9532 | whereer | 1 |
| 9533 | whelp | 1 |
| 9534 | whatsoever | 1 |
| 9535 | whalebone | 1 |
| 9536 | whale | 1 |
| 9537 | wet | 1 |
| 9538 | wells | 1 |
| 9539 | welkin | 1 |
| 9540 | welcoming | 1 |
| 9541 | weighs | 1 |
| 9542 | weighable | 1 |
| 9543 | weeps | 1 |
| 9544 | weeks | 1 |
| 9545 | weeds | 1 |
| 9546 | weeded | 1 |
| 9547 | weed | 1 |
| 9548 | weaver | 1 |
| 9549 | weathercock | 1 |
| 9550 | weariest | 1 |
| 9551 | wearies | 1 |
| 9552 | wearers | 1 |
| 9553 | wean | 1 |
| 9554 | weaklings | 1 |
| 9555 | weakens | 1 |
| 9556 | weakened | 1 |
| 9557 | wayside | 1 |
| 9558 | waylaying | 1 |
| 9559 | wayfarers | 1 |
| 9560 | waxed | 1 |
| 9561 | waving | 1 |
| 9562 | watery | 1 |
| 9563 | watchfulness | 1 |
| 9564 | wasps | 1 |
| 9565 | washes | 1 |
| 9566 | washerwoman | 1 |
| 9567 | wary | 1 |
| 9568 | warriors | 1 |
| 9569 | warmth | 1 |
| 9570 | warms | 1 |
| 9571 | warming | 1 |
| 9572 | warmer | 1 |
| 9573 | warfare | 1 |
| 9574 | wares | 1 |
| 9575 | ware | 1 |
| 9576 | wardrobes | 1 |
| 9577 | warder | 1 |
| 9578 | warden | 1 |
| 9579 | warded | 1 |
| 9580 | warble | 1 |
| 9581 | wantonness | 1 |
| 9582 | wantonly | 1 |
| 9583 | walnut | 1 |
| 9584 | walks | 1 |
| 9585 | walker | 1 |
| 9586 | wakes | 1 |
| 9587 | wakens | 1 |
| 9588 | wakened | 1 |
| 9589 | waive | 1 |
| 9590 | waistcoat | 1 |
| 9591 | wail | 1 |
| 9592 | wah | 1 |
| 9593 | wagon | 1 |
| 9594 | waggish | 1 |
| 9595 | wagging | 1 |
| 9596 | wafer | 1 |
| 9597 | vying | 1 |
| 9598 | vulgarity | 1 |
| 9599 | vulgarities | 1 |
| 9600 | vouchsafe | 1 |
| 9601 | vouch | 1 |
| 9602 | vote | 1 |
| 9603 | voracious | 1 |
| 9604 | vomited | 1 |
| 9605 | volunteered | 1 |
| 9606 | volunteer | 1 |
| 9607 | volley | 1 |
| 9608 | volente | 1 |
| 9609 | voided | 1 |
| 9610 | void | 1 |
| 9611 | vocation | 1 |
| 9612 | vobis | 1 |
| 9613 | vivar | 1 |
| 9614 | vivacity | 1 |
| 9615 | viso | 1 |
| 9616 | visage | 1 |
| 9617 | virues | 1 |
| 9618 | virtually | 1 |
| 9619 | viriatus | 1 |
| 9620 | virginity | 1 |
| 9621 | violets | 1 |
| 9622 | violate | 1 |
| 9623 | vinedressing | 1 |
| 9624 | vine | 1 |
| 9625 | vindicated | 1 |
| 9626 | villanovas | 1 |
| 9627 | villalpando | 1 |
| 9628 | villagers | 1 |
| 9629 | villadiego | 1 |
| 9630 | vileness | 1 |
| 9631 | vigil | 1 |
| 9632 | views | 1 |
| 9633 | victual | 1 |
| 9634 | victoriously | 1 |
| 9635 | victories | 1 |
| 9636 | victims | 1 |
| 9637 | viceroys | 1 |
| 9638 | vicecount | 1 |
| 9639 | vicaria | 1 |
| 9640 | viands | 1 |
| 9641 | vestros | 1 |
| 9642 | vespers | 1 |
| 9643 | vert | 1 |
| 9644 | versification | 1 |
| 9645 | vermin | 1 |
| 9646 | vermilion | 1 |
| 9647 | veritas | 1 |
| 9648 | verisimilitude | 1 |
| 9649 | verino | 1 |
| 9650 | verify | 1 |
| 9651 | verge | 1 |
| 9652 | verdure | 1 |
| 9653 | verdant | 1 |
| 9654 | verbs | 1 |
| 9655 | verbiage | 1 |
| 9656 | venturous | 1 |
| 9657 | venturesome | 1 |
| 9658 | ventures | 1 |
| 9659 | vented | 1 |
| 9660 | venom | 1 |
| 9661 | veneration | 1 |
| 9662 | venditur | 1 |
| 9663 | veintiquatro | 1 |
| 9664 | vehement | 1 |
| 9665 | vecinguerra | 1 |
| 9666 | vaunted | 1 |
| 9667 | vates | 1 |
| 9668 | vastly | 1 |
| 9669 | varying | 1 |
| 9670 | vanish | 1 |
| 9671 | van | 1 |
| 9672 | valuation | 1 |
| 9673 | valladolid | 1 |
| 9674 | vainglory | 1 |
| 9675 | vagary | 1 |
| 9676 | vacating | 1 |
| 9677 | uttermost | 1 |
| 9678 | utrique | 1 |
| 9679 | utility | 1 |
| 9680 | usque | 1 |
| 9681 | ushered | 1 |
| 9682 | usance | 1 |
| 9683 | usages | 1 |
| 9684 | urreas | 1 |
| 9685 | urraca | 1 |
| 9686 | urinary | 1 |
| 9687 | urchins | 1 |
| 9688 | urchin | 1 |
| 9689 | urbina | 1 |
| 9690 | urbanity | 1 |
| 9691 | ups | 1 |
| 9692 | upraised | 1 |
| 9693 | upholder | 1 |
| 9694 | upborne | 1 |
| 9695 | unwounded | 1 |
| 9696 | unworthily | 1 |
| 9697 | unwonted | 1 |
| 9698 | unwillingness | 1 |
| 9699 | unwillingly | 1 |
| 9700 | unwary | 1 |
| 9701 | unwalletted | 1 |
| 9702 | unveiled | 1 |
| 9703 | unveil | 1 |
| 9704 | unvanquished | 1 |
| 9705 | unutterable | 1 |
| 9706 | unused | 1 |
| 9707 | untutored | 1 |
| 9708 | untruths | 1 |
| 9709 | untruth | 1 |
| 9710 | untrussing | 1 |
| 9711 | untruss | 1 |
| 9712 | untroubled | 1 |
| 9713 | untried | 1 |
| 9714 | untranslated | 1 |
| 9715 | untiring | 1 |
| 9716 | unswerving | 1 |
| 9717 | unsustained | 1 |
| 9718 | unsuspiciously | 1 |
| 9719 | unsuspicious | 1 |
| 9720 | unsuspectingly | 1 |
| 9721 | unsuspected | 1 |
| 9722 | unsurpassable | 1 |
| 9723 | unstinting | 1 |
| 9724 | unstained | 1 |
| 9725 | unsought | 1 |
| 9726 | unshared | 1 |
| 9727 | unshaken | 1 |
| 9728 | unsatisfied | 1 |
| 9729 | unsated | 1 |
| 9730 | unsaid | 1 |
| 9731 | unsaddled | 1 |
| 9732 | unripe | 1 |
| 9733 | unrestricted | 1 |
| 9734 | unrestrainedly | 1 |
| 9735 | unrestrained | 1 |
| 9736 | unrest | 1 |
| 9737 | unreservedly | 1 |
| 9738 | unrelenting | 1 |
| 9739 | unrecognised | 1 |
| 9740 | unreasoning | 1 |
| 9741 | unreasonably | 1 |
| 9742 | unreason | 1 |
| 9743 | unreached | 1 |
| 9744 | unpromising | 1 |
| 9745 | unpretending | 1 |
| 9746 | unprepared | 1 |
| 9747 | unpolite | 1 |
| 9748 | unparagoned | 1 |
| 9749 | unpack | 1 |
| 9750 | unobserved | 1 |
| 9751 | uno | 1 |
| 9752 | unnosed | 1 |
| 9753 | unnapped | 1 |
| 9754 | unnamed | 1 |
| 9755 | unmoved | 1 |
| 9756 | unmixed | 1 |
| 9757 | unmercifully | 1 |
| 9758 | unmentioned | 1 |
| 9759 | unmeet | 1 |
| 9760 | unmatched | 1 |
| 9761 | unmask | 1 |
| 9762 | unmannerly | 1 |
| 9763 | unmade | 1 |
| 9764 | unloosing | 1 |
| 9765 | unloading | 1 |
| 9766 | unloaded | 1 |
| 9767 | unkept | 1 |
| 9768 | unkempt | 1 |
| 9769 | universities | 1 |
| 9770 | universally | 1 |
| 9771 | uniting | 1 |
| 9772 | unison | 1 |
| 9773 | union | 1 |
| 9774 | uninjured | 1 |
| 9775 | unicorn | 1 |
| 9776 | unhorsed | 1 |
| 9777 | unhooked | 1 |
| 9778 | unhinge | 1 |
| 9779 | unhesitatingly | 1 |
| 9780 | unharassed | 1 |
| 9781 | unguents | 1 |
| 9782 | ungrudgingly | 1 |
| 9783 | ungratefully | 1 |
| 9784 | ungoverned | 1 |
| 9785 | ungainly | 1 |
| 9786 | unfrequented | 1 |
| 9787 | unfortunates | 1 |
| 9788 | unforced | 1 |
| 9789 | unfold | 1 |
| 9790 | unfeeling | 1 |
| 9791 | unfavourable | 1 |
| 9792 | unfairly | 1 |
| 9793 | unfair | 1 |
| 9794 | unexamined | 1 |
| 9795 | unenforced | 1 |
| 9796 | uneasily | 1 |
| 9797 | unearthly | 1 |
| 9798 | undressing | 1 |
| 9799 | undismayed | 1 |
| 9800 | undisguised | 1 |
| 9801 | undiscerning | 1 |
| 9802 | undimmed | 1 |
| 9803 | undiminished | 1 |
| 9804 | undid | 1 |
| 9805 | underwent | 1 |
| 9806 | undervalued | 1 |
| 9807 | understander | 1 |
| 9808 | undermined | 1 |
| 9809 | undermine | 1 |
| 9810 | underlings | 1 |
| 9811 | undergoes | 1 |
| 9812 | underfoot | 1 |
| 9813 | underfed | 1 |
| 9814 | undelightful | 1 |
| 9815 | undaunted | 1 |
| 9816 | uncultured | 1 |
| 9817 | uncovering | 1 |
| 9818 | uncouth | 1 |
| 9819 | uncountable | 1 |
| 9820 | unconstrained | 1 |
| 9821 | unconscionable | 1 |
| 9822 | unconcernedly | 1 |
| 9823 | uncomfortable | 1 |
| 9824 | uncleanness | 1 |
| 9825 | unclasped | 1 |
| 9826 | unclad | 1 |
| 9827 | uncharitable | 1 |
| 9828 | uncertified | 1 |
| 9829 | unbroken | 1 |
| 9830 | unbosom | 1 |
| 9831 | unborn | 1 |
| 9832 | unblest | 1 |
| 9833 | unbind | 1 |
| 9834 | unbelieving | 1 |
| 9835 | unbelaboured | 1 |
| 9836 | unawares | 1 |
| 9837 | unavoidable | 1 |
| 9838 | unattained | 1 |
| 9839 | unassuming | 1 |
| 9840 | unassailed | 1 |
| 9841 | unapproached | 1 |
| 9842 | unanimous | 1 |
| 9843 | unadvisedly | 1 |
| 9844 | unadorned | 1 |
| 9845 | umbrella | 1 |
| 9846 | tyrians | 1 |
| 9847 | tyrian | 1 |
| 9848 | tyrannical | 1 |
| 9849 | twixt | 1 |
| 9850 | twitted | 1 |
| 9851 | twinges | 1 |
| 9852 | twined | 1 |
| 9853 | twilight | 1 |
| 9854 | twig | 1 |
| 9855 | twenties | 1 |
| 9856 | tutor | 1 |
| 9857 | tuto | 1 |
| 9858 | tut | 1 |
| 9859 | tusks | 1 |
| 9860 | tusked | 1 |
| 9861 | tusk | 1 |
| 9862 | tuscany | 1 |
| 9863 | tuscan | 1 |
| 9864 | turret | 1 |
| 9865 | turres | 1 |
| 9866 | turquesco | 1 |
| 9867 | turnips | 1 |
| 9868 | turnip | 1 |
| 9869 | turkeys | 1 |
| 9870 | turbans | 1 |
| 9871 | turban | 1 |
| 9872 | tunics | 1 |
| 9873 | tunic | 1 |
| 9874 | tune | 1 |
| 9875 | tumble | 1 |
| 9876 | tully | 1 |
| 9877 | tugged | 1 |
| 9878 | tudesqui | 1 |
| 9879 | ts | 1 |
| 9880 | truths | 1 |
| 9881 | truthfully | 1 |
| 9882 | trusts | 1 |
| 9883 | trustfulness | 1 |
| 9884 | trumped | 1 |
| 9885 | trujillo | 1 |
| 9886 | trow | 1 |
| 9887 | trove | 1 |
| 9888 | trophies | 1 |
| 9889 | trombones | 1 |
| 9890 | trojans | 1 |
| 9891 | trojan | 1 |
| 9892 | troglodytes | 1 |
| 9893 | trodden | 1 |
| 9894 | triumphed | 1 |
| 9895 | triumphantly | 1 |
| 9896 | tristram | 1 |
| 9897 | trips | 1 |
| 9898 | tripped | 1 |
| 9899 | trimmings | 1 |
| 9900 | trifled | 1 |
| 9901 | tricky | 1 |
| 9902 | trickster | 1 |
| 9903 | trickling | 1 |
| 9904 | tricked | 1 |
| 9905 | tributary | 1 |
| 9906 | tribulation | 1 |
| 9907 | tribes | 1 |
| 9908 | trials | 1 |
| 9909 | trestles | 1 |
| 9910 | trespassing | 1 |
| 9911 | trespassed | 1 |
| 9912 | trespass | 1 |
| 9913 | trenches | 1 |
| 9914 | tremor | 1 |
| 9915 | treasurer | 1 |
| 9916 | traverses | 1 |
| 9917 | trashy | 1 |
| 9918 | transports | 1 |
| 9919 | transmogrified | 1 |
| 9920 | translators | 1 |
| 9921 | transient | 1 |
| 9922 | transgressed | 1 |
| 9923 | transforms | 1 |
| 9924 | transforming | 1 |
| 9925 | transform | 1 |
| 9926 | transfixing | 1 |
| 9927 | transfixed | 1 |
| 9928 | transcribing | 1 |
| 9929 | transaction | 1 |
| 9930 | tranquillised | 1 |
| 9931 | tramped | 1 |
| 9932 | tramontana | 1 |
| 9933 | trajan | 1 |
| 9934 | traitress | 1 |
| 9935 | trains | 1 |
| 9936 | train | 1 |
| 9937 | trailing | 1 |
| 9938 | trail | 1 |
| 9939 | tradesman | 1 |
| 9940 | tracks | 1 |
| 9941 | trackless | 1 |
| 9942 | track | 1 |
| 9943 | traced | 1 |
| 9944 | trabajos | 1 |
| 9945 | townsfolk | 1 |
| 9946 | tournaments | 1 |
| 9947 | toughest | 1 |
| 9948 | touchy | 1 |
| 9949 | touchstone | 1 |
| 9950 | toto | 1 |
| 9951 | tostado | 1 |
| 9952 | toss | 1 |
| 9953 | tortolites | 1 |
| 9954 | tortoise | 1 |
| 9955 | torre | 1 |
| 9956 | torpid | 1 |
| 9957 | tormes | 1 |
| 9958 | tormentors | 1 |
| 9959 | tordesillesque | 1 |
| 9960 | toraquis | 1 |
| 9961 | toppling | 1 |
| 9962 | topmost | 1 |
| 9963 | topazes | 1 |
| 9964 | toothpick | 1 |
| 9965 | toothache | 1 |
| 9966 | tonsure | 1 |
| 9967 | toned | 1 |
| 9968 | ton | 1 |
| 9969 | tomillas | 1 |
| 9970 | tomboy | 1 |
| 9971 | tomasillo | 1 |
| 9972 | tologian | 1 |
| 9973 | toll | 1 |
| 9974 | toleration | 1 |
| 9975 | toledan | 1 |
| 9976 | toed | 1 |
| 9977 | tizona | 1 |
| 9978 | tityus | 1 |
| 9979 | titled | 1 |
| 9980 | tissues | 1 |
| 9981 | tissue | 1 |
| 9982 | tiresome | 1 |
| 9983 | tires | 1 |
| 9984 | tirantes | 1 |
| 9985 | tiquitoc | 1 |
| 9986 | tipstaff | 1 |
| 9987 | tiopieyo | 1 |
| 9988 | tints | 1 |
| 9989 | tinted | 1 |
| 9990 | timorous | 1 |
| 9991 | timonel | 1 |
| 9992 | timely | 1 |
| 9993 | timed | 1 |
| 9994 | timantes | 1 |
| 9995 | tillageland | 1 |
| 9996 | tillage | 1 |
| 9997 | tights | 1 |
| 9998 | ties | 1 |
| 9999 | tides | 1 |
| 10000 | tickle | 1 |
| 10001 | tibullus | 1 |
| 10002 | tiber | 1 |
| 10003 | tibar | 1 |
| 10004 | thyme | 1 |
| 10005 | thwart | 1 |
| 10006 | thwack | 1 |
| 10007 | thursday | 1 |
| 10008 | thunderer | 1 |
| 10009 | thunderbolts | 1 |
| 10010 | thumps | 1 |
| 10011 | thumbs | 1 |
| 10012 | thumbed | 1 |
| 10013 | thumb | 1 |
| 10014 | thrusting | 1 |
| 10015 | thrumming | 1 |
| 10016 | thrower | 1 |
| 10017 | throttling | 1 |
| 10018 | throttled | 1 |
| 10019 | throbbing | 1 |
| 10020 | thrilling | 1 |
| 10021 | thresholds | 1 |
| 10022 | threading | 1 |
| 10023 | thrash | 1 |
| 10024 | thraldom | 1 |
| 10025 | thracian | 1 |
| 10026 | thoughtlessness | 1 |
| 10027 | thoughtfully | 1 |
| 10028 | thoughtful | 1 |
| 10029 | thoroughfare | 1 |
| 10030 | thoroughbred | 1 |
| 10031 | thorough | 1 |
| 10032 | thong | 1 |
| 10033 | thomases | 1 |
| 10034 | thomas | 1 |
| 10035 | thistles | 1 |
| 10036 | thirties | 1 |
| 10037 | thirstiest | 1 |
| 10038 | thirstier | 1 |
| 10039 | thinness | 1 |
| 10040 | thinker | 1 |
| 10041 | thimbraeus | 1 |
| 10042 | thickheaded | 1 |
| 10043 | thicker | 1 |
| 10044 | thessaly | 1 |
| 10045 | thermodon | 1 |
| 10046 | thereon | 1 |
| 10047 | thereof | 1 |
| 10048 | therefrom | 1 |
| 10049 | thereabouts | 1 |
| 10050 | theory | 1 |
| 10051 | theological | 1 |
| 10052 | theologian | 1 |
| 10053 | thenceforth | 1 |
| 10054 | thefts | 1 |
| 10055 | theatres | 1 |
| 10056 | theatre | 1 |
| 10057 | thanksgivings | 1 |
| 10058 | thankless | 1 |
| 10059 | th | 1 |
| 10060 | tether | 1 |
| 10061 | testing | 1 |
| 10062 | testimonials | 1 |
| 10063 | testily | 1 |
| 10064 | testifying | 1 |
| 10065 | testified | 1 |
| 10066 | tersely | 1 |
| 10067 | terriers | 1 |
| 10068 | terrestrial | 1 |
| 10069 | terraqueous | 1 |
| 10070 | teresona | 1 |
| 10071 | teresaina | 1 |
| 10072 | terence | 1 |
| 10073 | terebinth | 1 |
| 10074 | tenth | 1 |
| 10075 | tent | 1 |
| 10076 | tenorio | 1 |
| 10077 | tenebras | 1 |
| 10078 | tenderest | 1 |
| 10079 | tenderer | 1 |
| 10080 | tendency | 1 |
| 10081 | temptingly | 1 |
| 10082 | tempora | 1 |
| 10083 | tempestuous | 1 |
| 10084 | temperet | 1 |
| 10085 | tellest | 1 |
| 10086 | tellers | 1 |
| 10087 | teller | 1 |
| 10088 | teens | 1 |
| 10089 | tedious | 1 |
| 10090 | tearfully | 1 |
| 10091 | teams | 1 |
| 10092 | teachers | 1 |
| 10093 | teacher | 1 |
| 10094 | tax | 1 |
| 10095 | taverns | 1 |
| 10096 | tasting | 1 |
| 10097 | tasteless | 1 |
| 10098 | tasks | 1 |
| 10099 | tartesians | 1 |
| 10100 | tartesian | 1 |
| 10101 | tarragona | 1 |
| 10102 | tarquin | 1 |
| 10103 | tarpeian | 1 |
| 10104 | tarnished | 1 |
| 10105 | tariff | 1 |
| 10106 | tapster | 1 |
| 10107 | tapping | 1 |
| 10108 | tap | 1 |
| 10109 | tantum | 1 |
| 10110 | tantalus | 1 |
| 10111 | tansillo | 1 |
| 10112 | tanneries | 1 |
| 10113 | tanned | 1 |
| 10114 | tangled | 1 |
| 10115 | tamper | 1 |
| 10116 | taming | 1 |
| 10117 | tambourine | 1 |
| 10118 | talons | 1 |
| 10119 | tally | 1 |
| 10120 | tallied | 1 |
| 10121 | tallest | 1 |
| 10122 | talker | 1 |
| 10123 | talia | 1 |
| 10124 | takest | 1 |
| 10125 | tainted | 1 |
| 10126 | taint | 1 |
| 10127 | tailors | 1 |
| 10128 | tailing | 1 |
| 10129 | tags | 1 |
| 10130 | tagarins | 1 |
| 10131 | taffeta | 1 |
| 10132 | tadpoles | 1 |
| 10133 | tacked | 1 |
| 10134 | tack | 1 |
| 10135 | taciturnity | 1 |
| 10136 | tacit | 1 |
| 10137 | tablantes | 1 |
| 10138 | tablante | 1 |
| 10139 | tabernas | 1 |
| 10140 | tabby | 1 |
| 10141 | tabarca | 1 |
| 10142 | systems | 1 |
| 10143 | syrup | 1 |
| 10144 | syrtes | 1 |
| 10145 | syriac | 1 |
| 10146 | sylvias | 1 |
| 10147 | sylla | 1 |
| 10148 | swordsmanship | 1 |
| 10149 | swoop | 1 |
| 10150 | swollen | 1 |
| 10151 | swish | 1 |
| 10152 | swineherd | 1 |
| 10153 | swindling | 1 |
| 10154 | swindles | 1 |
| 10155 | swindler | 1 |
| 10156 | swifts | 1 |
| 10157 | sweetness | 1 |
| 10158 | sweetly | 1 |
| 10159 | sweats | 1 |
| 10160 | sweated | 1 |
| 10161 | swaying | 1 |
| 10162 | swathing | 1 |
| 10163 | swathed | 1 |
| 10164 | swarms | 1 |
| 10165 | swap | 1 |
| 10166 | swallows | 1 |
| 10167 | swain | 1 |
| 10168 | sustained | 1 |
| 10169 | suspicious | 1 |
| 10170 | suspension | 1 |
| 10171 | suspend | 1 |
| 10172 | survive | 1 |
| 10173 | survey | 1 |
| 10174 | surrounds | 1 |
| 10175 | surrounding | 1 |
| 10176 | surrendering | 1 |
| 10177 | surprising | 1 |
| 10178 | surplices | 1 |
| 10179 | surpassingly | 1 |
| 10180 | surnamed | 1 |
| 10181 | surmounted | 1 |
| 10182 | surging | 1 |
| 10183 | surgeons | 1 |
| 10184 | surety | 1 |
| 10185 | sureties | 1 |
| 10186 | supremacy | 1 |
| 10187 | suppressing | 1 |
| 10188 | suppress | 1 |
| 10189 | supposition | 1 |
| 10190 | supposes | 1 |
| 10191 | supporter | 1 |
| 10192 | supplying | 1 |
| 10193 | supplication | 1 |
| 10194 | supple | 1 |
| 10195 | supping | 1 |
| 10196 | suppers | 1 |
| 10197 | superstitious | 1 |
| 10198 | superscription | 1 |
| 10199 | supernatural | 1 |
| 10200 | sunshade | 1 |
| 10201 | sunlight | 1 |
| 10202 | sundry | 1 |
| 10203 | sunburnt | 1 |
| 10204 | sums | 1 |
| 10205 | summum | 1 |
| 10206 | summons | 1 |
| 10207 | summoning | 1 |
| 10208 | sultry | 1 |
| 10209 | sulphur | 1 |
| 10210 | sully | 1 |
| 10211 | sulkily | 1 |
| 10212 | suite | 1 |
| 10213 | suggests | 1 |
| 10214 | suggestions | 1 |
| 10215 | suggestion | 1 |
| 10216 | suffereth | 1 |
| 10217 | suerte | 1 |
| 10218 | suero | 1 |
| 10219 | sueldos | 1 |
| 10220 | sucked | 1 |
| 10221 | suchlike | 1 |
| 10222 | subtlety | 1 |
| 10223 | subterfuges | 1 |
| 10224 | subsisted | 1 |
| 10225 | subsided | 1 |
| 10226 | submissively | 1 |
| 10227 | sublime | 1 |
| 10228 | sublimated | 1 |
| 10229 | subjection | 1 |
| 10230 | subduing | 1 |
| 10231 | sub | 1 |
| 10232 | suavity | 1 |
| 10233 | suadente | 1 |
| 10234 | su | 1 |
| 10235 | stygian | 1 |
| 10236 | sty | 1 |
| 10237 | stupefy | 1 |
| 10238 | stump | 1 |
| 10239 | stultorum | 1 |
| 10240 | stuffs | 1 |
| 10241 | studded | 1 |
| 10242 | stubborn | 1 |
| 10243 | stubbles | 1 |
| 10244 | stubble | 1 |
| 10245 | strumpets | 1 |
| 10246 | strongest | 1 |
| 10247 | stroked | 1 |
| 10248 | stript | 1 |
| 10249 | stringers | 1 |
| 10250 | stricter | 1 |
| 10251 | strewing | 1 |
| 10252 | strewed | 1 |
| 10253 | stretches | 1 |
| 10254 | strenuous | 1 |
| 10255 | strengthens | 1 |
| 10256 | streamers | 1 |
| 10257 | streamed | 1 |
| 10258 | streaks | 1 |
| 10259 | strayed | 1 |
| 10260 | straps | 1 |
| 10261 | strapping | 1 |
| 10262 | strappado | 1 |
| 10263 | strap | 1 |
| 10264 | strangely | 1 |
| 10265 | stranded | 1 |
| 10266 | straitness | 1 |
| 10267 | strains | 1 |
| 10268 | straightway | 1 |
| 10269 | straightforwardly | 1 |
| 10270 | straighter | 1 |
| 10271 | straighten | 1 |
| 10272 | stowing | 1 |
| 10273 | storming | 1 |
| 10274 | stork | 1 |
| 10275 | stored | 1 |
| 10276 | stooping | 1 |
| 10277 | stooped | 1 |
| 10278 | stoop | 1 |
| 10279 | stoodst | 1 |
| 10280 | stoning | 1 |
| 10281 | stomachs | 1 |
| 10282 | stolid | 1 |
| 10283 | stitching | 1 |
| 10284 | stitched | 1 |
| 10285 | stirs | 1 |
| 10286 | stipulation | 1 |
| 10287 | stipulated | 1 |
| 10288 | stint | 1 |
| 10289 | stinking | 1 |
| 10290 | stink | 1 |
| 10291 | stinging | 1 |
| 10292 | stimulator | 1 |
| 10293 | stimulant | 1 |
| 10294 | stilled | 1 |
| 10295 | stigmatised | 1 |
| 10296 | stifle | 1 |
| 10297 | stiffness | 1 |
| 10298 | stiffly | 1 |
| 10299 | stiffest | 1 |
| 10300 | stewpots | 1 |
| 10301 | stewed | 1 |
| 10302 | sternness | 1 |
| 10303 | sterile | 1 |
| 10304 | stepmother | 1 |
| 10305 | steering | 1 |
| 10306 | steered | 1 |
| 10307 | steam | 1 |
| 10308 | stealthy | 1 |
| 10309 | stealth | 1 |
| 10310 | stealest | 1 |
| 10311 | stealer | 1 |
| 10312 | stead | 1 |
| 10313 | staving | 1 |
| 10314 | staunch | 1 |
| 10315 | statues | 1 |
| 10316 | statements | 1 |
| 10317 | statement | 1 |
| 10318 | stateliness | 1 |
| 10319 | starvation | 1 |
| 10320 | starts | 1 |
| 10321 | startling | 1 |
| 10322 | starry | 1 |
| 10323 | starr | 1 |
| 10324 | starching | 1 |
| 10325 | starboard | 1 |
| 10326 | standstill | 1 |
| 10327 | stanched | 1 |
| 10328 | stamps | 1 |
| 10329 | stammering | 1 |
| 10330 | stalwart | 1 |
| 10331 | stall | 1 |
| 10332 | staking | 1 |
| 10333 | stairs | 1 |
| 10334 | stain | 1 |
| 10335 | staidness | 1 |
| 10336 | staggers | 1 |
| 10337 | staggered | 1 |
| 10338 | stabs | 1 |
| 10339 | stables | 1 |
| 10340 | squirissimus | 1 |
| 10341 | squirings | 1 |
| 10342 | squinted | 1 |
| 10343 | squibs | 1 |
| 10344 | squeamishly | 1 |
| 10345 | squat | 1 |
| 10346 | squares | 1 |
| 10347 | squalls | 1 |
| 10348 | squalling | 1 |
| 10349 | spurns | 1 |
| 10350 | spurning | 1 |
| 10351 | spurned | 1 |
| 10352 | spurn | 1 |
| 10353 | sprung | 1 |
| 10354 | sprout | 1 |
| 10355 | sprinkler | 1 |
| 10356 | sprinkled | 1 |
| 10357 | sprigs | 1 |
| 10358 | sprig | 1 |
| 10359 | spreads | 1 |
| 10360 | spray | 1 |
| 10361 | spout | 1 |
| 10362 | spotted | 1 |
| 10363 | sportsman | 1 |
| 10364 | sportive | 1 |
| 10365 | spoons | 1 |
| 10366 | spoon | 1 |
| 10367 | sponge | 1 |
| 10368 | spokesman | 1 |
| 10369 | splitting | 1 |
| 10370 | splinters | 1 |
| 10371 | splinter | 1 |
| 10372 | spittle | 1 |
| 10373 | spitted | 1 |
| 10374 | spit | 1 |
| 10375 | spiral | 1 |
| 10376 | spilorceria | 1 |
| 10377 | spilling | 1 |
| 10378 | spill | 1 |
| 10379 | spikes | 1 |
| 10380 | spiked | 1 |
| 10381 | spiced | 1 |
| 10382 | spero | 1 |
| 10383 | spends | 1 |
| 10384 | spellbound | 1 |
| 10385 | speeds | 1 |
| 10386 | speechifying | 1 |
| 10387 | spectres | 1 |
| 10388 | spectators | 1 |
| 10389 | spectator | 1 |
| 10390 | spectacled | 1 |
| 10391 | specify | 1 |
| 10392 | specified | 1 |
| 10393 | spearing | 1 |
| 10394 | spat | 1 |
| 10395 | spasms | 1 |
| 10396 | spasm | 1 |
| 10397 | sparse | 1 |
| 10398 | spareness | 1 |
| 10399 | spank | 1 |
| 10400 | spangles | 1 |
| 10401 | span | 1 |
| 10402 | spains | 1 |
| 10403 | sown | 1 |
| 10404 | sowing | 1 |
| 10405 | sowgelder | 1 |
| 10406 | southern | 1 |
| 10407 | south | 1 |
| 10408 | sour | 1 |
| 10409 | soup | 1 |
| 10410 | soulless | 1 |
| 10411 | souled | 1 |
| 10412 | sorrento | 1 |
| 10413 | sorest | 1 |
| 10414 | sorer | 1 |
| 10415 | sorcery | 1 |
| 10416 | sorceries | 1 |
| 10417 | sorceress | 1 |
| 10418 | sops | 1 |
| 10419 | sophistry | 1 |
| 10420 | sophisticated | 1 |
| 10421 | soothed | 1 |
| 10422 | soothe | 1 |
| 10423 | sooth | 1 |
| 10424 | songster | 1 |
| 10425 | sombreness | 1 |
| 10426 | sombre | 1 |
| 10427 | solution | 1 |
| 10428 | solus | 1 |
| 10429 | solstices | 1 |
| 10430 | solon | 1 |
| 10431 | solomon | 1 |
| 10432 | solisdan | 1 |
| 10433 | soliloquising | 1 |
| 10434 | soliloquise | 1 |
| 10435 | solicitous | 1 |
| 10436 | solicited | 1 |
| 10437 | solicitations | 1 |
| 10438 | solicit | 1 |
| 10439 | soles | 1 |
| 10440 | soldiering | 1 |
| 10441 | solder | 1 |
| 10442 | solaces | 1 |
| 10443 | solaced | 1 |
| 10444 | soiled | 1 |
| 10445 | softens | 1 |
| 10446 | socks | 1 |
| 10447 | sockets | 1 |
| 10448 | sobradisa | 1 |
| 10449 | sobbing | 1 |
| 10450 | soaring | 1 |
| 10451 | soar | 1 |
| 10452 | soapings | 1 |
| 10453 | soaping | 1 |
| 10454 | soaped | 1 |
| 10455 | soaked | 1 |
| 10456 | soak | 1 |
| 10457 | snuffled | 1 |
| 10458 | snuffing | 1 |
| 10459 | snowy | 1 |
| 10460 | snows | 1 |
| 10461 | sniffing | 1 |
| 10462 | sniffed | 1 |
| 10463 | sneers | 1 |
| 10464 | sneering | 1 |
| 10465 | sneered | 1 |
| 10466 | sneakingly | 1 |
| 10467 | sneak | 1 |
| 10468 | snatches | 1 |
| 10469 | snarling | 1 |
| 10470 | snarled | 1 |
| 10471 | snare | 1 |
| 10472 | snake | 1 |
| 10473 | snail | 1 |
| 10474 | smuggle | 1 |
| 10475 | smoothing | 1 |
| 10476 | smoother | 1 |
| 10477 | smoking | 1 |
| 10478 | smiting | 1 |
| 10479 | smithies | 1 |
| 10480 | smith | 1 |
| 10481 | smile | 1 |
| 10482 | smellest | 1 |
| 10483 | smear | 1 |
| 10484 | smattering | 1 |
| 10485 | smashing | 1 |
| 10486 | smartly | 1 |
| 10487 | smarter | 1 |
| 10488 | smarten | 1 |
| 10489 | smack | 1 |
| 10490 | slyly | 1 |
| 10491 | slut | 1 |
| 10492 | slur | 1 |
| 10493 | slumbering | 1 |
| 10494 | slumber | 1 |
| 10495 | slovenliness | 1 |
| 10496 | slothfully | 1 |
| 10497 | slothful | 1 |
| 10498 | slitting | 1 |
| 10499 | slit | 1 |
| 10500 | slips | 1 |
| 10501 | slippery | 1 |
| 10502 | slipper | 1 |
| 10503 | slings | 1 |
| 10504 | sling | 1 |
| 10505 | slim | 1 |
| 10506 | slide | 1 |
| 10507 | slid | 1 |
| 10508 | slices | 1 |
| 10509 | slice | 1 |
| 10510 | sleeve | 1 |
| 10511 | sleeplessness | 1 |
| 10512 | sleeper | 1 |
| 10513 | sleek | 1 |
| 10514 | slayest | 1 |
| 10515 | slaughtering | 1 |
| 10516 | slants | 1 |
| 10517 | slanderous | 1 |
| 10518 | slanderers | 1 |
| 10519 | slander | 1 |
| 10520 | slackened | 1 |
| 10521 | skipped | 1 |
| 10522 | skimmed | 1 |
| 10523 | skim | 1 |
| 10524 | skillful | 1 |
| 10525 | sketch | 1 |
| 10526 | skeleton | 1 |
| 10527 | skein | 1 |
| 10528 | sixth | 1 |
| 10529 | sixteenth | 1 |
| 10530 | sixes | 1 |
| 10531 | situations | 1 |
| 10532 | situation | 1 |
| 10533 | situated | 1 |
| 10534 | sittest | 1 |
| 10535 | sits | 1 |
| 10536 | site | 1 |
| 10537 | sisyphus | 1 |
| 10538 | sinon | 1 |
| 10539 | sinning | 1 |
| 10540 | sinks | 1 |
| 10541 | sinister | 1 |
| 10542 | singly | 1 |
| 10543 | singest | 1 |
| 10544 | singers | 1 |
| 10545 | sinful | 1 |
| 10546 | sinewy | 1 |
| 10547 | sinews | 1 |
| 10548 | sincerely | 1 |
| 10549 | simon | 1 |
| 10550 | simmering | 1 |
| 10551 | similitude | 1 |
| 10552 | silvato | 1 |
| 10553 | silva | 1 |
| 10554 | sillinesses | 1 |
| 10555 | sillier | 1 |
| 10556 | silenus | 1 |
| 10557 | siguenza | 1 |
| 10558 | sigismunda | 1 |
| 10559 | sightless | 1 |
| 10560 | sifted | 1 |
| 10561 | sift | 1 |
| 10562 | siestas | 1 |
| 10563 | siesta | 1 |
| 10564 | sickness | 1 |
| 10565 | sickle | 1 |
| 10566 | shylands | 1 |
| 10567 | shuts | 1 |
| 10568 | shuns | 1 |
| 10569 | shunning | 1 |
| 10570 | shrug | 1 |
| 10571 | shrovetide | 1 |
| 10572 | shroud | 1 |
| 10573 | shrivelled | 1 |
| 10574 | shrieks | 1 |
| 10575 | shrew | 1 |
| 10576 | shreds | 1 |
| 10577 | showered | 1 |
| 10578 | shovels | 1 |
| 10579 | shovel | 1 |
| 10580 | shouldered | 1 |
| 10581 | shortcoming | 1 |
| 10582 | shores | 1 |
| 10583 | shops | 1 |
| 10584 | shopkeeper | 1 |
| 10585 | shivers | 1 |
| 10586 | shiver | 1 |
| 10587 | shirk | 1 |
| 10588 | shipwrecks | 1 |
| 10589 | shine | 1 |
| 10590 | shifting | 1 |
| 10591 | shifted | 1 |
| 10592 | shielded | 1 |
| 10593 | shelf | 1 |
| 10594 | sheeted | 1 |
| 10595 | sheering | 1 |
| 10596 | sheepfold | 1 |
| 10597 | sheds | 1 |
| 10598 | sheathed | 1 |
| 10599 | sheathe | 1 |
| 10600 | shears | 1 |
| 10601 | sharply | 1 |
| 10602 | sharing | 1 |
| 10603 | shaped | 1 |
| 10604 | shanty | 1 |
| 10605 | shanties | 1 |
| 10606 | shanks | 1 |
| 10607 | shaming | 1 |
| 10608 | shamelessness | 1 |
| 10609 | shamefully | 1 |
| 10610 | shameful | 1 |
| 10611 | shallowness | 1 |
| 10612 | shakes | 1 |
| 10613 | shaded | 1 |
| 10614 | shad | 1 |
| 10615 | shackles | 1 |
| 10616 | shabbiness | 1 |
| 10617 | sewn | 1 |
| 10618 | sewer | 1 |
| 10619 | sew | 1 |
| 10620 | sevillian | 1 |
| 10621 | severities | 1 |
| 10622 | sever | 1 |
| 10623 | settles | 1 |
| 10624 | settest | 1 |
| 10625 | setter | 1 |
| 10626 | setoff | 1 |
| 10627 | servitors | 1 |
| 10628 | servissimus | 1 |
| 10629 | servile | 1 |
| 10630 | seriousness | 1 |
| 10631 | sergas | 1 |
| 10632 | serenity | 1 |
| 10633 | serenades | 1 |
| 10634 | seraglio | 1 |
| 10635 | sequence | 1 |
| 10636 | sentiments | 1 |
| 10637 | sensibly | 1 |
| 10638 | sendeth | 1 |
| 10639 | senate | 1 |
| 10640 | seminary | 1 |
| 10641 | semblances | 1 |
| 10642 | selim | 1 |
| 10643 | seizure | 1 |
| 10644 | seigniory | 1 |
| 10645 | seigniories | 1 |
| 10646 | seductive | 1 |
| 10647 | seduced | 1 |
| 10648 | sed | 1 |
| 10649 | securely | 1 |
| 10650 | sects | 1 |
| 10651 | sect | 1 |
| 10652 | seasoning | 1 |
| 10653 | seasoned | 1 |
| 10654 | seasonable | 1 |
| 10655 | seashore | 1 |
| 10656 | seaports | 1 |
| 10657 | seaport | 1 |
| 10658 | seamstress | 1 |
| 10659 | seams | 1 |
| 10660 | seam | 1 |
| 10661 | seacoast | 1 |
| 10662 | scythian | 1 |
| 10663 | scythe | 1 |
| 10664 | scyllas | 1 |
| 10665 | scuttled | 1 |
| 10666 | scum | 1 |
| 10667 | scuffles | 1 |
| 10668 | scud | 1 |
| 10669 | scrutinized | 1 |
| 10670 | scrutinised | 1 |
| 10671 | scruple | 1 |
| 10672 | scripserunt | 1 |
| 10673 | scrip | 1 |
| 10674 | scrimmage | 1 |
| 10675 | scribes | 1 |
| 10676 | screaming | 1 |
| 10677 | scream | 1 |
| 10678 | scrawl | 1 |
| 10679 | scrape | 1 |
| 10680 | scouts | 1 |
| 10681 | scourges | 1 |
| 10682 | scotched | 1 |
| 10683 | scorns | 1 |
| 10684 | scornfully | 1 |
| 10685 | scornful | 1 |
| 10686 | scornest | 1 |
| 10687 | scoldings | 1 |
| 10688 | scold | 1 |
| 10689 | scoffers | 1 |
| 10690 | scoffed | 1 |
| 10691 | scipios | 1 |
| 10692 | scipio | 1 |
| 10693 | schoolboys | 1 |
| 10694 | scholastic | 1 |
| 10695 | scholars | 1 |
| 10696 | schismatics | 1 |
| 10697 | sceptred | 1 |
| 10698 | scatterest | 1 |
| 10699 | scatterbrain | 1 |
| 10700 | scatter | 1 |
| 10701 | scars | 1 |
| 10702 | scarifying | 1 |
| 10703 | scarify | 1 |
| 10704 | scarf | 1 |
| 10705 | scares | 1 |
| 10706 | scapegraces | 1 |
| 10707 | scapegrace | 1 |
| 10708 | scant | 1 |
| 10709 | scanned | 1 |
| 10710 | scandals | 1 |
| 10711 | scandalous | 1 |
| 10712 | scandalised | 1 |
| 10713 | scandal | 1 |
| 10714 | scale | 1 |
| 10715 | scaffold | 1 |
| 10716 | saws | 1 |
| 10717 | savours | 1 |
| 10718 | savoured | 1 |
| 10719 | saves | 1 |
| 10720 | sauciness | 1 |
| 10721 | saucer | 1 |
| 10722 | saturnine | 1 |
| 10723 | saturdays | 1 |
| 10724 | saturday | 1 |
| 10725 | saturatio | 1 |
| 10726 | satisfies | 1 |
| 10727 | satirical | 1 |
| 10728 | satiety | 1 |
| 10729 | sated | 1 |
| 10730 | sardinian | 1 |
| 10731 | sardines | 1 |
| 10732 | sard | 1 |
| 10733 | sapping | 1 |
| 10734 | sapless | 1 |
| 10735 | sannazaro | 1 |
| 10736 | sank | 1 |
| 10737 | sanity | 1 |
| 10738 | sanguine | 1 |
| 10739 | sandy | 1 |
| 10740 | sandoval | 1 |
| 10741 | sandbags | 1 |
| 10742 | sandals | 1 |
| 10743 | sanctity | 1 |
| 10744 | sanctioning | 1 |
| 10745 | sancta | 1 |
| 10746 | sanchos | 1 |
| 10747 | sanchobienaya | 1 |
| 10748 | sanchico | 1 |
| 10749 | samsonino | 1 |
| 10750 | sambenito | 1 |
| 10751 | salves | 1 |
| 10752 | salutiferous | 1 |
| 10753 | salutary | 1 |
| 10754 | salting | 1 |
| 10755 | sallow | 1 |
| 10756 | salivation | 1 |
| 10757 | salazar | 1 |
| 10758 | salamander | 1 |
| 10759 | salable | 1 |
| 10760 | saker | 1 |
| 10761 | sainted | 1 |
| 10762 | sailed | 1 |
| 10763 | sagittarius | 1 |
| 10764 | safest | 1 |
| 10765 | safeguard | 1 |
| 10766 | sacristans | 1 |
| 10767 | sacrilege | 1 |
| 10768 | sacraments | 1 |
| 10769 | sackful | 1 |
| 10770 | sable | 1 |
| 10771 | sabaean | 1 |
| 10772 | rusty | 1 |
| 10773 | rustling | 1 |
| 10774 | rustle | 1 |
| 10775 | rusting | 1 |
| 10776 | rustics | 1 |
| 10777 | rusticity | 1 |
| 10778 | rushes | 1 |
| 10779 | rural | 1 |
| 10780 | runners | 1 |
| 10781 | rumours | 1 |
| 10782 | rumoured | 1 |
| 10783 | ruminating | 1 |
| 10784 | rumbling | 1 |
| 10785 | ruling | 1 |
| 10786 | rulers | 1 |
| 10787 | ruled | 1 |
| 10788 | ruins | 1 |
| 10789 | rugel | 1 |
| 10790 | rufo | 1 |
| 10791 | ruffles | 1 |
| 10792 | ruffled | 1 |
| 10793 | ruffians | 1 |
| 10794 | rue | 1 |
| 10795 | rudely | 1 |
| 10796 | ruddle | 1 |
| 10797 | rubicund | 1 |
| 10798 | rubicon | 1 |
| 10799 | rub | 1 |
| 10800 | royalty | 1 |
| 10801 | rower | 1 |
| 10802 | rove | 1 |
| 10803 | routing | 1 |
| 10804 | rout | 1 |
| 10805 | rousing | 1 |
| 10806 | rotunda | 1 |
| 10807 | rotting | 1 |
| 10808 | rottener | 1 |
| 10809 | rote | 1 |
| 10810 | rot | 1 |
| 10811 | ropy | 1 |
| 10812 | roomy | 1 |
| 10813 | rondilla | 1 |
| 10814 | rolands | 1 |
| 10815 | rojas | 1 |
| 10816 | roguishly | 1 |
| 10817 | rogues | 1 |
| 10818 | rogations | 1 |
| 10819 | rodamonte | 1 |
| 10820 | rocky | 1 |
| 10821 | rochelle | 1 |
| 10822 | rocabertis | 1 |
| 10823 | robs | 1 |
| 10824 | roarings | 1 |
| 10825 | roar | 1 |
| 10826 | rivulets | 1 |
| 10827 | rivulet | 1 |
| 10828 | rivalry | 1 |
| 10829 | rivalries | 1 |
| 10830 | risking | 1 |
| 10831 | risest | 1 |
| 10832 | riser | 1 |
| 10833 | ripple | 1 |
| 10834 | riphaean | 1 |
| 10835 | ripeness | 1 |
| 10836 | ripened | 1 |
| 10837 | riot | 1 |
| 10838 | rinsings | 1 |
| 10839 | rinsed | 1 |
| 10840 | rind | 1 |
| 10841 | rinconete | 1 |
| 10842 | rinaldo | 1 |
| 10843 | rills | 1 |
| 10844 | rigmarole | 1 |
| 10845 | rigid | 1 |
| 10846 | rightful | 1 |
| 10847 | rigged | 1 |
| 10848 | rifled | 1 |
| 10849 | rifle | 1 |
| 10850 | ridiculous | 1 |
| 10851 | ridge | 1 |
| 10852 | ridest | 1 |
| 10853 | riddles | 1 |
| 10854 | riddle | 1 |
| 10855 | rickety | 1 |
| 10856 | rice | 1 |
| 10857 | ricamonte | 1 |
| 10858 | ribbed | 1 |
| 10859 | ribald | 1 |
| 10860 | riaran | 1 |
| 10861 | rhyming | 1 |
| 10862 | rhubarb | 1 |
| 10863 | rheum | 1 |
| 10864 | revulgo | 1 |
| 10865 | revolts | 1 |
| 10866 | revolt | 1 |
| 10867 | revoked | 1 |
| 10868 | revoke | 1 |
| 10869 | revives | 1 |
| 10870 | reviver | 1 |
| 10871 | revival | 1 |
| 10872 | revising | 1 |
| 10873 | reviles | 1 |
| 10874 | reviewed | 1 |
| 10875 | reverie | 1 |
| 10876 | revere | 1 |
| 10877 | revenging | 1 |
| 10878 | revengeful | 1 |
| 10879 | revels | 1 |
| 10880 | revelled | 1 |
| 10881 | retreats | 1 |
| 10882 | retracted | 1 |
| 10883 | retorted | 1 |
| 10884 | reti | 1 |
| 10885 | rethoric | 1 |
| 10886 | retentive | 1 |
| 10887 | retchings | 1 |
| 10888 | retaliation | 1 |
| 10889 | retablo | 1 |
| 10890 | resuscitation | 1 |
| 10891 | restricts | 1 |
| 10892 | restraints | 1 |
| 10893 | restoreth | 1 |
| 10894 | restive | 1 |
| 10895 | responsibility | 1 |
| 10896 | response | 1 |
| 10897 | responded | 1 |
| 10898 | respite | 1 |
| 10899 | respecting | 1 |
| 10900 | respectful | 1 |
| 10901 | resounds | 1 |
| 10902 | resounding | 1 |
| 10903 | resolving | 1 |
| 10904 | resolves | 1 |
| 10905 | resists | 1 |
| 10906 | resistless | 1 |
| 10907 | resisting | 1 |
| 10908 | resisted | 1 |
| 10909 | resistance | 1 |
| 10910 | resin | 1 |
| 10911 | resent | 1 |
| 10912 | resemble | 1 |
| 10913 | rescuing | 1 |
| 10914 | rescued | 1 |
| 10915 | requisition | 1 |
| 10916 | requiring | 1 |
| 10917 | requesting | 1 |
| 10918 | requesenes | 1 |
| 10919 | reputable | 1 |
| 10920 | repulsive | 1 |
| 10921 | repugnance | 1 |
| 10922 | republic | 1 |
| 10923 | reproving | 1 |
| 10924 | reproduce | 1 |
| 10925 | reproachful | 1 |
| 10926 | reprieve | 1 |
| 10927 | repress | 1 |
| 10928 | representing | 1 |
| 10929 | reposing | 1 |
| 10930 | reposed | 1 |
| 10931 | reposada | 1 |
| 10932 | reports | 1 |
| 10933 | reporting | 1 |
| 10934 | repenting | 1 |
| 10935 | repentest | 1 |
| 10936 | repelling | 1 |
| 10937 | repelled | 1 |
| 10938 | repeatedly | 1 |
| 10939 | reopening | 1 |
| 10940 | renouncing | 1 |
| 10941 | renounced | 1 |
| 10942 | renews | 1 |
| 10943 | renewing | 1 |
| 10944 | rending | 1 |
| 10945 | renders | 1 |
| 10946 | remunerated | 1 |
| 10947 | removes | 1 |
| 10948 | removal | 1 |
| 10949 | remounted | 1 |
| 10950 | remotest | 1 |
| 10951 | remorseful | 1 |
| 10952 | remonstrated | 1 |
| 10953 | remonstrance | 1 |
| 10954 | remodel | 1 |
| 10955 | remitted | 1 |
| 10956 | remissness | 1 |
| 10957 | remission | 1 |
| 10958 | remesten | 1 |
| 10959 | remembrances | 1 |
| 10960 | remembering | 1 |
| 10961 | remedying | 1 |
| 10962 | remedies | 1 |
| 10963 | remarkably | 1 |
| 10964 | remands | 1 |
| 10965 | remainders | 1 |
| 10966 | remade | 1 |
| 10967 | reluctance | 1 |
| 10968 | reliance | 1 |
| 10969 | relaxing | 1 |
| 10970 | relax | 1 |
| 10971 | relatively | 1 |
| 10972 | relapsed | 1 |
| 10973 | rejoicing | 1 |
| 10974 | rejections | 1 |
| 10975 | rejection | 1 |
| 10976 | rejecting | 1 |
| 10977 | reinstate | 1 |
| 10978 | reined | 1 |
| 10979 | reigns | 1 |
| 10980 | regumque | 1 |
| 10981 | regulate | 1 |
| 10982 | regrets | 1 |
| 10983 | registries | 1 |
| 10984 | register | 1 |
| 10985 | regiment | 1 |
| 10986 | regardest | 1 |
| 10987 | regaling | 1 |
| 10988 | refutations | 1 |
| 10989 | refusal | 1 |
| 10990 | refulgence | 1 |
| 10991 | refreshment | 1 |
| 10992 | refreshed | 1 |
| 10993 | refrains | 1 |
| 10994 | reforming | 1 |
| 10995 | reform | 1 |
| 10996 | refinements | 1 |
| 10997 | refinement | 1 |
| 10998 | refectory | 1 |
| 10999 | reeling | 1 |
| 11000 | reeled | 1 |
| 11001 | reel | 1 |
| 11002 | reeking | 1 |
| 11003 | reduction | 1 |
| 11004 | reducing | 1 |
| 11005 | reduces | 1 |
| 11006 | redondillas | 1 |
| 11007 | redolence | 1 |
| 11008 | rectorships | 1 |
| 11009 | rectors | 1 |
| 11010 | rector | 1 |
| 11011 | recreations | 1 |
| 11012 | reconsidered | 1 |
| 11013 | recondite | 1 |
| 11014 | reconciling | 1 |
| 11015 | reconciled | 1 |
| 11016 | recommending | 1 |
| 11017 | recoils | 1 |
| 11018 | recognises | 1 |
| 11019 | recline | 1 |
| 11020 | reciting | 1 |
| 11021 | reciprocal | 1 |
| 11022 | recently | 1 |
| 11023 | recalls | 1 |
| 11024 | rebukes | 1 |
| 11025 | rebellas | 1 |
| 11026 | rebecks | 1 |
| 11027 | reasoned | 1 |
| 11028 | rearing | 1 |
| 11029 | reaps | 1 |
| 11030 | reappearance | 1 |
| 11031 | reaper | 1 |
| 11032 | reaped | 1 |
| 11033 | readmission | 1 |
| 11034 | readjusted | 1 |
| 11035 | readissimus | 1 |
| 11036 | rawness | 1 |
| 11037 | rawest | 1 |
| 11038 | ravishers | 1 |
| 11039 | ravens | 1 |
| 11040 | ravening | 1 |
| 11041 | ravena | 1 |
| 11042 | ravelin | 1 |
| 11043 | rave | 1 |
| 11044 | rattling | 1 |
| 11045 | rattle | 1 |
| 11046 | rationality | 1 |
| 11047 | rastrea | 1 |
| 11048 | rashers | 1 |
| 11049 | rasher | 1 |
| 11050 | rascality | 1 |
| 11051 | rarely | 1 |
| 11052 | rapturous | 1 |
| 11053 | raps | 1 |
| 11054 | rapped | 1 |
| 11055 | ranks | 1 |
| 11056 | ranged | 1 |
| 11057 | ramble | 1 |
| 11058 | raisins | 1 |
| 11059 | rains | 1 |
| 11060 | rails | 1 |
| 11061 | railed | 1 |
| 11062 | raggeder | 1 |
| 11063 | rag | 1 |
| 11064 | radical | 1 |
| 11065 | radiating | 1 |
| 11066 | radiant | 1 |
| 11067 | rackets | 1 |
| 11068 | rack | 1 |
| 11069 | racing | 1 |
| 11070 | quotes | 1 |
| 11071 | quoit | 1 |
| 11072 | quixotissimus | 1 |
| 11073 | quixotades | 1 |
| 11074 | quittest | 1 |
| 11075 | quirocia | 1 |
| 11076 | quintessence | 1 |
| 11077 | quinces | 1 |
| 11078 | quilted | 1 |
| 11079 | quilt | 1 |
| 11080 | quieting | 1 |
| 11081 | quietest | 1 |
| 11082 | quieter | 1 |
| 11083 | quidem | 1 |
| 11084 | quickening | 1 |
| 11085 | quickened | 1 |
| 11086 | quexana | 1 |
| 11087 | questioners | 1 |
| 11088 | questioner | 1 |
| 11089 | questionable | 1 |
| 11090 | query | 1 |
| 11091 | quartos | 1 |
| 11092 | quartan | 1 |
| 11093 | quart | 1 |
| 11094 | quarrelsome | 1 |
| 11095 | quando | 1 |
| 11096 | quandary | 1 |
| 11097 | qualms | 1 |
| 11098 | qualify | 1 |
| 11099 | quacks | 1 |
| 11100 | quack | 1 |
| 11101 | pyrenees | 1 |
| 11102 | pylades | 1 |
| 11103 | puzzles | 1 |
| 11104 | putrid | 1 |
| 11105 | pusillanimity | 1 |
| 11106 | purveyor | 1 |
| 11107 | pursuer | 1 |
| 11108 | purses | 1 |
| 11109 | purport | 1 |
| 11110 | puppets | 1 |
| 11111 | punishments | 1 |
| 11112 | punishing | 1 |
| 11113 | punctiliousness | 1 |
| 11114 | punched | 1 |
| 11115 | punch | 1 |
| 11116 | pummel | 1 |
| 11117 | pulsat | 1 |
| 11118 | pulpits | 1 |
| 11119 | pulling | 1 |
| 11120 | puff | 1 |
| 11121 | puertocarrero | 1 |
| 11122 | puebla | 1 |
| 11123 | puckered | 1 |
| 11124 | publishing | 1 |
| 11125 | publisher | 1 |
| 11126 | publicly | 1 |
| 11127 | ptolemies | 1 |
| 11128 | psalteries | 1 |
| 11129 | pry | 1 |
| 11130 | pruning | 1 |
| 11131 | prune | 1 |
| 11132 | prowling | 1 |
| 11133 | prow | 1 |
| 11134 | provisioned | 1 |
| 11135 | provides | 1 |
| 11136 | provender | 1 |
| 11137 | proven | 1 |
| 11138 | provant | 1 |
| 11139 | proudly | 1 |
| 11140 | protrude | 1 |
| 11141 | protesting | 1 |
| 11142 | protestations | 1 |
| 11143 | protectors | 1 |
| 11144 | prostration | 1 |
| 11145 | prospects | 1 |
| 11146 | prosecution | 1 |
| 11147 | props | 1 |
| 11148 | propping | 1 |
| 11149 | propped | 1 |
| 11150 | proposals | 1 |
| 11151 | prophesied | 1 |
| 11152 | properties | 1 |
| 11153 | propensities | 1 |
| 11154 | pronounce | 1 |
| 11155 | prompting | 1 |
| 11156 | prompted | 1 |
| 11157 | promoters | 1 |
| 11158 | promontory | 1 |
| 11159 | prominent | 1 |
| 11160 | prolonging | 1 |
| 11161 | prolonged | 1 |
| 11162 | prolong | 1 |
| 11163 | prolixity | 1 |
| 11164 | projector | 1 |
| 11165 | projections | 1 |
| 11166 | projecting | 1 |
| 11167 | prohibits | 1 |
| 11168 | profundities | 1 |
| 11169 | profits | 1 |
| 11170 | proficient | 1 |
| 11171 | professor | 1 |
| 11172 | professing | 1 |
| 11173 | profanity | 1 |
| 11174 | productions | 1 |
| 11175 | product | 1 |
| 11176 | producing | 1 |
| 11177 | prodigiously | 1 |
| 11178 | proddings | 1 |
| 11179 | procured | 1 |
| 11180 | proclaims | 1 |
| 11181 | processions | 1 |
| 11182 | processionists | 1 |
| 11183 | probation | 1 |
| 11184 | pro | 1 |
| 11185 | privity | 1 |
| 11186 | privet | 1 |
| 11187 | privacy | 1 |
| 11188 | prithee | 1 |
| 11189 | prioress | 1 |
| 11190 | priora | 1 |
| 11191 | printer | 1 |
| 11192 | principled | 1 |
| 11193 | principio | 1 |
| 11194 | principals | 1 |
| 11195 | primeval | 1 |
| 11196 | primera | 1 |
| 11197 | primed | 1 |
| 11198 | primaeval | 1 |
| 11199 | pricking | 1 |
| 11200 | prevaricator | 1 |
| 11201 | pretext | 1 |
| 11202 | pretends | 1 |
| 11203 | presumptuous | 1 |
| 11204 | presumed | 1 |
| 11205 | presume | 1 |
| 11206 | pressingly | 1 |
| 11207 | prescribes | 1 |
| 11208 | prepossessing | 1 |
| 11209 | preordination | 1 |
| 11210 | prematurely | 1 |
| 11211 | prelude | 1 |
| 11212 | preliminary | 1 |
| 11213 | prejudicial | 1 |
| 11214 | prejudiced | 1 |
| 11215 | preeminence | 1 |
| 11216 | predicted | 1 |
| 11217 | precipitately | 1 |
| 11218 | precipitate | 1 |
| 11219 | precinct | 1 |
| 11220 | precept | 1 |
| 11221 | preceeding | 1 |
| 11222 | preceding | 1 |
| 11223 | precedent | 1 |
| 11224 | precedence | 1 |
| 11225 | prearranged | 1 |
| 11226 | preambles | 1 |
| 11227 | preaches | 1 |
| 11228 | preachers | 1 |
| 11229 | preached | 1 |
| 11230 | pre | 1 |
| 11231 | prays | 1 |
| 11232 | prayed | 1 |
| 11233 | prate | 1 |
| 11234 | practical | 1 |
| 11235 | practicable | 1 |
| 11236 | pox | 1 |
| 11237 | powerfully | 1 |
| 11238 | powder | 1 |
| 11239 | pours | 1 |
| 11240 | pouring | 1 |
| 11241 | pounces | 1 |
| 11242 | poultry | 1 |
| 11243 | potter | 1 |
| 11244 | potions | 1 |
| 11245 | potful | 1 |
| 11246 | posture | 1 |
| 11247 | posting | 1 |
| 11248 | postillion | 1 |
| 11249 | postern | 1 |
| 11250 | postage | 1 |
| 11251 | possessors | 1 |
| 11252 | posadas | 1 |
| 11253 | posada | 1 |
| 11254 | portuguese | 1 |
| 11255 | ports | 1 |
| 11256 | portrays | 1 |
| 11257 | portraying | 1 |
| 11258 | portions | 1 |
| 11259 | portioned | 1 |
| 11260 | portico | 1 |
| 11261 | portia | 1 |
| 11262 | porters | 1 |
| 11263 | portcullis | 1 |
| 11264 | pores | 1 |
| 11265 | popes | 1 |
| 11266 | poorly | 1 |
| 11267 | poorer | 1 |
| 11268 | pontus | 1 |
| 11269 | pontifical | 1 |
| 11270 | pontiffs | 1 |
| 11271 | ponderous | 1 |
| 11272 | pommelled | 1 |
| 11273 | pommel | 1 |
| 11274 | polyphemes | 1 |
| 11275 | pollux | 1 |
| 11276 | politely | 1 |
| 11277 | polish | 1 |
| 11278 | policy | 1 |
| 11279 | poisonous | 1 |
| 11280 | poisoned | 1 |
| 11281 | poises | 1 |
| 11282 | poised | 1 |
| 11283 | pods | 1 |
| 11284 | pocketed | 1 |
| 11285 | plutarch | 1 |
| 11286 | plumaged | 1 |
| 11287 | plum | 1 |
| 11288 | plugs | 1 |
| 11289 | ploughs | 1 |
| 11290 | ploughing | 1 |
| 11291 | ploughed | 1 |
| 11292 | plodding | 1 |
| 11293 | plies | 1 |
| 11294 | plenteous | 1 |
| 11295 | plenary | 1 |
| 11296 | plectro | 1 |
| 11297 | plebeians | 1 |
| 11298 | pleasurable | 1 |
| 11299 | pleaded | 1 |
| 11300 | plea | 1 |
| 11301 | plazas | 1 |
| 11302 | plaything | 1 |
| 11303 | playful | 1 |
| 11304 | playest | 1 |
| 11305 | platter | 1 |
| 11306 | platirs | 1 |
| 11307 | plastering | 1 |
| 11308 | plants | 1 |
| 11309 | planks | 1 |
| 11310 | plaisance | 1 |
| 11311 | plaintiff | 1 |
| 11312 | placerdemivida | 1 |
| 11313 | pius | 1 |
| 11314 | piu | 1 |
| 11315 | pitted | 1 |
| 11316 | pits | 1 |
| 11317 | pitiful | 1 |
| 11318 | pith | 1 |
| 11319 | pitfall | 1 |
| 11320 | pisuerga | 1 |
| 11321 | pirates | 1 |
| 11322 | pips | 1 |
| 11323 | pipkinful | 1 |
| 11324 | piping | 1 |
| 11325 | piped | 1 |
| 11326 | pioneers | 1 |
| 11327 | piojo | 1 |
| 11328 | pintiquiniestra | 1 |
| 11329 | pint | 1 |
| 11330 | pinproddings | 1 |
| 11331 | pinprodding | 1 |
| 11332 | pinnacles | 1 |
| 11333 | pinked | 1 |
| 11334 | pink | 1 |
| 11335 | pineclad | 1 |
| 11336 | pinchbeck | 1 |
| 11337 | pinch | 1 |
| 11338 | pimping | 1 |
| 11339 | pillaged | 1 |
| 11340 | pillage | 1 |
| 11341 | pilfer | 1 |
| 11342 | piles | 1 |
| 11343 | piled | 1 |
| 11344 | pilchards | 1 |
| 11345 | pikes | 1 |
| 11346 | pignatta | 1 |
| 11347 | pigments | 1 |
| 11348 | piety | 1 |
| 11349 | piedrahita | 1 |
| 11350 | piedmont | 1 |
| 11351 | piecemeal | 1 |
| 11352 | piebald | 1 |
| 11353 | picturing | 1 |
| 11354 | pictured | 1 |
| 11355 | picks | 1 |
| 11356 | pickles | 1 |
| 11357 | pickled | 1 |
| 11358 | picking | 1 |
| 11359 | pickaxes | 1 |
| 11360 | pickaxe | 1 |
| 11361 | piace | 1 |
| 11362 | physicians | 1 |
| 11363 | phyllis | 1 |
| 11364 | phoebuses | 1 |
| 11365 | phlegmaties | 1 |
| 11366 | phlegmatics | 1 |
| 11367 | phlegmatically | 1 |
| 11368 | philosophies | 1 |
| 11369 | phillises | 1 |
| 11370 | pheasants | 1 |
| 11371 | pharaohs | 1 |
| 11372 | petticoats | 1 |
| 11373 | petronels | 1 |
| 11374 | petrals | 1 |
| 11375 | petition | 1 |
| 11376 | pet | 1 |
| 11377 | pestilent | 1 |
| 11378 | pestilence | 1 |
| 11379 | pessima | 1 |
| 11380 | perverter | 1 |
| 11381 | perverted | 1 |
| 11382 | perversity | 1 |
| 11383 | perverseness | 1 |
| 11384 | pervaded | 1 |
| 11385 | pervade | 1 |
| 11386 | perusing | 1 |
| 11387 | peru | 1 |
| 11388 | pertinent | 1 |
| 11389 | pertaining | 1 |
| 11390 | persuasive | 1 |
| 11391 | perspiring | 1 |
| 11392 | perspired | 1 |
| 11393 | personified | 1 |
| 11394 | persists | 1 |
| 11395 | persistent | 1 |
| 11396 | perseus | 1 |
| 11397 | persecutors | 1 |
| 11398 | perrillo | 1 |
| 11399 | perplexities | 1 |
| 11400 | perpetuity | 1 |
| 11401 | perogrullo | 1 |
| 11402 | pero | 1 |
| 11403 | permittest | 1 |
| 11404 | permits | 1 |
| 11405 | perlerino | 1 |
| 11406 | perlerina | 1 |
| 11407 | perjured | 1 |
| 11408 | peritoa | 1 |
| 11409 | perishing | 1 |
| 11410 | perishes | 1 |
| 11411 | periquillo | 1 |
| 11412 | perion | 1 |
| 11413 | periodical | 1 |
| 11414 | perfumes | 1 |
| 11415 | perfumery | 1 |
| 11416 | perfume | 1 |
| 11417 | perendenga | 1 |
| 11418 | peregrination | 1 |
| 11419 | perdition | 1 |
| 11420 | perdicis | 1 |
| 11421 | perched | 1 |
| 11422 | perception | 1 |
| 11423 | perceivest | 1 |
| 11424 | peralvillo | 1 |
| 11425 | per | 1 |
| 11426 | peppery | 1 |
| 11427 | pepin | 1 |
| 11428 | pent | 1 |
| 11429 | pennons | 1 |
| 11430 | penned | 1 |
| 11431 | penman | 1 |
| 11432 | penitent | 1 |
| 11433 | peneus | 1 |
| 11434 | penetrate | 1 |
| 11435 | penelope | 1 |
| 11436 | pending | 1 |
| 11437 | pencils | 1 |
| 11438 | pence | 1 |
| 11439 | pelt | 1 |
| 11440 | pellis | 1 |
| 11441 | peered | 1 |
| 11442 | peeled | 1 |
| 11443 | peel | 1 |
| 11444 | pedigrees | 1 |
| 11445 | pede | 1 |
| 11446 | pedants | 1 |
| 11447 | peculiarities | 1 |
| 11448 | peckish | 1 |
| 11449 | pecked | 1 |
| 11450 | pebble | 1 |
| 11451 | peas | 1 |
| 11452 | pearly | 1 |
| 11453 | pealing | 1 |
| 11454 | peal | 1 |
| 11455 | peaked | 1 |
| 11456 | peak | 1 |
| 11457 | peacemakers | 1 |
| 11458 | pawning | 1 |
| 11459 | pawing | 1 |
| 11460 | paved | 1 |
| 11461 | pauperum | 1 |
| 11462 | patrimony | 1 |
| 11463 | patrimonial | 1 |
| 11464 | patriarch | 1 |
| 11465 | pathetically | 1 |
| 11466 | paternity | 1 |
| 11467 | patena | 1 |
| 11468 | pata | 1 |
| 11469 | passionate | 1 |
| 11470 | passenger | 1 |
| 11471 | paso | 1 |
| 11472 | pasamaques | 1 |
| 11473 | partially | 1 |
| 11474 | parthians | 1 |
| 11475 | partes | 1 |
| 11476 | parsimonious | 1 |
| 11477 | parrhasius | 1 |
| 11478 | paroxysms | 1 |
| 11479 | paroxysm | 1 |
| 11480 | paropillo | 1 |
| 11481 | parley | 1 |
| 11482 | parishioners | 1 |
| 11483 | parish | 1 |
| 11484 | parenthesis | 1 |
| 11485 | parentage | 1 |
| 11486 | parent | 1 |
| 11487 | pardons | 1 |
| 11488 | pardoning | 1 |
| 11489 | parcel | 1 |
| 11490 | paralytics | 1 |
| 11491 | paralyses | 1 |
| 11492 | paralysed | 1 |
| 11493 | paralipomenon | 1 |
| 11494 | paradoxes | 1 |
| 11495 | parading | 1 |
| 11496 | papin | 1 |
| 11497 | pap | 1 |
| 11498 | panzino | 1 |
| 11499 | panting | 1 |
| 11500 | pannel | 1 |
| 11501 | panics | 1 |
| 11502 | panic | 1 |
| 11503 | paniaguado | 1 |
| 11504 | pang | 1 |
| 11505 | pane | 1 |
| 11506 | pandahilado | 1 |
| 11507 | pancino | 1 |
| 11508 | panchaia | 1 |
| 11509 | pancakes | 1 |
| 11510 | pamphlet | 1 |
| 11511 | palpable | 1 |
| 11512 | palomeque | 1 |
| 11513 | pallida | 1 |
| 11514 | palladium | 1 |
| 11515 | palinurus | 1 |
| 11516 | palaver | 1 |
| 11517 | palate | 1 |
| 11518 | palafoxes | 1 |
| 11519 | paladin | 1 |
| 11520 | paints | 1 |
| 11521 | painters | 1 |
| 11522 | pained | 1 |
| 11523 | pail | 1 |
| 11524 | paglia | 1 |
| 11525 | pageantry | 1 |
| 11526 | pagano | 1 |
| 11527 | paganism | 1 |
| 11528 | pads | 1 |
| 11529 | padre | 1 |
| 11530 | pactolus | 1 |
| 11531 | pact | 1 |
| 11532 | packing | 1 |
| 11533 | packets | 1 |
| 11534 | oxcart | 1 |
| 11535 | owns | 1 |
| 11536 | ownership | 1 |
| 11537 | oviedo | 1 |
| 11538 | overwork | 1 |
| 11539 | overweighted | 1 |
| 11540 | overweening | 1 |
| 11541 | overturns | 1 |
| 11542 | overtops | 1 |
| 11543 | overtop | 1 |
| 11544 | overthrowing | 1 |
| 11545 | overspread | 1 |
| 11546 | overshadowed | 1 |
| 11547 | overseers | 1 |
| 11548 | overseer | 1 |
| 11549 | overrun | 1 |
| 11550 | overpast | 1 |
| 11551 | overpass | 1 |
| 11552 | overmasters | 1 |
| 11553 | overmastered | 1 |
| 11554 | overlooked | 1 |
| 11555 | overlook | 1 |
| 11556 | overload | 1 |
| 11557 | overjoyed | 1 |
| 11558 | overhauled | 1 |
| 11559 | overhanging | 1 |
| 11560 | overgrown | 1 |
| 11561 | overflowings | 1 |
| 11562 | overcoming | 1 |
| 11563 | overcomes | 1 |
| 11564 | outweighs | 1 |
| 11565 | outwards | 1 |
| 11566 | outward | 1 |
| 11567 | outstretched | 1 |
| 11568 | outs | 1 |
| 11569 | outrageous | 1 |
| 11570 | outline | 1 |
| 11571 | outlaws | 1 |
| 11572 | outlasted | 1 |
| 11573 | outlast | 1 |
| 11574 | outlandish | 1 |
| 11575 | outdone | 1 |
| 11576 | outcast | 1 |
| 11577 | ounces | 1 |
| 11578 | ostentation | 1 |
| 11579 | ossa | 1 |
| 11580 | orsini | 1 |
| 11581 | ormsby | 1 |
| 11582 | orianas | 1 |
| 11583 | organising | 1 |
| 11584 | orestes | 1 |
| 11585 | orelia | 1 |
| 11586 | ordonez | 1 |
| 11587 | ordain | 1 |
| 11588 | oratory | 1 |
| 11589 | oratories | 1 |
| 11590 | oppressors | 1 |
| 11591 | oppressively | 1 |
| 11592 | oppression | 1 |
| 11593 | opposites | 1 |
| 11594 | opin | 1 |
| 11595 | openings | 1 |
| 11596 | onerous | 1 |
| 11597 | omnis | 1 |
| 11598 | omnipotent | 1 |
| 11599 | ominous | 1 |
| 11600 | omecils | 1 |
| 11601 | olivera | 1 |
| 11602 | olivantes | 1 |
| 11603 | olivante | 1 |
| 11604 | oliva | 1 |
| 11605 | oldest | 1 |
| 11606 | ointments | 1 |
| 11607 | ohs | 1 |
| 11608 | oftener | 1 |
| 11609 | offspring | 1 |
| 11610 | officious | 1 |
| 11611 | official | 1 |
| 11612 | offends | 1 |
| 11613 | offenders | 1 |
| 11614 | offender | 1 |
| 11615 | odours | 1 |
| 11616 | october | 1 |
| 11617 | octavianus | 1 |
| 11618 | octave | 1 |
| 11619 | oceans | 1 |
| 11620 | occupying | 1 |
| 11621 | occupations | 1 |
| 11622 | occupant | 1 |
| 11623 | occult | 1 |
| 11624 | occiput | 1 |
| 11625 | occidit | 1 |
| 11626 | occasionally | 1 |
| 11627 | obtuse | 1 |
| 11628 | obstructions | 1 |
| 11629 | obscuring | 1 |
| 11630 | obscene | 1 |
| 11631 | oblivious | 1 |
| 11632 | obliquely | 1 |
| 11633 | obliging | 1 |
| 11634 | obliges | 1 |
| 11635 | objections | 1 |
| 11636 | objectionable | 1 |
| 11637 | obeys | 1 |
| 11638 | obeisances | 1 |
| 11639 | oared | 1 |
| 11640 | nuzas | 1 |
| 11641 | nutshell | 1 |
| 11642 | nuncio | 1 |
| 11643 | numidians | 1 |
| 11644 | numerus | 1 |
| 11645 | numerabis | 1 |
| 11646 | numbered | 1 |
| 11647 | numantia | 1 |
| 11648 | num | 1 |
| 11649 | nulla | 1 |
| 11650 | nuisance | 1 |
| 11651 | nubila | 1 |
| 11652 | noxious | 1 |
| 11653 | nowise | 1 |
| 11654 | novitiate | 1 |
| 11655 | novelties | 1 |
| 11656 | nourishing | 1 |
| 11657 | nouns | 1 |
| 11658 | noted | 1 |
| 11659 | notebooks | 1 |
| 11660 | nosy | 1 |
| 11661 | nostrils | 1 |
| 11662 | noseless | 1 |
| 11663 | north | 1 |
| 11664 | noriz | 1 |
| 11665 | noodle | 1 |
| 11666 | nonsensical | 1 |
| 11667 | nona | 1 |
| 11668 | nomenclature | 1 |
| 11669 | noises | 1 |
| 11670 | nogales | 1 |
| 11671 | noddies | 1 |
| 11672 | noblest | 1 |
| 11673 | nobler | 1 |
| 11674 | nobis | 1 |
| 11675 | nizarani | 1 |
| 11676 | nisus | 1 |
| 11677 | nineteen | 1 |
| 11678 | nines | 1 |
| 11679 | nimrod | 1 |
| 11680 | nimbler | 1 |
| 11681 | nile | 1 |
| 11682 | nil | 1 |
| 11683 | nightmare | 1 |
| 11684 | niculoso | 1 |
| 11685 | nicolao | 1 |
| 11686 | niarros | 1 |
| 11687 | network | 1 |
| 11688 | net | 1 |
| 11689 | nestor | 1 |
| 11690 | nervous | 1 |
| 11691 | nerves | 1 |
| 11692 | nerved | 1 |
| 11693 | nerbia | 1 |
| 11694 | nemoroso | 1 |
| 11695 | neighs | 1 |
| 11696 | neighings | 1 |
| 11697 | neighbourly | 1 |
| 11698 | neighbouring | 1 |
| 11699 | neigh | 1 |
| 11700 | neigbbour | 1 |
| 11701 | negotiator | 1 |
| 11702 | negotiations | 1 |
| 11703 | negligent | 1 |
| 11704 | needlework | 1 |
| 11705 | needlewoman | 1 |
| 11706 | needles | 1 |
| 11707 | needing | 1 |
| 11708 | necklace | 1 |
| 11709 | necked | 1 |
| 11710 | neath | 1 |
| 11711 | neapolitan | 1 |
| 11712 | ne | 1 |
| 11713 | navarre | 1 |
| 11714 | naval | 1 |
| 11715 | nauseous | 1 |
| 11716 | naughty | 1 |
| 11717 | natives | 1 |
| 11718 | nastiness | 1 |
| 11719 | narrowness | 1 |
| 11720 | narrower | 1 |
| 11721 | narration | 1 |
| 11722 | narrated | 1 |
| 11723 | nape | 1 |
| 11724 | nailed | 1 |
| 11725 | nagging | 1 |
| 11726 | mystic | 1 |
| 11727 | mysteries | 1 |
| 11728 | myrtle | 1 |
| 11729 | muzaraque | 1 |
| 11730 | mutual | 1 |
| 11731 | mutton | 1 |
| 11732 | mutius | 1 |
| 11733 | mutilated | 1 |
| 11734 | mutatio | 1 |
| 11735 | mussel | 1 |
| 11736 | musketoon | 1 |
| 11737 | musketeers | 1 |
| 11738 | musing | 1 |
| 11739 | musically | 1 |
| 11740 | muscles | 1 |
| 11741 | murky | 1 |
| 11742 | murders | 1 |
| 11743 | murderously | 1 |
| 11744 | murdering | 1 |
| 11745 | murderers | 1 |
| 11746 | murder | 1 |
| 11747 | munitions | 1 |
| 11748 | muniment | 1 |
| 11749 | munaton | 1 |
| 11750 | mummied | 1 |
| 11751 | mummers | 1 |
| 11752 | mummer | 1 |
| 11753 | multos | 1 |
| 11754 | multitudes | 1 |
| 11755 | mulct | 1 |
| 11756 | muffling | 1 |
| 11757 | muffled | 1 |
| 11758 | muddled | 1 |
| 11759 | muddle | 1 |
| 11760 | moves | 1 |
| 11761 | moustached | 1 |
| 11762 | mourn | 1 |
| 11763 | mouldy | 1 |
| 11764 | mouldering | 1 |
| 11765 | motionless | 1 |
| 11766 | motherless | 1 |
| 11767 | moth | 1 |
| 11768 | motes | 1 |
| 11769 | mote | 1 |
| 11770 | mosques | 1 |
| 11771 | mortify | 1 |
| 11772 | mortification | 1 |
| 11773 | mortgaged | 1 |
| 11774 | mortally | 1 |
| 11775 | morsels | 1 |
| 11776 | mors | 1 |
| 11777 | moron | 1 |
| 11778 | moriscoes | 1 |
| 11779 | morally | 1 |
| 11780 | morality | 1 |
| 11781 | moorings | 1 |
| 11782 | moods | 1 |
| 11783 | moodily | 1 |
| 11784 | monument | 1 |
| 11785 | montserrate | 1 |
| 11786 | monotonous | 1 |
| 11787 | monjui | 1 |
| 11788 | monicongo | 1 |
| 11789 | moneys | 1 |
| 11790 | moneybox | 1 |
| 11791 | mondonedo | 1 |
| 11792 | moncadas | 1 |
| 11793 | monarchy | 1 |
| 11794 | monarchs | 1 |
| 11795 | monarchies | 1 |
| 11796 | molests | 1 |
| 11797 | moisten | 1 |
| 11798 | mohammed | 1 |
| 11799 | modon | 1 |
| 11800 | moderns | 1 |
| 11801 | moderately | 1 |
| 11802 | models | 1 |
| 11803 | mockingly | 1 |
| 11804 | mocking | 1 |
| 11805 | mockery | 1 |
| 11806 | mocked | 1 |
| 11807 | moanings | 1 |
| 11808 | mixes | 1 |
| 11809 | mitres | 1 |
| 11810 | mitigate | 1 |
| 11811 | misventures | 1 |
| 11812 | mists | 1 |
| 11813 | misguided | 1 |
| 11814 | misgivings | 1 |
| 11815 | misgiving | 1 |
| 11816 | misers | 1 |
| 11817 | miserly | 1 |
| 11818 | miserably | 1 |
| 11819 | misdemeanour | 1 |
| 11820 | misdeed | 1 |
| 11821 | misconduct | 1 |
| 11822 | mischances | 1 |
| 11823 | mischance | 1 |
| 11824 | misbehaviour | 1 |
| 11825 | miry | 1 |
| 11826 | miraguarda | 1 |
| 11827 | miraflores | 1 |
| 11828 | minuteness | 1 |
| 11829 | minguilla | 1 |
| 11830 | mingles | 1 |
| 11831 | mines | 1 |
| 11832 | mined | 1 |
| 11833 | miller | 1 |
| 11834 | milksops | 1 |
| 11835 | milking | 1 |
| 11836 | milesian | 1 |
| 11837 | mile | 1 |
| 11838 | miglior | 1 |
| 11839 | mightiest | 1 |
| 11840 | mightier | 1 |
| 11841 | midstream | 1 |
| 11842 | middling | 1 |
| 11843 | micocolembo | 1 |
| 11844 | michaelmas | 1 |
| 11845 | michael | 1 |
| 11846 | micer | 1 |
| 11847 | miaulina | 1 |
| 11848 | miau | 1 |
| 11849 | mi | 1 |
| 11850 | mezquino | 1 |
| 11851 | mexico | 1 |
| 11852 | mexican | 1 |
| 11853 | mewed | 1 |
| 11854 | mettlesome | 1 |
| 11855 | methods | 1 |
| 11856 | meted | 1 |
| 11857 | metaphysical | 1 |
| 11858 | metaphors | 1 |
| 11859 | metamorphosis | 1 |
| 11860 | metamorphoses | 1 |
| 11861 | messina | 1 |
| 11862 | messes | 1 |
| 11863 | messengers | 1 |
| 11864 | mess | 1 |
| 11865 | merrymaking | 1 |
| 11866 | merrier | 1 |
| 11867 | merlo | 1 |
| 11868 | merchandise | 1 |
| 11869 | meotides | 1 |
| 11870 | meona | 1 |
| 11871 | mentironiana | 1 |
| 11872 | mentions | 1 |
| 11873 | meneses | 1 |
| 11874 | menelaus | 1 |
| 11875 | mends | 1 |
| 11876 | mendozas | 1 |
| 11877 | mendoza | 1 |
| 11878 | mending | 1 |
| 11879 | mencia | 1 |
| 11880 | menaced | 1 |
| 11881 | memories | 1 |
| 11882 | memorial | 1 |
| 11883 | memento | 1 |
| 11884 | melting | 1 |
| 11885 | melons | 1 |
| 11886 | melon | 1 |
| 11887 | melody | 1 |
| 11888 | melodious | 1 |
| 11889 | mellifluous | 1 |
| 11890 | melisandra | 1 |
| 11891 | meets | 1 |
| 11892 | meekness | 1 |
| 11893 | meekly | 1 |
| 11894 | meed | 1 |
| 11895 | medusa | 1 |
| 11896 | medlars | 1 |
| 11897 | mediterranean | 1 |
| 11898 | meditations | 1 |
| 11899 | meditated | 1 |
| 11900 | medina | 1 |
| 11901 | medea | 1 |
| 11902 | meddler | 1 |
| 11903 | mechanism | 1 |
| 11904 | mecca | 1 |
| 11905 | measurements | 1 |
| 11906 | meanness | 1 |
| 11907 | meanly | 1 |
| 11908 | mealy | 1 |
| 11909 | meagre | 1 |
| 11910 | mazorca | 1 |
| 11911 | maze | 1 |
| 11912 | mausolus | 1 |
| 11913 | maundering | 1 |
| 11914 | mauling | 1 |
| 11915 | mauleon | 1 |
| 11916 | mauled | 1 |
| 11917 | mattresses | 1 |
| 11918 | matteo | 1 |
| 11919 | matted | 1 |
| 11920 | matrons | 1 |
| 11921 | matron | 1 |
| 11922 | matrimonial | 1 |
| 11923 | mathematics | 1 |
| 11924 | matchmaking | 1 |
| 11925 | matching | 1 |
| 11926 | masts | 1 |
| 11927 | mastiffs | 1 |
| 11928 | mastiff | 1 |
| 11929 | massy | 1 |
| 11930 | massive | 1 |
| 11931 | massilian | 1 |
| 11932 | masquerading | 1 |
| 11933 | mason | 1 |
| 11934 | maskers | 1 |
| 11935 | masked | 1 |
| 11936 | mash | 1 |
| 11937 | masculine | 1 |
| 11938 | mas | 1 |
| 11939 | marvellously | 1 |
| 11940 | martyrdom | 1 |
| 11941 | martos | 1 |
| 11942 | martino | 1 |
| 11943 | martinmas | 1 |
| 11944 | martinez | 1 |
| 11945 | martin | 1 |
| 11946 | martha | 1 |
| 11947 | marten | 1 |
| 11948 | marshalled | 1 |
| 11949 | marries | 1 |
| 11950 | marriages | 1 |
| 11951 | marred | 1 |
| 11952 | marquises | 1 |
| 11953 | marjoram | 1 |
| 11954 | marius | 1 |
| 11955 | marines | 1 |
| 11956 | mariner | 1 |
| 11957 | margins | 1 |
| 11958 | marco | 1 |
| 11959 | marchionesses | 1 |
| 11960 | maranon | 1 |
| 11961 | manzanares | 1 |
| 11962 | manure | 1 |
| 11963 | mantuan | 1 |
| 11964 | mantles | 1 |
| 11965 | mantible | 1 |
| 11966 | manriques | 1 |
| 11967 | manoeuvre | 1 |
| 11968 | manna | 1 |
| 11969 | manjar | 1 |
| 11970 | manifestly | 1 |
| 11971 | manifested | 1 |
| 11972 | manifestations | 1 |
| 11973 | manifestation | 1 |
| 11974 | maniac | 1 |
| 11975 | manchissima | 1 |
| 11976 | manchegans | 1 |
| 11977 | manager | 1 |
| 11978 | management | 1 |
| 11979 | mameluke | 1 |
| 11980 | mambrine | 1 |
| 11981 | maltreating | 1 |
| 11982 | maltese | 1 |
| 11983 | malo | 1 |
| 11984 | mallets | 1 |
| 11985 | malindrania | 1 |
| 11986 | malignity | 1 |
| 11987 | malfeasance | 1 |
| 11988 | malevolence | 1 |
| 11989 | malefactor | 1 |
| 11990 | maldonado | 1 |
| 11991 | malapert | 1 |
| 11992 | malandrino | 1 |
| 11993 | malaguero | 1 |
| 11994 | malae | 1 |
| 11995 | mala | 1 |
| 11996 | makers | 1 |
| 11997 | majority | 1 |
| 11998 | majimasa | 1 |
| 11999 | majalahonda | 1 |
| 12000 | mainstay | 1 |
| 12001 | mainly | 1 |
| 12002 | maiming | 1 |
| 12003 | maidenly | 1 |
| 12004 | maidenhood | 1 |
| 12005 | mahometan | 1 |
| 12006 | magnum | 1 |
| 12007 | magnified | 1 |
| 12008 | magnificently | 1 |
| 12009 | magnates | 1 |
| 12010 | magistrate | 1 |
| 12011 | magistracy | 1 |
| 12012 | magisterial | 1 |
| 12013 | magis | 1 |
| 12014 | magical | 1 |
| 12015 | magdalena | 1 |
| 12016 | magallanes | 1 |
| 12017 | madrigal | 1 |
| 12018 | madnesses | 1 |
| 12019 | madasimas | 1 |
| 12020 | maccabees | 1 |
| 12021 | macange | 1 |
| 12022 | lysippus | 1 |
| 12023 | lyric | 1 |
| 12024 | lynxes | 1 |
| 12025 | luxuriant | 1 |
| 12026 | lutes | 1 |
| 12027 | lustiest | 1 |
| 12028 | lusitanian | 1 |
| 12029 | lusitania | 1 |
| 12030 | lures | 1 |
| 12031 | lurchers | 1 |
| 12032 | lurch | 1 |
| 12033 | luncheon | 1 |
| 12034 | lunched | 1 |
| 12035 | lunatics | 1 |
| 12036 | lunas | 1 |
| 12037 | lunacies | 1 |
| 12038 | luna | 1 |
| 12039 | lumps | 1 |
| 12040 | luminary | 1 |
| 12041 | luminaries | 1 |
| 12042 | lull | 1 |
| 12043 | lukewarmly | 1 |
| 12044 | luigi | 1 |
| 12045 | luffing | 1 |
| 12046 | ludovico | 1 |
| 12047 | lucrando | 1 |
| 12048 | luckless | 1 |
| 12049 | luckily | 1 |
| 12050 | lucinda | 1 |
| 12051 | lucifer | 1 |
| 12052 | lucidity | 1 |
| 12053 | lucem | 1 |
| 12054 | loyally | 1 |
| 12055 | lowest | 1 |
| 12056 | lowers | 1 |
| 12057 | loveth | 1 |
| 12058 | lovest | 1 |
| 12059 | lovemakings | 1 |
| 12060 | lovemaking | 1 |
| 12061 | lovelorn | 1 |
| 12062 | loveliness | 1 |
| 12063 | lovelier | 1 |
| 12064 | loveletter | 1 |
| 12065 | loutish | 1 |
| 12066 | lousier | 1 |
| 12067 | loudest | 1 |
| 12068 | lots | 1 |
| 12069 | loses | 1 |
| 12070 | losers | 1 |
| 12071 | los | 1 |
| 12072 | lordlings | 1 |
| 12073 | loosening | 1 |
| 12074 | looseness | 1 |
| 12075 | loosener | 1 |
| 12076 | loosely | 1 |
| 12077 | loopholes | 1 |
| 12078 | loophole | 1 |
| 12079 | looped | 1 |
| 12080 | lookout | 1 |
| 12081 | lookers | 1 |
| 12082 | longest | 1 |
| 12083 | loneliness | 1 |
| 12084 | lone | 1 |
| 12085 | lombardy | 1 |
| 12086 | lolling | 1 |
| 12087 | loitered | 1 |
| 12088 | logiquous | 1 |
| 12089 | logic | 1 |
| 12090 | loggerheads | 1 |
| 12091 | log | 1 |
| 12092 | lofraso | 1 |
| 12093 | lodgings | 1 |
| 12094 | lodgers | 1 |
| 12095 | local | 1 |
| 12096 | lobo | 1 |
| 12097 | loaves | 1 |
| 12098 | loathsome | 1 |
| 12099 | loathed | 1 |
| 12100 | lladres | 1 |
| 12101 | liveliness | 1 |
| 12102 | livelihood | 1 |
| 12103 | littles | 1 |
| 12104 | littleness | 1 |
| 12105 | litters | 1 |
| 12106 | literally | 1 |
| 12107 | lisuarte | 1 |
| 12108 | listener | 1 |
| 12109 | lisbon | 1 |
| 12110 | linguist | 1 |
| 12111 | linger | 1 |
| 12112 | limps | 1 |
| 12113 | limned | 1 |
| 12114 | limitations | 1 |
| 12115 | likened | 1 |
| 12116 | lightnings | 1 |
| 12117 | lightest | 1 |
| 12118 | lightens | 1 |
| 12119 | lifelike | 1 |
| 12120 | lifeless | 1 |
| 12121 | liege | 1 |
| 12122 | licks | 1 |
| 12123 | license | 1 |
| 12124 | libya | 1 |
| 12125 | library | 1 |
| 12126 | libertine | 1 |
| 12127 | libertas | 1 |
| 12128 | liberator | 1 |
| 12129 | liberating | 1 |
| 12130 | liberated | 1 |
| 12131 | libels | 1 |
| 12132 | levying | 1 |
| 12133 | levelling | 1 |
| 12134 | lettered | 1 |
| 12135 | lessons | 1 |
| 12136 | lessened | 1 |
| 12137 | lese | 1 |
| 12138 | lepanto | 1 |
| 12139 | leonora | 1 |
| 12140 | leonese | 1 |
| 12141 | lentils | 1 |
| 12142 | legislator | 1 |
| 12143 | legible | 1 |
| 12144 | legends | 1 |
| 12145 | legend | 1 |
| 12146 | leganitos | 1 |
| 12147 | legal | 1 |
| 12148 | leeward | 1 |
| 12149 | leavings | 1 |
| 12150 | learnt | 1 |
| 12151 | leaner | 1 |
| 12152 | lealest | 1 |
| 12153 | leaked | 1 |
| 12154 | leaf | 1 |
| 12155 | leaders | 1 |
| 12156 | lazarillo | 1 |
| 12157 | lazaril | 1 |
| 12158 | layman | 1 |
| 12159 | laxities | 1 |
| 12160 | laxative | 1 |
| 12161 | lawlessness | 1 |
| 12162 | lawgiver | 1 |
| 12163 | lavishness | 1 |
| 12164 | lavished | 1 |
| 12165 | lavender | 1 |
| 12166 | lavapies | 1 |
| 12167 | lavajos | 1 |
| 12168 | lautrec | 1 |
| 12169 | laureate | 1 |
| 12170 | laurcalco | 1 |
| 12171 | laura | 1 |
| 12172 | launched | 1 |
| 12173 | launcelot | 1 |
| 12174 | lauding | 1 |
| 12175 | laudem | 1 |
| 12176 | lauded | 1 |
| 12177 | laudation | 1 |
| 12178 | laudable | 1 |
| 12179 | latino | 1 |
| 12180 | latest | 1 |
| 12181 | lateness | 1 |
| 12182 | lashings | 1 |
| 12183 | lashing | 1 |
| 12184 | lashed | 1 |
| 12185 | largess | 1 |
| 12186 | largely | 1 |
| 12187 | laredo | 1 |
| 12188 | larders | 1 |
| 12189 | lara | 1 |
| 12190 | lapse | 1 |
| 12191 | lapidaries | 1 |
| 12192 | lanner | 1 |
| 12193 | lanky | 1 |
| 12194 | lankness | 1 |
| 12195 | languishings | 1 |
| 12196 | languish | 1 |
| 12197 | lane | 1 |
| 12198 | landmarks | 1 |
| 12199 | lancers | 1 |
| 12200 | lamia | 1 |
| 12201 | lamented | 1 |
| 12202 | lair | 1 |
| 12203 | laida | 1 |
| 12204 | laguna | 1 |
| 12205 | lagoon | 1 |
| 12206 | ladylove | 1 |
| 12207 | ladle | 1 |
| 12208 | ladders | 1 |
| 12209 | ladder | 1 |
| 12210 | lacqueys | 1 |
| 12211 | lacquered | 1 |
| 12212 | lacking | 1 |
| 12213 | lackeys | 1 |
| 12214 | lachrymis | 1 |
| 12215 | lacerated | 1 |
| 12216 | lacedemonians | 1 |
| 12217 | labyrinths | 1 |
| 12218 | labourest | 1 |
| 12219 | label | 1 |
| 12220 | kyrieleison | 1 |
| 12221 | knoweth | 1 |
| 12222 | knotted | 1 |
| 12223 | knitted | 1 |
| 12224 | knighting | 1 |
| 12225 | knickknack | 1 |
| 12226 | knewest | 1 |
| 12227 | kneels | 1 |
| 12228 | kneads | 1 |
| 12229 | kneading | 1 |
| 12230 | knaves | 1 |
| 12231 | knaveries | 1 |
| 12232 | knack | 1 |
| 12233 | kits | 1 |
| 12234 | kinsfolk | 1 |
| 12235 | kindling | 1 |
| 12236 | kindliness | 1 |
| 12237 | kindles | 1 |
| 12238 | kindled | 1 |
| 12239 | kindle | 1 |
| 12240 | kin | 1 |
| 12241 | killer | 1 |
| 12242 | kidneys | 1 |
| 12243 | kicking | 1 |
| 12244 | kettles | 1 |
| 12245 | kettledrums | 1 |
| 12246 | kettle | 1 |
| 12247 | kestrel | 1 |
| 12248 | ken | 1 |
| 12249 | kegs | 1 |
| 12250 | kandian | 1 |
| 12251 | juxta | 1 |
| 12252 | juvenal | 1 |
| 12253 | justifiable | 1 |
| 12254 | jurists | 1 |
| 12255 | jurisdictions | 1 |
| 12256 | jur | 1 |
| 12257 | juncture | 1 |
| 12258 | jumbled | 1 |
| 12259 | jumble | 1 |
| 12260 | julys | 1 |
| 12261 | julian | 1 |
| 12262 | juguetes | 1 |
| 12263 | jugs | 1 |
| 12264 | juggling | 1 |
| 12265 | jugglery | 1 |
| 12266 | judiciary | 1 |
| 12267 | judicial | 1 |
| 12268 | judgeships | 1 |
| 12269 | jubilant | 1 |
| 12270 | juana | 1 |
| 12271 | joyous | 1 |
| 12272 | journeyman | 1 |
| 12273 | journeyed | 1 |
| 12274 | jot | 1 |
| 12275 | jollity | 1 |
| 12276 | joints | 1 |
| 12277 | joint | 1 |
| 12278 | joins | 1 |
| 12279 | jingling | 1 |
| 12280 | jingle | 1 |
| 12281 | jilted | 1 |
| 12282 | jews | 1 |
| 12283 | jesting | 1 |
| 12284 | jesters | 1 |
| 12285 | jessamine | 1 |
| 12286 | jerusalem | 1 |
| 12287 | jerkins | 1 |
| 12288 | jerking | 1 |
| 12289 | jennyasses | 1 |
| 12290 | jeered | 1 |
| 12291 | jeer | 1 |
| 12292 | jaw | 1 |
| 12293 | jauregui | 1 |
| 12294 | jason | 1 |
| 12295 | jargon | 1 |
| 12296 | jaramilla | 1 |
| 12297 | janizzaries | 1 |
| 12298 | jackdaws | 1 |
| 12299 | jackass | 1 |
| 12300 | jackals | 1 |
| 12301 | jacinth | 1 |
| 12302 | jaca | 1 |
| 12303 | jaboneros | 1 |
| 12304 | ixion | 1 |
| 12305 | items | 1 |
| 12306 | israel | 1 |
| 12307 | isolated | 1 |
| 12308 | isabella | 1 |
| 12309 | irritate | 1 |
| 12310 | irritable | 1 |
| 12311 | irretrievable | 1 |
| 12312 | irrepressible | 1 |
| 12313 | irregular | 1 |
| 12314 | irrationally | 1 |
| 12315 | inward | 1 |
| 12316 | invoking | 1 |
| 12317 | invoke | 1 |
| 12318 | invigorated | 1 |
| 12319 | investments | 1 |
| 12320 | investigator | 1 |
| 12321 | investigation | 1 |
| 12322 | investigated | 1 |
| 12323 | investigate | 1 |
| 12324 | invest | 1 |
| 12325 | inveighing | 1 |
| 12326 | invariable | 1 |
| 12327 | invade | 1 |
| 12328 | intruder | 1 |
| 12329 | introducing | 1 |
| 12330 | intrigues | 1 |
| 12331 | intimidate | 1 |
| 12332 | interwoven | 1 |
| 12333 | intervention | 1 |
| 12334 | interruption | 1 |
| 12335 | interrupted | 1 |
| 12336 | interrogations | 1 |
| 12337 | interred | 1 |
| 12338 | interpreted | 1 |
| 12339 | interpretation | 1 |
| 12340 | interpret | 1 |
| 12341 | intermission | 1 |
| 12342 | interlude | 1 |
| 12343 | interlacing | 1 |
| 12344 | interfering | 1 |
| 12345 | interferes | 1 |
| 12346 | interferences | 1 |
| 12347 | interference | 1 |
| 12348 | interfered | 1 |
| 12349 | interdict | 1 |
| 12350 | intercessory | 1 |
| 12351 | intercessor | 1 |
| 12352 | intently | 1 |
| 12353 | intentionally | 1 |
| 12354 | intent | 1 |
| 12355 | intends | 1 |
| 12356 | intemperance | 1 |
| 12357 | intelligibly | 1 |
| 12358 | intellects | 1 |
| 12359 | intact | 1 |
| 12360 | insuring | 1 |
| 12361 | insure | 1 |
| 12362 | insuperable | 1 |
| 12363 | insufficient | 1 |
| 12364 | insufferable | 1 |
| 12365 | instructive | 1 |
| 12366 | instructing | 1 |
| 12367 | instincts | 1 |
| 12368 | instinctively | 1 |
| 12369 | instilleth | 1 |
| 12370 | instil | 1 |
| 12371 | instigated | 1 |
| 12372 | instability | 1 |
| 12373 | inspires | 1 |
| 12374 | inspectors | 1 |
| 12375 | inspector | 1 |
| 12376 | inspect | 1 |
| 12377 | insolences | 1 |
| 12378 | insisting | 1 |
| 12379 | insist | 1 |
| 12380 | insignificant | 1 |
| 12381 | inserts | 1 |
| 12382 | inserting | 1 |
| 12383 | insensibility | 1 |
| 12384 | inscriptions | 1 |
| 12385 | insatiable | 1 |
| 12386 | insanity | 1 |
| 12387 | ins | 1 |
| 12388 | inquisitors | 1 |
| 12389 | inquisitiveness | 1 |
| 12390 | inquisition | 1 |
| 12391 | inquiry | 1 |
| 12392 | inquiries | 1 |
| 12393 | inopportune | 1 |
| 12394 | innocently | 1 |
| 12395 | innamorato | 1 |
| 12396 | inkstand | 1 |
| 12397 | iniquity | 1 |
| 12398 | iniquitous | 1 |
| 12399 | inimicos | 1 |
| 12400 | inherits | 1 |
| 12401 | inheriting | 1 |
| 12402 | inherited | 1 |
| 12403 | inherit | 1 |
| 12404 | ingulf | 1 |
| 12405 | ingrates | 1 |
| 12406 | infuses | 1 |
| 12407 | informs | 1 |
| 12408 | infliction | 1 |
| 12409 | infinitum | 1 |
| 12410 | infers | 1 |
| 12411 | infernal | 1 |
| 12412 | inferiors | 1 |
| 12413 | inferences | 1 |
| 12414 | inference | 1 |
| 12415 | infectious | 1 |
| 12416 | infantes | 1 |
| 12417 | infante | 1 |
| 12418 | infant | 1 |
| 12419 | infancy | 1 |
| 12420 | inexorably | 1 |
| 12421 | inexcusable | 1 |
| 12422 | inevitably | 1 |
| 12423 | inestimable | 1 |
| 12424 | inequality | 1 |
| 12425 | ineffectual | 1 |
| 12426 | industrious | 1 |
| 12427 | indulging | 1 |
| 12428 | indulgence | 1 |
| 12429 | inducements | 1 |
| 12430 | inducement | 1 |
| 12431 | indoors | 1 |
| 12432 | indoor | 1 |
| 12433 | indomitable | 1 |
| 12434 | indolent | 1 |
| 12435 | indivisible | 1 |
| 12436 | indites | 1 |
| 12437 | indisposition | 1 |
| 12438 | indirect | 1 |
| 12439 | indigestions | 1 |
| 12440 | indifferent | 1 |
| 12441 | indifference | 1 |
| 12442 | indictments | 1 |
| 12443 | indication | 1 |
| 12444 | indicated | 1 |
| 12445 | india | 1 |
| 12446 | indemnified | 1 |
| 12447 | indelible | 1 |
| 12448 | indecent | 1 |
| 12449 | incurs | 1 |
| 12450 | incurable | 1 |
| 12451 | incredulity | 1 |
| 12452 | incorrigible | 1 |
| 12453 | inconvenient | 1 |
| 12454 | incontinence | 1 |
| 12455 | inconstancy | 1 |
| 12456 | inconsiderate | 1 |
| 12457 | incoherent | 1 |
| 12458 | including | 1 |
| 12459 | includes | 1 |
| 12460 | inclosed | 1 |
| 12461 | incline | 1 |
| 12462 | incivility | 1 |
| 12463 | incidentally | 1 |
| 12464 | incidental | 1 |
| 12465 | incessant | 1 |
| 12466 | incentives | 1 |
| 12467 | incentive | 1 |
| 12468 | inarticulate | 1 |
| 12469 | inactivity | 1 |
| 12470 | inactive | 1 |
| 12471 | inaction | 1 |
| 12472 | inaccurate | 1 |
| 12473 | inaccessible | 1 |
| 12474 | imputation | 1 |
| 12475 | impurity | 1 |
| 12476 | impulsive | 1 |
| 12477 | imprudences | 1 |
| 12478 | improvised | 1 |
| 12479 | improvidence | 1 |
| 12480 | improves | 1 |
| 12481 | improved | 1 |
| 12482 | imprisonments | 1 |
| 12483 | imprisoned | 1 |
| 12484 | imprest | 1 |
| 12485 | impressing | 1 |
| 12486 | impressed | 1 |
| 12487 | imposture | 1 |
| 12488 | impostor | 1 |
| 12489 | implied | 1 |
| 12490 | implicit | 1 |
| 12491 | implements | 1 |
| 12492 | implement | 1 |
| 12493 | impious | 1 |
| 12494 | impetuous | 1 |
| 12495 | imperturbable | 1 |
| 12496 | impertinences | 1 |
| 12497 | imperishable | 1 |
| 12498 | imperious | 1 |
| 12499 | imperil | 1 |
| 12500 | imperial | 1 |
| 12501 | imperfect | 1 |
| 12502 | impenetrable | 1 |
| 12503 | impels | 1 |
| 12504 | impel | 1 |
| 12505 | impede | 1 |
| 12506 | impatiently | 1 |
| 12507 | immortalising | 1 |
| 12508 | immortalise | 1 |
| 12509 | immortal | 1 |
| 12510 | immemorial | 1 |
| 12511 | immaculatissimus | 1 |
| 12512 | immaculate | 1 |
| 12513 | imitator | 1 |
| 12514 | imagines | 1 |
| 12515 | imaginative | 1 |
| 12516 | imaginable | 1 |
| 12517 | imaged | 1 |
| 12518 | illusory | 1 |
| 12519 | illusion | 1 |
| 12520 | illud | 1 |
| 12521 | illtilled | 1 |
| 12522 | illness | 1 |
| 12523 | illiberal | 1 |
| 12524 | iliad | 1 |
| 12525 | ignoramus | 1 |
| 12526 | idiots | 1 |
| 12527 | identify | 1 |
| 12528 | identical | 1 |
| 12529 | ideal | 1 |
| 12530 | hyperbolical | 1 |
| 12531 | hussy | 1 |
| 12532 | hurriedly | 1 |
| 12533 | hurling | 1 |
| 12534 | hurl | 1 |
| 12535 | hurgada | 1 |
| 12536 | huntings | 1 |
| 12537 | huntingcoat | 1 |
| 12538 | hunted | 1 |
| 12539 | hungrily | 1 |
| 12540 | hungrier | 1 |
| 12541 | hundreds | 1 |
| 12542 | humpbacked | 1 |
| 12543 | humiliation | 1 |
| 12544 | humbleth | 1 |
| 12545 | humbles | 1 |
| 12546 | humbler | 1 |
| 12547 | humbled | 1 |
| 12548 | humanity | 1 |
| 12549 | humanist | 1 |
| 12550 | hugging | 1 |
| 12551 | hugest | 1 |
| 12552 | huddled | 1 |
| 12553 | hucksters | 1 |
| 12554 | hubbub | 1 |
| 12555 | howlings | 1 |
| 12556 | hovel | 1 |
| 12557 | housed | 1 |
| 12558 | hound | 1 |
| 12559 | hottest | 1 |
| 12560 | hospitably | 1 |
| 12561 | horror | 1 |
| 12562 | horrid | 1 |
| 12563 | horned | 1 |
| 12564 | horatius | 1 |
| 12565 | hops | 1 |
| 12566 | hooks | 1 |
| 12567 | hoofs | 1 |
| 12568 | hooded | 1 |
| 12569 | honeysuckle | 1 |
| 12570 | honeyed | 1 |
| 12571 | homicides | 1 |
| 12572 | homerus | 1 |
| 12573 | holly | 1 |
| 12574 | hollows | 1 |
| 12575 | holloa | 1 |
| 12576 | holder | 1 |
| 12577 | hoisting | 1 |
| 12578 | hogsheads | 1 |
| 12579 | hoc | 1 |
| 12580 | hoarser | 1 |
| 12581 | hive | 1 |
| 12582 | hitched | 1 |
| 12583 | historical | 1 |
| 12584 | hissings | 1 |
| 12585 | hissing | 1 |
| 12586 | hissed | 1 |
| 12587 | hire | 1 |
| 12588 | hipolito | 1 |
| 12589 | hillside | 1 |
| 12590 | hillock | 1 |
| 12591 | highbred | 1 |
| 12592 | hey | 1 |
| 12593 | hews | 1 |
| 12594 | hewing | 1 |
| 12595 | hew | 1 |
| 12596 | herradura | 1 |
| 12597 | heron | 1 |
| 12598 | herewith | 1 |
| 12599 | heretofore | 1 |
| 12600 | heretic | 1 |
| 12601 | hereby | 1 |
| 12602 | hereabouts | 1 |
| 12603 | herbalist | 1 |
| 12604 | herb | 1 |
| 12605 | heraclius | 1 |
| 12606 | hempen | 1 |
| 12607 | hemming | 1 |
| 12608 | helpmate | 1 |
| 12609 | helpful | 1 |
| 12610 | helper | 1 |
| 12611 | helmets | 1 |
| 12612 | helm | 1 |
| 12613 | heightened | 1 |
| 12614 | heeled | 1 |
| 12615 | heedful | 1 |
| 12616 | heeded | 1 |
| 12617 | hectors | 1 |
| 12618 | hebrew | 1 |
| 12619 | heaving | 1 |
| 12620 | heaviness | 1 |
| 12621 | heavily | 1 |
| 12622 | heaviest | 1 |
| 12623 | heavenward | 1 |
| 12624 | heavenly | 1 |
| 12625 | heave | 1 |
| 12626 | heats | 1 |
| 12627 | heaths | 1 |
| 12628 | heathenism | 1 |
| 12629 | heartrending | 1 |
| 12630 | heartfelt | 1 |
| 12631 | heaps | 1 |
| 12632 | healthy | 1 |
| 12633 | healthiest | 1 |
| 12634 | headforemost | 1 |
| 12635 | headaches | 1 |
| 12636 | haze | 1 |
| 12637 | hazards | 1 |
| 12638 | hawks | 1 |
| 12639 | havoc | 1 |
| 12640 | hautboys | 1 |
| 12641 | haunts | 1 |
| 12642 | haunting | 1 |
| 12643 | haunted | 1 |
| 12644 | hauled | 1 |
| 12645 | haul | 1 |
| 12646 | hauberk | 1 |
| 12647 | hates | 1 |
| 12648 | hater | 1 |
| 12649 | hassan | 1 |
| 12650 | hash | 1 |
| 12651 | harvests | 1 |
| 12652 | harquebusses | 1 |
| 12653 | harquebuss | 1 |
| 12654 | harps | 1 |
| 12655 | harnessing | 1 |
| 12656 | harmlessness | 1 |
| 12657 | harmed | 1 |
| 12658 | hark | 1 |
| 12659 | hardhearted | 1 |
| 12660 | hardest | 1 |
| 12661 | hankering | 1 |
| 12662 | hanker | 1 |
| 12663 | hangman | 1 |
| 12664 | handselled | 1 |
| 12665 | handmaidens | 1 |
| 12666 | handmaiden | 1 |
| 12667 | handles | 1 |
| 12668 | handkerchiefs | 1 |
| 12669 | handfuls | 1 |
| 12670 | hamlet | 1 |
| 12671 | hamida | 1 |
| 12672 | hamet | 1 |
| 12673 | ham | 1 |
| 12674 | halves | 1 |
| 12675 | halls | 1 |
| 12676 | hallooing | 1 |
| 12677 | haldudos | 1 |
| 12678 | haldudo | 1 |
| 12679 | hailstorm | 1 |
| 12680 | haggling | 1 |
| 12681 | haggard | 1 |
| 12682 | hagarene | 1 |
| 12683 | hadrian | 1 |
| 12684 | hacked | 1 |
| 12685 | habits | 1 |
| 12686 | gymnosophists | 1 |
| 12687 | guzmans | 1 |
| 12688 | guzman | 1 |
| 12689 | guy | 1 |
| 12690 | gutierre | 1 |
| 12691 | gushed | 1 |
| 12692 | gurreas | 1 |
| 12693 | gunshot | 1 |
| 12694 | gun | 1 |
| 12695 | gumption | 1 |
| 12696 | gulping | 1 |
| 12697 | gulped | 1 |
| 12698 | guisopete | 1 |
| 12699 | guides | 1 |
| 12700 | guidance | 1 |
| 12701 | guevara | 1 |
| 12702 | guesswork | 1 |
| 12703 | guarino | 1 |
| 12704 | guarding | 1 |
| 12705 | guarantee | 1 |
| 12706 | guadarrama | 1 |
| 12707 | grunted | 1 |
| 12708 | grumble | 1 |
| 12709 | grubs | 1 |
| 12710 | grows | 1 |
| 12711 | growling | 1 |
| 12712 | growler | 1 |
| 12713 | grovelling | 1 |
| 12714 | grouting | 1 |
| 12715 | group | 1 |
| 12716 | grotesque | 1 |
| 12717 | gross | 1 |
| 12718 | groomsman | 1 |
| 12719 | grooms | 1 |
| 12720 | grizzled | 1 |
| 12721 | grisly | 1 |
| 12722 | gripped | 1 |
| 12723 | gripings | 1 |
| 12724 | grinding | 1 |
| 12725 | grinder | 1 |
| 12726 | grijalba | 1 |
| 12727 | grievously | 1 |
| 12728 | greenwood | 1 |
| 12729 | greediness | 1 |
| 12730 | greaves | 1 |
| 12731 | greasy | 1 |
| 12732 | greased | 1 |
| 12733 | grease | 1 |
| 12734 | grazing | 1 |
| 12735 | graze | 1 |
| 12736 | graveyard | 1 |
| 12737 | gravest | 1 |
| 12738 | graver | 1 |
| 12739 | gravely | 1 |
| 12740 | gratis | 1 |
| 12741 | gratings | 1 |
| 12742 | gratification | 1 |
| 12743 | grate | 1 |
| 12744 | grappled | 1 |
| 12745 | grandiloquent | 1 |
| 12746 | grandeur | 1 |
| 12747 | granddaughter | 1 |
| 12748 | grammarian | 1 |
| 12749 | gram | 1 |
| 12750 | grail | 1 |
| 12751 | graduates | 1 |
| 12752 | graduated | 1 |
| 12753 | graciously | 1 |
| 12754 | graceless | 1 |
| 12755 | gownsman | 1 |
| 12756 | governorship | 1 |
| 12757 | governess | 1 |
| 12758 | goths | 1 |
| 12759 | gospels | 1 |
| 12760 | gospel | 1 |
| 12761 | gormandiser | 1 |
| 12762 | gorget | 1 |
| 12763 | gorge | 1 |
| 12764 | goose | 1 |
| 12765 | gonela | 1 |
| 12766 | golias | 1 |
| 12767 | goldfinch | 1 |
| 12768 | godspeed | 1 |
| 12769 | godsons | 1 |
| 12770 | godson | 1 |
| 12771 | godsend | 1 |
| 12772 | godliness | 1 |
| 12773 | godfrey | 1 |
| 12774 | godfathers | 1 |
| 12775 | godfather | 1 |
| 12776 | goaty | 1 |
| 12777 | goals | 1 |
| 12778 | goad | 1 |
| 12779 | gnawing | 1 |
| 12780 | gluttonous | 1 |
| 12781 | glowed | 1 |
| 12782 | glover | 1 |
| 12783 | glossing | 1 |
| 12784 | glosses | 1 |
| 12785 | glittered | 1 |
| 12786 | glimpses | 1 |
| 12787 | gliding | 1 |
| 12788 | glens | 1 |
| 12789 | gleam | 1 |
| 12790 | glasses | 1 |
| 12791 | glaring | 1 |
| 12792 | glamorous | 1 |
| 12793 | gladsome | 1 |
| 12794 | glade | 1 |
| 12795 | gladdening | 1 |
| 12796 | gladdened | 1 |
| 12797 | giu | 1 |
| 12798 | girth | 1 |
| 12799 | girds | 1 |
| 12800 | girdling | 1 |
| 12801 | gird | 1 |
| 12802 | giovanni | 1 |
| 12803 | gineta | 1 |
| 12804 | gills | 1 |
| 12805 | gilds | 1 |
| 12806 | gigote | 1 |
| 12807 | giddiness | 1 |
| 12808 | gibraltar | 1 |
| 12809 | gibraleon | 1 |
| 12810 | gibe | 1 |
| 12811 | gibberish | 1 |
| 12812 | gesture | 1 |
| 12813 | germane | 1 |
| 12814 | geometry | 1 |
| 12815 | gentry | 1 |
| 12816 | gentiles | 1 |
| 12817 | geniuses | 1 |
| 12818 | generations | 1 |
| 12819 | generated | 1 |
| 12820 | gazpacho | 1 |
| 12821 | gazes | 1 |
| 12822 | gauze | 1 |
| 12823 | gaudy | 1 |
| 12824 | gaudeamus | 1 |
| 12825 | gascons | 1 |
| 12826 | gasabal | 1 |
| 12827 | garnished | 1 |
| 12828 | garnish | 1 |
| 12829 | garner | 1 |
| 12830 | garment | 1 |
| 12831 | garci | 1 |
| 12832 | garaya | 1 |
| 12833 | garamantas | 1 |
| 12834 | garamanta | 1 |
| 12835 | gape | 1 |
| 12836 | gap | 1 |
| 12837 | gaols | 1 |
| 12838 | gang | 1 |
| 12839 | gambolling | 1 |
| 12840 | gambados | 1 |
| 12841 | galloon | 1 |
| 12842 | galliots | 1 |
| 12843 | galleries | 1 |
| 12844 | gallants | 1 |
| 12845 | gallantly | 1 |
| 12846 | gall | 1 |
| 12847 | galingale | 1 |
| 12848 | galician | 1 |
| 12849 | galiana | 1 |
| 12850 | gale | 1 |
| 12851 | galaors | 1 |
| 12852 | gadding | 1 |
| 12853 | gabrio | 1 |
| 12854 | fustian | 1 |
| 12855 | furze | 1 |
| 12856 | furthermore | 1 |
| 12857 | furtherance | 1 |
| 12858 | furry | 1 |
| 12859 | furrows | 1 |
| 12860 | furrowed | 1 |
| 12861 | furrow | 1 |
| 12862 | furbished | 1 |
| 12863 | fur | 1 |
| 12864 | funerals | 1 |
| 12865 | funeral | 1 |
| 12866 | functions | 1 |
| 12867 | fun | 1 |
| 12868 | fumes | 1 |
| 12869 | fuit | 1 |
| 12870 | fugite | 1 |
| 12871 | fuerint | 1 |
| 12872 | fuel | 1 |
| 12873 | fucar | 1 |
| 12874 | fruitlessly | 1 |
| 12875 | fruitful | 1 |
| 12876 | frozen | 1 |
| 12877 | froward | 1 |
| 12878 | frolicsome | 1 |
| 12879 | frogs | 1 |
| 12880 | frog | 1 |
| 12881 | frock | 1 |
| 12882 | frivolous | 1 |
| 12883 | frivolities | 1 |
| 12884 | friton | 1 |
| 12885 | frisking | 1 |
| 12886 | fringes | 1 |
| 12887 | frigate | 1 |
| 12888 | frieze | 1 |
| 12889 | frieslander | 1 |
| 12890 | fretting | 1 |
| 12891 | frets | 1 |
| 12892 | freshness | 1 |
| 12893 | freshly | 1 |
| 12894 | fresher | 1 |
| 12895 | freshened | 1 |
| 12896 | frequents | 1 |
| 12897 | frequenters | 1 |
| 12898 | frequency | 1 |
| 12899 | frenzied | 1 |
| 12900 | frenchified | 1 |
| 12901 | freeze | 1 |
| 12902 | frees | 1 |
| 12903 | fraudulent | 1 |
| 12904 | fratin | 1 |
| 12905 | frantic | 1 |
| 12906 | francolins | 1 |
| 12907 | francia | 1 |
| 12908 | francenia | 1 |
| 12909 | framer | 1 |
| 12910 | frail | 1 |
| 12911 | foxes | 1 |
| 12912 | fourfold | 1 |
| 12913 | fostered | 1 |
| 12914 | forwards | 1 |
| 12915 | forwardness | 1 |
| 12916 | fortunately | 1 |
| 12917 | forts | 1 |
| 12918 | fortresses | 1 |
| 12919 | fortifications | 1 |
| 12920 | forte | 1 |
| 12921 | forsooth | 1 |
| 12922 | forse | 1 |
| 12923 | forsaken | 1 |
| 12924 | formidable | 1 |
| 12925 | formally | 1 |
| 12926 | forked | 1 |
| 12927 | forgettest | 1 |
| 12928 | forgets | 1 |
| 12929 | forgetfulness | 1 |
| 12930 | forgetful | 1 |
| 12931 | forge | 1 |
| 12932 | forestalled | 1 |
| 12933 | foregoing | 1 |
| 12934 | forefinger | 1 |
| 12935 | forefathers | 1 |
| 12936 | forebodings | 1 |
| 12937 | forebode | 1 |
| 12938 | forcing | 1 |
| 12939 | forcibly | 1 |
| 12940 | forbearing | 1 |
| 12941 | foray | 1 |
| 12942 | footsore | 1 |
| 12943 | foots | 1 |
| 12944 | footpad | 1 |
| 12945 | footed | 1 |
| 12946 | foolishly | 1 |
| 12947 | foolishest | 1 |
| 12948 | followest | 1 |
| 12949 | folds | 1 |
| 12950 | folding | 1 |
| 12951 | foil | 1 |
| 12952 | foddering | 1 |
| 12953 | foces | 1 |
| 12954 | fluttered | 1 |
| 12955 | flutter | 1 |
| 12956 | flute | 1 |
| 12957 | flurry | 1 |
| 12958 | fluctuations | 1 |
| 12959 | flout | 1 |
| 12960 | flour | 1 |
| 12961 | floripes | 1 |
| 12962 | florentibus | 1 |
| 12963 | flora | 1 |
| 12964 | floors | 1 |
| 12965 | flogs | 1 |
| 12966 | floats | 1 |
| 12967 | flintlocks | 1 |
| 12968 | flinched | 1 |
| 12969 | flimsy | 1 |
| 12970 | flexible | 1 |
| 12971 | fleridas | 1 |
| 12972 | fleets | 1 |
| 12973 | flees | 1 |
| 12974 | flayed | 1 |
| 12975 | flay | 1 |
| 12976 | flaws | 1 |
| 12977 | flattered | 1 |
| 12978 | flattened | 1 |
| 12979 | flashed | 1 |
| 12980 | flappers | 1 |
| 12981 | flannel | 1 |
| 12982 | flam | 1 |
| 12983 | flakes | 1 |
| 12984 | flagging | 1 |
| 12985 | fixedly | 1 |
| 12986 | fives | 1 |
| 12987 | fittings | 1 |
| 12988 | fittingly | 1 |
| 12989 | fitment | 1 |
| 12990 | fishingrod | 1 |
| 12991 | fishes | 1 |
| 12992 | fishery | 1 |
| 12993 | firmest | 1 |
| 12994 | firma | 1 |
| 12995 | firewood | 1 |
| 12996 | firelocks | 1 |
| 12997 | finikin | 1 |
| 12998 | finer | 1 |
| 12999 | finely | 1 |
| 13000 | finders | 1 |
| 13001 | filthiest | 1 |
| 13002 | fillips | 1 |
| 13003 | fillies | 1 |
| 13004 | filida | 1 |
| 13005 | files | 1 |
| 13006 | filed | 1 |
| 13007 | figueroa | 1 |
| 13008 | fightest | 1 |
| 13009 | figged | 1 |
| 13010 | fifes | 1 |
| 13011 | fifer | 1 |
| 13012 | fido | 1 |
| 13013 | fidgets | 1 |
| 13014 | fez | 1 |
| 13015 | fetter | 1 |
| 13016 | fetlocks | 1 |
| 13017 | fetid | 1 |
| 13018 | fervently | 1 |
| 13019 | fertilising | 1 |
| 13020 | fertilises | 1 |
| 13021 | ferrara | 1 |
| 13022 | ferocity | 1 |
| 13023 | ferocious | 1 |
| 13024 | fernan | 1 |
| 13025 | ferment | 1 |
| 13026 | fencers | 1 |
| 13027 | felons | 1 |
| 13028 | felled | 1 |
| 13029 | felixmartes | 1 |
| 13030 | feliciano | 1 |
| 13031 | felicia | 1 |
| 13032 | fees | 1 |
| 13033 | feelest | 1 |
| 13034 | feeds | 1 |
| 13035 | feeder | 1 |
| 13036 | feasting | 1 |
| 13037 | feasted | 1 |
| 13038 | feasible | 1 |
| 13039 | fearful | 1 |
| 13040 | fearest | 1 |
| 13041 | fearer | 1 |
| 13042 | fealty | 1 |
| 13043 | fays | 1 |
| 13044 | favourites | 1 |
| 13045 | favor | 1 |
| 13046 | favila | 1 |
| 13047 | fauns | 1 |
| 13048 | faulty | 1 |
| 13049 | fatigued | 1 |
| 13050 | fathomed | 1 |
| 13051 | fatherly | 1 |
| 13052 | fatherless | 1 |
| 13053 | fathering | 1 |
| 13054 | fastest | 1 |
| 13055 | fastenings | 1 |
| 13056 | fashions | 1 |
| 13057 | fashioned | 1 |
| 13058 | fashionable | 1 |
| 13059 | fascinate | 1 |
| 13060 | farthingales | 1 |
| 13061 | fartax | 1 |
| 13062 | farmhouses | 1 |
| 13063 | farmers | 1 |
| 13064 | farce | 1 |
| 13065 | fantasies | 1 |
| 13066 | fando | 1 |
| 13067 | fanciest | 1 |
| 13068 | famine | 1 |
| 13069 | falter | 1 |
| 13070 | falsifying | 1 |
| 13071 | falsify | 1 |
| 13072 | falces | 1 |
| 13073 | fairies | 1 |
| 13074 | fainthearted | 1 |
| 13075 | faggots | 1 |
| 13076 | fading | 1 |
| 13077 | fade | 1 |
| 13078 | faculty | 1 |
| 13079 | faction | 1 |
| 13080 | facings | 1 |
| 13081 | facility | 1 |
| 13082 | facilities | 1 |
| 13083 | fabulous | 1 |
| 13084 | fabrication | 1 |
| 13085 | fa | 1 |
| 13086 | eyewitness | 1 |
| 13087 | eyelid | 1 |
| 13088 | exulting | 1 |
| 13089 | exult | 1 |
| 13090 | extremity | 1 |
| 13091 | extravagantly | 1 |
| 13092 | extract | 1 |
| 13093 | extols | 1 |
| 13094 | extolling | 1 |
| 13095 | extinguishing | 1 |
| 13096 | extended | 1 |
| 13097 | extant | 1 |
| 13098 | exquisite | 1 |
| 13099 | expressive | 1 |
| 13100 | expound | 1 |
| 13101 | exposures | 1 |
| 13102 | exposes | 1 |
| 13103 | explorer | 1 |
| 13104 | explode | 1 |
| 13105 | explains | 1 |
| 13106 | expire | 1 |
| 13107 | expiration | 1 |
| 13108 | expiate | 1 |
| 13109 | expelled | 1 |
| 13110 | expeditious | 1 |
| 13111 | expedients | 1 |
| 13112 | expectations | 1 |
| 13113 | expectant | 1 |
| 13114 | expatriation | 1 |
| 13115 | expatiate | 1 |
| 13116 | expansion | 1 |
| 13117 | exorbitant | 1 |
| 13118 | exhortations | 1 |
| 13119 | exhortation | 1 |
| 13120 | exhilarated | 1 |
| 13121 | exhibits | 1 |
| 13122 | exhibiting | 1 |
| 13123 | exhalations | 1 |
| 13124 | exhalation | 1 |
| 13125 | exeunt | 1 |
| 13126 | exerted | 1 |
| 13127 | exercises | 1 |
| 13128 | exercised | 1 |
| 13129 | exempts | 1 |
| 13130 | exemptions | 1 |
| 13131 | exemplary | 1 |
| 13132 | executing | 1 |
| 13133 | executes | 1 |
| 13134 | execrations | 1 |
| 13135 | execration | 1 |
| 13136 | excrescences | 1 |
| 13137 | excrements | 1 |
| 13138 | excommunication | 1 |
| 13139 | excesses | 1 |
| 13140 | excelled | 1 |
| 13141 | excel | 1 |
| 13142 | exceeds | 1 |
| 13143 | exasperation | 1 |
| 13144 | exasperated | 1 |
| 13145 | examiners | 1 |
| 13146 | examiner | 1 |
| 13147 | exalting | 1 |
| 13148 | exalteth | 1 |
| 13149 | exaltation | 1 |
| 13150 | exaggeration | 1 |
| 13151 | exaggerated | 1 |
| 13152 | exacting | 1 |
| 13153 | evildoing | 1 |
| 13154 | evildoer | 1 |
| 13155 | evens | 1 |
| 13156 | evenly | 1 |
| 13157 | eulogy | 1 |
| 13158 | ethiopians | 1 |
| 13159 | ethereal | 1 |
| 13160 | eternity | 1 |
| 13161 | essay | 1 |
| 13162 | esquires | 1 |
| 13163 | esquife | 1 |
| 13164 | esplandians | 1 |
| 13165 | espartafilardo | 1 |
| 13166 | espanoli | 1 |
| 13167 | escotillo | 1 |
| 13168 | escort | 1 |
| 13169 | eructations | 1 |
| 13170 | erst | 1 |
| 13171 | errs | 1 |
| 13172 | errants | 1 |
| 13173 | errands | 1 |
| 13174 | erostratus | 1 |
| 13175 | erecting | 1 |
| 13176 | ercilla | 1 |
| 13177 | eras | 1 |
| 13178 | equivalents | 1 |
| 13179 | equity | 1 |
| 13180 | equitably | 1 |
| 13181 | equitable | 1 |
| 13182 | equipment | 1 |
| 13183 | equinoxes | 1 |
| 13184 | equanimity | 1 |
| 13185 | equalised | 1 |
| 13186 | epigram | 1 |
| 13187 | enveloping | 1 |
| 13188 | entrusting | 1 |
| 13189 | entrap | 1 |
| 13190 | entrances | 1 |
| 13191 | entombs | 1 |
| 13192 | enticed | 1 |
| 13193 | enthusiasm | 1 |
| 13194 | enthrals | 1 |
| 13195 | entertainments | 1 |
| 13196 | enters | 1 |
| 13197 | entangle | 1 |
| 13198 | entails | 1 |
| 13199 | entailed | 1 |
| 13200 | entail | 1 |
| 13201 | ensnare | 1 |
| 13202 | enshrined | 1 |
| 13203 | enrique | 1 |
| 13204 | enriching | 1 |
| 13205 | enriched | 1 |
| 13206 | enormously | 1 |
| 13207 | enormity | 1 |
| 13208 | enmeshed | 1 |
| 13209 | enlist | 1 |
| 13210 | enlightened | 1 |
| 13211 | enjoyable | 1 |
| 13212 | enjoins | 1 |
| 13213 | enhancement | 1 |
| 13214 | engrossed | 1 |
| 13215 | englishman | 1 |
| 13216 | engineer | 1 |
| 13217 | engine | 1 |
| 13218 | engender | 1 |
| 13219 | engages | 1 |
| 13220 | engagements | 1 |
| 13221 | enforce | 1 |
| 13222 | enfold | 1 |
| 13223 | energies | 1 |
| 13224 | endurer | 1 |
| 13225 | endurance | 1 |
| 13226 | endowments | 1 |
| 13227 | endive | 1 |
| 13228 | endangering | 1 |
| 13229 | encumbered | 1 |
| 13230 | encouraging | 1 |
| 13231 | encounterer | 1 |
| 13232 | enclosure | 1 |
| 13233 | enclosed | 1 |
| 13234 | enclose | 1 |
| 13235 | encircling | 1 |
| 13236 | enchantresses | 1 |
| 13237 | encasing | 1 |
| 13238 | encampment | 1 |
| 13239 | encamped | 1 |
| 13240 | encamisado | 1 |
| 13241 | enamourned | 1 |
| 13242 | enactments | 1 |
| 13243 | enables | 1 |
| 13244 | emulation | 1 |
| 13245 | emptying | 1 |
| 13246 | empowered | 1 |
| 13247 | emotions | 1 |
| 13248 | embroidering | 1 |
| 13249 | embroider | 1 |
| 13250 | emblems | 1 |
| 13251 | emblem | 1 |
| 13252 | embers | 1 |
| 13253 | embellishment | 1 |
| 13254 | embassy | 1 |
| 13255 | embarrass | 1 |
| 13256 | embarkation | 1 |
| 13257 | elucidate | 1 |
| 13258 | eloquently | 1 |
| 13259 | eligible | 1 |
| 13260 | elephant | 1 |
| 13261 | elements | 1 |
| 13262 | elect | 1 |
| 13263 | elders | 1 |
| 13264 | elderly | 1 |
| 13265 | elches | 1 |
| 13266 | elapsed | 1 |
| 13267 | elaborately | 1 |
| 13268 | eighth | 1 |
| 13269 | egyptian | 1 |
| 13270 | ego | 1 |
| 13271 | egmont | 1 |
| 13272 | effigy | 1 |
| 13273 | efficacy | 1 |
| 13274 | effectual | 1 |
| 13275 | effective | 1 |
| 13276 | effacing | 1 |
| 13277 | eel | 1 |
| 13278 | edition | 1 |
| 13279 | edifice | 1 |
| 13280 | edicts | 1 |
| 13281 | edging | 1 |
| 13282 | edged | 1 |
| 13283 | ecstasy | 1 |
| 13284 | economy | 1 |
| 13285 | economical | 1 |
| 13286 | eclogue | 1 |
| 13287 | ecliptics | 1 |
| 13288 | eclipsed | 1 |
| 13289 | ebony | 1 |
| 13290 | ebbing | 1 |
| 13291 | eave | 1 |
| 13292 | eater | 1 |
| 13293 | eatables | 1 |
| 13294 | eastward | 1 |
| 13295 | eastertime | 1 |
| 13296 | earns | 1 |
| 13297 | earlier | 1 |
| 13298 | eagle | 1 |
| 13299 | e | 1 |
| 13300 | dyer | 1 |
| 13301 | dyed | 1 |
| 13302 | dwellings | 1 |
| 13303 | dutiful | 1 |
| 13304 | dutchman | 1 |
| 13305 | dusky | 1 |
| 13306 | durindana | 1 |
| 13307 | duration | 1 |
| 13308 | duped | 1 |
| 13309 | dunderhead | 1 |
| 13310 | dummy | 1 |
| 13311 | dullard | 1 |
| 13312 | dulcineae | 1 |
| 13313 | duero | 1 |
| 13314 | duenissima | 1 |
| 13315 | dubitat | 1 |
| 13316 | dubbing | 1 |
| 13317 | dryshod | 1 |
| 13318 | dryness | 1 |
| 13319 | dryads | 1 |
| 13320 | drummers | 1 |
| 13321 | drudgery | 1 |
| 13322 | drowsiness | 1 |
| 13323 | drovers | 1 |
| 13324 | dropsy | 1 |
| 13325 | droppest | 1 |
| 13326 | drooped | 1 |
| 13327 | drones | 1 |
| 13328 | drinker | 1 |
| 13329 | drifting | 1 |
| 13330 | drier | 1 |
| 13331 | dribble | 1 |
| 13332 | drest | 1 |
| 13333 | drenched | 1 |
| 13334 | dreadest | 1 |
| 13335 | drawest | 1 |
| 13336 | drapery | 1 |
| 13337 | draperies | 1 |
| 13338 | dramas | 1 |
| 13339 | drains | 1 |
| 13340 | drafted | 1 |
| 13341 | draft | 1 |
| 13342 | drachm | 1 |
| 13343 | dozed | 1 |
| 13344 | doxy | 1 |
| 13345 | dowry | 1 |
| 13346 | downtrodden | 1 |
| 13347 | downstrokes | 1 |
| 13348 | downs | 1 |
| 13349 | dough | 1 |
| 13350 | doubling | 1 |
| 13351 | doublets | 1 |
| 13352 | doubles | 1 |
| 13353 | dormouse | 1 |
| 13354 | dormitat | 1 |
| 13355 | dorado | 1 |
| 13356 | doom | 1 |
| 13357 | donoso | 1 |
| 13358 | donned | 1 |
| 13359 | donec | 1 |
| 13360 | donde | 1 |
| 13361 | domineering | 1 |
| 13362 | dominant | 1 |
| 13363 | domain | 1 |
| 13364 | doltish | 1 |
| 13365 | dolly | 1 |
| 13366 | dolfos | 1 |
| 13367 | dolet | 1 |
| 13368 | dogmatism | 1 |
| 13369 | dodging | 1 |
| 13370 | dodged | 1 |
| 13371 | document | 1 |
| 13372 | doctored | 1 |
| 13373 | dock | 1 |
| 13374 | docile | 1 |
| 13375 | diviners | 1 |
| 13376 | divinely | 1 |
| 13377 | divested | 1 |
| 13378 | diversity | 1 |
| 13379 | diverse | 1 |
| 13380 | ditties | 1 |
| 13381 | ditches | 1 |
| 13382 | disturbing | 1 |
| 13383 | disturber | 1 |
| 13384 | disturbances | 1 |
| 13385 | distrustful | 1 |
| 13386 | distrusted | 1 |
| 13387 | districts | 1 |
| 13388 | distribution | 1 |
| 13389 | distributes | 1 |
| 13390 | distribute | 1 |
| 13391 | distressing | 1 |
| 13392 | distressedest | 1 |
| 13393 | distractedly | 1 |
| 13394 | distils | 1 |
| 13395 | distilling | 1 |
| 13396 | distich | 1 |
| 13397 | distasteful | 1 |
| 13398 | distaff | 1 |
| 13399 | dissolved | 1 |
| 13400 | dissolve | 1 |
| 13401 | dissolute | 1 |
| 13402 | dissensions | 1 |
| 13403 | dissemble | 1 |
| 13404 | disrespectfully | 1 |
| 13405 | disrespect | 1 |
| 13406 | disreputable | 1 |
| 13407 | disregarding | 1 |
| 13408 | disregarded | 1 |
| 13409 | disquietude | 1 |
| 13410 | disquiets | 1 |
| 13411 | disquiet | 1 |
| 13412 | disputed | 1 |
| 13413 | disproportioned | 1 |
| 13414 | disproportion | 1 |
| 13415 | dispositions | 1 |
| 13416 | disport | 1 |
| 13417 | displeasing | 1 |
| 13418 | displease | 1 |
| 13419 | dispensations | 1 |
| 13420 | dispensation | 1 |
| 13421 | dispel | 1 |
| 13422 | dispassionate | 1 |
| 13423 | disparity | 1 |
| 13424 | disparaging | 1 |
| 13425 | disorderly | 1 |
| 13426 | disobeying | 1 |
| 13427 | dismissal | 1 |
| 13428 | dismantle | 1 |
| 13429 | disloyal | 1 |
| 13430 | disjointed | 1 |
| 13431 | disinherited | 1 |
| 13432 | disillusion | 1 |
| 13433 | dishwater | 1 |
| 13434 | dishonourably | 1 |
| 13435 | dishonourable | 1 |
| 13436 | dishevelled | 1 |
| 13437 | disheartened | 1 |
| 13438 | dishclouts | 1 |
| 13439 | disgusting | 1 |
| 13440 | disguising | 1 |
| 13441 | disgoverned | 1 |
| 13442 | disgorge | 1 |
| 13443 | diseases | 1 |
| 13444 | discoverest | 1 |
| 13445 | discoverer | 1 |
| 13446 | discourtesy | 1 |
| 13447 | discoursing | 1 |
| 13448 | discoursed | 1 |
| 13449 | discouraged | 1 |
| 13450 | discourage | 1 |
| 13451 | discontented | 1 |
| 13452 | discontent | 1 |
| 13453 | disconsolately | 1 |
| 13454 | discomforts | 1 |
| 13455 | discomfitures | 1 |
| 13456 | discomfiture | 1 |
| 13457 | discipline | 1 |
| 13458 | disciplinants | 1 |
| 13459 | disciples | 1 |
| 13460 | discerning | 1 |
| 13461 | discern | 1 |
| 13462 | discarded | 1 |
| 13463 | disbursement | 1 |
| 13464 | disbursed | 1 |
| 13465 | disburse | 1 |
| 13466 | disbelieve | 1 |
| 13467 | disarranged | 1 |
| 13468 | disapprove | 1 |
| 13469 | disadvantage | 1 |
| 13470 | disabusing | 1 |
| 13471 | dirt | 1 |
| 13472 | dirlos | 1 |
| 13473 | dirges | 1 |
| 13474 | dirge | 1 |
| 13475 | director | 1 |
| 13476 | dioscorides | 1 |
| 13477 | dinners | 1 |
| 13478 | dining | 1 |
| 13479 | dimity | 1 |
| 13480 | diminutive | 1 |
| 13481 | diminishing | 1 |
| 13482 | diminished | 1 |
| 13483 | diminish | 1 |
| 13484 | diligite | 1 |
| 13485 | diligent | 1 |
| 13486 | dilapidated | 1 |
| 13487 | dignitary | 1 |
| 13488 | digestion | 1 |
| 13489 | diffuse | 1 |
| 13490 | diffidence | 1 |
| 13491 | differed | 1 |
| 13492 | diere | 1 |
| 13493 | diction | 1 |
| 13494 | dico | 1 |
| 13495 | diamantine | 1 |
| 13496 | diabolo | 1 |
| 13497 | dexterously | 1 |
| 13498 | dews | 1 |
| 13499 | dew | 1 |
| 13500 | devotes | 1 |
| 13501 | devoir | 1 |
| 13502 | deus | 1 |
| 13503 | deum | 1 |
| 13504 | deuce | 1 |
| 13505 | detested | 1 |
| 13506 | detects | 1 |
| 13507 | detecting | 1 |
| 13508 | detected | 1 |
| 13509 | detained | 1 |
| 13510 | detailed | 1 |
| 13511 | detached | 1 |
| 13512 | desultory | 1 |
| 13513 | destructive | 1 |
| 13514 | destroyer | 1 |
| 13515 | destined | 1 |
| 13516 | dessert | 1 |
| 13517 | despondency | 1 |
| 13518 | despoiled | 1 |
| 13519 | despising | 1 |
| 13520 | despises | 1 |
| 13521 | desperado | 1 |
| 13522 | desolate | 1 |
| 13523 | desk | 1 |
| 13524 | designing | 1 |
| 13525 | designedly | 1 |
| 13526 | designations | 1 |
| 13527 | deservest | 1 |
| 13528 | descry | 1 |
| 13529 | derogatory | 1 |
| 13530 | deriving | 1 |
| 13531 | derives | 1 |
| 13532 | deranged | 1 |
| 13533 | derange | 1 |
| 13534 | depression | 1 |
| 13535 | depressed | 1 |
| 13536 | depreciation | 1 |
| 13537 | depravities | 1 |
| 13538 | depository | 1 |
| 13539 | depositary | 1 |
| 13540 | deposit | 1 |
| 13541 | deportment | 1 |
| 13542 | deplorable | 1 |
| 13543 | dependence | 1 |
| 13544 | departures | 1 |
| 13545 | departs | 1 |
| 13546 | departed | 1 |
| 13547 | denounce | 1 |
| 13548 | denmark | 1 |
| 13549 | demure | 1 |
| 13550 | demur | 1 |
| 13551 | demosthenes | 1 |
| 13552 | demonstration | 1 |
| 13553 | demonstrate | 1 |
| 13554 | demise | 1 |
| 13555 | demi | 1 |
| 13556 | demean | 1 |
| 13557 | deluge | 1 |
| 13558 | deluding | 1 |
| 13559 | della | 1 |
| 13560 | delinquents | 1 |
| 13561 | delicious | 1 |
| 13562 | delegated | 1 |
| 13563 | delaying | 1 |
| 13564 | deities | 1 |
| 13565 | defying | 1 |
| 13566 | defunct | 1 |
| 13567 | defrauded | 1 |
| 13568 | defraud | 1 |
| 13569 | defies | 1 |
| 13570 | deficiencies | 1 |
| 13571 | defiances | 1 |
| 13572 | defends | 1 |
| 13573 | defenceless | 1 |
| 13574 | defective | 1 |
| 13575 | defeated | 1 |
| 13576 | defamatory | 1 |
| 13577 | deeper | 1 |
| 13578 | deeming | 1 |
| 13579 | deduce | 1 |
| 13580 | dedicate | 1 |
| 13581 | decoy | 1 |
| 13582 | decoration | 1 |
| 13583 | decorated | 1 |
| 13584 | decline | 1 |
| 13585 | declarations | 1 |
| 13586 | declar | 1 |
| 13587 | decking | 1 |
| 13588 | deck | 1 |
| 13589 | decimas | 1 |
| 13590 | deciding | 1 |
| 13591 | deceptive | 1 |
| 13592 | decency | 1 |
| 13593 | deceitful | 1 |
| 13594 | decease | 1 |
| 13595 | decayed | 1 |
| 13596 | decay | 1 |
| 13597 | decapitating | 1 |
| 13598 | decapitated | 1 |
| 13599 | decanted | 1 |
| 13600 | debits | 1 |
| 13601 | debated | 1 |
| 13602 | debaseth | 1 |
| 13603 | dears | 1 |
| 13604 | dearest | 1 |
| 13605 | dearer | 1 |
| 13606 | deadened | 1 |
| 13607 | dazzling | 1 |
| 13608 | dazzle | 1 |
| 13609 | daytime | 1 |
| 13610 | david | 1 |
| 13611 | dauntlessly | 1 |
| 13612 | dates | 1 |
| 13613 | data | 1 |
| 13614 | darting | 1 |
| 13615 | dart | 1 |
| 13616 | darn | 1 |
| 13617 | darling | 1 |
| 13618 | darkish | 1 |
| 13619 | darkest | 1 |
| 13620 | darkening | 1 |
| 13621 | darkened | 1 |
| 13622 | darius | 1 |
| 13623 | darest | 1 |
| 13624 | daresay | 1 |
| 13625 | daraida | 1 |
| 13626 | dappled | 1 |
| 13627 | dancer | 1 |
| 13628 | danced | 1 |
| 13629 | danaes | 1 |
| 13630 | dampness | 1 |
| 13631 | damascus | 1 |
| 13632 | damages | 1 |
| 13633 | dallying | 1 |
| 13634 | dally | 1 |
| 13635 | dallied | 1 |
| 13636 | dalliance | 1 |
| 13637 | dale | 1 |
| 13638 | dais | 1 |
| 13639 | daintily | 1 |
| 13640 | daggers | 1 |
| 13641 | cuttlefish | 1 |
| 13642 | curvetting | 1 |
| 13643 | curves | 1 |
| 13644 | curtius | 1 |
| 13645 | curtii | 1 |
| 13646 | curtain | 1 |
| 13647 | curtailing | 1 |
| 13648 | curst | 1 |
| 13649 | curry | 1 |
| 13650 | curiously | 1 |
| 13651 | curiel | 1 |
| 13652 | cureless | 1 |
| 13653 | curdled | 1 |
| 13654 | curbed | 1 |
| 13655 | curambro | 1 |
| 13656 | curadillo | 1 |
| 13657 | cupbearer | 1 |
| 13658 | cunningly | 1 |
| 13659 | culture | 1 |
| 13660 | cultivate | 1 |
| 13661 | culprits | 1 |
| 13662 | cue | 1 |
| 13663 | cudgels | 1 |
| 13664 | cubits | 1 |
| 13665 | cuatrero | 1 |
| 13666 | cuartos | 1 |
| 13667 | cuartillos | 1 |
| 13668 | cruzadoes | 1 |
| 13669 | cruz | 1 |
| 13670 | crusts | 1 |
| 13671 | crushing | 1 |
| 13672 | crushes | 1 |
| 13673 | crumbling | 1 |
| 13674 | crumb | 1 |
| 13675 | cruisers | 1 |
| 13676 | cruiser | 1 |
| 13677 | cruise | 1 |
| 13678 | cruelties | 1 |
| 13679 | crucis | 1 |
| 13680 | crucifix | 1 |
| 13681 | crowning | 1 |
| 13682 | crowed | 1 |
| 13683 | crowds | 1 |
| 13684 | crowbar | 1 |
| 13685 | crocodile | 1 |
| 13686 | criticising | 1 |
| 13687 | criticise | 1 |
| 13688 | cristobal | 1 |
| 13689 | cripples | 1 |
| 13690 | cripple | 1 |
| 13691 | crinkled | 1 |
| 13692 | crimping | 1 |
| 13693 | criers | 1 |
| 13694 | crier | 1 |
| 13695 | crickets | 1 |
| 13696 | cribs | 1 |
| 13697 | cribbings | 1 |
| 13698 | crib | 1 |
| 13699 | crews | 1 |
| 13700 | crevices | 1 |
| 13701 | crete | 1 |
| 13702 | crestfallen | 1 |
| 13703 | crept | 1 |
| 13704 | creeping | 1 |
| 13705 | creek | 1 |
| 13706 | creed | 1 |
| 13707 | credulous | 1 |
| 13708 | credits | 1 |
| 13709 | creditor | 1 |
| 13710 | creatures | 1 |
| 13711 | creator | 1 |
| 13712 | creams | 1 |
| 13713 | craziness | 1 |
| 13714 | cravings | 1 |
| 13715 | crave | 1 |
| 13716 | crane | 1 |
| 13717 | cramps | 1 |
| 13718 | cramped | 1 |
| 13719 | craftsman | 1 |
| 13720 | crafts | 1 |
| 13721 | craftily | 1 |
| 13722 | cradled | 1 |
| 13723 | cradle | 1 |
| 13724 | cracks | 1 |
| 13725 | cracking | 1 |
| 13726 | crackers | 1 |
| 13727 | crack | 1 |
| 13728 | cowhide | 1 |
| 13729 | cowheels | 1 |
| 13730 | coveted | 1 |
| 13731 | covet | 1 |
| 13732 | cove | 1 |
| 13733 | courtships | 1 |
| 13734 | courtliness | 1 |
| 13735 | courtesies | 1 |
| 13736 | coursing | 1 |
| 13737 | coursers | 1 |
| 13738 | couples | 1 |
| 13739 | coupled | 1 |
| 13740 | countrymen | 1 |
| 13741 | counties | 1 |
| 13742 | countersign | 1 |
| 13743 | counterpoise | 1 |
| 13744 | counterpane | 1 |
| 13745 | counterbalanced | 1 |
| 13746 | counteract | 1 |
| 13747 | counter | 1 |
| 13748 | countenace | 1 |
| 13749 | counsellor | 1 |
| 13750 | counselled | 1 |
| 13751 | coughing | 1 |
| 13752 | coughed | 1 |
| 13753 | cough | 1 |
| 13754 | couched | 1 |
| 13755 | cottage | 1 |
| 13756 | cot | 1 |
| 13757 | costly | 1 |
| 13758 | costeth | 1 |
| 13759 | cortadillo | 1 |
| 13760 | corselet | 1 |
| 13761 | corse | 1 |
| 13762 | corruption | 1 |
| 13763 | corrupting | 1 |
| 13764 | corrupter | 1 |
| 13765 | corresponded | 1 |
| 13766 | correspond | 1 |
| 13767 | corps | 1 |
| 13768 | corns | 1 |
| 13769 | corking | 1 |
| 13770 | corellas | 1 |
| 13771 | cordiality | 1 |
| 13772 | corde | 1 |
| 13773 | copying | 1 |
| 13774 | cools | 1 |
| 13775 | cooling | 1 |
| 13776 | coolers | 1 |
| 13777 | cooler | 1 |
| 13778 | cooking | 1 |
| 13779 | cooings | 1 |
| 13780 | cooing | 1 |
| 13781 | convincing | 1 |
| 13782 | conveying | 1 |
| 13783 | conveyed | 1 |
| 13784 | conversion | 1 |
| 13785 | contumacy | 1 |
| 13786 | contrivers | 1 |
| 13787 | contrivances | 1 |
| 13788 | contributed | 1 |
| 13789 | contravention | 1 |
| 13790 | contravened | 1 |
| 13791 | contrasted | 1 |
| 13792 | contraries | 1 |
| 13793 | contradiction | 1 |
| 13794 | contradicted | 1 |
| 13795 | contradict | 1 |
| 13796 | contracted | 1 |
| 13797 | continuous | 1 |
| 13798 | continual | 1 |
| 13799 | contexture | 1 |
| 13800 | contests | 1 |
| 13801 | contenting | 1 |
| 13802 | contentedly | 1 |
| 13803 | contended | 1 |
| 13804 | contend | 1 |
| 13805 | contemplates | 1 |
| 13806 | contact | 1 |
| 13807 | consumption | 1 |
| 13808 | consummation | 1 |
| 13809 | consummate | 1 |
| 13810 | consuming | 1 |
| 13811 | consumes | 1 |
| 13812 | construct | 1 |
| 13813 | constrain | 1 |
| 13814 | constitutions | 1 |
| 13815 | constitutes | 1 |
| 13816 | constituted | 1 |
| 13817 | constellations | 1 |
| 13818 | consisting | 1 |
| 13819 | consistency | 1 |
| 13820 | considerate | 1 |
| 13821 | conscientious | 1 |
| 13822 | consciences | 1 |
| 13823 | conquest | 1 |
| 13824 | conquer | 1 |
| 13825 | connoisseur | 1 |
| 13826 | conjuring | 1 |
| 13827 | conjecturing | 1 |
| 13828 | conjecturally | 1 |
| 13829 | congregated | 1 |
| 13830 | congratulations | 1 |
| 13831 | confusing | 1 |
| 13832 | confounded | 1 |
| 13833 | conflicting | 1 |
| 13834 | confirmatory | 1 |
| 13835 | conferring | 1 |
| 13836 | conductors | 1 |
| 13837 | conductor | 1 |
| 13838 | condolent | 1 |
| 13839 | condole | 1 |
| 13840 | condemnation | 1 |
| 13841 | concoctor | 1 |
| 13842 | concocter | 1 |
| 13843 | concocted | 1 |
| 13844 | concoct | 1 |
| 13845 | conclusions | 1 |
| 13846 | conclave | 1 |
| 13847 | concert | 1 |
| 13848 | conceptions | 1 |
| 13849 | conception | 1 |
| 13850 | concentrated | 1 |
| 13851 | conceivable | 1 |
| 13852 | conceited | 1 |
| 13853 | conceit | 1 |
| 13854 | compunction | 1 |
| 13855 | comprehends | 1 |
| 13856 | comprehending | 1 |
| 13857 | compounding | 1 |
| 13858 | complying | 1 |
| 13859 | complutum | 1 |
| 13860 | complimented | 1 |
| 13861 | complimentary | 1 |
| 13862 | complicity | 1 |
| 13863 | complexioned | 1 |
| 13864 | completion | 1 |
| 13865 | completes | 1 |
| 13866 | complaisance | 1 |
| 13867 | complainant | 1 |
| 13868 | complacency | 1 |
| 13869 | compete | 1 |
| 13870 | compatriot | 1 |
| 13871 | compares | 1 |
| 13872 | companionship | 1 |
| 13873 | comorin | 1 |
| 13874 | commute | 1 |
| 13875 | communities | 1 |
| 13876 | communing | 1 |
| 13877 | communications | 1 |
| 13878 | communicating | 1 |
| 13879 | communicated | 1 |
| 13880 | commune | 1 |
| 13881 | commonwealth | 1 |
| 13882 | commoner | 1 |
| 13883 | commodity | 1 |
| 13884 | commissioned | 1 |
| 13885 | commission | 1 |
| 13886 | commissariat | 1 |
| 13887 | commiseration | 1 |
| 13888 | commingled | 1 |
| 13889 | commerce | 1 |
| 13890 | commentary | 1 |
| 13891 | commentaries | 1 |
| 13892 | commends | 1 |
| 13893 | commendatory | 1 |
| 13894 | commendation | 1 |
| 13895 | commenced | 1 |
| 13896 | commence | 1 |
| 13897 | comings | 1 |
| 13898 | comical | 1 |
| 13899 | comic | 1 |
| 13900 | comforter | 1 |
| 13901 | cometh | 1 |
| 13902 | comeliest | 1 |
| 13903 | combings | 1 |
| 13904 | combing | 1 |
| 13905 | combinations | 1 |
| 13906 | combed | 1 |
| 13907 | colures | 1 |
| 13908 | colonnas | 1 |
| 13909 | colocynth | 1 |
| 13910 | collegiate | 1 |
| 13911 | collector | 1 |
| 13912 | collectively | 1 |
| 13913 | collapse | 1 |
| 13914 | colds | 1 |
| 13915 | coldly | 1 |
| 13916 | coif | 1 |
| 13917 | cogitationes | 1 |
| 13918 | cogitation | 1 |
| 13919 | cocks | 1 |
| 13920 | cockering | 1 |
| 13921 | coats | 1 |
| 13922 | coasts | 1 |
| 13923 | coals | 1 |
| 13924 | clysters | 1 |
| 13925 | clusters | 1 |
| 13926 | clustering | 1 |
| 13927 | clumsily | 1 |
| 13928 | clubs | 1 |
| 13929 | clowns | 1 |
| 13930 | cloudy | 1 |
| 13931 | clouded | 1 |
| 13932 | closets | 1 |
| 13933 | closeted | 1 |
| 13934 | closeness | 1 |
| 13935 | cloister | 1 |
| 13936 | clogs | 1 |
| 13937 | clods | 1 |
| 13938 | clodhopper | 1 |
| 13939 | clodcrusher | 1 |
| 13940 | clip | 1 |
| 13941 | clime | 1 |
| 13942 | climbing | 1 |
| 13943 | climates | 1 |
| 13944 | cleverer | 1 |
| 13945 | clerks | 1 |
| 13946 | clergy | 1 |
| 13947 | clenched | 1 |
| 13948 | clenardo | 1 |
| 13949 | clefts | 1 |
| 13950 | cleaves | 1 |
| 13951 | cleave | 1 |
| 13952 | cleavage | 1 |
| 13953 | clears | 1 |
| 13954 | clearness | 1 |
| 13955 | clearing | 1 |
| 13956 | clearer | 1 |
| 13957 | cleanse | 1 |
| 13958 | cleaning | 1 |
| 13959 | clawed | 1 |
| 13960 | clauquel | 1 |
| 13961 | clasp | 1 |
| 13962 | clashing | 1 |
| 13963 | clarion | 1 |
| 13964 | claridiana | 1 |
| 13965 | clapping | 1 |
| 13966 | clapped | 1 |
| 13967 | claimed | 1 |
| 13968 | civilised | 1 |
| 13969 | citizens | 1 |
| 13970 | citest | 1 |
| 13971 | cite | 1 |
| 13972 | cirimony | 1 |
| 13973 | cirimonies | 1 |
| 13974 | circumstanced | 1 |
| 13975 | circumspectly | 1 |
| 13976 | circulated | 1 |
| 13977 | circe | 1 |
| 13978 | ciphers | 1 |
| 13979 | churned | 1 |
| 13980 | churls | 1 |
| 13981 | churchmen | 1 |
| 13982 | churches | 1 |
| 13983 | chronicles | 1 |
| 13984 | christus | 1 |
| 13985 | christobal | 1 |
| 13986 | christmas | 1 |
| 13987 | christianity | 1 |
| 13988 | christened | 1 |
| 13989 | choughs | 1 |
| 13990 | choke | 1 |
| 13991 | choir | 1 |
| 13992 | choicest | 1 |
| 13993 | choicely | 1 |
| 13994 | chisels | 1 |
| 13995 | chins | 1 |
| 13996 | chinese | 1 |
| 13997 | chimeras | 1 |
| 13998 | chimera | 1 |
| 13999 | chills | 1 |
| 14000 | childbirth | 1 |
| 14001 | chides | 1 |
| 14002 | chicory | 1 |
| 14003 | chickpea | 1 |
| 14004 | chick | 1 |
| 14005 | chews | 1 |
| 14006 | chewing | 1 |
| 14007 | chestnuts | 1 |
| 14008 | chestnut | 1 |
| 14009 | cherries | 1 |
| 14010 | cherishing | 1 |
| 14011 | cherished | 1 |
| 14012 | cheeses | 1 |
| 14013 | cheery | 1 |
| 14014 | checks | 1 |
| 14015 | cheated | 1 |
| 14016 | cheaper | 1 |
| 14017 | chattering | 1 |
| 14018 | chattered | 1 |
| 14019 | chatterbox | 1 |
| 14020 | chattels | 1 |
| 14021 | chastising | 1 |
| 14022 | chastised | 1 |
| 14023 | chastest | 1 |
| 14024 | chasing | 1 |
| 14025 | charybdises | 1 |
| 14026 | charter | 1 |
| 14027 | charon | 1 |
| 14028 | charny | 1 |
| 14029 | charcoal | 1 |
| 14030 | chaplet | 1 |
| 14031 | chaplains | 1 |
| 14032 | chapfallen | 1 |
| 14033 | chanting | 1 |
| 14034 | chanted | 1 |
| 14035 | chant | 1 |
| 14036 | changeable | 1 |
| 14037 | champaign | 1 |
| 14038 | chaldee | 1 |
| 14039 | chaldeans | 1 |
| 14040 | chagrin | 1 |
| 14041 | chafing | 1 |
| 14042 | chaff | 1 |
| 14043 | cessation | 1 |
| 14044 | certainties | 1 |
| 14045 | ceremoniousness | 1 |
| 14046 | ceremonious | 1 |
| 14047 | cerdas | 1 |
| 14048 | cerbellon | 1 |
| 14049 | century | 1 |
| 14050 | centred | 1 |
| 14051 | centre | 1 |
| 14052 | censure | 1 |
| 14053 | censorious | 1 |
| 14054 | cells | 1 |
| 14055 | cellar | 1 |
| 14056 | celesti | 1 |
| 14057 | celerity | 1 |
| 14058 | celebration | 1 |
| 14059 | ceilings | 1 |
| 14060 | ceases | 1 |
| 14061 | cazoleros | 1 |
| 14062 | cavilling | 1 |
| 14063 | caviar | 1 |
| 14064 | cavalry | 1 |
| 14065 | cautiousness | 1 |
| 14066 | cautery | 1 |
| 14067 | cauldron | 1 |
| 14068 | caudrillero | 1 |
| 14069 | catonian | 1 |
| 14070 | catiline | 1 |
| 14071 | catcher | 1 |
| 14072 | catapult | 1 |
| 14073 | catalonia | 1 |
| 14074 | catalogue | 1 |
| 14075 | casually | 1 |
| 14076 | castor | 1 |
| 14077 | castilians | 1 |
| 14078 | castigation | 1 |
| 14079 | cased | 1 |
| 14080 | casa | 1 |
| 14081 | carthagena | 1 |
| 14082 | carters | 1 |
| 14083 | cartels | 1 |
| 14084 | cartagena | 1 |
| 14085 | carrots | 1 |
| 14086 | carped | 1 |
| 14087 | carols | 1 |
| 14088 | carolea | 1 |
| 14089 | carobs | 1 |
| 14090 | carnal | 1 |
| 14091 | carmine | 1 |
| 14092 | carloto | 1 |
| 14093 | caressed | 1 |
| 14094 | carelessly | 1 |
| 14095 | careers | 1 |
| 14096 | careered | 1 |
| 14097 | cardinal | 1 |
| 14098 | carcass | 1 |
| 14099 | carcase | 1 |
| 14100 | carcajona | 1 |
| 14101 | carcajes | 1 |
| 14102 | carbuncles | 1 |
| 14103 | caraculiambro | 1 |
| 14104 | caput | 1 |
| 14105 | capturing | 1 |
| 14106 | captors | 1 |
| 14107 | captivated | 1 |
| 14108 | captivate | 1 |
| 14109 | capricious | 1 |
| 14110 | caprichoso | 1 |
| 14111 | caprices | 1 |
| 14112 | caprice | 1 |
| 14113 | capparum | 1 |
| 14114 | capons | 1 |
| 14115 | capitulated | 1 |
| 14116 | capilla | 1 |
| 14117 | cantle | 1 |
| 14118 | cantillana | 1 |
| 14119 | cantera | 1 |
| 14120 | canter | 1 |
| 14121 | canonry | 1 |
| 14122 | canonised | 1 |
| 14123 | cano | 1 |
| 14124 | cannonade | 1 |
| 14125 | cannibals | 1 |
| 14126 | cankerworm | 1 |
| 14127 | canine | 1 |
| 14128 | cancionero | 1 |
| 14129 | cancel | 1 |
| 14130 | canary | 1 |
| 14131 | campeador | 1 |
| 14132 | campaigns | 1 |
| 14133 | campaign | 1 |
| 14134 | camoens | 1 |
| 14135 | camlet | 1 |
| 14136 | camest | 1 |
| 14137 | camel | 1 |
| 14138 | calypso | 1 |
| 14139 | calumny | 1 |
| 14140 | calumniated | 1 |
| 14141 | calmed | 1 |
| 14142 | callow | 1 |
| 14143 | callings | 1 |
| 14144 | callest | 1 |
| 14145 | calle | 1 |
| 14146 | calculation | 1 |
| 14147 | calculated | 1 |
| 14148 | calatrava | 1 |
| 14149 | calamities | 1 |
| 14150 | calainos | 1 |
| 14151 | calabrian | 1 |
| 14152 | caii | 1 |
| 14153 | caesars | 1 |
| 14154 | cadells | 1 |
| 14155 | cackney | 1 |
| 14156 | cacique | 1 |
| 14157 | cachopins | 1 |
| 14158 | cachidiablo | 1 |
| 14159 | cabra | 1 |
| 14160 | cabins | 1 |
| 14161 | cabin | 1 |
| 14162 | cabbages | 1 |
| 14163 | bygone | 1 |
| 14164 | buzzard | 1 |
| 14165 | buxom | 1 |
| 14166 | button | 1 |
| 14167 | butron | 1 |
| 14168 | butchers | 1 |
| 14169 | busybodies | 1 |
| 14170 | busts | 1 |
| 14171 | bustle | 1 |
| 14172 | bustamante | 1 |
| 14173 | busiris | 1 |
| 14174 | businesses | 1 |
| 14175 | busily | 1 |
| 14176 | busiest | 1 |
| 14177 | burlador | 1 |
| 14178 | burguillos | 1 |
| 14179 | burdening | 1 |
| 14180 | bundred | 1 |
| 14181 | bunches | 1 |
| 14182 | bulwark | 1 |
| 14183 | bully | 1 |
| 14184 | bullocks | 1 |
| 14185 | bullets | 1 |
| 14186 | bulkier | 1 |
| 14187 | build | 1 |
| 14188 | bugle | 1 |
| 14189 | bugbear | 1 |
| 14190 | bug | 1 |
| 14191 | buffoons | 1 |
| 14192 | buff | 1 |
| 14193 | budging | 1 |
| 14194 | budget | 1 |
| 14195 | budding | 1 |
| 14196 | bucolics | 1 |
| 14197 | buckled | 1 |
| 14198 | bucketful | 1 |
| 14199 | bubbling | 1 |
| 14200 | brushwood | 1 |
| 14201 | brushing | 1 |
| 14202 | brush | 1 |
| 14203 | bruisers | 1 |
| 14204 | bruise | 1 |
| 14205 | browsing | 1 |
| 14206 | brow | 1 |
| 14207 | brotherly | 1 |
| 14208 | brotherhoods | 1 |
| 14209 | brooksides | 1 |
| 14210 | brookside | 1 |
| 14211 | brood | 1 |
| 14212 | brokers | 1 |
| 14213 | brocades | 1 |
| 14214 | brocaded | 1 |
| 14215 | brocabruno | 1 |
| 14216 | broadest | 1 |
| 14217 | broader | 1 |
| 14218 | broadcast | 1 |
| 14219 | broached | 1 |
| 14220 | brittleness | 1 |
| 14221 | bristling | 1 |
| 14222 | briskness | 1 |
| 14223 | briskish | 1 |
| 14224 | brine | 1 |
| 14225 | brindled | 1 |
| 14226 | brimstone | 1 |
| 14227 | brimming | 1 |
| 14228 | brimful | 1 |
| 14229 | brillador | 1 |
| 14230 | brigliador | 1 |
| 14231 | brightly | 1 |
| 14232 | brigands | 1 |
| 14233 | brigand | 1 |
| 14234 | brides | 1 |
| 14235 | bricklayers | 1 |
| 14236 | brickbats | 1 |
| 14237 | brick | 1 |
| 14238 | bribery | 1 |
| 14239 | bribed | 1 |
| 14240 | briars | 1 |
| 14241 | briareuses | 1 |
| 14242 | briareus | 1 |
| 14243 | breviaries | 1 |
| 14244 | bretons | 1 |
| 14245 | breezes | 1 |
| 14246 | breathed | 1 |
| 14247 | bream | 1 |
| 14248 | breakfasted | 1 |
| 14249 | breakfast | 1 |
| 14250 | brazier | 1 |
| 14251 | brazen | 1 |
| 14252 | brayers | 1 |
| 14253 | brayer | 1 |
| 14254 | brawl | 1 |
| 14255 | bravo | 1 |
| 14256 | braveries | 1 |
| 14257 | braver | 1 |
| 14258 | brandishing | 1 |
| 14259 | brandished | 1 |
| 14260 | brandabarbaran | 1 |
| 14261 | branching | 1 |
| 14262 | branched | 1 |
| 14263 | braids | 1 |
| 14264 | braided | 1 |
| 14265 | brahmans | 1 |
| 14266 | bradamante | 1 |
| 14267 | boxes | 1 |
| 14268 | bowshots | 1 |
| 14269 | bows | 1 |
| 14270 | bowl | 1 |
| 14271 | bouts | 1 |
| 14272 | bout | 1 |
| 14273 | bourbon | 1 |
| 14274 | bounding | 1 |
| 14275 | bouillon | 1 |
| 14276 | bottles | 1 |
| 14277 | bosque | 1 |
| 14278 | bosomed | 1 |
| 14279 | boscan | 1 |
| 14280 | bored | 1 |
| 14281 | bordering | 1 |
| 14282 | borcegui | 1 |
| 14283 | booty | 1 |
| 14284 | bootes | 1 |
| 14285 | boors | 1 |
| 14286 | boons | 1 |
| 14287 | bonus | 1 |
| 14288 | bonum | 1 |
| 14289 | bonny | 1 |
| 14290 | bonnet | 1 |
| 14291 | bonfires | 1 |
| 14292 | bonds | 1 |
| 14293 | bond | 1 |
| 14294 | bombazine | 1 |
| 14295 | bologna | 1 |
| 14296 | boliche | 1 |
| 14297 | bolder | 1 |
| 14298 | boiardo | 1 |
| 14299 | bodkin | 1 |
| 14300 | boding | 1 |
| 14301 | boasting | 1 |
| 14302 | boasted | 1 |
| 14303 | boars | 1 |
| 14304 | boarded | 1 |
| 14305 | blustering | 1 |
| 14306 | blurt | 1 |
| 14307 | blurred | 1 |
| 14308 | blunts | 1 |
| 14309 | blunter | 1 |
| 14310 | blunt | 1 |
| 14311 | blubbering | 1 |
| 14312 | blubber | 1 |
| 14313 | blot | 1 |
| 14314 | blossom | 1 |
| 14315 | bloom | 1 |
| 14316 | bloodstained | 1 |
| 14317 | bloodshed | 1 |
| 14318 | blockheads | 1 |
| 14319 | blits | 1 |
| 14320 | blithe | 1 |
| 14321 | blinding | 1 |
| 14322 | blindfolds | 1 |
| 14323 | blindfolded | 1 |
| 14324 | bleed | 1 |
| 14325 | bled | 1 |
| 14326 | bleating | 1 |
| 14327 | blasphemous | 1 |
| 14328 | blas | 1 |
| 14329 | blankets | 1 |
| 14330 | blanketers | 1 |
| 14331 | blanketeers | 1 |
| 14332 | blank | 1 |
| 14333 | blacksmiths | 1 |
| 14334 | blacksmith | 1 |
| 14335 | blackbreech | 1 |
| 14336 | blab | 1 |
| 14337 | bites | 1 |
| 14338 | births | 1 |
| 14339 | birthplace | 1 |
| 14340 | birdcages | 1 |
| 14341 | billows | 1 |
| 14342 | billings | 1 |
| 14343 | billing | 1 |
| 14344 | billiards | 1 |
| 14345 | bill | 1 |
| 14346 | bile | 1 |
| 14347 | biggest | 1 |
| 14348 | bewitch | 1 |
| 14349 | bewails | 1 |
| 14350 | bewailed | 1 |
| 14351 | bevy | 1 |
| 14352 | beverages | 1 |
| 14353 | beverage | 1 |
| 14354 | betters | 1 |
| 14355 | bethought | 1 |
| 14356 | betaking | 1 |
| 14357 | bestir | 1 |
| 14358 | bespangled | 1 |
| 14359 | besought | 1 |
| 14360 | beseeching | 1 |
| 14361 | berrueca | 1 |
| 14362 | berengeneros | 1 |
| 14363 | berengenas | 1 |
| 14364 | berengena | 1 |
| 14365 | benumbed | 1 |
| 14366 | benign | 1 |
| 14367 | benevolent | 1 |
| 14368 | beneficently | 1 |
| 14369 | beneficent | 1 |
| 14370 | benedictions | 1 |
| 14371 | benedictine | 1 |
| 14372 | benalcazar | 1 |
| 14373 | bemused | 1 |
| 14374 | belying | 1 |
| 14375 | bellyful | 1 |
| 14376 | bellowings | 1 |
| 14377 | bellow | 1 |
| 14378 | bellona | 1 |
| 14379 | bellerophon | 1 |
| 14380 | belisardas | 1 |
| 14381 | believers | 1 |
| 14382 | believer | 1 |
| 14383 | belfry | 1 |
| 14384 | beleaguered | 1 |
| 14385 | belches | 1 |
| 14386 | belabour | 1 |
| 14387 | behoves | 1 |
| 14388 | beholds | 1 |
| 14389 | beholdest | 1 |
| 14390 | beholder | 1 |
| 14391 | beholden | 1 |
| 14392 | beguiling | 1 |
| 14393 | beguiled | 1 |
| 14394 | begrudges | 1 |
| 14395 | beginnest | 1 |
| 14396 | begetteth | 1 |
| 14397 | begets | 1 |
| 14398 | befriends | 1 |
| 14399 | befitted | 1 |
| 14400 | befit | 1 |
| 14401 | befalling | 1 |
| 14402 | beehives | 1 |
| 14403 | beeches | 1 |
| 14404 | bedside | 1 |
| 14405 | bedecking | 1 |
| 14406 | bedeck | 1 |
| 14407 | bedclothes | 1 |
| 14408 | beautifully | 1 |
| 14409 | beaters | 1 |
| 14410 | bearings | 1 |
| 14411 | bearding | 1 |
| 14412 | bean | 1 |
| 14413 | beamest | 1 |
| 14414 | bead | 1 |
| 14415 | bazan | 1 |
| 14416 | baying | 1 |
| 14417 | baulked | 1 |
| 14418 | battlements | 1 |
| 14419 | battlefield | 1 |
| 14420 | batteries | 1 |
| 14421 | bats | 1 |
| 14422 | bating | 1 |
| 14423 | bathes | 1 |
| 14424 | bathe | 1 |
| 14425 | bath | 1 |
| 14426 | batches | 1 |
| 14427 | basted | 1 |
| 14428 | basle | 1 |
| 14429 | baskets | 1 |
| 14430 | basis | 1 |
| 14431 | basins | 1 |
| 14432 | basil | 1 |
| 14433 | bashful | 1 |
| 14434 | bas | 1 |
| 14435 | bartered | 1 |
| 14436 | barrier | 1 |
| 14437 | barricade | 1 |
| 14438 | baronies | 1 |
| 14439 | bargaining | 1 |
| 14440 | bareheaded | 1 |
| 14441 | bard | 1 |
| 14442 | barcino | 1 |
| 14443 | barbarian | 1 |
| 14444 | barba | 1 |
| 14445 | baratario | 1 |
| 14446 | baptist | 1 |
| 14447 | banos | 1 |
| 14448 | banners | 1 |
| 14449 | banishing | 1 |
| 14450 | banging | 1 |
| 14451 | bandying | 1 |
| 14452 | banares | 1 |
| 14453 | balvastro | 1 |
| 14454 | balmy | 1 |
| 14455 | balm | 1 |
| 14456 | ballenatos | 1 |
| 14457 | bales | 1 |
| 14458 | balbastro | 1 |
| 14459 | bakes | 1 |
| 14460 | bagpipes | 1 |
| 14461 | baggages | 1 |
| 14462 | badness | 1 |
| 14463 | badges | 1 |
| 14464 | badge | 1 |
| 14465 | backstrokes | 1 |
| 14466 | backstroke | 1 |
| 14467 | backbiter | 1 |
| 14468 | bachelors | 1 |
| 14469 | bacallao | 1 |
| 14470 | babie | 1 |
| 14471 | babes | 1 |
| 14472 | babe | 1 |
| 14473 | babbled | 1 |
| 14474 | babazon | 1 |
| 14475 | azpeitia | 1 |
| 14476 | azote | 1 |
| 14477 | awl | 1 |
| 14478 | awhile | 1 |
| 14479 | awesome | 1 |
| 14480 | aweary | 1 |
| 14481 | avowal | 1 |
| 14482 | avila | 1 |
| 14483 | avidity | 1 |
| 14484 | averted | 1 |
| 14485 | avert | 1 |
| 14486 | aversions | 1 |
| 14487 | avers | 1 |
| 14488 | averred | 1 |
| 14489 | average | 1 |
| 14490 | avellaneda | 1 |
| 14491 | authorised | 1 |
| 14492 | austriada | 1 |
| 14493 | auro | 1 |
| 14494 | aunt | 1 |
| 14495 | augustus | 1 |
| 14496 | augusts | 1 |
| 14497 | augustinus | 1 |
| 14498 | augury | 1 |
| 14499 | augsburg | 1 |
| 14500 | aughts | 1 |
| 14501 | audible | 1 |
| 14502 | attuned | 1 |
| 14503 | attorney | 1 |
| 14504 | attendeth | 1 |
| 14505 | attains | 1 |
| 14506 | attainment | 1 |
| 14507 | attaching | 1 |
| 14508 | attaches | 1 |
| 14509 | atrociously | 1 |
| 14510 | atoned | 1 |
| 14511 | athwart | 1 |
| 14512 | athirst | 1 |
| 14513 | athens | 1 |
| 14514 | asylum | 1 |
| 14515 | astute | 1 |
| 14516 | asturias | 1 |
| 14517 | astrolabe | 1 |
| 14518 | astraddle | 1 |
| 14519 | astound | 1 |
| 14520 | astonishing | 1 |
| 14521 | astolfo | 1 |
| 14522 | astern | 1 |
| 14523 | assyrians | 1 |
| 14524 | associated | 1 |
| 14525 | associate | 1 |
| 14526 | assign | 1 |
| 14527 | asseverations | 1 |
| 14528 | assessor | 1 |
| 14529 | assessed | 1 |
| 14530 | asserts | 1 |
| 14531 | assemble | 1 |
| 14532 | assaults | 1 |
| 14533 | asquint | 1 |
| 14534 | aspiring | 1 |
| 14535 | aspire | 1 |
| 14536 | aspirations | 1 |
| 14537 | asperity | 1 |
| 14538 | asparagus | 1 |
| 14539 | askew | 1 |
| 14540 | ash | 1 |
| 14541 | ascribe | 1 |
| 14542 | asceticism | 1 |
| 14543 | ascertaining | 1 |
| 14544 | ascent | 1 |
| 14545 | ascends | 1 |
| 14546 | artus | 1 |
| 14547 | artless | 1 |
| 14548 | artillery | 1 |
| 14549 | artfully | 1 |
| 14550 | artemisia | 1 |
| 14551 | arrobas | 1 |
| 14552 | arriba | 1 |
| 14553 | arras | 1 |
| 14554 | arrant | 1 |
| 14555 | arranges | 1 |
| 14556 | arraigned | 1 |
| 14557 | arming | 1 |
| 14558 | armenia | 1 |
| 14559 | armament | 1 |
| 14560 | arlanza | 1 |
| 14561 | arithmetician | 1 |
| 14562 | arisen | 1 |
| 14563 | arid | 1 |
| 14564 | ariadne | 1 |
| 14565 | argus | 1 |
| 14566 | arguing | 1 |
| 14567 | argent | 1 |
| 14568 | arevalo | 1 |
| 14569 | architecture | 1 |
| 14570 | archipiela | 1 |
| 14571 | archery | 1 |
| 14572 | archer | 1 |
| 14573 | archelaus | 1 |
| 14574 | archduke | 1 |
| 14575 | arcalaus | 1 |
| 14576 | arbitration | 1 |
| 14577 | araucana | 1 |
| 14578 | aras | 1 |
| 14579 | arabias | 1 |
| 14580 | aptitude | 1 |
| 14581 | april | 1 |
| 14582 | appurtenance | 1 |
| 14583 | appropriating | 1 |
| 14584 | apprentice | 1 |
| 14585 | appreciation | 1 |
| 14586 | appreciating | 1 |
| 14587 | appraisers | 1 |
| 14588 | apportioned | 1 |
| 14589 | applicants | 1 |
| 14590 | applicant | 1 |
| 14591 | appliances | 1 |
| 14592 | appetites | 1 |
| 14593 | appertains | 1 |
| 14594 | appertaining | 1 |
| 14595 | appellant | 1 |
| 14596 | appeasing | 1 |
| 14597 | appease | 1 |
| 14598 | appealing | 1 |
| 14599 | appealed | 1 |
| 14600 | apparent | 1 |
| 14601 | apparelled | 1 |
| 14602 | apothecaries | 1 |
| 14603 | apostasy | 1 |
| 14604 | apologue | 1 |
| 14605 | apologised | 1 |
| 14606 | apes | 1 |
| 14607 | apennine | 1 |
| 14608 | anvil | 1 |
| 14609 | antwerp | 1 |
| 14610 | antiquities | 1 |
| 14611 | antidote | 1 |
| 14612 | anticipation | 1 |
| 14613 | antechambers | 1 |
| 14614 | ante | 1 |
| 14615 | antagonists | 1 |
| 14616 | answerer | 1 |
| 14617 | answerable | 1 |
| 14618 | anon | 1 |
| 14619 | anoints | 1 |
| 14620 | annoyances | 1 |
| 14621 | annoy | 1 |
| 14622 | announce | 1 |
| 14623 | annotation | 1 |
| 14624 | annis | 1 |
| 14625 | annihilated | 1 |
| 14626 | annihilate | 1 |
| 14627 | ankle | 1 |
| 14628 | animate | 1 |
| 14629 | angulo | 1 |
| 14630 | angelo | 1 |
| 14631 | andrew | 1 |
| 14632 | andradilla | 1 |
| 14633 | andandona | 1 |
| 14634 | anatomy | 1 |
| 14635 | anarda | 1 |
| 14636 | amusements | 1 |
| 14637 | amounts | 1 |
| 14638 | amounted | 1 |
| 14639 | amongst | 1 |
| 14640 | aminta | 1 |
| 14641 | amidships | 1 |
| 14642 | amicus | 1 |
| 14643 | amicos | 1 |
| 14644 | amicably | 1 |
| 14645 | amica | 1 |
| 14646 | america | 1 |
| 14647 | ambushes | 1 |
| 14648 | ambling | 1 |
| 14649 | amblers | 1 |
| 14650 | amatory | 1 |
| 14651 | amarillises | 1 |
| 14652 | amarilises | 1 |
| 14653 | amaranth | 1 |
| 14654 | alway | 1 |
| 14655 | altro | 1 |
| 14656 | alternative | 1 |
| 14657 | alternate | 1 |
| 14658 | altar | 1 |
| 14659 | aloof | 1 |
| 14660 | aloes | 1 |
| 14661 | almorzar | 1 |
| 14662 | almonds | 1 |
| 14663 | almohaza | 1 |
| 14664 | almohades | 1 |
| 14665 | allusion | 1 |
| 14666 | alluding | 1 |
| 14667 | alludes | 1 |
| 14668 | allude | 1 |
| 14669 | alloy | 1 |
| 14670 | allowing | 1 |
| 14671 | allowance | 1 |
| 14672 | allotted | 1 |
| 14673 | allied | 1 |
| 14674 | alley | 1 |
| 14675 | allen | 1 |
| 14676 | allegories | 1 |
| 14677 | aljaferia | 1 |
| 14678 | aliquando | 1 |
| 14679 | alighting | 1 |
| 14680 | alighted | 1 |
| 14681 | alienated | 1 |
| 14682 | alhucema | 1 |
| 14683 | alhombra | 1 |
| 14684 | alheli | 1 |
| 14685 | algerine | 1 |
| 14686 | algarve | 1 |
| 14687 | alforias | 1 |
| 14688 | alfeniquen | 1 |
| 14689 | alfaqui | 1 |
| 14690 | alexandra | 1 |
| 14691 | alessandria | 1 |
| 14692 | alencastros | 1 |
| 14693 | alcocer | 1 |
| 14694 | alcobendas | 1 |
| 14695 | alchemy | 1 |
| 14696 | alcazar | 1 |
| 14697 | alcarria | 1 |
| 14698 | alcantara | 1 |
| 14699 | alcancia | 1 |
| 14700 | alcana | 1 |
| 14701 | alcala | 1 |
| 14702 | albraca | 1 |
| 14703 | albogue | 1 |
| 14704 | alastrajareas | 1 |
| 14705 | alamos | 1 |
| 14706 | alagones | 1 |
| 14707 | aha | 1 |
| 14708 | aguero | 1 |
| 14709 | agreeably | 1 |
| 14710 | agrajes | 1 |
| 14711 | agonies | 1 |
| 14712 | aglow | 1 |
| 14713 | agilers | 1 |
| 14714 | aggravate | 1 |
| 14715 | agents | 1 |
| 14716 | agent | 1 |
| 14717 | agape | 1 |
| 14718 | aga | 1 |
| 14719 | aftermost | 1 |
| 14720 | afloat | 1 |
| 14721 | affray | 1 |
| 14722 | affirming | 1 |
| 14723 | affirmed | 1 |
| 14724 | affirm | 1 |
| 14725 | affidavit | 1 |
| 14726 | affectations | 1 |
| 14727 | aequo | 1 |
| 14728 | advocacy | 1 |
| 14729 | adviser | 1 |
| 14730 | advices | 1 |
| 14731 | adversae | 1 |
| 14732 | adulterous | 1 |
| 14733 | adulation | 1 |
| 14734 | adriani | 1 |
| 14735 | adorns | 1 |
| 14736 | adornments | 1 |
| 14737 | adorning | 1 |
| 14738 | adoring | 1 |
| 14739 | adoration | 1 |
| 14740 | adopts | 1 |
| 14741 | admonition | 1 |
| 14742 | admonished | 1 |
| 14743 | admitting | 1 |
| 14744 | admittance | 1 |
| 14745 | admirer | 1 |
| 14746 | admiral | 1 |
| 14747 | administration | 1 |
| 14748 | adjured | 1 |
| 14749 | adjuncts | 1 |
| 14750 | adjoining | 1 |
| 14751 | adds | 1 |
| 14752 | adapting | 1 |
| 14753 | adaptation | 1 |
| 14754 | adamantine | 1 |
| 14755 | ad | 1 |
| 14756 | acutely | 1 |
| 14757 | actual | 1 |
| 14758 | actaeon | 1 |
| 14759 | acres | 1 |
| 14760 | acre | 1 |
| 14761 | acquiring | 1 |
| 14762 | acquires | 1 |
| 14763 | acquiesced | 1 |
| 14764 | aching | 1 |
| 14765 | achilleses | 1 |
| 14766 | ache | 1 |
| 14767 | accusing | 1 |
| 14768 | accurate | 1 |
| 14769 | accuracy | 1 |
| 14770 | accrue | 1 |
| 14771 | accoutred | 1 |
| 14772 | accountant | 1 |
| 14773 | accompanies | 1 |
| 14774 | accommodating | 1 |
| 14775 | accommodated | 1 |
| 14776 | accolade | 1 |
| 14777 | acceptance | 1 |
| 14778 | academies | 1 |
| 14779 | abusive | 1 |
| 14780 | abusing | 1 |
| 14781 | abuses | 1 |
| 14782 | abstracted | 1 |
| 14783 | abstaining | 1 |
| 14784 | abstain | 1 |
| 14785 | absorbing | 1 |
| 14786 | absolving | 1 |
| 14787 | absolves | 1 |
| 14788 | absolved | 1 |
| 14789 | absit | 1 |
| 14790 | absenting | 1 |
| 14791 | abscond | 1 |
| 14792 | abrenuncio | 1 |
| 14793 | abounding | 1 |
| 14794 | abounded | 1 |
| 14795 | abominate | 1 |
| 14796 | abominable | 1 |
| 14797 | abolishing | 1 |
| 14798 | abolished | 1 |
| 14799 | ablaze | 1 |
| 14800 | abjure | 1 |
| 14801 | abilities | 1 |
| 14802 | abideth | 1 |
| 14803 | abhors | 1 |
| 14804 | abhorred | 1 |
| 14805 | abhor | 1 |
| 14806 | abasement | 1 |
| 14807 | abandons | 1 |
| 14808 | abandoning | 1 |
| 14809 | abajo | 1 |
| 14810 | abadejo | 1 |
|
|
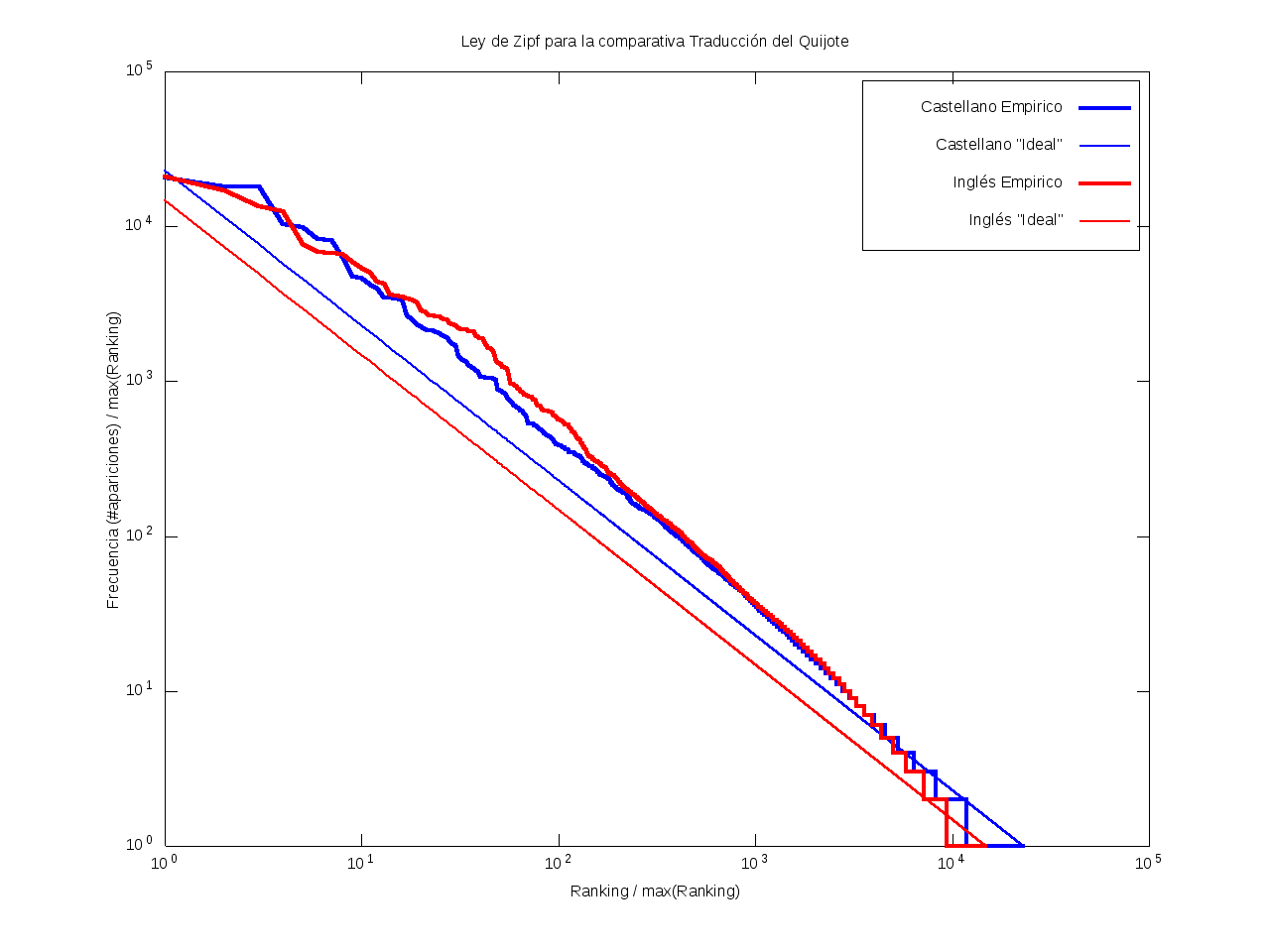
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará un conjunto (Castellano) (conjunto 1)
contra el otro (Inglés) (conjunto 2) y viceversa.
A continuación se muestra una lista de todas las palabras presentes en los textos,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
En este caso no tiene sentido aplicar el test de Dunning ya que los textos están en idiomas distintos.


