Comparativa: Quevedo contra Góngora
Índice
Información General
| Título: | * |
|---|
| Autor: | Francisco de Quevedo |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 21711 |
|---|
| #Palabras distintas: | 5385 |
|---|
| Type-Token ratio: | 24.80% |
|---|
|
| Título: | * |
|---|
| Autor: | Luis de Góngora |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 20168 |
|---|
| #Palabras distintas: | 5030 |
|---|
| Type-Token ratio: | 24.94% |
|---|
|
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| Quevedo | Góngora |
|---|
| #Palabras: | #Palabras distintas: |
|---|
| 1000 | 497 |
| 2000 | 895 |
| 3000 | 1248 |
| 4000 | 1568 |
| 5000 | 1883 |
| 6000 | 2079 |
| 7000 | 2275 |
| 8000 | 2477 |
| 9000 | 2712 |
| 10000 | 2980 |
| 11000 | 3284 |
| 12000 | 3510 |
| 13000 | 3786 |
| 14000 | 3984 |
| 15000 | 4200 |
| 16000 | 4396 |
| 17000 | 4570 |
| 18000 | 4753 |
| 19000 | 4929 |
| 20000 | 5118 |
| 21000 | 5273 |
| 21711 | 5385 |
|
| #Palabras: | #Palabras distintas: |
|---|
| 1000 | 507 |
| 2000 | 804 |
| 3000 | 1142 |
| 4000 | 1425 |
| 5000 | 1658 |
| 6000 | 1975 |
| 7000 | 2269 |
| 8000 | 2533 |
| 9000 | 2784 |
| 10000 | 3021 |
| 11000 | 3239 |
| 12000 | 3476 |
| 13000 | 3692 |
| 14000 | 3913 |
| 15000 | 4116 |
| 16000 | 4298 |
| 17000 | 4499 |
| 18000 | 4672 |
| 19000 | 4837 |
| 20000 | 5001 |
| 20168 | 5030 |
|
|
Ajuste por mínimos cuadrados de los datos a K*n^b: |
| Quevedo |
|
Góngora |
| K = 2.677 |
|
K = 2.167 |
| b = 0.764 |
|
b = 0.784 |

|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Quevedo | Góngora |
Ilustración del principio de mínimo esfuerzo: |
| Rank | Palabra | Frec |
|---|
| 1 | y | 956 |
| 2 | de | 860 |
| 3 | que | 855 |
| 4 | la | 650 |
| 5 | el | 589 |
| 6 | en | 577 |
| 7 | a | 390 |
| 8 | no | 304 |
| 9 | con | 279 |
| 10 | los | 273 |
| 11 | las | 255 |
| 12 | su | 215 |
| 13 | por | 195 |
| 14 | al | 195 |
| 15 | del | 188 |
| 16 | es | 168 |
| 17 | si | 152 |
| 18 | se | 146 |
| 19 | mi | 144 |
| 20 | lo | 125 |
| 21 | un | 117 |
| 22 | me | 116 |
| 23 | más | 111 |
| 24 | pues | 103 |
| 25 | tu | 100 |
| 26 | qué | 97 |
| 27 | le | 89 |
| 28 | te | 77 |
| 29 | sus | 75 |
| 30 | yo | 71 |
| 31 | ya | 71 |
| 32 | amor | 69 |
| 33 | para | 67 |
| 34 | son | 66 |
| 35 | sin | 65 |
| 36 | muerte | 65 |
| 37 | mis | 62 |
| 38 | vida | 60 |
| 39 | una | 60 |
| 40 | tan | 58 |
| 41 | ser | 57 |
| 42 | quien | 55 |
| 43 | ni | 55 |
| 44 | sol | 48 |
| 45 | ha | 47 |
| 46 | como | 46 |
| 47 | día | 43 |
| 48 | porque | 40 |
| 49 | cuando | 40 |
| 50 | alma | 39 |
| 51 | todo | 38 |
| 52 | luz | 38 |
| 53 | bien | 38 |
| 54 | tus | 37 |
| 55 | mas | 37 |
| 56 | mí | 36 |
| 57 | fuego | 36 |
| 58 | ojos | 35 |
| 59 | fue | 35 |
| 60 | soy | 33 |
| 61 | o | 33 |
| 62 | dios | 33 |
| 63 | cielo | 33 |
| 64 | he | 32 |
| 65 | él | 32 |
| 66 | oro | 31 |
| 67 | dar | 31 |
| 68 | tiempo | 30 |
| 69 | mal | 30 |
| 70 | este | 29 |
| 71 | dinero | 29 |
| 72 | don | 28 |
| 73 | ardiente | 28 |
| 74 | os | 27 |
| 75 | hay | 27 |
| 76 | donde | 27 |
| 77 | sólo | 26 |
| 78 | noche | 26 |
| 79 | entre | 26 |
| 80 | corazón | 26 |
| 81 | pero | 25 |
| 82 | hace | 25 |
| 83 | dos | 25 |
| 84 | amante | 25 |
| 85 | tierra | 24 |
| 86 | siempre | 24 |
| 87 | muy | 24 |
| 88 | tú | 23 |
| 89 | todos | 23 |
| 90 | llanto | 22 |
| 91 | llama | 22 |
| 92 | esta | 22 |
| 93 | cuanto | 22 |
| 94 | vos | 21 |
| 95 | tiene | 21 |
| 96 | sombra | 21 |
| 97 | nada | 21 |
| 98 | aunque | 21 |
| 99 | sueño | 20 |
| 100 | será | 20 |
| 101 | mar | 20 |
| 102 | está | 20 |
| 103 | ti | 19 |
| 104 | tanto | 19 |
| 105 | quién | 19 |
| 106 | mano | 19 |
| 107 | hombre | 19 |
| 108 | galán | 19 |
| 109 | fortuna | 19 |
| 110 | dama | 19 |
| 111 | voz | 18 |
| 112 | verdad | 18 |
| 113 | sí | 18 |
| 114 | quiero | 18 |
| 115 | menos | 18 |
| 116 | gran | 18 |
| 117 | da | 18 |
| 118 | oh | 17 |
| 119 | mujer | 17 |
| 120 | morir | 17 |
| 121 | mía | 17 |
| 122 | horas | 17 |
| 123 | hermosa | 17 |
| 124 | han | 17 |
| 125 | edad | 17 |
| 126 | boca | 17 |
| 127 | ver | 16 |
| 128 | siendo | 16 |
| 129 | puede | 16 |
| 130 | pena | 16 |
| 131 | mundo | 16 |
| 132 | hermosura | 16 |
| 133 | dulce | 16 |
| 134 | cuidado | 16 |
| 135 | sino | 15 |
| 136 | señor | 15 |
| 137 | puro | 15 |
| 138 | hoy | 15 |
| 139 | guerra | 15 |
| 140 | dolor | 15 |
| 141 | breve | 15 |
| 142 | vivir | 14 |
| 143 | tener | 14 |
| 144 | tal | 14 |
| 145 | sobre | 14 |
| 146 | sangre | 14 |
| 147 | poderoso | 14 |
| 148 | poco | 14 |
| 149 | negro | 14 |
| 150 | gloria | 14 |
| 151 | flores | 14 |
| 152 | camino | 14 |
| 153 | armas | 14 |
| 154 | rey | 13 |
| 155 | nunca | 13 |
| 156 | nieve | 13 |
| 157 | negra | 13 |
| 158 | muerto | 13 |
| 159 | miedo | 13 |
| 160 | mañana | 13 |
| 161 | luego | 13 |
| 162 | lisi | 13 |
| 163 | grande | 13 |
| 164 | gente | 13 |
| 165 | fría | 13 |
| 166 | estrellas | 13 |
| 167 | era | 13 |
| 168 | ella | 13 |
| 169 | dio | 13 |
| 170 | después | 13 |
| 171 | cuerpo | 13 |
| 172 | contra | 13 |
| 173 | ciego | 13 |
| 174 | agua | 13 |
| 175 | viento | 12 |
| 176 | ves | 12 |
| 177 | solamente | 12 |
| 178 | sola | 12 |
| 179 | pudo | 12 |
| 180 | paso | 12 |
| 181 | otro | 12 |
| 182 | nos | 12 |
| 183 | mejor | 12 |
| 184 | les | 12 |
| 185 | hasta | 12 |
| 186 | fuera | 12 |
| 187 | flor | 12 |
| 188 | cosa | 12 |
| 189 | consiente | 12 |
| 190 | aun | 12 |
| 191 | vino | 11 |
| 192 | venas | 11 |
| 193 | valiente | 11 |
| 194 | tengo | 11 |
| 195 | suerte | 11 |
| 196 | sombras | 11 |
| 197 | silencio | 11 |
| 198 | rico | 11 |
| 199 | manos | 11 |
| 200 | lágrimas | 11 |
| 201 | hora | 11 |
| 202 | caballero | 11 |
| 203 | amar | 11 |
| 204 | vio | 10 |
| 205 | viendo | 10 |
| 206 | todas | 10 |
| 207 | toda | 10 |
| 208 | tienes | 10 |
| 209 | suelo | 10 |
| 210 | sois | 10 |
| 211 | sé | 10 |
| 212 | mucho | 10 |
| 213 | mayor | 10 |
| 214 | malhaya | 10 |
| 215 | luna | 10 |
| 216 | letrilla | 10 |
| 217 | fin | 10 |
| 218 | eres | 10 |
| 219 | dura | 10 |
| 220 | cuán | 10 |
| 221 | cómo | 10 |
| 222 | cara | 10 |
| 223 | ausente | 10 |
| 224 | antes | 10 |
| 225 | alto | 10 |
| 226 | algún | 10 |
| 227 | yace | 9 |
| 228 | va | 9 |
| 229 | tenga | 9 |
| 230 | también | 9 |
| 231 | soberbia | 9 |
| 232 | quiere | 9 |
| 233 | pura | 9 |
| 234 | prisión | 9 |
| 235 | presunción | 9 |
| 236 | podido | 9 |
| 237 | pide | 9 |
| 238 | pensamiento | 9 |
| 239 | penas | 9 |
| 240 | paz | 9 |
| 241 | otra | 9 |
| 242 | oriente | 9 |
| 243 | nombre | 9 |
| 244 | memoria | 9 |
| 245 | llamas | 9 |
| 246 | ley | 9 |
| 247 | invierno | 9 |
| 248 | humo | 9 |
| 249 | hielo | 9 |
| 250 | hecho | 9 |
| 251 | ceniza | 9 |
| 252 | casa | 9 |
| 253 | campo | 9 |
| 254 | aquella | 9 |
| 255 | vuestra | 8 |
| 256 | vive | 8 |
| 257 | vi | 8 |
| 258 | tirano | 8 |
| 259 | serán | 8 |
| 260 | satírica | 8 |
| 261 | rosas | 8 |
| 262 | razón | 8 |
| 263 | rayo | 8 |
| 264 | púrpura | 8 |
| 265 | punto | 8 |
| 266 | primero | 8 |
| 267 | pobre | 8 |
| 268 | pies | 8 |
| 269 | pie | 8 |
| 270 | pasos | 8 |
| 271 | parte | 8 |
| 272 | olvido | 8 |
| 273 | mil | 8 |
| 274 | libertad | 8 |
| 275 | frente | 8 |
| 276 | están | 8 |
| 277 | espíritu | 8 |
| 278 | esa | 8 |
| 279 | entrañas | 8 |
| 280 | enamorado | 8 |
| 281 | doña | 8 |
| 282 | dan | 8 |
| 283 | cuenta | 8 |
| 284 | cristo | 8 |
| 285 | buen | 8 |
| 286 | boda | 8 |
| 287 | aún | 8 |
| 288 | años | 8 |
| 289 | aire | 8 |
| 290 | vuestro | 7 |
| 291 | vuelve | 7 |
| 292 | ven | 7 |
| 293 | veces | 7 |
| 294 | ve | 7 |
| 295 | triste | 7 |
| 296 | tras | 7 |
| 297 | toro | 7 |
| 298 | sosiego | 7 |
| 299 | sonoras | 7 |
| 300 | señora | 7 |
| 301 | sed | 7 |
| 302 | roma | 7 |
| 303 | risa | 7 |
| 304 | rigor | 7 |
| 305 | querido | 7 |
| 306 | pluma | 7 |
| 307 | piedad | 7 |
| 308 | persona | 7 |
| 309 | pecado | 7 |
| 310 | otros | 7 |
| 311 | oscura | 7 |
| 312 | mortaja | 7 |
| 313 | monte | 7 |
| 314 | mismo | 7 |
| 315 | misma | 7 |
| 316 | mira | 7 |
| 317 | lugar | 7 |
| 318 | llora | 7 |
| 319 | libre | 7 |
| 320 | infierno | 7 |
| 321 | hermoso | 7 |
| 322 | has | 7 |
| 323 | gusto | 7 |
| 324 | fuerza | 7 |
| 325 | estrella | 7 |
| 326 | españa | 7 |
| 327 | deseo | 7 |
| 328 | desde | 7 |
| 329 | descanso | 7 |
| 330 | dentro | 7 |
| 331 | cuidados | 7 |
| 332 | cualquier | 7 |
| 333 | corona | 7 |
| 334 | cada | 7 |
| 335 | bebe | 7 |
| 336 | ayer | 7 |
| 337 | aurora | 7 |
| 338 | atento | 7 |
| 339 | aminta | 7 |
| 340 | almas | 7 |
| 341 | alas | 7 |
| 342 | vuelo | 6 |
| 343 | vosotras | 6 |
| 344 | vivo | 6 |
| 345 | vista | 6 |
| 346 | virtud | 6 |
| 347 | vez | 6 |
| 348 | vergüenza | 6 |
| 349 | verdadero | 6 |
| 350 | vana | 6 |
| 351 | valentía | 6 |
| 352 | tuvo | 6 |
| 353 | toca | 6 |
| 354 | tesoro | 6 |
| 355 | solo | 6 |
| 356 | siente | 6 |
| 357 | sepulcro | 6 |
| 358 | sentidos | 6 |
| 359 | semblante | 6 |
| 360 | santo | 6 |
| 361 | rostro | 6 |
| 362 | rica | 6 |
| 363 | reloj | 6 |
| 364 | quiso | 6 |
| 365 | puedo | 6 |
| 366 | poder | 6 |
| 367 | pobreza | 6 |
| 368 | plata | 6 |
| 369 | piedras | 6 |
| 370 | perlas | 6 |
| 371 | peregrino | 6 |
| 372 | pecho | 6 |
| 373 | pasión | 6 |
| 374 | pasa | 6 |
| 375 | osuna | 6 |
| 376 | negros | 6 |
| 377 | nariz | 6 |
| 378 | nacido | 6 |
| 379 | metal | 6 |
| 380 | majestad | 6 |
| 381 | lleva | 6 |
| 382 | labios | 6 |
| 383 | jornada | 6 |
| 384 | invidia | 6 |
| 385 | imagen | 6 |
| 386 | hazañas | 6 |
| 387 | hacen | 6 |
| 388 | haber | 6 |
| 389 | gracias | 6 |
| 390 | goza | 6 |
| 391 | fuese | 6 |
| 392 | fuerte | 6 |
| 393 | fuente | 6 |
| 394 | estoy | 6 |
| 395 | esto | 6 |
| 396 | eso | 6 |
| 397 | érase | 6 |
| 398 | envía | 6 |
| 399 | entonces | 6 |
| 400 | engaños | 6 |
| 401 | debajo | 6 |
| 402 | dado | 6 |
| 403 | culpa | 6 |
| 404 | corriente | 6 |
| 405 | color | 6 |
| 406 | ciega | 6 |
| 407 | ceño | 6 |
| 408 | cárcel | 6 |
| 409 | caras | 6 |
| 410 | buena | 6 |
| 411 | blanco | 6 |
| 412 | avaro | 6 |
| 413 | aquel | 6 |
| 414 | año | 6 |
| 415 | antigua | 6 |
| 416 | anda | 6 |
| 417 | amores | 6 |
| 418 | altas | 6 |
| 419 | alguno | 6 |
| 420 | vuela | 5 |
| 421 | viste | 5 |
| 422 | vientos | 5 |
| 423 | viene | 5 |
| 424 | vestido | 5 |
| 425 | veo | 5 |
| 426 | vencer | 5 |
| 427 | unos | 5 |
| 428 | unas | 5 |
| 429 | tristeza | 5 |
| 430 | tres | 5 |
| 431 | treinta | 5 |
| 432 | toros | 5 |
| 433 | tienen | 5 |
| 434 | temor | 5 |
| 435 | temerosa | 5 |
| 436 | teme | 5 |
| 437 | suspiros | 5 |
| 438 | sonoro | 5 |
| 439 | soledad | 5 |
| 440 | sirve | 5 |
| 441 | sido | 5 |
| 442 | severo | 5 |
| 443 | san | 5 |
| 444 | salud | 5 |
| 445 | sabe | 5 |
| 446 | río | 5 |
| 447 | ricos | 5 |
| 448 | reino | 5 |
| 449 | quieres | 5 |
| 450 | quiera | 5 |
| 451 | pueden | 5 |
| 452 | propio | 5 |
| 453 | propia | 5 |
| 454 | principio | 5 |
| 455 | presumir | 5 |
| 456 | presente | 5 |
| 457 | postrer | 5 |
| 458 | polvo | 5 |
| 459 | podrá | 5 |
| 460 | patria | 5 |
| 461 | parto | 5 |
| 462 | orilla | 5 |
| 463 | oficio | 5 |
| 464 | nuevo | 5 |
| 465 | nueva | 5 |
| 466 | nuestro | 5 |
| 467 | nuestra | 5 |
| 468 | niña | 5 |
| 469 | muestra | 5 |
| 470 | mudas | 5 |
| 471 | movimiento | 5 |
| 472 | mostró | 5 |
| 473 | mortal | 5 |
| 474 | mío | 5 |
| 475 | ministro | 5 |
| 476 | mentiroso | 5 |
| 477 | manera | 5 |
| 478 | madre | 5 |
| 479 | luces | 5 |
| 480 | lloro | 5 |
| 481 | llena | 5 |
| 482 | llegó | 5 |
| 483 | llaman | 5 |
| 484 | lenguaje | 5 |
| 485 | largo | 5 |
| 486 | l | 5 |
| 487 | joyas | 5 |
| 488 | jardín | 5 |
| 489 | igual | 5 |
| 490 | huye | 5 |
| 491 | humana | 5 |
| 492 | hubiera | 5 |
| 493 | hombres | 5 |
| 494 | hizo | 5 |
| 495 | herida | 5 |
| 496 | grandes | 5 |
| 497 | fuí | 5 |
| 498 | fueron | 5 |
| 499 | flora | 5 |
| 500 | firme | 5 |
| 501 | firmamento | 5 |
| 502 | fama | 5 |
| 503 | eterno | 5 |
| 504 | estos | 5 |
| 505 | estilo | 5 |
| 506 | estas | 5 |
| 507 | estaba | 5 |
| 508 | espero | 5 |
| 509 | espaldas | 5 |
| 510 | espada | 5 |
| 511 | escudos | 5 |
| 512 | ellas | 5 |
| 513 | dueño | 5 |
| 514 | docta | 5 |
| 515 | dichoso | 5 |
| 516 | días | 5 |
| 517 | diablo | 5 |
| 518 | di | 5 |
| 519 | desprecia | 5 |
| 520 | desdichado | 5 |
| 521 | deja | 5 |
| 522 | decir | 5 |
| 523 | cuello | 5 |
| 524 | creo | 5 |
| 525 | cortés | 5 |
| 526 | conoce | 5 |
| 527 | compañía | 5 |
| 528 | clavel | 5 |
| 529 | cinco | 5 |
| 530 | cierra | 5 |
| 531 | cerco | 5 |
| 532 | caña | 5 |
| 533 | canto | 5 |
| 534 | cantas | 5 |
| 535 | cabeza | 5 |
| 536 | busca | 5 |
| 537 | brazos | 5 |
| 538 | blanca | 5 |
| 539 | belleza | 5 |
| 540 | basta | 5 |
| 541 | ay | 5 |
| 542 | aves | 5 |
| 543 | así | 5 |
| 544 | armado | 5 |
| 545 | arder | 5 |
| 546 | aquí | 5 |
| 547 | ansí | 5 |
| 548 | allá | 5 |
| 549 | aliento | 5 |
| 550 | algo | 5 |
| 551 | alegre | 5 |
| 552 | agrada | 5 |
| 553 | agora | 5 |
| 554 | advierte | 5 |
| 555 | vuelas | 4 |
| 556 | voluntad | 4 |
| 557 | voces | 4 |
| 558 | victoria | 4 |
| 559 | verte | 4 |
| 560 | verse | 4 |
| 561 | verde | 4 |
| 562 | verano | 4 |
| 563 | ventura | 4 |
| 564 | vencido | 4 |
| 565 | vela | 4 |
| 566 | vanidad | 4 |
| 567 | van | 4 |
| 568 | uno | 4 |
| 569 | tuve | 4 |
| 570 | tumba | 4 |
| 571 | traigo | 4 |
| 572 | trae | 4 |
| 573 | tormentos | 4 |
| 574 | tormento | 4 |
| 575 | tirana | 4 |
| 576 | supo | 4 |
| 577 | soplo | 4 |
| 578 | soldado | 4 |
| 579 | solas | 4 |
| 580 | siento | 4 |
| 581 | sepultada | 4 |
| 582 | señas | 4 |
| 583 | sentimiento | 4 |
| 584 | semejante | 4 |
| 585 | sea | 4 |
| 586 | santa | 4 |
| 587 | saber | 4 |
| 588 | rubio | 4 |
| 589 | rubíes | 4 |
| 590 | rosal | 4 |
| 591 | rosa | 4 |
| 592 | riqueza | 4 |
| 593 | ricas | 4 |
| 594 | reyes | 4 |
| 595 | revés | 4 |
| 596 | retrato | 4 |
| 597 | reales | 4 |
| 598 | rayos | 4 |
| 599 | quieren | 4 |
| 600 | puertas | 4 |
| 601 | puerta | 4 |
| 602 | pueblo | 4 |
| 603 | prisiones | 4 |
| 604 | primer | 4 |
| 605 | primaveras | 4 |
| 606 | primavera | 4 |
| 607 | presto | 4 |
| 608 | premio | 4 |
| 609 | precioso | 4 |
| 610 | prado | 4 |
| 611 | postrero | 4 |
| 612 | porfía | 4 |
| 613 | pobres | 4 |
| 614 | piedra | 4 |
| 615 | piadosa | 4 |
| 616 | perdido | 4 |
| 617 | perdición | 4 |
| 618 | pasados | 4 |
| 619 | pan | 4 |
| 620 | padre | 4 |
| 621 | padecer | 4 |
| 622 | padece | 4 |
| 623 | ostenta | 4 |
| 624 | orejas | 4 |
| 625 | ondas | 4 |
| 626 | nuestras | 4 |
| 627 | nubes | 4 |
| 628 | necios | 4 |
| 629 | necio | 4 |
| 630 | nadie | 4 |
| 631 | nadadores | 4 |
| 632 | murió | 4 |
| 633 | muerta | 4 |
| 634 | muero | 4 |
| 635 | muera | 4 |
| 636 | mudo | 4 |
| 637 | muda | 4 |
| 638 | muchos | 4 |
| 639 | muchas | 4 |
| 640 | montañas | 4 |
| 641 | miro | 4 |
| 642 | miras | 4 |
| 643 | mente | 4 |
| 644 | mata | 4 |
| 645 | martirio | 4 |
| 646 | mala | 4 |
| 647 | madrugas | 4 |
| 648 | lumbre | 4 |
| 649 | lozana | 4 |
| 650 | llorar | 4 |
| 651 | llegado | 4 |
| 652 | llega | 4 |
| 653 | leyes | 4 |
| 654 | lengua | 4 |
| 655 | laurel | 4 |
| 656 | larga | 4 |
| 657 | ladrón | 4 |
| 658 | jilguero | 4 |
| 659 | incendios | 4 |
| 660 | humos | 4 |
| 661 | humildad | 4 |
| 662 | humano | 4 |
| 663 | hubo | 4 |
| 664 | honra | 4 |
| 665 | honor | 4 |
| 666 | hierro | 4 |
| 667 | hambre | 4 |
| 668 | hacer | 4 |
| 669 | había | 4 |
| 670 | guardar | 4 |
| 671 | grandeza | 4 |
| 672 | gracia | 4 |
| 673 | glorioso | 4 |
| 674 | gemido | 4 |
| 675 | garganta | 4 |
| 676 | galas | 4 |
| 677 | gala | 4 |
| 678 | fuerzas | 4 |
| 679 | frío | 4 |
| 680 | flechas | 4 |
| 681 | familia | 4 |
| 682 | falta | 4 |
| 683 | facistol | 4 |
| 684 | espinas | 4 |
| 685 | enojos | 4 |
| 686 | engaño | 4 |
| 687 | enferma | 4 |
| 688 | enemigos | 4 |
| 689 | encendió | 4 |
| 690 | ellos | 4 |
| 691 | duro | 4 |
| 692 | duras | 4 |
| 693 | duque | 4 |
| 694 | duerme | 4 |
| 695 | doy | 4 |
| 696 | doliente | 4 |
| 697 | divertido | 4 |
| 698 | dineros | 4 |
| 699 | diles | 4 |
| 700 | dijo | 4 |
| 701 | digo | 4 |
| 702 | digasmé | 4 |
| 703 | dicho | 4 |
| 704 | dicen | 4 |
| 705 | dice | 4 |
| 706 | desvelas | 4 |
| 707 | deseos | 4 |
| 708 | desdén | 4 |
| 709 | delgada | 4 |
| 710 | dejó | 4 |
| 711 | dejas | 4 |
| 712 | dé | 4 |
| 713 | daños | 4 |
| 714 | dando | 4 |
| 715 | cuyos | 4 |
| 716 | cuya | 4 |
| 717 | cualquiera | 4 |
| 718 | cosas | 4 |
| 719 | comer | 4 |
| 720 | claveles | 4 |
| 721 | claustro | 4 |
| 722 | cierto | 4 |
| 723 | cielos | 4 |
| 724 | cayó | 4 |
| 725 | cautelas | 4 |
| 726 | causa | 4 |
| 727 | carne | 4 |
| 728 | carmesíes | 4 |
| 729 | cantar | 4 |
| 730 | cano | 4 |
| 731 | campos | 4 |
| 732 | caminante | 4 |
| 733 | cama | 4 |
| 734 | cadáver | 4 |
| 735 | cabello | 4 |
| 736 | brazo | 4 |
| 737 | blasones | 4 |
| 738 | blando | 4 |
| 739 | bella | 4 |
| 740 | baja | 4 |
| 741 | auroras | 4 |
| 742 | armonía | 4 |
| 743 | ardor | 4 |
| 744 | arde | 4 |
| 745 | amoroso | 4 |
| 746 | amigo | 4 |
| 747 | amenaza | 4 |
| 748 | amada | 4 |
| 749 | alimento | 4 |
| 750 | algunos | 4 |
| 751 | alcanza | 4 |
| 752 | aguas | 4 |
| 753 | agradecido | 4 |
| 754 | adán | 4 |
| 755 | acero | 4 |
| 756 | zagala | 3 |
| 757 | vuelvo | 3 |
| 758 | vuelta | 3 |
| 759 | vivido | 3 |
| 760 | viven | 3 |
| 761 | viva | 3 |
| 762 | vierte | 3 |
| 763 | vientre | 3 |
| 764 | vidas | 3 |
| 765 | vid | 3 |
| 766 | verme | 3 |
| 767 | verdes | 3 |
| 768 | verdadera | 3 |
| 769 | venido | 3 |
| 770 | venganza | 3 |
| 771 | veneno | 3 |
| 772 | vara | 3 |
| 773 | vano | 3 |
| 774 | valor | 3 |
| 775 | triunfante | 3 |
| 776 | traje | 3 |
| 777 | trabajo | 3 |
| 778 | torpe | 3 |
| 779 | tonos | 3 |
| 780 | tomar | 3 |
| 781 | tiro | 3 |
| 782 | tiranos | 3 |
| 783 | tinta | 3 |
| 784 | términos | 3 |
| 785 | tenía | 3 |
| 786 | tengan | 3 |
| 787 | tempestad | 3 |
| 788 | temo | 3 |
| 789 | temer | 3 |
| 790 | tela | 3 |
| 791 | tarde | 3 |
| 792 | tanta | 3 |
| 793 | suyo | 3 |
| 794 | sutil | 3 |
| 795 | suspiro | 3 |
| 796 | suma | 3 |
| 797 | sufrir | 3 |
| 798 | sueños | 3 |
| 799 | somos | 3 |
| 800 | solimán | 3 |
| 801 | soga | 3 |
| 802 | sirenas | 3 |
| 803 | siquiera | 3 |
| 804 | silla | 3 |
| 805 | siguieron | 3 |
| 806 | sigue | 3 |
| 807 | serás | 3 |
| 808 | sepoltura | 3 |
| 809 | sepa | 3 |
| 810 | séneca | 3 |
| 811 | sembrados | 3 |
| 812 | seguro | 3 |
| 813 | según | 3 |
| 814 | secreto | 3 |
| 815 | secos | 3 |
| 816 | sagrado | 3 |
| 817 | sacan | 3 |
| 818 | ruinas | 3 |
| 819 | ruego | 3 |
| 820 | rubí | 3 |
| 821 | ríos | 3 |
| 822 | ríes | 3 |
| 823 | respeto | 3 |
| 824 | resistencia | 3 |
| 825 | refiere | 3 |
| 826 | recién | 3 |
| 827 | quita | 3 |
| 828 | querer | 3 |
| 829 | queréis | 3 |
| 830 | quedó | 3 |
| 831 | puedes | 3 |
| 832 | pudiera | 3 |
| 833 | prosa | 3 |
| 834 | propias | 3 |
| 835 | primera | 3 |
| 836 | pretende | 3 |
| 837 | presumida | 3 |
| 838 | preciosa | 3 |
| 839 | precio | 3 |
| 840 | pólvora | 3 |
| 841 | poca | 3 |
| 842 | plumas | 3 |
| 843 | pisas | 3 |
| 844 | pienso | 3 |
| 845 | piense | 3 |
| 846 | pez | 3 |
| 847 | peso | 3 |
| 848 | personas | 3 |
| 849 | permite | 3 |
| 850 | perdidos | 3 |
| 851 | pequeño | 3 |
| 852 | peor | 3 |
| 853 | peñas | 3 |
| 854 | pedro | 3 |
| 855 | pecados | 3 |
| 856 | pasiones | 3 |
| 857 | pasajero | 3 |
| 858 | pasado | 3 |
| 859 | parecido | 3 |
| 860 | parecer | 3 |
| 861 | palabras | 3 |
| 862 | pájaro | 3 |
| 863 | paga | 3 |
| 864 | paciencia | 3 |
| 865 | otras | 3 |
| 866 | oscuro | 3 |
| 867 | osa | 3 |
| 868 | orfeo | 3 |
| 869 | olvida | 3 |
| 870 | oído | 3 |
| 871 | ofende | 3 |
| 872 | ocaso | 3 |
| 873 | ocasión | 3 |
| 874 | nuevas | 3 |
| 875 | nieves | 3 |
| 876 | nerón | 3 |
| 877 | negras | 3 |
| 878 | naturaleza | 3 |
| 879 | nadar | 3 |
| 880 | nació | 3 |
| 881 | nacimiento | 3 |
| 882 | nací | 3 |
| 883 | nace | 3 |
| 884 | músicos | 3 |
| 885 | mueve | 3 |
| 886 | muestre | 3 |
| 887 | mudos | 3 |
| 888 | mudanza | 3 |
| 889 | moza | 3 |
| 890 | mortales | 3 |
| 891 | moro | 3 |
| 892 | monumento | 3 |
| 893 | montes | 3 |
| 894 | molesto | 3 |
| 895 | modos | 3 |
| 896 | modo | 3 |
| 897 | míos | 3 |
| 898 | minas | 3 |
| 899 | milagro | 3 |
| 900 | mieses | 3 |
| 901 | mientras | 3 |
| 902 | miente | 3 |
| 903 | midas | 3 |
| 904 | mesa | 3 |
| 905 | merece | 3 |
| 906 | menester | 3 |
| 907 | mejores | 3 |
| 908 | medio | 3 |
| 909 | matar | 3 |
| 910 | marte | 3 |
| 911 | mármol | 3 |
| 912 | marido | 3 |
| 913 | máquina | 3 |
| 914 | locura | 3 |
| 915 | llueva | 3 |
| 916 | llorando | 3 |
| 917 | llevas | 3 |
| 918 | llano | 3 |
| 919 | lisonjera | 3 |
| 920 | lísida | 3 |
| 921 | limpieza | 3 |
| 922 | ligera | 3 |
| 923 | leandro | 3 |
| 924 | lanza | 3 |
| 925 | lado | 3 |
| 926 | labio | 3 |
| 927 | justo | 3 |
| 928 | juntos | 3 |
| 929 | junto | 3 |
| 930 | juicio | 3 |
| 931 | jesús | 3 |
| 932 | jamás | 3 |
| 933 | ir | 3 |
| 934 | instante | 3 |
| 935 | incendio | 3 |
| 936 | importuna | 3 |
| 937 | imperio | 3 |
| 938 | imita | 3 |
| 939 | horror | 3 |
| 940 | historia | 3 |
| 941 | hijos | 3 |
| 942 | heridas | 3 |
| 943 | hechos | 3 |
| 944 | haya | 3 |
| 945 | hallar | 3 |
| 946 | halla | 3 |
| 947 | hago | 3 |
| 948 | haciendo | 3 |
| 949 | hacienda | 3 |
| 950 | hacéis | 3 |
| 951 | habitación | 3 |
| 952 | gusano | 3 |
| 953 | guarda | 3 |
| 954 | golfo | 3 |
| 955 | girón | 3 |
| 956 | generosa | 3 |
| 957 | gemidos | 3 |
| 958 | gasta | 3 |
| 959 | gana | 3 |
| 960 | funesto | 3 |
| 961 | frágil | 3 |
| 962 | fiesta | 3 |
| 963 | fiero | 3 |
| 964 | feas | 3 |
| 965 | fea | 3 |
| 966 | fe | 3 |
| 967 | favor | 3 |
| 968 | exequias | 3 |
| 969 | etna | 3 |
| 970 | eterna | 3 |
| 971 | estando | 3 |
| 972 | espuma | 3 |
| 973 | esposo | 3 |
| 974 | espléndidas | 3 |
| 975 | esfuerzo | 3 |
| 976 | ese | 3 |
| 977 | escuadras | 3 |
| 978 | esconde | 3 |
| 979 | esclavo | 3 |
| 980 | esclava | 3 |
| 981 | esas | 3 |
| 982 | erase | 3 |
| 983 | eran | 3 |
| 984 | envidiosos | 3 |
| 985 | entendimiento | 3 |
| 986 | enseña | 3 |
| 987 | enjuga | 3 |
| 988 | enemigo | 3 |
| 989 | encendido | 3 |
| 990 | elocuente | 3 |
| 991 | elementos | 3 |
| 992 | elegante | 3 |
| 993 | ejército | 3 |
| 994 | ejemplo | 3 |
| 995 | e | 3 |
| 996 | duros | 3 |
| 997 | dureza | 3 |
| 998 | dulces | 3 |
| 999 | dudoso | 3 |
| 1000 | dote | 3 |
| 1001 | dormir | 3 |
| 1002 | dones | 3 |
| 1003 | doctos | 3 |
| 1004 | divina | 3 |
| 1005 | diste | 3 |
| 1006 | diome | 3 |
| 1007 | dije | 3 |
| 1008 | difunto | 3 |
| 1009 | diferentes | 3 |
| 1010 | diciendo | 3 |
| 1011 | dichosas | 3 |
| 1012 | diamante | 3 |
| 1013 | desvarío | 3 |
| 1014 | despojos | 3 |
| 1015 | despierto | 3 |
| 1016 | desnudo | 3 |
| 1017 | desdeñosa | 3 |
| 1018 | descansar | 3 |
| 1019 | derrama | 3 |
| 1020 | della | 3 |
| 1021 | delincuente | 3 |
| 1022 | delante | 3 |
| 1023 | dejan | 3 |
| 1024 | deidad | 3 |
| 1025 | defensa | 3 |
| 1026 | dedos | 3 |
| 1027 | dedo | 3 |
| 1028 | debo | 3 |
| 1029 | débil | 3 |
| 1030 | debe | 3 |
| 1031 | daros | 3 |
| 1032 | daré | 3 |
| 1033 | dame | 3 |
| 1034 | damas | 3 |
| 1035 | cuyas | 3 |
| 1036 | cuna | 3 |
| 1037 | culto | 3 |
| 1038 | cuitado | 3 |
| 1039 | cuerpos | 3 |
| 1040 | cuánto | 3 |
| 1041 | cuántas | 3 |
| 1042 | cuánta | 3 |
| 1043 | cuál | 3 |
| 1044 | cual | 3 |
| 1045 | cruz | 3 |
| 1046 | criada | 3 |
| 1047 | crece | 3 |
| 1048 | costumbres | 3 |
| 1049 | costa | 3 |
| 1050 | corta | 3 |
| 1051 | coroza | 3 |
| 1052 | coronado | 3 |
| 1053 | coro | 3 |
| 1054 | confío | 3 |
| 1055 | confiado | 3 |
| 1056 | conde | 3 |
| 1057 | come | 3 |
| 1058 | colores | 3 |
| 1059 | cohete | 3 |
| 1060 | codicia | 3 |
| 1061 | coche | 3 |
| 1062 | cobarde | 3 |
| 1063 | clavellinas | 3 |
| 1064 | cierta | 3 |
| 1065 | ciento | 3 |
| 1066 | chica | 3 |
| 1067 | cerrado | 3 |
| 1068 | cenizas | 3 |
| 1069 | celosos | 3 |
| 1070 | celos | 3 |
| 1071 | cañas | 3 |
| 1072 | camina | 3 |
| 1073 | calores | 3 |
| 1074 | callado | 3 |
| 1075 | calidad | 3 |
| 1076 | cadena | 3 |
| 1077 | burla | 3 |
| 1078 | bulto | 3 |
| 1079 | buenos | 3 |
| 1080 | bueno | 3 |
| 1081 | brevedad | 3 |
| 1082 | blasón | 3 |
| 1083 | bienes | 3 |
| 1084 | ave | 3 |
| 1085 | ausenta | 3 |
| 1086 | aura | 3 |
| 1087 | atiende | 3 |
| 1088 | asiste | 3 |
| 1089 | arriba | 3 |
| 1090 | arma | 3 |
| 1091 | arena | 3 |
| 1092 | ardiendo | 3 |
| 1093 | ardía | 3 |
| 1094 | aplauso | 3 |
| 1095 | apenas | 3 |
| 1096 | ansias | 3 |
| 1097 | amenazas | 3 |
| 1098 | amando | 3 |
| 1099 | alta | 3 |
| 1100 | alguna | 3 |
| 1101 | aleve | 3 |
| 1102 | alegría | 3 |
| 1103 | agravios | 3 |
| 1104 | agradable | 3 |
| 1105 | afecto | 3 |
| 1106 | adora | 3 |
| 1107 | admite | 3 |
| 1108 | acredita | 3 |
| 1109 | acerca | 3 |
| 1110 | acentos | 3 |
| 1111 | acá | 3 |
| 1112 | abreviado | 3 |
| 1113 | abrazos | 3 |
| 1114 | vuelvan | 2 |
| 1115 | volvió | 2 |
| 1116 | volcán | 2 |
| 1117 | vivos | 2 |
| 1118 | vives | 2 |
| 1119 | vivas | 2 |
| 1120 | viudas | 2 |
| 1121 | viuda | 2 |
| 1122 | vitoria | 2 |
| 1123 | visto | 2 |
| 1124 | vistió | 2 |
| 1125 | vine | 2 |
| 1126 | villano | 2 |
| 1127 | villa | 2 |
| 1128 | vil | 2 |
| 1129 | vieron | 2 |
| 1130 | vieres | 2 |
| 1131 | viere | 2 |
| 1132 | viéndote | 2 |
| 1133 | viejo | 2 |
| 1134 | vieja | 2 |
| 1135 | vicio | 2 |
| 1136 | vestidos | 2 |
| 1137 | vestidas | 2 |
| 1138 | versos | 2 |
| 1139 | veros | 2 |
| 1140 | veraste | 2 |
| 1141 | veras | 2 |
| 1142 | venir | 2 |
| 1143 | vengar | 2 |
| 1144 | venga | 2 |
| 1145 | vendrá | 2 |
| 1146 | veladores | 2 |
| 1147 | vejez | 2 |
| 1148 | veinticinco | 2 |
| 1149 | veinte | 2 |
| 1150 | vea | 2 |
| 1151 | vaya | 2 |
| 1152 | vanos | 2 |
| 1153 | valle | 2 |
| 1154 | vale | 2 |
| 1155 | vaca | 2 |
| 1156 | útil | 2 |
| 1157 | umbral | 2 |
| 1158 | tuyos | 2 |
| 1159 | tuvieron | 2 |
| 1160 | tuviera | 2 |
| 1161 | túmulo | 2 |
| 1162 | tudescos | 2 |
| 1163 | trujo | 2 |
| 1164 | truhán | 2 |
| 1165 | tristes | 2 |
| 1166 | tributo | 2 |
| 1167 | tregua | 2 |
| 1168 | trata | 2 |
| 1169 | traidora | 2 |
| 1170 | tracia | 2 |
| 1171 | trabajos | 2 |
| 1172 | tortilla | 2 |
| 1173 | torpes | 2 |
| 1174 | torno | 2 |
| 1175 | tomara | 2 |
| 1176 | tocas | 2 |
| 1177 | tizones | 2 |
| 1178 | tirsi | 2 |
| 1179 | tirio | 2 |
| 1180 | tinieblas | 2 |
| 1181 | tiernos | 2 |
| 1182 | tesoros | 2 |
| 1183 | tenéis | 2 |
| 1184 | tendrá | 2 |
| 1185 | templo | 2 |
| 1186 | temen | 2 |
| 1187 | techo | 2 |
| 1188 | tantos | 2 |
| 1189 | tantas | 2 |
| 1190 | tales | 2 |
| 1191 | talegos | 2 |
| 1192 | tajo | 2 |
| 1193 | tabernas | 2 |
| 1194 | suya | 2 |
| 1195 | surcos | 2 |
| 1196 | sumo | 2 |
| 1197 | suele | 2 |
| 1198 | sudor | 2 |
| 1199 | suceda | 2 |
| 1200 | subiste | 2 |
| 1201 | sospecho | 2 |
| 1202 | sordo | 2 |
| 1203 | solitario | 2 |
| 1204 | solares | 2 |
| 1205 | sobró | 2 |
| 1206 | soberbios | 2 |
| 1207 | sitio | 2 |
| 1208 | siguió | 2 |
| 1209 | sigo | 2 |
| 1210 | siglos | 2 |
| 1211 | siglo | 2 |
| 1212 | sierra | 2 |
| 1213 | severa | 2 |
| 1214 | servicios | 2 |
| 1215 | serena | 2 |
| 1216 | sentir | 2 |
| 1217 | sentido | 2 |
| 1218 | sentí | 2 |
| 1219 | sentaron | 2 |
| 1220 | senda | 2 |
| 1221 | semejantes | 2 |
| 1222 | semblantes | 2 |
| 1223 | seguros | 2 |
| 1224 | seguridad | 2 |
| 1225 | segura | 2 |
| 1226 | segundo | 2 |
| 1227 | sediento | 2 |
| 1228 | sean | 2 |
| 1229 | satisfacción | 2 |
| 1230 | sañas | 2 |
| 1231 | saña | 2 |
| 1232 | santera | 2 |
| 1233 | sano | 2 |
| 1234 | sangrienta | 2 |
| 1235 | salas | 2 |
| 1236 | sacrosanta | 2 |
| 1237 | sacar | 2 |
| 1238 | sabios | 2 |
| 1239 | ruiseñores | 2 |
| 1240 | ruido | 2 |
| 1241 | rompe | 2 |
| 1242 | romano | 2 |
| 1243 | romance | 2 |
| 1244 | robusta | 2 |
| 1245 | robar | 2 |
| 1246 | riyendo | 2 |
| 1247 | risueño | 2 |
| 1248 | rigurosas | 2 |
| 1249 | riberas | 2 |
| 1250 | ribera | 2 |
| 1251 | revueltos | 2 |
| 1252 | retiró | 2 |
| 1253 | retirado | 2 |
| 1254 | responde | 2 |
| 1255 | resplandeciente | 2 |
| 1256 | resistir | 2 |
| 1257 | resbalas | 2 |
| 1258 | representa | 2 |
| 1259 | reposo | 2 |
| 1260 | repente | 2 |
| 1261 | remos | 2 |
| 1262 | relámpagos | 2 |
| 1263 | reina | 2 |
| 1264 | regó | 2 |
| 1265 | regís | 2 |
| 1266 | regiones | 2 |
| 1267 | refrán | 2 |
| 1268 | redentor | 2 |
| 1269 | recuerdos | 2 |
| 1270 | recuerdo | 2 |
| 1271 | recata | 2 |
| 1272 | rato | 2 |
| 1273 | ramas | 2 |
| 1274 | quise | 2 |
| 1275 | quiebra | 2 |
| 1276 | quejosos | 2 |
| 1277 | quejas | 2 |
| 1278 | queja | 2 |
| 1279 | quede | 2 |
| 1280 | quedan | 2 |
| 1281 | quebranta | 2 |
| 1282 | quebrado | 2 |
| 1283 | puros | 2 |
| 1284 | punzón | 2 |
| 1285 | puntas | 2 |
| 1286 | puesto | 2 |
| 1287 | puente | 2 |
| 1288 | pudiendo | 2 |
| 1289 | prudente | 2 |
| 1290 | provecho | 2 |
| 1291 | prosigue | 2 |
| 1292 | proprio | 2 |
| 1293 | propiedades | 2 |
| 1294 | pronuncian | 2 |
| 1295 | prometo | 2 |
| 1296 | pródiga | 2 |
| 1297 | procura | 2 |
| 1298 | privanza | 2 |
| 1299 | prisa | 2 |
| 1300 | principales | 2 |
| 1301 | previene | 2 |
| 1302 | pretensión | 2 |
| 1303 | prestó | 2 |
| 1304 | prestado | 2 |
| 1305 | preso | 2 |
| 1306 | presentes | 2 |
| 1307 | preciosas | 2 |
| 1308 | porfiado | 2 |
| 1309 | poniente | 2 |
| 1310 | pocas | 2 |
| 1311 | plazos | 2 |
| 1312 | plantas | 2 |
| 1313 | planta | 2 |
| 1314 | pizorra | 2 |
| 1315 | pirámide | 2 |
| 1316 | pintado | 2 |
| 1317 | pintada | 2 |
| 1318 | pimiento | 2 |
| 1319 | pimienta | 2 |
| 1320 | piernas | 2 |
| 1321 | pierde | 2 |
| 1322 | piensa | 2 |
| 1323 | piélago | 2 |
| 1324 | pido | 2 |
| 1325 | pidan | 2 |
| 1326 | pida | 2 |
| 1327 | picado | 2 |
| 1328 | piadoso | 2 |
| 1329 | pesares | 2 |
| 1330 | pesar | 2 |
| 1331 | pesado | 2 |
| 1332 | persuadieron | 2 |
| 1333 | persuadida | 2 |
| 1334 | persuade | 2 |
| 1335 | persecución | 2 |
| 1336 | perros | 2 |
| 1337 | perderás | 2 |
| 1338 | pensión | 2 |
| 1339 | pensando | 2 |
| 1340 | pensamientos | 2 |
| 1341 | penar | 2 |
| 1342 | peje | 2 |
| 1343 | pasto | 2 |
| 1344 | pase | 2 |
| 1345 | pasar | 2 |
| 1346 | partes | 2 |
| 1347 | parecen | 2 |
| 1348 | pardas | 2 |
| 1349 | paraíso | 2 |
| 1350 | panza | 2 |
| 1351 | palma | 2 |
| 1352 | pálidos | 2 |
| 1353 | pálida | 2 |
| 1354 | palacio | 2 |
| 1355 | pago | 2 |
| 1356 | pagados | 2 |
| 1357 | padres | 2 |
| 1358 | padezco | 2 |
| 1359 | oyó | 2 |
| 1360 | ovidio | 2 |
| 1361 | osas | 2 |
| 1362 | osadía | 2 |
| 1363 | ornamento | 2 |
| 1364 | orbe | 2 |
| 1365 | omnipotente | 2 |
| 1366 | olvidos | 2 |
| 1367 | olmo | 2 |
| 1368 | ollas | 2 |
| 1369 | olas | 2 |
| 1370 | oirán | 2 |
| 1371 | oigas | 2 |
| 1372 | ofrece | 2 |
| 1373 | ofenden | 2 |
| 1374 | obstinado | 2 |
| 1375 | obras | 2 |
| 1376 | obediente | 2 |
| 1377 | número | 2 |
| 1378 | nuestros | 2 |
| 1379 | nube | 2 |
| 1380 | novia | 2 |
| 1381 | nobles | 2 |
| 1382 | noble | 2 |
| 1383 | niñez | 2 |
| 1384 | ninguno | 2 |
| 1385 | necesidad | 2 |
| 1386 | navega | 2 |
| 1387 | náufrago | 2 |
| 1388 | narciso | 2 |
| 1389 | nadando | 2 |
| 1390 | nacidos | 2 |
| 1391 | mustio | 2 |
| 1392 | músico | 2 |
| 1393 | música | 2 |
| 1394 | mulato | 2 |
| 1395 | mujeres | 2 |
| 1396 | muertas | 2 |
| 1397 | muere | 2 |
| 1398 | movimientos | 2 |
| 1399 | mostrar | 2 |
| 1400 | mostrando | 2 |
| 1401 | mostaza | 2 |
| 1402 | mosca | 2 |
| 1403 | mordido | 2 |
| 1404 | montaña | 2 |
| 1405 | mondada | 2 |
| 1406 | monarquía | 2 |
| 1407 | momento | 2 |
| 1408 | mismos | 2 |
| 1409 | mísero | 2 |
| 1410 | miraron | 2 |
| 1411 | mirar | 2 |
| 1412 | miráis | 2 |
| 1413 | mirad | 2 |
| 1414 | militar | 2 |
| 1415 | miércoles | 2 |
| 1416 | mezclaba | 2 |
| 1417 | mesmas | 2 |
| 1418 | méritos | 2 |
| 1419 | mercader | 2 |
| 1420 | mentiras | 2 |
| 1421 | mentira | 2 |
| 1422 | memorias | 2 |
| 1423 | mejora | 2 |
| 1424 | mejillas | 2 |
| 1425 | medulas | 2 |
| 1426 | médicos | 2 |
| 1427 | médico | 2 |
| 1428 | medicina | 2 |
| 1429 | martes | 2 |
| 1430 | mariposa | 2 |
| 1431 | marinero | 2 |
| 1432 | mari | 2 |
| 1433 | mares | 2 |
| 1434 | manto | 2 |
| 1435 | manso | 2 |
| 1436 | mandar | 2 |
| 1437 | manchó | 2 |
| 1438 | mancebo | 2 |
| 1439 | malos | 2 |
| 1440 | malas | 2 |
| 1441 | madrugan | 2 |
| 1442 | madrigal | 2 |
| 1443 | madres | 2 |
| 1444 | luto | 2 |
| 1445 | luciente | 2 |
| 1446 | loca | 2 |
| 1447 | lluvias | 2 |
| 1448 | llueve | 2 |
| 1449 | llevara | 2 |
| 1450 | llenos | 2 |
| 1451 | llanura | 2 |
| 1452 | llanos | 2 |
| 1453 | llame | 2 |
| 1454 | llamar | 2 |
| 1455 | liviana | 2 |
| 1456 | lisonjas | 2 |
| 1457 | lisa | 2 |
| 1458 | lírica | 2 |
| 1459 | lira | 2 |
| 1460 | líquido | 2 |
| 1461 | líquidas | 2 |
| 1462 | líquida | 2 |
| 1463 | linsojera | 2 |
| 1464 | lindas | 2 |
| 1465 | linaje | 2 |
| 1466 | limpio | 2 |
| 1467 | ligero | 2 |
| 1468 | licencia | 2 |
| 1469 | licas | 2 |
| 1470 | libra | 2 |
| 1471 | levantan | 2 |
| 1472 | levanta | 2 |
| 1473 | letras | 2 |
| 1474 | leonor | 2 |
| 1475 | león | 2 |
| 1476 | leño | 2 |
| 1477 | legiones | 2 |
| 1478 | lecho | 2 |
| 1479 | lección | 2 |
| 1480 | lazos | 2 |
| 1481 | lastimoso | 2 |
| 1482 | lástima | 2 |
| 1483 | labrador | 2 |
| 1484 | juventud | 2 |
| 1485 | justicia | 2 |
| 1486 | juez | 2 |
| 1487 | juego | 2 |
| 1488 | juan | 2 |
| 1489 | joya | 2 |
| 1490 | jove | 2 |
| 1491 | jordán | 2 |
| 1492 | jineta | 2 |
| 1493 | jasón | 2 |
| 1494 | irrevocable | 2 |
| 1495 | inútil | 2 |
| 1496 | interior | 2 |
| 1497 | interés | 2 |
| 1498 | intento | 2 |
| 1499 | intenté | 2 |
| 1500 | intenta | 2 |
| 1501 | instrumento | 2 |
| 1502 | inobedientes | 2 |
| 1503 | inobediencia | 2 |
| 1504 | ingrato | 2 |
| 1505 | infinitos | 2 |
| 1506 | infanzón | 2 |
| 1507 | indias | 2 |
| 1508 | inclinación | 2 |
| 1509 | inclina | 2 |
| 1510 | inadvertido | 2 |
| 1511 | impreso | 2 |
| 1512 | importa | 2 |
| 1513 | imite | 2 |
| 1514 | imitación | 2 |
| 1515 | ilustre | 2 |
| 1516 | humor | 2 |
| 1517 | humilde | 2 |
| 1518 | humanos | 2 |
| 1519 | hospedado | 2 |
| 1520 | honroso | 2 |
| 1521 | honras | 2 |
| 1522 | honrado | 2 |
| 1523 | hongos | 2 |
| 1524 | honesto | 2 |
| 1525 | hombro | 2 |
| 1526 | hidrópica | 2 |
| 1527 | hidropesía | 2 |
| 1528 | hicieron | 2 |
| 1529 | hervores | 2 |
| 1530 | hero | 2 |
| 1531 | herido | 2 |
| 1532 | hereje | 2 |
| 1533 | helado | 2 |
| 1534 | hechicera | 2 |
| 1535 | harto | 2 |
| 1536 | haré | 2 |
| 1537 | hanme | 2 |
| 1538 | hallan | 2 |
| 1539 | hagas | 2 |
| 1540 | hagan | 2 |
| 1541 | haga | 2 |
| 1542 | hados | 2 |
| 1543 | haces | 2 |
| 1544 | hacerme | 2 |
| 1545 | hable | 2 |
| 1546 | hablar | 2 |
| 1547 | hablan | 2 |
| 1548 | habita | 2 |
| 1549 | haberte | 2 |
| 1550 | gustas | 2 |
| 1551 | gusanos | 2 |
| 1552 | gula | 2 |
| 1553 | guijas | 2 |
| 1554 | guido | 2 |
| 1555 | güevos | 2 |
| 1556 | güeros | 2 |
| 1557 | guedejas | 2 |
| 1558 | güeco | 2 |
| 1559 | guardan | 2 |
| 1560 | guadaña | 2 |
| 1561 | granizos | 2 |
| 1562 | grandezas | 2 |
| 1563 | grajos | 2 |
| 1564 | gozo | 2 |
| 1565 | gozar | 2 |
| 1566 | golfos | 2 |
| 1567 | gobierno | 2 |
| 1568 | gimió | 2 |
| 1569 | gime | 2 |
| 1570 | gesto | 2 |
| 1571 | gentil | 2 |
| 1572 | gentes | 2 |
| 1573 | generoso | 2 |
| 1574 | gaznate | 2 |
| 1575 | gatos | 2 |
| 1576 | gastar | 2 |
| 1577 | ganados | 2 |
| 1578 | gallarda | 2 |
| 1579 | furias | 2 |
| 1580 | furia | 2 |
| 1581 | fulminar | 2 |
| 1582 | fuisteis | 2 |
| 1583 | fugitivo | 2 |
| 1584 | fugitivas | 2 |
| 1585 | fugitiva | 2 |
| 1586 | fuertes | 2 |
| 1587 | fuentes | 2 |
| 1588 | fruto | 2 |
| 1589 | fritos | 2 |
| 1590 | frentes | 2 |
| 1591 | fregona | 2 |
| 1592 | forzosos | 2 |
| 1593 | formidable | 2 |
| 1594 | floralva | 2 |
| 1595 | flaqueza | 2 |
| 1596 | flandes | 2 |
| 1597 | flagrante | 2 |
| 1598 | flaca | 2 |
| 1599 | firmeza | 2 |
| 1600 | fiestas | 2 |
| 1601 | fiera | 2 |
| 1602 | feo | 2 |
| 1603 | fénix | 2 |
| 1604 | felipe | 2 |
| 1605 | fatiga | 2 |
| 1606 | fantasma | 2 |
| 1607 | famoso | 2 |
| 1608 | falsa | 2 |
| 1609 | faldas | 2 |
| 1610 | faetón | 2 |
| 1611 | fábricas | 2 |
| 1612 | fabio | 2 |
| 1613 | exprimida | 2 |
| 1614 | examina | 2 |
| 1615 | europa | 2 |
| 1616 | eternidad | 2 |
| 1617 | eternamente | 2 |
| 1618 | estudios | 2 |
| 1619 | estrellada | 2 |
| 1620 | estrecha | 2 |
| 1621 | estorba | 2 |
| 1622 | estimación | 2 |
| 1623 | esté | 2 |
| 1624 | estás | 2 |
| 1625 | estarán | 2 |
| 1626 | estar | 2 |
| 1627 | estado | 2 |
| 1628 | estaban | 2 |
| 1629 | esquivo | 2 |
| 1630 | esperanzas | 2 |
| 1631 | esperanza | 2 |
| 1632 | espera | 2 |
| 1633 | español | 2 |
| 1634 | espanta | 2 |
| 1635 | esotra | 2 |
| 1636 | esforzado | 2 |
| 1637 | escuadrón | 2 |
| 1638 | escuadra | 2 |
| 1639 | escribo | 2 |
| 1640 | escribió | 2 |
| 1641 | escribe | 2 |
| 1642 | escondido | 2 |
| 1643 | errado | 2 |
| 1644 | epitafio | 2 |
| 1645 | envuelta | 2 |
| 1646 | envidia | 2 |
| 1647 | envejecen | 2 |
| 1648 | entierra | 2 |
| 1649 | entiendes | 2 |
| 1650 | entendidos | 2 |
| 1651 | enseñanza | 2 |
| 1652 | ennegreció | 2 |
| 1653 | enlutada | 2 |
| 1654 | enjuto | 2 |
| 1655 | engendró | 2 |
| 1656 | enfermedad | 2 |
| 1657 | enemiga | 2 |
| 1658 | encierra | 2 |
| 1659 | enciende | 2 |
| 1660 | encendidas | 2 |
| 1661 | encendida | 2 |
| 1662 | encender | 2 |
| 1663 | encarnado | 2 |
| 1664 | encarcelado | 2 |
| 1665 | enaguas | 2 |
| 1666 | empiezas | 2 |
| 1667 | elección | 2 |
| 1668 | ejecutoria | 2 |
| 1669 | egipto | 2 |
| 1670 | edades | 2 |
| 1671 | echen | 2 |
| 1672 | duplicado | 2 |
| 1673 | dueños | 2 |
| 1674 | dormida | 2 |
| 1675 | dónde | 2 |
| 1676 | doloroso | 2 |
| 1677 | dolores | 2 |
| 1678 | doctrina | 2 |
| 1679 | doctor | 2 |
| 1680 | doblones | 2 |
| 1681 | doblón | 2 |
| 1682 | divino | 2 |
| 1683 | dividido | 2 |
| 1684 | diversas | 2 |
| 1685 | disimulan | 2 |
| 1686 | discreto | 2 |
| 1687 | discreta | 2 |
| 1688 | dirá | 2 |
| 1689 | dile | 2 |
| 1690 | diferente | 2 |
| 1691 | dieron | 2 |
| 1692 | dichosos | 2 |
| 1693 | desvío | 2 |
| 1694 | desventuras | 2 |
| 1695 | desvelo | 2 |
| 1696 | destino | 2 |
| 1697 | destierro | 2 |
| 1698 | desprecio | 2 |
| 1699 | despreciada | 2 |
| 1700 | despide | 2 |
| 1701 | desperdicios | 2 |
| 1702 | despeñado | 2 |
| 1703 | desnudez | 2 |
| 1704 | desnudar | 2 |
| 1705 | desmayada | 2 |
| 1706 | desiguales | 2 |
| 1707 | desiertos | 2 |
| 1708 | desierto | 2 |
| 1709 | desesperada | 2 |
| 1710 | desengaños | 2 |
| 1711 | desecha | 2 |
| 1712 | desdichada | 2 |
| 1713 | desdicha | 2 |
| 1714 | desdeña | 2 |
| 1715 | desdenes | 2 |
| 1716 | descuido | 2 |
| 1717 | descubre | 2 |
| 1718 | descubierta | 2 |
| 1719 | desconsuelo | 2 |
| 1720 | desconocida | 2 |
| 1721 | desconcierto | 2 |
| 1722 | descendiente | 2 |
| 1723 | desatina | 2 |
| 1724 | desatado | 2 |
| 1725 | derramado | 2 |
| 1726 | derecho | 2 |
| 1727 | depare | 2 |
| 1728 | demonio | 2 |
| 1729 | dellas | 2 |
| 1730 | delito | 2 |
| 1731 | delicada | 2 |
| 1732 | deje | 2 |
| 1733 | dejaron | 2 |
| 1734 | dejar | 2 |
| 1735 | dejáis | 2 |
| 1736 | deis | 2 |
| 1737 | decoro | 2 |
| 1738 | décimas | 2 |
| 1739 | decente | 2 |
| 1740 | debidas | 2 |
| 1741 | deba | 2 |
| 1742 | das | 2 |
| 1743 | darme | 2 |
| 1744 | darán | 2 |
| 1745 | danubio | 2 |
| 1746 | dais | 2 |
| 1747 | daba | 2 |
| 1748 | cuyo | 2 |
| 1749 | curioso | 2 |
| 1750 | cura | 2 |
| 1751 | cuerdas | 2 |
| 1752 | cuerda | 2 |
| 1753 | cuentes | 2 |
| 1754 | cuentas | 2 |
| 1755 | cubrió | 2 |
| 1756 | cubiertos | 2 |
| 1757 | cuatro | 2 |
| 1758 | cuartos | 2 |
| 1759 | cuarenta | 2 |
| 1760 | cuantos | 2 |
| 1761 | cruel | 2 |
| 1762 | cristal | 2 |
| 1763 | criado | 2 |
| 1764 | crédito | 2 |
| 1765 | crecida | 2 |
| 1766 | crecer | 2 |
| 1767 | corto | 2 |
| 1768 | corte | 2 |
| 1769 | corrido | 2 |
| 1770 | correr | 2 |
| 1771 | corra | 2 |
| 1772 | coronas | 2 |
| 1773 | corazones | 2 |
| 1774 | coral | 2 |
| 1775 | convida | 2 |
| 1776 | contrario | 2 |
| 1777 | contigo | 2 |
| 1778 | contento | 2 |
| 1779 | contar | 2 |
| 1780 | contagio | 2 |
| 1781 | contaba | 2 |
| 1782 | cónsules | 2 |
| 1783 | consuelo | 2 |
| 1784 | constante | 2 |
| 1785 | consejo | 2 |
| 1786 | conozco | 2 |
| 1787 | conozca | 2 |
| 1788 | conocer | 2 |
| 1789 | conduce | 2 |
| 1790 | condición | 2 |
| 1791 | condestable | 2 |
| 1792 | concede | 2 |
| 1793 | competencia | 2 |
| 1794 | compara | 2 |
| 1795 | comieron | 2 |
| 1796 | cobardes | 2 |
| 1797 | clementes | 2 |
| 1798 | claro | 2 |
| 1799 | ciudad | 2 |
| 1800 | cincuenta | 2 |
| 1801 | ciegos | 2 |
| 1802 | chismes | 2 |
| 1803 | cetro | 2 |
| 1804 | cerros | 2 |
| 1805 | cerca | 2 |
| 1806 | ceñido | 2 |
| 1807 | centellas | 2 |
| 1808 | celo | 2 |
| 1809 | cautiverio | 2 |
| 1810 | caudal | 2 |
| 1811 | castigo | 2 |
| 1812 | casta | 2 |
| 1813 | caso | 2 |
| 1814 | casi | 2 |
| 1815 | carrera | 2 |
| 1816 | carnes | 2 |
| 1817 | carnero | 2 |
| 1818 | cargado | 2 |
| 1819 | cáñamo | 2 |
| 1820 | cantaron | 2 |
| 1821 | cansado | 2 |
| 1822 | canciones | 2 |
| 1823 | canas | 2 |
| 1824 | can | 2 |
| 1825 | campañas | 2 |
| 1826 | campana | 2 |
| 1827 | caminar | 2 |
| 1828 | calle | 2 |
| 1829 | callada | 2 |
| 1830 | calamidad | 2 |
| 1831 | cabañas | 2 |
| 1832 | caballo | 2 |
| 1833 | busque | 2 |
| 1834 | buscas | 2 |
| 1835 | burlas | 2 |
| 1836 | buida | 2 |
| 1837 | bruto | 2 |
| 1838 | bríos | 2 |
| 1839 | brilla | 2 |
| 1840 | bravatas | 2 |
| 1841 | borrasca | 2 |
| 1842 | bolsón | 2 |
| 1843 | bolsa | 2 |
| 1844 | blasonar | 2 |
| 1845 | blasona | 2 |
| 1846 | blanda | 2 |
| 1847 | blancura | 2 |
| 1848 | blancas | 2 |
| 1849 | bienaventuranza | 2 |
| 1850 | bendición | 2 |
| 1851 | basquiñas | 2 |
| 1852 | barbado | 2 |
| 1853 | balcones | 2 |
| 1854 | bajo | 2 |
| 1855 | azotaron | 2 |
| 1856 | avisan | 2 |
| 1857 | avariento | 2 |
| 1858 | ausencia | 2 |
| 1859 | atropella | 2 |
| 1860 | atrevida | 2 |
| 1861 | atreven | 2 |
| 1862 | atreve | 2 |
| 1863 | ásperos | 2 |
| 1864 | áspero | 2 |
| 1865 | asientos | 2 |
| 1866 | asco | 2 |
| 1867 | asados | 2 |
| 1868 | arroyuelos | 2 |
| 1869 | arroyos | 2 |
| 1870 | arroyo | 2 |
| 1871 | arrepentimiento | 2 |
| 1872 | armada | 2 |
| 1873 | arden | 2 |
| 1874 | aquesto | 2 |
| 1875 | aquesta | 2 |
| 1876 | aquellos | 2 |
| 1877 | apura | 2 |
| 1878 | aprisionado | 2 |
| 1879 | aprender | 2 |
| 1880 | aprende | 2 |
| 1881 | aposento | 2 |
| 1882 | apariencia | 2 |
| 1883 | apacibles | 2 |
| 1884 | anudado | 2 |
| 1885 | antiguo | 2 |
| 1886 | antaños | 2 |
| 1887 | animado | 2 |
| 1888 | anhelas | 2 |
| 1889 | andar | 2 |
| 1890 | anciana | 2 |
| 1891 | ancha | 2 |
| 1892 | amo | 2 |
| 1893 | amistad | 2 |
| 1894 | ambiciosa | 2 |
| 1895 | ambición | 2 |
| 1896 | amarillo | 2 |
| 1897 | amarillez | 2 |
| 1898 | amantes | 2 |
| 1899 | amanecer | 2 |
| 1900 | amado | 2 |
| 1901 | alumbra | 2 |
| 1902 | altura | 2 |
| 1903 | altos | 2 |
| 1904 | almendro | 2 |
| 1905 | aljaba | 2 |
| 1906 | alivio | 2 |
| 1907 | alimenta | 2 |
| 1908 | alexi | 2 |
| 1909 | aleje | 2 |
| 1910 | alcance | 2 |
| 1911 | albedrío | 2 |
| 1912 | alba | 2 |
| 1913 | alado | 2 |
| 1914 | alabanza | 2 |
| 1915 | airado | 2 |
| 1916 | ahorrar | 2 |
| 1917 | ahoga | 2 |
| 1918 | agudo | 2 |
| 1919 | aguarda | 2 |
| 1920 | agria | 2 |
| 1921 | afrenta | 2 |
| 1922 | afligido | 2 |
| 1923 | aflige | 2 |
| 1924 | afectos | 2 |
| 1925 | afán | 2 |
| 1926 | adonde | 2 |
| 1927 | admiten | 2 |
| 1928 | ademán | 2 |
| 1929 | acuerda | 2 |
| 1930 | acompañamiento | 2 |
| 1931 | acompaña | 2 |
| 1932 | acento | 2 |
| 1933 | acción | 2 |
| 1934 | acaso | 2 |
| 1935 | acabe | 2 |
| 1936 | acabar | 2 |
| 1937 | abril | 2 |
| 1938 | abrazado | 2 |
| 1939 | abraso | 2 |
| 1940 | ablanda | 2 |
| 1941 | abismo | 2 |
| 1942 | abajo | 2 |
| 1943 | zorras | 1 |
| 1944 | zenón | 1 |
| 1945 | zapatero | 1 |
| 1946 | zafir | 1 |
| 1947 | zabúllete | 1 |
| 1948 | yerto | 1 |
| 1949 | yerta | 1 |
| 1950 | yerre | 1 |
| 1951 | yerran | 1 |
| 1952 | yerra | 1 |
| 1953 | yendo | 1 |
| 1954 | yema | 1 |
| 1955 | yelos | 1 |
| 1956 | yelo | 1 |
| 1957 | vulcano | 1 |
| 1958 | vuestros | 1 |
| 1959 | vuestras | 1 |
| 1960 | vuélvete | 1 |
| 1961 | vuelves | 1 |
| 1962 | vuelvas | 1 |
| 1963 | vuélvanse | 1 |
| 1964 | vuelva | 1 |
| 1965 | vuelto | 1 |
| 1966 | vueltas | 1 |
| 1967 | voyme | 1 |
| 1968 | voy | 1 |
| 1969 | voto | 1 |
| 1970 | vosotros | 1 |
| 1971 | voraz | 1 |
| 1972 | vomita | 1 |
| 1973 | volvieron | 1 |
| 1974 | volvieran | 1 |
| 1975 | volvía | 1 |
| 1976 | volverte | 1 |
| 1977 | volvérmelo | 1 |
| 1978 | volverlo | 1 |
| 1979 | volverle | 1 |
| 1980 | volverán | 1 |
| 1981 | volver | 1 |
| 1982 | voló | 1 |
| 1983 | volcanes | 1 |
| 1984 | volante | 1 |
| 1985 | volando | 1 |
| 1986 | volador | 1 |
| 1987 | vocean | 1 |
| 1988 | vocablo | 1 |
| 1989 | vizcaya | 1 |
| 1990 | vivirán | 1 |
| 1991 | vivirá | 1 |
| 1992 | vivió | 1 |
| 1993 | viviente | 1 |
| 1994 | viviendo | 1 |
| 1995 | vivía | 1 |
| 1996 | viudo | 1 |
| 1997 | vituperios | 1 |
| 1998 | vitorioso | 1 |
| 1999 | vistiese | 1 |
| 2000 | vistiendo | 1 |
| 2001 | visten | 1 |
| 2002 | vísperas | 1 |
| 2003 | visión | 1 |
| 2004 | virtudes | 1 |
| 2005 | virgo | 1 |
| 2006 | virgen | 1 |
| 2007 | violento | 1 |
| 2008 | violenta | 1 |
| 2009 | violencia | 1 |
| 2010 | viole | 1 |
| 2011 | vinosas | 1 |
| 2012 | vinos | 1 |
| 2013 | vimos | 1 |
| 2014 | villanos | 1 |
| 2015 | vigüelas | 1 |
| 2016 | vieran | 1 |
| 2017 | viéneslo | 1 |
| 2018 | vienen | 1 |
| 2019 | viéndose | 1 |
| 2020 | viéndonos | 1 |
| 2021 | viéndome | 1 |
| 2022 | viéndole | 1 |
| 2023 | viejos | 1 |
| 2024 | viejas | 1 |
| 2025 | vidro | 1 |
| 2026 | vidrio | 1 |
| 2027 | victoriosa | 1 |
| 2028 | víctima | 1 |
| 2029 | vicios | 1 |
| 2030 | víbora | 1 |
| 2031 | viaje | 1 |
| 2032 | vete | 1 |
| 2033 | vesubio | 1 |
| 2034 | vestidito | 1 |
| 2035 | vestida | 1 |
| 2036 | vestía | 1 |
| 2037 | vestí | 1 |
| 2038 | veslos | 1 |
| 2039 | vertió | 1 |
| 2040 | vertido | 1 |
| 2041 | vergonzosos | 1 |
| 2042 | veréis | 1 |
| 2043 | verdura | 1 |
| 2044 | verdugos | 1 |
| 2045 | verdugo | 1 |
| 2046 | verdugado | 1 |
| 2047 | verdades | 1 |
| 2048 | verbo | 1 |
| 2049 | verás | 1 |
| 2050 | verá | 1 |
| 2051 | venzo | 1 |
| 2052 | venturoso | 1 |
| 2053 | venturosa | 1 |
| 2054 | ventana | 1 |
| 2055 | ventaja | 1 |
| 2056 | venta | 1 |
| 2057 | venidero | 1 |
| 2058 | venideras | 1 |
| 2059 | venida | 1 |
| 2060 | venïales | 1 |
| 2061 | vengole | 1 |
| 2062 | vengativos | 1 |
| 2063 | vengativa | 1 |
| 2064 | vengarse | 1 |
| 2065 | venganzas | 1 |
| 2066 | vengadora | 1 |
| 2067 | venerable | 1 |
| 2068 | vendré | 1 |
| 2069 | vendrán | 1 |
| 2070 | vendimia | 1 |
| 2071 | vendiendo | 1 |
| 2072 | vendido | 1 |
| 2073 | vendible | 1 |
| 2074 | vendederas | 1 |
| 2075 | véndanle | 1 |
| 2076 | venda | 1 |
| 2077 | venció | 1 |
| 2078 | vencimiento | 1 |
| 2079 | vencida | 1 |
| 2080 | vencerte | 1 |
| 2081 | vencedores | 1 |
| 2082 | vencedora | 1 |
| 2083 | vence | 1 |
| 2084 | venado | 1 |
| 2085 | vemos | 1 |
| 2086 | velocísima | 1 |
| 2087 | velloso | 1 |
| 2088 | vellones | 1 |
| 2089 | vella | 1 |
| 2090 | velillos | 1 |
| 2091 | velilla | 1 |
| 2092 | veleta | 1 |
| 2093 | velas | 1 |
| 2094 | velador | 1 |
| 2095 | vejigas | 1 |
| 2096 | veintidoseno | 1 |
| 2097 | ved | 1 |
| 2098 | vecindad | 1 |
| 2099 | vean | 1 |
| 2100 | vaso | 1 |
| 2101 | vasallos | 1 |
| 2102 | vasallaje | 1 |
| 2103 | vas | 1 |
| 2104 | varios | 1 |
| 2105 | varia | 1 |
| 2106 | vapores | 1 |
| 2107 | valonas | 1 |
| 2108 | valimiento | 1 |
| 2109 | valiera | 1 |
| 2110 | valeroso | 1 |
| 2111 | valen | 1 |
| 2112 | valdrá | 1 |
| 2113 | vais | 1 |
| 2114 | vainicas | 1 |
| 2115 | vacío | 1 |
| 2116 | vaciaba | 1 |
| 2117 | vacía | 1 |
| 2118 | vacado | 1 |
| 2119 | vacada | 1 |
| 2120 | v | 1 |
| 2121 | usurparon | 1 |
| 2122 | usurera | 1 |
| 2123 | usura | 1 |
| 2124 | urnas | 1 |
| 2125 | uña | 1 |
| 2126 | untándolos | 1 |
| 2127 | unidas | 1 |
| 2128 | unida | 1 |
| 2129 | única | 1 |
| 2130 | ungüento | 1 |
| 2131 | undoso | 1 |
| 2132 | umbrales | 1 |
| 2133 | último | 1 |
| 2134 | últimas | 1 |
| 2135 | última | 1 |
| 2136 | ulises | 1 |
| 2137 | ufanos | 1 |
| 2138 | ufana | 1 |
| 2139 | tuyo | 1 |
| 2140 | tuviste | 1 |
| 2141 | tuvieras | 1 |
| 2142 | tutelares | 1 |
| 2143 | turquíes | 1 |
| 2144 | turco | 1 |
| 2145 | turbio | 1 |
| 2146 | turbantes | 1 |
| 2147 | tumultos | 1 |
| 2148 | tuerces | 1 |
| 2149 | trujeron | 1 |
| 2150 | truenos | 1 |
| 2151 | trueno | 1 |
| 2152 | truena | 1 |
| 2153 | trueco | 1 |
| 2154 | trueca | 1 |
| 2155 | truchas | 1 |
| 2156 | trucha | 1 |
| 2157 | trote | 1 |
| 2158 | troquéis | 1 |
| 2159 | tropieza | 1 |
| 2160 | tropezará | 1 |
| 2161 | trono | 1 |
| 2162 | trongas | 1 |
| 2163 | troncos | 1 |
| 2164 | trompeta | 1 |
| 2165 | trofeos | 1 |
| 2166 | trocarme | 1 |
| 2167 | triunfará | 1 |
| 2168 | triunfadora | 1 |
| 2169 | triones | 1 |
| 2170 | trinacria | 1 |
| 2171 | tribus | 1 |
| 2172 | tretas | 1 |
| 2173 | trémulos | 1 |
| 2174 | trecho | 1 |
| 2175 | trazas | 1 |
| 2176 | traza | 1 |
| 2177 | travieso | 1 |
| 2178 | tratos | 1 |
| 2179 | trato | 1 |
| 2180 | tratable | 1 |
| 2181 | trastes | 1 |
| 2182 | traspasos | 1 |
| 2183 | trasgo | 1 |
| 2184 | traseros | 1 |
| 2185 | trapos | 1 |
| 2186 | transitoria | 1 |
| 2187 | tránsito | 1 |
| 2188 | transformadas | 1 |
| 2189 | tranquilidad | 1 |
| 2190 | tramposo | 1 |
| 2191 | traiga | 1 |
| 2192 | traidores | 1 |
| 2193 | traidor | 1 |
| 2194 | traiciones | 1 |
| 2195 | traía | 1 |
| 2196 | trago | 1 |
| 2197 | trágica | 1 |
| 2198 | tragar | 1 |
| 2199 | tragan | 1 |
| 2200 | traga | 1 |
| 2201 | traes | 1 |
| 2202 | traer | 1 |
| 2203 | trabaja | 1 |
| 2204 | total | 1 |
| 2205 | torva | 1 |
| 2206 | tórtolas | 1 |
| 2207 | torres | 1 |
| 2208 | torneos | 1 |
| 2209 | tormenta | 1 |
| 2210 | torcido | 1 |
| 2211 | toque | 1 |
| 2212 | tontas | 1 |
| 2213 | tómeme | 1 |
| 2214 | tomé | 1 |
| 2215 | tómate | 1 |
| 2216 | tomando | 1 |
| 2217 | tomá | 1 |
| 2218 | toma | 1 |
| 2219 | tocolas | 1 |
| 2220 | tocinos | 1 |
| 2221 | tocino | 1 |
| 2222 | tocarse | 1 |
| 2223 | tocando | 1 |
| 2224 | tocan | 1 |
| 2225 | tócame | 1 |
| 2226 | toalla | 1 |
| 2227 | titubeando | 1 |
| 2228 | tiria | 1 |
| 2229 | tiraniza | 1 |
| 2230 | tique | 1 |
| 2231 | tiña | 1 |
| 2232 | tinto | 1 |
| 2233 | tinteros | 1 |
| 2234 | tintero | 1 |
| 2235 | tiniebla | 1 |
| 2236 | timbre | 1 |
| 2237 | tiesa | 1 |
| 2238 | tierno | 1 |
| 2239 | tiernas | 1 |
| 2240 | tiernamente | 1 |
| 2241 | tierna | 1 |
| 2242 | tiempos | 1 |
| 2243 | tiembla | 1 |
| 2244 | tiburón | 1 |
| 2245 | tíber | 1 |
| 2246 | testimonio | 1 |
| 2247 | terror | 1 |
| 2248 | terrón | 1 |
| 2249 | ternezas | 1 |
| 2250 | terneza | 1 |
| 2251 | terciopelo | 1 |
| 2252 | tercianas | 1 |
| 2253 | tercero | 1 |
| 2254 | teñido | 1 |
| 2255 | tentación | 1 |
| 2256 | teniendo | 1 |
| 2257 | tenerla | 1 |
| 2258 | tenella | 1 |
| 2259 | tenebrosas | 1 |
| 2260 | tenebrosa | 1 |
| 2261 | tendría | 1 |
| 2262 | tendremos | 1 |
| 2263 | tendréis | 1 |
| 2264 | tendrán | 1 |
| 2265 | tendero | 1 |
| 2266 | tenca | 1 |
| 2267 | tenaz | 1 |
| 2268 | temprano | 1 |
| 2269 | temprana | 1 |
| 2270 | templarle | 1 |
| 2271 | templanza | 1 |
| 2272 | templando | 1 |
| 2273 | templado | 1 |
| 2274 | templada | 1 |
| 2275 | temiéndole | 1 |
| 2276 | temido | 1 |
| 2277 | temidas | 1 |
| 2278 | temida | 1 |
| 2279 | temerosos | 1 |
| 2280 | temeroso | 1 |
| 2281 | temerarios | 1 |
| 2282 | temblor | 1 |
| 2283 | temblaron | 1 |
| 2284 | temas | 1 |
| 2285 | telas | 1 |
| 2286 | tejieron | 1 |
| 2287 | teja | 1 |
| 2288 | taza | 1 |
| 2289 | tasado | 1 |
| 2290 | tasaba | 1 |
| 2291 | tasa | 1 |
| 2292 | tapetado | 1 |
| 2293 | tapadas | 1 |
| 2294 | tántalo | 1 |
| 2295 | tamaño | 1 |
| 2296 | talle | 1 |
| 2297 | tacto | 1 |
| 2298 | tachas | 1 |
| 2299 | tablados | 1 |
| 2300 | taberna | 1 |
| 2301 | t | 1 |
| 2302 | suyos | 1 |
| 2303 | sustento | 1 |
| 2304 | sustentarme | 1 |
| 2305 | sustentar | 1 |
| 2306 | sustentan | 1 |
| 2307 | sustenta | 1 |
| 2308 | suspirando | 1 |
| 2309 | suspiráis | 1 |
| 2310 | suspensión | 1 |
| 2311 | suspendiera | 1 |
| 2312 | suspenda | 1 |
| 2313 | supremo | 1 |
| 2314 | supliendo | 1 |
| 2315 | superlativa | 1 |
| 2316 | superior | 1 |
| 2317 | supe | 1 |
| 2318 | sumergirse | 1 |
| 2319 | sumas | 1 |
| 2320 | sujeto | 1 |
| 2321 | sujetas | 1 |
| 2322 | sujetarlo | 1 |
| 2323 | sujeta | 1 |
| 2324 | sufrimiento | 1 |
| 2325 | sufridos | 1 |
| 2326 | sufrido | 1 |
| 2327 | suenas | 1 |
| 2328 | suena | 1 |
| 2329 | sueltos | 1 |
| 2330 | suelta | 1 |
| 2331 | suelos | 1 |
| 2332 | suelen | 1 |
| 2333 | sucesores | 1 |
| 2334 | sucesiones | 1 |
| 2335 | sucedido | 1 |
| 2336 | subir | 1 |
| 2337 | subió | 1 |
| 2338 | subiéronse | 1 |
| 2339 | sube | 1 |
| 2340 | suba | 1 |
| 2341 | süave | 1 |
| 2342 | suave | 1 |
| 2343 | sospechas | 1 |
| 2344 | sospecha | 1 |
| 2345 | sosegó | 1 |
| 2346 | sosegar | 1 |
| 2347 | sortija | 1 |
| 2348 | soria | 1 |
| 2349 | sorbos | 1 |
| 2350 | sorben | 1 |
| 2351 | soplón | 1 |
| 2352 | soplillo | 1 |
| 2353 | soplando | 1 |
| 2354 | sopas | 1 |
| 2355 | sopa | 1 |
| 2356 | soñolientos | 1 |
| 2357 | soñé | 1 |
| 2358 | soñado | 1 |
| 2359 | soñaba | 1 |
| 2360 | sonora | 1 |
| 2361 | sonido | 1 |
| 2362 | soneto | 1 |
| 2363 | sombreros | 1 |
| 2364 | soltado | 1 |
| 2365 | solos | 1 |
| 2366 | sollozos | 1 |
| 2367 | solicitud | 1 |
| 2368 | soledades | 1 |
| 2369 | socorro | 1 |
| 2370 | socorrida | 1 |
| 2371 | socorres | 1 |
| 2372 | sobresaltos | 1 |
| 2373 | sobran | 1 |
| 2374 | sobra | 1 |
| 2375 | soberana | 1 |
| 2376 | sírvole | 1 |
| 2377 | sirven | 1 |
| 2378 | sirio | 1 |
| 2379 | sirena | 1 |
| 2380 | sincero | 1 |
| 2381 | simples | 1 |
| 2382 | símbolo | 1 |
| 2383 | silvio | 1 |
| 2384 | silvas | 1 |
| 2385 | sillas | 1 |
| 2386 | silbo | 1 |
| 2387 | sigues | 1 |
| 2388 | sígote | 1 |
| 2389 | signo | 1 |
| 2390 | significase | 1 |
| 2391 | significación | 1 |
| 2392 | sígate | 1 |
| 2393 | sigan | 1 |
| 2394 | siga | 1 |
| 2395 | sierpe | 1 |
| 2396 | sienes | 1 |
| 2397 | siciliana | 1 |
| 2398 | seso | 1 |
| 2399 | servís | 1 |
| 2400 | servir | 1 |
| 2401 | servicio | 1 |
| 2402 | servía | 1 |
| 2403 | serví | 1 |
| 2404 | serpiente | 1 |
| 2405 | sermones | 1 |
| 2406 | sería | 1 |
| 2407 | serenos | 1 |
| 2408 | serenado | 1 |
| 2409 | seráficas | 1 |
| 2410 | séquito | 1 |
| 2411 | sequen | 1 |
| 2412 | sepultura | 1 |
| 2413 | sepultado | 1 |
| 2414 | sepultadas | 1 |
| 2415 | sépase | 1 |
| 2416 | separa | 1 |
| 2417 | sepan | 1 |
| 2418 | seoto | 1 |
| 2419 | señorío | 1 |
| 2420 | señala | 1 |
| 2421 | señal | 1 |
| 2422 | seña | 1 |
| 2423 | sentirlas | 1 |
| 2424 | sentimientos | 1 |
| 2425 | sensitivo | 1 |
| 2426 | senos | 1 |
| 2427 | seno | 1 |
| 2428 | sencillo | 1 |
| 2429 | sencilla | 1 |
| 2430 | sembrar | 1 |
| 2431 | selvas | 1 |
| 2432 | selva | 1 |
| 2433 | sellaría | 1 |
| 2434 | segur | 1 |
| 2435 | seguir | 1 |
| 2436 | seguidme | 1 |
| 2437 | segadores | 1 |
| 2438 | sediciosos | 1 |
| 2439 | sedición | 1 |
| 2440 | seda | 1 |
| 2441 | secundan | 1 |
| 2442 | secretamente | 1 |
| 2443 | secreta | 1 |
| 2444 | seco | 1 |
| 2445 | secas | 1 |
| 2446 | seas | 1 |
| 2447 | sazonado | 1 |
| 2448 | sayón | 1 |
| 2449 | sayas | 1 |
| 2450 | saturno | 1 |
| 2451 | satisfecha | 1 |
| 2452 | satisfacer | 1 |
| 2453 | satírico | 1 |
| 2454 | sastre | 1 |
| 2455 | sarna | 1 |
| 2456 | sardinas | 1 |
| 2457 | saquearon | 1 |
| 2458 | saque | 1 |
| 2459 | sangriento | 1 |
| 2460 | sangrientas | 1 |
| 2461 | sangres | 1 |
| 2462 | salvaréis | 1 |
| 2463 | saludó | 1 |
| 2464 | saludaron | 1 |
| 2465 | saluda | 1 |
| 2466 | salteada | 1 |
| 2467 | salsa | 1 |
| 2468 | salmón | 1 |
| 2469 | salístele | 1 |
| 2470 | salió | 1 |
| 2471 | salime | 1 |
| 2472 | saliese | 1 |
| 2473 | salido | 1 |
| 2474 | salen | 1 |
| 2475 | salamandras | 1 |
| 2476 | salamandra | 1 |
| 2477 | salamanca | 1 |
| 2478 | salada | 1 |
| 2479 | sal | 1 |
| 2480 | sahagún | 1 |
| 2481 | sagrada | 1 |
| 2482 | sagaz | 1 |
| 2483 | sacudido | 1 |
| 2484 | sacrificios | 1 |
| 2485 | sacrificio | 1 |
| 2486 | sacramento | 1 |
| 2487 | saco | 1 |
| 2488 | sacarles | 1 |
| 2489 | saca | 1 |
| 2490 | sabroso | 1 |
| 2491 | sabrosas | 1 |
| 2492 | sabor | 1 |
| 2493 | sabio | 1 |
| 2494 | sabidor | 1 |
| 2495 | sabias | 1 |
| 2496 | sabia | 1 |
| 2497 | saben | 1 |
| 2498 | rústicos | 1 |
| 2499 | rumor | 1 |
| 2500 | rumia | 1 |
| 2501 | ruïdos | 1 |
| 2502 | ruegos | 1 |
| 2503 | ruedas | 1 |
| 2504 | rueda | 1 |
| 2505 | rudo | 1 |
| 2506 | rúbricas | 1 |
| 2507 | rubrica | 1 |
| 2508 | rubís | 1 |
| 2509 | rubias | 1 |
| 2510 | rubia | 1 |
| 2511 | roto | 1 |
| 2512 | roque | 1 |
| 2513 | ropa | 1 |
| 2514 | ronde | 1 |
| 2515 | ronda | 1 |
| 2516 | roncos | 1 |
| 2517 | roncha | 1 |
| 2518 | rompiera | 1 |
| 2519 | rompida | 1 |
| 2520 | romperse | 1 |
| 2521 | romper | 1 |
| 2522 | rompa | 1 |
| 2523 | rojos | 1 |
| 2524 | roja | 1 |
| 2525 | roída | 1 |
| 2526 | rogada | 1 |
| 2527 | rodelas | 1 |
| 2528 | rodéanle | 1 |
| 2529 | rodea | 1 |
| 2530 | rocas | 1 |
| 2531 | roca | 1 |
| 2532 | robles | 1 |
| 2533 | roballas | 1 |
| 2534 | robado | 1 |
| 2535 | rizos | 1 |
| 2536 | rizas | 1 |
| 2537 | rizado | 1 |
| 2538 | riscos | 1 |
| 2539 | risco | 1 |
| 2540 | risada | 1 |
| 2541 | rincón | 1 |
| 2542 | rin | 1 |
| 2543 | riguroso | 1 |
| 2544 | rigurosa | 1 |
| 2545 | rígido | 1 |
| 2546 | rígidas | 1 |
| 2547 | rige | 1 |
| 2548 | riéronse | 1 |
| 2549 | riendo | 1 |
| 2550 | riego | 1 |
| 2551 | riega | 1 |
| 2552 | ría | 1 |
| 2553 | revuelta | 1 |
| 2554 | revoca | 1 |
| 2555 | reviente | 1 |
| 2556 | reverberan | 1 |
| 2557 | retruécano | 1 |
| 2558 | retratada | 1 |
| 2559 | retraída | 1 |
| 2560 | retiro | 1 |
| 2561 | retirada | 1 |
| 2562 | retablo | 1 |
| 2563 | resucitola | 1 |
| 2564 | resucitó | 1 |
| 2565 | resucitado | 1 |
| 2566 | restituyes | 1 |
| 2567 | restituye | 1 |
| 2568 | restitúyanse | 1 |
| 2569 | restaurar | 1 |
| 2570 | restaurado | 1 |
| 2571 | resquicios | 1 |
| 2572 | respuestas | 1 |
| 2573 | respuesta | 1 |
| 2574 | respondió | 1 |
| 2575 | responder | 1 |
| 2576 | resplandor | 1 |
| 2577 | resplandecientes | 1 |
| 2578 | resplandece | 1 |
| 2579 | respiró | 1 |
| 2580 | respiras | 1 |
| 2581 | respetando | 1 |
| 2582 | respetaba | 1 |
| 2583 | respeta | 1 |
| 2584 | resonaron | 1 |
| 2585 | resistencias | 1 |
| 2586 | residencia | 1 |
| 2587 | rescate | 1 |
| 2588 | rescatar | 1 |
| 2589 | resbalar | 1 |
| 2590 | resbalando | 1 |
| 2591 | resabios | 1 |
| 2592 | requiebros | 1 |
| 2593 | requiebro | 1 |
| 2594 | requebrare | 1 |
| 2595 | reputación | 1 |
| 2596 | reputaban | 1 |
| 2597 | república | 1 |
| 2598 | represéntase | 1 |
| 2599 | reprensiones | 1 |
| 2600 | reprender | 1 |
| 2601 | repollo | 1 |
| 2602 | repitió | 1 |
| 2603 | repite | 1 |
| 2604 | repetir | 1 |
| 2605 | repetidas | 1 |
| 2606 | repetían | 1 |
| 2607 | repartido | 1 |
| 2608 | repartidas | 1 |
| 2609 | reparas | 1 |
| 2610 | reñido | 1 |
| 2611 | renunció | 1 |
| 2612 | renovado | 1 |
| 2613 | renglones | 1 |
| 2614 | rendido | 1 |
| 2615 | renacer | 1 |
| 2616 | remozar | 1 |
| 2617 | remontando | 1 |
| 2618 | remolino | 1 |
| 2619 | remite | 1 |
| 2620 | remiendo | 1 |
| 2621 | remedio | 1 |
| 2622 | remaba | 1 |
| 2623 | relumbrante | 1 |
| 2624 | religión | 1 |
| 2625 | relámpago | 1 |
| 2626 | rejones | 1 |
| 2627 | rejas | 1 |
| 2628 | rejalgar | 1 |
| 2629 | reír | 1 |
| 2630 | reinos | 1 |
| 2631 | reinó | 1 |
| 2632 | reinar | 1 |
| 2633 | reinaba | 1 |
| 2634 | rehusado | 1 |
| 2635 | regoldaba | 1 |
| 2636 | región | 1 |
| 2637 | regidas | 1 |
| 2638 | regalo | 1 |
| 2639 | regala | 1 |
| 2640 | reforzoles | 1 |
| 2641 | reduciéndole | 1 |
| 2642 | reducido | 1 |
| 2643 | redondillas | 1 |
| 2644 | rectos | 1 |
| 2645 | recostados | 1 |
| 2646 | recordada | 1 |
| 2647 | reconocimiento | 1 |
| 2648 | recocido | 1 |
| 2649 | recibirlo | 1 |
| 2650 | recibirle | 1 |
| 2651 | recibió | 1 |
| 2652 | recibille | 1 |
| 2653 | recibido | 1 |
| 2654 | recibes | 1 |
| 2655 | recíbeme | 1 |
| 2656 | recíbelo | 1 |
| 2657 | recelo | 1 |
| 2658 | recela | 1 |
| 2659 | recatos | 1 |
| 2660 | recato | 1 |
| 2661 | recataré | 1 |
| 2662 | recatado | 1 |
| 2663 | recatada | 1 |
| 2664 | recancanilla | 1 |
| 2665 | rebozo | 1 |
| 2666 | rebelde | 1 |
| 2667 | realzar | 1 |
| 2668 | razones | 1 |
| 2669 | razonan | 1 |
| 2670 | razonamientos | 1 |
| 2671 | razonamiento | 1 |
| 2672 | raudal | 1 |
| 2673 | rastillo | 1 |
| 2674 | raro | 1 |
| 2675 | rapiñas | 1 |
| 2676 | rapiña | 1 |
| 2677 | ranas | 1 |
| 2678 | rana | 1 |
| 2679 | ramplón | 1 |
| 2680 | ramos | 1 |
| 2681 | ramo | 1 |
| 2682 | ramillete | 1 |
| 2683 | rama | 1 |
| 2684 | raíz | 1 |
| 2685 | radïante | 1 |
| 2686 | rábano | 1 |
| 2687 | quitóseme | 1 |
| 2688 | quites | 1 |
| 2689 | quitas | 1 |
| 2690 | quitarme | 1 |
| 2691 | quitar | 1 |
| 2692 | quítame | 1 |
| 2693 | quisiese | 1 |
| 2694 | quisiere | 1 |
| 2695 | quisiera | 1 |
| 2696 | quince | 1 |
| 2697 | quietud | 1 |
| 2698 | quieras | 1 |
| 2699 | querrá | 1 |
| 2700 | quererte | 1 |
| 2701 | quereros | 1 |
| 2702 | querellas | 1 |
| 2703 | querella | 1 |
| 2704 | queredme | 1 |
| 2705 | quejado | 1 |
| 2706 | quedas | 1 |
| 2707 | quedaron | 1 |
| 2708 | quedarás | 1 |
| 2709 | quedar | 1 |
| 2710 | quedado | 1 |
| 2711 | queda | 1 |
| 2712 | quebrantan | 1 |
| 2713 | pusieron | 1 |
| 2714 | purpúrea | 1 |
| 2715 | puras | 1 |
| 2716 | puntiaguda | 1 |
| 2717 | punta | 1 |
| 2718 | pulpos | 1 |
| 2719 | pulgas | 1 |
| 2720 | pulga | 1 |
| 2721 | puja | 1 |
| 2722 | puerto | 1 |
| 2723 | puerco | 1 |
| 2724 | puédese | 1 |
| 2725 | pueda | 1 |
| 2726 | pueblos | 1 |
| 2727 | puebla | 1 |
| 2728 | pudieran | 1 |
| 2729 | pude | 1 |
| 2730 | publicando | 1 |
| 2731 | pruebo | 1 |
| 2732 | providencia | 1 |
| 2733 | proseguir | 1 |
| 2734 | propria | 1 |
| 2735 | proponga | 1 |
| 2736 | propios | 1 |
| 2737 | propicios | 1 |
| 2738 | pronunció | 1 |
| 2739 | pronostican | 1 |
| 2740 | pronostica | 1 |
| 2741 | prometerme | 1 |
| 2742 | promete | 1 |
| 2743 | prolongadas | 1 |
| 2744 | prolijidades | 1 |
| 2745 | profético | 1 |
| 2746 | profeta | 1 |
| 2747 | profeso | 1 |
| 2748 | produzca | 1 |
| 2749 | prodigios | 1 |
| 2750 | procurar | 1 |
| 2751 | proción | 1 |
| 2752 | procesos | 1 |
| 2753 | proceloso | 1 |
| 2754 | procede | 1 |
| 2755 | probar | 1 |
| 2756 | probado | 1 |
| 2757 | privó | 1 |
| 2758 | privar | 1 |
| 2759 | privado | 1 |
| 2760 | prisionero | 1 |
| 2761 | pringados | 1 |
| 2762 | pringadas | 1 |
| 2763 | príncipes | 1 |
| 2764 | princesa | 1 |
| 2765 | primogénita | 1 |
| 2766 | primeras | 1 |
| 2767 | prieto | 1 |
| 2768 | prevenir | 1 |
| 2769 | prevenido | 1 |
| 2770 | prevenida | 1 |
| 2771 | prevén | 1 |
| 2772 | pretensiones | 1 |
| 2773 | pretenmuela | 1 |
| 2774 | pretendiente | 1 |
| 2775 | pretendido | 1 |
| 2776 | pretenda | 1 |
| 2777 | presupuesto | 1 |
| 2778 | presumo | 1 |
| 2779 | presumiendo | 1 |
| 2780 | presumidas | 1 |
| 2781 | presuma | 1 |
| 2782 | prestarme | 1 |
| 2783 | prestar | 1 |
| 2784 | prestando | 1 |
| 2785 | prestadas | 1 |
| 2786 | presintiendo | 1 |
| 2787 | presencia | 1 |
| 2788 | prescribe | 1 |
| 2789 | preparen | 1 |
| 2790 | preñado | 1 |
| 2791 | prender | 1 |
| 2792 | prendas | 1 |
| 2793 | premios | 1 |
| 2794 | premió | 1 |
| 2795 | premiarte | 1 |
| 2796 | prefiero | 1 |
| 2797 | predicaré | 1 |
| 2798 | predicador | 1 |
| 2799 | precursor | 1 |
| 2800 | precipicios | 1 |
| 2801 | precias | 1 |
| 2802 | preciado | 1 |
| 2803 | preciada | 1 |
| 2804 | precia | 1 |
| 2805 | prados | 1 |
| 2806 | potente | 1 |
| 2807 | potencia | 1 |
| 2808 | postrera | 1 |
| 2809 | postre | 1 |
| 2810 | postigo | 1 |
| 2811 | posible | 1 |
| 2812 | poseo | 1 |
| 2813 | poseerte | 1 |
| 2814 | poseer | 1 |
| 2815 | posea | 1 |
| 2816 | portugal | 1 |
| 2817 | portento | 1 |
| 2818 | porfiando | 1 |
| 2819 | pordiosero | 1 |
| 2820 | popular | 1 |
| 2821 | popa | 1 |
| 2822 | ponzoña | 1 |
| 2823 | ponto | 1 |
| 2824 | pónganme | 1 |
| 2825 | poner | 1 |
| 2826 | pomposa | 1 |
| 2827 | pompa | 1 |
| 2828 | pomona | 1 |
| 2829 | polo | 1 |
| 2830 | poeta | 1 |
| 2831 | poemas | 1 |
| 2832 | poema | 1 |
| 2833 | podría | 1 |
| 2834 | podré | 1 |
| 2835 | podrás | 1 |
| 2836 | poderte | 1 |
| 2837 | poderosos | 1 |
| 2838 | pocos | 1 |
| 2839 | pobláronse | 1 |
| 2840 | poblaréis | 1 |
| 2841 | plumaje | 1 |
| 2842 | plectro | 1 |
| 2843 | plazas | 1 |
| 2844 | plaza | 1 |
| 2845 | platos | 1 |
| 2846 | platónica | 1 |
| 2847 | platón | 1 |
| 2848 | platicas | 1 |
| 2849 | platicantes | 1 |
| 2850 | platería | 1 |
| 2851 | planetas | 1 |
| 2852 | plaga | 1 |
| 2853 | placeres | 1 |
| 2854 | placer | 1 |
| 2855 | pitágoras | 1 |
| 2856 | pisó | 1 |
| 2857 | piso | 1 |
| 2858 | pisé | 1 |
| 2859 | pisar | 1 |
| 2860 | pisada | 1 |
| 2861 | piropos | 1 |
| 2862 | pirata | 1 |
| 2863 | piras | 1 |
| 2864 | piramidal | 1 |
| 2865 | pintora | 1 |
| 2866 | pintó | 1 |
| 2867 | pintando | 1 |
| 2868 | pincel | 1 |
| 2869 | pimientos | 1 |
| 2870 | piloto | 1 |
| 2871 | piezas | 1 |
| 2872 | pierdes | 1 |
| 2873 | pierden | 1 |
| 2874 | pierda | 1 |
| 2875 | piénsanse | 1 |
| 2876 | piensan | 1 |
| 2877 | pieles | 1 |
| 2878 | piel | 1 |
| 2879 | pidió | 1 |
| 2880 | pidiere | 1 |
| 2881 | pidiéndole | 1 |
| 2882 | pidiendo | 1 |
| 2883 | pides | 1 |
| 2884 | picos | 1 |
| 2885 | picar | 1 |
| 2886 | picantes | 1 |
| 2887 | picados | 1 |
| 2888 | pica | 1 |
| 2889 | piadosas | 1 |
| 2890 | pïadosa | 1 |
| 2891 | peto | 1 |
| 2892 | pestilencia | 1 |
| 2893 | peste | 1 |
| 2894 | pesco | 1 |
| 2895 | pescados | 1 |
| 2896 | pescada | 1 |
| 2897 | pesas | 1 |
| 2898 | persuadir | 1 |
| 2899 | persuadiéndola | 1 |
| 2900 | perseverad | 1 |
| 2901 | persevera | 1 |
| 2902 | perrengues | 1 |
| 2903 | perpetuamente | 1 |
| 2904 | permitía | 1 |
| 2905 | permites | 1 |
| 2906 | permanece | 1 |
| 2907 | perfumadas | 1 |
| 2908 | perfeta | 1 |
| 2909 | perfecto | 1 |
| 2910 | perfección | 1 |
| 2911 | perezosos | 1 |
| 2912 | perezoso | 1 |
| 2913 | perezosa | 1 |
| 2914 | pereza | 1 |
| 2915 | peregrinas | 1 |
| 2916 | peregrinando | 1 |
| 2917 | peregrinaciones | 1 |
| 2918 | perdone | 1 |
| 2919 | perdonaron | 1 |
| 2920 | perdona | 1 |
| 2921 | perdió | 1 |
| 2922 | perdiendo | 1 |
| 2923 | pérdida | 1 |
| 2924 | perder | 1 |
| 2925 | percibirse | 1 |
| 2926 | pequeña | 1 |
| 2927 | pepita | 1 |
| 2928 | pepino | 1 |
| 2929 | peonza | 1 |
| 2930 | penséis | 1 |
| 2931 | pensativa | 1 |
| 2932 | pensar | 1 |
| 2933 | penoso | 1 |
| 2934 | penitencias | 1 |
| 2935 | penitencia | 1 |
| 2936 | penando | 1 |
| 2937 | pelusas | 1 |
| 2938 | pelones | 1 |
| 2939 | peligroso | 1 |
| 2940 | peligro | 1 |
| 2941 | peligran | 1 |
| 2942 | pelayo | 1 |
| 2943 | pegan | 1 |
| 2944 | pegado | 1 |
| 2945 | pedradas | 1 |
| 2946 | pedidla | 1 |
| 2947 | pedí | 1 |
| 2948 | pedernal | 1 |
| 2949 | pedazos | 1 |
| 2950 | pechos | 1 |
| 2951 | pe | 1 |
| 2952 | pausa | 1 |
| 2953 | patrimonio | 1 |
| 2954 | patio | 1 |
| 2955 | pastora | 1 |
| 2956 | pastor | 1 |
| 2957 | pasó | 1 |
| 2958 | paseo | 1 |
| 2959 | pasas | 1 |
| 2960 | pasarás | 1 |
| 2961 | pasará | 1 |
| 2962 | pasadnos | 1 |
| 2963 | pasada | 1 |
| 2964 | partir | 1 |
| 2965 | partido | 1 |
| 2966 | partida | 1 |
| 2967 | parténope | 1 |
| 2968 | paro | 1 |
| 2969 | parlero | 1 |
| 2970 | parlera | 1 |
| 2971 | parlen | 1 |
| 2972 | pariome | 1 |
| 2973 | pariera | 1 |
| 2974 | pariente | 1 |
| 2975 | parezca | 1 |
| 2976 | pareciendo | 1 |
| 2977 | parecida | 1 |
| 2978 | parecía | 1 |
| 2979 | pareceres | 1 |
| 2980 | parecerán | 1 |
| 2981 | parece | 1 |
| 2982 | pardos | 1 |
| 2983 | parasismo | 1 |
| 2984 | parar | 1 |
| 2985 | parado | 1 |
| 2986 | par | 1 |
| 2987 | papel | 1 |
| 2988 | pápate | 1 |
| 2989 | pañales | 1 |
| 2990 | panzudo | 1 |
| 2991 | pantanos | 1 |
| 2992 | pancaya | 1 |
| 2993 | palustre | 1 |
| 2994 | palpe | 1 |
| 2995 | palos | 1 |
| 2996 | palor | 1 |
| 2997 | paloma | 1 |
| 2998 | palmas | 1 |
| 2999 | palinuro | 1 |
| 3000 | pálido | 1 |
| 3001 | paletilla | 1 |
| 3002 | palatino | 1 |
| 3003 | palabra | 1 |
| 3004 | paje | 1 |
| 3005 | pájaros | 1 |
| 3006 | paja | 1 |
| 3007 | pagase | 1 |
| 3008 | pagan | 1 |
| 3009 | padezca | 1 |
| 3010 | padecida | 1 |
| 3011 | padeces | 1 |
| 3012 | padecerás | 1 |
| 3013 | pacífico | 1 |
| 3014 | paces | 1 |
| 3015 | pacen | 1 |
| 3016 | pablillos | 1 |
| 3017 | pa | 1 |
| 3018 | oyere | 1 |
| 3019 | oyente | 1 |
| 3020 | oyen | 1 |
| 3021 | óyeme | 1 |
| 3022 | oye | 1 |
| 3023 | ovas | 1 |
| 3024 | ostentó | 1 |
| 3025 | ostentas | 1 |
| 3026 | ostentación | 1 |
| 3027 | osorio | 1 |
| 3028 | osé | 1 |
| 3029 | ose | 1 |
| 3030 | oscuros | 1 |
| 3031 | oscurecida | 1 |
| 3032 | oscuras | 1 |
| 3033 | osada | 1 |
| 3034 | oropel | 1 |
| 3035 | orión | 1 |
| 3036 | orillas | 1 |
| 3037 | originales | 1 |
| 3038 | origen | 1 |
| 3039 | orgullo | 1 |
| 3040 | organizando | 1 |
| 3041 | orfeos | 1 |
| 3042 | oreja | 1 |
| 3043 | ordene | 1 |
| 3044 | ordenas | 1 |
| 3045 | ordenad | 1 |
| 3046 | ordena | 1 |
| 3047 | oráis | 1 |
| 3048 | opuestas | 1 |
| 3049 | oprimido | 1 |
| 3050 | oprime | 1 |
| 3051 | opilación | 1 |
| 3052 | onzas | 1 |
| 3053 | onda | 1 |
| 3054 | omnipotencia | 1 |
| 3055 | olvide | 1 |
| 3056 | olvidaros | 1 |
| 3057 | olvidarle | 1 |
| 3058 | olvidares | 1 |
| 3059 | olvidado | 1 |
| 3060 | olvidadas | 1 |
| 3061 | oloroso | 1 |
| 3062 | olorosas | 1 |
| 3063 | olor | 1 |
| 3064 | olla | 1 |
| 3065 | olivares | 1 |
| 3066 | oliendo | 1 |
| 3067 | ojo | 1 |
| 3068 | ojalá | 1 |
| 3069 | oirás | 1 |
| 3070 | oír | 1 |
| 3071 | oídos | 1 |
| 3072 | oía | 1 |
| 3073 | oí | 1 |
| 3074 | ofrezca | 1 |
| 3075 | ofrecido | 1 |
| 3076 | ofreces | 1 |
| 3077 | ofensas | 1 |
| 3078 | ofensa | 1 |
| 3079 | ofenderos | 1 |
| 3080 | ofender | 1 |
| 3081 | ofendellas | 1 |
| 3082 | ofenda | 1 |
| 3083 | ocupa | 1 |
| 3084 | ocultarle | 1 |
| 3085 | ocioso | 1 |
| 3086 | ocio | 1 |
| 3087 | océano | 1 |
| 3088 | occidente | 1 |
| 3089 | ocasos | 1 |
| 3090 | ocasionas | 1 |
| 3091 | obstinación | 1 |
| 3092 | observante | 1 |
| 3093 | obra | 1 |
| 3094 | obligaros | 1 |
| 3095 | obligar | 1 |
| 3096 | obligación | 1 |
| 3097 | objeciones | 1 |
| 3098 | obedeces | 1 |
| 3099 | numerosa | 1 |
| 3100 | números | 1 |
| 3101 | nuez | 1 |
| 3102 | nuevos | 1 |
| 3103 | nubloso | 1 |
| 3104 | nublados | 1 |
| 3105 | noviembre | 1 |
| 3106 | notomía | 1 |
| 3107 | notifiques | 1 |
| 3108 | nota | 1 |
| 3109 | noruega | 1 |
| 3110 | nombro | 1 |
| 3111 | nombres | 1 |
| 3112 | nombrara | 1 |
| 3113 | nocturno | 1 |
| 3114 | nocturnas | 1 |
| 3115 | noches | 1 |
| 3116 | nobleza | 1 |
| 3117 | niños | 1 |
| 3118 | niño | 1 |
| 3119 | niñerías | 1 |
| 3120 | ninguna | 1 |
| 3121 | ningún | 1 |
| 3122 | ninfas | 1 |
| 3123 | ninfa | 1 |
| 3124 | nieto | 1 |
| 3125 | niego | 1 |
| 3126 | niégale | 1 |
| 3127 | niega | 1 |
| 3128 | nido | 1 |
| 3129 | nevado | 1 |
| 3130 | negociados | 1 |
| 3131 | negaste | 1 |
| 3132 | negáis | 1 |
| 3133 | necias | 1 |
| 3134 | necedad | 1 |
| 3135 | navegar | 1 |
| 3136 | nave | 1 |
| 3137 | natural | 1 |
| 3138 | nasón | 1 |
| 3139 | narizado | 1 |
| 3140 | naricísimo | 1 |
| 3141 | narices | 1 |
| 3142 | naranja | 1 |
| 3143 | nadará | 1 |
| 3144 | nadan | 1 |
| 3145 | nadador | 1 |
| 3146 | naciones | 1 |
| 3147 | nación | 1 |
| 3148 | naciese | 1 |
| 3149 | nacieron | 1 |
| 3150 | naciera | 1 |
| 3151 | naciendo | 1 |
| 3152 | nacida | 1 |
| 3153 | nacía | 1 |
| 3154 | naces | 1 |
| 3155 | nacer | 1 |
| 3156 | nabo | 1 |
| 3157 | muzas | 1 |
| 3158 | mustias | 1 |
| 3159 | músicas | 1 |
| 3160 | musas | 1 |
| 3161 | muros | 1 |
| 3162 | muro | 1 |
| 3163 | murmurando | 1 |
| 3164 | murmuran | 1 |
| 3165 | murieron | 1 |
| 3166 | muriendo | 1 |
| 3167 | múrice | 1 |
| 3168 | murciélagos | 1 |
| 3169 | murallas | 1 |
| 3170 | munición | 1 |
| 3171 | multiplique | 1 |
| 3172 | multiplicó | 1 |
| 3173 | multiplicas | 1 |
| 3174 | mula | 1 |
| 3175 | mueves | 1 |
| 3176 | muestran | 1 |
| 3177 | muertos | 1 |
| 3178 | muertes | 1 |
| 3179 | mueres | 1 |
| 3180 | mueren | 1 |
| 3181 | mueran | 1 |
| 3182 | mudarme | 1 |
| 3183 | mudando | 1 |
| 3184 | mudado | 1 |
| 3185 | muchísimo | 1 |
| 3186 | muchachuelos | 1 |
| 3187 | muchacha | 1 |
| 3188 | mucha | 1 |
| 3189 | mozo | 1 |
| 3190 | moverse | 1 |
| 3191 | motril | 1 |
| 3192 | mote | 1 |
| 3193 | motas | 1 |
| 3194 | mostraron | 1 |
| 3195 | mostrarme | 1 |
| 3196 | mostraba | 1 |
| 3197 | mosto | 1 |
| 3198 | mosquitos | 1 |
| 3199 | mosquito | 1 |
| 3200 | mosquetes | 1 |
| 3201 | mosquete | 1 |
| 3202 | moscos | 1 |
| 3203 | mosa | 1 |
| 3204 | morirse | 1 |
| 3205 | morirme | 1 |
| 3206 | moreno | 1 |
| 3207 | mordió | 1 |
| 3208 | morderle | 1 |
| 3209 | morder | 1 |
| 3210 | morcillas | 1 |
| 3211 | moralidad | 1 |
| 3212 | morado | 1 |
| 3213 | morada | 1 |
| 3214 | monumentos | 1 |
| 3215 | monstruo | 1 |
| 3216 | monjas | 1 |
| 3217 | mongibelo | 1 |
| 3218 | mondragón | 1 |
| 3219 | mondongo | 1 |
| 3220 | monda | 1 |
| 3221 | monarcas | 1 |
| 3222 | monarca | 1 |
| 3223 | molestan | 1 |
| 3224 | molesta | 1 |
| 3225 | molerlos | 1 |
| 3226 | mojarrilla | 1 |
| 3227 | mofen | 1 |
| 3228 | modestia | 1 |
| 3229 | mocedad | 1 |
| 3230 | mitigar | 1 |
| 3231 | mitad | 1 |
| 3232 | misterios | 1 |
| 3233 | misericordia | 1 |
| 3234 | miserias | 1 |
| 3235 | miseria | 1 |
| 3236 | miserable | 1 |
| 3237 | mísera | 1 |
| 3238 | misas | 1 |
| 3239 | miró | 1 |
| 3240 | mirlados | 1 |
| 3241 | miré | 1 |
| 3242 | mirasen | 1 |
| 3243 | mirares | 1 |
| 3244 | mirándoos | 1 |
| 3245 | mirando | 1 |
| 3246 | mirallos | 1 |
| 3247 | miraba | 1 |
| 3248 | mique | 1 |
| 3249 | mintió | 1 |
| 3250 | minero | 1 |
| 3251 | mimosas | 1 |
| 3252 | millares | 1 |
| 3253 | militando | 1 |
| 3254 | milagrosa | 1 |
| 3255 | milagros | 1 |
| 3256 | miembros | 1 |
| 3257 | mielgas | 1 |
| 3258 | miel | 1 |
| 3259 | mide | 1 |
| 3260 | mezquinos | 1 |
| 3261 | mesurado | 1 |
| 3262 | mesmos | 1 |
| 3263 | mesma | 1 |
| 3264 | mero | 1 |
| 3265 | merluzas | 1 |
| 3266 | meridiano | 1 |
| 3267 | merezco | 1 |
| 3268 | merézcate | 1 |
| 3269 | merecimiento | 1 |
| 3270 | mereciéndole | 1 |
| 3271 | merecidos | 1 |
| 3272 | merecido | 1 |
| 3273 | merecerte | 1 |
| 3274 | merecerlo | 1 |
| 3275 | merecer | 1 |
| 3276 | merecen | 1 |
| 3277 | merced | 1 |
| 3278 | menuda | 1 |
| 3279 | mentirosas | 1 |
| 3280 | mentirosa | 1 |
| 3281 | menea | 1 |
| 3282 | mendigando | 1 |
| 3283 | melón | 1 |
| 3284 | melodía | 1 |
| 3285 | melena | 1 |
| 3286 | melancólico | 1 |
| 3287 | mejorado | 1 |
| 3288 | medrosos | 1 |
| 3289 | medrosa | 1 |
| 3290 | medirlas | 1 |
| 3291 | medida | 1 |
| 3292 | medias | 1 |
| 3293 | media | 1 |
| 3294 | medallas | 1 |
| 3295 | mecha | 1 |
| 3296 | mayores | 1 |
| 3297 | mayo | 1 |
| 3298 | maullar | 1 |
| 3299 | matronas | 1 |
| 3300 | matrimonio | 1 |
| 3301 | mató | 1 |
| 3302 | matizar | 1 |
| 3303 | matiza | 1 |
| 3304 | materia | 1 |
| 3305 | matéis | 1 |
| 3306 | matarme | 1 |
| 3307 | matanza | 1 |
| 3308 | matando | 1 |
| 3309 | mataduras | 1 |
| 3310 | matada | 1 |
| 3311 | martos | 1 |
| 3312 | martín | 1 |
| 3313 | marta | 1 |
| 3314 | marlota | 1 |
| 3315 | marivinos | 1 |
| 3316 | mariposas | 1 |
| 3317 | márgenes | 1 |
| 3318 | margarita | 1 |
| 3319 | marcos | 1 |
| 3320 | marchitan | 1 |
| 3321 | marchando | 1 |
| 3322 | maravillas | 1 |
| 3323 | maravilla | 1 |
| 3324 | maravedís | 1 |
| 3325 | mantos | 1 |
| 3326 | mantilla | 1 |
| 3327 | mantiene | 1 |
| 3328 | mantenido | 1 |
| 3329 | manteles | 1 |
| 3330 | manjar | 1 |
| 3331 | mandome | 1 |
| 3332 | mande | 1 |
| 3333 | mandas | 1 |
| 3334 | mandarme | 1 |
| 3335 | mandallo | 1 |
| 3336 | mancillado | 1 |
| 3337 | mancilla | 1 |
| 3338 | manchado | 1 |
| 3339 | mancha | 1 |
| 3340 | mancebito | 1 |
| 3341 | malva | 1 |
| 3342 | maltrata | 1 |
| 3343 | malograrla | 1 |
| 3344 | malo | 1 |
| 3345 | malicias | 1 |
| 3346 | males | 1 |
| 3347 | maldice | 1 |
| 3348 | magra | 1 |
| 3349 | maestros | 1 |
| 3350 | madurando | 1 |
| 3351 | madura | 1 |
| 3352 | macilentos | 1 |
| 3353 | macilento | 1 |
| 3354 | macilenta | 1 |
| 3355 | luzbel | 1 |
| 3356 | lustre | 1 |
| 3357 | luquetes | 1 |
| 3358 | lumbres | 1 |
| 3359 | lujuria | 1 |
| 3360 | luisa | 1 |
| 3361 | lugares | 1 |
| 3362 | lucientes | 1 |
| 3363 | luciano | 1 |
| 3364 | luchando | 1 |
| 3365 | lúbricos | 1 |
| 3366 | lope | 1 |
| 3367 | lógrelas | 1 |
| 3368 | lógrala | 1 |
| 3369 | lograd | 1 |
| 3370 | lograba | 1 |
| 3371 | lodo | 1 |
| 3372 | loco | 1 |
| 3373 | locas | 1 |
| 3374 | loa | 1 |
| 3375 | lluvioso | 1 |
| 3376 | llueven | 1 |
| 3377 | lloroso | 1 |
| 3378 | llore | 1 |
| 3379 | lloras | 1 |
| 3380 | lloraron | 1 |
| 3381 | llevó | 1 |
| 3382 | llevo | 1 |
| 3383 | llévenme | 1 |
| 3384 | llevéis | 1 |
| 3385 | llévate | 1 |
| 3386 | llevaste | 1 |
| 3387 | llevarse | 1 |
| 3388 | llevaré | 1 |
| 3389 | llevarás | 1 |
| 3390 | llevar | 1 |
| 3391 | llevando | 1 |
| 3392 | llevada | 1 |
| 3393 | llenas | 1 |
| 3394 | llegue | 1 |
| 3395 | llego | 1 |
| 3396 | llegases | 1 |
| 3397 | llegase | 1 |
| 3398 | llegaron | 1 |
| 3399 | llegar | 1 |
| 3400 | llegan | 1 |
| 3401 | llantos | 1 |
| 3402 | llamo | 1 |
| 3403 | llámente | 1 |
| 3404 | llamé | 1 |
| 3405 | llámate | 1 |
| 3406 | llamaste | 1 |
| 3407 | llamáronme | 1 |
| 3408 | llamará | 1 |
| 3409 | llámanle | 1 |
| 3410 | llamado | 1 |
| 3411 | llamaba | 1 |
| 3412 | llagas | 1 |
| 3413 | litera | 1 |
| 3414 | lino | 1 |
| 3415 | líneas | 1 |
| 3416 | línea | 1 |
| 3417 | linda | 1 |
| 3418 | limpia | 1 |
| 3419 | limón | 1 |
| 3420 | límites | 1 |
| 3421 | limitados | 1 |
| 3422 | limbo | 1 |
| 3423 | limado | 1 |
| 3424 | limadas | 1 |
| 3425 | lima | 1 |
| 3426 | ligustre | 1 |
| 3427 | liguria | 1 |
| 3428 | ligas | 1 |
| 3429 | lienzo | 1 |
| 3430 | liendres | 1 |
| 3431 | lidora | 1 |
| 3432 | lid | 1 |
| 3433 | licor | 1 |
| 3434 | lico | 1 |
| 3435 | licenciosa | 1 |
| 3436 | libros | 1 |
| 3437 | libró | 1 |
| 3438 | libremente | 1 |
| 3439 | levantó | 1 |
| 3440 | levante | 1 |
| 3441 | levantar | 1 |
| 3442 | letrillas | 1 |
| 3443 | letrado | 1 |
| 3444 | lete | 1 |
| 3445 | lesna | 1 |
| 3446 | lento | 1 |
| 3447 | lenguas | 1 |
| 3448 | legítimos | 1 |
| 3449 | legión | 1 |
| 3450 | lector | 1 |
| 3451 | lechuga | 1 |
| 3452 | lazo | 1 |
| 3453 | laváronse | 1 |
| 3454 | lava | 1 |
| 3455 | laureles | 1 |
| 3456 | latinosa | 1 |
| 3457 | latino | 1 |
| 3458 | larvas | 1 |
| 3459 | largas | 1 |
| 3460 | lanzada | 1 |
| 3461 | langosta | 1 |
| 3462 | lance | 1 |
| 3463 | lana | 1 |
| 3464 | lampreas | 1 |
| 3465 | lamentos | 1 |
| 3466 | lamento | 1 |
| 3467 | lamentación | 1 |
| 3468 | lágrima | 1 |
| 3469 | ladridos | 1 |
| 3470 | ladrido | 1 |
| 3471 | ladrando | 1 |
| 3472 | laderas | 1 |
| 3473 | lacayos | 1 |
| 3474 | labradores | 1 |
| 3475 | labrada | 1 |
| 3476 | labra | 1 |
| 3477 | labores | 1 |
| 3478 | labor | 1 |
| 3479 | juzgarán | 1 |
| 3480 | justas | 1 |
| 3481 | justamente | 1 |
| 3482 | jure | 1 |
| 3483 | juraste | 1 |
| 3484 | júpiter | 1 |
| 3485 | juntara | 1 |
| 3486 | juntados | 1 |
| 3487 | juncos | 1 |
| 3488 | juglar | 1 |
| 3489 | jugar | 1 |
| 3490 | juegos | 1 |
| 3491 | juega | 1 |
| 3492 | jueces | 1 |
| 3493 | judea | 1 |
| 3494 | jubón | 1 |
| 3495 | joven | 1 |
| 3496 | josef | 1 |
| 3497 | jornalero | 1 |
| 3498 | jornal | 1 |
| 3499 | jetas | 1 |
| 3500 | jerez | 1 |
| 3501 | jaspes | 1 |
| 3502 | jardineros | 1 |
| 3503 | jarama | 1 |
| 3504 | jara | 1 |
| 3505 | jaque | 1 |
| 3506 | jácaras | 1 |
| 3507 | jácara | 1 |
| 3508 | iv | 1 |
| 3509 | italia | 1 |
| 3510 | irracionales | 1 |
| 3511 | iris | 1 |
| 3512 | iré | 1 |
| 3513 | iras | 1 |
| 3514 | invoca | 1 |
| 3515 | invisible | 1 |
| 3516 | invidioso | 1 |
| 3517 | invidiosas | 1 |
| 3518 | invidiosa | 1 |
| 3519 | invidias | 1 |
| 3520 | invidiada | 1 |
| 3521 | inventaran | 1 |
| 3522 | inundación | 1 |
| 3523 | inunda | 1 |
| 3524 | introduciendo | 1 |
| 3525 | interesada | 1 |
| 3526 | intercediendo | 1 |
| 3527 | intercadencia | 1 |
| 3528 | intentara | 1 |
| 3529 | intención | 1 |
| 3530 | inteligible | 1 |
| 3531 | intelectual | 1 |
| 3532 | insultos | 1 |
| 3533 | insolente | 1 |
| 3534 | inscripción | 1 |
| 3535 | insano | 1 |
| 3536 | insana | 1 |
| 3537 | inquiriendo | 1 |
| 3538 | inquietud | 1 |
| 3539 | inquietos | 1 |
| 3540 | inquieta | 1 |
| 3541 | inocente | 1 |
| 3542 | inmortales | 1 |
| 3543 | inmortal | 1 |
| 3544 | inmenso | 1 |
| 3545 | inmensidad | 1 |
| 3546 | inmensas | 1 |
| 3547 | injustas | 1 |
| 3548 | injurias | 1 |
| 3549 | injuriar | 1 |
| 3550 | injuria | 1 |
| 3551 | inhibitoria | 1 |
| 3552 | ingratas | 1 |
| 3553 | ingrata | 1 |
| 3554 | ingenio | 1 |
| 3555 | información | 1 |
| 3556 | influyendo | 1 |
| 3557 | influye | 1 |
| 3558 | inflama | 1 |
| 3559 | infinito | 1 |
| 3560 | infinita | 1 |
| 3561 | infiel | 1 |
| 3562 | inexorable | 1 |
| 3563 | industriosa | 1 |
| 3564 | indultos | 1 |
| 3565 | indignada | 1 |
| 3566 | indicios | 1 |
| 3567 | indicio | 1 |
| 3568 | inclinó | 1 |
| 3569 | incline | 1 |
| 3570 | inclinar | 1 |
| 3571 | inclinado | 1 |
| 3572 | inclemente | 1 |
| 3573 | incierto | 1 |
| 3574 | imprenta | 1 |
| 3575 | imposible | 1 |
| 3576 | importunan | 1 |
| 3577 | importar | 1 |
| 3578 | importantes | 1 |
| 3579 | implicación | 1 |
| 3580 | impida | 1 |
| 3581 | impensada | 1 |
| 3582 | impedida | 1 |
| 3583 | imiten | 1 |
| 3584 | imitarán | 1 |
| 3585 | imagina | 1 |
| 3586 | ilusión | 1 |
| 3587 | illana | 1 |
| 3588 | iii | 1 |
| 3589 | igualmente | 1 |
| 3590 | iguales | 1 |
| 3591 | igualase | 1 |
| 3592 | igualas | 1 |
| 3593 | ignoras | 1 |
| 3594 | ignorantes | 1 |
| 3595 | iglesia | 1 |
| 3596 | idolatre | 1 |
| 3597 | idolatrando | 1 |
| 3598 | idólatra | 1 |
| 3599 | ícaro | 1 |
| 3600 | iban | 1 |
| 3601 | iba | 1 |
| 3602 | huyó | 1 |
| 3603 | huyes | 1 |
| 3604 | huyeron | 1 |
| 3605 | huyen | 1 |
| 3606 | hurtó | 1 |
| 3607 | hurte | 1 |
| 3608 | hurtar | 1 |
| 3609 | hurtando | 1 |
| 3610 | hungría | 1 |
| 3611 | hundíase | 1 |
| 3612 | humosa | 1 |
| 3613 | humores | 1 |
| 3614 | humillo | 1 |
| 3615 | humildes | 1 |
| 3616 | humildemente | 1 |
| 3617 | humedezco | 1 |
| 3618 | humedecida | 1 |
| 3619 | humanidad | 1 |
| 3620 | huido | 1 |
| 3621 | huevo | 1 |
| 3622 | huestes | 1 |
| 3623 | hueste | 1 |
| 3624 | huésped | 1 |
| 3625 | huesos | 1 |
| 3626 | huerto | 1 |
| 3627 | huérfano | 1 |
| 3628 | hubieran | 1 |
| 3629 | hospedaron | 1 |
| 3630 | hospeda | 1 |
| 3631 | hosanna | 1 |
| 3632 | horrores | 1 |
| 3633 | horrendo | 1 |
| 3634 | horrenda | 1 |
| 3635 | horca | 1 |
| 3636 | honrosos | 1 |
| 3637 | honrosa | 1 |
| 3638 | honrados | 1 |
| 3639 | honradas | 1 |
| 3640 | honrada | 1 |
| 3641 | honores | 1 |
| 3642 | honestidad | 1 |
| 3643 | honesta | 1 |
| 3644 | hondos | 1 |
| 3645 | homero | 1 |
| 3646 | hollín | 1 |
| 3647 | hollé | 1 |
| 3648 | holandés | 1 |
| 3649 | holanda | 1 |
| 3650 | hoja | 1 |
| 3651 | hoguera | 1 |
| 3652 | historias | 1 |
| 3653 | hiriendo | 1 |
| 3654 | hipócritas | 1 |
| 3655 | hinchados | 1 |
| 3656 | hinchado | 1 |
| 3657 | hincársele | 1 |
| 3658 | himnos | 1 |
| 3659 | himno | 1 |
| 3660 | hile | 1 |
| 3661 | hilaba | 1 |
| 3662 | hijuelos | 1 |
| 3663 | hijas | 1 |
| 3664 | hijadas | 1 |
| 3665 | hija | 1 |
| 3666 | hierros | 1 |
| 3667 | hiere | 1 |
| 3668 | hierba | 1 |
| 3669 | hielos | 1 |
| 3670 | hiel | 1 |
| 3671 | hibla | 1 |
| 3672 | herreros | 1 |
| 3673 | herradores | 1 |
| 3674 | heroico | 1 |
| 3675 | hermosuras | 1 |
| 3676 | hermosos | 1 |
| 3677 | hermosísima | 1 |
| 3678 | hermosas | 1 |
| 3679 | herirme | 1 |
| 3680 | herencias | 1 |
| 3681 | herejes | 1 |
| 3682 | heredero | 1 |
| 3683 | heredada | 1 |
| 3684 | heredad | 1 |
| 3685 | helarle | 1 |
| 3686 | helada | 1 |
| 3687 | hechas | 1 |
| 3688 | hebras | 1 |
| 3689 | hebra | 1 |
| 3690 | hazaña | 1 |
| 3691 | haz | 1 |
| 3692 | hayas | 1 |
| 3693 | hayan | 1 |
| 3694 | hartura | 1 |
| 3695 | hartos | 1 |
| 3696 | hartaba | 1 |
| 3697 | haremos | 1 |
| 3698 | hará | 1 |
| 3699 | hambrienta | 1 |
| 3700 | hallo | 1 |
| 3701 | hálleme | 1 |
| 3702 | hallé | 1 |
| 3703 | halle | 1 |
| 3704 | hállate | 1 |
| 3705 | hallas | 1 |
| 3706 | hallarte | 1 |
| 3707 | hallarle | 1 |
| 3708 | hallaré | 1 |
| 3709 | halláramos | 1 |
| 3710 | halago | 1 |
| 3711 | hado | 1 |
| 3712 | hacia | 1 |
| 3713 | hacerte | 1 |
| 3714 | haced | 1 |
| 3715 | habrás | 1 |
| 3716 | habrán | 1 |
| 3717 | hablo | 1 |
| 3718 | hablen | 1 |
| 3719 | hablemos | 1 |
| 3720 | habláis | 1 |
| 3721 | hablado | 1 |
| 3722 | hablada | 1 |
| 3723 | habla | 1 |
| 3724 | hábito | 1 |
| 3725 | habitadas | 1 |
| 3726 | habiéndola | 1 |
| 3727 | habiendo | 1 |
| 3728 | haberse | 1 |
| 3729 | haberlo | 1 |
| 3730 | haberle | 1 |
| 3731 | habéis | 1 |
| 3732 | habas | 1 |
| 3733 | guzmanes | 1 |
| 3734 | guzmán | 1 |
| 3735 | gustoso | 1 |
| 3736 | gustos | 1 |
| 3737 | guirnalda | 1 |
| 3738 | guineo | 1 |
| 3739 | guinda | 1 |
| 3740 | guerrero | 1 |
| 3741 | guareció | 1 |
| 3742 | guárdese | 1 |
| 3743 | guarde | 1 |
| 3744 | guardasol | 1 |
| 3745 | guardas | 1 |
| 3746 | guardaría | 1 |
| 3747 | guardándole | 1 |
| 3748 | guardáis | 1 |
| 3749 | guardado | 1 |
| 3750 | guadañas | 1 |
| 3751 | grosero | 1 |
| 3752 | grosera | 1 |
| 3753 | grito | 1 |
| 3754 | grillos | 1 |
| 3755 | greña | 1 |
| 3756 | grecizante | 1 |
| 3757 | graves | 1 |
| 3758 | gravedad | 1 |
| 3759 | grave | 1 |
| 3760 | granjear | 1 |
| 3761 | granizado | 1 |
| 3762 | granada | 1 |
| 3763 | grana | 1 |
| 3764 | graduó | 1 |
| 3765 | grados | 1 |
| 3766 | gradas | 1 |
| 3767 | grabadas | 1 |
| 3768 | gozoso | 1 |
| 3769 | gozos | 1 |
| 3770 | gózante | 1 |
| 3771 | gozan | 1 |
| 3772 | gozaba | 1 |
| 3773 | gorrón | 1 |
| 3774 | gorja | 1 |
| 3775 | gordiviejas | 1 |
| 3776 | gonces | 1 |
| 3777 | golpes | 1 |
| 3778 | golondrina | 1 |
| 3779 | godos | 1 |
| 3780 | godo | 1 |
| 3781 | gocéis | 1 |
| 3782 | gobierna | 1 |
| 3783 | glotón | 1 |
| 3784 | glosado | 1 |
| 3785 | glorïoso | 1 |
| 3786 | gloriosas | 1 |
| 3787 | gloriosamente | 1 |
| 3788 | gloriosa | 1 |
| 3789 | glorias | 1 |
| 3790 | gimieron | 1 |
| 3791 | gimes | 1 |
| 3792 | gigante | 1 |
| 3793 | geometría | 1 |
| 3794 | génova | 1 |
| 3795 | generosas | 1 |
| 3796 | género | 1 |
| 3797 | gasté | 1 |
| 3798 | gaste | 1 |
| 3799 | gastáramos | 1 |
| 3800 | gastan | 1 |
| 3801 | gaspar | 1 |
| 3802 | garzota | 1 |
| 3803 | garras | 1 |
| 3804 | gargantas | 1 |
| 3805 | ganguea | 1 |
| 3806 | ganapán | 1 |
| 3807 | ganado | 1 |
| 3808 | ganadero | 1 |
| 3809 | gallo | 1 |
| 3810 | galeras | 1 |
| 3811 | galera | 1 |
| 3812 | galardón | 1 |
| 3813 | futuro | 1 |
| 3814 | furor | 1 |
| 3815 | furiosa | 1 |
| 3816 | funesta | 1 |
| 3817 | fundo | 1 |
| 3818 | fundido | 1 |
| 3819 | fundas | 1 |
| 3820 | fulminaron | 1 |
| 3821 | fulminante | 1 |
| 3822 | fulminando | 1 |
| 3823 | fulminan | 1 |
| 3824 | fulmina | 1 |
| 3825 | fuiste | 1 |
| 3826 | fui | 1 |
| 3827 | fuga | 1 |
| 3828 | fueses | 1 |
| 3829 | fuero | 1 |
| 3830 | fueres | 1 |
| 3831 | fuereis | 1 |
| 3832 | fuere | 1 |
| 3833 | fueras | 1 |
| 3834 | fuéramos | 1 |
| 3835 | frías | 1 |
| 3836 | fresno | 1 |
| 3837 | frescona | 1 |
| 3838 | frenética | 1 |
| 3839 | francisca | 1 |
| 3840 | fraile | 1 |
| 3841 | fragmentos | 1 |
| 3842 | fragilidad | 1 |
| 3843 | fragante | 1 |
| 3844 | forzosa | 1 |
| 3845 | fortalezas | 1 |
| 3846 | formidables | 1 |
| 3847 | formaran | 1 |
| 3848 | formar | 1 |
| 3849 | forjó | 1 |
| 3850 | forastero | 1 |
| 3851 | forastera | 1 |
| 3852 | fondos | 1 |
| 3853 | fluctuando | 1 |
| 3854 | floro | 1 |
| 3855 | flori | 1 |
| 3856 | florecilla | 1 |
| 3857 | florecidas | 1 |
| 3858 | flecha | 1 |
| 3859 | flaquezas | 1 |
| 3860 | flaco | 1 |
| 3861 | flacas | 1 |
| 3862 | firmada | 1 |
| 3863 | fío | 1 |
| 3864 | finos | 1 |
| 3865 | fingiendo | 1 |
| 3866 | fingida | 1 |
| 3867 | finge | 1 |
| 3868 | fineza | 1 |
| 3869 | finas | 1 |
| 3870 | fina | 1 |
| 3871 | filósofos | 1 |
| 3872 | filosofía | 1 |
| 3873 | filos | 1 |
| 3874 | fijas | 1 |
| 3875 | fijada | 1 |
| 3876 | figura | 1 |
| 3877 | fíes | 1 |
| 3878 | fiereza | 1 |
| 3879 | fieras | 1 |
| 3880 | fieltro | 1 |
| 3881 | fieles | 1 |
| 3882 | fiel | 1 |
| 3883 | fidalgos | 1 |
| 3884 | fía | 1 |
| 3885 | fez | 1 |
| 3886 | festivo | 1 |
| 3887 | feroz | 1 |
| 3888 | fembras | 1 |
| 3889 | feliz | 1 |
| 3890 | felicidades | 1 |
| 3891 | fecundo | 1 |
| 3892 | fecunda | 1 |
| 3893 | fatal | 1 |
| 3894 | farsante | 1 |
| 3895 | fantásticas | 1 |
| 3896 | fantasmas | 1 |
| 3897 | fanfarrones | 1 |
| 3898 | fanfarria | 1 |
| 3899 | faltas | 1 |
| 3900 | faltar | 1 |
| 3901 | fáltanme | 1 |
| 3902 | faltan | 1 |
| 3903 | falsete | 1 |
| 3904 | fallecida | 1 |
| 3905 | falda | 1 |
| 3906 | fajina | 1 |
| 3907 | facinorosas | 1 |
| 3908 | fácil | 1 |
| 3909 | facción | 1 |
| 3910 | fabricaste | 1 |
| 3911 | fabricando | 1 |
| 3912 | fabrican | 1 |
| 3913 | fabricado | 1 |
| 3914 | fabios | 1 |
| 3915 | extraños | 1 |
| 3916 | extrañas | 1 |
| 3917 | exterior | 1 |
| 3918 | extendida | 1 |
| 3919 | éxtasi | 1 |
| 3920 | explayose | 1 |
| 3921 | explayábase | 1 |
| 3922 | expiraba | 1 |
| 3923 | expira | 1 |
| 3924 | exhorta | 1 |
| 3925 | exhalando | 1 |
| 3926 | exhalación | 1 |
| 3927 | exentos | 1 |
| 3928 | exenta | 1 |
| 3929 | exclama | 1 |
| 3930 | exceso | 1 |
| 3931 | excelso | 1 |
| 3932 | excelentísimo | 1 |
| 3933 | excede | 1 |
| 3934 | exceda | 1 |
| 3935 | examinando | 1 |
| 3936 | examen | 1 |
| 3937 | exagere | 1 |
| 3938 | exageraciones | 1 |
| 3939 | exageración | 1 |
| 3940 | evasión | 1 |
| 3941 | eternas | 1 |
| 3942 | estuve | 1 |
| 3943 | estudioso | 1 |
| 3944 | estudio | 1 |
| 3945 | estudien | 1 |
| 3946 | estudiaron | 1 |
| 3947 | estudiara | 1 |
| 3948 | estudiante | 1 |
| 3949 | estudia | 1 |
| 3950 | estuche | 1 |
| 3951 | estrujada | 1 |
| 3952 | estrenad | 1 |
| 3953 | estremeció | 1 |
| 3954 | estrellado | 1 |
| 3955 | estrecho | 1 |
| 3956 | estrechas | 1 |
| 3957 | estrechamente | 1 |
| 3958 | estraza | 1 |
| 3959 | estraga | 1 |
| 3960 | estrado | 1 |
| 3961 | estotro | 1 |
| 3962 | estornudos | 1 |
| 3963 | estornudaba | 1 |
| 3964 | estornuda | 1 |
| 3965 | estorbo | 1 |
| 3966 | estimalde | 1 |
| 3967 | estima | 1 |
| 3968 | estilos | 1 |
| 3969 | estériles | 1 |
| 3970 | estén | 1 |
| 3971 | estéis | 1 |
| 3972 | estatua | 1 |
| 3973 | estaré | 1 |
| 3974 | estame | 1 |
| 3975 | estáis | 1 |
| 3976 | estacada | 1 |
| 3977 | estables | 1 |
| 3978 | esquivos | 1 |
| 3979 | esquivas | 1 |
| 3980 | esquiva | 1 |
| 3981 | esqueleto | 1 |
| 3982 | espumosos | 1 |
| 3983 | espumoso | 1 |
| 3984 | esposa | 1 |
| 3985 | esponja | 1 |
| 3986 | espolón | 1 |
| 3987 | esplendores | 1 |
| 3988 | espina | 1 |
| 3989 | espigas | 1 |
| 3990 | espías | 1 |
| 3991 | espiada | 1 |
| 3992 | espía | 1 |
| 3993 | espeso | 1 |
| 3994 | espere | 1 |
| 3995 | esperan | 1 |
| 3996 | espejo | 1 |
| 3997 | esparto | 1 |
| 3998 | españolas | 1 |
| 3999 | española | 1 |
| 4000 | españas | 1 |
| 4001 | espantoso | 1 |
| 4002 | espanto | 1 |
| 4003 | espantéis | 1 |
| 4004 | espadaña | 1 |
| 4005 | espacio | 1 |
| 4006 | esos | 1 |
| 4007 | esmeril | 1 |
| 4008 | esmeralda | 1 |
| 4009 | esmaltada | 1 |
| 4010 | esforzaban | 1 |
| 4011 | esfera | 1 |
| 4012 | escuro | 1 |
| 4013 | escuras | 1 |
| 4014 | escupido | 1 |
| 4015 | escudo | 1 |
| 4016 | escucho | 1 |
| 4017 | escuche | 1 |
| 4018 | escuchad | 1 |
| 4019 | escucha | 1 |
| 4020 | escuadrones | 1 |
| 4021 | escritor | 1 |
| 4022 | escrito | 1 |
| 4023 | escrita | 1 |
| 4024 | escribiré | 1 |
| 4025 | escribir | 1 |
| 4026 | escribiendo | 1 |
| 4027 | escríbase | 1 |
| 4028 | escribano | 1 |
| 4029 | escriba | 1 |
| 4030 | escorpión | 1 |
| 4031 | escorias | 1 |
| 4032 | escondieron | 1 |
| 4033 | escondidas | 1 |
| 4034 | escondida | 1 |
| 4035 | escondían | 1 |
| 4036 | esconderla | 1 |
| 4037 | esconda | 1 |
| 4038 | esclavitud | 1 |
| 4039 | esclarecido | 1 |
| 4040 | esclarecidas | 1 |
| 4041 | esclarecida | 1 |
| 4042 | escasamente | 1 |
| 4043 | escarmientos | 1 |
| 4044 | escapó | 1 |
| 4045 | escándalo | 1 |
| 4046 | escandalizan | 1 |
| 4047 | escandalice | 1 |
| 4048 | escamas | 1 |
| 4049 | escalas | 1 |
| 4050 | eruditos | 1 |
| 4051 | error | 1 |
| 4052 | errante | 1 |
| 4053 | errada | 1 |
| 4054 | erizo | 1 |
| 4055 | erizado | 1 |
| 4056 | equívocos | 1 |
| 4057 | equivocado | 1 |
| 4058 | equivoca | 1 |
| 4059 | epíteto | 1 |
| 4060 | epístolas | 1 |
| 4061 | epístola | 1 |
| 4062 | enzarza | 1 |
| 4063 | envuelto | 1 |
| 4064 | envío | 1 |
| 4065 | envidioso | 1 |
| 4066 | envidiosas | 1 |
| 4067 | envidien | 1 |
| 4068 | envidiados | 1 |
| 4069 | envejecer | 1 |
| 4070 | entró | 1 |
| 4071 | entretenme | 1 |
| 4072 | entretenidos | 1 |
| 4073 | entretener | 1 |
| 4074 | entresuelos | 1 |
| 4075 | entregué | 1 |
| 4076 | entregó | 1 |
| 4077 | entré | 1 |
| 4078 | entrare | 1 |
| 4079 | entrar | 1 |
| 4080 | entrando | 1 |
| 4081 | entráis | 1 |
| 4082 | entrada | 1 |
| 4083 | entierro | 1 |
| 4084 | entiendo | 1 |
| 4085 | entiendas | 1 |
| 4086 | enterrado | 1 |
| 4087 | enternecieron | 1 |
| 4088 | entera | 1 |
| 4089 | entendí | 1 |
| 4090 | entender | 1 |
| 4091 | entena | 1 |
| 4092 | entablo | 1 |
| 4093 | ensuciar | 1 |
| 4094 | ensordezca | 1 |
| 4095 | ensordeces | 1 |
| 4096 | ensangrientan | 1 |
| 4097 | ensangrentado | 1 |
| 4098 | ensalzar | 1 |
| 4099 | ensaladas | 1 |
| 4100 | ensalada | 1 |
| 4101 | enriquezco | 1 |
| 4102 | enriquecelde | 1 |
| 4103 | enredos | 1 |
| 4104 | enojo | 1 |
| 4105 | enojadas | 1 |
| 4106 | ennobleciste | 1 |
| 4107 | ennoblecido | 1 |
| 4108 | ennoblecerte | 1 |
| 4109 | ennegrecida | 1 |
| 4110 | enmudeció | 1 |
| 4111 | enmudecido | 1 |
| 4112 | enmiendan | 1 |
| 4113 | enmendastes | 1 |
| 4114 | enmendar | 1 |
| 4115 | enlutaron | 1 |
| 4116 | enjuta | 1 |
| 4117 | enhiesto | 1 |
| 4118 | engordar | 1 |
| 4119 | engendre | 1 |
| 4120 | engendrar | 1 |
| 4121 | engendrado | 1 |
| 4122 | engañoso | 1 |
| 4123 | engañosas | 1 |
| 4124 | engañe | 1 |
| 4125 | engañas | 1 |
| 4126 | engañada | 1 |
| 4127 | engaña | 1 |
| 4128 | enfurece | 1 |
| 4129 | enfado | 1 |
| 4130 | enemistad | 1 |
| 4131 | endureció | 1 |
| 4132 | encuentros | 1 |
| 4133 | encuentre | 1 |
| 4134 | encuéntrate | 1 |
| 4135 | encubrirnos | 1 |
| 4136 | encomienda | 1 |
| 4137 | encogido | 1 |
| 4138 | encina | 1 |
| 4139 | encerrar | 1 |
| 4140 | encerramiento | 1 |
| 4141 | encendieron | 1 |
| 4142 | encendidos | 1 |
| 4143 | encelado | 1 |
| 4144 | encargó | 1 |
| 4145 | encarece | 1 |
| 4146 | encarcelada | 1 |
| 4147 | encarado | 1 |
| 4148 | encaneces | 1 |
| 4149 | encaminado | 1 |
| 4150 | encajo | 1 |
| 4151 | encaje | 1 |
| 4152 | encájate | 1 |
| 4153 | encadena | 1 |
| 4154 | enamoran | 1 |
| 4155 | enamorada | 1 |
| 4156 | enamora | 1 |
| 4157 | enajena | 1 |
| 4158 | empréndenlos | 1 |
| 4159 | empobreces | 1 |
| 4160 | empleado | 1 |
| 4161 | empiézola | 1 |
| 4162 | empezará | 1 |
| 4163 | empezar | 1 |
| 4164 | empero | 1 |
| 4165 | empecé | 1 |
| 4166 | eminentes | 1 |
| 4167 | embudo | 1 |
| 4168 | embelequen | 1 |
| 4169 | embeleco | 1 |
| 4170 | embates | 1 |
| 4171 | embarazan | 1 |
| 4172 | embaraza | 1 |
| 4173 | embajadora | 1 |
| 4174 | elocuentes | 1 |
| 4175 | ello | 1 |
| 4176 | elemento | 1 |
| 4177 | elegantes | 1 |
| 4178 | elefante | 1 |
| 4179 | ejércitos | 1 |
| 4180 | ejercite | 1 |
| 4181 | ejercitar | 1 |
| 4182 | ejemplos | 1 |
| 4183 | ejecutivo | 1 |
| 4184 | ejecutar | 1 |
| 4185 | ejecuta | 1 |
| 4186 | ejecución | 1 |
| 4187 | efecto | 1 |
| 4188 | eco | 1 |
| 4189 | echolos | 1 |
| 4190 | echó | 1 |
| 4191 | échese | 1 |
| 4192 | echarla | 1 |
| 4193 | echaba | 1 |
| 4194 | echa | 1 |
| 4195 | ébano | 1 |
| 4196 | duró | 1 |
| 4197 | durmiese | 1 |
| 4198 | durmiendo | 1 |
| 4199 | durazno | 1 |
| 4200 | duración | 1 |
| 4201 | duermo | 1 |
| 4202 | duermen | 1 |
| 4203 | duerma | 1 |
| 4204 | duende | 1 |
| 4205 | duelos | 1 |
| 4206 | duele | 1 |
| 4207 | dudosos | 1 |
| 4208 | dudas | 1 |
| 4209 | duda | 1 |
| 4210 | dotrinada | 1 |
| 4211 | doseles | 1 |
| 4212 | dormido | 1 |
| 4213 | dorados | 1 |
| 4214 | dorado | 1 |
| 4215 | dorada | 1 |
| 4216 | doncellez | 1 |
| 4217 | doncella | 1 |
| 4218 | dominaba | 1 |
| 4219 | dolorosas | 1 |
| 4220 | dolorosa | 1 |
| 4221 | dolencia | 1 |
| 4222 | doctores | 1 |
| 4223 | docto | 1 |
| 4224 | doctas | 1 |
| 4225 | doce | 1 |
| 4226 | dobló | 1 |
| 4227 | dobles | 1 |
| 4228 | doblado | 1 |
| 4229 | do | 1 |
| 4230 | dixo | 1 |
| 4231 | divorcio | 1 |
| 4232 | divine | 1 |
| 4233 | divide | 1 |
| 4234 | divertida | 1 |
| 4235 | diversos | 1 |
| 4236 | distrito | 1 |
| 4237 | distes | 1 |
| 4238 | dispuesto | 1 |
| 4239 | dispensas | 1 |
| 4240 | dispensando | 1 |
| 4241 | dispensan | 1 |
| 4242 | dispensadores | 1 |
| 4243 | disparado | 1 |
| 4244 | disimuladas | 1 |
| 4245 | disimula | 1 |
| 4246 | disfraz | 1 |
| 4247 | disfavor | 1 |
| 4248 | discursos | 1 |
| 4249 | discurso | 1 |
| 4250 | discurrían | 1 |
| 4251 | discurren | 1 |
| 4252 | disculpa | 1 |
| 4253 | discretas | 1 |
| 4254 | discordia | 1 |
| 4255 | disciplinante | 1 |
| 4256 | disciplinado | 1 |
| 4257 | disciplina | 1 |
| 4258 | direlo | 1 |
| 4259 | dirás | 1 |
| 4260 | diole | 1 |
| 4261 | diolas | 1 |
| 4262 | dineras | 1 |
| 4263 | dime | 1 |
| 4264 | diluvios | 1 |
| 4265 | diluvio | 1 |
| 4266 | diligente | 1 |
| 4267 | diligencias | 1 |
| 4268 | diligencia | 1 |
| 4269 | dilató | 1 |
| 4270 | dilato | 1 |
| 4271 | dilatas | 1 |
| 4272 | dilata | 1 |
| 4273 | dijeron | 1 |
| 4274 | digno | 1 |
| 4275 | digas | 1 |
| 4276 | digan | 1 |
| 4277 | diga | 1 |
| 4278 | difuntos | 1 |
| 4279 | difuntas | 1 |
| 4280 | dificultosos | 1 |
| 4281 | diferiste | 1 |
| 4282 | diferencias | 1 |
| 4283 | diferenciaban | 1 |
| 4284 | diferencia | 1 |
| 4285 | diez | 1 |
| 4286 | diéronles | 1 |
| 4287 | diéronle | 1 |
| 4288 | diere | 1 |
| 4289 | diera | 1 |
| 4290 | diente | 1 |
| 4291 | diciembre | 1 |
| 4292 | dichosa | 1 |
| 4293 | dichas | 1 |
| 4294 | diamantes | 1 |
| 4295 | devotos | 1 |
| 4296 | devoción | 1 |
| 4297 | devaneos | 1 |
| 4298 | devanadera | 1 |
| 4299 | devana | 1 |
| 4300 | detúvose | 1 |
| 4301 | detrás | 1 |
| 4302 | detiene | 1 |
| 4303 | detenido | 1 |
| 4304 | detenida | 1 |
| 4305 | detenga | 1 |
| 4306 | detenerse | 1 |
| 4307 | desvíos | 1 |
| 4308 | desvíes | 1 |
| 4309 | desvía | 1 |
| 4310 | desventura | 1 |
| 4311 | desvelarme | 1 |
| 4312 | desvelan | 1 |
| 4313 | desvelado | 1 |
| 4314 | desvelada | 1 |
| 4315 | desvanece | 1 |
| 4316 | desvaído | 1 |
| 4317 | destrozos | 1 |
| 4318 | destrozo | 1 |
| 4319 | destinado | 1 |
| 4320 | destilando | 1 |
| 4321 | destierros | 1 |
| 4322 | destierra | 1 |
| 4323 | desterrado | 1 |
| 4324 | desta | 1 |
| 4325 | desquito | 1 |
| 4326 | despuebla | 1 |
| 4327 | desprecios | 1 |
| 4328 | despreció | 1 |
| 4329 | desprecié | 1 |
| 4330 | despreciarlo | 1 |
| 4331 | despreciado | 1 |
| 4332 | desposados | 1 |
| 4333 | despojado | 1 |
| 4334 | despoblado | 1 |
| 4335 | despiertos | 1 |
| 4336 | despierte | 1 |
| 4337 | desperté | 1 |
| 4338 | despeñadero | 1 |
| 4339 | despeñada | 1 |
| 4340 | despedirme | 1 |
| 4341 | despedazada | 1 |
| 4342 | desordenado | 1 |
| 4343 | desorden | 1 |
| 4344 | desollada | 1 |
| 4345 | desnudos | 1 |
| 4346 | desnudeces | 1 |
| 4347 | desnudas | 1 |
| 4348 | desnudando | 1 |
| 4349 | desnúdame | 1 |
| 4350 | desnudador | 1 |
| 4351 | desnuda | 1 |
| 4352 | desmoronados | 1 |
| 4353 | desmienten | 1 |
| 4354 | desmiente | 1 |
| 4355 | desmienta | 1 |
| 4356 | desmentirá | 1 |
| 4357 | desmayo | 1 |
| 4358 | deslizas | 1 |
| 4359 | deslazas | 1 |
| 4360 | desigual | 1 |
| 4361 | desiertas | 1 |
| 4362 | deshonesta | 1 |
| 4363 | deshojar | 1 |
| 4364 | deshecho | 1 |
| 4365 | deshace | 1 |
| 4366 | deshabitado | 1 |
| 4367 | desgreñado | 1 |
| 4368 | desgracias | 1 |
| 4369 | desgraciado | 1 |
| 4370 | desgracia | 1 |
| 4371 | desfigura | 1 |
| 4372 | desfallece | 1 |
| 4373 | desesperados | 1 |
| 4374 | desesperado | 1 |
| 4375 | desesperación | 1 |
| 4376 | desenvaina | 1 |
| 4377 | desenojada | 1 |
| 4378 | desengaño | 1 |
| 4379 | desengaña | 1 |
| 4380 | desenfrenado | 1 |
| 4381 | desembozo | 1 |
| 4382 | desembarazarnos | 1 |
| 4383 | desearla | 1 |
| 4384 | deseando | 1 |
| 4385 | deseado | 1 |
| 4386 | desdiga | 1 |
| 4387 | descuídate | 1 |
| 4388 | descuidado | 1 |
| 4389 | descubriendo | 1 |
| 4390 | descripción | 1 |
| 4391 | descortés | 1 |
| 4392 | desconsuelas | 1 |
| 4393 | desconsoladas | 1 |
| 4394 | desconocido | 1 |
| 4395 | desconfiar | 1 |
| 4396 | desconfianza | 1 |
| 4397 | descoloridos | 1 |
| 4398 | descoloridas | 1 |
| 4399 | descolorida | 1 |
| 4400 | descifra | 1 |
| 4401 | descendencias | 1 |
| 4402 | descaramiento | 1 |
| 4403 | descansen | 1 |
| 4404 | descanse | 1 |
| 4405 | descansarás | 1 |
| 4406 | descansaba | 1 |
| 4407 | descaminar | 1 |
| 4408 | descaminado | 1 |
| 4409 | descaminada | 1 |
| 4410 | desatar | 1 |
| 4411 | desatados | 1 |
| 4412 | desatadas | 1 |
| 4413 | desatada | 1 |
| 4414 | desataba | 1 |
| 4415 | desata | 1 |
| 4416 | desangrado | 1 |
| 4417 | desangradas | 1 |
| 4418 | desandar | 1 |
| 4419 | desamparada | 1 |
| 4420 | desamor | 1 |
| 4421 | desaliñada | 1 |
| 4422 | desafío | 1 |
| 4423 | desacredito | 1 |
| 4424 | desacordado | 1 |
| 4425 | desabrimientos | 1 |
| 4426 | desabrigan | 1 |
| 4427 | derriba | 1 |
| 4428 | derretir | 1 |
| 4429 | derramo | 1 |
| 4430 | derramaron | 1 |
| 4431 | derramada | 1 |
| 4432 | dependió | 1 |
| 4433 | deo | 1 |
| 4434 | denegridos | 1 |
| 4435 | den | 1 |
| 4436 | demudado | 1 |
| 4437 | demás | 1 |
| 4438 | demanda | 1 |
| 4439 | dellos | 1 |
| 4440 | delirio | 1 |
| 4441 | delicioso | 1 |
| 4442 | delgado | 1 |
| 4443 | delfín | 1 |
| 4444 | deleitar | 1 |
| 4445 | delata | 1 |
| 4446 | dejo | 1 |
| 4447 | dejes | 1 |
| 4448 | déjate | 1 |
| 4449 | déjase | 1 |
| 4450 | dejarle | 1 |
| 4451 | dejarán | 1 |
| 4452 | dejará | 1 |
| 4453 | dejara | 1 |
| 4454 | dejándola | 1 |
| 4455 | déjame | 1 |
| 4456 | dejad | 1 |
| 4457 | degollado | 1 |
| 4458 | defuera | 1 |
| 4459 | definiendo | 1 |
| 4460 | defiende | 1 |
| 4461 | defiéndaos | 1 |
| 4462 | decrépito | 1 |
| 4463 | decirte | 1 |
| 4464 | decios | 1 |
| 4465 | decilla | 1 |
| 4466 | debido | 1 |
| 4467 | debía | 1 |
| 4468 | deben | 1 |
| 4469 | débate | 1 |
| 4470 | dátil | 1 |
| 4471 | date | 1 |
| 4472 | dase | 1 |
| 4473 | darlo | 1 |
| 4474 | darles | 1 |
| 4475 | dareos | 1 |
| 4476 | dará | 1 |
| 4477 | danzas | 1 |
| 4478 | dallos | 1 |
| 4479 | dádivas | 1 |
| 4480 | dádiva | 1 |
| 4481 | dad | 1 |
| 4482 | dábanme | 1 |
| 4483 | custodia | 1 |
| 4484 | curiosidad | 1 |
| 4485 | curios | 1 |
| 4486 | curas | 1 |
| 4487 | curara | 1 |
| 4488 | curando | 1 |
| 4489 | curada | 1 |
| 4490 | cumplidos | 1 |
| 4491 | cumbres | 1 |
| 4492 | cumbre | 1 |
| 4493 | cultos | 1 |
| 4494 | culterana | 1 |
| 4495 | cultas | 1 |
| 4496 | culpas | 1 |
| 4497 | culpada | 1 |
| 4498 | cueva | 1 |
| 4499 | cuestas | 1 |
| 4500 | cuesta | 1 |
| 4501 | cuervos | 1 |
| 4502 | cueros | 1 |
| 4503 | cuero | 1 |
| 4504 | cuerdos | 1 |
| 4505 | cuento | 1 |
| 4506 | cuece | 1 |
| 4507 | cucurucho | 1 |
| 4508 | cubilete | 1 |
| 4509 | cuba | 1 |
| 4510 | cuarto | 1 |
| 4511 | cuartana | 1 |
| 4512 | cuarta | 1 |
| 4513 | cuaresma | 1 |
| 4514 | cuanta | 1 |
| 4515 | cuan | 1 |
| 4516 | cruentos | 1 |
| 4517 | cruenta | 1 |
| 4518 | crueles | 1 |
| 4519 | crucifijo | 1 |
| 4520 | cristianos | 1 |
| 4521 | cristiano | 1 |
| 4522 | cristïana | 1 |
| 4523 | cristalinas | 1 |
| 4524 | cristales | 1 |
| 4525 | crin | 1 |
| 4526 | cribas | 1 |
| 4527 | criaturas | 1 |
| 4528 | criara | 1 |
| 4529 | crespa | 1 |
| 4530 | creídas | 1 |
| 4531 | creer | 1 |
| 4532 | creció | 1 |
| 4533 | creciendo | 1 |
| 4534 | creces | 1 |
| 4535 | crecerte | 1 |
| 4536 | creas | 1 |
| 4537 | creación | 1 |
| 4538 | coyuntura | 1 |
| 4539 | cosechas | 1 |
| 4540 | corvo | 1 |
| 4541 | corvillo | 1 |
| 4542 | corva | 1 |
| 4543 | cortinas | 1 |
| 4544 | cortezas | 1 |
| 4545 | cortesía | 1 |
| 4546 | corteses | 1 |
| 4547 | cortesano | 1 |
| 4548 | cortesana | 1 |
| 4549 | cortan | 1 |
| 4550 | cortado | 1 |
| 4551 | cortad | 1 |
| 4552 | corsarios | 1 |
| 4553 | corrió | 1 |
| 4554 | corrientes | 1 |
| 4555 | corres | 1 |
| 4556 | corregidor | 1 |
| 4557 | corre | 1 |
| 4558 | corpus | 1 |
| 4559 | corpulento | 1 |
| 4560 | coronada | 1 |
| 4561 | cornudo | 1 |
| 4562 | cornado | 1 |
| 4563 | cordón | 1 |
| 4564 | cordero | 1 |
| 4565 | corcova | 1 |
| 4566 | corchete | 1 |
| 4567 | coraza | 1 |
| 4568 | copias | 1 |
| 4569 | copia | 1 |
| 4570 | copete | 1 |
| 4571 | conviene | 1 |
| 4572 | conversación | 1 |
| 4573 | convenía | 1 |
| 4574 | convencida | 1 |
| 4575 | convaleciente | 1 |
| 4576 | contrito | 1 |
| 4577 | contrarios | 1 |
| 4578 | contrapuntos | 1 |
| 4579 | contrapunto | 1 |
| 4580 | continúa | 1 |
| 4581 | contino | 1 |
| 4582 | contera | 1 |
| 4583 | contentos | 1 |
| 4584 | contarme | 1 |
| 4585 | contador | 1 |
| 4586 | contadas | 1 |
| 4587 | consumo | 1 |
| 4588 | consumir | 1 |
| 4589 | consumido | 1 |
| 4590 | consumida | 1 |
| 4591 | consume | 1 |
| 4592 | consuelos | 1 |
| 4593 | construye | 1 |
| 4594 | constelaciones | 1 |
| 4595 | constantes | 1 |
| 4596 | consortes | 1 |
| 4597 | consolarme | 1 |
| 4598 | considero | 1 |
| 4599 | considerándole | 1 |
| 4600 | considera | 1 |
| 4601 | consejos | 1 |
| 4602 | consejera | 1 |
| 4603 | conquistada | 1 |
| 4604 | conocimiento | 1 |
| 4605 | conocí | 1 |
| 4606 | conoces | 1 |
| 4607 | conocerte | 1 |
| 4608 | conoceros | 1 |
| 4609 | conjuro | 1 |
| 4610 | conjetura | 1 |
| 4611 | congrio | 1 |
| 4612 | congojoso | 1 |
| 4613 | congojosa | 1 |
| 4614 | confusos | 1 |
| 4615 | confuso | 1 |
| 4616 | confusión | 1 |
| 4617 | confundirle | 1 |
| 4618 | confundiendo | 1 |
| 4619 | conformes | 1 |
| 4620 | confines | 1 |
| 4621 | confieso | 1 |
| 4622 | confiese | 1 |
| 4623 | confianza | 1 |
| 4624 | confesión | 1 |
| 4625 | confesarse | 1 |
| 4626 | condeno | 1 |
| 4627 | condenada | 1 |
| 4628 | condena | 1 |
| 4629 | conciencia | 1 |
| 4630 | conciba | 1 |
| 4631 | conchas | 1 |
| 4632 | conceto | 1 |
| 4633 | concertaste | 1 |
| 4634 | concertando | 1 |
| 4635 | conceptos | 1 |
| 4636 | concento | 1 |
| 4637 | concediste | 1 |
| 4638 | concédele | 1 |
| 4639 | cóncavos | 1 |
| 4640 | cóncavas | 1 |
| 4641 | comunico | 1 |
| 4642 | comunera | 1 |
| 4643 | común | 1 |
| 4644 | compuesta | 1 |
| 4645 | compró | 1 |
| 4646 | comprar | 1 |
| 4647 | compra | 1 |
| 4648 | compiten | 1 |
| 4649 | compite | 1 |
| 4650 | compita | 1 |
| 4651 | competilla | 1 |
| 4652 | competidor | 1 |
| 4653 | comparados | 1 |
| 4654 | comparación | 1 |
| 4655 | compañías | 1 |
| 4656 | compadre | 1 |
| 4657 | compadecidos | 1 |
| 4658 | comió | 1 |
| 4659 | comiendo | 1 |
| 4660 | comían | 1 |
| 4661 | cometió | 1 |
| 4662 | cometa | 1 |
| 4663 | comercio | 1 |
| 4664 | comenzolos | 1 |
| 4665 | comen | 1 |
| 4666 | comedla | 1 |
| 4667 | combatido | 1 |
| 4668 | combatida | 1 |
| 4669 | combate | 1 |
| 4670 | colora | 1 |
| 4671 | colmados | 1 |
| 4672 | colegiales | 1 |
| 4673 | cola | 1 |
| 4674 | cohombro | 1 |
| 4675 | cofrades | 1 |
| 4676 | codicioso | 1 |
| 4677 | codiciaron | 1 |
| 4678 | codiciaba | 1 |
| 4679 | cocodrilo | 1 |
| 4680 | coco | 1 |
| 4681 | coces | 1 |
| 4682 | coca | 1 |
| 4683 | cobrador | 1 |
| 4684 | cobra | 1 |
| 4685 | clemencia | 1 |
| 4686 | cleantes | 1 |
| 4687 | clavos | 1 |
| 4688 | clavo | 1 |
| 4689 | clavado | 1 |
| 4690 | clavadas | 1 |
| 4691 | clava | 1 |
| 4692 | cláusulas | 1 |
| 4693 | claustros | 1 |
| 4694 | claros | 1 |
| 4695 | claras | 1 |
| 4696 | clara | 1 |
| 4697 | clamoreó | 1 |
| 4698 | clamor | 1 |
| 4699 | civil | 1 |
| 4700 | ciudadanos | 1 |
| 4701 | cítaras | 1 |
| 4702 | circunloquio | 1 |
| 4703 | círculos | 1 |
| 4704 | círculo | 1 |
| 4705 | cipreses | 1 |
| 4706 | ciñe | 1 |
| 4707 | cintas | 1 |
| 4708 | cimientos | 1 |
| 4709 | cimiento | 1 |
| 4710 | cierro | 1 |
| 4711 | ciencia | 1 |
| 4712 | cieguen | 1 |
| 4713 | ciegan | 1 |
| 4714 | cid | 1 |
| 4715 | chiste | 1 |
| 4716 | chiquilla | 1 |
| 4717 | chipre | 1 |
| 4718 | chillón | 1 |
| 4719 | chicas | 1 |
| 4720 | chapuzan | 1 |
| 4721 | chapitel | 1 |
| 4722 | chanzas | 1 |
| 4723 | césar | 1 |
| 4724 | cerúleos | 1 |
| 4725 | certeza | 1 |
| 4726 | cerriles | 1 |
| 4727 | cerrar | 1 |
| 4728 | cerrallos | 1 |
| 4729 | cerrada | 1 |
| 4730 | ceros | 1 |
| 4731 | cereza | 1 |
| 4732 | ceres | 1 |
| 4733 | ceremonias | 1 |
| 4734 | cercos | 1 |
| 4735 | cercano | 1 |
| 4736 | cercan | 1 |
| 4737 | cercado | 1 |
| 4738 | cerbero | 1 |
| 4739 | ceñir | 1 |
| 4740 | centelleante | 1 |
| 4741 | centellante | 1 |
| 4742 | centella | 1 |
| 4743 | censoria | 1 |
| 4744 | censo | 1 |
| 4745 | celoso | 1 |
| 4746 | celosa | 1 |
| 4747 | celestiales | 1 |
| 4748 | celebrarte | 1 |
| 4749 | celebralde | 1 |
| 4750 | céfiro | 1 |
| 4751 | cédula | 1 |
| 4752 | cedros | 1 |
| 4753 | cede | 1 |
| 4754 | cebolla | 1 |
| 4755 | cebo | 1 |
| 4756 | caza | 1 |
| 4757 | cavernas | 1 |
| 4758 | cavan | 1 |
| 4759 | cautivo | 1 |
| 4760 | cautelosos | 1 |
| 4761 | cautela | 1 |
| 4762 | catedrático | 1 |
| 4763 | cátedra | 1 |
| 4764 | cátate | 1 |
| 4765 | castillos | 1 |
| 4766 | castillas | 1 |
| 4767 | castilla | 1 |
| 4768 | castigas | 1 |
| 4769 | castigar | 1 |
| 4770 | castiga | 1 |
| 4771 | castidad | 1 |
| 4772 | castellanos | 1 |
| 4773 | castellano | 1 |
| 4774 | castañeta | 1 |
| 4775 | castaña | 1 |
| 4776 | caspa | 1 |
| 4777 | casos | 1 |
| 4778 | casimiro | 1 |
| 4779 | caseme | 1 |
| 4780 | casas | 1 |
| 4781 | casáronse | 1 |
| 4782 | casaron | 1 |
| 4783 | casarme | 1 |
| 4784 | casaos | 1 |
| 4785 | casan | 1 |
| 4786 | casamentero | 1 |
| 4787 | casados | 1 |
| 4788 | casado | 1 |
| 4789 | cartilla | 1 |
| 4790 | carriles | 1 |
| 4791 | carquesio | 1 |
| 4792 | carpas | 1 |
| 4793 | caro | 1 |
| 4794 | carmín | 1 |
| 4795 | carlos | 1 |
| 4796 | carininfos | 1 |
| 4797 | caricia | 1 |
| 4798 | cargó | 1 |
| 4799 | cargadas | 1 |
| 4800 | carga | 1 |
| 4801 | careciendo | 1 |
| 4802 | cárdeno | 1 |
| 4803 | cárdenas | 1 |
| 4804 | carcomida | 1 |
| 4805 | carbones | 1 |
| 4806 | carbonada | 1 |
| 4807 | carbón | 1 |
| 4808 | caracteres | 1 |
| 4809 | capaz | 1 |
| 4810 | capas | 1 |
| 4811 | capaces | 1 |
| 4812 | caos | 1 |
| 4813 | cañuto | 1 |
| 4814 | cañones | 1 |
| 4815 | cantor | 1 |
| 4816 | cantarle | 1 |
| 4817 | cantares | 1 |
| 4818 | cantanos | 1 |
| 4819 | cantándome | 1 |
| 4820 | cantando | 1 |
| 4821 | cántabro | 1 |
| 4822 | cantaba | 1 |
| 4823 | canta | 1 |
| 4824 | cansaré | 1 |
| 4825 | cansados | 1 |
| 4826 | cansa | 1 |
| 4827 | canos | 1 |
| 4828 | canoras | 1 |
| 4829 | canonice | 1 |
| 4830 | canicular | 1 |
| 4831 | canícula | 1 |
| 4832 | candores | 1 |
| 4833 | canción | 1 |
| 4834 | cana | 1 |
| 4835 | campeador | 1 |
| 4836 | campanilla | 1 |
| 4837 | caminos | 1 |
| 4838 | caminado | 1 |
| 4839 | cambio | 1 |
| 4840 | calzas | 1 |
| 4841 | calvas | 1 |
| 4842 | calor | 1 |
| 4843 | callar | 1 |
| 4844 | callados | 1 |
| 4845 | calladas | 1 |
| 4846 | cáliz | 1 |
| 4847 | calentura | 1 |
| 4848 | calendario | 1 |
| 4849 | caldero | 1 |
| 4850 | cálculo | 1 |
| 4851 | calcetero | 1 |
| 4852 | calavera | 1 |
| 4853 | calabazas | 1 |
| 4854 | calabaza | 1 |
| 4855 | cajas | 1 |
| 4856 | caimán | 1 |
| 4857 | caerse | 1 |
| 4858 | caerá | 1 |
| 4859 | caer | 1 |
| 4860 | caducan | 1 |
| 4861 | caducamente | 1 |
| 4862 | caducaban | 1 |
| 4863 | caduca | 1 |
| 4864 | cabo | 1 |
| 4865 | cabezas | 1 |
| 4866 | cabellos | 1 |
| 4867 | cabe | 1 |
| 4868 | cabaña | 1 |
| 4869 | caballeros | 1 |
| 4870 | caballeriza | 1 |
| 4871 | caballerías | 1 |
| 4872 | caballera | 1 |
| 4873 | buzano | 1 |
| 4874 | buscó | 1 |
| 4875 | busco | 1 |
| 4876 | buscarlos | 1 |
| 4877 | buscaré | 1 |
| 4878 | buscar | 1 |
| 4879 | buscado | 1 |
| 4880 | buscaba | 1 |
| 4881 | burlesca | 1 |
| 4882 | burlarme | 1 |
| 4883 | burlándose | 1 |
| 4884 | burlando | 1 |
| 4885 | búrlame | 1 |
| 4886 | burladora | 1 |
| 4887 | burlador | 1 |
| 4888 | buriel | 1 |
| 4889 | bultos | 1 |
| 4890 | bula | 1 |
| 4891 | bujía | 1 |
| 4892 | buenas | 1 |
| 4893 | bruja | 1 |
| 4894 | briosa | 1 |
| 4895 | brío | 1 |
| 4896 | brindis | 1 |
| 4897 | breves | 1 |
| 4898 | brevemente | 1 |
| 4899 | brava | 1 |
| 4900 | bramidos | 1 |
| 4901 | bracete | 1 |
| 4902 | botarga | 1 |
| 4903 | bota | 1 |
| 4904 | bostezo | 1 |
| 4905 | bosque | 1 |
| 4906 | borres | 1 |
| 4907 | borrascas | 1 |
| 4908 | borrachas | 1 |
| 4909 | bóreas | 1 |
| 4910 | bonito | 1 |
| 4911 | bonanza | 1 |
| 4912 | bombardas | 1 |
| 4913 | bolsas | 1 |
| 4914 | boloñés | 1 |
| 4915 | boga | 1 |
| 4916 | bocas | 1 |
| 4917 | blasonan | 1 |
| 4918 | blandos | 1 |
| 4919 | blandas | 1 |
| 4920 | blandamente | 1 |
| 4921 | blancos | 1 |
| 4922 | bizarría | 1 |
| 4923 | bizarra | 1 |
| 4924 | betún | 1 |
| 4925 | bestia | 1 |
| 4926 | beso | 1 |
| 4927 | besar | 1 |
| 4928 | besamanos | 1 |
| 4929 | berza | 1 |
| 4930 | berenjena | 1 |
| 4931 | benignas | 1 |
| 4932 | beneficios | 1 |
| 4933 | bendito | 1 |
| 4934 | benavente | 1 |
| 4935 | bellísima | 1 |
| 4936 | bellas | 1 |
| 4937 | belisa | 1 |
| 4938 | belicoso | 1 |
| 4939 | belicosa | 1 |
| 4940 | beldad | 1 |
| 4941 | bebiste | 1 |
| 4942 | bebió | 1 |
| 4943 | bebiéndoos | 1 |
| 4944 | bebido | 1 |
| 4945 | bebida | 1 |
| 4946 | bebía | 1 |
| 4947 | bébese | 1 |
| 4948 | bebería | 1 |
| 4949 | beberán | 1 |
| 4950 | bebéis | 1 |
| 4951 | baza | 1 |
| 4952 | bayetas | 1 |
| 4953 | bayeta | 1 |
| 4954 | bato | 1 |
| 4955 | batallas | 1 |
| 4956 | básteme | 1 |
| 4957 | baste | 1 |
| 4958 | bastábale | 1 |
| 4959 | bártulos | 1 |
| 4960 | barbo | 1 |
| 4961 | barbas | 1 |
| 4962 | barba | 1 |
| 4963 | baratas | 1 |
| 4964 | barata | 1 |
| 4965 | bañas | 1 |
| 4966 | bañado | 1 |
| 4967 | baña | 1 |
| 4968 | banquetes | 1 |
| 4969 | banderas | 1 |
| 4970 | bandera | 1 |
| 4971 | ballenas | 1 |
| 4972 | ballena | 1 |
| 4973 | balas | 1 |
| 4974 | bajeles | 1 |
| 4975 | bajel | 1 |
| 4976 | baje | 1 |
| 4977 | bajas | 1 |
| 4978 | bailes | 1 |
| 4979 | baile | 1 |
| 4980 | bailarín | 1 |
| 4981 | bailarán | 1 |
| 4982 | badajo | 1 |
| 4983 | báculo | 1 |
| 4984 | baco | 1 |
| 4985 | bachillera | 1 |
| 4986 | bacanales | 1 |
| 4987 | azumbres | 1 |
| 4988 | azufre | 1 |
| 4989 | azufrados | 1 |
| 4990 | azucena | 1 |
| 4991 | azúcar | 1 |
| 4992 | azotes | 1 |
| 4993 | azotan | 1 |
| 4994 | azadas | 1 |
| 4995 | azabache | 1 |
| 4996 | ayuno | 1 |
| 4997 | ayo | 1 |
| 4998 | aviso | 1 |
| 4999 | avises | 1 |
| 5000 | aventuró | 1 |
| 5001 | aventino | 1 |
| 5002 | aventajarse | 1 |
| 5003 | avaros | 1 |
| 5004 | avaricia | 1 |
| 5005 | avara | 1 |
| 5006 | autoridad | 1 |
| 5007 | autor | 1 |
| 5008 | ausentas | 1 |
| 5009 | ausencias | 1 |
| 5010 | aumento | 1 |
| 5011 | aumenta | 1 |
| 5012 | augusta | 1 |
| 5013 | atusada | 1 |
| 5014 | atunes | 1 |
| 5015 | atrevimiento | 1 |
| 5016 | atrevieron | 1 |
| 5017 | atrevidos | 1 |
| 5018 | atreverte | 1 |
| 5019 | atreverse | 1 |
| 5020 | atreva | 1 |
| 5021 | atrás | 1 |
| 5022 | átomos | 1 |
| 5023 | átomo | 1 |
| 5024 | atiendes | 1 |
| 5025 | atienden | 1 |
| 5026 | atiéndele | 1 |
| 5027 | atienda | 1 |
| 5028 | atesora | 1 |
| 5029 | atención | 1 |
| 5030 | atemorice | 1 |
| 5031 | atascan | 1 |
| 5032 | atarazaba | 1 |
| 5033 | asustado | 1 |
| 5034 | asuntos | 1 |
| 5035 | astros | 1 |
| 5036 | astrología | 1 |
| 5037 | asta | 1 |
| 5038 | aspiraste | 1 |
| 5039 | áspid | 1 |
| 5040 | ásperas | 1 |
| 5041 | áspera | 1 |
| 5042 | aspecto | 1 |
| 5043 | asombro | 1 |
| 5044 | asistió | 1 |
| 5045 | asistidos | 1 |
| 5046 | asirte | 1 |
| 5047 | asiento | 1 |
| 5048 | aseo | 1 |
| 5049 | aseguro | 1 |
| 5050 | aseguraros | 1 |
| 5051 | asegurado | 1 |
| 5052 | asciendes | 1 |
| 5053 | ascendiente | 1 |
| 5054 | asaltos | 1 |
| 5055 | asaltado | 1 |
| 5056 | arturo | 1 |
| 5057 | artificiosa | 1 |
| 5058 | artificial | 1 |
| 5059 | artífice | 1 |
| 5060 | articulada | 1 |
| 5061 | arte | 1 |
| 5062 | arrugada | 1 |
| 5063 | arrobas | 1 |
| 5064 | arrepentir | 1 |
| 5065 | arrendajo | 1 |
| 5066 | arremendando | 1 |
| 5067 | arrebol | 1 |
| 5068 | arrebata | 1 |
| 5069 | arrastro | 1 |
| 5070 | arrastran | 1 |
| 5071 | arrastra | 1 |
| 5072 | arracadas | 1 |
| 5073 | arpías | 1 |
| 5074 | aroma | 1 |
| 5075 | armadura | 1 |
| 5076 | aritmética | 1 |
| 5077 | argumentillo | 1 |
| 5078 | argumentaren | 1 |
| 5079 | argos | 1 |
| 5080 | argonauta | 1 |
| 5081 | arenas | 1 |
| 5082 | ardo | 1 |
| 5083 | ardió | 1 |
| 5084 | ardientes | 1 |
| 5085 | ardido | 1 |
| 5086 | árboles | 1 |
| 5087 | árbitros | 1 |
| 5088 | árbitro | 1 |
| 5089 | aras | 1 |
| 5090 | araña | 1 |
| 5091 | aranjuez | 1 |
| 5092 | aragón | 1 |
| 5093 | ara | 1 |
| 5094 | aqueste | 1 |
| 5095 | aqueje | 1 |
| 5096 | apurar | 1 |
| 5097 | apurado | 1 |
| 5098 | apruebo | 1 |
| 5099 | aprovechas | 1 |
| 5100 | aprisionada | 1 |
| 5101 | aprisiona | 1 |
| 5102 | aprietes | 1 |
| 5103 | apretada | 1 |
| 5104 | apresurado | 1 |
| 5105 | apresura | 1 |
| 5106 | aprendiz | 1 |
| 5107 | aprendiese | 1 |
| 5108 | aprenderemos | 1 |
| 5109 | aprenderán | 1 |
| 5110 | aprended | 1 |
| 5111 | aprendan | 1 |
| 5112 | apodos | 1 |
| 5113 | apocamiento | 1 |
| 5114 | aplique | 1 |
| 5115 | aplaudió | 1 |
| 5116 | apetecidos | 1 |
| 5117 | apetecido | 1 |
| 5118 | apetecer | 1 |
| 5119 | apasionáis | 1 |
| 5120 | aparte | 1 |
| 5121 | apartan | 1 |
| 5122 | aparta | 1 |
| 5123 | aparentes | 1 |
| 5124 | aparente | 1 |
| 5125 | apareció | 1 |
| 5126 | apago | 1 |
| 5127 | apagar | 1 |
| 5128 | apagada | 1 |
| 5129 | apaga | 1 |
| 5130 | añudado | 1 |
| 5131 | añadir | 1 |
| 5132 | antonio | 1 |
| 5133 | anticiparse | 1 |
| 5134 | ante | 1 |
| 5135 | ansioso | 1 |
| 5136 | anonadada | 1 |
| 5137 | animoso | 1 |
| 5138 | ánimo | 1 |
| 5139 | animar | 1 |
| 5140 | animal | 1 |
| 5141 | animada | 1 |
| 5142 | ánima | 1 |
| 5143 | anhélito | 1 |
| 5144 | anhelar | 1 |
| 5145 | anhelando | 1 |
| 5146 | anhela | 1 |
| 5147 | angosto | 1 |
| 5148 | angosta | 1 |
| 5149 | ángeles | 1 |
| 5150 | ángela | 1 |
| 5151 | ángel | 1 |
| 5152 | anegó | 1 |
| 5153 | anegadas | 1 |
| 5154 | anega | 1 |
| 5155 | anduvo | 1 |
| 5156 | andarán | 1 |
| 5157 | andante | 1 |
| 5158 | andan | 1 |
| 5159 | andaban | 1 |
| 5160 | andaba | 1 |
| 5161 | anchoba | 1 |
| 5162 | anás | 1 |
| 5163 | amortecido | 1 |
| 5164 | amortajado | 1 |
| 5165 | amorosa | 1 |
| 5166 | amolada | 1 |
| 5167 | amigos | 1 |
| 5168 | ameno | 1 |
| 5169 | amenazados | 1 |
| 5170 | amenaces | 1 |
| 5171 | amedrentando | 1 |
| 5172 | ambos | 1 |
| 5173 | ambiciosos | 1 |
| 5174 | ambiciones | 1 |
| 5175 | amasteis | 1 |
| 5176 | amase | 1 |
| 5177 | amas | 1 |
| 5178 | amartelar | 1 |
| 5179 | amartelado | 1 |
| 5180 | amarrada | 1 |
| 5181 | amarillos | 1 |
| 5182 | amarillas | 1 |
| 5183 | amarilis | 1 |
| 5184 | amargo | 1 |
| 5185 | amarga | 1 |
| 5186 | amaren | 1 |
| 5187 | amara | 1 |
| 5188 | amaneciese | 1 |
| 5189 | amaneciendo | 1 |
| 5190 | amanecida | 1 |
| 5191 | amanecerá | 1 |
| 5192 | amanece | 1 |
| 5193 | amancillada | 1 |
| 5194 | amados | 1 |
| 5195 | ama | 1 |
| 5196 | alza | 1 |
| 5197 | álvaro | 1 |
| 5198 | alumbraban | 1 |
| 5199 | altiva | 1 |
| 5200 | alteza | 1 |
| 5201 | altamente | 1 |
| 5202 | alquitara | 1 |
| 5203 | alquimista | 1 |
| 5204 | alivian | 1 |
| 5205 | aliño | 1 |
| 5206 | alindado | 1 |
| 5207 | alimente | 1 |
| 5208 | alientos | 1 |
| 5209 | alienta | 1 |
| 5210 | alhajas | 1 |
| 5211 | algunas | 1 |
| 5212 | alguaciles | 1 |
| 5213 | algodones | 1 |
| 5214 | alfombra | 1 |
| 5215 | alevoso | 1 |
| 5216 | alentado | 1 |
| 5217 | alentada | 1 |
| 5218 | alegrías | 1 |
| 5219 | alegoría | 1 |
| 5220 | alegan | 1 |
| 5221 | aldeas | 1 |
| 5222 | alce | 1 |
| 5223 | alcázares | 1 |
| 5224 | alcázar | 1 |
| 5225 | alcanzarla | 1 |
| 5226 | alcanzaras | 1 |
| 5227 | alcanzar | 1 |
| 5228 | alcachofa | 1 |
| 5229 | albricias | 1 |
| 5230 | alboroza | 1 |
| 5231 | alboroto | 1 |
| 5232 | alberga | 1 |
| 5233 | alargar | 1 |
| 5234 | alargan | 1 |
| 5235 | alanos | 1 |
| 5236 | alano | 1 |
| 5237 | alada | 1 |
| 5238 | alaben | 1 |
| 5239 | alabastrina | 1 |
| 5240 | alabanzas | 1 |
| 5241 | ajusticiar | 1 |
| 5242 | ajos | 1 |
| 5243 | ajenos | 1 |
| 5244 | ajenas | 1 |
| 5245 | ajena | 1 |
| 5246 | aires | 1 |
| 5247 | airada | 1 |
| 5248 | ahorro | 1 |
| 5249 | ahorcaron | 1 |
| 5250 | ahorcados | 1 |
| 5251 | ahogose | 1 |
| 5252 | ahogaron | 1 |
| 5253 | ah | 1 |
| 5254 | aguja | 1 |
| 5255 | águila | 1 |
| 5256 | aguijo | 1 |
| 5257 | agüeros | 1 |
| 5258 | agüero | 1 |
| 5259 | aguardan | 1 |
| 5260 | aguados | 1 |
| 5261 | agravio | 1 |
| 5262 | agravia | 1 |
| 5263 | agrado | 1 |
| 5264 | agradezca | 1 |
| 5265 | agradecida | 1 |
| 5266 | agradeces | 1 |
| 5267 | agradar | 1 |
| 5268 | agonizar | 1 |
| 5269 | agonía | 1 |
| 5270 | áfrica | 1 |
| 5271 | afrentarlos | 1 |
| 5272 | aflijo | 1 |
| 5273 | afirma | 1 |
| 5274 | afición | 1 |
| 5275 | afeitado | 1 |
| 5276 | afeitada | 1 |
| 5277 | afectado | 1 |
| 5278 | afanan | 1 |
| 5279 | advertidas | 1 |
| 5280 | advertencias | 1 |
| 5281 | advertencia | 1 |
| 5282 | adversidad | 1 |
| 5283 | adular | 1 |
| 5284 | adulador | 1 |
| 5285 | adulación | 1 |
| 5286 | adrede | 1 |
| 5287 | adoro | 1 |
| 5288 | adornome | 1 |
| 5289 | adorno | 1 |
| 5290 | adorne | 1 |
| 5291 | adormecido | 1 |
| 5292 | adormecen | 1 |
| 5293 | adoren | 1 |
| 5294 | adore | 1 |
| 5295 | adorase | 1 |
| 5296 | adorándote | 1 |
| 5297 | adorando | 1 |
| 5298 | adoran | 1 |
| 5299 | adorado | 1 |
| 5300 | adoración | 1 |
| 5301 | adónde | 1 |
| 5302 | admito | 1 |
| 5303 | admitirle | 1 |
| 5304 | admitió | 1 |
| 5305 | admitiéndole | 1 |
| 5306 | admitidos | 1 |
| 5307 | admitido | 1 |
| 5308 | admires | 1 |
| 5309 | admire | 1 |
| 5310 | admiras | 1 |
| 5311 | admirada | 1 |
| 5312 | admiración | 1 |
| 5313 | admira | 1 |
| 5314 | administrar | 1 |
| 5315 | adivine | 1 |
| 5316 | adelgaza | 1 |
| 5317 | adelantara | 1 |
| 5318 | acusen | 1 |
| 5319 | acusar | 1 |
| 5320 | acusaban | 1 |
| 5321 | acuéstanse | 1 |
| 5322 | acuerdas | 1 |
| 5323 | acrisolaron | 1 |
| 5324 | acreditada | 1 |
| 5325 | acrecentaban | 1 |
| 5326 | acostarse | 1 |
| 5327 | acostados | 1 |
| 5328 | acortarse | 1 |
| 5329 | acorde | 1 |
| 5330 | acontece | 1 |
| 5331 | aconsejando | 1 |
| 5332 | acondicionados | 1 |
| 5333 | acompañada | 1 |
| 5334 | acompañaba | 1 |
| 5335 | acometa | 1 |
| 5336 | acogimiento | 1 |
| 5337 | acobardar | 1 |
| 5338 | aciértanme | 1 |
| 5339 | acicalado | 1 |
| 5340 | acercarse | 1 |
| 5341 | acercáis | 1 |
| 5342 | aceite | 1 |
| 5343 | acebo | 1 |
| 5344 | acciones | 1 |
| 5345 | acariciarme | 1 |
| 5346 | acabas | 1 |
| 5347 | acabaron | 1 |
| 5348 | acábanlos | 1 |
| 5349 | acaban | 1 |
| 5350 | acabado | 1 |
| 5351 | abundancia | 1 |
| 5352 | abultan | 1 |
| 5353 | abuelo | 1 |
| 5354 | absorto | 1 |
| 5355 | absoluto | 1 |
| 5356 | abrojos | 1 |
| 5357 | abrió | 1 |
| 5358 | abrigado | 1 |
| 5359 | abriga | 1 |
| 5360 | abriéronse | 1 |
| 5361 | abrieron | 1 |
| 5362 | abreviar | 1 |
| 5363 | abréviame | 1 |
| 5364 | abres | 1 |
| 5365 | abre | 1 |
| 5366 | abrazada | 1 |
| 5367 | abrasar | 1 |
| 5368 | abrasándote | 1 |
| 5369 | abrasando | 1 |
| 5370 | abrasados | 1 |
| 5371 | abrasador | 1 |
| 5372 | abrasado | 1 |
| 5373 | abrasadas | 1 |
| 5374 | abrasaban | 1 |
| 5375 | abrasa | 1 |
| 5376 | aborta | 1 |
| 5377 | aborrecidos | 1 |
| 5378 | aborrecer | 1 |
| 5379 | aborrece | 1 |
| 5380 | abiertos | 1 |
| 5381 | abiertas | 1 |
| 5382 | abejas | 1 |
| 5383 | abalanzan | 1 |
| 5384 | abades | 1 |
| 5385 | abadejos | 1 |
|
| Rank | Palabra | Frec |
|---|
| 1 | de | 977 |
| 2 | que | 675 |
| 3 | la | 621 |
| 4 | el | 606 |
| 5 | y | 433 |
| 6 | en | 432 |
| 7 | a | 412 |
| 8 | no | 308 |
| 9 | al | 286 |
| 10 | del | 249 |
| 11 | su | 230 |
| 12 | las | 230 |
| 13 | los | 219 |
| 14 | con | 153 |
| 15 | más | 147 |
| 16 | sus | 130 |
| 17 | un | 122 |
| 18 | si | 114 |
| 19 | es | 114 |
| 20 | lo | 104 |
| 21 | o | 97 |
| 22 | se | 92 |
| 23 | ya | 91 |
| 24 | por | 91 |
| 25 | le | 83 |
| 26 | tadeo | 81 |
| 27 | mi | 66 |
| 28 | pues | 65 |
| 29 | dos | 58 |
| 30 | tu | 54 |
| 31 | fabio | 54 |
| 32 | una | 53 |
| 33 | cuando | 51 |
| 34 | camilo | 51 |
| 35 | bien | 51 |
| 36 | mar | 49 |
| 37 | tan | 45 |
| 38 | mas | 42 |
| 39 | me | 41 |
| 40 | donde | 41 |
| 41 | para | 40 |
| 42 | viento | 38 |
| 43 | sol | 38 |
| 44 | sin | 38 |
| 45 | dulce | 38 |
| 46 | día | 38 |
| 47 | son | 37 |
| 48 | entre | 37 |
| 49 | oh | 36 |
| 50 | menos | 36 |
| 51 | te | 35 |
| 52 | quien | 35 |
| 53 | marcelo | 35 |
| 54 | cuanto | 35 |
| 55 | aun | 34 |
| 56 | yo | 33 |
| 57 | otro | 33 |
| 58 | qué | 32 |
| 59 | ha | 32 |
| 60 | breve | 32 |
| 61 | fue | 31 |
| 62 | amor | 31 |
| 63 | siempre | 30 |
| 64 | tanto | 29 |
| 65 | ondas | 29 |
| 66 | aparte | 29 |
| 67 | plumas | 28 |
| 68 | pie | 28 |
| 69 | fin | 28 |
| 70 | aunque | 28 |
| 71 | verde | 27 |
| 72 | ven | 27 |
| 73 | mal | 27 |
| 74 | hoy | 27 |
| 75 | este | 27 |
| 76 | oro | 26 |
| 77 | como | 26 |
| 78 | violante | 25 |
| 79 | mis | 24 |
| 80 | bella | 24 |
| 81 | ahora | 24 |
| 82 | sobre | 23 |
| 83 | porque | 23 |
| 84 | otra | 23 |
| 85 | himeneo | 23 |
| 86 | esta | 23 |
| 87 | él | 23 |
| 88 | tus | 22 |
| 89 | ni | 22 |
| 90 | luego | 22 |
| 91 | cuyo | 22 |
| 92 | cielo | 22 |
| 93 | tal | 21 |
| 94 | dio | 21 |
| 95 | cristal | 21 |
| 96 | ser | 20 |
| 97 | ella | 20 |
| 98 | duro | 20 |
| 99 | da | 20 |
| 100 | cual | 20 |
| 101 | sueño | 19 |
| 102 | cuantos | 19 |
| 103 | rayos | 18 |
| 104 | ojos | 18 |
| 105 | joven | 18 |
| 106 | hijo | 18 |
| 107 | flores | 18 |
| 108 | era | 18 |
| 109 | cuya | 18 |
| 110 | aquel | 18 |
| 111 | sí | 17 |
| 112 | sea | 17 |
| 113 | pluma | 17 |
| 114 | os | 17 |
| 115 | octavio | 17 |
| 116 | nieve | 17 |
| 117 | muy | 17 |
| 118 | mano | 17 |
| 119 | frente | 17 |
| 120 | tierra | 16 |
| 121 | sino | 16 |
| 122 | luz | 16 |
| 123 | hizo | 16 |
| 124 | espuma | 16 |
| 125 | deja | 16 |
| 126 | cuantas | 16 |
| 127 | apenas | 16 |
| 128 | años | 16 |
| 129 | alas | 16 |
| 130 | veces | 15 |
| 131 | tanta | 15 |
| 132 | plata | 15 |
| 133 | mientras | 15 |
| 134 | les | 15 |
| 135 | estrellas | 15 |
| 136 | dulces | 15 |
| 137 | dios | 15 |
| 138 | ciento | 15 |
| 139 | aves | 15 |
| 140 | aún | 15 |
| 141 | agua | 15 |
| 142 | vano | 14 |
| 143 | tiene | 14 |
| 144 | nombre | 14 |
| 145 | mayor | 14 |
| 146 | fuego | 14 |
| 147 | antes | 14 |
| 148 | aire | 14 |
| 149 | vez | 13 |
| 150 | verdes | 13 |
| 151 | tiempo | 13 |
| 152 | tantas | 13 |
| 153 | sólo | 13 |
| 154 | solicita | 13 |
| 155 | playa | 13 |
| 156 | pesar | 13 |
| 157 | peregrino | 13 |
| 158 | número | 13 |
| 159 | ninfa | 13 |
| 160 | muchos | 13 |
| 161 | luciente | 13 |
| 162 | huésped | 13 |
| 163 | fe | 13 |
| 164 | escollo | 13 |
| 165 | casa | 13 |
| 166 | campo | 13 |
| 167 | bello | 13 |
| 168 | ardiente | 13 |
| 169 | voz | 12 |
| 170 | vista | 12 |
| 171 | uno | 12 |
| 172 | tú | 12 |
| 173 | señas | 12 |
| 174 | poca | 12 |
| 175 | pero | 12 |
| 176 | padre | 12 |
| 177 | leño | 12 |
| 178 | lelio | 12 |
| 179 | hay | 12 |
| 180 | hacer | 12 |
| 181 | graves | 12 |
| 182 | fiero | 12 |
| 183 | cuyas | 12 |
| 184 | aurora | 12 |
| 185 | vuelo | 11 |
| 186 | vuela | 11 |
| 187 | todos | 11 |
| 188 | rocas | 11 |
| 189 | pobre | 11 |
| 190 | muros | 11 |
| 191 | mudo | 11 |
| 192 | mucho | 11 |
| 193 | montes | 11 |
| 194 | mí | 11 |
| 195 | hija | 11 |
| 196 | he | 11 |
| 197 | esconde | 11 |
| 198 | corona | 11 |
| 199 | coro | 11 |
| 200 | camino | 11 |
| 201 | cabello | 11 |
| 202 | blancas | 11 |
| 203 | bellas | 11 |
| 204 | arenas | 11 |
| 205 | alta | 11 |
| 206 | albergue | 11 |
| 207 | vio | 10 |
| 208 | viejo | 10 |
| 209 | tres | 10 |
| 210 | todo | 10 |
| 211 | tantos | 10 |
| 212 | roca | 10 |
| 213 | ribera | 10 |
| 214 | quiere | 10 |
| 215 | prolijo | 10 |
| 216 | primero | 10 |
| 217 | poco | 10 |
| 218 | perdona | 10 |
| 219 | pasos | 10 |
| 220 | océano | 10 |
| 221 | miembros | 10 |
| 222 | mejor | 10 |
| 223 | madre | 10 |
| 224 | hierba | 10 |
| 225 | hecho | 10 |
| 226 | galatea | 10 |
| 227 | fiera | 10 |
| 228 | esto | 10 |
| 229 | edad | 10 |
| 230 | digo | 10 |
| 231 | días | 10 |
| 232 | deseo | 10 |
| 233 | deidad | 10 |
| 234 | cristales | 10 |
| 235 | contra | 10 |
| 236 | blando | 10 |
| 237 | arroyo | 10 |
| 238 | arena | 10 |
| 239 | voces | 9 |
| 240 | vestido | 9 |
| 241 | ti | 9 |
| 242 | términos | 9 |
| 243 | tarde | 9 |
| 244 | süave | 9 |
| 245 | sombra | 9 |
| 246 | sigue | 9 |
| 247 | seis | 9 |
| 248 | segundo | 9 |
| 249 | secreto | 9 |
| 250 | sangre | 9 |
| 251 | saber | 9 |
| 252 | robusto | 9 |
| 253 | quiero | 9 |
| 254 | pompa | 9 |
| 255 | neptuno | 9 |
| 256 | mundo | 9 |
| 257 | mía | 9 |
| 258 | lascivo | 9 |
| 259 | lágrimas | 9 |
| 260 | isabela | 9 |
| 261 | igual | 9 |
| 262 | hora | 9 |
| 263 | hace | 9 |
| 264 | grave | 9 |
| 265 | gran | 9 |
| 266 | está | 9 |
| 267 | espumas | 9 |
| 268 | ellas | 9 |
| 269 | después | 9 |
| 270 | debe | 9 |
| 271 | cuerno | 9 |
| 272 | cuál | 9 |
| 273 | carro | 9 |
| 274 | cáñamo | 9 |
| 275 | así | 9 |
| 276 | aguas | 9 |
| 277 | acero | 9 |
| 278 | viendo | 8 |
| 279 | troncos | 8 |
| 280 | toledo | 8 |
| 281 | templo | 8 |
| 282 | senos | 8 |
| 283 | robre | 8 |
| 284 | redes | 8 |
| 285 | púrpura | 8 |
| 286 | pino | 8 |
| 287 | piedras | 8 |
| 288 | persona | 8 |
| 289 | pecho | 8 |
| 290 | paso | 8 |
| 291 | otros | 8 |
| 292 | ofrece | 8 |
| 293 | nudos | 8 |
| 294 | niega | 8 |
| 295 | néctar | 8 |
| 296 | muerte | 8 |
| 297 | montaña | 8 |
| 298 | mil | 8 |
| 299 | marino | 8 |
| 300 | mancebo | 8 |
| 301 | invidia | 8 |
| 302 | instrumento | 8 |
| 303 | has | 8 |
| 304 | gloria | 8 |
| 305 | gente | 8 |
| 306 | fortuna | 8 |
| 307 | esplendor | 8 |
| 308 | esfera | 8 |
| 309 | di | 8 |
| 310 | dejó | 8 |
| 311 | copia | 8 |
| 312 | canoro | 8 |
| 313 | blancos | 8 |
| 314 | blanco | 8 |
| 315 | árboles | 8 |
| 316 | aquella | 8 |
| 317 | amigo | 8 |
| 318 | alma | 8 |
| 319 | alado | 8 |
| 320 | vida | 7 |
| 321 | vestida | 7 |
| 322 | vecina | 7 |
| 323 | va | 7 |
| 324 | turba | 7 |
| 325 | torpe | 7 |
| 326 | torcido | 7 |
| 327 | todas | 7 |
| 328 | tierno | 7 |
| 329 | término | 7 |
| 330 | silencio | 7 |
| 331 | sierra | 7 |
| 332 | señor | 7 |
| 333 | seno | 7 |
| 334 | rosas | 7 |
| 335 | rico | 7 |
| 336 | quién | 7 |
| 337 | pudo | 7 |
| 338 | plantas | 7 |
| 339 | pisa | 7 |
| 340 | pies | 7 |
| 341 | pastor | 7 |
| 342 | nunca | 7 |
| 343 | nuevo | 7 |
| 344 | nacido | 7 |
| 345 | muro | 7 |
| 346 | mucha | 7 |
| 347 | monte | 7 |
| 348 | mira | 7 |
| 349 | manos | 7 |
| 350 | luces | 7 |
| 351 | llano | 7 |
| 352 | ligero | 7 |
| 353 | lento | 7 |
| 354 | júpiter | 7 |
| 355 | honor | 7 |
| 356 | halló | 7 |
| 357 | gusto | 7 |
| 358 | fuente | 7 |
| 359 | forastero | 7 |
| 360 | estas | 7 |
| 361 | eran | 7 |
| 362 | encina | 7 |
| 363 | dijo | 7 |
| 364 | desde | 7 |
| 365 | desata | 7 |
| 366 | cuyos | 7 |
| 367 | cerro | 7 |
| 368 | cera | 7 |
| 369 | casi | 7 |
| 370 | carrera | 7 |
| 371 | cano | 7 |
| 372 | can | 7 |
| 373 | cada | 7 |
| 374 | cabras | 7 |
| 375 | boca | 7 |
| 376 | blanca | 7 |
| 377 | ave | 7 |
| 378 | armonía | 7 |
| 379 | zafiro | 6 |
| 380 | ver | 6 |
| 381 | venus | 6 |
| 382 | veneno | 6 |
| 383 | tronco | 6 |
| 384 | tras | 6 |
| 385 | teatro | 6 |
| 386 | süaves | 6 |
| 387 | sombras | 6 |
| 388 | rüido | 6 |
| 389 | río | 6 |
| 390 | remo | 6 |
| 391 | quejas | 6 |
| 392 | prolija | 6 |
| 393 | primavera | 6 |
| 394 | pocas | 6 |
| 395 | perlas | 6 |
| 396 | nuestra | 6 |
| 397 | nos | 6 |
| 398 | noche | 6 |
| 399 | noble | 6 |
| 400 | negras | 6 |
| 401 | muda | 6 |
| 402 | mío | 6 |
| 403 | micón | 6 |
| 404 | mercader | 6 |
| 405 | menor | 6 |
| 406 | memoria | 6 |
| 407 | lugar | 6 |
| 408 | lucientes | 6 |
| 409 | llegó | 6 |
| 410 | lisonja | 6 |
| 411 | líquido | 6 |
| 412 | lino | 6 |
| 413 | lilios | 6 |
| 414 | lícidas | 6 |
| 415 | leve | 6 |
| 416 | lengua | 6 |
| 417 | juncos | 6 |
| 418 | hondas | 6 |
| 419 | hombre | 6 |
| 420 | hojas | 6 |
| 421 | hijas | 6 |
| 422 | hermosura | 6 |
| 423 | hermana | 6 |
| 424 | hasta | 6 |
| 425 | haciendo | 6 |
| 426 | griego | 6 |
| 427 | gracias | 6 |
| 428 | galeazo | 6 |
| 429 | fuerte | 6 |
| 430 | fuera | 6 |
| 431 | extranjero | 6 |
| 432 | experiencia | 6 |
| 433 | escucha | 6 |
| 434 | escollos | 6 |
| 435 | errantes | 6 |
| 436 | entra | 6 |
| 437 | ellos | 6 |
| 438 | dulcemente | 6 |
| 439 | dueño | 6 |
| 440 | dorado | 6 |
| 441 | diez | 6 |
| 442 | diente | 6 |
| 443 | diamante | 6 |
| 444 | desnudo | 6 |
| 445 | desdén | 6 |
| 446 | dar | 6 |
| 447 | cupido | 6 |
| 448 | cumbre | 6 |
| 449 | culta | 6 |
| 450 | corvo | 6 |
| 451 | cien | 6 |
| 452 | ciego | 6 |
| 453 | cenizas | 6 |
| 454 | causa | 6 |
| 455 | canas | 6 |
| 456 | campos | 6 |
| 457 | campaña | 6 |
| 458 | bárbara | 6 |
| 459 | aljófar | 6 |
| 460 | alba | 6 |
| 461 | agradable | 6 |
| 462 | acis | 6 |
| 463 | voy | 5 |
| 464 | viste | 5 |
| 465 | vi | 5 |
| 466 | verdad | 5 |
| 467 | venerable | 5 |
| 468 | veloz | 5 |
| 469 | ve | 5 |
| 470 | urna | 5 |
| 471 | trompa | 5 |
| 472 | toda | 5 |
| 473 | templado | 5 |
| 474 | telas | 5 |
| 475 | tajo | 5 |
| 476 | suelo | 5 |
| 477 | sitio | 5 |
| 478 | serrano | 5 |
| 479 | será | 5 |
| 480 | segunda | 5 |
| 481 | sale | 5 |
| 482 | ruda | 5 |
| 483 | riquezas | 5 |
| 484 | remos | 5 |
| 485 | región | 5 |
| 486 | rayo | 5 |
| 487 | rato | 5 |
| 488 | ramas | 5 |
| 489 | quiso | 5 |
| 490 | puro | 5 |
| 491 | puedo | 5 |
| 492 | pudiera | 5 |
| 493 | primer | 5 |
| 494 | pocos | 5 |
| 495 | piel | 5 |
| 496 | perezoso | 5 |
| 497 | pendientes | 5 |
| 498 | pájaro | 5 |
| 499 | onda | 5 |
| 500 | noruega | 5 |
| 501 | norte | 5 |
| 502 | nido | 5 |
| 503 | nada | 5 |
| 504 | nácar | 5 |
| 505 | mozo | 5 |
| 506 | montañés | 5 |
| 507 | miente | 5 |
| 508 | mesas | 5 |
| 509 | mármol | 5 |
| 510 | llanto | 5 |
| 511 | llama | 5 |
| 512 | lasciva | 5 |
| 513 | labradores | 5 |
| 514 | isla | 5 |
| 515 | impedido | 5 |
| 516 | iguales | 5 |
| 517 | huye | 5 |
| 518 | humo | 5 |
| 519 | huesos | 5 |
| 520 | honra | 5 |
| 521 | hombro | 5 |
| 522 | hoja | 5 |
| 523 | hilos | 5 |
| 524 | hijos | 5 |
| 525 | hierro | 5 |
| 526 | halla | 5 |
| 527 | hablar | 5 |
| 528 | había | 5 |
| 529 | grutas | 5 |
| 530 | gruta | 5 |
| 531 | garzón | 5 |
| 532 | gallardo | 5 |
| 533 | fugitiva | 5 |
| 534 | fuerza | 5 |
| 535 | fruta | 5 |
| 536 | fresno | 5 |
| 537 | freno | 5 |
| 538 | florida | 5 |
| 539 | estrella | 5 |
| 540 | estoy | 5 |
| 541 | estilo | 5 |
| 542 | ésta | 5 |
| 543 | esposa | 5 |
| 544 | émulo | 5 |
| 545 | emilio | 5 |
| 546 | dura | 5 |
| 547 | do | 5 |
| 548 | discurso | 5 |
| 549 | dices | 5 |
| 550 | deste | 5 |
| 551 | dejar | 5 |
| 552 | dando | 5 |
| 553 | dan | 5 |
| 554 | cuna | 5 |
| 555 | culto | 5 |
| 556 | cuatro | 5 |
| 557 | cualquier | 5 |
| 558 | criado | 5 |
| 559 | cosas | 5 |
| 560 | cosa | 5 |
| 561 | consejo | 5 |
| 562 | conmigo | 5 |
| 563 | cisne | 5 |
| 564 | ceres | 5 |
| 565 | celo | 5 |
| 566 | capaz | 5 |
| 567 | canto | 5 |
| 568 | callar | 5 |
| 569 | cadenas | 5 |
| 570 | cabo | 5 |
| 571 | caballo | 5 |
| 572 | breves | 5 |
| 573 | bosque | 5 |
| 574 | bienaventurado | 5 |
| 575 | besa | 5 |
| 576 | azul | 5 |
| 577 | atento | 5 |
| 578 | arte | 5 |
| 579 | armas | 5 |
| 580 | ambos | 5 |
| 581 | amante | 5 |
| 582 | alto | 5 |
| 583 | allí | 5 |
| 584 | alimento | 5 |
| 585 | alguna | 5 |
| 586 | alcides | 5 |
| 587 | adusto | 5 |
| 588 | abeja | 5 |
| 589 | yugo | 4 |
| 590 | yace | 4 |
| 591 | vulto | 4 |
| 592 | vuestras | 4 |
| 593 | volantes | 4 |
| 594 | volante | 4 |
| 595 | virginal | 4 |
| 596 | villano | 4 |
| 597 | venera | 4 |
| 598 | venas | 4 |
| 599 | veloces | 4 |
| 600 | vello | 4 |
| 601 | vase | 4 |
| 602 | vana | 4 |
| 603 | valiente | 4 |
| 604 | vago | 4 |
| 605 | vacas | 4 |
| 606 | unos | 4 |
| 607 | undoso | 4 |
| 608 | undosa | 4 |
| 609 | umbrales | 4 |
| 610 | último | 4 |
| 611 | trofeo | 4 |
| 612 | trato | 4 |
| 613 | tetis | 4 |
| 614 | tercio | 4 |
| 615 | temor | 4 |
| 616 | tejió | 4 |
| 617 | tardo | 4 |
| 618 | tales | 4 |
| 619 | tálamo | 4 |
| 620 | sur | 4 |
| 621 | suma | 4 |
| 622 | sordo | 4 |
| 623 | sonante | 4 |
| 624 | soles | 4 |
| 625 | sienes | 4 |
| 626 | sido | 4 |
| 627 | señora | 4 |
| 628 | selvas | 4 |
| 629 | selva | 4 |
| 630 | seguro | 4 |
| 631 | sé | 4 |
| 632 | sañudo | 4 |
| 633 | sabe | 4 |
| 634 | rüina | 4 |
| 635 | rubio | 4 |
| 636 | rubíes | 4 |
| 637 | ronco | 4 |
| 638 | robusta | 4 |
| 639 | ríos | 4 |
| 640 | rigor | 4 |
| 641 | reales | 4 |
| 642 | real | 4 |
| 643 | rapaz | 4 |
| 644 | quisiera | 4 |
| 645 | purpúreos | 4 |
| 646 | puente | 4 |
| 647 | puede | 4 |
| 648 | polo | 4 |
| 649 | polifemo | 4 |
| 650 | planta | 4 |
| 651 | pisó | 4 |
| 652 | pisar | 4 |
| 653 | pescadores | 4 |
| 654 | pequeño | 4 |
| 655 | peor | 4 |
| 656 | peñas | 4 |
| 657 | peña | 4 |
| 658 | pensamiento | 4 |
| 659 | pendiente | 4 |
| 660 | pende | 4 |
| 661 | parte | 4 |
| 662 | pámpanos | 4 |
| 663 | palma | 4 |
| 664 | pales | 4 |
| 665 | ostenta | 4 |
| 666 | orejas | 4 |
| 667 | oreja | 4 |
| 668 | olmos | 4 |
| 669 | oído | 4 |
| 670 | occidente | 4 |
| 671 | nubes | 4 |
| 672 | nocturno | 4 |
| 673 | niño | 4 |
| 674 | ninfas | 4 |
| 675 | nilo | 4 |
| 676 | movimiento | 4 |
| 677 | misma | 4 |
| 678 | metal | 4 |
| 679 | menuda | 4 |
| 680 | medio | 4 |
| 681 | mancebos | 4 |
| 682 | luminoso | 4 |
| 683 | lucha | 4 |
| 684 | llave | 4 |
| 685 | ligera | 4 |
| 686 | licencia | 4 |
| 687 | libia | 4 |
| 688 | libertad | 4 |
| 689 | levantado | 4 |
| 690 | lecho | 4 |
| 691 | leche | 4 |
| 692 | lava | 4 |
| 693 | labrador | 4 |
| 694 | jayán | 4 |
| 695 | islas | 4 |
| 696 | inciertos | 4 |
| 697 | incierta | 4 |
| 698 | ilustra | 4 |
| 699 | huerto | 4 |
| 700 | horror | 4 |
| 701 | horas | 4 |
| 702 | hilo | 4 |
| 703 | hermosa | 4 |
| 704 | hermano | 4 |
| 705 | hará | 4 |
| 706 | han | 4 |
| 707 | haga | 4 |
| 708 | hacía | 4 |
| 709 | gusano | 4 |
| 710 | guijas | 4 |
| 711 | guardan | 4 |
| 712 | gime | 4 |
| 713 | fuga | 4 |
| 714 | fría | 4 |
| 715 | fresco | 4 |
| 716 | floresta | 4 |
| 717 | flaco | 4 |
| 718 | fácil | 4 |
| 719 | fábrica | 4 |
| 720 | extremos | 4 |
| 721 | extremo | 4 |
| 722 | europa | 4 |
| 723 | estaba | 4 |
| 724 | espumoso | 4 |
| 725 | espera | 4 |
| 726 | eso | 4 |
| 727 | ese | 4 |
| 728 | errante | 4 |
| 729 | enseña | 4 |
| 730 | enjuta | 4 |
| 731 | ello | 4 |
| 732 | elemento | 4 |
| 733 | duras | 4 |
| 734 | duda | 4 |
| 735 | dosel | 4 |
| 736 | dormido | 4 |
| 737 | dolor | 4 |
| 738 | distante | 4 |
| 739 | diligente | 4 |
| 740 | dice | 4 |
| 741 | desta | 4 |
| 742 | desnuda | 4 |
| 743 | desiguales | 4 |
| 744 | desengaños | 4 |
| 745 | desatada | 4 |
| 746 | dará | 4 |
| 747 | daño | 4 |
| 748 | dado | 4 |
| 749 | curso | 4 |
| 750 | cuidado | 4 |
| 751 | cuerdas | 4 |
| 752 | cuenta | 4 |
| 753 | cuanta | 4 |
| 754 | corte | 4 |
| 755 | coros | 4 |
| 756 | coronado | 4 |
| 757 | corchos | 4 |
| 758 | corcho | 4 |
| 759 | confuso | 4 |
| 760 | conchas | 4 |
| 761 | concento | 4 |
| 762 | cóncavo | 4 |
| 763 | colores | 4 |
| 764 | cola | 4 |
| 765 | ciega | 4 |
| 766 | choza | 4 |
| 767 | celoso | 4 |
| 768 | cela | 4 |
| 769 | caudal | 4 |
| 770 | candor | 4 |
| 771 | calzada | 4 |
| 772 | calle | 4 |
| 773 | cajero | 4 |
| 774 | buena | 4 |
| 775 | bellos | 4 |
| 776 | bebió | 4 |
| 777 | barquilla | 4 |
| 778 | bajel | 4 |
| 779 | baco | 4 |
| 780 | avara | 4 |
| 781 | augusto | 4 |
| 782 | áspid | 4 |
| 783 | arroyuelo | 4 |
| 784 | arboleda | 4 |
| 785 | aquí | 4 |
| 786 | aquellos | 4 |
| 787 | aquél | 4 |
| 788 | apacible | 4 |
| 789 | amores | 4 |
| 790 | amo | 4 |
| 791 | amistad | 4 |
| 792 | alterno | 4 |
| 793 | aljaba | 4 |
| 794 | alados | 4 |
| 795 | alada | 4 |
| 796 | agudo | 4 |
| 797 | aguda | 4 |
| 798 | agravio | 4 |
| 799 | agradecido | 4 |
| 800 | admiración | 4 |
| 801 | admira | 4 |
| 802 | zampoña | 3 |
| 803 | zaguán | 3 |
| 804 | yedras | 3 |
| 805 | vuestros | 3 |
| 806 | vuélvese | 3 |
| 807 | vistió | 3 |
| 808 | visten | 3 |
| 809 | virgen | 3 |
| 810 | vimos | 3 |
| 811 | vigilante | 3 |
| 812 | vides | 3 |
| 813 | vestidas | 3 |
| 814 | verdugo | 3 |
| 815 | veo | 3 |
| 816 | venido | 3 |
| 817 | venció | 3 |
| 818 | vencida | 3 |
| 819 | vecinos | 3 |
| 820 | vecino | 3 |
| 821 | vaquero | 3 |
| 822 | vanos | 3 |
| 823 | vacíos | 3 |
| 824 | uso | 3 |
| 825 | unió | 3 |
| 826 | unas | 3 |
| 827 | tuya | 3 |
| 828 | tumba | 3 |
| 829 | tropa | 3 |
| 830 | treguas | 3 |
| 831 | traslada | 3 |
| 832 | torrente | 3 |
| 833 | toro | 3 |
| 834 | topacios | 3 |
| 835 | tiro | 3 |
| 836 | tímido | 3 |
| 837 | tímida | 3 |
| 838 | tienda | 3 |
| 839 | testigo | 3 |
| 840 | tengo | 3 |
| 841 | tener | 3 |
| 842 | tejido | 3 |
| 843 | tardó | 3 |
| 844 | tabla | 3 |
| 845 | suyos | 3 |
| 846 | suyo | 3 |
| 847 | suya | 3 |
| 848 | supo | 3 |
| 849 | sufrir | 3 |
| 850 | sufre | 3 |
| 851 | suele | 3 |
| 852 | suegro | 3 |
| 853 | sudor | 3 |
| 854 | sudando | 3 |
| 855 | sublime | 3 |
| 856 | soy | 3 |
| 857 | sonoro | 3 |
| 858 | solo | 3 |
| 859 | solicitan | 3 |
| 860 | sobra | 3 |
| 861 | sirenas | 3 |
| 862 | singularidades | 3 |
| 863 | silbo | 3 |
| 864 | siguiendo | 3 |
| 865 | sierpe | 3 |
| 866 | siente | 3 |
| 867 | sevilla | 3 |
| 868 | serranos | 3 |
| 869 | serranas | 3 |
| 870 | según | 3 |
| 871 | sediento | 3 |
| 872 | seda | 3 |
| 873 | seca | 3 |
| 874 | sean | 3 |
| 875 | santa | 3 |
| 876 | salud | 3 |
| 877 | salto | 3 |
| 878 | salteó | 3 |
| 879 | sagrado | 3 |
| 880 | saetas | 3 |
| 881 | sacre | 3 |
| 882 | rústica | 3 |
| 883 | rosa | 3 |
| 884 | romper | 3 |
| 885 | robustos | 3 |
| 886 | rienda | 3 |
| 887 | ría | 3 |
| 888 | repetido | 3 |
| 889 | registra | 3 |
| 890 | regalo | 3 |
| 891 | regalado | 3 |
| 892 | rebelde | 3 |
| 893 | razón | 3 |
| 894 | raya | 3 |
| 895 | quizá | 3 |
| 896 | querría | 3 |
| 897 | quedó | 3 |
| 898 | purpúreo | 3 |
| 899 | purpúreas | 3 |
| 900 | puertas | 3 |
| 901 | pueblo | 3 |
| 902 | prudente | 3 |
| 903 | propio | 3 |
| 904 | propia | 3 |
| 905 | promontorio | 3 |
| 906 | prisión | 3 |
| 907 | prevenido | 3 |
| 908 | precipita | 3 |
| 909 | prado | 3 |
| 910 | polvo | 3 |
| 911 | pollo | 3 |
| 912 | plomo | 3 |
| 913 | pisando | 3 |
| 914 | pisan | 3 |
| 915 | piedra | 3 |
| 916 | piedad | 3 |
| 917 | perdida | 3 |
| 918 | pequeña | 3 |
| 919 | penda | 3 |
| 920 | penas | 3 |
| 921 | peligro | 3 |
| 922 | peinar | 3 |
| 923 | peinado | 3 |
| 924 | patriota | 3 |
| 925 | pasa | 3 |
| 926 | papel | 3 |
| 927 | palas | 3 |
| 928 | paga | 3 |
| 929 | paces | 3 |
| 930 | oyó | 3 |
| 931 | otras | 3 |
| 932 | orilla | 3 |
| 933 | orden | 3 |
| 934 | orbe | 3 |
| 935 | ojo | 3 |
| 936 | ofrecen | 3 |
| 937 | oculta | 3 |
| 938 | ocëano | 3 |
| 939 | ocasiones | 3 |
| 940 | numeroso | 3 |
| 941 | números | 3 |
| 942 | nuevas | 3 |
| 943 | nueva | 3 |
| 944 | nuestro | 3 |
| 945 | nube | 3 |
| 946 | novios | 3 |
| 947 | novio | 3 |
| 948 | niebla | 3 |
| 949 | negra | 3 |
| 950 | nave | 3 |
| 951 | nadante | 3 |
| 952 | nace | 3 |
| 953 | mujer | 3 |
| 954 | mueve | 3 |
| 955 | muere | 3 |
| 956 | muera | 3 |
| 957 | mudas | 3 |
| 958 | muchas | 3 |
| 959 | mortal | 3 |
| 960 | mora | 3 |
| 961 | montañas | 3 |
| 962 | modo | 3 |
| 963 | mitad | 3 |
| 964 | mísero | 3 |
| 965 | milano | 3 |
| 966 | mías | 3 |
| 967 | meta | 3 |
| 968 | mayores | 3 |
| 969 | mariposa | 3 |
| 970 | marinero | 3 |
| 971 | márgenes | 3 |
| 972 | marfil | 3 |
| 973 | mañana | 3 |
| 974 | malicia | 3 |
| 975 | mala | 3 |
| 976 | luna | 3 |
| 977 | lozano | 3 |
| 978 | lleva | 3 |
| 979 | liso | 3 |
| 980 | líquidos | 3 |
| 981 | lince | 3 |
| 982 | limpio | 3 |
| 983 | leda | 3 |
| 984 | labradora | 3 |
| 985 | juventud | 3 |
| 986 | junco | 3 |
| 987 | jazmines | 3 |
| 988 | jardín | 3 |
| 989 | isleño | 3 |
| 990 | inquïeta | 3 |
| 991 | inmóvil | 3 |
| 992 | inmortal | 3 |
| 993 | inconstantes | 3 |
| 994 | impide | 3 |
| 995 | ii | 3 |
| 996 | iglesia | 3 |
| 997 | i | 3 |
| 998 | humano | 3 |
| 999 | hospedaje | 3 |
| 1000 | hombros | 3 |
| 1001 | hielo | 3 |
| 1002 | heno | 3 |
| 1003 | harto | 3 |
| 1004 | haré | 3 |
| 1005 | hacienda | 3 |
| 1006 | guardó | 3 |
| 1007 | grillos | 3 |
| 1008 | granada | 3 |
| 1009 | grana | 3 |
| 1010 | globos | 3 |
| 1011 | generoso | 3 |
| 1012 | generosa | 3 |
| 1013 | ganado | 3 |
| 1014 | galán | 3 |
| 1015 | fulminante | 3 |
| 1016 | fuerzas | 3 |
| 1017 | fueran | 3 |
| 1018 | fragoso | 3 |
| 1019 | forma | 3 |
| 1020 | floreciente | 3 |
| 1021 | flor | 3 |
| 1022 | fïel | 3 |
| 1023 | fïado | 3 |
| 1024 | feroz | 3 |
| 1025 | fénix | 3 |
| 1026 | felices | 3 |
| 1027 | febo | 3 |
| 1028 | favores | 3 |
| 1029 | fatal | 3 |
| 1030 | fama | 3 |
| 1031 | experiencias | 3 |
| 1032 | examina | 3 |
| 1033 | estruendo | 3 |
| 1034 | éstos | 3 |
| 1035 | estos | 3 |
| 1036 | están | 3 |
| 1037 | estambre | 3 |
| 1038 | esquina | 3 |
| 1039 | espuela | 3 |
| 1040 | esposo | 3 |
| 1041 | españa | 3 |
| 1042 | espada | 3 |
| 1043 | escuadrón | 3 |
| 1044 | escuadra | 3 |
| 1045 | escondido | 3 |
| 1046 | esclarecido | 3 |
| 1047 | escamada | 3 |
| 1048 | escala | 3 |
| 1049 | esas | 3 |
| 1050 | esa | 3 |
| 1051 | engendra | 3 |
| 1052 | emulación | 3 |
| 1053 | eminente | 3 |
| 1054 | ejido | 3 |
| 1055 | ejercicio | 3 |
| 1056 | egipto | 3 |
| 1057 | éfire | 3 |
| 1058 | edificio | 3 |
| 1059 | eco | 3 |
| 1060 | dudosa | 3 |
| 1061 | dudo | 3 |
| 1062 | ducados | 3 |
| 1063 | dora | 3 |
| 1064 | dónde | 3 |
| 1065 | doliente | 3 |
| 1066 | doctrina | 3 |
| 1067 | dividido | 3 |
| 1068 | divide | 3 |
| 1069 | distancia | 3 |
| 1070 | diosa | 3 |
| 1071 | diga | 3 |
| 1072 | diera | 3 |
| 1073 | dicho | 3 |
| 1074 | dicha | 3 |
| 1075 | destas | 3 |
| 1076 | despedido | 3 |
| 1077 | desnudos | 3 |
| 1078 | desigual | 3 |
| 1079 | desengaño | 3 |
| 1080 | desatados | 3 |
| 1081 | desatado | 3 |
| 1082 | delfín | 3 |
| 1083 | dejo | 3 |
| 1084 | deidades | 3 |
| 1085 | decoro | 3 |
| 1086 | decir | 3 |
| 1087 | debajo | 3 |
| 1088 | damas | 3 |
| 1089 | cuerda | 3 |
| 1090 | cuello | 3 |
| 1091 | cuántas | 3 |
| 1092 | cruel | 3 |
| 1093 | cristalino | 3 |
| 1094 | creo | 3 |
| 1095 | cortesía | 3 |
| 1096 | corriente | 3 |
| 1097 | corre | 3 |
| 1098 | coronan | 3 |
| 1099 | coronada | 3 |
| 1100 | coral | 3 |
| 1101 | copa | 3 |
| 1102 | convoca | 3 |
| 1103 | confusión | 3 |
| 1104 | confusa | 3 |
| 1105 | conduce | 3 |
| 1106 | condición | 3 |
| 1107 | compañía | 3 |
| 1108 | comida | 3 |
| 1109 | columnas | 3 |
| 1110 | color | 3 |
| 1111 | clava | 3 |
| 1112 | clara | 3 |
| 1113 | cisnes | 3 |
| 1114 | ciñe | 3 |
| 1115 | cierta | 3 |
| 1116 | cielos | 3 |
| 1117 | cíclope | 3 |
| 1118 | chupa | 3 |
| 1119 | chopos | 3 |
| 1120 | cerúlea | 3 |
| 1121 | ceniza | 3 |
| 1122 | céfiro | 3 |
| 1123 | cebarse | 3 |
| 1124 | casta | 3 |
| 1125 | carroza | 3 |
| 1126 | carmesíes | 3 |
| 1127 | cansado | 3 |
| 1128 | cansada | 3 |
| 1129 | caminante | 3 |
| 1130 | caló | 3 |
| 1131 | cajas | 3 |
| 1132 | cabeza | 3 |
| 1133 | bronce | 3 |
| 1134 | brava | 3 |
| 1135 | bosques | 3 |
| 1136 | bodas | 3 |
| 1137 | bocas | 3 |
| 1138 | besó | 3 |
| 1139 | besar | 3 |
| 1140 | beldad | 3 |
| 1141 | batel | 3 |
| 1142 | bárbaros | 3 |
| 1143 | balcón | 3 |
| 1144 | baharí | 3 |
| 1145 | ay | 3 |
| 1146 | austro | 3 |
| 1147 | asta | 3 |
| 1148 | artificio | 3 |
| 1149 | artífice | 3 |
| 1150 | arrogante | 3 |
| 1151 | armados | 3 |
| 1152 | armado | 3 |
| 1153 | argenta | 3 |
| 1154 | arco | 3 |
| 1155 | árbol | 3 |
| 1156 | árbitro | 3 |
| 1157 | aquello | 3 |
| 1158 | apela | 3 |
| 1159 | animoso | 3 |
| 1160 | animal | 3 |
| 1161 | anciano | 3 |
| 1162 | amiga | 3 |
| 1163 | ambas | 3 |
| 1164 | amantes | 3 |
| 1165 | ama | 3 |
| 1166 | alterada | 3 |
| 1167 | altera | 3 |
| 1168 | almenas | 3 |
| 1169 | aliento | 3 |
| 1170 | algunas | 3 |
| 1171 | algún | 3 |
| 1172 | alegre | 3 |
| 1173 | aldea | 3 |
| 1174 | albogues | 3 |
| 1175 | albergues | 3 |
| 1176 | ala | 3 |
| 1177 | aires | 3 |
| 1178 | adora | 3 |
| 1179 | adonde | 3 |
| 1180 | acompañada | 3 |
| 1181 | acaba | 3 |
| 1182 | acá | 3 |
| 1183 | zurrón | 2 |
| 1184 | zagala | 2 |
| 1185 | yerro | 2 |
| 1186 | yedra | 2 |
| 1187 | vulgo | 2 |
| 1188 | vulcano | 2 |
| 1189 | vuestra | 2 |
| 1190 | vuelven | 2 |
| 1191 | voyme | 2 |
| 1192 | vos | 2 |
| 1193 | volando | 2 |
| 1194 | vivid | 2 |
| 1195 | vive | 2 |
| 1196 | viva | 2 |
| 1197 | violín | 2 |
| 1198 | violencia | 2 |
| 1199 | víolas | 2 |
| 1200 | vinos | 2 |
| 1201 | vínculo | 2 |
| 1202 | villanas | 2 |
| 1203 | villana | 2 |
| 1204 | vihuela | 2 |
| 1205 | vigilantes | 2 |
| 1206 | vientos | 2 |
| 1207 | viene | 2 |
| 1208 | vete | 2 |
| 1209 | vestir | 2 |
| 1210 | versos | 2 |
| 1211 | verdura | 2 |
| 1212 | venir | 2 |
| 1213 | venga | 2 |
| 1214 | vendado | 2 |
| 1215 | vencido | 2 |
| 1216 | vemos | 2 |
| 1217 | vaso | 2 |
| 1218 | vario | 2 |
| 1219 | vara | 2 |
| 1220 | valientes | 2 |
| 1221 | vagas | 2 |
| 1222 | vaca | 2 |
| 1223 | urbana | 2 |
| 1224 | único | 2 |
| 1225 | umbroso | 2 |
| 1226 | turbante | 2 |
| 1227 | trueno | 2 |
| 1228 | trompeta | 2 |
| 1229 | trofeos | 2 |
| 1230 | tritón | 2 |
| 1231 | tridente | 2 |
| 1232 | trenzas | 2 |
| 1233 | trémulos | 2 |
| 1234 | treinta | 2 |
| 1235 | travieso | 2 |
| 1236 | traidor | 2 |
| 1237 | traía | 2 |
| 1238 | torres | 2 |
| 1239 | torpes | 2 |
| 1240 | torneado | 2 |
| 1241 | torció | 2 |
| 1242 | tocas | 2 |
| 1243 | tirio | 2 |
| 1244 | tiria | 2 |
| 1245 | tirano | 2 |
| 1246 | tinieblas | 2 |
| 1247 | tibia | 2 |
| 1248 | terno | 2 |
| 1249 | tendido | 2 |
| 1250 | temer | 2 |
| 1251 | tejiendo | 2 |
| 1252 | tejía | 2 |
| 1253 | tejado | 2 |
| 1254 | tea | 2 |
| 1255 | suyas | 2 |
| 1256 | surcar | 2 |
| 1257 | surca | 2 |
| 1258 | sujeto | 2 |
| 1259 | sucede | 2 |
| 1260 | suceda | 2 |
| 1261 | sube | 2 |
| 1262 | sospecha | 2 |
| 1263 | sorda | 2 |
| 1264 | sonoroso | 2 |
| 1265 | sola | 2 |
| 1266 | soberano | 2 |
| 1267 | sitïal | 2 |
| 1268 | sirvieron | 2 |
| 1269 | sirve | 2 |
| 1270 | siendo | 2 |
| 1271 | servirte | 2 |
| 1272 | servido | 2 |
| 1273 | sepulcros | 2 |
| 1274 | sepa | 2 |
| 1275 | seña | 2 |
| 1276 | sella | 2 |
| 1277 | segur | 2 |
| 1278 | sed | 2 |
| 1279 | sayal | 2 |
| 1280 | sátiros | 2 |
| 1281 | sátiro | 2 |
| 1282 | santo | 2 |
| 1283 | saludó | 2 |
| 1284 | saluda | 2 |
| 1285 | salió | 2 |
| 1286 | salimos | 2 |
| 1287 | salía | 2 |
| 1288 | sacudido | 2 |
| 1289 | saca | 2 |
| 1290 | sabio | 2 |
| 1291 | sabes | 2 |
| 1292 | sabandijas | 2 |
| 1293 | ruiseñor | 2 |
| 1294 | rüinas | 2 |
| 1295 | ruin | 2 |
| 1296 | ruego | 2 |
| 1297 | rudos | 2 |
| 1298 | rudo | 2 |
| 1299 | rosicler | 2 |
| 1300 | ronca | 2 |
| 1301 | rompen | 2 |
| 1302 | rocío | 2 |
| 1303 | roble | 2 |
| 1304 | rival | 2 |
| 1305 | risueña | 2 |
| 1306 | riscos | 2 |
| 1307 | rindió | 2 |
| 1308 | riberas | 2 |
| 1309 | reyes | 2 |
| 1310 | rey | 2 |
| 1311 | revoca | 2 |
| 1312 | retórica | 2 |
| 1313 | resuelven | 2 |
| 1314 | restituyen | 2 |
| 1315 | restituye | 2 |
| 1316 | responda | 2 |
| 1317 | resplandeciente | 2 |
| 1318 | reposo | 2 |
| 1319 | religión | 2 |
| 1320 | reino | 2 |
| 1321 | reina | 2 |
| 1322 | regiones | 2 |
| 1323 | redujo | 2 |
| 1324 | redimió | 2 |
| 1325 | redil | 2 |
| 1326 | red | 2 |
| 1327 | reclamo | 2 |
| 1328 | rayaba | 2 |
| 1329 | raros | 2 |
| 1330 | ramo | 2 |
| 1331 | rabiar | 2 |
| 1332 | quería | 2 |
| 1333 | querellas | 2 |
| 1334 | queja | 2 |
| 1335 | quédese | 2 |
| 1336 | puso | 2 |
| 1337 | purpúrea | 2 |
| 1338 | punto | 2 |
| 1339 | puntas | 2 |
| 1340 | puesto | 2 |
| 1341 | puerto | 2 |
| 1342 | prora | 2 |
| 1343 | profundo | 2 |
| 1344 | profunda | 2 |
| 1345 | procura | 2 |
| 1346 | privilegios | 2 |
| 1347 | principio | 2 |
| 1348 | príncipe | 2 |
| 1349 | primera | 2 |
| 1350 | previno | 2 |
| 1351 | previene | 2 |
| 1352 | pretendida | 2 |
| 1353 | presuma | 2 |
| 1354 | presto | 2 |
| 1355 | prendas | 2 |
| 1356 | precisa | 2 |
| 1357 | precedente | 2 |
| 1358 | pórfidos | 2 |
| 1359 | ponzoña | 2 |
| 1360 | pomos | 2 |
| 1361 | pomona | 2 |
| 1362 | pólvora | 2 |
| 1363 | pollos | 2 |
| 1364 | político | 2 |
| 1365 | política | 2 |
| 1366 | policena | 2 |
| 1367 | podrá | 2 |
| 1368 | podías | 2 |
| 1369 | podía | 2 |
| 1370 | pobres | 2 |
| 1371 | pluvia | 2 |
| 1372 | piscatorio | 2 |
| 1373 | pisaba | 2 |
| 1374 | pirineo | 2 |
| 1375 | pintadas | 2 |
| 1376 | pinos | 2 |
| 1377 | pincel | 2 |
| 1378 | piloto | 2 |
| 1379 | pierde | 2 |
| 1380 | piélagos | 2 |
| 1381 | piélago | 2 |
| 1382 | pido | 2 |
| 1383 | pidió | 2 |
| 1384 | pide | 2 |
| 1385 | picos | 2 |
| 1386 | pico | 2 |
| 1387 | pías | 2 |
| 1388 | piadoso | 2 |
| 1389 | pesquisidor | 2 |
| 1390 | pesquería | 2 |
| 1391 | peso | 2 |
| 1392 | pescados | 2 |
| 1393 | pescador | 2 |
| 1394 | pesadumbre | 2 |
| 1395 | personas | 2 |
| 1396 | permitió | 2 |
| 1397 | perezosas | 2 |
| 1398 | peregrina | 2 |
| 1399 | perdonó | 2 |
| 1400 | pequeños | 2 |
| 1401 | peñasco | 2 |
| 1402 | penetra | 2 |
| 1403 | pena | 2 |
| 1404 | pelota | 2 |
| 1405 | pelo | 2 |
| 1406 | peligrosas | 2 |
| 1407 | peina | 2 |
| 1408 | pedernal | 2 |
| 1409 | pedazos | 2 |
| 1410 | paz | 2 |
| 1411 | partí | 2 |
| 1412 | partes | 2 |
| 1413 | parir | 2 |
| 1414 | pario | 2 |
| 1415 | paredes | 2 |
| 1416 | parece | 2 |
| 1417 | pardo | 2 |
| 1418 | pan | 2 |
| 1419 | palomas | 2 |
| 1420 | palios | 2 |
| 1421 | palestra | 2 |
| 1422 | palemo | 2 |
| 1423 | palacios | 2 |
| 1424 | palabras | 2 |
| 1425 | pace | 2 |
| 1426 | pabellón | 2 |
| 1427 | oya | 2 |
| 1428 | ovas | 2 |
| 1429 | otoño | 2 |
| 1430 | orillas | 2 |
| 1431 | opuesta | 2 |
| 1432 | olvido | 2 |
| 1433 | olas | 2 |
| 1434 | oía | 2 |
| 1435 | ofrenda | 2 |
| 1436 | ofreció | 2 |
| 1437 | oficina | 2 |
| 1438 | ocupando | 2 |
| 1439 | ocupa | 2 |
| 1440 | oculto | 2 |
| 1441 | ocioso | 2 |
| 1442 | ocasión | 2 |
| 1443 | obscuro | 2 |
| 1444 | obras | 2 |
| 1445 | oblicuos | 2 |
| 1446 | obeliscos | 2 |
| 1447 | obedeciendo | 2 |
| 1448 | nupcial | 2 |
| 1449 | nuevos | 2 |
| 1450 | nuestros | 2 |
| 1451 | nudoso | 2 |
| 1452 | nudo | 2 |
| 1453 | noto | 2 |
| 1454 | nocturnas | 2 |
| 1455 | ninguno | 2 |
| 1456 | nieblas | 2 |
| 1457 | nevada | 2 |
| 1458 | nervios | 2 |
| 1459 | negligente | 2 |
| 1460 | negar | 2 |
| 1461 | neblí | 2 |
| 1462 | náutica | 2 |
| 1463 | náufrago | 2 |
| 1464 | naufragio | 2 |
| 1465 | natural | 2 |
| 1466 | música | 2 |
| 1467 | musas | 2 |
| 1468 | musa | 2 |
| 1469 | muralla | 2 |
| 1470 | muerde | 2 |
| 1471 | mudos | 2 |
| 1472 | moro | 2 |
| 1473 | mordía | 2 |
| 1474 | morder | 2 |
| 1475 | moradores | 2 |
| 1476 | montañeses | 2 |
| 1477 | monstro | 2 |
| 1478 | monarquía | 2 |
| 1479 | mohína | 2 |
| 1480 | mismo | 2 |
| 1481 | miserablemente | 2 |
| 1482 | misa | 2 |
| 1483 | mirto | 2 |
| 1484 | mimbres | 2 |
| 1485 | mimbre | 2 |
| 1486 | mieses | 2 |
| 1487 | métrico | 2 |
| 1488 | mercedes | 2 |
| 1489 | merced | 2 |
| 1490 | mentir | 2 |
| 1491 | mentido | 2 |
| 1492 | memorias | 2 |
| 1493 | membrudo | 2 |
| 1494 | membrillo | 2 |
| 1495 | melancólico | 2 |
| 1496 | mejores | 2 |
| 1497 | media | 2 |
| 1498 | mayo | 2 |
| 1499 | matizado | 2 |
| 1500 | marte | 2 |
| 1501 | marina | 2 |
| 1502 | margen | 2 |
| 1503 | mapa | 2 |
| 1504 | manteles | 2 |
| 1505 | manera | 2 |
| 1506 | manchada | 2 |
| 1507 | malo | 2 |
| 1508 | malicias | 2 |
| 1509 | maestra | 2 |
| 1510 | lustro | 2 |
| 1511 | lunas | 2 |
| 1512 | luceros | 2 |
| 1513 | lúbrica | 2 |
| 1514 | loco | 2 |
| 1515 | lobo | 2 |
| 1516 | llora | 2 |
| 1517 | llevó | 2 |
| 1518 | llevas | 2 |
| 1519 | lleno | 2 |
| 1520 | llegaron | 2 |
| 1521 | llega | 2 |
| 1522 | llana | 2 |
| 1523 | llamo | 2 |
| 1524 | llamas | 2 |
| 1525 | llamarme | 2 |
| 1526 | llamar | 2 |
| 1527 | livia | 2 |
| 1528 | lisonjear | 2 |
| 1529 | líquidas | 2 |
| 1530 | limpia | 2 |
| 1531 | libre | 2 |
| 1532 | libra | 2 |
| 1533 | líbico | 2 |
| 1534 | liba | 2 |
| 1535 | leves | 2 |
| 1536 | leteo | 2 |
| 1537 | leños | 2 |
| 1538 | lejos | 2 |
| 1539 | lee | 2 |
| 1540 | laurel | 2 |
| 1541 | lastimosas | 2 |
| 1542 | lana | 2 |
| 1543 | lámina | 2 |
| 1544 | lambicando | 2 |
| 1545 | laguna | 2 |
| 1546 | labrado | 2 |
| 1547 | labio | 2 |
| 1548 | juntos | 2 |
| 1549 | junto | 2 |
| 1550 | juntar | 2 |
| 1551 | juno | 2 |
| 1552 | jóvenes | 2 |
| 1553 | jaspes | 2 |
| 1554 | istmo | 2 |
| 1555 | intonso | 2 |
| 1556 | intención | 2 |
| 1557 | intempestiva | 2 |
| 1558 | instante | 2 |
| 1559 | ingrato | 2 |
| 1560 | ingrata | 2 |
| 1561 | ingenïoso | 2 |
| 1562 | ingenïosa | 2 |
| 1563 | infamó | 2 |
| 1564 | industria | 2 |
| 1565 | indigna | 2 |
| 1566 | incierto | 2 |
| 1567 | incauto | 2 |
| 1568 | impulso | 2 |
| 1569 | improvisa | 2 |
| 1570 | importuno | 2 |
| 1571 | importa | 2 |
| 1572 | impedida | 2 |
| 1573 | imitar | 2 |
| 1574 | imitador | 2 |
| 1575 | imita | 2 |
| 1576 | imaginación | 2 |
| 1577 | igualmente | 2 |
| 1578 | iguala | 2 |
| 1579 | ignoran | 2 |
| 1580 | ignora | 2 |
| 1581 | iba | 2 |
| 1582 | huso | 2 |
| 1583 | hurta | 2 |
| 1584 | humor | 2 |
| 1585 | humilde | 2 |
| 1586 | huevos | 2 |
| 1587 | hueso | 2 |
| 1588 | hospedado | 2 |
| 1589 | horrenda | 2 |
| 1590 | hormigas | 2 |
| 1591 | horizontes | 2 |
| 1592 | honre | 2 |
| 1593 | honrado | 2 |
| 1594 | honesta | 2 |
| 1595 | hombres | 2 |
| 1596 | historia | 2 |
| 1597 | hierbas | 2 |
| 1598 | hiedras | 2 |
| 1599 | hicieron | 2 |
| 1600 | hermanos | 2 |
| 1601 | herida | 2 |
| 1602 | hércules | 2 |
| 1603 | hayas | 2 |
| 1604 | haya | 2 |
| 1605 | halle | 2 |
| 1606 | hablan | 2 |
| 1607 | guerra | 2 |
| 1608 | guarnición | 2 |
| 1609 | guarda | 2 |
| 1610 | guante | 2 |
| 1611 | guadaña | 2 |
| 1612 | gruesas | 2 |
| 1613 | grosero | 2 |
| 1614 | grillo | 2 |
| 1615 | greña | 2 |
| 1616 | granos | 2 |
| 1617 | grandezas | 2 |
| 1618 | grande | 2 |
| 1619 | grama | 2 |
| 1620 | gracia | 2 |
| 1621 | goza | 2 |
| 1622 | golpe | 2 |
| 1623 | gloriosas | 2 |
| 1624 | glorïosa | 2 |
| 1625 | glauco | 2 |
| 1626 | gimiendo | 2 |
| 1627 | gerifalte | 2 |
| 1628 | gentil | 2 |
| 1629 | generosos | 2 |
| 1630 | género | 2 |
| 1631 | gemidos | 2 |
| 1632 | gemido | 2 |
| 1633 | garzones | 2 |
| 1634 | ganges | 2 |
| 1635 | ganados | 2 |
| 1636 | gallarda | 2 |
| 1637 | gala | 2 |
| 1638 | fulminada | 2 |
| 1639 | fugitivos | 2 |
| 1640 | fugitivo | 2 |
| 1641 | fuertes | 2 |
| 1642 | fueron | 2 |
| 1643 | fuentes | 2 |
| 1644 | fuegos | 2 |
| 1645 | frondoso | 2 |
| 1646 | frío | 2 |
| 1647 | fresca | 2 |
| 1648 | fragosa | 2 |
| 1649 | frágil | 2 |
| 1650 | fragantes | 2 |
| 1651 | forzado | 2 |
| 1652 | formidable | 2 |
| 1653 | formando | 2 |
| 1654 | focas | 2 |
| 1655 | foca | 2 |
| 1656 | flamenco | 2 |
| 1657 | firmes | 2 |
| 1658 | firme | 2 |
| 1659 | finos | 2 |
| 1660 | fino | 2 |
| 1661 | finezas | 2 |
| 1662 | fina | 2 |
| 1663 | filos | 2 |
| 1664 | fijo | 2 |
| 1665 | fieras | 2 |
| 1666 | fïeles | 2 |
| 1667 | fía | 2 |
| 1668 | festivos | 2 |
| 1669 | fecundo | 2 |
| 1670 | fecunda | 2 |
| 1671 | fatiga | 2 |
| 1672 | farol | 2 |
| 1673 | fanal | 2 |
| 1674 | falta | 2 |
| 1675 | faetón | 2 |
| 1676 | extraño | 2 |
| 1677 | extranjeros | 2 |
| 1678 | exprimida | 2 |
| 1679 | experimentar | 2 |
| 1680 | exceda | 2 |
| 1681 | estrecha | 2 |
| 1682 | estigia | 2 |
| 1683 | éste | 2 |
| 1684 | estás | 2 |
| 1685 | espumosa | 2 |
| 1686 | esplendores | 2 |
| 1687 | espinas | 2 |
| 1688 | espigas | 2 |
| 1689 | espesura | 2 |
| 1690 | espejos | 2 |
| 1691 | espejo | 2 |
| 1692 | espaldas | 2 |
| 1693 | espacioso | 2 |
| 1694 | espacio | 2 |
| 1695 | escudero | 2 |
| 1696 | escrita | 2 |
| 1697 | escogió | 2 |
| 1698 | escena | 2 |
| 1699 | escariote | 2 |
| 1700 | escamas | 2 |
| 1701 | escamado | 2 |
| 1702 | erigió | 2 |
| 1703 | entrara | 2 |
| 1704 | entraos | 2 |
| 1705 | entonces | 2 |
| 1706 | enjugó | 2 |
| 1707 | enjambre | 2 |
| 1708 | engendradora | 2 |
| 1709 | engasta | 2 |
| 1710 | engaños | 2 |
| 1711 | engaña | 2 |
| 1712 | enemiga | 2 |
| 1713 | émula | 2 |
| 1714 | embiste | 2 |
| 1715 | elevada | 2 |
| 1716 | efecto | 2 |
| 1717 | edificios | 2 |
| 1718 | ecos | 2 |
| 1719 | eclíptica | 2 |
| 1720 | duque | 2 |
| 1721 | dulcísimas | 2 |
| 1722 | dueña | 2 |
| 1723 | doy | 2 |
| 1724 | dote | 2 |
| 1725 | doris | 2 |
| 1726 | doral | 2 |
| 1727 | dorada | 2 |
| 1728 | doce | 2 |
| 1729 | doble | 2 |
| 1730 | divina | 2 |
| 1731 | dividida | 2 |
| 1732 | disposición | 2 |
| 1733 | disonante | 2 |
| 1734 | disformes | 2 |
| 1735 | dirigió | 2 |
| 1736 | dilo | 2 |
| 1737 | diligencia | 2 |
| 1738 | digna | 2 |
| 1739 | digas | 2 |
| 1740 | dieron | 2 |
| 1741 | dictó | 2 |
| 1742 | dichosa | 2 |
| 1743 | dicen | 2 |
| 1744 | diáfanos | 2 |
| 1745 | dïáfano | 2 |
| 1746 | devoto | 2 |
| 1747 | desvíos | 2 |
| 1748 | desvarío | 2 |
| 1749 | destierro | 2 |
| 1750 | despliega | 2 |
| 1751 | desplegó | 2 |
| 1752 | despierto | 2 |
| 1753 | despidiendo | 2 |
| 1754 | deseando | 2 |
| 1755 | desdichas | 2 |
| 1756 | desdeña | 2 |
| 1757 | desciende | 2 |
| 1758 | desatarse | 2 |
| 1759 | desafía | 2 |
| 1760 | delicias | 2 |
| 1761 | déjate | 2 |
| 1762 | dejan | 2 |
| 1763 | dedos | 2 |
| 1764 | dédalo | 2 |
| 1765 | decillo | 2 |
| 1766 | debo | 2 |
| 1767 | deba | 2 |
| 1768 | dé | 2 |
| 1769 | dardo | 2 |
| 1770 | daños | 2 |
| 1771 | daba | 2 |
| 1772 | curiosa | 2 |
| 1773 | culpas | 2 |
| 1774 | culpa | 2 |
| 1775 | cueva | 2 |
| 1776 | cuernos | 2 |
| 1777 | cuchillo | 2 |
| 1778 | cristalina | 2 |
| 1779 | crepúsculos | 2 |
| 1780 | coyundas | 2 |
| 1781 | coturno | 2 |
| 1782 | cortinas | 2 |
| 1783 | cortezas | 2 |
| 1784 | corteses | 2 |
| 1785 | corta | 2 |
| 1786 | correspondido | 2 |
| 1787 | correr | 2 |
| 1788 | corren | 2 |
| 1789 | coronó | 2 |
| 1790 | corazón | 2 |
| 1791 | corales | 2 |
| 1792 | copos | 2 |
| 1793 | copo | 2 |
| 1794 | convida | 2 |
| 1795 | convecino | 2 |
| 1796 | contento | 2 |
| 1797 | contado | 2 |
| 1798 | consiente | 2 |
| 1799 | conoce | 2 |
| 1800 | conjunción | 2 |
| 1801 | confusos | 2 |
| 1802 | confusamente | 2 |
| 1803 | confunde | 2 |
| 1804 | confío | 2 |
| 1805 | conducidos | 2 |
| 1806 | conducida | 2 |
| 1807 | condenó | 2 |
| 1808 | concurso | 2 |
| 1809 | concurren | 2 |
| 1810 | conculcado | 2 |
| 1811 | concha | 2 |
| 1812 | concedió | 2 |
| 1813 | cómo | 2 |
| 1814 | coluna | 2 |
| 1815 | colorido | 2 |
| 1816 | codicia | 2 |
| 1817 | cloto | 2 |
| 1818 | clima | 2 |
| 1819 | claveles | 2 |
| 1820 | clavel | 2 |
| 1821 | claro | 2 |
| 1822 | civil | 2 |
| 1823 | ciudades | 2 |
| 1824 | ciudad | 2 |
| 1825 | cintia | 2 |
| 1826 | chozas | 2 |
| 1827 | chopo | 2 |
| 1828 | césped | 2 |
| 1829 | cerviz | 2 |
| 1830 | cerúleas | 2 |
| 1831 | cerros | 2 |
| 1832 | ceremonia | 2 |
| 1833 | cerdas | 2 |
| 1834 | cercado | 2 |
| 1835 | centro | 2 |
| 1836 | centellas | 2 |
| 1837 | cenit | 2 |
| 1838 | celosa | 2 |
| 1839 | celos | 2 |
| 1840 | celestial | 2 |
| 1841 | celdas | 2 |
| 1842 | céfiros | 2 |
| 1843 | cedió | 2 |
| 1844 | cayado | 2 |
| 1845 | cautelas | 2 |
| 1846 | caudales | 2 |
| 1847 | caso | 2 |
| 1848 | casamentero | 2 |
| 1849 | cartas | 2 |
| 1850 | cartago | 2 |
| 1851 | carrizos | 2 |
| 1852 | cargas | 2 |
| 1853 | carga | 2 |
| 1854 | caracoles | 2 |
| 1855 | caracol | 2 |
| 1856 | cañas | 2 |
| 1857 | caña | 2 |
| 1858 | canos | 2 |
| 1859 | canora | 2 |
| 1860 | candil | 2 |
| 1861 | cándidas | 2 |
| 1862 | canales | 2 |
| 1863 | cana | 2 |
| 1864 | camina | 2 |
| 1865 | cambaya | 2 |
| 1866 | cama | 2 |
| 1867 | calzó | 2 |
| 1868 | califique | 2 |
| 1869 | calidad | 2 |
| 1870 | caduco | 2 |
| 1871 | cadena | 2 |
| 1872 | cabrero | 2 |
| 1873 | caballos | 2 |
| 1874 | buscar | 2 |
| 1875 | buscaba | 2 |
| 1876 | burlado | 2 |
| 1877 | bulto | 2 |
| 1878 | bueyes | 2 |
| 1879 | bruñida | 2 |
| 1880 | brújula | 2 |
| 1881 | brazos | 2 |
| 1882 | brazo | 2 |
| 1883 | bozo | 2 |
| 1884 | bóvedas | 2 |
| 1885 | boj | 2 |
| 1886 | bienes | 2 |
| 1887 | betis | 2 |
| 1888 | bese | 2 |
| 1889 | bebe | 2 |
| 1890 | bastón | 2 |
| 1891 | basta | 2 |
| 1892 | basa | 2 |
| 1893 | bárbaro | 2 |
| 1894 | barba | 2 |
| 1895 | banderas | 2 |
| 1896 | baja | 2 |
| 1897 | baile | 2 |
| 1898 | bailando | 2 |
| 1899 | azules | 2 |
| 1900 | ayuno | 2 |
| 1901 | ausente | 2 |
| 1902 | ausencia | 2 |
| 1903 | aura | 2 |
| 1904 | atribuye | 2 |
| 1905 | atrevido | 2 |
| 1906 | atravesado | 2 |
| 1907 | atenta | 2 |
| 1908 | atención | 2 |
| 1909 | atalaya | 2 |
| 1910 | astrólogo | 2 |
| 1911 | áspides | 2 |
| 1912 | asombro | 2 |
| 1913 | aseo | 2 |
| 1914 | ascálafo | 2 |
| 1915 | artificiosa | 2 |
| 1916 | arrepentido | 2 |
| 1917 | arrebata | 2 |
| 1918 | arpón | 2 |
| 1919 | aromas | 2 |
| 1920 | armó | 2 |
| 1921 | argos | 2 |
| 1922 | ardientes | 2 |
| 1923 | arcos | 2 |
| 1924 | arabia | 2 |
| 1925 | aqueste | 2 |
| 1926 | aquéllos | 2 |
| 1927 | aquéllas | 2 |
| 1928 | apetito | 2 |
| 1929 | año | 2 |
| 1930 | anudado | 2 |
| 1931 | antiguo | 2 |
| 1932 | anotomía | 2 |
| 1933 | andas | 2 |
| 1934 | anda | 2 |
| 1935 | ameno | 2 |
| 1936 | ambición | 2 |
| 1937 | amada | 2 |
| 1938 | alterna | 2 |
| 1939 | alquerías | 2 |
| 1940 | aljófares | 2 |
| 1941 | algo | 2 |
| 1942 | alfombras | 2 |
| 1943 | aldehuela | 2 |
| 1944 | aldeas | 2 |
| 1945 | alcalde | 2 |
| 1946 | alcaide | 2 |
| 1947 | alcabala | 2 |
| 1948 | álamos | 2 |
| 1949 | aladas | 2 |
| 1950 | aguarda | 2 |
| 1951 | agricultura | 2 |
| 1952 | agradecida | 2 |
| 1953 | agilidad | 2 |
| 1954 | ágil | 2 |
| 1955 | aflija | 2 |
| 1956 | afición | 2 |
| 1957 | admire | 2 |
| 1958 | admirado | 2 |
| 1959 | acusando | 2 |
| 1960 | acento | 2 |
| 1961 | abril | 2 |
| 1962 | abriga | 2 |
| 1963 | abrevia | 2 |
| 1964 | abrazados | 2 |
| 1965 | abrazado | 2 |
| 1966 | abraza | 2 |
| 1967 | abra | 2 |
| 1968 | abetos | 2 |
| 1969 | abeto | 2 |
| 1970 | abaten | 2 |
| 1971 | zona | 1 |
| 1972 | zodíaco | 1 |
| 1973 | zaragoza | 1 |
| 1974 | zampoñas | 1 |
| 1975 | zahareña | 1 |
| 1976 | zagales | 1 |
| 1977 | zagalejas | 1 |
| 1978 | yerra | 1 |
| 1979 | yernos | 1 |
| 1980 | yerno | 1 |
| 1981 | yacen | 1 |
| 1982 | vulgares | 1 |
| 1983 | vulgar | 1 |
| 1984 | vuestro | 1 |
| 1985 | vuélvete | 1 |
| 1986 | vuelve | 1 |
| 1987 | vuelta | 1 |
| 1988 | vuelas | 1 |
| 1989 | voto | 1 |
| 1990 | votado | 1 |
| 1991 | vosotras | 1 |
| 1992 | voraz | 1 |
| 1993 | vomitó | 1 |
| 1994 | vomitar | 1 |
| 1995 | vomitando | 1 |
| 1996 | vomitado | 1 |
| 1997 | volvíase | 1 |
| 1998 | volverme | 1 |
| 1999 | voluntad | 1 |
| 2000 | volubles | 1 |
| 2001 | volga | 1 |
| 2002 | volcán | 1 |
| 2003 | vivo | 1 |
| 2004 | vivificando | 1 |
| 2005 | vividos | 1 |
| 2006 | vividores | 1 |
| 2007 | vivaz | 1 |
| 2008 | vital | 1 |
| 2009 | vistosa | 1 |
| 2010 | visto | 1 |
| 2011 | vistiendo | 1 |
| 2012 | vistan | 1 |
| 2013 | viscoso | 1 |
| 2014 | viscosamente | 1 |
| 2015 | virtud | 1 |
| 2016 | virotes | 1 |
| 2017 | viril | 1 |
| 2018 | vírgenes | 1 |
| 2019 | violentando | 1 |
| 2020 | vïolencia | 1 |
| 2021 | vïolas | 1 |
| 2022 | violaron | 1 |
| 2023 | vïolar | 1 |
| 2024 | violantes | 1 |
| 2025 | vïolador | 1 |
| 2026 | violado | 1 |
| 2027 | violada | 1 |
| 2028 | vínose | 1 |
| 2029 | vino | 1 |
| 2030 | viniera | 1 |
| 2031 | vinculó | 1 |
| 2032 | vinculen | 1 |
| 2033 | vincule | 1 |
| 2034 | vincular | 1 |
| 2035 | vinculan | 1 |
| 2036 | vinculados | 1 |
| 2037 | villanaje | 1 |
| 2038 | vil | 1 |
| 2039 | vierte | 1 |
| 2040 | vieras | 1 |
| 2041 | viejos | 1 |
| 2042 | vidrio | 1 |
| 2043 | vidrïera | 1 |
| 2044 | vid | 1 |
| 2045 | victoria | 1 |
| 2046 | viciosa | 1 |
| 2047 | vicio | 1 |
| 2048 | vibrante | 1 |
| 2049 | víbora | 1 |
| 2050 | viales | 1 |
| 2051 | vestidos | 1 |
| 2052 | ves | 1 |
| 2053 | vertumno | 1 |
| 2054 | verso | 1 |
| 2055 | vernos | 1 |
| 2056 | vergonzoso | 1 |
| 2057 | vergonzosas | 1 |
| 2058 | vergonzosa | 1 |
| 2059 | verdaderos | 1 |
| 2060 | verdadera | 1 |
| 2061 | verás | 1 |
| 2062 | veras | 1 |
| 2063 | verano | 1 |
| 2064 | venza | 1 |
| 2065 | venturoso | 1 |
| 2066 | venta | 1 |
| 2067 | venirse | 1 |
| 2068 | venida | 1 |
| 2069 | venían | 1 |
| 2070 | venía | 1 |
| 2071 | veneros | 1 |
| 2072 | veneras | 1 |
| 2073 | venerado | 1 |
| 2074 | veneradas | 1 |
| 2075 | venerables | 1 |
| 2076 | venenos | 1 |
| 2077 | vendimias | 1 |
| 2078 | vende | 1 |
| 2079 | venda | 1 |
| 2080 | vencidas | 1 |
| 2081 | vencedores | 1 |
| 2082 | vence | 1 |
| 2083 | venatorio | 1 |
| 2084 | venatorias | 1 |
| 2085 | venado | 1 |
| 2086 | venablos | 1 |
| 2087 | venablo | 1 |
| 2088 | vena | 1 |
| 2089 | vellones | 1 |
| 2090 | veleras | 1 |
| 2091 | velera | 1 |
| 2092 | velas | 1 |
| 2093 | vela | 1 |
| 2094 | veis | 1 |
| 2095 | veinte | 1 |
| 2096 | veía | 1 |
| 2097 | vega | 1 |
| 2098 | vedadas | 1 |
| 2099 | ved | 1 |
| 2100 | vea | 1 |
| 2101 | vaya | 1 |
| 2102 | vasos | 1 |
| 2103 | vas | 1 |
| 2104 | varia | 1 |
| 2105 | varas | 1 |
| 2106 | varada | 1 |
| 2107 | vaquera | 1 |
| 2108 | vanse | 1 |
| 2109 | valor | 1 |
| 2110 | vallete | 1 |
| 2111 | valles | 1 |
| 2112 | valenzuela | 1 |
| 2113 | valentía | 1 |
| 2114 | valen | 1 |
| 2115 | valelle | 1 |
| 2116 | valdrá | 1 |
| 2117 | vais | 1 |
| 2118 | vaina | 1 |
| 2119 | vagando | 1 |
| 2120 | vaga | 1 |
| 2121 | vadeando | 1 |
| 2122 | vacío | 1 |
| 2123 | vacilante | 1 |
| 2124 | vacía | 1 |
| 2125 | v | 1 |
| 2126 | útilmente | 1 |
| 2127 | usando | 1 |
| 2128 | usan | 1 |
| 2129 | usa | 1 |
| 2130 | urganda | 1 |
| 2131 | urca | 1 |
| 2132 | urbano | 1 |
| 2133 | untándoles | 1 |
| 2134 | umbrosa | 1 |
| 2135 | umbrío | 1 |
| 2136 | umbría | 1 |
| 2137 | ultramarino | 1 |
| 2138 | ultraje | 1 |
| 2139 | ubres | 1 |
| 2140 | tuyos | 1 |
| 2141 | tuyo | 1 |
| 2142 | tuvo | 1 |
| 2143 | tuviera | 1 |
| 2144 | tutora | 1 |
| 2145 | turquesco | 1 |
| 2146 | turquesadas | 1 |
| 2147 | turno | 1 |
| 2148 | turco | 1 |
| 2149 | turbóse | 1 |
| 2150 | turbó | 1 |
| 2151 | túmulos | 1 |
| 2152 | túmulo | 1 |
| 2153 | troyano | 1 |
| 2154 | troya | 1 |
| 2155 | trópicos | 1 |
| 2156 | trono | 1 |
| 2157 | tronchó | 1 |
| 2158 | trompas | 1 |
| 2159 | trocó | 1 |
| 2160 | trochas | 1 |
| 2161 | trocha | 1 |
| 2162 | trocara | 1 |
| 2163 | trocar | 1 |
| 2164 | trocalle | 1 |
| 2165 | triunfando | 1 |
| 2166 | triunfador | 1 |
| 2167 | triunfa | 1 |
| 2168 | tristes | 1 |
| 2169 | triplicado | 1 |
| 2170 | trïones | 1 |
| 2171 | trïón | 1 |
| 2172 | trinacria | 1 |
| 2173 | trillo | 1 |
| 2174 | trillado | 1 |
| 2175 | tributos | 1 |
| 2176 | tributó | 1 |
| 2177 | tributo | 1 |
| 2178 | tributaban | 1 |
| 2179 | tributa | 1 |
| 2180 | tribunal | 1 |
| 2181 | triaca | 1 |
| 2182 | trepó | 1 |
| 2183 | trepando | 1 |
| 2184 | trepa | 1 |
| 2185 | trenzándose | 1 |
| 2186 | trémula | 1 |
| 2187 | tremolantes | 1 |
| 2188 | tremola | 1 |
| 2189 | traza | 1 |
| 2190 | traviesos | 1 |
| 2191 | través | 1 |
| 2192 | tratos | 1 |
| 2193 | tratando | 1 |
| 2194 | tratamos | 1 |
| 2195 | trata | 1 |
| 2196 | tranquilidad | 1 |
| 2197 | tramontar | 1 |
| 2198 | tramontado | 1 |
| 2199 | traición | 1 |
| 2200 | trágicas | 1 |
| 2201 | trágica | 1 |
| 2202 | tradujo | 1 |
| 2203 | traducido | 1 |
| 2204 | tradición | 1 |
| 2205 | trabajo | 1 |
| 2206 | totalmente | 1 |
| 2207 | tostada | 1 |
| 2208 | tósigo | 1 |
| 2209 | tosco | 1 |
| 2210 | tosca | 1 |
| 2211 | tortüosa | 1 |
| 2212 | tortuga | 1 |
| 2213 | tórrida | 1 |
| 2214 | torre | 1 |
| 2215 | toros | 1 |
| 2216 | torno | 1 |
| 2217 | tormes | 1 |
| 2218 | tormentoso | 1 |
| 2219 | tormento | 1 |
| 2220 | tormenta | 1 |
| 2221 | torcidos | 1 |
| 2222 | torcida | 1 |
| 2223 | torbellinos | 1 |
| 2224 | topar | 1 |
| 2225 | tomo | 1 |
| 2226 | tomistas | 1 |
| 2227 | toledano | 1 |
| 2228 | toldado | 1 |
| 2229 | tocaban | 1 |
| 2230 | tizona | 1 |
| 2231 | titón | 1 |
| 2232 | tirsos | 1 |
| 2233 | tiraniza | 1 |
| 2234 | tiranía | 1 |
| 2235 | tïorba | 1 |
| 2236 | tinta | 1 |
| 2237 | tiniebla | 1 |
| 2238 | timón | 1 |
| 2239 | tijera | 1 |
| 2240 | tigre | 1 |
| 2241 | tifis | 1 |
| 2242 | tifeo | 1 |
| 2243 | tierras | 1 |
| 2244 | tiernos | 1 |
| 2245 | tiernas | 1 |
| 2246 | tierna | 1 |
| 2247 | tiento | 1 |
| 2248 | tienen | 1 |
| 2249 | tiburón | 1 |
| 2250 | tïara | 1 |
| 2251 | testamento | 1 |
| 2252 | terso | 1 |
| 2253 | terror | 1 |
| 2254 | terreno | 1 |
| 2255 | ternísimamente | 1 |
| 2256 | ternezuelo | 1 |
| 2257 | terneruela | 1 |
| 2258 | termodonte | 1 |
| 2259 | teñido | 1 |
| 2260 | tentarlo | 1 |
| 2261 | tenido | 1 |
| 2262 | tenían | 1 |
| 2263 | tenía | 1 |
| 2264 | tengáis | 1 |
| 2265 | tenéis | 1 |
| 2266 | tenebroso | 1 |
| 2267 | tendré | 1 |
| 2268 | tendrán | 1 |
| 2269 | tenaz | 1 |
| 2270 | tempranos | 1 |
| 2271 | templos | 1 |
| 2272 | templarte | 1 |
| 2273 | templarse | 1 |
| 2274 | templar | 1 |
| 2275 | templadamente | 1 |
| 2276 | templa | 1 |
| 2277 | temiendo | 1 |
| 2278 | temes | 1 |
| 2279 | temeroso | 1 |
| 2280 | temeridades | 1 |
| 2281 | teme | 1 |
| 2282 | temblando | 1 |
| 2283 | telar | 1 |
| 2284 | tela | 1 |
| 2285 | tejo | 1 |
| 2286 | tejen | 1 |
| 2287 | tejas | 1 |
| 2288 | tascando | 1 |
| 2289 | tardos | 1 |
| 2290 | tapiz | 1 |
| 2291 | tapices | 1 |
| 2292 | tapete | 1 |
| 2293 | también | 1 |
| 2294 | talle | 1 |
| 2295 | talía | 1 |
| 2296 | talares | 1 |
| 2297 | taladro | 1 |
| 2298 | taladra | 1 |
| 2299 | tafiletes | 1 |
| 2300 | tablas | 1 |
| 2301 | sutil | 1 |
| 2302 | susurrante | 1 |
| 2303 | suspiros | 1 |
| 2304 | suspiro | 1 |
| 2305 | suspensa | 1 |
| 2306 | suspendido | 1 |
| 2307 | suspender | 1 |
| 2308 | suspende | 1 |
| 2309 | surcó | 1 |
| 2310 | surco | 1 |
| 2311 | surcaron | 1 |
| 2312 | surcado | 1 |
| 2313 | surcada | 1 |
| 2314 | supremos | 1 |
| 2315 | supremo | 1 |
| 2316 | supla | 1 |
| 2317 | sumo | 1 |
| 2318 | sumas | 1 |
| 2319 | sufrirá | 1 |
| 2320 | sufrimiento | 1 |
| 2321 | sufren | 1 |
| 2322 | súfrala | 1 |
| 2323 | suerte | 1 |
| 2324 | suene | 1 |
| 2325 | sueltos | 1 |
| 2326 | suelto | 1 |
| 2327 | suelas | 1 |
| 2328 | sudar | 1 |
| 2329 | suda | 1 |
| 2330 | suceso | 1 |
| 2331 | sucedido | 1 |
| 2332 | sublimidad | 1 |
| 2333 | sublimes | 1 |
| 2334 | subjeto | 1 |
| 2335 | suaves | 1 |
| 2336 | süavemente | 1 |
| 2337 | soto | 1 |
| 2338 | sostuvo | 1 |
| 2339 | sosiego | 1 |
| 2340 | sordas | 1 |
| 2341 | sorbido | 1 |
| 2342 | soplo | 1 |
| 2343 | sonorosa | 1 |
| 2344 | sonoros | 1 |
| 2345 | sonoras | 1 |
| 2346 | sonora | 1 |
| 2347 | sollo | 1 |
| 2348 | solicitud | 1 |
| 2349 | solicitó | 1 |
| 2350 | solícito | 1 |
| 2351 | solicitar | 1 |
| 2352 | solicitando | 1 |
| 2353 | solicitado | 1 |
| 2354 | solicitada | 1 |
| 2355 | solícita | 1 |
| 2356 | solemniza | 1 |
| 2357 | soledad | 1 |
| 2358 | solas | 1 |
| 2359 | solamente | 1 |
| 2360 | sois | 1 |
| 2361 | sobrino | 1 |
| 2362 | sobrará | 1 |
| 2363 | sobran | 1 |
| 2364 | soberbios | 1 |
| 2365 | soberbia | 1 |
| 2366 | soberanos | 1 |
| 2367 | sísifo | 1 |
| 2368 | sirvió | 1 |
| 2369 | sirviendo | 1 |
| 2370 | sirven | 1 |
| 2371 | sirena | 1 |
| 2372 | sintió | 1 |
| 2373 | siniestra | 1 |
| 2374 | sincopan | 1 |
| 2375 | sinceridad | 1 |
| 2376 | simples | 1 |
| 2377 | símil | 1 |
| 2378 | simetis | 1 |
| 2379 | silla | 1 |
| 2380 | sileno | 1 |
| 2381 | silbos | 1 |
| 2382 | silbe | 1 |
| 2383 | silba | 1 |
| 2384 | sílaba | 1 |
| 2385 | siguió | 1 |
| 2386 | siguiente | 1 |
| 2387 | siguiéndole | 1 |
| 2388 | sigo | 1 |
| 2389 | siglos | 1 |
| 2390 | siglo | 1 |
| 2391 | siga | 1 |
| 2392 | sierpes | 1 |
| 2393 | siento | 1 |
| 2394 | sientes | 1 |
| 2395 | siegan | 1 |
| 2396 | sidón | 1 |
| 2397 | sicilïano | 1 |
| 2398 | sicilia | 1 |
| 2399 | sicana | 1 |
| 2400 | sexos | 1 |
| 2401 | sexo | 1 |
| 2402 | sevillanos | 1 |
| 2403 | seteno | 1 |
| 2404 | servir | 1 |
| 2405 | servidor | 1 |
| 2406 | serte | 1 |
| 2407 | serrana | 1 |
| 2408 | sereno | 1 |
| 2409 | serenidad | 1 |
| 2410 | serenara | 1 |
| 2411 | serenaba | 1 |
| 2412 | serena | 1 |
| 2413 | seréis | 1 |
| 2414 | serba | 1 |
| 2415 | serás | 1 |
| 2416 | serán | 1 |
| 2417 | serafín | 1 |
| 2418 | sepultura | 1 |
| 2419 | sepultar | 1 |
| 2420 | sepultados | 1 |
| 2421 | sepulcro | 1 |
| 2422 | señores | 1 |
| 2423 | sentados | 1 |
| 2424 | sentado | 1 |
| 2425 | senectud | 1 |
| 2426 | semicapro | 1 |
| 2427 | sembró | 1 |
| 2428 | sembrados | 1 |
| 2429 | semblante | 1 |
| 2430 | sellos | 1 |
| 2431 | selle | 1 |
| 2432 | sellar | 1 |
| 2433 | segura | 1 |
| 2434 | segundos | 1 |
| 2435 | segundas | 1 |
| 2436 | seguirás | 1 |
| 2437 | seguida | 1 |
| 2438 | seguía | 1 |
| 2439 | segando | 1 |
| 2440 | sedientas | 1 |
| 2441 | sedas | 1 |
| 2442 | secretos | 1 |
| 2443 | secretas | 1 |
| 2444 | secos | 1 |
| 2445 | seco | 1 |
| 2446 | saturno | 1 |
| 2447 | satisfecha | 1 |
| 2448 | satanás | 1 |
| 2449 | sarmiento | 1 |
| 2450 | sardo | 1 |
| 2451 | sañuda | 1 |
| 2452 | santos | 1 |
| 2453 | sangriento | 1 |
| 2454 | sanear | 1 |
| 2455 | salve | 1 |
| 2456 | salvas | 1 |
| 2457 | salvados | 1 |
| 2458 | saludolos | 1 |
| 2459 | saludar | 1 |
| 2460 | saludado | 1 |
| 2461 | salterio | 1 |
| 2462 | saltearon | 1 |
| 2463 | salteada | 1 |
| 2464 | salpicando | 1 |
| 2465 | salmón | 1 |
| 2466 | saliva | 1 |
| 2467 | salieron | 1 |
| 2468 | saliere | 1 |
| 2469 | salida | 1 |
| 2470 | salen | 1 |
| 2471 | salamandria | 1 |
| 2472 | sala | 1 |
| 2473 | sal | 1 |
| 2474 | sagrada | 1 |
| 2475 | sagitario | 1 |
| 2476 | saeta | 1 |
| 2477 | sacudir | 1 |
| 2478 | sacros | 1 |
| 2479 | sacro | 1 |
| 2480 | sacrílego | 1 |
| 2481 | sacrílegas | 1 |
| 2482 | sacrificios | 1 |
| 2483 | sacar | 1 |
| 2484 | sabrosa | 1 |
| 2485 | sabido | 1 |
| 2486 | sabía | 1 |
| 2487 | sabeo | 1 |
| 2488 | rumor | 1 |
| 2489 | rumbo | 1 |
| 2490 | ruiseñores | 1 |
| 2491 | ruinas | 1 |
| 2492 | rüído | 1 |
| 2493 | rugoso | 1 |
| 2494 | rugosas | 1 |
| 2495 | rugas | 1 |
| 2496 | ruedas | 1 |
| 2497 | ruecas | 1 |
| 2498 | rueca | 1 |
| 2499 | rudamente | 1 |
| 2500 | rubia | 1 |
| 2501 | rubí | 1 |
| 2502 | roto | 1 |
| 2503 | rota | 1 |
| 2504 | roscas | 1 |
| 2505 | rosado | 1 |
| 2506 | rompió | 1 |
| 2507 | rompieron | 1 |
| 2508 | rompida | 1 |
| 2509 | rompe | 1 |
| 2510 | rompa | 1 |
| 2511 | roma | 1 |
| 2512 | rojas | 1 |
| 2513 | roja | 1 |
| 2514 | roe | 1 |
| 2515 | rocín | 1 |
| 2516 | robustas | 1 |
| 2517 | robres | 1 |
| 2518 | robo | 1 |
| 2519 | robalo | 1 |
| 2520 | robador | 1 |
| 2521 | rizado | 1 |
| 2522 | risueños | 1 |
| 2523 | risueño | 1 |
| 2524 | risco | 1 |
| 2525 | riqueza | 1 |
| 2526 | rindiose | 1 |
| 2527 | rinden | 1 |
| 2528 | rinda | 1 |
| 2529 | rimas | 1 |
| 2530 | rigores | 1 |
| 2531 | ricos | 1 |
| 2532 | ricas | 1 |
| 2533 | rica | 1 |
| 2534 | ribazos | 1 |
| 2535 | revocó | 1 |
| 2536 | revocaban | 1 |
| 2537 | revelar | 1 |
| 2538 | retrógrado | 1 |
| 2539 | retrocediente | 1 |
| 2540 | retozando | 1 |
| 2541 | retozadores | 1 |
| 2542 | retórico | 1 |
| 2543 | retira | 1 |
| 2544 | retamas | 1 |
| 2545 | resuelto | 1 |
| 2546 | resto | 1 |
| 2547 | restituir | 1 |
| 2548 | restitüido | 1 |
| 2549 | restan | 1 |
| 2550 | respuesta | 1 |
| 2551 | respondón | 1 |
| 2552 | respondiste | 1 |
| 2553 | respondí | 1 |
| 2554 | responden | 1 |
| 2555 | responde | 1 |
| 2556 | respeto | 1 |
| 2557 | resonantes | 1 |
| 2558 | resistir | 1 |
| 2559 | resistencia | 1 |
| 2560 | resiste | 1 |
| 2561 | república | 1 |
| 2562 | replicáis | 1 |
| 2563 | repitiendo | 1 |
| 2564 | repite | 1 |
| 2565 | repita | 1 |
| 2566 | repetida | 1 |
| 2567 | repeló | 1 |
| 2568 | reparos | 1 |
| 2569 | reparo | 1 |
| 2570 | reparada | 1 |
| 2571 | reñir | 1 |
| 2572 | renunciar | 1 |
| 2573 | reniego | 1 |
| 2574 | renglones | 1 |
| 2575 | rendido | 1 |
| 2576 | remozado | 1 |
| 2577 | remotas | 1 |
| 2578 | remota | 1 |
| 2579 | rémora | 1 |
| 2580 | remolcó | 1 |
| 2581 | remitió | 1 |
| 2582 | remitiera | 1 |
| 2583 | remiten | 1 |
| 2584 | remite | 1 |
| 2585 | remiso | 1 |
| 2586 | remisión | 1 |
| 2587 | relinchos | 1 |
| 2588 | relincho | 1 |
| 2589 | relámpago | 1 |
| 2590 | relación | 1 |
| 2591 | reja | 1 |
| 2592 | reinos | 1 |
| 2593 | regulados | 1 |
| 2594 | regulada | 1 |
| 2595 | regocijo | 1 |
| 2596 | registró | 1 |
| 2597 | regalarte | 1 |
| 2598 | reflejo | 1 |
| 2599 | referidlo | 1 |
| 2600 | reduciendo | 1 |
| 2601 | reducido | 1 |
| 2602 | reducida | 1 |
| 2603 | reducía | 1 |
| 2604 | reduce | 1 |
| 2605 | redomas | 1 |
| 2606 | redomado | 1 |
| 2607 | redimir | 1 |
| 2608 | redimiendo | 1 |
| 2609 | redimidos | 1 |
| 2610 | rediman | 1 |
| 2611 | redima | 1 |
| 2612 | recurren | 1 |
| 2613 | recuerdan | 1 |
| 2614 | recuerda | 1 |
| 2615 | recordó | 1 |
| 2616 | reconocimiento | 1 |
| 2617 | reconociendo | 1 |
| 2618 | recoge | 1 |
| 2619 | recobrarle | 1 |
| 2620 | recline | 1 |
| 2621 | reclinarse | 1 |
| 2622 | reclinaron | 1 |
| 2623 | reclinados | 1 |
| 2624 | recíprocos | 1 |
| 2625 | reciente | 1 |
| 2626 | recién | 1 |
| 2627 | recibillo | 1 |
| 2628 | recibe | 1 |
| 2629 | recelar | 1 |
| 2630 | recelando | 1 |
| 2631 | recato | 1 |
| 2632 | rebela | 1 |
| 2633 | razones | 1 |
| 2634 | rayó | 1 |
| 2635 | rayando | 1 |
| 2636 | rayados | 1 |
| 2637 | rayada | 1 |
| 2638 | raudos | 1 |
| 2639 | rastro | 1 |
| 2640 | raso | 1 |
| 2641 | raro | 1 |
| 2642 | rara | 1 |
| 2643 | rápido | 1 |
| 2644 | rama | 1 |
| 2645 | racimos | 1 |
| 2646 | racimo | 1 |
| 2647 | quitaste | 1 |
| 2648 | quitan | 1 |
| 2649 | quitalla | 1 |
| 2650 | quintas | 1 |
| 2651 | quinas | 1 |
| 2652 | quilla | 1 |
| 2653 | quiés | 1 |
| 2654 | quieres | 1 |
| 2655 | quieren | 1 |
| 2656 | quicios | 1 |
| 2657 | quesillo | 1 |
| 2658 | quema | 1 |
| 2659 | queje | 1 |
| 2660 | quejarse | 1 |
| 2661 | quejándose | 1 |
| 2662 | quedos | 1 |
| 2663 | quedo | 1 |
| 2664 | quedara | 1 |
| 2665 | quedaba | 1 |
| 2666 | purpurear | 1 |
| 2667 | puros | 1 |
| 2668 | purísima | 1 |
| 2669 | purificación | 1 |
| 2670 | puridad | 1 |
| 2671 | purgarse | 1 |
| 2672 | puntualidad | 1 |
| 2673 | punta | 1 |
| 2674 | pululante | 1 |
| 2675 | pulsado | 1 |
| 2676 | pula | 1 |
| 2677 | puesta | 1 |
| 2678 | puerta | 1 |
| 2679 | pueda | 1 |
| 2680 | pueblos | 1 |
| 2681 | pudieron | 1 |
| 2682 | pudieran | 1 |
| 2683 | publicara | 1 |
| 2684 | publicando | 1 |
| 2685 | ptolomeos | 1 |
| 2686 | psiques | 1 |
| 2687 | prueba | 1 |
| 2688 | prudentes | 1 |
| 2689 | prudencia | 1 |
| 2690 | próxima | 1 |
| 2691 | provisiones | 1 |
| 2692 | provincias | 1 |
| 2693 | próvidas | 1 |
| 2694 | próvida | 1 |
| 2695 | provecho | 1 |
| 2696 | proteo | 1 |
| 2697 | próspera | 1 |
| 2698 | proserpina | 1 |
| 2699 | propios | 1 |
| 2700 | propiedad | 1 |
| 2701 | propias | 1 |
| 2702 | pronto | 1 |
| 2703 | pronosticada | 1 |
| 2704 | prometo | 1 |
| 2705 | prolijos | 1 |
| 2706 | prolijas | 1 |
| 2707 | progenie | 1 |
| 2708 | profundos | 1 |
| 2709 | profundas | 1 |
| 2710 | profana | 1 |
| 2711 | productor | 1 |
| 2712 | produce | 1 |
| 2713 | prodigïosos | 1 |
| 2714 | prodigioso | 1 |
| 2715 | pródiga | 1 |
| 2716 | procuran | 1 |
| 2717 | proceloso | 1 |
| 2718 | procede | 1 |
| 2719 | privilegió | 1 |
| 2720 | privilegien | 1 |
| 2721 | privilegie | 1 |
| 2722 | prisiones | 1 |
| 2723 | primores | 1 |
| 2724 | primicias | 1 |
| 2725 | primeros | 1 |
| 2726 | primeras | 1 |
| 2727 | primaveras | 1 |
| 2728 | prevista | 1 |
| 2729 | previniendo | 1 |
| 2730 | prevenidas | 1 |
| 2731 | prevenía | 1 |
| 2732 | pretendiendo | 1 |
| 2733 | pretende | 1 |
| 2734 | presurosa | 1 |
| 2735 | presuponiendo | 1 |
| 2736 | preste | 1 |
| 2737 | presta | 1 |
| 2738 | preso | 1 |
| 2739 | preside | 1 |
| 2740 | presentes | 1 |
| 2741 | presenta | 1 |
| 2742 | prescripto | 1 |
| 2743 | presago | 1 |
| 2744 | presagios | 1 |
| 2745 | prenden | 1 |
| 2746 | prenda | 1 |
| 2747 | premios | 1 |
| 2748 | premio | 1 |
| 2749 | premïados | 1 |
| 2750 | preguntas | 1 |
| 2751 | pregonero | 1 |
| 2752 | preciso | 1 |
| 2753 | precipitados | 1 |
| 2754 | precioso | 1 |
| 2755 | precïosamente | 1 |
| 2756 | potro | 1 |
| 2757 | postrimera | 1 |
| 2758 | postigo | 1 |
| 2759 | poso | 1 |
| 2760 | poro | 1 |
| 2761 | porfía | 1 |
| 2762 | populoso | 1 |
| 2763 | populosa | 1 |
| 2764 | popa | 1 |
| 2765 | ponzoñosa | 1 |
| 2766 | ponto | 1 |
| 2767 | poniéndole | 1 |
| 2768 | ponían | 1 |
| 2769 | pongan | 1 |
| 2770 | ponga | 1 |
| 2771 | poner | 1 |
| 2772 | ponen | 1 |
| 2773 | pone | 1 |
| 2774 | ponderosa | 1 |
| 2775 | pondero | 1 |
| 2776 | ponderé | 1 |
| 2777 | ponderador | 1 |
| 2778 | pondera | 1 |
| 2779 | pomo | 1 |
| 2780 | polvorosa | 1 |
| 2781 | poltronería | 1 |
| 2782 | polos | 1 |
| 2783 | poetas | 1 |
| 2784 | podría | 1 |
| 2785 | podéis | 1 |
| 2786 | pobos | 1 |
| 2787 | po | 1 |
| 2788 | plugo | 1 |
| 2789 | plomos | 1 |
| 2790 | plega | 1 |
| 2791 | plebeyo | 1 |
| 2792 | plaza | 1 |
| 2793 | playas | 1 |
| 2794 | platería | 1 |
| 2795 | platea | 1 |
| 2796 | planeta | 1 |
| 2797 | plancha | 1 |
| 2798 | pizarras | 1 |
| 2799 | pise | 1 |
| 2800 | piscatorias | 1 |
| 2801 | pisase | 1 |
| 2802 | pisaron | 1 |
| 2803 | pisada | 1 |
| 2804 | pisad | 1 |
| 2805 | piraterías | 1 |
| 2806 | pirámide | 1 |
| 2807 | pira | 1 |
| 2808 | pipotes | 1 |
| 2809 | pipas | 1 |
| 2810 | pío | 1 |
| 2811 | pihuela | 1 |
| 2812 | pierna | 1 |
| 2813 | pïérides | 1 |
| 2814 | pierda | 1 |
| 2815 | piensas | 1 |
| 2816 | piensa | 1 |
| 2817 | pieles | 1 |
| 2818 | pidiendo | 1 |
| 2819 | picas | 1 |
| 2820 | pïante | 1 |
| 2821 | piadosas | 1 |
| 2822 | piadosa | 1 |
| 2823 | pía | 1 |
| 2824 | pez | 1 |
| 2825 | petulante | 1 |
| 2826 | pestilencia | 1 |
| 2827 | pestañas | 1 |
| 2828 | pescar | 1 |
| 2829 | pesares | 1 |
| 2830 | pesadumbres | 1 |
| 2831 | pesado | 1 |
| 2832 | pesada | 1 |
| 2833 | peruana | 1 |
| 2834 | personajes | 1 |
| 2835 | perseguida | 1 |
| 2836 | perros | 1 |
| 2837 | permite | 1 |
| 2838 | perla | 1 |
| 2839 | perfectos | 1 |
| 2840 | perezosamente | 1 |
| 2841 | perezosa | 1 |
| 2842 | peregrinos | 1 |
| 2843 | perdonen | 1 |
| 2844 | perdone | 1 |
| 2845 | perdonara | 1 |
| 2846 | perdonando | 1 |
| 2847 | perdonados | 1 |
| 2848 | perdonado | 1 |
| 2849 | perdonaba | 1 |
| 2850 | perdón | 1 |
| 2851 | perdió | 1 |
| 2852 | perdidos | 1 |
| 2853 | perdido | 1 |
| 2854 | perdían | 1 |
| 2855 | perdí | 1 |
| 2856 | perderse | 1 |
| 2857 | perder | 1 |
| 2858 | pera | 1 |
| 2859 | peñascos | 1 |
| 2860 | pénsiles | 1 |
| 2861 | penséis | 1 |
| 2862 | pensé | 1 |
| 2863 | pensar | 1 |
| 2864 | penetraste | 1 |
| 2865 | penetraron | 1 |
| 2866 | penetran | 1 |
| 2867 | penetrador | 1 |
| 2868 | peneida | 1 |
| 2869 | pender | 1 |
| 2870 | penden | 1 |
| 2871 | penado | 1 |
| 2872 | pellico | 1 |
| 2873 | peligroso | 1 |
| 2874 | peinan | 1 |
| 2875 | peinados | 1 |
| 2876 | peinadas | 1 |
| 2877 | pegadlo | 1 |
| 2878 | pedir | 1 |
| 2879 | pedidos | 1 |
| 2880 | pedí | 1 |
| 2881 | pecadores | 1 |
| 2882 | pavón | 1 |
| 2883 | patrio | 1 |
| 2884 | patria | 1 |
| 2885 | pastores | 1 |
| 2886 | pastorales | 1 |
| 2887 | pastoral | 1 |
| 2888 | pasiones | 1 |
| 2889 | pasear | 1 |
| 2890 | pasas | 1 |
| 2891 | pasaron | 1 |
| 2892 | pasar | 1 |
| 2893 | partos | 1 |
| 2894 | parto | 1 |
| 2895 | partiré | 1 |
| 2896 | partimos | 1 |
| 2897 | partíme | 1 |
| 2898 | parnaso | 1 |
| 2899 | parlera | 1 |
| 2900 | parientas | 1 |
| 2901 | pareció | 1 |
| 2902 | parecía | 1 |
| 2903 | parecerse | 1 |
| 2904 | parecen | 1 |
| 2905 | pardas | 1 |
| 2906 | parda | 1 |
| 2907 | parca | 1 |
| 2908 | par | 1 |
| 2909 | paños | 1 |
| 2910 | panales | 1 |
| 2911 | panal | 1 |
| 2912 | pámpano | 1 |
| 2913 | paloma | 1 |
| 2914 | palizada | 1 |
| 2915 | palio | 1 |
| 2916 | palinuro | 1 |
| 2917 | pálidos | 1 |
| 2918 | pálido | 1 |
| 2919 | pálidas | 1 |
| 2920 | pálida | 1 |
| 2921 | paladïones | 1 |
| 2922 | palabra | 1 |
| 2923 | pajizo | 1 |
| 2924 | pajes | 1 |
| 2925 | paje | 1 |
| 2926 | paja | 1 |
| 2927 | pagando | 1 |
| 2928 | pagada | 1 |
| 2929 | pafo | 1 |
| 2930 | padrino | 1 |
| 2931 | padezco | 1 |
| 2932 | pacíficas | 1 |
| 2933 | pacientes | 1 |
| 2934 | paciencia | 1 |
| 2935 | pacen | 1 |
| 2936 | pabellones | 1 |
| 2937 | oyes | 1 |
| 2938 | oyendo | 1 |
| 2939 | overos | 1 |
| 2940 | overo | 1 |
| 2941 | ovejas | 1 |
| 2942 | óvalos | 1 |
| 2943 | óvalo | 1 |
| 2944 | otorgue | 1 |
| 2945 | otorga | 1 |
| 2946 | ostión | 1 |
| 2947 | ostente | 1 |
| 2948 | ostentado | 1 |
| 2949 | ostentación | 1 |
| 2950 | oso | 1 |
| 2951 | oscura | 1 |
| 2952 | osas | 1 |
| 2953 | osadía | 1 |
| 2954 | orza | 1 |
| 2955 | orlas | 1 |
| 2956 | orlado | 1 |
| 2957 | orladas | 1 |
| 2958 | orinales | 1 |
| 2959 | original | 1 |
| 2960 | orïente | 1 |
| 2961 | orientales | 1 |
| 2962 | orgullo | 1 |
| 2963 | órganos | 1 |
| 2964 | ordena | 1 |
| 2965 | orcas | 1 |
| 2966 | oraciones | 1 |
| 2967 | oración | 1 |
| 2968 | opulencias | 1 |
| 2969 | opuesto | 1 |
| 2970 | oprimió | 1 |
| 2971 | oprime | 1 |
| 2972 | oprima | 1 |
| 2973 | opresos | 1 |
| 2974 | opaca | 1 |
| 2975 | onceno | 1 |
| 2976 | omnium | 1 |
| 2977 | omiso | 1 |
| 2978 | olores | 1 |
| 2979 | olmo | 1 |
| 2980 | oliva | 1 |
| 2981 | olimpo | 1 |
| 2982 | olímpica | 1 |
| 2983 | oíste | 1 |
| 2984 | oirás | 1 |
| 2985 | oirán | 1 |
| 2986 | oílla | 1 |
| 2987 | oigo | 1 |
| 2988 | oídos | 1 |
| 2989 | ofrecido | 1 |
| 2990 | ofrecida | 1 |
| 2991 | ofrecerle | 1 |
| 2992 | ofrecerá | 1 |
| 2993 | ofrecer | 1 |
| 2994 | oficïosa | 1 |
| 2995 | oficio | 1 |
| 2996 | ofendido | 1 |
| 2997 | ofende | 1 |
| 2998 | ofenda | 1 |
| 2999 | odioso | 1 |
| 3000 | ocupó | 1 |
| 3001 | ocupar | 1 |
| 3002 | ocupan | 1 |
| 3003 | ocultos | 1 |
| 3004 | octava | 1 |
| 3005 | ociosos | 1 |
| 3006 | ociosa | 1 |
| 3007 | ocio | 1 |
| 3008 | ocho | 1 |
| 3009 | ocaso | 1 |
| 3010 | obstinada | 1 |
| 3011 | observador | 1 |
| 3012 | obscuras | 1 |
| 3013 | obligará | 1 |
| 3014 | obligación | 1 |
| 3015 | obelisco | 1 |
| 3016 | obedecía | 1 |
| 3017 | obedecen | 1 |
| 3018 | nuncio | 1 |
| 3019 | numerosamente | 1 |
| 3020 | nuez | 1 |
| 3021 | nueve | 1 |
| 3022 | nuestras | 1 |
| 3023 | nuero | 1 |
| 3024 | nuera | 1 |
| 3025 | novillos | 1 |
| 3026 | novillo | 1 |
| 3027 | novia | 1 |
| 3028 | novelas | 1 |
| 3029 | novedades | 1 |
| 3030 | noticia | 1 |
| 3031 | nota | 1 |
| 3032 | nombran | 1 |
| 3033 | nogal | 1 |
| 3034 | nocturna | 1 |
| 3035 | nocivo | 1 |
| 3036 | nísida | 1 |
| 3037 | níobe | 1 |
| 3038 | ningún | 1 |
| 3039 | nieven | 1 |
| 3040 | nieva | 1 |
| 3041 | nieto | 1 |
| 3042 | niegan | 1 |
| 3043 | nidos | 1 |
| 3044 | nevó | 1 |
| 3045 | nevadas | 1 |
| 3046 | neutro | 1 |
| 3047 | neutralidad | 1 |
| 3048 | neutra | 1 |
| 3049 | netas | 1 |
| 3050 | nesea | 1 |
| 3051 | nervïosos | 1 |
| 3052 | nereo | 1 |
| 3053 | negro | 1 |
| 3054 | negóme | 1 |
| 3055 | negocio | 1 |
| 3056 | negó | 1 |
| 3057 | negándose | 1 |
| 3058 | negallo | 1 |
| 3059 | necesidades | 1 |
| 3060 | necedad | 1 |
| 3061 | navíos | 1 |
| 3062 | navaja | 1 |
| 3063 | náuticas | 1 |
| 3064 | naufragios | 1 |
| 3065 | naufragante | 1 |
| 3066 | naturales | 1 |
| 3067 | natal | 1 |
| 3068 | nariz | 1 |
| 3069 | narcisos | 1 |
| 3070 | narciso | 1 |
| 3071 | nade | 1 |
| 3072 | nadando | 1 |
| 3073 | nadador | 1 |
| 3074 | naciones | 1 |
| 3075 | nació | 1 |
| 3076 | nácares | 1 |
| 3077 | músicos | 1 |
| 3078 | músico | 1 |
| 3079 | músicas | 1 |
| 3080 | musculosos | 1 |
| 3081 | músculos | 1 |
| 3082 | muró | 1 |
| 3083 | murmurara | 1 |
| 3084 | murió | 1 |
| 3085 | murieron | 1 |
| 3086 | múrelo | 1 |
| 3087 | murarse | 1 |
| 3088 | muran | 1 |
| 3089 | murada | 1 |
| 3090 | multiplica | 1 |
| 3091 | mula | 1 |
| 3092 | mujeres | 1 |
| 3093 | muflón | 1 |
| 3094 | muevas | 1 |
| 3095 | muestras | 1 |
| 3096 | muestra | 1 |
| 3097 | muertas | 1 |
| 3098 | muerta | 1 |
| 3099 | muela | 1 |
| 3100 | muebles | 1 |
| 3101 | moza | 1 |
| 3102 | mover | 1 |
| 3103 | motejóme | 1 |
| 3104 | mote | 1 |
| 3105 | mostrar | 1 |
| 3106 | mostrando | 1 |
| 3107 | mosto | 1 |
| 3108 | mosquetas | 1 |
| 3109 | mortaja | 1 |
| 3110 | morro | 1 |
| 3111 | morirme | 1 |
| 3112 | moren | 1 |
| 3113 | mordió | 1 |
| 3114 | mordiendo | 1 |
| 3115 | mordaza | 1 |
| 3116 | morados | 1 |
| 3117 | moradoras | 1 |
| 3118 | morador | 1 |
| 3119 | moradas | 1 |
| 3120 | montero | 1 |
| 3121 | montería | 1 |
| 3122 | montecillo | 1 |
| 3123 | montaraz | 1 |
| 3124 | montañesas | 1 |
| 3125 | montañesa | 1 |
| 3126 | monstruo | 1 |
| 3127 | monjes | 1 |
| 3128 | monja | 1 |
| 3129 | monarca | 1 |
| 3130 | momento | 1 |
| 3131 | molesta | 1 |
| 3132 | moja | 1 |
| 3133 | modos | 1 |
| 3134 | modestia | 1 |
| 3135 | modestas | 1 |
| 3136 | modesta | 1 |
| 3137 | moderno | 1 |
| 3138 | moderando | 1 |
| 3139 | moderador | 1 |
| 3140 | modelos | 1 |
| 3141 | mismos | 1 |
| 3142 | miseria | 1 |
| 3143 | mirtos | 1 |
| 3144 | miréme | 1 |
| 3145 | mírate | 1 |
| 3146 | mírasla | 1 |
| 3147 | mirarlo | 1 |
| 3148 | míos | 1 |
| 3149 | mintiendo | 1 |
| 3150 | ministril | 1 |
| 3151 | ministrar | 1 |
| 3152 | minerva | 1 |
| 3153 | minas | 1 |
| 3154 | minador | 1 |
| 3155 | milla | 1 |
| 3156 | militar | 1 |
| 3157 | milanés | 1 |
| 3158 | milagros | 1 |
| 3159 | mies | 1 |
| 3160 | miento | 1 |
| 3161 | miembro | 1 |
| 3162 | miel | 1 |
| 3163 | miedo | 1 |
| 3164 | midiendo | 1 |
| 3165 | mide | 1 |
| 3166 | midas | 1 |
| 3167 | mida | 1 |
| 3168 | mezquina | 1 |
| 3169 | mezcladas | 1 |
| 3170 | metros | 1 |
| 3171 | métrica | 1 |
| 3172 | metas | 1 |
| 3173 | metales | 1 |
| 3174 | meses | 1 |
| 3175 | meseguero | 1 |
| 3176 | mesa | 1 |
| 3177 | mes | 1 |
| 3178 | merece | 1 |
| 3179 | mercurio | 1 |
| 3180 | mercadante | 1 |
| 3181 | menudos | 1 |
| 3182 | menudas | 1 |
| 3183 | mentira | 1 |
| 3184 | mentidos | 1 |
| 3185 | mentida | 1 |
| 3186 | menosprecia | 1 |
| 3187 | menores | 1 |
| 3188 | menguando | 1 |
| 3189 | mengua | 1 |
| 3190 | menester | 1 |
| 3191 | melionesa | 1 |
| 3192 | melïona | 1 |
| 3193 | melancolías | 1 |
| 3194 | mejorada | 1 |
| 3195 | mejillas | 1 |
| 3196 | mejicano | 1 |
| 3197 | medina | 1 |
| 3198 | médico | 1 |
| 3199 | medianías | 1 |
| 3200 | meandro | 1 |
| 3201 | mazmorra | 1 |
| 3202 | mayos | 1 |
| 3203 | mauritania | 1 |
| 3204 | maullando | 1 |
| 3205 | matutinos | 1 |
| 3206 | matrimonio | 1 |
| 3207 | matiza | 1 |
| 3208 | matices | 1 |
| 3209 | maternas | 1 |
| 3210 | materia | 1 |
| 3211 | matadora | 1 |
| 3212 | mástiles | 1 |
| 3213 | máscara | 1 |
| 3214 | mascado | 1 |
| 3215 | marítimo | 1 |
| 3216 | marítima | 1 |
| 3217 | marinas | 1 |
| 3218 | mares | 1 |
| 3219 | marchita | 1 |
| 3220 | maravillas | 1 |
| 3221 | maravilla | 1 |
| 3222 | máquina | 1 |
| 3223 | mañosos | 1 |
| 3224 | manzana | 1 |
| 3225 | manto | 1 |
| 3226 | mantenía | 1 |
| 3227 | manteca | 1 |
| 3228 | manso | 1 |
| 3229 | manjares | 1 |
| 3230 | mande | 1 |
| 3231 | mandaron | 1 |
| 3232 | mandáisle | 1 |
| 3233 | mandado | 1 |
| 3234 | malsano | 1 |
| 3235 | mallas | 1 |
| 3236 | maliciosa | 1 |
| 3237 | males | 1 |
| 3238 | malaco | 1 |
| 3239 | majestüoso | 1 |
| 3240 | majestüosa | 1 |
| 3241 | majestad | 1 |
| 3242 | magnificencia | 1 |
| 3243 | madruga | 1 |
| 3244 | luto | 1 |
| 3245 | lunada | 1 |
| 3246 | luminosas | 1 |
| 3247 | luminosa | 1 |
| 3248 | luminarias | 1 |
| 3249 | lumbre | 1 |
| 3250 | luis | 1 |
| 3251 | lugarillo | 1 |
| 3252 | lucrecia | 1 |
| 3253 | lucir | 1 |
| 3254 | lucina | 1 |
| 3255 | lucidos | 1 |
| 3256 | luchadores | 1 |
| 3257 | lucero | 1 |
| 3258 | luce | 1 |
| 3259 | lonja | 1 |
| 3260 | londres | 1 |
| 3261 | lomo | 1 |
| 3262 | lograr | 1 |
| 3263 | lóbrego | 1 |
| 3264 | llueven | 1 |
| 3265 | llueve | 1 |
| 3266 | lloró | 1 |
| 3267 | llorada | 1 |
| 3268 | llevarte | 1 |
| 3269 | llevar | 1 |
| 3270 | llenos | 1 |
| 3271 | llegué | 1 |
| 3272 | llégase | 1 |
| 3273 | llegarme | 1 |
| 3274 | llegaran | 1 |
| 3275 | llegará | 1 |
| 3276 | llegan | 1 |
| 3277 | llegamos | 1 |
| 3278 | llamó | 1 |
| 3279 | llamáralo | 1 |
| 3280 | llaman | 1 |
| 3281 | llámame | 1 |
| 3282 | livor | 1 |
| 3283 | liviandad | 1 |
| 3284 | livianas | 1 |
| 3285 | liviana | 1 |
| 3286 | litoral | 1 |
| 3287 | lisonjeramente | 1 |
| 3288 | lisonjera | 1 |
| 3289 | lisonjean | 1 |
| 3290 | lisonjas | 1 |
| 3291 | lira | 1 |
| 3292 | liquido | 1 |
| 3293 | liquidar | 1 |
| 3294 | linterna | 1 |
| 3295 | límites | 1 |
| 3296 | limita | 1 |
| 3297 | lilio | 1 |
| 3298 | lilibeo | 1 |
| 3299 | ligurina | 1 |
| 3300 | ligeros | 1 |
| 3301 | ligereza | 1 |
| 3302 | ligeras | 1 |
| 3303 | liëo | 1 |
| 3304 | liebres | 1 |
| 3305 | liebre | 1 |
| 3306 | lides | 1 |
| 3307 | licote | 1 |
| 3308 | libro | 1 |
| 3309 | libres | 1 |
| 3310 | librada | 1 |
| 3311 | liberalmente | 1 |
| 3312 | liberal | 1 |
| 3313 | libar | 1 |
| 3314 | leyes | 1 |
| 3315 | levantó | 1 |
| 3316 | levantando | 1 |
| 3317 | levantan | 1 |
| 3318 | levantados | 1 |
| 3319 | levantadas | 1 |
| 3320 | levantada | 1 |
| 3321 | levanta | 1 |
| 3322 | levadiza | 1 |
| 3323 | leucipe | 1 |
| 3324 | letras | 1 |
| 3325 | letra | 1 |
| 3326 | lestrigones | 1 |
| 3327 | leopardo | 1 |
| 3328 | leones | 1 |
| 3329 | leona | 1 |
| 3330 | lentisco | 1 |
| 3331 | lenguas | 1 |
| 3332 | lenguaje | 1 |
| 3333 | lenguado | 1 |
| 3334 | leí | 1 |
| 3335 | legal | 1 |
| 3336 | lechos | 1 |
| 3337 | lección | 1 |
| 3338 | lebrel | 1 |
| 3339 | lean | 1 |
| 3340 | leal | 1 |
| 3341 | lea | 1 |
| 3342 | lazos | 1 |
| 3343 | lazo | 1 |
| 3344 | lavan | 1 |
| 3345 | laureta | 1 |
| 3346 | laureado | 1 |
| 3347 | latón | 1 |
| 3348 | latiendo | 1 |
| 3349 | lastimoso | 1 |
| 3350 | lastimosamente | 1 |
| 3351 | lascivos | 1 |
| 3352 | largos | 1 |
| 3353 | largo | 1 |
| 3354 | largas | 1 |
| 3355 | larga | 1 |
| 3356 | láquesis | 1 |
| 3357 | lapidosa | 1 |
| 3358 | lanas | 1 |
| 3359 | láminas | 1 |
| 3360 | lamiéndolo | 1 |
| 3361 | lamiendo | 1 |
| 3362 | laja | 1 |
| 3363 | lagrimoso | 1 |
| 3364 | lagrimosas | 1 |
| 3365 | lágrima | 1 |
| 3366 | lago | 1 |
| 3367 | lado | 1 |
| 3368 | labradoras | 1 |
| 3369 | labra | 1 |
| 3370 | labios | 1 |
| 3371 | laberinto | 1 |
| 3372 | juzga | 1 |
| 3373 | justo | 1 |
| 3374 | justiciero | 1 |
| 3375 | justicia | 1 |
| 3376 | juré | 1 |
| 3377 | juraré | 1 |
| 3378 | juntamente | 1 |
| 3379 | juntaba | 1 |
| 3380 | junta | 1 |
| 3381 | junón | 1 |
| 3382 | juncia | 1 |
| 3383 | jüicio | 1 |
| 3384 | juicio | 1 |
| 3385 | jugo | 1 |
| 3386 | jugar | 1 |
| 3387 | juez | 1 |
| 3388 | juega | 1 |
| 3389 | judiciosa | 1 |
| 3390 | jubileo | 1 |
| 3391 | jubilando | 1 |
| 3392 | joyas | 1 |
| 3393 | jinete | 1 |
| 3394 | java | 1 |
| 3395 | jaspe | 1 |
| 3396 | jarro | 1 |
| 3397 | jardines | 1 |
| 3398 | jamás | 1 |
| 3399 | jabalina | 1 |
| 3400 | jabalí | 1 |
| 3401 | istriadas | 1 |
| 3402 | islote | 1 |
| 3403 | ira | 1 |
| 3404 | invocan | 1 |
| 3405 | invoca | 1 |
| 3406 | invisible | 1 |
| 3407 | inviolable | 1 |
| 3408 | invidioso | 1 |
| 3409 | invidiosas | 1 |
| 3410 | invidïosa | 1 |
| 3411 | invidïado | 1 |
| 3412 | invidiado | 1 |
| 3413 | investigó | 1 |
| 3414 | invención | 1 |
| 3415 | invencibles | 1 |
| 3416 | inunde | 1 |
| 3417 | inundación | 1 |
| 3418 | inunda | 1 |
| 3419 | intüitivo | 1 |
| 3420 | introdujo | 1 |
| 3421 | introducirme | 1 |
| 3422 | introduce | 1 |
| 3423 | intrépida | 1 |
| 3424 | interrumpieron | 1 |
| 3425 | interrumpido | 1 |
| 3426 | interposición | 1 |
| 3427 | interno | 1 |
| 3428 | interïor | 1 |
| 3429 | interés | 1 |
| 3430 | intentó | 1 |
| 3431 | intento | 1 |
| 3432 | intentan | 1 |
| 3433 | intenta | 1 |
| 3434 | intempestivos | 1 |
| 3435 | insulto | 1 |
| 3436 | insultar | 1 |
| 3437 | instrumentos | 1 |
| 3438 | instinto | 1 |
| 3439 | instancia | 1 |
| 3440 | instable | 1 |
| 3441 | inspirados | 1 |
| 3442 | insignias | 1 |
| 3443 | insidia | 1 |
| 3444 | inocencia | 1 |
| 3445 | innumerables | 1 |
| 3446 | injusto | 1 |
| 3447 | injuria | 1 |
| 3448 | ingratitud | 1 |
| 3449 | inglés | 1 |
| 3450 | informe | 1 |
| 3451 | información | 1 |
| 3452 | informa | 1 |
| 3453 | infinita | 1 |
| 3454 | infierno | 1 |
| 3455 | infïeles | 1 |
| 3456 | inficionando | 1 |
| 3457 | infestador | 1 |
| 3458 | infernal | 1 |
| 3459 | inferïor | 1 |
| 3460 | infelizmente | 1 |
| 3461 | infelice | 1 |
| 3462 | infausto | 1 |
| 3463 | infantería | 1 |
| 3464 | infamen | 1 |
| 3465 | infame | 1 |
| 3466 | infamar | 1 |
| 3467 | inexpugnable | 1 |
| 3468 | indulto | 1 |
| 3469 | inducir | 1 |
| 3470 | indo | 1 |
| 3471 | indiscreto | 1 |
| 3472 | indignos | 1 |
| 3473 | indicio | 1 |
| 3474 | indeciso | 1 |
| 3475 | inculto | 1 |
| 3476 | inculta | 1 |
| 3477 | inculcar | 1 |
| 3478 | inconsiderado | 1 |
| 3479 | incluyes | 1 |
| 3480 | incluyen | 1 |
| 3481 | incluís | 1 |
| 3482 | inclinar | 1 |
| 3483 | inclinado | 1 |
| 3484 | inclinación | 1 |
| 3485 | inclina | 1 |
| 3486 | inciertas | 1 |
| 3487 | incentiva | 1 |
| 3488 | inca | 1 |
| 3489 | impreso | 1 |
| 3490 | impresa | 1 |
| 3491 | importunas | 1 |
| 3492 | importuna | 1 |
| 3493 | imponiéndole | 1 |
| 3494 | implicantes | 1 |
| 3495 | implica | 1 |
| 3496 | impido | 1 |
| 3497 | impidiéndole | 1 |
| 3498 | impetüoso | 1 |
| 3499 | impetre | 1 |
| 3500 | impertinentes | 1 |
| 3501 | impertinencias | 1 |
| 3502 | impertinencia | 1 |
| 3503 | imperïoso | 1 |
| 3504 | imperio | 1 |
| 3505 | impenetrable | 1 |
| 3506 | impedidos | 1 |
| 3507 | impedidas | 1 |
| 3508 | impacïente | 1 |
| 3509 | imito | 1 |
| 3510 | imite | 1 |
| 3511 | imitara | 1 |
| 3512 | imitada | 1 |
| 3513 | imán | 1 |
| 3514 | imaginaciones | 1 |
| 3515 | imagen | 1 |
| 3516 | ilustren | 1 |
| 3517 | ilustrar | 1 |
| 3518 | ilustraba | 1 |
| 3519 | igualarme | 1 |
| 3520 | igualara | 1 |
| 3521 | igualar | 1 |
| 3522 | ignoró | 1 |
| 3523 | ignorante | 1 |
| 3524 | ignorado | 1 |
| 3525 | ídolo | 1 |
| 3526 | idólatra | 1 |
| 3527 | idïomas | 1 |
| 3528 | ida | 1 |
| 3529 | ícaro | 1 |
| 3530 | huyera | 1 |
| 3531 | huyendo | 1 |
| 3532 | huyen | 1 |
| 3533 | huya | 1 |
| 3534 | hurtos | 1 |
| 3535 | hurtó | 1 |
| 3536 | hurto | 1 |
| 3537 | hurten | 1 |
| 3538 | hurtan | 1 |
| 3539 | humosos | 1 |
| 3540 | humildad | 1 |
| 3541 | húmido | 1 |
| 3542 | húmidas | 1 |
| 3543 | humeros | 1 |
| 3544 | humedecido | 1 |
| 3545 | humedecida | 1 |
| 3546 | humana | 1 |
| 3547 | huevo | 1 |
| 3548 | huelva | 1 |
| 3549 | huellas | 1 |
| 3550 | huella | 1 |
| 3551 | hueco | 1 |
| 3552 | hueca | 1 |
| 3553 | hospitalidad | 1 |
| 3554 | hospedó | 1 |
| 3555 | hospedajes | 1 |
| 3556 | hospedador | 1 |
| 3557 | hospeda | 1 |
| 3558 | hortelano | 1 |
| 3559 | horrores | 1 |
| 3560 | horrendo | 1 |
| 3561 | horizonte | 1 |
| 3562 | horca | 1 |
| 3563 | honrarás | 1 |
| 3564 | honrados | 1 |
| 3565 | honesto | 1 |
| 3566 | honestamente | 1 |
| 3567 | honda | 1 |
| 3568 | homicidas | 1 |
| 3569 | homicida | 1 |
| 3570 | holandas | 1 |
| 3571 | holanda | 1 |
| 3572 | hojaldrado | 1 |
| 3573 | hogaño | 1 |
| 3574 | hízote | 1 |
| 3575 | historias | 1 |
| 3576 | hircano | 1 |
| 3577 | hipócrita | 1 |
| 3578 | himno | 1 |
| 3579 | hiló | 1 |
| 3580 | hilan | 1 |
| 3581 | hilada | 1 |
| 3582 | hila | 1 |
| 3583 | hijuelos | 1 |
| 3584 | hierros | 1 |
| 3585 | hiere | 1 |
| 3586 | hidrópica | 1 |
| 3587 | hiciera | 1 |
| 3588 | hibleo | 1 |
| 3589 | hervir | 1 |
| 3590 | herradas | 1 |
| 3591 | héroe | 1 |
| 3592 | hermoso | 1 |
| 3593 | hermosas | 1 |
| 3594 | hermanas | 1 |
| 3595 | herido | 1 |
| 3596 | heredado | 1 |
| 3597 | hereda | 1 |
| 3598 | hercúleos | 1 |
| 3599 | hemisferio | 1 |
| 3600 | helvecias | 1 |
| 3601 | helada | 1 |
| 3602 | hechas | 1 |
| 3603 | hecha | 1 |
| 3604 | hartas | 1 |
| 3605 | harpía | 1 |
| 3606 | hambre | 1 |
| 3607 | hamadrías | 1 |
| 3608 | hallas | 1 |
| 3609 | hallar | 1 |
| 3610 | hallamos | 1 |
| 3611 | halcones | 1 |
| 3612 | halcón | 1 |
| 3613 | halagos | 1 |
| 3614 | hago | 1 |
| 3615 | hagan | 1 |
| 3616 | hado | 1 |
| 3617 | haciéndolo | 1 |
| 3618 | haciéndole | 1 |
| 3619 | hacían | 1 |
| 3620 | haces | 1 |
| 3621 | hacerlo | 1 |
| 3622 | hacerle | 1 |
| 3623 | hacerlas | 1 |
| 3624 | hacen | 1 |
| 3625 | hacello | 1 |
| 3626 | habló | 1 |
| 3627 | hablo | 1 |
| 3628 | hable | 1 |
| 3629 | hablaba | 1 |
| 3630 | habla | 1 |
| 3631 | habiendo | 1 |
| 3632 | habido | 1 |
| 3633 | habían | 1 |
| 3634 | habian | 1 |
| 3635 | haberle | 1 |
| 3636 | habéis | 1 |
| 3637 | gustos | 1 |
| 3638 | gulosos | 1 |
| 3639 | guloso | 1 |
| 3640 | gulosa | 1 |
| 3641 | guirnalda | 1 |
| 3642 | guido | 1 |
| 3643 | guía | 1 |
| 3644 | guarde | 1 |
| 3645 | guardarle | 1 |
| 3646 | guardaré | 1 |
| 3647 | guardaos | 1 |
| 3648 | guadalete | 1 |
| 3649 | grullas | 1 |
| 3650 | gruesos | 1 |
| 3651 | grueso | 1 |
| 3652 | gruesa | 1 |
| 3653 | groseramente | 1 |
| 3654 | grifaños | 1 |
| 3655 | grecia | 1 |
| 3656 | graznido | 1 |
| 3657 | grano | 1 |
| 3658 | granjerías | 1 |
| 3659 | granjeé | 1 |
| 3660 | grandísima | 1 |
| 3661 | grandeza | 1 |
| 3662 | grandes | 1 |
| 3663 | granates | 1 |
| 3664 | granadino | 1 |
| 3665 | gradüadamente | 1 |
| 3666 | gradas | 1 |
| 3667 | gracioso | 1 |
| 3668 | gozóla | 1 |
| 3669 | gozar | 1 |
| 3670 | gozando | 1 |
| 3671 | góngora | 1 |
| 3672 | gomas | 1 |
| 3673 | golpes | 1 |
| 3674 | golosos | 1 |
| 3675 | golosa | 1 |
| 3676 | golfo | 1 |
| 3677 | gnido | 1 |
| 3678 | glorïoso | 1 |
| 3679 | glorioso | 1 |
| 3680 | gloriosa | 1 |
| 3681 | globo | 1 |
| 3682 | gitano | 1 |
| 3683 | giros | 1 |
| 3684 | gira | 1 |
| 3685 | ginovés | 1 |
| 3686 | gima | 1 |
| 3687 | gigantes | 1 |
| 3688 | gëometría | 1 |
| 3689 | geómetra | 1 |
| 3690 | gentilhombre | 1 |
| 3691 | gentes | 1 |
| 3692 | genitivo | 1 |
| 3693 | genil | 1 |
| 3694 | gemir | 1 |
| 3695 | gémino | 1 |
| 3696 | gemidores | 1 |
| 3697 | gelanda | 1 |
| 3698 | gavia | 1 |
| 3699 | gatos | 1 |
| 3700 | gastó | 1 |
| 3701 | gastalle | 1 |
| 3702 | gasta | 1 |
| 3703 | garzas | 1 |
| 3704 | garza | 1 |
| 3705 | garrote | 1 |
| 3706 | garras | 1 |
| 3707 | garra | 1 |
| 3708 | garganta | 1 |
| 3709 | garbín | 1 |
| 3710 | gante | 1 |
| 3711 | ganimedes | 1 |
| 3712 | ganadero | 1 |
| 3713 | gamo | 1 |
| 3714 | gallinas | 1 |
| 3715 | gallardas | 1 |
| 3716 | galería | 1 |
| 3717 | galeras | 1 |
| 3718 | galeote | 1 |
| 3719 | galante | 1 |
| 3720 | gaita | 1 |
| 3721 | gabán | 1 |
| 3722 | furor | 1 |
| 3723 | funerales | 1 |
| 3724 | fundimos | 1 |
| 3725 | fulminó | 1 |
| 3726 | fulminando | 1 |
| 3727 | fulminado | 1 |
| 3728 | fuéramos | 1 |
| 3729 | fuelle | 1 |
| 3730 | fruto | 1 |
| 3731 | frutas | 1 |
| 3732 | frutales | 1 |
| 3733 | frustrados | 1 |
| 3734 | frondosas | 1 |
| 3735 | frondosa | 1 |
| 3736 | frigio | 1 |
| 3737 | fresnos | 1 |
| 3738 | frescas | 1 |
| 3739 | fraude | 1 |
| 3740 | francolín | 1 |
| 3741 | fraguas | 1 |
| 3742 | frágiles | 1 |
| 3743 | fragante | 1 |
| 3744 | fracaso | 1 |
| 3745 | foso | 1 |
| 3746 | forzarle | 1 |
| 3747 | fortaleza | 1 |
| 3748 | formidables | 1 |
| 3749 | formas | 1 |
| 3750 | fontanero | 1 |
| 3751 | fomenta | 1 |
| 3752 | fogosa | 1 |
| 3753 | flota | 1 |
| 3754 | florestas | 1 |
| 3755 | flora | 1 |
| 3756 | flexüosas | 1 |
| 3757 | flechen | 1 |
| 3758 | flechas | 1 |
| 3759 | flechados | 1 |
| 3760 | flecha | 1 |
| 3761 | flandes | 1 |
| 3762 | flamantes | 1 |
| 3763 | flacos | 1 |
| 3764 | flacas | 1 |
| 3765 | flaca | 1 |
| 3766 | fiscal | 1 |
| 3767 | firmezas | 1 |
| 3768 | firmeza | 1 |
| 3769 | firmé | 1 |
| 3770 | firmas | 1 |
| 3771 | firmamento | 1 |
| 3772 | firma | 1 |
| 3773 | fïó | 1 |
| 3774 | fió | 1 |
| 3775 | fío | 1 |
| 3776 | fingieron | 1 |
| 3777 | fingiendo | 1 |
| 3778 | fingido | 1 |
| 3779 | fingida | 1 |
| 3780 | fingen | 1 |
| 3781 | final | 1 |
| 3782 | filódoces | 1 |
| 3783 | fijas | 1 |
| 3784 | figura | 1 |
| 3785 | fiesta | 1 |
| 3786 | fierezas | 1 |
| 3787 | fíelas | 1 |
| 3788 | fiel | 1 |
| 3789 | fíe | 1 |
| 3790 | fidelium | 1 |
| 3791 | fiaré | 1 |
| 3792 | fiándose | 1 |
| 3793 | fïando | 1 |
| 3794 | festivo | 1 |
| 3795 | fértiles | 1 |
| 3796 | ferro | 1 |
| 3797 | feria | 1 |
| 3798 | feo | 1 |
| 3799 | femenil | 1 |
| 3800 | felicidad | 1 |
| 3801 | fecundas | 1 |
| 3802 | febeo | 1 |
| 3803 | favorecer | 1 |
| 3804 | favor | 1 |
| 3805 | favonio | 1 |
| 3806 | fausto | 1 |
| 3807 | faunos | 1 |
| 3808 | fauno | 1 |
| 3809 | fatigas | 1 |
| 3810 | fatigar | 1 |
| 3811 | fatigando | 1 |
| 3812 | fatigados | 1 |
| 3813 | fatigado | 1 |
| 3814 | faroles | 1 |
| 3815 | faro | 1 |
| 3816 | fantasía | 1 |
| 3817 | famulorum | 1 |
| 3818 | famularum | 1 |
| 3819 | famular | 1 |
| 3820 | famoso | 1 |
| 3821 | faltas | 1 |
| 3822 | falda | 1 |
| 3823 | falanges | 1 |
| 3824 | faisán | 1 |
| 3825 | facilidades | 1 |
| 3826 | fáciles | 1 |
| 3827 | fábula | 1 |
| 3828 | fabrican | 1 |
| 3829 | fabricado | 1 |
| 3830 | extraordinarias | 1 |
| 3831 | extiende | 1 |
| 3832 | expuso | 1 |
| 3833 | expulso | 1 |
| 3834 | expuesta | 1 |
| 3835 | exprimir | 1 |
| 3836 | exprimió | 1 |
| 3837 | exprimido | 1 |
| 3838 | expriman | 1 |
| 3839 | expone | 1 |
| 3840 | expedido | 1 |
| 3841 | exhalada | 1 |
| 3842 | excusa | 1 |
| 3843 | excelso | 1 |
| 3844 | excelsa | 1 |
| 3845 | excedida | 1 |
| 3846 | excedía | 1 |
| 3847 | excede | 1 |
| 3848 | examinando | 1 |
| 3849 | examinan | 1 |
| 3850 | evangelio | 1 |
| 3851 | euterpe | 1 |
| 3852 | eurota | 1 |
| 3853 | euro | 1 |
| 3854 | etón | 1 |
| 3855 | etïopia | 1 |
| 3856 | etíopes | 1 |
| 3857 | estuve | 1 |
| 3858 | estribos | 1 |
| 3859 | estrépito | 1 |
| 3860 | estremeciéndose | 1 |
| 3861 | estrellado | 1 |
| 3862 | estrecho | 1 |
| 3863 | estrechamente | 1 |
| 3864 | estragos | 1 |
| 3865 | estrago | 1 |
| 3866 | estoque | 1 |
| 3867 | estómagos | 1 |
| 3868 | estómago | 1 |
| 3869 | estival | 1 |
| 3870 | estimándolos | 1 |
| 3871 | estimando | 1 |
| 3872 | estigias | 1 |
| 3873 | estés | 1 |
| 3874 | estero | 1 |
| 3875 | estéril | 1 |
| 3876 | esté | 1 |
| 3877 | estatua | 1 |
| 3878 | éstas | 1 |
| 3879 | estanques | 1 |
| 3880 | estanque | 1 |
| 3881 | estáis | 1 |
| 3882 | estadista | 1 |
| 3883 | estaciones | 1 |
| 3884 | estación | 1 |
| 3885 | estacada | 1 |
| 3886 | estaban | 1 |
| 3887 | esquiva | 1 |
| 3888 | esquilmos | 1 |
| 3889 | esquilas | 1 |
| 3890 | esquilan | 1 |
| 3891 | espumosas | 1 |
| 3892 | espumar | 1 |
| 3893 | esposos | 1 |
| 3894 | esposas | 1 |
| 3895 | esponja | 1 |
| 3896 | espongïoso | 1 |
| 3897 | espolón | 1 |
| 3898 | espíritu | 1 |
| 3899 | espirante | 1 |
| 3900 | espío | 1 |
| 3901 | espina | 1 |
| 3902 | espigada | 1 |
| 3903 | espiga | 1 |
| 3904 | espía | 1 |
| 3905 | esperanza | 1 |
| 3906 | esperándoos | 1 |
| 3907 | esperaban | 1 |
| 3908 | especuló | 1 |
| 3909 | esparcido | 1 |
| 3910 | española | 1 |
| 3911 | español | 1 |
| 3912 | espadañas | 1 |
| 3913 | espacïoso | 1 |
| 3914 | espaciosas | 1 |
| 3915 | espacïosamente | 1 |
| 3916 | espacïosa | 1 |
| 3917 | esotras | 1 |
| 3918 | esos | 1 |
| 3919 | esmeralda | 1 |
| 3920 | esgrimirán | 1 |
| 3921 | esgrimida | 1 |
| 3922 | esfinge | 1 |
| 3923 | esféricos | 1 |
| 3924 | esencias | 1 |
| 3925 | escurecen | 1 |
| 3926 | esculturas | 1 |
| 3927 | escultores | 1 |
| 3928 | escuela | 1 |
| 3929 | escudos | 1 |
| 3930 | escudo | 1 |
| 3931 | escuderazo | 1 |
| 3932 | escuchas | 1 |
| 3933 | escucharan | 1 |
| 3934 | escuchar | 1 |
| 3935 | escuchad | 1 |
| 3936 | escrupulosa | 1 |
| 3937 | escribir | 1 |
| 3938 | escondia | 1 |
| 3939 | esconder | 1 |
| 3940 | escondas | 1 |
| 3941 | esconda | 1 |
| 3942 | escogen | 1 |
| 3943 | escila | 1 |
| 3944 | escasa | 1 |
| 3945 | escarlata | 1 |
| 3946 | escarchando | 1 |
| 3947 | escándalo | 1 |
| 3948 | escama | 1 |
| 3949 | escalones | 1 |
| 3950 | escaló | 1 |
| 3951 | escalar | 1 |
| 3952 | erudición | 1 |
| 3953 | erranti | 1 |
| 3954 | errado | 1 |
| 3955 | erraba | 1 |
| 3956 | erizo | 1 |
| 3957 | eritrea | 1 |
| 3958 | erige | 1 |
| 3959 | eres | 1 |
| 3960 | eral | 1 |
| 3961 | equinocios | 1 |
| 3962 | éolo | 1 |
| 3963 | entró | 1 |
| 3964 | entregar | 1 |
| 3965 | entregados | 1 |
| 3966 | entregado | 1 |
| 3967 | entredichos | 1 |
| 3968 | entré | 1 |
| 3969 | éntrase | 1 |
| 3970 | entrará | 1 |
| 3971 | entrar | 1 |
| 3972 | entran | 1 |
| 3973 | entrado | 1 |
| 3974 | entrada | 1 |
| 3975 | entiende | 1 |
| 3976 | entienda | 1 |
| 3977 | entero | 1 |
| 3978 | entera | 1 |
| 3979 | entendiste | 1 |
| 3980 | entena | 1 |
| 3981 | enseñó | 1 |
| 3982 | enroscada | 1 |
| 3983 | enriquece | 1 |
| 3984 | enramada | 1 |
| 3985 | enojos | 1 |
| 3986 | enoja | 1 |
| 3987 | enmudeció | 1 |
| 3988 | enmudecer | 1 |
| 3989 | enladrillados | 1 |
| 3990 | enjutas | 1 |
| 3991 | enjuga | 1 |
| 3992 | enjambres | 1 |
| 3993 | enhorabuena | 1 |
| 3994 | engolfó | 1 |
| 3995 | engendran | 1 |
| 3996 | engazando | 1 |
| 3997 | engaste | 1 |
| 3998 | engastados | 1 |
| 3999 | engastada | 1 |
| 4000 | engarza | 1 |
| 4001 | engañen | 1 |
| 4002 | engañada | 1 |
| 4003 | enfrenó | 1 |
| 4004 | enfrenara | 1 |
| 4005 | enfrenar | 1 |
| 4006 | enfrenado | 1 |
| 4007 | enfrenaba | 1 |
| 4008 | enfermera | 1 |
| 4009 | enfermedad | 1 |
| 4010 | enemigo | 1 |
| 4011 | endurecer | 1 |
| 4012 | encuentra | 1 |
| 4013 | encordonado | 1 |
| 4014 | encomienda | 1 |
| 4015 | encomendó | 1 |
| 4016 | encomendarme | 1 |
| 4017 | encomendada | 1 |
| 4018 | encinas | 1 |
| 4019 | encierra | 1 |
| 4020 | enciende | 1 |
| 4021 | encarcelada | 1 |
| 4022 | encanecido | 1 |
| 4023 | enamoróse | 1 |
| 4024 | enamora | 1 |
| 4025 | émulos | 1 |
| 4026 | emular | 1 |
| 4027 | empuñe | 1 |
| 4028 | empreña | 1 |
| 4029 | empolla | 1 |
| 4030 | empleé | 1 |
| 4031 | eminencia | 1 |
| 4032 | embravecido | 1 |
| 4033 | embistió | 1 |
| 4034 | embestille | 1 |
| 4035 | embebido | 1 |
| 4036 | embaraza | 1 |
| 4037 | elevado | 1 |
| 4038 | elegante | 1 |
| 4039 | ejército | 1 |
| 4040 | ejemplos | 1 |
| 4041 | ejemplo | 1 |
| 4042 | egito | 1 |
| 4043 | egipcia | 1 |
| 4044 | efemérides | 1 |
| 4045 | efectos | 1 |
| 4046 | edades | 1 |
| 4047 | eclíptico | 1 |
| 4048 | echó | 1 |
| 4049 | e | 1 |
| 4050 | duros | 1 |
| 4051 | durmió | 1 |
| 4052 | duramente | 1 |
| 4053 | dulcísimos | 1 |
| 4054 | dulcísimo | 1 |
| 4055 | duerme | 1 |
| 4056 | dudosos | 1 |
| 4057 | dudas | 1 |
| 4058 | dudaba | 1 |
| 4059 | drogas | 1 |
| 4060 | dormida | 1 |
| 4061 | doras | 1 |
| 4062 | dorándole | 1 |
| 4063 | dones | 1 |
| 4064 | doncella | 1 |
| 4065 | donato | 1 |
| 4066 | donaires | 1 |
| 4067 | don | 1 |
| 4068 | doméstico | 1 |
| 4069 | domésticas | 1 |
| 4070 | dome | 1 |
| 4071 | domadas | 1 |
| 4072 | dolores | 1 |
| 4073 | dolientes | 1 |
| 4074 | doctores | 1 |
| 4075 | docta | 1 |
| 4076 | doblones | 1 |
| 4077 | doblón | 1 |
| 4078 | dobles | 1 |
| 4079 | doblaste | 1 |
| 4080 | dobladuras | 1 |
| 4081 | divisa | 1 |
| 4082 | divino | 1 |
| 4083 | divierte | 1 |
| 4084 | dividiendo | 1 |
| 4085 | divididos | 1 |
| 4086 | disuelvan | 1 |
| 4087 | distinta | 1 |
| 4088 | distinguir | 1 |
| 4089 | distinguieron | 1 |
| 4090 | distilan | 1 |
| 4091 | distantes | 1 |
| 4092 | dispones | 1 |
| 4093 | dispensadora | 1 |
| 4094 | dispensa | 1 |
| 4095 | disolviéronse | 1 |
| 4096 | disolviendo | 1 |
| 4097 | disimules | 1 |
| 4098 | disimula | 1 |
| 4099 | discursiva | 1 |
| 4100 | discurriendo | 1 |
| 4101 | discurren | 1 |
| 4102 | discreto | 1 |
| 4103 | discreta | 1 |
| 4104 | dirimió | 1 |
| 4105 | dirigidos | 1 |
| 4106 | dirigido | 1 |
| 4107 | dirías | 1 |
| 4108 | diréoslo | 1 |
| 4109 | diré | 1 |
| 4110 | dirá | 1 |
| 4111 | dioses | 1 |
| 4112 | diomedes | 1 |
| 4113 | dineros | 1 |
| 4114 | dímela | 1 |
| 4115 | diluvio | 1 |
| 4116 | dilaciones | 1 |
| 4117 | dijera | 1 |
| 4118 | digno | 1 |
| 4119 | digerida | 1 |
| 4120 | díganlo | 1 |
| 4121 | difícil | 1 |
| 4122 | diferentes | 1 |
| 4123 | dido | 1 |
| 4124 | dictaba | 1 |
| 4125 | diciendo | 1 |
| 4126 | dichoso | 1 |
| 4127 | dichas | 1 |
| 4128 | dïana | 1 |
| 4129 | devotos | 1 |
| 4130 | devana | 1 |
| 4131 | deudo | 1 |
| 4132 | determina | 1 |
| 4133 | detenéis | 1 |
| 4134 | desvïada | 1 |
| 4135 | desvanecimiento | 1 |
| 4136 | desvanece | 1 |
| 4137 | destos | 1 |
| 4138 | destina | 1 |
| 4139 | destierros | 1 |
| 4140 | destierra | 1 |
| 4141 | desterrado | 1 |
| 4142 | destemplado | 1 |
| 4143 | despreciando | 1 |
| 4144 | desposados | 1 |
| 4145 | desposado | 1 |
| 4146 | desposada | 1 |
| 4147 | despojo | 1 |
| 4148 | desplumada | 1 |
| 4149 | desplegar | 1 |
| 4150 | despido | 1 |
| 4151 | despidió | 1 |
| 4152 | despejan | 1 |
| 4153 | despedida | 1 |
| 4154 | despecho | 1 |
| 4155 | desparezco | 1 |
| 4156 | desparece | 1 |
| 4157 | despaché | 1 |
| 4158 | despachando | 1 |
| 4159 | despacha | 1 |
| 4160 | despabilado | 1 |
| 4161 | desotro | 1 |
| 4162 | desnudó | 1 |
| 4163 | desnudas | 1 |
| 4164 | desmintieron | 1 |
| 4165 | desmintiendo | 1 |
| 4166 | desmiente | 1 |
| 4167 | desmentir | 1 |
| 4168 | desmentido | 1 |
| 4169 | desmantelando | 1 |
| 4170 | desliza | 1 |
| 4171 | desigualdad | 1 |
| 4172 | designios | 1 |
| 4173 | designio | 1 |
| 4174 | deshoja | 1 |
| 4175 | desgajó | 1 |
| 4176 | desfloren | 1 |
| 4177 | deseó | 1 |
| 4178 | desenlazado | 1 |
| 4179 | desembarcó | 1 |
| 4180 | desear | 1 |
| 4181 | desean | 1 |
| 4182 | deseado | 1 |
| 4183 | desea | 1 |
| 4184 | desdorados | 1 |
| 4185 | desdeñosa | 1 |
| 4186 | desdeñas | 1 |
| 4187 | desdeñar | 1 |
| 4188 | desdeñado | 1 |
| 4189 | desdenes | 1 |
| 4190 | descubro | 1 |
| 4191 | descubrió | 1 |
| 4192 | descubrieron | 1 |
| 4193 | describo | 1 |
| 4194 | desconfianza | 1 |
| 4195 | descendió | 1 |
| 4196 | descendientes | 1 |
| 4197 | descendía | 1 |
| 4198 | descargada | 1 |
| 4199 | descanso | 1 |
| 4200 | descansa | 1 |
| 4201 | desatinada | 1 |
| 4202 | desaten | 1 |
| 4203 | desate | 1 |
| 4204 | desatando | 1 |
| 4205 | desarmado | 1 |
| 4206 | desangró | 1 |
| 4207 | desafío | 1 |
| 4208 | derribarse | 1 |
| 4209 | derribados | 1 |
| 4210 | derramé | 1 |
| 4211 | derivados | 1 |
| 4212 | derecho | 1 |
| 4213 | deponiendo | 1 |
| 4214 | dentado | 1 |
| 4215 | densó | 1 |
| 4216 | denso | 1 |
| 4217 | densa | 1 |
| 4218 | den | 1 |
| 4219 | dellos | 1 |
| 4220 | delicioso | 1 |
| 4221 | delicia | 1 |
| 4222 | delgado | 1 |
| 4223 | delfines | 1 |
| 4224 | déjese | 1 |
| 4225 | deje | 1 |
| 4226 | dejas | 1 |
| 4227 | dejaron | 1 |
| 4228 | dejaréte | 1 |
| 4229 | dejándote | 1 |
| 4230 | dejando | 1 |
| 4231 | dejámosla | 1 |
| 4232 | dejado | 1 |
| 4233 | deforme | 1 |
| 4234 | defendidos | 1 |
| 4235 | dedo | 1 |
| 4236 | declina | 1 |
| 4237 | décimo | 1 |
| 4238 | décima | 1 |
| 4239 | decidiera | 1 |
| 4240 | decid | 1 |
| 4241 | débil | 1 |
| 4242 | debiera | 1 |
| 4243 | debido | 1 |
| 4244 | debía | 1 |
| 4245 | debes | 1 |
| 4246 | datilado | 1 |
| 4247 | dátil | 1 |
| 4248 | das | 1 |
| 4249 | darme | 1 |
| 4250 | darle | 1 |
| 4251 | darás | 1 |
| 4252 | danza | 1 |
| 4253 | damascó | 1 |
| 4254 | dales | 1 |
| 4255 | dais | 1 |
| 4256 | dados | 1 |
| 4257 | dadas | 1 |
| 4258 | dada | 1 |
| 4259 | daban | 1 |
| 4260 | curioso | 1 |
| 4261 | curiosidad | 1 |
| 4262 | cumbres | 1 |
| 4263 | cultamente | 1 |
| 4264 | culebra | 1 |
| 4265 | cuidados | 1 |
| 4266 | cuestiones | 1 |
| 4267 | cuestan | 1 |
| 4268 | cuesta | 1 |
| 4269 | cuervas | 1 |
| 4270 | cuerva | 1 |
| 4271 | cuerpo | 1 |
| 4272 | cuentas | 1 |
| 4273 | cuellos | 1 |
| 4274 | cuchillos | 1 |
| 4275 | cuchilla | 1 |
| 4276 | cuchara | 1 |
| 4277 | cúbrome | 1 |
| 4278 | cubrió | 1 |
| 4279 | cúbrete | 1 |
| 4280 | cubren | 1 |
| 4281 | cubran | 1 |
| 4282 | cuatriduano | 1 |
| 4283 | cuartos | 1 |
| 4284 | cuánto | 1 |
| 4285 | cuantía | 1 |
| 4286 | cuánta | 1 |
| 4287 | cuán | 1 |
| 4288 | cuan | 1 |
| 4289 | cuajado | 1 |
| 4290 | cuajada | 1 |
| 4291 | cuadrado | 1 |
| 4292 | cruza | 1 |
| 4293 | crujidos | 1 |
| 4294 | cruje | 1 |
| 4295 | cruja | 1 |
| 4296 | crüeldad | 1 |
| 4297 | cruces | 1 |
| 4298 | cristalinos | 1 |
| 4299 | crisólitos | 1 |
| 4300 | crisoles | 1 |
| 4301 | crisol | 1 |
| 4302 | cribando | 1 |
| 4303 | criados | 1 |
| 4304 | crïado | 1 |
| 4305 | criadas | 1 |
| 4306 | criada | 1 |
| 4307 | crestadas | 1 |
| 4308 | crespos | 1 |
| 4309 | crespo | 1 |
| 4310 | crespas | 1 |
| 4311 | creía | 1 |
| 4312 | creí | 1 |
| 4313 | crédito | 1 |
| 4314 | creciente | 1 |
| 4315 | creciendo | 1 |
| 4316 | crecidos | 1 |
| 4317 | crece | 1 |
| 4318 | coyunda | 1 |
| 4319 | coya | 1 |
| 4320 | cosultada | 1 |
| 4321 | costumbres | 1 |
| 4322 | costado | 1 |
| 4323 | cosido | 1 |
| 4324 | coscoja | 1 |
| 4325 | corzo | 1 |
| 4326 | corza | 1 |
| 4327 | corvos | 1 |
| 4328 | corva | 1 |
| 4329 | corteza | 1 |
| 4330 | cortésmente | 1 |
| 4331 | cortesano | 1 |
| 4332 | cortes | 1 |
| 4333 | corsario | 1 |
| 4334 | corros | 1 |
| 4335 | corrompe | 1 |
| 4336 | corrió | 1 |
| 4337 | corrido | 1 |
| 4338 | correspondencias | 1 |
| 4339 | corresponde | 1 |
| 4340 | corredor | 1 |
| 4341 | corpulento | 1 |
| 4342 | coronen | 1 |
| 4343 | corone | 1 |
| 4344 | coronados | 1 |
| 4345 | coronaban | 1 |
| 4346 | coronaba | 1 |
| 4347 | cordón | 1 |
| 4348 | corderos | 1 |
| 4349 | corderillos | 1 |
| 4350 | corcillo | 1 |
| 4351 | corazones | 1 |
| 4352 | copadas | 1 |
| 4353 | conyugal | 1 |
| 4354 | convocación | 1 |
| 4355 | convocaba | 1 |
| 4356 | convinieron | 1 |
| 4357 | convierte | 1 |
| 4358 | conviene | 1 |
| 4359 | convencida | 1 |
| 4360 | convecinó | 1 |
| 4361 | convecina | 1 |
| 4362 | convalecí | 1 |
| 4363 | continüada | 1 |
| 4364 | contina | 1 |
| 4365 | contera | 1 |
| 4366 | contenta | 1 |
| 4367 | contenía | 1 |
| 4368 | contar | 1 |
| 4369 | contagio | 1 |
| 4370 | contacto | 1 |
| 4371 | contaba | 1 |
| 4372 | consultado | 1 |
| 4373 | consulta | 1 |
| 4374 | cónsules | 1 |
| 4375 | consuela | 1 |
| 4376 | construyendo | 1 |
| 4377 | construyen | 1 |
| 4378 | construye | 1 |
| 4379 | constrüidos | 1 |
| 4380 | consolalle | 1 |
| 4381 | consignados | 1 |
| 4382 | conservarán | 1 |
| 4383 | consagrando | 1 |
| 4384 | conquistóle | 1 |
| 4385 | conoces | 1 |
| 4386 | conocer | 1 |
| 4387 | conocella | 1 |
| 4388 | conjuración | 1 |
| 4389 | congrio | 1 |
| 4390 | confunden | 1 |
| 4391 | confunda | 1 |
| 4392 | conformes | 1 |
| 4393 | confieso | 1 |
| 4394 | confiar | 1 |
| 4395 | conejuelos | 1 |
| 4396 | conejuelo | 1 |
| 4397 | conduzgo | 1 |
| 4398 | conduzgan | 1 |
| 4399 | condujo | 1 |
| 4400 | conducir | 1 |
| 4401 | conducidores | 1 |
| 4402 | conducen | 1 |
| 4403 | condolido | 1 |
| 4404 | condes | 1 |
| 4405 | condenado | 1 |
| 4406 | condena | 1 |
| 4407 | conde | 1 |
| 4408 | concurrientes | 1 |
| 4409 | concurría | 1 |
| 4410 | concordia | 1 |
| 4411 | concocelle | 1 |
| 4412 | concluya | 1 |
| 4413 | concitó | 1 |
| 4414 | conciencia | 1 |
| 4415 | concertada | 1 |
| 4416 | concepto | 1 |
| 4417 | concentüosa | 1 |
| 4418 | concediolo | 1 |
| 4419 | concediéndole | 1 |
| 4420 | concede | 1 |
| 4421 | concebir | 1 |
| 4422 | comunes | 1 |
| 4423 | compulsen | 1 |
| 4424 | comprados | 1 |
| 4425 | cómplice | 1 |
| 4426 | compitiendo | 1 |
| 4427 | competidoras | 1 |
| 4428 | competidor | 1 |
| 4429 | competentes | 1 |
| 4430 | competente | 1 |
| 4431 | comieron | 1 |
| 4432 | comience | 1 |
| 4433 | comido | 1 |
| 4434 | cometiendo | 1 |
| 4435 | cometer | 1 |
| 4436 | cometas | 1 |
| 4437 | comenzaran | 1 |
| 4438 | comenzando | 1 |
| 4439 | comarcanos | 1 |
| 4440 | comarcano | 1 |
| 4441 | comadreja | 1 |
| 4442 | comadre | 1 |
| 4443 | colora | 1 |
| 4444 | colmilluda | 1 |
| 4445 | colmillo | 1 |
| 4446 | coliseo | 1 |
| 4447 | colijo | 1 |
| 4448 | colgaré | 1 |
| 4449 | colérico | 1 |
| 4450 | cojea | 1 |
| 4451 | coja | 1 |
| 4452 | cogido | 1 |
| 4453 | cofres | 1 |
| 4454 | cofre | 1 |
| 4455 | cofrade | 1 |
| 4456 | codornices | 1 |
| 4457 | coches | 1 |
| 4458 | coche | 1 |
| 4459 | coces | 1 |
| 4460 | cobre | 1 |
| 4461 | cobrado | 1 |
| 4462 | cloris | 1 |
| 4463 | clicie | 1 |
| 4464 | clavó | 1 |
| 4465 | clavo | 1 |
| 4466 | clavijas | 1 |
| 4467 | clausura | 1 |
| 4468 | clarísimos | 1 |
| 4469 | clarísimo | 1 |
| 4470 | clarín | 1 |
| 4471 | claras | 1 |
| 4472 | ciudadanos | 1 |
| 4473 | ciudadano | 1 |
| 4474 | ciudadana | 1 |
| 4475 | cítaras | 1 |
| 4476 | cítara | 1 |
| 4477 | cisuras | 1 |
| 4478 | circunvestida | 1 |
| 4479 | círculos | 1 |
| 4480 | círculo | 1 |
| 4481 | cipria | 1 |
| 4482 | ciñen | 1 |
| 4483 | cíñalo | 1 |
| 4484 | cinco | 1 |
| 4485 | cimera | 1 |
| 4486 | cima | 1 |
| 4487 | cifre | 1 |
| 4488 | cierzos | 1 |
| 4489 | cierzo | 1 |
| 4490 | ciervo | 1 |
| 4491 | cierva | 1 |
| 4492 | cierto | 1 |
| 4493 | cierra | 1 |
| 4494 | ciencia | 1 |
| 4495 | ciegas | 1 |
| 4496 | chupar | 1 |
| 4497 | chiprïota | 1 |
| 4498 | cetro | 1 |
| 4499 | cetrería | 1 |
| 4500 | cetrera | 1 |
| 4501 | céspedes | 1 |
| 4502 | cervices | 1 |
| 4503 | certifico | 1 |
| 4504 | ceremonias | 1 |
| 4505 | cercanas | 1 |
| 4506 | cerca | 1 |
| 4507 | ceño | 1 |
| 4508 | ceñida | 1 |
| 4509 | centinela | 1 |
| 4510 | centauro | 1 |
| 4511 | cenizoso | 1 |
| 4512 | cenefa | 1 |
| 4513 | cenando | 1 |
| 4514 | cena | 1 |
| 4515 | celosías | 1 |
| 4516 | celosas | 1 |
| 4517 | celeste | 1 |
| 4518 | celebraban | 1 |
| 4519 | celebraba | 1 |
| 4520 | celaje | 1 |
| 4521 | cejas | 1 |
| 4522 | cefeo | 1 |
| 4523 | cédula | 1 |
| 4524 | cedí | 1 |
| 4525 | cecina | 1 |
| 4526 | cebo | 1 |
| 4527 | cébase | 1 |
| 4528 | ceba | 1 |
| 4529 | cazar | 1 |
| 4530 | cazadores | 1 |
| 4531 | caya | 1 |
| 4532 | cavernas | 1 |
| 4533 | caverna | 1 |
| 4534 | cavalcanti | 1 |
| 4535 | cavaglieri | 1 |
| 4536 | cavada | 1 |
| 4537 | cauto | 1 |
| 4538 | cautela | 1 |
| 4539 | cause | 1 |
| 4540 | caudaloso | 1 |
| 4541 | caudalosa | 1 |
| 4542 | catón | 1 |
| 4543 | católico | 1 |
| 4544 | cátedras | 1 |
| 4545 | catarribera | 1 |
| 4546 | casto | 1 |
| 4547 | castillo | 1 |
| 4548 | castigo | 1 |
| 4549 | castaña | 1 |
| 4550 | casos | 1 |
| 4551 | casero | 1 |
| 4552 | caseramente | 1 |
| 4553 | cascabel | 1 |
| 4554 | casas | 1 |
| 4555 | casarse | 1 |
| 4556 | casar | 1 |
| 4557 | casando | 1 |
| 4558 | cartujo | 1 |
| 4559 | carrizo | 1 |
| 4560 | carrizales | 1 |
| 4561 | caro | 1 |
| 4562 | caribes | 1 |
| 4563 | cardar | 1 |
| 4564 | cardada | 1 |
| 4565 | carcajes | 1 |
| 4566 | carcaj | 1 |
| 4567 | carbunclo | 1 |
| 4568 | caracteres | 1 |
| 4569 | cara | 1 |
| 4570 | capotes | 1 |
| 4571 | capiteles | 1 |
| 4572 | capilla | 1 |
| 4573 | capa | 1 |
| 4574 | cantuesos | 1 |
| 4575 | cántico | 1 |
| 4576 | cantar | 1 |
| 4577 | cantando | 1 |
| 4578 | cantan | 1 |
| 4579 | cansancio | 1 |
| 4580 | canicular | 1 |
| 4581 | cándidos | 1 |
| 4582 | candados | 1 |
| 4583 | canarias | 1 |
| 4584 | campañas | 1 |
| 4585 | campanilla | 1 |
| 4586 | caminos | 1 |
| 4587 | calzándole | 1 |
| 4588 | calzan | 1 |
| 4589 | calzadas | 1 |
| 4590 | calvo | 1 |
| 4591 | caluroso | 1 |
| 4592 | calor | 1 |
| 4593 | calmas | 1 |
| 4594 | calma | 1 |
| 4595 | callo | 1 |
| 4596 | calles | 1 |
| 4597 | callen | 1 |
| 4598 | callaron | 1 |
| 4599 | callaré | 1 |
| 4600 | callando | 1 |
| 4601 | callado | 1 |
| 4602 | caliginoso | 1 |
| 4603 | califican | 1 |
| 4604 | califica | 1 |
| 4605 | calientes | 1 |
| 4606 | calarse | 1 |
| 4607 | calaron | 1 |
| 4608 | caladas | 1 |
| 4609 | caístro | 1 |
| 4610 | cairela | 1 |
| 4611 | cairás | 1 |
| 4612 | caducar | 1 |
| 4613 | caduca | 1 |
| 4614 | caco | 1 |
| 4615 | cabritos | 1 |
| 4616 | cabrío | 1 |
| 4617 | cabra | 1 |
| 4618 | cabellos | 1 |
| 4619 | cabaña | 1 |
| 4620 | buzo | 1 |
| 4621 | busiris | 1 |
| 4622 | buscó | 1 |
| 4623 | buscarle | 1 |
| 4624 | burlas | 1 |
| 4625 | burlar | 1 |
| 4626 | burlándolo | 1 |
| 4627 | burla | 1 |
| 4628 | buril | 1 |
| 4629 | burgo | 1 |
| 4630 | bultos | 1 |
| 4631 | bullir | 1 |
| 4632 | buitres | 1 |
| 4633 | buitre | 1 |
| 4634 | bufando | 1 |
| 4635 | bueno | 1 |
| 4636 | buen | 1 |
| 4637 | bucólicos | 1 |
| 4638 | bucólica | 1 |
| 4639 | bruto | 1 |
| 4640 | bruta | 1 |
| 4641 | bruñidos | 1 |
| 4642 | bruñe | 1 |
| 4643 | brote | 1 |
| 4644 | brocados | 1 |
| 4645 | brocado | 1 |
| 4646 | britano | 1 |
| 4647 | brillante | 1 |
| 4648 | brillando | 1 |
| 4649 | brilla | 1 |
| 4650 | bravo | 1 |
| 4651 | brame | 1 |
| 4652 | bóveda | 1 |
| 4653 | botón | 1 |
| 4654 | boto | 1 |
| 4655 | botica | 1 |
| 4656 | bote | 1 |
| 4657 | bostezo | 1 |
| 4658 | bosquejó | 1 |
| 4659 | bosquejo | 1 |
| 4660 | bosquejado | 1 |
| 4661 | borró | 1 |
| 4662 | borní | 1 |
| 4663 | boreal | 1 |
| 4664 | borde | 1 |
| 4665 | bontà | 1 |
| 4666 | bondad | 1 |
| 4667 | blanqueando | 1 |
| 4668 | blandas | 1 |
| 4669 | blanda | 1 |
| 4670 | bizarro | 1 |
| 4671 | bisagra | 1 |
| 4672 | bipartido | 1 |
| 4673 | bipartida | 1 |
| 4674 | bicorne | 1 |
| 4675 | bestia | 1 |
| 4676 | beso | 1 |
| 4677 | besaste | 1 |
| 4678 | besando | 1 |
| 4679 | besan | 1 |
| 4680 | besaba | 1 |
| 4681 | berberiscos | 1 |
| 4682 | bengala | 1 |
| 4683 | benditísimo | 1 |
| 4684 | bendigo | 1 |
| 4685 | belleza | 1 |
| 4686 | bebo | 1 |
| 4687 | bebido | 1 |
| 4688 | bebida | 1 |
| 4689 | beberse | 1 |
| 4690 | beber | 1 |
| 4691 | bébelo | 1 |
| 4692 | beba | 1 |
| 4693 | bayos | 1 |
| 4694 | bayo | 1 |
| 4695 | batiendo | 1 |
| 4696 | batía | 1 |
| 4697 | bates | 1 |
| 4698 | baten | 1 |
| 4699 | batallas | 1 |
| 4700 | batalla | 1 |
| 4701 | bastó | 1 |
| 4702 | baste | 1 |
| 4703 | basiliscos | 1 |
| 4704 | basas | 1 |
| 4705 | barracas | 1 |
| 4706 | barraca | 1 |
| 4707 | barquillo | 1 |
| 4708 | barquillas | 1 |
| 4709 | barcas | 1 |
| 4710 | bárbaras | 1 |
| 4711 | barbado | 1 |
| 4712 | barato | 1 |
| 4713 | baña | 1 |
| 4714 | ballenas | 1 |
| 4715 | balido | 1 |
| 4716 | bala | 1 |
| 4717 | bajaran | 1 |
| 4718 | bajaba | 1 |
| 4719 | bailes | 1 |
| 4720 | bailar | 1 |
| 4721 | báculo | 1 |
| 4722 | bachillera | 1 |
| 4723 | bacantes | 1 |
| 4724 | bacanal | 1 |
| 4725 | babilonia | 1 |
| 4726 | azulísima | 1 |
| 4727 | azucenas | 1 |
| 4728 | azucena | 1 |
| 4729 | azotar | 1 |
| 4730 | azotadas | 1 |
| 4731 | azores | 1 |
| 4732 | azor | 1 |
| 4733 | azogue | 1 |
| 4734 | azahares | 1 |
| 4735 | azada | 1 |
| 4736 | ayude | 1 |
| 4737 | ayuda | 1 |
| 4738 | ayer | 1 |
| 4739 | aviso | 1 |
| 4740 | avecilla | 1 |
| 4741 | avariento | 1 |
| 4742 | avarienta | 1 |
| 4743 | auxilïar | 1 |
| 4744 | autor | 1 |
| 4745 | austros | 1 |
| 4746 | ausentarse | 1 |
| 4747 | augusta | 1 |
| 4748 | audaz | 1 |
| 4749 | audacia | 1 |
| 4750 | atunes | 1 |
| 4751 | atribüido | 1 |
| 4752 | atrevimiento | 1 |
| 4753 | atrevieron | 1 |
| 4754 | atreviera | 1 |
| 4755 | atreve | 1 |
| 4756 | atrás | 1 |
| 4757 | atractiva | 1 |
| 4758 | atlante | 1 |
| 4759 | ataúd | 1 |
| 4760 | atalayas | 1 |
| 4761 | atalanta | 1 |
| 4762 | atajo | 1 |
| 4763 | atados | 1 |
| 4764 | astros | 1 |
| 4765 | astronómicos | 1 |
| 4766 | astrología | 1 |
| 4767 | astillas | 1 |
| 4768 | aspiran | 1 |
| 4769 | aspira | 1 |
| 4770 | ásperas | 1 |
| 4771 | aspecto | 1 |
| 4772 | asido | 1 |
| 4773 | ascendiendo | 1 |
| 4774 | artificiosamente | 1 |
| 4775 | artículos | 1 |
| 4776 | articular | 1 |
| 4777 | articulado | 1 |
| 4778 | artesón | 1 |
| 4779 | artesa | 1 |
| 4780 | arrullo | 1 |
| 4781 | arrulla | 1 |
| 4782 | arrolló | 1 |
| 4783 | arrojadizo | 1 |
| 4784 | arrogancia | 1 |
| 4785 | arrogan | 1 |
| 4786 | arrimarle | 1 |
| 4787 | arrima | 1 |
| 4788 | arriba | 1 |
| 4789 | arrendara | 1 |
| 4790 | arreboza | 1 |
| 4791 | arreboles | 1 |
| 4792 | arrebolado | 1 |
| 4793 | arrebatamiento | 1 |
| 4794 | arrebatado | 1 |
| 4795 | arrastrados | 1 |
| 4796 | arrastraba | 1 |
| 4797 | arras | 1 |
| 4798 | arraigados | 1 |
| 4799 | arraiga | 1 |
| 4800 | arquitectura | 1 |
| 4801 | arquear | 1 |
| 4802 | arpías | 1 |
| 4803 | arpía | 1 |
| 4804 | aromática | 1 |
| 4805 | aroma | 1 |
| 4806 | arnés | 1 |
| 4807 | armonïoso | 1 |
| 4808 | armaron | 1 |
| 4809 | armar | 1 |
| 4810 | arman | 1 |
| 4811 | armada | 1 |
| 4812 | ariosto | 1 |
| 4813 | arïón | 1 |
| 4814 | argote | 1 |
| 4815 | argentando | 1 |
| 4816 | argentados | 1 |
| 4817 | argentada | 1 |
| 4818 | argel | 1 |
| 4819 | ardor | 1 |
| 4820 | arde | 1 |
| 4821 | arcaduz | 1 |
| 4822 | aras | 1 |
| 4823 | arados | 1 |
| 4824 | arador | 1 |
| 4825 | arado | 1 |
| 4826 | aracnes | 1 |
| 4827 | ara | 1 |
| 4828 | aquellas | 1 |
| 4829 | apurarle | 1 |
| 4830 | apurando | 1 |
| 4831 | apuntó | 1 |
| 4832 | aprisionado | 1 |
| 4833 | aprisionada | 1 |
| 4834 | aprisiona | 1 |
| 4835 | aprisa | 1 |
| 4836 | apresura | 1 |
| 4837 | aprender | 1 |
| 4838 | apremïado | 1 |
| 4839 | aprehender | 1 |
| 4840 | apolo | 1 |
| 4841 | apócrifa | 1 |
| 4842 | aplica | 1 |
| 4843 | aplausos | 1 |
| 4844 | aplauso | 1 |
| 4845 | apeó | 1 |
| 4846 | apelación | 1 |
| 4847 | apeado | 1 |
| 4848 | aparta | 1 |
| 4849 | aparecen | 1 |
| 4850 | añudando | 1 |
| 4851 | añado | 1 |
| 4852 | anunciando | 1 |
| 4853 | anuncia | 1 |
| 4854 | anudados | 1 |
| 4855 | anuda | 1 |
| 4856 | antoja | 1 |
| 4857 | antípodas | 1 |
| 4858 | antiguos | 1 |
| 4859 | antiguas | 1 |
| 4860 | antigua | 1 |
| 4861 | anticipa | 1 |
| 4862 | antárticas | 1 |
| 4863 | anocheció | 1 |
| 4864 | animosa | 1 |
| 4865 | ánimo | 1 |
| 4866 | anima | 1 |
| 4867 | anhelante | 1 |
| 4868 | anhelando | 1 |
| 4869 | ángel | 1 |
| 4870 | anegó | 1 |
| 4871 | anea | 1 |
| 4872 | andaluz | 1 |
| 4873 | andalucía | 1 |
| 4874 | áncora | 1 |
| 4875 | ancón | 1 |
| 4876 | ancha | 1 |
| 4877 | anales | 1 |
| 4878 | amorosos | 1 |
| 4879 | amorosa | 1 |
| 4880 | amó | 1 |
| 4881 | amigas | 1 |
| 4882 | américos | 1 |
| 4883 | amenazas | 1 |
| 4884 | amebeo | 1 |
| 4885 | ambrosía | 1 |
| 4886 | ambiguo | 1 |
| 4887 | ambicioso | 1 |
| 4888 | ambiciosas | 1 |
| 4889 | ámbar | 1 |
| 4890 | amazonas | 1 |
| 4891 | amazona | 1 |
| 4892 | amas | 1 |
| 4893 | amanezca | 1 |
| 4894 | amaltea | 1 |
| 4895 | alternar | 1 |
| 4896 | alternantes | 1 |
| 4897 | alternando | 1 |
| 4898 | alterando | 1 |
| 4899 | alteran | 1 |
| 4900 | alquería | 1 |
| 4901 | almendro | 1 |
| 4902 | almendra | 1 |
| 4903 | almejas | 1 |
| 4904 | almalafas | 1 |
| 4905 | allana | 1 |
| 4906 | alistar | 1 |
| 4907 | alisos | 1 |
| 4908 | aliso | 1 |
| 4909 | alimenten | 1 |
| 4910 | aliéntate | 1 |
| 4911 | alhelíes | 1 |
| 4912 | alhambra | 1 |
| 4913 | alguno | 1 |
| 4914 | alga | 1 |
| 4915 | alfombra | 1 |
| 4916 | alevosías | 1 |
| 4917 | aleto | 1 |
| 4918 | alegres | 1 |
| 4919 | aldabas | 1 |
| 4920 | alcornoque | 1 |
| 4921 | alcohole | 1 |
| 4922 | alcohola | 1 |
| 4923 | alcïón | 1 |
| 4924 | alcimedón | 1 |
| 4925 | alcázares | 1 |
| 4926 | alcázar | 1 |
| 4927 | alcanzan | 1 |
| 4928 | alcándara | 1 |
| 4929 | alcance | 1 |
| 4930 | albornoces | 1 |
| 4931 | albores | 1 |
| 4932 | álamo | 1 |
| 4933 | alameda | 1 |
| 4934 | alaba | 1 |
| 4935 | ajustando | 1 |
| 4936 | ajenos | 1 |
| 4937 | ajeno | 1 |
| 4938 | ajenas | 1 |
| 4939 | airoso | 1 |
| 4940 | aguja | 1 |
| 4941 | águila | 1 |
| 4942 | aguijón | 1 |
| 4943 | aguardo | 1 |
| 4944 | agregó | 1 |
| 4945 | agregados | 1 |
| 4946 | agraviando | 1 |
| 4947 | agravan | 1 |
| 4948 | agravado | 1 |
| 4949 | agrava | 1 |
| 4950 | agradecimiento | 1 |
| 4951 | agradecidas | 1 |
| 4952 | agradecidamente | 1 |
| 4953 | agradables | 1 |
| 4954 | aganipe | 1 |
| 4955 | africano | 1 |
| 4956 | afrenta | 1 |
| 4957 | aflojó | 1 |
| 4958 | aflijo | 1 |
| 4959 | afirmar | 1 |
| 4960 | afinidad | 1 |
| 4961 | afínese | 1 |
| 4962 | afectüoso | 1 |
| 4963 | afectos | 1 |
| 4964 | afecto | 1 |
| 4965 | afable | 1 |
| 4966 | advocaron | 1 |
| 4967 | adversidades | 1 |
| 4968 | adunco | 1 |
| 4969 | adulteraste | 1 |
| 4970 | adulación | 1 |
| 4971 | aduana | 1 |
| 4972 | adoro | 1 |
| 4973 | adorno | 1 |
| 4974 | adonis | 1 |
| 4975 | adónde | 1 |
| 4976 | adolescente | 1 |
| 4977 | admitir | 1 |
| 4978 | admitidos | 1 |
| 4979 | admita | 1 |
| 4980 | admiró | 1 |
| 4981 | admirando | 1 |
| 4982 | admiraciones | 1 |
| 4983 | adjudicas | 1 |
| 4984 | adivino | 1 |
| 4985 | adentro | 1 |
| 4986 | adarga | 1 |
| 4987 | acusándole | 1 |
| 4988 | acusaba | 1 |
| 4989 | acusa | 1 |
| 4990 | acuñados | 1 |
| 4991 | acude | 1 |
| 4992 | acuario | 1 |
| 4993 | acteón | 1 |
| 4994 | acrisola | 1 |
| 4995 | acordes | 1 |
| 4996 | acompañando | 1 |
| 4997 | acompañado | 1 |
| 4998 | acomodó | 1 |
| 4999 | acogió | 1 |
| 5000 | aclamó | 1 |
| 5001 | acertado | 1 |
| 5002 | acerados | 1 |
| 5003 | acequia | 1 |
| 5004 | acelerado | 1 |
| 5005 | acanto | 1 |
| 5006 | acabe | 1 |
| 5007 | acabarán | 1 |
| 5008 | absuelve | 1 |
| 5009 | absolvello | 1 |
| 5010 | abriles | 1 |
| 5011 | abrigados | 1 |
| 5012 | abriendo | 1 |
| 5013 | abrevïara | 1 |
| 5014 | abrevïada | 1 |
| 5015 | abre | 1 |
| 5016 | abrazó | 1 |
| 5017 | abrazo | 1 |
| 5018 | abrazáronse | 1 |
| 5019 | abrazaron | 1 |
| 5020 | abrazando | 1 |
| 5021 | abrazadora | 1 |
| 5022 | abrasar | 1 |
| 5023 | abrace | 1 |
| 5024 | abortaron | 1 |
| 5025 | abortada | 1 |
| 5026 | abogue | 1 |
| 5027 | abismo | 1 |
| 5028 | abierta | 1 |
| 5029 | abejas | 1 |
| 5030 | abades | 1 |
|
|
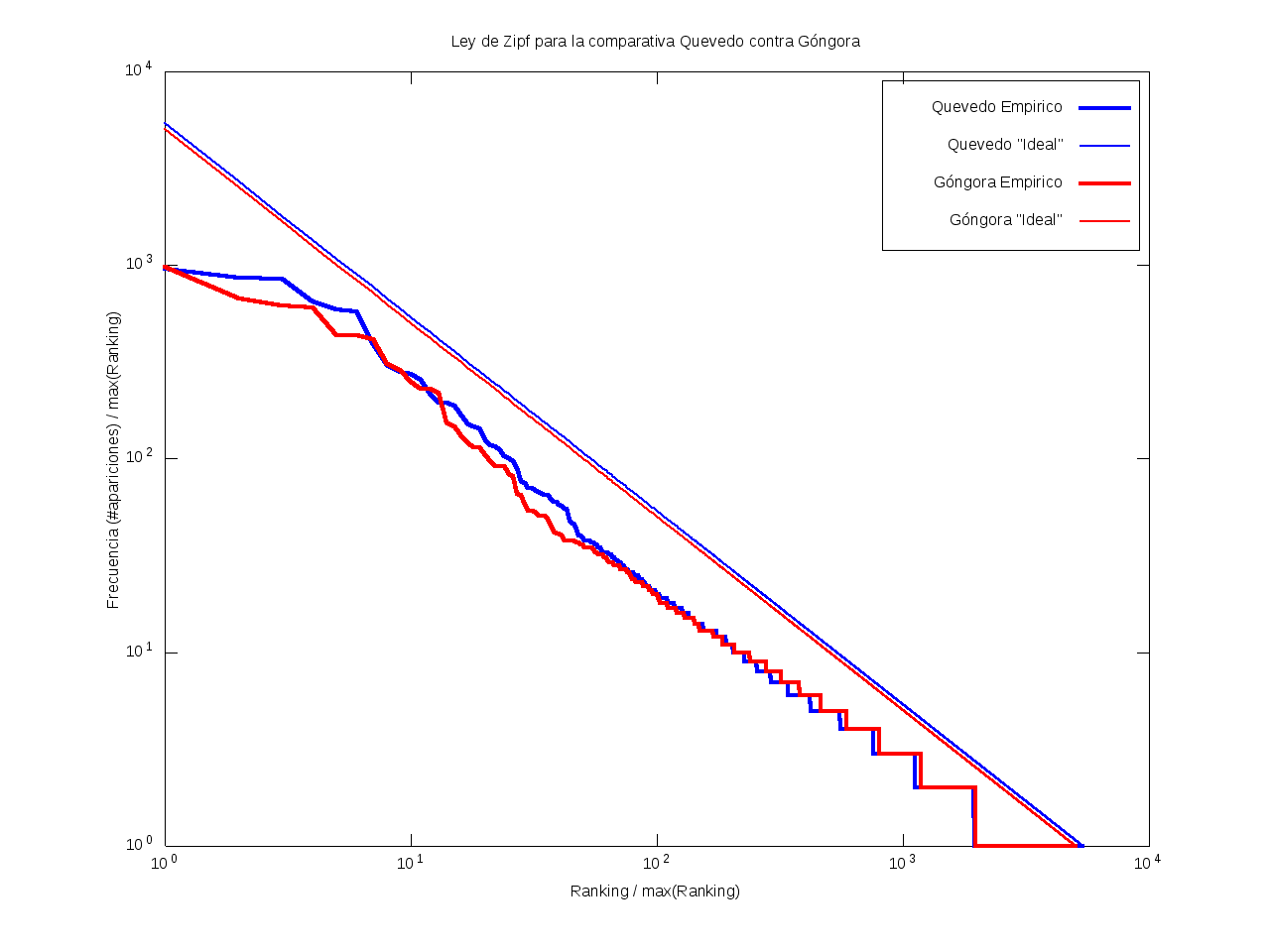
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará un conjunto (Quevedo) (conjunto 1)
contra el otro (Góngora) (conjunto 2) y viceversa.
A continuación se muestra una lista de todas las palabras presentes en los textos,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
Mostrar todo
Recoger


