Comparativa: Literatura española contra literatura inglesa
Índice
Información General
| Título: | * |
|---|
| Autor: | * |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 1800906 |
|---|
| #Palabras distintas: | 76810 |
|---|
| Type-Token ratio: | 4.27% |
|---|
|
| Título: | * |
|---|
| Autor: | * |
|---|
| Idioma: | Inglés |
|---|
| #Palabras total: | 1323714 |
|---|
| #Palabras distintas: | 28903 |
|---|
| Type-Token ratio: | 2.18% |
|---|
|
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| Castellano | Inglés |
|---|
| #Palabras: | #Palabras distintas: |
|---|
| 36018 | 5706 |
| 72036 | 11046 |
| 108054 | 14561 |
| 144072 | 17696 |
| 180090 | 20200 |
| 216108 | 21997 |
| 252126 | 23464 |
| 288144 | 24611 |
| 324162 | 25754 |
| 360180 | 27048 |
| 396198 | 28321 |
| 432216 | 29474 |
| 468234 | 30611 |
| 504252 | 31605 |
| 540270 | 32583 |
| 576288 | 34920 |
| 612306 | 36999 |
| 648324 | 38836 |
| 684342 | 40455 |
| 720360 | 41950 |
| 756378 | 43172 |
| 792396 | 44394 |
| 828414 | 45454 |
| 864432 | 46436 |
| 900450 | 47394 |
| 936468 | 48173 |
| 972486 | 50942 |
| 1008504 | 52746 |
| 1044522 | 54236 |
| 1080540 | 55220 |
| 1116558 | 56054 |
| 1152576 | 56826 |
| 1188594 | 57533 |
| 1224612 | 58207 |
| 1260630 | 58817 |
| 1296648 | 59339 |
| 1332666 | 60002 |
| 1368684 | 60926 |
| 1404702 | 61908 |
| 1440720 | 65447 |
| 1476738 | 68505 |
| 1512756 | 69268 |
| 1548774 | 70229 |
| 1584792 | 71196 |
| 1620810 | 71937 |
| 1656828 | 72696 |
| 1692846 | 73642 |
| 1728864 | 74555 |
| 1764882 | 75449 |
| 1800900 | 76810 |
| 1800906 | 76810 |
|
| #Palabras: | #Palabras distintas: |
|---|
| 26474 | 3967 |
| 52948 | 5917 |
| 79422 | 7099 |
| 105896 | 7964 |
| 132370 | 8728 |
| 158844 | 9468 |
| 185318 | 10064 |
| 211792 | 10928 |
| 238266 | 11577 |
| 264740 | 12214 |
| 291214 | 12727 |
| 317688 | 13241 |
| 344162 | 13764 |
| 370636 | 14146 |
| 397110 | 14572 |
| 423584 | 15237 |
| 450058 | 16085 |
| 476532 | 16923 |
| 503006 | 17544 |
| 529480 | 18110 |
| 555954 | 18664 |
| 582428 | 19148 |
| 608902 | 19847 |
| 635376 | 20541 |
| 661850 | 21042 |
| 688324 | 21698 |
| 714798 | 22294 |
| 741272 | 22702 |
| 767746 | 22999 |
| 794220 | 23299 |
| 820694 | 23573 |
| 847168 | 23841 |
| 873642 | 24255 |
| 900116 | 24715 |
| 926590 | 25059 |
| 953064 | 25366 |
| 979538 | 25674 |
| 1006012 | 26025 |
| 1032486 | 26261 |
| 1058960 | 26519 |
| 1085434 | 26745 |
| 1111908 | 26900 |
| 1138382 | 27158 |
| 1164856 | 27413 |
| 1191330 | 27656 |
| 1217804 | 27896 |
| 1244278 | 28178 |
| 1270752 | 28475 |
| 1297226 | 28666 |
| 1323700 | 28903 |
| 1323714 | 28903 |
|
|
Ajuste por mínimos cuadrados de los datos a K*n^b: |
| Castellano |
|
Inglés |
| K = 10.669 |
|
K = 18.351 |
| b = 0.615 |
|
b = 0.524 |

|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Castellano | Inglés |
Ilustración del principio de mínimo esfuerzo: |
| Rank | Palabra | Frec |
|---|
| 1 | de | 85641 |
| 2 | que | 74680 |
| 3 | y | 63032 |
| 4 | la | 58241 |
| 5 | a | 42958 |
| 6 | el | 40763 |
| 7 | en | 38512 |
| 8 | no | 30693 |
| 9 | se | 23495 |
| 10 | los | 21071 |
| 11 | con | 19945 |
| 12 | por | 17935 |
| 13 | las | 16539 |
| 14 | su | 16266 |
| 15 | lo | 15101 |
| 16 | un | 14496 |
| 17 | le | 13745 |
| 18 | del | 12449 |
| 19 | me | 11265 |
| 20 | es | 10752 |
| 21 | al | 10553 |
| 22 | una | 10216 |
| 23 | como | 10143 |
| 24 | más | 9589 |
| 25 | para | 8633 |
| 26 | si | 8463 |
| 27 | yo | 8220 |
| 28 | pero | 7155 |
| 29 | mi | 6800 |
| 30 | era | 6460 |
| 31 | había | 6030 |
| 32 | qué | 5858 |
| 33 | sus | 5244 |
| 34 | don | 5101 |
| 35 | él | 4823 |
| 36 | o | 4797 |
| 37 | sin | 4745 |
| 38 | dijo | 4739 |
| 39 | ya | 4738 |
| 40 | todo | 4713 |
| 41 | porque | 4609 |
| 42 | te | 4443 |
| 43 | ni | 4443 |
| 44 | tan | 4236 |
| 45 | usted | 4121 |
| 46 | bien | 3933 |
| 47 | ha | 3893 |
| 48 | ella | 3837 |
| 49 | pues | 3694 |
| 50 | cuando | 3603 |
| 51 | muy | 3555 |
| 52 | ser | 3315 |
| 53 | esto | 3306 |
| 54 | esta | 3178 |
| 55 | casa | 3019 |
| 56 | señor | 2901 |
| 57 | dos | 2901 |
| 58 | todos | 2884 |
| 59 | este | 2782 |
| 60 | e | 2695 |
| 61 | estaba | 2686 |
| 62 | aquel | 2680 |
| 63 | sí | 2661 |
| 64 | dios | 2600 |
| 65 | así | 2559 |
| 66 | sancho | 2414 |
| 67 | tu | 2378 |
| 68 | tenía | 2341 |
| 69 | aquella | 2291 |
| 70 | otra | 2236 |
| 71 | quien | 2221 |
| 72 | sobre | 2199 |
| 73 | quijote | 2198 |
| 74 | aquí | 2183 |
| 75 | hay | 2165 |
| 76 | poco | 2138 |
| 77 | otro | 2133 |
| 78 | he | 2114 |
| 79 | mí | 2083 |
| 80 | fue | 2038 |
| 81 | nos | 2023 |
| 82 | nada | 2017 |
| 83 | ver | 1997 |
| 84 | está | 1974 |
| 85 | hombre | 1952 |
| 86 | después | 1948 |
| 87 | mucho | 1947 |
| 88 | señora | 1946 |
| 89 | entre | 1942 |
| 90 | día | 1934 |
| 91 | vida | 1886 |
| 92 | donde | 1849 |
| 93 | decir | 1844 |
| 94 | tal | 1843 |
| 95 | cosa | 1841 |
| 96 | hasta | 1835 |
| 97 | mal | 1824 |
| 98 | tú | 1798 |
| 99 | son | 1782 |
| 100 | doña | 1754 |
| 101 | sino | 1728 |
| 102 | allí | 1727 |
| 103 | eso | 1725 |
| 104 | tiene | 1722 |
| 105 | é | 1704 |
| 106 | hacer | 1684 |
| 107 | cual | 1678 |
| 108 | también | 1650 |
| 109 | ahora | 1636 |
| 110 | mundo | 1587 |
| 111 | tiempo | 1564 |
| 112 | aunque | 1564 |
| 113 | todas | 1555 |
| 114 | ojos | 1549 |
| 115 | cosas | 1533 |
| 116 | gran | 1528 |
| 117 | tanto | 1525 |
| 118 | toda | 1497 |
| 119 | siempre | 1496 |
| 120 | mujer | 1469 |
| 121 | menos | 1465 |
| 122 | noche | 1435 |
| 123 | buen | 1429 |
| 124 | mismo | 1420 |
| 125 | les | 1418 |
| 126 | fin | 1413 |
| 127 | mas | 1385 |
| 128 | cómo | 1361 |
| 129 | vez | 1353 |
| 130 | mis | 1351 |
| 131 | verdad | 1344 |
| 132 | mano | 1332 |
| 133 | uno | 1318 |
| 134 | tengo | 1314 |
| 135 | algo | 1293 |
| 136 | mejor | 1284 |
| 137 | sé | 1282 |
| 138 | decía | 1269 |
| 139 | puede | 1265 |
| 140 | parte | 1263 |
| 141 | non | 1256 |
| 142 | luego | 1252 |
| 143 | d | 1249 |
| 144 | respondió | 1242 |
| 145 | buena | 1235 |
| 146 | cabeza | 1233 |
| 147 | dar | 1207 |
| 148 | dicho | 1202 |
| 149 | antes | 1192 |
| 150 | amor | 1192 |
| 151 | han | 1168 |
| 152 | alma | 1164 |
| 153 | eran | 1156 |
| 154 | desde | 1149 |
| 155 | soy | 1138 |
| 156 | hecho | 1134 |
| 157 | días | 1122 |
| 158 | otros | 1117 |
| 159 | iba | 1113 |
| 160 | estas | 1108 |
| 161 | podía | 1100 |
| 162 | fuera | 1100 |
| 163 | parece | 1077 |
| 164 | veces | 1072 |
| 165 | ellos | 1058 |
| 166 | quiero | 1053 |
| 167 | quién | 1041 |
| 168 | habían | 1028 |
| 169 | merced | 1027 |
| 170 | nunca | 1024 |
| 171 | vuestra | 1017 |
| 172 | tres | 1017 |
| 173 | sólo | 1016 |
| 174 | manos | 1008 |
| 175 | digo | 993 |
| 176 | cada | 993 |
| 177 | otras | 973 |
| 178 | madre | 973 |
| 179 | ana | 971 |
| 180 | visto | 967 |
| 181 | amigo | 966 |
| 182 | sea | 949 |
| 183 | alguna | 947 |
| 184 | voz | 940 |
| 185 | calle | 925 |
| 186 | ese | 919 |
| 187 | caballero | 919 |
| 188 | padre | 916 |
| 189 | parecía | 905 |
| 190 | os | 902 |
| 191 | estos | 874 |
| 192 | fortunata | 869 |
| 193 | á | 863 |
| 194 | tener | 855 |
| 195 | sido | 852 |
| 196 | años | 847 |
| 197 | manera | 835 |
| 198 | hizo | 832 |
| 199 | hacía | 830 |
| 200 | saber | 828 |
| 201 | tierra | 827 |
| 202 | hija | 824 |
| 203 | cuanto | 823 |
| 204 | puerta | 819 |
| 205 | va | 818 |
| 206 | esa | 817 |
| 207 | quiere | 813 |
| 208 | quería | 813 |
| 209 | pobre | 812 |
| 210 | sabe | 809 |
| 211 | hace | 804 |
| 212 | mañana | 801 |
| 213 | hijo | 797 |
| 214 | entonces | 797 |
| 215 | muchos | 796 |
| 216 | has | 796 |
| 217 | muchas | 788 |
| 218 | dice | 786 |
| 219 | dio | 781 |
| 220 | mayor | 780 |
| 221 | nadie | 777 |
| 222 | magistral | 775 |
| 223 | cielo | 771 |
| 224 | modo | 766 |
| 225 | grande | 765 |
| 226 | aquellos | 763 |
| 227 | algún | 758 |
| 228 | amo | 754 |
| 229 | haber | 745 |
| 230 | santa | 743 |
| 231 | cuerpo | 743 |
| 232 | palabras | 741 |
| 233 | allá | 735 |
| 234 | vio | 733 |
| 235 | camino | 731 |
| 236 | puesto | 726 |
| 237 | estoy | 719 |
| 238 | medio | 701 |
| 239 | cara | 695 |
| 240 | rey | 694 |
| 241 | muerte | 694 |
| 242 | sabía | 688 |
| 243 | ti | 687 |
| 244 | bueno | 683 |
| 245 | lugar | 680 |
| 246 | unos | 675 |
| 247 | mil | 672 |
| 248 | ay | 665 |
| 249 | vos | 663 |
| 250 | tarde | 662 |
| 251 | punto | 661 |
| 252 | hombres | 661 |
| 253 | hora | 659 |
| 254 | oh | 655 |
| 255 | hablar | 654 |
| 256 | boca | 652 |
| 257 | diciendo | 648 |
| 258 | palabra | 645 |
| 259 | daba | 645 |
| 260 | aun | 639 |
| 261 | primero | 637 |
| 262 | gente | 631 |
| 263 | caso | 630 |
| 264 | ir | 629 |
| 265 | será | 628 |
| 266 | contra | 628 |
| 267 | salir | 625 |
| 268 | corazón | 625 |
| 269 | cuatro | 623 |
| 270 | según | 620 |
| 271 | dentro | 620 |
| 272 | casi | 620 |
| 273 | marido | 617 |
| 274 | algunos | 617 |
| 275 | pie | 615 |
| 276 | misma | 615 |
| 277 | mala | 613 |
| 278 | estar | 613 |
| 279 | aquello | 610 |
| 280 | persona | 609 |
| 281 | da | 608 |
| 282 | estaban | 607 |
| 283 | nuestro | 604 |
| 284 | puso | 603 |
| 285 | mío | 603 |
| 286 | cura | 603 |
| 287 | hoy | 602 |
| 288 | cierto | 601 |
| 289 | cuenta | 600 |
| 290 | grandes | 593 |
| 291 | demás | 591 |
| 292 | hubiera | 588 |
| 293 | nombre | 585 |
| 294 | dado | 582 |
| 295 | mucha | 580 |
| 296 | idea | 579 |
| 297 | jacinta | 571 |
| 298 | volvió | 570 |
| 299 | tus | 562 |
| 300 | mía | 562 |
| 301 | creo | 560 |
| 302 | vino | 558 |
| 303 | juan | 556 |
| 304 | martín | 555 |
| 305 | razón | 551 |
| 306 | duda | 551 |
| 307 | pronto | 549 |
| 308 | fuerza | 549 |
| 309 | agua | 547 |
| 310 | ellas | 544 |
| 311 | nuestra | 540 |
| 312 | pueblo | 537 |
| 313 | luz | 535 |
| 314 | comer | 532 |
| 315 | gusto | 528 |
| 316 | aquellas | 525 |
| 317 | vamos | 524 |
| 318 | llegó | 522 |
| 319 | lupe | 521 |
| 320 | hacia | 521 |
| 321 | paso | 518 |
| 322 | eres | 515 |
| 323 | solo | 514 |
| 324 | voy | 513 |
| 325 | mientras | 513 |
| 326 | fuese | 513 |
| 327 | dónde | 512 |
| 328 | álvaro | 512 |
| 329 | historia | 507 |
| 330 | lado | 504 |
| 331 | tuvo | 503 |
| 332 | tienes | 502 |
| 333 | delante | 502 |
| 334 | debe | 501 |
| 335 | víctor | 498 |
| 336 | puedo | 498 |
| 337 | miedo | 498 |
| 338 | dinero | 496 |
| 339 | entró | 492 |
| 340 | pudo | 491 |
| 341 | pasar | 490 |
| 342 | suelo | 488 |
| 343 | unas | 486 |
| 344 | estado | 486 |
| 345 | entrar | 485 |
| 346 | algunas | 484 |
| 347 | poder | 483 |
| 348 | pies | 482 |
| 349 | tanta | 481 |
| 350 | regenta | 481 |
| 351 | triste | 478 |
| 352 | viene | 475 |
| 353 | falta | 473 |
| 354 | vetusta | 472 |
| 355 | momento | 472 |
| 356 | están | 472 |
| 357 | san | 471 |
| 358 | debía | 471 |
| 359 | vista | 470 |
| 360 | nuevo | 470 |
| 361 | tales | 467 |
| 362 | señores | 466 |
| 363 | sería | 464 |
| 364 | preguntó | 464 |
| 365 | joven | 464 |
| 366 | salió | 463 |
| 367 | amigos | 462 |
| 368 | rostro | 461 |
| 369 | ninguna | 461 |
| 370 | pensaba | 456 |
| 371 | nosotros | 455 |
| 372 | vaya | 452 |
| 373 | sol | 452 |
| 374 | primera | 452 |
| 375 | replicó | 449 |
| 376 | quiso | 449 |
| 377 | mira | 446 |
| 378 | adelante | 445 |
| 379 | fueron | 443 |
| 380 | aún | 440 |
| 381 | viendo | 439 |
| 382 | venía | 439 |
| 383 | hermano | 438 |
| 384 | ello | 437 |
| 385 | dando | 434 |
| 386 | sola | 431 |
| 387 | madrid | 431 |
| 388 | tomar | 429 |
| 389 | dicen | 422 |
| 390 | sabes | 420 |
| 391 | tienen | 419 |
| 392 | brazos | 419 |
| 393 | agora | 412 |
| 394 | poner | 410 |
| 395 | mar | 410 |
| 396 | cruz | 409 |
| 397 | quedó | 407 |
| 398 | horas | 407 |
| 399 | mesa | 406 |
| 400 | fuerte | 406 |
| 401 | fué | 405 |
| 402 | cerca | 405 |
| 403 | personas | 404 |
| 404 | media | 403 |
| 405 | causa | 403 |
| 406 | ante | 403 |
| 407 | pena | 397 |
| 408 | mujeres | 397 |
| 409 | además | 397 |
| 410 | oro | 395 |
| 411 | junto | 395 |
| 412 | veía | 394 |
| 413 | oído | 394 |
| 414 | caballeros | 393 |
| 415 | voluntad | 391 |
| 416 | todavía | 391 |
| 417 | tía | 391 |
| 418 | hermosa | 391 |
| 419 | buenas | 391 |
| 420 | trabajo | 384 |
| 421 | pasado | 384 |
| 422 | vieja | 381 |
| 423 | viejo | 379 |
| 424 | veo | 379 |
| 425 | venir | 379 |
| 426 | jamás | 379 |
| 427 | fuego | 379 |
| 428 | aire | 379 |
| 429 | volver | 378 |
| 430 | fe | 376 |
| 431 | esas | 376 |
| 432 | ideas | 375 |
| 433 | sangre | 373 |
| 434 | mesía | 373 |
| 435 | ah | 373 |
| 436 | apenas | 371 |
| 437 | llegar | 370 |
| 438 | deseo | 370 |
| 439 | posible | 369 |
| 440 | cuarto | 369 |
| 441 | vi | 367 |
| 442 | amiga | 367 |
| 443 | sentía | 366 |
| 444 | pensar | 366 |
| 445 | quieres | 365 |
| 446 | caballo | 365 |
| 447 | tenían | 364 |
| 448 | memoria | 364 |
| 449 | libro | 363 |
| 450 | suerte | 362 |
| 451 | dolor | 362 |
| 452 | desta | 362 |
| 453 | iglesia | 361 |
| 454 | familia | 361 |
| 455 | ahí | 359 |
| 456 | estás | 358 |
| 457 | año | 356 |
| 458 | muerto | 354 |
| 459 | fermín | 354 |
| 460 | pasó | 353 |
| 461 | vivir | 351 |
| 462 | razones | 351 |
| 463 | pesar | 351 |
| 464 | lengua | 351 |
| 465 | haciendo | 351 |
| 466 | espíritu | 351 |
| 467 | dije | 350 |
| 468 | parecer | 349 |
| 469 | obra | 349 |
| 470 | tantas | 348 |
| 471 | esos | 348 |
| 472 | éste | 347 |
| 473 | claro | 347 |
| 474 | rato | 346 |
| 475 | pasaba | 346 |
| 476 | orden | 346 |
| 477 | ve | 345 |
| 478 | diez | 345 |
| 479 | tras | 344 |
| 480 | remedio | 342 |
| 481 | nela | 341 |
| 482 | alto | 340 |
| 483 | panza | 339 |
| 484 | hubo | 339 |
| 485 | gracias | 339 |
| 486 | sintió | 337 |
| 487 | loco | 337 |
| 488 | buenos | 337 |
| 489 | silencio | 336 |
| 490 | creía | 336 |
| 491 | valor | 334 |
| 492 | pensamiento | 334 |
| 493 | hermosura | 333 |
| 494 | alguno | 333 |
| 495 | exclamó | 325 |
| 496 | conmigo | 325 |
| 497 | guillermina | 324 |
| 498 | brazo | 324 |
| 499 | nueva | 322 |
| 500 | niña | 322 |
| 501 | lejos | 322 |
| 502 | ido | 321 |
| 503 | cama | 319 |
| 504 | dejar | 318 |
| 505 | pudiera | 316 |
| 506 | hablaba | 316 |
| 507 | voces | 315 |
| 508 | podría | 315 |
| 509 | pecho | 315 |
| 510 | ocasión | 315 |
| 511 | dejó | 315 |
| 512 | rubín | 314 |
| 513 | libros | 314 |
| 514 | tantos | 313 |
| 515 | lágrimas | 313 |
| 516 | entender | 313 |
| 517 | benina | 313 |
| 518 | tenido | 311 |
| 519 | ama | 310 |
| 520 | quintanar | 309 |
| 521 | llama | 309 |
| 522 | siendo | 308 |
| 523 | nuño | 308 |
| 524 | hijos | 308 |
| 525 | estuvo | 308 |
| 526 | primer | 307 |
| 527 | oír | 307 |
| 528 | campo | 307 |
| 529 | natural | 305 |
| 530 | hemos | 305 |
| 531 | arriba | 305 |
| 532 | maxi | 304 |
| 533 | figura | 304 |
| 534 | cuales | 303 |
| 535 | gracia | 302 |
| 536 | armas | 301 |
| 537 | iban | 299 |
| 538 | edad | 299 |
| 539 | suyo | 298 |
| 540 | querer | 297 |
| 541 | partes | 297 |
| 542 | general | 297 |
| 543 | maximiliano | 295 |
| 544 | instante | 295 |
| 545 | frente | 295 |
| 546 | pan | 293 |
| 547 | seis | 292 |
| 548 | nuestros | 292 |
| 549 | mitad | 292 |
| 550 | ustedes | 291 |
| 551 | preciso | 290 |
| 552 | dulce | 290 |
| 553 | papel | 289 |
| 554 | llamaba | 289 |
| 555 | debajo | 289 |
| 556 | conciencia | 289 |
| 557 | vuestro | 288 |
| 558 | llevar | 288 |
| 559 | hacen | 287 |
| 560 | cabo | 287 |
| 561 | mirando | 286 |
| 562 | carlos | 285 |
| 563 | ciudad | 284 |
| 564 | sueño | 283 |
| 565 | dulcinea | 283 |
| 566 | abajo | 283 |
| 567 | ruido | 282 |
| 568 | obdulia | 282 |
| 569 | haya | 282 |
| 570 | cuidado | 282 |
| 571 | ciego | 282 |
| 572 | niño | 281 |
| 573 | cuya | 281 |
| 574 | creer | 280 |
| 575 | cel | 280 |
| 576 | carta | 280 |
| 577 | quisiera | 279 |
| 578 | ninguno | 279 |
| 579 | negro | 279 |
| 580 | llevaba | 279 |
| 581 | buscar | 279 |
| 582 | sr | 278 |
| 583 | andar | 277 |
| 584 | libre | 275 |
| 585 | santo | 274 |
| 586 | peor | 274 |
| 587 | pasos | 274 |
| 588 | fama | 274 |
| 589 | chico | 274 |
| 590 | tampoco | 273 |
| 591 | cinco | 273 |
| 592 | alegría | 273 |
| 593 | virtud | 272 |
| 594 | pepe | 272 |
| 595 | venido | 271 |
| 596 | seguro | 271 |
| 597 | ningún | 271 |
| 598 | suya | 270 |
| 599 | quiera | 268 |
| 600 | van | 267 |
| 601 | fortuna | 267 |
| 602 | españa | 267 |
| 603 | dan | 266 |
| 604 | contento | 266 |
| 605 | mozo | 265 |
| 606 | sala | 264 |
| 607 | querido | 264 |
| 608 | guerra | 264 |
| 609 | señoras | 263 |
| 610 | efecto | 263 |
| 611 | ropa | 262 |
| 612 | casas | 262 |
| 613 | caer | 262 |
| 614 | bajo | 262 |
| 615 | traía | 261 |
| 616 | quando | 261 |
| 617 | maría | 261 |
| 618 | malo | 261 |
| 619 | cualquier | 261 |
| 620 | pueden | 260 |
| 621 | pasa | 260 |
| 622 | largo | 260 |
| 623 | escudero | 260 |
| 624 | ven | 259 |
| 625 | culpa | 259 |
| 626 | paz | 258 |
| 627 | miraba | 258 |
| 628 | gloria | 258 |
| 629 | ventura | 257 |
| 630 | petra | 257 |
| 631 | mirar | 257 |
| 632 | llaman | 257 |
| 633 | gana | 257 |
| 634 | peligro | 256 |
| 635 | diablo | 256 |
| 636 | habría | 255 |
| 637 | encima | 254 |
| 638 | visita | 253 |
| 639 | siguiente | 253 |
| 640 | reales | 252 |
| 641 | ponía | 252 |
| 642 | viento | 250 |
| 643 | tomó | 249 |
| 644 | nin | 249 |
| 645 | añadió | 249 |
| 646 | tenga | 248 |
| 647 | gobierno | 248 |
| 648 | di | 248 |
| 649 | anda | 248 |
| 650 | alegre | 248 |
| 651 | último | 247 |
| 652 | perder | 247 |
| 653 | habrá | 247 |
| 654 | conversación | 247 |
| 655 | pedro | 246 |
| 656 | menester | 246 |
| 657 | hermana | 246 |
| 658 | coche | 246 |
| 659 | hambre | 245 |
| 660 | gobernador | 245 |
| 661 | doncella | 245 |
| 662 | propio | 244 |
| 663 | bastante | 244 |
| 664 | sentido | 243 |
| 665 | perdido | 243 |
| 666 | pareció | 243 |
| 667 | mesmo | 243 |
| 668 | comenzó | 243 |
| 669 | justicia | 242 |
| 670 | alta | 242 |
| 671 | esposa | 241 |
| 672 | enemigo | 241 |
| 673 | criado | 241 |
| 674 | siquiera | 240 |
| 675 | segunda | 240 |
| 676 | principio | 240 |
| 677 | ésta | 240 |
| 678 | detrás | 240 |
| 679 | cal | 239 |
| 680 | salud | 237 |
| 681 | pensó | 237 |
| 682 | pablo | 237 |
| 683 | derecho | 237 |
| 684 | cierta | 237 |
| 685 | pensamientos | 236 |
| 686 | perfecta | 235 |
| 687 | duque | 235 |
| 688 | dueña | 235 |
| 689 | color | 235 |
| 690 | deste | 234 |
| 691 | sale | 233 |
| 692 | libertad | 233 |
| 693 | vuesa | 232 |
| 694 | vuelta | 232 |
| 695 | espada | 232 |
| 696 | darle | 232 |
| 697 | carne | 232 |
| 698 | pobres | 231 |
| 699 | miró | 231 |
| 700 | cuyo | 231 |
| 701 | blanco | 231 |
| 702 | vestido | 230 |
| 703 | estamos | 230 |
| 704 | poca | 229 |
| 705 | haga | 229 |
| 706 | arte | 229 |
| 707 | risa | 228 |
| 708 | padres | 228 |
| 709 | habla | 228 |
| 710 | plaza | 227 |
| 711 | morir | 227 |
| 712 | pienso | 226 |
| 713 | oficio | 226 |
| 714 | hablando | 226 |
| 715 | dieron | 226 |
| 716 | verdadero | 224 |
| 717 | pocos | 224 |
| 718 | dama | 224 |
| 719 | v | 223 |
| 720 | sociedad | 223 |
| 721 | rico | 223 |
| 722 | josé | 223 |
| 723 | dormir | 223 |
| 724 | dejaba | 223 |
| 725 | tenemos | 222 |
| 726 | capítulo | 222 |
| 727 | pueda | 221 |
| 728 | presencia | 221 |
| 729 | diga | 221 |
| 730 | sobrino | 220 |
| 731 | segundo | 220 |
| 732 | naturaleza | 220 |
| 733 | grand | 220 |
| 734 | dé | 220 |
| 735 | salía | 219 |
| 736 | labios | 219 |
| 737 | frío | 219 |
| 738 | venga | 218 |
| 739 | nuevas | 218 |
| 740 | llegado | 218 |
| 741 | doce | 218 |
| 742 | honor | 217 |
| 743 | desgracia | 217 |
| 744 | tío | 216 |
| 745 | temor | 216 |
| 746 | principal | 216 |
| 747 | leer | 216 |
| 748 | acá | 216 |
| 749 | tono | 215 |
| 750 | basta | 215 |
| 751 | ves | 214 |
| 752 | propia | 214 |
| 753 | piedra | 214 |
| 754 | ánimo | 214 |
| 755 | oyó | 213 |
| 756 | ocho | 213 |
| 757 | semp | 212 |
| 758 | presto | 211 |
| 759 | presente | 211 |
| 760 | par | 211 |
| 761 | lástima | 211 |
| 762 | frígilis | 211 |
| 763 | sombra | 210 |
| 764 | pedir | 210 |
| 765 | acaso | 210 |
| 766 | público | 209 |
| 767 | obras | 209 |
| 768 | queda | 208 |
| 769 | esperanza | 208 |
| 770 | atención | 208 |
| 771 | teatro | 207 |
| 772 | señorita | 207 |
| 773 | pensando | 207 |
| 774 | rocinante | 206 |
| 775 | costumbre | 206 |
| 776 | tristeza | 205 |
| 777 | noble | 205 |
| 778 | dél | 205 |
| 779 | contestó | 205 |
| 780 | pocas | 204 |
| 781 | noches | 204 |
| 782 | diré | 204 |
| 783 | solía | 203 |
| 784 | lleno | 203 |
| 785 | compañía | 203 |
| 786 | andante | 203 |
| 787 | vea | 202 |
| 788 | real | 202 |
| 789 | gritó | 202 |
| 790 | tiempos | 201 |
| 791 | sacar | 201 |
| 792 | marqués | 201 |
| 793 | echar | 201 |
| 794 | amores | 201 |
| 795 | llamar | 200 |
| 796 | blanca | 200 |
| 797 | bautista | 200 |
| 798 | ayer | 200 |
| 799 | santos | 199 |
| 800 | meses | 199 |
| 801 | duquesa | 199 |
| 802 | canónigo | 199 |
| 803 | virgen | 198 |
| 804 | mancha | 198 |
| 805 | intención | 198 |
| 806 | dedos | 198 |
| 807 | contar | 198 |
| 808 | vergüenza | 197 |
| 809 | flores | 197 |
| 810 | della | 197 |
| 811 | autor | 197 |
| 812 | quieren | 196 |
| 813 | parecían | 196 |
| 814 | vn | 195 |
| 815 | verde | 195 |
| 816 | único | 195 |
| 817 | llena | 195 |
| 818 | cuantos | 195 |
| 819 | país | 194 |
| 820 | nuestras | 194 |
| 821 | podrá | 193 |
| 822 | narv | 193 |
| 823 | fernando | 193 |
| 824 | secreto | 192 |
| 825 | moreno | 192 |
| 826 | mauricia | 192 |
| 827 | importa | 192 |
| 828 | esposo | 192 |
| 829 | café | 192 |
| 830 | senora | 191 |
| 831 | durante | 191 |
| 832 | anita | 191 |
| 833 | volvía | 190 |
| 834 | vivo | 190 |
| 835 | imposible | 190 |
| 836 | honra | 190 |
| 837 | correr | 190 |
| 838 | barbarita | 190 |
| 839 | semejante | 189 |
| 840 | pecado | 189 |
| 841 | juicio | 189 |
| 842 | decían | 189 |
| 843 | sitio | 188 |
| 844 | silla | 188 |
| 845 | quanto | 188 |
| 846 | oía | 188 |
| 847 | chica | 188 |
| 848 | baja | 188 |
| 849 | río | 187 |
| 850 | piedad | 187 |
| 851 | mayores | 187 |
| 852 | mandó | 187 |
| 853 | veinte | 186 |
| 854 | empezó | 186 |
| 855 | criada | 186 |
| 856 | camila | 186 |
| 857 | calles | 186 |
| 858 | atrás | 186 |
| 859 | respeto | 185 |
| 860 | balcón | 185 |
| 861 | escalera | 184 |
| 862 | contrario | 184 |
| 863 | vale | 183 |
| 864 | toma | 183 |
| 865 | subir | 183 |
| 866 | opinión | 183 |
| 867 | médico | 183 |
| 868 | hago | 183 |
| 869 | forma | 183 |
| 870 | estando | 183 |
| 871 | echó | 183 |
| 872 | do | 183 |
| 873 | criados | 183 |
| 874 | vive | 182 |
| 875 | suele | 182 |
| 876 | escribir | 182 |
| 877 | entendimiento | 182 |
| 878 | pelayo | 181 |
| 879 | noticia | 181 |
| 880 | finalmente | 181 |
| 881 | veras | 180 |
| 882 | matar | 180 |
| 883 | ley | 180 |
| 884 | imaginación | 180 |
| 885 | favor | 180 |
| 886 | deja | 180 |
| 887 | conozco | 180 |
| 888 | barbero | 180 |
| 889 | venían | 179 |
| 890 | somos | 179 |
| 891 | puedes | 179 |
| 892 | necesidad | 179 |
| 893 | entraba | 179 |
| 894 | deseos | 179 |
| 895 | amistad | 179 |
| 896 | tienda | 178 |
| 897 | sobrina | 178 |
| 898 | podían | 178 |
| 899 | paseo | 178 |
| 900 | letras | 178 |
| 901 | cuento | 178 |
| 902 | aventura | 178 |
| 903 | vuelto | 177 |
| 904 | cualquiera | 177 |
| 905 | consejo | 177 |
| 906 | ansí | 177 |
| 907 | pone | 176 |
| 908 | paco | 176 |
| 909 | grave | 176 |
| 910 | duro | 176 |
| 911 | venta | 175 |
| 912 | querida | 175 |
| 913 | juntos | 175 |
| 914 | embargo | 175 |
| 915 | cocina | 175 |
| 916 | asno | 175 |
| 917 | verás | 174 |
| 918 | paula | 174 |
| 919 | pas | 174 |
| 920 | llegaba | 174 |
| 921 | hacían | 174 |
| 922 | fondo | 174 |
| 923 | dices | 174 |
| 924 | cuello | 174 |
| 925 | anselmo | 174 |
| 926 | alcoba | 174 |
| 927 | verle | 173 |
| 928 | pasión | 173 |
| 929 | paciencia | 173 |
| 930 | lleva | 173 |
| 931 | izquierdo | 173 |
| 932 | religión | 172 |
| 933 | esperar | 172 |
| 934 | decirle | 172 |
| 935 | vas | 171 |
| 936 | servir | 171 |
| 937 | quedaba | 171 |
| 938 | locura | 171 |
| 939 | hicieron | 171 |
| 940 | daban | 171 |
| 941 | primo | 170 |
| 942 | malos | 170 |
| 943 | lecho | 170 |
| 944 | l | 170 |
| 945 | haré | 170 |
| 946 | dientes | 170 |
| 947 | dejando | 170 |
| 948 | batalla | 170 |
| 949 | assi | 170 |
| 950 | viva | 169 |
| 951 | verdadera | 169 |
| 952 | marquesa | 169 |
| 953 | cristiano | 169 |
| 954 | supo | 168 |
| 955 | sombrero | 168 |
| 956 | expresión | 168 |
| 957 | castillo | 168 |
| 958 | sacó | 167 |
| 959 | negra | 167 |
| 960 | habéis | 167 |
| 961 | esperaba | 167 |
| 962 | cuánto | 167 |
| 963 | aventuras | 167 |
| 964 | tuviera | 166 |
| 965 | siento | 166 |
| 966 | seguía | 166 |
| 967 | puertas | 166 |
| 968 | perro | 166 |
| 969 | malas | 166 |
| 970 | infeliz | 166 |
| 971 | fuerzas | 166 |
| 972 | enfermo | 166 |
| 973 | cuál | 166 |
| 974 | verla | 165 |
| 975 | traje | 165 |
| 976 | ome | 165 |
| 977 | llorar | 165 |
| 978 | doy | 165 |
| 979 | dejado | 165 |
| 980 | contigo | 165 |
| 981 | propósito | 164 |
| 982 | obispo | 164 |
| 983 | hechos | 164 |
| 984 | enemigos | 164 |
| 985 | árboles | 164 |
| 986 | toboso | 163 |
| 987 | siete | 163 |
| 988 | señal | 163 |
| 989 | mire | 163 |
| 990 | espacio | 163 |
| 991 | enamorado | 163 |
| 992 | corte | 163 |
| 993 | conocía | 163 |
| 994 | catedral | 163 |
| 995 | negocio | 162 |
| 996 | daño | 162 |
| 997 | andantes | 162 |
| 998 | andaba | 162 |
| 999 | adonde | 162 |
| 1000 | versos | 161 |
| 1001 | siguió | 161 |
| 1002 | sentir | 161 |
| 1003 | sean | 161 |
| 1004 | salido | 161 |
| 1005 | sabio | 161 |
| 1006 | puro | 161 |
| 1007 | parm | 161 |
| 1008 | llevó | 161 |
| 1009 | jarifa | 161 |
| 1010 | derecha | 161 |
| 1011 | ángel | 161 |
| 1012 | viuda | 160 |
| 1013 | habló | 160 |
| 1014 | conocer | 160 |
| 1015 | confianza | 160 |
| 1016 | calisto | 160 |
| 1017 | sepa | 159 |
| 1018 | repente | 159 |
| 1019 | loca | 159 |
| 1020 | llegaron | 159 |
| 1021 | levantó | 159 |
| 1022 | habiendo | 159 |
| 1023 | creyó | 159 |
| 1024 | verá | 158 |
| 1025 | siglo | 158 |
| 1026 | mes | 158 |
| 1027 | larga | 158 |
| 1028 | género | 158 |
| 1029 | conocido | 158 |
| 1030 | cargo | 158 |
| 1031 | caballería | 158 |
| 1032 | terrible | 157 |
| 1033 | ojo | 156 |
| 1034 | moral | 156 |
| 1035 | mirada | 156 |
| 1036 | famoso | 156 |
| 1037 | demasiado | 156 |
| 1038 | sy | 155 |
| 1039 | provisor | 155 |
| 1040 | plata | 155 |
| 1041 | piernas | 155 |
| 1042 | fácil | 155 |
| 1043 | clase | 155 |
| 1044 | vivía | 154 |
| 1045 | rosario | 154 |
| 1046 | moro | 154 |
| 1047 | mamá | 154 |
| 1048 | juego | 154 |
| 1049 | grado | 154 |
| 1050 | capa | 154 |
| 1051 | vienen | 153 |
| 1052 | senor | 153 |
| 1053 | seguir | 153 |
| 1054 | poeta | 153 |
| 1055 | calor | 153 |
| 1056 | valiente | 152 |
| 1057 | luna | 152 |
| 1058 | hierro | 152 |
| 1059 | cerebro | 152 |
| 1060 | caridad | 152 |
| 1061 | ventana | 151 |
| 1062 | golpe | 151 |
| 1063 | ciertas | 151 |
| 1064 | cien | 151 |
| 1065 | belleza | 151 |
| 1066 | trae | 150 |
| 1067 | qual | 150 |
| 1068 | preciosa | 150 |
| 1069 | placer | 150 |
| 1070 | fueran | 150 |
| 1071 | damas | 150 |
| 1072 | curiosidad | 150 |
| 1073 | consigo | 150 |
| 1074 | busca | 150 |
| 1075 | acuerdo | 150 |
| 1076 | viaje | 149 |
| 1077 | oye | 149 |
| 1078 | melibea | 149 |
| 1079 | león | 149 |
| 1080 | cree | 149 |
| 1081 | condición | 149 |
| 1082 | suceso | 148 |
| 1083 | sentimiento | 148 |
| 1084 | niños | 148 |
| 1085 | mejores | 148 |
| 1086 | huésped | 148 |
| 1087 | hablado | 148 |
| 1088 | ambos | 148 |
| 1089 | dime | 147 |
| 1090 | cayó | 147 |
| 1091 | teresa | 146 |
| 1092 | servicio | 146 |
| 1093 | música | 146 |
| 1094 | mentira | 146 |
| 1095 | hermoso | 146 |
| 1096 | entra | 146 |
| 1097 | pura | 145 |
| 1098 | pelo | 145 |
| 1099 | dueño | 145 |
| 1100 | debo | 145 |
| 1101 | abind | 145 |
| 1102 | vna | 144 |
| 1103 | paca | 144 |
| 1104 | oyendo | 144 |
| 1105 | hombros | 144 |
| 1106 | ejemplo | 144 |
| 1107 | dura | 144 |
| 1108 | carrera | 144 |
| 1109 | podido | 143 |
| 1110 | monte | 143 |
| 1111 | miserable | 143 |
| 1112 | misa | 143 |
| 1113 | llamado | 143 |
| 1114 | faltaba | 143 |
| 1115 | espaldas | 143 |
| 1116 | casino | 143 |
| 1117 | segura | 142 |
| 1118 | saben | 142 |
| 1119 | rodillas | 142 |
| 1120 | ponerse | 142 |
| 1121 | muger | 142 |
| 1122 | lotario | 142 |
| 1123 | leído | 142 |
| 1124 | hubiese | 142 |
| 1125 | gabinete | 142 |
| 1126 | especie | 142 |
| 1127 | dellos | 142 |
| 1128 | abrió | 142 |
| 1129 | solos | 141 |
| 1130 | semejantes | 141 |
| 1131 | quizás | 141 |
| 1132 | licencia | 141 |
| 1133 | comedia | 141 |
| 1134 | clérigo | 141 |
| 1135 | cariño | 141 |
| 1136 | breve | 141 |
| 1137 | trato | 140 |
| 1138 | nicolás | 140 |
| 1139 | diz | 140 |
| 1140 | diciéndole | 140 |
| 1141 | celestina | 140 |
| 1142 | aposento | 140 |
| 1143 | acabó | 140 |
| 1144 | posada | 139 |
| 1145 | poniendo | 139 |
| 1146 | piedras | 139 |
| 1147 | comida | 139 |
| 1148 | ciencia | 139 |
| 1149 | bondad | 139 |
| 1150 | vieron | 138 |
| 1151 | suelen | 138 |
| 1152 | provecho | 138 |
| 1153 | muerta | 138 |
| 1154 | justo | 138 |
| 1155 | jesús | 138 |
| 1156 | disparates | 138 |
| 1157 | costumbres | 138 |
| 1158 | realidad | 137 |
| 1159 | interés | 137 |
| 1160 | hice | 137 |
| 1161 | comedor | 137 |
| 1162 | vueltas | 136 |
| 1163 | solas | 136 |
| 1164 | número | 136 |
| 1165 | manda | 136 |
| 1166 | estilo | 136 |
| 1167 | entiendo | 136 |
| 1168 | encontró | 136 |
| 1169 | conoce | 136 |
| 1170 | treinta | 135 |
| 1171 | situación | 135 |
| 1172 | sempronio | 135 |
| 1173 | orbajosa | 135 |
| 1174 | huerta | 135 |
| 1175 | encontraba | 135 |
| 1176 | reír | 134 |
| 1177 | humor | 134 |
| 1178 | humana | 134 |
| 1179 | gusta | 134 |
| 1180 | grandeza | 134 |
| 1181 | dicha | 134 |
| 1182 | byen | 134 |
| 1183 | ballester | 134 |
| 1184 | asunto | 134 |
| 1185 | antonio | 134 |
| 1186 | vuestras | 133 |
| 1187 | última | 133 |
| 1188 | traer | 133 |
| 1189 | toca | 133 |
| 1190 | talento | 133 |
| 1191 | oídos | 133 |
| 1192 | miseria | 133 |
| 1193 | discreto | 133 |
| 1194 | dió | 133 |
| 1195 | caído | 133 |
| 1196 | buscando | 133 |
| 1197 | vuelve | 132 |
| 1198 | vegallana | 132 |
| 1199 | prosiguió | 132 |
| 1200 | prisa | 132 |
| 1201 | objeto | 132 |
| 1202 | nacido | 132 |
| 1203 | leyes | 132 |
| 1204 | ira | 132 |
| 1205 | hacienda | 132 |
| 1206 | escrito | 132 |
| 1207 | cuán | 132 |
| 1208 | verse | 131 |
| 1209 | trataba | 131 |
| 1210 | subió | 131 |
| 1211 | ponte | 131 |
| 1212 | pañuelo | 131 |
| 1213 | movimiento | 131 |
| 1214 | duros | 131 |
| 1215 | carácter | 131 |
| 1216 | alcalde | 131 |
| 1217 | ronzal | 130 |
| 1218 | igual | 130 |
| 1219 | hecha | 130 |
| 1220 | banco | 130 |
| 1221 | varias | 129 |
| 1222 | soledad | 129 |
| 1223 | señas | 129 |
| 1224 | quitar | 129 |
| 1225 | patio | 129 |
| 1226 | navío | 129 |
| 1227 | miradas | 129 |
| 1228 | llevado | 129 |
| 1229 | gentes | 129 |
| 1230 | firme | 129 |
| 1231 | amante | 129 |
| 1232 | vestidos | 128 |
| 1233 | tomado | 128 |
| 1234 | reino | 128 |
| 1235 | puesta | 128 |
| 1236 | gritos | 128 |
| 1237 | entrado | 128 |
| 1238 | clara | 128 |
| 1239 | aldea | 128 |
| 1240 | uso | 127 |
| 1241 | sazón | 127 |
| 1242 | respuesta | 127 |
| 1243 | resolución | 127 |
| 1244 | paredes | 127 |
| 1245 | muchacho | 127 |
| 1246 | mandado | 127 |
| 1247 | llamó | 127 |
| 1248 | frasquito | 127 |
| 1249 | feliz | 127 |
| 1250 | entraron | 127 |
| 1251 | entrada | 127 |
| 1252 | ayuda | 127 |
| 1253 | andrés | 127 |
| 1254 | ricos | 126 |
| 1255 | pequeño | 126 |
| 1256 | palo | 126 |
| 1257 | esperando | 126 |
| 1258 | pompeyo | 125 |
| 1259 | dixo | 125 |
| 1260 | diego | 125 |
| 1261 | celos | 125 |
| 1262 | bosque | 125 |
| 1263 | primeros | 124 |
| 1264 | ozores | 124 |
| 1265 | fijo | 124 |
| 1266 | entusiasmo | 124 |
| 1267 | elvira | 124 |
| 1268 | dijeron | 124 |
| 1269 | diferentes | 124 |
| 1270 | bachiller | 124 |
| 1271 | tomando | 123 |
| 1272 | salieron | 123 |
| 1273 | parecido | 123 |
| 1274 | muchacha | 123 |
| 1275 | interior | 123 |
| 1276 | estupiñá | 123 |
| 1277 | admiración | 123 |
| 1278 | ventero | 122 |
| 1279 | tell | 122 |
| 1280 | sois | 122 |
| 1281 | salen | 122 |
| 1282 | pusieron | 122 |
| 1283 | pude | 122 |
| 1284 | polvo | 122 |
| 1285 | pide | 122 |
| 1286 | partida | 122 |
| 1287 | encontrar | 122 |
| 1288 | conviene | 122 |
| 1289 | contó | 122 |
| 1290 | burla | 122 |
| 1291 | barba | 122 |
| 1292 | aquél | 122 |
| 1293 | acerca | 122 |
| 1294 | tuve | 121 |
| 1295 | rucio | 121 |
| 1296 | prima | 121 |
| 1297 | piensa | 121 |
| 1298 | particular | 121 |
| 1299 | francisca | 121 |
| 1300 | dorotea | 121 |
| 1301 | viera | 120 |
| 1302 | salón | 120 |
| 1303 | salida | 120 |
| 1304 | quizá | 120 |
| 1305 | quedaron | 120 |
| 1306 | quedado | 120 |
| 1307 | pequeña | 120 |
| 1308 | pecados | 120 |
| 1309 | mente | 120 |
| 1310 | ínsula | 120 |
| 1311 | honrada | 120 |
| 1312 | halló | 120 |
| 1313 | ganas | 120 |
| 1314 | estrellas | 120 |
| 1315 | entiende | 120 |
| 1316 | difícil | 120 |
| 1317 | deseaba | 120 |
| 1318 | cuentas | 120 |
| 1319 | antiguo | 120 |
| 1320 | anoche | 120 |
| 1321 | pasaron | 119 |
| 1322 | papeles | 119 |
| 1323 | feijoo | 119 |
| 1324 | entrañas | 119 |
| 1325 | dineros | 119 |
| 1326 | cuándo | 119 |
| 1327 | capilla | 119 |
| 1328 | baldomero | 119 |
| 1329 | zalacaín | 118 |
| 1330 | traído | 118 |
| 1331 | toledo | 118 |
| 1332 | sucesos | 118 |
| 1333 | serlo | 118 |
| 1334 | querían | 118 |
| 1335 | nina | 118 |
| 1336 | infierno | 118 |
| 1337 | demonio | 118 |
| 1338 | acabar | 118 |
| 1339 | vengo | 117 |
| 1340 | vencido | 117 |
| 1341 | señorito | 117 |
| 1342 | rigor | 117 |
| 1343 | patria | 117 |
| 1344 | palos | 117 |
| 1345 | menor | 117 |
| 1346 | melib | 117 |
| 1347 | llega | 117 |
| 1348 | hará | 117 |
| 1349 | extranjero | 117 |
| 1350 | echando | 117 |
| 1351 | deben | 117 |
| 1352 | cuestión | 117 |
| 1353 | trata | 116 |
| 1354 | sucedió | 116 |
| 1355 | perdón | 116 |
| 1356 | haría | 116 |
| 1357 | ganado | 116 |
| 1358 | florentina | 116 |
| 1359 | esté | 116 |
| 1360 | enfermedad | 116 |
| 1361 | colores | 116 |
| 1362 | casta | 116 |
| 1363 | recuerdo | 115 |
| 1364 | motivo | 115 |
| 1365 | ladrón | 115 |
| 1366 | flor | 115 |
| 1367 | envidia | 115 |
| 1368 | cólera | 115 |
| 1369 | chicos | 115 |
| 1370 | casos | 115 |
| 1371 | aurora | 115 |
| 1372 | almas | 115 |
| 1373 | alas | 115 |
| 1374 | venganza | 114 |
| 1375 | teodoro | 114 |
| 1376 | servía | 114 |
| 1377 | sano | 114 |
| 1378 | punta | 114 |
| 1379 | prueba | 114 |
| 1380 | papitos | 114 |
| 1381 | maestro | 114 |
| 1382 | juro | 114 |
| 1383 | discurso | 114 |
| 1384 | aguas | 114 |
| 1385 | acababa | 114 |
| 1386 | espera | 113 |
| 1387 | diligencia | 113 |
| 1388 | creyendo | 113 |
| 1389 | cabellos | 113 |
| 1390 | antigua | 113 |
| 1391 | almudena | 113 |
| 1392 | adiós | 113 |
| 1393 | verano | 112 |
| 1394 | quedar | 112 |
| 1395 | pagar | 112 |
| 1396 | mismos | 112 |
| 1397 | labrador | 112 |
| 1398 | hacerse | 112 |
| 1399 | gesto | 112 |
| 1400 | frase | 112 |
| 1401 | costa | 112 |
| 1402 | cartas | 112 |
| 1403 | caballos | 112 |
| 1404 | vano | 111 |
| 1405 | término | 111 |
| 1406 | quince | 111 |
| 1407 | partido | 111 |
| 1408 | hacerle | 111 |
| 1409 | francés | 111 |
| 1410 | avnque | 111 |
| 1411 | ausencia | 111 |
| 1412 | aparte | 111 |
| 1413 | volviendo | 110 |
| 1414 | seguida | 110 |
| 1415 | reina | 110 |
| 1416 | querría | 110 |
| 1417 | presentes | 110 |
| 1418 | parmeno | 110 |
| 1419 | imagen | 110 |
| 1420 | hombro | 110 |
| 1421 | hijas | 110 |
| 1422 | cruel | 110 |
| 1423 | capaz | 110 |
| 1424 | tonto | 109 |
| 1425 | sabido | 109 |
| 1426 | repuso | 109 |
| 1427 | nuevos | 109 |
| 1428 | materia | 109 |
| 1429 | ii | 109 |
| 1430 | humano | 109 |
| 1431 | fui | 109 |
| 1432 | cantar | 109 |
| 1433 | calla | 109 |
| 1434 | arcipreste | 109 |
| 1435 | pidió | 108 |
| 1436 | pedazos | 108 |
| 1437 | llave | 108 |
| 1438 | fuere | 108 |
| 1439 | dirá | 108 |
| 1440 | bonita | 108 |
| 1441 | basilio | 108 |
| 1442 | ardiente | 108 |
| 1443 | visitación | 107 |
| 1444 | sacerdote | 107 |
| 1445 | pedía | 107 |
| 1446 | muestra | 107 |
| 1447 | mozos | 107 |
| 1448 | ingenio | 107 |
| 1449 | etc | 107 |
| 1450 | español | 107 |
| 1451 | cristianos | 107 |
| 1452 | cogió | 107 |
| 1453 | tuvieron | 106 |
| 1454 | seas | 106 |
| 1455 | rayo | 106 |
| 1456 | pregunta | 106 |
| 1457 | portal | 106 |
| 1458 | plácido | 106 |
| 1459 | pared | 106 |
| 1460 | negros | 106 |
| 1461 | francia | 106 |
| 1462 | extremo | 106 |
| 1463 | enferma | 106 |
| 1464 | diese | 106 |
| 1465 | despacho | 106 |
| 1466 | corría | 106 |
| 1467 | circunstancias | 106 |
| 1468 | ciertos | 106 |
| 1469 | suyos | 105 |
| 1470 | soldados | 105 |
| 1471 | sentimientos | 105 |
| 1472 | priesa | 105 |
| 1473 | pasaban | 105 |
| 1474 | parar | 105 |
| 1475 | orgullo | 105 |
| 1476 | nariz | 105 |
| 1477 | muestras | 105 |
| 1478 | mostraba | 105 |
| 1479 | limosna | 105 |
| 1480 | liberal | 105 |
| 1481 | lenguaje | 105 |
| 1482 | francisco | 105 |
| 1483 | empezaba | 105 |
| 1484 | doctor | 105 |
| 1485 | digno | 105 |
| 1486 | darme | 105 |
| 1487 | comido | 105 |
| 1488 | claridad | 105 |
| 1489 | callar | 105 |
| 1490 | ca | 105 |
| 1491 | parecen | 104 |
| 1492 | ora | 104 |
| 1493 | juanito | 104 |
| 1494 | indicó | 104 |
| 1495 | echado | 104 |
| 1496 | dormía | 104 |
| 1497 | dize | 104 |
| 1498 | daré | 104 |
| 1499 | cristo | 104 |
| 1500 | caminos | 104 |
| 1501 | animal | 104 |
| 1502 | tuviese | 103 |
| 1503 | tomaba | 103 |
| 1504 | siglos | 103 |
| 1505 | reloj | 103 |
| 1506 | necesitaba | 103 |
| 1507 | moros | 103 |
| 1508 | míos | 103 |
| 1509 | menudo | 103 |
| 1510 | ejercicio | 103 |
| 1511 | comía | 103 |
| 1512 | coger | 103 |
| 1513 | capitán | 103 |
| 1514 | acto | 103 |
| 1515 | términos | 102 |
| 1516 | syn | 102 |
| 1517 | soldado | 102 |
| 1518 | salían | 102 |
| 1519 | rincón | 102 |
| 1520 | rica | 102 |
| 1521 | quita | 102 |
| 1522 | niñas | 102 |
| 1523 | humilde | 102 |
| 1524 | gustaba | 102 |
| 1525 | evaristo | 102 |
| 1526 | entero | 102 |
| 1527 | elegante | 102 |
| 1528 | conforme | 102 |
| 1529 | ambas | 102 |
| 1530 | vicio | 101 |
| 1531 | venida | 101 |
| 1532 | sirve | 101 |
| 1533 | responder | 101 |
| 1534 | perros | 101 |
| 1535 | marcial | 101 |
| 1536 | i | 101 |
| 1537 | humo | 101 |
| 1538 | hablaban | 101 |
| 1539 | fuertes | 101 |
| 1540 | dueñas | 101 |
| 1541 | desque | 101 |
| 1542 | cardenio | 101 |
| 1543 | veremos | 100 |
| 1544 | verdaderamente | 100 |
| 1545 | servido | 100 |
| 1546 | palacio | 100 |
| 1547 | nubes | 100 |
| 1548 | mesma | 100 |
| 1549 | máquina | 100 |
| 1550 | hermanos | 100 |
| 1551 | golfín | 100 |
| 1552 | estómago | 100 |
| 1553 | ea | 100 |
| 1554 | diera | 100 |
| 1555 | confusión | 100 |
| 1556 | barbas | 100 |
| 1557 | acaba | 100 |
| 1558 | terror | 99 |
| 1559 | tendrá | 99 |
| 1560 | sentidos | 99 |
| 1561 | reyes | 99 |
| 1562 | repitió | 99 |
| 1563 | pluma | 99 |
| 1564 | moza | 99 |
| 1565 | luscinda | 99 |
| 1566 | ilustre | 99 |
| 1567 | harto | 99 |
| 1568 | éstos | 99 |
| 1569 | deje | 99 |
| 1570 | dedo | 99 |
| 1571 | cuartos | 99 |
| 1572 | cristiana | 99 |
| 1573 | coro | 99 |
| 1574 | común | 99 |
| 1575 | caza | 99 |
| 1576 | autoridad | 99 |
| 1577 | volvieron | 98 |
| 1578 | so | 98 |
| 1579 | seso | 98 |
| 1580 | serio | 98 |
| 1581 | señales | 98 |
| 1582 | política | 98 |
| 1583 | pieza | 98 |
| 1584 | mercedes | 98 |
| 1585 | lope | 98 |
| 1586 | llegando | 98 |
| 1587 | llanto | 98 |
| 1588 | ingleses | 98 |
| 1589 | hubieran | 98 |
| 1590 | herido | 98 |
| 1591 | gozar | 98 |
| 1592 | cuyas | 98 |
| 1593 | cortesía | 98 |
| 1594 | contado | 98 |
| 1595 | compañero | 98 |
| 1596 | cantidad | 98 |
| 1597 | vete | 97 |
| 1598 | tristes | 97 |
| 1599 | terreno | 97 |
| 1600 | ripamilán | 97 |
| 1601 | pasando | 97 |
| 1602 | noticias | 97 |
| 1603 | montes | 97 |
| 1604 | merece | 97 |
| 1605 | lanza | 97 |
| 1606 | gato | 97 |
| 1607 | fuesen | 97 |
| 1608 | existencia | 97 |
| 1609 | enojo | 97 |
| 1610 | emperador | 97 |
| 1611 | delfín | 97 |
| 1612 | cuerpos | 97 |
| 1613 | convento | 97 |
| 1614 | cambio | 97 |
| 1615 | azul | 97 |
| 1616 | árbol | 97 |
| 1617 | verdes | 96 |
| 1618 | quisiere | 96 |
| 1619 | olor | 96 |
| 1620 | observó | 96 |
| 1621 | necesario | 96 |
| 1622 | milagro | 96 |
| 1623 | hojas | 96 |
| 1624 | gozo | 96 |
| 1625 | engaño | 96 |
| 1626 | contaba | 96 |
| 1627 | anterior | 96 |
| 1628 | única | 95 |
| 1629 | sigue | 95 |
| 1630 | pastor | 95 |
| 1631 | narices | 95 |
| 1632 | muertos | 95 |
| 1633 | hidalgo | 95 |
| 1634 | haces | 95 |
| 1635 | fría | 95 |
| 1636 | experiencia | 95 |
| 1637 | encuentro | 95 |
| 1638 | corriente | 95 |
| 1639 | cayetano | 95 |
| 1640 | caballerías | 95 |
| 1641 | tuya | 94 |
| 1642 | temía | 94 |
| 1643 | sonriendo | 94 |
| 1644 | quieras | 94 |
| 1645 | qu | 94 |
| 1646 | matrimonio | 94 |
| 1647 | majestad | 94 |
| 1648 | hazañas | 94 |
| 1649 | curas | 94 |
| 1650 | cuerda | 94 |
| 1651 | carro | 94 |
| 1652 | bendito | 94 |
| 1653 | azotes | 94 |
| 1654 | vuelva | 93 |
| 1655 | verme | 93 |
| 1656 | tomás | 93 |
| 1657 | tendría | 93 |
| 1658 | ridículo | 93 |
| 1659 | ratos | 93 |
| 1660 | quedo | 93 |
| 1661 | penas | 93 |
| 1662 | metido | 93 |
| 1663 | llevaban | 93 |
| 1664 | juventud | 93 |
| 1665 | honrado | 93 |
| 1666 | hábito | 93 |
| 1667 | guarda | 93 |
| 1668 | foja | 93 |
| 1669 | fino | 93 |
| 1670 | discreción | 93 |
| 1671 | dejaron | 93 |
| 1672 | decirse | 93 |
| 1673 | darse | 93 |
| 1674 | dame | 93 |
| 1675 | cuyos | 93 |
| 1676 | come | 93 |
| 1677 | carga | 93 |
| 1678 | andan | 93 |
| 1679 | víctima | 92 |
| 1680 | varios | 92 |
| 1681 | rara | 92 |
| 1682 | pueblos | 92 |
| 1683 | parís | 92 |
| 1684 | nombres | 92 |
| 1685 | murmuró | 92 |
| 1686 | mata | 92 |
| 1687 | marcha | 92 |
| 1688 | malicia | 92 |
| 1689 | llamaban | 92 |
| 1690 | herida | 92 |
| 1691 | habitación | 92 |
| 1692 | guardar | 92 |
| 1693 | dormido | 92 |
| 1694 | diferencia | 92 |
| 1695 | descubierto | 92 |
| 1696 | debían | 92 |
| 1697 | cumplir | 92 |
| 1698 | corre | 92 |
| 1699 | consuelo | 92 |
| 1700 | comprar | 92 |
| 1701 | catalina | 92 |
| 1702 | vosotros | 91 |
| 1703 | tranquilo | 91 |
| 1704 | sentado | 91 |
| 1705 | piso | 91 |
| 1706 | periódicos | 91 |
| 1707 | limpio | 91 |
| 1708 | importancia | 91 |
| 1709 | hiciera | 91 |
| 1710 | hallaba | 91 |
| 1711 | fiesta | 91 |
| 1712 | espiritual | 91 |
| 1713 | escuela | 91 |
| 1714 | doncellas | 91 |
| 1715 | desto | 91 |
| 1716 | comercio | 91 |
| 1717 | caía | 91 |
| 1718 | amar | 91 |
| 1719 | alguien | 91 |
| 1720 | acercó | 91 |
| 1721 | tertulia | 90 |
| 1722 | tellagorri | 90 |
| 1723 | rayos | 90 |
| 1724 | puestos | 90 |
| 1725 | profundo | 90 |
| 1726 | profunda | 90 |
| 1727 | pongo | 90 |
| 1728 | peso | 90 |
| 1729 | llenos | 90 |
| 1730 | letra | 90 |
| 1731 | glocester | 90 |
| 1732 | galán | 90 |
| 1733 | esfuerzo | 90 |
| 1734 | escuadra | 90 |
| 1735 | energía | 90 |
| 1736 | educación | 90 |
| 1737 | echaba | 90 |
| 1738 | dispuesto | 90 |
| 1739 | cuantas | 90 |
| 1740 | cola | 90 |
| 1741 | cincuenta | 90 |
| 1742 | ciento | 90 |
| 1743 | asiento | 90 |
| 1744 | artículo | 90 |
| 1745 | aliento | 90 |
| 1746 | vanidad | 89 |
| 1747 | tratar | 89 |
| 1748 | tiro | 89 |
| 1749 | seda | 89 |
| 1750 | satisfecho | 89 |
| 1751 | murió | 89 |
| 1752 | licenciado | 89 |
| 1753 | jardín | 89 |
| 1754 | infame | 89 |
| 1755 | escena | 89 |
| 1756 | escándalo | 89 |
| 1757 | enfrente | 89 |
| 1758 | diría | 89 |
| 1759 | detuvo | 89 |
| 1760 | crea | 89 |
| 1761 | consejos | 89 |
| 1762 | compasión | 89 |
| 1763 | cárcel | 89 |
| 1764 | camisa | 89 |
| 1765 | traigo | 88 |
| 1766 | trabajos | 88 |
| 1767 | trabajar | 88 |
| 1768 | sonrisa | 88 |
| 1769 | seno | 88 |
| 1770 | sacaba | 88 |
| 1771 | respecto | 88 |
| 1772 | recordaba | 88 |
| 1773 | ó | 88 |
| 1774 | maldito | 88 |
| 1775 | iré | 88 |
| 1776 | invierno | 88 |
| 1777 | huesos | 88 |
| 1778 | hacerlo | 88 |
| 1779 | gentil | 88 |
| 1780 | estuviera | 88 |
| 1781 | espero | 88 |
| 1782 | destos | 88 |
| 1783 | criatura | 88 |
| 1784 | corrió | 88 |
| 1785 | compañeros | 88 |
| 1786 | buscaba | 88 |
| 1787 | blancas | 88 |
| 1788 | veían | 87 |
| 1789 | tonta | 87 |
| 1790 | tocar | 87 |
| 1791 | sentó | 87 |
| 1792 | pensado | 87 |
| 1793 | pedazo | 87 |
| 1794 | olvido | 87 |
| 1795 | nieve | 87 |
| 1796 | madera | 87 |
| 1797 | levantar | 87 |
| 1798 | jefe | 87 |
| 1799 | dignidad | 87 |
| 1800 | crees | 87 |
| 1801 | contenta | 87 |
| 1802 | altas | 87 |
| 1803 | abrir | 87 |
| 1804 | s | 86 |
| 1805 | relaciones | 86 |
| 1806 | primeras | 86 |
| 1807 | preguntar | 86 |
| 1808 | pase | 86 |
| 1809 | oyeron | 86 |
| 1810 | md | 86 |
| 1811 | luces | 86 |
| 1812 | felicidad | 86 |
| 1813 | excelente | 86 |
| 1814 | especialmente | 86 |
| 1815 | entendía | 86 |
| 1816 | conde | 86 |
| 1817 | casarse | 86 |
| 1818 | casar | 86 |
| 1819 | saca | 85 |
| 1820 | respondía | 85 |
| 1821 | ramos | 85 |
| 1822 | perdida | 85 |
| 1823 | orgaz | 85 |
| 1824 | nueve | 85 |
| 1825 | monjas | 85 |
| 1826 | levantarse | 85 |
| 1827 | leguas | 85 |
| 1828 | juez | 85 |
| 1829 | hallar | 85 |
| 1830 | fresco | 85 |
| 1831 | espejo | 85 |
| 1832 | espanto | 85 |
| 1833 | desdichado | 85 |
| 1834 | descanso | 85 |
| 1835 | cuasi | 85 |
| 1836 | creí | 85 |
| 1837 | confesar | 85 |
| 1838 | comedias | 85 |
| 1839 | aqui | 85 |
| 1840 | alegres | 85 |
| 1841 | abierto | 85 |
| 1842 | valía | 84 |
| 1843 | valeroso | 84 |
| 1844 | torre | 84 |
| 1845 | sucedido | 84 |
| 1846 | singular | 84 |
| 1847 | semblante | 84 |
| 1848 | pobreza | 84 |
| 1849 | olvidado | 84 |
| 1850 | momentos | 84 |
| 1851 | miraban | 84 |
| 1852 | mías | 84 |
| 1853 | figuras | 84 |
| 1854 | feo | 84 |
| 1855 | fecho | 84 |
| 1856 | entrando | 84 |
| 1857 | destas | 84 |
| 1858 | corredor | 84 |
| 1859 | conocimiento | 84 |
| 1860 | bella | 84 |
| 1861 | alonso | 84 |
| 1862 | vió | 83 |
| 1863 | templo | 83 |
| 1864 | sofá | 83 |
| 1865 | recibió | 83 |
| 1866 | poderoso | 83 |
| 1867 | necesito | 83 |
| 1868 | mostrar | 83 |
| 1869 | meter | 83 |
| 1870 | mandar | 83 |
| 1871 | fuente | 83 |
| 1872 | dulces | 83 |
| 1873 | cena | 83 |
| 1874 | bienes | 83 |
| 1875 | barco | 83 |
| 1876 | vuestros | 82 |
| 1877 | viejos | 82 |
| 1878 | subía | 82 |
| 1879 | queriendo | 82 |
| 1880 | prudente | 82 |
| 1881 | principales | 82 |
| 1882 | pierde | 82 |
| 1883 | páez | 82 |
| 1884 | órdenes | 82 |
| 1885 | linaje | 82 |
| 1886 | ligero | 82 |
| 1887 | hallado | 82 |
| 1888 | guimarán | 82 |
| 1889 | gritaba | 82 |
| 1890 | época | 82 |
| 1891 | dezir | 82 |
| 1892 | confesión | 82 |
| 1893 | centro | 82 |
| 1894 | cansado | 82 |
| 1895 | broma | 82 |
| 1896 | bajó | 82 |
| 1897 | baile | 82 |
| 1898 | amigas | 82 |
| 1899 | tendré | 81 |
| 1900 | tadeo | 81 |
| 1901 | superior | 81 |
| 1902 | sabían | 81 |
| 1903 | quise | 81 |
| 1904 | orejas | 81 |
| 1905 | norte | 81 |
| 1906 | nobleza | 81 |
| 1907 | necesita | 81 |
| 1908 | juntas | 81 |
| 1909 | inglés | 81 |
| 1910 | graves | 81 |
| 1911 | escudos | 81 |
| 1912 | escribe | 81 |
| 1913 | dizes | 81 |
| 1914 | distancia | 81 |
| 1915 | digna | 81 |
| 1916 | debió | 81 |
| 1917 | daría | 81 |
| 1918 | cuarenta | 81 |
| 1919 | carnes | 81 |
| 1920 | cadena | 81 |
| 1921 | botas | 81 |
| 1922 | alcanzar | 81 |
| 1923 | agradable | 81 |
| 1924 | ten | 80 |
| 1925 | suma | 80 |
| 1926 | salvo | 80 |
| 1927 | sacando | 80 |
| 1928 | ramas | 80 |
| 1929 | pierna | 80 |
| 1930 | periódico | 80 |
| 1931 | lobo | 80 |
| 1932 | junta | 80 |
| 1933 | golpes | 80 |
| 1934 | espalda | 80 |
| 1935 | discreta | 80 |
| 1936 | dijera | 80 |
| 1937 | digas | 80 |
| 1938 | dellas | 80 |
| 1939 | cuesta | 80 |
| 1940 | caras | 80 |
| 1941 | caña | 80 |
| 1942 | canto | 80 |
| 1943 | adónde | 80 |
| 1944 | acciones | 80 |
| 1945 | acabado | 80 |
| 1946 | vuelvo | 79 |
| 1947 | vela | 79 |
| 1948 | riendo | 79 |
| 1949 | prendas | 79 |
| 1950 | ponga | 79 |
| 1951 | poetas | 79 |
| 1952 | poesía | 79 |
| 1953 | pico | 79 |
| 1954 | ocasiones | 79 |
| 1955 | mandaba | 79 |
| 1956 | izquierda | 79 |
| 1957 | inútil | 79 |
| 1958 | forzoso | 79 |
| 1959 | estuvieron | 79 |
| 1960 | estará | 79 |
| 1961 | amantes | 79 |
| 1962 | acción | 79 |
| 1963 | zoraida | 78 |
| 1964 | tuyo | 78 |
| 1965 | tormento | 78 |
| 1966 | teniendo | 78 |
| 1967 | temprano | 78 |
| 1968 | tema | 78 |
| 1969 | sufrir | 78 |
| 1970 | solamente | 78 |
| 1971 | santísima | 78 |
| 1972 | sansón | 78 |
| 1973 | sabemos | 78 |
| 1974 | romualdo | 78 |
| 1975 | propios | 78 |
| 1976 | presa | 78 |
| 1977 | paga | 78 |
| 1978 | mancebo | 78 |
| 1979 | leche | 78 |
| 1980 | ganar | 78 |
| 1981 | fiera | 78 |
| 1982 | fiel | 78 |
| 1983 | falda | 78 |
| 1984 | fabla | 78 |
| 1985 | éstas | 78 |
| 1986 | dijese | 78 |
| 1987 | dándole | 78 |
| 1988 | casado | 78 |
| 1989 | cádiz | 78 |
| 1990 | bajar | 78 |
| 1991 | aspecto | 78 |
| 1992 | vivero | 77 |
| 1993 | visitas | 77 |
| 1994 | verte | 77 |
| 1995 | triunfo | 77 |
| 1996 | serán | 77 |
| 1997 | saliendo | 77 |
| 1998 | quitado | 77 |
| 1999 | puerto | 77 |
| 2000 | pudiese | 77 |
| 2001 | probar | 77 |
| 2002 | podré | 77 |
| 2003 | pesadumbre | 77 |
| 2004 | mostró | 77 |
| 2005 | mortal | 77 |
| 2006 | monja | 77 |
| 2007 | ministro | 77 |
| 2008 | males | 77 |
| 2009 | horrible | 77 |
| 2010 | historias | 77 |
| 2011 | fazer | 77 |
| 2012 | estuve | 77 |
| 2013 | estaría | 77 |
| 2014 | defensa | 77 |
| 2015 | dará | 77 |
| 2016 | conoció | 77 |
| 2017 | castigo | 77 |
| 2018 | calavera | 77 |
| 2019 | apareció | 77 |
| 2020 | acento | 77 |
| 2021 | vestida | 76 |
| 2022 | vendrá | 76 |
| 2023 | social | 76 |
| 2024 | siente | 76 |
| 2025 | seguridad | 76 |
| 2026 | roto | 76 |
| 2027 | presentó | 76 |
| 2028 | preguntas | 76 |
| 2029 | podemos | 76 |
| 2030 | plazer | 76 |
| 2031 | plato | 76 |
| 2032 | jumento | 76 |
| 2033 | jáuregui | 76 |
| 2034 | ja | 76 |
| 2035 | importaba | 76 |
| 2036 | huir | 76 |
| 2037 | genio | 76 |
| 2038 | divina | 76 |
| 2039 | disposición | 76 |
| 2040 | cristales | 76 |
| 2041 | corta | 76 |
| 2042 | corregidor | 76 |
| 2043 | cenar | 76 |
| 2044 | calma | 76 |
| 2045 | tocaba | 75 |
| 2046 | título | 75 |
| 2047 | sosiego | 75 |
| 2048 | seré | 75 |
| 2049 | nobles | 75 |
| 2050 | gordo | 75 |
| 2051 | esperanzas | 75 |
| 2052 | encontrado | 75 |
| 2053 | das | 75 |
| 2054 | combate | 75 |
| 2055 | atrevió | 75 |
| 2056 | apetito | 75 |
| 2057 | afirmó | 75 |
| 2058 | tercera | 74 |
| 2059 | suyas | 74 |
| 2060 | suspiros | 74 |
| 2061 | sor | 74 |
| 2062 | sierra | 74 |
| 2063 | semana | 74 |
| 2064 | queréis | 74 |
| 2065 | próxima | 74 |
| 2066 | prado | 74 |
| 2067 | plumas | 74 |
| 2068 | plática | 74 |
| 2069 | pasados | 74 |
| 2070 | oy | 74 |
| 2071 | mando | 74 |
| 2072 | limpia | 74 |
| 2073 | irse | 74 |
| 2074 | industria | 74 |
| 2075 | impresión | 74 |
| 2076 | ilusión | 74 |
| 2077 | humildad | 74 |
| 2078 | hable | 74 |
| 2079 | gravedad | 74 |
| 2080 | fija | 74 |
| 2081 | eh | 74 |
| 2082 | dia | 74 |
| 2083 | cristal | 74 |
| 2084 | corriendo | 74 |
| 2085 | coraçón | 74 |
| 2086 | comprender | 74 |
| 2087 | bromas | 74 |
| 2088 | bermúdez | 74 |
| 2089 | beber | 74 |
| 2090 | asimismo | 74 |
| 2091 | arma | 74 |
| 2092 | andando | 74 |
| 2093 | volviéndose | 73 |
| 2094 | villalonga | 73 |
| 2095 | supuesto | 73 |
| 2096 | suelta | 73 |
| 2097 | severiana | 73 |
| 2098 | seria | 73 |
| 2099 | samaniego | 73 |
| 2100 | revés | 73 |
| 2101 | provincia | 73 |
| 2102 | pintado | 73 |
| 2103 | perlas | 73 |
| 2104 | perfectamente | 73 |
| 2105 | paño | 73 |
| 2106 | pago | 73 |
| 2107 | locos | 73 |
| 2108 | largas | 73 |
| 2109 | haz | 73 |
| 2110 | gracioso | 73 |
| 2111 | extraño | 73 |
| 2112 | estudiante | 73 |
| 2113 | esquina | 73 |
| 2114 | disparate | 73 |
| 2115 | díjole | 73 |
| 2116 | dígame | 73 |
| 2117 | desnudo | 73 |
| 2118 | dejaban | 73 |
| 2119 | decís | 73 |
| 2120 | altar | 73 |
| 2121 | abierta | 73 |
| 2122 | vecino | 72 |
| 2123 | sed | 72 |
| 2124 | religiosa | 72 |
| 2125 | recibir | 72 |
| 2126 | paje | 72 |
| 2127 | mirad | 72 |
| 2128 | manifestó | 72 |
| 2129 | ladrones | 72 |
| 2130 | jugar | 72 |
| 2131 | joaquín | 72 |
| 2132 | inocencio | 72 |
| 2133 | hacerme | 72 |
| 2134 | garganta | 72 |
| 2135 | estancia | 72 |
| 2136 | efeto | 72 |
| 2137 | diablos | 72 |
| 2138 | destino | 72 |
| 2139 | dejo | 72 |
| 2140 | culto | 72 |
| 2141 | convenía | 72 |
| 2142 | casada | 72 |
| 2143 | caballuco | 72 |
| 2144 | boda | 72 |
| 2145 | balcones | 72 |
| 2146 | avn | 72 |
| 2147 | viese | 71 |
| 2148 | tratado | 71 |
| 2149 | tome | 71 |
| 2150 | sospecha | 71 |
| 2151 | plan | 71 |
| 2152 | pido | 71 |
| 2153 | papá | 71 |
| 2154 | oí | 71 |
| 2155 | negocios | 71 |
| 2156 | mulas | 71 |
| 2157 | maneras | 71 |
| 2158 | maldita | 71 |
| 2159 | lógica | 71 |
| 2160 | llevan | 71 |
| 2161 | leía | 71 |
| 2162 | evitar | 71 |
| 2163 | estuviese | 71 |
| 2164 | establecimiento | 71 |
| 2165 | entrambos | 71 |
| 2166 | digan | 71 |
| 2167 | dichoso | 71 |
| 2168 | desprecio | 71 |
| 2169 | cuántas | 71 |
| 2170 | calidad | 71 |
| 2171 | barca | 71 |
| 2172 | vinieron | 70 |
| 2173 | vencer | 70 |
| 2174 | vecinos | 70 |
| 2175 | temo | 70 |
| 2176 | sujeto | 70 |
| 2177 | rumor | 70 |
| 2178 | romper | 70 |
| 2179 | reía | 70 |
| 2180 | propias | 70 |
| 2181 | precio | 70 |
| 2182 | obligado | 70 |
| 2183 | minutos | 70 |
| 2184 | medios | 70 |
| 2185 | manto | 70 |
| 2186 | lucha | 70 |
| 2187 | llevo | 70 |
| 2188 | hiciese | 70 |
| 2189 | fresca | 70 |
| 2190 | falsa | 70 |
| 2191 | escuderos | 70 |
| 2192 | desdén | 70 |
| 2193 | corona | 70 |
| 2194 | clérigos | 70 |
| 2195 | cielos | 70 |
| 2196 | campos | 70 |
| 2197 | cabello | 70 |
| 2198 | burlas | 70 |
| 2199 | atrevido | 70 |
| 2200 | amos | 70 |
| 2201 | voto | 69 |
| 2202 | villa | 69 |
| 2203 | supiera | 69 |
| 2204 | sistema | 69 |
| 2205 | serían | 69 |
| 2206 | remedios | 69 |
| 2207 | quitó | 69 |
| 2208 | quedan | 69 |
| 2209 | parientes | 69 |
| 2210 | pálido | 69 |
| 2211 | pájaros | 69 |
| 2212 | ofreció | 69 |
| 2213 | ocurrió | 69 |
| 2214 | negar | 69 |
| 2215 | multitud | 69 |
| 2216 | muere | 69 |
| 2217 | muera | 69 |
| 2218 | mérito | 69 |
| 2219 | lugares | 69 |
| 2220 | llorando | 69 |
| 2221 | jóvenes | 69 |
| 2222 | inocente | 69 |
| 2223 | ex | 69 |
| 2224 | ejército | 69 |
| 2225 | den | 69 |
| 2226 | corazon | 69 |
| 2227 | cobarde | 69 |
| 2228 | celio | 69 |
| 2229 | cae | 69 |
| 2230 | ave | 69 |
| 2231 | asombro | 69 |
| 2232 | vivos | 68 |
| 2233 | viven | 68 |
| 2234 | tranquila | 68 |
| 2235 | tela | 68 |
| 2236 | sube | 68 |
| 2237 | sabiendo | 68 |
| 2238 | pública | 68 |
| 2239 | precisamente | 68 |
| 2240 | poniéndose | 68 |
| 2241 | piezas | 68 |
| 2242 | perdone | 68 |
| 2243 | pasiones | 68 |
| 2244 | nota | 68 |
| 2245 | nosotras | 68 |
| 2246 | movía | 68 |
| 2247 | frases | 68 |
| 2248 | empresa | 68 |
| 2249 | crédito | 68 |
| 2250 | comprendió | 68 |
| 2251 | cerró | 68 |
| 2252 | cerrar | 68 |
| 2253 | blancos | 68 |
| 2254 | bestia | 68 |
| 2255 | armado | 68 |
| 2256 | vuelo | 67 |
| 2257 | viniese | 67 |
| 2258 | viejas | 67 |
| 2259 | vetustenses | 67 |
| 2260 | techo | 67 |
| 2261 | suceder | 67 |
| 2262 | sublime | 67 |
| 2263 | simple | 67 |
| 2264 | quedaban | 67 |
| 2265 | prometido | 67 |
| 2266 | príncipe | 67 |
| 2267 | pecador | 67 |
| 2268 | pastores | 67 |
| 2269 | ofrecía | 67 |
| 2270 | mismas | 67 |
| 2271 | metió | 67 |
| 2272 | mejillas | 67 |
| 2273 | m | 67 |
| 2274 | libres | 67 |
| 2275 | leyó | 67 |
| 2276 | iguales | 67 |
| 2277 | hilo | 67 |
| 2278 | habido | 67 |
| 2279 | desgraciado | 67 |
| 2280 | demonios | 67 |
| 2281 | débil | 67 |
| 2282 | cueva | 67 |
| 2283 | castellano | 67 |
| 2284 | cabezas | 67 |
| 2285 | aya | 67 |
| 2286 | villano | 66 |
| 2287 | tomo | 66 |
| 2288 | tercero | 66 |
| 2289 | suspiro | 66 |
| 2290 | quede | 66 |
| 2291 | petronila | 66 |
| 2292 | permitía | 66 |
| 2293 | oración | 66 |
| 2294 | navíos | 66 |
| 2295 | maravillas | 66 |
| 2296 | madres | 66 |
| 2297 | llenas | 66 |
| 2298 | línea | 66 |
| 2299 | levantándose | 66 |
| 2300 | influencia | 66 |
| 2301 | imaginar | 66 |
| 2302 | iii | 66 |
| 2303 | gigante | 66 |
| 2304 | frutos | 66 |
| 2305 | filosofía | 66 |
| 2306 | figuraba | 66 |
| 2307 | faz | 66 |
| 2308 | error | 66 |
| 2309 | enteramente | 66 |
| 2310 | dizen | 66 |
| 2311 | despertó | 66 |
| 2312 | dejan | 66 |
| 2313 | deber | 66 |
| 2314 | crimen | 66 |
| 2315 | completamente | 66 |
| 2316 | cautivo | 66 |
| 2317 | caserón | 66 |
| 2318 | carretera | 66 |
| 2319 | bonito | 66 |
| 2320 | atrevía | 66 |
| 2321 | arnaiz | 66 |
| 2322 | areu | 66 |
| 2323 | altos | 66 |
| 2324 | aires | 66 |
| 2325 | tren | 65 |
| 2326 | sueños | 65 |
| 2327 | suave | 65 |
| 2328 | sotana | 65 |
| 2329 | sonreía | 65 |
| 2330 | salvaje | 65 |
| 2331 | salto | 65 |
| 2332 | sacado | 65 |
| 2333 | riqueza | 65 |
| 2334 | rabia | 65 |
| 2335 | principios | 65 |
| 2336 | preso | 65 |
| 2337 | prenda | 65 |
| 2338 | oreja | 65 |
| 2339 | obscuridad | 65 |
| 2340 | notó | 65 |
| 2341 | mia | 65 |
| 2342 | mentiras | 65 |
| 2343 | llevaron | 65 |
| 2344 | lenguas | 65 |
| 2345 | lector | 65 |
| 2346 | haberle | 65 |
| 2347 | graciosa | 65 |
| 2348 | formas | 65 |
| 2349 | fea | 65 |
| 2350 | estrecho | 65 |
| 2351 | española | 65 |
| 2352 | entera | 65 |
| 2353 | encantadores | 65 |
| 2354 | dirección | 65 |
| 2355 | creído | 65 |
| 2356 | cogido | 65 |
| 2357 | claramente | 65 |
| 2358 | cera | 65 |
| 2359 | barrio | 65 |
| 2360 | atento | 65 |
| 2361 | agravio | 65 |
| 2362 | acudir | 65 |
| 2363 | vetustense | 64 |
| 2364 | traían | 64 |
| 2365 | tenéis | 64 |
| 2366 | taberna | 64 |
| 2367 | susto | 64 |
| 2368 | sepultura | 64 |
| 2369 | seco | 64 |
| 2370 | recado | 64 |
| 2371 | procuraba | 64 |
| 2372 | princesa | 64 |
| 2373 | presteza | 64 |
| 2374 | negras | 64 |
| 2375 | muda | 64 |
| 2376 | muchachos | 64 |
| 2377 | mora | 64 |
| 2378 | medicina | 64 |
| 2379 | maese | 64 |
| 2380 | luis | 64 |
| 2381 | locuras | 64 |
| 2382 | hermosas | 64 |
| 2383 | furioso | 64 |
| 2384 | fantasía | 64 |
| 2385 | fácilmente | 64 |
| 2386 | escucha | 64 |
| 2387 | duelo | 64 |
| 2388 | continuó | 64 |
| 2389 | caja | 64 |
| 2390 | bolsillo | 64 |
| 2391 | besos | 64 |
| 2392 | asuntos | 64 |
| 2393 | antiguos | 64 |
| 2394 | ángeles | 64 |
| 2395 | andado | 64 |
| 2396 | vezes | 63 |
| 2397 | usar | 63 |
| 2398 | últimos | 63 |
| 2399 | tesoro | 63 |
| 2400 | temeroso | 63 |
| 2401 | talle | 63 |
| 2402 | soberbia | 63 |
| 2403 | sintiendo | 63 |
| 2404 | sevilla | 63 |
| 2405 | sereno | 63 |
| 2406 | salí | 63 |
| 2407 | renegado | 63 |
| 2408 | razon | 63 |
| 2409 | quisiese | 63 |
| 2410 | puntos | 63 |
| 2411 | premio | 63 |
| 2412 | piel | 63 |
| 2413 | pereza | 63 |
| 2414 | parque | 63 |
| 2415 | pariente | 63 |
| 2416 | nervios | 63 |
| 2417 | mona | 63 |
| 2418 | modos | 63 |
| 2419 | intento | 63 |
| 2420 | importante | 63 |
| 2421 | faltar | 63 |
| 2422 | estudio | 63 |
| 2423 | espolón | 63 |
| 2424 | diversas | 63 |
| 2425 | cuerdo | 63 |
| 2426 | comenzaron | 63 |
| 2427 | capital | 63 |
| 2428 | bárbara | 63 |
| 2429 | acudió | 63 |
| 2430 | virtudes | 62 |
| 2431 | victoria | 62 |
| 2432 | usaba | 62 |
| 2433 | tomé | 62 |
| 2434 | sentencia | 62 |
| 2435 | satisfacción | 62 |
| 2436 | responde | 62 |
| 2437 | repetía | 62 |
| 2438 | propuso | 62 |
| 2439 | principalmente | 62 |
| 2440 | pasan | 62 |
| 2441 | pasada | 62 |
| 2442 | honestidad | 62 |
| 2443 | fina | 62 |
| 2444 | fiebre | 62 |
| 2445 | escribió | 62 |
| 2446 | escribano | 62 |
| 2447 | encantado | 62 |
| 2448 | emoción | 62 |
| 2449 | cuentos | 62 |
| 2450 | cubierto | 62 |
| 2451 | confieso | 62 |
| 2452 | confesonario | 62 |
| 2453 | completo | 62 |
| 2454 | civil | 62 |
| 2455 | caída | 62 |
| 2456 | botica | 62 |
| 2457 | ataque | 62 |
| 2458 | arena | 62 |
| 2459 | animales | 62 |
| 2460 | alzó | 62 |
| 2461 | altisidora | 62 |
| 2462 | afición | 62 |
| 2463 | acero | 62 |
| 2464 | verso | 61 |
| 2465 | vara | 61 |
| 2466 | supe | 61 |
| 2467 | secretos | 61 |
| 2468 | saco | 61 |
| 2469 | penitencia | 61 |
| 2470 | pasillo | 61 |
| 2471 | ofrece | 61 |
| 2472 | muero | 61 |
| 2473 | movimientos | 61 |
| 2474 | isla | 61 |
| 2475 | hallo | 61 |
| 2476 | hallé | 61 |
| 2477 | hagas | 61 |
| 2478 | furia | 61 |
| 2479 | fatiga | 61 |
| 2480 | falso | 61 |
| 2481 | espectáculo | 61 |
| 2482 | escudo | 61 |
| 2483 | engañado | 61 |
| 2484 | disimular | 61 |
| 2485 | disgusto | 61 |
| 2486 | déjame | 61 |
| 2487 | defender | 61 |
| 2488 | decirlo | 61 |
| 2489 | consiguiente | 61 |
| 2490 | confesor | 61 |
| 2491 | chiquilla | 61 |
| 2492 | callaba | 61 |
| 2493 | bravo | 61 |
| 2494 | b | 61 |
| 2495 | argumento | 61 |
| 2496 | alrededor | 61 |
| 2497 | vejez | 60 |
| 2498 | vean | 60 |
| 2499 | vaso | 60 |
| 2500 | valientes | 60 |
| 2501 | testigo | 60 |
| 2502 | tello | 60 |
| 2503 | sombras | 60 |
| 2504 | seguramente | 60 |
| 2505 | rosa | 60 |
| 2506 | roma | 60 |
| 2507 | rojo | 60 |
| 2508 | resistir | 60 |
| 2509 | religioso | 60 |
| 2510 | perdió | 60 |
| 2511 | mula | 60 |
| 2512 | muebles | 60 |
| 2513 | militar | 60 |
| 2514 | medias | 60 |
| 2515 | mármol | 60 |
| 2516 | lumbre | 60 |
| 2517 | hola | 60 |
| 2518 | grandísimo | 60 |
| 2519 | españoles | 60 |
| 2520 | entré | 60 |
| 2521 | elic | 60 |
| 2522 | echa | 60 |
| 2523 | determinado | 60 |
| 2524 | despertar | 60 |
| 2525 | despacio | 60 |
| 2526 | deshonra | 60 |
| 2527 | compañera | 60 |
| 2528 | carrasco | 60 |
| 2529 | atrevimiento | 60 |
| 2530 | alcaide | 60 |
| 2531 | absolutamente | 60 |
| 2532 | zapatos | 59 |
| 2533 | ty | 59 |
| 2534 | salga | 59 |
| 2535 | rosas | 59 |
| 2536 | roque | 59 |
| 2537 | regular | 59 |
| 2538 | poquito | 59 |
| 2539 | ponen | 59 |
| 2540 | pituso | 59 |
| 2541 | piensas | 59 |
| 2542 | paseos | 59 |
| 2543 | ocurrido | 59 |
| 2544 | obscuro | 59 |
| 2545 | novela | 59 |
| 2546 | narváez | 59 |
| 2547 | moneda | 59 |
| 2548 | minas | 59 |
| 2549 | lucrecia | 59 |
| 2550 | limpieza | 59 |
| 2551 | levita | 59 |
| 2552 | ignorancia | 59 |
| 2553 | hoja | 59 |
| 2554 | habilidad | 59 |
| 2555 | haberse | 59 |
| 2556 | fecha | 59 |
| 2557 | faldas | 59 |
| 2558 | fabio | 59 |
| 2559 | entendido | 59 |
| 2560 | duerme | 59 |
| 2561 | decoro | 59 |
| 2562 | cubierta | 59 |
| 2563 | chocolate | 59 |
| 2564 | canta | 59 |
| 2565 | bolsa | 59 |
| 2566 | arroyo | 59 |
| 2567 | anuncia | 59 |
| 2568 | amada | 59 |
| 2569 | agujero | 59 |
| 2570 | ademán | 59 |
| 2571 | absurdo | 59 |
| 2572 | yr | 58 |
| 2573 | viste | 58 |
| 2574 | vienes | 58 |
| 2575 | vía | 58 |
| 2576 | velas | 58 |
| 2577 | uñas | 58 |
| 2578 | soltó | 58 |
| 2579 | sillón | 58 |
| 2580 | riquezas | 58 |
| 2581 | remediar | 58 |
| 2582 | quienes | 58 |
| 2583 | quedarse | 58 |
| 2584 | prudencia | 58 |
| 2585 | preguntaba | 58 |
| 2586 | posición | 58 |
| 2587 | pensé | 58 |
| 2588 | olvidar | 58 |
| 2589 | ohando | 58 |
| 2590 | odio | 58 |
| 2591 | medida | 58 |
| 2592 | maravilla | 58 |
| 2593 | maestra | 58 |
| 2594 | llegue | 58 |
| 2595 | llamas | 58 |
| 2596 | licurgo | 58 |
| 2597 | jamas | 58 |
| 2598 | ingeniero | 58 |
| 2599 | ideal | 58 |
| 2600 | humanidad | 58 |
| 2601 | hablaron | 58 |
| 2602 | hablan | 58 |
| 2603 | furor | 58 |
| 2604 | francamente | 58 |
| 2605 | flaco | 58 |
| 2606 | eterna | 58 |
| 2607 | estudiar | 58 |
| 2608 | estrella | 58 |
| 2609 | escondido | 58 |
| 2610 | engañar | 58 |
| 2611 | docena | 58 |
| 2612 | despecho | 58 |
| 2613 | dejase | 58 |
| 2614 | decente | 58 |
| 2615 | cuadro | 58 |
| 2616 | crespo | 58 |
| 2617 | consideración | 58 |
| 2618 | conducta | 58 |
| 2619 | calló | 58 |
| 2620 | aves | 58 |
| 2621 | ambición | 58 |
| 2622 | alcanza | 58 |
| 2623 | afán | 58 |
| 2624 | admirable | 58 |
| 2625 | volverse | 57 |
| 2626 | vestir | 57 |
| 2627 | verdades | 57 |
| 2628 | ventanas | 57 |
| 2629 | tardó | 57 |
| 2630 | sirven | 57 |
| 2631 | siguieron | 57 |
| 2632 | sesenta | 57 |
| 2633 | servicios | 57 |
| 2634 | saberlo | 57 |
| 2635 | recuerdos | 57 |
| 2636 | quitaba | 57 |
| 2637 | quedé | 57 |
| 2638 | puente | 57 |
| 2639 | pudieran | 57 |
| 2640 | penitenciario | 57 |
| 2641 | pareja | 57 |
| 2642 | ordinario | 57 |
| 2643 | naturales | 57 |
| 2644 | nación | 57 |
| 2645 | mesas | 57 |
| 2646 | manía | 57 |
| 2647 | malespina | 57 |
| 2648 | juliana | 57 |
| 2649 | juana | 57 |
| 2650 | jaula | 57 |
| 2651 | hallaron | 57 |
| 2652 | guardia | 57 |
| 2653 | felices | 57 |
| 2654 | estrecha | 57 |
| 2655 | entraban | 57 |
| 2656 | donaire | 57 |
| 2657 | demanda | 57 |
| 2658 | dejé | 57 |
| 2659 | debes | 57 |
| 2660 | criadas | 57 |
| 2661 | corto | 57 |
| 2662 | condiciones | 57 |
| 2663 | cerrada | 57 |
| 2664 | barinaga | 57 |
| 2665 | bah | 57 |
| 2666 | artículos | 57 |
| 2667 | yendo | 56 |
| 2668 | vulgar | 56 |
| 2669 | vimos | 56 |
| 2670 | viéndose | 56 |
| 2671 | tonterías | 56 |
| 2672 | tirar | 56 |
| 2673 | tinieblas | 56 |
| 2674 | sonaba | 56 |
| 2675 | sillas | 56 |
| 2676 | sentada | 56 |
| 2677 | retablo | 56 |
| 2678 | resto | 56 |
| 2679 | relación | 56 |
| 2680 | puse | 56 |
| 2681 | pudiendo | 56 |
| 2682 | perdía | 56 |
| 2683 | once | 56 |
| 2684 | novio | 56 |
| 2685 | necio | 56 |
| 2686 | mover | 56 |
| 2687 | mono | 56 |
| 2688 | llevando | 56 |
| 2689 | linda | 56 |
| 2690 | largos | 56 |
| 2691 | instrumento | 56 |
| 2692 | herencia | 56 |
| 2693 | hablo | 56 |
| 2694 | fábrica | 56 |
| 2695 | extraña | 56 |
| 2696 | díjome | 56 |
| 2697 | conseguir | 56 |
| 2698 | conocí | 56 |
| 2699 | confuso | 56 |
| 2700 | carlistas | 56 |
| 2701 | campaña | 56 |
| 2702 | breves | 56 |
| 2703 | averiguar | 56 |
| 2704 | andaban | 56 |
| 2705 | alabanzas | 56 |
| 2706 | vulgo | 55 |
| 2707 | vengan | 55 |
| 2708 | tropa | 55 |
| 2709 | tranquilidad | 55 |
| 2710 | torpe | 55 |
| 2711 | teresina | 55 |
| 2712 | socorro | 55 |
| 2713 | sabrá | 55 |
| 2714 | reposo | 55 |
| 2715 | profesión | 55 |
| 2716 | prisión | 55 |
| 2717 | pidiendo | 55 |
| 2718 | pechos | 55 |
| 2719 | obligación | 55 |
| 2720 | novia | 55 |
| 2721 | notar | 55 |
| 2722 | misericordia | 55 |
| 2723 | meterse | 55 |
| 2724 | lloraba | 55 |
| 2725 | llano | 55 |
| 2726 | juegos | 55 |
| 2727 | horror | 55 |
| 2728 | gallo | 55 |
| 2729 | franqueza | 55 |
| 2730 | filósofo | 55 |
| 2731 | fígaro | 55 |
| 2732 | facilidad | 55 |
| 2733 | estremo | 55 |
| 2734 | empleado | 55 |
| 2735 | efectivamente | 55 |
| 2736 | edificio | 55 |
| 2737 | dolores | 55 |
| 2738 | dificultades | 55 |
| 2739 | devoción | 55 |
| 2740 | despidió | 55 |
| 2741 | darte | 55 |
| 2742 | corrido | 55 |
| 2743 | copa | 55 |
| 2744 | clero | 55 |
| 2745 | círculo | 55 |
| 2746 | carnal | 55 |
| 2747 | carcajadas | 55 |
| 2748 | cantaba | 55 |
| 2749 | asco | 55 |
| 2750 | adentro | 55 |
| 2751 | actos | 55 |
| 2752 | acordaba | 55 |
| 2753 | yerba | 54 |
| 2754 | visitar | 54 |
| 2755 | verdaderas | 54 |
| 2756 | tipo | 54 |
| 2757 | temer | 54 |
| 2758 | sorpresa | 54 |
| 2759 | seres | 54 |
| 2760 | ruego | 54 |
| 2761 | rompió | 54 |
| 2762 | regente | 54 |
| 2763 | peligros | 54 |
| 2764 | pardo | 54 |
| 2765 | ondas | 54 |
| 2766 | ocurre | 54 |
| 2767 | nació | 54 |
| 2768 | modelo | 54 |
| 2769 | marcela | 54 |
| 2770 | lujo | 54 |
| 2771 | llegamos | 54 |
| 2772 | llamada | 54 |
| 2773 | justa | 54 |
| 2774 | invención | 54 |
| 2775 | inteligencia | 54 |
| 2776 | imágenes | 54 |
| 2777 | hueso | 54 |
| 2778 | hueco | 54 |
| 2779 | hazer | 54 |
| 2780 | guía | 54 |
| 2781 | galeras | 54 |
| 2782 | faltas | 54 |
| 2783 | esso | 54 |
| 2784 | esfuerzos | 54 |
| 2785 | empezar | 54 |
| 2786 | dudas | 54 |
| 2787 | desdichada | 54 |
| 2788 | debilidad | 54 |
| 2789 | cuidados | 54 |
| 2790 | contestaba | 54 |
| 2791 | conoces | 54 |
| 2792 | comprendía | 54 |
| 2793 | compra | 54 |
| 2794 | cerrado | 54 |
| 2795 | altura | 54 |
| 2796 | alara | 54 |
| 2797 | vivían | 53 |
| 2798 | tornó | 53 |
| 2799 | tierras | 53 |
| 2800 | testigos | 53 |
| 2801 | tenia | 53 |
| 2802 | temerosa | 53 |
| 2803 | tardanza | 53 |
| 2804 | serenidad | 53 |
| 2805 | saltó | 53 |
| 2806 | retiró | 53 |
| 2807 | quite | 53 |
| 2808 | promesas | 53 |
| 2809 | perdona | 53 |
| 2810 | oían | 53 |
| 2811 | montesinos | 53 |
| 2812 | llegué | 53 |
| 2813 | levantado | 53 |
| 2814 | lados | 53 |
| 2815 | joyas | 53 |
| 2816 | improviso | 53 |
| 2817 | humanas | 53 |
| 2818 | hogar | 53 |
| 2819 | halla | 53 |
| 2820 | fuentes | 53 |
| 2821 | freno | 53 |
| 2822 | fiestas | 53 |
| 2823 | estrépito | 53 |
| 2824 | estáis | 53 |
| 2825 | elicia | 53 |
| 2826 | edelmira | 53 |
| 2827 | diente | 53 |
| 2828 | desgracias | 53 |
| 2829 | descuido | 53 |
| 2830 | decirte | 53 |
| 2831 | cuántos | 53 |
| 2832 | creen | 53 |
| 2833 | corazones | 53 |
| 2834 | contando | 53 |
| 2835 | cintura | 53 |
| 2836 | ciega | 53 |
| 2837 | chiquillos | 53 |
| 2838 | cantando | 53 |
| 2839 | caminar | 53 |
| 2840 | cabra | 53 |
| 2841 | bulto | 53 |
| 2842 | bestias | 53 |
| 2843 | beso | 53 |
| 2844 | amable | 53 |
| 2845 | usan | 52 |
| 2846 | trance | 52 |
| 2847 | traición | 52 |
| 2848 | traen | 52 |
| 2849 | toros | 52 |
| 2850 | tentación | 52 |
| 2851 | seca | 52 |
| 2852 | regalo | 52 |
| 2853 | quejas | 52 |
| 2854 | pulso | 52 |
| 2855 | procesión | 52 |
| 2856 | ponerme | 52 |
| 2857 | podrían | 52 |
| 2858 | personaje | 52 |
| 2859 | peña | 52 |
| 2860 | pálida | 52 |
| 2861 | oficial | 52 |
| 2862 | nube | 52 |
| 2863 | muralla | 52 |
| 2864 | mirado | 52 |
| 2865 | miguel | 52 |
| 2866 | ligera | 52 |
| 2867 | inmenso | 52 |
| 2868 | grupo | 52 |
| 2869 | grito | 52 |
| 2870 | fruto | 52 |
| 2871 | famosa | 52 |
| 2872 | entierro | 52 |
| 2873 | encuentra | 52 |
| 2874 | enamorada | 52 |
| 2875 | desesperación | 52 |
| 2876 | declaró | 52 |
| 2877 | cortés | 52 |
| 2878 | claras | 52 |
| 2879 | casualidad | 52 |
| 2880 | capellán | 52 |
| 2881 | cabe | 52 |
| 2882 | bronce | 52 |
| 2883 | bajaba | 52 |
| 2884 | asilo | 52 |
| 2885 | artillería | 52 |
| 2886 | anciano | 52 |
| 2887 | ancho | 52 |
| 2888 | amparo | 52 |
| 2889 | acostumbrado | 52 |
| 2890 | acordó | 52 |
| 2891 | abrigo | 52 |
| 2892 | abría | 52 |
| 2893 | volviese | 51 |
| 2894 | ventaja | 51 |
| 2895 | tierna | 51 |
| 2896 | tiendas | 51 |
| 2897 | tengan | 51 |
| 2898 | tamaño | 51 |
| 2899 | solemne | 51 |
| 2900 | sofía | 51 |
| 2901 | sobresalto | 51 |
| 2902 | sentarse | 51 |
| 2903 | salimos | 51 |
| 2904 | rosarito | 51 |
| 2905 | roja | 51 |
| 2906 | rodríguez | 51 |
| 2907 | ricas | 51 |
| 2908 | rezar | 51 |
| 2909 | reja | 51 |
| 2910 | promesa | 51 |
| 2911 | nerviosa | 51 |
| 2912 | moverse | 51 |
| 2913 | jornada | 51 |
| 2914 | inmensa | 51 |
| 2915 | huéspedes | 51 |
| 2916 | gatos | 51 |
| 2917 | gallardo | 51 |
| 2918 | fonda | 51 |
| 2919 | faze | 51 |
| 2920 | estación | 51 |
| 2921 | ende | 51 |
| 2922 | dejarse | 51 |
| 2923 | camilo | 51 |
| 2924 | c | 51 |
| 2925 | buque | 51 |
| 2926 | artes | 51 |
| 2927 | arcediano | 51 |
| 2928 | admirado | 51 |
| 2929 | actitud | 51 |
| 2930 | vivido | 50 |
| 2931 | vemos | 50 |
| 2932 | varón | 50 |
| 2933 | trecho | 50 |
| 2934 | traza | 50 |
| 2935 | tías | 50 |
| 2936 | superiora | 50 |
| 2937 | somoza | 50 |
| 2938 | segun | 50 |
| 2939 | sal | 50 |
| 2940 | prados | 50 |
| 2941 | oiga | 50 |
| 2942 | moda | 50 |
| 2943 | miserables | 50 |
| 2944 | mill | 50 |
| 2945 | metía | 50 |
| 2946 | mantón | 50 |
| 2947 | llamo | 50 |
| 2948 | legua | 50 |
| 2949 | lacayo | 50 |
| 2950 | labradora | 50 |
| 2951 | juramento | 50 |
| 2952 | inconveniente | 50 |
| 2953 | hagan | 50 |
| 2954 | guardaba | 50 |
| 2955 | granada | 50 |
| 2956 | gozaba | 50 |
| 2957 | fortaleza | 50 |
| 2958 | empeño | 50 |
| 2959 | determinación | 50 |
| 2960 | despierto | 50 |
| 2961 | decirme | 50 |
| 2962 | custodio | 50 |
| 2963 | cumplido | 50 |
| 2964 | continuaba | 50 |
| 2965 | cogía | 50 |
| 2966 | cementerio | 50 |
| 2967 | casamiento | 50 |
| 2968 | canción | 50 |
| 2969 | blando | 50 |
| 2970 | aquesta | 50 |
| 2971 | abre | 50 |
| 2972 | abiertos | 50 |
| 2973 | volvían | 49 |
| 2974 | vil | 49 |
| 2975 | viéndole | 49 |
| 2976 | vestía | 49 |
| 2977 | veas | 49 |
| 2978 | tontería | 49 |
| 2979 | seguido | 49 |
| 2980 | saque | 49 |
| 2981 | ruiz | 49 |
| 2982 | retrato | 49 |
| 2983 | resultado | 49 |
| 2984 | redondo | 49 |
| 2985 | recibido | 49 |
| 2986 | quisieron | 49 |
| 2987 | puño | 49 |
| 2988 | puntas | 49 |
| 2989 | pudieron | 49 |
| 2990 | pruebas | 49 |
| 2991 | prometo | 49 |
| 2992 | presidente | 49 |
| 2993 | ponían | 49 |
| 2994 | peseta | 49 |
| 2995 | parezca | 49 |
| 2996 | paréceme | 49 |
| 2997 | olas | 49 |
| 2998 | oficiales | 49 |
| 2999 | objetos | 49 |
| 3000 | montaña | 49 |
| 3001 | mio | 49 |
| 3002 | miembros | 49 |
| 3003 | manuel | 49 |
| 3004 | lee | 49 |
| 3005 | hechas | 49 |
| 3006 | habíamos | 49 |
| 3007 | fundadora | 49 |
| 3008 | eterno | 49 |
| 3009 | esse | 49 |
| 3010 | espadas | 49 |
| 3011 | elegantes | 49 |
| 3012 | discretos | 49 |
| 3013 | dirigió | 49 |
| 3014 | dificultad | 49 |
| 3015 | determinó | 49 |
| 3016 | costanza | 49 |
| 3017 | consistía | 49 |
| 3018 | causas | 49 |
| 3019 | aviso | 49 |
| 3020 | autores | 49 |
| 3021 | aseguro | 49 |
| 3022 | armonía | 49 |
| 3023 | ansiedad | 49 |
| 3024 | actividad | 49 |
| 3025 | abismo | 49 |
| 3026 | trinidad | 48 |
| 3027 | total | 48 |
| 3028 | torquemada | 48 |
| 3029 | tocando | 48 |
| 3030 | suelto | 48 |
| 3031 | serás | 48 |
| 3032 | señá | 48 |
| 3033 | sana | 48 |
| 3034 | ronda | 48 |
| 3035 | primavera | 48 |
| 3036 | plantas | 48 |
| 3037 | origen | 48 |
| 3038 | novelas | 48 |
| 3039 | naturalmente | 48 |
| 3040 | nacimiento | 48 |
| 3041 | marineros | 48 |
| 3042 | manta | 48 |
| 3043 | lienzo | 48 |
| 3044 | impertinente | 48 |
| 3045 | honradez | 48 |
| 3046 | gestos | 48 |
| 3047 | fiero | 48 |
| 3048 | extraordinario | 48 |
| 3049 | explicaciones | 48 |
| 3050 | estábamos | 48 |
| 3051 | empezado | 48 |
| 3052 | descubrir | 48 |
| 3053 | des | 48 |
| 3054 | considerando | 48 |
| 3055 | cómoda | 48 |
| 3056 | clases | 48 |
| 3057 | castilla | 48 |
| 3058 | caían | 48 |
| 3059 | cabrero | 48 |
| 3060 | barcos | 48 |
| 3061 | ateo | 48 |
| 3062 | arrojó | 48 |
| 3063 | ardor | 48 |
| 3064 | apartar | 48 |
| 3065 | alla | 48 |
| 3066 | abindarráez | 48 |
| 3067 | vayas | 47 |
| 3068 | vase | 47 |
| 3069 | trajo | 47 |
| 3070 | sudor | 47 |
| 3071 | subieron | 47 |
| 3072 | sobra | 47 |
| 3073 | sienpre | 47 |
| 3074 | sentí | 47 |
| 3075 | salvación | 47 |
| 3076 | saliese | 47 |
| 3077 | quisieres | 47 |
| 3078 | prometió | 47 |
| 3079 | personal | 47 |
| 3080 | pausa | 47 |
| 3081 | ordenó | 47 |
| 3082 | oigo | 47 |
| 3083 | n | 47 |
| 3084 | mostrando | 47 |
| 3085 | morada | 47 |
| 3086 | montón | 47 |
| 3087 | miel | 47 |
| 3088 | marina | 47 |
| 3089 | lucr | 47 |
| 3090 | leal | 47 |
| 3091 | juntamente | 47 |
| 3092 | iremos | 47 |
| 3093 | in | 47 |
| 3094 | huyendo | 47 |
| 3095 | franceses | 47 |
| 3096 | familias | 47 |
| 3097 | expresar | 47 |
| 3098 | excelencia | 47 |
| 3099 | enorme | 47 |
| 3100 | echaron | 47 |
| 3101 | durmiendo | 47 |
| 3102 | diversos | 47 |
| 3103 | diligencias | 47 |
| 3104 | despues | 47 |
| 3105 | desdicha | 47 |
| 3106 | desconocido | 47 |
| 3107 | creas | 47 |
| 3108 | costado | 47 |
| 3109 | coronel | 47 |
| 3110 | cojo | 47 |
| 3111 | cobrar | 47 |
| 3112 | caro | 47 |
| 3113 | buscó | 47 |
| 3114 | anciana | 47 |
| 3115 | albarda | 47 |
| 3116 | agujeros | 47 |
| 3117 | absoluta | 47 |
| 3118 | vy | 46 |
| 3119 | vno | 46 |
| 3120 | verdugo | 46 |
| 3121 | vendría | 46 |
| 3122 | tendido | 46 |
| 3123 | soltar | 46 |
| 3124 | simpático | 46 |
| 3125 | sermón | 46 |
| 3126 | segismundo | 46 |
| 3127 | sabios | 46 |
| 3128 | redonda | 46 |
| 3129 | realmente | 46 |
| 3130 | púlpito | 46 |
| 3131 | puedan | 46 |
| 3132 | pozo | 46 |
| 3133 | pláticas | 46 |
| 3134 | pesado | 46 |
| 3135 | pesa | 46 |
| 3136 | pelos | 46 |
| 3137 | paja | 46 |
| 3138 | ordinaria | 46 |
| 3139 | observando | 46 |
| 3140 | muro | 46 |
| 3141 | mudo | 46 |
| 3142 | moría | 46 |
| 3143 | molido | 46 |
| 3144 | mayordomo | 46 |
| 3145 | lleve | 46 |
| 3146 | leyendo | 46 |
| 3147 | lectura | 46 |
| 3148 | latín | 46 |
| 3149 | instinto | 46 |
| 3150 | ingrata | 46 |
| 3151 | impulso | 46 |
| 3152 | haze | 46 |
| 3153 | guarde | 46 |
| 3154 | guapa | 46 |
| 3155 | generoso | 46 |
| 3156 | flaqueza | 46 |
| 3157 | estudios | 46 |
| 3158 | despedirse | 46 |
| 3159 | desear | 46 |
| 3160 | derechos | 46 |
| 3161 | delirio | 46 |
| 3162 | cuchillo | 46 |
| 3163 | convicción | 46 |
| 3164 | contraria | 46 |
| 3165 | conocían | 46 |
| 3166 | concierto | 46 |
| 3167 | comenzaba | 46 |
| 3168 | coge | 46 |
| 3169 | coches | 46 |
| 3170 | cipión | 46 |
| 3171 | cejas | 46 |
| 3172 | carraspique | 46 |
| 3173 | canas | 46 |
| 3174 | cámara | 46 |
| 3175 | borracho | 46 |
| 3176 | barro | 46 |
| 3177 | bailar | 46 |
| 3178 | aquélla | 46 |
| 3179 | amadís | 46 |
| 3180 | ajenas | 46 |
| 3181 | ajena | 46 |
| 3182 | acercaba | 46 |
| 3183 | volvería | 45 |
| 3184 | veréis | 45 |
| 3185 | vender | 45 |
| 3186 | veis | 45 |
| 3187 | valen | 45 |
| 3188 | tronco | 45 |
| 3189 | tomaron | 45 |
| 3190 | terciopelo | 45 |
| 3191 | temiendo | 45 |
| 3192 | subido | 45 |
| 3193 | santidad | 45 |
| 3194 | saltar | 45 |
| 3195 | sabré | 45 |
| 3196 | sábanas | 45 |
| 3197 | ronca | 45 |
| 3198 | respetable | 45 |
| 3199 | representaba | 45 |
| 3200 | razonable | 45 |
| 3201 | rápidamente | 45 |
| 3202 | próximo | 45 |
| 3203 | providencia | 45 |
| 3204 | presentaba | 45 |
| 3205 | pormenores | 45 |
| 3206 | ponerle | 45 |
| 3207 | pleito | 45 |
| 3208 | pensativo | 45 |
| 3209 | pelota | 45 |
| 3210 | original | 45 |
| 3211 | omes | 45 |
| 3212 | novedad | 45 |
| 3213 | molino | 45 |
| 3214 | micaelas | 45 |
| 3215 | marquesito | 45 |
| 3216 | mande | 45 |
| 3217 | maldad | 45 |
| 3218 | llegada | 45 |
| 3219 | lección | 45 |
| 3220 | jacinto | 45 |
| 3221 | iv | 45 |
| 3222 | iría | 45 |
| 3223 | impaciencia | 45 |
| 3224 | honesta | 45 |
| 3225 | heridos | 45 |
| 3226 | habrían | 45 |
| 3227 | gobernar | 45 |
| 3228 | facciones | 45 |
| 3229 | fablar | 45 |
| 3230 | engaña | 45 |
| 3231 | encantador | 45 |
| 3232 | duques | 45 |
| 3233 | divino | 45 |
| 3234 | desdichas | 45 |
| 3235 | cuentan | 45 |
| 3236 | cuánta | 45 |
| 3237 | contestar | 45 |
| 3238 | conocida | 45 |
| 3239 | chiquillo | 45 |
| 3240 | cava | 45 |
| 3241 | carlista | 45 |
| 3242 | cargado | 45 |
| 3243 | bruto | 45 |
| 3244 | briones | 45 |
| 3245 | blanda | 45 |
| 3246 | ausente | 45 |
| 3247 | amanecer | 45 |
| 3248 | acudieron | 45 |
| 3249 | yerro | 44 |
| 3250 | vuelven | 44 |
| 3251 | vidas | 44 |
| 3252 | véase | 44 |
| 3253 | valle | 44 |
| 3254 | valentía | 44 |
| 3255 | trató | 44 |
| 3256 | tiros | 44 |
| 3257 | suponer | 44 |
| 3258 | suplico | 44 |
| 3259 | sostener | 44 |
| 3260 | sentar | 44 |
| 3261 | satisfacer | 44 |
| 3262 | sacrificio | 44 |
| 3263 | rostros | 44 |
| 3264 | romance | 44 |
| 3265 | república | 44 |
| 3266 | regla | 44 |
| 3267 | recién | 44 |
| 3268 | quevedo | 44 |
| 3269 | pusiera | 44 |
| 3270 | piden | 44 |
| 3271 | paraba | 44 |
| 3272 | papa | 44 |
| 3273 | numancia | 44 |
| 3274 | nave | 44 |
| 3275 | merecía | 44 |
| 3276 | mate | 44 |
| 3277 | marinero | 44 |
| 3278 | lodo | 44 |
| 3279 | llegaban | 44 |
| 3280 | ligereza | 44 |
| 3281 | leonela | 44 |
| 3282 | hermanas | 44 |
| 3283 | heridas | 44 |
| 3284 | gas | 44 |
| 3285 | ganancia | 44 |
| 3286 | fasta | 44 |
| 3287 | familiar | 44 |
| 3288 | faltó | 44 |
| 3289 | empezaron | 44 |
| 3290 | dispuesta | 44 |
| 3291 | desea | 44 |
| 3292 | cuadros | 44 |
| 3293 | crianza | 44 |
| 3294 | comodidad | 44 |
| 3295 | comigo | 44 |
| 3296 | comiendo | 44 |
| 3297 | comían | 44 |
| 3298 | comen | 44 |
| 3299 | cabía | 44 |
| 3300 | benítez | 44 |
| 3301 | bendición | 44 |
| 3302 | bastaba | 44 |
| 3303 | atado | 44 |
| 3304 | apariencias | 44 |
| 3305 | añadir | 44 |
| 3306 | amarillo | 44 |
| 3307 | aceite | 44 |
| 3308 | zaragoza | 43 |
| 3309 | vine | 43 |
| 3310 | venus | 43 |
| 3311 | velo | 43 |
| 3312 | vecindad | 43 |
| 3313 | vacío | 43 |
| 3314 | u | 43 |
| 3315 | toro | 43 |
| 3316 | tablas | 43 |
| 3317 | sur | 43 |
| 3318 | sonrió | 43 |
| 3319 | sirvió | 43 |
| 3320 | siguiendo | 43 |
| 3321 | sesos | 43 |
| 3322 | saturnino | 43 |
| 3323 | salvar | 43 |
| 3324 | sacaron | 43 |
| 3325 | rubio | 43 |
| 3326 | rosita | 43 |
| 3327 | recibía | 43 |
| 3328 | prouecho | 43 |
| 3329 | prosigue | 43 |
| 3330 | posesión | 43 |
| 3331 | platón | 43 |
| 3332 | piadosa | 43 |
| 3333 | personajes | 43 |
| 3334 | pendiente | 43 |
| 3335 | pájaro | 43 |
| 3336 | orilla | 43 |
| 3337 | oidor | 43 |
| 3338 | ocurría | 43 |
| 3339 | observación | 43 |
| 3340 | nace | 43 |
| 3341 | montañas | 43 |
| 3342 | mentir | 43 |
| 3343 | melancolía | 43 |
| 3344 | mediodía | 43 |
| 3345 | material | 43 |
| 3346 | mangas | 43 |
| 3347 | líneas | 43 |
| 3348 | levantaba | 43 |
| 3349 | leones | 43 |
| 3350 | lana | 43 |
| 3351 | jaqueca | 43 |
| 3352 | imitar | 43 |
| 3353 | imagino | 43 |
| 3354 | hayan | 43 |
| 3355 | há | 43 |
| 3356 | galería | 43 |
| 3357 | flaca | 43 |
| 3358 | feliciana | 43 |
| 3359 | entramos | 43 |
| 3360 | enemiga | 43 |
| 3361 | duró | 43 |
| 3362 | duele | 43 |
| 3363 | ducados | 43 |
| 3364 | dixe | 43 |
| 3365 | dirán | 43 |
| 3366 | desesperado | 43 |
| 3367 | descubrió | 43 |
| 3368 | dello | 43 |
| 3369 | decidido | 43 |
| 3370 | curso | 43 |
| 3371 | coplas | 43 |
| 3372 | contener | 43 |
| 3373 | cigarro | 43 |
| 3374 | catorce | 43 |
| 3375 | caracteres | 43 |
| 3376 | capricho | 43 |
| 3377 | cansancio | 43 |
| 3378 | benito | 43 |
| 3379 | auxilio | 43 |
| 3380 | arrogante | 43 |
| 3381 | aparisi | 43 |
| 3382 | anochecer | 43 |
| 3383 | ancha | 43 |
| 3384 | ambiente | 43 |
| 3385 | amado | 43 |
| 3386 | advertir | 43 |
| 3387 | acabe | 43 |
| 3388 | abriendo | 43 |
| 3389 | viernes | 42 |
| 3390 | verlo | 42 |
| 3391 | verdaderos | 42 |
| 3392 | varas | 42 |
| 3393 | tristezas | 42 |
| 3394 | través | 42 |
| 3395 | trabuco | 42 |
| 3396 | tengas | 42 |
| 3397 | talante | 42 |
| 3398 | servían | 42 |
| 3399 | seriedad | 42 |
| 3400 | sentencias | 42 |
| 3401 | saludó | 42 |
| 3402 | romanos | 42 |
| 3403 | riendas | 42 |
| 3404 | refrán | 42 |
| 3405 | ratito | 42 |
| 3406 | ramo | 42 |
| 3407 | puños | 42 |
| 3408 | prefería | 42 |
| 3409 | porfía | 42 |
| 3410 | planta | 42 |
| 3411 | pintada | 42 |
| 3412 | pícaro | 42 |
| 3413 | pez | 42 |
| 3414 | perdidos | 42 |
| 3415 | perdición | 42 |
| 3416 | pares | 42 |
| 3417 | pagado | 42 |
| 3418 | oyes | 42 |
| 3419 | monedas | 42 |
| 3420 | milagros | 42 |
| 3421 | mete | 42 |
| 3422 | llegan | 42 |
| 3423 | lance | 42 |
| 3424 | joaquinito | 42 |
| 3425 | jarro | 42 |
| 3426 | infancia | 42 |
| 3427 | ignorante | 42 |
| 3428 | hospital | 42 |
| 3429 | hé | 42 |
| 3430 | hablarle | 42 |
| 3431 | formaban | 42 |
| 3432 | famosos | 42 |
| 3433 | exaltación | 42 |
| 3434 | espuma | 42 |
| 3435 | esperaban | 42 |
| 3436 | escape | 42 |
| 3437 | entiendes | 42 |
| 3438 | encontré | 42 |
| 3439 | elegancia | 42 |
| 3440 | ejecución | 42 |
| 3441 | dolorida | 42 |
| 3442 | dichosa | 42 |
| 3443 | diálogo | 42 |
| 3444 | despojos | 42 |
| 3445 | crueldad | 42 |
| 3446 | corral | 42 |
| 3447 | continuo | 42 |
| 3448 | considerar | 42 |
| 3449 | consideraba | 42 |
| 3450 | conque | 42 |
| 3451 | completa | 42 |
| 3452 | cesar | 42 |
| 3453 | capas | 42 |
| 3454 | bordo | 42 |
| 3455 | bello | 42 |
| 3456 | artista | 42 |
| 3457 | arr | 42 |
| 3458 | apartó | 42 |
| 3459 | alguacil | 42 |
| 3460 | alcázar | 42 |
| 3461 | acuerdas | 42 |
| 3462 | acompañado | 42 |
| 3463 | acera | 42 |
| 3464 | aca | 42 |
| 3465 | absoluto | 42 |
| 3466 | abrazó | 42 |
| 3467 | abandono | 42 |
| 3468 | vicios | 41 |
| 3469 | vayan | 41 |
| 3470 | valer | 41 |
| 3471 | tratando | 41 |
| 3472 | trapos | 41 |
| 3473 | tocan | 41 |
| 3474 | tocado | 41 |
| 3475 | tierno | 41 |
| 3476 | suspenso | 41 |
| 3477 | sospechas | 41 |
| 3478 | sopa | 41 |
| 3479 | solían | 41 |
| 3480 | severidad | 41 |
| 3481 | robado | 41 |
| 3482 | ridícula | 41 |
| 3483 | retirarse | 41 |
| 3484 | resuelto | 41 |
| 3485 | región | 41 |
| 3486 | raso | 41 |
| 3487 | quiteria | 41 |
| 3488 | querrá | 41 |
| 3489 | queja | 41 |
| 3490 | quedose | 41 |
| 3491 | puestas | 41 |
| 3492 | peregrino | 41 |
| 3493 | pedido | 41 |
| 3494 | partir | 41 |
| 3495 | operación | 41 |
| 3496 | observar | 41 |
| 3497 | nervioso | 41 |
| 3498 | nacer | 41 |
| 3499 | infinitos | 41 |
| 3500 | infinito | 41 |
| 3501 | indispensable | 41 |
| 3502 | inclinó | 41 |
| 3503 | humedad | 41 |
| 3504 | hermosos | 41 |
| 3505 | hacerla | 41 |
| 3506 | gota | 41 |
| 3507 | funciones | 41 |
| 3508 | fermosa | 41 |
| 3509 | felic | 41 |
| 3510 | farol | 41 |
| 3511 | estruendo | 41 |
| 3512 | espejos | 41 |
| 3513 | encanto | 41 |
| 3514 | domingo | 41 |
| 3515 | doctrina | 41 |
| 3516 | difunto | 41 |
| 3517 | delicado | 41 |
| 3518 | delicada | 41 |
| 3519 | delgado | 41 |
| 3520 | dada | 41 |
| 3521 | cuerno | 41 |
| 3522 | cortar | 41 |
| 3523 | corrían | 41 |
| 3524 | contemplando | 41 |
| 3525 | célebre | 41 |
| 3526 | celada | 41 |
| 3527 | cazador | 41 |
| 3528 | canalla | 41 |
| 3529 | bendita | 41 |
| 3530 | avendaño | 41 |
| 3531 | areusa | 41 |
| 3532 | aprender | 41 |
| 3533 | apreciar | 41 |
| 3534 | almorzar | 41 |
| 3535 | alforjas | 41 |
| 3536 | advirtió | 41 |
| 3537 | acercarse | 41 |
| 3538 | abundancia | 41 |
| 3539 | zapatero | 40 |
| 3540 | yerbas | 40 |
| 3541 | yelmo | 40 |
| 3542 | volar | 40 |
| 3543 | vii | 40 |
| 3544 | vido | 40 |
| 3545 | ventajas | 40 |
| 3546 | vencedor | 40 |
| 3547 | vee | 40 |
| 3548 | últimas | 40 |
| 3549 | terribles | 40 |
| 3550 | temblaba | 40 |
| 3551 | tardes | 40 |
| 3552 | sordo | 40 |
| 3553 | sirvo | 40 |
| 3554 | sera | 40 |
| 3555 | señoritas | 40 |
| 3556 | sentándose | 40 |
| 3557 | sencilla | 40 |
| 3558 | seguían | 40 |
| 3559 | saturno | 40 |
| 3560 | rueda | 40 |
| 3561 | romano | 40 |
| 3562 | reinos | 40 |
| 3563 | reían | 40 |
| 3564 | recordar | 40 |
| 3565 | recoger | 40 |
| 3566 | recebir | 40 |
| 3567 | raya | 40 |
| 3568 | raro | 40 |
| 3569 | quedándose | 40 |
| 3570 | propiedad | 40 |
| 3571 | probablemente | 40 |
| 3572 | presunción | 40 |
| 3573 | poderosa | 40 |
| 3574 | pobrecito | 40 |
| 3575 | permite | 40 |
| 3576 | pelea | 40 |
| 3577 | palma | 40 |
| 3578 | oso | 40 |
| 3579 | oriente | 40 |
| 3580 | oraciones | 40 |
| 3581 | olla | 40 |
| 3582 | notaba | 40 |
| 3583 | natura | 40 |
| 3584 | nací | 40 |
| 3585 | muros | 40 |
| 3586 | muñoz | 40 |
| 3587 | modestia | 40 |
| 3588 | metal | 40 |
| 3589 | llaves | 40 |
| 3590 | llamarse | 40 |
| 3591 | llamando | 40 |
| 3592 | límites | 40 |
| 3593 | jugando | 40 |
| 3594 | inocencia | 40 |
| 3595 | inmóvil | 40 |
| 3596 | inferior | 40 |
| 3597 | hielo | 40 |
| 3598 | gitana | 40 |
| 3599 | gastar | 40 |
| 3600 | gallinas | 40 |
| 3601 | fingiendo | 40 |
| 3602 | final | 40 |
| 3603 | estudiantes | 40 |
| 3604 | envuelto | 40 |
| 3605 | encendido | 40 |
| 3606 | encargo | 40 |
| 3607 | emplear | 40 |
| 3608 | diesen | 40 |
| 3609 | dias | 40 |
| 3610 | deseando | 40 |
| 3611 | debemos | 40 |
| 3612 | darles | 40 |
| 3613 | cuero | 40 |
| 3614 | cruces | 40 |
| 3615 | conveniente | 40 |
| 3616 | cesta | 40 |
| 3617 | cayendo | 40 |
| 3618 | cabras | 40 |
| 3619 | aver | 40 |
| 3620 | artificio | 40 |
| 3621 | armada | 40 |
| 3622 | añadía | 40 |
| 3623 | antiguas | 40 |
| 3624 | ánima | 40 |
| 3625 | alzando | 40 |
| 3626 | ally | 40 |
| 3627 | águeda | 40 |
| 3628 | agudo | 40 |
| 3629 | advierte | 40 |
| 3630 | admiraba | 40 |
| 3631 | acometer | 40 |
| 3632 | venerable | 39 |
| 3633 | trigo | 39 |
| 3634 | traidor | 39 |
| 3635 | toque | 39 |
| 3636 | tiró | 39 |
| 3637 | tabla | 39 |
| 3638 | subiendo | 39 |
| 3639 | sospechaba | 39 |
| 3640 | satisfecha | 39 |
| 3641 | salamanca | 39 |
| 3642 | sacristía | 39 |
| 3643 | resistencia | 39 |
| 3644 | recio | 39 |
| 3645 | raza | 39 |
| 3646 | púsose | 39 |
| 3647 | proyecto | 39 |
| 3648 | problema | 39 |
| 3649 | precioso | 39 |
| 3650 | permiso | 39 |
| 3651 | pequeños | 39 |
| 3652 | pedirle | 39 |
| 3653 | pedían | 39 |
| 3654 | padecer | 39 |
| 3655 | ocupado | 39 |
| 3656 | notas | 39 |
| 3657 | mugeres | 39 |
| 3658 | miraron | 39 |
| 3659 | mesón | 39 |
| 3660 | mayormente | 39 |
| 3661 | maridos | 39 |
| 3662 | marchar | 39 |
| 3663 | manteo | 39 |
| 3664 | literatura | 39 |
| 3665 | juzgar | 39 |
| 3666 | intereses | 39 |
| 3667 | idiota | 39 |
| 3668 | huye | 39 |
| 3669 | griego | 39 |
| 3670 | formidable | 39 |
| 3671 | formalidad | 39 |
| 3672 | firma | 39 |
| 3673 | faltado | 39 |
| 3674 | existe | 39 |
| 3675 | estraño | 39 |
| 3676 | escenas | 39 |
| 3677 | entendió | 39 |
| 3678 | elocuencia | 39 |
| 3679 | ejemplos | 39 |
| 3680 | eclesiástico | 39 |
| 3681 | domador | 39 |
| 3682 | disimulo | 39 |
| 3683 | dile | 39 |
| 3684 | desorden | 39 |
| 3685 | desafío | 39 |
| 3686 | dejarle | 39 |
| 3687 | consiste | 39 |
| 3688 | comparación | 39 |
| 3689 | comandante | 39 |
| 3690 | cogiendo | 39 |
| 3691 | carriazo | 39 |
| 3692 | cariñosa | 39 |
| 3693 | calumnia | 39 |
| 3694 | brío | 39 |
| 3695 | bocado | 39 |
| 3696 | batallas | 39 |
| 3697 | atmósfera | 39 |
| 3698 | arco | 39 |
| 3699 | anduvo | 39 |
| 3700 | amaba | 39 |
| 3701 | agradecido | 39 |
| 3702 | visiones | 38 |
| 3703 | veamos | 38 |
| 3704 | vanse | 38 |
| 3705 | trapo | 38 |
| 3706 | tira | 38 |
| 3707 | temblando | 38 |
| 3708 | suena | 38 |
| 3709 | sucia | 38 |
| 3710 | suavemente | 38 |
| 3711 | sonreír | 38 |
| 3712 | soneto | 38 |
| 3713 | sonaban | 38 |
| 3714 | sepulcro | 38 |
| 3715 | señalando | 38 |
| 3716 | respondí | 38 |
| 3717 | refranes | 38 |
| 3718 | prosa | 38 |
| 3719 | príncipes | 38 |
| 3720 | plazuela | 38 |
| 3721 | platos | 38 |
| 3722 | perdonar | 38 |
| 3723 | pasillos | 38 |
| 3724 | parroquia | 38 |
| 3725 | oírle | 38 |
| 3726 | oficios | 38 |
| 3727 | observaba | 38 |
| 3728 | obscura | 38 |
| 3729 | necios | 38 |
| 3730 | muelas | 38 |
| 3731 | muchachas | 38 |
| 3732 | motivos | 38 |
| 3733 | moscas | 38 |
| 3734 | misterio | 38 |
| 3735 | luto | 38 |
| 3736 | lazo | 38 |
| 3737 | labradores | 38 |
| 3738 | joya | 38 |
| 3739 | interesante | 38 |
| 3740 | inteligente | 38 |
| 3741 | haberme | 38 |
| 3742 | gustos | 38 |
| 3743 | guante | 38 |
| 3744 | grupos | 38 |
| 3745 | fieles | 38 |
| 3746 | fidelidad | 38 |
| 3747 | exigía | 38 |
| 3748 | escuchar | 38 |
| 3749 | enterado | 38 |
| 3750 | enfermedades | 38 |
| 3751 | encierra | 38 |
| 3752 | encerrado | 38 |
| 3753 | empieza | 38 |
| 3754 | desnuda | 38 |
| 3755 | deseado | 38 |
| 3756 | delito | 38 |
| 3757 | dejara | 38 |
| 3758 | dale | 38 |
| 3759 | curioso | 38 |
| 3760 | crecía | 38 |
| 3761 | correo | 38 |
| 3762 | contacto | 38 |
| 3763 | conferencia | 38 |
| 3764 | condesa | 38 |
| 3765 | concluir | 38 |
| 3766 | compuesto | 38 |
| 3767 | compras | 38 |
| 3768 | ciegos | 38 |
| 3769 | cide | 38 |
| 3770 | cañones | 38 |
| 3771 | cadenas | 38 |
| 3772 | bajando | 38 |
| 3773 | arreglo | 38 |
| 3774 | argumentos | 38 |
| 3775 | aparecía | 38 |
| 3776 | angustia | 38 |
| 3777 | alcalá | 38 |
| 3778 | álbum | 38 |
| 3779 | alba | 38 |
| 3780 | ajeno | 38 |
| 3781 | afrenta | 38 |
| 3782 | adelantado | 38 |
| 3783 | acostarse | 38 |
| 3784 | volví | 37 |
| 3785 | vientre | 37 |
| 3786 | varones | 37 |
| 3787 | trajes | 37 |
| 3788 | traes | 37 |
| 3789 | tirando | 37 |
| 3790 | testamento | 37 |
| 3791 | teme | 37 |
| 3792 | sutil | 37 |
| 3793 | suficiente | 37 |
| 3794 | sos | 37 |
| 3795 | soñaba | 37 |
| 3796 | socios | 37 |
| 3797 | sepas | 37 |
| 3798 | sagrada | 37 |
| 3799 | sabor | 37 |
| 3800 | ruegos | 37 |
| 3801 | rogó | 37 |
| 3802 | reconocer | 37 |
| 3803 | quieran | 37 |
| 3804 | quedará | 37 |
| 3805 | protección | 37 |
| 3806 | pesada | 37 |
| 3807 | peores | 37 |
| 3808 | penáguilas | 37 |
| 3809 | países | 37 |
| 3810 | notado | 37 |
| 3811 | niñez | 37 |
| 3812 | niega | 37 |
| 3813 | mesmos | 37 |
| 3814 | médicos | 37 |
| 3815 | mayo | 37 |
| 3816 | mañanas | 37 |
| 3817 | macho | 37 |
| 3818 | llevarle | 37 |
| 3819 | llamaron | 37 |
| 3820 | lista | 37 |
| 3821 | íntimo | 37 |
| 3822 | inmediatamente | 37 |
| 3823 | infinitas | 37 |
| 3824 | imperio | 37 |
| 3825 | huevos | 37 |
| 3826 | horizonte | 37 |
| 3827 | hondo | 37 |
| 3828 | hamete | 37 |
| 3829 | hallarse | 37 |
| 3830 | hablaremos | 37 |
| 3831 | gorro | 37 |
| 3832 | ginés | 37 |
| 3833 | gala | 37 |
| 3834 | fuertemente | 37 |
| 3835 | fisonomía | 37 |
| 3836 | físico | 37 |
| 3837 | faltaban | 37 |
| 3838 | europa | 37 |
| 3839 | estatua | 37 |
| 3840 | enamorados | 37 |
| 3841 | empleo | 37 |
| 3842 | doliente | 37 |
| 3843 | doble | 37 |
| 3844 | dichos | 37 |
| 3845 | desventura | 37 |
| 3846 | desconocida | 37 |
| 3847 | delicia | 37 |
| 3848 | cuna | 37 |
| 3849 | correspondencia | 37 |
| 3850 | convidados | 37 |
| 3851 | consiente | 37 |
| 3852 | concepto | 37 |
| 3853 | compás | 37 |
| 3854 | cómico | 37 |
| 3855 | cita | 37 |
| 3856 | castigar | 37 |
| 3857 | casó | 37 |
| 3858 | caricias | 37 |
| 3859 | caliente | 37 |
| 3860 | besar | 37 |
| 3861 | benigna | 37 |
| 3862 | barbaridad | 37 |
| 3863 | bala | 37 |
| 3864 | atentamente | 37 |
| 3865 | atender | 37 |
| 3866 | asegurar | 37 |
| 3867 | aprendido | 37 |
| 3868 | ancas | 37 |
| 3869 | algazara | 37 |
| 3870 | alfonso | 37 |
| 3871 | alegro | 37 |
| 3872 | aldeacorba | 37 |
| 3873 | aguardiente | 37 |
| 3874 | afuera | 37 |
| 3875 | aficionado | 37 |
| 3876 | acertado | 37 |
| 3877 | volveré | 36 |
| 3878 | universal | 36 |
| 3879 | uniforme | 36 |
| 3880 | tripas | 36 |
| 3881 | temas | 36 |
| 3882 | subían | 36 |
| 3883 | sociales | 36 |
| 3884 | secas | 36 |
| 3885 | salgo | 36 |
| 3886 | sagrado | 36 |
| 3887 | rogar | 36 |
| 3888 | rodrigo | 36 |
| 3889 | robustiano | 36 |
| 3890 | revolución | 36 |
| 3891 | respirar | 36 |
| 3892 | red | 36 |
| 3893 | recordó | 36 |
| 3894 | recogió | 36 |
| 3895 | recebido | 36 |
| 3896 | queso | 36 |
| 3897 | quedamos | 36 |
| 3898 | práctica | 36 |
| 3899 | pon | 36 |
| 3900 | playa | 36 |
| 3901 | pinzón | 36 |
| 3902 | pintura | 36 |
| 3903 | perdono | 36 |
| 3904 | pecadora | 36 |
| 3905 | patas | 36 |
| 3906 | palacios | 36 |
| 3907 | movió | 36 |
| 3908 | movido | 36 |
| 3909 | morena | 36 |
| 3910 | mientes | 36 |
| 3911 | miente | 36 |
| 3912 | masa | 36 |
| 3913 | marqueses | 36 |
| 3914 | marcharse | 36 |
| 3915 | lorenzo | 36 |
| 3916 | lloró | 36 |
| 3917 | llegóse | 36 |
| 3918 | llegase | 36 |
| 3919 | liberalidad | 36 |
| 3920 | levantaron | 36 |
| 3921 | juanín | 36 |
| 3922 | inquietud | 36 |
| 3923 | imperial | 36 |
| 3924 | hermandad | 36 |
| 3925 | hacemos | 36 |
| 3926 | habrás | 36 |
| 3927 | grosero | 36 |
| 3928 | grandezas | 36 |
| 3929 | gasta | 36 |
| 3930 | frialdad | 36 |
| 3931 | francesa | 36 |
| 3932 | formar | 36 |
| 3933 | formado | 36 |
| 3934 | estava | 36 |
| 3935 | estados | 36 |
| 3936 | especial | 36 |
| 3937 | escaleras | 36 |
| 3938 | envía | 36 |
| 3939 | enterarse | 36 |
| 3940 | encender | 36 |
| 3941 | encantada | 36 |
| 3942 | divertido | 36 |
| 3943 | dignos | 36 |
| 3944 | desierto | 36 |
| 3945 | delicadeza | 36 |
| 3946 | continente | 36 |
| 3947 | contentos | 36 |
| 3948 | conocidos | 36 |
| 3949 | conocen | 36 |
| 3950 | comprendo | 36 |
| 3951 | comprendido | 36 |
| 3952 | cochero | 36 |
| 3953 | ciertamente | 36 |
| 3954 | chicas | 36 |
| 3955 | católico | 36 |
| 3956 | castellana | 36 |
| 3957 | cañón | 36 |
| 3958 | campanilla | 36 |
| 3959 | brillaban | 36 |
| 3960 | besó | 36 |
| 3961 | berganza | 36 |
| 3962 | bellaco | 36 |
| 3963 | ayudar | 36 |
| 3964 | anchas | 36 |
| 3965 | alimento | 36 |
| 3966 | afecto | 36 |
| 3967 | acabaron | 36 |
| 3968 | vulgares | 35 |
| 3969 | vicente | 35 |
| 3970 | vería | 35 |
| 3971 | vais | 35 |
| 3972 | turbación | 35 |
| 3973 | torno | 35 |
| 3974 | toman | 35 |
| 3975 | tiento | 35 |
| 3976 | tendrás | 35 |
| 3977 | temores | 35 |
| 3978 | soga | 35 |
| 3979 | sinceridad | 35 |
| 3980 | semanas | 35 |
| 3981 | secretario | 35 |
| 3982 | saya | 35 |
| 3983 | sacristán | 35 |
| 3984 | sabéis | 35 |
| 3985 | rival | 35 |
| 3986 | ricote | 35 |
| 3987 | ribera | 35 |
| 3988 | remordimientos | 35 |
| 3989 | remordimiento | 35 |
| 3990 | profundamente | 35 |
| 3991 | probable | 35 |
| 3992 | poniéndole | 35 |
| 3993 | pondría | 35 |
| 3994 | podrás | 35 |
| 3995 | podéis | 35 |
| 3996 | pillo | 35 |
| 3997 | perjuicio | 35 |
| 3998 | pensarlo | 35 |
| 3999 | pegar | 35 |
| 4000 | olvidaba | 35 |
| 4001 | ocultar | 35 |
| 4002 | muriendo | 35 |
| 4003 | monstruo | 35 |
| 4004 | mató | 35 |
| 4005 | marcelo | 35 |
| 4006 | mantener | 35 |
| 4007 | lluvia | 35 |
| 4008 | leña | 35 |
| 4009 | jurar | 35 |
| 4010 | irá | 35 |
| 4011 | infantil | 35 |
| 4012 | impresiones | 35 |
| 4013 | hembra | 35 |
| 4014 | habrán | 35 |
| 4015 | habitaciones | 35 |
| 4016 | grandísima | 35 |
| 4017 | gigantes | 35 |
| 4018 | gasto | 35 |
| 4019 | gabán | 35 |
| 4020 | formal | 35 |
| 4021 | flora | 35 |
| 4022 | fieras | 35 |
| 4023 | falte | 35 |
| 4024 | facha | 35 |
| 4025 | expresaba | 35 |
| 4026 | éxito | 35 |
| 4027 | estraña | 35 |
| 4028 | estaré | 35 |
| 4029 | espinas | 35 |
| 4030 | escuadrón | 35 |
| 4031 | escritos | 35 |
| 4032 | entran | 35 |
| 4033 | encimada | 35 |
| 4034 | durmió | 35 |
| 4035 | dudar | 35 |
| 4036 | desmayada | 35 |
| 4037 | desgraciada | 35 |
| 4038 | descubre | 35 |
| 4039 | cubiertos | 35 |
| 4040 | crisis | 35 |
| 4041 | criminal | 35 |
| 4042 | cordero | 35 |
| 4043 | comisión | 35 |
| 4044 | colgado | 35 |
| 4045 | coja | 35 |
| 4046 | chispas | 35 |
| 4047 | canciones | 35 |
| 4048 | cajón | 35 |
| 4049 | cajas | 35 |
| 4050 | cabecera | 35 |
| 4051 | bodas | 35 |
| 4052 | billetes | 35 |
| 4053 | belén | 35 |
| 4054 | azules | 35 |
| 4055 | ayuntamiento | 35 |
| 4056 | asimesmo | 35 |
| 4057 | armados | 35 |
| 4058 | argel | 35 |
| 4059 | apretó | 35 |
| 4060 | amargo | 35 |
| 4061 | almuerzo | 35 |
| 4062 | alabanza | 35 |
| 4063 | aguja | 35 |
| 4064 | yra | 34 |
| 4065 | vivienda | 34 |
| 4066 | viajero | 34 |
| 4067 | veré | 34 |
| 4068 | veneno | 34 |
| 4069 | vecina | 34 |
| 4070 | turco | 34 |
| 4071 | trataban | 34 |
| 4072 | tontos | 34 |
| 4073 | tenorio | 34 |
| 4074 | temblar | 34 |
| 4075 | suertes | 34 |
| 4076 | sucede | 34 |
| 4077 | sosia | 34 |
| 4078 | soñado | 34 |
| 4079 | sirva | 34 |
| 4080 | señoría | 34 |
| 4081 | semejanza | 34 |
| 4082 | saqué | 34 |
| 4083 | sabiduría | 34 |
| 4084 | ruedas | 34 |
| 4085 | rubia | 34 |
| 4086 | risueña | 34 |
| 4087 | reñir | 34 |
| 4088 | regiones | 34 |
| 4089 | recordando | 34 |
| 4090 | recibe | 34 |
| 4091 | recato | 34 |
| 4092 | quedando | 34 |
| 4093 | quantos | 34 |
| 4094 | quantas | 34 |
| 4095 | quál | 34 |
| 4096 | procurando | 34 |
| 4097 | procura | 34 |
| 4098 | pones | 34 |
| 4099 | pondré | 34 |
| 4100 | político | 34 |
| 4101 | piense | 34 |
| 4102 | piadoso | 34 |
| 4103 | pesos | 34 |
| 4104 | perezoso | 34 |
| 4105 | pérdida | 34 |
| 4106 | peñas | 34 |
| 4107 | pegado | 34 |
| 4108 | paseaba | 34 |
| 4109 | pasará | 34 |
| 4110 | paraíso | 34 |
| 4111 | palomares | 34 |
| 4112 | pagaba | 34 |
| 4113 | ofrecer | 34 |
| 4114 | novedades | 34 |
| 4115 | necesaria | 34 |
| 4116 | misterios | 34 |
| 4117 | mezcla | 34 |
| 4118 | liberales | 34 |
| 4119 | levantóse | 34 |
| 4120 | lentamente | 34 |
| 4121 | lectores | 34 |
| 4122 | ji | 34 |
| 4123 | inglesa | 34 |
| 4124 | indudablemente | 34 |
| 4125 | indignación | 34 |
| 4126 | hábitos | 34 |
| 4127 | gustan | 34 |
| 4128 | gratitud | 34 |
| 4129 | grant | 34 |
| 4130 | gentileza | 34 |
| 4131 | fueras | 34 |
| 4132 | formando | 34 |
| 4133 | fijos | 34 |
| 4134 | faltan | 34 |
| 4135 | espíritus | 34 |
| 4136 | encontraron | 34 |
| 4137 | egoísmo | 34 |
| 4138 | duras | 34 |
| 4139 | dulzura | 34 |
| 4140 | dormida | 34 |
| 4141 | dorado | 34 |
| 4142 | deuda | 34 |
| 4143 | desseo | 34 |
| 4144 | despedida | 34 |
| 4145 | debiera | 34 |
| 4146 | cuestas | 34 |
| 4147 | corro | 34 |
| 4148 | conversaciones | 34 |
| 4149 | constante | 34 |
| 4150 | confusa | 34 |
| 4151 | comprende | 34 |
| 4152 | compadre | 34 |
| 4153 | cometido | 34 |
| 4154 | comentarios | 34 |
| 4155 | cobre | 34 |
| 4156 | circunstantes | 34 |
| 4157 | cerrados | 34 |
| 4158 | celo | 34 |
| 4159 | celipín | 34 |
| 4160 | celestial | 34 |
| 4161 | causaba | 34 |
| 4162 | cata | 34 |
| 4163 | camacho | 34 |
| 4164 | callando | 34 |
| 4165 | callado | 34 |
| 4166 | bellas | 34 |
| 4167 | balde | 34 |
| 4168 | bajos | 34 |
| 4169 | aristocracia | 34 |
| 4170 | apretaba | 34 |
| 4171 | apacible | 34 |
| 4172 | alzar | 34 |
| 4173 | alli | 34 |
| 4174 | albricias | 34 |
| 4175 | aborrecía | 34 |
| 4176 | vitoria | 33 |
| 4177 | vistas | 33 |
| 4178 | virtuosa | 33 |
| 4179 | violencia | 33 |
| 4180 | viniendo | 33 |
| 4181 | verán | 33 |
| 4182 | venas | 33 |
| 4183 | vámonos | 33 |
| 4184 | vaca | 33 |
| 4185 | urbia | 33 |
| 4186 | turbada | 33 |
| 4187 | torcido | 33 |
| 4188 | tocó | 33 |
| 4189 | timidez | 33 |
| 4190 | teniente | 33 |
| 4191 | tendremos | 33 |
| 4192 | t | 33 |
| 4193 | sustancia | 33 |
| 4194 | sotil | 33 |
| 4195 | sostenía | 33 |
| 4196 | sonó | 33 |
| 4197 | sollozos | 33 |
| 4198 | simpatía | 33 |
| 4199 | siguientes | 33 |
| 4200 | segund | 33 |
| 4201 | seamos | 33 |
| 4202 | saltando | 33 |
| 4203 | rincones | 33 |
| 4204 | rescate | 33 |
| 4205 | rendido | 33 |
| 4206 | quitarle | 33 |
| 4207 | queremos | 33 |
| 4208 | pro | 33 |
| 4209 | presta | 33 |
| 4210 | preparaba | 33 |
| 4211 | pregunté | 33 |
| 4212 | porvenir | 33 |
| 4213 | porción | 33 |
| 4214 | plomo | 33 |
| 4215 | pida | 33 |
| 4216 | perfección | 33 |
| 4217 | perdí | 33 |
| 4218 | pasear | 33 |
| 4219 | oyera | 33 |
| 4220 | olmedo | 33 |
| 4221 | ocupar | 33 |
| 4222 | obscuras | 33 |
| 4223 | necedades | 33 |
| 4224 | mudar | 33 |
| 4225 | mostrado | 33 |
| 4226 | misteriosa | 33 |
| 4227 | miren | 33 |
| 4228 | mirarle | 33 |
| 4229 | minuto | 33 |
| 4230 | ministros | 33 |
| 4231 | mesura | 33 |
| 4232 | merecido | 33 |
| 4233 | medicinas | 33 |
| 4234 | lloro | 33 |
| 4235 | llegándose | 33 |
| 4236 | lecciones | 33 |
| 4237 | labor | 33 |
| 4238 | instrumentos | 33 |
| 4239 | ingenioso | 33 |
| 4240 | infelices | 33 |
| 4241 | imitación | 33 |
| 4242 | ilusiones | 33 |
| 4243 | humildes | 33 |
| 4244 | hipócrita | 33 |
| 4245 | hayas | 33 |
| 4246 | furiosa | 33 |
| 4247 | extraordinaria | 33 |
| 4248 | exterior | 33 |
| 4249 | estúpido | 33 |
| 4250 | escuchando | 33 |
| 4251 | escritura | 33 |
| 4252 | escasa | 33 |
| 4253 | escala | 33 |
| 4254 | ésa | 33 |
| 4255 | enseñado | 33 |
| 4256 | encendida | 33 |
| 4257 | encantamento | 33 |
| 4258 | echan | 33 |
| 4259 | discursos | 33 |
| 4260 | delfina | 33 |
| 4261 | cualidades | 33 |
| 4262 | corren | 33 |
| 4263 | contemplación | 33 |
| 4264 | comió | 33 |
| 4265 | coma | 33 |
| 4266 | cierra | 33 |
| 4267 | carnero | 33 |
| 4268 | cañas | 33 |
| 4269 | cansada | 33 |
| 4270 | cadáver | 33 |
| 4271 | bruscamente | 33 |
| 4272 | bocas | 33 |
| 4273 | billete | 33 |
| 4274 | beneficio | 33 |
| 4275 | bailes | 33 |
| 4276 | bacía | 33 |
| 4277 | ayna | 33 |
| 4278 | arca | 33 |
| 4279 | aqueste | 33 |
| 4280 | aquéllos | 33 |
| 4281 | aparecer | 33 |
| 4282 | amas | 33 |
| 4283 | almohada | 33 |
| 4284 | alhajas | 33 |
| 4285 | aguda | 33 |
| 4286 | adoración | 33 |
| 4287 | acompañaba | 33 |
| 4288 | x | 32 |
| 4289 | vivamente | 32 |
| 4290 | vicario | 32 |
| 4291 | vencida | 32 |
| 4292 | vees | 32 |
| 4293 | vana | 32 |
| 4294 | trujo | 32 |
| 4295 | trazas | 32 |
| 4296 | tesoros | 32 |
| 4297 | ternura | 32 |
| 4298 | tenerla | 32 |
| 4299 | tarea | 32 |
| 4300 | ta | 32 |
| 4301 | syenpre | 32 |
| 4302 | solitario | 32 |
| 4303 | sigo | 32 |
| 4304 | sayo | 32 |
| 4305 | sacramento | 32 |
| 4306 | sabia | 32 |
| 4307 | ropas | 32 |
| 4308 | rodeado | 32 |
| 4309 | rezando | 32 |
| 4310 | reserva | 32 |
| 4311 | representa | 32 |
| 4312 | renta | 32 |
| 4313 | rastro | 32 |
| 4314 | quitarme | 32 |
| 4315 | pusiese | 32 |
| 4316 | propuesto | 32 |
| 4317 | progreso | 32 |
| 4318 | proceder | 32 |
| 4319 | pretexto | 32 |
| 4320 | presentarse | 32 |
| 4321 | pregunto | 32 |
| 4322 | preguntando | 32 |
| 4323 | pólvora | 32 |
| 4324 | podrán | 32 |
| 4325 | pintar | 32 |
| 4326 | pesaba | 32 |
| 4327 | periodista | 32 |
| 4328 | perfecto | 32 |
| 4329 | pasase | 32 |
| 4330 | pasara | 32 |
| 4331 | pareciéndole | 32 |
| 4332 | parecida | 32 |
| 4333 | parado | 32 |
| 4334 | palmo | 32 |
| 4335 | pa | 32 |
| 4336 | oyen | 32 |
| 4337 | ocupaba | 32 |
| 4338 | obligaba | 32 |
| 4339 | necedad | 32 |
| 4340 | napoleón | 32 |
| 4341 | músculos | 32 |
| 4342 | mudanza | 32 |
| 4343 | mozas | 32 |
| 4344 | morales | 32 |
| 4345 | modales | 32 |
| 4346 | mirándola | 32 |
| 4347 | millones | 32 |
| 4348 | militares | 32 |
| 4349 | maritornes | 32 |
| 4350 | manteles | 32 |
| 4351 | magnífico | 32 |
| 4352 | local | 32 |
| 4353 | llaga | 32 |
| 4354 | líquido | 32 |
| 4355 | julio | 32 |
| 4356 | ironía | 32 |
| 4357 | interrumpió | 32 |
| 4358 | insignificante | 32 |
| 4359 | inglaterra | 32 |
| 4360 | inclinado | 32 |
| 4361 | iglesias | 32 |
| 4362 | hízolo | 32 |
| 4363 | haciéndose | 32 |
| 4364 | hablas | 32 |
| 4365 | gritando | 32 |
| 4366 | gregorio | 32 |
| 4367 | gitanos | 32 |
| 4368 | fruta | 32 |
| 4369 | frescura | 32 |
| 4370 | franco | 32 |
| 4371 | fermo | 32 |
| 4372 | falto | 32 |
| 4373 | facultad | 32 |
| 4374 | expresó | 32 |
| 4375 | estima | 32 |
| 4376 | esposos | 32 |
| 4377 | espantosa | 32 |
| 4378 | esclavo | 32 |
| 4379 | entregó | 32 |
| 4380 | entrase | 32 |
| 4381 | enseñar | 32 |
| 4382 | encantos | 32 |
| 4383 | elemento | 32 |
| 4384 | eclesiástica | 32 |
| 4385 | drama | 32 |
| 4386 | dichas | 32 |
| 4387 | devota | 32 |
| 4388 | desconsuelo | 32 |
| 4389 | dende | 32 |
| 4390 | cuestiones | 32 |
| 4391 | crítica | 32 |
| 4392 | crió | 32 |
| 4393 | corrección | 32 |
| 4394 | contenerse | 32 |
| 4395 | contemplaba | 32 |
| 4396 | consentir | 32 |
| 4397 | concluyó | 32 |
| 4398 | codo | 32 |
| 4399 | codicia | 32 |
| 4400 | chimenea | 32 |
| 4401 | ceremonias | 32 |
| 4402 | ceniza | 32 |
| 4403 | cayeron | 32 |
| 4404 | católica | 32 |
| 4405 | carcajada | 32 |
| 4406 | capistun | 32 |
| 4407 | bonitas | 32 |
| 4408 | bastantes | 32 |
| 4409 | bajel | 32 |
| 4410 | atal | 32 |
| 4411 | asió | 32 |
| 4412 | as | 32 |
| 4413 | amorosa | 32 |
| 4414 | amarga | 32 |
| 4415 | alejandro | 32 |
| 4416 | águila | 32 |
| 4417 | adorno | 32 |
| 4418 | admirados | 32 |
| 4419 | acompañar | 32 |
| 4420 | acercándose | 32 |
| 4421 | zaro | 31 |
| 4422 | volverá | 31 |
| 4423 | vizcaíno | 31 |
| 4424 | vinagre | 31 |
| 4425 | vengas | 31 |
| 4426 | vecinas | 31 |
| 4427 | valencia | 31 |
| 4428 | usa | 31 |
| 4429 | tuvieran | 31 |
| 4430 | trujillo | 31 |
| 4431 | tiraba | 31 |
| 4432 | tienpo | 31 |
| 4433 | testimonio | 31 |
| 4434 | tenerle | 31 |
| 4435 | telas | 31 |
| 4436 | teatros | 31 |
| 4437 | sucio | 31 |
| 4438 | súbito | 31 |
| 4439 | suaves | 31 |
| 4440 | sosegado | 31 |
| 4441 | sonido | 31 |
| 4442 | solicitud | 31 |
| 4443 | seruicio | 31 |
| 4444 | sermones | 31 |
| 4445 | sebastián | 31 |
| 4446 | sabría | 31 |
| 4447 | ruina | 31 |
| 4448 | rufina | 31 |
| 4449 | robusto | 31 |
| 4450 | risas | 31 |
| 4451 | retiro | 31 |
| 4452 | restos | 31 |
| 4453 | regocijo | 31 |
| 4454 | recibieron | 31 |
| 4455 | recelo | 31 |
| 4456 | rápida | 31 |
| 4457 | quinto | 31 |
| 4458 | quier | 31 |
| 4459 | quejarse | 31 |
| 4460 | quedase | 31 |
| 4461 | puramente | 31 |
| 4462 | produjo | 31 |
| 4463 | procurar | 31 |
| 4464 | pretensiones | 31 |
| 4465 | preguntado | 31 |
| 4466 | postura | 31 |
| 4467 | pobrecita | 31 |
| 4468 | piano | 31 |
| 4469 | pescadores | 31 |
| 4470 | pequeñas | 31 |
| 4471 | pendencia | 31 |
| 4472 | paró | 31 |
| 4473 | orgullosa | 31 |
| 4474 | negaba | 31 |
| 4475 | músico | 31 |
| 4476 | muncho | 31 |
| 4477 | mueve | 31 |
| 4478 | mosca | 31 |
| 4479 | mortales | 31 |
| 4480 | misterioso | 31 |
| 4481 | mísero | 31 |
| 4482 | mijor | 31 |
| 4483 | mercado | 31 |
| 4484 | mercader | 31 |
| 4485 | mengua | 31 |
| 4486 | mañas | 31 |
| 4487 | maña | 31 |
| 4488 | luchar | 31 |
| 4489 | lío | 31 |
| 4490 | lecturas | 31 |
| 4491 | lanzó | 31 |
| 4492 | júpiter | 31 |
| 4493 | indiferencia | 31 |
| 4494 | ilustración | 31 |
| 4495 | honesto | 31 |
| 4496 | hipocresía | 31 |
| 4497 | hierba | 31 |
| 4498 | haberlo | 31 |
| 4499 | guardó | 31 |
| 4500 | guardado | 31 |
| 4501 | ganaba | 31 |
| 4502 | gallarda | 31 |
| 4503 | fuí | 31 |
| 4504 | extrañas | 31 |
| 4505 | examen | 31 |
| 4506 | escribía | 31 |
| 4507 | escondida | 31 |
| 4508 | entienda | 31 |
| 4509 | encina | 31 |
| 4510 | encargado | 31 |
| 4511 | efectos | 31 |
| 4512 | echarse | 31 |
| 4513 | echarle | 31 |
| 4514 | dudo | 31 |
| 4515 | distinguir | 31 |
| 4516 | discretas | 31 |
| 4517 | diferente | 31 |
| 4518 | dexa | 31 |
| 4519 | desmayo | 31 |
| 4520 | desengaño | 31 |
| 4521 | descansar | 31 |
| 4522 | desagradable | 31 |
| 4523 | desa | 31 |
| 4524 | dejes | 31 |
| 4525 | dejasen | 31 |
| 4526 | curar | 31 |
| 4527 | cuerdas | 31 |
| 4528 | cuente | 31 |
| 4529 | cuáles | 31 |
| 4530 | creían | 31 |
| 4531 | costillas | 31 |
| 4532 | conservaba | 31 |
| 4533 | conjunto | 31 |
| 4534 | concluido | 31 |
| 4535 | claros | 31 |
| 4536 | cervantes | 31 |
| 4537 | brevedad | 31 |
| 4538 | barato | 31 |
| 4539 | bandera | 31 |
| 4540 | azúcar | 31 |
| 4541 | asustado | 31 |
| 4542 | asomaba | 31 |
| 4543 | arrepentimiento | 31 |
| 4544 | armó | 31 |
| 4545 | apriesa | 31 |
| 4546 | aparato | 31 |
| 4547 | américa | 31 |
| 4548 | amenazas | 31 |
| 4549 | amén | 31 |
| 4550 | agradecimiento | 31 |
| 4551 | acuerda | 31 |
| 4552 | xxi | 30 |
| 4553 | vivas | 30 |
| 4554 | vestidas | 30 |
| 4555 | ventera | 30 |
| 4556 | venimos | 30 |
| 4557 | vencimiento | 30 |
| 4558 | vago | 30 |
| 4559 | universo | 30 |
| 4560 | turcos | 30 |
| 4561 | triunfante | 30 |
| 4562 | trabajaba | 30 |
| 4563 | tirano | 30 |
| 4564 | tendió | 30 |
| 4565 | tejado | 30 |
| 4566 | tafetán | 30 |
| 4567 | só | 30 |
| 4568 | sienta | 30 |
| 4569 | sentaba | 30 |
| 4570 | sensación | 30 |
| 4571 | sastre | 30 |
| 4572 | saliera | 30 |
| 4573 | saldrá | 30 |
| 4574 | sacarle | 30 |
| 4575 | romántico | 30 |
| 4576 | rodar | 30 |
| 4577 | ríos | 30 |
| 4578 | rienda | 30 |
| 4579 | revelaba | 30 |
| 4580 | remos | 30 |
| 4581 | redes | 30 |
| 4582 | recogidas | 30 |
| 4583 | raras | 30 |
| 4584 | quinta | 30 |
| 4585 | quédese | 30 |
| 4586 | puros | 30 |
| 4587 | protesta | 30 |
| 4588 | portero | 30 |
| 4589 | popa | 30 |
| 4590 | parentesco | 30 |
| 4591 | oyr | 30 |
| 4592 | ovejas | 30 |
| 4593 | obligó | 30 |
| 4594 | notable | 30 |
| 4595 | nones | 30 |
| 4596 | necessidad | 30 |
| 4597 | morirse | 30 |
| 4598 | moderna | 30 |
| 4599 | memorias | 30 |
| 4600 | materias | 30 |
| 4601 | matan | 30 |
| 4602 | mares | 30 |
| 4603 | maravedís | 30 |
| 4604 | llevas | 30 |
| 4605 | levanta | 30 |
| 4606 | lazos | 30 |
| 4607 | lámpara | 30 |
| 4608 | juárez | 30 |
| 4609 | isabel | 30 |
| 4610 | intenciones | 30 |
| 4611 | infernal | 30 |
| 4612 | huevo | 30 |
| 4613 | harán | 30 |
| 4614 | haciéndole | 30 |
| 4615 | gravina | 30 |
| 4616 | gitano | 30 |
| 4617 | fuesse | 30 |
| 4618 | fraile | 30 |
| 4619 | fortunato | 30 |
| 4620 | flandes | 30 |
| 4621 | fizo | 30 |
| 4622 | figúrate | 30 |
| 4623 | farmacia | 30 |
| 4624 | extremos | 30 |
| 4625 | expresiones | 30 |
| 4626 | explicaba | 30 |
| 4627 | estuvieran | 30 |
| 4628 | estan | 30 |
| 4629 | essa | 30 |
| 4630 | ése | 30 |
| 4631 | escrita | 30 |
| 4632 | entregado | 30 |
| 4633 | engañaba | 30 |
| 4634 | ejercicios | 30 |
| 4635 | eché | 30 |
| 4636 | dominaba | 30 |
| 4637 | dígolo | 30 |
| 4638 | devoto | 30 |
| 4639 | dejen | 30 |
| 4640 | dejaré | 30 |
| 4641 | dejará | 30 |
| 4642 | decírselo | 30 |
| 4643 | cubría | 30 |
| 4644 | cuarta | 30 |
| 4645 | costó | 30 |
| 4646 | costaba | 30 |
| 4647 | corredores | 30 |
| 4648 | contemplar | 30 |
| 4649 | conservar | 30 |
| 4650 | conseguido | 30 |
| 4651 | conceptos | 30 |
| 4652 | comprado | 30 |
| 4653 | comenzar | 30 |
| 4654 | comenzado | 30 |
| 4655 | columnas | 30 |
| 4656 | ciencias | 30 |
| 4657 | cerrando | 30 |
| 4658 | cebada | 30 |
| 4659 | caudal | 30 |
| 4660 | casados | 30 |
| 4661 | campanas | 30 |
| 4662 | camisas | 30 |
| 4663 | buscarle | 30 |
| 4664 | bastón | 30 |
| 4665 | barón | 30 |
| 4666 | barcelona | 30 |
| 4667 | bárbaro | 30 |
| 4668 | auto | 30 |
| 4669 | asustada | 30 |
| 4670 | arrojar | 30 |
| 4671 | arremetió | 30 |
| 4672 | armar | 30 |
| 4673 | aprovechar | 30 |
| 4674 | aprensión | 30 |
| 4675 | apariencia | 30 |
| 4676 | andas | 30 |
| 4677 | amoroso | 30 |
| 4678 | amistades | 30 |
| 4679 | alc | 30 |
| 4680 | ál | 30 |
| 4681 | aceptar | 30 |
| 4682 | accidente | 30 |
| 4683 | xiii | 29 |
| 4684 | vasallos | 29 |
| 4685 | valga | 29 |
| 4686 | usado | 29 |
| 4687 | turbado | 29 |
| 4688 | trampa | 29 |
| 4689 | torres | 29 |
| 4690 | tomaban | 29 |
| 4691 | tocas | 29 |
| 4692 | tocador | 29 |
| 4693 | timoteo | 29 |
| 4694 | tiernos | 29 |
| 4695 | tapia | 29 |
| 4696 | taller | 29 |
| 4697 | sexo | 29 |
| 4698 | sentirse | 29 |
| 4699 | sant | 29 |
| 4700 | salva | 29 |
| 4701 | sacan | 29 |
| 4702 | retórica | 29 |
| 4703 | repito | 29 |
| 4704 | rencor | 29 |
| 4705 | refugio | 29 |
| 4706 | puercos | 29 |
| 4707 | proposición | 29 |
| 4708 | pintor | 29 |
| 4709 | pierda | 29 |
| 4710 | pides | 29 |
| 4711 | pesetas | 29 |
| 4712 | pescuezo | 29 |
| 4713 | pasadas | 29 |
| 4714 | paresce | 29 |
| 4715 | pantalones | 29 |
| 4716 | paloma | 29 |
| 4717 | palco | 29 |
| 4718 | órgano | 29 |
| 4719 | oportuno | 29 |
| 4720 | opiniones | 29 |
| 4721 | ofrecimientos | 29 |
| 4722 | ofrecido | 29 |
| 4723 | ofendido | 29 |
| 4724 | obligaciones | 29 |
| 4725 | nido | 29 |
| 4726 | muchísimo | 29 |
| 4727 | molde | 29 |
| 4728 | miras | 29 |
| 4729 | miran | 29 |
| 4730 | mejilla | 29 |
| 4731 | marfil | 29 |
| 4732 | majadero | 29 |
| 4733 | londres | 29 |
| 4734 | llevase | 29 |
| 4735 | lejanos | 29 |
| 4736 | lázaro | 29 |
| 4737 | juicios | 29 |
| 4738 | joshé | 29 |
| 4739 | invidia | 29 |
| 4740 | íntima | 29 |
| 4741 | ínsulas | 29 |
| 4742 | inspiraba | 29 |
| 4743 | infinita | 29 |
| 4744 | individuos | 29 |
| 4745 | indigno | 29 |
| 4746 | imaginaba | 29 |
| 4747 | íbamos | 29 |
| 4748 | huerto | 29 |
| 4749 | hostia | 29 |
| 4750 | honrra | 29 |
| 4751 | hagamos | 29 |
| 4752 | hablemos | 29 |
| 4753 | guisa | 29 |
| 4754 | grisóstomo | 29 |
| 4755 | gobernadores | 29 |
| 4756 | gaula | 29 |
| 4757 | frías | 29 |
| 4758 | física | 29 |
| 4759 | finas | 29 |
| 4760 | farsa | 29 |
| 4761 | fantasmas | 29 |
| 4762 | f | 29 |
| 4763 | extraordinariamente | 29 |
| 4764 | et | 29 |
| 4765 | estella | 29 |
| 4766 | esperó | 29 |
| 4767 | escuchaba | 29 |
| 4768 | escrúpulo | 29 |
| 4769 | escoger | 29 |
| 4770 | encarnación | 29 |
| 4771 | eche | 29 |
| 4772 | echándose | 29 |
| 4773 | dudaba | 29 |
| 4774 | doloroso | 29 |
| 4775 | distraído | 29 |
| 4776 | distintos | 29 |
| 4777 | distintas | 29 |
| 4778 | dignas | 29 |
| 4779 | desventuras | 29 |
| 4780 | despierta | 29 |
| 4781 | despertaba | 29 |
| 4782 | desatino | 29 |
| 4783 | déjeme | 29 |
| 4784 | defendía | 29 |
| 4785 | decencia | 29 |
| 4786 | datos | 29 |
| 4787 | dándose | 29 |
| 4788 | daga | 29 |
| 4789 | cumple | 29 |
| 4790 | culpas | 29 |
| 4791 | convertido | 29 |
| 4792 | conquista | 29 |
| 4793 | conocemos | 29 |
| 4794 | condenada | 29 |
| 4795 | compuesta | 29 |
| 4796 | colmo | 29 |
| 4797 | colegio | 29 |
| 4798 | codos | 29 |
| 4799 | ciudades | 29 |
| 4800 | choto | 29 |
| 4801 | cerraba | 29 |
| 4802 | casarme | 29 |
| 4803 | carbón | 29 |
| 4804 | cantó | 29 |
| 4805 | brigadier | 29 |
| 4806 | bosques | 29 |
| 4807 | borde | 29 |
| 4808 | benevolencia | 29 |
| 4809 | audiencia | 29 |
| 4810 | asturiano | 29 |
| 4811 | asesino | 29 |
| 4812 | arçipreste | 29 |
| 4813 | aquesto | 29 |
| 4814 | antojaba | 29 |
| 4815 | aldeas | 29 |
| 4816 | alcance | 29 |
| 4817 | agregó | 29 |
| 4818 | agravios | 29 |
| 4819 | agradezco | 29 |
| 4820 | acostumbrada | 29 |
| 4821 | achaque | 29 |
| 4822 | acertó | 29 |
| 4823 | acabada | 29 |
| 4824 | abrazo | 29 |
| 4825 | volando | 28 |
| 4826 | vistió | 28 |
| 4827 | vestirse | 28 |
| 4828 | veinticinco | 28 |
| 4829 | vagamente | 28 |
| 4830 | trifaldi | 28 |
| 4831 | traiga | 28 |
| 4832 | torpes | 28 |
| 4833 | títulos | 28 |
| 4834 | tigre | 28 |
| 4835 | tendrán | 28 |
| 4836 | supiese | 28 |
| 4837 | suegra | 28 |
| 4838 | siga | 28 |
| 4839 | sientes | 28 |
| 4840 | serena | 28 |
| 4841 | sentaron | 28 |
| 4842 | sendas | 28 |
| 4843 | sencillo | 28 |
| 4844 | sencillez | 28 |
| 4845 | saña | 28 |
| 4846 | santas | 28 |
| 4847 | salta | 28 |
| 4848 | saldría | 28 |
| 4849 | salario | 28 |
| 4850 | sacerdotes | 28 |
| 4851 | retirado | 28 |
| 4852 | resulta | 28 |
| 4853 | respondido | 28 |
| 4854 | respiración | 28 |
| 4855 | repugnancia | 28 |
| 4856 | religiosos | 28 |
| 4857 | relato | 28 |
| 4858 | reinaba | 28 |
| 4859 | recinto | 28 |
| 4860 | rama | 28 |
| 4861 | raíces | 28 |
| 4862 | quejaba | 28 |
| 4863 | quedara | 28 |
| 4864 | pronunciar | 28 |
| 4865 | producía | 28 |
| 4866 | pitusa | 28 |
| 4867 | pensaban | 28 |
| 4868 | parto | 28 |
| 4869 | paños | 28 |
| 4870 | pajas | 28 |
| 4871 | padecía | 28 |
| 4872 | oscuro | 28 |
| 4873 | oscuridad | 28 |
| 4874 | ocupada | 28 |
| 4875 | ocupaciones | 28 |
| 4876 | necesidades | 28 |
| 4877 | murmuraba | 28 |
| 4878 | mística | 28 |
| 4879 | miserias | 28 |
| 4880 | miro | 28 |
| 4881 | mientra | 28 |
| 4882 | mato | 28 |
| 4883 | máscaras | 28 |
| 4884 | máscara | 28 |
| 4885 | marino | 28 |
| 4886 | máquinas | 28 |
| 4887 | manjares | 28 |
| 4888 | ligeramente | 28 |
| 4889 | lealtad | 28 |
| 4890 | judío | 28 |
| 4891 | inútiles | 28 |
| 4892 | infanta | 28 |
| 4893 | inclinación | 28 |
| 4894 | imposibles | 28 |
| 4895 | impaciente | 28 |
| 4896 | hucha | 28 |
| 4897 | hubieras | 28 |
| 4898 | hito | 28 |
| 4899 | héroe | 28 |
| 4900 | halle | 28 |
| 4901 | guitarra | 28 |
| 4902 | guapo | 28 |
| 4903 | guantes | 28 |
| 4904 | gorda | 28 |
| 4905 | globo | 28 |
| 4906 | función | 28 |
| 4907 | fuimos | 28 |
| 4908 | forastero | 28 |
| 4909 | firmeza | 28 |
| 4910 | fingía | 28 |
| 4911 | farmacéutico | 28 |
| 4912 | falsas | 28 |
| 4913 | facultades | 28 |
| 4914 | estimación | 28 |
| 4915 | espere | 28 |
| 4916 | esconde | 28 |
| 4917 | escapar | 28 |
| 4918 | errores | 28 |
| 4919 | entrambas | 28 |
| 4920 | entereza | 28 |
| 4921 | encogió | 28 |
| 4922 | domingos | 28 |
| 4923 | docenas | 28 |
| 4924 | dexar | 28 |
| 4925 | deshora | 28 |
| 4926 | desenvoltura | 28 |
| 4927 | depósito | 28 |
| 4928 | deleite | 28 |
| 4929 | decentes | 28 |
| 4930 | deberes | 28 |
| 4931 | dándome | 28 |
| 4932 | creerás | 28 |
| 4933 | corresponde | 28 |
| 4934 | cordel | 28 |
| 4935 | convencido | 28 |
| 4936 | contienda | 28 |
| 4937 | consintió | 28 |
| 4938 | confesaba | 28 |
| 4939 | compromiso | 28 |
| 4940 | comencé | 28 |
| 4941 | colonia | 28 |
| 4942 | civilización | 28 |
| 4943 | ceño | 28 |
| 4944 | cautivos | 28 |
| 4945 | causado | 28 |
| 4946 | botón | 28 |
| 4947 | bota | 28 |
| 4948 | bola | 28 |
| 4949 | baúl | 28 |
| 4950 | bancos | 28 |
| 4951 | balas | 28 |
| 4952 | ayudaba | 28 |
| 4953 | asistir | 28 |
| 4954 | aquestos | 28 |
| 4955 | apellido | 28 |
| 4956 | anos | 28 |
| 4957 | ande | 28 |
| 4958 | amorosas | 28 |
| 4959 | amenazaba | 28 |
| 4960 | alivio | 28 |
| 4961 | ajenos | 28 |
| 4962 | adoro | 28 |
| 4963 | admirar | 28 |
| 4964 | administración | 28 |
| 4965 | abril | 28 |
| 4966 | abandonado | 28 |
| 4967 | vuela | 27 |
| 4968 | vivimos | 27 |
| 4969 | viviendo | 27 |
| 4970 | visión | 27 |
| 4971 | visible | 27 |
| 4972 | vientos | 27 |
| 4973 | viajes | 27 |
| 4974 | verdat | 27 |
| 4975 | venid | 27 |
| 4976 | vende | 27 |
| 4977 | tosilos | 27 |
| 4978 | tomad | 27 |
| 4979 | tocante | 27 |
| 4980 | tinta | 27 |
| 4981 | superioridad | 27 |
| 4982 | sospechar | 27 |
| 4983 | solución | 27 |
| 4984 | sitios | 27 |
| 4985 | seremos | 27 |
| 4986 | señorío | 27 |
| 4987 | sensaciones | 27 |
| 4988 | senda | 27 |
| 4989 | ruin | 27 |
| 4990 | rompe | 27 |
| 4991 | robar | 27 |
| 4992 | risueño | 27 |
| 4993 | rezaba | 27 |
| 4994 | resignación | 27 |
| 4995 | representación | 27 |
| 4996 | reglas | 27 |
| 4997 | referido | 27 |
| 4998 | reconoció | 27 |
| 4999 | recibo | 27 |
| 5000 | quisieran | 27 |
| 5001 | quales | 27 |
| 5002 | propósitos | 27 |
| 5003 | promete | 27 |
| 5004 | prohibido | 27 |
| 5005 | procuró | 27 |
| 5006 | prestar | 27 |
| 5007 | preguntarle | 27 |
| 5008 | podremos | 27 |
| 5009 | pliegues | 27 |
| 5010 | pleberio | 27 |
| 5011 | planes | 27 |
| 5012 | placeres | 27 |
| 5013 | pino | 27 |
| 5014 | pierden | 27 |
| 5015 | picante | 27 |
| 5016 | perdiendo | 27 |
| 5017 | pastora | 27 |
| 5018 | olvida | 27 |
| 5019 | olía | 27 |
| 5020 | ojalá | 27 |
| 5021 | ofender | 27 |
| 5022 | novios | 27 |
| 5023 | nene | 27 |
| 5024 | naciones | 27 |
| 5025 | muertes | 27 |
| 5026 | muchedumbre | 27 |
| 5027 | mourelo | 27 |
| 5028 | misas | 27 |
| 5029 | miré | 27 |
| 5030 | mirase | 27 |
| 5031 | merlín | 27 |
| 5032 | mentecato | 27 |
| 5033 | matas | 27 |
| 5034 | maravilloso | 27 |
| 5035 | manifiesto | 27 |
| 5036 | loreto | 27 |
| 5037 | llora | 27 |
| 5038 | llenó | 27 |
| 5039 | lea | 27 |
| 5040 | lábaro | 27 |
| 5041 | juró | 27 |
| 5042 | jueves | 27 |
| 5043 | jaez | 27 |
| 5044 | irresistible | 27 |
| 5045 | insigne | 27 |
| 5046 | indicaba | 27 |
| 5047 | increíble | 27 |
| 5048 | impulsos | 27 |
| 5049 | imaginarse | 27 |
| 5050 | igualmente | 27 |
| 5051 | ignacia | 27 |
| 5052 | hermosísima | 27 |
| 5053 | hastío | 27 |
| 5054 | hábil | 27 |
| 5055 | guardan | 27 |
| 5056 | grano | 27 |
| 5057 | gozando | 27 |
| 5058 | galas | 27 |
| 5059 | fulano | 27 |
| 5060 | fío | 27 |
| 5061 | exclamaba | 27 |
| 5062 | espantado | 27 |
| 5063 | éramos | 27 |
| 5064 | encendidas | 27 |
| 5065 | encantados | 27 |
| 5066 | echaban | 27 |
| 5067 | dote | 27 |
| 5068 | divertirse | 27 |
| 5069 | disponer | 27 |
| 5070 | diana | 27 |
| 5071 | deudas | 27 |
| 5072 | determiné | 27 |
| 5073 | despreciaba | 27 |
| 5074 | desnudos | 27 |
| 5075 | desigual | 27 |
| 5076 | descubierta | 27 |
| 5077 | déjate | 27 |
| 5078 | cumbre | 27 |
| 5079 | criaturas | 27 |
| 5080 | cría | 27 |
| 5081 | cordura | 27 |
| 5082 | copas | 27 |
| 5083 | continua | 27 |
| 5084 | contenía | 27 |
| 5085 | contarle | 27 |
| 5086 | contaré | 27 |
| 5087 | constancia | 27 |
| 5088 | considera | 27 |
| 5089 | compañeras | 27 |
| 5090 | clavo | 27 |
| 5091 | cesaba | 27 |
| 5092 | castillos | 27 |
| 5093 | cascos | 27 |
| 5094 | casadas | 27 |
| 5095 | calzas | 27 |
| 5096 | calzado | 27 |
| 5097 | caen | 27 |
| 5098 | cacho | 27 |
| 5099 | botella | 27 |
| 5100 | biblioteca | 27 |
| 5101 | baño | 27 |
| 5102 | ayuno | 27 |
| 5103 | auditorio | 27 |
| 5104 | audacia | 27 |
| 5105 | atreverse | 27 |
| 5106 | atenta | 27 |
| 5107 | arrojaba | 27 |
| 5108 | aragón | 27 |
| 5109 | apartado | 27 |
| 5110 | ansias | 27 |
| 5111 | ánimos | 27 |
| 5112 | ancianos | 27 |
| 5113 | amorosos | 27 |
| 5114 | amarilla | 27 |
| 5115 | alora | 27 |
| 5116 | aguarda | 27 |
| 5117 | agradecida | 27 |
| 5118 | agrada | 27 |
| 5119 | adquirir | 27 |
| 5120 | adora | 27 |
| 5121 | adentros | 27 |
| 5122 | adarga | 27 |
| 5123 | acababan | 27 |
| 5124 | abuela | 27 |
| 5125 | abra | 27 |
| 5126 | yace | 26 |
| 5127 | viniere | 26 |
| 5128 | viajeros | 26 |
| 5129 | venda | 26 |
| 5130 | veen | 26 |
| 5131 | vacas | 26 |
| 5132 | útil | 26 |
| 5133 | unidos | 26 |
| 5134 | únicamente | 26 |
| 5135 | tyene | 26 |
| 5136 | tuerto | 26 |
| 5137 | trueno | 26 |
| 5138 | troncos | 26 |
| 5139 | trompeta | 26 |
| 5140 | tremendo | 26 |
| 5141 | tez | 26 |
| 5142 | tengamos | 26 |
| 5143 | tempestad | 26 |
| 5144 | sustentar | 26 |
| 5145 | sujetos | 26 |
| 5146 | sueltas | 26 |
| 5147 | suavidad | 26 |
| 5148 | socartes | 26 |
| 5149 | sincera | 26 |
| 5150 | señalado | 26 |
| 5151 | seña | 26 |
| 5152 | saltos | 26 |
| 5153 | sales | 26 |
| 5154 | sacrificios | 26 |
| 5155 | rota | 26 |
| 5156 | rodeada | 26 |
| 5157 | rocín | 26 |
| 5158 | roca | 26 |
| 5159 | responsabilidad | 26 |
| 5160 | resplandor | 26 |
| 5161 | representar | 26 |
| 5162 | repetir | 26 |
| 5163 | rejas | 26 |
| 5164 | reflexiones | 26 |
| 5165 | recogiendo | 26 |
| 5166 | rapidez | 26 |
| 5167 | rafael | 26 |
| 5168 | quia | 26 |
| 5169 | puta | 26 |
| 5170 | pudiere | 26 |
| 5171 | proponía | 26 |
| 5172 | prójima | 26 |
| 5173 | pretende | 26 |
| 5174 | presenta | 26 |
| 5175 | popular | 26 |
| 5176 | pompa | 26 |
| 5177 | pollos | 26 |
| 5178 | policía | 26 |
| 5179 | plega | 26 |
| 5180 | peligroso | 26 |
| 5181 | pelear | 26 |
| 5182 | pega | 26 |
| 5183 | pata | 26 |
| 5184 | pasas | 26 |
| 5185 | pasaje | 26 |
| 5186 | paisaje | 26 |
| 5187 | padrino | 26 |
| 5188 | oydo | 26 |
| 5189 | ovo | 26 |
| 5190 | oficina | 26 |
| 5191 | niebla | 26 |
| 5192 | moviendo | 26 |
| 5193 | ministerio | 26 |
| 5194 | merienda | 26 |
| 5195 | mental | 26 |
| 5196 | melancólico | 26 |
| 5197 | mayoría | 26 |
| 5198 | marzo | 26 |
| 5199 | marianela | 26 |
| 5200 | marchaba | 26 |
| 5201 | mantas | 26 |
| 5202 | manchas | 26 |
| 5203 | maestresala | 26 |
| 5204 | lucía | 26 |
| 5205 | lotería | 26 |
| 5206 | lópez | 26 |
| 5207 | lleven | 26 |
| 5208 | limpias | 26 |
| 5209 | leyenda | 26 |
| 5210 | leve | 26 |
| 5211 | levantando | 26 |
| 5212 | lejano | 26 |
| 5213 | lavar | 26 |
| 5214 | lanzas | 26 |
| 5215 | lamentable | 26 |
| 5216 | islas | 26 |
| 5217 | inspiración | 26 |
| 5218 | insistió | 26 |
| 5219 | inquieto | 26 |
| 5220 | inocentes | 26 |
| 5221 | injurias | 26 |
| 5222 | ingratitud | 26 |
| 5223 | ingenios | 26 |
| 5224 | infames | 26 |
| 5225 | infalible | 26 |
| 5226 | incapaz | 26 |
| 5227 | hubiere | 26 |
| 5228 | honrados | 26 |
| 5229 | hechura | 26 |
| 5230 | hazaña | 26 |
| 5231 | hauia | 26 |
| 5232 | hauer | 26 |
| 5233 | harta | 26 |
| 5234 | hallábase | 26 |
| 5235 | hablase | 26 |
| 5236 | hablador | 26 |
| 5237 | habías | 26 |
| 5238 | haberla | 26 |
| 5239 | glorias | 26 |
| 5240 | garras | 26 |
| 5241 | gallina | 26 |
| 5242 | frontera | 26 |
| 5243 | flacas | 26 |
| 5244 | finos | 26 |
| 5245 | fines | 26 |
| 5246 | felice | 26 |
| 5247 | febril | 26 |
| 5248 | favorable | 26 |
| 5249 | extensión | 26 |
| 5250 | explicar | 26 |
| 5251 | estarse | 26 |
| 5252 | espuelas | 26 |
| 5253 | esperan | 26 |
| 5254 | escrúpulos | 26 |
| 5255 | escritor | 26 |
| 5256 | escopeta | 26 |
| 5257 | enviado | 26 |
| 5258 | entretenimiento | 26 |
| 5259 | entretener | 26 |
| 5260 | entretanto | 26 |
| 5261 | enfermos | 26 |
| 5262 | encerrada | 26 |
| 5263 | empero | 26 |
| 5264 | emociones | 26 |
| 5265 | dureza | 26 |
| 5266 | dominio | 26 |
| 5267 | dogma | 26 |
| 5268 | diole | 26 |
| 5269 | diere | 26 |
| 5270 | detenerse | 26 |
| 5271 | descalza | 26 |
| 5272 | desapareció | 26 |
| 5273 | delicias | 26 |
| 5274 | dejarla | 26 |
| 5275 | declaraba | 26 |
| 5276 | debido | 26 |
| 5277 | cuñado | 26 |
| 5278 | culebra | 26 |
| 5279 | cuervo | 26 |
| 5280 | cueros | 26 |
| 5281 | crítico | 26 |
| 5282 | criterio | 26 |
| 5283 | creyeron | 26 |
| 5284 | creció | 26 |
| 5285 | cracasch | 26 |
| 5286 | cortes | 26 |
| 5287 | cortado | 26 |
| 5288 | corrida | 26 |
| 5289 | contrarios | 26 |
| 5290 | consecuencia | 26 |
| 5291 | comunes | 26 |
| 5292 | colorada | 26 |
| 5293 | colcha | 26 |
| 5294 | coín | 26 |
| 5295 | chasco | 26 |
| 5296 | chanfalla | 26 |
| 5297 | ceremonia | 26 |
| 5298 | centinela | 26 |
| 5299 | celoso | 26 |
| 5300 | celedonio | 26 |
| 5301 | casco | 26 |
| 5302 | carros | 26 |
| 5303 | cármenes | 26 |
| 5304 | cargada | 26 |
| 5305 | cantaban | 26 |
| 5306 | campana | 26 |
| 5307 | cafés | 26 |
| 5308 | cabildo | 26 |
| 5309 | bueyes | 26 |
| 5310 | brillante | 26 |
| 5311 | bóveda | 26 |
| 5312 | bigote | 26 |
| 5313 | atroz | 26 |
| 5314 | atreve | 26 |
| 5315 | asi | 26 |
| 5316 | aseguraba | 26 |
| 5317 | arranque | 26 |
| 5318 | amenaza | 26 |
| 5319 | amabilidad | 26 |
| 5320 | almohadas | 26 |
| 5321 | alabar | 26 |
| 5322 | agustín | 26 |
| 5323 | acabo | 26 |
| 5324 | abundante | 26 |
| 5325 | abogado | 26 |
| 5326 | vuesas | 25 |
| 5327 | vuelves | 25 |
| 5328 | volverme | 25 |
| 5329 | voluntades | 25 |
| 5330 | violento | 25 |
| 5331 | violante | 25 |
| 5332 | villuendas | 25 |
| 5333 | viii | 25 |
| 5334 | verlas | 25 |
| 5335 | vengarse | 25 |
| 5336 | vega | 25 |
| 5337 | vasco | 25 |
| 5338 | vaga | 25 |
| 5339 | vacía | 25 |
| 5340 | tuviesen | 25 |
| 5341 | turba | 25 |
| 5342 | tripulación | 25 |
| 5343 | tremenda | 25 |
| 5344 | torna | 25 |
| 5345 | temple | 25 |
| 5346 | té | 25 |
| 5347 | sustento | 25 |
| 5348 | supremo | 25 |
| 5349 | sumo | 25 |
| 5350 | síntomas | 25 |
| 5351 | siesta | 25 |
| 5352 | sentados | 25 |
| 5353 | secreta | 25 |
| 5354 | saltaba | 25 |
| 5355 | rústica | 25 |
| 5356 | robusta | 25 |
| 5357 | remo | 25 |
| 5358 | reducido | 25 |
| 5359 | recogido | 25 |
| 5360 | quatro | 25 |
| 5361 | púrpura | 25 |
| 5362 | probado | 25 |
| 5363 | prestigio | 25 |
| 5364 | prestado | 25 |
| 5365 | preguntóle | 25 |
| 5366 | posibles | 25 |
| 5367 | poseía | 25 |
| 5368 | pierdo | 25 |
| 5369 | pienses | 25 |
| 5370 | pícara | 25 |
| 5371 | persuadir | 25 |
| 5372 | perra | 25 |
| 5373 | perdonaba | 25 |
| 5374 | pensara | 25 |
| 5375 | pareciese | 25 |
| 5376 | parecerle | 25 |
| 5377 | padece | 25 |
| 5378 | pacheco | 25 |
| 5379 | oscuras | 25 |
| 5380 | orbe | 25 |
| 5381 | olvidó | 25 |
| 5382 | observaciones | 25 |
| 5383 | obligada | 25 |
| 5384 | números | 25 |
| 5385 | nombrar | 25 |
| 5386 | niñerías | 25 |
| 5387 | nicanora | 25 |
| 5388 | nacidos | 25 |
| 5389 | migo | 25 |
| 5390 | metiendo | 25 |
| 5391 | merecen | 25 |
| 5392 | matarme | 25 |
| 5393 | martirio | 25 |
| 5394 | marinos | 25 |
| 5395 | manjar | 25 |
| 5396 | mandamiento | 25 |
| 5397 | maleta | 25 |
| 5398 | llovía | 25 |
| 5399 | linajes | 25 |
| 5400 | limosnas | 25 |
| 5401 | licor | 25 |
| 5402 | labio | 25 |
| 5403 | justas | 25 |
| 5404 | júbilo | 25 |
| 5405 | isidro | 25 |
| 5406 | invisible | 25 |
| 5407 | intentar | 25 |
| 5408 | insolente | 25 |
| 5409 | insignificantes | 25 |
| 5410 | ingrato | 25 |
| 5411 | indicios | 25 |
| 5412 | indecente | 25 |
| 5413 | inclinaba | 25 |
| 5414 | imprenta | 25 |
| 5415 | importantes | 25 |
| 5416 | ignoraba | 25 |
| 5417 | humanos | 25 |
| 5418 | horribles | 25 |
| 5419 | haced | 25 |
| 5420 | hablamos | 25 |
| 5421 | gruesa | 25 |
| 5422 | gritar | 25 |
| 5423 | gris | 25 |
| 5424 | gloriosa | 25 |
| 5425 | gemidos | 25 |
| 5426 | frescas | 25 |
| 5427 | fregona | 25 |
| 5428 | frac | 25 |
| 5429 | feas | 25 |
| 5430 | fantasma | 25 |
| 5431 | falsos | 25 |
| 5432 | exige | 25 |
| 5433 | evangelio | 25 |
| 5434 | estrechas | 25 |
| 5435 | estimaba | 25 |
| 5436 | estén | 25 |
| 5437 | espeso | 25 |
| 5438 | espantoso | 25 |
| 5439 | entro | 25 |
| 5440 | entretenía | 25 |
| 5441 | elocuente | 25 |
| 5442 | eco | 25 |
| 5443 | dones | 25 |
| 5444 | dolía | 25 |
| 5445 | despensa | 25 |
| 5446 | deso | 25 |
| 5447 | desconfianza | 25 |
| 5448 | desaparecido | 25 |
| 5449 | delgada | 25 |
| 5450 | dejemos | 25 |
| 5451 | dejamos | 25 |
| 5452 | cuidar | 25 |
| 5453 | cuchilladas | 25 |
| 5454 | crueles | 25 |
| 5455 | coyuntura | 25 |
| 5456 | corrieron | 25 |
| 5457 | contraste | 25 |
| 5458 | contornos | 25 |
| 5459 | contestación | 25 |
| 5460 | conformidad | 25 |
| 5461 | condenado | 25 |
| 5462 | compuso | 25 |
| 5463 | comprendiendo | 25 |
| 5464 | comieron | 25 |
| 5465 | colorado | 25 |
| 5466 | coloquio | 25 |
| 5467 | cip | 25 |
| 5468 | churruca | 25 |
| 5469 | chulita | 25 |
| 5470 | cesto | 25 |
| 5471 | centeno | 25 |
| 5472 | calumnias | 25 |
| 5473 | bofetadas | 25 |
| 5474 | beneficiado | 25 |
| 5475 | bedoya | 25 |
| 5476 | bebe | 25 |
| 5477 | beatas | 25 |
| 5478 | beata | 25 |
| 5479 | azote | 25 |
| 5480 | avisar | 25 |
| 5481 | arrojando | 25 |
| 5482 | arráez | 25 |
| 5483 | ángulo | 25 |
| 5484 | amargura | 25 |
| 5485 | alfombra | 25 |
| 5486 | alcanzado | 25 |
| 5487 | acompañada | 25 |
| 5488 | acabando | 25 |
| 5489 | aburrimiento | 25 |
| 5490 | zapata | 24 |
| 5491 | yerra | 24 |
| 5492 | vuelvas | 24 |
| 5493 | vivió | 24 |
| 5494 | vísperas | 24 |
| 5495 | viniesen | 24 |
| 5496 | vigilancia | 24 |
| 5497 | venció | 24 |
| 5498 | váyase | 24 |
| 5499 | vanos | 24 |
| 5500 | uña | 24 |
| 5501 | últimamente | 24 |
| 5502 | tropezar | 24 |
| 5503 | tresillo | 24 |
| 5504 | tratan | 24 |
| 5505 | trajeron | 24 |
| 5506 | traeré | 24 |
| 5507 | tostada | 24 |
| 5508 | temblorosa | 24 |
| 5509 | tejados | 24 |
| 5510 | tasa | 24 |
| 5511 | tacto | 24 |
| 5512 | sutiles | 24 |
| 5513 | sueltos | 24 |
| 5514 | suba | 24 |
| 5515 | soltando | 24 |
| 5516 | solicita | 24 |
| 5517 | símbolo | 24 |
| 5518 | signo | 24 |
| 5519 | serviçio | 24 |
| 5520 | señoritos | 24 |
| 5521 | seguros | 24 |
| 5522 | segovia | 24 |
| 5523 | saludaba | 24 |
| 5524 | rumores | 24 |
| 5525 | ruda | 24 |
| 5526 | romanticismo | 24 |
| 5527 | roldán | 24 |
| 5528 | rodilla | 24 |
| 5529 | reverencia | 24 |
| 5530 | retirada | 24 |
| 5531 | respuestas | 24 |
| 5532 | respetar | 24 |
| 5533 | repitiendo | 24 |
| 5534 | repetidas | 24 |
| 5535 | recursos | 24 |
| 5536 | recorrer | 24 |
| 5537 | rata | 24 |
| 5538 | rápido | 24 |
| 5539 | rafaela | 24 |
| 5540 | r | 24 |
| 5541 | quitarse | 24 |
| 5542 | quedaré | 24 |
| 5543 | provincias | 24 |
| 5544 | presentar | 24 |
| 5545 | preocupaciones | 24 |
| 5546 | pongas | 24 |
| 5547 | pollo | 24 |
| 5548 | población | 24 |
| 5549 | pliego | 24 |
| 5550 | pisando | 24 |
| 5551 | picos | 24 |
| 5552 | persiguen | 24 |
| 5553 | permitió | 24 |
| 5554 | perfil | 24 |
| 5555 | perdóneme | 24 |
| 5556 | patricia | 24 |
| 5557 | passo | 24 |
| 5558 | paseando | 24 |
| 5559 | pasé | 24 |
| 5560 | particulares | 24 |
| 5561 | pareces | 24 |
| 5562 | palmadas | 24 |
| 5563 | pague | 24 |
| 5564 | pagó | 24 |
| 5565 | pacífico | 24 |
| 5566 | paces | 24 |
| 5567 | p | 24 |
| 5568 | otrosí | 24 |
| 5569 | orillas | 24 |
| 5570 | oportunidad | 24 |
| 5571 | ópera | 24 |
| 5572 | nueuas | 24 |
| 5573 | nacional | 24 |
| 5574 | murmurando | 24 |
| 5575 | mundos | 24 |
| 5576 | muertas | 24 |
| 5577 | mocedad | 24 |
| 5578 | mirarla | 24 |
| 5579 | ministerial | 24 |
| 5580 | merezco | 24 |
| 5581 | meditación | 24 |
| 5582 | maten | 24 |
| 5583 | marco | 24 |
| 5584 | manga | 24 |
| 5585 | magnífica | 24 |
| 5586 | madrugada | 24 |
| 5587 | lunes | 24 |
| 5588 | llevándose | 24 |
| 5589 | llame | 24 |
| 5590 | liebre | 24 |
| 5591 | laberinto | 24 |
| 5592 | jurado | 24 |
| 5593 | jueces | 24 |
| 5594 | jinete | 24 |
| 5595 | irás | 24 |
| 5596 | invencible | 24 |
| 5597 | intrigas | 24 |
| 5598 | íntimos | 24 |
| 5599 | intenso | 24 |
| 5600 | imprimir | 24 |
| 5601 | hurto | 24 |
| 5602 | huertas | 24 |
| 5603 | himeneo | 24 |
| 5604 | hilos | 24 |
| 5605 | hallazgo | 24 |
| 5606 | habré | 24 |
| 5607 | hables | 24 |
| 5608 | guardas | 24 |
| 5609 | guardando | 24 |
| 5610 | guardada | 24 |
| 5611 | grueso | 24 |
| 5612 | grosera | 24 |
| 5613 | gravemente | 24 |
| 5614 | goza | 24 |
| 5615 | glorioso | 24 |
| 5616 | fuero | 24 |
| 5617 | fingida | 24 |
| 5618 | filas | 24 |
| 5619 | feroz | 24 |
| 5620 | felizmente | 24 |
| 5621 | fazen | 24 |
| 5622 | favorecer | 24 |
| 5623 | fallo | 24 |
| 5624 | extendía | 24 |
| 5625 | estrado | 24 |
| 5626 | estés | 24 |
| 5627 | estatura | 24 |
| 5628 | estampa | 24 |
| 5629 | escapó | 24 |
| 5630 | envuelta | 24 |
| 5631 | enseñaba | 24 |
| 5632 | engaños | 24 |
| 5633 | encendió | 24 |
| 5634 | empleaba | 24 |
| 5635 | embuste | 24 |
| 5636 | edificios | 24 |
| 5637 | edades | 24 |
| 5638 | dueños | 24 |
| 5639 | dorada | 24 |
| 5640 | domicilio | 24 |
| 5641 | dolorosa | 24 |
| 5642 | disculpa | 24 |
| 5643 | diligente | 24 |
| 5644 | dieran | 24 |
| 5645 | deve | 24 |
| 5646 | desvarío | 24 |
| 5647 | desencanto | 24 |
| 5648 | dejarme | 24 |
| 5649 | dejaría | 24 |
| 5650 | daremos | 24 |
| 5651 | dádivas | 24 |
| 5652 | cumplimiento | 24 |
| 5653 | cuartel | 24 |
| 5654 | criar | 24 |
| 5655 | crecer | 24 |
| 5656 | cras | 24 |
| 5657 | costura | 24 |
| 5658 | coronado | 24 |
| 5659 | contino | 24 |
| 5660 | conozca | 24 |
| 5661 | confesó | 24 |
| 5662 | componer | 24 |
| 5663 | cifra | 24 |
| 5664 | césar | 24 |
| 5665 | ceja | 24 |
| 5666 | cédula | 24 |
| 5667 | cargados | 24 |
| 5668 | cantares | 24 |
| 5669 | canónigos | 24 |
| 5670 | caminante | 24 |
| 5671 | cambiar | 24 |
| 5672 | camas | 24 |
| 5673 | caldo | 24 |
| 5674 | brutal | 24 |
| 5675 | ayude | 24 |
| 5676 | asido | 24 |
| 5677 | arroz | 24 |
| 5678 | arroja | 24 |
| 5679 | arenas | 24 |
| 5680 | aprieta | 24 |
| 5681 | aprensiones | 24 |
| 5682 | apoyando | 24 |
| 5683 | añadiendo | 24 |
| 5684 | añadidura | 24 |
| 5685 | antoja | 24 |
| 5686 | ansia | 24 |
| 5687 | ando | 24 |
| 5688 | alegraba | 24 |
| 5689 | alcohol | 24 |
| 5690 | alcanzó | 24 |
| 5691 | ala | 24 |
| 5692 | ahínco | 24 |
| 5693 | aguardar | 24 |
| 5694 | aguantar | 24 |
| 5695 | agosto | 24 |
| 5696 | admite | 24 |
| 5697 | admiró | 24 |
| 5698 | admirables | 24 |
| 5699 | acostar | 24 |
| 5700 | abur | 24 |
| 5701 | abogados | 24 |
| 5702 | abiertas | 24 |
| 5703 | vosotras | 23 |
| 5704 | visorrey | 23 |
| 5705 | vengar | 23 |
| 5706 | ved | 23 |
| 5707 | válame | 23 |
| 5708 | vagas | 23 |
| 5709 | tumba | 23 |
| 5710 | troya | 23 |
| 5711 | trist | 23 |
| 5712 | trayendo | 23 |
| 5713 | trastos | 23 |
| 5714 | trabajando | 23 |
| 5715 | tormenta | 23 |
| 5716 | tomase | 23 |
| 5717 | tercer | 23 |
| 5718 | tarda | 23 |
| 5719 | tambor | 23 |
| 5720 | suponía | 23 |
| 5721 | sueldo | 23 |
| 5722 | sonriente | 23 |
| 5723 | solemnidad | 23 |
| 5724 | sofrir | 23 |
| 5725 | sofocada | 23 |
| 5726 | simples | 23 |
| 5727 | señana | 23 |
| 5728 | sentimental | 23 |
| 5729 | saludo | 23 |
| 5730 | salita | 23 |
| 5731 | sagrario | 23 |
| 5732 | robo | 23 |
| 5733 | riberas | 23 |
| 5734 | repugnante | 23 |
| 5735 | registro | 23 |
| 5736 | rayas | 23 |
| 5737 | ratón | 23 |
| 5738 | raíz | 23 |
| 5739 | querria | 23 |
| 5740 | puntillas | 23 |
| 5741 | puedas | 23 |
| 5742 | pudor | 23 |
| 5743 | pudiesen | 23 |
| 5744 | prometida | 23 |
| 5745 | prójimo | 23 |
| 5746 | presos | 23 |
| 5747 | preparado | 23 |
| 5748 | prender | 23 |
| 5749 | premios | 23 |
| 5750 | poderosos | 23 |
| 5751 | pistola | 23 |
| 5752 | piensan | 23 |
| 5753 | pesadilla | 23 |
| 5754 | permitido | 23 |
| 5755 | perales | 23 |
| 5756 | peinado | 23 |
| 5757 | pecar | 23 |
| 5758 | pavos | 23 |
| 5759 | partidas | 23 |
| 5760 | partía | 23 |
| 5761 | párpados | 23 |
| 5762 | parecíale | 23 |
| 5763 | paquito | 23 |
| 5764 | olimpia | 23 |
| 5765 | ofrecían | 23 |
| 5766 | ocupación | 23 |
| 5767 | oculta | 23 |
| 5768 | océano | 23 |
| 5769 | obstante | 23 |
| 5770 | obligados | 23 |
| 5771 | nuera | 23 |
| 5772 | neptuno | 23 |
| 5773 | nena | 23 |
| 5774 | nacida | 23 |
| 5775 | mur | 23 |
| 5776 | mundano | 23 |
| 5777 | munchos | 23 |
| 5778 | mueren | 23 |
| 5779 | mostrarse | 23 |
| 5780 | morisco | 23 |
| 5781 | molestaba | 23 |
| 5782 | menores | 23 |
| 5783 | mediano | 23 |
| 5784 | mecánica | 23 |
| 5785 | matarla | 23 |
| 5786 | matando | 23 |
| 5787 | margen | 23 |
| 5788 | maravillosa | 23 |
| 5789 | mancebos | 23 |
| 5790 | luciente | 23 |
| 5791 | lobos | 23 |
| 5792 | llevarse | 23 |
| 5793 | llenaba | 23 |
| 5794 | llego | 23 |
| 5795 | llamamos | 23 |
| 5796 | lela | 23 |
| 5797 | legítima | 23 |
| 5798 | juraba | 23 |
| 5799 | jugaba | 23 |
| 5800 | juega | 23 |
| 5801 | irme | 23 |
| 5802 | inmediata | 23 |
| 5803 | inefable | 23 |
| 5804 | individuo | 23 |
| 5805 | incomparable | 23 |
| 5806 | inclinada | 23 |
| 5807 | ídolo | 23 |
| 5808 | hierros | 23 |
| 5809 | hicieran | 23 |
| 5810 | heroico | 23 |
| 5811 | hallan | 23 |
| 5812 | habilidades | 23 |
| 5813 | guerras | 23 |
| 5814 | grana | 23 |
| 5815 | grados | 23 |
| 5816 | gozosa | 23 |
| 5817 | gotas | 23 |
| 5818 | gorra | 23 |
| 5819 | gitanas | 23 |
| 5820 | generosidad | 23 |
| 5821 | generosa | 23 |
| 5822 | géneros | 23 |
| 5823 | fusil | 23 |
| 5824 | fuga | 23 |
| 5825 | figurarse | 23 |
| 5826 | fermosura | 23 |
| 5827 | extranjeros | 23 |
| 5828 | existía | 23 |
| 5829 | evidente | 23 |
| 5830 | esclava | 23 |
| 5831 | escalones | 23 |
| 5832 | escalón | 23 |
| 5833 | escalofríos | 23 |
| 5834 | eras | 23 |
| 5835 | entrara | 23 |
| 5836 | entienden | 23 |
| 5837 | entendían | 23 |
| 5838 | entendí | 23 |
| 5839 | enseñanza | 23 |
| 5840 | enseña | 23 |
| 5841 | enfado | 23 |
| 5842 | enérgico | 23 |
| 5843 | encontrarse | 23 |
| 5844 | encontraban | 23 |
| 5845 | encarnado | 23 |
| 5846 | encargó | 23 |
| 5847 | empleados | 23 |
| 5848 | empezaban | 23 |
| 5849 | echo | 23 |
| 5850 | dominó | 23 |
| 5851 | divinidad | 23 |
| 5852 | dispuso | 23 |
| 5853 | discordia | 23 |
| 5854 | disciplina | 23 |
| 5855 | dirigiéndose | 23 |
| 5856 | dirigía | 23 |
| 5857 | dirás | 23 |
| 5858 | diócesis | 23 |
| 5859 | diamante | 23 |
| 5860 | detener | 23 |
| 5861 | destreza | 23 |
| 5862 | desir | 23 |
| 5863 | déjese | 23 |
| 5864 | dejas | 23 |
| 5865 | defecto | 23 |
| 5866 | declarar | 23 |
| 5867 | declaración | 23 |
| 5868 | daños | 23 |
| 5869 | danza | 23 |
| 5870 | dano | 23 |
| 5871 | dadas | 23 |
| 5872 | cuadrilleros | 23 |
| 5873 | cruzando | 23 |
| 5874 | cristóbal | 23 |
| 5875 | créame | 23 |
| 5876 | corteses | 23 |
| 5877 | corneta | 23 |
| 5878 | cordon | 23 |
| 5879 | continuar | 23 |
| 5880 | consideraciones | 23 |
| 5881 | conquistar | 23 |
| 5882 | conocieron | 23 |
| 5883 | conejo | 23 |
| 5884 | concertado | 23 |
| 5885 | comerciante | 23 |
| 5886 | columna | 23 |
| 5887 | colocar | 23 |
| 5888 | coces | 23 |
| 5889 | clavado | 23 |
| 5890 | cinta | 23 |
| 5891 | chato | 23 |
| 5892 | causó | 23 |
| 5893 | casero | 23 |
| 5894 | cariñoso | 23 |
| 5895 | caballeriza | 23 |
| 5896 | bellezas | 23 |
| 5897 | bebía | 23 |
| 5898 | barrios | 23 |
| 5899 | avía | 23 |
| 5900 | aturdido | 23 |
| 5901 | áspera | 23 |
| 5902 | arzobispo | 23 |
| 5903 | arreglar | 23 |
| 5904 | arrastraba | 23 |
| 5905 | apuntó | 23 |
| 5906 | apresuró | 23 |
| 5907 | apostaré | 23 |
| 5908 | aparición | 23 |
| 5909 | ánimas | 23 |
| 5910 | andamos | 23 |
| 5911 | andalucía | 23 |
| 5912 | aldeana | 23 |
| 5913 | afectos | 23 |
| 5914 | acudía | 23 |
| 5915 | acompañe | 23 |
| 5916 | acompañamiento | 23 |
| 5917 | acertar | 23 |
| 5918 | acaban | 23 |
| 5919 | abnegación | 23 |
| 5920 | volviera | 22 |
| 5921 | vnos | 22 |
| 5922 | viniera | 22 |
| 5923 | villanos | 22 |
| 5924 | viesen | 22 |
| 5925 | viere | 22 |
| 5926 | vendía | 22 |
| 5927 | varonil | 22 |
| 5928 | variedad | 22 |
| 5929 | vapor | 22 |
| 5930 | unión | 22 |
| 5931 | tunante | 22 |
| 5932 | trifón | 22 |
| 5933 | tragedia | 22 |
| 5934 | trabaja | 22 |
| 5935 | torpeza | 22 |
| 5936 | tiestos | 22 |
| 5937 | tiernas | 22 |
| 5938 | tentaciones | 22 |
| 5939 | tendida | 22 |
| 5940 | temblor | 22 |
| 5941 | suspensos | 22 |
| 5942 | sujeta | 22 |
| 5943 | sucesión | 22 |
| 5944 | suceda | 22 |
| 5945 | sosegada | 22 |
| 5946 | sonar | 22 |
| 5947 | socarrón | 22 |
| 5948 | sobras | 22 |
| 5949 | soberbios | 22 |
| 5950 | soberbio | 22 |
| 5951 | siniestro | 22 |
| 5952 | sima | 22 |
| 5953 | significaba | 22 |
| 5954 | sienes | 22 |
| 5955 | sequedad | 22 |
| 5956 | segundos | 22 |
| 5957 | salas | 22 |
| 5958 | ruidos | 22 |
| 5959 | rotas | 22 |
| 5960 | rompía | 22 |
| 5961 | rojas | 22 |
| 5962 | resultaba | 22 |
| 5963 | reposar | 22 |
| 5964 | regalos | 22 |
| 5965 | referir | 22 |
| 5966 | refería | 22 |
| 5967 | recurso | 22 |
| 5968 | reconocía | 22 |
| 5969 | recogimiento | 22 |
| 5970 | quitan | 22 |
| 5971 | quisiéredes | 22 |
| 5972 | quietud | 22 |
| 5973 | pureza | 22 |
| 5974 | puntualidad | 22 |
| 5975 | proa | 22 |
| 5976 | preguntaron | 22 |
| 5977 | prefiero | 22 |
| 5978 | polentinos | 22 |
| 5979 | pleitos | 22 |
| 5980 | pisar | 22 |
| 5981 | pique | 22 |
| 5982 | persecución | 22 |
| 5983 | pergamino | 22 |
| 5984 | perdonado | 22 |
| 5985 | pensador | 22 |
| 5986 | peligrosa | 22 |
| 5987 | partió | 22 |
| 5988 | parecieron | 22 |
| 5989 | paraguas | 22 |
| 5990 | orgulloso | 22 |
| 5991 | ordena | 22 |
| 5992 | ollas | 22 |
| 5993 | ocupaban | 22 |
| 5994 | nieto | 22 |
| 5995 | niego | 22 |
| 5996 | necesarias | 22 |
| 5997 | murmurar | 22 |
| 5998 | murieron | 22 |
| 5999 | mueble | 22 |
| 6000 | montañés | 22 |
| 6001 | molestia | 22 |
| 6002 | misticismo | 22 |
| 6003 | misión | 22 |
| 6004 | mirándole | 22 |
| 6005 | mina | 22 |
| 6006 | meto | 22 |
| 6007 | menudencias | 22 |
| 6008 | mentiroso | 22 |
| 6009 | materiales | 22 |
| 6010 | mártir | 22 |
| 6011 | martillo | 22 |
| 6012 | marchado | 22 |
| 6013 | mandas | 22 |
| 6014 | maldiciones | 22 |
| 6015 | llevarla | 22 |
| 6016 | llana | 22 |
| 6017 | limpiar | 22 |
| 6018 | libremente | 22 |
| 6019 | ix | 22 |
| 6020 | inclinándose | 22 |
| 6021 | ignorantes | 22 |
| 6022 | ida | 22 |
| 6023 | huérfana | 22 |
| 6024 | hubieron | 22 |
| 6025 | honradas | 22 |
| 6026 | hato | 22 |
| 6027 | harían | 22 |
| 6028 | haremos | 22 |
| 6029 | hacerte | 22 |
| 6030 | hablara | 22 |
| 6031 | habitantes | 22 |
| 6032 | habemos | 22 |
| 6033 | gustar | 22 |
| 6034 | grillos | 22 |
| 6035 | gozoso | 22 |
| 6036 | gonzález | 22 |
| 6037 | garbanzos | 22 |
| 6038 | galgo | 22 |
| 6039 | galeotes | 22 |
| 6040 | fuiste | 22 |
| 6041 | frutas | 22 |
| 6042 | frecuencia | 22 |
| 6043 | franca | 22 |
| 6044 | fórmula | 22 |
| 6045 | fiz | 22 |
| 6046 | firmes | 22 |
| 6047 | finura | 22 |
| 6048 | fila | 22 |
| 6049 | fijó | 22 |
| 6050 | fenómeno | 22 |
| 6051 | fee | 22 |
| 6052 | fealdad | 22 |
| 6053 | favores | 22 |
| 6054 | fatigado | 22 |
| 6055 | faroles | 22 |
| 6056 | faré | 22 |
| 6057 | fandiño | 22 |
| 6058 | excitación | 22 |
| 6059 | excepción | 22 |
| 6060 | exactitud | 22 |
| 6061 | equivocado | 22 |
| 6062 | enormes | 22 |
| 6063 | enmienda | 22 |
| 6064 | encuentran | 22 |
| 6065 | embustero | 22 |
| 6066 | dudoso | 22 |
| 6067 | dormían | 22 |
| 6068 | doradas | 22 |
| 6069 | docientos | 22 |
| 6070 | dó | 22 |
| 6071 | distinto | 22 |
| 6072 | distinta | 22 |
| 6073 | disputa | 22 |
| 6074 | disparó | 22 |
| 6075 | diario | 22 |
| 6076 | detuvieron | 22 |
| 6077 | detenía | 22 |
| 6078 | desventurado | 22 |
| 6079 | despreciar | 22 |
| 6080 | despedía | 22 |
| 6081 | desdenes | 22 |
| 6082 | descubrieron | 22 |
| 6083 | descubría | 22 |
| 6084 | descompuesto | 22 |
| 6085 | derrota | 22 |
| 6086 | derredor | 22 |
| 6087 | delincuente | 22 |
| 6088 | deleyte | 22 |
| 6089 | defenderse | 22 |
| 6090 | declara | 22 |
| 6091 | decid | 22 |
| 6092 | darían | 22 |
| 6093 | darán | 22 |
| 6094 | dados | 22 |
| 6095 | cuba | 22 |
| 6096 | creerlo | 22 |
| 6097 | creerá | 22 |
| 6098 | cosquillas | 22 |
| 6099 | coser | 22 |
| 6100 | corbata | 22 |
| 6101 | copia | 22 |
| 6102 | convencer | 22 |
| 6103 | contiene | 22 |
| 6104 | conocimientos | 22 |
| 6105 | conflicto | 22 |
| 6106 | compró | 22 |
| 6107 | componen | 22 |
| 6108 | compania | 22 |
| 6109 | comedido | 22 |
| 6110 | cocinero | 22 |
| 6111 | cocido | 22 |
| 6112 | charla | 22 |
| 6113 | celebrar | 22 |
| 6114 | cavilaciones | 22 |
| 6115 | cautela | 22 |
| 6116 | carreras | 22 |
| 6117 | carnaval | 22 |
| 6118 | carmen | 22 |
| 6119 | camina | 22 |
| 6120 | cambiado | 22 |
| 6121 | callo | 22 |
| 6122 | cállate | 22 |
| 6123 | callada | 22 |
| 6124 | caballerito | 22 |
| 6125 | botones | 22 |
| 6126 | borrachos | 22 |
| 6127 | bofetada | 22 |
| 6128 | boba | 22 |
| 6129 | blas | 22 |
| 6130 | bismarck | 22 |
| 6131 | berbería | 22 |
| 6132 | bata | 22 |
| 6133 | baños | 22 |
| 6134 | bálsamo | 22 |
| 6135 | auia | 22 |
| 6136 | atrevo | 22 |
| 6137 | aseo | 22 |
| 6138 | arriero | 22 |
| 6139 | arrastrando | 22 |
| 6140 | apoyó | 22 |
| 6141 | apodo | 22 |
| 6142 | antigüedad | 22 |
| 6143 | anima | 22 |
| 6144 | amri | 22 |
| 6145 | almacén | 22 |
| 6146 | algodón | 22 |
| 6147 | albergue | 22 |
| 6148 | agradecía | 22 |
| 6149 | agradar | 22 |
| 6150 | afable | 22 |
| 6151 | acompaña | 22 |
| 6152 | acierto | 22 |
| 6153 | acabase | 22 |
| 6154 | abrazar | 22 |
| 6155 | abandonada | 22 |
| 6156 | votos | 21 |
| 6157 | viéndome | 21 |
| 6158 | verja | 21 |
| 6159 | venden | 21 |
| 6160 | velar | 21 |
| 6161 | valladolid | 21 |
| 6162 | usando | 21 |
| 6163 | trotaconventos | 21 |
| 6164 | tribunal | 21 |
| 6165 | tratándose | 21 |
| 6166 | transeúntes | 21 |
| 6167 | traigan | 21 |
| 6168 | tormentos | 21 |
| 6169 | tolerancia | 21 |
| 6170 | tocino | 21 |
| 6171 | tino | 21 |
| 6172 | temporada | 21 |
| 6173 | temperamento | 21 |
| 6174 | taza | 21 |
| 6175 | tarasca | 21 |
| 6176 | tapaba | 21 |
| 6177 | tajo | 21 |
| 6178 | superiores | 21 |
| 6179 | sintieron | 21 |
| 6180 | sienten | 21 |
| 6181 | severo | 21 |
| 6182 | severa | 21 |
| 6183 | servirle | 21 |
| 6184 | serpiente | 21 |
| 6185 | sepan | 21 |
| 6186 | sendero | 21 |
| 6187 | sanos | 21 |
| 6188 | sanchica | 21 |
| 6189 | salve | 21 |
| 6190 | rompiendo | 21 |
| 6191 | romántica | 21 |
| 6192 | rodeaban | 21 |
| 6193 | ríe | 21 |
| 6194 | revólver | 21 |
| 6195 | restauración | 21 |
| 6196 | respondieron | 21 |
| 6197 | repentina | 21 |
| 6198 | recta | 21 |
| 6199 | reconozco | 21 |
| 6200 | ramón | 21 |
| 6201 | quitaron | 21 |
| 6202 | quinientos | 21 |
| 6203 | quieto | 21 |
| 6204 | quienquiera | 21 |
| 6205 | puñadas | 21 |
| 6206 | proyectos | 21 |
| 6207 | profesor | 21 |
| 6208 | produce | 21 |
| 6209 | pretensión | 21 |
| 6210 | pretendiente | 21 |
| 6211 | pretendía | 21 |
| 6212 | presupuesto | 21 |
| 6213 | presidio | 21 |
| 6214 | posee | 21 |
| 6215 | portugués | 21 |
| 6216 | poética | 21 |
| 6217 | pidieron | 21 |
| 6218 | piadosas | 21 |
| 6219 | pese | 21 |
| 6220 | pertenecía | 21 |
| 6221 | personalidad | 21 |
| 6222 | peregrinos | 21 |
| 6223 | pensión | 21 |
| 6224 | pavor | 21 |
| 6225 | passado | 21 |
| 6226 | pasamos | 21 |
| 6227 | pañuelos | 21 |
| 6228 | pantalón | 21 |
| 6229 | olvidada | 21 |
| 6230 | oler | 21 |
| 6231 | octubre | 21 |
| 6232 | obedecer | 21 |
| 6233 | nudo | 21 |
| 6234 | negó | 21 |
| 6235 | necia | 21 |
| 6236 | muñeca | 21 |
| 6237 | muestran | 21 |
| 6238 | movían | 21 |
| 6239 | mostrador | 21 |
| 6240 | mostraban | 21 |
| 6241 | mordejai | 21 |
| 6242 | moralidad | 21 |
| 6243 | montera | 21 |
| 6244 | místico | 21 |
| 6245 | mezquino | 21 |
| 6246 | meta | 21 |
| 6247 | menesterosos | 21 |
| 6248 | menéndez | 21 |
| 6249 | medir | 21 |
| 6250 | marte | 21 |
| 6251 | marroquí | 21 |
| 6252 | manso | 21 |
| 6253 | maestros | 21 |
| 6254 | luschía | 21 |
| 6255 | luengos | 21 |
| 6256 | llover | 21 |
| 6257 | llevamos | 21 |
| 6258 | llegara | 21 |
| 6259 | llamarla | 21 |
| 6260 | listo | 21 |
| 6261 | lili | 21 |
| 6262 | juramentos | 21 |
| 6263 | jugaban | 21 |
| 6264 | jesucristo | 21 |
| 6265 | jardines | 21 |
| 6266 | intentó | 21 |
| 6267 | injusticia | 21 |
| 6268 | indicio | 21 |
| 6269 | indecible | 21 |
| 6270 | inconvenientes | 21 |
| 6271 | implacable | 21 |
| 6272 | ilustrado | 21 |
| 6273 | héroes | 21 |
| 6274 | hazes | 21 |
| 6275 | hallándose | 21 |
| 6276 | hachas | 21 |
| 6277 | habiéndose | 21 |
| 6278 | grecia | 21 |
| 6279 | goze | 21 |
| 6280 | gobiernos | 21 |
| 6281 | germán | 21 |
| 6282 | generales | 21 |
| 6283 | ganó | 21 |
| 6284 | fuy | 21 |
| 6285 | fundamento | 21 |
| 6286 | fuegos | 21 |
| 6287 | fondos | 21 |
| 6288 | figurado | 21 |
| 6289 | fervor | 21 |
| 6290 | fatal | 21 |
| 6291 | explicó | 21 |
| 6292 | estribos | 21 |
| 6293 | estribo | 21 |
| 6294 | estaua | 21 |
| 6295 | espirituales | 21 |
| 6296 | escuelas | 21 |
| 6297 | escritas | 21 |
| 6298 | escribo | 21 |
| 6299 | escapaba | 21 |
| 6300 | ermitaño | 21 |
| 6301 | envidiaba | 21 |
| 6302 | encubrir | 21 |
| 6303 | encontrando | 21 |
| 6304 | empecé | 21 |
| 6305 | elementos | 21 |
| 6306 | ejemplar | 21 |
| 6307 | dulcemente | 21 |
| 6308 | dubda | 21 |
| 6309 | dotes | 21 |
| 6310 | doscientos | 21 |
| 6311 | doméstico | 21 |
| 6312 | diste | 21 |
| 6313 | discusión | 21 |
| 6314 | discretamente | 21 |
| 6315 | diremos | 21 |
| 6316 | diputado | 21 |
| 6317 | dijiste | 21 |
| 6318 | desprecia | 21 |
| 6319 | desesperada | 21 |
| 6320 | delantal | 21 |
| 6321 | defectos | 21 |
| 6322 | decidió | 21 |
| 6323 | damos | 21 |
| 6324 | custodia | 21 |
| 6325 | cubrió | 21 |
| 6326 | cuatrocientos | 21 |
| 6327 | creyera | 21 |
| 6328 | creerse | 21 |
| 6329 | creeríase | 21 |
| 6330 | creciendo | 21 |
| 6331 | cortinas | 21 |
| 6332 | corales | 21 |
| 6333 | conssejo | 21 |
| 6334 | consiguió | 21 |
| 6335 | conociera | 21 |
| 6336 | comienza | 21 |
| 6337 | cima | 21 |
| 6338 | chillidos | 21 |
| 6339 | cesó | 21 |
| 6340 | cercano | 21 |
| 6341 | ce | 21 |
| 6342 | castidad | 21 |
| 6343 | caprichos | 21 |
| 6344 | capitanes | 21 |
| 6345 | candil | 21 |
| 6346 | callaron | 21 |
| 6347 | calamidad | 21 |
| 6348 | burlada | 21 |
| 6349 | bullicio | 21 |
| 6350 | blancura | 21 |
| 6351 | bajaron | 21 |
| 6352 | atónito | 21 |
| 6353 | asomó | 21 |
| 6354 | asaz | 21 |
| 6355 | arquitectura | 21 |
| 6356 | aprovechaba | 21 |
| 6357 | aprobación | 21 |
| 6358 | apearse | 21 |
| 6359 | amita | 21 |
| 6360 | amiguita | 21 |
| 6361 | alteza | 21 |
| 6362 | alquiler | 21 |
| 6363 | almirante | 21 |
| 6364 | algun | 21 |
| 6365 | alboroto | 21 |
| 6366 | alarde | 21 |
| 6367 | alabado | 21 |
| 6368 | agujas | 21 |
| 6369 | agradaba | 21 |
| 6370 | admirablemente | 21 |
| 6371 | actores | 21 |
| 6372 | acompañaban | 21 |
| 6373 | abrían | 21 |
| 6374 | abrazos | 21 |
| 6375 | zarzas | 20 |
| 6376 | zapatillas | 20 |
| 6377 | xiv | 20 |
| 6378 | voluptuosidad | 20 |
| 6379 | viveza | 20 |
| 6380 | visitaba | 20 |
| 6381 | vinos | 20 |
| 6382 | villahorrenda | 20 |
| 6383 | viéndola | 20 |
| 6384 | vergonzoso | 20 |
| 6385 | venturoso | 20 |
| 6386 | vendido | 20 |
| 6387 | val | 20 |
| 6388 | urraca | 20 |
| 6389 | turbó | 20 |
| 6390 | trote | 20 |
| 6391 | trémula | 20 |
| 6392 | trecientos | 20 |
| 6393 | tratos | 20 |
| 6394 | terminó | 20 |
| 6395 | teología | 20 |
| 6396 | teníamos | 20 |
| 6397 | tendrían | 20 |
| 6398 | talla | 20 |
| 6399 | synon | 20 |
| 6400 | suspiró | 20 |
| 6401 | suspirar | 20 |
| 6402 | superficie | 20 |
| 6403 | sumisión | 20 |
| 6404 | sumamente | 20 |
| 6405 | suceden | 20 |
| 6406 | sorprendido | 20 |
| 6407 | sociedades | 20 |
| 6408 | setenta | 20 |
| 6409 | servidumbre | 20 |
| 6410 | seiscientos | 20 |
| 6411 | satanás | 20 |
| 6412 | sarcasmo | 20 |
| 6413 | sandeces | 20 |
| 6414 | sanar | 20 |
| 6415 | salvajes | 20 |
| 6416 | saludar | 20 |
| 6417 | salgan | 20 |
| 6418 | rodea | 20 |
| 6419 | rodando | 20 |
| 6420 | rocas | 20 |
| 6421 | roble | 20 |
| 6422 | resolvió | 20 |
| 6423 | recogida | 20 |
| 6424 | razonamiento | 20 |
| 6425 | ratones | 20 |
| 6426 | rasgos | 20 |
| 6427 | quemar | 20 |
| 6428 | quan | 20 |
| 6429 | purgatorio | 20 |
| 6430 | puras | 20 |
| 6431 | puñal | 20 |
| 6432 | pueril | 20 |
| 6433 | proseguir | 20 |
| 6434 | proporciones | 20 |
| 6435 | procede | 20 |
| 6436 | prisiones | 20 |
| 6437 | primitivo | 20 |
| 6438 | previsión | 20 |
| 6439 | presentado | 20 |
| 6440 | práctico | 20 |
| 6441 | pongan | 20 |
| 6442 | plazas | 20 |
| 6443 | periodo | 20 |
| 6444 | peregrina | 20 |
| 6445 | perderse | 20 |
| 6446 | penosa | 20 |
| 6447 | penitençia | 20 |
| 6448 | pendientes | 20 |
| 6449 | pavo | 20 |
| 6450 | passion | 20 |
| 6451 | parta | 20 |
| 6452 | parroquianos | 20 |
| 6453 | palomas | 20 |
| 6454 | palmas | 20 |
| 6455 | paisano | 20 |
| 6456 | oscura | 20 |
| 6457 | ordenado | 20 |
| 6458 | orador | 20 |
| 6459 | olvide | 20 |
| 6460 | oírse | 20 |
| 6461 | oírla | 20 |
| 6462 | oficinas | 20 |
| 6463 | ocupa | 20 |
| 6464 | ocultaba | 20 |
| 6465 | obrar | 20 |
| 6466 | obliga | 20 |
| 6467 | nuevamente | 20 |
| 6468 | novena | 20 |
| 6469 | notario | 20 |
| 6470 | ninfa | 20 |
| 6471 | natividad | 20 |
| 6472 | murmullo | 20 |
| 6473 | muestre | 20 |
| 6474 | morirme | 20 |
| 6475 | modas | 20 |
| 6476 | mezclado | 20 |
| 6477 | metros | 20 |
| 6478 | menuda | 20 |
| 6479 | melisendra | 20 |
| 6480 | mediante | 20 |
| 6481 | materialismo | 20 |
| 6482 | matado | 20 |
| 6483 | marras | 20 |
| 6484 | mandan | 20 |
| 6485 | maldades | 20 |
| 6486 | magistrado | 20 |
| 6487 | lujuria | 20 |
| 6488 | logrado | 20 |
| 6489 | llevada | 20 |
| 6490 | literaria | 20 |
| 6491 | lisonja | 20 |
| 6492 | liga | 20 |
| 6493 | ladrillos | 20 |
| 6494 | ladrillo | 20 |
| 6495 | labriego | 20 |
| 6496 | juzga | 20 |
| 6497 | justamente | 20 |
| 6498 | irritaba | 20 |
| 6499 | instintos | 20 |
| 6500 | insoportable | 20 |
| 6501 | infamia | 20 |
| 6502 | inexplicable | 20 |
| 6503 | indiferente | 20 |
| 6504 | indias | 20 |
| 6505 | incluso | 20 |
| 6506 | incienso | 20 |
| 6507 | impreso | 20 |
| 6508 | huyr | 20 |
| 6509 | huía | 20 |
| 6510 | hidalgos | 20 |
| 6511 | hiciste | 20 |
| 6512 | heredero | 20 |
| 6513 | heredado | 20 |
| 6514 | hablé | 20 |
| 6515 | hablaré | 20 |
| 6516 | habiéndole | 20 |
| 6517 | guardo | 20 |
| 6518 | graçia | 20 |
| 6519 | goce | 20 |
| 6520 | gastaba | 20 |
| 6521 | garcía | 20 |
| 6522 | gallardía | 20 |
| 6523 | futuro | 20 |
| 6524 | frailes | 20 |
| 6525 | figúrese | 20 |
| 6526 | ffué | 20 |
| 6527 | félix | 20 |
| 6528 | federico | 20 |
| 6529 | febrero | 20 |
| 6530 | fanatismo | 20 |
| 6531 | éxtasis | 20 |
| 6532 | examinar | 20 |
| 6533 | eternamente | 20 |
| 6534 | estúpida | 20 |
| 6535 | estrecheza | 20 |
| 6536 | estabas | 20 |
| 6537 | est | 20 |
| 6538 | esplendor | 20 |
| 6539 | espanta | 20 |
| 6540 | esfera | 20 |
| 6541 | esencial | 20 |
| 6542 | escusar | 20 |
| 6543 | escura | 20 |
| 6544 | escaso | 20 |
| 6545 | enxienplo | 20 |
| 6546 | enseñó | 20 |
| 6547 | engañada | 20 |
| 6548 | endrina | 20 |
| 6549 | encerraba | 20 |
| 6550 | emprender | 20 |
| 6551 | empeñado | 20 |
| 6552 | embustes | 20 |
| 6553 | economía | 20 |
| 6554 | dominar | 20 |
| 6555 | distraída | 20 |
| 6556 | distinguía | 20 |
| 6557 | discurriendo | 20 |
| 6558 | director | 20 |
| 6559 | dioses | 20 |
| 6560 | diestro | 20 |
| 6561 | dexo | 20 |
| 6562 | determinaron | 20 |
| 6563 | despertado | 20 |
| 6564 | desgraciadamente | 20 |
| 6565 | demostrando | 20 |
| 6566 | delirante | 20 |
| 6567 | delicadas | 20 |
| 6568 | darnos | 20 |
| 6569 | dad | 20 |
| 6570 | cuydado | 20 |
| 6571 | cuidaba | 20 |
| 6572 | cuaresma | 20 |
| 6573 | cruzadas | 20 |
| 6574 | costados | 20 |
| 6575 | cortos | 20 |
| 6576 | cortó | 20 |
| 6577 | convite | 20 |
| 6578 | contrabando | 20 |
| 6579 | constantino | 20 |
| 6580 | conociendo | 20 |
| 6581 | conjuro | 20 |
| 6582 | confesado | 20 |
| 6583 | concordia | 20 |
| 6584 | comúnmente | 20 |
| 6585 | competencia | 20 |
| 6586 | cobro | 20 |
| 6587 | clavos | 20 |
| 6588 | clavados | 20 |
| 6589 | chusma | 20 |
| 6590 | choque | 20 |
| 6591 | chaleco | 20 |
| 6592 | cavallo | 20 |
| 6593 | caserío | 20 |
| 6594 | carreta | 20 |
| 6595 | careta | 20 |
| 6596 | cansados | 20 |
| 6597 | can | 20 |
| 6598 | camara | 20 |
| 6599 | cálculos | 20 |
| 6600 | caiga | 20 |
| 6601 | cabos | 20 |
| 6602 | burro | 20 |
| 6603 | bula | 20 |
| 6604 | brillantes | 20 |
| 6605 | brillaba | 20 |
| 6606 | bribona | 20 |
| 6607 | brevemente | 20 |
| 6608 | besa | 20 |
| 6609 | bebido | 20 |
| 6610 | bebida | 20 |
| 6611 | atravesó | 20 |
| 6612 | atendía | 20 |
| 6613 | atados | 20 |
| 6614 | aspavientos | 20 |
| 6615 | arrojado | 20 |
| 6616 | arrebatado | 20 |
| 6617 | arranca | 20 |
| 6618 | ardía | 20 |
| 6619 | arcale | 20 |
| 6620 | aragonés | 20 |
| 6621 | apretado | 20 |
| 6622 | aprende | 20 |
| 6623 | apoyada | 20 |
| 6624 | aplicación | 20 |
| 6625 | aparejo | 20 |
| 6626 | anunciaba | 20 |
| 6627 | antaño | 20 |
| 6628 | animado | 20 |
| 6629 | animación | 20 |
| 6630 | andaluz | 20 |
| 6631 | americano | 20 |
| 6632 | amaneció | 20 |
| 6633 | altares | 20 |
| 6634 | ali | 20 |
| 6635 | alerta | 20 |
| 6636 | alcalle | 20 |
| 6637 | alargó | 20 |
| 6638 | alá | 20 |
| 6639 | ajo | 20 |
| 6640 | ahogaba | 20 |
| 6641 | aguador | 20 |
| 6642 | afligida | 20 |
| 6643 | acostó | 20 |
| 6644 | acordarse | 20 |
| 6645 | abuelo | 20 |
| 6646 | abismos | 20 |
| 6647 | abandonar | 20 |
| 6648 | zalamero | 19 |
| 6649 | ygual | 19 |
| 6650 | volvióse | 19 |
| 6651 | volvamos | 19 |
| 6652 | vocablos | 19 |
| 6653 | verdura | 19 |
| 6654 | ventanilla | 19 |
| 6655 | venís | 19 |
| 6656 | venidas | 19 |
| 6657 | vendrán | 19 |
| 6658 | variar | 19 |
| 6659 | vanas | 19 |
| 6660 | utilidad | 19 |
| 6661 | usanza | 19 |
| 6662 | trujeron | 19 |
| 6663 | trueco | 19 |
| 6664 | travesura | 19 |
| 6665 | tranquilamente | 19 |
| 6666 | traerle | 19 |
| 6667 | tomándole | 19 |
| 6668 | tocaban | 19 |
| 6669 | tente | 19 |
| 6670 | tardar | 19 |
| 6671 | tambien | 19 |
| 6672 | tablero | 19 |
| 6673 | suspiraba | 19 |
| 6674 | suprema | 19 |
| 6675 | supongo | 19 |
| 6676 | sudaba | 19 |
| 6677 | soplo | 19 |
| 6678 | sonrisas | 19 |
| 6679 | sonoro | 19 |
| 6680 | sólido | 19 |
| 6681 | soles | 19 |
| 6682 | socorrer | 19 |
| 6683 | soberano | 19 |
| 6684 | simplemente | 19 |
| 6685 | simón | 19 |
| 6686 | silenciosa | 19 |
| 6687 | senos | 19 |
| 6688 | senderos | 19 |
| 6689 | selvas | 19 |
| 6690 | secos | 19 |
| 6691 | sátira | 19 |
| 6692 | sargento | 19 |
| 6693 | santísimo | 19 |
| 6694 | salvado | 19 |
| 6695 | saliva | 19 |
| 6696 | sabed | 19 |
| 6697 | sábado | 19 |
| 6698 | rodeos | 19 |
| 6699 | riguroso | 19 |
| 6700 | riesgo | 19 |
| 6701 | revista | 19 |
| 6702 | revelación | 19 |
| 6703 | resultó | 19 |
| 6704 | reputación | 19 |
| 6705 | representan | 19 |
| 6706 | reparar | 19 |
| 6707 | rentas | 19 |
| 6708 | rendida | 19 |
| 6709 | reliquias | 19 |
| 6710 | religiosidad | 19 |
| 6711 | relámpago | 19 |
| 6712 | reírse | 19 |
| 6713 | recreo | 19 |
| 6714 | ración | 19 |
| 6715 | quito | 19 |
| 6716 | quisieren | 19 |
| 6717 | quedaría | 19 |
| 6718 | pusieran | 19 |
| 6719 | prólogo | 19 |
| 6720 | producido | 19 |
| 6721 | prisioneros | 19 |
| 6722 | preparar | 19 |
| 6723 | porqué | 19 |
| 6724 | ponerla | 19 |
| 6725 | polvos | 19 |
| 6726 | poético | 19 |
| 6727 | pintadas | 19 |
| 6728 | pinta | 19 |
| 6729 | pieles | 19 |
| 6730 | picar | 19 |
| 6731 | perezosa | 19 |
| 6732 | peras | 19 |
| 6733 | per | 19 |
| 6734 | peine | 19 |
| 6735 | pego | 19 |
| 6736 | pasmado | 19 |
| 6737 | paseaban | 19 |
| 6738 | pascua | 19 |
| 6739 | partidario | 19 |
| 6740 | párroco | 19 |
| 6741 | parió | 19 |
| 6742 | pág | 19 |
| 6743 | padrinos | 19 |
| 6744 | padecido | 19 |
| 6745 | oyese | 19 |
| 6746 | ovidio | 19 |
| 6747 | osaba | 19 |
| 6748 | ofensa | 19 |
| 6749 | octavio | 19 |
| 6750 | obtener | 19 |
| 6751 | obstáculos | 19 |
| 6752 | obreros | 19 |
| 6753 | ninfas | 19 |
| 6754 | necesitan | 19 |
| 6755 | naves | 19 |
| 6756 | nacen | 19 |
| 6757 | museo | 19 |
| 6758 | mudas | 19 |
| 6759 | montones | 19 |
| 6760 | monta | 19 |
| 6761 | modernos | 19 |
| 6762 | moderno | 19 |
| 6763 | mocha | 19 |
| 6764 | miles | 19 |
| 6765 | metida | 19 |
| 6766 | méritos | 19 |
| 6767 | menudas | 19 |
| 6768 | mendigo | 19 |
| 6769 | meditaba | 19 |
| 6770 | matemático | 19 |
| 6771 | manolo | 19 |
| 6772 | manifestar | 19 |
| 6773 | madura | 19 |
| 6774 | luenga | 19 |
| 6775 | logroño | 19 |
| 6776 | llegará | 19 |
| 6777 | llamase | 19 |
| 6778 | levantada | 19 |
| 6779 | leño | 19 |
| 6780 | laurel | 19 |
| 6781 | lastimoso | 19 |
| 6782 | lastimado | 19 |
| 6783 | lastimada | 19 |
| 6784 | largamente | 19 |
| 6785 | lanzón | 19 |
| 6786 | lago | 19 |
| 6787 | justos | 19 |
| 6788 | jubón | 19 |
| 6789 | italia | 19 |
| 6790 | intimidad | 19 |
| 6791 | instrucción | 19 |
| 6792 | inmediato | 19 |
| 6793 | indigna | 19 |
| 6794 | imponía | 19 |
| 6795 | húmeda | 19 |
| 6796 | huecos | 19 |
| 6797 | hiciesen | 19 |
| 6798 | hallase | 19 |
| 6799 | hallará | 19 |
| 6800 | gumersindo | 19 |
| 6801 | grosería | 19 |
| 6802 | groseras | 19 |
| 6803 | graciosas | 19 |
| 6804 | goces | 19 |
| 6805 | generosos | 19 |
| 6806 | garrote | 19 |
| 6807 | ganados | 19 |
| 6808 | fuerça | 19 |
| 6809 | fríos | 19 |
| 6810 | follaje | 19 |
| 6811 | finca | 19 |
| 6812 | figuró | 19 |
| 6813 | faser | 19 |
| 6814 | fantástico | 19 |
| 6815 | faga | 19 |
| 6816 | faena | 19 |
| 6817 | extraños | 19 |
| 6818 | expresarse | 19 |
| 6819 | excelentes | 19 |
| 6820 | exaltada | 19 |
| 6821 | estuvimos | 19 |
| 6822 | estacas | 19 |
| 6823 | esposas | 19 |
| 6824 | espesa | 19 |
| 6825 | esmero | 19 |
| 6826 | ermita | 19 |
| 6827 | épocas | 19 |
| 6828 | enviar | 19 |
| 6829 | ensueños | 19 |
| 6830 | enojado | 19 |
| 6831 | enhorabuena | 19 |
| 6832 | embozo | 19 |
| 6833 | eficaz | 19 |
| 6834 | donaires | 19 |
| 6835 | doméstica | 19 |
| 6836 | diziendo | 19 |
| 6837 | divinas | 19 |
| 6838 | distinción | 19 |
| 6839 | disposiciones | 19 |
| 6840 | disgustos | 19 |
| 6841 | discutía | 19 |
| 6842 | díjele | 19 |
| 6843 | digámoslo | 19 |
| 6844 | dichosos | 19 |
| 6845 | diamantes | 19 |
| 6846 | deteniéndose | 19 |
| 6847 | despidieron | 19 |
| 6848 | deshecho | 19 |
| 6849 | deseoso | 19 |
| 6850 | desaire | 19 |
| 6851 | dejándose | 19 |
| 6852 | decreto | 19 |
| 6853 | date | 19 |
| 6854 | dadme | 19 |
| 6855 | cubiertas | 19 |
| 6856 | crece | 19 |
| 6857 | cosillas | 19 |
| 6858 | cortesano | 19 |
| 6859 | coraje | 19 |
| 6860 | coquetería | 19 |
| 6861 | convidado | 19 |
| 6862 | convertir | 19 |
| 6863 | contaban | 19 |
| 6864 | constantemente | 19 |
| 6865 | consecuencias | 19 |
| 6866 | confiesa | 19 |
| 6867 | confidencias | 19 |
| 6868 | concluida | 19 |
| 6869 | concepción | 19 |
| 6870 | comienzo | 19 |
| 6871 | començó | 19 |
| 6872 | clavileño | 19 |
| 6873 | claudia | 19 |
| 6874 | cerco | 19 |
| 6875 | cenizas | 19 |
| 6876 | celebraba | 19 |
| 6877 | ceder | 19 |
| 6878 | castro | 19 |
| 6879 | carneros | 19 |
| 6880 | cargar | 19 |
| 6881 | caracoles | 19 |
| 6882 | cáñamo | 19 |
| 6883 | canela | 19 |
| 6884 | calzones | 19 |
| 6885 | cajones | 19 |
| 6886 | busque | 19 |
| 6887 | buscarme | 19 |
| 6888 | burlado | 19 |
| 6889 | bríos | 19 |
| 6890 | brincos | 19 |
| 6891 | bolsillos | 19 |
| 6892 | bobo | 19 |
| 6893 | bellotas | 19 |
| 6894 | bebió | 19 |
| 6895 | bayona | 19 |
| 6896 | barriga | 19 |
| 6897 | barra | 19 |
| 6898 | báculo | 19 |
| 6899 | ayudado | 19 |
| 6900 | atrevidos | 19 |
| 6901 | asperezas | 19 |
| 6902 | arrancaba | 19 |
| 6903 | arizmendi | 19 |
| 6904 | aquestas | 19 |
| 6905 | apuro | 19 |
| 6906 | apretar | 19 |
| 6907 | apóstol | 19 |
| 6908 | aparente | 19 |
| 6909 | anteriores | 19 |
| 6910 | anhelo | 19 |
| 6911 | angelical | 19 |
| 6912 | ambrosio | 19 |
| 6913 | alzaba | 19 |
| 6914 | alegria | 19 |
| 6915 | agüero | 19 |
| 6916 | aguardando | 19 |
| 6917 | agradeció | 19 |
| 6918 | afortunadamente | 19 |
| 6919 | advertido | 19 |
| 6920 | adoraba | 19 |
| 6921 | acordé | 19 |
| 6922 | acontecimiento | 19 |
| 6923 | acomodó | 19 |
| 6924 | aceptó | 19 |
| 6925 | zapato | 18 |
| 6926 | yeso | 18 |
| 6927 | xi | 18 |
| 6928 | vyno | 18 |
| 6929 | viuir | 18 |
| 6930 | villeneuve | 18 |
| 6931 | vieras | 18 |
| 6932 | vieran | 18 |
| 6933 | víctimas | 18 |
| 6934 | vegadas | 18 |
| 6935 | vallejo | 18 |
| 6936 | vagar | 18 |
| 6937 | vagabunda | 18 |
| 6938 | tuvimos | 18 |
| 6939 | trozos | 18 |
| 6940 | tropel | 18 |
| 6941 | triunfos | 18 |
| 6942 | traya | 18 |
| 6943 | tratara | 18 |
| 6944 | trapera | 18 |
| 6945 | transformación | 18 |
| 6946 | trampas | 18 |
| 6947 | tragar | 18 |
| 6948 | traemos | 18 |
| 6949 | tonos | 18 |
| 6950 | tomarse | 18 |
| 6951 | tomara | 18 |
| 6952 | tila | 18 |
| 6953 | terminar | 18 |
| 6954 | tenías | 18 |
| 6955 | techos | 18 |
| 6956 | supieron | 18 |
| 6957 | sufría | 18 |
| 6958 | sucedieron | 18 |
| 6959 | sorda | 18 |
| 6960 | soñar | 18 |
| 6961 | soñando | 18 |
| 6962 | sombrío | 18 |
| 6963 | solar | 18 |
| 6964 | síntoma | 18 |
| 6965 | simpática | 18 |
| 6966 | sílabas | 18 |
| 6967 | siguen | 18 |
| 6968 | signos | 18 |
| 6969 | sexos | 18 |
| 6970 | señalada | 18 |
| 6971 | seguirle | 18 |
| 6972 | seductor | 18 |
| 6973 | ruinas | 18 |
| 6974 | romero | 18 |
| 6975 | respondo | 18 |
| 6976 | respondiese | 18 |
| 6977 | respiraba | 18 |
| 6978 | repartir | 18 |
| 6979 | remediarlo | 18 |
| 6980 | reducida | 18 |
| 6981 | rebaño | 18 |
| 6982 | realizar | 18 |
| 6983 | re | 18 |
| 6984 | rasgo | 18 |
| 6985 | raros | 18 |
| 6986 | quierer | 18 |
| 6987 | querías | 18 |
| 6988 | quedarme | 18 |
| 6989 | pulgas | 18 |
| 6990 | puerco | 18 |
| 6991 | prosperidad | 18 |
| 6992 | prometer | 18 |
| 6993 | profundos | 18 |
| 6994 | prestaba | 18 |
| 6995 | prensa | 18 |
| 6996 | poquillo | 18 |
| 6997 | poema | 18 |
| 6998 | plazo | 18 |
| 6999 | píldoras | 18 |
| 7000 | pesados | 18 |
| 7001 | permitían | 18 |
| 7002 | perdones | 18 |
| 7003 | pepita | 18 |
| 7004 | penetrar | 18 |
| 7005 | peligrosas | 18 |
| 7006 | patadas | 18 |
| 7007 | parecerá | 18 |
| 7008 | parda | 18 |
| 7009 | paquetes | 18 |
| 7010 | palidez | 18 |
| 7011 | pacífica | 18 |
| 7012 | osuna | 18 |
| 7013 | osado | 18 |
| 7014 | orientales | 18 |
| 7015 | ordinarios | 18 |
| 7016 | opuesto | 18 |
| 7017 | oposición | 18 |
| 7018 | onzas | 18 |
| 7019 | onda | 18 |
| 7020 | ofrecen | 18 |
| 7021 | ociosidad | 18 |
| 7022 | observado | 18 |
| 7023 | obscurecer | 18 |
| 7024 | necesitas | 18 |
| 7025 | náufrago | 18 |
| 7026 | mueva | 18 |
| 7027 | muelle | 18 |
| 7028 | mostraron | 18 |
| 7029 | morisca | 18 |
| 7030 | morenos | 18 |
| 7031 | modesto | 18 |
| 7032 | ministra | 18 |
| 7033 | mesilla | 18 |
| 7034 | merecer | 18 |
| 7035 | menudos | 18 |
| 7036 | memorable | 18 |
| 7037 | melancólica | 18 |
| 7038 | manzana | 18 |
| 7039 | maliciosa | 18 |
| 7040 | malambruno | 18 |
| 7041 | lomo | 18 |
| 7042 | logró | 18 |
| 7043 | llevarme | 18 |
| 7044 | llevara | 18 |
| 7045 | llenar | 18 |
| 7046 | llamábase | 18 |
| 7047 | llagas | 18 |
| 7048 | literato | 18 |
| 7049 | lindas | 18 |
| 7050 | lícito | 18 |
| 7051 | libras | 18 |
| 7052 | librar | 18 |
| 7053 | librada | 18 |
| 7054 | legítimo | 18 |
| 7055 | leandra | 18 |
| 7056 | lanchas | 18 |
| 7057 | indudable | 18 |
| 7058 | independencia | 18 |
| 7059 | imposibilidad | 18 |
| 7060 | impedir | 18 |
| 7061 | hubiesen | 18 |
| 7062 | horca | 18 |
| 7063 | honroso | 18 |
| 7064 | historiador | 18 |
| 7065 | hideputa | 18 |
| 7066 | herir | 18 |
| 7067 | hazen | 18 |
| 7068 | harás | 18 |
| 7069 | hallara | 18 |
| 7070 | hablará | 18 |
| 7071 | guapas | 18 |
| 7072 | gramática | 18 |
| 7073 | gordos | 18 |
| 7074 | gobierna | 18 |
| 7075 | galerías | 18 |
| 7076 | fúnebre | 18 |
| 7077 | fuime | 18 |
| 7078 | frenesí | 18 |
| 7079 | finísimo | 18 |
| 7080 | fingido | 18 |
| 7081 | filósofos | 18 |
| 7082 | ferido | 18 |
| 7083 | fenelón | 18 |
| 7084 | felipe | 18 |
| 7085 | extendió | 18 |
| 7086 | explicación | 18 |
| 7087 | excursiones | 18 |
| 7088 | etiqueta | 18 |
| 7089 | estremeció | 18 |
| 7090 | estarían | 18 |
| 7091 | escritores | 18 |
| 7092 | escogido | 18 |
| 7093 | escoba | 18 |
| 7094 | envolvía | 18 |
| 7095 | entregar | 18 |
| 7096 | entrecejo | 18 |
| 7097 | enojos | 18 |
| 7098 | encantamentos | 18 |
| 7099 | enamora | 18 |
| 7100 | empresas | 18 |
| 7101 | embajada | 18 |
| 7102 | duermen | 18 |
| 7103 | dormirse | 18 |
| 7104 | dondequiera | 18 |
| 7105 | disimulando | 18 |
| 7106 | discutir | 18 |
| 7107 | discurrir | 18 |
| 7108 | difíciles | 18 |
| 7109 | diccionario | 18 |
| 7110 | deue | 18 |
| 7111 | desiertos | 18 |
| 7112 | dese | 18 |
| 7113 | descuidado | 18 |
| 7114 | descuida | 18 |
| 7115 | descubriese | 18 |
| 7116 | descubriendo | 18 |
| 7117 | descargó | 18 |
| 7118 | débiles | 18 |
| 7119 | darás | 18 |
| 7120 | cursi | 18 |
| 7121 | cupido | 18 |
| 7122 | cumpla | 18 |
| 7123 | culebras | 18 |
| 7124 | cuidadosamente | 18 |
| 7125 | cuervos | 18 |
| 7126 | cubrir | 18 |
| 7127 | cuadra | 18 |
| 7128 | correspondiente | 18 |
| 7129 | correspondía | 18 |
| 7130 | contentó | 18 |
| 7131 | consternación | 18 |
| 7132 | consolar | 18 |
| 7133 | consentía | 18 |
| 7134 | compostura | 18 |
| 7135 | complir | 18 |
| 7136 | comparar | 18 |
| 7137 | compañías | 18 |
| 7138 | combinaciones | 18 |
| 7139 | colocación | 18 |
| 7140 | colchones | 18 |
| 7141 | cogiéndola | 18 |
| 7142 | cocinera | 18 |
| 7143 | cobardes | 18 |
| 7144 | clavó | 18 |
| 7145 | claustro | 18 |
| 7146 | citas | 18 |
| 7147 | çielo | 18 |
| 7148 | chistes | 18 |
| 7149 | china | 18 |
| 7150 | céntimos | 18 |
| 7151 | cenador | 18 |
| 7152 | cautiverio | 18 |
| 7153 | cauallero | 18 |
| 7154 | case | 18 |
| 7155 | cántaro | 18 |
| 7156 | calleja | 18 |
| 7157 | caí | 18 |
| 7158 | cabreros | 18 |
| 7159 | cabestro | 18 |
| 7160 | cabeça | 18 |
| 7161 | cabal | 18 |
| 7162 | bulla | 18 |
| 7163 | boticario | 18 |
| 7164 | boina | 18 |
| 7165 | benengeli | 18 |
| 7166 | bayeta | 18 |
| 7167 | base | 18 |
| 7168 | bárbaros | 18 |
| 7169 | banderas | 18 |
| 7170 | ayo | 18 |
| 7171 | aventurero | 18 |
| 7172 | atentos | 18 |
| 7173 | atendiendo | 18 |
| 7174 | atada | 18 |
| 7175 | asy | 18 |
| 7176 | arrobas | 18 |
| 7177 | arrimado | 18 |
| 7178 | arrancó | 18 |
| 7179 | apuros | 18 |
| 7180 | apoyaba | 18 |
| 7181 | aparece | 18 |
| 7182 | amador | 18 |
| 7183 | alvar | 18 |
| 7184 | aldeano | 18 |
| 7185 | alborotado | 18 |
| 7186 | alargando | 18 |
| 7187 | ahorrar | 18 |
| 7188 | agradables | 18 |
| 7189 | ageno | 18 |
| 7190 | adulterio | 18 |
| 7191 | adquirido | 18 |
| 7192 | adelantó | 18 |
| 7193 | acordado | 18 |
| 7194 | acercaban | 18 |
| 7195 | acecho | 18 |
| 7196 | accidentes | 18 |
| 7197 | aburrido | 18 |
| 7198 | aburría | 18 |
| 7199 | aborrezco | 18 |
| 7200 | abencerraje | 18 |
| 7201 | zozobra | 17 |
| 7202 | yacía | 17 |
| 7203 | xvi | 17 |
| 7204 | xv | 17 |
| 7205 | vocación | 17 |
| 7206 | vives | 17 |
| 7207 | visera | 17 |
| 7208 | villana | 17 |
| 7209 | vidrio | 17 |
| 7210 | viciosa | 17 |
| 7211 | vernos | 17 |
| 7212 | vence | 17 |
| 7213 | vehemencia | 17 |
| 7214 | vecindario | 17 |
| 7215 | vasos | 17 |
| 7216 | vasallo | 17 |
| 7217 | vaciló | 17 |
| 7218 | turno | 17 |
| 7219 | tuertos | 17 |
| 7220 | troyas | 17 |
| 7221 | trono | 17 |
| 7222 | tratamiento | 17 |
| 7223 | trasto | 17 |
| 7224 | tragos | 17 |
| 7225 | trago | 17 |
| 7226 | tomarlo | 17 |
| 7227 | tomaría | 17 |
| 7228 | tocayo | 17 |
| 7229 | tintero | 17 |
| 7230 | ternera | 17 |
| 7231 | tercio | 17 |
| 7232 | temporal | 17 |
| 7233 | telón | 17 |
| 7234 | teja | 17 |
| 7235 | tálamo | 17 |
| 7236 | tabaco | 17 |
| 7237 | suplicio | 17 |
| 7238 | supersticioso | 17 |
| 7239 | sufrimiento | 17 |
| 7240 | sueno | 17 |
| 7241 | suegro | 17 |
| 7242 | sucediese | 17 |
| 7243 | sublimes | 17 |
| 7244 | sostenían | 17 |
| 7245 | soltaba | 17 |
| 7246 | sobrenatural | 17 |
| 7247 | sobremanera | 17 |
| 7248 | sirviendo | 17 |
| 7249 | simplicidad | 17 |
| 7250 | seriamente | 17 |
| 7251 | sentençia | 17 |
| 7252 | seducción | 17 |
| 7253 | seáis | 17 |
| 7254 | satisfechos | 17 |
| 7255 | sardinas | 17 |
| 7256 | saludable | 17 |
| 7257 | saldré | 17 |
| 7258 | sagaz | 17 |
| 7259 | sacarla | 17 |
| 7260 | sabroso | 17 |
| 7261 | sabrosa | 17 |
| 7262 | sabrás | 17 |
| 7263 | sábana | 17 |
| 7264 | rumbo | 17 |
| 7265 | rudo | 17 |
| 7266 | ronco | 17 |
| 7267 | rojos | 17 |
| 7268 | rodela | 17 |
| 7269 | rodeaba | 17 |
| 7270 | rió | 17 |
| 7271 | rinconada | 17 |
| 7272 | riéndose | 17 |
| 7273 | revolviendo | 17 |
| 7274 | resucitar | 17 |
| 7275 | responda | 17 |
| 7276 | residencia | 17 |
| 7277 | repuesto | 17 |
| 7278 | religiosas | 17 |
| 7279 | relativa | 17 |
| 7280 | referente | 17 |
| 7281 | quitándose | 17 |
| 7282 | quisiesen | 17 |
| 7283 | quema | 17 |
| 7284 | quedos | 17 |
| 7285 | queden | 17 |
| 7286 | quédate | 17 |
| 7287 | prudentes | 17 |
| 7288 | provisiones | 17 |
| 7289 | proposito | 17 |
| 7290 | propaganda | 17 |
| 7291 | programa | 17 |
| 7292 | prodigio | 17 |
| 7293 | probarlo | 17 |
| 7294 | privilegio | 17 |
| 7295 | privado | 17 |
| 7296 | preparada | 17 |
| 7297 | predicar | 17 |
| 7298 | predicador | 17 |
| 7299 | podríamos | 17 |
| 7300 | poderlo | 17 |
| 7301 | place | 17 |
| 7302 | pinturas | 17 |
| 7303 | pesadas | 17 |
| 7304 | perseguido | 17 |
| 7305 | perla | 17 |
| 7306 | perdices | 17 |
| 7307 | percal | 17 |
| 7308 | peldaños | 17 |
| 7309 | pecadores | 17 |
| 7310 | paternal | 17 |
| 7311 | paseándose | 17 |
| 7312 | parejas | 17 |
| 7313 | parayso | 17 |
| 7314 | palmada | 17 |
| 7315 | pajes | 17 |
| 7316 | pagaré | 17 |
| 7317 | pagan | 17 |
| 7318 | ofreciendo | 17 |
| 7319 | ofende | 17 |
| 7320 | oculto | 17 |
| 7321 | obstáculo | 17 |
| 7322 | obediencia | 17 |
| 7323 | navidad | 17 |
| 7324 | nata | 17 |
| 7325 | mudos | 17 |
| 7326 | mu | 17 |
| 7327 | monarquía | 17 |
| 7328 | molesto | 17 |
| 7329 | modista | 17 |
| 7330 | místicas | 17 |
| 7331 | mimos | 17 |
| 7332 | migas | 17 |
| 7333 | mensaje | 17 |
| 7334 | mejoría | 17 |
| 7335 | mediana | 17 |
| 7336 | mayorazgo | 17 |
| 7337 | mataron | 17 |
| 7338 | mantilla | 17 |
| 7339 | mansedumbre | 17 |
| 7340 | malicioso | 17 |
| 7341 | malicias | 17 |
| 7342 | malandrines | 17 |
| 7343 | maderas | 17 |
| 7344 | llorado | 17 |
| 7345 | llevaría | 17 |
| 7346 | llevaré | 17 |
| 7347 | llegaría | 17 |
| 7348 | llamarle | 17 |
| 7349 | lindos | 17 |
| 7350 | ligeros | 17 |
| 7351 | ligeras | 17 |
| 7352 | levantose | 17 |
| 7353 | letrado | 17 |
| 7354 | leopoldo | 17 |
| 7355 | lascivo | 17 |
| 7356 | lápiz | 17 |
| 7357 | lágrima | 17 |
| 7358 | juguetes | 17 |
| 7359 | jergón | 17 |
| 7360 | inverosímil | 17 |
| 7361 | intensa | 17 |
| 7362 | inmortal | 17 |
| 7363 | iniciativa | 17 |
| 7364 | infidelidad | 17 |
| 7365 | indulgencia | 17 |
| 7366 | incredulidad | 17 |
| 7367 | inclinando | 17 |
| 7368 | imaginó | 17 |
| 7369 | ilustres | 17 |
| 7370 | ideales | 17 |
| 7371 | huele | 17 |
| 7372 | hoyo | 17 |
| 7373 | horriblemente | 17 |
| 7374 | hondas | 17 |
| 7375 | honda | 17 |
| 7376 | hízose | 17 |
| 7377 | hereje | 17 |
| 7378 | hércules | 17 |
| 7379 | hebra | 17 |
| 7380 | hare | 17 |
| 7381 | hacernos | 17 |
| 7382 | hablarte | 17 |
| 7383 | gustado | 17 |
| 7384 | guíe | 17 |
| 7385 | gritaron | 17 |
| 7386 | gordas | 17 |
| 7387 | golosina | 17 |
| 7388 | generalmente | 17 |
| 7389 | gastado | 17 |
| 7390 | ganancias | 17 |
| 7391 | gallos | 17 |
| 7392 | galicia | 17 |
| 7393 | galera | 17 |
| 7394 | gaiferos | 17 |
| 7395 | fórmulas | 17 |
| 7396 | flaquezas | 17 |
| 7397 | flacos | 17 |
| 7398 | fazes | 17 |
| 7399 | excursión | 17 |
| 7400 | exclusivamente | 17 |
| 7401 | excitado | 17 |
| 7402 | examinando | 17 |
| 7403 | exaltado | 17 |
| 7404 | estremos | 17 |
| 7405 | estrañas | 17 |
| 7406 | estorbo | 17 |
| 7407 | espacioso | 17 |
| 7408 | escuadras | 17 |
| 7409 | escriba | 17 |
| 7410 | escapado | 17 |
| 7411 | equivocación | 17 |
| 7412 | envueltos | 17 |
| 7413 | entremos | 17 |
| 7414 | entendiendo | 17 |
| 7415 | ensalada | 17 |
| 7416 | engañas | 17 |
| 7417 | encerró | 17 |
| 7418 | enamorarse | 17 |
| 7419 | enaguas | 17 |
| 7420 | empiezan | 17 |
| 7421 | elogios | 17 |
| 7422 | elección | 17 |
| 7423 | ejércitos | 17 |
| 7424 | egipto | 17 |
| 7425 | duraba | 17 |
| 7426 | duermo | 17 |
| 7427 | disponía | 17 |
| 7428 | dispense | 17 |
| 7429 | disimulaba | 17 |
| 7430 | diome | 17 |
| 7431 | dijere | 17 |
| 7432 | digáis | 17 |
| 7433 | dificultoso | 17 |
| 7434 | diciéndome | 17 |
| 7435 | diariamente | 17 |
| 7436 | desvaríos | 17 |
| 7437 | destierro | 17 |
| 7438 | despedir | 17 |
| 7439 | desnudez | 17 |
| 7440 | desiguales | 17 |
| 7441 | deshacer | 17 |
| 7442 | desastre | 17 |
| 7443 | desaparecía | 17 |
| 7444 | desaparecer | 17 |
| 7445 | desaguisado | 17 |
| 7446 | dependientes | 17 |
| 7447 | delicados | 17 |
| 7448 | dejándole | 17 |
| 7449 | declarado | 17 |
| 7450 | decidme | 17 |
| 7451 | debieron | 17 |
| 7452 | curvas | 17 |
| 7453 | curado | 17 |
| 7454 | cuellos | 17 |
| 7455 | cubre | 17 |
| 7456 | cruzó | 17 |
| 7457 | crudo | 17 |
| 7458 | crímenes | 17 |
| 7459 | cosecha | 17 |
| 7460 | corteza | 17 |
| 7461 | cortada | 17 |
| 7462 | corrientes | 17 |
| 7463 | coronas | 17 |
| 7464 | corchetes | 17 |
| 7465 | convertía | 17 |
| 7466 | contesta | 17 |
| 7467 | contentaba | 17 |
| 7468 | consultar | 17 |
| 7469 | construcción | 17 |
| 7470 | conserva | 17 |
| 7471 | conocidas | 17 |
| 7472 | conocerle | 17 |
| 7473 | conduce | 17 |
| 7474 | concluía | 17 |
| 7475 | conchas | 17 |
| 7476 | comunicar | 17 |
| 7477 | comisario | 17 |
| 7478 | colocado | 17 |
| 7479 | colgando | 17 |
| 7480 | clavaba | 17 |
| 7481 | circunstancia | 17 |
| 7482 | choza | 17 |
| 7483 | chocar | 17 |
| 7484 | chiste | 17 |
| 7485 | charlando | 17 |
| 7486 | çerca | 17 |
| 7487 | ceñida | 17 |
| 7488 | cent | 17 |
| 7489 | celosía | 17 |
| 7490 | cazadores | 17 |
| 7491 | causar | 17 |
| 7492 | castelar | 17 |
| 7493 | casiana | 17 |
| 7494 | carecía | 17 |
| 7495 | capacho | 17 |
| 7496 | candor | 17 |
| 7497 | candelaria | 17 |
| 7498 | cállese | 17 |
| 7499 | calderón | 17 |
| 7500 | busto | 17 |
| 7501 | buscas | 17 |
| 7502 | buey | 17 |
| 7503 | bruja | 17 |
| 7504 | brocado | 17 |
| 7505 | bravos | 17 |
| 7506 | boz | 17 |
| 7507 | botellas | 17 |
| 7508 | bonitos | 17 |
| 7509 | bienestar | 17 |
| 7510 | bando | 17 |
| 7511 | bajeza | 17 |
| 7512 | avaricia | 17 |
| 7513 | atocha | 17 |
| 7514 | ataques | 17 |
| 7515 | asusta | 17 |
| 7516 | asombrado | 17 |
| 7517 | aseguró | 17 |
| 7518 | asalto | 17 |
| 7519 | arrojarse | 17 |
| 7520 | arrepentido | 17 |
| 7521 | arrancar | 17 |
| 7522 | arqueólogo | 17 |
| 7523 | armario | 17 |
| 7524 | ardientes | 17 |
| 7525 | apuntar | 17 |
| 7526 | apuesto | 17 |
| 7527 | aprovechó | 17 |
| 7528 | antojo | 17 |
| 7529 | ansy | 17 |
| 7530 | angustias | 17 |
| 7531 | andad | 17 |
| 7532 | aldeanos | 17 |
| 7533 | ajedrez | 17 |
| 7534 | airado | 17 |
| 7535 | agraviado | 17 |
| 7536 | africano | 17 |
| 7537 | afligido | 17 |
| 7538 | advierta | 17 |
| 7539 | advertid | 17 |
| 7540 | admirada | 17 |
| 7541 | adivinar | 17 |
| 7542 | ademanes | 17 |
| 7543 | acullá | 17 |
| 7544 | acostado | 17 |
| 7545 | acontecimientos | 17 |
| 7546 | acomodado | 17 |
| 7547 | acabara | 17 |
| 7548 | zoraid | 16 |
| 7549 | zas | 16 |
| 7550 | yugo | 16 |
| 7551 | xxiv | 16 |
| 7552 | viviera | 16 |
| 7553 | violín | 16 |
| 7554 | violenta | 16 |
| 7555 | vigor | 16 |
| 7556 | vieres | 16 |
| 7557 | vidrieras | 16 |
| 7558 | viajar | 16 |
| 7559 | verlos | 16 |
| 7560 | verbo | 16 |
| 7561 | veinticuatro | 16 |
| 7562 | vacíos | 16 |
| 7563 | uvas | 16 |
| 7564 | universidad | 16 |
| 7565 | tuyos | 16 |
| 7566 | tuviere | 16 |
| 7567 | truchas | 16 |
| 7568 | tropas | 16 |
| 7569 | traygo | 16 |
| 7570 | travieso | 16 |
| 7571 | traté | 16 |
| 7572 | tradición | 16 |
| 7573 | torné | 16 |
| 7574 | tontas | 16 |
| 7575 | tipos | 16 |
| 7576 | tibia | 16 |
| 7577 | tertulias | 16 |
| 7578 | tened | 16 |
| 7579 | tendidos | 16 |
| 7580 | templado | 16 |
| 7581 | tabique | 16 |
| 7582 | suplicó | 16 |
| 7583 | sufre | 16 |
| 7584 | suelos | 16 |
| 7585 | suela | 16 |
| 7586 | ssy | 16 |
| 7587 | sostengo | 16 |
| 7588 | solitaria | 16 |
| 7589 | sobrinas | 16 |
| 7590 | sobrado | 16 |
| 7591 | sintiéndose | 16 |
| 7592 | siéntate | 16 |
| 7593 | servidor | 16 |
| 7594 | servida | 16 |
| 7595 | serios | 16 |
| 7596 | serie | 16 |
| 7597 | sepamos | 16 |
| 7598 | seminario | 16 |
| 7599 | satisfación | 16 |
| 7600 | sarta | 16 |
| 7601 | santiago | 16 |
| 7602 | salvarse | 16 |
| 7603 | saltaban | 16 |
| 7604 | sacudir | 16 |
| 7605 | sacudiendo | 16 |
| 7606 | rufianes | 16 |
| 7607 | rotos | 16 |
| 7608 | ropilla | 16 |
| 7609 | rogado | 16 |
| 7610 | robustos | 16 |
| 7611 | robles | 16 |
| 7612 | rigurosa | 16 |
| 7613 | ría | 16 |
| 7614 | revuelto | 16 |
| 7615 | retor | 16 |
| 7616 | resumen | 16 |
| 7617 | respiró | 16 |
| 7618 | respectivas | 16 |
| 7619 | resolver | 16 |
| 7620 | requiere | 16 |
| 7621 | reposado | 16 |
| 7622 | repite | 16 |
| 7623 | renunciar | 16 |
| 7624 | renglón | 16 |
| 7625 | remate | 16 |
| 7626 | referidas | 16 |
| 7627 | recuerda | 16 |
| 7628 | reconociendo | 16 |
| 7629 | racional | 16 |
| 7630 | pucheros | 16 |
| 7631 | propiamente | 16 |
| 7632 | procedía | 16 |
| 7633 | presumir | 16 |
| 7634 | prestó | 16 |
| 7635 | presenciar | 16 |
| 7636 | preparando | 16 |
| 7637 | preciosas | 16 |
| 7638 | pontejos | 16 |
| 7639 | podrida | 16 |
| 7640 | podra | 16 |
| 7641 | pobrecilla | 16 |
| 7642 | pleb | 16 |
| 7643 | plano | 16 |
| 7644 | pizca | 16 |
| 7645 | pintó | 16 |
| 7646 | picaresca | 16 |
| 7647 | pescador | 16 |
| 7648 | perpetuo | 16 |
| 7649 | perpetua | 16 |
| 7650 | permanecer | 16 |
| 7651 | perdiz | 16 |
| 7652 | pensáis | 16 |
| 7653 | penitente | 16 |
| 7654 | pendencias | 16 |
| 7655 | penado | 16 |
| 7656 | pellizcos | 16 |
| 7657 | pegada | 16 |
| 7658 | pavimento | 16 |
| 7659 | patriotismo | 16 |
| 7660 | patente | 16 |
| 7661 | pasta | 16 |
| 7662 | passada | 16 |
| 7663 | parienta | 16 |
| 7664 | pardas | 16 |
| 7665 | paradero | 16 |
| 7666 | paquete | 16 |
| 7667 | papeletas | 16 |
| 7668 | panes | 16 |
| 7669 | palas | 16 |
| 7670 | oyose | 16 |
| 7671 | oydos | 16 |
| 7672 | oveja | 16 |
| 7673 | otoño | 16 |
| 7674 | oponerse | 16 |
| 7675 | olores | 16 |
| 7676 | ojuelos | 16 |
| 7677 | oir | 16 |
| 7678 | observador | 16 |
| 7679 | observa | 16 |
| 7680 | obscuros | 16 |
| 7681 | obligar | 16 |
| 7682 | numantinos | 16 |
| 7683 | numantino | 16 |
| 7684 | nudos | 16 |
| 7685 | nombrado | 16 |
| 7686 | necesitó | 16 |
| 7687 | necesarios | 16 |
| 7688 | narración | 16 |
| 7689 | naranja | 16 |
| 7690 | músicos | 16 |
| 7691 | murmuración | 16 |
| 7692 | municipal | 16 |
| 7693 | mudanzas | 16 |
| 7694 | mudado | 16 |
| 7695 | mostrándose | 16 |
| 7696 | mortificaba | 16 |
| 7697 | moribundo | 16 |
| 7698 | mordía | 16 |
| 7699 | morder | 16 |
| 7700 | moradas | 16 |
| 7701 | molestar | 16 |
| 7702 | mochas | 16 |
| 7703 | mineral | 16 |
| 7704 | miedos | 16 |
| 7705 | micomicona | 16 |
| 7706 | mezquina | 16 |
| 7707 | metieron | 16 |
| 7708 | mendigos | 16 |
| 7709 | meditar | 16 |
| 7710 | medianamente | 16 |
| 7711 | matemáticas | 16 |
| 7712 | marién | 16 |
| 7713 | marchó | 16 |
| 7714 | manolita | 16 |
| 7715 | manifestaba | 16 |
| 7716 | manías | 16 |
| 7717 | mandando | 16 |
| 7718 | manana | 16 |
| 7719 | maguer | 16 |
| 7720 | magdalena | 16 |
| 7721 | llevará | 16 |
| 7722 | llenaban | 16 |
| 7723 | limpios | 16 |
| 7724 | ligas | 16 |
| 7725 | libertino | 16 |
| 7726 | leyese | 16 |
| 7727 | levante | 16 |
| 7728 | levantan | 16 |
| 7729 | lento | 16 |
| 7730 | latines | 16 |
| 7731 | látigo | 16 |
| 7732 | lagrimas | 16 |
| 7733 | ladrona | 16 |
| 7734 | kempis | 16 |
| 7735 | jerónima | 16 |
| 7736 | interesaba | 16 |
| 7737 | inquieta | 16 |
| 7738 | injuria | 16 |
| 7739 | infanzón | 16 |
| 7740 | indulgente | 16 |
| 7741 | importuna | 16 |
| 7742 | impide | 16 |
| 7743 | igualdad | 16 |
| 7744 | huéspeda | 16 |
| 7745 | hube | 16 |
| 7746 | honrrada | 16 |
| 7747 | honrar | 16 |
| 7748 | hoguera | 16 |
| 7749 | histórico | 16 |
| 7750 | hiel | 16 |
| 7751 | helado | 16 |
| 7752 | hallando | 16 |
| 7753 | hala | 16 |
| 7754 | habitual | 16 |
| 7755 | gustaban | 16 |
| 7756 | gula | 16 |
| 7757 | grita | 16 |
| 7758 | griegos | 16 |
| 7759 | grata | 16 |
| 7760 | granos | 16 |
| 7761 | golosinas | 16 |
| 7762 | gitanilla | 16 |
| 7763 | gano | 16 |
| 7764 | galardon | 16 |
| 7765 | fundar | 16 |
| 7766 | fugitiva | 16 |
| 7767 | frecuentes | 16 |
| 7768 | fragata | 16 |
| 7769 | forzado | 16 |
| 7770 | forzada | 16 |
| 7771 | formada | 16 |
| 7772 | flamenco | 16 |
| 7773 | fingió | 16 |
| 7774 | finge | 16 |
| 7775 | filomenas | 16 |
| 7776 | fijas | 16 |
| 7777 | feos | 16 |
| 7778 | fechos | 16 |
| 7779 | famosas | 16 |
| 7780 | faltando | 16 |
| 7781 | exposición | 16 |
| 7782 | explicarse | 16 |
| 7783 | expedición | 16 |
| 7784 | etcétera | 16 |
| 7785 | estupor | 16 |
| 7786 | estudiado | 16 |
| 7787 | estudiaba | 16 |
| 7788 | estremecer | 16 |
| 7789 | estraños | 16 |
| 7790 | estéril | 16 |
| 7791 | estarás | 16 |
| 7792 | essas | 16 |
| 7793 | espinazo | 16 |
| 7794 | esencia | 16 |
| 7795 | escondidas | 16 |
| 7796 | esconder | 16 |
| 7797 | escenario | 16 |
| 7798 | escapa | 16 |
| 7799 | erudición | 16 |
| 7800 | envoltorio | 16 |
| 7801 | entregaba | 16 |
| 7802 | entrega | 16 |
| 7803 | enseñando | 16 |
| 7804 | enrique | 16 |
| 7805 | engañan | 16 |
| 7806 | énfasis | 16 |
| 7807 | eneas | 16 |
| 7808 | encuentre | 16 |
| 7809 | encinas | 16 |
| 7810 | encantadora | 16 |
| 7811 | elogio | 16 |
| 7812 | echase | 16 |
| 7813 | durar | 16 |
| 7814 | duermes | 16 |
| 7815 | duelos | 16 |
| 7816 | doblar | 16 |
| 7817 | divertía | 16 |
| 7818 | distracción | 16 |
| 7819 | dispone | 16 |
| 7820 | disparar | 16 |
| 7821 | digamos | 16 |
| 7822 | dígale | 16 |
| 7823 | difunta | 16 |
| 7824 | difícilmente | 16 |
| 7825 | diéronle | 16 |
| 7826 | diciéndoles | 16 |
| 7827 | diciembre | 16 |
| 7828 | devoraba | 16 |
| 7829 | detalles | 16 |
| 7830 | déstos | 16 |
| 7831 | desmayado | 16 |
| 7832 | desengaños | 16 |
| 7833 | descuide | 16 |
| 7834 | descomunal | 16 |
| 7835 | desatinos | 16 |
| 7836 | desahogo | 16 |
| 7837 | derribado | 16 |
| 7838 | derramar | 16 |
| 7839 | demasiadamente | 16 |
| 7840 | delitos | 16 |
| 7841 | deliciosa | 16 |
| 7842 | delantero | 16 |
| 7843 | delantera | 16 |
| 7844 | deis | 16 |
| 7845 | deidad | 16 |
| 7846 | defiende | 16 |
| 7847 | decisión | 16 |
| 7848 | decimos | 16 |
| 7849 | decide | 16 |
| 7850 | dalle | 16 |
| 7851 | dais | 16 |
| 7852 | cumplió | 16 |
| 7853 | culpable | 16 |
| 7854 | cuadrado | 16 |
| 7855 | crónica | 16 |
| 7856 | cristianas | 16 |
| 7857 | crepúsculo | 16 |
| 7858 | cráneo | 16 |
| 7859 | cosarios | 16 |
| 7860 | cortesías | 16 |
| 7861 | corrillo | 16 |
| 7862 | corra | 16 |
| 7863 | convirtió | 16 |
| 7864 | convinieron | 16 |
| 7865 | convenido | 16 |
| 7866 | contuvo | 16 |
| 7867 | contentarse | 16 |
| 7868 | contenido | 16 |
| 7869 | contarse | 16 |
| 7870 | consolaba | 16 |
| 7871 | consentimiento | 16 |
| 7872 | conpaña | 16 |
| 7873 | congoja | 16 |
| 7874 | confirmó | 16 |
| 7875 | condenados | 16 |
| 7876 | condena | 16 |
| 7877 | concedido | 16 |
| 7878 | comunidad | 16 |
| 7879 | comunicación | 16 |
| 7880 | comulgar | 16 |
| 7881 | comprendí | 16 |
| 7882 | comprendes | 16 |
| 7883 | cómplice | 16 |
| 7884 | cómicos | 16 |
| 7885 | cometer | 16 |
| 7886 | comes | 16 |
| 7887 | com | 16 |
| 7888 | colchón | 16 |
| 7889 | cibdad | 16 |
| 7890 | charcos | 16 |
| 7891 | chamberí | 16 |
| 7892 | cerros | 16 |
| 7893 | cerro | 16 |
| 7894 | cerebral | 16 |
| 7895 | cercana | 16 |
| 7896 | celind | 16 |
| 7897 | celda | 16 |
| 7898 | ceguera | 16 |
| 7899 | cedrón | 16 |
| 7900 | cazar | 16 |
| 7901 | cátedra | 16 |
| 7902 | catecismo | 16 |
| 7903 | catástrofe | 16 |
| 7904 | castiga | 16 |
| 7905 | castellanos | 16 |
| 7906 | cartama | 16 |
| 7907 | cargadas | 16 |
| 7908 | capaces | 16 |
| 7909 | cantan | 16 |
| 7910 | cándido | 16 |
| 7911 | callaban | 16 |
| 7912 | caigo | 16 |
| 7913 | caber | 16 |
| 7914 | cabaña | 16 |
| 7915 | buscan | 16 |
| 7916 | bultos | 16 |
| 7917 | brinco | 16 |
| 7918 | braulio | 16 |
| 7919 | blandura | 16 |
| 7920 | bernarda | 16 |
| 7921 | bellos | 16 |
| 7922 | basilisco | 16 |
| 7923 | banda | 16 |
| 7924 | bailando | 16 |
| 7925 | baila | 16 |
| 7926 | avergonzado | 16 |
| 7927 | avanzaba | 16 |
| 7928 | aumentó | 16 |
| 7929 | aumento | 16 |
| 7930 | aumentar | 16 |
| 7931 | atiende | 16 |
| 7932 | áspero | 16 |
| 7933 | asiéndole | 16 |
| 7934 | asida | 16 |
| 7935 | ardiendo | 16 |
| 7936 | apolo | 16 |
| 7937 | aplicar | 16 |
| 7938 | aplauso | 16 |
| 7939 | apartándose | 16 |
| 7940 | apartaba | 16 |
| 7941 | aparecieron | 16 |
| 7942 | anunció | 16 |
| 7943 | antipatía | 16 |
| 7944 | ansimesmo | 16 |
| 7945 | ano | 16 |
| 7946 | alegrar | 16 |
| 7947 | alegra | 16 |
| 7948 | alcornoque | 16 |
| 7949 | alcanzaba | 16 |
| 7950 | alborotada | 16 |
| 7951 | albedrío | 16 |
| 7952 | álava | 16 |
| 7953 | agudeza | 16 |
| 7954 | aguardaba | 16 |
| 7955 | agradecer | 16 |
| 7956 | agitación | 16 |
| 7957 | aflicción | 16 |
| 7958 | adivinaba | 16 |
| 7959 | acompañando | 16 |
| 7960 | acercando | 16 |
| 7961 | absorto | 16 |
| 7962 | xix | 15 |
| 7963 | volviose | 15 |
| 7964 | voló | 15 |
| 7965 | vnas | 15 |
| 7966 | vivan | 15 |
| 7967 | virrey | 15 |
| 7968 | vergonzosa | 15 |
| 7969 | vente | 15 |
| 7970 | venideros | 15 |
| 7971 | vello | 15 |
| 7972 | valles | 15 |
| 7973 | valerosa | 15 |
| 7974 | vagos | 15 |
| 7975 | usaban | 15 |
| 7976 | urgente | 15 |
| 7977 | tropezó | 15 |
| 7978 | tristan | 15 |
| 7979 | trastorno | 15 |
| 7980 | trascava | 15 |
| 7981 | traidores | 15 |
| 7982 | trabajado | 15 |
| 7983 | tostado | 15 |
| 7984 | toquilla | 15 |
| 7985 | topé | 15 |
| 7986 | tomas | 15 |
| 7987 | tomaré | 15 |
| 7988 | tirado | 15 |
| 7989 | tinte | 15 |
| 7990 | tímidamente | 15 |
| 7991 | terra | 15 |
| 7992 | tenerse | 15 |
| 7993 | tenderos | 15 |
| 7994 | tenazas | 15 |
| 7995 | temió | 15 |
| 7996 | temeridad | 15 |
| 7997 | temerario | 15 |
| 7998 | tembló | 15 |
| 7999 | temblaban | 15 |
| 8000 | tardaba | 15 |
| 8001 | tapa | 15 |
| 8002 | tabernas | 15 |
| 8003 | suspender | 15 |
| 8004 | sucedía | 15 |
| 8005 | subí | 15 |
| 8006 | suben | 15 |
| 8007 | sorprendió | 15 |
| 8008 | soplaba | 15 |
| 8009 | sonetos | 15 |
| 8010 | sombreros | 15 |
| 8011 | soltura | 15 |
| 8012 | solemnemente | 15 |
| 8013 | soledades | 15 |
| 8014 | siruientes | 15 |
| 8015 | serias | 15 |
| 8016 | señaló | 15 |
| 8017 | sentóse | 15 |
| 8018 | selva | 15 |
| 8019 | sarna | 15 |
| 8020 | sañudo | 15 |
| 8021 | sans | 15 |
| 8022 | salones | 15 |
| 8023 | saetas | 15 |
| 8024 | sacara | 15 |
| 8025 | sabrosas | 15 |
| 8026 | rrey | 15 |
| 8027 | rossini | 15 |
| 8028 | romana | 15 |
| 8029 | rodearon | 15 |
| 8030 | rocío | 15 |
| 8031 | rióse | 15 |
| 8032 | rianzares | 15 |
| 8033 | revueltos | 15 |
| 8034 | reunir | 15 |
| 8035 | reunión | 15 |
| 8036 | retiraron | 15 |
| 8037 | responsable | 15 |
| 8038 | resistía | 15 |
| 8039 | remota | 15 |
| 8040 | reído | 15 |
| 8041 | regalado | 15 |
| 8042 | reflejos | 15 |
| 8043 | redactor | 15 |
| 8044 | recompensa | 15 |
| 8045 | recibían | 15 |
| 8046 | reciba | 15 |
| 8047 | ras | 15 |
| 8048 | rancho | 15 |
| 8049 | racimo | 15 |
| 8050 | rabo | 15 |
| 8051 | quítate | 15 |
| 8052 | quieta | 15 |
| 8053 | quiebra | 15 |
| 8054 | querella | 15 |
| 8055 | quaresma | 15 |
| 8056 | puñetazo | 15 |
| 8057 | puntería | 15 |
| 8058 | pulmonía | 15 |
| 8059 | prontamente | 15 |
| 8060 | prometía | 15 |
| 8061 | profeso | 15 |
| 8062 | procurado | 15 |
| 8063 | préstamos | 15 |
| 8064 | presión | 15 |
| 8065 | presentaron | 15 |
| 8066 | preguntóme | 15 |
| 8067 | preguntaban | 15 |
| 8068 | posturas | 15 |
| 8069 | pondrá | 15 |
| 8070 | políticos | 15 |
| 8071 | polidura | 15 |
| 8072 | podréis | 15 |
| 8073 | poderosas | 15 |
| 8074 | pliegos | 15 |
| 8075 | pisos | 15 |
| 8076 | pisadas | 15 |
| 8077 | pillos | 15 |
| 8078 | pidiese | 15 |
| 8079 | picardías | 15 |
| 8080 | petróleo | 15 |
| 8081 | pescar | 15 |
| 8082 | persigue | 15 |
| 8083 | permaneció | 15 |
| 8084 | perdiese | 15 |
| 8085 | pequeñez | 15 |
| 8086 | pepa | 15 |
| 8087 | pegaba | 15 |
| 8088 | peces | 15 |
| 8089 | pater | 15 |
| 8090 | pasearse | 15 |
| 8091 | pascual | 15 |
| 8092 | pasatiempo | 15 |
| 8093 | pasamonte | 15 |
| 8094 | pasajero | 15 |
| 8095 | parroquiano | 15 |
| 8096 | parecerme | 15 |
| 8097 | pararon | 15 |
| 8098 | parada | 15 |
| 8099 | paliza | 15 |
| 8100 | palique | 15 |
| 8101 | palillo | 15 |
| 8102 | páginas | 15 |
| 8103 | pagarle | 15 |
| 8104 | oyentes | 15 |
| 8105 | ostentaba | 15 |
| 8106 | osadia | 15 |
| 8107 | oradores | 15 |
| 8108 | oprimía | 15 |
| 8109 | opinaba | 15 |
| 8110 | onrra | 15 |
| 8111 | ofrezco | 15 |
| 8112 | ofrecimiento | 15 |
| 8113 | ocurren | 15 |
| 8114 | ocupó | 15 |
| 8115 | ochoa | 15 |
| 8116 | nueuo | 15 |
| 8117 | noté | 15 |
| 8118 | nelson | 15 |
| 8119 | negativa | 15 |
| 8120 | navarra | 15 |
| 8121 | náuseas | 15 |
| 8122 | naturalidad | 15 |
| 8123 | nadando | 15 |
| 8124 | muslo | 15 |
| 8125 | musas | 15 |
| 8126 | motes | 15 |
| 8127 | mote | 15 |
| 8128 | mostrase | 15 |
| 8129 | moras | 15 |
| 8130 | molesta | 15 |
| 8131 | mochacho | 15 |
| 8132 | mismamente | 15 |
| 8133 | mirarse | 15 |
| 8134 | mezcladas | 15 |
| 8135 | metían | 15 |
| 8136 | meterme | 15 |
| 8137 | meterle | 15 |
| 8138 | mesías | 15 |
| 8139 | meditaciones | 15 |
| 8140 | matalerejo | 15 |
| 8141 | mambrino | 15 |
| 8142 | maltrecho | 15 |
| 8143 | lúgubre | 15 |
| 8144 | luchas | 15 |
| 8145 | loma | 15 |
| 8146 | llueve | 15 |
| 8147 | llevados | 15 |
| 8148 | llaneza | 15 |
| 8149 | llamados | 15 |
| 8150 | líquidos | 15 |
| 8151 | lindo | 15 |
| 8152 | limpiando | 15 |
| 8153 | liebres | 15 |
| 8154 | levantados | 15 |
| 8155 | leonero | 15 |
| 8156 | lavado | 15 |
| 8157 | lavaba | 15 |
| 8158 | lamentos | 15 |
| 8159 | jura | 15 |
| 8160 | juntar | 15 |
| 8161 | juncos | 15 |
| 8162 | jesu | 15 |
| 8163 | invisibles | 15 |
| 8164 | intensidad | 15 |
| 8165 | insultos | 15 |
| 8166 | índole | 15 |
| 8167 | índice | 15 |
| 8168 | importuno | 15 |
| 8169 | impedido | 15 |
| 8170 | imitando | 15 |
| 8171 | imaginando | 15 |
| 8172 | imaginaciones | 15 |
| 8173 | ilustrísima | 15 |
| 8174 | idealismo | 15 |
| 8175 | id | 15 |
| 8176 | huyó | 15 |
| 8177 | hurtar | 15 |
| 8178 | hotel | 15 |
| 8179 | horrores | 15 |
| 8180 | holanda | 15 |
| 8181 | hilado | 15 |
| 8182 | heroica | 15 |
| 8183 | hallamos | 15 |
| 8184 | hagáis | 15 |
| 8185 | habíase | 15 |
| 8186 | guerrero | 15 |
| 8187 | gruesos | 15 |
| 8188 | gruesas | 15 |
| 8189 | graciosos | 15 |
| 8190 | giro | 15 |
| 8191 | gibraltar | 15 |
| 8192 | gelo | 15 |
| 8193 | futura | 15 |
| 8194 | fugitivo | 15 |
| 8195 | frescos | 15 |
| 8196 | forman | 15 |
| 8197 | formaba | 15 |
| 8198 | flechas | 15 |
| 8199 | fíjate | 15 |
| 8200 | fijaba | 15 |
| 8201 | figuro | 15 |
| 8202 | fiar | 15 |
| 8203 | feria | 15 |
| 8204 | febo | 15 |
| 8205 | fallé | 15 |
| 8206 | fábula | 15 |
| 8207 | existen | 15 |
| 8208 | eternas | 15 |
| 8209 | estridente | 15 |
| 8210 | estribor | 15 |
| 8211 | estrechos | 15 |
| 8212 | estorbar | 15 |
| 8213 | estorbaba | 15 |
| 8214 | estimar | 15 |
| 8215 | estarán | 15 |
| 8216 | essos | 15 |
| 8217 | esperiencia | 15 |
| 8218 | esperança | 15 |
| 8219 | espantados | 15 |
| 8220 | espantada | 15 |
| 8221 | escuridad | 15 |
| 8222 | escritorio | 15 |
| 8223 | escribiendo | 15 |
| 8224 | esclavitud | 15 |
| 8225 | escándalos | 15 |
| 8226 | equilibrio | 15 |
| 8227 | entretenerse | 15 |
| 8228 | entere | 15 |
| 8229 | entendida | 15 |
| 8230 | engañó | 15 |
| 8231 | encontramos | 15 |
| 8232 | encogía | 15 |
| 8233 | encierro | 15 |
| 8234 | encerrados | 15 |
| 8235 | emperadores | 15 |
| 8236 | eliseo | 15 |
| 8237 | efusión | 15 |
| 8238 | educado | 15 |
| 8239 | económico | 15 |
| 8240 | duela | 15 |
| 8241 | dramas | 15 |
| 8242 | divide | 15 |
| 8243 | dijeran | 15 |
| 8244 | dexame | 15 |
| 8245 | detúvose | 15 |
| 8246 | determinaba | 15 |
| 8247 | despedido | 15 |
| 8248 | despedían | 15 |
| 8249 | desnudas | 15 |
| 8250 | deshizo | 15 |
| 8251 | deseaban | 15 |
| 8252 | desdeñado | 15 |
| 8253 | desdémona | 15 |
| 8254 | descargar | 15 |
| 8255 | descansa | 15 |
| 8256 | desasosiego | 15 |
| 8257 | desafíos | 15 |
| 8258 | derribar | 15 |
| 8259 | derramado | 15 |
| 8260 | denuedo | 15 |
| 8261 | demostrar | 15 |
| 8262 | dejaremos | 15 |
| 8263 | declaro | 15 |
| 8264 | deciros | 15 |
| 8265 | debida | 15 |
| 8266 | debaxo | 15 |
| 8267 | deán | 15 |
| 8268 | dársela | 15 |
| 8269 | damasco | 15 |
| 8270 | daca | 15 |
| 8271 | dábale | 15 |
| 8272 | cursis | 15 |
| 8273 | cuñada | 15 |
| 8274 | cumplidos | 15 |
| 8275 | cuentes | 15 |
| 8276 | cuchillada | 15 |
| 8277 | cubrían | 15 |
| 8278 | cuadrillero | 15 |
| 8279 | cuadrilla | 15 |
| 8280 | creyese | 15 |
| 8281 | creación | 15 |
| 8282 | corrillos | 15 |
| 8283 | corrí | 15 |
| 8284 | coronada | 15 |
| 8285 | córdoba | 15 |
| 8286 | convidaba | 15 |
| 8287 | convertirse | 15 |
| 8288 | convalecencia | 15 |
| 8289 | contempló | 15 |
| 8290 | consulta | 15 |
| 8291 | consejero | 15 |
| 8292 | conseguía | 15 |
| 8293 | conformes | 15 |
| 8294 | confesiones | 15 |
| 8295 | condenar | 15 |
| 8296 | condado | 15 |
| 8297 | concurso | 15 |
| 8298 | composición | 15 |
| 8299 | complexión | 15 |
| 8300 | comenzaban | 15 |
| 8301 | combatir | 15 |
| 8302 | coman | 15 |
| 8303 | comamos | 15 |
| 8304 | columpio | 15 |
| 8305 | cogote | 15 |
| 8306 | cogieron | 15 |
| 8307 | cofre | 15 |
| 8308 | cobardía | 15 |
| 8309 | clerical | 15 |
| 8310 | cintas | 15 |
| 8311 | cid | 15 |
| 8312 | chuletas | 15 |
| 8313 | cestas | 15 |
| 8314 | centurio | 15 |
| 8315 | celosa | 15 |
| 8316 | celindo | 15 |
| 8317 | católicos | 15 |
| 8318 | castaño | 15 |
| 8319 | carretero | 15 |
| 8320 | carcelero | 15 |
| 8321 | caracol | 15 |
| 8322 | capillas | 15 |
| 8323 | campanadas | 15 |
| 8324 | camoirán | 15 |
| 8325 | caminando | 15 |
| 8326 | camaradas | 15 |
| 8327 | calabozo | 15 |
| 8328 | buscaban | 15 |
| 8329 | burgos | 15 |
| 8330 | buques | 15 |
| 8331 | bunito | 15 |
| 8332 | bomba | 15 |
| 8333 | bocados | 15 |
| 8334 | billar | 15 |
| 8335 | bernardo | 15 |
| 8336 | bartolomé | 15 |
| 8337 | banquete | 15 |
| 8338 | bajas | 15 |
| 8339 | bajado | 15 |
| 8340 | ayes | 15 |
| 8341 | ayas | 15 |
| 8342 | avino | 15 |
| 8343 | avariento | 15 |
| 8344 | aureola | 15 |
| 8345 | aues | 15 |
| 8346 | aturdimiento | 15 |
| 8347 | atrevida | 15 |
| 8348 | atravesar | 15 |
| 8349 | atravesado | 15 |
| 8350 | atan | 15 |
| 8351 | asustó | 15 |
| 8352 | asustaba | 15 |
| 8353 | astucia | 15 |
| 8354 | aspirar | 15 |
| 8355 | aspereza | 15 |
| 8356 | asnos | 15 |
| 8357 | arrepentida | 15 |
| 8358 | arrastrar | 15 |
| 8359 | arrancarle | 15 |
| 8360 | arcos | 15 |
| 8361 | aquéllas | 15 |
| 8362 | apretando | 15 |
| 8363 | apagados | 15 |
| 8364 | apagado | 15 |
| 8365 | antipático | 15 |
| 8366 | anteojos | 15 |
| 8367 | animaba | 15 |
| 8368 | andava | 15 |
| 8369 | andadas | 15 |
| 8370 | an | 15 |
| 8371 | americana | 15 |
| 8372 | alturas | 15 |
| 8373 | alhaja | 15 |
| 8374 | alcanzan | 15 |
| 8375 | ajos | 15 |
| 8376 | áfrica | 15 |
| 8377 | afirmar | 15 |
| 8378 | adrede | 15 |
| 8379 | adornada | 15 |
| 8380 | acudían | 15 |
| 8381 | actual | 15 |
| 8382 | acreedores | 15 |
| 8383 | achaques | 15 |
| 8384 | absurdos | 15 |
| 8385 | absencia | 15 |
| 8386 | xii | 14 |
| 8387 | vuelvan | 14 |
| 8388 | volverán | 14 |
| 8389 | volaba | 14 |
| 8390 | viudas | 14 |
| 8391 | vírgenes | 14 |
| 8392 | violentamente | 14 |
| 8393 | viles | 14 |
| 8394 | vías | 14 |
| 8395 | verguenza | 14 |
| 8396 | verguença | 14 |
| 8397 | verdugos | 14 |
| 8398 | vendré | 14 |
| 8399 | vendiendo | 14 |
| 8400 | vencidos | 14 |
| 8401 | valido | 14 |
| 8402 | valían | 14 |
| 8403 | valerosos | 14 |
| 8404 | vacilar | 14 |
| 8405 | usos | 14 |
| 8406 | urbide | 14 |
| 8407 | umbral | 14 |
| 8408 | túnel | 14 |
| 8409 | trozo | 14 |
| 8410 | tributo | 14 |
| 8411 | trece | 14 |
| 8412 | tratamos | 14 |
| 8413 | trastornada | 14 |
| 8414 | tragaba | 14 |
| 8415 | traerme | 14 |
| 8416 | tos | 14 |
| 8417 | tornaron | 14 |
| 8418 | torcida | 14 |
| 8419 | torcer | 14 |
| 8420 | topo | 14 |
| 8421 | tomes | 14 |
| 8422 | tomarla | 14 |
| 8423 | tocantes | 14 |
| 8424 | tiranía | 14 |
| 8425 | timbre | 14 |
| 8426 | tieso | 14 |
| 8427 | tercia | 14 |
| 8428 | tenerme | 14 |
| 8429 | tendero | 14 |
| 8430 | temido | 14 |
| 8431 | tardo | 14 |
| 8432 | tapar | 14 |
| 8433 | tambores | 14 |
| 8434 | tajada | 14 |
| 8435 | suspensión | 14 |
| 8436 | supone | 14 |
| 8437 | sufrido | 14 |
| 8438 | suficiencia | 14 |
| 8439 | suenan | 14 |
| 8440 | sudando | 14 |
| 8441 | subida | 14 |
| 8442 | sostiene | 14 |
| 8443 | soslayo | 14 |
| 8444 | sonaron | 14 |
| 8445 | sobervia | 14 |
| 8446 | sirvieron | 14 |
| 8447 | sirves | 14 |
| 8448 | silvia | 14 |
| 8449 | sílaba | 14 |
| 8450 | significa | 14 |
| 8451 | serrana | 14 |
| 8452 | separarse | 14 |
| 8453 | separar | 14 |
| 8454 | separaba | 14 |
| 8455 | sentose | 14 |
| 8456 | sentíase | 14 |
| 8457 | sentáronse | 14 |
| 8458 | sensible | 14 |
| 8459 | sello | 14 |
| 8460 | salvador | 14 |
| 8461 | salteadores | 14 |
| 8462 | salidas | 14 |
| 8463 | sagacidad | 14 |
| 8464 | sacudía | 14 |
| 8465 | sacase | 14 |
| 8466 | sacaré | 14 |
| 8467 | rum | 14 |
| 8468 | rubios | 14 |
| 8469 | rogando | 14 |
| 8470 | roce | 14 |
| 8471 | rizos | 14 |
| 8472 | rindió | 14 |
| 8473 | revuelta | 14 |
| 8474 | resuelta | 14 |
| 8475 | resplandeciente | 14 |
| 8476 | respirando | 14 |
| 8477 | representaban | 14 |
| 8478 | reparo | 14 |
| 8479 | relucir | 14 |
| 8480 | refirió | 14 |
| 8481 | referida | 14 |
| 8482 | reduce | 14 |
| 8483 | reconocimiento | 14 |
| 8484 | reconoce | 14 |
| 8485 | recibimiento | 14 |
| 8486 | recibí | 14 |
| 8487 | reciben | 14 |
| 8488 | reacción | 14 |
| 8489 | ráfaga | 14 |
| 8490 | rabiar | 14 |
| 8491 | quitara | 14 |
| 8492 | quitaban | 14 |
| 8493 | querrás | 14 |
| 8494 | puntualmente | 14 |
| 8495 | pum | 14 |
| 8496 | pulmones | 14 |
| 8497 | pulcritud | 14 |
| 8498 | proximidad | 14 |
| 8499 | protestantes | 14 |
| 8500 | proporción | 14 |
| 8501 | propietario | 14 |
| 8502 | progresos | 14 |
| 8503 | probó | 14 |
| 8504 | primogénito | 14 |
| 8505 | presentimiento | 14 |
| 8506 | preparó | 14 |
| 8507 | preocupado | 14 |
| 8508 | preguntándole | 14 |
| 8509 | preguntan | 14 |
| 8510 | precipitadamente | 14 |
| 8511 | precauciones | 14 |
| 8512 | portería | 14 |
| 8513 | poridat | 14 |
| 8514 | poniente | 14 |
| 8515 | pongamos | 14 |
| 8516 | ponerte | 14 |
| 8517 | pondremos | 14 |
| 8518 | polo | 14 |
| 8519 | pío | 14 |
| 8520 | pícaros | 14 |
| 8521 | picaba | 14 |
| 8522 | pica | 14 |
| 8523 | pertenece | 14 |
| 8524 | perseguía | 14 |
| 8525 | permanecía | 14 |
| 8526 | perdieron | 14 |
| 8527 | pensase | 14 |
| 8528 | pensaron | 14 |
| 8529 | pensará | 14 |
| 8530 | pensamos | 14 |
| 8531 | pegó | 14 |
| 8532 | pedradas | 14 |
| 8533 | pedirme | 14 |
| 8534 | patios | 14 |
| 8535 | passos | 14 |
| 8536 | passados | 14 |
| 8537 | pasarse | 14 |
| 8538 | pasaría | 14 |
| 8539 | pasaporte | 14 |
| 8540 | partidos | 14 |
| 8541 | parezcan | 14 |
| 8542 | parecióle | 14 |
| 8543 | pardos | 14 |
| 8544 | pánico | 14 |
| 8545 | pálidos | 14 |
| 8546 | oyéndole | 14 |
| 8547 | olvides | 14 |
| 8548 | ojeriza | 14 |
| 8549 | ofrecieron | 14 |
| 8550 | ofreciéndole | 14 |
| 8551 | ocuparse | 14 |
| 8552 | ocioso | 14 |
| 8553 | ochenta | 14 |
| 8554 | obispos | 14 |
| 8555 | nuez | 14 |
| 8556 | nombraba | 14 |
| 8557 | nieves | 14 |
| 8558 | negarse | 14 |
| 8559 | necessario | 14 |
| 8560 | naval | 14 |
| 8561 | navaja | 14 |
| 8562 | na | 14 |
| 8563 | murallas | 14 |
| 8564 | muñecas | 14 |
| 8565 | muela | 14 |
| 8566 | movida | 14 |
| 8567 | mohíno | 14 |
| 8568 | miércoles | 14 |
| 8569 | metálico | 14 |
| 8570 | mesmas | 14 |
| 8571 | merecían | 14 |
| 8572 | mereces | 14 |
| 8573 | merçed | 14 |
| 8574 | menoscabo | 14 |
| 8575 | mendrugos | 14 |
| 8576 | mejorado | 14 |
| 8577 | meditando | 14 |
| 8578 | medidas | 14 |
| 8579 | materialista | 14 |
| 8580 | mataba | 14 |
| 8581 | marismas | 14 |
| 8582 | marca | 14 |
| 8583 | mandase | 14 |
| 8584 | mandarle | 14 |
| 8585 | malhaya | 14 |
| 8586 | malezas | 14 |
| 8587 | maíz | 14 |
| 8588 | magnificencia | 14 |
| 8589 | maestría | 14 |
| 8590 | madrugar | 14 |
| 8591 | lucido | 14 |
| 8592 | loores | 14 |
| 8593 | lontananza | 14 |
| 8594 | loçana | 14 |
| 8595 | llevaran | 14 |
| 8596 | llegasen | 14 |
| 8597 | literarias | 14 |
| 8598 | libra | 14 |
| 8599 | liberación | 14 |
| 8600 | levanto | 14 |
| 8601 | levantaban | 14 |
| 8602 | letrero | 14 |
| 8603 | leo | 14 |
| 8604 | lejana | 14 |
| 8605 | laureles | 14 |
| 8606 | lascivia | 14 |
| 8607 | lancha | 14 |
| 8608 | laguardia | 14 |
| 8609 | juzgó | 14 |
| 8610 | juyzio | 14 |
| 8611 | junio | 14 |
| 8612 | jugadores | 14 |
| 8613 | jugador | 14 |
| 8614 | jugado | 14 |
| 8615 | jota | 14 |
| 8616 | jesuitas | 14 |
| 8617 | jaulas | 14 |
| 8618 | jaquecas | 14 |
| 8619 | jabón | 14 |
| 8620 | inventado | 14 |
| 8621 | invenciones | 14 |
| 8622 | intriga | 14 |
| 8623 | interrumpido | 14 |
| 8624 | inspirado | 14 |
| 8625 | inspira | 14 |
| 8626 | insistía | 14 |
| 8627 | insana | 14 |
| 8628 | informe | 14 |
| 8629 | infante | 14 |
| 8630 | indecentes | 14 |
| 8631 | inaudito | 14 |
| 8632 | imprudente | 14 |
| 8633 | imprudencia | 14 |
| 8634 | impropio | 14 |
| 8635 | impertinentes | 14 |
| 8636 | ildefonso | 14 |
| 8637 | iguala | 14 |
| 8638 | idas | 14 |
| 8639 | ibas | 14 |
| 8640 | huérfanos | 14 |
| 8641 | horroroso | 14 |
| 8642 | horacio | 14 |
| 8643 | honestas | 14 |
| 8644 | homicida | 14 |
| 8645 | heno | 14 |
| 8646 | hembras | 14 |
| 8647 | hechicera | 14 |
| 8648 | hazte | 14 |
| 8649 | hacerlas | 14 |
| 8650 | habréis | 14 |
| 8651 | h | 14 |
| 8652 | guiaba | 14 |
| 8653 | guadalajara | 14 |
| 8654 | gobernación | 14 |
| 8655 | gentilhombre | 14 |
| 8656 | gentiles | 14 |
| 8657 | gastos | 14 |
| 8658 | ganarse | 14 |
| 8659 | galiano | 14 |
| 8660 | galatea | 14 |
| 8661 | galantería | 14 |
| 8662 | funesto | 14 |
| 8663 | fueros | 14 |
| 8664 | fueren | 14 |
| 8665 | fraternal | 14 |
| 8666 | foso | 14 |
| 8667 | formó | 14 |
| 8668 | finísima | 14 |
| 8669 | fijar | 14 |
| 8670 | fieros | 14 |
| 8671 | fía | 14 |
| 8672 | fermoso | 14 |
| 8673 | fatigada | 14 |
| 8674 | fase | 14 |
| 8675 | fará | 14 |
| 8676 | faltara | 14 |
| 8677 | facciosos | 14 |
| 8678 | extravagantes | 14 |
| 8679 | extravagancias | 14 |
| 8680 | extendiendo | 14 |
| 8681 | expediente | 14 |
| 8682 | existir | 14 |
| 8683 | exigencias | 14 |
| 8684 | exclamé | 14 |
| 8685 | exclamaciones | 14 |
| 8686 | exageración | 14 |
| 8687 | evidencia | 14 |
| 8688 | estupidez | 14 |
| 8689 | estrechó | 14 |
| 8690 | estrechamente | 14 |
| 8691 | estotro | 14 |
| 8692 | estorba | 14 |
| 8693 | estómagos | 14 |
| 8694 | estirar | 14 |
| 8695 | estimo | 14 |
| 8696 | estemos | 14 |
| 8697 | espina | 14 |
| 8698 | esperase | 14 |
| 8699 | esperado | 14 |
| 8700 | esparto | 14 |
| 8701 | esforzado | 14 |
| 8702 | escuchó | 14 |
| 8703 | escondite | 14 |
| 8704 | escollo | 14 |
| 8705 | escandalosa | 14 |
| 8706 | enteros | 14 |
| 8707 | entendemos | 14 |
| 8708 | enredos | 14 |
| 8709 | enojada | 14 |
| 8710 | enero | 14 |
| 8711 | endiablada | 14 |
| 8712 | encomendarse | 14 |
| 8713 | encendía | 14 |
| 8714 | encaminó | 14 |
| 8715 | encaje | 14 |
| 8716 | empuje | 14 |
| 8717 | empleada | 14 |
| 8718 | empezando | 14 |
| 8719 | empeñó | 14 |
| 8720 | egoísta | 14 |
| 8721 | edición | 14 |
| 8722 | echándole | 14 |
| 8723 | echada | 14 |
| 8724 | duena | 14 |
| 8725 | dramático | 14 |
| 8726 | dorados | 14 |
| 8727 | distracciones | 14 |
| 8728 | disputar | 14 |
| 8729 | disimulado | 14 |
| 8730 | disfrazado | 14 |
| 8731 | discípulo | 14 |
| 8732 | dire | 14 |
| 8733 | diras | 14 |
| 8734 | dióme | 14 |
| 8735 | dilo | 14 |
| 8736 | diferencias | 14 |
| 8737 | diabluras | 14 |
| 8738 | devociones | 14 |
| 8739 | despreciado | 14 |
| 8740 | despidiéndose | 14 |
| 8741 | desierta | 14 |
| 8742 | desempeñar | 14 |
| 8743 | desechar | 14 |
| 8744 | descubrirse | 14 |
| 8745 | descompuesta | 14 |
| 8746 | descalzos | 14 |
| 8747 | desazón | 14 |
| 8748 | desata | 14 |
| 8749 | desafiar | 14 |
| 8750 | derechas | 14 |
| 8751 | deprisa | 14 |
| 8752 | dependiente | 14 |
| 8753 | demostraciones | 14 |
| 8754 | demasiada | 14 |
| 8755 | demas | 14 |
| 8756 | demandadero | 14 |
| 8757 | dejarán | 14 |
| 8758 | dejaran | 14 |
| 8759 | decidida | 14 |
| 8760 | debí | 14 |
| 8761 | david | 14 |
| 8762 | dato | 14 |
| 8763 | dárselo | 14 |
| 8764 | dara | 14 |
| 8765 | cuyta | 14 |
| 8766 | cumplía | 14 |
| 8767 | cuidando | 14 |
| 8768 | cuan | 14 |
| 8769 | crujía | 14 |
| 8770 | cristiandad | 14 |
| 8771 | crecido | 14 |
| 8772 | costal | 14 |
| 8773 | cortina | 14 |
| 8774 | cortezas | 14 |
| 8775 | córcholis | 14 |
| 8776 | convino | 14 |
| 8777 | convierte | 14 |
| 8778 | convertida | 14 |
| 8779 | conventos | 14 |
| 8780 | convenga | 14 |
| 8781 | contestado | 14 |
| 8782 | contesçió | 14 |
| 8783 | consta | 14 |
| 8784 | considerado | 14 |
| 8785 | confirmar | 14 |
| 8786 | conferencias | 14 |
| 8787 | conducido | 14 |
| 8788 | condes | 14 |
| 8789 | conclusión | 14 |
| 8790 | comunicaba | 14 |
| 8791 | comprenderá | 14 |
| 8792 | compré | 14 |
| 8793 | compraba | 14 |
| 8794 | comparado | 14 |
| 8795 | comiese | 14 |
| 8796 | comienço | 14 |
| 8797 | comedimiento | 14 |
| 8798 | combinada | 14 |
| 8799 | combatientes | 14 |
| 8800 | comandanta | 14 |
| 8801 | colosal | 14 |
| 8802 | cogerla | 14 |
| 8803 | cobdiçia | 14 |
| 8804 | clarín | 14 |
| 8805 | cigarros | 14 |
| 8806 | çierto | 14 |
| 8807 | charco | 14 |
| 8808 | chaqueta | 14 |
| 8809 | champaña | 14 |
| 8810 | césped | 14 |
| 8811 | ceñido | 14 |
| 8812 | centauro | 14 |
| 8813 | censura | 14 |
| 8814 | cenaron | 14 |
| 8815 | célebres | 14 |
| 8816 | cecial | 14 |
| 8817 | causaban | 14 |
| 8818 | castigos | 14 |
| 8819 | castaños | 14 |
| 8820 | carretela | 14 |
| 8821 | caritativo | 14 |
| 8822 | carece | 14 |
| 8823 | capote | 14 |
| 8824 | cansarse | 14 |
| 8825 | cansa | 14 |
| 8826 | campanario | 14 |
| 8827 | calva | 14 |
| 8828 | callejón | 14 |
| 8829 | caletre | 14 |
| 8830 | cálculo | 14 |
| 8831 | cacochipi | 14 |
| 8832 | butacas | 14 |
| 8833 | butaca | 14 |
| 8834 | busqué | 14 |
| 8835 | buscado | 14 |
| 8836 | breue | 14 |
| 8837 | brasero | 14 |
| 8838 | borracha | 14 |
| 8839 | bigotes | 14 |
| 8840 | besando | 14 |
| 8841 | berlina | 14 |
| 8842 | bellaquería | 14 |
| 8843 | bellacos | 14 |
| 8844 | batería | 14 |
| 8845 | basura | 14 |
| 8846 | barquilla | 14 |
| 8847 | bardas | 14 |
| 8848 | barata | 14 |
| 8849 | bajito | 14 |
| 8850 | bajeles | 14 |
| 8851 | bajé | 14 |
| 8852 | bajaban | 14 |
| 8853 | bacalao | 14 |
| 8854 | baba | 14 |
| 8855 | averiguado | 14 |
| 8856 | avaro | 14 |
| 8857 | avanzada | 14 |
| 8858 | auristela | 14 |
| 8859 | aumentaba | 14 |
| 8860 | augusta | 14 |
| 8861 | atadas | 14 |
| 8862 | asentó | 14 |
| 8863 | ascos | 14 |
| 8864 | artistas | 14 |
| 8865 | arrogancia | 14 |
| 8866 | arregla | 14 |
| 8867 | arrastrado | 14 |
| 8868 | arder | 14 |
| 8869 | arde | 14 |
| 8870 | arcas | 14 |
| 8871 | araña | 14 |
| 8872 | apuesta | 14 |
| 8873 | aprovecha | 14 |
| 8874 | aprieto | 14 |
| 8875 | apretón | 14 |
| 8876 | aprendiendo | 14 |
| 8877 | aprendí | 14 |
| 8878 | aplicó | 14 |
| 8879 | aplausos | 14 |
| 8880 | apetitos | 14 |
| 8881 | apeándose | 14 |
| 8882 | apasionado | 14 |
| 8883 | apartarse | 14 |
| 8884 | aparta | 14 |
| 8885 | aparejos | 14 |
| 8886 | aparecido | 14 |
| 8887 | antonomasia | 14 |
| 8888 | antojos | 14 |
| 8889 | antequera | 14 |
| 8890 | angélica | 14 |
| 8891 | anarquía | 14 |
| 8892 | alza | 14 |
| 8893 | alteración | 14 |
| 8894 | alisa | 14 |
| 8895 | algeciras | 14 |
| 8896 | alejó | 14 |
| 8897 | alejaba | 14 |
| 8898 | alegrías | 14 |
| 8899 | alcanzo | 14 |
| 8900 | alcaldes | 14 |
| 8901 | alarma | 14 |
| 8902 | álamos | 14 |
| 8903 | aguardó | 14 |
| 8904 | aficiones | 14 |
| 8905 | afanes | 14 |
| 8906 | advertencia | 14 |
| 8907 | adulación | 14 |
| 8908 | adonai | 14 |
| 8909 | ado | 14 |
| 8910 | admitir | 14 |
| 8911 | admira | 14 |
| 8912 | adán | 14 |
| 8913 | activo | 14 |
| 8914 | activa | 14 |
| 8915 | acostumbrados | 14 |
| 8916 | acordar | 14 |
| 8917 | acordándose | 14 |
| 8918 | acontecido | 14 |
| 8919 | acompañaron | 14 |
| 8920 | acogimiento | 14 |
| 8921 | acertaba | 14 |
| 8922 | acaeció | 14 |
| 8923 | abrirle | 14 |
| 8924 | abanico | 14 |
| 8925 | zona | 13 |
| 8926 | zarzuela | 13 |
| 8927 | zapatería | 13 |
| 8928 | zaguán | 13 |
| 8929 | yegua | 13 |
| 8930 | viviese | 13 |
| 8931 | viviente | 13 |
| 8932 | viudo | 13 |
| 8933 | vistiendo | 13 |
| 8934 | vistazo | 13 |
| 8935 | visitado | 13 |
| 8936 | virgilio | 13 |
| 8937 | vidrios | 13 |
| 8938 | vidriera | 13 |
| 8939 | veses | 13 |
| 8940 | veros | 13 |
| 8941 | ventas | 13 |
| 8942 | venerables | 13 |
| 8943 | veloz | 13 |
| 8944 | vellaco | 13 |
| 8945 | vehemente | 13 |
| 8946 | vanidades | 13 |
| 8947 | válgame | 13 |
| 8948 | usurero | 13 |
| 8949 | urna | 13 |
| 8950 | únicos | 13 |
| 8951 | unción | 13 |
| 8952 | turbar | 13 |
| 8953 | tropezando | 13 |
| 8954 | trompetas | 13 |
| 8955 | trofeo | 13 |
| 8956 | tristesa | 13 |
| 8957 | tregua | 13 |
| 8958 | traye | 13 |
| 8959 | trataron | 13 |
| 8960 | transformaciones | 13 |
| 8961 | tranquilizó | 13 |
| 8962 | trágica | 13 |
| 8963 | topar | 13 |
| 8964 | tolosa | 13 |
| 8965 | tinto | 13 |
| 8966 | tintas | 13 |
| 8967 | tímido | 13 |
| 8968 | tijeras | 13 |
| 8969 | tientas | 13 |
| 8970 | tien | 13 |
| 8971 | tia | 13 |
| 8972 | texto | 13 |
| 8973 | tersa | 13 |
| 8974 | tenue | 13 |
| 8975 | tenerlo | 13 |
| 8976 | tenedor | 13 |
| 8977 | tardaron | 13 |
| 8978 | tardado | 13 |
| 8979 | sustentado | 13 |
| 8980 | suspirando | 13 |
| 8981 | suponiendo | 13 |
| 8982 | superstición | 13 |
| 8983 | suelas | 13 |
| 8984 | sudar | 13 |
| 8985 | sucias | 13 |
| 8986 | substancia | 13 |
| 8987 | sospecho | 13 |
| 8988 | sortija | 13 |
| 8989 | sopor | 13 |
| 8990 | sonoras | 13 |
| 8991 | somnolencia | 13 |
| 8992 | soltera | 13 |
| 8993 | sofismas | 13 |
| 8994 | socio | 13 |
| 8995 | sincero | 13 |
| 8996 | sierras | 13 |
| 8997 | separado | 13 |
| 8998 | separación | 13 |
| 8999 | sentaban | 13 |
| 9000 | seguidos | 13 |
| 9001 | salmón | 13 |
| 9002 | salesas | 13 |
| 9003 | sacudió | 13 |
| 9004 | sacudida | 13 |
| 9005 | sacramentos | 13 |
| 9006 | sacarme | 13 |
| 9007 | sacaban | 13 |
| 9008 | rústico | 13 |
| 9009 | rrespuesta | 13 |
| 9010 | rrazón | 13 |
| 9011 | roncesvalles | 13 |
| 9012 | romería | 13 |
| 9013 | románticas | 13 |
| 9014 | romances | 13 |
| 9015 | rita | 13 |
| 9016 | rige | 13 |
| 9017 | ridículas | 13 |
| 9018 | ricamente | 13 |
| 9019 | rezo | 13 |
| 9020 | reza | 13 |
| 9021 | reyna | 13 |
| 9022 | revolvía | 13 |
| 9023 | retira | 13 |
| 9024 | respiro | 13 |
| 9025 | respetando | 13 |
| 9026 | respetaba | 13 |
| 9027 | respectivos | 13 |
| 9028 | repentino | 13 |
| 9029 | reinas | 13 |
| 9030 | régimen | 13 |
| 9031 | regidor | 13 |
| 9032 | redentor | 13 |
| 9033 | recorrido | 13 |
| 9034 | recomendaciones | 13 |
| 9035 | recomendación | 13 |
| 9036 | recobrar | 13 |
| 9037 | reclamo | 13 |
| 9038 | reciente | 13 |
| 9039 | receta | 13 |
| 9040 | recados | 13 |
| 9041 | rabiosa | 13 |
| 9042 | quitarte | 13 |
| 9043 | quitará | 13 |
| 9044 | quitándole | 13 |
| 9045 | quitando | 13 |
| 9046 | queria | 13 |
| 9047 | quebraderos | 13 |
| 9048 | qualquier | 13 |
| 9049 | pulido | 13 |
| 9050 | públicas | 13 |
| 9051 | prosiguiendo | 13 |
| 9052 | prometen | 13 |
| 9053 | prolijo | 13 |
| 9054 | profanos | 13 |
| 9055 | procurador | 13 |
| 9056 | problemas | 13 |
| 9057 | primores | 13 |
| 9058 | préstamo | 13 |
| 9059 | presentan | 13 |
| 9060 | preparativos | 13 |
| 9061 | pregunte | 13 |
| 9062 | prácticas | 13 |
| 9063 | postrero | 13 |
| 9064 | positivo | 13 |
| 9065 | positiva | 13 |
| 9066 | portales | 13 |
| 9067 | portado | 13 |
| 9068 | pondrán | 13 |
| 9069 | poéticas | 13 |
| 9070 | pobrecitos | 13 |
| 9071 | plaser | 13 |
| 9072 | plaga | 13 |
| 9073 | pintaba | 13 |
| 9074 | pidiéndole | 13 |
| 9075 | picardía | 13 |
| 9076 | picantes | 13 |
| 9077 | picado | 13 |
| 9078 | pesimismo | 13 |
| 9079 | pescado | 13 |
| 9080 | pesca | 13 |
| 9081 | perseguir | 13 |
| 9082 | pernueces | 13 |
| 9083 | perfume | 13 |
| 9084 | pérez | 13 |
| 9085 | perdidas | 13 |
| 9086 | pensaría | 13 |
| 9087 | pellejo | 13 |
| 9088 | pedí | 13 |
| 9089 | pedernero | 13 |
| 9090 | patatas | 13 |
| 9091 | pastoral | 13 |
| 9092 | passe | 13 |
| 9093 | paseó | 13 |
| 9094 | pascuas | 13 |
| 9095 | pasatiempos | 13 |
| 9096 | partirse | 13 |
| 9097 | párrafos | 13 |
| 9098 | parecióme | 13 |
| 9099 | parecerse | 13 |
| 9100 | panorama | 13 |
| 9101 | página | 13 |
| 9102 | pagados | 13 |
| 9103 | padezco | 13 |
| 9104 | osaré | 13 |
| 9105 | osar | 13 |
| 9106 | oratorio | 13 |
| 9107 | olmo | 13 |
| 9108 | ola | 13 |
| 9109 | ofendida | 13 |
| 9110 | ocurrían | 13 |
| 9111 | ociosos | 13 |
| 9112 | ociosas | 13 |
| 9113 | obsequio | 13 |
| 9114 | nociones | 13 |
| 9115 | ningun | 13 |
| 9116 | nietos | 13 |
| 9117 | negarlo | 13 |
| 9118 | naturalismo | 13 |
| 9119 | narciso | 13 |
| 9120 | naipes | 13 |
| 9121 | nacieron | 13 |
| 9122 | murcia | 13 |
| 9123 | mudarse | 13 |
| 9124 | mortaja | 13 |
| 9125 | moriría | 13 |
| 9126 | morirá | 13 |
| 9127 | morado | 13 |
| 9128 | monesterio | 13 |
| 9129 | molinos | 13 |
| 9130 | millares | 13 |
| 9131 | milicia | 13 |
| 9132 | miento | 13 |
| 9133 | miembro | 13 |
| 9134 | método | 13 |
| 9135 | merino | 13 |
| 9136 | mercantil | 13 |
| 9137 | menear | 13 |
| 9138 | medroso | 13 |
| 9139 | matarle | 13 |
| 9140 | mantiene | 13 |
| 9141 | mandaban | 13 |
| 9142 | maldiciendo | 13 |
| 9143 | majestuoso | 13 |
| 9144 | mahoma | 13 |
| 9145 | magín | 13 |
| 9146 | luengas | 13 |
| 9147 | luchando | 13 |
| 9148 | longaniza | 13 |
| 9149 | llanos | 13 |
| 9150 | llamé | 13 |
| 9151 | lisonjas | 13 |
| 9152 | lisi | 13 |
| 9153 | linterna | 13 |
| 9154 | limpió | 13 |
| 9155 | lid | 13 |
| 9156 | librarse | 13 |
| 9157 | letrados | 13 |
| 9158 | lavarse | 13 |
| 9159 | latina | 13 |
| 9160 | lasciva | 13 |
| 9161 | lanzada | 13 |
| 9162 | ladridos | 13 |
| 9163 | juzgo | 13 |
| 9164 | jurando | 13 |
| 9165 | judías | 13 |
| 9166 | jovial | 13 |
| 9167 | jorge | 13 |
| 9168 | italiana | 13 |
| 9169 | iris | 13 |
| 9170 | inútilmente | 13 |
| 9171 | inundaba | 13 |
| 9172 | interrumpía | 13 |
| 9173 | interiores | 13 |
| 9174 | interesa | 13 |
| 9175 | instituciones | 13 |
| 9176 | insolencia | 13 |
| 9177 | insensible | 13 |
| 9178 | insensato | 13 |
| 9179 | innumerables | 13 |
| 9180 | inmensidad | 13 |
| 9181 | injusto | 13 |
| 9182 | influjo | 13 |
| 9183 | infiel | 13 |
| 9184 | indignado | 13 |
| 9185 | impresa | 13 |
| 9186 | iluminado | 13 |
| 9187 | ignora | 13 |
| 9188 | ignominia | 13 |
| 9189 | hy | 13 |
| 9190 | huelgo | 13 |
| 9191 | hornos | 13 |
| 9192 | honores | 13 |
| 9193 | hita | 13 |
| 9194 | hirió | 13 |
| 9195 | himno | 13 |
| 9196 | hiciere | 13 |
| 9197 | hermosuras | 13 |
| 9198 | heredera | 13 |
| 9199 | helada | 13 |
| 9200 | hazia | 13 |
| 9201 | hallaban | 13 |
| 9202 | hágame | 13 |
| 9203 | haciéndoles | 13 |
| 9204 | hacha | 13 |
| 9205 | hacéis | 13 |
| 9206 | habana | 13 |
| 9207 | guirnalda | 13 |
| 9208 | guardias | 13 |
| 9209 | guarden | 13 |
| 9210 | guardaré | 13 |
| 9211 | guardaban | 13 |
| 9212 | gruta | 13 |
| 9213 | gruñir | 13 |
| 9214 | grises | 13 |
| 9215 | grandioso | 13 |
| 9216 | golfo | 13 |
| 9217 | gobernadora | 13 |
| 9218 | gobernaba | 13 |
| 9219 | globos | 13 |
| 9220 | generación | 13 |
| 9221 | gemido | 13 |
| 9222 | gatas | 13 |
| 9223 | garbanzo | 13 |
| 9224 | ganando | 13 |
| 9225 | ganan | 13 |
| 9226 | galope | 13 |
| 9227 | furrier | 13 |
| 9228 | funda | 13 |
| 9229 | fuele | 13 |
| 9230 | frontero | 13 |
| 9231 | flexible | 13 |
| 9232 | fiso | 13 |
| 9233 | fiscal | 13 |
| 9234 | firmemente | 13 |
| 9235 | fingir | 13 |
| 9236 | fineza | 13 |
| 9237 | fijarse | 13 |
| 9238 | figurarte | 13 |
| 9239 | fiado | 13 |
| 9240 | festivo | 13 |
| 9241 | fenómenos | 13 |
| 9242 | felicísimo | 13 |
| 9243 | fatigas | 13 |
| 9244 | fango | 13 |
| 9245 | faltará | 13 |
| 9246 | faldriquera | 13 |
| 9247 | facunda | 13 |
| 9248 | fáciles | 13 |
| 9249 | facción | 13 |
| 9250 | extremada | 13 |
| 9251 | exquisito | 13 |
| 9252 | exquisita | 13 |
| 9253 | explica | 13 |
| 9254 | excelentísimo | 13 |
| 9255 | exactamente | 13 |
| 9256 | estudiando | 13 |
| 9257 | estate | 13 |
| 9258 | estanque | 13 |
| 9259 | estampas | 13 |
| 9260 | estallido | 13 |
| 9261 | estaciones | 13 |
| 9262 | espumas | 13 |
| 9263 | espléndida | 13 |
| 9264 | espesas | 13 |
| 9265 | escuchado | 13 |
| 9266 | escribí | 13 |
| 9267 | escriben | 13 |
| 9268 | escondía | 13 |
| 9269 | esconderse | 13 |
| 9270 | escogida | 13 |
| 9271 | ésas | 13 |
| 9272 | equipaje | 13 |
| 9273 | entrego | 13 |
| 9274 | entenderse | 13 |
| 9275 | enojosa | 13 |
| 9276 | enmendar | 13 |
| 9277 | enjambre | 13 |
| 9278 | enfada | 13 |
| 9279 | enemistad | 13 |
| 9280 | encuentras | 13 |
| 9281 | encontraría | 13 |
| 9282 | encomienda | 13 |
| 9283 | encendidos | 13 |
| 9284 | encarecer | 13 |
| 9285 | encantaba | 13 |
| 9286 | enamoró | 13 |
| 9287 | emprendió | 13 |
| 9288 | empeña | 13 |
| 9289 | eminente | 13 |
| 9290 | elocuentes | 13 |
| 9291 | elecciones | 13 |
| 9292 | ejercer | 13 |
| 9293 | echamos | 13 |
| 9294 | dobló | 13 |
| 9295 | díxome | 13 |
| 9296 | dixiste | 13 |
| 9297 | disimulada | 13 |
| 9298 | discurrió | 13 |
| 9299 | dimos | 13 |
| 9300 | diciéndose | 13 |
| 9301 | dexes | 13 |
| 9302 | devolver | 13 |
| 9303 | detiene | 13 |
| 9304 | determinar | 13 |
| 9305 | detenerme | 13 |
| 9306 | desposados | 13 |
| 9307 | despedirme | 13 |
| 9308 | despachó | 13 |
| 9309 | desgraciados | 13 |
| 9310 | desesperados | 13 |
| 9311 | descubrimiento | 13 |
| 9312 | describía | 13 |
| 9313 | desconcertó | 13 |
| 9314 | descender | 13 |
| 9315 | descanse | 13 |
| 9316 | desastres | 13 |
| 9317 | desaliento | 13 |
| 9318 | depende | 13 |
| 9319 | dentadura | 13 |
| 9320 | delicioso | 13 |
| 9321 | délai | 13 |
| 9322 | dejarlo | 13 |
| 9323 | dejadme | 13 |
| 9324 | décimo | 13 |
| 9325 | decíale | 13 |
| 9326 | debéis | 13 |
| 9327 | dátiles | 13 |
| 9328 | daros | 13 |
| 9329 | curia | 13 |
| 9330 | culta | 13 |
| 9331 | crucero | 13 |
| 9332 | créetelo | 13 |
| 9333 | creería | 13 |
| 9334 | coyta | 13 |
| 9335 | cosme | 13 |
| 9336 | cortésmente | 13 |
| 9337 | cortesanos | 13 |
| 9338 | cortedad | 13 |
| 9339 | cortas | 13 |
| 9340 | cortando | 13 |
| 9341 | corfín | 13 |
| 9342 | cordial | 13 |
| 9343 | corchete | 13 |
| 9344 | corazonada | 13 |
| 9345 | copla | 13 |
| 9346 | conversión | 13 |
| 9347 | conveniencia | 13 |
| 9348 | convencidos | 13 |
| 9349 | convencida | 13 |
| 9350 | contrariedad | 13 |
| 9351 | contentar | 13 |
| 9352 | contaron | 13 |
| 9353 | consuelos | 13 |
| 9354 | constitución | 13 |
| 9355 | consoló | 13 |
| 9356 | conservación | 13 |
| 9357 | conocerá | 13 |
| 9358 | confusos | 13 |
| 9359 | confiado | 13 |
| 9360 | confesarse | 13 |
| 9361 | conducto | 13 |
| 9362 | conducía | 13 |
| 9363 | conciencias | 13 |
| 9364 | concerniente | 13 |
| 9365 | concede | 13 |
| 9366 | compre | 13 |
| 9367 | compraré | 13 |
| 9368 | compasivo | 13 |
| 9369 | cómodo | 13 |
| 9370 | comidas | 13 |
| 9371 | cómica | 13 |
| 9372 | comerciantes | 13 |
| 9373 | comenzamos | 13 |
| 9374 | comadreja | 13 |
| 9375 | comadre | 13 |
| 9376 | colocaba | 13 |
| 9377 | colgados | 13 |
| 9378 | colgadas | 13 |
| 9379 | colgada | 13 |
| 9380 | colérico | 13 |
| 9381 | cojín | 13 |
| 9382 | cogidos | 13 |
| 9383 | clemencia | 13 |
| 9384 | ciudadanos | 13 |
| 9385 | círculos | 13 |
| 9386 | chozas | 13 |
| 9387 | chorro | 13 |
| 9388 | chillido | 13 |
| 9389 | chata | 13 |
| 9390 | cetro | 13 |
| 9391 | cesaron | 13 |
| 9392 | cerradas | 13 |
| 9393 | cebolla | 13 |
| 9394 | cayera | 13 |
| 9395 | caterva | 13 |
| 9396 | catalán | 13 |
| 9397 | casto | 13 |
| 9398 | castigado | 13 |
| 9399 | caseríos | 13 |
| 9400 | cartuchos | 13 |
| 9401 | carruaje | 13 |
| 9402 | cariñosas | 13 |
| 9403 | cariñosamente | 13 |
| 9404 | cañonazo | 13 |
| 9405 | cantidades | 13 |
| 9406 | cansar | 13 |
| 9407 | caminantes | 13 |
| 9408 | callejas | 13 |
| 9409 | calidades | 13 |
| 9410 | calentura | 13 |
| 9411 | caldero | 13 |
| 9412 | calamidades | 13 |
| 9413 | caerse | 13 |
| 9414 | burlesca | 13 |
| 9415 | burlar | 13 |
| 9416 | burdeos | 13 |
| 9417 | brutos | 13 |
| 9418 | brasas | 13 |
| 9419 | bonitamente | 13 |
| 9420 | bondadoso | 13 |
| 9421 | bondadosa | 13 |
| 9422 | bofetón | 13 |
| 9423 | blandas | 13 |
| 9424 | beneficios | 13 |
| 9425 | baste | 13 |
| 9426 | bastan | 13 |
| 9427 | barrer | 13 |
| 9428 | banqueta | 13 |
| 9429 | bahía | 13 |
| 9430 | bahama | 13 |
| 9431 | avrás | 13 |
| 9432 | autoridades | 13 |
| 9433 | aturdida | 13 |
| 9434 | atractivo | 13 |
| 9435 | ató | 13 |
| 9436 | ateísmo | 13 |
| 9437 | astros | 13 |
| 9438 | aspiraba | 13 |
| 9439 | asientos | 13 |
| 9440 | asensio | 13 |
| 9441 | asegura | 13 |
| 9442 | ascuas | 13 |
| 9443 | artístico | 13 |
| 9444 | arregló | 13 |
| 9445 | arreglado | 13 |
| 9446 | apuntes | 13 |
| 9447 | apretados | 13 |
| 9448 | apretada | 13 |
| 9449 | apoyo | 13 |
| 9450 | apagada | 13 |
| 9451 | anunciando | 13 |
| 9452 | antojó | 13 |
| 9453 | ángulos | 13 |
| 9454 | angosto | 13 |
| 9455 | andanada | 13 |
| 9456 | anchos | 13 |
| 9457 | amarillos | 13 |
| 9458 | aman | 13 |
| 9459 | alojamiento | 13 |
| 9460 | aljófar | 13 |
| 9461 | alegremente | 13 |
| 9462 | alargaba | 13 |
| 9463 | alabo | 13 |
| 9464 | ahorcado | 13 |
| 9465 | ágil | 13 |
| 9466 | advertí | 13 |
| 9467 | adorar | 13 |
| 9468 | ad | 13 |
| 9469 | acuerde | 13 |
| 9470 | acordaron | 13 |
| 9471 | acomodarse | 13 |
| 9472 | acercaron | 13 |
| 9473 | acentos | 13 |
| 9474 | abro | 13 |
| 9475 | abrazado | 13 |
| 9476 | aborrecer | 13 |
| 9477 | abandonó | 13 |
| 9478 | zagal | 12 |
| 9479 | yva | 12 |
| 9480 | yema | 12 |
| 9481 | yacían | 12 |
| 9482 | xvii | 12 |
| 9483 | vv | 12 |
| 9484 | volverle | 12 |
| 9485 | volveremos | 12 |
| 9486 | volcán | 12 |
| 9487 | vocablo | 12 |
| 9488 | viuo | 12 |
| 9489 | vituperios | 12 |
| 9490 | vistos | 12 |
| 9491 | vigilia | 12 |
| 9492 | vigas | 12 |
| 9493 | vestían | 12 |
| 9494 | vera | 12 |
| 9495 | venganzas | 12 |
| 9496 | vençer | 12 |
| 9497 | velaba | 12 |
| 9498 | vascuence | 12 |
| 9499 | vaina | 12 |
| 9500 | usó | 12 |
| 9501 | usada | 12 |
| 9502 | unido | 12 |
| 9503 | unida | 12 |
| 9504 | tuno | 12 |
| 9505 | tunantes | 12 |
| 9506 | túmulo | 12 |
| 9507 | tropiezo | 12 |
| 9508 | trocado | 12 |
| 9509 | tristemente | 12 |
| 9510 | trechos | 12 |
| 9511 | trayo | 12 |
| 9512 | travesuras | 12 |
| 9513 | trastornado | 12 |
| 9514 | trasladar | 12 |
| 9515 | transición | 12 |
| 9516 | tranquilos | 12 |
| 9517 | trágico | 12 |
| 9518 | traducir | 12 |
| 9519 | traducción | 12 |
| 9520 | trabajan | 12 |
| 9521 | tosca | 12 |
| 9522 | topó | 12 |
| 9523 | tontonelo | 12 |
| 9524 | tomamos | 12 |
| 9525 | tomada | 12 |
| 9526 | tirón | 12 |
| 9527 | tiras | 12 |
| 9528 | tiraban | 12 |
| 9529 | tiernamente | 12 |
| 9530 | tiembla | 12 |
| 9531 | tha | 12 |
| 9532 | tentar | 12 |
| 9533 | tenor | 12 |
| 9534 | templos | 12 |
| 9535 | temían | 12 |
| 9536 | temen | 12 |
| 9537 | talleres | 12 |
| 9538 | sustenta | 12 |
| 9539 | suspendió | 12 |
| 9540 | suicidio | 12 |
| 9541 | sueles | 12 |
| 9542 | suegros | 12 |
| 9543 | sucesivamente | 12 |
| 9544 | subo | 12 |
| 9545 | súbitamente | 12 |
| 9546 | súbita | 12 |
| 9547 | suaue | 12 |
| 9548 | sostuvo | 12 |
| 9549 | sosteniendo | 12 |
| 9550 | soraberri | 12 |
| 9551 | soportar | 12 |
| 9552 | soportales | 12 |
| 9553 | sonreían | 12 |
| 9554 | sonora | 12 |
| 9555 | sonajas | 12 |
| 9556 | sólidos | 12 |
| 9557 | solicitar | 12 |
| 9558 | sofrimiento | 12 |
| 9559 | sobresaltos | 12 |
| 9560 | soberana | 12 |
| 9561 | sinceramente | 12 |
| 9562 | siéntese | 12 |
| 9563 | setiembre | 12 |
| 9564 | serviros | 12 |
| 9565 | servidos | 12 |
| 9566 | seréis | 12 |
| 9567 | seras | 12 |
| 9568 | septiembre | 12 |
| 9569 | señalar | 12 |
| 9570 | sentida | 12 |
| 9571 | sentían | 12 |
| 9572 | seducir | 12 |
| 9573 | sastres | 12 |
| 9574 | sangrienta | 12 |
| 9575 | samdai | 12 |
| 9576 | salvaçión | 12 |
| 9577 | saludando | 12 |
| 9578 | sacristanes | 12 |
| 9579 | sacas | 12 |
| 9580 | rutina | 12 |
| 9581 | run | 12 |
| 9582 | rrico | 12 |
| 9583 | rodean | 12 |
| 9584 | riscos | 12 |
| 9585 | riquísimo | 12 |
| 9586 | rieron | 12 |
| 9587 | revolver | 12 |
| 9588 | retratos | 12 |
| 9589 | retiraba | 12 |
| 9590 | responderé | 12 |
| 9591 | responden | 12 |
| 9592 | respetos | 12 |
| 9593 | respetado | 12 |
| 9594 | respetables | 12 |
| 9595 | resbalando | 12 |
| 9596 | repugnaba | 12 |
| 9597 | representó | 12 |
| 9598 | reposada | 12 |
| 9599 | repetición | 12 |
| 9600 | remiendos | 12 |
| 9601 | regazo | 12 |
| 9602 | reflexionar | 12 |
| 9603 | refiero | 12 |
| 9604 | recurrir | 12 |
| 9605 | recto | 12 |
| 9606 | recorrió | 12 |
| 9607 | recorría | 12 |
| 9608 | reconciliación | 12 |
| 9609 | recibiera | 12 |
| 9610 | recibiendo | 12 |
| 9611 | rebelde | 12 |
| 9612 | rápidas | 12 |
| 9613 | quitárselo | 12 |
| 9614 | quinqué | 12 |
| 9615 | quiénes | 12 |
| 9616 | queridas | 12 |
| 9617 | quejándose | 12 |
| 9618 | quedóse | 12 |
| 9619 | qualquiera | 12 |
| 9620 | pusimos | 12 |
| 9621 | purísima | 12 |
| 9622 | pupilas | 12 |
| 9623 | puñalada | 12 |
| 9624 | puñados | 12 |
| 9625 | publicar | 12 |
| 9626 | profundas | 12 |
| 9627 | producir | 12 |
| 9628 | producían | 12 |
| 9629 | procuran | 12 |
| 9630 | priessa | 12 |
| 9631 | prevención | 12 |
| 9632 | pretendo | 12 |
| 9633 | presurosa | 12 |
| 9634 | preguntase | 12 |
| 9635 | preferido | 12 |
| 9636 | praderas | 12 |
| 9637 | potencia | 12 |
| 9638 | postrer | 12 |
| 9639 | postas | 12 |
| 9640 | poseo | 12 |
| 9641 | pos | 12 |
| 9642 | portugal | 12 |
| 9643 | portarse | 12 |
| 9644 | porrazo | 12 |
| 9645 | porquerías | 12 |
| 9646 | políticas | 12 |
| 9647 | poderío | 12 |
| 9648 | pintoresco | 12 |
| 9649 | pintados | 12 |
| 9650 | pinos | 12 |
| 9651 | pila | 12 |
| 9652 | pierdes | 12 |
| 9653 | piadosos | 12 |
| 9654 | pestilencia | 12 |
| 9655 | persuadido | 12 |
| 9656 | perras | 12 |
| 9657 | perfumes | 12 |
| 9658 | perfecciones | 12 |
| 9659 | perdicion | 12 |
| 9660 | pense | 12 |
| 9661 | penitencias | 12 |
| 9662 | penetrante | 12 |
| 9663 | penetraba | 12 |
| 9664 | penar | 12 |
| 9665 | peluca | 12 |
| 9666 | pellejos | 12 |
| 9667 | pechera | 12 |
| 9668 | patrona | 12 |
| 9669 | patada | 12 |
| 9670 | passar | 12 |
| 9671 | pasaremos | 12 |
| 9672 | paréntesis | 12 |
| 9673 | pareciéndome | 12 |
| 9674 | pardiez | 12 |
| 9675 | papas | 12 |
| 9676 | pagará | 12 |
| 9677 | oya | 12 |
| 9678 | ovillo | 12 |
| 9679 | ortuñ | 12 |
| 9680 | ordinariamente | 12 |
| 9681 | opuso | 12 |
| 9682 | oportuna | 12 |
| 9683 | oponer | 12 |
| 9684 | opinó | 12 |
| 9685 | operaciones | 12 |
| 9686 | onza | 12 |
| 9687 | oírme | 12 |
| 9688 | ocupan | 12 |
| 9689 | occidente | 12 |
| 9690 | ocaso | 12 |
| 9691 | obedecía | 12 |
| 9692 | nueua | 12 |
| 9693 | nueces | 12 |
| 9694 | notables | 12 |
| 9695 | nieta | 12 |
| 9696 | navegación | 12 |
| 9697 | narrador | 12 |
| 9698 | naranjas | 12 |
| 9699 | nápoles | 12 |
| 9700 | nacía | 12 |
| 9701 | músicas | 12 |
| 9702 | mudó | 12 |
| 9703 | mr | 12 |
| 9704 | morían | 12 |
| 9705 | montado | 12 |
| 9706 | monos | 12 |
| 9707 | monarca | 12 |
| 9708 | mole | 12 |
| 9709 | mirara | 12 |
| 9710 | mirándose | 12 |
| 9711 | mírala | 12 |
| 9712 | mezclando | 12 |
| 9713 | metiéndose | 12 |
| 9714 | metí | 12 |
| 9715 | mester | 12 |
| 9716 | mesquino | 12 |
| 9717 | merluza | 12 |
| 9718 | mercaderes | 12 |
| 9719 | mensajero | 12 |
| 9720 | menguada | 12 |
| 9721 | mejorar | 12 |
| 9722 | meditabundo | 12 |
| 9723 | maza | 12 |
| 9724 | maternidad | 12 |
| 9725 | maternal | 12 |
| 9726 | matadero | 12 |
| 9727 | mascar | 12 |
| 9728 | masas | 12 |
| 9729 | mariposa | 12 |
| 9730 | marcos | 12 |
| 9731 | maravillosas | 12 |
| 9732 | mantenía | 12 |
| 9733 | mantel | 12 |
| 9734 | manteca | 12 |
| 9735 | maniobras | 12 |
| 9736 | manila | 12 |
| 9737 | manifiesta | 12 |
| 9738 | manejar | 12 |
| 9739 | mandé | 12 |
| 9740 | manchego | 12 |
| 9741 | mamarracho | 12 |
| 9742 | lustre | 12 |
| 9743 | lozanía | 12 |
| 9744 | loxuria | 12 |
| 9745 | lomos | 12 |
| 9746 | loba | 12 |
| 9747 | lloras | 12 |
| 9748 | lloraban | 12 |
| 9749 | llegas | 12 |
| 9750 | llantos | 12 |
| 9751 | llamarme | 12 |
| 9752 | llamaría | 12 |
| 9753 | llamándole | 12 |
| 9754 | literatos | 12 |
| 9755 | literata | 12 |
| 9756 | límite | 12 |
| 9757 | librea | 12 |
| 9758 | lelo | 12 |
| 9759 | lelio | 12 |
| 9760 | leerla | 12 |
| 9761 | latino | 12 |
| 9762 | latigazos | 12 |
| 9763 | lata | 12 |
| 9764 | lanzando | 12 |
| 9765 | lances | 12 |
| 9766 | lanas | 12 |
| 9767 | lámparas | 12 |
| 9768 | labradoras | 12 |
| 9769 | labrado | 12 |
| 9770 | juntan | 12 |
| 9771 | juguete | 12 |
| 9772 | jornadas | 12 |
| 9773 | jerusalén | 12 |
| 9774 | jefes | 12 |
| 9775 | jabonero | 12 |
| 9776 | irritado | 12 |
| 9777 | inventar | 12 |
| 9778 | íntimas | 12 |
| 9779 | interesantes | 12 |
| 9780 | intelectual | 12 |
| 9781 | institución | 12 |
| 9782 | indica | 12 |
| 9783 | incierto | 12 |
| 9784 | incendio | 12 |
| 9785 | inaudita | 12 |
| 9786 | inagotable | 12 |
| 9787 | imponente | 12 |
| 9788 | ímpetu | 12 |
| 9789 | impertinencias | 12 |
| 9790 | impertinencia | 12 |
| 9791 | imparcial | 12 |
| 9792 | imita | 12 |
| 9793 | imágines | 12 |
| 9794 | idioma | 12 |
| 9795 | humillación | 12 |
| 9796 | humildemente | 12 |
| 9797 | huellas | 12 |
| 9798 | hubiéramos | 12 |
| 9799 | honrosa | 12 |
| 9800 | honradamente | 12 |
| 9801 | honestos | 12 |
| 9802 | hondos | 12 |
| 9803 | hipócritas | 12 |
| 9804 | hinojos | 12 |
| 9805 | higiene | 12 |
| 9806 | heroísmo | 12 |
| 9807 | herejes | 12 |
| 9808 | helechos | 12 |
| 9809 | hazme | 12 |
| 9810 | hados | 12 |
| 9811 | hacerles | 12 |
| 9812 | habrías | 12 |
| 9813 | hablillas | 12 |
| 9814 | hablándole | 12 |
| 9815 | haberte | 12 |
| 9816 | gustaría | 12 |
| 9817 | gusanos | 12 |
| 9818 | guiar | 12 |
| 9819 | groseros | 12 |
| 9820 | gritaban | 12 |
| 9821 | grato | 12 |
| 9822 | gozos | 12 |
| 9823 | gozan | 12 |
| 9824 | gozado | 12 |
| 9825 | goleta | 12 |
| 9826 | gobiernan | 12 |
| 9827 | glosa | 12 |
| 9828 | glorieta | 12 |
| 9829 | glacial | 12 |
| 9830 | gascón | 12 |
| 9831 | gancho | 12 |
| 9832 | ganadero | 12 |
| 9833 | gafas | 12 |
| 9834 | fusiles | 12 |
| 9835 | fumar | 12 |
| 9836 | fuéramos | 12 |
| 9837 | fuelle | 12 |
| 9838 | frecuente | 12 |
| 9839 | fray | 12 |
| 9840 | frasco | 12 |
| 9841 | frágil | 12 |
| 9842 | florida | 12 |
| 9843 | flojedad | 12 |
| 9844 | fincas | 12 |
| 9845 | filo | 12 |
| 9846 | filipinas | 12 |
| 9847 | figurar | 12 |
| 9848 | fernández | 12 |
| 9849 | fer | 12 |
| 9850 | fénix | 12 |
| 9851 | fatalidad | 12 |
| 9852 | fanático | 12 |
| 9853 | familiaridad | 12 |
| 9854 | faltase | 12 |
| 9855 | falsedad | 12 |
| 9856 | fábulas | 12 |
| 9857 | extiende | 12 |
| 9858 | expuso | 12 |
| 9859 | expresándose | 12 |
| 9860 | explico | 12 |
| 9861 | explanada | 12 |
| 9862 | expansiva | 12 |
| 9863 | exigían | 12 |
| 9864 | exclama | 12 |
| 9865 | exacta | 12 |
| 9866 | estuviesen | 12 |
| 9867 | estuche | 12 |
| 9868 | estrechez | 12 |
| 9869 | estragos | 12 |
| 9870 | estoria | 12 |
| 9871 | estadística | 12 |
| 9872 | esquinas | 12 |
| 9873 | espinosa | 12 |
| 9874 | espin | 12 |
| 9875 | espectadores | 12 |
| 9876 | espantable | 12 |
| 9877 | espaciosa | 12 |
| 9878 | esp | 12 |
| 9879 | escuro | 12 |
| 9880 | escuchaban | 12 |
| 9881 | escote | 12 |
| 9882 | escopetas | 12 |
| 9883 | escondidos | 12 |
| 9884 | escoge | 12 |
| 9885 | escaparse | 12 |
| 9886 | escandaloso | 12 |
| 9887 | erudito | 12 |
| 9888 | errante | 12 |
| 9889 | enviase | 12 |
| 9890 | entretenido | 12 |
| 9891 | enterrar | 12 |
| 9892 | enterrado | 12 |
| 9893 | enteras | 12 |
| 9894 | entendiera | 12 |
| 9895 | entendidos | 12 |
| 9896 | enseñan | 12 |
| 9897 | ensayo | 12 |
| 9898 | engañados | 12 |
| 9899 | enderezar | 12 |
| 9900 | enciende | 12 |
| 9901 | encerrarse | 12 |
| 9902 | encarnada | 12 |
| 9903 | enamorar | 12 |
| 9904 | empacho | 12 |
| 9905 | ejercía | 12 |
| 9906 | ejemplares | 12 |
| 9907 | eficacia | 12 |
| 9908 | dulcísima | 12 |
| 9909 | duerma | 12 |
| 9910 | duelen | 12 |
| 9911 | dormí | 12 |
| 9912 | doñ | 12 |
| 9913 | dolencia | 12 |
| 9914 | doblones | 12 |
| 9915 | doblado | 12 |
| 9916 | distrito | 12 |
| 9917 | distante | 12 |
| 9918 | disputas | 12 |
| 9919 | displicente | 12 |
| 9920 | disfrutaba | 12 |
| 9921 | dise | 12 |
| 9922 | dirigir | 12 |
| 9923 | directamente | 12 |
| 9924 | diniero | 12 |
| 9925 | diluvio | 12 |
| 9926 | dijesen | 12 |
| 9927 | difuntos | 12 |
| 9928 | diestra | 12 |
| 9929 | diega | 12 |
| 9930 | diabla | 12 |
| 9931 | devotos | 12 |
| 9932 | deudos | 12 |
| 9933 | detenidamente | 12 |
| 9934 | despotismo | 12 |
| 9935 | despachar | 12 |
| 9936 | desolación | 12 |
| 9937 | desesperaba | 12 |
| 9938 | deseosos | 12 |
| 9939 | deseas | 12 |
| 9940 | descripción | 12 |
| 9941 | describiendo | 12 |
| 9942 | desconsolada | 12 |
| 9943 | descobrir | 12 |
| 9944 | derrama | 12 |
| 9945 | demos | 12 |
| 9946 | dejarte | 12 |
| 9947 | decirles | 12 |
| 9948 | dándoles | 12 |
| 9949 | cuydados | 12 |
| 9950 | cuyda | 12 |
| 9951 | curiosos | 12 |
| 9952 | cupo | 12 |
| 9953 | cultura | 12 |
| 9954 | cuitas | 12 |
| 9955 | cuita | 12 |
| 9956 | cuernos | 12 |
| 9957 | cuerdos | 12 |
| 9958 | cuelga | 12 |
| 9959 | cuchicheo | 12 |
| 9960 | cruzados | 12 |
| 9961 | cruda | 12 |
| 9962 | creencias | 12 |
| 9963 | creencia | 12 |
| 9964 | creemos | 12 |
| 9965 | costas | 12 |
| 9966 | cortaba | 12 |
| 9967 | correos | 12 |
| 9968 | convidó | 12 |
| 9969 | convida | 12 |
| 9970 | convenció | 12 |
| 9971 | contradicción | 12 |
| 9972 | contigua | 12 |
| 9973 | conste | 12 |
| 9974 | considere | 12 |
| 9975 | confirmación | 12 |
| 9976 | confiese | 12 |
| 9977 | confesarlo | 12 |
| 9978 | concha | 12 |
| 9979 | conceder | 12 |
| 9980 | componía | 12 |
| 9981 | comezón | 12 |
| 9982 | comestibles | 12 |
| 9983 | comería | 12 |
| 9984 | comercial | 12 |
| 9985 | coloquios | 12 |
| 9986 | colgar | 12 |
| 9987 | circo | 12 |
| 9988 | chismes | 12 |
| 9989 | chirinos | 12 |
| 9990 | chateaubriand | 12 |
| 9991 | cerrojo | 12 |
| 9992 | cerraban | 12 |
| 9993 | cerezas | 12 |
| 9994 | celebro | 12 |
| 9995 | celebraron | 12 |
| 9996 | cayese | 12 |
| 9997 | cautiva | 12 |
| 9998 | catón | 12 |
| 9999 | casera | 12 |
| 10000 | casaron | 12 |
| 10001 | casaca | 12 |
| 10002 | cartón | 12 |
| 10003 | cartera | 12 |
| 10004 | caros | 12 |
| 10005 | carita | 12 |
| 10006 | cargando | 12 |
| 10007 | capones | 12 |
| 10008 | canten | 12 |
| 10009 | caminaba | 12 |
| 10010 | camarada | 12 |
| 10011 | calvario | 12 |
| 10012 | caleta | 12 |
| 10013 | busco | 12 |
| 10014 | burlarse | 12 |
| 10015 | burlaba | 12 |
| 10016 | bulas | 12 |
| 10017 | brusca | 12 |
| 10018 | brilla | 12 |
| 10019 | brava | 12 |
| 10020 | boulevard | 12 |
| 10021 | bordes | 12 |
| 10022 | bonifacio | 12 |
| 10023 | bonete | 12 |
| 10024 | bolas | 12 |
| 10025 | bodega | 12 |
| 10026 | blasfemias | 12 |
| 10027 | bienaventurado | 12 |
| 10028 | biblia | 12 |
| 10029 | bernardino | 12 |
| 10030 | beneficencia | 12 |
| 10031 | bebiendo | 12 |
| 10032 | bautismo | 12 |
| 10033 | batuecos | 12 |
| 10034 | batuecas | 12 |
| 10035 | batanes | 12 |
| 10036 | barullo | 12 |
| 10037 | barras | 12 |
| 10038 | baronesa | 12 |
| 10039 | barcas | 12 |
| 10040 | barataria | 12 |
| 10041 | balbució | 12 |
| 10042 | babor | 12 |
| 10043 | azucenas | 12 |
| 10044 | ayunas | 12 |
| 10045 | ayudó | 12 |
| 10046 | avisado | 12 |
| 10047 | avíe | 12 |
| 10048 | aventuró | 12 |
| 10049 | avanzó | 12 |
| 10050 | auer | 12 |
| 10051 | atributos | 12 |
| 10052 | atrevían | 12 |
| 10053 | atrevería | 12 |
| 10054 | atreva | 12 |
| 10055 | atravesaba | 12 |
| 10056 | atracción | 12 |
| 10057 | atormentaba | 12 |
| 10058 | atónita | 12 |
| 10059 | atentado | 12 |
| 10060 | atenciones | 12 |
| 10061 | atacar | 12 |
| 10062 | astuta | 12 |
| 10063 | asistía | 12 |
| 10064 | asegurando | 12 |
| 10065 | arzón | 12 |
| 10066 | artesa | 12 |
| 10067 | arroyos | 12 |
| 10068 | ardin | 12 |
| 10069 | ardían | 12 |
| 10070 | arábigo | 12 |
| 10071 | apurado | 12 |
| 10072 | apurada | 12 |
| 10073 | aptitud | 12 |
| 10074 | aprovechando | 12 |
| 10075 | apreciación | 12 |
| 10076 | aplica | 12 |
| 10077 | apear | 12 |
| 10078 | apartando | 12 |
| 10079 | aparecían | 12 |
| 10080 | anunciar | 12 |
| 10081 | antoñito | 12 |
| 10082 | antonia | 12 |
| 10083 | antipática | 12 |
| 10084 | antigüedades | 12 |
| 10085 | angosta | 12 |
| 10086 | amezqueta | 12 |
| 10087 | amarillas | 12 |
| 10088 | amando | 12 |
| 10089 | alvarado | 12 |
| 10090 | alumnos | 12 |
| 10091 | alfombras | 12 |
| 10092 | alfileres | 12 |
| 10093 | alfiler | 12 |
| 10094 | alemania | 12 |
| 10095 | alegró | 12 |
| 10096 | alcanzara | 12 |
| 10097 | alcahueta | 12 |
| 10098 | alborotar | 12 |
| 10099 | alarmada | 12 |
| 10100 | ajuar | 12 |
| 10101 | ahoga | 12 |
| 10102 | agonía | 12 |
| 10103 | afligidos | 12 |
| 10104 | aficionados | 12 |
| 10105 | afectación | 12 |
| 10106 | advirtiendo | 12 |
| 10107 | adornos | 12 |
| 10108 | admitía | 12 |
| 10109 | administrador | 12 |
| 10110 | adivino | 12 |
| 10111 | acude | 12 |
| 10112 | actor | 12 |
| 10113 | acostumbradas | 12 |
| 10114 | aconsejar | 12 |
| 10115 | acólito | 12 |
| 10116 | aceros | 12 |
| 10117 | acendrada | 12 |
| 10118 | académico | 12 |
| 10119 | acabamos | 12 |
| 10120 | abrieron | 12 |
| 10121 | abren | 12 |
| 10122 | abrazando | 12 |
| 10123 | abeja | 12 |
| 10124 | abanicos | 12 |
| 10125 | abad | 12 |
| 10126 | zorrilla | 11 |
| 10127 | zor | 11 |
| 10128 | yaze | 11 |
| 10129 | yantar | 11 |
| 10130 | volviesen | 11 |
| 10131 | voluptuosa | 11 |
| 10132 | voltaire | 11 |
| 10133 | víveres | 11 |
| 10134 | vivaldo | 11 |
| 10135 | víspera | 11 |
| 10136 | visajes | 11 |
| 10137 | viñas | 11 |
| 10138 | villamojada | 11 |
| 10139 | viéndote | 11 |
| 10140 | verna | 11 |
| 10141 | vereda | 11 |
| 10142 | venieron | 11 |
| 10143 | vencedora | 11 |
| 10144 | veleta | 11 |
| 10145 | vapores | 11 |
| 10146 | vanagloria | 11 |
| 10147 | valdría | 11 |
| 10148 | vagando | 11 |
| 10149 | vacilaba | 11 |
| 10150 | vacías | 11 |
| 10151 | trujese | 11 |
| 10152 | truenos | 11 |
| 10153 | trate | 11 |
| 10154 | transformada | 11 |
| 10155 | trafalgar | 11 |
| 10156 | toser | 11 |
| 10157 | torrente | 11 |
| 10158 | tornar | 11 |
| 10159 | tordo | 11 |
| 10160 | torbellino | 11 |
| 10161 | tomarle | 11 |
| 10162 | toldo | 11 |
| 10163 | tod | 11 |
| 10164 | toalla | 11 |
| 10165 | tirana | 11 |
| 10166 | timón | 11 |
| 10167 | tilín | 11 |
| 10168 | tigo | 11 |
| 10169 | tí | 11 |
| 10170 | teta | 11 |
| 10171 | terrones | 11 |
| 10172 | terquedad | 11 |
| 10173 | teoría | 11 |
| 10174 | temible | 11 |
| 10175 | temerosos | 11 |
| 10176 | tejas | 11 |
| 10177 | tedio | 11 |
| 10178 | tarjeta | 11 |
| 10179 | tapices | 11 |
| 10180 | talavera | 11 |
| 10181 | tacha | 11 |
| 10182 | sustos | 11 |
| 10183 | suplicante | 11 |
| 10184 | suplicaba | 11 |
| 10185 | supieran | 11 |
| 10186 | sujetó | 11 |
| 10187 | sueña | 11 |
| 10188 | sotanas | 11 |
| 10189 | sostenida | 11 |
| 10190 | sortijas | 11 |
| 10191 | sopas | 11 |
| 10192 | sollozando | 11 |
| 10193 | solícito | 11 |
| 10194 | solemnes | 11 |
| 10195 | sobrinito | 11 |
| 10196 | sintiera | 11 |
| 10197 | siniestra | 11 |
| 10198 | silbaba | 11 |
| 10199 | siguiese | 11 |
| 10200 | sierpe | 11 |
| 10201 | seys | 11 |
| 10202 | sesión | 11 |
| 10203 | servirte | 11 |
| 10204 | servilleta | 11 |
| 10205 | seruir | 11 |
| 10206 | serrano | 11 |
| 10207 | serenos | 11 |
| 10208 | sepultado | 11 |
| 10209 | sepáis | 11 |
| 10210 | sensibilidad | 11 |
| 10211 | semeja | 11 |
| 10212 | seguras | 11 |
| 10213 | seguimos | 11 |
| 10214 | seductores | 11 |
| 10215 | secta | 11 |
| 10216 | secretas | 11 |
| 10217 | secretamente | 11 |
| 10218 | satírico | 11 |
| 10219 | saquen | 11 |
| 10220 | sandez | 11 |
| 10221 | saltaron | 11 |
| 10222 | saldrán | 11 |
| 10223 | sacos | 11 |
| 10224 | saborear | 11 |
| 10225 | saboreaba | 11 |
| 10226 | sabidor | 11 |
| 10227 | saberse | 11 |
| 10228 | rústicos | 11 |
| 10229 | ruines | 11 |
| 10230 | rudeza | 11 |
| 10231 | rompieron | 11 |
| 10232 | rogaba | 11 |
| 10233 | rodear | 11 |
| 10234 | robustez | 11 |
| 10235 | robaba | 11 |
| 10236 | roba | 11 |
| 10237 | rigores | 11 |
| 10238 | ridículos | 11 |
| 10239 | revueltas | 11 |
| 10240 | revoluciones | 11 |
| 10241 | revolucionaria | 11 |
| 10242 | revelaciones | 11 |
| 10243 | reunidos | 11 |
| 10244 | reunido | 11 |
| 10245 | reunían | 11 |
| 10246 | retumbaban | 11 |
| 10247 | resiste | 11 |
| 10248 | res | 11 |
| 10249 | requiebros | 11 |
| 10250 | repugnantes | 11 |
| 10251 | repollo | 11 |
| 10252 | replicar | 11 |
| 10253 | repetían | 11 |
| 10254 | repasar | 11 |
| 10255 | repartió | 11 |
| 10256 | reparó | 11 |
| 10257 | reparación | 11 |
| 10258 | remotos | 11 |
| 10259 | relativo | 11 |
| 10260 | relámpagos | 11 |
| 10261 | regreso | 11 |
| 10262 | regidores | 11 |
| 10263 | regalar | 11 |
| 10264 | refiere | 11 |
| 10265 | redención | 11 |
| 10266 | rectitud | 11 |
| 10267 | recorriendo | 11 |
| 10268 | recogía | 11 |
| 10269 | recobraba | 11 |
| 10270 | rebuzno | 11 |
| 10271 | radical | 11 |
| 10272 | quijada | 11 |
| 10273 | qui | 11 |
| 10274 | queridos | 11 |
| 10275 | queredes | 11 |
| 10276 | quemado | 11 |
| 10277 | quehaceres | 11 |
| 10278 | quedas | 11 |
| 10279 | quebrar | 11 |
| 10280 | quebrantado | 11 |
| 10281 | quebrada | 11 |
| 10282 | pusiste | 11 |
| 10283 | pusiesen | 11 |
| 10284 | púseme | 11 |
| 10285 | puntual | 11 |
| 10286 | puertos | 11 |
| 10287 | pudieras | 11 |
| 10288 | pudiéramos | 11 |
| 10289 | puchero | 11 |
| 10290 | prurito | 11 |
| 10291 | protestas | 11 |
| 10292 | proprio | 11 |
| 10293 | pronunció | 11 |
| 10294 | prometiendo | 11 |
| 10295 | profeta | 11 |
| 10296 | profanación | 11 |
| 10297 | pródigo | 11 |
| 10298 | procedimientos | 11 |
| 10299 | prisionero | 11 |
| 10300 | primas | 11 |
| 10301 | pretextos | 11 |
| 10302 | presumía | 11 |
| 10303 | preste | 11 |
| 10304 | presbítero | 11 |
| 10305 | prepararse | 11 |
| 10306 | preguntéle | 11 |
| 10307 | preçio | 11 |
| 10308 | pozos | 11 |
| 10309 | postigo | 11 |
| 10310 | posibilidad | 11 |
| 10311 | porrazos | 11 |
| 10312 | porquero | 11 |
| 10313 | poníase | 11 |
| 10314 | poesías | 11 |
| 10315 | podria | 11 |
| 10316 | podamos | 11 |
| 10317 | plegarias | 11 |
| 10318 | plantón | 11 |
| 10319 | plantar | 11 |
| 10320 | pisa | 11 |
| 10321 | pirámide | 11 |
| 10322 | pipa | 11 |
| 10323 | pilar | 11 |
| 10324 | pierdas | 11 |
| 10325 | pestañas | 11 |
| 10326 | pescados | 11 |
| 10327 | persuasión | 11 |
| 10328 | personales | 11 |
| 10329 | peroque | 11 |
| 10330 | permitir | 11 |
| 10331 | perfeción | 11 |
| 10332 | perezosos | 11 |
| 10333 | perdería | 11 |
| 10334 | percha | 11 |
| 10335 | pepito | 11 |
| 10336 | penoso | 11 |
| 10337 | penitentes | 11 |
| 10338 | peligrosos | 11 |
| 10339 | pegan | 11 |
| 10340 | pedacitos | 11 |
| 10341 | pausadamente | 11 |
| 10342 | patrón | 11 |
| 10343 | particularmente | 11 |
| 10344 | partí | 11 |
| 10345 | pareciole | 11 |
| 10346 | parches | 11 |
| 10347 | paraje | 11 |
| 10348 | papelito | 11 |
| 10349 | palafrén | 11 |
| 10350 | pájara | 11 |
| 10351 | pagaría | 11 |
| 10352 | pagada | 11 |
| 10353 | padilla | 11 |
| 10354 | pablos | 11 |
| 10355 | pabellón | 11 |
| 10356 | oyrte | 11 |
| 10357 | ostentación | 11 |
| 10358 | ospitalech | 11 |
| 10359 | osos | 11 |
| 10360 | osadía | 11 |
| 10361 | osa | 11 |
| 10362 | ordenaron | 11 |
| 10363 | ordenanzas | 11 |
| 10364 | ordenaba | 11 |
| 10365 | oracion | 11 |
| 10366 | oliendo | 11 |
| 10367 | oirás | 11 |
| 10368 | oídas | 11 |
| 10369 | oída | 11 |
| 10370 | ofrenda | 11 |
| 10371 | obrador | 11 |
| 10372 | obedeciendo | 11 |
| 10373 | notorio | 11 |
| 10374 | noria | 11 |
| 10375 | nombró | 11 |
| 10376 | nogal | 11 |
| 10377 | niegues | 11 |
| 10378 | niegue | 11 |
| 10379 | nazareno | 11 |
| 10380 | navegar | 11 |
| 10381 | nadar | 11 |
| 10382 | nacían | 11 |
| 10383 | mugre | 11 |
| 10384 | mudando | 11 |
| 10385 | mostaza | 11 |
| 10386 | mosquitos | 11 |
| 10387 | monumento | 11 |
| 10388 | montiel | 11 |
| 10389 | molina | 11 |
| 10390 | místicos | 11 |
| 10391 | missa | 11 |
| 10392 | mísera | 11 |
| 10393 | millón | 11 |
| 10394 | mezclada | 11 |
| 10395 | mezclaban | 11 |
| 10396 | mezclaba | 11 |
| 10397 | merecimiento | 11 |
| 10398 | menosprecio | 11 |
| 10399 | menguado | 11 |
| 10400 | menesteres | 11 |
| 10401 | mend | 11 |
| 10402 | mención | 11 |
| 10403 | matrimonios | 11 |
| 10404 | matara | 11 |
| 10405 | mariposas | 11 |
| 10406 | mari | 11 |
| 10407 | mareaba | 11 |
| 10408 | marchando | 11 |
| 10409 | maravillado | 11 |
| 10410 | manicomio | 11 |
| 10411 | mandaron | 11 |
| 10412 | mandamos | 11 |
| 10413 | manchada | 11 |
| 10414 | maldición | 11 |
| 10415 | maldecir | 11 |
| 10416 | maldecía | 11 |
| 10417 | majo | 11 |
| 10418 | mágica | 11 |
| 10419 | maduro | 11 |
| 10420 | lunar | 11 |
| 10421 | lucir | 11 |
| 10422 | lucientes | 11 |
| 10423 | llevé | 11 |
| 10424 | llevasen | 11 |
| 10425 | llenado | 11 |
| 10426 | llamasen | 11 |
| 10427 | lino | 11 |
| 10428 | lince | 11 |
| 10429 | lienzos | 11 |
| 10430 | librería | 11 |
| 10431 | levántate | 11 |
| 10432 | letargo | 11 |
| 10433 | lenta | 11 |
| 10434 | leían | 11 |
| 10435 | leandro | 11 |
| 10436 | lazarillo | 11 |
| 10437 | lastimero | 11 |
| 10438 | lanzarote | 11 |
| 10439 | lamentaba | 11 |
| 10440 | laguna | 11 |
| 10441 | labrar | 11 |
| 10442 | labores | 11 |
| 10443 | juzgue | 11 |
| 10444 | juzgado | 11 |
| 10445 | juzgaba | 11 |
| 10446 | juvenil | 11 |
| 10447 | juntarse | 11 |
| 10448 | judíos | 11 |
| 10449 | judía | 11 |
| 10450 | judas | 11 |
| 10451 | jovialidad | 11 |
| 10452 | jaspe | 11 |
| 10453 | jaca | 11 |
| 10454 | italiano | 11 |
| 10455 | irán | 11 |
| 10456 | introducir | 11 |
| 10457 | intrépido | 11 |
| 10458 | intervenir | 11 |
| 10459 | intérprete | 11 |
| 10460 | insufrible | 11 |
| 10461 | instantes | 11 |
| 10462 | insistencia | 11 |
| 10463 | injusta | 11 |
| 10464 | ingenuidad | 11 |
| 10465 | infundía | 11 |
| 10466 | infernales | 11 |
| 10467 | inferir | 11 |
| 10468 | infançon | 11 |
| 10469 | infalibilidad | 11 |
| 10470 | inerte | 11 |
| 10471 | indecoroso | 11 |
| 10472 | inclusive | 11 |
| 10473 | inclusa | 11 |
| 10474 | impulsaba | 11 |
| 10475 | impresas | 11 |
| 10476 | impone | 11 |
| 10477 | imitaba | 11 |
| 10478 | imbécil | 11 |
| 10479 | ilustrada | 11 |
| 10480 | hundida | 11 |
| 10481 | hueca | 11 |
| 10482 | horrendo | 11 |
| 10483 | horrenda | 11 |
| 10484 | hongo | 11 |
| 10485 | homero | 11 |
| 10486 | holgara | 11 |
| 10487 | histórica | 11 |
| 10488 | hijito | 11 |
| 10489 | hidalguía | 11 |
| 10490 | herreruelo | 11 |
| 10491 | herederos | 11 |
| 10492 | haussonville | 11 |
| 10493 | hallarme | 11 |
| 10494 | hallábanse | 11 |
| 10495 | haldas | 11 |
| 10496 | hacíamos | 11 |
| 10497 | habíale | 11 |
| 10498 | gustoso | 11 |
| 10499 | gusano | 11 |
| 10500 | guinart | 11 |
| 10501 | guijarros | 11 |
| 10502 | guardase | 11 |
| 10503 | granuja | 11 |
| 10504 | goloso | 11 |
| 10505 | golondrina | 11 |
| 10506 | gloriosos | 11 |
| 10507 | geografía | 11 |
| 10508 | gemelos | 11 |
| 10509 | gata | 11 |
| 10510 | gastan | 11 |
| 10511 | gamo | 11 |
| 10512 | gaita | 11 |
| 10513 | fundado | 11 |
| 10514 | fundada | 11 |
| 10515 | fugaz | 11 |
| 10516 | fragua | 11 |
| 10517 | floresta | 11 |
| 10518 | flojo | 11 |
| 10519 | floja | 11 |
| 10520 | firmar | 11 |
| 10521 | firmamento | 11 |
| 10522 | filosófica | 11 |
| 10523 | filipe | 11 |
| 10524 | fiereza | 11 |
| 10525 | fiambre | 11 |
| 10526 | ferocidad | 11 |
| 10527 | felicísima | 11 |
| 10528 | fecunda | 11 |
| 10529 | favorezca | 11 |
| 10530 | fatigaba | 11 |
| 10531 | far | 11 |
| 10532 | faltriquera | 11 |
| 10533 | faltarán | 11 |
| 10534 | fablas | 11 |
| 10535 | expedientes | 11 |
| 10536 | existían | 11 |
| 10537 | exclamación | 11 |
| 10538 | excitada | 11 |
| 10539 | excesivo | 11 |
| 10540 | examinaba | 11 |
| 10541 | exageraciones | 11 |
| 10542 | exacto | 11 |
| 10543 | eucaliptus | 11 |
| 10544 | estuviere | 11 |
| 10545 | estudia | 11 |
| 10546 | estribillo | 11 |
| 10547 | estirado | 11 |
| 10548 | estera | 11 |
| 10549 | estatuas | 11 |
| 10550 | establecido | 11 |
| 10551 | espuela | 11 |
| 10552 | espías | 11 |
| 10553 | espiaba | 11 |
| 10554 | espérate | 11 |
| 10555 | espectáculos | 11 |
| 10556 | espacios | 11 |
| 10557 | esforzaba | 11 |
| 10558 | escusado | 11 |
| 10559 | escribirle | 11 |
| 10560 | escogió | 11 |
| 10561 | escocesa | 11 |
| 10562 | errar | 11 |
| 10563 | errado | 11 |
| 10564 | érale | 11 |
| 10565 | equivoco | 11 |
| 10566 | envió | 11 |
| 10567 | entrevista | 11 |
| 10568 | entretiene | 11 |
| 10569 | entretenida | 11 |
| 10570 | entregarse | 11 |
| 10571 | entrará | 11 |
| 10572 | entradas | 11 |
| 10573 | enteró | 11 |
| 10574 | enterada | 11 |
| 10575 | entendiese | 11 |
| 10576 | entendieron | 11 |
| 10577 | enseñarle | 11 |
| 10578 | enramada | 11 |
| 10579 | enjuto | 11 |
| 10580 | engendra | 11 |
| 10581 | engañarme | 11 |
| 10582 | engano | 11 |
| 10583 | enfadar | 11 |
| 10584 | enérgica | 11 |
| 10585 | endeble | 11 |
| 10586 | encuentros | 11 |
| 10587 | encogido | 11 |
| 10588 | encerrar | 11 |
| 10589 | enano | 11 |
| 10590 | empleos | 11 |
| 10591 | empeñaba | 11 |
| 10592 | emigración | 11 |
| 10593 | embozado | 11 |
| 10594 | elevarse | 11 |
| 10595 | económica | 11 |
| 10596 | dure | 11 |
| 10597 | durandarte | 11 |
| 10598 | dulçe | 11 |
| 10599 | dramática | 11 |
| 10600 | dormitorio | 11 |
| 10601 | dominios | 11 |
| 10602 | doctos | 11 |
| 10603 | doctores | 11 |
| 10604 | dividido | 11 |
| 10605 | diversidad | 11 |
| 10606 | distintamente | 11 |
| 10607 | distinguido | 11 |
| 10608 | distantes | 11 |
| 10609 | dispuestos | 11 |
| 10610 | displicencia | 11 |
| 10611 | disparado | 11 |
| 10612 | disparaba | 11 |
| 10613 | disimuladamente | 11 |
| 10614 | discurría | 11 |
| 10615 | disco | 11 |
| 10616 | diosa | 11 |
| 10617 | dijéramos | 11 |
| 10618 | dieren | 11 |
| 10619 | dibujos | 11 |
| 10620 | devaneos | 11 |
| 10621 | determina | 11 |
| 10622 | detenido | 11 |
| 10623 | destinada | 11 |
| 10624 | desterrado | 11 |
| 10625 | desposado | 11 |
| 10626 | despertaron | 11 |
| 10627 | despertando | 11 |
| 10628 | desonrra | 11 |
| 10629 | deslizándose | 11 |
| 10630 | deshonrado | 11 |
| 10631 | desfachatez | 11 |
| 10632 | desean | 11 |
| 10633 | deseamos | 11 |
| 10634 | desdeñosa | 11 |
| 10635 | descuidada | 11 |
| 10636 | descubra | 11 |
| 10637 | describir | 11 |
| 10638 | describe | 11 |
| 10639 | descontento | 11 |
| 10640 | descontenta | 11 |
| 10641 | descarga | 11 |
| 10642 | descansaba | 11 |
| 10643 | desaparecieron | 11 |
| 10644 | desamparado | 11 |
| 10645 | desaires | 11 |
| 10646 | derrotado | 11 |
| 10647 | demostraba | 11 |
| 10648 | demasía | 11 |
| 10649 | dejémonos | 11 |
| 10650 | decidirse | 11 |
| 10651 | deba | 11 |
| 10652 | darla | 11 |
| 10653 | curiosa | 11 |
| 10654 | cuitado | 11 |
| 10655 | cruzaban | 11 |
| 10656 | cruzaba | 11 |
| 10657 | criminales | 11 |
| 10658 | creeré | 11 |
| 10659 | créelo | 11 |
| 10660 | cortesana | 11 |
| 10661 | cortaron | 11 |
| 10662 | corpus | 11 |
| 10663 | corchuelo | 11 |
| 10664 | convidar | 11 |
| 10665 | convaleciente | 11 |
| 10666 | conté | 11 |
| 10667 | contara | 11 |
| 10668 | contándole | 11 |
| 10669 | contadas | 11 |
| 10670 | consumía | 11 |
| 10671 | consuela | 11 |
| 10672 | construir | 11 |
| 10673 | consorte | 11 |
| 10674 | consideró | 11 |
| 10675 | conservando | 11 |
| 10676 | conseguirlo | 11 |
| 10677 | consagrada | 11 |
| 10678 | conquistas | 11 |
| 10679 | conquistado | 11 |
| 10680 | confundir | 11 |
| 10681 | confío | 11 |
| 10682 | conejos | 11 |
| 10683 | conciertos | 11 |
| 10684 | comunicó | 11 |
| 10685 | comodidades | 11 |
| 10686 | comienzan | 11 |
| 10687 | combinación | 11 |
| 10688 | coleto | 11 |
| 10689 | colas | 11 |
| 10690 | cogida | 11 |
| 10691 | cogí | 11 |
| 10692 | codicioso | 11 |
| 10693 | coco | 11 |
| 10694 | cobró | 11 |
| 10695 | cobra | 11 |
| 10696 | clavija | 11 |
| 10697 | clavando | 11 |
| 10698 | clásicos | 11 |
| 10699 | clarito | 11 |
| 10700 | citado | 11 |
| 10701 | çierta | 11 |
| 10702 | cierre | 11 |
| 10703 | cient | 11 |
| 10704 | chirimías | 11 |
| 10705 | chimeneas | 11 |
| 10706 | cerveza | 11 |
| 10707 | cenado | 11 |
| 10708 | celosías | 11 |
| 10709 | cavilar | 11 |
| 10710 | catedrático | 11 |
| 10711 | casorio | 11 |
| 10712 | casilda | 11 |
| 10713 | cascabeles | 11 |
| 10714 | casase | 11 |
| 10715 | casaba | 11 |
| 10716 | cartilla | 11 |
| 10717 | cartagena | 11 |
| 10718 | carpio | 11 |
| 10719 | carmesí | 11 |
| 10720 | caritativa | 11 |
| 10721 | cargan | 11 |
| 10722 | carecer | 11 |
| 10723 | cardenal | 11 |
| 10724 | capitana | 11 |
| 10725 | capitales | 11 |
| 10726 | caos | 11 |
| 10727 | cante | 11 |
| 10728 | cantara | 11 |
| 10729 | cano | 11 |
| 10730 | canal | 11 |
| 10731 | campesino | 11 |
| 10732 | caminaban | 11 |
| 10733 | calzón | 11 |
| 10734 | callarse | 11 |
| 10735 | caería | 11 |
| 10736 | cadáveres | 11 |
| 10737 | buscase | 11 |
| 10738 | buscarla | 11 |
| 10739 | buscaré | 11 |
| 10740 | bufete | 11 |
| 10741 | bozes | 11 |
| 10742 | botín | 11 |
| 10743 | bote | 11 |
| 10744 | borrico | 11 |
| 10745 | bolsas | 11 |
| 10746 | besaba | 11 |
| 10747 | benditos | 11 |
| 10748 | bendiciones | 11 |
| 10749 | beldad | 11 |
| 10750 | baza | 11 |
| 10751 | batiendo | 11 |
| 10752 | bastó | 11 |
| 10753 | barniz | 11 |
| 10754 | barbarie | 11 |
| 10755 | baratijas | 11 |
| 10756 | azotar | 11 |
| 10757 | ayudarle | 11 |
| 10758 | ayudan | 11 |
| 10759 | avisos | 11 |
| 10760 | avergonzada | 11 |
| 10761 | avanzando | 11 |
| 10762 | augusto | 11 |
| 10763 | atrocidad | 11 |
| 10764 | atraía | 11 |
| 10765 | atienda | 11 |
| 10766 | atalaya | 11 |
| 10767 | astrología | 11 |
| 10768 | asquerosa | 11 |
| 10769 | asomaban | 11 |
| 10770 | asiendo | 11 |
| 10771 | ascensión | 11 |
| 10772 | artífice | 11 |
| 10773 | arrojan | 11 |
| 10774 | arrimó | 11 |
| 10775 | arremetieron | 11 |
| 10776 | arranques | 11 |
| 10777 | arrancado | 11 |
| 10778 | aristócrata | 11 |
| 10779 | ardite | 11 |
| 10780 | archivo | 11 |
| 10781 | arbustos | 11 |
| 10782 | apures | 11 |
| 10783 | aproximaba | 11 |
| 10784 | aprendió | 11 |
| 10785 | aprecio | 11 |
| 10786 | apoyar | 11 |
| 10787 | aposentos | 11 |
| 10788 | aplomo | 11 |
| 10789 | aplicaba | 11 |
| 10790 | apartaron | 11 |
| 10791 | anteojo | 11 |
| 10792 | ansimismo | 11 |
| 10793 | anillo | 11 |
| 10794 | angel | 11 |
| 10795 | andaría | 11 |
| 10796 | amenazando | 11 |
| 10797 | ámbar | 11 |
| 10798 | alzaron | 11 |
| 10799 | alumbraba | 11 |
| 10800 | alquilar | 11 |
| 10801 | almunia | 11 |
| 10802 | almirez | 11 |
| 10803 | aljaba | 11 |
| 10804 | albor | 11 |
| 10805 | albogues | 11 |
| 10806 | alado | 11 |
| 10807 | alababan | 11 |
| 10808 | alaba | 11 |
| 10809 | agudos | 11 |
| 10810 | agarró | 11 |
| 10811 | afirmaba | 11 |
| 10812 | afectando | 11 |
| 10813 | afectada | 11 |
| 10814 | afectaba | 11 |
| 10815 | adoptar | 11 |
| 10816 | admitido | 11 |
| 10817 | admiraron | 11 |
| 10818 | adelantos | 11 |
| 10819 | adela | 11 |
| 10820 | acostumbraba | 11 |
| 10821 | acosado | 11 |
| 10822 | aconsejaba | 11 |
| 10823 | acometido | 11 |
| 10824 | acometida | 11 |
| 10825 | acogió | 11 |
| 10826 | acceso | 11 |
| 10827 | acariciando | 11 |
| 10828 | academia | 11 |
| 10829 | acabóse | 11 |
| 10830 | absurda | 11 |
| 10831 | abreviar | 11 |
| 10832 | abrazaron | 11 |
| 10833 | abrasa | 11 |
| 10834 | aborrecido | 11 |
| 10835 | aborrece | 11 |
| 10836 | zarpa | 10 |
| 10837 | zalamerías | 10 |
| 10838 | zaga | 10 |
| 10839 | yéndose | 10 |
| 10840 | yelo | 10 |
| 10841 | yeguas | 10 |
| 10842 | yd | 10 |
| 10843 | vulgarmente | 10 |
| 10844 | vuélvete | 10 |
| 10845 | voluptuoso | 10 |
| 10846 | volado | 10 |
| 10847 | volaban | 10 |
| 10848 | vistoso | 10 |
| 10849 | visten | 10 |
| 10850 | visitaban | 10 |
| 10851 | virtuoso | 10 |
| 10852 | vigilar | 10 |
| 10853 | viga | 10 |
| 10854 | vien | 10 |
| 10855 | vicioso | 10 |
| 10856 | víbora | 10 |
| 10857 | viático | 10 |
| 10858 | vianda | 10 |
| 10859 | verles | 10 |
| 10860 | verían | 10 |
| 10861 | veríamos | 10 |
| 10862 | venturosa | 10 |
| 10863 | venecia | 10 |
| 10864 | vendedor | 10 |
| 10865 | vencedores | 10 |
| 10866 | velocidad | 10 |
| 10867 | vejer | 10 |
| 10868 | vayamos | 10 |
| 10869 | variado | 10 |
| 10870 | vales | 10 |
| 10871 | vacilando | 10 |
| 10872 | vacaciones | 10 |
| 10873 | útiles | 10 |
| 10874 | usadas | 10 |
| 10875 | urbanidad | 10 |
| 10876 | umbrales | 10 |
| 10877 | turrón | 10 |
| 10878 | trompa | 10 |
| 10879 | trocó | 10 |
| 10880 | trocar | 10 |
| 10881 | triunfa | 10 |
| 10882 | tristísimo | 10 |
| 10883 | trenzas | 10 |
| 10884 | trébol | 10 |
| 10885 | trastienda | 10 |
| 10886 | traspaso | 10 |
| 10887 | trasluce | 10 |
| 10888 | trasladó | 10 |
| 10889 | tránsito | 10 |
| 10890 | transigir | 10 |
| 10891 | trances | 10 |
| 10892 | traídos | 10 |
| 10893 | tortas | 10 |
| 10894 | torcidas | 10 |
| 10895 | toques | 10 |
| 10896 | topado | 10 |
| 10897 | tomen | 10 |
| 10898 | tomarme | 10 |
| 10899 | tolerar | 10 |
| 10900 | tocarle | 10 |
| 10901 | tocada | 10 |
| 10902 | tiranos | 10 |
| 10903 | tiran | 10 |
| 10904 | tinajas | 10 |
| 10905 | tesis | 10 |
| 10906 | tertulios | 10 |
| 10907 | terrado | 10 |
| 10908 | ternezas | 10 |
| 10909 | teólogo | 10 |
| 10910 | tenerte | 10 |
| 10911 | tenaz | 10 |
| 10912 | temiera | 10 |
| 10913 | temes | 10 |
| 10914 | tapándose | 10 |
| 10915 | tamaña | 10 |
| 10916 | talentos | 10 |
| 10917 | tachas | 10 |
| 10918 | tablado | 10 |
| 10919 | susurro | 10 |
| 10920 | suso | 10 |
| 10921 | sulpicia | 10 |
| 10922 | sujetaba | 10 |
| 10923 | subamos | 10 |
| 10924 | süave | 10 |
| 10925 | sserrana | 10 |
| 10926 | sospechando | 10 |
| 10927 | soplar | 10 |
| 10928 | soñé | 10 |
| 10929 | soñador | 10 |
| 10930 | sonrosada | 10 |
| 10931 | sonante | 10 |
| 10932 | sólida | 10 |
| 10933 | solemos | 10 |
| 10934 | solemnidades | 10 |
| 10935 | soldada | 10 |
| 10936 | sofocado | 10 |
| 10937 | sobrevino | 10 |
| 10938 | sobremesa | 10 |
| 10939 | sobran | 10 |
| 10940 | singulares | 10 |
| 10941 | simpleza | 10 |
| 10942 | significaban | 10 |
| 10943 | sigilo | 10 |
| 10944 | siéndolo | 10 |
| 10945 | sey | 10 |
| 10946 | sevillano | 10 |
| 10947 | servirá | 10 |
| 10948 | servanda | 10 |
| 10949 | serle | 10 |
| 10950 | separó | 10 |
| 10951 | señalaba | 10 |
| 10952 | sentirlo | 10 |
| 10953 | sentadas | 10 |
| 10954 | sendos | 10 |
| 10955 | senal | 10 |
| 10956 | semos | 10 |
| 10957 | semejaba | 10 |
| 10958 | seguirla | 10 |
| 10959 | seguiría | 10 |
| 10960 | seguí | 10 |
| 10961 | secar | 10 |
| 10962 | seades | 10 |
| 10963 | sanas | 10 |
| 10964 | salvarme | 10 |
| 10965 | saluda | 10 |
| 10966 | salteador | 10 |
| 10967 | saldremos | 10 |
| 10968 | salado | 10 |
| 10969 | sagaces | 10 |
| 10970 | saeta | 10 |
| 10971 | sacamos | 10 |
| 10972 | sabida | 10 |
| 10973 | sabias | 10 |
| 10974 | saavedra | 10 |
| 10975 | ruidosa | 10 |
| 10976 | rubor | 10 |
| 10977 | rubíes | 10 |
| 10978 | rraçón | 10 |
| 10979 | rompo | 10 |
| 10980 | rompiera | 10 |
| 10981 | rompen | 10 |
| 10982 | rodeo | 10 |
| 10983 | rodeados | 10 |
| 10984 | robaron | 10 |
| 10985 | rio | 10 |
| 10986 | ríes | 10 |
| 10987 | ríen | 10 |
| 10988 | revolvió | 10 |
| 10989 | revelar | 10 |
| 10990 | retirar | 10 |
| 10991 | retaguardia | 10 |
| 10992 | resultando | 10 |
| 10993 | resultados | 10 |
| 10994 | resta | 10 |
| 10995 | resquicios | 10 |
| 10996 | respondióme | 10 |
| 10997 | respondióle | 10 |
| 10998 | respaldo | 10 |
| 10999 | reservada | 10 |
| 11000 | rescatar | 10 |
| 11001 | requesones | 10 |
| 11002 | representante | 10 |
| 11003 | reprehensión | 10 |
| 11004 | replicaba | 10 |
| 11005 | repasaba | 10 |
| 11006 | repartía | 10 |
| 11007 | reparte | 10 |
| 11008 | reñido | 10 |
| 11009 | renglones | 10 |
| 11010 | remotas | 10 |
| 11011 | reluciente | 10 |
| 11012 | religiones | 10 |
| 11013 | reflexión | 10 |
| 11014 | reducir | 10 |
| 11015 | reconciliar | 10 |
| 11016 | recomendado | 10 |
| 11017 | recogieron | 10 |
| 11018 | recobrado | 10 |
| 11019 | recibida | 10 |
| 11020 | recia | 10 |
| 11021 | recebirle | 10 |
| 11022 | rebelión | 10 |
| 11023 | razonamientos | 10 |
| 11024 | rasa | 10 |
| 11025 | rapaz | 10 |
| 11026 | ranas | 10 |
| 11027 | rana | 10 |
| 11028 | ramsés | 10 |
| 11029 | rabiando | 10 |
| 11030 | querré | 10 |
| 11031 | querrán | 10 |
| 11032 | quererme | 10 |
| 11033 | quererle | 10 |
| 11034 | querellas | 10 |
| 11035 | quejo | 10 |
| 11036 | quejar | 10 |
| 11037 | quebranta | 10 |
| 11038 | pusiéronle | 10 |
| 11039 | puñaladas | 10 |
| 11040 | puerca | 10 |
| 11041 | publicado | 10 |
| 11042 | próximos | 10 |
| 11043 | próximamente | 10 |
| 11044 | proverbio | 10 |
| 11045 | protectora | 10 |
| 11046 | protector | 10 |
| 11047 | prosupuesto | 10 |
| 11048 | prosaica | 10 |
| 11049 | proposiciones | 10 |
| 11050 | propongo | 10 |
| 11051 | pronunciado | 10 |
| 11052 | prometí | 10 |
| 11053 | progresista | 10 |
| 11054 | profesa | 10 |
| 11055 | profecía | 10 |
| 11056 | producen | 10 |
| 11057 | prodigios | 10 |
| 11058 | proceso | 10 |
| 11059 | probabilidades | 10 |
| 11060 | primeramente | 10 |
| 11061 | prim | 10 |
| 11062 | prevenir | 10 |
| 11063 | prevenciones | 10 |
| 11064 | presumida | 10 |
| 11065 | prestada | 10 |
| 11066 | presenciado | 10 |
| 11067 | premática | 10 |
| 11068 | pregón | 10 |
| 11069 | preferencia | 10 |
| 11070 | precia | 10 |
| 11071 | poyo | 10 |
| 11072 | postre | 10 |
| 11073 | positivas | 10 |
| 11074 | poseído | 10 |
| 11075 | poseen | 10 |
| 11076 | portezuela | 10 |
| 11077 | portera | 10 |
| 11078 | porte | 10 |
| 11079 | porfiar | 10 |
| 11080 | populares | 10 |
| 11081 | poniéndome | 10 |
| 11082 | póngase | 10 |
| 11083 | ponerlo | 10 |
| 11084 | ponce | 10 |
| 11085 | pollinos | 10 |
| 11086 | polka | 10 |
| 11087 | podridos | 10 |
| 11088 | podías | 10 |
| 11089 | podíamos | 10 |
| 11090 | poderse | 10 |
| 11091 | poblado | 10 |
| 11092 | plebeyo | 10 |
| 11093 | plazeres | 10 |
| 11094 | plantado | 10 |
| 11095 | plancha | 10 |
| 11096 | pisaba | 10 |
| 11097 | pintores | 10 |
| 11098 | pinto | 10 |
| 11099 | pimienta | 10 |
| 11100 | pierres | 10 |
| 11101 | pidiera | 10 |
| 11102 | pichía | 10 |
| 11103 | petición | 10 |
| 11104 | pestes | 10 |
| 11105 | pesia | 10 |
| 11106 | pésame | 10 |
| 11107 | perspicacia | 10 |
| 11108 | periquito | 10 |
| 11109 | perdiera | 10 |
| 11110 | perdían | 10 |
| 11111 | perderla | 10 |
| 11112 | pequeñuelo | 10 |
| 11113 | pensaua | 10 |
| 11114 | pensativa | 10 |
| 11115 | penetró | 10 |
| 11116 | penada | 10 |
| 11117 | pellizco | 10 |
| 11118 | peines | 10 |
| 11119 | pegados | 10 |
| 11120 | pedr | 10 |
| 11121 | peca | 10 |
| 11122 | patros | 10 |
| 11123 | patrimonio | 10 |
| 11124 | passa | 10 |
| 11125 | pasmada | 10 |
| 11126 | pasadizo | 10 |
| 11127 | partieron | 10 |
| 11128 | partidarios | 10 |
| 11129 | participar | 10 |
| 11130 | parido | 10 |
| 11131 | parentela | 10 |
| 11132 | pareciera | 10 |
| 11133 | pareciendo | 10 |
| 11134 | parecería | 10 |
| 11135 | parándose | 10 |
| 11136 | paquita | 10 |
| 11137 | papás | 10 |
| 11138 | pantorrilla | 10 |
| 11139 | pana | 10 |
| 11140 | palomo | 10 |
| 11141 | palillos | 10 |
| 11142 | pálidas | 10 |
| 11143 | palcos | 10 |
| 11144 | pajarillos | 10 |
| 11145 | paisanos | 10 |
| 11146 | paguen | 10 |
| 11147 | pagas | 10 |
| 11148 | pagano | 10 |
| 11149 | padeció | 10 |
| 11150 | oyeran | 10 |
| 11151 | oviste | 10 |
| 11152 | oraçión | 10 |
| 11153 | olfato | 10 |
| 11154 | oleaje | 10 |
| 11155 | oímos | 10 |
| 11156 | oíase | 10 |
| 11157 | odiaba | 10 |
| 11158 | oda | 10 |
| 11159 | ocurrieron | 10 |
| 11160 | ocurrencia | 10 |
| 11161 | ocio | 10 |
| 11162 | ochavo | 10 |
| 11163 | obligaron | 10 |
| 11164 | obligan | 10 |
| 11165 | nublado | 10 |
| 11166 | noviembre | 10 |
| 11167 | notoria | 10 |
| 11168 | notando | 10 |
| 11169 | norabuena | 10 |
| 11170 | nonbre | 10 |
| 11171 | ningunas | 10 |
| 11172 | nidos | 10 |
| 11173 | nicolasa | 10 |
| 11174 | nepomuceno | 10 |
| 11175 | neçio | 10 |
| 11176 | necesariamente | 10 |
| 11177 | navarro | 10 |
| 11178 | nácar | 10 |
| 11179 | nabo | 10 |
| 11180 | mutuamente | 10 |
| 11181 | murmuraciones | 10 |
| 11182 | muncha | 10 |
| 11183 | muleta | 10 |
| 11184 | mueran | 10 |
| 11185 | mude | 10 |
| 11186 | movieron | 10 |
| 11187 | moviéndose | 10 |
| 11188 | mota | 10 |
| 11189 | moriré | 10 |
| 11190 | montemayor | 10 |
| 11191 | mojado | 10 |
| 11192 | moça | 10 |
| 11193 | mitra | 10 |
| 11194 | mitología | 10 |
| 11195 | misántropo | 10 |
| 11196 | millas | 10 |
| 11197 | migajas | 10 |
| 11198 | miga | 10 |
| 11199 | menudeaban | 10 |
| 11200 | mensajera | 10 |
| 11201 | melón | 10 |
| 11202 | mecánico | 10 |
| 11203 | matices | 10 |
| 11204 | materna | 10 |
| 11205 | mario | 10 |
| 11206 | marea | 10 |
| 11207 | marcho | 10 |
| 11208 | marcado | 10 |
| 11209 | maravillosamente | 10 |
| 11210 | mantua | 10 |
| 11211 | mantones | 10 |
| 11212 | manifestarse | 10 |
| 11213 | manifestación | 10 |
| 11214 | manejaba | 10 |
| 11215 | manden | 10 |
| 11216 | mandamientos | 10 |
| 11217 | manada | 10 |
| 11218 | maliciosos | 10 |
| 11219 | malditos | 10 |
| 11220 | maldiciente | 10 |
| 11221 | málaga | 10 |
| 11222 | maestrías | 10 |
| 11223 | luminosa | 10 |
| 11224 | luengo | 10 |
| 11225 | lograr | 10 |
| 11226 | lograba | 10 |
| 11227 | lóbrega | 10 |
| 11228 | loado | 10 |
| 11229 | llovido | 10 |
| 11230 | llore | 10 |
| 11231 | llegáronse | 10 |
| 11232 | llamaré | 10 |
| 11233 | llamaran | 10 |
| 11234 | llamadas | 10 |
| 11235 | liviandad | 10 |
| 11236 | liviana | 10 |
| 11237 | literario | 10 |
| 11238 | lisonjera | 10 |
| 11239 | lición | 10 |
| 11240 | levantadas | 10 |
| 11241 | letrilla | 10 |
| 11242 | leales | 10 |
| 11243 | lanzado | 10 |
| 11244 | ladrar | 10 |
| 11245 | lacayos | 10 |
| 11246 | juntando | 10 |
| 11247 | juntado | 10 |
| 11248 | josefinas | 10 |
| 11249 | jesuita | 10 |
| 11250 | jerónimo | 10 |
| 11251 | jerez | 10 |
| 11252 | jarabe | 10 |
| 11253 | jamón | 10 |
| 11254 | jacintito | 10 |
| 11255 | jabalí | 10 |
| 11256 | isabela | 10 |
| 11257 | inventó | 10 |
| 11258 | inventario | 10 |
| 11259 | interlocutor | 10 |
| 11260 | inspección | 10 |
| 11261 | insignes | 10 |
| 11262 | inquisición | 10 |
| 11263 | inquilinos | 10 |
| 11264 | inmaculada | 10 |
| 11265 | informado | 10 |
| 11266 | infiernos | 10 |
| 11267 | inferiores | 10 |
| 11268 | infaliblemente | 10 |
| 11269 | inés | 10 |
| 11270 | inercia | 10 |
| 11271 | inclinar | 10 |
| 11272 | inclemencias | 10 |
| 11273 | incierta | 10 |
| 11274 | impuso | 10 |
| 11275 | imposibilitado | 10 |
| 11276 | imperiosa | 10 |
| 11277 | impedía | 10 |
| 11278 | iluminada | 10 |
| 11279 | igualar | 10 |
| 11280 | ichtaber | 10 |
| 11281 | humos | 10 |
| 11282 | húmedos | 10 |
| 11283 | huella | 10 |
| 11284 | horrorizada | 10 |
| 11285 | honras | 10 |
| 11286 | holgazanes | 10 |
| 11287 | hojarasca | 10 |
| 11288 | hocicos | 10 |
| 11289 | hízole | 10 |
| 11290 | hijita | 10 |
| 11291 | higos | 10 |
| 11292 | hermosísimo | 10 |
| 11293 | hechizos | 10 |
| 11294 | haziendo | 10 |
| 11295 | hazienda | 10 |
| 11296 | harías | 10 |
| 11297 | hambriento | 10 |
| 11298 | hágase | 10 |
| 11299 | haciéndome | 10 |
| 11300 | haciendas | 10 |
| 11301 | hablaría | 10 |
| 11302 | habiéndome | 10 |
| 11303 | habiéndola | 10 |
| 11304 | haberlos | 10 |
| 11305 | guisado | 10 |
| 11306 | guirnaldas | 10 |
| 11307 | guapísima | 10 |
| 11308 | gruñido | 10 |
| 11309 | grotesco | 10 |
| 11310 | grasa | 10 |
| 11311 | grandiosa | 10 |
| 11312 | gr | 10 |
| 11313 | golosa | 10 |
| 11314 | gitanillas | 10 |
| 11315 | gil | 10 |
| 11316 | genero | 10 |
| 11317 | gemía | 10 |
| 11318 | gane | 10 |
| 11319 | ganada | 10 |
| 11320 | gallego | 10 |
| 11321 | galanes | 10 |
| 11322 | furto | 10 |
| 11323 | fúnebres | 10 |
| 11324 | fumaba | 10 |
| 11325 | fulgosio | 10 |
| 11326 | fuése | 10 |
| 11327 | fregar | 10 |
| 11328 | forzosamente | 10 |
| 11329 | formarse | 10 |
| 11330 | flotante | 10 |
| 11331 | flecha | 10 |
| 11332 | finuras | 10 |
| 11333 | filosófico | 10 |
| 11334 | filosóficas | 10 |
| 11335 | filos | 10 |
| 11336 | figurábase | 10 |
| 11337 | figuraban | 10 |
| 11338 | fíes | 10 |
| 11339 | fieltro | 10 |
| 11340 | fiaba | 10 |
| 11341 | fermosas | 10 |
| 11342 | familiares | 10 |
| 11343 | faltaron | 10 |
| 11344 | fallar | 10 |
| 11345 | falla | 10 |
| 11346 | faja | 10 |
| 11347 | extender | 10 |
| 11348 | expresando | 10 |
| 11349 | experiencias | 10 |
| 11350 | excitaba | 10 |
| 11351 | examinó | 10 |
| 11352 | examina | 10 |
| 11353 | eulalia | 10 |
| 11354 | estupenda | 10 |
| 11355 | estéis | 10 |
| 11356 | estaremos | 10 |
| 11357 | estaño | 10 |
| 11358 | establecer | 10 |
| 11359 | esperaron | 10 |
| 11360 | esperad | 10 |
| 11361 | especies | 10 |
| 11362 | especialidad | 10 |
| 11363 | esgrima | 10 |
| 11364 | esfuerço | 10 |
| 11365 | escudilla | 10 |
| 11366 | escondió | 10 |
| 11367 | escoja | 10 |
| 11368 | esclavos | 10 |
| 11369 | escaparate | 10 |
| 11370 | epístola | 10 |
| 11371 | envidiosos | 10 |
| 11372 | entrole | 10 |
| 11373 | entrever | 10 |
| 11374 | entretenidos | 10 |
| 11375 | entren | 10 |
| 11376 | entiendan | 10 |
| 11377 | entenderlo | 10 |
| 11378 | engendró | 10 |
| 11379 | endivido | 10 |
| 11380 | encubre | 10 |
| 11381 | encontrara | 10 |
| 11382 | encomendándose | 10 |
| 11383 | encierran | 10 |
| 11384 | encerramiento | 10 |
| 11385 | encargos | 10 |
| 11386 | emperatriz | 10 |
| 11387 | embriaguez | 10 |
| 11388 | embidia | 10 |
| 11389 | eléctrica | 10 |
| 11390 | eficaces | 10 |
| 11391 | echose | 10 |
| 11392 | echen | 10 |
| 11393 | echarlo | 10 |
| 11394 | echarla | 10 |
| 11395 | durará | 10 |
| 11396 | dulçes | 10 |
| 11397 | dosis | 10 |
| 11398 | dormitorios | 10 |
| 11399 | donzella | 10 |
| 11400 | domésticos | 10 |
| 11401 | documentos | 10 |
| 11402 | doctrinas | 10 |
| 11403 | doblón | 10 |
| 11404 | distinguidas | 10 |
| 11405 | distinguían | 10 |
| 11406 | distingue | 10 |
| 11407 | disputaban | 10 |
| 11408 | dispuestas | 10 |
| 11409 | disparatados | 10 |
| 11410 | disgustado | 10 |
| 11411 | disgustaba | 10 |
| 11412 | disen | 10 |
| 11413 | dirigían | 10 |
| 11414 | dirige | 10 |
| 11415 | dirían | 10 |
| 11416 | diplomático | 10 |
| 11417 | dímelo | 10 |
| 11418 | dilatado | 10 |
| 11419 | dijes | 10 |
| 11420 | dígase | 10 |
| 11421 | dígalo | 10 |
| 11422 | diéronme | 10 |
| 11423 | diciéndolo | 10 |
| 11424 | dialéctica | 10 |
| 11425 | diabólica | 10 |
| 11426 | dezia | 10 |
| 11427 | devotas | 10 |
| 11428 | devorar | 10 |
| 11429 | detenga | 10 |
| 11430 | desvanecía | 10 |
| 11431 | destruir | 10 |
| 11432 | destrozado | 10 |
| 11433 | destinado | 10 |
| 11434 | despierte | 10 |
| 11435 | despide | 10 |
| 11436 | despertaban | 10 |
| 11437 | despechado | 10 |
| 11438 | desnudar | 10 |
| 11439 | desinteresada | 10 |
| 11440 | desigualdad | 10 |
| 11441 | deshonrar | 10 |
| 11442 | desengañado | 10 |
| 11443 | deseada | 10 |
| 11444 | descubro | 10 |
| 11445 | descubiertos | 10 |
| 11446 | desconcierto | 10 |
| 11447 | descaro | 10 |
| 11448 | desarrollo | 10 |
| 11449 | desairado | 10 |
| 11450 | desabrido | 10 |
| 11451 | derechamente | 10 |
| 11452 | depositar | 10 |
| 11453 | departamento | 10 |
| 11454 | deogracias | 10 |
| 11455 | demetria | 10 |
| 11456 | demente | 10 |
| 11457 | déme | 10 |
| 11458 | dejad | 10 |
| 11459 | defendían | 10 |
| 11460 | dedal | 10 |
| 11461 | debiendo | 10 |
| 11462 | debate | 10 |
| 11463 | dava | 10 |
| 11464 | dantchari | 10 |
| 11465 | dádiva | 10 |
| 11466 | curva | 10 |
| 11467 | curó | 10 |
| 11468 | curarse | 10 |
| 11469 | curaba | 10 |
| 11470 | cuña | 10 |
| 11471 | cunple | 10 |
| 11472 | cuide | 10 |
| 11473 | cuidarse | 10 |
| 11474 | cuestan | 10 |
| 11475 | cuchara | 10 |
| 11476 | cuartito | 10 |
| 11477 | crujir | 10 |
| 11478 | cristina | 10 |
| 11479 | creías | 10 |
| 11480 | crecimiento | 10 |
| 11481 | creciente | 10 |
| 11482 | créalo | 10 |
| 11483 | cratilo | 10 |
| 11484 | costar | 10 |
| 11485 | cortadas | 10 |
| 11486 | corresponder | 10 |
| 11487 | convusco | 10 |
| 11488 | convendría | 10 |
| 11489 | convencía | 10 |
| 11490 | contratiempo | 10 |
| 11491 | contorsiones | 10 |
| 11492 | continuas | 10 |
| 11493 | continuando | 10 |
| 11494 | contesté | 10 |
| 11495 | conteniendo | 10 |
| 11496 | contenían | 10 |
| 11497 | contase | 10 |
| 11498 | contados | 10 |
| 11499 | constantinopla | 10 |
| 11500 | constaba | 10 |
| 11501 | considerable | 10 |
| 11502 | conserve | 10 |
| 11503 | consentido | 10 |
| 11504 | consagrar | 10 |
| 11505 | conplido | 10 |
| 11506 | conozcas | 10 |
| 11507 | conmovido | 10 |
| 11508 | conjeturas | 10 |
| 11509 | condestable | 10 |
| 11510 | concertada | 10 |
| 11511 | concavidad | 10 |
| 11512 | comunicado | 10 |
| 11513 | comprometido | 10 |
| 11514 | compone | 10 |
| 11515 | compinche | 10 |
| 11516 | compasiva | 10 |
| 11517 | comí | 10 |
| 11518 | comerse | 10 |
| 11519 | comenzando | 10 |
| 11520 | comas | 10 |
| 11521 | colorados | 10 |
| 11522 | colgó | 10 |
| 11523 | colegas | 10 |
| 11524 | cogían | 10 |
| 11525 | cobrando | 10 |
| 11526 | clavel | 10 |
| 11527 | clavar | 10 |
| 11528 | cláusulas | 10 |
| 11529 | clásica | 10 |
| 11530 | civiles | 10 |
| 11531 | citaba | 10 |
| 11532 | cirujano | 10 |
| 11533 | cinchas | 10 |
| 11534 | cieno | 10 |
| 11535 | çiençia | 10 |
| 11536 | chusco | 10 |
| 11537 | chocho | 10 |
| 11538 | chiquito | 10 |
| 11539 | chiquitín | 10 |
| 11540 | chillona | 10 |
| 11541 | chilló | 10 |
| 11542 | charlar | 10 |
| 11543 | chapa | 10 |
| 11544 | chal | 10 |
| 11545 | certeza | 10 |
| 11546 | central | 10 |
| 11547 | centinelas | 10 |
| 11548 | censor | 10 |
| 11549 | celebró | 10 |
| 11550 | celebrada | 10 |
| 11551 | cavalleros | 10 |
| 11552 | católicas | 10 |
| 11553 | catalejo | 10 |
| 11554 | catadura | 10 |
| 11555 | castos | 10 |
| 11556 | castel | 10 |
| 11557 | casamientos | 10 |
| 11558 | carrillos | 10 |
| 11559 | carlomagno | 10 |
| 11560 | cargos | 10 |
| 11561 | cargó | 10 |
| 11562 | cantos | 10 |
| 11563 | cánticos | 10 |
| 11564 | cantaron | 10 |
| 11565 | candoroso | 10 |
| 11566 | candaya | 10 |
| 11567 | camacha | 10 |
| 11568 | calzada | 10 |
| 11569 | calvo | 10 |
| 11570 | cabrón | 10 |
| 11571 | caben | 10 |
| 11572 | cabecilla | 10 |
| 11573 | buscarlo | 10 |
| 11574 | burlando | 10 |
| 11575 | bucentauro | 10 |
| 11576 | bruces | 10 |
| 11577 | brotar | 10 |
| 11578 | bronca | 10 |
| 11579 | brillo | 10 |
| 11580 | branco | 10 |
| 11581 | borró | 10 |
| 11582 | borrasca | 10 |
| 11583 | borda | 10 |
| 11584 | borbotones | 10 |
| 11585 | bonaparte | 10 |
| 11586 | besugo | 10 |
| 11587 | bergantín | 10 |
| 11588 | beneplácito | 10 |
| 11589 | belerma | 10 |
| 11590 | baxa | 10 |
| 11591 | batirse | 10 |
| 11592 | bastaban | 10 |
| 11593 | barruntos | 10 |
| 11594 | barrabás | 10 |
| 11595 | banca | 10 |
| 11596 | ballesta | 10 |
| 11597 | balanza | 10 |
| 11598 | baje | 10 |
| 11599 | bajan | 10 |
| 11600 | ayudase | 10 |
| 11601 | ayudarme | 10 |
| 11602 | averiguarlo | 10 |
| 11603 | averiguada | 10 |
| 11604 | aventureros | 10 |
| 11605 | avellanas | 10 |
| 11606 | avedes | 10 |
| 11607 | autora | 10 |
| 11608 | austria | 10 |
| 11609 | ausencias | 10 |
| 11610 | atrozmente | 10 |
| 11611 | atrocidades | 10 |
| 11612 | atreven | 10 |
| 11613 | atrasado | 10 |
| 11614 | atónitos | 10 |
| 11615 | atenerse | 10 |
| 11616 | atar | 10 |
| 11617 | astuto | 10 |
| 11618 | asturias | 10 |
| 11619 | asturiana | 10 |
| 11620 | astillas | 10 |
| 11621 | aspirando | 10 |
| 11622 | asoma | 10 |
| 11623 | asistido | 10 |
| 11624 | asegurarse | 10 |
| 11625 | asegurado | 10 |
| 11626 | arrimo | 10 |
| 11627 | arrieros | 10 |
| 11628 | arreglará | 10 |
| 11629 | arreglando | 10 |
| 11630 | arrebato | 10 |
| 11631 | arnés | 10 |
| 11632 | aristocrático | 10 |
| 11633 | arenga | 10 |
| 11634 | arcaz | 10 |
| 11635 | aras | 10 |
| 11636 | arado | 10 |
| 11637 | apunte | 10 |
| 11638 | apuntaba | 10 |
| 11639 | apunta | 10 |
| 11640 | aprisa | 10 |
| 11641 | apretones | 10 |
| 11642 | apresado | 10 |
| 11643 | apoyándose | 10 |
| 11644 | apostamos | 10 |
| 11645 | apartadas | 10 |
| 11646 | apaleado | 10 |
| 11647 | antojaban | 10 |
| 11648 | animo | 10 |
| 11649 | anhelos | 10 |
| 11650 | anduvieron | 10 |
| 11651 | anduve | 10 |
| 11652 | amoríos | 10 |
| 11653 | americanos | 10 |
| 11654 | amenazó | 10 |
| 11655 | amadeo | 10 |
| 11656 | alusiones | 10 |
| 11657 | alumbra | 10 |
| 11658 | alternativamente | 10 |
| 11659 | alimentos | 10 |
| 11660 | alegrarse | 10 |
| 11661 | alcanzaron | 10 |
| 11662 | alborozo | 10 |
| 11663 | alardes | 10 |
| 11664 | alameda | 10 |
| 11665 | ajustado | 10 |
| 11666 | airada | 10 |
| 11667 | ahorros | 10 |
| 11668 | agitado | 10 |
| 11669 | agilidad | 10 |
| 11670 | afirmación | 10 |
| 11671 | afirma | 10 |
| 11672 | afectuoso | 10 |
| 11673 | afabilidad | 10 |
| 11674 | adquiriendo | 10 |
| 11675 | adorado | 10 |
| 11676 | aderezado | 10 |
| 11677 | aderezada | 10 |
| 11678 | adelanta | 10 |
| 11679 | acudido | 10 |
| 11680 | acordose | 10 |
| 11681 | acontece | 10 |
| 11682 | aconsejado | 10 |
| 11683 | acompañase | 10 |
| 11684 | acompañarla | 10 |
| 11685 | acomodar | 10 |
| 11686 | açipreste | 10 |
| 11687 | acierta | 10 |
| 11688 | acercose | 10 |
| 11689 | abundantes | 10 |
| 11690 | absurdas | 10 |
| 11691 | abstracción | 10 |
| 11692 | abriese | 10 |
| 11693 | aborrecimiento | 10 |
| 11694 | abatimiento | 10 |
| 11695 | zara | 9 |
| 11696 | zancuda | 9 |
| 11697 | yre | 9 |
| 11698 | yras | 9 |
| 11699 | yerros | 9 |
| 11700 | vyda | 9 |
| 11701 | vozes | 9 |
| 11702 | vomitar | 9 |
| 11703 | volverla | 9 |
| 11704 | volverás | 9 |
| 11705 | vivísima | 9 |
| 11706 | vivieron | 9 |
| 11707 | viua | 9 |
| 11708 | virgos | 9 |
| 11709 | virginidad | 9 |
| 11710 | violentas | 9 |
| 11711 | viña | 9 |
| 11712 | vihuela | 9 |
| 11713 | vibraciones | 9 |
| 11714 | vestíbulo | 9 |
| 11715 | vértigo | 9 |
| 11716 | verídico | 9 |
| 11717 | vericuetos | 9 |
| 11718 | veredas | 9 |
| 11719 | verbigracia | 9 |
| 11720 | venturas | 9 |
| 11721 | ventanillo | 9 |
| 11722 | venirse | 9 |
| 11723 | venia | 9 |
| 11724 | véngase | 9 |
| 11725 | vengado | 9 |
| 11726 | vendían | 9 |
| 11727 | vena | 9 |
| 11728 | velos | 9 |
| 11729 | vehementes | 9 |
| 11730 | vástagos | 9 |
| 11731 | variedades | 9 |
| 11732 | valiéndose | 9 |
| 11733 | valerse | 9 |
| 11734 | vaguedad | 9 |
| 11735 | vagabundo | 9 |
| 11736 | usía | 9 |
| 11737 | tyenen | 9 |
| 11738 | tyenda | 9 |
| 11739 | tuviste | 9 |
| 11740 | tuue | 9 |
| 11741 | turbio | 9 |
| 11742 | tumulto | 9 |
| 11743 | truhán | 9 |
| 11744 | trucha | 9 |
| 11745 | tropezaba | 9 |
| 11746 | tremendas | 9 |
| 11747 | trebejo | 9 |
| 11748 | tratase | 9 |
| 11749 | traspasado | 9 |
| 11750 | trasnochadores | 9 |
| 11751 | trascoro | 9 |
| 11752 | transportado | 9 |
| 11753 | transparentes | 9 |
| 11754 | traidora | 9 |
| 11755 | traiciones | 9 |
| 11756 | tráfico | 9 |
| 11757 | traerá | 9 |
| 11758 | traductor | 9 |
| 11759 | trabaje | 9 |
| 11760 | trabajaban | 9 |
| 11761 | tortilla | 9 |
| 11762 | tordos | 9 |
| 11763 | tontín | 9 |
| 11764 | toméis | 9 |
| 11765 | tomate | 9 |
| 11766 | tom | 9 |
| 11767 | todavia | 9 |
| 11768 | tocase | 9 |
| 11769 | tocándole | 9 |
| 11770 | tirteafuera | 9 |
| 11771 | tirantes | 9 |
| 11772 | tíos | 9 |
| 11773 | tímida | 9 |
| 11774 | tiesas | 9 |
| 11775 | tiemblo | 9 |
| 11776 | tetuán | 9 |
| 11777 | terrenos | 9 |
| 11778 | terminante | 9 |
| 11779 | tenida | 9 |
| 11780 | tengáis | 9 |
| 11781 | tenerlos | 9 |
| 11782 | temporadas | 9 |
| 11783 | templar | 9 |
| 11784 | tejido | 9 |
| 11785 | teatral | 9 |
| 11786 | tarima | 9 |
| 11787 | tapias | 9 |
| 11788 | tapete | 9 |
| 11789 | tanda | 9 |
| 11790 | taludes | 9 |
| 11791 | tabacos | 9 |
| 11792 | suspensa | 9 |
| 11793 | suplir | 9 |
| 11794 | superchería | 9 |
| 11795 | sujetas | 9 |
| 11796 | sujetar | 9 |
| 11797 | suficientes | 9 |
| 11798 | sucios | 9 |
| 11799 | sucesor | 9 |
| 11800 | spíritu | 9 |
| 11801 | sospiros | 9 |
| 11802 | soso | 9 |
| 11803 | sosiégate | 9 |
| 11804 | sorprendía | 9 |
| 11805 | soñó | 9 |
| 11806 | sonidos | 9 |
| 11807 | sombría | 9 |
| 11808 | solteras | 9 |
| 11809 | soltaron | 9 |
| 11810 | solitarios | 9 |
| 11811 | solicitaba | 9 |
| 11812 | solaz | 9 |
| 11813 | sócrates | 9 |
| 11814 | socorros | 9 |
| 11815 | sobrinos | 9 |
| 11816 | sobresaltada | 9 |
| 11817 | sinvergüenza | 9 |
| 11818 | silencioso | 9 |
| 11819 | silbo | 9 |
| 11820 | siguiera | 9 |
| 11821 | significación | 9 |
| 11822 | sietemesino | 9 |
| 11823 | servirla | 9 |
| 11824 | separa | 9 |
| 11825 | sentiría | 9 |
| 11826 | sentimentalismo | 9 |
| 11827 | semblantes | 9 |
| 11828 | seductora | 9 |
| 11829 | sediento | 9 |
| 11830 | secretaría | 9 |
| 11831 | savia | 9 |
| 11832 | satisfizo | 9 |
| 11833 | satírica | 9 |
| 11834 | sarao | 9 |
| 11835 | sañuda | 9 |
| 11836 | santiguarse | 9 |
| 11837 | sancha | 9 |
| 11838 | sanch | 9 |
| 11839 | saludaron | 9 |
| 11840 | salsa | 9 |
| 11841 | sagunto | 9 |
| 11842 | sacudido | 9 |
| 11843 | sacaría | 9 |
| 11844 | sable | 9 |
| 11845 | rusia | 9 |
| 11846 | rroydo | 9 |
| 11847 | rondaba | 9 |
| 11848 | rompimiento | 9 |
| 11849 | rogaron | 9 |
| 11850 | roer | 9 |
| 11851 | roban | 9 |
| 11852 | rizado | 9 |
| 11853 | rítmico | 9 |
| 11854 | risueños | 9 |
| 11855 | rezos | 9 |
| 11856 | rezó | 9 |
| 11857 | rezio | 9 |
| 11858 | revienta | 9 |
| 11859 | reventar | 9 |
| 11860 | reventaba | 9 |
| 11861 | reúne | 9 |
| 11862 | retrocedió | 9 |
| 11863 | retroceder | 9 |
| 11864 | retirándose | 9 |
| 11865 | retahíla | 9 |
| 11866 | resumidas | 9 |
| 11867 | resoplidos | 9 |
| 11868 | resguardo | 9 |
| 11869 | resabios | 9 |
| 11870 | repúblicas | 9 |
| 11871 | representando | 9 |
| 11872 | repartidas | 9 |
| 11873 | renombre | 9 |
| 11874 | rendirse | 9 |
| 11875 | rendir | 9 |
| 11876 | rencores | 9 |
| 11877 | reinaldos | 9 |
| 11878 | refunfuñando | 9 |
| 11879 | refriega | 9 |
| 11880 | referidos | 9 |
| 11881 | recomendó | 9 |
| 11882 | recomendaba | 9 |
| 11883 | recobró | 9 |
| 11884 | reclamar | 9 |
| 11885 | recíprocamente | 9 |
| 11886 | recebida | 9 |
| 11887 | rebuznar | 9 |
| 11888 | raudal | 9 |
| 11889 | ralea | 9 |
| 11890 | quiza | 9 |
| 11891 | quisieras | 9 |
| 11892 | quimeras | 9 |
| 11893 | quijadas | 9 |
| 11894 | quiéreme | 9 |
| 11895 | quicio | 9 |
| 11896 | quexa | 9 |
| 11897 | querrían | 9 |
| 11898 | quererte | 9 |
| 11899 | quererla | 9 |
| 11900 | querencia | 9 |
| 11901 | quel | 9 |
| 11902 | quejó | 9 |
| 11903 | quejidos | 9 |
| 11904 | quejido | 9 |
| 11905 | quebrado | 9 |
| 11906 | quasi | 9 |
| 11907 | puto | 9 |
| 11908 | purísimo | 9 |
| 11909 | pulgar | 9 |
| 11910 | pudieres | 9 |
| 11911 | públicos | 9 |
| 11912 | publica | 9 |
| 11913 | pseudo | 9 |
| 11914 | prueva | 9 |
| 11915 | pruebe | 9 |
| 11916 | próximas | 9 |
| 11917 | provechoso | 9 |
| 11918 | protestante | 9 |
| 11919 | protestaba | 9 |
| 11920 | proteger | 9 |
| 11921 | próspero | 9 |
| 11922 | proponer | 9 |
| 11923 | propiedades | 9 |
| 11924 | pronunciando | 9 |
| 11925 | pronunciada | 9 |
| 11926 | prontitud | 9 |
| 11927 | profesaba | 9 |
| 11928 | prodigiosa | 9 |
| 11929 | procuro | 9 |
| 11930 | procure | 9 |
| 11931 | procurase | 9 |
| 11932 | procuraré | 9 |
| 11933 | privada | 9 |
| 11934 | previene | 9 |
| 11935 | pretina | 9 |
| 11936 | pretenden | 9 |
| 11937 | presentaban | 9 |
| 11938 | preocupación | 9 |
| 11939 | premiar | 9 |
| 11940 | preguntáronle | 9 |
| 11941 | prefirió | 9 |
| 11942 | preferían | 9 |
| 11943 | predicaba | 9 |
| 11944 | precisa | 9 |
| 11945 | preciosos | 9 |
| 11946 | preciaba | 9 |
| 11947 | potro | 9 |
| 11948 | postres | 9 |
| 11949 | poseer | 9 |
| 11950 | posadas | 9 |
| 11951 | portamonedas | 9 |
| 11952 | porfiado | 9 |
| 11953 | poned | 9 |
| 11954 | polémica | 9 |
| 11955 | poemas | 9 |
| 11956 | podrido | 9 |
| 11957 | podredumbre | 9 |
| 11958 | pobretería | 9 |
| 11959 | pobrecillo | 9 |
| 11960 | pluguiera | 9 |
| 11961 | plena | 9 |
| 11962 | platónico | 9 |
| 11963 | planeta | 9 |
| 11964 | plácida | 9 |
| 11965 | placeras | 9 |
| 11966 | plaça | 9 |
| 11967 | pitusín | 9 |
| 11968 | pito | 9 |
| 11969 | pintando | 9 |
| 11970 | pillín | 9 |
| 11971 | picó | 9 |
| 11972 | picando | 9 |
| 11973 | picada | 9 |
| 11974 | pi | 9 |
| 11975 | pestañear | 9 |
| 11976 | pesó | 9 |
| 11977 | pescante | 9 |
| 11978 | pesares | 9 |
| 11979 | perverso | 9 |
| 11980 | perversidad | 9 |
| 11981 | pertenecían | 9 |
| 11982 | pertenecer | 9 |
| 11983 | perseguida | 9 |
| 11984 | perseguían | 9 |
| 11985 | permitiera | 9 |
| 11986 | permita | 9 |
| 11987 | permanente | 9 |
| 11988 | periandro | 9 |
| 11989 | perfumado | 9 |
| 11990 | perfeta | 9 |
| 11991 | peresa | 9 |
| 11992 | perecer | 9 |
| 11993 | perdóname | 9 |
| 11994 | pendían | 9 |
| 11995 | pende | 9 |
| 11996 | pelleja | 9 |
| 11997 | peláez | 9 |
| 11998 | peinar | 9 |
| 11999 | pegarle | 9 |
| 12000 | pegajosa | 9 |
| 12001 | pedís | 9 |
| 12002 | pedernal | 9 |
| 12003 | pavón | 9 |
| 12004 | patriarca | 9 |
| 12005 | patético | 9 |
| 12006 | patética | 9 |
| 12007 | paterna | 9 |
| 12008 | pataditas | 9 |
| 12009 | pasto | 9 |
| 12010 | passan | 9 |
| 12011 | pasito | 9 |
| 12012 | pases | 9 |
| 12013 | pasen | 9 |
| 12014 | pasemos | 9 |
| 12015 | partiendo | 9 |
| 12016 | participación | 9 |
| 12017 | párrafo | 9 |
| 12018 | párpado | 9 |
| 12019 | pararse | 9 |
| 12020 | paran | 9 |
| 12021 | paraban | 9 |
| 12022 | pantalla | 9 |
| 12023 | panderetas | 9 |
| 12024 | padeciendo | 9 |
| 12025 | pacto | 9 |
| 12026 | oyóse | 9 |
| 12027 | oyere | 9 |
| 12028 | ovieron | 9 |
| 12029 | ove | 9 |
| 12030 | otorgado | 9 |
| 12031 | ostenta | 9 |
| 12032 | originales | 9 |
| 12033 | orgía | 9 |
| 12034 | orfandad | 9 |
| 12035 | oras | 9 |
| 12036 | orán | 9 |
| 12037 | opone | 9 |
| 12038 | opina | 9 |
| 12039 | olé | 9 |
| 12040 | oírte | 9 |
| 12041 | ohandos | 9 |
| 12042 | ofrecí | 9 |
| 12043 | ofrecerle | 9 |
| 12044 | ofiçio | 9 |
| 12045 | ofensas | 9 |
| 12046 | ofendía | 9 |
| 12047 | ofenden | 9 |
| 12048 | odiosa | 9 |
| 12049 | ocurrir | 9 |
| 12050 | ocupados | 9 |
| 12051 | ocultos | 9 |
| 12052 | ocultando | 9 |
| 12053 | observo | 9 |
| 12054 | obispado | 9 |
| 12055 | obediente | 9 |
| 12056 | obedeció | 9 |
| 12057 | obedecido | 9 |
| 12058 | obedecían | 9 |
| 12059 | nuca | 9 |
| 12060 | noventa | 9 |
| 12061 | nieblas | 9 |
| 12062 | nerviosas | 9 |
| 12063 | negociar | 9 |
| 12064 | néctar | 9 |
| 12065 | necesitar | 9 |
| 12066 | navajas | 9 |
| 12067 | nasçe | 9 |
| 12068 | naciendo | 9 |
| 12069 | muquier | 9 |
| 12070 | municiones | 9 |
| 12071 | mueven | 9 |
| 12072 | muelles | 9 |
| 12073 | mudan | 9 |
| 12074 | mosquito | 9 |
| 12075 | mortificación | 9 |
| 12076 | morros | 9 |
| 12077 | morrión | 9 |
| 12078 | mordió | 9 |
| 12079 | moño | 9 |
| 12080 | montaba | 9 |
| 12081 | monótona | 9 |
| 12082 | monosílabos | 9 |
| 12083 | monasterio | 9 |
| 12084 | monas | 9 |
| 12085 | monaguillo | 9 |
| 12086 | mollera | 9 |
| 12087 | molineros | 9 |
| 12088 | modernas | 9 |
| 12089 | misteriosas | 9 |
| 12090 | mires | 9 |
| 12091 | mirándome | 9 |
| 12092 | miranda | 9 |
| 12093 | mimo | 9 |
| 12094 | milagroso | 9 |
| 12095 | metralla | 9 |
| 12096 | metidos | 9 |
| 12097 | metas | 9 |
| 12098 | metamorfosis | 9 |
| 12099 | metáforas | 9 |
| 12100 | mercancía | 9 |
| 12101 | mentía | 9 |
| 12102 | mentar | 9 |
| 12103 | mendrugo | 9 |
| 12104 | mendiga | 9 |
| 12105 | mendicidad | 9 |
| 12106 | mechones | 9 |
| 12107 | matrimonial | 9 |
| 12108 | matase | 9 |
| 12109 | matador | 9 |
| 12110 | martirios | 9 |
| 12111 | martínez | 9 |
| 12112 | martes | 9 |
| 12113 | mariquilla | 9 |
| 12114 | mareo | 9 |
| 12115 | marauillo | 9 |
| 12116 | mantenga | 9 |
| 12117 | mansa | 9 |
| 12118 | manojo | 9 |
| 12119 | manil | 9 |
| 12120 | mandóme | 9 |
| 12121 | manadas | 9 |
| 12122 | malvados | 9 |
| 12123 | malva | 9 |
| 12124 | maltratado | 9 |
| 12125 | maligna | 9 |
| 12126 | maledicencia | 9 |
| 12127 | majestuosa | 9 |
| 12128 | magno | 9 |
| 12129 | lydiar | 9 |
| 12130 | luxuria | 9 |
| 12131 | luminoso | 9 |
| 12132 | lucero | 9 |
| 12133 | lozoya | 9 |
| 12134 | loza | 9 |
| 12135 | losa | 9 |
| 12136 | lógico | 9 |
| 12137 | locuaz | 9 |
| 12138 | locas | 9 |
| 12139 | loable | 9 |
| 12140 | llevándole | 9 |
| 12141 | llevándola | 9 |
| 12142 | lleuo | 9 |
| 12143 | llenarse | 9 |
| 12144 | llenan | 9 |
| 12145 | llegate | 9 |
| 12146 | llegaré | 9 |
| 12147 | llavín | 9 |
| 12148 | llamen | 9 |
| 12149 | llamara | 9 |
| 12150 | llamándome | 9 |
| 12151 | llamáis | 9 |
| 12152 | liso | 9 |
| 12153 | lírica | 9 |
| 12154 | lira | 9 |
| 12155 | limpiado | 9 |
| 12156 | licencias | 9 |
| 12157 | librillo | 9 |
| 12158 | leves | 9 |
| 12159 | levanté | 9 |
| 12160 | levantarme | 9 |
| 12161 | leva | 9 |
| 12162 | lentitud | 9 |
| 12163 | leí | 9 |
| 12164 | legislador | 9 |
| 12165 | legal | 9 |
| 12166 | lavandera | 9 |
| 12167 | lava | 9 |
| 12168 | latón | 9 |
| 12169 | lanzaba | 9 |
| 12170 | láminas | 9 |
| 12171 | labrada | 9 |
| 12172 | juzgando | 9 |
| 12173 | juuentud | 9 |
| 12174 | juicioso | 9 |
| 12175 | jornal | 9 |
| 12176 | joan | 9 |
| 12177 | jineta | 9 |
| 12178 | jacintillo | 9 |
| 12179 | ítem | 9 |
| 12180 | irían | 9 |
| 12181 | inventaba | 9 |
| 12182 | introdujo | 9 |
| 12183 | intervalos | 9 |
| 12184 | intenta | 9 |
| 12185 | intencionado | 9 |
| 12186 | insustancial | 9 |
| 12187 | insultar | 9 |
| 12188 | instancia | 9 |
| 12189 | insolentes | 9 |
| 12190 | insolencias | 9 |
| 12191 | inscripción | 9 |
| 12192 | inofensivo | 9 |
| 12193 | inmundicia | 9 |
| 12194 | inmortalidad | 9 |
| 12195 | información | 9 |
| 12196 | infantería | 9 |
| 12197 | inexpugnable | 9 |
| 12198 | inefables | 9 |
| 12199 | indispensables | 9 |
| 12200 | indignada | 9 |
| 12201 | indicar | 9 |
| 12202 | indeciso | 9 |
| 12203 | increíbles | 9 |
| 12204 | inclina | 9 |
| 12205 | incidente | 9 |
| 12206 | incendios | 9 |
| 12207 | incapaces | 9 |
| 12208 | incansable | 9 |
| 12209 | impossible | 9 |
| 12210 | importan | 9 |
| 12211 | impíos | 9 |
| 12212 | impiedad | 9 |
| 12213 | impedirlo | 9 |
| 12214 | imaginativo | 9 |
| 12215 | ilustrísimo | 9 |
| 12216 | iluminaba | 9 |
| 12217 | idos | 9 |
| 12218 | idolatría | 9 |
| 12219 | humillado | 9 |
| 12220 | húmedo | 9 |
| 12221 | hule | 9 |
| 12222 | huido | 9 |
| 12223 | hostilidad | 9 |
| 12224 | hospitalidad | 9 |
| 12225 | hospicio | 9 |
| 12226 | hospedaje | 9 |
| 12227 | horteras | 9 |
| 12228 | hormigas | 9 |
| 12229 | holgar | 9 |
| 12230 | históricos | 9 |
| 12231 | hincó | 9 |
| 12232 | hincar | 9 |
| 12233 | hígado | 9 |
| 12234 | herrero | 9 |
| 12235 | heladas | 9 |
| 12236 | haura | 9 |
| 12237 | hartzenbusch | 9 |
| 12238 | hartaba | 9 |
| 12239 | hallas | 9 |
| 12240 | hallarle | 9 |
| 12241 | halagos | 9 |
| 12242 | hacerlos | 9 |
| 12243 | habremos | 9 |
| 12244 | hablarla | 9 |
| 12245 | habladores | 9 |
| 12246 | habitante | 9 |
| 12247 | haberos | 9 |
| 12248 | gustó | 9 |
| 12249 | guedejas | 9 |
| 12250 | guárdese | 9 |
| 12251 | guárdate | 9 |
| 12252 | gruñía | 9 |
| 12253 | grietas | 9 |
| 12254 | griega | 9 |
| 12255 | gremio | 9 |
| 12256 | graduado | 9 |
| 12257 | grabados | 9 |
| 12258 | goma | 9 |
| 12259 | godoy | 9 |
| 12260 | gloriosas | 9 |
| 12261 | gimiendo | 9 |
| 12262 | gentuza | 9 |
| 12263 | gallegos | 9 |
| 12264 | galeote | 9 |
| 12265 | gaceta | 9 |
| 12266 | gabrielillo | 9 |
| 12267 | funesta | 9 |
| 12268 | fumando | 9 |
| 12269 | fuésemos | 9 |
| 12270 | fuensanta | 9 |
| 12271 | froilán | 9 |
| 12272 | fresno | 9 |
| 12273 | fresa | 9 |
| 12274 | fraude | 9 |
| 12275 | frágiles | 9 |
| 12276 | fragatas | 9 |
| 12277 | fragancia | 9 |
| 12278 | fracaso | 9 |
| 12279 | fósforo | 9 |
| 12280 | forro | 9 |
| 12281 | formidables | 9 |
| 12282 | floridos | 9 |
| 12283 | flema | 9 |
| 12284 | físicos | 9 |
| 12285 | firmado | 9 |
| 12286 | fingidos | 9 |
| 12287 | fingidas | 9 |
| 12288 | fijando | 9 |
| 12289 | fijado | 9 |
| 12290 | ficción | 9 |
| 12291 | feudal | 9 |
| 12292 | ferias | 9 |
| 12293 | fecundo | 9 |
| 12294 | favorecía | 9 |
| 12295 | favorece | 9 |
| 12296 | fausto | 9 |
| 12297 | farsante | 9 |
| 12298 | fardo | 9 |
| 12299 | fachada | 9 |
| 12300 | extravíos | 9 |
| 12301 | extranjera | 9 |
| 12302 | expresado | 9 |
| 12303 | explosión | 9 |
| 12304 | expansión | 9 |
| 12305 | existencias | 9 |
| 12306 | exijo | 9 |
| 12307 | exigir | 9 |
| 12308 | exclamar | 9 |
| 12309 | excesiva | 9 |
| 12310 | excepto | 9 |
| 12311 | excepciones | 9 |
| 12312 | eternidad | 9 |
| 12313 | estufa | 9 |
| 12314 | estiró | 9 |
| 12315 | estimaban | 9 |
| 12316 | estarlo | 9 |
| 12317 | estandarte | 9 |
| 12318 | estacada | 9 |
| 12319 | esquiva | 9 |
| 12320 | esqueleto | 9 |
| 12321 | esponja | 9 |
| 12322 | esperé | 9 |
| 12323 | esperaré | 9 |
| 12324 | esperamos | 9 |
| 12325 | españolas | 9 |
| 12326 | espante | 9 |
| 12327 | espantar | 9 |
| 12328 | esforzándose | 9 |
| 12329 | escuras | 9 |
| 12330 | escultura | 9 |
| 12331 | escucho | 9 |
| 12332 | escuchad | 9 |
| 12333 | escribiente | 9 |
| 12334 | escogidos | 9 |
| 12335 | escéptico | 9 |
| 12336 | escasas | 9 |
| 12337 | esbelto | 9 |
| 12338 | esbelta | 9 |
| 12339 | erguía | 9 |
| 12340 | érase | 9 |
| 12341 | equivale | 9 |
| 12342 | epitafio | 9 |
| 12343 | episodios | 9 |
| 12344 | episcopal | 9 |
| 12345 | epigramas | 9 |
| 12346 | enviarle | 9 |
| 12347 | enviaba | 9 |
| 12348 | entusiasmado | 9 |
| 12349 | entregada | 9 |
| 12350 | entraré | 9 |
| 12351 | entranas | 9 |
| 12352 | enterase | 9 |
| 12353 | enterando | 9 |
| 12354 | entendedor | 9 |
| 12355 | entablar | 9 |
| 12356 | enseñaré | 9 |
| 12357 | enriquecer | 9 |
| 12358 | enhoramala | 9 |
| 12359 | engracia | 9 |
| 12360 | engañando | 9 |
| 12361 | endiablado | 9 |
| 12362 | endereza | 9 |
| 12363 | encendieron | 9 |
| 12364 | encarnadas | 9 |
| 12365 | encajes | 9 |
| 12366 | empujaba | 9 |
| 12367 | emprendido | 9 |
| 12368 | empleó | 9 |
| 12369 | elíseos | 9 |
| 12370 | elena | 9 |
| 12371 | elegir | 9 |
| 12372 | eléctrico | 9 |
| 12373 | editor | 9 |
| 12374 | edificar | 9 |
| 12375 | ecos | 9 |
| 12376 | ebro | 9 |
| 12377 | dudosa | 9 |
| 12378 | dragón | 9 |
| 12379 | doze | 9 |
| 12380 | dormimos | 9 |
| 12381 | dómine | 9 |
| 12382 | dominante | 9 |
| 12383 | dominado | 9 |
| 12384 | doler | 9 |
| 12385 | documento | 9 |
| 12386 | divierte | 9 |
| 12387 | divididos | 9 |
| 12388 | diván | 9 |
| 12389 | distribución | 9 |
| 12390 | disputaba | 9 |
| 12391 | disponiéndose | 9 |
| 12392 | disparatado | 9 |
| 12393 | disimulados | 9 |
| 12394 | disgustó | 9 |
| 12395 | discutió | 9 |
| 12396 | dirigiendo | 9 |
| 12397 | diretes | 9 |
| 12398 | diplomacia | 9 |
| 12399 | dinástico | 9 |
| 12400 | dimes | 9 |
| 12401 | diligentes | 9 |
| 12402 | dijéronme | 9 |
| 12403 | díganme | 9 |
| 12404 | dibujo | 9 |
| 12405 | díaz | 9 |
| 12406 | dexemos | 9 |
| 12407 | deues | 9 |
| 12408 | detenerle | 9 |
| 12409 | desvergüenza | 9 |
| 12410 | desvanecido | 9 |
| 12411 | destrozo | 9 |
| 12412 | desprenderse | 9 |
| 12413 | desplegar | 9 |
| 12414 | despidiendo | 9 |
| 12415 | despejado | 9 |
| 12416 | despedí | 9 |
| 12417 | desparpajo | 9 |
| 12418 | desides | 9 |
| 12419 | deshechas | 9 |
| 12420 | deshace | 9 |
| 12421 | desenfado | 9 |
| 12422 | desdichados | 9 |
| 12423 | descuidos | 9 |
| 12424 | descubrí | 9 |
| 12425 | desconocidas | 9 |
| 12426 | descendió | 9 |
| 12427 | descendiente | 9 |
| 12428 | descargaba | 9 |
| 12429 | desatada | 9 |
| 12430 | desalmado | 9 |
| 12431 | desairada | 9 |
| 12432 | desafiado | 9 |
| 12433 | desabrida | 9 |
| 12434 | derribó | 9 |
| 12435 | deparó | 9 |
| 12436 | denme | 9 |
| 12437 | demostró | 9 |
| 12438 | demencia | 9 |
| 12439 | demandar | 9 |
| 12440 | delicadezas | 9 |
| 12441 | delgadas | 9 |
| 12442 | dejose | 9 |
| 12443 | dejándola | 9 |
| 12444 | déjale | 9 |
| 12445 | definitivamente | 9 |
| 12446 | defendido | 9 |
| 12447 | defenderme | 9 |
| 12448 | dedicó | 9 |
| 12449 | dedicarse | 9 |
| 12450 | dedicaba | 9 |
| 12451 | decoración | 9 |
| 12452 | decirlas | 9 |
| 12453 | decirla | 9 |
| 12454 | decías | 9 |
| 12455 | decíamos | 9 |
| 12456 | decadencia | 9 |
| 12457 | debilidades | 9 |
| 12458 | debieran | 9 |
| 12459 | darlos | 9 |
| 12460 | curarle | 9 |
| 12461 | curan | 9 |
| 12462 | cumplirá | 9 |
| 12463 | cumplimientos | 9 |
| 12464 | cumpliendo | 9 |
| 12465 | culpado | 9 |
| 12466 | cuéntame | 9 |
| 12467 | cuchillos | 9 |
| 12468 | cuchicheos | 9 |
| 12469 | cuartillo | 9 |
| 12470 | cuanta | 9 |
| 12471 | cruelmente | 9 |
| 12472 | crucificado | 9 |
| 12473 | creyéndose | 9 |
| 12474 | creçe | 9 |
| 12475 | corva | 9 |
| 12476 | corrupción | 9 |
| 12477 | corridos | 9 |
| 12478 | correrse | 9 |
| 12479 | correrías | 9 |
| 12480 | corregidora | 9 |
| 12481 | correa | 9 |
| 12482 | corporal | 9 |
| 12483 | cordón | 9 |
| 12484 | coral | 9 |
| 12485 | conyugal | 9 |
| 12486 | convido | 9 |
| 12487 | convertían | 9 |
| 12488 | convencimiento | 9 |
| 12489 | contrabandista | 9 |
| 12490 | continencia | 9 |
| 12491 | contienen | 9 |
| 12492 | contestaron | 9 |
| 12493 | contenida | 9 |
| 12494 | contagio | 9 |
| 12495 | consumados | 9 |
| 12496 | consultado | 9 |
| 12497 | consolarla | 9 |
| 12498 | consolado | 9 |
| 12499 | consintiera | 9 |
| 12500 | consigue | 9 |
| 12501 | consiento | 9 |
| 12502 | consienta | 9 |
| 12503 | considerablemente | 9 |
| 12504 | conservado | 9 |
| 12505 | conservaban | 9 |
| 12506 | conserje | 9 |
| 12507 | consentiré | 9 |
| 12508 | conpañas | 9 |
| 12509 | conocerla | 9 |
| 12510 | conjunción | 9 |
| 12511 | confusiones | 9 |
| 12512 | confundían | 9 |
| 12513 | confunde | 9 |
| 12514 | conformarse | 9 |
| 12515 | confidente | 9 |
| 12516 | confianzas | 9 |
| 12517 | concluyendo | 9 |
| 12518 | concertadas | 9 |
| 12519 | concejo | 9 |
| 12520 | concejal | 9 |
| 12521 | concedo | 9 |
| 12522 | comprendían | 9 |
| 12523 | cómplices | 9 |
| 12524 | complacer | 9 |
| 12525 | compararse | 9 |
| 12526 | comparaba | 9 |
| 12527 | companeros | 9 |
| 12528 | compadecía | 9 |
| 12529 | comiéndose | 9 |
| 12530 | comerá | 9 |
| 12531 | comentario | 9 |
| 12532 | comendador | 9 |
| 12533 | comarca | 9 |
| 12534 | colón | 9 |
| 12535 | colocó | 9 |
| 12536 | colocados | 9 |
| 12537 | colmillo | 9 |
| 12538 | colmena | 9 |
| 12539 | collingwood | 9 |
| 12540 | collar | 9 |
| 12541 | colgaban | 9 |
| 12542 | colgaba | 9 |
| 12543 | cogiéndole | 9 |
| 12544 | cocinas | 9 |
| 12545 | clavadas | 9 |
| 12546 | clava | 9 |
| 12547 | cisne | 9 |
| 12548 | cirios | 9 |
| 12549 | cipreses | 9 |
| 12550 | cimientos | 9 |
| 12551 | cimiento | 9 |
| 12552 | çiegos | 9 |
| 12553 | chupa | 9 |
| 12554 | chorreando | 9 |
| 12555 | chasquido | 9 |
| 12556 | charlatán | 9 |
| 12557 | cesantía | 9 |
| 12558 | certidumbre | 9 |
| 12559 | cereza | 9 |
| 12560 | cerdas | 9 |
| 12561 | ceñía | 9 |
| 12562 | cenas | 9 |
| 12563 | celeste | 9 |
| 12564 | celedonia | 9 |
| 12565 | celebrado | 9 |
| 12566 | cediendo | 9 |
| 12567 | cebo | 9 |
| 12568 | caverna | 9 |
| 12569 | caudales | 9 |
| 12570 | cauallos | 9 |
| 12571 | catiuo | 9 |
| 12572 | categoría | 9 |
| 12573 | catarro | 9 |
| 12574 | catarata | 9 |
| 12575 | catar | 9 |
| 12576 | casildea | 9 |
| 12577 | caseros | 9 |
| 12578 | cascote | 9 |
| 12579 | cáscara | 9 |
| 12580 | casarte | 9 |
| 12581 | casara | 9 |
| 12582 | carpinteros | 9 |
| 12583 | cargaba | 9 |
| 12584 | caramba | 9 |
| 12585 | caporala | 9 |
| 12586 | cañonazos | 9 |
| 12587 | cañizares | 9 |
| 12588 | cantón | 9 |
| 12589 | cantica | 9 |
| 12590 | cantado | 9 |
| 12591 | cansaba | 9 |
| 12592 | cánones | 9 |
| 12593 | campesinos | 9 |
| 12594 | cambroneras | 9 |
| 12595 | cambiaría | 9 |
| 12596 | calza | 9 |
| 12597 | calumniado | 9 |
| 12598 | calentarse | 9 |
| 12599 | calaveras | 9 |
| 12600 | calado | 9 |
| 12601 | caídos | 9 |
| 12602 | caerá | 9 |
| 12603 | caderas | 9 |
| 12604 | cadaque | 9 |
| 12605 | caçador | 9 |
| 12606 | cabritos | 9 |
| 12607 | cabellera | 9 |
| 12608 | cabalgadura | 9 |
| 12609 | buscarte | 9 |
| 12610 | buscarlos | 9 |
| 12611 | burlo | 9 |
| 12612 | bulliciosa | 9 |
| 12613 | buitre | 9 |
| 12614 | buelta | 9 |
| 12615 | brusco | 9 |
| 12616 | brito | 9 |
| 12617 | brisa | 9 |
| 12618 | brindis | 9 |
| 12619 | borla | 9 |
| 12620 | bodegón | 9 |
| 12621 | blandamente | 9 |
| 12622 | bizcocho | 9 |
| 12623 | bizarría | 9 |
| 12624 | birlocho | 9 |
| 12625 | bilis | 9 |
| 12626 | betún | 9 |
| 12627 | besarle | 9 |
| 12628 | benéfico | 9 |
| 12629 | bendiga | 9 |
| 12630 | bendiçión | 9 |
| 12631 | bebo | 9 |
| 12632 | barriles | 9 |
| 12633 | barbaridades | 9 |
| 12634 | barbado | 9 |
| 12635 | baraja | 9 |
| 12636 | bandos | 9 |
| 12637 | ballena | 9 |
| 12638 | balandrán | 9 |
| 12639 | azotado | 9 |
| 12640 | ayudante | 9 |
| 12641 | aventurar | 9 |
| 12642 | aumente | 9 |
| 12643 | aullidos | 9 |
| 12644 | auias | 9 |
| 12645 | atribuía | 9 |
| 12646 | atrevimientos | 9 |
| 12647 | atormenta | 9 |
| 12648 | aterraba | 9 |
| 12649 | atengo | 9 |
| 12650 | ata | 9 |
| 12651 | asqueroso | 9 |
| 12652 | asomar | 9 |
| 12653 | asistían | 9 |
| 12654 | asiste | 9 |
| 12655 | asfixia | 9 |
| 12656 | arruinado | 9 |
| 12657 | arroyuelo | 9 |
| 12658 | arrojaron | 9 |
| 12659 | arrastrada | 9 |
| 12660 | arrancada | 9 |
| 12661 | aroma | 9 |
| 12662 | aridez | 9 |
| 12663 | arguye | 9 |
| 12664 | arboleda | 9 |
| 12665 | arboladura | 9 |
| 12666 | arbitrio | 9 |
| 12667 | arañas | 9 |
| 12668 | arábiga | 9 |
| 12669 | arabia | 9 |
| 12670 | aprovecharse | 9 |
| 12671 | aprobó | 9 |
| 12672 | apretándole | 9 |
| 12673 | apreciaba | 9 |
| 12674 | apostura | 9 |
| 12675 | apeó | 9 |
| 12676 | aparté | 9 |
| 12677 | apartan | 9 |
| 12678 | aparentar | 9 |
| 12679 | apagaba | 9 |
| 12680 | anzuelo | 9 |
| 12681 | anuncios | 9 |
| 12682 | antrines | 9 |
| 12683 | antepecho | 9 |
| 12684 | anteayer | 9 |
| 12685 | ansiosa | 9 |
| 12686 | anochecido | 9 |
| 12687 | aniversario | 9 |
| 12688 | animó | 9 |
| 12689 | anhelaba | 9 |
| 12690 | angustioso | 9 |
| 12691 | angelito | 9 |
| 12692 | anegada | 9 |
| 12693 | andrajos | 9 |
| 12694 | andes | 9 |
| 12695 | anden | 9 |
| 12696 | andarse | 9 |
| 12697 | andará | 9 |
| 12698 | amidos | 9 |
| 12699 | amena | 9 |
| 12700 | amanece | 9 |
| 12701 | amables | 9 |
| 12702 | aludía | 9 |
| 12703 | altera | 9 |
| 12704 | altanería | 9 |
| 12705 | altamente | 9 |
| 12706 | alrededores | 9 |
| 12707 | almenas | 9 |
| 12708 | allende | 9 |
| 12709 | allega | 9 |
| 12710 | aliuio | 9 |
| 12711 | alientos | 9 |
| 12712 | alias | 9 |
| 12713 | alguaciles | 9 |
| 12714 | algos | 9 |
| 12715 | alfanje | 9 |
| 12716 | alejarse | 9 |
| 12717 | alejado | 9 |
| 12718 | aldonza | 9 |
| 12719 | alcides | 9 |
| 12720 | alcances | 9 |
| 12721 | alborotaba | 9 |
| 12722 | alamillos | 9 |
| 12723 | alambre | 9 |
| 12724 | alabando | 9 |
| 12725 | airoso | 9 |
| 12726 | ahumado | 9 |
| 12727 | aguarde | 9 |
| 12728 | aguanta | 9 |
| 12729 | aguadores | 9 |
| 12730 | agria | 9 |
| 12731 | agrado | 9 |
| 12732 | agitaba | 9 |
| 12733 | agente | 9 |
| 12734 | advertida | 9 |
| 12735 | advertencias | 9 |
| 12736 | adversario | 9 |
| 12737 | aduana | 9 |
| 12738 | adquisición | 9 |
| 12739 | adquirida | 9 |
| 12740 | adornaban | 9 |
| 12741 | admito | 9 |
| 12742 | admirando | 9 |
| 12743 | acusado | 9 |
| 12744 | acuestas | 9 |
| 12745 | acuérdate | 9 |
| 12746 | acuda | 9 |
| 12747 | acrecentar | 9 |
| 12748 | acorrer | 9 |
| 12749 | acordara | 9 |
| 12750 | acontecer | 9 |
| 12751 | aconsejo | 9 |
| 12752 | acompañados | 9 |
| 12753 | acompañadas | 9 |
| 12754 | acomodados | 9 |
| 12755 | aceitunas | 9 |
| 12756 | accesos | 9 |
| 12757 | acatamiento | 9 |
| 12758 | abuelos | 9 |
| 12759 | abrigado | 9 |
| 12760 | abrí | 9 |
| 12761 | abominable | 9 |
| 12762 | ablanda | 9 |
| 12763 | abatido | 9 |
| 12764 | abandonaba | 9 |
| 12765 | abades | 9 |
| 12766 | zoraide | 8 |
| 12767 | zagales | 8 |
| 12768 | zagala | 8 |
| 12769 | yguales | 8 |
| 12770 | yeruas | 8 |
| 12771 | yerran | 8 |
| 12772 | yermo | 8 |
| 12773 | yase | 8 |
| 12774 | xxx | 8 |
| 12775 | xxii | 8 |
| 12776 | xviii | 8 |
| 12777 | votación | 8 |
| 12778 | volvemos | 8 |
| 12779 | volved | 8 |
| 12780 | volváis | 8 |
| 12781 | voluntarios | 8 |
| 12782 | volumen | 8 |
| 12783 | vituperio | 8 |
| 12784 | visitó | 8 |
| 12785 | visiblemente | 8 |
| 12786 | virtuosos | 8 |
| 12787 | viose | 8 |
| 12788 | violentos | 8 |
| 12789 | viole | 8 |
| 12790 | vinieren | 8 |
| 12791 | vinieran | 8 |
| 12792 | victory | 8 |
| 12793 | victorias | 8 |
| 12794 | viceversa | 8 |
| 12795 | via | 8 |
| 12796 | veynte | 8 |
| 12797 | veya | 8 |
| 12798 | vestiglos | 8 |
| 12799 | venza | 8 |
| 12800 | vengarme | 8 |
| 12801 | vengamos | 8 |
| 12802 | veneración | 8 |
| 12803 | vendaval | 8 |
| 12804 | vencerme | 8 |
| 12805 | vencerle | 8 |
| 12806 | vélez | 8 |
| 12807 | velador | 8 |
| 12808 | veintisiete | 8 |
| 12809 | veíase | 8 |
| 12810 | vegez | 8 |
| 12811 | vegada | 8 |
| 12812 | veer | 8 |
| 12813 | vascongados | 8 |
| 12814 | varilla | 8 |
| 12815 | vanguardia | 8 |
| 12816 | valdrá | 8 |
| 12817 | vacilante | 8 |
| 12818 | vacante | 8 |
| 12819 | ultrajado | 8 |
| 12820 | tyenpo | 8 |
| 12821 | tuvieras | 8 |
| 12822 | turbarse | 8 |
| 12823 | túnica | 8 |
| 12824 | tuda | 8 |
| 12825 | trujillos | 8 |
| 12826 | trueque | 8 |
| 12827 | tropiece | 8 |
| 12828 | tropezones | 8 |
| 12829 | tropezado | 8 |
| 12830 | trocara | 8 |
| 12831 | triunfar | 8 |
| 12832 | tristísima | 8 |
| 12833 | trifaldín | 8 |
| 12834 | treynta | 8 |
| 12835 | trescientos | 8 |
| 12836 | treguas | 8 |
| 12837 | traydor | 8 |
| 12838 | trayan | 8 |
| 12839 | travesía | 8 |
| 12840 | tratándole | 8 |
| 12841 | trasaltar | 8 |
| 12842 | transparente | 8 |
| 12843 | transformado | 8 |
| 12844 | transacción | 8 |
| 12845 | tramo | 8 |
| 12846 | trajese | 8 |
| 12847 | traigas | 8 |
| 12848 | traída | 8 |
| 12849 | tragado | 8 |
| 12850 | tráeme | 8 |
| 12851 | trabó | 8 |
| 12852 | trabajosa | 8 |
| 12853 | trabajador | 8 |
| 12854 | tornaba | 8 |
| 12855 | tonillo | 8 |
| 12856 | tomóle | 8 |
| 12857 | tomemos | 8 |
| 12858 | tomasito | 8 |
| 12859 | tomándolo | 8 |
| 12860 | tomándola | 8 |
| 12861 | tocaron | 8 |
| 12862 | tocare | 8 |
| 12863 | tocadores | 8 |
| 12864 | to | 8 |
| 12865 | tirria | 8 |
| 12866 | tirase | 8 |
| 12867 | timo | 8 |
| 12868 | tesón | 8 |
| 12869 | terçero | 8 |
| 12870 | tentador | 8 |
| 12871 | tendiendo | 8 |
| 12872 | tender | 8 |
| 12873 | tenacidad | 8 |
| 12874 | telégrafo | 8 |
| 12875 | tarfe | 8 |
| 12876 | tareas | 8 |
| 12877 | tapujos | 8 |
| 12878 | tapiz | 8 |
| 12879 | taciturno | 8 |
| 12880 | tácito | 8 |
| 12881 | sutilezas | 8 |
| 12882 | suplicándole | 8 |
| 12883 | supersticiosa | 8 |
| 12884 | sufra | 8 |
| 12885 | sueldos | 8 |
| 12886 | sudores | 8 |
| 12887 | subterráneo | 8 |
| 12888 | sublevaba | 8 |
| 12889 | subjeto | 8 |
| 12890 | subimos | 8 |
| 12891 | subiese | 8 |
| 12892 | soto | 8 |
| 12893 | sostenido | 8 |
| 12894 | sospechosa | 8 |
| 12895 | sorprender | 8 |
| 12896 | sorprendente | 8 |
| 12897 | sordos | 8 |
| 12898 | soplando | 8 |
| 12899 | soñadora | 8 |
| 12900 | solicitudes | 8 |
| 12901 | solicitan | 8 |
| 12902 | solicitado | 8 |
| 12903 | solícita | 8 |
| 12904 | sofocaba | 8 |
| 12905 | soez | 8 |
| 12906 | socorrerla | 8 |
| 12907 | sobrenombre | 8 |
| 12908 | sobrante | 8 |
| 12909 | sirenas | 8 |
| 12910 | sinrazones | 8 |
| 12911 | sinon | 8 |
| 12912 | singularmente | 8 |
| 12913 | silenciosos | 8 |
| 12914 | silbidos | 8 |
| 12915 | siguro | 8 |
| 12916 | significar | 8 |
| 12917 | sientan | 8 |
| 12918 | sidra | 8 |
| 12919 | seya | 8 |
| 12920 | sexto | 8 |
| 12921 | serviría | 8 |
| 12922 | serías | 8 |
| 12923 | sepulturas | 8 |
| 12924 | sepoltura | 8 |
| 12925 | señala | 8 |
| 12926 | sentiré | 8 |
| 12927 | sentimos | 8 |
| 12928 | sentase | 8 |
| 12929 | senores | 8 |
| 12930 | senado | 8 |
| 12931 | semilla | 8 |
| 12932 | semejaban | 8 |
| 12933 | seguidas | 8 |
| 12934 | seglar | 8 |
| 12935 | seer | 8 |
| 12936 | secular | 8 |
| 12937 | saques | 8 |
| 12938 | sapos | 8 |
| 12939 | sapo | 8 |
| 12940 | santuario | 8 |
| 12941 | sandio | 8 |
| 12942 | sanctos | 8 |
| 12943 | samaniegas | 8 |
| 12944 | salvó | 8 |
| 12945 | saluo | 8 |
| 12946 | saludaban | 8 |
| 12947 | salmerón | 8 |
| 12948 | salirse | 8 |
| 12949 | saliesen | 8 |
| 12950 | salid | 8 |
| 12951 | salgas | 8 |
| 12952 | salgamos | 8 |
| 12953 | sacudirse | 8 |
| 12954 | saciar | 8 |
| 12955 | sacaste | 8 |
| 12956 | sacarlo | 8 |
| 12957 | sacará | 8 |
| 12958 | sabremos | 8 |
| 12959 | sabidurías | 8 |
| 12960 | ruydo | 8 |
| 12961 | rutinas | 8 |
| 12962 | ruiseñor | 8 |
| 12963 | ruidera | 8 |
| 12964 | rugió | 8 |
| 12965 | ruegan | 8 |
| 12966 | ruega | 8 |
| 12967 | rubí | 8 |
| 12968 | rótulo | 8 |
| 12969 | roquete | 8 |
| 12970 | rondeña | 8 |
| 12971 | rompa | 8 |
| 12972 | rogué | 8 |
| 12973 | roe | 8 |
| 12974 | rodado | 8 |
| 12975 | robre | 8 |
| 12976 | rizada | 8 |
| 12977 | riquísimas | 8 |
| 12978 | riñas | 8 |
| 12979 | ribetes | 8 |
| 12980 | rías | 8 |
| 12981 | revolucionario | 8 |
| 12982 | revelando | 8 |
| 12983 | revelaban | 8 |
| 12984 | retozaba | 8 |
| 12985 | retiróse | 8 |
| 12986 | retintín | 8 |
| 12987 | restaurant | 8 |
| 12988 | respondiendo | 8 |
| 12989 | respondían | 8 |
| 12990 | resplandecientes | 8 |
| 12991 | resplandecía | 8 |
| 12992 | réspice | 8 |
| 12993 | respetabilidad | 8 |
| 12994 | respeta | 8 |
| 12995 | resonó | 8 |
| 12996 | resonar | 8 |
| 12997 | resmas | 8 |
| 12998 | requieren | 8 |
| 12999 | reprimir | 8 |
| 13000 | repostero | 8 |
| 13001 | repartiendo | 8 |
| 13002 | reparaba | 8 |
| 13003 | repara | 8 |
| 13004 | renovar | 8 |
| 13005 | remilgos | 8 |
| 13006 | remedie | 8 |
| 13007 | relox | 8 |
| 13008 | relimpio | 8 |
| 13009 | relieve | 8 |
| 13010 | relativamente | 8 |
| 13011 | reírme | 8 |
| 13012 | reinar | 8 |
| 13013 | reinado | 8 |
| 13014 | regularmente | 8 |
| 13015 | regulares | 8 |
| 13016 | regir | 8 |
| 13017 | reforma | 8 |
| 13018 | referentes | 8 |
| 13019 | recrearse | 8 |
| 13020 | recreaba | 8 |
| 13021 | recordaban | 8 |
| 13022 | reconocieron | 8 |
| 13023 | reconocido | 8 |
| 13024 | reconocí | 8 |
| 13025 | recebidos | 8 |
| 13026 | recámara | 8 |
| 13027 | recadito | 8 |
| 13028 | reaccionario | 8 |
| 13029 | rayaba | 8 |
| 13030 | rascaba | 8 |
| 13031 | raposa | 8 |
| 13032 | ráfagas | 8 |
| 13033 | rabillo | 8 |
| 13034 | quod | 8 |
| 13035 | quo | 8 |
| 13036 | quitase | 8 |
| 13037 | quitársela | 8 |
| 13038 | quitarles | 8 |
| 13039 | quítame | 8 |
| 13040 | quisiste | 8 |
| 13041 | quisiéramos | 8 |
| 13042 | quexar | 8 |
| 13043 | quererlo | 8 |
| 13044 | quepa | 8 |
| 13045 | quemaba | 8 |
| 13046 | quedasen | 8 |
| 13047 | quedaremos | 8 |
| 13048 | quedaos | 8 |
| 13049 | quebranto | 8 |
| 13050 | quántos | 8 |
| 13051 | quanta | 8 |
| 13052 | pupitre | 8 |
| 13053 | pulcro | 8 |
| 13054 | púas | 8 |
| 13055 | provenía | 8 |
| 13056 | proveído | 8 |
| 13057 | provar | 8 |
| 13058 | protege | 8 |
| 13059 | prosiga | 8 |
| 13060 | propinas | 8 |
| 13061 | pronunciaba | 8 |
| 13062 | pronta | 8 |
| 13063 | prometes | 8 |
| 13064 | prolija | 8 |
| 13065 | prohibía | 8 |
| 13066 | prohíbe | 8 |
| 13067 | profundísimo | 8 |
| 13068 | profundidad | 8 |
| 13069 | profesan | 8 |
| 13070 | proezas | 8 |
| 13071 | producto | 8 |
| 13072 | procurarse | 8 |
| 13073 | procuraban | 8 |
| 13074 | procedencia | 8 |
| 13075 | probaba | 8 |
| 13076 | primos | 8 |
| 13077 | primor | 8 |
| 13078 | primitivos | 8 |
| 13079 | primitiva | 8 |
| 13080 | primerito | 8 |
| 13081 | prieto | 8 |
| 13082 | prevenido | 8 |
| 13083 | pretendientes | 8 |
| 13084 | presuroso | 8 |
| 13085 | presunciones | 8 |
| 13086 | prestamistas | 8 |
| 13087 | presento | 8 |
| 13088 | presentados | 8 |
| 13089 | prescindir | 8 |
| 13090 | presas | 8 |
| 13091 | preparándose | 8 |
| 13092 | preocupaba | 8 |
| 13093 | preñada | 8 |
| 13094 | prelado | 8 |
| 13095 | preguntara | 8 |
| 13096 | prefiriendo | 8 |
| 13097 | precursor | 8 |
| 13098 | precoz | 8 |
| 13099 | precipitación | 8 |
| 13100 | precios | 8 |
| 13101 | postrera | 8 |
| 13102 | portillo | 8 |
| 13103 | porfiaba | 8 |
| 13104 | poquitín | 8 |
| 13105 | ponerlos | 8 |
| 13106 | ponemos | 8 |
| 13107 | pondrás | 8 |
| 13108 | poncio | 8 |
| 13109 | pollina | 8 |
| 13110 | poblados | 8 |
| 13111 | plenitud | 8 |
| 13112 | plebeyos | 8 |
| 13113 | plebe | 8 |
| 13114 | plantó | 8 |
| 13115 | planchadora | 8 |
| 13116 | pisto | 8 |
| 13117 | piélago | 8 |
| 13118 | picarona | 8 |
| 13119 | pican | 8 |
| 13120 | peste | 8 |
| 13121 | pesebre | 8 |
| 13122 | perversión | 8 |
| 13123 | perspicaz | 8 |
| 13124 | persecuciones | 8 |
| 13125 | perrerías | 8 |
| 13126 | perplejidad | 8 |
| 13127 | permitiéndose | 8 |
| 13128 | perfiles | 8 |
| 13129 | perdonó | 8 |
| 13130 | perdiste | 8 |
| 13131 | pequeno | 8 |
| 13132 | peñasco | 8 |
| 13133 | pella | 8 |
| 13134 | pelean | 8 |
| 13135 | pegando | 8 |
| 13136 | pediría | 8 |
| 13137 | pecadoras | 8 |
| 13138 | pausada | 8 |
| 13139 | patriota | 8 |
| 13140 | pasolargo | 8 |
| 13141 | pasmosa | 8 |
| 13142 | paseíto | 8 |
| 13143 | pasajeros | 8 |
| 13144 | paro | 8 |
| 13145 | parezco | 8 |
| 13146 | parecidos | 8 |
| 13147 | parajes | 8 |
| 13148 | pañolería | 8 |
| 13149 | panzas | 8 |
| 13150 | panecillo | 8 |
| 13151 | pandero | 8 |
| 13152 | palmatoria | 8 |
| 13153 | pagase | 8 |
| 13154 | pagarés | 8 |
| 13155 | pagaban | 8 |
| 13156 | pacíficos | 8 |
| 13157 | paciente | 8 |
| 13158 | oygo | 8 |
| 13159 | oyéronse | 8 |
| 13160 | oscuros | 8 |
| 13161 | orquesta | 8 |
| 13162 | organismo | 8 |
| 13163 | ordenar | 8 |
| 13164 | ordenada | 8 |
| 13165 | optimismo | 8 |
| 13166 | oprimido | 8 |
| 13167 | oprimida | 8 |
| 13168 | oprime | 8 |
| 13169 | olvidaré | 8 |
| 13170 | oluido | 8 |
| 13171 | olorosas | 8 |
| 13172 | olorosa | 8 |
| 13173 | olmos | 8 |
| 13174 | olivares | 8 |
| 13175 | oírlo | 8 |
| 13176 | oírlas | 8 |
| 13177 | oirá | 8 |
| 13178 | oficiosidad | 8 |
| 13179 | odioso | 8 |
| 13180 | ocupadas | 8 |
| 13181 | ociosa | 8 |
| 13182 | obtuvo | 8 |
| 13183 | observadora | 8 |
| 13184 | novillo | 8 |
| 13185 | novenas | 8 |
| 13186 | noruega | 8 |
| 13187 | normal | 8 |
| 13188 | noé | 8 |
| 13189 | nocturno | 8 |
| 13190 | nocturnas | 8 |
| 13191 | nocturna | 8 |
| 13192 | ninos | 8 |
| 13193 | nilo | 8 |
| 13194 | nevada | 8 |
| 13195 | nerviosos | 8 |
| 13196 | negociante | 8 |
| 13197 | negligencia | 8 |
| 13198 | negado | 8 |
| 13199 | necesitados | 8 |
| 13200 | naufragio | 8 |
| 13201 | nascida | 8 |
| 13202 | nado | 8 |
| 13203 | nacionales | 8 |
| 13204 | musa | 8 |
| 13205 | murmurador | 8 |
| 13206 | murmullos | 8 |
| 13207 | muriese | 8 |
| 13208 | muñeco | 8 |
| 13209 | muletas | 8 |
| 13210 | muestres | 8 |
| 13211 | muerde | 8 |
| 13212 | muchísima | 8 |
| 13213 | mortuoria | 8 |
| 13214 | moriscos | 8 |
| 13215 | moribunda | 8 |
| 13216 | mordido | 8 |
| 13217 | montalbán | 8 |
| 13218 | monstruos | 8 |
| 13219 | monótono | 8 |
| 13220 | moldes | 8 |
| 13221 | mojicones | 8 |
| 13222 | mojados | 8 |
| 13223 | modesta | 8 |
| 13224 | mochachos | 8 |
| 13225 | mochachas | 8 |
| 13226 | mismísimo | 8 |
| 13227 | miradores | 8 |
| 13228 | mínimo | 8 |
| 13229 | mínima | 8 |
| 13230 | mimoso | 8 |
| 13231 | milagrosa | 8 |
| 13232 | micomicón | 8 |
| 13233 | mezclados | 8 |
| 13234 | metiose | 8 |
| 13235 | meten | 8 |
| 13236 | metafísica | 8 |
| 13237 | mesnada | 8 |
| 13238 | mentís | 8 |
| 13239 | mentirosos | 8 |
| 13240 | mentirosas | 8 |
| 13241 | menssajero | 8 |
| 13242 | memoriales | 8 |
| 13243 | melindres | 8 |
| 13244 | melezina | 8 |
| 13245 | melena | 8 |
| 13246 | meditabunda | 8 |
| 13247 | médica | 8 |
| 13248 | medianera | 8 |
| 13249 | mecha | 8 |
| 13250 | matadores | 8 |
| 13251 | mariuca | 8 |
| 13252 | márgenes | 8 |
| 13253 | marauillas | 8 |
| 13254 | maquinalmente | 8 |
| 13255 | mapa | 8 |
| 13256 | manteos | 8 |
| 13257 | mantenerse | 8 |
| 13258 | manotadas | 8 |
| 13259 | maniobra | 8 |
| 13260 | manifiestas | 8 |
| 13261 | mandil | 8 |
| 13262 | mandarla | 8 |
| 13263 | mandaría | 8 |
| 13264 | mandara | 8 |
| 13265 | mançebo | 8 |
| 13266 | mamás | 8 |
| 13267 | malla | 8 |
| 13268 | malditas | 8 |
| 13269 | maldicientes | 8 |
| 13270 | maldice | 8 |
| 13271 | magníficas | 8 |
| 13272 | maestras | 8 |
| 13273 | madrileños | 8 |
| 13274 | madero | 8 |
| 13275 | madeja | 8 |
| 13276 | lymosna | 8 |
| 13277 | luquitas | 8 |
| 13278 | lucirse | 8 |
| 13279 | luchaba | 8 |
| 13280 | luce | 8 |
| 13281 | lucas | 8 |
| 13282 | lúbrica | 8 |
| 13283 | lozana | 8 |
| 13284 | loro | 8 |
| 13285 | lloroso | 8 |
| 13286 | llores | 8 |
| 13287 | llevéis | 8 |
| 13288 | llevársela | 8 |
| 13289 | llevarlo | 8 |
| 13290 | llevarán | 8 |
| 13291 | llenando | 8 |
| 13292 | llegaremos | 8 |
| 13293 | llamarte | 8 |
| 13294 | listos | 8 |
| 13295 | limpiaba | 8 |
| 13296 | limitada | 8 |
| 13297 | libreas | 8 |
| 13298 | libertades | 8 |
| 13299 | levitas | 8 |
| 13300 | levemente | 8 |
| 13301 | levantase | 8 |
| 13302 | levantarle | 8 |
| 13303 | leonor | 8 |
| 13304 | leídos | 8 |
| 13305 | leganés | 8 |
| 13306 | leerlo | 8 |
| 13307 | lechuga | 8 |
| 13308 | lavó | 8 |
| 13309 | lastimosa | 8 |
| 13310 | lastima | 8 |
| 13311 | lámina | 8 |
| 13312 | laceria | 8 |
| 13313 | juntaba | 8 |
| 13314 | junco | 8 |
| 13315 | julián | 8 |
| 13316 | juegan | 8 |
| 13317 | judicial | 8 |
| 13318 | jilguero | 8 |
| 13319 | jarana | 8 |
| 13320 | iugurta | 8 |
| 13321 | inventor | 8 |
| 13322 | inutilidad | 8 |
| 13323 | intentos | 8 |
| 13324 | intentaba | 8 |
| 13325 | intemperie | 8 |
| 13326 | inteligentes | 8 |
| 13327 | insignias | 8 |
| 13328 | inquietudes | 8 |
| 13329 | inmensos | 8 |
| 13330 | informes | 8 |
| 13331 | informarse | 8 |
| 13332 | infinitamente | 8 |
| 13333 | infinidad | 8 |
| 13334 | inevitable | 8 |
| 13335 | indiscreto | 8 |
| 13336 | indiferentes | 8 |
| 13337 | indicado | 8 |
| 13338 | independiente | 8 |
| 13339 | incurable | 8 |
| 13340 | incorporó | 8 |
| 13341 | incomodidad | 8 |
| 13342 | incomodarse | 8 |
| 13343 | incomodado | 8 |
| 13344 | inclinaciones | 8 |
| 13345 | impropia | 8 |
| 13346 | impresionó | 8 |
| 13347 | importunos | 8 |
| 13348 | importunas | 8 |
| 13349 | importaban | 8 |
| 13350 | impío | 8 |
| 13351 | impidió | 8 |
| 13352 | impida | 8 |
| 13353 | imperturbable | 8 |
| 13354 | imaginado | 8 |
| 13355 | ignorar | 8 |
| 13356 | ignoran | 8 |
| 13357 | ídem | 8 |
| 13358 | huyeron | 8 |
| 13359 | huyen | 8 |
| 13360 | hundía | 8 |
| 13361 | humillar | 8 |
| 13362 | húmedas | 8 |
| 13363 | huían | 8 |
| 13364 | huérfano | 8 |
| 13365 | houo | 8 |
| 13366 | horrorosa | 8 |
| 13367 | horrísono | 8 |
| 13368 | horizontes | 8 |
| 13369 | hondonada | 8 |
| 13370 | homenaje | 8 |
| 13371 | holgando | 8 |
| 13372 | holgaba | 8 |
| 13373 | hocico | 8 |
| 13374 | hoc | 8 |
| 13375 | historiadores | 8 |
| 13376 | hipócrates | 8 |
| 13377 | hilaria | 8 |
| 13378 | hierbas | 8 |
| 13379 | hidalga | 8 |
| 13380 | herramientas | 8 |
| 13381 | hermenegildo | 8 |
| 13382 | hermanitas | 8 |
| 13383 | henares | 8 |
| 13384 | hechicero | 8 |
| 13385 | hase | 8 |
| 13386 | haréis | 8 |
| 13387 | haras | 8 |
| 13388 | hallóle | 8 |
| 13389 | hallen | 8 |
| 13390 | halléme | 8 |
| 13391 | halagaba | 8 |
| 13392 | hágalo | 8 |
| 13393 | hado | 8 |
| 13394 | haciéndolo | 8 |
| 13395 | haciéndola | 8 |
| 13396 | hacíase | 8 |
| 13397 | habláis | 8 |
| 13398 | guzmán | 8 |
| 13399 | gustase | 8 |
| 13400 | guarnición | 8 |
| 13401 | gruñidos | 8 |
| 13402 | groseramente | 8 |
| 13403 | greguescos | 8 |
| 13404 | gracejo | 8 |
| 13405 | gozosos | 8 |
| 13406 | godino | 8 |
| 13407 | gaznate | 8 |
| 13408 | gastó | 8 |
| 13409 | gasté | 8 |
| 13410 | gaste | 8 |
| 13411 | gastadas | 8 |
| 13412 | garçón | 8 |
| 13413 | gallardos | 8 |
| 13414 | gallardamente | 8 |
| 13415 | galeota | 8 |
| 13416 | futuras | 8 |
| 13417 | fundo | 8 |
| 13418 | fulminante | 8 |
| 13419 | fueste | 8 |
| 13420 | fueses | 8 |
| 13421 | fueres | 8 |
| 13422 | frotándose | 8 |
| 13423 | friolera | 8 |
| 13424 | frecuentaba | 8 |
| 13425 | frayle | 8 |
| 13426 | fraternidad | 8 |
| 13427 | fragmentos | 8 |
| 13428 | fornido | 8 |
| 13429 | follones | 8 |
| 13430 | folgura | 8 |
| 13431 | fingían | 8 |
| 13432 | finezas | 8 |
| 13433 | fijeza | 8 |
| 13434 | fíjese | 8 |
| 13435 | fijaron | 8 |
| 13436 | figurándose | 8 |
| 13437 | fibras | 8 |
| 13438 | ferrocarriles | 8 |
| 13439 | feridas | 8 |
| 13440 | felisa | 8 |
| 13441 | fechas | 8 |
| 13442 | fazía | 8 |
| 13443 | fazañas | 8 |
| 13444 | fastidio | 8 |
| 13445 | fases | 8 |
| 13446 | fascinación | 8 |
| 13447 | faría | 8 |
| 13448 | fantásticos | 8 |
| 13449 | fantástica | 8 |
| 13450 | faltaría | 8 |
| 13451 | faldones | 8 |
| 13452 | faetón | 8 |
| 13453 | fábricas | 8 |
| 13454 | extraviados | 8 |
| 13455 | extravagante | 8 |
| 13456 | extraordinarios | 8 |
| 13457 | extraordinarias | 8 |
| 13458 | extrañeza | 8 |
| 13459 | externo | 8 |
| 13460 | extendían | 8 |
| 13461 | expresiva | 8 |
| 13462 | exponía | 8 |
| 13463 | explique | 8 |
| 13464 | explicarme | 8 |
| 13465 | explicarlo | 8 |
| 13466 | explicaré | 8 |
| 13467 | exhalación | 8 |
| 13468 | exençión | 8 |
| 13469 | excusas | 8 |
| 13470 | excusa | 8 |
| 13471 | excitar | 8 |
| 13472 | excesos | 8 |
| 13473 | exceso | 8 |
| 13474 | excelencias | 8 |
| 13475 | excede | 8 |
| 13476 | exagerada | 8 |
| 13477 | exageraba | 8 |
| 13478 | evidentemente | 8 |
| 13479 | etiquetas | 8 |
| 13480 | estuviste | 8 |
| 13481 | estreno | 8 |
| 13482 | estranjeros | 8 |
| 13483 | estrago | 8 |
| 13484 | estorbase | 8 |
| 13485 | estopa | 8 |
| 13486 | estocadas | 8 |
| 13487 | estiman | 8 |
| 13488 | estimado | 8 |
| 13489 | estiende | 8 |
| 13490 | estancias | 8 |
| 13491 | estambre | 8 |
| 13492 | estallar | 8 |
| 13493 | estada | 8 |
| 13494 | esquivo | 8 |
| 13495 | esperas | 8 |
| 13496 | espectro | 8 |
| 13497 | espartero | 8 |
| 13498 | eses | 8 |
| 13499 | escupió | 8 |
| 13500 | escupía | 8 |
| 13501 | escrupuloso | 8 |
| 13502 | escribiese | 8 |
| 13503 | escribieron | 8 |
| 13504 | escondieron | 8 |
| 13505 | escollos | 8 |
| 13506 | esclavina | 8 |
| 13507 | escarnio | 8 |
| 13508 | escarlata | 8 |
| 13509 | errantes | 8 |
| 13510 | equivoca | 8 |
| 13511 | envíe | 8 |
| 13512 | envidioso | 8 |
| 13513 | entusiasta | 8 |
| 13514 | entretuvo | 8 |
| 13515 | entretenimientos | 8 |
| 13516 | entregas | 8 |
| 13517 | entraría | 8 |
| 13518 | entrad | 8 |
| 13519 | entornada | 8 |
| 13520 | enteraba | 8 |
| 13521 | entenderá | 8 |
| 13522 | entena | 8 |
| 13523 | ente | 8 |
| 13524 | ensilla | 8 |
| 13525 | enredo | 8 |
| 13526 | enr | 8 |
| 13527 | enojoso | 8 |
| 13528 | enjuta | 8 |
| 13529 | enigma | 8 |
| 13530 | engendrar | 8 |
| 13531 | energías | 8 |
| 13532 | enderezando | 8 |
| 13533 | encubridora | 8 |
| 13534 | encubierta | 8 |
| 13535 | encontrase | 8 |
| 13536 | encontrarla | 8 |
| 13537 | encogimiento | 8 |
| 13538 | encerrarle | 8 |
| 13539 | encerradas | 8 |
| 13540 | encarecimiento | 8 |
| 13541 | encarecidamente | 8 |
| 13542 | encaminar | 8 |
| 13543 | emplearía | 8 |
| 13544 | empleando | 8 |
| 13545 | empeñas | 8 |
| 13546 | empedrado | 8 |
| 13547 | eminentes | 8 |
| 13548 | embestir | 8 |
| 13549 | embelecos | 8 |
| 13550 | embarcarse | 8 |
| 13551 | elevar | 8 |
| 13552 | elevado | 8 |
| 13553 | elementales | 8 |
| 13554 | elemental | 8 |
| 13555 | efectivo | 8 |
| 13556 | echasen | 8 |
| 13557 | echarme | 8 |
| 13558 | durmieron | 8 |
| 13559 | duran | 8 |
| 13560 | duración | 8 |
| 13561 | dudosos | 8 |
| 13562 | dude | 8 |
| 13563 | doquiera | 8 |
| 13564 | dona | 8 |
| 13565 | domina | 8 |
| 13566 | dolorido | 8 |
| 13567 | dócil | 8 |
| 13568 | dixieron | 8 |
| 13569 | díxel | 8 |
| 13570 | divierten | 8 |
| 13571 | dividida | 8 |
| 13572 | divertida | 8 |
| 13573 | diversión | 8 |
| 13574 | distraídos | 8 |
| 13575 | distraía | 8 |
| 13576 | distraerse | 8 |
| 13577 | distancias | 8 |
| 13578 | disputando | 8 |
| 13579 | disparos | 8 |
| 13580 | disparada | 8 |
| 13581 | disfrazada | 8 |
| 13582 | discusiones | 8 |
| 13583 | disculpas | 8 |
| 13584 | discreciones | 8 |
| 13585 | discípulos | 8 |
| 13586 | dirigiose | 8 |
| 13587 | dirigido | 8 |
| 13588 | diose | 8 |
| 13589 | dióle | 8 |
| 13590 | diles | 8 |
| 13591 | díjoles | 8 |
| 13592 | dijimos | 8 |
| 13593 | dígote | 8 |
| 13594 | dignó | 8 |
| 13595 | diestros | 8 |
| 13596 | dido | 8 |
| 13597 | diciplinantes | 8 |
| 13598 | dicc | 8 |
| 13599 | diálogos | 8 |
| 13600 | deyuso | 8 |
| 13601 | deus | 8 |
| 13602 | deudor | 8 |
| 13603 | determinaciones | 8 |
| 13604 | detalle | 8 |
| 13605 | desvelado | 8 |
| 13606 | desusado | 8 |
| 13607 | desuariado | 8 |
| 13608 | desterrar | 8 |
| 13609 | despoblados | 8 |
| 13610 | despoblado | 8 |
| 13611 | despiertos | 8 |
| 13612 | despidiose | 8 |
| 13613 | despertador | 8 |
| 13614 | desperdicios | 8 |
| 13615 | desmejorado | 8 |
| 13616 | desmán | 8 |
| 13617 | deshonrada | 8 |
| 13618 | deshecha | 8 |
| 13619 | deseosa | 8 |
| 13620 | desecha | 8 |
| 13621 | descubiertas | 8 |
| 13622 | descrédito | 8 |
| 13623 | descortés | 8 |
| 13624 | desconsolado | 8 |
| 13625 | descollaba | 8 |
| 13626 | descendientes | 8 |
| 13627 | descendiendo | 8 |
| 13628 | descendía | 8 |
| 13629 | descarada | 8 |
| 13630 | descansado | 8 |
| 13631 | descalabrado | 8 |
| 13632 | desbordaba | 8 |
| 13633 | desayuno | 8 |
| 13634 | desatinada | 8 |
| 13635 | desatar | 8 |
| 13636 | desaparición | 8 |
| 13637 | desapacible | 8 |
| 13638 | desamor | 8 |
| 13639 | derramando | 8 |
| 13640 | deplorable | 8 |
| 13641 | deme | 8 |
| 13642 | delgados | 8 |
| 13643 | déjenme | 8 |
| 13644 | dejándome | 8 |
| 13645 | defienda | 8 |
| 13646 | defendiendo | 8 |
| 13647 | decoraciones | 8 |
| 13648 | decidor | 8 |
| 13649 | decíame | 8 |
| 13650 | daua | 8 |
| 13651 | dare | 8 |
| 13652 | danzas | 8 |
| 13653 | dante | 8 |
| 13654 | danos | 8 |
| 13655 | cutis | 8 |
| 13656 | cure | 8 |
| 13657 | cumpliría | 8 |
| 13658 | cultos | 8 |
| 13659 | cuida | 8 |
| 13660 | cuevas | 8 |
| 13661 | cueste | 8 |
| 13662 | cuenten | 8 |
| 13663 | cuclillas | 8 |
| 13664 | cuchufletas | 8 |
| 13665 | crucifijo | 8 |
| 13666 | crónico | 8 |
| 13667 | crónicas | 8 |
| 13668 | cristalino | 8 |
| 13669 | crían | 8 |
| 13670 | creyente | 8 |
| 13671 | creerán | 8 |
| 13672 | credulidad | 8 |
| 13673 | coxo | 8 |
| 13674 | cosiendo | 8 |
| 13675 | corvo | 8 |
| 13676 | corsé | 8 |
| 13677 | correspondientes | 8 |
| 13678 | correspondían | 8 |
| 13679 | correcta | 8 |
| 13680 | corpulento | 8 |
| 13681 | coroza | 8 |
| 13682 | coros | 8 |
| 13683 | coronados | 8 |
| 13684 | copos | 8 |
| 13685 | copioso | 8 |
| 13686 | convienen | 8 |
| 13687 | convicciones | 8 |
| 13688 | contravenir | 8 |
| 13689 | contrato | 8 |
| 13690 | contrahecha | 8 |
| 13691 | contracayes | 8 |
| 13692 | continuamente | 8 |
| 13693 | contentísimo | 8 |
| 13694 | contentado | 8 |
| 13695 | contemporáneos | 8 |
| 13696 | contemplaban | 8 |
| 13697 | consumo | 8 |
| 13698 | consume | 8 |
| 13699 | conspiración | 8 |
| 13700 | consolarme | 8 |
| 13701 | consideraban | 8 |
| 13702 | consagró | 8 |
| 13703 | conquistador | 8 |
| 13704 | conquistada | 8 |
| 13705 | conoscida | 8 |
| 13706 | conocimos | 8 |
| 13707 | conociese | 8 |
| 13708 | conocerse | 8 |
| 13709 | confusas | 8 |
| 13710 | confundía | 8 |
| 13711 | confitero | 8 |
| 13712 | confidencia | 8 |
| 13713 | confiaba | 8 |
| 13714 | confession | 8 |
| 13715 | condeno | 8 |
| 13716 | concluye | 8 |
| 13717 | concertó | 8 |
| 13718 | comunión | 8 |
| 13719 | comprada | 8 |
| 13720 | comportamiento | 8 |
| 13721 | componían | 8 |
| 13722 | complicada | 8 |
| 13723 | complacía | 8 |
| 13724 | complacencia | 8 |
| 13725 | competir | 8 |
| 13726 | comparaciones | 8 |
| 13727 | comoquiera | 8 |
| 13728 | comitiva | 8 |
| 13729 | comiença | 8 |
| 13730 | comensales | 8 |
| 13731 | combatido | 8 |
| 13732 | colocarse | 8 |
| 13733 | colocadas | 8 |
| 13734 | coloca | 8 |
| 13735 | colección | 8 |
| 13736 | colación | 8 |
| 13737 | cogerle | 8 |
| 13738 | cofradías | 8 |
| 13739 | cofradía | 8 |
| 13740 | cochino | 8 |
| 13741 | cobranza | 8 |
| 13742 | cobrador | 8 |
| 13743 | clori | 8 |
| 13744 | clavada | 8 |
| 13745 | cit | 8 |
| 13746 | cirio | 8 |
| 13747 | cirila | 8 |
| 13748 | chupar | 8 |
| 13749 | chistar | 8 |
| 13750 | chispa | 8 |
| 13751 | chino | 8 |
| 13752 | chillones | 8 |
| 13753 | chillando | 8 |
| 13754 | certifico | 8 |
| 13755 | cerdo | 8 |
| 13756 | cercanos | 8 |
| 13757 | cercado | 8 |
| 13758 | cenó | 8 |
| 13759 | cementerios | 8 |
| 13760 | celestiales | 8 |
| 13761 | cedido | 8 |
| 13762 | cazadora | 8 |
| 13763 | cavando | 8 |
| 13764 | cautelas | 8 |
| 13765 | cause | 8 |
| 13766 | castas | 8 |
| 13767 | casé | 8 |
| 13768 | casacones | 8 |
| 13769 | carruajes | 8 |
| 13770 | carretas | 8 |
| 13771 | cariños | 8 |
| 13772 | cargue | 8 |
| 13773 | carecían | 8 |
| 13774 | carbonero | 8 |
| 13775 | característico | 8 |
| 13776 | carabineros | 8 |
| 13777 | car | 8 |
| 13778 | capítulos | 8 |
| 13779 | capitulo | 8 |
| 13780 | cantor | 8 |
| 13781 | cantas | 8 |
| 13782 | cántaros | 8 |
| 13783 | canoro | 8 |
| 13784 | canonjía | 8 |
| 13785 | campea | 8 |
| 13786 | cambios | 8 |
| 13787 | calzaba | 8 |
| 13788 | calmarle | 8 |
| 13789 | callejuelas | 8 |
| 13790 | callaré | 8 |
| 13791 | callados | 8 |
| 13792 | calientes | 8 |
| 13793 | calaveradas | 8 |
| 13794 | calaverada | 8 |
| 13795 | cajita | 8 |
| 13796 | cachivaches | 8 |
| 13797 | cabizbajo | 8 |
| 13798 | cabían | 8 |
| 13799 | cabañas | 8 |
| 13800 | buscaría | 8 |
| 13801 | burros | 8 |
| 13802 | burlona | 8 |
| 13803 | burlándose | 8 |
| 13804 | burlador | 8 |
| 13805 | bulle | 8 |
| 13806 | buelue | 8 |
| 13807 | buche | 8 |
| 13808 | brutalidad | 8 |
| 13809 | brutales | 8 |
| 13810 | brujas | 8 |
| 13811 | brotaba | 8 |
| 13812 | bromuro | 8 |
| 13813 | brigadiera | 8 |
| 13814 | bretaña | 8 |
| 13815 | bóvedas | 8 |
| 13816 | botánico | 8 |
| 13817 | bondades | 8 |
| 13818 | boluer | 8 |
| 13819 | bolos | 8 |
| 13820 | blasfemia | 8 |
| 13821 | bicho | 8 |
| 13822 | bever | 8 |
| 13823 | bellaquerías | 8 |
| 13824 | beben | 8 |
| 13825 | basto | 8 |
| 13826 | bastimentos | 8 |
| 13827 | barquero | 8 |
| 13828 | bárbaras | 8 |
| 13829 | baratas | 8 |
| 13830 | banquetes | 8 |
| 13831 | bandeja | 8 |
| 13832 | balance | 8 |
| 13833 | bailaba | 8 |
| 13834 | baco | 8 |
| 13835 | azotaba | 8 |
| 13836 | azogue | 8 |
| 13837 | azares | 8 |
| 13838 | azahar | 8 |
| 13839 | ayunos | 8 |
| 13840 | ayre | 8 |
| 13841 | avisó | 8 |
| 13842 | averiguación | 8 |
| 13843 | averías | 8 |
| 13844 | aventaja | 8 |
| 13845 | avena | 8 |
| 13846 | avemarías | 8 |
| 13847 | avara | 8 |
| 13848 | ausentes | 8 |
| 13849 | audaz | 8 |
| 13850 | atrevieron | 8 |
| 13851 | atreviera | 8 |
| 13852 | atreuimiento | 8 |
| 13853 | atormentado | 8 |
| 13854 | atormentaban | 8 |
| 13855 | aterrada | 8 |
| 13856 | atavío | 8 |
| 13857 | asuste | 8 |
| 13858 | asustar | 8 |
| 13859 | asumpto | 8 |
| 13860 | asomos | 8 |
| 13861 | asombrada | 8 |
| 13862 | asomándose | 8 |
| 13863 | asomada | 8 |
| 13864 | asistencia | 8 |
| 13865 | asís | 8 |
| 13866 | asir | 8 |
| 13867 | asentimiento | 8 |
| 13868 | asentado | 8 |
| 13869 | ascendiente | 8 |
| 13870 | asaltos | 8 |
| 13871 | artillero | 8 |
| 13872 | arrugas | 8 |
| 13873 | arrugado | 8 |
| 13874 | arrojaban | 8 |
| 13875 | arrobamiento | 8 |
| 13876 | arrimada | 8 |
| 13877 | arreos | 8 |
| 13878 | arreglarse | 8 |
| 13879 | arrastra | 8 |
| 13880 | arrancarse | 8 |
| 13881 | arrancando | 8 |
| 13882 | arpa | 8 |
| 13883 | armarios | 8 |
| 13884 | armaba | 8 |
| 13885 | aristóteles | 8 |
| 13886 | aristócratas | 8 |
| 13887 | arenal | 8 |
| 13888 | ardores | 8 |
| 13889 | ardientemente | 8 |
| 13890 | arçobispo | 8 |
| 13891 | arcabuces | 8 |
| 13892 | aquiles | 8 |
| 13893 | apuntando | 8 |
| 13894 | aprovechado | 8 |
| 13895 | aprobaba | 8 |
| 13896 | apretadas | 8 |
| 13897 | aprenda | 8 |
| 13898 | apoyarse | 8 |
| 13899 | apoderado | 8 |
| 13900 | apeáronse | 8 |
| 13901 | apartamiento | 8 |
| 13902 | apaga | 8 |
| 13903 | anuncio | 8 |
| 13904 | antón | 8 |
| 13905 | antojadiza | 8 |
| 13906 | anticuario | 8 |
| 13907 | antecedentes | 8 |
| 13908 | ant | 8 |
| 13909 | anssy | 8 |
| 13910 | animoso | 8 |
| 13911 | angustiosa | 8 |
| 13912 | anejo | 8 |
| 13913 | anécdotas | 8 |
| 13914 | andemos | 8 |
| 13915 | anarquista | 8 |
| 13916 | ampare | 8 |
| 13917 | amonestaciones | 8 |
| 13918 | aminta | 8 |
| 13919 | amiguito | 8 |
| 13920 | ameno | 8 |
| 13921 | amargamente | 8 |
| 13922 | alzado | 8 |
| 13923 | alusión | 8 |
| 13924 | alternativas | 8 |
| 13925 | alternando | 8 |
| 13926 | alférez | 8 |
| 13927 | alexandre | 8 |
| 13928 | alentar | 8 |
| 13929 | alcuza | 8 |
| 13930 | alcurnia | 8 |
| 13931 | alcobas | 8 |
| 13932 | alburquerque | 8 |
| 13933 | alborozado | 8 |
| 13934 | alborotó | 8 |
| 13935 | alborote | 8 |
| 13936 | alborotados | 8 |
| 13937 | álamo | 8 |
| 13938 | airosa | 8 |
| 13939 | aguijón | 8 |
| 13940 | aguardo | 8 |
| 13941 | aguardaban | 8 |
| 13942 | agonías | 8 |
| 13943 | agenas | 8 |
| 13944 | afrentado | 8 |
| 13945 | afortunado | 8 |
| 13946 | aflige | 8 |
| 13947 | afirmativamente | 8 |
| 13948 | advirtiese | 8 |
| 13949 | advertía | 8 |
| 13950 | adusto | 8 |
| 13951 | adquirió | 8 |
| 13952 | adornar | 8 |
| 13953 | adorada | 8 |
| 13954 | admiraban | 8 |
| 13955 | aderezo | 8 |
| 13956 | aderezar | 8 |
| 13957 | adelantar | 8 |
| 13958 | acusa | 8 |
| 13959 | acuden | 8 |
| 13960 | acordarme | 8 |
| 13961 | aconteció | 8 |
| 13962 | aconseja | 8 |
| 13963 | acompañaré | 8 |
| 13964 | acomodo | 8 |
| 13965 | acomodaba | 8 |
| 13966 | acogida | 8 |
| 13967 | aclarar | 8 |
| 13968 | aciago | 8 |
| 13969 | acerté | 8 |
| 13970 | acepto | 8 |
| 13971 | aceptado | 8 |
| 13972 | aceptaba | 8 |
| 13973 | aceñas | 8 |
| 13974 | acémila | 8 |
| 13975 | acechando | 8 |
| 13976 | acarició | 8 |
| 13977 | acacias | 8 |
| 13978 | acabará | 8 |
| 13979 | acabamiento | 8 |
| 13980 | acabados | 8 |
| 13981 | abutarda | 8 |
| 13982 | abusos | 8 |
| 13983 | abuso | 8 |
| 13984 | abusando | 8 |
| 13985 | aburrirse | 8 |
| 13986 | abrojos | 8 |
| 13987 | abrid | 8 |
| 13988 | abrazada | 8 |
| 13989 | abraso | 8 |
| 13990 | abrasaba | 8 |
| 13991 | abras | 8 |
| 13992 | aborrecen | 8 |
| 13993 | abono | 8 |
| 13994 | abolengo | 8 |
| 13995 | abogacía | 8 |
| 13996 | abejas | 8 |
| 13997 | zugarramurdi | 7 |
| 13998 | zarandajas | 7 |
| 13999 | zagalas | 7 |
| 14000 | yedra | 7 |
| 14001 | ydo | 7 |
| 14002 | xx | 7 |
| 14003 | xristianos | 7 |
| 14004 | ximio | 7 |
| 14005 | wamba | 7 |
| 14006 | vydo | 7 |
| 14007 | vulgaris | 7 |
| 14008 | vulgaridades | 7 |
| 14009 | vueltos | 7 |
| 14010 | vuelos | 7 |
| 14011 | voyme | 7 |
| 14012 | voraz | 7 |
| 14013 | volverte | 7 |
| 14014 | volverlo | 7 |
| 14015 | volverían | 7 |
| 14016 | volante | 7 |
| 14017 | vocabulario | 7 |
| 14018 | vivirá | 7 |
| 14019 | vivientes | 7 |
| 14020 | vivaracha | 7 |
| 14021 | viue | 7 |
| 14022 | vistes | 7 |
| 14023 | visitarla | 7 |
| 14024 | viruelas | 7 |
| 14025 | virginal | 7 |
| 14026 | violencias | 7 |
| 14027 | villas | 7 |
| 14028 | villancicos | 7 |
| 14029 | vigilias | 7 |
| 14030 | vieren | 7 |
| 14031 | viçio | 7 |
| 14032 | vibrante | 7 |
| 14033 | vezina | 7 |
| 14034 | vestiglo | 7 |
| 14035 | vestiduras | 7 |
| 14036 | versión | 7 |
| 14037 | verosímil | 7 |
| 14038 | verná | 7 |
| 14039 | verjas | 7 |
| 14040 | verificó | 7 |
| 14041 | verificado | 7 |
| 14042 | vergonzosos | 7 |
| 14043 | veniste | 7 |
| 14044 | venidero | 7 |
| 14045 | vendrás | 7 |
| 14046 | vendió | 7 |
| 14047 | vendas | 7 |
| 14048 | vencía | 7 |
| 14049 | vençe | 7 |
| 14050 | vejigas | 7 |
| 14051 | vejarruco | 7 |
| 14052 | veáis | 7 |
| 14053 | vasto | 7 |
| 14054 | vasta | 7 |
| 14055 | válgate | 7 |
| 14056 | valentías | 7 |
| 14057 | válate | 7 |
| 14058 | vado | 7 |
| 14059 | usura | 7 |
| 14060 | unirse | 7 |
| 14061 | unidas | 7 |
| 14062 | únicas | 7 |
| 14063 | unía | 7 |
| 14064 | ultraje | 7 |
| 14065 | ulises | 7 |
| 14066 | tyenes | 7 |
| 14067 | tyen | 7 |
| 14068 | tuyas | 7 |
| 14069 | tubos | 7 |
| 14070 | tubo | 7 |
| 14071 | tropieza | 7 |
| 14072 | trofeos | 7 |
| 14073 | trocaba | 7 |
| 14074 | treta | 7 |
| 14075 | tresillistas | 7 |
| 14076 | traydo | 7 |
| 14077 | traviesa | 7 |
| 14078 | tratarme | 7 |
| 14079 | trasladado | 7 |
| 14080 | transcurrido | 7 |
| 14081 | tranquilizarse | 7 |
| 14082 | tranquilizaba | 7 |
| 14083 | tranquilas | 7 |
| 14084 | trajeran | 7 |
| 14085 | trajera | 7 |
| 14086 | tragando | 7 |
| 14087 | traería | 7 |
| 14088 | tradiciones | 7 |
| 14089 | tradicional | 7 |
| 14090 | tracia | 7 |
| 14091 | trabajoso | 7 |
| 14092 | trabajó | 7 |
| 14093 | tosco | 7 |
| 14094 | tortuga | 7 |
| 14095 | tórtola | 7 |
| 14096 | torralba | 7 |
| 14097 | torpemente | 7 |
| 14098 | tornillo | 7 |
| 14099 | tornado | 7 |
| 14100 | tornada | 7 |
| 14101 | torció | 7 |
| 14102 | torcidos | 7 |
| 14103 | topase | 7 |
| 14104 | topaba | 7 |
| 14105 | tomasen | 7 |
| 14106 | tomará | 7 |
| 14107 | tomados | 7 |
| 14108 | tolerable | 7 |
| 14109 | toledano | 7 |
| 14110 | todito | 7 |
| 14111 | tocara | 7 |
| 14112 | tisis | 7 |
| 14113 | tirones | 7 |
| 14114 | tiologías | 7 |
| 14115 | tiniente | 7 |
| 14116 | tiesa | 7 |
| 14117 | tiende | 7 |
| 14118 | tie | 7 |
| 14119 | tibio | 7 |
| 14120 | thesoros | 7 |
| 14121 | testero | 7 |
| 14122 | terrenal | 7 |
| 14123 | terminado | 7 |
| 14124 | terminada | 7 |
| 14125 | teorías | 7 |
| 14126 | tentó | 7 |
| 14127 | tentando | 7 |
| 14128 | teniéndole | 7 |
| 14129 | tenias | 7 |
| 14130 | teneys | 7 |
| 14131 | tendieron | 7 |
| 14132 | tendía | 7 |
| 14133 | temprana | 7 |
| 14134 | temporales | 7 |
| 14135 | templada | 7 |
| 14136 | temerón | 7 |
| 14137 | temerarios | 7 |
| 14138 | telarañas | 7 |
| 14139 | teje | 7 |
| 14140 | tardé | 7 |
| 14141 | tardaría | 7 |
| 14142 | tar | 7 |
| 14143 | tapó | 7 |
| 14144 | tañer | 7 |
| 14145 | tantísima | 7 |
| 14146 | taniendo | 7 |
| 14147 | tanasio | 7 |
| 14148 | talmente | 7 |
| 14149 | talente | 7 |
| 14150 | talar | 7 |
| 14151 | tajadas | 7 |
| 14152 | suspiritos | 7 |
| 14153 | supongamos | 7 |
| 14154 | suplicando | 7 |
| 14155 | supina | 7 |
| 14156 | supimos | 7 |
| 14157 | supersticiones | 7 |
| 14158 | sujeción | 7 |
| 14159 | sucesivo | 7 |
| 14160 | subterráneos | 7 |
| 14161 | sostenerse | 7 |
| 14162 | sospirando | 7 |
| 14163 | sosegar | 7 |
| 14164 | sosegados | 7 |
| 14165 | sosegadamente | 7 |
| 14166 | sosa | 7 |
| 14167 | sorprendida | 7 |
| 14168 | soñadas | 7 |
| 14169 | sonrosado | 7 |
| 14170 | sonrisilla | 7 |
| 14171 | sonbra | 7 |
| 14172 | solteronas | 7 |
| 14173 | soltado | 7 |
| 14174 | solitarias | 7 |
| 14175 | solás | 7 |
| 14176 | sogas | 7 |
| 14177 | soeces | 7 |
| 14178 | sodes | 7 |
| 14179 | socorriese | 7 |
| 14180 | socorrido | 7 |
| 14181 | socorre | 7 |
| 14182 | sobrinita | 7 |
| 14183 | sobriedad | 7 |
| 14184 | sobreponerse | 7 |
| 14185 | sobredicho | 7 |
| 14186 | sobraba | 7 |
| 14187 | sinrazón | 7 |
| 14188 | simpatías | 7 |
| 14189 | silvestres | 7 |
| 14190 | silbando | 7 |
| 14191 | signum | 7 |
| 14192 | significan | 7 |
| 14193 | sigamos | 7 |
| 14194 | sicilia | 7 |
| 14195 | serví | 7 |
| 14196 | seruidores | 7 |
| 14197 | serpientes | 7 |
| 14198 | seríe | 7 |
| 14199 | seríamos | 7 |
| 14200 | sepultados | 7 |
| 14201 | separadas | 7 |
| 14202 | señoril | 7 |
| 14203 | sentia | 7 |
| 14204 | sentéme | 7 |
| 14205 | sentaos | 7 |
| 14206 | sencillos | 7 |
| 14207 | semillas | 7 |
| 14208 | semi | 7 |
| 14209 | sembrar | 7 |
| 14210 | sembrados | 7 |
| 14211 | sembrado | 7 |
| 14212 | sedación | 7 |
| 14213 | seculares | 7 |
| 14214 | scribe | 7 |
| 14215 | satisfechas | 7 |
| 14216 | satisfaré | 7 |
| 14217 | sartén | 7 |
| 14218 | santiguada | 7 |
| 14219 | santidades | 7 |
| 14220 | sangriento | 7 |
| 14221 | sandoval | 7 |
| 14222 | samaritana | 7 |
| 14223 | salvarnos | 7 |
| 14224 | saludables | 7 |
| 14225 | salte | 7 |
| 14226 | saltado | 7 |
| 14227 | salíme | 7 |
| 14228 | salero | 7 |
| 14229 | salada | 7 |
| 14230 | sahumerio | 7 |
| 14231 | sacarnos | 7 |
| 14232 | sacarán | 7 |
| 14233 | sacadas | 7 |
| 14234 | sacada | 7 |
| 14235 | sábete | 7 |
| 14236 | ruyn | 7 |
| 14237 | rústicas | 7 |
| 14238 | ruso | 7 |
| 14239 | rüido | 7 |
| 14240 | rudos | 7 |
| 14241 | rubinius | 7 |
| 14242 | rubias | 7 |
| 14243 | rruego | 7 |
| 14244 | rranas | 7 |
| 14245 | rosarios | 7 |
| 14246 | rosal | 7 |
| 14247 | romperse | 7 |
| 14248 | robó | 7 |
| 14249 | ritmo | 7 |
| 14250 | riñón | 7 |
| 14251 | riña | 7 |
| 14252 | rinde | 7 |
| 14253 | rígido | 7 |
| 14254 | riego | 7 |
| 14255 | ricardo | 7 |
| 14256 | revolviéndose | 7 |
| 14257 | reveses | 7 |
| 14258 | revelado | 7 |
| 14259 | revela | 7 |
| 14260 | reunía | 7 |
| 14261 | retroceso | 7 |
| 14262 | reto | 7 |
| 14263 | retirose | 7 |
| 14264 | resurrección | 7 |
| 14265 | resultas | 7 |
| 14266 | resuelve | 7 |
| 14267 | resuello | 7 |
| 14268 | resucitado | 7 |
| 14269 | resquicio | 7 |
| 14270 | responderle | 7 |
| 14271 | respóndeme | 7 |
| 14272 | resortes | 7 |
| 14273 | resistió | 7 |
| 14274 | resistido | 7 |
| 14275 | resignado | 7 |
| 14276 | reservado | 7 |
| 14277 | rescatado | 7 |
| 14278 | reproducción | 7 |
| 14279 | representado | 7 |
| 14280 | reprensión | 7 |
| 14281 | reposa | 7 |
| 14282 | réplica | 7 |
| 14283 | repleto | 7 |
| 14284 | repitieron | 7 |
| 14285 | repetido | 7 |
| 14286 | repertorio | 7 |
| 14287 | renovaron | 7 |
| 14288 | renegando | 7 |
| 14289 | renacimiento | 7 |
| 14290 | rematado | 7 |
| 14291 | reliquia | 7 |
| 14292 | relinchos | 7 |
| 14293 | relieves | 7 |
| 14294 | regularidad | 7 |
| 14295 | registra | 7 |
| 14296 | regimiento | 7 |
| 14297 | regencia | 7 |
| 14298 | refresco | 7 |
| 14299 | reformas | 7 |
| 14300 | refiriendo | 7 |
| 14301 | referían | 7 |
| 14302 | redundar | 7 |
| 14303 | redondez | 7 |
| 14304 | redoma | 7 |
| 14305 | redobló | 7 |
| 14306 | recreándose | 7 |
| 14307 | recomienda | 7 |
| 14308 | recoletas | 7 |
| 14309 | recogían | 7 |
| 14310 | recobrando | 7 |
| 14311 | reclama | 7 |
| 14312 | recitar | 7 |
| 14313 | recibiría | 7 |
| 14314 | rechazaba | 7 |
| 14315 | recatada | 7 |
| 14316 | rebosando | 7 |
| 14317 | rebeldes | 7 |
| 14318 | realizado | 7 |
| 14319 | razonables | 7 |
| 14320 | rasón | 7 |
| 14321 | rasguño | 7 |
| 14322 | ramona | 7 |
| 14323 | ramiro | 7 |
| 14324 | radiante | 7 |
| 14325 | raciocinio | 7 |
| 14326 | rabiaba | 7 |
| 14327 | quiten | 7 |
| 14328 | quité | 7 |
| 14329 | quitasen | 7 |
| 14330 | quitas | 7 |
| 14331 | quitármela | 7 |
| 14332 | quitarán | 7 |
| 14333 | quiriendo | 7 |
| 14334 | quintas | 7 |
| 14335 | quiebre | 7 |
| 14336 | quicios | 7 |
| 14337 | quiá | 7 |
| 14338 | quexoso | 7 |
| 14339 | quemó | 7 |
| 14340 | quejumbrosa | 7 |
| 14341 | quedito | 7 |
| 14342 | quedáronse | 7 |
| 14343 | quebraba | 7 |
| 14344 | púsole | 7 |
| 14345 | pusiéronse | 7 |
| 14346 | pupilos | 7 |
| 14347 | pupilaje | 7 |
| 14348 | puñada | 7 |
| 14349 | punzantes | 7 |
| 14350 | puntapiés | 7 |
| 14351 | puntadas | 7 |
| 14352 | pulcra | 7 |
| 14353 | pugnaba | 7 |
| 14354 | pudimos | 7 |
| 14355 | publicidad | 7 |
| 14356 | proyectiles | 7 |
| 14357 | provocativa | 7 |
| 14358 | provisión | 7 |
| 14359 | provincial | 7 |
| 14360 | proveer | 7 |
| 14361 | protestó | 7 |
| 14362 | protagonista | 7 |
| 14363 | prostitución | 7 |
| 14364 | próspera | 7 |
| 14365 | prosaico | 7 |
| 14366 | propuse | 7 |
| 14367 | propria | 7 |
| 14368 | profesar | 7 |
| 14369 | profano | 7 |
| 14370 | prodigioso | 7 |
| 14371 | procedimiento | 7 |
| 14372 | proceden | 7 |
| 14373 | probaré | 7 |
| 14374 | probando | 7 |
| 14375 | probaban | 7 |
| 14376 | privados | 7 |
| 14377 | princesas | 7 |
| 14378 | primita | 7 |
| 14379 | primaveras | 7 |
| 14380 | pretendiendo | 7 |
| 14381 | pretendían | 7 |
| 14382 | prestamista | 7 |
| 14383 | presentose | 7 |
| 14384 | preparación | 7 |
| 14385 | preparaban | 7 |
| 14386 | prendió | 7 |
| 14387 | preguntarme | 7 |
| 14388 | pregúntale | 7 |
| 14389 | pregonero | 7 |
| 14390 | prefiere | 7 |
| 14391 | preferir | 7 |
| 14392 | preeminencias | 7 |
| 14393 | precisión | 7 |
| 14394 | preciosísima | 7 |
| 14395 | preciosidad | 7 |
| 14396 | preceptos | 7 |
| 14397 | precedieron | 7 |
| 14398 | postiza | 7 |
| 14399 | poste | 7 |
| 14400 | posta | 7 |
| 14401 | poseedor | 7 |
| 14402 | posadero | 7 |
| 14403 | pórtico | 7 |
| 14404 | porteros | 7 |
| 14405 | porquería | 7 |
| 14406 | ponerles | 7 |
| 14407 | polilla | 7 |
| 14408 | policarpo | 7 |
| 14409 | polainas | 7 |
| 14410 | podridas | 7 |
| 14411 | podras | 7 |
| 14412 | podia | 7 |
| 14413 | poderes | 7 |
| 14414 | plazos | 7 |
| 14415 | plazoleta | 7 |
| 14416 | planto | 7 |
| 14417 | pitas | 7 |
| 14418 | pisó | 7 |
| 14419 | piojín | 7 |
| 14420 | pintoresca | 7 |
| 14421 | pingajos | 7 |
| 14422 | pincel | 7 |
| 14423 | pim | 7 |
| 14424 | piloto | 7 |
| 14425 | pilletes | 7 |
| 14426 | pillería | 7 |
| 14427 | pieça | 7 |
| 14428 | pidas | 7 |
| 14429 | pidal | 7 |
| 14430 | picador | 7 |
| 14431 | piadat | 7 |
| 14432 | peticion | 7 |
| 14433 | petaca | 7 |
| 14434 | pessar | 7 |
| 14435 | pesquisidor | 7 |
| 14436 | pesquis | 7 |
| 14437 | pesas | 7 |
| 14438 | pesaroso | 7 |
| 14439 | pesadillas | 7 |
| 14440 | perteneciente | 7 |
| 14441 | perspectiva | 7 |
| 14442 | perseverancia | 7 |
| 14443 | perorata | 7 |
| 14444 | periodos | 7 |
| 14445 | perfumada | 7 |
| 14446 | perezosas | 7 |
| 14447 | perderme | 7 |
| 14448 | perderle | 7 |
| 14449 | peralta | 7 |
| 14450 | pequeñeces | 7 |
| 14451 | pensemos | 7 |
| 14452 | pensada | 7 |
| 14453 | pensabas | 7 |
| 14454 | penetra | 7 |
| 14455 | penando | 7 |
| 14456 | peldaño | 7 |
| 14457 | pelagatos | 7 |
| 14458 | pelado | 7 |
| 14459 | peinetas | 7 |
| 14460 | pedra | 7 |
| 14461 | paulinas | 7 |
| 14462 | patillas | 7 |
| 14463 | patenas | 7 |
| 14464 | patata | 7 |
| 14465 | pastoras | 7 |
| 14466 | pasmaba | 7 |
| 14467 | paseado | 7 |
| 14468 | pasasen | 7 |
| 14469 | pasaré | 7 |
| 14470 | pasaran | 7 |
| 14471 | pasajes | 7 |
| 14472 | pasábamos | 7 |
| 14473 | partos | 7 |
| 14474 | parroquias | 7 |
| 14475 | paresçe | 7 |
| 14476 | parentescos | 7 |
| 14477 | parecerles | 7 |
| 14478 | pareceres | 7 |
| 14479 | parche | 7 |
| 14480 | paraguay | 7 |
| 14481 | parados | 7 |
| 14482 | parabién | 7 |
| 14483 | pañizuelo | 7 |
| 14484 | pámpanos | 7 |
| 14485 | palotada | 7 |
| 14486 | palomar | 7 |
| 14487 | palmito | 7 |
| 14488 | palio | 7 |
| 14489 | palideció | 7 |
| 14490 | palideciendo | 7 |
| 14491 | palanca | 7 |
| 14492 | pajar | 7 |
| 14493 | paice | 7 |
| 14494 | pae | 7 |
| 14495 | padecimientos | 7 |
| 14496 | pacíficamente | 7 |
| 14497 | oyólo | 7 |
| 14498 | oyeres | 7 |
| 14499 | osó | 7 |
| 14500 | osada | 7 |
| 14501 | orlando | 7 |
| 14502 | oriental | 7 |
| 14503 | organista | 7 |
| 14504 | ordenanza | 7 |
| 14505 | ordenados | 7 |
| 14506 | orbajosenses | 7 |
| 14507 | oratoria | 7 |
| 14508 | oráculo | 7 |
| 14509 | opuesta | 7 |
| 14510 | oprimiendo | 7 |
| 14511 | opresión | 7 |
| 14512 | óperas | 7 |
| 14513 | oñate | 7 |
| 14514 | olvidos | 7 |
| 14515 | olvidarse | 7 |
| 14516 | olvidando | 7 |
| 14517 | oirse | 7 |
| 14518 | oirán | 7 |
| 14519 | ofreciese | 7 |
| 14520 | ofenda | 7 |
| 14521 | oeste | 7 |
| 14522 | odios | 7 |
| 14523 | ocultó | 7 |
| 14524 | ocultándose | 7 |
| 14525 | octava | 7 |
| 14526 | ochocientos | 7 |
| 14527 | observé | 7 |
| 14528 | obligue | 7 |
| 14529 | obligo | 7 |
| 14530 | ob | 7 |
| 14531 | numerosa | 7 |
| 14532 | notase | 7 |
| 14533 | notaron | 7 |
| 14534 | notaban | 7 |
| 14535 | nombra | 7 |
| 14536 | nesçio | 7 |
| 14537 | negligente | 7 |
| 14538 | necias | 7 |
| 14539 | necesitamos | 7 |
| 14540 | necesitado | 7 |
| 14541 | naturalistas | 7 |
| 14542 | naturalista | 7 |
| 14543 | naturalezas | 7 |
| 14544 | naipe | 7 |
| 14545 | naciste | 7 |
| 14546 | mustio | 7 |
| 14547 | muslos | 7 |
| 14548 | muscular | 7 |
| 14549 | murmuran | 7 |
| 14550 | murmuradores | 7 |
| 14551 | murmuraban | 7 |
| 14552 | murmura | 7 |
| 14553 | murillo | 7 |
| 14554 | mundogrande | 7 |
| 14555 | multiplicaba | 7 |
| 14556 | muladar | 7 |
| 14557 | mujercita | 7 |
| 14558 | mueca | 7 |
| 14559 | mudable | 7 |
| 14560 | movibles | 7 |
| 14561 | movible | 7 |
| 14562 | mostraré | 7 |
| 14563 | mostrándole | 7 |
| 14564 | morirás | 7 |
| 14565 | morato | 7 |
| 14566 | moratín | 7 |
| 14567 | moralmente | 7 |
| 14568 | moradores | 7 |
| 14569 | montaraz | 7 |
| 14570 | monsieur | 7 |
| 14571 | monotonía | 7 |
| 14572 | monólogo | 7 |
| 14573 | momia | 7 |
| 14574 | molimiento | 7 |
| 14575 | molestias | 7 |
| 14576 | mohín | 7 |
| 14577 | modistas | 7 |
| 14578 | moderación | 7 |
| 14579 | misteriosos | 7 |
| 14580 | mismito | 7 |
| 14581 | misericordioso | 7 |
| 14582 | miserablemente | 7 |
| 14583 | mirarme | 7 |
| 14584 | mirarlo | 7 |
| 14585 | miramientos | 7 |
| 14586 | mirábale | 7 |
| 14587 | mintroso | 7 |
| 14588 | mieses | 7 |
| 14589 | mienta | 7 |
| 14590 | midas | 7 |
| 14591 | mezclar | 7 |
| 14592 | mercurio | 7 |
| 14593 | mentirosa | 7 |
| 14594 | mentalmente | 7 |
| 14595 | menesterosa | 7 |
| 14596 | meneo | 7 |
| 14597 | meneando | 7 |
| 14598 | mendoza | 7 |
| 14599 | memorial | 7 |
| 14600 | melenas | 7 |
| 14601 | melancolías | 7 |
| 14602 | mejora | 7 |
| 14603 | medrar | 7 |
| 14604 | meditó | 7 |
| 14605 | médicis | 7 |
| 14606 | medicamentos | 7 |
| 14607 | medicamento | 7 |
| 14608 | mecedora | 7 |
| 14609 | mecanismo | 7 |
| 14610 | mds | 7 |
| 14611 | mazapán | 7 |
| 14612 | matorral | 7 |
| 14613 | materno | 7 |
| 14614 | mataría | 7 |
| 14615 | mártires | 7 |
| 14616 | marsilio | 7 |
| 14617 | marfusa | 7 |
| 14618 | marcharon | 7 |
| 14619 | marcada | 7 |
| 14620 | maravillo | 7 |
| 14621 | maravedí | 7 |
| 14622 | marauilla | 7 |
| 14623 | manzanares | 7 |
| 14624 | mansión | 7 |
| 14625 | manifestado | 7 |
| 14626 | mango | 7 |
| 14627 | maneja | 7 |
| 14628 | mandato | 7 |
| 14629 | mandarme | 7 |
| 14630 | mandaré | 7 |
| 14631 | mancilla | 7 |
| 14632 | manchado | 7 |
| 14633 | maná | 7 |
| 14634 | mamonas | 7 |
| 14635 | mama | 7 |
| 14636 | malvina | 7 |
| 14637 | malparado | 7 |
| 14638 | malferido | 7 |
| 14639 | maleficio | 7 |
| 14640 | malandrín | 7 |
| 14641 | maja | 7 |
| 14642 | magnitud | 7 |
| 14643 | magnánimo | 7 |
| 14644 | maduras | 7 |
| 14645 | madrugador | 7 |
| 14646 | madruga | 7 |
| 14647 | madrina | 7 |
| 14648 | madrileño | 7 |
| 14649 | machacar | 7 |
| 14650 | lygero | 7 |
| 14651 | lyd | 7 |
| 14652 | lunares | 7 |
| 14653 | lugareña | 7 |
| 14654 | luciendo | 7 |
| 14655 | lucida | 7 |
| 14656 | luchaban | 7 |
| 14657 | losas | 7 |
| 14658 | loor | 7 |
| 14659 | lonjas | 7 |
| 14660 | loçano | 7 |
| 14661 | llevarte | 7 |
| 14662 | lleváis | 7 |
| 14663 | lleguen | 7 |
| 14664 | llegaran | 7 |
| 14665 | llamará | 7 |
| 14666 | lívido | 7 |
| 14667 | litera | 7 |
| 14668 | lisa | 7 |
| 14669 | lírico | 7 |
| 14670 | limón | 7 |
| 14671 | librase | 7 |
| 14672 | librado | 7 |
| 14673 | liado | 7 |
| 14674 | leyere | 7 |
| 14675 | levantáronse | 7 |
| 14676 | levantara | 7 |
| 14677 | letura | 7 |
| 14678 | leona | 7 |
| 14679 | leñador | 7 |
| 14680 | lejanas | 7 |
| 14681 | leída | 7 |
| 14682 | lazeria | 7 |
| 14683 | lavatorio | 7 |
| 14684 | lavando | 7 |
| 14685 | languidez | 7 |
| 14686 | landre | 7 |
| 14687 | landó | 7 |
| 14688 | lamentables | 7 |
| 14689 | lagunas | 7 |
| 14690 | lag | 7 |
| 14691 | labradas | 7 |
| 14692 | laboratorio | 7 |
| 14693 | labia | 7 |
| 14694 | juridición | 7 |
| 14695 | jure | 7 |
| 14696 | juntaron | 7 |
| 14697 | juntaban | 7 |
| 14698 | jeta | 7 |
| 14699 | jerarquía | 7 |
| 14700 | jazmines | 7 |
| 14701 | jarras | 7 |
| 14702 | jai | 7 |
| 14703 | jadraque | 7 |
| 14704 | jadeante | 7 |
| 14705 | irritatio | 7 |
| 14706 | irritación | 7 |
| 14707 | irreverencia | 7 |
| 14708 | irónicamente | 7 |
| 14709 | iriarte | 7 |
| 14710 | iras | 7 |
| 14711 | invocando | 7 |
| 14712 | invitó | 7 |
| 14713 | invitado | 7 |
| 14714 | inveterada | 7 |
| 14715 | invento | 7 |
| 14716 | inventando | 7 |
| 14717 | inventa | 7 |
| 14718 | invasión | 7 |
| 14719 | inundada | 7 |
| 14720 | intranquilo | 7 |
| 14721 | intolerable | 7 |
| 14722 | intervención | 7 |
| 14723 | interno | 7 |
| 14724 | interna | 7 |
| 14725 | interminable | 7 |
| 14726 | interesado | 7 |
| 14727 | intachable | 7 |
| 14728 | insulanos | 7 |
| 14729 | instintivamente | 7 |
| 14730 | insomnio | 7 |
| 14731 | insistir | 7 |
| 14732 | insinuaciones | 7 |
| 14733 | insensiblemente | 7 |
| 14734 | inseguro | 7 |
| 14735 | inscripciones | 7 |
| 14736 | inmundo | 7 |
| 14737 | injustos | 7 |
| 14738 | ingenua | 7 |
| 14739 | ingeniosa | 7 |
| 14740 | infundir | 7 |
| 14741 | ínfulas | 7 |
| 14742 | infiere | 7 |
| 14743 | inferioridad | 7 |
| 14744 | industriales | 7 |
| 14745 | indiscreción | 7 |
| 14746 | indios | 7 |
| 14747 | indignos | 7 |
| 14748 | indicación | 7 |
| 14749 | indiano | 7 |
| 14750 | incorporarse | 7 |
| 14751 | incorporándose | 7 |
| 14752 | incomodidades | 7 |
| 14753 | inclinarse | 7 |
| 14754 | inciertos | 7 |
| 14755 | incertidumbre | 7 |
| 14756 | impuesto | 7 |
| 14757 | imprimiere | 7 |
| 14758 | impresos | 7 |
| 14759 | importunidades | 7 |
| 14760 | impiden | 7 |
| 14761 | imperceptible | 7 |
| 14762 | impedían | 7 |
| 14763 | imitaban | 7 |
| 14764 | imaginé | 7 |
| 14765 | iluminados | 7 |
| 14766 | iguale | 7 |
| 14767 | hurón | 7 |
| 14768 | huracán | 7 |
| 14769 | hunde | 7 |
| 14770 | humillarse | 7 |
| 14771 | humillaba | 7 |
| 14772 | humareda | 7 |
| 14773 | huida | 7 |
| 14774 | huelen | 7 |
| 14775 | hoz | 7 |
| 14776 | horno | 7 |
| 14777 | horn | 7 |
| 14778 | hormiga | 7 |
| 14779 | hondamente | 7 |
| 14780 | hízome | 7 |
| 14781 | hizieron | 7 |
| 14782 | hircania | 7 |
| 14783 | hilas | 7 |
| 14784 | hiere | 7 |
| 14785 | hiciéronlo | 7 |
| 14786 | hervía | 7 |
| 14787 | heroína | 7 |
| 14788 | hernani | 7 |
| 14789 | hermosísimas | 7 |
| 14790 | heredó | 7 |
| 14791 | heredada | 7 |
| 14792 | heredad | 7 |
| 14793 | hereda | 7 |
| 14794 | helados | 7 |
| 14795 | hechizera | 7 |
| 14796 | hebras | 7 |
| 14797 | hauias | 7 |
| 14798 | hasme | 7 |
| 14799 | hartas | 7 |
| 14800 | harina | 7 |
| 14801 | hambres | 7 |
| 14802 | hallaréis | 7 |
| 14803 | halagado | 7 |
| 14804 | hacello | 7 |
| 14805 | habríamos | 7 |
| 14806 | hablen | 7 |
| 14807 | hablaran | 7 |
| 14808 | habladora | 7 |
| 14809 | habérsela | 7 |
| 14810 | habernos | 7 |
| 14811 | habas | 7 |
| 14812 | gutural | 7 |
| 14813 | gutiérrez | 7 |
| 14814 | guste | 7 |
| 14815 | gustas | 7 |
| 14816 | guiomar | 7 |
| 14817 | guillermo | 7 |
| 14818 | guijas | 7 |
| 14819 | guijarro | 7 |
| 14820 | guerreros | 7 |
| 14821 | guardarse | 7 |
| 14822 | guardará | 7 |
| 14823 | guardadas | 7 |
| 14824 | guano | 7 |
| 14825 | guadiana | 7 |
| 14826 | grotesca | 7 |
| 14827 | gresca | 7 |
| 14828 | gratis | 7 |
| 14829 | grandísimos | 7 |
| 14830 | grajos | 7 |
| 14831 | gozó | 7 |
| 14832 | gozamos | 7 |
| 14833 | gonzalo | 7 |
| 14834 | golfines | 7 |
| 14835 | ginete | 7 |
| 14836 | gimnasia | 7 |
| 14837 | gime | 7 |
| 14838 | gentío | 7 |
| 14839 | gastados | 7 |
| 14840 | gaspar | 7 |
| 14841 | gases | 7 |
| 14842 | garza | 7 |
| 14843 | garbo | 7 |
| 14844 | gansos | 7 |
| 14845 | gangosa | 7 |
| 14846 | ganaron | 7 |
| 14847 | ganaban | 7 |
| 14848 | galgos | 7 |
| 14849 | galante | 7 |
| 14850 | furiosos | 7 |
| 14851 | furibundos | 7 |
| 14852 | fulgor | 7 |
| 14853 | fuéronse | 7 |
| 14854 | fuentecilla | 7 |
| 14855 | fritos | 7 |
| 14856 | frio | 7 |
| 14857 | frecuentemente | 7 |
| 14858 | frascos | 7 |
| 14859 | francos | 7 |
| 14860 | fotografías | 7 |
| 14861 | fósforos | 7 |
| 14862 | forzosa | 7 |
| 14863 | forzar | 7 |
| 14864 | formaron | 7 |
| 14865 | formalmente | 7 |
| 14866 | formales | 7 |
| 14867 | forasteros | 7 |
| 14868 | follón | 7 |
| 14869 | fogón | 7 |
| 14870 | flotando | 7 |
| 14871 | florecillas | 7 |
| 14872 | floreciente | 7 |
| 14873 | flamencos | 7 |
| 14874 | flamantes | 7 |
| 14875 | firmas | 7 |
| 14876 | firmadas | 7 |
| 14877 | finisterre | 7 |
| 14878 | fingirse | 7 |
| 14879 | fingen | 7 |
| 14880 | filosofías | 7 |
| 14881 | filis | 7 |
| 14882 | filípica | 7 |
| 14883 | fijamente | 7 |
| 14884 | fiarse | 7 |
| 14885 | feroces | 7 |
| 14886 | fermosos | 7 |
| 14887 | femenino | 7 |
| 14888 | felixmarte | 7 |
| 14889 | favorecido | 7 |
| 14890 | fatuo | 7 |
| 14891 | fatigues | 7 |
| 14892 | fatigados | 7 |
| 14893 | fatigaban | 7 |
| 14894 | fárrago | 7 |
| 14895 | fardos | 7 |
| 14896 | faltaran | 7 |
| 14897 | falló | 7 |
| 14898 | fagas | 7 |
| 14899 | facer | 7 |
| 14900 | fabricado | 7 |
| 14901 | fablando | 7 |
| 14902 | extremadura | 7 |
| 14903 | extraviado | 7 |
| 14904 | extrañaba | 7 |
| 14905 | extracto | 7 |
| 14906 | extenso | 7 |
| 14907 | extendido | 7 |
| 14908 | expuesto | 7 |
| 14909 | expresivo | 7 |
| 14910 | exponerse | 7 |
| 14911 | explotación | 7 |
| 14912 | experimentaba | 7 |
| 14913 | expectación | 7 |
| 14914 | existiera | 7 |
| 14915 | exhaló | 7 |
| 14916 | exequias | 7 |
| 14917 | excepcional | 7 |
| 14918 | evitarlo | 7 |
| 14919 | evangélica | 7 |
| 14920 | estuvieras | 7 |
| 14921 | estúpidos | 7 |
| 14922 | estupefacción | 7 |
| 14923 | estudo | 7 |
| 14924 | estrellado | 7 |
| 14925 | estocada | 7 |
| 14926 | estimada | 7 |
| 14927 | estavan | 7 |
| 14928 | estante | 7 |
| 14929 | estalló | 7 |
| 14930 | establecimientos | 7 |
| 14931 | espontaneidad | 7 |
| 14932 | espontáneamente | 7 |
| 14933 | espléndido | 7 |
| 14934 | espionaje | 7 |
| 14935 | espía | 7 |
| 14936 | espesura | 7 |
| 14937 | espesos | 7 |
| 14938 | esperaría | 7 |
| 14939 | especulación | 7 |
| 14940 | españas | 7 |
| 14941 | espantan | 7 |
| 14942 | espantajo | 7 |
| 14943 | espantaba | 7 |
| 14944 | esfuerza | 7 |
| 14945 | esforzados | 7 |
| 14946 | escusa | 7 |
| 14947 | escurría | 7 |
| 14948 | escuchan | 7 |
| 14949 | escuadrones | 7 |
| 14950 | escrutinio | 7 |
| 14951 | escriptura | 7 |
| 14952 | escripto | 7 |
| 14953 | escribanos | 7 |
| 14954 | escondrijos | 7 |
| 14955 | escondrijo | 7 |
| 14956 | escobas | 7 |
| 14957 | escarola | 7 |
| 14958 | escarnida | 7 |
| 14959 | escarmiento | 7 |
| 14960 | escaparates | 7 |
| 14961 | escalas | 7 |
| 14962 | equivocó | 7 |
| 14963 | equivocarse | 7 |
| 14964 | equivalía | 7 |
| 14965 | envidiable | 7 |
| 14966 | enviaré | 7 |
| 14967 | entresuelo | 7 |
| 14968 | entraremos | 7 |
| 14969 | entrañablemente | 7 |
| 14970 | enternecido | 7 |
| 14971 | entendimientos | 7 |
| 14972 | enseñe | 7 |
| 14973 | enseñaron | 7 |
| 14974 | enseñará | 7 |
| 14975 | enracimaban | 7 |
| 14976 | enoje | 7 |
| 14977 | enoja | 7 |
| 14978 | engullir | 7 |
| 14979 | engordar | 7 |
| 14980 | engañarse | 7 |
| 14981 | engañaban | 7 |
| 14982 | enganos | 7 |
| 14983 | enfadado | 7 |
| 14984 | end | 7 |
| 14985 | encrucijadas | 7 |
| 14986 | encontrará | 7 |
| 14987 | encomendó | 7 |
| 14988 | encogidos | 7 |
| 14989 | encaminase | 7 |
| 14990 | encaminaban | 7 |
| 14991 | enamoran | 7 |
| 14992 | émulo | 7 |
| 14993 | emulación | 7 |
| 14994 | empuñando | 7 |
| 14995 | empujón | 7 |
| 14996 | empujó | 7 |
| 14997 | emprendieron | 7 |
| 14998 | emprendía | 7 |
| 14999 | emplean | 7 |
| 15000 | empiezo | 7 |
| 15001 | emilio | 7 |
| 15002 | embarcación | 7 |
| 15003 | embalde | 7 |
| 15004 | embajador | 7 |
| 15005 | emanaciones | 7 |
| 15006 | elevando | 7 |
| 15007 | elevadas | 7 |
| 15008 | elevaba | 7 |
| 15009 | elefante | 7 |
| 15010 | elada | 7 |
| 15011 | ejercitar | 7 |
| 15012 | ejecutar | 7 |
| 15013 | egipcios | 7 |
| 15014 | efectiva | 7 |
| 15015 | edificante | 7 |
| 15016 | edecán | 7 |
| 15017 | echas | 7 |
| 15018 | echaría | 7 |
| 15019 | echaremos | 7 |
| 15020 | echaré | 7 |
| 15021 | durase | 7 |
| 15022 | duraría | 7 |
| 15023 | durara | 7 |
| 15024 | duradera | 7 |
| 15025 | dulzuras | 7 |
| 15026 | duérmete | 7 |
| 15027 | droguería | 7 |
| 15028 | donoso | 7 |
| 15029 | donosa | 7 |
| 15030 | dolían | 7 |
| 15031 | docto | 7 |
| 15032 | docta | 7 |
| 15033 | dobles | 7 |
| 15034 | divorcio | 7 |
| 15035 | divisa | 7 |
| 15036 | dividía | 7 |
| 15037 | distinguió | 7 |
| 15038 | distinguida | 7 |
| 15039 | dispénseme | 7 |
| 15040 | disparatadas | 7 |
| 15041 | disimules | 7 |
| 15042 | disimula | 7 |
| 15043 | disfrutar | 7 |
| 15044 | disfraz | 7 |
| 15045 | discrecion | 7 |
| 15046 | dirigirse | 7 |
| 15047 | directa | 7 |
| 15048 | diputados | 7 |
| 15049 | dineral | 7 |
| 15050 | dilatar | 7 |
| 15051 | dijésemos | 7 |
| 15052 | dijeren | 7 |
| 15053 | dignísimo | 7 |
| 15054 | diciplina | 7 |
| 15055 | dichosas | 7 |
| 15056 | diarios | 7 |
| 15057 | diablura | 7 |
| 15058 | deziendo | 7 |
| 15059 | dexó | 7 |
| 15060 | dexe | 7 |
| 15061 | dexado | 7 |
| 15062 | devuelve | 7 |
| 15063 | deuemos | 7 |
| 15064 | determinarse | 7 |
| 15065 | determinada | 7 |
| 15066 | deteneos | 7 |
| 15067 | desviados | 7 |
| 15068 | desventurada | 7 |
| 15069 | desvelos | 7 |
| 15070 | desvelada | 7 |
| 15071 | desvanecimiento | 7 |
| 15072 | desvanecerse | 7 |
| 15073 | desván | 7 |
| 15074 | destruyen | 7 |
| 15075 | destinos | 7 |
| 15076 | destinadas | 7 |
| 15077 | destacaba | 7 |
| 15078 | desprendimiento | 7 |
| 15079 | desposada | 7 |
| 15080 | despojo | 7 |
| 15081 | despojado | 7 |
| 15082 | desplegó | 7 |
| 15083 | despidiéronse | 7 |
| 15084 | despertase | 7 |
| 15085 | despertara | 7 |
| 15086 | despejada | 7 |
| 15087 | despego | 7 |
| 15088 | despacito | 7 |
| 15089 | despachado | 7 |
| 15090 | despabilado | 7 |
| 15091 | desocupado | 7 |
| 15092 | desmentir | 7 |
| 15093 | desmayos | 7 |
| 15094 | desmayados | 7 |
| 15095 | deslumbrar | 7 |
| 15096 | designios | 7 |
| 15097 | deshacía | 7 |
| 15098 | desenvuelta | 7 |
| 15099 | desenvolverse | 7 |
| 15100 | desencantada | 7 |
| 15101 | desempeñaba | 7 |
| 15102 | desembarazado | 7 |
| 15103 | desdeñoso | 7 |
| 15104 | desdeñar | 7 |
| 15105 | desdeña | 7 |
| 15106 | desculpa | 7 |
| 15107 | descuidados | 7 |
| 15108 | descrito | 7 |
| 15109 | descolorido | 7 |
| 15110 | descargo | 7 |
| 15111 | descalzo | 7 |
| 15112 | desató | 7 |
| 15113 | desatinado | 7 |
| 15114 | desatado | 7 |
| 15115 | desastrado | 7 |
| 15116 | desasirse | 7 |
| 15117 | desarmado | 7 |
| 15118 | desamparada | 7 |
| 15119 | desalmados | 7 |
| 15120 | desagradecido | 7 |
| 15121 | desafiando | 7 |
| 15122 | desafía | 7 |
| 15123 | derribo | 7 |
| 15124 | depositario | 7 |
| 15125 | denantes | 7 |
| 15126 | demuestra | 7 |
| 15127 | demandas | 7 |
| 15128 | deliberar | 7 |
| 15129 | deleytes | 7 |
| 15130 | dejos | 7 |
| 15131 | dejéis | 7 |
| 15132 | dejalle | 7 |
| 15133 | dejáis | 7 |
| 15134 | degradación | 7 |
| 15135 | defiendo | 7 |
| 15136 | defienden | 7 |
| 15137 | dedicado | 7 |
| 15138 | dedes | 7 |
| 15139 | declarase | 7 |
| 15140 | décimas | 7 |
| 15141 | decidir | 7 |
| 15142 | débilmente | 7 |
| 15143 | debíamos | 7 |
| 15144 | debdo | 7 |
| 15145 | dársele | 7 |
| 15146 | dardo | 7 |
| 15147 | dándote | 7 |
| 15148 | danar | 7 |
| 15149 | dábase | 7 |
| 15150 | curita | 7 |
| 15151 | cumplo | 7 |
| 15152 | cumplida | 7 |
| 15153 | cucurucho | 7 |
| 15154 | cucharón | 7 |
| 15155 | cucharada | 7 |
| 15156 | cruzar | 7 |
| 15157 | cruzan | 7 |
| 15158 | cruzado | 7 |
| 15159 | crueldades | 7 |
| 15160 | crudos | 7 |
| 15161 | críticos | 7 |
| 15162 | críticas | 7 |
| 15163 | cristianismo | 7 |
| 15164 | crío | 7 |
| 15165 | crio | 7 |
| 15166 | crines | 7 |
| 15167 | crié | 7 |
| 15168 | crías | 7 |
| 15169 | crescencia | 7 |
| 15170 | crecen | 7 |
| 15171 | coydando | 7 |
| 15172 | covarrubias | 7 |
| 15173 | couardia | 7 |
| 15174 | cotorra | 7 |
| 15175 | cota | 7 |
| 15176 | costará | 7 |
| 15177 | coscorrones | 7 |
| 15178 | cortijo | 7 |
| 15179 | corrigió | 7 |
| 15180 | corresponden | 7 |
| 15181 | corredora | 7 |
| 15182 | corporación | 7 |
| 15183 | cornudo | 7 |
| 15184 | corcho | 7 |
| 15185 | coqueta | 7 |
| 15186 | copo | 7 |
| 15187 | copias | 7 |
| 15188 | convulsiva | 7 |
| 15189 | convites | 7 |
| 15190 | convirtiera | 7 |
| 15191 | convenientes | 7 |
| 15192 | convéncete | 7 |
| 15193 | convencerle | 7 |
| 15194 | contrariedades | 7 |
| 15195 | contrahechas | 7 |
| 15196 | contradecía | 7 |
| 15197 | continuos | 7 |
| 15198 | continuaban | 7 |
| 15199 | contestaban | 7 |
| 15200 | contentas | 7 |
| 15201 | contemplarla | 7 |
| 15202 | contare | 7 |
| 15203 | consumido | 7 |
| 15204 | consumado | 7 |
| 15205 | constituye | 7 |
| 15206 | consienten | 7 |
| 15207 | considero | 7 |
| 15208 | conservador | 7 |
| 15209 | consejera | 7 |
| 15210 | conoscimiento | 7 |
| 15211 | conoscer | 7 |
| 15212 | conorte | 7 |
| 15213 | conocerlo | 7 |
| 15214 | conocedor | 7 |
| 15215 | congreso | 7 |
| 15216 | confundidos | 7 |
| 15217 | conformaba | 7 |
| 15218 | confiar | 7 |
| 15219 | confesaban | 7 |
| 15220 | conductor | 7 |
| 15221 | conducen | 7 |
| 15222 | condenadas | 7 |
| 15223 | concilio | 7 |
| 15224 | conçejo | 7 |
| 15225 | conceda | 7 |
| 15226 | concebido | 7 |
| 15227 | cóncavo | 7 |
| 15228 | conbrás | 7 |
| 15229 | comun | 7 |
| 15230 | compuestas | 7 |
| 15231 | compromisos | 7 |
| 15232 | comprando | 7 |
| 15233 | compara | 7 |
| 15234 | compaña | 7 |
| 15235 | comimos | 7 |
| 15236 | comiera | 7 |
| 15237 | comemos | 7 |
| 15238 | combés | 7 |
| 15239 | combates | 7 |
| 15240 | coluna | 7 |
| 15241 | colocada | 7 |
| 15242 | colinas | 7 |
| 15243 | colérica | 7 |
| 15244 | colegiales | 7 |
| 15245 | colecciones | 7 |
| 15246 | colada | 7 |
| 15247 | cogiera | 7 |
| 15248 | cogen | 7 |
| 15249 | codiciosos | 7 |
| 15250 | cobrado | 7 |
| 15251 | club | 7 |
| 15252 | clima | 7 |
| 15253 | cliente | 7 |
| 15254 | clem | 7 |
| 15255 | claveles | 7 |
| 15256 | clásico | 7 |
| 15257 | clamó | 7 |
| 15258 | ciudadela | 7 |
| 15259 | ciudadano | 7 |
| 15260 | citada | 7 |
| 15261 | circulación | 7 |
| 15262 | ciñe | 7 |
| 15263 | cigarrillo | 7 |
| 15264 | çiento | 7 |
| 15265 | ciegamente | 7 |
| 15266 | cicerón | 7 |
| 15267 | chucherías | 7 |
| 15268 | chorros | 7 |
| 15269 | chiquillas | 7 |
| 15270 | cherinos | 7 |
| 15271 | cháchara | 7 |
| 15272 | ceuo | 7 |
| 15273 | cesado | 7 |
| 15274 | cesaban | 7 |
| 15275 | cesa | 7 |
| 15276 | cerraron | 7 |
| 15277 | cerradura | 7 |
| 15278 | çerrada | 7 |
| 15279 | cerdos | 7 |
| 15280 | cerciorarse | 7 |
| 15281 | cenando | 7 |
| 15282 | celosos | 7 |
| 15283 | çelo | 7 |
| 15284 | celebraban | 7 |
| 15285 | cedió | 7 |
| 15286 | caudillo | 7 |
| 15287 | cauce | 7 |
| 15288 | cato | 7 |
| 15289 | casullas | 7 |
| 15290 | casualmente | 7 |
| 15291 | cásese | 7 |
| 15292 | caserones | 7 |
| 15293 | cáscaras | 7 |
| 15294 | cascada | 7 |
| 15295 | cascabel | 7 |
| 15296 | casaría | 7 |
| 15297 | casaré | 7 |
| 15298 | casaban | 7 |
| 15299 | cartucho | 7 |
| 15300 | carmesíes | 7 |
| 15301 | caritativas | 7 |
| 15302 | caricia | 7 |
| 15303 | cargas | 7 |
| 15304 | carecen | 7 |
| 15305 | carducha | 7 |
| 15306 | cardenales | 7 |
| 15307 | cárcamo | 7 |
| 15308 | carbones | 7 |
| 15309 | caramelo | 7 |
| 15310 | caperuzas | 7 |
| 15311 | capacidad | 7 |
| 15312 | cap | 7 |
| 15313 | canuto | 7 |
| 15314 | cántigas | 7 |
| 15315 | cansó | 7 |
| 15316 | canso | 7 |
| 15317 | canónico | 7 |
| 15318 | candeleros | 7 |
| 15319 | canario | 7 |
| 15320 | campanillas | 7 |
| 15321 | caminado | 7 |
| 15322 | cambió | 7 |
| 15323 | cambiaba | 7 |
| 15324 | calórico | 7 |
| 15325 | calores | 7 |
| 15326 | calorcillo | 7 |
| 15327 | calmar | 7 |
| 15328 | callas | 7 |
| 15329 | callad | 7 |
| 15330 | calificar | 7 |
| 15331 | calabazas | 7 |
| 15332 | calabaza | 7 |
| 15333 | cajero | 7 |
| 15334 | caídas | 7 |
| 15335 | caco | 7 |
| 15336 | caça | 7 |
| 15337 | cabezadas | 7 |
| 15338 | caballerescas | 7 |
| 15339 | caballeresca | 7 |
| 15340 | buscasen | 7 |
| 15341 | buscara | 7 |
| 15342 | buscalle | 7 |
| 15343 | burlaban | 7 |
| 15344 | bum | 7 |
| 15345 | buenamente | 7 |
| 15346 | bromitas | 7 |
| 15347 | brillar | 7 |
| 15348 | bribón | 7 |
| 15349 | brecha | 7 |
| 15350 | bramido | 7 |
| 15351 | boto | 7 |
| 15352 | borrascas | 7 |
| 15353 | borrar | 7 |
| 15354 | borrador | 7 |
| 15355 | borrado | 7 |
| 15356 | borrachera | 7 |
| 15357 | bordadas | 7 |
| 15358 | boga | 7 |
| 15359 | bobos | 7 |
| 15360 | bobas | 7 |
| 15361 | bizca | 7 |
| 15362 | bizarro | 7 |
| 15363 | besándole | 7 |
| 15364 | besan | 7 |
| 15365 | benditas | 7 |
| 15366 | bencerraje | 7 |
| 15367 | belianís | 7 |
| 15368 | bazar | 7 |
| 15369 | baxo | 7 |
| 15370 | bautizo | 7 |
| 15371 | bastones | 7 |
| 15372 | basílica | 7 |
| 15373 | barriada | 7 |
| 15374 | barraca | 7 |
| 15375 | bañaba | 7 |
| 15376 | bailarina | 7 |
| 15377 | bailado | 7 |
| 15378 | bagaje | 7 |
| 15379 | babilonia | 7 |
| 15380 | azar | 7 |
| 15381 | ayúdame | 7 |
| 15382 | ayan | 7 |
| 15383 | aventurado | 7 |
| 15384 | avanzaron | 7 |
| 15385 | auxiliar | 7 |
| 15386 | auténticos | 7 |
| 15387 | aut | 7 |
| 15388 | aura | 7 |
| 15389 | aula | 7 |
| 15390 | auiso | 7 |
| 15391 | atropelladamente | 7 |
| 15392 | atropella | 7 |
| 15393 | atreviéndose | 7 |
| 15394 | atrever | 7 |
| 15395 | atraviesa | 7 |
| 15396 | atravesando | 7 |
| 15397 | atraso | 7 |
| 15398 | atrasada | 7 |
| 15399 | atractivos | 7 |
| 15400 | átomos | 7 |
| 15401 | atierra | 7 |
| 15402 | atenas | 7 |
| 15403 | atanto | 7 |
| 15404 | atabales | 7 |
| 15405 | astrólogo | 7 |
| 15406 | asta | 7 |
| 15407 | aspiraciones | 7 |
| 15408 | ásperos | 7 |
| 15409 | aspas | 7 |
| 15410 | asidos | 7 |
| 15411 | asesinato | 7 |
| 15412 | aseguran | 7 |
| 15413 | ascuras | 7 |
| 15414 | artística | 7 |
| 15415 | arrugada | 7 |
| 15416 | arrojo | 7 |
| 15417 | arrojándose | 7 |
| 15418 | arrima | 7 |
| 15419 | arrebatos | 7 |
| 15420 | arrebató | 7 |
| 15421 | arranco | 7 |
| 15422 | arqueología | 7 |
| 15423 | árnica | 7 |
| 15424 | armiño | 7 |
| 15425 | armando | 7 |
| 15426 | arman | 7 |
| 15427 | aristocrática | 7 |
| 15428 | arden | 7 |
| 15429 | árbitro | 7 |
| 15430 | aquelarre | 7 |
| 15431 | apure | 7 |
| 15432 | apuntado | 7 |
| 15433 | aproximarse | 7 |
| 15434 | aprovechan | 7 |
| 15435 | aprenderá | 7 |
| 15436 | apreciable | 7 |
| 15437 | apoyado | 7 |
| 15438 | apólogos | 7 |
| 15439 | apoderó | 7 |
| 15440 | apoderarse | 7 |
| 15441 | aplacar | 7 |
| 15442 | apartarme | 7 |
| 15443 | apartados | 7 |
| 15444 | aparentes | 7 |
| 15445 | aparentando | 7 |
| 15446 | aparentaba | 7 |
| 15447 | aparejada | 7 |
| 15448 | apagó | 7 |
| 15449 | añoa | 7 |
| 15450 | antípodas | 7 |
| 15451 | antipáticos | 7 |
| 15452 | antesala | 7 |
| 15453 | anteanoche | 7 |
| 15454 | anís | 7 |
| 15455 | animalias | 7 |
| 15456 | animada | 7 |
| 15457 | andurriales | 7 |
| 15458 | andanza | 7 |
| 15459 | anales | 7 |
| 15460 | amorosamente | 7 |
| 15461 | amigotes | 7 |
| 15462 | ambicioso | 7 |
| 15463 | amarillez | 7 |
| 15464 | amarguras | 7 |
| 15465 | amanecía | 7 |
| 15466 | amados | 7 |
| 15467 | alvarito | 7 |
| 15468 | aludiendo | 7 |
| 15469 | alucinación | 7 |
| 15470 | altercado | 7 |
| 15471 | alterar | 7 |
| 15472 | alterada | 7 |
| 15473 | alteracion | 7 |
| 15474 | almendro | 7 |
| 15475 | almadrabas | 7 |
| 15476 | almacenes | 7 |
| 15477 | alimenta | 7 |
| 15478 | alhambra | 7 |
| 15479 | alevosía | 7 |
| 15480 | alemán | 7 |
| 15481 | alejándose | 7 |
| 15482 | alejaban | 7 |
| 15483 | alegraron | 7 |
| 15484 | alcé | 7 |
| 15485 | alcázares | 7 |
| 15486 | alcanzase | 7 |
| 15487 | alborota | 7 |
| 15488 | alborán | 7 |
| 15489 | albañiles | 7 |
| 15490 | alarmante | 7 |
| 15491 | alaridos | 7 |
| 15492 | alahe | 7 |
| 15493 | alabó | 7 |
| 15494 | alaban | 7 |
| 15495 | alababa | 7 |
| 15496 | ajustar | 7 |
| 15497 | ajustada | 7 |
| 15498 | ajetreo | 7 |
| 15499 | aislamiento | 7 |
| 15500 | ahorro | 7 |
| 15501 | ahorcar | 7 |
| 15502 | águilas | 7 |
| 15503 | agüeros | 7 |
| 15504 | aguardan | 7 |
| 15505 | agraviar | 7 |
| 15506 | agramante | 7 |
| 15507 | agradecidos | 7 |
| 15508 | agitaban | 7 |
| 15509 | agi | 7 |
| 15510 | agena | 7 |
| 15511 | afrentas | 7 |
| 15512 | advierto | 7 |
| 15513 | adquiría | 7 |
| 15514 | adornan | 7 |
| 15515 | adornado | 7 |
| 15516 | adornadas | 7 |
| 15517 | adoran | 7 |
| 15518 | adoptado | 7 |
| 15519 | adolescente | 7 |
| 15520 | admitió | 7 |
| 15521 | admiro | 7 |
| 15522 | administrar | 7 |
| 15523 | adivinó | 7 |
| 15524 | adherentes | 7 |
| 15525 | adelantaba | 7 |
| 15526 | acuesto | 7 |
| 15527 | acudiendo | 7 |
| 15528 | actriz | 7 |
| 15529 | acreditar | 7 |
| 15530 | acostada | 7 |
| 15531 | acostaba | 7 |
| 15532 | acordaos | 7 |
| 15533 | acontecía | 7 |
| 15534 | aconsejarte | 7 |
| 15535 | acompañó | 7 |
| 15536 | acompañarle | 7 |
| 15537 | acomodaron | 7 |
| 15538 | acomete | 7 |
| 15539 | acertada | 7 |
| 15540 | acercado | 7 |
| 15541 | acentuando | 7 |
| 15542 | acentuada | 7 |
| 15543 | acelerado | 7 |
| 15544 | acecha | 7 |
| 15545 | acarrea | 7 |
| 15546 | acalorada | 7 |
| 15547 | acaben | 7 |
| 15548 | acabemos | 7 |
| 15549 | acabadas | 7 |
| 15550 | abusar | 7 |
| 15551 | abstinencia | 7 |
| 15552 | absorta | 7 |
| 15553 | abriera | 7 |
| 15554 | abrazándola | 7 |
| 15555 | abonados | 7 |
| 15556 | abdicación | 7 |
| 15557 | abandonados | 7 |
| 15558 | zurrón | 6 |
| 15559 | zumbido | 6 |
| 15560 | zorros | 6 |
| 15561 | zorro | 6 |
| 15562 | zig | 6 |
| 15563 | zascandil | 6 |
| 15564 | zaragata | 6 |
| 15565 | zapateros | 6 |
| 15566 | zánganos | 6 |
| 15567 | zancas | 6 |
| 15568 | zafiro | 6 |
| 15569 | yua | 6 |
| 15570 | ymagen | 6 |
| 15571 | yglesia | 6 |
| 15572 | yerta | 6 |
| 15573 | yerno | 6 |
| 15574 | xxvii | 6 |
| 15575 | xxvi | 6 |
| 15576 | xristos | 6 |
| 15577 | vusté | 6 |
| 15578 | vulgaridad | 6 |
| 15579 | vso | 6 |
| 15580 | volvíme | 6 |
| 15581 | volvernos | 6 |
| 15582 | volvámonos | 6 |
| 15583 | volandas | 6 |
| 15584 | volada | 6 |
| 15585 | vizcaína | 6 |
| 15586 | viviré | 6 |
| 15587 | viviendas | 6 |
| 15588 | vivid | 6 |
| 15589 | viudita | 6 |
| 15590 | visual | 6 |
| 15591 | vistosos | 6 |
| 15592 | vistióse | 6 |
| 15593 | vistiese | 6 |
| 15594 | visos | 6 |
| 15595 | viso | 6 |
| 15596 | visitando | 6 |
| 15597 | violines | 6 |
| 15598 | vínole | 6 |
| 15599 | vínculo | 6 |
| 15600 | vinculete | 6 |
| 15601 | villegas | 6 |
| 15602 | villanía | 6 |
| 15603 | vigorosa | 6 |
| 15604 | viciosos | 6 |
| 15605 | vibración | 6 |
| 15606 | viajado | 6 |
| 15607 | vertud | 6 |
| 15608 | vergonzosas | 6 |
| 15609 | veredes | 6 |
| 15610 | veracidad | 6 |
| 15611 | ventilación | 6 |
| 15612 | vengada | 6 |
| 15613 | venera | 6 |
| 15614 | venenos | 6 |
| 15615 | vendrían | 6 |
| 15616 | vendado | 6 |
| 15617 | venciendo | 6 |
| 15618 | velando | 6 |
| 15619 | vejete | 6 |
| 15620 | vegetal | 6 |
| 15621 | vegetación | 6 |
| 15622 | vedes | 6 |
| 15623 | vedado | 6 |
| 15624 | vaquero | 6 |
| 15625 | vandalia | 6 |
| 15626 | valentísimo | 6 |
| 15627 | valenciano | 6 |
| 15628 | vacilación | 6 |
| 15629 | usara | 6 |
| 15630 | unió | 6 |
| 15631 | uniformes | 6 |
| 15632 | unidad | 6 |
| 15633 | ungüento | 6 |
| 15634 | undoso | 6 |
| 15635 | unánime | 6 |
| 15636 | ulmus | 6 |
| 15637 | ufano | 6 |
| 15638 | uchalí | 6 |
| 15639 | ubi | 6 |
| 15640 | úbeda | 6 |
| 15641 | tuviéramos | 6 |
| 15642 | turbe | 6 |
| 15643 | turbante | 6 |
| 15644 | turbacion | 6 |
| 15645 | tufo | 6 |
| 15646 | tudas | 6 |
| 15647 | truje | 6 |
| 15648 | trovador | 6 |
| 15649 | tronar | 6 |
| 15650 | trocaron | 6 |
| 15651 | trobar | 6 |
| 15652 | triunfaba | 6 |
| 15653 | tribunales | 6 |
| 15654 | tribulación | 6 |
| 15655 | tretas | 6 |
| 15656 | tremendos | 6 |
| 15657 | trazó | 6 |
| 15658 | trazar | 6 |
| 15659 | trazada | 6 |
| 15660 | trayecto | 6 |
| 15661 | traydora | 6 |
| 15662 | tratarse | 6 |
| 15663 | trastornos | 6 |
| 15664 | trastorna | 6 |
| 15665 | trastada | 6 |
| 15666 | trasladarse | 6 |
| 15667 | traslacerca | 6 |
| 15668 | traseros | 6 |
| 15669 | trasera | 6 |
| 15670 | trapitos | 6 |
| 15671 | trapisonda | 6 |
| 15672 | tranvía | 6 |
| 15673 | transformaba | 6 |
| 15674 | transeúnte | 6 |
| 15675 | tranquilizarla | 6 |
| 15676 | tranquilizar | 6 |
| 15677 | traídas | 6 |
| 15678 | trágicas | 6 |
| 15679 | traerte | 6 |
| 15680 | traéis | 6 |
| 15681 | traducido | 6 |
| 15682 | trabar | 6 |
| 15683 | trabajadores | 6 |
| 15684 | totalmente | 6 |
| 15685 | torpezas | 6 |
| 15686 | tornando | 6 |
| 15687 | tormes | 6 |
| 15688 | torciendo | 6 |
| 15689 | torcía | 6 |
| 15690 | topamos | 6 |
| 15691 | tomóla | 6 |
| 15692 | toleraba | 6 |
| 15693 | toga | 6 |
| 15694 | todopoderoso | 6 |
| 15695 | toco | 6 |
| 15696 | tocinos | 6 |
| 15697 | tocará | 6 |
| 15698 | toallas | 6 |
| 15699 | tirarle | 6 |
| 15700 | tirante | 6 |
| 15701 | tirador | 6 |
| 15702 | tintoreros | 6 |
| 15703 | tibieza | 6 |
| 15704 | textos | 6 |
| 15705 | tétrica | 6 |
| 15706 | testamentarios | 6 |
| 15707 | terminando | 6 |
| 15708 | terco | 6 |
| 15709 | teólogos | 6 |
| 15710 | teóg | 6 |
| 15711 | teñía | 6 |
| 15712 | tentativas | 6 |
| 15713 | tentativa | 6 |
| 15714 | tenidas | 6 |
| 15715 | ténganse | 6 |
| 15716 | tenerlas | 6 |
| 15717 | tenebrosa | 6 |
| 15718 | temperamentos | 6 |
| 15719 | temida | 6 |
| 15720 | temí | 6 |
| 15721 | tememos | 6 |
| 15722 | tellería | 6 |
| 15723 | telar | 6 |
| 15724 | tauerna | 6 |
| 15725 | tardança | 6 |
| 15726 | tapada | 6 |
| 15727 | tañe | 6 |
| 15728 | tantísimos | 6 |
| 15729 | talegas | 6 |
| 15730 | tajos | 6 |
| 15731 | taciturna | 6 |
| 15732 | sylvestris | 6 |
| 15733 | suspenden | 6 |
| 15734 | susceptible | 6 |
| 15735 | supremos | 6 |
| 15736 | suposición | 6 |
| 15737 | suponerse | 6 |
| 15738 | sumisa | 6 |
| 15739 | sufrió | 6 |
| 15740 | sufrimientos | 6 |
| 15741 | suene | 6 |
| 15742 | sucumbir | 6 |
| 15743 | suculento | 6 |
| 15744 | suciedad | 6 |
| 15745 | sucediere | 6 |
| 15746 | sucederá | 6 |
| 15747 | subleva | 6 |
| 15748 | süaves | 6 |
| 15749 | sotavento | 6 |
| 15750 | sospechosas | 6 |
| 15751 | sospechara | 6 |
| 15752 | sosona | 6 |
| 15753 | sopetón | 6 |
| 15754 | sonsonete | 6 |
| 15755 | sonríe | 6 |
| 15756 | solutamente | 6 |
| 15757 | solterón | 6 |
| 15758 | soltero | 6 |
| 15759 | soltarse | 6 |
| 15760 | soguilla | 6 |
| 15761 | sofisma | 6 |
| 15762 | socorrida | 6 |
| 15763 | socarronería | 6 |
| 15764 | sobró | 6 |
| 15765 | sobrenaturales | 6 |
| 15766 | sisona | 6 |
| 15767 | sirviese | 6 |
| 15768 | sirviente | 6 |
| 15769 | sirvan | 6 |
| 15770 | sine | 6 |
| 15771 | simulacro | 6 |
| 15772 | simplicidades | 6 |
| 15773 | silva | 6 |
| 15774 | sillares | 6 |
| 15775 | silbido | 6 |
| 15776 | silbar | 6 |
| 15777 | siguiéndole | 6 |
| 15778 | sigues | 6 |
| 15779 | significativo | 6 |
| 15780 | significado | 6 |
| 15781 | sigas | 6 |
| 15782 | sientas | 6 |
| 15783 | sien | 6 |
| 15784 | seto | 6 |
| 15785 | sesgo | 6 |
| 15786 | servidores | 6 |
| 15787 | servidora | 6 |
| 15788 | serafín | 6 |
| 15789 | séquito | 6 |
| 15790 | separando | 6 |
| 15791 | separados | 6 |
| 15792 | separaban | 6 |
| 15793 | señorías | 6 |
| 15794 | señero | 6 |
| 15795 | señaladas | 6 |
| 15796 | señalaban | 6 |
| 15797 | sentara | 6 |
| 15798 | sencillas | 6 |
| 15799 | sencillamente | 6 |
| 15800 | senales | 6 |
| 15801 | sellos | 6 |
| 15802 | segunt | 6 |
| 15803 | segundas | 6 |
| 15804 | seguiremos | 6 |
| 15805 | seguiré | 6 |
| 15806 | seguirán | 6 |
| 15807 | seguíale | 6 |
| 15808 | sanidad | 6 |
| 15809 | sánchez | 6 |
| 15810 | saludos | 6 |
| 15811 | salteó | 6 |
| 15812 | saltan | 6 |
| 15813 | salirme | 6 |
| 15814 | saladero | 6 |
| 15815 | sagrados | 6 |
| 15816 | sagradas | 6 |
| 15817 | sacrílego | 6 |
| 15818 | sacrificarse | 6 |
| 15819 | sacerdocio | 6 |
| 15820 | sacarte | 6 |
| 15821 | sacándole | 6 |
| 15822 | sabrosos | 6 |
| 15823 | sabidores | 6 |
| 15824 | sabíamos | 6 |
| 15825 | sabiamente | 6 |
| 15826 | sabandijas | 6 |
| 15827 | sábados | 6 |
| 15828 | rusticidad | 6 |
| 15829 | ruiseñores | 6 |
| 15830 | rugidos | 6 |
| 15831 | rufinita | 6 |
| 15832 | rúbrica | 6 |
| 15833 | rúa | 6 |
| 15834 | rrica | 6 |
| 15835 | rozagante | 6 |
| 15836 | royendo | 6 |
| 15837 | royal | 6 |
| 15838 | rouanet | 6 |
| 15839 | rosquillas | 6 |
| 15840 | ropillas | 6 |
| 15841 | ronquidos | 6 |
| 15842 | roncos | 6 |
| 15843 | roncas | 6 |
| 15844 | rollo | 6 |
| 15845 | rodeando | 6 |
| 15846 | robos | 6 |
| 15847 | robarle | 6 |
| 15848 | rivalidad | 6 |
| 15849 | risco | 6 |
| 15850 | riquísima | 6 |
| 15851 | riñendo | 6 |
| 15852 | rinden | 6 |
| 15853 | rigurosas | 6 |
| 15854 | rigodón | 6 |
| 15855 | ríete | 6 |
| 15856 | ribeteadora | 6 |
| 15857 | reyertas | 6 |
| 15858 | reyerta | 6 |
| 15859 | revolverse | 6 |
| 15860 | reverencias | 6 |
| 15861 | reventando | 6 |
| 15862 | retrocediendo | 6 |
| 15863 | retozar | 6 |
| 15864 | retóricas | 6 |
| 15865 | retorcidos | 6 |
| 15866 | retorcía | 6 |
| 15867 | retírate | 6 |
| 15868 | retina | 6 |
| 15869 | reticencias | 6 |
| 15870 | retazos | 6 |
| 15871 | resueltamente | 6 |
| 15872 | restituto | 6 |
| 15873 | responso | 6 |
| 15874 | respondiera | 6 |
| 15875 | respondes | 6 |
| 15876 | resplandores | 6 |
| 15877 | resplandece | 6 |
| 15878 | resorte | 6 |
| 15879 | resoplido | 6 |
| 15880 | resignada | 6 |
| 15881 | reses | 6 |
| 15882 | reservaba | 6 |
| 15883 | resbalar | 6 |
| 15884 | resbaladizo | 6 |
| 15885 | repugna | 6 |
| 15886 | republicano | 6 |
| 15887 | reprehender | 6 |
| 15888 | repóblica | 6 |
| 15889 | reparto | 6 |
| 15890 | repartido | 6 |
| 15891 | reparos | 6 |
| 15892 | reparado | 6 |
| 15893 | reñían | 6 |
| 15894 | reñía | 6 |
| 15895 | renunciaba | 6 |
| 15896 | renovó | 6 |
| 15897 | renegar | 6 |
| 15898 | rendijas | 6 |
| 15899 | rendición | 6 |
| 15900 | renacer | 6 |
| 15901 | remoto | 6 |
| 15902 | remordía | 6 |
| 15903 | remontarse | 6 |
| 15904 | remojo | 6 |
| 15905 | remiendo | 6 |
| 15906 | remedia | 6 |
| 15907 | reiría | 6 |
| 15908 | reirá | 6 |
| 15909 | regresó | 6 |
| 15910 | regocijos | 6 |
| 15911 | regocijados | 6 |
| 15912 | reglamento | 6 |
| 15913 | registrar | 6 |
| 15914 | regaló | 6 |
| 15915 | regalados | 6 |
| 15916 | reflejo | 6 |
| 15917 | reflejaban | 6 |
| 15918 | refieren | 6 |
| 15919 | referirse | 6 |
| 15920 | reduciendo | 6 |
| 15921 | reducidos | 6 |
| 15922 | redondillas | 6 |
| 15923 | redacción | 6 |
| 15924 | recuerdan | 6 |
| 15925 | rectoral | 6 |
| 15926 | rector | 6 |
| 15927 | recrear | 6 |
| 15928 | recorre | 6 |
| 15929 | recordado | 6 |
| 15930 | reconocerle | 6 |
| 15931 | recomiendo | 6 |
| 15932 | recoletos | 6 |
| 15933 | recoge | 6 |
| 15934 | reclamaba | 6 |
| 15935 | recitaba | 6 |
| 15936 | recetas | 6 |
| 15937 | recelosa | 6 |
| 15938 | recebían | 6 |
| 15939 | recebí | 6 |
| 15940 | rece | 6 |
| 15941 | rebuznos | 6 |
| 15942 | rebaños | 6 |
| 15943 | rebajo | 6 |
| 15944 | realismo | 6 |
| 15945 | realidades | 6 |
| 15946 | razonando | 6 |
| 15947 | rasgaba | 6 |
| 15948 | randas | 6 |
| 15949 | raimundo | 6 |
| 15950 | raído | 6 |
| 15951 | rafala | 6 |
| 15952 | radamanto | 6 |
| 15953 | racionales | 6 |
| 15954 | racimos | 6 |
| 15955 | rabioso | 6 |
| 15956 | quitándome | 6 |
| 15957 | quitamos | 6 |
| 15958 | quisto | 6 |
| 15959 | quiñones | 6 |
| 15960 | quintos | 6 |
| 15961 | quintana | 6 |
| 15962 | quimera | 6 |
| 15963 | quiebras | 6 |
| 15964 | quexura | 6 |
| 15965 | quexas | 6 |
| 15966 | querrías | 6 |
| 15967 | quererse | 6 |
| 15968 | quered | 6 |
| 15969 | queramos | 6 |
| 15970 | queráis | 6 |
| 15971 | quemarse | 6 |
| 15972 | quejado | 6 |
| 15973 | quedes | 6 |
| 15974 | quedaran | 6 |
| 15975 | quedábase | 6 |
| 15976 | quebrantada | 6 |
| 15977 | quáles | 6 |
| 15978 | pupila | 6 |
| 15979 | puntapié | 6 |
| 15980 | puertecilla | 6 |
| 15981 | pueriles | 6 |
| 15982 | pudiesse | 6 |
| 15983 | pud | 6 |
| 15984 | ps | 6 |
| 15985 | prudentísimo | 6 |
| 15986 | provechosas | 6 |
| 15987 | provada | 6 |
| 15988 | protestar | 6 |
| 15989 | protegido | 6 |
| 15990 | proporcionada | 6 |
| 15991 | propina | 6 |
| 15992 | propietarios | 6 |
| 15993 | propicia | 6 |
| 15994 | pronuncian | 6 |
| 15995 | prontito | 6 |
| 15996 | prometiste | 6 |
| 15997 | prohibir | 6 |
| 15998 | prohibida | 6 |
| 15999 | prohibición | 6 |
| 16000 | progresistas | 6 |
| 16001 | profundísima | 6 |
| 16002 | profesamos | 6 |
| 16003 | profesado | 6 |
| 16004 | profana | 6 |
| 16005 | prodigaba | 6 |
| 16006 | procures | 6 |
| 16007 | procedido | 6 |
| 16008 | probables | 6 |
| 16009 | privaciones | 6 |
| 16010 | prisionera | 6 |
| 16011 | principiaba | 6 |
| 16012 | prez | 6 |
| 16013 | previsto | 6 |
| 16014 | previo | 6 |
| 16015 | pretender | 6 |
| 16016 | presumo | 6 |
| 16017 | presté | 6 |
| 16018 | prestarle | 6 |
| 16019 | presona | 6 |
| 16020 | presentimientos | 6 |
| 16021 | presencié | 6 |
| 16022 | prendieron | 6 |
| 16023 | prenada | 6 |
| 16024 | preguntole | 6 |
| 16025 | preguntes | 6 |
| 16026 | pregúntaselo | 6 |
| 16027 | preguntáronme | 6 |
| 16028 | preguntare | 6 |
| 16029 | pregones | 6 |
| 16030 | pregonar | 6 |
| 16031 | pregonaba | 6 |
| 16032 | prefieres | 6 |
| 16033 | predilecto | 6 |
| 16034 | predicando | 6 |
| 16035 | predica | 6 |
| 16036 | precisas | 6 |
| 16037 | precipitó | 6 |
| 16038 | precepto | 6 |
| 16039 | precaución | 6 |
| 16040 | praschcu | 6 |
| 16041 | positivos | 6 |
| 16042 | posiciones | 6 |
| 16043 | portó | 6 |
| 16044 | portento | 6 |
| 16045 | porta | 6 |
| 16046 | porcelana | 6 |
| 16047 | ponernos | 6 |
| 16048 | pómulos | 6 |
| 16049 | pollas | 6 |
| 16050 | polla | 6 |
| 16051 | podieres | 6 |
| 16052 | podedes | 6 |
| 16053 | poble | 6 |
| 16054 | poblada | 6 |
| 16055 | poblachón | 6 |
| 16056 | pleyto | 6 |
| 16057 | platillo | 6 |
| 16058 | plataforma | 6 |
| 16059 | planchar | 6 |
| 16060 | pistolas | 6 |
| 16061 | pisan | 6 |
| 16062 | pirineo | 6 |
| 16063 | piojos | 6 |
| 16064 | pintan | 6 |
| 16065 | pinche | 6 |
| 16066 | pimientos | 6 |
| 16067 | pilares | 6 |
| 16068 | pidiéronle | 6 |
| 16069 | pidan | 6 |
| 16070 | picor | 6 |
| 16071 | picas | 6 |
| 16072 | pías | 6 |
| 16073 | pianito | 6 |
| 16074 | pianista | 6 |
| 16075 | pesara | 6 |
| 16076 | pesadumbres | 6 |
| 16077 | pertenecen | 6 |
| 16078 | perpendicular | 6 |
| 16079 | peros | 6 |
| 16080 | permitirle | 6 |
| 16081 | permitieron | 6 |
| 16082 | perjudicial | 6 |
| 16083 | perilla | 6 |
| 16084 | pérfido | 6 |
| 16085 | perece | 6 |
| 16086 | perdidoso | 6 |
| 16087 | pérdidas | 6 |
| 16088 | perderé | 6 |
| 16089 | pequeñuelos | 6 |
| 16090 | pequena | 6 |
| 16091 | pepina | 6 |
| 16092 | peón | 6 |
| 16093 | peñón | 6 |
| 16094 | peñaplata | 6 |
| 16095 | penumbra | 6 |
| 16096 | pensaré | 6 |
| 16097 | pensábamos | 6 |
| 16098 | penetraron | 6 |
| 16099 | pendía | 6 |
| 16100 | peinadas | 6 |
| 16101 | pegue | 6 |
| 16102 | pedrada | 6 |
| 16103 | pedirte | 6 |
| 16104 | pedirla | 6 |
| 16105 | pediré | 6 |
| 16106 | pedimos | 6 |
| 16107 | pedantería | 6 |
| 16108 | pedante | 6 |
| 16109 | pécora | 6 |
| 16110 | pecadillos | 6 |
| 16111 | pecaba | 6 |
| 16112 | pausas | 6 |
| 16113 | patíbulo | 6 |
| 16114 | pasteles | 6 |
| 16115 | pasmo | 6 |
| 16116 | pasean | 6 |
| 16117 | pasarle | 6 |
| 16118 | pasajera | 6 |
| 16119 | partimos | 6 |
| 16120 | particularidades | 6 |
| 16121 | parroquiana | 6 |
| 16122 | parrafito | 6 |
| 16123 | parlero | 6 |
| 16124 | parir | 6 |
| 16125 | pareciéndoles | 6 |
| 16126 | parecidas | 6 |
| 16127 | pare | 6 |
| 16128 | panadería | 6 |
| 16129 | panacea | 6 |
| 16130 | palpitaba | 6 |
| 16131 | palpando | 6 |
| 16132 | palmadita | 6 |
| 16133 | paladar | 6 |
| 16134 | palabritas | 6 |
| 16135 | palabrita | 6 |
| 16136 | págs | 6 |
| 16137 | paganismo | 6 |
| 16138 | padrastro | 6 |
| 16139 | padezca | 6 |
| 16140 | padecen | 6 |
| 16141 | oyéndola | 6 |
| 16142 | oyas | 6 |
| 16143 | otrosy | 6 |
| 16144 | otorgar | 6 |
| 16145 | ostentaban | 6 |
| 16146 | osé | 6 |
| 16147 | osadas | 6 |
| 16148 | ortografía | 6 |
| 16149 | oropel | 6 |
| 16150 | orillo | 6 |
| 16151 | originalidad | 6 |
| 16152 | órganos | 6 |
| 16153 | opuestas | 6 |
| 16154 | oprimió | 6 |
| 16155 | oprimían | 6 |
| 16156 | oponía | 6 |
| 16157 | onde | 6 |
| 16158 | omíllome | 6 |
| 16159 | olivo | 6 |
| 16160 | olías | 6 |
| 16161 | olían | 6 |
| 16162 | ojeras | 6 |
| 16163 | oíd | 6 |
| 16164 | ogano | 6 |
| 16165 | ofrezca | 6 |
| 16166 | oficiosa | 6 |
| 16167 | officio | 6 |
| 16168 | oferta | 6 |
| 16169 | ofensivas | 6 |
| 16170 | odiosos | 6 |
| 16171 | ocurrencias | 6 |
| 16172 | ocupe | 6 |
| 16173 | ocupando | 6 |
| 16174 | ochavos | 6 |
| 16175 | obsesión | 6 |
| 16176 | objetó | 6 |
| 16177 | objeciones | 6 |
| 16178 | obedientes | 6 |
| 16179 | obedezco | 6 |
| 16180 | obedece | 6 |
| 16181 | nupcial | 6 |
| 16182 | nuncio | 6 |
| 16183 | numerosos | 6 |
| 16184 | numeroso | 6 |
| 16185 | nueuamente | 6 |
| 16186 | novillos | 6 |
| 16187 | noviazgo | 6 |
| 16188 | note | 6 |
| 16189 | nonada | 6 |
| 16190 | nona | 6 |
| 16191 | nombrando | 6 |
| 16192 | niñería | 6 |
| 16193 | nino | 6 |
| 16194 | nelilla | 6 |
| 16195 | negarás | 6 |
| 16196 | necessidades | 6 |
| 16197 | necesitaban | 6 |
| 16198 | náutica | 6 |
| 16199 | nasçen | 6 |
| 16200 | narizes | 6 |
| 16201 | naranjos | 6 |
| 16202 | naida | 6 |
| 16203 | nahara | 6 |
| 16204 | nacimientos | 6 |
| 16205 | nabos | 6 |
| 16206 | musical | 6 |
| 16207 | mus | 6 |
| 16208 | muriera | 6 |
| 16209 | muramos | 6 |
| 16210 | municipio | 6 |
| 16211 | mundanos | 6 |
| 16212 | mundana | 6 |
| 16213 | mujercillas | 6 |
| 16214 | mugidos | 6 |
| 16215 | mugido | 6 |
| 16216 | muestrario | 6 |
| 16217 | mueres | 6 |
| 16218 | muecas | 6 |
| 16219 | mudaba | 6 |
| 16220 | muchísimos | 6 |
| 16221 | moviesen | 6 |
| 16222 | moviese | 6 |
| 16223 | motor | 6 |
| 16224 | mostro | 6 |
| 16225 | mostrarle | 6 |
| 16226 | mosto | 6 |
| 16227 | mortificaban | 6 |
| 16228 | mordiendo | 6 |
| 16229 | moraba | 6 |
| 16230 | monje | 6 |
| 16231 | molinero | 6 |
| 16232 | moler | 6 |
| 16233 | mojones | 6 |
| 16234 | mojarse | 6 |
| 16235 | mojaba | 6 |
| 16236 | modestamente | 6 |
| 16237 | moderaos | 6 |
| 16238 | moderado | 6 |
| 16239 | moço | 6 |
| 16240 | mocetón | 6 |
| 16241 | misteriosamente | 6 |
| 16242 | miserere | 6 |
| 16243 | miróle | 6 |
| 16244 | mírela | 6 |
| 16245 | miramos | 6 |
| 16246 | mirábanle | 6 |
| 16247 | mirá | 6 |
| 16248 | mios | 6 |
| 16249 | minero | 6 |
| 16250 | mimbres | 6 |
| 16251 | mimbre | 6 |
| 16252 | mimado | 6 |
| 16253 | millonario | 6 |
| 16254 | mieles | 6 |
| 16255 | micón | 6 |
| 16256 | mezquinos | 6 |
| 16257 | metro | 6 |
| 16258 | meterla | 6 |
| 16259 | metálica | 6 |
| 16260 | metafísico | 6 |
| 16261 | mesurado | 6 |
| 16262 | meseta | 6 |
| 16263 | merezca | 6 |
| 16264 | merecimientos | 6 |
| 16265 | mequetrefe | 6 |
| 16266 | menudillos | 6 |
| 16267 | mensuales | 6 |
| 16268 | mensual | 6 |
| 16269 | menguados | 6 |
| 16270 | meneses | 6 |
| 16271 | meneos | 6 |
| 16272 | menea | 6 |
| 16273 | membrillo | 6 |
| 16274 | meliflua | 6 |
| 16275 | melesina | 6 |
| 16276 | melancólicos | 6 |
| 16277 | melancólicas | 6 |
| 16278 | mejoras | 6 |
| 16279 | medre | 6 |
| 16280 | mediquillo | 6 |
| 16281 | medinasidonia | 6 |
| 16282 | mediados | 6 |
| 16283 | medía | 6 |
| 16284 | meca | 6 |
| 16285 | mazmorra | 6 |
| 16286 | máxima | 6 |
| 16287 | matorrales | 6 |
| 16288 | matemática | 6 |
| 16289 | matarte | 6 |
| 16290 | matarse | 6 |
| 16291 | mataré | 6 |
| 16292 | matará | 6 |
| 16293 | mase | 6 |
| 16294 | mascando | 6 |
| 16295 | martillazos | 6 |
| 16296 | marquesas | 6 |
| 16297 | marinería | 6 |
| 16298 | maria | 6 |
| 16299 | marear | 6 |
| 16300 | marchas | 6 |
| 16301 | marcharte | 6 |
| 16302 | marcharé | 6 |
| 16303 | marchaban | 6 |
| 16304 | mañanita | 6 |
| 16305 | manzanos | 6 |
| 16306 | mantillo | 6 |
| 16307 | mantienen | 6 |
| 16308 | manteado | 6 |
| 16309 | mansos | 6 |
| 16310 | mansilla | 6 |
| 16311 | manosear | 6 |
| 16312 | maniloro | 6 |
| 16313 | manifiestan | 6 |
| 16314 | manejo | 6 |
| 16315 | mandaste | 6 |
| 16316 | manco | 6 |
| 16317 | manchaba | 6 |
| 16318 | manantial | 6 |
| 16319 | mana | 6 |
| 16320 | mampara | 6 |
| 16321 | mamar | 6 |
| 16322 | malito | 6 |
| 16323 | maligno | 6 |
| 16324 | maliciosas | 6 |
| 16325 | malhechores | 6 |
| 16326 | maleante | 6 |
| 16327 | maldat | 6 |
| 16328 | magras | 6 |
| 16329 | magníficos | 6 |
| 16330 | magia | 6 |
| 16331 | magalona | 6 |
| 16332 | madr | 6 |
| 16333 | madalena | 6 |
| 16334 | lunas | 6 |
| 16335 | luminosas | 6 |
| 16336 | luminarias | 6 |
| 16337 | lulio | 6 |
| 16338 | lujosa | 6 |
| 16339 | lúgubres | 6 |
| 16340 | luejos | 6 |
| 16341 | lucidos | 6 |
| 16342 | lucían | 6 |
| 16343 | lord | 6 |
| 16344 | lona | 6 |
| 16345 | logar | 6 |
| 16346 | lodos | 6 |
| 16347 | lóbrego | 6 |
| 16348 | lluvias | 6 |
| 16349 | llueva | 6 |
| 16350 | lloros | 6 |
| 16351 | llorente | 6 |
| 16352 | lloran | 6 |
| 16353 | llévate | 6 |
| 16354 | llevarían | 6 |
| 16355 | llevábamos | 6 |
| 16356 | llenaron | 6 |
| 16357 | llegues | 6 |
| 16358 | llegose | 6 |
| 16359 | llegad | 6 |
| 16360 | llamaremos | 6 |
| 16361 | llamándola | 6 |
| 16362 | llagado | 6 |
| 16363 | lívida | 6 |
| 16364 | listas | 6 |
| 16365 | lirios | 6 |
| 16366 | líquidas | 6 |
| 16367 | liquidación | 6 |
| 16368 | líos | 6 |
| 16369 | lindezas | 6 |
| 16370 | limpiándose | 6 |
| 16371 | limbo | 6 |
| 16372 | lilios | 6 |
| 16373 | lides | 6 |
| 16374 | lícidas | 6 |
| 16375 | librero | 6 |
| 16376 | libertador | 6 |
| 16377 | liberalismo | 6 |
| 16378 | levi | 6 |
| 16379 | levar | 6 |
| 16380 | leños | 6 |
| 16381 | lentes | 6 |
| 16382 | lente | 6 |
| 16383 | legalidad | 6 |
| 16384 | leda | 6 |
| 16385 | lechos | 6 |
| 16386 | lean | 6 |
| 16387 | lavo | 6 |
| 16388 | lavan | 6 |
| 16389 | latidos | 6 |
| 16390 | laterales | 6 |
| 16391 | lascivos | 6 |
| 16392 | lara | 6 |
| 16393 | lanzar | 6 |
| 16394 | lampiño | 6 |
| 16395 | lamparilla | 6 |
| 16396 | lamentarse | 6 |
| 16397 | lamentaciones | 6 |
| 16398 | lagartija | 6 |
| 16399 | ladrido | 6 |
| 16400 | ladrando | 6 |
| 16401 | lacerado | 6 |
| 16402 | kilo | 6 |
| 16403 | juzgas | 6 |
| 16404 | juzgaron | 6 |
| 16405 | juyzios | 6 |
| 16406 | justiciero | 6 |
| 16407 | juntó | 6 |
| 16408 | juntáronse | 6 |
| 16409 | ju | 6 |
| 16410 | jordán | 6 |
| 16411 | job | 6 |
| 16412 | jinetes | 6 |
| 16413 | jhesuxristo | 6 |
| 16414 | jayán | 6 |
| 16415 | jarcias | 6 |
| 16416 | jabalíes | 6 |
| 16417 | j | 6 |
| 16418 | irritada | 6 |
| 16419 | irónica | 6 |
| 16420 | ipintza | 6 |
| 16421 | invicto | 6 |
| 16422 | inventé | 6 |
| 16423 | invencibles | 6 |
| 16424 | invariable | 6 |
| 16425 | inválido | 6 |
| 16426 | invadía | 6 |
| 16427 | introducción | 6 |
| 16428 | intimar | 6 |
| 16429 | intermitencias | 6 |
| 16430 | interminables | 6 |
| 16431 | interlocutora | 6 |
| 16432 | interesar | 6 |
| 16433 | interesada | 6 |
| 16434 | intenté | 6 |
| 16435 | intensísimo | 6 |
| 16436 | intendente | 6 |
| 16437 | insultado | 6 |
| 16438 | insultada | 6 |
| 16439 | insultaba | 6 |
| 16440 | instintiva | 6 |
| 16441 | instaló | 6 |
| 16442 | instalado | 6 |
| 16443 | inspiran | 6 |
| 16444 | inspiraban | 6 |
| 16445 | insisto | 6 |
| 16446 | insinuante | 6 |
| 16447 | insignia | 6 |
| 16448 | insensata | 6 |
| 16449 | insano | 6 |
| 16450 | insaciable | 6 |
| 16451 | inquirir | 6 |
| 16452 | inquebrantable | 6 |
| 16453 | inmundicias | 6 |
| 16454 | inminente | 6 |
| 16455 | inglesas | 6 |
| 16456 | ingeniosas | 6 |
| 16457 | ingalaterra | 6 |
| 16458 | infundió | 6 |
| 16459 | infortunios | 6 |
| 16460 | infortunio | 6 |
| 16461 | inflexiones | 6 |
| 16462 | inflexible | 6 |
| 16463 | indolencia | 6 |
| 16464 | individual | 6 |
| 16465 | indispensablemente | 6 |
| 16466 | indiscreta | 6 |
| 16467 | indirectas | 6 |
| 16468 | indignidad | 6 |
| 16469 | indianos | 6 |
| 16470 | india | 6 |
| 16471 | indefinible | 6 |
| 16472 | inconuenientes | 6 |
| 16473 | incontrastable | 6 |
| 16474 | inconstantes | 6 |
| 16475 | inconsolable | 6 |
| 16476 | incomprensibles | 6 |
| 16477 | incomodada | 6 |
| 16478 | incidentes | 6 |
| 16479 | impunemente | 6 |
| 16480 | impulsado | 6 |
| 16481 | imprudentes | 6 |
| 16482 | improvisa | 6 |
| 16483 | impresor | 6 |
| 16484 | imperfecto | 6 |
| 16485 | impedimento | 6 |
| 16486 | impacientaba | 6 |
| 16487 | imitador | 6 |
| 16488 | imaginarios | 6 |
| 16489 | imaginaria | 6 |
| 16490 | iluminó | 6 |
| 16491 | iluminar | 6 |
| 16492 | ilumina | 6 |
| 16493 | il | 6 |
| 16494 | ignoras | 6 |
| 16495 | idealista | 6 |
| 16496 | idealidad | 6 |
| 16497 | iconoclasta | 6 |
| 16498 | iceta | 6 |
| 16499 | íbase | 6 |
| 16500 | huso | 6 |
| 16501 | hurtos | 6 |
| 16502 | hurtó | 6 |
| 16503 | humorismo | 6 |
| 16504 | humores | 6 |
| 16505 | humorado | 6 |
| 16506 | humilla | 6 |
| 16507 | hortera | 6 |
| 16508 | horrorizaba | 6 |
| 16509 | hornachuelos | 6 |
| 16510 | honrrado | 6 |
| 16511 | honre | 6 |
| 16512 | homicidio | 6 |
| 16513 | hize | 6 |
| 16514 | históricas | 6 |
| 16515 | hipótesis | 6 |
| 16516 | hinchazón | 6 |
| 16517 | hileras | 6 |
| 16518 | higiénico | 6 |
| 16519 | hicimos | 6 |
| 16520 | hi | 6 |
| 16521 | herradura | 6 |
| 16522 | hernández | 6 |
| 16523 | herejías | 6 |
| 16524 | herejía | 6 |
| 16525 | heredar | 6 |
| 16526 | heredades | 6 |
| 16527 | hele | 6 |
| 16528 | héctor | 6 |
| 16529 | hebilla | 6 |
| 16530 | hara | 6 |
| 16531 | hanme | 6 |
| 16532 | hallóse | 6 |
| 16533 | hallaros | 6 |
| 16534 | hallares | 6 |
| 16535 | haceros | 6 |
| 16536 | hacendosa | 6 |
| 16537 | hablarse | 6 |
| 16538 | hablarme | 6 |
| 16539 | hablábamos | 6 |
| 16540 | habedes | 6 |
| 16541 | gustosa | 6 |
| 16542 | gustará | 6 |
| 16543 | guisados | 6 |
| 16544 | guiñaba | 6 |
| 16545 | guiase | 6 |
| 16546 | güevos | 6 |
| 16547 | guasa | 6 |
| 16548 | guardatvos | 6 |
| 16549 | guardaron | 6 |
| 16550 | guardaría | 6 |
| 16551 | guardados | 6 |
| 16552 | guapetona | 6 |
| 16553 | guadaña | 6 |
| 16554 | gruñendo | 6 |
| 16555 | gregüescos | 6 |
| 16556 | gravelinas | 6 |
| 16557 | granujas | 6 |
| 16558 | gradualmente | 6 |
| 16559 | graçias | 6 |
| 16560 | grabado | 6 |
| 16561 | gori | 6 |
| 16562 | golpecitos | 6 |
| 16563 | golpear | 6 |
| 16564 | gola | 6 |
| 16565 | gobernado | 6 |
| 16566 | girar | 6 |
| 16567 | ginesillo | 6 |
| 16568 | gilimón | 6 |
| 16569 | génova | 6 |
| 16570 | gemir | 6 |
| 16571 | gatitos | 6 |
| 16572 | garzón | 6 |
| 16573 | garrotes | 6 |
| 16574 | garrotazos | 6 |
| 16575 | garra | 6 |
| 16576 | garcilaso | 6 |
| 16577 | ganara | 6 |
| 16578 | ganapán | 6 |
| 16579 | galones | 6 |
| 16580 | galeazo | 6 |
| 16581 | galardón | 6 |
| 16582 | galápago | 6 |
| 16583 | galanterías | 6 |
| 16584 | fundadores | 6 |
| 16585 | fugitivos | 6 |
| 16586 | fues | 6 |
| 16587 | fuer | 6 |
| 16588 | frunció | 6 |
| 16589 | frunciendo | 6 |
| 16590 | frisaba | 6 |
| 16591 | friegas | 6 |
| 16592 | fríamente | 6 |
| 16593 | frayres | 6 |
| 16594 | franjas | 6 |
| 16595 | formación | 6 |
| 16596 | forca | 6 |
| 16597 | forado | 6 |
| 16598 | folletos | 6 |
| 16599 | flotaban | 6 |
| 16600 | florido | 6 |
| 16601 | florestas | 6 |
| 16602 | flauta | 6 |
| 16603 | flato | 6 |
| 16604 | flan | 6 |
| 16605 | flamante | 6 |
| 16606 | fize | 6 |
| 16607 | filosofar | 6 |
| 16608 | filial | 6 |
| 16609 | figurines | 6 |
| 16610 | figúrense | 6 |
| 16611 | figurando | 6 |
| 16612 | fierro | 6 |
| 16613 | fidalgo | 6 |
| 16614 | ffiz | 6 |
| 16615 | ffaze | 6 |
| 16616 | fértil | 6 |
| 16617 | fementido | 6 |
| 16618 | faziendo | 6 |
| 16619 | fazían | 6 |
| 16620 | fazia | 6 |
| 16621 | favorito | 6 |
| 16622 | favoreciese | 6 |
| 16623 | favorables | 6 |
| 16624 | fauor | 6 |
| 16625 | fatuos | 6 |
| 16626 | fatuidad | 6 |
| 16627 | fasen | 6 |
| 16628 | fas | 6 |
| 16629 | farsantes | 6 |
| 16630 | faro | 6 |
| 16631 | fantásticas | 6 |
| 16632 | fanáticos | 6 |
| 16633 | faltarle | 6 |
| 16634 | faltare | 6 |
| 16635 | fallarás | 6 |
| 16636 | fallado | 6 |
| 16637 | fados | 6 |
| 16638 | faciones | 6 |
| 16639 | facilitar | 6 |
| 16640 | fabricada | 6 |
| 16641 | fablado | 6 |
| 16642 | extremadamente | 6 |
| 16643 | extravío | 6 |
| 16644 | extraviada | 6 |
| 16645 | extienden | 6 |
| 16646 | exteriores | 6 |
| 16647 | exquisitos | 6 |
| 16648 | expuestos | 6 |
| 16649 | expuesta | 6 |
| 16650 | expreso | 6 |
| 16651 | expresa | 6 |
| 16652 | exponer | 6 |
| 16653 | explicarle | 6 |
| 16654 | explicando | 6 |
| 16655 | experto | 6 |
| 16656 | experimento | 6 |
| 16657 | expectativa | 6 |
| 16658 | expansiones | 6 |
| 16659 | existido | 6 |
| 16660 | exhibición | 6 |
| 16661 | exámenes | 6 |
| 16662 | exagerar | 6 |
| 16663 | estrumentos | 6 |
| 16664 | estrepitoso | 6 |
| 16665 | estremecimiento | 6 |
| 16666 | estrechar | 6 |
| 16667 | estrañeza | 6 |
| 16668 | estoque | 6 |
| 16669 | estonçe | 6 |
| 16670 | estó | 6 |
| 16671 | estirando | 6 |
| 16672 | estío | 6 |
| 16673 | estimadas | 6 |
| 16674 | estenso | 6 |
| 16675 | estender | 6 |
| 16676 | estatutos | 6 |
| 16677 | estantes | 6 |
| 16678 | estameña | 6 |
| 16679 | estallaban | 6 |
| 16680 | estades | 6 |
| 16681 | establo | 6 |
| 16682 | estableció | 6 |
| 16683 | establecida | 6 |
| 16684 | establecerse | 6 |
| 16685 | establece | 6 |
| 16686 | esplendores | 6 |
| 16687 | espigas | 6 |
| 16688 | espiar | 6 |
| 16689 | esperarle | 6 |
| 16690 | esperándole | 6 |
| 16691 | espectador | 6 |
| 16692 | esparció | 6 |
| 16693 | esparcidos | 6 |
| 16694 | esparcido | 6 |
| 16695 | espantó | 6 |
| 16696 | espaldar | 6 |
| 16697 | esmeraldas | 6 |
| 16698 | eslabón | 6 |
| 16699 | esferas | 6 |
| 16700 | escuálida | 6 |
| 16701 | escrupulosos | 6 |
| 16702 | escribiré | 6 |
| 16703 | escribiera | 6 |
| 16704 | escriban | 6 |
| 16705 | escrebir | 6 |
| 16706 | escorias | 6 |
| 16707 | escorial | 6 |
| 16708 | esconda | 6 |
| 16709 | escombros | 6 |
| 16710 | escolar | 6 |
| 16711 | escogía | 6 |
| 16712 | escasez | 6 |
| 16713 | escapase | 6 |
| 16714 | escandalosas | 6 |
| 16715 | escalofrío | 6 |
| 16716 | escabeche | 6 |
| 16717 | erutar | 6 |
| 16718 | errada | 6 |
| 16719 | erizo | 6 |
| 16720 | equivocada | 6 |
| 16721 | equidad | 6 |
| 16722 | envolvió | 6 |
| 16723 | envolvían | 6 |
| 16724 | envío | 6 |
| 16725 | envié | 6 |
| 16726 | envidiosa | 6 |
| 16727 | envidio | 6 |
| 16728 | envidiado | 6 |
| 16729 | enviaron | 6 |
| 16730 | envejecido | 6 |
| 16731 | entusiasmarse | 6 |
| 16732 | entres | 6 |
| 16733 | entremeto | 6 |
| 16734 | entrecano | 6 |
| 16735 | entrasen | 6 |
| 16736 | entras | 6 |
| 16737 | entiendas | 6 |
| 16738 | enterrados | 6 |
| 16739 | enterados | 6 |
| 16740 | entenderé | 6 |
| 16741 | entendederas | 6 |
| 16742 | ensimismada | 6 |
| 16743 | enseñé | 6 |
| 16744 | enseñarte | 6 |
| 16745 | enredadera | 6 |
| 16746 | enojóse | 6 |
| 16747 | enojar | 6 |
| 16748 | enlutada | 6 |
| 16749 | enjaulado | 6 |
| 16750 | engendrado | 6 |
| 16751 | engañoso | 6 |
| 16752 | engañes | 6 |
| 16753 | engañe | 6 |
| 16754 | enfermizo | 6 |
| 16755 | enfadosas | 6 |
| 16756 | enfade | 6 |
| 16757 | enfadada | 6 |
| 16758 | enfadaba | 6 |
| 16759 | enérgicamente | 6 |
| 16760 | encontraremos | 6 |
| 16761 | encomendarme | 6 |
| 16762 | encoger | 6 |
| 16763 | encobrir | 6 |
| 16764 | encerrarme | 6 |
| 16765 | encerrándose | 6 |
| 16766 | encendiendo | 6 |
| 16767 | encendían | 6 |
| 16768 | encaró | 6 |
| 16769 | encargaba | 6 |
| 16770 | encarándose | 6 |
| 16771 | encantadas | 6 |
| 16772 | encamisados | 6 |
| 16773 | encaminaron | 6 |
| 16774 | encaminando | 6 |
| 16775 | encaminado | 6 |
| 16776 | encaminadas | 6 |
| 16777 | encaja | 6 |
| 16778 | enbía | 6 |
| 16779 | enamoradas | 6 |
| 16780 | empuñó | 6 |
| 16781 | empuñaba | 6 |
| 16782 | empujando | 6 |
| 16783 | emplea | 6 |
| 16784 | empinada | 6 |
| 16785 | emperatrices | 6 |
| 16786 | empeños | 6 |
| 16787 | empeñadas | 6 |
| 16788 | empeñada | 6 |
| 16789 | empedernido | 6 |
| 16790 | empaque | 6 |
| 16791 | empapado | 6 |
| 16792 | eminencia | 6 |
| 16793 | emienda | 6 |
| 16794 | embustera | 6 |
| 16795 | embudo | 6 |
| 16796 | embriagado | 6 |
| 16797 | embrazó | 6 |
| 16798 | embobado | 6 |
| 16799 | emblema | 6 |
| 16800 | embelesamiento | 6 |
| 16801 | embebecido | 6 |
| 16802 | embarcar | 6 |
| 16803 | embarazo | 6 |
| 16804 | elizondo | 6 |
| 16805 | elevación | 6 |
| 16806 | elegía | 6 |
| 16807 | electricidad | 6 |
| 16808 | electoral | 6 |
| 16809 | ejecutoria | 6 |
| 16810 | educadas | 6 |
| 16811 | educada | 6 |
| 16812 | económicas | 6 |
| 16813 | eclesiásticos | 6 |
| 16814 | echará | 6 |
| 16815 | duraron | 6 |
| 16816 | durado | 6 |
| 16817 | dulcísimos | 6 |
| 16818 | dulcísimo | 6 |
| 16819 | duchas | 6 |
| 16820 | du | 6 |
| 16821 | drogas | 6 |
| 16822 | dotado | 6 |
| 16823 | dominarse | 6 |
| 16824 | doloridas | 6 |
| 16825 | doctora | 6 |
| 16826 | doblando | 6 |
| 16827 | doblaba | 6 |
| 16828 | divertir | 6 |
| 16829 | divertían | 6 |
| 16830 | diversiones | 6 |
| 16831 | distribuir | 6 |
| 16832 | distinguen | 6 |
| 16833 | distingo | 6 |
| 16834 | disponiendo | 6 |
| 16835 | dispensa | 6 |
| 16836 | disparo | 6 |
| 16837 | disparatada | 6 |
| 16838 | dispararon | 6 |
| 16839 | disparando | 6 |
| 16840 | disimulos | 6 |
| 16841 | disimuló | 6 |
| 16842 | disimulan | 6 |
| 16843 | discutieron | 6 |
| 16844 | discutían | 6 |
| 16845 | discurrido | 6 |
| 16846 | disculpaba | 6 |
| 16847 | disciplinas | 6 |
| 16848 | dirnos | 6 |
| 16849 | dira | 6 |
| 16850 | dimisión | 6 |
| 16851 | dimensiones | 6 |
| 16852 | dilema | 6 |
| 16853 | dilacion | 6 |
| 16854 | digresiones | 6 |
| 16855 | dignamente | 6 |
| 16856 | digestión | 6 |
| 16857 | digades | 6 |
| 16858 | dificultosa | 6 |
| 16859 | diesse | 6 |
| 16860 | dies | 6 |
| 16861 | diéronse | 6 |
| 16862 | dieciséis | 6 |
| 16863 | dictador | 6 |
| 16864 | devotamente | 6 |
| 16865 | determino | 6 |
| 16866 | determinamos | 6 |
| 16867 | deteniendo | 6 |
| 16868 | detenida | 6 |
| 16869 | destruye | 6 |
| 16870 | destrozar | 6 |
| 16871 | destemplado | 6 |
| 16872 | destempladas | 6 |
| 16873 | déste | 6 |
| 16874 | déstas | 6 |
| 16875 | désta | 6 |
| 16876 | dessean | 6 |
| 16877 | despreciaban | 6 |
| 16878 | déspota | 6 |
| 16879 | despojaron | 6 |
| 16880 | desplegaba | 6 |
| 16881 | desperté | 6 |
| 16882 | despejo | 6 |
| 16883 | despedirla | 6 |
| 16884 | despedidas | 6 |
| 16885 | despavorido | 6 |
| 16886 | despachaba | 6 |
| 16887 | despacha | 6 |
| 16888 | desos | 6 |
| 16889 | desordenado | 6 |
| 16890 | desnudarse | 6 |
| 16891 | desnudaba | 6 |
| 16892 | desmesurada | 6 |
| 16893 | desmedido | 6 |
| 16894 | desmaya | 6 |
| 16895 | desirvos | 6 |
| 16896 | deshonesta | 6 |
| 16897 | deshaciendo | 6 |
| 16898 | deshacerse | 6 |
| 16899 | desembarcar | 6 |
| 16900 | deseara | 6 |
| 16901 | descuelga | 6 |
| 16902 | descubrirme | 6 |
| 16903 | descubrirle | 6 |
| 16904 | descubrimos | 6 |
| 16905 | descubren | 6 |
| 16906 | descontentos | 6 |
| 16907 | desconcertado | 6 |
| 16908 | descomponía | 6 |
| 16909 | descansando | 6 |
| 16910 | descaminado | 6 |
| 16911 | descalzas | 6 |
| 16912 | desairar | 6 |
| 16913 | desagradecida | 6 |
| 16914 | desaforado | 6 |
| 16915 | desafiaba | 6 |
| 16916 | derribando | 6 |
| 16917 | derribada | 6 |
| 16918 | derrame | 6 |
| 16919 | derramaba | 6 |
| 16920 | depositó | 6 |
| 16921 | depare | 6 |
| 16922 | denuestos | 6 |
| 16923 | dentera | 6 |
| 16924 | densa | 6 |
| 16925 | demonches | 6 |
| 16926 | demandador | 6 |
| 16927 | deliraba | 6 |
| 16928 | deleitar | 6 |
| 16929 | déjela | 6 |
| 16930 | dejarnos | 6 |
| 16931 | dejarlas | 6 |
| 16932 | defuera | 6 |
| 16933 | deforme | 6 |
| 16934 | definitiva | 6 |
| 16935 | defenderle | 6 |
| 16936 | decorosa | 6 |
| 16937 | declive | 6 |
| 16938 | declaraban | 6 |
| 16939 | decisivo | 6 |
| 16940 | decirnos | 6 |
| 16941 | decille | 6 |
| 16942 | decida | 6 |
| 16943 | dechado | 6 |
| 16944 | debilitado | 6 |
| 16945 | debilitada | 6 |
| 16946 | debidas | 6 |
| 16947 | debías | 6 |
| 16948 | dart | 6 |
| 16949 | dario | 6 |
| 16950 | darín | 6 |
| 16951 | daqui | 6 |
| 16952 | dañoso | 6 |
| 16953 | dañada | 6 |
| 16954 | daniela | 6 |
| 16955 | dagas | 6 |
| 16956 | curo | 6 |
| 16957 | curarme | 6 |
| 16958 | curación | 6 |
| 16959 | cumplían | 6 |
| 16960 | cumplan | 6 |
| 16961 | cumbres | 6 |
| 16962 | cultivo | 6 |
| 16963 | cultivar | 6 |
| 16964 | cultivaba | 6 |
| 16965 | culpados | 6 |
| 16966 | culminante | 6 |
| 16967 | cuidarle | 6 |
| 16968 | cuenca | 6 |
| 16969 | cubrirse | 6 |
| 16970 | cubo | 6 |
| 16971 | cuarteles | 6 |
| 16972 | cuantito | 6 |
| 16973 | cualidad | 6 |
| 16974 | cuajados | 6 |
| 16975 | cuajada | 6 |
| 16976 | cuadras | 6 |
| 16977 | cruza | 6 |
| 16978 | cristianar | 6 |
| 16979 | crezca | 6 |
| 16980 | creíamos | 6 |
| 16981 | créete | 6 |
| 16982 | créeme | 6 |
| 16983 | creed | 6 |
| 16984 | credo | 6 |
| 16985 | credencial | 6 |
| 16986 | crear | 6 |
| 16987 | creado | 6 |
| 16988 | costra | 6 |
| 16989 | cossa | 6 |
| 16990 | cosita | 6 |
| 16991 | cosido | 6 |
| 16992 | cortejo | 6 |
| 16993 | cortaplumas | 6 |
| 16994 | cortan | 6 |
| 16995 | cortados | 6 |
| 16996 | corso | 6 |
| 16997 | corretaje | 6 |
| 16998 | correspondiendo | 6 |
| 16999 | correspondencias | 6 |
| 17000 | corregir | 6 |
| 17001 | correcto | 6 |
| 17002 | corporales | 6 |
| 17003 | coronista | 6 |
| 17004 | córdova | 6 |
| 17005 | cordobán | 6 |
| 17006 | cordeles | 6 |
| 17007 | corbatas | 6 |
| 17008 | corazas | 6 |
| 17009 | coraza | 6 |
| 17010 | convidaban | 6 |
| 17011 | convertidos | 6 |
| 17012 | convenio | 6 |
| 17013 | convencional | 6 |
| 17014 | conuiene | 6 |
| 17015 | controversia | 6 |
| 17016 | contribuir | 6 |
| 17017 | contribuciones | 6 |
| 17018 | contrarias | 6 |
| 17019 | contorno | 6 |
| 17020 | contiguo | 6 |
| 17021 | contestarle | 6 |
| 17022 | contestando | 6 |
| 17023 | contesçe | 6 |
| 17024 | contentísima | 6 |
| 17025 | contenerle | 6 |
| 17026 | contender | 6 |
| 17027 | contemplo | 6 |
| 17028 | contarla | 6 |
| 17029 | contará | 6 |
| 17030 | contabilidad | 6 |
| 17031 | consuma | 6 |
| 17032 | cónsul | 6 |
| 17033 | consuele | 6 |
| 17034 | construido | 6 |
| 17035 | constituyen | 6 |
| 17036 | constituían | 6 |
| 17037 | constituía | 6 |
| 17038 | consternada | 6 |
| 17039 | considerada | 6 |
| 17040 | conservan | 6 |
| 17041 | consejeros | 6 |
| 17042 | consagraba | 6 |
| 17043 | conplir | 6 |
| 17044 | conplida | 6 |
| 17045 | conpañía | 6 |
| 17046 | conozcan | 6 |
| 17047 | conocerte | 6 |
| 17048 | conocería | 6 |
| 17049 | conocerán | 6 |
| 17050 | conmovida | 6 |
| 17051 | conmiseración | 6 |
| 17052 | congojas | 6 |
| 17053 | confusamente | 6 |
| 17054 | confitería | 6 |
| 17055 | confirmo | 6 |
| 17056 | confiando | 6 |
| 17057 | confiados | 6 |
| 17058 | confesando | 6 |
| 17059 | conducidos | 6 |
| 17060 | conducida | 6 |
| 17061 | condicion | 6 |
| 17062 | concurrencia | 6 |
| 17063 | concordancia | 6 |
| 17064 | concluyo | 6 |
| 17065 | concluya | 6 |
| 17066 | concibe | 6 |
| 17067 | concertados | 6 |
| 17068 | concedió | 6 |
| 17069 | concediera | 6 |
| 17070 | concedía | 6 |
| 17071 | concebir | 6 |
| 17072 | concebía | 6 |
| 17073 | comunicativo | 6 |
| 17074 | comunica | 6 |
| 17075 | comprometía | 6 |
| 17076 | comprometer | 6 |
| 17077 | comprarle | 6 |
| 17078 | componiendo | 6 |
| 17079 | complot | 6 |
| 17080 | completar | 6 |
| 17081 | compendio | 6 |
| 17082 | comparando | 6 |
| 17083 | comparacion | 6 |
| 17084 | companero | 6 |
| 17085 | cómodamente | 6 |
| 17086 | cometidos | 6 |
| 17087 | cometía | 6 |
| 17088 | comeré | 6 |
| 17089 | comedimientos | 6 |
| 17090 | comadrón | 6 |
| 17091 | cóm | 6 |
| 17092 | coloso | 6 |
| 17093 | coloradas | 6 |
| 17094 | colondres | 6 |
| 17095 | colina | 6 |
| 17096 | colgaduras | 6 |
| 17097 | colega | 6 |
| 17098 | col | 6 |
| 17099 | coincidencia | 6 |
| 17100 | cohibida | 6 |
| 17101 | cohete | 6 |
| 17102 | cognac | 6 |
| 17103 | cogerlo | 6 |
| 17104 | cocidas | 6 |
| 17105 | cocía | 6 |
| 17106 | cochinos | 6 |
| 17107 | cloelia | 6 |
| 17108 | clerigalla | 6 |
| 17109 | clemente | 6 |
| 17110 | clavijo | 6 |
| 17111 | clave | 6 |
| 17112 | clavaban | 6 |
| 17113 | clareaba | 6 |
| 17114 | cisniega | 6 |
| 17115 | cisneros | 6 |
| 17116 | circular | 6 |
| 17117 | cinto | 6 |
| 17118 | cínico | 6 |
| 17119 | cierran | 6 |
| 17120 | ciegas | 6 |
| 17121 | chupando | 6 |
| 17122 | chorizos | 6 |
| 17123 | chirrido | 6 |
| 17124 | chipre | 6 |
| 17125 | chillar | 6 |
| 17126 | chicuela | 6 |
| 17127 | charol | 6 |
| 17128 | charlaban | 6 |
| 17129 | chanzas | 6 |
| 17130 | champagne | 6 |
| 17131 | chacota | 6 |
| 17132 | cesante | 6 |
| 17133 | cerillas | 6 |
| 17134 | cerilla | 6 |
| 17135 | ceres | 6 |
| 17136 | cerbatana | 6 |
| 17137 | centros | 6 |
| 17138 | céntimo | 6 |
| 17139 | centenares | 6 |
| 17140 | centellas | 6 |
| 17141 | celeridad | 6 |
| 17142 | ceguedad | 6 |
| 17143 | cebollas | 6 |
| 17144 | cazaba | 6 |
| 17145 | cayo | 6 |
| 17146 | cayeran | 6 |
| 17147 | cavidad | 6 |
| 17148 | cavernas | 6 |
| 17149 | causara | 6 |
| 17150 | caudaloso | 6 |
| 17151 | cauallo | 6 |
| 17152 | catequistas | 6 |
| 17153 | catedrales | 6 |
| 17154 | castigados | 6 |
| 17155 | castaña | 6 |
| 17156 | cassar | 6 |
| 17157 | casita | 6 |
| 17158 | casillas | 6 |
| 17159 | casilla | 6 |
| 17160 | cascarón | 6 |
| 17161 | casamos | 6 |
| 17162 | carteles | 6 |
| 17163 | cartel | 6 |
| 17164 | cartapacios | 6 |
| 17165 | cartapacio | 6 |
| 17166 | carreteras | 6 |
| 17167 | carpintero | 6 |
| 17168 | carnicería | 6 |
| 17169 | carmín | 6 |
| 17170 | carino | 6 |
| 17171 | cárdenas | 6 |
| 17172 | carcomida | 6 |
| 17173 | carca | 6 |
| 17174 | caravino | 6 |
| 17175 | caramelos | 6 |
| 17176 | característica | 6 |
| 17177 | caprichosa | 6 |
| 17178 | capón | 6 |
| 17179 | capirotes | 6 |
| 17180 | capellanías | 6 |
| 17181 | caño | 6 |
| 17182 | cañada | 6 |
| 17183 | cantinela | 6 |
| 17184 | cantero | 6 |
| 17185 | cantera | 6 |
| 17186 | cantase | 6 |
| 17187 | canséis | 6 |
| 17188 | canse | 6 |
| 17189 | cánovas | 6 |
| 17190 | canes | 6 |
| 17191 | candidato | 6 |
| 17192 | canarios | 6 |
| 17193 | campiña | 6 |
| 17194 | camorra | 6 |
| 17195 | cambiando | 6 |
| 17196 | cámaras | 6 |
| 17197 | calzonazos | 6 |
| 17198 | calvas | 6 |
| 17199 | callen | 6 |
| 17200 | callejones | 6 |
| 17201 | callase | 6 |
| 17202 | callandito | 6 |
| 17203 | calladita | 6 |
| 17204 | calibre | 6 |
| 17205 | calendario | 6 |
| 17206 | calderilla | 6 |
| 17207 | calderas | 6 |
| 17208 | caldera | 6 |
| 17209 | calatrava | 6 |
| 17210 | calada | 6 |
| 17211 | cacharros | 6 |
| 17212 | cabrito | 6 |
| 17213 | cabdal | 6 |
| 17214 | cabalgaduras | 6 |
| 17215 | busquemos | 6 |
| 17216 | buscón | 6 |
| 17217 | buscarse | 6 |
| 17218 | buscaron | 6 |
| 17219 | buscándole | 6 |
| 17220 | burras | 6 |
| 17221 | burladores | 6 |
| 17222 | bunita | 6 |
| 17223 | bulliciosos | 6 |
| 17224 | bufanda | 6 |
| 17225 | buenaventura | 6 |
| 17226 | bueltas | 6 |
| 17227 | bucólica | 6 |
| 17228 | broquel | 6 |
| 17229 | brazas | 6 |
| 17230 | brasa | 6 |
| 17231 | bramaba | 6 |
| 17232 | boua | 6 |
| 17233 | botes | 6 |
| 17234 | bostezos | 6 |
| 17235 | bostezo | 6 |
| 17236 | bostezar | 6 |
| 17237 | borrica | 6 |
| 17238 | bonísima | 6 |
| 17239 | bonilla | 6 |
| 17240 | bombo | 6 |
| 17241 | bombas | 6 |
| 17242 | boj | 6 |
| 17243 | bogar | 6 |
| 17244 | bodegones | 6 |
| 17245 | bochorno | 6 |
| 17246 | bocací | 6 |
| 17247 | bloque | 6 |
| 17248 | blanquecino | 6 |
| 17249 | blanquecina | 6 |
| 17250 | blanduras | 6 |
| 17251 | bizco | 6 |
| 17252 | bizarra | 6 |
| 17253 | biuir | 6 |
| 17254 | berzas | 6 |
| 17255 | bermejos | 6 |
| 17256 | bellísima | 6 |
| 17257 | bebieron | 6 |
| 17258 | bayetas | 6 |
| 17259 | batido | 6 |
| 17260 | baterías | 6 |
| 17261 | batallón | 6 |
| 17262 | batacazo | 6 |
| 17263 | bastimento | 6 |
| 17264 | bastara | 6 |
| 17265 | barrote | 6 |
| 17266 | barriendo | 6 |
| 17267 | barricadas | 6 |
| 17268 | barría | 6 |
| 17269 | barranco | 6 |
| 17270 | barlovento | 6 |
| 17271 | baratura | 6 |
| 17272 | baratos | 6 |
| 17273 | barandilla | 6 |
| 17274 | bañado | 6 |
| 17275 | banquero | 6 |
| 17276 | bandido | 6 |
| 17277 | baldosines | 6 |
| 17278 | balandra | 6 |
| 17279 | bajón | 6 |
| 17280 | bajamed | 6 |
| 17281 | baixo | 6 |
| 17282 | bailarinas | 6 |
| 17283 | badajo | 6 |
| 17284 | babel | 6 |
| 17285 | azufre | 6 |
| 17286 | azotando | 6 |
| 17287 | azeyte | 6 |
| 17288 | azahares | 6 |
| 17289 | azada | 6 |
| 17290 | ayuso | 6 |
| 17291 | ayún | 6 |
| 17292 | ayudara | 6 |
| 17293 | ayudando | 6 |
| 17294 | ayudaban | 6 |
| 17295 | ayrada | 6 |
| 17296 | avya | 6 |
| 17297 | avrá | 6 |
| 17298 | avisase | 6 |
| 17299 | ávila | 6 |
| 17300 | avían | 6 |
| 17301 | aversión | 6 |
| 17302 | averiguaciones | 6 |
| 17303 | avergonzaba | 6 |
| 17304 | aved | 6 |
| 17305 | avanzados | 6 |
| 17306 | autos | 6 |
| 17307 | ausentarse | 6 |
| 17308 | aumentando | 6 |
| 17309 | aumentan | 6 |
| 17310 | audaces | 6 |
| 17311 | atropello | 6 |
| 17312 | atroces | 6 |
| 17313 | atrio | 6 |
| 17314 | atribuye | 6 |
| 17315 | atrevidas | 6 |
| 17316 | atravesaron | 6 |
| 17317 | atravesada | 6 |
| 17318 | atras | 6 |
| 17319 | atrae | 6 |
| 17320 | átomo | 6 |
| 17321 | ateos | 6 |
| 17322 | atentas | 6 |
| 17323 | ataron | 6 |
| 17324 | atañe | 6 |
| 17325 | atando | 6 |
| 17326 | atambores | 6 |
| 17327 | atambor | 6 |
| 17328 | atacado | 6 |
| 17329 | atacaba | 6 |
| 17330 | ataca | 6 |
| 17331 | asustes | 6 |
| 17332 | asustarse | 6 |
| 17333 | astucias | 6 |
| 17334 | astorga | 6 |
| 17335 | asquerosas | 6 |
| 17336 | aspiración | 6 |
| 17337 | aspectos | 6 |
| 17338 | asomo | 6 |
| 17339 | asombroso | 6 |
| 17340 | asombrosa | 6 |
| 17341 | asombra | 6 |
| 17342 | asomaron | 6 |
| 17343 | asomando | 6 |
| 17344 | asomado | 6 |
| 17345 | asmodeo | 6 |
| 17346 | asistió | 6 |
| 17347 | asistenta | 6 |
| 17348 | asirle | 6 |
| 17349 | asienta | 6 |
| 17350 | asesor | 6 |
| 17351 | asesinos | 6 |
| 17352 | asentar | 6 |
| 17353 | asentada | 6 |
| 17354 | asendereado | 6 |
| 17355 | asegurándole | 6 |
| 17356 | asechanzas | 6 |
| 17357 | ascua | 6 |
| 17358 | asadores | 6 |
| 17359 | asado | 6 |
| 17360 | artísticas | 6 |
| 17361 | artificiosa | 6 |
| 17362 | artificios | 6 |
| 17363 | art | 6 |
| 17364 | arsénico | 6 |
| 17365 | arroyuelos | 6 |
| 17366 | arrostrar | 6 |
| 17367 | arrojase | 6 |
| 17368 | arrodillada | 6 |
| 17369 | arrimarse | 6 |
| 17370 | arrepiente | 6 |
| 17371 | arreglarlo | 6 |
| 17372 | arreglaré | 6 |
| 17373 | arreglada | 6 |
| 17374 | arrebatada | 6 |
| 17375 | arrastraban | 6 |
| 17376 | arrancaron | 6 |
| 17377 | aromas | 6 |
| 17378 | aro | 6 |
| 17379 | armónica | 6 |
| 17380 | armería | 6 |
| 17381 | armadura | 6 |
| 17382 | aritmética | 6 |
| 17383 | argos | 6 |
| 17384 | argonauta | 6 |
| 17385 | argamasilla | 6 |
| 17386 | arduo | 6 |
| 17387 | ardua | 6 |
| 17388 | ardit | 6 |
| 17389 | ardid | 6 |
| 17390 | arcángel | 6 |
| 17391 | arcadia | 6 |
| 17392 | apurar | 6 |
| 17393 | aprovechase | 6 |
| 17394 | aprouechar | 6 |
| 17395 | aprouecha | 6 |
| 17396 | apresurándose | 6 |
| 17397 | aprendiz | 6 |
| 17398 | aprenden | 6 |
| 17399 | apreciando | 6 |
| 17400 | aplicando | 6 |
| 17401 | aplaudía | 6 |
| 17402 | apiñados | 6 |
| 17403 | apeóse | 6 |
| 17404 | apelar | 6 |
| 17405 | apatía | 6 |
| 17406 | apasionados | 6 |
| 17407 | apasionada | 6 |
| 17408 | apartarle | 6 |
| 17409 | aparecen | 6 |
| 17410 | apalear | 6 |
| 17411 | apagar | 6 |
| 17412 | apacibles | 6 |
| 17413 | añadido | 6 |
| 17414 | añade | 6 |
| 17415 | anunciarse | 6 |
| 17416 | antoje | 6 |
| 17417 | ansioso | 6 |
| 17418 | ansiaba | 6 |
| 17419 | anochecía | 6 |
| 17420 | animándose | 6 |
| 17421 | animalito | 6 |
| 17422 | animados | 6 |
| 17423 | angeles | 6 |
| 17424 | anémico | 6 |
| 17425 | anejas | 6 |
| 17426 | andavan | 6 |
| 17427 | andadura | 6 |
| 17428 | ancianas | 6 |
| 17429 | amparar | 6 |
| 17430 | amistoso | 6 |
| 17431 | américas | 6 |
| 17432 | amenazado | 6 |
| 17433 | ambiciones | 6 |
| 17434 | amarillento | 6 |
| 17435 | amarillenta | 6 |
| 17436 | amaneciese | 6 |
| 17437 | amanecerá | 6 |
| 17438 | amalia | 6 |
| 17439 | amaban | 6 |
| 17440 | alzate | 6 |
| 17441 | alzarse | 6 |
| 17442 | alzacuello | 6 |
| 17443 | alvarez | 6 |
| 17444 | alumbrada | 6 |
| 17445 | alude | 6 |
| 17446 | altísimo | 6 |
| 17447 | alteró | 6 |
| 17448 | alterado | 6 |
| 17449 | alpargatas | 6 |
| 17450 | almorzaba | 6 |
| 17451 | almíbar | 6 |
| 17452 | almejas | 6 |
| 17453 | allegados | 6 |
| 17454 | alimentación | 6 |
| 17455 | algund | 6 |
| 17456 | algarabía | 6 |
| 17457 | alemanes | 6 |
| 17458 | alejar | 6 |
| 17459 | aldeanas | 6 |
| 17460 | alcahuete | 6 |
| 17461 | albert | 6 |
| 17462 | albañil | 6 |
| 17463 | alarmantes | 6 |
| 17464 | alargar | 6 |
| 17465 | alarga | 6 |
| 17466 | alano | 6 |
| 17467 | alabes | 6 |
| 17468 | alabe | 6 |
| 17469 | ahogó | 6 |
| 17470 | ahogando | 6 |
| 17471 | ahogado | 6 |
| 17472 | agudísimo | 6 |
| 17473 | agudas | 6 |
| 17474 | agraz | 6 |
| 17475 | agradó | 6 |
| 17476 | agotado | 6 |
| 17477 | agitada | 6 |
| 17478 | ágiles | 6 |
| 17479 | agarrándose | 6 |
| 17480 | agarrada | 6 |
| 17481 | afrontar | 6 |
| 17482 | afirmo | 6 |
| 17483 | afirmaciones | 6 |
| 17484 | afeaba | 6 |
| 17485 | advirtieron | 6 |
| 17486 | adversidades | 6 |
| 17487 | adúlteros | 6 |
| 17488 | aduar | 6 |
| 17489 | adornó | 6 |
| 17490 | adolescencia | 6 |
| 17491 | admiten | 6 |
| 17492 | admire | 6 |
| 17493 | admirarse | 6 |
| 17494 | adivina | 6 |
| 17495 | adelfas | 6 |
| 17496 | adelantados | 6 |
| 17497 | acusaciones | 6 |
| 17498 | acusaban | 6 |
| 17499 | acuesta | 6 |
| 17500 | acuerdan | 6 |
| 17501 | actualmente | 6 |
| 17502 | acostaron | 6 |
| 17503 | acordes | 6 |
| 17504 | acorde | 6 |
| 17505 | aconsejó | 6 |
| 17506 | aconsejarle | 6 |
| 17507 | acompañan | 6 |
| 17508 | acometía | 6 |
| 17509 | acoger | 6 |
| 17510 | acobardado | 6 |
| 17511 | acis | 6 |
| 17512 | achuchón | 6 |
| 17513 | acertare | 6 |
| 17514 | acepta | 6 |
| 17515 | acelerada | 6 |
| 17516 | acariciar | 6 |
| 17517 | acaesçe | 6 |
| 17518 | academias | 6 |
| 17519 | acad | 6 |
| 17520 | acabarse | 6 |
| 17521 | acabaría | 6 |
| 17522 | acabarás | 6 |
| 17523 | abundaba | 6 |
| 17524 | absolución | 6 |
| 17525 | abriéndose | 6 |
| 17526 | abreviado | 6 |
| 17527 | abrazándose | 6 |
| 17528 | abrazándole | 6 |
| 17529 | abrasó | 6 |
| 17530 | abrasar | 6 |
| 17531 | abrasados | 6 |
| 17532 | abrasada | 6 |
| 17533 | abran | 6 |
| 17534 | aborreciendo | 6 |
| 17535 | abogadillo | 6 |
| 17536 | abogada | 6 |
| 17537 | aberración | 6 |
| 17538 | abate | 6 |
| 17539 | abandona | 6 |
| 17540 | zumaya | 5 |
| 17541 | zapico | 5 |
| 17542 | zapatetas | 5 |
| 17543 | zángano | 5 |
| 17544 | zancajos | 5 |
| 17545 | zag | 5 |
| 17546 | yremos | 5 |
| 17547 | yorando | 5 |
| 17548 | ynfierno | 5 |
| 17549 | yernos | 5 |
| 17550 | yedras | 5 |
| 17551 | yda | 5 |
| 17552 | yangüeses | 5 |
| 17553 | yacen | 5 |
| 17554 | xxviii | 5 |
| 17555 | xxv | 5 |
| 17556 | xxix | 5 |
| 17557 | xxiii | 5 |
| 17558 | weigert | 5 |
| 17559 | wals | 5 |
| 17560 | vyeres | 5 |
| 17561 | vyanda | 5 |
| 17562 | vus | 5 |
| 17563 | vulto | 5 |
| 17564 | vuelas | 5 |
| 17565 | volviéndome | 5 |
| 17566 | voluble | 5 |
| 17567 | volteretas | 5 |
| 17568 | volantes | 5 |
| 17569 | vobis | 5 |
| 17570 | vo | 5 |
| 17571 | vivirás | 5 |
| 17572 | vivíamos | 5 |
| 17573 | viveros | 5 |
| 17574 | vivaracho | 5 |
| 17575 | vistosa | 5 |
| 17576 | vistieron | 5 |
| 17577 | vislumbres | 5 |
| 17578 | visitacion | 5 |
| 17579 | virtuosas | 5 |
| 17580 | viril | 5 |
| 17581 | virar | 5 |
| 17582 | vira | 5 |
| 17583 | violado | 5 |
| 17584 | vínose | 5 |
| 17585 | vime | 5 |
| 17586 | villanas | 5 |
| 17587 | villaamil | 5 |
| 17588 | vigoroso | 5 |
| 17589 | vigilante | 5 |
| 17590 | vigilaba | 5 |
| 17591 | vierte | 5 |
| 17592 | vid | 5 |
| 17593 | vicisitudes | 5 |
| 17594 | viandas | 5 |
| 17595 | viana | 5 |
| 17596 | viajante | 5 |
| 17597 | vezinas | 5 |
| 17598 | veyen | 5 |
| 17599 | vestigios | 5 |
| 17600 | vesle | 5 |
| 17601 | vesina | 5 |
| 17602 | vertiente | 5 |
| 17603 | verruga | 5 |
| 17604 | verosimilitud | 5 |
| 17605 | verídica | 5 |
| 17606 | vergonzante | 5 |
| 17607 | verbi | 5 |
| 17608 | veranos | 5 |
| 17609 | venian | 5 |
| 17610 | veníamos | 5 |
| 17611 | vengaba | 5 |
| 17612 | vendida | 5 |
| 17613 | vendemos | 5 |
| 17614 | vendedores | 5 |
| 17615 | venciste | 5 |
| 17616 | vencidas | 5 |
| 17617 | velón | 5 |
| 17618 | veloces | 5 |
| 17619 | velloso | 5 |
| 17620 | veleidades | 5 |
| 17621 | velamen | 5 |
| 17622 | vejiga | 5 |
| 17623 | veíanse | 5 |
| 17624 | vegetar | 5 |
| 17625 | véalo | 5 |
| 17626 | vastísimo | 5 |
| 17627 | vástago | 5 |
| 17628 | variando | 5 |
| 17629 | variados | 5 |
| 17630 | variaba | 5 |
| 17631 | varía | 5 |
| 17632 | vaqueros | 5 |
| 17633 | valiera | 5 |
| 17634 | valdovinos | 5 |
| 17635 | valdés | 5 |
| 17636 | vajilla | 5 |
| 17637 | vagón | 5 |
| 17638 | vagancia | 5 |
| 17639 | vagabundos | 5 |
| 17640 | vaciado | 5 |
| 17641 | usuales | 5 |
| 17642 | usté | 5 |
| 17643 | usados | 5 |
| 17644 | urge | 5 |
| 17645 | urganda | 5 |
| 17646 | urbana | 5 |
| 17647 | universidades | 5 |
| 17648 | unieron | 5 |
| 17649 | ungüentos | 5 |
| 17650 | unanimidad | 5 |
| 17651 | ultramarinos | 5 |
| 17652 | tuvieren | 5 |
| 17653 | tutelar | 5 |
| 17654 | tuteaba | 5 |
| 17655 | tute | 5 |
| 17656 | turquesas | 5 |
| 17657 | turbas | 5 |
| 17658 | turbamulta | 5 |
| 17659 | turbaba | 5 |
| 17660 | tuerce | 5 |
| 17661 | tudo | 5 |
| 17662 | trujesen | 5 |
| 17663 | trueca | 5 |
| 17664 | trovadores | 5 |
| 17665 | trotera | 5 |
| 17666 | tronchos | 5 |
| 17667 | trompetilla | 5 |
| 17668 | trivial | 5 |
| 17669 | triunfó | 5 |
| 17670 | triunfado | 5 |
| 17671 | triquiñuelas | 5 |
| 17672 | tripería | 5 |
| 17673 | trinquete | 5 |
| 17674 | trincheras | 5 |
| 17675 | trillado | 5 |
| 17676 | tricot | 5 |
| 17677 | trepidación | 5 |
| 17678 | trémulos | 5 |
| 17679 | trémulo | 5 |
| 17680 | trebejos | 5 |
| 17681 | trazando | 5 |
| 17682 | trazaba | 5 |
| 17683 | trayéndole | 5 |
| 17684 | traxo | 5 |
| 17685 | traviata | 5 |
| 17686 | trates | 5 |
| 17687 | traten | 5 |
| 17688 | tratasen | 5 |
| 17689 | tratas | 5 |
| 17690 | tratarla | 5 |
| 17691 | trataré | 5 |
| 17692 | tratados | 5 |
| 17693 | trastamara | 5 |
| 17694 | traslada | 5 |
| 17695 | trasbordo | 5 |
| 17696 | traqueteo | 5 |
| 17697 | trapisondas | 5 |
| 17698 | transijo | 5 |
| 17699 | transformó | 5 |
| 17700 | tranquilízate | 5 |
| 17701 | trama | 5 |
| 17702 | traigáis | 5 |
| 17703 | tragó | 5 |
| 17704 | tragedias | 5 |
| 17705 | tragaderas | 5 |
| 17706 | traerla | 5 |
| 17707 | tradujo | 5 |
| 17708 | trabajes | 5 |
| 17709 | trabada | 5 |
| 17710 | tosió | 5 |
| 17711 | tosía | 5 |
| 17712 | toscano | 5 |
| 17713 | tórtolas | 5 |
| 17714 | torneado | 5 |
| 17715 | torne | 5 |
| 17716 | toribio | 5 |
| 17717 | torero | 5 |
| 17718 | toquen | 5 |
| 17719 | tontuela | 5 |
| 17720 | tomare | 5 |
| 17721 | tocasen | 5 |
| 17722 | tocarla | 5 |
| 17723 | tocadas | 5 |
| 17724 | titubear | 5 |
| 17725 | titerero | 5 |
| 17726 | tísica | 5 |
| 17727 | tirso | 5 |
| 17728 | tiraron | 5 |
| 17729 | tirada | 5 |
| 17730 | tiñe | 5 |
| 17731 | tiita | 5 |
| 17732 | tiesos | 5 |
| 17733 | tibias | 5 |
| 17734 | tetrástrofo | 5 |
| 17735 | terso | 5 |
| 17736 | terrorífica | 5 |
| 17737 | terrón | 5 |
| 17738 | terremoto | 5 |
| 17739 | terminantemente | 5 |
| 17740 | terminaban | 5 |
| 17741 | terminaba | 5 |
| 17742 | terca | 5 |
| 17743 | teógenes | 5 |
| 17744 | teñido | 5 |
| 17745 | tenlo | 5 |
| 17746 | teniéndola | 5 |
| 17747 | teníades | 5 |
| 17748 | tenedes | 5 |
| 17749 | tendríamos | 5 |
| 17750 | tendidas | 5 |
| 17751 | tendencias | 5 |
| 17752 | tempranito | 5 |
| 17753 | templa | 5 |
| 17754 | tempestuoso | 5 |
| 17755 | temieron | 5 |
| 17756 | temibles | 5 |
| 17757 | temblaron | 5 |
| 17758 | tejió | 5 |
| 17759 | tejiendo | 5 |
| 17760 | tea | 5 |
| 17761 | tarugo | 5 |
| 17762 | tartera | 5 |
| 17763 | tardase | 5 |
| 17764 | tarambana | 5 |
| 17765 | tapaban | 5 |
| 17766 | tamaños | 5 |
| 17767 | talón | 5 |
| 17768 | tallado | 5 |
| 17769 | talega | 5 |
| 17770 | tahalí | 5 |
| 17771 | tacón | 5 |
| 17772 | tablillas | 5 |
| 17773 | tabernillas | 5 |
| 17774 | sutileza | 5 |
| 17775 | sustentaba | 5 |
| 17776 | sustancias | 5 |
| 17777 | suspira | 5 |
| 17778 | suspendieron | 5 |
| 17779 | suspendiendo | 5 |
| 17780 | suspendidos | 5 |
| 17781 | surtido | 5 |
| 17782 | surgió | 5 |
| 17783 | surcos | 5 |
| 17784 | supremacía | 5 |
| 17785 | supliqué | 5 |
| 17786 | súplicas | 5 |
| 17787 | supiere | 5 |
| 17788 | superficial | 5 |
| 17789 | sumido | 5 |
| 17790 | sumergirse | 5 |
| 17791 | sumergido | 5 |
| 17792 | sumas | 5 |
| 17793 | sujetarle | 5 |
| 17794 | suiza | 5 |
| 17795 | sugirió | 5 |
| 17796 | sufriendo | 5 |
| 17797 | suficientemente | 5 |
| 17798 | suenos | 5 |
| 17799 | suda | 5 |
| 17800 | sucesivos | 5 |
| 17801 | sucedióle | 5 |
| 17802 | sucedidas | 5 |
| 17803 | sucederme | 5 |
| 17804 | subiré | 5 |
| 17805 | sovereign | 5 |
| 17806 | sótanos | 5 |
| 17807 | sospiro | 5 |
| 17808 | sospechoso | 5 |
| 17809 | sospechó | 5 |
| 17810 | sospeche | 5 |
| 17811 | sosiega | 5 |
| 17812 | sosegó | 5 |
| 17813 | sorpresas | 5 |
| 17814 | sorprendidos | 5 |
| 17815 | sordidez | 5 |
| 17816 | soñolienta | 5 |
| 17817 | sonreído | 5 |
| 17818 | sonda | 5 |
| 17819 | sonado | 5 |
| 17820 | sonada | 5 |
| 17821 | someter | 5 |
| 17822 | sombríos | 5 |
| 17823 | solteros | 5 |
| 17824 | solté | 5 |
| 17825 | solomillo | 5 |
| 17826 | soliloquios | 5 |
| 17827 | soliloquio | 5 |
| 17828 | solidez | 5 |
| 17829 | solidaridad | 5 |
| 17830 | solícitos | 5 |
| 17831 | solicitó | 5 |
| 17832 | solicitada | 5 |
| 17833 | solercio | 5 |
| 17834 | solapa | 5 |
| 17835 | sofocar | 5 |
| 17836 | sofocados | 5 |
| 17837 | socorrerle | 5 |
| 17838 | socorra | 5 |
| 17839 | sobresaltado | 5 |
| 17840 | sobres | 5 |
| 17841 | sobrar | 5 |
| 17842 | sobrada | 5 |
| 17843 | sobervio | 5 |
| 17844 | soberanos | 5 |
| 17845 | sobejo | 5 |
| 17846 | situada | 5 |
| 17847 | situaciones | 5 |
| 17848 | sistemas | 5 |
| 17849 | sirvientes | 5 |
| 17850 | sinsabores | 5 |
| 17851 | sinfonía | 5 |
| 17852 | sinalefa | 5 |
| 17853 | simplezas | 5 |
| 17854 | símbolos | 5 |
| 17855 | sillería | 5 |
| 17856 | sigüenza | 5 |
| 17857 | siestas | 5 |
| 17858 | sicut | 5 |
| 17859 | seyendo | 5 |
| 17860 | severamente | 5 |
| 17861 | sesto | 5 |
| 17862 | servimos | 5 |
| 17863 | serviendo | 5 |
| 17864 | serui | 5 |
| 17865 | serte | 5 |
| 17866 | serme | 5 |
| 17867 | serenarse | 5 |
| 17868 | sepultada | 5 |
| 17869 | sepulcros | 5 |
| 17870 | sépase | 5 |
| 17871 | separaron | 5 |
| 17872 | sépalo | 5 |
| 17873 | señuelo | 5 |
| 17874 | señorona | 5 |
| 17875 | señalados | 5 |
| 17876 | sentiste | 5 |
| 17877 | sentís | 5 |
| 17878 | sentenciado | 5 |
| 17879 | sentémonos | 5 |
| 17880 | sensibles | 5 |
| 17881 | senquá | 5 |
| 17882 | senoras | 5 |
| 17883 | séneca | 5 |
| 17884 | senas | 5 |
| 17885 | selviana | 5 |
| 17886 | seguridades | 5 |
| 17887 | seguirá | 5 |
| 17888 | seguid | 5 |
| 17889 | seglares | 5 |
| 17890 | seducido | 5 |
| 17891 | secó | 5 |
| 17892 | sección | 5 |
| 17893 | secándose | 5 |
| 17894 | secando | 5 |
| 17895 | secamente | 5 |
| 17896 | sebo | 5 |
| 17897 | scott | 5 |
| 17898 | sazonada | 5 |
| 17899 | sayones | 5 |
| 17900 | sayal | 5 |
| 17901 | satisfaga | 5 |
| 17902 | satisface | 5 |
| 17903 | sartas | 5 |
| 17904 | santianes | 5 |
| 17905 | sanlúcar | 5 |
| 17906 | sangrías | 5 |
| 17907 | sangría | 5 |
| 17908 | sancta | 5 |
| 17909 | salyó | 5 |
| 17910 | saludarle | 5 |
| 17911 | saludarla | 5 |
| 17912 | saludado | 5 |
| 17913 | salterio | 5 |
| 17914 | saliste | 5 |
| 17915 | saliere | 5 |
| 17916 | salieran | 5 |
| 17917 | saldeoro | 5 |
| 17918 | salarios | 5 |
| 17919 | saint | 5 |
| 17920 | sacudidas | 5 |
| 17921 | sacro | 5 |
| 17922 | sacrílega | 5 |
| 17923 | sacrificar | 5 |
| 17924 | sacrificada | 5 |
| 17925 | sacre | 5 |
| 17926 | sacra | 5 |
| 17927 | saçón | 5 |
| 17928 | sacarlas | 5 |
| 17929 | sacarían | 5 |
| 17930 | sacaran | 5 |
| 17931 | sacándola | 5 |
| 17932 | sácalo | 5 |
| 17933 | sacados | 5 |
| 17934 | sabrosísimo | 5 |
| 17935 | sabras | 5 |
| 17936 | sables | 5 |
| 17937 | sablazo | 5 |
| 17938 | sabidoría | 5 |
| 17939 | sabías | 5 |
| 17940 | rumorcillo | 5 |
| 17941 | rüina | 5 |
| 17942 | ruidosas | 5 |
| 17943 | rufián | 5 |
| 17944 | ruégote | 5 |
| 17945 | rudas | 5 |
| 17946 | ruborizó | 5 |
| 17947 | rua | 5 |
| 17948 | rrudo | 5 |
| 17949 | rromanos | 5 |
| 17950 | rrío | 5 |
| 17951 | rrespondióle | 5 |
| 17952 | rrasones | 5 |
| 17953 | rrana | 5 |
| 17954 | rosellón | 5 |
| 17955 | rosales | 5 |
| 17956 | rosada | 5 |
| 17957 | ropita | 5 |
| 17958 | rondón | 5 |
| 17959 | ron | 5 |
| 17960 | rompería | 5 |
| 17961 | romancero | 5 |
| 17962 | rollizo | 5 |
| 17963 | rolliza | 5 |
| 17964 | rojizo | 5 |
| 17965 | rogóle | 5 |
| 17966 | rogada | 5 |
| 17967 | rodeadas | 5 |
| 17968 | robador | 5 |
| 17969 | robada | 5 |
| 17970 | rito | 5 |
| 17971 | riquísimos | 5 |
| 17972 | riñó | 5 |
| 17973 | riñen | 5 |
| 17974 | rindo | 5 |
| 17975 | rimero | 5 |
| 17976 | rigurosos | 5 |
| 17977 | rígida | 5 |
| 17978 | riéronse | 5 |
| 17979 | ríase | 5 |
| 17980 | rezan | 5 |
| 17981 | revivir | 5 |
| 17982 | reviento | 5 |
| 17983 | reviente | 5 |
| 17984 | reverendos | 5 |
| 17985 | reuniones | 5 |
| 17986 | reunieron | 5 |
| 17987 | reunidas | 5 |
| 17988 | reúnen | 5 |
| 17989 | retumbó | 5 |
| 17990 | retumbar | 5 |
| 17991 | retumbante | 5 |
| 17992 | rétulo | 5 |
| 17993 | retorno | 5 |
| 17994 | retiráronse | 5 |
| 17995 | resuelven | 5 |
| 17996 | restaurar | 5 |
| 17997 | restablecer | 5 |
| 17998 | respondíle | 5 |
| 17999 | responderme | 5 |
| 18000 | respondelle | 5 |
| 18001 | respondas | 5 |
| 18002 | respectivo | 5 |
| 18003 | resonantes | 5 |
| 18004 | resonaba | 5 |
| 18005 | resolverse | 5 |
| 18006 | resoluciones | 5 |
| 18007 | resistiéndose | 5 |
| 18008 | resignarse | 5 |
| 18009 | resentimiento | 5 |
| 18010 | resbalaban | 5 |
| 18011 | resaltar | 5 |
| 18012 | resabio | 5 |
| 18013 | requisitos | 5 |
| 18014 | requerido | 5 |
| 18015 | reputaba | 5 |
| 18016 | repulsivo | 5 |
| 18017 | reproches | 5 |
| 18018 | represente | 5 |
| 18019 | representaron | 5 |
| 18020 | representantes | 5 |
| 18021 | representadas | 5 |
| 18022 | representada | 5 |
| 18023 | representaciones | 5 |
| 18024 | reprendía | 5 |
| 18025 | reprehendido | 5 |
| 18026 | repostería | 5 |
| 18027 | reposaba | 5 |
| 18028 | repliques | 5 |
| 18029 | replico | 5 |
| 18030 | repleta | 5 |
| 18031 | repetida | 5 |
| 18032 | reparan | 5 |
| 18033 | reo | 5 |
| 18034 | reñida | 5 |
| 18035 | renunció | 5 |
| 18036 | renovación | 5 |
| 18037 | renovaban | 5 |
| 18038 | reniego | 5 |
| 18039 | renegaba | 5 |
| 18040 | remolinos | 5 |
| 18041 | remisión | 5 |
| 18042 | remeros | 5 |
| 18043 | remedialla | 5 |
| 18044 | remedando | 5 |
| 18045 | relucientes | 5 |
| 18046 | relojes | 5 |
| 18047 | relajación | 5 |
| 18048 | reir | 5 |
| 18049 | regocijado | 5 |
| 18050 | regocijada | 5 |
| 18051 | registros | 5 |
| 18052 | registrando | 5 |
| 18053 | regalitos | 5 |
| 18054 | regalaron | 5 |
| 18055 | refrigerio | 5 |
| 18056 | reflejaba | 5 |
| 18057 | refleja | 5 |
| 18058 | refinado | 5 |
| 18059 | refinada | 5 |
| 18060 | referencias | 5 |
| 18061 | reducía | 5 |
| 18062 | réditos | 5 |
| 18063 | rédito | 5 |
| 18064 | redil | 5 |
| 18065 | recuesto | 5 |
| 18066 | recua | 5 |
| 18067 | rectos | 5 |
| 18068 | rectificar | 5 |
| 18069 | recreaban | 5 |
| 18070 | recortar | 5 |
| 18071 | recorren | 5 |
| 18072 | reconocían | 5 |
| 18073 | reconocerlo | 5 |
| 18074 | recónditos | 5 |
| 18075 | recomendar | 5 |
| 18076 | recogiese | 5 |
| 18077 | recogen | 5 |
| 18078 | reclamaciones | 5 |
| 18079 | reclamaban | 5 |
| 18080 | recitando | 5 |
| 18081 | recibas | 5 |
| 18082 | rechinar | 5 |
| 18083 | receloso | 5 |
| 18084 | recela | 5 |
| 18085 | recebidas | 5 |
| 18086 | recebía | 5 |
| 18087 | razonar | 5 |
| 18088 | rasgó | 5 |
| 18089 | rasgar | 5 |
| 18090 | rasgados | 5 |
| 18091 | rasgado | 5 |
| 18092 | rascarse | 5 |
| 18093 | rarezas | 5 |
| 18094 | rapiña | 5 |
| 18095 | rapé | 5 |
| 18096 | ranchos | 5 |
| 18097 | ramaje | 5 |
| 18098 | raída | 5 |
| 18099 | raciones | 5 |
| 18100 | racha | 5 |
| 18101 | rabel | 5 |
| 18102 | quitóse | 5 |
| 18103 | quitose | 5 |
| 18104 | quítese | 5 |
| 18105 | quitarnos | 5 |
| 18106 | quitalle | 5 |
| 18107 | quisiesse | 5 |
| 18108 | quisicosa | 5 |
| 18109 | quis | 5 |
| 18110 | quintillas | 5 |
| 18111 | quintañona | 5 |
| 18112 | quincalla | 5 |
| 18113 | química | 5 |
| 18114 | quilla | 5 |
| 18115 | quilates | 5 |
| 18116 | quijano | 5 |
| 18117 | quietos | 5 |
| 18118 | quietecito | 5 |
| 18119 | quietas | 5 |
| 18120 | quid | 5 |
| 18121 | questiones | 5 |
| 18122 | quesieres | 5 |
| 18123 | quesido | 5 |
| 18124 | querras | 5 |
| 18125 | queridísimo | 5 |
| 18126 | queme | 5 |
| 18127 | quemas | 5 |
| 18128 | quejumbroso | 5 |
| 18129 | quejarme | 5 |
| 18130 | quedéme | 5 |
| 18131 | quebrantan | 5 |
| 18132 | quarto | 5 |
| 18133 | quán | 5 |
| 18134 | púsola | 5 |
| 18135 | purificación | 5 |
| 18136 | puñetazos | 5 |
| 18137 | puñado | 5 |
| 18138 | punzante | 5 |
| 18139 | puntiaguda | 5 |
| 18140 | pulpo | 5 |
| 18141 | pullas | 5 |
| 18142 | pulgada | 5 |
| 18143 | pulga | 5 |
| 18144 | puentes | 5 |
| 18145 | puédese | 5 |
| 18146 | pueblecillo | 5 |
| 18147 | pudre | 5 |
| 18148 | publicó | 5 |
| 18149 | publico | 5 |
| 18150 | públicamente | 5 |
| 18151 | publicaciones | 5 |
| 18152 | publicaba | 5 |
| 18153 | pruebo | 5 |
| 18154 | provisional | 5 |
| 18155 | proviene | 5 |
| 18156 | providencial | 5 |
| 18157 | proveídas | 5 |
| 18158 | protesto | 5 |
| 18159 | protegida | 5 |
| 18160 | protegía | 5 |
| 18161 | protectrices | 5 |
| 18162 | prospera | 5 |
| 18163 | prosiguieron | 5 |
| 18164 | prosiguen | 5 |
| 18165 | proseguía | 5 |
| 18166 | propuesta | 5 |
| 18167 | proponemos | 5 |
| 18168 | propone | 5 |
| 18169 | propasaba | 5 |
| 18170 | pronunciadas | 5 |
| 18171 | promontorio | 5 |
| 18172 | prometimientos | 5 |
| 18173 | prometían | 5 |
| 18174 | prométeme | 5 |
| 18175 | prometa | 5 |
| 18176 | prolongaba | 5 |
| 18177 | prohibidos | 5 |
| 18178 | profetizado | 5 |
| 18179 | profetas | 5 |
| 18180 | profanas | 5 |
| 18181 | profanaciones | 5 |
| 18182 | produzca | 5 |
| 18183 | produciendo | 5 |
| 18184 | producida | 5 |
| 18185 | pródiga | 5 |
| 18186 | procuré | 5 |
| 18187 | procuras | 5 |
| 18188 | procuraría | 5 |
| 18189 | procesiones | 5 |
| 18190 | próceres | 5 |
| 18191 | probarle | 5 |
| 18192 | privilegios | 5 |
| 18193 | privar | 5 |
| 18194 | priso | 5 |
| 18195 | principió | 5 |
| 18196 | primorosa | 5 |
| 18197 | primito | 5 |
| 18198 | prevengo | 5 |
| 18199 | pretextando | 5 |
| 18200 | prestos | 5 |
| 18201 | prestaban | 5 |
| 18202 | preseas | 5 |
| 18203 | prepárese | 5 |
| 18204 | preparan | 5 |
| 18205 | prepara | 5 |
| 18206 | preocupada | 5 |
| 18207 | prende | 5 |
| 18208 | premiado | 5 |
| 18209 | prematuro | 5 |
| 18210 | preliminares | 5 |
| 18211 | preferible | 5 |
| 18212 | predominio | 5 |
| 18213 | predicó | 5 |
| 18214 | precoces | 5 |
| 18215 | precisar | 5 |
| 18216 | precipita | 5 |
| 18217 | preciosísimas | 5 |
| 18218 | preciosidades | 5 |
| 18219 | preciados | 5 |
| 18220 | precedido | 5 |
| 18221 | prebendado | 5 |
| 18222 | preámbulo | 5 |
| 18223 | pragmáticas | 5 |
| 18224 | prácticos | 5 |
| 18225 | prácticamente | 5 |
| 18226 | practicaba | 5 |
| 18227 | potente | 5 |
| 18228 | postración | 5 |
| 18229 | positivismo | 5 |
| 18230 | positivamente | 5 |
| 18231 | poseían | 5 |
| 18232 | posaderas | 5 |
| 18233 | portentos | 5 |
| 18234 | porté | 5 |
| 18235 | portante | 5 |
| 18236 | portador | 5 |
| 18237 | porro | 5 |
| 18238 | porra | 5 |
| 18239 | poros | 5 |
| 18240 | porfiando | 5 |
| 18241 | pordiosero | 5 |
| 18242 | popularidad | 5 |
| 18243 | ponzoña | 5 |
| 18244 | pontífice | 5 |
| 18245 | ponme | 5 |
| 18246 | pongáis | 5 |
| 18247 | ponérselo | 5 |
| 18248 | ponérsela | 5 |
| 18249 | ponerlas | 5 |
| 18250 | ponello | 5 |
| 18251 | ponderar | 5 |
| 18252 | pompadour | 5 |
| 18253 | polvorosa | 5 |
| 18254 | polvareda | 5 |
| 18255 | pollino | 5 |
| 18256 | polifemo | 5 |
| 18257 | poéticos | 5 |
| 18258 | podre | 5 |
| 18259 | podiese | 5 |
| 18260 | podenco | 5 |
| 18261 | podáis | 5 |
| 18262 | poblaciones | 5 |
| 18263 | pliegue | 5 |
| 18264 | plebeya | 5 |
| 18265 | plazeme | 5 |
| 18266 | platillos | 5 |
| 18267 | platicar | 5 |
| 18268 | platerías | 5 |
| 18269 | platea | 5 |
| 18270 | planté | 5 |
| 18271 | planetas | 5 |
| 18272 | plaf | 5 |
| 18273 | placera | 5 |
| 18274 | plácemes | 5 |
| 18275 | piratas | 5 |
| 18276 | pintón | 5 |
| 18277 | pintiparada | 5 |
| 18278 | pintas | 5 |
| 18279 | pintaban | 5 |
| 18280 | pillete | 5 |
| 18281 | pillastre | 5 |
| 18282 | pilato | 5 |
| 18283 | pífaro | 5 |
| 18284 | pierdan | 5 |
| 18285 | petulante | 5 |
| 18286 | petitorio | 5 |
| 18287 | pesase | 5 |
| 18288 | pesándome | 5 |
| 18289 | pertrechos | 5 |
| 18290 | persuasiones | 5 |
| 18291 | persuadió | 5 |
| 18292 | perplejo | 5 |
| 18293 | permito | 5 |
| 18294 | permitirá | 5 |
| 18295 | permitiese | 5 |
| 18296 | permiten | 5 |
| 18297 | permitas | 5 |
| 18298 | permanecían | 5 |
| 18299 | peripecias | 5 |
| 18300 | perezosamente | 5 |
| 18301 | perentoria | 5 |
| 18302 | perenne | 5 |
| 18303 | peregrinación | 5 |
| 18304 | perecido | 5 |
| 18305 | perdulario | 5 |
| 18306 | perdonaría | 5 |
| 18307 | perdonara | 5 |
| 18308 | perdizes | 5 |
| 18309 | perdio | 5 |
| 18310 | perdiéndose | 5 |
| 18311 | perdi | 5 |
| 18312 | perderá | 5 |
| 18313 | pepitoria | 5 |
| 18314 | peones | 5 |
| 18315 | penuria | 5 |
| 18316 | penséis | 5 |
| 18317 | pensasen | 5 |
| 18318 | pensadas | 5 |
| 18319 | península | 5 |
| 18320 | penetraban | 5 |
| 18321 | peluquero | 5 |
| 18322 | peleando | 5 |
| 18323 | peinarse | 5 |
| 18324 | peinadora | 5 |
| 18325 | pegues | 5 |
| 18326 | pegarte | 5 |
| 18327 | pegarme | 5 |
| 18328 | pegadas | 5 |
| 18329 | pechuga | 5 |
| 18330 | pe | 5 |
| 18331 | paveses | 5 |
| 18332 | paúl | 5 |
| 18333 | patrones | 5 |
| 18334 | patrocinio | 5 |
| 18335 | patrióticas | 5 |
| 18336 | patriarcal | 5 |
| 18337 | pato | 5 |
| 18338 | pátina | 5 |
| 18339 | pateta | 5 |
| 18340 | pastelera | 5 |
| 18341 | pastas | 5 |
| 18342 | passadas | 5 |
| 18343 | pasóse | 5 |
| 18344 | pasmóse | 5 |
| 18345 | pasmaron | 5 |
| 18346 | pasmados | 5 |
| 18347 | pasee | 5 |
| 18348 | pasamanos | 5 |
| 18349 | participaban | 5 |
| 18350 | participaba | 5 |
| 18351 | parroquial | 5 |
| 18352 | parola | 5 |
| 18353 | parlamento | 5 |
| 18354 | paris | 5 |
| 18355 | pario | 5 |
| 18356 | pareciome | 5 |
| 18357 | pareciesen | 5 |
| 18358 | pareciere | 5 |
| 18359 | parecíame | 5 |
| 18360 | parecerlo | 5 |
| 18361 | parecéis | 5 |
| 18362 | parasismo | 5 |
| 18363 | parase | 5 |
| 18364 | papagayos | 5 |
| 18365 | panteón | 5 |
| 18366 | panteísmo | 5 |
| 18367 | pano | 5 |
| 18368 | panera | 5 |
| 18369 | panderos | 5 |
| 18370 | pandereta | 5 |
| 18371 | pamplinas | 5 |
| 18372 | palpitaciones | 5 |
| 18373 | palmos | 5 |
| 18374 | palmaditas | 5 |
| 18375 | palabrotas | 5 |
| 18376 | pala | 5 |
| 18377 | pajaritos | 5 |
| 18378 | pajarera | 5 |
| 18379 | paices | 5 |
| 18380 | pagos | 5 |
| 18381 | pagarás | 5 |
| 18382 | pagara | 5 |
| 18383 | paganos | 5 |
| 18384 | pagando | 5 |
| 18385 | pagamos | 5 |
| 18386 | pagador | 5 |
| 18387 | oyo | 5 |
| 18388 | oyesen | 5 |
| 18389 | óyeme | 5 |
| 18390 | oyeme | 5 |
| 18391 | otorgo | 5 |
| 18392 | otero | 5 |
| 18393 | otea | 5 |
| 18394 | ostensible | 5 |
| 18395 | osaría | 5 |
| 18396 | osados | 5 |
| 18397 | orza | 5 |
| 18398 | ornato | 5 |
| 18399 | ornamento | 5 |
| 18400 | orígenes | 5 |
| 18401 | organización | 5 |
| 18402 | orgánica | 5 |
| 18403 | orfeo | 5 |
| 18404 | ordinarias | 5 |
| 18405 | orbajosense | 5 |
| 18406 | oportunamente | 5 |
| 18407 | oponga | 5 |
| 18408 | opaco | 5 |
| 18409 | omnipotente | 5 |
| 18410 | omnia | 5 |
| 18411 | olviden | 5 |
| 18412 | olvidé | 5 |
| 18413 | olvidan | 5 |
| 18414 | olvidados | 5 |
| 18415 | olvidaban | 5 |
| 18416 | oliva | 5 |
| 18417 | oliente | 5 |
| 18418 | ojival | 5 |
| 18419 | ojitos | 5 |
| 18420 | ojeada | 5 |
| 18421 | oíste | 5 |
| 18422 | oílla | 5 |
| 18423 | óigame | 5 |
| 18424 | ofreciere | 5 |
| 18425 | ofenderte | 5 |
| 18426 | odoripherus | 5 |
| 18427 | ocurriole | 5 |
| 18428 | ocuparon | 5 |
| 18429 | ocultas | 5 |
| 18430 | ocultaban | 5 |
| 18431 | occidental | 5 |
| 18432 | obtuso | 5 |
| 18433 | obtenido | 5 |
| 18434 | obstinado | 5 |
| 18435 | obstinación | 5 |
| 18436 | obstina | 5 |
| 18437 | observe | 5 |
| 18438 | observaron | 5 |
| 18439 | obsequios | 5 |
| 18440 | obligaban | 5 |
| 18441 | objeción | 5 |
| 18442 | obedezca | 5 |
| 18443 | obedecerle | 5 |
| 18444 | obedecen | 5 |
| 18445 | obdulita | 5 |
| 18446 | núm | 5 |
| 18447 | nublaron | 5 |
| 18448 | noviciado | 5 |
| 18449 | novel | 5 |
| 18450 | nouedad | 5 |
| 18451 | notada | 5 |
| 18452 | nostalgia | 5 |
| 18453 | noroeste | 5 |
| 18454 | nominavito | 5 |
| 18455 | nombro | 5 |
| 18456 | nombran | 5 |
| 18457 | nogales | 5 |
| 18458 | nodriza | 5 |
| 18459 | nocturnos | 5 |
| 18460 | ningunos | 5 |
| 18461 | nimiedades | 5 |
| 18462 | niegas | 5 |
| 18463 | niegan | 5 |
| 18464 | nichos | 5 |
| 18465 | nerón | 5 |
| 18466 | negrura | 5 |
| 18467 | negrito | 5 |
| 18468 | negarme | 5 |
| 18469 | negarle | 5 |
| 18470 | negará | 5 |
| 18471 | negación | 5 |
| 18472 | nazcan | 5 |
| 18473 | navegando | 5 |
| 18474 | nauplia | 5 |
| 18475 | naufragios | 5 |
| 18476 | nativa | 5 |
| 18477 | natal | 5 |
| 18478 | nasçió | 5 |
| 18479 | nascio | 5 |
| 18480 | napoleónica | 5 |
| 18481 | naide | 5 |
| 18482 | naciente | 5 |
| 18483 | nacidas | 5 |
| 18484 | mutuos | 5 |
| 18485 | mutuo | 5 |
| 18486 | mutilado | 5 |
| 18487 | musgo | 5 |
| 18488 | músculo | 5 |
| 18489 | murciélago | 5 |
| 18490 | muñecos | 5 |
| 18491 | mundanas | 5 |
| 18492 | munchas | 5 |
| 18493 | muley | 5 |
| 18494 | mujeronas | 5 |
| 18495 | muevas | 5 |
| 18496 | mueras | 5 |
| 18497 | mudada | 5 |
| 18498 | muceta | 5 |
| 18499 | moviera | 5 |
| 18500 | movidos | 5 |
| 18501 | moverme | 5 |
| 18502 | motín | 5 |
| 18503 | mostrara | 5 |
| 18504 | mostráis | 5 |
| 18505 | mostrábase | 5 |
| 18506 | moryr | 5 |
| 18507 | morito | 5 |
| 18508 | morimos | 5 |
| 18509 | mordaza | 5 |
| 18510 | moralista | 5 |
| 18511 | morados | 5 |
| 18512 | moñas | 5 |
| 18513 | montería | 5 |
| 18514 | montar | 5 |
| 18515 | monstro | 5 |
| 18516 | monjil | 5 |
| 18517 | monísima | 5 |
| 18518 | monarcas | 5 |
| 18519 | molidos | 5 |
| 18520 | moleste | 5 |
| 18521 | molestas | 5 |
| 18522 | molestarle | 5 |
| 18523 | mojar | 5 |
| 18524 | mohína | 5 |
| 18525 | mocosos | 5 |
| 18526 | mixto | 5 |
| 18527 | miraré | 5 |
| 18528 | miramiento | 5 |
| 18529 | mírame | 5 |
| 18530 | miquis | 5 |
| 18531 | minerva | 5 |
| 18532 | mineros | 5 |
| 18533 | milano | 5 |
| 18534 | milagrosamente | 5 |
| 18535 | miiii | 5 |
| 18536 | mienten | 5 |
| 18537 | mezcló | 5 |
| 18538 | metiera | 5 |
| 18539 | metidas | 5 |
| 18540 | metales | 5 |
| 18541 | mesquina | 5 |
| 18542 | meson | 5 |
| 18543 | mesana | 5 |
| 18544 | mero | 5 |
| 18545 | meriendas | 5 |
| 18546 | merezcan | 5 |
| 18547 | merescimiento | 5 |
| 18548 | mereciera | 5 |
| 18549 | merecerlo | 5 |
| 18550 | merecéis | 5 |
| 18551 | mercados | 5 |
| 18552 | mentido | 5 |
| 18553 | menesteroso | 5 |
| 18554 | mena | 5 |
| 18555 | melitona | 5 |
| 18556 | melindroso | 5 |
| 18557 | melindrosa | 5 |
| 18558 | melindre | 5 |
| 18559 | mejorcito | 5 |
| 18560 | mejicano | 5 |
| 18561 | meditado | 5 |
| 18562 | medita | 5 |
| 18563 | medido | 5 |
| 18564 | medico | 5 |
| 18565 | medallas | 5 |
| 18566 | mecheros | 5 |
| 18567 | meaja | 5 |
| 18568 | mazos | 5 |
| 18569 | mazo | 5 |
| 18570 | mayoral | 5 |
| 18571 | matute | 5 |
| 18572 | matrona | 5 |
| 18573 | mates | 5 |
| 18574 | mateo | 5 |
| 18575 | mataduras | 5 |
| 18576 | mataban | 5 |
| 18577 | mástil | 5 |
| 18578 | masón | 5 |
| 18579 | martillos | 5 |
| 18580 | marsella | 5 |
| 18581 | marrullerías | 5 |
| 18582 | marruecos | 5 |
| 18583 | marquetería | 5 |
| 18584 | mármoles | 5 |
| 18585 | mariquita | 5 |
| 18586 | marimorena | 5 |
| 18587 | margarita | 5 |
| 18588 | mareado | 5 |
| 18589 | mareada | 5 |
| 18590 | marcando | 5 |
| 18591 | marauilles | 5 |
| 18592 | maquinaria | 5 |
| 18593 | manzanas | 5 |
| 18594 | manuscritos | 5 |
| 18595 | mantillas | 5 |
| 18596 | mansamente | 5 |
| 18597 | manifestaciones | 5 |
| 18598 | maniático | 5 |
| 18599 | maniática | 5 |
| 18600 | mandóle | 5 |
| 18601 | mandilón | 5 |
| 18602 | mandes | 5 |
| 18603 | mandava | 5 |
| 18604 | mandarlo | 5 |
| 18605 | mandare | 5 |
| 18606 | mandará | 5 |
| 18607 | mandándome | 5 |
| 18608 | mandándole | 5 |
| 18609 | mançebillo | 5 |
| 18610 | manceba | 5 |
| 18611 | mamarrachos | 5 |
| 18612 | malvado | 5 |
| 18613 | maluado | 5 |
| 18614 | maltrate | 5 |
| 18615 | maltratados | 5 |
| 18616 | malísimo | 5 |
| 18617 | maldecido | 5 |
| 18618 | malaventurado | 5 |
| 18619 | maguera | 5 |
| 18620 | magra | 5 |
| 18621 | magnate | 5 |
| 18622 | magistrados | 5 |
| 18623 | madurez | 5 |
| 18624 | madriles | 5 |
| 18625 | macilenta | 5 |
| 18626 | macetas | 5 |
| 18627 | ma | 5 |
| 18628 | lynaje | 5 |
| 18629 | lus | 5 |
| 18630 | lugarteniente | 5 |
| 18631 | lugareño | 5 |
| 18632 | lozanas | 5 |
| 18633 | lonja | 5 |
| 18634 | lograron | 5 |
| 18635 | logra | 5 |
| 18636 | locke | 5 |
| 18637 | localidad | 5 |
| 18638 | loa | 5 |
| 18639 | llueven | 5 |
| 18640 | lloviendo | 5 |
| 18641 | llorosos | 5 |
| 18642 | llorón | 5 |
| 18643 | lléveselo | 5 |
| 18644 | lleves | 5 |
| 18645 | llevárselo | 5 |
| 18646 | llevarás | 5 |
| 18647 | llevándome | 5 |
| 18648 | llevándolo | 5 |
| 18649 | lleuar | 5 |
| 18650 | lleguemos | 5 |
| 18651 | llegados | 5 |
| 18652 | llanura | 5 |
| 18653 | llamaradas | 5 |
| 18654 | llamándose | 5 |
| 18655 | livianas | 5 |
| 18656 | lisonjero | 5 |
| 18657 | lisonjeras | 5 |
| 18658 | lisiado | 5 |
| 18659 | lisas | 5 |
| 18660 | limpiarse | 5 |
| 18661 | limitó | 5 |
| 18662 | limitado | 5 |
| 18663 | lícitos | 5 |
| 18664 | libró | 5 |
| 18665 | librarle | 5 |
| 18666 | librara | 5 |
| 18667 | libranza | 5 |
| 18668 | libia | 5 |
| 18669 | leyeren | 5 |
| 18670 | leyera | 5 |
| 18671 | leydo | 5 |
| 18672 | levántese | 5 |
| 18673 | levanten | 5 |
| 18674 | levantéme | 5 |
| 18675 | levantaré | 5 |
| 18676 | letreros | 5 |
| 18677 | leonado | 5 |
| 18678 | legos | 5 |
| 18679 | leen | 5 |
| 18680 | lechuguino | 5 |
| 18681 | laven | 5 |
| 18682 | lavapiés | 5 |
| 18683 | lavándose | 5 |
| 18684 | lavadas | 5 |
| 18685 | lavabo | 5 |
| 18686 | lavaban | 5 |
| 18687 | laureado | 5 |
| 18688 | laúd | 5 |
| 18689 | latinos | 5 |
| 18690 | lastimeros | 5 |
| 18691 | lastimeras | 5 |
| 18692 | lástimas | 5 |
| 18693 | laseria | 5 |
| 18694 | lasala | 5 |
| 18695 | larvas | 5 |
| 18696 | larguísima | 5 |
| 18697 | lápida | 5 |
| 18698 | lanzaban | 5 |
| 18699 | langosta | 5 |
| 18700 | lamentó | 5 |
| 18701 | lamentándose | 5 |
| 18702 | lagartos | 5 |
| 18703 | ladraba | 5 |
| 18704 | ladra | 5 |
| 18705 | lacónica | 5 |
| 18706 | kock | 5 |
| 18707 | juzgué | 5 |
| 18708 | juzgada | 5 |
| 18709 | jurisdicción | 5 |
| 18710 | jurisconsulto | 5 |
| 18711 | juraré | 5 |
| 18712 | jugo | 5 |
| 18713 | juglar | 5 |
| 18714 | jirones | 5 |
| 18715 | jilgueros | 5 |
| 18716 | je | 5 |
| 18717 | jaco | 5 |
| 18718 | irún | 5 |
| 18719 | irte | 5 |
| 18720 | irrevocable | 5 |
| 18721 | irreverente | 5 |
| 18722 | irregular | 5 |
| 18723 | irías | 5 |
| 18724 | irguió | 5 |
| 18725 | invocaba | 5 |
| 18726 | invidiosos | 5 |
| 18727 | investigaciones | 5 |
| 18728 | invertir | 5 |
| 18729 | inventores | 5 |
| 18730 | invariablemente | 5 |
| 18731 | invadido | 5 |
| 18732 | inumerables | 5 |
| 18733 | introduciendo | 5 |
| 18734 | intranquila | 5 |
| 18735 | intitulado | 5 |
| 18736 | interrupciones | 5 |
| 18737 | interpretación | 5 |
| 18738 | interiormente | 5 |
| 18739 | intereso | 5 |
| 18740 | interese | 5 |
| 18741 | interesarse | 5 |
| 18742 | intentara | 5 |
| 18743 | intentaban | 5 |
| 18744 | intensos | 5 |
| 18745 | intencionada | 5 |
| 18746 | intempestiva | 5 |
| 18747 | inteligible | 5 |
| 18748 | intelectuales | 5 |
| 18749 | insulto | 5 |
| 18750 | instantánea | 5 |
| 18751 | instancias | 5 |
| 18752 | instalación | 5 |
| 18753 | insinuó | 5 |
| 18754 | inseparable | 5 |
| 18755 | insecto | 5 |
| 18756 | inquina | 5 |
| 18757 | inoportuno | 5 |
| 18758 | innata | 5 |
| 18759 | inmundos | 5 |
| 18760 | inmóviles | 5 |
| 18761 | inmensas | 5 |
| 18762 | inmemorial | 5 |
| 18763 | injusticias | 5 |
| 18764 | injustamente | 5 |
| 18765 | inicial | 5 |
| 18766 | inhabitable | 5 |
| 18767 | ingreso | 5 |
| 18768 | ingenieros | 5 |
| 18769 | infunde | 5 |
| 18770 | infieles | 5 |
| 18771 | infantiles | 5 |
| 18772 | infalibles | 5 |
| 18773 | inexperto | 5 |
| 18774 | inesperadamente | 5 |
| 18775 | inesperada | 5 |
| 18776 | industrias | 5 |
| 18777 | indumentaria | 5 |
| 18778 | indio | 5 |
| 18779 | indignaba | 5 |
| 18780 | indicando | 5 |
| 18781 | incurrir | 5 |
| 18782 | incumbencia | 5 |
| 18783 | inculto | 5 |
| 18784 | incrédulo | 5 |
| 18785 | inconstancia | 5 |
| 18786 | inconsciente | 5 |
| 18787 | inclinose | 5 |
| 18788 | incipiente | 5 |
| 18789 | incentivo | 5 |
| 18790 | inauguración | 5 |
| 18791 | inauditas | 5 |
| 18792 | inanición | 5 |
| 18793 | impulsa | 5 |
| 18794 | improvisó | 5 |
| 18795 | improvisada | 5 |
| 18796 | importe | 5 |
| 18797 | importará | 5 |
| 18798 | imponiendo | 5 |
| 18799 | ímpetus | 5 |
| 18800 | impetuosa | 5 |
| 18801 | imperfecta | 5 |
| 18802 | impasible | 5 |
| 18803 | imparcialmente | 5 |
| 18804 | imparcialidad | 5 |
| 18805 | imite | 5 |
| 18806 | imaginario | 5 |
| 18807 | imaginamos | 5 |
| 18808 | ijadas | 5 |
| 18809 | igualó | 5 |
| 18810 | igualarse | 5 |
| 18811 | igualara | 5 |
| 18812 | idólatra | 5 |
| 18813 | ibi | 5 |
| 18814 | hurta | 5 |
| 18815 | hundir | 5 |
| 18816 | hunda | 5 |
| 18817 | humorístico | 5 |
| 18818 | humillante | 5 |
| 18819 | humedecieron | 5 |
| 18820 | huesuda | 5 |
| 18821 | huessos | 5 |
| 18822 | hubimos | 5 |
| 18823 | houiesse | 5 |
| 18824 | hostias | 5 |
| 18825 | hospitales | 5 |
| 18826 | hortalizas | 5 |
| 18827 | horrorizado | 5 |
| 18828 | honrosos | 5 |
| 18829 | honran | 5 |
| 18830 | honduras | 5 |
| 18831 | hondura | 5 |
| 18832 | homo | 5 |
| 18833 | holgadamente | 5 |
| 18834 | hojuelas | 5 |
| 18835 | hiziera | 5 |
| 18836 | hipotecas | 5 |
| 18837 | hipocritona | 5 |
| 18838 | hipérboles | 5 |
| 18839 | hinchados | 5 |
| 18840 | hilaridad | 5 |
| 18841 | hiciéronse | 5 |
| 18842 | herreruelos | 5 |
| 18843 | herreros | 5 |
| 18844 | herraduras | 5 |
| 18845 | heroicamente | 5 |
| 18846 | herodes | 5 |
| 18847 | herméticamente | 5 |
| 18848 | hemistiquios | 5 |
| 18849 | hedat | 5 |
| 18850 | hauido | 5 |
| 18851 | haues | 5 |
| 18852 | hartura | 5 |
| 18853 | hartos | 5 |
| 18854 | haríamos | 5 |
| 18855 | haria | 5 |
| 18856 | harapos | 5 |
| 18857 | hame | 5 |
| 18858 | hambrientos | 5 |
| 18859 | hambrienta | 5 |
| 18860 | halo | 5 |
| 18861 | hallastes | 5 |
| 18862 | hallarte | 5 |
| 18863 | hallarla | 5 |
| 18864 | hallaré | 5 |
| 18865 | hallarás | 5 |
| 18866 | hallarán | 5 |
| 18867 | hallaran | 5 |
| 18868 | hallándome | 5 |
| 18869 | hallados | 5 |
| 18870 | halcón | 5 |
| 18871 | hágote | 5 |
| 18872 | hablarían | 5 |
| 18873 | habitaba | 5 |
| 18874 | gutierre | 5 |
| 18875 | gustosos | 5 |
| 18876 | gustando | 5 |
| 18877 | gustáis | 5 |
| 18878 | gusanillo | 5 |
| 18879 | gusanera | 5 |
| 18880 | gurapas | 5 |
| 18881 | guita | 5 |
| 18882 | guiñando | 5 |
| 18883 | guiando | 5 |
| 18884 | guerá | 5 |
| 18885 | guay | 5 |
| 18886 | guardarme | 5 |
| 18887 | guardarlos | 5 |
| 18888 | guardarlo | 5 |
| 18889 | guardarla | 5 |
| 18890 | guapos | 5 |
| 18891 | gu | 5 |
| 18892 | grutas | 5 |
| 18893 | gruñó | 5 |
| 18894 | grifo | 5 |
| 18895 | greñas | 5 |
| 18896 | gratas | 5 |
| 18897 | granizo | 5 |
| 18898 | grandísimas | 5 |
| 18899 | gradas | 5 |
| 18900 | graciosamente | 5 |
| 18901 | gozara | 5 |
| 18902 | gozaban | 5 |
| 18903 | gorriones | 5 |
| 18904 | golver | 5 |
| 18905 | golosos | 5 |
| 18906 | godos | 5 |
| 18907 | glotón | 5 |
| 18908 | ginebra | 5 |
| 18909 | gimió | 5 |
| 18910 | gigantescos | 5 |
| 18911 | gigantea | 5 |
| 18912 | germen | 5 |
| 18913 | generaciones | 5 |
| 18914 | gelas | 5 |
| 18915 | gaveta | 5 |
| 18916 | gatillos | 5 |
| 18917 | gatillo | 5 |
| 18918 | gastamos | 5 |
| 18919 | gasa | 5 |
| 18920 | gárrulo | 5 |
| 18921 | garrotazo | 5 |
| 18922 | garoça | 5 |
| 18923 | garantía | 5 |
| 18924 | garabatos | 5 |
| 18925 | ganga | 5 |
| 18926 | ganchos | 5 |
| 18927 | ganase | 5 |
| 18928 | ganaderos | 5 |
| 18929 | gallega | 5 |
| 18930 | galaor | 5 |
| 18931 | gaeta | 5 |
| 18932 | gacetilla | 5 |
| 18933 | gabriel | 5 |
| 18934 | fynca | 5 |
| 18935 | fuyme | 5 |
| 18936 | fusilar | 5 |
| 18937 | fusilado | 5 |
| 18938 | furtar | 5 |
| 18939 | furibunda | 5 |
| 18940 | funeral | 5 |
| 18941 | fundó | 5 |
| 18942 | fundándose | 5 |
| 18943 | fundaba | 5 |
| 18944 | fulleros | 5 |
| 18945 | fulana | 5 |
| 18946 | fuistes | 5 |
| 18947 | fuímonos | 5 |
| 18948 | fuíme | 5 |
| 18949 | fruncido | 5 |
| 18950 | frugal | 5 |
| 18951 | frotó | 5 |
| 18952 | frondosos | 5 |
| 18953 | franela | 5 |
| 18954 | francesas | 5 |
| 18955 | fragilidad | 5 |
| 18956 | foyr | 5 |
| 18957 | forzó | 5 |
| 18958 | forzados | 5 |
| 18959 | fortunas | 5 |
| 18960 | formados | 5 |
| 18961 | formadas | 5 |
| 18962 | forjado | 5 |
| 18963 | folgar | 5 |
| 18964 | fogoso | 5 |
| 18965 | fluxus | 5 |
| 18966 | flota | 5 |
| 18967 | flin | 5 |
| 18968 | fleche | 5 |
| 18969 | flautas | 5 |
| 18970 | físicas | 5 |
| 18971 | firmaba | 5 |
| 18972 | fingiéndose | 5 |
| 18973 | filosóficos | 5 |
| 18974 | fileno | 5 |
| 18975 | figurillas | 5 |
| 18976 | figuran | 5 |
| 18977 | figaro | 5 |
| 18978 | fielmente | 5 |
| 18979 | fianzas | 5 |
| 18980 | fiador | 5 |
| 18981 | ffueron | 5 |
| 18982 | ffabló | 5 |
| 18983 | feziera | 5 |
| 18984 | fez | 5 |
| 18985 | ferro | 5 |
| 18986 | ferida | 5 |
| 18987 | fenomenal | 5 |
| 18988 | fenecer | 5 |
| 18989 | fenbras | 5 |
| 18990 | femenil | 5 |
| 18991 | felicidades | 5 |
| 18992 | favorecida | 5 |
| 18993 | fauna | 5 |
| 18994 | fatigosa | 5 |
| 18995 | fatigar | 5 |
| 18996 | fasiendo | 5 |
| 18997 | farás | 5 |
| 18998 | fanegas | 5 |
| 18999 | familiarmente | 5 |
| 19000 | faltarme | 5 |
| 19001 | faltábale | 5 |
| 19002 | fallecimiento | 5 |
| 19003 | fado | 5 |
| 19004 | facturas | 5 |
| 19005 | facistol | 5 |
| 19006 | facilitaba | 5 |
| 19007 | facilita | 5 |
| 19008 | fabricar | 5 |
| 19009 | fabricante | 5 |
| 19010 | fabrican | 5 |
| 19011 | fabrica | 5 |
| 19012 | fablo | 5 |
| 19013 | fables | 5 |
| 19014 | exuberante | 5 |
| 19015 | extremidades | 5 |
| 19016 | extremado | 5 |
| 19017 | extravagancia | 5 |
| 19018 | extrañó | 5 |
| 19019 | extrañar | 5 |
| 19020 | extendidos | 5 |
| 19021 | extendida | 5 |
| 19022 | expulsión | 5 |
| 19023 | explotar | 5 |
| 19024 | explicara | 5 |
| 19025 | explicado | 5 |
| 19026 | expirar | 5 |
| 19027 | expansivo | 5 |
| 19028 | exigen | 5 |
| 19029 | exhalar | 5 |
| 19030 | exhalando | 5 |
| 19031 | execucion | 5 |
| 19032 | excusó | 5 |
| 19033 | exclamaron | 5 |
| 19034 | excitantes | 5 |
| 19035 | excelso | 5 |
| 19036 | examinado | 5 |
| 19037 | exaltaba | 5 |
| 19038 | exagerando | 5 |
| 19039 | exactas | 5 |
| 19040 | evitado | 5 |
| 19041 | eva | 5 |
| 19042 | eugenia | 5 |
| 19043 | eternos | 5 |
| 19044 | estuviéramos | 5 |
| 19045 | estuue | 5 |
| 19046 | estupendo | 5 |
| 19047 | estudie | 5 |
| 19048 | estudian | 5 |
| 19049 | estuco | 5 |
| 19050 | estrofas | 5 |
| 19051 | estrepitosa | 5 |
| 19052 | estrena | 5 |
| 19053 | estremecía | 5 |
| 19054 | estremadura | 5 |
| 19055 | estremado | 5 |
| 19056 | estremadas | 5 |
| 19057 | estremada | 5 |
| 19058 | estrema | 5 |
| 19059 | estrelleros | 5 |
| 19060 | estrellarse | 5 |
| 19061 | estrechando | 5 |
| 19062 | estrechaba | 5 |
| 19063 | estratagemas | 5 |
| 19064 | estranjero | 5 |
| 19065 | estrafalario | 5 |
| 19066 | estotra | 5 |
| 19067 | estilos | 5 |
| 19068 | estiércol | 5 |
| 19069 | esterilidad | 5 |
| 19070 | estériles | 5 |
| 19071 | estendió | 5 |
| 19072 | esten | 5 |
| 19073 | estallidos | 5 |
| 19074 | estad | 5 |
| 19075 | esquivaba | 5 |
| 19076 | esquife | 5 |
| 19077 | esquela | 5 |
| 19078 | espumoso | 5 |
| 19079 | espontánea | 5 |
| 19080 | espliego | 5 |
| 19081 | espléndidas | 5 |
| 19082 | esperemos | 5 |
| 19083 | esperaremos | 5 |
| 19084 | espérame | 5 |
| 19085 | especias | 5 |
| 19086 | esparcieron | 5 |
| 19087 | espantes | 5 |
| 19088 | espantas | 5 |
| 19089 | espantables | 5 |
| 19090 | esotro | 5 |
| 19091 | esforzaban | 5 |
| 19092 | esfinge | 5 |
| 19093 | esencias | 5 |
| 19094 | esenciales | 5 |
| 19095 | escupiendo | 5 |
| 19096 | escudriñar | 5 |
| 19097 | escudriñando | 5 |
| 19098 | escuderil | 5 |
| 19099 | escuchas | 5 |
| 19100 | escrituras | 5 |
| 19101 | escriptas | 5 |
| 19102 | esconden | 5 |
| 19103 | escogidas | 5 |
| 19104 | escogí | 5 |
| 19105 | escepticismo | 5 |
| 19106 | escarbando | 5 |
| 19107 | escaramuza | 5 |
| 19108 | escapatorias | 5 |
| 19109 | escapatoria | 5 |
| 19110 | escapan | 5 |
| 19111 | escapaban | 5 |
| 19112 | escandalizar | 5 |
| 19113 | escamas | 5 |
| 19114 | escalerilla | 5 |
| 19115 | eruditos | 5 |
| 19116 | erratas | 5 |
| 19117 | ero | 5 |
| 19118 | erizadas | 5 |
| 19119 | equivocarme | 5 |
| 19120 | equivocaciones | 5 |
| 19121 | equivalente | 5 |
| 19122 | epitafios | 5 |
| 19123 | episodio | 5 |
| 19124 | epiléptica | 5 |
| 19125 | épica | 5 |
| 19126 | envuelve | 5 |
| 19127 | envolver | 5 |
| 19128 | envite | 5 |
| 19129 | envidias | 5 |
| 19130 | envidiada | 5 |
| 19131 | envidiaban | 5 |
| 19132 | enumeración | 5 |
| 19133 | entusiasmos | 5 |
| 19134 | entróse | 5 |
| 19135 | entristeció | 5 |
| 19136 | entretenían | 5 |
| 19137 | entregue | 5 |
| 19138 | entregase | 5 |
| 19139 | entregarle | 5 |
| 19140 | entregarla | 5 |
| 19141 | entregara | 5 |
| 19142 | entregan | 5 |
| 19143 | entrauan | 5 |
| 19144 | entraste | 5 |
| 19145 | entrarse | 5 |
| 19146 | entrare | 5 |
| 19147 | entranse | 5 |
| 19148 | entr | 5 |
| 19149 | entonce | 5 |
| 19150 | entierros | 5 |
| 19151 | entiéndase | 5 |
| 19152 | entidad | 5 |
| 19153 | enterrarle | 5 |
| 19154 | enterneció | 5 |
| 19155 | enternecida | 5 |
| 19156 | enterándose | 5 |
| 19157 | entenderla | 5 |
| 19158 | entenderemos | 5 |
| 19159 | entenderás | 5 |
| 19160 | entendámonos | 5 |
| 19161 | entablaron | 5 |
| 19162 | ensuciar | 5 |
| 19163 | ensillar | 5 |
| 19164 | enseñarme | 5 |
| 19165 | enseñanzas | 5 |
| 19166 | enseñaban | 5 |
| 19167 | ensayos | 5 |
| 19168 | ensartando | 5 |
| 19169 | ensartados | 5 |
| 19170 | ensanchaba | 5 |
| 19171 | ensalmo | 5 |
| 19172 | enriquecido | 5 |
| 19173 | enredar | 5 |
| 19174 | enramadas | 5 |
| 19175 | enojados | 5 |
| 19176 | enmudeció | 5 |
| 19177 | enjugando | 5 |
| 19178 | engendraron | 5 |
| 19179 | engendran | 5 |
| 19180 | engañosa | 5 |
| 19181 | engañé | 5 |
| 19182 | engañador | 5 |
| 19183 | enganada | 5 |
| 19184 | enfriar | 5 |
| 19185 | enfermería | 5 |
| 19186 | enfático | 5 |
| 19187 | enfadarse | 5 |
| 19188 | enérgicos | 5 |
| 19189 | endurecida | 5 |
| 19190 | endiablados | 5 |
| 19191 | encubriendo | 5 |
| 19192 | encubría | 5 |
| 19193 | encubiertos | 5 |
| 19194 | encubierto | 5 |
| 19195 | encubiertas | 5 |
| 19196 | encontrose | 5 |
| 19197 | encontrarle | 5 |
| 19198 | encontrarás | 5 |
| 19199 | encontrábamos | 5 |
| 19200 | encomiendo | 5 |
| 19201 | encomendaba | 5 |
| 19202 | encogida | 5 |
| 19203 | encerraron | 5 |
| 19204 | encarnados | 5 |
| 19205 | encargando | 5 |
| 19206 | encarga | 5 |
| 19207 | encantan | 5 |
| 19208 | encajó | 5 |
| 19209 | encajado | 5 |
| 19210 | enbió | 5 |
| 19211 | enarboló | 5 |
| 19212 | enanos | 5 |
| 19213 | enana | 5 |
| 19214 | empiezas | 5 |
| 19215 | empezamos | 5 |
| 19216 | empeñarse | 5 |
| 19217 | emma | 5 |
| 19218 | embrazando | 5 |
| 19219 | embia | 5 |
| 19220 | embeleso | 5 |
| 19221 | embeleco | 5 |
| 19222 | embebido | 5 |
| 19223 | embarazos | 5 |
| 19224 | elegido | 5 |
| 19225 | elegantemente | 5 |
| 19226 | ejercitan | 5 |
| 19227 | eje | 5 |
| 19228 | eduardo | 5 |
| 19229 | échese | 5 |
| 19230 | echemos | 5 |
| 19231 | echarlos | 5 |
| 19232 | echara | 5 |
| 19233 | echados | 5 |
| 19234 | dyz | 5 |
| 19235 | durmiese | 5 |
| 19236 | duquesas | 5 |
| 19237 | dulzor | 5 |
| 19238 | dulcísimas | 5 |
| 19239 | dudó | 5 |
| 19240 | dudes | 5 |
| 19241 | dudando | 5 |
| 19242 | dramáticos | 5 |
| 19243 | dramáticas | 5 |
| 19244 | dotor | 5 |
| 19245 | dosel | 5 |
| 19246 | dormiré | 5 |
| 19247 | dormiendo | 5 |
| 19248 | doquier | 5 |
| 19249 | donzellas | 5 |
| 19250 | donayre | 5 |
| 19251 | donas | 5 |
| 19252 | domésticas | 5 |
| 19253 | dolorosos | 5 |
| 19254 | dolorosas | 5 |
| 19255 | doctorcillo | 5 |
| 19256 | docientas | 5 |
| 19257 | doblaron | 5 |
| 19258 | dobladas | 5 |
| 19259 | doblada | 5 |
| 19260 | dobla | 5 |
| 19261 | dízelo | 5 |
| 19262 | díxole | 5 |
| 19263 | dixere | 5 |
| 19264 | divisar | 5 |
| 19265 | divinos | 5 |
| 19266 | divinidades | 5 |
| 19267 | divierta | 5 |
| 19268 | divertirme | 5 |
| 19269 | diversa | 5 |
| 19270 | diuersas | 5 |
| 19271 | ditado | 5 |
| 19272 | distrajo | 5 |
| 19273 | distes | 5 |
| 19274 | disponga | 5 |
| 19275 | disparaban | 5 |
| 19276 | disolventes | 5 |
| 19277 | disminuir | 5 |
| 19278 | disminuía | 5 |
| 19279 | disimularlo | 5 |
| 19280 | disimulación | 5 |
| 19281 | disignio | 5 |
| 19282 | disgustar | 5 |
| 19283 | disformes | 5 |
| 19284 | díselo | 5 |
| 19285 | discurren | 5 |
| 19286 | disculpable | 5 |
| 19287 | diríase | 5 |
| 19288 | dirías | 5 |
| 19289 | diria | 5 |
| 19290 | directo | 5 |
| 19291 | diól | 5 |
| 19292 | dinamita | 5 |
| 19293 | dimpués | 5 |
| 19294 | dimelo | 5 |
| 19295 | dilata | 5 |
| 19296 | dijéronle | 5 |
| 19297 | dígole | 5 |
| 19298 | dificultosas | 5 |
| 19299 | dieta | 5 |
| 19300 | diéramos | 5 |
| 19301 | dieciocho | 5 |
| 19302 | diarias | 5 |
| 19303 | diaria | 5 |
| 19304 | dezirte | 5 |
| 19305 | dezía | 5 |
| 19306 | dexaua | 5 |
| 19307 | dexas | 5 |
| 19308 | dexaron | 5 |
| 19309 | devolvía | 5 |
| 19310 | devolverle | 5 |
| 19311 | deven | 5 |
| 19312 | devemos | 5 |
| 19313 | devaneo | 5 |
| 19314 | deuen | 5 |
| 19315 | deudo | 5 |
| 19316 | detuviese | 5 |
| 19317 | detuviéronse | 5 |
| 19318 | detractores | 5 |
| 19319 | detestables | 5 |
| 19320 | detestable | 5 |
| 19321 | determinéme | 5 |
| 19322 | detente | 5 |
| 19323 | detenernos | 5 |
| 19324 | desvío | 5 |
| 19325 | desviado | 5 |
| 19326 | desvergonzado | 5 |
| 19327 | desvergonzada | 5 |
| 19328 | desvelas | 5 |
| 19329 | desvanecida | 5 |
| 19330 | desvalidos | 5 |
| 19331 | desusada | 5 |
| 19332 | desuios | 5 |
| 19333 | destrozaba | 5 |
| 19334 | destroza | 5 |
| 19335 | destacándose | 5 |
| 19336 | destacaban | 5 |
| 19337 | desseos | 5 |
| 19338 | dessea | 5 |
| 19339 | despreocupación | 5 |
| 19340 | despreció | 5 |
| 19341 | despreciable | 5 |
| 19342 | desposorios | 5 |
| 19343 | desposorio | 5 |
| 19344 | despido | 5 |
| 19345 | despedíme | 5 |
| 19346 | desordenada | 5 |
| 19347 | desolada | 5 |
| 19348 | desnudó | 5 |
| 19349 | desmesurado | 5 |
| 19350 | desmejorada | 5 |
| 19351 | desmedrado | 5 |
| 19352 | desmayaba | 5 |
| 19353 | deslizó | 5 |
| 19354 | designio | 5 |
| 19355 | deshonre | 5 |
| 19356 | desfigurada | 5 |
| 19357 | deseó | 5 |
| 19358 | desengañar | 5 |
| 19359 | desempeñó | 5 |
| 19360 | desempeñado | 5 |
| 19361 | deseáis | 5 |
| 19362 | descubrían | 5 |
| 19363 | descubres | 5 |
| 19364 | desconoce | 5 |
| 19365 | desconfiaba | 5 |
| 19366 | descomponiéndose | 5 |
| 19367 | descomponerse | 5 |
| 19368 | descompone | 5 |
| 19369 | descolorida | 5 |
| 19370 | descolgar | 5 |
| 19371 | desciende | 5 |
| 19372 | descendemos | 5 |
| 19373 | descargado | 5 |
| 19374 | desbocado | 5 |
| 19375 | desbarajuste | 5 |
| 19376 | desayunado | 5 |
| 19377 | desatados | 5 |
| 19378 | desastroso | 5 |
| 19379 | desastrosa | 5 |
| 19380 | desarrolló | 5 |
| 19381 | desarrollarse | 5 |
| 19382 | desarrollando | 5 |
| 19383 | desaparece | 5 |
| 19384 | desalentada | 5 |
| 19385 | desalada | 5 |
| 19386 | desaforados | 5 |
| 19387 | desabrimiento | 5 |
| 19388 | derribados | 5 |
| 19389 | derriba | 5 |
| 19390 | derrengado | 5 |
| 19391 | derramó | 5 |
| 19392 | derivativo | 5 |
| 19393 | depósitos | 5 |
| 19394 | deo | 5 |
| 19395 | denostar | 5 |
| 19396 | demontres | 5 |
| 19397 | demasías | 5 |
| 19398 | delirando | 5 |
| 19399 | delincuentes | 5 |
| 19400 | deleites | 5 |
| 19401 | deleitaba | 5 |
| 19402 | dejóse | 5 |
| 19403 | déjele | 5 |
| 19404 | dejáronme | 5 |
| 19405 | dejáronle | 5 |
| 19406 | dejarles | 5 |
| 19407 | dejándote | 5 |
| 19408 | dejándonos | 5 |
| 19409 | degollado | 5 |
| 19410 | definitivo | 5 |
| 19411 | deferencia | 5 |
| 19412 | defensores | 5 |
| 19413 | defensor | 5 |
| 19414 | defendió | 5 |
| 19415 | dedillo | 5 |
| 19416 | decoroso | 5 |
| 19417 | declare | 5 |
| 19418 | declararse | 5 |
| 19419 | declarando | 5 |
| 19420 | declarados | 5 |
| 19421 | declarada | 5 |
| 19422 | decaimiento | 5 |
| 19423 | decadente | 5 |
| 19424 | débora | 5 |
| 19425 | debiste | 5 |
| 19426 | darvos | 5 |
| 19427 | darlo | 5 |
| 19428 | daréis | 5 |
| 19429 | dapño | 5 |
| 19430 | danzante | 5 |
| 19431 | dábanle | 5 |
| 19432 | cuzco | 5 |
| 19433 | cuytas | 5 |
| 19434 | cuytado | 5 |
| 19435 | cuytada | 5 |
| 19436 | curtidos | 5 |
| 19437 | curiosear | 5 |
| 19438 | curiosas | 5 |
| 19439 | curada | 5 |
| 19440 | cúmulo | 5 |
| 19441 | cumpliese | 5 |
| 19442 | cumplen | 5 |
| 19443 | culuebra | 5 |
| 19444 | cultivado | 5 |
| 19445 | cuidadito | 5 |
| 19446 | cueto | 5 |
| 19447 | cuerdamente | 5 |
| 19448 | cuéntase | 5 |
| 19449 | cucharilla | 5 |
| 19450 | cucharas | 5 |
| 19451 | cubren | 5 |
| 19452 | cubra | 5 |
| 19453 | cubil | 5 |
| 19454 | cubas | 5 |
| 19455 | cualesquiera | 5 |
| 19456 | cuadernas | 5 |
| 19457 | crudas | 5 |
| 19458 | crito | 5 |
| 19459 | criando | 5 |
| 19460 | criador | 5 |
| 19461 | criaba | 5 |
| 19462 | creyéndolo | 5 |
| 19463 | crey | 5 |
| 19464 | creídas | 5 |
| 19465 | creída | 5 |
| 19466 | creíase | 5 |
| 19467 | creerme | 5 |
| 19468 | creéis | 5 |
| 19469 | crecidos | 5 |
| 19470 | crean | 5 |
| 19471 | creados | 5 |
| 19472 | creador | 5 |
| 19473 | cráter | 5 |
| 19474 | coyunturas | 5 |
| 19475 | coytas | 5 |
| 19476 | coyda | 5 |
| 19477 | couarde | 5 |
| 19478 | cotarro | 5 |
| 19479 | costurera | 5 |
| 19480 | costancica | 5 |
| 19481 | cositas | 5 |
| 19482 | cortesanas | 5 |
| 19483 | corrimos | 5 |
| 19484 | corrigiendo | 5 |
| 19485 | corriese | 5 |
| 19486 | corriéndose | 5 |
| 19487 | corres | 5 |
| 19488 | corregido | 5 |
| 19489 | correas | 5 |
| 19490 | corran | 5 |
| 19491 | corrales | 5 |
| 19492 | coronilla | 5 |
| 19493 | coronan | 5 |
| 19494 | corneja | 5 |
| 19495 | corista | 5 |
| 19496 | cordones | 5 |
| 19497 | corcel | 5 |
| 19498 | corbacho | 5 |
| 19499 | corazonadas | 5 |
| 19500 | convirtieron | 5 |
| 19501 | convidando | 5 |
| 19502 | conversando | 5 |
| 19503 | convenza | 5 |
| 19504 | convencerse | 5 |
| 19505 | convencerla | 5 |
| 19506 | convencerá | 5 |
| 19507 | convence | 5 |
| 19508 | conuersacion | 5 |
| 19509 | contreras | 5 |
| 19510 | contratiempos | 5 |
| 19511 | contramaestre | 5 |
| 19512 | contradecir | 5 |
| 19513 | contiendas | 5 |
| 19514 | contera | 5 |
| 19515 | contentan | 5 |
| 19516 | contarlo | 5 |
| 19517 | contarles | 5 |
| 19518 | contante | 5 |
| 19519 | contagiado | 5 |
| 19520 | contador | 5 |
| 19521 | contada | 5 |
| 19522 | consunción | 5 |
| 19523 | consumida | 5 |
| 19524 | consolarle | 5 |
| 19525 | consolara | 5 |
| 19526 | consoladora | 5 |
| 19527 | consolaçión | 5 |
| 19528 | consola | 5 |
| 19529 | consejas | 5 |
| 19530 | consecuente | 5 |
| 19531 | consagración | 5 |
| 19532 | conosces | 5 |
| 19533 | conmovía | 5 |
| 19534 | congresos | 5 |
| 19535 | congoxa | 5 |
| 19536 | confundido | 5 |
| 19537 | confundidas | 5 |
| 19538 | confirmaron | 5 |
| 19539 | confirmaba | 5 |
| 19540 | confirma | 5 |
| 19541 | confiesas | 5 |
| 19542 | confía | 5 |
| 19543 | condujo | 5 |
| 19544 | conducir | 5 |
| 19545 | conducción | 5 |
| 19546 | condenó | 5 |
| 19547 | condenaba | 5 |
| 19548 | concurrir | 5 |
| 19549 | conciliar | 5 |
| 19550 | concertaron | 5 |
| 19551 | concertamos | 5 |
| 19552 | concertaba | 5 |
| 19553 | concento | 5 |
| 19554 | concejales | 5 |
| 19555 | comunique | 5 |
| 19556 | comunicarle | 5 |
| 19557 | comunicaciones | 5 |
| 19558 | comunal | 5 |
| 19559 | compuestos | 5 |
| 19560 | comprometo | 5 |
| 19561 | comprendieron | 5 |
| 19562 | complicados | 5 |
| 19563 | complicado | 5 |
| 19564 | complicadas | 5 |
| 19565 | complicaciones | 5 |
| 19566 | complicación | 5 |
| 19567 | completos | 5 |
| 19568 | completaban | 5 |
| 19569 | complemento | 5 |
| 19570 | complace | 5 |
| 19571 | compensaba | 5 |
| 19572 | comparo | 5 |
| 19573 | comparados | 5 |
| 19574 | comier | 5 |
| 19575 | comienzos | 5 |
| 19576 | comíamos | 5 |
| 19577 | cometió | 5 |
| 19578 | comete | 5 |
| 19579 | comérselo | 5 |
| 19580 | comenzóse | 5 |
| 19581 | comenzada | 5 |
| 19582 | comedidas | 5 |
| 19583 | combinados | 5 |
| 19584 | combinadas | 5 |
| 19585 | colorines | 5 |
| 19586 | colorido | 5 |
| 19587 | colodrillo | 5 |
| 19588 | colocándose | 5 |
| 19589 | coliseo | 5 |
| 19590 | coligió | 5 |
| 19591 | coleta | 5 |
| 19592 | colás | 5 |
| 19593 | cojita | 5 |
| 19594 | cojea | 5 |
| 19595 | coincidía | 5 |
| 19596 | coincide | 5 |
| 19597 | cohetes | 5 |
| 19598 | cohecho | 5 |
| 19599 | cogiese | 5 |
| 19600 | cogerte | 5 |
| 19601 | cogerlos | 5 |
| 19602 | cogeré | 5 |
| 19603 | cofres | 5 |
| 19604 | cofrades | 5 |
| 19605 | cocineros | 5 |
| 19606 | cobras | 5 |
| 19607 | cobraron | 5 |
| 19608 | cobran | 5 |
| 19609 | cobdicia | 5 |
| 19610 | clavándole | 5 |
| 19611 | clarísimo | 5 |
| 19612 | clarines | 5 |
| 19613 | clamor | 5 |
| 19614 | citar | 5 |
| 19615 | citan | 5 |
| 19616 | cisnes | 5 |
| 19617 | cirongilio | 5 |
| 19618 | circunspecto | 5 |
| 19619 | circunspección | 5 |
| 19620 | çinta | 5 |
| 19621 | cinismo | 5 |
| 19622 | çinco | 5 |
| 19623 | cimas | 5 |
| 19624 | çima | 5 |
| 19625 | cifras | 5 |
| 19626 | cierro | 5 |
| 19627 | cíclope | 5 |
| 19628 | cicerone | 5 |
| 19629 | chuzo | 5 |
| 19630 | chulos | 5 |
| 19631 | chulo | 5 |
| 19632 | chubasco | 5 |
| 19633 | chorreaban | 5 |
| 19634 | chitón | 5 |
| 19635 | chin | 5 |
| 19636 | chillonas | 5 |
| 19637 | chillaba | 5 |
| 19638 | chic | 5 |
| 19639 | chí | 5 |
| 19640 | chaveta | 5 |
| 19641 | charlaron | 5 |
| 19642 | chalequeras | 5 |
| 19643 | chalán | 5 |
| 19644 | cfr | 5 |
| 19645 | cero | 5 |
| 19646 | cerero | 5 |
| 19647 | censores | 5 |
| 19648 | cencerros | 5 |
| 19649 | cencerro | 5 |
| 19650 | cenceño | 5 |
| 19651 | çena | 5 |
| 19652 | celibato | 5 |
| 19653 | celemín | 5 |
| 19654 | celebran | 5 |
| 19655 | celebrados | 5 |
| 19656 | celdas | 5 |
| 19657 | celaje | 5 |
| 19658 | celadas | 5 |
| 19659 | céfiro | 5 |
| 19660 | cedía | 5 |
| 19661 | cede | 5 |
| 19662 | cazando | 5 |
| 19663 | cayda | 5 |
| 19664 | cayada | 5 |
| 19665 | caya | 5 |
| 19666 | caviloso | 5 |
| 19667 | cavar | 5 |
| 19668 | cavador | 5 |
| 19669 | cautivar | 5 |
| 19670 | cautelosamente | 5 |
| 19671 | causo | 5 |
| 19672 | catolicismo | 5 |
| 19673 | catiua | 5 |
| 19674 | cátate | 5 |
| 19675 | catado | 5 |
| 19676 | cataclismo | 5 |
| 19677 | casuchas | 5 |
| 19678 | casucha | 5 |
| 19679 | castañuelas | 5 |
| 19680 | castañas | 5 |
| 19681 | casia | 5 |
| 19682 | caseta | 5 |
| 19683 | cascajo | 5 |
| 19684 | casarnos | 5 |
| 19685 | casarla | 5 |
| 19686 | casan | 5 |
| 19687 | casamentero | 5 |
| 19688 | cartones | 5 |
| 19689 | cartitas | 5 |
| 19690 | carteras | 5 |
| 19691 | cartago | 5 |
| 19692 | carretillas | 5 |
| 19693 | carnicero | 5 |
| 19694 | carlismo | 5 |
| 19695 | cariñosos | 5 |
| 19696 | caridat | 5 |
| 19697 | caridades | 5 |
| 19698 | caricaturas | 5 |
| 19699 | caricatura | 5 |
| 19700 | cargaron | 5 |
| 19701 | cargamento | 5 |
| 19702 | cargaban | 5 |
| 19703 | careciendo | 5 |
| 19704 | cardos | 5 |
| 19705 | carátula | 5 |
| 19706 | capitan | 5 |
| 19707 | cantores | 5 |
| 19708 | canteros | 5 |
| 19709 | canpo | 5 |
| 19710 | canina | 5 |
| 19711 | candelas | 5 |
| 19712 | candela | 5 |
| 19713 | candado | 5 |
| 19714 | canciller | 5 |
| 19715 | canales | 5 |
| 19716 | cana | 5 |
| 19717 | camposanto | 5 |
| 19718 | campó | 5 |
| 19719 | campestres | 5 |
| 19720 | campechano | 5 |
| 19721 | campañas | 5 |
| 19722 | campanero | 5 |
| 19723 | campanarios | 5 |
| 19724 | camellos | 5 |
| 19725 | camello | 5 |
| 19726 | camelias | 5 |
| 19727 | calzarse | 5 |
| 19728 | calzados | 5 |
| 19729 | caló | 5 |
| 19730 | calmó | 5 |
| 19731 | calmado | 5 |
| 19732 | calmaba | 5 |
| 19733 | callos | 5 |
| 19734 | callamos | 5 |
| 19735 | calladito | 5 |
| 19736 | calladas | 5 |
| 19737 | caliza | 5 |
| 19738 | calienta | 5 |
| 19739 | calculo | 5 |
| 19740 | calculaba | 5 |
| 19741 | calandria | 5 |
| 19742 | calamina | 5 |
| 19743 | calabazadas | 5 |
| 19744 | caes | 5 |
| 19745 | caduca | 5 |
| 19746 | cachorros | 5 |
| 19747 | cachet | 5 |
| 19748 | cacharro | 5 |
| 19749 | cacerolas | 5 |
| 19750 | cabriolas | 5 |
| 19751 | cabr | 5 |
| 19752 | cabida | 5 |
| 19753 | cabezada | 5 |
| 19754 | caballerizas | 5 |
| 19755 | cabales | 5 |
| 19756 | burrero | 5 |
| 19757 | bullicioso | 5 |
| 19758 | bufando | 5 |
| 19759 | brotaban | 5 |
| 19760 | bronces | 5 |
| 19761 | breñas | 5 |
| 19762 | brebaje | 5 |
| 19763 | brea | 5 |
| 19764 | bravas | 5 |
| 19765 | bozo | 5 |
| 19766 | bouo | 5 |
| 19767 | borrosa | 5 |
| 19768 | borrón | 5 |
| 19769 | borricos | 5 |
| 19770 | borrachona | 5 |
| 19771 | borra | 5 |
| 19772 | bordados | 5 |
| 19773 | bordado | 5 |
| 19774 | borceguíes | 5 |
| 19775 | borbón | 5 |
| 19776 | boletín | 5 |
| 19777 | bodigo | 5 |
| 19778 | blasón | 5 |
| 19779 | blanquísimos | 5 |
| 19780 | blanquísimo | 5 |
| 19781 | blandos | 5 |
| 19782 | biuos | 5 |
| 19783 | biuo | 5 |
| 19784 | biua | 5 |
| 19785 | bilboquet | 5 |
| 19786 | bienhechora | 5 |
| 19787 | bienaventurados | 5 |
| 19788 | bicerra | 5 |
| 19789 | bevir | 5 |
| 19790 | beuer | 5 |
| 19791 | besándola | 5 |
| 19792 | besado | 5 |
| 19793 | bermejo | 5 |
| 19794 | bermejas | 5 |
| 19795 | benévola | 5 |
| 19796 | bendigo | 5 |
| 19797 | bendecía | 5 |
| 19798 | belcha | 5 |
| 19799 | be | 5 |
| 19800 | baztán | 5 |
| 19801 | baúles | 5 |
| 19802 | batallones | 5 |
| 19803 | bastero | 5 |
| 19804 | bases | 5 |
| 19805 | barrotes | 5 |
| 19806 | barcaza | 5 |
| 19807 | barbería | 5 |
| 19808 | barajar | 5 |
| 19809 | bañó | 5 |
| 19810 | bandoleros | 5 |
| 19811 | bandidos | 5 |
| 19812 | bancarrota | 5 |
| 19813 | balmes | 5 |
| 19814 | bajase | 5 |
| 19815 | bailarín | 5 |
| 19816 | bacantes | 5 |
| 19817 | babieca | 5 |
| 19818 | azumbre | 5 |
| 19819 | azotaron | 5 |
| 19820 | azotan | 5 |
| 19821 | azoramiento | 5 |
| 19822 | azorado | 5 |
| 19823 | azorada | 5 |
| 19824 | azor | 5 |
| 19825 | azafrán | 5 |
| 19826 | azabache | 5 |
| 19827 | ayúdeme | 5 |
| 19828 | ayudarte | 5 |
| 19829 | ayudarla | 5 |
| 19830 | ayudaría | 5 |
| 19831 | ayudaré | 5 |
| 19832 | ayrado | 5 |
| 19833 | avremos | 5 |
| 19834 | avínole | 5 |
| 19835 | avenía | 5 |
| 19836 | avellana | 5 |
| 19837 | auxilios | 5 |
| 19838 | autoriza | 5 |
| 19839 | auroras | 5 |
| 19840 | auras | 5 |
| 19841 | aumentaban | 5 |
| 19842 | auian | 5 |
| 19843 | atropellando | 5 |
| 19844 | atropellada | 5 |
| 19845 | atribulado | 5 |
| 19846 | atribuían | 5 |
| 19847 | atraer | 5 |
| 19848 | atormentando | 5 |
| 19849 | atontada | 5 |
| 19850 | atiza | 5 |
| 19851 | atienden | 5 |
| 19852 | aterradora | 5 |
| 19853 | atenuar | 5 |
| 19854 | atendió | 5 |
| 19855 | ataúdes | 5 |
| 19856 | ataúd | 5 |
| 19857 | atañen | 5 |
| 19858 | atajo | 5 |
| 19859 | ataja | 5 |
| 19860 | atacando | 5 |
| 19861 | ataba | 5 |
| 19862 | asustan | 5 |
| 19863 | asquerosos | 5 |
| 19864 | áspid | 5 |
| 19865 | ásperas | 5 |
| 19866 | asiduo | 5 |
| 19867 | asia | 5 |
| 19868 | asesinado | 5 |
| 19869 | ascendía | 5 |
| 19870 | asar | 5 |
| 19871 | asados | 5 |
| 19872 | asa | 5 |
| 19873 | artificial | 5 |
| 19874 | articular | 5 |
| 19875 | artesón | 5 |
| 19876 | arsenal | 5 |
| 19877 | arrullo | 5 |
| 19878 | arrullaba | 5 |
| 19879 | arroje | 5 |
| 19880 | arrimándose | 5 |
| 19881 | arrimaba | 5 |
| 19882 | arrepentirse | 5 |
| 19883 | arreo | 5 |
| 19884 | arreglos | 5 |
| 19885 | arreglaban | 5 |
| 19886 | arrabales | 5 |
| 19887 | arrabal | 5 |
| 19888 | arqueológico | 5 |
| 19889 | armoniosa | 5 |
| 19890 | armeros | 5 |
| 19891 | ariosto | 5 |
| 19892 | argumentación | 5 |
| 19893 | archivos | 5 |
| 19894 | arboledas | 5 |
| 19895 | arbitrios | 5 |
| 19896 | aquexa | 5 |
| 19897 | apuntación | 5 |
| 19898 | apuestas | 5 |
| 19899 | aptitudes | 5 |
| 19900 | aproximó | 5 |
| 19901 | aprovechamiento | 5 |
| 19902 | aprisionado | 5 |
| 19903 | apresuraba | 5 |
| 19904 | apresura | 5 |
| 19905 | aprensiva | 5 |
| 19906 | aprendan | 5 |
| 19907 | apostólico | 5 |
| 19908 | apóstoles | 5 |
| 19909 | apostado | 5 |
| 19910 | aporreado | 5 |
| 19911 | apócrifo | 5 |
| 19912 | aplicaciones | 5 |
| 19913 | aplacado | 5 |
| 19914 | apetecer | 5 |
| 19915 | apercebida | 5 |
| 19916 | apellidos | 5 |
| 19917 | apelación | 5 |
| 19918 | apearme | 5 |
| 19919 | apeado | 5 |
| 19920 | apartóse | 5 |
| 19921 | apartémonos | 5 |
| 19922 | apartada | 5 |
| 19923 | aparentemente | 5 |
| 19924 | aparejados | 5 |
| 19925 | apareciendo | 5 |
| 19926 | aparatos | 5 |
| 19927 | añado | 5 |
| 19928 | añadí | 5 |
| 19929 | anunciado | 5 |
| 19930 | anunciación | 5 |
| 19931 | anudado | 5 |
| 19932 | antona | 5 |
| 19933 | antología | 5 |
| 19934 | antiquísima | 5 |
| 19935 | antiespasmódica | 5 |
| 19936 | anticipo | 5 |
| 19937 | anti | 5 |
| 19938 | anteriormente | 5 |
| 19939 | ansiedades | 5 |
| 19940 | anotaciones | 5 |
| 19941 | anocheció | 5 |
| 19942 | animar | 5 |
| 19943 | animaban | 5 |
| 19944 | angostas | 5 |
| 19945 | angelitos | 5 |
| 19946 | anegado | 5 |
| 19947 | anduviesen | 5 |
| 19948 | anduviese | 5 |
| 19949 | anduviera | 5 |
| 19950 | andrea | 5 |
| 19951 | andrada | 5 |
| 19952 | ándese | 5 |
| 19953 | andaluza | 5 |
| 19954 | andábamos | 5 |
| 19955 | ancianidad | 5 |
| 19956 | anchusa | 5 |
| 19957 | anchuras | 5 |
| 19958 | anchura | 5 |
| 19959 | anatema | 5 |
| 19960 | ampuloso | 5 |
| 19961 | amplitud | 5 |
| 19962 | ampara | 5 |
| 19963 | amiguitas | 5 |
| 19964 | amenos | 5 |
| 19965 | amenidad | 5 |
| 19966 | amenazar | 5 |
| 19967 | amenazándole | 5 |
| 19968 | amen | 5 |
| 19969 | amberes | 5 |
| 19970 | amargos | 5 |
| 19971 | amapola | 5 |
| 19972 | amanezca | 5 |
| 19973 | amaneramiento | 5 |
| 19974 | amaltea | 5 |
| 19975 | amadises | 5 |
| 19976 | amadas | 5 |
| 19977 | alzada | 5 |
| 19978 | alzaban | 5 |
| 19979 | alumnas | 5 |
| 19980 | alumbrar | 5 |
| 19981 | aludir | 5 |
| 19982 | altísimos | 5 |
| 19983 | alternar | 5 |
| 19984 | alquilé | 5 |
| 19985 | alquilado | 5 |
| 19986 | alpiste | 5 |
| 19987 | alojado | 5 |
| 19988 | alojaba | 5 |
| 19989 | almudenilla | 5 |
| 19990 | almorzado | 5 |
| 19991 | almidón | 5 |
| 19992 | almendra | 5 |
| 19993 | almazen | 5 |
| 19994 | allegar | 5 |
| 19995 | allegado | 5 |
| 19996 | aliviado | 5 |
| 19997 | alimentarse | 5 |
| 19998 | alimentar | 5 |
| 19999 | alimaña | 5 |
| 20000 | alijo | 5 |
| 20001 | alianza | 5 |
| 20002 | algodones | 5 |
| 20003 | alfilerazos | 5 |
| 20004 | alevoso | 5 |
| 20005 | aleve | 5 |
| 20006 | alemana | 5 |
| 20007 | aleluya | 5 |
| 20008 | alegraría | 5 |
| 20009 | alcanzarle | 5 |
| 20010 | alcanzamos | 5 |
| 20011 | alcantarillas | 5 |
| 20012 | alborotóse | 5 |
| 20013 | alborotando | 5 |
| 20014 | alborotaban | 5 |
| 20015 | alados | 5 |
| 20016 | alada | 5 |
| 20017 | alaben | 5 |
| 20018 | alabastro | 5 |
| 20019 | alabardas | 5 |
| 20020 | airecillo | 5 |
| 20021 | ahorrarse | 5 |
| 20022 | ahorraba | 5 |
| 20023 | ahogándose | 5 |
| 20024 | ahogada | 5 |
| 20025 | ahechando | 5 |
| 20026 | agujerito | 5 |
| 20027 | aguijones | 5 |
| 20028 | aguija | 5 |
| 20029 | agudezas | 5 |
| 20030 | agrandaba | 5 |
| 20031 | agradecieron | 5 |
| 20032 | agradeciendo | 5 |
| 20033 | agradecidísimo | 5 |
| 20034 | agradece | 5 |
| 20035 | agradaban | 5 |
| 20036 | agraciada | 5 |
| 20037 | agitó | 5 |
| 20038 | agarrarse | 5 |
| 20039 | agarrando | 5 |
| 20040 | africa | 5 |
| 20041 | afortunada | 5 |
| 20042 | aforismos | 5 |
| 20043 | afligía | 5 |
| 20044 | afirman | 5 |
| 20045 | afilada | 5 |
| 20046 | aficionada | 5 |
| 20047 | aficion | 5 |
| 20048 | afectuosas | 5 |
| 20049 | afectuosa | 5 |
| 20050 | advertimientos | 5 |
| 20051 | advertimiento | 5 |
| 20052 | adúltero | 5 |
| 20053 | adorando | 5 |
| 20054 | adoradores | 5 |
| 20055 | adoraban | 5 |
| 20056 | adoptiva | 5 |
| 20057 | adondequiera | 5 |
| 20058 | admiren | 5 |
| 20059 | admiran | 5 |
| 20060 | adivinando | 5 |
| 20061 | adivinado | 5 |
| 20062 | adelantarse | 5 |
| 20063 | adefesios | 5 |
| 20064 | adargas | 5 |
| 20065 | adalid | 5 |
| 20066 | acusaba | 5 |
| 20067 | acumulando | 5 |
| 20068 | acuéstate | 5 |
| 20069 | acuérdome | 5 |
| 20070 | acudimos | 5 |
| 20071 | acudí | 5 |
| 20072 | acuchillado | 5 |
| 20073 | açúcar | 5 |
| 20074 | acta | 5 |
| 20075 | acreedor | 5 |
| 20076 | acreciente | 5 |
| 20077 | acostaré | 5 |
| 20078 | acostámonos | 5 |
| 20079 | acortar | 5 |
| 20080 | acordarás | 5 |
| 20081 | acordándome | 5 |
| 20082 | acordaban | 5 |
| 20083 | aconsejas | 5 |
| 20084 | acompañarme | 5 |
| 20085 | acompañara | 5 |
| 20086 | acompanado | 5 |
| 20087 | acomode | 5 |
| 20088 | acomodándose | 5 |
| 20089 | acomodada | 5 |
| 20090 | acometió | 5 |
| 20091 | acometieron | 5 |
| 20092 | acólitos | 5 |
| 20093 | aclaraba | 5 |
| 20094 | aciertas | 5 |
| 20095 | acidente | 5 |
| 20096 | acertara | 5 |
| 20097 | aceras | 5 |
| 20098 | acerada | 5 |
| 20099 | acentuado | 5 |
| 20100 | acentuaba | 5 |
| 20101 | acaecido | 5 |
| 20102 | acabose | 5 |
| 20103 | acabé | 5 |
| 20104 | acabasen | 5 |
| 20105 | acabas | 5 |
| 20106 | acabarla | 5 |
| 20107 | aburrida | 5 |
| 20108 | abundan | 5 |
| 20109 | abuelito | 5 |
| 20110 | abuelita | 5 |
| 20111 | absolutismo | 5 |
| 20112 | ábside | 5 |
| 20113 | abrumada | 5 |
| 20114 | abrirse | 5 |
| 20115 | abrióle | 5 |
| 20116 | abriéndole | 5 |
| 20117 | abrazarle | 5 |
| 20118 | abrazados | 5 |
| 20119 | aborrecida | 5 |
| 20120 | abordaje | 5 |
| 20121 | abandonarle | 5 |
| 20122 | abadesa | 5 |
| 20123 | à | 5 |
| 20124 | zutano | 4 |
| 20125 | zurriago | 4 |
| 20126 | zurdo | 4 |
| 20127 | zurcido | 4 |
| 20128 | zarabanda | 4 |
| 20129 | zapatones | 4 |
| 20130 | zapatilla | 4 |
| 20131 | zapatas | 4 |
| 20132 | zanja | 4 |
| 20133 | zancadilla | 4 |
| 20134 | zampoña | 4 |
| 20135 | yuy | 4 |
| 20136 | yuan | 4 |
| 20137 | yorar | 4 |
| 20138 | yervas | 4 |
| 20139 | yeciones | 4 |
| 20140 | yeción | 4 |
| 20141 | yago | 4 |
| 20142 | xxxviii | 4 |
| 20143 | xxxv | 4 |
| 20144 | xxxix | 4 |
| 20145 | xxxiv | 4 |
| 20146 | xxxiii | 4 |
| 20147 | xxxii | 4 |
| 20148 | xxxi | 4 |
| 20149 | xli | 4 |
| 20150 | walter | 4 |
| 20151 | vyl | 4 |
| 20152 | vyene | 4 |
| 20153 | vulcano | 4 |
| 20154 | vuélvese | 4 |
| 20155 | vuélvase | 4 |
| 20156 | vuelca | 4 |
| 20157 | vsar | 4 |
| 20158 | votó | 4 |
| 20159 | votar | 4 |
| 20160 | voracidad | 4 |
| 20161 | volviste | 4 |
| 20162 | volvimos | 4 |
| 20163 | volvías | 4 |
| 20164 | volveos | 4 |
| 20165 | volaron | 4 |
| 20166 | volaría | 4 |
| 20167 | vociferó | 4 |
| 20168 | vociferaba | 4 |
| 20169 | vó | 4 |
| 20170 | vizcaya | 4 |
| 20171 | vivísimo | 4 |
| 20172 | viviría | 4 |
| 20173 | viviremos | 4 |
| 20174 | viuiendo | 4 |
| 20175 | viudez | 4 |
| 20176 | viudedad | 4 |
| 20177 | viuas | 4 |
| 20178 | vitorias | 4 |
| 20179 | visito | 4 |
| 20180 | visionaria | 4 |
| 20181 | visibles | 4 |
| 20182 | viscoso | 4 |
| 20183 | virgo | 4 |
| 20184 | vireno | 4 |
| 20185 | violentísimo | 4 |
| 20186 | violentísima | 4 |
| 20187 | villajuán | 4 |
| 20188 | vilinch | 4 |
| 20189 | vileza | 4 |
| 20190 | vigorosas | 4 |
| 20191 | vigilantes | 4 |
| 20192 | vieses | 4 |
| 20193 | viéndolos | 4 |
| 20194 | viéndoles | 4 |
| 20195 | viedma | 4 |
| 20196 | vides | 4 |
| 20197 | vide | 4 |
| 20198 | vibraba | 4 |
| 20199 | vezindad | 4 |
| 20200 | veterano | 4 |
| 20201 | vestuario | 4 |
| 20202 | vestirme | 4 |
| 20203 | vestirle | 4 |
| 20204 | vestiré | 4 |
| 20205 | vestimos | 4 |
| 20206 | vestimenta | 4 |
| 20207 | veslo | 4 |
| 20208 | vesla | 4 |
| 20209 | vesindat | 4 |
| 20210 | vertientes | 4 |
| 20211 | vértice | 4 |
| 20212 | verter | 4 |
| 20213 | vertedero | 4 |
| 20214 | versó | 4 |
| 20215 | verisímiles | 4 |
| 20216 | verificose | 4 |
| 20217 | vergüenzas | 4 |
| 20218 | verdugado | 4 |
| 20219 | verdosa | 4 |
| 20220 | verdores | 4 |
| 20221 | verdor | 4 |
| 20222 | verbosidad | 4 |
| 20223 | verbos | 4 |
| 20224 | venzo | 4 |
| 20225 | venturosos | 4 |
| 20226 | venirnos | 4 |
| 20227 | venino | 4 |
| 20228 | veníe | 4 |
| 20229 | venideras | 4 |
| 20230 | venías | 4 |
| 20231 | vengue | 4 |
| 20232 | vengó | 4 |
| 20233 | vengativo | 4 |
| 20234 | vengaré | 4 |
| 20235 | vengara | 4 |
| 20236 | venenosa | 4 |
| 20237 | vendible | 4 |
| 20238 | vendí | 4 |
| 20239 | venderme | 4 |
| 20240 | vencieron | 4 |
| 20241 | vencerlos | 4 |
| 20242 | vencerla | 4 |
| 20243 | venado | 4 |
| 20244 | venablo | 4 |
| 20245 | vellacos | 4 |
| 20246 | vella | 4 |
| 20247 | veletas | 4 |
| 20248 | veintitrés | 4 |
| 20249 | veintiséis | 4 |
| 20250 | veíamos | 4 |
| 20251 | vehículo | 4 |
| 20252 | veda | 4 |
| 20253 | véala | 4 |
| 20254 | veades | 4 |
| 20255 | váyanse | 4 |
| 20256 | vastos | 4 |
| 20257 | varoniles | 4 |
| 20258 | varon | 4 |
| 20259 | varillas | 4 |
| 20260 | varia | 4 |
| 20261 | vargas | 4 |
| 20262 | vaquilla | 4 |
| 20263 | vanidat | 4 |
| 20264 | valyentes | 4 |
| 20265 | valya | 4 |
| 20266 | valla | 4 |
| 20267 | valió | 4 |
| 20268 | valgo | 4 |
| 20269 | valgan | 4 |
| 20270 | valerosas | 4 |
| 20271 | valerme | 4 |
| 20272 | valeriano | 4 |
| 20273 | valentón | 4 |
| 20274 | valenciana | 4 |
| 20275 | valcarlos | 4 |
| 20276 | vaivenes | 4 |
| 20277 | vagaban | 4 |
| 20278 | vademecum | 4 |
| 20279 | vaciedades | 4 |
| 20280 | vacantes | 4 |
| 20281 | uva | 4 |
| 20282 | utilizar | 4 |
| 20283 | usureros | 4 |
| 20284 | usé | 4 |
| 20285 | usaron | 4 |
| 20286 | uriarte | 4 |
| 20287 | urdax | 4 |
| 20288 | urbano | 4 |
| 20289 | untaba | 4 |
| 20290 | uníase | 4 |
| 20291 | undosa | 4 |
| 20292 | umanal | 4 |
| 20293 | ultramar | 4 |
| 20294 | ultra | 4 |
| 20295 | tuuo | 4 |
| 20296 | tutela | 4 |
| 20297 | turra | 4 |
| 20298 | turquesco | 4 |
| 20299 | turquesca | 4 |
| 20300 | turpín | 4 |
| 20301 | turgentes | 4 |
| 20302 | turbulenta | 4 |
| 20303 | turbia | 4 |
| 20304 | turbes | 4 |
| 20305 | turbaban | 4 |
| 20306 | tupido | 4 |
| 20307 | túnez | 4 |
| 20308 | tunanta | 4 |
| 20309 | tun | 4 |
| 20310 | tumbos | 4 |
| 20311 | tul | 4 |
| 20312 | tufillo | 4 |
| 20313 | tuerta | 4 |
| 20314 | truhanes | 4 |
| 20315 | truecan | 4 |
| 20316 | troyano | 4 |
| 20317 | tropicales | 4 |
| 20318 | tropezaron | 4 |
| 20319 | tropezaban | 4 |
| 20320 | tronado | 4 |
| 20321 | tronada | 4 |
| 20322 | trombón | 4 |
| 20323 | trocada | 4 |
| 20324 | trocaban | 4 |
| 20325 | trobador | 4 |
| 20326 | troba | 4 |
| 20327 | triviales | 4 |
| 20328 | triunfales | 4 |
| 20329 | tristura | 4 |
| 20330 | tristán | 4 |
| 20331 | tris | 4 |
| 20332 | tripulantes | 4 |
| 20333 | trinqué | 4 |
| 20334 | tributaba | 4 |
| 20335 | tribus | 4 |
| 20336 | trepar | 4 |
| 20337 | trecientas | 4 |
| 20338 | trazado | 4 |
| 20339 | traviesos | 4 |
| 20340 | tratarte | 4 |
| 20341 | tratarlo | 4 |
| 20342 | tratarle | 4 |
| 20343 | tratáredes | 4 |
| 20344 | tratare | 4 |
| 20345 | tratará | 4 |
| 20346 | tratante | 4 |
| 20347 | trasudando | 4 |
| 20348 | trastornaba | 4 |
| 20349 | traspasaba | 4 |
| 20350 | traslado | 4 |
| 20351 | trapicheos | 4 |
| 20352 | transmitido | 4 |
| 20353 | transformaron | 4 |
| 20354 | transforma | 4 |
| 20355 | transcurso | 4 |
| 20356 | tramando | 4 |
| 20357 | tráiganme | 4 |
| 20358 | tráigame | 4 |
| 20359 | traicionero | 4 |
| 20360 | traíamos | 4 |
| 20361 | tragué | 4 |
| 20362 | tragicomedia | 4 |
| 20363 | tráete | 4 |
| 20364 | traerse | 4 |
| 20365 | traerlo | 4 |
| 20366 | trabando | 4 |
| 20367 | trabajosamente | 4 |
| 20368 | trabajamos | 4 |
| 20369 | trabados | 4 |
| 20370 | trabado | 4 |
| 20371 | touiesse | 4 |
| 20372 | tosiendo | 4 |
| 20373 | toses | 4 |
| 20374 | torva | 4 |
| 20375 | torrentes | 4 |
| 20376 | torrellas | 4 |
| 20377 | torrecilla | 4 |
| 20378 | tornóle | 4 |
| 20379 | torneo | 4 |
| 20380 | tornen | 4 |
| 20381 | torneados | 4 |
| 20382 | tornate | 4 |
| 20383 | tornasoles | 4 |
| 20384 | tormentas | 4 |
| 20385 | toreros | 4 |
| 20386 | tordesillas | 4 |
| 20387 | toquillas | 4 |
| 20388 | toparon | 4 |
| 20389 | topacios | 4 |
| 20390 | tontaina | 4 |
| 20391 | tonel | 4 |
| 20392 | tomillo | 4 |
| 20393 | tómelo | 4 |
| 20394 | tomarían | 4 |
| 20395 | tomándose | 4 |
| 20396 | tolón | 4 |
| 20397 | tolomeo | 4 |
| 20398 | toditos | 4 |
| 20399 | toçino | 4 |
| 20400 | tocaya | 4 |
| 20401 | tocata | 4 |
| 20402 | tocarme | 4 |
| 20403 | tocamos | 4 |
| 20404 | titulo | 4 |
| 20405 | tito | 4 |
| 20406 | tisbe | 4 |
| 20407 | tirio | 4 |
| 20408 | tires | 4 |
| 20409 | tiren | 4 |
| 20410 | tiré | 4 |
| 20411 | tiraría | 4 |
| 20412 | tirantez | 4 |
| 20413 | tiniebla | 4 |
| 20414 | tinaja | 4 |
| 20415 | tin | 4 |
| 20416 | timorato | 4 |
| 20417 | times | 4 |
| 20418 | tijera | 4 |
| 20419 | tigres | 4 |
| 20420 | tiernísimo | 4 |
| 20421 | tiemblan | 4 |
| 20422 | tic | 4 |
| 20423 | tiara | 4 |
| 20424 | thesoro | 4 |
| 20425 | the | 4 |
| 20426 | tetis | 4 |
| 20427 | tetas | 4 |
| 20428 | testimonios | 4 |
| 20429 | tertulio | 4 |
| 20430 | tertulín | 4 |
| 20431 | terruño | 4 |
| 20432 | territorial | 4 |
| 20433 | terno | 4 |
| 20434 | ternia | 4 |
| 20435 | terne | 4 |
| 20436 | ternas | 4 |
| 20437 | terciando | 4 |
| 20438 | terçia | 4 |
| 20439 | tercas | 4 |
| 20440 | teñida | 4 |
| 20441 | tentado | 4 |
| 20442 | tenorios | 4 |
| 20443 | tenier | 4 |
| 20444 | tenidos | 4 |
| 20445 | tenerias | 4 |
| 20446 | teneos | 4 |
| 20447 | tenella | 4 |
| 20448 | teneatis | 4 |
| 20449 | tendimos | 4 |
| 20450 | tendencia | 4 |
| 20451 | tenacillas | 4 |
| 20452 | tempore | 4 |
| 20453 | temístocles | 4 |
| 20454 | temblorosas | 4 |
| 20455 | temblores | 4 |
| 20456 | telégrafos | 4 |
| 20457 | tejares | 4 |
| 20458 | técnicos | 4 |
| 20459 | teclas | 4 |
| 20460 | techado | 4 |
| 20461 | teatrales | 4 |
| 20462 | tate | 4 |
| 20463 | tasado | 4 |
| 20464 | tarsila | 4 |
| 20465 | tardía | 4 |
| 20466 | tardaremos | 4 |
| 20467 | tardará | 4 |
| 20468 | tardamos | 4 |
| 20469 | tararí | 4 |
| 20470 | tapizada | 4 |
| 20471 | taparse | 4 |
| 20472 | tapado | 4 |
| 20473 | tañía | 4 |
| 20474 | tantismas | 4 |
| 20475 | tantísimo | 4 |
| 20476 | tantísimas | 4 |
| 20477 | tantico | 4 |
| 20478 | tanteando | 4 |
| 20479 | tangible | 4 |
| 20480 | tane | 4 |
| 20481 | tamboril | 4 |
| 20482 | tambaleándose | 4 |
| 20483 | talud | 4 |
| 20484 | talonario | 4 |
| 20485 | talentazo | 4 |
| 20486 | talegos | 4 |
| 20487 | talego | 4 |
| 20488 | taimada | 4 |
| 20489 | tácitamente | 4 |
| 20490 | tácita | 4 |
| 20491 | tableros | 4 |
| 20492 | taberneros | 4 |
| 20493 | taba | 4 |
| 20494 | syervo | 4 |
| 20495 | sustituto | 4 |
| 20496 | sustituir | 4 |
| 20497 | sustentada | 4 |
| 20498 | sustentaban | 4 |
| 20499 | sustanciales | 4 |
| 20500 | suspicaz | 4 |
| 20501 | suspendido | 4 |
| 20502 | suspendida | 4 |
| 20503 | suscriciones | 4 |
| 20504 | susceptibilidad | 4 |
| 20505 | surgieron | 4 |
| 20506 | surgido | 4 |
| 20507 | surco | 4 |
| 20508 | suplicaron | 4 |
| 20509 | suplicar | 4 |
| 20510 | suplica | 4 |
| 20511 | supieres | 4 |
| 20512 | supieras | 4 |
| 20513 | superaba | 4 |
| 20514 | supera | 4 |
| 20515 | suntuosos | 4 |
| 20516 | suntuoso | 4 |
| 20517 | sunt | 4 |
| 20518 | sumida | 4 |
| 20519 | sum | 4 |
| 20520 | sujetaron | 4 |
| 20521 | sujetarme | 4 |
| 20522 | sujetándole | 4 |
| 20523 | suizo | 4 |
| 20524 | suicida | 4 |
| 20525 | sugestiones | 4 |
| 20526 | sufrirá | 4 |
| 20527 | sufridor | 4 |
| 20528 | suéltame | 4 |
| 20529 | sudorosa | 4 |
| 20530 | sucedidos | 4 |
| 20531 | sucederle | 4 |
| 20532 | subterránea | 4 |
| 20533 | subterfugios | 4 |
| 20534 | subordinación | 4 |
| 20535 | sublimidades | 4 |
| 20536 | subirse | 4 |
| 20537 | subirá | 4 |
| 20538 | subiéndose | 4 |
| 20539 | subidas | 4 |
| 20540 | subas | 4 |
| 20541 | subalternos | 4 |
| 20542 | ssyenpre | 4 |
| 20543 | sson | 4 |
| 20544 | sse | 4 |
| 20545 | soys | 4 |
| 20546 | souvenir | 4 |
| 20547 | sotileza | 4 |
| 20548 | sotiles | 4 |
| 20549 | sostendrá | 4 |
| 20550 | sospira | 4 |
| 20551 | sospeché | 4 |
| 20552 | sospechase | 4 |
| 20553 | sospecharlo | 4 |
| 20554 | sospechan | 4 |
| 20555 | sosos | 4 |
| 20556 | sosiéguese | 4 |
| 20557 | sosegarse | 4 |
| 20558 | sortijillas | 4 |
| 20559 | sorprendieron | 4 |
| 20560 | sorprende | 4 |
| 20561 | sorna | 4 |
| 20562 | sórdido | 4 |
| 20563 | sordas | 4 |
| 20564 | sorbetes | 4 |
| 20565 | soporífero | 4 |
| 20566 | soñolientos | 4 |
| 20567 | sonrieron | 4 |
| 20568 | sones | 4 |
| 20569 | sonara | 4 |
| 20570 | sometido | 4 |
| 20571 | sombrilla | 4 |
| 20572 | sollado | 4 |
| 20573 | solito | 4 |
| 20574 | solita | 4 |
| 20575 | soliman | 4 |
| 20576 | sólidas | 4 |
| 20577 | solicito | 4 |
| 20578 | solfa | 4 |
| 20579 | solares | 4 |
| 20580 | solapas | 4 |
| 20581 | solapada | 4 |
| 20582 | sojuzgada | 4 |
| 20583 | sofocante | 4 |
| 20584 | sofocadísima | 4 |
| 20585 | sodio | 4 |
| 20586 | socialistas | 4 |
| 20587 | socialista | 4 |
| 20588 | socarrona | 4 |
| 20589 | sobresaltó | 4 |
| 20590 | sobrepuja | 4 |
| 20591 | sobremodo | 4 |
| 20592 | sobrantes | 4 |
| 20593 | sobir | 4 |
| 20594 | sobado | 4 |
| 20595 | sobaco | 4 |
| 20596 | situado | 4 |
| 20597 | sitiada | 4 |
| 20598 | sistemática | 4 |
| 20599 | sirviera | 4 |
| 20600 | sirvas | 4 |
| 20601 | siruen | 4 |
| 20602 | sinónimo | 4 |
| 20603 | sinnúmero | 4 |
| 20604 | sinforosa | 4 |
| 20605 | sinceros | 4 |
| 20606 | simonía | 4 |
| 20607 | similitud | 4 |
| 20608 | símil | 4 |
| 20609 | simiente | 4 |
| 20610 | simbolizaba | 4 |
| 20611 | simbólico | 4 |
| 20612 | silvestre | 4 |
| 20613 | siluetas | 4 |
| 20614 | sillita | 4 |
| 20615 | silbante | 4 |
| 20616 | silban | 4 |
| 20617 | silba | 4 |
| 20618 | siguióle | 4 |
| 20619 | sígueme | 4 |
| 20620 | sigs | 4 |
| 20621 | sigan | 4 |
| 20622 | sieruo | 4 |
| 20623 | sierto | 4 |
| 20624 | sierpes | 4 |
| 20625 | sic | 4 |
| 20626 | seyle | 4 |
| 20627 | severas | 4 |
| 20628 | setecientas | 4 |
| 20629 | setas | 4 |
| 20630 | sesso | 4 |
| 20631 | sesiones | 4 |
| 20632 | servirse | 4 |
| 20633 | servirles | 4 |
| 20634 | servirían | 4 |
| 20635 | serviré | 4 |
| 20636 | servilletas | 4 |
| 20637 | seruida | 4 |
| 20638 | sernos | 4 |
| 20639 | serian | 4 |
| 20640 | serenó | 4 |
| 20641 | sere | 4 |
| 20642 | serafines | 4 |
| 20643 | sepultar | 4 |
| 20644 | sepulcral | 4 |
| 20645 | séptimo | 4 |
| 20646 | separarnos | 4 |
| 20647 | separándose | 4 |
| 20648 | separada | 4 |
| 20649 | señoronas | 4 |
| 20650 | señoríos | 4 |
| 20651 | señalo | 4 |
| 20652 | señale | 4 |
| 20653 | senyor | 4 |
| 20654 | senti | 4 |
| 20655 | sentándola | 4 |
| 20656 | sensual | 4 |
| 20657 | sensatas | 4 |
| 20658 | senectud | 4 |
| 20659 | semíramis | 4 |
| 20660 | semejas | 4 |
| 20661 | semejan | 4 |
| 20662 | segur | 4 |
| 20663 | seguimiento | 4 |
| 20664 | seguille | 4 |
| 20665 | seguidillas | 4 |
| 20666 | segadores | 4 |
| 20667 | seductoras | 4 |
| 20668 | seducía | 4 |
| 20669 | seduce | 4 |
| 20670 | seducciones | 4 |
| 20671 | sectario | 4 |
| 20672 | secciones | 4 |
| 20673 | seays | 4 |
| 20674 | scripsi | 4 |
| 20675 | sayas | 4 |
| 20676 | saúl | 4 |
| 20677 | satisfacían | 4 |
| 20678 | satisfacía | 4 |
| 20679 | sátiras | 4 |
| 20680 | sartenes | 4 |
| 20681 | sarmientos | 4 |
| 20682 | sargel | 4 |
| 20683 | sardina | 4 |
| 20684 | sáqueme | 4 |
| 20685 | santiguó | 4 |
| 20686 | sanó | 4 |
| 20687 | sangrientas | 4 |
| 20688 | sangrando | 4 |
| 20689 | sane | 4 |
| 20690 | sancto | 4 |
| 20691 | sanaba | 4 |
| 20692 | samaniegos | 4 |
| 20693 | salyr | 4 |
| 20694 | salya | 4 |
| 20695 | salvaría | 4 |
| 20696 | salvando | 4 |
| 20697 | salutaçión | 4 |
| 20698 | saludes | 4 |
| 20699 | saltimbanquis | 4 |
| 20700 | salté | 4 |
| 20701 | saltara | 4 |
| 20702 | salsas | 4 |
| 20703 | salpicaba | 4 |
| 20704 | salomón | 4 |
| 20705 | salióse | 4 |
| 20706 | salientes | 4 |
| 20707 | salidos | 4 |
| 20708 | salíamos | 4 |
| 20709 | saldrás | 4 |
| 20710 | saladas | 4 |
| 20711 | sahumar | 4 |
| 20712 | sacudiéndose | 4 |
| 20713 | sacudiéndole | 4 |
| 20714 | sacudían | 4 |
| 20715 | sacude | 4 |
| 20716 | sacripante | 4 |
| 20717 | sacrílegos | 4 |
| 20718 | sacrilegio | 4 |
| 20719 | sacrificado | 4 |
| 20720 | sacerdotal | 4 |
| 20721 | sacasen | 4 |
| 20722 | sacaros | 4 |
| 20723 | sácame | 4 |
| 20724 | sabrían | 4 |
| 20725 | sabrán | 4 |
| 20726 | saboreado | 4 |
| 20727 | sabiendas | 4 |
| 20728 | sabidora | 4 |
| 20729 | sabedes | 4 |
| 20730 | ruyndad | 4 |
| 20731 | ruy | 4 |
| 20732 | rurales | 4 |
| 20733 | rufian | 4 |
| 20734 | ruegote | 4 |
| 20735 | rueca | 4 |
| 20736 | rudamente | 4 |
| 20737 | ruborizarse | 4 |
| 20738 | rrostro | 4 |
| 20739 | rroma | 4 |
| 20740 | rriquesa | 4 |
| 20741 | rribera | 4 |
| 20742 | rrespondió | 4 |
| 20743 | rresçebir | 4 |
| 20744 | rredes | 4 |
| 20745 | rravia | 4 |
| 20746 | rraçones | 4 |
| 20747 | rracha | 4 |
| 20748 | roydo | 4 |
| 20749 | rótulos | 4 |
| 20750 | rosicler | 4 |
| 20751 | rosado | 4 |
| 20752 | ropero | 4 |
| 20753 | rondas | 4 |
| 20754 | rondar | 4 |
| 20755 | roncando | 4 |
| 20756 | romperla | 4 |
| 20757 | románticos | 4 |
| 20758 | romanas | 4 |
| 20759 | roídos | 4 |
| 20760 | roído | 4 |
| 20761 | roía | 4 |
| 20762 | rogarle | 4 |
| 20763 | rodaba | 4 |
| 20764 | rocino | 4 |
| 20765 | rocines | 4 |
| 20766 | robustas | 4 |
| 20767 | robledo | 4 |
| 20768 | robando | 4 |
| 20769 | rizoso | 4 |
| 20770 | risum | 4 |
| 20771 | risueñas | 4 |
| 20772 | ristre | 4 |
| 20773 | risilla | 4 |
| 20774 | riñones | 4 |
| 20775 | riño | 4 |
| 20776 | riñe | 4 |
| 20777 | rindiese | 4 |
| 20778 | rindieron | 4 |
| 20779 | rinda | 4 |
| 20780 | rifas | 4 |
| 20781 | rifa | 4 |
| 20782 | ries | 4 |
| 20783 | ridiculez | 4 |
| 20784 | riales | 4 |
| 20785 | rezaría | 4 |
| 20786 | rezado | 4 |
| 20787 | rezaban | 4 |
| 20788 | reyr | 4 |
| 20789 | reyno | 4 |
| 20790 | revuelven | 4 |
| 20791 | revuelve | 4 |
| 20792 | revolvieron | 4 |
| 20793 | revolvían | 4 |
| 20794 | revolucionarios | 4 |
| 20795 | revolcándose | 4 |
| 20796 | reventones | 4 |
| 20797 | reventó | 4 |
| 20798 | reveló | 4 |
| 20799 | reuma | 4 |
| 20800 | reuerencia | 4 |
| 20801 | retuvo | 4 |
| 20802 | retumbaba | 4 |
| 20803 | retratada | 4 |
| 20804 | retozos | 4 |
| 20805 | retozona | 4 |
| 20806 | retorcer | 4 |
| 20807 | retoños | 4 |
| 20808 | retírese | 4 |
| 20809 | retiré | 4 |
| 20810 | retirarme | 4 |
| 20811 | retiran | 4 |
| 20812 | reticencia | 4 |
| 20813 | retamas | 4 |
| 20814 | resultan | 4 |
| 20815 | resultaban | 4 |
| 20816 | resuelva | 4 |
| 20817 | resueltos | 4 |
| 20818 | resucita | 4 |
| 20819 | restituye | 4 |
| 20820 | respondiste | 4 |
| 20821 | respondería | 4 |
| 20822 | responderá | 4 |
| 20823 | respondéis | 4 |
| 20824 | respira | 4 |
| 20825 | respete | 4 |
| 20826 | respetada | 4 |
| 20827 | respetaban | 4 |
| 20828 | resonancias | 4 |
| 20829 | residir | 4 |
| 20830 | residen | 4 |
| 20831 | reside | 4 |
| 20832 | reservas | 4 |
| 20833 | reservándose | 4 |
| 20834 | resentimientos | 4 |
| 20835 | rescebido | 4 |
| 20836 | requisito | 4 |
| 20837 | requiebro | 4 |
| 20838 | requerir | 4 |
| 20839 | requerida | 4 |
| 20840 | reputado | 4 |
| 20841 | repuse | 4 |
| 20842 | repulgos | 4 |
| 20843 | repugnaban | 4 |
| 20844 | reproducía | 4 |
| 20845 | reprimenda | 4 |
| 20846 | representamos | 4 |
| 20847 | represar | 4 |
| 20848 | reprensible | 4 |
| 20849 | reprendió | 4 |
| 20850 | reprender | 4 |
| 20851 | reponerse | 4 |
| 20852 | repliqué | 4 |
| 20853 | repica | 4 |
| 20854 | repetirlo | 4 |
| 20855 | repetidos | 4 |
| 20856 | repentinas | 4 |
| 20857 | repasando | 4 |
| 20858 | repartieron | 4 |
| 20859 | repartidos | 4 |
| 20860 | reparten | 4 |
| 20861 | reparando | 4 |
| 20862 | reparador | 4 |
| 20863 | reñirle | 4 |
| 20864 | renuncio | 4 |
| 20865 | renqueando | 4 |
| 20866 | renovando | 4 |
| 20867 | renovado | 4 |
| 20868 | renovaba | 4 |
| 20869 | renegados | 4 |
| 20870 | rendidos | 4 |
| 20871 | rendía | 4 |
| 20872 | renacía | 4 |
| 20873 | remontaba | 4 |
| 20874 | remolque | 4 |
| 20875 | remolcar | 4 |
| 20876 | remediarlos | 4 |
| 20877 | reluce | 4 |
| 20878 | relojero | 4 |
| 20879 | religiosamente | 4 |
| 20880 | relator | 4 |
| 20881 | relativas | 4 |
| 20882 | relamía | 4 |
| 20883 | relacionadas | 4 |
| 20884 | rejuvenecido | 4 |
| 20885 | rejilla | 4 |
| 20886 | reiterar | 4 |
| 20887 | reíase | 4 |
| 20888 | reías | 4 |
| 20889 | rehusaba | 4 |
| 20890 | rehízo | 4 |
| 20891 | regresar | 4 |
| 20892 | regoldar | 4 |
| 20893 | regocijaba | 4 |
| 20894 | registró | 4 |
| 20895 | regida | 4 |
| 20896 | regía | 4 |
| 20897 | regeneración | 4 |
| 20898 | regaladas | 4 |
| 20899 | regalada | 4 |
| 20900 | regala | 4 |
| 20901 | refugiarse | 4 |
| 20902 | refuerzo | 4 |
| 20903 | refrescaba | 4 |
| 20904 | reforzar | 4 |
| 20905 | reformar | 4 |
| 20906 | refectorio | 4 |
| 20907 | refajo | 4 |
| 20908 | redunde | 4 |
| 20909 | redujo | 4 |
| 20910 | reducen | 4 |
| 20911 | redondas | 4 |
| 20912 | redomado | 4 |
| 20913 | redacciones | 4 |
| 20914 | recuesta | 4 |
| 20915 | recrearme | 4 |
| 20916 | recordarlo | 4 |
| 20917 | recordarás | 4 |
| 20918 | recordándole | 4 |
| 20919 | reconvención | 4 |
| 20920 | reconocida | 4 |
| 20921 | reconocerla | 4 |
| 20922 | recóndito | 4 |
| 20923 | reconciliarse | 4 |
| 20924 | recomendándole | 4 |
| 20925 | recogidos | 4 |
| 20926 | recogí | 4 |
| 20927 | recogerse | 4 |
| 20928 | recocho | 4 |
| 20929 | reclusión | 4 |
| 20930 | reclusa | 4 |
| 20931 | reclamando | 4 |
| 20932 | recitantes | 4 |
| 20933 | recios | 4 |
| 20934 | recientemente | 4 |
| 20935 | recibirla | 4 |
| 20936 | recibiré | 4 |
| 20937 | recibiéronme | 4 |
| 20938 | recibidas | 4 |
| 20939 | recibes | 4 |
| 20940 | reciamente | 4 |
| 20941 | rechazo | 4 |
| 20942 | rechazado | 4 |
| 20943 | recetó | 4 |
| 20944 | recelos | 4 |
| 20945 | recelando | 4 |
| 20946 | recebirla | 4 |
| 20947 | recebid | 4 |
| 20948 | recayó | 4 |
| 20949 | recatos | 4 |
| 20950 | recatado | 4 |
| 20951 | recatadas | 4 |
| 20952 | recargado | 4 |
| 20953 | recaída | 4 |
| 20954 | recabdo | 4 |
| 20955 | rebuznaron | 4 |
| 20956 | rebosa | 4 |
| 20957 | reboluer | 4 |
| 20958 | rebeldía | 4 |
| 20959 | rebelaba | 4 |
| 20960 | rebajarse | 4 |
| 20961 | reata | 4 |
| 20962 | realizando | 4 |
| 20963 | realización | 4 |
| 20964 | realista | 4 |
| 20965 | rayzes | 4 |
| 20966 | rayado | 4 |
| 20967 | ratonado | 4 |
| 20968 | ratas | 4 |
| 20969 | rascó | 4 |
| 20970 | rarísimo | 4 |
| 20971 | rareza | 4 |
| 20972 | raquítica | 4 |
| 20973 | rapaza | 4 |
| 20974 | rapavelas | 4 |
| 20975 | rancor | 4 |
| 20976 | ramplón | 4 |
| 20977 | ralo | 4 |
| 20978 | rajas | 4 |
| 20979 | raja | 4 |
| 20980 | rábano | 4 |
| 20981 | quitaste | 4 |
| 20982 | quitársele | 4 |
| 20983 | quitaré | 4 |
| 20984 | quitaran | 4 |
| 20985 | quisquilloso | 4 |
| 20986 | quirlis | 4 |
| 20987 | quirido | 4 |
| 20988 | quinientas | 4 |
| 20989 | quijotes | 4 |
| 20990 | quijana | 4 |
| 20991 | ques | 4 |
| 20992 | querrian | 4 |
| 20993 | querríamos | 4 |
| 20994 | querra | 4 |
| 20995 | quercus | 4 |
| 20996 | querades | 4 |
| 20997 | queje | 4 |
| 20998 | quejaban | 4 |
| 20999 | quédense | 4 |
| 21000 | quedéis | 4 |
| 21001 | quedaste | 4 |
| 21002 | quedarte | 4 |
| 21003 | quedaros | 4 |
| 21004 | quedarás | 4 |
| 21005 | quedamente | 4 |
| 21006 | quedábamos | 4 |
| 21007 | quebrantar | 4 |
| 21008 | quebrantamiento | 4 |
| 21009 | quebrantados | 4 |
| 21010 | quebrando | 4 |
| 21011 | quebradas | 4 |
| 21012 | quebraban | 4 |
| 21013 | quarta | 4 |
| 21014 | quantidad | 4 |
| 21015 | quam | 4 |
| 21016 | q | 4 |
| 21017 | puymaigre | 4 |
| 21018 | puy | 4 |
| 21019 | púsosela | 4 |
| 21020 | púsome | 4 |
| 21021 | purpúreos | 4 |
| 21022 | purpúreas | 4 |
| 21023 | purifica | 4 |
| 21024 | purga | 4 |
| 21025 | punzón | 4 |
| 21026 | puntiagudos | 4 |
| 21027 | puntales | 4 |
| 21028 | puntal | 4 |
| 21029 | puntada | 4 |
| 21030 | pundonor | 4 |
| 21031 | pulvisés | 4 |
| 21032 | pulquérrimo | 4 |
| 21033 | pulla | 4 |
| 21034 | pulgares | 4 |
| 21035 | pugnando | 4 |
| 21036 | puebla | 4 |
| 21037 | publique | 4 |
| 21038 | publicando | 4 |
| 21039 | publicada | 4 |
| 21040 | publicación | 4 |
| 21041 | púa | 4 |
| 21042 | psicológico | 4 |
| 21043 | psicología | 4 |
| 21044 | prudentemente | 4 |
| 21045 | proyectil | 4 |
| 21046 | provocar | 4 |
| 21047 | provocado | 4 |
| 21048 | provocada | 4 |
| 21049 | provinciano | 4 |
| 21050 | proveyó | 4 |
| 21051 | proveídos | 4 |
| 21052 | provechosos | 4 |
| 21053 | provechosa | 4 |
| 21054 | prouision | 4 |
| 21055 | prósperos | 4 |
| 21056 | prosopopeya | 4 |
| 21057 | proscenio | 4 |
| 21058 | prosaicas | 4 |
| 21059 | prórroga | 4 |
| 21060 | propusieron | 4 |
| 21061 | propriedad | 4 |
| 21062 | proporcionado | 4 |
| 21063 | proponiendo | 4 |
| 21064 | proponga | 4 |
| 21065 | proponerle | 4 |
| 21066 | propagandista | 4 |
| 21067 | pronunciamiento | 4 |
| 21068 | pronunciación | 4 |
| 21069 | pronuncia | 4 |
| 21070 | prontos | 4 |
| 21071 | pronósticos | 4 |
| 21072 | prometi | 4 |
| 21073 | prometerse | 4 |
| 21074 | promessa | 4 |
| 21075 | prolongar | 4 |
| 21076 | prolongándose | 4 |
| 21077 | prolongación | 4 |
| 21078 | prolijidad | 4 |
| 21079 | prolijas | 4 |
| 21080 | profético | 4 |
| 21081 | profesaron | 4 |
| 21082 | profesaban | 4 |
| 21083 | profanar | 4 |
| 21084 | productos | 4 |
| 21085 | produciéndole | 4 |
| 21086 | prodigar | 4 |
| 21087 | prodigalidad | 4 |
| 21088 | procuremos | 4 |
| 21089 | procuraron | 4 |
| 21090 | processo | 4 |
| 21091 | proceloso | 4 |
| 21092 | procaz | 4 |
| 21093 | probarme | 4 |
| 21094 | probarla | 4 |
| 21095 | probada | 4 |
| 21096 | privó | 4 |
| 21097 | privilegiado | 4 |
| 21098 | privilegiada | 4 |
| 21099 | privanza | 4 |
| 21100 | priuado | 4 |
| 21101 | priua | 4 |
| 21102 | pringue | 4 |
| 21103 | principia | 4 |
| 21104 | primitivas | 4 |
| 21105 | previno | 4 |
| 21106 | prevenida | 4 |
| 21107 | pretendida | 4 |
| 21108 | presumiendo | 4 |
| 21109 | presuma | 4 |
| 21110 | prestan | 4 |
| 21111 | prestados | 4 |
| 21112 | presintió | 4 |
| 21113 | presidir | 4 |
| 21114 | presidiendo | 4 |
| 21115 | presidida | 4 |
| 21116 | presidía | 4 |
| 21117 | presentase | 4 |
| 21118 | presentará | 4 |
| 21119 | presentándose | 4 |
| 21120 | presentándole | 4 |
| 21121 | presenció | 4 |
| 21122 | presagios | 4 |
| 21123 | prerrogativa | 4 |
| 21124 | prepararle | 4 |
| 21125 | preparados | 4 |
| 21126 | preocupaban | 4 |
| 21127 | preñado | 4 |
| 21128 | premiados | 4 |
| 21129 | preguntome | 4 |
| 21130 | preguntóles | 4 |
| 21131 | preguntarte | 4 |
| 21132 | preguntándoles | 4 |
| 21133 | preguntamos | 4 |
| 21134 | pregonando | 4 |
| 21135 | preferencias | 4 |
| 21136 | predominaba | 4 |
| 21137 | predilección | 4 |
| 21138 | predicadores | 4 |
| 21139 | predicado | 4 |
| 21140 | precipitados | 4 |
| 21141 | precipitaba | 4 |
| 21142 | precias | 4 |
| 21143 | preçiado | 4 |
| 21144 | preceder | 4 |
| 21145 | precedente | 4 |
| 21146 | pradecillo | 4 |
| 21147 | practicar | 4 |
| 21148 | postrada | 4 |
| 21149 | postizo | 4 |
| 21150 | postizas | 4 |
| 21151 | posteriormente | 4 |
| 21152 | posterior | 4 |
| 21153 | post | 4 |
| 21154 | possible | 4 |
| 21155 | possession | 4 |
| 21156 | pospuesto | 4 |
| 21157 | poso | 4 |
| 21158 | poseerlo | 4 |
| 21159 | posar | 4 |
| 21160 | posado | 4 |
| 21161 | portando | 4 |
| 21162 | portaba | 4 |
| 21163 | porradas | 4 |
| 21164 | porfías | 4 |
| 21165 | porfia | 4 |
| 21166 | poquísimo | 4 |
| 21167 | pontifical | 4 |
| 21168 | ponle | 4 |
| 21169 | poneros | 4 |
| 21170 | pompas | 4 |
| 21171 | pomada | 4 |
| 21172 | polvoriento | 4 |
| 21173 | pollinas | 4 |
| 21174 | polisón | 4 |
| 21175 | policías | 4 |
| 21176 | polémicas | 4 |
| 21177 | poique | 4 |
| 21178 | podrías | 4 |
| 21179 | podiere | 4 |
| 21180 | poderle | 4 |
| 21181 | poderlas | 4 |
| 21182 | podar | 4 |
| 21183 | pocilga | 4 |
| 21184 | pobrete | 4 |
| 21185 | pobremente | 4 |
| 21186 | plutarco | 4 |
| 21187 | plumaje | 4 |
| 21188 | pluguiese | 4 |
| 21189 | pleno | 4 |
| 21190 | plencia | 4 |
| 21191 | plazuelas | 4 |
| 21192 | plazía | 4 |
| 21193 | plazentera | 4 |
| 21194 | plaze | 4 |
| 21195 | playas | 4 |
| 21196 | platónicos | 4 |
| 21197 | plásticas | 4 |
| 21198 | plantaba | 4 |
| 21199 | planos | 4 |
| 21200 | planchas | 4 |
| 21201 | placidez | 4 |
| 21202 | pizarra | 4 |
| 21203 | pitillo | 4 |
| 21204 | pistoletazo | 4 |
| 21205 | pisas | 4 |
| 21206 | pisado | 4 |
| 21207 | piropos | 4 |
| 21208 | pintorescos | 4 |
| 21209 | pintarse | 4 |
| 21210 | pintarla | 4 |
| 21211 | pinitos | 4 |
| 21212 | pingo | 4 |
| 21213 | pinchazos | 4 |
| 21214 | pinchaban | 4 |
| 21215 | pince | 4 |
| 21216 | pimpollo | 4 |
| 21217 | pilón | 4 |
| 21218 | pilas | 4 |
| 21219 | piensos | 4 |
| 21220 | piensen | 4 |
| 21221 | piénselo | 4 |
| 21222 | pidióme | 4 |
| 21223 | pidiéronme | 4 |
| 21224 | picoteando | 4 |
| 21225 | picotazos | 4 |
| 21226 | picarón | 4 |
| 21227 | picaresco | 4 |
| 21228 | picadillo | 4 |
| 21229 | piar | 4 |
| 21230 | pía | 4 |
| 21231 | petrificada | 4 |
| 21232 | petiçión | 4 |
| 21233 | pescas | 4 |
| 21234 | pesando | 4 |
| 21235 | perversas | 4 |
| 21236 | perversa | 4 |
| 21237 | pertinaz | 4 |
| 21238 | pertinacia | 4 |
| 21239 | pertenecientes | 4 |
| 21240 | persuadirme | 4 |
| 21241 | persuadirle | 4 |
| 21242 | persuadida | 4 |
| 21243 | personilla | 4 |
| 21244 | persistía | 4 |
| 21245 | persiles | 4 |
| 21246 | persiguiendo | 4 |
| 21247 | perseverar | 4 |
| 21248 | perrito | 4 |
| 21249 | perrillo | 4 |
| 21250 | perrero | 4 |
| 21251 | perpetuamente | 4 |
| 21252 | peroles | 4 |
| 21253 | pernando | 4 |
| 21254 | permítaseme | 4 |
| 21255 | perjuicios | 4 |
| 21256 | peripecia | 4 |
| 21257 | periodistas | 4 |
| 21258 | pergenio | 4 |
| 21259 | pergaminos | 4 |
| 21260 | perfectos | 4 |
| 21261 | peresoso | 4 |
| 21262 | perecedero | 4 |
| 21263 | perdurable | 4 |
| 21264 | perdoñar | 4 |
| 21265 | perdonarla | 4 |
| 21266 | perdonará | 4 |
| 21267 | perdónala | 4 |
| 21268 | perdonadme | 4 |
| 21269 | perdon | 4 |
| 21270 | perdis | 4 |
| 21271 | perdióse | 4 |
| 21272 | perdimos | 4 |
| 21273 | perderte | 4 |
| 21274 | perderlo | 4 |
| 21275 | perderás | 4 |
| 21276 | perdamos | 4 |
| 21277 | percance | 4 |
| 21278 | pequeñitos | 4 |
| 21279 | pequeñito | 4 |
| 21280 | pentapolín | 4 |
| 21281 | pensándolo | 4 |
| 21282 | pensadores | 4 |
| 21283 | peno | 4 |
| 21284 | penetrado | 4 |
| 21285 | penetración | 4 |
| 21286 | penélope | 4 |
| 21287 | pendón | 4 |
| 21288 | penca | 4 |
| 21289 | peluquería | 4 |
| 21290 | peludo | 4 |
| 21291 | pellote | 4 |
| 21292 | pellico | 4 |
| 21293 | peje | 4 |
| 21294 | peinaba | 4 |
| 21295 | peina | 4 |
| 21296 | peguetas | 4 |
| 21297 | pegarse | 4 |
| 21298 | pegaron | 4 |
| 21299 | pegándose | 4 |
| 21300 | pegajoso | 4 |
| 21301 | pedregoso | 4 |
| 21302 | pedirles | 4 |
| 21303 | pediremos | 4 |
| 21304 | pedidos | 4 |
| 21305 | pedíale | 4 |
| 21306 | pedi | 4 |
| 21307 | pedestre | 4 |
| 21308 | pecosa | 4 |
| 21309 | pecó | 4 |
| 21310 | peco | 4 |
| 21311 | peçes | 4 |
| 21312 | pecaminosa | 4 |
| 21313 | pavorosa | 4 |
| 21314 | paul | 4 |
| 21315 | patriarcas | 4 |
| 21316 | patraña | 4 |
| 21317 | patochada | 4 |
| 21318 | patita | 4 |
| 21319 | paterno | 4 |
| 21320 | paternidad | 4 |
| 21321 | paternales | 4 |
| 21322 | pastoril | 4 |
| 21323 | pastorales | 4 |
| 21324 | pastillas | 4 |
| 21325 | pastelero | 4 |
| 21326 | pastel | 4 |
| 21327 | passava | 4 |
| 21328 | pasqua | 4 |
| 21329 | pásmese | 4 |
| 21330 | pasmadas | 4 |
| 21331 | pasmaban | 4 |
| 21332 | pasearon | 4 |
| 21333 | pasea | 4 |
| 21334 | pasarme | 4 |
| 21335 | pasarlo | 4 |
| 21336 | pasarla | 4 |
| 21337 | pasarían | 4 |
| 21338 | pasarás | 4 |
| 21339 | pasaportes | 4 |
| 21340 | pasándole | 4 |
| 21341 | pasajeras | 4 |
| 21342 | partirme | 4 |
| 21343 | partiré | 4 |
| 21344 | partióse | 4 |
| 21345 | partiesen | 4 |
| 21346 | particularidad | 4 |
| 21347 | participando | 4 |
| 21348 | participa | 4 |
| 21349 | partían | 4 |
| 21350 | parten | 4 |
| 21351 | parra | 4 |
| 21352 | paróse | 4 |
| 21353 | parlera | 4 |
| 21354 | pariste | 4 |
| 21355 | parientas | 4 |
| 21356 | parezcas | 4 |
| 21357 | parescen | 4 |
| 21358 | parecia | 4 |
| 21359 | parecerían | 4 |
| 21360 | paréceos | 4 |
| 21361 | parciales | 4 |
| 21362 | parcerisa | 4 |
| 21363 | parca | 4 |
| 21364 | parapilla | 4 |
| 21365 | paramento | 4 |
| 21366 | paralelos | 4 |
| 21367 | paralelas | 4 |
| 21368 | paradojas | 4 |
| 21369 | paradas | 4 |
| 21370 | parábolas | 4 |
| 21371 | parabienes | 4 |
| 21372 | pára | 4 |
| 21373 | paquetito | 4 |
| 21374 | papelera | 4 |
| 21375 | papagayo | 4 |
| 21376 | pañoles | 4 |
| 21377 | pañales | 4 |
| 21378 | pantorrillas | 4 |
| 21379 | panegírico | 4 |
| 21380 | pandillas | 4 |
| 21381 | palurdos | 4 |
| 21382 | palpitar | 4 |
| 21383 | palpitante | 4 |
| 21384 | palpitación | 4 |
| 21385 | palpables | 4 |
| 21386 | palpaba | 4 |
| 21387 | palomos | 4 |
| 21388 | palmetazos | 4 |
| 21389 | palmerín | 4 |
| 21390 | palmera | 4 |
| 21391 | palidecía | 4 |
| 21392 | paletilla | 4 |
| 21393 | paletas | 4 |
| 21394 | paleta | 4 |
| 21395 | pales | 4 |
| 21396 | palaçio | 4 |
| 21397 | palabrillas | 4 |
| 21398 | palabreja | 4 |
| 21399 | pajarillo | 4 |
| 21400 | paisana | 4 |
| 21401 | pagarlo | 4 |
| 21402 | pagare | 4 |
| 21403 | pagaras | 4 |
| 21404 | pagarán | 4 |
| 21405 | pagana | 4 |
| 21406 | padrón | 4 |
| 21407 | padrenuestros | 4 |
| 21408 | padrenuestro | 4 |
| 21409 | pachorra | 4 |
| 21410 | pacer | 4 |
| 21411 | pace | 4 |
| 21412 | pábulo | 4 |
| 21413 | pablicos | 4 |
| 21414 | oyda | 4 |
| 21415 | overo | 4 |
| 21416 | ouiesse | 4 |
| 21417 | otrosi | 4 |
| 21418 | otorgó | 4 |
| 21419 | oteros | 4 |
| 21420 | ostentoso | 4 |
| 21421 | ostentando | 4 |
| 21422 | osas | 4 |
| 21423 | osara | 4 |
| 21424 | ortuño | 4 |
| 21425 | ortiz | 4 |
| 21426 | orla | 4 |
| 21427 | oriana | 4 |
| 21428 | orgullosos | 4 |
| 21429 | ordenes | 4 |
| 21430 | ordene | 4 |
| 21431 | ordenase | 4 |
| 21432 | ordenarse | 4 |
| 21433 | ordenare | 4 |
| 21434 | ordenándome | 4 |
| 21435 | opulencia | 4 |
| 21436 | oportunos | 4 |
| 21437 | oportunas | 4 |
| 21438 | opio | 4 |
| 21439 | opinan | 4 |
| 21440 | opinaban | 4 |
| 21441 | opera | 4 |
| 21442 | onze | 4 |
| 21443 | onrrada | 4 |
| 21444 | ondulantes | 4 |
| 21445 | ondulaciones | 4 |
| 21446 | onbre | 4 |
| 21447 | omitir | 4 |
| 21448 | olvidéme | 4 |
| 21449 | olvidará | 4 |
| 21450 | olvidábaseme | 4 |
| 21451 | olorcillo | 4 |
| 21452 | olfatear | 4 |
| 21453 | olfateando | 4 |
| 21454 | ojazos | 4 |
| 21455 | ojales | 4 |
| 21456 | oíslo | 4 |
| 21457 | oigas | 4 |
| 21458 | oigan | 4 |
| 21459 | oigamos | 4 |
| 21460 | ofrezcan | 4 |
| 21461 | ofreciera | 4 |
| 21462 | ofrecida | 4 |
| 21463 | ofrecerse | 4 |
| 21464 | oficiando | 4 |
| 21465 | oficialmente | 4 |
| 21466 | oficialidad | 4 |
| 21467 | ofendo | 4 |
| 21468 | ofendidos | 4 |
| 21469 | ofenderle | 4 |
| 21470 | ocurriera | 4 |
| 21471 | ocupase | 4 |
| 21472 | ocuparme | 4 |
| 21473 | ocupándose | 4 |
| 21474 | ocultado | 4 |
| 21475 | octavo | 4 |
| 21476 | ocasionado | 4 |
| 21477 | ocampo | 4 |
| 21478 | observarla | 4 |
| 21479 | observancia | 4 |
| 21480 | observaban | 4 |
| 21481 | obsequiar | 4 |
| 21482 | obscurantista | 4 |
| 21483 | obrera | 4 |
| 21484 | obrando | 4 |
| 21485 | obrado | 4 |
| 21486 | obligarle | 4 |
| 21487 | oblicua | 4 |
| 21488 | obispa | 4 |
| 21489 | oan | 4 |
| 21490 | nula | 4 |
| 21491 | núcleo | 4 |
| 21492 | nubecillas | 4 |
| 21493 | nubecilla | 4 |
| 21494 | novicia | 4 |
| 21495 | novelistas | 4 |
| 21496 | novecientos | 4 |
| 21497 | notomía | 4 |
| 21498 | noto | 4 |
| 21499 | notarse | 4 |
| 21500 | notarlo | 4 |
| 21501 | nora | 4 |
| 21502 | nombramientos | 4 |
| 21503 | nombrada | 4 |
| 21504 | noción | 4 |
| 21505 | noblemente | 4 |
| 21506 | nobis | 4 |
| 21507 | niñita | 4 |
| 21508 | nihil | 4 |
| 21509 | nigromante | 4 |
| 21510 | nevado | 4 |
| 21511 | neptune | 4 |
| 21512 | neófita | 4 |
| 21513 | nenes | 4 |
| 21514 | nenas | 4 |
| 21515 | neira | 4 |
| 21516 | negativo | 4 |
| 21517 | negase | 4 |
| 21518 | negándose | 4 |
| 21519 | negaban | 4 |
| 21520 | nefando | 4 |
| 21521 | neçios | 4 |
| 21522 | necesite | 4 |
| 21523 | necesitará | 4 |
| 21524 | necesitara | 4 |
| 21525 | nazca | 4 |
| 21526 | navegantes | 4 |
| 21527 | navegante | 4 |
| 21528 | navegábamos | 4 |
| 21529 | navega | 4 |
| 21530 | navarros | 4 |
| 21531 | náufragos | 4 |
| 21532 | nato | 4 |
| 21533 | nativo | 4 |
| 21534 | nasce | 4 |
| 21535 | narrar | 4 |
| 21536 | narigudo | 4 |
| 21537 | narcissus | 4 |
| 21538 | naranjo | 4 |
| 21539 | nalgas | 4 |
| 21540 | nadadores | 4 |
| 21541 | nadador | 4 |
| 21542 | nacionalidad | 4 |
| 21543 | naciese | 4 |
| 21544 | naces | 4 |
| 21545 | musicales | 4 |
| 21546 | murrias | 4 |
| 21547 | murmure | 4 |
| 21548 | murio | 4 |
| 21549 | murciélagos | 4 |
| 21550 | munguía | 4 |
| 21551 | mujerzuela | 4 |
| 21552 | muevo | 4 |
| 21553 | muestren | 4 |
| 21554 | muele | 4 |
| 21555 | mudéjares | 4 |
| 21556 | mudéjar | 4 |
| 21557 | mudé | 4 |
| 21558 | mudase | 4 |
| 21559 | mudarme | 4 |
| 21560 | muchedumbres | 4 |
| 21561 | mozuela | 4 |
| 21562 | mozalbete | 4 |
| 21563 | móvil | 4 |
| 21564 | movidas | 4 |
| 21565 | motas | 4 |
| 21566 | mostrenco | 4 |
| 21567 | mostrarme | 4 |
| 21568 | mosen | 4 |
| 21569 | moscones | 4 |
| 21570 | mortuorios | 4 |
| 21571 | mortifica | 4 |
| 21572 | morió | 4 |
| 21573 | morfina | 4 |
| 21574 | mordaz | 4 |
| 21575 | morcilla | 4 |
| 21576 | moran | 4 |
| 21577 | moqueta | 4 |
| 21578 | monumentos | 4 |
| 21579 | monumental | 4 |
| 21580 | montaraces | 4 |
| 21581 | monstruoso | 4 |
| 21582 | monstruosidad | 4 |
| 21583 | monstruosas | 4 |
| 21584 | monserga | 4 |
| 21585 | monótonos | 4 |
| 21586 | monosílabo | 4 |
| 21587 | monopolio | 4 |
| 21588 | monjes | 4 |
| 21589 | monísimo | 4 |
| 21590 | monges | 4 |
| 21591 | monge | 4 |
| 21592 | monesterios | 4 |
| 21593 | monerías | 4 |
| 21594 | mondo | 4 |
| 21595 | momias | 4 |
| 21596 | molyno | 4 |
| 21597 | molió | 4 |
| 21598 | molinete | 4 |
| 21599 | molieron | 4 |
| 21600 | molida | 4 |
| 21601 | molestarte | 4 |
| 21602 | molestaban | 4 |
| 21603 | moles | 4 |
| 21604 | mojada | 4 |
| 21605 | mohosas | 4 |
| 21606 | moho | 4 |
| 21607 | modificación | 4 |
| 21608 | modelos | 4 |
| 21609 | mochacha | 4 |
| 21610 | mismísima | 4 |
| 21611 | misioneros | 4 |
| 21612 | míseros | 4 |
| 21613 | misericordias | 4 |
| 21614 | mírenlo | 4 |
| 21615 | miremos | 4 |
| 21616 | mírele | 4 |
| 21617 | mirasen | 4 |
| 21618 | mirarte | 4 |
| 21619 | mirarlos | 4 |
| 21620 | mirará | 4 |
| 21621 | míralos | 4 |
| 21622 | mirador | 4 |
| 21623 | mirábase | 4 |
| 21624 | minucioso | 4 |
| 21625 | minuciosamente | 4 |
| 21626 | ministración | 4 |
| 21627 | mínimas | 4 |
| 21628 | mimosas | 4 |
| 21629 | mimaba | 4 |
| 21630 | miliciano | 4 |
| 21631 | milán | 4 |
| 21632 | migaja | 4 |
| 21633 | mies | 4 |
| 21634 | midió | 4 |
| 21635 | midiendo | 4 |
| 21636 | mide | 4 |
| 21637 | mico | 4 |
| 21638 | mias | 4 |
| 21639 | miaja | 4 |
| 21640 | miá | 4 |
| 21641 | mezquinamente | 4 |
| 21642 | metrópoli | 4 |
| 21643 | métrico | 4 |
| 21644 | metióse | 4 |
| 21645 | metiéndole | 4 |
| 21646 | meternos | 4 |
| 21647 | metan | 4 |
| 21648 | metálicas | 4 |
| 21649 | mesurada | 4 |
| 21650 | mesturero | 4 |
| 21651 | merodeo | 4 |
| 21652 | meretrices | 4 |
| 21653 | merendar | 4 |
| 21654 | mereciese | 4 |
| 21655 | merecidos | 4 |
| 21656 | merecedora | 4 |
| 21657 | merecedor | 4 |
| 21658 | mequetrefes | 4 |
| 21659 | mensajes | 4 |
| 21660 | menguar | 4 |
| 21661 | menearse | 4 |
| 21662 | meneallo | 4 |
| 21663 | mendizábal | 4 |
| 21664 | mendicante | 4 |
| 21665 | memo | 4 |
| 21666 | melodrama | 4 |
| 21667 | melezinas | 4 |
| 21668 | melecina | 4 |
| 21669 | mejoró | 4 |
| 21670 | mejorando | 4 |
| 21671 | mejoraba | 4 |
| 21672 | méjico | 4 |
| 21673 | médula | 4 |
| 21674 | medrosa | 4 |
| 21675 | medraremos | 4 |
| 21676 | medrados | 4 |
| 21677 | medo | 4 |
| 21678 | medirse | 4 |
| 21679 | medina | 4 |
| 21680 | medea | 4 |
| 21681 | mayordoma | 4 |
| 21682 | matronas | 4 |
| 21683 | matiz | 4 |
| 21684 | matilde | 4 |
| 21685 | matías | 4 |
| 21686 | maternales | 4 |
| 21687 | mataste | 4 |
| 21688 | matarnos | 4 |
| 21689 | mastyn | 4 |
| 21690 | mastines | 4 |
| 21691 | masticando | 4 |
| 21692 | masca | 4 |
| 21693 | martos | 4 |
| 21694 | marinas | 4 |
| 21695 | marín | 4 |
| 21696 | marchita | 4 |
| 21697 | marché | 4 |
| 21698 | marcharme | 4 |
| 21699 | marchara | 4 |
| 21700 | marchan | 4 |
| 21701 | marcaba | 4 |
| 21702 | maravillarse | 4 |
| 21703 | marasmo | 4 |
| 21704 | maquinal | 4 |
| 21705 | maquiavelismo | 4 |
| 21706 | mapas | 4 |
| 21707 | mañoso | 4 |
| 21708 | manubrio | 4 |
| 21709 | mantuvo | 4 |
| 21710 | manteniéndose | 4 |
| 21711 | manteniendo | 4 |
| 21712 | mantenían | 4 |
| 21713 | mantenerlas | 4 |
| 21714 | manteamiento | 4 |
| 21715 | manoseadas | 4 |
| 21716 | manirroto | 4 |
| 21717 | manguito | 4 |
| 21718 | mangonear | 4 |
| 21719 | maneje | 4 |
| 21720 | manderecha | 4 |
| 21721 | mándeme | 4 |
| 21722 | mandaua | 4 |
| 21723 | mandasen | 4 |
| 21724 | mandándoles | 4 |
| 21725 | mandáis | 4 |
| 21726 | mandada | 4 |
| 21727 | manchega | 4 |
| 21728 | manchar | 4 |
| 21729 | mançebía | 4 |
| 21730 | manca | 4 |
| 21731 | maltratar | 4 |
| 21732 | maltratan | 4 |
| 21733 | maltratada | 4 |
| 21734 | malta | 4 |
| 21735 | mallorca | 4 |
| 21736 | malignos | 4 |
| 21737 | malhumorado | 4 |
| 21738 | maleza | 4 |
| 21739 | maletas | 4 |
| 21740 | malestar | 4 |
| 21741 | maldiga | 4 |
| 21742 | malandante | 4 |
| 21743 | malamente | 4 |
| 21744 | malagueñas | 4 |
| 21745 | majestuosamente | 4 |
| 21746 | majaderías | 4 |
| 21747 | majadería | 4 |
| 21748 | majada | 4 |
| 21749 | mainate | 4 |
| 21750 | maguncia | 4 |
| 21751 | magos | 4 |
| 21752 | magnates | 4 |
| 21753 | mágico | 4 |
| 21754 | madrugó | 4 |
| 21755 | madrugas | 4 |
| 21756 | madrugado | 4 |
| 21757 | madrugaba | 4 |
| 21758 | madriz | 4 |
| 21759 | madreselva | 4 |
| 21760 | madrecita | 4 |
| 21761 | madrastra | 4 |
| 21762 | maderos | 4 |
| 21763 | madásima | 4 |
| 21764 | macizo | 4 |
| 21765 | machos | 4 |
| 21766 | machacárselo | 4 |
| 21767 | machacando | 4 |
| 21768 | machacaba | 4 |
| 21769 | lysonjas | 4 |
| 21770 | lyeve | 4 |
| 21771 | luteranos | 4 |
| 21772 | lustroso | 4 |
| 21773 | lustrosa | 4 |
| 21774 | luminosos | 4 |
| 21775 | lumbres | 4 |
| 21776 | luégo | 4 |
| 21777 | lució | 4 |
| 21778 | lucifer | 4 |
| 21779 | luchó | 4 |
| 21780 | lozano | 4 |
| 21781 | lot | 4 |
| 21782 | loriga | 4 |
| 21783 | loquillo | 4 |
| 21784 | lomas | 4 |
| 21785 | lola | 4 |
| 21786 | lodazal | 4 |
| 21787 | locutorio | 4 |
| 21788 | loçanas | 4 |
| 21789 | locales | 4 |
| 21790 | loava | 4 |
| 21791 | loada | 4 |
| 21792 | load | 4 |
| 21793 | lluevan | 4 |
| 21794 | llorosa | 4 |
| 21795 | lloraron | 4 |
| 21796 | llevóme | 4 |
| 21797 | llévese | 4 |
| 21798 | llevaste | 4 |
| 21799 | llevársele | 4 |
| 21800 | llevarnos | 4 |
| 21801 | llevarles | 4 |
| 21802 | llevaremos | 4 |
| 21803 | llévame | 4 |
| 21804 | llevadas | 4 |
| 21805 | lleue | 4 |
| 21806 | lleuan | 4 |
| 21807 | lleua | 4 |
| 21808 | lléguese | 4 |
| 21809 | lleguéme | 4 |
| 21810 | llegaste | 4 |
| 21811 | llegarse | 4 |
| 21812 | llegarían | 4 |
| 21813 | llegarán | 4 |
| 21814 | llegaos | 4 |
| 21815 | llegándole | 4 |
| 21816 | llegadas | 4 |
| 21817 | llámase | 4 |
| 21818 | llamare | 4 |
| 21819 | llamarán | 4 |
| 21820 | llámame | 4 |
| 21821 | llámale | 4 |
| 21822 | llamad | 4 |
| 21823 | llagada | 4 |
| 21824 | liviano | 4 |
| 21825 | liuiano | 4 |
| 21826 | literarios | 4 |
| 21827 | lisura | 4 |
| 21828 | lisonjeros | 4 |
| 21829 | lisonjear | 4 |
| 21830 | líquida | 4 |
| 21831 | lindísimo | 4 |
| 21832 | lindamente | 4 |
| 21833 | limitados | 4 |
| 21834 | lima | 4 |
| 21835 | lieva | 4 |
| 21836 | licores | 4 |
| 21837 | lícita | 4 |
| 21838 | líbrame | 4 |
| 21839 | liberalmente | 4 |
| 21840 | li | 4 |
| 21841 | levantisca | 4 |
| 21842 | levántase | 4 |
| 21843 | levantarla | 4 |
| 21844 | levantaría | 4 |
| 21845 | levantaos | 4 |
| 21846 | levantamiento | 4 |
| 21847 | levadiza | 4 |
| 21848 | lesa | 4 |
| 21849 | lepra | 4 |
| 21850 | lepanto | 4 |
| 21851 | leoncia | 4 |
| 21852 | lemos | 4 |
| 21853 | legítimos | 4 |
| 21854 | legitimidad | 4 |
| 21855 | legión | 4 |
| 21856 | lees | 4 |
| 21857 | leerle | 4 |
| 21858 | leemos | 4 |
| 21859 | lebrel | 4 |
| 21860 | léase | 4 |
| 21861 | lauor | 4 |
| 21862 | láudano | 4 |
| 21863 | latía | 4 |
| 21864 | lastre | 4 |
| 21865 | lastimar | 4 |
| 21866 | laso | 4 |
| 21867 | largarse | 4 |
| 21868 | laredo | 4 |
| 21869 | lapurrá | 4 |
| 21870 | lápice | 4 |
| 21871 | lanzaron | 4 |
| 21872 | lanzándose | 4 |
| 21873 | lanilla | 4 |
| 21874 | lamparones | 4 |
| 21875 | lamentación | 4 |
| 21876 | laico | 4 |
| 21877 | lagrimita | 4 |
| 21878 | lagarto | 4 |
| 21879 | ladron | 4 |
| 21880 | ladino | 4 |
| 21881 | laderas | 4 |
| 21882 | labriegos | 4 |
| 21883 | labranza | 4 |
| 21884 | laboriosa | 4 |
| 21885 | laberintos | 4 |
| 21886 | kilómetro | 4 |
| 21887 | juzgues | 4 |
| 21888 | juzgan | 4 |
| 21889 | justicias | 4 |
| 21890 | justiçia | 4 |
| 21891 | jurisdición | 4 |
| 21892 | jurara | 4 |
| 21893 | juntillas | 4 |
| 21894 | jumentos | 4 |
| 21895 | juiciosos | 4 |
| 21896 | juiciosa | 4 |
| 21897 | jui | 4 |
| 21898 | jueguen | 4 |
| 21899 | judios | 4 |
| 21900 | jubones | 4 |
| 21901 | jubileo | 4 |
| 21902 | jubilado | 4 |
| 21903 | jubilación | 4 |
| 21904 | juanico | 4 |
| 21905 | jovialmente | 4 |
| 21906 | jofaina | 4 |
| 21907 | jayanes | 4 |
| 21908 | jáquima | 4 |
| 21909 | jaque | 4 |
| 21910 | jamona | 4 |
| 21911 | jaime | 4 |
| 21912 | jaeces | 4 |
| 21913 | jadeantes | 4 |
| 21914 | iug | 4 |
| 21915 | israel | 4 |
| 21916 | irrupción | 4 |
| 21917 | irritar | 4 |
| 21918 | irritaban | 4 |
| 21919 | irresponsable | 4 |
| 21920 | irrespetuoso | 4 |
| 21921 | irrespetuosas | 4 |
| 21922 | irreparable | 4 |
| 21923 | irracional | 4 |
| 21924 | irnos | 4 |
| 21925 | irene | 4 |
| 21926 | iracunda | 4 |
| 21927 | invidioso | 4 |
| 21928 | investigar | 4 |
| 21929 | investigación | 4 |
| 21930 | inverosímiles | 4 |
| 21931 | inventos | 4 |
| 21932 | inventaron | 4 |
| 21933 | inundación | 4 |
| 21934 | inundaban | 4 |
| 21935 | introducido | 4 |
| 21936 | intrepidez | 4 |
| 21937 | intransitable | 4 |
| 21938 | intimó | 4 |
| 21939 | íntimamente | 4 |
| 21940 | intervino | 4 |
| 21941 | intervenido | 4 |
| 21942 | intervenía | 4 |
| 21943 | interrupción | 4 |
| 21944 | interrumpiéndole | 4 |
| 21945 | interrogó | 4 |
| 21946 | interrogaba | 4 |
| 21947 | intermitentes | 4 |
| 21948 | intermedio | 4 |
| 21949 | interlocutores | 4 |
| 21950 | interesse | 4 |
| 21951 | intercession | 4 |
| 21952 | intentado | 4 |
| 21953 | intensísima | 4 |
| 21954 | intellectus | 4 |
| 21955 | intellectum | 4 |
| 21956 | integrante | 4 |
| 21957 | intachables | 4 |
| 21958 | insufribles | 4 |
| 21959 | instruirse | 4 |
| 21960 | instruido | 4 |
| 21961 | instó | 4 |
| 21962 | instituto | 4 |
| 21963 | insistiendo | 4 |
| 21964 | insectos | 4 |
| 21965 | inquietos | 4 |
| 21966 | inquietó | 4 |
| 21967 | inquietaba | 4 |
| 21968 | inoportuna | 4 |
| 21969 | inofensiva | 4 |
| 21970 | inodoro | 4 |
| 21971 | innocencia | 4 |
| 21972 | innatas | 4 |
| 21973 | inmundas | 4 |
| 21974 | inmuebles | 4 |
| 21975 | inmortales | 4 |
| 21976 | inmoral | 4 |
| 21977 | inmediatos | 4 |
| 21978 | inmediaciones | 4 |
| 21979 | injuriosas | 4 |
| 21980 | injertaba | 4 |
| 21981 | iniquidad | 4 |
| 21982 | inició | 4 |
| 21983 | iniciarse | 4 |
| 21984 | inhumano | 4 |
| 21985 | inherente | 4 |
| 21986 | ingratos | 4 |
| 21987 | infracción | 4 |
| 21988 | influye | 4 |
| 21989 | infatigable | 4 |
| 21990 | infamias | 4 |
| 21991 | inexorable | 4 |
| 21992 | inestimable | 4 |
| 21993 | inesperado | 4 |
| 21994 | inepto | 4 |
| 21995 | ineludible | 4 |
| 21996 | industrial | 4 |
| 21997 | induce | 4 |
| 21998 | indómito | 4 |
| 21999 | indiscutible | 4 |
| 22000 | indignó | 4 |
| 22001 | indicándole | 4 |
| 22002 | indicaciones | 4 |
| 22003 | indicaban | 4 |
| 22004 | independientes | 4 |
| 22005 | indefinidamente | 4 |
| 22006 | indecencias | 4 |
| 22007 | indagar | 4 |
| 22008 | incorporose | 4 |
| 22009 | inconstante | 4 |
| 22010 | inconsecuencia | 4 |
| 22011 | incomodaba | 4 |
| 22012 | incómoda | 4 |
| 22013 | incomoda | 4 |
| 22014 | incoherente | 4 |
| 22015 | inclino | 4 |
| 22016 | incitado | 4 |
| 22017 | inciso | 4 |
| 22018 | incauto | 4 |
| 22019 | inapreciable | 4 |
| 22020 | impuro | 4 |
| 22021 | impuesta | 4 |
| 22022 | improvisado | 4 |
| 22023 | imprimen | 4 |
| 22024 | imprime | 4 |
| 22025 | imposiciones | 4 |
| 22026 | importunado | 4 |
| 22027 | imponían | 4 |
| 22028 | imponerse | 4 |
| 22029 | imponer | 4 |
| 22030 | impidiera | 4 |
| 22031 | impetu | 4 |
| 22032 | imperioso | 4 |
| 22033 | imperios | 4 |
| 22034 | imperdible | 4 |
| 22035 | impacientes | 4 |
| 22036 | imitado | 4 |
| 22037 | imitaciones | 4 |
| 22038 | imantada | 4 |
| 22039 | imán | 4 |
| 22040 | imaginarla | 4 |
| 22041 | imaginados | 4 |
| 22042 | imaginada | 4 |
| 22043 | ilustradas | 4 |
| 22044 | ilustra | 4 |
| 22045 | iluminando | 4 |
| 22046 | illo | 4 |
| 22047 | illis | 4 |
| 22048 | ileso | 4 |
| 22049 | igualaban | 4 |
| 22050 | ignorando | 4 |
| 22051 | ignorado | 4 |
| 22052 | ignominioso | 4 |
| 22053 | ignominias | 4 |
| 22054 | ídolos | 4 |
| 22055 | idiotas | 4 |
| 22056 | íbanse | 4 |
| 22057 | hystoria | 4 |
| 22058 | huyes | 4 |
| 22059 | huya | 4 |
| 22060 | hurte | 4 |
| 22061 | hurtadillas | 4 |
| 22062 | huracanes | 4 |
| 22063 | hundirse | 4 |
| 22064 | hundió | 4 |
| 22065 | hundidos | 4 |
| 22066 | hundido | 4 |
| 22067 | humillados | 4 |
| 22068 | humedecer | 4 |
| 22069 | huiré | 4 |
| 22070 | huír | 4 |
| 22071 | hugo | 4 |
| 22072 | huertos | 4 |
| 22073 | huerfanito | 4 |
| 22074 | huérfanas | 4 |
| 22075 | huelga | 4 |
| 22076 | huchas | 4 |
| 22077 | hubiéredes | 4 |
| 22078 | houe | 4 |
| 22079 | hoteles | 4 |
| 22080 | hospedado | 4 |
| 22081 | hortaleza | 4 |
| 22082 | horrorosas | 4 |
| 22083 | horrorosamente | 4 |
| 22084 | horroriza | 4 |
| 22085 | horizontales | 4 |
| 22086 | horchata | 4 |
| 22087 | honrando | 4 |
| 22088 | honraba | 4 |
| 22089 | honestamente | 4 |
| 22090 | hondísimo | 4 |
| 22091 | hombruna | 4 |
| 22092 | holguemos | 4 |
| 22093 | holgó | 4 |
| 22094 | holgarse | 4 |
| 22095 | holgaría | 4 |
| 22096 | holandas | 4 |
| 22097 | hojalata | 4 |
| 22098 | hogueras | 4 |
| 22099 | hirviendo | 4 |
| 22100 | hinchando | 4 |
| 22101 | hinchado | 4 |
| 22102 | hinchada | 4 |
| 22103 | hilaza | 4 |
| 22104 | hidrópica | 4 |
| 22105 | hidropesía | 4 |
| 22106 | hidra | 4 |
| 22107 | hidalgas | 4 |
| 22108 | hicieras | 4 |
| 22109 | hete | 4 |
| 22110 | herrería | 4 |
| 22111 | herrar | 4 |
| 22112 | herramienta | 4 |
| 22113 | heroínas | 4 |
| 22114 | heroicos | 4 |
| 22115 | herodías | 4 |
| 22116 | hernando | 4 |
| 22117 | hermitano | 4 |
| 22118 | hermanita | 4 |
| 22119 | hermanico | 4 |
| 22120 | hería | 4 |
| 22121 | hecimos | 4 |
| 22122 | hechuras | 4 |
| 22123 | heces | 4 |
| 22124 | hazle | 4 |
| 22125 | hayamos | 4 |
| 22126 | hayáis | 4 |
| 22127 | hauras | 4 |
| 22128 | hauian | 4 |
| 22129 | hauemos | 4 |
| 22130 | harte | 4 |
| 22131 | hartarse | 4 |
| 22132 | hartar | 4 |
| 22133 | harpía | 4 |
| 22134 | hanse | 4 |
| 22135 | hallaste | 4 |
| 22136 | halláronle | 4 |
| 22137 | hallaría | 4 |
| 22138 | hallare | 4 |
| 22139 | hallaras | 4 |
| 22140 | hallábame | 4 |
| 22141 | haiga | 4 |
| 22142 | hadeduro | 4 |
| 22143 | hadas | 4 |
| 22144 | haciéndote | 4 |
| 22145 | hacíale | 4 |
| 22146 | hablarles | 4 |
| 22147 | hablame | 4 |
| 22148 | habladurías | 4 |
| 22149 | hablada | 4 |
| 22150 | habitar | 4 |
| 22151 | habitados | 4 |
| 22152 | habita | 4 |
| 22153 | hábiles | 4 |
| 22154 | habichuelas | 4 |
| 22155 | habíanle | 4 |
| 22156 | habíalo | 4 |
| 22157 | habíala | 4 |
| 22158 | habérselas | 4 |
| 22159 | haberles | 4 |
| 22160 | haberlas | 4 |
| 22161 | gustare | 4 |
| 22162 | gulhara | 4 |
| 22163 | guió | 4 |
| 22164 | guiñó | 4 |
| 22165 | guindillas | 4 |
| 22166 | guillotina | 4 |
| 22167 | guido | 4 |
| 22168 | guerrera | 4 |
| 22169 | guarte | 4 |
| 22170 | guarniciones | 4 |
| 22171 | guardes | 4 |
| 22172 | guárdeme | 4 |
| 22173 | guardé | 4 |
| 22174 | guardarropa | 4 |
| 22175 | guardarle | 4 |
| 22176 | guárdalo | 4 |
| 22177 | guadalupe | 4 |
| 22178 | guadalquivir | 4 |
| 22179 | guadalhajara | 4 |
| 22180 | grumete | 4 |
| 22181 | grotescas | 4 |
| 22182 | groserías | 4 |
| 22183 | gritan | 4 |
| 22184 | grillete | 4 |
| 22185 | greña | 4 |
| 22186 | greda | 4 |
| 22187 | gravísimo | 4 |
| 22188 | granjerías | 4 |
| 22189 | granjear | 4 |
| 22190 | granjeada | 4 |
| 22191 | granja | 4 |
| 22192 | grandor | 4 |
| 22193 | grandón | 4 |
| 22194 | grandemente | 4 |
| 22195 | granate | 4 |
| 22196 | granadas | 4 |
| 22197 | graja | 4 |
| 22198 | grada | 4 |
| 22199 | graciosísimo | 4 |
| 22200 | gozándose | 4 |
| 22201 | gótico | 4 |
| 22202 | góticas | 4 |
| 22203 | gótica | 4 |
| 22204 | gotera | 4 |
| 22205 | gorgueras | 4 |
| 22206 | gordura | 4 |
| 22207 | gómez | 4 |
| 22208 | golpeando | 4 |
| 22209 | golías | 4 |
| 22210 | golfos | 4 |
| 22211 | godo | 4 |
| 22212 | goda | 4 |
| 22213 | goço | 4 |
| 22214 | gobernaré | 4 |
| 22215 | gitanica | 4 |
| 22216 | girón | 4 |
| 22217 | giró | 4 |
| 22218 | gesticulando | 4 |
| 22219 | genuflexión | 4 |
| 22220 | genial | 4 |
| 22221 | generalizada | 4 |
| 22222 | generala | 4 |
| 22223 | gayo | 4 |
| 22224 | gavilanes | 4 |
| 22225 | gavilán | 4 |
| 22226 | gavia | 4 |
| 22227 | gaudeamus | 4 |
| 22228 | gastando | 4 |
| 22229 | gastaban | 4 |
| 22230 | gaseosos | 4 |
| 22231 | garzones | 4 |
| 22232 | garrotillo | 4 |
| 22233 | gárgaras | 4 |
| 22234 | gargantas | 4 |
| 22235 | garantías | 4 |
| 22236 | gañar | 4 |
| 22237 | gañán | 4 |
| 22238 | ganitas | 4 |
| 22239 | gangas | 4 |
| 22240 | ganancioso | 4 |
| 22241 | ganadas | 4 |
| 22242 | galleta | 4 |
| 22243 | galizia | 4 |
| 22244 | galanas | 4 |
| 22245 | gaitas | 4 |
| 22246 | gabinetes | 4 |
| 22247 | g | 4 |
| 22248 | fyn | 4 |
| 22249 | fuya | 4 |
| 22250 | fúxo | 4 |
| 22251 | fuste | 4 |
| 22252 | furores | 4 |
| 22253 | furibundo | 4 |
| 22254 | furibundas | 4 |
| 22255 | funestas | 4 |
| 22256 | funerales | 4 |
| 22257 | fundan | 4 |
| 22258 | fundamentos | 4 |
| 22259 | fundamental | 4 |
| 22260 | fundados | 4 |
| 22261 | fundación | 4 |
| 22262 | funcionario | 4 |
| 22263 | funcionaba | 4 |
| 22264 | fumador | 4 |
| 22265 | fulgores | 4 |
| 22266 | fuisteis | 4 |
| 22267 | fugitivas | 4 |
| 22268 | fuesses | 4 |
| 22269 | frutales | 4 |
| 22270 | fruente | 4 |
| 22271 | frotaba | 4 |
| 22272 | fronteras | 4 |
| 22273 | frívolo | 4 |
| 22274 | frivolidad | 4 |
| 22275 | fritas | 4 |
| 22276 | frenos | 4 |
| 22277 | frenético | 4 |
| 22278 | frenética | 4 |
| 22279 | fregado | 4 |
| 22280 | frecuentar | 4 |
| 22281 | frecuenta | 4 |
| 22282 | frayre | 4 |
| 22283 | franquezas | 4 |
| 22284 | franja | 4 |
| 22285 | francas | 4 |
| 22286 | fraganti | 4 |
| 22287 | fragancias | 4 |
| 22288 | fortísimo | 4 |
| 22289 | forrado | 4 |
| 22290 | forrada | 4 |
| 22291 | fomento | 4 |
| 22292 | folletito | 4 |
| 22293 | folletines | 4 |
| 22294 | fogosa | 4 |
| 22295 | fogonazo | 4 |
| 22296 | foe | 4 |
| 22297 | foco | 4 |
| 22298 | flotar | 4 |
| 22299 | flotaba | 4 |
| 22300 | florencia | 4 |
| 22301 | flojos | 4 |
| 22302 | firmó | 4 |
| 22303 | fingidamente | 4 |
| 22304 | filius | 4 |
| 22305 | filigranas | 4 |
| 22306 | fijan | 4 |
| 22307 | fijada | 4 |
| 22308 | fijaban | 4 |
| 22309 | figurón | 4 |
| 22310 | figurín | 4 |
| 22311 | figo | 4 |
| 22312 | fieres | 4 |
| 22313 | fierabrás | 4 |
| 22314 | fïel | 4 |
| 22315 | fideos | 4 |
| 22316 | ficóbriga | 4 |
| 22317 | ficieron | 4 |
| 22318 | fibra | 4 |
| 22319 | fianza | 4 |
| 22320 | ffizo | 4 |
| 22321 | feziese | 4 |
| 22322 | feuillet | 4 |
| 22323 | festivamente | 4 |
| 22324 | festín | 4 |
| 22325 | ferviente | 4 |
| 22326 | fertilidad | 4 |
| 22327 | ferrolana | 4 |
| 22328 | ferrocarril | 4 |
| 22329 | fernán | 4 |
| 22330 | ferir | 4 |
| 22331 | ferió | 4 |
| 22332 | féretro | 4 |
| 22333 | felpudo | 4 |
| 22334 | felicitó | 4 |
| 22335 | felicísimos | 4 |
| 22336 | felicemente | 4 |
| 22337 | feísima | 4 |
| 22338 | fecundidad | 4 |
| 22339 | fé | 4 |
| 22340 | fazie | 4 |
| 22341 | fazedes | 4 |
| 22342 | favorecían | 4 |
| 22343 | fastidiosa | 4 |
| 22344 | fastidiar | 4 |
| 22345 | fast | 4 |
| 22346 | fasía | 4 |
| 22347 | fasedes | 4 |
| 22348 | fascinada | 4 |
| 22349 | farina | 4 |
| 22350 | fardel | 4 |
| 22351 | fanática | 4 |
| 22352 | fanal | 4 |
| 22353 | famélico | 4 |
| 22354 | falsete | 4 |
| 22355 | falsedades | 4 |
| 22356 | falsamente | 4 |
| 22357 | falleció | 4 |
| 22358 | falle | 4 |
| 22359 | faldellín | 4 |
| 22360 | falaguera | 4 |
| 22361 | fajas | 4 |
| 22362 | fago | 4 |
| 22363 | fagamos | 4 |
| 22364 | fagades | 4 |
| 22365 | faenas | 4 |
| 22366 | facundia | 4 |
| 22367 | factor | 4 |
| 22368 | facilitado | 4 |
| 22369 | fachadas | 4 |
| 22370 | face | 4 |
| 22371 | fabricando | 4 |
| 22372 | fabricaba | 4 |
| 22373 | fabló | 4 |
| 22374 | fable | 4 |
| 22375 | fablad | 4 |
| 22376 | fa | 4 |
| 22377 | extremeño | 4 |
| 22378 | extrañe | 4 |
| 22379 | extrañado | 4 |
| 22380 | extranjeras | 4 |
| 22381 | extinguido | 4 |
| 22382 | exterminio | 4 |
| 22383 | extenderse | 4 |
| 22384 | exquisitas | 4 |
| 22385 | expulsado | 4 |
| 22386 | exprimida | 4 |
| 22387 | expresivos | 4 |
| 22388 | expresan | 4 |
| 22389 | expresaban | 4 |
| 22390 | explosiva | 4 |
| 22391 | explorar | 4 |
| 22392 | explíquese | 4 |
| 22393 | expliques | 4 |
| 22394 | explicase | 4 |
| 22395 | expirando | 4 |
| 22396 | expertos | 4 |
| 22397 | experimentar | 4 |
| 22398 | experimentado | 4 |
| 22399 | exóticas | 4 |
| 22400 | exigencia | 4 |
| 22401 | excusar | 4 |
| 22402 | excomunión | 4 |
| 22403 | excomulgar | 4 |
| 22404 | exclusivo | 4 |
| 22405 | exclusiva | 4 |
| 22406 | exclamo | 4 |
| 22407 | exclaman | 4 |
| 22408 | excitó | 4 |
| 22409 | excitaban | 4 |
| 22410 | excedía | 4 |
| 22411 | exceder | 4 |
| 22412 | exceda | 4 |
| 22413 | excavaciones | 4 |
| 22414 | exánime | 4 |
| 22415 | examinase | 4 |
| 22416 | examinarle | 4 |
| 22417 | exagerado | 4 |
| 22418 | exageradas | 4 |
| 22419 | evocando | 4 |
| 22420 | evasión | 4 |
| 22421 | europeo | 4 |
| 22422 | eup | 4 |
| 22423 | eugenio | 4 |
| 22424 | eufemismos | 4 |
| 22425 | estúpidas | 4 |
| 22426 | estupendos | 4 |
| 22427 | estupefacto | 4 |
| 22428 | estupefacta | 4 |
| 22429 | estudiada | 4 |
| 22430 | estropeado | 4 |
| 22431 | estricote | 4 |
| 22432 | estrenado | 4 |
| 22433 | estremecimientos | 4 |
| 22434 | estrellitas | 4 |
| 22435 | estrellada | 4 |
| 22436 | estrategia | 4 |
| 22437 | estratagema | 4 |
| 22438 | estorçer | 4 |
| 22439 | estorbó | 4 |
| 22440 | estorbarlo | 4 |
| 22441 | estorbarle | 4 |
| 22442 | estirpe | 4 |
| 22443 | estirón | 4 |
| 22444 | estirada | 4 |
| 22445 | estipendio | 4 |
| 22446 | estímulos | 4 |
| 22447 | estimas | 4 |
| 22448 | estimaré | 4 |
| 22449 | estimable | 4 |
| 22450 | estilan | 4 |
| 22451 | estido | 4 |
| 22452 | estético | 4 |
| 22453 | estética | 4 |
| 22454 | estese | 4 |
| 22455 | estertor | 4 |
| 22456 | esteras | 4 |
| 22457 | estendía | 4 |
| 22458 | estarias | 4 |
| 22459 | estaríamos | 4 |
| 22460 | estare | 4 |
| 22461 | estantigua | 4 |
| 22462 | estanquillo | 4 |
| 22463 | estanques | 4 |
| 22464 | estanco | 4 |
| 22465 | estampido | 4 |
| 22466 | estampía | 4 |
| 22467 | estampado | 4 |
| 22468 | estampadas | 4 |
| 22469 | estampada | 4 |
| 22470 | estallaba | 4 |
| 22471 | estafa | 4 |
| 22472 | establecía | 4 |
| 22473 | estábase | 4 |
| 22474 | esquilón | 4 |
| 22475 | esquelita | 4 |
| 22476 | esquelas | 4 |
| 22477 | espumar | 4 |
| 22478 | espulgar | 4 |
| 22479 | espritu | 4 |
| 22480 | esponjas | 4 |
| 22481 | esplendorosa | 4 |
| 22482 | espléndidamente | 4 |
| 22483 | espital | 4 |
| 22484 | espiritualidad | 4 |
| 22485 | espiritistas | 4 |
| 22486 | espiritista | 4 |
| 22487 | espirar | 4 |
| 22488 | espinos | 4 |
| 22489 | espino | 4 |
| 22490 | espiga | 4 |
| 22491 | espiando | 4 |
| 22492 | esperes | 4 |
| 22493 | esperaua | 4 |
| 22494 | esperarse | 4 |
| 22495 | esperara | 4 |
| 22496 | esperándote | 4 |
| 22497 | esperándola | 4 |
| 22498 | espejuelos | 4 |
| 22499 | especulaciones | 4 |
| 22500 | específico | 4 |
| 22501 | esparcir | 4 |
| 22502 | esparciendo | 4 |
| 22503 | esparcidas | 4 |
| 22504 | espantóse | 4 |
| 22505 | esotra | 4 |
| 22506 | ésos | 4 |
| 22507 | esgrimir | 4 |
| 22508 | esforzó | 4 |
| 22509 | esencialmente | 4 |
| 22510 | escusas | 4 |
| 22511 | escuros | 4 |
| 22512 | escurecen | 4 |
| 22513 | escultor | 4 |
| 22514 | escuderiles | 4 |
| 22515 | escuches | 4 |
| 22516 | escuche | 4 |
| 22517 | escucharte | 4 |
| 22518 | escrupulosa | 4 |
| 22519 | escribirse | 4 |
| 22520 | escribirlas | 4 |
| 22521 | escribas | 4 |
| 22522 | escotilla | 4 |
| 22523 | escondites | 4 |
| 22524 | escondiese | 4 |
| 22525 | escondían | 4 |
| 22526 | escolta | 4 |
| 22527 | escolares | 4 |
| 22528 | escogiese | 4 |
| 22529 | esclarecido | 4 |
| 22530 | escarmentado | 4 |
| 22531 | escaparnos | 4 |
| 22532 | escaparía | 4 |
| 22533 | escapara | 4 |
| 22534 | escaño | 4 |
| 22535 | escanto | 4 |
| 22536 | escandalosos | 4 |
| 22537 | escandalizó | 4 |
| 22538 | escandalizada | 4 |
| 22539 | escalona | 4 |
| 22540 | esbeltos | 4 |
| 22541 | erudita | 4 |
| 22542 | eróticas | 4 |
| 22543 | erguido | 4 |
| 22544 | erat | 4 |
| 22545 | equivocan | 4 |
| 22546 | equivocaba | 4 |
| 22547 | equívoca | 4 |
| 22548 | equilibrado | 4 |
| 22549 | envueltas | 4 |
| 22550 | envolviéndose | 4 |
| 22551 | envidió | 4 |
| 22552 | enviarte | 4 |
| 22553 | enviaría | 4 |
| 22554 | envían | 4 |
| 22555 | envenenado | 4 |
| 22556 | enumerar | 4 |
| 22557 | entyendo | 4 |
| 22558 | entusiastas | 4 |
| 22559 | entusiasmada | 4 |
| 22560 | entusiasmaba | 4 |
| 22561 | entristecía | 4 |
| 22562 | entretuvieron | 4 |
| 22563 | entretienen | 4 |
| 22564 | entretenidas | 4 |
| 22565 | entretengan | 4 |
| 22566 | entremeses | 4 |
| 22567 | entremés | 4 |
| 22568 | entregaron | 4 |
| 22569 | entregándole | 4 |
| 22570 | entregados | 4 |
| 22571 | entregaban | 4 |
| 22572 | entraran | 4 |
| 22573 | entrañable | 4 |
| 22574 | entrábamos | 4 |
| 22575 | entonçe | 4 |
| 22576 | entonado | 4 |
| 22577 | entonada | 4 |
| 22578 | entierren | 4 |
| 22579 | enterrasen | 4 |
| 22580 | enterraron | 4 |
| 22581 | enterrada | 4 |
| 22582 | enternecimiento | 4 |
| 22583 | enternecía | 4 |
| 22584 | enternecer | 4 |
| 22585 | entendidas | 4 |
| 22586 | entendedera | 4 |
| 22587 | entendamos | 4 |
| 22588 | ensimismado | 4 |
| 22589 | ensienplo | 4 |
| 22590 | enseñase | 4 |
| 22591 | enseñarles | 4 |
| 22592 | enseñándole | 4 |
| 22593 | enséñame | 4 |
| 22594 | ensayar | 4 |
| 22595 | ensayado | 4 |
| 22596 | ensangrentada | 4 |
| 22597 | ensalza | 4 |
| 22598 | ensaladera | 4 |
| 22599 | enredando | 4 |
| 22600 | enredan | 4 |
| 22601 | enredada | 4 |
| 22602 | enojes | 4 |
| 22603 | enmendado | 4 |
| 22604 | enlutados | 4 |
| 22605 | enlace | 4 |
| 22606 | enjugó | 4 |
| 22607 | enjuga | 4 |
| 22608 | enjambres | 4 |
| 22609 | enjalmas | 4 |
| 22610 | enim | 4 |
| 22611 | engáñaste | 4 |
| 22612 | engañarle | 4 |
| 22613 | enganado | 4 |
| 22614 | engana | 4 |
| 22615 | enfriaba | 4 |
| 22616 | enfermó | 4 |
| 22617 | enfermiza | 4 |
| 22618 | enfadosa | 4 |
| 22619 | enfadó | 4 |
| 22620 | enfades | 4 |
| 22621 | enfadas | 4 |
| 22622 | enfadan | 4 |
| 22623 | enemigas | 4 |
| 22624 | endriagos | 4 |
| 22625 | endemoniado | 4 |
| 22626 | endemoniada | 4 |
| 22627 | endechas | 4 |
| 22628 | encubren | 4 |
| 22629 | encubra | 4 |
| 22630 | encorvado | 4 |
| 22631 | encontrarte | 4 |
| 22632 | encontrarían | 4 |
| 22633 | encontradas | 4 |
| 22634 | encomendado | 4 |
| 22635 | ençima | 4 |
| 22636 | encienden | 4 |
| 22637 | encerronas | 4 |
| 22638 | ençerrada | 4 |
| 22639 | encerraban | 4 |
| 22640 | encenderse | 4 |
| 22641 | encargarse | 4 |
| 22642 | encargaría | 4 |
| 22643 | encargar | 4 |
| 22644 | encargándole | 4 |
| 22645 | encargada | 4 |
| 22646 | encargaban | 4 |
| 22647 | encarecimientos | 4 |
| 22648 | encaramarse | 4 |
| 22649 | encaramado | 4 |
| 22650 | encamine | 4 |
| 22651 | encaminaba | 4 |
| 22652 | encajar | 4 |
| 22653 | enbydia | 4 |
| 22654 | enbidia | 4 |
| 22655 | enbiada | 4 |
| 22656 | enajenación | 4 |
| 22657 | empujones | 4 |
| 22658 | empujar | 4 |
| 22659 | empujándole | 4 |
| 22660 | empujado | 4 |
| 22661 | empolvado | 4 |
| 22662 | emplee | 4 |
| 22663 | emplearse | 4 |
| 22664 | emplearon | 4 |
| 22665 | empleaban | 4 |
| 22666 | emplasto | 4 |
| 22667 | empezaría | 4 |
| 22668 | empeñan | 4 |
| 22669 | empaquetado | 4 |
| 22670 | empalagosas | 4 |
| 22671 | embueltas | 4 |
| 22672 | embozó | 4 |
| 22673 | emborracharse | 4 |
| 22674 | embistió | 4 |
| 22675 | embestida | 4 |
| 22676 | embelesado | 4 |
| 22677 | embelesada | 4 |
| 22678 | embargado | 4 |
| 22679 | embargaba | 4 |
| 22680 | embarcó | 4 |
| 22681 | embarcaciones | 4 |
| 22682 | embalsamado | 4 |
| 22683 | embajadores | 4 |
| 22684 | elogió | 4 |
| 22685 | elogiaba | 4 |
| 22686 | elisabat | 4 |
| 22687 | eligió | 4 |
| 22688 | elevada | 4 |
| 22689 | elegida | 4 |
| 22690 | elegantísima | 4 |
| 22691 | elasticidad | 4 |
| 22692 | ejido | 4 |
| 22693 | ejes | 4 |
| 22694 | ejercitarse | 4 |
| 22695 | ejemplaridad | 4 |
| 22696 | ejecutivo | 4 |
| 22697 | egoístas | 4 |
| 22698 | églogas | 4 |
| 22699 | efímero | 4 |
| 22700 | educar | 4 |
| 22701 | educaba | 4 |
| 22702 | edificación | 4 |
| 22703 | económicos | 4 |
| 22704 | eclipse | 4 |
| 22705 | eclipsado | 4 |
| 22706 | eclesiásticas | 4 |
| 22707 | echóse | 4 |
| 22708 | eches | 4 |
| 22709 | échense | 4 |
| 22710 | échate | 4 |
| 22711 | echarían | 4 |
| 22712 | echaran | 4 |
| 22713 | ebrio | 4 |
| 22714 | dyneros | 4 |
| 22715 | dya | 4 |
| 22716 | dy | 4 |
| 22717 | durmiera | 4 |
| 22718 | durán | 4 |
| 22719 | duramente | 4 |
| 22720 | dúo | 4 |
| 22721 | dumanoir | 4 |
| 22722 | dulzainas | 4 |
| 22723 | dulçor | 4 |
| 22724 | duendes | 4 |
| 22725 | ducha | 4 |
| 22726 | dubdando | 4 |
| 22727 | drôle | 4 |
| 22728 | dotores | 4 |
| 22729 | dotada | 4 |
| 22730 | doscientas | 4 |
| 22731 | dorronsoro | 4 |
| 22732 | dormidos | 4 |
| 22733 | dora | 4 |
| 22734 | donnell | 4 |
| 22735 | donna | 4 |
| 22736 | donayres | 4 |
| 22737 | donativos | 4 |
| 22738 | dominicales | 4 |
| 22739 | domine | 4 |
| 22740 | dominaron | 4 |
| 22741 | dominando | 4 |
| 22742 | dominada | 4 |
| 22743 | dolientes | 4 |
| 22744 | dolençia | 4 |
| 22745 | dogmas | 4 |
| 22746 | docilidad | 4 |
| 22747 | dobleces | 4 |
| 22748 | doblas | 4 |
| 22749 | doblándose | 4 |
| 22750 | dixol | 4 |
| 22751 | díxele | 4 |
| 22752 | dixel | 4 |
| 22753 | divulgóse | 4 |
| 22754 | división | 4 |
| 22755 | dividió | 4 |
| 22756 | dividían | 4 |
| 22757 | divertidos | 4 |
| 22758 | diuina | 4 |
| 22759 | diuersos | 4 |
| 22760 | ditados | 4 |
| 22761 | disuadirle | 4 |
| 22762 | distributiva | 4 |
| 22763 | distraer | 4 |
| 22764 | distrae | 4 |
| 22765 | distinguieron | 4 |
| 22766 | distinguiendo | 4 |
| 22767 | distinguidos | 4 |
| 22768 | disputan | 4 |
| 22769 | dispusieron | 4 |
| 22770 | disponible | 4 |
| 22771 | dispongo | 4 |
| 22772 | dispersaron | 4 |
| 22773 | dispensar | 4 |
| 22774 | disparatar | 4 |
| 22775 | disipar | 4 |
| 22776 | disfrazados | 4 |
| 22777 | disforme | 4 |
| 22778 | disfauor | 4 |
| 22779 | discurro | 4 |
| 22780 | discurre | 4 |
| 22781 | disculpó | 4 |
| 22782 | disculpar | 4 |
| 22783 | discorde | 4 |
| 22784 | dirigieron | 4 |
| 22785 | dirigidas | 4 |
| 22786 | dirigida | 4 |
| 22787 | dirigen | 4 |
| 22788 | direte | 4 |
| 22789 | diréis | 4 |
| 22790 | directora | 4 |
| 22791 | direcciones | 4 |
| 22792 | diran | 4 |
| 22793 | dir | 4 |
| 22794 | diplomática | 4 |
| 22795 | dionisio | 4 |
| 22796 | dinidá | 4 |
| 22797 | dinerales | 4 |
| 22798 | dinamarca | 4 |
| 22799 | dina | 4 |
| 22800 | dilatadas | 4 |
| 22801 | dilatada | 4 |
| 22802 | dilación | 4 |
| 22803 | dijeres | 4 |
| 22804 | digasmé | 4 |
| 22805 | díganlo | 4 |
| 22806 | difusa | 4 |
| 22807 | diferiencia | 4 |
| 22808 | diferenciaban | 4 |
| 22809 | diessen | 4 |
| 22810 | dieres | 4 |
| 22811 | dictando | 4 |
| 22812 | dictamen | 4 |
| 22813 | dictado | 4 |
| 22814 | dictaba | 4 |
| 22815 | dicir | 4 |
| 22816 | diciplinas | 4 |
| 22817 | diciéndoselo | 4 |
| 22818 | dícese | 4 |
| 22819 | dícenme | 4 |
| 22820 | dibuja | 4 |
| 22821 | diabólicos | 4 |
| 22822 | dexaste | 4 |
| 22823 | dexando | 4 |
| 22824 | dexan | 4 |
| 22825 | devuelto | 4 |
| 22826 | devorando | 4 |
| 22827 | devolvió | 4 |
| 22828 | devocionario | 4 |
| 22829 | devo | 4 |
| 22830 | devía | 4 |
| 22831 | deves | 4 |
| 22832 | deuotos | 4 |
| 22833 | deuo | 4 |
| 22834 | detuve | 4 |
| 22835 | detrimento | 4 |
| 22836 | detonación | 4 |
| 22837 | determinados | 4 |
| 22838 | determinadas | 4 |
| 22839 | detenimiento | 4 |
| 22840 | detenerla | 4 |
| 22841 | desvíos | 4 |
| 22842 | desviada | 4 |
| 22843 | desvelo | 4 |
| 22844 | desvanecidos | 4 |
| 22845 | desvanecidas | 4 |
| 22846 | desvanecer | 4 |
| 22847 | desvanece | 4 |
| 22848 | desuso | 4 |
| 22849 | desuellacaras | 4 |
| 22850 | destruyó | 4 |
| 22851 | destruyendo | 4 |
| 22852 | destrucción | 4 |
| 22853 | desterrados | 4 |
| 22854 | destartalado | 4 |
| 22855 | despropósitos | 4 |
| 22856 | despropósito | 4 |
| 22857 | despreocupado | 4 |
| 22858 | desprecie | 4 |
| 22859 | despreciando | 4 |
| 22860 | desprecian | 4 |
| 22861 | despreciada | 4 |
| 22862 | desplomado | 4 |
| 22863 | desplegando | 4 |
| 22864 | desplegaban | 4 |
| 22865 | despilfarro | 4 |
| 22866 | despídete | 4 |
| 22867 | despiden | 4 |
| 22868 | despejar | 4 |
| 22869 | despedimos | 4 |
| 22870 | despedazado | 4 |
| 22871 | despedazada | 4 |
| 22872 | despavorida | 4 |
| 22873 | despache | 4 |
| 22874 | despachados | 4 |
| 22875 | desollar | 4 |
| 22876 | desnudaron | 4 |
| 22877 | desmoronaba | 4 |
| 22878 | desmayó | 4 |
| 22879 | desmayarse | 4 |
| 22880 | desmayar | 4 |
| 22881 | deslumbrante | 4 |
| 22882 | deslumbrado | 4 |
| 22883 | deslumbraba | 4 |
| 22884 | deslizaba | 4 |
| 22885 | desliza | 4 |
| 22886 | desinteresado | 4 |
| 22887 | desigualdades | 4 |
| 22888 | desiendo | 4 |
| 22889 | desía | 4 |
| 22890 | deshonestos | 4 |
| 22891 | deshacían | 4 |
| 22892 | desgraciadas | 4 |
| 22893 | desgarrada | 4 |
| 22894 | desgajó | 4 |
| 22895 | desgaire | 4 |
| 22896 | desfigurado | 4 |
| 22897 | desfallecimientos | 4 |
| 22898 | desfacedor | 4 |
| 22899 | desesperarse | 4 |
| 22900 | desesperábase | 4 |
| 22901 | desenvainó | 4 |
| 22902 | desenvainando | 4 |
| 22903 | desengáñese | 4 |
| 22904 | desengañarle | 4 |
| 22905 | desenfadada | 4 |
| 22906 | desencantar | 4 |
| 22907 | desencajado | 4 |
| 22908 | desembarcó | 4 |
| 22909 | desembarazada | 4 |
| 22910 | desechan | 4 |
| 22911 | desechaba | 4 |
| 22912 | desearse | 4 |
| 22913 | dése | 4 |
| 22914 | desdiga | 4 |
| 22915 | desdichadas | 4 |
| 22916 | descuidadas | 4 |
| 22917 | descuidaba | 4 |
| 22918 | descubriera | 4 |
| 22919 | descubridor | 4 |
| 22920 | descriptiva | 4 |
| 22921 | descosido | 4 |
| 22922 | descoser | 4 |
| 22923 | desconfiar | 4 |
| 22924 | desconfiando | 4 |
| 22925 | desconfía | 4 |
| 22926 | desconcertada | 4 |
| 22927 | descomulgado | 4 |
| 22928 | descompuestas | 4 |
| 22929 | descomedidos | 4 |
| 22930 | descoloridas | 4 |
| 22931 | descolgó | 4 |
| 22932 | descolgarse | 4 |
| 22933 | descifrar | 4 |
| 22934 | descarnado | 4 |
| 22935 | descarnada | 4 |
| 22936 | descaradamente | 4 |
| 22937 | descansen | 4 |
| 22938 | descansada | 4 |
| 22939 | descabezar | 4 |
| 22940 | desayunarse | 4 |
| 22941 | desavenencia | 4 |
| 22942 | desarrollar | 4 |
| 22943 | desarmarle | 4 |
| 22944 | desarbolado | 4 |
| 22945 | desaparecían | 4 |
| 22946 | desaparecen | 4 |
| 22947 | desamparo | 4 |
| 22948 | desamparados | 4 |
| 22949 | desahogar | 4 |
| 22950 | desahogaba | 4 |
| 22951 | desagrado | 4 |
| 22952 | desagradecimiento | 4 |
| 22953 | desagradables | 4 |
| 22954 | desagradaba | 4 |
| 22955 | desafueros | 4 |
| 22956 | desaforadas | 4 |
| 22957 | derroche | 4 |
| 22958 | derribaron | 4 |
| 22959 | derramada | 4 |
| 22960 | deredor | 4 |
| 22961 | depositaban | 4 |
| 22962 | dependía | 4 |
| 22963 | departir | 4 |
| 22964 | deparase | 4 |
| 22965 | denotaban | 4 |
| 22966 | dengue | 4 |
| 22967 | demuestran | 4 |
| 22968 | demudado | 4 |
| 22969 | demostrarle | 4 |
| 22970 | demostración | 4 |
| 22971 | demostraban | 4 |
| 22972 | demandan | 4 |
| 22973 | demagogia | 4 |
| 22974 | déles | 4 |
| 22975 | delegación | 4 |
| 22976 | dele | 4 |
| 22977 | delata | 4 |
| 22978 | dejaste | 4 |
| 22979 | déjala | 4 |
| 22980 | dejábase | 4 |
| 22981 | dehesa | 4 |
| 22982 | degollar | 4 |
| 22983 | definición | 4 |
| 22984 | defensivas | 4 |
| 22985 | defensiva | 4 |
| 22986 | defendidos | 4 |
| 22987 | defendida | 4 |
| 22988 | defenderla | 4 |
| 22989 | defenderé | 4 |
| 22990 | dedicarme | 4 |
| 22991 | dedican | 4 |
| 22992 | dedicaban | 4 |
| 22993 | decorosamente | 4 |
| 22994 | declararme | 4 |
| 22995 | declaran | 4 |
| 22996 | declamando | 4 |
| 22997 | decidieron | 4 |
| 22998 | decidiera | 4 |
| 22999 | decididamente | 4 |
| 23000 | decentemente | 4 |
| 23001 | debidos | 4 |
| 23002 | debería | 4 |
| 23003 | dávale | 4 |
| 23004 | dauid | 4 |
| 23005 | dátil | 4 |
| 23006 | data | 4 |
| 23007 | dármele | 4 |
| 23008 | darlas | 4 |
| 23009 | daria | 4 |
| 23010 | dardos | 4 |
| 23011 | daras | 4 |
| 23012 | daña | 4 |
| 23013 | dandy | 4 |
| 23014 | dança | 4 |
| 23015 | danado | 4 |
| 23016 | dámaso | 4 |
| 23017 | dal | 4 |
| 23018 | dafne | 4 |
| 23019 | dadivoso | 4 |
| 23020 | dadiua | 4 |
| 23021 | dábanse | 4 |
| 23022 | cuydan | 4 |
| 23023 | cuydades | 4 |
| 23024 | custodiaban | 4 |
| 23025 | cursos | 4 |
| 23026 | curiosidades | 4 |
| 23027 | curaría | 4 |
| 23028 | curara | 4 |
| 23029 | curando | 4 |
| 23030 | curaban | 4 |
| 23031 | cunplido | 4 |
| 23032 | cuneta | 4 |
| 23033 | cundió | 4 |
| 23034 | cumplirlo | 4 |
| 23035 | cumplidas | 4 |
| 23036 | cumpláis | 4 |
| 23037 | cum | 4 |
| 23038 | culpar | 4 |
| 23039 | cuidó | 4 |
| 23040 | cuest | 4 |
| 23041 | cuelgan | 4 |
| 23042 | cuchitril | 4 |
| 23043 | cuchilleros | 4 |
| 23044 | cuchilla | 4 |
| 23045 | cuchichearon | 4 |
| 23046 | cubrieron | 4 |
| 23047 | cubriendo | 4 |
| 23048 | cúbrete | 4 |
| 23049 | cuartucho | 4 |
| 23050 | cuartana | 4 |
| 23051 | cuantía | 4 |
| 23052 | cuaderno | 4 |
| 23053 | cruzaron | 4 |
| 23054 | cruzada | 4 |
| 23055 | crucis | 4 |
| 23056 | crochet | 4 |
| 23057 | cristalinas | 4 |
| 23058 | crióse | 4 |
| 23059 | criaron | 4 |
| 23060 | criamos | 4 |
| 23061 | criaban | 4 |
| 23062 | cretonas | 4 |
| 23063 | cresta | 4 |
| 23064 | crespón | 4 |
| 23065 | creerte | 4 |
| 23066 | creerla | 4 |
| 23067 | creençia | 4 |
| 23068 | creedme | 4 |
| 23069 | credos | 4 |
| 23070 | crecidas | 4 |
| 23071 | crecida | 4 |
| 23072 | creces | 4 |
| 23073 | creáis | 4 |
| 23074 | creaba | 4 |
| 23075 | coyundas | 4 |
| 23076 | coytado | 4 |
| 23077 | cotufas | 4 |
| 23078 | costunbres | 4 |
| 23079 | costunbre | 4 |
| 23080 | costilla | 4 |
| 23081 | costase | 4 |
| 23082 | costantinopla | 4 |
| 23083 | costanilla | 4 |
| 23084 | cosmógrafo | 4 |
| 23085 | cosechas | 4 |
| 23086 | corujedo | 4 |
| 23087 | corten | 4 |
| 23088 | corté | 4 |
| 23089 | cortarle | 4 |
| 23090 | cortaban | 4 |
| 23091 | corrosiva | 4 |
| 23092 | corros | 4 |
| 23093 | corrompido | 4 |
| 23094 | corrige | 4 |
| 23095 | corridas | 4 |
| 23096 | corresponsal | 4 |
| 23097 | corresponda | 4 |
| 23098 | corregimiento | 4 |
| 23099 | corregía | 4 |
| 23100 | correcciones | 4 |
| 23101 | corras | 4 |
| 23102 | corporaciones | 4 |
| 23103 | coronadas | 4 |
| 23104 | coronaban | 4 |
| 23105 | coronaba | 4 |
| 23106 | cornisa | 4 |
| 23107 | cornetas | 4 |
| 23108 | cordonera | 4 |
| 23109 | cordialidad | 4 |
| 23110 | corderos | 4 |
| 23111 | corchos | 4 |
| 23112 | coraçones | 4 |
| 23113 | copón | 4 |
| 23114 | copete | 4 |
| 23115 | coñac | 4 |
| 23116 | convulsiones | 4 |
| 23117 | convulsión | 4 |
| 23118 | convirtiendo | 4 |
| 23119 | convierta | 4 |
| 23120 | convertirlos | 4 |
| 23121 | convertirle | 4 |
| 23122 | convenir | 4 |
| 23123 | conveniencias | 4 |
| 23124 | convenían | 4 |
| 23125 | convengo | 4 |
| 23126 | convencionales | 4 |
| 23127 | convencerás | 4 |
| 23128 | conueniente | 4 |
| 23129 | contyenda | 4 |
| 23130 | contusiones | 4 |
| 23131 | contribuye | 4 |
| 23132 | contribuido | 4 |
| 23133 | contribuía | 4 |
| 23134 | contrarrestar | 4 |
| 23135 | contrariar | 4 |
| 23136 | contrariado | 4 |
| 23137 | contrariada | 4 |
| 23138 | contradiga | 4 |
| 23139 | contradicciones | 4 |
| 23140 | contradecirla | 4 |
| 23141 | contracción | 4 |
| 23142 | contóles | 4 |
| 23143 | contingente | 4 |
| 23144 | contingencia | 4 |
| 23145 | contesto | 4 |
| 23146 | conteste | 4 |
| 23147 | contestarme | 4 |
| 23148 | contestara | 4 |
| 23149 | contestaciones | 4 |
| 23150 | contente | 4 |
| 23151 | conténtate | 4 |
| 23152 | contentaron | 4 |
| 23153 | conteniéndose | 4 |
| 23154 | contendientes | 4 |
| 23155 | contaste | 4 |
| 23156 | contarte | 4 |
| 23157 | contarme | 4 |
| 23158 | contarás | 4 |
| 23159 | contándose | 4 |
| 23160 | consumir | 4 |
| 23161 | consumió | 4 |
| 23162 | consumar | 4 |
| 23163 | consultas | 4 |
| 23164 | consultaba | 4 |
| 23165 | consuelan | 4 |
| 23166 | construida | 4 |
| 23167 | constipado | 4 |
| 23168 | constar | 4 |
| 23169 | conssejas | 4 |
| 23170 | conspiradores | 4 |
| 23171 | consortes | 4 |
| 23172 | consonante | 4 |
| 23173 | consolidado | 4 |
| 23174 | consolarse | 4 |
| 23175 | consolando | 4 |
| 23176 | consistir | 4 |
| 23177 | consigna | 4 |
| 23178 | consideres | 4 |
| 23179 | consideré | 4 |
| 23180 | considerándole | 4 |
| 23181 | considerados | 4 |
| 23182 | considerables | 4 |
| 23183 | conservo | 4 |
| 23184 | conservarse | 4 |
| 23185 | conseja | 4 |
| 23186 | consagrado | 4 |
| 23187 | consagra | 4 |
| 23188 | consabida | 4 |
| 23189 | conquistando | 4 |
| 23190 | conplyr | 4 |
| 23191 | conpañero | 4 |
| 23192 | conozcamos | 4 |
| 23193 | conosciste | 4 |
| 23194 | conosce | 4 |
| 23195 | conocieran | 4 |
| 23196 | conocedora | 4 |
| 23197 | conmovió | 4 |
| 23198 | conmoción | 4 |
| 23199 | conllevar | 4 |
| 23200 | conjurado | 4 |
| 23201 | conjuraba | 4 |
| 23202 | congrio | 4 |
| 23203 | congregados | 4 |
| 23204 | congoxas | 4 |
| 23205 | confundirle | 4 |
| 23206 | confunda | 4 |
| 23207 | confidencial | 4 |
| 23208 | confiada | 4 |
| 23209 | confesores | 4 |
| 23210 | confesora | 4 |
| 23211 | confesionario | 4 |
| 23212 | confesemos | 4 |
| 23213 | confesárselo | 4 |
| 23214 | confesarme | 4 |
| 23215 | confesaré | 4 |
| 23216 | conducían | 4 |
| 23217 | condicional | 4 |
| 23218 | condescendencia | 4 |
| 23219 | concurrían | 4 |
| 23220 | concurre | 4 |
| 23221 | concreto | 4 |
| 23222 | concluyeron | 4 |
| 23223 | concluían | 4 |
| 23224 | cónclave | 4 |
| 23225 | conciudadanos | 4 |
| 23226 | concibo | 4 |
| 23227 | concertando | 4 |
| 23228 | conçebiste | 4 |
| 23229 | conatos | 4 |
| 23230 | comunicados | 4 |
| 23231 | compuse | 4 |
| 23232 | comprometida | 4 |
| 23233 | compromete | 4 |
| 23234 | compro | 4 |
| 23235 | comprimidos | 4 |
| 23236 | comprenden | 4 |
| 23237 | comprendan | 4 |
| 23238 | comprenda | 4 |
| 23239 | compraron | 4 |
| 23240 | comprarlo | 4 |
| 23241 | comprados | 4 |
| 23242 | compradas | 4 |
| 23243 | composiciones | 4 |
| 23244 | compleja | 4 |
| 23245 | complaciente | 4 |
| 23246 | competidor | 4 |
| 23247 | compatriotas | 4 |
| 23248 | compassion | 4 |
| 23249 | comparanza | 4 |
| 23250 | comparable | 4 |
| 23251 | companera | 4 |
| 23252 | compadecida | 4 |
| 23253 | cómodos | 4 |
| 23254 | comité | 4 |
| 23255 | comistrajos | 4 |
| 23256 | comiste | 4 |
| 23257 | comisiones | 4 |
| 23258 | comiéndoselo | 4 |
| 23259 | comienças | 4 |
| 23260 | comidilla | 4 |
| 23261 | cometiendo | 4 |
| 23262 | cometa | 4 |
| 23263 | comerciales | 4 |
| 23264 | comerás | 4 |
| 23265 | comerán | 4 |
| 23266 | comella | 4 |
| 23267 | comedidamente | 4 |
| 23268 | combinar | 4 |
| 23269 | combinado | 4 |
| 23270 | combatida | 4 |
| 23271 | colunas | 4 |
| 23272 | colocaron | 4 |
| 23273 | colocara | 4 |
| 23274 | collares | 4 |
| 23275 | colgajos | 4 |
| 23276 | colegios | 4 |
| 23277 | colectiva | 4 |
| 23278 | coincidiendo | 4 |
| 23279 | cohechos | 4 |
| 23280 | coges | 4 |
| 23281 | cogería | 4 |
| 23282 | codornices | 4 |
| 23283 | código | 4 |
| 23284 | codiciado | 4 |
| 23285 | codiciada | 4 |
| 23286 | codearse | 4 |
| 23287 | codeándose | 4 |
| 23288 | cocinilla | 4 |
| 23289 | cocheras | 4 |
| 23290 | coadjutor | 4 |
| 23291 | clerecia | 4 |
| 23292 | clavándose | 4 |
| 23293 | clavan | 4 |
| 23294 | clasificar | 4 |
| 23295 | claraboya | 4 |
| 23296 | clamaron | 4 |
| 23297 | clamaba | 4 |
| 23298 | citando | 4 |
| 23299 | ciriales | 4 |
| 23300 | circustantes | 4 |
| 23301 | circunvecinas | 4 |
| 23302 | circunloquios | 4 |
| 23303 | ciprés | 4 |
| 23304 | cinturón | 4 |
| 23305 | cinchado | 4 |
| 23306 | cincel | 4 |
| 23307 | ciervo | 4 |
| 23308 | çiertas | 4 |
| 23309 | çiertamente | 4 |
| 23310 | cierras | 4 |
| 23311 | cientos | 4 |
| 23312 | científicas | 4 |
| 23313 | cicatero | 4 |
| 23314 | çibdat | 4 |
| 23315 | churrigueresco | 4 |
| 23316 | chupado | 4 |
| 23317 | chupaba | 4 |
| 23318 | chuletita | 4 |
| 23319 | chorreaba | 4 |
| 23320 | chopos | 4 |
| 23321 | chopo | 4 |
| 23322 | chistera | 4 |
| 23323 | chistaba | 4 |
| 23324 | chisme | 4 |
| 23325 | chirlos | 4 |
| 23326 | chiquita | 4 |
| 23327 | chinitas | 4 |
| 23328 | chillón | 4 |
| 23329 | chilla | 4 |
| 23330 | chifle | 4 |
| 23331 | chiflado | 4 |
| 23332 | chiflada | 4 |
| 23333 | chichones | 4 |
| 23334 | charló | 4 |
| 23335 | charlado | 4 |
| 23336 | charadas | 4 |
| 23337 | chaquetón | 4 |
| 23338 | chaparrón | 4 |
| 23339 | chanza | 4 |
| 23340 | chalecos | 4 |
| 23341 | cf | 4 |
| 23342 | cestona | 4 |
| 23343 | cese | 4 |
| 23344 | cerviz | 4 |
| 23345 | cerrillo | 4 |
| 23346 | cerril | 4 |
| 23347 | cerrazón | 4 |
| 23348 | cerrase | 4 |
| 23349 | cercan | 4 |
| 23350 | cepillo | 4 |
| 23351 | cepa | 4 |
| 23352 | ceñudo | 4 |
| 23353 | ceñuda | 4 |
| 23354 | ceñir | 4 |
| 23355 | centavo | 4 |
| 23356 | censurar | 4 |
| 23357 | censo | 4 |
| 23358 | cendal | 4 |
| 23359 | celestes | 4 |
| 23360 | celebra | 4 |
| 23361 | celador | 4 |
| 23362 | cela | 4 |
| 23363 | cegó | 4 |
| 23364 | cegaron | 4 |
| 23365 | cegado | 4 |
| 23366 | ceca | 4 |
| 23367 | cazuela | 4 |
| 23368 | cayóme | 4 |
| 23369 | caydo | 4 |
| 23370 | cayado | 4 |
| 23371 | cay | 4 |
| 23372 | cavilosa | 4 |
| 23373 | cavilación | 4 |
| 23374 | cautivaron | 4 |
| 23375 | cautivan | 4 |
| 23376 | causarme | 4 |
| 23377 | causarle | 4 |
| 23378 | cató | 4 |
| 23379 | categorías | 4 |
| 23380 | cataratas | 4 |
| 23381 | catafalco | 4 |
| 23382 | catad | 4 |
| 23383 | casual | 4 |
| 23384 | castrense | 4 |
| 23385 | castor | 4 |
| 23386 | castigó | 4 |
| 23387 | castigando | 4 |
| 23388 | castigada | 4 |
| 23389 | castellanas | 4 |
| 23390 | casteçao | 4 |
| 23391 | cassado | 4 |
| 23392 | caspa | 4 |
| 23393 | cases | 4 |
| 23394 | casarredonda | 4 |
| 23395 | carroza | 4 |
| 23396 | carromatos | 4 |
| 23397 | carreteros | 4 |
| 23398 | cargarse | 4 |
| 23399 | cargante | 4 |
| 23400 | carestía | 4 |
| 23401 | carecido | 4 |
| 23402 | cárdeno | 4 |
| 23403 | carcelera | 4 |
| 23404 | carcas | 4 |
| 23405 | carbonera | 4 |
| 23406 | carambita | 4 |
| 23407 | carabanchel | 4 |
| 23408 | capullos | 4 |
| 23409 | captivo | 4 |
| 23410 | caprichoso | 4 |
| 23411 | caprichosas | 4 |
| 23412 | capotes | 4 |
| 23413 | capota | 4 |
| 23414 | capitalista | 4 |
| 23415 | capita | 4 |
| 23416 | caperuza | 4 |
| 23417 | capellanes | 4 |
| 23418 | capataz | 4 |
| 23419 | çapatas | 4 |
| 23420 | cañuto | 4 |
| 23421 | cañoneo | 4 |
| 23422 | cantería | 4 |
| 23423 | cantaré | 4 |
| 23424 | cantará | 4 |
| 23425 | canses | 4 |
| 23426 | cansarme | 4 |
| 23427 | cansando | 4 |
| 23428 | cansadas | 4 |
| 23429 | canpana | 4 |
| 23430 | canos | 4 |
| 23431 | candelero | 4 |
| 23432 | candados | 4 |
| 23433 | canastillo | 4 |
| 23434 | canastillas | 4 |
| 23435 | canasta | 4 |
| 23436 | canallas | 4 |
| 23437 | camuza | 4 |
| 23438 | campillo | 4 |
| 23439 | campeón | 4 |
| 23440 | campanada | 4 |
| 23441 | caminaron | 4 |
| 23442 | caminan | 4 |
| 23443 | camastro | 4 |
| 23444 | camarote | 4 |
| 23445 | calzó | 4 |
| 23446 | calzadas | 4 |
| 23447 | calvicie | 4 |
| 23448 | calurosos | 4 |
| 23449 | calumniar | 4 |
| 23450 | calmarse | 4 |
| 23451 | callose | 4 |
| 23452 | callemos | 4 |
| 23453 | callejuela | 4 |
| 23454 | callejera | 4 |
| 23455 | callé | 4 |
| 23456 | callara | 4 |
| 23457 | callan | 4 |
| 23458 | calixta | 4 |
| 23459 | calenturas | 4 |
| 23460 | calentando | 4 |
| 23461 | calentaba | 4 |
| 23462 | caldos | 4 |
| 23463 | calcule | 4 |
| 23464 | calcular | 4 |
| 23465 | calcula | 4 |
| 23466 | cala | 4 |
| 23467 | cajistas | 4 |
| 23468 | caimán | 4 |
| 23469 | caerle | 4 |
| 23470 | caduco | 4 |
| 23471 | cadenilla | 4 |
| 23472 | cacique | 4 |
| 23473 | caca | 4 |
| 23474 | cabrillas | 4 |
| 23475 | cabría | 4 |
| 23476 | cabrera | 4 |
| 23477 | cabecita | 4 |
| 23478 | caballerosidad | 4 |
| 23479 | caballeresco | 4 |
| 23480 | caballera | 4 |
| 23481 | buscarnos | 4 |
| 23482 | buscarlas | 4 |
| 23483 | buscaremos | 4 |
| 23484 | buscamos | 4 |
| 23485 | buscada | 4 |
| 23486 | buscad | 4 |
| 23487 | burra | 4 |
| 23488 | burlonamente | 4 |
| 23489 | burlón | 4 |
| 23490 | burlados | 4 |
| 23491 | burladora | 4 |
| 23492 | burguillos | 4 |
| 23493 | bujeros | 4 |
| 23494 | búcaros | 4 |
| 23495 | brutalidades | 4 |
| 23496 | bruta | 4 |
| 23497 | bruscos | 4 |
| 23498 | bruñida | 4 |
| 23499 | bruma | 4 |
| 23500 | bromear | 4 |
| 23501 | bromeando | 4 |
| 23502 | bromazo | 4 |
| 23503 | brocados | 4 |
| 23504 | bringas | 4 |
| 23505 | brindaba | 4 |
| 23506 | brincar | 4 |
| 23507 | brincando | 4 |
| 23508 | brillando | 4 |
| 23509 | brigada | 4 |
| 23510 | brandalagas | 4 |
| 23511 | bramidos | 4 |
| 23512 | bramar | 4 |
| 23513 | boyero | 4 |
| 23514 | botijo | 4 |
| 23515 | botarate | 4 |
| 23516 | bostezó | 4 |
| 23517 | bostezando | 4 |
| 23518 | bosquejo | 4 |
| 23519 | borroso | 4 |
| 23520 | borrego | 4 |
| 23521 | borradas | 4 |
| 23522 | bordón | 4 |
| 23523 | bordada | 4 |
| 23524 | boquita | 4 |
| 23525 | boquirroto | 4 |
| 23526 | boquete | 4 |
| 23527 | bonos | 4 |
| 23528 | bonísimo | 4 |
| 23529 | bonanza | 4 |
| 23530 | bonachona | 4 |
| 23531 | bonachón | 4 |
| 23532 | bon | 4 |
| 23533 | bombardeo | 4 |
| 23534 | bolsón | 4 |
| 23535 | bolsín | 4 |
| 23536 | bogaban | 4 |
| 23537 | bodigos | 4 |
| 23538 | bocina | 4 |
| 23539 | bóbilis | 4 |
| 23540 | bobadas | 4 |
| 23541 | blasones | 4 |
| 23542 | blasfemo | 4 |
| 23543 | blasfemando | 4 |
| 23544 | blanchete | 4 |
| 23545 | bizmas | 4 |
| 23546 | biva | 4 |
| 23547 | biuora | 4 |
| 23548 | bienaventuranza | 4 |
| 23549 | bienauenturados | 4 |
| 23550 | bienauenturado | 4 |
| 23551 | bienandante | 4 |
| 23552 | bicicleta | 4 |
| 23553 | bíblico | 4 |
| 23554 | bibl | 4 |
| 23555 | biberón | 4 |
| 23556 | biarritz | 4 |
| 23557 | betis | 4 |
| 23558 | besárselas | 4 |
| 23559 | besaron | 4 |
| 23560 | besamanos | 4 |
| 23561 | besaban | 4 |
| 23562 | berroqueña | 4 |
| 23563 | berridos | 4 |
| 23564 | bermellón | 4 |
| 23565 | bermeja | 4 |
| 23566 | benigno | 4 |
| 23567 | benévolos | 4 |
| 23568 | benéfica | 4 |
| 23569 | beltrand | 4 |
| 23570 | bellaca | 4 |
| 23571 | bélicos | 4 |
| 23572 | beldat | 4 |
| 23573 | béjar | 4 |
| 23574 | bebiera | 4 |
| 23575 | bebiéndose | 4 |
| 23576 | bebían | 4 |
| 23577 | bebas | 4 |
| 23578 | beatos | 4 |
| 23579 | batista | 4 |
| 23580 | batía | 4 |
| 23581 | batel | 4 |
| 23582 | bate | 4 |
| 23583 | batán | 4 |
| 23584 | bastase | 4 |
| 23585 | bastas | 4 |
| 23586 | bastaría | 4 |
| 23587 | bastará | 4 |
| 23588 | bástame | 4 |
| 23589 | bastábale | 4 |
| 23590 | basa | 4 |
| 23591 | barrunta | 4 |
| 23592 | barros | 4 |
| 23593 | barricada | 4 |
| 23594 | barreño | 4 |
| 23595 | barrenderos | 4 |
| 23596 | barragana | 4 |
| 23597 | barracas | 4 |
| 23598 | barítono | 4 |
| 23599 | bañándose | 4 |
| 23600 | baña | 4 |
| 23601 | bandadas | 4 |
| 23602 | ballestas | 4 |
| 23603 | baldosa | 4 |
| 23604 | baldío | 4 |
| 23605 | balbuciente | 4 |
| 23606 | balances | 4 |
| 23607 | baladí | 4 |
| 23608 | bajen | 4 |
| 23609 | bajaré | 4 |
| 23610 | bajada | 4 |
| 23611 | bailador | 4 |
| 23612 | bailaban | 4 |
| 23613 | babia | 4 |
| 23614 | babero | 4 |
| 23615 | babas | 4 |
| 23616 | azpillaga | 4 |
| 23617 | azotó | 4 |
| 23618 | azotarse | 4 |
| 23619 | azotarme | 4 |
| 23620 | azota | 4 |
| 23621 | azogado | 4 |
| 23622 | ayuntamientos | 4 |
| 23623 | ayunar | 4 |
| 23624 | ayuden | 4 |
| 23625 | ayudasen | 4 |
| 23626 | ayudas | 4 |
| 23627 | ayudarse | 4 |
| 23628 | ayudaron | 4 |
| 23629 | ayudarnos | 4 |
| 23630 | ayudará | 4 |
| 23631 | ayudame | 4 |
| 23632 | ayudada | 4 |
| 23633 | ayamos | 4 |
| 23634 | avivó | 4 |
| 23635 | avivar | 4 |
| 23636 | avisé | 4 |
| 23637 | avise | 4 |
| 23638 | avisaré | 4 |
| 23639 | avisan | 4 |
| 23640 | aviene | 4 |
| 23641 | ávida | 4 |
| 23642 | avestruz | 4 |
| 23643 | averiguaré | 4 |
| 23644 | avergonzó | 4 |
| 23645 | averes | 4 |
| 23646 | aventurera | 4 |
| 23647 | avengas | 4 |
| 23648 | avellanado | 4 |
| 23649 | avecilla | 4 |
| 23650 | avaros | 4 |
| 23651 | avanza | 4 |
| 23652 | autorizar | 4 |
| 23653 | autócrata | 4 |
| 23654 | auténtico | 4 |
| 23655 | auténtica | 4 |
| 23656 | ausenta | 4 |
| 23657 | auria | 4 |
| 23658 | aullido | 4 |
| 23659 | auisado | 4 |
| 23660 | auemos | 4 |
| 23661 | aue | 4 |
| 23662 | auarienta | 4 |
| 23663 | aturdía | 4 |
| 23664 | aturde | 4 |
| 23665 | atropellos | 4 |
| 23666 | atropellar | 4 |
| 23667 | atropellado | 4 |
| 23668 | atribuyeron | 4 |
| 23669 | atribuyen | 4 |
| 23670 | atreverá | 4 |
| 23671 | atrevan | 4 |
| 23672 | atrayendo | 4 |
| 23673 | atravesados | 4 |
| 23674 | atrasados | 4 |
| 23675 | atrasadas | 4 |
| 23676 | atrajo | 4 |
| 23677 | atontado | 4 |
| 23678 | atleta | 4 |
| 23679 | atlante | 4 |
| 23680 | atizó | 4 |
| 23681 | atinar | 4 |
| 23682 | atenuado | 4 |
| 23683 | atenido | 4 |
| 23684 | atenga | 4 |
| 23685 | atacadas | 4 |
| 23686 | atacada | 4 |
| 23687 | ataban | 4 |
| 23688 | asustados | 4 |
| 23689 | astillazo | 4 |
| 23690 | assentar | 4 |
| 23691 | asomóse | 4 |
| 23692 | asomados | 4 |
| 23693 | asociaba | 4 |
| 23694 | asistiendo | 4 |
| 23695 | asisten | 4 |
| 23696 | asista | 4 |
| 23697 | asintió | 4 |
| 23698 | asimilarse | 4 |
| 23699 | asimilación | 4 |
| 23700 | asilos | 4 |
| 23701 | asieron | 4 |
| 23702 | asiéndola | 4 |
| 23703 | asentaba | 4 |
| 23704 | asenchio | 4 |
| 23705 | asegurándose | 4 |
| 23706 | asegurada | 4 |
| 23707 | ascendido | 4 |
| 23708 | ascender | 4 |
| 23709 | asaltaron | 4 |
| 23710 | asaltar | 4 |
| 23711 | asaltado | 4 |
| 23712 | asador | 4 |
| 23713 | asada | 4 |
| 23714 | artilleros | 4 |
| 23715 | artificiales | 4 |
| 23716 | artefacto | 4 |
| 23717 | arruina | 4 |
| 23718 | arrugando | 4 |
| 23719 | arrojé | 4 |
| 23720 | arrojados | 4 |
| 23721 | arrodillarse | 4 |
| 23722 | arrodillándose | 4 |
| 23723 | arrinconada | 4 |
| 23724 | arriesgar | 4 |
| 23725 | arriendo | 4 |
| 23726 | arrepiento | 4 |
| 23727 | arrepientes | 4 |
| 23728 | arrepentidas | 4 |
| 23729 | arrendador | 4 |
| 23730 | arremetida | 4 |
| 23731 | arremeter | 4 |
| 23732 | arreligión | 4 |
| 23733 | arreglaría | 4 |
| 23734 | arreglan | 4 |
| 23735 | arreglaba | 4 |
| 23736 | arrebata | 4 |
| 23737 | arrayua | 4 |
| 23738 | arrastró | 4 |
| 23739 | arrastren | 4 |
| 23740 | arrastran | 4 |
| 23741 | arrastradas | 4 |
| 23742 | arras | 4 |
| 23743 | arraigado | 4 |
| 23744 | arraigadas | 4 |
| 23745 | arquitectónico | 4 |
| 23746 | arqueológica | 4 |
| 23747 | aros | 4 |
| 23748 | armonizar | 4 |
| 23749 | armónico | 4 |
| 23750 | arminio | 4 |
| 23751 | armazón | 4 |
| 23752 | armatoste | 4 |
| 23753 | armamento | 4 |
| 23754 | armaban | 4 |
| 23755 | arisca | 4 |
| 23756 | áridos | 4 |
| 23757 | arguyó | 4 |
| 23758 | argüello | 4 |
| 23759 | argucias | 4 |
| 23760 | arganzuela | 4 |
| 23761 | argamasa | 4 |
| 23762 | ardites | 4 |
| 23763 | ardió | 4 |
| 23764 | ardino | 4 |
| 23765 | ardimiento | 4 |
| 23766 | ardentísima | 4 |
| 23767 | arcilla | 4 |
| 23768 | arboles | 4 |
| 23769 | arados | 4 |
| 23770 | ara | 4 |
| 23771 | aquéste | 4 |
| 23772 | apuraban | 4 |
| 23773 | apura | 4 |
| 23774 | aprueba | 4 |
| 23775 | aproximando | 4 |
| 23776 | aproximación | 4 |
| 23777 | aprovecharnos | 4 |
| 23778 | aprovecharme | 4 |
| 23779 | aprovechaban | 4 |
| 23780 | apropiarse | 4 |
| 23781 | apropiada | 4 |
| 23782 | aprobar | 4 |
| 23783 | aprietes | 4 |
| 23784 | apretaron | 4 |
| 23785 | apresurando | 4 |
| 23786 | aprendidas | 4 |
| 23787 | aprendía | 4 |
| 23788 | aprendería | 4 |
| 23789 | apremio | 4 |
| 23790 | apremiantes | 4 |
| 23791 | apreció | 4 |
| 23792 | apostolado | 4 |
| 23793 | apoderaba | 4 |
| 23794 | apócrifa | 4 |
| 23795 | apocamiento | 4 |
| 23796 | apocado | 4 |
| 23797 | aplique | 4 |
| 23798 | aplastar | 4 |
| 23799 | aplastada | 4 |
| 23800 | aplastaba | 4 |
| 23801 | apetecible | 4 |
| 23802 | apetece | 4 |
| 23803 | apestaba | 4 |
| 23804 | aperçebido | 4 |
| 23805 | apencar | 4 |
| 23806 | apelo | 4 |
| 23807 | apela | 4 |
| 23808 | apease | 4 |
| 23809 | apearon | 4 |
| 23810 | apático | 4 |
| 23811 | apasionadas | 4 |
| 23812 | aparto | 4 |
| 23813 | apartes | 4 |
| 23814 | apártense | 4 |
| 23815 | apartase | 4 |
| 23816 | apartáronse | 4 |
| 23817 | apartaban | 4 |
| 23818 | apariciones | 4 |
| 23819 | aparejadas | 4 |
| 23820 | aparatosa | 4 |
| 23821 | apagaban | 4 |
| 23822 | apaciguó | 4 |
| 23823 | añadiduras | 4 |
| 23824 | añada | 4 |
| 23825 | anunciaban | 4 |
| 23826 | antorcha | 4 |
| 23827 | antojase | 4 |
| 23828 | antojare | 4 |
| 23829 | antiquísimas | 4 |
| 23830 | antifaces | 4 |
| 23831 | anticipar | 4 |
| 23832 | anticipaba | 4 |
| 23833 | antero | 4 |
| 23834 | antemano | 4 |
| 23835 | antecogiendo | 4 |
| 23836 | ansiosos | 4 |
| 23837 | anque | 4 |
| 23838 | anotación | 4 |
| 23839 | anónimo | 4 |
| 23840 | anjeo | 4 |
| 23841 | aniquilar | 4 |
| 23842 | aniquilamiento | 4 |
| 23843 | animalitos | 4 |
| 23844 | anillos | 4 |
| 23845 | anhelante | 4 |
| 23846 | anhelando | 4 |
| 23847 | angustiada | 4 |
| 23848 | angelico | 4 |
| 23849 | angelica | 4 |
| 23850 | anemia | 4 |
| 23851 | anega | 4 |
| 23852 | anécdota | 4 |
| 23853 | anduvimos | 4 |
| 23854 | andrajo | 4 |
| 23855 | andén | 4 |
| 23856 | andarme | 4 |
| 23857 | andariega | 4 |
| 23858 | andares | 4 |
| 23859 | andarán | 4 |
| 23860 | andamio | 4 |
| 23861 | andáis | 4 |
| 23862 | anatomía | 4 |
| 23863 | anaquelería | 4 |
| 23864 | análogos | 4 |
| 23865 | analizar | 4 |
| 23866 | análisis | 4 |
| 23867 | anacreónticas | 4 |
| 23868 | anacleto | 4 |
| 23869 | amontonados | 4 |
| 23870 | amonestación | 4 |
| 23871 | amojamado | 4 |
| 23872 | amnistía | 4 |
| 23873 | amito | 4 |
| 23874 | amigote | 4 |
| 23875 | amigablemente | 4 |
| 23876 | ámexi | 4 |
| 23877 | amenazan | 4 |
| 23878 | amenazadora | 4 |
| 23879 | amenazada | 4 |
| 23880 | amenazaban | 4 |
| 23881 | ame | 4 |
| 23882 | ambulantes | 4 |
| 23883 | ambiciosos | 4 |
| 23884 | ambiciosa | 4 |
| 23885 | ambicionar | 4 |
| 23886 | amazona | 4 |
| 23887 | amartelado | 4 |
| 23888 | amarra | 4 |
| 23889 | amarle | 4 |
| 23890 | amarla | 4 |
| 23891 | amargor | 4 |
| 23892 | amaranto | 4 |
| 23893 | amará | 4 |
| 23894 | amara | 4 |
| 23895 | amanesce | 4 |
| 23896 | amaneradas | 4 |
| 23897 | amades | 4 |
| 23898 | amad | 4 |
| 23899 | álvarez | 4 |
| 23900 | alva | 4 |
| 23901 | alusivo | 4 |
| 23902 | alumbraban | 4 |
| 23903 | altivo | 4 |
| 23904 | altivez | 4 |
| 23905 | altiva | 4 |
| 23906 | altísima | 4 |
| 23907 | alterno | 4 |
| 23908 | alteraciones | 4 |
| 23909 | alteraba | 4 |
| 23910 | altanero | 4 |
| 23911 | alquilador | 4 |
| 23912 | alpaca | 4 |
| 23913 | alongado | 4 |
| 23914 | alojar | 4 |
| 23915 | almorzaron | 4 |
| 23916 | almoneda | 4 |
| 23917 | almohadillas | 4 |
| 23918 | almodóvar | 4 |
| 23919 | almendras | 4 |
| 23920 | almena | 4 |
| 23921 | alineadas | 4 |
| 23922 | alimañas | 4 |
| 23923 | alicante | 4 |
| 23924 | alheña | 4 |
| 23925 | alguazil | 4 |
| 23926 | alfonsismo | 4 |
| 23927 | alejandría | 4 |
| 23928 | alegrase | 4 |
| 23929 | alegras | 4 |
| 23930 | alegran | 4 |
| 23931 | alegraban | 4 |
| 23932 | alegorías | 4 |
| 23933 | alce | 4 |
| 23934 | alcayde | 4 |
| 23935 | alcarreño | 4 |
| 23936 | alcantarilla | 4 |
| 23937 | alcántara | 4 |
| 23938 | alcaldesa | 4 |
| 23939 | alcahuetas | 4 |
| 23940 | alarmarse | 4 |
| 23941 | alarmado | 4 |
| 23942 | alarido | 4 |
| 23943 | alanos | 4 |
| 23944 | alambres | 4 |
| 23945 | alahé | 4 |
| 23946 | alabaron | 4 |
| 23947 | alabardero | 4 |
| 23948 | alabados | 4 |
| 23949 | ajajá | 4 |
| 23950 | aislados | 4 |
| 23951 | airosos | 4 |
| 23952 | aína | 4 |
| 23953 | ahorcaron | 4 |
| 23954 | ahogos | 4 |
| 23955 | ahogo | 4 |
| 23956 | ahogaron | 4 |
| 23957 | ahogar | 4 |
| 23958 | ahogan | 4 |
| 23959 | agujereado | 4 |
| 23960 | agujereada | 4 |
| 23961 | aguileña | 4 |
| 23962 | aguilar | 4 |
| 23963 | agüelo | 4 |
| 23964 | aguárdese | 4 |
| 23965 | aguárdate | 4 |
| 23966 | aguardase | 4 |
| 23967 | aguanto | 4 |
| 23968 | aguamanil | 4 |
| 23969 | agrónomo | 4 |
| 23970 | agricultura | 4 |
| 23971 | agrias | 4 |
| 23972 | agradezca | 4 |
| 23973 | agradecidas | 4 |
| 23974 | agradeces | 4 |
| 23975 | agradeceré | 4 |
| 23976 | agradare | 4 |
| 23977 | agraciado | 4 |
| 23978 | agobiado | 4 |
| 23979 | agenda | 4 |
| 23980 | agasajo | 4 |
| 23981 | agarrado | 4 |
| 23982 | agarraban | 4 |
| 23983 | agarraba | 4 |
| 23984 | agarra | 4 |
| 23985 | agachó | 4 |
| 23986 | afueras | 4 |
| 23987 | afrentar | 4 |
| 23988 | afrentados | 4 |
| 23989 | aflija | 4 |
| 23990 | afligidas | 4 |
| 23991 | afirmativo | 4 |
| 23992 | afinidad | 4 |
| 23993 | afilados | 4 |
| 23994 | afeminado | 4 |
| 23995 | afeite | 4 |
| 23996 | afeitarse | 4 |
| 23997 | afeitado | 4 |
| 23998 | afecta | 4 |
| 23999 | afanaba | 4 |
| 24000 | afables | 4 |
| 24001 | advertirle | 4 |
| 24002 | adversa | 4 |
| 24003 | adúuultera | 4 |
| 24004 | adulterado | 4 |
| 24005 | adúltera | 4 |
| 24006 | adulona | 4 |
| 24007 | adulador | 4 |
| 24008 | adulaba | 4 |
| 24009 | aduersidades | 4 |
| 24010 | aduersa | 4 |
| 24011 | adquiridos | 4 |
| 24012 | adquiridas | 4 |
| 24013 | adquiere | 4 |
| 24014 | admitidos | 4 |
| 24015 | admitidas | 4 |
| 24016 | admita | 4 |
| 24017 | admiróse | 4 |
| 24018 | admiráronse | 4 |
| 24019 | admirarla | 4 |
| 24020 | admiraciones | 4 |
| 24021 | admiracion | 4 |
| 24022 | administre | 4 |
| 24023 | administrativa | 4 |
| 24024 | adivinanzas | 4 |
| 24025 | adivinación | 4 |
| 24026 | aderezos | 4 |
| 24027 | aderezados | 4 |
| 24028 | adereza | 4 |
| 24029 | adelantándose | 4 |
| 24030 | adefesio | 4 |
| 24031 | adarme | 4 |
| 24032 | acuso | 4 |
| 24033 | acusar | 4 |
| 24034 | aculla | 4 |
| 24035 | acuestes | 4 |
| 24036 | acuerdate | 4 |
| 24037 | acudid | 4 |
| 24038 | actitudes | 4 |
| 24039 | acritud | 4 |
| 24040 | acreditado | 4 |
| 24041 | acrecientan | 4 |
| 24042 | acostumbrando | 4 |
| 24043 | acostumbra | 4 |
| 24044 | acosté | 4 |
| 24045 | acostarme | 4 |
| 24046 | acostara | 4 |
| 24047 | acortando | 4 |
| 24048 | acorro | 4 |
| 24049 | acorre | 4 |
| 24050 | acordase | 4 |
| 24051 | acordarte | 4 |
| 24052 | acordará | 4 |
| 24053 | acordamos | 4 |
| 24054 | acordábase | 4 |
| 24055 | aconsejaría | 4 |
| 24056 | aconsejaré | 4 |
| 24057 | aconsejando | 4 |
| 24058 | acompañaría | 4 |
| 24059 | acompañamos | 4 |
| 24060 | acomoda | 4 |
| 24061 | acometiese | 4 |
| 24062 | acometiendo | 4 |
| 24063 | acometen | 4 |
| 24064 | acometa | 4 |
| 24065 | acobarda | 4 |
| 24066 | aclimatación | 4 |
| 24067 | aclaraban | 4 |
| 24068 | açidia | 4 |
| 24069 | acíbar | 4 |
| 24070 | achacoso | 4 |
| 24071 | achacaba | 4 |
| 24072 | acertaron | 4 |
| 24073 | acerqueme | 4 |
| 24074 | acercase | 4 |
| 24075 | acercábase | 4 |
| 24076 | acepté | 4 |
| 24077 | aceptaría | 4 |
| 24078 | acepción | 4 |
| 24079 | acémilas | 4 |
| 24080 | acechaba | 4 |
| 24081 | acataba | 4 |
| 24082 | acarrean | 4 |
| 24083 | acariciándole | 4 |
| 24084 | acariciaba | 4 |
| 24085 | acaloraba | 4 |
| 24086 | acaecimientos | 4 |
| 24087 | académica | 4 |
| 24088 | acabes | 4 |
| 24089 | acabarlo | 4 |
| 24090 | acabaremos | 4 |
| 24091 | acabadita | 4 |
| 24092 | abusaba | 4 |
| 24093 | aburrirás | 4 |
| 24094 | aburrían | 4 |
| 24095 | aburren | 4 |
| 24096 | aburre | 4 |
| 24097 | abundaban | 4 |
| 24098 | abultado | 4 |
| 24099 | abultadas | 4 |
| 24100 | abstracto | 4 |
| 24101 | abrumador | 4 |
| 24102 | abrumaba | 4 |
| 24103 | abrochó | 4 |
| 24104 | abriría | 4 |
| 24105 | abriose | 4 |
| 24106 | abriga | 4 |
| 24107 | abriéndola | 4 |
| 24108 | abres | 4 |
| 24109 | abrazóle | 4 |
| 24110 | abrazáronse | 4 |
| 24111 | abrazaba | 4 |
| 24112 | abrasado | 4 |
| 24113 | abrasadas | 4 |
| 24114 | aborrecerla | 4 |
| 24115 | abonado | 4 |
| 24116 | ablande | 4 |
| 24117 | ablandar | 4 |
| 24118 | abigarrado | 4 |
| 24119 | abertura | 4 |
| 24120 | aberraciones | 4 |
| 24121 | abenençia | 4 |
| 24122 | abaxo | 4 |
| 24123 | abatieron | 4 |
| 24124 | abaten | 4 |
| 24125 | abarcas | 4 |
| 24126 | abarca | 4 |
| 24127 | abandones | 4 |
| 24128 | abandone | 4 |
| 24129 | abandonaron | 4 |
| 24130 | abandonadas | 4 |
| 24131 | abandonaban | 4 |
| 24132 | abalorios | 4 |
| 24133 | zurriágame | 3 |
| 24134 | zumo | 3 |
| 24135 | zumbaron | 3 |
| 24136 | zuecos | 3 |
| 24137 | zorras | 3 |
| 24138 | zorra | 3 |
| 24139 | zócalo | 3 |
| 24140 | zipizape | 3 |
| 24141 | zás | 3 |
| 24142 | zarzuelas | 3 |
| 24143 | zarza | 3 |
| 24144 | zarazas | 3 |
| 24145 | zaragüelles | 3 |
| 24146 | zaquizamí | 3 |
| 24147 | zaque | 3 |
| 24148 | zanahorias | 3 |
| 24149 | zambulló | 3 |
| 24150 | zalemas | 3 |
| 24151 | zahareña | 3 |
| 24152 | zafiros | 3 |
| 24153 | zafio | 3 |
| 24154 | zafia | 3 |
| 24155 | z | 3 |
| 24156 | yt | 3 |
| 24157 | yrme | 3 |
| 24158 | yrás | 3 |
| 24159 | yran | 3 |
| 24160 | york | 3 |
| 24161 | yguale | 3 |
| 24162 | yerua | 3 |
| 24163 | yerre | 3 |
| 24164 | yemas | 3 |
| 24165 | yelos | 3 |
| 24166 | yécora | 3 |
| 24167 | ydos | 3 |
| 24168 | yaz | 3 |
| 24169 | yacente | 3 |
| 24170 | xxxvii | 3 |
| 24171 | xxxvi | 3 |
| 24172 | xristiano | 3 |
| 24173 | xlvii | 3 |
| 24174 | xlv | 3 |
| 24175 | xl | 3 |
| 24176 | werther | 3 |
| 24177 | vyeron | 3 |
| 24178 | vuélveme | 3 |
| 24179 | vuélvanse | 3 |
| 24180 | vuecencia | 3 |
| 24181 | vto | 3 |
| 24182 | vtilidad | 3 |
| 24183 | votaba | 3 |
| 24184 | vómitos | 3 |
| 24185 | vomitó | 3 |
| 24186 | vómito | 3 |
| 24187 | vomitando | 3 |
| 24188 | volviéronse | 3 |
| 24189 | volvíase | 3 |
| 24190 | voluptuosamente | 3 |
| 24191 | voluntat | 3 |
| 24192 | voluntario | 3 |
| 24193 | voluminoso | 3 |
| 24194 | volteando | 3 |
| 24195 | volteador | 3 |
| 24196 | volcados | 3 |
| 24197 | volara | 3 |
| 24198 | volador | 3 |
| 24199 | vocinglero | 3 |
| 24200 | vocales | 3 |
| 24201 | vnica | 3 |
| 24202 | vivieran | 3 |
| 24203 | vividor | 3 |
| 24204 | viví | 3 |
| 24205 | viváis | 3 |
| 24206 | viuos | 3 |
| 24207 | vital | 3 |
| 24208 | vistosas | 3 |
| 24209 | vistiéndome | 3 |
| 24210 | vislumbraba | 3 |
| 24211 | visitarnos | 3 |
| 24212 | visitarme | 3 |
| 24213 | visitarle | 3 |
| 24214 | visitada | 3 |
| 24215 | visanzón | 3 |
| 24216 | violeta | 3 |
| 24217 | vinir | 3 |
| 24218 | viniesse | 3 |
| 24219 | viniésemos | 3 |
| 24220 | vinieras | 3 |
| 24221 | víneme | 3 |
| 24222 | vínculos | 3 |
| 24223 | vinajeras | 3 |
| 24224 | vilo | 3 |
| 24225 | villadiego | 3 |
| 24226 | vilesa | 3 |
| 24227 | vigorosos | 3 |
| 24228 | vigilaban | 3 |
| 24229 | vies | 3 |
| 24230 | viéronle | 3 |
| 24231 | viéredes | 3 |
| 24232 | viéramos | 3 |
| 24233 | viena | 3 |
| 24234 | viejecillo | 3 |
| 24235 | vidro | 3 |
| 24236 | victorioso | 3 |
| 24237 | viçioso | 3 |
| 24238 | viciosas | 3 |
| 24239 | vibró | 3 |
| 24240 | vibraban | 3 |
| 24241 | viajantes | 3 |
| 24242 | viajan | 3 |
| 24243 | viajaban | 3 |
| 24244 | viaducto | 3 |
| 24245 | vezinos | 3 |
| 24246 | veyendo | 3 |
| 24247 | veye | 3 |
| 24248 | vetas | 3 |
| 24249 | vestidura | 3 |
| 24250 | vestidito | 3 |
| 24251 | vestí | 3 |
| 24252 | veslos | 3 |
| 24253 | vesino | 3 |
| 24254 | vertiginosas | 3 |
| 24255 | vertieron | 3 |
| 24256 | vertido | 3 |
| 24257 | vertida | 3 |
| 24258 | verticales | 3 |
| 24259 | vertederos | 3 |
| 24260 | versolari | 3 |
| 24261 | versado | 3 |
| 24262 | verosímiles | 3 |
| 24263 | veritas | 3 |
| 24264 | verídicamente | 3 |
| 24265 | veríais | 3 |
| 24266 | vergilio | 3 |
| 24267 | verduras | 3 |
| 24268 | véovos | 3 |
| 24269 | ventosa | 3 |
| 24270 | ventanillas | 3 |
| 24271 | ventajosa | 3 |
| 24272 | venit | 3 |
| 24273 | venis | 3 |
| 24274 | venirme | 3 |
| 24275 | veniere | 3 |
| 24276 | veníen | 3 |
| 24277 | venidos | 3 |
| 24278 | veniales | 3 |
| 24279 | vengarnos | 3 |
| 24280 | vengarle | 3 |
| 24281 | vengáis | 3 |
| 24282 | vengador | 3 |
| 24283 | venenosas | 3 |
| 24284 | vendó | 3 |
| 24285 | vendo | 3 |
| 24286 | vendimia | 3 |
| 24287 | venderlo | 3 |
| 24288 | venderle | 3 |
| 24289 | venciese | 3 |
| 24290 | vencían | 3 |
| 24291 | vencí | 3 |
| 24292 | vençen | 3 |
| 24293 | velludo | 3 |
| 24294 | vellones | 3 |
| 24295 | vellón | 3 |
| 24296 | vellido | 3 |
| 24297 | veladores | 3 |
| 24298 | velado | 3 |
| 24299 | veintidós | 3 |
| 24300 | vegetales | 3 |
| 24301 | veçino | 3 |
| 24302 | véanse | 3 |
| 24303 | vé | 3 |
| 24304 | vayades | 3 |
| 24305 | vate | 3 |
| 24306 | vasijas | 3 |
| 24307 | vasalla | 3 |
| 24308 | variaron | 3 |
| 24309 | variantes | 3 |
| 24310 | variada | 3 |
| 24311 | variación | 3 |
| 24312 | varapalo | 3 |
| 24313 | var | 3 |
| 24314 | vaquera | 3 |
| 24315 | vaporcito | 3 |
| 24316 | vanamente | 3 |
| 24317 | valores | 3 |
| 24318 | valones | 3 |
| 24319 | valona | 3 |
| 24320 | valme | 3 |
| 24321 | valiosas | 3 |
| 24322 | valiese | 3 |
| 24323 | validos | 3 |
| 24324 | valemos | 3 |
| 24325 | valedera | 3 |
| 24326 | váguidos | 3 |
| 24327 | vaguedades | 3 |
| 24328 | vagonetes | 3 |
| 24329 | vagamundos | 3 |
| 24330 | vagamundo | 3 |
| 24331 | vagaba | 3 |
| 24332 | vació | 3 |
| 24333 | vacilaciones | 3 |
| 24334 | vaciaba | 3 |
| 24335 | uy | 3 |
| 24336 | utilitaria | 3 |
| 24337 | usurpar | 3 |
| 24338 | usurpado | 3 |
| 24339 | use | 3 |
| 24340 | usava | 3 |
| 24341 | usarlo | 3 |
| 24342 | urías | 3 |
| 24343 | urdemalas | 3 |
| 24344 | urbs | 3 |
| 24345 | untar | 3 |
| 24346 | unir | 3 |
| 24347 | unían | 3 |
| 24348 | une | 3 |
| 24349 | ultrajar | 3 |
| 24350 | ulpiano | 3 |
| 24351 | uf | 3 |
| 24352 | uer | 3 |
| 24353 | ubeda | 3 |
| 24354 | túvole | 3 |
| 24355 | tuvistes | 3 |
| 24356 | tutti | 3 |
| 24357 | tutor | 3 |
| 24358 | turres | 3 |
| 24359 | turgente | 3 |
| 24360 | turgencias | 3 |
| 24361 | turcas | 3 |
| 24362 | turbóse | 3 |
| 24363 | turbias | 3 |
| 24364 | tuo | 3 |
| 24365 | túneles | 3 |
| 24366 | tumbado | 3 |
| 24367 | tulio | 3 |
| 24368 | tuerza | 3 |
| 24369 | troyanos | 3 |
| 24370 | trotes | 3 |
| 24371 | tropiezos | 3 |
| 24372 | tropezón | 3 |
| 24373 | troneras | 3 |
| 24374 | trompicones | 3 |
| 24375 | troche | 3 |
| 24376 | trocándose | 3 |
| 24377 | trocados | 3 |
| 24378 | trobas | 3 |
| 24379 | trizas | 3 |
| 24380 | triunfantes | 3 |
| 24381 | triunfal | 3 |
| 24382 | triunfador | 3 |
| 24383 | tristón | 3 |
| 24384 | tristanico | 3 |
| 24385 | triquitraque | 3 |
| 24386 | trincheas | 3 |
| 24387 | trimestre | 3 |
| 24388 | trigos | 3 |
| 24389 | trifulca | 3 |
| 24390 | trepando | 3 |
| 24391 | trepa | 3 |
| 24392 | trenes | 3 |
| 24393 | traynel | 3 |
| 24394 | trayes | 3 |
| 24395 | trayen | 3 |
| 24396 | traydores | 3 |
| 24397 | trayciones | 3 |
| 24398 | trayçión | 3 |
| 24399 | traycion | 3 |
| 24400 | travesaño | 3 |
| 24401 | trava | 3 |
| 24402 | trataría | 3 |
| 24403 | trataremos | 3 |
| 24404 | trasunto | 3 |
| 24405 | trastornar | 3 |
| 24406 | trasteando | 3 |
| 24407 | traspuso | 3 |
| 24408 | traspuesto | 3 |
| 24409 | trasponer | 3 |
| 24410 | traspassa | 3 |
| 24411 | traspasar | 3 |
| 24412 | traspasada | 3 |
| 24413 | traso | 3 |
| 24414 | trasnochar | 3 |
| 24415 | trasluz | 3 |
| 24416 | trasladándose | 3 |
| 24417 | traslación | 3 |
| 24418 | traseras | 3 |
| 24419 | trasbordar | 3 |
| 24420 | trapobana | 3 |
| 24421 | trapisondista | 3 |
| 24422 | trapillo | 3 |
| 24423 | transtiberina | 3 |
| 24424 | transporte | 3 |
| 24425 | transportar | 3 |
| 24426 | transacciones | 3 |
| 24427 | tramposo | 3 |
| 24428 | tramposa | 3 |
| 24429 | trámite | 3 |
| 24430 | tralla | 3 |
| 24431 | trajiste | 3 |
| 24432 | trajín | 3 |
| 24433 | trajecito | 3 |
| 24434 | traías | 3 |
| 24435 | trague | 3 |
| 24436 | tragón | 3 |
| 24437 | tragaluces | 3 |
| 24438 | tragadero | 3 |
| 24439 | traga | 3 |
| 24440 | traernos | 3 |
| 24441 | traerlos | 3 |
| 24442 | traerlas | 3 |
| 24443 | traeremos | 3 |
| 24444 | traerán | 3 |
| 24445 | traduzca | 3 |
| 24446 | tradución | 3 |
| 24447 | traducidas | 3 |
| 24448 | traduce | 3 |
| 24449 | trabamos | 3 |
| 24450 | trabajillos | 3 |
| 24451 | trabajen | 3 |
| 24452 | trabajara | 3 |
| 24453 | trabajadora | 3 |
| 24454 | trababa | 3 |
| 24455 | tovo | 3 |
| 24456 | touiste | 3 |
| 24457 | totalidad | 3 |
| 24458 | toscos | 3 |
| 24459 | toscas | 3 |
| 24460 | tortura | 3 |
| 24461 | tortuoso | 3 |
| 24462 | tortuosas | 3 |
| 24463 | tortuosa | 3 |
| 24464 | tortolilla | 3 |
| 24465 | torreznos | 3 |
| 24466 | torrezno | 3 |
| 24467 | torreón | 3 |
| 24468 | torpedat | 3 |
| 24469 | tornóse | 3 |
| 24470 | tornes | 3 |
| 24471 | tornéme | 3 |
| 24472 | tornase | 3 |
| 24473 | topasen | 3 |
| 24474 | toparemos | 3 |
| 24475 | topando | 3 |
| 24476 | toneladas | 3 |
| 24477 | tomedes | 3 |
| 24478 | tomaste | 3 |
| 24479 | tomarlos | 3 |
| 24480 | tomarlas | 3 |
| 24481 | tomares | 3 |
| 24482 | tomándome | 3 |
| 24483 | tómalo | 3 |
| 24484 | tomá | 3 |
| 24485 | toleraría | 3 |
| 24486 | toledanos | 3 |
| 24487 | toledana | 3 |
| 24488 | tole | 3 |
| 24489 | todita | 3 |
| 24490 | todd | 3 |
| 24491 | tocarse | 3 |
| 24492 | tocados | 3 |
| 24493 | tobillo | 3 |
| 24494 | tizona | 3 |
| 24495 | titulado | 3 |
| 24496 | tisú | 3 |
| 24497 | tísicos | 3 |
| 24498 | tirsos | 3 |
| 24499 | tiroteo | 3 |
| 24500 | tirita | 3 |
| 24501 | tiria | 3 |
| 24502 | tire | 3 |
| 24503 | tirarse | 3 |
| 24504 | tirarlos | 3 |
| 24505 | tiraré | 3 |
| 24506 | tirará | 3 |
| 24507 | tirándole | 3 |
| 24508 | tiradores | 3 |
| 24509 | tiorras | 3 |
| 24510 | tiñoso | 3 |
| 24511 | tinglado | 3 |
| 24512 | tifus | 3 |
| 24513 | tiernísima | 3 |
| 24514 | tiemblas | 3 |
| 24515 | tiburón | 3 |
| 24516 | tibi | 3 |
| 24517 | themis | 3 |
| 24518 | testo | 3 |
| 24519 | testarudo | 3 |
| 24520 | tesorero | 3 |
| 24521 | terrorífico | 3 |
| 24522 | territorio | 3 |
| 24523 | terrestre | 3 |
| 24524 | terrero | 3 |
| 24525 | terremotos | 3 |
| 24526 | terranova | 3 |
| 24527 | terquedades | 3 |
| 24528 | ternuras | 3 |
| 24529 | terna | 3 |
| 24530 | termómetro | 3 |
| 24531 | termasaltas | 3 |
| 24532 | tercios | 3 |
| 24533 | tercianas | 3 |
| 24534 | tercetos | 3 |
| 24535 | teológico | 3 |
| 24536 | teodosio | 3 |
| 24537 | teñir | 3 |
| 24538 | teñidas | 3 |
| 24539 | tenues | 3 |
| 24540 | tenuemente | 3 |
| 24541 | tentóse | 3 |
| 24542 | tentaba | 3 |
| 24543 | tensión | 3 |
| 24544 | tenprano | 3 |
| 24545 | tenle | 3 |
| 24546 | tenla | 3 |
| 24547 | tenientes | 3 |
| 24548 | teniéndose | 3 |
| 24549 | teniéndolo | 3 |
| 24550 | teníe | 3 |
| 24551 | teníale | 3 |
| 24552 | teníala | 3 |
| 24553 | teniades | 3 |
| 24554 | téngase | 3 |
| 24555 | téngala | 3 |
| 24556 | tenérsele | 3 |
| 24557 | teneros | 3 |
| 24558 | tenebroso | 3 |
| 24559 | tenducho | 3 |
| 24560 | tendrías | 3 |
| 24561 | tendréis | 3 |
| 24562 | tenderse | 3 |
| 24563 | tenderme | 3 |
| 24564 | tenaces | 3 |
| 24565 | tempora | 3 |
| 24566 | templó | 3 |
| 24567 | templanza | 3 |
| 24568 | templando | 3 |
| 24569 | temperatura | 3 |
| 24570 | temíamos | 3 |
| 24571 | temeridades | 3 |
| 24572 | temerary | 3 |
| 24573 | temeraria | 3 |
| 24574 | temblorosos | 3 |
| 24575 | tembloroso | 3 |
| 24576 | temblona | 3 |
| 24577 | teman | 3 |
| 24578 | téllez | 3 |
| 24579 | telegráfico | 3 |
| 24580 | tejida | 3 |
| 24581 | tejía | 3 |
| 24582 | techumbre | 3 |
| 24583 | tazas | 3 |
| 24584 | tartana | 3 |
| 24585 | tartán | 3 |
| 24586 | tarquino | 3 |
| 24587 | tardaré | 3 |
| 24588 | tardare | 3 |
| 24589 | tardaban | 3 |
| 24590 | tarascas | 3 |
| 24591 | tapón | 3 |
| 24592 | tapando | 3 |
| 24593 | tapan | 3 |
| 24594 | tapabocas | 3 |
| 24595 | tantismos | 3 |
| 24596 | tanteado | 3 |
| 24597 | tamiz | 3 |
| 24598 | tamborinos | 3 |
| 24599 | tambaleaba | 3 |
| 24600 | tamañitos | 3 |
| 24601 | tamañas | 3 |
| 24602 | talones | 3 |
| 24603 | tallos | 3 |
| 24604 | tallada | 3 |
| 24605 | talismán | 3 |
| 24606 | talía | 3 |
| 24607 | talco | 3 |
| 24608 | tajado | 3 |
| 24609 | tahur | 3 |
| 24610 | tahona | 3 |
| 24611 | tahelí | 3 |
| 24612 | tagarotes | 3 |
| 24613 | tagarino | 3 |
| 24614 | táctica | 3 |
| 24615 | tacos | 3 |
| 24616 | tacones | 3 |
| 24617 | taco | 3 |
| 24618 | tacita | 3 |
| 24619 | tacaño | 3 |
| 24620 | taburetes | 3 |
| 24621 | tabiques | 3 |
| 24622 | tabernario | 3 |
| 24623 | synple | 3 |
| 24624 | sygue | 3 |
| 24625 | sutilmente | 3 |
| 24626 | sustitución | 3 |
| 24627 | sustentase | 3 |
| 24628 | sustentaré | 3 |
| 24629 | sustentan | 3 |
| 24630 | sustancial | 3 |
| 24631 | suspiraban | 3 |
| 24632 | suspendía | 3 |
| 24633 | suspendan | 3 |
| 24634 | susodicho | 3 |
| 24635 | susio | 3 |
| 24636 | suscripción | 3 |
| 24637 | surtidores | 3 |
| 24638 | surgían | 3 |
| 24639 | supuso | 3 |
| 24640 | supuestos | 3 |
| 24641 | supuesta | 3 |
| 24642 | suprimir | 3 |
| 24643 | suprimido | 3 |
| 24644 | súpose | 3 |
| 24645 | suponerlo | 3 |
| 24646 | supliendo | 3 |
| 24647 | suplicarle | 3 |
| 24648 | suplicado | 3 |
| 24649 | suple | 3 |
| 24650 | supiesse | 3 |
| 24651 | supieses | 3 |
| 24652 | supiesen | 3 |
| 24653 | supersticiosas | 3 |
| 24654 | supersticiosamente | 3 |
| 24655 | sumergía | 3 |
| 24656 | sujetarse | 3 |
| 24657 | sujetarla | 3 |
| 24658 | sujetaban | 3 |
| 24659 | sugestión | 3 |
| 24660 | sugerido | 3 |
| 24661 | sugería | 3 |
| 24662 | sufridos | 3 |
| 24663 | sufrida | 3 |
| 24664 | sufres | 3 |
| 24665 | sufren | 3 |
| 24666 | sufragios | 3 |
| 24667 | suero | 3 |
| 24668 | sueltan | 3 |
| 24669 | sudo | 3 |
| 24670 | sudeste | 3 |
| 24671 | sudaban | 3 |
| 24672 | sucintamente | 3 |
| 24673 | sucessor | 3 |
| 24674 | sucesores | 3 |
| 24675 | sucedióme | 3 |
| 24676 | sucedían | 3 |
| 24677 | sucederles | 3 |
| 24678 | sucedería | 3 |
| 24679 | sucedan | 3 |
| 24680 | subsiste | 3 |
| 24681 | subsecretario | 3 |
| 24682 | subrepticiamente | 3 |
| 24683 | subrepticia | 3 |
| 24684 | sublimidad | 3 |
| 24685 | sublimemente | 3 |
| 24686 | sublimado | 3 |
| 24687 | sublevaban | 3 |
| 24688 | subiste | 3 |
| 24689 | subiera | 3 |
| 24690 | subid | 3 |
| 24691 | subes | 3 |
| 24692 | subasta | 3 |
| 24693 | stabat | 3 |
| 24694 | ssyn | 3 |
| 24695 | ssu | 3 |
| 24696 | ssobre | 3 |
| 24697 | ssé | 3 |
| 24698 | ssanta | 3 |
| 24699 | ssabe | 3 |
| 24700 | spritu | 3 |
| 24701 | sport | 3 |
| 24702 | spirto | 3 |
| 24703 | sótano | 3 |
| 24704 | sotabanco | 3 |
| 24705 | sostienen | 3 |
| 24706 | sostenimiento | 3 |
| 24707 | sostenga | 3 |
| 24708 | sostén | 3 |
| 24709 | sospechará | 3 |
| 24710 | sospechado | 3 |
| 24711 | sospechaban | 3 |
| 24712 | sosegóse | 3 |
| 24713 | sosegadas | 3 |
| 24714 | sortilegio | 3 |
| 24715 | sortear | 3 |
| 24716 | sorprendidas | 3 |
| 24717 | sorprendí | 3 |
| 24718 | sopló | 3 |
| 24719 | soplaron | 3 |
| 24720 | sopla | 3 |
| 24721 | sopicaldo | 3 |
| 24722 | soñoliento | 3 |
| 24723 | soñada | 3 |
| 24724 | sonrosadas | 3 |
| 24725 | sonriéndose | 3 |
| 24726 | sonaran | 3 |
| 24727 | sonando | 3 |
| 24728 | somo | 3 |
| 24729 | sometieron | 3 |
| 24730 | sometía | 3 |
| 24731 | sombrosos | 3 |
| 24732 | sombrillas | 3 |
| 24733 | sombrías | 3 |
| 24734 | sombrerito | 3 |
| 24735 | soltarle | 3 |
| 24736 | soltalle | 3 |
| 24737 | sollozar | 3 |
| 24738 | sollozaba | 3 |
| 24739 | solimán | 3 |
| 24740 | solido | 3 |
| 24741 | solicitadas | 3 |
| 24742 | solia | 3 |
| 24743 | solenes | 3 |
| 24744 | solemniza | 3 |
| 24745 | soldar | 3 |
| 24746 | soldadesca | 3 |
| 24747 | solazes | 3 |
| 24748 | soláz | 3 |
| 24749 | solariegas | 3 |
| 24750 | solana | 3 |
| 24751 | sofoques | 3 |
| 24752 | sofoco | 3 |
| 24753 | sofisterías | 3 |
| 24754 | socorrió | 3 |
| 24755 | socorriendo | 3 |
| 24756 | socorría | 3 |
| 24757 | socoa | 3 |
| 24758 | socialismo | 3 |
| 24759 | socaliñas | 3 |
| 24760 | sobro | 3 |
| 24761 | sobrio | 3 |
| 24762 | sobrinillo | 3 |
| 24763 | sobrinilla | 3 |
| 24764 | sobrescrito | 3 |
| 24765 | sobresaltan | 3 |
| 24766 | sobresaliente | 3 |
| 24767 | sobrenombres | 3 |
| 24768 | sobreescrito | 3 |
| 24769 | sobido | 3 |
| 24770 | soberuio | 3 |
| 24771 | soberanamente | 3 |
| 24772 | sobajada | 3 |
| 24773 | sobadas | 3 |
| 24774 | sitial | 3 |
| 24775 | sistemático | 3 |
| 24776 | sisar | 3 |
| 24777 | sisaba | 3 |
| 24778 | sisa | 3 |
| 24779 | siruiente | 3 |
| 24780 | sirgo | 3 |
| 24781 | sirena | 3 |
| 24782 | sinuosas | 3 |
| 24783 | sintiose | 3 |
| 24784 | sintieses | 3 |
| 24785 | sintiese | 3 |
| 24786 | sinodal | 3 |
| 24787 | siniestros | 3 |
| 24788 | singularísima | 3 |
| 24789 | singularidades | 3 |
| 24790 | singer | 3 |
| 24791 | singapore | 3 |
| 24792 | simultáneamente | 3 |
| 24793 | simpatizaba | 3 |
| 24794 | simpáticas | 3 |
| 24795 | simetría | 3 |
| 24796 | silverio | 3 |
| 24797 | silueta | 3 |
| 24798 | sillones | 3 |
| 24799 | sillar | 3 |
| 24800 | silenciosamente | 3 |
| 24801 | silbos | 3 |
| 24802 | silbaban | 3 |
| 24803 | siguiesen | 3 |
| 24804 | siguiéronle | 3 |
| 24805 | significativa | 3 |
| 24806 | sigámosle | 3 |
| 24807 | sígame | 3 |
| 24808 | siervos | 3 |
| 24809 | siéntense | 3 |
| 24810 | siéndole | 3 |
| 24811 | siega | 3 |
| 24812 | sibila | 3 |
| 24813 | shakespeare | 3 |
| 24814 | seydo | 3 |
| 24815 | sexta | 3 |
| 24816 | severos | 3 |
| 24817 | setos | 3 |
| 24818 | seteno | 3 |
| 24819 | setenas | 3 |
| 24820 | setecientos | 3 |
| 24821 | sestear | 3 |
| 24822 | sesta | 3 |
| 24823 | servirán | 3 |
| 24824 | servicial | 3 |
| 24825 | seruidor | 3 |
| 24826 | seruicios | 3 |
| 24827 | serranos | 3 |
| 24828 | serranillas | 3 |
| 24829 | serranas | 3 |
| 24830 | serpentón | 3 |
| 24831 | seretas | 3 |
| 24832 | seráfico | 3 |
| 24833 | seráfica | 3 |
| 24834 | sequen | 3 |
| 24835 | sepultó | 3 |
| 24836 | separose | 3 |
| 24837 | separes | 3 |
| 24838 | separaremos | 3 |
| 24839 | separan | 3 |
| 24840 | seor | 3 |
| 24841 | señalándole | 3 |
| 24842 | señalamos | 3 |
| 24843 | sentirme | 3 |
| 24844 | sentirla | 3 |
| 24845 | sentióse | 3 |
| 24846 | sentidas | 3 |
| 24847 | sentenciare | 3 |
| 24848 | sentenciar | 3 |
| 24849 | senté | 3 |
| 24850 | sentarme | 3 |
| 24851 | sentámonos | 3 |
| 24852 | sentadita | 3 |
| 24853 | sentábase | 3 |
| 24854 | sensuales | 3 |
| 24855 | sensata | 3 |
| 24856 | senil | 3 |
| 24857 | senén | 3 |
| 24858 | seminaristas | 3 |
| 24859 | seminarista | 3 |
| 24860 | semiente | 3 |
| 24861 | semestre | 3 |
| 24862 | sembrando | 3 |
| 24863 | sellado | 3 |
| 24864 | sellada | 3 |
| 24865 | selecto | 3 |
| 24866 | segundón | 3 |
| 24867 | segundar | 3 |
| 24868 | seguirme | 3 |
| 24869 | seguirlos | 3 |
| 24870 | seguidme | 3 |
| 24871 | seguidita | 3 |
| 24872 | seducirle | 3 |
| 24873 | sedentaria | 3 |
| 24874 | sede | 3 |
| 24875 | sedas | 3 |
| 24876 | secundum | 3 |
| 24877 | secularizar | 3 |
| 24878 | secuestrador | 3 |
| 24879 | secuaces | 3 |
| 24880 | secreteo | 3 |
| 24881 | secreteándose | 3 |
| 24882 | secado | 3 |
| 24883 | séanme | 3 |
| 24884 | scipión | 3 |
| 24885 | sciente | 3 |
| 24886 | sazonado | 3 |
| 24887 | sazonadas | 3 |
| 24888 | sazon | 3 |
| 24889 | saúco | 3 |
| 24890 | sauces | 3 |
| 24891 | sauanas | 3 |
| 24892 | satisfice | 3 |
| 24893 | satisfagas | 3 |
| 24894 | satisfacerse | 3 |
| 24895 | satisfaceros | 3 |
| 24896 | satisfacerlos | 3 |
| 24897 | satisfacciones | 3 |
| 24898 | sátiros | 3 |
| 24899 | satánico | 3 |
| 24900 | satánica | 3 |
| 24901 | satanases | 3 |
| 24902 | satán | 3 |
| 24903 | sastra | 3 |
| 24904 | sartal | 3 |
| 24905 | sarra | 3 |
| 24906 | sarcófago | 3 |
| 24907 | sarcástica | 3 |
| 24908 | saraos | 3 |
| 24909 | sarampión | 3 |
| 24910 | sanudo | 3 |
| 24911 | santurrona | 3 |
| 24912 | santiguaron | 3 |
| 24913 | santiguarme | 3 |
| 24914 | santiguar | 3 |
| 24915 | santiguándose | 3 |
| 24916 | santidat | 3 |
| 24917 | santiamén | 3 |
| 24918 | santamente | 3 |
| 24919 | sansueña | 3 |
| 24920 | sanguínea | 3 |
| 24921 | sanguinaria | 3 |
| 24922 | sanguijuelas | 3 |
| 24923 | sangrientos | 3 |
| 24924 | sandío | 3 |
| 24925 | sándalo | 3 |
| 24926 | sanase | 3 |
| 24927 | sanare | 3 |
| 24928 | sanado | 3 |
| 24929 | samaniega | 3 |
| 24930 | saly | 3 |
| 24931 | salvos | 3 |
| 24932 | salvoconduto | 3 |
| 24933 | sálvense | 3 |
| 24934 | salvedades | 3 |
| 24935 | salvarle | 3 |
| 24936 | salvan | 3 |
| 24937 | salvamos | 3 |
| 24938 | salvajismo | 3 |
| 24939 | salvados | 3 |
| 24940 | salvadora | 3 |
| 24941 | salvadera | 3 |
| 24942 | saltear | 3 |
| 24943 | salteada | 3 |
| 24944 | saltase | 3 |
| 24945 | salpicar | 3 |
| 24946 | salpicada | 3 |
| 24947 | salomon | 3 |
| 24948 | salmista | 3 |
| 24949 | salivazos | 3 |
| 24950 | salíos | 3 |
| 24951 | salio | 3 |
| 24952 | salidita | 3 |
| 24953 | saldo | 3 |
| 24954 | salacia | 3 |
| 24955 | sahumados | 3 |
| 24956 | sacuden | 3 |
| 24957 | sacrílegas | 3 |
| 24958 | sacramentado | 3 |
| 24959 | sacóle | 3 |
| 24960 | sacerdotisa | 3 |
| 24961 | sacaua | 3 |
| 24962 | sacarlos | 3 |
| 24963 | sacarles | 3 |
| 24964 | sacaremos | 3 |
| 24965 | sacaras | 3 |
| 24966 | sabydor | 3 |
| 24967 | sabréis | 3 |
| 24968 | sabre | 3 |
| 24969 | sabores | 3 |
| 24970 | saboreando | 3 |
| 24971 | sablazos | 3 |
| 24972 | saberlas | 3 |
| 24973 | saberla | 3 |
| 24974 | sábelo | 3 |
| 24975 | sabedor | 3 |
| 24976 | sabañones | 3 |
| 24977 | rutinario | 3 |
| 24978 | rutinaria | 3 |
| 24979 | rumiar | 3 |
| 24980 | rumia | 3 |
| 24981 | rumbos | 3 |
| 24982 | rumaldo | 3 |
| 24983 | ruinosos | 3 |
| 24984 | ruidosos | 3 |
| 24985 | rugiendo | 3 |
| 24986 | rugido | 3 |
| 24987 | ruégale | 3 |
| 24988 | ruedos | 3 |
| 24989 | rudimentos | 3 |
| 24990 | rúbricas | 3 |
| 24991 | ruborosa | 3 |
| 24992 | ruborizándose | 3 |
| 24993 | rubión | 3 |
| 24994 | rrosa | 3 |
| 24995 | rropa | 3 |
| 24996 | rromano | 3 |
| 24997 | rromançe | 3 |
| 24998 | rriso | 3 |
| 24999 | rricos | 3 |
| 25000 | rreyr | 3 |
| 25001 | rresplandor | 3 |
| 25002 | rresçíbenle | 3 |
| 25003 | rres | 3 |
| 25004 | rreguardan | 3 |
| 25005 | rrayz | 3 |
| 25006 | rrato | 3 |
| 25007 | rrasón | 3 |
| 25008 | rrapossa | 3 |
| 25009 | rraposa | 3 |
| 25010 | rozaban | 3 |
| 25011 | roza | 3 |
| 25012 | rousseau | 3 |
| 25013 | rosina | 3 |
| 25014 | rosetones | 3 |
| 25015 | rosca | 3 |
| 25016 | rosadas | 3 |
| 25017 | ropón | 3 |
| 25018 | rondeño | 3 |
| 25019 | ronde | 3 |
| 25020 | rondando | 3 |
| 25021 | roncaba | 3 |
| 25022 | rompida | 3 |
| 25023 | rompían | 3 |
| 25024 | rompí | 3 |
| 25025 | romperle | 3 |
| 25026 | romancistas | 3 |
| 25027 | rogaré | 3 |
| 25028 | rodilleras | 3 |
| 25029 | rodeó | 3 |
| 25030 | rodearse | 3 |
| 25031 | rociada | 3 |
| 25032 | robándome | 3 |
| 25033 | robados | 3 |
| 25034 | ro | 3 |
| 25035 | riyendo | 3 |
| 25036 | ritos | 3 |
| 25037 | risible | 3 |
| 25038 | ripio | 3 |
| 25039 | rioja | 3 |
| 25040 | rindiera | 3 |
| 25041 | rincon | 3 |
| 25042 | rimas | 3 |
| 25043 | rima | 3 |
| 25044 | rija | 3 |
| 25045 | riguridad | 3 |
| 25046 | riesgos | 3 |
| 25047 | riéndome | 3 |
| 25048 | rien | 3 |
| 25049 | ricota | 3 |
| 25050 | ricacho | 3 |
| 25051 | ribeteadoras | 3 |
| 25052 | ribete | 3 |
| 25053 | riachuelo | 3 |
| 25054 | rezaré | 3 |
| 25055 | rezagados | 3 |
| 25056 | reys | 3 |
| 25057 | revoltosos | 3 |
| 25058 | revoltoso | 3 |
| 25059 | revolcarse | 3 |
| 25060 | revoca | 3 |
| 25061 | revivió | 3 |
| 25062 | revistas | 3 |
| 25063 | revisión | 3 |
| 25064 | revisar | 3 |
| 25065 | revisando | 3 |
| 25066 | reventara | 3 |
| 25067 | reventaban | 3 |
| 25068 | revancha | 3 |
| 25069 | reunirse | 3 |
| 25070 | reunió | 3 |
| 25071 | reuniendo | 3 |
| 25072 | reunida | 3 |
| 25073 | reúma | 3 |
| 25074 | retumbaron | 3 |
| 25075 | retumbantes | 3 |
| 25076 | retuerce | 3 |
| 25077 | retrocedía | 3 |
| 25078 | retratar | 3 |
| 25079 | retratado | 3 |
| 25080 | retrasar | 3 |
| 25081 | retraimiento | 3 |
| 25082 | retraídos | 3 |
| 25083 | retozando | 3 |
| 25084 | retóricos | 3 |
| 25085 | retórico | 3 |
| 25086 | retorcida | 3 |
| 25087 | retoño | 3 |
| 25088 | retirémonos | 3 |
| 25089 | retire | 3 |
| 25090 | retener | 3 |
| 25091 | retencio | 3 |
| 25092 | retablos | 3 |
| 25093 | resultar | 3 |
| 25094 | restituyó | 3 |
| 25095 | restituya | 3 |
| 25096 | restituir | 3 |
| 25097 | restituido | 3 |
| 25098 | restantes | 3 |
| 25099 | restante | 3 |
| 25100 | restaba | 3 |
| 25101 | respondona | 3 |
| 25102 | respondióles | 3 |
| 25103 | respondiéronle | 3 |
| 25104 | respiraron | 3 |
| 25105 | respetuoso | 3 |
| 25106 | respeten | 3 |
| 25107 | respetabilísima | 3 |
| 25108 | respectos | 3 |
| 25109 | respectiva | 3 |
| 25110 | resonaron | 3 |
| 25111 | resolvieron | 3 |
| 25112 | resolvía | 3 |
| 25113 | resolví | 3 |
| 25114 | resolverán | 3 |
| 25115 | resoluta | 3 |
| 25116 | resistiendo | 3 |
| 25117 | resistencias | 3 |
| 25118 | resista | 3 |
| 25119 | resfriado | 3 |
| 25120 | reservar | 3 |
| 25121 | reservados | 3 |
| 25122 | resentirse | 3 |
| 25123 | reseco | 3 |
| 25124 | rescatados | 3 |
| 25125 | resbalas | 3 |
| 25126 | resbaladiza | 3 |
| 25127 | requiriendo | 3 |
| 25128 | requesito | 3 |
| 25129 | requebrando | 3 |
| 25130 | reputó | 3 |
| 25131 | reputaciones | 3 |
| 25132 | repulsión | 3 |
| 25133 | republicanos | 3 |
| 25134 | republicanismo | 3 |
| 25135 | reproducían | 3 |
| 25136 | reprimendas | 3 |
| 25137 | representé | 3 |
| 25138 | reprehensiones | 3 |
| 25139 | reprehende | 3 |
| 25140 | repolla | 3 |
| 25141 | replique | 3 |
| 25142 | replicarle | 3 |
| 25143 | repitiera | 3 |
| 25144 | repiten | 3 |
| 25145 | repique | 3 |
| 25146 | repetimos | 3 |
| 25147 | repentinamente | 3 |
| 25148 | repelones | 3 |
| 25149 | repecho | 3 |
| 25150 | repaso | 3 |
| 25151 | repartida | 3 |
| 25152 | repartición | 3 |
| 25153 | repartían | 3 |
| 25154 | reparta | 3 |
| 25155 | repares | 3 |
| 25156 | repare | 3 |
| 25157 | reparas | 3 |
| 25158 | repararon | 3 |
| 25159 | reparadora | 3 |
| 25160 | reparaciones | 3 |
| 25161 | reoyos | 3 |
| 25162 | reos | 3 |
| 25163 | renunciando | 3 |
| 25164 | renuncia | 3 |
| 25165 | renueva | 3 |
| 25166 | renovasen | 3 |
| 25167 | renováronse | 3 |
| 25168 | renir | 3 |
| 25169 | renialdos | 3 |
| 25170 | rendirle | 3 |
| 25171 | rendimiento | 3 |
| 25172 | rendidas | 3 |
| 25173 | rencuentros | 3 |
| 25174 | rencorosa | 3 |
| 25175 | rencorcillo | 3 |
| 25176 | renan | 3 |
| 25177 | remitió | 3 |
| 25178 | remite | 3 |
| 25179 | remiso | 3 |
| 25180 | remendón | 3 |
| 25181 | remendar | 3 |
| 25182 | remendados | 3 |
| 25183 | remendado | 3 |
| 25184 | remediaran | 3 |
| 25185 | remediara | 3 |
| 25186 | remediado | 3 |
| 25187 | rematar | 3 |
| 25188 | rematando | 3 |
| 25189 | rematados | 3 |
| 25190 | remataba | 3 |
| 25191 | remanso | 3 |
| 25192 | remando | 3 |
| 25193 | reluze | 3 |
| 25194 | relucía | 3 |
| 25195 | relincho | 3 |
| 25196 | relatos | 3 |
| 25197 | relacionarse | 3 |
| 25198 | reiteradas | 3 |
| 25199 | reírnos | 3 |
| 25200 | reíanse | 3 |
| 25201 | rehusó | 3 |
| 25202 | rehusado | 3 |
| 25203 | rehuía | 3 |
| 25204 | rehacerse | 3 |
| 25205 | regumque | 3 |
| 25206 | regresaban | 3 |
| 25207 | regocijar | 3 |
| 25208 | regio | 3 |
| 25209 | regimientos | 3 |
| 25210 | regatearon | 3 |
| 25211 | regar | 3 |
| 25212 | regañadientes | 3 |
| 25213 | regaliz | 3 |
| 25214 | regalista | 3 |
| 25215 | regalarte | 3 |
| 25216 | regalarle | 3 |
| 25217 | regalaba | 3 |
| 25218 | refunfuñó | 3 |
| 25219 | refugiándose | 3 |
| 25220 | refuerzos | 3 |
| 25221 | refrescó | 3 |
| 25222 | refrescar | 3 |
| 25223 | refrenar | 3 |
| 25224 | refran | 3 |
| 25225 | reflexivo | 3 |
| 25226 | reflexionó | 3 |
| 25227 | reflexiona | 3 |
| 25228 | reflejando | 3 |
| 25229 | refirieron | 3 |
| 25230 | refiriéndose | 3 |
| 25231 | refiera | 3 |
| 25232 | referirte | 3 |
| 25233 | referencia | 3 |
| 25234 | refajos | 3 |
| 25235 | redundase | 3 |
| 25236 | redunda | 3 |
| 25237 | reducirse | 3 |
| 25238 | reducirle | 3 |
| 25239 | redoblado | 3 |
| 25240 | rediós | 3 |
| 25241 | redimido | 3 |
| 25242 | redimía | 3 |
| 25243 | redactores | 3 |
| 25244 | redactar | 3 |
| 25245 | recurrido | 3 |
| 25246 | recurría | 3 |
| 25247 | recuerde | 3 |
| 25248 | rectificó | 3 |
| 25249 | rectas | 3 |
| 25250 | recreación | 3 |
| 25251 | recreacion | 3 |
| 25252 | recostó | 3 |
| 25253 | recostado | 3 |
| 25254 | recortada | 3 |
| 25255 | recorrieron | 3 |
| 25256 | recordarle | 3 |
| 25257 | recordación | 3 |
| 25258 | reconocería | 3 |
| 25259 | reconocen | 3 |
| 25260 | reconcilia | 3 |
| 25261 | recompensar | 3 |
| 25262 | recomendara | 3 |
| 25263 | recolección | 3 |
| 25264 | recogiesen | 3 |
| 25265 | recogiéndose | 3 |
| 25266 | recogerlo | 3 |
| 25267 | recogerla | 3 |
| 25268 | recodo | 3 |
| 25269 | recluta | 3 |
| 25270 | reclusas | 3 |
| 25271 | reclinar | 3 |
| 25272 | reclinada | 3 |
| 25273 | recíprocos | 3 |
| 25274 | recientes | 3 |
| 25275 | recibirlos | 3 |
| 25276 | recibirle | 3 |
| 25277 | recibirá | 3 |
| 25278 | recibiéronle | 3 |
| 25279 | rechoncho | 3 |
| 25280 | rechinaban | 3 |
| 25281 | rechinaba | 3 |
| 25282 | rechazar | 3 |
| 25283 | recetaba | 3 |
| 25284 | recaudo | 3 |
| 25285 | recaudador | 3 |
| 25286 | recatarse | 3 |
| 25287 | recata | 3 |
| 25288 | recaía | 3 |
| 25289 | recabdado | 3 |
| 25290 | rebuznando | 3 |
| 25291 | rebuznaba | 3 |
| 25292 | rebullir | 3 |
| 25293 | rebozo | 3 |
| 25294 | rebozada | 3 |
| 25295 | rebotica | 3 |
| 25296 | rebanadas | 3 |
| 25297 | reasumiendo | 3 |
| 25298 | reanudó | 3 |
| 25299 | realizó | 3 |
| 25300 | razonada | 3 |
| 25301 | razonaba | 3 |
| 25302 | rayó | 3 |
| 25303 | rayitas | 3 |
| 25304 | rayar | 3 |
| 25305 | rayaban | 3 |
| 25306 | ratonera | 3 |
| 25307 | ratoncillo | 3 |
| 25308 | rastros | 3 |
| 25309 | rastrear | 3 |
| 25310 | rastras | 3 |
| 25311 | rasguños | 3 |
| 25312 | rasguñar | 3 |
| 25313 | rasgueadas | 3 |
| 25314 | rasgaban | 3 |
| 25315 | rasero | 3 |
| 25316 | rasas | 3 |
| 25317 | rarísima | 3 |
| 25318 | raquítico | 3 |
| 25319 | raquíticas | 3 |
| 25320 | rapiñas | 3 |
| 25321 | rapina | 3 |
| 25322 | rápidos | 3 |
| 25323 | rapar | 3 |
| 25324 | rapacidad | 3 |
| 25325 | rapaces | 3 |
| 25326 | randa | 3 |
| 25327 | rancio | 3 |
| 25328 | ramoncita | 3 |
| 25329 | ramillete | 3 |
| 25330 | rameras | 3 |
| 25331 | rameado | 3 |
| 25332 | raigones | 3 |
| 25333 | rafaelito | 3 |
| 25334 | radicalmente | 3 |
| 25335 | raçón | 3 |
| 25336 | rabos | 3 |
| 25337 | rabien | 3 |
| 25338 | rabí | 3 |
| 25339 | quitóle | 3 |
| 25340 | quitáronle | 3 |
| 25341 | quitaría | 3 |
| 25342 | quitaremos | 3 |
| 25343 | quisieses | 3 |
| 25344 | quinze | 3 |
| 25345 | quintales | 3 |
| 25346 | quínola | 3 |
| 25347 | quin | 3 |
| 25348 | quijo | 3 |
| 25349 | quijera | 3 |
| 25350 | quiérote | 3 |
| 25351 | quiérome | 3 |
| 25352 | quierome | 3 |
| 25353 | quiérole | 3 |
| 25354 | quiebran | 3 |
| 25355 | quexosa | 3 |
| 25356 | quexo | 3 |
| 25357 | quesos | 3 |
| 25358 | quesiste | 3 |
| 25359 | quesada | 3 |
| 25360 | querrias | 3 |
| 25361 | queriéndole | 3 |
| 25362 | queríen | 3 |
| 25363 | querian | 3 |
| 25364 | queríamos | 3 |
| 25365 | quereros | 3 |
| 25366 | querençia | 3 |
| 25367 | quemo | 3 |
| 25368 | quemando | 3 |
| 25369 | quemados | 3 |
| 25370 | quemadas | 3 |
| 25371 | quelo | 3 |
| 25372 | quejosos | 3 |
| 25373 | quejarte | 3 |
| 25374 | quejara | 3 |
| 25375 | quejamos | 3 |
| 25376 | quedese | 3 |
| 25377 | quedaua | 3 |
| 25378 | quedate | 3 |
| 25379 | quedasse | 3 |
| 25380 | quedarán | 3 |
| 25381 | quedada | 3 |
| 25382 | quedad | 3 |
| 25383 | quedábanse | 3 |
| 25384 | quebró | 3 |
| 25385 | quebré | 3 |
| 25386 | quebrados | 3 |
| 25387 | quánto | 3 |
| 25388 | quand | 3 |
| 25389 | qualidad | 3 |
| 25390 | qua | 3 |
| 25391 | pyntor | 3 |
| 25392 | pusiere | 3 |
| 25393 | purpúreo | 3 |
| 25394 | purpúrea | 3 |
| 25395 | puridad | 3 |
| 25396 | punzadas | 3 |
| 25397 | punzada | 3 |
| 25398 | puntualidades | 3 |
| 25399 | puntuales | 3 |
| 25400 | puntilla | 3 |
| 25401 | puntiagudo | 3 |
| 25402 | pulsos | 3 |
| 25403 | púlpitos | 3 |
| 25404 | pulidas | 3 |
| 25405 | pulgadas | 3 |
| 25406 | pujar | 3 |
| 25407 | puja | 3 |
| 25408 | pugilato | 3 |
| 25409 | puff | 3 |
| 25410 | puf | 3 |
| 25411 | puerro | 3 |
| 25412 | pued | 3 |
| 25413 | pué | 3 |
| 25414 | pudra | 3 |
| 25415 | pudiésemos | 3 |
| 25416 | pudiéremos | 3 |
| 25417 | pudientes | 3 |
| 25418 | publicarse | 3 |
| 25419 | psicológica | 3 |
| 25420 | prusianos | 3 |
| 25421 | pruebes | 3 |
| 25422 | prueben | 3 |
| 25423 | proyectando | 3 |
| 25424 | proyectado | 3 |
| 25425 | proyectada | 3 |
| 25426 | proyectaba | 3 |
| 25427 | provocó | 3 |
| 25428 | provocativo | 3 |
| 25429 | provocase | 3 |
| 25430 | provocados | 3 |
| 25431 | provocaba | 3 |
| 25432 | provisto | 3 |
| 25433 | provista | 3 |
| 25434 | provincianos | 3 |
| 25435 | proveída | 3 |
| 25436 | provechos | 3 |
| 25437 | provados | 3 |
| 25438 | prouidencia | 3 |
| 25439 | proueer | 3 |
| 25440 | prouechoso | 3 |
| 25441 | prouechosa | 3 |
| 25442 | protestando | 3 |
| 25443 | protestado | 3 |
| 25444 | protejo | 3 |
| 25445 | protegiendo | 3 |
| 25446 | protegerle | 3 |
| 25447 | prosiguiese | 3 |
| 25448 | proseguí | 3 |
| 25449 | prorrumpió | 3 |
| 25450 | prorrumpiendo | 3 |
| 25451 | proprios | 3 |
| 25452 | propositos | 3 |
| 25453 | proporcionó | 3 |
| 25454 | proporcionaba | 3 |
| 25455 | proporciona | 3 |
| 25456 | proponían | 3 |
| 25457 | proponen | 3 |
| 25458 | propincua | 3 |
| 25459 | propicios | 3 |
| 25460 | propicio | 3 |
| 25461 | propasarse | 3 |
| 25462 | pronombre | 3 |
| 25463 | prometistes | 3 |
| 25464 | prometióselo | 3 |
| 25465 | prometióle | 3 |
| 25466 | prometimiento | 3 |
| 25467 | prometiéndole | 3 |
| 25468 | prometidas | 3 |
| 25469 | prolongó | 3 |
| 25470 | prolixidad | 3 |
| 25471 | prolijos | 3 |
| 25472 | prójimos | 3 |
| 25473 | prohibiendo | 3 |
| 25474 | prohibidas | 3 |
| 25475 | prohibí | 3 |
| 25476 | prohibe | 3 |
| 25477 | progresa | 3 |
| 25478 | profundidades | 3 |
| 25479 | profirió | 3 |
| 25480 | profesores | 3 |
| 25481 | profesiones | 3 |
| 25482 | profecta | 3 |
| 25483 | profecías | 3 |
| 25484 | profanado | 3 |
| 25485 | profanaba | 3 |
| 25486 | produjeron | 3 |
| 25487 | producidas | 3 |
| 25488 | producíale | 3 |
| 25489 | procurará | 3 |
| 25490 | procuradores | 3 |
| 25491 | procedió | 3 |
| 25492 | procedían | 3 |
| 25493 | procederes | 3 |
| 25494 | procedentes | 3 |
| 25495 | procedente | 3 |
| 25496 | probase | 3 |
| 25497 | probarse | 3 |
| 25498 | probará | 3 |
| 25499 | probabilidad | 3 |
| 25500 | privarse | 3 |
| 25501 | privación | 3 |
| 25502 | priva | 3 |
| 25503 | prístino | 3 |
| 25504 | prístina | 3 |
| 25505 | prisas | 3 |
| 25506 | pringadas | 3 |
| 25507 | primorosas | 3 |
| 25508 | primicias | 3 |
| 25509 | prietas | 3 |
| 25510 | priestley | 3 |
| 25511 | prevista | 3 |
| 25512 | previlegios | 3 |
| 25513 | previa | 3 |
| 25514 | preverlo | 3 |
| 25515 | prevenirse | 3 |
| 25516 | prevenía | 3 |
| 25517 | pretenda | 3 |
| 25518 | presumido | 3 |
| 25519 | prestarme | 3 |
| 25520 | prestará | 3 |
| 25521 | presidiario | 3 |
| 25522 | presidenta | 3 |
| 25523 | preside | 3 |
| 25524 | presenten | 3 |
| 25525 | presentaría | 3 |
| 25526 | presentara | 3 |
| 25527 | presentación | 3 |
| 25528 | presentable | 3 |
| 25529 | presenciaban | 3 |
| 25530 | presenciaba | 3 |
| 25531 | prescripciones | 3 |
| 25532 | prescribe | 3 |
| 25533 | presbiterio | 3 |
| 25534 | preposición | 3 |
| 25535 | preparen | 3 |
| 25536 | preparémonos | 3 |
| 25537 | prepare | 3 |
| 25538 | preparase | 3 |
| 25539 | prepararon | 3 |
| 25540 | preocupados | 3 |
| 25541 | preocupa | 3 |
| 25542 | preñadas | 3 |
| 25543 | prendiendo | 3 |
| 25544 | prendes | 3 |
| 25545 | prenderme | 3 |
| 25546 | prendado | 3 |
| 25547 | premia | 3 |
| 25548 | prematura | 3 |
| 25549 | preguntita | 3 |
| 25550 | pregunten | 3 |
| 25551 | preguntasen | 3 |
| 25552 | preguntárselo | 3 |
| 25553 | preguntarles | 3 |
| 25554 | preguntaré | 3 |
| 25555 | preguntante | 3 |
| 25556 | preguntándose | 3 |
| 25557 | preguntándome | 3 |
| 25558 | pregonan | 3 |
| 25559 | pregona | 3 |
| 25560 | preferiría | 3 |
| 25561 | predio | 3 |
| 25562 | predilecta | 3 |
| 25563 | precursores | 3 |
| 25564 | precocidad | 3 |
| 25565 | precipitarse | 3 |
| 25566 | precipitada | 3 |
| 25567 | precipitaban | 3 |
| 25568 | precipicio | 3 |
| 25569 | preçiosas | 3 |
| 25570 | preçian | 3 |
| 25571 | preciado | 3 |
| 25572 | preciada | 3 |
| 25573 | preçia | 3 |
| 25574 | preces | 3 |
| 25575 | precedió | 3 |
| 25576 | precedida | 3 |
| 25577 | preceden | 3 |
| 25578 | praxíteles | 3 |
| 25579 | pradera | 3 |
| 25580 | practicante | 3 |
| 25581 | practica | 3 |
| 25582 | potencias | 3 |
| 25583 | potásico | 3 |
| 25584 | potaje | 3 |
| 25585 | póstuma | 3 |
| 25586 | postremeria | 3 |
| 25587 | postizos | 3 |
| 25588 | postillón | 3 |
| 25589 | postergado | 3 |
| 25590 | posees | 3 |
| 25591 | poseerte | 3 |
| 25592 | posea | 3 |
| 25593 | posas | 3 |
| 25594 | posarse | 3 |
| 25595 | posados | 3 |
| 25596 | posadera | 3 |
| 25597 | portentosa | 3 |
| 25598 | portátil | 3 |
| 25599 | portas | 3 |
| 25600 | portarme | 3 |
| 25601 | portaré | 3 |
| 25602 | portar | 3 |
| 25603 | portalón | 3 |
| 25604 | portada | 3 |
| 25605 | pormenor | 3 |
| 25606 | porfió | 3 |
| 25607 | porfiaron | 3 |
| 25608 | porfían | 3 |
| 25609 | porcia | 3 |
| 25610 | porcell | 3 |
| 25611 | poquitito | 3 |
| 25612 | poquita | 3 |
| 25613 | poquilla | 3 |
| 25614 | ponzonoso | 3 |
| 25615 | ponzona | 3 |
| 25616 | ponto | 3 |
| 25617 | pontificia | 3 |
| 25618 | ponlo | 3 |
| 25619 | ponérsele | 3 |
| 25620 | ponérselas | 3 |
| 25621 | ponderaciones | 3 |
| 25622 | pomposo | 3 |
| 25623 | pomposa | 3 |
| 25624 | pomos | 3 |
| 25625 | pomona | 3 |
| 25626 | pomo | 3 |
| 25627 | pomaradas | 3 |
| 25628 | poluos | 3 |
| 25629 | poluo | 3 |
| 25630 | polos | 3 |
| 25631 | pollastres | 3 |
| 25632 | polkas | 3 |
| 25633 | polidoro | 3 |
| 25634 | polichinela | 3 |
| 25635 | poetisa | 3 |
| 25636 | poetillas | 3 |
| 25637 | podran | 3 |
| 25638 | podiste | 3 |
| 25639 | podimos | 3 |
| 25640 | podian | 3 |
| 25641 | poderte | 3 |
| 25642 | poderosísimo | 3 |
| 25643 | poderme | 3 |
| 25644 | poderla | 3 |
| 25645 | pobretes | 3 |
| 25646 | pobresa | 3 |
| 25647 | pobredat | 3 |
| 25648 | pobladas | 3 |
| 25649 | poblaba | 3 |
| 25650 | pluviales | 3 |
| 25651 | pluton | 3 |
| 25652 | pluralidad | 3 |
| 25653 | plural | 3 |
| 25654 | plumero | 3 |
| 25655 | plugo | 3 |
| 25656 | plomizo | 3 |
| 25657 | plinio | 3 |
| 25658 | pléyade | 3 |
| 25659 | plectro | 3 |
| 25660 | plazido | 3 |
| 25661 | plaz | 3 |
| 25662 | platónica | 3 |
| 25663 | platica | 3 |
| 25664 | platería | 3 |
| 25665 | plateresco | 3 |
| 25666 | plateas | 3 |
| 25667 | plasentero | 3 |
| 25668 | plasentería | 3 |
| 25669 | plasentera | 3 |
| 25670 | plase | 3 |
| 25671 | plantaron | 3 |
| 25672 | plantarle | 3 |
| 25673 | plantándose | 3 |
| 25674 | plantan | 3 |
| 25675 | plagio | 3 |
| 25676 | plaçer | 3 |
| 25677 | placenteras | 3 |
| 25678 | placentera | 3 |
| 25679 | plaças | 3 |
| 25680 | placas | 3 |
| 25681 | pitanza | 3 |
| 25682 | pitando | 3 |
| 25683 | pitágoras | 3 |
| 25684 | pistos | 3 |
| 25685 | pisotones | 3 |
| 25686 | pisotón | 3 |
| 25687 | pise | 3 |
| 25688 | pisaron | 3 |
| 25689 | pisada | 3 |
| 25690 | piropo | 3 |
| 25691 | píramo | 3 |
| 25692 | pirámides | 3 |
| 25693 | piquillo | 3 |
| 25694 | piñones | 3 |
| 25695 | piñón | 3 |
| 25696 | piñas | 3 |
| 25697 | pinté | 3 |
| 25698 | pintarte | 3 |
| 25699 | pingos | 3 |
| 25700 | pincha | 3 |
| 25701 | pinceles | 3 |
| 25702 | pincelada | 3 |
| 25703 | pináculo | 3 |
| 25704 | pimiento | 3 |
| 25705 | pilluelos | 3 |
| 25706 | píldora | 3 |
| 25707 | pilatos | 3 |
| 25708 | pílades | 3 |
| 25709 | pienssa | 3 |
| 25710 | pieldras | 3 |
| 25711 | piélagos | 3 |
| 25712 | piedeamigo | 3 |
| 25713 | piedat | 3 |
| 25714 | piececita | 3 |
| 25715 | pidióle | 3 |
| 25716 | pidiesen | 3 |
| 25717 | pidiere | 3 |
| 25718 | pidieran | 3 |
| 25719 | pídele | 3 |
| 25720 | picuda | 3 |
| 25721 | picota | 3 |
| 25722 | pichones | 3 |
| 25723 | picazones | 3 |
| 25724 | picazo | 3 |
| 25725 | picaron | 3 |
| 25726 | picarillo | 3 |
| 25727 | picarescos | 3 |
| 25728 | picará | 3 |
| 25729 | picados | 3 |
| 25730 | piara | 3 |
| 25731 | pianitos | 3 |
| 25732 | piache | 3 |
| 25733 | peto | 3 |
| 25734 | petitorios | 3 |
| 25735 | petit | 3 |
| 25736 | petimetre | 3 |
| 25737 | pestillo | 3 |
| 25738 | pestífera | 3 |
| 25739 | pestaña | 3 |
| 25740 | pesquisas | 3 |
| 25741 | pesquería | 3 |
| 25742 | pesóle | 3 |
| 25743 | pesimista | 3 |
| 25744 | pésima | 3 |
| 25745 | pescueço | 3 |
| 25746 | pescozones | 3 |
| 25747 | pesces | 3 |
| 25748 | pescadoras | 3 |
| 25749 | pesará | 3 |
| 25750 | pesan | 3 |
| 25751 | pesadito | 3 |
| 25752 | pesadez | 3 |
| 25753 | pesadamente | 3 |
| 25754 | perversos | 3 |
| 25755 | perturbación | 3 |
| 25756 | perteneció | 3 |
| 25757 | persuasiva | 3 |
| 25758 | persuadieron | 3 |
| 25759 | persuadiendo | 3 |
| 25760 | persuadía | 3 |
| 25761 | personificación | 3 |
| 25762 | personalidades | 3 |
| 25763 | perseuerancia | 3 |
| 25764 | perseguirme | 3 |
| 25765 | perseguidores | 3 |
| 25766 | perseguidor | 3 |
| 25767 | perruna | 3 |
| 25768 | perrera | 3 |
| 25769 | perradas | 3 |
| 25770 | perplexo | 3 |
| 25771 | perpleja | 3 |
| 25772 | perpetuas | 3 |
| 25773 | perniciosa | 3 |
| 25774 | permitiendo | 3 |
| 25775 | permítame | 3 |
| 25776 | permaneciendo | 3 |
| 25777 | perlerines | 3 |
| 25778 | perjuro | 3 |
| 25779 | perjura | 3 |
| 25780 | perjudiciales | 3 |
| 25781 | perjudicar | 3 |
| 25782 | perito | 3 |
| 25783 | períodos | 3 |
| 25784 | periódicamente | 3 |
| 25785 | perífrasis | 3 |
| 25786 | pérfidos | 3 |
| 25787 | perfeto | 3 |
| 25788 | perfectas | 3 |
| 25789 | peresçen | 3 |
| 25790 | perendengues | 3 |
| 25791 | perejil | 3 |
| 25792 | peregrinas | 3 |
| 25793 | peregrinaciones | 3 |
| 25794 | perdy | 3 |
| 25795 | perdoné | 3 |
| 25796 | perdonase | 3 |
| 25797 | perdonarle | 3 |
| 25798 | perdonaré | 3 |
| 25799 | perdoname | 3 |
| 25800 | perdigones | 3 |
| 25801 | perdigón | 3 |
| 25802 | perderíamos | 3 |
| 25803 | perdemos | 3 |
| 25804 | percibir | 3 |
| 25805 | percibió | 3 |
| 25806 | percibía | 3 |
| 25807 | percales | 3 |
| 25808 | pera | 3 |
| 25809 | pequeñuelas | 3 |
| 25810 | pequeñísima | 3 |
| 25811 | pepitas | 3 |
| 25812 | peonza | 3 |
| 25813 | peñascos | 3 |
| 25814 | peñascales | 3 |
| 25815 | pentecostés | 3 |
| 25816 | penssando | 3 |
| 25817 | pensays | 3 |
| 25818 | pensat | 3 |
| 25819 | pensarse | 3 |
| 25820 | pensarán | 3 |
| 25821 | pensados | 3 |
| 25822 | penosos | 3 |
| 25823 | penosamente | 3 |
| 25824 | penoles | 3 |
| 25825 | penita | 3 |
| 25826 | penetrando | 3 |
| 25827 | pene | 3 |
| 25828 | péndulo | 3 |
| 25829 | péndolas | 3 |
| 25830 | péndola | 3 |
| 25831 | penda | 3 |
| 25832 | penan | 3 |
| 25833 | penales | 3 |
| 25834 | peluda | 3 |
| 25835 | peloteras | 3 |
| 25836 | pelotas | 3 |
| 25837 | pelosmalos | 3 |
| 25838 | pellizcaron | 3 |
| 25839 | pellizcaba | 3 |
| 25840 | pellicos | 3 |
| 25841 | pelillos | 3 |
| 25842 | peleo | 3 |
| 25843 | pelearon | 3 |
| 25844 | pelada | 3 |
| 25845 | pelaban | 3 |
| 25846 | pela | 3 |
| 25847 | peineta | 3 |
| 25848 | pegotes | 3 |
| 25849 | pegarles | 3 |
| 25850 | pegaría | 3 |
| 25851 | pegadizo | 3 |
| 25852 | pegaban | 3 |
| 25853 | pedruscos | 3 |
| 25854 | pedíle | 3 |
| 25855 | pediere | 3 |
| 25856 | pedagógico | 3 |
| 25857 | pedacito | 3 |
| 25858 | peculiar | 3 |
| 25859 | pece | 3 |
| 25860 | pecaban | 3 |
| 25861 | peana | 3 |
| 25862 | payo | 3 |
| 25863 | pavoroso | 3 |
| 25864 | pavía | 3 |
| 25865 | pavero | 3 |
| 25866 | patrulla | 3 |
| 25867 | patrono | 3 |
| 25868 | patriótico | 3 |
| 25869 | patriarcales | 3 |
| 25870 | patos | 3 |
| 25871 | patochadas | 3 |
| 25872 | patitas | 3 |
| 25873 | patéticos | 3 |
| 25874 | paternostres | 3 |
| 25875 | pateo | 3 |
| 25876 | pateando | 3 |
| 25877 | pateada | 3 |
| 25878 | pataleta | 3 |
| 25879 | pataleo | 3 |
| 25880 | pataleando | 3 |
| 25881 | pastoriles | 3 |
| 25882 | pastilla | 3 |
| 25883 | pastelería | 3 |
| 25884 | passiones | 3 |
| 25885 | passaua | 3 |
| 25886 | passamos | 3 |
| 25887 | pasose | 3 |
| 25888 | pasmó | 3 |
| 25889 | pasmará | 3 |
| 25890 | pasma | 3 |
| 25891 | pasivo | 3 |
| 25892 | pasiva | 3 |
| 25893 | pasioncilla | 3 |
| 25894 | paseamos | 3 |
| 25895 | pasásemos | 3 |
| 25896 | pasarlas | 3 |
| 25897 | pasarán | 3 |
| 25898 | pasante | 3 |
| 25899 | pasándose | 3 |
| 25900 | pasabas | 3 |
| 25901 | parvas | 3 |
| 25902 | partíme | 3 |
| 25903 | partiese | 3 |
| 25904 | partidaria | 3 |
| 25905 | partición | 3 |
| 25906 | partezilla | 3 |
| 25907 | parterres | 3 |
| 25908 | parsimonia | 3 |
| 25909 | parrilla | 3 |
| 25910 | paroxismo | 3 |
| 25911 | parose | 3 |
| 25912 | parnaso | 3 |
| 25913 | parlando | 3 |
| 25914 | parisienses | 3 |
| 25915 | parisiense | 3 |
| 25916 | pariría | 3 |
| 25917 | pariera | 3 |
| 25918 | parezcamos | 3 |
| 25919 | paresçía | 3 |
| 25920 | parescera | 3 |
| 25921 | paréis | 3 |
| 25922 | parecióles | 3 |
| 25923 | parecíamos | 3 |
| 25924 | paré | 3 |
| 25925 | parcialidad | 3 |
| 25926 | pararrayos | 3 |
| 25927 | paráronse | 3 |
| 25928 | pararía | 3 |
| 25929 | parara | 3 |
| 25930 | páramos | 3 |
| 25931 | paralela | 3 |
| 25932 | parador | 3 |
| 25933 | paracaídas | 3 |
| 25934 | papilla | 3 |
| 25935 | papeleta | 3 |
| 25936 | papando | 3 |
| 25937 | papamoscas | 3 |
| 25938 | pañol | 3 |
| 25939 | panzuda | 3 |
| 25940 | panurgo | 3 |
| 25941 | pantallas | 3 |
| 25942 | paniaguados | 3 |
| 25943 | pánfilo | 3 |
| 25944 | pandafilando | 3 |
| 25945 | panadero | 3 |
| 25946 | pamphilus | 3 |
| 25947 | palpitando | 3 |
| 25948 | palpar | 3 |
| 25949 | palpable | 3 |
| 25950 | palominos | 3 |
| 25951 | palmotear | 3 |
| 25952 | palmitas | 3 |
| 25953 | palmetazo | 3 |
| 25954 | palmeras | 3 |
| 25955 | palito | 3 |
| 25956 | palinuro | 3 |
| 25957 | palidece | 3 |
| 25958 | palestra | 3 |
| 25959 | pajarito | 3 |
| 25960 | pajaritas | 3 |
| 25961 | pagué | 3 |
| 25962 | pagaros | 3 |
| 25963 | pagaron | 3 |
| 25964 | pagarla | 3 |
| 25965 | padecieron | 3 |
| 25966 | padecían | 3 |
| 25967 | padeces | 3 |
| 25968 | pactos | 3 |
| 25969 | pacíficas | 3 |
| 25970 | paciendo | 3 |
| 25971 | pacen | 3 |
| 25972 | pabellones | 3 |
| 25973 | oyste | 3 |
| 25974 | oyras | 3 |
| 25975 | oyente | 3 |
| 25976 | oyéndose | 3 |
| 25977 | oyéndolo | 3 |
| 25978 | oydme | 3 |
| 25979 | oyan | 3 |
| 25980 | óxido | 3 |
| 25981 | oviese | 3 |
| 25982 | ovas | 3 |
| 25983 | óvalo | 3 |
| 25984 | ouo | 3 |
| 25985 | ouieron | 3 |
| 25986 | otubre | 3 |
| 25987 | otrossy | 3 |
| 25988 | otorgue | 3 |
| 25989 | otorgan | 3 |
| 25990 | otorga | 3 |
| 25991 | otomana | 3 |
| 25992 | ostras | 3 |
| 25993 | ostentosa | 3 |
| 25994 | ostentar | 3 |
| 25995 | ostentan | 3 |
| 25996 | ose | 3 |
| 25997 | oscurísimo | 3 |
| 25998 | osaron | 3 |
| 25999 | orzar | 3 |
| 26000 | ortolano | 3 |
| 26001 | ortigas | 3 |
| 26002 | ortelano | 3 |
| 26003 | oriundo | 3 |
| 26004 | orificios | 3 |
| 26005 | orgías | 3 |
| 26006 | organizar | 3 |
| 26007 | organizado | 3 |
| 26008 | orestes | 3 |
| 26009 | ordené | 3 |
| 26010 | ordenas | 3 |
| 26011 | ordenares | 3 |
| 26012 | ordenadas | 3 |
| 26013 | ordalías | 3 |
| 26014 | órdago | 3 |
| 26015 | orar | 3 |
| 26016 | oraçiones | 3 |
| 26017 | opulenta | 3 |
| 26018 | optimistas | 3 |
| 26019 | optimista | 3 |
| 26020 | opresos | 3 |
| 26021 | oposiciones | 3 |
| 26022 | oponían | 3 |
| 26023 | opongo | 3 |
| 26024 | oponen | 3 |
| 26025 | opinion | 3 |
| 26026 | opinar | 3 |
| 26027 | opacas | 3 |
| 26028 | onesto | 3 |
| 26029 | ondulante | 3 |
| 26030 | omnium | 3 |
| 26031 | omnipotencia | 3 |
| 26032 | ómnibus | 3 |
| 26033 | omildat | 3 |
| 26034 | olvidito | 3 |
| 26035 | olvidase | 3 |
| 26036 | olvidas | 3 |
| 26037 | olvidaría | 3 |
| 26038 | olvidares | 3 |
| 26039 | olvidara | 3 |
| 26040 | olvidándose | 3 |
| 26041 | olvidadas | 3 |
| 26042 | oluidar | 3 |
| 26043 | oluidados | 3 |
| 26044 | oluidado | 3 |
| 26045 | oluida | 3 |
| 26046 | olorosos | 3 |
| 26047 | oloroso | 3 |
| 26048 | olivos | 3 |
| 26049 | olió | 3 |
| 26050 | olimpo | 3 |
| 26051 | olido | 3 |
| 26052 | olfateaba | 3 |
| 26053 | óleo | 3 |
| 26054 | olalla | 3 |
| 26055 | ojerosa | 3 |
| 26056 | ojeo | 3 |
| 26057 | ojal | 3 |
| 26058 | oístes | 3 |
| 26059 | oírlos | 3 |
| 26060 | oiré | 3 |
| 26061 | oíanse | 3 |
| 26062 | oíale | 3 |
| 26063 | ofresco | 3 |
| 26064 | ofreciósele | 3 |
| 26065 | ofreciéndose | 3 |
| 26066 | ofreces | 3 |
| 26067 | ofrecerles | 3 |
| 26068 | ofrecerá | 3 |
| 26069 | oficinistas | 3 |
| 26070 | ofendían | 3 |
| 26071 | ofenderse | 3 |
| 26072 | ofendería | 3 |
| 26073 | odiosas | 3 |
| 26074 | odas | 3 |
| 26075 | ocurrirle | 3 |
| 26076 | ocurriría | 3 |
| 26077 | ocurrirá | 3 |
| 26078 | ocurriósele | 3 |
| 26079 | ocurrida | 3 |
| 26080 | ocurra | 3 |
| 26081 | ocupes | 3 |
| 26082 | ocupemos | 3 |
| 26083 | ocuparía | 3 |
| 26084 | oculte | 3 |
| 26085 | ocultárselo | 3 |
| 26086 | ocultaron | 3 |
| 26087 | ocultarle | 3 |
| 26088 | ocultamente | 3 |
| 26089 | octavas | 3 |
| 26090 | ocre | 3 |
| 26091 | ocëano | 3 |
| 26092 | obvio | 3 |
| 26093 | obstrucciones | 3 |
| 26094 | obstinó | 3 |
| 26095 | observamos | 3 |
| 26096 | observadores | 3 |
| 26097 | observada | 3 |
| 26098 | obsequió | 3 |
| 26099 | obscurecía | 3 |
| 26100 | obrero | 3 |
| 26101 | obligase | 3 |
| 26102 | obligarme | 3 |
| 26103 | obligara | 3 |
| 26104 | obligándome | 3 |
| 26105 | obligándole | 3 |
| 26106 | obligacion | 3 |
| 26107 | oblicuos | 3 |
| 26108 | obesidad | 3 |
| 26109 | obenques | 3 |
| 26110 | obedeces | 3 |
| 26111 | obedecerla | 3 |
| 26112 | obedecelle | 3 |
| 26113 | nyn | 3 |
| 26114 | nuues | 3 |
| 26115 | núñez | 3 |
| 26116 | numerosas | 3 |
| 26117 | nulas | 3 |
| 26118 | nueue | 3 |
| 26119 | nueses | 3 |
| 26120 | nudoso | 3 |
| 26121 | nudillos | 3 |
| 26122 | nublados | 3 |
| 26123 | novísima | 3 |
| 26124 | novias | 3 |
| 26125 | novelescos | 3 |
| 26126 | novelda | 3 |
| 26127 | nostri | 3 |
| 26128 | noster | 3 |
| 26129 | norma | 3 |
| 26130 | nono | 3 |
| 26131 | nonbrada | 3 |
| 26132 | nonbles | 3 |
| 26133 | nombramiento | 3 |
| 26134 | nombraban | 3 |
| 26135 | nivel | 3 |
| 26136 | niñito | 3 |
| 26137 | niñera | 3 |
| 26138 | nieva | 3 |
| 26139 | nieue | 3 |
| 26140 | nicolasito | 3 |
| 26141 | nevadas | 3 |
| 26142 | neutral | 3 |
| 26143 | neurosis | 3 |
| 26144 | nesçios | 3 |
| 26145 | nero | 3 |
| 26146 | nenito | 3 |
| 26147 | nenín | 3 |
| 26148 | nembrot | 3 |
| 26149 | negruzca | 3 |
| 26150 | negociantes | 3 |
| 26151 | negociado | 3 |
| 26152 | negativas | 3 |
| 26153 | negarán | 3 |
| 26154 | negándome | 3 |
| 26155 | negando | 3 |
| 26156 | necesitase | 3 |
| 26157 | necesitaron | 3 |
| 26158 | necesitaría | 3 |
| 26159 | necesitarán | 3 |
| 26160 | necesitada | 3 |
| 26161 | nebulosa | 3 |
| 26162 | neblí | 3 |
| 26163 | navego | 3 |
| 26164 | navegado | 3 |
| 26165 | navegaba | 3 |
| 26166 | navas | 3 |
| 26167 | nauseabundo | 3 |
| 26168 | natas | 3 |
| 26169 | nasón | 3 |
| 26170 | nascidas | 3 |
| 26171 | nasci | 3 |
| 26172 | nasçer | 3 |
| 26173 | narrativa | 3 |
| 26174 | narrando | 3 |
| 26175 | narraba | 3 |
| 26176 | napolitano | 3 |
| 26177 | naharilla | 3 |
| 26178 | nadante | 3 |
| 26179 | nacimos | 3 |
| 26180 | my | 3 |
| 26181 | mutaciones | 3 |
| 26182 | mustios | 3 |
| 26183 | mustias | 3 |
| 26184 | murria | 3 |
| 26185 | muriéndose | 3 |
| 26186 | mures | 3 |
| 26187 | mundanal | 3 |
| 26188 | múltiples | 3 |
| 26189 | multa | 3 |
| 26190 | mullido | 3 |
| 26191 | muletilla | 3 |
| 26192 | mulato | 3 |
| 26193 | mulata | 3 |
| 26194 | mujerona | 3 |
| 26195 | mujeril | 3 |
| 26196 | mujercilla | 3 |
| 26197 | mugrienta | 3 |
| 26198 | muestro | 3 |
| 26199 | muérete | 3 |
| 26200 | muerdo | 3 |
| 26201 | mudaron | 3 |
| 26202 | mudaban | 3 |
| 26203 | mozuelo | 3 |
| 26204 | mozalvete | 3 |
| 26205 | movilidad | 3 |
| 26206 | moverlos | 3 |
| 26207 | movemos | 3 |
| 26208 | mouimientos | 3 |
| 26209 | motones | 3 |
| 26210 | motivado | 3 |
| 26211 | motivada | 3 |
| 26212 | motiuo | 3 |
| 26213 | mostré | 3 |
| 26214 | mostre | 3 |
| 26215 | mostraste | 3 |
| 26216 | mostráronse | 3 |
| 26217 | mostrarlo | 3 |
| 26218 | mostrare | 3 |
| 26219 | mostradme | 3 |
| 26220 | mosén | 3 |
| 26221 | mos | 3 |
| 26222 | mortificar | 3 |
| 26223 | mortificado | 3 |
| 26224 | mortificaciones | 3 |
| 26225 | mortero | 3 |
| 26226 | mortandad | 3 |
| 26227 | mortalmente | 3 |
| 26228 | mortajas | 3 |
| 26229 | morro | 3 |
| 26230 | morría | 3 |
| 26231 | morquecho | 3 |
| 26232 | morisquetas | 3 |
| 26233 | morisma | 3 |
| 26234 | moriones | 3 |
| 26235 | morillo | 3 |
| 26236 | morgante | 3 |
| 26237 | morería | 3 |
| 26238 | morenas | 3 |
| 26239 | morejón | 3 |
| 26240 | mordiéndose | 3 |
| 26241 | mordida | 3 |
| 26242 | morderse | 3 |
| 26243 | morderla | 3 |
| 26244 | morcillas | 3 |
| 26245 | morar | 3 |
| 26246 | moraleja | 3 |
| 26247 | monumentales | 3 |
| 26248 | montoncillo | 3 |
| 26249 | montilla | 3 |
| 26250 | montiela | 3 |
| 26251 | montico | 3 |
| 26252 | monteros | 3 |
| 26253 | montas | 3 |
| 26254 | montañesa | 3 |
| 26255 | montados | 3 |
| 26256 | montada | 3 |
| 26257 | monstruosa | 3 |
| 26258 | monótonas | 3 |
| 26259 | monferrado | 3 |
| 26260 | mondos | 3 |
| 26261 | mondongo | 3 |
| 26262 | móndame | 3 |
| 26263 | monda | 3 |
| 26264 | monaguillos | 3 |
| 26265 | monacillo | 3 |
| 26266 | molusco | 3 |
| 26267 | molinillos | 3 |
| 26268 | molière | 3 |
| 26269 | molestará | 3 |
| 26270 | moje | 3 |
| 26271 | mohosos | 3 |
| 26272 | mohosa | 3 |
| 26273 | mohínos | 3 |
| 26274 | mohines | 3 |
| 26275 | moharracho | 3 |
| 26276 | modosita | 3 |
| 26277 | modosa | 3 |
| 26278 | modificado | 3 |
| 26279 | moderando | 3 |
| 26280 | moderada | 3 |
| 26281 | moco | 3 |
| 26282 | moche | 3 |
| 26283 | moças | 3 |
| 26284 | mitras | 3 |
| 26285 | mitrado | 3 |
| 26286 | mitones | 3 |
| 26287 | mitigar | 3 |
| 26288 | mitades | 3 |
| 26289 | mister | 3 |
| 26290 | miss | 3 |
| 26291 | misiones | 3 |
| 26292 | míseras | 3 |
| 26293 | mirto | 3 |
| 26294 | mirra | 3 |
| 26295 | miróme | 3 |
| 26296 | mirlo | 3 |
| 26297 | míreme | 3 |
| 26298 | mírate | 3 |
| 26299 | miráronla | 3 |
| 26300 | mirarles | 3 |
| 26301 | mirarlas | 3 |
| 26302 | mirarias | 3 |
| 26303 | mirarían | 3 |
| 26304 | miraren | 3 |
| 26305 | mirame | 3 |
| 26306 | miralla | 3 |
| 26307 | miráis | 3 |
| 26308 | mirados | 3 |
| 26309 | mirábalas | 3 |
| 26310 | mirábala | 3 |
| 26311 | minuciosa | 3 |
| 26312 | mintrosa | 3 |
| 26313 | mintió | 3 |
| 26314 | minos | 3 |
| 26315 | minoría | 3 |
| 26316 | ministerios | 3 |
| 26317 | ministerialismo | 3 |
| 26318 | minio | 3 |
| 26319 | mingo | 3 |
| 26320 | minando | 3 |
| 26321 | mimosos | 3 |
| 26322 | mimaban | 3 |
| 26323 | militarismo | 3 |
| 26324 | milanos | 3 |
| 26325 | mienbros | 3 |
| 26326 | mida | 3 |
| 26327 | microscopio | 3 |
| 26328 | micos | 3 |
| 26329 | miasmas | 3 |
| 26330 | meytad | 3 |
| 26331 | mexía | 3 |
| 26332 | métrica | 3 |
| 26333 | metódicamente | 3 |
| 26334 | metódica | 3 |
| 26335 | metimos | 3 |
| 26336 | metíme | 3 |
| 26337 | metíle | 3 |
| 26338 | metiéndola | 3 |
| 26339 | metes | 3 |
| 26340 | meterte | 3 |
| 26341 | meteré | 3 |
| 26342 | metáis | 3 |
| 26343 | metafísicas | 3 |
| 26344 | messa | 3 |
| 26345 | mesonero | 3 |
| 26346 | mesonera | 3 |
| 26347 | mesándose | 3 |
| 26348 | meritorio | 3 |
| 26349 | merinos | 3 |
| 26350 | mereció | 3 |
| 26351 | merecemos | 3 |
| 26352 | merchandía | 3 |
| 26353 | mercancías | 3 |
| 26354 | mercaduria | 3 |
| 26355 | mercadería | 3 |
| 26356 | mercadal | 3 |
| 26357 | meramente | 3 |
| 26358 | mera | 3 |
| 26359 | meos | 3 |
| 26360 | meollo | 3 |
| 26361 | menudearon | 3 |
| 26362 | menudeando | 3 |
| 26363 | mentarle | 3 |
| 26364 | mensajeros | 3 |
| 26365 | mensajería | 3 |
| 26366 | menospreciado | 3 |
| 26367 | menoscaba | 3 |
| 26368 | menjurjes | 3 |
| 26369 | menguas | 3 |
| 26370 | menesterosas | 3 |
| 26371 | meneó | 3 |
| 26372 | menéese | 3 |
| 26373 | mendigando | 3 |
| 26374 | mencionados | 3 |
| 26375 | mençión | 3 |
| 26376 | memorables | 3 |
| 26377 | membrudo | 3 |
| 26378 | melunga | 3 |
| 26379 | melodía | 3 |
| 26380 | mellizos | 3 |
| 26381 | melchor | 3 |
| 26382 | mejorada | 3 |
| 26383 | mejía | 3 |
| 26384 | medrosos | 3 |
| 26385 | medra | 3 |
| 26386 | medoro | 3 |
| 26387 | mediocritas | 3 |
| 26388 | medicos | 3 |
| 26389 | medianeros | 3 |
| 26390 | medianería | 3 |
| 26391 | medianas | 3 |
| 26392 | medían | 3 |
| 26393 | mediación | 3 |
| 26394 | mediaba | 3 |
| 26395 | medallón | 3 |
| 26396 | medalla | 3 |
| 26397 | mechón | 3 |
| 26398 | mea | 3 |
| 26399 | mazorca | 3 |
| 26400 | mazas | 3 |
| 26401 | mayorales | 3 |
| 26402 | matinal | 3 |
| 26403 | mater | 3 |
| 26404 | matarlos | 3 |
| 26405 | matarás | 3 |
| 26406 | mataran | 3 |
| 26407 | matanza | 3 |
| 26408 | matamoros | 3 |
| 26409 | matalla | 3 |
| 26410 | matadlos | 3 |
| 26411 | mástiles | 3 |
| 26412 | mascullando | 3 |
| 26413 | masculino | 3 |
| 26414 | martinica | 3 |
| 26415 | martin | 3 |
| 26416 | martillazo | 3 |
| 26417 | marta | 3 |
| 26418 | marranos | 3 |
| 26419 | marquesch | 3 |
| 26420 | marmolillo | 3 |
| 26421 | marineras | 3 |
| 26422 | marica | 3 |
| 26423 | marianas | 3 |
| 26424 | mariana | 3 |
| 26425 | marees | 3 |
| 26426 | mareas | 3 |
| 26427 | mareante | 3 |
| 26428 | marean | 3 |
| 26429 | marcó | 3 |
| 26430 | março | 3 |
| 26431 | marchitos | 3 |
| 26432 | marchito | 3 |
| 26433 | márchese | 3 |
| 26434 | márchate | 3 |
| 26435 | marcharía | 3 |
| 26436 | marchándose | 3 |
| 26437 | maravillaron | 3 |
| 26438 | maravillaría | 3 |
| 26439 | maravillaba | 3 |
| 26440 | marauillada | 3 |
| 26441 | marañas | 3 |
| 26442 | maraña | 3 |
| 26443 | mañosa | 3 |
| 26444 | manzanilla | 3 |
| 26445 | manuela | 3 |
| 26446 | manual | 3 |
| 26447 | mantenimiento | 3 |
| 26448 | mantenido | 3 |
| 26449 | mantenençia | 3 |
| 26450 | mantellina | 3 |
| 26451 | manteleta | 3 |
| 26452 | manteaban | 3 |
| 26453 | mansas | 3 |
| 26454 | manoteando | 3 |
| 26455 | manotada | 3 |
| 26456 | manosearme | 3 |
| 26457 | manoseada | 3 |
| 26458 | manolito | 3 |
| 26459 | manolillo | 3 |
| 26460 | manojos | 3 |
| 26461 | maniquís | 3 |
| 26462 | maniquí | 3 |
| 26463 | manifiestos | 3 |
| 26464 | manifestarlo | 3 |
| 26465 | manifestábase | 3 |
| 26466 | manido | 3 |
| 26467 | manejando | 3 |
| 26468 | manejaban | 3 |
| 26469 | mandria | 3 |
| 26470 | mándote | 3 |
| 26471 | mandobles | 3 |
| 26472 | mandíbulas | 3 |
| 26473 | mandéis | 3 |
| 26474 | mandatos | 3 |
| 26475 | mandarte | 3 |
| 26476 | mandarines | 3 |
| 26477 | mandares | 3 |
| 26478 | mandaremos | 3 |
| 26479 | mandame | 3 |
| 26480 | mandados | 3 |
| 26481 | mandadero | 3 |
| 26482 | mandábamos | 3 |
| 26483 | mancos | 3 |
| 26484 | manchó | 3 |
| 26485 | mancharse | 3 |
| 26486 | manchadas | 3 |
| 26487 | mançebos | 3 |
| 26488 | mancebito | 3 |
| 26489 | mancebas | 3 |
| 26490 | mançana | 3 |
| 26491 | manazas | 3 |
| 26492 | manas | 3 |
| 26493 | manantiales | 3 |
| 26494 | mamotreto | 3 |
| 26495 | malum | 3 |
| 26496 | maltrató | 3 |
| 26497 | maltrates | 3 |
| 26498 | maltrata | 3 |
| 26499 | malsano | 3 |
| 26500 | malsana | 3 |
| 26501 | malita | 3 |
| 26502 | malísimas | 3 |
| 26503 | malísima | 3 |
| 26504 | malencólico | 3 |
| 26505 | maldecían | 3 |
| 26506 | malandantes | 3 |
| 26507 | malandança | 3 |
| 26508 | majaderos | 3 |
| 26509 | mahudes | 3 |
| 26510 | magullada | 3 |
| 26511 | mago | 3 |
| 26512 | magnifico | 3 |
| 26513 | magnificencias | 3 |
| 26514 | magníficamente | 3 |
| 26515 | magistratura | 3 |
| 26516 | mager | 3 |
| 26517 | magallanes | 3 |
| 26518 | madurando | 3 |
| 26519 | madrugones | 3 |
| 26520 | madrugón | 3 |
| 26521 | madrugan | 3 |
| 26522 | madriguera | 3 |
| 26523 | madrigales | 3 |
| 26524 | madrigal | 3 |
| 26525 | madona | 3 |
| 26526 | madejas | 3 |
| 26527 | madama | 3 |
| 26528 | máculas | 3 |
| 26529 | macilento | 3 |
| 26530 | maça | 3 |
| 26531 | lygera | 3 |
| 26532 | lyévate | 3 |
| 26533 | lyeva | 3 |
| 26534 | lydian | 3 |
| 26535 | luziente | 3 |
| 26536 | luzero | 3 |
| 26537 | lux | 3 |
| 26538 | lumbrera | 3 |
| 26539 | lugarón | 3 |
| 26540 | lueñes | 3 |
| 26541 | ludibrio | 3 |
| 26542 | luciría | 3 |
| 26543 | lucimiento | 3 |
| 26544 | lúcidos | 3 |
| 26545 | lucidas | 3 |
| 26546 | lucecillas | 3 |
| 26547 | lozanos | 3 |
| 26548 | loquito | 3 |
| 26549 | loquilla | 3 |
| 26550 | lombardas | 3 |
| 26551 | logrero | 3 |
| 26552 | locuacidad | 3 |
| 26553 | loçanos | 3 |
| 26554 | loçanía | 3 |
| 26555 | lóbregas | 3 |
| 26556 | loables | 3 |
| 26557 | lluvioso | 3 |
| 26558 | llovían | 3 |
| 26559 | lloriqueando | 3 |
| 26560 | lloré | 3 |
| 26561 | llorarla | 3 |
| 26562 | lloraras | 3 |
| 26563 | llevóse | 3 |
| 26564 | llevome | 3 |
| 26565 | llévenme | 3 |
| 26566 | lléveme | 3 |
| 26567 | lleváronme | 3 |
| 26568 | lleváronle | 3 |
| 26569 | llevarlas | 3 |
| 26570 | llevare | 3 |
| 26571 | llégate | 3 |
| 26572 | llegarte | 3 |
| 26573 | llegaren | 3 |
| 26574 | llegare | 3 |
| 26575 | llegábamos | 3 |
| 26576 | llanas | 3 |
| 26577 | llamole | 3 |
| 26578 | llamémosle | 3 |
| 26579 | llamauan | 3 |
| 26580 | llamaua | 3 |
| 26581 | llamaste | 3 |
| 26582 | llamáronle | 3 |
| 26583 | llamarada | 3 |
| 26584 | livio | 3 |
| 26585 | liturgia | 3 |
| 26586 | literalmente | 3 |
| 26587 | listones | 3 |
| 26588 | lisión | 3 |
| 26589 | lísida | 3 |
| 26590 | lisboa | 3 |
| 26591 | lirio | 3 |
| 26592 | linternas | 3 |
| 26593 | lindísimas | 3 |
| 26594 | linderos | 3 |
| 26595 | limpié | 3 |
| 26596 | limpiarle | 3 |
| 26597 | limpiamente | 3 |
| 26598 | limitarse | 3 |
| 26599 | limita | 3 |
| 26600 | lila | 3 |
| 26601 | ligítima | 3 |
| 26602 | ligadura | 3 |
| 26603 | lidiar | 3 |
| 26604 | liçión | 3 |
| 26605 | licenciosa | 3 |
| 26606 | librotes | 3 |
| 26607 | librote | 3 |
| 26608 | libreste | 3 |
| 26609 | librepensadores | 3 |
| 26610 | líbreme | 3 |
| 26611 | librarme | 3 |
| 26612 | librándose | 3 |
| 26613 | libertinos | 3 |
| 26614 | libertinaje | 3 |
| 26615 | liberté | 3 |
| 26616 | libaciones | 3 |
| 26617 | liada | 3 |
| 26618 | liaba | 3 |
| 26619 | leyeron | 3 |
| 26620 | leyda | 3 |
| 26621 | lexos | 3 |
| 26622 | levó | 3 |
| 26623 | levava | 3 |
| 26624 | levase | 3 |
| 26625 | levantasen | 3 |
| 26626 | levantarlas | 3 |
| 26627 | levantaran | 3 |
| 26628 | levantándome | 3 |
| 26629 | leuantate | 3 |
| 26630 | leuantar | 3 |
| 26631 | leuantado | 3 |
| 26632 | letuarios | 3 |
| 26633 | letanía | 3 |
| 26634 | leopardi | 3 |
| 26635 | leoneses | 3 |
| 26636 | leon | 3 |
| 26637 | lentejas | 3 |
| 26638 | lentas | 3 |
| 26639 | lengüetazos | 3 |
| 26640 | lema | 3 |
| 26641 | lejía | 3 |
| 26642 | leídas | 3 |
| 26643 | legislación | 3 |
| 26644 | legiones | 3 |
| 26645 | leerme | 3 |
| 26646 | leella | 3 |
| 26647 | léela | 3 |
| 26648 | leed | 3 |
| 26649 | lectoral | 3 |
| 26650 | lechones | 3 |
| 26651 | lazadas | 3 |
| 26652 | lazada | 3 |
| 26653 | lavaron | 3 |
| 26654 | lavanderas | 3 |
| 26655 | laura | 3 |
| 26656 | laudes | 3 |
| 26657 | lateral | 3 |
| 26658 | latas | 3 |
| 26659 | lastimosas | 3 |
| 26660 | lastime | 3 |
| 26661 | lastimados | 3 |
| 26662 | lascivas | 3 |
| 26663 | lasciami | 3 |
| 26664 | larrun | 3 |
| 26665 | lárgate | 3 |
| 26666 | largaba | 3 |
| 26667 | lapsus | 3 |
| 26668 | lanzarse | 3 |
| 26669 | lanzarla | 3 |
| 26670 | lanzan | 3 |
| 26671 | lanzadas | 3 |
| 26672 | lánguido | 3 |
| 26673 | lancé | 3 |
| 26674 | lança | 3 |
| 26675 | lamento | 3 |
| 26676 | lamentar | 3 |
| 26677 | lamenta | 3 |
| 26678 | lame | 3 |
| 26679 | lambicando | 3 |
| 26680 | lamartine | 3 |
| 26681 | lagos | 3 |
| 26682 | lagar | 3 |
| 26683 | ladronas | 3 |
| 26684 | ladró | 3 |
| 26685 | ladito | 3 |
| 26686 | lacónicamente | 3 |
| 26687 | lacio | 3 |
| 26688 | lácar | 3 |
| 26689 | labros | 3 |
| 26690 | labrando | 3 |
| 26691 | labrados | 3 |
| 26692 | labra | 3 |
| 26693 | kohler | 3 |
| 26694 | kilómetros | 3 |
| 26695 | juzgaban | 3 |
| 26696 | juveniles | 3 |
| 26697 | jurisprudencia | 3 |
| 26698 | jures | 3 |
| 26699 | juré | 3 |
| 26700 | juraste | 3 |
| 26701 | juraría | 3 |
| 26702 | jurare | 3 |
| 26703 | juraban | 3 |
| 26704 | junten | 3 |
| 26705 | juntándose | 3 |
| 26706 | juncia | 3 |
| 26707 | juguemos | 3 |
| 26708 | jugó | 3 |
| 26709 | juglares | 3 |
| 26710 | jugase | 3 |
| 26711 | jugaron | 3 |
| 26712 | jugada | 3 |
| 26713 | juegue | 3 |
| 26714 | judgar | 3 |
| 26715 | judea | 3 |
| 26716 | jubon | 3 |
| 26717 | jubilar | 3 |
| 26718 | jovenzuelo | 3 |
| 26719 | jovenzuela | 3 |
| 26720 | jotas | 3 |
| 26721 | josefa | 3 |
| 26722 | josef | 3 |
| 26723 | jornaleros | 3 |
| 26724 | jornalero | 3 |
| 26725 | jonás | 3 |
| 26726 | jocoso | 3 |
| 26727 | joco | 3 |
| 26728 | jo | 3 |
| 26729 | jirón | 3 |
| 26730 | jipijapa | 3 |
| 26731 | jimia | 3 |
| 26732 | jicarazo | 3 |
| 26733 | jerwis | 3 |
| 26734 | jerigonza | 3 |
| 26735 | jerarquías | 3 |
| 26736 | jazmín | 3 |
| 26737 | jaspes | 3 |
| 26738 | jasón | 3 |
| 26739 | jarros | 3 |
| 26740 | jardinero | 3 |
| 26741 | jarama | 3 |
| 26742 | japonesa | 3 |
| 26743 | jamones | 3 |
| 26744 | jamases | 3 |
| 26745 | jaleo | 3 |
| 26746 | jactarse | 3 |
| 26747 | jactancia | 3 |
| 26748 | jactaba | 3 |
| 26749 | jacintilla | 3 |
| 26750 | jacer | 3 |
| 26751 | jabonado | 3 |
| 26752 | istmo | 3 |
| 26753 | isleño | 3 |
| 26754 | isabelita | 3 |
| 26755 | irritante | 3 |
| 26756 | irritabilidad | 3 |
| 26757 | irrisoria | 3 |
| 26758 | irrevocables | 3 |
| 26759 | irregularidades | 3 |
| 26760 | irregulares | 3 |
| 26761 | irracionales | 3 |
| 26762 | irónico | 3 |
| 26763 | iréis | 3 |
| 26764 | iraeta | 3 |
| 26765 | iracundo | 3 |
| 26766 | ioduro | 3 |
| 26767 | io | 3 |
| 26768 | invoca | 3 |
| 26769 | invito | 3 |
| 26770 | invitados | 3 |
| 26771 | invitación | 3 |
| 26772 | invitaba | 3 |
| 26773 | invidiado | 3 |
| 26774 | inventas | 3 |
| 26775 | inventaran | 3 |
| 26776 | inventan | 3 |
| 26777 | inventada | 3 |
| 26778 | inválida | 3 |
| 26779 | inundó | 3 |
| 26780 | inundar | 3 |
| 26781 | inunda | 3 |
| 26782 | inuierno | 3 |
| 26783 | inuenciones | 3 |
| 26784 | intuición | 3 |
| 26785 | intrusos | 3 |
| 26786 | intrusa | 3 |
| 26787 | introducirse | 3 |
| 26788 | intrigantes | 3 |
| 26789 | intricados | 3 |
| 26790 | intricado | 3 |
| 26791 | intrépida | 3 |
| 26792 | intratable | 3 |
| 26793 | intranquilidad | 3 |
| 26794 | intitulaba | 3 |
| 26795 | intitula | 3 |
| 26796 | intimidades | 3 |
| 26797 | intervalo | 3 |
| 26798 | intersticio | 3 |
| 26799 | interrumpieron | 3 |
| 26800 | interrumpida | 3 |
| 26801 | interrumpían | 3 |
| 26802 | interrumpas | 3 |
| 26803 | interrogada | 3 |
| 26804 | interprete | 3 |
| 26805 | interpretar | 3 |
| 26806 | interponía | 3 |
| 26807 | interino | 3 |
| 26808 | interesantísimo | 3 |
| 26809 | interesantísima | 3 |
| 26810 | interesados | 3 |
| 26811 | interesaban | 3 |
| 26812 | intentaron | 3 |
| 26813 | intentaré | 3 |
| 26814 | intentando | 3 |
| 26815 | intentan | 3 |
| 26816 | intençión | 3 |
| 26817 | integridad | 3 |
| 26818 | intacto | 3 |
| 26819 | insultarle | 3 |
| 26820 | insultante | 3 |
| 26821 | insultando | 3 |
| 26822 | insultaban | 3 |
| 26823 | ínsulos | 3 |
| 26824 | insubordinaba | 3 |
| 26825 | instrucciones | 3 |
| 26826 | institutriz | 3 |
| 26827 | institutos | 3 |
| 26828 | instintivo | 3 |
| 26829 | instalar | 3 |
| 26830 | instalándose | 3 |
| 26831 | insoportables | 3 |
| 26832 | insomnios | 3 |
| 26833 | insistente | 3 |
| 26834 | inquisidora | 3 |
| 26835 | inquisidor | 3 |
| 26836 | inquiriendo | 3 |
| 26837 | inquilina | 3 |
| 26838 | inquietas | 3 |
| 26839 | inquietarse | 3 |
| 26840 | inquietaban | 3 |
| 26841 | inquïeta | 3 |
| 26842 | inoportunamente | 3 |
| 26843 | inopinadamente | 3 |
| 26844 | inopinada | 3 |
| 26845 | inocentona | 3 |
| 26846 | innominada | 3 |
| 26847 | innoble | 3 |
| 26848 | innegable | 3 |
| 26849 | inmutable | 3 |
| 26850 | inmodestia | 3 |
| 26851 | inmiscuirse | 3 |
| 26852 | inmejorable | 3 |
| 26853 | iniciales | 3 |
| 26854 | iniciada | 3 |
| 26855 | inicia | 3 |
| 26856 | ingerir | 3 |
| 26857 | ingenuo | 3 |
| 26858 | ingenuamente | 3 |
| 26859 | ingeniosos | 3 |
| 26860 | infundían | 3 |
| 26861 | infundan | 3 |
| 26862 | infortunado | 3 |
| 26863 | informándose | 3 |
| 26864 | informada | 3 |
| 26865 | informa | 3 |
| 26866 | influir | 3 |
| 26867 | influía | 3 |
| 26868 | influencias | 3 |
| 26869 | inflamados | 3 |
| 26870 | inflamado | 3 |
| 26871 | inflamada | 3 |
| 26872 | infestado | 3 |
| 26873 | infausto | 3 |
| 26874 | infanzones | 3 |
| 26875 | infamante | 3 |
| 26876 | inescrutables | 3 |
| 26877 | inequívocas | 3 |
| 26878 | ineficacia | 3 |
| 26879 | industriado | 3 |
| 26880 | indulgentes | 3 |
| 26881 | indubitablemente | 3 |
| 26882 | indomable | 3 |
| 26883 | individua | 3 |
| 26884 | indirecta | 3 |
| 26885 | indinos | 3 |
| 26886 | indino | 3 |
| 26887 | indico | 3 |
| 26888 | indicase | 3 |
| 26889 | indecisa | 3 |
| 26890 | indagaciones | 3 |
| 26891 | incurría | 3 |
| 26892 | incuria | 3 |
| 26893 | incurables | 3 |
| 26894 | inculta | 3 |
| 26895 | incorruptible | 3 |
| 26896 | incorrección | 3 |
| 26897 | incorporado | 3 |
| 26898 | incorporada | 3 |
| 26899 | incontestable | 3 |
| 26900 | inconsiderado | 3 |
| 26901 | inconscientemente | 3 |
| 26902 | incomprensible | 3 |
| 26903 | incompleta | 3 |
| 26904 | incomodó | 3 |
| 26905 | incómodo | 3 |
| 26906 | incomodarme | 3 |
| 26907 | incólume | 3 |
| 26908 | incoherentes | 3 |
| 26909 | inclito | 3 |
| 26910 | incliné | 3 |
| 26911 | inclinaban | 3 |
| 26912 | inclemencia | 3 |
| 26913 | incitó | 3 |
| 26914 | incitante | 3 |
| 26915 | incitan | 3 |
| 26916 | incita | 3 |
| 26917 | incentivos | 3 |
| 26918 | incensario | 3 |
| 26919 | incautos | 3 |
| 26920 | incapacidad | 3 |
| 26921 | inauguró | 3 |
| 26922 | inauditos | 3 |
| 26923 | inaguantable | 3 |
| 26924 | inacabables | 3 |
| 26925 | impurezas | 3 |
| 26926 | impulsaron | 3 |
| 26927 | impulsan | 3 |
| 26928 | impulsada | 3 |
| 26929 | improvisar | 3 |
| 26930 | impropias | 3 |
| 26931 | improper | 3 |
| 26932 | imprimieron | 3 |
| 26933 | imprimiendo | 3 |
| 26934 | impriman | 3 |
| 26935 | impresionables | 3 |
| 26936 | impresionable | 3 |
| 26937 | impotentes | 3 |
| 26938 | impotente | 3 |
| 26939 | imposibilitaban | 3 |
| 26940 | importunidad | 3 |
| 26941 | importunaba | 3 |
| 26942 | importaría | 3 |
| 26943 | importarán | 3 |
| 26944 | importación | 3 |
| 26945 | imponen | 3 |
| 26946 | implacables | 3 |
| 26947 | implacablemente | 3 |
| 26948 | imperiosos | 3 |
| 26949 | imperiosamente | 3 |
| 26950 | imperdonable | 3 |
| 26951 | impenetrable | 3 |
| 26952 | impelió | 3 |
| 26953 | impedirle | 3 |
| 26954 | impedirá | 3 |
| 26955 | impedimiento | 3 |
| 26956 | impedida | 3 |
| 26957 | impavidez | 3 |
| 26958 | impagable | 3 |
| 26959 | impacientarse | 3 |
| 26960 | imitaré | 3 |
| 26961 | imagines | 3 |
| 26962 | imagine | 3 |
| 26963 | imaginativos | 3 |
| 26964 | imaginaron | 3 |
| 26965 | imaginándose | 3 |
| 26966 | imaginadas | 3 |
| 26967 | imaginables | 3 |
| 26968 | imagina | 3 |
| 26969 | ilustrados | 3 |
| 26970 | ilustraciones | 3 |
| 26971 | ilusos | 3 |
| 26972 | ilegítimos | 3 |
| 26973 | igualen | 3 |
| 26974 | ignorada | 3 |
| 26975 | ignacio | 3 |
| 26976 | idolatrando | 3 |
| 26977 | idolatrado | 3 |
| 26978 | idolatrada | 3 |
| 26979 | idolatraba | 3 |
| 26980 | idilio | 3 |
| 26981 | ibaya | 3 |
| 26982 | íbame | 3 |
| 26983 | huyo | 3 |
| 26984 | huyera | 3 |
| 26985 | huyda | 3 |
| 26986 | huyan | 3 |
| 26987 | huraño | 3 |
| 26988 | huraña | 3 |
| 26989 | hundiendo | 3 |
| 26990 | humillaciones | 3 |
| 26991 | humildísimo | 3 |
| 26992 | humedecida | 3 |
| 26993 | humanidades | 3 |
| 26994 | humanamente | 3 |
| 26995 | huirse | 3 |
| 26996 | huevera | 3 |
| 26997 | hueles | 3 |
| 26998 | húchoho | 3 |
| 26999 | hubiérades | 3 |
| 27000 | hu | 3 |
| 27001 | houieras | 3 |
| 27002 | houiera | 3 |
| 27003 | hostil | 3 |
| 27004 | hosanna | 3 |
| 27005 | hortaliza | 3 |
| 27006 | horros | 3 |
| 27007 | horrorosos | 3 |
| 27008 | hormigueo | 3 |
| 27009 | horizontal | 3 |
| 27010 | horcajadas | 3 |
| 27011 | honrilla | 3 |
| 27012 | hongos | 3 |
| 27013 | home | 3 |
| 27014 | holocausto | 3 |
| 27015 | hollín | 3 |
| 27016 | holgura | 3 |
| 27017 | holgazanería | 3 |
| 27018 | holgazana | 3 |
| 27019 | holgazán | 3 |
| 27020 | holgaron | 3 |
| 27021 | holgaré | 3 |
| 27022 | holgado | 3 |
| 27023 | holgada | 3 |
| 27024 | hojeó | 3 |
| 27025 | hojeando | 3 |
| 27026 | hojaldres | 3 |
| 27027 | hogaza | 3 |
| 27028 | hogares | 3 |
| 27029 | hogaño | 3 |
| 27030 | hobiese | 3 |
| 27031 | hízonos | 3 |
| 27032 | hiziesse | 3 |
| 27033 | hiriendo | 3 |
| 27034 | hipógrifo | 3 |
| 27035 | hipocondría | 3 |
| 27036 | hiperbólicamente | 3 |
| 27037 | hiperbólica | 3 |
| 27038 | hipérbole | 3 |
| 27039 | hinque | 3 |
| 27040 | hinchó | 3 |
| 27041 | hinchar | 3 |
| 27042 | hincha | 3 |
| 27043 | hincapié | 3 |
| 27044 | hincando | 3 |
| 27045 | hincada | 3 |
| 27046 | himnos | 3 |
| 27047 | hilar | 3 |
| 27048 | hilada | 3 |
| 27049 | hilaba | 3 |
| 27050 | hijuelos | 3 |
| 27051 | hijodalgo | 3 |
| 27052 | hijitos | 3 |
| 27053 | higueras | 3 |
| 27054 | higo | 3 |
| 27055 | higiénicos | 3 |
| 27056 | higiénicas | 3 |
| 27057 | higa | 3 |
| 27058 | hierusalaim | 3 |
| 27059 | hieren | 3 |
| 27060 | hierbajos | 3 |
| 27061 | hiera | 3 |
| 27062 | hielos | 3 |
| 27063 | hiedras | 3 |
| 27064 | hiciésemos | 3 |
| 27065 | hiciéronle | 3 |
| 27066 | híceme | 3 |
| 27067 | hícelo | 3 |
| 27068 | hícele | 3 |
| 27069 | hícela | 3 |
| 27070 | híbrido | 3 |
| 27071 | hervores | 3 |
| 27072 | hervidero | 3 |
| 27073 | herradas | 3 |
| 27074 | heroicas | 3 |
| 27075 | hernán | 3 |
| 27076 | hermosean | 3 |
| 27077 | hermosea | 3 |
| 27078 | herejote | 3 |
| 27079 | heredé | 3 |
| 27080 | heráldico | 3 |
| 27081 | heráldica | 3 |
| 27082 | hendidura | 3 |
| 27083 | henchir | 3 |
| 27084 | hemistiquio | 3 |
| 27085 | helecho | 3 |
| 27086 | helar | 3 |
| 27087 | heciste | 3 |
| 27088 | hechizo | 3 |
| 27089 | hechiceros | 3 |
| 27090 | hechicería | 3 |
| 27091 | hebreo | 3 |
| 27092 | hebenes | 3 |
| 27093 | hazlo | 3 |
| 27094 | hastio | 3 |
| 27095 | hastiado | 3 |
| 27096 | hásele | 3 |
| 27097 | harnero | 3 |
| 27098 | hán | 3 |
| 27099 | hambrientas | 3 |
| 27100 | hallóla | 3 |
| 27101 | halles | 3 |
| 27102 | hallemos | 3 |
| 27103 | hallasen | 3 |
| 27104 | hállase | 3 |
| 27105 | hallarnos | 3 |
| 27106 | hallarían | 3 |
| 27107 | hallaren | 3 |
| 27108 | hallaremos | 3 |
| 27109 | hallándola | 3 |
| 27110 | halláis | 3 |
| 27111 | halda | 3 |
| 27112 | halago | 3 |
| 27113 | hagámonos | 3 |
| 27114 | hacinados | 3 |
| 27115 | hacías | 3 |
| 27116 | hacíalo | 3 |
| 27117 | hachazos | 3 |
| 27118 | hacelle | 3 |
| 27119 | hacaneas | 3 |
| 27120 | hacanea | 3 |
| 27121 | hac | 3 |
| 27122 | hablose | 3 |
| 27123 | hablasteis | 3 |
| 27124 | hablasen | 3 |
| 27125 | hablaros | 3 |
| 27126 | hablare | 3 |
| 27127 | habituales | 3 |
| 27128 | habito | 3 |
| 27129 | habitaban | 3 |
| 27130 | habiéndolos | 3 |
| 27131 | habíales | 3 |
| 27132 | habíais | 3 |
| 27133 | habíades | 3 |
| 27134 | haberes | 3 |
| 27135 | guzmanes | 3 |
| 27136 | guturales | 3 |
| 27137 | gustavito | 3 |
| 27138 | gustáredes | 3 |
| 27139 | gustara | 3 |
| 27140 | gulpeja | 3 |
| 27141 | guitarrillo | 3 |
| 27142 | guisas | 3 |
| 27143 | guisar | 3 |
| 27144 | guisantes | 3 |
| 27145 | guisando | 3 |
| 27146 | guipúzcoa | 3 |
| 27147 | guiador | 3 |
| 27148 | guiado | 3 |
| 27149 | guiada | 3 |
| 27150 | guevara | 3 |
| 27151 | güésped | 3 |
| 27152 | guerrilla | 3 |
| 27153 | güeros | 3 |
| 27154 | guarismo | 3 |
| 27155 | guarida | 3 |
| 27156 | guardianes | 3 |
| 27157 | guardesa | 3 |
| 27158 | guárdela | 3 |
| 27159 | guardat | 3 |
| 27160 | guardasol | 3 |
| 27161 | guardasen | 3 |
| 27162 | guardarte | 3 |
| 27163 | guardarlas | 3 |
| 27164 | guardares | 3 |
| 27165 | guardándose | 3 |
| 27166 | guardamos | 3 |
| 27167 | guardáis | 3 |
| 27168 | guardadito | 3 |
| 27169 | guapote | 3 |
| 27170 | guapezas | 3 |
| 27171 | guapetón | 3 |
| 27172 | gualardón | 3 |
| 27173 | grulla | 3 |
| 27174 | grosseros | 3 |
| 27175 | gritería | 3 |
| 27176 | grillo | 3 |
| 27177 | grillera | 3 |
| 27178 | grieta | 3 |
| 27179 | griegas | 3 |
| 27180 | greçia | 3 |
| 27181 | graznido | 3 |
| 27182 | graznar | 3 |
| 27183 | gravísimas | 3 |
| 27184 | gratos | 3 |
| 27185 | grasiento | 3 |
| 27186 | granjeado | 3 |
| 27187 | granito | 3 |
| 27188 | grandiosas | 3 |
| 27189 | granado | 3 |
| 27190 | grama | 3 |
| 27191 | graçiosa | 3 |
| 27192 | grabiel | 3 |
| 27193 | grabada | 3 |
| 27194 | gozase | 3 |
| 27195 | gozaros | 3 |
| 27196 | gozarme | 3 |
| 27197 | gozarla | 3 |
| 27198 | gozaré | 3 |
| 27199 | goteras | 3 |
| 27200 | gosos | 3 |
| 27201 | gorrón | 3 |
| 27202 | gordiano | 3 |
| 27203 | góndola | 3 |
| 27204 | gocen | 3 |
| 27205 | gobierne | 3 |
| 27206 | gobiernas | 3 |
| 27207 | gobernase | 3 |
| 27208 | gobernarse | 3 |
| 27209 | goberna | 3 |
| 27210 | glosó | 3 |
| 27211 | globulus | 3 |
| 27212 | gitanesca | 3 |
| 27213 | giros | 3 |
| 27214 | girifalte | 3 |
| 27215 | girando | 3 |
| 27216 | giralda | 3 |
| 27217 | gigantescas | 3 |
| 27218 | gigantazo | 3 |
| 27219 | gesticulaba | 3 |
| 27220 | gerundio | 3 |
| 27221 | gerifalte | 3 |
| 27222 | geométricas | 3 |
| 27223 | geología | 3 |
| 27224 | gentilidad | 3 |
| 27225 | genil | 3 |
| 27226 | generosas | 3 |
| 27227 | generalizaba | 3 |
| 27228 | genealogista | 3 |
| 27229 | gela | 3 |
| 27230 | gavias | 3 |
| 27231 | gaur | 3 |
| 27232 | gatito | 3 |
| 27233 | gatesca | 3 |
| 27234 | gateras | 3 |
| 27235 | gatera | 3 |
| 27236 | gastase | 3 |
| 27237 | gastas | 3 |
| 27238 | gastarla | 3 |
| 27239 | gascona | 3 |
| 27240 | gárrula | 3 |
| 27241 | garrida | 3 |
| 27242 | garita | 3 |
| 27243 | gargarismos | 3 |
| 27244 | garfios | 3 |
| 27245 | garçía | 3 |
| 27246 | garça | 3 |
| 27247 | garbosa | 3 |
| 27248 | garavatos | 3 |
| 27249 | garavato | 3 |
| 27250 | garatusas | 3 |
| 27251 | garabato | 3 |
| 27252 | ganzúas | 3 |
| 27253 | ganzúa | 3 |
| 27254 | gangoso | 3 |
| 27255 | ganen | 3 |
| 27256 | gané | 3 |
| 27257 | ganapanes | 3 |
| 27258 | ganamos | 3 |
| 27259 | galón | 3 |
| 27260 | gallynas | 3 |
| 27261 | gallyna | 3 |
| 27262 | gallegas | 3 |
| 27263 | galga | 3 |
| 27264 | galantes | 3 |
| 27265 | galanteo | 3 |
| 27266 | galalón | 3 |
| 27267 | gachas | 3 |
| 27268 | gacetillero | 3 |
| 27269 | gabinetito | 3 |
| 27270 | gabanes | 3 |
| 27271 | gabachos | 3 |
| 27272 | fynqué | 3 |
| 27273 | fynque | 3 |
| 27274 | fyncó | 3 |
| 27275 | fuyan | 3 |
| 27276 | futuros | 3 |
| 27277 | fusilería | 3 |
| 27278 | furtivas | 3 |
| 27279 | furiosas | 3 |
| 27280 | furias | 3 |
| 27281 | fundido | 3 |
| 27282 | fundador | 3 |
| 27283 | fundadas | 3 |
| 27284 | funcionar | 3 |
| 27285 | fuma | 3 |
| 27286 | fulminó | 3 |
| 27287 | fulgencia | 3 |
| 27288 | fulanito | 3 |
| 27289 | fuit | 3 |
| 27290 | fuercen | 3 |
| 27291 | fuérades | 3 |
| 27292 | fuemos | 3 |
| 27293 | fuelles | 3 |
| 27294 | fruncidas | 3 |
| 27295 | frotando | 3 |
| 27296 | frores | 3 |
| 27297 | frondoso | 3 |
| 27298 | frondosas | 3 |
| 27299 | frívola | 3 |
| 27300 | fritangas | 3 |
| 27301 | frita | 3 |
| 27302 | frisar | 3 |
| 27303 | friega | 3 |
| 27304 | frestón | 3 |
| 27305 | frescor | 3 |
| 27306 | fresas | 3 |
| 27307 | frentes | 3 |
| 27308 | frenéticos | 3 |
| 27309 | frenéticamente | 3 |
| 27310 | freír | 3 |
| 27311 | freía | 3 |
| 27312 | frecuentando | 3 |
| 27313 | frayles | 3 |
| 27314 | fraternales | 3 |
| 27315 | franquear | 3 |
| 27316 | fragoso | 3 |
| 27317 | fragmento | 3 |
| 27318 | fragante | 3 |
| 27319 | fraga | 3 |
| 27320 | fraco | 3 |
| 27321 | fosfato | 3 |
| 27322 | fosca | 3 |
| 27323 | forzosas | 3 |
| 27324 | forzaron | 3 |
| 27325 | forzarle | 3 |
| 27326 | forzando | 3 |
| 27327 | forzadas | 3 |
| 27328 | fortifica | 3 |
| 27329 | fortalezas | 3 |
| 27330 | forrados | 3 |
| 27331 | fornos | 3 |
| 27332 | forniçio | 3 |
| 27333 | formuló | 3 |
| 27334 | formulando | 3 |
| 27335 | forme | 3 |
| 27336 | formaría | 3 |
| 27337 | forjó | 3 |
| 27338 | forjar | 3 |
| 27339 | for | 3 |
| 27340 | fontana | 3 |
| 27341 | fomentan | 3 |
| 27342 | folleto | 3 |
| 27343 | folletín | 3 |
| 27344 | fol | 3 |
| 27345 | fofa | 3 |
| 27346 | fócil | 3 |
| 27347 | focas | 3 |
| 27348 | flujo | 3 |
| 27349 | fluctuando | 3 |
| 27350 | floreros | 3 |
| 27351 | fleco | 3 |
| 27352 | flechilla | 3 |
| 27353 | flamenca | 3 |
| 27354 | flagrante | 3 |
| 27355 | fízole | 3 |
| 27356 | físose | 3 |
| 27357 | fisonomías | 3 |
| 27358 | fisiológico | 3 |
| 27359 | físicamente | 3 |
| 27360 | fiscales | 3 |
| 27361 | firmezas | 3 |
| 27362 | firmada | 3 |
| 27363 | fió | 3 |
| 27364 | finito | 3 |
| 27365 | finísimas | 3 |
| 27366 | fingimientos | 3 |
| 27367 | fingimiento | 3 |
| 27368 | financieras | 3 |
| 27369 | filosofos | 3 |
| 27370 | filosofando | 3 |
| 27371 | filológica | 3 |
| 27372 | filipo | 3 |
| 27373 | filiación | 3 |
| 27374 | filantrópicos | 3 |
| 27375 | fil | 3 |
| 27376 | fijaremos | 3 |
| 27377 | fijándose | 3 |
| 27378 | figurósele | 3 |
| 27379 | figuritas | 3 |
| 27380 | figurémonos | 3 |
| 27381 | figurada | 3 |
| 27382 | figueroa | 3 |
| 27383 | figueras | 3 |
| 27384 | figón | 3 |
| 27385 | fíese | 3 |
| 27386 | fierecita | 3 |
| 27387 | fiere | 3 |
| 27388 | fíe | 3 |
| 27389 | fidias | 3 |
| 27390 | fichú | 3 |
| 27391 | fichas | 3 |
| 27392 | fiara | 3 |
| 27393 | fiambres | 3 |
| 27394 | fïado | 3 |
| 27395 | fiada | 3 |
| 27396 | ffazes | 3 |
| 27397 | ffasta | 3 |
| 27398 | ffablar | 3 |
| 27399 | fétido | 3 |
| 27400 | fétida | 3 |
| 27401 | férula | 3 |
| 27402 | fértiles | 3 |
| 27403 | ferruginosa | 3 |
| 27404 | ferreruelo | 3 |
| 27405 | feriendo | 3 |
| 27406 | feneció | 3 |
| 27407 | fementida | 3 |
| 27408 | femenina | 3 |
| 27409 | felonía | 3 |
| 27410 | feligreses | 3 |
| 27411 | fegura | 3 |
| 27412 | fecundas | 3 |
| 27413 | fechura | 3 |
| 27414 | fechorías | 3 |
| 27415 | fechoría | 3 |
| 27416 | febriles | 3 |
| 27417 | febeo | 3 |
| 27418 | favoreció | 3 |
| 27419 | favorecidos | 3 |
| 27420 | favorecerle | 3 |
| 27421 | favorecen | 3 |
| 27422 | favorcito | 3 |
| 27423 | fauces | 3 |
| 27424 | fatigue | 3 |
| 27425 | fatigoso | 3 |
| 27426 | fatigadísima | 3 |
| 27427 | fatigadas | 3 |
| 27428 | fatídicas | 3 |
| 27429 | fastidioso | 3 |
| 27430 | fastidiosas | 3 |
| 27431 | fascinaba | 3 |
| 27432 | fartar | 3 |
| 27433 | farolón | 3 |
| 27434 | farmacéuticos | 3 |
| 27435 | farmacéutica | 3 |
| 27436 | fariseos | 3 |
| 27437 | faredes | 3 |
| 27438 | fare | 3 |
| 27439 | faraones | 3 |
| 27440 | farándula | 3 |
| 27441 | fantásticamente | 3 |
| 27442 | fanbre | 3 |
| 27443 | fanatizado | 3 |
| 27444 | faltarían | 3 |
| 27445 | faltaré | 3 |
| 27446 | falsarios | 3 |
| 27447 | falsario | 3 |
| 27448 | fallecido | 3 |
| 27449 | fallava | 3 |
| 27450 | fallaras | 3 |
| 27451 | faldriqueras | 3 |
| 27452 | faldero | 3 |
| 27453 | falagos | 3 |
| 27454 | falagera | 3 |
| 27455 | falagava | 3 |
| 27456 | falagar | 3 |
| 27457 | faisán | 3 |
| 27458 | fagan | 3 |
| 27459 | facilitó | 3 |
| 27460 | facilitaban | 3 |
| 27461 | façia | 3 |
| 27462 | facetas | 3 |
| 27463 | fabulosos | 3 |
| 27464 | fabricación | 3 |
| 27465 | fablares | 3 |
| 27466 | ezguerra | 3 |
| 27467 | extremosa | 3 |
| 27468 | extrema | 3 |
| 27469 | extranquero | 3 |
| 27470 | extra | 3 |
| 27471 | extinguida | 3 |
| 27472 | extinguían | 3 |
| 27473 | externa | 3 |
| 27474 | extensos | 3 |
| 27475 | extendidas | 3 |
| 27476 | expuestas | 3 |
| 27477 | expresivas | 3 |
| 27478 | expresadas | 3 |
| 27479 | expongo | 3 |
| 27480 | exponga | 3 |
| 27481 | expone | 3 |
| 27482 | explotan | 3 |
| 27483 | exploró | 3 |
| 27484 | exploraba | 3 |
| 27485 | explícito | 3 |
| 27486 | explícate | 3 |
| 27487 | explicárselo | 3 |
| 27488 | explicaría | 3 |
| 27489 | expiraba | 3 |
| 27490 | experimentos | 3 |
| 27491 | experimentó | 3 |
| 27492 | expedito | 3 |
| 27493 | expectante | 3 |
| 27494 | exordio | 3 |
| 27495 | existirá | 3 |
| 27496 | exigido | 3 |
| 27497 | exhalaciones | 3 |
| 27498 | exentos | 3 |
| 27499 | exenta | 3 |
| 27500 | executar | 3 |
| 27501 | execrable | 3 |
| 27502 | excuso | 3 |
| 27503 | excusado | 3 |
| 27504 | excomulgado | 3 |
| 27505 | excluía | 3 |
| 27506 | excitante | 3 |
| 27507 | excitaciones | 3 |
| 27508 | excita | 3 |
| 27509 | excesivamente | 3 |
| 27510 | excepcionales | 3 |
| 27511 | excelsa | 3 |
| 27512 | exceden | 3 |
| 27513 | examinarse | 3 |
| 27514 | examinándole | 3 |
| 27515 | examinan | 3 |
| 27516 | examinadas | 3 |
| 27517 | exaltándose | 3 |
| 27518 | evolución | 3 |
| 27519 | evitarle | 3 |
| 27520 | evitaba | 3 |
| 27521 | evidentes | 3 |
| 27522 | evasivas | 3 |
| 27523 | evasivamente | 3 |
| 27524 | evangelista | 3 |
| 27525 | europeas | 3 |
| 27526 | europea | 3 |
| 27527 | euro | 3 |
| 27528 | euitar | 3 |
| 27529 | etna | 3 |
| 27530 | etiopía | 3 |
| 27531 | ética | 3 |
| 27532 | estúvose | 3 |
| 27533 | estuuiesse | 3 |
| 27534 | estupendas | 3 |
| 27535 | estudioso | 3 |
| 27536 | estudiarla | 3 |
| 27537 | estudiaré | 3 |
| 27538 | estudiadas | 3 |
| 27539 | estudiaban | 3 |
| 27540 | estucada | 3 |
| 27541 | estrumentes | 3 |
| 27542 | estrujón | 3 |
| 27543 | estropicio | 3 |
| 27544 | estropeados | 3 |
| 27545 | estropeada | 3 |
| 27546 | estricnina | 3 |
| 27547 | estrepitosos | 3 |
| 27548 | estrepitosas | 3 |
| 27549 | estrenó | 3 |
| 27550 | estremeciéndose | 3 |
| 27551 | estremecerse | 3 |
| 27552 | estremece | 3 |
| 27553 | estrellan | 3 |
| 27554 | estrechísima | 3 |
| 27555 | estrechezas | 3 |
| 27556 | estrecharle | 3 |
| 27557 | estrechándole | 3 |
| 27558 | estrechándola | 3 |
| 27559 | estrechado | 3 |
| 27560 | estraza | 3 |
| 27561 | estrangulado | 3 |
| 27562 | estrafalarios | 3 |
| 27563 | estouiesse | 3 |
| 27564 | estorva | 3 |
| 27565 | estoruar | 3 |
| 27566 | estornudo | 3 |
| 27567 | estorbasen | 3 |
| 27568 | estorbaran | 3 |
| 27569 | estorbara | 3 |
| 27570 | estorbado | 3 |
| 27571 | estorbaban | 3 |
| 27572 | estopas | 3 |
| 27573 | estoicismo | 3 |
| 27574 | estofado | 3 |
| 27575 | estirones | 3 |
| 27576 | estirarse | 3 |
| 27577 | estirándose | 3 |
| 27578 | estirados | 3 |
| 27579 | estiraba | 3 |
| 27580 | estímulo | 3 |
| 27581 | estimarse | 3 |
| 27582 | estimamos | 3 |
| 27583 | estigia | 3 |
| 27584 | estienden | 3 |
| 27585 | estése | 3 |
| 27586 | estes | 3 |
| 27587 | estercolero | 3 |
| 27588 | estentórea | 3 |
| 27589 | esténme | 3 |
| 27590 | estendido | 3 |
| 27591 | estela | 3 |
| 27592 | estéban | 3 |
| 27593 | esteban | 3 |
| 27594 | estaras | 3 |
| 27595 | estara | 3 |
| 27596 | estadme | 3 |
| 27597 | estacazo | 3 |
| 27598 | estaca | 3 |
| 27599 | establos | 3 |
| 27600 | establecerme | 3 |
| 27601 | estable | 3 |
| 27602 | esquivos | 3 |
| 27603 | esquivas | 3 |
| 27604 | esquilas | 3 |
| 27605 | esquila | 3 |
| 27606 | esqueletos | 3 |
| 27607 | espumosa | 3 |
| 27608 | espumarajos | 3 |
| 27609 | espontáneo | 3 |
| 27610 | esplín | 3 |
| 27611 | esplendoroso | 3 |
| 27612 | espléndidos | 3 |
| 27613 | esplandián | 3 |
| 27614 | espiritu | 3 |
| 27615 | espirales | 3 |
| 27616 | espinoso | 3 |
| 27617 | espín | 3 |
| 27618 | esperpento | 3 |
| 27619 | esperma | 3 |
| 27620 | espérenme | 3 |
| 27621 | espantos | 3 |
| 27622 | espanten | 3 |
| 27623 | espantase | 3 |
| 27624 | espantadas | 3 |
| 27625 | espalder | 3 |
| 27626 | espadachín | 3 |
| 27627 | esotras | 3 |
| 27628 | esmirriada | 3 |
| 27629 | esmeralda | 3 |
| 27630 | esmerado | 3 |
| 27631 | esmerada | 3 |
| 27632 | esme | 3 |
| 27633 | esgrimía | 3 |
| 27634 | esforzar | 3 |
| 27635 | esforcé | 3 |
| 27636 | escusare | 3 |
| 27637 | escusara | 3 |
| 27638 | escurriendo | 3 |
| 27639 | escurecer | 3 |
| 27640 | escupir | 3 |
| 27641 | escupidera | 3 |
| 27642 | escupe | 3 |
| 27643 | escueta | 3 |
| 27644 | escuece | 3 |
| 27645 | escudriñador | 3 |
| 27646 | escucharlo | 3 |
| 27647 | escúchame | 3 |
| 27648 | escuchada | 3 |
| 27649 | escrupulosidad | 3 |
| 27650 | escriuir | 3 |
| 27651 | escribirme | 3 |
| 27652 | escribirla | 3 |
| 27653 | escribiere | 3 |
| 27654 | escribían | 3 |
| 27655 | escrevir | 3 |
| 27656 | escotillas | 3 |
| 27657 | esconderme | 3 |
| 27658 | esconderla | 3 |
| 27659 | escojo | 3 |
| 27660 | escogieron | 3 |
| 27661 | escocia | 3 |
| 27662 | escocés | 3 |
| 27663 | escobillón | 3 |
| 27664 | esclavinas | 3 |
| 27665 | escépticos | 3 |
| 27666 | escénico | 3 |
| 27667 | escayolas | 3 |
| 27668 | escasos | 3 |
| 27669 | escarpines | 3 |
| 27670 | escarnido | 3 |
| 27671 | escarda | 3 |
| 27672 | escarcha | 3 |
| 27673 | escarabajos | 3 |
| 27674 | escapes | 3 |
| 27675 | escapas | 3 |
| 27676 | escaparon | 3 |
| 27677 | escaparme | 3 |
| 27678 | escandalizarse | 3 |
| 27679 | escandalizan | 3 |
| 27680 | escandalizado | 3 |
| 27681 | escanciar | 3 |
| 27682 | escamada | 3 |
| 27683 | escalonados | 3 |
| 27684 | escalonada | 3 |
| 27685 | escalo | 3 |
| 27686 | escalar | 3 |
| 27687 | esbeltez | 3 |
| 27688 | esbeltas | 3 |
| 27689 | erre | 3 |
| 27690 | errados | 3 |
| 27691 | ermilio | 3 |
| 27692 | erizados | 3 |
| 27693 | erizado | 3 |
| 27694 | erigió | 3 |
| 27695 | erase | 3 |
| 27696 | éranle | 3 |
| 27697 | éralo | 3 |
| 27698 | er | 3 |
| 27699 | equívocos | 3 |
| 27700 | equipajes | 3 |
| 27701 | epopeya | 3 |
| 27702 | epiléptico | 3 |
| 27703 | epigastrio | 3 |
| 27704 | epidermis | 3 |
| 27705 | epidemia | 3 |
| 27706 | épico | 3 |
| 27707 | épicas | 3 |
| 27708 | enxemplo | 3 |
| 27709 | envuelven | 3 |
| 27710 | envolviendo | 3 |
| 27711 | envolverse | 3 |
| 27712 | envíeme | 3 |
| 27713 | envido | 3 |
| 27714 | envidiar | 3 |
| 27715 | envidiados | 3 |
| 27716 | enviarme | 3 |
| 27717 | enviará | 3 |
| 27718 | enviando | 3 |
| 27719 | envenenar | 3 |
| 27720 | envenenamiento | 3 |
| 27721 | envenenada | 3 |
| 27722 | envejecía | 3 |
| 27723 | envejecen | 3 |
| 27724 | envalentonó | 3 |
| 27725 | envainó | 3 |
| 27726 | enumeraba | 3 |
| 27727 | entusiasmó | 3 |
| 27728 | enturbió | 3 |
| 27729 | entronizado | 3 |
| 27730 | entrometida | 3 |
| 27731 | entristezca | 3 |
| 27732 | entristecían | 3 |
| 27733 | entristece | 3 |
| 27734 | entretuviese | 3 |
| 27735 | entremeterse | 3 |
| 27736 | entremeter | 3 |
| 27737 | entregarme | 3 |
| 27738 | entregarlos | 3 |
| 27739 | entregaría | 3 |
| 27740 | entregaran | 3 |
| 27741 | entregándose | 3 |
| 27742 | entregando | 3 |
| 27743 | entregadas | 3 |
| 27744 | entreabiertos | 3 |
| 27745 | entreabiertas | 3 |
| 27746 | entrava | 3 |
| 27747 | entrauas | 3 |
| 27748 | éntrate | 3 |
| 27749 | entráronle | 3 |
| 27750 | entrarnos | 3 |
| 27751 | entrarme | 3 |
| 27752 | entrábale | 3 |
| 27753 | entornados | 3 |
| 27754 | entono | 3 |
| 27755 | entonación | 3 |
| 27756 | entona | 3 |
| 27757 | entierre | 3 |
| 27758 | entierra | 3 |
| 27759 | entiéndelo | 3 |
| 27760 | enterose | 3 |
| 27761 | enternecimientos | 3 |
| 27762 | enternece | 3 |
| 27763 | entérese | 3 |
| 27764 | enteré | 3 |
| 27765 | enterasen | 3 |
| 27766 | enteraron | 3 |
| 27767 | enterara | 3 |
| 27768 | enterar | 3 |
| 27769 | entendióle | 3 |
| 27770 | entendiere | 3 |
| 27771 | entendernos | 3 |
| 27772 | entenderle | 3 |
| 27773 | entenderlas | 3 |
| 27774 | entabló | 3 |
| 27775 | ensueño | 3 |
| 27776 | enssienplo | 3 |
| 27777 | ensillase | 3 |
| 27778 | enseñóle | 3 |
| 27779 | enseñes | 3 |
| 27780 | enseñen | 3 |
| 27781 | enseñas | 3 |
| 27782 | enseñarla | 3 |
| 27783 | enseñaría | 3 |
| 27784 | ensanche | 3 |
| 27785 | ensalzar | 3 |
| 27786 | enroscándose | 3 |
| 27787 | enroscadas | 3 |
| 27788 | enroscada | 3 |
| 27789 | enristró | 3 |
| 27790 | enriquecen | 3 |
| 27791 | enrejados | 3 |
| 27792 | enredado | 3 |
| 27793 | enredaba | 3 |
| 27794 | enperador | 3 |
| 27795 | enojosas | 3 |
| 27796 | enojó | 3 |
| 27797 | enojarse | 3 |
| 27798 | enojaba | 3 |
| 27799 | ennoblece | 3 |
| 27800 | ennegrecida | 3 |
| 27801 | enmudecer | 3 |
| 27802 | enmendó | 3 |
| 27803 | enlutadas | 3 |
| 27804 | enlazados | 3 |
| 27805 | enlazaba | 3 |
| 27806 | enjutos | 3 |
| 27807 | enjugaba | 3 |
| 27808 | enhorabuenas | 3 |
| 27809 | enguantada | 3 |
| 27810 | engrandecer | 3 |
| 27811 | engordado | 3 |
| 27812 | engorda | 3 |
| 27813 | engomado | 3 |
| 27814 | engastado | 3 |
| 27815 | engañosas | 3 |
| 27816 | engañarte | 3 |
| 27817 | engañara | 3 |
| 27818 | engañadas | 3 |
| 27819 | enganchadas | 3 |
| 27820 | enganar | 3 |
| 27821 | enfurruñaba | 3 |
| 27822 | enfriase | 3 |
| 27823 | enfriado | 3 |
| 27824 | enfría | 3 |
| 27825 | enfrenar | 3 |
| 27826 | enfermera | 3 |
| 27827 | enfáticamente | 3 |
| 27828 | enfática | 3 |
| 27829 | enérgicas | 3 |
| 27830 | endurecido | 3 |
| 27831 | endurecidas | 3 |
| 27832 | endilgó | 3 |
| 27833 | endiabladas | 3 |
| 27834 | enderezan | 3 |
| 27835 | encontreme | 3 |
| 27836 | encontraste | 3 |
| 27837 | encontrarme | 3 |
| 27838 | encontraran | 3 |
| 27839 | encontrándose | 3 |
| 27840 | encontrados | 3 |
| 27841 | encono | 3 |
| 27842 | encomio | 3 |
| 27843 | encomendo | 3 |
| 27844 | encoge | 3 |
| 27845 | encinta | 3 |
| 27846 | ençiende | 3 |
| 27847 | encharcados | 3 |
| 27848 | encerrase | 3 |
| 27849 | encarece | 3 |
| 27850 | encarcelado | 3 |
| 27851 | encarcelada | 3 |
| 27852 | encarado | 3 |
| 27853 | encapotado | 3 |
| 27854 | encantó | 3 |
| 27855 | encanta | 3 |
| 27856 | encandilados | 3 |
| 27857 | encaminóse | 3 |
| 27858 | encamina | 3 |
| 27859 | encajaba | 3 |
| 27860 | encadenados | 3 |
| 27861 | enbya | 3 |
| 27862 | enarbolando | 3 |
| 27863 | enamoro | 3 |
| 27864 | enamorando | 3 |
| 27865 | émula | 3 |
| 27866 | empuño | 3 |
| 27867 | empujándola | 3 |
| 27868 | empresario | 3 |
| 27869 | emprenta | 3 |
| 27870 | emprenderla | 3 |
| 27871 | emprendedor | 3 |
| 27872 | emprende | 3 |
| 27873 | empotrado | 3 |
| 27874 | empos | 3 |
| 27875 | empleomanía | 3 |
| 27876 | empleara | 3 |
| 27877 | empleadas | 3 |
| 27878 | emplastos | 3 |
| 27879 | empiece | 3 |
| 27880 | empezará | 3 |
| 27881 | empeoraba | 3 |
| 27882 | empeñe | 3 |
| 27883 | empeñaron | 3 |
| 27884 | empeñar | 3 |
| 27885 | empeñados | 3 |
| 27886 | empeñaban | 3 |
| 27887 | empellones | 3 |
| 27888 | empedrados | 3 |
| 27889 | empedrada | 3 |
| 27890 | empecer | 3 |
| 27891 | empecemos | 3 |
| 27892 | empecatada | 3 |
| 27893 | emparentado | 3 |
| 27894 | emparentada | 3 |
| 27895 | empapelar | 3 |
| 27896 | empañados | 3 |
| 27897 | empalagaba | 3 |
| 27898 | emisión | 3 |
| 27899 | emendar | 3 |
| 27900 | embutido | 3 |
| 27901 | embusteros | 3 |
| 27902 | embrutecimiento | 3 |
| 27903 | embrujado | 3 |
| 27904 | embromar | 3 |
| 27905 | embriagada | 3 |
| 27906 | embriagaba | 3 |
| 27907 | embozos | 3 |
| 27908 | embozándose | 3 |
| 27909 | embozada | 3 |
| 27910 | emboscó | 3 |
| 27911 | emboscar | 3 |
| 27912 | emborrachado | 3 |
| 27913 | emborrachaba | 3 |
| 27914 | embocó | 3 |
| 27915 | embocadura | 3 |
| 27916 | embobados | 3 |
| 27917 | embiste | 3 |
| 27918 | embie | 3 |
| 27919 | embiar | 3 |
| 27920 | embestido | 3 |
| 27921 | embarqué | 3 |
| 27922 | embarque | 3 |
| 27923 | embarga | 3 |
| 27924 | embarcaron | 3 |
| 27925 | embarcados | 3 |
| 27926 | embarazosa | 3 |
| 27927 | embarazada | 3 |
| 27928 | embaraza | 3 |
| 27929 | emanciparse | 3 |
| 27930 | emanaba | 3 |
| 27931 | emana | 3 |
| 27932 | elevan | 3 |
| 27933 | elevaban | 3 |
| 27934 | electrizaba | 3 |
| 27935 | elástica | 3 |
| 27936 | ejercitando | 3 |
| 27937 | ejercían | 3 |
| 27938 | ejercen | 3 |
| 27939 | ejerce | 3 |
| 27940 | ejecutor | 3 |
| 27941 | ejecutado | 3 |
| 27942 | ejecuta | 3 |
| 27943 | egipcia | 3 |
| 27944 | éfire | 3 |
| 27945 | efímeras | 3 |
| 27946 | efigie | 3 |
| 27947 | efetos | 3 |
| 27948 | efectuarse | 3 |
| 27949 | editores | 3 |
| 27950 | edipo | 3 |
| 27951 | edificantes | 3 |
| 27952 | edificado | 3 |
| 27953 | ediciones | 3 |
| 27954 | edic | 3 |
| 27955 | economías | 3 |
| 27956 | echóme | 3 |
| 27957 | echóle | 3 |
| 27958 | echeneis | 3 |
| 27959 | écheme | 3 |
| 27960 | echaste | 3 |
| 27961 | echásemos | 3 |
| 27962 | echarte | 3 |
| 27963 | echárselas | 3 |
| 27964 | echarles | 3 |
| 27965 | echándoselas | 3 |
| 27966 | echándosela | 3 |
| 27967 | echándome | 3 |
| 27968 | echándola | 3 |
| 27969 | écarté | 3 |
| 27970 | ébano | 3 |
| 27971 | è | 3 |
| 27972 | dyxo | 3 |
| 27973 | dyos | 3 |
| 27974 | dyó | 3 |
| 27975 | duz | 3 |
| 27976 | durmiose | 3 |
| 27977 | durmiente | 3 |
| 27978 | durmamos | 3 |
| 27979 | durable | 3 |
| 27980 | duraban | 3 |
| 27981 | dumas | 3 |
| 27982 | dueñesco | 3 |
| 27983 | duende | 3 |
| 27984 | dudarlo | 3 |
| 27985 | dudaban | 3 |
| 27986 | dubdosa | 3 |
| 27987 | dromedarios | 3 |
| 27988 | droga | 3 |
| 27989 | dozena | 3 |
| 27990 | doto | 3 |
| 27991 | dormirme | 3 |
| 27992 | dormiremos | 3 |
| 27993 | doñeos | 3 |
| 27994 | doñear | 3 |
| 27995 | doñeador | 3 |
| 27996 | donosas | 3 |
| 27997 | doncellez | 3 |
| 27998 | dominum | 3 |
| 27999 | domini | 3 |
| 28000 | dominarle | 3 |
| 28001 | dominan | 3 |
| 28002 | domiciliaria | 3 |
| 28003 | domar | 3 |
| 28004 | domado | 3 |
| 28005 | domada | 3 |
| 28006 | doma | 3 |
| 28007 | dolo | 3 |
| 28008 | doliera | 3 |
| 28009 | dolerse | 3 |
| 28010 | dogal | 3 |
| 28011 | doctas | 3 |
| 28012 | díxol | 3 |
| 28013 | dixiéronle | 3 |
| 28014 | dixeron | 3 |
| 28015 | dix | 3 |
| 28016 | divisó | 3 |
| 28017 | dividirse | 3 |
| 28018 | dividieron | 3 |
| 28019 | divididas | 3 |
| 28020 | divertidas | 3 |
| 28021 | diva | 3 |
| 28022 | distintivo | 3 |
| 28023 | distingos | 3 |
| 28024 | distinciones | 3 |
| 28025 | dissimular | 3 |
| 28026 | dissimulado | 3 |
| 28027 | disputaron | 3 |
| 28028 | dispuse | 3 |
| 28029 | dispersos | 3 |
| 28030 | dispensas | 3 |
| 28031 | dispensado | 3 |
| 28032 | disparadero | 3 |
| 28033 | disolviendo | 3 |
| 28034 | disolvente | 3 |
| 28035 | disoluta | 3 |
| 28036 | dislocado | 3 |
| 28037 | dislocada | 3 |
| 28038 | disipado | 3 |
| 28039 | disimularon | 3 |
| 28040 | disimularla | 3 |
| 28041 | disimuladas | 3 |
| 28042 | disimulaban | 3 |
| 28043 | disgustada | 3 |
| 28044 | disgusta | 3 |
| 28045 | disfrazaron | 3 |
| 28046 | disfavor | 3 |
| 28047 | dises | 3 |
| 28048 | disertación | 3 |
| 28049 | diser | 3 |
| 28050 | discutiendo | 3 |
| 28051 | disculpo | 3 |
| 28052 | disculpando | 3 |
| 28053 | discordantes | 3 |
| 28054 | discipulo | 3 |
| 28055 | discernir | 3 |
| 28056 | dirigióse | 3 |
| 28057 | dirigidos | 3 |
| 28058 | dirigí | 3 |
| 28059 | diríe | 3 |
| 28060 | dirévos | 3 |
| 28061 | direvos | 3 |
| 28062 | directiva | 3 |
| 28063 | diplomáticos | 3 |
| 28064 | díos | 3 |
| 28065 | dionos | 3 |
| 28066 | dioles | 3 |
| 28067 | dinastía | 3 |
| 28068 | diminuto | 3 |
| 28069 | dímela | 3 |
| 28070 | dilatas | 3 |
| 28071 | dilatando | 3 |
| 28072 | dilaciones | 3 |
| 28073 | dijistes | 3 |
| 28074 | dijímosle | 3 |
| 28075 | digestiones | 3 |
| 28076 | digerir | 3 |
| 28077 | digería | 3 |
| 28078 | dificultaba | 3 |
| 28079 | dificilillo | 3 |
| 28080 | dificil | 3 |
| 28081 | diferenciaba | 3 |
| 28082 | diéronselos | 3 |
| 28083 | diéredes | 3 |
| 28084 | dieras | 3 |
| 28085 | diecinueve | 3 |
| 28086 | dictó | 3 |
| 28087 | dictar | 3 |
| 28088 | dicta | 3 |
| 28089 | dicharachos | 3 |
| 28090 | dibujó | 3 |
| 28091 | diapasón | 3 |
| 28092 | diantres | 3 |
| 28093 | dializado | 3 |
| 28094 | diagonales | 3 |
| 28095 | diabólicas | 3 |
| 28096 | diablillos | 3 |
| 28097 | dezidme | 3 |
| 28098 | dezian | 3 |
| 28099 | dexóme | 3 |
| 28100 | dexieron | 3 |
| 28101 | dexen | 3 |
| 28102 | dexat | 3 |
| 28103 | dexare | 3 |
| 28104 | dexale | 3 |
| 28105 | dexala | 3 |
| 28106 | dexadas | 3 |
| 28107 | devorándola | 3 |
| 28108 | devorado | 3 |
| 28109 | devoraban | 3 |
| 28110 | devoçión | 3 |
| 28111 | devezes | 3 |
| 28112 | devanaba | 3 |
| 28113 | deuociones | 3 |
| 28114 | deudores | 3 |
| 28115 | detuviera | 3 |
| 28116 | detienen | 3 |
| 28117 | determinan | 3 |
| 28118 | deteniéndole | 3 |
| 28119 | detenían | 3 |
| 28120 | detengamos | 3 |
| 28121 | detén | 3 |
| 28122 | desvióse | 3 |
| 28123 | desvió | 3 |
| 28124 | desviarse | 3 |
| 28125 | desvía | 3 |
| 28126 | desvergüenzas | 3 |
| 28127 | desventurados | 3 |
| 28128 | desvencijadas | 3 |
| 28129 | desvencijada | 3 |
| 28130 | desvariado | 3 |
| 28131 | desvanecieron | 3 |
| 28132 | desvaneciéndose | 3 |
| 28133 | desvanecen | 3 |
| 28134 | desuariar | 3 |
| 28135 | destruya | 3 |
| 28136 | destrozos | 3 |
| 28137 | destraído | 3 |
| 28138 | destinados | 3 |
| 28139 | destinaba | 3 |
| 28140 | destierra | 3 |
| 28141 | destellos | 3 |
| 28142 | destello | 3 |
| 28143 | destajo | 3 |
| 28144 | desso | 3 |
| 28145 | desse | 3 |
| 28146 | desquite | 3 |
| 28147 | desputar | 3 |
| 28148 | desputaçión | 3 |
| 28149 | desproporción | 3 |
| 28150 | desprendido | 3 |
| 28151 | desprende | 3 |
| 28152 | despojar | 3 |
| 28153 | desplomó | 3 |
| 28154 | desplomarse | 3 |
| 28155 | despilfarros | 3 |
| 28156 | despidese | 3 |
| 28157 | despiadado | 3 |
| 28158 | despiadada | 3 |
| 28159 | despertarle | 3 |
| 28160 | despertarla | 3 |
| 28161 | despertalle | 3 |
| 28162 | desperezándose | 3 |
| 28163 | despeñado | 3 |
| 28164 | despeñada | 3 |
| 28165 | despenseros | 3 |
| 28166 | despensero | 3 |
| 28167 | despenado | 3 |
| 28168 | despega | 3 |
| 28169 | despedazaba | 3 |
| 28170 | despavoridos | 3 |
| 28171 | despaché | 3 |
| 28172 | despachando | 3 |
| 28173 | despabilarse | 3 |
| 28174 | despabilar | 3 |
| 28175 | desórdenes | 3 |
| 28176 | desocupados | 3 |
| 28177 | desocupada | 3 |
| 28178 | desobediencia | 3 |
| 28179 | desnudeces | 3 |
| 28180 | desnudándose | 3 |
| 28181 | desmiento | 3 |
| 28182 | desmiente | 3 |
| 28183 | desmenuzar | 3 |
| 28184 | desmenuzaba | 3 |
| 28185 | desmentía | 3 |
| 28186 | desmedrada | 3 |
| 28187 | desmedida | 3 |
| 28188 | desmañado | 3 |
| 28189 | deslomo | 3 |
| 28190 | deslizarse | 3 |
| 28191 | deslizaban | 3 |
| 28192 | desliz | 3 |
| 28193 | deslenguado | 3 |
| 28194 | desleído | 3 |
| 28195 | desirte | 3 |
| 28196 | desires | 3 |
| 28197 | desinterés | 3 |
| 28198 | desiertas | 3 |
| 28199 | desid | 3 |
| 28200 | deshoras | 3 |
| 28201 | deshonor | 3 |
| 28202 | deshojar | 3 |
| 28203 | deshilachada | 3 |
| 28204 | deshiciese | 3 |
| 28205 | deshago | 3 |
| 28206 | deshacen | 3 |
| 28207 | desgobernado | 3 |
| 28208 | desfavorables | 3 |
| 28209 | desfavorable | 3 |
| 28210 | desfaga | 3 |
| 28211 | desfacer | 3 |
| 28212 | desface | 3 |
| 28213 | desesperacion | 3 |
| 28214 | deseosas | 3 |
| 28215 | desenvuelto | 3 |
| 28216 | desenvainada | 3 |
| 28217 | desentonada | 3 |
| 28218 | desenlace | 3 |
| 28219 | desengañarse | 3 |
| 28220 | desenfadado | 3 |
| 28221 | desencantarla | 3 |
| 28222 | desempeñara | 3 |
| 28223 | desembarazaron | 3 |
| 28224 | desembarazar | 3 |
| 28225 | desechos | 3 |
| 28226 | desecho | 3 |
| 28227 | deseche | 3 |
| 28228 | desechados | 3 |
| 28229 | desearía | 3 |
| 28230 | desdoro | 3 |
| 28231 | desdeñaba | 3 |
| 28232 | descuidarse | 3 |
| 28233 | descuentos | 3 |
| 28234 | descuento | 3 |
| 28235 | descubrieran | 3 |
| 28236 | descubras | 3 |
| 28237 | describirla | 3 |
| 28238 | desconsoladas | 3 |
| 28239 | desconocimiento | 3 |
| 28240 | desconocía | 3 |
| 28241 | desconfianzas | 3 |
| 28242 | desconfiados | 3 |
| 28243 | desconfiada | 3 |
| 28244 | descomunales | 3 |
| 28245 | descompuestos | 3 |
| 28246 | descompostura | 3 |
| 28247 | descollaban | 3 |
| 28248 | descenso | 3 |
| 28249 | descendían | 3 |
| 28250 | descendencia | 3 |
| 28251 | descarriada | 3 |
| 28252 | descargada | 3 |
| 28253 | descarado | 3 |
| 28254 | descansadamente | 3 |
| 28255 | descaminada | 3 |
| 28256 | descaecimiento | 3 |
| 28257 | desbaratar | 3 |
| 28258 | desbaratado | 3 |
| 28259 | desbarataba | 3 |
| 28260 | desazones | 3 |
| 28261 | desavenencias | 3 |
| 28262 | desatinar | 3 |
| 28263 | desatarse | 3 |
| 28264 | desataron | 3 |
| 28265 | desataban | 3 |
| 28266 | desataba | 3 |
| 28267 | desastrada | 3 |
| 28268 | desasosegado | 3 |
| 28269 | desasosegada | 3 |
| 28270 | desarmada | 3 |
| 28271 | desanimado | 3 |
| 28272 | desanimaba | 3 |
| 28273 | desamparó | 3 |
| 28274 | desampare | 3 |
| 28275 | desamparar | 3 |
| 28276 | desamorado | 3 |
| 28277 | desalquilado | 3 |
| 28278 | desaliño | 3 |
| 28279 | desalado | 3 |
| 28280 | desahogan | 3 |
| 28281 | desahogada | 3 |
| 28282 | desaforada | 3 |
| 28283 | desafió | 3 |
| 28284 | desafiarle | 3 |
| 28285 | desacreditar | 3 |
| 28286 | desacreditan | 3 |
| 28287 | desacato | 3 |
| 28288 | desabridos | 3 |
| 28289 | derrumbadas | 3 |
| 28290 | derrotados | 3 |
| 28291 | derribóle | 3 |
| 28292 | derrames | 3 |
| 28293 | derramaron | 3 |
| 28294 | derramamiento | 3 |
| 28295 | derechito | 3 |
| 28296 | derechita | 3 |
| 28297 | depresiones | 3 |
| 28298 | depositando | 3 |
| 28299 | depositado | 3 |
| 28300 | deploraba | 3 |
| 28301 | depender | 3 |
| 28302 | departe | 3 |
| 28303 | departa | 3 |
| 28304 | denunciaba | 3 |
| 28305 | denuesto | 3 |
| 28306 | denostada | 3 |
| 28307 | denominación | 3 |
| 28308 | denle | 3 |
| 28309 | dengues | 3 |
| 28310 | demostrado | 3 |
| 28311 | demostina | 3 |
| 28312 | demonche | 3 |
| 28313 | demasiadas | 3 |
| 28314 | demandó | 3 |
| 28315 | demandado | 3 |
| 28316 | delinquente | 3 |
| 28317 | delicto | 3 |
| 28318 | delicadísimo | 3 |
| 28319 | delicadamente | 3 |
| 28320 | deliberadamente | 3 |
| 28321 | deliberada | 3 |
| 28322 | deletérea | 3 |
| 28323 | delanteros | 3 |
| 28324 | delanteras | 3 |
| 28325 | dejónos | 3 |
| 28326 | déjenmos | 3 |
| 28327 | dejémosle | 3 |
| 28328 | déjase | 3 |
| 28329 | dejaros | 3 |
| 28330 | dejarlos | 3 |
| 28331 | dejarás | 3 |
| 28332 | dejándolos | 3 |
| 28333 | déjalo | 3 |
| 28334 | deidades | 3 |
| 28335 | degradante | 3 |
| 28336 | degollados | 3 |
| 28337 | definir | 3 |
| 28338 | defiéndete | 3 |
| 28339 | defiendan | 3 |
| 28340 | defensas | 3 |
| 28341 | defenderá | 3 |
| 28342 | defectillos | 3 |
| 28343 | deducirse | 3 |
| 28344 | deduce | 3 |
| 28345 | dedicaron | 3 |
| 28346 | dedicar | 3 |
| 28347 | dedica | 3 |
| 28348 | decretos | 3 |
| 28349 | decretales | 3 |
| 28350 | decretado | 3 |
| 28351 | decrépito | 3 |
| 28352 | decoraban | 3 |
| 28353 | declinación | 3 |
| 28354 | declina | 3 |
| 28355 | declararte | 3 |
| 28356 | declararon | 3 |
| 28357 | declarándole | 3 |
| 28358 | declaraciones | 3 |
| 28359 | decírsela | 3 |
| 28360 | decírmelo | 3 |
| 28361 | decirlos | 3 |
| 28362 | décima | 3 |
| 28363 | decillo | 3 |
| 28364 | decilla | 3 |
| 28365 | deciendo | 3 |
| 28366 | decido | 3 |
| 28367 | decidía | 3 |
| 28368 | decíase | 3 |
| 28369 | decantado | 3 |
| 28370 | decálogo | 3 |
| 28371 | decaído | 3 |
| 28372 | decaer | 3 |
| 28373 | debieras | 3 |
| 28374 | deberían | 3 |
| 28375 | debates | 3 |
| 28376 | davan | 3 |
| 28377 | dat | 3 |
| 28378 | dáselo | 3 |
| 28379 | darwinismo | 3 |
| 28380 | darwin | 3 |
| 28381 | dártela | 3 |
| 28382 | dárselos | 3 |
| 28383 | dárselas | 3 |
| 28384 | darl | 3 |
| 28385 | darias | 3 |
| 28386 | dares | 3 |
| 28387 | dañan | 3 |
| 28388 | dañados | 3 |
| 28389 | danzando | 3 |
| 28390 | danle | 3 |
| 28391 | daniel | 3 |
| 28392 | dándosela | 3 |
| 28393 | dándonos | 3 |
| 28394 | danada | 3 |
| 28395 | dami | 3 |
| 28396 | dalde | 3 |
| 28397 | dador | 3 |
| 28398 | dadnos | 3 |
| 28399 | dádmele | 3 |
| 28400 | dadle | 3 |
| 28401 | dabo | 3 |
| 28402 | dábanme | 3 |
| 28403 | dábamos | 3 |
| 28404 | dábame | 3 |
| 28405 | dábales | 3 |
| 28406 | cuydós | 3 |
| 28407 | cuydé | 3 |
| 28408 | cuydar | 3 |
| 28409 | cúya | 3 |
| 28410 | curtidores | 3 |
| 28411 | curtido | 3 |
| 28412 | curial | 3 |
| 28413 | cures | 3 |
| 28414 | curen | 3 |
| 28415 | curase | 3 |
| 28416 | curadas | 3 |
| 28417 | cúpula | 3 |
| 28418 | cupiese | 3 |
| 28419 | cunplir | 3 |
| 28420 | cunplen | 3 |
| 28421 | cundía | 3 |
| 28422 | cumplirse | 3 |
| 28423 | cumplirla | 3 |
| 28424 | cumplirás | 3 |
| 28425 | cumples | 3 |
| 28426 | cultivada | 3 |
| 28427 | culpada | 3 |
| 28428 | culpabilidad | 3 |
| 28429 | culpaba | 3 |
| 28430 | culinario | 3 |
| 28431 | culinaria | 3 |
| 28432 | cuidaban | 3 |
| 28433 | cuerpecillo | 3 |
| 28434 | cuece | 3 |
| 28435 | cuchicheaban | 3 |
| 28436 | cubriese | 3 |
| 28437 | cuatralbo | 3 |
| 28438 | cuartillos | 3 |
| 28439 | cuarterones | 3 |
| 28440 | cuartas | 3 |
| 28441 | cuantiosos | 3 |
| 28442 | cuajo | 3 |
| 28443 | cuadritos | 3 |
| 28444 | cuadre | 3 |
| 28445 | cuadratura | 3 |
| 28446 | cuadraba | 3 |
| 28447 | crujió | 3 |
| 28448 | crujieron | 3 |
| 28449 | crujientes | 3 |
| 28450 | cronista | 3 |
| 28451 | cromos | 3 |
| 28452 | cromo | 3 |
| 28453 | cristos | 3 |
| 28454 | cristianamente | 3 |
| 28455 | cristalina | 3 |
| 28456 | críe | 3 |
| 28457 | cribas | 3 |
| 28458 | creyentes | 3 |
| 28459 | creyéndome | 3 |
| 28460 | creyéndola | 3 |
| 28461 | crepuscular | 3 |
| 28462 | creó | 3 |
| 28463 | creímos | 3 |
| 28464 | creerle | 3 |
| 28465 | creeréis | 3 |
| 28466 | crédula | 3 |
| 28467 | créditos | 3 |
| 28468 | crecían | 3 |
| 28469 | créanmelo | 3 |
| 28470 | creades | 3 |
| 28471 | creaciones | 3 |
| 28472 | crasa | 3 |
| 28473 | covarde | 3 |
| 28474 | coto | 3 |
| 28475 | costurones | 3 |
| 28476 | costureras | 3 |
| 28477 | costras | 3 |
| 28478 | costosas | 3 |
| 28479 | costosa | 3 |
| 28480 | costo | 3 |
| 28481 | costara | 3 |
| 28482 | cossas | 3 |
| 28483 | cosidos | 3 |
| 28484 | cosida | 3 |
| 28485 | cose | 3 |
| 28486 | coscorrón | 3 |
| 28487 | cosario | 3 |
| 28488 | corvillo | 3 |
| 28489 | corvetas | 3 |
| 28490 | cortinaje | 3 |
| 28491 | cortesia | 3 |
| 28492 | cortesanías | 3 |
| 28493 | cortarse | 3 |
| 28494 | cortarme | 3 |
| 28495 | cortante | 3 |
| 28496 | cortándole | 3 |
| 28497 | cortadillo | 3 |
| 28498 | corsario | 3 |
| 28499 | corrupto | 3 |
| 28500 | corrompida | 3 |
| 28501 | corriste | 3 |
| 28502 | corrigen | 3 |
| 28503 | correspondió | 3 |
| 28504 | correrla | 3 |
| 28505 | corregida | 3 |
| 28506 | corredera | 3 |
| 28507 | correctas | 3 |
| 28508 | correctamente | 3 |
| 28509 | correción | 3 |
| 28510 | corralada | 3 |
| 28511 | corpulenta | 3 |
| 28512 | corpulencia | 3 |
| 28513 | corpiños | 3 |
| 28514 | corpachón | 3 |
| 28515 | cornisas | 3 |
| 28516 | cornejo | 3 |
| 28517 | cornado | 3 |
| 28518 | coristas | 3 |
| 28519 | corinto | 3 |
| 28520 | coria | 3 |
| 28521 | cordialmente | 3 |
| 28522 | cordiales | 3 |
| 28523 | cordera | 3 |
| 28524 | corder | 3 |
| 28525 | cordales | 3 |
| 28526 | corcovos | 3 |
| 28527 | corbatines | 3 |
| 28528 | coquetona | 3 |
| 28529 | coqueterías | 3 |
| 28530 | copiado | 3 |
| 28531 | cooperación | 3 |
| 28532 | cónyuges | 3 |
| 28533 | conyugales | 3 |
| 28534 | convoca | 3 |
| 28535 | convide | 3 |
| 28536 | convidaron | 3 |
| 28537 | convertirla | 3 |
| 28538 | convertidas | 3 |
| 28539 | converso | 3 |
| 28540 | conversar | 3 |
| 28541 | convengan | 3 |
| 28542 | convengamos | 3 |
| 28543 | convencieron | 3 |
| 28544 | convenciendo | 3 |
| 28545 | contusión | 3 |
| 28546 | contundentes | 3 |
| 28547 | contrito | 3 |
| 28548 | contrición | 3 |
| 28549 | contribución | 3 |
| 28550 | contreçión | 3 |
| 28551 | contrecho | 3 |
| 28552 | contravenido | 3 |
| 28553 | contratos | 3 |
| 28554 | contratas | 3 |
| 28555 | contrariaba | 3 |
| 28556 | contrapunto | 3 |
| 28557 | contrapuestos | 3 |
| 28558 | contraído | 3 |
| 28559 | contraía | 3 |
| 28560 | contrahacer | 3 |
| 28561 | contradictorias | 3 |
| 28562 | contradecían | 3 |
| 28563 | contrabandistas | 3 |
| 28564 | contr | 3 |
| 28565 | contoneo | 3 |
| 28566 | contole | 3 |
| 28567 | continuidad | 3 |
| 28568 | continuase | 3 |
| 28569 | continuaron | 3 |
| 28570 | continuado | 3 |
| 28571 | continuación | 3 |
| 28572 | contina | 3 |
| 28573 | contestole | 3 |
| 28574 | contestas | 3 |
| 28575 | contéstame | 3 |
| 28576 | contentóme | 3 |
| 28577 | contentísimas | 3 |
| 28578 | contentase | 3 |
| 28579 | contentarle | 3 |
| 28580 | contentaría | 3 |
| 28581 | contentará | 3 |
| 28582 | contentándose | 3 |
| 28583 | contentamos | 3 |
| 28584 | contenidas | 3 |
| 28585 | contemporizar | 3 |
| 28586 | contemporáneo | 3 |
| 28587 | contemporánea | 3 |
| 28588 | contemplé | 3 |
| 28589 | contemplado | 3 |
| 28590 | contéles | 3 |
| 28591 | contárselo | 3 |
| 28592 | contaros | 3 |
| 28593 | contármelo | 3 |
| 28594 | contarlas | 3 |
| 28595 | contaría | 3 |
| 28596 | contaria | 3 |
| 28597 | contándolos | 3 |
| 28598 | contándoles | 3 |
| 28599 | contamos | 3 |
| 28600 | contadme | 3 |
| 28601 | contad | 3 |
| 28602 | contábamos | 3 |
| 28603 | consumiendo | 3 |
| 28604 | consumidores | 3 |
| 28605 | consumían | 3 |
| 28606 | consumen | 3 |
| 28607 | consultarle | 3 |
| 28608 | consultando | 3 |
| 28609 | cónsules | 3 |
| 28610 | consuetudinaria | 3 |
| 28611 | construiría | 3 |
| 28612 | construían | 3 |
| 28613 | construía | 3 |
| 28614 | construcciones | 3 |
| 28615 | constituir | 3 |
| 28616 | constituida | 3 |
| 28617 | constituçión | 3 |
| 28618 | consternado | 3 |
| 28619 | constelaciones | 3 |
| 28620 | constantes | 3 |
| 28621 | consseja | 3 |
| 28622 | conspirar | 3 |
| 28623 | conspirador | 3 |
| 28624 | consorcio | 3 |
| 28625 | consonantes | 3 |
| 28626 | consolé | 3 |
| 28627 | consolas | 3 |
| 28628 | consolador | 3 |
| 28629 | consolaban | 3 |
| 28630 | consistente | 3 |
| 28631 | consiguiendo | 3 |
| 28632 | considerase | 3 |
| 28633 | considerarse | 3 |
| 28634 | considerarme | 3 |
| 28635 | conservas | 3 |
| 28636 | conservarla | 3 |
| 28637 | consentiría | 3 |
| 28638 | consentirá | 3 |
| 28639 | consentían | 3 |
| 28640 | conseguiría | 3 |
| 28641 | conseguimos | 3 |
| 28642 | consagrados | 3 |
| 28643 | conplidamente | 3 |
| 28644 | conpaño | 3 |
| 28645 | conoscido | 3 |
| 28646 | conosçía | 3 |
| 28647 | conoscia | 3 |
| 28648 | conocíla | 3 |
| 28649 | conocerme | 3 |
| 28650 | conocerlos | 3 |
| 28651 | conocelle | 3 |
| 28652 | conjúrote | 3 |
| 28653 | conjurar | 3 |
| 28654 | conjuración | 3 |
| 28655 | conjetura | 3 |
| 28656 | congojosa | 3 |
| 28657 | congojó | 3 |
| 28658 | congojado | 3 |
| 28659 | confundirse | 3 |
| 28660 | confundiese | 3 |
| 28661 | confundiéndose | 3 |
| 28662 | confundida | 3 |
| 28663 | confunden | 3 |
| 28664 | conformarnos | 3 |
| 28665 | conformado | 3 |
| 28666 | confonda | 3 |
| 28667 | confirmándose | 3 |
| 28668 | confirman | 3 |
| 28669 | confió | 3 |
| 28670 | confines | 3 |
| 28671 | configuración | 3 |
| 28672 | confiésame | 3 |
| 28673 | confianzudo | 3 |
| 28674 | confessar | 3 |
| 28675 | confesonarios | 3 |
| 28676 | confesarle | 3 |
| 28677 | conferenciando | 3 |
| 28678 | confabulado | 3 |
| 28679 | conduta | 3 |
| 28680 | condumio | 3 |
| 28681 | condimento | 3 |
| 28682 | condicionales | 3 |
| 28683 | condesas | 3 |
| 28684 | condenes | 3 |
| 28685 | condene | 3 |
| 28686 | condenando | 3 |
| 28687 | condenaban | 3 |
| 28688 | concurridos | 3 |
| 28689 | concurría | 3 |
| 28690 | concurrentes | 3 |
| 28691 | concurren | 3 |
| 28692 | concretas | 3 |
| 28693 | concluyese | 3 |
| 28694 | concluyera | 3 |
| 28695 | concluyente | 3 |
| 28696 | concluyen | 3 |
| 28697 | conclusiones | 3 |
| 28698 | concluiremos | 3 |
| 28699 | concluirá | 3 |
| 28700 | concluído | 3 |
| 28701 | conciliador | 3 |
| 28702 | conciliación | 3 |
| 28703 | concierta | 3 |
| 28704 | concernientes | 3 |
| 28705 | conceptuaba | 3 |
| 28706 | concentrada | 3 |
| 28707 | concediste | 3 |
| 28708 | concediese | 3 |
| 28709 | concedieron | 3 |
| 28710 | concedían | 3 |
| 28711 | concederle | 3 |
| 28712 | concebí | 3 |
| 28713 | conbid | 3 |
| 28714 | conato | 3 |
| 28715 | comunidades | 3 |
| 28716 | comunico | 3 |
| 28717 | comunicativa | 3 |
| 28718 | comunicase | 3 |
| 28719 | comunicarse | 3 |
| 28720 | comunicándose | 3 |
| 28721 | comunicando | 3 |
| 28722 | comunican | 3 |
| 28723 | comunicaban | 3 |
| 28724 | comte | 3 |
| 28725 | compungido | 3 |
| 28726 | compuertas | 3 |
| 28727 | comprometen | 3 |
| 28728 | comprobar | 3 |
| 28729 | compres | 3 |
| 28730 | comprendiera | 3 |
| 28731 | comprendida | 3 |
| 28732 | comprendemos | 3 |
| 28733 | comprarme | 3 |
| 28734 | comprarla | 3 |
| 28735 | comprara | 3 |
| 28736 | compran | 3 |
| 28737 | compramos | 3 |
| 28738 | compradores | 3 |
| 28739 | compraban | 3 |
| 28740 | comprábamos | 3 |
| 28741 | composturas | 3 |
| 28742 | compongo | 3 |
| 28743 | componerle | 3 |
| 28744 | complido | 3 |
| 28745 | complida | 3 |
| 28746 | complicidad | 3 |
| 28747 | completaba | 3 |
| 28748 | complaciéndose | 3 |
| 28749 | complacido | 3 |
| 28750 | complacerle | 3 |
| 28751 | competente | 3 |
| 28752 | compensar | 3 |
| 28753 | compatrioto | 3 |
| 28754 | compatible | 3 |
| 28755 | comparsas | 3 |
| 28756 | comparó | 3 |
| 28757 | compare | 3 |
| 28758 | compararme | 3 |
| 28759 | comparada | 3 |
| 28760 | compaño | 3 |
| 28761 | compaginar | 3 |
| 28762 | compadres | 3 |
| 28763 | compadeció | 3 |
| 28764 | compadecerse | 3 |
| 28765 | compadece | 3 |
| 28766 | comp | 3 |
| 28767 | comisionados | 3 |
| 28768 | comilonas | 3 |
| 28769 | comilón | 3 |
| 28770 | comiesen | 3 |
| 28771 | comience | 3 |
| 28772 | comidos | 3 |
| 28773 | cómicas | 3 |
| 28774 | cometieron | 3 |
| 28775 | cometiera | 3 |
| 28776 | cometían | 3 |
| 28777 | cometas | 3 |
| 28778 | comeremos | 3 |
| 28779 | comenzaría | 3 |
| 28780 | comentar | 3 |
| 28781 | començé | 3 |
| 28782 | comedidos | 3 |
| 28783 | comedida | 3 |
| 28784 | comediantes | 3 |
| 28785 | combustible | 3 |
| 28786 | combinando | 3 |
| 28787 | combinaba | 3 |
| 28788 | combatió | 3 |
| 28789 | combatiente | 3 |
| 28790 | comarcanos | 3 |
| 28791 | columbrar | 3 |
| 28792 | colosales | 3 |
| 28793 | coloradita | 3 |
| 28794 | coloque | 3 |
| 28795 | colonos | 3 |
| 28796 | colonias | 3 |
| 28797 | colocando | 3 |
| 28798 | colmó | 3 |
| 28799 | colmada | 3 |
| 28800 | colindantes | 3 |
| 28801 | colijo | 3 |
| 28802 | coligiendo | 3 |
| 28803 | colgadura | 3 |
| 28804 | colegir | 3 |
| 28805 | colchas | 3 |
| 28806 | colarse | 3 |
| 28807 | colapso | 3 |
| 28808 | colán | 3 |
| 28809 | cojeando | 3 |
| 28810 | coincidir | 3 |
| 28811 | coincidido | 3 |
| 28812 | cogidas | 3 |
| 28813 | coetáneo | 3 |
| 28814 | codorniz | 3 |
| 28815 | codillo | 3 |
| 28816 | codiciosa | 3 |
| 28817 | codicilo | 3 |
| 28818 | cocos | 3 |
| 28819 | cocineras | 3 |
| 28820 | cochinada | 3 |
| 28821 | cochina | 3 |
| 28822 | cobrase | 3 |
| 28823 | cobraba | 3 |
| 28824 | cobija | 3 |
| 28825 | cobertura | 3 |
| 28826 | cobertera | 3 |
| 28827 | cobdiciosa | 3 |
| 28828 | cobdiçian | 3 |
| 28829 | cleriguito | 3 |
| 28830 | clericales | 3 |
| 28831 | clementina | 3 |
| 28832 | clavellinas | 3 |
| 28833 | clavazón | 3 |
| 28834 | clavarle | 3 |
| 28835 | claudio | 3 |
| 28836 | clás | 3 |
| 28837 | claritas | 3 |
| 28838 | clarísimos | 3 |
| 28839 | claridat | 3 |
| 28840 | claridades | 3 |
| 28841 | clarear | 3 |
| 28842 | claraboyas | 3 |
| 28843 | claques | 3 |
| 28844 | clac | 3 |
| 28845 | civilizados | 3 |
| 28846 | citó | 3 |
| 28847 | cito | 3 |
| 28848 | cítara | 3 |
| 28849 | citados | 3 |
| 28850 | citadas | 3 |
| 28851 | cisterna | 3 |
| 28852 | cisco | 3 |
| 28853 | circunvecinos | 3 |
| 28854 | circe | 3 |
| 28855 | ciñó | 3 |
| 28856 | ciñen | 3 |
| 28857 | cínicos | 3 |
| 28858 | cilicios | 3 |
| 28859 | cilicio | 3 |
| 28860 | çiertos | 3 |
| 28861 | científica | 3 |
| 28862 | çient | 3 |
| 28863 | ciegan | 3 |
| 28864 | ciclistas | 3 |
| 28865 | ciceroniana | 3 |
| 28866 | cicatrices | 3 |
| 28867 | cibera | 3 |
| 28868 | çibdad | 3 |
| 28869 | chuscadas | 3 |
| 28870 | churrigueresca | 3 |
| 28871 | chupan | 3 |
| 28872 | chun | 3 |
| 28873 | chuleta | 3 |
| 28874 | chufas | 3 |
| 28875 | chuchería | 3 |
| 28876 | chocolatera | 3 |
| 28877 | chocante | 3 |
| 28878 | chocando | 3 |
| 28879 | chocaban | 3 |
| 28880 | chocaba | 3 |
| 28881 | choça | 3 |
| 28882 | choca | 3 |
| 28883 | chistoso | 3 |
| 28884 | chistó | 3 |
| 28885 | chisteras | 3 |
| 28886 | chis | 3 |
| 28887 | chinita | 3 |
| 28888 | chinescas | 3 |
| 28889 | chinche | 3 |
| 28890 | chichón | 3 |
| 28891 | chascos | 3 |
| 28892 | chartreuse | 3 |
| 28893 | charretera | 3 |
| 28894 | charlatana | 3 |
| 28895 | charca | 3 |
| 28896 | chapas | 3 |
| 28897 | chantre | 3 |
| 28898 | chançonetas | 3 |
| 28899 | chamusquina | 3 |
| 28900 | çevo | 3 |
| 28901 | cevil | 3 |
| 28902 | ceuta | 3 |
| 28903 | cesse | 3 |
| 28904 | céspedes | 3 |
| 28905 | cesen | 3 |
| 28906 | cesantes | 3 |
| 28907 | cerúlea | 3 |
| 28908 | certamen | 3 |
| 28909 | cerrojos | 3 |
| 28910 | cerré | 3 |
| 28911 | cerrad | 3 |
| 28912 | ceremoniosa | 3 |
| 28913 | ceremonial | 3 |
| 28914 | cerebrales | 3 |
| 28915 | cercos | 3 |
| 28916 | cercenando | 3 |
| 28917 | cercen | 3 |
| 28918 | cercanas | 3 |
| 28919 | çercado | 3 |
| 28920 | ceptro | 3 |
| 28921 | cepillar | 3 |
| 28922 | çenteno | 3 |
| 28923 | centella | 3 |
| 28924 | centavos | 3 |
| 28925 | ceno | 3 |
| 28926 | çeniza | 3 |
| 28927 | cenit | 3 |
| 28928 | cenir | 3 |
| 28929 | cenicienta | 3 |
| 28930 | cené | 3 |
| 28931 | cenamos | 3 |
| 28932 | cenaba | 3 |
| 28933 | celebrarse | 3 |
| 28934 | cejijunto | 3 |
| 28935 | cejijunta | 3 |
| 28936 | cejar | 3 |
| 28937 | ceguezuelo | 3 |
| 28938 | cegaba | 3 |
| 28939 | cédulas | 3 |
| 28940 | cedes | 3 |
| 28941 | cedazo | 3 |
| 28942 | çeçina | 3 |
| 28943 | cebra | 3 |
| 28944 | cebolletas | 3 |
| 28945 | cebarse | 3 |
| 28946 | ceba | 3 |
| 28947 | cazuelo | 3 |
| 28948 | cazo | 3 |
| 28949 | cazadas | 3 |
| 28950 | cayósele | 3 |
| 28951 | cayga | 3 |
| 28952 | cayere | 3 |
| 28953 | caydas | 3 |
| 28954 | cayan | 3 |
| 28955 | cavilo | 3 |
| 28956 | cavilando | 3 |
| 28957 | cavilaba | 3 |
| 28958 | cavernosa | 3 |
| 28959 | cavallero | 3 |
| 28960 | cauto | 3 |
| 28961 | cautivaban | 3 |
| 28962 | cautivaba | 3 |
| 28963 | cauterio | 3 |
| 28964 | cautelosa | 3 |
| 28965 | causaron | 3 |
| 28966 | causante | 3 |
| 28967 | causan | 3 |
| 28968 | catre | 3 |
| 28969 | cathólica | 3 |
| 28970 | categórica | 3 |
| 28971 | cátedras | 3 |
| 28972 | cate | 3 |
| 28973 | catat | 3 |
| 28974 | catástrofes | 3 |
| 28975 | catarros | 3 |
| 28976 | catando | 3 |
| 28977 | catan | 3 |
| 28978 | catálogo | 3 |
| 28979 | catalanes | 3 |
| 28980 | casualidades | 3 |
| 28981 | castiza | 3 |
| 28982 | castita | 3 |
| 28983 | castigarme | 3 |
| 28984 | castigarle | 3 |
| 28985 | castigaba | 3 |
| 28986 | casteçaos | 3 |
| 28987 | castamente | 3 |
| 28988 | cast | 3 |
| 28989 | casinos | 3 |
| 28990 | casería | 3 |
| 28991 | caseras | 3 |
| 28992 | cascaciruelas | 3 |
| 28993 | casarían | 3 |
| 28994 | casarás | 3 |
| 28995 | casarán | 3 |
| 28996 | casará | 3 |
| 28997 | casaderas | 3 |
| 28998 | carúnculas | 3 |
| 28999 | cartuchera | 3 |
| 29000 | cartero | 3 |
| 29001 | carrozas | 3 |
| 29002 | carromato | 3 |
| 29003 | carrillo | 3 |
| 29004 | carriles | 3 |
| 29005 | carricoche | 3 |
| 29006 | carrascón | 3 |
| 29007 | carrasca | 3 |
| 29008 | carpanta | 3 |
| 29009 | carnoso | 3 |
| 29010 | carnavales | 3 |
| 29011 | carnales | 3 |
| 29012 | caribes | 3 |
| 29013 | cariacontecido | 3 |
| 29014 | cárceles | 3 |
| 29015 | carcajes | 3 |
| 29016 | carbonería | 3 |
| 29017 | carantoñas | 3 |
| 29018 | capuz | 3 |
| 29019 | capua | 3 |
| 29020 | cápsulas | 3 |
| 29021 | caprichosos | 3 |
| 29022 | capitular | 3 |
| 29023 | capitaneaba | 3 |
| 29024 | caoba | 3 |
| 29025 | cañaheja | 3 |
| 29026 | cantoras | 3 |
| 29027 | cantora | 3 |
| 29028 | cántico | 3 |
| 29029 | cantadera | 3 |
| 29030 | cantabria | 3 |
| 29031 | cansaron | 3 |
| 29032 | canónicas | 3 |
| 29033 | canillas | 3 |
| 29034 | candorosa | 3 |
| 29035 | candidez | 3 |
| 29036 | cándidas | 3 |
| 29037 | candelillas | 3 |
| 29038 | candelabros | 3 |
| 29039 | candeal | 3 |
| 29040 | cancionero | 3 |
| 29041 | canamor | 3 |
| 29042 | canaleja | 3 |
| 29043 | camps | 3 |
| 29044 | campestre | 3 |
| 29045 | campeador | 3 |
| 29046 | campar | 3 |
| 29047 | campante | 3 |
| 29048 | campanillazo | 3 |
| 29049 | campaneros | 3 |
| 29050 | campamento | 3 |
| 29051 | camisería | 3 |
| 29052 | caminito | 3 |
| 29053 | camineros | 3 |
| 29054 | caminemos | 3 |
| 29055 | caminé | 3 |
| 29056 | caminata | 3 |
| 29057 | caminase | 3 |
| 29058 | camilla | 3 |
| 29059 | cambiazo | 3 |
| 29060 | cambiaron | 3 |
| 29061 | cambian | 3 |
| 29062 | cambiaban | 3 |
| 29063 | cambia | 3 |
| 29064 | camaranchón | 3 |
| 29065 | camaraíta | 3 |
| 29066 | camaleones | 3 |
| 29067 | calzo | 3 |
| 29068 | calo | 3 |
| 29069 | cálmese | 3 |
| 29070 | callaría | 3 |
| 29071 | cáliz | 3 |
| 29072 | calientan | 3 |
| 29073 | cálices | 3 |
| 29074 | calesero | 3 |
| 29075 | calenturienta | 3 |
| 29076 | calentar | 3 |
| 29077 | calentaban | 3 |
| 29078 | calculan | 3 |
| 29079 | calcetín | 3 |
| 29080 | calatayud | 3 |
| 29081 | calandrias | 3 |
| 29082 | calados | 3 |
| 29083 | calaba | 3 |
| 29084 | caíste | 3 |
| 29085 | caín | 3 |
| 29086 | cafetera | 3 |
| 29087 | caerán | 3 |
| 29088 | caducan | 3 |
| 29089 | cadete | 3 |
| 29090 | cadera | 3 |
| 29091 | cadaldía | 3 |
| 29092 | caciques | 3 |
| 29093 | cachipote | 3 |
| 29094 | cachetes | 3 |
| 29095 | cachete | 3 |
| 29096 | cachemira | 3 |
| 29097 | caçar | 3 |
| 29098 | cabrones | 3 |
| 29099 | cabrío | 3 |
| 29100 | cabrerizo | 3 |
| 29101 | cable | 3 |
| 29102 | cabizbaja | 3 |
| 29103 | cabido | 3 |
| 29104 | cabelleras | 3 |
| 29105 | caballucos | 3 |
| 29106 | caballerizos | 3 |
| 29107 | caballerescos | 3 |
| 29108 | cábalas | 3 |
| 29109 | cab | 3 |
| 29110 | byenes | 3 |
| 29111 | butrón | 3 |
| 29112 | bustamante | 3 |
| 29113 | búsquela | 3 |
| 29114 | busilis | 3 |
| 29115 | buscándola | 3 |
| 29116 | burreros | 3 |
| 29117 | burrada | 3 |
| 29118 | burocráticas | 3 |
| 29119 | burlonas | 3 |
| 29120 | burlesco | 3 |
| 29121 | burlan | 3 |
| 29122 | burladas | 3 |
| 29123 | bureo | 3 |
| 29124 | burbujas | 3 |
| 29125 | bulliendo | 3 |
| 29126 | bullen | 3 |
| 29127 | bujías | 3 |
| 29128 | bujía | 3 |
| 29129 | buhona | 3 |
| 29130 | bugía | 3 |
| 29131 | bufidos | 3 |
| 29132 | buenazo | 3 |
| 29133 | buenandança | 3 |
| 29134 | buelan | 3 |
| 29135 | bucólicos | 3 |
| 29136 | bucólico | 3 |
| 29137 | brujo | 3 |
| 29138 | brujería | 3 |
| 29139 | brotó | 3 |
| 29140 | bronco | 3 |
| 29141 | bromista | 3 |
| 29142 | brocha | 3 |
| 29143 | brisas | 3 |
| 29144 | brindó | 3 |
| 29145 | brindando | 3 |
| 29146 | brincaba | 3 |
| 29147 | brillaron | 3 |
| 29148 | brillantez | 3 |
| 29149 | brígida | 3 |
| 29150 | brida | 3 |
| 29151 | bribonaza | 3 |
| 29152 | breva | 3 |
| 29153 | breuemente | 3 |
| 29154 | bregar | 3 |
| 29155 | bravura | 3 |
| 29156 | bravatas | 3 |
| 29157 | braua | 3 |
| 29158 | bragas | 3 |
| 29159 | braços | 3 |
| 29160 | botines | 3 |
| 29161 | botijos | 3 |
| 29162 | boticas | 3 |
| 29163 | boticarios | 3 |
| 29164 | boteros | 3 |
| 29165 | botánica | 3 |
| 29166 | botafuego | 3 |
| 29167 | boses | 3 |
| 29168 | borrosas | 3 |
| 29169 | borran | 3 |
| 29170 | borraba | 3 |
| 29171 | borlas | 3 |
| 29172 | borgoña | 3 |
| 29173 | bordones | 3 |
| 29174 | bordando | 3 |
| 29175 | borbollones | 3 |
| 29176 | bonus | 3 |
| 29177 | bonico | 3 |
| 29178 | bonetillo | 3 |
| 29179 | bonetes | 3 |
| 29180 | bondat | 3 |
| 29181 | bona | 3 |
| 29182 | bom | 3 |
| 29183 | bolver | 3 |
| 29184 | bolso | 3 |
| 29185 | bolsistas | 3 |
| 29186 | bolsilla | 3 |
| 29187 | bollos | 3 |
| 29188 | bolar | 3 |
| 29189 | bogando | 3 |
| 29190 | bogadores | 3 |
| 29191 | bofes | 3 |
| 29192 | bocona | 3 |
| 29193 | bochornosa | 3 |
| 29194 | bobalicones | 3 |
| 29195 | bobalicón | 3 |
| 29196 | blusa | 3 |
| 29197 | blanquísimas | 3 |
| 29198 | blanquísima | 3 |
| 29199 | blandones | 3 |
| 29200 | biuen | 3 |
| 29201 | biuda | 3 |
| 29202 | biriatu | 3 |
| 29203 | biografía | 3 |
| 29204 | billares | 3 |
| 29205 | bilbao | 3 |
| 29206 | bigotillo | 3 |
| 29207 | bienvenido | 3 |
| 29208 | bienvenida | 3 |
| 29209 | bienauenturanza | 3 |
| 29210 | bienandanzas | 3 |
| 29211 | bevíe | 3 |
| 29212 | bestial | 3 |
| 29213 | besóle | 3 |
| 29214 | bese | 3 |
| 29215 | berrinchín | 3 |
| 29216 | berrinche | 3 |
| 29217 | berrido | 3 |
| 29218 | bergante | 3 |
| 29219 | berenjena | 3 |
| 29220 | berberiscos | 3 |
| 29221 | benignidad | 3 |
| 29222 | beneméritos | 3 |
| 29223 | beneficiados | 3 |
| 29224 | benéficas | 3 |
| 29225 | bendijo | 3 |
| 29226 | bendicha | 3 |
| 29227 | bendecirán | 3 |
| 29228 | bendecir | 3 |
| 29229 | bendeçión | 3 |
| 29230 | beltenebros | 3 |
| 29231 | bellota | 3 |
| 29232 | belisario | 3 |
| 29233 | belianises | 3 |
| 29234 | belga | 3 |
| 29235 | belenes | 3 |
| 29236 | behetría | 3 |
| 29237 | bebimos | 3 |
| 29238 | bebiese | 3 |
| 29239 | bebidas | 3 |
| 29240 | bebí | 3 |
| 29241 | beberse | 3 |
| 29242 | bebería | 3 |
| 29243 | beberé | 3 |
| 29244 | bebedor | 3 |
| 29245 | beaumarchais | 3 |
| 29246 | beatífica | 3 |
| 29247 | bazares | 3 |
| 29248 | bayo | 3 |
| 29249 | baylando | 3 |
| 29250 | bavieca | 3 |
| 29251 | batueco | 3 |
| 29252 | batirme | 3 |
| 29253 | batín | 3 |
| 29254 | batiéndose | 3 |
| 29255 | batían | 3 |
| 29256 | baten | 3 |
| 29257 | bastos | 3 |
| 29258 | bastidores | 3 |
| 29259 | bastaron | 3 |
| 29260 | bastardo | 3 |
| 29261 | bastamos | 3 |
| 29262 | bastado | 3 |
| 29263 | basilea | 3 |
| 29264 | bascas | 3 |
| 29265 | barrunto | 3 |
| 29266 | barruntaba | 3 |
| 29267 | barrionuevo | 3 |
| 29268 | barril | 3 |
| 29269 | barrido | 3 |
| 29270 | barreno | 3 |
| 29271 | barre | 3 |
| 29272 | barrancos | 3 |
| 29273 | barquitos | 3 |
| 29274 | baroncito | 3 |
| 29275 | bardales | 3 |
| 29276 | barcino | 3 |
| 29277 | barbuda | 3 |
| 29278 | barbilla | 3 |
| 29279 | barbián | 3 |
| 29280 | barberos | 3 |
| 29281 | barbechos | 3 |
| 29282 | barbada | 3 |
| 29283 | barandal | 3 |
| 29284 | barajas | 3 |
| 29285 | baqueta | 3 |
| 29286 | bañan | 3 |
| 29287 | bañados | 3 |
| 29288 | bañada | 3 |
| 29289 | bandolero | 3 |
| 29290 | bandada | 3 |
| 29291 | banasta | 3 |
| 29292 | balumba | 3 |
| 29293 | baluarte | 3 |
| 29294 | baltasar | 3 |
| 29295 | balsa | 3 |
| 29296 | baldonado | 3 |
| 29297 | baldón | 3 |
| 29298 | baldomerito | 3 |
| 29299 | balazos | 3 |
| 29300 | bajemos | 3 |
| 29301 | bájate | 3 |
| 29302 | bajam | 3 |
| 29303 | bailad | 3 |
| 29304 | baigorri | 3 |
| 29305 | baharí | 3 |
| 29306 | bagatele | 3 |
| 29307 | bagatela | 3 |
| 29308 | badulaques | 3 |
| 29309 | badil | 3 |
| 29310 | bactriana | 3 |
| 29311 | bacín | 3 |
| 29312 | bachillera | 3 |
| 29313 | baches | 3 |
| 29314 | bacante | 3 |
| 29315 | bacallao | 3 |
| 29316 | babosos | 3 |
| 29317 | ba | 3 |
| 29318 | azuzaba | 3 |
| 29319 | azumbres | 3 |
| 29320 | azulada | 3 |
| 29321 | azucena | 3 |
| 29322 | azucarillos | 3 |
| 29323 | azucarada | 3 |
| 29324 | azpeitia | 3 |
| 29325 | azoten | 3 |
| 29326 | azotea | 3 |
| 29327 | azotada | 3 |
| 29328 | azotaban | 3 |
| 29329 | azófar | 3 |
| 29330 | azevedo | 3 |
| 29331 | azero | 3 |
| 29332 | azadón | 3 |
| 29333 | azadas | 3 |
| 29334 | azacán | 3 |
| 29335 | ayudo | 3 |
| 29336 | ayudarles | 3 |
| 29337 | ayudarás | 3 |
| 29338 | ayudados | 3 |
| 29339 | ayres | 3 |
| 29340 | ayades | 3 |
| 29341 | avydo | 3 |
| 29342 | avisaron | 3 |
| 29343 | avisarme | 3 |
| 29344 | avisarle | 3 |
| 29345 | avisando | 3 |
| 29346 | avisadas | 3 |
| 29347 | avisa | 3 |
| 29348 | avío | 3 |
| 29349 | ávido | 3 |
| 29350 | aviado | 3 |
| 29351 | avia | 3 |
| 29352 | averiguo | 3 |
| 29353 | averigüé | 3 |
| 29354 | averigüe | 3 |
| 29355 | averiguando | 3 |
| 29356 | aventurillas | 3 |
| 29357 | aventurarse | 3 |
| 29358 | aventuraba | 3 |
| 29359 | aventajaba | 3 |
| 29360 | avenían | 3 |
| 29361 | avenencia | 3 |
| 29362 | avemos | 3 |
| 29363 | avemaría | 3 |
| 29364 | avarizia | 3 |
| 29365 | avariçia | 3 |
| 29366 | avanzar | 3 |
| 29367 | avanzado | 3 |
| 29368 | avanzaban | 3 |
| 29369 | autorizado | 3 |
| 29370 | autorizada | 3 |
| 29371 | autorizaba | 3 |
| 29372 | autoritario | 3 |
| 29373 | autoritaria | 3 |
| 29374 | austro | 3 |
| 29375 | austerlitz | 3 |
| 29376 | aumentaron | 3 |
| 29377 | aumenta | 3 |
| 29378 | auisos | 3 |
| 29379 | auido | 3 |
| 29380 | audiencias | 3 |
| 29381 | atusada | 3 |
| 29382 | aturdirse | 3 |
| 29383 | aturdió | 3 |
| 29384 | aturdían | 3 |
| 29385 | atropellarse | 3 |
| 29386 | atronaba | 3 |
| 29387 | atribuyendo | 3 |
| 29388 | atribuir | 3 |
| 29389 | atrevíme | 3 |
| 29390 | atreví | 3 |
| 29391 | atreverías | 3 |
| 29392 | atreveré | 3 |
| 29393 | atrayéndola | 3 |
| 29394 | atravesaban | 3 |
| 29395 | atrasos | 3 |
| 29396 | atraían | 3 |
| 29397 | atracones | 3 |
| 29398 | atormenten | 3 |
| 29399 | atormentarme | 3 |
| 29400 | atormentarla | 3 |
| 29401 | atormentada | 3 |
| 29402 | atolondramiento | 3 |
| 29403 | atolladero | 3 |
| 29404 | atisbando | 3 |
| 29405 | atienen | 3 |
| 29406 | atiendes | 3 |
| 29407 | atestados | 3 |
| 29408 | atesora | 3 |
| 29409 | aterrados | 3 |
| 29410 | aterrador | 3 |
| 29411 | aterrado | 3 |
| 29412 | atenuada | 3 |
| 29413 | atenuaba | 3 |
| 29414 | atentísimamente | 3 |
| 29415 | atenía | 3 |
| 29416 | atener | 3 |
| 29417 | ateneo | 3 |
| 29418 | atendiese | 3 |
| 29419 | atemperar | 3 |
| 29420 | ate | 3 |
| 29421 | atauios | 3 |
| 29422 | atareada | 3 |
| 29423 | atajar | 3 |
| 29424 | atacarnos | 3 |
| 29425 | atacados | 3 |
| 29426 | atacaban | 3 |
| 29427 | asusto | 3 |
| 29428 | asustarle | 3 |
| 29429 | asuntillo | 3 |
| 29430 | asunción | 3 |
| 29431 | astronomía | 3 |
| 29432 | astro | 3 |
| 29433 | assentóse | 3 |
| 29434 | aspiro | 3 |
| 29435 | aspira | 3 |
| 29436 | aspero | 3 |
| 29437 | ásperamente | 3 |
| 29438 | aspa | 3 |
| 29439 | asomose | 3 |
| 29440 | asomé | 3 |
| 29441 | asombró | 3 |
| 29442 | asombres | 3 |
| 29443 | asombre | 3 |
| 29444 | asombrarse | 3 |
| 29445 | asombrados | 3 |
| 29446 | asombraba | 3 |
| 29447 | asomarse | 3 |
| 29448 | asomáronse | 3 |
| 29449 | asomara | 3 |
| 29450 | asolado | 3 |
| 29451 | asociar | 3 |
| 29452 | asociados | 3 |
| 29453 | asociaciones | 3 |
| 29454 | asociación | 3 |
| 29455 | asistirle | 3 |
| 29456 | asistieron | 3 |
| 29457 | asistente | 3 |
| 29458 | asiéndome | 3 |
| 29459 | asiáticos | 3 |
| 29460 | asiático | 3 |
| 29461 | aseveración | 3 |
| 29462 | asenté | 3 |
| 29463 | asendereados | 3 |
| 29464 | asegure | 3 |
| 29465 | asegurarte | 3 |
| 29466 | asegurarlo | 3 |
| 29467 | asegurarle | 3 |
| 29468 | asedio | 3 |
| 29469 | ascondido | 3 |
| 29470 | ascenso | 3 |
| 29471 | ascendientes | 3 |
| 29472 | asaltaba | 3 |
| 29473 | asalariado | 3 |
| 29474 | asadas | 3 |
| 29475 | artús | 3 |
| 29476 | artísticos | 3 |
| 29477 | artimañas | 3 |
| 29478 | artificioso | 3 |
| 29479 | articulista | 3 |
| 29480 | artesones | 3 |
| 29481 | artesas | 3 |
| 29482 | artesanos | 3 |
| 29483 | artesano | 3 |
| 29484 | arrullado | 3 |
| 29485 | arruinando | 3 |
| 29486 | arrugaba | 3 |
| 29487 | arropó | 3 |
| 29488 | arrollado | 3 |
| 29489 | arrojasen | 3 |
| 29490 | arrojas | 3 |
| 29491 | arrojarme | 3 |
| 29492 | arrojarle | 3 |
| 29493 | arrojaré | 3 |
| 29494 | arrojara | 3 |
| 29495 | arrojada | 3 |
| 29496 | arrogantísima | 3 |
| 29497 | arrogantes | 3 |
| 29498 | arrogancias | 3 |
| 29499 | arroba | 3 |
| 29500 | arriesgado | 3 |
| 29501 | arrepintiéndose | 3 |
| 29502 | arrepiéntete | 3 |
| 29503 | arrepentidos | 3 |
| 29504 | arrendamiento | 3 |
| 29505 | arremetiendo | 3 |
| 29506 | arremangado | 3 |
| 29507 | arreglaremos | 3 |
| 29508 | arreglador | 3 |
| 29509 | arreció | 3 |
| 29510 | arrechucho | 3 |
| 29511 | arrastrara | 3 |
| 29512 | arrastrándose | 3 |
| 29513 | arrastrados | 3 |
| 29514 | arrancan | 3 |
| 29515 | arrancados | 3 |
| 29516 | arrancaban | 3 |
| 29517 | arraigada | 3 |
| 29518 | arquitecto | 3 |
| 29519 | arqueando | 3 |
| 29520 | arqueadas | 3 |
| 29521 | arpón | 3 |
| 29522 | arpillera | 3 |
| 29523 | arpías | 3 |
| 29524 | aromática | 3 |
| 29525 | arneguy | 3 |
| 29526 | arnaúte | 3 |
| 29527 | armoniosas | 3 |
| 29528 | armonia | 3 |
| 29529 | armaron | 3 |
| 29530 | armara | 3 |
| 29531 | armadas | 3 |
| 29532 | aritmético | 3 |
| 29533 | aristocráticas | 3 |
| 29534 | arias | 3 |
| 29535 | argolla | 3 |
| 29536 | argentina | 3 |
| 29537 | argenta | 3 |
| 29538 | argales | 3 |
| 29539 | arengas | 3 |
| 29540 | ardo | 3 |
| 29541 | ardides | 3 |
| 29542 | arçobispos | 3 |
| 29543 | arciprestazgo | 3 |
| 29544 | arcaduz | 3 |
| 29545 | arcabuz | 3 |
| 29546 | arboricultura | 3 |
| 29547 | árbitros | 3 |
| 29548 | arávigo | 3 |
| 29549 | aragonesa | 3 |
| 29550 | arábigos | 3 |
| 29551 | árabe | 3 |
| 29552 | aquiescencia | 3 |
| 29553 | aquexaua | 3 |
| 29554 | aqueso | 3 |
| 29555 | aquesa | 3 |
| 29556 | apuró | 3 |
| 29557 | apuras | 3 |
| 29558 | apurarse | 3 |
| 29559 | apunto | 3 |
| 29560 | apuntaron | 3 |
| 29561 | apuntador | 3 |
| 29562 | apuntadas | 3 |
| 29563 | apuntaciones | 3 |
| 29564 | aproximaban | 3 |
| 29565 | aproueche | 3 |
| 29566 | apropiado | 3 |
| 29567 | aprisita | 3 |
| 29568 | aprisco | 3 |
| 29569 | aprietos | 3 |
| 29570 | apresure | 3 |
| 29571 | apresuraron | 3 |
| 29572 | apresurado | 3 |
| 29573 | apresuradamente | 3 |
| 29574 | apresados | 3 |
| 29575 | aprendo | 3 |
| 29576 | aprendiese | 3 |
| 29577 | aprendieron | 3 |
| 29578 | aprendían | 3 |
| 29579 | aprenderás | 3 |
| 29580 | aprendas | 3 |
| 29581 | apremiante | 3 |
| 29582 | apremiado | 3 |
| 29583 | aprehensión | 3 |
| 29584 | apreciadas | 3 |
| 29585 | apreciaciones | 3 |
| 29586 | aprecia | 3 |
| 29587 | apoyadas | 3 |
| 29588 | apoya | 3 |
| 29589 | apoteosis | 3 |
| 29590 | apóstrofes | 3 |
| 29591 | apostar | 3 |
| 29592 | apostaba | 3 |
| 29593 | aposta | 3 |
| 29594 | apolonia | 3 |
| 29595 | apogeo | 3 |
| 29596 | apocados | 3 |
| 29597 | aplicara | 3 |
| 29598 | aplicándole | 3 |
| 29599 | aplicado | 3 |
| 29600 | aplazar | 3 |
| 29601 | aplaudir | 3 |
| 29602 | aplaudió | 3 |
| 29603 | aplaude | 3 |
| 29604 | aplasto | 3 |
| 29605 | aplastado | 3 |
| 29606 | aplacarle | 3 |
| 29607 | aplacarla | 3 |
| 29608 | aplacara | 3 |
| 29609 | apilados | 3 |
| 29610 | ápice | 3 |
| 29611 | apetecido | 3 |
| 29612 | apetecía | 3 |
| 29613 | apesta | 3 |
| 29614 | apero | 3 |
| 29615 | apéndice | 3 |
| 29616 | apego | 3 |
| 29617 | apegada | 3 |
| 29618 | apeé | 3 |
| 29619 | apee | 3 |
| 29620 | apedrear | 3 |
| 29621 | apeaos | 3 |
| 29622 | apeadero | 3 |
| 29623 | apassionados | 3 |
| 29624 | apartara | 3 |
| 29625 | aparezca | 3 |
| 29626 | aparentó | 3 |
| 29627 | aparejar | 3 |
| 29628 | aparejaos | 3 |
| 29629 | apareja | 3 |
| 29630 | aparadores | 3 |
| 29631 | apañado | 3 |
| 29632 | apaleaban | 3 |
| 29633 | apagaron | 3 |
| 29634 | apagadas | 3 |
| 29635 | añadiré | 3 |
| 29636 | añadiéndose | 3 |
| 29637 | anunciarle | 3 |
| 29638 | anuncian | 3 |
| 29639 | anulación | 3 |
| 29640 | anubló | 3 |
| 29641 | antojósele | 3 |
| 29642 | antojaron | 3 |
| 29643 | antojadizo | 3 |
| 29644 | antiquísimo | 3 |
| 29645 | antipatías | 3 |
| 29646 | antiguedad | 3 |
| 29647 | antiguamente | 3 |
| 29648 | antifaz | 3 |
| 29649 | anticuado | 3 |
| 29650 | anticiparse | 3 |
| 29651 | anticipado | 3 |
| 29652 | anthoni | 3 |
| 29653 | antepasados | 3 |
| 29654 | antecesores | 3 |
| 29655 | antecedente | 3 |
| 29656 | ansuelo | 3 |
| 29657 | anónimos | 3 |
| 29658 | anonadada | 3 |
| 29659 | anocheciese | 3 |
| 29660 | animas | 3 |
| 29661 | animalejo | 3 |
| 29662 | angustiado | 3 |
| 29663 | anguloso | 3 |
| 29664 | angulosa | 3 |
| 29665 | anguila | 3 |
| 29666 | angelina | 3 |
| 29667 | ángela | 3 |
| 29668 | anegó | 3 |
| 29669 | andré | 3 |
| 29670 | andrajosos | 3 |
| 29671 | andrajosa | 3 |
| 29672 | ándeme | 3 |
| 29673 | ándate | 3 |
| 29674 | andarían | 3 |
| 29675 | andaríamos | 3 |
| 29676 | andaré | 3 |
| 29677 | andantesca | 3 |
| 29678 | andana | 3 |
| 29679 | andamiaje | 3 |
| 29680 | andaluces | 3 |
| 29681 | anbos | 3 |
| 29682 | anaqueles | 3 |
| 29683 | análogas | 3 |
| 29684 | análoga | 3 |
| 29685 | anacronismos | 3 |
| 29686 | anacoreta | 3 |
| 29687 | amoratados | 3 |
| 29688 | amoratada | 3 |
| 29689 | amontonada | 3 |
| 29690 | amonesta | 3 |
| 29691 | amó | 3 |
| 29692 | amenazador | 3 |
| 29693 | amelia | 3 |
| 29694 | ambulante | 3 |
| 29695 | ámbito | 3 |
| 29696 | amazonas | 3 |
| 29697 | amatar | 3 |
| 29698 | amasijo | 3 |
| 29699 | amase | 3 |
| 29700 | amasando | 3 |
| 29701 | amasado | 3 |
| 29702 | amarillentas | 3 |
| 29703 | amarilis | 3 |
| 29704 | amargas | 3 |
| 29705 | amaré | 3 |
| 29706 | amansar | 3 |
| 29707 | amansa | 3 |
| 29708 | amanerado | 3 |
| 29709 | amanecido | 3 |
| 29710 | amancebada | 3 |
| 29711 | amáis | 3 |
| 29712 | amago | 3 |
| 29713 | alzóse | 3 |
| 29714 | alzándose | 3 |
| 29715 | alzados | 3 |
| 29716 | alzadas | 3 |
| 29717 | alunbrar | 3 |
| 29718 | alumbrado | 3 |
| 29719 | aludido | 3 |
| 29720 | altozanos | 3 |
| 29721 | alternaban | 3 |
| 29722 | alterna | 3 |
| 29723 | alteres | 3 |
| 29724 | altere | 3 |
| 29725 | altercar | 3 |
| 29726 | altercados | 3 |
| 29727 | alterando | 3 |
| 29728 | alteran | 3 |
| 29729 | altaneros | 3 |
| 29730 | altanera | 3 |
| 29731 | alquimia | 3 |
| 29732 | alquiló | 3 |
| 29733 | alquileres | 3 |
| 29734 | alpargateros | 3 |
| 29735 | alonsito | 3 |
| 29736 | alojaron | 3 |
| 29737 | almorcemos | 3 |
| 29738 | almoraima | 3 |
| 29739 | almonedas | 3 |
| 29740 | almohaza | 3 |
| 29741 | almohadones | 3 |
| 29742 | almirantes | 3 |
| 29743 | almíbares | 3 |
| 29744 | almete | 3 |
| 29745 | almalafa | 3 |
| 29746 | almacenistas | 3 |
| 29747 | allegue | 3 |
| 29748 | aljófares | 3 |
| 29749 | alivió | 3 |
| 29750 | aliviar | 3 |
| 29751 | alivian | 3 |
| 29752 | alimentan | 3 |
| 29753 | alimentado | 3 |
| 29754 | alimentada | 3 |
| 29755 | alimentaba | 3 |
| 29756 | aliados | 3 |
| 29757 | alhombra | 3 |
| 29758 | algarrobos | 3 |
| 29759 | algalia | 3 |
| 29760 | alfombrado | 3 |
| 29761 | alfenique | 3 |
| 29762 | alfaquí | 3 |
| 29763 | alfamar | 3 |
| 29764 | aleteo | 3 |
| 29765 | aletargada | 3 |
| 29766 | aletargaba | 3 |
| 29767 | aleros | 3 |
| 29768 | alentando | 3 |
| 29769 | alentado | 3 |
| 29770 | alentaba | 3 |
| 29771 | aleluyas | 3 |
| 29772 | alejandros | 3 |
| 29773 | alégrate | 3 |
| 29774 | alegrará | 3 |
| 29775 | alegrando | 3 |
| 29776 | alegoría | 3 |
| 29777 | alegando | 3 |
| 29778 | alegaba | 3 |
| 29779 | aldabonazos | 3 |
| 29780 | aldabón | 3 |
| 29781 | alcoy | 3 |
| 29782 | alcornoques | 3 |
| 29783 | alcoholismo | 3 |
| 29784 | alcedo | 3 |
| 29785 | alcarreña | 3 |
| 29786 | alcaravanes | 3 |
| 29787 | alcanzas | 3 |
| 29788 | alcanzarla | 3 |
| 29789 | alcanzare | 3 |
| 29790 | alcanzará | 3 |
| 29791 | alcanzada | 3 |
| 29792 | alcanzaban | 3 |
| 29793 | alcancen | 3 |
| 29794 | alcancé | 3 |
| 29795 | alcança | 3 |
| 29796 | alcabalas | 3 |
| 29797 | alcabala | 3 |
| 29798 | albraca | 3 |
| 29799 | alborotase | 3 |
| 29800 | alborotan | 3 |
| 29801 | albergues | 3 |
| 29802 | albergarse | 3 |
| 29803 | albaceas | 3 |
| 29804 | alaveses | 3 |
| 29805 | alarmó | 3 |
| 29806 | alarmas | 3 |
| 29807 | alarmar | 3 |
| 29808 | alarmadísima | 3 |
| 29809 | alárabes | 3 |
| 29810 | alambique | 3 |
| 29811 | alambicados | 3 |
| 29812 | alambicada | 3 |
| 29813 | alabóle | 3 |
| 29814 | alabarla | 3 |
| 29815 | ajustarle | 3 |
| 29816 | ajeros | 3 |
| 29817 | ajadas | 3 |
| 29818 | aislado | 3 |
| 29819 | airosas | 3 |
| 29820 | ahuyenta | 3 |
| 29821 | ahumadas | 3 |
| 29822 | ahorrado | 3 |
| 29823 | ahorquen | 3 |
| 29824 | ahorita | 3 |
| 29825 | ahorcarle | 3 |
| 29826 | ahogue | 3 |
| 29827 | ahogarse | 3 |
| 29828 | ahogarle | 3 |
| 29829 | ahogados | 3 |
| 29830 | aguisado | 3 |
| 29831 | aguirre | 3 |
| 29832 | aguilas | 3 |
| 29833 | aguijar | 3 |
| 29834 | agüela | 3 |
| 29835 | aguardé | 3 |
| 29836 | aguante | 3 |
| 29837 | aguántate | 3 |
| 29838 | aguantando | 3 |
| 29839 | aguamanos | 3 |
| 29840 | aguacero | 3 |
| 29841 | agrícola | 3 |
| 29842 | agresión | 3 |
| 29843 | agregada | 3 |
| 29844 | agravaba | 3 |
| 29845 | agradecerle | 3 |
| 29846 | agradecemos | 3 |
| 29847 | agradan | 3 |
| 29848 | agradablemente | 3 |
| 29849 | agradábale | 3 |
| 29850 | agraciados | 3 |
| 29851 | agotó | 3 |
| 29852 | agorero | 3 |
| 29853 | agonizante | 3 |
| 29854 | agonizaba | 3 |
| 29855 | agolpaban | 3 |
| 29856 | agitarse | 3 |
| 29857 | agitando | 3 |
| 29858 | agitan | 3 |
| 29859 | agitadas | 3 |
| 29860 | agencia | 3 |
| 29861 | agasajar | 3 |
| 29862 | agasajado | 3 |
| 29863 | agasajaba | 3 |
| 29864 | agarré | 3 |
| 29865 | agarraron | 3 |
| 29866 | agapita | 3 |
| 29867 | agallas | 3 |
| 29868 | afruenta | 3 |
| 29869 | africana | 3 |
| 29870 | aforro | 3 |
| 29871 | aforrado | 3 |
| 29872 | aforismo | 3 |
| 29873 | afogar | 3 |
| 29874 | aflojó | 3 |
| 29875 | aflijas | 3 |
| 29876 | afligir | 3 |
| 29877 | afligíme | 3 |
| 29878 | aflictivo | 3 |
| 29879 | aflictiva | 3 |
| 29880 | aflición | 3 |
| 29881 | afirmativa | 3 |
| 29882 | afirmarse | 3 |
| 29883 | afincamiento | 3 |
| 29884 | afinar | 3 |
| 29885 | afilado | 3 |
| 29886 | aficionó | 3 |
| 29887 | afeytes | 3 |
| 29888 | afeó | 3 |
| 29889 | afeminados | 3 |
| 29890 | afeitar | 3 |
| 29891 | afeitada | 3 |
| 29892 | afeitaba | 3 |
| 29893 | afectuosos | 3 |
| 29894 | afectuosamente | 3 |
| 29895 | afectó | 3 |
| 29896 | afectado | 3 |
| 29897 | afectadas | 3 |
| 29898 | advertidos | 3 |
| 29899 | advertidas | 3 |
| 29900 | adversos | 3 |
| 29901 | adversidad | 3 |
| 29902 | adusta | 3 |
| 29903 | aduersidad | 3 |
| 29904 | adquirí | 3 |
| 29905 | adorna | 3 |
| 29906 | adormecido | 3 |
| 29907 | adorarte | 3 |
| 29908 | adoraron | 3 |
| 29909 | adorador | 3 |
| 29910 | adoquines | 3 |
| 29911 | adoptivo | 3 |
| 29912 | adoptamos | 3 |
| 29913 | adonis | 3 |
| 29914 | adocenados | 3 |
| 29915 | adobo | 3 |
| 29916 | adobes | 3 |
| 29917 | admitirle | 3 |
| 29918 | admitirla | 3 |
| 29919 | admitieron | 3 |
| 29920 | admitiera | 3 |
| 29921 | admitida | 3 |
| 29922 | admiras | 3 |
| 29923 | admirándose | 3 |
| 29924 | admiradas | 3 |
| 29925 | admirábase | 3 |
| 29926 | admirábanse | 3 |
| 29927 | administrativo | 3 |
| 29928 | administradora | 3 |
| 29929 | administraba | 3 |
| 29930 | administra | 3 |
| 29931 | adjetivo | 3 |
| 29932 | adios | 3 |
| 29933 | adevinaba | 3 |
| 29934 | aderezó | 3 |
| 29935 | aderece | 3 |
| 29936 | adelanto | 3 |
| 29937 | adelantada | 3 |
| 29938 | adecuado | 3 |
| 29939 | adaptación | 3 |
| 29940 | acusón | 3 |
| 29941 | acuse | 3 |
| 29942 | acusarse | 3 |
| 29943 | acusador | 3 |
| 29944 | acusaçión | 3 |
| 29945 | acudiesen | 3 |
| 29946 | acudas | 3 |
| 29947 | acuçioso | 3 |
| 29948 | acuchillados | 3 |
| 29949 | acuarelas | 3 |
| 29950 | actuales | 3 |
| 29951 | activamente | 3 |
| 29952 | acreditó | 3 |
| 29953 | acredite | 3 |
| 29954 | acreditados | 3 |
| 29955 | acreditada | 3 |
| 29956 | acredita | 3 |
| 29957 | acrecentó | 3 |
| 29958 | acotaciones | 3 |
| 29959 | acostumbró | 3 |
| 29960 | acostumbro | 3 |
| 29961 | acostumbres | 3 |
| 29962 | acostose | 3 |
| 29963 | acostase | 3 |
| 29964 | acostarte | 3 |
| 29965 | acostáronse | 3 |
| 29966 | acostarle | 3 |
| 29967 | acostamos | 3 |
| 29968 | acostados | 3 |
| 29969 | acosa | 3 |
| 29970 | acordeón | 3 |
| 29971 | acordáis | 3 |
| 29972 | aconsejóle | 3 |
| 29973 | aconsejé | 3 |
| 29974 | aconseje | 3 |
| 29975 | aconsejada | 3 |
| 29976 | acompasados | 3 |
| 29977 | acompaño | 3 |
| 29978 | acompañasen | 3 |
| 29979 | acompañarse | 3 |
| 29980 | acompañará | 3 |
| 29981 | acompañantes | 3 |
| 29982 | acompañante | 3 |
| 29983 | acompañándola | 3 |
| 29984 | acompanar | 3 |
| 29985 | acompana | 3 |
| 29986 | acomodé | 3 |
| 29987 | acometimientos | 3 |
| 29988 | acometerla | 3 |
| 29989 | acogiese | 3 |
| 29990 | acobardó | 3 |
| 29991 | acierte | 3 |
| 29992 | aciertan | 3 |
| 29993 | ácido | 3 |
| 29994 | aciagos | 3 |
| 29995 | achilles | 3 |
| 29996 | acertaré | 3 |
| 29997 | acertando | 3 |
| 29998 | acertaban | 3 |
| 29999 | acerqué | 3 |
| 30000 | acercóse | 3 |
| 30001 | acercar | 3 |
| 30002 | acercamos | 3 |
| 30003 | acerados | 3 |
| 30004 | acequia | 3 |
| 30005 | aceptando | 3 |
| 30006 | aceptación | 3 |
| 30007 | acentuó | 3 |
| 30008 | acendrado | 3 |
| 30009 | acelerados | 3 |
| 30010 | acechar | 3 |
| 30011 | accionando | 3 |
| 30012 | accidental | 3 |
| 30013 | accesible | 3 |
| 30014 | accedió | 3 |
| 30015 | acariciaban | 3 |
| 30016 | acantonamos | 3 |
| 30017 | acallarle | 3 |
| 30018 | acaesçió | 3 |
| 30019 | académicos | 3 |
| 30020 | acabaste | 3 |
| 30021 | acabarle | 3 |
| 30022 | acabaré | 3 |
| 30023 | acabándola | 3 |
| 30024 | acabad | 3 |
| 30025 | abyección | 3 |
| 30026 | aburridos | 3 |
| 30027 | abundoso | 3 |
| 30028 | abundantemente | 3 |
| 30029 | abunda | 3 |
| 30030 | absuelve | 3 |
| 30031 | abstraído | 3 |
| 30032 | abstracta | 3 |
| 30033 | abstracciones | 3 |
| 30034 | abstengo | 3 |
| 30035 | absorbente | 3 |
| 30036 | absorbedero | 3 |
| 30037 | absentes | 3 |
| 30038 | abrumados | 3 |
| 30039 | abrumaban | 3 |
| 30040 | abruma | 3 |
| 30041 | abrirme | 3 |
| 30042 | abrirla | 3 |
| 30043 | abrirá | 3 |
| 30044 | abrigadito | 3 |
| 30045 | abrigada | 3 |
| 30046 | abreuia | 3 |
| 30047 | abrazarme | 3 |
| 30048 | abrazara | 3 |
| 30049 | abrazándome | 3 |
| 30050 | abraza | 3 |
| 30051 | abrasan | 3 |
| 30052 | abracé | 3 |
| 30053 | abrace | 3 |
| 30054 | aborrida | 3 |
| 30055 | aborrecidos | 3 |
| 30056 | abordar | 3 |
| 30057 | abollada | 3 |
| 30058 | abigarrada | 3 |
| 30059 | abiertamente | 3 |
| 30060 | abencerrajes | 3 |
| 30061 | abecedario | 3 |
| 30062 | abdomen | 3 |
| 30063 | abdicar | 3 |
| 30064 | abc | 3 |
| 30065 | abbas | 3 |
| 30066 | abbad | 3 |
| 30067 | abarcar | 3 |
| 30068 | abandonarme | 3 |
| 30069 | abandonarla | 3 |
| 30070 | abandonará | 3 |
| 30071 | abandonando | 3 |
| 30072 | abalanzó | 3 |
| 30073 | abadejo | 3 |
| 30074 | ab | 3 |
| 30075 | zurita | 2 |
| 30076 | zurda | 2 |
| 30077 | zurcir | 2 |
| 30078 | zurcidos | 2 |
| 30079 | zúñiga | 2 |
| 30080 | zumbón | 2 |
| 30081 | zumbar | 2 |
| 30082 | zumban | 2 |
| 30083 | zumbaban | 2 |
| 30084 | zumbaba | 2 |
| 30085 | zucena | 2 |
| 30086 | zu | 2 |
| 30087 | zozobras | 2 |
| 30088 | zortzico | 2 |
| 30089 | zoquetes | 2 |
| 30090 | zopencos | 2 |
| 30091 | zoología | 2 |
| 30092 | zonas | 2 |
| 30093 | zocodover | 2 |
| 30094 | zinc | 2 |
| 30095 | zi | 2 |
| 30096 | zeugma | 2 |
| 30097 | zeloso | 2 |
| 30098 | zegríes | 2 |
| 30099 | zarzamora | 2 |
| 30100 | zarzal | 2 |
| 30101 | zarandearte | 2 |
| 30102 | zaques | 2 |
| 30103 | zapatito | 2 |
| 30104 | zapateado | 2 |
| 30105 | zanjas | 2 |
| 30106 | zancarrón | 2 |
| 30107 | zampoñas | 2 |
| 30108 | zampado | 2 |
| 30109 | zamora | 2 |
| 30110 | zambra | 2 |
| 30111 | zaleas | 2 |
| 30112 | zalamera | 2 |
| 30113 | zalagarda | 2 |
| 30114 | zalá | 2 |
| 30115 | zaide | 2 |
| 30116 | zahorí | 2 |
| 30117 | zahara | 2 |
| 30118 | zaguero | 2 |
| 30119 | zagalona | 2 |
| 30120 | zagalillo | 2 |
| 30121 | zagalejas | 2 |
| 30122 | zafir | 2 |
| 30123 | zafarrancho | 2 |
| 30124 | yvan | 2 |
| 30125 | yuso | 2 |
| 30126 | yuas | 2 |
| 30127 | yredes | 2 |
| 30128 | yrado | 2 |
| 30129 | yrada | 2 |
| 30130 | yoduro | 2 |
| 30131 | ymágenes | 2 |
| 30132 | yjares | 2 |
| 30133 | yjadas | 2 |
| 30134 | yio | 2 |
| 30135 | yia | 2 |
| 30136 | ygualmente | 2 |
| 30137 | ygualara | 2 |
| 30138 | yerva | 2 |
| 30139 | yertos | 2 |
| 30140 | yerto | 2 |
| 30141 | yermos | 2 |
| 30142 | yéndome | 2 |
| 30143 | yéndoles | 2 |
| 30144 | yéndole | 2 |
| 30145 | ydvos | 2 |
| 30146 | yazía | 2 |
| 30147 | yazeys | 2 |
| 30148 | yaser | 2 |
| 30149 | yantava | 2 |
| 30150 | yantares | 2 |
| 30151 | yanta | 2 |
| 30152 | yaga | 2 |
| 30153 | xlviii | 2 |
| 30154 | xlvi | 2 |
| 30155 | xlix | 2 |
| 30156 | xliv | 2 |
| 30157 | xliii | 2 |
| 30158 | xlii | 2 |
| 30159 | xergas | 2 |
| 30160 | xarope | 2 |
| 30161 | xarifa | 2 |
| 30162 | xaquima | 2 |
| 30163 | whig | 2 |
| 30164 | wagner | 2 |
| 30165 | w | 2 |
| 30166 | vyñas | 2 |
| 30167 | vynome | 2 |
| 30168 | vyn | 2 |
| 30169 | vyeja | 2 |
| 30170 | vya | 2 |
| 30171 | vult | 2 |
| 30172 | vulgarísimo | 2 |
| 30173 | vulgarísima | 2 |
| 30174 | vuelcos | 2 |
| 30175 | vous | 2 |
| 30176 | votando | 2 |
| 30177 | vomita | 2 |
| 30178 | volvíle | 2 |
| 30179 | volviéronle | 2 |
| 30180 | volvieran | 2 |
| 30181 | volviéndoselo | 2 |
| 30182 | volviéndolo | 2 |
| 30183 | volviéndole | 2 |
| 30184 | volvíame | 2 |
| 30185 | volvérselos | 2 |
| 30186 | volvérsela | 2 |
| 30187 | volveros | 2 |
| 30188 | volverlos | 2 |
| 30189 | volveríamos | 2 |
| 30190 | voluptuosas | 2 |
| 30191 | voluntariamente | 2 |
| 30192 | voluntaria | 2 |
| 30193 | voluminosa | 2 |
| 30194 | voltear | 2 |
| 30195 | volo | 2 |
| 30196 | volcar | 2 |
| 30197 | volatines | 2 |
| 30198 | volatería | 2 |
| 30199 | volarse | 2 |
| 30200 | volados | 2 |
| 30201 | vociferando | 2 |
| 30202 | vocerrón | 2 |
| 30203 | vocería | 2 |
| 30204 | vocecilla | 2 |
| 30205 | voacé | 2 |
| 30206 | vnico | 2 |
| 30207 | vnguentos | 2 |
| 30208 | vizconde | 2 |
| 30209 | vizcaínos | 2 |
| 30210 | vivit | 2 |
| 30211 | vivísimos | 2 |
| 30212 | vivís | 2 |
| 30213 | vivirían | 2 |
| 30214 | vivieras | 2 |
| 30215 | vividos | 2 |
| 30216 | vividores | 2 |
| 30217 | vivet | 2 |
| 30218 | vivendi | 2 |
| 30219 | vivarachos | 2 |
| 30220 | vivamos | 2 |
| 30221 | vivacidad | 2 |
| 30222 | vivaaaa | 2 |
| 30223 | viuiria | 2 |
| 30224 | viuia | 2 |
| 30225 | viues | 2 |
| 30226 | vitupera | 2 |
| 30227 | vitrina | 2 |
| 30228 | vítreo | 2 |
| 30229 | vitis | 2 |
| 30230 | vítimas | 2 |
| 30231 | vitalicia | 2 |
| 30232 | vistiose | 2 |
| 30233 | vistillas | 2 |
| 30234 | vistiéronse | 2 |
| 30235 | vistiéndose | 2 |
| 30236 | vistelos | 2 |
| 30237 | vistalegre | 2 |
| 30238 | vislumbrar | 2 |
| 30239 | visiten | 2 |
| 30240 | visité | 2 |
| 30241 | visite | 2 |
| 30242 | visitasse | 2 |
| 30243 | visitarte | 2 |
| 30244 | visitaron | 2 |
| 30245 | visitaciones | 2 |
| 30246 | visionario | 2 |
| 30247 | vision | 2 |
| 30248 | viscosa | 2 |
| 30249 | virtutis | 2 |
| 30250 | virtut | 2 |
| 30251 | virtuosísima | 2 |
| 30252 | virotes | 2 |
| 30253 | virote | 2 |
| 30254 | viró | 2 |
| 30255 | virilidad | 2 |
| 30256 | virgines | 2 |
| 30257 | virgillio | 2 |
| 30258 | vióse | 2 |
| 30259 | violo | 2 |
| 30260 | violetas | 2 |
| 30261 | violentísimas | 2 |
| 30262 | violentar | 2 |
| 30263 | violentando | 2 |
| 30264 | víolas | 2 |
| 30265 | violadas | 2 |
| 30266 | viola | 2 |
| 30267 | viñedos | 2 |
| 30268 | vínosele | 2 |
| 30269 | vinosas | 2 |
| 30270 | vínome | 2 |
| 30271 | viniessedes | 2 |
| 30272 | vinier | 2 |
| 30273 | viniéndosele | 2 |
| 30274 | viner | 2 |
| 30275 | vinas | 2 |
| 30276 | vímonos | 2 |
| 30277 | villorete | 2 |
| 30278 | villavieja | 2 |
| 30279 | villabona | 2 |
| 30280 | vilezas | 2 |
| 30281 | vile | 2 |
| 30282 | vigilarla | 2 |
| 30283 | vigilara | 2 |
| 30284 | vigía | 2 |
| 30285 | viesses | 2 |
| 30286 | viessen | 2 |
| 30287 | viésemos | 2 |
| 30288 | vientres | 2 |
| 30289 | vientecillo | 2 |
| 30290 | viendote | 2 |
| 30291 | viendome | 2 |
| 30292 | viéndolo | 2 |
| 30293 | viéndolas | 2 |
| 30294 | viendola | 2 |
| 30295 | viejecito | 2 |
| 30296 | vie | 2 |
| 30297 | vidrioso | 2 |
| 30298 | vidente | 2 |
| 30299 | victoriosos | 2 |
| 30300 | victoriosa | 2 |
| 30301 | vicisitud | 2 |
| 30302 | viciado | 2 |
| 30303 | vicaría | 2 |
| 30304 | vibrantes | 2 |
| 30305 | viandantes | 2 |
| 30306 | viajeras | 2 |
| 30307 | viajecito | 2 |
| 30308 | viajando | 2 |
| 30309 | vfano | 2 |
| 30310 | veys | 2 |
| 30311 | veyalo | 2 |
| 30312 | vey | 2 |
| 30313 | vetustas | 2 |
| 30314 | vestros | 2 |
| 30315 | vestirte | 2 |
| 30316 | vestirnos | 2 |
| 30317 | vestirla | 2 |
| 30318 | vestíme | 2 |
| 30319 | vespucios | 2 |
| 30320 | vespucio | 2 |
| 30321 | vesinas | 2 |
| 30322 | vertió | 2 |
| 30323 | vertiginoso | 2 |
| 30324 | vertiginosa | 2 |
| 30325 | vertical | 2 |
| 30326 | versificar | 2 |
| 30327 | verrugas | 2 |
| 30328 | vero | 2 |
| 30329 | vernía | 2 |
| 30330 | vernet | 2 |
| 30331 | verificará | 2 |
| 30332 | verificar | 2 |
| 30333 | verifican | 2 |
| 30334 | verificaba | 2 |
| 30335 | verídicos | 2 |
| 30336 | verídicas | 2 |
| 30337 | verías | 2 |
| 30338 | veria | 2 |
| 30339 | vergueña | 2 |
| 30340 | vergüença | 2 |
| 30341 | vergeles | 2 |
| 30342 | verga | 2 |
| 30343 | vereys | 2 |
| 30344 | vere | 2 |
| 30345 | verduleras | 2 |
| 30346 | verdoso | 2 |
| 30347 | verdosas | 2 |
| 30348 | verdinegro | 2 |
| 30349 | verças | 2 |
| 30350 | verbum | 2 |
| 30351 | verbis | 2 |
| 30352 | veraz | 2 |
| 30353 | veraste | 2 |
| 30354 | veranillo | 2 |
| 30355 | véome | 2 |
| 30356 | venzan | 2 |
| 30357 | ventrera | 2 |
| 30358 | ventorro | 2 |
| 30359 | ventorrillos | 2 |
| 30360 | ventillas | 2 |
| 30361 | ventilen | 2 |
| 30362 | ventilarse | 2 |
| 30363 | ventilar | 2 |
| 30364 | vénme | 2 |
| 30365 | venme | 2 |
| 30366 | veniera | 2 |
| 30367 | venier | 2 |
| 30368 | venie | 2 |
| 30369 | venialmente | 2 |
| 30370 | vengativos | 2 |
| 30371 | vengaros | 2 |
| 30372 | vengábase | 2 |
| 30373 | venero | 2 |
| 30374 | venerando | 2 |
| 30375 | venerado | 2 |
| 30376 | veneradas | 2 |
| 30377 | venenoso | 2 |
| 30378 | veneciano | 2 |
| 30379 | veneciana | 2 |
| 30380 | vendieron | 2 |
| 30381 | vendiere | 2 |
| 30382 | vendidas | 2 |
| 30383 | vendia | 2 |
| 30384 | vendes | 2 |
| 30385 | venderse | 2 |
| 30386 | venderlos | 2 |
| 30387 | venderla | 2 |
| 30388 | vendaje | 2 |
| 30389 | vendados | 2 |
| 30390 | vençido | 2 |
| 30391 | vencerlo | 2 |
| 30392 | vencerían | 2 |
| 30393 | venceremos | 2 |
| 30394 | vencerás | 2 |
| 30395 | vencerá | 2 |
| 30396 | vencéis | 2 |
| 30397 | vencedoras | 2 |
| 30398 | vençamos | 2 |
| 30399 | venablos | 2 |
| 30400 | velozmente | 2 |
| 30401 | velle | 2 |
| 30402 | vellaca | 2 |
| 30403 | velis | 2 |
| 30404 | velera | 2 |
| 30405 | veleidoso | 2 |
| 30406 | vele | 2 |
| 30407 | velche | 2 |
| 30408 | velasco | 2 |
| 30409 | velarle | 2 |
| 30410 | velarla | 2 |
| 30411 | velaban | 2 |
| 30412 | vejezuela | 2 |
| 30413 | vejamen | 2 |
| 30414 | vejación | 2 |
| 30415 | veintiuno | 2 |
| 30416 | veíalos | 2 |
| 30417 | veíala | 2 |
| 30418 | veíais | 2 |
| 30419 | vegilia | 2 |
| 30420 | vegedat | 2 |
| 30421 | veemos | 2 |
| 30422 | veedor | 2 |
| 30423 | vedados | 2 |
| 30424 | vecindades | 2 |
| 30425 | veçina | 2 |
| 30426 | veçes | 2 |
| 30427 | veays | 2 |
| 30428 | vazios | 2 |
| 30429 | vazio | 2 |
| 30430 | vayo | 2 |
| 30431 | vaumare | 2 |
| 30432 | vates | 2 |
| 30433 | vaste | 2 |
| 30434 | vassallos | 2 |
| 30435 | vassallo | 2 |
| 30436 | vasito | 2 |
| 30437 | vasija | 2 |
| 30438 | vascular | 2 |
| 30439 | vascos | 2 |
| 30440 | vasares | 2 |
| 30441 | varruntan | 2 |
| 30442 | varitas | 2 |
| 30443 | varita | 2 |
| 30444 | vario | 2 |
| 30445 | variato | 2 |
| 30446 | variadísima | 2 |
| 30447 | variadas | 2 |
| 30448 | variaciones | 2 |
| 30449 | variacion | 2 |
| 30450 | variable | 2 |
| 30451 | varazos | 2 |
| 30452 | varapalos | 2 |
| 30453 | vaqueta | 2 |
| 30454 | vápulo | 2 |
| 30455 | vapulamiento | 2 |
| 30456 | vaporoso | 2 |
| 30457 | vánse | 2 |
| 30458 | vanidoso | 2 |
| 30459 | vanidosa | 2 |
| 30460 | vandera | 2 |
| 30461 | vanagloriarse | 2 |
| 30462 | vampiro | 2 |
| 30463 | valyente | 2 |
| 30464 | valonas | 2 |
| 30465 | valmont | 2 |
| 30466 | vallena | 2 |
| 30467 | valioso | 2 |
| 30468 | valimiento | 2 |
| 30469 | valija | 2 |
| 30470 | valieran | 2 |
| 30471 | válidos | 2 |
| 30472 | valetudinario | 2 |
| 30473 | valerte | 2 |
| 30474 | valerle | 2 |
| 30475 | valera | 2 |
| 30476 | valenzuela | 2 |
| 30477 | valentísimos | 2 |
| 30478 | valentísima | 2 |
| 30479 | valençia | 2 |
| 30480 | valedores | 2 |
| 30481 | valedero | 2 |
| 30482 | valdrían | 2 |
| 30483 | valdíos | 2 |
| 30484 | valdepeñas | 2 |
| 30485 | valcerrado | 2 |
| 30486 | valala | 2 |
| 30487 | vainillas | 2 |
| 30488 | vagones | 2 |
| 30489 | vagaroso | 2 |
| 30490 | vagan | 2 |
| 30491 | vade | 2 |
| 30492 | vacilantes | 2 |
| 30493 | vacilado | 2 |
| 30494 | vacada | 2 |
| 30495 | uvias | 2 |
| 30496 | utilísimas | 2 |
| 30497 | usurpan | 2 |
| 30498 | usurpación | 2 |
| 30499 | usurera | 2 |
| 30500 | usufructo | 2 |
| 30501 | usual | 2 |
| 30502 | uste | 2 |
| 30503 | ustáriz | 2 |
| 30504 | uses | 2 |
| 30505 | usase | 2 |
| 30506 | usarse | 2 |
| 30507 | usaré | 2 |
| 30508 | usaran | 2 |
| 30509 | usará | 2 |
| 30510 | usad | 2 |
| 30511 | úrsula | 2 |
| 30512 | urruña | 2 |
| 30513 | urosas | 2 |
| 30514 | urola | 2 |
| 30515 | urnas | 2 |
| 30516 | urgía | 2 |
| 30517 | urgencias | 2 |
| 30518 | urgencia | 2 |
| 30519 | urbanos | 2 |
| 30520 | urbanas | 2 |
| 30521 | urbanamente | 2 |
| 30522 | untersuchungen | 2 |
| 30523 | untados | 2 |
| 30524 | untado | 2 |
| 30525 | untada | 2 |
| 30526 | universitario | 2 |
| 30527 | universalmente | 2 |
| 30528 | unísono | 2 |
| 30529 | uniones | 2 |
| 30530 | uniéndose | 2 |
| 30531 | uniendo | 2 |
| 30532 | unicornio | 2 |
| 30533 | ungento | 2 |
| 30534 | unen | 2 |
| 30535 | undécimo | 2 |
| 30536 | unció | 2 |
| 30537 | unánimemente | 2 |
| 30538 | umbroso | 2 |
| 30539 | ultramontanos | 2 |
| 30540 | ultramarino | 2 |
| 30541 | ultrajes | 2 |
| 30542 | ultrajados | 2 |
| 30543 | ultima | 2 |
| 30544 | ulixes | 2 |
| 30545 | ujier | 2 |
| 30546 | ujeros | 2 |
| 30547 | ufana | 2 |
| 30548 | uéspet | 2 |
| 30549 | ueso | 2 |
| 30550 | ubre | 2 |
| 30551 | tyrat | 2 |
| 30552 | tyra | 2 |
| 30553 | tynta | 2 |
| 30554 | tyento | 2 |
| 30555 | tuvímoslo | 2 |
| 30556 | tuviésemos | 2 |
| 30557 | tuviéronle | 2 |
| 30558 | tuviéronla | 2 |
| 30559 | tutora | 2 |
| 30560 | tutelares | 2 |
| 30561 | tuteándola | 2 |
| 30562 | tuteaban | 2 |
| 30563 | tutea | 2 |
| 30564 | tusca | 2 |
| 30565 | turulato | 2 |
| 30566 | turris | 2 |
| 30567 | turquí | 2 |
| 30568 | turquescos | 2 |
| 30569 | turquesa | 2 |
| 30570 | turbose | 2 |
| 30571 | turbios | 2 |
| 30572 | turbéme | 2 |
| 30573 | turbarle | 2 |
| 30574 | turbantes | 2 |
| 30575 | turbándose | 2 |
| 30576 | turban | 2 |
| 30577 | turbados | 2 |
| 30578 | tupé | 2 |
| 30579 | túnicas | 2 |
| 30580 | tumor | 2 |
| 30581 | tumbas | 2 |
| 30582 | tumban | 2 |
| 30583 | tumbaba | 2 |
| 30584 | tuis | 2 |
| 30585 | tugurios | 2 |
| 30586 | tuerces | 2 |
| 30587 | tudescos | 2 |
| 30588 | tudesco | 2 |
| 30589 | tubinga | 2 |
| 30590 | tuberculosis | 2 |
| 30591 | tuae | 2 |
| 30592 | truxiste | 2 |
| 30593 | truquage | 2 |
| 30594 | trun | 2 |
| 30595 | trújole | 2 |
| 30596 | trujiste | 2 |
| 30597 | trujéronle | 2 |
| 30598 | trujéronla | 2 |
| 30599 | trujeres | 2 |
| 30600 | trujere | 2 |
| 30601 | trufas | 2 |
| 30602 | truena | 2 |
| 30603 | trucos | 2 |
| 30604 | truchuelas | 2 |
| 30605 | truchuela | 2 |
| 30606 | truchimán | 2 |
| 30607 | troxo | 2 |
| 30608 | troxieron | 2 |
| 30609 | trovas | 2 |
| 30610 | trova | 2 |
| 30611 | trousseaux | 2 |
| 30612 | troteras | 2 |
| 30613 | trota | 2 |
| 30614 | tropical | 2 |
| 30615 | tropezaras | 2 |
| 30616 | tropelías | 2 |
| 30617 | tronchón | 2 |
| 30618 | tronados | 2 |
| 30619 | trómpogelas | 2 |
| 30620 | trompas | 2 |
| 30621 | troco | 2 |
| 30622 | trochas | 2 |
| 30623 | trocha | 2 |
| 30624 | trocaría | 2 |
| 30625 | trocalle | 2 |
| 30626 | trobando | 2 |
| 30627 | triunfe | 2 |
| 30628 | triunfará | 2 |
| 30629 | triunfando | 2 |
| 30630 | triunfaban | 2 |
| 30631 | tritones | 2 |
| 30632 | tritón | 2 |
| 30633 | tristísimos | 2 |
| 30634 | triquete | 2 |
| 30635 | trípode | 2 |
| 30636 | triple | 2 |
| 30637 | tripa | 2 |
| 30638 | trinquetada | 2 |
| 30639 | trinos | 2 |
| 30640 | trincó | 2 |
| 30641 | trinchador | 2 |
| 30642 | trincando | 2 |
| 30643 | trinando | 2 |
| 30644 | trinacria | 2 |
| 30645 | trinaba | 2 |
| 30646 | trimestral | 2 |
| 30647 | trillando | 2 |
| 30648 | tridente | 2 |
| 30649 | tributó | 2 |
| 30650 | tributarios | 2 |
| 30651 | tributar | 2 |
| 30652 | tributando | 2 |
| 30653 | tributaban | 2 |
| 30654 | tribuna | 2 |
| 30655 | tribulança | 2 |
| 30656 | tribulacion | 2 |
| 30657 | triángulos | 2 |
| 30658 | triangular | 2 |
| 30659 | triaca | 2 |
| 30660 | treze | 2 |
| 30661 | tresquilen | 2 |
| 30662 | trepó | 2 |
| 30663 | trepaban | 2 |
| 30664 | trenzados | 2 |
| 30665 | trenza | 2 |
| 30666 | tremolina | 2 |
| 30667 | tremola | 2 |
| 30668 | tremer | 2 |
| 30669 | trefudo | 2 |
| 30670 | trechón | 2 |
| 30671 | trazo | 2 |
| 30672 | trazados | 2 |
| 30673 | trayle | 2 |
| 30674 | trayas | 2 |
| 30675 | traxeron | 2 |
| 30676 | traxe | 2 |
| 30677 | trax | 2 |
| 30678 | travas | 2 |
| 30679 | travando | 2 |
| 30680 | trauiesos | 2 |
| 30681 | tratóse | 2 |
| 30682 | tratemos | 2 |
| 30683 | tratarlos | 2 |
| 30684 | tratarles | 2 |
| 30685 | tratarían | 2 |
| 30686 | tratarán | 2 |
| 30687 | tratándola | 2 |
| 30688 | tratamientos | 2 |
| 30689 | tratable | 2 |
| 30690 | tratábame | 2 |
| 30691 | tratábala | 2 |
| 30692 | trasudar | 2 |
| 30693 | trasudaba | 2 |
| 30694 | trastrigo | 2 |
| 30695 | trastorné | 2 |
| 30696 | trastorne | 2 |
| 30697 | trastornase | 2 |
| 30698 | trastornan | 2 |
| 30699 | trastornaban | 2 |
| 30700 | trastes | 2 |
| 30701 | traste | 2 |
| 30702 | trastadas | 2 |
| 30703 | trasquilar | 2 |
| 30704 | traspuesta | 2 |
| 30705 | trasposiciones | 2 |
| 30706 | traspillados | 2 |
| 30707 | traspiés | 2 |
| 30708 | traspasó | 2 |
| 30709 | traspasados | 2 |
| 30710 | traspasaban | 2 |
| 30711 | traspasa | 2 |
| 30712 | trasparente | 2 |
| 30713 | trasnochada | 2 |
| 30714 | trasladose | 2 |
| 30715 | traslados | 2 |
| 30716 | trasladé | 2 |
| 30717 | trasladaron | 2 |
| 30718 | trasladarle | 2 |
| 30719 | trasladándola | 2 |
| 30720 | trasladaba | 2 |
| 30721 | trasgo | 2 |
| 30722 | trasero | 2 |
| 30723 | trasegando | 2 |
| 30724 | trascendencia | 2 |
| 30725 | trapalona | 2 |
| 30726 | trapajos | 2 |
| 30727 | trapa | 2 |
| 30728 | tranzados | 2 |
| 30729 | tranzado | 2 |
| 30730 | tranvías | 2 |
| 30731 | transportaron | 2 |
| 30732 | transportada | 2 |
| 30733 | transparentarse | 2 |
| 30734 | transparencias | 2 |
| 30735 | transparencia | 2 |
| 30736 | transmitirlo | 2 |
| 30737 | transido | 2 |
| 30738 | transformismo | 2 |
| 30739 | transformase | 2 |
| 30740 | transformarse | 2 |
| 30741 | transformar | 2 |
| 30742 | transfigurado | 2 |
| 30743 | transfigurada | 2 |
| 30744 | transferencia | 2 |
| 30745 | transeuntes | 2 |
| 30746 | transcurrió | 2 |
| 30747 | tranquilizadores | 2 |
| 30748 | tranquilizado | 2 |
| 30749 | tranquilícese | 2 |
| 30750 | trangullones | 2 |
| 30751 | trancos | 2 |
| 30752 | trancazo | 2 |
| 30753 | tranca | 2 |
| 30754 | trampilla | 2 |
| 30755 | trámites | 2 |
| 30756 | trajesen | 2 |
| 30757 | trajéronle | 2 |
| 30758 | trajecitos | 2 |
| 30759 | trajeado | 2 |
| 30760 | trajano | 2 |
| 30761 | trailla | 2 |
| 30762 | traigamos | 2 |
| 30763 | traidoras | 2 |
| 30764 | traicionera | 2 |
| 30765 | traíame | 2 |
| 30766 | trahedes | 2 |
| 30767 | trágicos | 2 |
| 30768 | tragi | 2 |
| 30769 | tragas | 2 |
| 30770 | tragarse | 2 |
| 30771 | tragarme | 2 |
| 30772 | tragan | 2 |
| 30773 | tragaldabas | 2 |
| 30774 | trafagos | 2 |
| 30775 | tráfago | 2 |
| 30776 | tráetelo | 2 |
| 30777 | traere | 2 |
| 30778 | traella | 2 |
| 30779 | tráele | 2 |
| 30780 | traedme | 2 |
| 30781 | traed | 2 |
| 30782 | tradutor | 2 |
| 30783 | traduje | 2 |
| 30784 | traductores | 2 |
| 30785 | traduciendo | 2 |
| 30786 | traducidos | 2 |
| 30787 | traducida | 2 |
| 30788 | tradicionalista | 2 |
| 30789 | tradicionales | 2 |
| 30790 | tractado | 2 |
| 30791 | trabillas | 2 |
| 30792 | trabazón | 2 |
| 30793 | trabase | 2 |
| 30794 | trabaron | 2 |
| 30795 | traban | 2 |
| 30796 | trabajillo | 2 |
| 30797 | trabajase | 2 |
| 30798 | trabajaron | 2 |
| 30799 | trabajaré | 2 |
| 30800 | trabajadoras | 2 |
| 30801 | trabadas | 2 |
| 30802 | trababan | 2 |
| 30803 | tozino | 2 |
| 30804 | tovyeres | 2 |
| 30805 | toviese | 2 |
| 30806 | toviere | 2 |
| 30807 | toviera | 2 |
| 30808 | tout | 2 |
| 30809 | touieron | 2 |
| 30810 | toue | 2 |
| 30811 | tostados | 2 |
| 30812 | tostadas | 2 |
| 30813 | tosquedad | 2 |
| 30814 | tósigo | 2 |
| 30815 | tosían | 2 |
| 30816 | tose | 2 |
| 30817 | toscana | 2 |
| 30818 | toscamente | 2 |
| 30819 | tosa | 2 |
| 30820 | tortuosos | 2 |
| 30821 | tortolas | 2 |
| 30822 | tortillas | 2 |
| 30823 | torso | 2 |
| 30824 | tornóla | 2 |
| 30825 | tornillos | 2 |
| 30826 | tornera | 2 |
| 30827 | torneos | 2 |
| 30828 | torneada | 2 |
| 30829 | tornaste | 2 |
| 30830 | tornasse | 2 |
| 30831 | tórnase | 2 |
| 30832 | tornas | 2 |
| 30833 | tornarse | 2 |
| 30834 | tornare | 2 |
| 30835 | tornará | 2 |
| 30836 | tornara | 2 |
| 30837 | tornándose | 2 |
| 30838 | tornándole | 2 |
| 30839 | tornados | 2 |
| 30840 | tornaban | 2 |
| 30841 | tordilla | 2 |
| 30842 | torciéndose | 2 |
| 30843 | torcaças | 2 |
| 30844 | toquéis | 2 |
| 30845 | toqué | 2 |
| 30846 | topóme | 2 |
| 30847 | tópico | 2 |
| 30848 | topete | 2 |
| 30849 | topetazo | 2 |
| 30850 | tope | 2 |
| 30851 | toparéis | 2 |
| 30852 | topare | 2 |
| 30853 | toos | 2 |
| 30854 | tontito | 2 |
| 30855 | tontiloco | 2 |
| 30856 | tontamente | 2 |
| 30857 | tontainas | 2 |
| 30858 | tonsurado | 2 |
| 30859 | tonadilla | 2 |
| 30860 | tonadas | 2 |
| 30861 | tón | 2 |
| 30862 | ton | 2 |
| 30863 | tomóse | 2 |
| 30864 | tomos | 2 |
| 30865 | tomóme | 2 |
| 30866 | tomólo | 2 |
| 30867 | tomole | 2 |
| 30868 | tomillares | 2 |
| 30869 | tómese | 2 |
| 30870 | tómeme | 2 |
| 30871 | tomauas | 2 |
| 30872 | tómate | 2 |
| 30873 | tomases | 2 |
| 30874 | tomaros | 2 |
| 30875 | tomáronse | 2 |
| 30876 | tomarnos | 2 |
| 30877 | tomaremos | 2 |
| 30878 | tomaréis | 2 |
| 30879 | tomarás | 2 |
| 30880 | tomaras | 2 |
| 30881 | tomarán | 2 |
| 30882 | tomaran | 2 |
| 30883 | tomándolas | 2 |
| 30884 | tomalla | 2 |
| 30885 | tómala | 2 |
| 30886 | tomadme | 2 |
| 30887 | tomadas | 2 |
| 30888 | tolondrones | 2 |
| 30889 | tolerarlas | 2 |
| 30890 | tolerante | 2 |
| 30891 | tolera | 2 |
| 30892 | toledos | 2 |
| 30893 | toldilla | 2 |
| 30894 | toíto | 2 |
| 30895 | tocho | 2 |
| 30896 | tocarlos | 2 |
| 30897 | tocarlas | 2 |
| 30898 | tocaré | 2 |
| 30899 | tocándose | 2 |
| 30900 | tobillos | 2 |
| 30901 | tizones | 2 |
| 30902 | tizne | 2 |
| 30903 | tiznado | 2 |
| 30904 | tiznada | 2 |
| 30905 | titulada | 2 |
| 30906 | titulaba | 2 |
| 30907 | titubeando | 2 |
| 30908 | titanes | 2 |
| 30909 | tísico | 2 |
| 30910 | tirsi | 2 |
| 30911 | tirotearse | 2 |
| 30912 | tirito | 2 |
| 30913 | tirarte | 2 |
| 30914 | tirarlo | 2 |
| 30915 | tiraniza | 2 |
| 30916 | tiránica | 2 |
| 30917 | tirándose | 2 |
| 30918 | tiradas | 2 |
| 30919 | tiqui | 2 |
| 30920 | tiple | 2 |
| 30921 | tio | 2 |
| 30922 | tinturas | 2 |
| 30923 | tinteros | 2 |
| 30924 | tinelo | 2 |
| 30925 | tinacrio | 2 |
| 30926 | tímpano | 2 |
| 30927 | timideces | 2 |
| 30928 | tímidas | 2 |
| 30929 | timbales | 2 |
| 30930 | timaba | 2 |
| 30931 | tilos | 2 |
| 30932 | tijeretazo | 2 |
| 30933 | tijeretas | 2 |
| 30934 | tiito | 2 |
| 30935 | tientes | 2 |
| 30936 | tienta | 2 |
| 30937 | tienpos | 2 |
| 30938 | tiénenlo | 2 |
| 30939 | tiendo | 2 |
| 30940 | tié | 2 |
| 30941 | tibulo | 2 |
| 30942 | tibios | 2 |
| 30943 | tíber | 2 |
| 30944 | thorum | 2 |
| 30945 | thiers | 2 |
| 30946 | texido | 2 |
| 30947 | tétrico | 2 |
| 30948 | testamentaría | 2 |
| 30949 | testaférreo | 2 |
| 30950 | testador | 2 |
| 30951 | tesorera | 2 |
| 30952 | teseo | 2 |
| 30953 | tesalia | 2 |
| 30954 | teruel | 2 |
| 30955 | tersos | 2 |
| 30956 | tersas | 2 |
| 30957 | terrores | 2 |
| 30958 | terrenas | 2 |
| 30959 | terrae | 2 |
| 30960 | terrados | 2 |
| 30961 | terradillo | 2 |
| 30962 | ternísimamente | 2 |
| 30963 | ternía | 2 |
| 30964 | terneza | 2 |
| 30965 | ternero | 2 |
| 30966 | ternemos | 2 |
| 30967 | terné | 2 |
| 30968 | termodonte | 2 |
| 30969 | terminos | 2 |
| 30970 | termino | 2 |
| 30971 | termine | 2 |
| 30972 | terminase | 2 |
| 30973 | terminantes | 2 |
| 30974 | terminan | 2 |
| 30975 | terminados | 2 |
| 30976 | terminadas | 2 |
| 30977 | terencio | 2 |
| 30978 | terció | 2 |
| 30979 | terciar | 2 |
| 30980 | terciado | 2 |
| 30981 | terceronas | 2 |
| 30982 | terçera | 2 |
| 30983 | terçer | 2 |
| 30984 | terapéutica | 2 |
| 30985 | teóricos | 2 |
| 30986 | teórica | 2 |
| 30987 | teológicos | 2 |
| 30988 | teológica | 2 |
| 30989 | teologías | 2 |
| 30990 | teogonía | 2 |
| 30991 | teogenes | 2 |
| 30992 | teodora | 2 |
| 30993 | teócrito | 2 |
| 30994 | teñidos | 2 |
| 30995 | teñían | 2 |
| 30996 | tentada | 2 |
| 30997 | tenme | 2 |
| 30998 | teníase | 2 |
| 30999 | tenian | 2 |
| 31000 | tengote | 2 |
| 31001 | téngolo | 2 |
| 31002 | ténganme | 2 |
| 31003 | téngalo | 2 |
| 31004 | tengades | 2 |
| 31005 | tenes | 2 |
| 31006 | tenerles | 2 |
| 31007 | tené | 2 |
| 31008 | tendiéronse | 2 |
| 31009 | tendían | 2 |
| 31010 | tenblar | 2 |
| 31011 | tenazicas | 2 |
| 31012 | tenacidades | 2 |
| 31013 | tén | 2 |
| 31014 | tempranos | 2 |
| 31015 | templarle | 2 |
| 31016 | templados | 2 |
| 31017 | templaba | 2 |
| 31018 | tempestades | 2 |
| 31019 | temidas | 2 |
| 31020 | temerosas | 2 |
| 31021 | temerarias | 2 |
| 31022 | teméis | 2 |
| 31023 | temblonas | 2 |
| 31024 | tembleque | 2 |
| 31025 | temamos | 2 |
| 31026 | tellagorris | 2 |
| 31027 | telegrafiado | 2 |
| 31028 | tejo | 2 |
| 31029 | tejieron | 2 |
| 31030 | tejidos | 2 |
| 31031 | tejidas | 2 |
| 31032 | tejer | 2 |
| 31033 | tejen | 2 |
| 31034 | tejar | 2 |
| 31035 | tecum | 2 |
| 31036 | técnicas | 2 |
| 31037 | teclado | 2 |
| 31038 | tecla | 2 |
| 31039 | tebas | 2 |
| 31040 | teatino | 2 |
| 31041 | teas | 2 |
| 31042 | tascando | 2 |
| 31043 | tasaron | 2 |
| 31044 | tasajo | 2 |
| 31045 | tasada | 2 |
| 31046 | tasaba | 2 |
| 31047 | tarumba | 2 |
| 31048 | tartesios | 2 |
| 31049 | tartamudo | 2 |
| 31050 | tartamudea | 2 |
| 31051 | tartamuda | 2 |
| 31052 | tarsa | 2 |
| 31053 | tarro | 2 |
| 31054 | tarragona | 2 |
| 31055 | tarpeya | 2 |
| 31056 | tarjetas | 2 |
| 31057 | tarifas | 2 |
| 31058 | tardío | 2 |
| 31059 | tardinero | 2 |
| 31060 | tardemos | 2 |
| 31061 | tardasse | 2 |
| 31062 | tardas | 2 |
| 31063 | tardarían | 2 |
| 31064 | tardara | 2 |
| 31065 | tardando | 2 |
| 31066 | taravilla | 2 |
| 31067 | tapicero | 2 |
| 31068 | tapiadas | 2 |
| 31069 | tápenme | 2 |
| 31070 | taparrabo | 2 |
| 31071 | taparle | 2 |
| 31072 | tapados | 2 |
| 31073 | tapadillo | 2 |
| 31074 | tapadas | 2 |
| 31075 | tapaboca | 2 |
| 31076 | tañidos | 2 |
| 31077 | tañido | 2 |
| 31078 | tañida | 2 |
| 31079 | tañían | 2 |
| 31080 | tañendo | 2 |
| 31081 | tantum | 2 |
| 31082 | tánto | 2 |
| 31083 | tantismo | 2 |
| 31084 | tantearemos | 2 |
| 31085 | tántalo | 2 |
| 31086 | tanida | 2 |
| 31087 | tanga | 2 |
| 31088 | taner | 2 |
| 31089 | tanbién | 2 |
| 31090 | tamizada | 2 |
| 31091 | tamborín | 2 |
| 31092 | tamborilero | 2 |
| 31093 | tamaza | 2 |
| 31094 | tamar | 2 |
| 31095 | tamañita | 2 |
| 31096 | talles | 2 |
| 31097 | talares | 2 |
| 31098 | talabarte | 2 |
| 31099 | tala | 2 |
| 31100 | tajador | 2 |
| 31101 | tagarote | 2 |
| 31102 | tafetanes | 2 |
| 31103 | taciturnos | 2 |
| 31104 | tácitos | 2 |
| 31105 | tachuelas | 2 |
| 31106 | tacho | 2 |
| 31107 | taças | 2 |
| 31108 | tac | 2 |
| 31109 | tablones | 2 |
| 31110 | tablitas | 2 |
| 31111 | tablilla | 2 |
| 31112 | tableado | 2 |
| 31113 | tablajero | 2 |
| 31114 | tablada | 2 |
| 31115 | tabernero | 2 |
| 31116 | tabardo | 2 |
| 31117 | syrvo | 2 |
| 31118 | syrve | 2 |
| 31119 | synples | 2 |
| 31120 | susurró | 2 |
| 31121 | susurraba | 2 |
| 31122 | sustraerse | 2 |
| 31123 | sustituído | 2 |
| 31124 | sustente | 2 |
| 31125 | sustentarse | 2 |
| 31126 | sustentarme | 2 |
| 31127 | sustentadas | 2 |
| 31128 | sustantivo | 2 |
| 31129 | suspirona | 2 |
| 31130 | suspire | 2 |
| 31131 | suspiras | 2 |
| 31132 | suspirado | 2 |
| 31133 | suspicacia | 2 |
| 31134 | suspenderse | 2 |
| 31135 | suspende | 2 |
| 31136 | suspenda | 2 |
| 31137 | suscrición | 2 |
| 31138 | susana | 2 |
| 31139 | surtú | 2 |
| 31140 | surto | 2 |
| 31141 | surtían | 2 |
| 31142 | surgir | 2 |
| 31143 | surgen | 2 |
| 31144 | surge | 2 |
| 31145 | surcó | 2 |
| 31146 | surcar | 2 |
| 31147 | surcaban | 2 |
| 31148 | surca | 2 |
| 31149 | suprimían | 2 |
| 31150 | suprime | 2 |
| 31151 | suponían | 2 |
| 31152 | suponga | 2 |
| 31153 | supón | 2 |
| 31154 | súpolo | 2 |
| 31155 | suplió | 2 |
| 31156 | suplícote | 2 |
| 31157 | suplícoos | 2 |
| 31158 | suplicastes | 2 |
| 31159 | suplicamos | 2 |
| 31160 | súplica | 2 |
| 31161 | suplía | 2 |
| 31162 | suplia | 2 |
| 31163 | suplemento | 2 |
| 31164 | suplan | 2 |
| 31165 | supla | 2 |
| 31166 | supito | 2 |
| 31167 | supiste | 2 |
| 31168 | supiessen | 2 |
| 31169 | superpuestas | 2 |
| 31170 | superposición | 2 |
| 31171 | superlativos | 2 |
| 31172 | superfluidades | 2 |
| 31173 | superficiales | 2 |
| 31174 | superabundancia | 2 |
| 31175 | super | 2 |
| 31176 | suntuaria | 2 |
| 31177 | summum | 2 |
| 31178 | summa | 2 |
| 31179 | sumiso | 2 |
| 31180 | suministrarle | 2 |
| 31181 | sumidos | 2 |
| 31182 | sumidas | 2 |
| 31183 | sumía | 2 |
| 31184 | sumergida | 2 |
| 31185 | sumerge | 2 |
| 31186 | sumaria | 2 |
| 31187 | sultán | 2 |
| 31188 | sulfato | 2 |
| 31189 | sujetara | 2 |
| 31190 | sui | 2 |
| 31191 | sugirieron | 2 |
| 31192 | sugiriéndole | 2 |
| 31193 | sugestivo | 2 |
| 31194 | sugerían | 2 |
| 31195 | sugeríale | 2 |
| 31196 | sufro | 2 |
| 31197 | sufrirle | 2 |
| 31198 | sufriría | 2 |
| 31199 | sufriré | 2 |
| 31200 | sufrieron | 2 |
| 31201 | sufrible | 2 |
| 31202 | sufras | 2 |
| 31203 | súfrala | 2 |
| 31204 | sufragio | 2 |
| 31205 | suffrir | 2 |
| 31206 | suez | 2 |
| 31207 | sueras | 2 |
| 31208 | sueñan | 2 |
| 31209 | suenen | 2 |
| 31210 | suelten | 2 |
| 31211 | suéltela | 2 |
| 31212 | suelte | 2 |
| 31213 | suegras | 2 |
| 31214 | suecia | 2 |
| 31215 | sudario | 2 |
| 31216 | sucumbiría | 2 |
| 31217 | suculentos | 2 |
| 31218 | suculenta | 2 |
| 31219 | sucesiva | 2 |
| 31220 | sucedernos | 2 |
| 31221 | sucédele | 2 |
| 31222 | sucedáneos | 2 |
| 31223 | subterráneas | 2 |
| 31224 | subteniente | 2 |
| 31225 | substituir | 2 |
| 31226 | subsistir | 2 |
| 31227 | subsistía | 2 |
| 31228 | subsistencia | 2 |
| 31229 | subsiguientes | 2 |
| 31230 | subsidios | 2 |
| 31231 | subsidio | 2 |
| 31232 | subrepticio | 2 |
| 31233 | submarina | 2 |
| 31234 | sublimada | 2 |
| 31235 | sublevó | 2 |
| 31236 | sublevado | 2 |
| 31237 | subjetivo | 2 |
| 31238 | súbitas | 2 |
| 31239 | subirme | 2 |
| 31240 | subiría | 2 |
| 31241 | subio | 2 |
| 31242 | subiéronse | 2 |
| 31243 | subiéronle | 2 |
| 31244 | súbeme | 2 |
| 31245 | súbditos | 2 |
| 31246 | subastas | 2 |
| 31247 | suavizar | 2 |
| 31248 | suavizando | 2 |
| 31249 | suavizaba | 2 |
| 31250 | suárez | 2 |
| 31251 | suarés | 2 |
| 31252 | statu | 2 |
| 31253 | ssus | 2 |
| 31254 | ssierra | 2 |
| 31255 | ssienpre | 2 |
| 31256 | ssi | 2 |
| 31257 | sser | 2 |
| 31258 | sseñora | 2 |
| 31259 | ssea | 2 |
| 31260 | ssaña | 2 |
| 31261 | ssanto | 2 |
| 31262 | spiritu | 2 |
| 31263 | speranza | 2 |
| 31264 | sperança | 2 |
| 31265 | spanischen | 2 |
| 31266 | sotilmente | 2 |
| 31267 | sotilezas | 2 |
| 31268 | soterranos | 2 |
| 31269 | sotar | 2 |
| 31270 | sotanilla | 2 |
| 31271 | sota | 2 |
| 31272 | sostienes | 2 |
| 31273 | sosteniéndose | 2 |
| 31274 | sostenerme | 2 |
| 31275 | sostendré | 2 |
| 31276 | sostendrás | 2 |
| 31277 | sossegada | 2 |
| 31278 | sospirar | 2 |
| 31279 | sospechosos | 2 |
| 31280 | sospechaste | 2 |
| 31281 | sospecharse | 2 |
| 31282 | sospechabas | 2 |
| 31283 | sosón | 2 |
| 31284 | sosiegue | 2 |
| 31285 | sosegase | 2 |
| 31286 | sosegaron | 2 |
| 31287 | sosegaos | 2 |
| 31288 | sosegad | 2 |
| 31289 | sorteando | 2 |
| 31290 | sorprendo | 2 |
| 31291 | soria | 2 |
| 31292 | sordomuda | 2 |
| 31293 | sordina | 2 |
| 31294 | sordera | 2 |
| 31295 | sorbos | 2 |
| 31296 | sorbo | 2 |
| 31297 | sorbido | 2 |
| 31298 | soporífera | 2 |
| 31299 | sopo | 2 |
| 31300 | soplos | 2 |
| 31301 | soplón | 2 |
| 31302 | soplándose | 2 |
| 31303 | sopieres | 2 |
| 31304 | sopera | 2 |
| 31305 | soñolientas | 2 |
| 31306 | soñadores | 2 |
| 31307 | soñaban | 2 |
| 31308 | sonsacado | 2 |
| 31309 | sonrojo | 2 |
| 31310 | sonrisita | 2 |
| 31311 | sonorosos | 2 |
| 31312 | sonoroso | 2 |
| 31313 | sonorosa | 2 |
| 31314 | sonoros | 2 |
| 31315 | sonetes | 2 |
| 31316 | sondear | 2 |
| 31317 | sonaua | 2 |
| 31318 | sonatas | 2 |
| 31319 | sonase | 2 |
| 31320 | sonarse | 2 |
| 31321 | sonantes | 2 |
| 31322 | sonámbulo | 2 |
| 31323 | sonámbula | 2 |
| 31324 | sonados | 2 |
| 31325 | sonadas | 2 |
| 31326 | somnolencias | 2 |
| 31327 | sometida | 2 |
| 31328 | someterse | 2 |
| 31329 | somete | 2 |
| 31330 | someros | 2 |
| 31331 | sombrerero | 2 |
| 31332 | sombrajos | 2 |
| 31333 | soltaste | 2 |
| 31334 | soltarme | 2 |
| 31335 | soltarlo | 2 |
| 31336 | soltarla | 2 |
| 31337 | soltara | 2 |
| 31338 | soltamos | 2 |
| 31339 | soltaban | 2 |
| 31340 | solón | 2 |
| 31341 | sollozo | 2 |
| 31342 | sollo | 2 |
| 31343 | sólidamente | 2 |
| 31344 | solicite | 2 |
| 31345 | solicitantes | 2 |
| 31346 | solicitante | 2 |
| 31347 | solíamos | 2 |
| 31348 | solfeo | 2 |
| 31349 | solenizar | 2 |
| 31350 | solenidá | 2 |
| 31351 | solemnizar | 2 |
| 31352 | solemnísimo | 2 |
| 31353 | solecismos | 2 |
| 31354 | soldadura | 2 |
| 31355 | soldadotes | 2 |
| 31356 | soldadote | 2 |
| 31357 | soldaditos | 2 |
| 31358 | soldadesco | 2 |
| 31359 | soldadas | 2 |
| 31360 | solazarse | 2 |
| 31361 | solazando | 2 |
| 31362 | sofrire | 2 |
| 31363 | sofocó | 2 |
| 31364 | sofocando | 2 |
| 31365 | sofocaban | 2 |
| 31366 | socorrerme | 2 |
| 31367 | socorred | 2 |
| 31368 | socarronamente | 2 |
| 31369 | socapa | 2 |
| 31370 | sobrinitos | 2 |
| 31371 | sobrinejo | 2 |
| 31372 | sobrevive | 2 |
| 31373 | sobreviniese | 2 |
| 31374 | sobrevenir | 2 |
| 31375 | sobrevenido | 2 |
| 31376 | sobreuiene | 2 |
| 31377 | sobresaltóse | 2 |
| 31378 | sobresalte | 2 |
| 31379 | sobresaltaron | 2 |
| 31380 | sobresaltadas | 2 |
| 31381 | sobresalta | 2 |
| 31382 | sobresalir | 2 |
| 31383 | sobresalientes | 2 |
| 31384 | sobresalían | 2 |
| 31385 | sobreponían | 2 |
| 31386 | sobreponen | 2 |
| 31387 | sobrepone | 2 |
| 31388 | sobrentendido | 2 |
| 31389 | sobrehumana | 2 |
| 31390 | sobrecogido | 2 |
| 31391 | sobrecogía | 2 |
| 31392 | sobraron | 2 |
| 31393 | sobraran | 2 |
| 31394 | sobrará | 2 |
| 31395 | sobrando | 2 |
| 31396 | sobramos | 2 |
| 31397 | sobrados | 2 |
| 31398 | soborno | 2 |
| 31399 | sobones | 2 |
| 31400 | sobón | 2 |
| 31401 | sobire | 2 |
| 31402 | sobió | 2 |
| 31403 | sobía | 2 |
| 31404 | soberanía | 2 |
| 31405 | sobar | 2 |
| 31406 | soba | 2 |
| 31407 | sl | 2 |
| 31408 | situó | 2 |
| 31409 | sito | 2 |
| 31410 | sitïal | 2 |
| 31411 | sistemáticamente | 2 |
| 31412 | sísifo | 2 |
| 31413 | sisas | 2 |
| 31414 | sirviesen | 2 |
| 31415 | sirviéndoles | 2 |
| 31416 | sirviéndole | 2 |
| 31417 | siruiendo | 2 |
| 31418 | sirue | 2 |
| 31419 | siruan | 2 |
| 31420 | sirtes | 2 |
| 31421 | sinuosidades | 2 |
| 31422 | sintiólo | 2 |
| 31423 | sintio | 2 |
| 31424 | sintéticas | 2 |
| 31425 | síntesis | 2 |
| 31426 | singularizarme | 2 |
| 31427 | singularísimo | 2 |
| 31428 | singularísimas | 2 |
| 31429 | singularidad | 2 |
| 31430 | síncope | 2 |
| 31431 | sinceras | 2 |
| 31432 | sinapismos | 2 |
| 31433 | sinaí | 2 |
| 31434 | simultáneos | 2 |
| 31435 | simultáneo | 2 |
| 31436 | simulado | 2 |
| 31437 | simpáticos | 2 |
| 31438 | simoníaco | 2 |
| 31439 | simoniaco | 2 |
| 31440 | similor | 2 |
| 31441 | símiles | 2 |
| 31442 | simétricos | 2 |
| 31443 | simétrico | 2 |
| 31444 | silos | 2 |
| 31445 | silogismos | 2 |
| 31446 | silleta | 2 |
| 31447 | sillero | 2 |
| 31448 | sílfide | 2 |
| 31449 | sileno | 2 |
| 31450 | silenciosas | 2 |
| 31451 | silbó | 2 |
| 31452 | silbe | 2 |
| 31453 | silbato | 2 |
| 31454 | silbas | 2 |
| 31455 | silbantes | 2 |
| 31456 | silbada | 2 |
| 31457 | sil | 2 |
| 31458 | siguiole | 2 |
| 31459 | siguiola | 2 |
| 31460 | siguiéndoles | 2 |
| 31461 | siguiéndola | 2 |
| 31462 | síguese | 2 |
| 31463 | sigua | 2 |
| 31464 | significara | 2 |
| 31465 | significantes | 2 |
| 31466 | sigismunda | 2 |
| 31467 | sietes | 2 |
| 31468 | siervo | 2 |
| 31469 | sierva | 2 |
| 31470 | sienbra | 2 |
| 31471 | siemprevivas | 2 |
| 31472 | siembran | 2 |
| 31473 | siella | 2 |
| 31474 | sibarita | 2 |
| 31475 | séville | 2 |
| 31476 | setentón | 2 |
| 31477 | séte | 2 |
| 31478 | sesudos | 2 |
| 31479 | sesudo | 2 |
| 31480 | sesudas | 2 |
| 31481 | sesuda | 2 |
| 31482 | sesga | 2 |
| 31483 | sesada | 2 |
| 31484 | servís | 2 |
| 31485 | servirme | 2 |
| 31486 | servirlos | 2 |
| 31487 | servirlas | 2 |
| 31488 | serviremos | 2 |
| 31489 | servilla | 2 |
| 31490 | serviles | 2 |
| 31491 | servila | 2 |
| 31492 | servil | 2 |
| 31493 | servienta | 2 |
| 31494 | servíale | 2 |
| 31495 | seruido | 2 |
| 31496 | serre | 2 |
| 31497 | serrar | 2 |
| 31498 | serranía | 2 |
| 31499 | serrallo | 2 |
| 31500 | serpentino | 2 |
| 31501 | serones | 2 |
| 31502 | sermonearle | 2 |
| 31503 | serenísimo | 2 |
| 31504 | serenado | 2 |
| 31505 | seran | 2 |
| 31506 | sequía | 2 |
| 31507 | sepultan | 2 |
| 31508 | sepultadas | 2 |
| 31509 | séptima | 2 |
| 31510 | separas | 2 |
| 31511 | separarme | 2 |
| 31512 | separarlos | 2 |
| 31513 | sepades | 2 |
| 31514 | seo | 2 |
| 31515 | señorón | 2 |
| 31516 | señoritingo | 2 |
| 31517 | señorial | 2 |
| 31518 | señó | 2 |
| 31519 | señalen | 2 |
| 31520 | señalé | 2 |
| 31521 | señalaron | 2 |
| 31522 | señalaría | 2 |
| 31523 | señaladamente | 2 |
| 31524 | senuelo | 2 |
| 31525 | sentyr | 2 |
| 31526 | sentirle | 2 |
| 31527 | sentirlas | 2 |
| 31528 | sentina | 2 |
| 31529 | sentimentales | 2 |
| 31530 | sentible | 2 |
| 31531 | sentíalo | 2 |
| 31532 | sentemos | 2 |
| 31533 | sentarnos | 2 |
| 31534 | sentarla | 2 |
| 31535 | sentando | 2 |
| 31536 | sentamos | 2 |
| 31537 | sentaditas | 2 |
| 31538 | sensatos | 2 |
| 31539 | sensato | 2 |
| 31540 | sensatez | 2 |
| 31541 | sensacional | 2 |
| 31542 | senorio | 2 |
| 31543 | senhor | 2 |
| 31544 | senetud | 2 |
| 31545 | seneca | 2 |
| 31546 | senador | 2 |
| 31547 | sementales | 2 |
| 31548 | seméjase | 2 |
| 31549 | semejar | 2 |
| 31550 | semejanzas | 2 |
| 31551 | sembró | 2 |
| 31552 | sembrara | 2 |
| 31553 | sembradura | 2 |
| 31554 | sembrada | 2 |
| 31555 | sembraba | 2 |
| 31556 | selló | 2 |
| 31557 | sellar | 2 |
| 31558 | sella | 2 |
| 31559 | selectas | 2 |
| 31560 | segurança | 2 |
| 31561 | segurado | 2 |
| 31562 | segurada | 2 |
| 31563 | seguistes | 2 |
| 31564 | seguís | 2 |
| 31565 | seguirse | 2 |
| 31566 | seguirlas | 2 |
| 31567 | seguirás | 2 |
| 31568 | seguiendo | 2 |
| 31569 | segoviana | 2 |
| 31570 | segar | 2 |
| 31571 | segada | 2 |
| 31572 | sedujeron | 2 |
| 31573 | seducida | 2 |
| 31574 | sedienta | 2 |
| 31575 | sedero | 2 |
| 31576 | secundario | 2 |
| 31577 | secuestrada | 2 |
| 31578 | sectas | 2 |
| 31579 | secretillo | 2 |
| 31580 | secretaria | 2 |
| 31581 | secaron | 2 |
| 31582 | secara | 2 |
| 31583 | secadero | 2 |
| 31584 | secaban | 2 |
| 31585 | secaba | 2 |
| 31586 | séate | 2 |
| 31587 | séase | 2 |
| 31588 | séalo | 2 |
| 31589 | scortum | 2 |
| 31590 | scipion | 2 |
| 31591 | scinta | 2 |
| 31592 | sciencia | 2 |
| 31593 | sayón | 2 |
| 31594 | sayago | 2 |
| 31595 | sauce | 2 |
| 31596 | saturada | 2 |
| 31597 | satisfazer | 2 |
| 31598 | satisfará | 2 |
| 31599 | satisfago | 2 |
| 31600 | satisfactoria | 2 |
| 31601 | satisfacerte | 2 |
| 31602 | satisfacerme | 2 |
| 31603 | satisfacerles | 2 |
| 31604 | satisfacerle | 2 |
| 31605 | satisfacerla | 2 |
| 31606 | sátiro | 2 |
| 31607 | satirizar | 2 |
| 31608 | satíricos | 2 |
| 31609 | satín | 2 |
| 31610 | satén | 2 |
| 31611 | sarpullo | 2 |
| 31612 | sargas | 2 |
| 31613 | sardo | 2 |
| 31614 | sarcasmos | 2 |
| 31615 | saquito | 2 |
| 31616 | saquear | 2 |
| 31617 | saqueaban | 2 |
| 31618 | sañas | 2 |
| 31619 | sanz | 2 |
| 31620 | santito | 2 |
| 31621 | santiguas | 2 |
| 31622 | santiguaba | 2 |
| 31623 | santificación | 2 |
| 31624 | santera | 2 |
| 31625 | sanguinolenta | 2 |
| 31626 | sanguino | 2 |
| 31627 | sanguinarios | 2 |
| 31628 | sanguijuela | 2 |
| 31629 | sandía | 2 |
| 31630 | sancionado | 2 |
| 31631 | sanchos | 2 |
| 31632 | sanará | 2 |
| 31633 | sanara | 2 |
| 31634 | sanan | 2 |
| 31635 | samos | 2 |
| 31636 | samaritanas | 2 |
| 31637 | salves | 2 |
| 31638 | salvé | 2 |
| 31639 | salvas | 2 |
| 31640 | salvarte | 2 |
| 31641 | salvaron | 2 |
| 31642 | salvarla | 2 |
| 31643 | salvará | 2 |
| 31644 | salvara | 2 |
| 31645 | salvamento | 2 |
| 31646 | sálvamelo | 2 |
| 31647 | salvadores | 2 |
| 31648 | salvaban | 2 |
| 31649 | salutífero | 2 |
| 31650 | salutífera | 2 |
| 31651 | salut | 2 |
| 31652 | salue | 2 |
| 31653 | saludónos | 2 |
| 31654 | saludé | 2 |
| 31655 | salude | 2 |
| 31656 | saludáronse | 2 |
| 31657 | saludarles | 2 |
| 31658 | saludarlas | 2 |
| 31659 | saludándola | 2 |
| 31660 | saludan | 2 |
| 31661 | saludamos | 2 |
| 31662 | saltes | 2 |
| 31663 | salterios | 2 |
| 31664 | saltearon | 2 |
| 31665 | salteados | 2 |
| 31666 | saltaría | 2 |
| 31667 | saltaembarca | 2 |
| 31668 | salpicón | 2 |
| 31669 | salpicado | 2 |
| 31670 | salpicadas | 2 |
| 31671 | salobre | 2 |
| 31672 | salmones | 2 |
| 31673 | salmantino | 2 |
| 31674 | salitre | 2 |
| 31675 | salitas | 2 |
| 31676 | salís | 2 |
| 31677 | salirnos | 2 |
| 31678 | salímonos | 2 |
| 31679 | saliesse | 2 |
| 31680 | saliéronse | 2 |
| 31681 | saliéndose | 2 |
| 31682 | saliéndole | 2 |
| 31683 | salicilato | 2 |
| 31684 | salgáis | 2 |
| 31685 | saldrían | 2 |
| 31686 | salchichón | 2 |
| 31687 | sajón | 2 |
| 31688 | sainete | 2 |
| 31689 | said | 2 |
| 31690 | sahumaremos | 2 |
| 31691 | sagra | 2 |
| 31692 | sagitario | 2 |
| 31693 | sagasta | 2 |
| 31694 | sacudimientos | 2 |
| 31695 | sacudimiento | 2 |
| 31696 | sacudiéndola | 2 |
| 31697 | sacrosanta | 2 |
| 31698 | sacristías | 2 |
| 31699 | sacris | 2 |
| 31700 | sacrilegios | 2 |
| 31701 | sacrifiçio | 2 |
| 31702 | sacrificarme | 2 |
| 31703 | sacrificándose | 2 |
| 31704 | sacrificaban | 2 |
| 31705 | sacrificaba | 2 |
| 31706 | sacrifica | 2 |
| 31707 | sacramental | 2 |
| 31708 | sacóla | 2 |
| 31709 | sacola | 2 |
| 31710 | sacól | 2 |
| 31711 | saciedad | 2 |
| 31712 | saciaba | 2 |
| 31713 | sacasses | 2 |
| 31714 | sacarse | 2 |
| 31715 | sacáronme | 2 |
| 31716 | sacaren | 2 |
| 31717 | sacándose | 2 |
| 31718 | sacándolos | 2 |
| 31719 | sácala | 2 |
| 31720 | sacábale | 2 |
| 31721 | sabyo | 2 |
| 31722 | sabya | 2 |
| 31723 | sabrosamente | 2 |
| 31724 | sabrías | 2 |
| 31725 | sabria | 2 |
| 31726 | sabra | 2 |
| 31727 | saborearle | 2 |
| 31728 | saborea | 2 |
| 31729 | saborcillo | 2 |
| 31730 | sabogas | 2 |
| 31731 | sabina | 2 |
| 31732 | sabihondo | 2 |
| 31733 | sabiéndolas | 2 |
| 31734 | sabidos | 2 |
| 31735 | sabidas | 2 |
| 31736 | sabian | 2 |
| 31737 | saberlos | 2 |
| 31738 | saberle | 2 |
| 31739 | sabeo | 2 |
| 31740 | sabedme | 2 |
| 31741 | sabandija | 2 |
| 31742 | sa | 2 |
| 31743 | ryo | 2 |
| 31744 | ruydos | 2 |
| 31745 | rutinarios | 2 |
| 31746 | rutinarias | 2 |
| 31747 | ruptura | 2 |
| 31748 | rumía | 2 |
| 31749 | rumboso | 2 |
| 31750 | rumbosa | 2 |
| 31751 | ruinoso | 2 |
| 31752 | ruinosa | 2 |
| 31753 | ruindad | 2 |
| 31754 | rüinas | 2 |
| 31755 | ruidosamente | 2 |
| 31756 | ruibarbo | 2 |
| 31757 | rugosos | 2 |
| 31758 | rugoso | 2 |
| 31759 | rugir | 2 |
| 31760 | rugía | 2 |
| 31761 | rugero | 2 |
| 31762 | ruegue | 2 |
| 31763 | ruegovos | 2 |
| 31764 | ruedo | 2 |
| 31765 | rucia | 2 |
| 31766 | rubricado | 2 |
| 31767 | ruborizada | 2 |
| 31768 | rubiles | 2 |
| 31769 | rubén | 2 |
| 31770 | rruys | 2 |
| 31771 | rruega | 2 |
| 31772 | rroyn | 2 |
| 31773 | rrosado | 2 |
| 31774 | rromeros | 2 |
| 31775 | rrogué | 2 |
| 31776 | rrogar | 2 |
| 31777 | rrogando | 2 |
| 31778 | rrodiella | 2 |
| 31779 | rrocío | 2 |
| 31780 | rroçín | 2 |
| 31781 | rrobar | 2 |
| 31782 | rriqueza | 2 |
| 31783 | rrimas | 2 |
| 31784 | rrimar | 2 |
| 31785 | rriendo | 2 |
| 31786 | rríe | 2 |
| 31787 | rribal | 2 |
| 31788 | rri | 2 |
| 31789 | rreyes | 2 |
| 31790 | rretrayas | 2 |
| 31791 | rretraheres | 2 |
| 31792 | rretoçar | 2 |
| 31793 | rresuçitado | 2 |
| 31794 | rrespuso | 2 |
| 31795 | rresponder | 2 |
| 31796 | rrespondas | 2 |
| 31797 | rresplandeçiente | 2 |
| 31798 | rreservados | 2 |
| 31799 | rresçibiera | 2 |
| 31800 | rresçiben | 2 |
| 31801 | rresçebiste | 2 |
| 31802 | rrequieres | 2 |
| 31803 | rrencura | 2 |
| 31804 | rrelusiente | 2 |
| 31805 | rreligiosos | 2 |
| 31806 | rrehierta | 2 |
| 31807 | rrehez | 2 |
| 31808 | rreheses | 2 |
| 31809 | rrefertero | 2 |
| 31810 | rred | 2 |
| 31811 | rreçio | 2 |
| 31812 | rreçelo | 2 |
| 31813 | rrecabda | 2 |
| 31814 | rramos | 2 |
| 31815 | rrama | 2 |
| 31816 | rraçión | 2 |
| 31817 | rrachona | 2 |
| 31818 | rrabé | 2 |
| 31819 | rozzos | 2 |
| 31820 | rozagantes | 2 |
| 31821 | royan | 2 |
| 31822 | roturas | 2 |
| 31823 | rotura | 2 |
| 31824 | rotunda | 2 |
| 31825 | rotolando | 2 |
| 31826 | rose | 2 |
| 31827 | rorró | 2 |
| 31828 | ropaje | 2 |
| 31829 | roñoso | 2 |
| 31830 | rondó | 2 |
| 31831 | roncar | 2 |
| 31832 | rompiese | 2 |
| 31833 | rompiéndose | 2 |
| 31834 | romperlo | 2 |
| 31835 | rompella | 2 |
| 31836 | rompáis | 2 |
| 31837 | romo | 2 |
| 31838 | romerías | 2 |
| 31839 | románico | 2 |
| 31840 | romancico | 2 |
| 31841 | romadizo | 2 |
| 31842 | rollos | 2 |
| 31843 | rolando | 2 |
| 31844 | rojizos | 2 |
| 31845 | roída | 2 |
| 31846 | roían | 2 |
| 31847 | roguéle | 2 |
| 31848 | rogativas | 2 |
| 31849 | rogaste | 2 |
| 31850 | rogase | 2 |
| 31851 | rogarte | 2 |
| 31852 | rogare | 2 |
| 31853 | rogara | 2 |
| 31854 | rogándole | 2 |
| 31855 | rogámosle | 2 |
| 31856 | rogamos | 2 |
| 31857 | rogad | 2 |
| 31858 | roen | 2 |
| 31859 | roedores | 2 |
| 31860 | rodrigón | 2 |
| 31861 | rodó | 2 |
| 31862 | rodo | 2 |
| 31863 | rodelas | 2 |
| 31864 | rodee | 2 |
| 31865 | rodease | 2 |
| 31866 | rodeándola | 2 |
| 31867 | rodaron | 2 |
| 31868 | rodamos | 2 |
| 31869 | rodajas | 2 |
| 31870 | roció | 2 |
| 31871 | roces | 2 |
| 31872 | robes | 2 |
| 31873 | roben | 2 |
| 31874 | robe | 2 |
| 31875 | robastes | 2 |
| 31876 | robase | 2 |
| 31877 | robara | 2 |
| 31878 | roballa | 2 |
| 31879 | robaban | 2 |
| 31880 | rizo | 2 |
| 31881 | rizados | 2 |
| 31882 | rivero | 2 |
| 31883 | rivalizar | 2 |
| 31884 | rivalidades | 2 |
| 31885 | rivales | 2 |
| 31886 | ritmos | 2 |
| 31887 | ristras | 2 |
| 31888 | risita | 2 |
| 31889 | risada | 2 |
| 31890 | rire | 2 |
| 31891 | riose | 2 |
| 31892 | riñonadas | 2 |
| 31893 | riñese | 2 |
| 31894 | riñeron | 2 |
| 31895 | riñan | 2 |
| 31896 | ringorrangos | 2 |
| 31897 | rindióse | 2 |
| 31898 | rindiose | 2 |
| 31899 | rindiesen | 2 |
| 31900 | rinconadas | 2 |
| 31901 | rijoso | 2 |
| 31902 | rigoroso | 2 |
| 31903 | rigorosa | 2 |
| 31904 | riges | 2 |
| 31905 | riffeño | 2 |
| 31906 | riese | 2 |
| 31907 | riera | 2 |
| 31908 | rientes | 2 |
| 31909 | ridiculizar | 2 |
| 31910 | ridiculizando | 2 |
| 31911 | ridiculeces | 2 |
| 31912 | ridicula | 2 |
| 31913 | ribazo | 2 |
| 31914 | ríanse | 2 |
| 31915 | rían | 2 |
| 31916 | rezumo | 2 |
| 31917 | rezongar | 2 |
| 31918 | rezongando | 2 |
| 31919 | rezonas | 2 |
| 31920 | rezios | 2 |
| 31921 | rezia | 2 |
| 31922 | rezas | 2 |
| 31923 | rezaron | 2 |
| 31924 | rezarle | 2 |
| 31925 | rezarían | 2 |
| 31926 | rezagadas | 2 |
| 31927 | reynas | 2 |
| 31928 | revulsivos | 2 |
| 31929 | revoltosa | 2 |
| 31930 | revoltijo | 2 |
| 31931 | revoloteaban | 2 |
| 31932 | revolcar | 2 |
| 31933 | revoco | 2 |
| 31934 | revisten | 2 |
| 31935 | revisó | 2 |
| 31936 | revientan | 2 |
| 31937 | revestido | 2 |
| 31938 | revestían | 2 |
| 31939 | revestía | 2 |
| 31940 | reverendo | 2 |
| 31941 | reverendísimo | 2 |
| 31942 | reverendas | 2 |
| 31943 | reverenda | 2 |
| 31944 | reverencio | 2 |
| 31945 | reverdecer | 2 |
| 31946 | reverberos | 2 |
| 31947 | reverbero | 2 |
| 31948 | reventaran | 2 |
| 31949 | reventado | 2 |
| 31950 | revele | 2 |
| 31951 | revelaron | 2 |
| 31952 | revelarle | 2 |
| 31953 | reveladas | 2 |
| 31954 | revelada | 2 |
| 31955 | revalidar | 2 |
| 31956 | reunirme | 2 |
| 31957 | reúna | 2 |
| 31958 | reuistas | 2 |
| 31959 | retuvieron | 2 |
| 31960 | retumban | 2 |
| 31961 | retrospectivos | 2 |
| 31962 | retrocedido | 2 |
| 31963 | retro | 2 |
| 31964 | retraymiento | 2 |
| 31965 | retraso | 2 |
| 31966 | retrasaba | 2 |
| 31967 | retraía | 2 |
| 31968 | retraer | 2 |
| 31969 | retrae | 2 |
| 31970 | retozonas | 2 |
| 31971 | retorta | 2 |
| 31972 | retorciéndose | 2 |
| 31973 | retorciendo | 2 |
| 31974 | retorcidas | 2 |
| 31975 | retorcían | 2 |
| 31976 | retorcerse | 2 |
| 31977 | retó | 2 |
| 31978 | retires | 2 |
| 31979 | retirasen | 2 |
| 31980 | retirarnos | 2 |
| 31981 | retiraría | 2 |
| 31982 | retiraré | 2 |
| 31983 | retirara | 2 |
| 31984 | retirando | 2 |
| 31985 | retenido | 2 |
| 31986 | retén | 2 |
| 31987 | retebién | 2 |
| 31988 | retardar | 2 |
| 31989 | retardaba | 2 |
| 31990 | retama | 2 |
| 31991 | retado | 2 |
| 31992 | retacillos | 2 |
| 31993 | retaba | 2 |
| 31994 | resurreción | 2 |
| 31995 | resume | 2 |
| 31996 | resulte | 2 |
| 31997 | resultase | 2 |
| 31998 | resultaron | 2 |
| 31999 | resultaría | 2 |
| 32000 | resultare | 2 |
| 32001 | resultará | 2 |
| 32002 | resultara | 2 |
| 32003 | resuenan | 2 |
| 32004 | resuena | 2 |
| 32005 | resucitó | 2 |
| 32006 | resucitase | 2 |
| 32007 | resucitara | 2 |
| 32008 | resucitando | 2 |
| 32009 | restregándose | 2 |
| 32010 | restregaba | 2 |
| 32011 | restori | 2 |
| 32012 | restituyen | 2 |
| 32013 | restituiría | 2 |
| 32014 | restituida | 2 |
| 32015 | restitución | 2 |
| 32016 | restaurado | 2 |
| 32017 | restaura | 2 |
| 32018 | restallido | 2 |
| 32019 | restablecido | 2 |
| 32020 | restablecía | 2 |
| 32021 | restablecería | 2 |
| 32022 | responsos | 2 |
| 32023 | responsables | 2 |
| 32024 | responsabilidades | 2 |
| 32025 | respondistes | 2 |
| 32026 | respondiole | 2 |
| 32027 | respondiéndose | 2 |
| 32028 | responderles | 2 |
| 32029 | responderla | 2 |
| 32030 | responderán | 2 |
| 32031 | resplandescientes | 2 |
| 32032 | resplandescen | 2 |
| 32033 | resplandeció | 2 |
| 32034 | resplandecían | 2 |
| 32035 | respiros | 2 |
| 32036 | respiras | 2 |
| 32037 | respetuosos | 2 |
| 32038 | respetuosa | 2 |
| 32039 | respetó | 2 |
| 32040 | respetaran | 2 |
| 32041 | respetadas | 2 |
| 32042 | respectivamente | 2 |
| 32043 | respecta | 2 |
| 32044 | resonando | 2 |
| 32045 | resonancia | 2 |
| 32046 | resonaban | 2 |
| 32047 | resolviose | 2 |
| 32048 | resolviéndose | 2 |
| 32049 | resolvería | 2 |
| 32050 | resolverá | 2 |
| 32051 | resma | 2 |
| 32052 | resisto | 2 |
| 32053 | resistiese | 2 |
| 32054 | resintió | 2 |
| 32055 | resina | 2 |
| 32056 | resignaban | 2 |
| 32057 | resido | 2 |
| 32058 | residían | 2 |
| 32059 | residía | 2 |
| 32060 | residentes | 2 |
| 32061 | resia | 2 |
| 32062 | resguardándose | 2 |
| 32063 | resguardado | 2 |
| 32064 | resfría | 2 |
| 32065 | reservo | 2 |
| 32066 | reservarle | 2 |
| 32067 | reservando | 2 |
| 32068 | reservadas | 2 |
| 32069 | resentido | 2 |
| 32070 | rescoldo | 2 |
| 32071 | rescibo | 2 |
| 32072 | resciben | 2 |
| 32073 | rescibe | 2 |
| 32074 | rescató | 2 |
| 32075 | rescaté | 2 |
| 32076 | resbaló | 2 |
| 32077 | resbalan | 2 |
| 32078 | resbalaba | 2 |
| 32079 | resbala | 2 |
| 32080 | resaltando | 2 |
| 32081 | rerum | 2 |
| 32082 | requirió | 2 |
| 32083 | requiriese | 2 |
| 32084 | requiescat | 2 |
| 32085 | requetefinos | 2 |
| 32086 | requería | 2 |
| 32087 | requerí | 2 |
| 32088 | requemada | 2 |
| 32089 | requemaba | 2 |
| 32090 | reputaban | 2 |
| 32091 | reps | 2 |
| 32092 | reprodujo | 2 |
| 32093 | reproducir | 2 |
| 32094 | reproducen | 2 |
| 32095 | representóla | 2 |
| 32096 | representasen | 2 |
| 32097 | representársela | 2 |
| 32098 | representarse | 2 |
| 32099 | representará | 2 |
| 32100 | representándose | 2 |
| 32101 | representábasele | 2 |
| 32102 | represa | 2 |
| 32103 | reprendo | 2 |
| 32104 | reprenden | 2 |
| 32105 | reprehension | 2 |
| 32106 | repreciosa | 2 |
| 32107 | reposteros | 2 |
| 32108 | reposando | 2 |
| 32109 | reposadas | 2 |
| 32110 | reposadamente | 2 |
| 32111 | reportes | 2 |
| 32112 | reportarse | 2 |
| 32113 | reponiéndose | 2 |
| 32114 | repoblicanos | 2 |
| 32115 | repliquéis | 2 |
| 32116 | repliegues | 2 |
| 32117 | repliegue | 2 |
| 32118 | réplicas | 2 |
| 32119 | replicáis | 2 |
| 32120 | replicaban | 2 |
| 32121 | replica | 2 |
| 32122 | replegó | 2 |
| 32123 | repitiéndose | 2 |
| 32124 | repitiéndole | 2 |
| 32125 | repicar | 2 |
| 32126 | repetí | 2 |
| 32127 | repentinos | 2 |
| 32128 | repatriación | 2 |
| 32129 | repasa | 2 |
| 32130 | repartos | 2 |
| 32131 | repartirse | 2 |
| 32132 | repartirlo | 2 |
| 32133 | repartio | 2 |
| 32134 | repararía | 2 |
| 32135 | reñiría | 2 |
| 32136 | renzilla | 2 |
| 32137 | renunciara | 2 |
| 32138 | renunciado | 2 |
| 32139 | renuevan | 2 |
| 32140 | renovóse | 2 |
| 32141 | renovados | 2 |
| 32142 | renovada | 2 |
| 32143 | reniremos | 2 |
| 32144 | reniegue | 2 |
| 32145 | reniega | 2 |
| 32146 | renegó | 2 |
| 32147 | renegada | 2 |
| 32148 | renegaban | 2 |
| 32149 | rendirnos | 2 |
| 32150 | rendirme | 2 |
| 32151 | rendija | 2 |
| 32152 | rencura | 2 |
| 32153 | rencuentro | 2 |
| 32154 | rencoroso | 2 |
| 32155 | rencillas | 2 |
| 32156 | remunerado | 2 |
| 32157 | removía | 2 |
| 32158 | remotamente | 2 |
| 32159 | remontarnos | 2 |
| 32160 | remontar | 2 |
| 32161 | remontándose | 2 |
| 32162 | remolino | 2 |
| 32163 | remolcado | 2 |
| 32164 | remito | 2 |
| 32165 | remitirle | 2 |
| 32166 | remitieron | 2 |
| 32167 | remitido | 2 |
| 32168 | remiten | 2 |
| 32169 | remirando | 2 |
| 32170 | remira | 2 |
| 32171 | reminiscencias | 2 |
| 32172 | remesas | 2 |
| 32173 | remedo | 2 |
| 32174 | remedió | 2 |
| 32175 | remedies | 2 |
| 32176 | remediarlas | 2 |
| 32177 | remediarla | 2 |
| 32178 | remediará | 2 |
| 32179 | remediallo | 2 |
| 32180 | remediados | 2 |
| 32181 | remedándole | 2 |
| 32182 | remeda | 2 |
| 32183 | remató | 2 |
| 32184 | remates | 2 |
| 32185 | remataron | 2 |
| 32186 | rematan | 2 |
| 32187 | rematadamente | 2 |
| 32188 | remanece | 2 |
| 32189 | remachó | 2 |
| 32190 | relumbrante | 2 |
| 32191 | relumbraban | 2 |
| 32192 | relumbraba | 2 |
| 32193 | relucida | 2 |
| 32194 | relucían | 2 |
| 32195 | relojera | 2 |
| 32196 | reloja | 2 |
| 32197 | rellenas | 2 |
| 32198 | rellano | 2 |
| 32199 | relinchar | 2 |
| 32200 | relieua | 2 |
| 32201 | relevado | 2 |
| 32202 | relente | 2 |
| 32203 | relatores | 2 |
| 32204 | relatando | 2 |
| 32205 | relampagueo | 2 |
| 32206 | relamida | 2 |
| 32207 | relacionados | 2 |
| 32208 | relacionaba | 2 |
| 32209 | rejuvenecía | 2 |
| 32210 | rejo | 2 |
| 32211 | reirse | 2 |
| 32212 | reirían | 2 |
| 32213 | reirás | 2 |
| 32214 | reintegro | 2 |
| 32215 | reinó | 2 |
| 32216 | reinase | 2 |
| 32217 | reinando | 2 |
| 32218 | reinan | 2 |
| 32219 | reinaban | 2 |
| 32220 | rehuir | 2 |
| 32221 | rehenes | 2 |
| 32222 | rehacer | 2 |
| 32223 | regurgitación | 2 |
| 32224 | regueros | 2 |
| 32225 | reguapo | 2 |
| 32226 | regresaría | 2 |
| 32227 | regresaba | 2 |
| 32228 | regordete | 2 |
| 32229 | regordeta | 2 |
| 32230 | regocijó | 2 |
| 32231 | regocijadas | 2 |
| 32232 | regó | 2 |
| 32233 | registran | 2 |
| 32234 | registrado | 2 |
| 32235 | registrada | 2 |
| 32236 | regís | 2 |
| 32237 | regirle | 2 |
| 32238 | regil | 2 |
| 32239 | regidos | 2 |
| 32240 | regia | 2 |
| 32241 | regateo | 2 |
| 32242 | regateaba | 2 |
| 32243 | regatas | 2 |
| 32244 | regañona | 2 |
| 32245 | regañón | 2 |
| 32246 | regaño | 2 |
| 32247 | regalito | 2 |
| 32248 | regalen | 2 |
| 32249 | regalase | 2 |
| 32250 | regalarse | 2 |
| 32251 | regalan | 2 |
| 32252 | regaladamente | 2 |
| 32253 | regalaban | 2 |
| 32254 | regaba | 2 |
| 32255 | refunfuños | 2 |
| 32256 | refugiose | 2 |
| 32257 | refugió | 2 |
| 32258 | refugiaron | 2 |
| 32259 | refugiadas | 2 |
| 32260 | refrigerios | 2 |
| 32261 | refriegas | 2 |
| 32262 | refrescarle | 2 |
| 32263 | refregones | 2 |
| 32264 | refregándose | 2 |
| 32265 | reforzó | 2 |
| 32266 | reforzados | 2 |
| 32267 | reformó | 2 |
| 32268 | reformista | 2 |
| 32269 | reformada | 2 |
| 32270 | reflujo | 2 |
| 32271 | reflexiva | 2 |
| 32272 | reflexiono | 2 |
| 32273 | reflexionando | 2 |
| 32274 | refistolera | 2 |
| 32275 | refiriéndole | 2 |
| 32276 | refiriéndola | 2 |
| 32277 | refiérome | 2 |
| 32278 | referirlos | 2 |
| 32279 | referirle | 2 |
| 32280 | referirlas | 2 |
| 32281 | referiré | 2 |
| 32282 | reemplazar | 2 |
| 32283 | reedificaba | 2 |
| 32284 | redundó | 2 |
| 32285 | redundará | 2 |
| 32286 | redundara | 2 |
| 32287 | redundaba | 2 |
| 32288 | reducirla | 2 |
| 32289 | reducidas | 2 |
| 32290 | reducían | 2 |
| 32291 | redoutable | 2 |
| 32292 | redondeaban | 2 |
| 32293 | redoble | 2 |
| 32294 | redoblar | 2 |
| 32295 | redimir | 2 |
| 32296 | redimió | 2 |
| 32297 | redentora | 2 |
| 32298 | rededor | 2 |
| 32299 | redactada | 2 |
| 32300 | recuento | 2 |
| 32301 | rectificaba | 2 |
| 32302 | rectifica | 2 |
| 32303 | rectamente | 2 |
| 32304 | recrudecimiento | 2 |
| 32305 | recrea | 2 |
| 32306 | recostaba | 2 |
| 32307 | recortes | 2 |
| 32308 | recortarlo | 2 |
| 32309 | recortados | 2 |
| 32310 | recortadas | 2 |
| 32311 | recortaba | 2 |
| 32312 | recorta | 2 |
| 32313 | recorrían | 2 |
| 32314 | recordarme | 2 |
| 32315 | recordamos | 2 |
| 32316 | recordable | 2 |
| 32317 | recórcholis | 2 |
| 32318 | recontar | 2 |
| 32319 | recontaba | 2 |
| 32320 | reconozca | 2 |
| 32321 | reconocióle | 2 |
| 32322 | reconocidos | 2 |
| 32323 | reconocidas | 2 |
| 32324 | reconoces | 2 |
| 32325 | reconocerse | 2 |
| 32326 | reconocerían | 2 |
| 32327 | recónditas | 2 |
| 32328 | recóndita | 2 |
| 32329 | reconcomio | 2 |
| 32330 | reconciliaron | 2 |
| 32331 | reconciliado | 2 |
| 32332 | reconciliaciones | 2 |
| 32333 | reconcentrar | 2 |
| 32334 | recomendé | 2 |
| 32335 | recomendados | 2 |
| 32336 | recomendadas | 2 |
| 32337 | recomendada | 2 |
| 32338 | recomendables | 2 |
| 32339 | recojo | 2 |
| 32340 | recoja | 2 |
| 32341 | recogióse | 2 |
| 32342 | recogimos | 2 |
| 32343 | recogiera | 2 |
| 32344 | recógete | 2 |
| 32345 | recogerlos | 2 |
| 32346 | recogerlas | 2 |
| 32347 | recogeremos | 2 |
| 32348 | recogeré | 2 |
| 32349 | recogemos | 2 |
| 32350 | recobro | 2 |
| 32351 | recobrada | 2 |
| 32352 | reclutas | 2 |
| 32353 | reclaman | 2 |
| 32354 | reclamado | 2 |
| 32355 | reclamación | 2 |
| 32356 | recitó | 2 |
| 32357 | recita | 2 |
| 32358 | recíproca | 2 |
| 32359 | recipiente | 2 |
| 32360 | reçio | 2 |
| 32361 | recibirme | 2 |
| 32362 | recibirlo | 2 |
| 32363 | recibióme | 2 |
| 32364 | recibióle | 2 |
| 32365 | recibiese | 2 |
| 32366 | recibiente | 2 |
| 32367 | recíbeme | 2 |
| 32368 | recias | 2 |
| 32369 | recherches | 2 |
| 32370 | rechazó | 2 |
| 32371 | rechazando | 2 |
| 32372 | rechazada | 2 |
| 32373 | receptividad | 2 |
| 32374 | recepción | 2 |
| 32375 | reçelo | 2 |
| 32376 | recé | 2 |
| 32377 | recaudado | 2 |
| 32378 | recatados | 2 |
| 32379 | recatadamente | 2 |
| 32380 | recataba | 2 |
| 32381 | recargada | 2 |
| 32382 | reçar | 2 |
| 32383 | recaer | 2 |
| 32384 | recaen | 2 |
| 32385 | recaditos | 2 |
| 32386 | recadista | 2 |
| 32387 | recabdat | 2 |
| 32388 | recabdarás | 2 |
| 32389 | recabdar | 2 |
| 32390 | rebuznó | 2 |
| 32391 | rebuscó | 2 |
| 32392 | rebtedes | 2 |
| 32393 | rebozado | 2 |
| 32394 | rebosar | 2 |
| 32395 | rebién | 2 |
| 32396 | rebenque | 2 |
| 32397 | rebelarse | 2 |
| 32398 | rebela | 2 |
| 32399 | rebeca | 2 |
| 32400 | rebajarme | 2 |
| 32401 | rebajar | 2 |
| 32402 | rebaja | 2 |
| 32403 | reapareció | 2 |
| 32404 | reanimar | 2 |
| 32405 | reanimaba | 2 |
| 32406 | realizarse | 2 |
| 32407 | realizarlos | 2 |
| 32408 | realizarlo | 2 |
| 32409 | realizada | 2 |
| 32410 | realice | 2 |
| 32411 | realce | 2 |
| 32412 | razonablemente | 2 |
| 32413 | rayz | 2 |
| 32414 | rayados | 2 |
| 32415 | rayada | 2 |
| 32416 | raudales | 2 |
| 32417 | ratero | 2 |
| 32418 | rastrojos | 2 |
| 32419 | rastrillando | 2 |
| 32420 | rásquese | 2 |
| 32421 | rasos | 2 |
| 32422 | rasguñaban | 2 |
| 32423 | rasguear | 2 |
| 32424 | rasgueando | 2 |
| 32425 | rasgando | 2 |
| 32426 | rascarle | 2 |
| 32427 | rascar | 2 |
| 32428 | rascándose | 2 |
| 32429 | rarísimas | 2 |
| 32430 | rapista | 2 |
| 32431 | rapes | 2 |
| 32432 | rape | 2 |
| 32433 | rapantes | 2 |
| 32434 | rapamiento | 2 |
| 32435 | rapadas | 2 |
| 32436 | rapada | 2 |
| 32437 | rapacejos | 2 |
| 32438 | randera | 2 |
| 32439 | rancores | 2 |
| 32440 | rancios | 2 |
| 32441 | rancias | 2 |
| 32442 | rampantes | 2 |
| 32443 | rampa | 2 |
| 32444 | ramitos | 2 |
| 32445 | ramírez | 2 |
| 32446 | ramilletes | 2 |
| 32447 | ramera | 2 |
| 32448 | ralos | 2 |
| 32449 | rails | 2 |
| 32450 | radío | 2 |
| 32451 | raçones | 2 |
| 32452 | racionero | 2 |
| 32453 | raciocinios | 2 |
| 32454 | raciocinar | 2 |
| 32455 | rabiosos | 2 |
| 32456 | rabió | 2 |
| 32457 | rabietina | 2 |
| 32458 | rabie | 2 |
| 32459 | rabeles | 2 |
| 32460 | rabadilla | 2 |
| 32461 | ra | 2 |
| 32462 | quites | 2 |
| 32463 | quitate | 2 |
| 32464 | quitasoles | 2 |
| 32465 | quitarvos | 2 |
| 32466 | quitárselos | 2 |
| 32467 | quitaros | 2 |
| 32468 | quitáronse | 2 |
| 32469 | quitármelo | 2 |
| 32470 | quitármele | 2 |
| 32471 | quitarlos | 2 |
| 32472 | quitarlo | 2 |
| 32473 | quitarla | 2 |
| 32474 | quitarían | 2 |
| 32475 | quitándonos | 2 |
| 32476 | quítale | 2 |
| 32477 | quitadle | 2 |
| 32478 | quitadas | 2 |
| 32479 | quitábale | 2 |
| 32480 | quistión | 2 |
| 32481 | quista | 2 |
| 32482 | quísome | 2 |
| 32483 | quisimos | 2 |
| 32484 | quisiesses | 2 |
| 32485 | quisiésemos | 2 |
| 32486 | quisiéremos | 2 |
| 32487 | quisierdes | 2 |
| 32488 | quisierais | 2 |
| 32489 | quíseme | 2 |
| 32490 | quirier | 2 |
| 32491 | quintín | 2 |
| 32492 | quintero | 2 |
| 32493 | quincena | 2 |
| 32494 | quinçe | 2 |
| 32495 | químicos | 2 |
| 32496 | químico | 2 |
| 32497 | quilate | 2 |
| 32498 | quijotiz | 2 |
| 32499 | quijotadas | 2 |
| 32500 | quietó | 2 |
| 32501 | quietecitos | 2 |
| 32502 | quiés | 2 |
| 32503 | quierole | 2 |
| 32504 | quiéreslo | 2 |
| 32505 | quiéranme | 2 |
| 32506 | quiebro | 2 |
| 32507 | quiebren | 2 |
| 32508 | quicumque | 2 |
| 32509 | quiçá | 2 |
| 32510 | quexan | 2 |
| 32511 | quevedos | 2 |
| 32512 | question | 2 |
| 32513 | quesiere | 2 |
| 32514 | querindango | 2 |
| 32515 | querier | 2 |
| 32516 | queriéndose | 2 |
| 32517 | queriéndolo | 2 |
| 32518 | queridísima | 2 |
| 32519 | querias | 2 |
| 32520 | quererlos | 2 |
| 32521 | querencias | 2 |
| 32522 | querellando | 2 |
| 32523 | queredme | 2 |
| 32524 | quequier | 2 |
| 32525 | quemasen | 2 |
| 32526 | quemaron | 2 |
| 32527 | quemaría | 2 |
| 32528 | quemaran | 2 |
| 32529 | quejosa | 2 |
| 32530 | quejarás | 2 |
| 32531 | quejándome | 2 |
| 32532 | quejando | 2 |
| 32533 | quehazer | 2 |
| 32534 | quedeme | 2 |
| 32535 | quedasteis | 2 |
| 32536 | quedarías | 2 |
| 32537 | quedare | 2 |
| 32538 | quedaras | 2 |
| 32539 | quebrose | 2 |
| 32540 | quebrarse | 2 |
| 32541 | quebrantos | 2 |
| 32542 | quebrantó | 2 |
| 32543 | quebrándose | 2 |
| 32544 | quebradiza | 2 |
| 32545 | quarenta | 2 |
| 32546 | quantía | 2 |
| 32547 | pytas | 2 |
| 32548 | pyntados | 2 |
| 32549 | pyntado | 2 |
| 32550 | pyntadas | 2 |
| 32551 | pynta | 2 |
| 32552 | pyerde | 2 |
| 32553 | pyden | 2 |
| 32554 | pyco | 2 |
| 32555 | pycaça | 2 |
| 32556 | puyol | 2 |
| 32557 | puteria | 2 |
| 32558 | putativa | 2 |
| 32559 | pusímonos | 2 |
| 32560 | pusiéronme | 2 |
| 32561 | pusiéronlos | 2 |
| 32562 | pusieras | 2 |
| 32563 | pus | 2 |
| 32564 | purita | 2 |
| 32565 | purísimas | 2 |
| 32566 | purificarse | 2 |
| 32567 | purificada | 2 |
| 32568 | purgarse | 2 |
| 32569 | purgando | 2 |
| 32570 | purezas | 2 |
| 32571 | pur | 2 |
| 32572 | pupilo | 2 |
| 32573 | pupilero | 2 |
| 32574 | puntualísimo | 2 |
| 32575 | puntuación | 2 |
| 32576 | puntoso | 2 |
| 32577 | puntillosa | 2 |
| 32578 | puntillos | 2 |
| 32579 | puntera | 2 |
| 32580 | puntadita | 2 |
| 32581 | puno | 2 |
| 32582 | punir | 2 |
| 32583 | pundonoroso | 2 |
| 32584 | puncen | 2 |
| 32585 | pun | 2 |
| 32586 | pululan | 2 |
| 32587 | pulsat | 2 |
| 32588 | pulsación | 2 |
| 32589 | pulsa | 2 |
| 32590 | pulpitillo | 2 |
| 32591 | pulmonías | 2 |
| 32592 | pulmón | 2 |
| 32593 | pulir | 2 |
| 32594 | pulcras | 2 |
| 32595 | pula | 2 |
| 32596 | pujos | 2 |
| 32597 | pujanza | 2 |
| 32598 | pujante | 2 |
| 32599 | pugnan | 2 |
| 32600 | pugnaban | 2 |
| 32601 | pugna | 2 |
| 32602 | puéstose | 2 |
| 32603 | puerilidad | 2 |
| 32604 | puédense | 2 |
| 32605 | puédelos | 2 |
| 32606 | puebro | 2 |
| 32607 | pueblecito | 2 |
| 32608 | pueblas | 2 |
| 32609 | pue | 2 |
| 32610 | pudren | 2 |
| 32611 | púdolo | 2 |
| 32612 | pudiste | 2 |
| 32613 | pudiente | 2 |
| 32614 | pucheritos | 2 |
| 32615 | publicos | 2 |
| 32616 | publicaua | 2 |
| 32617 | publicaban | 2 |
| 32618 | ptolomeo | 2 |
| 32619 | psicológicos | 2 |
| 32620 | pse | 2 |
| 32621 | pruritos | 2 |
| 32622 | prueua | 2 |
| 32623 | prueban | 2 |
| 32624 | prudencio | 2 |
| 32625 | proyecta | 2 |
| 32626 | proyección | 2 |
| 32627 | provocativos | 2 |
| 32628 | provocando | 2 |
| 32629 | provocaciones | 2 |
| 32630 | provoca | 2 |
| 32631 | provó | 2 |
| 32632 | provisorato | 2 |
| 32633 | provisionalmente | 2 |
| 32634 | provincialismo | 2 |
| 32635 | provinciales | 2 |
| 32636 | proverbios | 2 |
| 32637 | provenir | 2 |
| 32638 | proveía | 2 |
| 32639 | proveerse | 2 |
| 32640 | proveeré | 2 |
| 32641 | proveedor | 2 |
| 32642 | provaron | 2 |
| 32643 | provado | 2 |
| 32644 | prouisiones | 2 |
| 32645 | prouerbio | 2 |
| 32646 | prouar | 2 |
| 32647 | prototipo | 2 |
| 32648 | protestaron | 2 |
| 32649 | protestanta | 2 |
| 32650 | protestaban | 2 |
| 32651 | proteja | 2 |
| 32652 | protegían | 2 |
| 32653 | protegerla | 2 |
| 32654 | protectoras | 2 |
| 32655 | prostituida | 2 |
| 32656 | prosperidades | 2 |
| 32657 | prospere | 2 |
| 32658 | prosperar | 2 |
| 32659 | prósperamente | 2 |
| 32660 | prospectos | 2 |
| 32661 | prosistas | 2 |
| 32662 | prosélitos | 2 |
| 32663 | proseguimos | 2 |
| 32664 | proseguid | 2 |
| 32665 | prosapia | 2 |
| 32666 | prosaicos | 2 |
| 32667 | prorrumpir | 2 |
| 32668 | prorrumpieron | 2 |
| 32669 | prora | 2 |
| 32670 | propusieran | 2 |
| 32671 | proporcionaría | 2 |
| 32672 | proporcion | 2 |
| 32673 | proponerte | 2 |
| 32674 | proponerles | 2 |
| 32675 | propietaria | 2 |
| 32676 | propenso | 2 |
| 32677 | propensión | 2 |
| 32678 | propalar | 2 |
| 32679 | propala | 2 |
| 32680 | propagar | 2 |
| 32681 | propagan | 2 |
| 32682 | pronunciaron | 2 |
| 32683 | pronunciara | 2 |
| 32684 | pronunciaban | 2 |
| 32685 | pronosticando | 2 |
| 32686 | pronosticado | 2 |
| 32687 | prompta | 2 |
| 32688 | prometióles | 2 |
| 32689 | prometio | 2 |
| 32690 | prometieron | 2 |
| 32691 | prometiéndome | 2 |
| 32692 | prometerme | 2 |
| 32693 | prometemos | 2 |
| 32694 | prometas | 2 |
| 32695 | prométame | 2 |
| 32696 | prolongado | 2 |
| 32697 | prolongadas | 2 |
| 32698 | prolongada | 2 |
| 32699 | prolonga | 2 |
| 32700 | prole | 2 |
| 32701 | prohibirle | 2 |
| 32702 | prohibió | 2 |
| 32703 | prohibían | 2 |
| 32704 | prohíban | 2 |
| 32705 | progenie | 2 |
| 32706 | profusión | 2 |
| 32707 | prófuga | 2 |
| 32708 | profetizando | 2 |
| 32709 | profetizadas | 2 |
| 32710 | profesora | 2 |
| 32711 | profesando | 2 |
| 32712 | profería | 2 |
| 32713 | productivo | 2 |
| 32714 | producirse | 2 |
| 32715 | producirme | 2 |
| 32716 | producidos | 2 |
| 32717 | prodigiosamente | 2 |
| 32718 | prodigarse | 2 |
| 32719 | prodigando | 2 |
| 32720 | prodigado | 2 |
| 32721 | procuréis | 2 |
| 32722 | procurarían | 2 |
| 32723 | procurad | 2 |
| 32724 | procul | 2 |
| 32725 | procomún | 2 |
| 32726 | proclamo | 2 |
| 32727 | proclamación | 2 |
| 32728 | proclama | 2 |
| 32729 | proçesión | 2 |
| 32730 | procedencias | 2 |
| 32731 | probósele | 2 |
| 32732 | probeza | 2 |
| 32733 | probemos | 2 |
| 32734 | probaremos | 2 |
| 32735 | probara | 2 |
| 32736 | probanza | 2 |
| 32737 | probamos | 2 |
| 32738 | proas | 2 |
| 32739 | privadas | 2 |
| 32740 | priuados | 2 |
| 32741 | prioste | 2 |
| 32742 | priores | 2 |
| 32743 | priora | 2 |
| 32744 | pringado | 2 |
| 32745 | principiar | 2 |
| 32746 | principian | 2 |
| 32747 | principalidad | 2 |
| 32748 | prinçipales | 2 |
| 32749 | primordiales | 2 |
| 32750 | primaria | 2 |
| 32751 | priesas | 2 |
| 32752 | previsor | 2 |
| 32753 | previniendo | 2 |
| 32754 | previamente | 2 |
| 32755 | preveo | 2 |
| 32756 | prevenidos | 2 |
| 32757 | prevengamos | 2 |
| 32758 | preveía | 2 |
| 32759 | prevaricador | 2 |
| 32760 | prevaleció | 2 |
| 32761 | pretil | 2 |
| 32762 | pretéritas | 2 |
| 32763 | pretérita | 2 |
| 32764 | pretendió | 2 |
| 32765 | pretendido | 2 |
| 32766 | pretendí | 2 |
| 32767 | pretendes | 2 |
| 32768 | presurosos | 2 |
| 32769 | presurosas | 2 |
| 32770 | presupone | 2 |
| 32771 | presuntuosa | 2 |
| 32772 | presuncion | 2 |
| 32773 | presumirá | 2 |
| 32774 | presumes | 2 |
| 32775 | presumen | 2 |
| 32776 | presumas | 2 |
| 32777 | prestóme | 2 |
| 32778 | prestidigitador | 2 |
| 32779 | prestasen | 2 |
| 32780 | prestase | 2 |
| 32781 | prestas | 2 |
| 32782 | prestarse | 2 |
| 32783 | prestando | 2 |
| 32784 | presonajes | 2 |
| 32785 | presiones | 2 |
| 32786 | presidido | 2 |
| 32787 | presidencia | 2 |
| 32788 | preservado | 2 |
| 32789 | presentía | 2 |
| 32790 | preséntese | 2 |
| 32791 | preséntele | 2 |
| 32792 | presentéis | 2 |
| 32793 | presentáronse | 2 |
| 32794 | presentarme | 2 |
| 32795 | presentarles | 2 |
| 32796 | presentarle | 2 |
| 32797 | presentaré | 2 |
| 32798 | presentando | 2 |
| 32799 | presentalle | 2 |
| 32800 | presentábase | 2 |
| 32801 | presencias | 2 |
| 32802 | presenciaron | 2 |
| 32803 | presenciara | 2 |
| 32804 | presea | 2 |
| 32805 | prescripción | 2 |
| 32806 | prescindiendo | 2 |
| 32807 | prescindía | 2 |
| 32808 | prescinde | 2 |
| 32809 | presagio | 2 |
| 32810 | presagiar | 2 |
| 32811 | prerrogativas | 2 |
| 32812 | preponderancia | 2 |
| 32813 | preparo | 2 |
| 32814 | prepárate | 2 |
| 32815 | preparasen | 2 |
| 32816 | preparadas | 2 |
| 32817 | preocuparse | 2 |
| 32818 | preñados | 2 |
| 32819 | prendido | 2 |
| 32820 | prendidas | 2 |
| 32821 | prendida | 2 |
| 32822 | prendían | 2 |
| 32823 | prenderle | 2 |
| 32824 | prenden | 2 |
| 32825 | prendedle | 2 |
| 32826 | prendarse | 2 |
| 32827 | prendada | 2 |
| 32828 | premian | 2 |
| 32829 | premeditación | 2 |
| 32830 | prematuramente | 2 |
| 32831 | premáticas | 2 |
| 32832 | prehistórica | 2 |
| 32833 | preguntarnos | 2 |
| 32834 | preguntará | 2 |
| 32835 | preguntale | 2 |
| 32836 | pregon | 2 |
| 32837 | prefirieron | 2 |
| 32838 | prefieren | 2 |
| 32839 | preferiré | 2 |
| 32840 | prefación | 2 |
| 32841 | preeminencia | 2 |
| 32842 | predomina | 2 |
| 32843 | predisposición | 2 |
| 32844 | predios | 2 |
| 32845 | preclaros | 2 |
| 32846 | precisos | 2 |
| 32847 | precisado | 2 |
| 32848 | precipitemos | 2 |
| 32849 | precipitaste | 2 |
| 32850 | precipitar | 2 |
| 32851 | precipicios | 2 |
| 32852 | preciosísimo | 2 |
| 32853 | preciosica | 2 |
| 32854 | preçiosa | 2 |
| 32855 | preciarte | 2 |
| 32856 | precian | 2 |
| 32857 | preçiados | 2 |
| 32858 | preçiada | 2 |
| 32859 | preciábase | 2 |
| 32860 | preciaban | 2 |
| 32861 | precedidas | 2 |
| 32862 | precedía | 2 |
| 32863 | precede | 2 |
| 32864 | prebendados | 2 |
| 32865 | prebenda | 2 |
| 32866 | práxedes | 2 |
| 32867 | prancha | 2 |
| 32868 | pragmática | 2 |
| 32869 | praga | 2 |
| 32870 | practico | 2 |
| 32871 | practicado | 2 |
| 32872 | practicable | 2 |
| 32873 | pr | 2 |
| 32874 | pp | 2 |
| 32875 | pozquidac | 2 |
| 32876 | pour | 2 |
| 32877 | potros | 2 |
| 32878 | potra | 2 |
| 32879 | potosí | 2 |
| 32880 | potestades | 2 |
| 32881 | potestad | 2 |
| 32882 | poternas | 2 |
| 32883 | potacion | 2 |
| 32884 | postulación | 2 |
| 32885 | postro | 2 |
| 32886 | postrimeria | 2 |
| 32887 | postigos | 2 |
| 32888 | posteriores | 2 |
| 32889 | posteridad | 2 |
| 32890 | postemas | 2 |
| 32891 | postema | 2 |
| 32892 | possesion | 2 |
| 32893 | pospone | 2 |
| 32894 | posó | 2 |
| 32895 | positivista | 2 |
| 32896 | posiste | 2 |
| 32897 | posesor | 2 |
| 32898 | posesiones | 2 |
| 32899 | posesionarse | 2 |
| 32900 | posesionaron | 2 |
| 32901 | posesion | 2 |
| 32902 | poseemos | 2 |
| 32903 | poseedores | 2 |
| 32904 | posa | 2 |
| 32905 | portugueses | 2 |
| 32906 | portuguesa | 2 |
| 32907 | portiello | 2 |
| 32908 | pórticos | 2 |
| 32909 | portear | 2 |
| 32910 | portazos | 2 |
| 32911 | portazo | 2 |
| 32912 | portazgo | 2 |
| 32913 | portaua | 2 |
| 32914 | portan | 2 |
| 32915 | portamanteo | 2 |
| 32916 | portalada | 2 |
| 32917 | porras | 2 |
| 32918 | porquerizo | 2 |
| 32919 | porné | 2 |
| 32920 | pornan | 2 |
| 32921 | porna | 2 |
| 32922 | poridad | 2 |
| 32923 | pórfidos | 2 |
| 32924 | porfias | 2 |
| 32925 | porfiados | 2 |
| 32926 | pordioseros | 2 |
| 32927 | pordioseo | 2 |
| 32928 | poquísimas | 2 |
| 32929 | poquillejo | 2 |
| 32930 | populoso | 2 |
| 32931 | populosa | 2 |
| 32932 | populacho | 2 |
| 32933 | pontón | 2 |
| 32934 | pontífices | 2 |
| 32935 | pontes | 2 |
| 32936 | ponla | 2 |
| 32937 | poniéndosele | 2 |
| 32938 | poniéndonos | 2 |
| 32939 | poniéndolos | 2 |
| 32940 | poniéndoles | 2 |
| 32941 | ponías | 2 |
| 32942 | poníale | 2 |
| 32943 | ponia | 2 |
| 32944 | póngome | 2 |
| 32945 | póngolo | 2 |
| 32946 | pónganme | 2 |
| 32947 | pongámonos | 2 |
| 32948 | póngame | 2 |
| 32949 | ponferrada | 2 |
| 32950 | pónese | 2 |
| 32951 | ponese | 2 |
| 32952 | ponert | 2 |
| 32953 | ponérmela | 2 |
| 32954 | ponense | 2 |
| 32955 | ponelle | 2 |
| 32956 | ponella | 2 |
| 32957 | ponéis | 2 |
| 32958 | ponedla | 2 |
| 32959 | pondrían | 2 |
| 32960 | pondríamos | 2 |
| 32961 | ponderando | 2 |
| 32962 | ponderaba | 2 |
| 32963 | pomposos | 2 |
| 32964 | pomposas | 2 |
| 32965 | pomares | 2 |
| 32966 | polvorosas | 2 |
| 32967 | polvorín | 2 |
| 32968 | polvorienta | 2 |
| 32969 | polvillo | 2 |
| 32970 | polluelo | 2 |
| 32971 | pollería | 2 |
| 32972 | polizonte | 2 |
| 32973 | politiquilla | 2 |
| 32974 | polisones | 2 |
| 32975 | polígono | 2 |
| 32976 | polido | 2 |
| 32977 | policena | 2 |
| 32978 | polacos | 2 |
| 32979 | polaco | 2 |
| 32980 | podrian | 2 |
| 32981 | podies | 2 |
| 32982 | podíen | 2 |
| 32983 | podie | 2 |
| 32984 | podert | 2 |
| 32985 | poderosamente | 2 |
| 32986 | poderíos | 2 |
| 32987 | poderio | 2 |
| 32988 | podencos | 2 |
| 32989 | podaba | 2 |
| 32990 | poço | 2 |
| 32991 | poc | 2 |
| 32992 | pobrísimo | 2 |
| 32993 | pobrísima | 2 |
| 32994 | pobrezas | 2 |
| 32995 | pobretín | 2 |
| 32996 | pobrecitas | 2 |
| 32997 | pluvia | 2 |
| 32998 | plus | 2 |
| 32999 | plum | 2 |
| 33000 | plomos | 2 |
| 33001 | plomizas | 2 |
| 33002 | plin | 2 |
| 33003 | plieguecitos | 2 |
| 33004 | pleytesía | 2 |
| 33005 | plenamente | 2 |
| 33006 | plegaria | 2 |
| 33007 | plegar | 2 |
| 33008 | plegando | 2 |
| 33009 | plazera | 2 |
| 33010 | plauto | 2 |
| 33011 | platónicamente | 2 |
| 33012 | platito | 2 |
| 33013 | platir | 2 |
| 33014 | platicando | 2 |
| 33015 | platerescos | 2 |
| 33016 | plateadas | 2 |
| 33017 | plastón | 2 |
| 33018 | plástico | 2 |
| 33019 | plasticidad | 2 |
| 33020 | plástica | 2 |
| 33021 | plasta | 2 |
| 33022 | plaseres | 2 |
| 33023 | plasenteras | 2 |
| 33024 | plasencia | 2 |
| 33025 | plañideros | 2 |
| 33026 | plañidero | 2 |
| 33027 | plantose | 2 |
| 33028 | plantones | 2 |
| 33029 | planteó | 2 |
| 33030 | plantear | 2 |
| 33031 | planteando | 2 |
| 33032 | plante | 2 |
| 33033 | plantarse | 2 |
| 33034 | plantados | 2 |
| 33035 | plantadas | 2 |
| 33036 | plantación | 2 |
| 33037 | plancheta | 2 |
| 33038 | plancharle | 2 |
| 33039 | planchando | 2 |
| 33040 | planchado | 2 |
| 33041 | planas | 2 |
| 33042 | plana | 2 |
| 33043 | plam | 2 |
| 33044 | plaço | 2 |
| 33045 | plaçentero | 2 |
| 33046 | placa | 2 |
| 33047 | pla | 2 |
| 33048 | pizpireta | 2 |
| 33049 | pizorra | 2 |
| 33050 | pizarras | 2 |
| 33051 | pivote | 2 |
| 33052 | pittore | 2 |
| 33053 | pitos | 2 |
| 33054 | pitonisa | 2 |
| 33055 | pitillos | 2 |
| 33056 | pisuerga | 2 |
| 33057 | pistoletes | 2 |
| 33058 | pistilos | 2 |
| 33059 | pista | 2 |
| 33060 | pisoteando | 2 |
| 33061 | pisoteado | 2 |
| 33062 | pises | 2 |
| 33063 | piscatorio | 2 |
| 33064 | pisarle | 2 |
| 33065 | pisándose | 2 |
| 33066 | pisaban | 2 |
| 33067 | piruetas | 2 |
| 33068 | pirran | 2 |
| 33069 | pirraba | 2 |
| 33070 | piros | 2 |
| 33071 | pirineos | 2 |
| 33072 | piratería | 2 |
| 33073 | pirata | 2 |
| 33074 | pira | 2 |
| 33075 | piquito | 2 |
| 33076 | piquen | 2 |
| 33077 | piores | 2 |
| 33078 | pior | 2 |
| 33079 | piojoso | 2 |
| 33080 | piojo | 2 |
| 33081 | piña | 2 |
| 33082 | pinturera | 2 |
| 33083 | pintaua | 2 |
| 33084 | pintase | 2 |
| 33085 | pintarnos | 2 |
| 33086 | pintarle | 2 |
| 33087 | pintao | 2 |
| 33088 | pintándole | 2 |
| 33089 | pingües | 2 |
| 33090 | pindongona | 2 |
| 33091 | pinchas | 2 |
| 33092 | pinchar | 2 |
| 33093 | pinares | 2 |
| 33094 | pin | 2 |
| 33095 | piltrafas | 2 |
| 33096 | pillastres | 2 |
| 33097 | pildoritas | 2 |
| 33098 | pildora | 2 |
| 33099 | pigault | 2 |
| 33100 | pif | 2 |
| 33101 | piérdese | 2 |
| 33102 | pieldra | 2 |
| 33103 | piecho | 2 |
| 33104 | piececitas | 2 |
| 33105 | pidiole | 2 |
| 33106 | pidieren | 2 |
| 33107 | pidiéndome | 2 |
| 33108 | pidiéndoles | 2 |
| 33109 | pídeselo | 2 |
| 33110 | pidámosle | 2 |
| 33111 | pid | 2 |
| 33112 | pictórica | 2 |
| 33113 | píctima | 2 |
| 33114 | picotear | 2 |
| 33115 | picón | 2 |
| 33116 | pícome | 2 |
| 33117 | picazos | 2 |
| 33118 | picazón | 2 |
| 33119 | picazas | 2 |
| 33120 | picarse | 2 |
| 33121 | picarescas | 2 |
| 33122 | pícaras | 2 |
| 33123 | picaporte | 2 |
| 33124 | picaña | 2 |
| 33125 | picadura | 2 |
| 33126 | phenix | 2 |
| 33127 | pezón | 2 |
| 33128 | petrolero | 2 |
| 33129 | petrica | 2 |
| 33130 | peticiones | 2 |
| 33131 | petafio | 2 |
| 33132 | pessima | 2 |
| 33133 | pesquisa | 2 |
| 33134 | pesimistas | 2 |
| 33135 | pescuda | 2 |
| 33136 | pescó | 2 |
| 33137 | pesco | 2 |
| 33138 | pescaron | 2 |
| 33139 | pescando | 2 |
| 33140 | pescadillas | 2 |
| 33141 | pescadilla | 2 |
| 33142 | pescadero | 2 |
| 33143 | pescaba | 2 |
| 33144 | pesarosa | 2 |
| 33145 | pesaría | 2 |
| 33146 | pésales | 2 |
| 33147 | pesaban | 2 |
| 33148 | perú | 2 |
| 33149 | perturbar | 2 |
| 33150 | perturban | 2 |
| 33151 | perturbado | 2 |
| 33152 | pertinentes | 2 |
| 33153 | pertinente | 2 |
| 33154 | pertenezca | 2 |
| 33155 | pertenecido | 2 |
| 33156 | persuadirles | 2 |
| 33157 | persuadiese | 2 |
| 33158 | persuadiéndose | 2 |
| 33159 | persuadí | 2 |
| 33160 | persuades | 2 |
| 33161 | persuade | 2 |
| 33162 | perspectivas | 2 |
| 33163 | personó | 2 |
| 33164 | personificado | 2 |
| 33165 | personalmente | 2 |
| 33166 | persiguió | 2 |
| 33167 | persiguieron | 2 |
| 33168 | persignó | 2 |
| 33169 | persignándose | 2 |
| 33170 | persignaba | 2 |
| 33171 | persia | 2 |
| 33172 | perseueras | 2 |
| 33173 | perseuerar | 2 |
| 33174 | perseguidos | 2 |
| 33175 | perseguidora | 2 |
| 33176 | perseguidas | 2 |
| 33177 | persas | 2 |
| 33178 | persa | 2 |
| 33179 | perrilla | 2 |
| 33180 | perrazos | 2 |
| 33181 | perplexidad | 2 |
| 33182 | perplejos | 2 |
| 33183 | perpetuos | 2 |
| 33184 | perpetuidad | 2 |
| 33185 | perpetuase | 2 |
| 33186 | perpetuar | 2 |
| 33187 | peroraba | 2 |
| 33188 | perol | 2 |
| 33189 | pernil | 2 |
| 33190 | permuta | 2 |
| 33191 | permitirse | 2 |
| 33192 | permitirme | 2 |
| 33193 | permitirían | 2 |
| 33194 | permitieran | 2 |
| 33195 | permitidme | 2 |
| 33196 | permites | 2 |
| 33197 | permanecieron | 2 |
| 33198 | permanecí | 2 |
| 33199 | perjudica | 2 |
| 33200 | periquitos | 2 |
| 33201 | periquillo | 2 |
| 33202 | periquete | 2 |
| 33203 | período | 2 |
| 33204 | periodísticos | 2 |
| 33205 | periodismo | 2 |
| 33206 | periódica | 2 |
| 33207 | periglo | 2 |
| 33208 | perifollo | 2 |
| 33209 | peri | 2 |
| 33210 | perfumería | 2 |
| 33211 | perfumadas | 2 |
| 33212 | perfidia | 2 |
| 33213 | pérfida | 2 |
| 33214 | perfeccionando | 2 |
| 33215 | perezcan | 2 |
| 33216 | perezca | 2 |
| 33217 | peresosso | 2 |
| 33218 | peresçe | 2 |
| 33219 | perenal | 2 |
| 33220 | pereçoso | 2 |
| 33221 | perecio | 2 |
| 33222 | perecieron | 2 |
| 33223 | pereciendo | 2 |
| 33224 | pereceríamos | 2 |
| 33225 | perecen | 2 |
| 33226 | pereçe | 2 |
| 33227 | perdularios | 2 |
| 33228 | perdonen | 2 |
| 33229 | perdonéis | 2 |
| 33230 | perdonas | 2 |
| 33231 | perdonarte | 2 |
| 33232 | perdonarán | 2 |
| 33233 | perdonando | 2 |
| 33234 | perdonamos | 2 |
| 33235 | perdonalle | 2 |
| 33236 | perdonados | 2 |
| 33237 | perdonad | 2 |
| 33238 | perdimiento | 2 |
| 33239 | perdiesen | 2 |
| 33240 | perdiere | 2 |
| 33241 | perdiçes | 2 |
| 33242 | perdet | 2 |
| 33243 | perderas | 2 |
| 33244 | perdays | 2 |
| 33245 | percibe | 2 |
| 33246 | percheles | 2 |
| 33247 | perceptible | 2 |
| 33248 | peral | 2 |
| 33249 | pequeñita | 2 |
| 33250 | pequenas | 2 |
| 33251 | peque | 2 |
| 33252 | pepión | 2 |
| 33253 | pepino | 2 |
| 33254 | pepillo | 2 |
| 33255 | pepes | 2 |
| 33256 | peoría | 2 |
| 33257 | peorcito | 2 |
| 33258 | péñola | 2 |
| 33259 | penúltimo | 2 |
| 33260 | pentagrama | 2 |
| 33261 | penssé | 2 |
| 33262 | penssaré | 2 |
| 33263 | penso | 2 |
| 33264 | pensavan | 2 |
| 33265 | pensauas | 2 |
| 33266 | pensaste | 2 |
| 33267 | pensares | 2 |
| 33268 | pensaras | 2 |
| 33269 | pensaran | 2 |
| 33270 | pensallo | 2 |
| 33271 | peniques | 2 |
| 33272 | penetrantes | 2 |
| 33273 | penes | 2 |
| 33274 | peneque | 2 |
| 33275 | penelope | 2 |
| 33276 | pendones | 2 |
| 33277 | pender | 2 |
| 33278 | pencas | 2 |
| 33279 | penaua | 2 |
| 33280 | penase | 2 |
| 33281 | penaredes | 2 |
| 33282 | penados | 2 |
| 33283 | penadas | 2 |
| 33284 | peluconas | 2 |
| 33285 | peluche | 2 |
| 33286 | pelotera | 2 |
| 33287 | pelotazo | 2 |
| 33288 | peló | 2 |
| 33289 | pelmazos | 2 |
| 33290 | pelmazo | 2 |
| 33291 | pellizcado | 2 |
| 33292 | pellizcaban | 2 |
| 33293 | pellis | 2 |
| 33294 | pelitos | 2 |
| 33295 | pelito | 2 |
| 33296 | peligrosísima | 2 |
| 33297 | peligrar | 2 |
| 33298 | peligran | 2 |
| 33299 | peligra | 2 |
| 33300 | peleto | 2 |
| 33301 | peletería | 2 |
| 33302 | peleen | 2 |
| 33303 | peleé | 2 |
| 33304 | peleantes | 2 |
| 33305 | peleador | 2 |
| 33306 | peleado | 2 |
| 33307 | pele | 2 |
| 33308 | pelarnos | 2 |
| 33309 | pelaría | 2 |
| 33310 | pelar | 2 |
| 33311 | pelando | 2 |
| 33312 | pelan | 2 |
| 33313 | pelaje | 2 |
| 33314 | peladilla | 2 |
| 33315 | peladas | 2 |
| 33316 | peinó | 2 |
| 33317 | peinándose | 2 |
| 33318 | peinados | 2 |
| 33319 | peinadoras | 2 |
| 33320 | peinada | 2 |
| 33321 | pegujares | 2 |
| 33322 | pegué | 2 |
| 33323 | pegaso | 2 |
| 33324 | pegas | 2 |
| 33325 | pegará | 2 |
| 33326 | pegamos | 2 |
| 33327 | pégame | 2 |
| 33328 | pegajosos | 2 |
| 33329 | pedroso | 2 |
| 33330 | pedrisco | 2 |
| 33331 | pedricar | 2 |
| 33332 | pedrería | 2 |
| 33333 | pedreñales | 2 |
| 33334 | pedis | 2 |
| 33335 | pedírsela | 2 |
| 33336 | pedirse | 2 |
| 33337 | pediros | 2 |
| 33338 | pedirlo | 2 |
| 33339 | pedirás | 2 |
| 33340 | pedirá | 2 |
| 33341 | pedillo | 2 |
| 33342 | pedilla | 2 |
| 33343 | pedigüeño | 2 |
| 33344 | pediduras | 2 |
| 33345 | pedides | 2 |
| 33346 | pedida | 2 |
| 33347 | pedestal | 2 |
| 33348 | pedem | 2 |
| 33349 | pede | 2 |
| 33350 | pedantes | 2 |
| 33351 | pedal | 2 |
| 33352 | pedaço | 2 |
| 33353 | peculiares | 2 |
| 33354 | pecheros | 2 |
| 33355 | pechar | 2 |
| 33356 | pecha | 2 |
| 33357 | pecas | 2 |
| 33358 | pecará | 2 |
| 33359 | pecando | 2 |
| 33360 | pecaminosos | 2 |
| 33361 | pecaminoso | 2 |
| 33362 | pecaminosas | 2 |
| 33363 | payas | 2 |
| 33364 | paxaros | 2 |
| 33365 | pavones | 2 |
| 33366 | pavés | 2 |
| 33367 | paveros | 2 |
| 33368 | pava | 2 |
| 33369 | pausadas | 2 |
| 33370 | pauperum | 2 |
| 33371 | paulo | 2 |
| 33372 | patulea | 2 |
| 33373 | patriótica | 2 |
| 33374 | patricio | 2 |
| 33375 | patrias | 2 |
| 33376 | patrañas | 2 |
| 33377 | paternalmente | 2 |
| 33378 | patentes | 2 |
| 33379 | patena | 2 |
| 33380 | patatitas | 2 |
| 33381 | patatín | 2 |
| 33382 | patatán | 2 |
| 33383 | pataplum | 2 |
| 33384 | pataleos | 2 |
| 33385 | patá | 2 |
| 33386 | pastrañas | 2 |
| 33387 | pastraña | 2 |
| 33388 | pastoreo | 2 |
| 33389 | pasteleras | 2 |
| 33390 | pastaban | 2 |
| 33391 | passaste | 2 |
| 33392 | passaren | 2 |
| 33393 | passando | 2 |
| 33394 | pasmoso | 2 |
| 33395 | pasmosas | 2 |
| 33396 | pasmos | 2 |
| 33397 | pásmense | 2 |
| 33398 | pasmarote | 2 |
| 33399 | pasmáronse | 2 |
| 33400 | pasmábase | 2 |
| 33401 | pasividad | 2 |
| 33402 | pasiegos | 2 |
| 33403 | páselo | 2 |
| 33404 | paséis | 2 |
| 33405 | pasava | 2 |
| 33406 | pasaste | 2 |
| 33407 | pasases | 2 |
| 33408 | pasaríamos | 2 |
| 33409 | pasarero | 2 |
| 33410 | pasare | 2 |
| 33411 | pasaras | 2 |
| 33412 | pasadizos | 2 |
| 33413 | pasadera | 2 |
| 33414 | pasábamoslo | 2 |
| 33415 | party | 2 |
| 33416 | partirás | 2 |
| 33417 | partio | 2 |
| 33418 | partieses | 2 |
| 33419 | partiésemos | 2 |
| 33420 | partículas | 2 |
| 33421 | participó | 2 |
| 33422 | partícipes | 2 |
| 33423 | partícipe | 2 |
| 33424 | participantes | 2 |
| 33425 | participacion | 2 |
| 33426 | parteras | 2 |
| 33427 | partas | 2 |
| 33428 | partan | 2 |
| 33429 | partamos | 2 |
| 33430 | parson | 2 |
| 33431 | parroquianas | 2 |
| 33432 | parroquiales | 2 |
| 33433 | párrocos | 2 |
| 33434 | parras | 2 |
| 33435 | parrales | 2 |
| 33436 | parques | 2 |
| 33437 | parodias | 2 |
| 33438 | parlar | 2 |
| 33439 | parlanchina | 2 |
| 33440 | paridas | 2 |
| 33441 | parida | 2 |
| 33442 | parían | 2 |
| 33443 | paría | 2 |
| 33444 | parí | 2 |
| 33445 | pargamino | 2 |
| 33446 | párese | 2 |
| 33447 | paresciesse | 2 |
| 33448 | parescian | 2 |
| 33449 | parescia | 2 |
| 33450 | paresçer | 2 |
| 33451 | paresçen | 2 |
| 33452 | paresceme | 2 |
| 33453 | paren | 2 |
| 33454 | parejo | 2 |
| 33455 | pareciéronle | 2 |
| 33456 | pareciéndose | 2 |
| 33457 | parecíanle | 2 |
| 33458 | parecí | 2 |
| 33459 | parécese | 2 |
| 33460 | parecérselo | 2 |
| 33461 | parecerán | 2 |
| 33462 | parecemos | 2 |
| 33463 | pardon | 2 |
| 33464 | pardios | 2 |
| 33465 | pardillo | 2 |
| 33466 | pardales | 2 |
| 33467 | parcería | 2 |
| 33468 | párate | 2 |
| 33469 | parásito | 2 |
| 33470 | paras | 2 |
| 33471 | parará | 2 |
| 33472 | parapetan | 2 |
| 33473 | paranzas | 2 |
| 33474 | parando | 2 |
| 33475 | paranças | 2 |
| 33476 | páramo | 2 |
| 33477 | paralizada | 2 |
| 33478 | parálisis | 2 |
| 33479 | paralelo | 2 |
| 33480 | paradójico | 2 |
| 33481 | paradójica | 2 |
| 33482 | parábola | 2 |
| 33483 | papirotazo | 2 |
| 33484 | papelista | 2 |
| 33485 | papelillo | 2 |
| 33486 | papelejo | 2 |
| 33487 | papelaos | 2 |
| 33488 | paparruchas | 2 |
| 33489 | paparrucha | 2 |
| 33490 | papanatas | 2 |
| 33491 | papalina | 2 |
| 33492 | pañosa | 2 |
| 33493 | pañolón | 2 |
| 33494 | pañolito | 2 |
| 33495 | pañizuelos | 2 |
| 33496 | pañería | 2 |
| 33497 | panzudo | 2 |
| 33498 | panzudas | 2 |
| 33499 | pantoja | 2 |
| 33500 | panteísta | 2 |
| 33501 | paniaguado | 2 |
| 33502 | panfilona | 2 |
| 33503 | pane | 2 |
| 33504 | panderetazos | 2 |
| 33505 | pancino | 2 |
| 33506 | pancaya | 2 |
| 33507 | panal | 2 |
| 33508 | pámpano | 2 |
| 33509 | pamema | 2 |
| 33510 | pam | 2 |
| 33511 | palurdo | 2 |
| 33512 | palpe | 2 |
| 33513 | palotes | 2 |
| 33514 | palosanto | 2 |
| 33515 | palomeque | 2 |
| 33516 | palmilla | 2 |
| 33517 | palitroque | 2 |
| 33518 | palitos | 2 |
| 33519 | palios | 2 |
| 33520 | palidecer | 2 |
| 33521 | paletos | 2 |
| 33522 | paletada | 2 |
| 33523 | palemo | 2 |
| 33524 | palatino | 2 |
| 33525 | palamenta | 2 |
| 33526 | palais | 2 |
| 33527 | paladión | 2 |
| 33528 | palación | 2 |
| 33529 | palaciegas | 2 |
| 33530 | palaciega | 2 |
| 33531 | palabrilla | 2 |
| 33532 | palabrería | 2 |
| 33533 | palabrejas | 2 |
| 33534 | pajizo | 2 |
| 33535 | pajeles | 2 |
| 33536 | pajecillo | 2 |
| 33537 | pajarillas | 2 |
| 33538 | pajarete | 2 |
| 33539 | pajares | 2 |
| 33540 | paicía | 2 |
| 33541 | pagaste | 2 |
| 33542 | págase | 2 |
| 33543 | pagárselo | 2 |
| 33544 | pagarse | 2 |
| 33545 | pagarme | 2 |
| 33546 | pagaos | 2 |
| 33547 | págam | 2 |
| 33548 | pagalle | 2 |
| 33549 | pagadas | 2 |
| 33550 | pagad | 2 |
| 33551 | padillita | 2 |
| 33552 | padezcamos | 2 |
| 33553 | pacotilla | 2 |
| 33554 | pacos | 2 |
| 33555 | pacientes | 2 |
| 33556 | paçiençia | 2 |
| 33557 | pacían | 2 |
| 33558 | pablillos | 2 |
| 33559 | oystes | 2 |
| 33560 | oyrlo | 2 |
| 33561 | oyredes | 2 |
| 33562 | oyran | 2 |
| 33563 | oyón | 2 |
| 33564 | oyolo | 2 |
| 33565 | oymos | 2 |
| 33566 | oyeren | 2 |
| 33567 | oyéndote | 2 |
| 33568 | oyéndolas | 2 |
| 33569 | oydas | 2 |
| 33570 | oyd | 2 |
| 33571 | oyarzun | 2 |
| 33572 | oxte | 2 |
| 33573 | ovyeron | 2 |
| 33574 | óvose | 2 |
| 33575 | oviesen | 2 |
| 33576 | ovies | 2 |
| 33577 | oviera | 2 |
| 33578 | overos | 2 |
| 33579 | oval | 2 |
| 33580 | ov | 2 |
| 33581 | ouiere | 2 |
| 33582 | ouejas | 2 |
| 33583 | oue | 2 |
| 33584 | où | 2 |
| 33585 | otramente | 2 |
| 33586 | otorgóle | 2 |
| 33587 | otorgase | 2 |
| 33588 | otorgaría | 2 |
| 33589 | otorgaba | 2 |
| 33590 | oteo | 2 |
| 33591 | otelo | 2 |
| 33592 | oteas | 2 |
| 33593 | ostugo | 2 |
| 33594 | ostende | 2 |
| 33595 | ossa | 2 |
| 33596 | oscurece | 2 |
| 33597 | oscilando | 2 |
| 33598 | oscilaba | 2 |
| 33599 | osaste | 2 |
| 33600 | osase | 2 |
| 33601 | osan | 2 |
| 33602 | osamos | 2 |
| 33603 | osamenta | 2 |
| 33604 | osadias | 2 |
| 33605 | oruga | 2 |
| 33606 | ortodoxos | 2 |
| 33607 | ortodoxo | 2 |
| 33608 | orondas | 2 |
| 33609 | ornitólogo | 2 |
| 33610 | orladas | 2 |
| 33611 | orlada | 2 |
| 33612 | orinales | 2 |
| 33613 | orín | 2 |
| 33614 | origine | 2 |
| 33615 | originado | 2 |
| 33616 | oria | 2 |
| 33617 | ori | 2 |
| 33618 | orgullya | 2 |
| 33619 | orgullosas | 2 |
| 33620 | organizadas | 2 |
| 33621 | organizada | 2 |
| 33622 | organizaba | 2 |
| 33623 | organdí | 2 |
| 33624 | orfila | 2 |
| 33625 | orellana | 2 |
| 33626 | orejudo | 2 |
| 33627 | orégano | 2 |
| 33628 | ordine | 2 |
| 33629 | ordeñar | 2 |
| 33630 | ordeñando | 2 |
| 33631 | ordenara | 2 |
| 33632 | ordenan | 2 |
| 33633 | ordenación | 2 |
| 33634 | orça | 2 |
| 33635 | órbitas | 2 |
| 33636 | orbaneja | 2 |
| 33637 | oratorios | 2 |
| 33638 | oratorias | 2 |
| 33639 | orangutanes | 2 |
| 33640 | orabuena | 2 |
| 33641 | or | 2 |
| 33642 | opúsculo | 2 |
| 33643 | opulentos | 2 |
| 33644 | opuestos | 2 |
| 33645 | óptico | 2 |
| 33646 | óptica | 2 |
| 33647 | oprobrio | 2 |
| 33648 | oprimiéndose | 2 |
| 33649 | oprimidos | 2 |
| 33650 | oprimidas | 2 |
| 33651 | oprimen | 2 |
| 33652 | opresiones | 2 |
| 33653 | oponiendo | 2 |
| 33654 | opondrá | 2 |
| 33655 | opino | 2 |
| 33656 | opinas | 2 |
| 33657 | opinado | 2 |
| 33658 | operibus | 2 |
| 33659 | opacidad | 2 |
| 33660 | opaca | 2 |
| 33661 | onrrar | 2 |
| 33662 | onrrados | 2 |
| 33663 | onrrado | 2 |
| 33664 | onestidad | 2 |
| 33665 | onestad | 2 |
| 33666 | onera | 2 |
| 33667 | ondeando | 2 |
| 33668 | onceno | 2 |
| 33669 | omnes | 2 |
| 33670 | ombligo | 2 |
| 33671 | olvidósele | 2 |
| 33672 | olvidaron | 2 |
| 33673 | olvidarlas | 2 |
| 33674 | olvidarla | 2 |
| 33675 | olvidándome | 2 |
| 33676 | oluidaua | 2 |
| 33677 | olivar | 2 |
| 33678 | olfatorios | 2 |
| 33679 | olfateado | 2 |
| 33680 | oleada | 2 |
| 33681 | ojivas | 2 |
| 33682 | ojivales | 2 |
| 33683 | ojillos | 2 |
| 33684 | ojeroso | 2 |
| 33685 | ojeadas | 2 |
| 33686 | oís | 2 |
| 33687 | oírnos | 2 |
| 33688 | oirle | 2 |
| 33689 | oiremos | 2 |
| 33690 | oiréis | 2 |
| 33691 | oíllo | 2 |
| 33692 | oílle | 2 |
| 33693 | oíle | 2 |
| 33694 | oidores | 2 |
| 33695 | oídme | 2 |
| 33696 | oidium | 2 |
| 33697 | ogaño | 2 |
| 33698 | ofuscan | 2 |
| 33699 | ofuscado | 2 |
| 33700 | oftálmica | 2 |
| 33701 | ofrendas | 2 |
| 33702 | ofrecíle | 2 |
| 33703 | ofreciéndosele | 2 |
| 33704 | ofrecerme | 2 |
| 33705 | ofrecerla | 2 |
| 33706 | ofiçios | 2 |
| 33707 | oficiar | 2 |
| 33708 | oficialas | 2 |
| 33709 | oficiala | 2 |
| 33710 | oficiaba | 2 |
| 33711 | ofertorio | 2 |
| 33712 | ofensiva | 2 |
| 33713 | ofendió | 2 |
| 33714 | ofenderos | 2 |
| 33715 | ofenderá | 2 |
| 33716 | ofendellas | 2 |
| 33717 | odreçillo | 2 |
| 33718 | odisea | 2 |
| 33719 | odiar | 2 |
| 33720 | odia | 2 |
| 33721 | odalisca | 2 |
| 33722 | ocurrírseme | 2 |
| 33723 | ocurrírsele | 2 |
| 33724 | ocurrirme | 2 |
| 33725 | ocurriome | 2 |
| 33726 | ocurrieran | 2 |
| 33727 | ocurriendo | 2 |
| 33728 | ocurridos | 2 |
| 33729 | ocurridas | 2 |
| 33730 | ocupo | 2 |
| 33731 | ocupen | 2 |
| 33732 | ocupas | 2 |
| 33733 | ocuparte | 2 |
| 33734 | ocupadísimo | 2 |
| 33735 | ocupábase | 2 |
| 33736 | ocultes | 2 |
| 33737 | ocultarte | 2 |
| 33738 | ocultarlos | 2 |
| 33739 | ocultarlo | 2 |
| 33740 | ocultan | 2 |
| 33741 | oculos | 2 |
| 33742 | ocular | 2 |
| 33743 | ocin | 2 |
| 33744 | ochocientas | 2 |
| 33745 | ocasionó | 2 |
| 33746 | ocasional | 2 |
| 33747 | ocasionadas | 2 |
| 33748 | ocasionada | 2 |
| 33749 | ocasion | 2 |
| 33750 | ocaña | 2 |
| 33751 | obteniendo | 2 |
| 33752 | obtenerla | 2 |
| 33753 | obstrucción | 2 |
| 33754 | obstinada | 2 |
| 33755 | obstinaba | 2 |
| 33756 | obstara | 2 |
| 33757 | observándole | 2 |
| 33758 | observándola | 2 |
| 33759 | obsérvala | 2 |
| 33760 | obsequias | 2 |
| 33761 | obsequiarle | 2 |
| 33762 | obsequiándote | 2 |
| 33763 | obsequiadas | 2 |
| 33764 | obscenidades | 2 |
| 33765 | obre | 2 |
| 33766 | obrase | 2 |
| 33767 | oblonga | 2 |
| 33768 | obligas | 2 |
| 33769 | obligarles | 2 |
| 33770 | obligando | 2 |
| 33771 | oblicuas | 2 |
| 33772 | objetivo | 2 |
| 33773 | objetaba | 2 |
| 33774 | obeso | 2 |
| 33775 | obeliscos | 2 |
| 33776 | obedecí | 2 |
| 33777 | obedecerte | 2 |
| 33778 | obedeceré | 2 |
| 33779 | ñudos | 2 |
| 33780 | ñ | 2 |
| 33781 | nutrias | 2 |
| 33782 | nutria | 2 |
| 33783 | numero | 2 |
| 33784 | numérico | 2 |
| 33785 | numérica | 2 |
| 33786 | numeradas | 2 |
| 33787 | numen | 2 |
| 33788 | nulos | 2 |
| 33789 | nuezes | 2 |
| 33790 | nueuos | 2 |
| 33791 | nublosas | 2 |
| 33792 | nubarrones | 2 |
| 33793 | novísimos | 2 |
| 33794 | noveno | 2 |
| 33795 | novelesco | 2 |
| 33796 | novelesca | 2 |
| 33797 | novelería | 2 |
| 33798 | novelera | 2 |
| 33799 | novar | 2 |
| 33800 | nouedades | 2 |
| 33801 | noturnas | 2 |
| 33802 | notorias | 2 |
| 33803 | nótese | 2 |
| 33804 | notarios | 2 |
| 33805 | notadas | 2 |
| 33806 | notad | 2 |
| 33807 | notablemente | 2 |
| 33808 | notabilidades | 2 |
| 33809 | notabilidad | 2 |
| 33810 | not | 2 |
| 33811 | normalmente | 2 |
| 33812 | normalidad | 2 |
| 33813 | nordeste | 2 |
| 33814 | noramala | 2 |
| 33815 | nonbrado | 2 |
| 33816 | nonble | 2 |
| 33817 | nomine | 2 |
| 33818 | nombras | 2 |
| 33819 | nombrarse | 2 |
| 33820 | nombrara | 2 |
| 33821 | nómbrame | 2 |
| 33822 | nombrados | 2 |
| 33823 | nombradía | 2 |
| 33824 | nolis | 2 |
| 33825 | nodrizas | 2 |
| 33826 | nocivo | 2 |
| 33827 | nocibles | 2 |
| 33828 | nochecita | 2 |
| 33829 | nocharniegos | 2 |
| 33830 | noblezas | 2 |
| 33831 | noblesas | 2 |
| 33832 | noblesa | 2 |
| 33833 | nobiscum | 2 |
| 33834 | nobilísima | 2 |
| 33835 | nigromancia | 2 |
| 33836 | nietecillos | 2 |
| 33837 | nief | 2 |
| 33838 | nicarona | 2 |
| 33839 | newton | 2 |
| 33840 | neutralidad | 2 |
| 33841 | neutra | 2 |
| 33842 | neuralgia | 2 |
| 33843 | netos | 2 |
| 33844 | neto | 2 |
| 33845 | neta | 2 |
| 33846 | néstor | 2 |
| 33847 | nescio | 2 |
| 33848 | nerviosilla | 2 |
| 33849 | neri | 2 |
| 33850 | neos | 2 |
| 33851 | neo | 2 |
| 33852 | nemiga | 2 |
| 33853 | neísmo | 2 |
| 33854 | neguilla | 2 |
| 33855 | negruzcos | 2 |
| 33856 | negruzco | 2 |
| 33857 | negose | 2 |
| 33858 | negociara | 2 |
| 33859 | negociando | 2 |
| 33860 | negociaciones | 2 |
| 33861 | negligencias | 2 |
| 33862 | negároslo | 2 |
| 33863 | negaron | 2 |
| 33864 | negaría | 2 |
| 33865 | negara | 2 |
| 33866 | negaciones | 2 |
| 33867 | nefasto | 2 |
| 33868 | necessarias | 2 |
| 33869 | necesiten | 2 |
| 33870 | necesitaremos | 2 |
| 33871 | necesitáis | 2 |
| 33872 | necesitábamos | 2 |
| 33873 | neçesidat | 2 |
| 33874 | neblina | 2 |
| 33875 | nea | 2 |
| 33876 | nazarena | 2 |
| 33877 | nayean | 2 |
| 33878 | navidades | 2 |
| 33879 | navegamos | 2 |
| 33880 | navarino | 2 |
| 33881 | navancos | 2 |
| 33882 | navales | 2 |
| 33883 | náutico | 2 |
| 33884 | náuticas | 2 |
| 33885 | nauios | 2 |
| 33886 | nauio | 2 |
| 33887 | naufragado | 2 |
| 33888 | náufraga | 2 |
| 33889 | natillas | 2 |
| 33890 | nasçieron | 2 |
| 33891 | nasciendo | 2 |
| 33892 | nasçido | 2 |
| 33893 | nascido | 2 |
| 33894 | nasçida | 2 |
| 33895 | nascer | 2 |
| 33896 | nasca | 2 |
| 33897 | nasal | 2 |
| 33898 | narraciones | 2 |
| 33899 | nardos | 2 |
| 33900 | nardo | 2 |
| 33901 | narcisos | 2 |
| 33902 | narbaez | 2 |
| 33903 | naranjeros | 2 |
| 33904 | naranjero | 2 |
| 33905 | naranjera | 2 |
| 33906 | napoleones | 2 |
| 33907 | nao | 2 |
| 33908 | nadaban | 2 |
| 33909 | nacistes | 2 |
| 33910 | naciera | 2 |
| 33911 | naçe | 2 |
| 33912 | nabucodonosor | 2 |
| 33913 | muzas | 2 |
| 33914 | mutuas | 2 |
| 33915 | mutatis | 2 |
| 33916 | mutandis | 2 |
| 33917 | mutación | 2 |
| 33918 | mustia | 2 |
| 33919 | musica | 2 |
| 33920 | musgosas | 2 |
| 33921 | musculatura | 2 |
| 33922 | murmuros | 2 |
| 33923 | murmuro | 2 |
| 33924 | murmuren | 2 |
| 33925 | murmurase | 2 |
| 33926 | murmuras | 2 |
| 33927 | murmuradora | 2 |
| 33928 | murmurado | 2 |
| 33929 | muriere | 2 |
| 33930 | muradal | 2 |
| 33931 | muove | 2 |
| 33932 | muñón | 2 |
| 33933 | muñidor | 2 |
| 33934 | munificencia | 2 |
| 33935 | municipales | 2 |
| 33936 | mundanales | 2 |
| 33937 | multiplicas | 2 |
| 33938 | multiplica | 2 |
| 33939 | multas | 2 |
| 33940 | mulos | 2 |
| 33941 | mulo | 2 |
| 33942 | muletillas | 2 |
| 33943 | mujerzuelas | 2 |
| 33944 | mujeriego | 2 |
| 33945 | mujeriegas | 2 |
| 33946 | muías | 2 |
| 33947 | mugriento | 2 |
| 33948 | muge | 2 |
| 33949 | mugas | 2 |
| 33950 | muéveme | 2 |
| 33951 | muevan | 2 |
| 33952 | muévale | 2 |
| 33953 | muéstrese | 2 |
| 33954 | muestrame | 2 |
| 33955 | muertto | 2 |
| 33956 | muertecito | 2 |
| 33957 | muérese | 2 |
| 33958 | muerdan | 2 |
| 33959 | muerda | 2 |
| 33960 | múdese | 2 |
| 33961 | muden | 2 |
| 33962 | mudasen | 2 |
| 33963 | mudáronse | 2 |
| 33964 | mudándose | 2 |
| 33965 | mudables | 2 |
| 33966 | muchísimas | 2 |
| 33967 | muchachuelas | 2 |
| 33968 | mucetas | 2 |
| 33969 | mozalbetes | 2 |
| 33970 | moysen | 2 |
| 33971 | móviles | 2 |
| 33972 | movile | 2 |
| 33973 | moviéndola | 2 |
| 33974 | movíase | 2 |
| 33975 | moví | 2 |
| 33976 | moverte | 2 |
| 33977 | moveros | 2 |
| 33978 | moverle | 2 |
| 33979 | moverla | 2 |
| 33980 | movediza | 2 |
| 33981 | mouio | 2 |
| 33982 | mouimiento | 2 |
| 33983 | mouime | 2 |
| 33984 | mouer | 2 |
| 33985 | mots | 2 |
| 33986 | mostróse | 2 |
| 33987 | mostrencos | 2 |
| 33988 | mostréle | 2 |
| 33989 | mostréis | 2 |
| 33990 | mostrasen | 2 |
| 33991 | mostraros | 2 |
| 33992 | mostrará | 2 |
| 33993 | mostrándome | 2 |
| 33994 | mostradas | 2 |
| 33995 | mostrad | 2 |
| 33996 | mosquita | 2 |
| 33997 | mosquetes | 2 |
| 33998 | mosquetas | 2 |
| 33999 | mosqueo | 2 |
| 34000 | mortificó | 2 |
| 34001 | mortificarle | 2 |
| 34002 | mortificarla | 2 |
| 34003 | mortífero | 2 |
| 34004 | mortecina | 2 |
| 34005 | morriña | 2 |
| 34006 | morredes | 2 |
| 34007 | morrazo | 2 |
| 34008 | morralla | 2 |
| 34009 | morón | 2 |
| 34010 | moró | 2 |
| 34011 | mormón | 2 |
| 34012 | moriscas | 2 |
| 34013 | moriremos | 2 |
| 34014 | morigerado | 2 |
| 34015 | morieron | 2 |
| 34016 | morí | 2 |
| 34017 | moreto | 2 |
| 34018 | morenito | 2 |
| 34019 | mordiera | 2 |
| 34020 | mordían | 2 |
| 34021 | morboso | 2 |
| 34022 | morbidez | 2 |
| 34023 | moralizar | 2 |
| 34024 | moráez | 2 |
| 34025 | morador | 2 |
| 34026 | mor | 2 |
| 34027 | moñuca | 2 |
| 34028 | moños | 2 |
| 34029 | moña | 2 |
| 34030 | monuiedro | 2 |
| 34031 | montserrat | 2 |
| 34032 | montó | 2 |
| 34033 | montiña | 2 |
| 34034 | montijo | 2 |
| 34035 | montés | 2 |
| 34036 | montero | 2 |
| 34037 | montepío | 2 |
| 34038 | montaron | 2 |
| 34039 | montañeses | 2 |
| 34040 | montaban | 2 |
| 34041 | mont | 2 |
| 34042 | monstruosos | 2 |
| 34043 | monserrat | 2 |
| 34044 | monomaníaco | 2 |
| 34045 | monomanía | 2 |
| 34046 | monjío | 2 |
| 34047 | mongolfieras | 2 |
| 34048 | mongas | 2 |
| 34049 | monedita | 2 |
| 34050 | monedero | 2 |
| 34051 | monde | 2 |
| 34052 | mondas | 2 |
| 34053 | mondar | 2 |
| 34054 | mondada | 2 |
| 34055 | monástica | 2 |
| 34056 | monarquías | 2 |
| 34057 | monadas | 2 |
| 34058 | momentito | 2 |
| 34059 | momentáneamente | 2 |
| 34060 | momentánea | 2 |
| 34061 | molinera | 2 |
| 34062 | molicie | 2 |
| 34063 | molía | 2 |
| 34064 | molestos | 2 |
| 34065 | molestó | 2 |
| 34066 | molestísimas | 2 |
| 34067 | molestarse | 2 |
| 34068 | molestarme | 2 |
| 34069 | molestarla | 2 |
| 34070 | molestaré | 2 |
| 34071 | molestaran | 2 |
| 34072 | molestan | 2 |
| 34073 | molestado | 2 |
| 34074 | moléculas | 2 |
| 34075 | mojigatos | 2 |
| 34076 | mojigatería | 2 |
| 34077 | mojigata | 2 |
| 34078 | mojicón | 2 |
| 34079 | mojamos | 2 |
| 34080 | mojadura | 2 |
| 34081 | moja | 2 |
| 34082 | moisén | 2 |
| 34083 | mohínas | 2 |
| 34084 | modus | 2 |
| 34085 | modulaciones | 2 |
| 34086 | modorra | 2 |
| 34087 | modismos | 2 |
| 34088 | modificaron | 2 |
| 34089 | modificar | 2 |
| 34090 | modestita | 2 |
| 34091 | moderados | 2 |
| 34092 | modelado | 2 |
| 34093 | modelada | 2 |
| 34094 | moçuelo | 2 |
| 34095 | mocosa | 2 |
| 34096 | mochuelos | 2 |
| 34097 | mochuelo | 2 |
| 34098 | mochila | 2 |
| 34099 | mocedades | 2 |
| 34100 | mobiliario | 2 |
| 34101 | mo | 2 |
| 34102 | mitón | 2 |
| 34103 | missas | 2 |
| 34104 | misiva | 2 |
| 34105 | misitas | 2 |
| 34106 | misita | 2 |
| 34107 | misionero | 2 |
| 34108 | miseros | 2 |
| 34109 | miscelánea | 2 |
| 34110 | misantropía | 2 |
| 34111 | misal | 2 |
| 34112 | mirosté | 2 |
| 34113 | mirose | 2 |
| 34114 | mirones | 2 |
| 34115 | mirólos | 2 |
| 34116 | mirolo | 2 |
| 34117 | miróla | 2 |
| 34118 | mirilla | 2 |
| 34119 | mírese | 2 |
| 34120 | mírenos | 2 |
| 34121 | mírelos | 2 |
| 34122 | miréla | 2 |
| 34123 | miréis | 2 |
| 34124 | miraste | 2 |
| 34125 | mirasse | 2 |
| 34126 | miraría | 2 |
| 34127 | mirarás | 2 |
| 34128 | miraran | 2 |
| 34129 | míranse | 2 |
| 34130 | mirándoos | 2 |
| 34131 | mirándolos | 2 |
| 34132 | míralo | 2 |
| 34133 | mirallos | 2 |
| 34134 | miralle | 2 |
| 34135 | mírale | 2 |
| 34136 | miraglos | 2 |
| 34137 | miradlo | 2 |
| 34138 | miradle | 2 |
| 34139 | mirábanse | 2 |
| 34140 | miope | 2 |
| 34141 | mintrosos | 2 |
| 34142 | mínguez | 2 |
| 34143 | mineralogía | 2 |
| 34144 | minarle | 2 |
| 34145 | minar | 2 |
| 34146 | mimosa | 2 |
| 34147 | mimir | 2 |
| 34148 | mímicas | 2 |
| 34149 | mímica | 2 |
| 34150 | mimar | 2 |
| 34151 | mimando | 2 |
| 34152 | mimada | 2 |
| 34153 | mima | 2 |
| 34154 | millonaria | 2 |
| 34155 | milla | 2 |
| 34156 | militante | 2 |
| 34157 | milanés | 2 |
| 34158 | milagrosos | 2 |
| 34159 | mijt | 2 |
| 34160 | mijo | 2 |
| 34161 | mientas | 2 |
| 34162 | mielgas | 2 |
| 34163 | miedosos | 2 |
| 34164 | miedosa | 2 |
| 34165 | micor | 2 |
| 34166 | micolalde | 2 |
| 34167 | micho | 2 |
| 34168 | miajita | 2 |
| 34169 | mezquita | 2 |
| 34170 | mezquindad | 2 |
| 34171 | mezclaron | 2 |
| 34172 | mezclan | 2 |
| 34173 | mezclábase | 2 |
| 34174 | metz | 2 |
| 34175 | metrificar | 2 |
| 34176 | metódico | 2 |
| 34177 | metódicas | 2 |
| 34178 | metióme | 2 |
| 34179 | metio | 2 |
| 34180 | metímoslos | 2 |
| 34181 | metimiento | 2 |
| 34182 | metiese | 2 |
| 34183 | metieran | 2 |
| 34184 | metiéndolo | 2 |
| 34185 | meticulosa | 2 |
| 34186 | metíame | 2 |
| 34187 | metérselo | 2 |
| 34188 | meterlo | 2 |
| 34189 | meterá | 2 |
| 34190 | mételo | 2 |
| 34191 | metamos | 2 |
| 34192 | metamorfóseos | 2 |
| 34193 | metad | 2 |
| 34194 | messes | 2 |
| 34195 | mesones | 2 |
| 34196 | mesita | 2 |
| 34197 | mesiellas | 2 |
| 34198 | mesajera | 2 |
| 34199 | meryenda | 2 |
| 34200 | meros | 2 |
| 34201 | mermar | 2 |
| 34202 | mermaba | 2 |
| 34203 | merlo | 2 |
| 34204 | meritoria | 2 |
| 34205 | meriendo | 2 |
| 34206 | meretriz | 2 |
| 34207 | meresçimiento | 2 |
| 34208 | meresçíen | 2 |
| 34209 | meresçían | 2 |
| 34210 | meresçes | 2 |
| 34211 | meresçer | 2 |
| 34212 | meresçen | 2 |
| 34213 | merengues | 2 |
| 34214 | merengue | 2 |
| 34215 | merendaron | 2 |
| 34216 | merendado | 2 |
| 34217 | mereciesen | 2 |
| 34218 | merecieron | 2 |
| 34219 | merecida | 2 |
| 34220 | merecías | 2 |
| 34221 | mercaduría | 2 |
| 34222 | mercadero | 2 |
| 34223 | mercachifle | 2 |
| 34224 | meñique | 2 |
| 34225 | menudillo | 2 |
| 34226 | menudeo | 2 |
| 34227 | menudear | 2 |
| 34228 | mentyra | 2 |
| 34229 | mentor | 2 |
| 34230 | mentirás | 2 |
| 34231 | mentirán | 2 |
| 34232 | mentille | 2 |
| 34233 | mentida | 2 |
| 34234 | mentecatos | 2 |
| 34235 | mentarlo | 2 |
| 34236 | mentarla | 2 |
| 34237 | mentales | 2 |
| 34238 | menosprecia | 2 |
| 34239 | menoscaban | 2 |
| 34240 | menjuy | 2 |
| 34241 | menguará | 2 |
| 34242 | menguan | 2 |
| 34243 | menguaba | 2 |
| 34244 | menga | 2 |
| 34245 | menestrales | 2 |
| 34246 | menestrala | 2 |
| 34247 | menestra | 2 |
| 34248 | menease | 2 |
| 34249 | meneaba | 2 |
| 34250 | mendozas | 2 |
| 34251 | méndez | 2 |
| 34252 | mencionar | 2 |
| 34253 | mencionado | 2 |
| 34254 | menaje | 2 |
| 34255 | memos | 2 |
| 34256 | memorialito | 2 |
| 34257 | melosa | 2 |
| 34258 | melopea | 2 |
| 34259 | melodramáticos | 2 |
| 34260 | melódica | 2 |
| 34261 | melocotoneros | 2 |
| 34262 | melocotón | 2 |
| 34263 | mella | 2 |
| 34264 | melindrosas | 2 |
| 34265 | melibeo | 2 |
| 34266 | meléndez | 2 |
| 34267 | melancólicamente | 2 |
| 34268 | mejorarse | 2 |
| 34269 | mejorará | 2 |
| 34270 | mejorados | 2 |
| 34271 | meis | 2 |
| 34272 | mefistófeles | 2 |
| 34273 | medulas | 2 |
| 34274 | medrosica | 2 |
| 34275 | medrando | 2 |
| 34276 | medran | 2 |
| 34277 | medos | 2 |
| 34278 | mediterráneo | 2 |
| 34279 | mediterránea | 2 |
| 34280 | meditemos | 2 |
| 34281 | meditaría | 2 |
| 34282 | medioeval | 2 |
| 34283 | medió | 2 |
| 34284 | mediaron | 2 |
| 34285 | mediar | 2 |
| 34286 | medianos | 2 |
| 34287 | medianoche | 2 |
| 34288 | medianías | 2 |
| 34289 | medianero | 2 |
| 34290 | medelín | 2 |
| 34291 | mecía | 2 |
| 34292 | mechas | 2 |
| 34293 | mechada | 2 |
| 34294 | mecedoras | 2 |
| 34295 | meajas | 2 |
| 34296 | mazorcas | 2 |
| 34297 | mazmorras | 2 |
| 34298 | maya | 2 |
| 34299 | máximas | 2 |
| 34300 | mausoleos | 2 |
| 34301 | maulas | 2 |
| 34302 | matutinos | 2 |
| 34303 | matutinas | 2 |
| 34304 | matusalén | 2 |
| 34305 | matritenses | 2 |
| 34306 | matrícula | 2 |
| 34307 | matizar | 2 |
| 34308 | matizado | 2 |
| 34309 | matiza | 2 |
| 34310 | materialistas | 2 |
| 34311 | matemos | 2 |
| 34312 | matemáticos | 2 |
| 34313 | maté | 2 |
| 34314 | matava | 2 |
| 34315 | mataronle | 2 |
| 34316 | matarles | 2 |
| 34317 | matanzas | 2 |
| 34318 | mátanse | 2 |
| 34319 | matame | 2 |
| 34320 | mátale | 2 |
| 34321 | matadora | 2 |
| 34322 | matad | 2 |
| 34323 | matacanes | 2 |
| 34324 | mastín | 2 |
| 34325 | masticación | 2 |
| 34326 | masteleros | 2 |
| 34327 | maste | 2 |
| 34328 | massa | 2 |
| 34329 | masónica | 2 |
| 34330 | masillero | 2 |
| 34331 | masculina | 2 |
| 34332 | mascó | 2 |
| 34333 | mascarillas | 2 |
| 34334 | mascaba | 2 |
| 34335 | martirizarle | 2 |
| 34336 | martirizada | 2 |
| 34337 | martirizaba | 2 |
| 34338 | martelo | 2 |
| 34339 | martas | 2 |
| 34340 | marrullero | 2 |
| 34341 | marrullera | 2 |
| 34342 | marrón | 2 |
| 34343 | marrasquino | 2 |
| 34344 | marquilla | 2 |
| 34345 | maroto | 2 |
| 34346 | maroma | 2 |
| 34347 | marmotona | 2 |
| 34348 | marlota | 2 |
| 34349 | marítimas | 2 |
| 34350 | mariscos | 2 |
| 34351 | mariposita | 2 |
| 34352 | marimachos | 2 |
| 34353 | maridillo | 2 |
| 34354 | maridada | 2 |
| 34355 | margaritas | 2 |
| 34356 | mareos | 2 |
| 34357 | marejada | 2 |
| 34358 | marearle | 2 |
| 34359 | mareados | 2 |
| 34360 | mareaban | 2 |
| 34361 | mare | 2 |
| 34362 | marciales | 2 |
| 34363 | marchóse | 2 |
| 34364 | marchitas | 2 |
| 34365 | marchitan | 2 |
| 34366 | marchase | 2 |
| 34367 | marcharnos | 2 |
| 34368 | marcar | 2 |
| 34369 | marcan | 2 |
| 34370 | marcados | 2 |
| 34371 | marcaban | 2 |
| 34372 | maravillosos | 2 |
| 34373 | maravillase | 2 |
| 34374 | maravillar | 2 |
| 34375 | maravillada | 2 |
| 34376 | maravillaban | 2 |
| 34377 | marauillosa | 2 |
| 34378 | marauillar | 2 |
| 34379 | marandro | 2 |
| 34380 | maragatos | 2 |
| 34381 | maquinaciones | 2 |
| 34382 | maquiavelo | 2 |
| 34383 | maquiavélico | 2 |
| 34384 | mañosos | 2 |
| 34385 | mañero | 2 |
| 34386 | manuscrito | 2 |
| 34387 | manuales | 2 |
| 34388 | mantuve | 2 |
| 34389 | mantos | 2 |
| 34390 | mantita | 2 |
| 34391 | mantequillas | 2 |
| 34392 | mantengo | 2 |
| 34393 | mantengas | 2 |
| 34394 | manténgaos | 2 |
| 34395 | mantenerle | 2 |
| 34396 | mantenerla | 2 |
| 34397 | mantenedor | 2 |
| 34398 | mantelería | 2 |
| 34399 | mantecadas | 2 |
| 34400 | mantearon | 2 |
| 34401 | manteamientos | 2 |
| 34402 | manteadores | 2 |
| 34403 | mansyllas | 2 |
| 34404 | manssa | 2 |
| 34405 | manriques | 2 |
| 34406 | manrique | 2 |
| 34407 | manquedad | 2 |
| 34408 | manque | 2 |
| 34409 | manotazos | 2 |
| 34410 | manosee | 2 |
| 34411 | manolé | 2 |
| 34412 | manola | 2 |
| 34413 | manjavacas | 2 |
| 34414 | manisch | 2 |
| 34415 | maniqueos | 2 |
| 34416 | maniobrar | 2 |
| 34417 | manillas | 2 |
| 34418 | manilla | 2 |
| 34419 | manifieste | 2 |
| 34420 | manifiestamente | 2 |
| 34421 | manifestauan | 2 |
| 34422 | manifestase | 2 |
| 34423 | manifestaron | 2 |
| 34424 | manifestarlas | 2 |
| 34425 | manifestara | 2 |
| 34426 | manifestamos | 2 |
| 34427 | manifestaban | 2 |
| 34428 | manida | 2 |
| 34429 | maniáticas | 2 |
| 34430 | maníaco | 2 |
| 34431 | manguitos | 2 |
| 34432 | mangoneo | 2 |
| 34433 | manejos | 2 |
| 34434 | manejan | 2 |
| 34435 | manecita | 2 |
| 34436 | mane | 2 |
| 34437 | mandos | 2 |
| 34438 | mandóles | 2 |
| 34439 | mándoles | 2 |
| 34440 | mandoles | 2 |
| 34441 | mandole | 2 |
| 34442 | mandól | 2 |
| 34443 | mandilona | 2 |
| 34444 | mandéle | 2 |
| 34445 | mandásemos | 2 |
| 34446 | mandarles | 2 |
| 34447 | mandarín | 2 |
| 34448 | mandaran | 2 |
| 34449 | mándalos | 2 |
| 34450 | mandad | 2 |
| 34451 | manchegos | 2 |
| 34452 | manche | 2 |
| 34453 | máncharras | 2 |
| 34454 | mançebya | 2 |
| 34455 | mançanas | 2 |
| 34456 | manar | 2 |
| 34457 | mamona | 2 |
| 34458 | mamón | 2 |
| 34459 | mamí | 2 |
| 34460 | mameluco | 2 |
| 34461 | mamando | 2 |
| 34462 | mamado | 2 |
| 34463 | malvas | 2 |
| 34464 | maluada | 2 |
| 34465 | maltratase | 2 |
| 34466 | maltratas | 2 |
| 34467 | maltratarme | 2 |
| 34468 | maltratadas | 2 |
| 34469 | maltrataba | 2 |
| 34470 | malsanos | 2 |
| 34471 | malsabyda | 2 |
| 34472 | malquisto | 2 |
| 34473 | malquerençia | 2 |
| 34474 | malparada | 2 |
| 34475 | malorum | 2 |
| 34476 | malograse | 2 |
| 34477 | malogrado | 2 |
| 34478 | malintencionado | 2 |
| 34479 | malilla | 2 |
| 34480 | malheficios | 2 |
| 34481 | malhadado | 2 |
| 34482 | malfetría | 2 |
| 34483 | malévolo | 2 |
| 34484 | malévolas | 2 |
| 34485 | maletilla | 2 |
| 34486 | malencónico | 2 |
| 34487 | malenconía | 2 |
| 34488 | malencolía | 2 |
| 34489 | maléfica | 2 |
| 34490 | maldonado | 2 |
| 34491 | maldonadas | 2 |
| 34492 | maldizen | 2 |
| 34493 | maldijo | 2 |
| 34494 | maldigo | 2 |
| 34495 | maldicion | 2 |
| 34496 | maldecidos | 2 |
| 34497 | maldecida | 2 |
| 34498 | malaventurados | 2 |
| 34499 | malauenturado | 2 |
| 34500 | malapresas | 2 |
| 34501 | malandanzas | 2 |
| 34502 | majestades | 2 |
| 34503 | majar | 2 |
| 34504 | majalahonda | 2 |
| 34505 | majagranzas | 2 |
| 34506 | maizales | 2 |
| 34507 | maitines | 2 |
| 34508 | maitia | 2 |
| 34509 | mais | 2 |
| 34510 | magullaba | 2 |
| 34511 | magon | 2 |
| 34512 | magnitudes | 2 |
| 34513 | magnetismo | 2 |
| 34514 | magnética | 2 |
| 34515 | magnánimos | 2 |
| 34516 | magnanimidad | 2 |
| 34517 | magnánima | 2 |
| 34518 | mágicas | 2 |
| 34519 | magestat | 2 |
| 34520 | magera | 2 |
| 34521 | maeso | 2 |
| 34522 | maduros | 2 |
| 34523 | madure | 2 |
| 34524 | madrugue | 2 |
| 34525 | madrugo | 2 |
| 34526 | madrugaron | 2 |
| 34527 | madrugamos | 2 |
| 34528 | madrileñas | 2 |
| 34529 | madrileña | 2 |
| 34530 | madrigueras | 2 |
| 34531 | madreselvas | 2 |
| 34532 | madapolanes | 2 |
| 34533 | maços | 2 |
| 34534 | maço | 2 |
| 34535 | macizos | 2 |
| 34536 | macizas | 2 |
| 34537 | maciza | 2 |
| 34538 | macilentos | 2 |
| 34539 | macias | 2 |
| 34540 | machuelo | 2 |
| 34541 | machuca | 2 |
| 34542 | machacones | 2 |
| 34543 | machacona | 2 |
| 34544 | machacan | 2 |
| 34545 | macha | 2 |
| 34546 | macedonia | 2 |
| 34547 | macana | 2 |
| 34548 | maçada | 2 |
| 34549 | macabeos | 2 |
| 34550 | lyviano | 2 |
| 34551 | lysa | 2 |
| 34552 | lynage | 2 |
| 34553 | lyebre | 2 |
| 34554 | lybro | 2 |
| 34555 | lxviii | 2 |
| 34556 | lxii | 2 |
| 34557 | luzbel | 2 |
| 34558 | lutero | 2 |
| 34559 | luterano | 2 |
| 34560 | lutera | 2 |
| 34561 | lustro | 2 |
| 34562 | luneta | 2 |
| 34563 | lune | 2 |
| 34564 | lunbre | 2 |
| 34565 | lunática | 2 |
| 34566 | lujosas | 2 |
| 34567 | lujos | 2 |
| 34568 | luján | 2 |
| 34569 | lúgubremente | 2 |
| 34570 | lugarnoble | 2 |
| 34571 | lugareños | 2 |
| 34572 | lugarcito | 2 |
| 34573 | ludovico | 2 |
| 34574 | lucrecio | 2 |
| 34575 | lucrativa | 2 |
| 34576 | lucrando | 2 |
| 34577 | lucios | 2 |
| 34578 | lucio | 2 |
| 34579 | lucinda | 2 |
| 34580 | luciera | 2 |
| 34581 | lucí | 2 |
| 34582 | luché | 2 |
| 34583 | luchadores | 2 |
| 34584 | luchador | 2 |
| 34585 | luchado | 2 |
| 34586 | luceros | 2 |
| 34587 | lucerna | 2 |
| 34588 | lúbricos | 2 |
| 34589 | lozanías | 2 |
| 34590 | lotes | 2 |
| 34591 | lotérica | 2 |
| 34592 | loterías | 2 |
| 34593 | lote | 2 |
| 34594 | loros | 2 |
| 34595 | lorenzana | 2 |
| 34596 | loquinaria | 2 |
| 34597 | loquillas | 2 |
| 34598 | lontananzas | 2 |
| 34599 | longura | 2 |
| 34600 | longincuos | 2 |
| 34601 | longevidad | 2 |
| 34602 | longanizas | 2 |
| 34603 | lonas | 2 |
| 34604 | logro | 2 |
| 34605 | logre | 2 |
| 34606 | lograría | 2 |
| 34607 | logrando | 2 |
| 34608 | lograda | 2 |
| 34609 | lógicamente | 2 |
| 34610 | logares | 2 |
| 34611 | locutorios | 2 |
| 34612 | locuaces | 2 |
| 34613 | loçoya | 2 |
| 34614 | locomotoras | 2 |
| 34615 | locamente | 2 |
| 34616 | lobuna | 2 |
| 34617 | lobreguez | 2 |
| 34618 | lobas | 2 |
| 34619 | loan | 2 |
| 34620 | lloviznaba | 2 |
| 34621 | llovió | 2 |
| 34622 | lloviese | 2 |
| 34623 | llovidos | 2 |
| 34624 | llovería | 2 |
| 34625 | lloveré | 2 |
| 34626 | llorosas | 2 |
| 34627 | llorona | 2 |
| 34628 | lloréis | 2 |
| 34629 | llorava | 2 |
| 34630 | lloraste | 2 |
| 34631 | llorarle | 2 |
| 34632 | llorara | 2 |
| 34633 | lloramos | 2 |
| 34634 | llévelo | 2 |
| 34635 | llévaste | 2 |
| 34636 | llevárselos | 2 |
| 34637 | llevárnosle | 2 |
| 34638 | llevarlos | 2 |
| 34639 | llevándolas | 2 |
| 34640 | llévalo | 2 |
| 34641 | llevallos | 2 |
| 34642 | llevadme | 2 |
| 34643 | llevadle | 2 |
| 34644 | llevadera | 2 |
| 34645 | llevábase | 2 |
| 34646 | lleuaua | 2 |
| 34647 | lleuaronla | 2 |
| 34648 | llenero | 2 |
| 34649 | llene | 2 |
| 34650 | llenarla | 2 |
| 34651 | llenaría | 2 |
| 34652 | llenaran | 2 |
| 34653 | llenara | 2 |
| 34654 | llenándome | 2 |
| 34655 | llenábase | 2 |
| 34656 | lleguémonos | 2 |
| 34657 | llegóme | 2 |
| 34658 | llegé | 2 |
| 34659 | llegava | 2 |
| 34660 | llegásemos | 2 |
| 34661 | llegábase | 2 |
| 34662 | llaues | 2 |
| 34663 | llamóse | 2 |
| 34664 | llamóme | 2 |
| 34665 | llamola | 2 |
| 34666 | llámese | 2 |
| 34667 | llames | 2 |
| 34668 | llamémoslo | 2 |
| 34669 | llámeme | 2 |
| 34670 | llamarlo | 2 |
| 34671 | llamarlas | 2 |
| 34672 | llámanse | 2 |
| 34673 | llamándolos | 2 |
| 34674 | llamador | 2 |
| 34675 | llamadle | 2 |
| 34676 | llamabas | 2 |
| 34677 | llamábanla | 2 |
| 34678 | llamábamos | 2 |
| 34679 | lizos | 2 |
| 34680 | lizárraga | 2 |
| 34681 | livianos | 2 |
| 34682 | livia | 2 |
| 34683 | liverpool | 2 |
| 34684 | litteræ | 2 |
| 34685 | litigante | 2 |
| 34686 | literatas | 2 |
| 34687 | lite | 2 |
| 34688 | litado | 2 |
| 34689 | listón | 2 |
| 34690 | listado | 2 |
| 34691 | lisonjea | 2 |
| 34692 | lirón | 2 |
| 34693 | lirgandeo | 2 |
| 34694 | liquidar | 2 |
| 34695 | lipendi | 2 |
| 34696 | linsojera | 2 |
| 34697 | linpio | 2 |
| 34698 | lindísimos | 2 |
| 34699 | lindísima | 2 |
| 34700 | linajudos | 2 |
| 34701 | linajudo | 2 |
| 34702 | linajuda | 2 |
| 34703 | limpísima | 2 |
| 34704 | limpióse | 2 |
| 34705 | limpión | 2 |
| 34706 | limpie | 2 |
| 34707 | limpiasen | 2 |
| 34708 | limpiase | 2 |
| 34709 | limpiárselos | 2 |
| 34710 | limpiaron | 2 |
| 34711 | limpiarme | 2 |
| 34712 | limpiarlos | 2 |
| 34713 | limpiarlas | 2 |
| 34714 | limpiara | 2 |
| 34715 | limpiad | 2 |
| 34716 | limpiaban | 2 |
| 34717 | limosnita | 2 |
| 34718 | limones | 2 |
| 34719 | limitaré | 2 |
| 34720 | limitaban | 2 |
| 34721 | limitaba | 2 |
| 34722 | lililíes | 2 |
| 34723 | lilas | 2 |
| 34724 | lii | 2 |
| 34725 | ligorio | 2 |
| 34726 | ligerezas | 2 |
| 34727 | ligaduras | 2 |
| 34728 | ligados | 2 |
| 34729 | ligado | 2 |
| 34730 | ligaba | 2 |
| 34731 | liévastelo | 2 |
| 34732 | liendres | 2 |
| 34733 | lié | 2 |
| 34734 | liciones | 2 |
| 34735 | licenciados | 2 |
| 34736 | licas | 2 |
| 34737 | libritos | 2 |
| 34738 | librito | 2 |
| 34739 | librete | 2 |
| 34740 | libreros | 2 |
| 34741 | librerías | 2 |
| 34742 | libré | 2 |
| 34743 | librasen | 2 |
| 34744 | librarla | 2 |
| 34745 | librados | 2 |
| 34746 | libraba | 2 |
| 34747 | líbico | 2 |
| 34748 | liberaremos | 2 |
| 34749 | liberar | 2 |
| 34750 | liberalotes | 2 |
| 34751 | liberalote | 2 |
| 34752 | liberalidades | 2 |
| 34753 | liba | 2 |
| 34754 | liar | 2 |
| 34755 | lía | 2 |
| 34756 | leznas | 2 |
| 34757 | leyva | 2 |
| 34758 | leyentes | 2 |
| 34759 | leyéndolas | 2 |
| 34760 | leyéndola | 2 |
| 34761 | leyendas | 2 |
| 34762 | leydas | 2 |
| 34763 | lexias | 2 |
| 34764 | lexia | 2 |
| 34765 | levóme | 2 |
| 34766 | levólos | 2 |
| 34767 | levóla | 2 |
| 34768 | levitín | 2 |
| 34769 | levítico | 2 |
| 34770 | levantéle | 2 |
| 34771 | levantarles | 2 |
| 34772 | levantándolo | 2 |
| 34773 | levantándole | 2 |
| 34774 | levantándola | 2 |
| 34775 | levantámonos | 2 |
| 34776 | levantador | 2 |
| 34777 | levantad | 2 |
| 34778 | levantábase | 2 |
| 34779 | levadas | 2 |
| 34780 | leuanta | 2 |
| 34781 | letuario | 2 |
| 34782 | letu | 2 |
| 34783 | lettres | 2 |
| 34784 | letrina | 2 |
| 34785 | letradillo | 2 |
| 34786 | leteo | 2 |
| 34787 | lesna | 2 |
| 34788 | lesión | 2 |
| 34789 | lesaca | 2 |
| 34790 | leopardo | 2 |
| 34791 | leoncitos | 2 |
| 34792 | leoncillo | 2 |
| 34793 | lentos | 2 |
| 34794 | lentejuelas | 2 |
| 34795 | lengüeta | 2 |
| 34796 | lenguaza | 2 |
| 34797 | lenguaraz | 2 |
| 34798 | legumbres | 2 |
| 34799 | lego | 2 |
| 34800 | legitimistas | 2 |
| 34801 | legisladores | 2 |
| 34802 | legalmente | 2 |
| 34803 | legado | 2 |
| 34804 | legación | 2 |
| 34805 | leerse | 2 |
| 34806 | leerlos | 2 |
| 34807 | leerlas | 2 |
| 34808 | leeré | 2 |
| 34809 | leerás | 2 |
| 34810 | leeldo | 2 |
| 34811 | ledo | 2 |
| 34812 | ledanía | 2 |
| 34813 | lectoras | 2 |
| 34814 | lectora | 2 |
| 34815 | lechuzas | 2 |
| 34816 | lechuza | 2 |
| 34817 | lechugas | 2 |
| 34818 | lebrun | 2 |
| 34819 | lear | 2 |
| 34820 | leamos | 2 |
| 34821 | lealtat | 2 |
| 34822 | lazerio | 2 |
| 34823 | lavatorios | 2 |
| 34824 | lavas | 2 |
| 34825 | lavarme | 2 |
| 34826 | lavaderos | 2 |
| 34827 | lavadero | 2 |
| 34828 | lavada | 2 |
| 34829 | lauro | 2 |
| 34830 | laurent | 2 |
| 34831 | laúdes | 2 |
| 34832 | laud | 2 |
| 34833 | latrocinio | 2 |
| 34834 | latorre | 2 |
| 34835 | latitud | 2 |
| 34836 | latinas | 2 |
| 34837 | latigazo | 2 |
| 34838 | latente | 2 |
| 34839 | latamente | 2 |
| 34840 | lastimera | 2 |
| 34841 | lastiman | 2 |
| 34842 | lastimaban | 2 |
| 34843 | lastimaba | 2 |
| 34844 | lasrados | 2 |
| 34845 | lasos | 2 |
| 34846 | lasciuos | 2 |
| 34847 | lasa | 2 |
| 34848 | larrau | 2 |
| 34849 | larguísimas | 2 |
| 34850 | largueza | 2 |
| 34851 | largó | 2 |
| 34852 | largado | 2 |
| 34853 | lardo | 2 |
| 34854 | lápidas | 2 |
| 34855 | lanzarme | 2 |
| 34856 | lanudo | 2 |
| 34857 | lanternas | 2 |
| 34858 | lanterna | 2 |
| 34859 | lantejas | 2 |
| 34860 | lanillas | 2 |
| 34861 | lánguidos | 2 |
| 34862 | lánguida | 2 |
| 34863 | lançó | 2 |
| 34864 | lanciego | 2 |
| 34865 | lampiñas | 2 |
| 34866 | lamiendo | 2 |
| 34867 | lamían | 2 |
| 34868 | lamía | 2 |
| 34869 | lamentando | 2 |
| 34870 | lamentaban | 2 |
| 34871 | laissez | 2 |
| 34872 | lagrimones | 2 |
| 34873 | lagarta | 2 |
| 34874 | ladre | 2 |
| 34875 | ladradores | 2 |
| 34876 | laços | 2 |
| 34877 | lacónico | 2 |
| 34878 | laço | 2 |
| 34879 | lacedemonios | 2 |
| 34880 | labró | 2 |
| 34881 | labrios | 2 |
| 34882 | labranzas | 2 |
| 34883 | labrandera | 2 |
| 34884 | laborioso | 2 |
| 34885 | laberíntico | 2 |
| 34886 | king | 2 |
| 34887 | juzgarse | 2 |
| 34888 | juzgarme | 2 |
| 34889 | juzgarlo | 2 |
| 34890 | juzgarle | 2 |
| 34891 | juzgará | 2 |
| 34892 | juzgara | 2 |
| 34893 | juzgad | 2 |
| 34894 | juxta | 2 |
| 34895 | juvenal | 2 |
| 34896 | justillo | 2 |
| 34897 | justificar | 2 |
| 34898 | justiciada | 2 |
| 34899 | jusga | 2 |
| 34900 | jurisperito | 2 |
| 34901 | jurisconsultos | 2 |
| 34902 | juras | 2 |
| 34903 | juran | 2 |
| 34904 | juramos | 2 |
| 34905 | júramelo | 2 |
| 34906 | jurados | 2 |
| 34907 | jurábamos | 2 |
| 34908 | junturas | 2 |
| 34909 | juntitos | 2 |
| 34910 | juntase | 2 |
| 34911 | juntados | 2 |
| 34912 | juntadas | 2 |
| 34913 | juno | 2 |
| 34914 | junde | 2 |
| 34915 | junda | 2 |
| 34916 | jumo | 2 |
| 34917 | jumentiles | 2 |
| 34918 | jumá | 2 |
| 34919 | julepe | 2 |
| 34920 | juimos | 2 |
| 34921 | juiciosas | 2 |
| 34922 | jüicio | 2 |
| 34923 | juguetona | 2 |
| 34924 | juglaria | 2 |
| 34925 | jugarle | 2 |
| 34926 | jugaría | 2 |
| 34927 | jugaremos | 2 |
| 34928 | jugara | 2 |
| 34929 | jugadas | 2 |
| 34930 | jugábamos | 2 |
| 34931 | juegas | 2 |
| 34932 | judiós | 2 |
| 34933 | judiciario | 2 |
| 34934 | judgaron | 2 |
| 34935 | judgando | 2 |
| 34936 | judaísmo | 2 |
| 34937 | jubiló | 2 |
| 34938 | jubilada | 2 |
| 34939 | joventud | 2 |
| 34940 | jovencito | 2 |
| 34941 | jovellanos | 2 |
| 34942 | jove | 2 |
| 34943 | jorobas | 2 |
| 34944 | jorobar | 2 |
| 34945 | jorobado | 2 |
| 34946 | jorobada | 2 |
| 34947 | joroba | 2 |
| 34948 | jograría | 2 |
| 34949 | joglares | 2 |
| 34950 | jodíos | 2 |
| 34951 | jironado | 2 |
| 34952 | jiménez | 2 |
| 34953 | jícara | 2 |
| 34954 | jhesúxristo | 2 |
| 34955 | jhesú | 2 |
| 34956 | jhesu | 2 |
| 34957 | jesuitismo | 2 |
| 34958 | jerusalem | 2 |
| 34959 | jeroglífico | 2 |
| 34960 | jericó | 2 |
| 34961 | jergones | 2 |
| 34962 | jerezano | 2 |
| 34963 | jeremías | 2 |
| 34964 | javiera | 2 |
| 34965 | javier | 2 |
| 34966 | jaunchos | 2 |
| 34967 | jaspeados | 2 |
| 34968 | jarrones | 2 |
| 34969 | jarrillo | 2 |
| 34970 | jarrazo | 2 |
| 34971 | jardineros | 2 |
| 34972 | jardineras | 2 |
| 34973 | jarcia | 2 |
| 34974 | jarabes | 2 |
| 34975 | jara | 2 |
| 34976 | jáquimas | 2 |
| 34977 | jaquet | 2 |
| 34978 | japoneses | 2 |
| 34979 | japonés | 2 |
| 34980 | japón | 2 |
| 34981 | jamonas | 2 |
| 34982 | jamelgo | 2 |
| 34983 | jadeando | 2 |
| 34984 | jactose | 2 |
| 34985 | jactándose | 2 |
| 34986 | jactancioso | 2 |
| 34987 | jactábase | 2 |
| 34988 | jacos | 2 |
| 34989 | jacob | 2 |
| 34990 | jaciendo | 2 |
| 34991 | jabonaduras | 2 |
| 34992 | jabonadura | 2 |
| 34993 | itinerario | 2 |
| 34994 | italias | 2 |
| 34995 | israelita | 2 |
| 34996 | isquiña | 2 |
| 34997 | ispania | 2 |
| 34998 | isopo | 2 |
| 34999 | islote | 2 |
| 35000 | írsele | 2 |
| 35001 | irritó | 2 |
| 35002 | irritase | 2 |
| 35003 | irritarse | 2 |
| 35004 | irritara | 2 |
| 35005 | irritados | 2 |
| 35006 | irritábase | 2 |
| 35007 | irrespetuosa | 2 |
| 35008 | irresistibles | 2 |
| 35009 | irreprochables | 2 |
| 35010 | irremisiblemente | 2 |
| 35011 | irremediables | 2 |
| 35012 | irremediable | 2 |
| 35013 | irregularmente | 2 |
| 35014 | irregularidad | 2 |
| 35015 | irreflexiva | 2 |
| 35016 | irreductible | 2 |
| 35017 | irrecusables | 2 |
| 35018 | irrecusable | 2 |
| 35019 | irreconciliable | 2 |
| 35020 | irradiación | 2 |
| 35021 | irradiaba | 2 |
| 35022 | ironías | 2 |
| 35023 | irlos | 2 |
| 35024 | irlandeses | 2 |
| 35025 | irisados | 2 |
| 35026 | iriartea | 2 |
| 35027 | iria | 2 |
| 35028 | irguiéndose | 2 |
| 35029 | irascible | 2 |
| 35030 | invulnerable | 2 |
| 35031 | involuntario | 2 |
| 35032 | involucremos | 2 |
| 35033 | involucrar | 2 |
| 35034 | invocó | 2 |
| 35035 | invocar | 2 |
| 35036 | invocan | 2 |
| 35037 | invocaciones | 2 |
| 35038 | invite | 2 |
| 35039 | invitar | 2 |
| 35040 | invitando | 2 |
| 35041 | invita | 2 |
| 35042 | inviernos | 2 |
| 35043 | invidiosas | 2 |
| 35044 | invidiada | 2 |
| 35045 | invictísimo | 2 |
| 35046 | inviar | 2 |
| 35047 | investigó | 2 |
| 35048 | inventora | 2 |
| 35049 | inventiva | 2 |
| 35050 | invente | 2 |
| 35051 | invasor | 2 |
| 35052 | inválidas | 2 |
| 35053 | invadiendo | 2 |
| 35054 | invadían | 2 |
| 35055 | inusitadas | 2 |
| 35056 | inusitada | 2 |
| 35057 | inundaron | 2 |
| 35058 | inundado | 2 |
| 35059 | inuidia | 2 |
| 35060 | inuentar | 2 |
| 35061 | inuencion | 2 |
| 35062 | intruso | 2 |
| 35063 | introibo | 2 |
| 35064 | introdujese | 2 |
| 35065 | introducirme | 2 |
| 35066 | introducirlo | 2 |
| 35067 | introducidos | 2 |
| 35068 | introducen | 2 |
| 35069 | introduce | 2 |
| 35070 | intrincados | 2 |
| 35071 | intrigante | 2 |
| 35072 | intricadas | 2 |
| 35073 | intricada | 2 |
| 35074 | intrépidamente | 2 |
| 35075 | intransigencia | 2 |
| 35076 | intonso | 2 |
| 35077 | intolerancia | 2 |
| 35078 | intitulada | 2 |
| 35079 | intimo | 2 |
| 35080 | intervengo | 2 |
| 35081 | intersticios | 2 |
| 35082 | interrumpir | 2 |
| 35083 | interrumpiera | 2 |
| 35084 | interrumpiendo | 2 |
| 35085 | interrumpidas | 2 |
| 35086 | interrumpí | 2 |
| 35087 | interrumpe | 2 |
| 35088 | interrumpáis | 2 |
| 35089 | interromper | 2 |
| 35090 | interrogar | 2 |
| 35091 | interrogaciones | 2 |
| 35092 | interpuesto | 2 |
| 35093 | interpretado | 2 |
| 35094 | interpretaciones | 2 |
| 35095 | interpretaba | 2 |
| 35096 | internándose | 2 |
| 35097 | intermitente | 2 |
| 35098 | intermisión | 2 |
| 35099 | intermediario | 2 |
| 35100 | interjecciones | 2 |
| 35101 | interina | 2 |
| 35102 | interesara | 2 |
| 35103 | interesan | 2 |
| 35104 | interceptaban | 2 |
| 35105 | inter | 2 |
| 35106 | intentona | 2 |
| 35107 | intentase | 2 |
| 35108 | intentas | 2 |
| 35109 | intentarlas | 2 |
| 35110 | intentaría | 2 |
| 35111 | intentaremos | 2 |
| 35112 | intensas | 2 |
| 35113 | intensamente | 2 |
| 35114 | intencionados | 2 |
| 35115 | intencionadas | 2 |
| 35116 | intencion | 2 |
| 35117 | intempestivo | 2 |
| 35118 | intellectu | 2 |
| 35119 | intelectualmente | 2 |
| 35120 | intactas | 2 |
| 35121 | insustanciales | 2 |
| 35122 | insurrección | 2 |
| 35123 | insultó | 2 |
| 35124 | insulta | 2 |
| 35125 | insulso | 2 |
| 35126 | insulsa | 2 |
| 35127 | insuficiente | 2 |
| 35128 | insubordinación | 2 |
| 35129 | instructivo | 2 |
| 35130 | instruam | 2 |
| 35131 | instigado | 2 |
| 35132 | instaron | 2 |
| 35133 | instantáneo | 2 |
| 35134 | instantáneamente | 2 |
| 35135 | instalarse | 2 |
| 35136 | instaláronse | 2 |
| 35137 | instalados | 2 |
| 35138 | instalada | 2 |
| 35139 | instado | 2 |
| 35140 | instable | 2 |
| 35141 | instabilidad | 2 |
| 35142 | inspiró | 2 |
| 35143 | inspirarse | 2 |
| 35144 | inspirar | 2 |
| 35145 | inspirados | 2 |
| 35146 | inspiradas | 2 |
| 35147 | inspiraciones | 2 |
| 35148 | inspirábale | 2 |
| 35149 | inspector | 2 |
| 35150 | insociable | 2 |
| 35151 | insistido | 2 |
| 35152 | insistían | 2 |
| 35153 | insisten | 2 |
| 35154 | insiste | 2 |
| 35155 | insípidos | 2 |
| 35156 | insípida | 2 |
| 35157 | insinuarle | 2 |
| 35158 | insinuantes | 2 |
| 35159 | insinuación | 2 |
| 35160 | insinuaba | 2 |
| 35161 | inservibles | 2 |
| 35162 | inservible | 2 |
| 35163 | inseparables | 2 |
| 35164 | insensatos | 2 |
| 35165 | insensatez | 2 |
| 35166 | inseguridad | 2 |
| 35167 | inseguras | 2 |
| 35168 | inreparable | 2 |
| 35169 | inquisidores | 2 |
| 35170 | inquilinas | 2 |
| 35171 | inquietísima | 2 |
| 35172 | inquerir | 2 |
| 35173 | inorme | 2 |
| 35174 | inoportunidad | 2 |
| 35175 | inopinado | 2 |
| 35176 | inocentadas | 2 |
| 35177 | inobedientes | 2 |
| 35178 | inobediencia | 2 |
| 35179 | innumerable | 2 |
| 35180 | innovador | 2 |
| 35181 | innobles | 2 |
| 35182 | inmunda | 2 |
| 35183 | inmovilidad | 2 |
| 35184 | inmoralidad | 2 |
| 35185 | inmensamente | 2 |
| 35186 | injustas | 2 |
| 35187 | injuriar | 2 |
| 35188 | injuriado | 2 |
| 35189 | injertar | 2 |
| 35190 | ininteligibles | 2 |
| 35191 | ininteligible | 2 |
| 35192 | inimitable | 2 |
| 35193 | iniciativas | 2 |
| 35194 | iniciado | 2 |
| 35195 | iniciación | 2 |
| 35196 | inhumana | 2 |
| 35197 | inhabitables | 2 |
| 35198 | ingresos | 2 |
| 35199 | ingresa | 2 |
| 35200 | ingredientes | 2 |
| 35201 | ingratas | 2 |
| 35202 | ingénito | 2 |
| 35203 | ingénita | 2 |
| 35204 | ingenïoso | 2 |
| 35205 | ingenïosa | 2 |
| 35206 | infundirle | 2 |
| 35207 | infundiéndole | 2 |
| 35208 | infructuosa | 2 |
| 35209 | infranqueable | 2 |
| 35210 | infortunada | 2 |
| 35211 | informó | 2 |
| 35212 | informase | 2 |
| 35213 | informaros | 2 |
| 35214 | informaba | 2 |
| 35215 | influyó | 2 |
| 35216 | influyentes | 2 |
| 35217 | influyente | 2 |
| 35218 | influyendo | 2 |
| 35219 | inflo | 2 |
| 35220 | inflado | 2 |
| 35221 | infinitivo | 2 |
| 35222 | ínfimos | 2 |
| 35223 | ínfimo | 2 |
| 35224 | ínfimas | 2 |
| 35225 | infiltraba | 2 |
| 35226 | infiera | 2 |
| 35227 | infestados | 2 |
| 35228 | inferimos | 2 |
| 35229 | infelice | 2 |
| 35230 | infamó | 2 |
| 35231 | infamatorio | 2 |
| 35232 | infamar | 2 |
| 35233 | inexplicables | 2 |
| 35234 | inexpertas | 2 |
| 35235 | inexperta | 2 |
| 35236 | inexcusables | 2 |
| 35237 | inesperadas | 2 |
| 35238 | inertes | 2 |
| 35239 | ineptitud | 2 |
| 35240 | inepta | 2 |
| 35241 | ineficaz | 2 |
| 35242 | induziendole | 2 |
| 35243 | industriosos | 2 |
| 35244 | industrioso | 2 |
| 35245 | industriosa | 2 |
| 35246 | indultos | 2 |
| 35247 | indulto | 2 |
| 35248 | indujo | 2 |
| 35249 | indubitables | 2 |
| 35250 | indomptable | 2 |
| 35251 | indómitos | 2 |
| 35252 | indolentes | 2 |
| 35253 | individualismo | 2 |
| 35254 | indispuesta | 2 |
| 35255 | indisoluble | 2 |
| 35256 | indiscretos | 2 |
| 35257 | indisciplina | 2 |
| 35258 | indirectamente | 2 |
| 35259 | indiqué | 2 |
| 35260 | indilugencias | 2 |
| 35261 | indignes | 2 |
| 35262 | indigne | 2 |
| 35263 | indignamente | 2 |
| 35264 | indignaban | 2 |
| 35265 | indigesta | 2 |
| 35266 | indicaron | 2 |
| 35267 | indicarle | 2 |
| 35268 | indican | 2 |
| 35269 | indicada | 2 |
| 35270 | indeterminado | 2 |
| 35271 | indescriptible | 2 |
| 35272 | indemnización | 2 |
| 35273 | indelebles | 2 |
| 35274 | indefectiblemente | 2 |
| 35275 | indecorosas | 2 |
| 35276 | indecorosa | 2 |
| 35277 | indecencia | 2 |
| 35278 | indagación | 2 |
| 35279 | incurrido | 2 |
| 35280 | incurra | 2 |
| 35281 | incumbencias | 2 |
| 35282 | incrustaba | 2 |
| 35283 | increpar | 2 |
| 35284 | incrédula | 2 |
| 35285 | incorregible | 2 |
| 35286 | incorrecta | 2 |
| 35287 | inconvinientes | 2 |
| 35288 | inconveniencia | 2 |
| 35289 | inconsiderada | 2 |
| 35290 | inconmensurable | 2 |
| 35291 | incomportable | 2 |
| 35292 | incompleto | 2 |
| 35293 | incompatibles | 2 |
| 35294 | incompatible | 2 |
| 35295 | incomparables | 2 |
| 35296 | incomparablemente | 2 |
| 35297 | incómodos | 2 |
| 35298 | incomodo | 2 |
| 35299 | incomode | 2 |
| 35300 | incómodas | 2 |
| 35301 | incomodar | 2 |
| 35302 | incoherencia | 2 |
| 35303 | incógnito | 2 |
| 35304 | incogitado | 2 |
| 35305 | ínclito | 2 |
| 35306 | inclinóse | 2 |
| 35307 | incline | 2 |
| 35308 | inclinaron | 2 |
| 35309 | inclinarme | 2 |
| 35310 | inclinándome | 2 |
| 35311 | inclinan | 2 |
| 35312 | inclinados | 2 |
| 35313 | inclinadas | 2 |
| 35314 | incitar | 2 |
| 35315 | inchado | 2 |
| 35316 | incalificable | 2 |
| 35317 | incalculable | 2 |
| 35318 | inaugurar | 2 |
| 35319 | inaugural | 2 |
| 35320 | inapreciables | 2 |
| 35321 | inapetencia | 2 |
| 35322 | inamovible | 2 |
| 35323 | inadvertidos | 2 |
| 35324 | inadvertido | 2 |
| 35325 | inadvertidamente | 2 |
| 35326 | inacción | 2 |
| 35327 | inacabable | 2 |
| 35328 | impuse | 2 |
| 35329 | impura | 2 |
| 35330 | impugnar | 2 |
| 35331 | impuestas | 2 |
| 35332 | impúdica | 2 |
| 35333 | imprudencias | 2 |
| 35334 | improvisaron | 2 |
| 35335 | improvisamente | 2 |
| 35336 | improvisadas | 2 |
| 35337 | improvisación | 2 |
| 35338 | improvisaba | 2 |
| 35339 | impropiedades | 2 |
| 35340 | imprimo | 2 |
| 35341 | imprimirse | 2 |
| 35342 | imprimió | 2 |
| 35343 | imprimían | 2 |
| 35344 | imprimía | 2 |
| 35345 | imprima | 2 |
| 35346 | impression | 2 |
| 35347 | impresores | 2 |
| 35348 | impresionaron | 2 |
| 35349 | impresionar | 2 |
| 35350 | impresionado | 2 |
| 35351 | impresionada | 2 |
| 35352 | imprescindibles | 2 |
| 35353 | imprescindible | 2 |
| 35354 | impregnadas | 2 |
| 35355 | imprecaciones | 2 |
| 35356 | impotencia | 2 |
| 35357 | imposición | 2 |
| 35358 | imposibilitada | 2 |
| 35359 | imposibilita | 2 |
| 35360 | importunó | 2 |
| 35361 | importunarla | 2 |
| 35362 | importunan | 2 |
| 35363 | importunaciones | 2 |
| 35364 | importunaban | 2 |
| 35365 | importarle | 2 |
| 35366 | importara | 2 |
| 35367 | importar | 2 |
| 35368 | importantísimo | 2 |
| 35369 | importado | 2 |
| 35370 | imponiéndole | 2 |
| 35371 | imponerme | 2 |
| 35372 | imponentes | 2 |
| 35373 | impondría | 2 |
| 35374 | implorar | 2 |
| 35375 | implícitamente | 2 |
| 35376 | impido | 2 |
| 35377 | impidieron | 2 |
| 35378 | impidan | 2 |
| 35379 | impía | 2 |
| 35380 | impetuoso | 2 |
| 35381 | impetrando | 2 |
| 35382 | impericia | 2 |
| 35383 | imperiales | 2 |
| 35384 | imperfección | 2 |
| 35385 | imperecedera | 2 |
| 35386 | imperativo | 2 |
| 35387 | impensada | 2 |
| 35388 | impenetrables | 2 |
| 35389 | impelidos | 2 |
| 35390 | impedirme | 2 |
| 35391 | impediré | 2 |
| 35392 | impedidos | 2 |
| 35393 | impávido | 2 |
| 35394 | impávida | 2 |
| 35395 | imparciales | 2 |
| 35396 | immerito | 2 |
| 35397 | imito | 2 |
| 35398 | imitarlos | 2 |
| 35399 | imitarán | 2 |
| 35400 | imitara | 2 |
| 35401 | imitáis | 2 |
| 35402 | imitada | 2 |
| 35403 | imaginara | 2 |
| 35404 | ilusorios | 2 |
| 35405 | ilusorio | 2 |
| 35406 | iluminen | 2 |
| 35407 | ilumine | 2 |
| 35408 | iluminaron | 2 |
| 35409 | iluminarme | 2 |
| 35410 | iluminará | 2 |
| 35411 | iluminadas | 2 |
| 35412 | iluminaban | 2 |
| 35413 | illescas | 2 |
| 35414 | ilíada | 2 |
| 35415 | ilesa | 2 |
| 35416 | ilegibles | 2 |
| 35417 | ilegal | 2 |
| 35418 | ilcienso | 2 |
| 35419 | ihesuxristo | 2 |
| 35420 | igualé | 2 |
| 35421 | igualarían | 2 |
| 35422 | igualará | 2 |
| 35423 | igualan | 2 |
| 35424 | igreja | 2 |
| 35425 | ignoró | 2 |
| 35426 | ignoro | 2 |
| 35427 | ignores | 2 |
| 35428 | ignore | 2 |
| 35429 | ignorarlo | 2 |
| 35430 | ignoramos | 2 |
| 35431 | ignorados | 2 |
| 35432 | ignoraban | 2 |
| 35433 | íes | 2 |
| 35434 | idumeo | 2 |
| 35435 | idolillo | 2 |
| 35436 | idolatraré | 2 |
| 35437 | idiotismo | 2 |
| 35438 | idílico | 2 |
| 35439 | ideólogos | 2 |
| 35440 | ideó | 2 |
| 35441 | idéntico | 2 |
| 35442 | idéntica | 2 |
| 35443 | idear | 2 |
| 35444 | ideación | 2 |
| 35445 | ictericia | 2 |
| 35446 | ícaro | 2 |
| 35447 | ibérica | 2 |
| 35448 | iberia | 2 |
| 35449 | ibantelly | 2 |
| 35450 | huygamos | 2 |
| 35451 | huyese | 2 |
| 35452 | huyas | 2 |
| 35453 | husmear | 2 |
| 35454 | hurten | 2 |
| 35455 | hurtarle | 2 |
| 35456 | hurtando | 2 |
| 35457 | hurtado | 2 |
| 35458 | hurtada | 2 |
| 35459 | hurtaba | 2 |
| 35460 | húrgale | 2 |
| 35461 | hundirme | 2 |
| 35462 | hundirá | 2 |
| 35463 | hundiose | 2 |
| 35464 | hundiera | 2 |
| 35465 | hundían | 2 |
| 35466 | humorísticas | 2 |
| 35467 | humorística | 2 |
| 35468 | humilmente | 2 |
| 35469 | humilló | 2 |
| 35470 | humíllate | 2 |
| 35471 | humillan | 2 |
| 35472 | húmera | 2 |
| 35473 | humedeciendo | 2 |
| 35474 | humeante | 2 |
| 35475 | humazo | 2 |
| 35476 | humaredas | 2 |
| 35477 | humanitario | 2 |
| 35478 | humanista | 2 |
| 35479 | humani | 2 |
| 35480 | humanal | 2 |
| 35481 | huidos | 2 |
| 35482 | huído | 2 |
| 35483 | huí | 2 |
| 35484 | huesudo | 2 |
| 35485 | huestes | 2 |
| 35486 | hueste | 2 |
| 35487 | huéspedas | 2 |
| 35488 | huesped | 2 |
| 35489 | huesca | 2 |
| 35490 | huertecillo | 2 |
| 35491 | huerte | 2 |
| 35492 | huerfanitos | 2 |
| 35493 | huerco | 2 |
| 35494 | huelva | 2 |
| 35495 | huelo | 2 |
| 35496 | huélgome | 2 |
| 35497 | huelgas | 2 |
| 35498 | huelgan | 2 |
| 35499 | huelan | 2 |
| 35500 | huela | 2 |
| 35501 | huego | 2 |
| 35502 | huecas | 2 |
| 35503 | hubieren | 2 |
| 35504 | hubiérase | 2 |
| 35505 | hoyos | 2 |
| 35506 | hospedó | 2 |
| 35507 | hospeda | 2 |
| 35508 | horticultura | 2 |
| 35509 | hortelano | 2 |
| 35510 | horripilaba | 2 |
| 35511 | horquillas | 2 |
| 35512 | hornillo | 2 |
| 35513 | hornilla | 2 |
| 35514 | hornacinas | 2 |
| 35515 | hormiguero | 2 |
| 35516 | hordas | 2 |
| 35517 | horadados | 2 |
| 35518 | horada | 2 |
| 35519 | honrras | 2 |
| 35520 | honrarle | 2 |
| 35521 | honralle | 2 |
| 35522 | honorario | 2 |
| 35523 | hondísimas | 2 |
| 35524 | hondísima | 2 |
| 35525 | hominis | 2 |
| 35526 | homicidios | 2 |
| 35527 | homicidas | 2 |
| 35528 | hombrunas | 2 |
| 35529 | hombrón | 2 |
| 35530 | hombría | 2 |
| 35531 | hombrada | 2 |
| 35532 | hollar | 2 |
| 35533 | holguéme | 2 |
| 35534 | holgué | 2 |
| 35535 | holgue | 2 |
| 35536 | holgaua | 2 |
| 35537 | holgase | 2 |
| 35538 | holgarme | 2 |
| 35539 | holgaran | 2 |
| 35540 | holgándose | 2 |
| 35541 | holgados | 2 |
| 35542 | hocicuda | 2 |
| 35543 | hocicada | 2 |
| 35544 | hoces | 2 |
| 35545 | hobiera | 2 |
| 35546 | hiziste | 2 |
| 35547 | hiziere | 2 |
| 35548 | histrionismo | 2 |
| 35549 | histerismo | 2 |
| 35550 | hispanos | 2 |
| 35551 | hispano | 2 |
| 35552 | hisopos | 2 |
| 35553 | hisopo | 2 |
| 35554 | hirieron | 2 |
| 35555 | hipóstasis | 2 |
| 35556 | hiponax | 2 |
| 35557 | hipogrifo | 2 |
| 35558 | hiperbólicos | 2 |
| 35559 | hiperbólico | 2 |
| 35560 | hiperbólicas | 2 |
| 35561 | hinojales | 2 |
| 35562 | hinchadas | 2 |
| 35563 | hincarse | 2 |
| 35564 | hincándose | 2 |
| 35565 | hincado | 2 |
| 35566 | hincaba | 2 |
| 35567 | hinca | 2 |
| 35568 | hile | 2 |
| 35569 | hilan | 2 |
| 35570 | hilachas | 2 |
| 35571 | hijastra | 2 |
| 35572 | higuera | 2 |
| 35573 | higienista | 2 |
| 35574 | higas | 2 |
| 35575 | hieres | 2 |
| 35576 | hierático | 2 |
| 35577 | hierática | 2 |
| 35578 | hieran | 2 |
| 35579 | hiedra | 2 |
| 35580 | hicistes | 2 |
| 35581 | hiciéronnos | 2 |
| 35582 | hicieres | 2 |
| 35583 | hicieren | 2 |
| 35584 | hiciérades | 2 |
| 35585 | heziste | 2 |
| 35586 | hevos | 2 |
| 35587 | heterogéneos | 2 |
| 35588 | heterogeneidad | 2 |
| 35589 | heterogénea | 2 |
| 35590 | hervir | 2 |
| 35591 | herrerías | 2 |
| 35592 | herrados | 2 |
| 35593 | herradores | 2 |
| 35594 | herós | 2 |
| 35595 | heroísmos | 2 |
| 35596 | hero | 2 |
| 35597 | hermosota | 2 |
| 35598 | hermosísimos | 2 |
| 35599 | hermoseado | 2 |
| 35600 | hermosamente | 2 |
| 35601 | hermanito | 2 |
| 35602 | herirnos | 2 |
| 35603 | herirme | 2 |
| 35604 | herirle | 2 |
| 35605 | herías | 2 |
| 35606 | herían | 2 |
| 35607 | herencias | 2 |
| 35608 | heredo | 2 |
| 35609 | herederas | 2 |
| 35610 | herede | 2 |
| 35611 | heredara | 2 |
| 35612 | heredáis | 2 |
| 35613 | hercúleos | 2 |
| 35614 | herbolario | 2 |
| 35615 | herbario | 2 |
| 35616 | hendido | 2 |
| 35617 | hendida | 2 |
| 35618 | hender | 2 |
| 35619 | henchido | 2 |
| 35620 | hémosle | 2 |
| 35621 | heme | 2 |
| 35622 | hemanuel | 2 |
| 35623 | helos | 2 |
| 35624 | heló | 2 |
| 35625 | helo | 2 |
| 35626 | helas | 2 |
| 35627 | hela | 2 |
| 35628 | hediondo | 2 |
| 35629 | heda | 2 |
| 35630 | hechizado | 2 |
| 35631 | hechiceras | 2 |
| 35632 | hebdomadario | 2 |
| 35633 | hazialo | 2 |
| 35634 | havas | 2 |
| 35635 | hava | 2 |
| 35636 | haurias | 2 |
| 35637 | haure | 2 |
| 35638 | hauiendo | 2 |
| 35639 | hauiamos | 2 |
| 35640 | hauerla | 2 |
| 35641 | hatchisschina | 2 |
| 35642 | hastiaba | 2 |
| 35643 | hartazgo | 2 |
| 35644 | hartarme | 2 |
| 35645 | hartaré | 2 |
| 35646 | hartaban | 2 |
| 35647 | harpa | 2 |
| 35648 | harmonium | 2 |
| 35649 | harias | 2 |
| 35650 | harian | 2 |
| 35651 | harele | 2 |
| 35652 | harbar | 2 |
| 35653 | haraposa | 2 |
| 35654 | harapo | 2 |
| 35655 | harapiento | 2 |
| 35656 | haraganes | 2 |
| 35657 | hanegas | 2 |
| 35658 | hamos | 2 |
| 35659 | hamlet | 2 |
| 35660 | hallose | 2 |
| 35661 | hálleme | 2 |
| 35662 | hallaua | 2 |
| 35663 | hallásemos | 2 |
| 35664 | halláronse | 2 |
| 35665 | halláronla | 2 |
| 35666 | hallarlo | 2 |
| 35667 | halláredes | 2 |
| 35668 | halláramos | 2 |
| 35669 | hallándonos | 2 |
| 35670 | hallándole | 2 |
| 35671 | halladas | 2 |
| 35672 | hallada | 2 |
| 35673 | hallabas | 2 |
| 35674 | hálito | 2 |
| 35675 | haldeando | 2 |
| 35676 | halcones | 2 |
| 35677 | halagasen | 2 |
| 35678 | halagaría | 2 |
| 35679 | halagando | 2 |
| 35680 | halagaban | 2 |
| 35681 | haigan | 2 |
| 35682 | hagote | 2 |
| 35683 | hágale | 2 |
| 35684 | hacinadas | 2 |
| 35685 | haciéndonos | 2 |
| 35686 | hacíala | 2 |
| 35687 | hache | 2 |
| 35688 | hacérselo | 2 |
| 35689 | hacérsele | 2 |
| 35690 | hacérsela | 2 |
| 35691 | haceos | 2 |
| 35692 | hacellas | 2 |
| 35693 | hacella | 2 |
| 35694 | hacedor | 2 |
| 35695 | habraba | 2 |
| 35696 | háblele | 2 |
| 35697 | habléla | 2 |
| 35698 | habléis | 2 |
| 35699 | hablauan | 2 |
| 35700 | hablaua | 2 |
| 35701 | hablaronte | 2 |
| 35702 | hablarnos | 2 |
| 35703 | hablarlo | 2 |
| 35704 | hablaríamos | 2 |
| 35705 | hablarán | 2 |
| 35706 | hâblar | 2 |
| 35707 | hablándose | 2 |
| 35708 | hablándonos | 2 |
| 35709 | hablándoles | 2 |
| 35710 | háblame | 2 |
| 35711 | hablalle | 2 |
| 35712 | hablale | 2 |
| 35713 | habladme | 2 |
| 35714 | hablad | 2 |
| 35715 | habitaron | 2 |
| 35716 | habitamos | 2 |
| 35717 | habitadores | 2 |
| 35718 | habitadoras | 2 |
| 35719 | habitado | 2 |
| 35720 | habitable | 2 |
| 35721 | hábilmente | 2 |
| 35722 | habilitado | 2 |
| 35723 | habilidoso | 2 |
| 35724 | habiéndosele | 2 |
| 35725 | habiéndolo | 2 |
| 35726 | habidos | 2 |
| 35727 | habíanse | 2 |
| 35728 | habérsele | 2 |
| 35729 | habérmelo | 2 |
| 35730 | habéisla | 2 |
| 35731 | habano | 2 |
| 35732 | habaneras | 2 |
| 35733 | gutapercha | 2 |
| 35734 | gustosamente | 2 |
| 35735 | gustes | 2 |
| 35736 | gustazo | 2 |
| 35737 | gustaron | 2 |
| 35738 | gustarme | 2 |
| 35739 | gustarle | 2 |
| 35740 | gustarán | 2 |
| 35741 | gustábale | 2 |
| 35742 | guitarreo | 2 |
| 35743 | guitarras | 2 |
| 35744 | guisotes | 2 |
| 35745 | guiso | 2 |
| 35746 | guisadas | 2 |
| 35747 | guisaban | 2 |
| 35748 | guisaba | 2 |
| 35749 | guiñar | 2 |
| 35750 | guinea | 2 |
| 35751 | guindilla | 2 |
| 35752 | guinderos | 2 |
| 35753 | guillén | 2 |
| 35754 | guillati | 2 |
| 35755 | guilla | 2 |
| 35756 | guíete | 2 |
| 35757 | guie | 2 |
| 35758 | guías | 2 |
| 35759 | guiarte | 2 |
| 35760 | guiarse | 2 |
| 35761 | guiarla | 2 |
| 35762 | guiados | 2 |
| 35763 | guiaban | 2 |
| 35764 | guerrilleros | 2 |
| 35765 | guerr | 2 |
| 35766 | güena | 2 |
| 35767 | guelte | 2 |
| 35768 | güeco | 2 |
| 35769 | guasoncita | 2 |
| 35770 | guasón | 2 |
| 35771 | guasitas | 2 |
| 35772 | guasas | 2 |
| 35773 | guarecidos | 2 |
| 35774 | guarecer | 2 |
| 35775 | guárdevos | 2 |
| 35776 | guárdense | 2 |
| 35777 | guardemos | 2 |
| 35778 | guárdelo | 2 |
| 35779 | guardarvos | 2 |
| 35780 | guardara | 2 |
| 35781 | guárdame | 2 |
| 35782 | guardamalletas | 2 |
| 35783 | guardalla | 2 |
| 35784 | guardador | 2 |
| 35785 | guardábala | 2 |
| 35786 | guapines | 2 |
| 35787 | guapetonas | 2 |
| 35788 | guadalerce | 2 |
| 35789 | grupa | 2 |
| 35790 | gruñían | 2 |
| 35791 | gruñen | 2 |
| 35792 | grumetes | 2 |
| 35793 | grullas | 2 |
| 35794 | grotescos | 2 |
| 35795 | gro | 2 |
| 35796 | grites | 2 |
| 35797 | grité | 2 |
| 35798 | gritase | 2 |
| 35799 | gritarle | 2 |
| 35800 | gritaré | 2 |
| 35801 | gritador | 2 |
| 35802 | gritado | 2 |
| 35803 | grey | 2 |
| 35804 | grebas | 2 |
| 35805 | grava | 2 |
| 35806 | grauedad | 2 |
| 35807 | gratuitos | 2 |
| 35808 | gratificación | 2 |
| 35809 | grasientos | 2 |
| 35810 | granujería | 2 |
| 35811 | granjería | 2 |
| 35812 | granjeé | 2 |
| 35813 | granjearon | 2 |
| 35814 | granjearme | 2 |
| 35815 | granjea | 2 |
| 35816 | granizos | 2 |
| 35817 | granizada | 2 |
| 35818 | grandissimo | 2 |
| 35819 | grandecitas | 2 |
| 35820 | gramáticas | 2 |
| 35821 | gramatical | 2 |
| 35822 | grajal | 2 |
| 35823 | graduó | 2 |
| 35824 | gradual | 2 |
| 35825 | gradieris | 2 |
| 35826 | gradaciones | 2 |
| 35827 | graciosísima | 2 |
| 35828 | grabar | 2 |
| 35829 | grabadas | 2 |
| 35830 | goznes | 2 |
| 35831 | gozasen | 2 |
| 35832 | gozarlo | 2 |
| 35833 | gozaría | 2 |
| 35834 | gozaremos | 2 |
| 35835 | gozarán | 2 |
| 35836 | gozaran | 2 |
| 35837 | goyri | 2 |
| 35838 | goya | 2 |
| 35839 | gotitas | 2 |
| 35840 | götinga | 2 |
| 35841 | goteando | 2 |
| 35842 | gostar | 2 |
| 35843 | goso | 2 |
| 35844 | gorros | 2 |
| 35845 | gorrita | 2 |
| 35846 | gorrero | 2 |
| 35847 | gorras | 2 |
| 35848 | gorjeo | 2 |
| 35849 | góngora | 2 |
| 35850 | gomia | 2 |
| 35851 | gomecillos | 2 |
| 35852 | golpeja | 2 |
| 35853 | golpecito | 2 |
| 35854 | golpeándose | 2 |
| 35855 | golpeaban | 2 |
| 35856 | golpeaba | 2 |
| 35857 | golpazos | 2 |
| 35858 | golossyna | 2 |
| 35859 | gollerías | 2 |
| 35860 | golía | 2 |
| 35861 | golhin | 2 |
| 35862 | goberno | 2 |
| 35863 | gobernaor | 2 |
| 35864 | gobernantes | 2 |
| 35865 | gobernante | 2 |
| 35866 | gobernando | 2 |
| 35867 | gobernada | 2 |
| 35868 | glosas | 2 |
| 35869 | glorïoso | 2 |
| 35870 | gloriosamente | 2 |
| 35871 | glorïosa | 2 |
| 35872 | glauco | 2 |
| 35873 | girones | 2 |
| 35874 | girifaltes | 2 |
| 35875 | girasol | 2 |
| 35876 | gira | 2 |
| 35877 | gineta | 2 |
| 35878 | gimieron | 2 |
| 35879 | gigantesco | 2 |
| 35880 | gigantesca | 2 |
| 35881 | giganta | 2 |
| 35882 | getafe | 2 |
| 35883 | gesticulaban | 2 |
| 35884 | gestas | 2 |
| 35885 | gestación | 2 |
| 35886 | gertrudis | 2 |
| 35887 | george | 2 |
| 35888 | geometría | 2 |
| 35889 | geológicas | 2 |
| 35890 | genyeis | 2 |
| 35891 | genui | 2 |
| 35892 | genuflexiones | 2 |
| 35893 | genta | 2 |
| 35894 | genios | 2 |
| 35895 | genieys | 2 |
| 35896 | geniecillo | 2 |
| 35897 | geniazo | 2 |
| 35898 | geniales | 2 |
| 35899 | generos | 2 |
| 35900 | generis | 2 |
| 35901 | generalife | 2 |
| 35902 | generalidades | 2 |
| 35903 | generalidad | 2 |
| 35904 | genealógico | 2 |
| 35905 | gelatinosas | 2 |
| 35906 | gazmoñería | 2 |
| 35907 | gayta | 2 |
| 35908 | gayos | 2 |
| 35909 | gavota | 2 |
| 35910 | gatuperio | 2 |
| 35911 | gatuno | 2 |
| 35912 | gastrónomo | 2 |
| 35913 | gastaua | 2 |
| 35914 | gastarse | 2 |
| 35915 | gastarlo | 2 |
| 35916 | gastarlas | 2 |
| 35917 | gastara | 2 |
| 35918 | gastador | 2 |
| 35919 | gastada | 2 |
| 35920 | gaseosa | 2 |
| 35921 | gasas | 2 |
| 35922 | gárrulos | 2 |
| 35923 | gárrulas | 2 |
| 35924 | garrucha | 2 |
| 35925 | garrapatos | 2 |
| 35926 | garrafas | 2 |
| 35927 | garrafales | 2 |
| 35928 | garnacho | 2 |
| 35929 | garfio | 2 |
| 35930 | gardoqui | 2 |
| 35931 | garçones | 2 |
| 35932 | garbín | 2 |
| 35933 | gante | 2 |
| 35934 | ganso | 2 |
| 35935 | ganosas | 2 |
| 35936 | ganita | 2 |
| 35937 | ganges | 2 |
| 35938 | gandulones | 2 |
| 35939 | gande | 2 |
| 35940 | gandalín | 2 |
| 35941 | ganarme | 2 |
| 35942 | ganarle | 2 |
| 35943 | ganarla | 2 |
| 35944 | ganaría | 2 |
| 35945 | ganaria | 2 |
| 35946 | ganare | 2 |
| 35947 | ganarás | 2 |
| 35948 | gananciosos | 2 |
| 35949 | gamos | 2 |
| 35950 | gama | 2 |
| 35951 | galopar | 2 |
| 35952 | galocha | 2 |
| 35953 | gallinero | 2 |
| 35954 | galletas | 2 |
| 35955 | gallardas | 2 |
| 35956 | galileo | 2 |
| 35957 | galdós | 2 |
| 35958 | galchagorri | 2 |
| 35959 | galateas | 2 |
| 35960 | galardonada | 2 |
| 35961 | galapaguito | 2 |
| 35962 | galan | 2 |
| 35963 | gaitero | 2 |
| 35964 | gaha | 2 |
| 35965 | gadea | 2 |
| 35966 | gacha | 2 |
| 35967 | gacetilleros | 2 |
| 35968 | gacetas | 2 |
| 35969 | gabrielito | 2 |
| 35970 | fyna | 2 |
| 35971 | fuyó | 2 |
| 35972 | fuyendo | 2 |
| 35973 | fuyen | 2 |
| 35974 | fuxieron | 2 |
| 35975 | fustes | 2 |
| 35976 | fustán | 2 |
| 35977 | fusión | 2 |
| 35978 | fusilen | 2 |
| 35979 | fusilaron | 2 |
| 35980 | furtos | 2 |
| 35981 | furtas | 2 |
| 35982 | furiosamente | 2 |
| 35983 | furgón | 2 |
| 35984 | fuoco | 2 |
| 35985 | funestamente | 2 |
| 35986 | funerario | 2 |
| 35987 | fundir | 2 |
| 35988 | funde | 2 |
| 35989 | fundarme | 2 |
| 35990 | fundadoras | 2 |
| 35991 | funcionaban | 2 |
| 35992 | fumándose | 2 |
| 35993 | fuman | 2 |
| 35994 | fumaban | 2 |
| 35995 | fulminaron | 2 |
| 35996 | fulminar | 2 |
| 35997 | fulminantes | 2 |
| 35998 | fulminando | 2 |
| 35999 | fulminada | 2 |
| 36000 | fulmina | 2 |
| 36001 | fullero | 2 |
| 36002 | fulastre | 2 |
| 36003 | fuguilla | 2 |
| 36004 | fugó | 2 |
| 36005 | fugado | 2 |
| 36006 | fugaces | 2 |
| 36007 | fuessen | 2 |
| 36008 | fuessemos | 2 |
| 36009 | fuésele | 2 |
| 36010 | fuesa | 2 |
| 36011 | fuerzan | 2 |
| 36012 | fuertecillo | 2 |
| 36013 | fuéronle | 2 |
| 36014 | fuencarral | 2 |
| 36015 | fueme | 2 |
| 36016 | fuéles | 2 |
| 36017 | fuéle | 2 |
| 36018 | fuas | 2 |
| 36019 | fu | 2 |
| 36020 | frustrado | 2 |
| 36021 | fruslerías | 2 |
| 36022 | fruncimiento | 2 |
| 36023 | fruncidos | 2 |
| 36024 | fruncida | 2 |
| 36025 | fruición | 2 |
| 36026 | frotado | 2 |
| 36027 | frota | 2 |
| 36028 | frontis | 2 |
| 36029 | frontino | 2 |
| 36030 | fronterizos | 2 |
| 36031 | frontal | 2 |
| 36032 | frondosa | 2 |
| 36033 | frito | 2 |
| 36034 | frisones | 2 |
| 36035 | frisonas | 2 |
| 36036 | friscal | 2 |
| 36037 | frisada | 2 |
| 36038 | frioleras | 2 |
| 36039 | frey | 2 |
| 36040 | frecuentaban | 2 |
| 36041 | frecha | 2 |
| 36042 | fraternizaban | 2 |
| 36043 | fraternalmente | 2 |
| 36044 | frasecilla | 2 |
| 36045 | fraques | 2 |
| 36046 | franquearon | 2 |
| 36047 | franqueaban | 2 |
| 36048 | frandes | 2 |
| 36049 | françisco | 2 |
| 36050 | francesota | 2 |
| 36051 | francesilla | 2 |
| 36052 | fraguas | 2 |
| 36053 | fragosa | 2 |
| 36054 | fragantes | 2 |
| 36055 | fracasos | 2 |
| 36056 | foyas | 2 |
| 36057 | fougueux | 2 |
| 36058 | fotográfico | 2 |
| 36059 | fotografía | 2 |
| 36060 | fósil | 2 |
| 36061 | forzosos | 2 |
| 36062 | forzalla | 2 |
| 36063 | forzaba | 2 |
| 36064 | fortu | 2 |
| 36065 | fortísima | 2 |
| 36066 | fortificar | 2 |
| 36067 | fortificados | 2 |
| 36068 | fortificaba | 2 |
| 36069 | fortalecen | 2 |
| 36070 | fortalece | 2 |
| 36071 | forros | 2 |
| 36072 | forraría | 2 |
| 36073 | forraje | 2 |
| 36074 | forraba | 2 |
| 36075 | foro | 2 |
| 36076 | forno | 2 |
| 36077 | fornidos | 2 |
| 36078 | formular | 2 |
| 36079 | forminge | 2 |
| 36080 | formarla | 2 |
| 36081 | formara | 2 |
| 36082 | formamos | 2 |
| 36083 | formalito | 2 |
| 36084 | forçó | 2 |
| 36085 | forcejeando | 2 |
| 36086 | forcejeaba | 2 |
| 36087 | forçar | 2 |
| 36088 | forasteras | 2 |
| 36089 | forajidos | 2 |
| 36090 | fontanero | 2 |
| 36091 | fonseca | 2 |
| 36092 | foncé | 2 |
| 36093 | fomentaba | 2 |
| 36094 | fols | 2 |
| 36095 | folía | 2 |
| 36096 | fogosas | 2 |
| 36097 | fogonadura | 2 |
| 36098 | foca | 2 |
| 36099 | fluxión | 2 |
| 36100 | flux | 2 |
| 36101 | fluctuaba | 2 |
| 36102 | floxo | 2 |
| 36103 | flote | 2 |
| 36104 | flotas | 2 |
| 36105 | florín | 2 |
| 36106 | florimorte | 2 |
| 36107 | floricultura | 2 |
| 36108 | florete | 2 |
| 36109 | florentinilla | 2 |
| 36110 | florecer | 2 |
| 36111 | floreados | 2 |
| 36112 | floralva | 2 |
| 36113 | flojilla | 2 |
| 36114 | flo | 2 |
| 36115 | flexibilidad | 2 |
| 36116 | flequillo | 2 |
| 36117 | flemáticos | 2 |
| 36118 | flecos | 2 |
| 36119 | flechaba | 2 |
| 36120 | flauteados | 2 |
| 36121 | flaqueça | 2 |
| 36122 | flaqueaban | 2 |
| 36123 | flanqueada | 2 |
| 36124 | flammarión | 2 |
| 36125 | flammarion | 2 |
| 36126 | flamencas | 2 |
| 36127 | flácida | 2 |
| 36128 | fízol | 2 |
| 36129 | fiziste | 2 |
| 36130 | fita | 2 |
| 36131 | fisura | 2 |
| 36132 | fisonómico | 2 |
| 36133 | fisiólogos | 2 |
| 36134 | fisiólogo | 2 |
| 36135 | fisiológicos | 2 |
| 36136 | fisiológica | 2 |
| 36137 | fisgoneo | 2 |
| 36138 | fisgona | 2 |
| 36139 | fiscalizadora | 2 |
| 36140 | fírmela | 2 |
| 36141 | firmara | 2 |
| 36142 | firmando | 2 |
| 36143 | firmabo | 2 |
| 36144 | finja | 2 |
| 36145 | finitas | 2 |
| 36146 | fingiera | 2 |
| 36147 | fingí | 2 |
| 36148 | finalizar | 2 |
| 36149 | finales | 2 |
| 36150 | finados | 2 |
| 36151 | filtrándose | 2 |
| 36152 | filtraba | 2 |
| 36153 | filosofo | 2 |
| 36154 | filosóficamente | 2 |
| 36155 | filosofia | 2 |
| 36156 | filomena | 2 |
| 36157 | filisteo | 2 |
| 36158 | fili | 2 |
| 36159 | filete | 2 |
| 36160 | filarmónico | 2 |
| 36161 | filantrópico | 2 |
| 36162 | filantrópica | 2 |
| 36163 | filantropía | 2 |
| 36164 | fijuelos | 2 |
| 36165 | fijose | 2 |
| 36166 | fijé | 2 |
| 36167 | fije | 2 |
| 36168 | fijáronse | 2 |
| 36169 | fijarla | 2 |
| 36170 | fijadalgo | 2 |
| 36171 | figurilla | 2 |
| 36172 | figurarme | 2 |
| 36173 | figuradas | 2 |
| 36174 | figuración | 2 |
| 36175 | fies | 2 |
| 36176 | fierezas | 2 |
| 36177 | fieren | 2 |
| 36178 | fieramente | 2 |
| 36179 | fïeles | 2 |
| 36180 | fielato | 2 |
| 36181 | fiebres | 2 |
| 36182 | fidelísimo | 2 |
| 36183 | fidei | 2 |
| 36184 | ficciones | 2 |
| 36185 | fíate | 2 |
| 36186 | fiat | 2 |
| 36187 | fías | 2 |
| 36188 | fiarme | 2 |
| 36189 | fiando | 2 |
| 36190 | fiança | 2 |
| 36191 | fían | 2 |
| 36192 | fiambrera | 2 |
| 36193 | fiados | 2 |
| 36194 | fiadores | 2 |
| 36195 | ffuese | 2 |
| 36196 | ffuego | 2 |
| 36197 | ffize | 2 |
| 36198 | ffija | 2 |
| 36199 | ffeciste | 2 |
| 36200 | ffazíe | 2 |
| 36201 | ffazen | 2 |
| 36202 | ffallo | 2 |
| 36203 | feudalismo | 2 |
| 36204 | feudales | 2 |
| 36205 | fétidas | 2 |
| 36206 | festivos | 2 |
| 36207 | festividá | 2 |
| 36208 | festiva | 2 |
| 36209 | fesistes | 2 |
| 36210 | fervorosamente | 2 |
| 36211 | fervorosa | 2 |
| 36212 | fervientes | 2 |
| 36213 | ferruginoso | 2 |
| 36214 | ferreros | 2 |
| 36215 | férreas | 2 |
| 36216 | ferrand | 2 |
| 36217 | ferradas | 2 |
| 36218 | fermento | 2 |
| 36219 | ferirla | 2 |
| 36220 | feriólo | 2 |
| 36221 | fería | 2 |
| 36222 | fenelona | 2 |
| 36223 | fenbra | 2 |
| 36224 | femeninas | 2 |
| 36225 | femeniles | 2 |
| 36226 | femençia | 2 |
| 36227 | felpudos | 2 |
| 36228 | felpa | 2 |
| 36229 | felicito | 2 |
| 36230 | felicitaron | 2 |
| 36231 | felicitar | 2 |
| 36232 | felicitaciones | 2 |
| 36233 | felicitaban | 2 |
| 36234 | felicitaba | 2 |
| 36235 | felicísimamente | 2 |
| 36236 | federal | 2 |
| 36237 | fecit | 2 |
| 36238 | feçiese | 2 |
| 36239 | fechurías | 2 |
| 36240 | fealdat | 2 |
| 36241 | fealdades | 2 |
| 36242 | fazienda | 2 |
| 36243 | fazíe | 2 |
| 36244 | fazerlos | 2 |
| 36245 | fazaña | 2 |
| 36246 | faysanes | 2 |
| 36247 | faya | 2 |
| 36248 | favoritas | 2 |
| 36249 | favorita | 2 |
| 36250 | favoreciesen | 2 |
| 36251 | favoreciendo | 2 |
| 36252 | favorecíanme | 2 |
| 36253 | favorecerme | 2 |
| 36254 | favoreced | 2 |
| 36255 | faut | 2 |
| 36256 | faustino | 2 |
| 36257 | fauorecer | 2 |
| 36258 | fauorable | 2 |
| 36259 | faunos | 2 |
| 36260 | fatua | 2 |
| 36261 | fatigo | 2 |
| 36262 | fatigando | 2 |
| 36263 | fatales | 2 |
| 36264 | fastidien | 2 |
| 36265 | fasienda | 2 |
| 36266 | fasia | 2 |
| 36267 | fascinado | 2 |
| 36268 | fascina | 2 |
| 36269 | fasaña | 2 |
| 36270 | fartes | 2 |
| 36271 | farsas | 2 |
| 36272 | farsalia | 2 |
| 36273 | farolillos | 2 |
| 36274 | farolero | 2 |
| 36275 | farolear | 2 |
| 36276 | farias | 2 |
| 36277 | fantasmona | 2 |
| 36278 | fantasmagorías | 2 |
| 36279 | fantasías | 2 |
| 36280 | fangosos | 2 |
| 36281 | fanfarrones | 2 |
| 36282 | fanfarronería | 2 |
| 36283 | fanfarronadas | 2 |
| 36284 | fanfarrón | 2 |
| 36285 | fanatizados | 2 |
| 36286 | fanales | 2 |
| 36287 | famosísimo | 2 |
| 36288 | familiarizado | 2 |
| 36289 | faltos | 2 |
| 36290 | faltóles | 2 |
| 36291 | faltaua | 2 |
| 36292 | faltaria | 2 |
| 36293 | faltarás | 2 |
| 36294 | falsificado | 2 |
| 36295 | falsificada | 2 |
| 36296 | falsificación | 2 |
| 36297 | falsedat | 2 |
| 36298 | fallyr | 2 |
| 36299 | fallido | 2 |
| 36300 | fallesçidas | 2 |
| 36301 | fallesçen | 2 |
| 36302 | fallesçe | 2 |
| 36303 | falléme | 2 |
| 36304 | fallaredes | 2 |
| 36305 | fallarán | 2 |
| 36306 | fallan | 2 |
| 36307 | fallamos | 2 |
| 36308 | faldón | 2 |
| 36309 | faldamentos | 2 |
| 36310 | falansterio | 2 |
| 36311 | falange | 2 |
| 36312 | fajos | 2 |
| 36313 | faisanes | 2 |
| 36314 | fadas | 2 |
| 36315 | fadaron | 2 |
| 36316 | factum | 2 |
| 36317 | factible | 2 |
| 36318 | facinoroso | 2 |
| 36319 | facilitaran | 2 |
| 36320 | facilillo | 2 |
| 36321 | facienda | 2 |
| 36322 | facial | 2 |
| 36323 | faccioso | 2 |
| 36324 | facciosa | 2 |
| 36325 | fabuloso | 2 |
| 36326 | fabulosas | 2 |
| 36327 | fabulosa | 2 |
| 36328 | fabulista | 2 |
| 36329 | fabrique | 2 |
| 36330 | fabricó | 2 |
| 36331 | fabricaste | 2 |
| 36332 | fabricador | 2 |
| 36333 | fablévos | 2 |
| 36334 | fablavan | 2 |
| 36335 | fablava | 2 |
| 36336 | fablaua | 2 |
| 36337 | fablat | 2 |
| 36338 | fablasse | 2 |
| 36339 | fablare | 2 |
| 36340 | fablamos | 2 |
| 36341 | ez | 2 |
| 36342 | exultemus | 2 |
| 36343 | exuberantes | 2 |
| 36344 | extremis | 2 |
| 36345 | extremidad | 2 |
| 36346 | extremas | 2 |
| 36347 | extraviarse | 2 |
| 36348 | extravían | 2 |
| 36349 | extraviadas | 2 |
| 36350 | extrañará | 2 |
| 36351 | extranjerizado | 2 |
| 36352 | extrajo | 2 |
| 36353 | extraído | 2 |
| 36354 | extraer | 2 |
| 36355 | extirpación | 2 |
| 36356 | extinguirse | 2 |
| 36357 | extinguir | 2 |
| 36358 | extinguió | 2 |
| 36359 | externos | 2 |
| 36360 | extenuado | 2 |
| 36361 | extendiéndose | 2 |
| 36362 | extasiado | 2 |
| 36363 | exseminarista | 2 |
| 36364 | exsecretario | 2 |
| 36365 | expuse | 2 |
| 36366 | exprofeso | 2 |
| 36367 | exprisiones | 2 |
| 36368 | exprimido | 2 |
| 36369 | expresada | 2 |
| 36370 | exponerte | 2 |
| 36371 | exponemos | 2 |
| 36372 | exploraciones | 2 |
| 36373 | expliquen | 2 |
| 36374 | expliquemos | 2 |
| 36375 | expliqué | 2 |
| 36376 | explicas | 2 |
| 36377 | explicársela | 2 |
| 36378 | explicaron | 2 |
| 36379 | explican | 2 |
| 36380 | explícame | 2 |
| 36381 | explicaban | 2 |
| 36382 | expiró | 2 |
| 36383 | expiriencia | 2 |
| 36384 | expiraron | 2 |
| 36385 | expirado | 2 |
| 36386 | expira | 2 |
| 36387 | expiatoria | 2 |
| 36388 | expertas | 2 |
| 36389 | experta | 2 |
| 36390 | experimentaron | 2 |
| 36391 | experimentando | 2 |
| 36392 | experimentados | 2 |
| 36393 | experimenta | 2 |
| 36394 | expeditivo | 2 |
| 36395 | expedir | 2 |
| 36396 | expediciones | 2 |
| 36397 | expedicionario | 2 |
| 36398 | éxitos | 2 |
| 36399 | existió | 2 |
| 36400 | existieran | 2 |
| 36401 | existentes | 2 |
| 36402 | existente | 2 |
| 36403 | exista | 2 |
| 36404 | exigiría | 2 |
| 36405 | exigió | 2 |
| 36406 | exigieron | 2 |
| 36407 | exiges | 2 |
| 36408 | exhortación | 2 |
| 36409 | exhala | 2 |
| 36410 | exemplos | 2 |
| 36411 | exemplo | 2 |
| 36412 | execrables | 2 |
| 36413 | excusaba | 2 |
| 36414 | exclusión | 2 |
| 36415 | excitarlo | 2 |
| 36416 | excitara | 2 |
| 36417 | excitados | 2 |
| 36418 | excitadísima | 2 |
| 36419 | excesivos | 2 |
| 36420 | excelsas | 2 |
| 36421 | examinemos | 2 |
| 36422 | examine | 2 |
| 36423 | exaltados | 2 |
| 36424 | exaltadas | 2 |
| 36425 | exaltaciones | 2 |
| 36426 | exageradamente | 2 |
| 36427 | exagera | 2 |
| 36428 | exabrupto | 2 |
| 36429 | evocaba | 2 |
| 36430 | evitarlos | 2 |
| 36431 | evitarlas | 2 |
| 36432 | evitando | 2 |
| 36433 | evita | 2 |
| 36434 | evangelios | 2 |
| 36435 | evangélicos | 2 |
| 36436 | evangélico | 2 |
| 36437 | europeos | 2 |
| 36438 | eunuco | 2 |
| 36439 | eudoro | 2 |
| 36440 | eucaristía | 2 |
| 36441 | étrangère | 2 |
| 36442 | etorri | 2 |
| 36443 | eternidades | 2 |
| 36444 | etéreas | 2 |
| 36445 | etelvina | 2 |
| 36446 | etapas | 2 |
| 36447 | etapa | 2 |
| 36448 | était | 2 |
| 36449 | estuviésemos | 2 |
| 36450 | estuviéremos | 2 |
| 36451 | estuuiera | 2 |
| 36452 | estúpidamente | 2 |
| 36453 | estufas | 2 |
| 36454 | estudió | 2 |
| 36455 | estudien | 2 |
| 36456 | estudié | 2 |
| 36457 | estudiarse | 2 |
| 36458 | estudiara | 2 |
| 36459 | estudiantón | 2 |
| 36460 | estudiados | 2 |
| 36461 | estuches | 2 |
| 36462 | estucadas | 2 |
| 36463 | estrujaron | 2 |
| 36464 | estrujar | 2 |
| 36465 | estrujada | 2 |
| 36466 | estrujaba | 2 |
| 36467 | estropajosa | 2 |
| 36468 | estrofa | 2 |
| 36469 | estricta | 2 |
| 36470 | estribillos | 2 |
| 36471 | estribando | 2 |
| 36472 | estrenar | 2 |
| 36473 | estrenada | 2 |
| 36474 | estremecido | 2 |
| 36475 | estrelló | 2 |
| 36476 | estrello | 2 |
| 36477 | estrecheces | 2 |
| 36478 | estratificación | 2 |
| 36479 | estratégico | 2 |
| 36480 | estratégica | 2 |
| 36481 | estraordinario | 2 |
| 36482 | estrañezas | 2 |
| 36483 | estrano | 2 |
| 36484 | estrana | 2 |
| 36485 | estragados | 2 |
| 36486 | estraga | 2 |
| 36487 | estrados | 2 |
| 36488 | estrada | 2 |
| 36489 | estornudos | 2 |
| 36490 | estordido | 2 |
| 36491 | estorbos | 2 |
| 36492 | estorbarse | 2 |
| 36493 | estorbarme | 2 |
| 36494 | estorbaré | 2 |
| 36495 | estorban | 2 |
| 36496 | estoraque | 2 |
| 36497 | estomago | 2 |
| 36498 | estólida | 2 |
| 36499 | estola | 2 |
| 36500 | estofa | 2 |
| 36501 | estiraran | 2 |
| 36502 | estiradas | 2 |
| 36503 | estimulaba | 2 |
| 36504 | estimula | 2 |
| 36505 | estimen | 2 |
| 36506 | estimarme | 2 |
| 36507 | estimaran | 2 |
| 36508 | estimara | 2 |
| 36509 | estimando | 2 |
| 36510 | estimados | 2 |
| 36511 | estil | 2 |
| 36512 | estigma | 2 |
| 36513 | estiercol | 2 |
| 36514 | esterior | 2 |
| 36515 | ester | 2 |
| 36516 | estepas | 2 |
| 36517 | estepa | 2 |
| 36518 | estendiendo | 2 |
| 36519 | estenderse | 2 |
| 36520 | estebanillo | 2 |
| 36521 | estays | 2 |
| 36522 | estavas | 2 |
| 36523 | estatuto | 2 |
| 36524 | estaturas | 2 |
| 36525 | estáte | 2 |
| 36526 | estarte | 2 |
| 36527 | estarme | 2 |
| 36528 | estarla | 2 |
| 36529 | estaréis | 2 |
| 36530 | estaos | 2 |
| 36531 | estanterol | 2 |
| 36532 | estanquillos | 2 |
| 36533 | estándome | 2 |
| 36534 | estándola | 2 |
| 36535 | estança | 2 |
| 36536 | estampidos | 2 |
| 36537 | estampe | 2 |
| 36538 | estampar | 2 |
| 36539 | estamentos | 2 |
| 36540 | estáme | 2 |
| 36541 | estalle | 2 |
| 36542 | estafar | 2 |
| 36543 | estadista | 2 |
| 36544 | establecidas | 2 |
| 36545 | establecen | 2 |
| 36546 | estábale | 2 |
| 36547 | essotro | 2 |
| 36548 | esquivando | 2 |
| 36549 | esquiuo | 2 |
| 36550 | esquite | 2 |
| 36551 | esquilmos | 2 |
| 36552 | esquilman | 2 |
| 36553 | esquelitas | 2 |
| 36554 | esputo | 2 |
| 36555 | esprit | 2 |
| 36556 | espoz | 2 |
| 36557 | espontáneos | 2 |
| 36558 | espolear | 2 |
| 36559 | esplendidez | 2 |
| 36560 | espiritui | 2 |
| 36561 | espiritualmente | 2 |
| 36562 | espiritualista | 2 |
| 36563 | espiritualismo | 2 |
| 36564 | espiritismo | 2 |
| 36565 | espirando | 2 |
| 36566 | espiral | 2 |
| 36567 | espío | 2 |
| 36568 | espinal | 2 |
| 36569 | espetos | 2 |
| 36570 | espetéme | 2 |
| 36571 | espeta | 2 |
| 36572 | espesísima | 2 |
| 36573 | esperimentado | 2 |
| 36574 | espérese | 2 |
| 36575 | esperen | 2 |
| 36576 | esperasen | 2 |
| 36577 | esperarte | 2 |
| 36578 | esperarme | 2 |
| 36579 | esperarían | 2 |
| 36580 | esperándome | 2 |
| 36581 | esperados | 2 |
| 36582 | esperada | 2 |
| 36583 | esperabas | 2 |
| 36584 | espectros | 2 |
| 36585 | especificar | 2 |
| 36586 | espasmódico | 2 |
| 36587 | espasmódica | 2 |
| 36588 | esparteros | 2 |
| 36589 | espartano | 2 |
| 36590 | espárragos | 2 |
| 36591 | esparcimiento | 2 |
| 36592 | esparcían | 2 |
| 36593 | esparcía | 2 |
| 36594 | esparce | 2 |
| 36595 | espantosos | 2 |
| 36596 | espantosas | 2 |
| 36597 | espantando | 2 |
| 36598 | espantadiza | 2 |
| 36599 | espaldarazos | 2 |
| 36600 | espaldarazo | 2 |
| 36601 | espadañas | 2 |
| 36602 | espadaña | 2 |
| 36603 | espaciosos | 2 |
| 36604 | espaciosas | 2 |
| 36605 | espaciar | 2 |
| 36606 | esotros | 2 |
| 36607 | esmerose | 2 |
| 36608 | esmeradamente | 2 |
| 36609 | esfuércese | 2 |
| 36610 | esforzada | 2 |
| 36611 | esforzábase | 2 |
| 36612 | esforçado | 2 |
| 36613 | esférica | 2 |
| 36614 | esenta | 2 |
| 36615 | escusó | 2 |
| 36616 | escuses | 2 |
| 36617 | escusarás | 2 |
| 36618 | escusandose | 2 |
| 36619 | escusados | 2 |
| 36620 | escusadas | 2 |
| 36621 | escusada | 2 |
| 36622 | escurrían | 2 |
| 36623 | escurre | 2 |
| 36624 | escurísima | 2 |
| 36625 | escureció | 2 |
| 36626 | escurecerse | 2 |
| 36627 | escurecerlos | 2 |
| 36628 | escupo | 2 |
| 36629 | escupirle | 2 |
| 36630 | escupiría | 2 |
| 36631 | escupieron | 2 |
| 36632 | esculturas | 2 |
| 36633 | esculturales | 2 |
| 36634 | escultóricos | 2 |
| 36635 | escultores | 2 |
| 36636 | esculpido | 2 |
| 36637 | escuezan | 2 |
| 36638 | escueza | 2 |
| 36639 | escudriñaba | 2 |
| 36640 | escudillar | 2 |
| 36641 | escuda | 2 |
| 36642 | escuchen | 2 |
| 36643 | escuchemos | 2 |
| 36644 | escúcheme | 2 |
| 36645 | escuchéis | 2 |
| 36646 | escuchase | 2 |
| 36647 | escucharle | 2 |
| 36648 | escucharemos | 2 |
| 36649 | escuchare | 2 |
| 36650 | escuchara | 2 |
| 36651 | escuchándole | 2 |
| 36652 | escuálido | 2 |
| 36653 | escualidez | 2 |
| 36654 | escrutadora | 2 |
| 36655 | escriuo | 2 |
| 36656 | escriuio | 2 |
| 36657 | escriuieron | 2 |
| 36658 | escripta | 2 |
| 36659 | escribirlo | 2 |
| 36660 | escribiría | 2 |
| 36661 | escribióme | 2 |
| 36662 | escribieran | 2 |
| 36663 | escribiéndose | 2 |
| 36664 | escríbame | 2 |
| 36665 | escreví | 2 |
| 36666 | escotar | 2 |
| 36667 | escotada | 2 |
| 36668 | escota | 2 |
| 36669 | escoria | 2 |
| 36670 | escoplos | 2 |
| 36671 | escondiéndose | 2 |
| 36672 | escondiendo | 2 |
| 36673 | escóndese | 2 |
| 36674 | escondería | 2 |
| 36675 | escondas | 2 |
| 36676 | escombrera | 2 |
| 36677 | escolásticos | 2 |
| 36678 | escolapios | 2 |
| 36679 | escojas | 2 |
| 36680 | escogiendo | 2 |
| 36681 | escogerme | 2 |
| 36682 | escogen | 2 |
| 36683 | escocias | 2 |
| 36684 | esclavas | 2 |
| 36685 | esclarecidos | 2 |
| 36686 | escéptica | 2 |
| 36687 | escatimar | 2 |
| 36688 | escaseza | 2 |
| 36689 | escasean | 2 |
| 36690 | escasamente | 2 |
| 36691 | escarva | 2 |
| 36692 | escarpias | 2 |
| 36693 | escarnios | 2 |
| 36694 | escarnecía | 2 |
| 36695 | escarnecerle | 2 |
| 36696 | escarmientos | 2 |
| 36697 | escarmientan | 2 |
| 36698 | escarmentar | 2 |
| 36699 | escarmentados | 2 |
| 36700 | escariote | 2 |
| 36701 | escarceos | 2 |
| 36702 | escarba | 2 |
| 36703 | escapularios | 2 |
| 36704 | escapé | 2 |
| 36705 | escaparte | 2 |
| 36706 | escaparedes | 2 |
| 36707 | escapará | 2 |
| 36708 | escapadas | 2 |
| 36709 | escandalosamente | 2 |
| 36710 | escandalizes | 2 |
| 36711 | escandalizando | 2 |
| 36712 | escandalera | 2 |
| 36713 | escamosa | 2 |
| 36714 | escamado | 2 |
| 36715 | escama | 2 |
| 36716 | escalon | 2 |
| 36717 | escaló | 2 |
| 36718 | escalinata | 2 |
| 36719 | escalaron | 2 |
| 36720 | escajos | 2 |
| 36721 | escabulló | 2 |
| 36722 | escabroso | 2 |
| 36723 | escabrosas | 2 |
| 36724 | esbeltísimo | 2 |
| 36725 | erupciones | 2 |
| 36726 | errónea | 2 |
| 36727 | erró | 2 |
| 36728 | erraran | 2 |
| 36729 | erradas | 2 |
| 36730 | erradamente | 2 |
| 36731 | eróticos | 2 |
| 36732 | erótico | 2 |
| 36733 | erótica | 2 |
| 36734 | erizaron | 2 |
| 36735 | erizando | 2 |
| 36736 | erizada | 2 |
| 36737 | eriza | 2 |
| 36738 | eris | 2 |
| 36739 | erigido | 2 |
| 36740 | erías | 2 |
| 36741 | eriales | 2 |
| 36742 | ergotina | 2 |
| 36743 | ergo | 2 |
| 36744 | ercilla | 2 |
| 36745 | erario | 2 |
| 36746 | erard | 2 |
| 36747 | érales | 2 |
| 36748 | érades | 2 |
| 36749 | equivoqué | 2 |
| 36750 | equivocas | 2 |
| 36751 | equivocadamente | 2 |
| 36752 | equinocios | 2 |
| 36753 | equinocial | 2 |
| 36754 | epilépticos | 2 |
| 36755 | epilépticas | 2 |
| 36756 | epilepsia | 2 |
| 36757 | epígrafe | 2 |
| 36758 | epaminondas | 2 |
| 36759 | enzias | 2 |
| 36760 | enzarzando | 2 |
| 36761 | enxerir | 2 |
| 36762 | enviudar | 2 |
| 36763 | envilecen | 2 |
| 36764 | enviéle | 2 |
| 36765 | envidiosona | 2 |
| 36766 | envidiara | 2 |
| 36767 | envidiables | 2 |
| 36768 | enviaremos | 2 |
| 36769 | envíame | 2 |
| 36770 | enviados | 2 |
| 36771 | enviad | 2 |
| 36772 | envenena | 2 |
| 36773 | envejecida | 2 |
| 36774 | envejecer | 2 |
| 36775 | envejece | 2 |
| 36776 | envasó | 2 |
| 36777 | envalentonándose | 2 |
| 36778 | envalentonado | 2 |
| 36779 | envainen | 2 |
| 36780 | entyende | 2 |
| 36781 | entyenda | 2 |
| 36782 | entusiástico | 2 |
| 36783 | entusiasman | 2 |
| 36784 | enturbiar | 2 |
| 36785 | entrometidos | 2 |
| 36786 | entrometidas | 2 |
| 36787 | entrometerse | 2 |
| 36788 | entristecióse | 2 |
| 36789 | entristecerse | 2 |
| 36790 | entristeçer | 2 |
| 36791 | entrevistas | 2 |
| 36792 | entrevió | 2 |
| 36793 | entreverado | 2 |
| 36794 | entreveía | 2 |
| 36795 | entretuviesen | 2 |
| 36796 | entretuviera | 2 |
| 36797 | entretienes | 2 |
| 36798 | entreteniéndose | 2 |
| 36799 | entreteniendo | 2 |
| 36800 | entretengo | 2 |
| 36801 | entretenga | 2 |
| 36802 | entretenerme | 2 |
| 36803 | entretenerle | 2 |
| 36804 | entretalladura | 2 |
| 36805 | entresacando | 2 |
| 36806 | entrepuentes | 2 |
| 36807 | entrepuente | 2 |
| 36808 | entrepiernas | 2 |
| 36809 | entreoído | 2 |
| 36810 | entremezclaban | 2 |
| 36811 | entremeten | 2 |
| 36812 | entremedio | 2 |
| 36813 | entréme | 2 |
| 36814 | entregué | 2 |
| 36815 | entregóse | 2 |
| 36816 | entregarás | 2 |
| 36817 | entregará | 2 |
| 36818 | entregamos | 2 |
| 36819 | entredicho | 2 |
| 36820 | entrecortadas | 2 |
| 36821 | entrecortada | 2 |
| 36822 | entreacto | 2 |
| 36823 | éntre | 2 |
| 36824 | entráronse | 2 |
| 36825 | entrarle | 2 |
| 36826 | entraos | 2 |
| 36827 | entrañaban | 2 |
| 36828 | entramado | 2 |
| 36829 | entráis | 2 |
| 36830 | entrados | 2 |
| 36831 | entrábase | 2 |
| 36832 | entorpecimientos | 2 |
| 36833 | entorpecimiento | 2 |
| 36834 | entorpece | 2 |
| 36835 | entornaba | 2 |
| 36836 | entonó | 2 |
| 36837 | entonaban | 2 |
| 36838 | entierran | 2 |
| 36839 | entiéndete | 2 |
| 36840 | entidades | 2 |
| 36841 | entibiaba | 2 |
| 36842 | entibia | 2 |
| 36843 | enterró | 2 |
| 36844 | enterrarte | 2 |
| 36845 | enterrarse | 2 |
| 36846 | enterramos | 2 |
| 36847 | enterramientos | 2 |
| 36848 | enterrador | 2 |
| 36849 | enternecieron | 2 |
| 36850 | enternecían | 2 |
| 36851 | enternecerse | 2 |
| 36852 | entérate | 2 |
| 36853 | enteraros | 2 |
| 36854 | enterarme | 2 |
| 36855 | entendieran | 2 |
| 36856 | entendet | 2 |
| 36857 | entenderías | 2 |
| 36858 | entenderían | 2 |
| 36859 | entenderán | 2 |
| 36860 | entendemiento | 2 |
| 36861 | entended | 2 |
| 36862 | entençión | 2 |
| 36863 | entavía | 2 |
| 36864 | entallado | 2 |
| 36865 | entablo | 2 |
| 36866 | entablado | 2 |
| 36867 | entablada | 2 |
| 36868 | entablaba | 2 |
| 36869 | ensuziar | 2 |
| 36870 | ensuciado | 2 |
| 36871 | ensilló | 2 |
| 36872 | ensillando | 2 |
| 36873 | enseñorearse | 2 |
| 36874 | enseñóme | 2 |
| 36875 | enséñemela | 2 |
| 36876 | enseñarlas | 2 |
| 36877 | enseñándosela | 2 |
| 36878 | enseñándola | 2 |
| 36879 | enseñadas | 2 |
| 36880 | enseñábale | 2 |
| 36881 | enseguida | 2 |
| 36882 | ensayarse | 2 |
| 36883 | ensayándose | 2 |
| 36884 | ensartar | 2 |
| 36885 | ensartadas | 2 |
| 36886 | ensarta | 2 |
| 36887 | ensano | 2 |
| 36888 | ensangrentar | 2 |
| 36889 | ensangrentado | 2 |
| 36890 | ensanchar | 2 |
| 36891 | ensanchándose | 2 |
| 36892 | ensancha | 2 |
| 36893 | ensalzo | 2 |
| 36894 | ensalmador | 2 |
| 36895 | enroscado | 2 |
| 36896 | enroscaban | 2 |
| 36897 | enronquecido | 2 |
| 36898 | enrizados | 2 |
| 36899 | enriquece | 2 |
| 36900 | enrevesado | 2 |
| 36901 | enrejada | 2 |
| 36902 | enredó | 2 |
| 36903 | enredarse | 2 |
| 36904 | enredaron | 2 |
| 36905 | enredarme | 2 |
| 36906 | enredadora | 2 |
| 36907 | enredador | 2 |
| 36908 | enredaderas | 2 |
| 36909 | enredaban | 2 |
| 36910 | enreda | 2 |
| 36911 | enperadores | 2 |
| 36912 | enormísima | 2 |
| 36913 | enorgullecía | 2 |
| 36914 | enojé | 2 |
| 36915 | enojaste | 2 |
| 36916 | enojadas | 2 |
| 36917 | ennoblecía | 2 |
| 36918 | ennegreció | 2 |
| 36919 | ennegrecidas | 2 |
| 36920 | ennegrecían | 2 |
| 36921 | enmudece | 2 |
| 36922 | enmendarse | 2 |
| 36923 | enmendaré | 2 |
| 36924 | enmendando | 2 |
| 36925 | enmendados | 2 |
| 36926 | enmedio | 2 |
| 36927 | enmascarado | 2 |
| 36928 | enloquecer | 2 |
| 36929 | enlazadas | 2 |
| 36930 | enlazada | 2 |
| 36931 | enlaces | 2 |
| 36932 | enlaças | 2 |
| 36933 | enjutas | 2 |
| 36934 | enjundia | 2 |
| 36935 | enhiesto | 2 |
| 36936 | enhebrada | 2 |
| 36937 | engrudo | 2 |
| 36938 | engrosando | 2 |
| 36939 | engrandecen | 2 |
| 36940 | engranados | 2 |
| 36941 | engrana | 2 |
| 36942 | engorres | 2 |
| 36943 | engordarla | 2 |
| 36944 | engolosinar | 2 |
| 36945 | engolfó | 2 |
| 36946 | engolfarse | 2 |
| 36947 | engolfado | 2 |
| 36948 | engendro | 2 |
| 36949 | engendré | 2 |
| 36950 | engendre | 2 |
| 36951 | engendradora | 2 |
| 36952 | engendraban | 2 |
| 36953 | engatusas | 2 |
| 36954 | engatusarás | 2 |
| 36955 | engaste | 2 |
| 36956 | engastados | 2 |
| 36957 | engasta | 2 |
| 36958 | engarza | 2 |
| 36959 | engañóse | 2 |
| 36960 | engañen | 2 |
| 36961 | engañáis | 2 |
| 36962 | enganosa | 2 |
| 36963 | enganchó | 2 |
| 36964 | enganchaba | 2 |
| 36965 | enganase | 2 |
| 36966 | enfureció | 2 |
| 36967 | enfurecido | 2 |
| 36968 | enfurecía | 2 |
| 36969 | enfriara | 2 |
| 36970 | enfrenó | 2 |
| 36971 | enfrenado | 2 |
| 36972 | enfrenada | 2 |
| 36973 | enfrenaba | 2 |
| 36974 | enfrascados | 2 |
| 36975 | enfrascado | 2 |
| 36976 | enfraquesçes | 2 |
| 36977 | enforcaron | 2 |
| 36978 | enforcar | 2 |
| 36979 | enforcado | 2 |
| 36980 | enfiesta | 2 |
| 36981 | enfermero | 2 |
| 36982 | enfermar | 2 |
| 36983 | enfant | 2 |
| 36984 | enfadoso | 2 |
| 36985 | enfaden | 2 |
| 36986 | enfadará | 2 |
| 36987 | enfadara | 2 |
| 36988 | energúmeno | 2 |
| 36989 | enemistades | 2 |
| 36990 | enea | 2 |
| 36991 | endurecidos | 2 |
| 36992 | endurecía | 2 |
| 36993 | enderezó | 2 |
| 36994 | enderezo | 2 |
| 36995 | enderezase | 2 |
| 36996 | enderezarse | 2 |
| 36997 | enderezado | 2 |
| 36998 | enderécese | 2 |
| 36999 | endemoniados | 2 |
| 37000 | endemoniadas | 2 |
| 37001 | endecasílabos | 2 |
| 37002 | encumbrados | 2 |
| 37003 | encumbrada | 2 |
| 37004 | encuentres | 2 |
| 37005 | encuentren | 2 |
| 37006 | encuéntrase | 2 |
| 37007 | encubrirlo | 2 |
| 37008 | encubrió | 2 |
| 37009 | encubriera | 2 |
| 37010 | encubria | 2 |
| 37011 | encuadernados | 2 |
| 37012 | encuadernado | 2 |
| 37013 | encrucijada | 2 |
| 37014 | encopetadas | 2 |
| 37015 | encontrones | 2 |
| 37016 | encontronazo | 2 |
| 37017 | encontrola | 2 |
| 37018 | encontremos | 2 |
| 37019 | encontrasen | 2 |
| 37020 | encontrarlos | 2 |
| 37021 | encontrarlo | 2 |
| 37022 | encontraré | 2 |
| 37023 | encontrare | 2 |
| 37024 | encontradizo | 2 |
| 37025 | encontrábase | 2 |
| 37026 | enconada | 2 |
| 37027 | encomiende | 2 |
| 37028 | encomiendas | 2 |
| 37029 | encomiendan | 2 |
| 37030 | encomiástico | 2 |
| 37031 | encomiando | 2 |
| 37032 | encomendarnos | 2 |
| 37033 | encomendándonos | 2 |
| 37034 | encomendados | 2 |
| 37035 | encomendadas | 2 |
| 37036 | encolerizado | 2 |
| 37037 | encogiendo | 2 |
| 37038 | encogerse | 2 |
| 37039 | encobyerto | 2 |
| 37040 | encobierto | 2 |
| 37041 | encobiertas | 2 |
| 37042 | enclenque | 2 |
| 37043 | encierren | 2 |
| 37044 | ençienso | 2 |
| 37045 | encienda | 2 |
| 37046 | encías | 2 |
| 37047 | encerróse | 2 |
| 37048 | encerrose | 2 |
| 37049 | encerrona | 2 |
| 37050 | encerráronse | 2 |
| 37051 | encerrarla | 2 |
| 37052 | encerrando | 2 |
| 37053 | ençerrado | 2 |
| 37054 | encerradita | 2 |
| 37055 | encerados | 2 |
| 37056 | encendería | 2 |
| 37057 | ençendemiento | 2 |
| 37058 | encefalitis | 2 |
| 37059 | encarnizamiento | 2 |
| 37060 | encarnizados | 2 |
| 37061 | encarnizada | 2 |
| 37062 | encariñada | 2 |
| 37063 | encariñaba | 2 |
| 37064 | encargué | 2 |
| 37065 | encargase | 2 |
| 37066 | encargarte | 2 |
| 37067 | encargadas | 2 |
| 37068 | encareció | 2 |
| 37069 | encareciendo | 2 |
| 37070 | encarecida | 2 |
| 37071 | encarecía | 2 |
| 37072 | encarecerlos | 2 |
| 37073 | encarecerlo | 2 |
| 37074 | encarecen | 2 |
| 37075 | encarar | 2 |
| 37076 | encaramándose | 2 |
| 37077 | encantar | 2 |
| 37078 | encantaban | 2 |
| 37079 | encanecido | 2 |
| 37080 | encanallamiento | 2 |
| 37081 | encaminara | 2 |
| 37082 | encaminan | 2 |
| 37083 | encallar | 2 |
| 37084 | encalabrinado | 2 |
| 37085 | encajarse | 2 |
| 37086 | encajaron | 2 |
| 37087 | encajándole | 2 |
| 37088 | encajan | 2 |
| 37089 | encajados | 2 |
| 37090 | encadenamiento | 2 |
| 37091 | encadenadas | 2 |
| 37092 | enbuelvas | 2 |
| 37093 | enbióme | 2 |
| 37094 | enbióles | 2 |
| 37095 | enbiava | 2 |
| 37096 | enbiar | 2 |
| 37097 | enbargue | 2 |
| 37098 | enatío | 2 |
| 37099 | enarta | 2 |
| 37100 | enardece | 2 |
| 37101 | enarbolaron | 2 |
| 37102 | enamorarla | 2 |
| 37103 | enamoramiento | 2 |
| 37104 | enamoraban | 2 |
| 37105 | enaltecer | 2 |
| 37106 | enalbardase | 2 |
| 37107 | enalbardado | 2 |
| 37108 | enajenado | 2 |
| 37109 | émulos | 2 |
| 37110 | emular | 2 |
| 37111 | empuñar | 2 |
| 37112 | empuñadura | 2 |
| 37113 | empujaron | 2 |
| 37114 | empujan | 2 |
| 37115 | empujaban | 2 |
| 37116 | empuja | 2 |
| 37117 | empréstito | 2 |
| 37118 | empreñaría | 2 |
| 37119 | empreñar | 2 |
| 37120 | emprentas | 2 |
| 37121 | emprendiese | 2 |
| 37122 | emprendían | 2 |
| 37123 | empotrados | 2 |
| 37124 | emporio | 2 |
| 37125 | empolla | 2 |
| 37126 | emplumada | 2 |
| 37127 | emplearán | 2 |
| 37128 | empleará | 2 |
| 37129 | empirismo | 2 |
| 37130 | empinados | 2 |
| 37131 | empinado | 2 |
| 37132 | empinadas | 2 |
| 37133 | empida | 2 |
| 37134 | empezaré | 2 |
| 37135 | empezada | 2 |
| 37136 | emperifollada | 2 |
| 37137 | emperante | 2 |
| 37138 | empequeñecido | 2 |
| 37139 | empeñé | 2 |
| 37140 | empeñará | 2 |
| 37141 | empeñando | 2 |
| 37142 | empecible | 2 |
| 37143 | empecéle | 2 |
| 37144 | empece | 2 |
| 37145 | emparejando | 2 |
| 37146 | emparedado | 2 |
| 37147 | emparedada | 2 |
| 37148 | empaquetados | 2 |
| 37149 | empapada | 2 |
| 37150 | empanadas | 2 |
| 37151 | empanada | 2 |
| 37152 | empalme | 2 |
| 37153 | empalagosos | 2 |
| 37154 | empalagosa | 2 |
| 37155 | empadronamiento | 2 |
| 37156 | empache | 2 |
| 37157 | empachado | 2 |
| 37158 | emisarios | 2 |
| 37159 | eminentemente | 2 |
| 37160 | eminencias | 2 |
| 37161 | emigrar | 2 |
| 37162 | emerencia | 2 |
| 37163 | emendada | 2 |
| 37164 | embutidos | 2 |
| 37165 | embuelto | 2 |
| 37166 | embuelta | 2 |
| 37167 | embrutecía | 2 |
| 37168 | embriagarse | 2 |
| 37169 | embrazado | 2 |
| 37170 | embozarse | 2 |
| 37171 | embozados | 2 |
| 37172 | embozadamente | 2 |
| 37173 | embotan | 2 |
| 37174 | embotado | 2 |
| 37175 | embosque | 2 |
| 37176 | emborronar | 2 |
| 37177 | emborracharon | 2 |
| 37178 | emborrachaban | 2 |
| 37179 | emboquéme | 2 |
| 37180 | embisten | 2 |
| 37181 | embista | 2 |
| 37182 | embió | 2 |
| 37183 | embio | 2 |
| 37184 | embidioso | 2 |
| 37185 | embestirse | 2 |
| 37186 | embestidas | 2 |
| 37187 | embellecía | 2 |
| 37188 | embelesan | 2 |
| 37189 | embelesaba | 2 |
| 37190 | embebecía | 2 |
| 37191 | embaxada | 2 |
| 37192 | embaular | 2 |
| 37193 | embargó | 2 |
| 37194 | embarcarnos | 2 |
| 37195 | embarcarme | 2 |
| 37196 | embarcamos | 2 |
| 37197 | embarcado | 2 |
| 37198 | embarazoso | 2 |
| 37199 | embarazan | 2 |
| 37200 | embajadas | 2 |
| 37201 | embaixos | 2 |
| 37202 | embadurnadas | 2 |
| 37203 | emancipación | 2 |
| 37204 | emanada | 2 |
| 37205 | emanación | 2 |
| 37206 | elogiarle | 2 |
| 37207 | elogiando | 2 |
| 37208 | elogian | 2 |
| 37209 | elocución | 2 |
| 37210 | elle | 2 |
| 37211 | eliso | 2 |
| 37212 | eliminar | 2 |
| 37213 | elevados | 2 |
| 37214 | elegías | 2 |
| 37215 | elegantón | 2 |
| 37216 | elegantísimo | 2 |
| 37217 | elegancias | 2 |
| 37218 | electorales | 2 |
| 37219 | eleción | 2 |
| 37220 | elduayen | 2 |
| 37221 | elástico | 2 |
| 37222 | elaboración | 2 |
| 37223 | ejercitada | 2 |
| 37224 | ejercitaban | 2 |
| 37225 | ejerció | 2 |
| 37226 | ejerciendo | 2 |
| 37227 | ejecutase | 2 |
| 37228 | ejecutaron | 2 |
| 37229 | ejecutando | 2 |
| 37230 | ejecutan | 2 |
| 37231 | egypto | 2 |
| 37232 | egualdad | 2 |
| 37233 | egozcue | 2 |
| 37234 | egoistón | 2 |
| 37235 | ego | 2 |
| 37236 | égloga | 2 |
| 37237 | égida | 2 |
| 37238 | efluvios | 2 |
| 37239 | eficazmente | 2 |
| 37240 | eficacísimo | 2 |
| 37241 | efemérides | 2 |
| 37242 | efectuar | 2 |
| 37243 | efectivos | 2 |
| 37244 | educó | 2 |
| 37245 | educatriz | 2 |
| 37246 | educativas | 2 |
| 37247 | educarla | 2 |
| 37248 | educandas | 2 |
| 37249 | educados | 2 |
| 37250 | edredón | 2 |
| 37251 | edificó | 2 |
| 37252 | edificarse | 2 |
| 37253 | edificando | 2 |
| 37254 | edificada | 2 |
| 37255 | edificaba | 2 |
| 37256 | edifica | 2 |
| 37257 | ed | 2 |
| 37258 | economista | 2 |
| 37259 | eclíptica | 2 |
| 37260 | eclipses | 2 |
| 37261 | eclipsaba | 2 |
| 37262 | echéle | 2 |
| 37263 | echéis | 2 |
| 37264 | echehun | 2 |
| 37265 | echaua | 2 |
| 37266 | échase | 2 |
| 37267 | echártela | 2 |
| 37268 | echársela | 2 |
| 37269 | echarri | 2 |
| 37270 | echarpe | 2 |
| 37271 | echáronse | 2 |
| 37272 | echáronnos | 2 |
| 37273 | echarás | 2 |
| 37274 | echarán | 2 |
| 37275 | echándolos | 2 |
| 37276 | echallo | 2 |
| 37277 | echáis | 2 |
| 37278 | echadito | 2 |
| 37279 | echadas | 2 |
| 37280 | echábaselas | 2 |
| 37281 | echábalo | 2 |
| 37282 | eceto | 2 |
| 37283 | ecce | 2 |
| 37284 | ecbátana | 2 |
| 37285 | ecarté | 2 |
| 37286 | dyme | 2 |
| 37287 | dyeres | 2 |
| 37288 | dyablo | 2 |
| 37289 | durmiesen | 2 |
| 37290 | durmientes | 2 |
| 37291 | durmiéndola | 2 |
| 37292 | durito | 2 |
| 37293 | durísimos | 2 |
| 37294 | durísima | 2 |
| 37295 | durare | 2 |
| 37296 | duplicar | 2 |
| 37297 | duplicado | 2 |
| 37298 | duplicaban | 2 |
| 37299 | dulzona | 2 |
| 37300 | dulzón | 2 |
| 37301 | dulcineas | 2 |
| 37302 | dulçemente | 2 |
| 37303 | duguay | 2 |
| 37304 | dufour | 2 |
| 37305 | duerman | 2 |
| 37306 | duenas | 2 |
| 37307 | dudosas | 2 |
| 37308 | duden | 2 |
| 37309 | dudéis | 2 |
| 37310 | dudarse | 2 |
| 37311 | dudara | 2 |
| 37312 | dudan | 2 |
| 37313 | dúctil | 2 |
| 37314 | dubdas | 2 |
| 37315 | dubdar | 2 |
| 37316 | dubdança | 2 |
| 37317 | dreadnoutgh | 2 |
| 37318 | dragones | 2 |
| 37319 | drago | 2 |
| 37320 | dozenas | 2 |
| 37321 | dotrina | 2 |
| 37322 | dotó | 2 |
| 37323 | dotados | 2 |
| 37324 | dotación | 2 |
| 37325 | doseles | 2 |
| 37326 | dorregaray | 2 |
| 37327 | dornajos | 2 |
| 37328 | dornajo | 2 |
| 37329 | dormitar | 2 |
| 37330 | dormitaban | 2 |
| 37331 | dormitaba | 2 |
| 37332 | dormirla | 2 |
| 37333 | dormiría | 2 |
| 37334 | dormirá | 2 |
| 37335 | dormíos | 2 |
| 37336 | dormilones | 2 |
| 37337 | dormilona | 2 |
| 37338 | dormieron | 2 |
| 37339 | dormidito | 2 |
| 37340 | dormidita | 2 |
| 37341 | dormidas | 2 |
| 37342 | doris | 2 |
| 37343 | dorar | 2 |
| 37344 | dorando | 2 |
| 37345 | doral | 2 |
| 37346 | doñeguil | 2 |
| 37347 | doñea | 2 |
| 37348 | donosura | 2 |
| 37349 | dono | 2 |
| 37350 | donçella | 2 |
| 37351 | donativo | 2 |
| 37352 | domó | 2 |
| 37353 | dominus | 2 |
| 37354 | dominós | 2 |
| 37355 | domingueras | 2 |
| 37356 | dominados | 2 |
| 37357 | domiciliarios | 2 |
| 37358 | domesticos | 2 |
| 37359 | domesticidad | 2 |
| 37360 | domeñar | 2 |
| 37361 | doman | 2 |
| 37362 | domadas | 2 |
| 37363 | doloridos | 2 |
| 37364 | dolió | 2 |
| 37365 | doliese | 2 |
| 37366 | doliendo | 2 |
| 37367 | dolido | 2 |
| 37368 | dolia | 2 |
| 37369 | dolerme | 2 |
| 37370 | doleos | 2 |
| 37371 | dolençias | 2 |
| 37372 | doblo | 2 |
| 37373 | doblega | 2 |
| 37374 | doblan | 2 |
| 37375 | doblados | 2 |
| 37376 | díxoles | 2 |
| 37377 | dixiere | 2 |
| 37378 | dixessen | 2 |
| 37379 | dixesse | 2 |
| 37380 | dixeres | 2 |
| 37381 | dixele | 2 |
| 37382 | divulgar | 2 |
| 37383 | divisoria | 2 |
| 37384 | divisas | 2 |
| 37385 | divisaron | 2 |
| 37386 | divirtió | 2 |
| 37387 | divirtiéndote | 2 |
| 37388 | divirtiendo | 2 |
| 37389 | divinamente | 2 |
| 37390 | divierto | 2 |
| 37391 | diviertas | 2 |
| 37392 | diviertan | 2 |
| 37393 | dividiéndose | 2 |
| 37394 | dividiendo | 2 |
| 37395 | dividen | 2 |
| 37396 | divertirte | 2 |
| 37397 | divertiría | 2 |
| 37398 | divertimos | 2 |
| 37399 | divertimiento | 2 |
| 37400 | divagaciones | 2 |
| 37401 | diuersidad | 2 |
| 37402 | dituzu | 2 |
| 37403 | dite | 2 |
| 37404 | disuadir | 2 |
| 37405 | distritos | 2 |
| 37406 | distrajeron | 2 |
| 37407 | distrajera | 2 |
| 37408 | distraerme | 2 |
| 37409 | distraerle | 2 |
| 37410 | distinguirla | 2 |
| 37411 | distinguíamos | 2 |
| 37412 | distender | 2 |
| 37413 | disputó | 2 |
| 37414 | disputilla | 2 |
| 37415 | disputárselo | 2 |
| 37416 | dispusiese | 2 |
| 37417 | disponían | 2 |
| 37418 | dispongas | 2 |
| 37419 | disponen | 2 |
| 37420 | dispersión | 2 |
| 37421 | dispersado | 2 |
| 37422 | dispensadora | 2 |
| 37423 | disparidad | 2 |
| 37424 | disparé | 2 |
| 37425 | dispararse | 2 |
| 37426 | disparan | 2 |
| 37427 | dispara | 2 |
| 37428 | disonante | 2 |
| 37429 | disolvían | 2 |
| 37430 | disolutos | 2 |
| 37431 | disolución | 2 |
| 37432 | disminuyendo | 2 |
| 37433 | disminuído | 2 |
| 37434 | disloque | 2 |
| 37435 | disipó | 2 |
| 37436 | disinios | 2 |
| 37437 | disimulé | 2 |
| 37438 | disimule | 2 |
| 37439 | disimulase | 2 |
| 37440 | disignios | 2 |
| 37441 | disfruto | 2 |
| 37442 | disfrutan | 2 |
| 37443 | disfrutaban | 2 |
| 37444 | disfruta | 2 |
| 37445 | disfrazar | 2 |
| 37446 | disfrazadas | 2 |
| 37447 | disfrazaba | 2 |
| 37448 | disfamar | 2 |
| 37449 | disertaciones | 2 |
| 37450 | disertaba | 2 |
| 37451 | diselo | 2 |
| 37452 | disecado | 2 |
| 37453 | discutido | 2 |
| 37454 | discurriera | 2 |
| 37455 | discurres | 2 |
| 37456 | discurra | 2 |
| 37457 | disculpen | 2 |
| 37458 | disculparlo | 2 |
| 37459 | disculpan | 2 |
| 37460 | discretísimo | 2 |
| 37461 | discrecional | 2 |
| 37462 | discordias | 2 |
| 37463 | díscola | 2 |
| 37464 | discípula | 2 |
| 37465 | disciplinarias | 2 |
| 37466 | disciplinadas | 2 |
| 37467 | discernimiento | 2 |
| 37468 | discantaba | 2 |
| 37469 | dirija | 2 |
| 37470 | dirigirlos | 2 |
| 37471 | dirigirlo | 2 |
| 37472 | dirigieran | 2 |
| 37473 | diríale | 2 |
| 37474 | diréte | 2 |
| 37475 | diréisle | 2 |
| 37476 | diputó | 2 |
| 37477 | diputación | 2 |
| 37478 | diplomáticas | 2 |
| 37479 | dióselos | 2 |
| 37480 | diósela | 2 |
| 37481 | diosas | 2 |
| 37482 | diónos | 2 |
| 37483 | dióm | 2 |
| 37484 | dióla | 2 |
| 37485 | dintel | 2 |
| 37486 | dinos | 2 |
| 37487 | dino | 2 |
| 37488 | dinerillo | 2 |
| 37489 | dímosle | 2 |
| 37490 | diminutivos | 2 |
| 37491 | diminutivo | 2 |
| 37492 | diminuta | 2 |
| 37493 | dilucidar | 2 |
| 37494 | dilitoria | 2 |
| 37495 | dilexi | 2 |
| 37496 | dilato | 2 |
| 37497 | dilates | 2 |
| 37498 | dilate | 2 |
| 37499 | dilatados | 2 |
| 37500 | dilatación | 2 |
| 37501 | dilataba | 2 |
| 37502 | dilas | 2 |
| 37503 | dila | 2 |
| 37504 | dil | 2 |
| 37505 | díjose | 2 |
| 37506 | dijole | 2 |
| 37507 | díjeles | 2 |
| 37508 | digresión | 2 |
| 37509 | digolo | 2 |
| 37510 | dignísima | 2 |
| 37511 | dignidades | 2 |
| 37512 | dignase | 2 |
| 37513 | dignarse | 2 |
| 37514 | dígasenos | 2 |
| 37515 | dígamelo | 2 |
| 37516 | dígales | 2 |
| 37517 | difuntas | 2 |
| 37518 | difundió | 2 |
| 37519 | difundida | 2 |
| 37520 | difinición | 2 |
| 37521 | difiere | 2 |
| 37522 | dificile | 2 |
| 37523 | differencia | 2 |
| 37524 | diferentemente | 2 |
| 37525 | diferencio | 2 |
| 37526 | diferenciar | 2 |
| 37527 | diferencian | 2 |
| 37528 | diezmos | 2 |
| 37529 | diezmo | 2 |
| 37530 | diestras | 2 |
| 37531 | diestramente | 2 |
| 37532 | dieses | 2 |
| 37533 | diésemos | 2 |
| 37534 | diés | 2 |
| 37535 | diéronsela | 2 |
| 37536 | diéronles | 2 |
| 37537 | dientecillos | 2 |
| 37538 | dieces | 2 |
| 37539 | dictan | 2 |
| 37540 | dictadas | 2 |
| 37541 | dico | 2 |
| 37542 | diciéndote | 2 |
| 37543 | dicermi | 2 |
| 37544 | dicer | 2 |
| 37545 | diccionarios | 2 |
| 37546 | dibujando | 2 |
| 37547 | dibujado | 2 |
| 37548 | dibujada | 2 |
| 37549 | dibujaban | 2 |
| 37550 | diaquilón | 2 |
| 37551 | diantre | 2 |
| 37552 | dianas | 2 |
| 37553 | dïana | 2 |
| 37554 | diamantinos | 2 |
| 37555 | diáfanos | 2 |
| 37556 | dïáfano | 2 |
| 37557 | diáfano | 2 |
| 37558 | diadema | 2 |
| 37559 | diacitron | 2 |
| 37560 | diabro | 2 |
| 37561 | diabólico | 2 |
| 37562 | dezirt | 2 |
| 37563 | dezirme | 2 |
| 37564 | dezían | 2 |
| 37565 | dexistes | 2 |
| 37566 | dexiere | 2 |
| 37567 | dexenme | 2 |
| 37568 | dexemplo | 2 |
| 37569 | dexarle | 2 |
| 37570 | dexarasme | 2 |
| 37571 | déxame | 2 |
| 37572 | dexalos | 2 |
| 37573 | déxalo | 2 |
| 37574 | dexallo | 2 |
| 37575 | dexades | 2 |
| 37576 | dexada | 2 |
| 37577 | dexad | 2 |
| 37578 | devoró | 2 |
| 37579 | devorarle | 2 |
| 37580 | devolviendo | 2 |
| 37581 | devolución | 2 |
| 37582 | devocionarios | 2 |
| 37583 | deviersas | 2 |
| 37584 | deviera | 2 |
| 37585 | devíe | 2 |
| 37586 | deveses | 2 |
| 37587 | devedes | 2 |
| 37588 | devane | 2 |
| 37589 | devanadera | 2 |
| 37590 | devana | 2 |
| 37591 | deuocion | 2 |
| 37592 | deudora | 2 |
| 37593 | deudillas | 2 |
| 37594 | deuanea | 2 |
| 37595 | detyen | 2 |
| 37596 | detúvole | 2 |
| 37597 | detuviesen | 2 |
| 37598 | detuvieran | 2 |
| 37599 | determinose | 2 |
| 37600 | determinante | 2 |
| 37601 | determinándose | 2 |
| 37602 | determinando | 2 |
| 37603 | deteniéndola | 2 |
| 37604 | detenidos | 2 |
| 37605 | deteníase | 2 |
| 37606 | detengas | 2 |
| 37607 | detenerlo | 2 |
| 37608 | detenemos | 2 |
| 37609 | detenéis | 2 |
| 37610 | detalladas | 2 |
| 37611 | detalladamente | 2 |
| 37612 | desyr | 2 |
| 37613 | desvíate | 2 |
| 37614 | desviaron | 2 |
| 37615 | desviarle | 2 |
| 37616 | desviándose | 2 |
| 37617 | desviadas | 2 |
| 37618 | desviaban | 2 |
| 37619 | desvergonzados | 2 |
| 37620 | desvergonzadas | 2 |
| 37621 | desvencijado | 2 |
| 37622 | desvela | 2 |
| 37623 | desvariados | 2 |
| 37624 | desvariadas | 2 |
| 37625 | desvanes | 2 |
| 37626 | desvalijando | 2 |
| 37627 | desvalijado | 2 |
| 37628 | desusados | 2 |
| 37629 | desunció | 2 |
| 37630 | desuelle | 2 |
| 37631 | destruyr | 2 |
| 37632 | destruyese | 2 |
| 37633 | destruirme | 2 |
| 37634 | destruirlo | 2 |
| 37635 | destruido | 2 |
| 37636 | destruía | 2 |
| 37637 | destrozando | 2 |
| 37638 | destrozados | 2 |
| 37639 | destrozada | 2 |
| 37640 | destornillada | 2 |
| 37641 | destituir | 2 |
| 37642 | destituído | 2 |
| 37643 | destitución | 2 |
| 37644 | destinillo | 2 |
| 37645 | destina | 2 |
| 37646 | destilando | 2 |
| 37647 | destilación | 2 |
| 37648 | destilaban | 2 |
| 37649 | destilaba | 2 |
| 37650 | destierros | 2 |
| 37651 | destierran | 2 |
| 37652 | desterrando | 2 |
| 37653 | desterrada | 2 |
| 37654 | desteñido | 2 |
| 37655 | destartaladas | 2 |
| 37656 | destapaba | 2 |
| 37657 | destaja | 2 |
| 37658 | destacó | 2 |
| 37659 | destacarse | 2 |
| 37660 | desseas | 2 |
| 37661 | desseado | 2 |
| 37662 | dessas | 2 |
| 37663 | dessa | 2 |
| 37664 | desquitarse | 2 |
| 37665 | desquiciada | 2 |
| 37666 | despuntes | 2 |
| 37667 | despuntan | 2 |
| 37668 | despuntaba | 2 |
| 37669 | despuelas | 2 |
| 37670 | desprovista | 2 |
| 37671 | desproporcionadas | 2 |
| 37672 | despreocupados | 2 |
| 37673 | desprendió | 2 |
| 37674 | desprendiese | 2 |
| 37675 | desprendía | 2 |
| 37676 | desprenderme | 2 |
| 37677 | desprenden | 2 |
| 37678 | desprecios | 2 |
| 37679 | desprecies | 2 |
| 37680 | desprecié | 2 |
| 37681 | despreciarle | 2 |
| 37682 | despreciará | 2 |
| 37683 | despreciara | 2 |
| 37684 | despotricar | 2 |
| 37685 | despose | 2 |
| 37686 | desposarte | 2 |
| 37687 | desposarse | 2 |
| 37688 | desposar | 2 |
| 37689 | despojó | 2 |
| 37690 | desplumar | 2 |
| 37691 | desplumaban | 2 |
| 37692 | desplomose | 2 |
| 37693 | desplome | 2 |
| 37694 | despliega | 2 |
| 37695 | despintado | 2 |
| 37696 | despintadas | 2 |
| 37697 | despiértele | 2 |
| 37698 | despiertas | 2 |
| 37699 | despidióse | 2 |
| 37700 | despidiente | 2 |
| 37701 | despídase | 2 |
| 37702 | despidámonos | 2 |
| 37703 | despertamos | 2 |
| 37704 | despertadora | 2 |
| 37705 | desperta | 2 |
| 37706 | despernado | 2 |
| 37707 | desperezos | 2 |
| 37708 | desperezarse | 2 |
| 37709 | despereza | 2 |
| 37710 | desperdiciar | 2 |
| 37711 | desperdiciado | 2 |
| 37712 | despeñó | 2 |
| 37713 | despeñarse | 2 |
| 37714 | despeñar | 2 |
| 37715 | despeñadero | 2 |
| 37716 | despeñaba | 2 |
| 37717 | despeña | 2 |
| 37718 | despellejar | 2 |
| 37719 | despejan | 2 |
| 37720 | despeinada | 2 |
| 37721 | despegado | 2 |
| 37722 | despedirlos | 2 |
| 37723 | despedió | 2 |
| 37724 | despedazar | 2 |
| 37725 | despechéis | 2 |
| 37726 | despartir | 2 |
| 37727 | desparramados | 2 |
| 37728 | despachos | 2 |
| 37729 | despácheme | 2 |
| 37730 | despachase | 2 |
| 37731 | despachara | 2 |
| 37732 | despachan | 2 |
| 37733 | despachaderas | 2 |
| 37734 | despabiló | 2 |
| 37735 | despabilo | 2 |
| 37736 | despabile | 2 |
| 37737 | despabilarme | 2 |
| 37738 | despabilándose | 2 |
| 37739 | despabilada | 2 |
| 37740 | desollado | 2 |
| 37741 | desocupadas | 2 |
| 37742 | desnudando | 2 |
| 37743 | desmoronar | 2 |
| 37744 | desmorona | 2 |
| 37745 | desmoralizados | 2 |
| 37746 | desmintió | 2 |
| 37747 | desmintiendo | 2 |
| 37748 | desmenuzadas | 2 |
| 37749 | desmentirse | 2 |
| 37750 | desmentirle | 2 |
| 37751 | desmentiría | 2 |
| 37752 | desmentirá | 2 |
| 37753 | desmentido | 2 |
| 37754 | desmelenada | 2 |
| 37755 | desmazalado | 2 |
| 37756 | desmayes | 2 |
| 37757 | desmaye | 2 |
| 37758 | desmayadas | 2 |
| 37759 | desmantelados | 2 |
| 37760 | desmande | 2 |
| 37761 | desmandarse | 2 |
| 37762 | desmandada | 2 |
| 37763 | desmanda | 2 |
| 37764 | deslumbrantes | 2 |
| 37765 | deslumbran | 2 |
| 37766 | deslumbrador | 2 |
| 37767 | deslumbrada | 2 |
| 37768 | deslucían | 2 |
| 37769 | deslocado | 2 |
| 37770 | deslizose | 2 |
| 37771 | deslizaron | 2 |
| 37772 | deslicen | 2 |
| 37773 | desliáronle | 2 |
| 37774 | desleían | 2 |
| 37775 | desleal | 2 |
| 37776 | desistiese | 2 |
| 37777 | desirme | 2 |
| 37778 | desinteresados | 2 |
| 37779 | desinteresadamente | 2 |
| 37780 | desimos | 2 |
| 37781 | desilusionó | 2 |
| 37782 | desildo | 2 |
| 37783 | desilde | 2 |
| 37784 | designación | 2 |
| 37785 | desíe | 2 |
| 37786 | desidme | 2 |
| 37787 | desidia | 2 |
| 37788 | desídesme | 2 |
| 37789 | deshonroso | 2 |
| 37790 | deshonró | 2 |
| 37791 | deshonras | 2 |
| 37792 | deshonran | 2 |
| 37793 | deshonraba | 2 |
| 37794 | deshonesto | 2 |
| 37795 | deshonestidades | 2 |
| 37796 | deshonestidad | 2 |
| 37797 | deshilachados | 2 |
| 37798 | deshilachado | 2 |
| 37799 | deshielo | 2 |
| 37800 | deshiciéronse | 2 |
| 37801 | deshechos | 2 |
| 37802 | deshaciéndose | 2 |
| 37803 | deshacerle | 2 |
| 37804 | desgreñado | 2 |
| 37805 | desgreñada | 2 |
| 37806 | desgastadas | 2 |
| 37807 | desgarrarse | 2 |
| 37808 | desgarrado | 2 |
| 37809 | desgarradas | 2 |
| 37810 | desgarraba | 2 |
| 37811 | desgarbado | 2 |
| 37812 | desganada | 2 |
| 37813 | desgana | 2 |
| 37814 | desgajaba | 2 |
| 37815 | desfloren | 2 |
| 37816 | desflorar | 2 |
| 37817 | desflorando | 2 |
| 37818 | desfile | 2 |
| 37819 | desfilar | 2 |
| 37820 | desfilando | 2 |
| 37821 | desfilaban | 2 |
| 37822 | desfigurar | 2 |
| 37823 | desfigurando | 2 |
| 37824 | desfiguradas | 2 |
| 37825 | desfiguraba | 2 |
| 37826 | desfecho | 2 |
| 37827 | desfavorecido | 2 |
| 37828 | desfallecimiento | 2 |
| 37829 | desfallecía | 2 |
| 37830 | desfallecer | 2 |
| 37831 | desfaciendo | 2 |
| 37832 | desfachatada | 2 |
| 37833 | desesperó | 2 |
| 37834 | desespero | 2 |
| 37835 | desespérese | 2 |
| 37836 | desesperes | 2 |
| 37837 | desesperarme | 2 |
| 37838 | desesperaban | 2 |
| 37839 | desequilibrio | 2 |
| 37840 | desenvuelve | 2 |
| 37841 | desenvueltas | 2 |
| 37842 | desenvolturas | 2 |
| 37843 | desenvainadas | 2 |
| 37844 | desentonar | 2 |
| 37845 | desenterradas | 2 |
| 37846 | desengañó | 2 |
| 37847 | desengañen | 2 |
| 37848 | desengañados | 2 |
| 37849 | desengañadas | 2 |
| 37850 | desengañada | 2 |
| 37851 | desenganchar | 2 |
| 37852 | desenfreno | 2 |
| 37853 | desenfrenada | 2 |
| 37854 | desencantó | 2 |
| 37855 | desencante | 2 |
| 37856 | desencantase | 2 |
| 37857 | desencantados | 2 |
| 37858 | desencajó | 2 |
| 37859 | desencajaron | 2 |
| 37860 | desencajados | 2 |
| 37861 | desempeñarla | 2 |
| 37862 | desembuchaba | 2 |
| 37863 | desembozándose | 2 |
| 37864 | desembolsó | 2 |
| 37865 | desembolsase | 2 |
| 37866 | desembarco | 2 |
| 37867 | desembarcado | 2 |
| 37868 | desembarcadero | 2 |
| 37869 | desembarazo | 2 |
| 37870 | deseches | 2 |
| 37871 | desecharla | 2 |
| 37872 | desecharán | 2 |
| 37873 | desechado | 2 |
| 37874 | desechadas | 2 |
| 37875 | desearme | 2 |
| 37876 | desearle | 2 |
| 37877 | desearla | 2 |
| 37878 | desdigo | 2 |
| 37879 | desdice | 2 |
| 37880 | desdeñosas | 2 |
| 37881 | desdeñarse | 2 |
| 37882 | desdeñando | 2 |
| 37883 | descumunión | 2 |
| 37884 | descuidillo | 2 |
| 37885 | descuidar | 2 |
| 37886 | descuidaban | 2 |
| 37887 | descuelgas | 2 |
| 37888 | descubrirlo | 2 |
| 37889 | descubriría | 2 |
| 37890 | descubriremos | 2 |
| 37891 | descubrimientos | 2 |
| 37892 | descubrillo | 2 |
| 37893 | descubriesse | 2 |
| 37894 | descubriésemos | 2 |
| 37895 | descubriéndose | 2 |
| 37896 | descubríamos | 2 |
| 37897 | descúbrese | 2 |
| 37898 | descubran | 2 |
| 37899 | descuartizar | 2 |
| 37900 | descrita | 2 |
| 37901 | descripciones | 2 |
| 37902 | describirse | 2 |
| 37903 | describirlo | 2 |
| 37904 | descreimiento | 2 |
| 37905 | descreídos | 2 |
| 37906 | descoyuntado | 2 |
| 37907 | descosiese | 2 |
| 37908 | descortesía | 2 |
| 37909 | descorteses | 2 |
| 37910 | descortes | 2 |
| 37911 | descorrido | 2 |
| 37912 | descorazonado | 2 |
| 37913 | descontente | 2 |
| 37914 | descontentamiento | 2 |
| 37915 | descontar | 2 |
| 37916 | desconsuelos | 2 |
| 37917 | desconsolados | 2 |
| 37918 | desconsolador | 2 |
| 37919 | desconocidos | 2 |
| 37920 | desconoces | 2 |
| 37921 | desconocer | 2 |
| 37922 | desconfie | 2 |
| 37923 | desconfías | 2 |
| 37924 | desconfiado | 2 |
| 37925 | desconciertos | 2 |
| 37926 | desconcertados | 2 |
| 37927 | descomulgados | 2 |
| 37928 | descompuso | 2 |
| 37929 | descompusiera | 2 |
| 37930 | descomposición | 2 |
| 37931 | descomponían | 2 |
| 37932 | descomedimiento | 2 |
| 37933 | descoloridos | 2 |
| 37934 | descolgarlos | 2 |
| 37935 | descolgándose | 2 |
| 37936 | descolgado | 2 |
| 37937 | descobriria | 2 |
| 37938 | descobria | 2 |
| 37939 | descienden | 2 |
| 37940 | descastada | 2 |
| 37941 | descarriado | 2 |
| 37942 | descarriadas | 2 |
| 37943 | descarnados | 2 |
| 37944 | descansos | 2 |
| 37945 | descansó | 2 |
| 37946 | descanses | 2 |
| 37947 | descansemos | 2 |
| 37948 | descansase | 2 |
| 37949 | descansará | 2 |
| 37950 | descansan | 2 |
| 37951 | descansados | 2 |
| 37952 | descansad | 2 |
| 37953 | descansaban | 2 |
| 37954 | descalabrar | 2 |
| 37955 | descalabrados | 2 |
| 37956 | descabezando | 2 |
| 37957 | descabezado | 2 |
| 37958 | descabellada | 2 |
| 37959 | desbordarse | 2 |
| 37960 | desbordaban | 2 |
| 37961 | desbarató | 2 |
| 37962 | desbaratarse | 2 |
| 37963 | desbaratando | 2 |
| 37964 | desbaratada | 2 |
| 37965 | desbarata | 2 |
| 37966 | desbandada | 2 |
| 37967 | desayuné | 2 |
| 37968 | desayunar | 2 |
| 37969 | desavenidos | 2 |
| 37970 | desatinadas | 2 |
| 37971 | desatina | 2 |
| 37972 | desatender | 2 |
| 37973 | desaté | 2 |
| 37974 | desate | 2 |
| 37975 | desatando | 2 |
| 37976 | desatacarse | 2 |
| 37977 | desasosiegos | 2 |
| 37978 | desaseado | 2 |
| 37979 | desas | 2 |
| 37980 | desarrollada | 2 |
| 37981 | desarreglos | 2 |
| 37982 | desarraigar | 2 |
| 37983 | desarmaron | 2 |
| 37984 | desarmar | 2 |
| 37985 | desarmando | 2 |
| 37986 | desarbolados | 2 |
| 37987 | desapercebido | 2 |
| 37988 | desapasionado | 2 |
| 37989 | desaparezca | 2 |
| 37990 | desapareciera | 2 |
| 37991 | desapareciendo | 2 |
| 37992 | desapacibles | 2 |
| 37993 | desandar | 2 |
| 37994 | desamar | 2 |
| 37995 | desalmada | 2 |
| 37996 | desahogos | 2 |
| 37997 | desahogó | 2 |
| 37998 | desahogadamente | 2 |
| 37999 | desagravios | 2 |
| 38000 | desagravio | 2 |
| 38001 | desagradecidos | 2 |
| 38002 | desafuero | 2 |
| 38003 | desafióme | 2 |
| 38004 | desafio | 2 |
| 38005 | desafinado | 2 |
| 38006 | desafiedes | 2 |
| 38007 | desafiase | 2 |
| 38008 | desafiador | 2 |
| 38009 | desafiaban | 2 |
| 38010 | desacuerdo | 2 |
| 38011 | desacredito | 2 |
| 38012 | desacreditado | 2 |
| 38013 | desacordadas | 2 |
| 38014 | desacompanada | 2 |
| 38015 | desabrimientos | 2 |
| 38016 | desabrigado | 2 |
| 38017 | derrumbadero | 2 |
| 38018 | derrumbaba | 2 |
| 38019 | derroteros | 2 |
| 38020 | derrocar | 2 |
| 38021 | derribarse | 2 |
| 38022 | derribarle | 2 |
| 38023 | derriban | 2 |
| 38024 | derretía | 2 |
| 38025 | derrengada | 2 |
| 38026 | derramóse | 2 |
| 38027 | derramo | 2 |
| 38028 | derrámasele | 2 |
| 38029 | derramarse | 2 |
| 38030 | derivan | 2 |
| 38031 | derivados | 2 |
| 38032 | derivado | 2 |
| 38033 | deriva | 2 |
| 38034 | depurar | 2 |
| 38035 | depreciación | 2 |
| 38036 | depravada | 2 |
| 38037 | depravación | 2 |
| 38038 | depositaría | 2 |
| 38039 | depositados | 2 |
| 38040 | depositaba | 2 |
| 38041 | deponer | 2 |
| 38042 | deplorar | 2 |
| 38043 | deplorando | 2 |
| 38044 | dependiese | 2 |
| 38045 | dependen | 2 |
| 38046 | departyr | 2 |
| 38047 | departiendo | 2 |
| 38048 | depararme | 2 |
| 38049 | deparara | 2 |
| 38050 | denuncias | 2 |
| 38051 | denuestan | 2 |
| 38052 | denso | 2 |
| 38053 | densidad | 2 |
| 38054 | denostadas | 2 |
| 38055 | denodado | 2 |
| 38056 | denodadamente | 2 |
| 38057 | dénle | 2 |
| 38058 | dengoso | 2 |
| 38059 | dengosa | 2 |
| 38060 | denegación | 2 |
| 38061 | demudar | 2 |
| 38062 | demudada | 2 |
| 38063 | demostrarlo | 2 |
| 38064 | démosle | 2 |
| 38065 | démonos | 2 |
| 38066 | democrático | 2 |
| 38067 | demócratas | 2 |
| 38068 | demócrata | 2 |
| 38069 | deméritos | 2 |
| 38070 | demandes | 2 |
| 38071 | demande | 2 |
| 38072 | demandase | 2 |
| 38073 | demandare | 2 |
| 38074 | demandaba | 2 |
| 38075 | demagogo | 2 |
| 38076 | demagógica | 2 |
| 38077 | delirios | 2 |
| 38078 | deliquio | 2 |
| 38079 | delineantes | 2 |
| 38080 | deliciosos | 2 |
| 38081 | deliberemos | 2 |
| 38082 | deliberado | 2 |
| 38083 | deliberacion | 2 |
| 38084 | delgadísimo | 2 |
| 38085 | delfines | 2 |
| 38086 | deleznable | 2 |
| 38087 | deleytoso | 2 |
| 38088 | deleytosas | 2 |
| 38089 | deleytosa | 2 |
| 38090 | deleytava | 2 |
| 38091 | deleiten | 2 |
| 38092 | deleitan | 2 |
| 38093 | deleitable | 2 |
| 38094 | delegado | 2 |
| 38095 | delectable | 2 |
| 38096 | déle | 2 |
| 38097 | delaciones | 2 |
| 38098 | dejosas | 2 |
| 38099 | dejóle | 2 |
| 38100 | dejóla | 2 |
| 38101 | déjense | 2 |
| 38102 | déjenle | 2 |
| 38103 | dejémoslos | 2 |
| 38104 | dejémoslo | 2 |
| 38105 | déjelo | 2 |
| 38106 | dejéle | 2 |
| 38107 | dejarían | 2 |
| 38108 | dejaréis | 2 |
| 38109 | dejaras | 2 |
| 38110 | dejáramos | 2 |
| 38111 | dejárame | 2 |
| 38112 | déjanse | 2 |
| 38113 | déjanos | 2 |
| 38114 | dejándolo | 2 |
| 38115 | dejándoles | 2 |
| 38116 | dejallos | 2 |
| 38117 | déjales | 2 |
| 38118 | dejados | 2 |
| 38119 | dejadas | 2 |
| 38120 | dejada | 2 |
| 38121 | degollando | 2 |
| 38122 | degollada | 2 |
| 38123 | degenerar | 2 |
| 38124 | degeneración | 2 |
| 38125 | defuntos | 2 |
| 38126 | defraudar | 2 |
| 38127 | defraudando | 2 |
| 38128 | definiendo | 2 |
| 38129 | definido | 2 |
| 38130 | definida | 2 |
| 38131 | deficiencias | 2 |
| 38132 | deffiende | 2 |
| 38133 | deffendimiento | 2 |
| 38134 | defetos | 2 |
| 38135 | defensiones | 2 |
| 38136 | defendiera | 2 |
| 38137 | defenderte | 2 |
| 38138 | defenderos | 2 |
| 38139 | defendernos | 2 |
| 38140 | defenderlas | 2 |
| 38141 | defenderás | 2 |
| 38142 | defendays | 2 |
| 38143 | deducía | 2 |
| 38144 | deditos | 2 |
| 38145 | dedito | 2 |
| 38146 | dedico | 2 |
| 38147 | dédalo | 2 |
| 38148 | dedalo | 2 |
| 38149 | decretó | 2 |
| 38150 | decrépita | 2 |
| 38151 | decorativas | 2 |
| 38152 | decorar | 2 |
| 38153 | declinar | 2 |
| 38154 | declaréle | 2 |
| 38155 | declarasen | 2 |
| 38156 | declaras | 2 |
| 38157 | declararnos | 2 |
| 38158 | declararlo | 2 |
| 38159 | declararle | 2 |
| 38160 | declararé | 2 |
| 38161 | declarador | 2 |
| 38162 | declamatorio | 2 |
| 38163 | declamado | 2 |
| 38164 | declamaciones | 2 |
| 38165 | declamación | 2 |
| 38166 | decisiva | 2 |
| 38167 | decírtelo | 2 |
| 38168 | décimos | 2 |
| 38169 | decillas | 2 |
| 38170 | decildes | 2 |
| 38171 | decienden | 2 |
| 38172 | deciende | 2 |
| 38173 | decidirme | 2 |
| 38174 | decidirá | 2 |
| 38175 | decidiose | 2 |
| 38176 | decidimos | 2 |
| 38177 | decidí | 2 |
| 38178 | decídete | 2 |
| 38179 | decíanle | 2 |
| 38180 | decendió | 2 |
| 38181 | decendientes | 2 |
| 38182 | decender | 2 |
| 38183 | decendencia | 2 |
| 38184 | decaída | 2 |
| 38185 | debuxo | 2 |
| 38186 | debría | 2 |
| 38187 | débitos | 2 |
| 38188 | debistes | 2 |
| 38189 | debda | 2 |
| 38190 | deban | 2 |
| 38191 | deambulación | 2 |
| 38192 | dávanle | 2 |
| 38193 | dávales | 2 |
| 38194 | daudé | 2 |
| 38195 | dauan | 2 |
| 38196 | datme | 2 |
| 38197 | datilados | 2 |
| 38198 | databa | 2 |
| 38199 | dasme | 2 |
| 38200 | dasle | 2 |
| 38201 | dase | 2 |
| 38202 | darwinista | 2 |
| 38203 | dártelo | 2 |
| 38204 | darrer | 2 |
| 38205 | dárosla | 2 |
| 38206 | dármelos | 2 |
| 38207 | dármelas | 2 |
| 38208 | darinel | 2 |
| 38209 | dapno | 2 |
| 38210 | daos | 2 |
| 38211 | dañosas | 2 |
| 38212 | dañosa | 2 |
| 38213 | dañino | 2 |
| 38214 | dañe | 2 |
| 38215 | dañar | 2 |
| 38216 | dañadores | 2 |
| 38217 | dañado | 2 |
| 38218 | dañaba | 2 |
| 38219 | danzar | 2 |
| 38220 | danubio | 2 |
| 38221 | danosos | 2 |
| 38222 | danles | 2 |
| 38223 | dane | 2 |
| 38224 | dándoselos | 2 |
| 38225 | dándolo | 2 |
| 38226 | dándolas | 2 |
| 38227 | dándola | 2 |
| 38228 | damiselas | 2 |
| 38229 | dámele | 2 |
| 38230 | dámela | 2 |
| 38231 | damascos | 2 |
| 38232 | dam | 2 |
| 38233 | daldes | 2 |
| 38234 | dala | 2 |
| 38235 | dago | 2 |
| 38236 | dadiuas | 2 |
| 38237 | cyerto | 2 |
| 38238 | cuz | 2 |
| 38239 | cuytar | 2 |
| 38240 | cúyos | 2 |
| 38241 | cúyo | 2 |
| 38242 | cuydéme | 2 |
| 38243 | custunbre | 2 |
| 38244 | custodiaba | 2 |
| 38245 | curtis | 2 |
| 38246 | curtida | 2 |
| 38247 | cursilería | 2 |
| 38248 | cursado | 2 |
| 38249 | curis | 2 |
| 38250 | curiambro | 2 |
| 38251 | curiales | 2 |
| 38252 | curé | 2 |
| 38253 | curarte | 2 |
| 38254 | curaron | 2 |
| 38255 | curaré | 2 |
| 38256 | curánganos | 2 |
| 38257 | curándose | 2 |
| 38258 | curándome | 2 |
| 38259 | cupiera | 2 |
| 38260 | cuota | 2 |
| 38261 | cunplidas | 2 |
| 38262 | cundiendo | 2 |
| 38263 | cunde | 2 |
| 38264 | cunas | 2 |
| 38265 | cumplís | 2 |
| 38266 | cumpliré | 2 |
| 38267 | cumplio | 2 |
| 38268 | cumplieron | 2 |
| 38269 | cumpliera | 2 |
| 38270 | cumplidísima | 2 |
| 38271 | cumplidamente | 2 |
| 38272 | cumpleaños | 2 |
| 38273 | cúmplase | 2 |
| 38274 | cumplas | 2 |
| 38275 | cultivando | 2 |
| 38276 | cultas | 2 |
| 38277 | culpo | 2 |
| 38278 | culpes | 2 |
| 38279 | culparle | 2 |
| 38280 | culpables | 2 |
| 38281 | culminantes | 2 |
| 38282 | cuitada | 2 |
| 38283 | cuidé | 2 |
| 38284 | cuidaré | 2 |
| 38285 | cueza | 2 |
| 38286 | cueruo | 2 |
| 38287 | cuerpecito | 2 |
| 38288 | cuentecita | 2 |
| 38289 | cuentame | 2 |
| 38290 | cuéntalos | 2 |
| 38291 | cuéntale | 2 |
| 38292 | cuentale | 2 |
| 38293 | cuelgo | 2 |
| 38294 | cuela | 2 |
| 38295 | cucuruchos | 2 |
| 38296 | cuchillas | 2 |
| 38297 | cuchicheando | 2 |
| 38298 | cuchicheaba | 2 |
| 38299 | cucharones | 2 |
| 38300 | cucharadas | 2 |
| 38301 | cucaña | 2 |
| 38302 | cubrirla | 2 |
| 38303 | cubrióse | 2 |
| 38304 | cubrimos | 2 |
| 38305 | cubriesse | 2 |
| 38306 | cubriera | 2 |
| 38307 | cubriéndola | 2 |
| 38308 | cubríale | 2 |
| 38309 | cubran | 2 |
| 38310 | cubiletes | 2 |
| 38311 | cubilete | 2 |
| 38312 | cúbicos | 2 |
| 38313 | cúbico | 2 |
| 38314 | cuartetos | 2 |
| 38315 | cuarteto | 2 |
| 38316 | cuarterón | 2 |
| 38317 | cuarentena | 2 |
| 38318 | cualsiquiera | 2 |
| 38319 | cualque | 2 |
| 38320 | cuajarones | 2 |
| 38321 | cuajado | 2 |
| 38322 | cuadrote | 2 |
| 38323 | cuadró | 2 |
| 38324 | cuadrito | 2 |
| 38325 | cuadrilátero | 2 |
| 38326 | cuadrada | 2 |
| 38327 | cuadraban | 2 |
| 38328 | cuadernillos | 2 |
| 38329 | cruzarse | 2 |
| 38330 | crujiendo | 2 |
| 38331 | crujidos | 2 |
| 38332 | crujido | 2 |
| 38333 | crudezas | 2 |
| 38334 | crudeza | 2 |
| 38335 | crucifícale | 2 |
| 38336 | cruce | 2 |
| 38337 | cronicones | 2 |
| 38338 | critico | 2 |
| 38339 | criticar | 2 |
| 38340 | criterios | 2 |
| 38341 | criste | 2 |
| 38342 | cristalitos | 2 |
| 38343 | cristalinos | 2 |
| 38344 | crispaba | 2 |
| 38345 | crisóstomo | 2 |
| 38346 | crisol | 2 |
| 38347 | crisálida | 2 |
| 38348 | cris | 2 |
| 38349 | cripta | 2 |
| 38350 | crin | 2 |
| 38351 | criminala | 2 |
| 38352 | crie | 2 |
| 38353 | cribando | 2 |
| 38354 | criba | 2 |
| 38355 | criaturita | 2 |
| 38356 | criase | 2 |
| 38357 | criarlos | 2 |
| 38358 | criarle | 2 |
| 38359 | crian | 2 |
| 38360 | criadita | 2 |
| 38361 | criaderos | 2 |
| 38362 | cria | 2 |
| 38363 | creyóle | 2 |
| 38364 | creyeras | 2 |
| 38365 | creyeran | 2 |
| 38366 | cretona | 2 |
| 38367 | cretáceas | 2 |
| 38368 | cretácea | 2 |
| 38369 | crestas | 2 |
| 38370 | crespos | 2 |
| 38371 | crespa | 2 |
| 38372 | crescer | 2 |
| 38373 | cresçe | 2 |
| 38374 | cresce | 2 |
| 38375 | crepúsculos | 2 |
| 38376 | crema | 2 |
| 38377 | creídos | 2 |
| 38378 | creíale | 2 |
| 38379 | creet | 2 |
| 38380 | creerlos | 2 |
| 38381 | creerían | 2 |
| 38382 | créemelo | 2 |
| 38383 | creedes | 2 |
| 38384 | credite | 2 |
| 38385 | creciese | 2 |
| 38386 | crecieron | 2 |
| 38387 | creciera | 2 |
| 38388 | crecería | 2 |
| 38389 | creçen | 2 |
| 38390 | crearía | 2 |
| 38391 | créanme | 2 |
| 38392 | créanlo | 2 |
| 38393 | creamos | 2 |
| 38394 | créamelo | 2 |
| 38395 | creadas | 2 |
| 38396 | creada | 2 |
| 38397 | crasitud | 2 |
| 38398 | crac | 2 |
| 38399 | coz | 2 |
| 38400 | coyunda | 2 |
| 38401 | coytoso | 2 |
| 38402 | coytados | 2 |
| 38403 | coydó | 2 |
| 38404 | coydas | 2 |
| 38405 | coydado | 2 |
| 38406 | coxquillas | 2 |
| 38407 | coxqueas | 2 |
| 38408 | covil | 2 |
| 38409 | covacha | 2 |
| 38410 | coturno | 2 |
| 38411 | cotorrearon | 2 |
| 38412 | cotorras | 2 |
| 38413 | cotidiano | 2 |
| 38414 | costuras | 2 |
| 38415 | costera | 2 |
| 38416 | costeó | 2 |
| 38417 | costeando | 2 |
| 38418 | costaron | 2 |
| 38419 | costarme | 2 |
| 38420 | costaría | 2 |
| 38421 | costaban | 2 |
| 38422 | cossario | 2 |
| 38423 | coso | 2 |
| 38424 | cosméticos | 2 |
| 38425 | cosilla | 2 |
| 38426 | cosieron | 2 |
| 38427 | cosidas | 2 |
| 38428 | cosía | 2 |
| 38429 | cosecheros | 2 |
| 38430 | coscoja | 2 |
| 38431 | corzo | 2 |
| 38432 | coruñas | 2 |
| 38433 | corujedos | 2 |
| 38434 | cortinones | 2 |
| 38435 | cortesanía | 2 |
| 38436 | cortaste | 2 |
| 38437 | cortase | 2 |
| 38438 | cortaría | 2 |
| 38439 | cortaré | 2 |
| 38440 | cortaran | 2 |
| 38441 | cortadoras | 2 |
| 38442 | corruptor | 2 |
| 38443 | corromper | 2 |
| 38444 | corrompe | 2 |
| 38445 | corroe | 2 |
| 38446 | corroboró | 2 |
| 38447 | corroborar | 2 |
| 38448 | corroborando | 2 |
| 38449 | corriesen | 2 |
| 38450 | corriera | 2 |
| 38451 | corrienda | 2 |
| 38452 | corretor | 2 |
| 38453 | corretear | 2 |
| 38454 | correspondido | 2 |
| 38455 | correspondes | 2 |
| 38456 | corresponderle | 2 |
| 38457 | correría | 2 |
| 38458 | corremos | 2 |
| 38459 | correligionario | 2 |
| 38460 | correligionarias | 2 |
| 38461 | corregirla | 2 |
| 38462 | corrediza | 2 |
| 38463 | correderas | 2 |
| 38464 | corred | 2 |
| 38465 | correctos | 2 |
| 38466 | correccional | 2 |
| 38467 | corralón | 2 |
| 38468 | corpulentos | 2 |
| 38469 | corpulentas | 2 |
| 38470 | corpórea | 2 |
| 38471 | corpezuelo | 2 |
| 38472 | corpacho | 2 |
| 38473 | coronó | 2 |
| 38474 | corónicas | 2 |
| 38475 | coronica | 2 |
| 38476 | coronen | 2 |
| 38477 | coronar | 2 |
| 38478 | cornudos | 2 |
| 38479 | cornucopias | 2 |
| 38480 | cornezuelo | 2 |
| 38481 | corizas | 2 |
| 38482 | coriza | 2 |
| 38483 | corifeos | 2 |
| 38484 | coreaban | 2 |
| 38485 | cordobés | 2 |
| 38486 | cordillera | 2 |
| 38487 | cordelería | 2 |
| 38488 | corcovada | 2 |
| 38489 | corbatín | 2 |
| 38490 | corazoncito | 2 |
| 38491 | coquetear | 2 |
| 38492 | coqueteaba | 2 |
| 38493 | copudo | 2 |
| 38494 | coplitas | 2 |
| 38495 | copita | 2 |
| 38496 | copiosísimo | 2 |
| 38497 | copiosas | 2 |
| 38498 | copiosamente | 2 |
| 38499 | copiaba | 2 |
| 38500 | coordinar | 2 |
| 38501 | cooper | 2 |
| 38502 | convulsamente | 2 |
| 38503 | convocando | 2 |
| 38504 | convirtiose | 2 |
| 38505 | convirtiéndose | 2 |
| 38506 | conviniese | 2 |
| 38507 | conviniera | 2 |
| 38508 | conviniendo | 2 |
| 38509 | convincente | 2 |
| 38510 | convierten | 2 |
| 38511 | convidase | 2 |
| 38512 | convidadas | 2 |
| 38513 | convertirían | 2 |
| 38514 | convertimos | 2 |
| 38515 | conversaban | 2 |
| 38516 | conversaba | 2 |
| 38517 | convénzase | 2 |
| 38518 | convenirle | 2 |
| 38519 | convenimos | 2 |
| 38520 | convenible | 2 |
| 38521 | conveníale | 2 |
| 38522 | convendrá | 2 |
| 38523 | convencionalismo | 2 |
| 38524 | convenciera | 2 |
| 38525 | convencerme | 2 |
| 38526 | convencerías | 2 |
| 38527 | convenceré | 2 |
| 38528 | convecino | 2 |
| 38529 | conuierte | 2 |
| 38530 | conuiertan | 2 |
| 38531 | contuso | 2 |
| 38532 | contundente | 2 |
| 38533 | contumaz | 2 |
| 38534 | contrista | 2 |
| 38535 | contrincantes | 2 |
| 38536 | contriçión | 2 |
| 38537 | contribuían | 2 |
| 38538 | contraventanas | 2 |
| 38539 | contratantes | 2 |
| 38540 | contratación | 2 |
| 38541 | contrata | 2 |
| 38542 | contrastes | 2 |
| 38543 | contrastando | 2 |
| 38544 | contrastado | 2 |
| 38545 | contrastaba | 2 |
| 38546 | contraseño | 2 |
| 38547 | contrasentidos | 2 |
| 38548 | contrasentido | 2 |
| 38549 | contrariarme | 2 |
| 38550 | contrariarle | 2 |
| 38551 | contrapuntos | 2 |
| 38552 | contrapeso | 2 |
| 38553 | contramaestres | 2 |
| 38554 | contrahecho | 2 |
| 38555 | contrafuerte | 2 |
| 38556 | contraen | 2 |
| 38557 | contradijo | 2 |
| 38558 | contradictorio | 2 |
| 38559 | contradiciéndole | 2 |
| 38560 | contradice | 2 |
| 38561 | contradezir | 2 |
| 38562 | contradecirse | 2 |
| 38563 | contradecirle | 2 |
| 38564 | contracciones | 2 |
| 38565 | continúo | 2 |
| 38566 | continuemos | 2 |
| 38567 | continuasen | 2 |
| 38568 | continuara | 2 |
| 38569 | continuadamente | 2 |
| 38570 | continúa | 2 |
| 38571 | contingibles | 2 |
| 38572 | continentes | 2 |
| 38573 | contezca | 2 |
| 38574 | contesció | 2 |
| 38575 | contesca | 2 |
| 38576 | contertulios | 2 |
| 38577 | conteras | 2 |
| 38578 | contentóse | 2 |
| 38579 | contentón | 2 |
| 38580 | contenti | 2 |
| 38581 | contentarme | 2 |
| 38582 | contentare | 2 |
| 38583 | contentara | 2 |
| 38584 | contentamiento | 2 |
| 38585 | contentaban | 2 |
| 38586 | contenidos | 2 |
| 38587 | contengo | 2 |
| 38588 | contenga | 2 |
| 38589 | contenerlos | 2 |
| 38590 | contenerla | 2 |
| 38591 | contendor | 2 |
| 38592 | contendiente | 2 |
| 38593 | contemplativa | 2 |
| 38594 | contemplarse | 2 |
| 38595 | contemplándole | 2 |
| 38596 | contemplaciones | 2 |
| 38597 | contéle | 2 |
| 38598 | conteçe | 2 |
| 38599 | contártelo | 2 |
| 38600 | contarlos | 2 |
| 38601 | contándonos | 2 |
| 38602 | contalle | 2 |
| 38603 | contáis | 2 |
| 38604 | contagiosa | 2 |
| 38605 | contagiada | 2 |
| 38606 | consygo | 2 |
| 38607 | consuno | 2 |
| 38608 | consumos | 2 |
| 38609 | consumidos | 2 |
| 38610 | consumidor | 2 |
| 38611 | consumaría | 2 |
| 38612 | consumada | 2 |
| 38613 | consultó | 2 |
| 38614 | consulté | 2 |
| 38615 | consultarme | 2 |
| 38616 | consultara | 2 |
| 38617 | consultan | 2 |
| 38618 | consuene | 2 |
| 38619 | constunbres | 2 |
| 38620 | construyendo | 2 |
| 38621 | construye | 2 |
| 38622 | construidos | 2 |
| 38623 | construidas | 2 |
| 38624 | constituyéndose | 2 |
| 38625 | constituidos | 2 |
| 38626 | constituido | 2 |
| 38627 | constituidas | 2 |
| 38628 | constituciones | 2 |
| 38629 | constipar | 2 |
| 38630 | constanza | 2 |
| 38631 | conssolaçión | 2 |
| 38632 | conssejó | 2 |
| 38633 | conssejado | 2 |
| 38634 | conspirando | 2 |
| 38635 | conspiraciones | 2 |
| 38636 | conspiraba | 2 |
| 38637 | consonancia | 2 |
| 38638 | consolóse | 2 |
| 38639 | consolase | 2 |
| 38640 | consolaría | 2 |
| 38641 | consolaré | 2 |
| 38642 | consoladoras | 2 |
| 38643 | consolábase | 2 |
| 38644 | consistió | 2 |
| 38645 | consistiera | 2 |
| 38646 | consistencia | 2 |
| 38647 | consisten | 2 |
| 38648 | consista | 2 |
| 38649 | consiguiese | 2 |
| 38650 | consiguieron | 2 |
| 38651 | consiguen | 2 |
| 38652 | consignados | 2 |
| 38653 | consignado | 2 |
| 38654 | consignada | 2 |
| 38655 | consientes | 2 |
| 38656 | consideren | 2 |
| 38657 | consideras | 2 |
| 38658 | considerarle | 2 |
| 38659 | considerándose | 2 |
| 38660 | consideran | 2 |
| 38661 | consideradas | 2 |
| 38662 | considerábase | 2 |
| 38663 | conservó | 2 |
| 38664 | conservatorio | 2 |
| 38665 | conservándose | 2 |
| 38666 | conservadores | 2 |
| 38667 | conservadora | 2 |
| 38668 | conservada | 2 |
| 38669 | conserue | 2 |
| 38670 | conserua | 2 |
| 38671 | consentyr | 2 |
| 38672 | consentimos | 2 |
| 38673 | consentí | 2 |
| 38674 | consejaua | 2 |
| 38675 | conseguirle | 2 |
| 38676 | conseguían | 2 |
| 38677 | consecutivos | 2 |
| 38678 | consagro | 2 |
| 38679 | consagré | 2 |
| 38680 | consagrando | 2 |
| 38681 | conquisto | 2 |
| 38682 | conquistaron | 2 |
| 38683 | conquistaba | 2 |
| 38684 | conpusiçión | 2 |
| 38685 | conpuesta | 2 |
| 38686 | conpradme | 2 |
| 38687 | conpletas | 2 |
| 38688 | conplado | 2 |
| 38689 | conpañon | 2 |
| 38690 | conpanía | 2 |
| 38691 | conosco | 2 |
| 38692 | conosciendo | 2 |
| 38693 | conosçí | 2 |
| 38694 | conosçen | 2 |
| 38695 | conortan | 2 |
| 38696 | conorta | 2 |
| 38697 | conociste | 2 |
| 38698 | conocíle | 2 |
| 38699 | conociesen | 2 |
| 38700 | conocierle | 2 |
| 38701 | conociéramos | 2 |
| 38702 | conociéndola | 2 |
| 38703 | conocíamos | 2 |
| 38704 | conoceros | 2 |
| 38705 | conocerían | 2 |
| 38706 | conoceré | 2 |
| 38707 | conocerás | 2 |
| 38708 | conocéis | 2 |
| 38709 | connusco | 2 |
| 38710 | connaturalizada | 2 |
| 38711 | conmueve | 2 |
| 38712 | conmovedora | 2 |
| 38713 | conmovedor | 2 |
| 38714 | conjurote | 2 |
| 38715 | conjuran | 2 |
| 38716 | conjurados | 2 |
| 38717 | conjuraban | 2 |
| 38718 | conjeturar | 2 |
| 38719 | congregado | 2 |
| 38720 | congoxoso | 2 |
| 38721 | congoxes | 2 |
| 38722 | congojoso | 2 |
| 38723 | congo | 2 |
| 38724 | congestión | 2 |
| 38725 | congénita | 2 |
| 38726 | congéneres | 2 |
| 38727 | confundo | 2 |
| 38728 | confundirla | 2 |
| 38729 | confundió | 2 |
| 38730 | confundieron | 2 |
| 38731 | confundieran | 2 |
| 38732 | confundiendo | 2 |
| 38733 | confundan | 2 |
| 38734 | confundamos | 2 |
| 38735 | confuerto | 2 |
| 38736 | confortante | 2 |
| 38737 | confortable | 2 |
| 38738 | conforta | 2 |
| 38739 | confort | 2 |
| 38740 | conformas | 2 |
| 38741 | confiscalles | 2 |
| 38742 | confirmase | 2 |
| 38743 | confirmado | 2 |
| 38744 | confirmada | 2 |
| 38745 | confirmábase | 2 |
| 38746 | confín | 2 |
| 38747 | confiesso | 2 |
| 38748 | confiéselo | 2 |
| 38749 | confiésamelo | 2 |
| 38750 | confidentes | 2 |
| 38751 | confiaron | 2 |
| 38752 | confianzuda | 2 |
| 38753 | confiaban | 2 |
| 38754 | confeso | 2 |
| 38755 | confesé | 2 |
| 38756 | confesata | 2 |
| 38757 | confesase | 2 |
| 38758 | confesaron | 2 |
| 38759 | confesáis | 2 |
| 38760 | confecciones | 2 |
| 38761 | confeccionar | 2 |
| 38762 | confección | 2 |
| 38763 | confadre | 2 |
| 38764 | conductos | 2 |
| 38765 | conducirse | 2 |
| 38766 | conducirlo | 2 |
| 38767 | conduciendo | 2 |
| 38768 | conducidas | 2 |
| 38769 | condoliéndose | 2 |
| 38770 | condolido | 2 |
| 38771 | condiscípulos | 2 |
| 38772 | condiscípulo | 2 |
| 38773 | condescendiente | 2 |
| 38774 | condescendencias | 2 |
| 38775 | condensaba | 2 |
| 38776 | condensa | 2 |
| 38777 | condenarse | 2 |
| 38778 | condenación | 2 |
| 38779 | condecoraciones | 2 |
| 38780 | concurrida | 2 |
| 38781 | conculcado | 2 |
| 38782 | concubinato | 2 |
| 38783 | concubina | 2 |
| 38784 | concretamente | 2 |
| 38785 | concordando | 2 |
| 38786 | concordaba | 2 |
| 38787 | concomiéndose | 2 |
| 38788 | concluydo | 2 |
| 38789 | concluyamos | 2 |
| 38790 | conclusyón | 2 |
| 38791 | concluirse | 2 |
| 38792 | concluidas | 2 |
| 38793 | concluída | 2 |
| 38794 | concluí | 2 |
| 38795 | concilios | 2 |
| 38796 | conciliadora | 2 |
| 38797 | conciliábulos | 2 |
| 38798 | conciliábulo | 2 |
| 38799 | conciliaba | 2 |
| 38800 | conciertan | 2 |
| 38801 | conçiençia | 2 |
| 38802 | conçiença | 2 |
| 38803 | concibió | 2 |
| 38804 | concetos | 2 |
| 38805 | concertáronse | 2 |
| 38806 | concertar | 2 |
| 38807 | concepciones | 2 |
| 38808 | concediesse | 2 |
| 38809 | concediendo | 2 |
| 38810 | concedérsele | 2 |
| 38811 | concebida | 2 |
| 38812 | cóncavos | 2 |
| 38813 | concausas | 2 |
| 38814 | concatenación | 2 |
| 38815 | conbides | 2 |
| 38816 | comyençan | 2 |
| 38817 | comunicárselo | 2 |
| 38818 | comunicaron | 2 |
| 38819 | comunicaré | 2 |
| 38820 | comunicada | 2 |
| 38821 | comunicable | 2 |
| 38822 | comunales | 2 |
| 38823 | comulgaría | 2 |
| 38824 | comulgan | 2 |
| 38825 | comulgaba | 2 |
| 38826 | comulga | 2 |
| 38827 | cómputo | 2 |
| 38828 | compusiera | 2 |
| 38829 | compungida | 2 |
| 38830 | compromisario | 2 |
| 38831 | comprometiéndose | 2 |
| 38832 | comprometerle | 2 |
| 38833 | comprometerla | 2 |
| 38834 | comprometas | 2 |
| 38835 | comprimió | 2 |
| 38836 | comprimiéndose | 2 |
| 38837 | comprimido | 2 |
| 38838 | comprimidas | 2 |
| 38839 | comprimida | 2 |
| 38840 | comprendimos | 2 |
| 38841 | comprenderlo | 2 |
| 38842 | comprenderla | 2 |
| 38843 | comprenderías | 2 |
| 38844 | comprenderían | 2 |
| 38845 | comprenderás | 2 |
| 38846 | compremos | 2 |
| 38847 | compraste | 2 |
| 38848 | comprase | 2 |
| 38849 | comprárselo | 2 |
| 38850 | comprarse | 2 |
| 38851 | compraría | 2 |
| 38852 | compraran | 2 |
| 38853 | compradora | 2 |
| 38854 | compota | 2 |
| 38855 | componíase | 2 |
| 38856 | componerse | 2 |
| 38857 | componerme | 2 |
| 38858 | componendas | 2 |
| 38859 | compondría | 2 |
| 38860 | compondrá | 2 |
| 38861 | complidos | 2 |
| 38862 | completas | 2 |
| 38863 | completando | 2 |
| 38864 | completan | 2 |
| 38865 | completado | 2 |
| 38866 | complejas | 2 |
| 38867 | complazer | 2 |
| 38868 | complacerla | 2 |
| 38869 | complacencias | 2 |
| 38870 | complacemos | 2 |
| 38871 | competidoras | 2 |
| 38872 | competentes | 2 |
| 38873 | compensara | 2 |
| 38874 | compensación | 2 |
| 38875 | compensaban | 2 |
| 38876 | compatibles | 2 |
| 38877 | compasivos | 2 |
| 38878 | compasivas | 2 |
| 38879 | compartido | 2 |
| 38880 | compartía | 2 |
| 38881 | comparsa | 2 |
| 38882 | comparolo | 2 |
| 38883 | compareció | 2 |
| 38884 | comparan | 2 |
| 38885 | comparaban | 2 |
| 38886 | compadezco | 2 |
| 38887 | compadecidos | 2 |
| 38888 | compadecían | 2 |
| 38889 | compadecerle | 2 |
| 38890 | compadecer | 2 |
| 38891 | compacto | 2 |
| 38892 | compactas | 2 |
| 38893 | comodón | 2 |
| 38894 | cómodas | 2 |
| 38895 | comm | 2 |
| 38896 | cómitre | 2 |
| 38897 | comisuras | 2 |
| 38898 | comiso | 2 |
| 38899 | comisionista | 2 |
| 38900 | comino | 2 |
| 38901 | comienzas | 2 |
| 38902 | comiences | 2 |
| 38903 | comíe | 2 |
| 38904 | comezones | 2 |
| 38905 | cometida | 2 |
| 38906 | cometí | 2 |
| 38907 | comérselas | 2 |
| 38908 | comeros | 2 |
| 38909 | comerlos | 2 |
| 38910 | comerlo | 2 |
| 38911 | comerlas | 2 |
| 38912 | comerla | 2 |
| 38913 | comerías | 2 |
| 38914 | comercios | 2 |
| 38915 | comercianta | 2 |
| 38916 | comercian | 2 |
| 38917 | comenzóme | 2 |
| 38918 | comenzase | 2 |
| 38919 | comenzara | 2 |
| 38920 | comenzados | 2 |
| 38921 | comentando | 2 |
| 38922 | comentada | 2 |
| 38923 | comentaban | 2 |
| 38924 | comentaba | 2 |
| 38925 | començóle | 2 |
| 38926 | començól | 2 |
| 38927 | començaron | 2 |
| 38928 | coméme | 2 |
| 38929 | comedyr | 2 |
| 38930 | comediante | 2 |
| 38931 | comedianta | 2 |
| 38932 | comedero | 2 |
| 38933 | comed | 2 |
| 38934 | combustión | 2 |
| 38935 | combínense | 2 |
| 38936 | combina | 2 |
| 38937 | combatirle | 2 |
| 38938 | combatirla | 2 |
| 38939 | combatidos | 2 |
| 38940 | combatían | 2 |
| 38941 | comandantes | 2 |
| 38942 | cómalos | 2 |
| 38943 | comadronas | 2 |
| 38944 | comadres | 2 |
| 38945 | columpia | 2 |
| 38946 | columbró | 2 |
| 38947 | colorista | 2 |
| 38948 | colorete | 2 |
| 38949 | colora | 2 |
| 38950 | colones | 2 |
| 38951 | colocase | 2 |
| 38952 | colocarlas | 2 |
| 38953 | colocan | 2 |
| 38954 | colocaciones | 2 |
| 38955 | colocaban | 2 |
| 38956 | coló | 2 |
| 38957 | colmenas | 2 |
| 38958 | colmar | 2 |
| 38959 | colmados | 2 |
| 38960 | colmado | 2 |
| 38961 | colleras | 2 |
| 38962 | collera | 2 |
| 38963 | collarines | 2 |
| 38964 | collaços | 2 |
| 38965 | colilla | 2 |
| 38966 | coligieron | 2 |
| 38967 | colige | 2 |
| 38968 | coliflor | 2 |
| 38969 | colguemos | 2 |
| 38970 | colgarle | 2 |
| 38971 | colgara | 2 |
| 38972 | colgantes | 2 |
| 38973 | colgándose | 2 |
| 38974 | coléricas | 2 |
| 38975 | colegirse | 2 |
| 38976 | colegial | 2 |
| 38977 | colectivo | 2 |
| 38978 | coleccionistas | 2 |
| 38979 | coleccionador | 2 |
| 38980 | colar | 2 |
| 38981 | colacion | 2 |
| 38982 | cojos | 2 |
| 38983 | cojeaba | 2 |
| 38984 | coimbra | 2 |
| 38985 | cohonestarse | 2 |
| 38986 | coheche | 2 |
| 38987 | cohechan | 2 |
| 38988 | cogitationes | 2 |
| 38989 | cogitaciones | 2 |
| 38990 | cogiste | 2 |
| 38991 | cogiéronle | 2 |
| 38992 | cogieran | 2 |
| 38993 | cogiéndose | 2 |
| 38994 | cogerá | 2 |
| 38995 | cofrecillo | 2 |
| 38996 | cofrade | 2 |
| 38997 | cofín | 2 |
| 38998 | cofas | 2 |
| 38999 | codiçioso | 2 |
| 39000 | codiciosas | 2 |
| 39001 | codazos | 2 |
| 39002 | codazo | 2 |
| 39003 | cocodrilo | 2 |
| 39004 | cocinerita | 2 |
| 39005 | coçina | 2 |
| 39006 | cociendo | 2 |
| 39007 | cochera | 2 |
| 39008 | coçes | 2 |
| 39009 | coca | 2 |
| 39010 | cobros | 2 |
| 39011 | cobré | 2 |
| 39012 | cobrarla | 2 |
| 39013 | cobraría | 2 |
| 39014 | cobrarán | 2 |
| 39015 | cobradores | 2 |
| 39016 | cobierto | 2 |
| 39017 | cobertor | 2 |
| 39018 | cobertizo | 2 |
| 39019 | cobdiçiar | 2 |
| 39020 | coalición | 2 |
| 39021 | co | 2 |
| 39022 | clubs | 2 |
| 39023 | cloto | 2 |
| 39024 | clorótica | 2 |
| 39025 | clorhidrato | 2 |
| 39026 | cloaca | 2 |
| 39027 | clínicas | 2 |
| 39028 | clerezia | 2 |
| 39029 | clementes | 2 |
| 39030 | clavijas | 2 |
| 39031 | claveteando | 2 |
| 39032 | claveteado | 2 |
| 39033 | claves | 2 |
| 39034 | clavelero | 2 |
| 39035 | clavarse | 2 |
| 39036 | clavaron | 2 |
| 39037 | cláusula | 2 |
| 39038 | claustral | 2 |
| 39039 | clauos | 2 |
| 39040 | clauo | 2 |
| 39041 | claudicante | 2 |
| 39042 | clasificado | 2 |
| 39043 | clasificaciones | 2 |
| 39044 | clarita | 2 |
| 39045 | clarísima | 2 |
| 39046 | clarisas | 2 |
| 39047 | clarinetes | 2 |
| 39048 | clareando | 2 |
| 39049 | claque | 2 |
| 39050 | clandestino | 2 |
| 39051 | clandestinamente | 2 |
| 39052 | clamoreo | 2 |
| 39053 | clamaban | 2 |
| 39054 | clama | 2 |
| 39055 | claire | 2 |
| 39056 | civilizado | 2 |
| 39057 | civilizada | 2 |
| 39058 | çivera | 2 |
| 39059 | ciudadanas | 2 |
| 39060 | citunas | 2 |
| 39061 | çítola | 2 |
| 39062 | citarte | 2 |
| 39063 | citaré | 2 |
| 39064 | cítaras | 2 |
| 39065 | citaban | 2 |
| 39066 | cirujeda | 2 |
| 39067 | cirujanos | 2 |
| 39068 | cirugía | 2 |
| 39069 | ciruelas | 2 |
| 39070 | cirino | 2 |
| 39071 | cirimonias | 2 |
| 39072 | circunscrita | 2 |
| 39073 | circunflejo | 2 |
| 39074 | circunferencia | 2 |
| 39075 | circundado | 2 |
| 39076 | circunda | 2 |
| 39077 | circulante | 2 |
| 39078 | circulaban | 2 |
| 39079 | circuito | 2 |
| 39080 | circos | 2 |
| 39081 | cipiones | 2 |
| 39082 | ciñóse | 2 |
| 39083 | ciño | 2 |
| 39084 | cintia | 2 |
| 39085 | cintajos | 2 |
| 39086 | çinquenta | 2 |
| 39087 | çinfonía | 2 |
| 39088 | cincha | 2 |
| 39089 | cimera | 2 |
| 39090 | cimenterios | 2 |
| 39091 | cimenterio | 2 |
| 39092 | cilindros | 2 |
| 39093 | cilíndricas | 2 |
| 39094 | cigüeña | 2 |
| 39095 | cigarrito | 2 |
| 39096 | cigarrillos | 2 |
| 39097 | cigarras | 2 |
| 39098 | cierzo | 2 |
| 39099 | çiervo | 2 |
| 39100 | cierva | 2 |
| 39101 | científico | 2 |
| 39102 | çiencia | 2 |
| 39103 | çien | 2 |
| 39104 | çielos | 2 |
| 39105 | ciegue | 2 |
| 39106 | çiego | 2 |
| 39107 | çiegan | 2 |
| 39108 | çiega | 2 |
| 39109 | cicuta | 2 |
| 39110 | ciclón | 2 |
| 39111 | cicatriz | 2 |
| 39112 | çibdades | 2 |
| 39113 | cianíis | 2 |
| 39114 | chuscas | 2 |
| 39115 | churumbé | 2 |
| 39116 | churros | 2 |
| 39117 | chupe | 2 |
| 39118 | chumbos | 2 |
| 39119 | chulas | 2 |
| 39120 | chufa | 2 |
| 39121 | chubascos | 2 |
| 39122 | chubasca | 2 |
| 39123 | christus | 2 |
| 39124 | christianos | 2 |
| 39125 | chorrea | 2 |
| 39126 | chocolatito | 2 |
| 39127 | chocolates | 2 |
| 39128 | chocheces | 2 |
| 39129 | chocarrero | 2 |
| 39130 | chocaron | 2 |
| 39131 | chito | 2 |
| 39132 | chitito | 2 |
| 39133 | chisté | 2 |
| 39134 | chispita | 2 |
| 39135 | chispeantes | 2 |
| 39136 | chismosos | 2 |
| 39137 | chismosas | 2 |
| 39138 | chismosa | 2 |
| 39139 | chirris | 2 |
| 39140 | chirridos | 2 |
| 39141 | chirriar | 2 |
| 39142 | chirles | 2 |
| 39143 | chiripa | 2 |
| 39144 | chiquititas | 2 |
| 39145 | chiquitas | 2 |
| 39146 | chiquilladas | 2 |
| 39147 | chiquillada | 2 |
| 39148 | chipiona | 2 |
| 39149 | chinto | 2 |
| 39150 | chinos | 2 |
| 39151 | chinesca | 2 |
| 39152 | chinelas | 2 |
| 39153 | chínchirri | 2 |
| 39154 | chinches | 2 |
| 39155 | chillería | 2 |
| 39156 | chiflarse | 2 |
| 39157 | chifladura | 2 |
| 39158 | chiflados | 2 |
| 39159 | chifla | 2 |
| 39160 | chiclana | 2 |
| 39161 | chi | 2 |
| 39162 | cheong | 2 |
| 39163 | chavales | 2 |
| 39164 | chavala | 2 |
| 39165 | chasqueados | 2 |
| 39166 | chasqueado | 2 |
| 39167 | chascarrillos | 2 |
| 39168 | chas | 2 |
| 39169 | charreteras | 2 |
| 39170 | charlatánicas | 2 |
| 39171 | charlatanas | 2 |
| 39172 | charlaba | 2 |
| 39173 | charanga | 2 |
| 39174 | chaquetas | 2 |
| 39175 | chaqué | 2 |
| 39176 | chapuzón | 2 |
| 39177 | chapines | 2 |
| 39178 | chaparrones | 2 |
| 39179 | chapapote | 2 |
| 39180 | chanzonetas | 2 |
| 39181 | chanclos | 2 |
| 39182 | chanchullos | 2 |
| 39183 | chamuscados | 2 |
| 39184 | chamelote | 2 |
| 39185 | chambras | 2 |
| 39186 | chambra | 2 |
| 39187 | chambergo | 2 |
| 39188 | chambelanes | 2 |
| 39189 | chalet | 2 |
| 39190 | chales | 2 |
| 39191 | chalana | 2 |
| 39192 | chafalditas | 2 |
| 39193 | chafado | 2 |
| 39194 | chafada | 2 |
| 39195 | chacorrero | 2 |
| 39196 | chacona | 2 |
| 39197 | chabacana | 2 |
| 39198 | ceux | 2 |
| 39199 | cetros | 2 |
| 39200 | cetrería | 2 |
| 39201 | cetina | 2 |
| 39202 | cetera | 2 |
| 39203 | cesses | 2 |
| 39204 | cessa | 2 |
| 39205 | cesé | 2 |
| 39206 | césares | 2 |
| 39207 | cesárea | 2 |
| 39208 | cesando | 2 |
| 39209 | cervices | 2 |
| 39210 | cerúleas | 2 |
| 39211 | certificados | 2 |
| 39212 | certificado | 2 |
| 39213 | çertero | 2 |
| 39214 | certero | 2 |
| 39215 | çertera | 2 |
| 39216 | cerriles | 2 |
| 39217 | cerrera | 2 |
| 39218 | cerremos | 2 |
| 39219 | cerrasen | 2 |
| 39220 | cerrarse | 2 |
| 39221 | cerráronse | 2 |
| 39222 | cerrarlos | 2 |
| 39223 | çerrar | 2 |
| 39224 | cerrándolos | 2 |
| 39225 | cerrándole | 2 |
| 39226 | cerraduras | 2 |
| 39227 | çerrado | 2 |
| 39228 | ceros | 2 |
| 39229 | cernido | 2 |
| 39230 | cernícalo | 2 |
| 39231 | cernadero | 2 |
| 39232 | ceremonioso | 2 |
| 39233 | ceremoniosas | 2 |
| 39234 | cerda | 2 |
| 39235 | cerciorose | 2 |
| 39236 | cercioró | 2 |
| 39237 | cercén | 2 |
| 39238 | cercedilla | 2 |
| 39239 | cercada | 2 |
| 39240 | cerbelo | 2 |
| 39241 | ceptros | 2 |
| 39242 | cepo | 2 |
| 39243 | ceñidos | 2 |
| 39244 | ceñidas | 2 |
| 39245 | ceñían | 2 |
| 39246 | centrífuga | 2 |
| 39247 | centrales | 2 |
| 39248 | centigramo | 2 |
| 39249 | centén | 2 |
| 39250 | centelleante | 2 |
| 39251 | çentella | 2 |
| 39252 | censuras | 2 |
| 39253 | cenidero | 2 |
| 39254 | cenefas | 2 |
| 39255 | cene | 2 |
| 39256 | cencerrada | 2 |
| 39257 | cenase | 2 |
| 39258 | cenarían | 2 |
| 39259 | cenaremos | 2 |
| 39260 | cenaban | 2 |
| 39261 | celucos | 2 |
| 39262 | çeloso | 2 |
| 39263 | celosas | 2 |
| 39264 | çelos | 2 |
| 39265 | celipe | 2 |
| 39266 | celestinas | 2 |
| 39267 | celebros | 2 |
| 39268 | celebridad | 2 |
| 39269 | celebrarla | 2 |
| 39270 | celebrara | 2 |
| 39271 | celebrando | 2 |
| 39272 | celebérrimo | 2 |
| 39273 | celauro | 2 |
| 39274 | celar | 2 |
| 39275 | celajes | 2 |
| 39276 | çelada | 2 |
| 39277 | celaba | 2 |
| 39278 | çejas | 2 |
| 39279 | çeja | 2 |
| 39280 | çeguedat | 2 |
| 39281 | cegata | 2 |
| 39282 | cegase | 2 |
| 39283 | céfiros | 2 |
| 39284 | cefalalgia | 2 |
| 39285 | cedros | 2 |
| 39286 | cedro | 2 |
| 39287 | cedo | 2 |
| 39288 | cedí | 2 |
| 39289 | cederá | 2 |
| 39290 | cecina | 2 |
| 39291 | ceceoso | 2 |
| 39292 | cebollino | 2 |
| 39293 | cebollinas | 2 |
| 39294 | cebáronse | 2 |
| 39295 | cebado | 2 |
| 39296 | cazolones | 2 |
| 39297 | cazas | 2 |
| 39298 | cazado | 2 |
| 39299 | cayesen | 2 |
| 39300 | caxquete | 2 |
| 39301 | caxco | 2 |
| 39302 | cavan | 2 |
| 39303 | cavadores | 2 |
| 39304 | cavada | 2 |
| 39305 | cautivó | 2 |
| 39306 | cautivé | 2 |
| 39307 | cautivado | 2 |
| 39308 | causóles | 2 |
| 39309 | causándome | 2 |
| 39310 | causadora | 2 |
| 39311 | causábale | 2 |
| 39312 | caudalosa | 2 |
| 39313 | caualleros | 2 |
| 39314 | cativo | 2 |
| 39315 | çatico | 2 |
| 39316 | catequizas | 2 |
| 39317 | caten | 2 |
| 39318 | categórico | 2 |
| 39319 | categóricas | 2 |
| 39320 | categóricamente | 2 |
| 39321 | caté | 2 |
| 39322 | catay | 2 |
| 39323 | catase | 2 |
| 39324 | catarroso | 2 |
| 39325 | cataron | 2 |
| 39326 | catarlo | 2 |
| 39327 | catara | 2 |
| 39328 | cataluña | 2 |
| 39329 | catálogos | 2 |
| 39330 | catalana | 2 |
| 39331 | cataduras | 2 |
| 39332 | catador | 2 |
| 39333 | cataclismos | 2 |
| 39334 | casulla | 2 |
| 39335 | castiguen | 2 |
| 39336 | castíguele | 2 |
| 39337 | castigue | 2 |
| 39338 | castigas | 2 |
| 39339 | castigaros | 2 |
| 39340 | castigarlos | 2 |
| 39341 | castigara | 2 |
| 39342 | castigándome | 2 |
| 39343 | castígame | 2 |
| 39344 | castigalle | 2 |
| 39345 | castigaldo | 2 |
| 39346 | castigaban | 2 |
| 39347 | castiella | 2 |
| 39348 | castañeteo | 2 |
| 39349 | castañetazos | 2 |
| 39350 | castañetas | 2 |
| 39351 | cassas | 2 |
| 39352 | cassarse | 2 |
| 39353 | cassamientos | 2 |
| 39354 | cassamiento | 2 |
| 39355 | cassa | 2 |
| 39356 | cáspita | 2 |
| 39357 | casose | 2 |
| 39358 | casillero | 2 |
| 39359 | cásense | 2 |
| 39360 | cásate | 2 |
| 39361 | casarlos | 2 |
| 39362 | casarías | 2 |
| 39363 | casaréis | 2 |
| 39364 | casare | 2 |
| 39365 | casaras | 2 |
| 39366 | casaos | 2 |
| 39367 | casando | 2 |
| 39368 | casadera | 2 |
| 39369 | carvajal | 2 |
| 39370 | carunculosa | 2 |
| 39371 | cartulina | 2 |
| 39372 | cartujos | 2 |
| 39373 | cartujo | 2 |
| 39374 | cartuja | 2 |
| 39375 | cartelones | 2 |
| 39376 | cartea | 2 |
| 39377 | carronadas | 2 |
| 39378 | carromatero | 2 |
| 39379 | carrizos | 2 |
| 39380 | carrizo | 2 |
| 39381 | carril | 2 |
| 39382 | carreterona | 2 |
| 39383 | carretadas | 2 |
| 39384 | carpeta | 2 |
| 39385 | carniceros | 2 |
| 39386 | carniçero | 2 |
| 39387 | carniçerías | 2 |
| 39388 | carnicerías | 2 |
| 39389 | carnestolendas | 2 |
| 39390 | carnaza | 2 |
| 39391 | carlancas | 2 |
| 39392 | cariz | 2 |
| 39393 | caritativos | 2 |
| 39394 | carísimos | 2 |
| 39395 | carísimo | 2 |
| 39396 | cariñitos | 2 |
| 39397 | carillas | 2 |
| 39398 | cargué | 2 |
| 39399 | carezca | 2 |
| 39400 | caretas | 2 |
| 39401 | caresciendo | 2 |
| 39402 | carencia | 2 |
| 39403 | careció | 2 |
| 39404 | carecieron | 2 |
| 39405 | careces | 2 |
| 39406 | carecería | 2 |
| 39407 | cardo | 2 |
| 39408 | cárdenos | 2 |
| 39409 | cárdena | 2 |
| 39410 | cardado | 2 |
| 39411 | carcunda | 2 |
| 39412 | carcaños | 2 |
| 39413 | carcaj | 2 |
| 39414 | carbuncos | 2 |
| 39415 | carboneras | 2 |
| 39416 | caravana | 2 |
| 39417 | caramillo | 2 |
| 39418 | caramiello | 2 |
| 39419 | carámbano | 2 |
| 39420 | caramanchón | 2 |
| 39421 | caracuel | 2 |
| 39422 | caracterizar | 2 |
| 39423 | caracterizaba | 2 |
| 39424 | característicos | 2 |
| 39425 | caracolear | 2 |
| 39426 | carabina | 2 |
| 39427 | capullo | 2 |
| 39428 | captura | 2 |
| 39429 | captiva | 2 |
| 39430 | captar | 2 |
| 39431 | caprichillos | 2 |
| 39432 | capotillo | 2 |
| 39433 | capitoné | 2 |
| 39434 | capiteles | 2 |
| 39435 | capitalito | 2 |
| 39436 | capirote | 2 |
| 39437 | capellina | 2 |
| 39438 | capciosas | 2 |
| 39439 | capciosa | 2 |
| 39440 | çapatos | 2 |
| 39441 | capatazo | 2 |
| 39442 | capataces | 2 |
| 39443 | capacete | 2 |
| 39444 | cañonear | 2 |
| 39445 | cañizo | 2 |
| 39446 | cañavera | 2 |
| 39447 | cañamones | 2 |
| 39448 | cañamón | 2 |
| 39449 | canturia | 2 |
| 39450 | cantonales | 2 |
| 39451 | cantillo | 2 |
| 39452 | cantigas | 2 |
| 39453 | cantía | 2 |
| 39454 | cantatriz | 2 |
| 39455 | cantarle | 2 |
| 39456 | cantarillo | 2 |
| 39457 | cantarilla | 2 |
| 39458 | cantaría | 2 |
| 39459 | cantaran | 2 |
| 39460 | cantante | 2 |
| 39461 | cantándole | 2 |
| 39462 | cántale | 2 |
| 39463 | cantados | 2 |
| 39464 | cantador | 2 |
| 39465 | cantadas | 2 |
| 39466 | cantábrico | 2 |
| 39467 | cansóse | 2 |
| 39468 | cansé | 2 |
| 39469 | cansase | 2 |
| 39470 | cansas | 2 |
| 39471 | cansarte | 2 |
| 39472 | cansaros | 2 |
| 39473 | cansaría | 2 |
| 39474 | cansaré | 2 |
| 39475 | cansará | 2 |
| 39476 | cansan | 2 |
| 39477 | cansamos | 2 |
| 39478 | cánsala | 2 |
| 39479 | cansadita | 2 |
| 39480 | çanpoña | 2 |
| 39481 | canpanas | 2 |
| 39482 | canora | 2 |
| 39483 | canonizar | 2 |
| 39484 | canoniza | 2 |
| 39485 | canon | 2 |
| 39486 | caninos | 2 |
| 39487 | canino | 2 |
| 39488 | canijo | 2 |
| 39489 | canicular | 2 |
| 39490 | cangrejo | 2 |
| 39491 | candorosamente | 2 |
| 39492 | candiles | 2 |
| 39493 | candidatura | 2 |
| 39494 | cándida | 2 |
| 39495 | cancre | 2 |
| 39496 | cancion | 2 |
| 39497 | cancerbero | 2 |
| 39498 | cáncer | 2 |
| 39499 | canceles | 2 |
| 39500 | cancel | 2 |
| 39501 | canastos | 2 |
| 39502 | canarias | 2 |
| 39503 | canapé | 2 |
| 39504 | cananeas | 2 |
| 39505 | canallada | 2 |
| 39506 | campesina | 2 |
| 39507 | campechana | 2 |
| 39508 | campeaba | 2 |
| 39509 | campanuda | 2 |
| 39510 | camita | 2 |
| 39511 | camisolas | 2 |
| 39512 | camisola | 2 |
| 39513 | camine | 2 |
| 39514 | caminatas | 2 |
| 39515 | caminasen | 2 |
| 39516 | caminamos | 2 |
| 39517 | caminad | 2 |
| 39518 | caminábamos | 2 |
| 39519 | camilia | 2 |
| 39520 | cambrí | 2 |
| 39521 | cambie | 2 |
| 39522 | cambiazos | 2 |
| 39523 | cambiarlo | 2 |
| 39524 | cambiaran | 2 |
| 39525 | cambiara | 2 |
| 39526 | cambiante | 2 |
| 39527 | cambiada | 2 |
| 39528 | cambaya | 2 |
| 39529 | camastrón | 2 |
| 39530 | camarones | 2 |
| 39531 | camarín | 2 |
| 39532 | camarilla | 2 |
| 39533 | camareros | 2 |
| 39534 | camarero | 2 |
| 39535 | camarera | 2 |
| 39536 | calzar | 2 |
| 39537 | calzan | 2 |
| 39538 | calzaban | 2 |
| 39539 | calvos | 2 |
| 39540 | calumnió | 2 |
| 39541 | calumniadores | 2 |
| 39542 | calumniador | 2 |
| 39543 | calumniaba | 2 |
| 39544 | calmaron | 2 |
| 39545 | calmándose | 2 |
| 39546 | callosa | 2 |
| 39547 | callenta | 2 |
| 39548 | callejero | 2 |
| 39549 | callejeras | 2 |
| 39550 | callasen | 2 |
| 39551 | callare | 2 |
| 39552 | callarán | 2 |
| 39553 | callará | 2 |
| 39554 | caliginosas | 2 |
| 39555 | califique | 2 |
| 39556 | calificados | 2 |
| 39557 | calificada | 2 |
| 39558 | calificaba | 2 |
| 39559 | califas | 2 |
| 39560 | cálida | 2 |
| 39561 | calentarme | 2 |
| 39562 | calentándose | 2 |
| 39563 | calentado | 2 |
| 39564 | calé | 2 |
| 39565 | calderos | 2 |
| 39566 | calderonianas | 2 |
| 39567 | caldeos | 2 |
| 39568 | caldeado | 2 |
| 39569 | caldeada | 2 |
| 39570 | caldeaba | 2 |
| 39571 | calculé | 2 |
| 39572 | calculada | 2 |
| 39573 | calceta | 2 |
| 39574 | calcañares | 2 |
| 39575 | calatravas | 2 |
| 39576 | calar | 2 |
| 39577 | calándose | 2 |
| 39578 | calamitosos | 2 |
| 39579 | calambres | 2 |
| 39580 | calambre | 2 |
| 39581 | calaínos | 2 |
| 39582 | calabrés | 2 |
| 39583 | calabazada | 2 |
| 39584 | cajuela | 2 |
| 39585 | cajitas | 2 |
| 39586 | cajista | 2 |
| 39587 | cairás | 2 |
| 39588 | caíme | 2 |
| 39589 | caigas | 2 |
| 39590 | caigan | 2 |
| 39591 | cafres | 2 |
| 39592 | çafir | 2 |
| 39593 | cáfila | 2 |
| 39594 | cafeteros | 2 |
| 39595 | cafetero | 2 |
| 39596 | caere | 2 |
| 39597 | caerás | 2 |
| 39598 | caducar | 2 |
| 39599 | cadencia | 2 |
| 39600 | cadavérica | 2 |
| 39601 | cadahalso | 2 |
| 39602 | caçurros | 2 |
| 39603 | caçones | 2 |
| 39604 | cachorro | 2 |
| 39605 | cachaza | 2 |
| 39606 | cacareo | 2 |
| 39607 | cacarear | 2 |
| 39608 | cacao | 2 |
| 39609 | cabritillos | 2 |
| 39610 | cabriolé | 2 |
| 39611 | cabriola | 2 |
| 39612 | cabrían | 2 |
| 39613 | cabezudo | 2 |
| 39614 | cabestrillo | 2 |
| 39615 | cabeças | 2 |
| 39616 | cabalmente | 2 |
| 39617 | caballista | 2 |
| 39618 | caballete | 2 |
| 39619 | caballerizo | 2 |
| 39620 | caballeritos | 2 |
| 39621 | caballerete | 2 |
| 39622 | byvrás | 2 |
| 39623 | byron | 2 |
| 39624 | bustos | 2 |
| 39625 | bustamente | 2 |
| 39626 | busques | 2 |
| 39627 | busquen | 2 |
| 39628 | busquéis | 2 |
| 39629 | busiris | 2 |
| 39630 | buscasse | 2 |
| 39631 | buscármelo | 2 |
| 39632 | buscarles | 2 |
| 39633 | buscaran | 2 |
| 39634 | buscáis | 2 |
| 39635 | buscador | 2 |
| 39636 | buscadas | 2 |
| 39637 | buscábamos | 2 |
| 39638 | burumbum | 2 |
| 39639 | burradas | 2 |
| 39640 | burlones | 2 |
| 39641 | burló | 2 |
| 39642 | burles | 2 |
| 39643 | burléis | 2 |
| 39644 | burlé | 2 |
| 39645 | burle | 2 |
| 39646 | burlaste | 2 |
| 39647 | burlasen | 2 |
| 39648 | burláis | 2 |
| 39649 | burguete | 2 |
| 39650 | burgueses | 2 |
| 39651 | burdos | 2 |
| 39652 | burda | 2 |
| 39653 | buñuelos | 2 |
| 39654 | bullón | 2 |
| 39655 | bullir | 2 |
| 39656 | bullían | 2 |
| 39657 | bullía | 2 |
| 39658 | bullanguera | 2 |
| 39659 | buldero | 2 |
| 39660 | buida | 2 |
| 39661 | buhonería | 2 |
| 39662 | buhonas | 2 |
| 39663 | bufos | 2 |
| 39664 | bufones | 2 |
| 39665 | buffon | 2 |
| 39666 | buexes | 2 |
| 39667 | buenora | 2 |
| 39668 | buenavista | 2 |
| 39669 | buenafé | 2 |
| 39670 | buelues | 2 |
| 39671 | bueluas | 2 |
| 39672 | buelto | 2 |
| 39673 | buela | 2 |
| 39674 | bucólicas | 2 |
| 39675 | bucéfalo | 2 |
| 39676 | bu | 2 |
| 39677 | brutalmente | 2 |
| 39678 | brusquedad | 2 |
| 39679 | bruselas | 2 |
| 39680 | bruscas | 2 |
| 39681 | bruñidos | 2 |
| 39682 | brunelo | 2 |
| 39683 | brumario | 2 |
| 39684 | brumado | 2 |
| 39685 | brumadas | 2 |
| 39686 | brújula | 2 |
| 39687 | brotes | 2 |
| 39688 | brotando | 2 |
| 39689 | brota | 2 |
| 39690 | broqueles | 2 |
| 39691 | broches | 2 |
| 39692 | brochar | 2 |
| 39693 | brochado | 2 |
| 39694 | brocal | 2 |
| 39695 | británico | 2 |
| 39696 | brioso | 2 |
| 39697 | briosa | 2 |
| 39698 | brindose | 2 |
| 39699 | brindar | 2 |
| 39700 | brincadora | 2 |
| 39701 | brilló | 2 |
| 39702 | brillase | 2 |
| 39703 | brillan | 2 |
| 39704 | brilladoro | 2 |
| 39705 | bribones | 2 |
| 39706 | bribonas | 2 |
| 39707 | breviario | 2 |
| 39708 | brest | 2 |
| 39709 | bregó | 2 |
| 39710 | bregando | 2 |
| 39711 | brega | 2 |
| 39712 | brecolera | 2 |
| 39713 | brazadas | 2 |
| 39714 | braveza | 2 |
| 39715 | bravamente | 2 |
| 39716 | braueza | 2 |
| 39717 | braseros | 2 |
| 39718 | branca | 2 |
| 39719 | bramuras | 2 |
| 39720 | bramava | 2 |
| 39721 | bramante | 2 |
| 39722 | bramando | 2 |
| 39723 | brama | 2 |
| 39724 | braço | 2 |
| 39725 | bracete | 2 |
| 39726 | bracero | 2 |
| 39727 | bozal | 2 |
| 39728 | bouos | 2 |
| 39729 | botoneras | 2 |
| 39730 | botonaduras | 2 |
| 39731 | botitas | 2 |
| 39732 | botinas | 2 |
| 39733 | botellita | 2 |
| 39734 | botarga | 2 |
| 39735 | bostezaban | 2 |
| 39736 | bostezaba | 2 |
| 39737 | borro | 2 |
| 39738 | borricas | 2 |
| 39739 | borrando | 2 |
| 39740 | borrada | 2 |
| 39741 | borracherías | 2 |
| 39742 | borracheras | 2 |
| 39743 | borrachas | 2 |
| 39744 | borraban | 2 |
| 39745 | bordeando | 2 |
| 39746 | bordar | 2 |
| 39747 | borceguí | 2 |
| 39748 | borbones | 2 |
| 39749 | boquilla | 2 |
| 39750 | boquiabierta | 2 |
| 39751 | bonum | 2 |
| 39752 | bonitísimos | 2 |
| 39753 | bonitísimo | 2 |
| 39754 | bonísimas | 2 |
| 39755 | bónibus | 2 |
| 39756 | bondadosos | 2 |
| 39757 | bondadosamente | 2 |
| 39758 | bomberos | 2 |
| 39759 | bombé | 2 |
| 39760 | boluerse | 2 |
| 39761 | boluera | 2 |
| 39762 | bolued | 2 |
| 39763 | boluamos | 2 |
| 39764 | bollo | 2 |
| 39765 | bolitas | 2 |
| 39766 | bolita | 2 |
| 39767 | boleo | 2 |
| 39768 | bolando | 2 |
| 39769 | bol | 2 |
| 39770 | bojío | 2 |
| 39771 | bogasen | 2 |
| 39772 | bodrio | 2 |
| 39773 | bodegas | 2 |
| 39774 | bocinas | 2 |
| 39775 | bochornos | 2 |
| 39776 | bocaza | 2 |
| 39777 | bocanadas | 2 |
| 39778 | bocanada | 2 |
| 39779 | bobito | 2 |
| 39780 | boberías | 2 |
| 39781 | bobería | 2 |
| 39782 | bo | 2 |
| 39783 | bloques | 2 |
| 39784 | bloqueo | 2 |
| 39785 | blindado | 2 |
| 39786 | blasonar | 2 |
| 39787 | blasona | 2 |
| 39788 | blason | 2 |
| 39789 | blasfemar | 2 |
| 39790 | blanquecinas | 2 |
| 39791 | blanquear | 2 |
| 39792 | blanquean | 2 |
| 39793 | blandiendo | 2 |
| 39794 | blandía | 2 |
| 39795 | blanc | 2 |
| 39796 | bizmar | 2 |
| 39797 | bizcos | 2 |
| 39798 | bizarramente | 2 |
| 39799 | bivo | 2 |
| 39800 | biven | 2 |
| 39801 | bivda | 2 |
| 39802 | bistec | 2 |
| 39803 | bisperas | 2 |
| 39804 | bis | 2 |
| 39805 | birrete | 2 |
| 39806 | birla | 2 |
| 39807 | biliosa | 2 |
| 39808 | bijou | 2 |
| 39809 | bierzo | 2 |
| 39810 | bienquisto | 2 |
| 39811 | bienobrar | 2 |
| 39812 | bienhechor | 2 |
| 39813 | bienempleado | 2 |
| 39814 | bicoca | 2 |
| 39815 | bichos | 2 |
| 39816 | bibliófilo | 2 |
| 39817 | bevido | 2 |
| 39818 | beve | 2 |
| 39819 | beuo | 2 |
| 39820 | besuqueos | 2 |
| 39821 | besuqueo | 2 |
| 39822 | bestión | 2 |
| 39823 | bestialidad | 2 |
| 39824 | bestezuela | 2 |
| 39825 | bésoos | 2 |
| 39826 | besárselos | 2 |
| 39827 | besarse | 2 |
| 39828 | besarme | 2 |
| 39829 | besarla | 2 |
| 39830 | besará | 2 |
| 39831 | besándoselas | 2 |
| 39832 | besada | 2 |
| 39833 | besad | 2 |
| 39834 | berza | 2 |
| 39835 | berrueco | 2 |
| 39836 | berreaba | 2 |
| 39837 | bernesga | 2 |
| 39838 | berlín | 2 |
| 39839 | berenjenas | 2 |
| 39840 | bere | 2 |
| 39841 | berdan | 2 |
| 39842 | berceras | 2 |
| 39843 | beodo | 2 |
| 39844 | benjuí | 2 |
| 39845 | benignos | 2 |
| 39846 | bengala | 2 |
| 39847 | benévolo | 2 |
| 39848 | benevolencias | 2 |
| 39849 | benévolamente | 2 |
| 39850 | beneficioso | 2 |
| 39851 | beneficiao | 2 |
| 39852 | benedictus | 2 |
| 39853 | bene | 2 |
| 39854 | benditísimo | 2 |
| 39855 | bendigate | 2 |
| 39856 | bendecían | 2 |
| 39857 | bencerrajes | 2 |
| 39858 | benavides | 2 |
| 39859 | benavente | 2 |
| 39860 | belvedere | 2 |
| 39861 | beltz | 2 |
| 39862 | belona | 2 |
| 39863 | belicosas | 2 |
| 39864 | bélico | 2 |
| 39865 | beleño | 2 |
| 39866 | beethoven | 2 |
| 39867 | bedmar | 2 |
| 39868 | bébese | 2 |
| 39869 | bebés | 2 |
| 39870 | beberemos | 2 |
| 39871 | bebedizo | 2 |
| 39872 | bebamos | 2 |
| 39873 | beba | 2 |
| 39874 | beatriz | 2 |
| 39875 | beatería | 2 |
| 39876 | bazofias | 2 |
| 39877 | bayonetazos | 2 |
| 39878 | bayonetas | 2 |
| 39879 | baxar | 2 |
| 39880 | bavoquía | 2 |
| 39881 | bautizar | 2 |
| 39882 | bautistas | 2 |
| 39883 | baudilio | 2 |
| 39884 | bato | 2 |
| 39885 | batistas | 2 |
| 39886 | batir | 2 |
| 39887 | batieron | 2 |
| 39888 | batidor | 2 |
| 39889 | bateas | 2 |
| 39890 | batanado | 2 |
| 39891 | batallar | 2 |
| 39892 | batallador | 2 |
| 39893 | batahola | 2 |
| 39894 | basurero | 2 |
| 39895 | bastonazos | 2 |
| 39896 | bastidor | 2 |
| 39897 | bastiat | 2 |
| 39898 | basten | 2 |
| 39899 | bastare | 2 |
| 39900 | bastar | 2 |
| 39901 | bastantemente | 2 |
| 39902 | basquiñas | 2 |
| 39903 | basas | 2 |
| 39904 | barvas | 2 |
| 39905 | baruuda | 2 |
| 39906 | baruas | 2 |
| 39907 | bártulos | 2 |
| 39908 | bartolillos | 2 |
| 39909 | barruntan | 2 |
| 39910 | barroquismo | 2 |
| 39911 | barroco | 2 |
| 39912 | barricas | 2 |
| 39913 | barrían | 2 |
| 39914 | barreras | 2 |
| 39915 | barreduras | 2 |
| 39916 | barrabasadas | 2 |
| 39917 | baronesita | 2 |
| 39918 | baronesas | 2 |
| 39919 | barómetro | 2 |
| 39920 | barnizada | 2 |
| 39921 | barbudo | 2 |
| 39922 | barbiponiente | 2 |
| 39923 | barbilucio | 2 |
| 39924 | barbilindo | 2 |
| 39925 | barbier | 2 |
| 39926 | barbarroja | 2 |
| 39927 | barajaban | 2 |
| 39928 | baos | 2 |
| 39929 | bañe | 2 |
| 39930 | bañas | 2 |
| 39931 | bañarse | 2 |
| 39932 | bañadas | 2 |
| 39933 | bañaban | 2 |
| 39934 | banquetas | 2 |
| 39935 | banderillas | 2 |
| 39936 | bandas | 2 |
| 39937 | banastas | 2 |
| 39938 | bambino | 2 |
| 39939 | balsamo | 2 |
| 39940 | ballenas | 2 |
| 39941 | balidos | 2 |
| 39942 | balduque | 2 |
| 39943 | baldosín | 2 |
| 39944 | baldones | 2 |
| 39945 | baldon | 2 |
| 39946 | baldíos | 2 |
| 39947 | baldía | 2 |
| 39948 | baldado | 2 |
| 39949 | balda | 2 |
| 39950 | balbucientes | 2 |
| 39951 | balbuceó | 2 |
| 39952 | balbucear | 2 |
| 39953 | balazo | 2 |
| 39954 | balaustrada | 2 |
| 39955 | balanceos | 2 |
| 39956 | balanceo | 2 |
| 39957 | balancearse | 2 |
| 39958 | balanceaban | 2 |
| 39959 | baladronadas | 2 |
| 39960 | bajezas | 2 |
| 39961 | bajera | 2 |
| 39962 | bajarme | 2 |
| 39963 | bajarlo | 2 |
| 39964 | bajarle | 2 |
| 39965 | bajarla | 2 |
| 39966 | bajarán | 2 |
| 39967 | bajará | 2 |
| 39968 | bajara | 2 |
| 39969 | bajamos | 2 |
| 39970 | bajadlos | 2 |
| 39971 | bailoteando | 2 |
| 39972 | bailó | 2 |
| 39973 | bailé | 2 |
| 39974 | bailasen | 2 |
| 39975 | bailas | 2 |
| 39976 | bailaron | 2 |
| 39977 | bailan | 2 |
| 39978 | bailadora | 2 |
| 39979 | bailábamos | 2 |
| 39980 | baidejos | 2 |
| 39981 | bagarinos | 2 |
| 39982 | baeza | 2 |
| 39983 | badeas | 2 |
| 39984 | bachilleres | 2 |
| 39985 | bacanal | 2 |
| 39986 | babuchas | 2 |
| 39987 | babosa | 2 |
| 39988 | babilónico | 2 |
| 39989 | babilla | 2 |
| 39990 | baberos | 2 |
| 39991 | babador | 2 |
| 39992 | azulejos | 2 |
| 39993 | azuleaba | 2 |
| 39994 | azucarero | 2 |
| 39995 | azqueta | 2 |
| 39996 | azotaina | 2 |
| 39997 | azoróse | 2 |
| 39998 | azeytes | 2 |
| 39999 | azemilero | 2 |
| 40000 | azafranada | 2 |
| 40001 | ayuntan | 2 |
| 40002 | ayunav | 2 |
| 40003 | ayuna | 2 |
| 40004 | ayudéis | 2 |
| 40005 | ayudaremos | 2 |
| 40006 | ayudaran | 2 |
| 40007 | ayudantes | 2 |
| 40008 | ayudándole | 2 |
| 40009 | ayudadas | 2 |
| 40010 | ayudábala | 2 |
| 40011 | ayrados | 2 |
| 40012 | axuar | 2 |
| 40013 | axioma | 2 |
| 40014 | avríe | 2 |
| 40015 | avredes | 2 |
| 40016 | avizor | 2 |
| 40017 | avivando | 2 |
| 40018 | avivaban | 2 |
| 40019 | avivaba | 2 |
| 40020 | avistamos | 2 |
| 40021 | avispada | 2 |
| 40022 | avíseme | 2 |
| 40023 | avisas | 2 |
| 40024 | avisarte | 2 |
| 40025 | avisaría | 2 |
| 40026 | avísame | 2 |
| 40027 | avisados | 2 |
| 40028 | avisada | 2 |
| 40029 | avisaba | 2 |
| 40030 | aviñón | 2 |
| 40031 | avinagrado | 2 |
| 40032 | avieso | 2 |
| 40033 | aviesa | 2 |
| 40034 | aviendo | 2 |
| 40035 | avie | 2 |
| 40036 | ávidos | 2 |
| 40037 | ávidas | 2 |
| 40038 | aviada | 2 |
| 40039 | averiguó | 2 |
| 40040 | averiguase | 2 |
| 40041 | averiguarse | 2 |
| 40042 | averiguaron | 2 |
| 40043 | averiados | 2 |
| 40044 | averiado | 2 |
| 40045 | avería | 2 |
| 40046 | avergüenza | 2 |
| 40047 | avergüence | 2 |
| 40048 | avergonzados | 2 |
| 40049 | avergonzaban | 2 |
| 40050 | aventurilla | 2 |
| 40051 | aventurándose | 2 |
| 40052 | aventajarse | 2 |
| 40053 | aventajarme | 2 |
| 40054 | aventajados | 2 |
| 40055 | aventajado | 2 |
| 40056 | aventajada | 2 |
| 40057 | aventado | 2 |
| 40058 | avenidos | 2 |
| 40059 | avenido | 2 |
| 40060 | avenida | 2 |
| 40061 | avenid | 2 |
| 40062 | avellaneda | 2 |
| 40063 | avasallador | 2 |
| 40064 | avanzara | 2 |
| 40065 | avanzadas | 2 |
| 40066 | avancuerda | 2 |
| 40067 | auxiliarnos | 2 |
| 40068 | auxiliarla | 2 |
| 40069 | auxiliado | 2 |
| 40070 | autres | 2 |
| 40071 | autorizan | 2 |
| 40072 | autorice | 2 |
| 40073 | autonomía | 2 |
| 40074 | automático | 2 |
| 40075 | autenticidad | 2 |
| 40076 | auténticas | 2 |
| 40077 | autem | 2 |
| 40078 | auspicios | 2 |
| 40079 | ausentó | 2 |
| 40080 | ausentas | 2 |
| 40081 | ausentar | 2 |
| 40082 | ausentado | 2 |
| 40083 | auricular | 2 |
| 40084 | auremos | 2 |
| 40085 | aurea | 2 |
| 40086 | aure | 2 |
| 40087 | aúnan | 2 |
| 40088 | aumentase | 2 |
| 40089 | aumentarla | 2 |
| 40090 | aumentado | 2 |
| 40091 | aumentada | 2 |
| 40092 | aullar | 2 |
| 40093 | aulas | 2 |
| 40094 | aujeritos | 2 |
| 40095 | augustas | 2 |
| 40096 | auge | 2 |
| 40097 | aufa | 2 |
| 40098 | aueys | 2 |
| 40099 | auentaja | 2 |
| 40100 | auaricia | 2 |
| 40101 | au | 2 |
| 40102 | atyende | 2 |
| 40103 | atusaba | 2 |
| 40104 | atura | 2 |
| 40105 | atunes | 2 |
| 40106 | atufado | 2 |
| 40107 | atufa | 2 |
| 40108 | atropina | 2 |
| 40109 | atropellan | 2 |
| 40110 | atropellados | 2 |
| 40111 | atronador | 2 |
| 40112 | atronaban | 2 |
| 40113 | atrición | 2 |
| 40114 | atribuyas | 2 |
| 40115 | atribuyan | 2 |
| 40116 | atribuya | 2 |
| 40117 | atributo | 2 |
| 40118 | atribulados | 2 |
| 40119 | atribulada | 2 |
| 40120 | atribuciones | 2 |
| 40121 | atrevudo | 2 |
| 40122 | atreviose | 2 |
| 40123 | atrevíase | 2 |
| 40124 | atrévete | 2 |
| 40125 | atreves | 2 |
| 40126 | atreverme | 2 |
| 40127 | atraviesan | 2 |
| 40128 | atravesara | 2 |
| 40129 | atrasadilla | 2 |
| 40130 | atrapar | 2 |
| 40131 | atraillado | 2 |
| 40132 | atraídos | 2 |
| 40133 | atraído | 2 |
| 40134 | atraída | 2 |
| 40135 | atragantó | 2 |
| 40136 | atragantaban | 2 |
| 40137 | atraerle | 2 |
| 40138 | atracón | 2 |
| 40139 | atormentes | 2 |
| 40140 | atormente | 2 |
| 40141 | atormentarse | 2 |
| 40142 | atormentarle | 2 |
| 40143 | atormentar | 2 |
| 40144 | atontadas | 2 |
| 40145 | atónitas | 2 |
| 40146 | atonía | 2 |
| 40147 | atolondrado | 2 |
| 40148 | atlas | 2 |
| 40149 | atino | 2 |
| 40150 | atinadas | 2 |
| 40151 | atildada | 2 |
| 40152 | atiene | 2 |
| 40153 | atiendo | 2 |
| 40154 | atiéndele | 2 |
| 40155 | atice | 2 |
| 40156 | atestadas | 2 |
| 40157 | atestada | 2 |
| 40158 | atesoraba | 2 |
| 40159 | aterra | 2 |
| 40160 | atenuación | 2 |
| 40161 | atentísimo | 2 |
| 40162 | ateniense | 2 |
| 40163 | ateneos | 2 |
| 40164 | atendidas | 2 |
| 40165 | atendida | 2 |
| 40166 | atendían | 2 |
| 40167 | atended | 2 |
| 40168 | atencion | 2 |
| 40169 | áteme | 2 |
| 40170 | atavismo | 2 |
| 40171 | atavíos | 2 |
| 40172 | atarse | 2 |
| 40173 | atarme | 2 |
| 40174 | atarles | 2 |
| 40175 | atarlas | 2 |
| 40176 | atarla | 2 |
| 40177 | atareado | 2 |
| 40178 | atanta | 2 |
| 40179 | atándole | 2 |
| 40180 | atanbor | 2 |
| 40181 | atales | 2 |
| 40182 | atalayas | 2 |
| 40183 | atajes | 2 |
| 40184 | atajen | 2 |
| 40185 | atajarla | 2 |
| 40186 | atajan | 2 |
| 40187 | atajadores | 2 |
| 40188 | atajado | 2 |
| 40189 | atahonas | 2 |
| 40190 | ataduras | 2 |
| 40191 | atadero | 2 |
| 40192 | atacó | 2 |
| 40193 | atacan | 2 |
| 40194 | asusté | 2 |
| 40195 | asustaría | 2 |
| 40196 | asustara | 2 |
| 40197 | asustando | 2 |
| 40198 | asustadizo | 2 |
| 40199 | asustadiza | 2 |
| 40200 | asustadísimo | 2 |
| 40201 | asustadísima | 2 |
| 40202 | asustadas | 2 |
| 40203 | asuelven | 2 |
| 40204 | astroso | 2 |
| 40205 | astrólogos | 2 |
| 40206 | astraga | 2 |
| 40207 | astillero | 2 |
| 40208 | astas | 2 |
| 40209 | assy | 2 |
| 40210 | assentado | 2 |
| 40211 | assegurando | 2 |
| 40212 | assecha | 2 |
| 40213 | assaz | 2 |
| 40214 | aspiran | 2 |
| 40215 | aspiraban | 2 |
| 40216 | aspilleras | 2 |
| 40217 | áspides | 2 |
| 40218 | asperos | 2 |
| 40219 | aspera | 2 |
| 40220 | aspado | 2 |
| 40221 | asombrar | 2 |
| 40222 | asombran | 2 |
| 40223 | asombradizos | 2 |
| 40224 | asomase | 2 |
| 40225 | asolviese | 2 |
| 40226 | asocio | 2 |
| 40227 | asociando | 2 |
| 40228 | asociadas | 2 |
| 40229 | asociada | 2 |
| 40230 | asocia | 2 |
| 40231 | asó | 2 |
| 40232 | asnal | 2 |
| 40233 | asistirla | 2 |
| 40234 | asistiera | 2 |
| 40235 | asistí | 2 |
| 40236 | asistentes | 2 |
| 40237 | asirse | 2 |
| 40238 | asirios | 2 |
| 40239 | asintiendo | 2 |
| 40240 | asignación | 2 |
| 40241 | asientate | 2 |
| 40242 | asientan | 2 |
| 40243 | asiduos | 2 |
| 40244 | asidas | 2 |
| 40245 | asían | 2 |
| 40246 | asfixiaba | 2 |
| 40247 | asestaban | 2 |
| 40248 | asesinatos | 2 |
| 40249 | asesinaron | 2 |
| 40250 | asesinarme | 2 |
| 40251 | asesinar | 2 |
| 40252 | asesinaban | 2 |
| 40253 | aserto | 2 |
| 40254 | asentaron | 2 |
| 40255 | asentaré | 2 |
| 40256 | asentadores | 2 |
| 40257 | asendereada | 2 |
| 40258 | asemejaban | 2 |
| 40259 | asegúrote | 2 |
| 40260 | aseguren | 2 |
| 40261 | asegurártelo | 2 |
| 40262 | aseguraron | 2 |
| 40263 | aseguraría | 2 |
| 40264 | aseguraran | 2 |
| 40265 | asegurara | 2 |
| 40266 | asegurados | 2 |
| 40267 | aseguradas | 2 |
| 40268 | aseguraban | 2 |
| 40269 | asedian | 2 |
| 40270 | asediaban | 2 |
| 40271 | aseados | 2 |
| 40272 | ase | 2 |
| 40273 | ascona | 2 |
| 40274 | ascetismo | 2 |
| 40275 | asceta | 2 |
| 40276 | ascensiones | 2 |
| 40277 | ascendiendo | 2 |
| 40278 | ascálafo | 2 |
| 40279 | asañes | 2 |
| 40280 | asamblea | 2 |
| 40281 | asaltó | 2 |
| 40282 | asaltan | 2 |
| 40283 | asaltada | 2 |
| 40284 | asalta | 2 |
| 40285 | arzones | 2 |
| 40286 | arzobispos | 2 |
| 40287 | arvejas | 2 |
| 40288 | aruños | 2 |
| 40289 | arturo | 2 |
| 40290 | artífices | 2 |
| 40291 | articulejo | 2 |
| 40292 | articulado | 2 |
| 40293 | articuladas | 2 |
| 40294 | articulada | 2 |
| 40295 | artesonado | 2 |
| 40296 | artesillas | 2 |
| 40297 | artero | 2 |
| 40298 | artera | 2 |
| 40299 | arrumacos | 2 |
| 40300 | arrullos | 2 |
| 40301 | arrulló | 2 |
| 40302 | arrullándole | 2 |
| 40303 | arrullaban | 2 |
| 40304 | arrulla | 2 |
| 40305 | arruinada | 2 |
| 40306 | arrugó | 2 |
| 40307 | arrugar | 2 |
| 40308 | arrugados | 2 |
| 40309 | arrostre | 2 |
| 40310 | arrope | 2 |
| 40311 | arrojóle | 2 |
| 40312 | arrojes | 2 |
| 40313 | arrojarte | 2 |
| 40314 | arrojáronse | 2 |
| 40315 | arrojarlo | 2 |
| 40316 | arrojarla | 2 |
| 40317 | arrojaría | 2 |
| 40318 | arrojándole | 2 |
| 40319 | arrojadizo | 2 |
| 40320 | arrojadas | 2 |
| 40321 | arrodilladas | 2 |
| 40322 | arrinconados | 2 |
| 40323 | arrinconado | 2 |
| 40324 | arriméme | 2 |
| 40325 | arrimarme | 2 |
| 40326 | arrimados | 2 |
| 40327 | arrimadito | 2 |
| 40328 | arriesgados | 2 |
| 40329 | arriesgada | 2 |
| 40330 | arribita | 2 |
| 40331 | arribar | 2 |
| 40332 | arriar | 2 |
| 40333 | arrepintió | 2 |
| 40334 | arrepienta | 2 |
| 40335 | arrepentyr | 2 |
| 40336 | arrepentir | 2 |
| 40337 | arrepentimientos | 2 |
| 40338 | arrepentía | 2 |
| 40339 | arrendara | 2 |
| 40340 | arrendar | 2 |
| 40341 | arremeto | 2 |
| 40342 | arremetí | 2 |
| 40343 | arremete | 2 |
| 40344 | arremangó | 2 |
| 40345 | arrellanado | 2 |
| 40346 | arreglito | 2 |
| 40347 | arregle | 2 |
| 40348 | arreglarme | 2 |
| 40349 | arreglarle | 2 |
| 40350 | arreglarían | 2 |
| 40351 | arreglara | 2 |
| 40352 | arreglándose | 2 |
| 40353 | arreglados | 2 |
| 40354 | arregladito | 2 |
| 40355 | arregimientos | 2 |
| 40356 | arredrado | 2 |
| 40357 | arredraba | 2 |
| 40358 | arreciaba | 2 |
| 40359 | arrebozado | 2 |
| 40360 | arrebolada | 2 |
| 40361 | arrebates | 2 |
| 40362 | arrebatar | 2 |
| 40363 | arrebatando | 2 |
| 40364 | arrebatan | 2 |
| 40365 | arrebatamiento | 2 |
| 40366 | arrebatadas | 2 |
| 40367 | arrastro | 2 |
| 40368 | arrastre | 2 |
| 40369 | arrastrase | 2 |
| 40370 | arrastrarse | 2 |
| 40371 | arrastrándome | 2 |
| 40372 | arrasados | 2 |
| 40373 | arrancose | 2 |
| 40374 | arrancas | 2 |
| 40375 | arrancarles | 2 |
| 40376 | arrancarla | 2 |
| 40377 | arrancadas | 2 |
| 40378 | arraigo | 2 |
| 40379 | arraigados | 2 |
| 40380 | arraigaba | 2 |
| 40381 | arraiga | 2 |
| 40382 | arquitrabe | 2 |
| 40383 | arquitectónica | 2 |
| 40384 | arquilla | 2 |
| 40385 | arpía | 2 |
| 40386 | arpegios | 2 |
| 40387 | aromático | 2 |
| 40388 | aromáticas | 2 |
| 40389 | arnes | 2 |
| 40390 | arnaldo | 2 |
| 40391 | armóse | 2 |
| 40392 | armonioso | 2 |
| 40393 | armo | 2 |
| 40394 | armisticio | 2 |
| 40395 | armesto | 2 |
| 40396 | ármese | 2 |
| 40397 | armen | 2 |
| 40398 | armase | 2 |
| 40399 | armarse | 2 |
| 40400 | armagnac | 2 |
| 40401 | arlequín | 2 |
| 40402 | aristoteles | 2 |
| 40403 | aristocráticos | 2 |
| 40404 | arista | 2 |
| 40405 | arisco | 2 |
| 40406 | arichulegui | 2 |
| 40407 | arguyéndole | 2 |
| 40408 | arguyen | 2 |
| 40409 | argumosa | 2 |
| 40410 | argumentando | 2 |
| 40411 | argumentaba | 2 |
| 40412 | argüía | 2 |
| 40413 | argollas | 2 |
| 40414 | argentino | 2 |
| 40415 | argentada | 2 |
| 40416 | argado | 2 |
| 40417 | areo | 2 |
| 40418 | arenques | 2 |
| 40419 | arenisca | 2 |
| 40420 | arenilla | 2 |
| 40421 | arengaba | 2 |
| 40422 | área | 2 |
| 40423 | arduos | 2 |
| 40424 | arduas | 2 |
| 40425 | ardentísimo | 2 |
| 40426 | arcones | 2 |
| 40427 | arcón | 2 |
| 40428 | archipi | 2 |
| 40429 | arceas | 2 |
| 40430 | arcano | 2 |
| 40431 | arcaláus | 2 |
| 40432 | arcaísmo | 2 |
| 40433 | arcaduces | 2 |
| 40434 | arcadas | 2 |
| 40435 | arbolito | 2 |
| 40436 | arbolillos | 2 |
| 40437 | arbolas | 2 |
| 40438 | arbolado | 2 |
| 40439 | araucana | 2 |
| 40440 | arar | 2 |
| 40441 | arañazos | 2 |
| 40442 | arañaron | 2 |
| 40443 | arañada | 2 |
| 40444 | aranjuez | 2 |
| 40445 | aranda | 2 |
| 40446 | aranceles | 2 |
| 40447 | aranaz | 2 |
| 40448 | aragoneses | 2 |
| 40449 | aradas | 2 |
| 40450 | arabescos | 2 |
| 40451 | árabes | 2 |
| 40452 | aquexan | 2 |
| 40453 | aquéstos | 2 |
| 40454 | aquésta | 2 |
| 40455 | aquese | 2 |
| 40456 | aquesas | 2 |
| 40457 | aquéllo | 2 |
| 40458 | apuren | 2 |
| 40459 | apurando | 2 |
| 40460 | apuran | 2 |
| 40461 | apurados | 2 |
| 40462 | apuradas | 2 |
| 40463 | apuñeado | 2 |
| 40464 | apunté | 2 |
| 40465 | apuntarlas | 2 |
| 40466 | apuntaré | 2 |
| 40467 | apuntara | 2 |
| 40468 | apuntan | 2 |
| 40469 | apuntamiento | 2 |
| 40470 | apuntalada | 2 |
| 40471 | apuestos | 2 |
| 40472 | apto | 2 |
| 40473 | aproximadamente | 2 |
| 40474 | aproximada | 2 |
| 40475 | aproximaciones | 2 |
| 40476 | aprovecho | 2 |
| 40477 | aprovechemos | 2 |
| 40478 | aprovechará | 2 |
| 40479 | aprovechara | 2 |
| 40480 | aprovechándose | 2 |
| 40481 | aprovechamos | 2 |
| 40482 | aprovechados | 2 |
| 40483 | aprovechadas | 2 |
| 40484 | apropiándose | 2 |
| 40485 | apropiadas | 2 |
| 40486 | aprobé | 2 |
| 40487 | aprobadas | 2 |
| 40488 | aprisionados | 2 |
| 40489 | aprisionada | 2 |
| 40490 | aprisiona | 2 |
| 40491 | apriscos | 2 |
| 40492 | apriete | 2 |
| 40493 | apriétate | 2 |
| 40494 | aprietas | 2 |
| 40495 | aprietan | 2 |
| 40496 | apreturas | 2 |
| 40497 | apretarse | 2 |
| 40498 | apretarla | 2 |
| 40499 | apretándosela | 2 |
| 40500 | apretándose | 2 |
| 40501 | apresures | 2 |
| 40502 | apresurar | 2 |
| 40503 | apresurados | 2 |
| 40504 | aprensivo | 2 |
| 40505 | aprendizaje | 2 |
| 40506 | aprendiera | 2 |
| 40507 | aprendidos | 2 |
| 40508 | aprendices | 2 |
| 40509 | aprenderán | 2 |
| 40510 | aprendemos | 2 |
| 40511 | aprended | 2 |
| 40512 | aprendamos | 2 |
| 40513 | apreciarse | 2 |
| 40514 | apreciaban | 2 |
| 40515 | apoyan | 2 |
| 40516 | apoyados | 2 |
| 40517 | apoyaban | 2 |
| 40518 | apostólicos | 2 |
| 40519 | apóstata | 2 |
| 40520 | apostasía | 2 |
| 40521 | apostaría | 2 |
| 40522 | apostados | 2 |
| 40523 | aposentamiento | 2 |
| 40524 | aposentados | 2 |
| 40525 | aposentado | 2 |
| 40526 | aporrear | 2 |
| 40527 | aporrean | 2 |
| 40528 | aporrea | 2 |
| 40529 | apoplético | 2 |
| 40530 | apolillados | 2 |
| 40531 | apodos | 2 |
| 40532 | apoderose | 2 |
| 40533 | apodere | 2 |
| 40534 | apoderaron | 2 |
| 40535 | apoderaban | 2 |
| 40536 | apodaca | 2 |
| 40537 | apoca | 2 |
| 40538 | aplícate | 2 |
| 40539 | aplicarse | 2 |
| 40540 | aplicándose | 2 |
| 40541 | aplican | 2 |
| 40542 | aplicados | 2 |
| 40543 | aplazó | 2 |
| 40544 | aplazible | 2 |
| 40545 | aplaze | 2 |
| 40546 | aplazada | 2 |
| 40547 | aplaudo | 2 |
| 40548 | aplaudieron | 2 |
| 40549 | aplaudidos | 2 |
| 40550 | aplaudían | 2 |
| 40551 | aplastó | 2 |
| 40552 | aplastadas | 2 |
| 40553 | aplanado | 2 |
| 40554 | aplacó | 2 |
| 40555 | aplace | 2 |
| 40556 | aplacada | 2 |
| 40557 | apiñadas | 2 |
| 40558 | apiñaban | 2 |
| 40559 | apetitosos | 2 |
| 40560 | apetitoso | 2 |
| 40561 | apetitosa | 2 |
| 40562 | apetecida | 2 |
| 40563 | apestas | 2 |
| 40564 | apestando | 2 |
| 40565 | apersonado | 2 |
| 40566 | apercibimiento | 2 |
| 40567 | apercibía | 2 |
| 40568 | apercibete | 2 |
| 40569 | apercibe | 2 |
| 40570 | aperçebudo | 2 |
| 40571 | aperçebidos | 2 |
| 40572 | apercebido | 2 |
| 40573 | apercebidas | 2 |
| 40574 | aperçebida | 2 |
| 40575 | apenado | 2 |
| 40576 | apenada | 2 |
| 40577 | apellidado | 2 |
| 40578 | apeles | 2 |
| 40579 | apelativo | 2 |
| 40580 | apelando | 2 |
| 40581 | apechugar | 2 |
| 40582 | apéate | 2 |
| 40583 | apeámonos | 2 |
| 40584 | apasionadamente | 2 |
| 40585 | apartóle | 2 |
| 40586 | apártese | 2 |
| 40587 | apártate | 2 |
| 40588 | apartate | 2 |
| 40589 | apartas | 2 |
| 40590 | apartaos | 2 |
| 40591 | apartándome | 2 |
| 40592 | apartámonos | 2 |
| 40593 | aparentarla | 2 |
| 40594 | aparéjese | 2 |
| 40595 | aparejado | 2 |
| 40596 | apareciera | 2 |
| 40597 | aparecérsele | 2 |
| 40598 | aparador | 2 |
| 40599 | apañaditos | 2 |
| 40600 | apañaditas | 2 |
| 40601 | apalabrado | 2 |
| 40602 | apagarse | 2 |
| 40603 | apagarla | 2 |
| 40604 | apagando | 2 |
| 40605 | apacentaba | 2 |
| 40606 | añejos | 2 |
| 40607 | añejo | 2 |
| 40608 | añasca | 2 |
| 40609 | añal | 2 |
| 40610 | añadiría | 2 |
| 40611 | añadióse | 2 |
| 40612 | añadimos | 2 |
| 40613 | añadieron | 2 |
| 40614 | añadían | 2 |
| 40615 | añades | 2 |
| 40616 | anunciarme | 2 |
| 40617 | anunciará | 2 |
| 40618 | anunciándole | 2 |
| 40619 | anunciadas | 2 |
| 40620 | anulo | 2 |
| 40621 | antro | 2 |
| 40622 | antorchas | 2 |
| 40623 | antojado | 2 |
| 40624 | antitéticos | 2 |
| 40625 | antiparras | 2 |
| 40626 | antinoo | 2 |
| 40627 | antinomia | 2 |
| 40628 | antiguallas | 2 |
| 40629 | antigo | 2 |
| 40630 | antífrasis | 2 |
| 40631 | anticuarios | 2 |
| 40632 | anticipos | 2 |
| 40633 | anticipada | 2 |
| 40634 | anterioridad | 2 |
| 40635 | antepuerta | 2 |
| 40636 | anteón | 2 |
| 40637 | anteo | 2 |
| 40638 | antecogió | 2 |
| 40639 | antecesor | 2 |
| 40640 | antaños | 2 |
| 40641 | antagonista | 2 |
| 40642 | antagonismo | 2 |
| 40643 | ansiosas | 2 |
| 40644 | ansiada | 2 |
| 40645 | ansarones | 2 |
| 40646 | anotomía | 2 |
| 40647 | anotarse | 2 |
| 40648 | anotar | 2 |
| 40649 | anonadado | 2 |
| 40650 | anonada | 2 |
| 40651 | anomalías | 2 |
| 40652 | anoeta | 2 |
| 40653 | annatas | 2 |
| 40654 | anises | 2 |
| 40655 | aniquile | 2 |
| 40656 | aniquilan | 2 |
| 40657 | aniquilado | 2 |
| 40658 | aniquilada | 2 |
| 40659 | animosos | 2 |
| 40660 | animosidad | 2 |
| 40661 | anímese | 2 |
| 40662 | animes | 2 |
| 40663 | animase | 2 |
| 40664 | animando | 2 |
| 40665 | animadora | 2 |
| 40666 | anibal | 2 |
| 40667 | anhelas | 2 |
| 40668 | anhelar | 2 |
| 40669 | anhelantes | 2 |
| 40670 | anhelaban | 2 |
| 40671 | anhela | 2 |
| 40672 | angustiosos | 2 |
| 40673 | angustiadas | 2 |
| 40674 | angulema | 2 |
| 40675 | anguilas | 2 |
| 40676 | angosturas | 2 |
| 40677 | angelote | 2 |
| 40678 | angelón | 2 |
| 40679 | angelillo | 2 |
| 40680 | angélico | 2 |
| 40681 | angelicales | 2 |
| 40682 | ánfora | 2 |
| 40683 | anfitrión | 2 |
| 40684 | anfiteatro | 2 |
| 40685 | anexas | 2 |
| 40686 | aneurisma | 2 |
| 40687 | anegue | 2 |
| 40688 | anegar | 2 |
| 40689 | anduvieran | 2 |
| 40690 | andróminas | 2 |
| 40691 | andrómaca | 2 |
| 40692 | andoain | 2 |
| 40693 | ándense | 2 |
| 40694 | andaua | 2 |
| 40695 | andarte | 2 |
| 40696 | andariego | 2 |
| 40697 | andanadas | 2 |
| 40698 | andá | 2 |
| 40699 | and | 2 |
| 40700 | áncoras | 2 |
| 40701 | áncora | 2 |
| 40702 | ancla | 2 |
| 40703 | anchísima | 2 |
| 40704 | ancheta | 2 |
| 40705 | anch | 2 |
| 40706 | anatómicos | 2 |
| 40707 | anatemas | 2 |
| 40708 | anascote | 2 |
| 40709 | análogo | 2 |
| 40710 | analogía | 2 |
| 40711 | anafrodita | 2 |
| 40712 | ánades | 2 |
| 40713 | anacronismo | 2 |
| 40714 | anacreóntica | 2 |
| 40715 | amxy | 2 |
| 40716 | amueblada | 2 |
| 40717 | ampuero | 2 |
| 40718 | ampolla | 2 |
| 40719 | amplios | 2 |
| 40720 | amplio | 2 |
| 40721 | ampliación | 2 |
| 40722 | amplia | 2 |
| 40723 | ampararse | 2 |
| 40724 | amparará | 2 |
| 40725 | amparando | 2 |
| 40726 | ampárame | 2 |
| 40727 | amparado | 2 |
| 40728 | amoscándose | 2 |
| 40729 | amortiguados | 2 |
| 40730 | amortajó | 2 |
| 40731 | amoratado | 2 |
| 40732 | amora | 2 |
| 40733 | amontonaban | 2 |
| 40734 | amonestando | 2 |
| 40735 | amistosas | 2 |
| 40736 | amistosamente | 2 |
| 40737 | amistosa | 2 |
| 40738 | amiguitos | 2 |
| 40739 | amiclas | 2 |
| 40740 | ameste | 2 |
| 40741 | ames | 2 |
| 40742 | amengua | 2 |
| 40743 | amenazándola | 2 |
| 40744 | amenazadoras | 2 |
| 40745 | amenas | 2 |
| 40746 | amenaças | 2 |
| 40747 | amenaçar | 2 |
| 40748 | amemos | 2 |
| 40749 | amedrentado | 2 |
| 40750 | amé | 2 |
| 40751 | ambrosía | 2 |
| 40752 | ámbitos | 2 |
| 40753 | ambicionaba | 2 |
| 40754 | amays | 2 |
| 40755 | amavan | 2 |
| 40756 | amava | 2 |
| 40757 | amaua | 2 |
| 40758 | amasara | 2 |
| 40759 | amartelar | 2 |
| 40760 | amarrada | 2 |
| 40761 | amarlas | 2 |
| 40762 | amariella | 2 |
| 40763 | amarguen | 2 |
| 40764 | amargan | 2 |
| 40765 | amargaban | 2 |
| 40766 | amapolas | 2 |
| 40767 | amansado | 2 |
| 40768 | amanerada | 2 |
| 40769 | amanecidos | 2 |
| 40770 | amancebamiento | 2 |
| 40771 | amancebados | 2 |
| 40772 | amamos | 2 |
| 40773 | amalgama | 2 |
| 40774 | amainar | 2 |
| 40775 | amagos | 2 |
| 40776 | amagado | 2 |
| 40777 | amadores | 2 |
| 40778 | amablemente | 2 |
| 40779 | amabilísimo | 2 |
| 40780 | am | 2 |
| 40781 | alzaste | 2 |
| 40782 | álzase | 2 |
| 40783 | alzase | 2 |
| 40784 | alzarme | 2 |
| 40785 | alzamiento | 2 |
| 40786 | alvos | 2 |
| 40787 | alvarín | 2 |
| 40788 | alvarda | 2 |
| 40789 | alusivos | 2 |
| 40790 | aluorada | 2 |
| 40791 | alumna | 2 |
| 40792 | alumbre | 2 |
| 40793 | aludió | 2 |
| 40794 | alucinar | 2 |
| 40795 | aluayalde | 2 |
| 40796 | aluanares | 2 |
| 40797 | alua | 2 |
| 40798 | altruista | 2 |
| 40799 | altra | 2 |
| 40800 | altitud | 2 |
| 40801 | altisonante | 2 |
| 40802 | altísimas | 2 |
| 40803 | altibajos | 2 |
| 40804 | alteras | 2 |
| 40805 | alterarse | 2 |
| 40806 | alterados | 2 |
| 40807 | alteraban | 2 |
| 40808 | altarito | 2 |
| 40809 | altanerías | 2 |
| 40810 | alquitrán | 2 |
| 40811 | alquilaba | 2 |
| 40812 | alquila | 2 |
| 40813 | alquife | 2 |
| 40814 | alquerías | 2 |
| 40815 | alpes | 2 |
| 40816 | alpargatero | 2 |
| 40817 | alongó | 2 |
| 40818 | alones | 2 |
| 40819 | alojarse | 2 |
| 40820 | alocución | 2 |
| 40821 | almuerzos | 2 |
| 40822 | almuerzas | 2 |
| 40823 | almuerço | 2 |
| 40824 | almudenita | 2 |
| 40825 | almorzando | 2 |
| 40826 | almohadón | 2 |
| 40827 | almohadilla | 2 |
| 40828 | almo | 2 |
| 40829 | almidonada | 2 |
| 40830 | almibarados | 2 |
| 40831 | almibarado | 2 |
| 40832 | almibaradas | 2 |
| 40833 | almeja | 2 |
| 40834 | almanzor | 2 |
| 40835 | almanaques | 2 |
| 40836 | almanaque | 2 |
| 40837 | almagre | 2 |
| 40838 | allego | 2 |
| 40839 | allegate | 2 |
| 40840 | allegando | 2 |
| 40841 | allegadas | 2 |
| 40842 | alivia | 2 |
| 40843 | aliuiado | 2 |
| 40844 | aliso | 2 |
| 40845 | aliño | 2 |
| 40846 | alimentados | 2 |
| 40847 | aligeraba | 2 |
| 40848 | aligera | 2 |
| 40849 | aliciente | 2 |
| 40850 | aliagas | 2 |
| 40851 | aliada | 2 |
| 40852 | alhelíes | 2 |
| 40853 | alhelí | 2 |
| 40854 | algúnd | 2 |
| 40855 | alguaçil | 2 |
| 40856 | algecireño | 2 |
| 40857 | algebrista | 2 |
| 40858 | algas | 2 |
| 40859 | alga | 2 |
| 40860 | alforja | 2 |
| 40861 | alfonsino | 2 |
| 40862 | alfombrada | 2 |
| 40863 | alfeñique | 2 |
| 40864 | alfayate | 2 |
| 40865 | alfanjes | 2 |
| 40866 | alfana | 2 |
| 40867 | alexi | 2 |
| 40868 | alevosías | 2 |
| 40869 | alevosa | 2 |
| 40870 | aleto | 2 |
| 40871 | aletargados | 2 |
| 40872 | aletargado | 2 |
| 40873 | alero | 2 |
| 40874 | alentó | 2 |
| 40875 | alentara | 2 |
| 40876 | alentada | 2 |
| 40877 | alejose | 2 |
| 40878 | aleje | 2 |
| 40879 | alejaron | 2 |
| 40880 | alejarme | 2 |
| 40881 | alejarle | 2 |
| 40882 | alejandrino | 2 |
| 40883 | alejando | 2 |
| 40884 | alejábase | 2 |
| 40885 | aleja | 2 |
| 40886 | alegróse | 2 |
| 40887 | alegrose | 2 |
| 40888 | alégrome | 2 |
| 40889 | alegrasen | 2 |
| 40890 | alegrarte | 2 |
| 40891 | alegráronse | 2 |
| 40892 | alegrarle | 2 |
| 40893 | alegramos | 2 |
| 40894 | alegrado | 2 |
| 40895 | alegrábanse | 2 |
| 40896 | alegórica | 2 |
| 40897 | alegaron | 2 |
| 40898 | alegar | 2 |
| 40899 | alega | 2 |
| 40900 | alefanfarón | 2 |
| 40901 | aleación | 2 |
| 40902 | alduides | 2 |
| 40903 | aldehuela | 2 |
| 40904 | aldaba | 2 |
| 40905 | alcotín | 2 |
| 40906 | alcohólico | 2 |
| 40907 | alcibíades | 2 |
| 40908 | alcatifa | 2 |
| 40909 | alcarria | 2 |
| 40910 | alcaraz | 2 |
| 40911 | alcanzarlos | 2 |
| 40912 | alcanzaría | 2 |
| 40913 | alcanzaren | 2 |
| 40914 | alcanzando | 2 |
| 40915 | alcanzados | 2 |
| 40916 | alçando | 2 |
| 40917 | alcancías | 2 |
| 40918 | alcancía | 2 |
| 40919 | alcançarían | 2 |
| 40920 | alcaidía | 2 |
| 40921 | alcagüete | 2 |
| 40922 | alcachofas | 2 |
| 40923 | álbums | 2 |
| 40924 | álbumes | 2 |
| 40925 | alborotes | 2 |
| 40926 | alboroten | 2 |
| 40927 | alborotasen | 2 |
| 40928 | alborotarse | 2 |
| 40929 | alborotáronse | 2 |
| 40930 | alborotaría | 2 |
| 40931 | alborotara | 2 |
| 40932 | alborotadores | 2 |
| 40933 | albornoz | 2 |
| 40934 | alborada | 2 |
| 40935 | albóndigas | 2 |
| 40936 | albo | 2 |
| 40937 | albis | 2 |
| 40938 | albillo | 2 |
| 40939 | alberto | 2 |
| 40940 | albergar | 2 |
| 40941 | albardero | 2 |
| 40942 | albardas | 2 |
| 40943 | albaicín | 2 |
| 40944 | alarmose | 2 |
| 40945 | alarmando | 2 |
| 40946 | alarmaba | 2 |
| 40947 | alargue | 2 |
| 40948 | alargarle | 2 |
| 40949 | alargándole | 2 |
| 40950 | alargan | 2 |
| 40951 | alardo | 2 |
| 40952 | alardeaba | 2 |
| 40953 | alarcón | 2 |
| 40954 | alana | 2 |
| 40955 | alambicado | 2 |
| 40956 | alambicadas | 2 |
| 40957 | aladas | 2 |
| 40958 | alabé | 2 |
| 40959 | alabarle | 2 |
| 40960 | alabada | 2 |
| 40961 | ajusto | 2 |
| 40962 | ajusticiar | 2 |
| 40963 | ajuste | 2 |
| 40964 | ajustando | 2 |
| 40965 | ajustamos | 2 |
| 40966 | ajusta | 2 |
| 40967 | ajumao | 2 |
| 40968 | ajorcas | 2 |
| 40969 | ajado | 2 |
| 40970 | airados | 2 |
| 40971 | airadas | 2 |
| 40972 | aibar | 2 |
| 40973 | ahuecar | 2 |
| 40974 | ahuecando | 2 |
| 40975 | ahuecados | 2 |
| 40976 | ahuecado | 2 |
| 40977 | ahueca | 2 |
| 40978 | ahorró | 2 |
| 40979 | ahorrarme | 2 |
| 40980 | ahorraréis | 2 |
| 40981 | ahorran | 2 |
| 40982 | ahorcarse | 2 |
| 40983 | ahorcarme | 2 |
| 40984 | ahorcan | 2 |
| 40985 | ahorcados | 2 |
| 40986 | ahondaba | 2 |
| 40987 | ahogas | 2 |
| 40988 | ahogarme | 2 |
| 40989 | ahogara | 2 |
| 40990 | ahogaban | 2 |
| 40991 | ahíta | 2 |
| 40992 | ahinco | 2 |
| 40993 | ahilada | 2 |
| 40994 | ahijados | 2 |
| 40995 | ahijado | 2 |
| 40996 | aguzando | 2 |
| 40997 | aguzan | 2 |
| 40998 | aguzado | 2 |
| 40999 | agujetas | 2 |
| 41000 | agujeta | 2 |
| 41001 | aguijó | 2 |
| 41002 | aguijo | 2 |
| 41003 | aguijando | 2 |
| 41004 | aguerrido | 2 |
| 41005 | agueros | 2 |
| 41006 | aguardentazo | 2 |
| 41007 | aguardasen | 2 |
| 41008 | aguardaron | 2 |
| 41009 | aguardarle | 2 |
| 41010 | aguardándome | 2 |
| 41011 | aguardamos | 2 |
| 41012 | aguardad | 2 |
| 41013 | aguantó | 2 |
| 41014 | aguantaba | 2 |
| 41015 | aguaceros | 2 |
| 41016 | agrietada | 2 |
| 41017 | agridulce | 2 |
| 41018 | agriado | 2 |
| 41019 | agresora | 2 |
| 41020 | agresor | 2 |
| 41021 | agregarse | 2 |
| 41022 | agregaron | 2 |
| 41023 | agregar | 2 |
| 41024 | agregado | 2 |
| 41025 | agravó | 2 |
| 41026 | agravias | 2 |
| 41027 | agraviarle | 2 |
| 41028 | agravian | 2 |
| 41029 | agravan | 2 |
| 41030 | agras | 2 |
| 41031 | agrandarse | 2 |
| 41032 | agradezcas | 2 |
| 41033 | agradecióselo | 2 |
| 41034 | agradecimientos | 2 |
| 41035 | agradecíle | 2 |
| 41036 | agradeciéndole | 2 |
| 41037 | agradecí | 2 |
| 41038 | agradecérselo | 2 |
| 41039 | agradecerlo | 2 |
| 41040 | agradecería | 2 |
| 41041 | agradecen | 2 |
| 41042 | agrade | 2 |
| 41043 | agradarle | 2 |
| 41044 | agradarla | 2 |
| 41045 | agradado | 2 |
| 41046 | agostado | 2 |
| 41047 | agolpaba | 2 |
| 41048 | agobiada | 2 |
| 41049 | agobia | 2 |
| 41050 | agitándose | 2 |
| 41051 | agita | 2 |
| 41052 | agentes | 2 |
| 41053 | agenos | 2 |
| 41054 | agazapándose | 2 |
| 41055 | agazapado | 2 |
| 41056 | agasajaditos | 2 |
| 41057 | agasajada | 2 |
| 41058 | agárrate | 2 |
| 41059 | agarrarlo | 2 |
| 41060 | agarrándole | 2 |
| 41061 | agarran | 2 |
| 41062 | agarrados | 2 |
| 41063 | agarenos | 2 |
| 41064 | agachar | 2 |
| 41065 | agachándose | 2 |
| 41066 | agachado | 2 |
| 41067 | agacha | 2 |
| 41068 | africanas | 2 |
| 41069 | afrento | 2 |
| 41070 | afrente | 2 |
| 41071 | afrentarse | 2 |
| 41072 | afortunados | 2 |
| 41073 | afluía | 2 |
| 41074 | afloxase | 2 |
| 41075 | afloxara | 2 |
| 41076 | afloxa | 2 |
| 41077 | aflojarse | 2 |
| 41078 | aflojaba | 2 |
| 41079 | afloja | 2 |
| 41080 | afloencias | 2 |
| 41081 | aflijo | 2 |
| 41082 | afligirse | 2 |
| 41083 | afligióse | 2 |
| 41084 | afligió | 2 |
| 41085 | afirmativas | 2 |
| 41086 | afirmas | 2 |
| 41087 | afirmándose | 2 |
| 41088 | afines | 2 |
| 41089 | afinaban | 2 |
| 41090 | afiló | 2 |
| 41091 | afiladas | 2 |
| 41092 | afila | 2 |
| 41093 | aficionadas | 2 |
| 41094 | afeto | 2 |
| 41095 | aferradas | 2 |
| 41096 | afeminamiento | 2 |
| 41097 | afeites | 2 |
| 41098 | afeiten | 2 |
| 41099 | afeitados | 2 |
| 41100 | afectísimo | 2 |
| 41101 | afectan | 2 |
| 41102 | afecciones | 2 |
| 41103 | afección | 2 |
| 41104 | afeaban | 2 |
| 41105 | afanan | 2 |
| 41106 | afan | 2 |
| 41107 | aéreo | 2 |
| 41108 | advirtiesen | 2 |
| 41109 | advirtiéndole | 2 |
| 41110 | adviertes | 2 |
| 41111 | adviertas | 2 |
| 41112 | advertirte | 2 |
| 41113 | advenediza | 2 |
| 41114 | aduxo | 2 |
| 41115 | adustas | 2 |
| 41116 | adulterios | 2 |
| 41117 | aduló | 2 |
| 41118 | adular | 2 |
| 41119 | adulaban | 2 |
| 41120 | aducía | 2 |
| 41121 | aduares | 2 |
| 41122 | adriano | 2 |
| 41123 | adquirieron | 2 |
| 41124 | adquiera | 2 |
| 41125 | adoró | 2 |
| 41126 | adornes | 2 |
| 41127 | adorne | 2 |
| 41128 | adornarse | 2 |
| 41129 | adornados | 2 |
| 41130 | adornaba | 2 |
| 41131 | adormeció | 2 |
| 41132 | adormecida | 2 |
| 41133 | adoren | 2 |
| 41134 | adore | 2 |
| 41135 | adoratrices | 2 |
| 41136 | adorase | 2 |
| 41137 | adoras | 2 |
| 41138 | adorarla | 2 |
| 41139 | adoramos | 2 |
| 41140 | adorabas | 2 |
| 41141 | adoquier | 2 |
| 41142 | adobar | 2 |
| 41143 | adoban | 2 |
| 41144 | admitirlos | 2 |
| 41145 | admitirlo | 2 |
| 41146 | admitiendo | 2 |
| 41147 | admitían | 2 |
| 41148 | admisión | 2 |
| 41149 | admiróle | 2 |
| 41150 | admiremos | 2 |
| 41151 | admiré | 2 |
| 41152 | admiraría | 2 |
| 41153 | admiramos | 2 |
| 41154 | admiradores | 2 |
| 41155 | administraron | 2 |
| 41156 | administrando | 2 |
| 41157 | administrado | 2 |
| 41158 | adjudicó | 2 |
| 41159 | adjudicado | 2 |
| 41160 | adivinarle | 2 |
| 41161 | adivinaciones | 2 |
| 41162 | adiestra | 2 |
| 41163 | adiciones | 2 |
| 41164 | adhiere | 2 |
| 41165 | adhesión | 2 |
| 41166 | adherirme | 2 |
| 41167 | adevino | 2 |
| 41168 | aderezasen | 2 |
| 41169 | aderezaron | 2 |
| 41170 | aderezando | 2 |
| 41171 | aderezan | 2 |
| 41172 | aderezaban | 2 |
| 41173 | adeliñado | 2 |
| 41174 | adelgaza | 2 |
| 41175 | adelantaron | 2 |
| 41176 | adelantara | 2 |
| 41177 | adelantan | 2 |
| 41178 | adecuados | 2 |
| 41179 | adecuada | 2 |
| 41180 | adaptada | 2 |
| 41181 | adamar | 2 |
| 41182 | adamado | 2 |
| 41183 | adam | 2 |
| 41184 | adagio | 2 |
| 41185 | acusen | 2 |
| 41186 | acusarme | 2 |
| 41187 | acusare | 2 |
| 41188 | acusando | 2 |
| 41189 | acusadora | 2 |
| 41190 | acusación | 2 |
| 41191 | acurrucó | 2 |
| 41192 | acumular | 2 |
| 41193 | acumulados | 2 |
| 41194 | acumulado | 2 |
| 41195 | acuéstese | 2 |
| 41196 | acuerdos | 2 |
| 41197 | acuérdese | 2 |
| 41198 | acuchillador | 2 |
| 41199 | actualidad | 2 |
| 41200 | actrices | 2 |
| 41201 | actividades | 2 |
| 41202 | act | 2 |
| 41203 | acribillado | 2 |
| 41204 | acreditadas | 2 |
| 41205 | acreditaban | 2 |
| 41206 | acreditaba | 2 |
| 41207 | acrecientas | 2 |
| 41208 | acrecentaba | 2 |
| 41209 | acre | 2 |
| 41210 | acostumbre | 2 |
| 41211 | acostumbrarse | 2 |
| 41212 | acostumbran | 2 |
| 41213 | acostumbraban | 2 |
| 41214 | acostóse | 2 |
| 41215 | acostéme | 2 |
| 41216 | acostaría | 2 |
| 41217 | acostábase | 2 |
| 41218 | acosados | 2 |
| 41219 | acortarse | 2 |
| 41220 | acorrucó | 2 |
| 41221 | acorres | 2 |
| 41222 | acorralada | 2 |
| 41223 | acordo | 2 |
| 41224 | acordaría | 2 |
| 41225 | acordando | 2 |
| 41226 | acordados | 2 |
| 41227 | acordada | 2 |
| 41228 | acoquinar | 2 |
| 41229 | acontecieron | 2 |
| 41230 | acontecerles | 2 |
| 41231 | acontecerle | 2 |
| 41232 | acontecen | 2 |
| 41233 | aconsejes | 2 |
| 41234 | aconsejaron | 2 |
| 41235 | aconsejarme | 2 |
| 41236 | aconsejaremos | 2 |
| 41237 | aconsejara | 2 |
| 41238 | aconsejan | 2 |
| 41239 | aconsejaban | 2 |
| 41240 | acongojadísima | 2 |
| 41241 | acondicionado | 2 |
| 41242 | acompañé | 2 |
| 41243 | acompañaros | 2 |
| 41244 | acompañarles | 2 |
| 41245 | acompañándose | 2 |
| 41246 | acompáñale | 2 |
| 41247 | acompanemos | 2 |
| 41248 | acompanada | 2 |
| 41249 | acomodóse | 2 |
| 41250 | acomoden | 2 |
| 41251 | acomodasen | 2 |
| 41252 | acomodáronme | 2 |
| 41253 | acomodarme | 2 |
| 41254 | acomodarle | 2 |
| 41255 | acomodaría | 2 |
| 41256 | acomodándome | 2 |
| 41257 | acomodándole | 2 |
| 41258 | acomodando | 2 |
| 41259 | acomodadas | 2 |
| 41260 | acomiendo | 2 |
| 41261 | acometieran | 2 |
| 41262 | acometidos | 2 |
| 41263 | acometidas | 2 |
| 41264 | acometí | 2 |
| 41265 | acometería | 2 |
| 41266 | acometedor | 2 |
| 41267 | acoje | 2 |
| 41268 | acoja | 2 |
| 41269 | acogoto | 2 |
| 41270 | acogido | 2 |
| 41271 | acogidas | 2 |
| 41272 | acogerse | 2 |
| 41273 | acoge | 2 |
| 41274 | acoceando | 2 |
| 41275 | acobardes | 2 |
| 41276 | aclaró | 2 |
| 41277 | aclare | 2 |
| 41278 | aclarado | 2 |
| 41279 | aclaración | 2 |
| 41280 | aclara | 2 |
| 41281 | aclamaciones | 2 |
| 41282 | açiprestes | 2 |
| 41283 | acicates | 2 |
| 41284 | achico | 2 |
| 41285 | achacaban | 2 |
| 41286 | acetar | 2 |
| 41287 | acertarle | 2 |
| 41288 | acertados | 2 |
| 41289 | acertadas | 2 |
| 41290 | acerque | 2 |
| 41291 | acerico | 2 |
| 41292 | acercósele | 2 |
| 41293 | acerco | 2 |
| 41294 | acércate | 2 |
| 41295 | acercara | 2 |
| 41296 | acercándosele | 2 |
| 41297 | acercan | 2 |
| 41298 | acercáis | 2 |
| 41299 | acerbas | 2 |
| 41300 | aceptaron | 2 |
| 41301 | aceptarlo | 2 |
| 41302 | aceptadas | 2 |
| 41303 | aceptada | 2 |
| 41304 | aceptables | 2 |
| 41305 | aceptable | 2 |
| 41306 | aceña | 2 |
| 41307 | acelgas | 2 |
| 41308 | aceleró | 2 |
| 41309 | aceituna | 2 |
| 41310 | aceitosas | 2 |
| 41311 | aceitera | 2 |
| 41312 | aceita | 2 |
| 41313 | aceda | 2 |
| 41314 | acechador | 2 |
| 41315 | acebo | 2 |
| 41316 | accionistas | 2 |
| 41317 | accidentada | 2 |
| 41318 | accesorios | 2 |
| 41319 | accesorio | 2 |
| 41320 | accediendo | 2 |
| 41321 | acatarrado | 2 |
| 41322 | acatar | 2 |
| 41323 | acarreado | 2 |
| 41324 | acariciarle | 2 |
| 41325 | acaricia | 2 |
| 41326 | acanaladas | 2 |
| 41327 | acamuzado | 2 |
| 41328 | acaloró | 2 |
| 41329 | acaloradamente | 2 |
| 41330 | acallar | 2 |
| 41331 | acaescido | 2 |
| 41332 | acaescer | 2 |
| 41333 | acaecieron | 2 |
| 41334 | acaece | 2 |
| 41335 | acábese | 2 |
| 41336 | acabasse | 2 |
| 41337 | acabársele | 2 |
| 41338 | acabarán | 2 |
| 41339 | acabaran | 2 |
| 41340 | acabándose | 2 |
| 41341 | acaballa | 2 |
| 41342 | abyerta | 2 |
| 41343 | abuse | 2 |
| 41344 | abusas | 2 |
| 41345 | abusado | 2 |
| 41346 | abusa | 2 |
| 41347 | aburrirme | 2 |
| 41348 | aburrirle | 2 |
| 41349 | aburrió | 2 |
| 41350 | aburriéndose | 2 |
| 41351 | aburridas | 2 |
| 41352 | aburres | 2 |
| 41353 | aburra | 2 |
| 41354 | abundosa | 2 |
| 41355 | abundamiento | 2 |
| 41356 | abultaba | 2 |
| 41357 | abta | 2 |
| 41358 | absuelta | 2 |
| 41359 | abstinençia | 2 |
| 41360 | absorbiendo | 2 |
| 41361 | absorbían | 2 |
| 41362 | absorbía | 2 |
| 41363 | absolvía | 2 |
| 41364 | absolutas | 2 |
| 41365 | absente | 2 |
| 41366 | abrumadora | 2 |
| 41367 | abroño | 2 |
| 41368 | abrochándose | 2 |
| 41369 | abrochado | 2 |
| 41370 | abrochaba | 2 |
| 41371 | abrirían | 2 |
| 41372 | abriremos | 2 |
| 41373 | abriré | 2 |
| 41374 | abrióse | 2 |
| 41375 | abriles | 2 |
| 41376 | abrigos | 2 |
| 41377 | abrígate | 2 |
| 41378 | abrigara | 2 |
| 41379 | abrigar | 2 |
| 41380 | abrigados | 2 |
| 41381 | abrigadas | 2 |
| 41382 | abriesen | 2 |
| 41383 | abrieran | 2 |
| 41384 | abriéndolos | 2 |
| 41385 | abreviaturas | 2 |
| 41386 | abrevia | 2 |
| 41387 | abrenos | 2 |
| 41388 | abreme | 2 |
| 41389 | abrazólos | 2 |
| 41390 | abrázate | 2 |
| 41391 | abrazase | 2 |
| 41392 | abrazarte | 2 |
| 41393 | abrazarla | 2 |
| 41394 | abrase | 2 |
| 41395 | abrasarse | 2 |
| 41396 | abrasarme | 2 |
| 41397 | abrasadores | 2 |
| 41398 | abrasador | 2 |
| 41399 | aborresçer | 2 |
| 41400 | aborreció | 2 |
| 41401 | aborrecían | 2 |
| 41402 | aborreces | 2 |
| 41403 | aborrecerte | 2 |
| 41404 | aborreceré | 2 |
| 41405 | aborrecerá | 2 |
| 41406 | abordó | 2 |
| 41407 | abonadas | 2 |
| 41408 | abona | 2 |
| 41409 | abomino | 2 |
| 41410 | abominado | 2 |
| 41411 | abolladuras | 2 |
| 41412 | abollado | 2 |
| 41413 | abolida | 2 |
| 41414 | aboliciones | 2 |
| 41415 | abogue | 2 |
| 41416 | abofetear | 2 |
| 41417 | ablandaros | 2 |
| 41418 | ablandara | 2 |
| 41419 | ablandado | 2 |
| 41420 | abiua | 2 |
| 41421 | abito | 2 |
| 41422 | abismarse | 2 |
| 41423 | abigarradas | 2 |
| 41424 | abeytar | 2 |
| 41425 | abetos | 2 |
| 41426 | abeto | 2 |
| 41427 | abernuncio | 2 |
| 41428 | abejón | 2 |
| 41429 | abdiençia | 2 |
| 41430 | abaxóse | 2 |
| 41431 | abaxar | 2 |
| 41432 | abatir | 2 |
| 41433 | abatiendo | 2 |
| 41434 | abatida | 2 |
| 41435 | abastasse | 2 |
| 41436 | abastado | 2 |
| 41437 | abandonase | 2 |
| 41438 | abandonarse | 2 |
| 41439 | abandonarlo | 2 |
| 41440 | abandonan | 2 |
| 41441 | abalanzándose | 2 |
| 41442 | abajó | 2 |
| 41443 | abajarse | 2 |
| 41444 | abajar | 2 |
| 41445 | abaco | 2 |
| 41446 | aba | 2 |
| 41447 | zuzaban | 1 |
| 41448 | zutanos | 1 |
| 41449 | zurujanos | 1 |
| 41450 | zurujano | 1 |
| 41451 | zurrio | 1 |
| 41452 | zurriagazo | 1 |
| 41453 | zurriaga | 1 |
| 41454 | zurrar | 1 |
| 41455 | zurra | 1 |
| 41456 | zuri | 1 |
| 41457 | zurcidora | 1 |
| 41458 | zurcidor | 1 |
| 41459 | zurcen | 1 |
| 41460 | zurbarán | 1 |
| 41461 | zur | 1 |
| 41462 | zumos | 1 |
| 41463 | zumbona | 1 |
| 41464 | zumbidillo | 1 |
| 41465 | zumbando | 1 |
| 41466 | zumbadores | 1 |
| 41467 | zumba | 1 |
| 41468 | zumarri | 1 |
| 41469 | zulema | 1 |
| 41470 | zufro | 1 |
| 41471 | zufre | 1 |
| 41472 | zufaina | 1 |
| 41473 | zuen | 1 |
| 41474 | zueco | 1 |
| 41475 | zuazté | 1 |
| 41476 | zuaz | 1 |
| 41477 | zuavo | 1 |
| 41478 | zozobró | 1 |
| 41479 | zozobrado | 1 |
| 41480 | zote | 1 |
| 41481 | zortzicos | 1 |
| 41482 | zorruna | 1 |
| 41483 | zorrocloco | 1 |
| 41484 | zoroástrica | 1 |
| 41485 | zoroastes | 1 |
| 41486 | zoquete | 1 |
| 41487 | zopiro | 1 |
| 41488 | zoológica | 1 |
| 41489 | zonzorino | 1 |
| 41490 | zoltanís | 1 |
| 41491 | zoílo | 1 |
| 41492 | zofrirte | 1 |
| 41493 | zofrir | 1 |
| 41494 | zodíacos | 1 |
| 41495 | zodíaco | 1 |
| 41496 | zodiaco | 1 |
| 41497 | zoca | 1 |
| 41498 | zeuxis | 1 |
| 41499 | zenón | 1 |
| 41500 | zenit | 1 |
| 41501 | zementerio | 1 |
| 41502 | zelador | 1 |
| 41503 | zeitschrift | 1 |
| 41504 | zegrí | 1 |
| 41505 | zazosita | 1 |
| 41506 | zarzo | 1 |
| 41507 | zarzaparrilla | 1 |
| 41508 | zarzales | 1 |
| 41509 | zarrapastrosas | 1 |
| 41510 | zarpasen | 1 |
| 41511 | zarpaban | 1 |
| 41512 | zaros | 1 |
| 41513 | zarandeo | 1 |
| 41514 | zarandearse | 1 |
| 41515 | zarandeando | 1 |
| 41516 | zarandean | 1 |
| 41517 | zarandeaban | 1 |
| 41518 | zarabandas | 1 |
| 41519 | zapo | 1 |
| 41520 | zapiaín | 1 |
| 41521 | zape | 1 |
| 41522 | zapatitos | 1 |
| 41523 | zapaticos | 1 |
| 41524 | zapatescas | 1 |
| 41525 | zapateo | 1 |
| 41526 | zapatear | 1 |
| 41527 | zapateadores | 1 |
| 41528 | zapataplús | 1 |
| 41529 | zanoguera | 1 |
| 41530 | zanjón | 1 |
| 41531 | zanjó | 1 |
| 41532 | zancos | 1 |
| 41533 | zancadas | 1 |
| 41534 | zampó | 1 |
| 41535 | zampo | 1 |
| 41536 | zamparon | 1 |
| 41537 | zamparme | 1 |
| 41538 | zampamos | 1 |
| 41539 | zampa | 1 |
| 41540 | zamoranos | 1 |
| 41541 | zamorano | 1 |
| 41542 | zamoranas | 1 |
| 41543 | zamorana | 1 |
| 41544 | zambullida | 1 |
| 41545 | zambullen | 1 |
| 41546 | zambombazos | 1 |
| 41547 | zambo | 1 |
| 41548 | zambas | 1 |
| 41549 | zamarro | 1 |
| 41550 | zamarreé | 1 |
| 41551 | zamarras | 1 |
| 41552 | zamarra | 1 |
| 41553 | zamacois | 1 |
| 41554 | zalea | 1 |
| 41555 | zalameras | 1 |
| 41556 | zalamea | 1 |
| 41557 | zaino | 1 |
| 41558 | zaides | 1 |
| 41559 | zahúrdas | 1 |
| 41560 | zahúrda | 1 |
| 41561 | zahumadores | 1 |
| 41562 | zahones | 1 |
| 41563 | zahinas | 1 |
| 41564 | zaheriendo | 1 |
| 41565 | zaharenas | 1 |
| 41566 | zagalote | 1 |
| 41567 | zagalón | 1 |
| 41568 | zafiote | 1 |
| 41569 | zafias | 1 |
| 41570 | zafarnos | 1 |
| 41571 | zafarme | 1 |
| 41572 | zaceaba | 1 |
| 41573 | zacarías | 1 |
| 41574 | zabullir | 1 |
| 41575 | zabullían | 1 |
| 41576 | zabúllete | 1 |
| 41577 | yzquierdo | 1 |
| 41578 | yz | 1 |
| 41579 | yverniso | 1 |
| 41580 | yvase | 1 |
| 41581 | yvas | 1 |
| 41582 | yvalo | 1 |
| 41583 | yvagela | 1 |
| 41584 | yuntas | 1 |
| 41585 | yuntar | 1 |
| 41586 | yúgo | 1 |
| 41587 | yugero | 1 |
| 41588 | yugadas | 1 |
| 41589 | yuamos | 1 |
| 41590 | ystorias | 1 |
| 41591 | ystoriales | 1 |
| 41592 | ysrael | 1 |
| 41593 | ysquierdo | 1 |
| 41594 | ysquierda | 1 |
| 41595 | ysopete | 1 |
| 41596 | ysayas | 1 |
| 41597 | ysac | 1 |
| 41598 | yrvos | 1 |
| 41599 | yrse | 1 |
| 41600 | yrritados | 1 |
| 41601 | yrnos | 1 |
| 41602 | yrm | 1 |
| 41603 | yrle | 1 |
| 41604 | yrien | 1 |
| 41605 | yrian | 1 |
| 41606 | yrgyendo | 1 |
| 41607 | yrés | 1 |
| 41608 | yrán | 1 |
| 41609 | yrados | 1 |
| 41610 | yradas | 1 |
| 41611 | ypocrita | 1 |
| 41612 | ypocresía | 1 |
| 41613 | ypocrás | 1 |
| 41614 | ypermestra | 1 |
| 41615 | yoguieren | 1 |
| 41616 | yogásemos | 1 |
| 41617 | yogase | 1 |
| 41618 | yogar | 1 |
| 41619 | yodo | 1 |
| 41620 | yoaten | 1 |
| 41621 | ynojos | 1 |
| 41622 | ynojo | 1 |
| 41623 | ynoçente | 1 |
| 41624 | ynocente | 1 |
| 41625 | ynfernal | 1 |
| 41626 | ynes | 1 |
| 41627 | yncan | 1 |
| 41628 | ymos | 1 |
| 41629 | ymitauas | 1 |
| 41630 | ymajen | 1 |
| 41631 | ymaginamientos | 1 |
| 41632 | ymaginacion | 1 |
| 41633 | ymagina | 1 |
| 41634 | ylustrantes | 1 |
| 41635 | ylicito | 1 |
| 41636 | ygualdad | 1 |
| 41637 | ygualas | 1 |
| 41638 | ygualar | 1 |
| 41639 | ygualadera | 1 |
| 41640 | ygualada | 1 |
| 41641 | yglesias | 1 |
| 41642 | yezgo | 1 |
| 41643 | yesos | 1 |
| 41644 | yesones | 1 |
| 41645 | yesón | 1 |
| 41646 | yeserías | 1 |
| 41647 | yesca | 1 |
| 41648 | yerres | 1 |
| 41649 | yérralo | 1 |
| 41650 | yermas | 1 |
| 41651 | yerguen | 1 |
| 41652 | yergue | 1 |
| 41653 | yergos | 1 |
| 41654 | yéndonos | 1 |
| 41655 | yen | 1 |
| 41656 | yele | 1 |
| 41657 | yelan | 1 |
| 41658 | yela | 1 |
| 41659 | yeguerisa | 1 |
| 41660 | ydras | 1 |
| 41661 | ydolo | 1 |
| 41662 | ydas | 1 |
| 41663 | yazíe | 1 |
| 41664 | yazes | 1 |
| 41665 | yasía | 1 |
| 41666 | yases | 1 |
| 41667 | yas | 1 |
| 41668 | yantes | 1 |
| 41669 | yantaría | 1 |
| 41670 | yantado | 1 |
| 41671 | yacimiento | 1 |
| 41672 | yaçiendo | 1 |
| 41673 | yacer | 1 |
| 41674 | yaçe | 1 |
| 41675 | xymio | 1 |
| 41676 | xristo | 1 |
| 41677 | xriste | 1 |
| 41678 | xo | 1 |
| 41679 | xiij | 1 |
| 41680 | xiiij | 1 |
| 41681 | xerga | 1 |
| 41682 | xenofonte | 1 |
| 41683 | xenofon | 1 |
| 41684 | xarcias | 1 |
| 41685 | xaques | 1 |
| 41686 | wisseman | 1 |
| 41687 | wieland | 1 |
| 41688 | whigs | 1 |
| 41689 | werke | 1 |
| 41690 | wéllington | 1 |
| 41691 | wellington | 1 |
| 41692 | washingtonia | 1 |
| 41693 | walses | 1 |
| 41694 | wagón | 1 |
| 41695 | wad | 1 |
| 41696 | vyyuela | 1 |
| 41697 | vyudas | 1 |
| 41698 | vysta | 1 |
| 41699 | vyó | 1 |
| 41700 | vyña | 1 |
| 41701 | vynose | 1 |
| 41702 | vynóme | 1 |
| 41703 | vynieron | 1 |
| 41704 | vyllenchón | 1 |
| 41705 | vyllanos | 1 |
| 41706 | vyllanía | 1 |
| 41707 | vyllanchón | 1 |
| 41708 | vylezas | 1 |
| 41709 | vylesa | 1 |
| 41710 | vyga | 1 |
| 41711 | vyese | 1 |
| 41712 | vyento | 1 |
| 41713 | vyenen | 1 |
| 41714 | vydose | 1 |
| 41715 | vydol | 1 |
| 41716 | vyd | 1 |
| 41717 | vyçyos | 1 |
| 41718 | vyçyo | 1 |
| 41719 | vyçios | 1 |
| 41720 | vyçio | 1 |
| 41721 | vyandas | 1 |
| 41722 | vulnerant | 1 |
| 41723 | vulgarote | 1 |
| 41724 | vuestr | 1 |
| 41725 | vueso | 1 |
| 41726 | vueseñoría | 1 |
| 41727 | vuélvemelo | 1 |
| 41728 | vuélvele | 1 |
| 41729 | vuélvela | 1 |
| 41730 | vuélvate | 1 |
| 41731 | vuélvala | 1 |
| 41732 | vueltecita | 1 |
| 41733 | vuelco | 1 |
| 41734 | vuelcas | 1 |
| 41735 | vuelan | 1 |
| 41736 | vucedes | 1 |
| 41737 | vucé | 1 |
| 41738 | vuacé | 1 |
| 41739 | vu | 1 |
| 41740 | vse | 1 |
| 41741 | vsaste | 1 |
| 41742 | vsaron | 1 |
| 41743 | vsan | 1 |
| 41744 | vsado | 1 |
| 41745 | vs | 1 |
| 41746 | vrdio | 1 |
| 41747 | vrai | 1 |
| 41748 | voyez | 1 |
| 41749 | voyageur | 1 |
| 41750 | vox | 1 |
| 41751 | vótote | 1 |
| 41752 | votivas | 1 |
| 41753 | votaron | 1 |
| 41754 | votantes | 1 |
| 41755 | votado | 1 |
| 41756 | votaciones | 1 |
| 41757 | vostra | 1 |
| 41758 | voses | 1 |
| 41759 | vorazmente | 1 |
| 41760 | voquibles | 1 |
| 41761 | vomito | 1 |
| 41762 | vomitivos | 1 |
| 41763 | vomitase | 1 |
| 41764 | vomitan | 1 |
| 41765 | vomitado | 1 |
| 41766 | vóme | 1 |
| 41767 | volvistes | 1 |
| 41768 | volviósela | 1 |
| 41769 | volvióme | 1 |
| 41770 | volviolos | 1 |
| 41771 | volviole | 1 |
| 41772 | volvióla | 1 |
| 41773 | volvímosle | 1 |
| 41774 | volvime | 1 |
| 41775 | volviéronme | 1 |
| 41776 | volviéronla | 1 |
| 41777 | volviéredes | 1 |
| 41778 | volviere | 1 |
| 41779 | volvieras | 1 |
| 41780 | volviéramos | 1 |
| 41781 | volviéndolos | 1 |
| 41782 | volviéndoles | 1 |
| 41783 | volviéndola | 1 |
| 41784 | volvíamos | 1 |
| 41785 | volvíale | 1 |
| 41786 | volvérsele | 1 |
| 41787 | volvérmelos | 1 |
| 41788 | volvérmelo | 1 |
| 41789 | volveréme | 1 |
| 41790 | volveréis | 1 |
| 41791 | volvedme | 1 |
| 41792 | volvedle | 1 |
| 41793 | volutas | 1 |
| 41794 | voluntariosa | 1 |
| 41795 | volúmenes | 1 |
| 41796 | volume | 1 |
| 41797 | volubles | 1 |
| 41798 | volubilidad | 1 |
| 41799 | volteriano | 1 |
| 41800 | volteo | 1 |
| 41801 | voltearle | 1 |
| 41802 | volteadores | 1 |
| 41803 | volteadas | 1 |
| 41804 | volteaban | 1 |
| 41805 | volteaba | 1 |
| 41806 | voltaria | 1 |
| 41807 | vollaz | 1 |
| 41808 | volk | 1 |
| 41809 | volga | 1 |
| 41810 | voleo | 1 |
| 41811 | volente | 1 |
| 41812 | volé | 1 |
| 41813 | volcó | 1 |
| 41814 | volcara | 1 |
| 41815 | volcánicas | 1 |
| 41816 | volcanes | 1 |
| 41817 | volcándola | 1 |
| 41818 | volcando | 1 |
| 41819 | volcado | 1 |
| 41820 | volatineros | 1 |
| 41821 | volatinera | 1 |
| 41822 | volatilizándolo | 1 |
| 41823 | volátiles | 1 |
| 41824 | volátil | 1 |
| 41825 | volaterías | 1 |
| 41826 | volasen | 1 |
| 41827 | volaré | 1 |
| 41828 | volarán | 1 |
| 41829 | volapiés | 1 |
| 41830 | volandillas | 1 |
| 41831 | volandera | 1 |
| 41832 | voladura | 1 |
| 41833 | voladora | 1 |
| 41834 | voladeros | 1 |
| 41835 | volábanle | 1 |
| 41836 | volábamos | 1 |
| 41837 | voime | 1 |
| 41838 | voi | 1 |
| 41839 | vogt | 1 |
| 41840 | vocis | 1 |
| 41841 | vocinglera | 1 |
| 41842 | vociferes | 1 |
| 41843 | vociferarla | 1 |
| 41844 | vociferar | 1 |
| 41845 | vociferaban | 1 |
| 41846 | vocifera | 1 |
| 41847 | vocerío | 1 |
| 41848 | vocear | 1 |
| 41849 | voceando | 1 |
| 41850 | vocean | 1 |
| 41851 | voceaba | 1 |
| 41852 | vocal | 1 |
| 41853 | vocaciones | 1 |
| 41854 | vnturillas | 1 |
| 41855 | vnturas | 1 |
| 41856 | vntos | 1 |
| 41857 | vnto | 1 |
| 41858 | vntasnos | 1 |
| 41859 | vniversa | 1 |
| 41860 | vnicornio | 1 |
| 41861 | vltimas | 1 |
| 41862 | vltima | 1 |
| 41863 | vizina | 1 |
| 41864 | vivito | 1 |
| 41865 | vivísimas | 1 |
| 41866 | vivísimamente | 1 |
| 41867 | vivirlas | 1 |
| 41868 | vivirías | 1 |
| 41869 | vivirán | 1 |
| 41870 | vivificó | 1 |
| 41871 | vivificando | 1 |
| 41872 | vivieres | 1 |
| 41873 | viviere | 1 |
| 41874 | vivíe | 1 |
| 41875 | vivideros | 1 |
| 41876 | vividera | 1 |
| 41877 | vivías | 1 |
| 41878 | vivent | 1 |
| 41879 | vivendum | 1 |
| 41880 | vivaz | 1 |
| 41881 | vivar | 1 |
| 41882 | vivaqueaba | 1 |
| 41883 | vívame | 1 |
| 41884 | vivaces | 1 |
| 41885 | vivaaa | 1 |
| 41886 | viuiremos | 1 |
| 41887 | viuiras | 1 |
| 41888 | viuimos | 1 |
| 41889 | viuificar | 1 |
| 41890 | viuificacion | 1 |
| 41891 | viuiere | 1 |
| 41892 | viuido | 1 |
| 41893 | viuen | 1 |
| 41894 | viuela | 1 |
| 41895 | viudos | 1 |
| 41896 | vituperoso | 1 |
| 41897 | vituperosas | 1 |
| 41898 | vituperóme | 1 |
| 41899 | vituperó | 1 |
| 41900 | vituperarte | 1 |
| 41901 | vituperaré | 1 |
| 41902 | vituperar | 1 |
| 41903 | vituperadores | 1 |
| 41904 | vituperado | 1 |
| 41905 | vituperaba | 1 |
| 41906 | vituallas | 1 |
| 41907 | vitriolo | 1 |
| 41908 | vitoriosos | 1 |
| 41909 | vitorioso | 1 |
| 41910 | vítores | 1 |
| 41911 | vítor | 1 |
| 41912 | vitela | 1 |
| 41913 | vitandos | 1 |
| 41914 | vitalidad | 1 |
| 41915 | vitalicio | 1 |
| 41916 | vita | 1 |
| 41917 | vit | 1 |
| 41918 | vístose | 1 |
| 41919 | vistosamente | 1 |
| 41920 | vístome | 1 |
| 41921 | vistiré | 1 |
| 41922 | vistióme | 1 |
| 41923 | vistióle | 1 |
| 41924 | vistieren | 1 |
| 41925 | vistiere | 1 |
| 41926 | vistiera | 1 |
| 41927 | vistiéndonos | 1 |
| 41928 | vistiéndolo | 1 |
| 41929 | vistiéndola | 1 |
| 41930 | vistía | 1 |
| 41931 | vistetele | 1 |
| 41932 | vístete | 1 |
| 41933 | vístesos | 1 |
| 41934 | vístese | 1 |
| 41935 | vístelo | 1 |
| 41936 | vístele | 1 |
| 41937 | vístase | 1 |
| 41938 | vistanse | 1 |
| 41939 | vístanme | 1 |
| 41940 | vistan | 1 |
| 41941 | vistámosle | 1 |
| 41942 | vispera | 1 |
| 41943 | vislumbró | 1 |
| 41944 | vislumbran | 1 |
| 41945 | visitenos | 1 |
| 41946 | visítela | 1 |
| 41947 | visitaua | 1 |
| 41948 | visitase | 1 |
| 41949 | visitáronle | 1 |
| 41950 | visitarlos | 1 |
| 41951 | visitare | 1 |
| 41952 | visitara | 1 |
| 41953 | visitante | 1 |
| 41954 | visitándola | 1 |
| 41955 | visitan | 1 |
| 41956 | visitamos | 1 |
| 41957 | visitalla | 1 |
| 41958 | visitadas | 1 |
| 41959 | visitábale | 1 |
| 41960 | visillos | 1 |
| 41961 | vishenta | 1 |
| 41962 | viseo | 1 |
| 41963 | viscosos | 1 |
| 41964 | viscosamente | 1 |
| 41965 | viscocho | 1 |
| 41966 | visaje | 1 |
| 41967 | visagras | 1 |
| 41968 | visagra | 1 |
| 41969 | vis | 1 |
| 41970 | virutas | 1 |
| 41971 | virus | 1 |
| 41972 | virués | 1 |
| 41973 | viruela | 1 |
| 41974 | virtus | 1 |
| 41975 | virtuosísimo | 1 |
| 41976 | virtualmente | 1 |
| 41977 | virreyes | 1 |
| 41978 | virosos | 1 |
| 41979 | viriles | 1 |
| 41980 | viribus | 1 |
| 41981 | viriato | 1 |
| 41982 | vírgulas | 1 |
| 41983 | virgiliana | 1 |
| 41984 | virgam | 1 |
| 41985 | vireinato | 1 |
| 41986 | virchov | 1 |
| 41987 | virase | 1 |
| 41988 | viras | 1 |
| 41989 | virada | 1 |
| 41990 | viraba | 1 |
| 41991 | vir | 1 |
| 41992 | viperina | 1 |
| 41993 | vióme | 1 |
| 41994 | viome | 1 |
| 41995 | violó | 1 |
| 41996 | violentó | 1 |
| 41997 | violentes | 1 |
| 41998 | violentarse | 1 |
| 41999 | vïolencia | 1 |
| 42000 | vióle | 1 |
| 42001 | vïolas | 1 |
| 42002 | violas | 1 |
| 42003 | violaron | 1 |
| 42004 | vïolar | 1 |
| 42005 | violantes | 1 |
| 42006 | violados | 1 |
| 42007 | vïolador | 1 |
| 42008 | violada | 1 |
| 42009 | violación | 1 |
| 42010 | violácea | 1 |
| 42011 | vióla | 1 |
| 42012 | viñadero | 1 |
| 42013 | vinoso | 1 |
| 42014 | vínoseme | 1 |
| 42015 | vinosa | 1 |
| 42016 | viniste | 1 |
| 42017 | viniesses | 1 |
| 42018 | viniessen | 1 |
| 42019 | vinieses | 1 |
| 42020 | viniésedes | 1 |
| 42021 | viniéronse | 1 |
| 42022 | vinieronlos | 1 |
| 42023 | viniéronle | 1 |
| 42024 | viniérale | 1 |
| 42025 | viniéndole | 1 |
| 42026 | viniendola | 1 |
| 42027 | vinelo | 1 |
| 42028 | vinele | 1 |
| 42029 | vindicta | 1 |
| 42030 | vinculó | 1 |
| 42031 | vinculen | 1 |
| 42032 | vincule | 1 |
| 42033 | vincular | 1 |
| 42034 | vinculan | 1 |
| 42035 | vinculados | 1 |
| 42036 | vinci | 1 |
| 42037 | vinazo | 1 |
| 42038 | vinateros | 1 |
| 42039 | vinajeroso | 1 |
| 42040 | vinagrillo | 1 |
| 42041 | vinader | 1 |
| 42042 | vina | 1 |
| 42043 | vin | 1 |
| 42044 | vímoslo | 1 |
| 42045 | vímosle | 1 |
| 42046 | víme | 1 |
| 42047 | vilmente | 1 |
| 42048 | villorrio | 1 |
| 42049 | villiegris | 1 |
| 42050 | villeza | 1 |
| 42051 | villena | 1 |
| 42052 | villaviciosa | 1 |
| 42053 | villarreal | 1 |
| 42054 | villarica | 1 |
| 42055 | villanovas | 1 |
| 42056 | villanías | 1 |
| 42057 | villanesco | 1 |
| 42058 | villanescas | 1 |
| 42059 | villanería | 1 |
| 42060 | villanaje | 1 |
| 42061 | villalpando | 1 |
| 42062 | villahermosa | 1 |
| 42063 | villafranca | 1 |
| 42064 | villafangosa | 1 |
| 42065 | villadie | 1 |
| 42066 | vilipendio | 1 |
| 42067 | vilipendiar | 1 |
| 42068 | vila | 1 |
| 42069 | vigüelas | 1 |
| 42070 | vigüela | 1 |
| 42071 | vigorizó | 1 |
| 42072 | vigorizar | 1 |
| 42073 | vigorizan | 1 |
| 42074 | vigorización | 1 |
| 42075 | vigorizaba | 1 |
| 42076 | vigisuela | 1 |
| 42077 | vigilo | 1 |
| 42078 | vigilase | 1 |
| 42079 | vigilarlas | 1 |
| 42080 | vigilaré | 1 |
| 42081 | vigilando | 1 |
| 42082 | vigilado | 1 |
| 42083 | vigilada | 1 |
| 42084 | vigentes | 1 |
| 42085 | vigente | 1 |
| 42086 | vieux | 1 |
| 42087 | viesse | 1 |
| 42088 | viésedes | 1 |
| 42089 | viés | 1 |
| 42090 | vierten | 1 |
| 42091 | viertan | 1 |
| 42092 | vierta | 1 |
| 42093 | vieronte | 1 |
| 42094 | viéronse | 1 |
| 42095 | vierais | 1 |
| 42096 | viente | 1 |
| 42097 | viénesme | 1 |
| 42098 | vienesme | 1 |
| 42099 | viéneslo | 1 |
| 42100 | viener | 1 |
| 42101 | viénenseme | 1 |
| 42102 | viéndoselo | 1 |
| 42103 | viéndoos | 1 |
| 42104 | viendoos | 1 |
| 42105 | viéndonos | 1 |
| 42106 | viejona | 1 |
| 42107 | viejísimo | 1 |
| 42108 | viejecitos | 1 |
| 42109 | viejecitas | 1 |
| 42110 | viejecillos | 1 |
| 42111 | viejecilla | 1 |
| 42112 | viejecica | 1 |
| 42113 | vidros | 1 |
| 42114 | vidriosa | 1 |
| 42115 | vidrïera | 1 |
| 42116 | vidriada | 1 |
| 42117 | vídote | 1 |
| 42118 | vídolo | 1 |
| 42119 | vidita | 1 |
| 42120 | vidit | 1 |
| 42121 | videor | 1 |
| 42122 | videncia | 1 |
| 42123 | videare | 1 |
| 42124 | vidaña | 1 |
| 42125 | vidania | 1 |
| 42126 | vicuña | 1 |
| 42127 | victo | 1 |
| 42128 | victis | 1 |
| 42129 | victimario | 1 |
| 42130 | viciosote | 1 |
| 42131 | viçiosos | 1 |
| 42132 | viciosonas | 1 |
| 42133 | vicia | 1 |
| 42134 | vicepresidente | 1 |
| 42135 | vicarios | 1 |
| 42136 | vibratorio | 1 |
| 42137 | vibrando | 1 |
| 42138 | vibran | 1 |
| 42139 | vibra | 1 |
| 42140 | viborezno | 1 |
| 42141 | víboras | 1 |
| 42142 | vibdas | 1 |
| 42143 | vían | 1 |
| 42144 | víamos | 1 |
| 42145 | víame | 1 |
| 42146 | viam | 1 |
| 42147 | viales | 1 |
| 42148 | viajo | 1 |
| 42149 | viajatas | 1 |
| 42150 | viajaba | 1 |
| 42151 | viaductos | 1 |
| 42152 | viable | 1 |
| 42153 | viabilidad | 1 |
| 42154 | vfana | 1 |
| 42155 | vezino | 1 |
| 42156 | vezindat | 1 |
| 42157 | vezindades | 1 |
| 42158 | vezado | 1 |
| 42159 | vezada | 1 |
| 42160 | veza | 1 |
| 42161 | veyo | 1 |
| 42162 | veynteno | 1 |
| 42163 | veyla | 1 |
| 42164 | veyes | 1 |
| 42165 | veyeron | 1 |
| 42166 | veyan | 1 |
| 42167 | veyalos | 1 |
| 42168 | veyades | 1 |
| 42169 | vevir | 1 |
| 42170 | vevido | 1 |
| 42171 | vevía | 1 |
| 42172 | veví | 1 |
| 42173 | vetustos | 1 |
| 42174 | vetusto | 1 |
| 42175 | vetustente | 1 |
| 42176 | veto | 1 |
| 42177 | veterinaria | 1 |
| 42178 | veteranos | 1 |
| 42179 | vesugos | 1 |
| 42180 | vesubio | 1 |
| 42181 | vestusta | 1 |
| 42182 | vestra | 1 |
| 42183 | vestirlo | 1 |
| 42184 | vestirlas | 1 |
| 42185 | vestiría | 1 |
| 42186 | vestirás | 1 |
| 42187 | vestirá | 1 |
| 42188 | vestió | 1 |
| 42189 | vestímonos | 1 |
| 42190 | vestíle | 1 |
| 42191 | vestigio | 1 |
| 42192 | vestiéronle | 1 |
| 42193 | vestiéndose | 1 |
| 42194 | vestíe | 1 |
| 42195 | vestidla | 1 |
| 42196 | vestidita | 1 |
| 42197 | vestíame | 1 |
| 42198 | vesti | 1 |
| 42199 | vestal | 1 |
| 42200 | vesme | 1 |
| 42201 | vesinos | 1 |
| 42202 | vésela | 1 |
| 42203 | vervos | 1 |
| 42204 | vertyendo | 1 |
| 42205 | vertumno | 1 |
| 42206 | vertu | 1 |
| 42207 | vértigos | 1 |
| 42208 | vertiginosos | 1 |
| 42209 | vertidas | 1 |
| 42210 | verti | 1 |
| 42211 | verterse | 1 |
| 42212 | verterlas | 1 |
| 42213 | verterla | 1 |
| 42214 | verssos | 1 |
| 42215 | versitos | 1 |
| 42216 | versito | 1 |
| 42217 | versiones | 1 |
| 42218 | versificado | 1 |
| 42219 | versificación | 1 |
| 42220 | versículo | 1 |
| 42221 | vérsele | 1 |
| 42222 | versecillos | 1 |
| 42223 | versate | 1 |
| 42224 | versalles | 1 |
| 42225 | versados | 1 |
| 42226 | verruguita | 1 |
| 42227 | vernia | 1 |
| 42228 | vernemos | 1 |
| 42229 | verné | 1 |
| 42230 | verne | 1 |
| 42231 | vernas | 1 |
| 42232 | vernan | 1 |
| 42233 | vermis | 1 |
| 42234 | vermejas | 1 |
| 42235 | veritatis | 1 |
| 42236 | verisimilitud | 1 |
| 42237 | verino | 1 |
| 42238 | verificarse | 1 |
| 42239 | verificaron | 1 |
| 42240 | verificaría | 1 |
| 42241 | verificara | 1 |
| 42242 | verificada | 1 |
| 42243 | verificábase | 1 |
| 42244 | veríedes | 1 |
| 42245 | verias | 1 |
| 42246 | veríades | 1 |
| 42247 | verguenças | 1 |
| 42248 | vergoñosa | 1 |
| 42249 | vergoña | 1 |
| 42250 | vergonzantes | 1 |
| 42251 | vergonçoso | 1 |
| 42252 | vergel | 1 |
| 42253 | vergas | 1 |
| 42254 | vergara | 1 |
| 42255 | veremundo | 1 |
| 42256 | verémonos | 1 |
| 42257 | veréisos | 1 |
| 42258 | veréislo | 1 |
| 42259 | verduricas | 1 |
| 42260 | verdulera | 1 |
| 42261 | verdiniales | 1 |
| 42262 | verdín | 1 |
| 42263 | verdi | 1 |
| 42264 | verdeles | 1 |
| 42265 | verdegueados | 1 |
| 42266 | verdear | 1 |
| 42267 | verçuelas | 1 |
| 42268 | verbasco | 1 |
| 42269 | verbales | 1 |
| 42270 | verba | 1 |
| 42271 | verásme | 1 |
| 42272 | veráslos | 1 |
| 42273 | veráslo | 1 |
| 42274 | veraniega | 1 |
| 42275 | veraneo | 1 |
| 42276 | veranear | 1 |
| 42277 | veraneado | 1 |
| 42278 | veraneaban | 1 |
| 42279 | veraneaba | 1 |
| 42280 | veote | 1 |
| 42281 | véole | 1 |
| 42282 | veole | 1 |
| 42283 | venya | 1 |
| 42284 | venturosas | 1 |
| 42285 | ventrudos | 1 |
| 42286 | ventris | 1 |
| 42287 | ventrílocuo | 1 |
| 42288 | ventosear | 1 |
| 42289 | ventorrillo | 1 |
| 42290 | ventores | 1 |
| 42291 | ventolera | 1 |
| 42292 | ventisca | 1 |
| 42293 | ventilara | 1 |
| 42294 | ventilados | 1 |
| 42295 | ventilado | 1 |
| 42296 | ventilaba | 1 |
| 42297 | ventidós | 1 |
| 42298 | venticuatro | 1 |
| 42299 | venti | 1 |
| 42300 | venteros | 1 |
| 42301 | venternía | 1 |
| 42302 | venternero | 1 |
| 42303 | venternera | 1 |
| 42304 | venteriles | 1 |
| 42305 | venteril | 1 |
| 42306 | venteaba | 1 |
| 42307 | ventanuchos | 1 |
| 42308 | ventanucha | 1 |
| 42309 | ventanaje | 1 |
| 42310 | ventajoso | 1 |
| 42311 | ventajosamente | 1 |
| 42312 | vense | 1 |
| 42313 | veno | 1 |
| 42314 | venle | 1 |
| 42315 | venite | 1 |
| 42316 | venistes | 1 |
| 42317 | venirte | 1 |
| 42318 | veniros | 1 |
| 42319 | venirle | 1 |
| 42320 | veniessen | 1 |
| 42321 | veniésedes | 1 |
| 42322 | veniéronse | 1 |
| 42323 | venienl | 1 |
| 42324 | venien | 1 |
| 42325 | venides | 1 |
| 42326 | venidera | 1 |
| 42327 | venias | 1 |
| 42328 | venïales | 1 |
| 42329 | veníale | 1 |
| 42330 | veníades | 1 |
| 42331 | veniades | 1 |
| 42332 | vengues | 1 |
| 42333 | venguéis | 1 |
| 42334 | vengué | 1 |
| 42335 | véngote | 1 |
| 42336 | vengole | 1 |
| 42337 | vengativa | 1 |
| 42338 | vengasen | 1 |
| 42339 | véngante | 1 |
| 42340 | vénganse | 1 |
| 42341 | vengándose | 1 |
| 42342 | vengando | 1 |
| 42343 | vengados | 1 |
| 42344 | vengadores | 1 |
| 42345 | vengadora | 1 |
| 42346 | vengades | 1 |
| 42347 | vengadas | 1 |
| 42348 | vengad | 1 |
| 42349 | vengaban | 1 |
| 42350 | veneros | 1 |
| 42351 | veneras | 1 |
| 42352 | venerandas | 1 |
| 42353 | veneranda | 1 |
| 42354 | veneran | 1 |
| 42355 | venerada | 1 |
| 42356 | veneraba | 1 |
| 42357 | venenosos | 1 |
| 42358 | venecianos | 1 |
| 42359 | vendremos | 1 |
| 42360 | vendréis | 1 |
| 42361 | venditur | 1 |
| 42362 | vendióse | 1 |
| 42363 | vendio | 1 |
| 42364 | vendimos | 1 |
| 42365 | vendimie | 1 |
| 42366 | vendimias | 1 |
| 42367 | vendimiar | 1 |
| 42368 | vendimiador | 1 |
| 42369 | vendiese | 1 |
| 42370 | vendiéndolos | 1 |
| 42371 | vendíe | 1 |
| 42372 | vendidos | 1 |
| 42373 | vendibles | 1 |
| 42374 | vendíamosles | 1 |
| 42375 | vendíalos | 1 |
| 42376 | venderte | 1 |
| 42377 | venderían | 1 |
| 42378 | vendería | 1 |
| 42379 | venderia | 1 |
| 42380 | venderás | 1 |
| 42381 | venderá | 1 |
| 42382 | vendemiento | 1 |
| 42383 | vendehumos | 1 |
| 42384 | vendée | 1 |
| 42385 | vendedoras | 1 |
| 42386 | vendederas | 1 |
| 42387 | vendeanos | 1 |
| 42388 | vendeano | 1 |
| 42389 | vendar | 1 |
| 42390 | véndanle | 1 |
| 42391 | vendan | 1 |
| 42392 | vendáis | 1 |
| 42393 | vendada | 1 |
| 42394 | vencistes | 1 |
| 42395 | vençimiento | 1 |
| 42396 | vencíla | 1 |
| 42397 | venciéronse | 1 |
| 42398 | vencieres | 1 |
| 42399 | venciere | 1 |
| 42400 | venciéndose | 1 |
| 42401 | vençida | 1 |
| 42402 | vencerte | 1 |
| 42403 | vençerse | 1 |
| 42404 | venceros | 1 |
| 42405 | vencerlas | 1 |
| 42406 | vencería | 1 |
| 42407 | vençeremos | 1 |
| 42408 | vençerás | 1 |
| 42409 | vencen | 1 |
| 42410 | vençemos | 1 |
| 42411 | vencellos | 1 |
| 42412 | vencejos | 1 |
| 42413 | vençedor | 1 |
| 42414 | vença | 1 |
| 42415 | venatorio | 1 |
| 42416 | venatorias | 1 |
| 42417 | venaspre | 1 |
| 42418 | venales | 1 |
| 42419 | venados | 1 |
| 42420 | veme | 1 |
| 42421 | veluci | 1 |
| 42422 | velocísimo | 1 |
| 42423 | velocísima | 1 |
| 42424 | velludos | 1 |
| 42425 | velluda | 1 |
| 42426 | vellosas | 1 |
| 42427 | vellosa | 1 |
| 42428 | vellorí | 1 |
| 42429 | vellas | 1 |
| 42430 | vellaquillo | 1 |
| 42431 | velito | 1 |
| 42432 | velitas | 1 |
| 42433 | velillos | 1 |
| 42434 | velilla | 1 |
| 42435 | veleras | 1 |
| 42436 | veleidosa | 1 |
| 42437 | veldo | 1 |
| 42438 | veldat | 1 |
| 42439 | velate | 1 |
| 42440 | velase | 1 |
| 42441 | velarte | 1 |
| 42442 | velaron | 1 |
| 42443 | velarlo | 1 |
| 42444 | velaría | 1 |
| 42445 | velaremos | 1 |
| 42446 | velaré | 1 |
| 42447 | velándosele | 1 |
| 42448 | velan | 1 |
| 42449 | velamos | 1 |
| 42450 | velámenes | 1 |
| 42451 | velados | 1 |
| 42452 | velada | 1 |
| 42453 | vejote | 1 |
| 42454 | vejezuelo | 1 |
| 42455 | vejezuelas | 1 |
| 42456 | vejéz | 1 |
| 42457 | vejetes | 1 |
| 42458 | vejestorios | 1 |
| 42459 | vejestorio | 1 |
| 42460 | vejedat | 1 |
| 42461 | vejeces | 1 |
| 42462 | vejanconas | 1 |
| 42463 | veisme | 1 |
| 42464 | véisle | 1 |
| 42465 | veisle | 1 |
| 42466 | veislas | 1 |
| 42467 | veisla | 1 |
| 42468 | veintiocho | 1 |
| 42469 | veintinueve | 1 |
| 42470 | veintidoseno | 1 |
| 42471 | veíaselas | 1 |
| 42472 | veías | 1 |
| 42473 | veíalo | 1 |
| 42474 | veíale | 1 |
| 42475 | veíalas | 1 |
| 42476 | vehículos | 1 |
| 42477 | vehementísimos | 1 |
| 42478 | vehemencias | 1 |
| 42479 | veguellinas | 1 |
| 42480 | vegetativa | 1 |
| 42481 | vegetatiuo | 1 |
| 42482 | vegetando | 1 |
| 42483 | vegetaba | 1 |
| 42484 | vegeta | 1 |
| 42485 | vegallanas | 1 |
| 42486 | véese | 1 |
| 42487 | veela | 1 |
| 42488 | veee | 1 |
| 42489 | veedores | 1 |
| 42490 | veedes | 1 |
| 42491 | veed | 1 |
| 42492 | veduño | 1 |
| 42493 | vedriado | 1 |
| 42494 | vedo | 1 |
| 42495 | vedlo | 1 |
| 42496 | vedle | 1 |
| 42497 | vedlas | 1 |
| 42498 | vedijas | 1 |
| 42499 | vedija | 1 |
| 42500 | veder | 1 |
| 42501 | vedeganbre | 1 |
| 42502 | vedava | 1 |
| 42503 | vedan | 1 |
| 42504 | vedadas | 1 |
| 42505 | vedada | 1 |
| 42506 | vécu | 1 |
| 42507 | vecinguerra | 1 |
| 42508 | veçindades | 1 |
| 42509 | vecinal | 1 |
| 42510 | veci | 1 |
| 42511 | vecchia | 1 |
| 42512 | véate | 1 |
| 42513 | veate | 1 |
| 42514 | veámoslo | 1 |
| 42515 | veámosle | 1 |
| 42516 | veámosla | 1 |
| 42517 | veámonos | 1 |
| 42518 | véame | 1 |
| 42519 | veale | 1 |
| 42520 | veádeslas | 1 |
| 42521 | vazian | 1 |
| 42522 | vaziado | 1 |
| 42523 | vayle | 1 |
| 42524 | vayladas | 1 |
| 42525 | vayase | 1 |
| 42526 | vayáis | 1 |
| 42527 | vauban | 1 |
| 42528 | vatum | 1 |
| 42529 | vaticinó | 1 |
| 42530 | vaticinios | 1 |
| 42531 | vaticinar | 1 |
| 42532 | vaticinan | 1 |
| 42533 | vaticinaba | 1 |
| 42534 | vastísimos | 1 |
| 42535 | vastas | 1 |
| 42536 | vassalo | 1 |
| 42537 | vasqueaua | 1 |
| 42538 | vasío | 1 |
| 42539 | vasías | 1 |
| 42540 | vasía | 1 |
| 42541 | váselo | 1 |
| 42542 | vasconia | 1 |
| 42543 | vascongadas | 1 |
| 42544 | vascas | 1 |
| 42545 | vasallaje | 1 |
| 42546 | varruntólo | 1 |
| 42547 | varrón | 1 |
| 42548 | varraganes | 1 |
| 42549 | varraco | 1 |
| 42550 | varoncitos | 1 |
| 42551 | varona | 1 |
| 42552 | varisis | 1 |
| 42553 | varió | 1 |
| 42554 | variarle | 1 |
| 42555 | variaran | 1 |
| 42556 | variará | 1 |
| 42557 | variadísimas | 1 |
| 42558 | vargueño | 1 |
| 42559 | varga | 1 |
| 42560 | vareó | 1 |
| 42561 | vareo | 1 |
| 42562 | varear | 1 |
| 42563 | vareando | 1 |
| 42564 | varde | 1 |
| 42565 | vardara | 1 |
| 42566 | varajas | 1 |
| 42567 | varada | 1 |
| 42568 | vaqueriso | 1 |
| 42569 | vaquerisa | 1 |
| 42570 | vaqueriços | 1 |
| 42571 | vapuleo | 1 |
| 42572 | vapuleándome | 1 |
| 42573 | vapulean | 1 |
| 42574 | vapularon | 1 |
| 42575 | vapularme | 1 |
| 42576 | vapulaba | 1 |
| 42577 | vaporosos | 1 |
| 42578 | vaporosa | 1 |
| 42579 | vapora | 1 |
| 42580 | vánseme | 1 |
| 42581 | vanle | 1 |
| 42582 | vanidosos | 1 |
| 42583 | vanegas | 1 |
| 42584 | vandurria | 1 |
| 42585 | vandero | 1 |
| 42586 | vanagloriosos | 1 |
| 42587 | vanaglorioso | 1 |
| 42588 | vanaglorió | 1 |
| 42589 | vanagloriarnos | 1 |
| 42590 | vanagloriaba | 1 |
| 42591 | vanæ | 1 |
| 42592 | vampiros | 1 |
| 42593 | vámosle | 1 |
| 42594 | vámo | 1 |
| 42595 | vame | 1 |
| 42596 | valyere | 1 |
| 42597 | valyan | 1 |
| 42598 | valy | 1 |
| 42599 | válvula | 1 |
| 42600 | valsavin | 1 |
| 42601 | valoraciones | 1 |
| 42602 | valoncica | 1 |
| 42603 | valón | 1 |
| 42604 | valo | 1 |
| 42605 | válme | 1 |
| 42606 | vallete | 1 |
| 42607 | vallesteros | 1 |
| 42608 | vallestero | 1 |
| 42609 | vallejos | 1 |
| 42610 | vallehermoso | 1 |
| 42611 | valledor | 1 |
| 42612 | vallecas | 1 |
| 42613 | valleameno | 1 |
| 42614 | valladares | 1 |
| 42615 | valladar | 1 |
| 42616 | valiesen | 1 |
| 42617 | valieron | 1 |
| 42618 | valientemente | 1 |
| 42619 | valiéndome | 1 |
| 42620 | valiéndole | 1 |
| 42621 | valíe | 1 |
| 42622 | valie | 1 |
| 42623 | validas | 1 |
| 42624 | válida | 1 |
| 42625 | válganos | 1 |
| 42626 | valgamos | 1 |
| 42627 | valeur | 1 |
| 42628 | válete | 1 |
| 42629 | valerosísimos | 1 |
| 42630 | valerosamente | 1 |
| 42631 | valernos | 1 |
| 42632 | valeriana | 1 |
| 42633 | valentya | 1 |
| 42634 | valentones | 1 |
| 42635 | valentísimamente | 1 |
| 42636 | valenciennes | 1 |
| 42637 | valencianos | 1 |
| 42638 | váleme | 1 |
| 42639 | valelle | 1 |
| 42640 | valedor | 1 |
| 42641 | valedes | 1 |
| 42642 | valederas | 1 |
| 42643 | valdrías | 1 |
| 42644 | valdria | 1 |
| 42645 | valdrí | 1 |
| 42646 | valdré | 1 |
| 42647 | valdrán | 1 |
| 42648 | valdivielso | 1 |
| 42649 | valdiñón | 1 |
| 42650 | valdía | 1 |
| 42651 | valdevacas | 1 |
| 42652 | valdemoro | 1 |
| 42653 | valdemoriello | 1 |
| 42654 | valdeflores | 1 |
| 42655 | valde | 1 |
| 42656 | valcázar | 1 |
| 42657 | valasme | 1 |
| 42658 | valas | 1 |
| 42659 | valança | 1 |
| 42660 | valan | 1 |
| 42661 | valame | 1 |
| 42662 | valadí | 1 |
| 42663 | vala | 1 |
| 42664 | vaivén | 1 |
| 42665 | vainicas | 1 |
| 42666 | vaiga | 1 |
| 42667 | vahos | 1 |
| 42668 | vaho | 1 |
| 42669 | vahídos | 1 |
| 42670 | vaharada | 1 |
| 42671 | vahando | 1 |
| 42672 | vagidos | 1 |
| 42673 | vagarosa | 1 |
| 42674 | vagaren | 1 |
| 42675 | vagamunda | 1 |
| 42676 | vagado | 1 |
| 42677 | vae | 1 |
| 42678 | vadita | 1 |
| 42679 | vadearon | 1 |
| 42680 | vadear | 1 |
| 42681 | vadeando | 1 |
| 42682 | vacuna | 1 |
| 42683 | vacilo | 1 |
| 42684 | vacilé | 1 |
| 42685 | vacile | 1 |
| 42686 | vacilaron | 1 |
| 42687 | vacilará | 1 |
| 42688 | vaciamos | 1 |
| 42689 | vaciad | 1 |
| 42690 | vaciaban | 1 |
| 42691 | vacase | 1 |
| 42692 | vacado | 1 |
| 42693 | uvia | 1 |
| 42694 | utrique | 1 |
| 42695 | utrilla | 1 |
| 42696 | utrera | 1 |
| 42697 | utrecht | 1 |
| 42698 | utopias | 1 |
| 42699 | utopía | 1 |
| 42700 | útilmente | 1 |
| 42701 | utilizó | 1 |
| 42702 | utilizo | 1 |
| 42703 | utilizado | 1 |
| 42704 | utilizaban | 1 |
| 42705 | utilizaba | 1 |
| 42706 | utilitario | 1 |
| 42707 | utilísimos | 1 |
| 42708 | utilidades | 1 |
| 42709 | utile | 1 |
| 42710 | utero | 1 |
| 42711 | uter | 1 |
| 42712 | utensilios | 1 |
| 42713 | ut | 1 |
| 42714 | usurparon | 1 |
| 42715 | usurparle | 1 |
| 42716 | usurpador | 1 |
| 42717 | usurpadas | 1 |
| 42718 | usurbil | 1 |
| 42719 | usuras | 1 |
| 42720 | usurarias | 1 |
| 42721 | usuraria | 1 |
| 42722 | usufructuaria | 1 |
| 42723 | ustés | 1 |
| 42724 | usque | 1 |
| 42725 | usen | 1 |
| 42726 | usemos | 1 |
| 42727 | úsase | 1 |
| 42728 | usarlas | 1 |
| 42729 | usarla | 1 |
| 42730 | usaría | 1 |
| 42731 | usaréis | 1 |
| 42732 | usare | 1 |
| 42733 | usanzas | 1 |
| 42734 | usamos | 1 |
| 42735 | usaje | 1 |
| 42736 | usadla | 1 |
| 42737 | usábalo | 1 |
| 42738 | us | 1 |
| 42739 | urzo | 1 |
| 42740 | ursinos | 1 |
| 42741 | urruca | 1 |
| 42742 | urreas | 1 |
| 42743 | uribe | 1 |
| 42744 | urgentísimo | 1 |
| 42745 | urgentes | 1 |
| 42746 | urepel | 1 |
| 42747 | urdir | 1 |
| 42748 | urdimbres | 1 |
| 42749 | urdiendo | 1 |
| 42750 | urdido | 1 |
| 42751 | urdidas | 1 |
| 42752 | urdiales | 1 |
| 42753 | urde | 1 |
| 42754 | urca | 1 |
| 42755 | urbsaugustense | 1 |
| 42756 | urbsaugustana | 1 |
| 42757 | urbina | 1 |
| 42758 | urbicesorbi | 1 |
| 42759 | urbi | 1 |
| 42760 | urbanidades | 1 |
| 42761 | upero | 1 |
| 42762 | uosotros | 1 |
| 42763 | uos | 1 |
| 42764 | uñadas | 1 |
| 42765 | untura | 1 |
| 42766 | untó | 1 |
| 42767 | unto | 1 |
| 42768 | untarse | 1 |
| 42769 | untarle | 1 |
| 42770 | untaos | 1 |
| 42771 | untándolos | 1 |
| 42772 | untándoles | 1 |
| 42773 | untando | 1 |
| 42774 | untaban | 1 |
| 42775 | uns | 1 |
| 42776 | universitarios | 1 |
| 42777 | universi | 1 |
| 42778 | universario | 1 |
| 42779 | uniste | 1 |
| 42780 | unirte | 1 |
| 42781 | unirles | 1 |
| 42782 | unióse | 1 |
| 42783 | uniformidad | 1 |
| 42784 | uniformados | 1 |
| 42785 | uniéronse | 1 |
| 42786 | uniera | 1 |
| 42787 | uniéndonos | 1 |
| 42788 | unicuique | 1 |
| 42789 | unicornios | 1 |
| 42790 | uníanse | 1 |
| 42791 | uní | 1 |
| 42792 | ungidas | 1 |
| 42793 | ungente | 1 |
| 42794 | únense | 1 |
| 42795 | uncir | 1 |
| 42796 | unciones | 1 |
| 42797 | unçión | 1 |
| 42798 | umiçidio | 1 |
| 42799 | umbrosa | 1 |
| 42800 | umbrío | 1 |
| 42801 | umbría | 1 |
| 42802 | umano | 1 |
| 42803 | umanidad | 1 |
| 42804 | umana | 1 |
| 42805 | ulysse | 1 |
| 42806 | ultratumba | 1 |
| 42807 | ultratelúrica | 1 |
| 42808 | ultramundanos | 1 |
| 42809 | ultramontano | 1 |
| 42810 | ultramontanismo | 1 |
| 42811 | ultramontanas | 1 |
| 42812 | ultrajando | 1 |
| 42813 | ultrajada | 1 |
| 42814 | ultraja | 1 |
| 42815 | ultimo | 1 |
| 42816 | ultimadamente | 1 |
| 42817 | ulterior | 1 |
| 42818 | ulm | 1 |
| 42819 | ulloa | 1 |
| 42820 | ullah | 1 |
| 42821 | úlceras | 1 |
| 42822 | ujieres | 1 |
| 42823 | ujeritos | 1 |
| 42824 | ui | 1 |
| 42825 | ugarona | 1 |
| 42826 | ufanos | 1 |
| 42827 | ufanidad | 1 |
| 42828 | ufánese | 1 |
| 42829 | ufane | 1 |
| 42830 | ufanas | 1 |
| 42831 | ufanarte | 1 |
| 42832 | úes | 1 |
| 42833 | uerte | 1 |
| 42834 | uertas | 1 |
| 42835 | uerse | 1 |
| 42836 | uerme | 1 |
| 42837 | uerco | 1 |
| 42838 | uenecia | 1 |
| 42839 | ue | 1 |
| 42840 | ubres | 1 |
| 42841 | uale | 1 |
| 42842 | tyzones | 1 |
| 42843 | tyzonadores | 1 |
| 42844 | tyznado | 1 |
| 42845 | tysones | 1 |
| 42846 | tyról | 1 |
| 42847 | tyró | 1 |
| 42848 | tyrava | 1 |
| 42849 | tyras | 1 |
| 42850 | tyrarías | 1 |
| 42851 | tyrares | 1 |
| 42852 | tyña | 1 |
| 42853 | tyntos | 1 |
| 42854 | tynto | 1 |
| 42855 | tyntas | 1 |
| 42856 | tyesta | 1 |
| 42857 | tyerra | 1 |
| 42858 | tyénese | 1 |
| 42859 | tyénenle | 1 |
| 42860 | tyénelas | 1 |
| 42861 | tyenden | 1 |
| 42862 | tyenbla | 1 |
| 42863 | tyempo | 1 |
| 42864 | tya | 1 |
| 42865 | tuy | 1 |
| 42866 | túvose | 1 |
| 42867 | túvolos | 1 |
| 42868 | túvola | 1 |
| 42869 | tuvímoslos | 1 |
| 42870 | tuvímosla | 1 |
| 42871 | tuvieses | 1 |
| 42872 | tuviésedes | 1 |
| 42873 | tuviéronme | 1 |
| 42874 | tuviéronlo | 1 |
| 42875 | tuviéralo | 1 |
| 42876 | tuviérades | 1 |
| 42877 | tuum | 1 |
| 42878 | tuuiesse | 1 |
| 42879 | tuuiese | 1 |
| 42880 | tuuiera | 1 |
| 42881 | tutriz | 1 |
| 42882 | tutores | 1 |
| 42883 | tuto | 1 |
| 42884 | tutearle | 1 |
| 42885 | tuteándose | 1 |
| 42886 | tururú | 1 |
| 42887 | turulatos | 1 |
| 42888 | turuino | 1 |
| 42889 | turuias | 1 |
| 42890 | turuada | 1 |
| 42891 | turrones | 1 |
| 42892 | turroneras | 1 |
| 42893 | turquíes | 1 |
| 42894 | turquía | 1 |
| 42895 | turquescas | 1 |
| 42896 | turquesadas | 1 |
| 42897 | turpia | 1 |
| 42898 | turóme | 1 |
| 42899 | turnaban | 1 |
| 42900 | turistas | 1 |
| 42901 | turián | 1 |
| 42902 | turgencia | 1 |
| 42903 | turégano | 1 |
| 42904 | turca | 1 |
| 42905 | turbulento | 1 |
| 42906 | turbulencia | 1 |
| 42907 | turbo | 1 |
| 42908 | turbión | 1 |
| 42909 | turbian | 1 |
| 42910 | turbiamente | 1 |
| 42911 | turbaua | 1 |
| 42912 | turbasse | 1 |
| 42913 | turbasen | 1 |
| 42914 | túrbase | 1 |
| 42915 | turbarte | 1 |
| 42916 | turbarme | 1 |
| 42917 | turbaré | 1 |
| 42918 | turbara | 1 |
| 42919 | turbando | 1 |
| 42920 | turbamos | 1 |
| 42921 | turbame | 1 |
| 42922 | turbadísima | 1 |
| 42923 | turbadamente | 1 |
| 42924 | turbaciones | 1 |
| 42925 | turbábalo | 1 |
| 42926 | turbábala | 1 |
| 42927 | turan | 1 |
| 42928 | turaba | 1 |
| 42929 | tupidas | 1 |
| 42930 | tupida | 1 |
| 42931 | tunicela | 1 |
| 42932 | tundiéndole | 1 |
| 42933 | tundidores | 1 |
| 42934 | tundidor | 1 |
| 42935 | tundido | 1 |
| 42936 | tundida | 1 |
| 42937 | tundas | 1 |
| 42938 | tunda | 1 |
| 42939 | tunbal | 1 |
| 42940 | tunanterías | 1 |
| 42941 | tunantas | 1 |
| 42942 | tuna | 1 |
| 42943 | tumultuosos | 1 |
| 42944 | tumultuoso | 1 |
| 42945 | tumultos | 1 |
| 42946 | túmulos | 1 |
| 42947 | tumefacta | 1 |
| 42948 | tumbo | 1 |
| 42949 | tumbando | 1 |
| 42950 | tumbados | 1 |
| 42951 | tullido | 1 |
| 42952 | tullida | 1 |
| 42953 | tullerías | 1 |
| 42954 | tui | 1 |
| 42955 | tuho | 1 |
| 42956 | tuétanos | 1 |
| 42957 | tuétano | 1 |
| 42958 | tuetano | 1 |
| 42959 | tuesta | 1 |
| 42960 | túes | 1 |
| 42961 | tuero | 1 |
| 42962 | tuercen | 1 |
| 42963 | tuerca | 1 |
| 42964 | tueras | 1 |
| 42965 | tuelte | 1 |
| 42966 | tuelle | 1 |
| 42967 | tuelga | 1 |
| 42968 | tudesqui | 1 |
| 42969 | tubería | 1 |
| 42970 | tualeta | 1 |
| 42971 | tuæ | 1 |
| 42972 | tua | 1 |
| 42973 | tsión | 1 |
| 42974 | trusas | 1 |
| 42975 | truqueurs | 1 |
| 42976 | trunfó | 1 |
| 42977 | trunfo | 1 |
| 42978 | trunfar | 1 |
| 42979 | truncados | 1 |
| 42980 | truncado | 1 |
| 42981 | truncadas | 1 |
| 42982 | truncada | 1 |
| 42983 | trújome | 1 |
| 42984 | trujistes | 1 |
| 42985 | trujillete | 1 |
| 42986 | trujillesca | 1 |
| 42987 | trujillas | 1 |
| 42988 | trujéronsele | 1 |
| 42989 | trujera | 1 |
| 42990 | trujamán | 1 |
| 42991 | truhanería | 1 |
| 42992 | truhana | 1 |
| 42993 | trufados | 1 |
| 42994 | trueques | 1 |
| 42995 | truenan | 1 |
| 42996 | truécale | 1 |
| 42997 | truculento | 1 |
| 42998 | troyana | 1 |
| 42999 | tróxovos | 1 |
| 43000 | tróxote | 1 |
| 43001 | tróxolo | 1 |
| 43002 | tróxole | 1 |
| 43003 | tróxo | 1 |
| 43004 | troxistes | 1 |
| 43005 | troxies | 1 |
| 43006 | troxiéronlos | 1 |
| 43007 | troxiéronlo | 1 |
| 43008 | troxiello | 1 |
| 43009 | trouvait | 1 |
| 43010 | trouin | 1 |
| 43011 | trotón | 1 |
| 43012 | trotico | 1 |
| 43013 | trotero | 1 |
| 43014 | trotas | 1 |
| 43015 | trotando | 1 |
| 43016 | trotalla | 1 |
| 43017 | trotaconuentos | 1 |
| 43018 | trot | 1 |
| 43019 | troquemos | 1 |
| 43020 | troquel | 1 |
| 43021 | troquéis | 1 |
| 43022 | tropos | 1 |
| 43023 | tropo | 1 |
| 43024 | trópicos | 1 |
| 43025 | tropezóme | 1 |
| 43026 | tropezasse | 1 |
| 43027 | tropezasen | 1 |
| 43028 | tropezase | 1 |
| 43029 | tropezarme | 1 |
| 43030 | tropezará | 1 |
| 43031 | tropezara | 1 |
| 43032 | tropezamos | 1 |
| 43033 | tropecé | 1 |
| 43034 | tropece | 1 |
| 43035 | tronque | 1 |
| 43036 | tronpas | 1 |
| 43037 | tronos | 1 |
| 43038 | tronó | 1 |
| 43039 | trongas | 1 |
| 43040 | tronchó | 1 |
| 43041 | troncho | 1 |
| 43042 | tronchado | 1 |
| 43043 | tronaron | 1 |
| 43044 | tronadores | 1 |
| 43045 | tronaba | 1 |
| 43046 | trompo | 1 |
| 43047 | trompicando | 1 |
| 43048 | trompetitas | 1 |
| 43049 | trompetillas | 1 |
| 43050 | trompeteada | 1 |
| 43051 | trompetada | 1 |
| 43052 | trompazos | 1 |
| 43053 | trompadas | 1 |
| 43054 | trompada | 1 |
| 43055 | trompacios | 1 |
| 43056 | trojes | 1 |
| 43057 | trojae | 1 |
| 43058 | trogloditas | 1 |
| 43059 | trocitos | 1 |
| 43060 | trocaste | 1 |
| 43061 | trocasse | 1 |
| 43062 | trocasen | 1 |
| 43063 | trocase | 1 |
| 43064 | trocarse | 1 |
| 43065 | trocáronse | 1 |
| 43066 | trocarme | 1 |
| 43067 | trocarlos | 1 |
| 43068 | trocarlas | 1 |
| 43069 | trocáreme | 1 |
| 43070 | trocarán | 1 |
| 43071 | trocaran | 1 |
| 43072 | trocando | 1 |
| 43073 | trocadas | 1 |
| 43074 | trocábase | 1 |
| 43075 | troca | 1 |
| 43076 | trobo | 1 |
| 43077 | trobase | 1 |
| 43078 | trobaríades | 1 |
| 43079 | trobara | 1 |
| 43080 | trobadores | 1 |
| 43081 | trobada | 1 |
| 43082 | triunvirato | 1 |
| 43083 | triunmphe | 1 |
| 43084 | triunfen | 1 |
| 43085 | triunfase | 1 |
| 43086 | triunfaría | 1 |
| 43087 | triunfara | 1 |
| 43088 | triunfan | 1 |
| 43089 | triunfalmente | 1 |
| 43090 | triunfadora | 1 |
| 43091 | trituro | 1 |
| 43092 | triturar | 1 |
| 43093 | triturada | 1 |
| 43094 | tristísimamente | 1 |
| 43095 | tristis | 1 |
| 43096 | tristençia | 1 |
| 43097 | trisca | 1 |
| 43098 | triquiñuela | 1 |
| 43099 | tripulando | 1 |
| 43100 | tripulados | 1 |
| 43101 | tripulaciones | 1 |
| 43102 | tripulaban | 1 |
| 43103 | tripudas | 1 |
| 43104 | triplicar | 1 |
| 43105 | triplicado | 1 |
| 43106 | triples | 1 |
| 43107 | tripicallero | 1 |
| 43108 | triperas | 1 |
| 43109 | trïones | 1 |
| 43110 | triones | 1 |
| 43111 | trïón | 1 |
| 43112 | trinquis | 1 |
| 43113 | trinquen | 1 |
| 43114 | trinitarias | 1 |
| 43115 | trinco | 1 |
| 43116 | trinchera | 1 |
| 43117 | trinchéense | 1 |
| 43118 | trincheado | 1 |
| 43119 | trincharon | 1 |
| 43120 | trinchante | 1 |
| 43121 | trinchándome | 1 |
| 43122 | trinchado | 1 |
| 43123 | trincha | 1 |
| 43124 | trincaron | 1 |
| 43125 | trincan | 1 |
| 43126 | trinca | 1 |
| 43127 | trinar | 1 |
| 43128 | trinan | 1 |
| 43129 | trimestres | 1 |
| 43130 | trimestralmente | 1 |
| 43131 | trillo | 1 |
| 43132 | trillar | 1 |
| 43133 | trillan | 1 |
| 43134 | trilladoras | 1 |
| 43135 | trillada | 1 |
| 43136 | trilla | 1 |
| 43137 | triguillos | 1 |
| 43138 | trifulcas | 1 |
| 43139 | trifoncito | 1 |
| 43140 | trifoncillo | 1 |
| 43141 | trifona | 1 |
| 43142 | tridentino | 1 |
| 43143 | triçesimo | 1 |
| 43144 | tributos | 1 |
| 43145 | tributaria | 1 |
| 43146 | tributa | 1 |
| 43147 | tribunicia | 1 |
| 43148 | tribulaçión | 1 |
| 43149 | tribu | 1 |
| 43150 | triasandalos | 1 |
| 43151 | triángulo | 1 |
| 43152 | triana | 1 |
| 43153 | trexnada | 1 |
| 43154 | trexna | 1 |
| 43155 | trevo | 1 |
| 43156 | trestaurar | 1 |
| 43157 | tresquillar | 1 |
| 43158 | tresquilanme | 1 |
| 43159 | tresquilados | 1 |
| 43160 | tresquilado | 1 |
| 43161 | tresientos | 1 |
| 43162 | treseño | 1 |
| 43163 | trescientas | 1 |
| 43164 | trepidaba | 1 |
| 43165 | treperas | 1 |
| 43166 | trepadores | 1 |
| 43167 | trepadora | 1 |
| 43168 | trepador | 1 |
| 43169 | trepado | 1 |
| 43170 | trepaba | 1 |
| 43171 | trenzándose | 1 |
| 43172 | trento | 1 |
| 43173 | trente | 1 |
| 43174 | trentanario | 1 |
| 43175 | trenidat | 1 |
| 43176 | trencilla | 1 |
| 43177 | trença | 1 |
| 43178 | trena | 1 |
| 43179 | tremunt | 1 |
| 43180 | tremor | 1 |
| 43181 | trémolo | 1 |
| 43182 | tremolantes | 1 |
| 43183 | tremolaban | 1 |
| 43184 | tremo | 1 |
| 43185 | trementina | 1 |
| 43186 | tremente | 1 |
| 43187 | tremens | 1 |
| 43188 | tremen | 1 |
| 43189 | trefuda | 1 |
| 43190 | treçientos | 1 |
| 43191 | treçientas | 1 |
| 43192 | trechel | 1 |
| 43193 | trechadas | 1 |
| 43194 | trebol | 1 |
| 43195 | trebejando | 1 |
| 43196 | trazasen | 1 |
| 43197 | trazáronla | 1 |
| 43198 | trazaron | 1 |
| 43199 | trazarle | 1 |
| 43200 | trazaré | 1 |
| 43201 | trazamos | 1 |
| 43202 | trazador | 1 |
| 43203 | trazadas | 1 |
| 43204 | trazaban | 1 |
| 43205 | tráyoles | 1 |
| 43206 | traylla | 1 |
| 43207 | traygays | 1 |
| 43208 | traygas | 1 |
| 43209 | traygan | 1 |
| 43210 | trayéndoselo | 1 |
| 43211 | trayéndome | 1 |
| 43212 | trayéndola | 1 |
| 43213 | trayeme | 1 |
| 43214 | trayedes | 1 |
| 43215 | traydos | 1 |
| 43216 | trayale | 1 |
| 43217 | tray | 1 |
| 43218 | traxeran | 1 |
| 43219 | travó | 1 |
| 43220 | traviessa | 1 |
| 43221 | traviesas | 1 |
| 43222 | traviatta | 1 |
| 43223 | traviatonas | 1 |
| 43224 | travesurilla | 1 |
| 43225 | travesías | 1 |
| 43226 | traveseros | 1 |
| 43227 | travesemos | 1 |
| 43228 | travesaños | 1 |
| 43229 | travé | 1 |
| 43230 | travava | 1 |
| 43231 | travaron | 1 |
| 43232 | travar | 1 |
| 43233 | trával | 1 |
| 43234 | travadas | 1 |
| 43235 | trauiessa | 1 |
| 43236 | trauan | 1 |
| 43237 | tratose | 1 |
| 43238 | tratóle | 1 |
| 43239 | tratólas | 1 |
| 43240 | trátele | 1 |
| 43241 | tratéis | 1 |
| 43242 | tratays | 1 |
| 43243 | trataua | 1 |
| 43244 | tratásemos | 1 |
| 43245 | trátase | 1 |
| 43246 | tratáronse | 1 |
| 43247 | tratáronle | 1 |
| 43248 | tratarnos | 1 |
| 43249 | tratarlas | 1 |
| 43250 | tratares | 1 |
| 43251 | trataréis | 1 |
| 43252 | trátanse | 1 |
| 43253 | tratándoles | 1 |
| 43254 | tratándolas | 1 |
| 43255 | trátame | 1 |
| 43256 | tratame | 1 |
| 43257 | trátalos | 1 |
| 43258 | tratalle | 1 |
| 43259 | tratáis | 1 |
| 43260 | tratadistas | 1 |
| 43261 | tratadas | 1 |
| 43262 | tratada | 1 |
| 43263 | tratables | 1 |
| 43264 | tratábase | 1 |
| 43265 | tratábamos | 1 |
| 43266 | tratábale | 1 |
| 43267 | trasvolado | 1 |
| 43268 | trasversal | 1 |
| 43269 | trasudores | 1 |
| 43270 | trasudor | 1 |
| 43271 | trastulo | 1 |
| 43272 | trastrueques | 1 |
| 43273 | trastrueque | 1 |
| 43274 | trastruecan | 1 |
| 43275 | trastrocame | 1 |
| 43276 | trastrocada | 1 |
| 43277 | trastornóla | 1 |
| 43278 | trastornaron | 1 |
| 43279 | trastornarle | 1 |
| 43280 | trastornándome | 1 |
| 43281 | trastornando | 1 |
| 43282 | trastornadas | 1 |
| 43283 | trastornábalas | 1 |
| 43284 | trastocar | 1 |
| 43285 | trastejarse | 1 |
| 43286 | trasteaba | 1 |
| 43287 | trastea | 1 |
| 43288 | trastazos | 1 |
| 43289 | trastazo | 1 |
| 43290 | trasquilón | 1 |
| 43291 | trasquiló | 1 |
| 43292 | trasquilen | 1 |
| 43293 | trasquilase | 1 |
| 43294 | trasquilaremos | 1 |
| 43295 | trasquilados | 1 |
| 43296 | trasquilada | 1 |
| 43297 | trasquila | 1 |
| 43298 | traspusiesen | 1 |
| 43299 | trasportan | 1 |
| 43300 | trasportado | 1 |
| 43301 | trasponga | 1 |
| 43302 | trasponen | 1 |
| 43303 | trasponella | 1 |
| 43304 | trasplantar | 1 |
| 43305 | trasplantan | 1 |
| 43306 | trasplantadas | 1 |
| 43307 | trasplantada | 1 |
| 43308 | trasplantaba | 1 |
| 43309 | traspié | 1 |
| 43310 | traspasso | 1 |
| 43311 | traspasse | 1 |
| 43312 | traspassaron | 1 |
| 43313 | traspasos | 1 |
| 43314 | traspásenme | 1 |
| 43315 | traspase | 1 |
| 43316 | traspásasele | 1 |
| 43317 | traspasaron | 1 |
| 43318 | traspasarla | 1 |
| 43319 | traspasara | 1 |
| 43320 | traspasándole | 1 |
| 43321 | traspasando | 1 |
| 43322 | traspasan | 1 |
| 43323 | trasparentes | 1 |
| 43324 | trasparencia | 1 |
| 43325 | trasnochados | 1 |
| 43326 | trasnochado | 1 |
| 43327 | trasnochadas | 1 |
| 43328 | trasnochaban | 1 |
| 43329 | trasmutación | 1 |
| 43330 | trasmitiendo | 1 |
| 43331 | traslucirse | 1 |
| 43332 | traslucir | 1 |
| 43333 | trasluciendo | 1 |
| 43334 | traslucido | 1 |
| 43335 | traslucían | 1 |
| 43336 | trasládola | 1 |
| 43337 | trasladen | 1 |
| 43338 | traslade | 1 |
| 43339 | trasladarme | 1 |
| 43340 | trasladarlos | 1 |
| 43341 | trasladaríamos | 1 |
| 43342 | trasladaría | 1 |
| 43343 | trasladaremos | 1 |
| 43344 | trasladaré | 1 |
| 43345 | trasladará | 1 |
| 43346 | trasladándonos | 1 |
| 43347 | trasladando | 1 |
| 43348 | trasladan | 1 |
| 43349 | trasladalla | 1 |
| 43350 | trasladada | 1 |
| 43351 | trasladaban | 1 |
| 43352 | trasijadas | 1 |
| 43353 | trasiego | 1 |
| 43354 | trasiega | 1 |
| 43355 | trasformación | 1 |
| 43356 | trasfagos | 1 |
| 43357 | trasegarlo | 1 |
| 43358 | trasegaba | 1 |
| 43359 | trascienden | 1 |
| 43360 | trascender | 1 |
| 43361 | trascendental | 1 |
| 43362 | trascala | 1 |
| 43363 | trasbordamos | 1 |
| 43364 | trasbordados | 1 |
| 43365 | trasbordábamos | 1 |
| 43366 | trapicheo | 1 |
| 43367 | trapeo | 1 |
| 43368 | trapearon | 1 |
| 43369 | trapaza | 1 |
| 43370 | trapalón | 1 |
| 43371 | trapacero | 1 |
| 43372 | trap | 1 |
| 43373 | tranzada | 1 |
| 43374 | transversales | 1 |
| 43375 | transversal | 1 |
| 43376 | transportes | 1 |
| 43377 | transportase | 1 |
| 43378 | transportaba | 1 |
| 43379 | transporta | 1 |
| 43380 | transpirar | 1 |
| 43381 | transparentar | 1 |
| 43382 | transparentando | 1 |
| 43383 | transparentado | 1 |
| 43384 | transmitir | 1 |
| 43385 | transmitió | 1 |
| 43386 | transmitiendo | 1 |
| 43387 | transmitidos | 1 |
| 43388 | transmitían | 1 |
| 43389 | transmitía | 1 |
| 43390 | transmiten | 1 |
| 43391 | transmite | 1 |
| 43392 | transmisión | 1 |
| 43393 | transmigrar | 1 |
| 43394 | transmigración | 1 |
| 43395 | transmigraban | 1 |
| 43396 | transladado | 1 |
| 43397 | translaciones | 1 |
| 43398 | tránsitos | 1 |
| 43399 | transitorio | 1 |
| 43400 | transitoria | 1 |
| 43401 | transigió | 1 |
| 43402 | transigiendo | 1 |
| 43403 | transigido | 1 |
| 43404 | transigían | 1 |
| 43405 | transigía | 1 |
| 43406 | transiciones | 1 |
| 43407 | transfusiones | 1 |
| 43408 | transfusión | 1 |
| 43409 | transformóse | 1 |
| 43410 | transforme | 1 |
| 43411 | transformas | 1 |
| 43412 | transformáramos | 1 |
| 43413 | transformándose | 1 |
| 43414 | transformando | 1 |
| 43415 | transformadas | 1 |
| 43416 | transformaban | 1 |
| 43417 | transfiguraciones | 1 |
| 43418 | transfiguración | 1 |
| 43419 | transfiguraba | 1 |
| 43420 | transferido | 1 |
| 43421 | transeunte | 1 |
| 43422 | transcurridos | 1 |
| 43423 | transcurrían | 1 |
| 43424 | transbordarse | 1 |
| 43425 | tranquilizaron | 1 |
| 43426 | tranquilizarme | 1 |
| 43427 | tranquilizarle | 1 |
| 43428 | tranquilizaré | 1 |
| 43429 | tranquilizara | 1 |
| 43430 | tranquilizándose | 1 |
| 43431 | tranquilizándola | 1 |
| 43432 | tranquilizando | 1 |
| 43433 | tranquilizan | 1 |
| 43434 | tranquilizadora | 1 |
| 43435 | tranquilizador | 1 |
| 43436 | tranquilices | 1 |
| 43437 | tranquen | 1 |
| 43438 | trançe | 1 |
| 43439 | trança | 1 |
| 43440 | tramposos | 1 |
| 43441 | trampista | 1 |
| 43442 | trampear | 1 |
| 43443 | trampantojos | 1 |
| 43444 | tramoyas | 1 |
| 43445 | tramos | 1 |
| 43446 | tramontar | 1 |
| 43447 | tramontana | 1 |
| 43448 | tramontado | 1 |
| 43449 | tramito | 1 |
| 43450 | tramasen | 1 |
| 43451 | tramas | 1 |
| 43452 | tramaban | 1 |
| 43453 | trajines | 1 |
| 43454 | trajineros | 1 |
| 43455 | trajinan | 1 |
| 43456 | trajeras | 1 |
| 43457 | trajerais | 1 |
| 43458 | trairé | 1 |
| 43459 | traílla | 1 |
| 43460 | tráiganos | 1 |
| 43461 | traíganme | 1 |
| 43462 | traigámosle | 1 |
| 43463 | tráigamela | 1 |
| 43464 | tráigala | 1 |
| 43465 | traídole | 1 |
| 43466 | traídola | 1 |
| 43467 | traido | 1 |
| 43468 | traida | 1 |
| 43469 | traicioneros | 1 |
| 43470 | traíanla | 1 |
| 43471 | traíalas | 1 |
| 43472 | traíais | 1 |
| 43473 | trai | 1 |
| 43474 | trahes | 1 |
| 43475 | traheré | 1 |
| 43476 | trahens | 1 |
| 43477 | trahe | 1 |
| 43478 | traguito | 1 |
| 43479 | tragose | 1 |
| 43480 | tragonía | 1 |
| 43481 | tragona | 1 |
| 43482 | tragineros | 1 |
| 43483 | tragicómicos | 1 |
| 43484 | tragico | 1 |
| 43485 | tragaron | 1 |
| 43486 | tragármela | 1 |
| 43487 | tragaría | 1 |
| 43488 | tragara | 1 |
| 43489 | tragantón | 1 |
| 43490 | tragándose | 1 |
| 43491 | tragándole | 1 |
| 43492 | tragamos | 1 |
| 43493 | trágame | 1 |
| 43494 | tragaluz | 1 |
| 43495 | tragallos | 1 |
| 43496 | tragallo | 1 |
| 43497 | trágala | 1 |
| 43498 | tragáis | 1 |
| 43499 | tragaderos | 1 |
| 43500 | tragada | 1 |
| 43501 | tragacanto | 1 |
| 43502 | tragaban | 1 |
| 43503 | tragábamos | 1 |
| 43504 | traficante | 1 |
| 43505 | traficaban | 1 |
| 43506 | traéslos | 1 |
| 43507 | tráeslos | 1 |
| 43508 | traés | 1 |
| 43509 | traérosle | 1 |
| 43510 | traérosla | 1 |
| 43511 | traérnosle | 1 |
| 43512 | traérmele | 1 |
| 43513 | traérmelas | 1 |
| 43514 | traergela | 1 |
| 43515 | traerás | 1 |
| 43516 | tráemelo | 1 |
| 43517 | traelle | 1 |
| 43518 | traele | 1 |
| 43519 | traeldos | 1 |
| 43520 | tráela | 1 |
| 43521 | traédmelos | 1 |
| 43522 | traedle | 1 |
| 43523 | traduzga | 1 |
| 43524 | traduzco | 1 |
| 43525 | tradújose | 1 |
| 43526 | traductora | 1 |
| 43527 | traducirse | 1 |
| 43528 | traducírmelo | 1 |
| 43529 | traducirlos | 1 |
| 43530 | traducirlo | 1 |
| 43531 | traducirla | 1 |
| 43532 | traduciré | 1 |
| 43533 | traducía | 1 |
| 43534 | traducciones | 1 |
| 43535 | tradicionalmente | 1 |
| 43536 | tracy | 1 |
| 43537 | tractaua | 1 |
| 43538 | tracista | 1 |
| 43539 | tracemos | 1 |
| 43540 | tracamundana | 1 |
| 43541 | trabucos | 1 |
| 43542 | trabucazos | 1 |
| 43543 | trabucan | 1 |
| 43544 | trabucaban | 1 |
| 43545 | trabé | 1 |
| 43546 | trabe | 1 |
| 43547 | trabazones | 1 |
| 43548 | trabándose | 1 |
| 43549 | trabándole | 1 |
| 43550 | trabajemos | 1 |
| 43551 | trabajedes | 1 |
| 43552 | trabajé | 1 |
| 43553 | trabajava | 1 |
| 43554 | trabajauas | 1 |
| 43555 | trabajat | 1 |
| 43556 | trabajaste | 1 |
| 43557 | trabajarla | 1 |
| 43558 | trabajarías | 1 |
| 43559 | trabajarían | 1 |
| 43560 | trabajaría | 1 |
| 43561 | trabajarás | 1 |
| 43562 | trabájalo | 1 |
| 43563 | trabajada | 1 |
| 43564 | trabacuentas | 1 |
| 43565 | traba | 1 |
| 43566 | toy | 1 |
| 43567 | tóxicos | 1 |
| 43568 | toxicación | 1 |
| 43569 | tóvose | 1 |
| 43570 | tóvos | 1 |
| 43571 | tovistes | 1 |
| 43572 | tovillos | 1 |
| 43573 | tovieses | 1 |
| 43574 | tovies | 1 |
| 43575 | tovieron | 1 |
| 43576 | tovieres | 1 |
| 43577 | tóvel | 1 |
| 43578 | tove | 1 |
| 43579 | tous | 1 |
| 43580 | tournefort | 1 |
| 43581 | touo | 1 |
| 43582 | toujours | 1 |
| 43583 | touistes | 1 |
| 43584 | touiesses | 1 |
| 43585 | touiessen | 1 |
| 43586 | touieremos | 1 |
| 43587 | touieras | 1 |
| 43588 | touiera | 1 |
| 43589 | toto | 1 |
| 43590 | tostasen | 1 |
| 43591 | tostar | 1 |
| 43592 | tostadores | 1 |
| 43593 | tostadita | 1 |
| 43594 | tostaban | 1 |
| 43595 | tostaba | 1 |
| 43596 | toso | 1 |
| 43597 | tosino | 1 |
| 43598 | tosidura | 1 |
| 43599 | tosido | 1 |
| 43600 | toséis | 1 |
| 43601 | tosecilla | 1 |
| 43602 | torzales | 1 |
| 43603 | tory | 1 |
| 43604 | torvo | 1 |
| 43605 | torvamente | 1 |
| 43606 | toruellinos | 1 |
| 43607 | tortüosa | 1 |
| 43608 | tórtolos | 1 |
| 43609 | tortolitos | 1 |
| 43610 | tortolitas | 1 |
| 43611 | tortoleo | 1 |
| 43612 | tortillita | 1 |
| 43613 | tortícolis | 1 |
| 43614 | tortarosa | 1 |
| 43615 | torta | 1 |
| 43616 | torrijos | 1 |
| 43617 | tórrida | 1 |
| 43618 | torresno | 1 |
| 43619 | torrero | 1 |
| 43620 | torrentera | 1 |
| 43621 | torrejón | 1 |
| 43622 | torregorda | 1 |
| 43623 | torraé | 1 |
| 43624 | torrados | 1 |
| 43625 | torote | 1 |
| 43626 | toronja | 1 |
| 43627 | tórnote | 1 |
| 43628 | tornose | 1 |
| 43629 | tornos | 1 |
| 43630 | tornóme | 1 |
| 43631 | tórnome | 1 |
| 43632 | torniscones | 1 |
| 43633 | torniscón | 1 |
| 43634 | torniquete | 1 |
| 43635 | tornillándola | 1 |
| 43636 | torneses | 1 |
| 43637 | tórnese | 1 |
| 43638 | tornese | 1 |
| 43639 | tornero | 1 |
| 43640 | torneras | 1 |
| 43641 | torner | 1 |
| 43642 | tornemos | 1 |
| 43643 | tornémonos | 1 |
| 43644 | tornedes | 1 |
| 43645 | tornear | 1 |
| 43646 | torneando | 1 |
| 43647 | torneadita | 1 |
| 43648 | tornays | 1 |
| 43649 | tornava | 1 |
| 43650 | tornaua | 1 |
| 43651 | tórnate | 1 |
| 43652 | tornasolados | 1 |
| 43653 | tornasol | 1 |
| 43654 | tornásemos | 1 |
| 43655 | tornarte | 1 |
| 43656 | tornaros | 1 |
| 43657 | tornáronla | 1 |
| 43658 | tornarme | 1 |
| 43659 | tornarlo | 1 |
| 43660 | tornarle | 1 |
| 43661 | tornaríe | 1 |
| 43662 | tornarían | 1 |
| 43663 | tornares | 1 |
| 43664 | tornaremos | 1 |
| 43665 | tornaré | 1 |
| 43666 | tornarase | 1 |
| 43667 | tornaras | 1 |
| 43668 | tornarán | 1 |
| 43669 | tórnanse | 1 |
| 43670 | tornanla | 1 |
| 43671 | tornandome | 1 |
| 43672 | tornan | 1 |
| 43673 | tornamos | 1 |
| 43674 | tornallo | 1 |
| 43675 | tornalle | 1 |
| 43676 | tórnale | 1 |
| 43677 | tornalas | 1 |
| 43678 | tornadiza | 1 |
| 43679 | tornadas | 1 |
| 43680 | tornad | 1 |
| 43681 | tornábase | 1 |
| 43682 | tornábale | 1 |
| 43683 | tornábala | 1 |
| 43684 | tormentoso | 1 |
| 43685 | torméntasle | 1 |
| 43686 | torillo | 1 |
| 43687 | toril | 1 |
| 43688 | toretes | 1 |
| 43689 | torear | 1 |
| 43690 | toreando | 1 |
| 43691 | toreado | 1 |
| 43692 | toreaban | 1 |
| 43693 | toreaba | 1 |
| 43694 | tordillo | 1 |
| 43695 | tordesillesco | 1 |
| 43696 | torda | 1 |
| 43697 | torcuato | 1 |
| 43698 | torciesen | 1 |
| 43699 | torcieron | 1 |
| 43700 | torcidamente | 1 |
| 43701 | torcerse | 1 |
| 43702 | torcera | 1 |
| 43703 | torcella | 1 |
| 43704 | torceduras | 1 |
| 43705 | torcedor | 1 |
| 43706 | torce | 1 |
| 43707 | torcato | 1 |
| 43708 | torcaces | 1 |
| 43709 | torbellinos | 1 |
| 43710 | tórax | 1 |
| 43711 | toraquís | 1 |
| 43712 | toral | 1 |
| 43713 | torácica | 1 |
| 43714 | toraces | 1 |
| 43715 | tora | 1 |
| 43716 | toquiblanca | 1 |
| 43717 | tóquenme | 1 |
| 43718 | toquecito | 1 |
| 43719 | topos | 1 |
| 43720 | topome | 1 |
| 43721 | topográficos | 1 |
| 43722 | tópicos | 1 |
| 43723 | topemos | 1 |
| 43724 | topéme | 1 |
| 43725 | topauamos | 1 |
| 43726 | topasses | 1 |
| 43727 | topásemos | 1 |
| 43728 | topáronme | 1 |
| 43729 | toparía | 1 |
| 43730 | topares | 1 |
| 43731 | toparen | 1 |
| 43732 | topáredes | 1 |
| 43733 | topáramos | 1 |
| 43734 | topacio | 1 |
| 43735 | topaban | 1 |
| 43736 | topa | 1 |
| 43737 | too | 1 |
| 43738 | tontunas | 1 |
| 43739 | tontuna | 1 |
| 43740 | tontonela | 1 |
| 43741 | tontita | 1 |
| 43742 | tontina | 1 |
| 43743 | tontees | 1 |
| 43744 | tontear | 1 |
| 43745 | tonteando | 1 |
| 43746 | tontadas | 1 |
| 43747 | tonsurados | 1 |
| 43748 | tonito | 1 |
| 43749 | tonina | 1 |
| 43750 | tónicos | 1 |
| 43751 | tónica | 1 |
| 43752 | toneles | 1 |
| 43753 | tonelada | 1 |
| 43754 | tonante | 1 |
| 43755 | tonadillas | 1 |
| 43756 | tomóm | 1 |
| 43757 | tomola | 1 |
| 43758 | tomistas | 1 |
| 43759 | tomillos | 1 |
| 43760 | tomillas | 1 |
| 43761 | tomeste | 1 |
| 43762 | tomeras | 1 |
| 43763 | tómense | 1 |
| 43764 | tómenlas | 1 |
| 43765 | tomemosselo | 1 |
| 43766 | tomélos | 1 |
| 43767 | tómelos | 1 |
| 43768 | tomélo | 1 |
| 43769 | tómela | 1 |
| 43770 | tómbola | 1 |
| 43771 | tomazo | 1 |
| 43772 | tomays | 1 |
| 43773 | tomavan | 1 |
| 43774 | tomava | 1 |
| 43775 | tomaua | 1 |
| 43776 | tomatlo | 1 |
| 43777 | tomates | 1 |
| 43778 | tomat | 1 |
| 43779 | tomastes | 1 |
| 43780 | tomasse | 1 |
| 43781 | tomasillo | 1 |
| 43782 | tomáronlo | 1 |
| 43783 | tomáronle | 1 |
| 43784 | tomarles | 1 |
| 43785 | tomarías | 1 |
| 43786 | tomarias | 1 |
| 43787 | tomaríamos | 1 |
| 43788 | tomaríale | 1 |
| 43789 | tomaréle | 1 |
| 43790 | tomárase | 1 |
| 43791 | tomáramos | 1 |
| 43792 | tomaos | 1 |
| 43793 | tómanse | 1 |
| 43794 | tomámoslas | 1 |
| 43795 | tomalle | 1 |
| 43796 | tómale | 1 |
| 43797 | tomáis | 1 |
| 43798 | tomadora | 1 |
| 43799 | tomador | 1 |
| 43800 | tomadlos | 1 |
| 43801 | tomadle | 1 |
| 43802 | tomábase | 1 |
| 43803 | tomabas | 1 |
| 43804 | tomábamos | 1 |
| 43805 | tomábala | 1 |
| 43806 | tolú | 1 |
| 43807 | tolosano | 1 |
| 43808 | tolondrón | 1 |
| 43809 | tolomeos | 1 |
| 43810 | tólogo | 1 |
| 43811 | tologías | 1 |
| 43812 | tollina | 1 |
| 43813 | tollidos | 1 |
| 43814 | tollerar | 1 |
| 43815 | toleres | 1 |
| 43816 | toleraron | 1 |
| 43817 | tolerarlo | 1 |
| 43818 | tolerancias | 1 |
| 43819 | toleran | 1 |
| 43820 | toleradas | 1 |
| 43821 | toleraban | 1 |
| 43822 | tolentino | 1 |
| 43823 | toldado | 1 |
| 43824 | tolaido | 1 |
| 43825 | toilette | 1 |
| 43826 | togados | 1 |
| 43827 | tocón | 1 |
| 43828 | tocolas | 1 |
| 43829 | tocaua | 1 |
| 43830 | tocati | 1 |
| 43831 | tocastes | 1 |
| 43832 | tocasse | 1 |
| 43833 | tocaros | 1 |
| 43834 | tocarlo | 1 |
| 43835 | tocarían | 1 |
| 43836 | tocaría | 1 |
| 43837 | tocarás | 1 |
| 43838 | tocarán | 1 |
| 43839 | tocaran | 1 |
| 43840 | tocárades | 1 |
| 43841 | tocándonos | 1 |
| 43842 | tocándolos | 1 |
| 43843 | tocándoles | 1 |
| 43844 | tocándola | 1 |
| 43845 | tocamientos | 1 |
| 43846 | tocamiento | 1 |
| 43847 | tócame | 1 |
| 43848 | tocame | 1 |
| 43849 | tócalos | 1 |
| 43850 | tocalla | 1 |
| 43851 | tocábamos | 1 |
| 43852 | tobosina | 1 |
| 43853 | tobosescas | 1 |
| 43854 | tobosa | 1 |
| 43855 | tobo | 1 |
| 43856 | tob | 1 |
| 43857 | tó | 1 |
| 43858 | tlemcén | 1 |
| 43859 | tiznes | 1 |
| 43860 | tiznándole | 1 |
| 43861 | tiznando | 1 |
| 43862 | tivolis | 1 |
| 43863 | titulos | 1 |
| 43864 | titulillos | 1 |
| 43865 | titulillo | 1 |
| 43866 | títulas | 1 |
| 43867 | titulará | 1 |
| 43868 | titular | 1 |
| 43869 | titulados | 1 |
| 43870 | titula | 1 |
| 43871 | titubeaba | 1 |
| 43872 | titón | 1 |
| 43873 | titiriteros | 1 |
| 43874 | titilar | 1 |
| 43875 | títeres | 1 |
| 43876 | titerera | 1 |
| 43877 | titán | 1 |
| 43878 | tissot | 1 |
| 43879 | tísicas | 1 |
| 43880 | tiróse | 1 |
| 43881 | tirole | 1 |
| 43882 | tiritos | 1 |
| 43883 | tiritar | 1 |
| 43884 | tiritando | 1 |
| 43885 | tiritaba | 1 |
| 43886 | tirios | 1 |
| 43887 | tirilla | 1 |
| 43888 | tiréle | 1 |
| 43889 | tírele | 1 |
| 43890 | tirava | 1 |
| 43891 | tirauan | 1 |
| 43892 | tiraste | 1 |
| 43893 | tirárselos | 1 |
| 43894 | tirársela | 1 |
| 43895 | tirarme | 1 |
| 43896 | tirarlas | 1 |
| 43897 | tirarla | 1 |
| 43898 | tirare | 1 |
| 43899 | tirarás | 1 |
| 43900 | tirarán | 1 |
| 43901 | tiranístico | 1 |
| 43902 | tiránico | 1 |
| 43903 | tirándolos | 1 |
| 43904 | tirándoles | 1 |
| 43905 | tirándola | 1 |
| 43906 | tiranas | 1 |
| 43907 | tirámosla | 1 |
| 43908 | tiramira | 1 |
| 43909 | tírale | 1 |
| 43910 | tirajos | 1 |
| 43911 | tiradvos | 1 |
| 43912 | tirados | 1 |
| 43913 | tirádola | 1 |
| 43914 | tirad | 1 |
| 43915 | tirabuzones | 1 |
| 43916 | tirabas | 1 |
| 43917 | tirábanle | 1 |
| 43918 | tirábalo | 1 |
| 43919 | tiquitoc | 1 |
| 43920 | tiquitique | 1 |
| 43921 | tique | 1 |
| 43922 | tipografía | 1 |
| 43923 | tipito | 1 |
| 43924 | tiote | 1 |
| 43925 | tiotas | 1 |
| 43926 | tiota | 1 |
| 43927 | tiorra | 1 |
| 43928 | tïorba | 1 |
| 43929 | tiopieyo | 1 |
| 43930 | tiona | 1 |
| 43931 | tiólogos | 1 |
| 43932 | tiñosa | 1 |
| 43933 | tiñó | 1 |
| 43934 | tiñéndosela | 1 |
| 43935 | tiñéndolo | 1 |
| 43936 | tiñéndole | 1 |
| 43937 | tiñendo | 1 |
| 43938 | tiña | 1 |
| 43939 | tintura | 1 |
| 43940 | tintos | 1 |
| 43941 | tintineo | 1 |
| 43942 | tintes | 1 |
| 43943 | tinosa | 1 |
| 43944 | tinientes | 1 |
| 43945 | tinagica | 1 |
| 43946 | tina | 1 |
| 43947 | timos | 1 |
| 43948 | timoratos | 1 |
| 43949 | timorata | 1 |
| 43950 | timor | 1 |
| 43951 | timonero | 1 |
| 43952 | timonel | 1 |
| 43953 | timonear | 1 |
| 43954 | tímidos | 1 |
| 43955 | timidos | 1 |
| 43956 | timet | 1 |
| 43957 | timbrio | 1 |
| 43958 | timbrado | 1 |
| 43959 | timarte | 1 |
| 43960 | timarse | 1 |
| 43961 | timantes | 1 |
| 43962 | timan | 1 |
| 43963 | timadora | 1 |
| 43964 | timaban | 1 |
| 43965 | tilo | 1 |
| 43966 | tílburi | 1 |
| 43967 | tifoidea | 1 |
| 43968 | tifis | 1 |
| 43969 | tifeo | 1 |
| 43970 | tiesto | 1 |
| 43971 | tiestamente | 1 |
| 43972 | tiesta | 1 |
| 43973 | tiernísimos | 1 |
| 43974 | tientan | 1 |
| 43975 | tienete | 1 |
| 43976 | tiénesla | 1 |
| 43977 | tiénese | 1 |
| 43978 | tienente | 1 |
| 43979 | tiénennos | 1 |
| 43980 | tienenle | 1 |
| 43981 | tieneme | 1 |
| 43982 | tiénele | 1 |
| 43983 | tienele | 1 |
| 43984 | tienden | 1 |
| 43985 | tienblan | 1 |
| 43986 | tíen | 1 |
| 43987 | tiemplate | 1 |
| 43988 | tiempla | 1 |
| 43989 | tiemble | 1 |
| 43990 | ticio | 1 |
| 43991 | tica | 1 |
| 43992 | tiburones | 1 |
| 43993 | tiburonas | 1 |
| 43994 | tibre | 1 |
| 43995 | tibores | 1 |
| 43996 | tibidabo | 1 |
| 43997 | tibial | 1 |
| 43998 | tíbi | 1 |
| 43999 | tiberio | 1 |
| 44000 | tíbar | 1 |
| 44001 | tibar | 1 |
| 44002 | tïara | 1 |
| 44003 | thunderer | 1 |
| 44004 | tholomeo | 1 |
| 44005 | thinville | 1 |
| 44006 | thessoreros | 1 |
| 44007 | thesorero | 1 |
| 44008 | thesaurum | 1 |
| 44009 | thamar | 1 |
| 44010 | thackeray | 1 |
| 44011 | textualmente | 1 |
| 44012 | textes | 1 |
| 44013 | texon | 1 |
| 44014 | texo | 1 |
| 44015 | texedores | 1 |
| 44016 | texedor | 1 |
| 44017 | tétricas | 1 |
| 44018 | tetrarca | 1 |
| 44019 | tetita | 1 |
| 44020 | tetilla | 1 |
| 44021 | tetera | 1 |
| 44022 | tetástrofo | 1 |
| 44023 | tetánica | 1 |
| 44024 | testuz | 1 |
| 44025 | testos | 1 |
| 44026 | testimoniar | 1 |
| 44027 | testeros | 1 |
| 44028 | testera | 1 |
| 44029 | testas | 1 |
| 44030 | testarudos | 1 |
| 44031 | testar | 1 |
| 44032 | testantur | 1 |
| 44033 | tessitura | 1 |
| 44034 | tesorería | 1 |
| 44035 | tesifone | 1 |
| 44036 | tertuliantes | 1 |
| 44037 | tertuliaba | 1 |
| 44038 | tersan | 1 |
| 44039 | terruños | 1 |
| 44040 | terroso | 1 |
| 44041 | terrorista | 1 |
| 44042 | terroríficos | 1 |
| 44043 | terron | 1 |
| 44044 | terrier | 1 |
| 44045 | terriblemente | 1 |
| 44046 | terrestres | 1 |
| 44047 | terreros | 1 |
| 44048 | terrenales | 1 |
| 44049 | terrena | 1 |
| 44050 | terraza | 1 |
| 44051 | terras | 1 |
| 44052 | terráqueo | 1 |
| 44053 | terraplenes | 1 |
| 44054 | terraplén | 1 |
| 44055 | terpsícore | 1 |
| 44056 | ternos | 1 |
| 44057 | terníe | 1 |
| 44058 | ternias | 1 |
| 44059 | ternezuelo | 1 |
| 44060 | terneruela | 1 |
| 44061 | ternerito | 1 |
| 44062 | terneras | 1 |
| 44063 | ternasme | 1 |
| 44064 | ternan | 1 |
| 44065 | terná | 1 |
| 44066 | termópilas | 1 |
| 44067 | termómetros | 1 |
| 44068 | terminasen | 1 |
| 44069 | terminarse | 1 |
| 44070 | terminarle | 1 |
| 44071 | terminarlas | 1 |
| 44072 | terminaría | 1 |
| 44073 | terminaciones | 1 |
| 44074 | terminación | 1 |
| 44075 | terminachos | 1 |
| 44076 | termal | 1 |
| 44077 | tergiversemos | 1 |
| 44078 | tergiversando | 1 |
| 44079 | teresona | 1 |
| 44080 | teresaina | 1 |
| 44081 | terenciana | 1 |
| 44082 | terebinto | 1 |
| 44083 | tercos | 1 |
| 44084 | terciopelos | 1 |
| 44085 | tercié | 1 |
| 44086 | terciándose | 1 |
| 44087 | terciana | 1 |
| 44088 | terciaba | 1 |
| 44089 | terceros | 1 |
| 44090 | tercerones | 1 |
| 44091 | tercería | 1 |
| 44092 | terceras | 1 |
| 44093 | tercamente | 1 |
| 44094 | terapéutico | 1 |
| 44095 | terapéuticas | 1 |
| 44096 | teóricas | 1 |
| 44097 | teológicas | 1 |
| 44098 | teologales | 1 |
| 44099 | teóloga | 1 |
| 44100 | teogonías | 1 |
| 44101 | teodolitos | 1 |
| 44102 | teodolito | 1 |
| 44103 | teocrático | 1 |
| 44104 | teñirse | 1 |
| 44105 | tenuidad | 1 |
| 44106 | tentólos | 1 |
| 44107 | tentóle | 1 |
| 44108 | tentóla | 1 |
| 44109 | tenté | 1 |
| 44110 | tentarte | 1 |
| 44111 | tentarse | 1 |
| 44112 | tentarme | 1 |
| 44113 | tentarlo | 1 |
| 44114 | tentarían | 1 |
| 44115 | tentaré | 1 |
| 44116 | tentare | 1 |
| 44117 | tentados | 1 |
| 44118 | tentadores | 1 |
| 44119 | tentadora | 1 |
| 44120 | tentáculos | 1 |
| 44121 | tentaçión | 1 |
| 44122 | tentábala | 1 |
| 44123 | tenreiro | 1 |
| 44124 | tenptaçiones | 1 |
| 44125 | tenpro | 1 |
| 44126 | tenpradas | 1 |
| 44127 | tenprad | 1 |
| 44128 | tenporal | 1 |
| 44129 | tenporadas | 1 |
| 44130 | tenporada | 1 |
| 44131 | tenplano | 1 |
| 44132 | tenplamiento | 1 |
| 44133 | tenientejo | 1 |
| 44134 | tenienta | 1 |
| 44135 | teniéndonos | 1 |
| 44136 | teniéndomela | 1 |
| 44137 | teniéndome | 1 |
| 44138 | teniéndolos | 1 |
| 44139 | teniéndoles | 1 |
| 44140 | teniéndolas | 1 |
| 44141 | teníen | 1 |
| 44142 | tenien | 1 |
| 44143 | teníanse | 1 |
| 44144 | teníanle | 1 |
| 44145 | teniamos | 1 |
| 44146 | teníalos | 1 |
| 44147 | teníalo | 1 |
| 44148 | teníalas | 1 |
| 44149 | teníal | 1 |
| 44150 | teníais | 1 |
| 44151 | tení | 1 |
| 44152 | teni | 1 |
| 44153 | tenhan | 1 |
| 44154 | tengotelo | 1 |
| 44155 | tengolo | 1 |
| 44156 | téngole | 1 |
| 44157 | ténganos | 1 |
| 44158 | tengámoslo | 1 |
| 44159 | tengámosle | 1 |
| 44160 | téngame | 1 |
| 44161 | téngale | 1 |
| 44162 | tenert | 1 |
| 44163 | tenérsela | 1 |
| 44164 | tenernos | 1 |
| 44165 | tenerías | 1 |
| 44166 | tenelle | 1 |
| 44167 | tenéisla | 1 |
| 44168 | tenedores | 1 |
| 44169 | tenedoras | 1 |
| 44170 | tenedme | 1 |
| 44171 | tenedlos | 1 |
| 44172 | tenedle | 1 |
| 44173 | tenebrosos | 1 |
| 44174 | tenebrosas | 1 |
| 44175 | tenebras | 1 |
| 44176 | tenebrario | 1 |
| 44177 | tendrásla | 1 |
| 44178 | tendralos | 1 |
| 44179 | tendones | 1 |
| 44180 | tendióse | 1 |
| 44181 | tendillas | 1 |
| 44182 | tendiéronle | 1 |
| 44183 | tendiera | 1 |
| 44184 | tendíanse | 1 |
| 44185 | tenderil | 1 |
| 44186 | tenderijos | 1 |
| 44187 | tenderete | 1 |
| 44188 | tendera | 1 |
| 44189 | tendeos | 1 |
| 44190 | tendente | 1 |
| 44191 | tendemos | 1 |
| 44192 | tendejones | 1 |
| 44193 | tenca | 1 |
| 44194 | tenblores | 1 |
| 44195 | tenazuelas | 1 |
| 44196 | tenasas | 1 |
| 44197 | tenante | 1 |
| 44198 | tenaças | 1 |
| 44199 | temps | 1 |
| 44200 | temporis | 1 |
| 44201 | temporibus | 1 |
| 44202 | temporera | 1 |
| 44203 | temporadillas | 1 |
| 44204 | temporadilla | 1 |
| 44205 | templóse | 1 |
| 44206 | templóla | 1 |
| 44207 | templete | 1 |
| 44208 | templásemos | 1 |
| 44209 | templase | 1 |
| 44210 | templarte | 1 |
| 44211 | templarse | 1 |
| 44212 | templarles | 1 |
| 44213 | templarla | 1 |
| 44214 | templaréis | 1 |
| 44215 | templara | 1 |
| 44216 | templadita | 1 |
| 44217 | templadico | 1 |
| 44218 | templadas | 1 |
| 44219 | templadamente | 1 |
| 44220 | templad | 1 |
| 44221 | tempestuosos | 1 |
| 44222 | temperet | 1 |
| 44223 | temperaturas | 1 |
| 44224 | temperancia | 1 |
| 44225 | temperado | 1 |
| 44226 | tempé | 1 |
| 44227 | témpanos | 1 |
| 44228 | temorosos | 1 |
| 44229 | témome | 1 |
| 44230 | temiste | 1 |
| 44231 | temis | 1 |
| 44232 | temióte | 1 |
| 44233 | temio | 1 |
| 44234 | temiésemos | 1 |
| 44235 | temiese | 1 |
| 44236 | temiéramos | 1 |
| 44237 | temiéndolo | 1 |
| 44238 | temiéndole | 1 |
| 44239 | temíase | 1 |
| 44240 | temías | 1 |
| 44241 | temíades | 1 |
| 44242 | temia | 1 |
| 44243 | temerones | 1 |
| 44244 | temerlo | 1 |
| 44245 | temerle | 1 |
| 44246 | temeríe | 1 |
| 44247 | temería | 1 |
| 44248 | temere | 1 |
| 44249 | temerás | 1 |
| 44250 | témense | 1 |
| 44251 | temedes | 1 |
| 44252 | temed | 1 |
| 44253 | temblorcico | 1 |
| 44254 | temblo | 1 |
| 44255 | temblase | 1 |
| 44256 | tembláronle | 1 |
| 44257 | temblarán | 1 |
| 44258 | temblara | 1 |
| 44259 | temblándome | 1 |
| 44260 | tembladores | 1 |
| 44261 | tembladora | 1 |
| 44262 | temblábale | 1 |
| 44263 | temáis | 1 |
| 44264 | temades | 1 |
| 44265 | telones | 1 |
| 44266 | telo | 1 |
| 44267 | tellagori | 1 |
| 44268 | telilla | 1 |
| 44269 | telescopio | 1 |
| 44270 | telegramas | 1 |
| 44271 | telegráficos | 1 |
| 44272 | telegráficas | 1 |
| 44273 | telegrafías | 1 |
| 44274 | telegrafiarse | 1 |
| 44275 | telegrafía | 1 |
| 44276 | telares | 1 |
| 44277 | telarana | 1 |
| 44278 | tejos | 1 |
| 44279 | tejes | 1 |
| 44280 | tejedora | 1 |
| 44281 | tejedor | 1 |
| 44282 | tejavana | 1 |
| 44283 | tejadillos | 1 |
| 44284 | tejadillo | 1 |
| 44285 | tejada | 1 |
| 44286 | tegel | 1 |
| 44287 | tediosas | 1 |
| 44288 | tediosa | 1 |
| 44289 | técnico | 1 |
| 44290 | tecnicismo | 1 |
| 44291 | técnica | 1 |
| 44292 | tecleando | 1 |
| 44293 | tecleaban | 1 |
| 44294 | tecleaba | 1 |
| 44295 | teces | 1 |
| 44296 | tebano | 1 |
| 44297 | tazón | 1 |
| 44298 | taverna | 1 |
| 44299 | távano | 1 |
| 44300 | tauromaquia | 1 |
| 44301 | taurómacas | 1 |
| 44302 | taurina | 1 |
| 44303 | tatiste | 1 |
| 44304 | tática | 1 |
| 44305 | tati | 1 |
| 44306 | tasso | 1 |
| 44307 | tassa | 1 |
| 44308 | tase | 1 |
| 44309 | tascaba | 1 |
| 44310 | tasaran | 1 |
| 44311 | tasajos | 1 |
| 44312 | tartamudeó | 1 |
| 44313 | tartamudeando | 1 |
| 44314 | tártagos | 1 |
| 44315 | tarso | 1 |
| 44316 | tarsilita | 1 |
| 44317 | tarjetazos | 1 |
| 44318 | tarifa | 1 |
| 44319 | tardos | 1 |
| 44320 | tardíos | 1 |
| 44321 | tardineros | 1 |
| 44322 | tardecillo | 1 |
| 44323 | tardecica | 1 |
| 44324 | tardaríamos | 1 |
| 44325 | tardárades | 1 |
| 44326 | tardan | 1 |
| 44327 | tardamiento | 1 |
| 44328 | tardábamos | 1 |
| 44329 | tarazón | 1 |
| 44330 | taraza | 1 |
| 44331 | tarato | 1 |
| 44332 | tarascona | 1 |
| 44333 | tararear | 1 |
| 44334 | tarareando | 1 |
| 44335 | tarareaba | 1 |
| 44336 | tarantaina | 1 |
| 44337 | tarancón | 1 |
| 44338 | taraguntia | 1 |
| 44339 | tarabilla | 1 |
| 44340 | tapujo | 1 |
| 44341 | tapujito | 1 |
| 44342 | tapujas | 1 |
| 44343 | tapones | 1 |
| 44344 | tapiceros | 1 |
| 44345 | tapicería | 1 |
| 44346 | tapiasen | 1 |
| 44347 | tapiar | 1 |
| 44348 | tapetes | 1 |
| 44349 | tapetado | 1 |
| 44350 | tápese | 1 |
| 44351 | tapemos | 1 |
| 44352 | tape | 1 |
| 44353 | tapase | 1 |
| 44354 | tapas | 1 |
| 44355 | tapárselos | 1 |
| 44356 | taparrabos | 1 |
| 44357 | taparlo | 1 |
| 44358 | taparelli | 1 |
| 44359 | tapará | 1 |
| 44360 | tapaos | 1 |
| 44361 | tapándoselo | 1 |
| 44362 | tápalotodo | 1 |
| 44363 | tápala | 1 |
| 44364 | tapadita | 1 |
| 44365 | tapadillos | 1 |
| 44366 | tapadera | 1 |
| 44367 | tapábase | 1 |
| 44368 | tañen | 1 |
| 44369 | tañedores | 1 |
| 44370 | tañedor | 1 |
| 44371 | tantooo | 1 |
| 44372 | tantica | 1 |
| 44373 | tanteó | 1 |
| 44374 | tanteo | 1 |
| 44375 | tantees | 1 |
| 44376 | tanteé | 1 |
| 44377 | tantear | 1 |
| 44378 | tanteaban | 1 |
| 44379 | tanteaba | 1 |
| 44380 | tant | 1 |
| 44381 | tansilo | 1 |
| 44382 | tanía | 1 |
| 44383 | tania | 1 |
| 44384 | tangente | 1 |
| 44385 | tangan | 1 |
| 44386 | tanen | 1 |
| 44387 | tanbyén | 1 |
| 44388 | tanbyen | 1 |
| 44389 | tanbien | 1 |
| 44390 | tamorlán | 1 |
| 44391 | tamíen | 1 |
| 44392 | tamerlán | 1 |
| 44393 | tamente | 1 |
| 44394 | tamborines | 1 |
| 44395 | tamborazos | 1 |
| 44396 | tambaleábase | 1 |
| 44397 | támaras | 1 |
| 44398 | tamañitas | 1 |
| 44399 | talyón | 1 |
| 44400 | talludo | 1 |
| 44401 | talluditos | 1 |
| 44402 | talludito | 1 |
| 44403 | tallo | 1 |
| 44404 | tallas | 1 |
| 44405 | tallarla | 1 |
| 44406 | tallarín | 1 |
| 44407 | tallar | 1 |
| 44408 | tallando | 1 |
| 44409 | tallados | 1 |
| 44410 | talladas | 1 |
| 44411 | talis | 1 |
| 44412 | talia | 1 |
| 44413 | taleguito | 1 |
| 44414 | taleguillo | 1 |
| 44415 | talegazos | 1 |
| 44416 | talcualita | 1 |
| 44417 | talaveranos | 1 |
| 44418 | talas | 1 |
| 44419 | taladro | 1 |
| 44420 | taladrar | 1 |
| 44421 | taladraban | 1 |
| 44422 | taladra | 1 |
| 44423 | take | 1 |
| 44424 | tajones | 1 |
| 44425 | tajava | 1 |
| 44426 | tajar | 1 |
| 44427 | tajantes | 1 |
| 44428 | tajadores | 1 |
| 44429 | tajadora | 1 |
| 44430 | tajadicas | 1 |
| 44431 | tajadero | 1 |
| 44432 | taja | 1 |
| 44433 | taimado | 1 |
| 44434 | taigeto | 1 |
| 44435 | tahures | 1 |
| 44436 | tahúr | 1 |
| 44437 | tahonas | 1 |
| 44438 | tagarninas | 1 |
| 44439 | tagarnina | 1 |
| 44440 | tagarinos | 1 |
| 44441 | tafurerias | 1 |
| 44442 | tafurería | 1 |
| 44443 | tafiletes | 1 |
| 44444 | táctico | 1 |
| 44445 | tácticas | 1 |
| 44446 | taconeo | 1 |
| 44447 | taconeando | 1 |
| 44448 | taciturnas | 1 |
| 44449 | tácitas | 1 |
| 44450 | tachonado | 1 |
| 44451 | tachó | 1 |
| 44452 | taché | 1 |
| 44453 | tacharle | 1 |
| 44454 | tachar | 1 |
| 44455 | tachado | 1 |
| 44456 | tacendo | 1 |
| 44457 | tacaños | 1 |
| 44458 | tacaña | 1 |
| 44459 | taça | 1 |
| 44460 | taburete | 1 |
| 44461 | taborete | 1 |
| 44462 | tabor | 1 |
| 44463 | tabletas | 1 |
| 44464 | tablax | 1 |
| 44465 | tablantes | 1 |
| 44466 | tablante | 1 |
| 44467 | tablajeros | 1 |
| 44468 | tablajera | 1 |
| 44469 | tablagero | 1 |
| 44470 | tablados | 1 |
| 44471 | tabladillo | 1 |
| 44472 | tabí | 1 |
| 44473 | tabernuca | 1 |
| 44474 | tabernera | 1 |
| 44475 | tabernáculo | 1 |
| 44476 | tabarra | 1 |
| 44477 | tabarca | 1 |
| 44478 | tabaque | 1 |
| 44479 | tabacazo | 1 |
| 44480 | syrviendo | 1 |
| 44481 | syrvela | 1 |
| 44482 | synventura | 1 |
| 44483 | syntax | 1 |
| 44484 | synrazón | 1 |
| 44485 | synpleza | 1 |
| 44486 | sylvar | 1 |
| 44487 | sylva | 1 |
| 44488 | syllo | 1 |
| 44489 | syllas | 1 |
| 44490 | syguirán | 1 |
| 44491 | sygnos | 1 |
| 44492 | syete | 1 |
| 44493 | syesta | 1 |
| 44494 | syerva | 1 |
| 44495 | syerra | 1 |
| 44496 | syente | 1 |
| 44497 | syendo | 1 |
| 44498 | syenbra | 1 |
| 44499 | syempre | 1 |
| 44500 | swift | 1 |
| 44501 | suziuelo | 1 |
| 44502 | suziedades | 1 |
| 44503 | suziedad | 1 |
| 44504 | suzidad | 1 |
| 44505 | suzias | 1 |
| 44506 | suzia | 1 |
| 44507 | suviste | 1 |
| 44508 | suum | 1 |
| 44509 | sutilizaron | 1 |
| 44510 | sutilizado | 1 |
| 44511 | sutilísimo | 1 |
| 44512 | sutilísimas | 1 |
| 44513 | susurros | 1 |
| 44514 | susurrays | 1 |
| 44515 | susurraron | 1 |
| 44516 | susurrante | 1 |
| 44517 | susurrando | 1 |
| 44518 | susurra | 1 |
| 44519 | sustraérsele | 1 |
| 44520 | sustraernos | 1 |
| 44521 | sustraer | 1 |
| 44522 | sustracción | 1 |
| 44523 | sustituyeron | 1 |
| 44524 | sustituyéndoles | 1 |
| 44525 | sustituyendo | 1 |
| 44526 | sustituye | 1 |
| 44527 | sustituirla | 1 |
| 44528 | sustituiremos | 1 |
| 44529 | sustentó | 1 |
| 44530 | sustentéis | 1 |
| 44531 | sustentarlos | 1 |
| 44532 | sustentarla | 1 |
| 44533 | sustentaría | 1 |
| 44534 | sustentaran | 1 |
| 44535 | sustentará | 1 |
| 44536 | sustentara | 1 |
| 44537 | sustentándome | 1 |
| 44538 | sustentándola | 1 |
| 44539 | sustentamos | 1 |
| 44540 | sustentámonos | 1 |
| 44541 | sustentalla | 1 |
| 44542 | sustentáculo | 1 |
| 44543 | sustentación | 1 |
| 44544 | sustentábame | 1 |
| 44545 | susté | 1 |
| 44546 | sustancioso | 1 |
| 44547 | sustanciosa | 1 |
| 44548 | suspirón | 1 |
| 44549 | suspiraron | 1 |
| 44550 | suspirante | 1 |
| 44551 | suspiráis | 1 |
| 44552 | suspicacias | 1 |
| 44553 | suspensas | 1 |
| 44554 | suspendo | 1 |
| 44555 | suspendióse | 1 |
| 44556 | suspendióme | 1 |
| 44557 | suspendióles | 1 |
| 44558 | suspendiesen | 1 |
| 44559 | suspendiera | 1 |
| 44560 | suspendían | 1 |
| 44561 | suspenderme | 1 |
| 44562 | suspenderlo | 1 |
| 44563 | suspended | 1 |
| 44564 | susodichos | 1 |
| 44565 | susodicha | 1 |
| 44566 | suscritoras | 1 |
| 44567 | suscritor | 1 |
| 44568 | suscripciones | 1 |
| 44569 | suscricioncita | 1 |
| 44570 | suscribió | 1 |
| 44571 | suscitara | 1 |
| 44572 | suscitar | 1 |
| 44573 | suscitaba | 1 |
| 44574 | suscipe | 1 |
| 44575 | susceptibles | 1 |
| 44576 | suscepciones | 1 |
| 44577 | susaña | 1 |
| 44578 | surugiano | 1 |
| 44579 | surtidos | 1 |
| 44580 | surtidor | 1 |
| 44581 | surtía | 1 |
| 44582 | sursillos | 1 |
| 44583 | surgiesen | 1 |
| 44584 | surgieran | 1 |
| 44585 | surgiendo | 1 |
| 44586 | surgía | 1 |
| 44587 | sure | 1 |
| 44588 | surcaron | 1 |
| 44589 | surcando | 1 |
| 44590 | surcan | 1 |
| 44591 | surcado | 1 |
| 44592 | surcadas | 1 |
| 44593 | surcada | 1 |
| 44594 | surcaba | 1 |
| 44595 | surbicesorbi | 1 |
| 44596 | supusieron | 1 |
| 44597 | supusiera | 1 |
| 44598 | suprímomela | 1 |
| 44599 | suprimo | 1 |
| 44600 | suprimirse | 1 |
| 44601 | suprimirlo | 1 |
| 44602 | suprimiría | 1 |
| 44603 | suprimiese | 1 |
| 44604 | suprimiendo | 1 |
| 44605 | suprimidos | 1 |
| 44606 | suprimida | 1 |
| 44607 | suprimía | 1 |
| 44608 | supra | 1 |
| 44609 | supportant | 1 |
| 44610 | supplico | 1 |
| 44611 | suponiéndolo | 1 |
| 44612 | suponiéndoles | 1 |
| 44613 | suponiéndole | 1 |
| 44614 | suponiéndolas | 1 |
| 44615 | suponíanla | 1 |
| 44616 | suponíalo | 1 |
| 44617 | suponíales | 1 |
| 44618 | supóngola | 1 |
| 44619 | supóngase | 1 |
| 44620 | supones | 1 |
| 44621 | suponérseles | 1 |
| 44622 | suponérsela | 1 |
| 44623 | suponerle | 1 |
| 44624 | suponeres | 1 |
| 44625 | suponen | 1 |
| 44626 | suponemos | 1 |
| 44627 | súpome | 1 |
| 44628 | suplo | 1 |
| 44629 | suplirse | 1 |
| 44630 | suplirla | 1 |
| 44631 | supliquémosle | 1 |
| 44632 | supliquéle | 1 |
| 44633 | supliera | 1 |
| 44634 | suplido | 1 |
| 44635 | suplicóle | 1 |
| 44636 | suplicasen | 1 |
| 44637 | suplicase | 1 |
| 44638 | suplicarte | 1 |
| 44639 | suplicáronle | 1 |
| 44640 | suplicarme | 1 |
| 44641 | suplicándome | 1 |
| 44642 | suplicalle | 1 |
| 44643 | suplicad | 1 |
| 44644 | suplicaciones | 1 |
| 44645 | suplicación | 1 |
| 44646 | suplían | 1 |
| 44647 | suplementos | 1 |
| 44648 | suplementario | 1 |
| 44649 | supitos | 1 |
| 44650 | súpitas | 1 |
| 44651 | supistes | 1 |
| 44652 | supinos | 1 |
| 44653 | supinador | 1 |
| 44654 | supiesses | 1 |
| 44655 | supiésemos | 1 |
| 44656 | supieseis | 1 |
| 44657 | supiésedes | 1 |
| 44658 | supiéronlo | 1 |
| 44659 | supiérades | 1 |
| 44660 | supersticiosos | 1 |
| 44661 | superlativa | 1 |
| 44662 | superiormente | 1 |
| 44663 | superintendente | 1 |
| 44664 | supérieur | 1 |
| 44665 | superfluidad | 1 |
| 44666 | superflua | 1 |
| 44667 | superfirolíticos | 1 |
| 44668 | superfirolíticas | 1 |
| 44669 | superfino | 1 |
| 44670 | superficies | 1 |
| 44671 | superficialidades | 1 |
| 44672 | superficialidad | 1 |
| 44673 | superciliar | 1 |
| 44674 | supercherías | 1 |
| 44675 | superávit | 1 |
| 44676 | superaron | 1 |
| 44677 | superarla | 1 |
| 44678 | superan | 1 |
| 44679 | superaban | 1 |
| 44680 | supeditar | 1 |
| 44681 | supeditado | 1 |
| 44682 | supeditada | 1 |
| 44683 | suñera | 1 |
| 44684 | suntuosas | 1 |
| 44685 | suntuosa | 1 |
| 44686 | súmum | 1 |
| 44687 | súmulas | 1 |
| 44688 | sumptuosamente | 1 |
| 44689 | sumptuosa | 1 |
| 44690 | sumisos | 1 |
| 44691 | sumisiones | 1 |
| 44692 | sumirlo | 1 |
| 44693 | suministre | 1 |
| 44694 | suministrado | 1 |
| 44695 | suministrada | 1 |
| 44696 | suministraba | 1 |
| 44697 | suministra | 1 |
| 44698 | sumiese | 1 |
| 44699 | sumiéronnos | 1 |
| 44700 | sumergirla | 1 |
| 44701 | sumergió | 1 |
| 44702 | sumergieron | 1 |
| 44703 | sumergiendo | 1 |
| 44704 | sumergen | 1 |
| 44705 | sumarios | 1 |
| 44706 | sumar | 1 |
| 44707 | sumando | 1 |
| 44708 | sumados | 1 |
| 44709 | sumaban | 1 |
| 44710 | sultana | 1 |
| 44711 | sulfurosas | 1 |
| 44712 | sulfurosa | 1 |
| 44713 | sulfureos | 1 |
| 44714 | sulfure | 1 |
| 44715 | sulfurar | 1 |
| 44716 | sulfurándose | 1 |
| 44717 | sulfonal | 1 |
| 44718 | sujetose | 1 |
| 44719 | sujetarlo | 1 |
| 44720 | sujetarles | 1 |
| 44721 | sujetaré | 1 |
| 44722 | sujetaran | 1 |
| 44723 | sujetándome | 1 |
| 44724 | sujetándolas | 1 |
| 44725 | sujetando | 1 |
| 44726 | sujetan | 1 |
| 44727 | sujétale | 1 |
| 44728 | sujetáis | 1 |
| 44729 | sujetada | 1 |
| 44730 | sujecion | 1 |
| 44731 | suizos | 1 |
| 44732 | suizas | 1 |
| 44733 | suis | 1 |
| 44734 | suicidó | 1 |
| 44735 | suicido | 1 |
| 44736 | suicide | 1 |
| 44737 | suicidarnos | 1 |
| 44738 | sugiriole | 1 |
| 44739 | sugiriese | 1 |
| 44740 | sugiriera | 1 |
| 44741 | sugiere | 1 |
| 44742 | sugieran | 1 |
| 44743 | sugestionada | 1 |
| 44744 | sugerirle | 1 |
| 44745 | sugeridas | 1 |
| 44746 | sugerida | 1 |
| 44747 | sugeríanle | 1 |
| 44748 | sufrirte | 1 |
| 44749 | sufrirlos | 1 |
| 44750 | sufrirlas | 1 |
| 44751 | sufrirían | 1 |
| 44752 | sufrirás | 1 |
| 44753 | sufrio | 1 |
| 44754 | sufriese | 1 |
| 44755 | sufriere | 1 |
| 44756 | sufriera | 1 |
| 44757 | sufrían | 1 |
| 44758 | sufria | 1 |
| 44759 | sufrí | 1 |
| 44760 | sufrete | 1 |
| 44761 | sufrela | 1 |
| 44762 | sufran | 1 |
| 44763 | sufraja | 1 |
| 44764 | sufragar | 1 |
| 44765 | suetonio | 1 |
| 44766 | sueñecitos | 1 |
| 44767 | sueñecito | 1 |
| 44768 | sueñecillo | 1 |
| 44769 | sueñas | 1 |
| 44770 | suenas | 1 |
| 44771 | suéltese | 1 |
| 44772 | sueltes | 1 |
| 44773 | sueltecito | 1 |
| 44774 | suéltase | 1 |
| 44775 | suéleselos | 1 |
| 44776 | suélense | 1 |
| 44777 | suélenles | 1 |
| 44778 | sueldecillo | 1 |
| 44779 | suelan | 1 |
| 44780 | suecos | 1 |
| 44781 | sueco | 1 |
| 44782 | sué | 1 |
| 44783 | sudoroso | 1 |
| 44784 | sudava | 1 |
| 44785 | sudase | 1 |
| 44786 | sudan | 1 |
| 44787 | sudado | 1 |
| 44788 | sudadas | 1 |
| 44789 | sudada | 1 |
| 44790 | sucursal | 1 |
| 44791 | sucumbió | 1 |
| 44792 | sucumbido | 1 |
| 44793 | sucumbían | 1 |
| 44794 | sucumbe | 1 |
| 44795 | sucinta | 1 |
| 44796 | sucieder | 1 |
| 44797 | sucesivas | 1 |
| 44798 | sucesiones | 1 |
| 44799 | sucer | 1 |
| 44800 | sucedióles | 1 |
| 44801 | sucediéronse | 1 |
| 44802 | sucedieren | 1 |
| 44803 | sucedieran | 1 |
| 44804 | sucediera | 1 |
| 44805 | sucediéndose | 1 |
| 44806 | sucediéndoles | 1 |
| 44807 | sucediendo | 1 |
| 44808 | sucedida | 1 |
| 44809 | sucederse | 1 |
| 44810 | sucederán | 1 |
| 44811 | sucedáneo | 1 |
| 44812 | succedieron | 1 |
| 44813 | subyugando | 1 |
| 44814 | subyugada | 1 |
| 44815 | subversivo | 1 |
| 44816 | subversiva | 1 |
| 44817 | subvenciones | 1 |
| 44818 | suburbios | 1 |
| 44819 | subtiles | 1 |
| 44820 | subsuelo | 1 |
| 44821 | substituyéndole | 1 |
| 44822 | substituye | 1 |
| 44823 | substituyamos | 1 |
| 44824 | substituirles | 1 |
| 44825 | substituídos | 1 |
| 44826 | substituido | 1 |
| 44827 | substituía | 1 |
| 44828 | substantivo | 1 |
| 44829 | substanciosos | 1 |
| 44830 | substance | 1 |
| 44831 | subsistirán | 1 |
| 44832 | subsistirá | 1 |
| 44833 | subsistiendo | 1 |
| 44834 | subsistentes | 1 |
| 44835 | subsistencias | 1 |
| 44836 | subsiguiente | 1 |
| 44837 | subsecretarios | 1 |
| 44838 | subscripto | 1 |
| 44839 | subscripta | 1 |
| 44840 | subscripciones | 1 |
| 44841 | subscripción | 1 |
| 44842 | subscribió | 1 |
| 44843 | subscribe | 1 |
| 44844 | subrepticios | 1 |
| 44845 | subrayó | 1 |
| 44846 | subrayando | 1 |
| 44847 | subrayadas | 1 |
| 44848 | subrayaba | 1 |
| 44849 | subprefectos | 1 |
| 44850 | sublimizado | 1 |
| 44851 | sublimiza | 1 |
| 44852 | sublimarán | 1 |
| 44853 | subliman | 1 |
| 44854 | sublimación | 1 |
| 44855 | sublimaban | 1 |
| 44856 | sublimaba | 1 |
| 44857 | sublevo | 1 |
| 44858 | sublevasen | 1 |
| 44859 | sublevarse | 1 |
| 44860 | sublevaron | 1 |
| 44861 | sublevadas | 1 |
| 44862 | sublevaciones | 1 |
| 44863 | subjetos | 1 |
| 44864 | subjecto | 1 |
| 44865 | subjecion | 1 |
| 44866 | subito | 1 |
| 44867 | subirte | 1 |
| 44868 | subirlas | 1 |
| 44869 | subirla | 1 |
| 44870 | subióse | 1 |
| 44871 | subímonos | 1 |
| 44872 | subíme | 1 |
| 44873 | subieres | 1 |
| 44874 | subiéndosele | 1 |
| 44875 | subiéndome | 1 |
| 44876 | subiéndole | 1 |
| 44877 | subidos | 1 |
| 44878 | subias | 1 |
| 44879 | subi | 1 |
| 44880 | súbete | 1 |
| 44881 | súbese | 1 |
| 44882 | suberbiosa | 1 |
| 44883 | subdividirse | 1 |
| 44884 | subdividido | 1 |
| 44885 | subdividen | 1 |
| 44886 | subdivide | 1 |
| 44887 | súbdito | 1 |
| 44888 | súbdita | 1 |
| 44889 | súbante | 1 |
| 44890 | suban | 1 |
| 44891 | subalterno | 1 |
| 44892 | subalterna | 1 |
| 44893 | subáis | 1 |
| 44894 | suaviza | 1 |
| 44895 | suavitatem | 1 |
| 44896 | suavísimamente | 1 |
| 44897 | suavísima | 1 |
| 44898 | suavicen | 1 |
| 44899 | suavice | 1 |
| 44900 | süavemente | 1 |
| 44901 | suauissimo | 1 |
| 44902 | suauidad | 1 |
| 44903 | suaues | 1 |
| 44904 | suaré | 1 |
| 44905 | suadente | 1 |
| 44906 | sua | 1 |
| 44907 | stupendo | 1 |
| 44908 | stultorum | 1 |
| 44909 | stulta | 1 |
| 44910 | studio | 1 |
| 44911 | stream | 1 |
| 44912 | strauss | 1 |
| 44913 | stoa | 1 |
| 44914 | stigie | 1 |
| 44915 | stellae | 1 |
| 44916 | stage | 1 |
| 44917 | sta | 1 |
| 44918 | ssyl | 1 |
| 44919 | ssyga | 1 |
| 44920 | ssusiedad | 1 |
| 44921 | ssuerte | 1 |
| 44922 | ssoto | 1 |
| 44923 | ssotileza | 1 |
| 44924 | ssotierra | 1 |
| 44925 | ssospiros | 1 |
| 44926 | ssospecha | 1 |
| 44927 | ssoria | 1 |
| 44928 | ssopo | 1 |
| 44929 | ssonar | 1 |
| 44930 | ssoltura | 1 |
| 44931 | ssolás | 1 |
| 44932 | ssogas | 1 |
| 44933 | ssodes | 1 |
| 44934 | ssobervia | 1 |
| 44935 | ssiete | 1 |
| 44936 | ssevilla | 1 |
| 44937 | ssesos | 1 |
| 44938 | sseso | 1 |
| 44939 | sseñor | 1 |
| 44940 | ssenty | 1 |
| 44941 | ssenda | 1 |
| 44942 | ssenbré | 1 |
| 44943 | ssenbrar | 1 |
| 44944 | ssemejava | 1 |
| 44945 | sseméjasme | 1 |
| 44946 | ssellada | 1 |
| 44947 | sseguro | 1 |
| 44948 | ssegura | 1 |
| 44949 | ssegovia | 1 |
| 44950 | sseda | 1 |
| 44951 | ssecarás | 1 |
| 44952 | sseas | 1 |
| 44953 | ssávalos | 1 |
| 44954 | ssant | 1 |
| 44955 | ssangre | 1 |
| 44956 | ssangrar | 1 |
| 44957 | ssan | 1 |
| 44958 | ssalyó | 1 |
| 44959 | ssalvo | 1 |
| 44960 | ssalve | 1 |
| 44961 | ssalvar | 1 |
| 44962 | ssalió | 1 |
| 44963 | ssalga | 1 |
| 44964 | ssalen | 1 |
| 44965 | ssacóme | 1 |
| 44966 | ssácasla | 1 |
| 44967 | ssabuesos | 1 |
| 44968 | ssabría | 1 |
| 44969 | ssabores | 1 |
| 44970 | ssabios | 1 |
| 44971 | ssabido | 1 |
| 44972 | ssabedes | 1 |
| 44973 | ssabed | 1 |
| 44974 | squieleto | 1 |
| 44975 | sprit | 1 |
| 44976 | sposa | 1 |
| 44977 | splendorum | 1 |
| 44978 | spirital | 1 |
| 44979 | spínolas | 1 |
| 44980 | spero | 1 |
| 44981 | species | 1 |
| 44982 | spantalobos | 1 |
| 44983 | spanish | 1 |
| 44984 | spain | 1 |
| 44985 | sovart | 1 |
| 44986 | sousa | 1 |
| 44987 | soulié | 1 |
| 44988 | soul | 1 |
| 44989 | sotylesa | 1 |
| 44990 | sotyl | 1 |
| 44991 | sots | 1 |
| 44992 | sotove | 1 |
| 44993 | sotos | 1 |
| 44994 | sotilesa | 1 |
| 44995 | sotiéranlo | 1 |
| 44996 | soterremos | 1 |
| 44997 | soterrar | 1 |
| 44998 | soterraña | 1 |
| 44999 | soterranas | 1 |
| 45000 | soterrados | 1 |
| 45001 | soterrado | 1 |
| 45002 | soterraba | 1 |
| 45003 | soterrá | 1 |
| 45004 | sotero | 1 |
| 45005 | soterné | 1 |
| 45006 | sotecho | 1 |
| 45007 | sotaventó | 1 |
| 45008 | sotaventados | 1 |
| 45009 | sotaermitaño | 1 |
| 45010 | sostuvimos | 1 |
| 45011 | sostuviera | 1 |
| 45012 | sostuve | 1 |
| 45013 | sostuuo | 1 |
| 45014 | sostienta | 1 |
| 45015 | sosteniéndola | 1 |
| 45016 | sostenías | 1 |
| 45017 | sostengas | 1 |
| 45018 | sostenerlo | 1 |
| 45019 | sostenemos | 1 |
| 45020 | sostenéis | 1 |
| 45021 | sossiego | 1 |
| 45022 | sossegar | 1 |
| 45023 | sossegado | 1 |
| 45024 | sossegadas | 1 |
| 45025 | sospiró | 1 |
| 45026 | sospiré | 1 |
| 45027 | sospiravas | 1 |
| 45028 | sospirará | 1 |
| 45029 | sospesas | 1 |
| 45030 | sospechuela | 1 |
| 45031 | sospechen | 1 |
| 45032 | sospecharon | 1 |
| 45033 | sospecháis | 1 |
| 45034 | sospechábase | 1 |
| 45035 | sosieguen | 1 |
| 45036 | sosería | 1 |
| 45037 | soseguéis | 1 |
| 45038 | sosegases | 1 |
| 45039 | sosegasen | 1 |
| 45040 | sosegáronse | 1 |
| 45041 | sosegarle | 1 |
| 45042 | sosegándole | 1 |
| 45043 | sosegando | 1 |
| 45044 | sosegadvos | 1 |
| 45045 | sosegadilla | 1 |
| 45046 | sosas | 1 |
| 45047 | sosaños | 1 |
| 45048 | sosaño | 1 |
| 45049 | sosañar | 1 |
| 45050 | sosañada | 1 |
| 45051 | sosamente | 1 |
| 45052 | soruos | 1 |
| 45053 | sortyja | 1 |
| 45054 | sortilegios | 1 |
| 45055 | sortearlo | 1 |
| 45056 | sortearle | 1 |
| 45057 | sorteaba | 1 |
| 45058 | sortea | 1 |
| 45059 | sort | 1 |
| 45060 | sorrento | 1 |
| 45061 | sorpresita | 1 |
| 45062 | sorprendiese | 1 |
| 45063 | sorprendiera | 1 |
| 45064 | sorprendiéndola | 1 |
| 45065 | sorprendían | 1 |
| 45066 | sorprenderle | 1 |
| 45067 | sorprenderla | 1 |
| 45068 | sorprenderéis | 1 |
| 45069 | sorprenderán | 1 |
| 45070 | sorprenderá | 1 |
| 45071 | sorprendentes | 1 |
| 45072 | sorprendan | 1 |
| 45073 | sorprenda | 1 |
| 45074 | sordomudos | 1 |
| 45075 | sordomudo | 1 |
| 45076 | sórdidos | 1 |
| 45077 | sórdidas | 1 |
| 45078 | sórdida | 1 |
| 45079 | sordamente | 1 |
| 45080 | sorbióse | 1 |
| 45081 | sorbió | 1 |
| 45082 | sorbiese | 1 |
| 45083 | sorbieran | 1 |
| 45084 | sorbiendo | 1 |
| 45085 | sorbete | 1 |
| 45086 | sorberla | 1 |
| 45087 | sorber | 1 |
| 45088 | sorben | 1 |
| 45089 | sorbe | 1 |
| 45090 | soprepujando | 1 |
| 45091 | soporto | 1 |
| 45092 | soportas | 1 |
| 45093 | soportando | 1 |
| 45094 | soportan | 1 |
| 45095 | soportado | 1 |
| 45096 | soportable | 1 |
| 45097 | soportaba | 1 |
| 45098 | soporíferos | 1 |
| 45099 | soponcio | 1 |
| 45100 | sopón | 1 |
| 45101 | sópom | 1 |
| 45102 | soplillo | 1 |
| 45103 | soplarse | 1 |
| 45104 | soplao | 1 |
| 45105 | soplándole | 1 |
| 45106 | soplado | 1 |
| 45107 | sopitaña | 1 |
| 45108 | sopiesen | 1 |
| 45109 | sopiésedes | 1 |
| 45110 | sopiese | 1 |
| 45111 | sopiere | 1 |
| 45112 | sopessa | 1 |
| 45113 | sopesarlos | 1 |
| 45114 | sopesando | 1 |
| 45115 | sopesa | 1 |
| 45116 | sopelana | 1 |
| 45117 | sopalandas | 1 |
| 45118 | sop | 1 |
| 45119 | soñava | 1 |
| 45120 | soñaron | 1 |
| 45121 | soñarlo | 1 |
| 45122 | soñaremos | 1 |
| 45123 | soñaré | 1 |
| 45124 | soñamos | 1 |
| 45125 | soñados | 1 |
| 45126 | sonsoniche | 1 |
| 45127 | sonsaques | 1 |
| 45128 | sonsacarles | 1 |
| 45129 | sonsacar | 1 |
| 45130 | sonsaca | 1 |
| 45131 | sonrosados | 1 |
| 45132 | sonrojos | 1 |
| 45133 | sonrojaba | 1 |
| 45134 | sonrisillas | 1 |
| 45135 | sonriose | 1 |
| 45136 | sonríes | 1 |
| 45137 | sonriéndome | 1 |
| 45138 | sonriéndoles | 1 |
| 45139 | sonríeme | 1 |
| 45140 | sonríasele | 1 |
| 45141 | sonreyendo | 1 |
| 45142 | sonreírse | 1 |
| 45143 | sonreíme | 1 |
| 45144 | sonoridad | 1 |
| 45145 | sono | 1 |
| 45146 | sonetuelo | 1 |
| 45147 | sonete | 1 |
| 45148 | sonelo | 1 |
| 45149 | sondéela | 1 |
| 45150 | sondearle | 1 |
| 45151 | sondeado | 1 |
| 45152 | sondeaba | 1 |
| 45153 | sondaje | 1 |
| 45154 | sonbriella | 1 |
| 45155 | sonbrero | 1 |
| 45156 | sonauas | 1 |
| 45157 | sonasen | 1 |
| 45158 | sonarme | 1 |
| 45159 | sonarían | 1 |
| 45160 | sonará | 1 |
| 45161 | sonándose | 1 |
| 45162 | sonándola | 1 |
| 45163 | sonámbulos | 1 |
| 45164 | sonambulismo | 1 |
| 45165 | sonajero | 1 |
| 45166 | sonajear | 1 |
| 45167 | sonador | 1 |
| 45168 | sonable | 1 |
| 45169 | són | 1 |
| 45170 | sompesóla | 1 |
| 45171 | somovióla | 1 |
| 45172 | somovimientos | 1 |
| 45173 | somosierra | 1 |
| 45174 | somióse | 1 |
| 45175 | somieda | 1 |
| 45176 | somidas | 1 |
| 45177 | sometiera | 1 |
| 45178 | sometiéndose | 1 |
| 45179 | sometiéndolo | 1 |
| 45180 | sometidos | 1 |
| 45181 | sometidas | 1 |
| 45182 | sometían | 1 |
| 45183 | sometes | 1 |
| 45184 | someterte | 1 |
| 45185 | someterlas | 1 |
| 45186 | someten | 1 |
| 45187 | someta | 1 |
| 45188 | someras | 1 |
| 45189 | somera | 1 |
| 45190 | sombrillazo | 1 |
| 45191 | sombríamente | 1 |
| 45192 | sombrerote | 1 |
| 45193 | sombreritos | 1 |
| 45194 | sombrerete | 1 |
| 45195 | sombrereros | 1 |
| 45196 | sombrerera | 1 |
| 45197 | sombreo | 1 |
| 45198 | sombreada | 1 |
| 45199 | soma | 1 |
| 45200 | solyan | 1 |
| 45201 | solventar | 1 |
| 45202 | solus | 1 |
| 45203 | soluciones | 1 |
| 45204 | soltole | 1 |
| 45205 | soltola | 1 |
| 45206 | solterones | 1 |
| 45207 | solterona | 1 |
| 45208 | soltería | 1 |
| 45209 | soltasen | 1 |
| 45210 | soltarte | 1 |
| 45211 | soltáronle | 1 |
| 45212 | soltarlos | 1 |
| 45213 | soltarles | 1 |
| 45214 | soltarían | 1 |
| 45215 | soltándole | 1 |
| 45216 | soltándola | 1 |
| 45217 | soltalde | 1 |
| 45218 | soltados | 1 |
| 45219 | soltada | 1 |
| 45220 | solsticios | 1 |
| 45221 | solórzana | 1 |
| 45222 | soló | 1 |
| 45223 | sollozó | 1 |
| 45224 | sollozante | 1 |
| 45225 | sollao | 1 |
| 45226 | sollados | 1 |
| 45227 | soliviantados | 1 |
| 45228 | soliviantada | 1 |
| 45229 | solitos | 1 |
| 45230 | sólito | 1 |
| 45231 | solitas | 1 |
| 45232 | solisdán | 1 |
| 45233 | solís | 1 |
| 45234 | sólidum | 1 |
| 45235 | solidificación | 1 |
| 45236 | solidificaba | 1 |
| 45237 | solidifica | 1 |
| 45238 | solideo | 1 |
| 45239 | solidaria | 1 |
| 45240 | solicitos | 1 |
| 45241 | soliciten | 1 |
| 45242 | solicitaste | 1 |
| 45243 | solícitas | 1 |
| 45244 | solicitas | 1 |
| 45245 | solicitaron | 1 |
| 45246 | solicitarle | 1 |
| 45247 | solicitares | 1 |
| 45248 | solicitaré | 1 |
| 45249 | solicitara | 1 |
| 45250 | solicitando | 1 |
| 45251 | solicitallo | 1 |
| 45252 | solicitalla | 1 |
| 45253 | solicitados | 1 |
| 45254 | solicitación | 1 |
| 45255 | solías | 1 |
| 45256 | soliadisa | 1 |
| 45257 | solíades | 1 |
| 45258 | solfeó | 1 |
| 45259 | solfeen | 1 |
| 45260 | solfas | 1 |
| 45261 | soleys | 1 |
| 45262 | soletas | 1 |
| 45263 | soleta | 1 |
| 45264 | soler | 1 |
| 45265 | solenniza | 1 |
| 45266 | solenizarle | 1 |
| 45267 | solenizalle | 1 |
| 45268 | solenizados | 1 |
| 45269 | solenizadas | 1 |
| 45270 | solenizaban | 1 |
| 45271 | solenísimas | 1 |
| 45272 | solenidat | 1 |
| 45273 | solene | 1 |
| 45274 | solemnizase | 1 |
| 45275 | solemnice | 1 |
| 45276 | soleado | 1 |
| 45277 | soldevilla | 1 |
| 45278 | soldase | 1 |
| 45279 | soldarse | 1 |
| 45280 | soldarla | 1 |
| 45281 | soldaremos | 1 |
| 45282 | soldara | 1 |
| 45283 | soldadico | 1 |
| 45284 | solazasen | 1 |
| 45285 | solazaron | 1 |
| 45286 | solazándose | 1 |
| 45287 | solasar | 1 |
| 45288 | solariega | 1 |
| 45289 | solapar | 1 |
| 45290 | solapados | 1 |
| 45291 | solapadas | 1 |
| 45292 | solapadamente | 1 |
| 45293 | solano | 1 |
| 45294 | solamiente | 1 |
| 45295 | sojuzgaste | 1 |
| 45296 | sojuzgado | 1 |
| 45297 | sojuzgadas | 1 |
| 45298 | sojorno | 1 |
| 45299 | soit | 1 |
| 45300 | sogazos | 1 |
| 45301 | sofrite | 1 |
| 45302 | sofrirte | 1 |
| 45303 | sofrirse | 1 |
| 45304 | sofrirle | 1 |
| 45305 | sofrillas | 1 |
| 45306 | sofrido | 1 |
| 45307 | soforas | 1 |
| 45308 | sofocones | 1 |
| 45309 | sofocase | 1 |
| 45310 | sofocarse | 1 |
| 45311 | sofocaciones | 1 |
| 45312 | sofisticos | 1 |
| 45313 | sofístico | 1 |
| 45314 | sofistica | 1 |
| 45315 | sofistería | 1 |
| 45316 | sofiones | 1 |
| 45317 | soficiente | 1 |
| 45318 | soffrir | 1 |
| 45319 | sofás | 1 |
| 45320 | sodoma | 1 |
| 45321 | socrates | 1 |
| 45322 | socorrito | 1 |
| 45323 | socorriome | 1 |
| 45324 | socorrieran | 1 |
| 45325 | socorridas | 1 |
| 45326 | socorrías | 1 |
| 45327 | socorres | 1 |
| 45328 | socorreros | 1 |
| 45329 | socorrerles | 1 |
| 45330 | socorrería | 1 |
| 45331 | socorreremos | 1 |
| 45332 | socorrerá | 1 |
| 45333 | socorren | 1 |
| 45334 | socorrelle | 1 |
| 45335 | socorrella | 1 |
| 45336 | socorredor | 1 |
| 45337 | socorran | 1 |
| 45338 | socórrale | 1 |
| 45339 | société | 1 |
| 45340 | socias | 1 |
| 45341 | sociable | 1 |
| 45342 | socia | 1 |
| 45343 | sochantres | 1 |
| 45344 | sochantre | 1 |
| 45345 | socavados | 1 |
| 45346 | socavación | 1 |
| 45347 | socavaban | 1 |
| 45348 | socarronas | 1 |
| 45349 | socaliñado | 1 |
| 45350 | sobyr | 1 |
| 45351 | sobrón | 1 |
| 45352 | sobrios | 1 |
| 45353 | sobrinitas | 1 |
| 45354 | sobria | 1 |
| 45355 | sobrevivirían | 1 |
| 45356 | sobrevivirá | 1 |
| 45357 | sobrevivir | 1 |
| 45358 | sobrevivido | 1 |
| 45359 | sobrevista | 1 |
| 45360 | sobrevirgos | 1 |
| 45361 | sobrevinieron | 1 |
| 45362 | sobrevienta | 1 |
| 45363 | sobreviene | 1 |
| 45364 | sobrevenirle | 1 |
| 45365 | sobrevenía | 1 |
| 45366 | sobreuino | 1 |
| 45367 | sobrestante | 1 |
| 45368 | sobresolados | 1 |
| 45369 | sobresaltes | 1 |
| 45370 | sobresaltase | 1 |
| 45371 | sobresaltarse | 1 |
| 45372 | sobresaltarme | 1 |
| 45373 | sobresaltar | 1 |
| 45374 | sobresalieron | 1 |
| 45375 | sobresalientemente | 1 |
| 45376 | sobresaliendo | 1 |
| 45377 | sobresalen | 1 |
| 45378 | sobrerropa | 1 |
| 45379 | sobrepuso | 1 |
| 45380 | sobrepujó | 1 |
| 45381 | sobrepujaron | 1 |
| 45382 | sobrepujar | 1 |
| 45383 | sobrepujaban | 1 |
| 45384 | sobrepuestos | 1 |
| 45385 | sobreponiéndose | 1 |
| 45386 | sobreponía | 1 |
| 45387 | sobrepones | 1 |
| 45388 | sobrepondrás | 1 |
| 45389 | sobrepellices | 1 |
| 45390 | sobreparto | 1 |
| 45391 | sobrenadó | 1 |
| 45392 | sobrelleve | 1 |
| 45393 | sobrellevaban | 1 |
| 45394 | sobrehumanos | 1 |
| 45395 | sobrehumano | 1 |
| 45396 | sobreescribidla | 1 |
| 45397 | sobredorada | 1 |
| 45398 | sobrecogió | 1 |
| 45399 | sobrecogiéronla | 1 |
| 45400 | sobrecogida | 1 |
| 45401 | sobrecogían | 1 |
| 45402 | sobrecogería | 1 |
| 45403 | sobrecoge | 1 |
| 45404 | sobreçejas | 1 |
| 45405 | sobrecargar | 1 |
| 45406 | sobrecargado | 1 |
| 45407 | sobrecarga | 1 |
| 45408 | sobrebarbero | 1 |
| 45409 | sobraua | 1 |
| 45410 | sobrase | 1 |
| 45411 | sobraria | 1 |
| 45412 | sobrare | 1 |
| 45413 | sobrara | 1 |
| 45414 | sobradamente | 1 |
| 45415 | sobraban | 1 |
| 45416 | sobr | 1 |
| 45417 | sobornos | 1 |
| 45418 | sobornó | 1 |
| 45419 | sobornar | 1 |
| 45420 | soboncita | 1 |
| 45421 | sobiese | 1 |
| 45422 | sobieron | 1 |
| 45423 | sobida | 1 |
| 45424 | sobi | 1 |
| 45425 | soberviosa | 1 |
| 45426 | sobervios | 1 |
| 45427 | sobervientas | 1 |
| 45428 | sobervi | 1 |
| 45429 | soberuia | 1 |
| 45430 | soberuezcas | 1 |
| 45431 | soberbias | 1 |
| 45432 | sobejos | 1 |
| 45433 | sobejas | 1 |
| 45434 | sobándolas | 1 |
| 45435 | sobacos | 1 |
| 45436 | sobaba | 1 |
| 45437 | smith | 1 |
| 45438 | sketches | 1 |
| 45439 | sixto | 1 |
| 45440 | situados | 1 |
| 45441 | situadas | 1 |
| 45442 | sitiando | 1 |
| 45443 | sitiaba | 1 |
| 45444 | sita | 1 |
| 45445 | sit | 1 |
| 45446 | sístole | 1 |
| 45447 | sistematizar | 1 |
| 45448 | sisonas | 1 |
| 45449 | sisenta | 1 |
| 45450 | sisara | 1 |
| 45451 | sisando | 1 |
| 45452 | sisado | 1 |
| 45453 | sisada | 1 |
| 45454 | sisabas | 1 |
| 45455 | sisábamos | 1 |
| 45456 | sírvole | 1 |
| 45457 | sirviríe | 1 |
| 45458 | sirviéremos | 1 |
| 45459 | sirviere | 1 |
| 45460 | sirvieran | 1 |
| 45461 | sirvienta | 1 |
| 45462 | sirviéndose | 1 |
| 45463 | sirviéndola | 1 |
| 45464 | sirvi | 1 |
| 45465 | sírvate | 1 |
| 45466 | sírvase | 1 |
| 45467 | sírvale | 1 |
| 45468 | siruienta | 1 |
| 45469 | siruas | 1 |
| 45470 | siruamos | 1 |
| 45471 | sirio | 1 |
| 45472 | siríaca | 1 |
| 45473 | siria | 1 |
| 45474 | siquera | 1 |
| 45475 | siñor | 1 |
| 45476 | sinvergüenzones | 1 |
| 45477 | sinvergüenzonaza | 1 |
| 45478 | sinvergüenzonas | 1 |
| 45479 | sinvergonzonazos | 1 |
| 45480 | sinuoso | 1 |
| 45481 | sinuosa | 1 |
| 45482 | sintióse | 1 |
| 45483 | sintióme | 1 |
| 45484 | sintiole | 1 |
| 45485 | sintiesses | 1 |
| 45486 | sintiessen | 1 |
| 45487 | sintiessedes | 1 |
| 45488 | sintiesse | 1 |
| 45489 | sintiéronse | 1 |
| 45490 | sintieras | 1 |
| 45491 | sintieran | 1 |
| 45492 | sintiéndonos | 1 |
| 45493 | sintiéndolo | 1 |
| 45494 | sintetizó | 1 |
| 45495 | sintetizarse | 1 |
| 45496 | sintetizaremos | 1 |
| 45497 | sintetizan | 1 |
| 45498 | sintético | 1 |
| 45499 | sintaxis | 1 |
| 45500 | sintáctica | 1 |
| 45501 | sinsabor | 1 |
| 45502 | sinrazon | 1 |
| 45503 | sinpre | 1 |
| 45504 | sinples | 1 |
| 45505 | sinple | 1 |
| 45506 | sínople | 1 |
| 45507 | sinónimos | 1 |
| 45508 | sinón | 1 |
| 45509 | sinodales | 1 |
| 45510 | sinjusticia | 1 |
| 45511 | sinificativo | 1 |
| 45512 | sinificancia | 1 |
| 45513 | siniestras | 1 |
| 45514 | singula | 1 |
| 45515 | sinforoso | 1 |
| 45516 | sinfonías | 1 |
| 45517 | sinfinidá | 1 |
| 45518 | sinfín | 1 |
| 45519 | sindicado | 1 |
| 45520 | sincopieses | 1 |
| 45521 | sincopiés | 1 |
| 45522 | síncopes | 1 |
| 45523 | síncopas | 1 |
| 45524 | sincopan | 1 |
| 45525 | sinceridades | 1 |
| 45526 | sincerarse | 1 |
| 45527 | sinabafas | 1 |
| 45528 | simultánea | 1 |
| 45529 | simular | 1 |
| 45530 | simulacros | 1 |
| 45531 | simulaba | 1 |
| 45532 | simpson | 1 |
| 45533 | simplota | 1 |
| 45534 | simplona | 1 |
| 45535 | simplín | 1 |
| 45536 | simplicitas | 1 |
| 45537 | simplicísimo | 1 |
| 45538 | simplicio | 1 |
| 45539 | simplezico | 1 |
| 45540 | simpatizase | 1 |
| 45541 | simpatizado | 1 |
| 45542 | simpáticamente | 1 |
| 45543 | simonías | 1 |
| 45544 | simones | 1 |
| 45545 | similares | 1 |
| 45546 | simétricas | 1 |
| 45547 | simetis | 1 |
| 45548 | simeón | 1 |
| 45549 | simbolismos | 1 |
| 45550 | simbolismo | 1 |
| 45551 | simbólica | 1 |
| 45552 | simancas | 1 |
| 45553 | silvoso | 1 |
| 45554 | silvó | 1 |
| 45555 | silvio | 1 |
| 45556 | silvias | 1 |
| 45557 | silvato | 1 |
| 45558 | silvas | 1 |
| 45559 | silvanos | 1 |
| 45560 | siluo | 1 |
| 45561 | silo | 1 |
| 45562 | silletazo | 1 |
| 45563 | silinçio | 1 |
| 45564 | silicios | 1 |
| 45565 | silicato | 1 |
| 45566 | silguero | 1 |
| 45567 | silfos | 1 |
| 45568 | silfidones | 1 |
| 45569 | silfidona | 1 |
| 45570 | silere | 1 |
| 45571 | silencios | 1 |
| 45572 | silbaría | 1 |
| 45573 | silbaré | 1 |
| 45574 | silbándoles | 1 |
| 45575 | silbándole | 1 |
| 45576 | silbamos | 1 |
| 45577 | silbados | 1 |
| 45578 | silbado | 1 |
| 45579 | silabeo | 1 |
| 45580 | sila | 1 |
| 45581 | siguole | 1 |
| 45582 | sigunda | 1 |
| 45583 | siguiose | 1 |
| 45584 | siguiólas | 1 |
| 45585 | siguióla | 1 |
| 45586 | siguimiento | 1 |
| 45587 | siguiéndome | 1 |
| 45588 | siguia | 1 |
| 45589 | siguez | 1 |
| 45590 | siguese | 1 |
| 45591 | síguelos | 1 |
| 45592 | síguele | 1 |
| 45593 | sigts | 1 |
| 45594 | sígote | 1 |
| 45595 | signis | 1 |
| 45596 | significó | 1 |
| 45597 | significativos | 1 |
| 45598 | significativas | 1 |
| 45599 | significase | 1 |
| 45600 | significarme | 1 |
| 45601 | significarle | 1 |
| 45602 | significaría | 1 |
| 45603 | significáis | 1 |
| 45604 | significada | 1 |
| 45605 | signatarios | 1 |
| 45606 | sigiloso | 1 |
| 45607 | sígate | 1 |
| 45608 | siganos | 1 |
| 45609 | sigámosla | 1 |
| 45610 | sigáis | 1 |
| 45611 | sietemesinos | 1 |
| 45612 | sietecientas | 1 |
| 45613 | síes | 1 |
| 45614 | siervas | 1 |
| 45615 | sieruas | 1 |
| 45616 | sierua | 1 |
| 45617 | siéntase | 1 |
| 45618 | siéntanse | 1 |
| 45619 | sienpr | 1 |
| 45620 | siéndote | 1 |
| 45621 | siéndoles | 1 |
| 45622 | siembra | 1 |
| 45623 | siego | 1 |
| 45624 | siegan | 1 |
| 45625 | sieben | 1 |
| 45626 | sidrería | 1 |
| 45627 | sidonio | 1 |
| 45628 | sidón | 1 |
| 45629 | sicilïano | 1 |
| 45630 | sicilianas | 1 |
| 45631 | siciliana | 1 |
| 45632 | sicario | 1 |
| 45633 | sicana | 1 |
| 45634 | sibias | 1 |
| 45635 | sian | 1 |
| 45636 | sharraren | 1 |
| 45637 | shangai | 1 |
| 45638 | seyme | 1 |
| 45639 | sexagenario | 1 |
| 45640 | sevillanos | 1 |
| 45641 | sevillana | 1 |
| 45642 | sevigné | 1 |
| 45643 | sevicia | 1 |
| 45644 | severísimos | 1 |
| 45645 | severísimamente | 1 |
| 45646 | severísima | 1 |
| 45647 | severidades | 1 |
| 45648 | severiano | 1 |
| 45649 | seuilla | 1 |
| 45650 | seueridad | 1 |
| 45651 | seudo | 1 |
| 45652 | setoain | 1 |
| 45653 | sétimo | 1 |
| 45654 | setimo | 1 |
| 45655 | set | 1 |
| 45656 | sesudamente | 1 |
| 45657 | sesteando | 1 |
| 45658 | sesostris | 1 |
| 45659 | sesito | 1 |
| 45660 | sesgando | 1 |
| 45661 | sesgaba | 1 |
| 45662 | sesera | 1 |
| 45663 | sesentona | 1 |
| 45664 | servos | 1 |
| 45665 | servivos | 1 |
| 45666 | servirt | 1 |
| 45667 | servíos | 1 |
| 45668 | serviola | 1 |
| 45669 | servió | 1 |
| 45670 | servímosle | 1 |
| 45671 | servilón | 1 |
| 45672 | servilmente | 1 |
| 45673 | servilletero | 1 |
| 45674 | servillas | 1 |
| 45675 | servíle | 1 |
| 45676 | serviera | 1 |
| 45677 | servientes | 1 |
| 45678 | servíe | 1 |
| 45679 | servidumbres | 1 |
| 45680 | servídose | 1 |
| 45681 | servidorísimos | 1 |
| 45682 | servidas | 1 |
| 45683 | serviçios | 1 |
| 45684 | servibles | 1 |
| 45685 | servíanos | 1 |
| 45686 | servíanle | 1 |
| 45687 | servian | 1 |
| 45688 | servíamos | 1 |
| 45689 | serviam | 1 |
| 45690 | servíalas | 1 |
| 45691 | serven | 1 |
| 45692 | seruis | 1 |
| 45693 | seruiremos | 1 |
| 45694 | seruientes | 1 |
| 45695 | seruidora | 1 |
| 45696 | seruias | 1 |
| 45697 | seruia | 1 |
| 45698 | sert | 1 |
| 45699 | serrezuela | 1 |
| 45700 | serranilla | 1 |
| 45701 | serpentones | 1 |
| 45702 | serpentine | 1 |
| 45703 | serpentear | 1 |
| 45704 | serpenteaba | 1 |
| 45705 | serpentea | 1 |
| 45706 | serpeando | 1 |
| 45707 | serpeaba | 1 |
| 45708 | serpea | 1 |
| 45709 | serosa | 1 |
| 45710 | seros | 1 |
| 45711 | sermoneo | 1 |
| 45712 | sermonearla | 1 |
| 45713 | sermonearé | 1 |
| 45714 | sermoneaba | 1 |
| 45715 | sermoncito | 1 |
| 45716 | sermoncillos | 1 |
| 45717 | sermoncillo | 1 |
| 45718 | sermoncico | 1 |
| 45719 | sermonazo | 1 |
| 45720 | sermonarias | 1 |
| 45721 | sermon | 1 |
| 45722 | serles | 1 |
| 45723 | series | 1 |
| 45724 | seríale | 1 |
| 45725 | seríades | 1 |
| 45726 | seriades | 1 |
| 45727 | sergas | 1 |
| 45728 | sereys | 1 |
| 45729 | sereta | 1 |
| 45730 | serenissimo | 1 |
| 45731 | serenissima | 1 |
| 45732 | serenísima | 1 |
| 45733 | serénese | 1 |
| 45734 | serené | 1 |
| 45735 | serene | 1 |
| 45736 | serénate | 1 |
| 45737 | serenatas | 1 |
| 45738 | serenata | 1 |
| 45739 | serenase | 1 |
| 45740 | serenaron | 1 |
| 45741 | serenarás | 1 |
| 45742 | serenara | 1 |
| 45743 | serenar | 1 |
| 45744 | serenaba | 1 |
| 45745 | serba | 1 |
| 45746 | serafinita | 1 |
| 45747 | seráficas | 1 |
| 45748 | sequuntur | 1 |
| 45749 | sequedades | 1 |
| 45750 | seque | 1 |
| 45751 | sepulturero | 1 |
| 45752 | sepultarse | 1 |
| 45753 | sepultarnos | 1 |
| 45754 | sepultarlas | 1 |
| 45755 | septeno | 1 |
| 45756 | sepolcro | 1 |
| 45757 | sepárese | 1 |
| 45758 | separé | 1 |
| 45759 | separasen | 1 |
| 45760 | separase | 1 |
| 45761 | separáronse | 1 |
| 45762 | separarlo | 1 |
| 45763 | separarlas | 1 |
| 45764 | separarla | 1 |
| 45765 | separaría | 1 |
| 45766 | separarás | 1 |
| 45767 | separamos | 1 |
| 45768 | separadamente | 1 |
| 45769 | separábanse | 1 |
| 45770 | separábais | 1 |
| 45771 | sépanlo | 1 |
| 45772 | sepámoslo | 1 |
| 45773 | seoto | 1 |
| 45774 | séos | 1 |
| 45775 | señorones | 1 |
| 45776 | señoriticas | 1 |
| 45777 | señorísimas | 1 |
| 45778 | señoriles | 1 |
| 45779 | señorete | 1 |
| 45780 | señoreándole | 1 |
| 45781 | señoreaba | 1 |
| 45782 | señorea | 1 |
| 45783 | señorazos | 1 |
| 45784 | señoa | 1 |
| 45785 | señeros | 1 |
| 45786 | señeras | 1 |
| 45787 | señera | 1 |
| 45788 | señalóse | 1 |
| 45789 | señalole | 1 |
| 45790 | señálensele | 1 |
| 45791 | señalémosle | 1 |
| 45792 | señalas | 1 |
| 45793 | señalarse | 1 |
| 45794 | señaláronme | 1 |
| 45795 | señaláronle | 1 |
| 45796 | señalarle | 1 |
| 45797 | señalaré | 1 |
| 45798 | señalaran | 1 |
| 45799 | señalándote | 1 |
| 45800 | señalándose | 1 |
| 45801 | señaladísima | 1 |
| 45802 | señalábanse | 1 |
| 45803 | senzilla | 1 |
| 45804 | sentirlos | 1 |
| 45805 | sentiríades | 1 |
| 45806 | sentiriades | 1 |
| 45807 | sentiria | 1 |
| 45808 | sentirás | 1 |
| 45809 | sentirán | 1 |
| 45810 | sentiran | 1 |
| 45811 | sentirá | 1 |
| 45812 | sentira | 1 |
| 45813 | sentinas | 1 |
| 45814 | sentillo | 1 |
| 45815 | sentibles | 1 |
| 45816 | sentías | 1 |
| 45817 | sentíamos | 1 |
| 45818 | sentíame | 1 |
| 45819 | sentíala | 1 |
| 45820 | sentenciosos | 1 |
| 45821 | sentencioso | 1 |
| 45822 | sentenciosamente | 1 |
| 45823 | sentenciosa | 1 |
| 45824 | sentenció | 1 |
| 45825 | sentenciéla | 1 |
| 45826 | sentenciáronme | 1 |
| 45827 | sentenciaron | 1 |
| 45828 | sentencian | 1 |
| 45829 | sentenciador | 1 |
| 45830 | sentarte | 1 |
| 45831 | sentarle | 1 |
| 45832 | sentaremos | 1 |
| 45833 | sentareme | 1 |
| 45834 | sentaré | 1 |
| 45835 | sentaran | 1 |
| 45836 | sentao | 1 |
| 45837 | sentándosele | 1 |
| 45838 | sentaditos | 1 |
| 45839 | sentad | 1 |
| 45840 | sentábanse | 1 |
| 45841 | sentábamos | 1 |
| 45842 | sentábame | 1 |
| 45843 | sensyllas | 1 |
| 45844 | sensualista | 1 |
| 45845 | sensualismo | 1 |
| 45846 | sensualidad | 1 |
| 45847 | sensu | 1 |
| 45848 | sensitivo | 1 |
| 45849 | sensitiva | 1 |
| 45850 | sensiblerías | 1 |
| 45851 | sensiblería | 1 |
| 45852 | sensiblemente | 1 |
| 45853 | sensatamente | 1 |
| 45854 | senetú | 1 |
| 45855 | sendebar | 1 |
| 45856 | sencillísimo | 1 |
| 45857 | sencillísima | 1 |
| 45858 | senbrar | 1 |
| 45859 | senbrada | 1 |
| 45860 | senaleja | 1 |
| 45861 | senalan | 1 |
| 45862 | sempiterno | 1 |
| 45863 | sempiternas | 1 |
| 45864 | sempiterna | 1 |
| 45865 | semítica | 1 |
| 45866 | semiramis | 1 |
| 45867 | semioscura | 1 |
| 45868 | semínimas | 1 |
| 45869 | semine | 1 |
| 45870 | semillero | 1 |
| 45871 | semidoncellas | 1 |
| 45872 | semicírculo | 1 |
| 45873 | semicientífico | 1 |
| 45874 | semicapro | 1 |
| 45875 | semiaristocracia | 1 |
| 45876 | semestres | 1 |
| 45877 | semeje | 1 |
| 45878 | semejava | 1 |
| 45879 | semejassen | 1 |
| 45880 | semejará | 1 |
| 45881 | semejança | 1 |
| 45882 | semejable | 1 |
| 45883 | semejábades | 1 |
| 45884 | seme | 1 |
| 45885 | sembradas | 1 |
| 45886 | sembrad | 1 |
| 45887 | semanita | 1 |
| 45888 | semá | 1 |
| 45889 | selvicultura | 1 |
| 45890 | selvatoquez | 1 |
| 45891 | selvática | 1 |
| 45892 | sélo | 1 |
| 45893 | selmana | 1 |
| 45894 | selle | 1 |
| 45895 | sellaron | 1 |
| 45896 | sellaría | 1 |
| 45897 | sellaíto | 1 |
| 45898 | sellados | 1 |
| 45899 | selladas | 1 |
| 45900 | sellad | 1 |
| 45901 | selimo | 1 |
| 45902 | selim | 1 |
| 45903 | selectos | 1 |
| 45904 | selección | 1 |
| 45905 | séle | 1 |
| 45906 | seiscientas | 1 |
| 45907 | seidor | 1 |
| 45908 | seiás | 1 |
| 45909 | segurar | 1 |
| 45910 | seguramiente | 1 |
| 45911 | segundara | 1 |
| 45912 | seguirte | 1 |
| 45913 | seguirían | 1 |
| 45914 | seguiríamos | 1 |
| 45915 | seguirela | 1 |
| 45916 | seguiréis | 1 |
| 45917 | seguira | 1 |
| 45918 | seguío | 1 |
| 45919 | seguimientos | 1 |
| 45920 | seguíle | 1 |
| 45921 | seguíla | 1 |
| 45922 | seguiéremos | 1 |
| 45923 | seguiente | 1 |
| 45924 | seguiendol | 1 |
| 45925 | seguidores | 1 |
| 45926 | seguidor | 1 |
| 45927 | seguidlos | 1 |
| 45928 | seguidla | 1 |
| 45929 | seguidamente | 1 |
| 45930 | seguíamos | 1 |
| 45931 | seguíales | 1 |
| 45932 | seguíala | 1 |
| 45933 | seguia | 1 |
| 45934 | segovianos | 1 |
| 45935 | segmento | 1 |
| 45936 | segidor | 1 |
| 45937 | segida | 1 |
| 45938 | segava | 1 |
| 45939 | segarme | 1 |
| 45940 | segándole | 1 |
| 45941 | segando | 1 |
| 45942 | segados | 1 |
| 45943 | segadora | 1 |
| 45944 | segador | 1 |
| 45945 | segadas | 1 |
| 45946 | segaban | 1 |
| 45947 | seduzco | 1 |
| 45948 | sedúzcanmela | 1 |
| 45949 | sedujo | 1 |
| 45950 | sedujeran | 1 |
| 45951 | seducírselo | 1 |
| 45952 | seducirla | 1 |
| 45953 | seduciré | 1 |
| 45954 | seduciendo | 1 |
| 45955 | seducidas | 1 |
| 45956 | sedoso | 1 |
| 45957 | sedimentos | 1 |
| 45958 | sedimento | 1 |
| 45959 | sedimentado | 1 |
| 45960 | sedientos | 1 |
| 45961 | sedientas | 1 |
| 45962 | sediciosos | 1 |
| 45963 | sedición | 1 |
| 45964 | sedeño | 1 |
| 45965 | sedentarismo | 1 |
| 45966 | sedentario | 1 |
| 45967 | sedante | 1 |
| 45968 | sedanes | 1 |
| 45969 | sedán | 1 |
| 45970 | secutoria | 1 |
| 45971 | secundase | 1 |
| 45972 | secundarias | 1 |
| 45973 | secundaria | 1 |
| 45974 | secundar | 1 |
| 45975 | secundan | 1 |
| 45976 | secundaba | 1 |
| 45977 | secum | 1 |
| 45978 | secularizándose | 1 |
| 45979 | secularización | 1 |
| 45980 | secuestrarlo | 1 |
| 45981 | secuestramos | 1 |
| 45982 | secuestradoras | 1 |
| 45983 | secuestrado | 1 |
| 45984 | secuestradas | 1 |
| 45985 | secuentia | 1 |
| 45986 | secuelas | 1 |
| 45987 | secuela | 1 |
| 45988 | secretito | 1 |
| 45989 | secreteos | 1 |
| 45990 | secreteó | 1 |
| 45991 | secretearse | 1 |
| 45992 | secreteara | 1 |
| 45993 | secretarios | 1 |
| 45994 | secchi | 1 |
| 45995 | secarte | 1 |
| 45996 | secarse | 1 |
| 45997 | secáronse | 1 |
| 45998 | secarme | 1 |
| 45999 | secarlo | 1 |
| 46000 | secarle | 1 |
| 46001 | sécanse | 1 |
| 46002 | secaderos | 1 |
| 46003 | sebosa | 1 |
| 46004 | sebastopol | 1 |
| 46005 | séavos | 1 |
| 46006 | séale | 1 |
| 46007 | scriptores | 1 |
| 46008 | scripserunt | 1 |
| 46009 | screuir | 1 |
| 46010 | scolares | 1 |
| 46011 | scitas | 1 |
| 46012 | scirroso | 1 |
| 46013 | scilas | 1 |
| 46014 | schopenhauer | 1 |
| 46015 | schiller | 1 |
| 46016 | schevill | 1 |
| 46017 | sc | 1 |
| 46018 | sazones | 1 |
| 46019 | sazonarla | 1 |
| 46020 | sazonados | 1 |
| 46021 | sayos | 1 |
| 46022 | sayete | 1 |
| 46023 | sayazo | 1 |
| 46024 | sayagués | 1 |
| 46025 | say | 1 |
| 46026 | sauses | 1 |
| 46027 | saurios | 1 |
| 46028 | saudades | 1 |
| 46029 | saúcos | 1 |
| 46030 | sauco | 1 |
| 46031 | satysfaçión | 1 |
| 46032 | saturninos | 1 |
| 46033 | saturnillo | 1 |
| 46034 | saturnales | 1 |
| 46035 | saturatio | 1 |
| 46036 | saturadas | 1 |
| 46037 | saturación | 1 |
| 46038 | satisficieron | 1 |
| 46039 | satisficiera | 1 |
| 46040 | satisfaze | 1 |
| 46041 | satisfaría | 1 |
| 46042 | satisfare | 1 |
| 46043 | satisfarás | 1 |
| 46044 | satisfagan | 1 |
| 46045 | satisfagáis | 1 |
| 46046 | satisfaciones | 1 |
| 46047 | satisfaçión | 1 |
| 46048 | satisfaciendo | 1 |
| 46049 | satisfacíamos | 1 |
| 46050 | satisfaces | 1 |
| 46051 | satisfacerlo | 1 |
| 46052 | satisfacerlas | 1 |
| 46053 | satisfacelle | 1 |
| 46054 | satisfacéis | 1 |
| 46055 | satíricas | 1 |
| 46056 | satinado | 1 |
| 46057 | satenes | 1 |
| 46058 | satélites | 1 |
| 46059 | satélite | 1 |
| 46060 | sastrerías | 1 |
| 46061 | sastrería | 1 |
| 46062 | sasón | 1 |
| 46063 | sas | 1 |
| 46064 | sarten | 1 |
| 46065 | sarraceno | 1 |
| 46066 | sarnosos | 1 |
| 46067 | sarnosa | 1 |
| 46068 | sarmiento | 1 |
| 46069 | sargentua | 1 |
| 46070 | sargentos | 1 |
| 46071 | sardou | 1 |
| 46072 | sardónica | 1 |
| 46073 | sardiniya | 1 |
| 46074 | sardesco | 1 |
| 46075 | sarcástico | 1 |
| 46076 | sara | 1 |
| 46077 | saquitos | 1 |
| 46078 | saqueo | 1 |
| 46079 | saquemos | 1 |
| 46080 | saquéle | 1 |
| 46081 | saqueen | 1 |
| 46082 | saquearon | 1 |
| 46083 | sapientísimas | 1 |
| 46084 | sapientísima | 1 |
| 46085 | sapientiæ | 1 |
| 46086 | sapiençia | 1 |
| 46087 | sapho | 1 |
| 46088 | sañudamente | 1 |
| 46089 | sañoso | 1 |
| 46090 | sañosa | 1 |
| 46091 | sanzio | 1 |
| 46092 | santurrón | 1 |
| 46093 | santuarios | 1 |
| 46094 | santu | 1 |
| 46095 | santona | 1 |
| 46096 | santolalla | 1 |
| 46097 | santisma | 1 |
| 46098 | santiscario | 1 |
| 46099 | santina | 1 |
| 46100 | santimperie | 1 |
| 46101 | santillana | 1 |
| 46102 | santillán | 1 |
| 46103 | santiguávame | 1 |
| 46104 | santiguáronse | 1 |
| 46105 | santiguarnos | 1 |
| 46106 | santiguando | 1 |
| 46107 | santiguamos | 1 |
| 46108 | santiguaduras | 1 |
| 46109 | santiguado | 1 |
| 46110 | santigua | 1 |
| 46111 | santiga | 1 |
| 46112 | santifiquísimas | 1 |
| 46113 | santificarnos | 1 |
| 46114 | santificar | 1 |
| 46115 | santificante | 1 |
| 46116 | santero | 1 |
| 46117 | santeras | 1 |
| 46118 | santarén | 1 |
| 46119 | santángel | 1 |
| 46120 | santander | 1 |
| 46121 | sanssón | 1 |
| 46122 | sansonino | 1 |
| 46123 | sanson | 1 |
| 46124 | sansol | 1 |
| 46125 | sansimoniano | 1 |
| 46126 | sanitarismo | 1 |
| 46127 | sanitario | 1 |
| 46128 | sanidat | 1 |
| 46129 | sangustiado | 1 |
| 46130 | sanguis | 1 |
| 46131 | sanguinosas | 1 |
| 46132 | sanguinolento | 1 |
| 46133 | sanguinario | 1 |
| 46134 | sangrientamente | 1 |
| 46135 | sangres | 1 |
| 46136 | sangren | 1 |
| 46137 | sangrarse | 1 |
| 46138 | sangraran | 1 |
| 46139 | sangrar | 1 |
| 46140 | sangran | 1 |
| 46141 | sangraban | 1 |
| 46142 | sangraba | 1 |
| 46143 | sangr | 1 |
| 46144 | sanes | 1 |
| 46145 | sanen | 1 |
| 46146 | sanear | 1 |
| 46147 | saneando | 1 |
| 46148 | saneamiento | 1 |
| 46149 | saneaba | 1 |
| 46150 | sandunga | 1 |
| 46151 | sandalio | 1 |
| 46152 | sandalias | 1 |
| 46153 | sanctus | 1 |
| 46154 | sanctorum | 1 |
| 46155 | sancti | 1 |
| 46156 | sanctas | 1 |
| 46157 | sancristán | 1 |
| 46158 | sancionaría | 1 |
| 46159 | sancionadora | 1 |
| 46160 | sanción | 1 |
| 46161 | sanchuelo | 1 |
| 46162 | sanchico | 1 |
| 46163 | sanazaro | 1 |
| 46164 | sanaua | 1 |
| 46165 | sanarte | 1 |
| 46166 | sanarlo | 1 |
| 46167 | sanarlas | 1 |
| 46168 | sanaría | 1 |
| 46169 | sanaremos | 1 |
| 46170 | sanarás | 1 |
| 46171 | sanamos | 1 |
| 46172 | samuel | 1 |
| 46173 | samnita | 1 |
| 46174 | sambenito | 1 |
| 46175 | salyrá | 1 |
| 46176 | salyda | 1 |
| 46177 | salvóse | 1 |
| 46178 | salvoconducto | 1 |
| 46179 | salvilla | 1 |
| 46180 | salvedad | 1 |
| 46181 | salvava | 1 |
| 46182 | salvatucó | 1 |
| 46183 | sálvaslo | 1 |
| 46184 | salvarías | 1 |
| 46185 | salvaremos | 1 |
| 46186 | salvaréis | 1 |
| 46187 | salvaré | 1 |
| 46188 | salvarás | 1 |
| 46189 | sálvanos | 1 |
| 46190 | salvamiento | 1 |
| 46191 | salvamano | 1 |
| 46192 | salvajito | 1 |
| 46193 | salvajita | 1 |
| 46194 | salvajina | 1 |
| 46195 | salvajadas | 1 |
| 46196 | salvaguardia | 1 |
| 46197 | salvadoras | 1 |
| 46198 | salvada | 1 |
| 46199 | salvaba | 1 |
| 46200 | salutaciones | 1 |
| 46201 | salutación | 1 |
| 46202 | salutacion | 1 |
| 46203 | salustio | 1 |
| 46204 | salus | 1 |
| 46205 | saludóme | 1 |
| 46206 | saludolos | 1 |
| 46207 | saludóles | 1 |
| 46208 | saludóle | 1 |
| 46209 | saludéle | 1 |
| 46210 | salúdele | 1 |
| 46211 | salúdavos | 1 |
| 46212 | saludava | 1 |
| 46213 | saludarte | 1 |
| 46214 | saludarse | 1 |
| 46215 | saludáronle | 1 |
| 46216 | saludarme | 1 |
| 46217 | saludaran | 1 |
| 46218 | saludándome | 1 |
| 46219 | saludándolos | 1 |
| 46220 | saludándole | 1 |
| 46221 | saludame | 1 |
| 46222 | saludalle | 1 |
| 46223 | saludadores | 1 |
| 46224 | saludador | 1 |
| 46225 | saludada | 1 |
| 46226 | saludábamos | 1 |
| 46227 | saluar | 1 |
| 46228 | saluaje | 1 |
| 46229 | saluados | 1 |
| 46230 | saltonas | 1 |
| 46231 | saltón | 1 |
| 46232 | salteóm | 1 |
| 46233 | salten | 1 |
| 46234 | saltemos | 1 |
| 46235 | saltee | 1 |
| 46236 | salteasen | 1 |
| 46237 | saltearlos | 1 |
| 46238 | salteándosele | 1 |
| 46239 | salteándole | 1 |
| 46240 | saltea | 1 |
| 46241 | saltas | 1 |
| 46242 | saltarlo | 1 |
| 46243 | saltarla | 1 |
| 46244 | saltarines | 1 |
| 46245 | saltaran | 1 |
| 46246 | saltará | 1 |
| 46247 | saltaparedes | 1 |
| 46248 | saltándosele | 1 |
| 46249 | saltándola | 1 |
| 46250 | saltamontes | 1 |
| 46251 | saltados | 1 |
| 46252 | saltá | 1 |
| 46253 | salpreso | 1 |
| 46254 | salpresas | 1 |
| 46255 | salpresa | 1 |
| 46256 | salpimentar | 1 |
| 46257 | salpicó | 1 |
| 46258 | salpicaron | 1 |
| 46259 | salpicando | 1 |
| 46260 | salomónicas | 1 |
| 46261 | salmuera | 1 |
| 46262 | salmos | 1 |
| 46263 | salmorejo | 1 |
| 46264 | salmo | 1 |
| 46265 | salmistas | 1 |
| 46266 | salmanticenses | 1 |
| 46267 | salmanca | 1 |
| 46268 | salivita | 1 |
| 46269 | salivazo | 1 |
| 46270 | salistes | 1 |
| 46271 | salístele | 1 |
| 46272 | salírsele | 1 |
| 46273 | salirle | 1 |
| 46274 | salirá | 1 |
| 46275 | saliónos | 1 |
| 46276 | salióle | 1 |
| 46277 | salime | 1 |
| 46278 | saliessen | 1 |
| 46279 | salieses | 1 |
| 46280 | saliésemos | 1 |
| 46281 | saliéronle | 1 |
| 46282 | salieres | 1 |
| 46283 | saliéredes | 1 |
| 46284 | saliente | 1 |
| 46285 | saliéndome | 1 |
| 46286 | salie | 1 |
| 46287 | saliditas | 1 |
| 46288 | salidad | 1 |
| 46289 | salíase | 1 |
| 46290 | salías | 1 |
| 46291 | salias | 1 |
| 46292 | salian | 1 |
| 46293 | saliamos | 1 |
| 46294 | salíale | 1 |
| 46295 | salia | 1 |
| 46296 | sali | 1 |
| 46297 | sálgome | 1 |
| 46298 | salgome | 1 |
| 46299 | sálgase | 1 |
| 46300 | salgámosles | 1 |
| 46301 | salgámonos | 1 |
| 46302 | sálese | 1 |
| 46303 | saleroso | 1 |
| 46304 | salenle | 1 |
| 46305 | saledizos | 1 |
| 46306 | saldréis | 1 |
| 46307 | saldra | 1 |
| 46308 | saldos | 1 |
| 46309 | saldar | 1 |
| 46310 | saldan | 1 |
| 46311 | saldados | 1 |
| 46312 | saldaba | 1 |
| 46313 | salchichas | 1 |
| 46314 | salazar | 1 |
| 46315 | salaremos | 1 |
| 46316 | salar | 1 |
| 46317 | salamo | 1 |
| 46318 | salamanquesa | 1 |
| 46319 | salamandria | 1 |
| 46320 | salamandras | 1 |
| 46321 | salamandra | 1 |
| 46322 | saladísimo | 1 |
| 46323 | sajones | 1 |
| 46324 | sajonas | 1 |
| 46325 | sajona | 1 |
| 46326 | sahumerios | 1 |
| 46327 | sahuméme | 1 |
| 46328 | sahagún | 1 |
| 46329 | sagude | 1 |
| 46330 | saguda | 1 |
| 46331 | sagriado | 1 |
| 46332 | sagrarios | 1 |
| 46333 | sagital | 1 |
| 46334 | sagacísimo | 1 |
| 46335 | safo | 1 |
| 46336 | saetilla | 1 |
| 46337 | saetazos | 1 |
| 46338 | saet | 1 |
| 46339 | sacudo | 1 |
| 46340 | sacudirme | 1 |
| 46341 | sacudirles | 1 |
| 46342 | sacudirlas | 1 |
| 46343 | sacudiré | 1 |
| 46344 | sacudimos | 1 |
| 46345 | sacudíme | 1 |
| 46346 | sacudieron | 1 |
| 46347 | sacudieran | 1 |
| 46348 | sacudiéndoles | 1 |
| 46349 | sacudí | 1 |
| 46350 | sacuda | 1 |
| 46351 | sacrosanto | 1 |
| 46352 | sacros | 1 |
| 46353 | sacristanía | 1 |
| 46354 | sacristanejo | 1 |
| 46355 | sacristando | 1 |
| 46356 | sacristana | 1 |
| 46357 | sacristan | 1 |
| 46358 | sacrilegos | 1 |
| 46359 | sacrilega | 1 |
| 46360 | sacrifíquese | 1 |
| 46361 | sacrifique | 1 |
| 46362 | sacrifico | 1 |
| 46363 | sacrificase | 1 |
| 46364 | sacrificarnos | 1 |
| 46365 | sacrificaría | 1 |
| 46366 | sacrificando | 1 |
| 46367 | sacrifican | 1 |
| 46368 | sacrificadores | 1 |
| 46369 | sacrefiçios | 1 |
| 46370 | sacras | 1 |
| 46371 | sacramentales | 1 |
| 46372 | sacóme | 1 |
| 46373 | sacólos | 1 |
| 46374 | sacol | 1 |
| 46375 | sacógelo | 1 |
| 46376 | sacias | 1 |
| 46377 | saciarse | 1 |
| 46378 | saciadas | 1 |
| 46379 | sacerdotisas | 1 |
| 46380 | sacerdotales | 1 |
| 46381 | saçerdotal | 1 |
| 46382 | sacatrapos | 1 |
| 46383 | sacástelo | 1 |
| 46384 | sacasse | 1 |
| 46385 | sacasla | 1 |
| 46386 | sacársele | 1 |
| 46387 | sacáronle | 1 |
| 46388 | sacáronla | 1 |
| 46389 | sacármela | 1 |
| 46390 | sacaria | 1 |
| 46391 | sacares | 1 |
| 46392 | sacaréis | 1 |
| 46393 | sacáredes | 1 |
| 46394 | sacaredes | 1 |
| 46395 | sacáramos | 1 |
| 46396 | sacapotras | 1 |
| 46397 | sacao | 1 |
| 46398 | sácanos | 1 |
| 46399 | sacándomele | 1 |
| 46400 | sacándomela | 1 |
| 46401 | sacándome | 1 |
| 46402 | sácalos | 1 |
| 46403 | sacallos | 1 |
| 46404 | sacallas | 1 |
| 46405 | sacáis | 1 |
| 46406 | sacádoos | 1 |
| 46407 | sacádole | 1 |
| 46408 | sacabuches | 1 |
| 46409 | sacabuche | 1 |
| 46410 | sacabó | 1 |
| 46411 | sacábanlos | 1 |
| 46412 | sacábala | 1 |
| 46413 | sabyendas | 1 |
| 46414 | sabyençia | 1 |
| 46415 | sabyduría | 1 |
| 46416 | sabydores | 1 |
| 46417 | sabusté | 1 |
| 46418 | sabuesos | 1 |
| 46419 | sabueso | 1 |
| 46420 | sabríame | 1 |
| 46421 | sabríais | 1 |
| 46422 | sabréisme | 1 |
| 46423 | sabráslo | 1 |
| 46424 | sabran | 1 |
| 46425 | saboyanas | 1 |
| 46426 | saboyana | 1 |
| 46427 | saboya | 1 |
| 46428 | saboreó | 1 |
| 46429 | saboréate | 1 |
| 46430 | saborearon | 1 |
| 46431 | saboreándose | 1 |
| 46432 | saboreadas | 1 |
| 46433 | saboreaban | 1 |
| 46434 | saborado | 1 |
| 46435 | sabihondos | 1 |
| 46436 | sabihonda | 1 |
| 46437 | sabier | 1 |
| 46438 | sabiente | 1 |
| 46439 | sabiençia | 1 |
| 46440 | sabíen | 1 |
| 46441 | sabíe | 1 |
| 46442 | sabie | 1 |
| 46443 | sabíanlo | 1 |
| 46444 | sabialo | 1 |
| 46445 | sabete | 1 |
| 46446 | sabeslas | 1 |
| 46447 | sábese | 1 |
| 46448 | sabernos | 1 |
| 46449 | sábenlas | 1 |
| 46450 | sabençia | 1 |
| 46451 | sabello | 1 |
| 46452 | sabella | 1 |
| 46453 | sábelas | 1 |
| 46454 | sabeees | 1 |
| 46455 | sabedoras | 1 |
| 46456 | sabçe | 1 |
| 46457 | sabañón | 1 |
| 46458 | sabanas | 1 |
| 46459 | sabado | 1 |
| 46460 | ryos | 1 |
| 46461 | ryome | 1 |
| 46462 | ryncón | 1 |
| 46463 | ryma | 1 |
| 46464 | rye | 1 |
| 46465 | ryco | 1 |
| 46466 | ryca | 1 |
| 46467 | ruyz | 1 |
| 46468 | ruyseñores | 1 |
| 46469 | ruysenores | 1 |
| 46470 | ruynmente | 1 |
| 46471 | ruynes | 1 |
| 46472 | ruyndades | 1 |
| 46473 | ruuios | 1 |
| 46474 | ruuia | 1 |
| 46475 | rutilio | 1 |
| 46476 | rutilantes | 1 |
| 46477 | rusticación | 1 |
| 46478 | rusos | 1 |
| 46479 | rus | 1 |
| 46480 | rural | 1 |
| 46481 | rura | 1 |
| 46482 | rupertito | 1 |
| 46483 | runrún | 1 |
| 46484 | rumpantes | 1 |
| 46485 | rumorosa | 1 |
| 46486 | rumiase | 1 |
| 46487 | rumiarlas | 1 |
| 46488 | rumiara | 1 |
| 46489 | rumiantes | 1 |
| 46490 | rumiaban | 1 |
| 46491 | rumiaba | 1 |
| 46492 | rumbeles | 1 |
| 46493 | ruleta | 1 |
| 46494 | ruinosas | 1 |
| 46495 | ruinmente | 1 |
| 46496 | ruïdos | 1 |
| 46497 | rüído | 1 |
| 46498 | ruído | 1 |
| 46499 | ruidito | 1 |
| 46500 | ruidillo | 1 |
| 46501 | rugosas | 1 |
| 46502 | rugosa | 1 |
| 46503 | rugiente | 1 |
| 46504 | rugel | 1 |
| 46505 | rugas | 1 |
| 46506 | rufo | 1 |
| 46507 | rueguen | 1 |
| 46508 | ruégole | 1 |
| 46509 | ruegas | 1 |
| 46510 | ruegal | 1 |
| 46511 | ruedita | 1 |
| 46512 | ruede | 1 |
| 46513 | ruecas | 1 |
| 46514 | rudimentarios | 1 |
| 46515 | rudimentario | 1 |
| 46516 | rudimentaria | 1 |
| 46517 | rudesinda | 1 |
| 46518 | rudentes | 1 |
| 46519 | rucutucua | 1 |
| 46520 | ruciarse | 1 |
| 46521 | rubricas | 1 |
| 46522 | rubrica | 1 |
| 46523 | ruborizadas | 1 |
| 46524 | rubores | 1 |
| 46525 | rubita | 1 |
| 46526 | rubís | 1 |
| 46527 | rubines | 1 |
| 46528 | rubies | 1 |
| 46529 | rubicundos | 1 |
| 46530 | rubicundo | 1 |
| 46531 | rubicón | 1 |
| 46532 | ruana | 1 |
| 46533 | rrysueña | 1 |
| 46534 | rruysynor | 1 |
| 46535 | rruydo | 1 |
| 46536 | rruybarvo | 1 |
| 46537 | rrumiar | 1 |
| 46538 | rruégovos | 1 |
| 46539 | rruegos | 1 |
| 46540 | rruéganle | 1 |
| 46541 | rruegan | 1 |
| 46542 | rruegal | 1 |
| 46543 | rrudos | 1 |
| 46544 | rrudeza | 1 |
| 46545 | rruçío | 1 |
| 46546 | rrúçio | 1 |
| 46547 | rruby | 1 |
| 46548 | rroysyñor | 1 |
| 46549 | rroydos | 1 |
| 46550 | rroto | 1 |
| 46551 | rrotas | 1 |
| 46552 | rrota | 1 |
| 46553 | rrostros | 1 |
| 46554 | rrosata | 1 |
| 46555 | rrosario | 1 |
| 46556 | rrondón | 1 |
| 46557 | rronda | 1 |
| 46558 | rronçesvalles | 1 |
| 46559 | rromero | 1 |
| 46560 | rromerías | 1 |
| 46561 | rromería | 1 |
| 46562 | rromanze | 1 |
| 46563 | rroldán | 1 |
| 46564 | rrogueste | 1 |
| 46565 | rrogó | 1 |
| 46566 | rrogele | 1 |
| 46567 | rrogela | 1 |
| 46568 | rrogarle | 1 |
| 46569 | rrogándote | 1 |
| 46570 | rrogamos | 1 |
| 46571 | rroer | 1 |
| 46572 | rroe | 1 |
| 46573 | rrodillas | 1 |
| 46574 | rrodilla | 1 |
| 46575 | rrodesno | 1 |
| 46576 | rrodas | 1 |
| 46577 | rrodando | 1 |
| 46578 | rroby | 1 |
| 46579 | rrobos | 1 |
| 46580 | rroble | 1 |
| 46581 | rrobas | 1 |
| 46582 | rroban | 1 |
| 46583 | rrixo | 1 |
| 46584 | rrisetes | 1 |
| 46585 | rriquesas | 1 |
| 46586 | rriplicaçiones | 1 |
| 46587 | rriofrío | 1 |
| 46588 | rrientes | 1 |
| 46589 | rríen | 1 |
| 46590 | rriega | 1 |
| 46591 | rricamente | 1 |
| 46592 | rribaldo | 1 |
| 46593 | rreyres | 1 |
| 46594 | rreyerien | 1 |
| 46595 | rreyendo | 1 |
| 46596 | rreye | 1 |
| 46597 | rrevolviendo | 1 |
| 46598 | rrevierta | 1 |
| 46599 | rreveses | 1 |
| 46600 | rrevatado | 1 |
| 46601 | rretuvo | 1 |
| 46602 | rretrayda | 1 |
| 46603 | rretraya | 1 |
| 46604 | rretraes | 1 |
| 46605 | rretraer | 1 |
| 46606 | rretorno | 1 |
| 46607 | rretoçando | 1 |
| 46608 | rretientas | 1 |
| 46609 | rreteñir | 1 |
| 46610 | rretentóle | 1 |
| 46611 | rretentar | 1 |
| 46612 | rretenientes | 1 |
| 46613 | rretaço | 1 |
| 46614 | rrestrojos | 1 |
| 46615 | rresses | 1 |
| 46616 | rrespuestas | 1 |
| 46617 | rrespondióme | 1 |
| 46618 | rrespondile | 1 |
| 46619 | rrespondieron | 1 |
| 46620 | rrespondiera | 1 |
| 46621 | rresponderán | 1 |
| 46622 | rresponden | 1 |
| 46623 | rresponde | 1 |
| 46624 | rrespondades | 1 |
| 46625 | rresplandesçería | 1 |
| 46626 | rresplandesçer | 1 |
| 46627 | rresio | 1 |
| 46628 | rreses | 1 |
| 46629 | rresellosa | 1 |
| 46630 | rresçibo | 1 |
| 46631 | rresçibióme | 1 |
| 46632 | rresçibiéronle | 1 |
| 46633 | rresçibieron | 1 |
| 46634 | rresçibidas | 1 |
| 46635 | rresçibida | 1 |
| 46636 | rresçibían | 1 |
| 46637 | rresçibe | 1 |
| 46638 | rresçélome | 1 |
| 46639 | rresçelades | 1 |
| 46640 | rresçebyr | 1 |
| 46641 | rresçebirlos | 1 |
| 46642 | rresçebirle | 1 |
| 46643 | rresçebiól | 1 |
| 46644 | rresçebidas | 1 |
| 46645 | rresaron | 1 |
| 46646 | rresaré | 1 |
| 46647 | rrequerida | 1 |
| 46648 | rrequena | 1 |
| 46649 | rrepuntan | 1 |
| 46650 | rrepunta | 1 |
| 46651 | rrepuesto | 1 |
| 46652 | rrepuesta | 1 |
| 46653 | rrepto | 1 |
| 46654 | rreportorio | 1 |
| 46655 | rrepiso | 1 |
| 46656 | rrepiente | 1 |
| 46657 | rrepetido | 1 |
| 46658 | rrepeso | 1 |
| 46659 | rrepara | 1 |
| 46660 | rreñidor | 1 |
| 46661 | rreñid | 1 |
| 46662 | rrenuevo | 1 |
| 46663 | rrenta | 1 |
| 46664 | rrensyllas | 1 |
| 46665 | rrensilla | 1 |
| 46666 | rrensellosa | 1 |
| 46667 | rrenir | 1 |
| 46668 | rrencor | 1 |
| 46669 | rrençilla | 1 |
| 46670 | rremira | 1 |
| 46671 | rremesçe | 1 |
| 46672 | rremendar | 1 |
| 46673 | rremenbrança | 1 |
| 46674 | rrematar | 1 |
| 46675 | rrematan | 1 |
| 46676 | rremaneçiste | 1 |
| 46677 | rrelusíe | 1 |
| 46678 | rrelijosas | 1 |
| 46679 | rreligioso | 1 |
| 46680 | rreligiosas | 1 |
| 46681 | rreligiosa | 1 |
| 46682 | rrehiertas | 1 |
| 46683 | rrehertero | 1 |
| 46684 | rrehertado | 1 |
| 46685 | rrehazer | 1 |
| 46686 | rrehallas | 1 |
| 46687 | rreguardava | 1 |
| 46688 | rreguarda | 1 |
| 46689 | rregno | 1 |
| 46690 | rregnando | 1 |
| 46691 | rregistro | 1 |
| 46692 | rregava | 1 |
| 46693 | rregateras | 1 |
| 46694 | rregañada | 1 |
| 46695 | rregaço | 1 |
| 46696 | rrefusando | 1 |
| 46697 | rrefitorios | 1 |
| 46698 | rrefitor | 1 |
| 46699 | rrefierto | 1 |
| 46700 | rrefezes | 1 |
| 46701 | rrefés | 1 |
| 46702 | rreferteras | 1 |
| 46703 | rrefaze | 1 |
| 46704 | rrefases | 1 |
| 46705 | rredréme | 1 |
| 46706 | rredrado | 1 |
| 46707 | rredrada | 1 |
| 46708 | rredondos | 1 |
| 46709 | rredondo | 1 |
| 46710 | rredero | 1 |
| 46711 | rrecudyr | 1 |
| 46712 | rrecudas | 1 |
| 46713 | rrecuda | 1 |
| 46714 | rrecreçer | 1 |
| 46715 | rreconvençión | 1 |
| 46716 | rrecíbenle | 1 |
| 46717 | rrecelose | 1 |
| 46718 | rreçeledes | 1 |
| 46719 | rreçelan | 1 |
| 46720 | rrecaudo | 1 |
| 46721 | rreçando | 1 |
| 46722 | rrecado | 1 |
| 46723 | rrecabo | 1 |
| 46724 | rrecabdos | 1 |
| 46725 | rrecabdo | 1 |
| 46726 | rrecabdeste | 1 |
| 46727 | rrecabdava | 1 |
| 46728 | rrecabdan | 1 |
| 46729 | rrecabdamos | 1 |
| 46730 | rrecabado | 1 |
| 46731 | rrecaba | 1 |
| 46732 | rrebuznar | 1 |
| 46733 | rrebuélveslo | 1 |
| 46734 | rrebtedes | 1 |
| 46735 | rrebtado | 1 |
| 46736 | rrebolvedor | 1 |
| 46737 | rrebevió | 1 |
| 46738 | rrebató | 1 |
| 46739 | rrebatado | 1 |
| 46740 | rrebatadas | 1 |
| 46741 | rreales | 1 |
| 46742 | rreal | 1 |
| 46743 | rrazonó | 1 |
| 46744 | rrazones | 1 |
| 46745 | rrays | 1 |
| 46746 | rrayo | 1 |
| 46747 | rraviosa | 1 |
| 46748 | rraviará | 1 |
| 46749 | rratiello | 1 |
| 46750 | rrastrojo | 1 |
| 46751 | rrastro | 1 |
| 46752 | rrasonaron | 1 |
| 46753 | rrasonar | 1 |
| 46754 | rrason | 1 |
| 46755 | rrasgaredes | 1 |
| 46756 | rrascan | 1 |
| 46757 | rrasa | 1 |
| 46758 | rraposya | 1 |
| 46759 | rraposo | 1 |
| 46760 | rraposilla | 1 |
| 46761 | rrapáz | 1 |
| 46762 | rrapás | 1 |
| 46763 | rrando | 1 |
| 46764 | rralas | 1 |
| 46765 | rrahez | 1 |
| 46766 | rrafezes | 1 |
| 46767 | rradío | 1 |
| 46768 | rradía | 1 |
| 46769 | rraçiones | 1 |
| 46770 | rrachonas | 1 |
| 46771 | rracho | 1 |
| 46772 | rraça | 1 |
| 46773 | rraby | 1 |
| 46774 | rrabíes | 1 |
| 46775 | rrabí | 1 |
| 46776 | rozzo | 1 |
| 46777 | rozó | 1 |
| 46778 | roznar | 1 |
| 46779 | rozase | 1 |
| 46780 | rozas | 1 |
| 46781 | rozarte | 1 |
| 46782 | rozarse | 1 |
| 46783 | rozarnos | 1 |
| 46784 | rozando | 1 |
| 46785 | rozan | 1 |
| 46786 | rozamiento | 1 |
| 46787 | rozadura | 1 |
| 46788 | rozados | 1 |
| 46789 | rozado | 1 |
| 46790 | rozada | 1 |
| 46791 | rozaba | 1 |
| 46792 | royesen | 1 |
| 46793 | royéndose | 1 |
| 46794 | royéndome | 1 |
| 46795 | royéndolo | 1 |
| 46796 | roy | 1 |
| 46797 | rout | 1 |
| 46798 | rotundo | 1 |
| 46799 | rotundamente | 1 |
| 46800 | rotonda | 1 |
| 46801 | rotin | 1 |
| 46802 | rothschild | 1 |
| 46803 | roten | 1 |
| 46804 | rotación | 1 |
| 46805 | rostriquemados | 1 |
| 46806 | rostchild | 1 |
| 46807 | rossiniano | 1 |
| 46808 | rospeni | 1 |
| 46809 | roses | 1 |
| 46810 | rosendo | 1 |
| 46811 | roscas | 1 |
| 46812 | rosaura | 1 |
| 46813 | rosarita | 1 |
| 46814 | rosarillo | 1 |
| 46815 | rosariazo | 1 |
| 46816 | rosados | 1 |
| 46817 | ros | 1 |
| 46818 | rorrooó | 1 |
| 46819 | rorro | 1 |
| 46820 | roquetes | 1 |
| 46821 | roquetas | 1 |
| 46822 | roques | 1 |
| 46823 | roquero | 1 |
| 46824 | roquefort | 1 |
| 46825 | ropones | 1 |
| 46826 | ropería | 1 |
| 46827 | ropavejeros | 1 |
| 46828 | ropavejero | 1 |
| 46829 | roñosas | 1 |
| 46830 | roña | 1 |
| 46831 | ronzalillo | 1 |
| 46832 | ronzalesco | 1 |
| 46833 | ronzalesca | 1 |
| 46834 | ronquilla | 1 |
| 46835 | ronquido | 1 |
| 46836 | ronquera | 1 |
| 46837 | rondo | 1 |
| 46838 | rondilla | 1 |
| 46839 | rondeños | 1 |
| 46840 | rondemos | 1 |
| 46841 | rondara | 1 |
| 46842 | rondadores | 1 |
| 46843 | rondábanos | 1 |
| 46844 | rondábamos | 1 |
| 46845 | ronchas | 1 |
| 46846 | roncha | 1 |
| 46847 | ronces | 1 |
| 46848 | roncante | 1 |
| 46849 | roncaban | 1 |
| 46850 | romulo | 1 |
| 46851 | rompiose | 1 |
| 46852 | rompiéndomela | 1 |
| 46853 | rompiéndome | 1 |
| 46854 | rompiéndolos | 1 |
| 46855 | rompidos | 1 |
| 46856 | rompido | 1 |
| 46857 | rompidas | 1 |
| 46858 | rompíanse | 1 |
| 46859 | rómpete | 1 |
| 46860 | rómpese | 1 |
| 46861 | romperte | 1 |
| 46862 | romperme | 1 |
| 46863 | romperlos | 1 |
| 46864 | romperlas | 1 |
| 46865 | rompenecios | 1 |
| 46866 | rompemos | 1 |
| 46867 | rómpeme | 1 |
| 46868 | rompelle | 1 |
| 46869 | rompelanzas | 1 |
| 46870 | rompecabezas | 1 |
| 46871 | rómpaselas | 1 |
| 46872 | rompan | 1 |
| 46873 | rompamos | 1 |
| 46874 | romos | 1 |
| 46875 | romolinos | 1 |
| 46876 | romeros | 1 |
| 46877 | romea | 1 |
| 46878 | rombos | 1 |
| 46879 | romboides | 1 |
| 46880 | rombo | 1 |
| 46881 | romas | 1 |
| 46882 | romanzas | 1 |
| 46883 | romanus | 1 |
| 46884 | romantismo | 1 |
| 46885 | romanische | 1 |
| 46886 | románicos | 1 |
| 46887 | románica | 1 |
| 46888 | romancito | 1 |
| 46889 | romancesco | 1 |
| 46890 | romancesca | 1 |
| 46891 | romanceros | 1 |
| 46892 | romançe | 1 |
| 46893 | roman | 1 |
| 46894 | romadizado | 1 |
| 46895 | rollizos | 1 |
| 46896 | roldanes | 1 |
| 46897 | roldanejo | 1 |
| 46898 | rojizas | 1 |
| 46899 | rojiza | 1 |
| 46900 | rohan | 1 |
| 46901 | roguéla | 1 |
| 46902 | rogue | 1 |
| 46903 | rogóme | 1 |
| 46904 | rogome | 1 |
| 46905 | rogo | 1 |
| 46906 | roger | 1 |
| 46907 | rogavan | 1 |
| 46908 | rogava | 1 |
| 46909 | rogauan | 1 |
| 46910 | rogárselo | 1 |
| 46911 | rogaros | 1 |
| 46912 | rogarían | 1 |
| 46913 | rogaremos | 1 |
| 46914 | rogarán | 1 |
| 46915 | rogarále | 1 |
| 46916 | rogándonos | 1 |
| 46917 | rogándome | 1 |
| 46918 | rogandome | 1 |
| 46919 | rogándoles | 1 |
| 46920 | rogáis | 1 |
| 46921 | rogadores | 1 |
| 46922 | rogaciones | 1 |
| 46923 | rogaban | 1 |
| 46924 | rogábamos | 1 |
| 46925 | roerá | 1 |
| 46926 | roelas | 1 |
| 46927 | roedor | 1 |
| 46928 | roed | 1 |
| 46929 | rodriguito | 1 |
| 46930 | rodré | 1 |
| 46931 | rodillazos | 1 |
| 46932 | rodil | 1 |
| 46933 | rodeóme | 1 |
| 46934 | rodeen | 1 |
| 46935 | rodeemos | 1 |
| 46936 | rodéele | 1 |
| 46937 | rodeé | 1 |
| 46938 | rodeasen | 1 |
| 46939 | rodearte | 1 |
| 46940 | rodearemos | 1 |
| 46941 | rodéanle | 1 |
| 46942 | rodeamos | 1 |
| 46943 | rodeámonos | 1 |
| 46944 | rodeábanse | 1 |
| 46945 | rodarían | 1 |
| 46946 | rodara | 1 |
| 46947 | rodamontes | 1 |
| 46948 | rodamonte | 1 |
| 46949 | rodaja | 1 |
| 46950 | rodadas | 1 |
| 46951 | rococó | 1 |
| 46952 | rocíe | 1 |
| 46953 | rociarias | 1 |
| 46954 | rociándose | 1 |
| 46955 | rociaba | 1 |
| 46956 | rocía | 1 |
| 46957 | rocho | 1 |
| 46958 | rochela | 1 |
| 46959 | roçapoco | 1 |
| 46960 | rocadero | 1 |
| 46961 | rocabertis | 1 |
| 46962 | roça | 1 |
| 46963 | robustiana | 1 |
| 46964 | robustecer | 1 |
| 46965 | robres | 1 |
| 46966 | robré | 1 |
| 46967 | robledales | 1 |
| 46968 | roberto | 1 |
| 46969 | robaste | 1 |
| 46970 | robas | 1 |
| 46971 | robármelo | 1 |
| 46972 | robarlo | 1 |
| 46973 | robarla | 1 |
| 46974 | robaré | 1 |
| 46975 | robarán | 1 |
| 46976 | robaran | 1 |
| 46977 | robará | 1 |
| 46978 | robándoselo | 1 |
| 46979 | robándole | 1 |
| 46980 | robamos | 1 |
| 46981 | robalo | 1 |
| 46982 | roballas | 1 |
| 46983 | robadores | 1 |
| 46984 | robadas | 1 |
| 46985 | roastbeef | 1 |
| 46986 | road | 1 |
| 46987 | rizosa | 1 |
| 46988 | rizas | 1 |
| 46989 | rizarse | 1 |
| 46990 | rizar | 1 |
| 46991 | rizando | 1 |
| 46992 | riza | 1 |
| 46993 | riyó | 1 |
| 46994 | riyeron | 1 |
| 46995 | rixoso | 1 |
| 46996 | rixo | 1 |
| 46997 | rivalizaba | 1 |
| 46998 | rivaliza | 1 |
| 46999 | ritual | 1 |
| 47000 | ritornellos | 1 |
| 47001 | ritómico | 1 |
| 47002 | ritólicas | 1 |
| 47003 | rítmicos | 1 |
| 47004 | risuena | 1 |
| 47005 | risotadas | 1 |
| 47006 | riso | 1 |
| 47007 | risitas | 1 |
| 47008 | risibles | 1 |
| 47009 | risete | 1 |
| 47010 | riquísimamente | 1 |
| 47011 | riquesa | 1 |
| 47012 | riotinto | 1 |
| 47013 | rios | 1 |
| 47014 | ríome | 1 |
| 47015 | riome | 1 |
| 47016 | riñosas | 1 |
| 47017 | riñiremos | 1 |
| 47018 | riñes | 1 |
| 47019 | riñeren | 1 |
| 47020 | riñeran | 1 |
| 47021 | ríñeme | 1 |
| 47022 | riñamos | 1 |
| 47023 | ríñame | 1 |
| 47024 | ríñale | 1 |
| 47025 | rinieron | 1 |
| 47026 | rinen | 1 |
| 47027 | rine | 1 |
| 47028 | rindan | 1 |
| 47029 | rinconete | 1 |
| 47030 | rinconcito | 1 |
| 47031 | rin | 1 |
| 47032 | rimpuesta | 1 |
| 47033 | rimna | 1 |
| 47034 | rimeros | 1 |
| 47035 | rimar | 1 |
| 47036 | riman | 1 |
| 47037 | rimados | 1 |
| 47038 | rijo | 1 |
| 47039 | rigurosísima | 1 |
| 47040 | rigurosamente | 1 |
| 47041 | rigorosamente | 1 |
| 47042 | rigoristas | 1 |
| 47043 | rigolución | 1 |
| 47044 | rigolade | 1 |
| 47045 | rigodones | 1 |
| 47046 | rígidos | 1 |
| 47047 | rigidez | 1 |
| 47048 | rígidas | 1 |
| 47049 | rígidamente | 1 |
| 47050 | rigera | 1 |
| 47051 | rigen | 1 |
| 47052 | rifle | 1 |
| 47053 | riff | 1 |
| 47054 | rifeas | 1 |
| 47055 | rifárselos | 1 |
| 47056 | rifarla | 1 |
| 47057 | rifar | 1 |
| 47058 | rieto | 1 |
| 47059 | rieste | 1 |
| 47060 | riesen | 1 |
| 47061 | riéronla | 1 |
| 47062 | rieres | 1 |
| 47063 | rieras | 1 |
| 47064 | rieran | 1 |
| 47065 | riéndole | 1 |
| 47066 | riegan | 1 |
| 47067 | riega | 1 |
| 47068 | ridículamente | 1 |
| 47069 | ridente | 1 |
| 47070 | ricome | 1 |
| 47071 | rich | 1 |
| 47072 | ricardos | 1 |
| 47073 | ricarda | 1 |
| 47074 | ricamonte | 1 |
| 47075 | ricahembra | 1 |
| 47076 | ricachos | 1 |
| 47077 | ricachonas | 1 |
| 47078 | ricachón | 1 |
| 47079 | ricacha | 1 |
| 47080 | ribeteados | 1 |
| 47081 | ribeteada | 1 |
| 47082 | ribereño | 1 |
| 47083 | ribazos | 1 |
| 47084 | ribalde | 1 |
| 47085 | ribadavia | 1 |
| 47086 | riarán | 1 |
| 47087 | rezumos | 1 |
| 47088 | rezumía | 1 |
| 47089 | rezumando | 1 |
| 47090 | rezumados | 1 |
| 47091 | rezumaba | 1 |
| 47092 | rezongó | 1 |
| 47093 | rezongadores | 1 |
| 47094 | rezongaba | 1 |
| 47095 | reze | 1 |
| 47096 | rezaste | 1 |
| 47097 | rezaremos | 1 |
| 47098 | rezare | 1 |
| 47099 | rezarán | 1 |
| 47100 | rezándole | 1 |
| 47101 | rezamos | 1 |
| 47102 | rézale | 1 |
| 47103 | rezagándose | 1 |
| 47104 | rezagada | 1 |
| 47105 | rezadora | 1 |
| 47106 | reyrme | 1 |
| 47107 | reynos | 1 |
| 47108 | reynar | 1 |
| 47109 | reyentes | 1 |
| 47110 | reya | 1 |
| 47111 | rex | 1 |
| 47112 | rewólver | 1 |
| 47113 | revulgo | 1 |
| 47114 | revuelvo | 1 |
| 47115 | revuelves | 1 |
| 47116 | revuelvan | 1 |
| 47117 | revuelva | 1 |
| 47118 | revuelcos | 1 |
| 47119 | revuelco | 1 |
| 47120 | revue | 1 |
| 47121 | revóquela | 1 |
| 47122 | revolviese | 1 |
| 47123 | revolviéndosele | 1 |
| 47124 | revolviéndola | 1 |
| 47125 | revolví | 1 |
| 47126 | revolverlas | 1 |
| 47127 | revolveré | 1 |
| 47128 | revolvéis | 1 |
| 47129 | revoltosilla | 1 |
| 47130 | revoltosas | 1 |
| 47131 | revoltillos | 1 |
| 47132 | revoloteó | 1 |
| 47133 | revolotear | 1 |
| 47134 | revolcose | 1 |
| 47135 | revolcase | 1 |
| 47136 | revolando | 1 |
| 47137 | revocó | 1 |
| 47138 | revocarle | 1 |
| 47139 | revocar | 1 |
| 47140 | revocado | 1 |
| 47141 | revocaban | 1 |
| 47142 | reviviendo | 1 |
| 47143 | revistó | 1 |
| 47144 | revistió | 1 |
| 47145 | revistiera | 1 |
| 47146 | revistiéndolas | 1 |
| 47147 | revistiéndola | 1 |
| 47148 | revístase | 1 |
| 47149 | revistar | 1 |
| 47150 | revisaré | 1 |
| 47151 | reviradas | 1 |
| 47152 | revilla | 1 |
| 47153 | revientes | 1 |
| 47154 | revienten | 1 |
| 47155 | revestirse | 1 |
| 47156 | revestir | 1 |
| 47157 | revestimiento | 1 |
| 47158 | revestidas | 1 |
| 47159 | revesado | 1 |
| 47160 | revesada | 1 |
| 47161 | revesa | 1 |
| 47162 | revertida | 1 |
| 47163 | reverso | 1 |
| 47164 | reversión | 1 |
| 47165 | reverente | 1 |
| 47166 | reverendísimas | 1 |
| 47167 | reverendísima | 1 |
| 47168 | reverencien | 1 |
| 47169 | reverenciar | 1 |
| 47170 | reverdeció | 1 |
| 47171 | reverdeciendo | 1 |
| 47172 | reverdecidas | 1 |
| 47173 | reverdece | 1 |
| 47174 | reverberar | 1 |
| 47175 | reverberan | 1 |
| 47176 | reverberada | 1 |
| 47177 | reventazón | 1 |
| 47178 | reventasen | 1 |
| 47179 | reventas | 1 |
| 47180 | reventaría | 1 |
| 47181 | revenidos | 1 |
| 47182 | revenge | 1 |
| 47183 | revender | 1 |
| 47184 | revendedores | 1 |
| 47185 | revendederas | 1 |
| 47186 | revellín | 1 |
| 47187 | revelé | 1 |
| 47188 | revelase | 1 |
| 47189 | revelarte | 1 |
| 47190 | revelarse | 1 |
| 47191 | revelara | 1 |
| 47192 | revelándose | 1 |
| 47193 | revelan | 1 |
| 47194 | revatamiento | 1 |
| 47195 | rev | 1 |
| 47196 | reuolucion | 1 |
| 47197 | reuniose | 1 |
| 47198 | reuniéronse | 1 |
| 47199 | reunieran | 1 |
| 47200 | reuniera | 1 |
| 47201 | reuní | 1 |
| 47202 | reunen | 1 |
| 47203 | reumáticos | 1 |
| 47204 | reumático | 1 |
| 47205 | reuisto | 1 |
| 47206 | reuista | 1 |
| 47207 | reui | 1 |
| 47208 | reuessar | 1 |
| 47209 | reuesar | 1 |
| 47210 | reues | 1 |
| 47211 | reuerenda | 1 |
| 47212 | reuerberar | 1 |
| 47213 | reuana | 1 |
| 47214 | retuviera | 1 |
| 47215 | retumbando | 1 |
| 47216 | retumbado | 1 |
| 47217 | retumba | 1 |
| 47218 | rétulos | 1 |
| 47219 | retule | 1 |
| 47220 | retular | 1 |
| 47221 | retruécanos | 1 |
| 47222 | retruécano | 1 |
| 47223 | retrospectivo | 1 |
| 47224 | retrospectiva | 1 |
| 47225 | retrógrado | 1 |
| 47226 | retrogradaba | 1 |
| 47227 | retrocediente | 1 |
| 47228 | retrocedí | 1 |
| 47229 | retrocede | 1 |
| 47230 | retrocedamos | 1 |
| 47231 | retroacción | 1 |
| 47232 | retribuido | 1 |
| 47233 | retretes | 1 |
| 47234 | retrete | 1 |
| 47235 | retraydo | 1 |
| 47236 | retrayas | 1 |
| 47237 | retrató | 1 |
| 47238 | retratistas | 1 |
| 47239 | retratista | 1 |
| 47240 | retráteme | 1 |
| 47241 | retrate | 1 |
| 47242 | retratarse | 1 |
| 47243 | retratarle | 1 |
| 47244 | retrataba | 1 |
| 47245 | retrataaar | 1 |
| 47246 | retrata | 1 |
| 47247 | retrasó | 1 |
| 47248 | retrasen | 1 |
| 47249 | retrasados | 1 |
| 47250 | retrasada | 1 |
| 47251 | retraída | 1 |
| 47252 | retraete | 1 |
| 47253 | retraerse | 1 |
| 47254 | retraerían | 1 |
| 47255 | retractase | 1 |
| 47256 | retractarse | 1 |
| 47257 | retractación | 1 |
| 47258 | retozo | 1 |
| 47259 | retozala | 1 |
| 47260 | retozadores | 1 |
| 47261 | retozaban | 1 |
| 47262 | retour | 1 |
| 47263 | retortijado | 1 |
| 47264 | retortero | 1 |
| 47265 | retornarían | 1 |
| 47266 | retóricamente | 1 |
| 47267 | retores | 1 |
| 47268 | retorció | 1 |
| 47269 | retorcieron | 1 |
| 47270 | retorcido | 1 |
| 47271 | retorcedura | 1 |
| 47272 | retoque | 1 |
| 47273 | retoñado | 1 |
| 47274 | retólicas | 1 |
| 47275 | retocó | 1 |
| 47276 | retocarla | 1 |
| 47277 | retocar | 1 |
| 47278 | retocando | 1 |
| 47279 | retocados | 1 |
| 47280 | retocada | 1 |
| 47281 | retireme | 1 |
| 47282 | retiréis | 1 |
| 47283 | retirases | 1 |
| 47284 | retirásemos | 1 |
| 47285 | retírase | 1 |
| 47286 | retirase | 1 |
| 47287 | retirarte | 1 |
| 47288 | retirarlos | 1 |
| 47289 | retirarlo | 1 |
| 47290 | retirarle | 1 |
| 47291 | retiraran | 1 |
| 47292 | retirándolo | 1 |
| 47293 | retiramos | 1 |
| 47294 | retiradas | 1 |
| 47295 | retiradamente | 1 |
| 47296 | retirábase | 1 |
| 47297 | retiraban | 1 |
| 47298 | retiñendo | 1 |
| 47299 | retinto | 1 |
| 47300 | retinta | 1 |
| 47301 | retiniana | 1 |
| 47302 | retinens | 1 |
| 47303 | retiente | 1 |
| 47304 | retientan | 1 |
| 47305 | reteñido | 1 |
| 47306 | retentar | 1 |
| 47307 | reteniéndole | 1 |
| 47308 | reteniéndola | 1 |
| 47309 | retenida | 1 |
| 47310 | retenían | 1 |
| 47311 | retenerlo | 1 |
| 47312 | retenerle | 1 |
| 47313 | retención | 1 |
| 47314 | retembló | 1 |
| 47315 | retemblaron | 1 |
| 47316 | retemblar | 1 |
| 47317 | retemblando | 1 |
| 47318 | retemblaba | 1 |
| 47319 | retardemos | 1 |
| 47320 | retarde | 1 |
| 47321 | retara | 1 |
| 47322 | retar | 1 |
| 47323 | retándole | 1 |
| 47324 | retahila | 1 |
| 47325 | retaçar | 1 |
| 47326 | reta | 1 |
| 47327 | resuscitaba | 1 |
| 47328 | resurrecion | 1 |
| 47329 | resurgía | 1 |
| 47330 | resumo | 1 |
| 47331 | resumirse | 1 |
| 47332 | resumía | 1 |
| 47333 | resulución | 1 |
| 47334 | resultole | 1 |
| 47335 | resultasen | 1 |
| 47336 | resultarle | 1 |
| 47337 | resultarán | 1 |
| 47338 | resuelvas | 1 |
| 47339 | resueltas | 1 |
| 47340 | resuella | 1 |
| 47341 | resucitola | 1 |
| 47342 | resucito | 1 |
| 47343 | resucites | 1 |
| 47344 | resucite | 1 |
| 47345 | resucitaran | 1 |
| 47346 | resucitan | 1 |
| 47347 | resucitador | 1 |
| 47348 | resucitaban | 1 |
| 47349 | resucitaba | 1 |
| 47350 | restuarar | 1 |
| 47351 | restriñimientos | 1 |
| 47352 | restringido | 1 |
| 47353 | restreñimientos | 1 |
| 47354 | restregones | 1 |
| 47355 | restregón | 1 |
| 47356 | restregó | 1 |
| 47357 | restregáronle | 1 |
| 47358 | restregado | 1 |
| 47359 | restituyo | 1 |
| 47360 | restituyes | 1 |
| 47361 | restitúyanse | 1 |
| 47362 | restituirse | 1 |
| 47363 | restituirlo | 1 |
| 47364 | restituímos | 1 |
| 47365 | restitüido | 1 |
| 47366 | restituía | 1 |
| 47367 | restitucion | 1 |
| 47368 | restaurarse | 1 |
| 47369 | restaurara | 1 |
| 47370 | restaurants | 1 |
| 47371 | restauranes | 1 |
| 47372 | restaurando | 1 |
| 47373 | restauradas | 1 |
| 47374 | restaurada | 1 |
| 47375 | restauraba | 1 |
| 47376 | restaron | 1 |
| 47377 | restar | 1 |
| 47378 | restañar | 1 |
| 47379 | restañándole | 1 |
| 47380 | restañadas | 1 |
| 47381 | restañaba | 1 |
| 47382 | restan | 1 |
| 47383 | réstame | 1 |
| 47384 | restallar | 1 |
| 47385 | restallando | 1 |
| 47386 | restallaban | 1 |
| 47387 | restait | 1 |
| 47388 | restablezca | 1 |
| 47389 | restablecimiento | 1 |
| 47390 | restablece | 1 |
| 47391 | restaban | 1 |
| 47392 | resquiebro | 1 |
| 47393 | resquiebra | 1 |
| 47394 | resquebrajos | 1 |
| 47395 | resquebrajaba | 1 |
| 47396 | responsión | 1 |
| 47397 | respondón | 1 |
| 47398 | respondiome | 1 |
| 47399 | respondiolos | 1 |
| 47400 | respondioles | 1 |
| 47401 | respondio | 1 |
| 47402 | respondílo | 1 |
| 47403 | respondiesen | 1 |
| 47404 | respondiéronme | 1 |
| 47405 | respondieran | 1 |
| 47406 | respondiente | 1 |
| 47407 | respondiéndome | 1 |
| 47408 | respondiéndole | 1 |
| 47409 | respondiéndola | 1 |
| 47410 | respondida | 1 |
| 47411 | respondias | 1 |
| 47412 | responderte | 1 |
| 47413 | responderse | 1 |
| 47414 | responderia | 1 |
| 47415 | responderemos | 1 |
| 47416 | responderás | 1 |
| 47417 | respondera | 1 |
| 47418 | respóndenos | 1 |
| 47419 | respondemos | 1 |
| 47420 | respondeme | 1 |
| 47421 | respondelles | 1 |
| 47422 | respóndele | 1 |
| 47423 | respondedme | 1 |
| 47424 | responded | 1 |
| 47425 | respondan | 1 |
| 47426 | respóndame | 1 |
| 47427 | respóndale | 1 |
| 47428 | respondáis | 1 |
| 47429 | resplandesciente | 1 |
| 47430 | resplandecieron | 1 |
| 47431 | resplandeçiente | 1 |
| 47432 | resplandeciendo | 1 |
| 47433 | resplandecen | 1 |
| 47434 | respiré | 1 |
| 47435 | respirase | 1 |
| 47436 | respirado | 1 |
| 47437 | respiraderos | 1 |
| 47438 | respirable | 1 |
| 47439 | respiraban | 1 |
| 47440 | respirábamos | 1 |
| 47441 | respingar | 1 |
| 47442 | respingados | 1 |
| 47443 | respingadas | 1 |
| 47444 | réspices | 1 |
| 47445 | respetuosamente | 1 |
| 47446 | respetosa | 1 |
| 47447 | respetemos | 1 |
| 47448 | respéteme | 1 |
| 47449 | respetas | 1 |
| 47450 | respetarse | 1 |
| 47451 | respetaron | 1 |
| 47452 | respetaremos | 1 |
| 47453 | respetan | 1 |
| 47454 | respetados | 1 |
| 47455 | respetad | 1 |
| 47456 | respetabilísimos | 1 |
| 47457 | respetabilísimo | 1 |
| 47458 | respetabilísimas | 1 |
| 47459 | respectaban | 1 |
| 47460 | respaldos | 1 |
| 47461 | resoplo | 1 |
| 47462 | resonarán | 1 |
| 47463 | resonante | 1 |
| 47464 | resonado | 1 |
| 47465 | resolvióse | 1 |
| 47466 | resolvimos | 1 |
| 47467 | resolviéronse | 1 |
| 47468 | resolviera | 1 |
| 47469 | resolviéndola | 1 |
| 47470 | resolviendo | 1 |
| 47471 | resolvíase | 1 |
| 47472 | resolvían | 1 |
| 47473 | resolvíame | 1 |
| 47474 | resolvérsele | 1 |
| 47475 | resolverme | 1 |
| 47476 | resolverlos | 1 |
| 47477 | resolverlo | 1 |
| 47478 | resolverle | 1 |
| 47479 | resolverlas | 1 |
| 47480 | resolverían | 1 |
| 47481 | resolvamos | 1 |
| 47482 | resolvámonos | 1 |
| 47483 | resollos | 1 |
| 47484 | resolló | 1 |
| 47485 | resobándose | 1 |
| 47486 | resobado | 1 |
| 47487 | resobaba | 1 |
| 47488 | resistirlo | 1 |
| 47489 | resistirle | 1 |
| 47490 | resistiría | 1 |
| 47491 | resistimos | 1 |
| 47492 | resistiesen | 1 |
| 47493 | resistieras | 1 |
| 47494 | resistiera | 1 |
| 47495 | resistíase | 1 |
| 47496 | resistían | 1 |
| 47497 | resistes | 1 |
| 47498 | resistente | 1 |
| 47499 | resisten | 1 |
| 47500 | resistas | 1 |
| 47501 | resio | 1 |
| 47502 | resinas | 1 |
| 47503 | resignó | 1 |
| 47504 | resigno | 1 |
| 47505 | resígnese | 1 |
| 47506 | resigne | 1 |
| 47507 | resignaron | 1 |
| 47508 | resignarnos | 1 |
| 47509 | resignan | 1 |
| 47510 | resignados | 1 |
| 47511 | resignadas | 1 |
| 47512 | resignábase | 1 |
| 47513 | residuos | 1 |
| 47514 | residiera | 1 |
| 47515 | residíamos | 1 |
| 47516 | residencias | 1 |
| 47517 | resguardar | 1 |
| 47518 | resfriaron | 1 |
| 47519 | resfriarme | 1 |
| 47520 | reservó | 1 |
| 47521 | reservase | 1 |
| 47522 | reservarse | 1 |
| 47523 | reservarme | 1 |
| 47524 | reservarían | 1 |
| 47525 | reservadísimo | 1 |
| 47526 | reservaban | 1 |
| 47527 | reseñada | 1 |
| 47528 | reseña | 1 |
| 47529 | reselles | 1 |
| 47530 | resecaban | 1 |
| 47531 | rescibió | 1 |
| 47532 | resçibida | 1 |
| 47533 | resciba | 1 |
| 47534 | resçelé | 1 |
| 47535 | rescebiste | 1 |
| 47536 | rescebir | 1 |
| 47537 | resçebido | 1 |
| 47538 | rescatemos | 1 |
| 47539 | rescátate | 1 |
| 47540 | rescatasen | 1 |
| 47541 | rescatase | 1 |
| 47542 | rescatarlos | 1 |
| 47543 | rescataré | 1 |
| 47544 | rescataos | 1 |
| 47545 | rescatando | 1 |
| 47546 | rescatamos | 1 |
| 47547 | rescataba | 1 |
| 47548 | resbaloso | 1 |
| 47549 | resbalósele | 1 |
| 47550 | resbalón | 1 |
| 47551 | resbalaron | 1 |
| 47552 | resbalándose | 1 |
| 47553 | resbaladizos | 1 |
| 47554 | resalao | 1 |
| 47555 | requirimientos | 1 |
| 47556 | requirieron | 1 |
| 47557 | requiriera | 1 |
| 47558 | requirido | 1 |
| 47559 | requiría | 1 |
| 47560 | requiero | 1 |
| 47561 | requiem | 1 |
| 47562 | requiébranse | 1 |
| 47563 | requetefinas | 1 |
| 47564 | requesón | 1 |
| 47565 | requesenes | 1 |
| 47566 | requerirlos | 1 |
| 47567 | requerimientos | 1 |
| 47568 | requerimiento | 1 |
| 47569 | requeridos | 1 |
| 47570 | requerid | 1 |
| 47571 | requemo | 1 |
| 47572 | requemado | 1 |
| 47573 | requejo | 1 |
| 47574 | requebróme | 1 |
| 47575 | requebrarla | 1 |
| 47576 | requebrare | 1 |
| 47577 | requebrar | 1 |
| 47578 | requebrábanle | 1 |
| 47579 | reputas | 1 |
| 47580 | reputaron | 1 |
| 47581 | reputándole | 1 |
| 47582 | reputan | 1 |
| 47583 | reputados | 1 |
| 47584 | reputábala | 1 |
| 47585 | repusieron | 1 |
| 47586 | repuntaba | 1 |
| 47587 | repulsiva | 1 |
| 47588 | repulsa | 1 |
| 47589 | repulgo | 1 |
| 47590 | repulgadas | 1 |
| 47591 | repulgada | 1 |
| 47592 | repugne | 1 |
| 47593 | repugnaría | 1 |
| 47594 | repugnándole | 1 |
| 47595 | repugnancias | 1 |
| 47596 | repugnan | 1 |
| 47597 | repuestos | 1 |
| 47598 | repuesta | 1 |
| 47599 | république | 1 |
| 47600 | repúblico | 1 |
| 47601 | republicanitos | 1 |
| 47602 | republicana | 1 |
| 47603 | republica | 1 |
| 47604 | repto | 1 |
| 47605 | reptilias | 1 |
| 47606 | reptilia | 1 |
| 47607 | reptiles | 1 |
| 47608 | reptil | 1 |
| 47609 | reptar | 1 |
| 47610 | reprueua | 1 |
| 47611 | repruebas | 1 |
| 47612 | reprueba | 1 |
| 47613 | reproduzca | 1 |
| 47614 | reprodujeron | 1 |
| 47615 | reprodujera | 1 |
| 47616 | reproducirme | 1 |
| 47617 | reproduciéndose | 1 |
| 47618 | reproduciéndolo | 1 |
| 47619 | reproduciendo | 1 |
| 47620 | reproducídose | 1 |
| 47621 | reproducido | 1 |
| 47622 | reproducidas | 1 |
| 47623 | reproducida | 1 |
| 47624 | reprochó | 1 |
| 47625 | reproche | 1 |
| 47626 | reprocharme | 1 |
| 47627 | reprocharle | 1 |
| 47628 | reprochándole | 1 |
| 47629 | reprochador | 1 |
| 47630 | reprochado | 1 |
| 47631 | reprochaban | 1 |
| 47632 | réprobo | 1 |
| 47633 | reprobas | 1 |
| 47634 | reprobación | 1 |
| 47635 | reprobables | 1 |
| 47636 | reprimiré | 1 |
| 47637 | reprimió | 1 |
| 47638 | reprimiendo | 1 |
| 47639 | reprimen | 1 |
| 47640 | reprima | 1 |
| 47641 | represiva | 1 |
| 47642 | represento | 1 |
| 47643 | representes | 1 |
| 47644 | representélo | 1 |
| 47645 | representativos | 1 |
| 47646 | representativo | 1 |
| 47647 | representativas | 1 |
| 47648 | represéntase | 1 |
| 47649 | representas | 1 |
| 47650 | representarnos | 1 |
| 47651 | representarme | 1 |
| 47652 | representarían | 1 |
| 47653 | representaría | 1 |
| 47654 | representaran | 1 |
| 47655 | representallas | 1 |
| 47656 | representados | 1 |
| 47657 | representábase | 1 |
| 47658 | represando | 1 |
| 47659 | reprensiones | 1 |
| 47660 | reprendiese | 1 |
| 47661 | reprendieran | 1 |
| 47662 | reprendiéndome | 1 |
| 47663 | reprendiendolo | 1 |
| 47664 | reprendido | 1 |
| 47665 | reprendíales | 1 |
| 47666 | reprenderle | 1 |
| 47667 | reprenderla | 1 |
| 47668 | reprende | 1 |
| 47669 | reprehensores | 1 |
| 47670 | reprehensor | 1 |
| 47671 | reprehendiólos | 1 |
| 47672 | reprehendió | 1 |
| 47673 | reprehendiéndome | 1 |
| 47674 | reprehendiendo | 1 |
| 47675 | reprehendidos | 1 |
| 47676 | reprehendidas | 1 |
| 47677 | reprehendida | 1 |
| 47678 | reprehendía | 1 |
| 47679 | reprehendas | 1 |
| 47680 | reprehendáis | 1 |
| 47681 | reprehenda | 1 |
| 47682 | repreguntas | 1 |
| 47683 | reposterías | 1 |
| 47684 | reposen | 1 |
| 47685 | reposemos | 1 |
| 47686 | reposé | 1 |
| 47687 | repose | 1 |
| 47688 | reposaría | 1 |
| 47689 | reposan | 1 |
| 47690 | reposad | 1 |
| 47691 | reposaban | 1 |
| 47692 | reportóse | 1 |
| 47693 | reportorio | 1 |
| 47694 | repórtola | 1 |
| 47695 | reporters | 1 |
| 47696 | reporte | 1 |
| 47697 | reportase | 1 |
| 47698 | reportaré | 1 |
| 47699 | reponiendo | 1 |
| 47700 | reponían | 1 |
| 47701 | reponerte | 1 |
| 47702 | reponerme | 1 |
| 47703 | reponer | 1 |
| 47704 | repone | 1 |
| 47705 | repondió | 1 |
| 47706 | repollos | 1 |
| 47707 | repoblicanas | 1 |
| 47708 | repliégate | 1 |
| 47709 | repliegan | 1 |
| 47710 | replicóme | 1 |
| 47711 | replicase | 1 |
| 47712 | replicáronle | 1 |
| 47713 | replicaron | 1 |
| 47714 | replicaré | 1 |
| 47715 | replicare | 1 |
| 47716 | replicará | 1 |
| 47717 | replicara | 1 |
| 47718 | replicalle | 1 |
| 47719 | replicado | 1 |
| 47720 | repletos | 1 |
| 47721 | repletas | 1 |
| 47722 | replegándose | 1 |
| 47723 | replegando | 1 |
| 47724 | repitiese | 1 |
| 47725 | repítelas | 1 |
| 47726 | repita | 1 |
| 47727 | repisar | 1 |
| 47728 | repiqueteo | 1 |
| 47729 | repiquete | 1 |
| 47730 | repiques | 1 |
| 47731 | repiquen | 1 |
| 47732 | repicó | 1 |
| 47733 | repicando | 1 |
| 47734 | repican | 1 |
| 47735 | repicallas | 1 |
| 47736 | repetirvos | 1 |
| 47737 | repetírselo | 1 |
| 47738 | repetirla | 1 |
| 47739 | repetirías | 1 |
| 47740 | repetiría | 1 |
| 47741 | repetidme | 1 |
| 47742 | repetid | 1 |
| 47743 | repeticiones | 1 |
| 47744 | repercutiendo | 1 |
| 47745 | repercutía | 1 |
| 47746 | repentista | 1 |
| 47747 | repentimiento | 1 |
| 47748 | repelón | 1 |
| 47749 | repeló | 1 |
| 47750 | repelándome | 1 |
| 47751 | repelado | 1 |
| 47752 | repega | 1 |
| 47753 | repasó | 1 |
| 47754 | repasarlos | 1 |
| 47755 | repasarles | 1 |
| 47756 | repasarle | 1 |
| 47757 | repasándola | 1 |
| 47758 | repasaban | 1 |
| 47759 | repartiros | 1 |
| 47760 | repartirlos | 1 |
| 47761 | repartiría | 1 |
| 47762 | repartirá | 1 |
| 47763 | repartióse | 1 |
| 47764 | repartijaban | 1 |
| 47765 | repartiéronlo | 1 |
| 47766 | repartiéronle | 1 |
| 47767 | repartiéndolas | 1 |
| 47768 | repartidor | 1 |
| 47769 | repartible | 1 |
| 47770 | repártela | 1 |
| 47771 | repártase | 1 |
| 47772 | repartan | 1 |
| 47773 | repartamos | 1 |
| 47774 | repártalas | 1 |
| 47775 | reparona | 1 |
| 47776 | repáresela | 1 |
| 47777 | reparemos | 1 |
| 47778 | reparé | 1 |
| 47779 | reparatrices | 1 |
| 47780 | repararé | 1 |
| 47781 | reparamos | 1 |
| 47782 | reparáis | 1 |
| 47783 | reparadas | 1 |
| 47784 | reparada | 1 |
| 47785 | reparaban | 1 |
| 47786 | reparábamos | 1 |
| 47787 | repapile | 1 |
| 47788 | repantigado | 1 |
| 47789 | reorganice | 1 |
| 47790 | reojo | 1 |
| 47791 | reñirles | 1 |
| 47792 | reñiremos | 1 |
| 47793 | reñirá | 1 |
| 47794 | reñimos | 1 |
| 47795 | reñiendo | 1 |
| 47796 | reñíamos | 1 |
| 47797 | renzillas | 1 |
| 47798 | renuncie | 1 |
| 47799 | renunciaron | 1 |
| 47800 | renunciarla | 1 |
| 47801 | renunçiaría | 1 |
| 47802 | renunciaré | 1 |
| 47803 | renuévese | 1 |
| 47804 | renueves | 1 |
| 47805 | rentoy | 1 |
| 47806 | rentita | 1 |
| 47807 | rentístico | 1 |
| 47808 | renteros | 1 |
| 47809 | rentará | 1 |
| 47810 | rentada | 1 |
| 47811 | rensilla | 1 |
| 47812 | renovase | 1 |
| 47813 | renovarse | 1 |
| 47814 | renovarle | 1 |
| 47815 | renovará | 1 |
| 47816 | renovad | 1 |
| 47817 | renovaciones | 1 |
| 47818 | renouaras | 1 |
| 47819 | renouar | 1 |
| 47820 | renouado | 1 |
| 47821 | renombrada | 1 |
| 47822 | rennert | 1 |
| 47823 | renieguen | 1 |
| 47824 | reniegos | 1 |
| 47825 | renia | 1 |
| 47826 | rengloncito | 1 |
| 47827 | renglon | 1 |
| 47828 | renegué | 1 |
| 47829 | renegadas | 1 |
| 47830 | renegad | 1 |
| 47831 | rendondilla | 1 |
| 47832 | rendiros | 1 |
| 47833 | rendirla | 1 |
| 47834 | rendiría | 1 |
| 47835 | rendíos | 1 |
| 47836 | rendidísimo | 1 |
| 47837 | rendidísima | 1 |
| 47838 | rendían | 1 |
| 47839 | rendí | 1 |
| 47840 | renda | 1 |
| 47841 | rencorosas | 1 |
| 47842 | rencilla | 1 |
| 47843 | renca | 1 |
| 47844 | renascence | 1 |
| 47845 | renacuajos | 1 |
| 47846 | renaciera | 1 |
| 47847 | renacían | 1 |
| 47848 | renacen | 1 |
| 47849 | remunerar | 1 |
| 47850 | remunera | 1 |
| 47851 | remueve | 1 |
| 47852 | remuerde | 1 |
| 47853 | remudar | 1 |
| 47854 | remozar | 1 |
| 47855 | remozado | 1 |
| 47856 | removió | 1 |
| 47857 | removieran | 1 |
| 47858 | removiendo | 1 |
| 47859 | removido | 1 |
| 47860 | removidas | 1 |
| 47861 | removida | 1 |
| 47862 | removían | 1 |
| 47863 | remover | 1 |
| 47864 | remotísimo | 1 |
| 47865 | remordiera | 1 |
| 47866 | remordiéndole | 1 |
| 47867 | rémora | 1 |
| 47868 | remoquete | 1 |
| 47869 | remontó | 1 |
| 47870 | remonte | 1 |
| 47871 | remóntate | 1 |
| 47872 | remontarte | 1 |
| 47873 | remontarme | 1 |
| 47874 | remontara | 1 |
| 47875 | remontando | 1 |
| 47876 | remontado | 1 |
| 47877 | remontabas | 1 |
| 47878 | remonta | 1 |
| 47879 | remonona | 1 |
| 47880 | remono | 1 |
| 47881 | remonísima | 1 |
| 47882 | remondóse | 1 |
| 47883 | remón | 1 |
| 47884 | remolones | 1 |
| 47885 | remolcó | 1 |
| 47886 | remolcándola | 1 |
| 47887 | remolcados | 1 |
| 47888 | remolcadora | 1 |
| 47889 | remolacha | 1 |
| 47890 | remoje | 1 |
| 47891 | remojado | 1 |
| 47892 | remítome | 1 |
| 47893 | remitirlo | 1 |
| 47894 | remitirán | 1 |
| 47895 | remitir | 1 |
| 47896 | remitiese | 1 |
| 47897 | remitiera | 1 |
| 47898 | remitiéndome | 1 |
| 47899 | remitidos | 1 |
| 47900 | remitidas | 1 |
| 47901 | remitía | 1 |
| 47902 | remitamos | 1 |
| 47903 | remisos | 1 |
| 47904 | remirólos | 1 |
| 47905 | remiro | 1 |
| 47906 | remírenos | 1 |
| 47907 | remire | 1 |
| 47908 | remírase | 1 |
| 47909 | remirarle | 1 |
| 47910 | remiralla | 1 |
| 47911 | remirado | 1 |
| 47912 | reminiscencia | 1 |
| 47913 | remilgadas | 1 |
| 47914 | remilgada | 1 |
| 47915 | remilga | 1 |
| 47916 | remiente | 1 |
| 47917 | remienda | 1 |
| 47918 | remetieron | 1 |
| 47919 | remestán | 1 |
| 47920 | remesa | 1 |
| 47921 | remendona | 1 |
| 47922 | remendarnos | 1 |
| 47923 | remendarla | 1 |
| 47924 | remendando | 1 |
| 47925 | remendadas | 1 |
| 47926 | remendada | 1 |
| 47927 | remembranza | 1 |
| 47928 | remedos | 1 |
| 47929 | remedien | 1 |
| 47930 | remediaua | 1 |
| 47931 | remediásedes | 1 |
| 47932 | remediase | 1 |
| 47933 | remediarse | 1 |
| 47934 | remediaros | 1 |
| 47935 | remediaron | 1 |
| 47936 | remediarme | 1 |
| 47937 | remediarán | 1 |
| 47938 | remediárades | 1 |
| 47939 | remediando | 1 |
| 47940 | remedian | 1 |
| 47941 | remediador | 1 |
| 47942 | remediadlo | 1 |
| 47943 | remediadas | 1 |
| 47944 | remediaban | 1 |
| 47945 | remedé | 1 |
| 47946 | remedasses | 1 |
| 47947 | remedar | 1 |
| 47948 | remedaban | 1 |
| 47949 | remeçe | 1 |
| 47950 | rematarnos | 1 |
| 47951 | rematarlo | 1 |
| 47952 | rematadas | 1 |
| 47953 | remataban | 1 |
| 47954 | remangó | 1 |
| 47955 | remanga | 1 |
| 47956 | remaneció | 1 |
| 47957 | remanecer | 1 |
| 47958 | remala | 1 |
| 47959 | remadera | 1 |
| 47960 | remachando | 1 |
| 47961 | remaba | 1 |
| 47962 | relusiente | 1 |
| 47963 | relumbrones | 1 |
| 47964 | relumbrón | 1 |
| 47965 | relumbrays | 1 |
| 47966 | relumbrantes | 1 |
| 47967 | relumbra | 1 |
| 47968 | reluçientes | 1 |
| 47969 | relojería | 1 |
| 47970 | rellenó | 1 |
| 47971 | rellenan | 1 |
| 47972 | relinche | 1 |
| 47973 | relincharán | 1 |
| 47974 | relinchaba | 1 |
| 47975 | religion | 1 |
| 47976 | relieuan | 1 |
| 47977 | relicario | 1 |
| 47978 | relevase | 1 |
| 47979 | relevarle | 1 |
| 47980 | relevaban | 1 |
| 47981 | releva | 1 |
| 47982 | releídas | 1 |
| 47983 | relegada | 1 |
| 47984 | releerlo | 1 |
| 47985 | releerla | 1 |
| 47986 | relatoras | 1 |
| 47987 | relativos | 1 |
| 47988 | relate | 1 |
| 47989 | relatares | 1 |
| 47990 | relatar | 1 |
| 47991 | relataba | 1 |
| 47992 | relata | 1 |
| 47993 | relasos | 1 |
| 47994 | relampagueaban | 1 |
| 47995 | relamiendo | 1 |
| 47996 | relámete | 1 |
| 47997 | relamerse | 1 |
| 47998 | relajar | 1 |
| 47999 | relajamiento | 1 |
| 48000 | relajado | 1 |
| 48001 | relajadas | 1 |
| 48002 | relacionase | 1 |
| 48003 | relacionara | 1 |
| 48004 | relacionar | 1 |
| 48005 | relacionado | 1 |
| 48006 | relacionada | 1 |
| 48007 | relacionaban | 1 |
| 48008 | relaciona | 1 |
| 48009 | relacion | 1 |
| 48010 | rejuvenecimiento | 1 |
| 48011 | rejuveneciendo | 1 |
| 48012 | rejuvenecerle | 1 |
| 48013 | rejuvenece | 1 |
| 48014 | rejones | 1 |
| 48015 | rejalgar | 1 |
| 48016 | reivindicar | 1 |
| 48017 | reivindicación | 1 |
| 48018 | reiteráronse | 1 |
| 48019 | reiterándole | 1 |
| 48020 | reiterando | 1 |
| 48021 | reiteraban | 1 |
| 48022 | reírte | 1 |
| 48023 | reíros | 1 |
| 48024 | reírlas | 1 |
| 48025 | reirías | 1 |
| 48026 | reiré | 1 |
| 48027 | reirán | 1 |
| 48028 | reintegraría | 1 |
| 48029 | reintegrado | 1 |
| 48030 | reintegracion | 1 |
| 48031 | reincorporóse | 1 |
| 48032 | reincidir | 1 |
| 48033 | reincidiese | 1 |
| 48034 | reincidente | 1 |
| 48035 | reinaría | 1 |
| 48036 | reinara | 1 |
| 48037 | reimunda | 1 |
| 48038 | reimprimirlo | 1 |
| 48039 | reimpresiones | 1 |
| 48040 | reímos | 1 |
| 48041 | reíme | 1 |
| 48042 | reílle | 1 |
| 48043 | reídas | 1 |
| 48044 | reíamos | 1 |
| 48045 | reí | 1 |
| 48046 | rehuyria | 1 |
| 48047 | rehuyre | 1 |
| 48048 | rehuyr | 1 |
| 48049 | rehúya | 1 |
| 48050 | rehusólo | 1 |
| 48051 | rehúso | 1 |
| 48052 | rehusé | 1 |
| 48053 | rehusaua | 1 |
| 48054 | rehusaron | 1 |
| 48055 | rehusaremos | 1 |
| 48056 | rehusar | 1 |
| 48057 | rehusa | 1 |
| 48058 | rehuido | 1 |
| 48059 | rehú | 1 |
| 48060 | rehinchays | 1 |
| 48061 | rehína | 1 |
| 48062 | rehecho | 1 |
| 48063 | rehacerla | 1 |
| 48064 | rehabilitarse | 1 |
| 48065 | reguridad | 1 |
| 48066 | regulam | 1 |
| 48067 | regulados | 1 |
| 48068 | regulada | 1 |
| 48069 | regüeldos | 1 |
| 48070 | regué | 1 |
| 48071 | reguapa | 1 |
| 48072 | regrese | 1 |
| 48073 | regresase | 1 |
| 48074 | regresando | 1 |
| 48075 | regresamos | 1 |
| 48076 | regresa | 1 |
| 48077 | regrande | 1 |
| 48078 | regostóse | 1 |
| 48079 | regolver | 1 |
| 48080 | regoldaba | 1 |
| 48081 | regodeo | 1 |
| 48082 | regocijen | 1 |
| 48083 | regocíjate | 1 |
| 48084 | regocijarse | 1 |
| 48085 | regocijarnos | 1 |
| 48086 | regocijándose | 1 |
| 48087 | regocijan | 1 |
| 48088 | regocijalle | 1 |
| 48089 | regocijadores | 1 |
| 48090 | regocijador | 1 |
| 48091 | regocijadísima | 1 |
| 48092 | regocijadamente | 1 |
| 48093 | regocijad | 1 |
| 48094 | regocijación | 1 |
| 48095 | regocijaban | 1 |
| 48096 | regocija | 1 |
| 48097 | regno | 1 |
| 48098 | regnarent | 1 |
| 48099 | reglamentarios | 1 |
| 48100 | reglamentario | 1 |
| 48101 | reglamentadas | 1 |
| 48102 | reglamentaba | 1 |
| 48103 | regladamente | 1 |
| 48104 | reglada | 1 |
| 48105 | regisvos | 1 |
| 48106 | registre | 1 |
| 48107 | registraron | 1 |
| 48108 | registraremos | 1 |
| 48109 | registrarán | 1 |
| 48110 | registrándole | 1 |
| 48111 | registrados | 1 |
| 48112 | registraban | 1 |
| 48113 | regional | 1 |
| 48114 | region | 1 |
| 48115 | regina | 1 |
| 48116 | regido | 1 |
| 48117 | regidas | 1 |
| 48118 | reges | 1 |
| 48119 | regenerarte | 1 |
| 48120 | regenerarlas | 1 |
| 48121 | regenerado | 1 |
| 48122 | regenerada | 1 |
| 48123 | regeneraciones | 1 |
| 48124 | regeneracion | 1 |
| 48125 | regeneraba | 1 |
| 48126 | rege | 1 |
| 48127 | regazados | 1 |
| 48128 | regatones | 1 |
| 48129 | regato | 1 |
| 48130 | regatear | 1 |
| 48131 | regateando | 1 |
| 48132 | regatean | 1 |
| 48133 | regateado | 1 |
| 48134 | regare | 1 |
| 48135 | regaños | 1 |
| 48136 | regañó | 1 |
| 48137 | regañar | 1 |
| 48138 | regañaban | 1 |
| 48139 | regando | 1 |
| 48140 | regalona | 1 |
| 48141 | regales | 1 |
| 48142 | regalé | 1 |
| 48143 | regale | 1 |
| 48144 | regalaua | 1 |
| 48145 | regalastes | 1 |
| 48146 | regalasen | 1 |
| 48147 | regalas | 1 |
| 48148 | regaláronle | 1 |
| 48149 | regalarnos | 1 |
| 48150 | regalarme | 1 |
| 48151 | regalaremos | 1 |
| 48152 | regalaré | 1 |
| 48153 | regalaran | 1 |
| 48154 | regaláramos | 1 |
| 48155 | regalándose | 1 |
| 48156 | regalalle | 1 |
| 48157 | regalalla | 1 |
| 48158 | regaladísimo | 1 |
| 48159 | regalábame | 1 |
| 48160 | regado | 1 |
| 48161 | regaderas | 1 |
| 48162 | regadera | 1 |
| 48163 | regada | 1 |
| 48164 | refutaría | 1 |
| 48165 | refutara | 1 |
| 48166 | refutación | 1 |
| 48167 | refunfuñas | 1 |
| 48168 | refunfuñan | 1 |
| 48169 | refundiéndose | 1 |
| 48170 | refundida | 1 |
| 48171 | refulgentes | 1 |
| 48172 | refugié | 1 |
| 48173 | refugiándonos | 1 |
| 48174 | refugiados | 1 |
| 48175 | refugiado | 1 |
| 48176 | refugiábanse | 1 |
| 48177 | refugiaban | 1 |
| 48178 | refugiaba | 1 |
| 48179 | refugia | 1 |
| 48180 | refuerza | 1 |
| 48181 | refrigerado | 1 |
| 48182 | refriegues | 1 |
| 48183 | refrescando | 1 |
| 48184 | refrescan | 1 |
| 48185 | refrénate | 1 |
| 48186 | refrenase | 1 |
| 48187 | refrenarse | 1 |
| 48188 | refrenada | 1 |
| 48189 | refregarte | 1 |
| 48190 | refregar | 1 |
| 48191 | refregándole | 1 |
| 48192 | refrancico | 1 |
| 48193 | refractario | 1 |
| 48194 | refractaban | 1 |
| 48195 | reforzoles | 1 |
| 48196 | reforzando | 1 |
| 48197 | reforzado | 1 |
| 48198 | reforzada | 1 |
| 48199 | reformistas | 1 |
| 48200 | reforme | 1 |
| 48201 | reformase | 1 |
| 48202 | reformando | 1 |
| 48203 | refociló | 1 |
| 48204 | refocilo | 1 |
| 48205 | refocilarse | 1 |
| 48206 | refocilarían | 1 |
| 48207 | reflexivos | 1 |
| 48208 | reflexionemos | 1 |
| 48209 | reflexionaba | 1 |
| 48210 | reflejar | 1 |
| 48211 | reflejándose | 1 |
| 48212 | reflejados | 1 |
| 48213 | reflejado | 1 |
| 48214 | reflejadas | 1 |
| 48215 | reflejábase | 1 |
| 48216 | refiriese | 1 |
| 48217 | refirieran | 1 |
| 48218 | refiriera | 1 |
| 48219 | refiriéndolo | 1 |
| 48220 | refirencias | 1 |
| 48221 | refiramos | 1 |
| 48222 | refinarlos | 1 |
| 48223 | refinar | 1 |
| 48224 | refinamientos | 1 |
| 48225 | refinamiento | 1 |
| 48226 | refinados | 1 |
| 48227 | refinadas | 1 |
| 48228 | refiérela | 1 |
| 48229 | refertyr | 1 |
| 48230 | refero | 1 |
| 48231 | referírselas | 1 |
| 48232 | referirme | 1 |
| 48233 | referirían | 1 |
| 48234 | referiría | 1 |
| 48235 | referimos | 1 |
| 48236 | referidlo | 1 |
| 48237 | referíanse | 1 |
| 48238 | referí | 1 |
| 48239 | refeos | 1 |
| 48240 | refacción | 1 |
| 48241 | reencarnación | 1 |
| 48242 | reemplazo | 1 |
| 48243 | reemplazaron | 1 |
| 48244 | reemplazarlas | 1 |
| 48245 | reemplazado | 1 |
| 48246 | reedificada | 1 |
| 48247 | reduzido | 1 |
| 48248 | redúzgase | 1 |
| 48249 | reduze | 1 |
| 48250 | reduxiste | 1 |
| 48251 | reduplicado | 1 |
| 48252 | redundantes | 1 |
| 48253 | redundancia | 1 |
| 48254 | redundan | 1 |
| 48255 | redújose | 1 |
| 48256 | redujeron | 1 |
| 48257 | reduje | 1 |
| 48258 | réduite | 1 |
| 48259 | reductos | 1 |
| 48260 | reducto | 1 |
| 48261 | reducirte | 1 |
| 48262 | reducirme | 1 |
| 48263 | reducirlo | 1 |
| 48264 | reducirá | 1 |
| 48265 | reduçir | 1 |
| 48266 | reducille | 1 |
| 48267 | reduciéndose | 1 |
| 48268 | reduciéndolo | 1 |
| 48269 | reduciéndole | 1 |
| 48270 | reduciéndolas | 1 |
| 48271 | reducíansele | 1 |
| 48272 | redúcese | 1 |
| 48273 | redruejas | 1 |
| 48274 | redropelo | 1 |
| 48275 | redrar | 1 |
| 48276 | redondos | 1 |
| 48277 | redondita | 1 |
| 48278 | redondeza | 1 |
| 48279 | redondel | 1 |
| 48280 | redondear | 1 |
| 48281 | redondeado | 1 |
| 48282 | redondamente | 1 |
| 48283 | redomillas | 1 |
| 48284 | redomilla | 1 |
| 48285 | redomas | 1 |
| 48286 | redomadona | 1 |
| 48287 | redoblaron | 1 |
| 48288 | redoblaba | 1 |
| 48289 | redivivo | 1 |
| 48290 | rediviva | 1 |
| 48291 | redingote | 1 |
| 48292 | redimirse | 1 |
| 48293 | redimirle | 1 |
| 48294 | redimiendo | 1 |
| 48295 | redimidos | 1 |
| 48296 | redimidas | 1 |
| 48297 | rediman | 1 |
| 48298 | redima | 1 |
| 48299 | redentorista | 1 |
| 48300 | redenciones | 1 |
| 48301 | redencion | 1 |
| 48302 | redemir | 1 |
| 48303 | redecilla | 1 |
| 48304 | reddes | 1 |
| 48305 | redaño | 1 |
| 48306 | redada | 1 |
| 48307 | redactaré | 1 |
| 48308 | redactándolo | 1 |
| 48309 | redactado | 1 |
| 48310 | redactaban | 1 |
| 48311 | redactaba | 1 |
| 48312 | recurrió | 1 |
| 48313 | recurren | 1 |
| 48314 | recuperó | 1 |
| 48315 | reculó | 1 |
| 48316 | recuéstate | 1 |
| 48317 | recuestando | 1 |
| 48318 | recuestaban | 1 |
| 48319 | recueros | 1 |
| 48320 | recuerden | 1 |
| 48321 | recuérdanme | 1 |
| 48322 | recuenta | 1 |
| 48323 | recudieron | 1 |
| 48324 | rectórico | 1 |
| 48325 | rectorías | 1 |
| 48326 | rectilíneas | 1 |
| 48327 | rectificando | 1 |
| 48328 | recte | 1 |
| 48329 | rectángulos | 1 |
| 48330 | rectángulo | 1 |
| 48331 | rectangular | 1 |
| 48332 | rectae | 1 |
| 48333 | recrudecía | 1 |
| 48334 | recriminación | 1 |
| 48335 | recreos | 1 |
| 48336 | recrearía | 1 |
| 48337 | recrearan | 1 |
| 48338 | recreándonos | 1 |
| 48339 | recreando | 1 |
| 48340 | recreado | 1 |
| 48341 | recreábase | 1 |
| 48342 | recostole | 1 |
| 48343 | recosté | 1 |
| 48344 | recostase | 1 |
| 48345 | recostarme | 1 |
| 48346 | recostándose | 1 |
| 48347 | recostados | 1 |
| 48348 | recortaran | 1 |
| 48349 | recortándolo | 1 |
| 48350 | recortado | 1 |
| 48351 | recorro | 1 |
| 48352 | recorriese | 1 |
| 48353 | recorridos | 1 |
| 48354 | recorrida | 1 |
| 48355 | recorrí | 1 |
| 48356 | recorrerá | 1 |
| 48357 | recorred | 1 |
| 48358 | recordasen | 1 |
| 48359 | recordasedes | 1 |
| 48360 | recordase | 1 |
| 48361 | recordarlas | 1 |
| 48362 | recordarla | 1 |
| 48363 | recordaremos | 1 |
| 48364 | recordaré | 1 |
| 48365 | recordará | 1 |
| 48366 | recordara | 1 |
| 48367 | recordándote | 1 |
| 48368 | recordadas | 1 |
| 48369 | recordada | 1 |
| 48370 | recopilación | 1 |
| 48371 | reconvenyr | 1 |
| 48372 | reconvengas | 1 |
| 48373 | reconvençión | 1 |
| 48374 | reconstruí | 1 |
| 48375 | reconstituyentes | 1 |
| 48376 | reconquistar | 1 |
| 48377 | reconquista | 1 |
| 48378 | reconozcamos | 1 |
| 48379 | reconoscimiento | 1 |
| 48380 | reconociole | 1 |
| 48381 | reconocimos | 1 |
| 48382 | reconocimientos | 1 |
| 48383 | reconociera | 1 |
| 48384 | reconociéndolos | 1 |
| 48385 | reconociéndole | 1 |
| 48386 | reconocíamos | 1 |
| 48387 | reconocerlos | 1 |
| 48388 | reconocerlas | 1 |
| 48389 | reconoceremos | 1 |
| 48390 | reconoceré | 1 |
| 48391 | reconocerá | 1 |
| 48392 | reconocemos | 1 |
| 48393 | recondenada | 1 |
| 48394 | reconcilió | 1 |
| 48395 | reconciliémonos | 1 |
| 48396 | reconciliase | 1 |
| 48397 | reconciliarme | 1 |
| 48398 | reconciliaría | 1 |
| 48399 | reconciliaré | 1 |
| 48400 | reconciliarás | 1 |
| 48401 | reconcilian | 1 |
| 48402 | reconciliaban | 1 |
| 48403 | reconciliábamos | 1 |
| 48404 | reconcentrado | 1 |
| 48405 | reconcentradas | 1 |
| 48406 | reconcentrada | 1 |
| 48407 | recomponía | 1 |
| 48408 | recompensó | 1 |
| 48409 | recompensas | 1 |
| 48410 | recompensarte | 1 |
| 48411 | recompensara | 1 |
| 48412 | recompensallas | 1 |
| 48413 | recompensados | 1 |
| 48414 | recompensado | 1 |
| 48415 | recompensaba | 1 |
| 48416 | recomiendan | 1 |
| 48417 | recomendase | 1 |
| 48418 | recomendarles | 1 |
| 48419 | recomendarle | 1 |
| 48420 | recomendarla | 1 |
| 48421 | recomendaremos | 1 |
| 48422 | recomendando | 1 |
| 48423 | recomendable | 1 |
| 48424 | recomendaban | 1 |
| 48425 | recolectado | 1 |
| 48426 | recojas | 1 |
| 48427 | recojan | 1 |
| 48428 | recogímonos | 1 |
| 48429 | recogiéronse | 1 |
| 48430 | recogiéndome | 1 |
| 48431 | recogiéndolos | 1 |
| 48432 | recogiéndolo | 1 |
| 48433 | recogiéndole | 1 |
| 48434 | recogiéndolas | 1 |
| 48435 | recogidamente | 1 |
| 48436 | recogia | 1 |
| 48437 | recogernos | 1 |
| 48438 | recogerles | 1 |
| 48439 | recogerían | 1 |
| 48440 | recogería | 1 |
| 48441 | recogerá | 1 |
| 48442 | recogeos | 1 |
| 48443 | recogella | 1 |
| 48444 | recodos | 1 |
| 48445 | recocido | 1 |
| 48446 | recobré | 1 |
| 48447 | recobre | 1 |
| 48448 | recobraste | 1 |
| 48449 | recobrarle | 1 |
| 48450 | recobraría | 1 |
| 48451 | recobrará | 1 |
| 48452 | recobrara | 1 |
| 48453 | recobran | 1 |
| 48454 | recoba | 1 |
| 48455 | reclutaba | 1 |
| 48456 | recluso | 1 |
| 48457 | reclinó | 1 |
| 48458 | recline | 1 |
| 48459 | reclinatorios | 1 |
| 48460 | reclinarse | 1 |
| 48461 | reclinaron | 1 |
| 48462 | reclinados | 1 |
| 48463 | reclinado | 1 |
| 48464 | reclamos | 1 |
| 48465 | reclamola | 1 |
| 48466 | reclamó | 1 |
| 48467 | reclamas | 1 |
| 48468 | reclamarlo | 1 |
| 48469 | reclamaríamos | 1 |
| 48470 | reclamará | 1 |
| 48471 | reciura | 1 |
| 48472 | recitante | 1 |
| 48473 | recitándolas | 1 |
| 48474 | recitados | 1 |
| 48475 | recitábale | 1 |
| 48476 | reciprocidad | 1 |
| 48477 | reçios | 1 |
| 48478 | recintos | 1 |
| 48479 | recibiste | 1 |
| 48480 | recibirnos | 1 |
| 48481 | recibirlas | 1 |
| 48482 | recibiria | 1 |
| 48483 | recibirás | 1 |
| 48484 | recibira | 1 |
| 48485 | recibiome | 1 |
| 48486 | recibiólo | 1 |
| 48487 | recibióla | 1 |
| 48488 | recibio | 1 |
| 48489 | recibimos | 1 |
| 48490 | recibillo | 1 |
| 48491 | recibille | 1 |
| 48492 | recibiesse | 1 |
| 48493 | recibiesen | 1 |
| 48494 | recibiéronse | 1 |
| 48495 | recibiere | 1 |
| 48496 | recibiéndome | 1 |
| 48497 | recibiéndole | 1 |
| 48498 | recibiéndolas | 1 |
| 48499 | recibidos | 1 |
| 48500 | recibías | 1 |
| 48501 | recibíamos | 1 |
| 48502 | recibeme | 1 |
| 48503 | recíbelo | 1 |
| 48504 | recíbele | 1 |
| 48505 | reciban | 1 |
| 48506 | reçiamente | 1 |
| 48507 | rechupidos | 1 |
| 48508 | rechupete | 1 |
| 48509 | rechupando | 1 |
| 48510 | rechupado | 1 |
| 48511 | rechinó | 1 |
| 48512 | rechinido | 1 |
| 48513 | rechinasen | 1 |
| 48514 | rechinaran | 1 |
| 48515 | rechinantes | 1 |
| 48516 | rechinando | 1 |
| 48517 | rechinan | 1 |
| 48518 | rechina | 1 |
| 48519 | rechazaua | 1 |
| 48520 | rechazarlo | 1 |
| 48521 | rechazarle | 1 |
| 48522 | rechazaría | 1 |
| 48523 | rechazara | 1 |
| 48524 | rechazándola | 1 |
| 48525 | rechazadas | 1 |
| 48526 | rechaza | 1 |
| 48527 | rechacemos | 1 |
| 48528 | reçevirlo | 1 |
| 48529 | recetes | 1 |
| 48530 | recetáronsele | 1 |
| 48531 | recetaría | 1 |
| 48532 | recetado | 1 |
| 48533 | recetada | 1 |
| 48534 | recetábale | 1 |
| 48535 | recento | 1 |
| 48536 | recentales | 1 |
| 48537 | recemos | 1 |
| 48538 | recelosas | 1 |
| 48539 | receló | 1 |
| 48540 | recelaua | 1 |
| 48541 | recelarme | 1 |
| 48542 | recelar | 1 |
| 48543 | recelaba | 1 |
| 48544 | recebiros | 1 |
| 48545 | recebirme | 1 |
| 48546 | recebirlas | 1 |
| 48547 | recebiremos | 1 |
| 48548 | recebiran | 1 |
| 48549 | reçebir | 1 |
| 48550 | recebimiento | 1 |
| 48551 | recebillos | 1 |
| 48552 | recebillo | 1 |
| 48553 | recebidme | 1 |
| 48554 | recebíale | 1 |
| 48555 | recebia | 1 |
| 48556 | recebi | 1 |
| 48557 | recayese | 1 |
| 48558 | recayera | 1 |
| 48559 | recaudados | 1 |
| 48560 | recaudación | 1 |
| 48561 | recataré | 1 |
| 48562 | recatándose | 1 |
| 48563 | recargo | 1 |
| 48564 | recargaba | 1 |
| 48565 | recapitule | 1 |
| 48566 | recapitulando | 1 |
| 48567 | recapacité | 1 |
| 48568 | recapacite | 1 |
| 48569 | recapacitando | 1 |
| 48570 | reçando | 1 |
| 48571 | recancanilla | 1 |
| 48572 | recambio | 1 |
| 48573 | recaló | 1 |
| 48574 | recalentándolos | 1 |
| 48575 | recalentaban | 1 |
| 48576 | recalcitrantes | 1 |
| 48577 | recalcar | 1 |
| 48578 | recalcando | 1 |
| 48579 | recalado | 1 |
| 48580 | recaerá | 1 |
| 48581 | recae | 1 |
| 48582 | recabo | 1 |
| 48583 | recabé | 1 |
| 48584 | recabdó | 1 |
| 48585 | recabde | 1 |
| 48586 | recabdares | 1 |
| 48587 | rebuznasen | 1 |
| 48588 | rebuznase | 1 |
| 48589 | rebuznaréis | 1 |
| 48590 | rebuznaré | 1 |
| 48591 | rebuznara | 1 |
| 48592 | rebuznadores | 1 |
| 48593 | rebuznador | 1 |
| 48594 | rebuznado | 1 |
| 48595 | rebuznaban | 1 |
| 48596 | rebuzna | 1 |
| 48597 | rebusquémosle | 1 |
| 48598 | rebusque | 1 |
| 48599 | rebusnar | 1 |
| 48600 | rebusnando | 1 |
| 48601 | rebuscar | 1 |
| 48602 | rebuscado | 1 |
| 48603 | rebuscada | 1 |
| 48604 | rebuscaban | 1 |
| 48605 | rebuscaba | 1 |
| 48606 | rebullicio | 1 |
| 48607 | rebullía | 1 |
| 48608 | rebulléndose | 1 |
| 48609 | rebullen | 1 |
| 48610 | rebulle | 1 |
| 48611 | rebueluo | 1 |
| 48612 | rebueluas | 1 |
| 48613 | rebuelto | 1 |
| 48614 | rebrinquen | 1 |
| 48615 | rebozados | 1 |
| 48616 | rebozadas | 1 |
| 48617 | rebotaron | 1 |
| 48618 | rebotaban | 1 |
| 48619 | rebosaban | 1 |
| 48620 | rebosaba | 1 |
| 48621 | reboluedores | 1 |
| 48622 | rebolcado | 1 |
| 48623 | reblandeció | 1 |
| 48624 | reblandecimiento | 1 |
| 48625 | reblandecido | 1 |
| 48626 | reblandecerlos | 1 |
| 48627 | reblandecer | 1 |
| 48628 | rebentasse | 1 |
| 48629 | rebentarias | 1 |
| 48630 | rebentar | 1 |
| 48631 | rebenacq | 1 |
| 48632 | rebeló | 1 |
| 48633 | rebellas | 1 |
| 48634 | rebeliones | 1 |
| 48635 | rebato | 1 |
| 48636 | rebatada | 1 |
| 48637 | rebata | 1 |
| 48638 | rebasaron | 1 |
| 48639 | rebasaría | 1 |
| 48640 | rebasara | 1 |
| 48641 | rebasar | 1 |
| 48642 | rebasados | 1 |
| 48643 | rebasado | 1 |
| 48644 | rebañaduras | 1 |
| 48645 | rebañaba | 1 |
| 48646 | rebaña | 1 |
| 48647 | rebanaría | 1 |
| 48648 | rebanada | 1 |
| 48649 | rebajos | 1 |
| 48650 | rebajó | 1 |
| 48651 | rebajes | 1 |
| 48652 | rebajase | 1 |
| 48653 | rebajaremos | 1 |
| 48654 | rebajando | 1 |
| 48655 | rebajado | 1 |
| 48656 | rebajada | 1 |
| 48657 | reapertura | 1 |
| 48658 | reaparecieron | 1 |
| 48659 | reaparecía | 1 |
| 48660 | reaparecer | 1 |
| 48661 | reaparecen | 1 |
| 48662 | reanudar | 1 |
| 48663 | reanudados | 1 |
| 48664 | reanuda | 1 |
| 48665 | reanimó | 1 |
| 48666 | reanimase | 1 |
| 48667 | reanimaron | 1 |
| 48668 | reanimarle | 1 |
| 48669 | reanimarla | 1 |
| 48670 | reanima | 1 |
| 48671 | realzarla | 1 |
| 48672 | realzar | 1 |
| 48673 | realzamiento | 1 |
| 48674 | realzado | 1 |
| 48675 | realizase | 1 |
| 48676 | realizarla | 1 |
| 48677 | realizaría | 1 |
| 48678 | realizara | 1 |
| 48679 | realizan | 1 |
| 48680 | realizados | 1 |
| 48681 | realizadas | 1 |
| 48682 | realizable | 1 |
| 48683 | realizaban | 1 |
| 48684 | realizaba | 1 |
| 48685 | realito | 1 |
| 48686 | realistas | 1 |
| 48687 | realetes | 1 |
| 48688 | reacias | 1 |
| 48689 | reacciones | 1 |
| 48690 | reaccionarios | 1 |
| 48691 | razonan | 1 |
| 48692 | razonador | 1 |
| 48693 | razona | 1 |
| 48694 | razas | 1 |
| 48695 | rayuela | 1 |
| 48696 | raynela | 1 |
| 48697 | raydo | 1 |
| 48698 | rayauan | 1 |
| 48699 | rayando | 1 |
| 48700 | rayana | 1 |
| 48701 | rayaditas | 1 |
| 48702 | ravia | 1 |
| 48703 | rávena | 1 |
| 48704 | rauio | 1 |
| 48705 | rauia | 1 |
| 48706 | raudos | 1 |
| 48707 | raudo | 1 |
| 48708 | raube | 1 |
| 48709 | ratopes | 1 |
| 48710 | ratoneras | 1 |
| 48711 | ratonar | 1 |
| 48712 | ratonados | 1 |
| 48713 | ratonada | 1 |
| 48714 | raton | 1 |
| 48715 | ratitos | 1 |
| 48716 | ratificó | 1 |
| 48717 | ratifico | 1 |
| 48718 | rateros | 1 |
| 48719 | rateras | 1 |
| 48720 | ratera | 1 |
| 48721 | rasuras | 1 |
| 48722 | rastrojo | 1 |
| 48723 | rastrillos | 1 |
| 48724 | rastrillado | 1 |
| 48725 | rastreros | 1 |
| 48726 | rastrero | 1 |
| 48727 | rastrera | 1 |
| 48728 | rastreando | 1 |
| 48729 | rastrea | 1 |
| 48730 | rastillo | 1 |
| 48731 | rasque | 1 |
| 48732 | raspe | 1 |
| 48733 | raspándolo | 1 |
| 48734 | raspados | 1 |
| 48735 | raspaba | 1 |
| 48736 | raspa | 1 |
| 48737 | rasión | 1 |
| 48738 | rasgues | 1 |
| 48739 | rasgueos | 1 |
| 48740 | rasgueo | 1 |
| 48741 | rasguearlo | 1 |
| 48742 | rasgueada | 1 |
| 48743 | rasgases | 1 |
| 48744 | rasgarse | 1 |
| 48745 | rasgarla | 1 |
| 48746 | rasgare | 1 |
| 48747 | rasgará | 1 |
| 48748 | rasgara | 1 |
| 48749 | rasgándome | 1 |
| 48750 | rasgadas | 1 |
| 48751 | rascuñado | 1 |
| 48752 | rascuno | 1 |
| 48753 | rascunes | 1 |
| 48754 | rascóse | 1 |
| 48755 | rascarnos | 1 |
| 48756 | rascarme | 1 |
| 48757 | rascaría | 1 |
| 48758 | rascaña | 1 |
| 48759 | rascándote | 1 |
| 48760 | rascándonos | 1 |
| 48761 | rascando | 1 |
| 48762 | rascan | 1 |
| 48763 | rascamos | 1 |
| 48764 | ráscame | 1 |
| 48765 | rascador | 1 |
| 48766 | rascado | 1 |
| 48767 | rascacauallos | 1 |
| 48768 | rarificaciones | 1 |
| 48769 | raridad | 1 |
| 48770 | raquitismo | 1 |
| 48771 | raquíticos | 1 |
| 48772 | raptos | 1 |
| 48773 | rapto | 1 |
| 48774 | rapsodias | 1 |
| 48775 | rapossa | 1 |
| 48776 | raposas | 1 |
| 48777 | rapido | 1 |
| 48778 | rapidísimo | 1 |
| 48779 | rapidísimamente | 1 |
| 48780 | rapidísima | 1 |
| 48781 | rapidas | 1 |
| 48782 | rapazuelo | 1 |
| 48783 | rapasen | 1 |
| 48784 | rapase | 1 |
| 48785 | rapas | 1 |
| 48786 | raparte | 1 |
| 48787 | raparía | 1 |
| 48788 | rapando | 1 |
| 48789 | rapador | 1 |
| 48790 | rapado | 1 |
| 48791 | rapacería | 1 |
| 48792 | rapaça | 1 |
| 48793 | rapaba | 1 |
| 48794 | rapa | 1 |
| 48795 | ranero | 1 |
| 48796 | ranelagh | 1 |
| 48797 | randado | 1 |
| 48798 | ranciosos | 1 |
| 48799 | rancioso | 1 |
| 48800 | rancia | 1 |
| 48801 | ramplona | 1 |
| 48802 | rampas | 1 |
| 48803 | ramojo | 1 |
| 48804 | ramificaciones | 1 |
| 48805 | ramerilla | 1 |
| 48806 | rameados | 1 |
| 48807 | rameaditas | 1 |
| 48808 | rameadas | 1 |
| 48809 | ramayana | 1 |
| 48810 | ramalazo | 1 |
| 48811 | ramal | 1 |
| 48812 | rallando | 1 |
| 48813 | ralla | 1 |
| 48814 | raleza | 1 |
| 48815 | raldo | 1 |
| 48816 | ralas | 1 |
| 48817 | rala | 1 |
| 48818 | rajitas | 1 |
| 48819 | rajatabla | 1 |
| 48820 | rajada | 1 |
| 48821 | raíles | 1 |
| 48822 | raídos | 1 |
| 48823 | raídas | 1 |
| 48824 | raheses | 1 |
| 48825 | raheces | 1 |
| 48826 | rafigurarle | 1 |
| 48827 | rafaelesco | 1 |
| 48828 | radio | 1 |
| 48829 | radicaba | 1 |
| 48830 | radïante | 1 |
| 48831 | rada | 1 |
| 48832 | racionó | 1 |
| 48833 | racioncita | 1 |
| 48834 | racionarse | 1 |
| 48835 | racionarnos | 1 |
| 48836 | racionalmente | 1 |
| 48837 | racionalistas | 1 |
| 48838 | racionalismo | 1 |
| 48839 | raciona | 1 |
| 48840 | racion | 1 |
| 48841 | raciocinó | 1 |
| 48842 | raciocina | 1 |
| 48843 | racimillos | 1 |
| 48844 | raças | 1 |
| 48845 | rabygalga | 1 |
| 48846 | rabultados | 1 |
| 48847 | rabito | 1 |
| 48848 | rabiosito | 1 |
| 48849 | rabiosilla | 1 |
| 48850 | rabietinas | 1 |
| 48851 | rabias | 1 |
| 48852 | rabiará | 1 |
| 48853 | rabian | 1 |
| 48854 | rabiaban | 1 |
| 48855 | rabagones | 1 |
| 48856 | rabadán | 1 |
| 48857 | quum | 1 |
| 48858 | quomodo | 1 |
| 48859 | quixotes | 1 |
| 48860 | quixera | 1 |
| 48861 | quixadas | 1 |
| 48862 | quivoquiar | 1 |
| 48863 | quitóseme | 1 |
| 48864 | quitósele | 1 |
| 48865 | quitóme | 1 |
| 48866 | quitole | 1 |
| 48867 | quíteseme | 1 |
| 48868 | quítesele | 1 |
| 48869 | quítenseme | 1 |
| 48870 | quítensele | 1 |
| 48871 | quitemos | 1 |
| 48872 | quíteme | 1 |
| 48873 | quítele | 1 |
| 48874 | quitat | 1 |
| 48875 | quitasteme | 1 |
| 48876 | quitasse | 1 |
| 48877 | quitasol | 1 |
| 48878 | quitases | 1 |
| 48879 | quitásemos | 1 |
| 48880 | quítaselo | 1 |
| 48881 | quitártelo | 1 |
| 48882 | quitártela | 1 |
| 48883 | quitárselas | 1 |
| 48884 | quitárosle | 1 |
| 48885 | quitárosla | 1 |
| 48886 | quitáronselo | 1 |
| 48887 | quitáronsela | 1 |
| 48888 | quitáronme | 1 |
| 48889 | quitáronlas | 1 |
| 48890 | quitárnosle | 1 |
| 48891 | quitármelos | 1 |
| 48892 | quitarleslas | 1 |
| 48893 | quitaríase | 1 |
| 48894 | quitaren | 1 |
| 48895 | quitare | 1 |
| 48896 | quitáramos | 1 |
| 48897 | quitaos | 1 |
| 48898 | quítanme | 1 |
| 48899 | quitanles | 1 |
| 48900 | quitándoselas | 1 |
| 48901 | quitándosela | 1 |
| 48902 | quitándola | 1 |
| 48903 | quitámossele | 1 |
| 48904 | quitamela | 1 |
| 48905 | quitame | 1 |
| 48906 | quitalla | 1 |
| 48907 | quítalas | 1 |
| 48908 | quitáis | 1 |
| 48909 | quitaguas | 1 |
| 48910 | quitádote | 1 |
| 48911 | quitados | 1 |
| 48912 | quitádmelo | 1 |
| 48913 | quitádmele | 1 |
| 48914 | quitada | 1 |
| 48915 | quitación | 1 |
| 48916 | quitábamos | 1 |
| 48917 | quisyese | 1 |
| 48918 | quisyeres | 1 |
| 48919 | quisque | 1 |
| 48920 | quisome | 1 |
| 48921 | quísole | 1 |
| 48922 | quisistes | 1 |
| 48923 | quisístelo | 1 |
| 48924 | quisímosle | 1 |
| 48925 | quisiessen | 1 |
| 48926 | quisiésedes | 1 |
| 48927 | quisiéronse | 1 |
| 48928 | quisiéronle | 1 |
| 48929 | quisieridísimis | 1 |
| 48930 | quisierades | 1 |
| 48931 | quiselo | 1 |
| 48932 | quísele | 1 |
| 48933 | quisá | 1 |
| 48934 | quirúrgicamente | 1 |
| 48935 | quirúrgica | 1 |
| 48936 | quirocia | 1 |
| 48937 | quirieleisón | 1 |
| 48938 | quiquiriquí | 1 |
| 48939 | quintiliano | 1 |
| 48940 | quinti | 1 |
| 48941 | quintan | 1 |
| 48942 | quintal | 1 |
| 48943 | quintaesencia | 1 |
| 48944 | quinolicas | 1 |
| 48945 | quinina | 1 |
| 48946 | quincallería | 1 |
| 48947 | quinas | 1 |
| 48948 | quina | 1 |
| 48949 | quimeristas | 1 |
| 48950 | quiméricos | 1 |
| 48951 | quima | 1 |
| 48952 | quilo | 1 |
| 48953 | quilata | 1 |
| 48954 | quijotísimo | 1 |
| 48955 | quijotescos | 1 |
| 48956 | quijotesco | 1 |
| 48957 | quijotada | 1 |
| 48958 | quij | 1 |
| 48959 | quigéredes | 1 |
| 48960 | quietismo | 1 |
| 48961 | quietarse | 1 |
| 48962 | quiérovos | 1 |
| 48963 | quierovos | 1 |
| 48964 | quierote | 1 |
| 48965 | quiéroos | 1 |
| 48966 | quiérom | 1 |
| 48967 | quierolo | 1 |
| 48968 | quiérolas | 1 |
| 48969 | quiérola | 1 |
| 48970 | quierola | 1 |
| 48971 | quiería | 1 |
| 48972 | quiéreste | 1 |
| 48973 | quiereslo | 1 |
| 48974 | quiereseles | 1 |
| 48975 | quiérente | 1 |
| 48976 | quierénse | 1 |
| 48977 | quiérenme | 1 |
| 48978 | quiérem | 1 |
| 48979 | quiérelo | 1 |
| 48980 | quiérasme | 1 |
| 48981 | quiéralo | 1 |
| 48982 | quiérala | 1 |
| 48983 | quieles | 1 |
| 48984 | quiebros | 1 |
| 48985 | quiébrome | 1 |
| 48986 | quiebrasnos | 1 |
| 48987 | quidprocuos | 1 |
| 48988 | quidem | 1 |
| 48989 | quibus | 1 |
| 48990 | quexosos | 1 |
| 48991 | quexóse | 1 |
| 48992 | quexome | 1 |
| 48993 | quexaua | 1 |
| 48994 | quexasseme | 1 |
| 48995 | quexase | 1 |
| 48996 | quexarme | 1 |
| 48997 | quexaran | 1 |
| 48998 | quexades | 1 |
| 48999 | quevedesca | 1 |
| 49000 | quesyste | 1 |
| 49001 | quesuelos | 1 |
| 49002 | questioncillas | 1 |
| 49003 | quessiese | 1 |
| 49004 | quésome | 1 |
| 49005 | quesitos | 1 |
| 49006 | quesito | 1 |
| 49007 | quesistes | 1 |
| 49008 | quesillo | 1 |
| 49009 | quesieron | 1 |
| 49010 | quese | 1 |
| 49011 | querríes | 1 |
| 49012 | querríedes | 1 |
| 49013 | querríades | 1 |
| 49014 | querremos | 1 |
| 49015 | querrello | 1 |
| 49016 | querráse | 1 |
| 49017 | querránme | 1 |
| 49018 | querran | 1 |
| 49019 | queriéndome | 1 |
| 49020 | queriéndolos | 1 |
| 49021 | queriéndola | 1 |
| 49022 | queriéndol | 1 |
| 49023 | queríe | 1 |
| 49024 | queridísimos | 1 |
| 49025 | queríanle | 1 |
| 49026 | queríalos | 1 |
| 49027 | queríalo | 1 |
| 49028 | queríale | 1 |
| 49029 | queríala | 1 |
| 49030 | querí | 1 |
| 49031 | quereys | 1 |
| 49032 | queretnos | 1 |
| 49033 | queretmos | 1 |
| 49034 | queret | 1 |
| 49035 | querérselas | 1 |
| 49036 | quereres | 1 |
| 49037 | querencioso | 1 |
| 49038 | querenciosa | 1 |
| 49039 | querémoslas | 1 |
| 49040 | querelloso | 1 |
| 49041 | querellarse | 1 |
| 49042 | querellar | 1 |
| 49043 | querellante | 1 |
| 49044 | queréllanse | 1 |
| 49045 | querellándos | 1 |
| 49046 | querellan | 1 |
| 49047 | querellado | 1 |
| 49048 | quereldo | 1 |
| 49049 | queréislo | 1 |
| 49050 | queredla | 1 |
| 49051 | querays | 1 |
| 49052 | querámonos | 1 |
| 49053 | quequiera | 1 |
| 49054 | quepan | 1 |
| 49055 | quepamos | 1 |
| 49056 | quenerral | 1 |
| 49057 | quemé | 1 |
| 49058 | quemazón | 1 |
| 49059 | quemaua | 1 |
| 49060 | quémate | 1 |
| 49061 | quemasteis | 1 |
| 49062 | quemaste | 1 |
| 49063 | quémasle | 1 |
| 49064 | quemarnos | 1 |
| 49065 | quemarlo | 1 |
| 49066 | quemarle | 1 |
| 49067 | quemaré | 1 |
| 49068 | quémanse | 1 |
| 49069 | quemándose | 1 |
| 49070 | quemándolas | 1 |
| 49071 | quemallos | 1 |
| 49072 | quemadura | 1 |
| 49073 | quemada | 1 |
| 49074 | quemaban | 1 |
| 49075 | quem | 1 |
| 49076 | quejumbrosos | 1 |
| 49077 | quejumbrosas | 1 |
| 49078 | quejóse | 1 |
| 49079 | quéjese | 1 |
| 49080 | quejes | 1 |
| 49081 | quejéis | 1 |
| 49082 | quejáronse | 1 |
| 49083 | quejaron | 1 |
| 49084 | quejaré | 1 |
| 49085 | quejaos | 1 |
| 49086 | quejana | 1 |
| 49087 | quejábaseme | 1 |
| 49088 | quejábase | 1 |
| 49089 | quejabas | 1 |
| 49090 | quejábamonos | 1 |
| 49091 | quejábades | 1 |
| 49092 | quefia | 1 |
| 49093 | quedóme | 1 |
| 49094 | quédome | 1 |
| 49095 | quedillo | 1 |
| 49096 | quédesele | 1 |
| 49097 | quédente | 1 |
| 49098 | quedemos | 1 |
| 49099 | quedémonos | 1 |
| 49100 | quedava | 1 |
| 49101 | quedauanle | 1 |
| 49102 | quedauan | 1 |
| 49103 | quedásemos | 1 |
| 49104 | quedásedes | 1 |
| 49105 | quedarlo | 1 |
| 49106 | quedarían | 1 |
| 49107 | quedaríamos | 1 |
| 49108 | quedaria | 1 |
| 49109 | quedaréme | 1 |
| 49110 | quedaréis | 1 |
| 49111 | quedaráse | 1 |
| 49112 | quedáramos | 1 |
| 49113 | quedárades | 1 |
| 49114 | quedándome | 1 |
| 49115 | quedándoles | 1 |
| 49116 | quedáis | 1 |
| 49117 | quedábame | 1 |
| 49118 | queças | 1 |
| 49119 | queça | 1 |
| 49120 | quebro | 1 |
| 49121 | quebreys | 1 |
| 49122 | quebremos | 1 |
| 49123 | quebréis | 1 |
| 49124 | quebredes | 1 |
| 49125 | quebre | 1 |
| 49126 | quebraste | 1 |
| 49127 | quebrasses | 1 |
| 49128 | quebraron | 1 |
| 49129 | quebrarle | 1 |
| 49130 | quebrarla | 1 |
| 49131 | quebraría | 1 |
| 49132 | quebraria | 1 |
| 49133 | quebrare | 1 |
| 49134 | quebraras | 1 |
| 49135 | quebrará | 1 |
| 49136 | quebrantarse | 1 |
| 49137 | quebrantáredes | 1 |
| 49138 | quebrantara | 1 |
| 49139 | quebrantamientos | 1 |
| 49140 | quebrantadas | 1 |
| 49141 | quebradizo | 1 |
| 49142 | queblantedes | 1 |
| 49143 | queblantada | 1 |
| 49144 | quatorzeno | 1 |
| 49145 | quatorçe | 1 |
| 49146 | quatitur | 1 |
| 49147 | quartero | 1 |
| 49148 | quaresm | 1 |
| 49149 | quantioso | 1 |
| 49150 | quantias | 1 |
| 49151 | quanti | 1 |
| 49152 | quánta | 1 |
| 49153 | quant | 1 |
| 49154 | quándo | 1 |
| 49155 | qualsequier | 1 |
| 49156 | qualis | 1 |
| 49157 | qualidades | 1 |
| 49158 | quærite | 1 |
| 49159 | quæ | 1 |
| 49160 | quadrupea | 1 |
| 49161 | quadrillos | 1 |
| 49162 | quadrilla | 1 |
| 49163 | quadriles | 1 |
| 49164 | quadriella | 1 |
| 49165 | quadrado | 1 |
| 49166 | quadernos | 1 |
| 49167 | quaderna | 1 |
| 49168 | qartos | 1 |
| 49169 | pytofleras | 1 |
| 49170 | pyñones | 1 |
| 49171 | pyntóle | 1 |
| 49172 | pyntol | 1 |
| 49173 | pynté | 1 |
| 49174 | pyntase | 1 |
| 49175 | pyntalla | 1 |
| 49176 | pyntada | 1 |
| 49177 | pyno | 1 |
| 49178 | pynar | 1 |
| 49179 | pydote | 1 |
| 49180 | putrefacción | 1 |
| 49181 | putos | 1 |
| 49182 | putona | 1 |
| 49183 | putillos | 1 |
| 49184 | putillo | 1 |
| 49185 | putico | 1 |
| 49186 | putería | 1 |
| 49187 | putativo | 1 |
| 49188 | putas | 1 |
| 49189 | pústulas | 1 |
| 49190 | pússome | 1 |
| 49191 | pusso | 1 |
| 49192 | pusque | 1 |
| 49193 | púsoseme | 1 |
| 49194 | púsosele | 1 |
| 49195 | pusose | 1 |
| 49196 | púsonos | 1 |
| 49197 | pusome | 1 |
| 49198 | púsolos | 1 |
| 49199 | púsolas | 1 |
| 49200 | pusle | 1 |
| 49201 | pusistes | 1 |
| 49202 | pusilánimo | 1 |
| 49203 | pusilanimo | 1 |
| 49204 | pusilanimidad | 1 |
| 49205 | pusilánime | 1 |
| 49206 | pusiesse | 1 |
| 49207 | pusieses | 1 |
| 49208 | pusiéronsele | 1 |
| 49209 | pusierónse | 1 |
| 49210 | pusiéronmele | 1 |
| 49211 | pusiéronlas | 1 |
| 49212 | pusiéronla | 1 |
| 49213 | pusieres | 1 |
| 49214 | pusieren | 1 |
| 49215 | pusiéredes | 1 |
| 49216 | pusiéramos | 1 |
| 49217 | pusete | 1 |
| 49218 | purulentas | 1 |
| 49219 | purpurinos | 1 |
| 49220 | purpurina | 1 |
| 49221 | purpurear | 1 |
| 49222 | purito | 1 |
| 49223 | puristas | 1 |
| 49224 | purificó | 1 |
| 49225 | purificarla | 1 |
| 49226 | purificará | 1 |
| 49227 | purificado | 1 |
| 49228 | puribus | 1 |
| 49229 | purgó | 1 |
| 49230 | purgo | 1 |
| 49231 | purgara | 1 |
| 49232 | purgar | 1 |
| 49233 | purés | 1 |
| 49234 | puppim | 1 |
| 49235 | puñé | 1 |
| 49236 | puñales | 1 |
| 49237 | puñalero | 1 |
| 49238 | puñadito | 1 |
| 49239 | puña | 1 |
| 49240 | punzamiento | 1 |
| 49241 | punzadoras | 1 |
| 49242 | punzadora | 1 |
| 49243 | punzado | 1 |
| 49244 | punzaban | 1 |
| 49245 | punzaba | 1 |
| 49246 | punturas | 1 |
| 49247 | puntuosas | 1 |
| 49248 | puntualísima | 1 |
| 49249 | puntillo | 1 |
| 49250 | puntillazos | 1 |
| 49251 | puntiagudas | 1 |
| 49252 | puntear | 1 |
| 49253 | punteados | 1 |
| 49254 | punteado | 1 |
| 49255 | puntarme | 1 |
| 49256 | puntares | 1 |
| 49257 | puntado | 1 |
| 49258 | punido | 1 |
| 49259 | punicion | 1 |
| 49260 | pungidos | 1 |
| 49261 | pungido | 1 |
| 49262 | puné | 1 |
| 49263 | pundonorosos | 1 |
| 49264 | pundonorosas | 1 |
| 49265 | pundonores | 1 |
| 49266 | punase | 1 |
| 49267 | punan | 1 |
| 49268 | punaladas | 1 |
| 49269 | punadas | 1 |
| 49270 | puna | 1 |
| 49271 | pumaradas | 1 |
| 49272 | pumarada | 1 |
| 49273 | pulvis | 1 |
| 49274 | pulverizo | 1 |
| 49275 | pulverizarse | 1 |
| 49276 | pulverizar | 1 |
| 49277 | pulverizándose | 1 |
| 49278 | pulverizando | 1 |
| 49279 | pulverizado | 1 |
| 49280 | pulverizadas | 1 |
| 49281 | pulverices | 1 |
| 49282 | pululante | 1 |
| 49283 | pululáis | 1 |
| 49284 | pulsó | 1 |
| 49285 | pulsera | 1 |
| 49286 | pulsado | 1 |
| 49287 | pulsaciones | 1 |
| 49288 | pulpos | 1 |
| 49289 | pulpito | 1 |
| 49290 | pulpitante | 1 |
| 49291 | pulpejo | 1 |
| 49292 | pulpa | 1 |
| 49293 | pulirte | 1 |
| 49294 | pulirse | 1 |
| 49295 | pulió | 1 |
| 49296 | pulimentado | 1 |
| 49297 | puliéndola | 1 |
| 49298 | puliendo | 1 |
| 49299 | pulicena | 1 |
| 49300 | pulen | 1 |
| 49301 | pulchra | 1 |
| 49302 | pulcela | 1 |
| 49303 | pujaste | 1 |
| 49304 | pujada | 1 |
| 49305 | pujaba | 1 |
| 49306 | pugnó | 1 |
| 49307 | pugnes | 1 |
| 49308 | pugnaré | 1 |
| 49309 | pugnado | 1 |
| 49310 | puez | 1 |
| 49311 | puéstoos | 1 |
| 49312 | puéstome | 1 |
| 49313 | puéstole | 1 |
| 49314 | puestecico | 1 |
| 49315 | pués | 1 |
| 49316 | puertocarrero | 1 |
| 49317 | puerte | 1 |
| 49318 | puerros | 1 |
| 49319 | puerquísima | 1 |
| 49320 | puerperio | 1 |
| 49321 | puerperales | 1 |
| 49322 | puerilidades | 1 |
| 49323 | puericia | 1 |
| 49324 | puercas | 1 |
| 49325 | puercamente | 1 |
| 49326 | puercachones | 1 |
| 49327 | puenta | 1 |
| 49328 | puelbro | 1 |
| 49329 | puediera | 1 |
| 49330 | puédevos | 1 |
| 49331 | puédeslo | 1 |
| 49332 | puédesele | 1 |
| 49333 | puedense | 1 |
| 49334 | puédelo | 1 |
| 49335 | puédela | 1 |
| 49336 | puédel | 1 |
| 49337 | pueblecitos | 1 |
| 49338 | pueblecillos | 1 |
| 49339 | pueble | 1 |
| 49340 | pudrirse | 1 |
| 49341 | pudriría | 1 |
| 49342 | pudrirán | 1 |
| 49343 | pudrirá | 1 |
| 49344 | pudriesen | 1 |
| 49345 | pudrían | 1 |
| 49346 | pudorosa | 1 |
| 49347 | pudistes | 1 |
| 49348 | pudieses | 1 |
| 49349 | pudieren | 1 |
| 49350 | pudieremos | 1 |
| 49351 | pudiéredes | 1 |
| 49352 | pudiérate | 1 |
| 49353 | pudiérasele | 1 |
| 49354 | pudiérase | 1 |
| 49355 | pudierais | 1 |
| 49356 | pudiérades | 1 |
| 49357 | pudiéndose | 1 |
| 49358 | púdico | 1 |
| 49359 | pudibundo | 1 |
| 49360 | pudía | 1 |
| 49361 | pucheta | 1 |
| 49362 | pucherito | 1 |
| 49363 | publiquen | 1 |
| 49364 | publiquemos | 1 |
| 49365 | publicista | 1 |
| 49366 | publicase | 1 |
| 49367 | publicas | 1 |
| 49368 | publicaron | 1 |
| 49369 | publicarlos | 1 |
| 49370 | publicarlas | 1 |
| 49371 | publicaría | 1 |
| 49372 | publicará | 1 |
| 49373 | publicara | 1 |
| 49374 | publicantones | 1 |
| 49375 | publicanos | 1 |
| 49376 | publican | 1 |
| 49377 | publicamente | 1 |
| 49378 | publicador | 1 |
| 49379 | ptolomeos | 1 |
| 49380 | psoas | 1 |
| 49381 | psíquico | 1 |
| 49382 | psiques | 1 |
| 49383 | psicólogo | 1 |
| 49384 | psicológicas | 1 |
| 49385 | psicológicamente | 1 |
| 49386 | psicologías | 1 |
| 49387 | pseudomórfico | 1 |
| 49388 | pseudoclásico | 1 |
| 49389 | psé | 1 |
| 49390 | psch | 1 |
| 49391 | psalmo | 1 |
| 49392 | prymera | 1 |
| 49393 | pruuun | 1 |
| 49394 | prusiana | 1 |
| 49395 | prum | 1 |
| 49396 | pruévolo | 1 |
| 49397 | pruevo | 1 |
| 49398 | pruévalo | 1 |
| 49399 | prueuas | 1 |
| 49400 | pruébensela | 1 |
| 49401 | pruébemelo | 1 |
| 49402 | prudhonianas | 1 |
| 49403 | prudencial | 1 |
| 49404 | proyectillo | 1 |
| 49405 | proyectan | 1 |
| 49406 | proyecho | 1 |
| 49407 | proximos | 1 |
| 49408 | provorás | 1 |
| 49409 | provólo | 1 |
| 49410 | provocaron | 1 |
| 49411 | provocarlo | 1 |
| 49412 | provocarlas | 1 |
| 49413 | provocándose | 1 |
| 49414 | provocan | 1 |
| 49415 | provocador | 1 |
| 49416 | provocaban | 1 |
| 49417 | provistos | 1 |
| 49418 | provisores | 1 |
| 49419 | provino | 1 |
| 49420 | provinciana | 1 |
| 49421 | próvidas | 1 |
| 49422 | próvida | 1 |
| 49423 | proveyóse | 1 |
| 49424 | proveyéronse | 1 |
| 49425 | proveyéronles | 1 |
| 49426 | proveste | 1 |
| 49427 | proverse | 1 |
| 49428 | proverbyo | 1 |
| 49429 | proverbial | 1 |
| 49430 | provenirle | 1 |
| 49431 | provenido | 1 |
| 49432 | provenían | 1 |
| 49433 | provendrá | 1 |
| 49434 | provéme | 1 |
| 49435 | provélo | 1 |
| 49436 | proveernos | 1 |
| 49437 | proveerme | 1 |
| 49438 | proveeréis | 1 |
| 49439 | proveemos | 1 |
| 49440 | provee | 1 |
| 49441 | provecta | 1 |
| 49442 | provechossa | 1 |
| 49443 | provechosamente | 1 |
| 49444 | provéase | 1 |
| 49445 | provea | 1 |
| 49446 | prové | 1 |
| 49447 | provarse | 1 |
| 49448 | provares | 1 |
| 49449 | provaredes | 1 |
| 49450 | provare | 1 |
| 49451 | provadlo | 1 |
| 49452 | prouoques | 1 |
| 49453 | prouocasme | 1 |
| 49454 | prouocas | 1 |
| 49455 | prouocara | 1 |
| 49456 | prouienen | 1 |
| 49457 | prouiene | 1 |
| 49458 | proueyste | 1 |
| 49459 | proueyesse | 1 |
| 49460 | proueydas | 1 |
| 49461 | prouey | 1 |
| 49462 | proueo | 1 |
| 49463 | proueamos | 1 |
| 49464 | protoplasma | 1 |
| 49465 | protomiseria | 1 |
| 49466 | protoioduro | 1 |
| 49467 | protoencantador | 1 |
| 49468 | protocolos | 1 |
| 49469 | proto | 1 |
| 49470 | protestase | 1 |
| 49471 | protestara | 1 |
| 49472 | protestan | 1 |
| 49473 | protestamos | 1 |
| 49474 | proteo | 1 |
| 49475 | protegió | 1 |
| 49476 | protegiéndole | 1 |
| 49477 | protegidos | 1 |
| 49478 | protegidas | 1 |
| 49479 | protegerte | 1 |
| 49480 | protegerlo | 1 |
| 49481 | protegería | 1 |
| 49482 | protegeré | 1 |
| 49483 | protegerá | 1 |
| 49484 | protegen | 1 |
| 49485 | protectores | 1 |
| 49486 | proteción | 1 |
| 49487 | proteccionistas | 1 |
| 49488 | protecciones | 1 |
| 49489 | prosupuesta | 1 |
| 49490 | prosuponga | 1 |
| 49491 | prostituyese | 1 |
| 49492 | prostituta | 1 |
| 49493 | prosterne | 1 |
| 49494 | prosternaban | 1 |
| 49495 | prosperos | 1 |
| 49496 | prospero | 1 |
| 49497 | prosperete | 1 |
| 49498 | prósperas | 1 |
| 49499 | prosperaría | 1 |
| 49500 | prosperamente | 1 |
| 49501 | prosperaba | 1 |
| 49502 | prosigas | 1 |
| 49503 | prosigamos | 1 |
| 49504 | proserpina | 1 |
| 49505 | prosélito | 1 |
| 49506 | proseguirla | 1 |
| 49507 | proseguido | 1 |
| 49508 | proseguían | 1 |
| 49509 | proscritas | 1 |
| 49510 | prosas | 1 |
| 49511 | prorrumpiéramos | 1 |
| 49512 | prorrumpe | 1 |
| 49513 | prórrogas | 1 |
| 49514 | prorogarle | 1 |
| 49515 | propusso | 1 |
| 49516 | propúsole | 1 |
| 49517 | propusimos | 1 |
| 49518 | propusiera | 1 |
| 49519 | propuestos | 1 |
| 49520 | propter | 1 |
| 49521 | proprietario | 1 |
| 49522 | propriedades | 1 |
| 49523 | proprias | 1 |
| 49524 | proporna | 1 |
| 49525 | proporciónele | 1 |
| 49526 | proporcionase | 1 |
| 49527 | proporcionarme | 1 |
| 49528 | proporcionarán | 1 |
| 49529 | proporcionara | 1 |
| 49530 | proporcionar | 1 |
| 49531 | proporcionándose | 1 |
| 49532 | proporcionando | 1 |
| 49533 | proporcionales | 1 |
| 49534 | proporcional | 1 |
| 49535 | proporcionadamente | 1 |
| 49536 | proporcionábale | 1 |
| 49537 | proponiéndose | 1 |
| 49538 | proponíamos | 1 |
| 49539 | proponia | 1 |
| 49540 | propongan | 1 |
| 49541 | propongámosla | 1 |
| 49542 | propongamos | 1 |
| 49543 | propones | 1 |
| 49544 | proponérselo | 1 |
| 49545 | proponerse | 1 |
| 49546 | proponernos | 1 |
| 49547 | propónense | 1 |
| 49548 | propinó | 1 |
| 49549 | propinillas | 1 |
| 49550 | propinilla | 1 |
| 49551 | propingos | 1 |
| 49552 | propincuo | 1 |
| 49553 | propincuas | 1 |
| 49554 | propinaron | 1 |
| 49555 | propinado | 1 |
| 49556 | propiedat | 1 |
| 49557 | propici | 1 |
| 49558 | propiadat | 1 |
| 49559 | propheta | 1 |
| 49560 | prophani | 1 |
| 49561 | propensa | 1 |
| 49562 | propendían | 1 |
| 49563 | propendía | 1 |
| 49564 | propenden | 1 |
| 49565 | propemodum | 1 |
| 49566 | propedéutica | 1 |
| 49567 | propasó | 1 |
| 49568 | propase | 1 |
| 49569 | propasase | 1 |
| 49570 | propasado | 1 |
| 49571 | propasa | 1 |
| 49572 | propalo | 1 |
| 49573 | propalando | 1 |
| 49574 | propalaba | 1 |
| 49575 | propague | 1 |
| 49576 | propagandistas | 1 |
| 49577 | propagaban | 1 |
| 49578 | propaga | 1 |
| 49579 | pronunçio | 1 |
| 49580 | pronunçie | 1 |
| 49581 | pronunciasen | 1 |
| 49582 | pronunciarlo | 1 |
| 49583 | pronunciarle | 1 |
| 49584 | pronunciaran | 1 |
| 49585 | pronunciándolas | 1 |
| 49586 | pronunciamos | 1 |
| 49587 | pronunçiaçión | 1 |
| 49588 | prontísimo | 1 |
| 49589 | prontas | 1 |
| 49590 | pronóstico | 1 |
| 49591 | pronosticaste | 1 |
| 49592 | pronostican | 1 |
| 49593 | pronosticada | 1 |
| 49594 | pronostica | 1 |
| 49595 | promulgó | 1 |
| 49596 | promulgando | 1 |
| 49597 | promulga | 1 |
| 49598 | promovió | 1 |
| 49599 | promoviera | 1 |
| 49600 | promovido | 1 |
| 49601 | promouera | 1 |
| 49602 | promotor | 1 |
| 49603 | promisiones | 1 |
| 49604 | promisión | 1 |
| 49605 | prominentes | 1 |
| 49606 | prominencias | 1 |
| 49607 | promety | 1 |
| 49608 | prometiól | 1 |
| 49609 | prometímosselo | 1 |
| 49610 | prometímosle | 1 |
| 49611 | prometimos | 1 |
| 49612 | prometíle | 1 |
| 49613 | prometílas | 1 |
| 49614 | prometil | 1 |
| 49615 | prometieres | 1 |
| 49616 | prometiéndolo | 1 |
| 49617 | prometíe | 1 |
| 49618 | prometidos | 1 |
| 49619 | prometíaselas | 1 |
| 49620 | prometías | 1 |
| 49621 | prometia | 1 |
| 49622 | prometeslo | 1 |
| 49623 | prometérselo | 1 |
| 49624 | prometerla | 1 |
| 49625 | prometería | 1 |
| 49626 | prometeo | 1 |
| 49627 | prometem | 1 |
| 49628 | prométela | 1 |
| 49629 | prometéisme | 1 |
| 49630 | prometedor | 1 |
| 49631 | prometedes | 1 |
| 49632 | prométase | 1 |
| 49633 | prometades | 1 |
| 49634 | promessas | 1 |
| 49635 | prolongase | 1 |
| 49636 | prolongarse | 1 |
| 49637 | prolongando | 1 |
| 49638 | prolongan | 1 |
| 49639 | prolongados | 1 |
| 49640 | prolongaban | 1 |
| 49641 | prólogos | 1 |
| 49642 | prologo | 1 |
| 49643 | prolixos | 1 |
| 49644 | prolixo | 1 |
| 49645 | prolixas | 1 |
| 49646 | prolixa | 1 |
| 49647 | prolijidades | 1 |
| 49648 | prolijamente | 1 |
| 49649 | prolífica | 1 |
| 49650 | proletarios | 1 |
| 49651 | proletarias | 1 |
| 49652 | proles | 1 |
| 49653 | prójimas | 1 |
| 49654 | proive | 1 |
| 49655 | prohijar | 1 |
| 49656 | prohijalla | 1 |
| 49657 | prohibo | 1 |
| 49658 | prohibirse | 1 |
| 49659 | prohibirlos | 1 |
| 49660 | prohibiría | 1 |
| 49661 | prohibiera | 1 |
| 49662 | prohibiciones | 1 |
| 49663 | prohíben | 1 |
| 49664 | prohiban | 1 |
| 49665 | progresivo | 1 |
| 49666 | progresistón | 1 |
| 49667 | progresado | 1 |
| 49668 | profundum | 1 |
| 49669 | profundísimos | 1 |
| 49670 | profundísimamente | 1 |
| 49671 | profiriese | 1 |
| 49672 | profinas | 1 |
| 49673 | proficias | 1 |
| 49674 | proffeçía | 1 |
| 49675 | profetizaron | 1 |
| 49676 | profética | 1 |
| 49677 | profesionales | 1 |
| 49678 | profesen | 1 |
| 49679 | profesas | 1 |
| 49680 | profesadas | 1 |
| 49681 | proferir | 1 |
| 49682 | proferido | 1 |
| 49683 | profectas | 1 |
| 49684 | profeçías | 1 |
| 49685 | profeçía | 1 |
| 49686 | profanó | 1 |
| 49687 | profanidad | 1 |
| 49688 | profanarte | 1 |
| 49689 | profanarlo | 1 |
| 49690 | profanaran | 1 |
| 49691 | profanada | 1 |
| 49692 | profanaban | 1 |
| 49693 | proeza | 1 |
| 49694 | proeto | 1 |
| 49695 | prodújose | 1 |
| 49696 | prodújole | 1 |
| 49697 | produjeran | 1 |
| 49698 | produjera | 1 |
| 49699 | productores | 1 |
| 49700 | productor | 1 |
| 49701 | producirlos | 1 |
| 49702 | producirían | 1 |
| 49703 | producirán | 1 |
| 49704 | produciéndose | 1 |
| 49705 | producíase | 1 |
| 49706 | producíala | 1 |
| 49707 | produces | 1 |
| 49708 | producciones | 1 |
| 49709 | prodromos | 1 |
| 49710 | prodrómico | 1 |
| 49711 | prodigole | 1 |
| 49712 | prodigó | 1 |
| 49713 | prodigïosos | 1 |
| 49714 | prodigiosos | 1 |
| 49715 | prodigiosas | 1 |
| 49716 | prodigara | 1 |
| 49717 | prodigándole | 1 |
| 49718 | prodigalidades | 1 |
| 49719 | prodigaban | 1 |
| 49720 | procurose | 1 |
| 49721 | procúrolas | 1 |
| 49722 | procuraste | 1 |
| 49723 | procurarlo | 1 |
| 49724 | procurarles | 1 |
| 49725 | procurarle | 1 |
| 49726 | procurarla | 1 |
| 49727 | procuraran | 1 |
| 49728 | procurárades | 1 |
| 49729 | procurara | 1 |
| 49730 | procurándose | 1 |
| 49731 | procurándolo | 1 |
| 49732 | procuramos | 1 |
| 49733 | procuralle | 1 |
| 49734 | procuraçiones | 1 |
| 49735 | procreen | 1 |
| 49736 | procrearon | 1 |
| 49737 | procónsul | 1 |
| 49738 | proclamas | 1 |
| 49739 | proclamarse | 1 |
| 49740 | proclamar | 1 |
| 49741 | proclamamos | 1 |
| 49742 | proclamado | 1 |
| 49743 | proclamaba | 1 |
| 49744 | proción | 1 |
| 49745 | prócida | 1 |
| 49746 | proçesso | 1 |
| 49747 | processiones | 1 |
| 49748 | procesos | 1 |
| 49749 | proçeso | 1 |
| 49750 | proçesiones | 1 |
| 49751 | procesionalmente | 1 |
| 49752 | procesada | 1 |
| 49753 | proceroso | 1 |
| 49754 | procelosa | 1 |
| 49755 | procediera | 1 |
| 49756 | procederé | 1 |
| 49757 | procedas | 1 |
| 49758 | procedamos | 1 |
| 49759 | proceda | 1 |
| 49760 | procacidad | 1 |
| 49761 | probreza | 1 |
| 49762 | probrecilla | 1 |
| 49763 | probóseme | 1 |
| 49764 | proboscidio | 1 |
| 49765 | probole | 1 |
| 49766 | probieza | 1 |
| 49767 | probidad | 1 |
| 49768 | probes | 1 |
| 49769 | probedat | 1 |
| 49770 | probecicos | 1 |
| 49771 | probe | 1 |
| 49772 | probatica | 1 |
| 49773 | probasen | 1 |
| 49774 | probásemos | 1 |
| 49775 | probártelo | 1 |
| 49776 | probarnos | 1 |
| 49777 | probaría | 1 |
| 49778 | probare | 1 |
| 49779 | probarás | 1 |
| 49780 | probaran | 1 |
| 49781 | probanzas | 1 |
| 49782 | probándola | 1 |
| 49783 | proballa | 1 |
| 49784 | probáis | 1 |
| 49785 | probadas | 1 |
| 49786 | proba | 1 |
| 49787 | proaza | 1 |
| 49788 | pró | 1 |
| 49789 | prizes | 1 |
| 49790 | privilegió | 1 |
| 49791 | privilegien | 1 |
| 49792 | privilegie | 1 |
| 49793 | privilegiados | 1 |
| 49794 | privilegiadas | 1 |
| 49795 | prive | 1 |
| 49796 | privaste | 1 |
| 49797 | privasen | 1 |
| 49798 | privaron | 1 |
| 49799 | privarle | 1 |
| 49800 | privándose | 1 |
| 49801 | privándome | 1 |
| 49802 | privándole | 1 |
| 49803 | privándola | 1 |
| 49804 | privan | 1 |
| 49805 | privaba | 1 |
| 49806 | prius | 1 |
| 49807 | priuas | 1 |
| 49808 | priuaria | 1 |
| 49809 | priuar | 1 |
| 49810 | priuanza | 1 |
| 49811 | prisso | 1 |
| 49812 | prísole | 1 |
| 49813 | prismáticos | 1 |
| 49814 | prismáticas | 1 |
| 49815 | prismática | 1 |
| 49816 | prisma | 1 |
| 49817 | prisioncilla | 1 |
| 49818 | prisionado | 1 |
| 49819 | prisco | 1 |
| 49820 | prior | 1 |
| 49821 | pringosa | 1 |
| 49822 | pringaron | 1 |
| 49823 | pringao | 1 |
| 49824 | pringados | 1 |
| 49825 | principium | 1 |
| 49826 | principié | 1 |
| 49827 | principiante | 1 |
| 49828 | principiado | 1 |
| 49829 | principado | 1 |
| 49830 | prince | 1 |
| 49831 | primus | 1 |
| 49832 | primorosos | 1 |
| 49833 | primoroso | 1 |
| 49834 | primorosamente | 1 |
| 49835 | primordial | 1 |
| 49836 | primogénita | 1 |
| 49837 | primiero | 1 |
| 49838 | primerizos | 1 |
| 49839 | primerizo | 1 |
| 49840 | primeriza | 1 |
| 49841 | primarias | 1 |
| 49842 | prigny | 1 |
| 49843 | prietos | 1 |
| 49844 | prieta | 1 |
| 49845 | priestar | 1 |
| 49846 | priegos | 1 |
| 49847 | priego | 1 |
| 49848 | priebarlo | 1 |
| 49849 | priebar | 1 |
| 49850 | price | 1 |
| 49851 | priado | 1 |
| 49852 | preyto | 1 |
| 49853 | previstos | 1 |
| 49854 | previsora | 1 |
| 49855 | previsiones | 1 |
| 49856 | previos | 1 |
| 49857 | previnieron | 1 |
| 49858 | previniera | 1 |
| 49859 | previne | 1 |
| 49860 | previlegio | 1 |
| 49861 | previlegiado | 1 |
| 49862 | previendo | 1 |
| 49863 | previas | 1 |
| 49864 | prever | 1 |
| 49865 | preventivo | 1 |
| 49866 | prevenirnos | 1 |
| 49867 | prevenirme | 1 |
| 49868 | prevenirlo | 1 |
| 49869 | prevenirle | 1 |
| 49870 | prevenirlas | 1 |
| 49871 | prevenimos | 1 |
| 49872 | prevenídose | 1 |
| 49873 | prevenidas | 1 |
| 49874 | prevenid | 1 |
| 49875 | prevén | 1 |
| 49876 | prevaricaciones | 1 |
| 49877 | prevaricaban | 1 |
| 49878 | prevaliéndose | 1 |
| 49879 | prevalido | 1 |
| 49880 | prevalerse | 1 |
| 49881 | prevaleciese | 1 |
| 49882 | prevalecido | 1 |
| 49883 | prevalecer | 1 |
| 49884 | prevalece | 1 |
| 49885 | prevale | 1 |
| 49886 | preux | 1 |
| 49887 | preuenir | 1 |
| 49888 | preuenidos | 1 |
| 49889 | preuaricadora | 1 |
| 49890 | pretinazos | 1 |
| 49891 | pretextó | 1 |
| 49892 | pretextado | 1 |
| 49893 | pretexta | 1 |
| 49894 | pretéritos | 1 |
| 49895 | pretericiones | 1 |
| 49896 | pretenmuela | 1 |
| 49897 | pretendieron | 1 |
| 49898 | pretendiera | 1 |
| 49899 | pretenderás | 1 |
| 49900 | pretendemos | 1 |
| 49901 | presuras | 1 |
| 49902 | presupuesta | 1 |
| 49903 | presuponiendo | 1 |
| 49904 | presupongamos | 1 |
| 49905 | presuntuosos | 1 |
| 49906 | presuntuoso | 1 |
| 49907 | presunta | 1 |
| 49908 | presumptuosa | 1 |
| 49909 | presumís | 1 |
| 49910 | presumiese | 1 |
| 49911 | presumiera | 1 |
| 49912 | presumidillas | 1 |
| 49913 | presumidas | 1 |
| 49914 | presumían | 1 |
| 49915 | presumíamos | 1 |
| 49916 | presumí | 1 |
| 49917 | presume | 1 |
| 49918 | prestósele | 1 |
| 49919 | prestose | 1 |
| 49920 | prestóle | 1 |
| 49921 | prestidigitaciones | 1 |
| 49922 | prestes | 1 |
| 49923 | prestaros | 1 |
| 49924 | prestaron | 1 |
| 49925 | prestarnos | 1 |
| 49926 | prestarlos | 1 |
| 49927 | prestaríamos | 1 |
| 49928 | prestaría | 1 |
| 49929 | prestaré | 1 |
| 49930 | prestara | 1 |
| 49931 | prestándole | 1 |
| 49932 | prestadas | 1 |
| 49933 | pressuroso | 1 |
| 49934 | pressura | 1 |
| 49935 | presso | 1 |
| 49936 | presse | 1 |
| 49937 | pressa | 1 |
| 49938 | presonas | 1 |
| 49939 | presno | 1 |
| 49940 | presiste | 1 |
| 49941 | presintiendo | 1 |
| 49942 | presillas | 1 |
| 49943 | presiese | 1 |
| 49944 | presiento | 1 |
| 49945 | presientes | 1 |
| 49946 | presienten | 1 |
| 49947 | presidios | 1 |
| 49948 | presidió | 1 |
| 49949 | presidieron | 1 |
| 49950 | presidieran | 1 |
| 49951 | presidiera | 1 |
| 49952 | presididos | 1 |
| 49953 | presidiarios | 1 |
| 49954 | presidentes | 1 |
| 49955 | presidencial | 1 |
| 49956 | preservativo | 1 |
| 49957 | preservarle | 1 |
| 49958 | presentósela | 1 |
| 49959 | presentóle | 1 |
| 49960 | presentól | 1 |
| 49961 | presentir | 1 |
| 49962 | presentido | 1 |
| 49963 | presentían | 1 |
| 49964 | presentava | 1 |
| 49965 | preséntate | 1 |
| 49966 | preséntase | 1 |
| 49967 | presentárselo | 1 |
| 49968 | presentársele | 1 |
| 49969 | presentaros | 1 |
| 49970 | presentarlo | 1 |
| 49971 | presentaren | 1 |
| 49972 | presentándonos | 1 |
| 49973 | presentándome | 1 |
| 49974 | presentándoles | 1 |
| 49975 | presentándola | 1 |
| 49976 | presentada | 1 |
| 49977 | presenciarlo | 1 |
| 49978 | presenciarían | 1 |
| 49979 | presenciará | 1 |
| 49980 | presenciando | 1 |
| 49981 | presencian | 1 |
| 49982 | presenciamos | 1 |
| 49983 | presenciados | 1 |
| 49984 | presençia | 1 |
| 49985 | prescrito | 1 |
| 49986 | prescripto | 1 |
| 49987 | prescindirían | 1 |
| 49988 | prescindiría | 1 |
| 49989 | prescindiré | 1 |
| 49990 | prescindido | 1 |
| 49991 | prescindamos | 1 |
| 49992 | presbiterus | 1 |
| 49993 | presbíteros | 1 |
| 49994 | presago | 1 |
| 49995 | presagiara | 1 |
| 49996 | prerogativas | 1 |
| 49997 | preparé | 1 |
| 49998 | preparatorias | 1 |
| 49999 | preparas | 1 |
| 50000 | prepararnos | 1 |
| 50001 | prepararme | 1 |
| 50002 | prepararla | 1 |
| 50003 | prepararían | 1 |
| 50004 | prepararía | 1 |
| 50005 | prepararemos | 1 |
| 50006 | preparándolos | 1 |
| 50007 | preparándole | 1 |
| 50008 | preparamos | 1 |
| 50009 | prepárame | 1 |
| 50010 | preparábase | 1 |
| 50011 | preocupó | 1 |
| 50012 | preocupes | 1 |
| 50013 | preocupándole | 1 |
| 50014 | preocupan | 1 |
| 50015 | preñez | 1 |
| 50016 | prenuncio | 1 |
| 50017 | prensas | 1 |
| 50018 | prensados | 1 |
| 50019 | prensada | 1 |
| 50020 | prendose | 1 |
| 50021 | prendióseme | 1 |
| 50022 | prendiómelo | 1 |
| 50023 | prendiól | 1 |
| 50024 | prendimos | 1 |
| 50025 | prendiesen | 1 |
| 50026 | prendiese | 1 |
| 50027 | prendieran | 1 |
| 50028 | prendiera | 1 |
| 50029 | prendíe | 1 |
| 50030 | prendía | 1 |
| 50031 | prenderte | 1 |
| 50032 | prendérseme | 1 |
| 50033 | prenderos | 1 |
| 50034 | prenderlo | 1 |
| 50035 | prenderla | 1 |
| 50036 | prenderas | 1 |
| 50037 | prendelos | 1 |
| 50038 | prendéis | 1 |
| 50039 | prendedero | 1 |
| 50040 | prended | 1 |
| 50041 | prendara | 1 |
| 50042 | prendan | 1 |
| 50043 | prendaba | 1 |
| 50044 | premura | 1 |
| 50045 | premiten | 1 |
| 50046 | premite | 1 |
| 50047 | premissas | 1 |
| 50048 | premiso | 1 |
| 50049 | premioso | 1 |
| 50050 | premiosas | 1 |
| 50051 | premió | 1 |
| 50052 | premien | 1 |
| 50053 | premie | 1 |
| 50054 | premias | 1 |
| 50055 | premiarte | 1 |
| 50056 | premiároslo | 1 |
| 50057 | premiaron | 1 |
| 50058 | premiarle | 1 |
| 50059 | premïados | 1 |
| 50060 | premiaba | 1 |
| 50061 | premeditada | 1 |
| 50062 | prematuras | 1 |
| 50063 | preludios | 1 |
| 50064 | preliminar | 1 |
| 50065 | prejuro | 1 |
| 50066 | prejuicios | 1 |
| 50067 | prehistoria | 1 |
| 50068 | preguntónos | 1 |
| 50069 | preguntonas | 1 |
| 50070 | pregúntolo | 1 |
| 50071 | preguntólas | 1 |
| 50072 | preguntitas | 1 |
| 50073 | preguntillas | 1 |
| 50074 | pregúnteselo | 1 |
| 50075 | pregúntenme | 1 |
| 50076 | pregúntenle | 1 |
| 50077 | preguntémosle | 1 |
| 50078 | pregúntemelo | 1 |
| 50079 | pregúntelo | 1 |
| 50080 | preguntéles | 1 |
| 50081 | pregúntele | 1 |
| 50082 | preguntélas | 1 |
| 50083 | preguntaste | 1 |
| 50084 | preguntártelo | 1 |
| 50085 | preguntársela | 1 |
| 50086 | preguntarse | 1 |
| 50087 | preguntáronla | 1 |
| 50088 | préguntaron | 1 |
| 50089 | preguntarlo | 1 |
| 50090 | preguntaría | 1 |
| 50091 | preguntaren | 1 |
| 50092 | preguntaremos | 1 |
| 50093 | preguntáredes | 1 |
| 50094 | preguntaras | 1 |
| 50095 | preguntarán | 1 |
| 50096 | preguntantes | 1 |
| 50097 | preguntanta | 1 |
| 50098 | preguntándoselo | 1 |
| 50099 | preguntandome | 1 |
| 50100 | preguntámosle | 1 |
| 50101 | preguntalle | 1 |
| 50102 | preguntáis | 1 |
| 50103 | preguntador | 1 |
| 50104 | preguntadle | 1 |
| 50105 | preguntada | 1 |
| 50106 | preguntad | 1 |
| 50107 | preguntábamos | 1 |
| 50108 | preguntábame | 1 |
| 50109 | preguntábales | 1 |
| 50110 | pregonedes | 1 |
| 50111 | pregone | 1 |
| 50112 | pregonas | 1 |
| 50113 | pregonarlos | 1 |
| 50114 | pregonábanlos | 1 |
| 50115 | pregonaban | 1 |
| 50116 | prefieras | 1 |
| 50117 | prefiera | 1 |
| 50118 | preferiremos | 1 |
| 50119 | prefacio | 1 |
| 50120 | preeminentes | 1 |
| 50121 | preeminente | 1 |
| 50122 | predominar | 1 |
| 50123 | predominaban | 1 |
| 50124 | predístesle | 1 |
| 50125 | predisponerme | 1 |
| 50126 | predisponen | 1 |
| 50127 | prediquen | 1 |
| 50128 | predique | 1 |
| 50129 | predilectos | 1 |
| 50130 | predilecciones | 1 |
| 50131 | predico | 1 |
| 50132 | predicas | 1 |
| 50133 | predicaré | 1 |
| 50134 | predicará | 1 |
| 50135 | predicara | 1 |
| 50136 | predican | 1 |
| 50137 | predicamento | 1 |
| 50138 | predicaçiones | 1 |
| 50139 | predicaciones | 1 |
| 50140 | predicación | 1 |
| 50141 | predicaban | 1 |
| 50142 | predestinados | 1 |
| 50143 | predecesores | 1 |
| 50144 | predecesoras | 1 |
| 50145 | precursoras | 1 |
| 50146 | precursora | 1 |
| 50147 | precozmente | 1 |
| 50148 | preconizan | 1 |
| 50149 | preclara | 1 |
| 50150 | precisarlo | 1 |
| 50151 | precipitosamente | 1 |
| 50152 | precipítome | 1 |
| 50153 | precipites | 1 |
| 50154 | precipiten | 1 |
| 50155 | precipite | 1 |
| 50156 | precipitase | 1 |
| 50157 | precipitaron | 1 |
| 50158 | precipitara | 1 |
| 50159 | preçioso | 1 |
| 50160 | preciosita | 1 |
| 50161 | preciosísimos | 1 |
| 50162 | precïosamente | 1 |
| 50163 | preció | 1 |
| 50164 | preçiedes | 1 |
| 50165 | precié | 1 |
| 50166 | precie | 1 |
| 50167 | preçiava | 1 |
| 50168 | preciauan | 1 |
| 50169 | préciate | 1 |
| 50170 | preciarse | 1 |
| 50171 | preçiará | 1 |
| 50172 | preciará | 1 |
| 50173 | preciar | 1 |
| 50174 | preciamos | 1 |
| 50175 | préçiala | 1 |
| 50176 | preçiadas | 1 |
| 50177 | preceto | 1 |
| 50178 | preçes | 1 |
| 50179 | precediera | 1 |
| 50180 | precedidos | 1 |
| 50181 | precedencia | 1 |
| 50182 | precavido | 1 |
| 50183 | precavernos | 1 |
| 50184 | precaria | 1 |
| 50185 | prebendas | 1 |
| 50186 | preámbulos | 1 |
| 50187 | preambulos | 1 |
| 50188 | preambulo | 1 |
| 50189 | prea | 1 |
| 50190 | prazga | 1 |
| 50191 | praser | 1 |
| 50192 | pradoluengo | 1 |
| 50193 | pradillo | 1 |
| 50194 | practicaron | 1 |
| 50195 | practicarla | 1 |
| 50196 | practicantes | 1 |
| 50197 | practicando | 1 |
| 50198 | practican | 1 |
| 50199 | practicadas | 1 |
| 50200 | practicada | 1 |
| 50201 | practicables | 1 |
| 50202 | poussin | 1 |
| 50203 | pourtalés | 1 |
| 50204 | potrillo | 1 |
| 50205 | potrero | 1 |
| 50206 | potingues | 1 |
| 50207 | potingue | 1 |
| 50208 | potest | 1 |
| 50209 | potes | 1 |
| 50210 | potentes | 1 |
| 50211 | potentado | 1 |
| 50212 | potentadas | 1 |
| 50213 | potentada | 1 |
| 50214 | potasio | 1 |
| 50215 | postulante | 1 |
| 50216 | postró | 1 |
| 50217 | postrimerías | 1 |
| 50218 | postrimera | 1 |
| 50219 | postreras | 1 |
| 50220 | postrar | 1 |
| 50221 | postrado | 1 |
| 50222 | postólico | 1 |
| 50223 | postillones | 1 |
| 50224 | postilla | 1 |
| 50225 | posteriori | 1 |
| 50226 | postdata | 1 |
| 50227 | postales | 1 |
| 50228 | postal | 1 |
| 50229 | possunt | 1 |
| 50230 | possumus | 1 |
| 50231 | posseydos | 1 |
| 50232 | posseydo | 1 |
| 50233 | posseido | 1 |
| 50234 | posseerian | 1 |
| 50235 | posseen | 1 |
| 50236 | possaríe | 1 |
| 50237 | possada | 1 |
| 50238 | posponerle | 1 |
| 50239 | pospelo | 1 |
| 50240 | posma | 1 |
| 50241 | posístete | 1 |
| 50242 | posistes | 1 |
| 50243 | posiéronle | 1 |
| 50244 | posibilitado | 1 |
| 50245 | poseyéndolo | 1 |
| 50246 | poseyendo | 1 |
| 50247 | poseydos | 1 |
| 50248 | posesivo | 1 |
| 50249 | posesionarían | 1 |
| 50250 | posentado | 1 |
| 50251 | poseídas | 1 |
| 50252 | poseída | 1 |
| 50253 | poseerme | 1 |
| 50254 | poseerle | 1 |
| 50255 | poseerlas | 1 |
| 50256 | poseerla | 1 |
| 50257 | poseeremos | 1 |
| 50258 | poseerás | 1 |
| 50259 | poseello | 1 |
| 50260 | poseellas | 1 |
| 50261 | poseedora | 1 |
| 50262 | posarle | 1 |
| 50263 | posadería | 1 |
| 50264 | posaban | 1 |
| 50265 | posaba | 1 |
| 50266 | porydat | 1 |
| 50267 | portuna | 1 |
| 50268 | portugales | 1 |
| 50269 | portón | 1 |
| 50270 | portogal | 1 |
| 50271 | portocarrero | 1 |
| 50272 | porto | 1 |
| 50273 | portier | 1 |
| 50274 | portiellos | 1 |
| 50275 | portezuelo | 1 |
| 50276 | portes | 1 |
| 50277 | portentoso | 1 |
| 50278 | portátiles | 1 |
| 50279 | pórtate | 1 |
| 50280 | portarte | 1 |
| 50281 | portarnos | 1 |
| 50282 | portantes | 1 |
| 50283 | portamos | 1 |
| 50284 | portalones | 1 |
| 50285 | portados | 1 |
| 50286 | portadores | 1 |
| 50287 | portadgo | 1 |
| 50288 | portabas | 1 |
| 50289 | portaban | 1 |
| 50290 | port | 1 |
| 50291 | porrumpió | 1 |
| 50292 | porros | 1 |
| 50293 | porrada | 1 |
| 50294 | porquerón | 1 |
| 50295 | poro | 1 |
| 50296 | porne | 1 |
| 50297 | pormandado | 1 |
| 50298 | poridades | 1 |
| 50299 | porfya | 1 |
| 50300 | porfiosos | 1 |
| 50301 | porfioso | 1 |
| 50302 | porfíes | 1 |
| 50303 | porfiedes | 1 |
| 50304 | porfiarle | 1 |
| 50305 | porfiaré | 1 |
| 50306 | porfiare | 1 |
| 50307 | porfiada | 1 |
| 50308 | porfaçaría | 1 |
| 50309 | porfaçaba | 1 |
| 50310 | pordiosear | 1 |
| 50311 | pordioseando | 1 |
| 50312 | pordioseaba | 1 |
| 50313 | porciones | 1 |
| 50314 | porches | 1 |
| 50315 | porcelanescas | 1 |
| 50316 | pór | 1 |
| 50317 | poquyllo | 1 |
| 50318 | poquitos | 1 |
| 50319 | poquitas | 1 |
| 50320 | poquísimos | 1 |
| 50321 | poquísima | 1 |
| 50322 | poquillas | 1 |
| 50323 | poquiello | 1 |
| 50324 | populosas | 1 |
| 50325 | populi | 1 |
| 50326 | popen | 1 |
| 50327 | poño | 1 |
| 50328 | ponzoñoso | 1 |
| 50329 | ponzoñosa | 1 |
| 50330 | pontificii | 1 |
| 50331 | pontificado | 1 |
| 50332 | pontevedra | 1 |
| 50333 | ponlas | 1 |
| 50334 | ponío | 1 |
| 50335 | poniéndote | 1 |
| 50336 | poniéndoselos | 1 |
| 50337 | poniéndosela | 1 |
| 50338 | poniéndomela | 1 |
| 50339 | poniéndolo | 1 |
| 50340 | poniéndolas | 1 |
| 50341 | poniéndola | 1 |
| 50342 | poníe | 1 |
| 50343 | poníasele | 1 |
| 50344 | poníanse | 1 |
| 50345 | poníamos | 1 |
| 50346 | poníala | 1 |
| 50347 | póngole | 1 |
| 50348 | pongelo | 1 |
| 50349 | póngasele | 1 |
| 50350 | pónganos | 1 |
| 50351 | pongámosle | 1 |
| 50352 | póngalo | 1 |
| 50353 | poneysme | 1 |
| 50354 | ponesme | 1 |
| 50355 | póneslos | 1 |
| 50356 | ponérteme | 1 |
| 50357 | poneos | 1 |
| 50358 | ponente | 1 |
| 50359 | pónenos | 1 |
| 50360 | pónenle | 1 |
| 50361 | pónelo | 1 |
| 50362 | ponellos | 1 |
| 50363 | poneldos | 1 |
| 50364 | poneldo | 1 |
| 50365 | ponedme | 1 |
| 50366 | ponedle | 1 |
| 50367 | pondrías | 1 |
| 50368 | pondríala | 1 |
| 50369 | pondrémela | 1 |
| 50370 | pondréme | 1 |
| 50371 | pondréla | 1 |
| 50372 | pondréis | 1 |
| 50373 | ponderosa | 1 |
| 50374 | pondero | 1 |
| 50375 | ponderes | 1 |
| 50376 | ponderen | 1 |
| 50377 | ponderemos | 1 |
| 50378 | ponderé | 1 |
| 50379 | ponderaron | 1 |
| 50380 | ponderarle | 1 |
| 50381 | ponderan | 1 |
| 50382 | ponderador | 1 |
| 50383 | ponderado | 1 |
| 50384 | ponderaban | 1 |
| 50385 | pondera | 1 |
| 50386 | ponçoñar | 1 |
| 50387 | ponçoña | 1 |
| 50388 | ponchera | 1 |
| 50389 | ponche | 1 |
| 50390 | pomposidad | 1 |
| 50391 | pomposamente | 1 |
| 50392 | pompones | 1 |
| 50393 | pómez | 1 |
| 50394 | pomarada | 1 |
| 50395 | polvorosos | 1 |
| 50396 | polvoroso | 1 |
| 50397 | polvoro | 1 |
| 50398 | polvorientos | 1 |
| 50399 | polvorientas | 1 |
| 50400 | pólux | 1 |
| 50401 | poluorizadas | 1 |
| 50402 | poluillos | 1 |
| 50403 | poltrones | 1 |
| 50404 | poltronería | 1 |
| 50405 | poltrón | 1 |
| 50406 | polso | 1 |
| 50407 | polonia | 1 |
| 50408 | polluela | 1 |
| 50409 | pollitos | 1 |
| 50410 | pollita | 1 |
| 50411 | pollinesca | 1 |
| 50412 | polleros | 1 |
| 50413 | pollerías | 1 |
| 50414 | pollera | 1 |
| 50415 | pollastre | 1 |
| 50416 | polizontes | 1 |
| 50417 | pólizas | 1 |
| 50418 | poliuto | 1 |
| 50419 | politiquejos | 1 |
| 50420 | politicastros | 1 |
| 50421 | pólipo | 1 |
| 50422 | poliphemus | 1 |
| 50423 | polinesia | 1 |
| 50424 | polifemos | 1 |
| 50425 | polidas | 1 |
| 50426 | policiacos | 1 |
| 50427 | policíaca | 1 |
| 50428 | policarpa | 1 |
| 50429 | poleo | 1 |
| 50430 | polemista | 1 |
| 50431 | poleas | 1 |
| 50432 | polea | 1 |
| 50433 | polavieja | 1 |
| 50434 | polares | 1 |
| 50435 | polanco | 1 |
| 50436 | polaca | 1 |
| 50437 | poetizados | 1 |
| 50438 | poetilla | 1 |
| 50439 | poesias | 1 |
| 50440 | poe | 1 |
| 50441 | podrir | 1 |
| 50442 | podríe | 1 |
| 50443 | podrias | 1 |
| 50444 | podriala | 1 |
| 50445 | podri | 1 |
| 50446 | podréislo | 1 |
| 50447 | podredumbres | 1 |
| 50448 | podredes | 1 |
| 50449 | podrásme | 1 |
| 50450 | podráse | 1 |
| 50451 | podiesse | 1 |
| 50452 | podíese | 1 |
| 50453 | podieren | 1 |
| 50454 | podierdes | 1 |
| 50455 | podiendolos | 1 |
| 50456 | podias | 1 |
| 50457 | podíanse | 1 |
| 50458 | podíades | 1 |
| 50459 | podi | 1 |
| 50460 | podervos | 1 |
| 50461 | poderosso | 1 |
| 50462 | poderosísima | 1 |
| 50463 | podernos | 1 |
| 50464 | poderlos | 1 |
| 50465 | podémoslos | 1 |
| 50466 | pode | 1 |
| 50467 | podades | 1 |
| 50468 | podadera | 1 |
| 50469 | poda | 1 |
| 50470 | pocula | 1 |
| 50471 | pocritona | 1 |
| 50472 | poción | 1 |
| 50473 | pócima | 1 |
| 50474 | pocillo | 1 |
| 50475 | pocilgas | 1 |
| 50476 | poche | 1 |
| 50477 | pobrísimos | 1 |
| 50478 | pobreto | 1 |
| 50479 | pobrecillas | 1 |
| 50480 | pobos | 1 |
| 50481 | pobló | 1 |
| 50482 | pobleza | 1 |
| 50483 | pobles | 1 |
| 50484 | pobledat | 1 |
| 50485 | pobláronse | 1 |
| 50486 | poblarla | 1 |
| 50487 | poblaréis | 1 |
| 50488 | poblare | 1 |
| 50489 | poblar | 1 |
| 50490 | poblachones | 1 |
| 50491 | poblacho | 1 |
| 50492 | poblaban | 1 |
| 50493 | po | 1 |
| 50494 | plymouth | 1 |
| 50495 | pluvias | 1 |
| 50496 | pluuias | 1 |
| 50497 | plun | 1 |
| 50498 | plumonía | 1 |
| 50499 | plumear | 1 |
| 50500 | plumajes | 1 |
| 50501 | plumacho | 1 |
| 50502 | pluguieron | 1 |
| 50503 | pluguiere | 1 |
| 50504 | plúgo | 1 |
| 50505 | plu | 1 |
| 50506 | plomiza | 1 |
| 50507 | plomados | 1 |
| 50508 | plógo | 1 |
| 50509 | plo | 1 |
| 50510 | plintos | 1 |
| 50511 | plinmuf | 1 |
| 50512 | plinios | 1 |
| 50513 | plim | 1 |
| 50514 | pleytés | 1 |
| 50515 | pleyteamiento | 1 |
| 50516 | pleuresía | 1 |
| 50517 | pleurer | 1 |
| 50518 | pletórico | 1 |
| 50519 | pletisía | 1 |
| 50520 | pleticó | 1 |
| 50521 | pleticar | 1 |
| 50522 | pletesía | 1 |
| 50523 | pletea | 1 |
| 50524 | plenos | 1 |
| 50525 | pleniputenciano | 1 |
| 50526 | plenipotenciario | 1 |
| 50527 | pleitista | 1 |
| 50528 | pléiticas | 1 |
| 50529 | pleiteará | 1 |
| 50530 | pleitear | 1 |
| 50531 | pleiteantes | 1 |
| 50532 | pleiteando | 1 |
| 50533 | pleitazo | 1 |
| 50534 | plegarse | 1 |
| 50535 | plégaos | 1 |
| 50536 | plegado | 1 |
| 50537 | plegadera | 1 |
| 50538 | plegaba | 1 |
| 50539 | plectio | 1 |
| 50540 | plebis | 1 |
| 50541 | plebeyas | 1 |
| 50542 | pleberico | 1 |
| 50543 | plazia | 1 |
| 50544 | plázete | 1 |
| 50545 | plazes | 1 |
| 50546 | plázeme | 1 |
| 50547 | plazca | 1 |
| 50548 | platónicas | 1 |
| 50549 | platonazo | 1 |
| 50550 | platires | 1 |
| 50551 | platicas | 1 |
| 50552 | platicantes | 1 |
| 50553 | platicante | 1 |
| 50554 | platican | 1 |
| 50555 | platicaban | 1 |
| 50556 | plateros | 1 |
| 50557 | platero | 1 |
| 50558 | plateresca | 1 |
| 50559 | plateó | 1 |
| 50560 | plateado | 1 |
| 50561 | plateada | 1 |
| 50562 | platao | 1 |
| 50563 | plataformas | 1 |
| 50564 | plásticos | 1 |
| 50565 | plasmador | 1 |
| 50566 | plasíe | 1 |
| 50567 | plasia | 1 |
| 50568 | plases | 1 |
| 50569 | plasera | 1 |
| 50570 | plasenteros | 1 |
| 50571 | plasençia | 1 |
| 50572 | plañosa | 1 |
| 50573 | plañirla | 1 |
| 50574 | plañidera | 1 |
| 50575 | plañendo | 1 |
| 50576 | plantóse | 1 |
| 50577 | plantilla | 1 |
| 50578 | plantigrado | 1 |
| 50579 | plantifiquen | 1 |
| 50580 | plántese | 1 |
| 50581 | planteo | 1 |
| 50582 | planteándole | 1 |
| 50583 | planteado | 1 |
| 50584 | planteada | 1 |
| 50585 | planteaba | 1 |
| 50586 | plantea | 1 |
| 50587 | plantarte | 1 |
| 50588 | plantársele | 1 |
| 50589 | plantarme | 1 |
| 50590 | plantarla | 1 |
| 50591 | plantaría | 1 |
| 50592 | plantaremos | 1 |
| 50593 | plantando | 1 |
| 50594 | plantada | 1 |
| 50595 | planicies | 1 |
| 50596 | planicie | 1 |
| 50597 | planetario | 1 |
| 50598 | planche | 1 |
| 50599 | planchándole | 1 |
| 50600 | planchadoras | 1 |
| 50601 | planchada | 1 |
| 50602 | planchaba | 1 |
| 50603 | plaira | 1 |
| 50604 | plafagonia | 1 |
| 50605 | plado | 1 |
| 50606 | plácticos | 1 |
| 50607 | plaços | 1 |
| 50608 | placita | 1 |
| 50609 | placidito | 1 |
| 50610 | placeros | 1 |
| 50611 | placerdemivida | 1 |
| 50612 | placerá | 1 |
| 50613 | plaçenteros | 1 |
| 50614 | placenteros | 1 |
| 50615 | placentero | 1 |
| 50616 | plaçenterías | 1 |
| 50617 | plaçentera | 1 |
| 50618 | plácenos | 1 |
| 50619 | plaçe | 1 |
| 50620 | pl | 1 |
| 50621 | pizpirigaña | 1 |
| 50622 | pizpiretas | 1 |
| 50623 | pizmiento | 1 |
| 50624 | pizmienta | 1 |
| 50625 | pizarro | 1 |
| 50626 | pixota | 1 |
| 50627 | più | 1 |
| 50628 | pitusiana | 1 |
| 50629 | pituitaria | 1 |
| 50630 | pitt | 1 |
| 50631 | pitón | 1 |
| 50632 | pitoja | 1 |
| 50633 | pitofufito | 1 |
| 50634 | pitoflero | 1 |
| 50635 | pitita | 1 |
| 50636 | pitisa | 1 |
| 50637 | pítima | 1 |
| 50638 | pitidos | 1 |
| 50639 | pitarás | 1 |
| 50640 | pitañosos | 1 |
| 50641 | pitañosas | 1 |
| 50642 | pita | 1 |
| 50643 | pistolitas | 1 |
| 50644 | pissa | 1 |
| 50645 | pisotearla | 1 |
| 50646 | pisoteadas | 1 |
| 50647 | pisoteada | 1 |
| 50648 | pisotea | 1 |
| 50649 | pisen | 1 |
| 50650 | pisé | 1 |
| 50651 | piscis | 1 |
| 50652 | piscina | 1 |
| 50653 | piscicultura | 1 |
| 50654 | piscatorias | 1 |
| 50655 | písase | 1 |
| 50656 | pisase | 1 |
| 50657 | pisárselas | 1 |
| 50658 | pisarlas | 1 |
| 50659 | pisara | 1 |
| 50660 | pisándoles | 1 |
| 50661 | pisamos | 1 |
| 50662 | pisad | 1 |
| 50663 | pisacorto | 1 |
| 50664 | piruétanos | 1 |
| 50665 | piruétano | 1 |
| 50666 | pirueta | 1 |
| 50667 | pirú | 1 |
| 50668 | pirroquia | 1 |
| 50669 | pirra | 1 |
| 50670 | pirotécnicas | 1 |
| 50671 | pirmes | 1 |
| 50672 | piraterías | 1 |
| 50673 | piras | 1 |
| 50674 | piramo | 1 |
| 50675 | piramidal | 1 |
| 50676 | piquillos | 1 |
| 50677 | piques | 1 |
| 50678 | piquemos | 1 |
| 50679 | piqué | 1 |
| 50680 | pipotes | 1 |
| 50681 | pipote | 1 |
| 50682 | pipirijaina | 1 |
| 50683 | pipas | 1 |
| 50684 | pionono | 1 |
| 50685 | piojosa | 1 |
| 50686 | piñonate | 1 |
| 50687 | piñata | 1 |
| 50688 | pinzones | 1 |
| 50689 | pinzas | 1 |
| 50690 | pintósela | 1 |
| 50691 | pintorreado | 1 |
| 50692 | pintorreadas | 1 |
| 50693 | pintorescas | 1 |
| 50694 | pintora | 1 |
| 50695 | píntola | 1 |
| 50696 | pintiquiniestra | 1 |
| 50697 | pintiparados | 1 |
| 50698 | pintiparado | 1 |
| 50699 | pintemos | 1 |
| 50700 | pinte | 1 |
| 50701 | pintaste | 1 |
| 50702 | pintasse | 1 |
| 50703 | pintasen | 1 |
| 50704 | pintarrajeados | 1 |
| 50705 | pintarrajeadas | 1 |
| 50706 | pintarlo | 1 |
| 50707 | pintarlas | 1 |
| 50708 | pintaría | 1 |
| 50709 | píntaos | 1 |
| 50710 | pintándose | 1 |
| 50711 | pintándonos | 1 |
| 50712 | pintándolo | 1 |
| 50713 | pintamos | 1 |
| 50714 | pintad | 1 |
| 50715 | pinreles | 1 |
| 50716 | pinones | 1 |
| 50717 | pinón | 1 |
| 50718 | pinicos | 1 |
| 50719 | pinganitos | 1 |
| 50720 | pingajo | 1 |
| 50721 | pinedo | 1 |
| 50722 | pindonga | 1 |
| 50723 | pindárico | 1 |
| 50724 | pinchó | 1 |
| 50725 | pinchase | 1 |
| 50726 | pincharle | 1 |
| 50727 | pincharlas | 1 |
| 50728 | pinchándole | 1 |
| 50729 | pinchamos | 1 |
| 50730 | pinchado | 1 |
| 50731 | pinchacitos | 1 |
| 50732 | pinchaba | 1 |
| 50733 | pimpollos | 1 |
| 50734 | pimpinela | 1 |
| 50735 | pimenteles | 1 |
| 50736 | piltrafa | 1 |
| 50737 | pilotos | 1 |
| 50738 | pilosa | 1 |
| 50739 | pillines | 1 |
| 50740 | pillincito | 1 |
| 50741 | pillinadas | 1 |
| 50742 | pille | 1 |
| 50743 | pillaremos | 1 |
| 50744 | pillar | 1 |
| 50745 | pillamo | 1 |
| 50746 | pillaje | 1 |
| 50747 | pilastrones | 1 |
| 50748 | pilades | 1 |
| 50749 | pihuelas | 1 |
| 50750 | pihuela | 1 |
| 50751 | pignoró | 1 |
| 50752 | pignorado | 1 |
| 50753 | pigmentario | 1 |
| 50754 | pifias | 1 |
| 50755 | pifia | 1 |
| 50756 | pífaros | 1 |
| 50757 | pietista | 1 |
| 50758 | piesetas | 1 |
| 50759 | pieseta | 1 |
| 50760 | pierro | 1 |
| 50761 | piernazas | 1 |
| 50762 | pïérides | 1 |
| 50763 | piérdense | 1 |
| 50764 | pierdase | 1 |
| 50765 | piensso | 1 |
| 50766 | pienssas | 1 |
| 50767 | piensasté | 1 |
| 50768 | piénsanse | 1 |
| 50769 | piénsalo | 1 |
| 50770 | pielago | 1 |
| 50771 | piegar | 1 |
| 50772 | piedrecitas | 1 |
| 50773 | piedrecita | 1 |
| 50774 | piedrecillas | 1 |
| 50775 | piedrecilla | 1 |
| 50776 | piedrahíta | 1 |
| 50777 | pied | 1 |
| 50778 | piececitos | 1 |
| 50779 | piececilla | 1 |
| 50780 | pié | 1 |
| 50781 | pidyeron | 1 |
| 50782 | pidré | 1 |
| 50783 | pidistes | 1 |
| 50784 | pidiría | 1 |
| 50785 | pidióselo | 1 |
| 50786 | pidiósele | 1 |
| 50787 | pidióles | 1 |
| 50788 | pidio | 1 |
| 50789 | pidiésemos | 1 |
| 50790 | pidiésedes | 1 |
| 50791 | pidieres | 1 |
| 50792 | pidieras | 1 |
| 50793 | pidiéndotelo | 1 |
| 50794 | pidiéndoos | 1 |
| 50795 | pidiendome | 1 |
| 50796 | pidiendole | 1 |
| 50797 | pidiéndola | 1 |
| 50798 | pidías | 1 |
| 50799 | pídese | 1 |
| 50800 | pidenles | 1 |
| 50801 | pídeme | 1 |
| 50802 | pidelo | 1 |
| 50803 | pídanmelo | 1 |
| 50804 | picudilla | 1 |
| 50805 | picotera | 1 |
| 50806 | picotearon | 1 |
| 50807 | picoteaba | 1 |
| 50808 | picote | 1 |
| 50809 | picóse | 1 |
| 50810 | picose | 1 |
| 50811 | picorcillo | 1 |
| 50812 | picona | 1 |
| 50813 | picóle | 1 |
| 50814 | picio | 1 |
| 50815 | pichoncitos | 1 |
| 50816 | pichona | 1 |
| 50817 | pichón | 1 |
| 50818 | piche | 1 |
| 50819 | picaza | 1 |
| 50820 | picase | 1 |
| 50821 | picarones | 1 |
| 50822 | picaronaza | 1 |
| 50823 | picarísima | 1 |
| 50824 | picarilla | 1 |
| 50825 | picáredes | 1 |
| 50826 | picardease | 1 |
| 50827 | picarás | 1 |
| 50828 | picaran | 1 |
| 50829 | pícaramente | 1 |
| 50830 | picapedreros | 1 |
| 50831 | picapedrero | 1 |
| 50832 | picaño | 1 |
| 50833 | picañas | 1 |
| 50834 | picáis | 1 |
| 50835 | picadito | 1 |
| 50836 | picadilly | 1 |
| 50837 | picadas | 1 |
| 50838 | picachos | 1 |
| 50839 | picaças | 1 |
| 50840 | picaça | 1 |
| 50841 | picaban | 1 |
| 50842 | piazo | 1 |
| 50843 | pias | 1 |
| 50844 | pïante | 1 |
| 50845 | pianino | 1 |
| 50846 | pianillo | 1 |
| 50847 | pían | 1 |
| 50848 | pian | 1 |
| 50849 | piamonte | 1 |
| 50850 | piafar | 1 |
| 50851 | piadosísimos | 1 |
| 50852 | pïadosa | 1 |
| 50853 | piadad | 1 |
| 50854 | piaban | 1 |
| 50855 | pia | 1 |
| 50856 | phrates | 1 |
| 50857 | phorminx | 1 |
| 50858 | philósophos | 1 |
| 50859 | philosophos | 1 |
| 50860 | philosophie | 1 |
| 50861 | philosophi | 1 |
| 50862 | philosopharentur | 1 |
| 50863 | philosomia | 1 |
| 50864 | philosofía | 1 |
| 50865 | philologie | 1 |
| 50866 | philloxera | 1 |
| 50867 | philipo | 1 |
| 50868 | phebo | 1 |
| 50869 | phebeo | 1 |
| 50870 | peyrohade | 1 |
| 50871 | peyne | 1 |
| 50872 | peynde | 1 |
| 50873 | peynanla | 1 |
| 50874 | peynados | 1 |
| 50875 | peynadores | 1 |
| 50876 | peur | 1 |
| 50877 | peu | 1 |
| 50878 | petulancia | 1 |
| 50879 | petril | 1 |
| 50880 | petrificó | 1 |
| 50881 | petrificaron | 1 |
| 50882 | petrificado | 1 |
| 50883 | petrificación | 1 |
| 50884 | petrifica | 1 |
| 50885 | petreras | 1 |
| 50886 | pétreo | 1 |
| 50887 | petrarcha | 1 |
| 50888 | petrarca | 1 |
| 50889 | petrales | 1 |
| 50890 | petiseca | 1 |
| 50891 | petirrojos | 1 |
| 50892 | petimetres | 1 |
| 50893 | petid | 1 |
| 50894 | petiçiones | 1 |
| 50895 | petatur | 1 |
| 50896 | petate | 1 |
| 50897 | petardos | 1 |
| 50898 | pétalos | 1 |
| 50899 | petacas | 1 |
| 50900 | petaba | 1 |
| 50901 | pestorejo | 1 |
| 50902 | pestilentes | 1 |
| 50903 | pestilenciales | 1 |
| 50904 | pestilençia | 1 |
| 50905 | pestíferos | 1 |
| 50906 | pestiferos | 1 |
| 50907 | pestífero | 1 |
| 50908 | pestanas | 1 |
| 50909 | pessó | 1 |
| 50910 | pessas | 1 |
| 50911 | pessa | 1 |
| 50912 | pesquisar | 1 |
| 50913 | pesques | 1 |
| 50914 | pesque | 1 |
| 50915 | pespunteados | 1 |
| 50916 | pespuntar | 1 |
| 50917 | pespuntaba | 1 |
| 50918 | pespunta | 1 |
| 50919 | pespetiva | 1 |
| 50920 | pésimos | 1 |
| 50921 | pésimamente | 1 |
| 50922 | pesi | 1 |
| 50923 | pesetillas | 1 |
| 50924 | pesetilla | 1 |
| 50925 | pésetes | 1 |
| 50926 | peseteros | 1 |
| 50927 | peses | 1 |
| 50928 | pesen | 1 |
| 50929 | pésemelo | 1 |
| 50930 | péselo | 1 |
| 50931 | pesebres | 1 |
| 50932 | pesé | 1 |
| 50933 | pescuezos | 1 |
| 50934 | pescudar | 1 |
| 50935 | pescuçudo | 1 |
| 50936 | pescozón | 1 |
| 50937 | pescozada | 1 |
| 50938 | pescarse | 1 |
| 50939 | pescaremos | 1 |
| 50940 | pescan | 1 |
| 50941 | pescadora | 1 |
| 50942 | pescada | 1 |
| 50943 | pescaban | 1 |
| 50944 | pesassen | 1 |
| 50945 | pesarosos | 1 |
| 50946 | pesarme | 1 |
| 50947 | pesarle | 1 |
| 50948 | pesare | 1 |
| 50949 | pesándole | 1 |
| 50950 | pésames | 1 |
| 50951 | pesame | 1 |
| 50952 | pesadita | 1 |
| 50953 | pesadísimo | 1 |
| 50954 | pesadísima | 1 |
| 50955 | pesábame | 1 |
| 50956 | pes | 1 |
| 50957 | pervertírsele | 1 |
| 50958 | pervertir | 1 |
| 50959 | pervertimos | 1 |
| 50960 | pervertidos | 1 |
| 50961 | pervertido | 1 |
| 50962 | pervertidas | 1 |
| 50963 | pervertida | 1 |
| 50964 | pervertía | 1 |
| 50965 | peruertieras | 1 |
| 50966 | peruertido | 1 |
| 50967 | peruana | 1 |
| 50968 | perturben | 1 |
| 50969 | perturbe | 1 |
| 50970 | perturbase | 1 |
| 50971 | perturbaron | 1 |
| 50972 | perturbadora | 1 |
| 50973 | perturbadas | 1 |
| 50974 | perturbada | 1 |
| 50975 | perturbaciones | 1 |
| 50976 | perturbaba | 1 |
| 50977 | perturba | 1 |
| 50978 | pertrecharle | 1 |
| 50979 | pertrechando | 1 |
| 50980 | pertinencia | 1 |
| 50981 | pertinaces | 1 |
| 50982 | pertenezco | 1 |
| 50983 | pertenezcan | 1 |
| 50984 | pertenesçen | 1 |
| 50985 | pertenesçe | 1 |
| 50986 | pertenesce | 1 |
| 50987 | pertenencias | 1 |
| 50988 | pertenençia | 1 |
| 50989 | pertenencia | 1 |
| 50990 | perteneciese | 1 |
| 50991 | perteneciera | 1 |
| 50992 | perteneciendo | 1 |
| 50993 | pertenecí | 1 |
| 50994 | perteneces | 1 |
| 50995 | pertenecerle | 1 |
| 50996 | pertenecería | 1 |
| 50997 | persygues | 1 |
| 50998 | persuasivo | 1 |
| 50999 | persuasivas | 1 |
| 51000 | persuadirte | 1 |
| 51001 | persuadirnos | 1 |
| 51002 | persuadille | 1 |
| 51003 | persuadiéronse | 1 |
| 51004 | persuadieran | 1 |
| 51005 | persuadiéndome | 1 |
| 51006 | persuadiéndole | 1 |
| 51007 | persuadiéndola | 1 |
| 51008 | persuadidos | 1 |
| 51009 | persuadían | 1 |
| 51010 | persuádeles | 1 |
| 51011 | persuada | 1 |
| 51012 | perspicaces | 1 |
| 51013 | personificar | 1 |
| 51014 | personifican | 1 |
| 51015 | personificada | 1 |
| 51016 | personificaciones | 1 |
| 51017 | personificaba | 1 |
| 51018 | personifica | 1 |
| 51019 | personarse | 1 |
| 51020 | personaron | 1 |
| 51021 | personalizarlos | 1 |
| 51022 | personalizar | 1 |
| 51023 | personalizando | 1 |
| 51024 | personalidá | 1 |
| 51025 | persistió | 1 |
| 51026 | persistieron | 1 |
| 51027 | persistiendo | 1 |
| 51028 | persistían | 1 |
| 51029 | persistentes | 1 |
| 51030 | persistente | 1 |
| 51031 | persiste | 1 |
| 51032 | persio | 1 |
| 51033 | persinó | 1 |
| 51034 | persiguirán | 1 |
| 51035 | persiguiese | 1 |
| 51036 | persiguiéronle | 1 |
| 51037 | persiguiéndose | 1 |
| 51038 | persiguiéndole | 1 |
| 51039 | persigues | 1 |
| 51040 | persignarse | 1 |
| 51041 | persigáis | 1 |
| 51042 | persiga | 1 |
| 51043 | pérsica | 1 |
| 51044 | persianas | 1 |
| 51045 | persiana | 1 |
| 51046 | persevero | 1 |
| 51047 | perseveré | 1 |
| 51048 | perseverando | 1 |
| 51049 | perseverad | 1 |
| 51050 | persevera | 1 |
| 51051 | perseuerando | 1 |
| 51052 | perseueran | 1 |
| 51053 | perseueracion | 1 |
| 51054 | perseuera | 1 |
| 51055 | persépolis | 1 |
| 51056 | perseguís | 1 |
| 51057 | perseguirte | 1 |
| 51058 | perseguirnos | 1 |
| 51059 | perseguirlas | 1 |
| 51060 | perseguirla | 1 |
| 51061 | perseguirá | 1 |
| 51062 | perseguimiento | 1 |
| 51063 | perseguíale | 1 |
| 51064 | persecutorio | 1 |
| 51065 | persecucion | 1 |
| 51066 | perruno | 1 |
| 51067 | perroquia | 1 |
| 51068 | perrochianos | 1 |
| 51069 | perrochano | 1 |
| 51070 | perritos | 1 |
| 51071 | perritas | 1 |
| 51072 | perrita | 1 |
| 51073 | perricos | 1 |
| 51074 | perrica | 1 |
| 51075 | perrería | 1 |
| 51076 | perrengues | 1 |
| 51077 | perrazo | 1 |
| 51078 | perpiñá | 1 |
| 51079 | perpetuó | 1 |
| 51080 | perpetuarse | 1 |
| 51081 | perpetuadores | 1 |
| 51082 | perpetúa | 1 |
| 51083 | perpendicularmente | 1 |
| 51084 | perpendiculares | 1 |
| 51085 | perpe | 1 |
| 51086 | peroré | 1 |
| 51087 | perorar | 1 |
| 51088 | perorando | 1 |
| 51089 | perorador | 1 |
| 51090 | perora | 1 |
| 51091 | peroqu | 1 |
| 51092 | perona | 1 |
| 51093 | perogrullo | 1 |
| 51094 | perogrulladas | 1 |
| 51095 | pernoctar | 1 |
| 51096 | perno | 1 |
| 51097 | perniquiebres | 1 |
| 51098 | perniles | 1 |
| 51099 | pernetas | 1 |
| 51100 | perneras | 1 |
| 51101 | permitiste | 1 |
| 51102 | permitírselo | 1 |
| 51103 | permitirnos | 1 |
| 51104 | permitirlos | 1 |
| 51105 | permitirles | 1 |
| 51106 | permitiría | 1 |
| 51107 | permitiremos | 1 |
| 51108 | permitiole | 1 |
| 51109 | permitiéndonos | 1 |
| 51110 | permitiéndoles | 1 |
| 51111 | permitiéndole | 1 |
| 51112 | permitida | 1 |
| 51113 | permitíale | 1 |
| 51114 | permítesele | 1 |
| 51115 | permíteme | 1 |
| 51116 | permítase | 1 |
| 51117 | permitáis | 1 |
| 51118 | permission | 1 |
| 51119 | permanezca | 1 |
| 51120 | permanesce | 1 |
| 51121 | permanentes | 1 |
| 51122 | permanecido | 1 |
| 51123 | permanecerán | 1 |
| 51124 | permanecen | 1 |
| 51125 | permanece | 1 |
| 51126 | perlica | 1 |
| 51127 | perlerino | 1 |
| 51128 | perlerina | 1 |
| 51129 | perláticos | 1 |
| 51130 | perlático | 1 |
| 51131 | perlados | 1 |
| 51132 | perlado | 1 |
| 51133 | perladas | 1 |
| 51134 | perjuros | 1 |
| 51135 | perjureste | 1 |
| 51136 | perjurar | 1 |
| 51137 | perjurando | 1 |
| 51138 | perjuran | 1 |
| 51139 | perjuraba | 1 |
| 51140 | perjudiquen | 1 |
| 51141 | perjudicaría | 1 |
| 51142 | perjudicado | 1 |
| 51143 | peritos | 1 |
| 51144 | peritonitis | 1 |
| 51145 | peritoa | 1 |
| 51146 | peripatético | 1 |
| 51147 | peripatética | 1 |
| 51148 | perión | 1 |
| 51149 | periodiquillo | 1 |
| 51150 | periodiqueros | 1 |
| 51151 | periódicas | 1 |
| 51152 | perigueux | 1 |
| 51153 | périgord | 1 |
| 51154 | periféricos | 1 |
| 51155 | periferia | 1 |
| 51156 | periespíritu | 1 |
| 51157 | perictos | 1 |
| 51158 | pericos | 1 |
| 51159 | perico | 1 |
| 51160 | pericles | 1 |
| 51161 | pericial | 1 |
| 51162 | perhenales | 1 |
| 51163 | pergeño | 1 |
| 51164 | pergeñadas | 1 |
| 51165 | pergeñada | 1 |
| 51166 | perfumera | 1 |
| 51167 | perfumados | 1 |
| 51168 | perfuma | 1 |
| 51169 | perfilados | 1 |
| 51170 | perfidias | 1 |
| 51171 | pérfidas | 1 |
| 51172 | perficiónala | 1 |
| 51173 | perficion | 1 |
| 51174 | perfetos | 1 |
| 51175 | perfetísimo | 1 |
| 51176 | perfectísimamente | 1 |
| 51177 | perfeciones | 1 |
| 51178 | perfecion | 1 |
| 51179 | perfeccionarse | 1 |
| 51180 | perfeccionar | 1 |
| 51181 | perfeccionándose | 1 |
| 51182 | perfeccionamiento | 1 |
| 51183 | perfeccionado | 1 |
| 51184 | perfec | 1 |
| 51185 | perezco | 1 |
| 51186 | perezcas | 1 |
| 51187 | perezas | 1 |
| 51188 | peresosos | 1 |
| 51189 | peresosas | 1 |
| 51190 | peresciessen | 1 |
| 51191 | peresceria | 1 |
| 51192 | peresas | 1 |
| 51193 | perendenga | 1 |
| 51194 | perencejo | 1 |
| 51195 | peregrinando | 1 |
| 51196 | peregrinamos | 1 |
| 51197 | peregrinado | 1 |
| 51198 | pereda | 1 |
| 51199 | perecieran | 1 |
| 51200 | pereciéndome | 1 |
| 51201 | perecida | 1 |
| 51202 | perecían | 1 |
| 51203 | perecía | 1 |
| 51204 | perecería | 1 |
| 51205 | perecerán | 1 |
| 51206 | pereçer | 1 |
| 51207 | perecemos | 1 |
| 51208 | pereça | 1 |
| 51209 | perdurado | 1 |
| 51210 | perdurables | 1 |
| 51211 | perdudo | 1 |
| 51212 | perdredes | 1 |
| 51213 | perdoñando | 1 |
| 51214 | perdonóselos | 1 |
| 51215 | perdonóla | 1 |
| 51216 | perdónesenos | 1 |
| 51217 | perdóneseme | 1 |
| 51218 | perdónenos | 1 |
| 51219 | perdónenme | 1 |
| 51220 | perdonemos | 1 |
| 51221 | perdónemelo | 1 |
| 51222 | perdonelos | 1 |
| 51223 | perdonele | 1 |
| 51224 | perdonastes | 1 |
| 51225 | perdonasen | 1 |
| 51226 | perdonárselos | 1 |
| 51227 | perdonaros | 1 |
| 51228 | perdonaron | 1 |
| 51229 | perdonarnos | 1 |
| 51230 | perdonarlo | 1 |
| 51231 | perdonáramos | 1 |
| 51232 | perdonándoselo | 1 |
| 51233 | perdonándosela | 1 |
| 51234 | perdonan | 1 |
| 51235 | perdonadle | 1 |
| 51236 | perdonadas | 1 |
| 51237 | perdonada | 1 |
| 51238 | perdonaban | 1 |
| 51239 | perdistes | 1 |
| 51240 | perdises | 1 |
| 51241 | perdiose | 1 |
| 51242 | perdióla | 1 |
| 51243 | perdío | 1 |
| 51244 | perdiguero | 1 |
| 51245 | perdigonada | 1 |
| 51246 | perdieras | 1 |
| 51247 | perdierades | 1 |
| 51248 | perdiéndoseme | 1 |
| 51249 | perdiendose | 1 |
| 51250 | perdidamente | 1 |
| 51251 | perdiciosas | 1 |
| 51252 | perdiçión | 1 |
| 51253 | perdian | 1 |
| 51254 | perdíame | 1 |
| 51255 | perdeys | 1 |
| 51256 | perderos | 1 |
| 51257 | perderlos | 1 |
| 51258 | perderles | 1 |
| 51259 | perderías | 1 |
| 51260 | perderias | 1 |
| 51261 | perderiamos | 1 |
| 51262 | perderemos | 1 |
| 51263 | perderedes | 1 |
| 51264 | perdere | 1 |
| 51265 | perderán | 1 |
| 51266 | perdera | 1 |
| 51267 | perdella | 1 |
| 51268 | perdéis | 1 |
| 51269 | perdédesvos | 1 |
| 51270 | perded | 1 |
| 51271 | percusión | 1 |
| 51272 | percloruro | 1 |
| 51273 | percibirse | 1 |
| 51274 | percibieron | 1 |
| 51275 | percibida | 1 |
| 51276 | percibían | 1 |
| 51277 | percibí | 1 |
| 51278 | perciben | 1 |
| 51279 | perciban | 1 |
| 51280 | percheros | 1 |
| 51281 | perchero | 1 |
| 51282 | perchel | 1 |
| 51283 | perceptivas | 1 |
| 51284 | perceptibles | 1 |
| 51285 | perçebydvos | 1 |
| 51286 | percebir | 1 |
| 51287 | percebe | 1 |
| 51288 | percatáramos | 1 |
| 51289 | percalina | 1 |
| 51290 | perbreue | 1 |
| 51291 | peratiñen | 1 |
| 51292 | peralvillo | 1 |
| 51293 | peraltados | 1 |
| 51294 | peralitos | 1 |
| 51295 | perailes | 1 |
| 51296 | peques | 1 |
| 51297 | pequeñitas | 1 |
| 51298 | pequeñísimo | 1 |
| 51299 | pequenos | 1 |
| 51300 | pequemos | 1 |
| 51301 | pequé | 1 |
| 51302 | peptona | 1 |
| 51303 | pepiones | 1 |
| 51304 | pepinillos | 1 |
| 51305 | pepilla | 1 |
| 51306 | peoncillo | 1 |
| 51307 | peñuelas | 1 |
| 51308 | peñolas | 1 |
| 51309 | peñol | 1 |
| 51310 | peñíscola | 1 |
| 51311 | peñavera | 1 |
| 51312 | peñaranda | 1 |
| 51313 | peñacerrada | 1 |
| 51314 | penúltima | 1 |
| 51315 | pentapolén | 1 |
| 51316 | penssó | 1 |
| 51317 | penssemos | 1 |
| 51318 | penssavan | 1 |
| 51319 | penssar | 1 |
| 51320 | penssamiento | 1 |
| 51321 | pensiono | 1 |
| 51322 | pensionista | 1 |
| 51323 | pensiones | 1 |
| 51324 | pénsiles | 1 |
| 51325 | pensil | 1 |
| 51326 | penséme | 1 |
| 51327 | pensedes | 1 |
| 51328 | pensatiuo | 1 |
| 51329 | pensastes | 1 |
| 51330 | pensarnos | 1 |
| 51331 | pensarle | 1 |
| 51332 | pensarían | 1 |
| 51333 | pensarian | 1 |
| 51334 | pensaren | 1 |
| 51335 | pensaréis | 1 |
| 51336 | pensarás | 1 |
| 51337 | pensadorzuelo | 1 |
| 51338 | pensad | 1 |
| 51339 | pensábanlo | 1 |
| 51340 | penosísimos | 1 |
| 51341 | penosísima | 1 |
| 51342 | penosas | 1 |
| 51343 | penitenciarias | 1 |
| 51344 | penitencial | 1 |
| 51345 | penitenciados | 1 |
| 51346 | penitas | 1 |
| 51347 | penintençia | 1 |
| 51348 | penetro | 1 |
| 51349 | penetres | 1 |
| 51350 | penetremos | 1 |
| 51351 | penetré | 1 |
| 51352 | penetre | 1 |
| 51353 | penetraste | 1 |
| 51354 | penetrase | 1 |
| 51355 | penetrarse | 1 |
| 51356 | penetraras | 1 |
| 51357 | penetrándose | 1 |
| 51358 | penetran | 1 |
| 51359 | penetrados | 1 |
| 51360 | penetrador | 1 |
| 51361 | penetradas | 1 |
| 51362 | penetrada | 1 |
| 51363 | penetrad | 1 |
| 51364 | peneste | 1 |
| 51365 | peneo | 1 |
| 51366 | penen | 1 |
| 51367 | penéis | 1 |
| 51368 | peneida | 1 |
| 51369 | péndulos | 1 |
| 51370 | pendoncillo | 1 |
| 51371 | pendonazas | 1 |
| 51372 | pendon | 1 |
| 51373 | pendolista | 1 |
| 51374 | pendiere | 1 |
| 51375 | pendíanle | 1 |
| 51376 | pendenzuela | 1 |
| 51377 | penden | 1 |
| 51378 | pendebat | 1 |
| 51379 | pendangas | 1 |
| 51380 | penauas | 1 |
| 51381 | penates | 1 |
| 51382 | penaste | 1 |
| 51383 | penasse | 1 |
| 51384 | penaria | 1 |
| 51385 | penarás | 1 |
| 51386 | penarán | 1 |
| 51387 | penara | 1 |
| 51388 | penantes | 1 |
| 51389 | penalidad | 1 |
| 51390 | penal | 1 |
| 51391 | penadilla | 1 |
| 51392 | penades | 1 |
| 51393 | penachos | 1 |
| 51394 | penacho | 1 |
| 51395 | pelygros | 1 |
| 51396 | pelusas | 1 |
| 51397 | pelusa | 1 |
| 51398 | peludas | 1 |
| 51399 | pelucas | 1 |
| 51400 | pelras | 1 |
| 51401 | pelotones | 1 |
| 51402 | pelotilla | 1 |
| 51403 | peloteando | 1 |
| 51404 | pelotada | 1 |
| 51405 | pelones | 1 |
| 51406 | pelón | 1 |
| 51407 | pelon | 1 |
| 51408 | pelól | 1 |
| 51409 | pelmaços | 1 |
| 51410 | pellota | 1 |
| 51411 | pello | 1 |
| 51412 | pellizcar | 1 |
| 51413 | pellizcándole | 1 |
| 51414 | pellizcando | 1 |
| 51415 | pellizcacen | 1 |
| 51416 | pellizca | 1 |
| 51417 | pelliza | 1 |
| 51418 | pelligeros | 1 |
| 51419 | pellejas | 1 |
| 51420 | pelleas | 1 |
| 51421 | pelinegra | 1 |
| 51422 | pelillo | 1 |
| 51423 | peligrosísimo | 1 |
| 51424 | peligró | 1 |
| 51425 | peligre | 1 |
| 51426 | peligrara | 1 |
| 51427 | pelicano | 1 |
| 51428 | peliagudo | 1 |
| 51429 | peliaguda | 1 |
| 51430 | peleón | 1 |
| 51431 | peleó | 1 |
| 51432 | pelecharan | 1 |
| 51433 | pelechar | 1 |
| 51434 | peleares | 1 |
| 51435 | peleante | 1 |
| 51436 | peleamos | 1 |
| 51437 | peleada | 1 |
| 51438 | peleaba | 1 |
| 51439 | pelaza | 1 |
| 51440 | pelastes | 1 |
| 51441 | pelarvos | 1 |
| 51442 | pelarruecas | 1 |
| 51443 | peláronle | 1 |
| 51444 | pelarme | 1 |
| 51445 | pelambre | 1 |
| 51446 | pelafustán | 1 |
| 51447 | pelados | 1 |
| 51448 | pelacejas | 1 |
| 51449 | pelaça | 1 |
| 51450 | pejugar | 1 |
| 51451 | pejiguera | 1 |
| 51452 | peinóse | 1 |
| 51453 | peinose | 1 |
| 51454 | peino | 1 |
| 51455 | peinarte | 1 |
| 51456 | peinarme | 1 |
| 51457 | peinarla | 1 |
| 51458 | peinando | 1 |
| 51459 | peinan | 1 |
| 51460 | peinamos | 1 |
| 51461 | peinador | 1 |
| 51462 | peguen | 1 |
| 51463 | pégueme | 1 |
| 51464 | pegote | 1 |
| 51465 | pegóseme | 1 |
| 51466 | pegósele | 1 |
| 51467 | pegóse | 1 |
| 51468 | pegones | 1 |
| 51469 | pégate | 1 |
| 51470 | pegatas | 1 |
| 51471 | pegasteis | 1 |
| 51472 | pegase | 1 |
| 51473 | pegárselo | 1 |
| 51474 | pegársela | 1 |
| 51475 | pegarnos | 1 |
| 51476 | pegármela | 1 |
| 51477 | pegaré | 1 |
| 51478 | pegaras | 1 |
| 51479 | pegarán | 1 |
| 51480 | pegara | 1 |
| 51481 | pegándoselos | 1 |
| 51482 | pegándomela | 1 |
| 51483 | pegajosas | 1 |
| 51484 | pegadlo | 1 |
| 51485 | pegadizas | 1 |
| 51486 | pegadiza | 1 |
| 51487 | pegábasele | 1 |
| 51488 | pedruzco | 1 |
| 51489 | pedrusco | 1 |
| 51490 | pedrilla | 1 |
| 51491 | pedricas | 1 |
| 51492 | pedricadores | 1 |
| 51493 | pedricaderas | 1 |
| 51494 | pedrezuelas | 1 |
| 51495 | pedrero | 1 |
| 51496 | pedrerías | 1 |
| 51497 | pedregosos | 1 |
| 51498 | pedregosas | 1 |
| 51499 | pedreas | 1 |
| 51500 | pedrea | 1 |
| 51501 | pedorreras | 1 |
| 51502 | pedistes | 1 |
| 51503 | pediste | 1 |
| 51504 | pedírselos | 1 |
| 51505 | pedírsele | 1 |
| 51506 | pedirlos | 1 |
| 51507 | pediréte | 1 |
| 51508 | pedirán | 1 |
| 51509 | pedió | 1 |
| 51510 | pedímosle | 1 |
| 51511 | pedimiento | 1 |
| 51512 | pedilde | 1 |
| 51513 | pedigüeñas | 1 |
| 51514 | pedigüeña | 1 |
| 51515 | pediese | 1 |
| 51516 | pedieres | 1 |
| 51517 | pediendo | 1 |
| 51518 | pedidor | 1 |
| 51519 | pedídole | 1 |
| 51520 | pedídmela | 1 |
| 51521 | pedidla | 1 |
| 51522 | pedidas | 1 |
| 51523 | pedid | 1 |
| 51524 | pedibus | 1 |
| 51525 | pedías | 1 |
| 51526 | pedias | 1 |
| 51527 | pedíanme | 1 |
| 51528 | pedíamos | 1 |
| 51529 | pedestres | 1 |
| 51530 | pedernalinas | 1 |
| 51531 | pedernales | 1 |
| 51532 | pedantón | 1 |
| 51533 | pedantesco | 1 |
| 51534 | pedantesca | 1 |
| 51535 | pedanteado | 1 |
| 51536 | pedaleando | 1 |
| 51537 | pedagogo | 1 |
| 51538 | pedagógicas | 1 |
| 51539 | pedaços | 1 |
| 51540 | pecuniarios | 1 |
| 51541 | pecuniario | 1 |
| 51542 | peculio | 1 |
| 51543 | pecoso | 1 |
| 51544 | pecilga | 1 |
| 51545 | pechugón | 1 |
| 51546 | pechona | 1 |
| 51547 | pechinas | 1 |
| 51548 | pechero | 1 |
| 51549 | pececillos | 1 |
| 51550 | pecco | 1 |
| 51551 | peccata | 1 |
| 51552 | pecase | 1 |
| 51553 | pecaron | 1 |
| 51554 | pecare | 1 |
| 51555 | pecaran | 1 |
| 51556 | pecara | 1 |
| 51557 | pecamos | 1 |
| 51558 | peçados | 1 |
| 51559 | pecadorcico | 1 |
| 51560 | pecadillo | 1 |
| 51561 | pecadesno | 1 |
| 51562 | pecada | 1 |
| 51563 | pebetero | 1 |
| 51564 | peau | 1 |
| 51565 | peanas | 1 |
| 51566 | pche | 1 |
| 51567 | pazpuerca | 1 |
| 51568 | pazguatos | 1 |
| 51569 | payaso | 1 |
| 51570 | payasa | 1 |
| 51571 | paya | 1 |
| 51572 | paxarera | 1 |
| 51573 | paxaras | 1 |
| 51574 | pavura | 1 |
| 51575 | pavorosos | 1 |
| 51576 | pavorosamente | 1 |
| 51577 | pavonadas | 1 |
| 51578 | pavonada | 1 |
| 51579 | pavisosa | 1 |
| 51580 | paviotes | 1 |
| 51581 | paviotas | 1 |
| 51582 | pavillo | 1 |
| 51583 | paveznos | 1 |
| 51584 | pavesnos | 1 |
| 51585 | pauta | 1 |
| 51586 | pauso | 1 |
| 51587 | pausanias | 1 |
| 51588 | pausado | 1 |
| 51589 | páuperum | 1 |
| 51590 | pauorosas | 1 |
| 51591 | pauor | 1 |
| 51592 | paúles | 1 |
| 51593 | paulatinos | 1 |
| 51594 | paulatinamente | 1 |
| 51595 | pau | 1 |
| 51596 | patronato | 1 |
| 51597 | patrocinado | 1 |
| 51598 | patris | 1 |
| 51599 | patrióticos | 1 |
| 51600 | patriotas | 1 |
| 51601 | patrio | 1 |
| 51602 | patrimos | 1 |
| 51603 | patrimonial | 1 |
| 51604 | patricidas | 1 |
| 51605 | patriarcalismo | 1 |
| 51606 | patoso | 1 |
| 51607 | patológicos | 1 |
| 51608 | patológico | 1 |
| 51609 | patología | 1 |
| 51610 | patito | 1 |
| 51611 | patinillo | 1 |
| 51612 | patincour | 1 |
| 51613 | patinar | 1 |
| 51614 | patinadores | 1 |
| 51615 | patinación | 1 |
| 51616 | patigurbiar | 1 |
| 51617 | patiecillo | 1 |
| 51618 | patibulario | 1 |
| 51619 | patharra | 1 |
| 51620 | paternidades | 1 |
| 51621 | patentemente | 1 |
| 51622 | patencures | 1 |
| 51623 | patee | 1 |
| 51624 | patearle | 1 |
| 51625 | pateándole | 1 |
| 51626 | pateado | 1 |
| 51627 | patatosa | 1 |
| 51628 | patás | 1 |
| 51629 | patarata | 1 |
| 51630 | pataplús | 1 |
| 51631 | patanes | 1 |
| 51632 | patán | 1 |
| 51633 | pataleaban | 1 |
| 51634 | patalea | 1 |
| 51635 | patagonia | 1 |
| 51636 | patadillas | 1 |
| 51637 | pataba | 1 |
| 51638 | pastrija | 1 |
| 51639 | pastosidad | 1 |
| 51640 | pastos | 1 |
| 51641 | pastoreaba | 1 |
| 51642 | pastorcillo | 1 |
| 51643 | pastorcico | 1 |
| 51644 | pastija | 1 |
| 51645 | pasteur | 1 |
| 51646 | pastelón | 1 |
| 51647 | pastellera | 1 |
| 51648 | pasteleros | 1 |
| 51649 | passó | 1 |
| 51650 | passionados | 1 |
| 51651 | passes | 1 |
| 51652 | passer | 1 |
| 51653 | passea | 1 |
| 51654 | passauan | 1 |
| 51655 | passatiempo | 1 |
| 51656 | passasse | 1 |
| 51657 | passarse | 1 |
| 51658 | passaremos | 1 |
| 51659 | passare | 1 |
| 51660 | passaran | 1 |
| 51661 | passara | 1 |
| 51662 | pasola | 1 |
| 51663 | pasmose | 1 |
| 51664 | pasmosamente | 1 |
| 51665 | pasméme | 1 |
| 51666 | pasmasen | 1 |
| 51667 | pasmarte | 1 |
| 51668 | pasmarotes | 1 |
| 51669 | pasmarías | 1 |
| 51670 | pasmaré | 1 |
| 51671 | pasmaran | 1 |
| 51672 | pasman | 1 |
| 51673 | pasivos | 1 |
| 51674 | pasivas | 1 |
| 51675 | pasitos | 1 |
| 51676 | pasitamente | 1 |
| 51677 | pasita | 1 |
| 51678 | pasiphe | 1 |
| 51679 | pasion | 1 |
| 51680 | pasillas | 1 |
| 51681 | pasife | 1 |
| 51682 | pasiega | 1 |
| 51683 | paseóse | 1 |
| 51684 | pasémosle | 1 |
| 51685 | paseítos | 1 |
| 51686 | paséese | 1 |
| 51687 | pasees | 1 |
| 51688 | paséate | 1 |
| 51689 | pasearnos | 1 |
| 51690 | paseantes | 1 |
| 51691 | paseante | 1 |
| 51692 | paseándolos | 1 |
| 51693 | paseándola | 1 |
| 51694 | paseáis | 1 |
| 51695 | paseábanse | 1 |
| 51696 | paseábamos | 1 |
| 51697 | paseábame | 1 |
| 51698 | pasçía | 1 |
| 51699 | pascia | 1 |
| 51700 | pasce | 1 |
| 51701 | pascasio | 1 |
| 51702 | pascal | 1 |
| 51703 | pasaua | 1 |
| 51704 | pásate | 1 |
| 51705 | pasaros | 1 |
| 51706 | pasáronsenos | 1 |
| 51707 | pasáronse | 1 |
| 51708 | pasáronle | 1 |
| 51709 | pasaréte | 1 |
| 51710 | pasáramos | 1 |
| 51711 | pasao | 1 |
| 51712 | pasándoseme | 1 |
| 51713 | pasándolos | 1 |
| 51714 | pasándoles | 1 |
| 51715 | pasándola | 1 |
| 51716 | pasamiento | 1 |
| 51717 | pasamaques | 1 |
| 51718 | pasamano | 1 |
| 51719 | pasamanería | 1 |
| 51720 | pásalas | 1 |
| 51721 | pasáis | 1 |
| 51722 | pasagonzalo | 1 |
| 51723 | pasadnos | 1 |
| 51724 | pasadita | 1 |
| 51725 | pasádesvos | 1 |
| 51726 | pasaderas | 1 |
| 51727 | pasad | 1 |
| 51728 | pasacalles | 1 |
| 51729 | pasábanse | 1 |
| 51730 | pasábalas | 1 |
| 51731 | pasá | 1 |
| 51732 | paryentes | 1 |
| 51733 | párvulos | 1 |
| 51734 | párvulas | 1 |
| 51735 | parves | 1 |
| 51736 | parvedad | 1 |
| 51737 | parva | 1 |
| 51738 | partyrle | 1 |
| 51739 | partyr | 1 |
| 51740 | partyóse | 1 |
| 51741 | partyme | 1 |
| 51742 | pártome | 1 |
| 51743 | partome | 1 |
| 51744 | partiste | 1 |
| 51745 | partirnos | 1 |
| 51746 | partirle | 1 |
| 51747 | partirías | 1 |
| 51748 | partiríamos | 1 |
| 51749 | partiremos | 1 |
| 51750 | partiquino | 1 |
| 51751 | partíos | 1 |
| 51752 | partióles | 1 |
| 51753 | partillo | 1 |
| 51754 | partiesses | 1 |
| 51755 | partiessen | 1 |
| 51756 | partiéronse | 1 |
| 51757 | partiere | 1 |
| 51758 | partieran | 1 |
| 51759 | partiéndoseme | 1 |
| 51760 | partiéndole | 1 |
| 51761 | partidor | 1 |
| 51762 | partidita | 1 |
| 51763 | partidillas | 1 |
| 51764 | partid | 1 |
| 51765 | particularizar | 1 |
| 51766 | partícula | 1 |
| 51767 | participé | 1 |
| 51768 | participe | 1 |
| 51769 | participaste | 1 |
| 51770 | participaron | 1 |
| 51771 | participarme | 1 |
| 51772 | participante | 1 |
| 51773 | participan | 1 |
| 51774 | participaciones | 1 |
| 51775 | particion | 1 |
| 51776 | parti | 1 |
| 51777 | parthos | 1 |
| 51778 | partezica | 1 |
| 51779 | párteslo | 1 |
| 51780 | pártese | 1 |
| 51781 | partesanas | 1 |
| 51782 | parterre | 1 |
| 51783 | partera | 1 |
| 51784 | parténope | 1 |
| 51785 | partenón | 1 |
| 51786 | parteçión | 1 |
| 51787 | partámonos | 1 |
| 51788 | parsimoniosa | 1 |
| 51789 | parriba | 1 |
| 51790 | parrasio | 1 |
| 51791 | parral | 1 |
| 51792 | paroxismos | 1 |
| 51793 | parósem | 1 |
| 51794 | paropillo | 1 |
| 51795 | parodiar | 1 |
| 51796 | parodiaba | 1 |
| 51797 | parodia | 1 |
| 51798 | parmenico | 1 |
| 51799 | parlylla | 1 |
| 51800 | parlotear | 1 |
| 51801 | parloteando | 1 |
| 51802 | parló | 1 |
| 51803 | parlinas | 1 |
| 51804 | parleria | 1 |
| 51805 | parlen | 1 |
| 51806 | parlava | 1 |
| 51807 | parlatorio | 1 |
| 51808 | parlas | 1 |
| 51809 | parlares | 1 |
| 51810 | parlanchinear | 1 |
| 51811 | parlanchín | 1 |
| 51812 | parlan | 1 |
| 51813 | parlamentos | 1 |
| 51814 | parlamentaron | 1 |
| 51815 | parlamentarismo | 1 |
| 51816 | parlamentarios | 1 |
| 51817 | parlamentario | 1 |
| 51818 | parlamentaria | 1 |
| 51819 | parlamentando | 1 |
| 51820 | parlador | 1 |
| 51821 | parlado | 1 |
| 51822 | parladera | 1 |
| 51823 | park | 1 |
| 51824 | parisién | 1 |
| 51825 | parióme | 1 |
| 51826 | pariome | 1 |
| 51827 | parihuela | 1 |
| 51828 | pariese | 1 |
| 51829 | parieres | 1 |
| 51830 | parieran | 1 |
| 51831 | pariendo | 1 |
| 51832 | paridad | 1 |
| 51833 | parias | 1 |
| 51834 | paresciere | 1 |
| 51835 | paresçiente | 1 |
| 51836 | parescido | 1 |
| 51837 | paresçían | 1 |
| 51838 | parescete | 1 |
| 51839 | paresçes | 1 |
| 51840 | paresces | 1 |
| 51841 | paresçerá | 1 |
| 51842 | parésçeme | 1 |
| 51843 | parescas | 1 |
| 51844 | paresca | 1 |
| 51845 | parens | 1 |
| 51846 | parejos | 1 |
| 51847 | parejita | 1 |
| 51848 | paredones | 1 |
| 51849 | paredón | 1 |
| 51850 | pareciónos | 1 |
| 51851 | pareciólas | 1 |
| 51852 | parecieran | 1 |
| 51853 | pareciéralo | 1 |
| 51854 | pareciendote | 1 |
| 51855 | parecidísimo | 1 |
| 51856 | parecías | 1 |
| 51857 | parecíanme | 1 |
| 51858 | parecíales | 1 |
| 51859 | parécete | 1 |
| 51860 | parecérsele | 1 |
| 51861 | parecernos | 1 |
| 51862 | parecerla | 1 |
| 51863 | pareceré | 1 |
| 51864 | parecerás | 1 |
| 51865 | pareçeme | 1 |
| 51866 | pareceme | 1 |
| 51867 | parécelo | 1 |
| 51868 | pareçe | 1 |
| 51869 | parduzco | 1 |
| 51870 | parduzcas | 1 |
| 51871 | pardiós | 1 |
| 51872 | pardessus | 1 |
| 51873 | pardeaba | 1 |
| 51874 | pardal | 1 |
| 51875 | parçioneros | 1 |
| 51876 | parcialmente | 1 |
| 51877 | parcialidades | 1 |
| 51878 | parcial | 1 |
| 51879 | parcas | 1 |
| 51880 | parava | 1 |
| 51881 | parate | 1 |
| 51882 | parasti | 1 |
| 51883 | parasitismo | 1 |
| 51884 | parasitario | 1 |
| 51885 | parasismos | 1 |
| 51886 | pararvos | 1 |
| 51887 | pararé | 1 |
| 51888 | pararán | 1 |
| 51889 | pararan | 1 |
| 51890 | parapetos | 1 |
| 51891 | parapeta | 1 |
| 51892 | parangón | 1 |
| 51893 | parança | 1 |
| 51894 | paramos | 1 |
| 51895 | paramentos | 1 |
| 51896 | paramentados | 1 |
| 51897 | paramal | 1 |
| 51898 | paralizó | 1 |
| 51899 | paralizan | 1 |
| 51900 | paralizado | 1 |
| 51901 | paralizadas | 1 |
| 51902 | paralizaba | 1 |
| 51903 | paralíticos | 1 |
| 51904 | paralítico | 1 |
| 51905 | paralítica | 1 |
| 51906 | paralipomenón | 1 |
| 51907 | paralelamente | 1 |
| 51908 | paral | 1 |
| 51909 | paraguazo | 1 |
| 51910 | paráfrasis | 1 |
| 51911 | parafraseando | 1 |
| 51912 | paradójicas | 1 |
| 51913 | paradillas | 1 |
| 51914 | paraderos | 1 |
| 51915 | parábase | 1 |
| 51916 | parábanse | 1 |
| 51917 | paquetitos | 1 |
| 51918 | paquetillo | 1 |
| 51919 | papos | 1 |
| 51920 | papo | 1 |
| 51921 | papista | 1 |
| 51922 | papisa | 1 |
| 51923 | pápiros | 1 |
| 51924 | papín | 1 |
| 51925 | papesa | 1 |
| 51926 | papen | 1 |
| 51927 | papeluchos | 1 |
| 51928 | papelucho | 1 |
| 51929 | papelotes | 1 |
| 51930 | papelorios | 1 |
| 51931 | papelón | 1 |
| 51932 | papelitos | 1 |
| 51933 | papelistas | 1 |
| 51934 | papelillos | 1 |
| 51935 | papeletitas | 1 |
| 51936 | papelejos | 1 |
| 51937 | papé | 1 |
| 51938 | pape | 1 |
| 51939 | pápate | 1 |
| 51940 | paparos | 1 |
| 51941 | papar | 1 |
| 51942 | papal | 1 |
| 51943 | papaíto | 1 |
| 51944 | papahígo | 1 |
| 51945 | pañolones | 1 |
| 51946 | pañolero | 1 |
| 51947 | pañero | 1 |
| 51948 | pantuflos | 1 |
| 51949 | pantuflas | 1 |
| 51950 | pantorriiiilla | 1 |
| 51951 | panteras | 1 |
| 51952 | panteones | 1 |
| 51953 | panteísticos | 1 |
| 51954 | panteística | 1 |
| 51955 | panteístas | 1 |
| 51956 | panteísmos | 1 |
| 51957 | pantasmas | 1 |
| 51958 | pantanos | 1 |
| 51959 | pantano | 1 |
| 51960 | pantaloncitos | 1 |
| 51961 | pantalia | 1 |
| 51962 | pantaleón | 1 |
| 51963 | panoplia | 1 |
| 51964 | panoli | 1 |
| 51965 | panificación | 1 |
| 51966 | pánfila | 1 |
| 51967 | paneras | 1 |
| 51968 | panenteísmo | 1 |
| 51969 | panegíricos | 1 |
| 51970 | pandora | 1 |
| 51971 | pandilla | 1 |
| 51972 | panderete | 1 |
| 51973 | pandemonio | 1 |
| 51974 | pandahilado | 1 |
| 51975 | pancorvo | 1 |
| 51976 | pancorbo | 1 |
| 51977 | panares | 1 |
| 51978 | panar | 1 |
| 51979 | panales | 1 |
| 51980 | panadizo | 1 |
| 51981 | panadera | 1 |
| 51982 | panaceas | 1 |
| 51983 | pamplona | 1 |
| 51984 | palustre | 1 |
| 51985 | palurdas | 1 |
| 51986 | paludismo | 1 |
| 51987 | palúdicas | 1 |
| 51988 | palta | 1 |
| 51989 | palsa | 1 |
| 51990 | palpó | 1 |
| 51991 | palpitantes | 1 |
| 51992 | palpitaban | 1 |
| 51993 | palpita | 1 |
| 51994 | palparles | 1 |
| 51995 | palpándose | 1 |
| 51996 | pálpalos | 1 |
| 51997 | palpaban | 1 |
| 51998 | palpa | 1 |
| 51999 | paloteadico | 1 |
| 52000 | palote | 1 |
| 52001 | palotadas | 1 |
| 52002 | palor | 1 |
| 52003 | palomino | 1 |
| 52004 | palomina | 1 |
| 52005 | palmoteándole | 1 |
| 52006 | palmitos | 1 |
| 52007 | palmease | 1 |
| 52008 | palmearon | 1 |
| 52009 | palmarios | 1 |
| 52010 | palmario | 1 |
| 52011 | palmaria | 1 |
| 52012 | palmar | 1 |
| 52013 | palmadicas | 1 |
| 52014 | pallida | 1 |
| 52015 | pallavicini | 1 |
| 52016 | pallas | 1 |
| 52017 | palla | 1 |
| 52018 | palizas | 1 |
| 52019 | palizada | 1 |
| 52020 | palisandro | 1 |
| 52021 | palinodia | 1 |
| 52022 | palillero | 1 |
| 52023 | paliducha | 1 |
| 52024 | palido | 1 |
| 52025 | palideces | 1 |
| 52026 | paliativos | 1 |
| 52027 | paliar | 1 |
| 52028 | paliabra | 1 |
| 52029 | paletot | 1 |
| 52030 | paletoque | 1 |
| 52031 | paleto | 1 |
| 52032 | palestina | 1 |
| 52033 | paleontología | 1 |
| 52034 | palastro | 1 |
| 52035 | palante | 1 |
| 52036 | palanquín | 1 |
| 52037 | palanganita | 1 |
| 52038 | palanciano | 1 |
| 52039 | palançiana | 1 |
| 52040 | palafrenes | 1 |
| 52041 | palafreneros | 1 |
| 52042 | palafoxes | 1 |
| 52043 | paladïones | 1 |
| 52044 | paladino | 1 |
| 52045 | paladines | 1 |
| 52046 | paladina | 1 |
| 52047 | paladares | 1 |
| 52048 | palacimás | 1 |
| 52049 | palaciegos | 1 |
| 52050 | palabrero | 1 |
| 52051 | palabreo | 1 |
| 52052 | pal | 1 |
| 52053 | pajuelas | 1 |
| 52054 | pajiza | 1 |
| 52055 | pajita | 1 |
| 52056 | pajezico | 1 |
| 52057 | pajés | 1 |
| 52058 | pajecillos | 1 |
| 52059 | pajatamo | 1 |
| 52060 | pajarracos | 1 |
| 52061 | pajarraco | 1 |
| 52062 | pajarita | 1 |
| 52063 | pajaricas | 1 |
| 52064 | paixa | 1 |
| 52065 | paix | 1 |
| 52066 | paisajista | 1 |
| 52067 | paisajes | 1 |
| 52068 | paicían | 1 |
| 52069 | paicerse | 1 |
| 52070 | paicen | 1 |
| 52071 | pahería | 1 |
| 52072 | págueseme | 1 |
| 52073 | pagues | 1 |
| 52074 | paguéle | 1 |
| 52075 | pagúele | 1 |
| 52076 | pagós | 1 |
| 52077 | paginitas | 1 |
| 52078 | pagina | 1 |
| 52079 | pagé | 1 |
| 52080 | pagávas | 1 |
| 52081 | pagavan | 1 |
| 52082 | págate | 1 |
| 52083 | pagastes | 1 |
| 52084 | pagasse | 1 |
| 52085 | pagarte | 1 |
| 52086 | pagároslo | 1 |
| 52087 | pagárnoslo | 1 |
| 52088 | pagarnos | 1 |
| 52089 | pagarías | 1 |
| 52090 | pagaríamos | 1 |
| 52091 | pagares | 1 |
| 52092 | pagaremos | 1 |
| 52093 | pagaréis | 1 |
| 52094 | pagaran | 1 |
| 52095 | pagándoselo | 1 |
| 52096 | pagándole | 1 |
| 52097 | pagandole | 1 |
| 52098 | pagán | 1 |
| 52099 | pagamentos | 1 |
| 52100 | pagalla | 1 |
| 52101 | pagadle | 1 |
| 52102 | pagaderos | 1 |
| 52103 | pagaderas | 1 |
| 52104 | pafo | 1 |
| 52105 | paf | 1 |
| 52106 | paella | 1 |
| 52107 | paece | 1 |
| 52108 | padrazo | 1 |
| 52109 | padezcase | 1 |
| 52110 | padezcas | 1 |
| 52111 | padescido | 1 |
| 52112 | padescian | 1 |
| 52113 | padescer | 1 |
| 52114 | padescemos | 1 |
| 52115 | padecimiento | 1 |
| 52116 | padecida | 1 |
| 52117 | padecí | 1 |
| 52118 | padecerla | 1 |
| 52119 | padecerías | 1 |
| 52120 | padecería | 1 |
| 52121 | padecerás | 1 |
| 52122 | padecerá | 1 |
| 52123 | padécense | 1 |
| 52124 | padecellas | 1 |
| 52125 | padan | 1 |
| 52126 | pactolo | 1 |
| 52127 | pacificos | 1 |
| 52128 | pacificar | 1 |
| 52129 | pacificadores | 1 |
| 52130 | pacificadoras | 1 |
| 52131 | pacienzudas | 1 |
| 52132 | paçiendo | 1 |
| 52133 | paciençia | 1 |
| 52134 | pachecos | 1 |
| 52135 | pacem | 1 |
| 52136 | pablito | 1 |
| 52137 | pábilos | 1 |
| 52138 | pábilo | 1 |
| 52139 | pabilo | 1 |
| 52140 | pá | 1 |
| 52141 | oytme | 1 |
| 52142 | oyrle | 1 |
| 52143 | oyremos | 1 |
| 52144 | oyre | 1 |
| 52145 | oyrá | 1 |
| 52146 | oyra | 1 |
| 52147 | óyote | 1 |
| 52148 | oyome | 1 |
| 52149 | oyoles | 1 |
| 52150 | oyóle | 1 |
| 52151 | oyola | 1 |
| 52152 | oylla | 1 |
| 52153 | óyle | 1 |
| 52154 | oylda | 1 |
| 52155 | oygas | 1 |
| 52156 | oyga | 1 |
| 52157 | oyete | 1 |
| 52158 | oyessen | 1 |
| 52159 | oyéronme | 1 |
| 52160 | oyeredes | 1 |
| 52161 | oyeras | 1 |
| 52162 | óyense | 1 |
| 52163 | oyéndotelo | 1 |
| 52164 | oyéndonos | 1 |
| 52165 | oyéndolos | 1 |
| 52166 | oyéndoles | 1 |
| 52167 | oyendole | 1 |
| 52168 | oydores | 1 |
| 52169 | oydor | 1 |
| 52170 | oydes | 1 |
| 52171 | oyáis | 1 |
| 52172 | oxígeno | 1 |
| 52173 | oxidadas | 1 |
| 52174 | oxear | 1 |
| 52175 | owen | 1 |
| 52176 | ovyste | 1 |
| 52177 | ovydyo | 1 |
| 52178 | ovydio | 1 |
| 52179 | óvosele | 1 |
| 52180 | ovóse | 1 |
| 52181 | óvomelo | 1 |
| 52182 | óvolas | 1 |
| 52183 | oviesse | 1 |
| 52184 | ovieses | 1 |
| 52185 | ovieralos | 1 |
| 52186 | oviérades | 1 |
| 52187 | ovier | 1 |
| 52188 | oviedo | 1 |
| 52189 | ovid | 1 |
| 52190 | ovejuno | 1 |
| 52191 | ovejero | 1 |
| 52192 | óvalos | 1 |
| 52193 | ovaladas | 1 |
| 52194 | ovación | 1 |
| 52195 | ouiessemos | 1 |
| 52196 | ouieres | 1 |
| 52197 | ouiera | 1 |
| 52198 | ouidio | 1 |
| 52199 | oueja | 1 |
| 52200 | otrie | 1 |
| 52201 | otri | 1 |
| 52202 | otr | 1 |
| 52203 | otórgeselo | 1 |
| 52204 | otorgatme | 1 |
| 52205 | otorgáronlo | 1 |
| 52206 | otorgarme | 1 |
| 52207 | otorgarle | 1 |
| 52208 | otorgándose | 1 |
| 52209 | otorgamos | 1 |
| 52210 | otoños | 1 |
| 52211 | otoñada | 1 |
| 52212 | otonio | 1 |
| 52213 | oteóme | 1 |
| 52214 | oteé | 1 |
| 52215 | otear | 1 |
| 52216 | otéame | 1 |
| 52217 | otaviano | 1 |
| 52218 | ostyas | 1 |
| 52219 | ostutzale | 1 |
| 52220 | ostracismo | 1 |
| 52221 | ostra | 1 |
| 52222 | ostión | 1 |
| 52223 | ostiense | 1 |
| 52224 | ostentosos | 1 |
| 52225 | ostentosas | 1 |
| 52226 | ostentó | 1 |
| 52227 | ostente | 1 |
| 52228 | ostentas | 1 |
| 52229 | ostentado | 1 |
| 52230 | ostensiblemente | 1 |
| 52231 | ostatu | 1 |
| 52232 | ostalaje | 1 |
| 52233 | ostabat | 1 |
| 52234 | osso | 1 |
| 52235 | osses | 1 |
| 52236 | ospital | 1 |
| 52237 | ospedado | 1 |
| 52238 | osorio | 1 |
| 52239 | osol | 1 |
| 52240 | osiris | 1 |
| 52241 | oscuridades | 1 |
| 52242 | oscurecida | 1 |
| 52243 | oscurecían | 1 |
| 52244 | oscurecerlos | 1 |
| 52245 | oscurecen | 1 |
| 52246 | oscilantes | 1 |
| 52247 | oscilante | 1 |
| 52248 | oscilaban | 1 |
| 52249 | oscar | 1 |
| 52250 | osauan | 1 |
| 52251 | osaua | 1 |
| 52252 | osasen | 1 |
| 52253 | osarvos | 1 |
| 52254 | osarse | 1 |
| 52255 | osare | 1 |
| 52256 | osará | 1 |
| 52257 | osándome | 1 |
| 52258 | osando | 1 |
| 52259 | osadamente | 1 |
| 52260 | osaban | 1 |
| 52261 | orzó | 1 |
| 52262 | orzando | 1 |
| 52263 | oruela | 1 |
| 52264 | ortógrafo | 1 |
| 52265 | ortodoxas | 1 |
| 52266 | ortodoxa | 1 |
| 52267 | orto | 1 |
| 52268 | ortiga | 1 |
| 52269 | ortelana | 1 |
| 52270 | ortaliza | 1 |
| 52271 | orsini | 1 |
| 52272 | orrela | 1 |
| 52273 | orra | 1 |
| 52274 | orpheo | 1 |
| 52275 | oros | 1 |
| 52276 | oropesa | 1 |
| 52277 | oropéndola | 1 |
| 52278 | orode | 1 |
| 52279 | oró | 1 |
| 52280 | ornitológicas | 1 |
| 52281 | ornatos | 1 |
| 52282 | ornamentos | 1 |
| 52283 | ormaiztegui | 1 |
| 52284 | orlas | 1 |
| 52285 | orlado | 1 |
| 52286 | orlaban | 1 |
| 52287 | oriundos | 1 |
| 52288 | oris | 1 |
| 52289 | orior | 1 |
| 52290 | orión | 1 |
| 52291 | orinó | 1 |
| 52292 | orina | 1 |
| 52293 | orihuela | 1 |
| 52294 | originó | 1 |
| 52295 | originarse | 1 |
| 52296 | originalmente | 1 |
| 52297 | originalísimo | 1 |
| 52298 | originalísima | 1 |
| 52299 | originada | 1 |
| 52300 | origina | 1 |
| 52301 | oriflama | 1 |
| 52302 | orïente | 1 |
| 52303 | orientarse | 1 |
| 52304 | orientándose | 1 |
| 52305 | orientalista | 1 |
| 52306 | orientada | 1 |
| 52307 | oriella | 1 |
| 52308 | orianas | 1 |
| 52309 | orgullosamente | 1 |
| 52310 | orgullos | 1 |
| 52311 | orgullito | 1 |
| 52312 | orgasmo | 1 |
| 52313 | organo | 1 |
| 52314 | organizó | 1 |
| 52315 | organizarse | 1 |
| 52316 | organizaremos | 1 |
| 52317 | organizando | 1 |
| 52318 | organizados | 1 |
| 52319 | organizador | 1 |
| 52320 | organizaciones | 1 |
| 52321 | organismos | 1 |
| 52322 | organillo | 1 |
| 52323 | orgánico | 1 |
| 52324 | orfeos | 1 |
| 52325 | oreos | 1 |
| 52326 | orenean | 1 |
| 52327 | orelia | 1 |
| 52328 | orejón | 1 |
| 52329 | orejitas | 1 |
| 52330 | orejita | 1 |
| 52331 | orejeras | 1 |
| 52332 | orearme | 1 |
| 52333 | orearan | 1 |
| 52334 | oreando | 1 |
| 52335 | orea | 1 |
| 52336 | ore | 1 |
| 52337 | ordóñez | 1 |
| 52338 | ordo | 1 |
| 52339 | ordinaro | 1 |
| 52340 | ordinariotes | 1 |
| 52341 | ordinariota | 1 |
| 52342 | ordinarieces | 1 |
| 52343 | ordenólo | 1 |
| 52344 | ordenola | 1 |
| 52345 | ordeno | 1 |
| 52346 | ordenemos | 1 |
| 52347 | ordenaste | 1 |
| 52348 | ordenarle | 1 |
| 52349 | ordenaría | 1 |
| 52350 | ordenaremos | 1 |
| 52351 | ordenando | 1 |
| 52352 | ordenador | 1 |
| 52353 | ordenadito | 1 |
| 52354 | ordenadísimo | 1 |
| 52355 | ordenad | 1 |
| 52356 | ordenaban | 1 |
| 52357 | ordeales | 1 |
| 52358 | orcas | 1 |
| 52359 | órbita | 1 |
| 52360 | orates | 1 |
| 52361 | orate | 1 |
| 52362 | orangután | 1 |
| 52363 | oráis | 1 |
| 52364 | orain | 1 |
| 52365 | oradoras | 1 |
| 52366 | orado | 1 |
| 52367 | oraba | 1 |
| 52368 | oquerra | 1 |
| 52369 | oquedad | 1 |
| 52370 | opusimos | 1 |
| 52371 | opusiesen | 1 |
| 52372 | opusiéronse | 1 |
| 52373 | opusieron | 1 |
| 52374 | opusiera | 1 |
| 52375 | opúsculos | 1 |
| 52376 | opulento | 1 |
| 52377 | opulentísimo | 1 |
| 52378 | opulencias | 1 |
| 52379 | optó | 1 |
| 52380 | optimismos | 1 |
| 52381 | optimi | 1 |
| 52382 | óptima | 1 |
| 52383 | ópticas | 1 |
| 52384 | opte | 1 |
| 52385 | optativa | 1 |
| 52386 | optase | 1 |
| 52387 | optaron | 1 |
| 52388 | optar | 1 |
| 52389 | opta | 1 |
| 52390 | oprobios | 1 |
| 52391 | oprobio | 1 |
| 52392 | oprimo | 1 |
| 52393 | oprimirse | 1 |
| 52394 | oprimiría | 1 |
| 52395 | oprimir | 1 |
| 52396 | oprimiéndole | 1 |
| 52397 | oprimiéndola | 1 |
| 52398 | oprima | 1 |
| 52399 | opresor | 1 |
| 52400 | oppert | 1 |
| 52401 | opositor | 1 |
| 52402 | oportunista | 1 |
| 52403 | oportunísimo | 1 |
| 52404 | oponiéndose | 1 |
| 52405 | opóngase | 1 |
| 52406 | oponérsele | 1 |
| 52407 | opondría | 1 |
| 52408 | opondremos | 1 |
| 52409 | opine | 1 |
| 52410 | opinaron | 1 |
| 52411 | opinando | 1 |
| 52412 | opinables | 1 |
| 52413 | opilación | 1 |
| 52414 | opiáceo | 1 |
| 52415 | operistas | 1 |
| 52416 | operista | 1 |
| 52417 | operan | 1 |
| 52418 | operador | 1 |
| 52419 | operacion | 1 |
| 52420 | ópalo | 1 |
| 52421 | opalina | 1 |
| 52422 | opacos | 1 |
| 52423 | ooooh | 1 |
| 52424 | oocampo | 1 |
| 52425 | oñez | 1 |
| 52426 | onzeno | 1 |
| 52427 | onrren | 1 |
| 52428 | onrrava | 1 |
| 52429 | onrraría | 1 |
| 52430 | onrradas | 1 |
| 52431 | onrr | 1 |
| 52432 | onofre | 1 |
| 52433 | ongui | 1 |
| 52434 | onesta | 1 |
| 52435 | onerá | 1 |
| 52436 | onduladas | 1 |
| 52437 | ondulaba | 1 |
| 52438 | onduan | 1 |
| 52439 | ondosos | 1 |
| 52440 | ondó | 1 |
| 52441 | ondinas | 1 |
| 52442 | ondean | 1 |
| 52443 | ondeado | 1 |
| 52444 | ondeadas | 1 |
| 52445 | ondeada | 1 |
| 52446 | onctan | 1 |
| 52447 | onces | 1 |
| 52448 | onbros | 1 |
| 52449 | onbligo | 1 |
| 52450 | omyl | 1 |
| 52451 | omoplatos | 1 |
| 52452 | omoplato | 1 |
| 52453 | omnis | 1 |
| 52454 | omnímodo | 1 |
| 52455 | omnímodas | 1 |
| 52456 | omnilateral | 1 |
| 52457 | omnibus | 1 |
| 52458 | omitimos | 1 |
| 52459 | omitida | 1 |
| 52460 | omiten | 1 |
| 52461 | omite | 1 |
| 52462 | omissis | 1 |
| 52463 | omiso | 1 |
| 52464 | omisiones | 1 |
| 52465 | omisión | 1 |
| 52466 | ominosos | 1 |
| 52467 | ominoso | 1 |
| 52468 | omilmente | 1 |
| 52469 | omillava | 1 |
| 52470 | omillan | 1 |
| 52471 | omilla | 1 |
| 52472 | omilidat | 1 |
| 52473 | omildes | 1 |
| 52474 | omil | 1 |
| 52475 | omenaje | 1 |
| 52476 | omecillos | 1 |
| 52477 | omecillo | 1 |
| 52478 | omeçida | 1 |
| 52479 | omar | 1 |
| 52480 | omanidat | 1 |
| 52481 | olvyda | 1 |
| 52482 | olvidóse | 1 |
| 52483 | olvidés | 1 |
| 52484 | olvidemos | 1 |
| 52485 | olvidéis | 1 |
| 52486 | olvídate | 1 |
| 52487 | olvidastes | 1 |
| 52488 | olvidaste | 1 |
| 52489 | olvidasen | 1 |
| 52490 | olvídaseme | 1 |
| 52491 | olvidarte | 1 |
| 52492 | olvidárseles | 1 |
| 52493 | olvidársele | 1 |
| 52494 | olvidaros | 1 |
| 52495 | olvidáronsele | 1 |
| 52496 | olvidarme | 1 |
| 52497 | olvidarlo | 1 |
| 52498 | olvidarle | 1 |
| 52499 | olvidaran | 1 |
| 52500 | olvidáramos | 1 |
| 52501 | olvidamos | 1 |
| 52502 | olvidalla | 1 |
| 52503 | olvidadizos | 1 |
| 52504 | oluides | 1 |
| 52505 | oluidemos | 1 |
| 52506 | oluidases | 1 |
| 52507 | oluidas | 1 |
| 52508 | oluidaron | 1 |
| 52509 | oluidaras | 1 |
| 52510 | oluidan | 1 |
| 52511 | oluidada | 1 |
| 52512 | olózaga | 1 |
| 52513 | olorosísimas | 1 |
| 52514 | olivífero | 1 |
| 52515 | olivera | 1 |
| 52516 | oliveira | 1 |
| 52517 | olivas | 1 |
| 52518 | olivantes | 1 |
| 52519 | olivante | 1 |
| 52520 | olistes | 1 |
| 52521 | oliscan | 1 |
| 52522 | olisca | 1 |
| 52523 | olímpicos | 1 |
| 52524 | olímpica | 1 |
| 52525 | olimpa | 1 |
| 52526 | oligisto | 1 |
| 52527 | oligárquico | 1 |
| 52528 | oliese | 1 |
| 52529 | oliéndole | 1 |
| 52530 | oliéndolas | 1 |
| 52531 | olias | 1 |
| 52532 | olfatorias | 1 |
| 52533 | olfateo | 1 |
| 52534 | olfatea | 1 |
| 52535 | olerme | 1 |
| 52536 | óleos | 1 |
| 52537 | oleeé | 1 |
| 52538 | oleadas | 1 |
| 52539 | olave | 1 |
| 52540 | olaberri | 1 |
| 52541 | ojoz | 1 |
| 52542 | ojiva | 1 |
| 52543 | ojitas | 1 |
| 52544 | ojinegra | 1 |
| 52545 | ojeándole | 1 |
| 52546 | ojeados | 1 |
| 52547 | ojeador | 1 |
| 52548 | ojazo | 1 |
| 52549 | ojalateros | 1 |
| 52550 | ojala | 1 |
| 52551 | oiste | 1 |
| 52552 | oíros | 1 |
| 52553 | oírles | 1 |
| 52554 | oirían | 1 |
| 52555 | oiría | 1 |
| 52556 | oiquina | 1 |
| 52557 | oímosla | 1 |
| 52558 | oílos | 1 |
| 52559 | oílas | 1 |
| 52560 | oíganme | 1 |
| 52561 | óiganme | 1 |
| 52562 | oigámoslo | 1 |
| 52563 | oígame | 1 |
| 52564 | óigalo | 1 |
| 52565 | oid | 1 |
| 52566 | oíanme | 1 |
| 52567 | oíanle | 1 |
| 52568 | oíamos | 1 |
| 52569 | oíales | 1 |
| 52570 | oi | 1 |
| 52571 | ogni | 1 |
| 52572 | ofuscaras | 1 |
| 52573 | ofuscándose | 1 |
| 52574 | ofrezcáis | 1 |
| 52575 | ofrescimientos | 1 |
| 52576 | ofrescimiento | 1 |
| 52577 | ofrescido | 1 |
| 52578 | ofrescia | 1 |
| 52579 | ofrescer | 1 |
| 52580 | ofrescele | 1 |
| 52581 | ofrescas | 1 |
| 52582 | ofreciste | 1 |
| 52583 | ofrecióseme | 1 |
| 52584 | ofreciósela | 1 |
| 52585 | ofrecióse | 1 |
| 52586 | ofrecióme | 1 |
| 52587 | ofrecióle | 1 |
| 52588 | ofreçiol | 1 |
| 52589 | ofreçió | 1 |
| 52590 | ofrecímele | 1 |
| 52591 | ofrecílas | 1 |
| 52592 | ofrecil | 1 |
| 52593 | ofreciesen | 1 |
| 52594 | ofreciéronsele | 1 |
| 52595 | ofreciéronme | 1 |
| 52596 | ofreciéndoseles | 1 |
| 52597 | ofreciéndolo | 1 |
| 52598 | ofreciéndoles | 1 |
| 52599 | ofrecíase | 1 |
| 52600 | ofrecian | 1 |
| 52601 | ofrecíame | 1 |
| 52602 | ofrécesele | 1 |
| 52603 | ofreçervos | 1 |
| 52604 | ofrecérseme | 1 |
| 52605 | ofrecérselo | 1 |
| 52606 | ofrecérseles | 1 |
| 52607 | ofrecería | 1 |
| 52608 | ofreçeremos | 1 |
| 52609 | ofreceré | 1 |
| 52610 | ofrecerán | 1 |
| 52611 | ofreçémostelo | 1 |
| 52612 | ofrecemos | 1 |
| 52613 | ofrecelle | 1 |
| 52614 | ofrécele | 1 |
| 52615 | ofrecedme | 1 |
| 52616 | ofre | 1 |
| 52617 | ofidiana | 1 |
| 52618 | oficiosos | 1 |
| 52619 | oficioso | 1 |
| 52620 | oficiosas | 1 |
| 52621 | oficïosa | 1 |
| 52622 | oficinista | 1 |
| 52623 | oficinalis | 1 |
| 52624 | oficialillo | 1 |
| 52625 | ofícialas | 1 |
| 52626 | offrezco | 1 |
| 52627 | offrescimientos | 1 |
| 52628 | offrescer | 1 |
| 52629 | offresce | 1 |
| 52630 | offreçió | 1 |
| 52631 | offrecimientos | 1 |
| 52632 | officios | 1 |
| 52633 | offiçia | 1 |
| 52634 | offertas | 1 |
| 52635 | offensione | 1 |
| 52636 | offension | 1 |
| 52637 | offendio | 1 |
| 52638 | offendido | 1 |
| 52639 | offendes | 1 |
| 52640 | offenderte | 1 |
| 52641 | offender | 1 |
| 52642 | offendedor | 1 |
| 52643 | ofensores | 1 |
| 52644 | ofensor | 1 |
| 52645 | ofensivo | 1 |
| 52646 | ofendiese | 1 |
| 52647 | ofendiera | 1 |
| 52648 | ofendiendo | 1 |
| 52649 | ofendidas | 1 |
| 52650 | ofendí | 1 |
| 52651 | ofendes | 1 |
| 52652 | ofenderles | 1 |
| 52653 | ofenderé | 1 |
| 52654 | ofenderán | 1 |
| 52655 | ofendellos | 1 |
| 52656 | ofendelle | 1 |
| 52657 | ofendedme | 1 |
| 52658 | oes | 1 |
| 52659 | odresillo | 1 |
| 52660 | odoríferas | 1 |
| 52661 | odite | 1 |
| 52662 | odiosamente | 1 |
| 52663 | odié | 1 |
| 52664 | odias | 1 |
| 52665 | odiarme | 1 |
| 52666 | odiado | 1 |
| 52667 | odiaban | 1 |
| 52668 | oderunt | 1 |
| 52669 | odaliscas | 1 |
| 52670 | ocurrirían | 1 |
| 52671 | ocurrirán | 1 |
| 52672 | ocurriese | 1 |
| 52673 | ocurrieren | 1 |
| 52674 | ocurrente | 1 |
| 52675 | ocurran | 1 |
| 52676 | ocupose | 1 |
| 52677 | ocuparnos | 1 |
| 52678 | ocuparle | 1 |
| 52679 | ocuparían | 1 |
| 52680 | ocuparé | 1 |
| 52681 | ocupare | 1 |
| 52682 | ocuparan | 1 |
| 52683 | ocuparála | 1 |
| 52684 | ocupará | 1 |
| 52685 | ocupaos | 1 |
| 52686 | ocupándola | 1 |
| 52687 | ocupador | 1 |
| 52688 | ocupábanse | 1 |
| 52689 | ocultis | 1 |
| 52690 | ocultémonos | 1 |
| 52691 | ocultéis | 1 |
| 52692 | ocultase | 1 |
| 52693 | ocultarse | 1 |
| 52694 | ocultáronse | 1 |
| 52695 | ocultármelo | 1 |
| 52696 | ocultarme | 1 |
| 52697 | ocultarlas | 1 |
| 52698 | ocultarían | 1 |
| 52699 | ocultaras | 1 |
| 52700 | ocultara | 1 |
| 52701 | ocultándome | 1 |
| 52702 | ocultándolo | 1 |
| 52703 | ocultándole | 1 |
| 52704 | ocultaciones | 1 |
| 52705 | ocultación | 1 |
| 52706 | octosílabos | 1 |
| 52707 | octogenario | 1 |
| 52708 | octauo | 1 |
| 52709 | ocios | 1 |
| 52710 | ochos | 1 |
| 52711 | ochentón | 1 |
| 52712 | ochentines | 1 |
| 52713 | ochavito | 1 |
| 52714 | ochavado | 1 |
| 52715 | ocerin | 1 |
| 52716 | océanos | 1 |
| 52717 | oceano | 1 |
| 52718 | occupado | 1 |
| 52719 | occidit | 1 |
| 52720 | ocasyón | 1 |
| 52721 | ocasos | 1 |
| 52722 | ocasionas | 1 |
| 52723 | ocasionarme | 1 |
| 52724 | ocasionarán | 1 |
| 52725 | ocasionando | 1 |
| 52726 | ocasionan | 1 |
| 52727 | ocasionaban | 1 |
| 52728 | ocasiona | 1 |
| 52729 | ocación | 1 |
| 52730 | obviant | 1 |
| 52731 | obuses | 1 |
| 52732 | obtinados | 1 |
| 52733 | obtienen | 1 |
| 52734 | obtenidas | 1 |
| 52735 | obtenía | 1 |
| 52736 | obtenerlo | 1 |
| 52737 | obstruido | 1 |
| 52738 | obstruían | 1 |
| 52739 | obstino | 1 |
| 52740 | obstinas | 1 |
| 52741 | obstinados | 1 |
| 52742 | obstetricia | 1 |
| 52743 | obseso | 1 |
| 52744 | observole | 1 |
| 52745 | observémosle | 1 |
| 52746 | observatorios | 1 |
| 52747 | observatorio | 1 |
| 52748 | observaste | 1 |
| 52749 | observas | 1 |
| 52750 | observarse | 1 |
| 52751 | observarle | 1 |
| 52752 | observaría | 1 |
| 52753 | observara | 1 |
| 52754 | observante | 1 |
| 52755 | observándose | 1 |
| 52756 | observándome | 1 |
| 52757 | observándolo | 1 |
| 52758 | observan | 1 |
| 52759 | obsérvale | 1 |
| 52760 | observados | 1 |
| 52761 | observábale | 1 |
| 52762 | observábala | 1 |
| 52763 | obsequiosissimus | 1 |
| 52764 | obsequiarse | 1 |
| 52765 | obsequiarles | 1 |
| 52766 | obsequiarla | 1 |
| 52767 | obsequiaremos | 1 |
| 52768 | obsequiando | 1 |
| 52769 | obsequian | 1 |
| 52770 | obsequiado | 1 |
| 52771 | obsequiada | 1 |
| 52772 | obsequiaban | 1 |
| 52773 | obsequiaba | 1 |
| 52774 | obscurezca | 1 |
| 52775 | obscureció | 1 |
| 52776 | obscurecieron | 1 |
| 52777 | obscurecida | 1 |
| 52778 | obscurantismo | 1 |
| 52779 | obscuramente | 1 |
| 52780 | obsceno | 1 |
| 52781 | obscenas | 1 |
| 52782 | obro | 1 |
| 52783 | obrita | 1 |
| 52784 | obren | 1 |
| 52785 | obrastes | 1 |
| 52786 | obrarse | 1 |
| 52787 | obraron | 1 |
| 52788 | obrarlo | 1 |
| 52789 | obraré | 1 |
| 52790 | obrare | 1 |
| 52791 | obrara | 1 |
| 52792 | obran | 1 |
| 52793 | obrallo | 1 |
| 52794 | obrad | 1 |
| 52795 | obraban | 1 |
| 52796 | obraba | 1 |
| 52797 | óbolo | 1 |
| 52798 | obliguen | 1 |
| 52799 | obligué | 1 |
| 52800 | obligole | 1 |
| 52801 | obligé | 1 |
| 52802 | obligatorio | 1 |
| 52803 | obligaste | 1 |
| 52804 | obligasen | 1 |
| 52805 | obligarte | 1 |
| 52806 | obligarse | 1 |
| 52807 | obligaros | 1 |
| 52808 | obligarnos | 1 |
| 52809 | obligarlos | 1 |
| 52810 | obligarla | 1 |
| 52811 | obligaríanles | 1 |
| 52812 | obligaran | 1 |
| 52813 | obligará | 1 |
| 52814 | obliganseles | 1 |
| 52815 | obligándonos | 1 |
| 52816 | obligándoles | 1 |
| 52817 | obligadísimo | 1 |
| 52818 | obligábale | 1 |
| 52819 | oblicuo | 1 |
| 52820 | oblicuidad | 1 |
| 52821 | obladas | 1 |
| 52822 | oblada | 1 |
| 52823 | oblaçiones | 1 |
| 52824 | oblaciones | 1 |
| 52825 | oblaçión | 1 |
| 52826 | oblación | 1 |
| 52827 | obla | 1 |
| 52828 | objetivos | 1 |
| 52829 | objetiva | 1 |
| 52830 | objetado | 1 |
| 52831 | objecto | 1 |
| 52832 | obispillo | 1 |
| 52833 | obelisco | 1 |
| 52834 | obediençia | 1 |
| 52835 | obedicido | 1 |
| 52836 | obedezcan | 1 |
| 52837 | obedescian | 1 |
| 52838 | obedescerian | 1 |
| 52839 | obedesçer | 1 |
| 52840 | obedescer | 1 |
| 52841 | obedesçen | 1 |
| 52842 | obedeciese | 1 |
| 52843 | obedeciéronle | 1 |
| 52844 | obedecieron | 1 |
| 52845 | obedeciéramos | 1 |
| 52846 | obedecidos | 1 |
| 52847 | obedecidas | 1 |
| 52848 | obedecida | 1 |
| 52849 | obedecerlos | 1 |
| 52850 | obedecería | 1 |
| 52851 | obedeceremos | 1 |
| 52852 | obedecerás | 1 |
| 52853 | obedecerá | 1 |
| 52854 | obedecera | 1 |
| 52855 | obedéceme | 1 |
| 52856 | obedecellos | 1 |
| 52857 | obedecella | 1 |
| 52858 | obdulias | 1 |
| 52859 | obcecado | 1 |
| 52860 | obcecada | 1 |
| 52861 | ñora | 1 |
| 52862 | ñoños | 1 |
| 52863 | ñoñeces | 1 |
| 52864 | ny | 1 |
| 52865 | nuzía | 1 |
| 52866 | nuzas | 1 |
| 52867 | nutrirse | 1 |
| 52868 | nutrir | 1 |
| 52869 | nutrido | 1 |
| 52870 | nutría | 1 |
| 52871 | nunc | 1 |
| 52872 | numismático | 1 |
| 52873 | númidas | 1 |
| 52874 | numerus | 1 |
| 52875 | numerosísimos | 1 |
| 52876 | numerosamente | 1 |
| 52877 | numéricas | 1 |
| 52878 | numerales | 1 |
| 52879 | numerabis | 1 |
| 52880 | numa | 1 |
| 52881 | num | 1 |
| 52882 | nulo | 1 |
| 52883 | nulidades | 1 |
| 52884 | nulidad | 1 |
| 52885 | nuevecitos | 1 |
| 52886 | nuevecito | 1 |
| 52887 | nuevecitas | 1 |
| 52888 | nuevecita | 1 |
| 52889 | nuevam | 1 |
| 52890 | nuestramo | 1 |
| 52891 | nuestr | 1 |
| 52892 | nueso | 1 |
| 52893 | nués | 1 |
| 52894 | nues | 1 |
| 52895 | nuero | 1 |
| 52896 | nueras | 1 |
| 52897 | nubloso | 1 |
| 52898 | nublos | 1 |
| 52899 | nubló | 1 |
| 52900 | nublo | 1 |
| 52901 | nublada | 1 |
| 52902 | nublaba | 1 |
| 52903 | nubila | 1 |
| 52904 | novo | 1 |
| 52905 | novísimo | 1 |
| 52906 | novilla | 1 |
| 52907 | noviçios | 1 |
| 52908 | novicios | 1 |
| 52909 | novicio | 1 |
| 52910 | noviazgos | 1 |
| 52911 | novenario | 1 |
| 52912 | novelitas | 1 |
| 52913 | novelita | 1 |
| 52914 | novelista | 1 |
| 52915 | novelicas | 1 |
| 52916 | noveles | 1 |
| 52917 | noveladores | 1 |
| 52918 | novelador | 1 |
| 52919 | novato | 1 |
| 52920 | nouicios | 1 |
| 52921 | noueno | 1 |
| 52922 | noturnos | 1 |
| 52923 | noturna | 1 |
| 52924 | nôtre | 1 |
| 52925 | notorios | 1 |
| 52926 | notifiques | 1 |
| 52927 | notifiqué | 1 |
| 52928 | notificar | 1 |
| 52929 | notificándoles | 1 |
| 52930 | notificado | 1 |
| 52931 | noticioso | 1 |
| 52932 | noticiero | 1 |
| 52933 | noticierismo | 1 |
| 52934 | notes | 1 |
| 52935 | noten | 1 |
| 52936 | notaste | 1 |
| 52937 | notasen | 1 |
| 52938 | notáronlo | 1 |
| 52939 | notaría | 1 |
| 52940 | notara | 1 |
| 52941 | notándose | 1 |
| 52942 | notamos | 1 |
| 52943 | notador | 1 |
| 52944 | notabilísima | 1 |
| 52945 | notábase | 1 |
| 52946 | notábamos | 1 |
| 52947 | nostres | 1 |
| 52948 | nostras | 1 |
| 52949 | nostra | 1 |
| 52950 | north | 1 |
| 52951 | nortes | 1 |
| 52952 | normandos | 1 |
| 52953 | normandía | 1 |
| 52954 | normalizar | 1 |
| 52955 | normales | 1 |
| 52956 | noriz | 1 |
| 52957 | norias | 1 |
| 52958 | norbait | 1 |
| 52959 | noramaza | 1 |
| 52960 | nor | 1 |
| 52961 | nonbrar | 1 |
| 52962 | nominativo | 1 |
| 52963 | nominativas | 1 |
| 52964 | nominal | 1 |
| 52965 | nómina | 1 |
| 52966 | nomenclaturas | 1 |
| 52967 | nomenclátor | 1 |
| 52968 | nombremos | 1 |
| 52969 | nombréme | 1 |
| 52970 | nombrays | 1 |
| 52971 | nombrastes | 1 |
| 52972 | nombrase | 1 |
| 52973 | nombrarte | 1 |
| 52974 | nombraron | 1 |
| 52975 | nombrarme | 1 |
| 52976 | nombrarle | 1 |
| 52977 | nombrarla | 1 |
| 52978 | nombráredes | 1 |
| 52979 | nombraras | 1 |
| 52980 | nombrándome | 1 |
| 52981 | nombramos | 1 |
| 52982 | nombrallos | 1 |
| 52983 | nombráis | 1 |
| 52984 | nombrábase | 1 |
| 52985 | nómadas | 1 |
| 52986 | nómada | 1 |
| 52987 | nolite | 1 |
| 52988 | noli | 1 |
| 52989 | nol | 1 |
| 52990 | noiz | 1 |
| 52991 | nogera | 1 |
| 52992 | noctibus | 1 |
| 52993 | nocivas | 1 |
| 52994 | nociva | 1 |
| 52995 | nocherniegos | 1 |
| 52996 | nocherniego | 1 |
| 52997 | nochebuena | 1 |
| 52998 | nocedal | 1 |
| 52999 | nobre | 1 |
| 53000 | nobilísimos | 1 |
| 53001 | nobilísimo | 1 |
| 53002 | nobiliario | 1 |
| 53003 | nobiliarias | 1 |
| 53004 | nizarani | 1 |
| 53005 | nizán | 1 |
| 53006 | nivelle | 1 |
| 53007 | niveles | 1 |
| 53008 | nivelarse | 1 |
| 53009 | nivelando | 1 |
| 53010 | nivelamiento | 1 |
| 53011 | niveladora | 1 |
| 53012 | nivelado | 1 |
| 53013 | nivelación | 1 |
| 53014 | nivelaba | 1 |
| 53015 | nitro | 1 |
| 53016 | nísperos | 1 |
| 53017 | niso | 1 |
| 53018 | nísida | 1 |
| 53019 | nisi | 1 |
| 53020 | níquel | 1 |
| 53021 | nipresas | 1 |
| 53022 | niporesas | 1 |
| 53023 | nipis | 1 |
| 53024 | níobe | 1 |
| 53025 | niñeras | 1 |
| 53026 | niñeces | 1 |
| 53027 | ninón | 1 |
| 53028 | ninon | 1 |
| 53029 | nínive | 1 |
| 53030 | ningund | 1 |
| 53031 | nimia | 1 |
| 53032 | nimbo | 1 |
| 53033 | nigromántico | 1 |
| 53034 | nigromantesa | 1 |
| 53035 | nieven | 1 |
| 53036 | niev | 1 |
| 53037 | nietecito | 1 |
| 53038 | niéguesenos | 1 |
| 53039 | niéguenme | 1 |
| 53040 | niégale | 1 |
| 53041 | nidada | 1 |
| 53042 | nicot | 1 |
| 53043 | nicolao | 1 |
| 53044 | nic | 1 |
| 53045 | niarros | 1 |
| 53046 | new | 1 |
| 53047 | nevó | 1 |
| 53048 | nevatilla | 1 |
| 53049 | nevase | 1 |
| 53050 | nevar | 1 |
| 53051 | nevando | 1 |
| 53052 | nevaba | 1 |
| 53053 | neutro | 1 |
| 53054 | neutralizado | 1 |
| 53055 | neutrales | 1 |
| 53056 | neurosismo | 1 |
| 53057 | neuralgias | 1 |
| 53058 | neuio | 1 |
| 53059 | neuf | 1 |
| 53060 | neu | 1 |
| 53061 | netezuelos | 1 |
| 53062 | netas | 1 |
| 53063 | nesea | 1 |
| 53064 | nescios | 1 |
| 53065 | nesçia | 1 |
| 53066 | nesçesidat | 1 |
| 53067 | nesçedat | 1 |
| 53068 | nescatzale | 1 |
| 53069 | nervudos | 1 |
| 53070 | nervuda | 1 |
| 53071 | nervosa | 1 |
| 53072 | nervïosos | 1 |
| 53073 | nerviosísima | 1 |
| 53074 | nerviosidades | 1 |
| 53075 | nerviosidad | 1 |
| 53076 | nereo | 1 |
| 53077 | nerbia | 1 |
| 53078 | nenita | 1 |
| 53079 | nenbrar | 1 |
| 53080 | nemrod | 1 |
| 53081 | nemorosos | 1 |
| 53082 | nemoroso | 1 |
| 53083 | nemo | 1 |
| 53084 | némine | 1 |
| 53085 | nelsones | 1 |
| 53086 | neguijón | 1 |
| 53087 | negruzcas | 1 |
| 53088 | negruras | 1 |
| 53089 | negrísima | 1 |
| 53090 | negrillo | 1 |
| 53091 | negregura | 1 |
| 53092 | negrazo | 1 |
| 53093 | negósela | 1 |
| 53094 | negóme | 1 |
| 53095 | negociarlo | 1 |
| 53096 | negocianta | 1 |
| 53097 | negociados | 1 |
| 53098 | negociacion | 1 |
| 53099 | negocia | 1 |
| 53100 | negligentes | 1 |
| 53101 | négligé | 1 |
| 53102 | negedes | 1 |
| 53103 | negativos | 1 |
| 53104 | negaste | 1 |
| 53105 | negarte | 1 |
| 53106 | negarles | 1 |
| 53107 | negarla | 1 |
| 53108 | negaré | 1 |
| 53109 | negare | 1 |
| 53110 | negaras | 1 |
| 53111 | negaran | 1 |
| 53112 | negándoles | 1 |
| 53113 | negamos | 1 |
| 53114 | negallo | 1 |
| 53115 | negáis | 1 |
| 53116 | negadas | 1 |
| 53117 | negábase | 1 |
| 53118 | nefastos | 1 |
| 53119 | nefasta | 1 |
| 53120 | nefas | 1 |
| 53121 | nefarios | 1 |
| 53122 | nefandos | 1 |
| 53123 | nefandas | 1 |
| 53124 | nefanda | 1 |
| 53125 | neçuelo | 1 |
| 53126 | neciuelo | 1 |
| 53127 | neçias | 1 |
| 53128 | neciamente | 1 |
| 53129 | neçiacha | 1 |
| 53130 | necessitada | 1 |
| 53131 | necessarios | 1 |
| 53132 | necessaria | 1 |
| 53133 | necesites | 1 |
| 53134 | necesité | 1 |
| 53135 | necesitasen | 1 |
| 53136 | necesitásemos | 1 |
| 53137 | necesitarlos | 1 |
| 53138 | necesitarlas | 1 |
| 53139 | necesitarías | 1 |
| 53140 | necesitaré | 1 |
| 53141 | necesitando | 1 |
| 53142 | necesitadas | 1 |
| 53143 | necesarísimo | 1 |
| 53144 | neçedat | 1 |
| 53145 | neceda | 1 |
| 53146 | necat | 1 |
| 53147 | nec | 1 |
| 53148 | nebuloso | 1 |
| 53149 | nebli | 1 |
| 53150 | neas | 1 |
| 53151 | ne | 1 |
| 53152 | nazco | 1 |
| 53153 | nazareth | 1 |
| 53154 | nazaret | 1 |
| 53155 | nazarenus | 1 |
| 53156 | naypes | 1 |
| 53157 | nay | 1 |
| 53158 | navegue | 1 |
| 53159 | navegan | 1 |
| 53160 | navegados | 1 |
| 53161 | navegaban | 1 |
| 53162 | navascués | 1 |
| 53163 | navajazos | 1 |
| 53164 | náusea | 1 |
| 53165 | nauidad | 1 |
| 53166 | naufragar | 1 |
| 53167 | naufragante | 1 |
| 53168 | nauegando | 1 |
| 53169 | náu | 1 |
| 53170 | natus | 1 |
| 53171 | naturas | 1 |
| 53172 | naturans | 1 |
| 53173 | naturalísimo | 1 |
| 53174 | naturaleça | 1 |
| 53175 | natalicio | 1 |
| 53176 | natalia | 1 |
| 53177 | natación | 1 |
| 53178 | nason | 1 |
| 53179 | nasional | 1 |
| 53180 | nasçistes | 1 |
| 53181 | nasciste | 1 |
| 53182 | nasçióle | 1 |
| 53183 | nascimiento | 1 |
| 53184 | nasçiera | 1 |
| 53185 | nasciera | 1 |
| 53186 | nascidos | 1 |
| 53187 | nasçía | 1 |
| 53188 | nasçí | 1 |
| 53189 | nascí | 1 |
| 53190 | nasçemiento | 1 |
| 53191 | nasas | 1 |
| 53192 | nasales | 1 |
| 53193 | naryz | 1 |
| 53194 | narrados | 1 |
| 53195 | narradora | 1 |
| 53196 | narrado | 1 |
| 53197 | narraban | 1 |
| 53198 | narra | 1 |
| 53199 | narizilla | 1 |
| 53200 | narizado | 1 |
| 53201 | narina | 1 |
| 53202 | narigudos | 1 |
| 53203 | narigante | 1 |
| 53204 | naricísimo | 1 |
| 53205 | naricillas | 1 |
| 53206 | naricilla | 1 |
| 53207 | nariçes | 1 |
| 53208 | narcótico | 1 |
| 53209 | narcisus | 1 |
| 53210 | narbáez | 1 |
| 53211 | naranjazos | 1 |
| 53212 | naranjado | 1 |
| 53213 | napoleónicas | 1 |
| 53214 | napoleonen | 1 |
| 53215 | napeas | 1 |
| 53216 | nansouk | 1 |
| 53217 | nanita | 1 |
| 53218 | nalgadas | 1 |
| 53219 | nalga | 1 |
| 53220 | najo | 1 |
| 53221 | najabao | 1 |
| 53222 | nagoga | 1 |
| 53223 | nados | 1 |
| 53224 | nadé | 1 |
| 53225 | nade | 1 |
| 53226 | nadasen | 1 |
| 53227 | nadase | 1 |
| 53228 | nadará | 1 |
| 53229 | nadan | 1 |
| 53230 | nadamos | 1 |
| 53231 | nadaba | 1 |
| 53232 | nacisteis | 1 |
| 53233 | naçiste | 1 |
| 53234 | nacionalismo | 1 |
| 53235 | nacion | 1 |
| 53236 | nacientes | 1 |
| 53237 | naçido | 1 |
| 53238 | nacerle | 1 |
| 53239 | nacerá | 1 |
| 53240 | nácenle | 1 |
| 53241 | naçençia | 1 |
| 53242 | nacemos | 1 |
| 53243 | nácares | 1 |
| 53244 | nacarada | 1 |
| 53245 | nabucodonossor | 1 |
| 53246 | nabuco | 1 |
| 53247 | nabal | 1 |
| 53248 | mys | 1 |
| 53249 | myrrha | 1 |
| 53250 | myo | 1 |
| 53251 | myll | 1 |
| 53252 | myércoles | 1 |
| 53253 | muzgosa | 1 |
| 53254 | muzaraque | 1 |
| 53255 | muza | 1 |
| 53256 | muyta | 1 |
| 53257 | muymaigre | 1 |
| 53258 | muvió | 1 |
| 53259 | mutua | 1 |
| 53260 | mutismo | 1 |
| 53261 | mutiladas | 1 |
| 53262 | mutilación | 1 |
| 53263 | mutilaban | 1 |
| 53264 | mutatio | 1 |
| 53265 | musotros | 1 |
| 53266 | muslito | 1 |
| 53267 | musiqueo | 1 |
| 53268 | musicos | 1 |
| 53269 | musico | 1 |
| 53270 | musicas | 1 |
| 53271 | musgosos | 1 |
| 53272 | musgos | 1 |
| 53273 | museos | 1 |
| 53274 | musculosos | 1 |
| 53275 | musculosa | 1 |
| 53276 | musarañas | 1 |
| 53277 | muru | 1 |
| 53278 | muró | 1 |
| 53279 | murmurio | 1 |
| 53280 | murmures | 1 |
| 53281 | murmureo | 1 |
| 53282 | murmuremos | 1 |
| 53283 | murmuraron | 1 |
| 53284 | murmuraría | 1 |
| 53285 | murmurara | 1 |
| 53286 | murmurantes | 1 |
| 53287 | murmurante | 1 |
| 53288 | murisillo | 1 |
| 53289 | muriésemos | 1 |
| 53290 | murierme | 1 |
| 53291 | muriérase | 1 |
| 53292 | murieras | 1 |
| 53293 | muriéndonos | 1 |
| 53294 | muriéndome | 1 |
| 53295 | múrice | 1 |
| 53296 | murgas | 1 |
| 53297 | múrelo | 1 |
| 53298 | murciana | 1 |
| 53299 | murasen | 1 |
| 53300 | murarse | 1 |
| 53301 | muran | 1 |
| 53302 | murada | 1 |
| 53303 | mura | 1 |
| 53304 | muquieres | 1 |
| 53305 | muñós | 1 |
| 53306 | muñidos | 1 |
| 53307 | muñequito | 1 |
| 53308 | muñeira | 1 |
| 53309 | muñatones | 1 |
| 53310 | muñatón | 1 |
| 53311 | munición | 1 |
| 53312 | mundum | 1 |
| 53313 | mundanamente | 1 |
| 53314 | munda | 1 |
| 53315 | mund | 1 |
| 53316 | mulus | 1 |
| 53317 | multos | 1 |
| 53318 | multitudes | 1 |
| 53319 | multiplique | 1 |
| 53320 | multiplicó | 1 |
| 53321 | multiplicaron | 1 |
| 53322 | multiplicándose | 1 |
| 53323 | multiplican | 1 |
| 53324 | multiplicadas | 1 |
| 53325 | multiplicaciones | 1 |
| 53326 | multiplicación | 1 |
| 53327 | multiplicaban | 1 |
| 53328 | müller | 1 |
| 53329 | mulieribus | 1 |
| 53330 | muliere | 1 |
| 53331 | muleteros | 1 |
| 53332 | mulatazo | 1 |
| 53333 | muladares | 1 |
| 53334 | mujerota | 1 |
| 53335 | mujeriega | 1 |
| 53336 | mujeraza | 1 |
| 53337 | muito | 1 |
| 53338 | mugrones | 1 |
| 53339 | mugrientos | 1 |
| 53340 | mugrientas | 1 |
| 53341 | mugres | 1 |
| 53342 | mugir | 1 |
| 53343 | muflón | 1 |
| 53344 | muévete | 1 |
| 53345 | mueves | 1 |
| 53346 | muévenos | 1 |
| 53347 | muévate | 1 |
| 53348 | muévaos | 1 |
| 53349 | mueues | 1 |
| 53350 | mueuen | 1 |
| 53351 | mueue | 1 |
| 53352 | muéstrateles | 1 |
| 53353 | muéstratele | 1 |
| 53354 | muestrarios | 1 |
| 53355 | muestramela | 1 |
| 53356 | muéstrale | 1 |
| 53357 | muesca | 1 |
| 53358 | muertte | 1 |
| 53359 | muérome | 1 |
| 53360 | muérense | 1 |
| 53361 | muerdes | 1 |
| 53362 | muerden | 1 |
| 53363 | muerdas | 1 |
| 53364 | muérame | 1 |
| 53365 | muellemente | 1 |
| 53366 | muedo | 1 |
| 53367 | mueblista | 1 |
| 53368 | mueblaje | 1 |
| 53369 | mudemos | 1 |
| 53370 | mudaua | 1 |
| 53371 | múdaste | 1 |
| 53372 | mudarte | 1 |
| 53373 | mudaras | 1 |
| 53374 | mudarán | 1 |
| 53375 | mudara | 1 |
| 53376 | mudanse | 1 |
| 53377 | mudándoles | 1 |
| 53378 | mudamos | 1 |
| 53379 | mudamiento | 1 |
| 53380 | mudad | 1 |
| 53381 | mucosa | 1 |
| 53382 | mucio | 1 |
| 53383 | mucílago | 1 |
| 53384 | muchismos | 1 |
| 53385 | muchachuelos | 1 |
| 53386 | muchachones | 1 |
| 53387 | muchachón | 1 |
| 53388 | muchacherías | 1 |
| 53389 | mozart | 1 |
| 53390 | mozárabe | 1 |
| 53391 | moysén | 1 |
| 53392 | moyna | 1 |
| 53393 | moyano | 1 |
| 53394 | moya | 1 |
| 53395 | moxtrenco | 1 |
| 53396 | moxquito | 1 |
| 53397 | moxquete | 1 |
| 53398 | moxcas | 1 |
| 53399 | moviste | 1 |
| 53400 | moviose | 1 |
| 53401 | movías | 1 |
| 53402 | movería | 1 |
| 53403 | moveremos | 1 |
| 53404 | moverán | 1 |
| 53405 | movedizo | 1 |
| 53406 | movedizas | 1 |
| 53407 | mováis | 1 |
| 53408 | moustiques | 1 |
| 53409 | mouible | 1 |
| 53410 | mouia | 1 |
| 53411 | moueysme | 1 |
| 53412 | mouediza | 1 |
| 53413 | motril | 1 |
| 53414 | motivaran | 1 |
| 53415 | motivados | 1 |
| 53416 | motivadas | 1 |
| 53417 | motiva | 1 |
| 53418 | motines | 1 |
| 53419 | motilón | 1 |
| 53420 | motete | 1 |
| 53421 | motejóme | 1 |
| 53422 | motejar | 1 |
| 53423 | motejándoles | 1 |
| 53424 | motejan | 1 |
| 53425 | motejaban | 1 |
| 53426 | moteja | 1 |
| 53427 | mostrósela | 1 |
| 53428 | mostrose | 1 |
| 53429 | mostróme | 1 |
| 53430 | mostróle | 1 |
| 53431 | mostréme | 1 |
| 53432 | mostredes | 1 |
| 53433 | mostrava | 1 |
| 53434 | mostraua | 1 |
| 53435 | mostratme | 1 |
| 53436 | mostrarte | 1 |
| 53437 | mostrart | 1 |
| 53438 | mostráronle | 1 |
| 53439 | mostrarnos | 1 |
| 53440 | mostrarlas | 1 |
| 53441 | mostrarla | 1 |
| 53442 | mostraría | 1 |
| 53443 | mostrares | 1 |
| 53444 | mostraréis | 1 |
| 53445 | mostrarásme | 1 |
| 53446 | mostrarás | 1 |
| 53447 | mostraras | 1 |
| 53448 | mostrárades | 1 |
| 53449 | mostrándoselos | 1 |
| 53450 | mostrándoselo | 1 |
| 53451 | mostrándonos | 1 |
| 53452 | mostrándomelo | 1 |
| 53453 | mostrándolos | 1 |
| 53454 | mostrándolo | 1 |
| 53455 | mostrandoles | 1 |
| 53456 | mostrandole | 1 |
| 53457 | mostrándola | 1 |
| 53458 | mostrámosle | 1 |
| 53459 | mostralle | 1 |
| 53460 | mostrádnosla | 1 |
| 53461 | mostra | 1 |
| 53462 | mostacilla | 1 |
| 53463 | mostachos | 1 |
| 53464 | mosquitero | 1 |
| 53465 | mosqueteros | 1 |
| 53466 | mosquete | 1 |
| 53467 | mosqueó | 1 |
| 53468 | mosquearme | 1 |
| 53469 | mosquear | 1 |
| 53470 | moscos | 1 |
| 53471 | mosco | 1 |
| 53472 | moscatel | 1 |
| 53473 | mosa | 1 |
| 53474 | mortuorio | 1 |
| 53475 | mortuorias | 1 |
| 53476 | mortui | 1 |
| 53477 | mortifiques | 1 |
| 53478 | mortifique | 1 |
| 53479 | mortificóle | 1 |
| 53480 | mortificasen | 1 |
| 53481 | mortificarnos | 1 |
| 53482 | mortificarme | 1 |
| 53483 | mortificarles | 1 |
| 53484 | mortificaré | 1 |
| 53485 | mortificara | 1 |
| 53486 | mortificantes | 1 |
| 53487 | mortificándole | 1 |
| 53488 | mortificando | 1 |
| 53489 | mortifican | 1 |
| 53490 | mortíferos | 1 |
| 53491 | mortífera | 1 |
| 53492 | mortecinos | 1 |
| 53493 | morteçino | 1 |
| 53494 | mortecino | 1 |
| 53495 | mortecinas | 1 |
| 53496 | mors | 1 |
| 53497 | morrones | 1 |
| 53498 | morrocotuda | 1 |
| 53499 | morritos | 1 |
| 53500 | morris | 1 |
| 53501 | morrioncete | 1 |
| 53502 | morrás | 1 |
| 53503 | morral | 1 |
| 53504 | morradas | 1 |
| 53505 | morrada | 1 |
| 53506 | morrá | 1 |
| 53507 | morosos | 1 |
| 53508 | morosidades | 1 |
| 53509 | moriuntur | 1 |
| 53510 | moriste | 1 |
| 53511 | morírseme | 1 |
| 53512 | morirnos | 1 |
| 53513 | morirían | 1 |
| 53514 | moriríamos | 1 |
| 53515 | morires | 1 |
| 53516 | morire | 1 |
| 53517 | morillos | 1 |
| 53518 | morigerada | 1 |
| 53519 | moriere | 1 |
| 53520 | moriendo | 1 |
| 53521 | morides | 1 |
| 53522 | moríame | 1 |
| 53523 | moria | 1 |
| 53524 | morganero | 1 |
| 53525 | morfeo | 1 |
| 53526 | moresillo | 1 |
| 53527 | mores | 1 |
| 53528 | morenísimo | 1 |
| 53529 | morenico | 1 |
| 53530 | morendo | 1 |
| 53531 | moren | 1 |
| 53532 | morellanas | 1 |
| 53533 | moré | 1 |
| 53534 | more | 1 |
| 53535 | mordiscos | 1 |
| 53536 | mordiscar | 1 |
| 53537 | mordiscada | 1 |
| 53538 | mordio | 1 |
| 53539 | mordiese | 1 |
| 53540 | mordieron | 1 |
| 53541 | mordiéndome | 1 |
| 53542 | mordidas | 1 |
| 53543 | mordian | 1 |
| 53544 | morderles | 1 |
| 53545 | morderle | 1 |
| 53546 | mordería | 1 |
| 53547 | mordentes | 1 |
| 53548 | mordellas | 1 |
| 53549 | mordedura | 1 |
| 53550 | mordedora | 1 |
| 53551 | mordaças | 1 |
| 53552 | morcilludo | 1 |
| 53553 | morcillones | 1 |
| 53554 | morcillo | 1 |
| 53555 | morcillero | 1 |
| 53556 | morciegalo | 1 |
| 53557 | morbosa | 1 |
| 53558 | morbo | 1 |
| 53559 | mórbido | 1 |
| 53560 | mórbida | 1 |
| 53561 | morazo | 1 |
| 53562 | morava | 1 |
| 53563 | morauas | 1 |
| 53564 | moraua | 1 |
| 53565 | morarme | 1 |
| 53566 | moraré | 1 |
| 53567 | morara | 1 |
| 53568 | morando | 1 |
| 53569 | moralizarla | 1 |
| 53570 | moralizadora | 1 |
| 53571 | moralistas | 1 |
| 53572 | moráis | 1 |
| 53573 | moradoras | 1 |
| 53574 | moraban | 1 |
| 53575 | moquito | 1 |
| 53576 | moquillo | 1 |
| 53577 | moquant | 1 |
| 53578 | monumentalidad | 1 |
| 53579 | monturas | 1 |
| 53580 | montuosos | 1 |
| 53581 | montpensier | 1 |
| 53582 | montose | 1 |
| 53583 | montoncitos | 1 |
| 53584 | monto | 1 |
| 53585 | montïel | 1 |
| 53586 | montevideo | 1 |
| 53587 | montesyna | 1 |
| 53588 | montessas | 1 |
| 53589 | monteses | 1 |
| 53590 | montesa | 1 |
| 53591 | monterilla | 1 |
| 53592 | montemuru | 1 |
| 53593 | monteleón | 1 |
| 53594 | montecristo | 1 |
| 53595 | montecillo | 1 |
| 53596 | montblanch | 1 |
| 53597 | montazgo | 1 |
| 53598 | montase | 1 |
| 53599 | montarse | 1 |
| 53600 | montarlo | 1 |
| 53601 | montaremos | 1 |
| 53602 | montare | 1 |
| 53603 | montañuelas | 1 |
| 53604 | montañuela | 1 |
| 53605 | montañesas | 1 |
| 53606 | montante | 1 |
| 53607 | montando | 1 |
| 53608 | montan | 1 |
| 53609 | montadas | 1 |
| 53610 | monstruosidades | 1 |
| 53611 | monstrua | 1 |
| 53612 | monstros | 1 |
| 53613 | monsseñer | 1 |
| 53614 | monssener | 1 |
| 53615 | monsiur | 1 |
| 53616 | monserrato | 1 |
| 53617 | monseñer | 1 |
| 53618 | monsener | 1 |
| 53619 | monpeller | 1 |
| 53620 | monopolizaron | 1 |
| 53621 | monopolizar | 1 |
| 53622 | monopolizando | 1 |
| 53623 | monopolizadores | 1 |
| 53624 | monopolizaban | 1 |
| 53625 | monomanías | 1 |
| 53626 | monomaniacos | 1 |
| 53627 | monomaniacas | 1 |
| 53628 | monomaniaca | 1 |
| 53629 | monologue | 1 |
| 53630 | monólogos | 1 |
| 53631 | monolito | 1 |
| 53632 | monocromos | 1 |
| 53633 | monjuí | 1 |
| 53634 | monjitas | 1 |
| 53635 | monjiles | 1 |
| 53636 | monita | 1 |
| 53637 | monísimos | 1 |
| 53638 | monísimas | 1 |
| 53639 | monises | 1 |
| 53640 | monín | 1 |
| 53641 | monillo | 1 |
| 53642 | monilla | 1 |
| 53643 | monigote | 1 |
| 53644 | monicongo | 1 |
| 53645 | mónica | 1 |
| 53646 | mongólico | 1 |
| 53647 | mongibelo | 1 |
| 53648 | mongibel | 1 |
| 53649 | mongía | 1 |
| 53650 | monetaria | 1 |
| 53651 | monescillo | 1 |
| 53652 | monería | 1 |
| 53653 | moneditas | 1 |
| 53654 | monederos | 1 |
| 53655 | moneca | 1 |
| 53656 | monea | 1 |
| 53657 | mondragón | 1 |
| 53658 | mondoñedo | 1 |
| 53659 | mondes | 1 |
| 53660 | mondarnos | 1 |
| 53661 | mondarajas | 1 |
| 53662 | mondándose | 1 |
| 53663 | mondaduras | 1 |
| 53664 | moncloa | 1 |
| 53665 | moncayo | 1 |
| 53666 | moncadas | 1 |
| 53667 | monamente | 1 |
| 53668 | monagos | 1 |
| 53669 | monada | 1 |
| 53670 | monacillos | 1 |
| 53671 | mon | 1 |
| 53672 | momos | 1 |
| 53673 | momificaba | 1 |
| 53674 | momentitos | 1 |
| 53675 | momentico | 1 |
| 53676 | momentaneos | 1 |
| 53677 | momentáneas | 1 |
| 53678 | molto | 1 |
| 53679 | moltke | 1 |
| 53680 | molletes | 1 |
| 53681 | mollejar | 1 |
| 53682 | molleja | 1 |
| 53683 | molins | 1 |
| 53684 | molinillo | 1 |
| 53685 | molimientos | 1 |
| 53686 | molificar | 1 |
| 53687 | molifica | 1 |
| 53688 | moliesen | 1 |
| 53689 | moliera | 1 |
| 53690 | molientes | 1 |
| 53691 | moliente | 1 |
| 53692 | moliendo | 1 |
| 53693 | molienda | 1 |
| 53694 | molían | 1 |
| 53695 | molestísimo | 1 |
| 53696 | molestísima | 1 |
| 53697 | molestes | 1 |
| 53698 | molesten | 1 |
| 53699 | molestasen | 1 |
| 53700 | molestase | 1 |
| 53701 | molestándolos | 1 |
| 53702 | molestándoles | 1 |
| 53703 | molestándole | 1 |
| 53704 | molestando | 1 |
| 53705 | molestamos | 1 |
| 53706 | molestados | 1 |
| 53707 | molestábale | 1 |
| 53708 | moleslo | 1 |
| 53709 | moleschott | 1 |
| 53710 | molerlos | 1 |
| 53711 | molerle | 1 |
| 53712 | molerá | 1 |
| 53713 | molelle | 1 |
| 53714 | moledor | 1 |
| 53715 | molécula | 1 |
| 53716 | molduras | 1 |
| 53717 | moldearla | 1 |
| 53718 | mojón | 1 |
| 53719 | mojó | 1 |
| 53720 | mojino | 1 |
| 53721 | mojigangas | 1 |
| 53722 | mojarte | 1 |
| 53723 | mojarrilla | 1 |
| 53724 | mojaría | 1 |
| 53725 | mojándole | 1 |
| 53726 | mojando | 1 |
| 53727 | mojama | 1 |
| 53728 | mojadas | 1 |
| 53729 | moi | 1 |
| 53730 | mohino | 1 |
| 53731 | mohinísimo | 1 |
| 53732 | mohicanos | 1 |
| 53733 | mohatra | 1 |
| 53734 | mohar | 1 |
| 53735 | mohalinar | 1 |
| 53736 | mogollón | 1 |
| 53737 | mofen | 1 |
| 53738 | mofarse | 1 |
| 53739 | mofante | 1 |
| 53740 | mofador | 1 |
| 53741 | mofa | 1 |
| 53742 | modular | 1 |
| 53743 | modulando | 1 |
| 53744 | modulado | 1 |
| 53745 | modulaba | 1 |
| 53746 | modorría | 1 |
| 53747 | modón | 1 |
| 53748 | moditos | 1 |
| 53749 | modito | 1 |
| 53750 | modistos | 1 |
| 53751 | modistillas | 1 |
| 53752 | modistilla | 1 |
| 53753 | modificó | 1 |
| 53754 | modificara | 1 |
| 53755 | modificaciones | 1 |
| 53756 | modificaba | 1 |
| 53757 | módica | 1 |
| 53758 | modestísimo | 1 |
| 53759 | modestas | 1 |
| 53760 | moderó | 1 |
| 53761 | modérese | 1 |
| 53762 | modere | 1 |
| 53763 | moderarse | 1 |
| 53764 | moderaron | 1 |
| 53765 | moderaré | 1 |
| 53766 | moderar | 1 |
| 53767 | moderantismo | 1 |
| 53768 | moderaísmo | 1 |
| 53769 | moderador | 1 |
| 53770 | modelito | 1 |
| 53771 | modele | 1 |
| 53772 | modelarlos | 1 |
| 53773 | modelaban | 1 |
| 53774 | moçuela | 1 |
| 53775 | mocoso | 1 |
| 53776 | moços | 1 |
| 53777 | moclin | 1 |
| 53778 | mocito | 1 |
| 53779 | mocho | 1 |
| 53780 | mochilas | 1 |
| 53781 | moçetas | 1 |
| 53782 | moçedat | 1 |
| 53783 | moca | 1 |
| 53784 | miz | 1 |
| 53785 | mixtura | 1 |
| 53786 | mixtificación | 1 |
| 53787 | mixta | 1 |
| 53788 | mixía | 1 |
| 53789 | miulina | 1 |
| 53790 | mitroso | 1 |
| 53791 | mitos | 1 |
| 53792 | mitológicos | 1 |
| 53793 | mitológico | 1 |
| 53794 | mitológica | 1 |
| 53795 | mitologías | 1 |
| 53796 | mito | 1 |
| 53797 | mitigarlo | 1 |
| 53798 | mitigado | 1 |
| 53799 | mitigada | 1 |
| 53800 | mitchell | 1 |
| 53801 | mitas | 1 |
| 53802 | misturas | 1 |
| 53803 | mistress | 1 |
| 53804 | mistos | 1 |
| 53805 | misto | 1 |
| 53806 | mistiquerías | 1 |
| 53807 | mistificaciones | 1 |
| 53808 | místicamente | 1 |
| 53809 | misté | 1 |
| 53810 | missericordia | 1 |
| 53811 | mismísimos | 1 |
| 53812 | misérrimo | 1 |
| 53813 | misericordiosos | 1 |
| 53814 | misericordiosas | 1 |
| 53815 | míseramente | 1 |
| 53816 | misera | 1 |
| 53817 | misales | 1 |
| 53818 | misacantano | 1 |
| 53819 | mirtos | 1 |
| 53820 | mironas | 1 |
| 53821 | miroles | 1 |
| 53822 | mirola | 1 |
| 53823 | mirlados | 1 |
| 53824 | mirlaba | 1 |
| 53825 | miriñaque | 1 |
| 53826 | miréme | 1 |
| 53827 | mireme | 1 |
| 53828 | mírelo | 1 |
| 53829 | mirava | 1 |
| 53830 | miraua | 1 |
| 53831 | mirate | 1 |
| 53832 | mírasla | 1 |
| 53833 | miraros | 1 |
| 53834 | miráronse | 1 |
| 53835 | mirares | 1 |
| 53836 | mirare | 1 |
| 53837 | miraras | 1 |
| 53838 | mirante | 1 |
| 53839 | mirándonos | 1 |
| 53840 | mirandome | 1 |
| 53841 | mirándolo | 1 |
| 53842 | mirandole | 1 |
| 53843 | mirándolas | 1 |
| 53844 | miralo | 1 |
| 53845 | miraldo | 1 |
| 53846 | míralas | 1 |
| 53847 | miraguarda | 1 |
| 53848 | miraflores | 1 |
| 53849 | miradora | 1 |
| 53850 | miradla | 1 |
| 53851 | miradilla | 1 |
| 53852 | mirabilia | 1 |
| 53853 | mirábanme | 1 |
| 53854 | mirábanla | 1 |
| 53855 | mirábamos | 1 |
| 53856 | mirábalo | 1 |
| 53857 | mirábales | 1 |
| 53858 | miqueletes | 1 |
| 53859 | mique | 1 |
| 53860 | miopía | 1 |
| 53861 | miología | 1 |
| 53862 | minutillo | 1 |
| 53863 | minuta | 1 |
| 53864 | minueto | 1 |
| 53865 | minué | 1 |
| 53866 | minuciosos | 1 |
| 53867 | minuciosidades | 1 |
| 53868 | minuciosas | 1 |
| 53869 | mintyendo | 1 |
| 53870 | mintrosas | 1 |
| 53871 | mintira | 1 |
| 53872 | mintiome | 1 |
| 53873 | mintiese | 1 |
| 53874 | mintiendo | 1 |
| 53875 | minó | 1 |
| 53876 | ministril | 1 |
| 53877 | ministraron | 1 |
| 53878 | ministrar | 1 |
| 53879 | ministeriales | 1 |
| 53880 | ministérial | 1 |
| 53881 | minino | 1 |
| 53882 | mínimos | 1 |
| 53883 | miniaturita | 1 |
| 53884 | miniatura | 1 |
| 53885 | minguilla | 1 |
| 53886 | minerua | 1 |
| 53887 | minería | 1 |
| 53888 | mineralógicas | 1 |
| 53889 | minerales | 1 |
| 53890 | minera | 1 |
| 53891 | minaron | 1 |
| 53892 | minador | 1 |
| 53893 | minada | 1 |
| 53894 | mimosidad | 1 |
| 53895 | mimitos | 1 |
| 53896 | mímicos | 1 |
| 53897 | mime | 1 |
| 53898 | mimarle | 1 |
| 53899 | mimados | 1 |
| 53900 | mimadito | 1 |
| 53901 | mimadita | 1 |
| 53902 | milo | 1 |
| 53903 | millonas | 1 |
| 53904 | millonarios | 1 |
| 53905 | millifolia | 1 |
| 53906 | millán | 1 |
| 53907 | milito | 1 |
| 53908 | mílites | 1 |
| 53909 | mílite | 1 |
| 53910 | militarote | 1 |
| 53911 | militarmente | 1 |
| 53912 | militantes | 1 |
| 53913 | militando | 1 |
| 53914 | militamos | 1 |
| 53915 | militáis | 1 |
| 53916 | militaba | 1 |
| 53917 | milienta | 1 |
| 53918 | milicianos | 1 |
| 53919 | miliboee | 1 |
| 53920 | miliarias | 1 |
| 53921 | milesias | 1 |
| 53922 | milenta | 1 |
| 53923 | milaneses | 1 |
| 53924 | milanesa | 1 |
| 53925 | milan | 1 |
| 53926 | milagrosas | 1 |
| 53927 | mijoría | 1 |
| 53928 | mijores | 1 |
| 53929 | miiiii | 1 |
| 53930 | miglior | 1 |
| 53931 | migel | 1 |
| 53932 | migao | 1 |
| 53933 | mierca | 1 |
| 53934 | mientan | 1 |
| 53935 | miénbresevos | 1 |
| 53936 | mienbre | 1 |
| 53937 | mienbran | 1 |
| 53938 | miémbresele | 1 |
| 53939 | mielero | 1 |
| 53940 | miela | 1 |
| 53941 | miedoso | 1 |
| 53942 | miedosilla | 1 |
| 53943 | mieditis | 1 |
| 53944 | mied | 1 |
| 53945 | mido | 1 |
| 53946 | midiesse | 1 |
| 53947 | midiesen | 1 |
| 53948 | midiere | 1 |
| 53949 | midiéramos | 1 |
| 53950 | midiera | 1 |
| 53951 | midiéndolos | 1 |
| 53952 | midiéndole | 1 |
| 53953 | mides | 1 |
| 53954 | miden | 1 |
| 53955 | midámoslo | 1 |
| 53956 | miculoso | 1 |
| 53957 | microscopios | 1 |
| 53958 | microscópico | 1 |
| 53959 | micocolembo | 1 |
| 53960 | michita | 1 |
| 53961 | michi | 1 |
| 53962 | micer | 1 |
| 53963 | micaela | 1 |
| 53964 | micael | 1 |
| 53965 | mica | 1 |
| 53966 | miau | 1 |
| 53967 | miajitas | 1 |
| 53968 | mezquitas | 1 |
| 53969 | mezquinidad | 1 |
| 53970 | mezcolanza | 1 |
| 53971 | mezclóse | 1 |
| 53972 | mezcles | 1 |
| 53973 | mezclen | 1 |
| 53974 | mezclase | 1 |
| 53975 | mezclarse | 1 |
| 53976 | mezclarme | 1 |
| 53977 | mezclarle | 1 |
| 53978 | mezclarla | 1 |
| 53979 | mezclaras | 1 |
| 53980 | mezclándose | 1 |
| 53981 | mezclándolos | 1 |
| 53982 | mezclándolo | 1 |
| 53983 | mezcládose | 1 |
| 53984 | meyer | 1 |
| 53985 | mexilla | 1 |
| 53986 | mexías | 1 |
| 53987 | meus | 1 |
| 53988 | meum | 1 |
| 53989 | metydo | 1 |
| 53990 | metropolitano | 1 |
| 53991 | metrificadas | 1 |
| 53992 | métricas | 1 |
| 53993 | métricamente | 1 |
| 53994 | métome | 1 |
| 53995 | metodizando | 1 |
| 53996 | metodista | 1 |
| 53997 | metódicos | 1 |
| 53998 | metiósele | 1 |
| 53999 | metiole | 1 |
| 54000 | metingos | 1 |
| 54001 | metime | 1 |
| 54002 | metílos | 1 |
| 54003 | metiéronme | 1 |
| 54004 | metiéronlos | 1 |
| 54005 | metiéndoselos | 1 |
| 54006 | metiéndolos | 1 |
| 54007 | metídose | 1 |
| 54008 | metídome | 1 |
| 54009 | metídolas | 1 |
| 54010 | metiditos | 1 |
| 54011 | metidito | 1 |
| 54012 | metidita | 1 |
| 54013 | metidillo | 1 |
| 54014 | metíase | 1 |
| 54015 | metíala | 1 |
| 54016 | métete | 1 |
| 54017 | metete | 1 |
| 54018 | meterlos | 1 |
| 54019 | meteorológicos | 1 |
| 54020 | meteorología | 1 |
| 54021 | meteoro | 1 |
| 54022 | métense | 1 |
| 54023 | metenla | 1 |
| 54024 | metempsícosis | 1 |
| 54025 | metemos | 1 |
| 54026 | mételos | 1 |
| 54027 | metelo | 1 |
| 54028 | metella | 1 |
| 54029 | mételes | 1 |
| 54030 | métele | 1 |
| 54031 | metela | 1 |
| 54032 | metedle | 1 |
| 54033 | métanse | 1 |
| 54034 | metalurgia | 1 |
| 54035 | metalizado | 1 |
| 54036 | metalización | 1 |
| 54037 | metálicos | 1 |
| 54038 | metálicamente | 1 |
| 54039 | metafóricamente | 1 |
| 54040 | metafísicamente | 1 |
| 54041 | metá | 1 |
| 54042 | mesturárardes | 1 |
| 54043 | mesturado | 1 |
| 54044 | mesturada | 1 |
| 54045 | messurada | 1 |
| 54046 | messonero | 1 |
| 54047 | messe | 1 |
| 54048 | mesquita | 1 |
| 54049 | mesquindat | 1 |
| 54050 | mesquinas | 1 |
| 54051 | mesoneras | 1 |
| 54052 | mesocrático | 1 |
| 54053 | mesnadas | 1 |
| 54054 | mesianitis | 1 |
| 54055 | mesetas | 1 |
| 54056 | mesericordia | 1 |
| 54057 | meseguero | 1 |
| 54058 | mescolanzas | 1 |
| 54059 | mescolanza | 1 |
| 54060 | mescláronme | 1 |
| 54061 | mescladores | 1 |
| 54062 | mescer | 1 |
| 54063 | mesarse | 1 |
| 54064 | mesaron | 1 |
| 54065 | mesajero | 1 |
| 54066 | mesada | 1 |
| 54067 | mesábame | 1 |
| 54068 | mesaba | 1 |
| 54069 | meryno | 1 |
| 54070 | mermó | 1 |
| 54071 | mermas | 1 |
| 54072 | mermando | 1 |
| 54073 | mermados | 1 |
| 54074 | merluzas | 1 |
| 54075 | merjelina | 1 |
| 54076 | meritos | 1 |
| 54077 | méritamente | 1 |
| 54078 | meriendan | 1 |
| 54079 | meridionales | 1 |
| 54080 | meridional | 1 |
| 54081 | meridiano | 1 |
| 54082 | merézcate | 1 |
| 54083 | merezcas | 1 |
| 54084 | merescieron | 1 |
| 54085 | meresçiente | 1 |
| 54086 | merescias | 1 |
| 54087 | meresçería | 1 |
| 54088 | meresçeré | 1 |
| 54089 | merescer | 1 |
| 54090 | merescen | 1 |
| 54091 | meresçedes | 1 |
| 54092 | meresçe | 1 |
| 54093 | merescas | 1 |
| 54094 | meresca | 1 |
| 54095 | merengada | 1 |
| 54096 | merenderos | 1 |
| 54097 | merendaba | 1 |
| 54098 | mereçiste | 1 |
| 54099 | merecio | 1 |
| 54100 | merecieren | 1 |
| 54101 | mereciéndole | 1 |
| 54102 | merecidísimo | 1 |
| 54103 | merecidas | 1 |
| 54104 | merecíalo | 1 |
| 54105 | mereciades | 1 |
| 54106 | merecerte | 1 |
| 54107 | merecerles | 1 |
| 54108 | merecerla | 1 |
| 54109 | merecería | 1 |
| 54110 | mereceré | 1 |
| 54111 | merecerá | 1 |
| 54112 | merecedores | 1 |
| 54113 | mereçedes | 1 |
| 54114 | merecedes | 1 |
| 54115 | mercuriales | 1 |
| 54116 | mercurial | 1 |
| 54117 | merçet | 1 |
| 54118 | mercería | 1 |
| 54119 | mercenarias | 1 |
| 54120 | merçedes | 1 |
| 54121 | mercarlo | 1 |
| 54122 | mercar | 1 |
| 54123 | mercantiles | 1 |
| 54124 | mercantes | 1 |
| 54125 | mercadurias | 1 |
| 54126 | mercadores | 1 |
| 54127 | mercadillo | 1 |
| 54128 | mercaderías | 1 |
| 54129 | mercadera | 1 |
| 54130 | mercadante | 1 |
| 54131 | mercachifles | 1 |
| 54132 | merca | 1 |
| 54133 | mequínez | 1 |
| 54134 | mépris | 1 |
| 54135 | meótides | 1 |
| 54136 | meona | 1 |
| 54137 | meón | 1 |
| 54138 | meo | 1 |
| 54139 | menudeóse | 1 |
| 54140 | menudean | 1 |
| 54141 | menudeábanse | 1 |
| 54142 | menudamente | 1 |
| 54143 | mentyras | 1 |
| 54144 | mentyr | 1 |
| 54145 | menty | 1 |
| 54146 | mentos | 1 |
| 54147 | mentón | 1 |
| 54148 | mentó | 1 |
| 54149 | mentises | 1 |
| 54150 | mentirosito | 1 |
| 54151 | mentirosísimo | 1 |
| 54152 | mentirosamente | 1 |
| 54153 | mentironiana | 1 |
| 54154 | mentirola | 1 |
| 54155 | mentirilla | 1 |
| 54156 | mentirijillas | 1 |
| 54157 | mentirijilla | 1 |
| 54158 | mentiré | 1 |
| 54159 | mentidos | 1 |
| 54160 | mentían | 1 |
| 54161 | mentéis | 1 |
| 54162 | mentecaterías | 1 |
| 54163 | mentecata | 1 |
| 54164 | mentaré | 1 |
| 54165 | mentalle | 1 |
| 54166 | menta | 1 |
| 54167 | ménsula | 1 |
| 54168 | menstrua | 1 |
| 54169 | menssajera | 1 |
| 54170 | mensil | 1 |
| 54171 | mensajerías | 1 |
| 54172 | mensaj | 1 |
| 54173 | mens | 1 |
| 54174 | menosprecios | 1 |
| 54175 | menosprecie | 1 |
| 54176 | menospreciase | 1 |
| 54177 | menospreciaron | 1 |
| 54178 | menospreciar | 1 |
| 54179 | menospreciando | 1 |
| 54180 | menospreciadas | 1 |
| 54181 | menospreçiada | 1 |
| 54182 | menospreçia | 1 |
| 54183 | menoscabe | 1 |
| 54184 | menoscabasen | 1 |
| 54185 | menoscábase | 1 |
| 54186 | menoscabaron | 1 |
| 54187 | menoscabar | 1 |
| 54188 | menoscabando | 1 |
| 54189 | menoscabado | 1 |
| 54190 | menoscabadas | 1 |
| 54191 | menoretas | 1 |
| 54192 | menjurje | 1 |
| 54193 | menistro | 1 |
| 54194 | menistrada | 1 |
| 54195 | meningo | 1 |
| 54196 | meningitis | 1 |
| 54197 | menina | 1 |
| 54198 | mengüe | 1 |
| 54199 | mengue | 1 |
| 54200 | menguaua | 1 |
| 54201 | menguare | 1 |
| 54202 | menguando | 1 |
| 54203 | menguamos | 1 |
| 54204 | menguadas | 1 |
| 54205 | menguaban | 1 |
| 54206 | mengías | 1 |
| 54207 | mengía | 1 |
| 54208 | menge | 1 |
| 54209 | mengana | 1 |
| 54210 | menearon | 1 |
| 54211 | menearán | 1 |
| 54212 | menéalas | 1 |
| 54213 | meneada | 1 |
| 54214 | meneaban | 1 |
| 54215 | mendiry | 1 |
| 54216 | mendigas | 1 |
| 54217 | mendigar | 1 |
| 54218 | mendian | 1 |
| 54219 | mendi | 1 |
| 54220 | mencionarlo | 1 |
| 54221 | mencionaré | 1 |
| 54222 | mencionada | 1 |
| 54223 | menciona | 1 |
| 54224 | mencion | 1 |
| 54225 | mencía | 1 |
| 54226 | mençebillo | 1 |
| 54227 | menbratvos | 1 |
| 54228 | menandro | 1 |
| 54229 | menando | 1 |
| 54230 | menalao | 1 |
| 54231 | memueria | 1 |
| 54232 | memorioso | 1 |
| 54233 | memorialista | 1 |
| 54234 | memento | 1 |
| 54235 | membraros | 1 |
| 54236 | membranosas | 1 |
| 54237 | membibres | 1 |
| 54238 | melosos | 1 |
| 54239 | meloso | 1 |
| 54240 | melosilla | 1 |
| 54241 | melosas | 1 |
| 54242 | melon | 1 |
| 54243 | melómanos | 1 |
| 54244 | melómano | 1 |
| 54245 | melodramática | 1 |
| 54246 | melodiosa | 1 |
| 54247 | melodías | 1 |
| 54248 | melodia | 1 |
| 54249 | melle | 1 |
| 54250 | mellados | 1 |
| 54251 | mellado | 1 |
| 54252 | melitar | 1 |
| 54253 | meliora | 1 |
| 54254 | melionesa | 1 |
| 54255 | melïona | 1 |
| 54256 | melindrosos | 1 |
| 54257 | melindrán | 1 |
| 54258 | melinas | 1 |
| 54259 | melifluo | 1 |
| 54260 | melifluamente | 1 |
| 54261 | melificada | 1 |
| 54262 | melicianos | 1 |
| 54263 | melesinas | 1 |
| 54264 | melenudos | 1 |
| 54265 | melenudo | 1 |
| 54266 | melenuda | 1 |
| 54267 | melenita | 1 |
| 54268 | melecinas | 1 |
| 54269 | mêle | 1 |
| 54270 | melchior | 1 |
| 54271 | melanconía | 1 |
| 54272 | melaera | 1 |
| 54273 | mela | 1 |
| 54274 | mel | 1 |
| 54275 | mejorías | 1 |
| 54276 | mejoria | 1 |
| 54277 | mejoréis | 1 |
| 54278 | mejorcita | 1 |
| 54279 | mejorasen | 1 |
| 54280 | mejorase | 1 |
| 54281 | mejorarla | 1 |
| 54282 | mejoraría | 1 |
| 54283 | mejorares | 1 |
| 54284 | mejoraré | 1 |
| 54285 | mejorarán | 1 |
| 54286 | mejorándose | 1 |
| 54287 | mejoran | 1 |
| 54288 | mejoradas | 1 |
| 54289 | mejicana | 1 |
| 54290 | meitad | 1 |
| 54291 | mei | 1 |
| 54292 | meharín | 1 |
| 54293 | megera | 1 |
| 54294 | mefistofélicos | 1 |
| 54295 | meetings | 1 |
| 54296 | medusa | 1 |
| 54297 | medrugos | 1 |
| 54298 | medrosicos | 1 |
| 54299 | medrosas | 1 |
| 54300 | medró | 1 |
| 54301 | medro | 1 |
| 54302 | medremos | 1 |
| 54303 | medraua | 1 |
| 54304 | medras | 1 |
| 54305 | medrará | 1 |
| 54306 | medrado | 1 |
| 54307 | medradas | 1 |
| 54308 | medité | 1 |
| 54309 | medite | 1 |
| 54310 | meditarlo | 1 |
| 54311 | meditan | 1 |
| 54312 | meditabuntur | 1 |
| 54313 | meditabor | 1 |
| 54314 | meditaban | 1 |
| 54315 | medirlas | 1 |
| 54316 | mediré | 1 |
| 54317 | medíos | 1 |
| 54318 | mediodia | 1 |
| 54319 | medinaceli | 1 |
| 54320 | medimos | 1 |
| 54321 | medíme | 1 |
| 54322 | mediis | 1 |
| 54323 | medievales | 1 |
| 54324 | médiese | 1 |
| 54325 | medidos | 1 |
| 54326 | medidor | 1 |
| 54327 | medicinales | 1 |
| 54328 | mediasen | 1 |
| 54329 | mediase | 1 |
| 54330 | mediascañas | 1 |
| 54331 | medianía | 1 |
| 54332 | medianeras | 1 |
| 54333 | mediando | 1 |
| 54334 | medíamos | 1 |
| 54335 | medíalas | 1 |
| 54336 | mediaban | 1 |
| 54337 | meder | 1 |
| 54338 | medecinas | 1 |
| 54339 | mecina | 1 |
| 54340 | meciéndose | 1 |
| 54341 | meciéndola | 1 |
| 54342 | meciendo | 1 |
| 54343 | mecida | 1 |
| 54344 | mechero | 1 |
| 54345 | méchants | 1 |
| 54346 | meces | 1 |
| 54347 | mécele | 1 |
| 54348 | mecánicos | 1 |
| 54349 | mecánicas | 1 |
| 54350 | mecánicamente | 1 |
| 54351 | mecachis | 1 |
| 54352 | mearuberry | 1 |
| 54353 | meandro | 1 |
| 54354 | meaca | 1 |
| 54355 | mdlxii | 1 |
| 54356 | mdccxcii | 1 |
| 54357 | mcmxx | 1 |
| 54358 | mazurca | 1 |
| 54359 | mayúscula | 1 |
| 54360 | maytines | 1 |
| 54361 | máys | 1 |
| 54362 | mayos | 1 |
| 54363 | mayoridad | 1 |
| 54364 | mayorazguetes | 1 |
| 54365 | mayorazguete | 1 |
| 54366 | mayorazgos | 1 |
| 54367 | mayonesa | 1 |
| 54368 | mayer | 1 |
| 54369 | mayar | 1 |
| 54370 | mayando | 1 |
| 54371 | mayadores | 1 |
| 54372 | mayaban | 1 |
| 54373 | mayaba | 1 |
| 54374 | maxmordos | 1 |
| 54375 | máximo | 1 |
| 54376 | maximiliana | 1 |
| 54377 | maxilar | 1 |
| 54378 | mauvais | 1 |
| 54379 | mausoleo | 1 |
| 54380 | mauro | 1 |
| 54381 | mauritania | 1 |
| 54382 | maullar | 1 |
| 54383 | maullando | 1 |
| 54384 | maulería | 1 |
| 54385 | mauleón | 1 |
| 54386 | mauleon | 1 |
| 54387 | maudsley | 1 |
| 54388 | matynes | 1 |
| 54389 | matutino | 1 |
| 54390 | matutina | 1 |
| 54391 | matuteros | 1 |
| 54392 | maturana | 1 |
| 54393 | matriz | 1 |
| 54394 | matritense | 1 |
| 54395 | matrimoñesco | 1 |
| 54396 | matrimoñesca | 1 |
| 54397 | matricularse | 1 |
| 54398 | matriculados | 1 |
| 54399 | matriculadas | 1 |
| 54400 | matrices | 1 |
| 54401 | matraca | 1 |
| 54402 | matóse | 1 |
| 54403 | matona | 1 |
| 54404 | matólo | 1 |
| 54405 | matóla | 1 |
| 54406 | matizes | 1 |
| 54407 | matizadas | 1 |
| 54408 | matitas | 1 |
| 54409 | matinée | 1 |
| 54410 | matinales | 1 |
| 54411 | matina | 1 |
| 54412 | matin | 1 |
| 54413 | matiella | 1 |
| 54414 | mathieu | 1 |
| 54415 | mateste | 1 |
| 54416 | maternas | 1 |
| 54417 | materialmente | 1 |
| 54418 | materializado | 1 |
| 54419 | materialidades | 1 |
| 54420 | materialidad | 1 |
| 54421 | mátenme | 1 |
| 54422 | matemáticamente | 1 |
| 54423 | matelot | 1 |
| 54424 | matele | 1 |
| 54425 | matéis | 1 |
| 54426 | match | 1 |
| 54427 | matauan | 1 |
| 54428 | mátate | 1 |
| 54429 | matásteme | 1 |
| 54430 | matástel | 1 |
| 54431 | matasses | 1 |
| 54432 | matasse | 1 |
| 54433 | matases | 1 |
| 54434 | matasen | 1 |
| 54435 | matarya | 1 |
| 54436 | matáronlo | 1 |
| 54437 | matarm | 1 |
| 54438 | matarlo | 1 |
| 54439 | mataríe | 1 |
| 54440 | matarían | 1 |
| 54441 | matarian | 1 |
| 54442 | mataremos | 1 |
| 54443 | mataréme | 1 |
| 54444 | matare | 1 |
| 54445 | mataras | 1 |
| 54446 | matarále | 1 |
| 54447 | matanla | 1 |
| 54448 | matándote | 1 |
| 54449 | matándol | 1 |
| 54450 | matamos | 1 |
| 54451 | matamigos | 1 |
| 54452 | mátameles | 1 |
| 54453 | mátame | 1 |
| 54454 | matalote | 1 |
| 54455 | matalotaje | 1 |
| 54456 | matalones | 1 |
| 54457 | matadme | 1 |
| 54458 | matada | 1 |
| 54459 | matachines | 1 |
| 54460 | mastuerço | 1 |
| 54461 | mastina | 1 |
| 54462 | masticarlos | 1 |
| 54463 | mástel | 1 |
| 54464 | massarnau | 1 |
| 54465 | massanielo | 1 |
| 54466 | masqué | 1 |
| 54467 | masque | 1 |
| 54468 | masónico | 1 |
| 54469 | masones | 1 |
| 54470 | masnada | 1 |
| 54471 | masini | 1 |
| 54472 | masílicos | 1 |
| 54473 | masiella | 1 |
| 54474 | maselleras | 1 |
| 54475 | masdeu | 1 |
| 54476 | mascullones | 1 |
| 54477 | mascullándolos | 1 |
| 54478 | masculinos | 1 |
| 54479 | masculinas | 1 |
| 54480 | mascota | 1 |
| 54481 | mascase | 1 |
| 54482 | mascarón | 1 |
| 54483 | mascarla | 1 |
| 54484 | mascaran | 1 |
| 54485 | mascara | 1 |
| 54486 | mascado | 1 |
| 54487 | masarnau | 1 |
| 54488 | masalanca | 1 |
| 54489 | marynero | 1 |
| 54490 | maryna | 1 |
| 54491 | marydo | 1 |
| 54492 | marya | 1 |
| 54493 | martyriada | 1 |
| 54494 | martirizaron | 1 |
| 54495 | martirizando | 1 |
| 54496 | martirizados | 1 |
| 54497 | martirizado | 1 |
| 54498 | martirizaban | 1 |
| 54499 | martirice | 1 |
| 54500 | martino | 1 |
| 54501 | martina | 1 |
| 54502 | martilogio | 1 |
| 54503 | martillea | 1 |
| 54504 | martillase | 1 |
| 54505 | martillando | 1 |
| 54506 | márteres | 1 |
| 54507 | marsilla | 1 |
| 54508 | marsilios | 1 |
| 54509 | marrullería | 1 |
| 54510 | marrubios | 1 |
| 54511 | marroquia | 1 |
| 54512 | marrido | 1 |
| 54513 | marrano | 1 |
| 54514 | marranadas | 1 |
| 54515 | marranada | 1 |
| 54516 | marrakesh | 1 |
| 54517 | marrajotes | 1 |
| 54518 | márquez | 1 |
| 54519 | marquesitas | 1 |
| 54520 | marquesita | 1 |
| 54521 | marquesina | 1 |
| 54522 | maromas | 1 |
| 54523 | marmota | 1 |
| 54524 | mármores | 1 |
| 54525 | marmóreo | 1 |
| 54526 | marmóles | 1 |
| 54527 | marmolejo | 1 |
| 54528 | marmol | 1 |
| 54529 | marmitón | 1 |
| 54530 | marlborough | 1 |
| 54531 | marivinos | 1 |
| 54532 | marítimos | 1 |
| 54533 | marítimo | 1 |
| 54534 | marítima | 1 |
| 54535 | maritales | 1 |
| 54536 | marital | 1 |
| 54537 | marisabidilla | 1 |
| 54538 | marirramos | 1 |
| 54539 | marinilla | 1 |
| 54540 | maringouins | 1 |
| 54541 | marinerillos | 1 |
| 54542 | marine | 1 |
| 54543 | marinándolas | 1 |
| 54544 | marinados | 1 |
| 54545 | marimacho | 1 |
| 54546 | marien | 1 |
| 54547 | maricón | 1 |
| 54548 | marichu | 1 |
| 54549 | maricastaña | 1 |
| 54550 | marías | 1 |
| 54551 | mariage | 1 |
| 54552 | marfyl | 1 |
| 54553 | marfúz | 1 |
| 54554 | marfuz | 1 |
| 54555 | marfuces | 1 |
| 54556 | mareta | 1 |
| 54557 | maremagno | 1 |
| 54558 | marearse | 1 |
| 54559 | marearlos | 1 |
| 54560 | marearla | 1 |
| 54561 | marearán | 1 |
| 54562 | mareantes | 1 |
| 54563 | mareando | 1 |
| 54564 | marcialidad | 1 |
| 54565 | marchose | 1 |
| 54566 | marchitarse | 1 |
| 54567 | marchitaban | 1 |
| 54568 | marchena | 1 |
| 54569 | marche | 1 |
| 54570 | marchasen | 1 |
| 54571 | marcháronse | 1 |
| 54572 | marcharemos | 1 |
| 54573 | marcharan | 1 |
| 54574 | marcháos | 1 |
| 54575 | marchante | 1 |
| 54576 | marchamos | 1 |
| 54577 | marchámonos | 1 |
| 54578 | marchádose | 1 |
| 54579 | marchabas | 1 |
| 54580 | marchábamos | 1 |
| 54581 | marcelino | 1 |
| 54582 | marcelica | 1 |
| 54583 | marcas | 1 |
| 54584 | marcaron | 1 |
| 54585 | marcarlos | 1 |
| 54586 | marcarles | 1 |
| 54587 | marcándolos | 1 |
| 54588 | marcador | 1 |
| 54589 | marcadas | 1 |
| 54590 | marcadamente | 1 |
| 54591 | maravillose | 1 |
| 54592 | maravillós | 1 |
| 54593 | maravíllome | 1 |
| 54594 | maravilles | 1 |
| 54595 | maravillemos | 1 |
| 54596 | maravilléme | 1 |
| 54597 | maravillé | 1 |
| 54598 | maraville | 1 |
| 54599 | maravillásemos | 1 |
| 54600 | maravillarme | 1 |
| 54601 | maravillarán | 1 |
| 54602 | maravillárame | 1 |
| 54603 | maravillándose | 1 |
| 54604 | maravillan | 1 |
| 54605 | maravillados | 1 |
| 54606 | maravillábase | 1 |
| 54607 | maravedy | 1 |
| 54608 | marauillome | 1 |
| 54609 | marauille | 1 |
| 54610 | marauillarme | 1 |
| 54611 | marauillarias | 1 |
| 54612 | marauedi | 1 |
| 54613 | marañón | 1 |
| 54614 | maragato | 1 |
| 54615 | maragatería | 1 |
| 54616 | maquinillas | 1 |
| 54617 | maquinase | 1 |
| 54618 | maquinales | 1 |
| 54619 | maquinación | 1 |
| 54620 | maquina | 1 |
| 54621 | maquiavélicos | 1 |
| 54622 | maqueda | 1 |
| 54623 | mañosito | 1 |
| 54624 | mañosas | 1 |
| 54625 | mañosamente | 1 |
| 54626 | maño | 1 |
| 54627 | mañeruelas | 1 |
| 54628 | mañanitas | 1 |
| 54629 | mañanicas | 1 |
| 54630 | manzilla | 1 |
| 54631 | manzanedo | 1 |
| 54632 | manutención | 1 |
| 54633 | manueles | 1 |
| 54634 | manuelacho | 1 |
| 54635 | manu | 1 |
| 54636 | mantyene | 1 |
| 54637 | mantúvose | 1 |
| 54638 | mantuviese | 1 |
| 54639 | mantuvieron | 1 |
| 54640 | mantuviera | 1 |
| 54641 | mantuano | 1 |
| 54642 | mantoviste | 1 |
| 54643 | mantienes | 1 |
| 54644 | mantién | 1 |
| 54645 | mantible | 1 |
| 54646 | manterola | 1 |
| 54647 | mantequilla | 1 |
| 54648 | mantenimientos | 1 |
| 54649 | mantenidos | 1 |
| 54650 | mantenídoos | 1 |
| 54651 | manténgame | 1 |
| 54652 | mantenerte | 1 |
| 54653 | mantenerme | 1 |
| 54654 | mantenerlo | 1 |
| 54655 | mantendría | 1 |
| 54656 | mantecas | 1 |
| 54657 | manteandome | 1 |
| 54658 | mansillera | 1 |
| 54659 | mansellero | 1 |
| 54660 | mansedumbres | 1 |
| 54661 | mansalva | 1 |
| 54662 | manparado | 1 |
| 54663 | manoteaba | 1 |
| 54664 | manotazo | 1 |
| 54665 | manoso | 1 |
| 54666 | manoseóse | 1 |
| 54667 | manoseó | 1 |
| 54668 | manosearle | 1 |
| 54669 | manoseándole | 1 |
| 54670 | manoseando | 1 |
| 54671 | manosean | 1 |
| 54672 | manoseaba | 1 |
| 54673 | manoplazo | 1 |
| 54674 | manolos | 1 |
| 54675 | manolitos | 1 |
| 54676 | manolesco | 1 |
| 54677 | manolas | 1 |
| 54678 | manjá | 1 |
| 54679 | manivelas | 1 |
| 54680 | manirrota | 1 |
| 54681 | maniqueo | 1 |
| 54682 | maniobrando | 1 |
| 54683 | maniobraba | 1 |
| 54684 | manifiesten | 1 |
| 54685 | manifiestase | 1 |
| 54686 | manífica | 1 |
| 54687 | manifestose | 1 |
| 54688 | manifesté | 1 |
| 54689 | manifestasen | 1 |
| 54690 | manifestarte | 1 |
| 54691 | manifestárselo | 1 |
| 54692 | manifestármelo | 1 |
| 54693 | manifestarme | 1 |
| 54694 | manifestarle | 1 |
| 54695 | manifestaran | 1 |
| 54696 | manifestándose | 1 |
| 54697 | manifestándole | 1 |
| 54698 | manifestando | 1 |
| 54699 | manifestallos | 1 |
| 54700 | manifestada | 1 |
| 54701 | manifatura | 1 |
| 54702 | maniatar | 1 |
| 54703 | mangueros | 1 |
| 54704 | mangonee | 1 |
| 54705 | mangoneando | 1 |
| 54706 | mangonean | 1 |
| 54707 | mangoneado | 1 |
| 54708 | manglares | 1 |
| 54709 | manetizan | 1 |
| 54710 | manejes | 1 |
| 54711 | manejarte | 1 |
| 54712 | manejarse | 1 |
| 54713 | manejarlo | 1 |
| 54714 | manejarla | 1 |
| 54715 | manejaré | 1 |
| 54716 | manejándole | 1 |
| 54717 | manejamos | 1 |
| 54718 | manejada | 1 |
| 54719 | manecar | 1 |
| 54720 | manebunt | 1 |
| 54721 | mandrágoras | 1 |
| 54722 | mandote | 1 |
| 54723 | mandóselos | 1 |
| 54724 | mandona | 1 |
| 54725 | mandome | 1 |
| 54726 | mandólos | 1 |
| 54727 | mandólo | 1 |
| 54728 | mándole | 1 |
| 54729 | mandóla | 1 |
| 54730 | mandola | 1 |
| 54731 | mandingas | 1 |
| 54732 | mandiles | 1 |
| 54733 | mándelas | 1 |
| 54734 | mandel | 1 |
| 54735 | mandávale | 1 |
| 54736 | mandauas | 1 |
| 54737 | mandauan | 1 |
| 54738 | mandatle | 1 |
| 54739 | mandatis | 1 |
| 54740 | mandastes | 1 |
| 54741 | mandárselo | 1 |
| 54742 | mandarse | 1 |
| 54743 | mandáronme | 1 |
| 54744 | mandáronles | 1 |
| 54745 | mandárnoslo | 1 |
| 54746 | mandarlos | 1 |
| 54747 | mandaren | 1 |
| 54748 | mandaras | 1 |
| 54749 | mandallo | 1 |
| 54750 | mandallas | 1 |
| 54751 | mándales | 1 |
| 54752 | mándale | 1 |
| 54753 | mandalas | 1 |
| 54754 | mandáisle | 1 |
| 54755 | mandadlos | 1 |
| 54756 | mandadería | 1 |
| 54757 | mandadas | 1 |
| 54758 | mandábalo | 1 |
| 54759 | mandábale | 1 |
| 54760 | mandábala | 1 |
| 54761 | mancuerda | 1 |
| 54762 | mancillado | 1 |
| 54763 | mançilla | 1 |
| 54764 | manchurrones | 1 |
| 54765 | mancho | 1 |
| 54766 | manchitas | 1 |
| 54767 | manchísima | 1 |
| 54768 | manches | 1 |
| 54769 | manchegazo | 1 |
| 54770 | manchase | 1 |
| 54771 | manchara | 1 |
| 54772 | manchándolos | 1 |
| 54773 | manchan | 1 |
| 54774 | mancháis | 1 |
| 54775 | manchaban | 1 |
| 54776 | mancebitos | 1 |
| 54777 | mançebillos | 1 |
| 54778 | mançebilla | 1 |
| 54779 | mançebiello | 1 |
| 54780 | mancebia | 1 |
| 54781 | mançebéz | 1 |
| 54782 | mançebez | 1 |
| 54783 | mançeba | 1 |
| 54784 | mançeb | 1 |
| 54785 | mancase | 1 |
| 54786 | mançanedo | 1 |
| 54787 | manaza | 1 |
| 54788 | manan | 1 |
| 54789 | manahora | 1 |
| 54790 | manadilla | 1 |
| 54791 | manadiellas | 1 |
| 54792 | manaba | 1 |
| 54793 | mampostería | 1 |
| 54794 | mamotretos | 1 |
| 54795 | mamonado | 1 |
| 54796 | mamo | 1 |
| 54797 | mamen | 1 |
| 54798 | mamé | 1 |
| 54799 | mambruc | 1 |
| 54800 | mamas | 1 |
| 54801 | mamaron | 1 |
| 54802 | mamándose | 1 |
| 54803 | mamaíta | 1 |
| 54804 | mamaba | 1 |
| 54805 | mam | 1 |
| 54806 | malvices | 1 |
| 54807 | malvada | 1 |
| 54808 | maluauiscos | 1 |
| 54809 | maltrechos | 1 |
| 54810 | maltrecha | 1 |
| 54811 | maltraten | 1 |
| 54812 | maltratara | 1 |
| 54813 | maltratando | 1 |
| 54814 | maltratamiento | 1 |
| 54815 | maltrataban | 1 |
| 54816 | maltrajeao | 1 |
| 54817 | maltraher | 1 |
| 54818 | malsufrido | 1 |
| 54819 | malsonantes | 1 |
| 54820 | malsonante | 1 |
| 54821 | malsofridas | 1 |
| 54822 | malsinar | 1 |
| 54823 | malsañudo | 1 |
| 54824 | malsabydas | 1 |
| 54825 | malsaber | 1 |
| 54826 | malquistarle | 1 |
| 54827 | malqueriente | 1 |
| 54828 | malquerido | 1 |
| 54829 | malquerencia | 1 |
| 54830 | malquebrantó | 1 |
| 54831 | malquebrantado | 1 |
| 54832 | malproueyda | 1 |
| 54833 | malpintado | 1 |
| 54834 | malpegado | 1 |
| 54835 | malparir | 1 |
| 54836 | malparió | 1 |
| 54837 | malparados | 1 |
| 54838 | malpagar | 1 |
| 54839 | malora | 1 |
| 54840 | malogró | 1 |
| 54841 | malograrla | 1 |
| 54842 | malogrados | 1 |
| 54843 | malnacida | 1 |
| 54844 | malmordiendo | 1 |
| 54845 | malmaxcada | 1 |
| 54846 | mallogrado | 1 |
| 54847 | mallas | 1 |
| 54848 | malitos | 1 |
| 54849 | malintencionados | 1 |
| 54850 | malino | 1 |
| 54851 | malindrania | 1 |
| 54852 | malignidad | 1 |
| 54853 | maliciosamente | 1 |
| 54854 | maliçiosa | 1 |
| 54855 | maliciado | 1 |
| 54856 | maliciaban | 1 |
| 54857 | malhumor | 1 |
| 54858 | malhizieron | 1 |
| 54859 | malheureux | 1 |
| 54860 | malheur | 1 |
| 54861 | malheridos | 1 |
| 54862 | malherido | 1 |
| 54863 | malherbe | 1 |
| 54864 | malhechora | 1 |
| 54865 | malhechor | 1 |
| 54866 | malhadadas | 1 |
| 54867 | malhadada | 1 |
| 54868 | malgré | 1 |
| 54869 | malgastado | 1 |
| 54870 | malgastada | 1 |
| 54871 | malganados | 1 |
| 54872 | malferida | 1 |
| 54873 | malfecho | 1 |
| 54874 | malfado | 1 |
| 54875 | malface | 1 |
| 54876 | malevolencia | 1 |
| 54877 | malestorvar | 1 |
| 54878 | malespantados | 1 |
| 54879 | malesculcada | 1 |
| 54880 | malengañada | 1 |
| 54881 | malencónicos | 1 |
| 54882 | malencónicas | 1 |
| 54883 | maléfico | 1 |
| 54884 | malefiçios | 1 |
| 54885 | malefiçio | 1 |
| 54886 | maleficiar | 1 |
| 54887 | maledicencias | 1 |
| 54888 | malecones | 1 |
| 54889 | maleantes | 1 |
| 54890 | maleador | 1 |
| 54891 | maleada | 1 |
| 54892 | maleables | 1 |
| 54893 | maleable | 1 |
| 54894 | maldolyente | 1 |
| 54895 | maldoladas | 1 |
| 54896 | maldo | 1 |
| 54897 | maldizientes | 1 |
| 54898 | maldiziente | 1 |
| 54899 | maldiziendo | 1 |
| 54900 | maldizes | 1 |
| 54901 | maldize | 1 |
| 54902 | maldíxole | 1 |
| 54903 | malditamente | 1 |
| 54904 | maldíjose | 1 |
| 54905 | maldíjome | 1 |
| 54906 | maldíjeme | 1 |
| 54907 | maldigan | 1 |
| 54908 | maldiciéndola | 1 |
| 54909 | maldicha | 1 |
| 54910 | maldices | 1 |
| 54911 | maldicen | 1 |
| 54912 | maldezir | 1 |
| 54913 | maldezientes | 1 |
| 54914 | maldesir | 1 |
| 54915 | maldesiente | 1 |
| 54916 | maldenostada | 1 |
| 54917 | maldecirte | 1 |
| 54918 | maldecirá | 1 |
| 54919 | maldecidas | 1 |
| 54920 | maldecíamos | 1 |
| 54921 | malcriado | 1 |
| 54922 | malchufados | 1 |
| 54923 | malchara | 1 |
| 54924 | malcasar | 1 |
| 54925 | malcasado | 1 |
| 54926 | malcasadas | 1 |
| 54927 | malcasa | 1 |
| 54928 | malbaratándolas | 1 |
| 54929 | malbaratado | 1 |
| 54930 | malayas | 1 |
| 54931 | malaventura | 1 |
| 54932 | malauenturada | 1 |
| 54933 | malapresso | 1 |
| 54934 | malapreso | 1 |
| 54935 | malapresa | 1 |
| 54936 | malangosto | 1 |
| 54937 | malandrino | 1 |
| 54938 | malandrina | 1 |
| 54939 | malandar | 1 |
| 54940 | malandanza | 1 |
| 54941 | malakoff | 1 |
| 54942 | malae | 1 |
| 54943 | malaco | 1 |
| 54944 | malabares | 1 |
| 54945 | majuelos | 1 |
| 54946 | majos | 1 |
| 54947 | majometana | 1 |
| 54948 | majestuosos | 1 |
| 54949 | majestüoso | 1 |
| 54950 | majestuosas | 1 |
| 54951 | majestüosa | 1 |
| 54952 | majestat | 1 |
| 54953 | majas | 1 |
| 54954 | majadera | 1 |
| 54955 | majadas | 1 |
| 54956 | maistral | 1 |
| 54957 | mairena | 1 |
| 54958 | mainates | 1 |
| 54959 | mahones | 1 |
| 54960 | mahón | 1 |
| 54961 | mahométicos | 1 |
| 54962 | mahomético | 1 |
| 54963 | maheridas | 1 |
| 54964 | mahamate | 1 |
| 54965 | magyares | 1 |
| 54966 | magulló | 1 |
| 54967 | magullasen | 1 |
| 54968 | magullar | 1 |
| 54969 | magullándose | 1 |
| 54970 | magulladuras | 1 |
| 54971 | magullados | 1 |
| 54972 | magullado | 1 |
| 54973 | magulladas | 1 |
| 54974 | magros | 1 |
| 54975 | magrillo | 1 |
| 54976 | magrilla | 1 |
| 54977 | magnum | 1 |
| 54978 | magnolias | 1 |
| 54979 | magnificamente | 1 |
| 54980 | magnificado | 1 |
| 54981 | magnético | 1 |
| 54982 | magnéticas | 1 |
| 54983 | magnesia | 1 |
| 54984 | magnes | 1 |
| 54985 | magistrales | 1 |
| 54986 | magisterio | 1 |
| 54987 | magis | 1 |
| 54988 | magimasa | 1 |
| 54989 | mágicos | 1 |
| 54990 | mágicamente | 1 |
| 54991 | magestad | 1 |
| 54992 | magazo | 1 |
| 54993 | magadaña | 1 |
| 54994 | magadana | 1 |
| 54995 | magada | 1 |
| 54996 | maga | 1 |
| 54997 | maestrya | 1 |
| 54998 | maestrita | 1 |
| 54999 | maestrique | 1 |
| 55000 | maestre | 1 |
| 55001 | maesecoral | 1 |
| 55002 | madurar | 1 |
| 55003 | maduran | 1 |
| 55004 | madurado | 1 |
| 55005 | madurada | 1 |
| 55006 | madrugues | 1 |
| 55007 | madruguemos | 1 |
| 55008 | madrugeste | 1 |
| 55009 | madrugava | 1 |
| 55010 | madrugaría | 1 |
| 55011 | madrugadores | 1 |
| 55012 | madrugadas | 1 |
| 55013 | madroños | 1 |
| 55014 | madroñaje | 1 |
| 55015 | madrileñitos | 1 |
| 55016 | madrigalete | 1 |
| 55017 | madreselua | 1 |
| 55018 | madrejón | 1 |
| 55019 | madrastras | 1 |
| 55020 | madrás | 1 |
| 55021 | madra | 1 |
| 55022 | madoz | 1 |
| 55023 | madexitas | 1 |
| 55024 | madexas | 1 |
| 55025 | madexa | 1 |
| 55026 | madésima | 1 |
| 55027 | maderita | 1 |
| 55028 | madásimas | 1 |
| 55029 | madapolán | 1 |
| 55030 | macuquinas | 1 |
| 55031 | macitos | 1 |
| 55032 | macías | 1 |
| 55033 | machucándole | 1 |
| 55034 | machito | 1 |
| 55035 | machichaco | 1 |
| 55036 | machete | 1 |
| 55037 | machetazos | 1 |
| 55038 | machaquen | 1 |
| 55039 | machaqué | 1 |
| 55040 | machamartillo | 1 |
| 55041 | machacó | 1 |
| 55042 | machacaron | 1 |
| 55043 | machacarla | 1 |
| 55044 | machacante | 1 |
| 55045 | machacado | 1 |
| 55046 | machacada | 1 |
| 55047 | macedónico | 1 |
| 55048 | macedón | 1 |
| 55049 | macdonell | 1 |
| 55050 | macas | 1 |
| 55051 | macarrones | 1 |
| 55052 | macario | 1 |
| 55053 | maçar | 1 |
| 55054 | macange | 1 |
| 55055 | macacona | 1 |
| 55056 | macabra | 1 |
| 55057 | macabeo | 1 |
| 55058 | mabille | 1 |
| 55059 | lyxa | 1 |
| 55060 | lyviandat | 1 |
| 55061 | lystada | 1 |
| 55062 | lysongia | 1 |
| 55063 | lyon | 1 |
| 55064 | lynpio | 1 |
| 55065 | lynpiesa | 1 |
| 55066 | lynpieça | 1 |
| 55067 | lynpiar | 1 |
| 55068 | lynpia | 1 |
| 55069 | lyndero | 1 |
| 55070 | lynaj | 1 |
| 55071 | lymosma | 1 |
| 55072 | lygerezas | 1 |
| 55073 | lyévela | 1 |
| 55074 | lyevas | 1 |
| 55075 | lyevan | 1 |
| 55076 | lyévalos | 1 |
| 55077 | lyendo | 1 |
| 55078 | lydié | 1 |
| 55079 | lydiando | 1 |
| 55080 | lydia | 1 |
| 55081 | lyçión | 1 |
| 55082 | lyçion | 1 |
| 55083 | lyçençia | 1 |
| 55084 | lyçencia | 1 |
| 55085 | lybrados | 1 |
| 55086 | lybertat | 1 |
| 55087 | lxxvi | 1 |
| 55088 | lxxiv | 1 |
| 55089 | lxxiii | 1 |
| 55090 | lxxii | 1 |
| 55091 | lxxi | 1 |
| 55092 | lxx | 1 |
| 55093 | lxvii | 1 |
| 55094 | lxvi | 1 |
| 55095 | lxv | 1 |
| 55096 | lxix | 1 |
| 55097 | lxiv | 1 |
| 55098 | lxiii | 1 |
| 55099 | lxi | 1 |
| 55100 | lx | 1 |
| 55101 | lviii | 1 |
| 55102 | lvii | 1 |
| 55103 | lvi | 1 |
| 55104 | lv | 1 |
| 55105 | luzgan | 1 |
| 55106 | luzentores | 1 |
| 55107 | luys | 1 |
| 55108 | luvias | 1 |
| 55109 | lutosa | 1 |
| 55110 | lutos | 1 |
| 55111 | luteras | 1 |
| 55112 | lutecia | 1 |
| 55113 | lustrosos | 1 |
| 55114 | lustrosas | 1 |
| 55115 | lustros | 1 |
| 55116 | lustres | 1 |
| 55117 | lustrada | 1 |
| 55118 | lusitano | 1 |
| 55119 | lusitania | 1 |
| 55120 | lusitana | 1 |
| 55121 | lusiente | 1 |
| 55122 | lurrean | 1 |
| 55123 | lur | 1 |
| 55124 | luquetes | 1 |
| 55125 | luque | 1 |
| 55126 | lupus | 1 |
| 55127 | lupercio | 1 |
| 55128 | lupanares | 1 |
| 55129 | lunetas | 1 |
| 55130 | lunada | 1 |
| 55131 | lumpia | 1 |
| 55132 | lumínicos | 1 |
| 55133 | luminaria | 1 |
| 55134 | luminares | 1 |
| 55135 | lumbreras | 1 |
| 55136 | lujuriosas | 1 |
| 55137 | lujosos | 1 |
| 55138 | lujoso | 1 |
| 55139 | lujanes | 1 |
| 55140 | luisa | 1 |
| 55141 | lugo | 1 |
| 55142 | lugartenientes | 1 |
| 55143 | lugarillo | 1 |
| 55144 | lugareñas | 1 |
| 55145 | lugarejo | 1 |
| 55146 | lueñe | 1 |
| 55147 | lueñas | 1 |
| 55148 | lucura | 1 |
| 55149 | lucubraciones | 1 |
| 55150 | lucro | 1 |
| 55151 | lucrativos | 1 |
| 55152 | lucrativo | 1 |
| 55153 | lucrar | 1 |
| 55154 | lucis | 1 |
| 55155 | lucirme | 1 |
| 55156 | lucirlo | 1 |
| 55157 | lucina | 1 |
| 55158 | luciferum | 1 |
| 55159 | luciéramos | 1 |
| 55160 | lucidísimo | 1 |
| 55161 | lucidez | 1 |
| 55162 | luciano | 1 |
| 55163 | lucho | 1 |
| 55164 | luchemos | 1 |
| 55165 | luchase | 1 |
| 55166 | lucharían | 1 |
| 55167 | lucharía | 1 |
| 55168 | luchana | 1 |
| 55169 | luchan | 1 |
| 55170 | luchamos | 1 |
| 55171 | luceroz | 1 |
| 55172 | lucem | 1 |
| 55173 | lucecita | 1 |
| 55174 | lucanor | 1 |
| 55175 | lucano | 1 |
| 55176 | lucaaam | 1 |
| 55177 | lubricidad | 1 |
| 55178 | lúbricas | 1 |
| 55179 | lu | 1 |
| 55180 | loz | 1 |
| 55181 | loyola | 1 |
| 55182 | lovelace | 1 |
| 55183 | lourdes | 1 |
| 55184 | loups | 1 |
| 55185 | loué | 1 |
| 55186 | lotero | 1 |
| 55187 | lotéricas | 1 |
| 55188 | lorito | 1 |
| 55189 | lorigas | 1 |
| 55190 | loretas | 1 |
| 55191 | lores | 1 |
| 55192 | lorda | 1 |
| 55193 | lora | 1 |
| 55194 | loquitur | 1 |
| 55195 | loquillos | 1 |
| 55196 | loquesco | 1 |
| 55197 | loquear | 1 |
| 55198 | loo | 1 |
| 55199 | longitud | 1 |
| 55200 | longísima | 1 |
| 55201 | longino | 1 |
| 55202 | longe | 1 |
| 55203 | londonenses | 1 |
| 55204 | london | 1 |
| 55205 | lombriz | 1 |
| 55206 | lombardía | 1 |
| 55207 | lombarda | 1 |
| 55208 | loja | 1 |
| 55209 | lógrelas | 1 |
| 55210 | logré | 1 |
| 55211 | lograse | 1 |
| 55212 | logras | 1 |
| 55213 | lograrlos | 1 |
| 55214 | lograrlo | 1 |
| 55215 | lograrla | 1 |
| 55216 | lograrán | 1 |
| 55217 | logrará | 1 |
| 55218 | logran | 1 |
| 55219 | logramos | 1 |
| 55220 | lógrala | 1 |
| 55221 | logradas | 1 |
| 55222 | lograd | 1 |
| 55223 | logomaquias | 1 |
| 55224 | logicuos | 1 |
| 55225 | lógicos | 1 |
| 55226 | lógicas | 1 |
| 55227 | logia | 1 |
| 55228 | lofraso | 1 |
| 55229 | loemos | 1 |
| 55230 | loe | 1 |
| 55231 | lodazales | 1 |
| 55232 | locus | 1 |
| 55233 | locurilla | 1 |
| 55234 | locomoción | 1 |
| 55235 | loçan | 1 |
| 55236 | localidades | 1 |
| 55237 | lobuno | 1 |
| 55238 | lóbulos | 1 |
| 55239 | lobitos | 1 |
| 55240 | lobezno | 1 |
| 55241 | loberos | 1 |
| 55242 | lobanillo | 1 |
| 55243 | loas | 1 |
| 55244 | loaré | 1 |
| 55245 | loar | 1 |
| 55246 | loandolos | 1 |
| 55247 | loador | 1 |
| 55248 | loades | 1 |
| 55249 | loadas | 1 |
| 55250 | loaba | 1 |
| 55251 | ló | 1 |
| 55252 | llueue | 1 |
| 55253 | lluengua | 1 |
| 55254 | llovizna | 1 |
| 55255 | lloviere | 1 |
| 55256 | lloviera | 1 |
| 55257 | llovidas | 1 |
| 55258 | llovida | 1 |
| 55259 | lloverá | 1 |
| 55260 | llouia | 1 |
| 55261 | llorones | 1 |
| 55262 | lloriqueos | 1 |
| 55263 | lloriqueo | 1 |
| 55264 | lloriquear | 1 |
| 55265 | lloricones | 1 |
| 55266 | lloricón | 1 |
| 55267 | lloremos | 1 |
| 55268 | lloraua | 1 |
| 55269 | llorase | 1 |
| 55270 | llorarlas | 1 |
| 55271 | lloraríedes | 1 |
| 55272 | llorarían | 1 |
| 55273 | lloraría | 1 |
| 55274 | lloraré | 1 |
| 55275 | lloraran | 1 |
| 55276 | lloráralas | 1 |
| 55277 | llorará | 1 |
| 55278 | llorándome | 1 |
| 55279 | llorandola | 1 |
| 55280 | lloramicos | 1 |
| 55281 | llorados | 1 |
| 55282 | lloradera | 1 |
| 55283 | lloradas | 1 |
| 55284 | llorada | 1 |
| 55285 | llobregat | 1 |
| 55286 | llirio | 1 |
| 55287 | llevose | 1 |
| 55288 | llevómele | 1 |
| 55289 | llevóle | 1 |
| 55290 | llévola | 1 |
| 55291 | llevola | 1 |
| 55292 | llévete | 1 |
| 55293 | lléveselas | 1 |
| 55294 | llévense | 1 |
| 55295 | llevemos | 1 |
| 55296 | llevéme | 1 |
| 55297 | llevélo | 1 |
| 55298 | llévele | 1 |
| 55299 | llevava | 1 |
| 55300 | llévatelas | 1 |
| 55301 | llevastes | 1 |
| 55302 | llevártela | 1 |
| 55303 | llevárselas | 1 |
| 55304 | llevaros | 1 |
| 55305 | llevarónse | 1 |
| 55306 | lleváronse | 1 |
| 55307 | lleváronles | 1 |
| 55308 | llevárnoslo | 1 |
| 55309 | llevármelo | 1 |
| 55310 | llevármele | 1 |
| 55311 | llevármela | 1 |
| 55312 | llevaríamos | 1 |
| 55313 | llevaréis | 1 |
| 55314 | llevarássela | 1 |
| 55315 | lleváramos | 1 |
| 55316 | llevárades | 1 |
| 55317 | llevaos | 1 |
| 55318 | llevantan | 1 |
| 55319 | llévanla | 1 |
| 55320 | llevándoselo | 1 |
| 55321 | llevándoselas | 1 |
| 55322 | llevándoos | 1 |
| 55323 | llevándonos | 1 |
| 55324 | llevándolos | 1 |
| 55325 | llevámoslas | 1 |
| 55326 | llevámonoslas | 1 |
| 55327 | llévalos | 1 |
| 55328 | llevallo | 1 |
| 55329 | llevalle | 1 |
| 55330 | llevalla | 1 |
| 55331 | llévale | 1 |
| 55332 | llevalde | 1 |
| 55333 | llévala | 1 |
| 55334 | llevádolos | 1 |
| 55335 | llevádole | 1 |
| 55336 | llevaderos | 1 |
| 55337 | llevadero | 1 |
| 55338 | llevad | 1 |
| 55339 | llevabas | 1 |
| 55340 | llevábale | 1 |
| 55341 | llevábalas | 1 |
| 55342 | llevábala | 1 |
| 55343 | lleues | 1 |
| 55344 | lleuemos | 1 |
| 55345 | lleueme | 1 |
| 55346 | lleuauan | 1 |
| 55347 | lleuaste | 1 |
| 55348 | lleuassen | 1 |
| 55349 | lleuasse | 1 |
| 55350 | lleuas | 1 |
| 55351 | lleuarla | 1 |
| 55352 | lleuaria | 1 |
| 55353 | lleuaras | 1 |
| 55354 | lleuaran | 1 |
| 55355 | lleuara | 1 |
| 55356 | lleuamela | 1 |
| 55357 | lleuame | 1 |
| 55358 | lleuada | 1 |
| 55359 | lleuad | 1 |
| 55360 | lleña | 1 |
| 55361 | llenósele | 1 |
| 55362 | llenóse | 1 |
| 55363 | llenola | 1 |
| 55364 | llengua | 1 |
| 55365 | llénese | 1 |
| 55366 | llénense | 1 |
| 55367 | llenen | 1 |
| 55368 | llenéis | 1 |
| 55369 | llené | 1 |
| 55370 | llenase | 1 |
| 55371 | llenaros | 1 |
| 55372 | llenáronse | 1 |
| 55373 | llenarles | 1 |
| 55374 | llenarlas | 1 |
| 55375 | llenarán | 1 |
| 55376 | llenará | 1 |
| 55377 | llenándosele | 1 |
| 55378 | llenándose | 1 |
| 55379 | llenándole | 1 |
| 55380 | llenándolas | 1 |
| 55381 | llenamos | 1 |
| 55382 | lléguense | 1 |
| 55383 | lleguéis | 1 |
| 55384 | llegósenos | 1 |
| 55385 | llégome | 1 |
| 55386 | llegastes | 1 |
| 55387 | llegasse | 1 |
| 55388 | llegases | 1 |
| 55389 | llégase | 1 |
| 55390 | llegáronle | 1 |
| 55391 | llegarme | 1 |
| 55392 | llegarlo | 1 |
| 55393 | llegarla | 1 |
| 55394 | llegaria | 1 |
| 55395 | llegares | 1 |
| 55396 | llegarás | 1 |
| 55397 | llegaraos | 1 |
| 55398 | llegáramos | 1 |
| 55399 | lléganse | 1 |
| 55400 | llegándosele | 1 |
| 55401 | llegándola | 1 |
| 55402 | llegadme | 1 |
| 55403 | llegábame | 1 |
| 55404 | llaue | 1 |
| 55405 | llanuras | 1 |
| 55406 | llanillas | 1 |
| 55407 | llanamente | 1 |
| 55408 | llanada | 1 |
| 55409 | llámome | 1 |
| 55410 | llamólos | 1 |
| 55411 | llamóle | 1 |
| 55412 | llámola | 1 |
| 55413 | llameys | 1 |
| 55414 | llámente | 1 |
| 55415 | llamemos | 1 |
| 55416 | llámelo | 1 |
| 55417 | llaméle | 1 |
| 55418 | llamela | 1 |
| 55419 | llaméis | 1 |
| 55420 | llamedes | 1 |
| 55421 | llamavan | 1 |
| 55422 | llamava | 1 |
| 55423 | llamatme | 1 |
| 55424 | llamativos | 1 |
| 55425 | llamativo | 1 |
| 55426 | llamativa | 1 |
| 55427 | llámate | 1 |
| 55428 | llamasse | 1 |
| 55429 | llamases | 1 |
| 55430 | llamárselo | 1 |
| 55431 | llamársela | 1 |
| 55432 | llamáronme | 1 |
| 55433 | llamáronla | 1 |
| 55434 | llamarnos | 1 |
| 55435 | llamarles | 1 |
| 55436 | llamaríamos | 1 |
| 55437 | llamáremos | 1 |
| 55438 | llamarásme | 1 |
| 55439 | llamarás | 1 |
| 55440 | llamáralo | 1 |
| 55441 | llámanme | 1 |
| 55442 | llámanlos | 1 |
| 55443 | llámanle | 1 |
| 55444 | llamándonos | 1 |
| 55445 | llamandome | 1 |
| 55446 | llamándoles | 1 |
| 55447 | llámandola | 1 |
| 55448 | llamamiento | 1 |
| 55449 | llamame | 1 |
| 55450 | llámalos | 1 |
| 55451 | llámalo | 1 |
| 55452 | llamalda | 1 |
| 55453 | llamadme | 1 |
| 55454 | llamadla | 1 |
| 55455 | llamábanle | 1 |
| 55456 | llamábala | 1 |
| 55457 | llagaron | 1 |
| 55458 | llagar | 1 |
| 55459 | llagados | 1 |
| 55460 | lladres | 1 |
| 55461 | lla | 1 |
| 55462 | ll | 1 |
| 55463 | lixo | 1 |
| 55464 | lix | 1 |
| 55465 | livrés | 1 |
| 55466 | livor | 1 |
| 55467 | liviandades | 1 |
| 55468 | liv | 1 |
| 55469 | liuiandad | 1 |
| 55470 | liuianamente | 1 |
| 55471 | liuiana | 1 |
| 55472 | littérature | 1 |
| 55473 | litros | 1 |
| 55474 | litro | 1 |
| 55475 | litoral | 1 |
| 55476 | litografía | 1 |
| 55477 | litigioso | 1 |
| 55478 | litigios | 1 |
| 55479 | litigio | 1 |
| 55480 | litigantes | 1 |
| 55481 | litigan | 1 |
| 55482 | litigado | 1 |
| 55483 | literatazos | 1 |
| 55484 | literas | 1 |
| 55485 | literal | 1 |
| 55486 | litem | 1 |
| 55487 | lita | 1 |
| 55488 | lisyón | 1 |
| 55489 | lisuarte | 1 |
| 55490 | listurria | 1 |
| 55491 | listillas | 1 |
| 55492 | listados | 1 |
| 55493 | listada | 1 |
| 55494 | lisonjeramente | 1 |
| 55495 | lisonjee | 1 |
| 55496 | lisonjean | 1 |
| 55497 | lisonjeado | 1 |
| 55498 | lisongero | 1 |
| 55499 | lisonga | 1 |
| 55500 | lisipo | 1 |
| 55501 | lision | 1 |
| 55502 | lisiados | 1 |
| 55503 | lisiadas | 1 |
| 55504 | liríope | 1 |
| 55505 | líricamente | 1 |
| 55506 | liras | 1 |
| 55507 | liquor | 1 |
| 55508 | liquido | 1 |
| 55509 | liquidado | 1 |
| 55510 | liquidada | 1 |
| 55511 | liquidaban | 1 |
| 55512 | liquida | 1 |
| 55513 | liquescer | 1 |
| 55514 | líquenes | 1 |
| 55515 | liquen | 1 |
| 55516 | liquefacta | 1 |
| 55517 | lionense | 1 |
| 55518 | liólas | 1 |
| 55519 | lió | 1 |
| 55520 | liñán | 1 |
| 55521 | linpiarme | 1 |
| 55522 | linpia | 1 |
| 55523 | linón | 1 |
| 55524 | linneo | 1 |
| 55525 | lingüístico | 1 |
| 55526 | lingua | 1 |
| 55527 | lingotes | 1 |
| 55528 | linfático | 1 |
| 55529 | linfática | 1 |
| 55530 | linfas | 1 |
| 55531 | lindoro | 1 |
| 55532 | lindero | 1 |
| 55533 | lindaba | 1 |
| 55534 | linces | 1 |
| 55535 | linaloel | 1 |
| 55536 | linajudas | 1 |
| 55537 | limpiólas | 1 |
| 55538 | limpienle | 1 |
| 55539 | limpien | 1 |
| 55540 | limpiémelos | 1 |
| 55541 | límpido | 1 |
| 55542 | límpida | 1 |
| 55543 | limpiaste | 1 |
| 55544 | limpiarte | 1 |
| 55545 | limpiáronle | 1 |
| 55546 | limpiarlo | 1 |
| 55547 | limpiarían | 1 |
| 55548 | limpiaos | 1 |
| 55549 | limpiándome | 1 |
| 55550 | limpiándolos | 1 |
| 55551 | limpiamos | 1 |
| 55552 | límpiale | 1 |
| 55553 | limpiados | 1 |
| 55554 | limpiadera | 1 |
| 55555 | limosnera | 1 |
| 55556 | limonita | 1 |
| 55557 | limoneros | 1 |
| 55558 | limonada | 1 |
| 55559 | limon | 1 |
| 55560 | limítrofes | 1 |
| 55561 | limítrofe | 1 |
| 55562 | limitose | 1 |
| 55563 | limites | 1 |
| 55564 | limiten | 1 |
| 55565 | limiteme | 1 |
| 55566 | limite | 1 |
| 55567 | limitando | 1 |
| 55568 | limitan | 1 |
| 55569 | limitámonos | 1 |
| 55570 | limitadas | 1 |
| 55571 | limitadamente | 1 |
| 55572 | límiste | 1 |
| 55573 | limas | 1 |
| 55574 | limado | 1 |
| 55575 | limadas | 1 |
| 55576 | lilio | 1 |
| 55577 | lilíes | 1 |
| 55578 | lilibeo | 1 |
| 55579 | lija | 1 |
| 55580 | liii | 1 |
| 55581 | ligustre | 1 |
| 55582 | ligurina | 1 |
| 55583 | liguria | 1 |
| 55584 | ligue | 1 |
| 55585 | ligongero | 1 |
| 55586 | lignitos | 1 |
| 55587 | ligítimo | 1 |
| 55588 | ligítimamente | 1 |
| 55589 | ligión | 1 |
| 55590 | ligerísimos | 1 |
| 55591 | ligerísimas | 1 |
| 55592 | ligar | 1 |
| 55593 | ligan | 1 |
| 55594 | ligamiento | 1 |
| 55595 | ligamen | 1 |
| 55596 | life | 1 |
| 55597 | lieves | 1 |
| 55598 | lieve | 1 |
| 55599 | liévastela | 1 |
| 55600 | lievas | 1 |
| 55601 | liévanle | 1 |
| 55602 | lievanle | 1 |
| 55603 | liévagelos | 1 |
| 55604 | liëo | 1 |
| 55605 | lienda | 1 |
| 55606 | lidora | 1 |
| 55607 | lidió | 1 |
| 55608 | lidiase | 1 |
| 55609 | lidiando | 1 |
| 55610 | lidian | 1 |
| 55611 | lidiadores | 1 |
| 55612 | lidiador | 1 |
| 55613 | lidiaban | 1 |
| 55614 | lidiaba | 1 |
| 55615 | licote | 1 |
| 55616 | lico | 1 |
| 55617 | lícitas | 1 |
| 55618 | lícitamente | 1 |
| 55619 | licita | 1 |
| 55620 | liçionario | 1 |
| 55621 | lichiga | 1 |
| 55622 | licencioso | 1 |
| 55623 | licenciatura | 1 |
| 55624 | licenciarse | 1 |
| 55625 | licenciarla | 1 |
| 55626 | licenciadillo | 1 |
| 55627 | liçençia | 1 |
| 55628 | liçencia | 1 |
| 55629 | libruchos | 1 |
| 55630 | librillos | 1 |
| 55631 | librico | 1 |
| 55632 | libretas | 1 |
| 55633 | libreta | 1 |
| 55634 | líbrese | 1 |
| 55635 | librepensamiento | 1 |
| 55636 | librepensador | 1 |
| 55637 | libren | 1 |
| 55638 | librecambista | 1 |
| 55639 | libraros | 1 |
| 55640 | libraron | 1 |
| 55641 | librarnos | 1 |
| 55642 | librarlas | 1 |
| 55643 | librarian | 1 |
| 55644 | libraría | 1 |
| 55645 | libraré | 1 |
| 55646 | librándome | 1 |
| 55647 | libralla | 1 |
| 55648 | librairie | 1 |
| 55649 | libraires | 1 |
| 55650 | librador | 1 |
| 55651 | libraco | 1 |
| 55652 | librábamos | 1 |
| 55653 | libio | 1 |
| 55654 | libidinosa | 1 |
| 55655 | libertó | 1 |
| 55656 | liberticidas | 1 |
| 55657 | libertas | 1 |
| 55658 | libertanza | 1 |
| 55659 | libertados | 1 |
| 55660 | libertado | 1 |
| 55661 | libertada | 1 |
| 55662 | liberó | 1 |
| 55663 | liberalescos | 1 |
| 55664 | liber | 1 |
| 55665 | libelos | 1 |
| 55666 | libelo | 1 |
| 55667 | libellus | 1 |
| 55668 | libea | 1 |
| 55669 | libar | 1 |
| 55670 | lib | 1 |
| 55671 | liarte | 1 |
| 55672 | liaron | 1 |
| 55673 | liándose | 1 |
| 55674 | liándolos | 1 |
| 55675 | liados | 1 |
| 55676 | liadas | 1 |
| 55677 | lezna | 1 |
| 55678 | lezaun | 1 |
| 55679 | leys | 1 |
| 55680 | leyóle | 1 |
| 55681 | leyólas | 1 |
| 55682 | leyóla | 1 |
| 55683 | leylo | 1 |
| 55684 | leyesen | 1 |
| 55685 | leyerlo | 1 |
| 55686 | leyeres | 1 |
| 55687 | leyeras | 1 |
| 55688 | leyeran | 1 |
| 55689 | leyer | 1 |
| 55690 | leyéndolos | 1 |
| 55691 | leyéndolo | 1 |
| 55692 | leyéndole | 1 |
| 55693 | leye | 1 |
| 55694 | leya | 1 |
| 55695 | léxico | 1 |
| 55696 | levosa | 1 |
| 55697 | levómelo | 1 |
| 55698 | levome | 1 |
| 55699 | levólo | 1 |
| 55700 | levol | 1 |
| 55701 | levógelos | 1 |
| 55702 | levítica | 1 |
| 55703 | leventes | 1 |
| 55704 | levatose | 1 |
| 55705 | levaryas | 1 |
| 55706 | levarla | 1 |
| 55707 | levaremos | 1 |
| 55708 | levaré | 1 |
| 55709 | levará | 1 |
| 55710 | levántose | 1 |
| 55711 | levantós | 1 |
| 55712 | levantóle | 1 |
| 55713 | levantóla | 1 |
| 55714 | levantola | 1 |
| 55715 | levantiscas | 1 |
| 55716 | levantes | 1 |
| 55717 | levántenme | 1 |
| 55718 | levanteme | 1 |
| 55719 | levantéis | 1 |
| 55720 | levantate | 1 |
| 55721 | levantastes | 1 |
| 55722 | levantaste | 1 |
| 55723 | levántasles | 1 |
| 55724 | levántasle | 1 |
| 55725 | levantarte | 1 |
| 55726 | levantáronme | 1 |
| 55727 | levantarnos | 1 |
| 55728 | levantarlo | 1 |
| 55729 | levantaríamos | 1 |
| 55730 | levantares | 1 |
| 55731 | levantará | 1 |
| 55732 | levantándoles | 1 |
| 55733 | levantamos | 1 |
| 55734 | levantalla | 1 |
| 55735 | levantadores | 1 |
| 55736 | levantábamonos | 1 |
| 55737 | levándol | 1 |
| 55738 | levando | 1 |
| 55739 | levadura | 1 |
| 55740 | levado | 1 |
| 55741 | levadlo | 1 |
| 55742 | levadizos | 1 |
| 55743 | levad | 1 |
| 55744 | leur | 1 |
| 55745 | leues | 1 |
| 55746 | leucipe | 1 |
| 55747 | leuays | 1 |
| 55748 | leuauas | 1 |
| 55749 | leuaua | 1 |
| 55750 | leuaste | 1 |
| 55751 | leuaron | 1 |
| 55752 | leuante | 1 |
| 55753 | leuantasse | 1 |
| 55754 | leuantase | 1 |
| 55755 | leuantarse | 1 |
| 55756 | leuantaron | 1 |
| 55757 | leuantarme | 1 |
| 55758 | leuantanles | 1 |
| 55759 | leuantada | 1 |
| 55760 | leuamos | 1 |
| 55761 | leuado | 1 |
| 55762 | leuada | 1 |
| 55763 | letrillas | 1 |
| 55764 | letrada | 1 |
| 55765 | letores | 1 |
| 55766 | letor | 1 |
| 55767 | lete | 1 |
| 55768 | letargos | 1 |
| 55769 | letanías | 1 |
| 55770 | letania | 1 |
| 55771 | letal | 1 |
| 55772 | lestrigones | 1 |
| 55773 | lesnedri | 1 |
| 55774 | lesmes | 1 |
| 55775 | lesiones | 1 |
| 55776 | lesbos | 1 |
| 55777 | lesbas | 1 |
| 55778 | lerrumburo | 1 |
| 55779 | lérida | 1 |
| 55780 | lercha | 1 |
| 55781 | leproso | 1 |
| 55782 | leprosas | 1 |
| 55783 | leonora | 1 |
| 55784 | leoninos | 1 |
| 55785 | leonesismos | 1 |
| 55786 | leonera | 1 |
| 55787 | leonardo | 1 |
| 55788 | leonada | 1 |
| 55789 | leñeras | 1 |
| 55790 | leñera | 1 |
| 55791 | lentura | 1 |
| 55792 | lentísimamente | 1 |
| 55793 | lentisco | 1 |
| 55794 | lenitivo | 1 |
| 55795 | lenitivas | 1 |
| 55796 | lenidad | 1 |
| 55797 | lengüetería | 1 |
| 55798 | lengüetazo | 1 |
| 55799 | lengüetas | 1 |
| 55800 | lengüecita | 1 |
| 55801 | lenguaraces | 1 |
| 55802 | lenguados | 1 |
| 55803 | lenguado | 1 |
| 55804 | lenclós | 1 |
| 55805 | lenclos | 1 |
| 55806 | lencería | 1 |
| 55807 | lena | 1 |
| 55808 | lelos | 1 |
| 55809 | lelilíes | 1 |
| 55810 | lejas | 1 |
| 55811 | lejanamente | 1 |
| 55812 | leivas | 1 |
| 55813 | leitoral | 1 |
| 55814 | leímos | 1 |
| 55815 | leíla | 1 |
| 55816 | leguminosa | 1 |
| 55817 | legualá | 1 |
| 55818 | legría | 1 |
| 55819 | legitimista | 1 |
| 55820 | legitimidades | 1 |
| 55821 | legítimas | 1 |
| 55822 | legítimamente | 1 |
| 55823 | legitima | 1 |
| 55824 | legistas | 1 |
| 55825 | legibus | 1 |
| 55826 | legía | 1 |
| 55827 | legendarios | 1 |
| 55828 | lege | 1 |
| 55829 | legar | 1 |
| 55830 | leganitos | 1 |
| 55831 | legalizado | 1 |
| 55832 | legalizadas | 1 |
| 55833 | legajos | 1 |
| 55834 | legajo | 1 |
| 55835 | lega | 1 |
| 55836 | leerte | 1 |
| 55837 | leería | 1 |
| 55838 | leerán | 1 |
| 55839 | leerálo | 1 |
| 55840 | leellos | 1 |
| 55841 | leelle | 1 |
| 55842 | leellas | 1 |
| 55843 | léele | 1 |
| 55844 | leelde | 1 |
| 55845 | leedle | 1 |
| 55846 | ledanías | 1 |
| 55847 | leçión | 1 |
| 55848 | leción | 1 |
| 55849 | leçion | 1 |
| 55850 | lechuzos | 1 |
| 55851 | lechuguinos | 1 |
| 55852 | lechoso | 1 |
| 55853 | lechosa | 1 |
| 55854 | lechón | 1 |
| 55855 | lechigada | 1 |
| 55856 | lechetrezna | 1 |
| 55857 | lecheros | 1 |
| 55858 | leçençia | 1 |
| 55859 | leccioncita | 1 |
| 55860 | lebrero | 1 |
| 55861 | lebanón | 1 |
| 55862 | léanla | 1 |
| 55863 | léamela | 1 |
| 55864 | léalos | 1 |
| 55865 | lealmente | 1 |
| 55866 | lealdad | 1 |
| 55867 | lazraron | 1 |
| 55868 | lazrado | 1 |
| 55869 | lazrada | 1 |
| 55870 | lazari | 1 |
| 55871 | lazaretos | 1 |
| 55872 | lazareto | 1 |
| 55873 | lazar | 1 |
| 55874 | laxitud | 1 |
| 55875 | lavóse | 1 |
| 55876 | lavose | 1 |
| 55877 | lavor | 1 |
| 55878 | lavóme | 1 |
| 55879 | laves | 1 |
| 55880 | lavemos | 1 |
| 55881 | lave | 1 |
| 55882 | lavater | 1 |
| 55883 | lavaste | 1 |
| 55884 | lavase | 1 |
| 55885 | lavarte | 1 |
| 55886 | laváronse | 1 |
| 55887 | laváronme | 1 |
| 55888 | lavarle | 1 |
| 55889 | lavaría | 1 |
| 55890 | lavaré | 1 |
| 55891 | lavaran | 1 |
| 55892 | lavaos | 1 |
| 55893 | lavándola | 1 |
| 55894 | lavajos | 1 |
| 55895 | lavaduras | 1 |
| 55896 | lavados | 1 |
| 55897 | lavadme | 1 |
| 55898 | lautrec | 1 |
| 55899 | lautamente | 1 |
| 55900 | laus | 1 |
| 55901 | lauros | 1 |
| 55902 | laureta | 1 |
| 55903 | laurea | 1 |
| 55904 | laurcalco | 1 |
| 55905 | laudem | 1 |
| 55906 | laudatorio | 1 |
| 55907 | laudatores | 1 |
| 55908 | laudaron | 1 |
| 55909 | laudamus | 1 |
| 55910 | laudable | 1 |
| 55911 | lauadas | 1 |
| 55912 | latrocinios | 1 |
| 55913 | latro | 1 |
| 55914 | latonero | 1 |
| 55915 | latitudinario | 1 |
| 55916 | latitudes | 1 |
| 55917 | latió | 1 |
| 55918 | latinosa | 1 |
| 55919 | latinista | 1 |
| 55920 | latinidad | 1 |
| 55921 | latinicos | 1 |
| 55922 | latinajos | 1 |
| 55923 | latieron | 1 |
| 55924 | latiendo | 1 |
| 55925 | latido | 1 |
| 55926 | lati | 1 |
| 55927 | látere | 1 |
| 55928 | laten | 1 |
| 55929 | late | 1 |
| 55930 | latanias | 1 |
| 55931 | latamque | 1 |
| 55932 | lastro | 1 |
| 55933 | lastraba | 1 |
| 55934 | lastimosísimo | 1 |
| 55935 | lastimosísima | 1 |
| 55936 | lastimóse | 1 |
| 55937 | lastimosamente | 1 |
| 55938 | lastimó | 1 |
| 55939 | lastimo | 1 |
| 55940 | lastimes | 1 |
| 55941 | lastimen | 1 |
| 55942 | lastimasteme | 1 |
| 55943 | lastimas | 1 |
| 55944 | lastimaron | 1 |
| 55945 | lastimarla | 1 |
| 55946 | lastimaran | 1 |
| 55947 | lastimara | 1 |
| 55948 | lastimándose | 1 |
| 55949 | lastimandome | 1 |
| 55950 | lastimadas | 1 |
| 55951 | lastarás | 1 |
| 55952 | lastan | 1 |
| 55953 | lastamos | 1 |
| 55954 | lasrada | 1 |
| 55955 | laserios | 1 |
| 55956 | laserío | 1 |
| 55957 | lasciuo | 1 |
| 55958 | lasciate | 1 |
| 55959 | lasaro | 1 |
| 55960 | lasao | 1 |
| 55961 | larratecoeguia | 1 |
| 55962 | larrañaga | 1 |
| 55963 | larralde | 1 |
| 55964 | laringe | 1 |
| 55965 | larguísimos | 1 |
| 55966 | larguísimo | 1 |
| 55967 | larguilucho | 1 |
| 55968 | larguillo | 1 |
| 55969 | larguea | 1 |
| 55970 | largue | 1 |
| 55971 | largaron | 1 |
| 55972 | largaran | 1 |
| 55973 | largara | 1 |
| 55974 | largar | 1 |
| 55975 | largándote | 1 |
| 55976 | largamos | 1 |
| 55977 | lares | 1 |
| 55978 | lardero | 1 |
| 55979 | lardeen | 1 |
| 55980 | laras | 1 |
| 55981 | laranjas | 1 |
| 55982 | láquesis | 1 |
| 55983 | lapsos | 1 |
| 55984 | lapso | 1 |
| 55985 | lapidosa | 1 |
| 55986 | lapide | 1 |
| 55987 | lapidarios | 1 |
| 55988 | lapidaria | 1 |
| 55989 | lápices | 1 |
| 55990 | lapa | 1 |
| 55991 | laodice | 1 |
| 55992 | lañador | 1 |
| 55993 | lanzones | 1 |
| 55994 | lanzo | 1 |
| 55995 | lánzate | 1 |
| 55996 | lanzasen | 1 |
| 55997 | lanzarlo | 1 |
| 55998 | lanzará | 1 |
| 55999 | lanzara | 1 |
| 56000 | lanzándole | 1 |
| 56001 | lanzados | 1 |
| 56002 | lanuza | 1 |
| 56003 | lantigua | 1 |
| 56004 | lante | 1 |
| 56005 | lanprea | 1 |
| 56006 | languidecía | 1 |
| 56007 | languidecer | 1 |
| 56008 | lánguidas | 1 |
| 56009 | lánguidamente | 1 |
| 56010 | langue | 1 |
| 56011 | langostino | 1 |
| 56012 | langostas | 1 |
| 56013 | landrezilla | 1 |
| 56014 | landas | 1 |
| 56015 | lancilla | 1 |
| 56016 | lanchita | 1 |
| 56017 | lanceta | 1 |
| 56018 | láncese | 1 |
| 56019 | lanceros | 1 |
| 56020 | lançe | 1 |
| 56021 | lanças | 1 |
| 56022 | lampreas | 1 |
| 56023 | lampiños | 1 |
| 56024 | lampazos | 1 |
| 56025 | laminotas | 1 |
| 56026 | laminitas | 1 |
| 56027 | laminero | 1 |
| 56028 | laminada | 1 |
| 56029 | lamieron | 1 |
| 56030 | lamiéndoselos | 1 |
| 56031 | lamiéndose | 1 |
| 56032 | lamiéndolo | 1 |
| 56033 | lamido | 1 |
| 56034 | lamidas | 1 |
| 56035 | lamia | 1 |
| 56036 | lamería | 1 |
| 56037 | lamer | 1 |
| 56038 | lamentes | 1 |
| 56039 | lamente | 1 |
| 56040 | lamentaron | 1 |
| 56041 | lamentarme | 1 |
| 56042 | lamentamos | 1 |
| 56043 | lamentador | 1 |
| 56044 | lamentacion | 1 |
| 56045 | lamentábase | 1 |
| 56046 | lamen | 1 |
| 56047 | lamego | 1 |
| 56048 | lamedor | 1 |
| 56049 | lambas | 1 |
| 56050 | laja | 1 |
| 56051 | lain | 1 |
| 56052 | laida | 1 |
| 56053 | laicos | 1 |
| 56054 | laica | 1 |
| 56055 | lagrimosos | 1 |
| 56056 | lagrimoso | 1 |
| 56057 | lagrimosas | 1 |
| 56058 | lagrimitas | 1 |
| 56059 | lagrimillas | 1 |
| 56060 | lagrimeo | 1 |
| 56061 | lagrimear | 1 |
| 56062 | lagrimean | 1 |
| 56063 | lagrimeaban | 1 |
| 56064 | lagrimales | 1 |
| 56065 | lagartona | 1 |
| 56066 | lagartijo | 1 |
| 56067 | lagartijero | 1 |
| 56068 | lagartijeras | 1 |
| 56069 | lagares | 1 |
| 56070 | lagañoso | 1 |
| 56071 | lagañas | 1 |
| 56072 | laganitos | 1 |
| 56073 | laganas | 1 |
| 56074 | laga | 1 |
| 56075 | lafourchette | 1 |
| 56076 | lætemur | 1 |
| 56077 | laetatus | 1 |
| 56078 | ladronzuelo | 1 |
| 56079 | ladronicio | 1 |
| 56080 | ladrillazos | 1 |
| 56081 | ladrillazo | 1 |
| 56082 | ladrillados | 1 |
| 56083 | ladrándole | 1 |
| 56084 | ladran | 1 |
| 56085 | ladrado | 1 |
| 56086 | ladinamente | 1 |
| 56087 | ladina | 1 |
| 56088 | ladi | 1 |
| 56089 | ladera | 1 |
| 56090 | ladearme | 1 |
| 56091 | ladeando | 1 |
| 56092 | ladeado | 1 |
| 56093 | ladeaba | 1 |
| 56094 | lacto | 1 |
| 56095 | lactancia | 1 |
| 56096 | lacrimosos | 1 |
| 56097 | lacrimoso | 1 |
| 56098 | lacrimosa | 1 |
| 56099 | lacrimae | 1 |
| 56100 | lacre | 1 |
| 56101 | lacónicas | 1 |
| 56102 | laçio | 1 |
| 56103 | laçias | 1 |
| 56104 | lachrymis | 1 |
| 56105 | lachrimarum | 1 |
| 56106 | laçerio | 1 |
| 56107 | lacerias | 1 |
| 56108 | lacería | 1 |
| 56109 | lacerante | 1 |
| 56110 | lacedemonio | 1 |
| 56111 | lacayuna | 1 |
| 56112 | lacayuelos | 1 |
| 56113 | labruscas | 1 |
| 56114 | labre | 1 |
| 56115 | labrarse | 1 |
| 56116 | labrança | 1 |
| 56117 | labran | 1 |
| 56118 | labradorescas | 1 |
| 56119 | labraba | 1 |
| 56120 | laboriosos | 1 |
| 56121 | laboriosidad | 1 |
| 56122 | labiano | 1 |
| 56123 | labe | 1 |
| 56124 | là | 1 |
| 56125 | kyries | 1 |
| 56126 | krupp | 1 |
| 56127 | kirschen | 1 |
| 56128 | kilos | 1 |
| 56129 | kermesas | 1 |
| 56130 | kaleidoscopio | 1 |
| 56131 | kader | 1 |
| 56132 | k | 1 |
| 56133 | júzguenlo | 1 |
| 56134 | júzguelo | 1 |
| 56135 | juzguéis | 1 |
| 56136 | juzgóse | 1 |
| 56137 | juzgólo | 1 |
| 56138 | juzgaua | 1 |
| 56139 | juzgat | 1 |
| 56140 | juzgasses | 1 |
| 56141 | juzgase | 1 |
| 56142 | juzgares | 1 |
| 56143 | juzgaremos | 1 |
| 56144 | juzgarás | 1 |
| 56145 | juzgarán | 1 |
| 56146 | juzgaran | 1 |
| 56147 | juzgándose | 1 |
| 56148 | juzgandome | 1 |
| 56149 | juzgamos | 1 |
| 56150 | juzgáis | 1 |
| 56151 | juzgados | 1 |
| 56152 | juzgador | 1 |
| 56153 | juzgábase | 1 |
| 56154 | juysio | 1 |
| 56155 | juyando | 1 |
| 56156 | justyçia | 1 |
| 56157 | justó | 1 |
| 56158 | justizia | 1 |
| 56159 | justísimas | 1 |
| 56160 | justísima | 1 |
| 56161 | justiniano | 1 |
| 56162 | justificarás | 1 |
| 56163 | justificadas | 1 |
| 56164 | justificación | 1 |
| 56165 | justificables | 1 |
| 56166 | justificaban | 1 |
| 56167 | justificaba | 1 |
| 56168 | justifica | 1 |
| 56169 | justicieros | 1 |
| 56170 | justicieras | 1 |
| 56171 | justiciera | 1 |
| 56172 | justiciar | 1 |
| 56173 | justiçiado | 1 |
| 56174 | justemos | 1 |
| 56175 | justavan | 1 |
| 56176 | justaré | 1 |
| 56177 | justador | 1 |
| 56178 | jusieu | 1 |
| 56179 | jusgar | 1 |
| 56180 | jusgador | 1 |
| 56181 | jus | 1 |
| 56182 | jurydiçión | 1 |
| 56183 | jurre | 1 |
| 56184 | juros | 1 |
| 56185 | jurista | 1 |
| 56186 | juris | 1 |
| 56187 | jurídicos | 1 |
| 56188 | jurídico | 1 |
| 56189 | jurídicas | 1 |
| 56190 | jurídicamente | 1 |
| 56191 | jurídica | 1 |
| 56192 | juren | 1 |
| 56193 | juremos | 1 |
| 56194 | jurasen | 1 |
| 56195 | jurase | 1 |
| 56196 | jurarte | 1 |
| 56197 | jurarse | 1 |
| 56198 | juraron | 1 |
| 56199 | jurarme | 1 |
| 56200 | jurarlo | 1 |
| 56201 | jurarle | 1 |
| 56202 | jurarias | 1 |
| 56203 | juráramos | 1 |
| 56204 | jurándote | 1 |
| 56205 | jurándose | 1 |
| 56206 | júrame | 1 |
| 56207 | juráis | 1 |
| 56208 | jurada | 1 |
| 56209 | juntura | 1 |
| 56210 | juntóseme | 1 |
| 56211 | juntose | 1 |
| 56212 | juntona | 1 |
| 56213 | júntese | 1 |
| 56214 | juntemos | 1 |
| 56215 | juntéme | 1 |
| 56216 | junteme | 1 |
| 56217 | junte | 1 |
| 56218 | juntava | 1 |
| 56219 | júntate | 1 |
| 56220 | juntassen | 1 |
| 56221 | juntarnos | 1 |
| 56222 | juntarias | 1 |
| 56223 | juntaren | 1 |
| 56224 | juntaremos | 1 |
| 56225 | juntarás | 1 |
| 56226 | juntaran | 1 |
| 56227 | juntara | 1 |
| 56228 | juntándonos | 1 |
| 56229 | juntándome | 1 |
| 56230 | juntamos | 1 |
| 56231 | juntamiento | 1 |
| 56232 | juntalos | 1 |
| 56233 | juntades | 1 |
| 56234 | juntábansele | 1 |
| 56235 | juntábanse | 1 |
| 56236 | junón | 1 |
| 56237 | junios | 1 |
| 56238 | jumeras | 1 |
| 56239 | jumenta | 1 |
| 56240 | jum | 1 |
| 56241 | julios | 1 |
| 56242 | julianita | 1 |
| 56243 | julia | 1 |
| 56244 | juisio | 1 |
| 56245 | juiciosísimo | 1 |
| 56246 | juiciosillo | 1 |
| 56247 | juiciosamente | 1 |
| 56248 | juguetoncica | 1 |
| 56249 | jugueteando | 1 |
| 56250 | jugueteaban | 1 |
| 56251 | jugué | 1 |
| 56252 | jugosos | 1 |
| 56253 | juglarías | 1 |
| 56254 | juglara | 1 |
| 56255 | jugavan | 1 |
| 56256 | jugava | 1 |
| 56257 | jugaste | 1 |
| 56258 | jugasen | 1 |
| 56259 | jugásemos | 1 |
| 56260 | jugarreta | 1 |
| 56261 | jugares | 1 |
| 56262 | jugaras | 1 |
| 56263 | jugándose | 1 |
| 56264 | jugáis | 1 |
| 56265 | juga | 1 |
| 56266 | jueues | 1 |
| 56267 | juergas | 1 |
| 56268 | judit | 1 |
| 56269 | judiciosa | 1 |
| 56270 | judiciarias | 1 |
| 56271 | judiciaria | 1 |
| 56272 | judgó | 1 |
| 56273 | judgan | 1 |
| 56274 | judgador | 1 |
| 56275 | judería | 1 |
| 56276 | judæorum | 1 |
| 56277 | jucunde | 1 |
| 56278 | júcar | 1 |
| 56279 | jubonazo | 1 |
| 56280 | jubileos | 1 |
| 56281 | jubilé | 1 |
| 56282 | jubilarte | 1 |
| 56283 | jubilarse | 1 |
| 56284 | jubilarle | 1 |
| 56285 | jubilando | 1 |
| 56286 | jubiladas | 1 |
| 56287 | jubilaba | 1 |
| 56288 | juanetes | 1 |
| 56289 | juanes | 1 |
| 56290 | juanelo | 1 |
| 56291 | juanazo | 1 |
| 56292 | juán | 1 |
| 56293 | joyero | 1 |
| 56294 | joviales | 1 |
| 56295 | jovenzuelas | 1 |
| 56296 | jovencitos | 1 |
| 56297 | jovellar | 1 |
| 56298 | jouy | 1 |
| 56299 | josué | 1 |
| 56300 | joshepe | 1 |
| 56301 | josés | 1 |
| 56302 | joseph | 1 |
| 56303 | josafat | 1 |
| 56304 | josafad | 1 |
| 56305 | jorobarnos | 1 |
| 56306 | jorobándonos | 1 |
| 56307 | jorobados | 1 |
| 56308 | jorobadita | 1 |
| 56309 | jornales | 1 |
| 56310 | jormiguita | 1 |
| 56311 | jonjabaron | 1 |
| 56312 | jónico | 1 |
| 56313 | joloanas | 1 |
| 56314 | jollines | 1 |
| 56315 | johán | 1 |
| 56316 | joffre | 1 |
| 56317 | joeces | 1 |
| 56318 | jocunda | 1 |
| 56319 | jocoserio | 1 |
| 56320 | jocasta | 1 |
| 56321 | joca | 1 |
| 56322 | joaquina | 1 |
| 56323 | joanelo | 1 |
| 56324 | joab | 1 |
| 56325 | jira | 1 |
| 56326 | jipíos | 1 |
| 56327 | jinojo | 1 |
| 56328 | jimioso | 1 |
| 56329 | jimio | 1 |
| 56330 | jiferos | 1 |
| 56331 | jifería | 1 |
| 56332 | jierros | 1 |
| 56333 | jierro | 1 |
| 56334 | jicarón | 1 |
| 56335 | jícaras | 1 |
| 56336 | jhesús | 1 |
| 56337 | jevilla | 1 |
| 56338 | jetas | 1 |
| 56339 | jetafe | 1 |
| 56340 | jesuxristo | 1 |
| 56341 | jesuítico | 1 |
| 56342 | jesuíticamente | 1 |
| 56343 | jesuítica | 1 |
| 56344 | jesú | 1 |
| 56345 | jerónimos | 1 |
| 56346 | jeroma | 1 |
| 56347 | jeroglíficos | 1 |
| 56348 | jermosura | 1 |
| 56349 | jeringas | 1 |
| 56350 | jerida | 1 |
| 56351 | jerga | 1 |
| 56352 | jerezanos | 1 |
| 56353 | jerárquicos | 1 |
| 56354 | jenízaros | 1 |
| 56355 | jena | 1 |
| 56356 | jehová | 1 |
| 56357 | jean | 1 |
| 56358 | jazmin | 1 |
| 56359 | javanesas | 1 |
| 56360 | javalyn | 1 |
| 56361 | javali | 1 |
| 56362 | java | 1 |
| 56363 | jáurigui | 1 |
| 56364 | jaulones | 1 |
| 56365 | játiva | 1 |
| 56366 | jaspeada | 1 |
| 56367 | jaspeaban | 1 |
| 56368 | jasmin | 1 |
| 56369 | jarrito | 1 |
| 56370 | jarrillos | 1 |
| 56371 | jarretiera | 1 |
| 56372 | jaropes | 1 |
| 56373 | jarife | 1 |
| 56374 | jardinillo | 1 |
| 56375 | jardinería | 1 |
| 56376 | jaramilla | 1 |
| 56377 | jarales | 1 |
| 56378 | jaquecoso | 1 |
| 56379 | janto | 1 |
| 56380 | janos | 1 |
| 56381 | james | 1 |
| 56382 | jamelgos | 1 |
| 56383 | jambas | 1 |
| 56384 | jamais | 1 |
| 56385 | jaleos | 1 |
| 56386 | jaleadores | 1 |
| 56387 | jaldetas | 1 |
| 56388 | jaldes | 1 |
| 56389 | jalapa | 1 |
| 56390 | jaffa | 1 |
| 56391 | jafet | 1 |
| 56392 | jaén | 1 |
| 56393 | jactanciosa | 1 |
| 56394 | jacquard | 1 |
| 56395 | jacometrenzo | 1 |
| 56396 | jacintos | 1 |
| 56397 | jacieron | 1 |
| 56398 | jaccoud | 1 |
| 56399 | jacas | 1 |
| 56400 | jácaras | 1 |
| 56401 | jacarandina | 1 |
| 56402 | jácara | 1 |
| 56403 | jaboneros | 1 |
| 56404 | jabonarse | 1 |
| 56405 | jabonaron | 1 |
| 56406 | jablao | 1 |
| 56407 | jábega | 1 |
| 56408 | jabé | 1 |
| 56409 | jabalyn | 1 |
| 56410 | jabalina | 1 |
| 56411 | izquierdos | 1 |
| 56412 | izquierdeaba | 1 |
| 56413 | izpegui | 1 |
| 56414 | izó | 1 |
| 56415 | izatecó | 1 |
| 56416 | izarse | 1 |
| 56417 | izaron | 1 |
| 56418 | izarle | 1 |
| 56419 | izar | 1 |
| 56420 | izado | 1 |
| 56421 | izadas | 1 |
| 56422 | izada | 1 |
| 56423 | iustus | 1 |
| 56424 | iuan | 1 |
| 56425 | itzarroiz | 1 |
| 56426 | itzalac | 1 |
| 56427 | iturbide | 1 |
| 56428 | itur | 1 |
| 56429 | itinerarios | 1 |
| 56430 | iten | 1 |
| 56431 | ite | 1 |
| 56432 | itálico | 1 |
| 56433 | italianos | 1 |
| 56434 | ita | 1 |
| 56435 | isuribere | 1 |
| 56436 | istriadas | 1 |
| 56437 | iste | 1 |
| 56438 | israelitas | 1 |
| 56439 | isprisiones | 1 |
| 56440 | isopete | 1 |
| 56441 | isomórfico | 1 |
| 56442 | islitas | 1 |
| 56443 | islilla | 1 |
| 56444 | islamismo | 1 |
| 56445 | isis | 1 |
| 56446 | ishat | 1 |
| 56447 | iseo | 1 |
| 56448 | iscariote | 1 |
| 56449 | isaías | 1 |
| 56450 | isabeu | 1 |
| 56451 | is | 1 |
| 56452 | irura | 1 |
| 56453 | irujo | 1 |
| 56454 | írseme | 1 |
| 56455 | irrupciones | 1 |
| 56456 | irrito | 1 |
| 56457 | irrites | 1 |
| 56458 | irriteme | 1 |
| 56459 | irritarlos | 1 |
| 56460 | irritarle | 1 |
| 56461 | irritarla | 1 |
| 56462 | irritándome | 1 |
| 56463 | irritadas | 1 |
| 56464 | irritable | 1 |
| 56465 | irritabile | 1 |
| 56466 | irrita | 1 |
| 56467 | irrisión | 1 |
| 56468 | irrintzi | 1 |
| 56469 | irreverentes | 1 |
| 56470 | irreverentemente | 1 |
| 56471 | irreverencias | 1 |
| 56472 | irresponsabilidad | 1 |
| 56473 | irresolutos | 1 |
| 56474 | irreprochable | 1 |
| 56475 | irreparables | 1 |
| 56476 | irreligiosidades | 1 |
| 56477 | irreligiosidad | 1 |
| 56478 | irregularidadotro | 1 |
| 56479 | irrefragable | 1 |
| 56480 | irreflexivas | 1 |
| 56481 | irreflexivamente | 1 |
| 56482 | irrecuperables | 1 |
| 56483 | irrecuperable | 1 |
| 56484 | irrebatible | 1 |
| 56485 | irradió | 1 |
| 56486 | irradiando | 1 |
| 56487 | irradiaban | 1 |
| 56488 | irónicos | 1 |
| 56489 | irlo | 1 |
| 56490 | irle | 1 |
| 56491 | irlas | 1 |
| 56492 | irlandas | 1 |
| 56493 | irlanda | 1 |
| 56494 | irla | 1 |
| 56495 | irisarri | 1 |
| 56496 | iraty | 1 |
| 56497 | irato | 1 |
| 56498 | irati | 1 |
| 56499 | irascibilidad | 1 |
| 56500 | iracundia | 1 |
| 56501 | ipso | 1 |
| 56502 | ipsa | 1 |
| 56503 | iñon | 1 |
| 56504 | iñíguez | 1 |
| 56505 | iñigo | 1 |
| 56506 | iñasi | 1 |
| 56507 | inza | 1 |
| 56508 | inyectados | 1 |
| 56509 | inyectaban | 1 |
| 56510 | invóqueles | 1 |
| 56511 | involuntarios | 1 |
| 56512 | involuntariamente | 1 |
| 56513 | involucre | 1 |
| 56514 | involución | 1 |
| 56515 | invocación | 1 |
| 56516 | invitole | 1 |
| 56517 | inviten | 1 |
| 56518 | invitele | 1 |
| 56519 | invitase | 1 |
| 56520 | invitaron | 1 |
| 56521 | invitarle | 1 |
| 56522 | invitarla | 1 |
| 56523 | invitará | 1 |
| 56524 | invitándolo | 1 |
| 56525 | invitándole | 1 |
| 56526 | invitaciones | 1 |
| 56527 | invirtieron | 1 |
| 56528 | invirtiéndole | 1 |
| 56529 | inviolable | 1 |
| 56530 | inviolabilidad | 1 |
| 56531 | invidïosa | 1 |
| 56532 | invidiosa | 1 |
| 56533 | invidio | 1 |
| 56534 | invidias | 1 |
| 56535 | invidiara | 1 |
| 56536 | invidïado | 1 |
| 56537 | invicta | 1 |
| 56538 | inviaba | 1 |
| 56539 | inveterado | 1 |
| 56540 | inveteradas | 1 |
| 56541 | investigase | 1 |
| 56542 | investigando | 1 |
| 56543 | investigador | 1 |
| 56544 | invertidos | 1 |
| 56545 | invertía | 1 |
| 56546 | inversa | 1 |
| 56547 | invernante | 1 |
| 56548 | invernadero | 1 |
| 56549 | invernáculo | 1 |
| 56550 | inventivo | 1 |
| 56551 | inventéis | 1 |
| 56552 | inventase | 1 |
| 56553 | inventarme | 1 |
| 56554 | inventarlo | 1 |
| 56555 | inventarle | 1 |
| 56556 | inventarla | 1 |
| 56557 | inventariar | 1 |
| 56558 | inventará | 1 |
| 56559 | inventados | 1 |
| 56560 | inventadas | 1 |
| 56561 | inventaban | 1 |
| 56562 | invenerable | 1 |
| 56563 | invectiva | 1 |
| 56564 | invasores | 1 |
| 56565 | invasiones | 1 |
| 56566 | inválidos | 1 |
| 56567 | invadió | 1 |
| 56568 | invadieron | 1 |
| 56569 | invadida | 1 |
| 56570 | invaden | 1 |
| 56571 | inutilizado | 1 |
| 56572 | inutilizada | 1 |
| 56573 | inusitado | 1 |
| 56574 | inundose | 1 |
| 56575 | inunde | 1 |
| 56576 | inundarle | 1 |
| 56577 | inundara | 1 |
| 56578 | inundándola | 1 |
| 56579 | inundando | 1 |
| 56580 | inundan | 1 |
| 56581 | inundados | 1 |
| 56582 | inumerable | 1 |
| 56583 | inumerabilidad | 1 |
| 56584 | inuisible | 1 |
| 56585 | inuicem | 1 |
| 56586 | inuestigar | 1 |
| 56587 | inuernales | 1 |
| 56588 | inuentor | 1 |
| 56589 | intüitivo | 1 |
| 56590 | intuitiva | 1 |
| 56591 | intuiciones | 1 |
| 56592 | intrumentos | 1 |
| 56593 | introito | 1 |
| 56594 | introduzco | 1 |
| 56595 | introduzcan | 1 |
| 56596 | introdújelo | 1 |
| 56597 | introduje | 1 |
| 56598 | introductora | 1 |
| 56599 | introducida | 1 |
| 56600 | introducía | 1 |
| 56601 | introd | 1 |
| 56602 | intrinseco | 1 |
| 56603 | intrínsecamente | 1 |
| 56604 | intríngulis | 1 |
| 56605 | intrigüelas | 1 |
| 56606 | intrigar | 1 |
| 56607 | intrigantas | 1 |
| 56608 | intrigado | 1 |
| 56609 | intrigaba | 1 |
| 56610 | intricarlos | 1 |
| 56611 | intricadamente | 1 |
| 56612 | intricable | 1 |
| 56613 | intrépidos | 1 |
| 56614 | intrépide | 1 |
| 56615 | intrépidas | 1 |
| 56616 | intrate | 1 |
| 56617 | intransitables | 1 |
| 56618 | intransigentes | 1 |
| 56619 | intranquilizó | 1 |
| 56620 | intra | 1 |
| 56621 | intonsos | 1 |
| 56622 | intollerable | 1 |
| 56623 | intolerante | 1 |
| 56624 | intolerables | 1 |
| 56625 | intimido | 1 |
| 56626 | intimidado | 1 |
| 56627 | intimase | 1 |
| 56628 | intimaron | 1 |
| 56629 | intimarle | 1 |
| 56630 | intimándole | 1 |
| 56631 | intimando | 1 |
| 56632 | intimado | 1 |
| 56633 | intimaciones | 1 |
| 56634 | intimación | 1 |
| 56635 | intimaba | 1 |
| 56636 | intestinal | 1 |
| 56637 | interviniesen | 1 |
| 56638 | intervinieron | 1 |
| 56639 | intervinieran | 1 |
| 56640 | interviene | 1 |
| 56641 | intervenían | 1 |
| 56642 | intervenga | 1 |
| 56643 | interrumpirla | 1 |
| 56644 | interrumpiese | 1 |
| 56645 | interrumpiéndome | 1 |
| 56646 | interrumpiéndola | 1 |
| 56647 | interrumper | 1 |
| 56648 | interrumpen | 1 |
| 56649 | interrumpeles | 1 |
| 56650 | interrumpan | 1 |
| 56651 | interrotos | 1 |
| 56652 | interrompiendo | 1 |
| 56653 | interromperéis | 1 |
| 56654 | interrogué | 1 |
| 56655 | interrogatorios | 1 |
| 56656 | interrogatorio | 1 |
| 56657 | interrogativa | 1 |
| 56658 | interrogarlos | 1 |
| 56659 | interrogarle | 1 |
| 56660 | interrogantes | 1 |
| 56661 | interrogante | 1 |
| 56662 | interrogándose | 1 |
| 56663 | interrogándola | 1 |
| 56664 | interrogando | 1 |
| 56665 | interrogadores | 1 |
| 56666 | interrogador | 1 |
| 56667 | interrogadas | 1 |
| 56668 | interrogación | 1 |
| 56669 | interregno | 1 |
| 56670 | interpuso | 1 |
| 56671 | interpusieron | 1 |
| 56672 | interpretó | 1 |
| 56673 | intérpretes | 1 |
| 56674 | interpretase | 1 |
| 56675 | interpretándolos | 1 |
| 56676 | interpretándola | 1 |
| 56677 | interpretando | 1 |
| 56678 | interpretacion | 1 |
| 56679 | interpretabas | 1 |
| 56680 | interpreta | 1 |
| 56681 | interposición | 1 |
| 56682 | interposicion | 1 |
| 56683 | interponiéndose | 1 |
| 56684 | interponiendo | 1 |
| 56685 | interpone | 1 |
| 56686 | interpolador | 1 |
| 56687 | interpeló | 1 |
| 56688 | interpelaron | 1 |
| 56689 | interpelaciones | 1 |
| 56690 | interpelación | 1 |
| 56691 | internos | 1 |
| 56692 | internaron | 1 |
| 56693 | internaban | 1 |
| 56694 | intermedios | 1 |
| 56695 | intermedia | 1 |
| 56696 | interjección | 1 |
| 56697 | interioridades | 1 |
| 56698 | interioridad | 1 |
| 56699 | interïor | 1 |
| 56700 | interinos | 1 |
| 56701 | interinas | 1 |
| 56702 | interinamente | 1 |
| 56703 | ínterin | 1 |
| 56704 | interfezto | 1 |
| 56705 | interesó | 1 |
| 56706 | interesase | 1 |
| 56707 | interesaron | 1 |
| 56708 | interesarla | 1 |
| 56709 | interesal | 1 |
| 56710 | interesadas | 1 |
| 56711 | interdum | 1 |
| 56712 | intercolumnios | 1 |
| 56713 | intercolumnio | 1 |
| 56714 | intercessor | 1 |
| 56715 | intercesor | 1 |
| 56716 | intercesión | 1 |
| 56717 | interceptaron | 1 |
| 56718 | interceptando | 1 |
| 56719 | interceptado | 1 |
| 56720 | interceptadas | 1 |
| 56721 | intercediendo | 1 |
| 56722 | intercedí | 1 |
| 56723 | interceder | 1 |
| 56724 | intercede | 1 |
| 56725 | interceda | 1 |
| 56726 | intercalada | 1 |
| 56727 | intercala | 1 |
| 56728 | intercadencia | 1 |
| 56729 | intentes | 1 |
| 56730 | intente | 1 |
| 56731 | intentarse | 1 |
| 56732 | intentarlo | 1 |
| 56733 | intentarla | 1 |
| 56734 | intentare | 1 |
| 56735 | intentaran | 1 |
| 56736 | intentalla | 1 |
| 56737 | intensísimas | 1 |
| 56738 | intendencia | 1 |
| 56739 | intende | 1 |
| 56740 | intempestivos | 1 |
| 56741 | intempestivas | 1 |
| 56742 | intellectuales | 1 |
| 56743 | inteligibles | 1 |
| 56744 | inteligentísimo | 1 |
| 56745 | inteligencias | 1 |
| 56746 | intelegibles | 1 |
| 56747 | íntegro | 1 |
| 56748 | integrar | 1 |
| 56749 | integral | 1 |
| 56750 | intacta | 1 |
| 56751 | insurrectos | 1 |
| 56752 | insurreccionó | 1 |
| 56753 | insurreccional | 1 |
| 56754 | insurgentes | 1 |
| 56755 | insurgente | 1 |
| 56756 | insultillos | 1 |
| 56757 | insulté | 1 |
| 56758 | insultase | 1 |
| 56759 | insultaron | 1 |
| 56760 | insultarías | 1 |
| 56761 | insultara | 1 |
| 56762 | insultantemente | 1 |
| 56763 | insultan | 1 |
| 56764 | insulsos | 1 |
| 56765 | insulsez | 1 |
| 56766 | insulsas | 1 |
| 56767 | ínsulo | 1 |
| 56768 | insulano | 1 |
| 56769 | insuficientes | 1 |
| 56770 | insuficiencia | 1 |
| 56771 | insubordina | 1 |
| 56772 | instruyeses | 1 |
| 56773 | instruyera | 1 |
| 56774 | instruyen | 1 |
| 56775 | instruye | 1 |
| 56776 | instruyda | 1 |
| 56777 | instruya | 1 |
| 56778 | instrutos | 1 |
| 56779 | instrumentista | 1 |
| 56780 | instrumentes | 1 |
| 56781 | instrumente | 1 |
| 56782 | instruirte | 1 |
| 56783 | instruirme | 1 |
| 56784 | instruído | 1 |
| 56785 | instruidas | 1 |
| 56786 | instruída | 1 |
| 56787 | instructiva | 1 |
| 56788 | instructa | 1 |
| 56789 | instósele | 1 |
| 56790 | instituyó | 1 |
| 56791 | instituido | 1 |
| 56792 | instituídas | 1 |
| 56793 | instituida | 1 |
| 56794 | instintivas | 1 |
| 56795 | instigo | 1 |
| 56796 | instigara | 1 |
| 56797 | instigados | 1 |
| 56798 | instalose | 1 |
| 56799 | instalaban | 1 |
| 56800 | instalaba | 1 |
| 56801 | instaban | 1 |
| 56802 | instaba | 1 |
| 56803 | inspirole | 1 |
| 56804 | inspiro | 1 |
| 56805 | inspiren | 1 |
| 56806 | inspire | 1 |
| 56807 | inspirase | 1 |
| 56808 | inspiraron | 1 |
| 56809 | inspirarle | 1 |
| 56810 | inspirará | 1 |
| 56811 | inspirándome | 1 |
| 56812 | inspirada | 1 |
| 56813 | inspirabas | 1 |
| 56814 | insperiencia | 1 |
| 56815 | inspeccionando | 1 |
| 56816 | inspecciona | 1 |
| 56817 | insolvente | 1 |
| 56818 | insolvencias | 1 |
| 56819 | insolvencia | 1 |
| 56820 | insoluble | 1 |
| 56821 | insólito | 1 |
| 56822 | insolenta | 1 |
| 56823 | insociables | 1 |
| 56824 | insistiré | 1 |
| 56825 | insistimos | 1 |
| 56826 | insistiese | 1 |
| 56827 | insistieron | 1 |
| 56828 | insistes | 1 |
| 56829 | insipiente | 1 |
| 56830 | insípido | 1 |
| 56831 | insinuarse | 1 |
| 56832 | insinuar | 1 |
| 56833 | insinuándose | 1 |
| 56834 | insinuado | 1 |
| 56835 | insignificancia | 1 |
| 56836 | insigna | 1 |
| 56837 | insienplo | 1 |
| 56838 | insidiosos | 1 |
| 56839 | insidias | 1 |
| 56840 | insidia | 1 |
| 56841 | inserto | 1 |
| 56842 | insértemelo | 1 |
| 56843 | insertarlo | 1 |
| 56844 | insertar | 1 |
| 56845 | insere | 1 |
| 56846 | insepulto | 1 |
| 56847 | insensibles | 1 |
| 56848 | inseguros | 1 |
| 56849 | insectívoro | 1 |
| 56850 | insecticidas | 1 |
| 56851 | insectes | 1 |
| 56852 | insanos | 1 |
| 56853 | inresolutas | 1 |
| 56854 | inremediables | 1 |
| 56855 | inremediable | 1 |
| 56856 | inquisitorial | 1 |
| 56857 | inquirió | 1 |
| 56858 | inquiriese | 1 |
| 56859 | inquilino | 1 |
| 56860 | inquietes | 1 |
| 56861 | inquietaron | 1 |
| 56862 | inquietarle | 1 |
| 56863 | inquietara | 1 |
| 56864 | inquietar | 1 |
| 56865 | inquietan | 1 |
| 56866 | inquietamente | 1 |
| 56867 | inportunidad | 1 |
| 56868 | inormes | 1 |
| 56869 | inoportunos | 1 |
| 56870 | inoportunas | 1 |
| 56871 | inopia | 1 |
| 56872 | inominiosos | 1 |
| 56873 | inominia | 1 |
| 56874 | inolvidable | 1 |
| 56875 | inojos | 1 |
| 56876 | inogar | 1 |
| 56877 | inodoras | 1 |
| 56878 | inocentemente | 1 |
| 56879 | inocentada | 1 |
| 56880 | inoçençio | 1 |
| 56881 | inobediente | 1 |
| 56882 | innúmeros | 1 |
| 56883 | innovación | 1 |
| 56884 | innocentes | 1 |
| 56885 | innocente | 1 |
| 56886 | innegables | 1 |
| 56887 | innecesario | 1 |
| 56888 | innato | 1 |
| 56889 | inmutó | 1 |
| 56890 | inmutarse | 1 |
| 56891 | inmutara | 1 |
| 56892 | inmutada | 1 |
| 56893 | inmutables | 1 |
| 56894 | inmunidad | 1 |
| 56895 | inmueble | 1 |
| 56896 | inmovilizó | 1 |
| 56897 | inmovibles | 1 |
| 56898 | inmortalizar | 1 |
| 56899 | inmorales | 1 |
| 56900 | inmobles | 1 |
| 56901 | inmigración | 1 |
| 56902 | inmerito | 1 |
| 56903 | inmemoriales | 1 |
| 56904 | inmaculados | 1 |
| 56905 | inmaculado | 1 |
| 56906 | injustísima | 1 |
| 56907 | injustificado | 1 |
| 56908 | injuriosa | 1 |
| 56909 | injuriando | 1 |
| 56910 | injurian | 1 |
| 56911 | injuriada | 1 |
| 56912 | injertos | 1 |
| 56913 | injerto | 1 |
| 56914 | injertándole | 1 |
| 56915 | injertado | 1 |
| 56916 | injerido | 1 |
| 56917 | injerencias | 1 |
| 56918 | initium | 1 |
| 56919 | iniquo | 1 |
| 56920 | iniqua | 1 |
| 56921 | inimicos | 1 |
| 56922 | inimicis | 1 |
| 56923 | inifica | 1 |
| 56924 | inicuos | 1 |
| 56925 | iniciose | 1 |
| 56926 | iniciase | 1 |
| 56927 | iniciaron | 1 |
| 56928 | iniciarlo | 1 |
| 56929 | iniciarle | 1 |
| 56930 | iniciar | 1 |
| 56931 | iniciándose | 1 |
| 56932 | iniciándole | 1 |
| 56933 | inician | 1 |
| 56934 | iniciados | 1 |
| 56935 | iniciadoras | 1 |
| 56936 | iniciadora | 1 |
| 56937 | iniciadas | 1 |
| 56938 | iniciábasele | 1 |
| 56939 | iniciábase | 1 |
| 56940 | iniciaba | 1 |
| 56941 | inhumanidad | 1 |
| 56942 | inhumanas | 1 |
| 56943 | inhonesta | 1 |
| 56944 | inhibitoria | 1 |
| 56945 | inhibirse | 1 |
| 56946 | inhibía | 1 |
| 56947 | inhabilitado | 1 |
| 56948 | inhábiles | 1 |
| 56949 | inhábil | 1 |
| 56950 | ingrrr | 1 |
| 56951 | ingresara | 1 |
| 56952 | ingresar | 1 |
| 56953 | ingresamos | 1 |
| 56954 | ingrediente | 1 |
| 56955 | ingratuelo | 1 |
| 56956 | ingratona | 1 |
| 56957 | inglorius | 1 |
| 56958 | inglesotes | 1 |
| 56959 | inglesote | 1 |
| 56960 | inglesones | 1 |
| 56961 | inglesona | 1 |
| 56962 | inglaterras | 1 |
| 56963 | ingiere | 1 |
| 56964 | ingestión | 1 |
| 56965 | ingertos | 1 |
| 56966 | ingertar | 1 |
| 56967 | ingerta | 1 |
| 56968 | ingerirse | 1 |
| 56969 | ingenuos | 1 |
| 56970 | ingenuas | 1 |
| 56971 | ingénuamente | 1 |
| 56972 | ingentes | 1 |
| 56973 | ingente | 1 |
| 56974 | ingénitos | 1 |
| 56975 | ingeniosísimos | 1 |
| 56976 | ingeniosísimo | 1 |
| 56977 | ingeniara | 1 |
| 56978 | infusorios | 1 |
| 56979 | infundirte | 1 |
| 56980 | infundirse | 1 |
| 56981 | infundirles | 1 |
| 56982 | infundios | 1 |
| 56983 | infundio | 1 |
| 56984 | infundiendo | 1 |
| 56985 | infundido | 1 |
| 56986 | infundidas | 1 |
| 56987 | infundíanle | 1 |
| 56988 | infundíamos | 1 |
| 56989 | infundíale | 1 |
| 56990 | infundes | 1 |
| 56991 | infunden | 1 |
| 56992 | infunda | 1 |
| 56993 | infructuoso | 1 |
| 56994 | infringir | 1 |
| 56995 | infringido | 1 |
| 56996 | infringe | 1 |
| 56997 | infranqueables | 1 |
| 56998 | infraganti | 1 |
| 56999 | informóse | 1 |
| 57000 | infórmate | 1 |
| 57001 | informarlo | 1 |
| 57002 | informaremos | 1 |
| 57003 | informarásle | 1 |
| 57004 | informar | 1 |
| 57005 | informante | 1 |
| 57006 | informando | 1 |
| 57007 | informamos | 1 |
| 57008 | informalle | 1 |
| 57009 | informados | 1 |
| 57010 | informadora | 1 |
| 57011 | informaciones | 1 |
| 57012 | informábase | 1 |
| 57013 | infolios | 1 |
| 57014 | influyese | 1 |
| 57015 | influyera | 1 |
| 57016 | influyen | 1 |
| 57017 | influya | 1 |
| 57018 | influido | 1 |
| 57019 | influían | 1 |
| 57020 | infló | 1 |
| 57021 | infligir | 1 |
| 57022 | inflexibles | 1 |
| 57023 | inflexibilidad | 1 |
| 57024 | inflándose | 1 |
| 57025 | inflamó | 1 |
| 57026 | inflamarse | 1 |
| 57027 | inflamar | 1 |
| 57028 | inflamándose | 1 |
| 57029 | inflaman | 1 |
| 57030 | inflamación | 1 |
| 57031 | inflamable | 1 |
| 57032 | inflamaban | 1 |
| 57033 | inflamaba | 1 |
| 57034 | inflama | 1 |
| 57035 | inflados | 1 |
| 57036 | inflada | 1 |
| 57037 | inflaban | 1 |
| 57038 | inflaba | 1 |
| 57039 | infiráis | 1 |
| 57040 | infinjas | 1 |
| 57041 | infinitus | 1 |
| 57042 | infinitivos | 1 |
| 57043 | ínfima | 1 |
| 57044 | infiesto | 1 |
| 57045 | infiero | 1 |
| 57046 | infïeles | 1 |
| 57047 | inficionando | 1 |
| 57048 | infestarse | 1 |
| 57049 | infestador | 1 |
| 57050 | infestadas | 1 |
| 57051 | infestada | 1 |
| 57052 | inferïor | 1 |
| 57053 | infelizote | 1 |
| 57054 | infelizmente | 1 |
| 57055 | infélices | 1 |
| 57056 | infecundos | 1 |
| 57057 | infecundidad | 1 |
| 57058 | infecunda | 1 |
| 57059 | infausta | 1 |
| 57060 | infanzona | 1 |
| 57061 | infantes | 1 |
| 57062 | infançones | 1 |
| 57063 | infamen | 1 |
| 57064 | infamado | 1 |
| 57065 | infamaba | 1 |
| 57066 | infalibidad | 1 |
| 57067 | infali | 1 |
| 57068 | infacundo | 1 |
| 57069 | inextricable | 1 |
| 57070 | inextinguible | 1 |
| 57071 | inexpresiva | 1 |
| 57072 | inexplorado | 1 |
| 57073 | inexpertos | 1 |
| 57074 | inexperiencia | 1 |
| 57075 | inevitablemente | 1 |
| 57076 | inesperados | 1 |
| 57077 | inescrutable | 1 |
| 57078 | inervación | 1 |
| 57079 | inequívoca | 1 |
| 57080 | ineptos | 1 |
| 57081 | ineptas | 1 |
| 57082 | ineficaces | 1 |
| 57083 | ineducado | 1 |
| 57084 | ineducada | 1 |
| 57085 | inédita | 1 |
| 57086 | induzir | 1 |
| 57087 | industriaremos | 1 |
| 57088 | industriándole | 1 |
| 57089 | industriadas | 1 |
| 57090 | indumentario | 1 |
| 57091 | indultan | 1 |
| 57092 | indulta | 1 |
| 57093 | indulgençias | 1 |
| 57094 | indújole | 1 |
| 57095 | indujeran | 1 |
| 57096 | indudables | 1 |
| 57097 | inductor | 1 |
| 57098 | inductivo | 1 |
| 57099 | inducir | 1 |
| 57100 | inducidos | 1 |
| 57101 | inducción | 1 |
| 57102 | indubitadamente | 1 |
| 57103 | indómitas | 1 |
| 57104 | indolentemente | 1 |
| 57105 | indolente | 1 |
| 57106 | indoctos | 1 |
| 57107 | indócil | 1 |
| 57108 | indo | 1 |
| 57109 | indivudua | 1 |
| 57110 | indivisible | 1 |
| 57111 | individualizar | 1 |
| 57112 | individualista | 1 |
| 57113 | individualidades | 1 |
| 57114 | individuales | 1 |
| 57115 | indistintamente | 1 |
| 57116 | indisputable | 1 |
| 57117 | indisposición | 1 |
| 57118 | indisponiendo | 1 |
| 57119 | indiscutibles | 1 |
| 57120 | indiscretas | 1 |
| 57121 | indiscreciones | 1 |
| 57122 | indisciplinado | 1 |
| 57123 | indirectos | 1 |
| 57124 | indirecto | 1 |
| 57125 | indirecte | 1 |
| 57126 | indique | 1 |
| 57127 | indinas | 1 |
| 57128 | indina | 1 |
| 57129 | indilugencia | 1 |
| 57130 | indignas | 1 |
| 57131 | indignarse | 1 |
| 57132 | indignarían | 1 |
| 57133 | indignaría | 1 |
| 57134 | indignara | 1 |
| 57135 | indignacion | 1 |
| 57136 | indigestos | 1 |
| 57137 | indigestiones | 1 |
| 57138 | indigestión | 1 |
| 57139 | indigéstate | 1 |
| 57140 | indigestan | 1 |
| 57141 | indigestada | 1 |
| 57142 | indigestaba | 1 |
| 57143 | indigentes | 1 |
| 57144 | indigente | 1 |
| 57145 | indígena | 1 |
| 57146 | índices | 1 |
| 57147 | indicarse | 1 |
| 57148 | indicáronle | 1 |
| 57149 | indicarme | 1 |
| 57150 | indicarla | 1 |
| 57151 | indicarán | 1 |
| 57152 | indicara | 1 |
| 57153 | indicados | 1 |
| 57154 | indicadas | 1 |
| 57155 | indiana | 1 |
| 57156 | indeterminada | 1 |
| 57157 | indestructibles | 1 |
| 57158 | indestructible | 1 |
| 57159 | indescifrable | 1 |
| 57160 | indemnizarse | 1 |
| 57161 | indemnizaciones | 1 |
| 57162 | indemnizaba | 1 |
| 57163 | indemnice | 1 |
| 57164 | indeleble | 1 |
| 57165 | indefinidos | 1 |
| 57166 | indefinido | 1 |
| 57167 | indefensos | 1 |
| 57168 | indefenso | 1 |
| 57169 | indecisas | 1 |
| 57170 | indecibles | 1 |
| 57171 | indecentonas | 1 |
| 57172 | indecentísimos | 1 |
| 57173 | indecentemente | 1 |
| 57174 | indagatorias | 1 |
| 57175 | indagando | 1 |
| 57176 | indagador | 1 |
| 57177 | indagadas | 1 |
| 57178 | indagaba | 1 |
| 57179 | incuses | 1 |
| 57180 | incusarnos | 1 |
| 57181 | incusarla | 1 |
| 57182 | incurrió | 1 |
| 57183 | incumbía | 1 |
| 57184 | incultura | 1 |
| 57185 | incultos | 1 |
| 57186 | incultivados | 1 |
| 57187 | incultísimo | 1 |
| 57188 | incultas | 1 |
| 57189 | inculpación | 1 |
| 57190 | inculpabilidad | 1 |
| 57191 | inculcó | 1 |
| 57192 | inculcaron | 1 |
| 57193 | inculcará | 1 |
| 57194 | inculcar | 1 |
| 57195 | inculcado | 1 |
| 57196 | incuestionable | 1 |
| 57197 | incrustando | 1 |
| 57198 | incrustadas | 1 |
| 57199 | incrusta | 1 |
| 57200 | incruentos | 1 |
| 57201 | incruentas | 1 |
| 57202 | increyble | 1 |
| 57203 | increparle | 1 |
| 57204 | increpandole | 1 |
| 57205 | increpaba | 1 |
| 57206 | incremento | 1 |
| 57207 | incorregibles | 1 |
| 57208 | incorrecto | 1 |
| 57209 | incorrectas | 1 |
| 57210 | incorrectamente | 1 |
| 57211 | incorrecciones | 1 |
| 57212 | incorporé | 1 |
| 57213 | incorporarle | 1 |
| 57214 | incorporan | 1 |
| 57215 | incorporábase | 1 |
| 57216 | incorporaban | 1 |
| 57217 | incorpora | 1 |
| 57218 | inconueniente | 1 |
| 57219 | incontrovertibles | 1 |
| 57220 | incontrovertible | 1 |
| 57221 | incontrastables | 1 |
| 57222 | incontinente | 1 |
| 57223 | incontestablemente | 1 |
| 57224 | inconsolables | 1 |
| 57225 | inconscientes | 1 |
| 57226 | inconsciencia | 1 |
| 57227 | inconmensurables | 1 |
| 57228 | incongruente | 1 |
| 57229 | inconfesables | 1 |
| 57230 | inconexos | 1 |
| 57231 | inconcuso | 1 |
| 57232 | inconcusas | 1 |
| 57233 | incomunicado | 1 |
| 57234 | incomunicación | 1 |
| 57235 | incompletos | 1 |
| 57236 | incompletas | 1 |
| 57237 | incompatibilidades | 1 |
| 57238 | incomoden | 1 |
| 57239 | incomodé | 1 |
| 57240 | incomodase | 1 |
| 57241 | incomodara | 1 |
| 57242 | incomodándose | 1 |
| 57243 | incomodan | 1 |
| 57244 | incomodadísima | 1 |
| 57245 | incomodadas | 1 |
| 57246 | incomeniente | 1 |
| 57247 | incombustible | 1 |
| 57248 | incoloras | 1 |
| 57249 | incognito | 1 |
| 57250 | incógnita | 1 |
| 57251 | incogitada | 1 |
| 57252 | incluyese | 1 |
| 57253 | incluyes | 1 |
| 57254 | incluyeran | 1 |
| 57255 | incluyen | 1 |
| 57256 | incluya | 1 |
| 57257 | inclusero | 1 |
| 57258 | incluís | 1 |
| 57259 | incluírla | 1 |
| 57260 | incluido | 1 |
| 57261 | ínclitas | 1 |
| 57262 | inclinósele | 1 |
| 57263 | inclinas | 1 |
| 57264 | inclinará | 1 |
| 57265 | inclinamos | 1 |
| 57266 | inclinábase | 1 |
| 57267 | inclemente | 1 |
| 57268 | incito | 1 |
| 57269 | incité | 1 |
| 57270 | incite | 1 |
| 57271 | incitativo | 1 |
| 57272 | incitativas | 1 |
| 57273 | incitaros | 1 |
| 57274 | incitará | 1 |
| 57275 | incitantes | 1 |
| 57276 | incitándoles | 1 |
| 57277 | incitándole | 1 |
| 57278 | incitando | 1 |
| 57279 | incitados | 1 |
| 57280 | incitada | 1 |
| 57281 | incitaban | 1 |
| 57282 | incitaba | 1 |
| 57283 | incisos | 1 |
| 57284 | inciertas | 1 |
| 57285 | incidencia | 1 |
| 57286 | inchillas | 1 |
| 57287 | inche | 1 |
| 57288 | incestuosos | 1 |
| 57289 | incesantemente | 1 |
| 57290 | incesante | 1 |
| 57291 | incesable | 1 |
| 57292 | incertidumbres | 1 |
| 57293 | incertedumbre | 1 |
| 57294 | incentiva | 1 |
| 57295 | incendiar | 1 |
| 57296 | incendiando | 1 |
| 57297 | incendiada | 1 |
| 57298 | incautas | 1 |
| 57299 | incautado | 1 |
| 57300 | incautación | 1 |
| 57301 | incautaba | 1 |
| 57302 | incasables | 1 |
| 57303 | incapacitaba | 1 |
| 57304 | incandescente | 1 |
| 57305 | incalificables | 1 |
| 57306 | inca | 1 |
| 57307 | inaveriguable | 1 |
| 57308 | inauguren | 1 |
| 57309 | inaugurando | 1 |
| 57310 | inauguraban | 1 |
| 57311 | inasociables | 1 |
| 57312 | inarticulada | 1 |
| 57313 | inarmónica | 1 |
| 57314 | inarco | 1 |
| 57315 | inapetente | 1 |
| 57316 | inapetencias | 1 |
| 57317 | inanimados | 1 |
| 57318 | inalterada | 1 |
| 57319 | inalterables | 1 |
| 57320 | inalterable | 1 |
| 57321 | inalienables | 1 |
| 57322 | inadvertencia | 1 |
| 57323 | inactivo | 1 |
| 57324 | inactividad | 1 |
| 57325 | inactiva | 1 |
| 57326 | inacesible | 1 |
| 57327 | inaccesible | 1 |
| 57328 | imputado | 1 |
| 57329 | imputaban | 1 |
| 57330 | imputaba | 1 |
| 57331 | impúsome | 1 |
| 57332 | impusiese | 1 |
| 57333 | impusieron | 1 |
| 57334 | impusiere | 1 |
| 57335 | impusiera | 1 |
| 57336 | impuros | 1 |
| 57337 | impureza | 1 |
| 57338 | impuras | 1 |
| 57339 | impune | 1 |
| 57340 | impulsión | 1 |
| 57341 | impulsarán | 1 |
| 57342 | impulsar | 1 |
| 57343 | impulsábala | 1 |
| 57344 | impúdicas | 1 |
| 57345 | impúber | 1 |
| 57346 | imprudentemente | 1 |
| 57347 | improvisará | 1 |
| 57348 | improvisados | 1 |
| 57349 | improvisador | 1 |
| 57350 | improvisaban | 1 |
| 57351 | improuisos | 1 |
| 57352 | improuiso | 1 |
| 57353 | improrrogable | 1 |
| 57354 | impropios | 1 |
| 57355 | impropiamente | 1 |
| 57356 | improperios | 1 |
| 57357 | improductivas | 1 |
| 57358 | ímprobo | 1 |
| 57359 | improbable | 1 |
| 57360 | imprimirlo | 1 |
| 57361 | imprimirle | 1 |
| 57362 | imprimirla | 1 |
| 57363 | imprimio | 1 |
| 57364 | imprimiéronseme | 1 |
| 57365 | imprimid | 1 |
| 57366 | imprímese | 1 |
| 57367 | imprevistos | 1 |
| 57368 | imprevista | 1 |
| 57369 | imprevisor | 1 |
| 57370 | impressores | 1 |
| 57371 | impresso | 1 |
| 57372 | impresione | 1 |
| 57373 | impresionados | 1 |
| 57374 | impresionaban | 1 |
| 57375 | impresionaba | 1 |
| 57376 | impresiona | 1 |
| 57377 | impregnarse | 1 |
| 57378 | impregnado | 1 |
| 57379 | imprecación | 1 |
| 57380 | imprecaba | 1 |
| 57381 | impostura | 1 |
| 57382 | imposta | 1 |
| 57383 | imposibilitó | 1 |
| 57384 | imposibilitara | 1 |
| 57385 | imposibilitar | 1 |
| 57386 | imposibilitándola | 1 |
| 57387 | importunes | 1 |
| 57388 | importunase | 1 |
| 57389 | importunarle | 1 |
| 57390 | importunar | 1 |
| 57391 | importunando | 1 |
| 57392 | importunada | 1 |
| 57393 | importó | 1 |
| 57394 | importasen | 1 |
| 57395 | importase | 1 |
| 57396 | importare | 1 |
| 57397 | importantísima | 1 |
| 57398 | importadores | 1 |
| 57399 | importadoras | 1 |
| 57400 | importador | 1 |
| 57401 | impopularidad | 1 |
| 57402 | imponíase | 1 |
| 57403 | imponíale | 1 |
| 57404 | impongan | 1 |
| 57405 | imponerte | 1 |
| 57406 | imponérsele | 1 |
| 57407 | imponerle | 1 |
| 57408 | impondrá | 1 |
| 57409 | impolítica | 1 |
| 57410 | imploró | 1 |
| 57411 | imploro | 1 |
| 57412 | implorando | 1 |
| 57413 | implícito | 1 |
| 57414 | implícitas | 1 |
| 57415 | implicaría | 1 |
| 57416 | implicantes | 1 |
| 57417 | implicación | 1 |
| 57418 | implica | 1 |
| 57419 | implantado | 1 |
| 57420 | impíreas | 1 |
| 57421 | impidiesen | 1 |
| 57422 | impidiese | 1 |
| 57423 | impidieran | 1 |
| 57424 | impidiéndose | 1 |
| 57425 | impidiéndole | 1 |
| 57426 | impidía | 1 |
| 57427 | impides | 1 |
| 57428 | impías | 1 |
| 57429 | impíamente | 1 |
| 57430 | impetus | 1 |
| 57431 | impetuosos | 1 |
| 57432 | impetüoso | 1 |
| 57433 | impetre | 1 |
| 57434 | impetrado | 1 |
| 57435 | imperuio | 1 |
| 57436 | imperturbabilidad | 1 |
| 57437 | impersonal | 1 |
| 57438 | impermeable | 1 |
| 57439 | imperïoso | 1 |
| 57440 | imperiosas | 1 |
| 57441 | imperficion | 1 |
| 57442 | imperfeto | 1 |
| 57443 | imperfeta | 1 |
| 57444 | imperfectísima | 1 |
| 57445 | imperfectas | 1 |
| 57446 | imperfectamente | 1 |
| 57447 | imperfecion | 1 |
| 57448 | imperfecciones | 1 |
| 57449 | imperatoria | 1 |
| 57450 | imperando | 1 |
| 57451 | imperaba | 1 |
| 57452 | impensado | 1 |
| 57453 | impenetrabilidad | 1 |
| 57454 | impeliendo | 1 |
| 57455 | impelidas | 1 |
| 57456 | impelían | 1 |
| 57457 | impelen | 1 |
| 57458 | impele | 1 |
| 57459 | impedirte | 1 |
| 57460 | impedírselo | 1 |
| 57461 | impedirlos | 1 |
| 57462 | impedirles | 1 |
| 57463 | impedirla | 1 |
| 57464 | impedimentos | 1 |
| 57465 | impedidas | 1 |
| 57466 | impecable | 1 |
| 57467 | impasibles | 1 |
| 57468 | impasibilidad | 1 |
| 57469 | impares | 1 |
| 57470 | impalpable | 1 |
| 57471 | impagables | 1 |
| 57472 | impacïente | 1 |
| 57473 | impacientase | 1 |
| 57474 | impacienta | 1 |
| 57475 | immortale | 1 |
| 57476 | imiten | 1 |
| 57477 | imítela | 1 |
| 57478 | imitativa | 1 |
| 57479 | imitaste | 1 |
| 57480 | imitarse | 1 |
| 57481 | imitaros | 1 |
| 57482 | imitarlo | 1 |
| 57483 | imitarle | 1 |
| 57484 | imitarla | 1 |
| 57485 | imitari | 1 |
| 57486 | imitare | 1 |
| 57487 | imitándola | 1 |
| 57488 | imitalle | 1 |
| 57489 | imitados | 1 |
| 57490 | imitadores | 1 |
| 57491 | imitadoras | 1 |
| 57492 | imitadora | 1 |
| 57493 | imediatamente | 1 |
| 57494 | imbuyen | 1 |
| 57495 | imbuirlas | 1 |
| 57496 | imbécilmente | 1 |
| 57497 | imbecilidad | 1 |
| 57498 | imbéciles | 1 |
| 57499 | imanes | 1 |
| 57500 | imagínole | 1 |
| 57501 | imagínese | 1 |
| 57502 | imaginativa | 1 |
| 57503 | imagínate | 1 |
| 57504 | imaginase | 1 |
| 57505 | imaginas | 1 |
| 57506 | imaginársela | 1 |
| 57507 | imaginarme | 1 |
| 57508 | imaginarlo | 1 |
| 57509 | imaginaren | 1 |
| 57510 | imaginaremos | 1 |
| 57511 | imaginan | 1 |
| 57512 | imaginallas | 1 |
| 57513 | imaginaldo | 1 |
| 57514 | imagináis | 1 |
| 57515 | imaginacioncilla | 1 |
| 57516 | imaginable | 1 |
| 57517 | imaginábase | 1 |
| 57518 | imaginabas | 1 |
| 57519 | imaginaban | 1 |
| 57520 | im | 1 |
| 57521 | ilustren | 1 |
| 57522 | ilustrarse | 1 |
| 57523 | ilustrará | 1 |
| 57524 | ilustrar | 1 |
| 57525 | ilustrando | 1 |
| 57526 | ilustran | 1 |
| 57527 | ilustraba | 1 |
| 57528 | ilusionó | 1 |
| 57529 | ilusioncita | 1 |
| 57530 | ilusionarse | 1 |
| 57531 | ilusionándose | 1 |
| 57532 | ilusionan | 1 |
| 57533 | ilusionado | 1 |
| 57534 | ilusionaba | 1 |
| 57535 | ilumino | 1 |
| 57536 | iluminase | 1 |
| 57537 | iluminándolo | 1 |
| 57538 | ilumíname | 1 |
| 57539 | iluminaciones | 1 |
| 57540 | iluminación | 1 |
| 57541 | ilógica | 1 |
| 57542 | ilmo | 1 |
| 57543 | illud | 1 |
| 57544 | illuc | 1 |
| 57545 | illos | 1 |
| 57546 | illorum | 1 |
| 57547 | illi | 1 |
| 57548 | ille | 1 |
| 57549 | illana | 1 |
| 57550 | iliteratas | 1 |
| 57551 | ilimitado | 1 |
| 57552 | ilícitos | 1 |
| 57553 | ilesos | 1 |
| 57554 | ilegítima | 1 |
| 57555 | ilegible | 1 |
| 57556 | ilcobalizaque | 1 |
| 57557 | ijas | 1 |
| 57558 | ijares | 1 |
| 57559 | ijadeando | 1 |
| 57560 | iiii | 1 |
| 57561 | igusquiza | 1 |
| 57562 | iguesí | 1 |
| 57563 | igualo | 1 |
| 57564 | igualitos | 1 |
| 57565 | igualdades | 1 |
| 57566 | igualasen | 1 |
| 57567 | igualase | 1 |
| 57568 | igualas | 1 |
| 57569 | igualarme | 1 |
| 57570 | igualaran | 1 |
| 57571 | igualáis | 1 |
| 57572 | igualado | 1 |
| 57573 | igualada | 1 |
| 57574 | ignotos | 1 |
| 57575 | ignoto | 1 |
| 57576 | ignoréis | 1 |
| 57577 | ignoraste | 1 |
| 57578 | ignorarlas | 1 |
| 57579 | ignorarla | 1 |
| 57580 | ignoraría | 1 |
| 57581 | ignorándolos | 1 |
| 57582 | ignorancias | 1 |
| 57583 | ignoráis | 1 |
| 57584 | ignoradas | 1 |
| 57585 | ignominiosamente | 1 |
| 57586 | ignominiosa | 1 |
| 57587 | ignacita | 1 |
| 57588 | iglesita | 1 |
| 57589 | iesus | 1 |
| 57590 | idóneo | 1 |
| 57591 | idolatro | 1 |
| 57592 | idolatrías | 1 |
| 57593 | idolatre | 1 |
| 57594 | idolatrar | 1 |
| 57595 | idolatra | 1 |
| 57596 | idïomas | 1 |
| 57597 | idiomas | 1 |
| 57598 | idio | 1 |
| 57599 | idilios | 1 |
| 57600 | idiazabal | 1 |
| 57601 | ides | 1 |
| 57602 | identificar | 1 |
| 57603 | identifican | 1 |
| 57604 | identificaba | 1 |
| 57605 | identidad | 1 |
| 57606 | idénticos | 1 |
| 57607 | idénticas | 1 |
| 57608 | idem | 1 |
| 57609 | ideítas | 1 |
| 57610 | idease | 1 |
| 57611 | idearon | 1 |
| 57612 | idealizar | 1 |
| 57613 | ideado | 1 |
| 57614 | ideadas | 1 |
| 57615 | ideada | 1 |
| 57616 | ideaban | 1 |
| 57617 | ideaba | 1 |
| 57618 | íd | 1 |
| 57619 | iconografía | 1 |
| 57620 | iconoclastas | 1 |
| 57621 | icena | 1 |
| 57622 | icasi | 1 |
| 57623 | ícaros | 1 |
| 57624 | ibilli | 1 |
| 57625 | íberos | 1 |
| 57626 | ibamos | 1 |
| 57627 | íbales | 1 |
| 57628 | íbades | 1 |
| 57629 | iaz | 1 |
| 57630 | huyriales | 1 |
| 57631 | huyóse | 1 |
| 57632 | huygas | 1 |
| 57633 | huyere | 1 |
| 57634 | huyeran | 1 |
| 57635 | huyamos | 1 |
| 57636 | huviesse | 1 |
| 57637 | huvieron | 1 |
| 57638 | huuieron | 1 |
| 57639 | husmeó | 1 |
| 57640 | hurtes | 1 |
| 57641 | hurté | 1 |
| 57642 | hurtase | 1 |
| 57643 | hurtaron | 1 |
| 57644 | hurtarían | 1 |
| 57645 | hurtan | 1 |
| 57646 | hurtamos | 1 |
| 57647 | hurtallo | 1 |
| 57648 | hurtados | 1 |
| 57649 | hurtacordel | 1 |
| 57650 | hurtaban | 1 |
| 57651 | hurtábamos | 1 |
| 57652 | hurtábades | 1 |
| 57653 | hurra | 1 |
| 57654 | huronera | 1 |
| 57655 | huroneaba | 1 |
| 57656 | hurgoneo | 1 |
| 57657 | hurgado | 1 |
| 57658 | hurgada | 1 |
| 57659 | hurgaba | 1 |
| 57660 | hungría | 1 |
| 57661 | hundo | 1 |
| 57662 | hundire | 1 |
| 57663 | hundimos | 1 |
| 57664 | hundimientos | 1 |
| 57665 | hundimiento | 1 |
| 57666 | hundiéronse | 1 |
| 57667 | hundiéndola | 1 |
| 57668 | hundidas | 1 |
| 57669 | hundíase | 1 |
| 57670 | hundíamos | 1 |
| 57671 | húndete | 1 |
| 57672 | hundes | 1 |
| 57673 | hunden | 1 |
| 57674 | humour | 1 |
| 57675 | humosos | 1 |
| 57676 | humosa | 1 |
| 57677 | humorados | 1 |
| 57678 | humoradas | 1 |
| 57679 | humorada | 1 |
| 57680 | humíllome | 1 |
| 57681 | humillo | 1 |
| 57682 | humillen | 1 |
| 57683 | humillarlo | 1 |
| 57684 | humillarles | 1 |
| 57685 | humillarle | 1 |
| 57686 | humillaría | 1 |
| 57687 | humillaos | 1 |
| 57688 | humillándose | 1 |
| 57689 | humilladas | 1 |
| 57690 | humillada | 1 |
| 57691 | humilísima | 1 |
| 57692 | humildades | 1 |
| 57693 | húmidos | 1 |
| 57694 | húmido | 1 |
| 57695 | húmidas | 1 |
| 57696 | húmida | 1 |
| 57697 | humi | 1 |
| 57698 | humeros | 1 |
| 57699 | humero | 1 |
| 57700 | humedezco | 1 |
| 57701 | humedecido | 1 |
| 57702 | humedecía | 1 |
| 57703 | humedecerse | 1 |
| 57704 | humedece | 1 |
| 57705 | humear | 1 |
| 57706 | humeantes | 1 |
| 57707 | humeando | 1 |
| 57708 | humea | 1 |
| 57709 | humboldt | 1 |
| 57710 | humanizada | 1 |
| 57711 | humanizaban | 1 |
| 57712 | humanitarias | 1 |
| 57713 | humanado | 1 |
| 57714 | huma | 1 |
| 57715 | hum | 1 |
| 57716 | hulleras | 1 |
| 57717 | hullera | 1 |
| 57718 | hules | 1 |
| 57719 | huírnos | 1 |
| 57720 | huirme | 1 |
| 57721 | huiría | 1 |
| 57722 | huilla | 1 |
| 57723 | huid | 1 |
| 57724 | huías | 1 |
| 57725 | hugonotes | 1 |
| 57726 | huevitos | 1 |
| 57727 | hueverito | 1 |
| 57728 | huevería | 1 |
| 57729 | hueveras | 1 |
| 57730 | huevecillo | 1 |
| 57731 | hueuos | 1 |
| 57732 | huestantigua | 1 |
| 57733 | huesso | 1 |
| 57734 | huesecito | 1 |
| 57735 | huesecillo | 1 |
| 57736 | huerza | 1 |
| 57737 | hueros | 1 |
| 57738 | huerfanilla | 1 |
| 57739 | huerfanas | 1 |
| 57740 | huente | 1 |
| 57741 | huelgues | 1 |
| 57742 | huelguen | 1 |
| 57743 | huelgue | 1 |
| 57744 | hue | 1 |
| 57745 | huço | 1 |
| 57746 | húbolo | 1 |
| 57747 | hubistes | 1 |
| 57748 | hubiste | 1 |
| 57749 | hubieses | 1 |
| 57750 | hubiésemos | 1 |
| 57751 | hubiéranos | 1 |
| 57752 | hubiérame | 1 |
| 57753 | hubiéralo | 1 |
| 57754 | hubiérales | 1 |
| 57755 | hubiérale | 1 |
| 57756 | hubiéralas | 1 |
| 57757 | hubiá | 1 |
| 57758 | húbele | 1 |
| 57759 | hozando | 1 |
| 57760 | houiste | 1 |
| 57761 | houinhoins | 1 |
| 57762 | houiesses | 1 |
| 57763 | houiessen | 1 |
| 57764 | houieremos | 1 |
| 57765 | houiere | 1 |
| 57766 | hoto | 1 |
| 57767 | hostilizar | 1 |
| 57768 | hostilidades | 1 |
| 57769 | hostiles | 1 |
| 57770 | hostigó | 1 |
| 57771 | hostigándole | 1 |
| 57772 | hostalero | 1 |
| 57773 | hostal | 1 |
| 57774 | hospitalera | 1 |
| 57775 | hospitalario | 1 |
| 57776 | hospicios | 1 |
| 57777 | hospiciano | 1 |
| 57778 | hospedóm | 1 |
| 57779 | hospedáronme | 1 |
| 57780 | hospedaron | 1 |
| 57781 | hospedajes | 1 |
| 57782 | hospedador | 1 |
| 57783 | hoscos | 1 |
| 57784 | hosco | 1 |
| 57785 | hosca | 1 |
| 57786 | horrorizo | 1 |
| 57787 | horrorizadas | 1 |
| 57788 | horrorice | 1 |
| 57789 | horrísona | 1 |
| 57790 | horripilé | 1 |
| 57791 | horripilan | 1 |
| 57792 | horripilado | 1 |
| 57793 | horripiladas | 1 |
| 57794 | horripila | 1 |
| 57795 | horridus | 1 |
| 57796 | horrendos | 1 |
| 57797 | horrendas | 1 |
| 57798 | horras | 1 |
| 57799 | horra | 1 |
| 57800 | horquilla | 1 |
| 57801 | hornito | 1 |
| 57802 | hornillos | 1 |
| 57803 | hormiguilla | 1 |
| 57804 | hormiguean | 1 |
| 57805 | hormigonazos | 1 |
| 57806 | hormas | 1 |
| 57807 | horma | 1 |
| 57808 | horita | 1 |
| 57809 | horchaterías | 1 |
| 57810 | horchatería | 1 |
| 57811 | horcas | 1 |
| 57812 | horcajadura | 1 |
| 57813 | horario | 1 |
| 57814 | horaña | 1 |
| 57815 | horadó | 1 |
| 57816 | horado | 1 |
| 57817 | horadara | 1 |
| 57818 | horadado | 1 |
| 57819 | horadación | 1 |
| 57820 | horadaban | 1 |
| 57821 | horacianas | 1 |
| 57822 | horaca | 1 |
| 57823 | hopo | 1 |
| 57824 | honrrauan | 1 |
| 57825 | honrraua | 1 |
| 57826 | honrramos | 1 |
| 57827 | honrrados | 1 |
| 57828 | honrosísima | 1 |
| 57829 | honrosas | 1 |
| 57830 | honrosamente | 1 |
| 57831 | honren | 1 |
| 57832 | honratu | 1 |
| 57833 | honraste | 1 |
| 57834 | honrás | 1 |
| 57835 | honrarte | 1 |
| 57836 | honrarse | 1 |
| 57837 | honraros | 1 |
| 57838 | honraron | 1 |
| 57839 | honrarnos | 1 |
| 57840 | honrarme | 1 |
| 57841 | honrarlos | 1 |
| 57842 | honraremos | 1 |
| 57843 | honraré | 1 |
| 57844 | honrarás | 1 |
| 57845 | honrara | 1 |
| 57846 | honrándola | 1 |
| 57847 | honradote | 1 |
| 57848 | honradito | 1 |
| 57849 | honradísimos | 1 |
| 57850 | honradísimo | 1 |
| 57851 | honradísima | 1 |
| 57852 | honradeces | 1 |
| 57853 | honrad | 1 |
| 57854 | honraban | 1 |
| 57855 | honorarios | 1 |
| 57856 | honorabilidad | 1 |
| 57857 | honni | 1 |
| 57858 | honguito | 1 |
| 57859 | honestísimos | 1 |
| 57860 | honestísima | 1 |
| 57861 | honestad | 1 |
| 57862 | hondonadas | 1 |
| 57863 | hondón | 1 |
| 57864 | hondísimos | 1 |
| 57865 | hondero | 1 |
| 57866 | hominum | 1 |
| 57867 | homini | 1 |
| 57868 | homilía | 1 |
| 57869 | homerus | 1 |
| 57870 | homedes | 1 |
| 57871 | homeçida | 1 |
| 57872 | hombruno | 1 |
| 57873 | hombretón | 1 |
| 57874 | hombrecito | 1 |
| 57875 | hombrecillo | 1 |
| 57876 | hombreándose | 1 |
| 57877 | hombreaba | 1 |
| 57878 | hombrachón | 1 |
| 57879 | hollen | 1 |
| 57880 | hollé | 1 |
| 57881 | holgóse | 1 |
| 57882 | holgo | 1 |
| 57883 | holgazanote | 1 |
| 57884 | holgazanotas | 1 |
| 57885 | holgazan | 1 |
| 57886 | holgays | 1 |
| 57887 | holgastes | 1 |
| 57888 | holgasse | 1 |
| 57889 | holgasen | 1 |
| 57890 | holgáronse | 1 |
| 57891 | holgares | 1 |
| 57892 | holgaremos | 1 |
| 57893 | holgaréme | 1 |
| 57894 | holgáredes | 1 |
| 57895 | holgáramos | 1 |
| 57896 | holgárame | 1 |
| 57897 | holgará | 1 |
| 57898 | holgáis | 1 |
| 57899 | holgadísimas | 1 |
| 57900 | holgábase | 1 |
| 57901 | holgábanse | 1 |
| 57902 | holgábame | 1 |
| 57903 | holandés | 1 |
| 57904 | hojosos | 1 |
| 57905 | hojitas | 1 |
| 57906 | hojita | 1 |
| 57907 | hojeo | 1 |
| 57908 | hojeé | 1 |
| 57909 | hojearlos | 1 |
| 57910 | hojearle | 1 |
| 57911 | hojear | 1 |
| 57912 | hojeándolo | 1 |
| 57913 | hojeado | 1 |
| 57914 | hojaplasma | 1 |
| 57915 | hojaldrado | 1 |
| 57916 | hojalateros | 1 |
| 57917 | hojadelata | 1 |
| 57918 | hogazas | 1 |
| 57919 | hogaças | 1 |
| 57920 | hodie | 1 |
| 57921 | hociquitos | 1 |
| 57922 | hociquearemos | 1 |
| 57923 | hocicando | 1 |
| 57924 | hocicadas | 1 |
| 57925 | hobiere | 1 |
| 57926 | hízote | 1 |
| 57927 | hizolo | 1 |
| 57928 | hízoles | 1 |
| 57929 | hízola | 1 |
| 57930 | hizimos | 1 |
| 57931 | histriónica | 1 |
| 57932 | historiado | 1 |
| 57933 | histérico | 1 |
| 57934 | histéricas | 1 |
| 57935 | histérica | 1 |
| 57936 | hispanófilo | 1 |
| 57937 | hispana | 1 |
| 57938 | his | 1 |
| 57939 | hirviente | 1 |
| 57940 | hirióle | 1 |
| 57941 | hiriese | 1 |
| 57942 | hirieran | 1 |
| 57943 | hiriera | 1 |
| 57944 | hircano | 1 |
| 57945 | hipotéticos | 1 |
| 57946 | hipotéticamente | 1 |
| 57947 | hipotérmico | 1 |
| 57948 | hipotecan | 1 |
| 57949 | hipotecado | 1 |
| 57950 | hipotecada | 1 |
| 57951 | hipoteca | 1 |
| 57952 | hipoquitropíticas | 1 |
| 57953 | hipopótamos | 1 |
| 57954 | hipólito | 1 |
| 57955 | hipódromos | 1 |
| 57956 | hipódromo | 1 |
| 57957 | hipocritón | 1 |
| 57958 | hipócritamente | 1 |
| 57959 | hipocráticos | 1 |
| 57960 | hipocráticas | 1 |
| 57961 | hipo | 1 |
| 57962 | hípica | 1 |
| 57963 | hiperquinesia | 1 |
| 57964 | hinquéme | 1 |
| 57965 | hinojo | 1 |
| 57966 | hindostán | 1 |
| 57967 | hincósele | 1 |
| 57968 | hinco | 1 |
| 57969 | hinchir | 1 |
| 57970 | hinches | 1 |
| 57971 | hinchen | 1 |
| 57972 | hinche | 1 |
| 57973 | hincharte | 1 |
| 57974 | hinchándose | 1 |
| 57975 | hinchan | 1 |
| 57976 | hinchaba | 1 |
| 57977 | híncate | 1 |
| 57978 | hincársele | 1 |
| 57979 | hincaron | 1 |
| 57980 | hincarme | 1 |
| 57981 | hincarle | 1 |
| 57982 | hincan | 1 |
| 57983 | hincados | 1 |
| 57984 | hincábame | 1 |
| 57985 | hilvanarlos | 1 |
| 57986 | hilvanada | 1 |
| 57987 | hiló | 1 |
| 57988 | hillo | 1 |
| 57989 | hill | 1 |
| 57990 | hilito | 1 |
| 57991 | hilillos | 1 |
| 57992 | hilera | 1 |
| 57993 | hildebrando | 1 |
| 57994 | hilando | 1 |
| 57995 | hilanderas | 1 |
| 57996 | hiladito | 1 |
| 57997 | hiladillo | 1 |
| 57998 | hilacha | 1 |
| 57999 | hilaban | 1 |
| 58000 | hila | 1 |
| 58001 | hijadas | 1 |
| 58002 | hij | 1 |
| 58003 | higuí | 1 |
| 58004 | higueruela | 1 |
| 58005 | high | 1 |
| 58006 | hígados | 1 |
| 58007 | higado | 1 |
| 58008 | hierven | 1 |
| 58009 | hieruen | 1 |
| 58010 | hierue | 1 |
| 58011 | hierrecillo | 1 |
| 58012 | hieroglí | 1 |
| 58013 | hierocrático | 1 |
| 58014 | hiero | 1 |
| 58015 | hieráticos | 1 |
| 58016 | hieras | 1 |
| 58017 | hieles | 1 |
| 58018 | hiede | 1 |
| 58019 | hiebre | 1 |
| 58020 | hidrostática | 1 |
| 58021 | hidrógeno | 1 |
| 58022 | hidiondas | 1 |
| 58023 | hideperro | 1 |
| 58024 | hide | 1 |
| 58025 | hidalguete | 1 |
| 58026 | hicímoslos | 1 |
| 58027 | hiciésedes | 1 |
| 58028 | hiciéronte | 1 |
| 58029 | hiciéronme | 1 |
| 58030 | hiciéremos | 1 |
| 58031 | hiciéredes | 1 |
| 58032 | hiciéramos | 1 |
| 58033 | hiciendo | 1 |
| 58034 | hic | 1 |
| 58035 | híbridas | 1 |
| 58036 | hibleo | 1 |
| 58037 | hibla | 1 |
| 58038 | hibernia | 1 |
| 58039 | hían | 1 |
| 58040 | hialoides | 1 |
| 58041 | hía | 1 |
| 58042 | hezimos | 1 |
| 58043 | hez | 1 |
| 58044 | hexasílabos | 1 |
| 58045 | hévoslo | 1 |
| 58046 | heviella | 1 |
| 58047 | hétores | 1 |
| 58048 | hétor | 1 |
| 58049 | hético | 1 |
| 58050 | heterogéneo | 1 |
| 58051 | heterogéneas | 1 |
| 58052 | heterodoxo | 1 |
| 58053 | heterodoxa | 1 |
| 58054 | hétenos | 1 |
| 58055 | hételo | 1 |
| 58056 | hétele | 1 |
| 58057 | hesperia | 1 |
| 58058 | hes | 1 |
| 58059 | hervor | 1 |
| 58060 | hervidor | 1 |
| 58061 | heruolarios | 1 |
| 58062 | heruir | 1 |
| 58063 | heruientes | 1 |
| 58064 | heruia | 1 |
| 58065 | herroso | 1 |
| 58066 | herror | 1 |
| 58067 | herrerias | 1 |
| 58068 | herrera | 1 |
| 58069 | herren | 1 |
| 58070 | herré | 1 |
| 58071 | herraje | 1 |
| 58072 | herrada | 1 |
| 58073 | herpéticos | 1 |
| 58074 | héros | 1 |
| 58075 | heroicidades | 1 |
| 58076 | heroicidad | 1 |
| 58077 | herodiana | 1 |
| 58078 | hernio | 1 |
| 58079 | hermosotes | 1 |
| 58080 | hermosismo | 1 |
| 58081 | hermita | 1 |
| 58082 | hermanitos | 1 |
| 58083 | hermanillo | 1 |
| 58084 | hermandades | 1 |
| 58085 | hermanados | 1 |
| 58086 | hermanaba | 1 |
| 58087 | hermafrodita | 1 |
| 58088 | herizo | 1 |
| 58089 | herirse | 1 |
| 58090 | herirles | 1 |
| 58091 | herirla | 1 |
| 58092 | herire | 1 |
| 58093 | herirá | 1 |
| 58094 | herimos | 1 |
| 58095 | heria | 1 |
| 58096 | herético | 1 |
| 58097 | heréticas | 1 |
| 58098 | herética | 1 |
| 58099 | heresiarcas | 1 |
| 58100 | heresiarca | 1 |
| 58101 | herençia | 1 |
| 58102 | herejotes | 1 |
| 58103 | heregia | 1 |
| 58104 | herege | 1 |
| 58105 | heredónos | 1 |
| 58106 | hereditario | 1 |
| 58107 | hereden | 1 |
| 58108 | heredase | 1 |
| 58109 | heredaron | 1 |
| 58110 | heredarlo | 1 |
| 58111 | heredaran | 1 |
| 58112 | heredan | 1 |
| 58113 | heredamos | 1 |
| 58114 | heredamientos | 1 |
| 58115 | heredamiento | 1 |
| 58116 | heredadas | 1 |
| 58117 | hercúleo | 1 |
| 58118 | hercúlea | 1 |
| 58119 | herculano | 1 |
| 58120 | herboso | 1 |
| 58121 | herborizando | 1 |
| 58122 | hérauts | 1 |
| 58123 | heraclio | 1 |
| 58124 | heptasílabos | 1 |
| 58125 | hepila | 1 |
| 58126 | hepatitis | 1 |
| 58127 | hepáticas | 1 |
| 58128 | henos | 1 |
| 58129 | hendija | 1 |
| 58130 | hendiduras | 1 |
| 58131 | hendía | 1 |
| 58132 | hendí | 1 |
| 58133 | hendaya | 1 |
| 58134 | henchirse | 1 |
| 58135 | henchidos | 1 |
| 58136 | henao | 1 |
| 58137 | hemostática | 1 |
| 58138 | hemorragia | 1 |
| 58139 | hemoptisis | 1 |
| 58140 | hemisferio | 1 |
| 58141 | hemicráneo | 1 |
| 58142 | hemençia | 1 |
| 58143 | helyçes | 1 |
| 58144 | helvecias | 1 |
| 58145 | heliotropo | 1 |
| 58146 | heliogábalo | 1 |
| 58147 | hélice | 1 |
| 58148 | helias | 1 |
| 58149 | helénico | 1 |
| 58150 | helénicas | 1 |
| 58151 | helénica | 1 |
| 58152 | helena | 1 |
| 58153 | helase | 1 |
| 58154 | helárseme | 1 |
| 58155 | helaron | 1 |
| 58156 | helarle | 1 |
| 58157 | helara | 1 |
| 58158 | helándole | 1 |
| 58159 | helando | 1 |
| 58160 | helaban | 1 |
| 58161 | héla | 1 |
| 58162 | heis | 1 |
| 58163 | heine | 1 |
| 58164 | hegemonía | 1 |
| 58165 | hedores | 1 |
| 58166 | hedor | 1 |
| 58167 | hediondos | 1 |
| 58168 | hediondas | 1 |
| 58169 | hedifiçio | 1 |
| 58170 | hedian | 1 |
| 58171 | hedia | 1 |
| 58172 | heder | 1 |
| 58173 | hedad | 1 |
| 58174 | héchoos | 1 |
| 58175 | héchole | 1 |
| 58176 | hechizerias | 1 |
| 58177 | hechizeras | 1 |
| 58178 | hechizaba | 1 |
| 58179 | hechicerías | 1 |
| 58180 | hechiceresca | 1 |
| 58181 | hebrero | 1 |
| 58182 | hebreos | 1 |
| 58183 | hebrea | 1 |
| 58184 | hebraizante | 1 |
| 58185 | hebraicas | 1 |
| 58186 | hebillas | 1 |
| 58187 | hazmerreír | 1 |
| 58188 | hazientes | 1 |
| 58189 | haziendose | 1 |
| 58190 | haziendola | 1 |
| 58191 | haziendas | 1 |
| 58192 | haziades | 1 |
| 58193 | hazese | 1 |
| 58194 | hazértela | 1 |
| 58195 | hazerte | 1 |
| 58196 | hazerme | 1 |
| 58197 | hazerlos | 1 |
| 58198 | hazerlo | 1 |
| 58199 | hazerla | 1 |
| 58200 | hazense | 1 |
| 58201 | hazén | 1 |
| 58202 | hazemos | 1 |
| 58203 | hazelo | 1 |
| 58204 | hazelas | 1 |
| 58205 | hazedor | 1 |
| 58206 | hazed | 1 |
| 58207 | hazañosos | 1 |
| 58208 | hazanas | 1 |
| 58209 | hazalvaro | 1 |
| 58210 | haymarket | 1 |
| 58211 | hayar | 1 |
| 58212 | háyamos | 1 |
| 58213 | hayades | 1 |
| 58214 | havía | 1 |
| 58215 | hauria | 1 |
| 58216 | hauran | 1 |
| 58217 | hauiale | 1 |
| 58218 | haueys | 1 |
| 58219 | hauerte | 1 |
| 58220 | hauerlo | 1 |
| 58221 | hauas | 1 |
| 58222 | hauada | 1 |
| 58223 | haua | 1 |
| 58224 | hatos | 1 |
| 58225 | hatillo | 1 |
| 58226 | hatchiss | 1 |
| 58227 | hastía | 1 |
| 58228 | haste | 1 |
| 58229 | hasparren | 1 |
| 58230 | hasle | 1 |
| 58231 | hasla | 1 |
| 58232 | háselo | 1 |
| 58233 | háseles | 1 |
| 58234 | hascas | 1 |
| 58235 | hasalejas | 1 |
| 58236 | hás | 1 |
| 58237 | hártome | 1 |
| 58238 | hartó | 1 |
| 58239 | hartmann | 1 |
| 58240 | hartes | 1 |
| 58241 | hartazga | 1 |
| 58242 | hártate | 1 |
| 58243 | hartarte | 1 |
| 58244 | hartaran | 1 |
| 58245 | hartándose | 1 |
| 58246 | hartan | 1 |
| 58247 | hartamos | 1 |
| 58248 | harro | 1 |
| 58249 | harriero | 1 |
| 58250 | harre | 1 |
| 58251 | harpillera | 1 |
| 58252 | harpías | 1 |
| 58253 | harpias | 1 |
| 58254 | harpar | 1 |
| 58255 | harpado | 1 |
| 58256 | harpadas | 1 |
| 58257 | harpada | 1 |
| 58258 | harón | 1 |
| 58259 | harinas | 1 |
| 58260 | haríale | 1 |
| 58261 | haríades | 1 |
| 58262 | hariades | 1 |
| 58263 | harélo | 1 |
| 58264 | haréislo | 1 |
| 58265 | hareís | 1 |
| 58266 | hardy | 1 |
| 58267 | harda | 1 |
| 58268 | harásme | 1 |
| 58269 | harásela | 1 |
| 58270 | haráse | 1 |
| 58271 | haraposos | 1 |
| 58272 | haraposas | 1 |
| 58273 | haran | 1 |
| 58274 | haragán | 1 |
| 58275 | háosla | 1 |
| 58276 | hanos | 1 |
| 58277 | hanla | 1 |
| 58278 | hanega | 1 |
| 58279 | handrajoso | 1 |
| 58280 | handora | 1 |
| 58281 | hamida | 1 |
| 58282 | hamet | 1 |
| 58283 | hámela | 1 |
| 58284 | hamburgo | 1 |
| 58285 | hambr | 1 |
| 58286 | hámago | 1 |
| 58287 | hamadrías | 1 |
| 58288 | hamaca | 1 |
| 58289 | hallóme | 1 |
| 58290 | hallole | 1 |
| 58291 | halléle | 1 |
| 58292 | halléla | 1 |
| 58293 | hallazgos | 1 |
| 58294 | hállate | 1 |
| 58295 | hallástete | 1 |
| 58296 | hallármela | 1 |
| 58297 | hallaríamos | 1 |
| 58298 | hallaria | 1 |
| 58299 | hallareys | 1 |
| 58300 | hallaráse | 1 |
| 58301 | hállanse | 1 |
| 58302 | hallanle | 1 |
| 58303 | hallámonos | 1 |
| 58304 | hallador | 1 |
| 58305 | hallábamos | 1 |
| 58306 | halía | 1 |
| 58307 | hale | 1 |
| 58308 | haldudos | 1 |
| 58309 | haldudo | 1 |
| 58310 | haldear | 1 |
| 58311 | halaguero | 1 |
| 58312 | halagüeños | 1 |
| 58313 | halagüeño | 1 |
| 58314 | halagaron | 1 |
| 58315 | halagarme | 1 |
| 58316 | halagarle | 1 |
| 58317 | halagare | 1 |
| 58318 | halagar | 1 |
| 58319 | halagador | 1 |
| 58320 | halagada | 1 |
| 58321 | halaga | 1 |
| 58322 | hais | 1 |
| 58323 | hágome | 1 |
| 58324 | hágolo | 1 |
| 58325 | hágole | 1 |
| 58326 | hagays | 1 |
| 58327 | háganme | 1 |
| 58328 | háganle | 1 |
| 58329 | hagámosle | 1 |
| 58330 | hagamosle | 1 |
| 58331 | hagámosela | 1 |
| 58332 | hágalas | 1 |
| 58333 | haeckel | 1 |
| 58334 | haec | 1 |
| 58335 | hadriani | 1 |
| 58336 | hadedur | 1 |
| 58337 | hacirlo | 1 |
| 58338 | haçina | 1 |
| 58339 | haciéndosele | 1 |
| 58340 | haciéndomelo | 1 |
| 58341 | haciéndolos | 1 |
| 58342 | hacíanles | 1 |
| 58343 | hacíanle | 1 |
| 58344 | hacíanla | 1 |
| 58345 | hacíales | 1 |
| 58346 | hacíais | 1 |
| 58347 | hacíades | 1 |
| 58348 | hachones | 1 |
| 58349 | haches | 1 |
| 58350 | hácese | 1 |
| 58351 | hacérsenos | 1 |
| 58352 | hacérselos | 1 |
| 58353 | hacérmele | 1 |
| 58354 | haçerio | 1 |
| 58355 | hácense | 1 |
| 58356 | hacenes | 1 |
| 58357 | hacendista | 1 |
| 58358 | hacendados | 1 |
| 58359 | hacémoslas | 1 |
| 58360 | háceme | 1 |
| 58361 | hacelde | 1 |
| 58362 | hacednos | 1 |
| 58363 | hacedme | 1 |
| 58364 | hacedles | 1 |
| 58365 | hacedero | 1 |
| 58366 | hacedera | 1 |
| 58367 | hacas | 1 |
| 58368 | haça | 1 |
| 58369 | habro | 1 |
| 58370 | habríase | 1 |
| 58371 | habríale | 1 |
| 58372 | habríades | 1 |
| 58373 | habrélas | 1 |
| 58374 | habréla | 1 |
| 58375 | habrase | 1 |
| 58376 | habraré | 1 |
| 58377 | habra | 1 |
| 58378 | hablóse | 1 |
| 58379 | hablóme | 1 |
| 58380 | hablóle | 1 |
| 58381 | hablilla | 1 |
| 58382 | háblesele | 1 |
| 58383 | háblese | 1 |
| 58384 | hábleme | 1 |
| 58385 | hábleles | 1 |
| 58386 | hablays | 1 |
| 58387 | hablaste | 1 |
| 58388 | habláronse | 1 |
| 58389 | hablaria | 1 |
| 58390 | hablaréis | 1 |
| 58391 | hablarás | 1 |
| 58392 | hablaras | 1 |
| 58393 | habláramos | 1 |
| 58394 | hablantes | 1 |
| 58395 | hablanse | 1 |
| 58396 | háblanos | 1 |
| 58397 | hablándote | 1 |
| 58398 | hablándome | 1 |
| 58399 | hablándolos | 1 |
| 58400 | hablanco | 1 |
| 58401 | hablalla | 1 |
| 58402 | háblale | 1 |
| 58403 | hablados | 1 |
| 58404 | habladoras | 1 |
| 58405 | habladas | 1 |
| 58406 | hablabas | 1 |
| 58407 | habitude | 1 |
| 58408 | habituarse | 1 |
| 58409 | habitualmente | 1 |
| 58410 | habituado | 1 |
| 58411 | habitan | 1 |
| 58412 | habitadas | 1 |
| 58413 | habitáculo | 1 |
| 58414 | habitabilidad | 1 |
| 58415 | habitabas | 1 |
| 58416 | habilitándole | 1 |
| 58417 | habilita | 1 |
| 58418 | habilísimos | 1 |
| 58419 | habilísimas | 1 |
| 58420 | habilísima | 1 |
| 58421 | habiéndote | 1 |
| 58422 | habiéndoselos | 1 |
| 58423 | habiéndoos | 1 |
| 58424 | habiéndonos | 1 |
| 58425 | habiéndolas | 1 |
| 58426 | habíasele | 1 |
| 58427 | habíapresentado | 1 |
| 58428 | habíanme | 1 |
| 58429 | habian | 1 |
| 58430 | habíamonos | 1 |
| 58431 | habíame | 1 |
| 58432 | habíalos | 1 |
| 58433 | habíalas | 1 |
| 58434 | habia | 1 |
| 58435 | habet | 1 |
| 58436 | habértelo | 1 |
| 58437 | habérselo | 1 |
| 58438 | habérosla | 1 |
| 58439 | habérmelos | 1 |
| 58440 | habérmelas | 1 |
| 58441 | habérmela | 1 |
| 58442 | habello | 1 |
| 58443 | habelle | 1 |
| 58444 | habéisme | 1 |
| 58445 | habares | 1 |
| 58446 | habanos | 1 |
| 58447 | habalí | 1 |
| 58448 | hab | 1 |
| 58449 | guzques | 1 |
| 58450 | guya | 1 |
| 58451 | guy | 1 |
| 58452 | guttenberg | 1 |
| 58453 | gutier | 1 |
| 58454 | gutenberg | 1 |
| 58455 | gutarrac | 1 |
| 58456 | gustote | 1 |
| 58457 | gustosas | 1 |
| 58458 | gusté | 1 |
| 58459 | gustarían | 1 |
| 58460 | gustares | 1 |
| 58461 | gustaré | 1 |
| 58462 | gustaran | 1 |
| 58463 | gustamos | 1 |
| 58464 | gustable | 1 |
| 58465 | gusanito | 1 |
| 58466 | gusanillos | 1 |
| 58467 | gurreas | 1 |
| 58468 | gure | 1 |
| 58469 | guras | 1 |
| 58470 | guluzmear | 1 |
| 58471 | gulosos | 1 |
| 58472 | guloso | 1 |
| 58473 | gulosa | 1 |
| 58474 | gullurías | 1 |
| 58475 | gulliver | 1 |
| 58476 | gulilla | 1 |
| 58477 | gulfara | 1 |
| 58478 | gulf | 1 |
| 58479 | gules | 1 |
| 58480 | guitarro | 1 |
| 58481 | guitarristas | 1 |
| 58482 | guitarrista | 1 |
| 58483 | guissasen | 1 |
| 58484 | guisos | 1 |
| 58485 | guisopete | 1 |
| 58486 | guise | 1 |
| 58487 | guisase | 1 |
| 58488 | guisandera | 1 |
| 58489 | guisalle | 1 |
| 58490 | guiris | 1 |
| 58491 | guirigay | 1 |
| 58492 | guipuzcoanos | 1 |
| 58493 | guío | 1 |
| 58494 | guiños | 1 |
| 58495 | guiño | 1 |
| 58496 | guiñapo | 1 |
| 58497 | guiñados | 1 |
| 58498 | guiñada | 1 |
| 58499 | guiña | 1 |
| 58500 | guineo | 1 |
| 58501 | guindó | 1 |
| 58502 | guindas | 1 |
| 58503 | guindalera | 1 |
| 58504 | guinda | 1 |
| 58505 | guinando | 1 |
| 58506 | guillotinadas | 1 |
| 58507 | guillado | 1 |
| 58508 | guijeñas | 1 |
| 58509 | guija | 1 |
| 58510 | guíes | 1 |
| 58511 | guies | 1 |
| 58512 | guibeleguieta | 1 |
| 58513 | guiasen | 1 |
| 58514 | guias | 1 |
| 58515 | guiaré | 1 |
| 58516 | guiándolos | 1 |
| 58517 | guiándole | 1 |
| 58518 | guiándolas | 1 |
| 58519 | guían | 1 |
| 58520 | guíame | 1 |
| 58521 | guiadas | 1 |
| 58522 | guiábanle | 1 |
| 58523 | guiábalas | 1 |
| 58524 | guia | 1 |
| 58525 | güevo | 1 |
| 58526 | guevaras | 1 |
| 58527 | guetaria | 1 |
| 58528 | güéspedes | 1 |
| 58529 | güéspeda | 1 |
| 58530 | güesos | 1 |
| 58531 | güesa | 1 |
| 58532 | guerrillero | 1 |
| 58533 | guerrea | 1 |
| 58534 | gueró | 1 |
| 58535 | güero | 1 |
| 58536 | guère | 1 |
| 58537 | güeno | 1 |
| 58538 | güelvo | 1 |
| 58539 | güélvete | 1 |
| 58540 | guelbenzu | 1 |
| 58541 | guedeja | 1 |
| 58542 | guealés | 1 |
| 58543 | guciac | 1 |
| 58544 | gubernativo | 1 |
| 58545 | gubernamentales | 1 |
| 58546 | gubernamental | 1 |
| 58547 | gubernación | 1 |
| 58548 | guayaquileño | 1 |
| 58549 | guatepeor | 1 |
| 58550 | guatemala | 1 |
| 58551 | guasones | 1 |
| 58552 | guasee | 1 |
| 58553 | guárte | 1 |
| 58554 | guarnimientos | 1 |
| 58555 | guarnidos | 1 |
| 58556 | guarnecidos | 1 |
| 58557 | guarnecido | 1 |
| 58558 | guarnecidas | 1 |
| 58559 | guarnecida | 1 |
| 58560 | guarnecía | 1 |
| 58561 | guarismos | 1 |
| 58562 | guarir | 1 |
| 58563 | guarino | 1 |
| 58564 | guaridas | 1 |
| 58565 | guarescer | 1 |
| 58566 | guaresçe | 1 |
| 58567 | guareció | 1 |
| 58568 | guarecieron | 1 |
| 58569 | guarecerse | 1 |
| 58570 | guarecerles | 1 |
| 58571 | guardolo | 1 |
| 58572 | guardillas | 1 |
| 58573 | guardilla | 1 |
| 58574 | guardiano | 1 |
| 58575 | guardiana | 1 |
| 58576 | guardián | 1 |
| 58577 | guardete | 1 |
| 58578 | guardeste | 1 |
| 58579 | guardese | 1 |
| 58580 | guardesas | 1 |
| 58581 | guárdes | 1 |
| 58582 | guárdenos | 1 |
| 58583 | guardémoslo | 1 |
| 58584 | guárdelos | 1 |
| 58585 | guardava | 1 |
| 58586 | guardaua | 1 |
| 58587 | guardaste | 1 |
| 58588 | guardárselo | 1 |
| 58589 | guardarropas | 1 |
| 58590 | guardarnos | 1 |
| 58591 | guardarían | 1 |
| 58592 | guardaos | 1 |
| 58593 | guárdanlo | 1 |
| 58594 | guardándonos | 1 |
| 58595 | guardándolo | 1 |
| 58596 | guardándole | 1 |
| 58597 | guardámonos | 1 |
| 58598 | guardamano | 1 |
| 58599 | guardalle | 1 |
| 58600 | guárdale | 1 |
| 58601 | guárdalas | 1 |
| 58602 | guárdala | 1 |
| 58603 | guardadora | 1 |
| 58604 | guardadme | 1 |
| 58605 | guardadla | 1 |
| 58606 | guardades | 1 |
| 58607 | guardaderas | 1 |
| 58608 | guardad | 1 |
| 58609 | guardacantón | 1 |
| 58610 | guardabrisas | 1 |
| 58611 | guardábase | 1 |
| 58612 | guardábalo | 1 |
| 58613 | guardaamigo | 1 |
| 58614 | guapito | 1 |
| 58615 | guapísimos | 1 |
| 58616 | guapín | 1 |
| 58617 | guapillas | 1 |
| 58618 | guapeza | 1 |
| 58619 | guapetones | 1 |
| 58620 | guapamente | 1 |
| 58621 | guantero | 1 |
| 58622 | gualdrapa | 1 |
| 58623 | gualá | 1 |
| 58624 | guadarrama | 1 |
| 58625 | guadañas | 1 |
| 58626 | guadameciles | 1 |
| 58627 | guadamací | 1 |
| 58628 | guadalete | 1 |
| 58629 | grytadera | 1 |
| 58630 | gruyer | 1 |
| 58631 | grupito | 1 |
| 58632 | gruñidora | 1 |
| 58633 | gruñeron | 1 |
| 58634 | gruñe | 1 |
| 58635 | grund | 1 |
| 58636 | gruesísimos | 1 |
| 58637 | gruesísima | 1 |
| 58638 | gruesecillo | 1 |
| 58639 | grúas | 1 |
| 58640 | groya | 1 |
| 58641 | grossero | 1 |
| 58642 | grosezuelos | 1 |
| 58643 | gros | 1 |
| 58644 | groma | 1 |
| 58645 | grolia | 1 |
| 58646 | grojear | 1 |
| 58647 | grite | 1 |
| 58648 | gritas | 1 |
| 58649 | gritarme | 1 |
| 58650 | gritaremos | 1 |
| 58651 | gritarán | 1 |
| 58652 | gritará | 1 |
| 58653 | gritándonos | 1 |
| 58654 | grítale | 1 |
| 58655 | gritábamos | 1 |
| 58656 | gritábale | 1 |
| 58657 | grima | 1 |
| 58658 | grilletes | 1 |
| 58659 | grilleras | 1 |
| 58660 | grilla | 1 |
| 58661 | grijalte | 1 |
| 58662 | grijalba | 1 |
| 58663 | grifos | 1 |
| 58664 | grifaños | 1 |
| 58665 | grial | 1 |
| 58666 | gressus | 1 |
| 58667 | grenelle | 1 |
| 58668 | gremios | 1 |
| 58669 | gredoso | 1 |
| 58670 | greco | 1 |
| 58671 | grecizante | 1 |
| 58672 | greales | 1 |
| 58673 | graznado | 1 |
| 58674 | graziella | 1 |
| 58675 | gravosa | 1 |
| 58676 | gravitó | 1 |
| 58677 | gravitativo | 1 |
| 58678 | gravitaba | 1 |
| 58679 | gravita | 1 |
| 58680 | gravísima | 1 |
| 58681 | graullé | 1 |
| 58682 | graue | 1 |
| 58683 | gratuitamente | 1 |
| 58684 | gratuita | 1 |
| 58685 | gratituda | 1 |
| 58686 | gratísima | 1 |
| 58687 | gratificallas | 1 |
| 58688 | gratificado | 1 |
| 58689 | gratia | 1 |
| 58690 | grasientas | 1 |
| 58691 | granzones | 1 |
| 58692 | granuloso | 1 |
| 58693 | granulosa | 1 |
| 58694 | granulaciones | 1 |
| 58695 | granujita | 1 |
| 58696 | granujerías | 1 |
| 58697 | granjeó | 1 |
| 58698 | granjeen | 1 |
| 58699 | granjee | 1 |
| 58700 | granjeamos | 1 |
| 58701 | granjeadas | 1 |
| 58702 | granizaron | 1 |
| 58703 | granizado | 1 |
| 58704 | granítico | 1 |
| 58705 | graniso | 1 |
| 58706 | granisava | 1 |
| 58707 | granillo | 1 |
| 58708 | graneado | 1 |
| 58709 | grandullón | 1 |
| 58710 | grandones | 1 |
| 58711 | grandiosidad | 1 |
| 58712 | grandilocuentes | 1 |
| 58713 | grandilocuente | 1 |
| 58714 | grandílocua | 1 |
| 58715 | grandías | 1 |
| 58716 | grandecitos | 1 |
| 58717 | grandecita | 1 |
| 58718 | granda | 1 |
| 58719 | granava | 1 |
| 58720 | granates | 1 |
| 58721 | granadino | 1 |
| 58722 | granadinas | 1 |
| 58723 | gramos | 1 |
| 58724 | gramonilla | 1 |
| 58725 | gramo | 1 |
| 58726 | gramático | 1 |
| 58727 | gramaticales | 1 |
| 58728 | gram | 1 |
| 58729 | grajeas | 1 |
| 58730 | grajas | 1 |
| 58731 | grajales | 1 |
| 58732 | gragea | 1 |
| 58733 | gráficas | 1 |
| 58734 | gráficamente | 1 |
| 58735 | grafía | 1 |
| 58736 | graduarse | 1 |
| 58737 | graduaron | 1 |
| 58738 | graduaría | 1 |
| 58739 | graduados | 1 |
| 58740 | graduador | 1 |
| 58741 | gradüadamente | 1 |
| 58742 | graduación | 1 |
| 58743 | graduaba | 1 |
| 58744 | gradesçido | 1 |
| 58745 | gradésçegelo | 1 |
| 58746 | gradan | 1 |
| 58747 | grad | 1 |
| 58748 | graciosita | 1 |
| 58749 | graciosísimos | 1 |
| 58750 | graciosísimas | 1 |
| 58751 | graciosidad | 1 |
| 58752 | graciosico | 1 |
| 58753 | graciado | 1 |
| 58754 | grace | 1 |
| 58755 | grabó | 1 |
| 58756 | grabe | 1 |
| 58757 | grabarla | 1 |
| 58758 | grabaremos | 1 |
| 58759 | grabando | 1 |
| 58760 | grababan | 1 |
| 58761 | gozques | 1 |
| 58762 | gozquecillo | 1 |
| 58763 | gozose | 1 |
| 58764 | gozosas | 1 |
| 58765 | gozón | 1 |
| 58766 | gozome | 1 |
| 58767 | gozóla | 1 |
| 58768 | gozemos | 1 |
| 58769 | gozemonos | 1 |
| 58770 | gózate | 1 |
| 58771 | gozasse | 1 |
| 58772 | gozas | 1 |
| 58773 | gozarse | 1 |
| 58774 | gozaron | 1 |
| 58775 | gozarle | 1 |
| 58776 | gozarian | 1 |
| 58777 | gozariamos | 1 |
| 58778 | gozaréis | 1 |
| 58779 | gozarás | 1 |
| 58780 | gozaras | 1 |
| 58781 | gozará | 1 |
| 58782 | gózante | 1 |
| 58783 | gózala | 1 |
| 58784 | gozadas | 1 |
| 58785 | gozada | 1 |
| 58786 | gouernador | 1 |
| 58787 | gotoso | 1 |
| 58788 | gotita | 1 |
| 58789 | goterones | 1 |
| 58790 | gotear | 1 |
| 58791 | goteaban | 1 |
| 58792 | goste | 1 |
| 58793 | gostarlas | 1 |
| 58794 | gostaduras | 1 |
| 58795 | gosaste | 1 |
| 58796 | gorronería | 1 |
| 58797 | gorronazo | 1 |
| 58798 | gorrona | 1 |
| 58799 | gorritas | 1 |
| 58800 | gorrión | 1 |
| 58801 | gorrinos | 1 |
| 58802 | gorrinaza | 1 |
| 58803 | gorrina | 1 |
| 58804 | gorrilla | 1 |
| 58805 | gorrete | 1 |
| 58806 | gorjeos | 1 |
| 58807 | gorjear | 1 |
| 58808 | gorjeador | 1 |
| 58809 | gorjeaban | 1 |
| 58810 | gorja | 1 |
| 58811 | gorgoteo | 1 |
| 58812 | gorgee | 1 |
| 58813 | gordiviejas | 1 |
| 58814 | gordito | 1 |
| 58815 | gordita | 1 |
| 58816 | gordísimo | 1 |
| 58817 | gordilla | 1 |
| 58818 | gorde | 1 |
| 58819 | gora | 1 |
| 58820 | goñi | 1 |
| 58821 | gongorismo | 1 |
| 58822 | gongorino | 1 |
| 58823 | gonela | 1 |
| 58824 | gonces | 1 |
| 58825 | gomogga | 1 |
| 58826 | gomez | 1 |
| 58827 | gomeles | 1 |
| 58828 | gomel | 1 |
| 58829 | gomas | 1 |
| 58830 | golviésemos | 1 |
| 58831 | golvier | 1 |
| 58832 | golpetazos | 1 |
| 58833 | golpeó | 1 |
| 58834 | golpecillo | 1 |
| 58835 | golpearse | 1 |
| 58836 | golpea | 1 |
| 58837 | golpado | 1 |
| 58838 | golpad | 1 |
| 58839 | golp | 1 |
| 58840 | golosyna | 1 |
| 58841 | golosinar | 1 |
| 58842 | golosidad | 1 |
| 58843 | golosazo | 1 |
| 58844 | golondryna | 1 |
| 58845 | golondrinas | 1 |
| 58846 | gollería | 1 |
| 58847 | golido | 1 |
| 58848 | goliat | 1 |
| 58849 | golhines | 1 |
| 58850 | golfin | 1 |
| 58851 | golfas | 1 |
| 58852 | golfa | 1 |
| 58853 | goletas | 1 |
| 58854 | goled | 1 |
| 58855 | gold | 1 |
| 58856 | goiri | 1 |
| 58857 | gofes | 1 |
| 58858 | goëthe | 1 |
| 58859 | godofredo | 1 |
| 58860 | godofre | 1 |
| 58861 | gocémosla | 1 |
| 58862 | gocemos | 1 |
| 58863 | gocéis | 1 |
| 58864 | gocé | 1 |
| 58865 | gobiernito | 1 |
| 58866 | goberné | 1 |
| 58867 | gobernases | 1 |
| 58868 | gobernarte | 1 |
| 58869 | gobernarlos | 1 |
| 58870 | gobernarlo | 1 |
| 58871 | gobernarle | 1 |
| 58872 | gobernarla | 1 |
| 58873 | gobernaría | 1 |
| 58874 | gobernares | 1 |
| 58875 | gobernare | 1 |
| 58876 | gobernarás | 1 |
| 58877 | gobernara | 1 |
| 58878 | gobernamos | 1 |
| 58879 | gobernadoresco | 1 |
| 58880 | gobernad | 1 |
| 58881 | gobernable | 1 |
| 58882 | gobernaban | 1 |
| 58883 | gobernábala | 1 |
| 58884 | goárdame | 1 |
| 58885 | gnomos | 1 |
| 58886 | gnómica | 1 |
| 58887 | gnido | 1 |
| 58888 | glúteos | 1 |
| 58889 | gluten | 1 |
| 58890 | glotona | 1 |
| 58891 | glosar | 1 |
| 58892 | glosan | 1 |
| 58893 | glosados | 1 |
| 58894 | glosado | 1 |
| 58895 | glosaba | 1 |
| 58896 | gloriya | 1 |
| 58897 | gloriosísima | 1 |
| 58898 | glorifico | 1 |
| 58899 | glorifican | 1 |
| 58900 | glorificado | 1 |
| 58901 | glorifica | 1 |
| 58902 | gloriado | 1 |
| 58903 | glóbulos | 1 |
| 58904 | glóbulo | 1 |
| 58905 | glaucoma | 1 |
| 58906 | gladiolos | 1 |
| 58907 | gladiador | 1 |
| 58908 | glacis | 1 |
| 58909 | giù | 1 |
| 58910 | gitarra | 1 |
| 58911 | gitar | 1 |
| 58912 | gitanismo | 1 |
| 58913 | gitanillos | 1 |
| 58914 | gitani | 1 |
| 58915 | gitanescas | 1 |
| 58916 | gitanerías | 1 |
| 58917 | gitaneaba | 1 |
| 58918 | gisada | 1 |
| 58919 | girgonça | 1 |
| 58920 | giratorio | 1 |
| 58921 | girasoles | 1 |
| 58922 | girase | 1 |
| 58923 | giras | 1 |
| 58924 | girara | 1 |
| 58925 | giran | 1 |
| 58926 | giraldi | 1 |
| 58927 | giraba | 1 |
| 58928 | ginoveses | 1 |
| 58929 | ginovesa | 1 |
| 58930 | ginovés | 1 |
| 58931 | ginosofistas | 1 |
| 58932 | ginetes | 1 |
| 58933 | ginebrino | 1 |
| 58934 | ginasios | 1 |
| 58935 | gimnásticos | 1 |
| 58936 | gimnástica | 1 |
| 58937 | gimnasio | 1 |
| 58938 | gimnasias | 1 |
| 58939 | gimes | 1 |
| 58940 | gimen | 1 |
| 58941 | gima | 1 |
| 58942 | gilís | 1 |
| 58943 | gilí | 1 |
| 58944 | gilecuelco | 1 |
| 58945 | gigote | 1 |
| 58946 | gigantones | 1 |
| 58947 | gigantona | 1 |
| 58948 | gigantón | 1 |
| 58949 | gigantillo | 1 |
| 58950 | giganteos | 1 |
| 58951 | gigantazos | 1 |
| 58952 | gibraleón | 1 |
| 58953 | giar | 1 |
| 58954 | gestionemos | 1 |
| 58955 | gestionaban | 1 |
| 58956 | gestión | 1 |
| 58957 | gesticularíamos | 1 |
| 58958 | gesticular | 1 |
| 58959 | gesticulación | 1 |
| 58960 | gestico | 1 |
| 58961 | gessler | 1 |
| 58962 | gerunt | 1 |
| 58963 | gerona | 1 |
| 58964 | gérmenes | 1 |
| 58965 | germanos | 1 |
| 58966 | germanía | 1 |
| 58967 | gerifaltes | 1 |
| 58968 | geraya | 1 |
| 58969 | geórgicas | 1 |
| 58970 | geométricos | 1 |
| 58971 | geométrica | 1 |
| 58972 | gëometría | 1 |
| 58973 | geómetra | 1 |
| 58974 | geológicos | 1 |
| 58975 | geológica | 1 |
| 58976 | geógrafos | 1 |
| 58977 | geográficos | 1 |
| 58978 | geográfica | 1 |
| 58979 | genus | 1 |
| 58980 | genuit | 1 |
| 58981 | genuino | 1 |
| 58982 | genuinamente | 1 |
| 58983 | gentualla | 1 |
| 58984 | gentleman | 1 |
| 58985 | gentileshombres | 1 |
| 58986 | gentezuelas | 1 |
| 58987 | gentezuela | 1 |
| 58988 | gentezilla | 1 |
| 58989 | gentecilla | 1 |
| 58990 | gentecica | 1 |
| 58991 | gens | 1 |
| 58992 | genoveses | 1 |
| 58993 | genovés | 1 |
| 58994 | genivito | 1 |
| 58995 | genitivo | 1 |
| 58996 | genialidades | 1 |
| 58997 | gengibrante | 1 |
| 58998 | generosidades | 1 |
| 58999 | generosamente | 1 |
| 59000 | generalizar | 1 |
| 59001 | generalización | 1 |
| 59002 | generalísimo | 1 |
| 59003 | generadora | 1 |
| 59004 | gendarmes | 1 |
| 59005 | gendarme | 1 |
| 59006 | genaro | 1 |
| 59007 | gemirían | 1 |
| 59008 | gémino | 1 |
| 59009 | gemidores | 1 |
| 59010 | gemidicos | 1 |
| 59011 | gemelas | 1 |
| 59012 | gelves | 1 |
| 59013 | gelsemina | 1 |
| 59014 | gelanda | 1 |
| 59015 | gazul | 1 |
| 59016 | gazpachos | 1 |
| 59017 | gaznatico | 1 |
| 59018 | gaznates | 1 |
| 59019 | gaznápiro | 1 |
| 59020 | gazmoño | 1 |
| 59021 | gazmoña | 1 |
| 59022 | gazapos | 1 |
| 59023 | gayón | 1 |
| 59024 | gayola | 1 |
| 59025 | gayarre | 1 |
| 59026 | gayado | 1 |
| 59027 | gayadas | 1 |
| 59028 | gaya | 1 |
| 59029 | gaviellas | 1 |
| 59030 | gavetas | 1 |
| 59031 | gauzcatzu | 1 |
| 59032 | gauthier | 1 |
| 59033 | gaume | 1 |
| 59034 | gauilanes | 1 |
| 59035 | gaudia | 1 |
| 59036 | gau | 1 |
| 59037 | gatuperios | 1 |
| 59038 | gatunos | 1 |
| 59039 | gatita | 1 |
| 59040 | gatescas | 1 |
| 59041 | gaterías | 1 |
| 59042 | gatería | 1 |
| 59043 | gatéenme | 1 |
| 59044 | gatearon | 1 |
| 59045 | gateando | 1 |
| 59046 | gateamiento | 1 |
| 59047 | gateado | 1 |
| 59048 | gâté | 1 |
| 59049 | gatazo | 1 |
| 59050 | gatada | 1 |
| 59051 | gastronómicos | 1 |
| 59052 | gastronómico | 1 |
| 59053 | gastronómicas | 1 |
| 59054 | gastroenteritis | 1 |
| 59055 | gástrico | 1 |
| 59056 | gastón | 1 |
| 59057 | gastes | 1 |
| 59058 | gasten | 1 |
| 59059 | gastasse | 1 |
| 59060 | gastarías | 1 |
| 59061 | gastarían | 1 |
| 59062 | gastaríamos | 1 |
| 59063 | gastaré | 1 |
| 59064 | gastarás | 1 |
| 59065 | gastáramos | 1 |
| 59066 | gastará | 1 |
| 59067 | gastándolo | 1 |
| 59068 | gastalle | 1 |
| 59069 | gastalla | 1 |
| 59070 | gastala | 1 |
| 59071 | gastadores | 1 |
| 59072 | gastadora | 1 |
| 59073 | gastábamos | 1 |
| 59074 | gasparón | 1 |
| 59075 | gasparito | 1 |
| 59076 | gasnar | 1 |
| 59077 | gasifica | 1 |
| 59078 | gascones | 1 |
| 59079 | gasajos | 1 |
| 59080 | gasajo | 1 |
| 59081 | gasaje | 1 |
| 59082 | gasajados | 1 |
| 59083 | gasajado | 1 |
| 59084 | gasabal | 1 |
| 59085 | garzota | 1 |
| 59086 | garzos | 1 |
| 59087 | garzas | 1 |
| 59088 | garvanços | 1 |
| 59089 | garuines | 1 |
| 59090 | garrulería | 1 |
| 59091 | garruchas | 1 |
| 59092 | garrota | 1 |
| 59093 | garroso | 1 |
| 59094 | garrofales | 1 |
| 59095 | garró | 1 |
| 59096 | garrido | 1 |
| 59097 | garranchos | 1 |
| 59098 | garrancho | 1 |
| 59099 | garramar | 1 |
| 59100 | garrama | 1 |
| 59101 | garraiz | 1 |
| 59102 | garnidos | 1 |
| 59103 | garnidas | 1 |
| 59104 | garniçiones | 1 |
| 59105 | garni | 1 |
| 59106 | garnachas | 1 |
| 59107 | garnacha | 1 |
| 59108 | garlochín | 1 |
| 59109 | garitos | 1 |
| 59110 | garitas | 1 |
| 59111 | gariofelata | 1 |
| 59112 | garibay | 1 |
| 59113 | gargantilla | 1 |
| 59114 | gargantero | 1 |
| 59115 | gargajos | 1 |
| 59116 | gargajo | 1 |
| 59117 | garfiñé | 1 |
| 59118 | garfiñaran | 1 |
| 59119 | garden | 1 |
| 59120 | gardatla | 1 |
| 59121 | garçonía | 1 |
| 59122 | garci | 1 |
| 59123 | garças | 1 |
| 59124 | garbeare | 1 |
| 59125 | garantíceme | 1 |
| 59126 | garante | 1 |
| 59127 | garanón | 1 |
| 59128 | garamantas | 1 |
| 59129 | garamanta | 1 |
| 59130 | garabito | 1 |
| 59131 | garabí | 1 |
| 59132 | garabateados | 1 |
| 59133 | garabateada | 1 |
| 59134 | gañir | 1 |
| 59135 | gañecoechia | 1 |
| 59136 | gañadora | 1 |
| 59137 | gansirula | 1 |
| 59138 | ganosos | 1 |
| 59139 | ganoso | 1 |
| 59140 | ganóselos | 1 |
| 59141 | ganosa | 1 |
| 59142 | ganimedes | 1 |
| 59143 | ganguea | 1 |
| 59144 | gangrenada | 1 |
| 59145 | ganes | 1 |
| 59146 | ganemos | 1 |
| 59147 | ganéles | 1 |
| 59148 | gandules | 1 |
| 59149 | gandía | 1 |
| 59150 | ganchuda | 1 |
| 59151 | ganaste | 1 |
| 59152 | ganáronsela | 1 |
| 59153 | ganarnos | 1 |
| 59154 | ganarlo | 1 |
| 59155 | ganaremos | 1 |
| 59156 | ganarán | 1 |
| 59157 | ganará | 1 |
| 59158 | ganándose | 1 |
| 59159 | ganándola | 1 |
| 59160 | gananciales | 1 |
| 59161 | ganançia | 1 |
| 59162 | gáname | 1 |
| 59163 | ganades | 1 |
| 59164 | ganadería | 1 |
| 59165 | ganadera | 1 |
| 59166 | ganábamos | 1 |
| 59167 | ganábalo | 1 |
| 59168 | gamuzas | 1 |
| 59169 | gamones | 1 |
| 59170 | gamellas | 1 |
| 59171 | gamella | 1 |
| 59172 | gamboa | 1 |
| 59173 | galparzasoro | 1 |
| 59174 | galonado | 1 |
| 59175 | gallofero | 1 |
| 59176 | gallofería | 1 |
| 59177 | gallofas | 1 |
| 59178 | gallipavos | 1 |
| 59179 | gallineros | 1 |
| 59180 | gallinejera | 1 |
| 59181 | gallineja | 1 |
| 59182 | gallináceas | 1 |
| 59183 | gallillo | 1 |
| 59184 | gallarín | 1 |
| 59185 | gallardísimo | 1 |
| 59186 | gallardísima | 1 |
| 59187 | gallardetes | 1 |
| 59188 | gallardete | 1 |
| 59189 | gallardeó | 1 |
| 59190 | gallardearme | 1 |
| 59191 | gallardeaba | 1 |
| 59192 | gallarde | 1 |
| 59193 | gall | 1 |
| 59194 | galindo | 1 |
| 59195 | galimatías | 1 |
| 59196 | galilea | 1 |
| 59197 | gálico | 1 |
| 59198 | galicismos | 1 |
| 59199 | galicianas | 1 |
| 59200 | galiana | 1 |
| 59201 | galguito | 1 |
| 59202 | galgamentos | 1 |
| 59203 | galerna | 1 |
| 59204 | galeones | 1 |
| 59205 | galeno | 1 |
| 59206 | galdezazu | 1 |
| 59207 | galchagorris | 1 |
| 59208 | galardones | 1 |
| 59209 | galardone | 1 |
| 59210 | galardonaste | 1 |
| 59211 | galardonas | 1 |
| 59212 | galardonaron | 1 |
| 59213 | galardonare | 1 |
| 59214 | galardonados | 1 |
| 59215 | galardonado | 1 |
| 59216 | galaores | 1 |
| 59217 | galantina | 1 |
| 59218 | galantemente | 1 |
| 59219 | galantear | 1 |
| 59220 | galant | 1 |
| 59221 | galanos | 1 |
| 59222 | galana | 1 |
| 59223 | gaiztoac | 1 |
| 59224 | gaie | 1 |
| 59225 | gaho | 1 |
| 59226 | gafo | 1 |
| 59227 | gaditana | 1 |
| 59228 | gacetillas | 1 |
| 59229 | gacela | 1 |
| 59230 | gabrio | 1 |
| 59231 | gabino | 1 |
| 59232 | gabinetillo | 1 |
| 59233 | gabiltzanac | 1 |
| 59234 | gabe | 1 |
| 59235 | gabancito | 1 |
| 59236 | gabancillo | 1 |
| 59237 | gabacho | 1 |
| 59238 | gabachas | 1 |
| 59239 | fyz | 1 |
| 59240 | fyta | 1 |
| 59241 | fyrmado | 1 |
| 59242 | fyno | 1 |
| 59243 | fynco | 1 |
| 59244 | fynchyr | 1 |
| 59245 | fynchadas | 1 |
| 59246 | fynchada | 1 |
| 59247 | fyncavades | 1 |
| 59248 | fyncava | 1 |
| 59249 | fyncase | 1 |
| 59250 | fyncaron | 1 |
| 59251 | fyncar | 1 |
| 59252 | fyncando | 1 |
| 59253 | fyncados | 1 |
| 59254 | fyncado | 1 |
| 59255 | fyncada | 1 |
| 59256 | fygura | 1 |
| 59257 | fygueras | 1 |
| 59258 | fygado | 1 |
| 59259 | fyesta | 1 |
| 59260 | fyere | 1 |
| 59261 | fyende | 1 |
| 59262 | fydalgo | 1 |
| 59263 | fyará | 1 |
| 59264 | fyar | 1 |
| 59265 | fyança | 1 |
| 59266 | fuyr | 1 |
| 59267 | fuylo | 1 |
| 59268 | fuyáis | 1 |
| 59269 | fuyades | 1 |
| 59270 | futraque | 1 |
| 59271 | fútiles | 1 |
| 59272 | fútil | 1 |
| 59273 | fustis | 1 |
| 59274 | fustas | 1 |
| 59275 | fusta | 1 |
| 59276 | fusileros | 1 |
| 59277 | fusilémosle | 1 |
| 59278 | fusilaremos | 1 |
| 59279 | fusilan | 1 |
| 59280 | fusilados | 1 |
| 59281 | fusilaba | 1 |
| 59282 | fusia | 1 |
| 59283 | furtó | 1 |
| 59284 | furtivos | 1 |
| 59285 | furtivo | 1 |
| 59286 | furtillos | 1 |
| 59287 | furtes | 1 |
| 59288 | furte | 1 |
| 59289 | fúrtasle | 1 |
| 59290 | furtase | 1 |
| 59291 | furtaron | 1 |
| 59292 | furtarías | 1 |
| 59293 | furtando | 1 |
| 59294 | furtallo | 1 |
| 59295 | furtados | 1 |
| 59296 | furtadas | 1 |
| 59297 | furniçio | 1 |
| 59298 | furio | 1 |
| 59299 | für | 1 |
| 59300 | fungosa | 1 |
| 59301 | funestos | 1 |
| 59302 | funestísimas | 1 |
| 59303 | funestísima | 1 |
| 59304 | funerarios | 1 |
| 59305 | funera | 1 |
| 59306 | funebridad | 1 |
| 59307 | fundirnos | 1 |
| 59308 | fundimos | 1 |
| 59309 | fundiéndose | 1 |
| 59310 | fundidas | 1 |
| 59311 | fundición | 1 |
| 59312 | fundes | 1 |
| 59313 | fundas | 1 |
| 59314 | fundarse | 1 |
| 59315 | fundándonos | 1 |
| 59316 | fundándome | 1 |
| 59317 | fundando | 1 |
| 59318 | fundamentales | 1 |
| 59319 | fundamenta | 1 |
| 59320 | fundaciones | 1 |
| 59321 | fundábase | 1 |
| 59322 | fundabas | 1 |
| 59323 | funcionó | 1 |
| 59324 | funcionarios | 1 |
| 59325 | funcionaria | 1 |
| 59326 | funcionara | 1 |
| 59327 | funcionante | 1 |
| 59328 | funcionando | 1 |
| 59329 | funcionan | 1 |
| 59330 | funciona | 1 |
| 59331 | funámbula | 1 |
| 59332 | fumigarte | 1 |
| 59333 | fumero | 1 |
| 59334 | fumas | 1 |
| 59335 | fumarse | 1 |
| 59336 | fumadores | 1 |
| 59337 | fumado | 1 |
| 59338 | fumada | 1 |
| 59339 | fulminan | 1 |
| 59340 | fulminado | 1 |
| 59341 | fulanos | 1 |
| 59342 | fulanita | 1 |
| 59343 | fuisteme | 1 |
| 59344 | fuilo | 1 |
| 59345 | fuile | 1 |
| 59346 | fuguillas | 1 |
| 59347 | fugite | 1 |
| 59348 | fugir | 1 |
| 59349 | fugas | 1 |
| 59350 | fuey | 1 |
| 59351 | fuesedes | 1 |
| 59352 | fuérzame | 1 |
| 59353 | fuertecilla | 1 |
| 59354 | fuert | 1 |
| 59355 | fuéronselo | 1 |
| 59356 | fueronse | 1 |
| 59357 | fuéronlo | 1 |
| 59358 | fuéronles | 1 |
| 59359 | fuerit | 1 |
| 59360 | fuerint | 1 |
| 59361 | fuereis | 1 |
| 59362 | fuerço | 1 |
| 59363 | fuerce | 1 |
| 59364 | fuerças | 1 |
| 59365 | fuérale | 1 |
| 59366 | fuerais | 1 |
| 59367 | füera | 1 |
| 59368 | fuentfría | 1 |
| 59369 | fuenterrabía | 1 |
| 59370 | fuentecillas | 1 |
| 59371 | fuenos | 1 |
| 59372 | fuémosnos | 1 |
| 59373 | fuémosle | 1 |
| 59374 | fuéme | 1 |
| 59375 | fuélo | 1 |
| 59376 | fuelo | 1 |
| 59377 | fuelga | 1 |
| 59378 | fueles | 1 |
| 59379 | fúcar | 1 |
| 59380 | fuca | 1 |
| 59381 | frutuosas | 1 |
| 59382 | frutificando | 1 |
| 59383 | frutero | 1 |
| 59384 | fruteras | 1 |
| 59385 | frustrar | 1 |
| 59386 | frustrados | 1 |
| 59387 | frustó | 1 |
| 59388 | fruncir | 1 |
| 59389 | fruncía | 1 |
| 59390 | frugalmente | 1 |
| 59391 | frugalidad | 1 |
| 59392 | fruela | 1 |
| 59393 | fructus | 1 |
| 59394 | fructa | 1 |
| 59395 | fru | 1 |
| 59396 | froten | 1 |
| 59397 | frote | 1 |
| 59398 | frotasen | 1 |
| 59399 | frotáronle | 1 |
| 59400 | frotar | 1 |
| 59401 | frotándole | 1 |
| 59402 | frotándola | 1 |
| 59403 | frotamientos | 1 |
| 59404 | frotábase | 1 |
| 59405 | frotaban | 1 |
| 59406 | fror | 1 |
| 59407 | frontones | 1 |
| 59408 | frontispicios | 1 |
| 59409 | frontispicio | 1 |
| 59410 | frontiles | 1 |
| 59411 | frontil | 1 |
| 59412 | fronterizo | 1 |
| 59413 | frontales | 1 |
| 59414 | frondosidad | 1 |
| 59415 | fronçidas | 1 |
| 59416 | from | 1 |
| 59417 | frojaz | 1 |
| 59418 | froga | 1 |
| 59419 | frívolos | 1 |
| 59420 | frívolas | 1 |
| 59421 | friuras | 1 |
| 59422 | friura | 1 |
| 59423 | frituras | 1 |
| 59424 | fritón | 1 |
| 59425 | fritanga | 1 |
| 59426 | frisón | 1 |
| 59427 | frisado | 1 |
| 59428 | frisaban | 1 |
| 59429 | frios | 1 |
| 59430 | frión | 1 |
| 59431 | frigorífico | 1 |
| 59432 | frigio | 1 |
| 59433 | frigidísimo | 1 |
| 59434 | fríes | 1 |
| 59435 | frieron | 1 |
| 59436 | frida | 1 |
| 59437 | freyr | 1 |
| 59438 | fresquísima | 1 |
| 59439 | fresquecito | 1 |
| 59440 | fresquecita | 1 |
| 59441 | fresnos | 1 |
| 59442 | frescuras | 1 |
| 59443 | frescona | 1 |
| 59444 | frescachona | 1 |
| 59445 | frescachón | 1 |
| 59446 | frenopático | 1 |
| 59447 | frenillados | 1 |
| 59448 | frenéticas | 1 |
| 59449 | frema | 1 |
| 59450 | freidera | 1 |
| 59451 | frei | 1 |
| 59452 | fregoteo | 1 |
| 59453 | fregotee | 1 |
| 59454 | fregones | 1 |
| 59455 | fregaste | 1 |
| 59456 | fregaron | 1 |
| 59457 | fregarlas | 1 |
| 59458 | fregaré | 1 |
| 59459 | fregando | 1 |
| 59460 | fregaban | 1 |
| 59461 | fregaba | 1 |
| 59462 | freeeesero | 1 |
| 59463 | frecuentó | 1 |
| 59464 | frecuentase | 1 |
| 59465 | frecuentan | 1 |
| 59466 | frecuentador | 1 |
| 59467 | frecuentado | 1 |
| 59468 | frechas | 1 |
| 59469 | freatas | 1 |
| 59470 | fraze | 1 |
| 59471 | frazadas | 1 |
| 59472 | frazada | 1 |
| 59473 | frayría | 1 |
| 59474 | fraylía | 1 |
| 59475 | frayla | 1 |
| 59476 | fraudulenta | 1 |
| 59477 | fraudes | 1 |
| 59478 | fratín | 1 |
| 59479 | frática | 1 |
| 59480 | fraternizar | 1 |
| 59481 | frasquita | 1 |
| 59482 | frasquetes | 1 |
| 59483 | frasis | 1 |
| 59484 | frasecillas | 1 |
| 59485 | frasecicas | 1 |
| 59486 | frasear | 1 |
| 59487 | frascuelo | 1 |
| 59488 | frascueeeelo | 1 |
| 59489 | franqueó | 1 |
| 59490 | francote | 1 |
| 59491 | francolines | 1 |
| 59492 | francolín | 1 |
| 59493 | francolí | 1 |
| 59494 | francklin | 1 |
| 59495 | franciscos | 1 |
| 59496 | franciscas | 1 |
| 59497 | françia | 1 |
| 59498 | franchote | 1 |
| 59499 | francesitos | 1 |
| 59500 | francesillas | 1 |
| 59501 | frances | 1 |
| 59502 | francenia | 1 |
| 59503 | français | 1 |
| 59504 | francachelas | 1 |
| 59505 | frailecitos | 1 |
| 59506 | frailecito | 1 |
| 59507 | frailecicos | 1 |
| 59508 | fraigerundio | 1 |
| 59509 | fraguó | 1 |
| 59510 | fraguar | 1 |
| 59511 | fraguado | 1 |
| 59512 | fragrancia | 1 |
| 59513 | fragile | 1 |
| 59514 | fragatonas | 1 |
| 59515 | frade | 1 |
| 59516 | fracasó | 1 |
| 59517 | fracasar | 1 |
| 59518 | fracasado | 1 |
| 59519 | fr | 1 |
| 59520 | foz | 1 |
| 59521 | foydor | 1 |
| 59522 | foydas | 1 |
| 59523 | foyd | 1 |
| 59524 | foya | 1 |
| 59525 | foxieron | 1 |
| 59526 | fourchette | 1 |
| 59527 | fouquier | 1 |
| 59528 | foto | 1 |
| 59529 | fostigarás | 1 |
| 59530 | fosos | 1 |
| 59531 | fósiles | 1 |
| 59532 | fosforito | 1 |
| 59533 | fosfórica | 1 |
| 59534 | fosforeras | 1 |
| 59535 | foscos | 1 |
| 59536 | fosco | 1 |
| 59537 | foscas | 1 |
| 59538 | forzudo | 1 |
| 59539 | forzo | 1 |
| 59540 | forzaua | 1 |
| 59541 | forzaste | 1 |
| 59542 | forzasen | 1 |
| 59543 | forzarles | 1 |
| 59544 | forzarán | 1 |
| 59545 | forzara | 1 |
| 59546 | forzándose | 1 |
| 59547 | forzamos | 1 |
| 59548 | forzador | 1 |
| 59549 | forzadamente | 1 |
| 59550 | forzábame | 1 |
| 59551 | forza | 1 |
| 59552 | fortunilla | 1 |
| 59553 | fortunatita | 1 |
| 59554 | fortunatas | 1 |
| 59555 | fortunaaá | 1 |
| 59556 | fortuitos | 1 |
| 59557 | fortísimos | 1 |
| 59558 | fortísimas | 1 |
| 59559 | fortísimamente | 1 |
| 59560 | fortificó | 1 |
| 59561 | fortificase | 1 |
| 59562 | fortificaron | 1 |
| 59563 | fortifican | 1 |
| 59564 | fortificado | 1 |
| 59565 | fortificaciones | 1 |
| 59566 | fortificación | 1 |
| 59567 | forte | 1 |
| 59568 | fortalecimiento | 1 |
| 59569 | fortaleciéronlas | 1 |
| 59570 | fortalecídose | 1 |
| 59571 | fortalecidos | 1 |
| 59572 | fortalecido | 1 |
| 59573 | fortalecidas | 1 |
| 59574 | fortalecían | 1 |
| 59575 | fortalecía | 1 |
| 59576 | fortalecerá | 1 |
| 59577 | fortalecer | 1 |
| 59578 | forsi | 1 |
| 59579 | forró | 1 |
| 59580 | forradas | 1 |
| 59581 | foros | 1 |
| 59582 | forner | 1 |
| 59583 | fornachos | 1 |
| 59584 | formulismo | 1 |
| 59585 | formularlo | 1 |
| 59586 | formose | 1 |
| 59587 | formo | 1 |
| 59588 | fórmico | 1 |
| 59589 | formeste | 1 |
| 59590 | formemos | 1 |
| 59591 | forméis | 1 |
| 59592 | formasen | 1 |
| 59593 | formarte | 1 |
| 59594 | formarle | 1 |
| 59595 | formarlas | 1 |
| 59596 | formaremos | 1 |
| 59597 | formaran | 1 |
| 59598 | formará | 1 |
| 59599 | formándose | 1 |
| 59600 | formalizarse | 1 |
| 59601 | formalita | 1 |
| 59602 | formalidades | 1 |
| 59603 | formalice | 1 |
| 59604 | forjarse | 1 |
| 59605 | forjaron | 1 |
| 59606 | forjaría | 1 |
| 59607 | forjándose | 1 |
| 59608 | forjan | 1 |
| 59609 | forjaba | 1 |
| 59610 | foribundo | 1 |
| 59611 | forera | 1 |
| 59612 | forcejearon | 1 |
| 59613 | forcejear | 1 |
| 59614 | forcejeaban | 1 |
| 59615 | forcejea | 1 |
| 59616 | forcejaba | 1 |
| 59617 | forcé | 1 |
| 59618 | forçaste | 1 |
| 59619 | forçados | 1 |
| 59620 | forçado | 1 |
| 59621 | forçada | 1 |
| 59622 | forastera | 1 |
| 59623 | forajido | 1 |
| 59624 | foragidos | 1 |
| 59625 | forados | 1 |
| 59626 | fontezicas | 1 |
| 59627 | fontezica | 1 |
| 59628 | fontecilla | 1 |
| 59629 | fontainebleau | 1 |
| 59630 | fonsarios | 1 |
| 59631 | fonético | 1 |
| 59632 | fondistas | 1 |
| 59633 | fondista | 1 |
| 59634 | fondear | 1 |
| 59635 | fondeados | 1 |
| 59636 | fondeaban | 1 |
| 59637 | fondas | 1 |
| 59638 | fomenten | 1 |
| 59639 | fomentas | 1 |
| 59640 | fomentar | 1 |
| 59641 | fomentada | 1 |
| 59642 | fomenta | 1 |
| 59643 | follya | 1 |
| 59644 | folloncicos | 1 |
| 59645 | follis | 1 |
| 59646 | folletitos | 1 |
| 59647 | follajes | 1 |
| 59648 | folios | 1 |
| 59649 | folio | 1 |
| 59650 | folguras | 1 |
| 59651 | folgavan | 1 |
| 59652 | folgaron | 1 |
| 59653 | folgaremos | 1 |
| 59654 | folgaredes | 1 |
| 59655 | folgad | 1 |
| 59656 | fojas | 1 |
| 59657 | foguera | 1 |
| 59658 | fogosos | 1 |
| 59659 | fogosidad | 1 |
| 59660 | fogonero | 1 |
| 59661 | fogonazos | 1 |
| 59662 | fogar | 1 |
| 59663 | fofo | 1 |
| 59664 | foces | 1 |
| 59665 | fluye | 1 |
| 59666 | flutuoso | 1 |
| 59667 | flutuosa | 1 |
| 59668 | fluir | 1 |
| 59669 | fluidos | 1 |
| 59670 | fluido | 1 |
| 59671 | fluidez | 1 |
| 59672 | fluctuant | 1 |
| 59673 | fluctuación | 1 |
| 59674 | floxa | 1 |
| 59675 | flotantes | 1 |
| 59676 | flotación | 1 |
| 59677 | floro | 1 |
| 59678 | floriture | 1 |
| 59679 | florista | 1 |
| 59680 | florisel | 1 |
| 59681 | floripes | 1 |
| 59682 | florilogios | 1 |
| 59683 | floridas | 1 |
| 59684 | floricultor | 1 |
| 59685 | florian | 1 |
| 59686 | flori | 1 |
| 59687 | florezilla | 1 |
| 59688 | flórez | 1 |
| 59689 | floresci | 1 |
| 59690 | florescen | 1 |
| 59691 | florero | 1 |
| 59692 | floreos | 1 |
| 59693 | florentino | 1 |
| 59694 | florentibus | 1 |
| 59695 | florecitas | 1 |
| 59696 | floreció | 1 |
| 59697 | florecilla | 1 |
| 59698 | florecieron | 1 |
| 59699 | florecidos | 1 |
| 59700 | florecido | 1 |
| 59701 | florecidas | 1 |
| 59702 | florecían | 1 |
| 59703 | flojita | 1 |
| 59704 | flojillos | 1 |
| 59705 | flojillo | 1 |
| 59706 | flojas | 1 |
| 59707 | flojamente | 1 |
| 59708 | flexüosas | 1 |
| 59709 | flexiones | 1 |
| 59710 | fléridas | 1 |
| 59711 | flemosa | 1 |
| 59712 | flemático | 1 |
| 59713 | flemáticamente | 1 |
| 59714 | flemática | 1 |
| 59715 | flegmasías | 1 |
| 59716 | flegmasía | 1 |
| 59717 | flechen | 1 |
| 59718 | flechazo | 1 |
| 59719 | flecharla | 1 |
| 59720 | flechados | 1 |
| 59721 | flechadas | 1 |
| 59722 | flebotomía | 1 |
| 59723 | flébiles | 1 |
| 59724 | flayres | 1 |
| 59725 | flayre | 1 |
| 59726 | flatus | 1 |
| 59727 | flatulento | 1 |
| 59728 | flatulenta | 1 |
| 59729 | flaquísimo | 1 |
| 59730 | flaquearon | 1 |
| 59731 | flaquear | 1 |
| 59732 | flaqueaba | 1 |
| 59733 | flaquea | 1 |
| 59734 | flaque | 1 |
| 59735 | flanqueándola | 1 |
| 59736 | flanes | 1 |
| 59737 | flaneo | 1 |
| 59738 | flanco | 1 |
| 59739 | flámulas | 1 |
| 59740 | flammae | 1 |
| 59741 | flamígeros | 1 |
| 59742 | flameando | 1 |
| 59743 | flamas | 1 |
| 59744 | flagrantes | 1 |
| 59745 | fláccido | 1 |
| 59746 | fláccidas | 1 |
| 59747 | fláccida | 1 |
| 59748 | fízose | 1 |
| 59749 | fízos | 1 |
| 59750 | fízome | 1 |
| 59751 | fizome | 1 |
| 59752 | fízom | 1 |
| 59753 | fízolos | 1 |
| 59754 | fízoles | 1 |
| 59755 | fizle | 1 |
| 59756 | fiziesse | 1 |
| 59757 | fizieran | 1 |
| 59758 | fiziera | 1 |
| 59759 | fiunt | 1 |
| 59760 | fito | 1 |
| 59761 | fisonomista | 1 |
| 59762 | fisonómicos | 1 |
| 59763 | fisonómica | 1 |
| 59764 | físole | 1 |
| 59765 | fisnos | 1 |
| 59766 | fisle | 1 |
| 59767 | fisiológicas | 1 |
| 59768 | fisiológicamente | 1 |
| 59769 | fisiognómicos | 1 |
| 59770 | fisico | 1 |
| 59771 | fisica | 1 |
| 59772 | fisgonear | 1 |
| 59773 | fisgando | 1 |
| 59774 | fisga | 1 |
| 59775 | fiscalizar | 1 |
| 59776 | fiscalización | 1 |
| 59777 | fiscalías | 1 |
| 59778 | firmísima | 1 |
| 59779 | firmen | 1 |
| 59780 | firmé | 1 |
| 59781 | firmaron | 1 |
| 59782 | firmarla | 1 |
| 59783 | firmaré | 1 |
| 59784 | firman | 1 |
| 59785 | firmados | 1 |
| 59786 | fióle | 1 |
| 59787 | fïó | 1 |
| 59788 | fio | 1 |
| 59789 | finta | 1 |
| 59790 | finojos | 1 |
| 59791 | finojo | 1 |
| 59792 | fínisimo | 1 |
| 59793 | finis | 1 |
| 59794 | finiquito | 1 |
| 59795 | finiqueleando | 1 |
| 59796 | finibusterræ | 1 |
| 59797 | fingirían | 1 |
| 59798 | fingiremos | 1 |
| 59799 | fingiré | 1 |
| 59800 | fingire | 1 |
| 59801 | fingieron | 1 |
| 59802 | fingiendote | 1 |
| 59803 | fingiéndome | 1 |
| 59804 | fingiéndole | 1 |
| 59805 | finges | 1 |
| 59806 | fingendo | 1 |
| 59807 | find | 1 |
| 59808 | finco | 1 |
| 59809 | finchida | 1 |
| 59810 | finchados | 1 |
| 59811 | finchada | 1 |
| 59812 | fincaste | 1 |
| 59813 | fincar | 1 |
| 59814 | fincan | 1 |
| 59815 | fincada | 1 |
| 59816 | finara | 1 |
| 59817 | financiero | 1 |
| 59818 | financiera | 1 |
| 59819 | finamente | 1 |
| 59820 | finado | 1 |
| 59821 | finada | 1 |
| 59822 | finaba | 1 |
| 59823 | filtro | 1 |
| 59824 | filtrar | 1 |
| 59825 | filtrando | 1 |
| 59826 | filtrado | 1 |
| 59827 | filtrada | 1 |
| 59828 | filtraciones | 1 |
| 59829 | filtración | 1 |
| 59830 | filosomia | 1 |
| 59831 | filosofismo | 1 |
| 59832 | filosofea | 1 |
| 59833 | filosofastros | 1 |
| 59834 | filosofales | 1 |
| 59835 | filosofal | 1 |
| 59836 | filosofaba | 1 |
| 59837 | filósofa | 1 |
| 59838 | filón | 1 |
| 59839 | filología | 1 |
| 59840 | filódoces | 1 |
| 59841 | filó | 1 |
| 59842 | filisteazo | 1 |
| 59843 | filipina | 1 |
| 59844 | filigres | 1 |
| 59845 | filigrana | 1 |
| 59846 | fílidas | 1 |
| 59847 | fílida | 1 |
| 59848 | filibustero | 1 |
| 59849 | filetes | 1 |
| 59850 | filatería | 1 |
| 59851 | filaretes | 1 |
| 59852 | filar | 1 |
| 59853 | filantrópicas | 1 |
| 59854 | filado | 1 |
| 59855 | fijuelo | 1 |
| 59856 | fijóse | 1 |
| 59857 | fijosdalgo | 1 |
| 59858 | fijodalgo | 1 |
| 59859 | fijemos | 1 |
| 59860 | fijase | 1 |
| 59861 | fijasdalgo | 1 |
| 59862 | fijarlo | 1 |
| 59863 | fijarle | 1 |
| 59864 | fijarlas | 1 |
| 59865 | fijaría | 1 |
| 59866 | fijarán | 1 |
| 59867 | fijara | 1 |
| 59868 | fijándome | 1 |
| 59869 | fijados | 1 |
| 59870 | fijadas | 1 |
| 59871 | fijación | 1 |
| 59872 | figuróseme | 1 |
| 59873 | figurose | 1 |
| 59874 | figurones | 1 |
| 59875 | figuronas | 1 |
| 59876 | figurita | 1 |
| 59877 | figúreselo | 1 |
| 59878 | figúresela | 1 |
| 59879 | figures | 1 |
| 59880 | figureros | 1 |
| 59881 | figúrenselo | 1 |
| 59882 | figuremos | 1 |
| 59883 | figuré | 1 |
| 59884 | figure | 1 |
| 59885 | figuraseme | 1 |
| 59886 | figurársele | 1 |
| 59887 | figurármelo | 1 |
| 59888 | figuraríamos | 1 |
| 59889 | figurare | 1 |
| 59890 | figuraran | 1 |
| 59891 | figurándoselo | 1 |
| 59892 | figurándosela | 1 |
| 59893 | figurándonos | 1 |
| 59894 | figurándome | 1 |
| 59895 | figurados | 1 |
| 59896 | figuraciones | 1 |
| 59897 | figurábaseme | 1 |
| 59898 | figuerola | 1 |
| 59899 | figu | 1 |
| 59900 | figos | 1 |
| 59901 | fígados | 1 |
| 59902 | fierísimo | 1 |
| 59903 | fieri | 1 |
| 59904 | fierecilla | 1 |
| 59905 | fierbe | 1 |
| 59906 | fielding | 1 |
| 59907 | fieldad | 1 |
| 59908 | fielatos | 1 |
| 59909 | fíelas | 1 |
| 59910 | fiéis | 1 |
| 59911 | fiedes | 1 |
| 59912 | fie | 1 |
| 59913 | fido | 1 |
| 59914 | fideputa | 1 |
| 59915 | fideo | 1 |
| 59916 | fidelium | 1 |
| 59917 | fidelísima | 1 |
| 59918 | fidelidades | 1 |
| 59919 | fidedigno | 1 |
| 59920 | fidedignas | 1 |
| 59921 | fidalguía | 1 |
| 59922 | fidalgos | 1 |
| 59923 | ficus | 1 |
| 59924 | ficticios | 1 |
| 59925 | ficticio | 1 |
| 59926 | ficticia | 1 |
| 59927 | fictas | 1 |
| 59928 | ficion | 1 |
| 59929 | ficiesen | 1 |
| 59930 | ficarás | 1 |
| 59931 | fiauan | 1 |
| 59932 | fiásemos | 1 |
| 59933 | fiase | 1 |
| 59934 | fiasco | 1 |
| 59935 | fiaron | 1 |
| 59936 | fiaré | 1 |
| 59937 | fiano | 1 |
| 59938 | fiándose | 1 |
| 59939 | fïando | 1 |
| 59940 | fiancó | 1 |
| 59941 | fiambreras | 1 |
| 59942 | fiadura | 1 |
| 59943 | fiadora | 1 |
| 59944 | fiad | 1 |
| 59945 | fiaban | 1 |
| 59946 | ffyz | 1 |
| 59947 | ffyncó | 1 |
| 59948 | ffuy | 1 |
| 59949 | ffurtól | 1 |
| 59950 | ffurtava | 1 |
| 59951 | ffurtar | 1 |
| 59952 | ffurón | 1 |
| 59953 | ffuime | 1 |
| 59954 | ffuerte | 1 |
| 59955 | ffuéronse | 1 |
| 59956 | ffrançés | 1 |
| 59957 | fforadóse | 1 |
| 59958 | ffollya | 1 |
| 59959 | ffizvos | 1 |
| 59960 | ffízose | 1 |
| 59961 | ffiestas | 1 |
| 59962 | ffesieron | 1 |
| 59963 | ffecho | 1 |
| 59964 | ffazle | 1 |
| 59965 | ffázeslo | 1 |
| 59966 | ffázesles | 1 |
| 59967 | ffázele | 1 |
| 59968 | ffaz | 1 |
| 59969 | ffasíe | 1 |
| 59970 | ffases | 1 |
| 59971 | ffasaña | 1 |
| 59972 | ffaría | 1 |
| 59973 | ffallyr | 1 |
| 59974 | ffallarás | 1 |
| 59975 | ffaciendo | 1 |
| 59976 | ffabla | 1 |
| 59977 | feziste | 1 |
| 59978 | feziesen | 1 |
| 59979 | fezieron | 1 |
| 59980 | feziere | 1 |
| 59981 | fey | 1 |
| 59982 | feuillistes | 1 |
| 59983 | feúcha | 1 |
| 59984 | fetiches | 1 |
| 59985 | fesyeron | 1 |
| 59986 | festones | 1 |
| 59987 | festoneados | 1 |
| 59988 | festividad | 1 |
| 59989 | festivas | 1 |
| 59990 | festiuidad | 1 |
| 59991 | festino | 1 |
| 59992 | festejó | 1 |
| 59993 | festéjase | 1 |
| 59994 | festejando | 1 |
| 59995 | festejalle | 1 |
| 59996 | feste | 1 |
| 59997 | fesieron | 1 |
| 59998 | fesiere | 1 |
| 59999 | feses | 1 |
| 60000 | fervos | 1 |
| 60001 | fervoroso | 1 |
| 60002 | fertilizar | 1 |
| 60003 | fertiliza | 1 |
| 60004 | ferruje | 1 |
| 60005 | ferretero | 1 |
| 60006 | ferretería | 1 |
| 60007 | ferretera | 1 |
| 60008 | ferrero | 1 |
| 60009 | férrea | 1 |
| 60010 | ferre | 1 |
| 60011 | ferrava | 1 |
| 60012 | ferrara | 1 |
| 60013 | ferrant | 1 |
| 60014 | ferrando | 1 |
| 60015 | ferrandez | 1 |
| 60016 | ferrado | 1 |
| 60017 | ferrada | 1 |
| 60018 | ferozmente | 1 |
| 60019 | ferocísimo | 1 |
| 60020 | ferocidades | 1 |
| 60021 | fernand | 1 |
| 60022 | fermosuras | 1 |
| 60023 | fermosur | 1 |
| 60024 | fermosillos | 1 |
| 60025 | fermentaron | 1 |
| 60026 | fermentando | 1 |
| 60027 | fermentados | 1 |
| 60028 | fermenta | 1 |
| 60029 | ferieron | 1 |
| 60030 | feríen | 1 |
| 60031 | feridos | 1 |
| 60032 | ferid | 1 |
| 60033 | feriar | 1 |
| 60034 | feríanlo | 1 |
| 60035 | ferdinand | 1 |
| 60036 | feotes | 1 |
| 60037 | feona | 1 |
| 60038 | feón | 1 |
| 60039 | fenómenas | 1 |
| 60040 | feno | 1 |
| 60041 | feniestras | 1 |
| 60042 | fénico | 1 |
| 60043 | fenicias | 1 |
| 60044 | fenicia | 1 |
| 60045 | fengir | 1 |
| 60046 | fengidos | 1 |
| 60047 | fenestras | 1 |
| 60048 | fenescieron | 1 |
| 60049 | fenesçer | 1 |
| 60050 | fenescer | 1 |
| 60051 | fendientes | 1 |
| 60052 | fenderían | 1 |
| 60053 | femineo | 1 |
| 60054 | féme | 1 |
| 60055 | fembras | 1 |
| 60056 | felpilla | 1 |
| 60057 | felpas | 1 |
| 60058 | felonías | 1 |
| 60059 | felix | 1 |
| 60060 | felinos | 1 |
| 60061 | felino | 1 |
| 60062 | felinas | 1 |
| 60063 | felina | 1 |
| 60064 | feligrés | 1 |
| 60065 | felicíteme | 1 |
| 60066 | felicitarme | 1 |
| 60067 | felicitándose | 1 |
| 60068 | felicitado | 1 |
| 60069 | felicísimas | 1 |
| 60070 | feliciano | 1 |
| 60071 | felicia | 1 |
| 60072 | félices | 1 |
| 60073 | feíto | 1 |
| 60074 | feíta | 1 |
| 60075 | feísimo | 1 |
| 60076 | feijóo | 1 |
| 60077 | fehacientes | 1 |
| 60078 | fegurada | 1 |
| 60079 | fees | 1 |
| 60080 | fedro | 1 |
| 60081 | fediondo | 1 |
| 60082 | federación | 1 |
| 60083 | feçystelos | 1 |
| 60084 | feçyste | 1 |
| 60085 | fecundísimo | 1 |
| 60086 | fecundar | 1 |
| 60087 | feculentos | 1 |
| 60088 | fecistes | 1 |
| 60089 | feciste | 1 |
| 60090 | feçiesen | 1 |
| 60091 | feçieron | 1 |
| 60092 | feçiéredes | 1 |
| 60093 | fechuría | 1 |
| 60094 | fechadura | 1 |
| 60095 | febre | 1 |
| 60096 | febos | 1 |
| 60097 | feblero | 1 |
| 60098 | featón | 1 |
| 60099 | fazte | 1 |
| 60100 | fazlo | 1 |
| 60101 | fazles | 1 |
| 60102 | faziones | 1 |
| 60103 | fazíes | 1 |
| 60104 | faziente | 1 |
| 60105 | fazíen | 1 |
| 60106 | faziase | 1 |
| 60107 | fazías | 1 |
| 60108 | fazias | 1 |
| 60109 | fazíansele | 1 |
| 60110 | fazíanme | 1 |
| 60111 | fazianl | 1 |
| 60112 | fazet | 1 |
| 60113 | fázeste | 1 |
| 60114 | fázesme | 1 |
| 60115 | fázeslos | 1 |
| 60116 | fázeslo | 1 |
| 60117 | fázesle | 1 |
| 60118 | fazeslas | 1 |
| 60119 | fázesla | 1 |
| 60120 | fázes | 1 |
| 60121 | fazerte | 1 |
| 60122 | fazert | 1 |
| 60123 | fazerse | 1 |
| 60124 | fazerme | 1 |
| 60125 | fazerlo | 1 |
| 60126 | fazerle | 1 |
| 60127 | fazemos | 1 |
| 60128 | fázelo | 1 |
| 60129 | fázelas | 1 |
| 60130 | fazela | 1 |
| 60131 | fazel | 1 |
| 60132 | fazedor | 1 |
| 60133 | fazañero | 1 |
| 60134 | faza | 1 |
| 60135 | fayle | 1 |
| 60136 | fay | 1 |
| 60137 | favoritos | 1 |
| 60138 | favoridos | 1 |
| 60139 | favorézcate | 1 |
| 60140 | favorezcas | 1 |
| 60141 | favorezcan | 1 |
| 60142 | favoreciéndome | 1 |
| 60143 | favoreciéndoles | 1 |
| 60144 | favoreciéndola | 1 |
| 60145 | favoreces | 1 |
| 60146 | favorecerse | 1 |
| 60147 | favorecernos | 1 |
| 60148 | favorecerla | 1 |
| 60149 | favorecedoras | 1 |
| 60150 | favorablemente | 1 |
| 60151 | favonio | 1 |
| 60152 | favila | 1 |
| 60153 | favas | 1 |
| 60154 | fausta | 1 |
| 60155 | fauoreceme | 1 |
| 60156 | fauorables | 1 |
| 60157 | fauno | 1 |
| 60158 | fatuidades | 1 |
| 60159 | fatigosos | 1 |
| 60160 | fatigóse | 1 |
| 60161 | fatigosas | 1 |
| 60162 | fatigó | 1 |
| 60163 | fatigarte | 1 |
| 60164 | fatigaron | 1 |
| 60165 | fatigarnos | 1 |
| 60166 | fatigaría | 1 |
| 60167 | fatigara | 1 |
| 60168 | fatigándose | 1 |
| 60169 | fatigan | 1 |
| 60170 | fatigalles | 1 |
| 60171 | fatigadísimo | 1 |
| 60172 | fatigábase | 1 |
| 60173 | fatídicos | 1 |
| 60174 | fatídico | 1 |
| 60175 | fatídica | 1 |
| 60176 | fatalista | 1 |
| 60177 | fatalidades | 1 |
| 60178 | fasyendo | 1 |
| 60179 | fastuosidad | 1 |
| 60180 | fastos | 1 |
| 60181 | fastio | 1 |
| 60182 | fastidiosos | 1 |
| 60183 | fastídiese | 1 |
| 60184 | fastidie | 1 |
| 60185 | fastidiarle | 1 |
| 60186 | fastidiando | 1 |
| 60187 | fastidian | 1 |
| 60188 | fastidiado | 1 |
| 60189 | faste | 1 |
| 60190 | fasle | 1 |
| 60191 | fasiéndola | 1 |
| 60192 | fasie | 1 |
| 60193 | fashionables | 1 |
| 60194 | faset | 1 |
| 60195 | fasert | 1 |
| 60196 | faserle | 1 |
| 60197 | fásenos | 1 |
| 60198 | fasemos | 1 |
| 60199 | fasedores | 1 |
| 60200 | fasedor | 1 |
| 60201 | fasedlo | 1 |
| 60202 | fascinadores | 1 |
| 60203 | fascinador | 1 |
| 60204 | fascinaban | 1 |
| 60205 | fascas | 1 |
| 60206 | fasañero | 1 |
| 60207 | fasañas | 1 |
| 60208 | faryna | 1 |
| 60209 | farto | 1 |
| 60210 | farte | 1 |
| 60211 | fartax | 1 |
| 60212 | fartarás | 1 |
| 60213 | fartará | 1 |
| 60214 | farta | 1 |
| 60215 | farseto | 1 |
| 60216 | farsantuelo | 1 |
| 60217 | farsanta | 1 |
| 60218 | faronía | 1 |
| 60219 | farón | 1 |
| 60220 | farolona | 1 |
| 60221 | farolillo | 1 |
| 60222 | farnesios | 1 |
| 60223 | farmacopea | 1 |
| 60224 | farmacias | 1 |
| 60225 | fariseas | 1 |
| 60226 | faringe | 1 |
| 60227 | faríemos | 1 |
| 60228 | farías | 1 |
| 60229 | faria | 1 |
| 60230 | farfantonas | 1 |
| 60231 | farfantona | 1 |
| 60232 | fares | 1 |
| 60233 | faremos | 1 |
| 60234 | farece | 1 |
| 60235 | fardida | 1 |
| 60236 | fardeles | 1 |
| 60237 | faras | 1 |
| 60238 | faraón | 1 |
| 60239 | farán | 1 |
| 60240 | faquín | 1 |
| 60241 | fantesía | 1 |
| 60242 | fantasya | 1 |
| 60243 | fantastica | 1 |
| 60244 | fantasmones | 1 |
| 60245 | fantasmonas | 1 |
| 60246 | fantasmón | 1 |
| 60247 | fantasmagórica | 1 |
| 60248 | fantasmagoría | 1 |
| 60249 | fantasiosa | 1 |
| 60250 | fantasiar | 1 |
| 60251 | fantasia | 1 |
| 60252 | fantaseado | 1 |
| 60253 | fantaseaba | 1 |
| 60254 | fangoso | 1 |
| 60255 | fanfarronada | 1 |
| 60256 | fanfarria | 1 |
| 60257 | fanegadas | 1 |
| 60258 | fando | 1 |
| 60259 | fandanguero | 1 |
| 60260 | fandangos | 1 |
| 60261 | fandangona | 1 |
| 60262 | fandango | 1 |
| 60263 | fancy | 1 |
| 60264 | fanbriento | 1 |
| 60265 | fanatizada | 1 |
| 60266 | fanáticas | 1 |
| 60267 | famulorum | 1 |
| 60268 | famularum | 1 |
| 60269 | famular | 1 |
| 60270 | famosísimos | 1 |
| 60271 | famo | 1 |
| 60272 | familiona | 1 |
| 60273 | familión | 1 |
| 60274 | familiarizarse | 1 |
| 60275 | familiarizaran | 1 |
| 60276 | familiarizara | 1 |
| 60277 | familiarizados | 1 |
| 60278 | familiarizadas | 1 |
| 60279 | familiaridades | 1 |
| 60280 | famélicos | 1 |
| 60281 | famélicas | 1 |
| 60282 | fambre | 1 |
| 60283 | famas | 1 |
| 60284 | falúa | 1 |
| 60285 | faltriqueras | 1 |
| 60286 | faltoncito | 1 |
| 60287 | faltón | 1 |
| 60288 | faltole | 1 |
| 60289 | faltes | 1 |
| 60290 | falten | 1 |
| 60291 | faltemos | 1 |
| 60292 | falteme | 1 |
| 60293 | faltasse | 1 |
| 60294 | faltasen | 1 |
| 60295 | faltarte | 1 |
| 60296 | faltarse | 1 |
| 60297 | faltarnos | 1 |
| 60298 | faltaren | 1 |
| 60299 | faltaremos | 1 |
| 60300 | fáltanme | 1 |
| 60301 | faltandome | 1 |
| 60302 | faltandoles | 1 |
| 60303 | faltalle | 1 |
| 60304 | faltales | 1 |
| 60305 | faltábanle | 1 |
| 60306 | falssedat | 1 |
| 60307 | falssas | 1 |
| 60308 | falsopecto | 1 |
| 60309 | falsó | 1 |
| 60310 | falsísimo | 1 |
| 60311 | falsísima | 1 |
| 60312 | falsificó | 1 |
| 60313 | falsificadas | 1 |
| 60314 | falsías | 1 |
| 60315 | falsía | 1 |
| 60316 | falsear | 1 |
| 60317 | falsean | 1 |
| 60318 | falseamiento | 1 |
| 60319 | falsaua | 1 |
| 60320 | falsaste | 1 |
| 60321 | falsarias | 1 |
| 60322 | fallós | 1 |
| 60323 | fallir | 1 |
| 60324 | fallidas | 1 |
| 60325 | fallías | 1 |
| 60326 | fallía | 1 |
| 60327 | fallese | 1 |
| 60328 | fallesçer | 1 |
| 60329 | fallesce | 1 |
| 60330 | falles | 1 |
| 60331 | fallençia | 1 |
| 60332 | fallen | 1 |
| 60333 | fallecieron | 1 |
| 60334 | fallecida | 1 |
| 60335 | fallecen | 1 |
| 60336 | falleçedero | 1 |
| 60337 | falleçe | 1 |
| 60338 | fallece | 1 |
| 60339 | fallaste | 1 |
| 60340 | fallase | 1 |
| 60341 | fallas | 1 |
| 60342 | fallaron | 1 |
| 60343 | fallares | 1 |
| 60344 | fallare | 1 |
| 60345 | fallará | 1 |
| 60346 | fallara | 1 |
| 60347 | fállanse | 1 |
| 60348 | falladas | 1 |
| 60349 | falimente | 1 |
| 60350 | faldragas | 1 |
| 60351 | faldonada | 1 |
| 60352 | faldillas | 1 |
| 60353 | faldetas | 1 |
| 60354 | falderillo | 1 |
| 60355 | faldellines | 1 |
| 60356 | falcón | 1 |
| 60357 | falcon | 1 |
| 60358 | falces | 1 |
| 60359 | falaris | 1 |
| 60360 | falanges | 1 |
| 60361 | falanga | 1 |
| 60362 | falaguero | 1 |
| 60363 | falagaré | 1 |
| 60364 | falagada | 1 |
| 60365 | falagábale | 1 |
| 60366 | falacias | 1 |
| 60367 | falacia | 1 |
| 60368 | fajo | 1 |
| 60369 | fajita | 1 |
| 60370 | fajina | 1 |
| 60371 | fajaron | 1 |
| 60372 | fajarlo | 1 |
| 60373 | fajados | 1 |
| 60374 | fajado | 1 |
| 60375 | fajaban | 1 |
| 60376 | fágote | 1 |
| 60377 | fagollaga | 1 |
| 60378 | fagase | 1 |
| 60379 | fadrique | 1 |
| 60380 | fadiga | 1 |
| 60381 | fadar | 1 |
| 60382 | fadado | 1 |
| 60383 | facultativos | 1 |
| 60384 | facultativa | 1 |
| 60385 | factus | 1 |
| 60386 | factura | 1 |
| 60387 | factorías | 1 |
| 60388 | factores | 1 |
| 60389 | facto | 1 |
| 60390 | facta | 1 |
| 60391 | facsímile | 1 |
| 60392 | façon | 1 |
| 60393 | facinorosos | 1 |
| 60394 | facinorosas | 1 |
| 60395 | facinorosa | 1 |
| 60396 | facimus | 1 |
| 60397 | facilité | 1 |
| 60398 | facilitarlo | 1 |
| 60399 | facilitaría | 1 |
| 60400 | facilitando | 1 |
| 60401 | facilitan | 1 |
| 60402 | facilitación | 1 |
| 60403 | facilísima | 1 |
| 60404 | facilidades | 1 |
| 60405 | facile | 1 |
| 60406 | facil | 1 |
| 60407 | façiet | 1 |
| 60408 | facientibus | 1 |
| 60409 | façienda | 1 |
| 60410 | façien | 1 |
| 60411 | façías | 1 |
| 60412 | faciales | 1 |
| 60413 | façía | 1 |
| 60414 | fachenda | 1 |
| 60415 | fachas | 1 |
| 60416 | faceto | 1 |
| 60417 | fáçete | 1 |
| 60418 | faces | 1 |
| 60419 | façerte | 1 |
| 60420 | faceros | 1 |
| 60421 | facerle | 1 |
| 60422 | facere | 1 |
| 60423 | façer | 1 |
| 60424 | fáçenlo | 1 |
| 60425 | façen | 1 |
| 60426 | facen | 1 |
| 60427 | façemos | 1 |
| 60428 | façedes | 1 |
| 60429 | faced | 1 |
| 60430 | façe | 1 |
| 60431 | facas | 1 |
| 60432 | façañas | 1 |
| 60433 | fabulistas | 1 |
| 60434 | fabulearse | 1 |
| 60435 | fabrilla | 1 |
| 60436 | fabricio | 1 |
| 60437 | fabricase | 1 |
| 60438 | fabricarse | 1 |
| 60439 | fabricarla | 1 |
| 60440 | fabricarían | 1 |
| 60441 | fabricamos | 1 |
| 60442 | fabricados | 1 |
| 60443 | fabricadas | 1 |
| 60444 | fabrasen | 1 |
| 60445 | fabrar | 1 |
| 60446 | fablóme | 1 |
| 60447 | fablóle | 1 |
| 60448 | fablilla | 1 |
| 60449 | fabliella | 1 |
| 60450 | fabliau | 1 |
| 60451 | fableste | 1 |
| 60452 | fablen | 1 |
| 60453 | fablémoslo | 1 |
| 60454 | fablemos | 1 |
| 60455 | fabléla | 1 |
| 60456 | fablél | 1 |
| 60457 | fabledes | 1 |
| 60458 | fablé | 1 |
| 60459 | fablatle | 1 |
| 60460 | fablastes | 1 |
| 60461 | fablassen | 1 |
| 60462 | fáblasles | 1 |
| 60463 | fablarvos | 1 |
| 60464 | fablarnos | 1 |
| 60465 | fablarme | 1 |
| 60466 | fablaredes | 1 |
| 60467 | fablaré | 1 |
| 60468 | fablardes | 1 |
| 60469 | fablarás | 1 |
| 60470 | fablan | 1 |
| 60471 | fáblales | 1 |
| 60472 | fáblale | 1 |
| 60473 | fablador | 1 |
| 60474 | fabladme | 1 |
| 60475 | fabladla | 1 |
| 60476 | fabládesme | 1 |
| 60477 | fablaban | 1 |
| 60478 | fabios | 1 |
| 60479 | fabiolita | 1 |
| 60480 | fabiola | 1 |
| 60481 | ezquerdo | 1 |
| 60482 | ezpeleta | 1 |
| 60483 | ezpaniaco | 1 |
| 60484 | ezechías | 1 |
| 60485 | ezcon | 1 |
| 60486 | eyvernada | 1 |
| 60487 | eylau | 1 |
| 60488 | ey | 1 |
| 60489 | extrememos | 1 |
| 60490 | extremando | 1 |
| 60491 | extremaba | 1 |
| 60492 | extrayendo | 1 |
| 60493 | extravió | 1 |
| 60494 | extraviasen | 1 |
| 60495 | extraviarle | 1 |
| 60496 | extraviaba | 1 |
| 60497 | extravagantísimos | 1 |
| 60498 | extravagantísimas | 1 |
| 60499 | extratante | 1 |
| 60500 | extrañísimas | 1 |
| 60501 | extrañísima | 1 |
| 60502 | extrañase | 1 |
| 60503 | extrañaron | 1 |
| 60504 | extrañarían | 1 |
| 60505 | extrañando | 1 |
| 60506 | extrañamos | 1 |
| 60507 | extrañados | 1 |
| 60508 | extranjis | 1 |
| 60509 | extranjerote | 1 |
| 60510 | extranjerismo | 1 |
| 60511 | extramuros | 1 |
| 60512 | extralimitarse | 1 |
| 60513 | extralimitándome | 1 |
| 60514 | extrajeron | 1 |
| 60515 | extraída | 1 |
| 60516 | extraía | 1 |
| 60517 | extraerle | 1 |
| 60518 | extractor | 1 |
| 60519 | extracciones | 1 |
| 60520 | extracción | 1 |
| 60521 | extollite | 1 |
| 60522 | extirparla | 1 |
| 60523 | extirpar | 1 |
| 60524 | extirpados | 1 |
| 60525 | extinguiose | 1 |
| 60526 | extinguieran | 1 |
| 60527 | extinguiera | 1 |
| 60528 | extinguía | 1 |
| 60529 | extingue | 1 |
| 60530 | extinción | 1 |
| 60531 | exterminios | 1 |
| 60532 | exteriorizarse | 1 |
| 60533 | exterioridades | 1 |
| 60534 | extenuada | 1 |
| 60535 | extenuación | 1 |
| 60536 | extensísimo | 1 |
| 60537 | extensiones | 1 |
| 60538 | extensas | 1 |
| 60539 | extensamente | 1 |
| 60540 | extensa | 1 |
| 60541 | extendióseles | 1 |
| 60542 | extendieron | 1 |
| 60543 | extendiera | 1 |
| 60544 | extendiéndome | 1 |
| 60545 | extendiéndolas | 1 |
| 60546 | extendí | 1 |
| 60547 | extenderlas | 1 |
| 60548 | extendería | 1 |
| 60549 | extenderemos | 1 |
| 60550 | extáticos | 1 |
| 60551 | extática | 1 |
| 60552 | extasían | 1 |
| 60553 | extasiada | 1 |
| 60554 | extasía | 1 |
| 60555 | éxtasi | 1 |
| 60556 | expusiera | 1 |
| 60557 | expúsele | 1 |
| 60558 | expurgar | 1 |
| 60559 | expurgación | 1 |
| 60560 | expulso | 1 |
| 60561 | expulsarla | 1 |
| 60562 | expulsados | 1 |
| 60563 | expulsadas | 1 |
| 60564 | expugnarla | 1 |
| 60565 | expugnador | 1 |
| 60566 | expropiado | 1 |
| 60567 | expropiación | 1 |
| 60568 | exprimir | 1 |
| 60569 | exprimió | 1 |
| 60570 | exprimieron | 1 |
| 60571 | exprimidas | 1 |
| 60572 | exprimían | 1 |
| 60573 | expriman | 1 |
| 60574 | exprima | 1 |
| 60575 | express | 1 |
| 60576 | exprese | 1 |
| 60577 | expresase | 1 |
| 60578 | expresas | 1 |
| 60579 | expresaron | 1 |
| 60580 | expresarlo | 1 |
| 60581 | expresarle | 1 |
| 60582 | expresarlas | 1 |
| 60583 | expresándole | 1 |
| 60584 | expresamente | 1 |
| 60585 | expresados | 1 |
| 60586 | expresábase | 1 |
| 60587 | expositor | 1 |
| 60588 | expositio | 1 |
| 60589 | exposiciones | 1 |
| 60590 | exportado | 1 |
| 60591 | exponiendo | 1 |
| 60592 | exponían | 1 |
| 60593 | expones | 1 |
| 60594 | exponerme | 1 |
| 60595 | exponerla | 1 |
| 60596 | exponente | 1 |
| 60597 | expondría | 1 |
| 60598 | expondré | 1 |
| 60599 | explotarse | 1 |
| 60600 | explotarlos | 1 |
| 60601 | explotarlo | 1 |
| 60602 | explotaré | 1 |
| 60603 | explotados | 1 |
| 60604 | explotada | 1 |
| 60605 | exploremos | 1 |
| 60606 | explore | 1 |
| 60607 | explorando | 1 |
| 60608 | exploradores | 1 |
| 60609 | explíquenos | 1 |
| 60610 | explíquemelo | 1 |
| 60611 | explíqueme | 1 |
| 60612 | explicole | 1 |
| 60613 | explícitamente | 1 |
| 60614 | explícita | 1 |
| 60615 | explicit | 1 |
| 60616 | explicártelo | 1 |
| 60617 | explicárselas | 1 |
| 60618 | explicármelo | 1 |
| 60619 | explicaran | 1 |
| 60620 | explicará | 1 |
| 60621 | explicados | 1 |
| 60622 | explicada | 1 |
| 60623 | explayose | 1 |
| 60624 | explaye | 1 |
| 60625 | explayándose | 1 |
| 60626 | explayábase | 1 |
| 60627 | explanó | 1 |
| 60628 | explanara | 1 |
| 60629 | explana | 1 |
| 60630 | expirantes | 1 |
| 60631 | expirante | 1 |
| 60632 | expiraban | 1 |
| 60633 | expiar | 1 |
| 60634 | expiad | 1 |
| 60635 | expiación | 1 |
| 60636 | expertísimo | 1 |
| 60637 | experimenté | 1 |
| 60638 | experimente | 1 |
| 60639 | experimentamos | 1 |
| 60640 | experimentales | 1 |
| 60641 | experimentada | 1 |
| 60642 | experimentábamos | 1 |
| 60643 | expensas | 1 |
| 60644 | expenden | 1 |
| 60645 | expelía | 1 |
| 60646 | expeditiva | 1 |
| 60647 | expedita | 1 |
| 60648 | expedido | 1 |
| 60649 | expedicionarios | 1 |
| 60650 | expatriación | 1 |
| 60651 | expartidario | 1 |
| 60652 | expansivos | 1 |
| 60653 | expansivas | 1 |
| 60654 | expansivamente | 1 |
| 60655 | exótica | 1 |
| 60656 | exornados | 1 |
| 60657 | exorcismos | 1 |
| 60658 | exorcice | 1 |
| 60659 | exorbitantes | 1 |
| 60660 | exorbitante | 1 |
| 60661 | exorbitancia | 1 |
| 60662 | exitazo | 1 |
| 60663 | existís | 1 |
| 60664 | existiría | 1 |
| 60665 | existiesen | 1 |
| 60666 | existiese | 1 |
| 60667 | existiendo | 1 |
| 60668 | existes | 1 |
| 60669 | existencía | 1 |
| 60670 | existan | 1 |
| 60671 | eximios | 1 |
| 60672 | eximio | 1 |
| 60673 | exíjase | 1 |
| 60674 | exija | 1 |
| 60675 | exigüidad | 1 |
| 60676 | exigua | 1 |
| 60677 | exigirle | 1 |
| 60678 | exigiendo | 1 |
| 60679 | exigí | 1 |
| 60680 | exigente | 1 |
| 60681 | exido | 1 |
| 60682 | exhortándoles | 1 |
| 60683 | exhortándole | 1 |
| 60684 | exhortaba | 1 |
| 60685 | exhorta | 1 |
| 60686 | exhibir | 1 |
| 60687 | exhibe | 1 |
| 60688 | exhaustas | 1 |
| 60689 | exhausta | 1 |
| 60690 | exhalaron | 1 |
| 60691 | exhalada | 1 |
| 60692 | exhalaban | 1 |
| 60693 | exhalaba | 1 |
| 60694 | exguerrillero | 1 |
| 60695 | exeunt | 1 |
| 60696 | exercicio | 1 |
| 60697 | exequatur | 1 |
| 60698 | exento | 1 |
| 60699 | exentarse | 1 |
| 60700 | exegéticas | 1 |
| 60701 | executaste | 1 |
| 60702 | execración | 1 |
| 60703 | excusemos | 1 |
| 60704 | excúsase | 1 |
| 60705 | excusarme | 1 |
| 60706 | excusarlo | 1 |
| 60707 | excusaremos | 1 |
| 60708 | excusáramos | 1 |
| 60709 | excusallo | 1 |
| 60710 | excusadas | 1 |
| 60711 | excusada | 1 |
| 60712 | excumunión | 1 |
| 60713 | excrecencia | 1 |
| 60714 | excosechero | 1 |
| 60715 | excluyó | 1 |
| 60716 | excluye | 1 |
| 60717 | exclusivismo | 1 |
| 60718 | exclusivas | 1 |
| 60719 | excluían | 1 |
| 60720 | exclaustrar | 1 |
| 60721 | exclaustrados | 1 |
| 60722 | exclaustrado | 1 |
| 60723 | exclaustración | 1 |
| 60724 | exclamará | 1 |
| 60725 | exclamando | 1 |
| 60726 | exclamado | 1 |
| 60727 | exclamábamos | 1 |
| 60728 | excites | 1 |
| 60729 | excite | 1 |
| 60730 | excitase | 1 |
| 60731 | excitaron | 1 |
| 60732 | excitarle | 1 |
| 60733 | excitando | 1 |
| 60734 | excitadota | 1 |
| 60735 | excitadísimo | 1 |
| 60736 | excitadilla | 1 |
| 60737 | excitadas | 1 |
| 60738 | exceto | 1 |
| 60739 | excetado | 1 |
| 60740 | excesso | 1 |
| 60741 | exceptúen | 1 |
| 60742 | exceptuando | 1 |
| 60743 | exceptuaba | 1 |
| 60744 | excéntricos | 1 |
| 60745 | excentricidades | 1 |
| 60746 | excéntricas | 1 |
| 60747 | excelsos | 1 |
| 60748 | excellencia | 1 |
| 60749 | excelentissimo | 1 |
| 60750 | excelentísimos | 1 |
| 60751 | excelentísima | 1 |
| 60752 | excelentemente | 1 |
| 60753 | excedió | 1 |
| 60754 | excedio | 1 |
| 60755 | excediese | 1 |
| 60756 | excedida | 1 |
| 60757 | excedería | 1 |
| 60758 | exasperaba | 1 |
| 60759 | examino | 1 |
| 60760 | examinarme | 1 |
| 60761 | examinarlo | 1 |
| 60762 | examinarlas | 1 |
| 60763 | examinarla | 1 |
| 60764 | examinaré | 1 |
| 60765 | examinándolos | 1 |
| 60766 | examínalo | 1 |
| 60767 | examínale | 1 |
| 60768 | examinador | 1 |
| 60769 | examinádole | 1 |
| 60770 | exaltó | 1 |
| 60771 | exaltas | 1 |
| 60772 | exaltarse | 1 |
| 60773 | exaltando | 1 |
| 60774 | exaltaban | 1 |
| 60775 | exalta | 1 |
| 60776 | exagero | 1 |
| 60777 | exageres | 1 |
| 60778 | exagere | 1 |
| 60779 | exageras | 1 |
| 60780 | exagerarlos | 1 |
| 60781 | exageradísima | 1 |
| 60782 | exageraban | 1 |
| 60783 | exactos | 1 |
| 60784 | exabruptos | 1 |
| 60785 | evocó | 1 |
| 60786 | evocaron | 1 |
| 60787 | evocarla | 1 |
| 60788 | evocar | 1 |
| 60789 | evocados | 1 |
| 60790 | evocadas | 1 |
| 60791 | evocada | 1 |
| 60792 | evocación | 1 |
| 60793 | evitó | 1 |
| 60794 | eviten | 1 |
| 60795 | evite | 1 |
| 60796 | evitarse | 1 |
| 60797 | evitarles | 1 |
| 60798 | evitara | 1 |
| 60799 | evitándole | 1 |
| 60800 | evitaban | 1 |
| 60801 | everniso | 1 |
| 60802 | eventuales | 1 |
| 60803 | evento | 1 |
| 60804 | événements | 1 |
| 60805 | evasivos | 1 |
| 60806 | evasiva | 1 |
| 60807 | evaporara | 1 |
| 60808 | evaporado | 1 |
| 60809 | evaporación | 1 |
| 60810 | evaporaban | 1 |
| 60811 | evaporaba | 1 |
| 60812 | evapora | 1 |
| 60813 | evangelísticos | 1 |
| 60814 | evangelistas | 1 |
| 60815 | evangelii | 1 |
| 60816 | evadirse | 1 |
| 60817 | evadí | 1 |
| 60818 | evacuar | 1 |
| 60819 | euterpe | 1 |
| 60820 | euscal | 1 |
| 60821 | eurygalus | 1 |
| 60822 | eurota | 1 |
| 60823 | euríalo | 1 |
| 60824 | eurialio | 1 |
| 60825 | eureka | 1 |
| 60826 | eum | 1 |
| 60827 | euliyac | 1 |
| 60828 | eugenie | 1 |
| 60829 | éufrates | 1 |
| 60830 | eufemismo | 1 |
| 60831 | eucologio | 1 |
| 60832 | euclides | 1 |
| 60833 | eucaliptos | 1 |
| 60834 | eua | 1 |
| 60835 | eu | 1 |
| 60836 | etruscos | 1 |
| 60837 | être | 1 |
| 60838 | etor | 1 |
| 60839 | etón | 1 |
| 60840 | eton | 1 |
| 60841 | etnógrafo | 1 |
| 60842 | etnográfico | 1 |
| 60843 | etnicos | 1 |
| 60844 | etiquetillas | 1 |
| 60845 | etiquetera | 1 |
| 60846 | etiópico | 1 |
| 60847 | etïopia | 1 |
| 60848 | etíopes | 1 |
| 60849 | etiopes | 1 |
| 60850 | etíope | 1 |
| 60851 | etimologistas | 1 |
| 60852 | etimología | 1 |
| 60853 | éticas | 1 |
| 60854 | eternizarlos | 1 |
| 60855 | eternizar | 1 |
| 60856 | eternizaba | 1 |
| 60857 | eterniza | 1 |
| 60858 | eternice | 1 |
| 60859 | etéreo | 1 |
| 60860 | etchehun | 1 |
| 60861 | etalaje | 1 |
| 60862 | estuvímonos | 1 |
| 60863 | estuvieses | 1 |
| 60864 | estuviésedes | 1 |
| 60865 | estuviéronse | 1 |
| 60866 | estuvieres | 1 |
| 60867 | estuvieren | 1 |
| 60868 | estuviéredes | 1 |
| 60869 | estuuieron | 1 |
| 60870 | estuuieren | 1 |
| 60871 | estupro | 1 |
| 60872 | estupores | 1 |
| 60873 | estupideces | 1 |
| 60874 | estupendamente | 1 |
| 60875 | estupefactos | 1 |
| 60876 | estudos | 1 |
| 60877 | estudiosos | 1 |
| 60878 | estudiosa | 1 |
| 60879 | estudiase | 1 |
| 60880 | estudias | 1 |
| 60881 | estudiaron | 1 |
| 60882 | estudiarle | 1 |
| 60883 | estudiaría | 1 |
| 60884 | estudiantillo | 1 |
| 60885 | estudiantiles | 1 |
| 60886 | estudiantil | 1 |
| 60887 | estudiantado | 1 |
| 60888 | estudiándole | 1 |
| 60889 | estudiamos | 1 |
| 60890 | estucos | 1 |
| 60891 | estuchitos | 1 |
| 60892 | estuchito | 1 |
| 60893 | estucado | 1 |
| 60894 | estrujarse | 1 |
| 60895 | estrujarle | 1 |
| 60896 | estrujarla | 1 |
| 60897 | estrujándose | 1 |
| 60898 | estrujado | 1 |
| 60899 | estruendoso | 1 |
| 60900 | estructura | 1 |
| 60901 | estropeó | 1 |
| 60902 | estropeasen | 1 |
| 60903 | estropearon | 1 |
| 60904 | estropear | 1 |
| 60905 | estropeándose | 1 |
| 60906 | estropeando | 1 |
| 60907 | estropean | 1 |
| 60908 | estropeadísima | 1 |
| 60909 | estropeadas | 1 |
| 60910 | estropeaba | 1 |
| 60911 | estropea | 1 |
| 60912 | estropajosas | 1 |
| 60913 | estropajos | 1 |
| 60914 | estropajo | 1 |
| 60915 | estrólogos | 1 |
| 60916 | estro | 1 |
| 60917 | estripaterrones | 1 |
| 60918 | estriego | 1 |
| 60919 | estridentes | 1 |
| 60920 | estridencia | 1 |
| 60921 | estrictamente | 1 |
| 60922 | estriban | 1 |
| 60923 | estribación | 1 |
| 60924 | estriba | 1 |
| 60925 | estrepitosamente | 1 |
| 60926 | estrepito | 1 |
| 60927 | estrenose | 1 |
| 60928 | estrenas | 1 |
| 60929 | estrenaríamos | 1 |
| 60930 | estrenaré | 1 |
| 60931 | estrenare | 1 |
| 60932 | estrenara | 1 |
| 60933 | estrenad | 1 |
| 60934 | estrenaba | 1 |
| 60935 | estremeçió | 1 |
| 60936 | estremeciéndome | 1 |
| 60937 | estremeciendo | 1 |
| 60938 | estremecen | 1 |
| 60939 | estremarme | 1 |
| 60940 | estremadamente | 1 |
| 60941 | estrelleras | 1 |
| 60942 | estrellarte | 1 |
| 60943 | estrellarla | 1 |
| 60944 | estrellaré | 1 |
| 60945 | estrellar | 1 |
| 60946 | estrellándose | 1 |
| 60947 | estrellándolas | 1 |
| 60948 | estrellaban | 1 |
| 60949 | estrellaba | 1 |
| 60950 | estrego | 1 |
| 60951 | estregársela | 1 |
| 60952 | estrechísimamente | 1 |
| 60953 | estreche | 1 |
| 60954 | estrecharon | 1 |
| 60955 | estrecharme | 1 |
| 60956 | estrechándose | 1 |
| 60957 | estrechan | 1 |
| 60958 | estrechaban | 1 |
| 60959 | estre | 1 |
| 60960 | estratégicos | 1 |
| 60961 | estratégicas | 1 |
| 60962 | estraordinarios | 1 |
| 60963 | estraordinariamente | 1 |
| 60964 | estranos | 1 |
| 60965 | estranjeras | 1 |
| 60966 | estrangularme | 1 |
| 60967 | estrangulara | 1 |
| 60968 | estrangular | 1 |
| 60969 | estrangulándola | 1 |
| 60970 | estrangulada | 1 |
| 60971 | estrangulación | 1 |
| 60972 | estranezas | 1 |
| 60973 | estrambóticas | 1 |
| 60974 | estrambótica | 1 |
| 60975 | estrambotes | 1 |
| 60976 | estragarlo | 1 |
| 60977 | estragaría | 1 |
| 60978 | estragado | 1 |
| 60979 | estrafalaria | 1 |
| 60980 | estrabismo | 1 |
| 60981 | estoyte | 1 |
| 60982 | estoyle | 1 |
| 60983 | estouo | 1 |
| 60984 | estouimos | 1 |
| 60985 | estouiesedes | 1 |
| 60986 | estouiese | 1 |
| 60987 | estouiere | 1 |
| 60988 | estote | 1 |
| 60989 | estorves | 1 |
| 60990 | estorvador | 1 |
| 60991 | estorvado | 1 |
| 60992 | estoruays | 1 |
| 60993 | estoruasse | 1 |
| 60994 | estoruarte | 1 |
| 60995 | estoruaras | 1 |
| 60996 | estoruan | 1 |
| 60997 | estoruales | 1 |
| 60998 | estorua | 1 |
| 60999 | estornudar | 1 |
| 61000 | estornudaba | 1 |
| 61001 | estornuda | 1 |
| 61002 | estorninos | 1 |
| 61003 | estorcer | 1 |
| 61004 | estorbóselo | 1 |
| 61005 | estorben | 1 |
| 61006 | estorbe | 1 |
| 61007 | estorbársela | 1 |
| 61008 | estorbáronlo | 1 |
| 61009 | estorbaron | 1 |
| 61010 | estorbarla | 1 |
| 61011 | estorbaren | 1 |
| 61012 | estorbando | 1 |
| 61013 | estorbábanselo | 1 |
| 61014 | estoraques | 1 |
| 61015 | estoposa | 1 |
| 61016 | estonçes | 1 |
| 61017 | estomaticón | 1 |
| 61018 | estólidos | 1 |
| 61019 | estolidez | 1 |
| 61020 | estoico | 1 |
| 61021 | estoica | 1 |
| 61022 | estofados | 1 |
| 61023 | estofadas | 1 |
| 61024 | estodieron | 1 |
| 61025 | estodieres | 1 |
| 61026 | estobarlo | 1 |
| 61027 | estivo | 1 |
| 61028 | estival | 1 |
| 61029 | estirpes | 1 |
| 61030 | estiróse | 1 |
| 61031 | estiren | 1 |
| 61032 | estirase | 1 |
| 61033 | estirarme | 1 |
| 61034 | estirarlo | 1 |
| 61035 | estiraré | 1 |
| 61036 | estirándole | 1 |
| 61037 | estiradito | 1 |
| 61038 | estiradamente | 1 |
| 61039 | estirábase | 1 |
| 61040 | estira | 1 |
| 61041 | estimuló | 1 |
| 61042 | estimule | 1 |
| 61043 | estimular | 1 |
| 61044 | estimulante | 1 |
| 61045 | estimulándole | 1 |
| 61046 | estimulando | 1 |
| 61047 | estimulada | 1 |
| 61048 | estimó | 1 |
| 61049 | estimes | 1 |
| 61050 | estime | 1 |
| 61051 | estimase | 1 |
| 61052 | estimaron | 1 |
| 61053 | estimándose | 1 |
| 61054 | estimándolos | 1 |
| 61055 | estimándole | 1 |
| 61056 | estímalos | 1 |
| 61057 | estimalde | 1 |
| 61058 | estimalda | 1 |
| 61059 | estimáis | 1 |
| 61060 | estimadla | 1 |
| 61061 | estimables | 1 |
| 61062 | estillo | 1 |
| 61063 | estilita | 1 |
| 61064 | estilista | 1 |
| 61065 | estila | 1 |
| 61066 | estigio | 1 |
| 61067 | estigias | 1 |
| 61068 | estiendes | 1 |
| 61069 | estiendan | 1 |
| 61070 | estid | 1 |
| 61071 | estevado | 1 |
| 61072 | estéticos | 1 |
| 61073 | estéticas | 1 |
| 61074 | estéticamente | 1 |
| 61075 | estero | 1 |
| 61076 | esternón | 1 |
| 61077 | esterlinas | 1 |
| 61078 | esteritas | 1 |
| 61079 | esterita | 1 |
| 61080 | esteriores | 1 |
| 61081 | esterilla | 1 |
| 61082 | esterilizando | 1 |
| 61083 | estereotipada | 1 |
| 61084 | esterensuby | 1 |
| 61085 | estercuela | 1 |
| 61086 | estercolar | 1 |
| 61087 | estercolándolas | 1 |
| 61088 | esteraran | 1 |
| 61089 | esteparios | 1 |
| 61090 | estendiese | 1 |
| 61091 | estendieron | 1 |
| 61092 | estendiéndose | 1 |
| 61093 | estendidos | 1 |
| 61094 | estendidas | 1 |
| 61095 | estendida | 1 |
| 61096 | estendería | 1 |
| 61097 | estenderá | 1 |
| 61098 | estéme | 1 |
| 61099 | estedes | 1 |
| 61100 | estav | 1 |
| 61101 | estauas | 1 |
| 61102 | estatuido | 1 |
| 61103 | estatuario | 1 |
| 61104 | estático | 1 |
| 61105 | estática | 1 |
| 61106 | estáste | 1 |
| 61107 | estarle | 1 |
| 61108 | estaribel | 1 |
| 61109 | estarías | 1 |
| 61110 | estaria | 1 |
| 61111 | estarcidos | 1 |
| 61112 | estarcido | 1 |
| 61113 | estarce | 1 |
| 61114 | estaran | 1 |
| 61115 | estáos | 1 |
| 61116 | estantillos | 1 |
| 61117 | estantiguas | 1 |
| 61118 | estantería | 1 |
| 61119 | estanquero | 1 |
| 61120 | estano | 1 |
| 61121 | estándosele | 1 |
| 61122 | estándose | 1 |
| 61123 | estándole | 1 |
| 61124 | estandartes | 1 |
| 61125 | estancarse | 1 |
| 61126 | estancamiento | 1 |
| 61127 | estancado | 1 |
| 61128 | estancadas | 1 |
| 61129 | estanbre | 1 |
| 61130 | estampó | 1 |
| 61131 | estampitas | 1 |
| 61132 | estampilla | 1 |
| 61133 | estampes | 1 |
| 61134 | estampero | 1 |
| 61135 | estámpelo | 1 |
| 61136 | estampárselo | 1 |
| 61137 | estamparse | 1 |
| 61138 | estampados | 1 |
| 61139 | estampaba | 1 |
| 61140 | estámosle | 1 |
| 61141 | estame | 1 |
| 61142 | estambres | 1 |
| 61143 | estallo | 1 |
| 61144 | estallase | 1 |
| 61145 | estallaron | 1 |
| 61146 | estallarme | 1 |
| 61147 | estallando | 1 |
| 61148 | estafón | 1 |
| 61149 | estafetas | 1 |
| 61150 | estafase | 1 |
| 61151 | estafarme | 1 |
| 61152 | estafarles | 1 |
| 61153 | estafamos | 1 |
| 61154 | estaçión | 1 |
| 61155 | estacazos | 1 |
| 61156 | establyas | 1 |
| 61157 | establía | 1 |
| 61158 | establezcan | 1 |
| 61159 | establezcamos | 1 |
| 61160 | estables | 1 |
| 61161 | estableciéndose | 1 |
| 61162 | estableciendo | 1 |
| 61163 | establecidos | 1 |
| 61164 | establecí | 1 |
| 61165 | establecerá | 1 |
| 61166 | estabilidad | 1 |
| 61167 | estábaselo | 1 |
| 61168 | estábanlo | 1 |
| 61169 | estábanle | 1 |
| 61170 | estábalas | 1 |
| 61171 | essotra | 1 |
| 61172 | esquivias | 1 |
| 61173 | esquiveza | 1 |
| 61174 | esquivedes | 1 |
| 61175 | esquive | 1 |
| 61176 | esquivarse | 1 |
| 61177 | esquivar | 1 |
| 61178 | esquivan | 1 |
| 61179 | esquiuidad | 1 |
| 61180 | esquiuedad | 1 |
| 61181 | esquiuas | 1 |
| 61182 | esquiuandose | 1 |
| 61183 | esquiua | 1 |
| 61184 | esquistosa | 1 |
| 61185 | esquistos | 1 |
| 61186 | esquisitos | 1 |
| 61187 | esquirla | 1 |
| 61188 | esquinen | 1 |
| 61189 | esquine | 1 |
| 61190 | esquinazo | 1 |
| 61191 | esquinado | 1 |
| 61192 | esquilo | 1 |
| 61193 | esquilan | 1 |
| 61194 | esquilache | 1 |
| 61195 | esqueros | 1 |
| 61196 | espyciales | 1 |
| 61197 | espurgo | 1 |
| 61198 | espumosos | 1 |
| 61199 | espumosas | 1 |
| 61200 | espumante | 1 |
| 61201 | espumajoso | 1 |
| 61202 | espumajos | 1 |
| 61203 | espumad | 1 |
| 61204 | espúlguenos | 1 |
| 61205 | espulguen | 1 |
| 61206 | espulgarse | 1 |
| 61207 | espulgan | 1 |
| 61208 | espulgador | 1 |
| 61209 | espulgado | 1 |
| 61210 | espulgadero | 1 |
| 61211 | espuerta | 1 |
| 61212 | espressare | 1 |
| 61213 | espreso | 1 |
| 61214 | espresion | 1 |
| 61215 | espresaste | 1 |
| 61216 | espresa | 1 |
| 61217 | espotrique | 1 |
| 61218 | espotricarás | 1 |
| 61219 | espotrica | 1 |
| 61220 | esportonas | 1 |
| 61221 | esportillas | 1 |
| 61222 | esportilla | 1 |
| 61223 | espontáneas | 1 |
| 61224 | espontanearse | 1 |
| 61225 | esponjosa | 1 |
| 61226 | esponjan | 1 |
| 61227 | espongïoso | 1 |
| 61228 | espolvoreada | 1 |
| 61229 | espolique | 1 |
| 61230 | espolios | 1 |
| 61231 | espolines | 1 |
| 61232 | espoleando | 1 |
| 61233 | esplines | 1 |
| 61234 | esplinado | 1 |
| 61235 | esplendorosos | 1 |
| 61236 | esplendideces | 1 |
| 61237 | esplandianes | 1 |
| 61238 | espirtos | 1 |
| 61239 | espirituosos | 1 |
| 61240 | espirituosa | 1 |
| 61241 | espiritualizar | 1 |
| 61242 | espiritualísima | 1 |
| 61243 | espiritillo | 1 |
| 61244 | espiritado | 1 |
| 61245 | espiritada | 1 |
| 61246 | espirante | 1 |
| 61247 | espirado | 1 |
| 61248 | espionajes | 1 |
| 61249 | espinosas | 1 |
| 61250 | espinel | 1 |
| 61251 | espinaças | 1 |
| 61252 | espinacas | 1 |
| 61253 | espilorchería | 1 |
| 61254 | espigado | 1 |
| 61255 | espigadita | 1 |
| 61256 | espigada | 1 |
| 61257 | espifor | 1 |
| 61258 | espienden | 1 |
| 61259 | espiçial | 1 |
| 61260 | espicharon | 1 |
| 61261 | espichamos | 1 |
| 61262 | espichaba | 1 |
| 61263 | espich | 1 |
| 61264 | espiarlos | 1 |
| 61265 | espiándole | 1 |
| 61266 | espiados | 1 |
| 61267 | espiado | 1 |
| 61268 | espiada | 1 |
| 61269 | espiaban | 1 |
| 61270 | espetó | 1 |
| 61271 | espetera | 1 |
| 61272 | espetarle | 1 |
| 61273 | espetaría | 1 |
| 61274 | espetar | 1 |
| 61275 | espetándonos | 1 |
| 61276 | espetando | 1 |
| 61277 | espetado | 1 |
| 61278 | espetáculo | 1 |
| 61279 | espetaba | 1 |
| 61280 | espesuras | 1 |
| 61281 | espessura | 1 |
| 61282 | espessos | 1 |
| 61283 | espesísimo | 1 |
| 61284 | esperta | 1 |
| 61285 | esperpentos | 1 |
| 61286 | esperimiento | 1 |
| 61287 | esperimentados | 1 |
| 61288 | esperezóse | 1 |
| 61289 | esperezándose | 1 |
| 61290 | espéreme | 1 |
| 61291 | esperéis | 1 |
| 61292 | esperat | 1 |
| 61293 | esperasses | 1 |
| 61294 | esperasse | 1 |
| 61295 | esperásemos | 1 |
| 61296 | esperaros | 1 |
| 61297 | esperarles | 1 |
| 61298 | esperarla | 1 |
| 61299 | esperaréis | 1 |
| 61300 | esperarás | 1 |
| 61301 | esperaramos | 1 |
| 61302 | esperarades | 1 |
| 61303 | esperará | 1 |
| 61304 | esperaos | 1 |
| 61305 | esperante | 1 |
| 61306 | esperandote | 1 |
| 61307 | esperándoos | 1 |
| 61308 | esperame | 1 |
| 61309 | esperallo | 1 |
| 61310 | esperalle | 1 |
| 61311 | esperallas | 1 |
| 61312 | esperalla | 1 |
| 61313 | esperadme | 1 |
| 61314 | esperades | 1 |
| 61315 | esperadas | 1 |
| 61316 | esperábamos | 1 |
| 61317 | esperábalos | 1 |
| 61318 | esperabais | 1 |
| 61319 | espendí | 1 |
| 61320 | espeluznó | 1 |
| 61321 | espelúznase | 1 |
| 61322 | espeluznante | 1 |
| 61323 | espeleta | 1 |
| 61324 | espele | 1 |
| 61325 | espejito | 1 |
| 61326 | espejismo | 1 |
| 61327 | espejillo | 1 |
| 61328 | espediente | 1 |
| 61329 | especuló | 1 |
| 61330 | espéculo | 1 |
| 61331 | especulo | 1 |
| 61332 | especule | 1 |
| 61333 | especulativas | 1 |
| 61334 | especulador | 1 |
| 61335 | especulacion | 1 |
| 61336 | espectación | 1 |
| 61337 | específicos | 1 |
| 61338 | especificaron | 1 |
| 61339 | específicamente | 1 |
| 61340 | especificado | 1 |
| 61341 | especificaba | 1 |
| 61342 | específica | 1 |
| 61343 | especialistas | 1 |
| 61344 | especialista | 1 |
| 61345 | especialísimo | 1 |
| 61346 | especialísima | 1 |
| 61347 | especiales | 1 |
| 61348 | espeçia | 1 |
| 61349 | especerías | 1 |
| 61350 | espauorecian | 1 |
| 61351 | espátula | 1 |
| 61352 | espatarrándose | 1 |
| 61353 | espatarrados | 1 |
| 61354 | espasmos | 1 |
| 61355 | espasmo | 1 |
| 61356 | espartana | 1 |
| 61357 | espartafilardo | 1 |
| 61358 | esparsido | 1 |
| 61359 | esparrancló | 1 |
| 61360 | esparraguera | 1 |
| 61361 | esparcirán | 1 |
| 61362 | esparcimientos | 1 |
| 61363 | esparciéndose | 1 |
| 61364 | esparcida | 1 |
| 61365 | esparavanes | 1 |
| 61366 | españolizada | 1 |
| 61367 | españolismo | 1 |
| 61368 | españita | 1 |
| 61369 | espantóme | 1 |
| 61370 | espantemosla | 1 |
| 61371 | espantéis | 1 |
| 61372 | espanté | 1 |
| 61373 | espantava | 1 |
| 61374 | espantaste | 1 |
| 61375 | espantáronse | 1 |
| 61376 | espantaron | 1 |
| 61377 | espantarlo | 1 |
| 61378 | espantaría | 1 |
| 61379 | espantaras | 1 |
| 61380 | espantaran | 1 |
| 61381 | espantara | 1 |
| 61382 | espantajos | 1 |
| 61383 | espantadizos | 1 |
| 61384 | espantadizo | 1 |
| 61385 | espantábase | 1 |
| 61386 | espantabas | 1 |
| 61387 | espaldilla | 1 |
| 61388 | espaldera | 1 |
| 61389 | espaldazaro | 1 |
| 61390 | espagnol | 1 |
| 61391 | espagne | 1 |
| 61392 | espadilla | 1 |
| 61393 | espacïoso | 1 |
| 61394 | espaciosísimo | 1 |
| 61395 | espaciosísima | 1 |
| 61396 | espaciosidad | 1 |
| 61397 | espacïosamente | 1 |
| 61398 | espacïosa | 1 |
| 61399 | espació | 1 |
| 61400 | espaçio | 1 |
| 61401 | espaçias | 1 |
| 61402 | espaciarse | 1 |
| 61403 | espaciada | 1 |
| 61404 | espachurrar | 1 |
| 61405 | espace | 1 |
| 61406 | espa | 1 |
| 61407 | esotéricos | 1 |
| 61408 | esorbitante | 1 |
| 61409 | esófago | 1 |
| 61410 | esmeró | 1 |
| 61411 | esmeril | 1 |
| 61412 | esmerándose | 1 |
| 61413 | esmeran | 1 |
| 61414 | esmeradísimos | 1 |
| 61415 | esmeradísima | 1 |
| 61416 | esmeraba | 1 |
| 61417 | esmera | 1 |
| 61418 | esmaltadas | 1 |
| 61419 | esmaltada | 1 |
| 61420 | eslora | 1 |
| 61421 | eslauones | 1 |
| 61422 | eslabonando | 1 |
| 61423 | eslabonado | 1 |
| 61424 | eslabonaba | 1 |
| 61425 | esgrimirla | 1 |
| 61426 | esgrimirán | 1 |
| 61427 | esgrimió | 1 |
| 61428 | esgrimieron | 1 |
| 61429 | esgrimiéndola | 1 |
| 61430 | esgrimidor | 1 |
| 61431 | esgrimida | 1 |
| 61432 | esgremir | 1 |
| 61433 | esgremidor | 1 |
| 61434 | esgarrochados | 1 |
| 61435 | esgamoches | 1 |
| 61436 | esfuérzate | 1 |
| 61437 | esfuerzate | 1 |
| 61438 | esfuerzas | 1 |
| 61439 | esfuerzan | 1 |
| 61440 | esfuerçe | 1 |
| 61441 | esfuerça | 1 |
| 61442 | esforzaua | 1 |
| 61443 | esforzarte | 1 |
| 61444 | esforzarse | 1 |
| 61445 | esforzaré | 1 |
| 61446 | esforzare | 1 |
| 61447 | esforzándome | 1 |
| 61448 | esforzando | 1 |
| 61449 | esforçados | 1 |
| 61450 | esfogue | 1 |
| 61451 | esfinges | 1 |
| 61452 | esféricos | 1 |
| 61453 | esfericidad | 1 |
| 61454 | eserina | 1 |
| 61455 | esentos | 1 |
| 61456 | esentas | 1 |
| 61457 | esençiones | 1 |
| 61458 | esenciones | 1 |
| 61459 | esencialísimo | 1 |
| 61460 | esencialísimas | 1 |
| 61461 | esenciada | 1 |
| 61462 | escusóse | 1 |
| 61463 | escusóme | 1 |
| 61464 | escuso | 1 |
| 61465 | escuseras | 1 |
| 61466 | escuse | 1 |
| 61467 | escusarvos | 1 |
| 61468 | escusarte | 1 |
| 61469 | escusarla | 1 |
| 61470 | escusarían | 1 |
| 61471 | escusaré | 1 |
| 61472 | escusaran | 1 |
| 61473 | escusará | 1 |
| 61474 | escúsanos | 1 |
| 61475 | escurro | 1 |
| 61476 | escurriesen | 1 |
| 61477 | escurriésedes | 1 |
| 61478 | escurrieron | 1 |
| 61479 | escurriduras | 1 |
| 61480 | escurridizo | 1 |
| 61481 | escurridiza | 1 |
| 61482 | escurrí | 1 |
| 61483 | escurren | 1 |
| 61484 | escurezcan | 1 |
| 61485 | escuresce | 1 |
| 61486 | escureçió | 1 |
| 61487 | escureciesen | 1 |
| 61488 | escurecieron | 1 |
| 61489 | escurecida | 1 |
| 61490 | escurecía | 1 |
| 61491 | escureçes | 1 |
| 61492 | escurecerla | 1 |
| 61493 | escurece | 1 |
| 61494 | escupirme | 1 |
| 61495 | escupirán | 1 |
| 61496 | escupirá | 1 |
| 61497 | escupióme | 1 |
| 61498 | escupiera | 1 |
| 61499 | escupido | 1 |
| 61500 | escúpenl | 1 |
| 61501 | escupen | 1 |
| 61502 | escupan | 1 |
| 61503 | escultural | 1 |
| 61504 | escultórico | 1 |
| 61505 | esculpirse | 1 |
| 61506 | esculpidos | 1 |
| 61507 | esculpidas | 1 |
| 61508 | esculares | 1 |
| 61509 | esculapio | 1 |
| 61510 | escuetos | 1 |
| 61511 | escueto | 1 |
| 61512 | escuetas | 1 |
| 61513 | escuerzo | 1 |
| 61514 | escuerço | 1 |
| 61515 | escuecen | 1 |
| 61516 | escudriñó | 1 |
| 61517 | escudriño | 1 |
| 61518 | escudriñéle | 1 |
| 61519 | escudriñase | 1 |
| 61520 | escudriñas | 1 |
| 61521 | escudriñáronse | 1 |
| 61522 | escudriñarla | 1 |
| 61523 | escudriñan | 1 |
| 61524 | escudriñadoras | 1 |
| 61525 | escudriñado | 1 |
| 61526 | escudrina | 1 |
| 61527 | escudó | 1 |
| 61528 | escudito | 1 |
| 61529 | escudillos | 1 |
| 61530 | escudillas | 1 |
| 61531 | escudiellas | 1 |
| 61532 | escuderón | 1 |
| 61533 | escuderísimo | 1 |
| 61534 | escuderilmente | 1 |
| 61535 | escuderías | 1 |
| 61536 | escuderazo | 1 |
| 61537 | escudera | 1 |
| 61538 | escude | 1 |
| 61539 | escudávanse | 1 |
| 61540 | escudar | 1 |
| 61541 | escudados | 1 |
| 61542 | escuchólas | 1 |
| 61543 | escuchóla | 1 |
| 61544 | escuchémosle | 1 |
| 61545 | escuchéle | 1 |
| 61546 | escuché | 1 |
| 61547 | escuchauas | 1 |
| 61548 | escuchatelo | 1 |
| 61549 | escuchastes | 1 |
| 61550 | escuchasen | 1 |
| 61551 | escucharon | 1 |
| 61552 | escucharme | 1 |
| 61553 | escucharían | 1 |
| 61554 | escucharé | 1 |
| 61555 | escucharan | 1 |
| 61556 | escuchantes | 1 |
| 61557 | escuchandote | 1 |
| 61558 | escuchalle | 1 |
| 61559 | escuchale | 1 |
| 61560 | escuchala | 1 |
| 61561 | escuchados | 1 |
| 61562 | escuchadas | 1 |
| 61563 | escuchábamos | 1 |
| 61564 | escuálidos | 1 |
| 61565 | escuálidas | 1 |
| 61566 | escu | 1 |
| 61567 | escrutiñador | 1 |
| 61568 | escrutinios | 1 |
| 61569 | escrutador | 1 |
| 61570 | escrupulosamente | 1 |
| 61571 | escrivir | 1 |
| 61572 | escriviese | 1 |
| 61573 | escriva | 1 |
| 61574 | escriuiendo | 1 |
| 61575 | escriue | 1 |
| 61576 | escritorios | 1 |
| 61577 | escritoras | 1 |
| 61578 | escribístesla | 1 |
| 61579 | escribistes | 1 |
| 61580 | escribiste | 1 |
| 61581 | escribirte | 1 |
| 61582 | escribirlos | 1 |
| 61583 | escribirían | 1 |
| 61584 | escribiremos | 1 |
| 61585 | escribirás | 1 |
| 61586 | escribirá | 1 |
| 61587 | escribimos | 1 |
| 61588 | escribillos | 1 |
| 61589 | escribille | 1 |
| 61590 | escribilla | 1 |
| 61591 | escribiesen | 1 |
| 61592 | escribiésemos | 1 |
| 61593 | escribieren | 1 |
| 61594 | escribiéndole | 1 |
| 61595 | escribidores | 1 |
| 61596 | escribido | 1 |
| 61597 | escribida | 1 |
| 61598 | escribíamos | 1 |
| 61599 | escribes | 1 |
| 61600 | escríbeme | 1 |
| 61601 | escríbele | 1 |
| 61602 | escríbase | 1 |
| 61603 | escribamos | 1 |
| 61604 | escríbala | 1 |
| 61605 | escrementos | 1 |
| 61606 | escremento | 1 |
| 61607 | escrebirse | 1 |
| 61608 | escrebiré | 1 |
| 61609 | escozorcillo | 1 |
| 61610 | escozor | 1 |
| 61611 | escoziote | 1 |
| 61612 | escotillón | 1 |
| 61613 | escotillo | 1 |
| 61614 | escotes | 1 |
| 61615 | escoté | 1 |
| 61616 | escotan | 1 |
| 61617 | escotados | 1 |
| 61618 | escosura | 1 |
| 61619 | escorzos | 1 |
| 61620 | escorzaba | 1 |
| 61621 | escorpionaza | 1 |
| 61622 | escorpión | 1 |
| 61623 | escoplo | 1 |
| 61624 | escopieron | 1 |
| 61625 | escopetilla | 1 |
| 61626 | escopeteros | 1 |
| 61627 | escondo | 1 |
| 61628 | escondiste | 1 |
| 61629 | escondimiento | 1 |
| 61630 | escondiesen | 1 |
| 61631 | escondidita | 1 |
| 61632 | escondidísimo | 1 |
| 61633 | escondíase | 1 |
| 61634 | escondíamos | 1 |
| 61635 | escondia | 1 |
| 61636 | escondí | 1 |
| 61637 | escóndete | 1 |
| 61638 | escondete | 1 |
| 61639 | esconderé | 1 |
| 61640 | esconderás | 1 |
| 61641 | escóndelo | 1 |
| 61642 | escondamos | 1 |
| 61643 | escondáis | 1 |
| 61644 | esconbra | 1 |
| 61645 | escomonión | 1 |
| 61646 | escomienzo | 1 |
| 61647 | escombreras | 1 |
| 61648 | escombramos | 1 |
| 61649 | escoltaron | 1 |
| 61650 | escoltando | 1 |
| 61651 | escoltados | 1 |
| 61652 | escoltado | 1 |
| 61653 | escoltadas | 1 |
| 61654 | escoltada | 1 |
| 61655 | escolios | 1 |
| 61656 | escolástico | 1 |
| 61657 | escolasticismo | 1 |
| 61658 | escolástica | 1 |
| 61659 | escoje | 1 |
| 61660 | escojan | 1 |
| 61661 | escogitar | 1 |
| 61662 | escogio | 1 |
| 61663 | escogieres | 1 |
| 61664 | escogiere | 1 |
| 61665 | escogidísimos | 1 |
| 61666 | escogidísimo | 1 |
| 61667 | escogían | 1 |
| 61668 | escogian | 1 |
| 61669 | escoges | 1 |
| 61670 | escogería | 1 |
| 61671 | escogerá | 1 |
| 61672 | escogella | 1 |
| 61673 | escogedes | 1 |
| 61674 | escofyna | 1 |
| 61675 | escocióme | 1 |
| 61676 | escocía | 1 |
| 61677 | escocer | 1 |
| 61678 | escobones | 1 |
| 61679 | escobilla | 1 |
| 61680 | escobazos | 1 |
| 61681 | escobazo | 1 |
| 61682 | escobajo | 1 |
| 61683 | escluya | 1 |
| 61684 | esclavizarles | 1 |
| 61685 | esclavizar | 1 |
| 61686 | esclavizan | 1 |
| 61687 | esclavitudes | 1 |
| 61688 | esclaua | 1 |
| 61689 | esclareciendo | 1 |
| 61690 | esclarecidas | 1 |
| 61691 | esclarecida | 1 |
| 61692 | esclarecerla | 1 |
| 61693 | escila | 1 |
| 61694 | escenita | 1 |
| 61695 | escenarios | 1 |
| 61696 | escayola | 1 |
| 61697 | escatimados | 1 |
| 61698 | escatima | 1 |
| 61699 | escaseces | 1 |
| 61700 | escasearían | 1 |
| 61701 | escaseando | 1 |
| 61702 | escaseaban | 1 |
| 61703 | escasayozu | 1 |
| 61704 | escarvas | 1 |
| 61705 | escarrar | 1 |
| 61706 | escarpas | 1 |
| 61707 | escarolero | 1 |
| 61708 | escarolados | 1 |
| 61709 | escarnidos | 1 |
| 61710 | escarnidor | 1 |
| 61711 | escarnecido | 1 |
| 61712 | escarnecida | 1 |
| 61713 | escarneçerla | 1 |
| 61714 | escarnecen | 1 |
| 61715 | escarmiente | 1 |
| 61716 | escarmentó | 1 |
| 61717 | escarmenté | 1 |
| 61718 | escarmentase | 1 |
| 61719 | escarmentará | 1 |
| 61720 | escarmentando | 1 |
| 61721 | escarmentada | 1 |
| 61722 | escarmenase | 1 |
| 61723 | escarlatina | 1 |
| 61724 | escardilla | 1 |
| 61725 | escarde | 1 |
| 61726 | escardaré | 1 |
| 61727 | escardara | 1 |
| 61728 | escarchas | 1 |
| 61729 | escarchando | 1 |
| 61730 | escarbar | 1 |
| 61731 | escarbaba | 1 |
| 61732 | escaray | 1 |
| 61733 | escarapela | 1 |
| 61734 | escaramuzas | 1 |
| 61735 | escarabajo | 1 |
| 61736 | escapose | 1 |
| 61737 | escapome | 1 |
| 61738 | escapo | 1 |
| 61739 | escapeme | 1 |
| 61740 | escapava | 1 |
| 61741 | escapasen | 1 |
| 61742 | escapárseme | 1 |
| 61743 | escapársele | 1 |
| 61744 | escaparían | 1 |
| 61745 | escaparé | 1 |
| 61746 | escaparan | 1 |
| 61747 | escapándose | 1 |
| 61748 | escapando | 1 |
| 61749 | escapalla | 1 |
| 61750 | escapada | 1 |
| 61751 | escaños | 1 |
| 61752 | escantan | 1 |
| 61753 | escantamente | 1 |
| 61754 | escantaderas | 1 |
| 61755 | escantada | 1 |
| 61756 | escandalizase | 1 |
| 61757 | escandalizarte | 1 |
| 61758 | escandalizará | 1 |
| 61759 | escandalizadas | 1 |
| 61760 | escandalizaba | 1 |
| 61761 | escandalicéme | 1 |
| 61762 | escandalice | 1 |
| 61763 | escancie | 1 |
| 61764 | escanciando | 1 |
| 61765 | escanciadora | 1 |
| 61766 | escanciaba | 1 |
| 61767 | escamoteos | 1 |
| 61768 | escamoteó | 1 |
| 61769 | escamotees | 1 |
| 61770 | escamoteándoles | 1 |
| 61771 | escamoteadas | 1 |
| 61772 | escamosas | 1 |
| 61773 | escamones | 1 |
| 61774 | escamonea | 1 |
| 61775 | escamonde | 1 |
| 61776 | escamón | 1 |
| 61777 | escamo | 1 |
| 61778 | escaminado | 1 |
| 61779 | escamilla | 1 |
| 61780 | escame | 1 |
| 61781 | escamarse | 1 |
| 61782 | escamandro | 1 |
| 61783 | escamaba | 1 |
| 61784 | escalpelo | 1 |
| 61785 | escallentar | 1 |
| 61786 | escallentador | 1 |
| 61787 | escalerillas | 1 |
| 61788 | escaldado | 1 |
| 61789 | escalasen | 1 |
| 61790 | escalando | 1 |
| 61791 | escalafón | 1 |
| 61792 | escaladores | 1 |
| 61793 | escalado | 1 |
| 61794 | escabullo | 1 |
| 61795 | escabullirse | 1 |
| 61796 | escabecharnos | 1 |
| 61797 | escabecharla | 1 |
| 61798 | escabechado | 1 |
| 61799 | escabechadas | 1 |
| 61800 | esbozarse | 1 |
| 61801 | esbirros | 1 |
| 61802 | esbirro | 1 |
| 61803 | esbeltísimas | 1 |
| 61804 | esaú | 1 |
| 61805 | esango | 1 |
| 61806 | esaminados | 1 |
| 61807 | esaminadores | 1 |
| 61808 | esaminado | 1 |
| 61809 | és | 1 |
| 61810 | erveras | 1 |
| 61811 | erutaciones | 1 |
| 61812 | eruptos | 1 |
| 61813 | eruditamente | 1 |
| 61814 | erudiciones | 1 |
| 61815 | eructaba | 1 |
| 61816 | erte | 1 |
| 61817 | ersía | 1 |
| 61818 | erróneamente | 1 |
| 61819 | erroitza | 1 |
| 61820 | errien | 1 |
| 61821 | errides | 1 |
| 61822 | errico | 1 |
| 61823 | erreste | 1 |
| 61824 | erres | 1 |
| 61825 | erremos | 1 |
| 61826 | erreguiñen | 1 |
| 61827 | erreguiña | 1 |
| 61828 | errazu | 1 |
| 61829 | errátil | 1 |
| 61830 | errática | 1 |
| 61831 | errata | 1 |
| 61832 | errarte | 1 |
| 61833 | errarse | 1 |
| 61834 | erraría | 1 |
| 61835 | erraren | 1 |
| 61836 | errare | 1 |
| 61837 | errara | 1 |
| 61838 | erranti | 1 |
| 61839 | errando | 1 |
| 61840 | errança | 1 |
| 61841 | errábades | 1 |
| 61842 | erraba | 1 |
| 61843 | erotismo | 1 |
| 61844 | eróstrato | 1 |
| 61845 | eroísma | 1 |
| 61846 | ermitas | 1 |
| 61847 | ermitaños | 1 |
| 61848 | ermada | 1 |
| 61849 | erm | 1 |
| 61850 | erizó | 1 |
| 61851 | erizarse | 1 |
| 61852 | erizándose | 1 |
| 61853 | erizan | 1 |
| 61854 | erizábansele | 1 |
| 61855 | erizaban | 1 |
| 61856 | erizaba | 1 |
| 61857 | eritrea | 1 |
| 61858 | eriso | 1 |
| 61859 | erisipelada | 1 |
| 61860 | eriotzac | 1 |
| 61861 | erigirlo | 1 |
| 61862 | erigen | 1 |
| 61863 | erige | 1 |
| 61864 | erguir | 1 |
| 61865 | erguidas | 1 |
| 61866 | erguida | 1 |
| 61867 | erguían | 1 |
| 61868 | erencia | 1 |
| 61869 | ereje | 1 |
| 61870 | eregias | 1 |
| 61871 | eregia | 1 |
| 61872 | eredades | 1 |
| 61873 | erección | 1 |
| 61874 | erdi | 1 |
| 61875 | ercules | 1 |
| 61876 | erçer | 1 |
| 61877 | erba | 1 |
| 61878 | erantzale | 1 |
| 61879 | eral | 1 |
| 61880 | erais | 1 |
| 61881 | erades | 1 |
| 61882 | eraclito | 1 |
| 61883 | equus | 1 |
| 61884 | equo | 1 |
| 61885 | equivoques | 1 |
| 61886 | equivoque | 1 |
| 61887 | equívocas | 1 |
| 61888 | equivocarte | 1 |
| 61889 | equivocaría | 1 |
| 61890 | equivocar | 1 |
| 61891 | equivocando | 1 |
| 61892 | equivocamos | 1 |
| 61893 | equivocados | 1 |
| 61894 | equivocadas | 1 |
| 61895 | equivalentes | 1 |
| 61896 | equitativo | 1 |
| 61897 | equis | 1 |
| 61898 | equipos | 1 |
| 61899 | equipo | 1 |
| 61900 | equiparando | 1 |
| 61901 | equiparaba | 1 |
| 61902 | equinoccio | 1 |
| 61903 | equilibrios | 1 |
| 61904 | equilibrarás | 1 |
| 61905 | equilibrara | 1 |
| 61906 | equilibradas | 1 |
| 61907 | equilibraban | 1 |
| 61908 | equi | 1 |
| 61909 | equercito | 1 |
| 61910 | epopeyas | 1 |
| 61911 | epoca | 1 |
| 61912 | epíteto | 1 |
| 61913 | epístolas | 1 |
| 61914 | epiro | 1 |
| 61915 | epinicio | 1 |
| 61916 | epílogo | 1 |
| 61917 | epigramático | 1 |
| 61918 | epigrama | 1 |
| 61919 | epígrafes | 1 |
| 61920 | epigenesis | 1 |
| 61921 | epifanía | 1 |
| 61922 | epidérmicas | 1 |
| 61923 | epicuro | 1 |
| 61924 | epicurista | 1 |
| 61925 | epicúreo | 1 |
| 61926 | epicureísmo | 1 |
| 61927 | epiceno | 1 |
| 61928 | epicena | 1 |
| 61929 | epanadiplosis | 1 |
| 61930 | éolo | 1 |
| 61931 | eñadió | 1 |
| 61932 | enzarzó | 1 |
| 61933 | enzarzaran | 1 |
| 61934 | enzarzados | 1 |
| 61935 | enzarzado | 1 |
| 61936 | enzarzaban | 1 |
| 61937 | enzarza | 1 |
| 61938 | enxutos | 1 |
| 61939 | enxuto | 1 |
| 61940 | enxundias | 1 |
| 61941 | enxiridores | 1 |
| 61942 | enxienpro | 1 |
| 61943 | enxerida | 1 |
| 61944 | enxería | 1 |
| 61945 | enxanbre | 1 |
| 61946 | enxalvega | 1 |
| 61947 | envuelvo | 1 |
| 61948 | envuelvas | 1 |
| 61949 | envuelva | 1 |
| 61950 | envueltitos | 1 |
| 61951 | envolviole | 1 |
| 61952 | envolviéronme | 1 |
| 61953 | envolvieron | 1 |
| 61954 | envolviéndonos | 1 |
| 61955 | envolvíase | 1 |
| 61956 | envolví | 1 |
| 61957 | envolverlos | 1 |
| 61958 | envolverla | 1 |
| 61959 | envoltorios | 1 |
| 61960 | enviudó | 1 |
| 61961 | enviudé | 1 |
| 61962 | enviudaste | 1 |
| 61963 | enviudares | 1 |
| 61964 | envistieron | 1 |
| 61965 | enviso | 1 |
| 61966 | enviole | 1 |
| 61967 | envio | 1 |
| 61968 | envilecimiento | 1 |
| 61969 | envilecidos | 1 |
| 61970 | envilecido | 1 |
| 61971 | envileçes | 1 |
| 61972 | envilece | 1 |
| 61973 | envieux | 1 |
| 61974 | envíemelos | 1 |
| 61975 | envidiosas | 1 |
| 61976 | envidien | 1 |
| 61977 | envidiaros | 1 |
| 61978 | envidiarían | 1 |
| 61979 | envidiando | 1 |
| 61980 | envidar | 1 |
| 61981 | envidado | 1 |
| 61982 | enviciados | 1 |
| 61983 | enviciadas | 1 |
| 61984 | enviaste | 1 |
| 61985 | enviasen | 1 |
| 61986 | envías | 1 |
| 61987 | enviársela | 1 |
| 61988 | enviarla | 1 |
| 61989 | enviaran | 1 |
| 61990 | enviara | 1 |
| 61991 | envíanos | 1 |
| 61992 | enviándole | 1 |
| 61993 | enviallo | 1 |
| 61994 | enviádselo | 1 |
| 61995 | enviádole | 1 |
| 61996 | enviábame | 1 |
| 61997 | enviábades | 1 |
| 61998 | envi | 1 |
| 61999 | envés | 1 |
| 62000 | envergonçada | 1 |
| 62001 | envenene | 1 |
| 62002 | envenenas | 1 |
| 62003 | envenenarse | 1 |
| 62004 | envenenara | 1 |
| 62005 | envenenando | 1 |
| 62006 | envenenaban | 1 |
| 62007 | envelyñas | 1 |
| 62008 | enveleñó | 1 |
| 62009 | envejesçen | 1 |
| 62010 | envejeciendo | 1 |
| 62011 | envejecidas | 1 |
| 62012 | envejecerá | 1 |
| 62013 | envejeçedes | 1 |
| 62014 | envegeçí | 1 |
| 62015 | envásole | 1 |
| 62016 | envasar | 1 |
| 62017 | envásala | 1 |
| 62018 | envaramiento | 1 |
| 62019 | envanecían | 1 |
| 62020 | envanecerme | 1 |
| 62021 | envanece | 1 |
| 62022 | envalentonaron | 1 |
| 62023 | envalentonados | 1 |
| 62024 | envalentonaban | 1 |
| 62025 | envainar | 1 |
| 62026 | envainados | 1 |
| 62027 | envainada | 1 |
| 62028 | envade | 1 |
| 62029 | enunciar | 1 |
| 62030 | enunciado | 1 |
| 62031 | enunciada | 1 |
| 62032 | enuncia | 1 |
| 62033 | enumeraciones | 1 |
| 62034 | enuistiendolas | 1 |
| 62035 | enuiste | 1 |
| 62036 | enues | 1 |
| 62037 | enuergonzantes | 1 |
| 62038 | enuelesada | 1 |
| 62039 | enuejecida | 1 |
| 62040 | enuejeci | 1 |
| 62041 | enuejecer | 1 |
| 62042 | enuejece | 1 |
| 62043 | enuegescen | 1 |
| 62044 | enuegece | 1 |
| 62045 | entyéndolos | 1 |
| 62046 | entyéndelo | 1 |
| 62047 | entyéndela | 1 |
| 62048 | entyendas | 1 |
| 62049 | entusiasmes | 1 |
| 62050 | entusiasmas | 1 |
| 62051 | entusiasmarán | 1 |
| 62052 | entusiasmándose | 1 |
| 62053 | entusiasmados | 1 |
| 62054 | entusiasmaban | 1 |
| 62055 | entusiasma | 1 |
| 62056 | enturuies | 1 |
| 62057 | enturbiando | 1 |
| 62058 | enturbiada | 1 |
| 62059 | entumecimiento | 1 |
| 62060 | entumecidos | 1 |
| 62061 | entumecida | 1 |
| 62062 | entumecían | 1 |
| 62063 | entumecía | 1 |
| 62064 | entumecer | 1 |
| 62065 | entropeçar | 1 |
| 62066 | entroncar | 1 |
| 62067 | entrometo | 1 |
| 62068 | entrometimiento | 1 |
| 62069 | entrometido | 1 |
| 62070 | entrometa | 1 |
| 62071 | éntrome | 1 |
| 62072 | entristézese | 1 |
| 62073 | entristesco | 1 |
| 62074 | entristeçieron | 1 |
| 62075 | entristecieron | 1 |
| 62076 | entristeciendo | 1 |
| 62077 | entristeçes | 1 |
| 62078 | entristecerme | 1 |
| 62079 | entristecer | 1 |
| 62080 | entristeçe | 1 |
| 62081 | entriégame | 1 |
| 62082 | entricadas | 1 |
| 62083 | entrexeridas | 1 |
| 62084 | entreviese | 1 |
| 62085 | entreviendo | 1 |
| 62086 | entrevía | 1 |
| 62087 | entreveró | 1 |
| 62088 | entreverar | 1 |
| 62089 | entreverando | 1 |
| 62090 | entreverados | 1 |
| 62091 | entrevé | 1 |
| 62092 | entreueniendo | 1 |
| 62093 | entretúvose | 1 |
| 62094 | entretúvonos | 1 |
| 62095 | entretuvímonos | 1 |
| 62096 | entretuviésemos | 1 |
| 62097 | entretúveme | 1 |
| 62098 | entretuve | 1 |
| 62099 | entretenme | 1 |
| 62100 | entretenle | 1 |
| 62101 | entreteníale | 1 |
| 62102 | entreténgase | 1 |
| 62103 | entretengamos | 1 |
| 62104 | entretengámonos | 1 |
| 62105 | entreteneros | 1 |
| 62106 | entretenerlas | 1 |
| 62107 | entretenerla | 1 |
| 62108 | entretenellos | 1 |
| 62109 | entretenelle | 1 |
| 62110 | entretenedla | 1 |
| 62111 | entretendría | 1 |
| 62112 | entretendré | 1 |
| 62113 | entretelas | 1 |
| 62114 | entretejióse | 1 |
| 62115 | entretejidos | 1 |
| 62116 | entretejidas | 1 |
| 62117 | entresuelos | 1 |
| 62118 | entresemana | 1 |
| 62119 | éntrese | 1 |
| 62120 | entresaque | 1 |
| 62121 | entresacan | 1 |
| 62122 | entresacada | 1 |
| 62123 | entreponga | 1 |
| 62124 | entreparecía | 1 |
| 62125 | entreoyóle | 1 |
| 62126 | entreoí | 1 |
| 62127 | entremezcladas | 1 |
| 62128 | entremezclada | 1 |
| 62129 | entremety | 1 |
| 62130 | entremetiesse | 1 |
| 62131 | entremetiesen | 1 |
| 62132 | entremetieren | 1 |
| 62133 | entremetiera | 1 |
| 62134 | entremetidos | 1 |
| 62135 | entremetido | 1 |
| 62136 | entremetidas | 1 |
| 62137 | entremetida | 1 |
| 62138 | entremétete | 1 |
| 62139 | entremeternos | 1 |
| 62140 | entremeterme | 1 |
| 62141 | entremete | 1 |
| 62142 | entremetas | 1 |
| 62143 | entremedias | 1 |
| 62144 | entrelazaban | 1 |
| 62145 | entréis | 1 |
| 62146 | entregues | 1 |
| 62147 | entreguéme | 1 |
| 62148 | entregaste | 1 |
| 62149 | entregarte | 1 |
| 62150 | entregárselos | 1 |
| 62151 | entregárselo | 1 |
| 62152 | entregarlo | 1 |
| 62153 | entregarlas | 1 |
| 62154 | entregarían | 1 |
| 62155 | entregáredes | 1 |
| 62156 | entregaré | 1 |
| 62157 | entregándoselo | 1 |
| 62158 | entregándolos | 1 |
| 62159 | entregándolas | 1 |
| 62160 | entregámosla | 1 |
| 62161 | entregalle | 1 |
| 62162 | entregábase | 1 |
| 62163 | entregábalos | 1 |
| 62164 | entredichos | 1 |
| 62165 | entredes | 1 |
| 62166 | entrecuesto | 1 |
| 62167 | entrecortaba | 1 |
| 62168 | entreclara | 1 |
| 62169 | entrecanos | 1 |
| 62170 | entreactos | 1 |
| 62171 | entreabrió | 1 |
| 62172 | entreabriendo | 1 |
| 62173 | entreabierta | 1 |
| 62174 | entrauamos | 1 |
| 62175 | entraua | 1 |
| 62176 | entrate | 1 |
| 62177 | entrásemos | 1 |
| 62178 | éntrase | 1 |
| 62179 | entraros | 1 |
| 62180 | entrarla | 1 |
| 62181 | entrarían | 1 |
| 62182 | entraríamos | 1 |
| 62183 | entraréis | 1 |
| 62184 | entraras | 1 |
| 62185 | entrarán | 1 |
| 62186 | entrapajadas | 1 |
| 62187 | entrapajada | 1 |
| 62188 | entrañan | 1 |
| 62189 | entrañaba | 1 |
| 62190 | entraña | 1 |
| 62191 | entrantes | 1 |
| 62192 | éntranse | 1 |
| 62193 | éntranle | 1 |
| 62194 | entrándose | 1 |
| 62195 | entranable | 1 |
| 62196 | entrámonos | 1 |
| 62197 | éntrale | 1 |
| 62198 | entrabase | 1 |
| 62199 | entrábame | 1 |
| 62200 | entortolarse | 1 |
| 62201 | entorreadas | 1 |
| 62202 | entorpecidos | 1 |
| 62203 | entorpecido | 1 |
| 62204 | entorpecían | 1 |
| 62205 | entorpecía | 1 |
| 62206 | entorpecerle | 1 |
| 62207 | entorpecería | 1 |
| 62208 | entorpecen | 1 |
| 62209 | entornó | 1 |
| 62210 | entornándolos | 1 |
| 62211 | entornado | 1 |
| 62212 | entornadas | 1 |
| 62213 | entonos | 1 |
| 62214 | entonaos | 1 |
| 62215 | entonan | 1 |
| 62216 | entonadas | 1 |
| 62217 | entonaba | 1 |
| 62218 | entomólogo | 1 |
| 62219 | entomológicas | 1 |
| 62220 | entomecen | 1 |
| 62221 | entomece | 1 |
| 62222 | entoldado | 1 |
| 62223 | entiesaba | 1 |
| 62224 | entiéndese | 1 |
| 62225 | entiéndela | 1 |
| 62226 | entiéndala | 1 |
| 62227 | entibie | 1 |
| 62228 | entes | 1 |
| 62229 | enterráronla | 1 |
| 62230 | enterrarme | 1 |
| 62231 | enterraré | 1 |
| 62232 | enterrarán | 1 |
| 62233 | enterraran | 1 |
| 62234 | enterrándonos | 1 |
| 62235 | enterrando | 1 |
| 62236 | enterrámosle | 1 |
| 62237 | enterradas | 1 |
| 62238 | enterrábamos | 1 |
| 62239 | enterraba | 1 |
| 62240 | enternidad | 1 |
| 62241 | enternezco | 1 |
| 62242 | enternézcaos | 1 |
| 62243 | enternezca | 1 |
| 62244 | enternecióse | 1 |
| 62245 | enternecíme | 1 |
| 62246 | enterneciera | 1 |
| 62247 | enterneciéndose | 1 |
| 62248 | enternecerme | 1 |
| 62249 | enternecerlos | 1 |
| 62250 | enternecerle | 1 |
| 62251 | enternecerían | 1 |
| 62252 | enternecen | 1 |
| 62253 | enternazcaos | 1 |
| 62254 | entern | 1 |
| 62255 | entermiza | 1 |
| 62256 | enterizo | 1 |
| 62257 | enterita | 1 |
| 62258 | enteres | 1 |
| 62259 | enteren | 1 |
| 62260 | enteremos | 1 |
| 62261 | enteraste | 1 |
| 62262 | enterarnos | 1 |
| 62263 | enterarle | 1 |
| 62264 | enteraría | 1 |
| 62265 | enteraré | 1 |
| 62266 | enteradas | 1 |
| 62267 | entenebreciéndome | 1 |
| 62268 | entenebrecidos | 1 |
| 62269 | entendy | 1 |
| 62270 | entendudo | 1 |
| 62271 | entendrían | 1 |
| 62272 | entendrian | 1 |
| 62273 | entendredes | 1 |
| 62274 | entendrán | 1 |
| 62275 | entendiste | 1 |
| 62276 | entendiose | 1 |
| 62277 | entendimos | 1 |
| 62278 | entendíles | 1 |
| 62279 | entendiesen | 1 |
| 62280 | entendieren | 1 |
| 62281 | entendiérades | 1 |
| 62282 | entendiéndolos | 1 |
| 62283 | entendíen | 1 |
| 62284 | entendíasele | 1 |
| 62285 | entendíalo | 1 |
| 62286 | entendíais | 1 |
| 62287 | entendia | 1 |
| 62288 | entendetlo | 1 |
| 62289 | entenderte | 1 |
| 62290 | entenderos | 1 |
| 62291 | entenderlos | 1 |
| 62292 | entenderles | 1 |
| 62293 | entendería | 1 |
| 62294 | entendéis | 1 |
| 62295 | entendáis | 1 |
| 62296 | entendades | 1 |
| 62297 | entenas | 1 |
| 62298 | entenado | 1 |
| 62299 | entenada | 1 |
| 62300 | enteca | 1 |
| 62301 | entarimado | 1 |
| 62302 | entapujarse | 1 |
| 62303 | entapujadita | 1 |
| 62304 | entalles | 1 |
| 62305 | entallarse | 1 |
| 62306 | entallada | 1 |
| 62307 | entallad | 1 |
| 62308 | entablose | 1 |
| 62309 | entable | 1 |
| 62310 | entablarle | 1 |
| 62311 | entabladura | 1 |
| 62312 | ensyenpro | 1 |
| 62313 | ensyenplo | 1 |
| 62314 | ensueña | 1 |
| 62315 | ensúciome | 1 |
| 62316 | ensució | 1 |
| 62317 | ensucio | 1 |
| 62318 | ensuciarlo | 1 |
| 62319 | ensuciaré | 1 |
| 62320 | ensucian | 1 |
| 62321 | ensuciados | 1 |
| 62322 | ensuciaba | 1 |
| 62323 | ensucia | 1 |
| 62324 | enssienpro | 1 |
| 62325 | ensotanado | 1 |
| 62326 | ensortijado | 1 |
| 62327 | ensordezca | 1 |
| 62328 | ensordecieron | 1 |
| 62329 | ensordecían | 1 |
| 62330 | ensordeces | 1 |
| 62331 | ensordecedor | 1 |
| 62332 | ensordece | 1 |
| 62333 | ensorde | 1 |
| 62334 | ensoñadora | 1 |
| 62335 | ensoñación | 1 |
| 62336 | ensombrezcan | 1 |
| 62337 | ensogados | 1 |
| 62338 | ensoberuecerse | 1 |
| 62339 | ensoberbezca | 1 |
| 62340 | ensoberbecido | 1 |
| 62341 | ensoberbecía | 1 |
| 62342 | ensoberbecerse | 1 |
| 62343 | ensoberbecerlos | 1 |
| 62344 | ensina | 1 |
| 62345 | ensimisme | 1 |
| 62346 | ensillen | 1 |
| 62347 | ensille | 1 |
| 62348 | ensillarse | 1 |
| 62349 | ensillaron | 1 |
| 62350 | ensillarásme | 1 |
| 62351 | ensíllame | 1 |
| 62352 | ensillada | 1 |
| 62353 | ensillaba | 1 |
| 62354 | ensiladas | 1 |
| 62355 | ensienpro | 1 |
| 62356 | ensías | 1 |
| 62357 | enseres | 1 |
| 62358 | enseñorease | 1 |
| 62359 | enseñoreando | 1 |
| 62360 | enseñoreados | 1 |
| 62361 | enseñólos | 1 |
| 62362 | enseño | 1 |
| 62363 | enséñenme | 1 |
| 62364 | enseñemos | 1 |
| 62365 | enséñemelo | 1 |
| 62366 | enseñéis | 1 |
| 62367 | enseñásemos | 1 |
| 62368 | enseñárselo | 1 |
| 62369 | enseñársele | 1 |
| 62370 | enseñáronme | 1 |
| 62371 | enseñarnos | 1 |
| 62372 | enseñármele | 1 |
| 62373 | enseñaremos | 1 |
| 62374 | enseñare | 1 |
| 62375 | enseñaran | 1 |
| 62376 | enseñara | 1 |
| 62377 | enseñándosele | 1 |
| 62378 | enseñándoselas | 1 |
| 62379 | enseñándome | 1 |
| 62380 | enséñale | 1 |
| 62381 | enséñala | 1 |
| 62382 | enseñadme | 1 |
| 62383 | enseñabas | 1 |
| 62384 | ensenoreado | 1 |
| 62385 | ensena | 1 |
| 62386 | ense | 1 |
| 62387 | ensayó | 1 |
| 62388 | ensayaremos | 1 |
| 62389 | ensayara | 1 |
| 62390 | ensayados | 1 |
| 62391 | ensayaba | 1 |
| 62392 | ensartaron | 1 |
| 62393 | ensártalos | 1 |
| 62394 | ensartado | 1 |
| 62395 | ensarriá | 1 |
| 62396 | ensarmentar | 1 |
| 62397 | ensaño | 1 |
| 62398 | ensañas | 1 |
| 62399 | ensañar | 1 |
| 62400 | ensangriento | 1 |
| 62401 | ensangrientan | 1 |
| 62402 | ensangrienta | 1 |
| 62403 | ensangrentando | 1 |
| 62404 | ensangrentados | 1 |
| 62405 | ensangrentadas | 1 |
| 62406 | ensangosta | 1 |
| 62407 | ensanchó | 1 |
| 62408 | ensancho | 1 |
| 62409 | ensancharse | 1 |
| 62410 | ensanchara | 1 |
| 62411 | ensanchan | 1 |
| 62412 | ensanchaban | 1 |
| 62413 | ensanar | 1 |
| 62414 | ensananse | 1 |
| 62415 | ensanada | 1 |
| 62416 | ensalzaron | 1 |
| 62417 | ensalzarás | 1 |
| 62418 | ensalzaos | 1 |
| 62419 | ensalzamiento | 1 |
| 62420 | ensalmaderas | 1 |
| 62421 | ensalmaba | 1 |
| 62422 | ensalçamientos | 1 |
| 62423 | ensalçada | 1 |
| 62424 | ensaladas | 1 |
| 62425 | ensabanados | 1 |
| 62426 | enrubiar | 1 |
| 62427 | enroscarse | 1 |
| 62428 | enroscados | 1 |
| 62429 | enroscaba | 1 |
| 62430 | enronqueciéronse | 1 |
| 62431 | enronquecieron | 1 |
| 62432 | enronquecían | 1 |
| 62433 | enronquece | 1 |
| 62434 | enrojecidos | 1 |
| 62435 | enrojecidas | 1 |
| 62436 | enrojecía | 1 |
| 62437 | enriza | 1 |
| 62438 | enristrando | 1 |
| 62439 | enriquezco | 1 |
| 62440 | enríquez | 1 |
| 62441 | enriqueta | 1 |
| 62442 | enriquecieron | 1 |
| 62443 | enriqueciéndose | 1 |
| 62444 | enriqueciendo | 1 |
| 62445 | enriquecíanse | 1 |
| 62446 | enriquecerse | 1 |
| 62447 | enriquecelde | 1 |
| 62448 | enrevesados | 1 |
| 62449 | enrevesadas | 1 |
| 62450 | enrevesada | 1 |
| 62451 | enrejado | 1 |
| 62452 | enrejadas | 1 |
| 62453 | enredosas | 1 |
| 62454 | enredes | 1 |
| 62455 | enredaríamos | 1 |
| 62456 | enredándose | 1 |
| 62457 | enredados | 1 |
| 62458 | enredadoras | 1 |
| 62459 | enranciaran | 1 |
| 62460 | enramar | 1 |
| 62461 | enramaban | 1 |
| 62462 | enpuesta | 1 |
| 62463 | enprestadlo | 1 |
| 62464 | enpresta | 1 |
| 62465 | enprea | 1 |
| 62466 | enpós | 1 |
| 62467 | enpos | 1 |
| 62468 | enplea | 1 |
| 62469 | enplazóla | 1 |
| 62470 | enplasto | 1 |
| 62471 | enpiuelan | 1 |
| 62472 | enpieça | 1 |
| 62473 | enpesçer | 1 |
| 62474 | enpesçe | 1 |
| 62475 | enpero | 1 |
| 62476 | enperios | 1 |
| 62477 | enperesedes | 1 |
| 62478 | enpereçes | 1 |
| 62479 | enperante | 1 |
| 62480 | enpendolados | 1 |
| 62481 | enpeesçer | 1 |
| 62482 | enpeesçen | 1 |
| 62483 | enpecen | 1 |
| 62484 | enpeçe | 1 |
| 62485 | enpavonada | 1 |
| 62486 | enormidades | 1 |
| 62487 | enormemente | 1 |
| 62488 | enorgulleciéndose | 1 |
| 62489 | enoramala | 1 |
| 62490 | enojote | 1 |
| 62491 | enojosos | 1 |
| 62492 | enojosísimos | 1 |
| 62493 | enojedes | 1 |
| 62494 | enójase | 1 |
| 62495 | enojase | 1 |
| 62496 | enojártela | 1 |
| 62497 | enojarte | 1 |
| 62498 | enojaré | 1 |
| 62499 | enojara | 1 |
| 62500 | enojan | 1 |
| 62501 | enojalla | 1 |
| 62502 | enojábanla | 1 |
| 62503 | enojaban | 1 |
| 62504 | enoblecer | 1 |
| 62505 | ennuyé | 1 |
| 62506 | ennobleza | 1 |
| 62507 | ennobleciste | 1 |
| 62508 | ennobleciendo | 1 |
| 62509 | ennoblecido | 1 |
| 62510 | ennoblecerte | 1 |
| 62511 | ennoblecerse | 1 |
| 62512 | ennoblecerles | 1 |
| 62513 | ennoblecer | 1 |
| 62514 | ennoblecemos | 1 |
| 62515 | ennegrecidos | 1 |
| 62516 | ennegrecido | 1 |
| 62517 | enmudescerias | 1 |
| 62518 | enmudecióse | 1 |
| 62519 | enmudeciera | 1 |
| 62520 | enmudecido | 1 |
| 62521 | enmudecía | 1 |
| 62522 | enmudecí | 1 |
| 62523 | enmudeçes | 1 |
| 62524 | enmohecido | 1 |
| 62525 | enmohecidas | 1 |
| 62526 | enmohecían | 1 |
| 62527 | enmiendes | 1 |
| 62528 | enmiende | 1 |
| 62529 | enmiendan | 1 |
| 62530 | enmendastes | 1 |
| 62531 | enmendaron | 1 |
| 62532 | enmendarme | 1 |
| 62533 | enmendarlo | 1 |
| 62534 | enmendarla | 1 |
| 62535 | enmendaren | 1 |
| 62536 | enmendada | 1 |
| 62537 | enmascarando | 1 |
| 62538 | enmaromado | 1 |
| 62539 | enmantaban | 1 |
| 62540 | enmagresçen | 1 |
| 62541 | enluto | 1 |
| 62542 | enlutaron | 1 |
| 62543 | enlucía | 1 |
| 62544 | enloquesçes | 1 |
| 62545 | enloqueçidos | 1 |
| 62546 | enloquecidas | 1 |
| 62547 | enloqueçida | 1 |
| 62548 | enloquecía | 1 |
| 62549 | enloquecerme | 1 |
| 62550 | enloquece | 1 |
| 62551 | enlaze | 1 |
| 62552 | enlazastes | 1 |
| 62553 | enlazarte | 1 |
| 62554 | enlazar | 1 |
| 62555 | enlazándose | 1 |
| 62556 | enlazan | 1 |
| 62557 | enlase | 1 |
| 62558 | enladrillados | 1 |
| 62559 | enlaçes | 1 |
| 62560 | enlabiadoras | 1 |
| 62561 | enjutísimas | 1 |
| 62562 | enjuiciar | 1 |
| 62563 | enjugue | 1 |
| 62564 | enjugase | 1 |
| 62565 | enjugar | 1 |
| 62566 | enjugándose | 1 |
| 62567 | enjugan | 1 |
| 62568 | enjugadlas | 1 |
| 62569 | enjuagóse | 1 |
| 62570 | enjerto | 1 |
| 62571 | enjaulasen | 1 |
| 62572 | enjaularme | 1 |
| 62573 | enjaulados | 1 |
| 62574 | enjauladas | 1 |
| 62575 | enjaulada | 1 |
| 62576 | enjareto | 1 |
| 62577 | enjaretarle | 1 |
| 62578 | enjaretándose | 1 |
| 62579 | enjalma | 1 |
| 62580 | enjaguar | 1 |
| 62581 | enjaguaduras | 1 |
| 62582 | enjaezó | 1 |
| 62583 | enjaezándole | 1 |
| 62584 | enjaezado | 1 |
| 62585 | enjaezada | 1 |
| 62586 | enjabonáronle | 1 |
| 62587 | enimigo | 1 |
| 62588 | enigmáticas | 1 |
| 62589 | enigmática | 1 |
| 62590 | enigmas | 1 |
| 62591 | enhoto | 1 |
| 62592 | enhilas | 1 |
| 62593 | enhilar | 1 |
| 62594 | enhila | 1 |
| 62595 | enhebras | 1 |
| 62596 | enharinados | 1 |
| 62597 | enharinado | 1 |
| 62598 | engullía | 1 |
| 62599 | engulleron | 1 |
| 62600 | engulle | 1 |
| 62601 | enguí | 1 |
| 62602 | engrosaba | 1 |
| 62603 | engrescan | 1 |
| 62604 | engreírse | 1 |
| 62605 | engrasado | 1 |
| 62606 | engrandezca | 1 |
| 62607 | engrandecimiento | 1 |
| 62608 | engrandecía | 1 |
| 62609 | engrandecerte | 1 |
| 62610 | engrandecerlas | 1 |
| 62611 | engrandecerla | 1 |
| 62612 | engrandeced | 1 |
| 62613 | engrandece | 1 |
| 62614 | engranaje | 1 |
| 62615 | engraçio | 1 |
| 62616 | engraçias | 1 |
| 62617 | engorrosísimo | 1 |
| 62618 | engorrosa | 1 |
| 62619 | engorden | 1 |
| 62620 | engordase | 1 |
| 62621 | engordas | 1 |
| 62622 | engordara | 1 |
| 62623 | engordando | 1 |
| 62624 | engomada | 1 |
| 62625 | engolosinaron | 1 |
| 62626 | engolosina | 1 |
| 62627 | engolfarte | 1 |
| 62628 | engolfados | 1 |
| 62629 | engolfada | 1 |
| 62630 | englobado | 1 |
| 62631 | engeño | 1 |
| 62632 | engendros | 1 |
| 62633 | engendraua | 1 |
| 62634 | engendraren | 1 |
| 62635 | engendrara | 1 |
| 62636 | engendrando | 1 |
| 62637 | engendrados | 1 |
| 62638 | engendrador | 1 |
| 62639 | engendrada | 1 |
| 62640 | engazando | 1 |
| 62641 | engazado | 1 |
| 62642 | engatusar | 1 |
| 62643 | engatusando | 1 |
| 62644 | engatusa | 1 |
| 62645 | engastonar | 1 |
| 62646 | engastada | 1 |
| 62647 | engarzó | 1 |
| 62648 | engarzada | 1 |
| 62649 | engarnos | 1 |
| 62650 | engarfiñaron | 1 |
| 62651 | engañosos | 1 |
| 62652 | engañólo | 1 |
| 62653 | engañifas | 1 |
| 62654 | engañedes | 1 |
| 62655 | engañaste | 1 |
| 62656 | engañase | 1 |
| 62657 | engañarnos | 1 |
| 62658 | engañarlos | 1 |
| 62659 | engañarla | 1 |
| 62660 | engañaría | 1 |
| 62661 | engañare | 1 |
| 62662 | engañarás | 1 |
| 62663 | engañándose | 1 |
| 62664 | engañándonos | 1 |
| 62665 | engañamos | 1 |
| 62666 | engañalle | 1 |
| 62667 | engañadores | 1 |
| 62668 | engañadora | 1 |
| 62669 | engañades | 1 |
| 62670 | engañábase | 1 |
| 62671 | enganoso | 1 |
| 62672 | enganosas | 1 |
| 62673 | enganchole | 1 |
| 62674 | enganche | 1 |
| 62675 | enganchará | 1 |
| 62676 | enganchan | 1 |
| 62677 | enganchados | 1 |
| 62678 | enganchado | 1 |
| 62679 | enganchada | 1 |
| 62680 | enganchaban | 1 |
| 62681 | engancha | 1 |
| 62682 | enganando | 1 |
| 62683 | enganan | 1 |
| 62684 | enganados | 1 |
| 62685 | enganador | 1 |
| 62686 | engalanó | 1 |
| 62687 | engalanarse | 1 |
| 62688 | engalanadas | 1 |
| 62689 | enfychisó | 1 |
| 62690 | enfurruñas | 1 |
| 62691 | enfurruñados | 1 |
| 62692 | enfurruñado | 1 |
| 62693 | enfureciendo | 1 |
| 62694 | enfureces | 1 |
| 62695 | enfurecen | 1 |
| 62696 | enfurece | 1 |
| 62697 | enfundadas | 1 |
| 62698 | enfríe | 1 |
| 62699 | enfriarás | 1 |
| 62700 | enfriaran | 1 |
| 62701 | enfriándose | 1 |
| 62702 | enfriando | 1 |
| 62703 | enfrían | 1 |
| 62704 | enfriada | 1 |
| 62705 | enfriaban | 1 |
| 62706 | enfreno | 1 |
| 62707 | enfrenase | 1 |
| 62708 | enfrenara | 1 |
| 62709 | enfrenados | 1 |
| 62710 | enfrena | 1 |
| 62711 | enfrascó | 1 |
| 62712 | enfrascarse | 1 |
| 62713 | enfrascaron | 1 |
| 62714 | enforma | 1 |
| 62715 | enforce | 1 |
| 62716 | enforcavan | 1 |
| 62717 | enforcados | 1 |
| 62718 | enforcada | 1 |
| 62719 | enflautadora | 1 |
| 62720 | enflaquidas | 1 |
| 62721 | enflaquezes | 1 |
| 62722 | enflaquesçes | 1 |
| 62723 | enflaquesçen | 1 |
| 62724 | enflaquecieron | 1 |
| 62725 | enflaquecido | 1 |
| 62726 | enflaquecía | 1 |
| 62727 | enflaqueçe | 1 |
| 62728 | enflaquece | 1 |
| 62729 | enflama | 1 |
| 62730 | enfin | 1 |
| 62731 | enfiló | 1 |
| 62732 | enfilarla | 1 |
| 62733 | enfilar | 1 |
| 62734 | enfilándose | 1 |
| 62735 | enfilándolos | 1 |
| 62736 | enfiestos | 1 |
| 62737 | enfernal | 1 |
| 62738 | enfermucho | 1 |
| 62739 | enfermemos | 1 |
| 62740 | enfermaste | 1 |
| 62741 | enfermaran | 1 |
| 62742 | enfermara | 1 |
| 62743 | enfermando | 1 |
| 62744 | enfermado | 1 |
| 62745 | enfáticos | 1 |
| 62746 | enfáticas | 1 |
| 62747 | enfaronea | 1 |
| 62748 | enfamedes | 1 |
| 62749 | enfamaron | 1 |
| 62750 | enfaman | 1 |
| 62751 | enfamamiento | 1 |
| 62752 | enfamado | 1 |
| 62753 | enfamada | 1 |
| 62754 | enfadé | 1 |
| 62755 | enfádate | 1 |
| 62756 | enfadase | 1 |
| 62757 | enfadaros | 1 |
| 62758 | enfadaron | 1 |
| 62759 | enfadarle | 1 |
| 62760 | enfadarías | 1 |
| 62761 | enfadarían | 1 |
| 62762 | enfadaré | 1 |
| 62763 | enfadáis | 1 |
| 62764 | enfadados | 1 |
| 62765 | enfadadito | 1 |
| 62766 | enfadadas | 1 |
| 62767 | enfadábase | 1 |
| 62768 | enf | 1 |
| 62769 | enervolas | 1 |
| 62770 | enerve | 1 |
| 62771 | enerisan | 1 |
| 62772 | energúmenos | 1 |
| 62773 | enemistarnos | 1 |
| 62774 | enefable | 1 |
| 62775 | enecido | 1 |
| 62776 | enduxo | 1 |
| 62777 | endureció | 1 |
| 62778 | endurecimiento | 1 |
| 62779 | endurecer | 1 |
| 62780 | endurece | 1 |
| 62781 | endurar | 1 |
| 62782 | endulzó | 1 |
| 62783 | endulzara | 1 |
| 62784 | endryna | 1 |
| 62785 | endrino | 1 |
| 62786 | endrinas | 1 |
| 62787 | endrin | 1 |
| 62788 | endrigos | 1 |
| 62789 | endriago | 1 |
| 62790 | endomingados | 1 |
| 62791 | endividos | 1 |
| 62792 | endiosas | 1 |
| 62793 | endiosarse | 1 |
| 62794 | endiñarles | 1 |
| 62795 | endilgue | 1 |
| 62796 | endilgarle | 1 |
| 62797 | endiablo | 1 |
| 62798 | enderredor | 1 |
| 62799 | enderlaza | 1 |
| 62800 | enderezarle | 1 |
| 62801 | enderezarán | 1 |
| 62802 | enderezaran | 1 |
| 62803 | enderezándole | 1 |
| 62804 | enderezador | 1 |
| 62805 | enderezaba | 1 |
| 62806 | enderedor | 1 |
| 62807 | enderecé | 1 |
| 62808 | enderece | 1 |
| 62809 | endémicos | 1 |
| 62810 | endechando | 1 |
| 62811 | endechado | 1 |
| 62812 | endechaderas | 1 |
| 62813 | endecha | 1 |
| 62814 | encumbres | 1 |
| 62815 | encuéntrome | 1 |
| 62816 | encuéntrate | 1 |
| 62817 | encuentrarla | 1 |
| 62818 | encuentrar | 1 |
| 62819 | encubro | 1 |
| 62820 | encubrís | 1 |
| 62821 | encubrirte | 1 |
| 62822 | encubrírsela | 1 |
| 62823 | encubrirse | 1 |
| 62824 | encubrirnos | 1 |
| 62825 | encubrirme | 1 |
| 62826 | encubrirles | 1 |
| 62827 | encubrirle | 1 |
| 62828 | encubrio | 1 |
| 62829 | encubrimiento | 1 |
| 62830 | encubriese | 1 |
| 62831 | encubriéndosela | 1 |
| 62832 | encubriéndola | 1 |
| 62833 | encubridoras | 1 |
| 62834 | encubridor | 1 |
| 62835 | encubrian | 1 |
| 62836 | encubresme | 1 |
| 62837 | encúbrese | 1 |
| 62838 | encubras | 1 |
| 62839 | encubiertamente | 1 |
| 62840 | encubertadas | 1 |
| 62841 | encuadrar | 1 |
| 62842 | encuadernadas | 1 |
| 62843 | encruzijada | 1 |
| 62844 | encrucejadas | 1 |
| 62845 | encrespándose | 1 |
| 62846 | encorvarse | 1 |
| 62847 | encorvar | 1 |
| 62848 | encorvamiento | 1 |
| 62849 | encorvadas | 1 |
| 62850 | encorporados | 1 |
| 62851 | encorozada | 1 |
| 62852 | encore | 1 |
| 62853 | encordonado | 1 |
| 62854 | encordado | 1 |
| 62855 | encopetados | 1 |
| 62856 | encopetado | 1 |
| 62857 | encopetada | 1 |
| 62858 | encontronazos | 1 |
| 62859 | encontrolo | 1 |
| 62860 | encontrole | 1 |
| 62861 | encontrémela | 1 |
| 62862 | encontréme | 1 |
| 62863 | encontrém | 1 |
| 62864 | encontrele | 1 |
| 62865 | encontrásemos | 1 |
| 62866 | encontrársele | 1 |
| 62867 | encontrársela | 1 |
| 62868 | encontrarnos | 1 |
| 62869 | encontrarlas | 1 |
| 62870 | encontraras | 1 |
| 62871 | encontrarán | 1 |
| 62872 | encontrándome | 1 |
| 62873 | encontrándole | 1 |
| 62874 | encontrámosle | 1 |
| 62875 | encontrádole | 1 |
| 62876 | encontrada | 1 |
| 62877 | encontinente | 1 |
| 62878 | enconos | 1 |
| 62879 | encone | 1 |
| 62880 | enconar | 1 |
| 62881 | enconan | 1 |
| 62882 | enconado | 1 |
| 62883 | encomparablemente | 1 |
| 62884 | encomiéndole | 1 |
| 62885 | encomiéndese | 1 |
| 62886 | encomiéndenme | 1 |
| 62887 | encomiéndeme | 1 |
| 62888 | encomiéndate | 1 |
| 62889 | encomiéndame | 1 |
| 62890 | encomiéndalo | 1 |
| 62891 | encomiarlo | 1 |
| 62892 | encomiados | 1 |
| 62893 | encomendóme | 1 |
| 62894 | encomendole | 1 |
| 62895 | encomendémoslo | 1 |
| 62896 | encomendauan | 1 |
| 62897 | encomendasen | 1 |
| 62898 | encomendarte | 1 |
| 62899 | encomendaros | 1 |
| 62900 | encomendaron | 1 |
| 62901 | encomendarles | 1 |
| 62902 | encomendarle | 1 |
| 62903 | encomendar | 1 |
| 62904 | encomendándome | 1 |
| 62905 | encomendadlo | 1 |
| 62906 | encomendada | 1 |
| 62907 | encomendaban | 1 |
| 62908 | encomendábame | 1 |
| 62909 | encoje | 1 |
| 62910 | encojan | 1 |
| 62911 | encogimientos | 1 |
| 62912 | encogiera | 1 |
| 62913 | encogiéndose | 1 |
| 62914 | encogidas | 1 |
| 62915 | encogerlo | 1 |
| 62916 | encogemos | 1 |
| 62917 | encobyerta | 1 |
| 62918 | encobrid | 1 |
| 62919 | encobrias | 1 |
| 62920 | encobria | 1 |
| 62921 | encobrí | 1 |
| 62922 | encobo | 1 |
| 62923 | encoba | 1 |
| 62924 | enclinando | 1 |
| 62925 | enclina | 1 |
| 62926 | enclenques | 1 |
| 62927 | enclavóme | 1 |
| 62928 | enclavó | 1 |
| 62929 | enclavijar | 1 |
| 62930 | enclavijan | 1 |
| 62931 | enclavijados | 1 |
| 62932 | enclavijadas | 1 |
| 62933 | enclavijaba | 1 |
| 62934 | enclave | 1 |
| 62935 | enclavársela | 1 |
| 62936 | enclavaron | 1 |
| 62937 | enclauijadas | 1 |
| 62938 | enclaresçía | 1 |
| 62939 | encintado | 1 |
| 62940 | encinar | 1 |
| 62941 | encierros | 1 |
| 62942 | enciérrome | 1 |
| 62943 | encierre | 1 |
| 62944 | enciérrate | 1 |
| 62945 | encierras | 1 |
| 62946 | encienso | 1 |
| 62947 | enciendes | 1 |
| 62948 | enciclopédica | 1 |
| 62949 | encía | 1 |
| 62950 | enchufaban | 1 |
| 62951 | encharcadas | 1 |
| 62952 | encharcada | 1 |
| 62953 | encharcad | 1 |
| 62954 | encerro | 1 |
| 62955 | encerré | 1 |
| 62956 | encerrasen | 1 |
| 62957 | encerrarte | 1 |
| 62958 | ençerraron | 1 |
| 62959 | encerrarlo | 1 |
| 62960 | encerrarán | 1 |
| 62961 | encerrándonos | 1 |
| 62962 | encerrándoles | 1 |
| 62963 | encerrándole | 1 |
| 62964 | encerrad | 1 |
| 62965 | encerado | 1 |
| 62966 | enceradas | 1 |
| 62967 | encenegándose | 1 |
| 62968 | encendiósele | 1 |
| 62969 | encendios | 1 |
| 62970 | ençendimiento | 1 |
| 62971 | encendiese | 1 |
| 62972 | encendiera | 1 |
| 62973 | encendiéndolas | 1 |
| 62974 | ençendíen | 1 |
| 62975 | ençendíe | 1 |
| 62976 | ençendidos | 1 |
| 62977 | ençendidas | 1 |
| 62978 | ençendida | 1 |
| 62979 | ençendían | 1 |
| 62980 | encenderme | 1 |
| 62981 | encenderlos | 1 |
| 62982 | encenderle | 1 |
| 62983 | encenderlas | 1 |
| 62984 | encenderla | 1 |
| 62985 | encenderá | 1 |
| 62986 | encendera | 1 |
| 62987 | ençender | 1 |
| 62988 | encendello | 1 |
| 62989 | encenagó | 1 |
| 62990 | encenágate | 1 |
| 62991 | encenagados | 1 |
| 62992 | encenagaba | 1 |
| 62993 | ençelado | 1 |
| 62994 | encelado | 1 |
| 62995 | encefálico | 1 |
| 62996 | encaxado | 1 |
| 62997 | encauzarlo | 1 |
| 62998 | encauzada | 1 |
| 62999 | encastilló | 1 |
| 63000 | encastilladas | 1 |
| 63001 | encasquetóse | 1 |
| 63002 | encasquetose | 1 |
| 63003 | encasquetarme | 1 |
| 63004 | encasquetándose | 1 |
| 63005 | encasquetan | 1 |
| 63006 | encasquetado | 1 |
| 63007 | encasquetada | 1 |
| 63008 | encasquetaban | 1 |
| 63009 | encasquetaba | 1 |
| 63010 | encasqueta | 1 |
| 63011 | encasillado | 1 |
| 63012 | encarzaron | 1 |
| 63013 | encarrilarle | 1 |
| 63014 | encarose | 1 |
| 63015 | encarnarse | 1 |
| 63016 | encarnándose | 1 |
| 63017 | encarnaciones | 1 |
| 63018 | encarnaba | 1 |
| 63019 | encarna | 1 |
| 63020 | encariñarte | 1 |
| 63021 | encariñándose | 1 |
| 63022 | encariñan | 1 |
| 63023 | encariñado | 1 |
| 63024 | encárguese | 1 |
| 63025 | encarguemos | 1 |
| 63026 | encargue | 1 |
| 63027 | encargóse | 1 |
| 63028 | encargóles | 1 |
| 63029 | encárgate | 1 |
| 63030 | encargármelo | 1 |
| 63031 | encargarle | 1 |
| 63032 | encargaremos | 1 |
| 63033 | encargaras | 1 |
| 63034 | encargárale | 1 |
| 63035 | encargará | 1 |
| 63036 | encargara | 1 |
| 63037 | encargándonos | 1 |
| 63038 | encargándome | 1 |
| 63039 | encargándoles | 1 |
| 63040 | encargándolas | 1 |
| 63041 | encárgale | 1 |
| 63042 | encargados | 1 |
| 63043 | encargábase | 1 |
| 63044 | encareciéronme | 1 |
| 63045 | encareciéndole | 1 |
| 63046 | encarecido | 1 |
| 63047 | encarecíales | 1 |
| 63048 | encareces | 1 |
| 63049 | encarecerte | 1 |
| 63050 | encareceros | 1 |
| 63051 | encarecerlas | 1 |
| 63052 | encareceré | 1 |
| 63053 | encarecella | 1 |
| 63054 | encaré | 1 |
| 63055 | encare | 1 |
| 63056 | encarcela | 1 |
| 63057 | encararon | 1 |
| 63058 | encaramó | 1 |
| 63059 | encaramar | 1 |
| 63060 | encaramando | 1 |
| 63061 | encaraman | 1 |
| 63062 | encaramados | 1 |
| 63063 | encaramadas | 1 |
| 63064 | encaramaban | 1 |
| 63065 | encaramaba | 1 |
| 63066 | encaradas | 1 |
| 63067 | encaprichó | 1 |
| 63068 | encapricharte | 1 |
| 63069 | encaprichara | 1 |
| 63070 | encaprichado | 1 |
| 63071 | encaprichadas | 1 |
| 63072 | encantorio | 1 |
| 63073 | encantóla | 1 |
| 63074 | encanten | 1 |
| 63075 | encanté | 1 |
| 63076 | encante | 1 |
| 63077 | encantáronla | 1 |
| 63078 | encantaron | 1 |
| 63079 | encantando | 1 |
| 63080 | encantamientos | 1 |
| 63081 | encantalla | 1 |
| 63082 | encantadoras | 1 |
| 63083 | encanijados | 1 |
| 63084 | encanijado | 1 |
| 63085 | encanijada | 1 |
| 63086 | encaneci | 1 |
| 63087 | encaneces | 1 |
| 63088 | encandelado | 1 |
| 63089 | encanallan | 1 |
| 63090 | encanallado | 1 |
| 63091 | encamisado | 1 |
| 63092 | encaminose | 1 |
| 63093 | encamino | 1 |
| 63094 | encaminen | 1 |
| 63095 | encaminéis | 1 |
| 63096 | encaminé | 1 |
| 63097 | encaminarlos | 1 |
| 63098 | encaminarla | 1 |
| 63099 | encaminarían | 1 |
| 63100 | encaminare | 1 |
| 63101 | encaminados | 1 |
| 63102 | encambronado | 1 |
| 63103 | encamarme | 1 |
| 63104 | encamada | 1 |
| 63105 | encallaría | 1 |
| 63106 | encallado | 1 |
| 63107 | encalabrinó | 1 |
| 63108 | encalabrinada | 1 |
| 63109 | encajona | 1 |
| 63110 | encajo | 1 |
| 63111 | encajería | 1 |
| 63112 | encajera | 1 |
| 63113 | encájenme | 1 |
| 63114 | encájate | 1 |
| 63115 | encajarte | 1 |
| 63116 | encajársela | 1 |
| 63117 | encajarle | 1 |
| 63118 | encajamos | 1 |
| 63119 | encajallo | 1 |
| 63120 | encajalle | 1 |
| 63121 | encajador | 1 |
| 63122 | encajadas | 1 |
| 63123 | encajada | 1 |
| 63124 | encadenando | 1 |
| 63125 | encadena | 1 |
| 63126 | encabrilló | 1 |
| 63127 | encabezar | 1 |
| 63128 | encabezan | 1 |
| 63129 | encabezamos | 1 |
| 63130 | enbyote | 1 |
| 63131 | enbyo | 1 |
| 63132 | enbyamos | 1 |
| 63133 | enbuelto | 1 |
| 63134 | enbudo | 1 |
| 63135 | enbriagos | 1 |
| 63136 | enbota | 1 |
| 63137 | enbióte | 1 |
| 63138 | enbiéle | 1 |
| 63139 | enbiél | 1 |
| 63140 | enbié | 1 |
| 63141 | enbidiosos | 1 |
| 63142 | enbidioso | 1 |
| 63143 | enbíavos | 1 |
| 63144 | enbiátgelo | 1 |
| 63145 | enbiares | 1 |
| 63146 | enbían | 1 |
| 63147 | enbargo | 1 |
| 63148 | enbargan | 1 |
| 63149 | enbarga | 1 |
| 63150 | enbalde | 1 |
| 63151 | enbaçado | 1 |
| 63152 | enartar | 1 |
| 63153 | enartan | 1 |
| 63154 | enardecido | 1 |
| 63155 | enardecida | 1 |
| 63156 | enardecía | 1 |
| 63157 | enarcó | 1 |
| 63158 | enarcar | 1 |
| 63159 | enarcando | 1 |
| 63160 | enarbolada | 1 |
| 63161 | enante | 1 |
| 63162 | enanita | 1 |
| 63163 | enamoróse | 1 |
| 63164 | enamoróme | 1 |
| 63165 | enamoróle | 1 |
| 63166 | enamoróla | 1 |
| 63167 | enamorisca | 1 |
| 63168 | enamoren | 1 |
| 63169 | enamoréme | 1 |
| 63170 | enamoréla | 1 |
| 63171 | enamoré | 1 |
| 63172 | enamore | 1 |
| 63173 | enamorasen | 1 |
| 63174 | enamorarte | 1 |
| 63175 | enamoraron | 1 |
| 63176 | enamoraran | 1 |
| 63177 | enamorara | 1 |
| 63178 | enamorándome | 1 |
| 63179 | enamoramos | 1 |
| 63180 | enamoradizo | 1 |
| 63181 | enamoradito | 1 |
| 63182 | enamorad | 1 |
| 63183 | enamorábala | 1 |
| 63184 | enamoraba | 1 |
| 63185 | enamistad | 1 |
| 63186 | enaltecido | 1 |
| 63187 | enaltecerlo | 1 |
| 63188 | enaltecerla | 1 |
| 63189 | enalbardó | 1 |
| 63190 | enalbardando | 1 |
| 63191 | enajenas | 1 |
| 63192 | enajena | 1 |
| 63193 | enagenación | 1 |
| 63194 | emulsión | 1 |
| 63195 | empuñe | 1 |
| 63196 | empuñaron | 1 |
| 63197 | empuñará | 1 |
| 63198 | empuñamos | 1 |
| 63199 | empuñado | 1 |
| 63200 | empujoncillos | 1 |
| 63201 | empujole | 1 |
| 63202 | empujola | 1 |
| 63203 | empujasen | 1 |
| 63204 | empujarse | 1 |
| 63205 | empujaran | 1 |
| 63206 | empujará | 1 |
| 63207 | empujara | 1 |
| 63208 | empujándose | 1 |
| 63209 | empuerque | 1 |
| 63210 | empuerca | 1 |
| 63211 | emprincipio | 1 |
| 63212 | empréstitos | 1 |
| 63213 | empresta | 1 |
| 63214 | empreñastes | 1 |
| 63215 | empreñaba | 1 |
| 63216 | empreña | 1 |
| 63217 | emprendo | 1 |
| 63218 | emprendiesen | 1 |
| 63219 | emprendiera | 1 |
| 63220 | empréndenlos | 1 |
| 63221 | emprendemos | 1 |
| 63222 | emprendella | 1 |
| 63223 | emprenda | 1 |
| 63224 | empozarme | 1 |
| 63225 | empozado | 1 |
| 63226 | empotrarse | 1 |
| 63227 | empotradas | 1 |
| 63228 | empotrada | 1 |
| 63229 | emponzonado | 1 |
| 63230 | empolvarme | 1 |
| 63231 | empolvar | 1 |
| 63232 | empolvados | 1 |
| 63233 | empolvadas | 1 |
| 63234 | empolvada | 1 |
| 63235 | empolva | 1 |
| 63236 | empollar | 1 |
| 63237 | empollándola | 1 |
| 63238 | empollados | 1 |
| 63239 | empoçonas | 1 |
| 63240 | empobreciesen | 1 |
| 63241 | empobrecieron | 1 |
| 63242 | empobrecida | 1 |
| 63243 | empobreces | 1 |
| 63244 | empobrecerla | 1 |
| 63245 | empobrecer | 1 |
| 63246 | emplumenla | 1 |
| 63247 | emplumadas | 1 |
| 63248 | emplumaba | 1 |
| 63249 | emplomados | 1 |
| 63250 | emplomadas | 1 |
| 63251 | empleolo | 1 |
| 63252 | empleíto | 1 |
| 63253 | empleitas | 1 |
| 63254 | empleíllos | 1 |
| 63255 | empleíllo | 1 |
| 63256 | emplees | 1 |
| 63257 | empleen | 1 |
| 63258 | empleé | 1 |
| 63259 | empleasen | 1 |
| 63260 | empleas | 1 |
| 63261 | emplearla | 1 |
| 63262 | emplearé | 1 |
| 63263 | emplearan | 1 |
| 63264 | empleamos | 1 |
| 63265 | empleadísima | 1 |
| 63266 | empleadillo | 1 |
| 63267 | empleábale | 1 |
| 63268 | emplazamiento | 1 |
| 63269 | emplastaron | 1 |
| 63270 | emplastado | 1 |
| 63271 | emplastada | 1 |
| 63272 | empinó | 1 |
| 63273 | empingorotó | 1 |
| 63274 | empingorotados | 1 |
| 63275 | empingorotado | 1 |
| 63276 | empingorotadas | 1 |
| 63277 | empingorotada | 1 |
| 63278 | empínase | 1 |
| 63279 | empinarse | 1 |
| 63280 | empinarnos | 1 |
| 63281 | empinándose | 1 |
| 63282 | empinándola | 1 |
| 63283 | empinadísimo | 1 |
| 63284 | empinaba | 1 |
| 63285 | empina | 1 |
| 63286 | empiézola | 1 |
| 63287 | empiézate | 1 |
| 63288 | empiedran | 1 |
| 63289 | empieces | 1 |
| 63290 | empicotaron | 1 |
| 63291 | empezóse | 1 |
| 63292 | empezca | 1 |
| 63293 | empezaste | 1 |
| 63294 | empezase | 1 |
| 63295 | empezáronme | 1 |
| 63296 | empezaremos | 1 |
| 63297 | empezarás | 1 |
| 63298 | empezarán | 1 |
| 63299 | empezara | 1 |
| 63300 | empezámosla | 1 |
| 63301 | empezados | 1 |
| 63302 | empezadas | 1 |
| 63303 | emperrado | 1 |
| 63304 | emperifolladas | 1 |
| 63305 | emperejilarse | 1 |
| 63306 | emperejilado | 1 |
| 63307 | emperegilado | 1 |
| 63308 | emperadora | 1 |
| 63309 | empeoró | 1 |
| 63310 | empeorarse | 1 |
| 63311 | empeorar | 1 |
| 63312 | empeora | 1 |
| 63313 | empeñose | 1 |
| 63314 | empeñemos | 1 |
| 63315 | empeñaste | 1 |
| 63316 | empeñáronse | 1 |
| 63317 | empeñarme | 1 |
| 63318 | empeñaríamos | 1 |
| 63319 | empeñaría | 1 |
| 63320 | empeñarás | 1 |
| 63321 | empeñadamente | 1 |
| 63322 | empeñábase | 1 |
| 63323 | empenar | 1 |
| 63324 | empenachados | 1 |
| 63325 | empellón | 1 |
| 63326 | empelladas | 1 |
| 63327 | empedré | 1 |
| 63328 | empedrarle | 1 |
| 63329 | empedrar | 1 |
| 63330 | empedradas | 1 |
| 63331 | empediria | 1 |
| 63332 | empedernidas | 1 |
| 63333 | empecía | 1 |
| 63334 | empecatado | 1 |
| 63335 | empecatadas | 1 |
| 63336 | empastados | 1 |
| 63337 | emparrados | 1 |
| 63338 | emparrado | 1 |
| 63339 | emparentarme | 1 |
| 63340 | emparejó | 1 |
| 63341 | emparejarse | 1 |
| 63342 | emparejaron | 1 |
| 63343 | emparejará | 1 |
| 63344 | emparejar | 1 |
| 63345 | emparejan | 1 |
| 63346 | emparejada | 1 |
| 63347 | emparejaba | 1 |
| 63348 | empareja | 1 |
| 63349 | emparedaran | 1 |
| 63350 | emparedados | 1 |
| 63351 | emparán | 1 |
| 63352 | empaquetaron | 1 |
| 63353 | empaquetadas | 1 |
| 63354 | empaqueta | 1 |
| 63355 | empapelado | 1 |
| 63356 | empapando | 1 |
| 63357 | empañarse | 1 |
| 63358 | empañado | 1 |
| 63359 | empaña | 1 |
| 63360 | empalmaste | 1 |
| 63361 | empalmándose | 1 |
| 63362 | empalmaban | 1 |
| 63363 | empalmaba | 1 |
| 63364 | empalizadas | 1 |
| 63365 | empalagoso | 1 |
| 63366 | empalagara | 1 |
| 63367 | empalado | 1 |
| 63368 | empalaba | 1 |
| 63369 | empadronar | 1 |
| 63370 | empachaua | 1 |
| 63371 | empachados | 1 |
| 63372 | emolumentos | 1 |
| 63373 | emoliente | 1 |
| 63374 | emocional | 1 |
| 63375 | emocionado | 1 |
| 63376 | emitir | 1 |
| 63377 | emitida | 1 |
| 63378 | emitía | 1 |
| 63379 | emite | 1 |
| 63380 | emisario | 1 |
| 63381 | emilion | 1 |
| 63382 | emigró | 1 |
| 63383 | emigrado | 1 |
| 63384 | emigrada | 1 |
| 63385 | emigraciones | 1 |
| 63386 | emiendes | 1 |
| 63387 | emiende | 1 |
| 63388 | eméticos | 1 |
| 63389 | emético | 1 |
| 63390 | emersión | 1 |
| 63391 | emendarse | 1 |
| 63392 | emendarme | 1 |
| 63393 | emendaçión | 1 |
| 63394 | emenche | 1 |
| 63395 | embutirse | 1 |
| 63396 | embutir | 1 |
| 63397 | embutiendo | 1 |
| 63398 | embutida | 1 |
| 63399 | embute | 1 |
| 63400 | embustidores | 1 |
| 63401 | embusteras | 1 |
| 63402 | embueluas | 1 |
| 63403 | embueltos | 1 |
| 63404 | embuchados | 1 |
| 63405 | embruteció | 1 |
| 63406 | embrutecido | 1 |
| 63407 | embrutecida | 1 |
| 63408 | embrutecían | 1 |
| 63409 | embrutecerse | 1 |
| 63410 | embrutecedor | 1 |
| 63411 | embrome | 1 |
| 63412 | embromándole | 1 |
| 63413 | embromando | 1 |
| 63414 | embrollo | 1 |
| 63415 | embrollaran | 1 |
| 63416 | embrollado | 1 |
| 63417 | embrollada | 1 |
| 63418 | embrollaba | 1 |
| 63419 | embrionario | 1 |
| 63420 | embrión | 1 |
| 63421 | embriagueces | 1 |
| 63422 | embriagó | 1 |
| 63423 | embriago | 1 |
| 63424 | embriagarle | 1 |
| 63425 | embriagan | 1 |
| 63426 | embriagadoras | 1 |
| 63427 | embriagador | 1 |
| 63428 | embriaga | 1 |
| 63429 | embreados | 1 |
| 63430 | embravecido | 1 |
| 63431 | embozando | 1 |
| 63432 | embozan | 1 |
| 63433 | embozadito | 1 |
| 63434 | embozadas | 1 |
| 63435 | embozaban | 1 |
| 63436 | embozaba | 1 |
| 63437 | embotó | 1 |
| 63438 | embotellada | 1 |
| 63439 | embotarse | 1 |
| 63440 | embotar | 1 |
| 63441 | embota | 1 |
| 63442 | emboscasen | 1 |
| 63443 | emboscarse | 1 |
| 63444 | emboscadas | 1 |
| 63445 | emboscada | 1 |
| 63446 | emborrachen | 1 |
| 63447 | emborráchate | 1 |
| 63448 | emborracharle | 1 |
| 63449 | emborrachan | 1 |
| 63450 | emborracha | 1 |
| 63451 | emborbota | 1 |
| 63452 | embolsó | 1 |
| 63453 | embolsé | 1 |
| 63454 | emboce | 1 |
| 63455 | embocar | 1 |
| 63456 | embobar | 1 |
| 63457 | embobadas | 1 |
| 63458 | embobada | 1 |
| 63459 | embiude | 1 |
| 63460 | embistiéronle | 1 |
| 63461 | embistieron | 1 |
| 63462 | embistiera | 1 |
| 63463 | embiome | 1 |
| 63464 | embies | 1 |
| 63465 | embiemosle | 1 |
| 63466 | embidiosos | 1 |
| 63467 | embidiosas | 1 |
| 63468 | embidias | 1 |
| 63469 | embidiar | 1 |
| 63470 | embiauan | 1 |
| 63471 | embiasse | 1 |
| 63472 | embiarte | 1 |
| 63473 | embiarme | 1 |
| 63474 | embiaría | 1 |
| 63475 | embiara | 1 |
| 63476 | embiado | 1 |
| 63477 | embeuecimiento | 1 |
| 63478 | embetunadas | 1 |
| 63479 | embestirle | 1 |
| 63480 | embestirla | 1 |
| 63481 | embestimos | 1 |
| 63482 | embestille | 1 |
| 63483 | embelleció | 1 |
| 63484 | embelleciéndose | 1 |
| 63485 | embellecida | 1 |
| 63486 | embellecían | 1 |
| 63487 | embellecer | 1 |
| 63488 | embelesarse | 1 |
| 63489 | embelesara | 1 |
| 63490 | embelesados | 1 |
| 63491 | embelesadas | 1 |
| 63492 | embelequen | 1 |
| 63493 | embelecadores | 1 |
| 63494 | embebidos | 1 |
| 63495 | embebían | 1 |
| 63496 | embeber | 1 |
| 63497 | embebecimiento | 1 |
| 63498 | embebecidos | 1 |
| 63499 | embebecida | 1 |
| 63500 | embebecí | 1 |
| 63501 | embebe | 1 |
| 63502 | embazó | 1 |
| 63503 | embaymientos | 1 |
| 63504 | embaxador | 1 |
| 63505 | embaularan | 1 |
| 63506 | embaulará | 1 |
| 63507 | embaulando | 1 |
| 63508 | embaulaban | 1 |
| 63509 | embaucas | 1 |
| 63510 | embaucara | 1 |
| 63511 | embaucar | 1 |
| 63512 | embaucando | 1 |
| 63513 | embaucador | 1 |
| 63514 | embaucado | 1 |
| 63515 | embates | 1 |
| 63516 | embarulló | 1 |
| 63517 | embarullarse | 1 |
| 63518 | embarullar | 1 |
| 63519 | embarullaba | 1 |
| 63520 | embarquemos | 1 |
| 63521 | embarquéme | 1 |
| 63522 | embargué | 1 |
| 63523 | embargósele | 1 |
| 63524 | embargaron | 1 |
| 63525 | embargaría | 1 |
| 63526 | embargar | 1 |
| 63527 | embargaban | 1 |
| 63528 | embarcose | 1 |
| 63529 | embarco | 1 |
| 63530 | embárcate | 1 |
| 63531 | embarcase | 1 |
| 63532 | embarcarte | 1 |
| 63533 | embarcarlos | 1 |
| 63534 | embarcándome | 1 |
| 63535 | embarcan | 1 |
| 63536 | embarcadero | 1 |
| 63537 | embarcada | 1 |
| 63538 | embarcaban | 1 |
| 63539 | embarazosos | 1 |
| 63540 | embarazosas | 1 |
| 63541 | embarazara | 1 |
| 63542 | embarazáis | 1 |
| 63543 | embarazado | 1 |
| 63544 | embalsamen | 1 |
| 63545 | embalsamamientos | 1 |
| 63546 | embalsamaban | 1 |
| 63547 | embalsa | 1 |
| 63548 | embaldosados | 1 |
| 63549 | embalajes | 1 |
| 63550 | embajadora | 1 |
| 63551 | embaidora | 1 |
| 63552 | embaidor | 1 |
| 63553 | embaído | 1 |
| 63554 | embadurnar | 1 |
| 63555 | embadurnado | 1 |
| 63556 | embadurnada | 1 |
| 63557 | emancipaste | 1 |
| 63558 | emanciparía | 1 |
| 63559 | emancipado | 1 |
| 63560 | emanara | 1 |
| 63561 | emanaban | 1 |
| 63562 | elurrez | 1 |
| 63563 | eludir | 1 |
| 63564 | eludiendo | 1 |
| 63565 | eludí | 1 |
| 63566 | elorrieta | 1 |
| 63567 | eloquendi | 1 |
| 63568 | eloïm | 1 |
| 63569 | elohino | 1 |
| 63570 | elogiaron | 1 |
| 63571 | elogiara | 1 |
| 63572 | elogiar | 1 |
| 63573 | elogiados | 1 |
| 63574 | eliz | 1 |
| 63575 | élite | 1 |
| 63576 | eliseos | 1 |
| 63577 | elíseo | 1 |
| 63578 | elisa | 1 |
| 63579 | elimine | 1 |
| 63580 | eliminación | 1 |
| 63581 | eliminaba | 1 |
| 63582 | elija | 1 |
| 63583 | eligrosas | 1 |
| 63584 | eligiesen | 1 |
| 63585 | eligen | 1 |
| 63586 | elige | 1 |
| 63587 | élices | 1 |
| 63588 | elevó | 1 |
| 63589 | elevo | 1 |
| 63590 | elevé | 1 |
| 63591 | elevarla | 1 |
| 63592 | elevándote | 1 |
| 63593 | elevándose | 1 |
| 63594 | elevamiento | 1 |
| 63595 | elevaciones | 1 |
| 63596 | eleva | 1 |
| 63597 | elementa | 1 |
| 63598 | elegirte | 1 |
| 63599 | elegiría | 1 |
| 63600 | elegíaca | 1 |
| 63601 | elegantona | 1 |
| 63602 | elefantes | 1 |
| 63603 | electriza | 1 |
| 63604 | eléctricos | 1 |
| 63605 | eléctricas | 1 |
| 63606 | electores | 1 |
| 63607 | elector | 1 |
| 63608 | electo | 1 |
| 63609 | elches | 1 |
| 63610 | elásticos | 1 |
| 63611 | elásticas | 1 |
| 63612 | elásticamente | 1 |
| 63613 | elado | 1 |
| 63614 | elaborados | 1 |
| 63615 | elaboradas | 1 |
| 63616 | elaboraba | 1 |
| 63617 | eklogen | 1 |
| 63618 | ejerzo | 1 |
| 63619 | ejerza | 1 |
| 63620 | ejercite | 1 |
| 63621 | ejercitastes | 1 |
| 63622 | ejercitasen | 1 |
| 63623 | ejercitarlo | 1 |
| 63624 | ejercitarle | 1 |
| 63625 | ejercitándose | 1 |
| 63626 | ejercitallos | 1 |
| 63627 | ejercitados | 1 |
| 63628 | ejercitado | 1 |
| 63629 | ejercitad | 1 |
| 63630 | ejercitaba | 1 |
| 63631 | ejercita | 1 |
| 63632 | ejercido | 1 |
| 63633 | ejecutorias | 1 |
| 63634 | ejecutores | 1 |
| 63635 | ejecutivos | 1 |
| 63636 | ejecutivas | 1 |
| 63637 | ejecutiva | 1 |
| 63638 | ejecute | 1 |
| 63639 | ejecutarme | 1 |
| 63640 | ejecutarla | 1 |
| 63641 | ejecutallos | 1 |
| 63642 | ejecutaba | 1 |
| 63643 | eick | 1 |
| 63644 | eibrío | 1 |
| 63645 | eguin | 1 |
| 63646 | eguia | 1 |
| 63647 | eguemón | 1 |
| 63648 | eguales | 1 |
| 63649 | egualar | 1 |
| 63650 | egualança | 1 |
| 63651 | egual | 1 |
| 63652 | eguado | 1 |
| 63653 | egregios | 1 |
| 63654 | egregio | 1 |
| 63655 | egito | 1 |
| 63656 | egisto | 1 |
| 63657 | egipcias | 1 |
| 63658 | egïón | 1 |
| 63659 | egida | 1 |
| 63660 | egeria | 1 |
| 63661 | ega | 1 |
| 63662 | efusivo | 1 |
| 63663 | efusiones | 1 |
| 63664 | efímeros | 1 |
| 63665 | efímera | 1 |
| 63666 | eficacísimas | 1 |
| 63667 | eficacísimamente | 1 |
| 63668 | eficacísima | 1 |
| 63669 | eficacemente | 1 |
| 63670 | effecto | 1 |
| 63671 | efetuase | 1 |
| 63672 | efetuar | 1 |
| 63673 | efetivo | 1 |
| 63674 | efetiva | 1 |
| 63675 | efes | 1 |
| 63676 | efeméride | 1 |
| 63677 | efectuó | 1 |
| 63678 | efectuase | 1 |
| 63679 | efectuado | 1 |
| 63680 | efectuaba | 1 |
| 63681 | efectúa | 1 |
| 63682 | efectividad | 1 |
| 63683 | efectivas | 1 |
| 63684 | eduqué | 1 |
| 63685 | educatrices | 1 |
| 63686 | educativa | 1 |
| 63687 | educarse | 1 |
| 63688 | educarle | 1 |
| 63689 | educarlas | 1 |
| 63690 | educaré | 1 |
| 63691 | educaran | 1 |
| 63692 | educan | 1 |
| 63693 | educadito | 1 |
| 63694 | educa | 1 |
| 63695 | edifique | 1 |
| 63696 | edificársenos | 1 |
| 63697 | edificara | 1 |
| 63698 | edifican | 1 |
| 63699 | edificados | 1 |
| 63700 | edificadas | 1 |
| 63701 | edicto | 1 |
| 63702 | edgar | 1 |
| 63703 | eder | 1 |
| 63704 | edemíaca | 1 |
| 63705 | edematosos | 1 |
| 63706 | ecuménico | 1 |
| 63707 | ecuestre | 1 |
| 63708 | ecónomo | 1 |
| 63709 | economizarlo | 1 |
| 63710 | economizar | 1 |
| 63711 | economizaba | 1 |
| 63712 | economistas | 1 |
| 63713 | economato | 1 |
| 63714 | écloga | 1 |
| 63715 | eclís | 1 |
| 63716 | eclíptico | 1 |
| 63717 | eclipsó | 1 |
| 63718 | eclipsar | 1 |
| 63719 | eclipsan | 1 |
| 63720 | eclipsaban | 1 |
| 63721 | eclipsa | 1 |
| 63722 | eclampsia | 1 |
| 63723 | eciomo | 1 |
| 63724 | eci | 1 |
| 63725 | echósele | 1 |
| 63726 | echómelo | 1 |
| 63727 | echome | 1 |
| 63728 | echolos | 1 |
| 63729 | echólo | 1 |
| 63730 | echóles | 1 |
| 63731 | echole | 1 |
| 63732 | echóla | 1 |
| 63733 | echól | 1 |
| 63734 | échesele | 1 |
| 63735 | échenme | 1 |
| 63736 | échenle | 1 |
| 63737 | echemosle | 1 |
| 63738 | echemendi | 1 |
| 63739 | echeme | 1 |
| 63740 | échele | 1 |
| 63741 | echeberrigaray | 1 |
| 63742 | echebarría | 1 |
| 63743 | echean | 1 |
| 63744 | echat | 1 |
| 63745 | echasse | 1 |
| 63746 | echasnos | 1 |
| 63747 | echaros | 1 |
| 63748 | echáronm | 1 |
| 63749 | echárnosla | 1 |
| 63750 | echarnos | 1 |
| 63751 | echármele | 1 |
| 63752 | echaréis | 1 |
| 63753 | echare | 1 |
| 63754 | echaras | 1 |
| 63755 | échar | 1 |
| 63756 | echanse | 1 |
| 63757 | echanlos | 1 |
| 63758 | échanle | 1 |
| 63759 | echanle | 1 |
| 63760 | echanlas | 1 |
| 63761 | echanla | 1 |
| 63762 | echándotelas | 1 |
| 63763 | echándotela | 1 |
| 63764 | echándote | 1 |
| 63765 | echándonos | 1 |
| 63766 | echándoles | 1 |
| 63767 | échame | 1 |
| 63768 | echame | 1 |
| 63769 | échalos | 1 |
| 63770 | echalos | 1 |
| 63771 | echalle | 1 |
| 63772 | echalla | 1 |
| 63773 | échale | 1 |
| 63774 | echalar | 1 |
| 63775 | echagüe | 1 |
| 63776 | echador | 1 |
| 63777 | echádmelos | 1 |
| 63778 | echadme | 1 |
| 63779 | echadle | 1 |
| 63780 | echadiza | 1 |
| 63781 | echad | 1 |
| 63782 | echacuervos | 1 |
| 63783 | echacuervo | 1 |
| 63784 | echábase | 1 |
| 63785 | echabas | 1 |
| 63786 | echábamos | 1 |
| 63787 | echábalas | 1 |
| 63788 | ecetuando | 1 |
| 63789 | ecequiel | 1 |
| 63790 | eceptar | 1 |
| 63791 | ecco | 1 |
| 63792 | ecclesiae | 1 |
| 63793 | ecarri | 1 |
| 63794 | eburneo | 1 |
| 63795 | ebrios | 1 |
| 63796 | ebria | 1 |
| 63797 | êbase | 1 |
| 63798 | ebanista | 1 |
| 63799 | dyzes | 1 |
| 63800 | dyspensa | 1 |
| 63801 | dyrévos | 1 |
| 63802 | dyóle | 1 |
| 63803 | dyna | 1 |
| 63804 | dyl | 1 |
| 63805 | dyez | 1 |
| 63806 | dyentes | 1 |
| 63807 | dus | 1 |
| 63808 | durro | 1 |
| 63809 | duróle | 1 |
| 63810 | durmiéronse | 1 |
| 63811 | durmieran | 1 |
| 63812 | durmades | 1 |
| 63813 | durlindana | 1 |
| 63814 | duritos | 1 |
| 63815 | durindana | 1 |
| 63816 | duretes | 1 |
| 63817 | durete | 1 |
| 63818 | duresa | 1 |
| 63819 | dürer | 1 |
| 63820 | durazos | 1 |
| 63821 | duraznos | 1 |
| 63822 | durazno | 1 |
| 63823 | durasnos | 1 |
| 63824 | durasen | 1 |
| 63825 | duraren | 1 |
| 63826 | durarán | 1 |
| 63827 | durando | 1 |
| 63828 | durador | 1 |
| 63829 | duraderos | 1 |
| 63830 | durables | 1 |
| 63831 | durábale | 1 |
| 63832 | duplicaron | 1 |
| 63833 | dupanloup | 1 |
| 63834 | duodécimo | 1 |
| 63835 | dumio | 1 |
| 63836 | dum | 1 |
| 63837 | dulzores | 1 |
| 63838 | dulzones | 1 |
| 63839 | dulcineae | 1 |
| 63840 | dulcina | 1 |
| 63841 | dulcificó | 1 |
| 63842 | dulcificarla | 1 |
| 63843 | dulcificando | 1 |
| 63844 | dulcia | 1 |
| 63845 | duero | 1 |
| 63846 | dueñísima | 1 |
| 63847 | dueñesca | 1 |
| 63848 | duelitos | 1 |
| 63849 | duelistas | 1 |
| 63850 | duélase | 1 |
| 63851 | duelan | 1 |
| 63852 | duecho | 1 |
| 63853 | dudillas | 1 |
| 63854 | dudilla | 1 |
| 63855 | dudemos | 1 |
| 63856 | dudase | 1 |
| 63857 | dudaron | 1 |
| 63858 | dudare | 1 |
| 63859 | dudaran | 1 |
| 63860 | dudará | 1 |
| 63861 | dudança | 1 |
| 63862 | dudamos | 1 |
| 63863 | ducientos | 1 |
| 63864 | duchos | 1 |
| 63865 | ducho | 1 |
| 63866 | ducal | 1 |
| 63867 | ducado | 1 |
| 63868 | dubitativo | 1 |
| 63869 | dubitat | 1 |
| 63870 | dubdosos | 1 |
| 63871 | dubdoso | 1 |
| 63872 | dubarry | 1 |
| 63873 | dualista | 1 |
| 63874 | dualismos | 1 |
| 63875 | dromedario | 1 |
| 63876 | droguista | 1 |
| 63877 | drizas | 1 |
| 63878 | dríadas | 1 |
| 63879 | drástico | 1 |
| 63880 | dramón | 1 |
| 63881 | dramita | 1 |
| 63882 | dramaturgo | 1 |
| 63883 | dramatiza | 1 |
| 63884 | dramatische | 1 |
| 63885 | dragut | 1 |
| 63886 | dragon | 1 |
| 63887 | dracmático | 1 |
| 63888 | dozy | 1 |
| 63889 | dozeno | 1 |
| 63890 | doz | 1 |
| 63891 | doyte | 1 |
| 63892 | doyme | 1 |
| 63893 | doyla | 1 |
| 63894 | dover | 1 |
| 63895 | dovelas | 1 |
| 63896 | dotrinada | 1 |
| 63897 | dotos | 1 |
| 63898 | dótelo | 1 |
| 63899 | dotasse | 1 |
| 63900 | dotarle | 1 |
| 63901 | dotar | 1 |
| 63902 | dosimétrico | 1 |
| 63903 | doseno | 1 |
| 63904 | doseletes | 1 |
| 63905 | dorso | 1 |
| 63906 | dorsal | 1 |
| 63907 | dormitat | 1 |
| 63908 | dormitando | 1 |
| 63909 | dormitan | 1 |
| 63910 | dormiste | 1 |
| 63911 | dormirte | 1 |
| 63912 | dormirnos | 1 |
| 63913 | dormirlas | 1 |
| 63914 | dormiriemos | 1 |
| 63915 | dormíme | 1 |
| 63916 | dormilón | 1 |
| 63917 | dormilera | 1 |
| 63918 | dormidillos | 1 |
| 63919 | dormías | 1 |
| 63920 | dormias | 1 |
| 63921 | dormiamos | 1 |
| 63922 | dórico | 1 |
| 63923 | doras | 1 |
| 63924 | dorándole | 1 |
| 63925 | dorador | 1 |
| 63926 | doraba | 1 |
| 63927 | doñosa | 1 |
| 63928 | doñeo | 1 |
| 63929 | doñegil | 1 |
| 63930 | doñas | 1 |
| 63931 | donsella | 1 |
| 63932 | donos | 1 |
| 63933 | donné | 1 |
| 63934 | donec | 1 |
| 63935 | donear | 1 |
| 63936 | doneaderas | 1 |
| 63937 | dondyr | 1 |
| 63938 | doncellicas | 1 |
| 63939 | donceles | 1 |
| 63940 | donçel | 1 |
| 63941 | doncel | 1 |
| 63942 | donce | 1 |
| 63943 | donato | 1 |
| 63944 | donairoso | 1 |
| 63945 | donados | 1 |
| 63946 | donación | 1 |
| 63947 | donable | 1 |
| 63948 | domo | 1 |
| 63949 | dóminus | 1 |
| 63950 | domino | 1 |
| 63951 | domínguez | 1 |
| 63952 | domingueros | 1 |
| 63953 | dominé | 1 |
| 63954 | dominase | 1 |
| 63955 | dominarnos | 1 |
| 63956 | dominarla | 1 |
| 63957 | dominantes | 1 |
| 63958 | dominanta | 1 |
| 63959 | dominándolos | 1 |
| 63960 | dominándola | 1 |
| 63961 | domicilium | 1 |
| 63962 | domicilios | 1 |
| 63963 | domiciliada | 1 |
| 63964 | domestiquen | 1 |
| 63965 | domestiquéme | 1 |
| 63966 | domesticaremos | 1 |
| 63967 | domesticar | 1 |
| 63968 | domesticado | 1 |
| 63969 | domesticación | 1 |
| 63970 | dome | 1 |
| 63971 | domas | 1 |
| 63972 | domarle | 1 |
| 63973 | domaríamos | 1 |
| 63974 | domara | 1 |
| 63975 | domados | 1 |
| 63976 | domadores | 1 |
| 63977 | domadora | 1 |
| 63978 | domaba | 1 |
| 63979 | dolyente | 1 |
| 63980 | dolyéndome | 1 |
| 63981 | dolyendo | 1 |
| 63982 | dolorosísima | 1 |
| 63983 | dolorosamente | 1 |
| 63984 | doloriosas | 1 |
| 63985 | dolorcillos | 1 |
| 63986 | dolomía | 1 |
| 63987 | döllinger | 1 |
| 63988 | dolioso | 1 |
| 63989 | dolióse | 1 |
| 63990 | dolióme | 1 |
| 63991 | doliesen | 1 |
| 63992 | dolieron | 1 |
| 63993 | dolieran | 1 |
| 63994 | dolier | 1 |
| 63995 | dolíale | 1 |
| 63996 | dolfos | 1 |
| 63997 | dolet | 1 |
| 63998 | dolernos | 1 |
| 63999 | dolerle | 1 |
| 64000 | dolería | 1 |
| 64001 | dolerá | 1 |
| 64002 | doledes | 1 |
| 64003 | dolçor | 1 |
| 64004 | dolamas | 1 |
| 64005 | dóla | 1 |
| 64006 | dola | 1 |
| 64007 | doite | 1 |
| 64008 | doile | 1 |
| 64009 | dogmatizador | 1 |
| 64010 | dogmáticos | 1 |
| 64011 | dogmático | 1 |
| 64012 | dogmáticas | 1 |
| 64013 | dogales | 1 |
| 64014 | dodecasílabos | 1 |
| 64015 | doctrino | 1 |
| 64016 | doctrinarios | 1 |
| 64017 | doctrinario | 1 |
| 64018 | doctrínala | 1 |
| 64019 | doctoral | 1 |
| 64020 | docilota | 1 |
| 64021 | dócilmente | 1 |
| 64022 | docente | 1 |
| 64023 | doceañista | 1 |
| 64024 | doçe | 1 |
| 64025 | docampo | 1 |
| 64026 | doblóse | 1 |
| 64027 | dobloncito | 1 |
| 64028 | doblólos | 1 |
| 64029 | dobler | 1 |
| 64030 | doblemos | 1 |
| 64031 | doblegarse | 1 |
| 64032 | doblaste | 1 |
| 64033 | doblase | 1 |
| 64034 | doblarse | 1 |
| 64035 | doblarnos | 1 |
| 64036 | doblarlos | 1 |
| 64037 | doblarlo | 1 |
| 64038 | doblares | 1 |
| 64039 | doblará | 1 |
| 64040 | doblándole | 1 |
| 64041 | doblamos | 1 |
| 64042 | dobladuras | 1 |
| 64043 | dobladle | 1 |
| 64044 | dobladitos | 1 |
| 64045 | dobladillar | 1 |
| 64046 | dizut | 1 |
| 64047 | dizna | 1 |
| 64048 | diziendole | 1 |
| 64049 | dízenlo | 1 |
| 64050 | dízenle | 1 |
| 64051 | dizeles | 1 |
| 64052 | díxote | 1 |
| 64053 | dixom | 1 |
| 64054 | dixogelo | 1 |
| 64055 | dixit | 1 |
| 64056 | dixistes | 1 |
| 64057 | dixiesses | 1 |
| 64058 | dixiessen | 1 |
| 64059 | dixiesen | 1 |
| 64060 | dixiese | 1 |
| 64061 | dixieronle | 1 |
| 64062 | dixieren | 1 |
| 64063 | dixiera | 1 |
| 64064 | díxiel | 1 |
| 64065 | dixeses | 1 |
| 64066 | dixesen | 1 |
| 64067 | dixera | 1 |
| 64068 | díxela | 1 |
| 64069 | díx | 1 |
| 64070 | divulgasen | 1 |
| 64071 | divulgara | 1 |
| 64072 | divulgándose | 1 |
| 64073 | divulgado | 1 |
| 64074 | diviso | 1 |
| 64075 | divisibles | 1 |
| 64076 | divisible | 1 |
| 64077 | divisara | 1 |
| 64078 | divisamos | 1 |
| 64079 | divisado | 1 |
| 64080 | divisaban | 1 |
| 64081 | divisábamos | 1 |
| 64082 | divirtióse | 1 |
| 64083 | divirtiera | 1 |
| 64084 | divinísima | 1 |
| 64085 | divinidat | 1 |
| 64086 | divine | 1 |
| 64087 | divinam | 1 |
| 64088 | diviesos | 1 |
| 64089 | divido | 1 |
| 64090 | dividirían | 1 |
| 64091 | dividir | 1 |
| 64092 | dividiesen | 1 |
| 64093 | dividiéndolos | 1 |
| 64094 | dividiéndolas | 1 |
| 64095 | dividíanse | 1 |
| 64096 | divides | 1 |
| 64097 | dividendos | 1 |
| 64098 | dividendo | 1 |
| 64099 | dividan | 1 |
| 64100 | divida | 1 |
| 64101 | divi | 1 |
| 64102 | divertirnos | 1 |
| 64103 | divertirles | 1 |
| 64104 | divertirle | 1 |
| 64105 | divertirla | 1 |
| 64106 | divertimientos | 1 |
| 64107 | divertille | 1 |
| 64108 | divertiesen | 1 |
| 64109 | divertiéndose | 1 |
| 64110 | divertidísima | 1 |
| 64111 | divertíanla | 1 |
| 64112 | divertíamos | 1 |
| 64113 | divertíale | 1 |
| 64114 | divertí | 1 |
| 64115 | diverssas | 1 |
| 64116 | diverso | 1 |
| 64117 | diversidades | 1 |
| 64118 | divergencias | 1 |
| 64119 | divagar | 1 |
| 64120 | divagando | 1 |
| 64121 | diurno | 1 |
| 64122 | diurna | 1 |
| 64123 | diuréticos | 1 |
| 64124 | diuision | 1 |
| 64125 | diuisible | 1 |
| 64126 | diuerso | 1 |
| 64127 | ditu | 1 |
| 64128 | diteque | 1 |
| 64129 | disuene | 1 |
| 64130 | disuelven | 1 |
| 64131 | disuelve | 1 |
| 64132 | disuélvase | 1 |
| 64133 | disuelvan | 1 |
| 64134 | disuelto | 1 |
| 64135 | disueltas | 1 |
| 64136 | disuelta | 1 |
| 64137 | disuadirse | 1 |
| 64138 | disuadirme | 1 |
| 64139 | disuadiendo | 1 |
| 64140 | disuadía | 1 |
| 64141 | disturbios | 1 |
| 64142 | distribuyendo | 1 |
| 64143 | distribuirse | 1 |
| 64144 | distribuidos | 1 |
| 64145 | distribuido | 1 |
| 64146 | distribuida | 1 |
| 64147 | distrayendo | 1 |
| 64148 | distraydo | 1 |
| 64149 | distrajeran | 1 |
| 64150 | distraje | 1 |
| 64151 | distraigo | 1 |
| 64152 | distráiganme | 1 |
| 64153 | distraidita | 1 |
| 64154 | distraídas | 1 |
| 64155 | distraídamente | 1 |
| 64156 | distraían | 1 |
| 64157 | distráete | 1 |
| 64158 | distraerte | 1 |
| 64159 | distraerla | 1 |
| 64160 | distraerían | 1 |
| 64161 | distraería | 1 |
| 64162 | distraedme | 1 |
| 64163 | disto | 1 |
| 64164 | distintivos | 1 |
| 64165 | distinguirse | 1 |
| 64166 | distinguirlos | 1 |
| 64167 | distinguirlo | 1 |
| 64168 | distinguirle | 1 |
| 64169 | distinguieran | 1 |
| 64170 | distinguiéndose | 1 |
| 64171 | distinguidísimo | 1 |
| 64172 | distinguíase | 1 |
| 64173 | distinguíanse | 1 |
| 64174 | distinguí | 1 |
| 64175 | distilar | 1 |
| 64176 | distilan | 1 |
| 64177 | distilada | 1 |
| 64178 | dístico | 1 |
| 64179 | disticha | 1 |
| 64180 | distan | 1 |
| 64181 | distábamos | 1 |
| 64182 | distaba | 1 |
| 64183 | dista | 1 |
| 64184 | dissonos | 1 |
| 64185 | dissimulando | 1 |
| 64186 | dissimulaciones | 1 |
| 64187 | dissimula | 1 |
| 64188 | dissensiones | 1 |
| 64189 | dissension | 1 |
| 64190 | disquisiciones | 1 |
| 64191 | disputen | 1 |
| 64192 | disputase | 1 |
| 64193 | disputarle | 1 |
| 64194 | disputara | 1 |
| 64195 | disputándose | 1 |
| 64196 | disputaçión | 1 |
| 64197 | disputábanse | 1 |
| 64198 | dispusiesen | 1 |
| 64199 | dispusiera | 1 |
| 64200 | dispusición | 1 |
| 64201 | dispusicion | 1 |
| 64202 | dispuestilla | 1 |
| 64203 | dispreciar | 1 |
| 64204 | disposicion | 1 |
| 64205 | disponiéndola | 1 |
| 64206 | disponibles | 1 |
| 64207 | disponíase | 1 |
| 64208 | dispónese | 1 |
| 64209 | dispones | 1 |
| 64210 | disponerse | 1 |
| 64211 | disponerme | 1 |
| 64212 | disponed | 1 |
| 64213 | dispón | 1 |
| 64214 | displicentes | 1 |
| 64215 | displicencias | 1 |
| 64216 | dispersas | 1 |
| 64217 | dispersarse | 1 |
| 64218 | dispersar | 1 |
| 64219 | dispersándose | 1 |
| 64220 | dispersados | 1 |
| 64221 | dispersaban | 1 |
| 64222 | dispersaba | 1 |
| 64223 | dispersa | 1 |
| 64224 | dispepsias | 1 |
| 64225 | dispepsia | 1 |
| 64226 | dispenssar | 1 |
| 64227 | dispensó | 1 |
| 64228 | dispénsenme | 1 |
| 64229 | dispénsele | 1 |
| 64230 | dispensase | 1 |
| 64231 | dispensarme | 1 |
| 64232 | dispensará | 1 |
| 64233 | dispensando | 1 |
| 64234 | dispensan | 1 |
| 64235 | dispensadores | 1 |
| 64236 | dispensada | 1 |
| 64237 | dispensaciones | 1 |
| 64238 | dispendiosos | 1 |
| 64239 | dispendiosas | 1 |
| 64240 | disparze | 1 |
| 64241 | disparósela | 1 |
| 64242 | disparitas | 1 |
| 64243 | dispárese | 1 |
| 64244 | disparatando | 1 |
| 64245 | disparatadamente | 1 |
| 64246 | disparataba | 1 |
| 64247 | dispararlos | 1 |
| 64248 | dispararles | 1 |
| 64249 | dispararé | 1 |
| 64250 | dispararán | 1 |
| 64251 | disparándole | 1 |
| 64252 | disparalla | 1 |
| 64253 | disparados | 1 |
| 64254 | disparadas | 1 |
| 64255 | disonancia | 1 |
| 64256 | disolvió | 1 |
| 64257 | disolviéronse | 1 |
| 64258 | disolviera | 1 |
| 64259 | disolvía | 1 |
| 64260 | disolverse | 1 |
| 64261 | disolverla | 1 |
| 64262 | disoluto | 1 |
| 64263 | disoluble | 1 |
| 64264 | disminuyó | 1 |
| 64265 | disminuyen | 1 |
| 64266 | disminuye | 1 |
| 64267 | disminuya | 1 |
| 64268 | disminuían | 1 |
| 64269 | disminución | 1 |
| 64270 | disloquemos | 1 |
| 64271 | dislocaron | 1 |
| 64272 | dislocará | 1 |
| 64273 | dislocación | 1 |
| 64274 | dislates | 1 |
| 64275 | dislate | 1 |
| 64276 | disipose | 1 |
| 64277 | disiparan | 1 |
| 64278 | disipará | 1 |
| 64279 | disipando | 1 |
| 64280 | disipación | 1 |
| 64281 | disipábanse | 1 |
| 64282 | disipaban | 1 |
| 64283 | disipaba | 1 |
| 64284 | disipa | 1 |
| 64285 | disinio | 1 |
| 64286 | disinificantes | 1 |
| 64287 | disimulas | 1 |
| 64288 | disimularse | 1 |
| 64289 | disimularlos | 1 |
| 64290 | disimularle | 1 |
| 64291 | disimilo | 1 |
| 64292 | disimilar | 1 |
| 64293 | disiendo | 1 |
| 64294 | disíen | 1 |
| 64295 | disgustillo | 1 |
| 64296 | disguste | 1 |
| 64297 | disgustarse | 1 |
| 64298 | disgustaron | 1 |
| 64299 | disgustarle | 1 |
| 64300 | disgustarla | 1 |
| 64301 | disgustan | 1 |
| 64302 | disgustaban | 1 |
| 64303 | disgrega | 1 |
| 64304 | disfrutó | 1 |
| 64305 | disfrute | 1 |
| 64306 | disfrutando | 1 |
| 64307 | disfrázate | 1 |
| 64308 | disfrazasen | 1 |
| 64309 | disfrazase | 1 |
| 64310 | disfrazarían | 1 |
| 64311 | disfrazando | 1 |
| 64312 | disfrazan | 1 |
| 64313 | disformísima | 1 |
| 64314 | disfigurado | 1 |
| 64315 | disfigura | 1 |
| 64316 | disertaron | 1 |
| 64317 | disertar | 1 |
| 64318 | disertaban | 1 |
| 64319 | diseño | 1 |
| 64320 | disentimiento | 1 |
| 64321 | disensiones | 1 |
| 64322 | dísenlo | 1 |
| 64323 | diseminaban | 1 |
| 64324 | díselos | 1 |
| 64325 | disección | 1 |
| 64326 | discutirla | 1 |
| 64327 | discutiría | 1 |
| 64328 | discutiremos | 1 |
| 64329 | discutiré | 1 |
| 64330 | discutirá | 1 |
| 64331 | discutiose | 1 |
| 64332 | discutíamos | 1 |
| 64333 | discute | 1 |
| 64334 | discursiva | 1 |
| 64335 | discursito | 1 |
| 64336 | discursiones | 1 |
| 64337 | discursazo | 1 |
| 64338 | discurrirán | 1 |
| 64339 | discurrimos | 1 |
| 64340 | discurrimientos | 1 |
| 64341 | discurrían | 1 |
| 64342 | discurrí | 1 |
| 64343 | discurras | 1 |
| 64344 | disculpose | 1 |
| 64345 | disculpéme | 1 |
| 64346 | disculpé | 1 |
| 64347 | disculparse | 1 |
| 64348 | disculparme | 1 |
| 64349 | disculparía | 1 |
| 64350 | disculparé | 1 |
| 64351 | disculparan | 1 |
| 64352 | disculpándose | 1 |
| 64353 | disculpado | 1 |
| 64354 | disculpables | 1 |
| 64355 | disculpábase | 1 |
| 64356 | discuido | 1 |
| 64357 | discubrierlo | 1 |
| 64358 | discricion | 1 |
| 64359 | discretísimos | 1 |
| 64360 | discretísimas | 1 |
| 64361 | discreteo | 1 |
| 64362 | discrepante | 1 |
| 64363 | discrepando | 1 |
| 64364 | discrepaban | 1 |
| 64365 | discre | 1 |
| 64366 | discordes | 1 |
| 64367 | discorda | 1 |
| 64368 | disçípulo | 1 |
| 64369 | discípulas | 1 |
| 64370 | disciplinaria | 1 |
| 64371 | disciplinante | 1 |
| 64372 | disciplinado | 1 |
| 64373 | disciplentes | 1 |
| 64374 | discerneys | 1 |
| 64375 | disc | 1 |
| 64376 | disanto | 1 |
| 64377 | disantero | 1 |
| 64378 | dis | 1 |
| 64379 | dirti | 1 |
| 64380 | dirlos | 1 |
| 64381 | dirimió | 1 |
| 64382 | dirijo | 1 |
| 64383 | diríjala | 1 |
| 64384 | dirigirte | 1 |
| 64385 | dirigirme | 1 |
| 64386 | dirigirle | 1 |
| 64387 | dirigirla | 1 |
| 64388 | dirigirá | 1 |
| 64389 | dirigimos | 1 |
| 64390 | dirigímonos | 1 |
| 64391 | dirigiese | 1 |
| 64392 | dirigiera | 1 |
| 64393 | dirigiéndome | 1 |
| 64394 | dirigíamos | 1 |
| 64395 | diretorio | 1 |
| 64396 | dires | 1 |
| 64397 | diréoslo | 1 |
| 64398 | direlo | 1 |
| 64399 | diréle | 1 |
| 64400 | dirélas | 1 |
| 64401 | directores | 1 |
| 64402 | directe | 1 |
| 64403 | directas | 1 |
| 64404 | dirásle | 1 |
| 64405 | dirasle | 1 |
| 64406 | diranle | 1 |
| 64407 | dirame | 1 |
| 64408 | diráles | 1 |
| 64409 | diralaco | 1 |
| 64410 | diquiá | 1 |
| 64411 | diputo | 1 |
| 64412 | dipósito | 1 |
| 64413 | diplomacias | 1 |
| 64414 | diploma | 1 |
| 64415 | dióte | 1 |
| 64416 | dióselo | 1 |
| 64417 | diosecito | 1 |
| 64418 | dioscórides | 1 |
| 64419 | dionisíacas | 1 |
| 64420 | diómelo | 1 |
| 64421 | diomedes | 1 |
| 64422 | dióles | 1 |
| 64423 | diolas | 1 |
| 64424 | diola | 1 |
| 64425 | diógenes | 1 |
| 64426 | diógela | 1 |
| 64427 | diños | 1 |
| 64428 | dínosla | 1 |
| 64429 | diniera | 1 |
| 64430 | dinidad | 1 |
| 64431 | dineroso | 1 |
| 64432 | dineras | 1 |
| 64433 | dineradas | 1 |
| 64434 | dinásticos | 1 |
| 64435 | dinastías | 1 |
| 64436 | dímosles | 1 |
| 64437 | dímosla | 1 |
| 64438 | dimoños | 1 |
| 64439 | dimittere | 1 |
| 64440 | dimisionario | 1 |
| 64441 | diminuyóla | 1 |
| 64442 | diminuyessen | 1 |
| 64443 | diminuyelas | 1 |
| 64444 | diminuya | 1 |
| 64445 | diminutos | 1 |
| 64446 | diminutio | 1 |
| 64447 | diminutas | 1 |
| 64448 | diminuirse | 1 |
| 64449 | diminuirla | 1 |
| 64450 | diminuiendo | 1 |
| 64451 | diminuido | 1 |
| 64452 | diminucion | 1 |
| 64453 | dimetria | 1 |
| 64454 | dímelas | 1 |
| 64455 | diluvios | 1 |
| 64456 | diluviaba | 1 |
| 64457 | diluído | 1 |
| 64458 | dilucidemos | 1 |
| 64459 | dilucide | 1 |
| 64460 | diligitis | 1 |
| 64461 | diligite | 1 |
| 64462 | diligentísima | 1 |
| 64463 | dilicada | 1 |
| 64464 | dilatóse | 1 |
| 64465 | dilatoria | 1 |
| 64466 | dilató | 1 |
| 64467 | dilatemos | 1 |
| 64468 | dilátelo | 1 |
| 64469 | dilatase | 1 |
| 64470 | dilatarme | 1 |
| 64471 | dilatarlo | 1 |
| 64472 | dilatándose | 1 |
| 64473 | dilataban | 1 |
| 64474 | dilacerar | 1 |
| 64475 | dilaceran | 1 |
| 64476 | díjoselo | 1 |
| 64477 | díjonos | 1 |
| 64478 | dijon | 1 |
| 64479 | dijóme | 1 |
| 64480 | díjolo | 1 |
| 64481 | dijóle | 1 |
| 64482 | dijeras | 1 |
| 64483 | dijéralo | 1 |
| 64484 | díjelas | 1 |
| 64485 | dija | 1 |
| 64486 | digovos | 1 |
| 64487 | digotelo | 1 |
| 64488 | dígoos | 1 |
| 64489 | dígoles | 1 |
| 64490 | digole | 1 |
| 64491 | dignificar | 1 |
| 64492 | dignatario | 1 |
| 64493 | dignara | 1 |
| 64494 | dignándose | 1 |
| 64495 | dignado | 1 |
| 64496 | dignaba | 1 |
| 64497 | digitalina | 1 |
| 64498 | digitales | 1 |
| 64499 | digital | 1 |
| 64500 | digiere | 1 |
| 64501 | digiera | 1 |
| 64502 | digestivo | 1 |
| 64503 | digestivas | 1 |
| 64504 | digerido | 1 |
| 64505 | digerida | 1 |
| 64506 | dígante | 1 |
| 64507 | díganos | 1 |
| 64508 | diganos | 1 |
| 64509 | díganle | 1 |
| 64510 | dígamela | 1 |
| 64511 | dígalos | 1 |
| 64512 | digalo | 1 |
| 64513 | dígalas | 1 |
| 64514 | dígal | 1 |
| 64515 | difundirse | 1 |
| 64516 | difundiéndose | 1 |
| 64517 | difundido | 1 |
| 64518 | difundían | 1 |
| 64519 | difunde | 1 |
| 64520 | difunda | 1 |
| 64521 | difinitiva | 1 |
| 64522 | difieren | 1 |
| 64523 | dificultosos | 1 |
| 64524 | dificultó | 1 |
| 64525 | dificulto | 1 |
| 64526 | dificultara | 1 |
| 64527 | dificultar | 1 |
| 64528 | dificultaban | 1 |
| 64529 | dificilísima | 1 |
| 64530 | difficultad | 1 |
| 64531 | differentes | 1 |
| 64532 | differencias | 1 |
| 64533 | diferiste | 1 |
| 64534 | diferirias | 1 |
| 64535 | diferir | 1 |
| 64536 | diferenciaros | 1 |
| 64537 | diferenciarían | 1 |
| 64538 | diferenciamos | 1 |
| 64539 | diferenciados | 1 |
| 64540 | difamatorios | 1 |
| 64541 | diezocho | 1 |
| 64542 | díez | 1 |
| 64543 | dietético | 1 |
| 64544 | dietas | 1 |
| 64545 | diesemos | 1 |
| 64546 | dierum | 1 |
| 64547 | diéronlos | 1 |
| 64548 | dieronle | 1 |
| 64549 | dierdes | 1 |
| 64550 | dierasme | 1 |
| 64551 | diéranle | 1 |
| 64552 | diérale | 1 |
| 64553 | diéral | 1 |
| 64554 | diérais | 1 |
| 64555 | dierais | 1 |
| 64556 | dier | 1 |
| 64557 | dieguito | 1 |
| 64558 | diecisiete | 1 |
| 64559 | die | 1 |
| 64560 | didáctico | 1 |
| 64561 | dícteme | 1 |
| 64562 | dicte | 1 |
| 64563 | dictatorial | 1 |
| 64564 | dictaría | 1 |
| 64565 | dictadura | 1 |
| 64566 | dictadora | 1 |
| 64567 | dickens | 1 |
| 64568 | diçípulos | 1 |
| 64569 | dicípulo | 1 |
| 64570 | dicipline | 1 |
| 64571 | diciplinante | 1 |
| 64572 | diçió | 1 |
| 64573 | dicier | 1 |
| 64574 | diciéndoos | 1 |
| 64575 | diciéndonos | 1 |
| 64576 | diciéndolas | 1 |
| 64577 | dichosísimo | 1 |
| 64578 | díchoselo | 1 |
| 64579 | dichosamente | 1 |
| 64580 | dicharacheros | 1 |
| 64581 | dicharachera | 1 |
| 64582 | diçes | 1 |
| 64583 | dícenlo | 1 |
| 64584 | dícenle | 1 |
| 64585 | diçen | 1 |
| 64586 | díceme | 1 |
| 64587 | diçe | 1 |
| 64588 | dicat | 1 |
| 64589 | dibujose | 1 |
| 64590 | dibujar | 1 |
| 64591 | dibujándose | 1 |
| 64592 | dibujan | 1 |
| 64593 | dibujadas | 1 |
| 64594 | dibujaba | 1 |
| 64595 | dibu | 1 |
| 64596 | diátesis | 1 |
| 64597 | diasaturión | 1 |
| 64598 | diarrodon | 1 |
| 64599 | diantoso | 1 |
| 64600 | dianches | 1 |
| 64601 | diametralmente | 1 |
| 64602 | diamargaritón | 1 |
| 64603 | diamantino | 1 |
| 64604 | diamanta | 1 |
| 64605 | dialécticas | 1 |
| 64606 | diagragante | 1 |
| 64607 | diagnóstico | 1 |
| 64608 | diaforético | 1 |
| 64609 | diafanidad | 1 |
| 64610 | diáfana | 1 |
| 64611 | diademas | 1 |
| 64612 | diaçymino | 1 |
| 64613 | diácono | 1 |
| 64614 | diaçitrón | 1 |
| 64615 | diabolo | 1 |
| 64616 | diablillo | 1 |
| 64617 | diablesca | 1 |
| 64618 | diablesas | 1 |
| 64619 | diablejo | 1 |
| 64620 | dí | 1 |
| 64621 | dezmar | 1 |
| 64622 | dezmaban | 1 |
| 64623 | dezit | 1 |
| 64624 | dezis | 1 |
| 64625 | dezirtelo | 1 |
| 64626 | dezirlo | 1 |
| 64627 | dezirles | 1 |
| 64628 | dezires | 1 |
| 64629 | dézir | 1 |
| 64630 | dezildes | 1 |
| 64631 | deziéndole | 1 |
| 64632 | dezíen | 1 |
| 64633 | dezidores | 1 |
| 64634 | dezidor | 1 |
| 64635 | dezidle | 1 |
| 64636 | dezid | 1 |
| 64637 | dezias | 1 |
| 64638 | deziades | 1 |
| 64639 | dezeno | 1 |
| 64640 | deydat | 1 |
| 64641 | deydad | 1 |
| 64642 | dextrina | 1 |
| 64643 | dexós | 1 |
| 64644 | dexólo | 1 |
| 64645 | dexóla | 1 |
| 64646 | dexiste | 1 |
| 64647 | dexiese | 1 |
| 64648 | dexies | 1 |
| 64649 | dexieronle | 1 |
| 64650 | dexier | 1 |
| 64651 | déxevos | 1 |
| 64652 | dexemosle | 1 |
| 64653 | dexava | 1 |
| 64654 | dexauas | 1 |
| 64655 | dexauan | 1 |
| 64656 | déxatme | 1 |
| 64657 | dexate | 1 |
| 64658 | dexastes | 1 |
| 64659 | dexassen | 1 |
| 64660 | déxasle | 1 |
| 64661 | dexase | 1 |
| 64662 | dexarse | 1 |
| 64663 | dexarme | 1 |
| 64664 | dexarm | 1 |
| 64665 | dexarlo | 1 |
| 64666 | dexarla | 1 |
| 64667 | dexaríe | 1 |
| 64668 | dexarían | 1 |
| 64669 | dexaré | 1 |
| 64670 | dexaras | 1 |
| 64671 | dexarán | 1 |
| 64672 | dexaran | 1 |
| 64673 | dexara | 1 |
| 64674 | dexaos | 1 |
| 64675 | déxanl | 1 |
| 64676 | dexandola | 1 |
| 64677 | dexamos | 1 |
| 64678 | dexamele | 1 |
| 64679 | dexalo | 1 |
| 64680 | déxala | 1 |
| 64681 | devuelves | 1 |
| 64682 | devuelva | 1 |
| 64683 | devríen | 1 |
| 64684 | devotísima | 1 |
| 64685 | devorarla | 1 |
| 64686 | devoran | 1 |
| 64687 | devorados | 1 |
| 64688 | devoradora | 1 |
| 64689 | devorador | 1 |
| 64690 | devorada | 1 |
| 64691 | devora | 1 |
| 64692 | devolviese | 1 |
| 64693 | devolvieran | 1 |
| 64694 | devolviéndoselo | 1 |
| 64695 | devolviéndoles | 1 |
| 64696 | devolviéndole | 1 |
| 64697 | devolvían | 1 |
| 64698 | devolvérselos | 1 |
| 64699 | devolverme | 1 |
| 64700 | devolverlos | 1 |
| 64701 | devolverlas | 1 |
| 64702 | devolvería | 1 |
| 64703 | devolveré | 1 |
| 64704 | devolverán | 1 |
| 64705 | devolverá | 1 |
| 64706 | devoluciones | 1 |
| 64707 | devisa | 1 |
| 64708 | deviersos | 1 |
| 64709 | devier | 1 |
| 64710 | devie | 1 |
| 64711 | devidirse | 1 |
| 64712 | dévense | 1 |
| 64713 | dévenlo | 1 |
| 64714 | devengar | 1 |
| 64715 | devengado | 1 |
| 64716 | devengadas | 1 |
| 64717 | dévelo | 1 |
| 64718 | devegadas | 1 |
| 64719 | devédeslos | 1 |
| 64720 | devastadores | 1 |
| 64721 | devastación | 1 |
| 64722 | devastaba | 1 |
| 64723 | devanó | 1 |
| 64724 | devano | 1 |
| 64725 | devaneando | 1 |
| 64726 | devanarse | 1 |
| 64727 | devanar | 1 |
| 64728 | devanamos | 1 |
| 64729 | devanado | 1 |
| 64730 | devanábamos | 1 |
| 64731 | devallen | 1 |
| 64732 | deuzic | 1 |
| 64733 | deux | 1 |
| 64734 | deuria | 1 |
| 64735 | deuoto | 1 |
| 64736 | deuotas | 1 |
| 64737 | deuota | 1 |
| 64738 | deum | 1 |
| 64739 | deuido | 1 |
| 64740 | deuida | 1 |
| 64741 | deuia | 1 |
| 64742 | deueys | 1 |
| 64743 | deuaneen | 1 |
| 64744 | deuanear | 1 |
| 64745 | deuaneando | 1 |
| 64746 | deuan | 1 |
| 64747 | detuvimos | 1 |
| 64748 | detúveme | 1 |
| 64749 | detuuiesse | 1 |
| 64750 | detuue | 1 |
| 64751 | detras | 1 |
| 64752 | detóvome | 1 |
| 64753 | detove | 1 |
| 64754 | detiénese | 1 |
| 64755 | detiénense | 1 |
| 64756 | detesto | 1 |
| 64757 | detestación | 1 |
| 64758 | detestablemente | 1 |
| 64759 | determinen | 1 |
| 64760 | determinemos | 1 |
| 64761 | determinasse | 1 |
| 64762 | determinase | 1 |
| 64763 | determinas | 1 |
| 64764 | determináronse | 1 |
| 64765 | determinaría | 1 |
| 64766 | determinaremos | 1 |
| 64767 | determinantes | 1 |
| 64768 | determinámonos | 1 |
| 64769 | determinacion | 1 |
| 64770 | determinaban | 1 |
| 64771 | deterioro | 1 |
| 64772 | deteriorando | 1 |
| 64773 | deteriorado | 1 |
| 64774 | deteniéndolos | 1 |
| 64775 | deteníamos | 1 |
| 64776 | deteníamonos | 1 |
| 64777 | deteníame | 1 |
| 64778 | deténgome | 1 |
| 64779 | deténgase | 1 |
| 64780 | detengan | 1 |
| 64781 | detenerlos | 1 |
| 64782 | detenerles | 1 |
| 64783 | detenelle | 1 |
| 64784 | detened | 1 |
| 64785 | detendrían | 1 |
| 64786 | detendría | 1 |
| 64787 | detendremos | 1 |
| 64788 | detención | 1 |
| 64789 | déte | 1 |
| 64790 | dete | 1 |
| 64791 | detchesarry | 1 |
| 64792 | detallistas | 1 |
| 64793 | detallado | 1 |
| 64794 | desyerra | 1 |
| 64795 | desyéndole | 1 |
| 64796 | desvivo | 1 |
| 64797 | desviviéndote | 1 |
| 64798 | desvivido | 1 |
| 64799 | desvivían | 1 |
| 64800 | desviven | 1 |
| 64801 | desvirtuaran | 1 |
| 64802 | desvirtuada | 1 |
| 64803 | desvirtuábalos | 1 |
| 64804 | desvirgué | 1 |
| 64805 | desvíes | 1 |
| 64806 | desviemos | 1 |
| 64807 | desvié | 1 |
| 64808 | desvíe | 1 |
| 64809 | desviases | 1 |
| 64810 | desviase | 1 |
| 64811 | desvías | 1 |
| 64812 | desviarnos | 1 |
| 64813 | desviar | 1 |
| 64814 | desviaos | 1 |
| 64815 | desviándome | 1 |
| 64816 | desvïada | 1 |
| 64817 | desviaba | 1 |
| 64818 | desvergonzó | 1 |
| 64819 | desvergonzarse | 1 |
| 64820 | desvergonçada | 1 |
| 64821 | desventuradas | 1 |
| 64822 | desventajosa | 1 |
| 64823 | desventajas | 1 |
| 64824 | desventaja | 1 |
| 64825 | desvengonzado | 1 |
| 64826 | desvelen | 1 |
| 64827 | desvelarse | 1 |
| 64828 | desvelaron | 1 |
| 64829 | desvelarme | 1 |
| 64830 | desvelará | 1 |
| 64831 | desvelara | 1 |
| 64832 | desvelan | 1 |
| 64833 | desvelados | 1 |
| 64834 | desvelábase | 1 |
| 64835 | desvelaban | 1 |
| 64836 | desvariar | 1 |
| 64837 | desvariando | 1 |
| 64838 | desvariada | 1 |
| 64839 | desvaría | 1 |
| 64840 | desvaneció | 1 |
| 64841 | desvanecimientos | 1 |
| 64842 | desvaneciendo | 1 |
| 64843 | desvanecíase | 1 |
| 64844 | desvanecían | 1 |
| 64845 | desvanécese | 1 |
| 64846 | desvalijaron | 1 |
| 64847 | desvalijar | 1 |
| 64848 | desvalido | 1 |
| 64849 | desvaído | 1 |
| 64850 | desusar | 1 |
| 64851 | desusando | 1 |
| 64852 | desuncir | 1 |
| 64853 | desunce | 1 |
| 64854 | desuio | 1 |
| 64855 | desuiados | 1 |
| 64856 | desuia | 1 |
| 64857 | desuerguenza | 1 |
| 64858 | desuergonzado | 1 |
| 64859 | desuergonzadas | 1 |
| 64860 | desuergonzada | 1 |
| 64861 | desuentura | 1 |
| 64862 | desuellen | 1 |
| 64863 | desuellan | 1 |
| 64864 | desueles | 1 |
| 64865 | desuarios | 1 |
| 64866 | desuariados | 1 |
| 64867 | destutt | 1 |
| 64868 | destruyste | 1 |
| 64869 | destruyrlo | 1 |
| 64870 | destruyras | 1 |
| 64871 | destruyo | 1 |
| 64872 | destruymiento | 1 |
| 64873 | destrúyeslo | 1 |
| 64874 | destrúyese | 1 |
| 64875 | destruyes | 1 |
| 64876 | destruyeron | 1 |
| 64877 | destruyera | 1 |
| 64878 | destruydor | 1 |
| 64879 | destruydas | 1 |
| 64880 | destruycion | 1 |
| 64881 | destruirnos | 1 |
| 64882 | destruirlos | 1 |
| 64883 | destruiré | 1 |
| 64884 | destruille | 1 |
| 64885 | destruidos | 1 |
| 64886 | destruida | 1 |
| 64887 | destruición | 1 |
| 64888 | destruían | 1 |
| 64889 | destrues | 1 |
| 64890 | destructoras | 1 |
| 64891 | destrución | 1 |
| 64892 | destrozas | 1 |
| 64893 | destrozarme | 1 |
| 64894 | destrozará | 1 |
| 64895 | destrozándose | 1 |
| 64896 | destrozan | 1 |
| 64897 | destrozáis | 1 |
| 64898 | destrozadas | 1 |
| 64899 | destrozaban | 1 |
| 64900 | destroyr | 1 |
| 64901 | destroncaron | 1 |
| 64902 | destroncada | 1 |
| 64903 | destronamiento | 1 |
| 64904 | destroces | 1 |
| 64905 | destris | 1 |
| 64906 | destripaterrones | 1 |
| 64907 | destraídas | 1 |
| 64908 | destraída | 1 |
| 64909 | destrae | 1 |
| 64910 | destotro | 1 |
| 64911 | destotra | 1 |
| 64912 | destorvo | 1 |
| 64913 | destorcieron | 1 |
| 64914 | destocándose | 1 |
| 64915 | destocado | 1 |
| 64916 | destituirle | 1 |
| 64917 | destinósele | 1 |
| 64918 | destinó | 1 |
| 64919 | destinguir | 1 |
| 64920 | destinejo | 1 |
| 64921 | destinatario | 1 |
| 64922 | destinarme | 1 |
| 64923 | destinarle | 1 |
| 64924 | destinar | 1 |
| 64925 | destillarme | 1 |
| 64926 | destiladera | 1 |
| 64927 | destiladas | 1 |
| 64928 | destierren | 1 |
| 64929 | destiento | 1 |
| 64930 | destetan | 1 |
| 64931 | desterráronlos | 1 |
| 64932 | desterrarme | 1 |
| 64933 | desterrarlo | 1 |
| 64934 | desterraremos | 1 |
| 64935 | desterrándoles | 1 |
| 64936 | desterraban | 1 |
| 64937 | desternillaba | 1 |
| 64938 | desteñía | 1 |
| 64939 | destemplose | 1 |
| 64940 | destemplanza | 1 |
| 64941 | destempladamente | 1 |
| 64942 | destar | 1 |
| 64943 | destaponados | 1 |
| 64944 | destapéme | 1 |
| 64945 | destape | 1 |
| 64946 | destapas | 1 |
| 64947 | destapar | 1 |
| 64948 | destapado | 1 |
| 64949 | destapada | 1 |
| 64950 | destacose | 1 |
| 64951 | destaca | 1 |
| 64952 | dessos | 1 |
| 64953 | dessollando | 1 |
| 64954 | dessolladas | 1 |
| 64955 | desseosos | 1 |
| 64956 | desseoso | 1 |
| 64957 | dessee | 1 |
| 64958 | dessecha | 1 |
| 64959 | desseays | 1 |
| 64960 | desseauamos | 1 |
| 64961 | dessearla | 1 |
| 64962 | dessear | 1 |
| 64963 | dessabrido | 1 |
| 64964 | desrayas | 1 |
| 64965 | desquito | 1 |
| 64966 | desquitándonos | 1 |
| 64967 | desquitados | 1 |
| 64968 | desquitaba | 1 |
| 64969 | desquita | 1 |
| 64970 | desquicien | 1 |
| 64971 | desquicie | 1 |
| 64972 | desquiciaron | 1 |
| 64973 | desquiciamiento | 1 |
| 64974 | desquiciadores | 1 |
| 64975 | desqu | 1 |
| 64976 | desputasen | 1 |
| 64977 | despuntas | 1 |
| 64978 | despuntarás | 1 |
| 64979 | despuntando | 1 |
| 64980 | despuntaban | 1 |
| 64981 | despueblas | 1 |
| 64982 | despuebla | 1 |
| 64983 | desprovistos | 1 |
| 64984 | desprovisto | 1 |
| 64985 | desproporcionadamente | 1 |
| 64986 | desproporcionada | 1 |
| 64987 | despriuasse | 1 |
| 64988 | desprevenidos | 1 |
| 64989 | desprevenida | 1 |
| 64990 | desprestigio | 1 |
| 64991 | desprestigiarte | 1 |
| 64992 | desprestigiaría | 1 |
| 64993 | desprestigiar | 1 |
| 64994 | desprestigiado | 1 |
| 64995 | despreocupadas | 1 |
| 64996 | despreocupada | 1 |
| 64997 | desprendiéndose | 1 |
| 64998 | desprendiendo | 1 |
| 64999 | desprecien | 1 |
| 65000 | despreciéis | 1 |
| 65001 | despreciativa | 1 |
| 65002 | despreciase | 1 |
| 65003 | despreçias | 1 |
| 65004 | desprecias | 1 |
| 65005 | despreciarse | 1 |
| 65006 | despreciaros | 1 |
| 65007 | despreciaron | 1 |
| 65008 | despreciarlos | 1 |
| 65009 | despreciarlo | 1 |
| 65010 | despreciarás | 1 |
| 65011 | despreçiarán | 1 |
| 65012 | despreciándolos | 1 |
| 65013 | despreciándole | 1 |
| 65014 | despreciándolas | 1 |
| 65015 | despreciándola | 1 |
| 65016 | despreciador | 1 |
| 65017 | despreciadas | 1 |
| 65018 | despreciables | 1 |
| 65019 | despotriques | 1 |
| 65020 | despotrique | 1 |
| 65021 | despotricaron | 1 |
| 65022 | despóticos | 1 |
| 65023 | despótico | 1 |
| 65024 | despóticas | 1 |
| 65025 | despóticamente | 1 |
| 65026 | despótica | 1 |
| 65027 | déspotas | 1 |
| 65028 | desposó | 1 |
| 65029 | desposarme | 1 |
| 65030 | desposara | 1 |
| 65031 | desposadas | 1 |
| 65032 | desposa | 1 |
| 65033 | despolvoreó | 1 |
| 65034 | despolvorearnos | 1 |
| 65035 | despojes | 1 |
| 65036 | despoje | 1 |
| 65037 | despojarse | 1 |
| 65038 | despojarme | 1 |
| 65039 | despojarías | 1 |
| 65040 | despójanse | 1 |
| 65041 | despojaban | 1 |
| 65042 | despojaba | 1 |
| 65043 | despoja | 1 |
| 65044 | despoblaste | 1 |
| 65045 | despoblada | 1 |
| 65046 | desplumó | 1 |
| 65047 | desplumarle | 1 |
| 65048 | desplumados | 1 |
| 65049 | desplumadoras | 1 |
| 65050 | desplumada | 1 |
| 65051 | desplomada | 1 |
| 65052 | desplomaban | 1 |
| 65053 | desplomaba | 1 |
| 65054 | despliéguese | 1 |
| 65055 | desplieguen | 1 |
| 65056 | despliegue | 1 |
| 65057 | desplegase | 1 |
| 65058 | desplegarás | 1 |
| 65059 | desplegado | 1 |
| 65060 | desplegadas | 1 |
| 65061 | desplantes | 1 |
| 65062 | desplace | 1 |
| 65063 | despintada | 1 |
| 65064 | despinta | 1 |
| 65065 | despilfarrada | 1 |
| 65066 | despiertísima | 1 |
| 65067 | despierten | 1 |
| 65068 | despiertan | 1 |
| 65069 | despiértame | 1 |
| 65070 | despidiólos | 1 |
| 65071 | despidio | 1 |
| 65072 | despidiese | 1 |
| 65073 | despidiéronla | 1 |
| 65074 | despidiera | 1 |
| 65075 | despidiéndolos | 1 |
| 65076 | despídese | 1 |
| 65077 | despides | 1 |
| 65078 | despidense | 1 |
| 65079 | despidays | 1 |
| 65080 | despídame | 1 |
| 65081 | despida | 1 |
| 65082 | despiadadamente | 1 |
| 65083 | despertose | 1 |
| 65084 | despertóme | 1 |
| 65085 | desperto | 1 |
| 65086 | despertays | 1 |
| 65087 | despertastes | 1 |
| 65088 | despertáronse | 1 |
| 65089 | despertáronlos | 1 |
| 65090 | despertarnos | 1 |
| 65091 | despertarme | 1 |
| 65092 | despertaría | 1 |
| 65093 | despertaré | 1 |
| 65094 | despertará | 1 |
| 65095 | despertándose | 1 |
| 65096 | despertadores | 1 |
| 65097 | desperna | 1 |
| 65098 | desperfectos | 1 |
| 65099 | desperezo | 1 |
| 65100 | desperezara | 1 |
| 65101 | desperdigada | 1 |
| 65102 | desperdicio | 1 |
| 65103 | despercudir | 1 |
| 65104 | despercudida | 1 |
| 65105 | despepita | 1 |
| 65106 | despeñéme | 1 |
| 65107 | despeñas | 1 |
| 65108 | despeñarme | 1 |
| 65109 | despeñaperros | 1 |
| 65110 | despeñándose | 1 |
| 65111 | despeñándome | 1 |
| 65112 | despeñan | 1 |
| 65113 | despeñaderos | 1 |
| 65114 | despensas | 1 |
| 65115 | despensadores | 1 |
| 65116 | despender | 1 |
| 65117 | despenar | 1 |
| 65118 | despenada | 1 |
| 65119 | despeluznado | 1 |
| 65120 | despellejo | 1 |
| 65121 | despellejarse | 1 |
| 65122 | despellejaban | 1 |
| 65123 | despellejaba | 1 |
| 65124 | despejó | 1 |
| 65125 | despejarse | 1 |
| 65126 | despejaría | 1 |
| 65127 | despejará | 1 |
| 65128 | despejándole | 1 |
| 65129 | despejalle | 1 |
| 65130 | despejados | 1 |
| 65131 | despejadísimo | 1 |
| 65132 | despejadas | 1 |
| 65133 | despejaban | 1 |
| 65134 | despeinarse | 1 |
| 65135 | despegó | 1 |
| 65136 | despegarse | 1 |
| 65137 | despegar | 1 |
| 65138 | despegador | 1 |
| 65139 | despegaba | 1 |
| 65140 | despedirte | 1 |
| 65141 | despedirles | 1 |
| 65142 | despedirlas | 1 |
| 65143 | despedirá | 1 |
| 65144 | despedímonos | 1 |
| 65145 | despedimientos | 1 |
| 65146 | despedille | 1 |
| 65147 | despediéndose | 1 |
| 65148 | despedazaua | 1 |
| 65149 | despedazarse | 1 |
| 65150 | despedazaría | 1 |
| 65151 | despedazara | 1 |
| 65152 | despedazados | 1 |
| 65153 | despedazadores | 1 |
| 65154 | despedazadas | 1 |
| 65155 | despedazaban | 1 |
| 65156 | despedazábamos | 1 |
| 65157 | despedaces | 1 |
| 65158 | despechoso | 1 |
| 65159 | despecharon | 1 |
| 65160 | despechados | 1 |
| 65161 | despechada | 1 |
| 65162 | despearse | 1 |
| 65163 | despeado | 1 |
| 65164 | despeada | 1 |
| 65165 | despavoridas | 1 |
| 65166 | despartirla | 1 |
| 65167 | despartió | 1 |
| 65168 | despartidores | 1 |
| 65169 | desparte | 1 |
| 65170 | desparramó | 1 |
| 65171 | desparramasen | 1 |
| 65172 | desparramar | 1 |
| 65173 | desparramándose | 1 |
| 65174 | desparramadas | 1 |
| 65175 | desparramaban | 1 |
| 65176 | desparrama | 1 |
| 65177 | desparezco | 1 |
| 65178 | despareció | 1 |
| 65179 | desparecíla | 1 |
| 65180 | desparecido | 1 |
| 65181 | desparecían | 1 |
| 65182 | desparecer | 1 |
| 65183 | desparece | 1 |
| 65184 | desparcir | 1 |
| 65185 | desparatado | 1 |
| 65186 | despalmado | 1 |
| 65187 | despalmadas | 1 |
| 65188 | despaldado | 1 |
| 65189 | despagar | 1 |
| 65190 | despaga | 1 |
| 65191 | despaçio | 1 |
| 65192 | despachito | 1 |
| 65193 | despáchenme | 1 |
| 65194 | despachen | 1 |
| 65195 | despachélos | 1 |
| 65196 | despáchate | 1 |
| 65197 | despachasen | 1 |
| 65198 | despacharme | 1 |
| 65199 | despacharlo | 1 |
| 65200 | despacharle | 1 |
| 65201 | despachará | 1 |
| 65202 | despáchanse | 1 |
| 65203 | despachada | 1 |
| 65204 | despabilé | 1 |
| 65205 | despabilasen | 1 |
| 65206 | despabilaron | 1 |
| 65207 | despabilaré | 1 |
| 65208 | despabilados | 1 |
| 65209 | despabilaban | 1 |
| 65210 | despabilaba | 1 |
| 65211 | despabila | 1 |
| 65212 | desotros | 1 |
| 65213 | desotro | 1 |
| 65214 | desorientar | 1 |
| 65215 | desorientados | 1 |
| 65216 | desorientada | 1 |
| 65217 | desorientaba | 1 |
| 65218 | desorganización | 1 |
| 65219 | desorejado | 1 |
| 65220 | desorejaba | 1 |
| 65221 | desordenados | 1 |
| 65222 | desordenadas | 1 |
| 65223 | desonrrado | 1 |
| 65224 | desonrrada | 1 |
| 65225 | desoluto | 1 |
| 65226 | desollaros | 1 |
| 65227 | desollaron | 1 |
| 65228 | desollarnos | 1 |
| 65229 | desolladas | 1 |
| 65230 | desollada | 1 |
| 65231 | desollaba | 1 |
| 65232 | desolado | 1 |
| 65233 | desojaban | 1 |
| 65234 | desocuparme | 1 |
| 65235 | desobligaba | 1 |
| 65236 | desobedientes | 1 |
| 65237 | desobedezco | 1 |
| 65238 | desobedecían | 1 |
| 65239 | desobedecería | 1 |
| 65240 | desnudóse | 1 |
| 65241 | desnudillo | 1 |
| 65242 | desnúdese | 1 |
| 65243 | desnudé | 1 |
| 65244 | desnude | 1 |
| 65245 | desnudaua | 1 |
| 65246 | desnudasen | 1 |
| 65247 | desnudase | 1 |
| 65248 | desnudarnos | 1 |
| 65249 | desnudarme | 1 |
| 65250 | desnudarlas | 1 |
| 65251 | desnudan | 1 |
| 65252 | desnúdame | 1 |
| 65253 | desnudador | 1 |
| 65254 | desnudado | 1 |
| 65255 | desnudabas | 1 |
| 65256 | desnuca | 1 |
| 65257 | desniveles | 1 |
| 65258 | desnivel | 1 |
| 65259 | desnatan | 1 |
| 65260 | desnarigados | 1 |
| 65261 | desnarigado | 1 |
| 65262 | desnarigada | 1 |
| 65263 | desmuele | 1 |
| 65264 | desmoronarse | 1 |
| 65265 | desmoronan | 1 |
| 65266 | desmoronados | 1 |
| 65267 | desmoronado | 1 |
| 65268 | desmoralizadoras | 1 |
| 65269 | desmoralización | 1 |
| 65270 | desmontó | 1 |
| 65271 | desmontados | 1 |
| 65272 | desmochadas | 1 |
| 65273 | desmochada | 1 |
| 65274 | desminuyen | 1 |
| 65275 | desmintiese | 1 |
| 65276 | desmintieron | 1 |
| 65277 | desmintieran | 1 |
| 65278 | desmintiéndome | 1 |
| 65279 | desmigajé | 1 |
| 65280 | desmigajar | 1 |
| 65281 | desmienten | 1 |
| 65282 | desmienta | 1 |
| 65283 | desmesurados | 1 |
| 65284 | desmesuradas | 1 |
| 65285 | desmesuradamente | 1 |
| 65286 | desmerecía | 1 |
| 65287 | desmerecerías | 1 |
| 65288 | desmerecer | 1 |
| 65289 | desmerece | 1 |
| 65290 | desmentirla | 1 |
| 65291 | desmentiré | 1 |
| 65292 | desmentille | 1 |
| 65293 | desmentíla | 1 |
| 65294 | desmentidas | 1 |
| 65295 | desmengue | 1 |
| 65296 | desmengua | 1 |
| 65297 | desmemoriado | 1 |
| 65298 | desmembramos | 1 |
| 65299 | desmejorarse | 1 |
| 65300 | desmejoramiento | 1 |
| 65301 | desmejoradillo | 1 |
| 65302 | desmejoraba | 1 |
| 65303 | desmedidas | 1 |
| 65304 | desmedidamente | 1 |
| 65305 | desmayóse | 1 |
| 65306 | desmayé | 1 |
| 65307 | desmayasen | 1 |
| 65308 | desmayaron | 1 |
| 65309 | desmayaráse | 1 |
| 65310 | desmayan | 1 |
| 65311 | desmayábase | 1 |
| 65312 | desmantelar | 1 |
| 65313 | desmantelando | 1 |
| 65314 | desmantelado | 1 |
| 65315 | desmantelada | 1 |
| 65316 | desmanes | 1 |
| 65317 | desmandó | 1 |
| 65318 | desmando | 1 |
| 65319 | desmandes | 1 |
| 65320 | desmandase | 1 |
| 65321 | desmandas | 1 |
| 65322 | desmandarme | 1 |
| 65323 | desmandara | 1 |
| 65324 | desmandaba | 1 |
| 65325 | desmadejado | 1 |
| 65326 | desmadejadas | 1 |
| 65327 | desmadejada | 1 |
| 65328 | deslustrar | 1 |
| 65329 | deslumbro | 1 |
| 65330 | deslumbradora | 1 |
| 65331 | deslumbraban | 1 |
| 65332 | deslucida | 1 |
| 65333 | deslomar | 1 |
| 65334 | deslizase | 1 |
| 65335 | deslizas | 1 |
| 65336 | deslizarme | 1 |
| 65337 | deslizar | 1 |
| 65338 | deslizando | 1 |
| 65339 | deslizan | 1 |
| 65340 | deslizado | 1 |
| 65341 | deslindase | 1 |
| 65342 | deslindar | 1 |
| 65343 | deslindan | 1 |
| 65344 | desligó | 1 |
| 65345 | desligado | 1 |
| 65346 | desligada | 1 |
| 65347 | deslices | 1 |
| 65348 | desliando | 1 |
| 65349 | desliaba | 1 |
| 65350 | desleznadera | 1 |
| 65351 | deslenguó | 1 |
| 65352 | deslenguamiento | 1 |
| 65353 | deslenguados | 1 |
| 65354 | desleída | 1 |
| 65355 | deslealtades | 1 |
| 65356 | deslealtad | 1 |
| 65357 | desleales | 1 |
| 65358 | deslazas | 1 |
| 65359 | desjarrete | 1 |
| 65360 | desjarretaron | 1 |
| 65361 | desitme | 1 |
| 65362 | desit | 1 |
| 65363 | desisto | 1 |
| 65364 | desistiré | 1 |
| 65365 | desistirás | 1 |
| 65366 | desistir | 1 |
| 65367 | desistió | 1 |
| 65368 | desistieron | 1 |
| 65369 | desistido | 1 |
| 65370 | desistía | 1 |
| 65371 | desirse | 1 |
| 65372 | desirnos | 1 |
| 65373 | desírgelo | 1 |
| 65374 | desinios | 1 |
| 65375 | desilusiones | 1 |
| 65376 | desilusionada | 1 |
| 65377 | desilusión | 1 |
| 65378 | designó | 1 |
| 65379 | designo | 1 |
| 65380 | designarlos | 1 |
| 65381 | designarlas | 1 |
| 65382 | designarla | 1 |
| 65383 | designaré | 1 |
| 65384 | designaran | 1 |
| 65385 | designará | 1 |
| 65386 | designado | 1 |
| 65387 | designada | 1 |
| 65388 | designaba | 1 |
| 65389 | designa | 1 |
| 65390 | desíenme | 1 |
| 65391 | desiderátum | 1 |
| 65392 | desían | 1 |
| 65393 | desí | 1 |
| 65394 | deshonrra | 1 |
| 65395 | deshonré | 1 |
| 65396 | deshonrarnos | 1 |
| 65397 | deshonrarme | 1 |
| 65398 | deshonrarle | 1 |
| 65399 | deshonrarán | 1 |
| 65400 | deshonrabuenos | 1 |
| 65401 | deshonestas | 1 |
| 65402 | deshojadas | 1 |
| 65403 | deshoja | 1 |
| 65404 | deshogar | 1 |
| 65405 | deshinchándose | 1 |
| 65406 | deshilados | 1 |
| 65407 | deshilachaban | 1 |
| 65408 | deshicieron | 1 |
| 65409 | deshice | 1 |
| 65410 | desherraba | 1 |
| 65411 | desheredados | 1 |
| 65412 | desheredado | 1 |
| 65413 | desheredada | 1 |
| 65414 | deshelaba | 1 |
| 65415 | deshaziendo | 1 |
| 65416 | deshaze | 1 |
| 65417 | desharía | 1 |
| 65418 | desharé | 1 |
| 65419 | deshambridos | 1 |
| 65420 | deshaciéndola | 1 |
| 65421 | deshacerte | 1 |
| 65422 | deshacerme | 1 |
| 65423 | deshacerlos | 1 |
| 65424 | deshacello | 1 |
| 65425 | deshacedor | 1 |
| 65426 | deshaced | 1 |
| 65427 | deshabitado | 1 |
| 65428 | deshabitada | 1 |
| 65429 | desgreñadas | 1 |
| 65430 | desgrenado | 1 |
| 65431 | desgranadas | 1 |
| 65432 | desgranábasele | 1 |
| 65433 | desgradesçí | 1 |
| 65434 | desgozne | 1 |
| 65435 | desgoznarse | 1 |
| 65436 | desgobernando | 1 |
| 65437 | desgobernador | 1 |
| 65438 | desgobernada | 1 |
| 65439 | desgaste | 1 |
| 65440 | desgastase | 1 |
| 65441 | desgastará | 1 |
| 65442 | desgastada | 1 |
| 65443 | desgarróse | 1 |
| 65444 | desgarrones | 1 |
| 65445 | desgarrón | 1 |
| 65446 | desgarró | 1 |
| 65447 | desgarro | 1 |
| 65448 | desgarrase | 1 |
| 65449 | desgarrándose | 1 |
| 65450 | desgarrando | 1 |
| 65451 | desgarran | 1 |
| 65452 | desgarrador | 1 |
| 65453 | desgarraban | 1 |
| 65454 | desgarbada | 1 |
| 65455 | desgañite | 1 |
| 65456 | desgañitarse | 1 |
| 65457 | desgañifando | 1 |
| 65458 | desganas | 1 |
| 65459 | desgajarse | 1 |
| 65460 | desgajaron | 1 |
| 65461 | desgajar | 1 |
| 65462 | desgajada | 1 |
| 65463 | desfuzia | 1 |
| 65464 | desfogaré | 1 |
| 65465 | desfízos | 1 |
| 65466 | desfilaron | 1 |
| 65467 | desfiladero | 1 |
| 65468 | desfigurarse | 1 |
| 65469 | desfigurarla | 1 |
| 65470 | desfigurándose | 1 |
| 65471 | desfigurándolo | 1 |
| 65472 | desfigurados | 1 |
| 65473 | desfiguraban | 1 |
| 65474 | desfigura | 1 |
| 65475 | desferrar | 1 |
| 65476 | desfegurado | 1 |
| 65477 | desfegurada | 1 |
| 65478 | desfeas | 1 |
| 65479 | desfazer | 1 |
| 65480 | desfavorecer | 1 |
| 65481 | desfavorablemente | 1 |
| 65482 | desfases | 1 |
| 65483 | desfase | 1 |
| 65484 | desfaré | 1 |
| 65485 | desfanbrido | 1 |
| 65486 | desfallydo | 1 |
| 65487 | desfallezca | 1 |
| 65488 | desfallesçen | 1 |
| 65489 | desfalleciendo | 1 |
| 65490 | desfallecidos | 1 |
| 65491 | desfallecido | 1 |
| 65492 | desfallecida | 1 |
| 65493 | desfallece | 1 |
| 65494 | desfalcaré | 1 |
| 65495 | desfagan | 1 |
| 65496 | desfacelle | 1 |
| 65497 | desestimase | 1 |
| 65498 | desestero | 1 |
| 65499 | desespere | 1 |
| 65500 | desesperas | 1 |
| 65501 | desesperars | 1 |
| 65502 | desesperaron | 1 |
| 65503 | desesperaría | 1 |
| 65504 | desesperar | 1 |
| 65505 | desesperanza | 1 |
| 65506 | desesperante | 1 |
| 65507 | desesperadas | 1 |
| 65508 | desesperadamente | 1 |
| 65509 | desesperábame | 1 |
| 65510 | desespera | 1 |
| 65511 | deservicios | 1 |
| 65512 | deservicio | 1 |
| 65513 | deserví | 1 |
| 65514 | desertor | 1 |
| 65515 | desertar | 1 |
| 65516 | desertaban | 1 |
| 65517 | deserrado | 1 |
| 65518 | deserradas | 1 |
| 65519 | deserción | 1 |
| 65520 | desequilibrios | 1 |
| 65521 | desequilibraba | 1 |
| 65522 | deseñoraba | 1 |
| 65523 | desenvuelvo | 1 |
| 65524 | desenvueltamente | 1 |
| 65525 | desenvolvíle | 1 |
| 65526 | desenvolviese | 1 |
| 65527 | desenvolviéndole | 1 |
| 65528 | desenvolviéndolas | 1 |
| 65529 | desenvolvía | 1 |
| 65530 | desenvolveros | 1 |
| 65531 | desenvolverme | 1 |
| 65532 | desenvolver | 1 |
| 65533 | desenvoltísima | 1 |
| 65534 | desenvainen | 1 |
| 65535 | desenvaine | 1 |
| 65536 | desenvainaron | 1 |
| 65537 | desenvainar | 1 |
| 65538 | desenvaina | 1 |
| 65539 | desentumecían | 1 |
| 65540 | desentumecía | 1 |
| 65541 | desentrañarles | 1 |
| 65542 | desentrañaremos | 1 |
| 65543 | desentrañar | 1 |
| 65544 | desentrañaban | 1 |
| 65545 | desentrañaba | 1 |
| 65546 | desentono | 1 |
| 65547 | desentonadas | 1 |
| 65548 | desentonaba | 1 |
| 65549 | desentona | 1 |
| 65550 | desentido | 1 |
| 65551 | desenterraua | 1 |
| 65552 | desenterrar | 1 |
| 65553 | desenterrándonos | 1 |
| 65554 | desenterrado | 1 |
| 65555 | desenterraba | 1 |
| 65556 | desentendido | 1 |
| 65557 | desentendida | 1 |
| 65558 | desensillado | 1 |
| 65559 | desensartó | 1 |
| 65560 | desenroscarse | 1 |
| 65561 | desenrosca | 1 |
| 65562 | desenredarle | 1 |
| 65563 | desenredándose | 1 |
| 65564 | desenojaros | 1 |
| 65565 | desenojarla | 1 |
| 65566 | desenojaría | 1 |
| 65567 | desenojar | 1 |
| 65568 | desenojada | 1 |
| 65569 | desenmascaré | 1 |
| 65570 | desenlazarle | 1 |
| 65571 | desenlazando | 1 |
| 65572 | desenlazado | 1 |
| 65573 | desenjaularon | 1 |
| 65574 | desengonzado | 1 |
| 65575 | desengañóse | 1 |
| 65576 | desengañónos | 1 |
| 65577 | desengañes | 1 |
| 65578 | desengáñate | 1 |
| 65579 | desengañasen | 1 |
| 65580 | desengañarme | 1 |
| 65581 | desengañara | 1 |
| 65582 | desengañaos | 1 |
| 65583 | desengañaban | 1 |
| 65584 | desengaña | 1 |
| 65585 | desenganchó | 1 |
| 65586 | desengancharemos | 1 |
| 65587 | desenganchad | 1 |
| 65588 | desenfundando | 1 |
| 65589 | desenfundan | 1 |
| 65590 | desenfrenado | 1 |
| 65591 | desenfadadamente | 1 |
| 65592 | desencuadernarse | 1 |
| 65593 | desenconan | 1 |
| 65594 | desenclavijó | 1 |
| 65595 | desencinta | 1 |
| 65596 | desencasquetándose | 1 |
| 65597 | desencarna | 1 |
| 65598 | desencantos | 1 |
| 65599 | desencantes | 1 |
| 65600 | desencantarte | 1 |
| 65601 | desencantado | 1 |
| 65602 | desencajarle | 1 |
| 65603 | desencajaba | 1 |
| 65604 | desencadenó | 1 |
| 65605 | desencadenáronse | 1 |
| 65606 | desencadenado | 1 |
| 65607 | desenamorado | 1 |
| 65608 | desenalbardar | 1 |
| 65609 | desempeños | 1 |
| 65610 | desempeño | 1 |
| 65611 | desempeñes | 1 |
| 65612 | desempeñaron | 1 |
| 65613 | desempeñarlo | 1 |
| 65614 | desempeñarlas | 1 |
| 65615 | desempeñaran | 1 |
| 65616 | desempeñará | 1 |
| 65617 | desempeñando | 1 |
| 65618 | desempeñan | 1 |
| 65619 | desempeñados | 1 |
| 65620 | desempeña | 1 |
| 65621 | desempenado | 1 |
| 65622 | desemejanza | 1 |
| 65623 | desemejable | 1 |
| 65624 | déseme | 1 |
| 65625 | desembuelta | 1 |
| 65626 | desembuchas | 1 |
| 65627 | desembuchando | 1 |
| 65628 | desembozo | 1 |
| 65629 | desemboltura | 1 |
| 65630 | desembolsos | 1 |
| 65631 | desembolsar | 1 |
| 65632 | desembolsado | 1 |
| 65633 | desembolsada | 1 |
| 65634 | desembocar | 1 |
| 65635 | desemboca | 1 |
| 65636 | desembaúle | 1 |
| 65637 | desembaular | 1 |
| 65638 | desembarcos | 1 |
| 65639 | desembarcásemos | 1 |
| 65640 | desembarazarnos | 1 |
| 65641 | desembarazándose | 1 |
| 65642 | desembarazando | 1 |
| 65643 | desembarazadas | 1 |
| 65644 | desembarazadamente | 1 |
| 65645 | desembaraza | 1 |
| 65646 | desembanastasen | 1 |
| 65647 | déselo | 1 |
| 65648 | desellando | 1 |
| 65649 | déseles | 1 |
| 65650 | désele | 1 |
| 65651 | deseen | 1 |
| 65652 | deseemos | 1 |
| 65653 | deseé | 1 |
| 65654 | desechóme | 1 |
| 65655 | desechéisla | 1 |
| 65656 | desechéis | 1 |
| 65657 | deseché | 1 |
| 65658 | desechásteme | 1 |
| 65659 | desechase | 1 |
| 65660 | desechas | 1 |
| 65661 | desecharon | 1 |
| 65662 | desecharle | 1 |
| 65663 | desechando | 1 |
| 65664 | deséchalo | 1 |
| 65665 | desechalla | 1 |
| 65666 | desechada | 1 |
| 65667 | desechaban | 1 |
| 65668 | deseavos | 1 |
| 65669 | deseaste | 1 |
| 65670 | deseasse | 1 |
| 65671 | desease | 1 |
| 65672 | desearon | 1 |
| 65673 | desearen | 1 |
| 65674 | desearan | 1 |
| 65675 | deseándolo | 1 |
| 65676 | deseándole | 1 |
| 65677 | deseados | 1 |
| 65678 | deseábamos | 1 |
| 65679 | desdore | 1 |
| 65680 | desdorados | 1 |
| 65681 | desdonada | 1 |
| 65682 | desdobló | 1 |
| 65683 | desdoblas | 1 |
| 65684 | desdoblarse | 1 |
| 65685 | desdobláronse | 1 |
| 65686 | desdoblado | 1 |
| 65687 | desdoblaba | 1 |
| 65688 | desdiré | 1 |
| 65689 | desdijese | 1 |
| 65690 | desdijera | 1 |
| 65691 | desdigan | 1 |
| 65692 | desdiciéndose | 1 |
| 65693 | desdichadísimas | 1 |
| 65694 | desdichadísima | 1 |
| 65695 | desdichadamente | 1 |
| 65696 | desdezía | 1 |
| 65697 | desdesir | 1 |
| 65698 | desdeñosamente | 1 |
| 65699 | desdeñedes | 1 |
| 65700 | desdeñé | 1 |
| 65701 | desdeñase | 1 |
| 65702 | desdeñas | 1 |
| 65703 | desdeñará | 1 |
| 65704 | desdeñara | 1 |
| 65705 | desdeñándose | 1 |
| 65706 | desdeñamientos | 1 |
| 65707 | desdeñados | 1 |
| 65708 | desdeñada | 1 |
| 65709 | desdentado | 1 |
| 65710 | desdentada | 1 |
| 65711 | desden | 1 |
| 65712 | desdecirme | 1 |
| 65713 | desdecir | 1 |
| 65714 | desd | 1 |
| 65715 | descuydar | 1 |
| 65716 | descuydados | 1 |
| 65717 | descuydado | 1 |
| 65718 | descumunales | 1 |
| 65719 | descumulgado | 1 |
| 65720 | descumulgada | 1 |
| 65721 | descumplir | 1 |
| 65722 | desculpó | 1 |
| 65723 | desculparte | 1 |
| 65724 | desculpada | 1 |
| 65725 | desculpaba | 1 |
| 65726 | descuidó | 1 |
| 65727 | descuidillos | 1 |
| 65728 | descuides | 1 |
| 65729 | descuidero | 1 |
| 65730 | descuidera | 1 |
| 65731 | descuídate | 1 |
| 65732 | descuidasen | 1 |
| 65733 | descuidase | 1 |
| 65734 | descuente | 1 |
| 65735 | descuella | 1 |
| 65736 | descuelgue | 1 |
| 65737 | descuelgan | 1 |
| 65738 | descuchar | 1 |
| 65739 | descubrirte | 1 |
| 65740 | descubrirnos | 1 |
| 65741 | descubrirlos | 1 |
| 65742 | descubrirla | 1 |
| 65743 | descubriríamos | 1 |
| 65744 | descubriré | 1 |
| 65745 | descubriose | 1 |
| 65746 | descubriolo | 1 |
| 65747 | descubrióla | 1 |
| 65748 | descubrio | 1 |
| 65749 | descubrille | 1 |
| 65750 | descubriesen | 1 |
| 65751 | descubriéronle | 1 |
| 65752 | descubrieres | 1 |
| 65753 | descubrieras | 1 |
| 65754 | descubriéndome | 1 |
| 65755 | descubriéndolo | 1 |
| 65756 | descubriéndole | 1 |
| 65757 | descúbrete | 1 |
| 65758 | descubresnos | 1 |
| 65759 | descúbreme | 1 |
| 65760 | descubrele | 1 |
| 65761 | descubráis | 1 |
| 65762 | descuartizarlos | 1 |
| 65763 | descuartizarla | 1 |
| 65764 | descuartizan | 1 |
| 65765 | descuartizada | 1 |
| 65766 | descuartizaba | 1 |
| 65767 | descuartice | 1 |
| 65768 | descuajaraba | 1 |
| 65769 | descuadernado | 1 |
| 65770 | descriue | 1 |
| 65771 | descritas | 1 |
| 65772 | descrismándose | 1 |
| 65773 | descriptivos | 1 |
| 65774 | descriptivo | 1 |
| 65775 | descriptivas | 1 |
| 65776 | descríe | 1 |
| 65777 | describo | 1 |
| 65778 | describirlos | 1 |
| 65779 | describirle | 1 |
| 65780 | describió | 1 |
| 65781 | describiese | 1 |
| 65782 | describen | 1 |
| 65783 | describa | 1 |
| 65784 | descreído | 1 |
| 65785 | descreídas | 1 |
| 65786 | descreída | 1 |
| 65787 | descreer | 1 |
| 65788 | descrece | 1 |
| 65789 | descotada | 1 |
| 65790 | descosía | 1 |
| 65791 | descoserse | 1 |
| 65792 | descorrió | 1 |
| 65793 | descorrían | 1 |
| 65794 | descorrer | 1 |
| 65795 | descordia | 1 |
| 65796 | descorazonó | 1 |
| 65797 | descorazonamiento | 1 |
| 65798 | descontó | 1 |
| 65799 | descontentó | 1 |
| 65800 | descontentas | 1 |
| 65801 | descontentar | 1 |
| 65802 | descontentamientos | 1 |
| 65803 | descontentadizo | 1 |
| 65804 | descontándole | 1 |
| 65805 | descontando | 1 |
| 65806 | descontadas | 1 |
| 65807 | descontaba | 1 |
| 65808 | desconsuele | 1 |
| 65809 | desconsuelas | 1 |
| 65810 | desconsuela | 1 |
| 65811 | desconsolóle | 1 |
| 65812 | desconsoladoras | 1 |
| 65813 | desconsoladora | 1 |
| 65814 | desconsoladísima | 1 |
| 65815 | desconsoladamente | 1 |
| 65816 | desconsolaba | 1 |
| 65817 | desconsideradas | 1 |
| 65818 | desconsideradamente | 1 |
| 65819 | desconsiderá | 1 |
| 65820 | desconpón | 1 |
| 65821 | desconozco | 1 |
| 65822 | desconoscido | 1 |
| 65823 | desconosçida | 1 |
| 65824 | desconociesen | 1 |
| 65825 | desconociéronme | 1 |
| 65826 | desconocieron | 1 |
| 65827 | desconociendo | 1 |
| 65828 | desconocíamos | 1 |
| 65829 | desconocen | 1 |
| 65830 | desconfuerta | 1 |
| 65831 | desconformidad | 1 |
| 65832 | desconfío | 1 |
| 65833 | desconfies | 1 |
| 65834 | desconfíen | 1 |
| 65835 | desconfié | 1 |
| 65836 | desconfiaua | 1 |
| 65837 | desconfiaron | 1 |
| 65838 | desconciertan | 1 |
| 65839 | desconcierta | 1 |
| 65840 | desconchadas | 1 |
| 65841 | desconcertadas | 1 |
| 65842 | desconcertaban | 1 |
| 65843 | desconcertaba | 1 |
| 65844 | descomunión | 1 |
| 65845 | descomulgó | 1 |
| 65846 | descomulgadas | 1 |
| 65847 | descomponiéndole | 1 |
| 65848 | descomponerlo | 1 |
| 65849 | descomponerla | 1 |
| 65850 | descomponemos | 1 |
| 65851 | descompondría | 1 |
| 65852 | descompasado | 1 |
| 65853 | descomonión | 1 |
| 65854 | descomodidades | 1 |
| 65855 | descomer | 1 |
| 65856 | descomedida | 1 |
| 65857 | descollaría | 1 |
| 65858 | descollar | 1 |
| 65859 | descollando | 1 |
| 65860 | descolgásedes | 1 |
| 65861 | descolgarte | 1 |
| 65862 | descolgáronlos | 1 |
| 65863 | descolgaron | 1 |
| 65864 | descolgarla | 1 |
| 65865 | descolgando | 1 |
| 65866 | descolgadas | 1 |
| 65867 | descolgaba | 1 |
| 65868 | descogidos | 1 |
| 65869 | descogido | 1 |
| 65870 | descogerá | 1 |
| 65871 | descoger | 1 |
| 65872 | descoco | 1 |
| 65873 | descobyerta | 1 |
| 65874 | descobryr | 1 |
| 65875 | descobrire | 1 |
| 65876 | descobrimientos | 1 |
| 65877 | descobrilla | 1 |
| 65878 | descobrides | 1 |
| 65879 | descobrid | 1 |
| 65880 | descobrades | 1 |
| 65881 | descobierto | 1 |
| 65882 | descobiertamente | 1 |
| 65883 | descobierta | 1 |
| 65884 | desclavar | 1 |
| 65885 | desçiplina | 1 |
| 65886 | desciñó | 1 |
| 65887 | desciñéronse | 1 |
| 65888 | descifró | 1 |
| 65889 | descifremos | 1 |
| 65890 | descifrarlas | 1 |
| 65891 | descifrable | 1 |
| 65892 | descifraba | 1 |
| 65893 | descifra | 1 |
| 65894 | descerrajaré | 1 |
| 65895 | desceñido | 1 |
| 65896 | desceñida | 1 |
| 65897 | descensos | 1 |
| 65898 | desçenir | 1 |
| 65899 | descendyó | 1 |
| 65900 | descendy | 1 |
| 65901 | desçendió | 1 |
| 65902 | desçendimiento | 1 |
| 65903 | descendimiento | 1 |
| 65904 | desçendido | 1 |
| 65905 | descendido | 1 |
| 65906 | descendente | 1 |
| 65907 | descendencias | 1 |
| 65908 | descastar | 1 |
| 65909 | descastado | 1 |
| 65910 | descascaraba | 1 |
| 65911 | descasaua | 1 |
| 65912 | descartes | 1 |
| 65913 | descártense | 1 |
| 65914 | descarten | 1 |
| 65915 | descartarse | 1 |
| 65916 | descartaba | 1 |
| 65917 | descarta | 1 |
| 65918 | descarne | 1 |
| 65919 | descarnadas | 1 |
| 65920 | descarnaba | 1 |
| 65921 | descargos | 1 |
| 65922 | descargasen | 1 |
| 65923 | descargase | 1 |
| 65924 | descargas | 1 |
| 65925 | descargaría | 1 |
| 65926 | descargaré | 1 |
| 65927 | descargándosela | 1 |
| 65928 | descargándose | 1 |
| 65929 | descargando | 1 |
| 65930 | descargados | 1 |
| 65931 | descaramiento | 1 |
| 65932 | descaperuzados | 1 |
| 65933 | descaperuzado | 1 |
| 65934 | descanssa | 1 |
| 65935 | descanséis | 1 |
| 65936 | descansas | 1 |
| 65937 | descansaron | 1 |
| 65938 | descansarle | 1 |
| 65939 | descansare | 1 |
| 65940 | descansarás | 1 |
| 65941 | descansara | 1 |
| 65942 | descansamos | 1 |
| 65943 | descamisado | 1 |
| 65944 | descaminos | 1 |
| 65945 | descaminar | 1 |
| 65946 | descaminadas | 1 |
| 65947 | descalzó | 1 |
| 65948 | descalzarte | 1 |
| 65949 | descalzarse | 1 |
| 65950 | descalzarle | 1 |
| 65951 | descalzar | 1 |
| 65952 | descalzándose | 1 |
| 65953 | descalzaba | 1 |
| 65954 | descalcitos | 1 |
| 65955 | descalce | 1 |
| 65956 | descalabro | 1 |
| 65957 | descalabréle | 1 |
| 65958 | descalabré | 1 |
| 65959 | descalabraron | 1 |
| 65960 | descalabradura | 1 |
| 65961 | descalabra | 1 |
| 65962 | descaezcas | 1 |
| 65963 | descaescimiento | 1 |
| 65964 | descabullir | 1 |
| 65965 | descabezó | 1 |
| 65966 | descabezados | 1 |
| 65967 | descabezaban | 1 |
| 65968 | descabellado | 1 |
| 65969 | descabelladas | 1 |
| 65970 | descabalar | 1 |
| 65971 | descabalado | 1 |
| 65972 | descabaladas | 1 |
| 65973 | descabalada | 1 |
| 65974 | desbuélvete | 1 |
| 65975 | desbuchase | 1 |
| 65976 | desbuchar | 1 |
| 65977 | desbravase | 1 |
| 65978 | desbraue | 1 |
| 65979 | desbordase | 1 |
| 65980 | desbordar | 1 |
| 65981 | desbordamientos | 1 |
| 65982 | desbordamiento | 1 |
| 65983 | desbordado | 1 |
| 65984 | desbordada | 1 |
| 65985 | desbocándose | 1 |
| 65986 | desbocada | 1 |
| 65987 | desbauando | 1 |
| 65988 | desbastaron | 1 |
| 65989 | desbastar | 1 |
| 65990 | desbastándola | 1 |
| 65991 | desbástala | 1 |
| 65992 | desbarro | 1 |
| 65993 | desbarraba | 1 |
| 65994 | desbarbada | 1 |
| 65995 | desbarato | 1 |
| 65996 | desbarate | 1 |
| 65997 | desbaratáronse | 1 |
| 65998 | desbaratarlos | 1 |
| 65999 | desbaratan | 1 |
| 66000 | desbaratados | 1 |
| 66001 | desbaratadas | 1 |
| 66002 | desbarataban | 1 |
| 66003 | desbanquen | 1 |
| 66004 | desbanque | 1 |
| 66005 | desbandó | 1 |
| 66006 | desbandan | 1 |
| 66007 | desbandamos | 1 |
| 66008 | desbancado | 1 |
| 66009 | desazonada | 1 |
| 66010 | desazonaba | 1 |
| 66011 | desayunemos | 1 |
| 66012 | desayune | 1 |
| 66013 | desayunase | 1 |
| 66014 | desayunarnos | 1 |
| 66015 | desayunaos | 1 |
| 66016 | desayunan | 1 |
| 66017 | desayudo | 1 |
| 66018 | desayudaba | 1 |
| 66019 | desayuda | 1 |
| 66020 | desavío | 1 |
| 66021 | desaventuras | 1 |
| 66022 | desaventura | 1 |
| 66023 | desautorizar | 1 |
| 66024 | desauenturado | 1 |
| 66025 | desauenturadas | 1 |
| 66026 | desauenturada | 1 |
| 66027 | desauentura | 1 |
| 66028 | desauenires | 1 |
| 66029 | desatyrisiendo | 1 |
| 66030 | desatose | 1 |
| 66031 | desatólas | 1 |
| 66032 | desatinó | 1 |
| 66033 | desatinaba | 1 |
| 66034 | desati | 1 |
| 66035 | desatentado | 1 |
| 66036 | desatentadamente | 1 |
| 66037 | desaten | 1 |
| 66038 | desatasen | 1 |
| 66039 | desataros | 1 |
| 66040 | desatarlos | 1 |
| 66041 | desatarle | 1 |
| 66042 | desatamos | 1 |
| 66043 | desatadlo | 1 |
| 66044 | desatadas | 1 |
| 66045 | desatácate | 1 |
| 66046 | desatacar | 1 |
| 66047 | desatacados | 1 |
| 66048 | desastrosos | 1 |
| 66049 | desastradas | 1 |
| 66050 | desasosiega | 1 |
| 66051 | desasosegarles | 1 |
| 66052 | desasosegar | 1 |
| 66053 | desasosegaba | 1 |
| 66054 | desasna | 1 |
| 66055 | desasir | 1 |
| 66056 | desasía | 1 |
| 66057 | desasí | 1 |
| 66058 | desaseo | 1 |
| 66059 | désas | 1 |
| 66060 | desarropado | 1 |
| 66061 | desarróllase | 1 |
| 66062 | desarrollaron | 1 |
| 66063 | desarrollándosele | 1 |
| 66064 | desarrollándose | 1 |
| 66065 | desarrollan | 1 |
| 66066 | desarrollado | 1 |
| 66067 | desarrolladas | 1 |
| 66068 | desarrollaban | 1 |
| 66069 | desarrollaba | 1 |
| 66070 | desarrolla | 1 |
| 66071 | desarreglo | 1 |
| 66072 | desarreglado | 1 |
| 66073 | desarregladas | 1 |
| 66074 | desarreglada | 1 |
| 66075 | desarrebozóse | 1 |
| 66076 | desarrebozaba | 1 |
| 66077 | desarrapadas | 1 |
| 66078 | desarrapada | 1 |
| 66079 | desarraigó | 1 |
| 66080 | desarmóle | 1 |
| 66081 | desarmare | 1 |
| 66082 | desarman | 1 |
| 66083 | desarmados | 1 |
| 66084 | desarmaban | 1 |
| 66085 | desarma | 1 |
| 66086 | desarbolar | 1 |
| 66087 | desaprueba | 1 |
| 66088 | desaprovechada | 1 |
| 66089 | desaprobar | 1 |
| 66090 | desaprobación | 1 |
| 66091 | desaprensando | 1 |
| 66092 | desapártese | 1 |
| 66093 | desapartarse | 1 |
| 66094 | desapartaísos | 1 |
| 66095 | desapartada | 1 |
| 66096 | desapariciones | 1 |
| 66097 | desapareciose | 1 |
| 66098 | desapareciese | 1 |
| 66099 | desaparecida | 1 |
| 66100 | desaparecíamos | 1 |
| 66101 | desaparecí | 1 |
| 66102 | desaparecerse | 1 |
| 66103 | desaparecería | 1 |
| 66104 | desanimó | 1 |
| 66105 | desanime | 1 |
| 66106 | desanimarte | 1 |
| 66107 | desanimar | 1 |
| 66108 | desanimándose | 1 |
| 66109 | desanimados | 1 |
| 66110 | desangró | 1 |
| 66111 | desangrado | 1 |
| 66112 | desangradas | 1 |
| 66113 | desanduvo | 1 |
| 66114 | desandaré | 1 |
| 66115 | desandando | 1 |
| 66116 | desandado | 1 |
| 66117 | desamparé | 1 |
| 66118 | desamparasse | 1 |
| 66119 | desampararos | 1 |
| 66120 | desampararme | 1 |
| 66121 | desamparándole | 1 |
| 66122 | desamparando | 1 |
| 66123 | desamparan | 1 |
| 66124 | desamparadas | 1 |
| 66125 | desamparaba | 1 |
| 66126 | desampara | 1 |
| 66127 | desamortización | 1 |
| 66128 | desaminar | 1 |
| 66129 | desamigos | 1 |
| 66130 | desamen | 1 |
| 66131 | desama | 1 |
| 66132 | desalyña | 1 |
| 66133 | desalumbrados | 1 |
| 66134 | desalumbradamente | 1 |
| 66135 | desalojar | 1 |
| 66136 | desalojando | 1 |
| 66137 | desalojaban | 1 |
| 66138 | desalmadas | 1 |
| 66139 | desaliñase | 1 |
| 66140 | desaliñando | 1 |
| 66141 | desaliñada | 1 |
| 66142 | desalinada | 1 |
| 66143 | desalientos | 1 |
| 66144 | desalforjó | 1 |
| 66145 | desalentados | 1 |
| 66146 | desalentado | 1 |
| 66147 | desalentaban | 1 |
| 66148 | desalbardara | 1 |
| 66149 | desalabauas | 1 |
| 66150 | desalabas | 1 |
| 66151 | desairarte | 1 |
| 66152 | desairarlos | 1 |
| 66153 | desairarle | 1 |
| 66154 | desairarla | 1 |
| 66155 | desairados | 1 |
| 66156 | desairadas | 1 |
| 66157 | desairaban | 1 |
| 66158 | desahucios | 1 |
| 66159 | desahucio | 1 |
| 66160 | desahuciarlo | 1 |
| 66161 | desahuciado | 1 |
| 66162 | desahogue | 1 |
| 66163 | desahógate | 1 |
| 66164 | desahogaran | 1 |
| 66165 | desahogará | 1 |
| 66166 | desahogándola | 1 |
| 66167 | desahogando | 1 |
| 66168 | desahogaban | 1 |
| 66169 | desahoga | 1 |
| 66170 | desaguisada | 1 |
| 66171 | desagüe | 1 |
| 66172 | desaguarse | 1 |
| 66173 | desaguaderos | 1 |
| 66174 | desagua | 1 |
| 66175 | desagraviarte | 1 |
| 66176 | desagraviarme | 1 |
| 66177 | desagraviada | 1 |
| 66178 | desagradó | 1 |
| 66179 | desagradescido | 1 |
| 66180 | desagradesçida | 1 |
| 66181 | desagradesçer | 1 |
| 66182 | desagradescen | 1 |
| 66183 | desagrade | 1 |
| 66184 | desagradaron | 1 |
| 66185 | desagradablemente | 1 |
| 66186 | desaforadamente | 1 |
| 66187 | desafinar | 1 |
| 66188 | desafinamos | 1 |
| 66189 | desafíe | 1 |
| 66190 | desafiásedes | 1 |
| 66191 | desafiarse | 1 |
| 66192 | desafiaron | 1 |
| 66193 | desafiaría | 1 |
| 66194 | desafiaré | 1 |
| 66195 | desafiaran | 1 |
| 66196 | desafiamos | 1 |
| 66197 | desafiamiento | 1 |
| 66198 | desafialle | 1 |
| 66199 | desafiadas | 1 |
| 66200 | desadormescieron | 1 |
| 66201 | desadonas | 1 |
| 66202 | desacreditó | 1 |
| 66203 | desacreditasen | 1 |
| 66204 | desacreditarse | 1 |
| 66205 | desacreditándote | 1 |
| 66206 | desacreditaban | 1 |
| 66207 | desacredita | 1 |
| 66208 | desacordes | 1 |
| 66209 | desacordemente | 1 |
| 66210 | desacorde | 1 |
| 66211 | desacordados | 1 |
| 66212 | desacordado | 1 |
| 66213 | desacordada | 1 |
| 66214 | desaconsejaban | 1 |
| 66215 | desacompanados | 1 |
| 66216 | desacompanado | 1 |
| 66217 | desaciertos | 1 |
| 66218 | desacierto | 1 |
| 66219 | desabrochó | 1 |
| 66220 | desabrocharon | 1 |
| 66221 | desabrocharle | 1 |
| 66222 | desabrochar | 1 |
| 66223 | desabrochándose | 1 |
| 66224 | desabrochándole | 1 |
| 66225 | desabrigues | 1 |
| 66226 | desabrigo | 1 |
| 66227 | desabrigara | 1 |
| 66228 | desabrigan | 1 |
| 66229 | desabrigada | 1 |
| 66230 | desabridísimo | 1 |
| 66231 | desabridamente | 1 |
| 66232 | desabotonar | 1 |
| 66233 | desabotonados | 1 |
| 66234 | desaborida | 1 |
| 66235 | dés | 1 |
| 66236 | derrumbarse | 1 |
| 66237 | derrumbara | 1 |
| 66238 | derrumbar | 1 |
| 66239 | derrumbado | 1 |
| 66240 | derrumbaban | 1 |
| 66241 | derrumba | 1 |
| 66242 | derruído | 1 |
| 66243 | derrueca | 1 |
| 66244 | derrotó | 1 |
| 66245 | derrotero | 1 |
| 66246 | derroté | 1 |
| 66247 | derrotar | 1 |
| 66248 | derrotada | 1 |
| 66249 | derrocóm | 1 |
| 66250 | derrocharla | 1 |
| 66251 | derrochar | 1 |
| 66252 | derrochador | 1 |
| 66253 | derrochaban | 1 |
| 66254 | derrocha | 1 |
| 66255 | derritieran | 1 |
| 66256 | derritiéndose | 1 |
| 66257 | derritiendo | 1 |
| 66258 | derriten | 1 |
| 66259 | derribóme | 1 |
| 66260 | derríbol | 1 |
| 66261 | derribes | 1 |
| 66262 | derriben | 1 |
| 66263 | derríbela | 1 |
| 66264 | derribé | 1 |
| 66265 | derribaste | 1 |
| 66266 | derribas | 1 |
| 66267 | derribarte | 1 |
| 66268 | derribáronme | 1 |
| 66269 | derribáronles | 1 |
| 66270 | derribarme | 1 |
| 66271 | derribarán | 1 |
| 66272 | derríbanse | 1 |
| 66273 | derribándote | 1 |
| 66274 | derribamos | 1 |
| 66275 | derríbame | 1 |
| 66276 | derriballes | 1 |
| 66277 | derriballe | 1 |
| 66278 | derribadas | 1 |
| 66279 | derribaban | 1 |
| 66280 | derribaba | 1 |
| 66281 | derretirse | 1 |
| 66282 | derretirle | 1 |
| 66283 | derretirá | 1 |
| 66284 | derretir | 1 |
| 66285 | derretidos | 1 |
| 66286 | derretida | 1 |
| 66287 | derretían | 1 |
| 66288 | derrengar | 1 |
| 66289 | derrengados | 1 |
| 66290 | derramóselas | 1 |
| 66291 | derramóle | 1 |
| 66292 | derramen | 1 |
| 66293 | derramé | 1 |
| 66294 | derramaua | 1 |
| 66295 | derramarme | 1 |
| 66296 | derramaré | 1 |
| 66297 | derramándose | 1 |
| 66298 | derraman | 1 |
| 66299 | derramados | 1 |
| 66300 | derramaban | 1 |
| 66301 | derogando | 1 |
| 66302 | derogada | 1 |
| 66303 | dernière | 1 |
| 66304 | dermatológicas | 1 |
| 66305 | derivadas | 1 |
| 66306 | derivaciones | 1 |
| 66307 | derivación | 1 |
| 66308 | derivaba | 1 |
| 66309 | derechitos | 1 |
| 66310 | derechero | 1 |
| 66311 | der | 1 |
| 66312 | deputado | 1 |
| 66313 | depusiese | 1 |
| 66314 | depurados | 1 |
| 66315 | deprimía | 1 |
| 66316 | depriesa | 1 |
| 66317 | depresivo | 1 |
| 66318 | deprender | 1 |
| 66319 | deprenden | 1 |
| 66320 | deprecatorias | 1 |
| 66321 | deprecaciones | 1 |
| 66322 | deprecación | 1 |
| 66323 | deprecaba | 1 |
| 66324 | depravados | 1 |
| 66325 | depravado | 1 |
| 66326 | depravaciones | 1 |
| 66327 | deposito | 1 |
| 66328 | depositen | 1 |
| 66329 | deposité | 1 |
| 66330 | deposite | 1 |
| 66331 | depositasen | 1 |
| 66332 | depositaron | 1 |
| 66333 | depositarlos | 1 |
| 66334 | depositarías | 1 |
| 66335 | depositarias | 1 |
| 66336 | depositadas | 1 |
| 66337 | deposita | 1 |
| 66338 | deportment | 1 |
| 66339 | deportes | 1 |
| 66340 | deponiendo | 1 |
| 66341 | deploró | 1 |
| 66342 | deploro | 1 |
| 66343 | deplorables | 1 |
| 66344 | deplorablemente | 1 |
| 66345 | dependió | 1 |
| 66346 | dependiera | 1 |
| 66347 | dependencias | 1 |
| 66348 | departiremos | 1 |
| 66349 | departiré | 1 |
| 66350 | departió | 1 |
| 66351 | departiese | 1 |
| 66352 | departiera | 1 |
| 66353 | departidos | 1 |
| 66354 | departido | 1 |
| 66355 | departían | 1 |
| 66356 | departen | 1 |
| 66357 | departamos | 1 |
| 66358 | departamentos | 1 |
| 66359 | départ | 1 |
| 66360 | deparare | 1 |
| 66361 | deparará | 1 |
| 66362 | deparándote | 1 |
| 66363 | deparándole | 1 |
| 66364 | deparan | 1 |
| 66365 | deparado | 1 |
| 66366 | depara | 1 |
| 66367 | déosle | 1 |
| 66368 | deña | 1 |
| 66369 | denunció | 1 |
| 66370 | denuncies | 1 |
| 66371 | denunciarlos | 1 |
| 66372 | denunciare | 1 |
| 66373 | denunciado | 1 |
| 66374 | denunciaban | 1 |
| 66375 | denuncia | 1 |
| 66376 | denuestas | 1 |
| 66377 | denueda | 1 |
| 66378 | dentrellas | 1 |
| 66379 | dentre | 1 |
| 66380 | dentición | 1 |
| 66381 | denteras | 1 |
| 66382 | dentellear | 1 |
| 66383 | dentelladas | 1 |
| 66384 | dentado | 1 |
| 66385 | dentadas | 1 |
| 66386 | densó | 1 |
| 66387 | densísimo | 1 |
| 66388 | dénsele | 1 |
| 66389 | dense | 1 |
| 66390 | denque | 1 |
| 66391 | denotando | 1 |
| 66392 | denostemos | 1 |
| 66393 | denostava | 1 |
| 66394 | denostat | 1 |
| 66395 | denostando | 1 |
| 66396 | denostador | 1 |
| 66397 | denostado | 1 |
| 66398 | dénoslo | 1 |
| 66399 | dénos | 1 |
| 66400 | denonado | 1 |
| 66401 | denominó | 1 |
| 66402 | denominaciones | 1 |
| 66403 | denominacion | 1 |
| 66404 | denominaba | 1 |
| 66405 | denodados | 1 |
| 66406 | denodada | 1 |
| 66407 | dénmelos | 1 |
| 66408 | denimaniyoc | 1 |
| 66409 | denigrarlo | 1 |
| 66410 | denidades | 1 |
| 66411 | dengosas | 1 |
| 66412 | denegridos | 1 |
| 66413 | denegaciones | 1 |
| 66414 | demuestras | 1 |
| 66415 | demudó | 1 |
| 66416 | demudeste | 1 |
| 66417 | demudé | 1 |
| 66418 | demude | 1 |
| 66419 | demuda | 1 |
| 66420 | dempressa | 1 |
| 66421 | demostré | 1 |
| 66422 | demostrava | 1 |
| 66423 | demostrativas | 1 |
| 66424 | demostraría | 1 |
| 66425 | demostraré | 1 |
| 66426 | demostrara | 1 |
| 66427 | demostrándome | 1 |
| 66428 | demostrándolo | 1 |
| 66429 | demostrador | 1 |
| 66430 | demostrada | 1 |
| 66431 | demóstenes | 1 |
| 66432 | demosle | 1 |
| 66433 | demontre | 1 |
| 66434 | demonstrativos | 1 |
| 66435 | demolieron | 1 |
| 66436 | demolición | 1 |
| 66437 | demoler | 1 |
| 66438 | demodoco | 1 |
| 66439 | democráticas | 1 |
| 66440 | democrática | 1 |
| 66441 | demi | 1 |
| 66442 | demesuras | 1 |
| 66443 | demencias | 1 |
| 66444 | démelos | 1 |
| 66445 | démele | 1 |
| 66446 | démela | 1 |
| 66447 | demediase | 1 |
| 66448 | demediara | 1 |
| 66449 | demediaba | 1 |
| 66450 | demasias | 1 |
| 66451 | demasiados | 1 |
| 66452 | demarcando | 1 |
| 66453 | demandudieres | 1 |
| 66454 | demándovos | 1 |
| 66455 | demandóle | 1 |
| 66456 | demandól | 1 |
| 66457 | demandol | 1 |
| 66458 | demando | 1 |
| 66459 | demandéle | 1 |
| 66460 | demandavan | 1 |
| 66461 | demandava | 1 |
| 66462 | demandaua | 1 |
| 66463 | demandaron | 1 |
| 66464 | demandantes | 1 |
| 66465 | demandante | 1 |
| 66466 | demandaderas | 1 |
| 66467 | demandadas | 1 |
| 66468 | demandada | 1 |
| 66469 | demagógicas | 1 |
| 66470 | demagoga | 1 |
| 66471 | demacrados | 1 |
| 66472 | demacración | 1 |
| 66473 | deltoides | 1 |
| 66474 | delta | 1 |
| 66475 | delos | 1 |
| 66476 | delo | 1 |
| 66477 | dellante | 1 |
| 66478 | deliró | 1 |
| 66479 | delirium | 1 |
| 66480 | deliriosas | 1 |
| 66481 | deliriosa | 1 |
| 66482 | delirara | 1 |
| 66483 | delirar | 1 |
| 66484 | delirado | 1 |
| 66485 | delira | 1 |
| 66486 | deliñada | 1 |
| 66487 | delinquentes | 1 |
| 66488 | delinease | 1 |
| 66489 | delinear | 1 |
| 66490 | delineado | 1 |
| 66491 | delineadas | 1 |
| 66492 | delictos | 1 |
| 66493 | deliciosas | 1 |
| 66494 | delicadito | 1 |
| 66495 | delicadísima | 1 |
| 66496 | delicadillo | 1 |
| 66497 | delibre | 1 |
| 66498 | deliberó | 1 |
| 66499 | deliberase | 1 |
| 66500 | deliberaron | 1 |
| 66501 | delgadísimos | 1 |
| 66502 | delgadilla | 1 |
| 66503 | delgadez | 1 |
| 66504 | delfinito | 1 |
| 66505 | deleznables | 1 |
| 66506 | deléytase | 1 |
| 66507 | deleytan | 1 |
| 66508 | deleytables | 1 |
| 66509 | deletreaba | 1 |
| 66510 | deletéreos | 1 |
| 66511 | deles | 1 |
| 66512 | deleitoso | 1 |
| 66513 | deleitasen | 1 |
| 66514 | deleitarse | 1 |
| 66515 | deleitándome | 1 |
| 66516 | deleitables | 1 |
| 66517 | deleitábale | 1 |
| 66518 | deleita | 1 |
| 66519 | delegando | 1 |
| 66520 | delegados | 1 |
| 66521 | delavigne | 1 |
| 66522 | delatores | 1 |
| 66523 | delator | 1 |
| 66524 | delató | 1 |
| 66525 | delaten | 1 |
| 66526 | delatase | 1 |
| 66527 | delatarse | 1 |
| 66528 | delataron | 1 |
| 66529 | delatarla | 1 |
| 66530 | delatar | 1 |
| 66531 | delatando | 1 |
| 66532 | delataban | 1 |
| 66533 | delataba | 1 |
| 66534 | delantito | 1 |
| 66535 | delant | 1 |
| 66536 | delación | 1 |
| 66537 | déla | 1 |
| 66538 | dejoso | 1 |
| 66539 | dejóme | 1 |
| 66540 | déjome | 1 |
| 66541 | dejólos | 1 |
| 66542 | dejolo | 1 |
| 66543 | dejoles | 1 |
| 66544 | déjola | 1 |
| 66545 | dejola | 1 |
| 66546 | déjeseme | 1 |
| 66547 | déjennos | 1 |
| 66548 | déjenmela | 1 |
| 66549 | déjemelo | 1 |
| 66550 | dejéles | 1 |
| 66551 | déjelas | 1 |
| 66552 | dejastes | 1 |
| 66553 | dejártela | 1 |
| 66554 | dejárselos | 1 |
| 66555 | dejársele | 1 |
| 66556 | dejarretaron | 1 |
| 66557 | dejáronmele | 1 |
| 66558 | dejáronles | 1 |
| 66559 | dejáronla | 1 |
| 66560 | dejaréte | 1 |
| 66561 | dejares | 1 |
| 66562 | dejaren | 1 |
| 66563 | dejarémosle | 1 |
| 66564 | dejare | 1 |
| 66565 | dejaos | 1 |
| 66566 | déjanme | 1 |
| 66567 | dejándotela | 1 |
| 66568 | dejándoselas | 1 |
| 66569 | dejándonoslo | 1 |
| 66570 | dejándolas | 1 |
| 66571 | dejámosla | 1 |
| 66572 | déjamele | 1 |
| 66573 | déjamela | 1 |
| 66574 | dejálos | 1 |
| 66575 | déjalos | 1 |
| 66576 | dejallas | 1 |
| 66577 | dejádolos | 1 |
| 66578 | dejadnos | 1 |
| 66579 | dejadlos | 1 |
| 66580 | dejadlo | 1 |
| 66581 | dejadle | 1 |
| 66582 | dejadez | 1 |
| 66583 | dejabas | 1 |
| 66584 | dejábamela | 1 |
| 66585 | dejábame | 1 |
| 66586 | dejábalos | 1 |
| 66587 | déjà | 1 |
| 66588 | deísmo | 1 |
| 66589 | déis | 1 |
| 66590 | deicidas | 1 |
| 66591 | dei | 1 |
| 66592 | dehesas | 1 |
| 66593 | degüello | 1 |
| 66594 | degüellan | 1 |
| 66595 | degüella | 1 |
| 66596 | degradarse | 1 |
| 66597 | degradarme | 1 |
| 66598 | degradarla | 1 |
| 66599 | degradan | 1 |
| 66600 | degradado | 1 |
| 66601 | degradadas | 1 |
| 66602 | degrada | 1 |
| 66603 | dégoûté | 1 |
| 66604 | degollina | 1 |
| 66605 | degollava | 1 |
| 66606 | degollaron | 1 |
| 66607 | degollarla | 1 |
| 66608 | degolladas | 1 |
| 66609 | deglutaba | 1 |
| 66610 | degli | 1 |
| 66611 | degeneraba | 1 |
| 66612 | degenera | 1 |
| 66613 | defyendo | 1 |
| 66614 | defyendavos | 1 |
| 66615 | defunción | 1 |
| 66616 | defraudó | 1 |
| 66617 | defraude | 1 |
| 66618 | defraudaros | 1 |
| 66619 | defraudarme | 1 |
| 66620 | defraudarle | 1 |
| 66621 | defraudados | 1 |
| 66622 | defraudadas | 1 |
| 66623 | defraudada | 1 |
| 66624 | defraudaciones | 1 |
| 66625 | defraudaba | 1 |
| 66626 | defrauda | 1 |
| 66627 | deformes | 1 |
| 66628 | defondar | 1 |
| 66629 | definirse | 1 |
| 66630 | definía | 1 |
| 66631 | define | 1 |
| 66632 | defiéndonos | 1 |
| 66633 | defiéndeme | 1 |
| 66634 | defiendas | 1 |
| 66635 | defiéndaos | 1 |
| 66636 | déficit | 1 |
| 66637 | defiance | 1 |
| 66638 | deffenssiones | 1 |
| 66639 | deffendióse | 1 |
| 66640 | defeto | 1 |
| 66641 | defesa | 1 |
| 66642 | deferimos | 1 |
| 66643 | defensivo | 1 |
| 66644 | defensiuas | 1 |
| 66645 | defension | 1 |
| 66646 | defendrá | 1 |
| 66647 | defendióme | 1 |
| 66648 | defendiole | 1 |
| 66649 | defendiese | 1 |
| 66650 | defendieron | 1 |
| 66651 | defendiéndose | 1 |
| 66652 | defendiéndonos | 1 |
| 66653 | defendiéndolo | 1 |
| 66654 | defendiéndola | 1 |
| 66655 | defendidas | 1 |
| 66656 | defendia | 1 |
| 66657 | defenderlos | 1 |
| 66658 | defenderlo | 1 |
| 66659 | defenderemos | 1 |
| 66660 | defendemos | 1 |
| 66661 | defendedor | 1 |
| 66662 | defectuosísima | 1 |
| 66663 | defectillo | 1 |
| 66664 | deesas | 1 |
| 66665 | deduzco | 1 |
| 66666 | deduje | 1 |
| 66667 | deducimos | 1 |
| 66668 | deduciendo | 1 |
| 66669 | deducen | 1 |
| 66670 | deducciones | 1 |
| 66671 | deducción | 1 |
| 66672 | dedique | 1 |
| 66673 | dedin | 1 |
| 66674 | dedicose | 1 |
| 66675 | dedicóle | 1 |
| 66676 | dedicatorias | 1 |
| 66677 | dedicatoria | 1 |
| 66678 | dedicas | 1 |
| 66679 | dedicaría | 1 |
| 66680 | dedicara | 1 |
| 66681 | dedicándonos | 1 |
| 66682 | dedicada | 1 |
| 66683 | dédalos | 1 |
| 66684 | dedales | 1 |
| 66685 | decurión | 1 |
| 66686 | decuere | 1 |
| 66687 | decretar | 1 |
| 66688 | decretal | 1 |
| 66689 | decreta | 1 |
| 66690 | decrépitos | 1 |
| 66691 | decrépitas | 1 |
| 66692 | decorosos | 1 |
| 66693 | decorosas | 1 |
| 66694 | decoró | 1 |
| 66695 | decorativos | 1 |
| 66696 | decorativo | 1 |
| 66697 | decorativamente | 1 |
| 66698 | decorarse | 1 |
| 66699 | decoran | 1 |
| 66700 | decorámosla | 1 |
| 66701 | decoraba | 1 |
| 66702 | decomisura | 1 |
| 66703 | decomisador | 1 |
| 66704 | declinauan | 1 |
| 66705 | declinando | 1 |
| 66706 | declaróme | 1 |
| 66707 | declaren | 1 |
| 66708 | declaré | 1 |
| 66709 | declararlos | 1 |
| 66710 | declararía | 1 |
| 66711 | declarare | 1 |
| 66712 | declarará | 1 |
| 66713 | declarara | 1 |
| 66714 | declaraos | 1 |
| 66715 | declarándolo | 1 |
| 66716 | declaramos | 1 |
| 66717 | declarame | 1 |
| 66718 | decláralo | 1 |
| 66719 | declarale | 1 |
| 66720 | declarad | 1 |
| 66721 | declamar | 1 |
| 66722 | declamador | 1 |
| 66723 | declamaba | 1 |
| 66724 | decisivas | 1 |
| 66725 | decisiones | 1 |
| 66726 | deciséis | 1 |
| 66727 | decírsele | 1 |
| 66728 | decírselas | 1 |
| 66729 | decírosla | 1 |
| 66730 | decios | 1 |
| 66731 | decimosesto | 1 |
| 66732 | decimoseptimo | 1 |
| 66733 | decimoquinto | 1 |
| 66734 | decimooctauo | 1 |
| 66735 | decimonono | 1 |
| 66736 | decimo | 1 |
| 66737 | decimito | 1 |
| 66738 | decimales | 1 |
| 66739 | decilles | 1 |
| 66740 | decildo | 1 |
| 66741 | deciembre | 1 |
| 66742 | decídselo | 1 |
| 66743 | decidores | 1 |
| 66744 | decidles | 1 |
| 66745 | decidle | 1 |
| 66746 | decidirle | 1 |
| 66747 | decidirla | 1 |
| 66748 | decidirían | 1 |
| 66749 | decidiría | 1 |
| 66750 | decidirás | 1 |
| 66751 | decidiéronse | 1 |
| 66752 | decidiéndose | 1 |
| 66753 | decidiendo | 1 |
| 66754 | decididos | 1 |
| 66755 | decididas | 1 |
| 66756 | decides | 1 |
| 66757 | deciden | 1 |
| 66758 | decidáis | 1 |
| 66759 | decible | 1 |
| 66760 | decíanse | 1 |
| 66761 | decíanme | 1 |
| 66762 | decíalas | 1 |
| 66763 | decia | 1 |
| 66764 | déchiqueter | 1 |
| 66765 | deceplinantes | 1 |
| 66766 | decentísimo | 1 |
| 66767 | decendiente | 1 |
| 66768 | decendiendo | 1 |
| 66769 | decendían | 1 |
| 66770 | decendía | 1 |
| 66771 | decendencias | 1 |
| 66772 | decenario | 1 |
| 66773 | decayendo | 1 |
| 66774 | decantase | 1 |
| 66775 | decantada | 1 |
| 66776 | decaimientos | 1 |
| 66777 | decaídos | 1 |
| 66778 | decaía | 1 |
| 66779 | decae | 1 |
| 66780 | decadencias | 1 |
| 66781 | debióse | 1 |
| 66782 | debióle | 1 |
| 66783 | debilucho | 1 |
| 66784 | debilité | 1 |
| 66785 | debilitarse | 1 |
| 66786 | debiere | 1 |
| 66787 | debiérase | 1 |
| 66788 | debiéramos | 1 |
| 66789 | debiéndonos | 1 |
| 66790 | debiéndolo | 1 |
| 66791 | debíase | 1 |
| 66792 | debérsela | 1 |
| 66793 | deberíamos | 1 |
| 66794 | deberá | 1 |
| 66795 | débelo | 1 |
| 66796 | debdores | 1 |
| 66797 | debdas | 1 |
| 66798 | debatido | 1 |
| 66799 | débate | 1 |
| 66800 | debatas | 1 |
| 66801 | débat | 1 |
| 66802 | debas | 1 |
| 66803 | debajito | 1 |
| 66804 | dcc | 1 |
| 66805 | days | 1 |
| 66806 | dax | 1 |
| 66807 | davito | 1 |
| 66808 | davidson | 1 |
| 66809 | davídicas | 1 |
| 66810 | dávame | 1 |
| 66811 | dávades | 1 |
| 66812 | daualo | 1 |
| 66813 | datnos | 1 |
| 66814 | datla | 1 |
| 66815 | dativo | 1 |
| 66816 | datilado | 1 |
| 66817 | dásme | 1 |
| 66818 | dásle | 1 |
| 66819 | dasla | 1 |
| 66820 | dáselos | 1 |
| 66821 | dásela | 1 |
| 66822 | dársena | 1 |
| 66823 | dárseme | 1 |
| 66824 | darro | 1 |
| 66825 | dárnoslo | 1 |
| 66826 | dárnosle | 1 |
| 66827 | dármelo | 1 |
| 66828 | dármela | 1 |
| 66829 | darío | 1 |
| 66830 | dário | 1 |
| 66831 | daríe | 1 |
| 66832 | darías | 1 |
| 66833 | daréte | 1 |
| 66834 | dareos | 1 |
| 66835 | darémoste | 1 |
| 66836 | darémosles | 1 |
| 66837 | daréle | 1 |
| 66838 | daráte | 1 |
| 66839 | darásme | 1 |
| 66840 | darásela | 1 |
| 66841 | daránnos | 1 |
| 66842 | darálo | 1 |
| 66843 | daraida | 1 |
| 66844 | dapñosa | 1 |
| 66845 | dapñas | 1 |
| 66846 | dapnos | 1 |
| 66847 | dañó | 1 |
| 66848 | dañina | 1 |
| 66849 | dañarnos | 1 |
| 66850 | dañaría | 1 |
| 66851 | dañador | 1 |
| 66852 | danzantes | 1 |
| 66853 | danzadores | 1 |
| 66854 | danse | 1 |
| 66855 | danoso | 1 |
| 66856 | danosa | 1 |
| 66857 | danme | 1 |
| 66858 | dánle | 1 |
| 66859 | danes | 1 |
| 66860 | dandys | 1 |
| 66861 | dándoselo | 1 |
| 66862 | dándosele | 1 |
| 66863 | dandoos | 1 |
| 66864 | dándomela | 1 |
| 66865 | dándolos | 1 |
| 66866 | dándol | 1 |
| 66867 | dancharinea | 1 |
| 66868 | dançar | 1 |
| 66869 | danauan | 1 |
| 66870 | danara | 1 |
| 66871 | danan | 1 |
| 66872 | dánaes | 1 |
| 66873 | danados | 1 |
| 66874 | dana | 1 |
| 66875 | damián | 1 |
| 66876 | dámelo | 1 |
| 66877 | dáme | 1 |
| 66878 | damasquino | 1 |
| 66879 | damasquería | 1 |
| 66880 | damascó | 1 |
| 66881 | dalyla | 1 |
| 66882 | dalo | 1 |
| 66883 | dallos | 1 |
| 66884 | dalli | 1 |
| 66885 | dallas | 1 |
| 66886 | dalla | 1 |
| 66887 | dalila | 1 |
| 66888 | dalgueva | 1 |
| 66889 | dales | 1 |
| 66890 | dalda | 1 |
| 66891 | dalas | 1 |
| 66892 | daganzo | 1 |
| 66893 | dádselos | 1 |
| 66894 | dádselo | 1 |
| 66895 | dádome | 1 |
| 66896 | dádole | 1 |
| 66897 | dadivosos | 1 |
| 66898 | dades | 1 |
| 66899 | dácame | 1 |
| 66900 | dabas | 1 |
| 66901 | dábannos | 1 |
| 66902 | dábanmelos | 1 |
| 66903 | dábanlas | 1 |
| 66904 | dábamelos | 1 |
| 66905 | dábalo | 1 |
| 66906 | dábalas | 1 |
| 66907 | dábala | 1 |
| 66908 | çynta | 1 |
| 66909 | çynió | 1 |
| 66910 | cxxxix | 1 |
| 66911 | cx | 1 |
| 66912 | cuytoso | 1 |
| 66913 | cuytados | 1 |
| 66914 | cuytadillas | 1 |
| 66915 | cuytadas | 1 |
| 66916 | cuydóse | 1 |
| 66917 | cuydosa | 1 |
| 66918 | cuydó | 1 |
| 66919 | cuydés | 1 |
| 66920 | cuydedes | 1 |
| 66921 | cuydavan | 1 |
| 66922 | cuydas | 1 |
| 66923 | cuydares | 1 |
| 66924 | cuydará | 1 |
| 66925 | cuydára | 1 |
| 66926 | cuydando | 1 |
| 66927 | cúyas | 1 |
| 66928 | cuvier | 1 |
| 66929 | cutiré | 1 |
| 66930 | cutíes | 1 |
| 66931 | custodire | 1 |
| 66932 | custodiarla | 1 |
| 66933 | custodiar | 1 |
| 66934 | custodiados | 1 |
| 66935 | custodiada | 1 |
| 66936 | custodi | 1 |
| 66937 | custituçión | 1 |
| 66938 | cúspide | 1 |
| 66939 | curtir | 1 |
| 66940 | curtía | 1 |
| 66941 | cursso | 1 |
| 66942 | cursilona | 1 |
| 66943 | cursilerías | 1 |
| 66944 | cursar | 1 |
| 66945 | cursaban | 1 |
| 66946 | çurrón | 1 |
| 66947 | currito | 1 |
| 66948 | currente | 1 |
| 66949 | curra | 1 |
| 66950 | curóme | 1 |
| 66951 | curiosona | 1 |
| 66952 | curiosón | 1 |
| 66953 | curiosísimo | 1 |
| 66954 | curioseo | 1 |
| 66955 | curiosamente | 1 |
| 66956 | curios | 1 |
| 66957 | curio | 1 |
| 66958 | curiel | 1 |
| 66959 | curemos | 1 |
| 66960 | curémonos | 1 |
| 66961 | curéis | 1 |
| 66962 | curdela | 1 |
| 66963 | curda | 1 |
| 66964 | curcios | 1 |
| 66965 | curcio | 1 |
| 66966 | curays | 1 |
| 66967 | curauas | 1 |
| 66968 | curaua | 1 |
| 66969 | curato | 1 |
| 66970 | curaste | 1 |
| 66971 | curárselas | 1 |
| 66972 | curaremos | 1 |
| 66973 | curanderas | 1 |
| 66974 | curamos | 1 |
| 66975 | curambro | 1 |
| 66976 | curador | 1 |
| 66977 | curadillo | 1 |
| 66978 | curad | 1 |
| 66979 | curábale | 1 |
| 66980 | cuquero | 1 |
| 66981 | cupulín | 1 |
| 66982 | cúpulas | 1 |
| 66983 | cúpome | 1 |
| 66984 | cupiesse | 1 |
| 66985 | cupiesen | 1 |
| 66986 | cupieron | 1 |
| 66987 | cupieran | 1 |
| 66988 | cupe | 1 |
| 66989 | cuotidiana | 1 |
| 66990 | cuotas | 1 |
| 66991 | cuños | 1 |
| 66992 | cuñas | 1 |
| 66993 | cuñados | 1 |
| 66994 | cuñadita | 1 |
| 66995 | cunplió | 1 |
| 66996 | cunplidos | 1 |
| 66997 | cunplida | 1 |
| 66998 | cunplan | 1 |
| 66999 | cunitas | 1 |
| 67000 | cunita | 1 |
| 67001 | cunero | 1 |
| 67002 | cundiese | 1 |
| 67003 | cundido | 1 |
| 67004 | cumunal | 1 |
| 67005 | cúmulus | 1 |
| 67006 | cumulus | 1 |
| 67007 | cumplíselos | 1 |
| 67008 | cumplirle | 1 |
| 67009 | cumplirlas | 1 |
| 67010 | cumplióse | 1 |
| 67011 | cumpliólo | 1 |
| 67012 | cumplillos | 1 |
| 67013 | cumplille | 1 |
| 67014 | cumplilla | 1 |
| 67015 | cumpliesse | 1 |
| 67016 | cumpliere | 1 |
| 67017 | cumplieran | 1 |
| 67018 | cumpliéndosela | 1 |
| 67019 | cumplidle | 1 |
| 67020 | cumplidísimo | 1 |
| 67021 | cumplid | 1 |
| 67022 | cumplia | 1 |
| 67023 | cumplí | 1 |
| 67024 | cumplamos | 1 |
| 67025 | cumín | 1 |
| 67026 | cultus | 1 |
| 67027 | cultive | 1 |
| 67028 | cultivarlo | 1 |
| 67029 | cultivara | 1 |
| 67030 | cultivándolas | 1 |
| 67031 | cultivan | 1 |
| 67032 | cultívalos | 1 |
| 67033 | cultivación | 1 |
| 67034 | culterana | 1 |
| 67035 | cultamente | 1 |
| 67036 | culpeys | 1 |
| 67037 | culpe | 1 |
| 67038 | culparte | 1 |
| 67039 | culparles | 1 |
| 67040 | culparas | 1 |
| 67041 | culpante | 1 |
| 67042 | culpando | 1 |
| 67043 | culpan | 1 |
| 67044 | culpadas | 1 |
| 67045 | culpábase | 1 |
| 67046 | culotte | 1 |
| 67047 | culito | 1 |
| 67048 | culinarias | 1 |
| 67049 | culebro | 1 |
| 67050 | culebrear | 1 |
| 67051 | culebreaban | 1 |
| 67052 | culebrazo | 1 |
| 67053 | culcusirse | 1 |
| 67054 | culata | 1 |
| 67055 | culantrillo | 1 |
| 67056 | cuitísima | 1 |
| 67057 | cuitadas | 1 |
| 67058 | cuistión | 1 |
| 67059 | cuiste | 1 |
| 67060 | cuique | 1 |
| 67061 | cuido | 1 |
| 67062 | cuides | 1 |
| 67063 | cuidase | 1 |
| 67064 | cuidarnos | 1 |
| 67065 | cuidarme | 1 |
| 67066 | cuidarlos | 1 |
| 67067 | cuidarla | 1 |
| 67068 | cuidará | 1 |
| 67069 | cuidara | 1 |
| 67070 | cuidándole | 1 |
| 67071 | cuidándolas | 1 |
| 67072 | cuidan | 1 |
| 67073 | cuidadoso | 1 |
| 67074 | cuidadosa | 1 |
| 67075 | cuidadas | 1 |
| 67076 | cuidada | 1 |
| 67077 | cuibdaba | 1 |
| 67078 | cueze | 1 |
| 67079 | cuévanos | 1 |
| 67080 | cuestores | 1 |
| 67081 | cuestionar | 1 |
| 67082 | cuestionando | 1 |
| 67083 | cuestionaban | 1 |
| 67084 | cuesten | 1 |
| 67085 | cuestalada | 1 |
| 67086 | cuesco | 1 |
| 67087 | cuervas | 1 |
| 67088 | cuerva | 1 |
| 67089 | çuero | 1 |
| 67090 | cuernecitos | 1 |
| 67091 | cuernecillos | 1 |
| 67092 | cuerdamiente | 1 |
| 67093 | cuerbo | 1 |
| 67094 | cuera | 1 |
| 67095 | cuentera | 1 |
| 67096 | cuéntenosla | 1 |
| 67097 | cuéntenos | 1 |
| 67098 | cuéntenme | 1 |
| 67099 | cuénteme | 1 |
| 67100 | cuentecillo | 1 |
| 67101 | cuéntaste | 1 |
| 67102 | cuéntaselo | 1 |
| 67103 | cuéntanos | 1 |
| 67104 | cuéntamelo | 1 |
| 67105 | cuentamelo | 1 |
| 67106 | cuéntalo | 1 |
| 67107 | cuentalo | 1 |
| 67108 | cuéntala | 1 |
| 67109 | cuencas | 1 |
| 67110 | cuelloalvo | 1 |
| 67111 | cuéllar | 1 |
| 67112 | cuell | 1 |
| 67113 | cuélguense | 1 |
| 67114 | cuelguen | 1 |
| 67115 | cuélgueme | 1 |
| 67116 | cuelgue | 1 |
| 67117 | cuélgente | 1 |
| 67118 | cuedo | 1 |
| 67119 | cuecen | 1 |
| 67120 | cue | 1 |
| 67121 | cudiciosa | 1 |
| 67122 | cudicia | 1 |
| 67123 | cuco | 1 |
| 67124 | cuchipanda | 1 |
| 67125 | cuchillote | 1 |
| 67126 | cuchillito | 1 |
| 67127 | cuchicheó | 1 |
| 67128 | cucharillas | 1 |
| 67129 | cucharetazos | 1 |
| 67130 | cuchares | 1 |
| 67131 | cucaracha | 1 |
| 67132 | cucamonas | 1 |
| 67133 | cúbrome | 1 |
| 67134 | cubro | 1 |
| 67135 | cubrirte | 1 |
| 67136 | cubrirá | 1 |
| 67137 | cubriose | 1 |
| 67138 | cubriole | 1 |
| 67139 | cubrióla | 1 |
| 67140 | cubrio | 1 |
| 67141 | cubríme | 1 |
| 67142 | cubriéronse | 1 |
| 67143 | cubriéronle | 1 |
| 67144 | cubrieran | 1 |
| 67145 | cubriéndose | 1 |
| 67146 | cubriéndolos | 1 |
| 67147 | cubriéndole | 1 |
| 67148 | cubríalas | 1 |
| 67149 | cubrí | 1 |
| 67150 | cubres | 1 |
| 67151 | cúbrele | 1 |
| 67152 | cúbrase | 1 |
| 67153 | cubras | 1 |
| 67154 | cubranos | 1 |
| 67155 | cubramos | 1 |
| 67156 | cubital | 1 |
| 67157 | cubicularia | 1 |
| 67158 | cúbicas | 1 |
| 67159 | cúbica | 1 |
| 67160 | cuatros | 1 |
| 67161 | cuatropea | 1 |
| 67162 | cuatrocientas | 1 |
| 67163 | cuatrociensos | 1 |
| 67164 | cuatrines | 1 |
| 67165 | cuatrín | 1 |
| 67166 | cuatrillones | 1 |
| 67167 | cuatriduano | 1 |
| 67168 | cuatrero | 1 |
| 67169 | cuartuchos | 1 |
| 67170 | cuartillas | 1 |
| 67171 | cuartilla | 1 |
| 67172 | cuartelillo | 1 |
| 67173 | cuartelesco | 1 |
| 67174 | cuartean | 1 |
| 67175 | cuarteada | 1 |
| 67176 | cuartea | 1 |
| 67177 | cuartal | 1 |
| 67178 | cuartago | 1 |
| 67179 | cuáqueros | 1 |
| 67180 | cuantiosas | 1 |
| 67181 | cuantimás | 1 |
| 67182 | cuanti | 1 |
| 67183 | cuande | 1 |
| 67184 | cualquiere | 1 |
| 67185 | cualisquiera | 1 |
| 67186 | cualificada | 1 |
| 67187 | cualesquier | 1 |
| 67188 | cuaje | 1 |
| 67189 | cuajarse | 1 |
| 67190 | cuajadas | 1 |
| 67191 | cuádruple | 1 |
| 67192 | cuadrúpedo | 1 |
| 67193 | cuadrumana | 1 |
| 67194 | cuadróle | 1 |
| 67195 | cuadrilongo | 1 |
| 67196 | cuadrillas | 1 |
| 67197 | cuadriláteros | 1 |
| 67198 | cuadril | 1 |
| 67199 | cuadriculado | 1 |
| 67200 | cuadren | 1 |
| 67201 | cuadrase | 1 |
| 67202 | cuadraría | 1 |
| 67203 | cuadraren | 1 |
| 67204 | cuadrare | 1 |
| 67205 | cuadraran | 1 |
| 67206 | cuadrantes | 1 |
| 67207 | cuadrante | 1 |
| 67208 | cuadrángano | 1 |
| 67209 | cuadran | 1 |
| 67210 | cuadrados | 1 |
| 67211 | cuadradillos | 1 |
| 67212 | cuadradas | 1 |
| 67213 | cuadernos | 1 |
| 67214 | cuaderna | 1 |
| 67215 | cryador | 1 |
| 67216 | cruzniego | 1 |
| 67217 | cruzes | 1 |
| 67218 | cruzáronse | 1 |
| 67219 | cruzarnos | 1 |
| 67220 | cruzándose | 1 |
| 67221 | cruzamiento | 1 |
| 67222 | cruzábanse | 1 |
| 67223 | cruyziava | 1 |
| 67224 | crusología | 1 |
| 67225 | crus | 1 |
| 67226 | crujiéndole | 1 |
| 67227 | crujida | 1 |
| 67228 | crujías | 1 |
| 67229 | crujían | 1 |
| 67230 | crujen | 1 |
| 67231 | cruje | 1 |
| 67232 | cruja | 1 |
| 67233 | cruentos | 1 |
| 67234 | cruento | 1 |
| 67235 | cruenta | 1 |
| 67236 | cruelísimo | 1 |
| 67237 | cruelísimas | 1 |
| 67238 | cruelísima | 1 |
| 67239 | crueldat | 1 |
| 67240 | crüeldad | 1 |
| 67241 | crudísimo | 1 |
| 67242 | crudillo | 1 |
| 67243 | crucifixión | 1 |
| 67244 | crucifique | 1 |
| 67245 | crucificó | 1 |
| 67246 | crucificarme | 1 |
| 67247 | crucificando | 1 |
| 67248 | crucificados | 1 |
| 67249 | crucifica | 1 |
| 67250 | cruceta | 1 |
| 67251 | crucecita | 1 |
| 67252 | croto | 1 |
| 67253 | croquetita | 1 |
| 67254 | cronométrica | 1 |
| 67255 | cronologías | 1 |
| 67256 | cromwell | 1 |
| 67257 | cromáticas | 1 |
| 67258 | croiset | 1 |
| 67259 | critiques | 1 |
| 67260 | critiquen | 1 |
| 67261 | criticona | 1 |
| 67262 | criticó | 1 |
| 67263 | criticaron | 1 |
| 67264 | criticando | 1 |
| 67265 | criticados | 1 |
| 67266 | criticado | 1 |
| 67267 | critica | 1 |
| 67268 | cristus | 1 |
| 67269 | cristinos | 1 |
| 67270 | cristinica | 1 |
| 67271 | cristianesca | 1 |
| 67272 | cristïana | 1 |
| 67273 | cristián | 1 |
| 67274 | cristel | 1 |
| 67275 | cristalizada | 1 |
| 67276 | cristalización | 1 |
| 67277 | cristalizaban | 1 |
| 67278 | cristalerías | 1 |
| 67279 | crispan | 1 |
| 67280 | crispamientos | 1 |
| 67281 | crispaduras | 1 |
| 67282 | crispados | 1 |
| 67283 | crispadas | 1 |
| 67284 | crispada | 1 |
| 67285 | crisólitos | 1 |
| 67286 | crisoles | 1 |
| 67287 | crióme | 1 |
| 67288 | criome | 1 |
| 67289 | crinolinas | 1 |
| 67290 | crinados | 1 |
| 67291 | crimines | 1 |
| 67292 | crimine | 1 |
| 67293 | criminalmente | 1 |
| 67294 | crillon | 1 |
| 67295 | criera | 1 |
| 67296 | críen | 1 |
| 67297 | criéme | 1 |
| 67298 | criban | 1 |
| 67299 | criava | 1 |
| 67300 | criaste | 1 |
| 67301 | criasen | 1 |
| 67302 | crias | 1 |
| 67303 | criáronle | 1 |
| 67304 | criarme | 1 |
| 67305 | criarlo | 1 |
| 67306 | criarla | 1 |
| 67307 | criaré | 1 |
| 67308 | criara | 1 |
| 67309 | criaos | 1 |
| 67310 | criao | 1 |
| 67311 | críanse | 1 |
| 67312 | criança | 1 |
| 67313 | crïado | 1 |
| 67314 | criad | 1 |
| 67315 | crezcan | 1 |
| 67316 | creyóse | 1 |
| 67317 | creyólo | 1 |
| 67318 | creyolo | 1 |
| 67319 | creyeses | 1 |
| 67320 | creyesen | 1 |
| 67321 | creyérase | 1 |
| 67322 | creyen | 1 |
| 67323 | creydo | 1 |
| 67324 | creyan | 1 |
| 67325 | creta | 1 |
| 67326 | crestadas | 1 |
| 67327 | crespones | 1 |
| 67328 | crespas | 1 |
| 67329 | crescimientos | 1 |
| 67330 | cresciéndo | 1 |
| 67331 | cresciendo | 1 |
| 67332 | crescidos | 1 |
| 67333 | crescido | 1 |
| 67334 | crescidas | 1 |
| 67335 | cresçer | 1 |
| 67336 | crescen | 1 |
| 67337 | cres | 1 |
| 67338 | crepant | 1 |
| 67339 | creóselos | 1 |
| 67340 | creóselo | 1 |
| 67341 | creolo | 1 |
| 67342 | crenchas | 1 |
| 67343 | creminales | 1 |
| 67344 | cremes | 1 |
| 67345 | crementinas | 1 |
| 67346 | creímoslo | 1 |
| 67347 | creimos | 1 |
| 67348 | creíble | 1 |
| 67349 | creíanle | 1 |
| 67350 | creíala | 1 |
| 67351 | creetme | 1 |
| 67352 | creételo | 1 |
| 67353 | creeslo | 1 |
| 67354 | creernos | 1 |
| 67355 | creérmelo | 1 |
| 67356 | creerlas | 1 |
| 67357 | creeria | 1 |
| 67358 | creeremos | 1 |
| 67359 | creere | 1 |
| 67360 | creeras | 1 |
| 67361 | creéme | 1 |
| 67362 | creeme | 1 |
| 67363 | creedoras | 1 |
| 67364 | crédulo | 1 |
| 67365 | crédulas | 1 |
| 67366 | credencialeja | 1 |
| 67367 | crecióles | 1 |
| 67368 | creçió | 1 |
| 67369 | creçieron | 1 |
| 67370 | crecidito | 1 |
| 67371 | creciditas | 1 |
| 67372 | crecidita | 1 |
| 67373 | crecíale | 1 |
| 67374 | creci | 1 |
| 67375 | crecerte | 1 |
| 67376 | creceria | 1 |
| 67377 | créçenme | 1 |
| 67378 | crearemos | 1 |
| 67379 | crearán | 1 |
| 67380 | creánmelo | 1 |
| 67381 | creámosle | 1 |
| 67382 | créamela | 1 |
| 67383 | creadoras | 1 |
| 67384 | creadora | 1 |
| 67385 | crato | 1 |
| 67386 | cratino | 1 |
| 67387 | cráneos | 1 |
| 67388 | cozina | 1 |
| 67389 | cozido | 1 |
| 67390 | cozes | 1 |
| 67391 | coytral | 1 |
| 67392 | coytándome | 1 |
| 67393 | coytada | 1 |
| 67394 | coys | 1 |
| 67395 | coydo | 1 |
| 67396 | coydedes | 1 |
| 67397 | coydé | 1 |
| 67398 | coydavan | 1 |
| 67399 | coydares | 1 |
| 67400 | coydar | 1 |
| 67401 | coydan | 1 |
| 67402 | coydados | 1 |
| 67403 | coya | 1 |
| 67404 | coy | 1 |
| 67405 | coxquillosicas | 1 |
| 67406 | coxqueays | 1 |
| 67407 | coxqueaba | 1 |
| 67408 | coxquea | 1 |
| 67409 | coxixo | 1 |
| 67410 | coxín | 1 |
| 67411 | coxeades | 1 |
| 67412 | coxcorrones | 1 |
| 67413 | coxa | 1 |
| 67414 | covent | 1 |
| 67415 | covardo | 1 |
| 67416 | covadonga | 1 |
| 67417 | covachuelismo | 1 |
| 67418 | cousins | 1 |
| 67419 | courtray | 1 |
| 67420 | cotta | 1 |
| 67421 | cotorrones | 1 |
| 67422 | cotorrón | 1 |
| 67423 | cotorrear | 1 |
| 67424 | cotorreaban | 1 |
| 67425 | cotonía | 1 |
| 67426 | cotizaciones | 1 |
| 67427 | cotización | 1 |
| 67428 | cotiza | 1 |
| 67429 | cotidianas | 1 |
| 67430 | cotidiana | 1 |
| 67431 | cotejáronse | 1 |
| 67432 | cotejando | 1 |
| 67433 | cotejado | 1 |
| 67434 | cotas | 1 |
| 67435 | cosultada | 1 |
| 67436 | costureros | 1 |
| 67437 | costurero | 1 |
| 67438 | costumeros | 1 |
| 67439 | costumero | 1 |
| 67440 | costumera | 1 |
| 67441 | costribado | 1 |
| 67442 | costosos | 1 |
| 67443 | costoso | 1 |
| 67444 | costillajes | 1 |
| 67445 | costiellas | 1 |
| 67446 | costiella | 1 |
| 67447 | costezuela | 1 |
| 67448 | costeo | 1 |
| 67449 | costellaçión | 1 |
| 67450 | costellación | 1 |
| 67451 | costear | 1 |
| 67452 | costasse | 1 |
| 67453 | costáronme | 1 |
| 67454 | costarles | 1 |
| 67455 | costarle | 1 |
| 67456 | costaria | 1 |
| 67457 | costarán | 1 |
| 67458 | costanera | 1 |
| 67459 | costando | 1 |
| 67460 | costales | 1 |
| 67461 | cosseras | 1 |
| 67462 | cosquilleo | 1 |
| 67463 | cosqueamos | 1 |
| 67464 | cosmografía | 1 |
| 67465 | cósmico | 1 |
| 67466 | cosmético | 1 |
| 67467 | cosmao | 1 |
| 67468 | cosió | 1 |
| 67469 | cosineras | 1 |
| 67470 | cosina | 1 |
| 67471 | cosíme | 1 |
| 67472 | cosideración | 1 |
| 67473 | cosían | 1 |
| 67474 | cosestorio | 1 |
| 67475 | coses | 1 |
| 67476 | coserse | 1 |
| 67477 | coseme | 1 |
| 67478 | coselete | 1 |
| 67479 | cosejador | 1 |
| 67480 | cosedoras | 1 |
| 67481 | cosed | 1 |
| 67482 | cosechero | 1 |
| 67483 | corzos | 1 |
| 67484 | corza | 1 |
| 67485 | corvos | 1 |
| 67486 | corvejones | 1 |
| 67487 | coruña | 1 |
| 67488 | cortólas | 1 |
| 67489 | cortóla | 1 |
| 67490 | cortito | 1 |
| 67491 | cortísimo | 1 |
| 67492 | cortísima | 1 |
| 67493 | cortinón | 1 |
| 67494 | cortinillas | 1 |
| 67495 | cortinilla | 1 |
| 67496 | cortinajes | 1 |
| 67497 | cortimos | 1 |
| 67498 | cortiella | 1 |
| 67499 | corticales | 1 |
| 67500 | cortezon | 1 |
| 67501 | cortez | 1 |
| 67502 | cortesísimo | 1 |
| 67503 | cortesísimamente | 1 |
| 67504 | cortesias | 1 |
| 67505 | cortejar | 1 |
| 67506 | cortecilla | 1 |
| 67507 | corteça | 1 |
| 67508 | cortarte | 1 |
| 67509 | cortáronles | 1 |
| 67510 | cortaronle | 1 |
| 67511 | cortarlas | 1 |
| 67512 | cortarla | 1 |
| 67513 | cortarían | 1 |
| 67514 | cortares | 1 |
| 67515 | cortarémosle | 1 |
| 67516 | cortare | 1 |
| 67517 | cortará | 1 |
| 67518 | cortara | 1 |
| 67519 | cortapisas | 1 |
| 67520 | cortándose | 1 |
| 67521 | cortamente | 1 |
| 67522 | córtame | 1 |
| 67523 | cortafuegos | 1 |
| 67524 | cortaduras | 1 |
| 67525 | cortadores | 1 |
| 67526 | cortadito | 1 |
| 67527 | cortadísima | 1 |
| 67528 | cortad | 1 |
| 67529 | cortábale | 1 |
| 67530 | corsés | 1 |
| 67531 | corsarios | 1 |
| 67532 | corruto | 1 |
| 67533 | corruscos | 1 |
| 67534 | corrusco | 1 |
| 67535 | corruptora | 1 |
| 67536 | corruptio | 1 |
| 67537 | corruptelas | 1 |
| 67538 | corruptela | 1 |
| 67539 | corrupta | 1 |
| 67540 | corrupciones | 1 |
| 67541 | corrupcion | 1 |
| 67542 | corrumpas | 1 |
| 67543 | corrosivo | 1 |
| 67544 | çorrón | 1 |
| 67545 | corrompio | 1 |
| 67546 | corrompiera | 1 |
| 67547 | corrompiendo | 1 |
| 67548 | corrompidas | 1 |
| 67549 | corrompía | 1 |
| 67550 | corromperla | 1 |
| 67551 | corroía | 1 |
| 67552 | corroborarla | 1 |
| 67553 | corrobóranse | 1 |
| 67554 | corroborada | 1 |
| 67555 | corroboraba | 1 |
| 67556 | corrióse | 1 |
| 67557 | corriole | 1 |
| 67558 | corrijan | 1 |
| 67559 | corrija | 1 |
| 67560 | corrígete | 1 |
| 67561 | corriesse | 1 |
| 67562 | corriéronse | 1 |
| 67563 | corriere | 1 |
| 67564 | corrieran | 1 |
| 67565 | corriéndola | 1 |
| 67566 | corriendito | 1 |
| 67567 | corríe | 1 |
| 67568 | corridísimo | 1 |
| 67569 | corridica | 1 |
| 67570 | corríase | 1 |
| 67571 | corríanse | 1 |
| 67572 | corríamos | 1 |
| 67573 | corríale | 1 |
| 67574 | correveidile | 1 |
| 67575 | correteando | 1 |
| 67576 | correspondiesen | 1 |
| 67577 | correspondiese | 1 |
| 67578 | correspondiera | 1 |
| 67579 | correspondiéndoles | 1 |
| 67580 | correspondidos | 1 |
| 67581 | corresponderos | 1 |
| 67582 | corresponderás | 1 |
| 67583 | corresponderá | 1 |
| 67584 | correspondéis | 1 |
| 67585 | correspondas | 1 |
| 67586 | correspondan | 1 |
| 67587 | correrte | 1 |
| 67588 | correrían | 1 |
| 67589 | correria | 1 |
| 67590 | correosa | 1 |
| 67591 | correntona | 1 |
| 67592 | correntío | 1 |
| 67593 | corrella | 1 |
| 67594 | correligionarios | 1 |
| 67595 | correlarios | 1 |
| 67596 | corregirte | 1 |
| 67597 | corregirse | 1 |
| 67598 | corregimos | 1 |
| 67599 | corregieres | 1 |
| 67600 | corregidores | 1 |
| 67601 | corregían | 1 |
| 67602 | corredizos | 1 |
| 67603 | corredizo | 1 |
| 67604 | corrector | 1 |
| 67605 | correctivos | 1 |
| 67606 | correctivo | 1 |
| 67607 | correctísima | 1 |
| 67608 | correccionalista | 1 |
| 67609 | corraladas | 1 |
| 67610 | corráis | 1 |
| 67611 | corpúsculo | 1 |
| 67612 | corpudo | 1 |
| 67613 | corpóreas | 1 |
| 67614 | corporalmente | 1 |
| 67615 | corpiño | 1 |
| 67616 | coronillas | 1 |
| 67617 | corónica | 1 |
| 67618 | corone | 1 |
| 67619 | coronarte | 1 |
| 67620 | coronarse | 1 |
| 67621 | coronaron | 1 |
| 67622 | coronarlo | 1 |
| 67623 | coronarán | 1 |
| 67624 | coronando | 1 |
| 67625 | coronamiento | 1 |
| 67626 | corolas | 1 |
| 67627 | corolario | 1 |
| 67628 | coroides | 1 |
| 67629 | cornuda | 1 |
| 67630 | córnea | 1 |
| 67631 | cornamenta | 1 |
| 67632 | cornada | 1 |
| 67633 | cormano | 1 |
| 67634 | cormana | 1 |
| 67635 | corma | 1 |
| 67636 | corito | 1 |
| 67637 | corintio | 1 |
| 67638 | corellas | 1 |
| 67639 | cordu | 1 |
| 67640 | cordojo | 1 |
| 67641 | cordillita | 1 |
| 67642 | cordilleras | 1 |
| 67643 | cordilla | 1 |
| 67644 | corderito | 1 |
| 67645 | corderillos | 1 |
| 67646 | corderilla | 1 |
| 67647 | corderica | 1 |
| 67648 | corderas | 1 |
| 67649 | cordellate | 1 |
| 67650 | cordelero | 1 |
| 67651 | cordelejos | 1 |
| 67652 | cordelejo | 1 |
| 67653 | corde | 1 |
| 67654 | cordal | 1 |
| 67655 | corcovados | 1 |
| 67656 | corcova | 1 |
| 67657 | corcillo | 1 |
| 67658 | corças | 1 |
| 67659 | corbona | 1 |
| 67660 | corbeta | 1 |
| 67661 | corazoncillo | 1 |
| 67662 | corambres | 1 |
| 67663 | corambre | 1 |
| 67664 | coram | 1 |
| 67665 | corages | 1 |
| 67666 | coraceros | 1 |
| 67667 | coraça | 1 |
| 67668 | cór | 1 |
| 67669 | coquetismo | 1 |
| 67670 | coqueteando | 1 |
| 67671 | coqueteaban | 1 |
| 67672 | coquetas | 1 |
| 67673 | coquera | 1 |
| 67674 | copulativas | 1 |
| 67675 | copones | 1 |
| 67676 | copleros | 1 |
| 67677 | coplee | 1 |
| 67678 | copistas | 1 |
| 67679 | copiosa | 1 |
| 67680 | copio | 1 |
| 67681 | copilla | 1 |
| 67682 | cópielo | 1 |
| 67683 | copié | 1 |
| 67684 | copiaremos | 1 |
| 67685 | copiar | 1 |
| 67686 | copiantes | 1 |
| 67687 | copiando | 1 |
| 67688 | copiamos | 1 |
| 67689 | copiados | 1 |
| 67690 | copiadores | 1 |
| 67691 | copiada | 1 |
| 67692 | cophta | 1 |
| 67693 | copadas | 1 |
| 67694 | coordiné | 1 |
| 67695 | coordinado | 1 |
| 67696 | coordinadas | 1 |
| 67697 | cooperar | 1 |
| 67698 | coooosa | 1 |
| 67699 | conzolación | 1 |
| 67700 | conwallis | 1 |
| 67701 | convyene | 1 |
| 67702 | convyén | 1 |
| 67703 | convulsos | 1 |
| 67704 | convulso | 1 |
| 67705 | convulsivo | 1 |
| 67706 | convulsivas | 1 |
| 67707 | convoy | 1 |
| 67708 | convoqué | 1 |
| 67709 | convocándole | 1 |
| 67710 | convocados | 1 |
| 67711 | convocación | 1 |
| 67712 | convocaba | 1 |
| 67713 | convivencia | 1 |
| 67714 | convirtiésemos | 1 |
| 67715 | convirtieran | 1 |
| 67716 | convirtiéndoseles | 1 |
| 67717 | conviniesen | 1 |
| 67718 | convierto | 1 |
| 67719 | conviértese | 1 |
| 67720 | conviertan | 1 |
| 67721 | conviértalas | 1 |
| 67722 | conviéneos | 1 |
| 67723 | convien | 1 |
| 67724 | convidóme | 1 |
| 67725 | convidólas | 1 |
| 67726 | convídesele | 1 |
| 67727 | convidemos | 1 |
| 67728 | convidéme | 1 |
| 67729 | convidé | 1 |
| 67730 | convidarles | 1 |
| 67731 | convidaría | 1 |
| 67732 | convidará | 1 |
| 67733 | convidara | 1 |
| 67734 | convídanos | 1 |
| 67735 | convidándonos | 1 |
| 67736 | convidándoles | 1 |
| 67737 | convidan | 1 |
| 67738 | convidalle | 1 |
| 67739 | convidadores | 1 |
| 67740 | convidadora | 1 |
| 67741 | convidador | 1 |
| 67742 | convidábale | 1 |
| 67743 | convexos | 1 |
| 67744 | convexo | 1 |
| 67745 | convexidad | 1 |
| 67746 | convertyr | 1 |
| 67747 | convertirlo | 1 |
| 67748 | convertirlas | 1 |
| 67749 | convertirías | 1 |
| 67750 | convertiría | 1 |
| 67751 | convertiremos | 1 |
| 67752 | convertiré | 1 |
| 67753 | converte | 1 |
| 67754 | conversos | 1 |
| 67755 | conversiones | 1 |
| 67756 | convergencia | 1 |
| 67757 | conventual | 1 |
| 67758 | convenirles | 1 |
| 67759 | convenientemente | 1 |
| 67760 | conveníe | 1 |
| 67761 | convenida | 1 |
| 67762 | convenencia | 1 |
| 67763 | convención | 1 |
| 67764 | convencimientos | 1 |
| 67765 | convenciéndole | 1 |
| 67766 | convencían | 1 |
| 67767 | convences | 1 |
| 67768 | convencerte | 1 |
| 67769 | convencernos | 1 |
| 67770 | convenceréis | 1 |
| 67771 | convencen | 1 |
| 67772 | convéncele | 1 |
| 67773 | convecinos | 1 |
| 67774 | convecinó | 1 |
| 67775 | convecina | 1 |
| 67776 | convalecí | 1 |
| 67777 | convalecer | 1 |
| 67778 | convalecencias | 1 |
| 67779 | conuiniente | 1 |
| 67780 | conuierta | 1 |
| 67781 | conuertir | 1 |
| 67782 | conuertio | 1 |
| 67783 | conuertido | 1 |
| 67784 | conuersar | 1 |
| 67785 | conuenibles | 1 |
| 67786 | conuencion | 1 |
| 67787 | conualesce | 1 |
| 67788 | contyendas | 1 |
| 67789 | contúvose | 1 |
| 67790 | contúveme | 1 |
| 67791 | contusos | 1 |
| 67792 | conturbado | 1 |
| 67793 | contuerçe | 1 |
| 67794 | controvertía | 1 |
| 67795 | controversias | 1 |
| 67796 | contritos | 1 |
| 67797 | contrincante | 1 |
| 67798 | contribuyo | 1 |
| 67799 | contribuyente | 1 |
| 67800 | contribuya | 1 |
| 67801 | contribuirá | 1 |
| 67802 | contribuído | 1 |
| 67803 | contre | 1 |
| 67804 | contrayendo | 1 |
| 67805 | contray | 1 |
| 67806 | contraviniendo | 1 |
| 67807 | contraventores | 1 |
| 67808 | contratista | 1 |
| 67809 | contratar | 1 |
| 67810 | contratado | 1 |
| 67811 | contrastar | 1 |
| 67812 | contrastan | 1 |
| 67813 | contrastaban | 1 |
| 67814 | contrasta | 1 |
| 67815 | contraseña | 1 |
| 67816 | contrarrestarla | 1 |
| 67817 | contrariaron | 1 |
| 67818 | contrariarla | 1 |
| 67819 | contrariaran | 1 |
| 67820 | contrariará | 1 |
| 67821 | contrarían | 1 |
| 67822 | contrariábala | 1 |
| 67823 | contrapuestas | 1 |
| 67824 | contraproyecto | 1 |
| 67825 | contraponer | 1 |
| 67826 | contraminale | 1 |
| 67827 | contramina | 1 |
| 67828 | contraltos | 1 |
| 67829 | contralto | 1 |
| 67830 | contrallos | 1 |
| 67831 | contrallo | 1 |
| 67832 | contrallavalo | 1 |
| 67833 | contrajudías | 1 |
| 67834 | contrajo | 1 |
| 67835 | contraídas | 1 |
| 67836 | contraída | 1 |
| 67837 | contraían | 1 |
| 67838 | contrafalda | 1 |
| 67839 | contraerse | 1 |
| 67840 | contraer | 1 |
| 67841 | contrae | 1 |
| 67842 | contradize | 1 |
| 67843 | contradixo | 1 |
| 67844 | contradiré | 1 |
| 67845 | contradigo | 1 |
| 67846 | contradición | 1 |
| 67847 | contradiciéndose | 1 |
| 67848 | contradiciendo | 1 |
| 67849 | contradecirme | 1 |
| 67850 | contradecirlo | 1 |
| 67851 | contradanzas | 1 |
| 67852 | contradanza | 1 |
| 67853 | contractibilidad | 1 |
| 67854 | contóselo | 1 |
| 67855 | contorsión | 1 |
| 67856 | contorneada | 1 |
| 67857 | contonean | 1 |
| 67858 | contóme | 1 |
| 67859 | contome | 1 |
| 67860 | contólo | 1 |
| 67861 | contóle | 1 |
| 67862 | contóla | 1 |
| 67863 | continuaremos | 1 |
| 67864 | continúan | 1 |
| 67865 | continuadas | 1 |
| 67866 | continüada | 1 |
| 67867 | continuada | 1 |
| 67868 | continuaa | 1 |
| 67869 | contínua | 1 |
| 67870 | continos | 1 |
| 67871 | continiéndose | 1 |
| 67872 | contienden | 1 |
| 67873 | contiende | 1 |
| 67874 | contexto | 1 |
| 67875 | contestura | 1 |
| 67876 | contestarte | 1 |
| 67877 | contestarse | 1 |
| 67878 | contestarles | 1 |
| 67879 | contestaría | 1 |
| 67880 | contestaras | 1 |
| 67881 | contestará | 1 |
| 67882 | contestándolos | 1 |
| 67883 | contestan | 1 |
| 67884 | contestada | 1 |
| 67885 | contestábale | 1 |
| 67886 | contescimientos | 1 |
| 67887 | contescimiento | 1 |
| 67888 | contésçete | 1 |
| 67889 | contesçervos | 1 |
| 67890 | contésçel | 1 |
| 67891 | contésçal | 1 |
| 67892 | conterraneos | 1 |
| 67893 | conterráneo | 1 |
| 67894 | contentose | 1 |
| 67895 | contentona | 1 |
| 67896 | contentes | 1 |
| 67897 | contentemonos | 1 |
| 67898 | contenté | 1 |
| 67899 | contentate | 1 |
| 67900 | contentasen | 1 |
| 67901 | contentaremos | 1 |
| 67902 | contentáredes | 1 |
| 67903 | contentardes | 1 |
| 67904 | contentarás | 1 |
| 67905 | contentándonos | 1 |
| 67906 | contentando | 1 |
| 67907 | contentalle | 1 |
| 67908 | contentadiza | 1 |
| 67909 | contentada | 1 |
| 67910 | contentábase | 1 |
| 67911 | conteniéndome | 1 |
| 67912 | contenia | 1 |
| 67913 | contenerte | 1 |
| 67914 | contenerme | 1 |
| 67915 | contendré | 1 |
| 67916 | contendrán | 1 |
| 67917 | contendiesen | 1 |
| 67918 | contendieron | 1 |
| 67919 | contendíendo | 1 |
| 67920 | contemporizador | 1 |
| 67921 | contemporáneas | 1 |
| 67922 | contempléis | 1 |
| 67923 | contemple | 1 |
| 67924 | contemplaua | 1 |
| 67925 | contemplativo | 1 |
| 67926 | contemplasse | 1 |
| 67927 | contemplas | 1 |
| 67928 | contemplarlo | 1 |
| 67929 | contemplarle | 1 |
| 67930 | contemplarían | 1 |
| 67931 | contemplándonos | 1 |
| 67932 | contemplándolo | 1 |
| 67933 | contemplándola | 1 |
| 67934 | contemplan | 1 |
| 67935 | contemplacion | 1 |
| 67936 | contemplábase | 1 |
| 67937 | contemplábamos | 1 |
| 67938 | contempla | 1 |
| 67939 | contemos | 1 |
| 67940 | contélos | 1 |
| 67941 | contélas | 1 |
| 67942 | contéla | 1 |
| 67943 | contéis | 1 |
| 67944 | conteçióme | 1 |
| 67945 | conteciom | 1 |
| 67946 | conteçió | 1 |
| 67947 | contecido | 1 |
| 67948 | contártela | 1 |
| 67949 | contársele | 1 |
| 67950 | contárselas | 1 |
| 67951 | contároslo | 1 |
| 67952 | contáronle | 1 |
| 67953 | contarnos | 1 |
| 67954 | contarían | 1 |
| 67955 | contaremos | 1 |
| 67956 | contaran | 1 |
| 67957 | contándote | 1 |
| 67958 | contándoselo | 1 |
| 67959 | contándoseles | 1 |
| 67960 | contándome | 1 |
| 67961 | contaminado | 1 |
| 67962 | contaminaba | 1 |
| 67963 | contalla | 1 |
| 67964 | contaldes | 1 |
| 67965 | contairé | 1 |
| 67966 | contagioso | 1 |
| 67967 | contagiosas | 1 |
| 67968 | contagió | 1 |
| 67969 | contagie | 1 |
| 67970 | contagiarse | 1 |
| 67971 | contagiar | 1 |
| 67972 | contaduría | 1 |
| 67973 | contadnos | 1 |
| 67974 | contadísimas | 1 |
| 67975 | contadero | 1 |
| 67976 | contactos | 1 |
| 67977 | contábase | 1 |
| 67978 | contabas | 1 |
| 67979 | contábales | 1 |
| 67980 | contábale | 1 |
| 67981 | consyntyrá | 1 |
| 67982 | consustancial | 1 |
| 67983 | consumirte | 1 |
| 67984 | consumiosse | 1 |
| 67985 | consumieron | 1 |
| 67986 | consumiéndose | 1 |
| 67987 | consumes | 1 |
| 67988 | consumero | 1 |
| 67989 | consuman | 1 |
| 67990 | consumadamente | 1 |
| 67991 | consultárselo | 1 |
| 67992 | consultaron | 1 |
| 67993 | consultarlo | 1 |
| 67994 | consultaría | 1 |
| 67995 | consultaré | 1 |
| 67996 | consultándose | 1 |
| 67997 | consultándolo | 1 |
| 67998 | consúltalo | 1 |
| 67999 | consultados | 1 |
| 68000 | consultada | 1 |
| 68001 | consules | 1 |
| 68002 | consuélome | 1 |
| 68003 | consuelate | 1 |
| 68004 | consuélase | 1 |
| 68005 | consuelala | 1 |
| 68006 | consuegro | 1 |
| 68007 | construyó | 1 |
| 68008 | construyéndole | 1 |
| 68009 | construyen | 1 |
| 68010 | construyan | 1 |
| 68011 | construirse | 1 |
| 68012 | construirlo | 1 |
| 68013 | construiré | 1 |
| 68014 | constrüidos | 1 |
| 68015 | constructoras | 1 |
| 68016 | constructivo | 1 |
| 68017 | constructiva | 1 |
| 68018 | constreñida | 1 |
| 68019 | constituyó | 1 |
| 68020 | constituyo | 1 |
| 68021 | constituyesen | 1 |
| 68022 | constituyeron | 1 |
| 68023 | constituyéndolos | 1 |
| 68024 | constituyendo | 1 |
| 68025 | constituydas | 1 |
| 68026 | constitutivos | 1 |
| 68027 | constitutivo | 1 |
| 68028 | constitutiva | 1 |
| 68029 | constituirse | 1 |
| 68030 | constituído | 1 |
| 68031 | constituías | 1 |
| 68032 | constitucion | 1 |
| 68033 | constipase | 1 |
| 68034 | constipada | 1 |
| 68035 | constipaba | 1 |
| 68036 | consternó | 1 |
| 68037 | consternados | 1 |
| 68038 | consternadas | 1 |
| 68039 | constelaçión | 1 |
| 68040 | constelación | 1 |
| 68041 | constelacion | 1 |
| 68042 | constara | 1 |
| 68043 | constantina | 1 |
| 68044 | constaban | 1 |
| 68045 | conssentyd | 1 |
| 68046 | conssentir | 1 |
| 68047 | conssejavan | 1 |
| 68048 | consséjasme | 1 |
| 68049 | conssejar | 1 |
| 68050 | conspiran | 1 |
| 68051 | conspicuo | 1 |
| 68052 | conspicuas | 1 |
| 68053 | consolóle | 1 |
| 68054 | consolidó | 1 |
| 68055 | consolidase | 1 |
| 68056 | consolemos | 1 |
| 68057 | consolémonos | 1 |
| 68058 | consoléme | 1 |
| 68059 | consolatorias | 1 |
| 68060 | consolasse | 1 |
| 68061 | consolasen | 1 |
| 68062 | consolarte | 1 |
| 68063 | consoláronme | 1 |
| 68064 | consolarnos | 1 |
| 68065 | consolarías | 1 |
| 68066 | consolarán | 1 |
| 68067 | consolará | 1 |
| 68068 | consolándole | 1 |
| 68069 | consolalle | 1 |
| 68070 | consoladores | 1 |
| 68071 | consolada | 1 |
| 68072 | consolación | 1 |
| 68073 | consolacion | 1 |
| 68074 | consolábale | 1 |
| 68075 | consistorios | 1 |
| 68076 | consistirá | 1 |
| 68077 | consistiese | 1 |
| 68078 | consistían | 1 |
| 68079 | consistentes | 1 |
| 68080 | consistan | 1 |
| 68081 | consintré | 1 |
| 68082 | consintiría | 1 |
| 68083 | consintio | 1 |
| 68084 | consintiesse | 1 |
| 68085 | consintiese | 1 |
| 68086 | consintiéronselo | 1 |
| 68087 | consintieron | 1 |
| 68088 | consintientes | 1 |
| 68089 | consintiéndoselo | 1 |
| 68090 | consintiendo | 1 |
| 68091 | consiguiran | 1 |
| 68092 | consiguira | 1 |
| 68093 | consiguiesen | 1 |
| 68094 | consiguiera | 1 |
| 68095 | consiguientes | 1 |
| 68096 | consignó | 1 |
| 68097 | consignar | 1 |
| 68098 | consignadas | 1 |
| 68099 | consigas | 1 |
| 68100 | consiga | 1 |
| 68101 | consientas | 1 |
| 68102 | considérelo | 1 |
| 68103 | consideraste | 1 |
| 68104 | considerasse | 1 |
| 68105 | considerasen | 1 |
| 68106 | considerarte | 1 |
| 68107 | consideraría | 1 |
| 68108 | considerara | 1 |
| 68109 | considerándome | 1 |
| 68110 | consideramos | 1 |
| 68111 | considérame | 1 |
| 68112 | considéralo | 1 |
| 68113 | considérale | 1 |
| 68114 | consideráis | 1 |
| 68115 | considerad | 1 |
| 68116 | considerábanla | 1 |
| 68117 | considerábamos | 1 |
| 68118 | conserven | 1 |
| 68119 | consérvele | 1 |
| 68120 | conservarlos | 1 |
| 68121 | conservarlo | 1 |
| 68122 | conservaré | 1 |
| 68123 | conservarán | 1 |
| 68124 | conservándome | 1 |
| 68125 | conservamos | 1 |
| 68126 | conservaduría | 1 |
| 68127 | conservados | 1 |
| 68128 | conservadoras | 1 |
| 68129 | conservadas | 1 |
| 68130 | conservábase | 1 |
| 68131 | conseruar | 1 |
| 68132 | conseruado | 1 |
| 68133 | conserjería | 1 |
| 68134 | consequencia | 1 |
| 68135 | consentría | 1 |
| 68136 | consentirse | 1 |
| 68137 | consentirlo | 1 |
| 68138 | consentirán | 1 |
| 68139 | consentidas | 1 |
| 68140 | conséjote | 1 |
| 68141 | consejóme | 1 |
| 68142 | consejó | 1 |
| 68143 | consejeras | 1 |
| 68144 | consejate | 1 |
| 68145 | conséjame | 1 |
| 68146 | conseguistes | 1 |
| 68147 | conseguirse | 1 |
| 68148 | conseguiré | 1 |
| 68149 | conseguirán | 1 |
| 68150 | conseguieron | 1 |
| 68151 | conseguida | 1 |
| 68152 | conseguí | 1 |
| 68153 | consecutivamente | 1 |
| 68154 | consecuentes | 1 |
| 68155 | consciente | 1 |
| 68156 | consagre | 1 |
| 68157 | consagrarte | 1 |
| 68158 | consagrarse | 1 |
| 68159 | consagráronle | 1 |
| 68160 | consagrarlos | 1 |
| 68161 | consagrarle | 1 |
| 68162 | consagraría | 1 |
| 68163 | consagraremos | 1 |
| 68164 | consagrándose | 1 |
| 68165 | consagran | 1 |
| 68166 | consabidos | 1 |
| 68167 | consabidores | 1 |
| 68168 | consabido | 1 |
| 68169 | conquistóle | 1 |
| 68170 | conquistó | 1 |
| 68171 | conquistarla | 1 |
| 68172 | conquistaría | 1 |
| 68173 | conquistara | 1 |
| 68174 | conquistándolo | 1 |
| 68175 | conquistan | 1 |
| 68176 | conquistados | 1 |
| 68177 | conquistadores | 1 |
| 68178 | conquirense | 1 |
| 68179 | conquibules | 1 |
| 68180 | conqueridora | 1 |
| 68181 | conpusso | 1 |
| 68182 | conpuso | 1 |
| 68183 | conpuse | 1 |
| 68184 | conpuesto | 1 |
| 68185 | conprarien | 1 |
| 68186 | conpraríe | 1 |
| 68187 | conpraría | 1 |
| 68188 | conprarás | 1 |
| 68189 | conprar | 1 |
| 68190 | conprador | 1 |
| 68191 | conpradas | 1 |
| 68192 | conprad | 1 |
| 68193 | conpósele | 1 |
| 68194 | conponer | 1 |
| 68195 | conpone | 1 |
| 68196 | conpón | 1 |
| 68197 | conplyda | 1 |
| 68198 | conplóla | 1 |
| 68199 | conplit | 1 |
| 68200 | conpliste | 1 |
| 68201 | conplisión | 1 |
| 68202 | conplieron | 1 |
| 68203 | conplidos | 1 |
| 68204 | conplid | 1 |
| 68205 | conpleta | 1 |
| 68206 | conplarás | 1 |
| 68207 | conpasión | 1 |
| 68208 | conparty | 1 |
| 68209 | conpareciera | 1 |
| 68210 | conparaçión | 1 |
| 68211 | conparación | 1 |
| 68212 | conpañones | 1 |
| 68213 | conpañeras | 1 |
| 68214 | conpanón | 1 |
| 68215 | conpanero | 1 |
| 68216 | conpadre | 1 |
| 68217 | conozcays | 1 |
| 68218 | conozan | 1 |
| 68219 | conosço | 1 |
| 68220 | conosçiste | 1 |
| 68221 | conoscio | 1 |
| 68222 | conosciesses | 1 |
| 68223 | conosçiere | 1 |
| 68224 | conosciente | 1 |
| 68225 | conosçienta | 1 |
| 68226 | conoscidos | 1 |
| 68227 | conosçido | 1 |
| 68228 | conoscidas | 1 |
| 68229 | conosciasme | 1 |
| 68230 | conoscias | 1 |
| 68231 | conosçervos | 1 |
| 68232 | conoscerte | 1 |
| 68233 | conoscerlo | 1 |
| 68234 | conosceras | 1 |
| 68235 | conosçemiento | 1 |
| 68236 | conoscan | 1 |
| 68237 | conortar | 1 |
| 68238 | conortadvos | 1 |
| 68239 | conortadme | 1 |
| 68240 | conocístela | 1 |
| 68241 | conocisteis | 1 |
| 68242 | conocióme | 1 |
| 68243 | conociólos | 1 |
| 68244 | conocióle | 1 |
| 68245 | conociole | 1 |
| 68246 | conociola | 1 |
| 68247 | conocio | 1 |
| 68248 | conocímonos | 1 |
| 68249 | conociessen | 1 |
| 68250 | conoçieses | 1 |
| 68251 | conociésemos | 1 |
| 68252 | conociésedes | 1 |
| 68253 | conociéronle | 1 |
| 68254 | conociere | 1 |
| 68255 | conocieras | 1 |
| 68256 | conociéndole | 1 |
| 68257 | conocías | 1 |
| 68258 | conocíalo | 1 |
| 68259 | conocia | 1 |
| 68260 | conócesme | 1 |
| 68261 | conocesme | 1 |
| 68262 | conócesle | 1 |
| 68263 | conocernos | 1 |
| 68264 | conocerles | 1 |
| 68265 | conocerlas | 1 |
| 68266 | conoceremos | 1 |
| 68267 | conoceréis | 1 |
| 68268 | conocere | 1 |
| 68269 | conoçer | 1 |
| 68270 | conocella | 1 |
| 68271 | conocedores | 1 |
| 68272 | conocedoras | 1 |
| 68273 | cono | 1 |
| 68274 | connivencia | 1 |
| 68275 | conmutó | 1 |
| 68276 | conmoviera | 1 |
| 68277 | conmovidísima | 1 |
| 68278 | conmoverse | 1 |
| 68279 | conmoverá | 1 |
| 68280 | conmovedores | 1 |
| 68281 | conmociones | 1 |
| 68282 | conminó | 1 |
| 68283 | conminación | 1 |
| 68284 | conmemoraban | 1 |
| 68285 | conmemora | 1 |
| 68286 | conllevando | 1 |
| 68287 | conllevador | 1 |
| 68288 | conjuros | 1 |
| 68289 | conjure | 1 |
| 68290 | conjurasen | 1 |
| 68291 | conjurarte | 1 |
| 68292 | conjurarse | 1 |
| 68293 | conjurarme | 1 |
| 68294 | conjurada | 1 |
| 68295 | conjurábame | 1 |
| 68296 | conjunciones | 1 |
| 68297 | conjugar | 1 |
| 68298 | conjugal | 1 |
| 68299 | conjeturo | 1 |
| 68300 | conjeturaron | 1 |
| 68301 | conjeturando | 1 |
| 68302 | conjeturamos | 1 |
| 68303 | conjecturar | 1 |
| 68304 | conil | 1 |
| 68305 | cónicos | 1 |
| 68306 | cónica | 1 |
| 68307 | congruas | 1 |
| 68308 | congrua | 1 |
| 68309 | congrios | 1 |
| 68310 | congriogaciones | 1 |
| 68311 | congrieso | 1 |
| 68312 | congregarse | 1 |
| 68313 | congregarla | 1 |
| 68314 | congregaciones | 1 |
| 68315 | congregación | 1 |
| 68316 | congregaba | 1 |
| 68317 | congratularse | 1 |
| 68318 | congratulándose | 1 |
| 68319 | congraciándose | 1 |
| 68320 | congoxosa | 1 |
| 68321 | congojóse | 1 |
| 68322 | congojosas | 1 |
| 68323 | congoje | 1 |
| 68324 | congojarte | 1 |
| 68325 | congojadísima | 1 |
| 68326 | congojaban | 1 |
| 68327 | congojaba | 1 |
| 68328 | congestione | 1 |
| 68329 | congestionaba | 1 |
| 68330 | congestiona | 1 |
| 68331 | congénitas | 1 |
| 68332 | congenialidad | 1 |
| 68333 | congeniaban | 1 |
| 68334 | congeniábamos | 1 |
| 68335 | congelaron | 1 |
| 68336 | congeladas | 1 |
| 68337 | confutación | 1 |
| 68338 | confundirme | 1 |
| 68339 | confundirles | 1 |
| 68340 | confundirías | 1 |
| 68341 | confundirían | 1 |
| 68342 | confundiría | 1 |
| 68343 | confundiera | 1 |
| 68344 | confundiéndole | 1 |
| 68345 | confuerte | 1 |
| 68346 | confrontar | 1 |
| 68347 | confrontándolas | 1 |
| 68348 | confradias | 1 |
| 68349 | confortativo | 1 |
| 68350 | confortativas | 1 |
| 68351 | confortaron | 1 |
| 68352 | confortar | 1 |
| 68353 | confortantes | 1 |
| 68354 | confortado | 1 |
| 68355 | conformó | 1 |
| 68356 | conformo | 1 |
| 68357 | confórmese | 1 |
| 68358 | conformaron | 1 |
| 68359 | conformaran | 1 |
| 68360 | conformará | 1 |
| 68361 | conformándose | 1 |
| 68362 | conforman | 1 |
| 68363 | conformación | 1 |
| 68364 | conformábase | 1 |
| 68365 | confluencia | 1 |
| 68366 | conflito | 1 |
| 68367 | confligunt | 1 |
| 68368 | conflictos | 1 |
| 68369 | confituras | 1 |
| 68370 | confitó | 1 |
| 68371 | confites | 1 |
| 68372 | confiterías | 1 |
| 68373 | confitera | 1 |
| 68374 | confite | 1 |
| 68375 | confisión | 1 |
| 68376 | confiscación | 1 |
| 68377 | confirmóse | 1 |
| 68378 | confirmólo | 1 |
| 68379 | confirmóle | 1 |
| 68380 | confírmole | 1 |
| 68381 | confirmen | 1 |
| 68382 | confirme | 1 |
| 68383 | confirmarlo | 1 |
| 68384 | confirmarlas | 1 |
| 68385 | confirmará | 1 |
| 68386 | confirmando | 1 |
| 68387 | confirmamos | 1 |
| 68388 | confirmaçión | 1 |
| 68389 | confirmaban | 1 |
| 68390 | confirieron | 1 |
| 68391 | confirencia | 1 |
| 68392 | confinantes | 1 |
| 68393 | confiessas | 1 |
| 68394 | confieses | 1 |
| 68395 | confiesen | 1 |
| 68396 | confiéseme | 1 |
| 68397 | confíese | 1 |
| 68398 | confiesan | 1 |
| 68399 | confiésalo | 1 |
| 68400 | confíes | 1 |
| 68401 | confies | 1 |
| 68402 | confiemos | 1 |
| 68403 | confíe | 1 |
| 68404 | conficionados | 1 |
| 68405 | confíate | 1 |
| 68406 | confiase | 1 |
| 68407 | confías | 1 |
| 68408 | confiarse | 1 |
| 68409 | confiarme | 1 |
| 68410 | confiarle | 1 |
| 68411 | confiaría | 1 |
| 68412 | confiara | 1 |
| 68413 | confían | 1 |
| 68414 | confiadote | 1 |
| 68415 | confiadas | 1 |
| 68416 | confiadamente | 1 |
| 68417 | confiad | 1 |
| 68418 | confia | 1 |
| 68419 | conffisión | 1 |
| 68420 | conffieso | 1 |
| 68421 | conffesor | 1 |
| 68422 | conffesión | 1 |
| 68423 | confessor | 1 |
| 68424 | confessado | 1 |
| 68425 | confesos | 1 |
| 68426 | confesóme | 1 |
| 68427 | confesóle | 1 |
| 68428 | confesaste | 1 |
| 68429 | confesarte | 1 |
| 68430 | confesarlas | 1 |
| 68431 | confesarla | 1 |
| 68432 | confesarían | 1 |
| 68433 | confesaría | 1 |
| 68434 | confesaremos | 1 |
| 68435 | confesarás | 1 |
| 68436 | confesándote | 1 |
| 68437 | confesándose | 1 |
| 68438 | confesados | 1 |
| 68439 | confesada | 1 |
| 68440 | confesad | 1 |
| 68441 | confesábades | 1 |
| 68442 | conferir | 1 |
| 68443 | conferenciaban | 1 |
| 68444 | conferenciaba | 1 |
| 68445 | confederacion | 1 |
| 68446 | confectu | 1 |
| 68447 | confecionar | 1 |
| 68448 | confeccionados | 1 |
| 68449 | confeccionada | 1 |
| 68450 | confeccionaba | 1 |
| 68451 | confecciona | 1 |
| 68452 | confaciones | 1 |
| 68453 | confabulada | 1 |
| 68454 | confabulación | 1 |
| 68455 | confabulaban | 1 |
| 68456 | conexión | 1 |
| 68457 | conejuelos | 1 |
| 68458 | conejuelo | 1 |
| 68459 | conejero | 1 |
| 68460 | coneja | 1 |
| 68461 | conduzgo | 1 |
| 68462 | conduzgan | 1 |
| 68463 | conduzca | 1 |
| 68464 | condutor | 1 |
| 68465 | condújole | 1 |
| 68466 | condújola | 1 |
| 68467 | condujeron | 1 |
| 68468 | condujera | 1 |
| 68469 | conduit | 1 |
| 68470 | conductores | 1 |
| 68471 | conducís | 1 |
| 68472 | conducirme | 1 |
| 68473 | conducirle | 1 |
| 68474 | conduciría | 1 |
| 68475 | conduciéndolo | 1 |
| 68476 | conducidores | 1 |
| 68477 | conduces | 1 |
| 68478 | condolíme | 1 |
| 68479 | condolidos | 1 |
| 68480 | condolernos | 1 |
| 68481 | condimentados | 1 |
| 68482 | condimentado | 1 |
| 68483 | condillac | 1 |
| 68484 | condido | 1 |
| 68485 | condiçión | 1 |
| 68486 | condesita | 1 |
| 68487 | condesil | 1 |
| 68488 | condeses | 1 |
| 68489 | condescender | 1 |
| 68490 | condesados | 1 |
| 68491 | condesado | 1 |
| 68492 | condepñar | 1 |
| 68493 | condepnar | 1 |
| 68494 | condeñado | 1 |
| 68495 | condensarse | 1 |
| 68496 | condensaron | 1 |
| 68497 | condensándose | 1 |
| 68498 | condensando | 1 |
| 68499 | condensados | 1 |
| 68500 | condensadas | 1 |
| 68501 | condensada | 1 |
| 68502 | condensación | 1 |
| 68503 | condensaban | 1 |
| 68504 | condenedes | 1 |
| 68505 | condenasen | 1 |
| 68506 | condenase | 1 |
| 68507 | condenáronme | 1 |
| 68508 | condenaron | 1 |
| 68509 | condenarme | 1 |
| 68510 | condenarlos | 1 |
| 68511 | condenarlo | 1 |
| 68512 | condenarle | 1 |
| 68513 | condenaría | 1 |
| 68514 | condenaré | 1 |
| 68515 | condenarás | 1 |
| 68516 | condenan | 1 |
| 68517 | condenáis | 1 |
| 68518 | condenaciones | 1 |
| 68519 | condemnada | 1 |
| 68520 | condedijos | 1 |
| 68521 | condecendió | 1 |
| 68522 | condecender | 1 |
| 68523 | condecenció | 1 |
| 68524 | condazo | 1 |
| 68525 | condados | 1 |
| 68526 | concurrieron | 1 |
| 68527 | concurrientes | 1 |
| 68528 | concurriendo | 1 |
| 68529 | concurridas | 1 |
| 68530 | concurrente | 1 |
| 68531 | concupiscente | 1 |
| 68532 | concupiscencias | 1 |
| 68533 | conculcar | 1 |
| 68534 | concuerdan | 1 |
| 68535 | concuerda | 1 |
| 68536 | concreten | 1 |
| 68537 | concretar | 1 |
| 68538 | concretándose | 1 |
| 68539 | concretándome | 1 |
| 68540 | concretando | 1 |
| 68541 | concretan | 1 |
| 68542 | concordes | 1 |
| 68543 | concordato | 1 |
| 68544 | concordarnos | 1 |
| 68545 | concordaban | 1 |
| 68546 | concomitancias | 1 |
| 68547 | concomen | 1 |
| 68548 | concocelle | 1 |
| 68549 | concluyr | 1 |
| 68550 | concluyóse | 1 |
| 68551 | concluyesen | 1 |
| 68552 | concluyeran | 1 |
| 68553 | concluyentes | 1 |
| 68554 | concluydas | 1 |
| 68555 | concluyas | 1 |
| 68556 | concluirlas | 1 |
| 68557 | concluirla | 1 |
| 68558 | concluirían | 1 |
| 68559 | concluiría | 1 |
| 68560 | concluiré | 1 |
| 68561 | concluimos | 1 |
| 68562 | concluídos | 1 |
| 68563 | concluídas | 1 |
| 68564 | concitó | 1 |
| 68565 | concitando | 1 |
| 68566 | conciso | 1 |
| 68567 | concisión | 1 |
| 68568 | concilió | 1 |
| 68569 | conciliasen | 1 |
| 68570 | conciliarse | 1 |
| 68571 | conciliario | 1 |
| 68572 | conciliadoras | 1 |
| 68573 | concilia | 1 |
| 68574 | concierte | 1 |
| 68575 | conciértase | 1 |
| 68576 | conciertame | 1 |
| 68577 | concierne | 1 |
| 68578 | concienzudas | 1 |
| 68579 | concienzudamente | 1 |
| 68580 | concibiendo | 1 |
| 68581 | concibas | 1 |
| 68582 | concibamos | 1 |
| 68583 | conciba | 1 |
| 68584 | conchitas | 1 |
| 68585 | concheta | 1 |
| 68586 | conceto | 1 |
| 68587 | concession | 1 |
| 68588 | concesiones | 1 |
| 68589 | concesión | 1 |
| 68590 | concerto | 1 |
| 68591 | concertéme | 1 |
| 68592 | concerte | 1 |
| 68593 | concertauan | 1 |
| 68594 | concertaste | 1 |
| 68595 | concertaremos | 1 |
| 68596 | concertant | 1 |
| 68597 | concertadamente | 1 |
| 68598 | concertaban | 1 |
| 68599 | conceptuosos | 1 |
| 68600 | conceptum | 1 |
| 68601 | conceptuándola | 1 |
| 68602 | conceptista | 1 |
| 68603 | concepta | 1 |
| 68604 | concentüosa | 1 |
| 68605 | concentrándose | 1 |
| 68606 | concentrado | 1 |
| 68607 | concentración | 1 |
| 68608 | concejil | 1 |
| 68609 | concéitos | 1 |
| 68610 | concedióselo | 1 |
| 68611 | concediolo | 1 |
| 68612 | concedieran | 1 |
| 68613 | concediéndole | 1 |
| 68614 | concedida | 1 |
| 68615 | concederemos | 1 |
| 68616 | concederé | 1 |
| 68617 | concederán | 1 |
| 68618 | concedemos | 1 |
| 68619 | concédeme | 1 |
| 68620 | concédele | 1 |
| 68621 | concedas | 1 |
| 68622 | concebirse | 1 |
| 68623 | concebiría | 1 |
| 68624 | concebidos | 1 |
| 68625 | concebían | 1 |
| 68626 | concavidades | 1 |
| 68627 | cóncavas | 1 |
| 68628 | cóncava | 1 |
| 68629 | conbydes | 1 |
| 68630 | conbydar | 1 |
| 68631 | conbyd | 1 |
| 68632 | conbusco | 1 |
| 68633 | conbrían | 1 |
| 68634 | conbrí | 1 |
| 68635 | conbredes | 1 |
| 68636 | conblueça | 1 |
| 68637 | conbites | 1 |
| 68638 | conbite | 1 |
| 68639 | conbidól | 1 |
| 68640 | conbidó | 1 |
| 68641 | conbidas | 1 |
| 68642 | conbidáronle | 1 |
| 68643 | conbidado | 1 |
| 68644 | comutativa | 1 |
| 68645 | comunmente | 1 |
| 68646 | comunistas | 1 |
| 68647 | comuniquemos | 1 |
| 68648 | comunicaua | 1 |
| 68649 | comunícase | 1 |
| 68650 | comunicarlas | 1 |
| 68651 | comunicarán | 1 |
| 68652 | comunicaran | 1 |
| 68653 | comunicará | 1 |
| 68654 | comunicara | 1 |
| 68655 | comunicándolo | 1 |
| 68656 | comunicandola | 1 |
| 68657 | comunicamos | 1 |
| 68658 | comunicallo | 1 |
| 68659 | comunicalle | 1 |
| 68660 | comunicadas | 1 |
| 68661 | comunicables | 1 |
| 68662 | comunera | 1 |
| 68663 | comulgué | 1 |
| 68664 | comulgó | 1 |
| 68665 | comulgas | 1 |
| 68666 | comulgaron | 1 |
| 68667 | comulgando | 1 |
| 68668 | comulgado | 1 |
| 68669 | cómputos | 1 |
| 68670 | compusiesen | 1 |
| 68671 | compusiese | 1 |
| 68672 | compusieron | 1 |
| 68673 | compungióse | 1 |
| 68674 | compungidas | 1 |
| 68675 | compunción | 1 |
| 68676 | compulsen | 1 |
| 68677 | compulsar | 1 |
| 68678 | comprometió | 1 |
| 68679 | comprometían | 1 |
| 68680 | comprometernos | 1 |
| 68681 | comprometerme | 1 |
| 68682 | comprometerles | 1 |
| 68683 | comprobarse | 1 |
| 68684 | comprobados | 1 |
| 68685 | comprobado | 1 |
| 68686 | comprobación | 1 |
| 68687 | comprimiéndosela | 1 |
| 68688 | comprime | 1 |
| 68689 | compriar | 1 |
| 68690 | compresión | 1 |
| 68691 | comprensible | 1 |
| 68692 | comprendiolo | 1 |
| 68693 | comprendiéramos | 1 |
| 68694 | comprendiéndolo | 1 |
| 68695 | comprenderme | 1 |
| 68696 | comprenderle | 1 |
| 68697 | comprenderlas | 1 |
| 68698 | comprenderíamos | 1 |
| 68699 | comprendería | 1 |
| 68700 | comprendéis | 1 |
| 68701 | cómpreme | 1 |
| 68702 | compréle | 1 |
| 68703 | compréis | 1 |
| 68704 | comprehendo | 1 |
| 68705 | comprehender | 1 |
| 68706 | comprehenden | 1 |
| 68707 | comprasen | 1 |
| 68708 | comprarmi | 1 |
| 68709 | comprarlos | 1 |
| 68710 | comprarían | 1 |
| 68711 | compraremos | 1 |
| 68712 | compráramos | 1 |
| 68713 | comprará | 1 |
| 68714 | comprallo | 1 |
| 68715 | comprábale | 1 |
| 68716 | compotas | 1 |
| 68717 | compositores | 1 |
| 68718 | composicioncita | 1 |
| 68719 | composicioncilla | 1 |
| 68720 | comportable | 1 |
| 68721 | componiéndose | 1 |
| 68722 | compongas | 1 |
| 68723 | compongan | 1 |
| 68724 | compones | 1 |
| 68725 | componerlo | 1 |
| 68726 | componerlas | 1 |
| 68727 | componerla | 1 |
| 68728 | componenda | 1 |
| 68729 | componedores | 1 |
| 68730 | compondremos | 1 |
| 68731 | compondré | 1 |
| 68732 | compo | 1 |
| 68733 | compluto | 1 |
| 68734 | compliste | 1 |
| 68735 | compliras | 1 |
| 68736 | compliran | 1 |
| 68737 | complira | 1 |
| 68738 | complimos | 1 |
| 68739 | complidas | 1 |
| 68740 | complicar | 1 |
| 68741 | complicadísima | 1 |
| 68742 | complica | 1 |
| 68743 | completó | 1 |
| 68744 | complesion | 1 |
| 68745 | complazerte | 1 |
| 68746 | complaze | 1 |
| 68747 | complazco | 1 |
| 68748 | complacientes | 1 |
| 68749 | complacidísima | 1 |
| 68750 | complacida | 1 |
| 68751 | complacíase | 1 |
| 68752 | complaces | 1 |
| 68753 | complacerte | 1 |
| 68754 | complaceros | 1 |
| 68755 | complacéis | 1 |
| 68756 | compitiendo | 1 |
| 68757 | compiten | 1 |
| 68758 | compite | 1 |
| 68759 | compita | 1 |
| 68760 | compilase | 1 |
| 68761 | compilar | 1 |
| 68762 | compilando | 1 |
| 68763 | competilla | 1 |
| 68764 | competientes | 1 |
| 68765 | competidores | 1 |
| 68766 | competían | 1 |
| 68767 | competía | 1 |
| 68768 | competencias | 1 |
| 68769 | compère | 1 |
| 68770 | compensó | 1 |
| 68771 | compensarme | 1 |
| 68772 | compensarla | 1 |
| 68773 | compensaciones | 1 |
| 68774 | compensacion | 1 |
| 68775 | compenetraron | 1 |
| 68776 | compenetrando | 1 |
| 68777 | compenetran | 1 |
| 68778 | compendioso | 1 |
| 68779 | compelidos | 1 |
| 68780 | compelido | 1 |
| 68781 | compelía | 1 |
| 68782 | compelia | 1 |
| 68783 | compatriotos | 1 |
| 68784 | compatriote | 1 |
| 68785 | compatibilidad | 1 |
| 68786 | compasivamente | 1 |
| 68787 | compasiones | 1 |
| 68788 | compasion | 1 |
| 68789 | compases | 1 |
| 68790 | compasaba | 1 |
| 68791 | compartir | 1 |
| 68792 | compartimientos | 1 |
| 68793 | compartieron | 1 |
| 68794 | comparten | 1 |
| 68795 | compares | 1 |
| 68796 | comparen | 1 |
| 68797 | comparemos | 1 |
| 68798 | comparéis | 1 |
| 68799 | comparecieron | 1 |
| 68800 | comparativos | 1 |
| 68801 | comparativo | 1 |
| 68802 | comparativamente | 1 |
| 68803 | comparaste | 1 |
| 68804 | compararon | 1 |
| 68805 | compararlo | 1 |
| 68806 | compararlas | 1 |
| 68807 | compararla | 1 |
| 68808 | compararíamos | 1 |
| 68809 | comparará | 1 |
| 68810 | comparara | 1 |
| 68811 | comparándolos | 1 |
| 68812 | comparamos | 1 |
| 68813 | comparables | 1 |
| 68814 | compañerismo | 1 |
| 68815 | compaginadas | 1 |
| 68816 | compagina | 1 |
| 68817 | compadecióse | 1 |
| 68818 | compadeciéndose | 1 |
| 68819 | compadecido | 1 |
| 68820 | compadecí | 1 |
| 68821 | compadécete | 1 |
| 68822 | compadecerte | 1 |
| 68823 | compacta | 1 |
| 68824 | comorín | 1 |
| 68825 | comoquier | 1 |
| 68826 | comodoro | 1 |
| 68827 | comodísimas | 1 |
| 68828 | commis | 1 |
| 68829 | comme | 1 |
| 68830 | comités | 1 |
| 68831 | comitentes | 1 |
| 68832 | comiteles | 1 |
| 68833 | comistrajo | 1 |
| 68834 | comistraje | 1 |
| 68835 | comisionado | 1 |
| 68836 | comiquito | 1 |
| 68837 | comiquería | 1 |
| 68838 | comiólos | 1 |
| 68839 | comiólo | 1 |
| 68840 | comio | 1 |
| 68841 | cominos | 1 |
| 68842 | comineros | 1 |
| 68843 | cominad | 1 |
| 68844 | comímela | 1 |
| 68845 | comiesses | 1 |
| 68846 | comiésemos | 1 |
| 68847 | comiere | 1 |
| 68848 | comieras | 1 |
| 68849 | comiéramos | 1 |
| 68850 | comiénzanme | 1 |
| 68851 | comiéndosele | 1 |
| 68852 | comiéndoselas | 1 |
| 68853 | comiéndomelas | 1 |
| 68854 | comiéndolo | 1 |
| 68855 | comiendolo | 1 |
| 68856 | comiençe | 1 |
| 68857 | comiençan | 1 |
| 68858 | comíen | 1 |
| 68859 | comídose | 1 |
| 68860 | comidir | 1 |
| 68861 | comides | 1 |
| 68862 | cómicamente | 1 |
| 68863 | comica | 1 |
| 68864 | comías | 1 |
| 68865 | comíanse | 1 |
| 68866 | comiamos | 1 |
| 68867 | comia | 1 |
| 68868 | cometiese | 1 |
| 68869 | cometidas | 1 |
| 68870 | cometerlas | 1 |
| 68871 | cometerías | 1 |
| 68872 | cometerá | 1 |
| 68873 | cometen | 1 |
| 68874 | cometemos | 1 |
| 68875 | cómetela | 1 |
| 68876 | cómete | 1 |
| 68877 | cometan | 1 |
| 68878 | comestible | 1 |
| 68879 | comérsele | 1 |
| 68880 | comérsela | 1 |
| 68881 | comere | 1 |
| 68882 | comerciando | 1 |
| 68883 | comerciaban | 1 |
| 68884 | comerciaba | 1 |
| 68885 | comercia | 1 |
| 68886 | comenzolos | 1 |
| 68887 | comenzóle | 1 |
| 68888 | comenzole | 1 |
| 68889 | comenzo | 1 |
| 68890 | comenzauas | 1 |
| 68891 | comenzaste | 1 |
| 68892 | comenzasen | 1 |
| 68893 | comenzásemos | 1 |
| 68894 | comenzaremos | 1 |
| 68895 | comenzaran | 1 |
| 68896 | comenzará | 1 |
| 68897 | comenzáis | 1 |
| 68898 | comenzad | 1 |
| 68899 | comentos | 1 |
| 68900 | comento | 1 |
| 68901 | comentase | 1 |
| 68902 | comentarlos | 1 |
| 68903 | comentarlas | 1 |
| 68904 | comentarla | 1 |
| 68905 | comentado | 1 |
| 68906 | cómense | 1 |
| 68907 | comensalía | 1 |
| 68908 | comensal | 1 |
| 68909 | comenencias | 1 |
| 68910 | comenencia | 1 |
| 68911 | comendón | 1 |
| 68912 | comendado | 1 |
| 68913 | començós | 1 |
| 68914 | començol | 1 |
| 68915 | comencemos | 1 |
| 68916 | comencélo | 1 |
| 68917 | començel | 1 |
| 68918 | començava | 1 |
| 68919 | començaríen | 1 |
| 68920 | començare | 1 |
| 68921 | començar | 1 |
| 68922 | començallo | 1 |
| 68923 | començada | 1 |
| 68924 | cómeme | 1 |
| 68925 | comellas | 1 |
| 68926 | cómela | 1 |
| 68927 | comehostias | 1 |
| 68928 | comedla | 1 |
| 68929 | comedirse | 1 |
| 68930 | comedirme | 1 |
| 68931 | comediría | 1 |
| 68932 | comedir | 1 |
| 68933 | comedio | 1 |
| 68934 | comedieta | 1 |
| 68935 | comediendo | 1 |
| 68936 | comedid | 1 |
| 68937 | comedías | 1 |
| 68938 | comedí | 1 |
| 68939 | comedes | 1 |
| 68940 | combustibles | 1 |
| 68941 | combinen | 1 |
| 68942 | combinan | 1 |
| 68943 | combinaban | 1 |
| 68944 | combide | 1 |
| 68945 | combidauan | 1 |
| 68946 | combidasses | 1 |
| 68947 | combidar | 1 |
| 68948 | combidan | 1 |
| 68949 | combidame | 1 |
| 68950 | combidada | 1 |
| 68951 | combida | 1 |
| 68952 | combatistes | 1 |
| 68953 | combatiré | 1 |
| 68954 | combatiéndose | 1 |
| 68955 | combatiendo | 1 |
| 68956 | combatía | 1 |
| 68957 | combaten | 1 |
| 68958 | comático | 1 |
| 68959 | comarcas | 1 |
| 68960 | comarcano | 1 |
| 68961 | comanditaria | 1 |
| 68962 | comámoslo | 1 |
| 68963 | comáis | 1 |
| 68964 | comadreaban | 1 |
| 68965 | coluros | 1 |
| 68966 | columpios | 1 |
| 68967 | columpiaron | 1 |
| 68968 | columpiar | 1 |
| 68969 | columpiándose | 1 |
| 68970 | columpiándonos | 1 |
| 68971 | columpiaban | 1 |
| 68972 | columpiábame | 1 |
| 68973 | columnarias | 1 |
| 68974 | columbro | 1 |
| 68975 | columbraron | 1 |
| 68976 | columbrando | 1 |
| 68977 | columbraba | 1 |
| 68978 | columbra | 1 |
| 68979 | colosos | 1 |
| 68980 | colose | 1 |
| 68981 | coloreó | 1 |
| 68982 | coloreando | 1 |
| 68983 | coloreaba | 1 |
| 68984 | colorcito | 1 |
| 68985 | colorastes | 1 |
| 68986 | colorasse | 1 |
| 68987 | colorao | 1 |
| 68988 | colorante | 1 |
| 68989 | coloran | 1 |
| 68990 | coloradilla | 1 |
| 68991 | colóqueme | 1 |
| 68992 | coloqué | 1 |
| 68993 | colophón | 1 |
| 68994 | colono | 1 |
| 68995 | colonizadas | 1 |
| 68996 | colonial | 1 |
| 68997 | colonas | 1 |
| 68998 | colodra | 1 |
| 68999 | colocose | 1 |
| 69000 | colocártelos | 1 |
| 69001 | colocáronme | 1 |
| 69002 | colocarme | 1 |
| 69003 | colocarlo | 1 |
| 69004 | colocarle | 1 |
| 69005 | colocaran | 1 |
| 69006 | colocará | 1 |
| 69007 | colocao | 1 |
| 69008 | colocaditas | 1 |
| 69009 | colmilludo | 1 |
| 69010 | colmilluda | 1 |
| 69011 | colmillos | 1 |
| 69012 | colmiellos | 1 |
| 69013 | cólmese | 1 |
| 69014 | colmeneros | 1 |
| 69015 | colmen | 1 |
| 69016 | colmaron | 1 |
| 69017 | colmando | 1 |
| 69018 | colmadas | 1 |
| 69019 | colmaba | 1 |
| 69020 | collores | 1 |
| 69021 | collis | 1 |
| 69022 | collingwoodes | 1 |
| 69023 | collarada | 1 |
| 69024 | collados | 1 |
| 69025 | collacion | 1 |
| 69026 | colisión | 1 |
| 69027 | colindante | 1 |
| 69028 | colillas | 1 |
| 69029 | colija | 1 |
| 69030 | coligidas | 1 |
| 69031 | coligen | 1 |
| 69032 | coliflores | 1 |
| 69033 | colguélo | 1 |
| 69034 | colgasen | 1 |
| 69035 | colgaron | 1 |
| 69036 | colgarlos | 1 |
| 69037 | colgarlo | 1 |
| 69038 | colgarien | 1 |
| 69039 | colgaría | 1 |
| 69040 | colgaré | 1 |
| 69041 | colgante | 1 |
| 69042 | colgándosele | 1 |
| 69043 | colgándoos | 1 |
| 69044 | colgándome | 1 |
| 69045 | colgajo | 1 |
| 69046 | colgador | 1 |
| 69047 | colgadizos | 1 |
| 69048 | coletos | 1 |
| 69049 | coletazos | 1 |
| 69050 | coles | 1 |
| 69051 | colerilla | 1 |
| 69052 | colera | 1 |
| 69053 | colegido | 1 |
| 69054 | colegiata | 1 |
| 69055 | colegiala | 1 |
| 69056 | colegía | 1 |
| 69057 | colegí | 1 |
| 69058 | colectividades | 1 |
| 69059 | colectivas | 1 |
| 69060 | colectivamente | 1 |
| 69061 | colectas | 1 |
| 69062 | coleccionista | 1 |
| 69063 | coleccionarlos | 1 |
| 69064 | coleccionado | 1 |
| 69065 | colé | 1 |
| 69066 | colchado | 1 |
| 69067 | colasa | 1 |
| 69068 | colaríamos | 1 |
| 69069 | colaría | 1 |
| 69070 | colambre | 1 |
| 69071 | coladores | 1 |
| 69072 | colado | 1 |
| 69073 | colaboración | 1 |
| 69074 | colaboraba | 1 |
| 69075 | colaban | 1 |
| 69076 | colaba | 1 |
| 69077 | cojuelo | 1 |
| 69078 | cojines | 1 |
| 69079 | cojera | 1 |
| 69080 | cojeéis | 1 |
| 69081 | cojearás | 1 |
| 69082 | cojear | 1 |
| 69083 | cojeaban | 1 |
| 69084 | cojas | 1 |
| 69085 | cojan | 1 |
| 69086 | cójala | 1 |
| 69087 | coincidiese | 1 |
| 69088 | coincidencias | 1 |
| 69089 | coin | 1 |
| 69090 | coima | 1 |
| 69091 | cohyta | 1 |
| 69092 | cohonestar | 1 |
| 69093 | cohonda | 1 |
| 69094 | cohombro | 1 |
| 69095 | cohibidos | 1 |
| 69096 | cohibido | 1 |
| 69097 | cohibían | 1 |
| 69098 | cohibía | 1 |
| 69099 | cohecharme | 1 |
| 69100 | cohecharemos | 1 |
| 69101 | cohechadores | 1 |
| 69102 | cohechado | 1 |
| 69103 | cogollo | 1 |
| 69104 | cogitacions | 1 |
| 69105 | cogióle | 1 |
| 69106 | cogióla | 1 |
| 69107 | cogiola | 1 |
| 69108 | cogines | 1 |
| 69109 | cogiessen | 1 |
| 69110 | cogiéronse | 1 |
| 69111 | cogiéronlos | 1 |
| 69112 | cogiéndonos | 1 |
| 69113 | cogiéndolos | 1 |
| 69114 | cogiéndolo | 1 |
| 69115 | cogiéndolas | 1 |
| 69116 | cogiditos | 1 |
| 69117 | cogérsela | 1 |
| 69118 | cogernos | 1 |
| 69119 | cogerme | 1 |
| 69120 | cogerás | 1 |
| 69121 | cogerán | 1 |
| 69122 | cogemos | 1 |
| 69123 | cógeme | 1 |
| 69124 | cógelo | 1 |
| 69125 | cógele | 1 |
| 69126 | cogéis | 1 |
| 69127 | cofreros | 1 |
| 69128 | cofrecico | 1 |
| 69129 | cofonda | 1 |
| 69130 | cofias | 1 |
| 69131 | cofia | 1 |
| 69132 | coffya | 1 |
| 69133 | cofadría | 1 |
| 69134 | coeteris | 1 |
| 69135 | coetáneos | 1 |
| 69136 | coetánea | 1 |
| 69137 | coercitivo | 1 |
| 69138 | coello | 1 |
| 69139 | coeda | 1 |
| 69140 | codyçyossos | 1 |
| 69141 | codornizes | 1 |
| 69142 | codorniçes | 1 |
| 69143 | codonate | 1 |
| 69144 | codillos | 1 |
| 69145 | codificación | 1 |
| 69146 | codiçiosa | 1 |
| 69147 | codicióme | 1 |
| 69148 | codiçio | 1 |
| 69149 | codicio | 1 |
| 69150 | codiçies | 1 |
| 69151 | codiçiava | 1 |
| 69152 | codiciaron | 1 |
| 69153 | codiciar | 1 |
| 69154 | codiciaba | 1 |
| 69155 | codiçia | 1 |
| 69156 | codean | 1 |
| 69157 | codeaban | 1 |
| 69158 | codeaba | 1 |
| 69159 | çoda | 1 |
| 69160 | cocotte | 1 |
| 69161 | çoçobra | 1 |
| 69162 | coclearia | 1 |
| 69163 | coçinas | 1 |
| 69164 | cocinar | 1 |
| 69165 | cocinaba | 1 |
| 69166 | cociéndolos | 1 |
| 69167 | cocidos | 1 |
| 69168 | cocida | 1 |
| 69169 | cocho | 1 |
| 69170 | cochinamente | 1 |
| 69171 | cochinadas | 1 |
| 69172 | cochilo | 1 |
| 69173 | cochillo | 1 |
| 69174 | cochiello | 1 |
| 69175 | cochecito | 1 |
| 69176 | cochecillo | 1 |
| 69177 | cocea | 1 |
| 69178 | cocas | 1 |
| 69179 | cobyerto | 1 |
| 69180 | cobrire | 1 |
| 69181 | cobrir | 1 |
| 69182 | cobrimos | 1 |
| 69183 | cobri | 1 |
| 69184 | cobres | 1 |
| 69185 | cobraste | 1 |
| 69186 | cobrásedes | 1 |
| 69187 | cobrárselo | 1 |
| 69188 | cobrarse | 1 |
| 69189 | cobrarlos | 1 |
| 69190 | cobrarlo | 1 |
| 69191 | cobrarle | 1 |
| 69192 | cobrarían | 1 |
| 69193 | cobraremos | 1 |
| 69194 | cobraré | 1 |
| 69195 | cobranzas | 1 |
| 69196 | cobrándole | 1 |
| 69197 | cobrallo | 1 |
| 69198 | cobrábale | 1 |
| 69199 | cobos | 1 |
| 69200 | cobijo | 1 |
| 69201 | cobijados | 1 |
| 69202 | cobijaba | 1 |
| 69203 | cobierta | 1 |
| 69204 | cobi | 1 |
| 69205 | cobertizos | 1 |
| 69206 | coberteras | 1 |
| 69207 | cobdyçia | 1 |
| 69208 | cobdiçiosso | 1 |
| 69209 | cobdiçiosos | 1 |
| 69210 | cobdiciosos | 1 |
| 69211 | cobdicioso | 1 |
| 69212 | cobdiçióla | 1 |
| 69213 | cobdiçió | 1 |
| 69214 | cobdiçio | 1 |
| 69215 | cobdicio | 1 |
| 69216 | cobdiçie | 1 |
| 69217 | cobdiçiava | 1 |
| 69218 | cobdiçiaron | 1 |
| 69219 | cobdiciando | 1 |
| 69220 | cobdiçi | 1 |
| 69221 | cobardón | 1 |
| 69222 | cobarden | 1 |
| 69223 | cobalto | 1 |
| 69224 | coartar | 1 |
| 69225 | coadjutores | 1 |
| 69226 | coacción | 1 |
| 69227 | cnde | 1 |
| 69228 | cloris | 1 |
| 69229 | cloral | 1 |
| 69230 | cloacas | 1 |
| 69231 | clizan | 1 |
| 69232 | clíticas | 1 |
| 69233 | clistenestra | 1 |
| 69234 | climatológica | 1 |
| 69235 | climas | 1 |
| 69236 | clientula | 1 |
| 69237 | clientes | 1 |
| 69238 | clientela | 1 |
| 69239 | clicie | 1 |
| 69240 | cleto | 1 |
| 69241 | clerófobo | 1 |
| 69242 | clerofobia | 1 |
| 69243 | clerófoba | 1 |
| 69244 | clerizones | 1 |
| 69245 | clerisones | 1 |
| 69246 | clerigos | 1 |
| 69247 | clerigo | 1 |
| 69248 | clericalis | 1 |
| 69249 | clerezía | 1 |
| 69250 | cleresía | 1 |
| 69251 | clerecía | 1 |
| 69252 | cleopatra | 1 |
| 69253 | clenardo | 1 |
| 69254 | clemencín | 1 |
| 69255 | cleantes | 1 |
| 69256 | clavósele | 1 |
| 69257 | clavetee | 1 |
| 69258 | claveteara | 1 |
| 69259 | claveteados | 1 |
| 69260 | claveteada | 1 |
| 69261 | claven | 1 |
| 69262 | clavásedes | 1 |
| 69263 | clavase | 1 |
| 69264 | clavársele | 1 |
| 69265 | clavarlos | 1 |
| 69266 | clavarles | 1 |
| 69267 | clavarla | 1 |
| 69268 | clavarás | 1 |
| 69269 | clavaran | 1 |
| 69270 | clavamos | 1 |
| 69271 | clavá | 1 |
| 69272 | clausura | 1 |
| 69273 | claustros | 1 |
| 69274 | claustras | 1 |
| 69275 | claustra | 1 |
| 69276 | clauquel | 1 |
| 69277 | clauellinas | 1 |
| 69278 | claudina | 1 |
| 69279 | claudicantes | 1 |
| 69280 | claudiana | 1 |
| 69281 | classense | 1 |
| 69282 | class | 1 |
| 69283 | clasificarse | 1 |
| 69284 | clasificarla | 1 |
| 69285 | clasificando | 1 |
| 69286 | clasificación | 1 |
| 69287 | clasifica | 1 |
| 69288 | clasicismo | 1 |
| 69289 | clásicas | 1 |
| 69290 | clarus | 1 |
| 69291 | clarucho | 1 |
| 69292 | claror | 1 |
| 69293 | claroescuro | 1 |
| 69294 | clarinete | 1 |
| 69295 | clarimientes | 1 |
| 69296 | clarificado | 1 |
| 69297 | claridiana | 1 |
| 69298 | claréate | 1 |
| 69299 | clarea | 1 |
| 69300 | claquín | 1 |
| 69301 | claqueteo | 1 |
| 69302 | clandestinos | 1 |
| 69303 | clamores | 1 |
| 69304 | clamoreó | 1 |
| 69305 | clamoreaba | 1 |
| 69306 | clamen | 1 |
| 69307 | clamas | 1 |
| 69308 | clamar | 1 |
| 69309 | clamando | 1 |
| 69310 | clamamos | 1 |
| 69311 | cladera | 1 |
| 69312 | clabos | 1 |
| 69313 | clabar | 1 |
| 69314 | cla | 1 |
| 69315 | cizañoso | 1 |
| 69316 | civita | 1 |
| 69317 | civis | 1 |
| 69318 | civilizo | 1 |
| 69319 | civilizadas | 1 |
| 69320 | civilizaciones | 1 |
| 69321 | ciutti | 1 |
| 69322 | ciudadana | 1 |
| 69323 | citutina | 1 |
| 69324 | cítola | 1 |
| 69325 | citola | 1 |
| 69326 | citita | 1 |
| 69327 | citia | 1 |
| 69328 | citen | 1 |
| 69329 | cite | 1 |
| 69330 | citarse | 1 |
| 69331 | citaron | 1 |
| 69332 | citación | 1 |
| 69333 | cisuras | 1 |
| 69334 | çistel | 1 |
| 69335 | çisne | 1 |
| 69336 | cismáticos | 1 |
| 69337 | ciscos | 1 |
| 69338 | cirujanitos | 1 |
| 69339 | ciruelo | 1 |
| 69340 | cirrus | 1 |
| 69341 | cirineo | 1 |
| 69342 | cirilo | 1 |
| 69343 | circustancias | 1 |
| 69344 | circuspición | 1 |
| 69345 | circunvestida | 1 |
| 69346 | circunvecina | 1 |
| 69347 | circunstante | 1 |
| 69348 | circunstanciales | 1 |
| 69349 | circunspecta | 1 |
| 69350 | circunloquio | 1 |
| 69351 | circunferencias | 1 |
| 69352 | circundan | 1 |
| 69353 | circundaba | 1 |
| 69354 | circulo | 1 |
| 69355 | circulito | 1 |
| 69356 | circulillos | 1 |
| 69357 | circulando | 1 |
| 69358 | circula | 1 |
| 69359 | ciquiña | 1 |
| 69360 | cipria | 1 |
| 69361 | cipresses | 1 |
| 69362 | cipion | 1 |
| 69363 | ciñósela | 1 |
| 69364 | ciñiéndole | 1 |
| 69365 | ciñese | 1 |
| 69366 | ciñéndonos | 1 |
| 69367 | ciñendo | 1 |
| 69368 | cíñalo | 1 |
| 69369 | ciña | 1 |
| 69370 | cinturas | 1 |
| 69371 | cintita | 1 |
| 69372 | cintillo | 1 |
| 69373 | çintas | 1 |
| 69374 | cintarearlo | 1 |
| 69375 | cintarazos | 1 |
| 69376 | cintajo | 1 |
| 69377 | çinorias | 1 |
| 69378 | cínicamente | 1 |
| 69379 | cínica | 1 |
| 69380 | cinen | 1 |
| 69381 | cinegético | 1 |
| 69382 | cinegéticas | 1 |
| 69383 | cincuentona | 1 |
| 69384 | cinchar | 1 |
| 69385 | cinchalle | 1 |
| 69386 | cinammomo | 1 |
| 69387 | cimodocea | 1 |
| 69388 | cimitarra | 1 |
| 69389 | çiminteryo | 1 |
| 69390 | çiminterios | 1 |
| 69391 | çiminterio | 1 |
| 69392 | çimiento | 1 |
| 69393 | cimentador | 1 |
| 69394 | cimentadas | 1 |
| 69395 | cimbros | 1 |
| 69396 | cimbréis | 1 |
| 69397 | cimarrón | 1 |
| 69398 | cimarra | 1 |
| 69399 | çillero | 1 |
| 69400 | cilipín | 1 |
| 69401 | cilindro | 1 |
| 69402 | cilíndricos | 1 |
| 69403 | cigüeñas | 1 |
| 69404 | çigueña | 1 |
| 69405 | cigueña | 1 |
| 69406 | ciguenas | 1 |
| 69407 | ciguena | 1 |
| 69408 | cigoñinos | 1 |
| 69409 | cigarreras | 1 |
| 69410 | cifró | 1 |
| 69411 | cifre | 1 |
| 69412 | cifrarse | 1 |
| 69413 | cifrado | 1 |
| 69414 | cifradas | 1 |
| 69415 | cifraba | 1 |
| 69416 | cierzos | 1 |
| 69417 | ciervas | 1 |
| 69418 | çierva | 1 |
| 69419 | cieruo | 1 |
| 69420 | çierro | 1 |
| 69421 | ciérrese | 1 |
| 69422 | cierren | 1 |
| 69423 | çiérrate | 1 |
| 69424 | ciérrase | 1 |
| 69425 | cierrase | 1 |
| 69426 | ciérranse | 1 |
| 69427 | ciérralos | 1 |
| 69428 | çierra | 1 |
| 69429 | ciernes | 1 |
| 69430 | científicos | 1 |
| 69431 | cienfuegos | 1 |
| 69432 | çiençias | 1 |
| 69433 | ciençia | 1 |
| 69434 | cielito | 1 |
| 69435 | ciel | 1 |
| 69436 | cieguito | 1 |
| 69437 | cieguen | 1 |
| 69438 | çiégaslos | 1 |
| 69439 | ciégale | 1 |
| 69440 | cidras | 1 |
| 69441 | cides | 1 |
| 69442 | cicutina | 1 |
| 69443 | ciclopios | 1 |
| 69444 | ciclópea | 1 |
| 69445 | ciclones | 1 |
| 69446 | ciclo | 1 |
| 69447 | cíclades | 1 |
| 69448 | ciceronianca | 1 |
| 69449 | cicatrizar | 1 |
| 69450 | cicateros | 1 |
| 69451 | cibeles | 1 |
| 69452 | cibdat | 1 |
| 69453 | cibdades | 1 |
| 69454 | çibdadano | 1 |
| 69455 | cibdadana | 1 |
| 69456 | cianuro | 1 |
| 69457 | ci | 1 |
| 69458 | chycos | 1 |
| 69459 | chycas | 1 |
| 69460 | chyca | 1 |
| 69461 | chusquin | 1 |
| 69462 | chuscada | 1 |
| 69463 | chusca | 1 |
| 69464 | churumbeles | 1 |
| 69465 | churumbelas | 1 |
| 69466 | churrillera | 1 |
| 69467 | churriguerescos | 1 |
| 69468 | churras | 1 |
| 69469 | churia | 1 |
| 69470 | chupó | 1 |
| 69471 | chupío | 1 |
| 69472 | chupetín | 1 |
| 69473 | chupé | 1 |
| 69474 | chupase | 1 |
| 69475 | chupas | 1 |
| 69476 | chuparse | 1 |
| 69477 | chuparle | 1 |
| 69478 | chuparla | 1 |
| 69479 | chupándose | 1 |
| 69480 | chupándolos | 1 |
| 69481 | chupándole | 1 |
| 69482 | chupados | 1 |
| 69483 | chupada | 1 |
| 69484 | chupaban | 1 |
| 69485 | chumbo | 1 |
| 69486 | chulito | 1 |
| 69487 | chulesco | 1 |
| 69488 | chulesca | 1 |
| 69489 | chula | 1 |
| 69490 | chufetas | 1 |
| 69491 | chufeta | 1 |
| 69492 | chuferos | 1 |
| 69493 | chu | 1 |
| 69494 | christophorus | 1 |
| 69495 | christo | 1 |
| 69496 | christiano | 1 |
| 69497 | christi | 1 |
| 69498 | chozo | 1 |
| 69499 | chovelar | 1 |
| 69500 | chorritos | 1 |
| 69501 | chorretadas | 1 |
| 69502 | chorreras | 1 |
| 69503 | chorrear | 1 |
| 69504 | chorrean | 1 |
| 69505 | choquezuelas | 1 |
| 69506 | choquezuela | 1 |
| 69507 | choques | 1 |
| 69508 | chopa | 1 |
| 69509 | chomel | 1 |
| 69510 | chollas | 1 |
| 69511 | choconos | 1 |
| 69512 | chocome | 1 |
| 69513 | chocolatero | 1 |
| 69514 | chocoa | 1 |
| 69515 | chocó | 1 |
| 69516 | chocló | 1 |
| 69517 | chochos | 1 |
| 69518 | chocheemos | 1 |
| 69519 | chochas | 1 |
| 69520 | chocasen | 1 |
| 69521 | chocarrerías | 1 |
| 69522 | chocarrera | 1 |
| 69523 | chocarrear | 1 |
| 69524 | chocarían | 1 |
| 69525 | chocantes | 1 |
| 69526 | chocamos | 1 |
| 69527 | chistosos | 1 |
| 69528 | chistosísima | 1 |
| 69529 | chisto | 1 |
| 69530 | chisterómetro | 1 |
| 69531 | chistasen | 1 |
| 69532 | chistaré | 1 |
| 69533 | chistara | 1 |
| 69534 | chispos | 1 |
| 69535 | chisporroteos | 1 |
| 69536 | chisporroteó | 1 |
| 69537 | chisporroteo | 1 |
| 69538 | chisporroteaba | 1 |
| 69539 | chisporrotea | 1 |
| 69540 | chispillas | 1 |
| 69541 | chispazos | 1 |
| 69542 | chismorreo | 1 |
| 69543 | chismorreando | 1 |
| 69544 | chismorreaban | 1 |
| 69545 | chismográfico | 1 |
| 69546 | chismografías | 1 |
| 69547 | chismajos | 1 |
| 69548 | chisgarabís | 1 |
| 69549 | chirrión | 1 |
| 69550 | chirrío | 1 |
| 69551 | chirlería | 1 |
| 69552 | chirlava | 1 |
| 69553 | chirlata | 1 |
| 69554 | chirlando | 1 |
| 69555 | chiripón | 1 |
| 69556 | chirimía | 1 |
| 69557 | chirimbolos | 1 |
| 69558 | chirigotas | 1 |
| 69559 | chiries | 1 |
| 69560 | chiquitos | 1 |
| 69561 | chiquitito | 1 |
| 69562 | chiquitita | 1 |
| 69563 | chiquirrininas | 1 |
| 69564 | chiquillín | 1 |
| 69565 | chiquillería | 1 |
| 69566 | chiquierdi | 1 |
| 69567 | chiquiella | 1 |
| 69568 | chiprïota | 1 |
| 69569 | chingurria | 1 |
| 69570 | chinescos | 1 |
| 69571 | chinela | 1 |
| 69572 | chinchoso | 1 |
| 69573 | chinchorro | 1 |
| 69574 | chinchón | 1 |
| 69575 | chinchillas | 1 |
| 69576 | chinchilla | 1 |
| 69577 | chincharse | 1 |
| 69578 | chinas | 1 |
| 69579 | chillo | 1 |
| 69580 | chille | 1 |
| 69581 | chillaron | 1 |
| 69582 | chilladores | 1 |
| 69583 | chilindrón | 1 |
| 69584 | chifló | 1 |
| 69585 | chiflao | 1 |
| 69586 | chiflaba | 1 |
| 69587 | chicuelos | 1 |
| 69588 | chicoria | 1 |
| 69589 | chicooo | 1 |
| 69590 | chicoleos | 1 |
| 69591 | chicheaban | 1 |
| 69592 | chicha | 1 |
| 69593 | chiaror | 1 |
| 69594 | chevrière | 1 |
| 69595 | cherriadores | 1 |
| 69596 | cherevías | 1 |
| 69597 | che | 1 |
| 69598 | chaza | 1 |
| 69599 | chavo | 1 |
| 69600 | chauvinisme | 1 |
| 69601 | chaubandidegui | 1 |
| 69602 | chatas | 1 |
| 69603 | chassepot | 1 |
| 69604 | chasquidos | 1 |
| 69605 | chasqueada | 1 |
| 69606 | chasqueaba | 1 |
| 69607 | chascarrillo | 1 |
| 69608 | charrán | 1 |
| 69609 | charoles | 1 |
| 69610 | charoladas | 1 |
| 69611 | charní | 1 |
| 69612 | charlatanes | 1 |
| 69613 | charlas | 1 |
| 69614 | charlaría | 1 |
| 69615 | charlaremos | 1 |
| 69616 | charada | 1 |
| 69617 | chaquetillas | 1 |
| 69618 | chaquet | 1 |
| 69619 | chapuzarse | 1 |
| 69620 | chapuzan | 1 |
| 69621 | chapuzaba | 1 |
| 69622 | chapurraba | 1 |
| 69623 | chapoteo | 1 |
| 69624 | chapoteaban | 1 |
| 69625 | chapiteles | 1 |
| 69626 | chapitel | 1 |
| 69627 | chapinazos | 1 |
| 69628 | chapín | 1 |
| 69629 | chapin | 1 |
| 69630 | chapeo | 1 |
| 69631 | chapeados | 1 |
| 69632 | chapalangarra | 1 |
| 69633 | chapada | 1 |
| 69634 | chanto | 1 |
| 69635 | chantal | 1 |
| 69636 | chanson | 1 |
| 69637 | chanflones | 1 |
| 69638 | chanfaina | 1 |
| 69639 | chandan | 1 |
| 69640 | chancleta | 1 |
| 69641 | chancillerías | 1 |
| 69642 | chancee | 1 |
| 69643 | chance | 1 |
| 69644 | chamuscan | 1 |
| 69645 | chamuscamos | 1 |
| 69646 | chamuscado | 1 |
| 69647 | champignons | 1 |
| 69648 | chambritas | 1 |
| 69649 | chambones | 1 |
| 69650 | chambelán | 1 |
| 69651 | chamartín | 1 |
| 69652 | chalets | 1 |
| 69653 | chalanesco | 1 |
| 69654 | chalanescas | 1 |
| 69655 | chalanes | 1 |
| 69656 | chalaneaba | 1 |
| 69657 | chafé | 1 |
| 69658 | chafarrinones | 1 |
| 69659 | chafarote | 1 |
| 69660 | chafaron | 1 |
| 69661 | chafarle | 1 |
| 69662 | chacxu | 1 |
| 69663 | chacorrerías | 1 |
| 69664 | chacó | 1 |
| 69665 | chachito | 1 |
| 69666 | ch | 1 |
| 69667 | çevera | 1 |
| 69668 | çevadas | 1 |
| 69669 | ceuasnos | 1 |
| 69670 | ceuara | 1 |
| 69671 | ceuan | 1 |
| 69672 | cette | 1 |
| 69673 | cetrino | 1 |
| 69674 | cetrera | 1 |
| 69675 | cestos | 1 |
| 69676 | çesto | 1 |
| 69677 | cestito | 1 |
| 69678 | çestilla | 1 |
| 69679 | çestil | 1 |
| 69680 | çesta | 1 |
| 69681 | cesso | 1 |
| 69682 | cessen | 1 |
| 69683 | cessasse | 1 |
| 69684 | cessara | 1 |
| 69685 | cessar | 1 |
| 69686 | cesitas | 1 |
| 69687 | cesarían | 1 |
| 69688 | cesaría | 1 |
| 69689 | cesarán | 1 |
| 69690 | cesaran | 1 |
| 69691 | cesara | 1 |
| 69692 | cesantías | 1 |
| 69693 | cesan | 1 |
| 69694 | cervino | 1 |
| 69695 | çerviçes | 1 |
| 69696 | cerviçes | 1 |
| 69697 | cervellón | 1 |
| 69698 | cervantesca | 1 |
| 69699 | cervántes | 1 |
| 69700 | cerúleos | 1 |
| 69701 | ceruiz | 1 |
| 69702 | certísimos | 1 |
| 69703 | certísimo | 1 |
| 69704 | certísimas | 1 |
| 69705 | certísima | 1 |
| 69706 | certificóme | 1 |
| 69707 | certificarse | 1 |
| 69708 | certificáronle | 1 |
| 69709 | certificaron | 1 |
| 69710 | certificarme | 1 |
| 69711 | certificándose | 1 |
| 69712 | certificándoles | 1 |
| 69713 | certificame | 1 |
| 69714 | certificación | 1 |
| 69715 | certifica | 1 |
| 69716 | certería | 1 |
| 69717 | certera | 1 |
| 69718 | çertenidad | 1 |
| 69719 | certenidad | 1 |
| 69720 | çerteficado | 1 |
| 69721 | certámenes | 1 |
| 69722 | cerróse | 1 |
| 69723 | çerros | 1 |
| 69724 | cerrole | 1 |
| 69725 | çerro | 1 |
| 69726 | cerréme | 1 |
| 69727 | cerras | 1 |
| 69728 | çerraron | 1 |
| 69729 | cerrarle | 1 |
| 69730 | cerrarla | 1 |
| 69731 | çerrarías | 1 |
| 69732 | çerraré | 1 |
| 69733 | cerraré | 1 |
| 69734 | cerrarán | 1 |
| 69735 | cerrará | 1 |
| 69736 | cerrara | 1 |
| 69737 | cerrándose | 1 |
| 69738 | cerrándoles | 1 |
| 69739 | cerramiento | 1 |
| 69740 | cerrallos | 1 |
| 69741 | çerraduras | 1 |
| 69742 | çerrados | 1 |
| 69743 | cerrábase | 1 |
| 69744 | cerora | 1 |
| 69745 | cernida | 1 |
| 69746 | cernía | 1 |
| 69747 | çermeña | 1 |
| 69748 | cerimonia | 1 |
| 69749 | cerería | 1 |
| 69750 | cereras | 1 |
| 69751 | ceremoniosos | 1 |
| 69752 | ceremoniosamente | 1 |
| 69753 | çereça | 1 |
| 69754 | cerebros | 1 |
| 69755 | cereales | 1 |
| 69756 | cerdosa | 1 |
| 69757 | cerdear | 1 |
| 69758 | cerdea | 1 |
| 69759 | çercól | 1 |
| 69760 | cercioraba | 1 |
| 69761 | cercenarla | 1 |
| 69762 | cercenara | 1 |
| 69763 | cercenar | 1 |
| 69764 | cercenadora | 1 |
| 69765 | cercenado | 1 |
| 69766 | çercava | 1 |
| 69767 | çercanos | 1 |
| 69768 | cercanías | 1 |
| 69769 | çercanas | 1 |
| 69770 | çercana | 1 |
| 69771 | cercados | 1 |
| 69772 | cercadas | 1 |
| 69773 | çercada | 1 |
| 69774 | cerbero | 1 |
| 69775 | cerbatanas | 1 |
| 69776 | cerámica | 1 |
| 69777 | cerá | 1 |
| 69778 | çera | 1 |
| 69779 | çepos | 1 |
| 69780 | cepos | 1 |
| 69781 | cepillos | 1 |
| 69782 | cepilla | 1 |
| 69783 | cepas | 1 |
| 69784 | cepacauallo | 1 |
| 69785 | çepa | 1 |
| 69786 | ceñudos | 1 |
| 69787 | ceños | 1 |
| 69788 | ceñores | 1 |
| 69789 | ceñirme | 1 |
| 69790 | ceñirle | 1 |
| 69791 | çeñiglo | 1 |
| 69792 | ceñidor | 1 |
| 69793 | çeñida | 1 |
| 69794 | ceñíale | 1 |
| 69795 | centuria | 1 |
| 69796 | centuplicado | 1 |
| 69797 | centuplica | 1 |
| 69798 | centrípeto | 1 |
| 69799 | céntrica | 1 |
| 69800 | centralizar | 1 |
| 69801 | centón | 1 |
| 69802 | centímetros | 1 |
| 69803 | centímetro | 1 |
| 69804 | centésimo | 1 |
| 69805 | centésima | 1 |
| 69806 | çentenos | 1 |
| 69807 | centenos | 1 |
| 69808 | centenil | 1 |
| 69809 | centenes | 1 |
| 69810 | centenario | 1 |
| 69811 | centenar | 1 |
| 69812 | centelleo | 1 |
| 69813 | centellearon | 1 |
| 69814 | centellear | 1 |
| 69815 | centelleantes | 1 |
| 69816 | centelleaba | 1 |
| 69817 | centellante | 1 |
| 69818 | censuró | 1 |
| 69819 | censuren | 1 |
| 69820 | censurando | 1 |
| 69821 | censuradores | 1 |
| 69822 | censos | 1 |
| 69823 | censoria | 1 |
| 69824 | censeurs | 1 |
| 69825 | cenóse | 1 |
| 69826 | çenorias | 1 |
| 69827 | cenizoso | 1 |
| 69828 | cenital | 1 |
| 69829 | cenido | 1 |
| 69830 | çenico | 1 |
| 69831 | ceniciento | 1 |
| 69832 | cenicientas | 1 |
| 69833 | cenemos | 1 |
| 69834 | cenefa | 1 |
| 69835 | cencerruna | 1 |
| 69836 | çençerros | 1 |
| 69837 | çencerro | 1 |
| 69838 | cencerril | 1 |
| 69839 | cencerreo | 1 |
| 69840 | cencerrar | 1 |
| 69841 | cençeño | 1 |
| 69842 | çenava | 1 |
| 69843 | cenaste | 1 |
| 69844 | cenásemos | 1 |
| 69845 | çenas | 1 |
| 69846 | çenaría | 1 |
| 69847 | cenaréis | 1 |
| 69848 | cenaré | 1 |
| 69849 | çenarás | 1 |
| 69850 | cenarás | 1 |
| 69851 | cenará | 1 |
| 69852 | çenar | 1 |
| 69853 | cenan | 1 |
| 69854 | cenagosa | 1 |
| 69855 | cenadas | 1 |
| 69856 | cenábamos | 1 |
| 69857 | çemiento | 1 |
| 69858 | çementerio | 1 |
| 69859 | celtíberos | 1 |
| 69860 | celtas | 1 |
| 69861 | celsitud | 1 |
| 69862 | celonio | 1 |
| 69863 | celle | 1 |
| 69864 | celitos | 1 |
| 69865 | celiplinas | 1 |
| 69866 | celipinillo | 1 |
| 69867 | celipillo | 1 |
| 69868 | celillos | 1 |
| 69869 | çeliçio | 1 |
| 69870 | célicas | 1 |
| 69871 | célibe | 1 |
| 69872 | celibatarios | 1 |
| 69873 | celesti | 1 |
| 69874 | celesta | 1 |
| 69875 | celeres | 1 |
| 69876 | celenque | 1 |
| 69877 | celenio | 1 |
| 69878 | celemines | 1 |
| 69879 | çeledes | 1 |
| 69880 | celebróse | 1 |
| 69881 | celebridades | 1 |
| 69882 | celebremos | 1 |
| 69883 | celebre | 1 |
| 69884 | celebrarte | 1 |
| 69885 | celebrarlos | 1 |
| 69886 | celebrarlo | 1 |
| 69887 | celebrarles | 1 |
| 69888 | celebraría | 1 |
| 69889 | celebraré | 1 |
| 69890 | celebrarán | 1 |
| 69891 | celebrándote | 1 |
| 69892 | celebrándose | 1 |
| 69893 | celebrándola | 1 |
| 69894 | celebralo | 1 |
| 69895 | celebralde | 1 |
| 69896 | celebérrimos | 1 |
| 69897 | çelares | 1 |
| 69898 | celaré | 1 |
| 69899 | çelar | 1 |
| 69900 | çelan | 1 |
| 69901 | çelado | 1 |
| 69902 | çela | 1 |
| 69903 | cejó | 1 |
| 69904 | çejo | 1 |
| 69905 | cejijuntos | 1 |
| 69906 | cejase | 1 |
| 69907 | cejaría | 1 |
| 69908 | cejaba | 1 |
| 69909 | cegué | 1 |
| 69910 | cegarse | 1 |
| 69911 | cegarla | 1 |
| 69912 | cegaras | 1 |
| 69913 | cegara | 1 |
| 69914 | çegar | 1 |
| 69915 | cegar | 1 |
| 69916 | cegalle | 1 |
| 69917 | cefiso | 1 |
| 69918 | cefeo | 1 |
| 69919 | cefalálgicos | 1 |
| 69920 | cefalálgico | 1 |
| 69921 | cedulilla | 1 |
| 69922 | cedieruédas | 1 |
| 69923 | cedas | 1 |
| 69924 | çedaçuelo | 1 |
| 69925 | ceda | 1 |
| 69926 | çeçinas | 1 |
| 69927 | ceçina | 1 |
| 69928 | çeçial | 1 |
| 69929 | ceceo | 1 |
| 69930 | cecear | 1 |
| 69931 | ceceando | 1 |
| 69932 | cebreros | 1 |
| 69933 | cebón | 1 |
| 69934 | cebolluda | 1 |
| 69935 | cébase | 1 |
| 69936 | cebaron | 1 |
| 69937 | cebarla | 1 |
| 69938 | cebar | 1 |
| 69939 | cebados | 1 |
| 69940 | cebadas | 1 |
| 69941 | cebaba | 1 |
| 69942 | cazurro | 1 |
| 69943 | cazuelillo | 1 |
| 69944 | cazuelas | 1 |
| 69945 | cazos | 1 |
| 69946 | cazolón | 1 |
| 69947 | cazoletas | 1 |
| 69948 | cazoleros | 1 |
| 69949 | cazó | 1 |
| 69950 | cazcarrias | 1 |
| 69951 | cazaron | 1 |
| 69952 | cazarlo | 1 |
| 69953 | cazarle | 1 |
| 69954 | cazarla | 1 |
| 69955 | cazara | 1 |
| 69956 | cazan | 1 |
| 69957 | cazaderos | 1 |
| 69958 | cazable | 1 |
| 69959 | cayose | 1 |
| 69960 | cayn | 1 |
| 69961 | caygo | 1 |
| 69962 | caygas | 1 |
| 69963 | caygan | 1 |
| 69964 | cayéronle | 1 |
| 69965 | cayeras | 1 |
| 69966 | cayer | 1 |
| 69967 | cayen | 1 |
| 69968 | caye | 1 |
| 69969 | cayas | 1 |
| 69970 | cayaras | 1 |
| 69971 | caxuela | 1 |
| 69972 | caxquillo | 1 |
| 69973 | caxquetes | 1 |
| 69974 | cavour | 1 |
| 69975 | cavó | 1 |
| 69976 | caviles | 1 |
| 69977 | cavilarás | 1 |
| 69978 | cavila | 1 |
| 69979 | cavidades | 1 |
| 69980 | cavial | 1 |
| 69981 | cavernoso | 1 |
| 69982 | cavernosas | 1 |
| 69983 | caveant | 1 |
| 69984 | cavase | 1 |
| 69985 | cavas | 1 |
| 69986 | cavallunos | 1 |
| 69987 | cavallos | 1 |
| 69988 | cavallerías | 1 |
| 69989 | cavallar | 1 |
| 69990 | cavalgo | 1 |
| 69991 | cavalgar | 1 |
| 69992 | cavalgaduras | 1 |
| 69993 | cavalgadas | 1 |
| 69994 | cavalga | 1 |
| 69995 | cavalcanti | 1 |
| 69996 | cavaglieri | 1 |
| 69997 | cavadura | 1 |
| 69998 | cavaban | 1 |
| 69999 | cavaba | 1 |
| 70000 | cautivastes | 1 |
| 70001 | cautivas | 1 |
| 70002 | cautivarla | 1 |
| 70003 | cautivamos | 1 |
| 70004 | cautivábale | 1 |
| 70005 | cautiuo | 1 |
| 70006 | cautiuaste | 1 |
| 70007 | cauterios | 1 |
| 70008 | cautelosos | 1 |
| 70009 | cauteloso | 1 |
| 70010 | causóme | 1 |
| 70011 | causóle | 1 |
| 70012 | causaste | 1 |
| 70013 | causaría | 1 |
| 70014 | causarán | 1 |
| 70015 | causaran | 1 |
| 70016 | causantes | 1 |
| 70017 | causándole | 1 |
| 70018 | causados | 1 |
| 70019 | causadores | 1 |
| 70020 | causada | 1 |
| 70021 | causábanle | 1 |
| 70022 | caulis | 1 |
| 70023 | caudalosos | 1 |
| 70024 | caudalosas | 1 |
| 70025 | caudalito | 1 |
| 70026 | caualleria | 1 |
| 70027 | catyvos | 1 |
| 70028 | catyva | 1 |
| 70029 | catorze | 1 |
| 70030 | catorceno | 1 |
| 70031 | catóptrico | 1 |
| 70032 | catóptrica | 1 |
| 70033 | catonis | 1 |
| 70034 | catonianas | 1 |
| 70035 | caton | 1 |
| 70036 | catoliquísima | 1 |
| 70037 | católicamente | 1 |
| 70038 | catiuos | 1 |
| 70039 | catiuome | 1 |
| 70040 | catiuanse | 1 |
| 70041 | catiuan | 1 |
| 70042 | catiuadola | 1 |
| 70043 | catiuada | 1 |
| 70044 | catilinario | 1 |
| 70045 | catilina | 1 |
| 70046 | cathreda | 1 |
| 70047 | cathólico | 1 |
| 70048 | catholicæ | 1 |
| 70049 | cathelineau | 1 |
| 70050 | cathedra | 1 |
| 70051 | cates | 1 |
| 70052 | catequizó | 1 |
| 70053 | catequizador | 1 |
| 70054 | categóricarnente | 1 |
| 70055 | catedráticos | 1 |
| 70056 | catedrática | 1 |
| 70057 | catedra | 1 |
| 70058 | catedes | 1 |
| 70059 | catecúmenos | 1 |
| 70060 | catecúmeno | 1 |
| 70061 | catecúmena | 1 |
| 70062 | cataste | 1 |
| 70063 | catas | 1 |
| 70064 | catarrosos | 1 |
| 70065 | catarriberas | 1 |
| 70066 | catarribera | 1 |
| 70067 | catarral | 1 |
| 70068 | cátaros | 1 |
| 70069 | catarle | 1 |
| 70070 | catarían | 1 |
| 70071 | cataré | 1 |
| 70072 | cataplasma | 1 |
| 70073 | catándole | 1 |
| 70074 | cátame | 1 |
| 70075 | catalunga | 1 |
| 70076 | cátalo | 1 |
| 70077 | cataliñ | 1 |
| 70078 | catale | 1 |
| 70079 | cátalas | 1 |
| 70080 | catalanas | 1 |
| 70081 | catafalcos | 1 |
| 70082 | catades | 1 |
| 70083 | catacumbas | 1 |
| 70084 | cataba | 1 |
| 70085 | casus | 1 |
| 70086 | casuismo | 1 |
| 70087 | castros | 1 |
| 70088 | castraron | 1 |
| 70089 | castrametación | 1 |
| 70090 | castrador | 1 |
| 70091 | cástor | 1 |
| 70092 | castizo | 1 |
| 70093 | castimonia | 1 |
| 70094 | castillito | 1 |
| 70095 | castillete | 1 |
| 70096 | castillas | 1 |
| 70097 | castillans | 1 |
| 70098 | castíguese | 1 |
| 70099 | castigues | 1 |
| 70100 | castíguense | 1 |
| 70101 | castigué | 1 |
| 70102 | castiglione | 1 |
| 70103 | castígate | 1 |
| 70104 | castigase | 1 |
| 70105 | castigarnos | 1 |
| 70106 | castigarles | 1 |
| 70107 | castigarias | 1 |
| 70108 | castigaría | 1 |
| 70109 | castigaré | 1 |
| 70110 | castigaran | 1 |
| 70111 | castigan | 1 |
| 70112 | castígalos | 1 |
| 70113 | castigallos | 1 |
| 70114 | castigadvos | 1 |
| 70115 | castiello | 1 |
| 70116 | castidat | 1 |
| 70117 | castella | 1 |
| 70118 | castelet | 1 |
| 70119 | castañetazo | 1 |
| 70120 | castañeta | 1 |
| 70121 | castañeras | 1 |
| 70122 | castañedos | 1 |
| 70123 | castañares | 1 |
| 70124 | castanas | 1 |
| 70125 | casseras | 1 |
| 70126 | cassase | 1 |
| 70127 | cassarme | 1 |
| 70128 | cassadas | 1 |
| 70129 | cassada | 1 |
| 70130 | casquivano | 1 |
| 70131 | casquillo | 1 |
| 70132 | casquería | 1 |
| 70133 | caspitina | 1 |
| 70134 | caspe | 1 |
| 70135 | casmines | 1 |
| 70136 | casitas | 1 |
| 70137 | casimodo | 1 |
| 70138 | casimiro | 1 |
| 70139 | casimir | 1 |
| 70140 | casetón | 1 |
| 70141 | casetas | 1 |
| 70142 | caserías | 1 |
| 70143 | caseramente | 1 |
| 70144 | caseosa | 1 |
| 70145 | casen | 1 |
| 70146 | casémonos | 1 |
| 70147 | caseme | 1 |
| 70148 | casedes | 1 |
| 70149 | cascotes | 1 |
| 70150 | cascaveles | 1 |
| 70151 | cascarones | 1 |
| 70152 | cascarla | 1 |
| 70153 | cascarilla | 1 |
| 70154 | cascarazo | 1 |
| 70155 | cascara | 1 |
| 70156 | cascado | 1 |
| 70157 | cascadas | 1 |
| 70158 | casca | 1 |
| 70159 | casasen | 1 |
| 70160 | casarvos | 1 |
| 70161 | casáronse | 1 |
| 70162 | casarón | 1 |
| 70163 | casarmiento | 1 |
| 70164 | casármela | 1 |
| 70165 | casarm | 1 |
| 70166 | casarlo | 1 |
| 70167 | casarle | 1 |
| 70168 | casarlas | 1 |
| 70169 | casárase | 1 |
| 70170 | casáramos | 1 |
| 70171 | casándose | 1 |
| 70172 | casándola | 1 |
| 70173 | casámonos | 1 |
| 70174 | casamenteras | 1 |
| 70175 | casamentera | 1 |
| 70176 | casamatas | 1 |
| 70177 | casallas | 1 |
| 70178 | cásale | 1 |
| 70179 | casadla | 1 |
| 70180 | casaditas | 1 |
| 70181 | casadita | 1 |
| 70182 | casacón | 1 |
| 70183 | casacas | 1 |
| 70184 | casabas | 1 |
| 70185 | cas | 1 |
| 70186 | cartuchería | 1 |
| 70187 | cartoncejo | 1 |
| 70188 | cartita | 1 |
| 70189 | cartica | 1 |
| 70190 | carteta | 1 |
| 70191 | carteros | 1 |
| 70192 | cartelón | 1 |
| 70193 | cartelero | 1 |
| 70194 | cartelas | 1 |
| 70195 | cartela | 1 |
| 70196 | carteaba | 1 |
| 70197 | cártama | 1 |
| 70198 | cartajena | 1 |
| 70199 | carromateros | 1 |
| 70200 | carrizales | 1 |
| 70201 | carrión | 1 |
| 70202 | carriola | 1 |
| 70203 | carrilleras | 1 |
| 70204 | carrillera | 1 |
| 70205 | carrilladas | 1 |
| 70206 | carricoches | 1 |
| 70207 | carrick | 1 |
| 70208 | carricaburo | 1 |
| 70209 | carretón | 1 |
| 70210 | carretes | 1 |
| 70211 | carreritas | 1 |
| 70212 | carraspiques | 1 |
| 70213 | carraspera | 1 |
| 70214 | carraspeó | 1 |
| 70215 | carraspeo | 1 |
| 70216 | carraspeaba | 1 |
| 70217 | carrash | 1 |
| 70218 | carrascas | 1 |
| 70219 | carrascales | 1 |
| 70220 | carrancas | 1 |
| 70221 | carrales | 1 |
| 70222 | carracas | 1 |
| 70223 | carraca | 1 |
| 70224 | carquesio | 1 |
| 70225 | carpían | 1 |
| 70226 | carpetazo | 1 |
| 70227 | carpetas | 1 |
| 70228 | carpas | 1 |
| 70229 | carón | 1 |
| 70230 | carolo | 1 |
| 70231 | carolina | 1 |
| 70232 | carolea | 1 |
| 70233 | carnosos | 1 |
| 70234 | carnosas | 1 |
| 70235 | carnosa | 1 |
| 70236 | carnieras | 1 |
| 70237 | carniçeros | 1 |
| 70238 | carniçería | 1 |
| 70239 | carner | 1 |
| 70240 | carnecitas | 1 |
| 70241 | carnazas | 1 |
| 70242 | carnavalescos | 1 |
| 70243 | carnavalesco | 1 |
| 70244 | carnavalesca | 1 |
| 70245 | carn | 1 |
| 70246 | carminoso | 1 |
| 70247 | carloto | 1 |
| 70248 | carlo | 1 |
| 70249 | carlistona | 1 |
| 70250 | carlistón | 1 |
| 70251 | carlanca | 1 |
| 70252 | carirredondo | 1 |
| 70253 | carirredonda | 1 |
| 70254 | cariñena | 1 |
| 70255 | carininfos | 1 |
| 70256 | carilleno | 1 |
| 70257 | carilla | 1 |
| 70258 | caricato | 1 |
| 70259 | caribe | 1 |
| 70260 | caribdis | 1 |
| 70261 | caria | 1 |
| 70262 | cargues | 1 |
| 70263 | cárguenlo | 1 |
| 70264 | cargase | 1 |
| 70265 | cargarlo | 1 |
| 70266 | cargaría | 1 |
| 70267 | cargarás | 1 |
| 70268 | cargaran | 1 |
| 70269 | cargara | 1 |
| 70270 | cargantísimo | 1 |
| 70271 | cargantes | 1 |
| 70272 | cargándole | 1 |
| 70273 | cargandola | 1 |
| 70274 | cargamos | 1 |
| 70275 | cargalle | 1 |
| 70276 | cargadita | 1 |
| 70277 | cargábanle | 1 |
| 70278 | carezco | 1 |
| 70279 | carezcan | 1 |
| 70280 | carezcamos | 1 |
| 70281 | carescia | 1 |
| 70282 | caresceys | 1 |
| 70283 | caresce | 1 |
| 70284 | carencias | 1 |
| 70285 | carena | 1 |
| 70286 | careciessen | 1 |
| 70287 | careciese | 1 |
| 70288 | careciere | 1 |
| 70289 | carecieran | 1 |
| 70290 | careciera | 1 |
| 70291 | carecíamos | 1 |
| 70292 | careceras | 1 |
| 70293 | carecemos | 1 |
| 70294 | careaba | 1 |
| 70295 | cardona | 1 |
| 70296 | cardiopatía | 1 |
| 70297 | cardinales | 1 |
| 70298 | cardíacos | 1 |
| 70299 | cardiaca | 1 |
| 70300 | cardec | 1 |
| 70301 | cardarle | 1 |
| 70302 | cardar | 1 |
| 70303 | cardan | 1 |
| 70304 | cardada | 1 |
| 70305 | carcundas | 1 |
| 70306 | carcomido | 1 |
| 70307 | carcomidas | 1 |
| 70308 | carcomen | 1 |
| 70309 | carcoma | 1 |
| 70310 | çarçillo | 1 |
| 70311 | çarçiellos | 1 |
| 70312 | carceres | 1 |
| 70313 | carceleros | 1 |
| 70314 | cárçel | 1 |
| 70315 | carcaño | 1 |
| 70316 | carcañares | 1 |
| 70317 | carcamal | 1 |
| 70318 | carcajona | 1 |
| 70319 | carcajadita | 1 |
| 70320 | çarça | 1 |
| 70321 | carbunclo | 1 |
| 70322 | carbonizaban | 1 |
| 70323 | carboniento | 1 |
| 70324 | carbonatadas | 1 |
| 70325 | carbonada | 1 |
| 70326 | carbayeda | 1 |
| 70327 | caravanas | 1 |
| 70328 | carátulas | 1 |
| 70329 | caráteres | 1 |
| 70330 | çarapico | 1 |
| 70331 | caramillos | 1 |
| 70332 | carambolas | 1 |
| 70333 | caraiter | 1 |
| 70334 | carado | 1 |
| 70335 | caraculiambro | 1 |
| 70336 | caracterizan | 1 |
| 70337 | caracterizados | 1 |
| 70338 | caracterizadas | 1 |
| 70339 | caracteriza | 1 |
| 70340 | características | 1 |
| 70341 | carácteres | 1 |
| 70342 | caracolitos | 1 |
| 70343 | çaraças | 1 |
| 70344 | çaraça | 1 |
| 70345 | carabinero | 1 |
| 70346 | caraballo | 1 |
| 70347 | caput | 1 |
| 70348 | capuchoncitos | 1 |
| 70349 | capuchón | 1 |
| 70350 | capuchino | 1 |
| 70351 | captivos | 1 |
| 70352 | captividad | 1 |
| 70353 | caps | 1 |
| 70354 | caprichosamente | 1 |
| 70355 | caprichillo | 1 |
| 70356 | capotón | 1 |
| 70357 | capotillos | 1 |
| 70358 | capotas | 1 |
| 70359 | caporalas | 1 |
| 70360 | capitulares | 1 |
| 70361 | capitis | 1 |
| 70362 | capitaneadas | 1 |
| 70363 | capitaneaban | 1 |
| 70364 | capitanas | 1 |
| 70365 | capitalizaba | 1 |
| 70366 | capitalazo | 1 |
| 70367 | capitación | 1 |
| 70368 | capisco | 1 |
| 70369 | capilar | 1 |
| 70370 | caperu | 1 |
| 70371 | capelo | 1 |
| 70372 | capellynas | 1 |
| 70373 | capellyna | 1 |
| 70374 | capellar | 1 |
| 70375 | capelina | 1 |
| 70376 | capearlo | 1 |
| 70377 | capear | 1 |
| 70378 | capean | 1 |
| 70379 | capeadores | 1 |
| 70380 | capeador | 1 |
| 70381 | capeábanle | 1 |
| 70382 | capcioso | 1 |
| 70383 | çapatero | 1 |
| 70384 | caparum | 1 |
| 70385 | capalleja | 1 |
| 70386 | capadocia | 1 |
| 70387 | capada | 1 |
| 70388 | capachos | 1 |
| 70389 | capacha | 1 |
| 70390 | capacetes | 1 |
| 70391 | caótico | 1 |
| 70392 | cañutos | 1 |
| 70393 | cañutillos | 1 |
| 70394 | cañutillo | 1 |
| 70395 | cañoncito | 1 |
| 70396 | cañitas | 1 |
| 70397 | cañilleras | 1 |
| 70398 | cañí | 1 |
| 70399 | cañerías | 1 |
| 70400 | cañedo | 1 |
| 70401 | cañamoncito | 1 |
| 70402 | cañamazo | 1 |
| 70403 | cañadas | 1 |
| 70404 | cantusado | 1 |
| 70405 | canturriaba | 1 |
| 70406 | cantuesos | 1 |
| 70407 | cantueso | 1 |
| 70408 | cantorrios | 1 |
| 70409 | cantorio | 1 |
| 70410 | cantones | 1 |
| 70411 | cantoneros | 1 |
| 70412 | cantonera | 1 |
| 70413 | cantonalismo | 1 |
| 70414 | cantonada | 1 |
| 70415 | cantineros | 1 |
| 70416 | cantina | 1 |
| 70417 | cantimploras | 1 |
| 70418 | cantillana | 1 |
| 70419 | cantil | 1 |
| 70420 | cántiga | 1 |
| 70421 | cantidá | 1 |
| 70422 | canticio | 1 |
| 70423 | canticas | 1 |
| 70424 | cántic | 1 |
| 70425 | cantes | 1 |
| 70426 | canteras | 1 |
| 70427 | canterac | 1 |
| 70428 | canterà | 1 |
| 70429 | cantemos | 1 |
| 70430 | cantéis | 1 |
| 70431 | cantazo | 1 |
| 70432 | cantays | 1 |
| 70433 | cantavan | 1 |
| 70434 | cantávalo | 1 |
| 70435 | cantava | 1 |
| 70436 | cantats | 1 |
| 70437 | cantatrices | 1 |
| 70438 | cantate | 1 |
| 70439 | cantasses | 1 |
| 70440 | cantasen | 1 |
| 70441 | cantarte | 1 |
| 70442 | cantarse | 1 |
| 70443 | cantarranas | 1 |
| 70444 | cantarla | 1 |
| 70445 | cantare | 1 |
| 70446 | cantarcillos | 1 |
| 70447 | cantarcicos | 1 |
| 70448 | cantaras | 1 |
| 70449 | cántara | 1 |
| 70450 | cantantes | 1 |
| 70451 | cantanos | 1 |
| 70452 | cantanla | 1 |
| 70453 | cantándome | 1 |
| 70454 | cantamos | 1 |
| 70455 | cantáis | 1 |
| 70456 | cantadores | 1 |
| 70457 | cantaderas | 1 |
| 70458 | cantada | 1 |
| 70459 | cantad | 1 |
| 70460 | cántabro | 1 |
| 70461 | cantables | 1 |
| 70462 | cantabile | 1 |
| 70463 | cantábamos | 1 |
| 70464 | cansses | 1 |
| 70465 | canssedes | 1 |
| 70466 | canssar | 1 |
| 70467 | canssada | 1 |
| 70468 | canssa | 1 |
| 70469 | cansóme | 1 |
| 70470 | cansóle | 1 |
| 70471 | cansemos | 1 |
| 70472 | canseco | 1 |
| 70473 | cansarle | 1 |
| 70474 | cansarás | 1 |
| 70475 | cansaran | 1 |
| 70476 | cansara | 1 |
| 70477 | cánsanme | 1 |
| 70478 | cansándome | 1 |
| 70479 | cansadito | 1 |
| 70480 | cansábase | 1 |
| 70481 | cansábanse | 1 |
| 70482 | cansaban | 1 |
| 70483 | canoso | 1 |
| 70484 | canosa | 1 |
| 70485 | canoras | 1 |
| 70486 | canonjías | 1 |
| 70487 | canonizaron | 1 |
| 70488 | canonizarlas | 1 |
| 70489 | canonizaremos | 1 |
| 70490 | canonizan | 1 |
| 70491 | canonizado | 1 |
| 70492 | canonizada | 1 |
| 70493 | canonizable | 1 |
| 70494 | canonizaban | 1 |
| 70495 | canonistas | 1 |
| 70496 | canonista | 1 |
| 70497 | canonigo | 1 |
| 70498 | canónigas | 1 |
| 70499 | canóniga | 1 |
| 70500 | canónicos | 1 |
| 70501 | canonice | 1 |
| 70502 | canonicato | 1 |
| 70503 | canjilón | 1 |
| 70504 | canjeamos | 1 |
| 70505 | canistillo | 1 |
| 70506 | canísima | 1 |
| 70507 | caniculares | 1 |
| 70508 | canícula | 1 |
| 70509 | caníbales | 1 |
| 70510 | cangrejos | 1 |
| 70511 | cangreja | 1 |
| 70512 | cangilones | 1 |
| 70513 | canequí | 1 |
| 70514 | canelones | 1 |
| 70515 | candy | 1 |
| 70516 | candores | 1 |
| 70517 | candolle | 1 |
| 70518 | candilones | 1 |
| 70519 | candilean | 1 |
| 70520 | candilazos | 1 |
| 70521 | candilazo | 1 |
| 70522 | cándidos | 1 |
| 70523 | candideces | 1 |
| 70524 | candidaturas | 1 |
| 70525 | candentes | 1 |
| 70526 | candelicas | 1 |
| 70527 | candelabro | 1 |
| 70528 | candayesca | 1 |
| 70529 | cancillerías | 1 |
| 70530 | cánçeres | 1 |
| 70531 | cancelación | 1 |
| 70532 | cancamurria | 1 |
| 70533 | çancadiella | 1 |
| 70534 | çanca | 1 |
| 70535 | canc | 1 |
| 70536 | canbio | 1 |
| 70537 | canasto | 1 |
| 70538 | canastiello | 1 |
| 70539 | canastas | 1 |
| 70540 | canasce | 1 |
| 70541 | canariera | 1 |
| 70542 | canapés | 1 |
| 70543 | cananea | 1 |
| 70544 | canana | 1 |
| 70545 | cánamo | 1 |
| 70546 | canalones | 1 |
| 70547 | canalejas | 1 |
| 70548 | canadas | 1 |
| 70549 | camús | 1 |
| 70550 | camuesa | 1 |
| 70551 | camuçia | 1 |
| 70552 | camposantos | 1 |
| 70553 | campomanes | 1 |
| 70554 | campesinas | 1 |
| 70555 | campeó | 1 |
| 70556 | campear | 1 |
| 70557 | campean | 1 |
| 70558 | campbell | 1 |
| 70559 | campanudo | 1 |
| 70560 | campanudamente | 1 |
| 70561 | campanillazos | 1 |
| 70562 | campaneo | 1 |
| 70563 | camoes | 1 |
| 70564 | camissas | 1 |
| 70565 | camisolín | 1 |
| 70566 | camiones | 1 |
| 70567 | caminó | 1 |
| 70568 | caminen | 1 |
| 70569 | caminejo | 1 |
| 70570 | caminéis | 1 |
| 70571 | caminas | 1 |
| 70572 | caminallas | 1 |
| 70573 | caminador | 1 |
| 70574 | camillas | 1 |
| 70575 | camera | 1 |
| 70576 | cameio | 1 |
| 70577 | cambiasen | 1 |
| 70578 | cambiase | 1 |
| 70579 | cambias | 1 |
| 70580 | cambiarte | 1 |
| 70581 | cambiáronse | 1 |
| 70582 | cambiantes | 1 |
| 70583 | cambiándolos | 1 |
| 70584 | cambiándolo | 1 |
| 70585 | cambiáis | 1 |
| 70586 | cambiadas | 1 |
| 70587 | camastros | 1 |
| 70588 | çamarras | 1 |
| 70589 | çamarón | 1 |
| 70590 | camareta | 1 |
| 70591 | camaranchones | 1 |
| 70592 | camará | 1 |
| 70593 | camaleón | 1 |
| 70594 | calzoncillos | 1 |
| 70595 | calzarme | 1 |
| 70596 | calzaré | 1 |
| 70597 | calzare | 1 |
| 70598 | calzará | 1 |
| 70599 | calzándose | 1 |
| 70600 | calzándole | 1 |
| 70601 | calypso | 1 |
| 70602 | calyenta | 1 |
| 70603 | calvinista | 1 |
| 70604 | calvicies | 1 |
| 70605 | calvera | 1 |
| 70606 | calvatrueno | 1 |
| 70607 | caluroso | 1 |
| 70608 | calurosa | 1 |
| 70609 | calunien | 1 |
| 70610 | caluniar | 1 |
| 70611 | calumniosas | 1 |
| 70612 | calumniosa | 1 |
| 70613 | calumniaste | 1 |
| 70614 | calumnian | 1 |
| 70615 | calumniadoras | 1 |
| 70616 | calumniadora | 1 |
| 70617 | calumniaban | 1 |
| 70618 | calorosa | 1 |
| 70619 | calora | 1 |
| 70620 | calóñenme | 1 |
| 70621 | caloñas | 1 |
| 70622 | caloña | 1 |
| 70623 | calonjía | 1 |
| 70624 | calomarde | 1 |
| 70625 | calofrío | 1 |
| 70626 | calmose | 1 |
| 70627 | calme | 1 |
| 70628 | calmazo | 1 |
| 70629 | cálmate | 1 |
| 70630 | calmas | 1 |
| 70631 | calmará | 1 |
| 70632 | calmando | 1 |
| 70633 | calman | 1 |
| 70634 | calmada | 1 |
| 70635 | callis | 1 |
| 70636 | calleys | 1 |
| 70637 | cállense | 1 |
| 70638 | callémonos | 1 |
| 70639 | callejeros | 1 |
| 70640 | calléis | 1 |
| 70641 | calledes | 1 |
| 70642 | callaz | 1 |
| 70643 | callaua | 1 |
| 70644 | cállatela | 1 |
| 70645 | callarte | 1 |
| 70646 | callarme | 1 |
| 70647 | callarlos | 1 |
| 70648 | callarlo | 1 |
| 70649 | callaras | 1 |
| 70650 | callao | 1 |
| 70651 | callandico | 1 |
| 70652 | callande | 1 |
| 70653 | callaíto | 1 |
| 70654 | calladitos | 1 |
| 70655 | callades | 1 |
| 70656 | callabas | 1 |
| 70657 | callábamos | 1 |
| 70658 | callá | 1 |
| 70659 | calipso | 1 |
| 70660 | calíope | 1 |
| 70661 | caligráficos | 1 |
| 70662 | caligrafía | 1 |
| 70663 | caliginoso | 1 |
| 70664 | california | 1 |
| 70665 | calificó | 1 |
| 70666 | calificativos | 1 |
| 70667 | calificase | 1 |
| 70668 | calificaron | 1 |
| 70669 | califican | 1 |
| 70670 | calificado | 1 |
| 70671 | calificadas | 1 |
| 70672 | calificación | 1 |
| 70673 | califica | 1 |
| 70674 | calienten | 1 |
| 70675 | caliéntat | 1 |
| 70676 | cálidas | 1 |
| 70677 | calidá | 1 |
| 70678 | calesín | 1 |
| 70679 | calesa | 1 |
| 70680 | calepino | 1 |
| 70681 | calenturillas | 1 |
| 70682 | calentó | 1 |
| 70683 | calentito | 1 |
| 70684 | calentitas | 1 |
| 70685 | calentita | 1 |
| 70686 | calenté | 1 |
| 70687 | calentaste | 1 |
| 70688 | calentarte | 1 |
| 70689 | calentaron | 1 |
| 70690 | calentármela | 1 |
| 70691 | calentarlo | 1 |
| 70692 | calentarle | 1 |
| 70693 | calentándome | 1 |
| 70694 | calentándolo | 1 |
| 70695 | calentador | 1 |
| 70696 | calentábamos | 1 |
| 70697 | calendas | 1 |
| 70698 | calefacción | 1 |
| 70699 | caldito | 1 |
| 70700 | calderuela | 1 |
| 70701 | calderon | 1 |
| 70702 | caldereros | 1 |
| 70703 | calderero | 1 |
| 70704 | calderería | 1 |
| 70705 | calderadas | 1 |
| 70706 | calder | 1 |
| 70707 | caldedero | 1 |
| 70708 | caldeas | 1 |
| 70709 | caldeando | 1 |
| 70710 | caldea | 1 |
| 70711 | calculó | 1 |
| 70712 | calculista | 1 |
| 70713 | calculas | 1 |
| 70714 | calculando | 1 |
| 70715 | calculador | 1 |
| 70716 | calculado | 1 |
| 70717 | calco | 1 |
| 70718 | calcinación | 1 |
| 70719 | calcetines | 1 |
| 70720 | calcetero | 1 |
| 70721 | calcárea | 1 |
| 70722 | calçar | 1 |
| 70723 | calcaño | 1 |
| 70724 | calcañar | 1 |
| 70725 | calcanar | 1 |
| 70726 | calbi | 1 |
| 70727 | calaverilla | 1 |
| 70728 | calataút | 1 |
| 70729 | calarse | 1 |
| 70730 | calaron | 1 |
| 70731 | calándoselos | 1 |
| 70732 | calamo | 1 |
| 70733 | calamitosa | 1 |
| 70734 | calaminíferas | 1 |
| 70735 | calaminífera | 1 |
| 70736 | calambuco | 1 |
| 70737 | calamares | 1 |
| 70738 | calais | 1 |
| 70739 | calainos | 1 |
| 70740 | çalagarda | 1 |
| 70741 | calafateado | 1 |
| 70742 | caladas | 1 |
| 70743 | calabozos | 1 |
| 70744 | calábase | 1 |
| 70745 | calabacillas | 1 |
| 70746 | calabaça | 1 |
| 70747 | cajonería | 1 |
| 70748 | cajoncito | 1 |
| 70749 | cajilla | 1 |
| 70750 | cajigal | 1 |
| 70751 | cajetillas | 1 |
| 70752 | cajetilla | 1 |
| 70753 | caístro | 1 |
| 70754 | cairela | 1 |
| 70755 | caímos | 1 |
| 70756 | caíale | 1 |
| 70757 | çahorar | 1 |
| 70758 | cahen | 1 |
| 70759 | çafyr | 1 |
| 70760 | cafre | 1 |
| 70761 | cafia | 1 |
| 70762 | cafeteras | 1 |
| 70763 | cáesete | 1 |
| 70764 | caerías | 1 |
| 70765 | caeremos | 1 |
| 70766 | caera | 1 |
| 70767 | caenas | 1 |
| 70768 | caemos | 1 |
| 70769 | caelumque | 1 |
| 70770 | caducos | 1 |
| 70771 | caducamente | 1 |
| 70772 | caducado | 1 |
| 70773 | caducaban | 1 |
| 70774 | cadmio | 1 |
| 70775 | cader | 1 |
| 70776 | cadenillas | 1 |
| 70777 | cadencioso | 1 |
| 70778 | cadenciosas | 1 |
| 70779 | cadencias | 1 |
| 70780 | cadenaaa | 1 |
| 70781 | cadells | 1 |
| 70782 | cadávere | 1 |
| 70783 | cadalso | 1 |
| 70784 | caçurro | 1 |
| 70785 | caçurrías | 1 |
| 70786 | caçurra | 1 |
| 70787 | cacumen | 1 |
| 70788 | cacos | 1 |
| 70789 | caçorría | 1 |
| 70790 | cacofónico | 1 |
| 70791 | caço | 1 |
| 70792 | caciquismo | 1 |
| 70793 | caciquil | 1 |
| 70794 | cachucha | 1 |
| 70795 | cachos | 1 |
| 70796 | cachopines | 1 |
| 70797 | cachondas | 1 |
| 70798 | cachidiablo | 1 |
| 70799 | cachazudas | 1 |
| 70800 | cachazuda | 1 |
| 70801 | cacharrería | 1 |
| 70802 | cacerola | 1 |
| 70803 | cacerías | 1 |
| 70804 | cacería | 1 |
| 70805 | caças | 1 |
| 70806 | cacarearlo | 1 |
| 70807 | cacareaba | 1 |
| 70808 | cacahuetes | 1 |
| 70809 | caçadores | 1 |
| 70810 | caç | 1 |
| 70811 | cabtivo | 1 |
| 70812 | cabron | 1 |
| 70813 | cabrilla | 1 |
| 70814 | cabríe | 1 |
| 70815 | cabrestantes | 1 |
| 70816 | cabremos | 1 |
| 70817 | cabrán | 1 |
| 70818 | cabrahígos | 1 |
| 70819 | cabrahígo | 1 |
| 70820 | cabotaje | 1 |
| 70821 | cables | 1 |
| 70822 | cabileño | 1 |
| 70823 | cabezota | 1 |
| 70824 | cabezón | 1 |
| 70825 | cabestros | 1 |
| 70826 | cabes | 1 |
| 70827 | cabemos | 1 |
| 70828 | cabellerías | 1 |
| 70829 | cabel | 1 |
| 70830 | cabeçudo | 1 |
| 70831 | cabecillas | 1 |
| 70832 | cabeceras | 1 |
| 70833 | cabeçeó | 1 |
| 70834 | cabçe | 1 |
| 70835 | caballuna | 1 |
| 70836 | caballote | 1 |
| 70837 | caballito | 1 |
| 70838 | caballistas | 1 |
| 70839 | caballico | 1 |
| 70840 | caballerote | 1 |
| 70841 | caballerosos | 1 |
| 70842 | caballeroso | 1 |
| 70843 | caballeretes | 1 |
| 70844 | caballeras | 1 |
| 70845 | caballe | 1 |
| 70846 | cabalitos | 1 |
| 70847 | cabalística | 1 |
| 70848 | cabalgaba | 1 |
| 70849 | cabaiero | 1 |
| 70850 | cabacera | 1 |
| 70851 | caba | 1 |
| 70852 | byvos | 1 |
| 70853 | byvo | 1 |
| 70854 | byviredes | 1 |
| 70855 | byvió | 1 |
| 70856 | byvierdes | 1 |
| 70857 | byve | 1 |
| 70858 | byvas | 1 |
| 70859 | byvamos | 1 |
| 70860 | byva | 1 |
| 70861 | byuda | 1 |
| 70862 | byroniano | 1 |
| 70863 | byenfaser | 1 |
| 70864 | byenapreso | 1 |
| 70865 | byenandante | 1 |
| 70866 | buzo | 1 |
| 70867 | buzcorona | 1 |
| 70868 | buzano | 1 |
| 70869 | buytrera | 1 |
| 70870 | buy | 1 |
| 70871 | buxyes | 1 |
| 70872 | buxía | 1 |
| 70873 | buxes | 1 |
| 70874 | búsquenle | 1 |
| 70875 | búsquelo | 1 |
| 70876 | busquéle | 1 |
| 70877 | buscones | 1 |
| 70878 | buscona | 1 |
| 70879 | buscólo | 1 |
| 70880 | buscava | 1 |
| 70881 | buscat | 1 |
| 70882 | buscaste | 1 |
| 70883 | buscases | 1 |
| 70884 | buscásemos | 1 |
| 70885 | buscárselos | 1 |
| 70886 | buscaros | 1 |
| 70887 | buscarían | 1 |
| 70888 | buscaríamos | 1 |
| 70889 | buscaren | 1 |
| 70890 | buscarás | 1 |
| 70891 | buscáramos | 1 |
| 70892 | buscárale | 1 |
| 70893 | buscará | 1 |
| 70894 | buscanse | 1 |
| 70895 | buscándote | 1 |
| 70896 | buscándoos | 1 |
| 70897 | buscándome | 1 |
| 70898 | búscalos | 1 |
| 70899 | buscallos | 1 |
| 70900 | buscallo | 1 |
| 70901 | buscala | 1 |
| 70902 | buscadores | 1 |
| 70903 | buscadora | 1 |
| 70904 | buscadla | 1 |
| 70905 | buscabas | 1 |
| 70906 | búsca | 1 |
| 70907 | burtos | 1 |
| 70908 | bursia | 1 |
| 70909 | burris | 1 |
| 70910 | burrera | 1 |
| 70911 | burocracia | 1 |
| 70912 | burlescos | 1 |
| 70913 | burlescas | 1 |
| 70914 | burlería | 1 |
| 70915 | burlen | 1 |
| 70916 | burlemos | 1 |
| 70917 | burleme | 1 |
| 70918 | búrlate | 1 |
| 70919 | burlaros | 1 |
| 70920 | burlaron | 1 |
| 70921 | burlarme | 1 |
| 70922 | burlarían | 1 |
| 70923 | burlaremos | 1 |
| 70924 | burlárase | 1 |
| 70925 | burlarán | 1 |
| 70926 | burlándolo | 1 |
| 70927 | búrlame | 1 |
| 70928 | burlábase | 1 |
| 70929 | burke | 1 |
| 70930 | buriles | 1 |
| 70931 | buril | 1 |
| 70932 | buriel | 1 |
| 70933 | burguesía | 1 |
| 70934 | burguesa | 1 |
| 70935 | burgués | 1 |
| 70936 | burgo | 1 |
| 70937 | burgeses | 1 |
| 70938 | burgés | 1 |
| 70939 | burel | 1 |
| 70940 | burdeles | 1 |
| 70941 | burdas | 1 |
| 70942 | burbujeaba | 1 |
| 70943 | buquinista | 1 |
| 70944 | buñuelo | 1 |
| 70945 | bunsen | 1 |
| 70946 | bulrra | 1 |
| 70947 | bulló | 1 |
| 70948 | bullidores | 1 |
| 70949 | bulliciosas | 1 |
| 70950 | bullente | 1 |
| 70951 | bullendote | 1 |
| 70952 | bullendo | 1 |
| 70953 | bullanguero | 1 |
| 70954 | bullangas | 1 |
| 70955 | bullanga | 1 |
| 70956 | bull | 1 |
| 70957 | bulevares | 1 |
| 70958 | buleros | 1 |
| 70959 | bujelladas | 1 |
| 70960 | bujarrón | 1 |
| 70961 | buitres | 1 |
| 70962 | buidos | 1 |
| 70963 | buido | 1 |
| 70964 | buidas | 1 |
| 70965 | buhoneros | 1 |
| 70966 | buhón | 1 |
| 70967 | búho | 1 |
| 70968 | buhardillones | 1 |
| 70969 | bufonesca | 1 |
| 70970 | bufonas | 1 |
| 70971 | bufón | 1 |
| 70972 | bufo | 1 |
| 70973 | buffet | 1 |
| 70974 | bufar | 1 |
| 70975 | bufandas | 1 |
| 70976 | búfalo | 1 |
| 70977 | bufaban | 1 |
| 70978 | bufaba | 1 |
| 70979 | bueycencia | 1 |
| 70980 | buenísima | 1 |
| 70981 | buenaval | 1 |
| 70982 | buenasventuras | 1 |
| 70983 | buenamiente | 1 |
| 70984 | buelve | 1 |
| 70985 | bueluen | 1 |
| 70986 | buelo | 1 |
| 70987 | bue | 1 |
| 70988 | budistas | 1 |
| 70989 | budista | 1 |
| 70990 | buchner | 1 |
| 70991 | buces | 1 |
| 70992 | búas | 1 |
| 70993 | bryo | 1 |
| 70994 | bruyère | 1 |
| 70995 | bruxa | 1 |
| 70996 | brutesco | 1 |
| 70997 | brusquer | 1 |
| 70998 | brusista | 1 |
| 70999 | bruños | 1 |
| 71000 | bruñido | 1 |
| 71001 | bruñidas | 1 |
| 71002 | bruñe | 1 |
| 71003 | bruno | 1 |
| 71004 | brumó | 1 |
| 71005 | brumada | 1 |
| 71006 | brumaban | 1 |
| 71007 | brújulas | 1 |
| 71008 | brujerías | 1 |
| 71009 | brrrr | 1 |
| 71010 | brrr | 1 |
| 71011 | brr | 1 |
| 71012 | brozna | 1 |
| 71013 | broza | 1 |
| 71014 | brotecillo | 1 |
| 71015 | brote | 1 |
| 71016 | brotaron | 1 |
| 71017 | brotaran | 1 |
| 71018 | brotan | 1 |
| 71019 | brotado | 1 |
| 71020 | brooke | 1 |
| 71021 | broncos | 1 |
| 71022 | broncíneos | 1 |
| 71023 | broncínea | 1 |
| 71024 | broncha | 1 |
| 71025 | bronch | 1 |
| 71026 | broncas | 1 |
| 71027 | bromees | 1 |
| 71028 | bromee | 1 |
| 71029 | bromeas | 1 |
| 71030 | brodio | 1 |
| 71031 | brochazos | 1 |
| 71032 | brochase | 1 |
| 71033 | brochada | 1 |
| 71034 | brocabruno | 1 |
| 71035 | briznas | 1 |
| 71036 | britano | 1 |
| 71037 | briscus | 1 |
| 71038 | briscada | 1 |
| 71039 | brisca | 1 |
| 71040 | briosos | 1 |
| 71041 | brindóme | 1 |
| 71042 | brindasen | 1 |
| 71043 | brindaron | 1 |
| 71044 | brindarles | 1 |
| 71045 | brindado | 1 |
| 71046 | brindaban | 1 |
| 71047 | brincó | 1 |
| 71048 | brincan | 1 |
| 71049 | brincaban | 1 |
| 71050 | brillos | 1 |
| 71051 | brillará | 1 |
| 71052 | brillantísimos | 1 |
| 71053 | brillantísima | 1 |
| 71054 | brihuega | 1 |
| 71055 | bribonazo | 1 |
| 71056 | bribonada | 1 |
| 71057 | briareos | 1 |
| 71058 | briareo | 1 |
| 71059 | briador | 1 |
| 71060 | brevísimo | 1 |
| 71061 | brevísima | 1 |
| 71062 | breviarios | 1 |
| 71063 | brevas | 1 |
| 71064 | breuissima | 1 |
| 71065 | breuedad | 1 |
| 71066 | bretones | 1 |
| 71067 | bretón | 1 |
| 71068 | brete | 1 |
| 71069 | bretañia | 1 |
| 71070 | bretador | 1 |
| 71071 | breñales | 1 |
| 71072 | breguet | 1 |
| 71073 | bregué | 1 |
| 71074 | bregaron | 1 |
| 71075 | brechas | 1 |
| 71076 | brebajes | 1 |
| 71077 | brazaletes | 1 |
| 71078 | bravuras | 1 |
| 71079 | bravucones | 1 |
| 71080 | bravucón | 1 |
| 71081 | bravant | 1 |
| 71082 | brauos | 1 |
| 71083 | brauas | 1 |
| 71084 | braserón | 1 |
| 71085 | brandabarbarán | 1 |
| 71086 | brancos | 1 |
| 71087 | bramó | 1 |
| 71088 | brame | 1 |
| 71089 | bragueta | 1 |
| 71090 | braguero | 1 |
| 71091 | bragado | 1 |
| 71092 | braga | 1 |
| 71093 | brafuneras | 1 |
| 71094 | bradamante | 1 |
| 71095 | bracmánica | 1 |
| 71096 | bracmanes | 1 |
| 71097 | bracitos | 1 |
| 71098 | braceando | 1 |
| 71099 | braceaban | 1 |
| 71100 | bra | 1 |
| 71101 | bozeas | 1 |
| 71102 | bozear | 1 |
| 71103 | bozeando | 1 |
| 71104 | bozeador | 1 |
| 71105 | boyzuelo | 1 |
| 71106 | boyerizos | 1 |
| 71107 | boyardo | 1 |
| 71108 | boya | 1 |
| 71109 | boxear | 1 |
| 71110 | box | 1 |
| 71111 | boutade | 1 |
| 71112 | bouquet | 1 |
| 71113 | boulou | 1 |
| 71114 | bouilla | 1 |
| 71115 | bouas | 1 |
| 71116 | botonazos | 1 |
| 71117 | botita | 1 |
| 71118 | botiquines | 1 |
| 71119 | botillerías | 1 |
| 71120 | botillería | 1 |
| 71121 | botiller | 1 |
| 71122 | boticarito | 1 |
| 71123 | boticarín | 1 |
| 71124 | boticaria | 1 |
| 71125 | botellazo | 1 |
| 71126 | botecillo | 1 |
| 71127 | botaratadas | 1 |
| 71128 | botaratada | 1 |
| 71129 | botánicas | 1 |
| 71130 | botando | 1 |
| 71131 | botanas | 1 |
| 71132 | bostezara | 1 |
| 71133 | bostezado | 1 |
| 71134 | bosteza | 1 |
| 71135 | bossuet | 1 |
| 71136 | bosqueril | 1 |
| 71137 | bosquejó | 1 |
| 71138 | bosquejar | 1 |
| 71139 | bosquejado | 1 |
| 71140 | bosquejada | 1 |
| 71141 | bosqueja | 1 |
| 71142 | bosquecillos | 1 |
| 71143 | bosquecillo | 1 |
| 71144 | bosio | 1 |
| 71145 | bosco | 1 |
| 71146 | boscán | 1 |
| 71147 | boscajes | 1 |
| 71148 | bos | 1 |
| 71149 | borzeguies | 1 |
| 71150 | borte | 1 |
| 71151 | borrosos | 1 |
| 71152 | borriquitas | 1 |
| 71153 | borriquillo | 1 |
| 71154 | borriqueros | 1 |
| 71155 | borriqueñas | 1 |
| 71156 | borricote | 1 |
| 71157 | borricales | 1 |
| 71158 | borricada | 1 |
| 71159 | borres | 1 |
| 71160 | borremos | 1 |
| 71161 | borrell | 1 |
| 71162 | borrega | 1 |
| 71163 | borre | 1 |
| 71164 | borrase | 1 |
| 71165 | borrascosos | 1 |
| 71166 | borrarse | 1 |
| 71167 | borraron | 1 |
| 71168 | borrarme | 1 |
| 71169 | borrarle | 1 |
| 71170 | borrarlas | 1 |
| 71171 | borrarla | 1 |
| 71172 | borrarán | 1 |
| 71173 | borrara | 1 |
| 71174 | borrachón | 1 |
| 71175 | borona | 1 |
| 71176 | borní | 1 |
| 71177 | borlita | 1 |
| 71178 | borleo | 1 |
| 71179 | borgias | 1 |
| 71180 | bóreas | 1 |
| 71181 | boreal | 1 |
| 71182 | bordó | 1 |
| 71183 | bordeaba | 1 |
| 71184 | bordea | 1 |
| 71185 | bordaron | 1 |
| 71186 | bordará | 1 |
| 71187 | bordan | 1 |
| 71188 | bordagorri | 1 |
| 71189 | bordaduras | 1 |
| 71190 | bordadores | 1 |
| 71191 | bordador | 1 |
| 71192 | bordaban | 1 |
| 71193 | boquirrubios | 1 |
| 71194 | boquirru | 1 |
| 71195 | boquirris | 1 |
| 71196 | boquetes | 1 |
| 71197 | boqueás | 1 |
| 71198 | boquear | 1 |
| 71199 | boqueadas | 1 |
| 71200 | boquea | 1 |
| 71201 | bootes | 1 |
| 71202 | bontà | 1 |
| 71203 | bonitísima | 1 |
| 71204 | bonísimos | 1 |
| 71205 | bonillas | 1 |
| 71206 | bonibus | 1 |
| 71207 | bonetón | 1 |
| 71208 | bonetero | 1 |
| 71209 | bondadosas | 1 |
| 71210 | bonancibles | 1 |
| 71211 | bombonera | 1 |
| 71212 | bombés | 1 |
| 71213 | bombardeada | 1 |
| 71214 | bombardas | 1 |
| 71215 | bolvieron | 1 |
| 71216 | bolviéndole | 1 |
| 71217 | bolví | 1 |
| 71218 | bolvérmela | 1 |
| 71219 | bolverás | 1 |
| 71220 | boluieron | 1 |
| 71221 | boluia | 1 |
| 71222 | bolsicos | 1 |
| 71223 | bolsico | 1 |
| 71224 | boloñés | 1 |
| 71225 | boloña | 1 |
| 71226 | bolonia | 1 |
| 71227 | bollyçio | 1 |
| 71228 | bolliçio | 1 |
| 71229 | bollicio | 1 |
| 71230 | bollero | 1 |
| 71231 | bollería | 1 |
| 71232 | bólido | 1 |
| 71233 | boliche | 1 |
| 71234 | bolera | 1 |
| 71235 | bolava | 1 |
| 71236 | bolaua | 1 |
| 71237 | bolantes | 1 |
| 71238 | bojiganga | 1 |
| 71239 | bois | 1 |
| 71240 | boire | 1 |
| 71241 | boileau | 1 |
| 71242 | bohonero | 1 |
| 71243 | bohemia | 1 |
| 71244 | bohardillón | 1 |
| 71245 | bohardillas | 1 |
| 71246 | bohardilla | 1 |
| 71247 | bogó | 1 |
| 71248 | bogase | 1 |
| 71249 | bogado | 1 |
| 71250 | bogábamos | 1 |
| 71251 | bofetones | 1 |
| 71252 | bofetá | 1 |
| 71253 | bodorrio | 1 |
| 71254 | bodoques | 1 |
| 71255 | bodilla | 1 |
| 71256 | bodeguero | 1 |
| 71257 | bodegonero | 1 |
| 71258 | bodegoneras | 1 |
| 71259 | bodegonera | 1 |
| 71260 | bodego | 1 |
| 71261 | boconas | 1 |
| 71262 | boço | 1 |
| 71263 | bock | 1 |
| 71264 | bochornosos | 1 |
| 71265 | bochas | 1 |
| 71266 | boceto | 1 |
| 71267 | boçes | 1 |
| 71268 | bocaditos | 1 |
| 71269 | bocadillos | 1 |
| 71270 | bocacalle | 1 |
| 71271 | bocabierto | 1 |
| 71272 | bobones | 1 |
| 71273 | bobona | 1 |
| 71274 | bobón | 1 |
| 71275 | bobillo | 1 |
| 71276 | bobalicona | 1 |
| 71277 | bobadilla | 1 |
| 71278 | bloquear | 1 |
| 71279 | bloquean | 1 |
| 71280 | bloqueadas | 1 |
| 71281 | blondos | 1 |
| 71282 | blondas | 1 |
| 71283 | blindaje | 1 |
| 71284 | blinco | 1 |
| 71285 | bledos | 1 |
| 71286 | bledo | 1 |
| 71287 | blav | 1 |
| 71288 | blasonan | 1 |
| 71289 | blasonados | 1 |
| 71290 | blasfemos | 1 |
| 71291 | blasfemó | 1 |
| 71292 | blasfeme | 1 |
| 71293 | blasfemases | 1 |
| 71294 | blasfemas | 1 |
| 71295 | blasfemaban | 1 |
| 71296 | blasfemaba | 1 |
| 71297 | blasfema | 1 |
| 71298 | blaré | 1 |
| 71299 | blanquita | 1 |
| 71300 | blanquinegras | 1 |
| 71301 | blanquette | 1 |
| 71302 | blanqueará | 1 |
| 71303 | blanqueando | 1 |
| 71304 | blanqueado | 1 |
| 71305 | blanqueaban | 1 |
| 71306 | blanqueaba | 1 |
| 71307 | blanducho | 1 |
| 71308 | blandón | 1 |
| 71309 | blandió | 1 |
| 71310 | blandiéndolo | 1 |
| 71311 | blandeando | 1 |
| 71312 | blanchetes | 1 |
| 71313 | blâmé | 1 |
| 71314 | blago | 1 |
| 71315 | blaços | 1 |
| 71316 | blaço | 1 |
| 71317 | biznietos | 1 |
| 71318 | bizmarse | 1 |
| 71319 | bizmarle | 1 |
| 71320 | bizmalle | 1 |
| 71321 | bizmado | 1 |
| 71322 | bizmada | 1 |
| 71323 | bizma | 1 |
| 71324 | bizcochitos | 1 |
| 71325 | bizcochito | 1 |
| 71326 | bizcas | 1 |
| 71327 | bizcarretic | 1 |
| 71328 | bizcando | 1 |
| 71329 | bizcaba | 1 |
| 71330 | bizarras | 1 |
| 71331 | bizantinas | 1 |
| 71332 | bizantina | 1 |
| 71333 | bive | 1 |
| 71334 | bivalvo | 1 |
| 71335 | biuoras | 1 |
| 71336 | biuimos | 1 |
| 71337 | biuiessen | 1 |
| 71338 | biuiesse | 1 |
| 71339 | biuieran | 1 |
| 71340 | biuiera | 1 |
| 71341 | biui | 1 |
| 71342 | biuas | 1 |
| 71343 | biuamos | 1 |
| 71344 | bituania | 1 |
| 71345 | bitinia | 1 |
| 71346 | bisunto | 1 |
| 71347 | bisteques | 1 |
| 71348 | bisperada | 1 |
| 71349 | bisoño | 1 |
| 71350 | bisoñé | 1 |
| 71351 | bisnieto | 1 |
| 71352 | bisnieta | 1 |
| 71353 | bismark | 1 |
| 71354 | bisiesto | 1 |
| 71355 | bishiño | 1 |
| 71356 | bisagra | 1 |
| 71357 | bisabuelos | 1 |
| 71358 | birretillo | 1 |
| 71359 | birmingham | 1 |
| 71360 | birló | 1 |
| 71361 | birlado | 1 |
| 71362 | biricornio | 1 |
| 71363 | bípedo | 1 |
| 71364 | bipartido | 1 |
| 71365 | bipartida | 1 |
| 71366 | bion | 1 |
| 71367 | biombo | 1 |
| 71368 | biógrafo | 1 |
| 71369 | biografías | 1 |
| 71370 | billetito | 1 |
| 71371 | billetico | 1 |
| 71372 | billarista | 1 |
| 71373 | billa | 1 |
| 71374 | bill | 1 |
| 71375 | bilioso | 1 |
| 71376 | bilingüe | 1 |
| 71377 | bílbilis | 1 |
| 71378 | bilateral | 1 |
| 71379 | bigotudo | 1 |
| 71380 | bigotito | 1 |
| 71381 | bigotera | 1 |
| 71382 | bigotejo | 1 |
| 71383 | bigarren | 1 |
| 71384 | bigardón | 1 |
| 71385 | bifurcación | 1 |
| 71386 | biftec | 1 |
| 71387 | bifrontes | 1 |
| 71388 | bifronte | 1 |
| 71389 | bientratados | 1 |
| 71390 | bienrrazonada | 1 |
| 71391 | bienquista | 1 |
| 71392 | bienquerençia | 1 |
| 71393 | bienparado | 1 |
| 71394 | bienllegada | 1 |
| 71395 | bienintencionadamente | 1 |
| 71396 | bienhechores | 1 |
| 71397 | bienfechores | 1 |
| 71398 | bienfecha | 1 |
| 71399 | bienfasyentes | 1 |
| 71400 | bienempleada | 1 |
| 71401 | bienaya | 1 |
| 71402 | bienaventuranzas | 1 |
| 71403 | bienaventurada | 1 |
| 71404 | bienauenturadas | 1 |
| 71405 | bienauenturada | 1 |
| 71406 | bienandanza | 1 |
| 71407 | bienamada | 1 |
| 71408 | bién | 1 |
| 71409 | bidasoa | 1 |
| 71410 | bicorne | 1 |
| 71411 | bicocas | 1 |
| 71412 | bicicletas | 1 |
| 71413 | bichito | 1 |
| 71414 | bíceps | 1 |
| 71415 | bibliotecas | 1 |
| 71416 | bibelot | 1 |
| 71417 | bi | 1 |
| 71418 | bezes | 1 |
| 71419 | bexiga | 1 |
| 71420 | bevras | 1 |
| 71421 | bevió | 1 |
| 71422 | bevimos | 1 |
| 71423 | beviera | 1 |
| 71424 | beviendo | 1 |
| 71425 | beverría | 1 |
| 71426 | bevería | 1 |
| 71427 | beven | 1 |
| 71428 | bevedor | 1 |
| 71429 | bev | 1 |
| 71430 | beuiendo | 1 |
| 71431 | beuia | 1 |
| 71432 | beuen | 1 |
| 71433 | beuemos | 1 |
| 71434 | beudos | 1 |
| 71435 | beua | 1 |
| 71436 | betsabée | 1 |
| 71437 | beticó | 1 |
| 71438 | beti | 1 |
| 71439 | bethlehem | 1 |
| 71440 | beteac | 1 |
| 71441 | besuqueó | 1 |
| 71442 | besuqueándose | 1 |
| 71443 | besuqueaba | 1 |
| 71444 | besugos | 1 |
| 71445 | besole | 1 |
| 71446 | besóla | 1 |
| 71447 | beserro | 1 |
| 71448 | beserrillo | 1 |
| 71449 | bésele | 1 |
| 71450 | beséla | 1 |
| 71451 | beséis | 1 |
| 71452 | besé | 1 |
| 71453 | besava | 1 |
| 71454 | besaste | 1 |
| 71455 | besas | 1 |
| 71456 | besársela | 1 |
| 71457 | besáronle | 1 |
| 71458 | besarlas | 1 |
| 71459 | besaré | 1 |
| 71460 | besara | 1 |
| 71461 | besaos | 1 |
| 71462 | besándose | 1 |
| 71463 | besamos | 1 |
| 71464 | bésalos | 1 |
| 71465 | besadle | 1 |
| 71466 | besadlas | 1 |
| 71467 | besadera | 1 |
| 71468 | besabas | 1 |
| 71469 | berwick | 1 |
| 71470 | bervo | 1 |
| 71471 | berssabe | 1 |
| 71472 | berruguete | 1 |
| 71473 | berrugones | 1 |
| 71474 | berrueca | 1 |
| 71475 | berros | 1 |
| 71476 | berroqueño | 1 |
| 71477 | berroqueñas | 1 |
| 71478 | berrocal | 1 |
| 71479 | berro | 1 |
| 71480 | berriyac | 1 |
| 71481 | berrinches | 1 |
| 71482 | berreando | 1 |
| 71483 | berracas | 1 |
| 71484 | bernouville | 1 |
| 71485 | bernard | 1 |
| 71486 | bermudo | 1 |
| 71487 | bermingán | 1 |
| 71488 | bermeo | 1 |
| 71489 | bermellones | 1 |
| 71490 | bermellonadas | 1 |
| 71491 | bermellonada | 1 |
| 71492 | bermellon | 1 |
| 71493 | bergia | 1 |
| 71494 | bergel | 1 |
| 71495 | bergantón | 1 |
| 71496 | bergantines | 1 |
| 71497 | bergantes | 1 |
| 71498 | bergantas | 1 |
| 71499 | berganta | 1 |
| 71500 | berenjeneros | 1 |
| 71501 | berenjenal | 1 |
| 71502 | berenguela | 1 |
| 71503 | berdones | 1 |
| 71504 | berdáriz | 1 |
| 71505 | bercera | 1 |
| 71506 | berceo | 1 |
| 71507 | berá | 1 |
| 71508 | bera | 1 |
| 71509 | beo | 1 |
| 71510 | beno | 1 |
| 71511 | benitos | 1 |
| 71512 | beninas | 1 |
| 71513 | benignita | 1 |
| 71514 | benignas | 1 |
| 71515 | bengalas | 1 |
| 71516 | benemérito | 1 |
| 71517 | benéficos | 1 |
| 71518 | beneficiar | 1 |
| 71519 | beneditos | 1 |
| 71520 | benedicto | 1 |
| 71521 | benedicta | 1 |
| 71522 | bendixo | 1 |
| 71523 | benditísima | 1 |
| 71524 | benditamente | 1 |
| 71525 | bendije | 1 |
| 71526 | bendigaos | 1 |
| 71527 | bendigamos | 1 |
| 71528 | bendiciendo | 1 |
| 71529 | bendichos | 1 |
| 71530 | bendicho | 1 |
| 71531 | bendiçen | 1 |
| 71532 | bendicen | 1 |
| 71533 | bendice | 1 |
| 71534 | bendexiese | 1 |
| 71535 | bendeciré | 1 |
| 71536 | bendecirá | 1 |
| 71537 | bendecidas | 1 |
| 71538 | bencina | 1 |
| 71539 | benalcázar | 1 |
| 71540 | bemol | 1 |
| 71541 | beltrán | 1 |
| 71542 | beltran | 1 |
| 71543 | belorofonte | 1 |
| 71544 | belo | 1 |
| 71545 | belmonte | 1 |
| 71546 | belméz | 1 |
| 71547 | bellum | 1 |
| 71548 | bellotes | 1 |
| 71549 | bellosa | 1 |
| 71550 | belloritas | 1 |
| 71551 | bellísimo | 1 |
| 71552 | belli | 1 |
| 71553 | bellegarde | 1 |
| 71554 | belle | 1 |
| 71555 | bellaquillo | 1 |
| 71556 | belladona | 1 |
| 71557 | bellacuelo | 1 |
| 71558 | bellaconazo | 1 |
| 71559 | bellacón | 1 |
| 71560 | bellacas | 1 |
| 71561 | belitre | 1 |
| 71562 | belisardas | 1 |
| 71563 | belisa | 1 |
| 71564 | beligerantes | 1 |
| 71565 | belífero | 1 |
| 71566 | belicosos | 1 |
| 71567 | belicoso | 1 |
| 71568 | belicosa | 1 |
| 71569 | bélica | 1 |
| 71570 | bélgica | 1 |
| 71571 | belfort | 1 |
| 71572 | belencita | 1 |
| 71573 | belen | 1 |
| 71574 | belem | 1 |
| 71575 | beldando | 1 |
| 71576 | bel | 1 |
| 71577 | begonias | 1 |
| 71578 | begonia | 1 |
| 71579 | befa | 1 |
| 71580 | beefteck | 1 |
| 71581 | beefstek | 1 |
| 71582 | beefsteak | 1 |
| 71583 | beduinos | 1 |
| 71584 | bécquer | 1 |
| 71585 | becoquín | 1 |
| 71586 | beçerros | 1 |
| 71587 | becerro | 1 |
| 71588 | becerril | 1 |
| 71589 | becerradas | 1 |
| 71590 | beca | 1 |
| 71591 | bebiste | 1 |
| 71592 | bebiere | 1 |
| 71593 | bebiéndoos | 1 |
| 71594 | bebiéndola | 1 |
| 71595 | bebidos | 1 |
| 71596 | bebíase | 1 |
| 71597 | bebérsele | 1 |
| 71598 | beberle | 1 |
| 71599 | beberlas | 1 |
| 71600 | beberías | 1 |
| 71601 | beberán | 1 |
| 71602 | bebemos | 1 |
| 71603 | bébelo | 1 |
| 71604 | bebéis | 1 |
| 71605 | bebedores | 1 |
| 71606 | bebed | 1 |
| 71607 | bebé | 1 |
| 71608 | bébase | 1 |
| 71609 | beban | 1 |
| 71610 | beau | 1 |
| 71611 | beatuela | 1 |
| 71612 | beato | 1 |
| 71613 | beatífico | 1 |
| 71614 | beatificaron | 1 |
| 71615 | beati | 1 |
| 71616 | bearn | 1 |
| 71617 | bé | 1 |
| 71618 | bazofia | 1 |
| 71619 | bazanes | 1 |
| 71620 | bazán | 1 |
| 71621 | bazan | 1 |
| 71622 | bayos | 1 |
| 71623 | bayonetazo | 1 |
| 71624 | bayarte | 1 |
| 71625 | bayardo | 1 |
| 71626 | baxes | 1 |
| 71627 | baxaua | 1 |
| 71628 | baxas | 1 |
| 71629 | baxarme | 1 |
| 71630 | baxame | 1 |
| 71631 | baviecas | 1 |
| 71632 | bautysta | 1 |
| 71633 | bautizos | 1 |
| 71634 | bautizó | 1 |
| 71635 | bautizaron | 1 |
| 71636 | bautizaré | 1 |
| 71637 | bautizan | 1 |
| 71638 | bautizada | 1 |
| 71639 | bautismal | 1 |
| 71640 | bautisma | 1 |
| 71641 | bautisat | 1 |
| 71642 | bautice | 1 |
| 71643 | bausanes | 1 |
| 71644 | bausana | 1 |
| 71645 | batuta | 1 |
| 71646 | battistini | 1 |
| 71647 | batrania | 1 |
| 71648 | batón | 1 |
| 71649 | batlló | 1 |
| 71650 | batita | 1 |
| 71651 | batirnos | 1 |
| 71652 | batiría | 1 |
| 71653 | batiremos | 1 |
| 71654 | batiréis | 1 |
| 71655 | batió | 1 |
| 71656 | batieran | 1 |
| 71657 | batiéndola | 1 |
| 71658 | batidas | 1 |
| 71659 | batida | 1 |
| 71660 | batíamos | 1 |
| 71661 | bates | 1 |
| 71662 | batas | 1 |
| 71663 | batanee | 1 |
| 71664 | batallitas | 1 |
| 71665 | batallen | 1 |
| 71666 | basureros | 1 |
| 71667 | basuras | 1 |
| 71668 | bastoncito | 1 |
| 71669 | bastome | 1 |
| 71670 | bastiones | 1 |
| 71671 | bastete | 1 |
| 71672 | básteme | 1 |
| 71673 | bastecida | 1 |
| 71674 | basteado | 1 |
| 71675 | basteada | 1 |
| 71676 | bastaua | 1 |
| 71677 | bastasse | 1 |
| 71678 | bastaros | 1 |
| 71679 | bastarme | 1 |
| 71680 | bastarle | 1 |
| 71681 | bastarían | 1 |
| 71682 | bastardos | 1 |
| 71683 | bastardea | 1 |
| 71684 | bastarda | 1 |
| 71685 | bastarán | 1 |
| 71686 | bastaran | 1 |
| 71687 | bastaráme | 1 |
| 71688 | bastantísima | 1 |
| 71689 | bastándoles | 1 |
| 71690 | bastándole | 1 |
| 71691 | bastando | 1 |
| 71692 | bástale | 1 |
| 71693 | basquiña | 1 |
| 71694 | basiliscos | 1 |
| 71695 | basilisa | 1 |
| 71696 | báscula | 1 |
| 71697 | basamento | 1 |
| 71698 | basado | 1 |
| 71699 | basadas | 1 |
| 71700 | barvos | 1 |
| 71701 | barvechos | 1 |
| 71702 | barvecho | 1 |
| 71703 | barva | 1 |
| 71704 | barullón | 1 |
| 71705 | barullero | 1 |
| 71706 | barua | 1 |
| 71707 | barruntó | 1 |
| 71708 | barruntas | 1 |
| 71709 | barruntar | 1 |
| 71710 | barrúntanos | 1 |
| 71711 | barruntado | 1 |
| 71712 | barrot | 1 |
| 71713 | barroso | 1 |
| 71714 | barroca | 1 |
| 71715 | barrizales | 1 |
| 71716 | barrizal | 1 |
| 71717 | barrió | 1 |
| 71718 | barrimos | 1 |
| 71719 | barrilitos | 1 |
| 71720 | barrilejos | 1 |
| 71721 | barriguera | 1 |
| 71722 | barrigón | 1 |
| 71723 | barrigas | 1 |
| 71724 | barrieran | 1 |
| 71725 | barriera | 1 |
| 71726 | barrida | 1 |
| 71727 | barríamos | 1 |
| 71728 | barriadas | 1 |
| 71729 | barrerme | 1 |
| 71730 | barrerle | 1 |
| 71731 | barreremos | 1 |
| 71732 | barrere | 1 |
| 71733 | barrera | 1 |
| 71734 | barreños | 1 |
| 71735 | barrenos | 1 |
| 71736 | barrenó | 1 |
| 71737 | barrendero | 1 |
| 71738 | barrenaba | 1 |
| 71739 | barrancas | 1 |
| 71740 | barraganía | 1 |
| 71741 | barragán | 1 |
| 71742 | barrabasada | 1 |
| 71743 | barquito | 1 |
| 71744 | barquinazo | 1 |
| 71745 | barquillo | 1 |
| 71746 | barquillas | 1 |
| 71747 | baronías | 1 |
| 71748 | barnizados | 1 |
| 71749 | barnices | 1 |
| 71750 | bargueño | 1 |
| 71751 | bardo | 1 |
| 71752 | bardal | 1 |
| 71753 | barcus | 1 |
| 71754 | barçilona | 1 |
| 71755 | barcia | 1 |
| 71756 | barcasiyua | 1 |
| 71757 | barcadas | 1 |
| 71758 | barbuquejo | 1 |
| 71759 | barbos | 1 |
| 71760 | barbo | 1 |
| 71761 | barbitaheño | 1 |
| 71762 | barbirrubio | 1 |
| 71763 | barbinegro | 1 |
| 71764 | barbilampiño | 1 |
| 71765 | barbianas | 1 |
| 71766 | barbiana | 1 |
| 71767 | barbera | 1 |
| 71768 | barbecho | 1 |
| 71769 | barbarlas | 1 |
| 71770 | barbaridadas | 1 |
| 71771 | bárbaramente | 1 |
| 71772 | barbados | 1 |
| 71773 | barbadas | 1 |
| 71774 | barbacanas | 1 |
| 71775 | baraturas | 1 |
| 71776 | báratro | 1 |
| 71777 | baratito | 1 |
| 71778 | baratillos | 1 |
| 71779 | baratillo | 1 |
| 71780 | baratario | 1 |
| 71781 | baratan | 1 |
| 71782 | barástolis | 1 |
| 71783 | barandado | 1 |
| 71784 | baranda | 1 |
| 71785 | barajara | 1 |
| 71786 | barajando | 1 |
| 71787 | barajan | 1 |
| 71788 | barajados | 1 |
| 71789 | barahúnda | 1 |
| 71790 | barahunda | 1 |
| 71791 | bar | 1 |
| 71792 | báquico | 1 |
| 71793 | baqueteados | 1 |
| 71794 | baquerisa | 1 |
| 71795 | baptizalla | 1 |
| 71796 | baptizada | 1 |
| 71797 | baptista | 1 |
| 71798 | bañeros | 1 |
| 71799 | bañaron | 1 |
| 71800 | bañarme | 1 |
| 71801 | bañarle | 1 |
| 71802 | bañares | 1 |
| 71803 | bañará | 1 |
| 71804 | bañar | 1 |
| 71805 | bañándoselas | 1 |
| 71806 | bañando | 1 |
| 71807 | bañábala | 1 |
| 71808 | banquillo | 1 |
| 71809 | banqueros | 1 |
| 71810 | banos | 1 |
| 71811 | bandurria | 1 |
| 71812 | bandonar | 1 |
| 71813 | bandolerismo | 1 |
| 71814 | bandines | 1 |
| 71815 | banderos | 1 |
| 71816 | banderita | 1 |
| 71817 | banderillero | 1 |
| 71818 | banderetas | 1 |
| 71819 | bandejita | 1 |
| 71820 | bandejas | 1 |
| 71821 | bandear | 1 |
| 71822 | bandeando | 1 |
| 71823 | ban | 1 |
| 71824 | bamboleo | 1 |
| 71825 | bamboleas | 1 |
| 71826 | bamboleaban | 1 |
| 71827 | bambochadas | 1 |
| 71828 | bambalinas | 1 |
| 71829 | balzac | 1 |
| 71830 | balvastro | 1 |
| 71831 | balsain | 1 |
| 71832 | ballestta | 1 |
| 71833 | ballestilla | 1 |
| 71834 | ballesteros | 1 |
| 71835 | ballenatos | 1 |
| 71836 | balitas | 1 |
| 71837 | balita | 1 |
| 71838 | balística | 1 |
| 71839 | balija | 1 |
| 71840 | balido | 1 |
| 71841 | balentía | 1 |
| 71842 | baleares | 1 |
| 71843 | baldovinos | 1 |
| 71844 | baldonada | 1 |
| 71845 | baldo | 1 |
| 71846 | baldeo | 1 |
| 71847 | baldadito | 1 |
| 71848 | baldada | 1 |
| 71849 | balconea | 1 |
| 71850 | balconcillo | 1 |
| 71851 | balconajes | 1 |
| 71852 | balconaje | 1 |
| 71853 | balbucir | 1 |
| 71854 | balbucieron | 1 |
| 71855 | balbuciendo | 1 |
| 71856 | balbucía | 1 |
| 71857 | balbastro | 1 |
| 71858 | balaustres | 1 |
| 71859 | balar | 1 |
| 71860 | balanzas | 1 |
| 71861 | balandras | 1 |
| 71862 | balandranes | 1 |
| 71863 | balando | 1 |
| 71864 | balancines | 1 |
| 71865 | balancín | 1 |
| 71866 | balanceó | 1 |
| 71867 | balanceara | 1 |
| 71868 | balanceándose | 1 |
| 71869 | balanceando | 1 |
| 71870 | balancean | 1 |
| 71871 | balanceaba | 1 |
| 71872 | balança | 1 |
| 71873 | bálago | 1 |
| 71874 | baladros | 1 |
| 71875 | baladronada | 1 |
| 71876 | baladro | 1 |
| 71877 | bajoncito | 1 |
| 71878 | bajita | 1 |
| 71879 | bajísimos | 1 |
| 71880 | bájese | 1 |
| 71881 | bajes | 1 |
| 71882 | bájense | 1 |
| 71883 | bajarte | 1 |
| 71884 | bajarían | 1 |
| 71885 | bajaría | 1 |
| 71886 | bajaremos | 1 |
| 71887 | bajaran | 1 |
| 71888 | bajándose | 1 |
| 71889 | bajándolas | 1 |
| 71890 | bajándola | 1 |
| 71891 | bajáis | 1 |
| 71892 | bajados | 1 |
| 71893 | bajad | 1 |
| 71894 | bajábale | 1 |
| 71895 | bajábala | 1 |
| 71896 | bailoteos | 1 |
| 71897 | bailoteo | 1 |
| 71898 | bailo | 1 |
| 71899 | bailly | 1 |
| 71900 | baillière | 1 |
| 71901 | bailén | 1 |
| 71902 | bailéis | 1 |
| 71903 | bailarines | 1 |
| 71904 | bailarían | 1 |
| 71905 | bailaré | 1 |
| 71906 | bailarán | 1 |
| 71907 | bailara | 1 |
| 71908 | bailadores | 1 |
| 71909 | bailadoras | 1 |
| 71910 | bailadas | 1 |
| 71911 | bailábanle | 1 |
| 71912 | baicic | 1 |
| 71913 | bahareros | 1 |
| 71914 | baguetilla | 1 |
| 71915 | baglivio | 1 |
| 71916 | bagatelas | 1 |
| 71917 | bagajes | 1 |
| 71918 | baena | 1 |
| 71919 | badulaque | 1 |
| 71920 | badila | 1 |
| 71921 | badezu | 1 |
| 71922 | badajoz | 1 |
| 71923 | badajes | 1 |
| 71924 | badajadas | 1 |
| 71925 | baço | 1 |
| 71926 | baciyelmo | 1 |
| 71927 | baçines | 1 |
| 71928 | bacines | 1 |
| 71929 | baçín | 1 |
| 71930 | bachillería | 1 |
| 71931 | bachillerada | 1 |
| 71932 | bachillear | 1 |
| 71933 | bacanales | 1 |
| 71934 | bacalareus | 1 |
| 71935 | babylonia | 1 |
| 71936 | babilónicos | 1 |
| 71937 | babilónicas | 1 |
| 71938 | babilón | 1 |
| 71939 | babie | 1 |
| 71940 | babera | 1 |
| 71941 | babeaba | 1 |
| 71942 | babazón | 1 |
| 71943 | azuzarlas | 1 |
| 71944 | azuzándole | 1 |
| 71945 | azuzan | 1 |
| 71946 | azuzáis | 1 |
| 71947 | azuzado | 1 |
| 71948 | azutea | 1 |
| 71949 | azur | 1 |
| 71950 | azulísima | 1 |
| 71951 | azulejo | 1 |
| 71952 | azulados | 1 |
| 71953 | azulado | 1 |
| 71954 | azufrados | 1 |
| 71955 | azuda | 1 |
| 71956 | azucarillo | 1 |
| 71957 | azucarera | 1 |
| 71958 | azucarados | 1 |
| 71959 | azucarado | 1 |
| 71960 | azucaradas | 1 |
| 71961 | azpetia | 1 |
| 71962 | azparrain | 1 |
| 71963 | azotesca | 1 |
| 71964 | azótate | 1 |
| 71965 | azotase | 1 |
| 71966 | azotarte | 1 |
| 71967 | azotarle | 1 |
| 71968 | azotarla | 1 |
| 71969 | azotarás | 1 |
| 71970 | azótanme | 1 |
| 71971 | azotándome | 1 |
| 71972 | azotandome | 1 |
| 71973 | azotados | 1 |
| 71974 | azotadas | 1 |
| 71975 | azotacalles | 1 |
| 71976 | azores | 1 |
| 71977 | azoradísima | 1 |
| 71978 | azoguejo | 1 |
| 71979 | azofeyfas | 1 |
| 71980 | aziago | 1 |
| 71981 | azí | 1 |
| 71982 | azemileros | 1 |
| 71983 | azeca | 1 |
| 71984 | azcona | 1 |
| 71985 | azcarat | 1 |
| 71986 | azcain | 1 |
| 71987 | azaroso | 1 |
| 71988 | azarado | 1 |
| 71989 | azaraba | 1 |
| 71990 | azán | 1 |
| 71991 | azalea | 1 |
| 71992 | azagayas | 1 |
| 71993 | azafran | 1 |
| 71994 | azadonada | 1 |
| 71995 | azadon | 1 |
| 71996 | aza | 1 |
| 71997 | ayusso | 1 |
| 71998 | ayunten | 1 |
| 71999 | ayuntamos | 1 |
| 72000 | ayuntados | 1 |
| 72001 | ayunta | 1 |
| 72002 | ayunque | 1 |
| 72003 | ayunes | 1 |
| 72004 | ayunava | 1 |
| 72005 | ayunase | 1 |
| 72006 | ayunarle | 1 |
| 72007 | ayunaría | 1 |
| 72008 | ayunara | 1 |
| 72009 | ayunador | 1 |
| 72010 | ayunado | 1 |
| 72011 | ayunaba | 1 |
| 72012 | ayúdome | 1 |
| 72013 | ayudóle | 1 |
| 72014 | ayudole | 1 |
| 72015 | ayúdevos | 1 |
| 72016 | ayudéte | 1 |
| 72017 | ayudes | 1 |
| 72018 | ayúdenos | 1 |
| 72019 | ayudemos | 1 |
| 72020 | ayudémonos | 1 |
| 72021 | ayúdele | 1 |
| 72022 | ayudé | 1 |
| 72023 | ayudava | 1 |
| 72024 | ayudaros | 1 |
| 72025 | ayudáronle | 1 |
| 72026 | ayudáronla | 1 |
| 72027 | ayudarlos | 1 |
| 72028 | ayudaríamos | 1 |
| 72029 | ayudares | 1 |
| 72030 | ayudare | 1 |
| 72031 | ayudarais | 1 |
| 72032 | ayudaos | 1 |
| 72033 | ayudándose | 1 |
| 72034 | ayudándoos | 1 |
| 72035 | ayudándome | 1 |
| 72036 | ayudándolas | 1 |
| 72037 | ayudándola | 1 |
| 72038 | ayudandola | 1 |
| 72039 | ayudalle | 1 |
| 72040 | ayúdala | 1 |
| 72041 | ayudador | 1 |
| 72042 | ayudadles | 1 |
| 72043 | ayudábanse | 1 |
| 72044 | ayudábamos | 1 |
| 72045 | ayud | 1 |
| 72046 | ayraste | 1 |
| 72047 | ayras | 1 |
| 72048 | ayala | 1 |
| 72049 | axis | 1 |
| 72050 | axiensos | 1 |
| 72051 | axenúz | 1 |
| 72052 | axabeba | 1 |
| 72053 | avyva | 1 |
| 72054 | avyene | 1 |
| 72055 | avye | 1 |
| 72056 | avría | 1 |
| 72057 | avoleza | 1 |
| 72058 | avizores | 1 |
| 72059 | avivo | 1 |
| 72060 | avives | 1 |
| 72061 | avive | 1 |
| 72062 | avivarse | 1 |
| 72063 | avivan | 1 |
| 72064 | avivado | 1 |
| 72065 | avistarme | 1 |
| 72066 | avistados | 1 |
| 72067 | avispas | 1 |
| 72068 | avispados | 1 |
| 72069 | avispado | 1 |
| 72070 | avísote | 1 |
| 72071 | avisón | 1 |
| 72072 | avisillo | 1 |
| 72073 | avises | 1 |
| 72074 | avísenme | 1 |
| 72075 | avisen | 1 |
| 72076 | avisasteis | 1 |
| 72077 | avisaste | 1 |
| 72078 | avisasen | 1 |
| 72079 | avisásemos | 1 |
| 72080 | avisarla | 1 |
| 72081 | avisaréte | 1 |
| 72082 | avisaremos | 1 |
| 72083 | avisarás | 1 |
| 72084 | avisarán | 1 |
| 72085 | avisara | 1 |
| 72086 | avisándome | 1 |
| 72087 | avisándole | 1 |
| 72088 | avisamos | 1 |
| 72089 | avisad | 1 |
| 72090 | avisaban | 1 |
| 72091 | avíos | 1 |
| 72092 | avinieran | 1 |
| 72093 | aviniendo | 1 |
| 72094 | avine | 1 |
| 72095 | avindarraez | 1 |
| 72096 | avinagrados | 1 |
| 72097 | aviesos | 1 |
| 72098 | aviesas | 1 |
| 72099 | avienes | 1 |
| 72100 | avienen | 1 |
| 72101 | avién | 1 |
| 72102 | avíen | 1 |
| 72103 | avidez | 1 |
| 72104 | aviarme | 1 |
| 72105 | aviarla | 1 |
| 72106 | aviar | 1 |
| 72107 | avian | 1 |
| 72108 | avíala | 1 |
| 72109 | avet | 1 |
| 72110 | averte | 1 |
| 72111 | avérsevos | 1 |
| 72112 | averla | 1 |
| 72113 | averigüen | 1 |
| 72114 | averigüemos | 1 |
| 72115 | averígüelo | 1 |
| 72116 | averigüéle | 1 |
| 72117 | averiguarle | 1 |
| 72118 | averiguaría | 1 |
| 72119 | averiguare | 1 |
| 72120 | averiguan | 1 |
| 72121 | averiguamos | 1 |
| 72122 | averiguallo | 1 |
| 72123 | averiguadores | 1 |
| 72124 | averiguador | 1 |
| 72125 | averiguadas | 1 |
| 72126 | averigua | 1 |
| 72127 | averiada | 1 |
| 72128 | avergüenzo | 1 |
| 72129 | avergonzóse | 1 |
| 72130 | avergonzose | 1 |
| 72131 | avergonzarse | 1 |
| 72132 | avergonzáronse | 1 |
| 72133 | avergonzarme | 1 |
| 72134 | avergonzarla | 1 |
| 72135 | avergonzaos | 1 |
| 72136 | avergonzando | 1 |
| 72137 | avergonzadísimo | 1 |
| 72138 | avergonzadas | 1 |
| 72139 | aventureras | 1 |
| 72140 | aventuremos | 1 |
| 72141 | aventuréis | 1 |
| 72142 | aventuré | 1 |
| 72143 | aventure | 1 |
| 72144 | aventurarnos | 1 |
| 72145 | aventurarme | 1 |
| 72146 | aventurarlo | 1 |
| 72147 | aventurarías | 1 |
| 72148 | aventuraría | 1 |
| 72149 | aventurándote | 1 |
| 72150 | aventurándolo | 1 |
| 72151 | aventurando | 1 |
| 72152 | aventuran | 1 |
| 72153 | aventuralla | 1 |
| 72154 | aventurados | 1 |
| 72155 | aventuradas | 1 |
| 72156 | aventurábase | 1 |
| 72157 | aventu | 1 |
| 72158 | aventino | 1 |
| 72159 | aventajó | 1 |
| 72160 | aventajase | 1 |
| 72161 | aventajaron | 1 |
| 72162 | aventajarán | 1 |
| 72163 | aventajará | 1 |
| 72164 | aventajar | 1 |
| 72165 | aventajaban | 1 |
| 72166 | avenirse | 1 |
| 72167 | avenir | 1 |
| 72168 | avengo | 1 |
| 72169 | avenga | 1 |
| 72170 | avendría | 1 |
| 72171 | avendremos | 1 |
| 72172 | avendré | 1 |
| 72173 | avémoslo | 1 |
| 72174 | avellanos | 1 |
| 72175 | avellano | 1 |
| 72176 | avellanadas | 1 |
| 72177 | avellanada | 1 |
| 72178 | avecitas | 1 |
| 72179 | avecindados | 1 |
| 72180 | avasallen | 1 |
| 72181 | avasallase | 1 |
| 72182 | avasallara | 1 |
| 72183 | avasallan | 1 |
| 72184 | avasalladores | 1 |
| 72185 | avasallado | 1 |
| 72186 | avarisia | 1 |
| 72187 | avarientas | 1 |
| 72188 | avarienta | 1 |
| 72189 | avariciosa | 1 |
| 72190 | avaras | 1 |
| 72191 | avapiés | 1 |
| 72192 | avalora | 1 |
| 72193 | auxiliase | 1 |
| 72194 | auxiliarse | 1 |
| 72195 | auxiliaron | 1 |
| 72196 | auxiliarle | 1 |
| 72197 | auxiliaran | 1 |
| 72198 | auxilïar | 1 |
| 72199 | auxiliándoles | 1 |
| 72200 | auxiliada | 1 |
| 72201 | aux | 1 |
| 72202 | autorzuelos | 1 |
| 72203 | autorizo | 1 |
| 72204 | autorizarme | 1 |
| 72205 | autorizantes | 1 |
| 72206 | autorizados | 1 |
| 72207 | autoritarios | 1 |
| 72208 | autoritarias | 1 |
| 72209 | autoritariamente | 1 |
| 72210 | autorices | 1 |
| 72211 | autorcillos | 1 |
| 72212 | autorcillo | 1 |
| 72213 | autopsia | 1 |
| 72214 | automóviles | 1 |
| 72215 | automóvil | 1 |
| 72216 | autómatas | 1 |
| 72217 | autolatría | 1 |
| 72218 | autocrático | 1 |
| 72219 | autocrática | 1 |
| 72220 | autobiográfica | 1 |
| 72221 | autobiografía | 1 |
| 72222 | auteurs | 1 |
| 72223 | auténticamente | 1 |
| 72224 | austros | 1 |
| 72225 | austríada | 1 |
| 72226 | austríacos | 1 |
| 72227 | austriacos | 1 |
| 72228 | austriacas | 1 |
| 72229 | austeridad | 1 |
| 72230 | austeras | 1 |
| 72231 | aussi | 1 |
| 72232 | auspicio | 1 |
| 72233 | ausonio | 1 |
| 72234 | ausento | 1 |
| 72235 | ausentasen | 1 |
| 72236 | ausentase | 1 |
| 72237 | ausentaros | 1 |
| 72238 | ausentarme | 1 |
| 72239 | ausentándose | 1 |
| 72240 | ausentádose | 1 |
| 72241 | ausculte | 1 |
| 72242 | auscultarle | 1 |
| 72243 | aurrena | 1 |
| 72244 | aurorita | 1 |
| 72245 | auro | 1 |
| 72246 | aúpa | 1 |
| 72247 | auñón | 1 |
| 72248 | aunqu | 1 |
| 72249 | aunq | 1 |
| 72250 | aunarme | 1 |
| 72251 | aumentos | 1 |
| 72252 | auméntase | 1 |
| 72253 | aumentas | 1 |
| 72254 | aumentármela | 1 |
| 72255 | aumentarlas | 1 |
| 72256 | aumentarás | 1 |
| 72257 | aumentarán | 1 |
| 72258 | auméntame | 1 |
| 72259 | aumentáis | 1 |
| 72260 | aumentados | 1 |
| 72261 | aulló | 1 |
| 72262 | aullando | 1 |
| 72263 | aullado | 1 |
| 72264 | áulico | 1 |
| 72265 | auiuas | 1 |
| 72266 | auiuadora | 1 |
| 72267 | auisote | 1 |
| 72268 | auise | 1 |
| 72269 | auisauate | 1 |
| 72270 | auisarte | 1 |
| 72271 | auisar | 1 |
| 72272 | auisale | 1 |
| 72273 | auisada | 1 |
| 72274 | auiendo | 1 |
| 72275 | auiaseme | 1 |
| 72276 | auiame | 1 |
| 72277 | auiades | 1 |
| 72278 | augustísima | 1 |
| 72279 | augustinus | 1 |
| 72280 | augustina | 1 |
| 72281 | augurios | 1 |
| 72282 | augurio | 1 |
| 72283 | augurando | 1 |
| 72284 | augmentado | 1 |
| 72285 | augmenta | 1 |
| 72286 | auf | 1 |
| 72287 | auerte | 1 |
| 72288 | aueran | 1 |
| 72289 | auenture | 1 |
| 72290 | auenturauan | 1 |
| 72291 | auenturado | 1 |
| 72292 | auelo | 1 |
| 72293 | audición | 1 |
| 72294 | audiat | 1 |
| 72295 | audacísimo | 1 |
| 72296 | audacias | 1 |
| 72297 | auctoridad | 1 |
| 72298 | auctor | 1 |
| 72299 | aucto | 1 |
| 72300 | aube | 1 |
| 72301 | auariento | 1 |
| 72302 | auantaja | 1 |
| 72303 | atyncar | 1 |
| 72304 | atyenden | 1 |
| 72305 | atusó | 1 |
| 72306 | atusarte | 1 |
| 72307 | atusándole | 1 |
| 72308 | atusando | 1 |
| 72309 | aturullo | 1 |
| 72310 | aturullada | 1 |
| 72311 | aturdiré | 1 |
| 72312 | aturdieron | 1 |
| 72313 | aturdiendo | 1 |
| 72314 | aturdidos | 1 |
| 72315 | aturdidísima | 1 |
| 72316 | aturdíase | 1 |
| 72317 | aturdí | 1 |
| 72318 | atún | 1 |
| 72319 | atufo | 1 |
| 72320 | atufándonos | 1 |
| 72321 | attend | 1 |
| 72322 | attache | 1 |
| 72323 | atruena | 1 |
| 72324 | atropelló | 1 |
| 72325 | atropellas | 1 |
| 72326 | atropellaron | 1 |
| 72327 | atropellaré | 1 |
| 72328 | atropellarás | 1 |
| 72329 | atropellaras | 1 |
| 72330 | atropellarán | 1 |
| 72331 | atropellándolo | 1 |
| 72332 | atropelladas | 1 |
| 72333 | atropellaban | 1 |
| 72334 | atronaron | 1 |
| 72335 | atronar | 1 |
| 72336 | atronando | 1 |
| 72337 | atronadora | 1 |
| 72338 | atrofian | 1 |
| 72339 | atrincherado | 1 |
| 72340 | atriles | 1 |
| 72341 | atril | 1 |
| 72342 | atribuyo | 1 |
| 72343 | atribuyese | 1 |
| 72344 | atribuyes | 1 |
| 72345 | atribuyéndolos | 1 |
| 72346 | atribuyéndolo | 1 |
| 72347 | atribuyéndole | 1 |
| 72348 | atribuyéndolas | 1 |
| 72349 | atribularon | 1 |
| 72350 | atribuladas | 1 |
| 72351 | atribuirse | 1 |
| 72352 | atribuirme | 1 |
| 72353 | atribuirlo | 1 |
| 72354 | atribuirle | 1 |
| 72355 | atribuídos | 1 |
| 72356 | atribüido | 1 |
| 72357 | atribuí | 1 |
| 72358 | atribución | 1 |
| 72359 | atrevyme | 1 |
| 72360 | atrevuda | 1 |
| 72361 | atrevióse | 1 |
| 72362 | atrevieres | 1 |
| 72363 | atrevieren | 1 |
| 72364 | atreviere | 1 |
| 72365 | atrevidísima | 1 |
| 72366 | atrevidillo | 1 |
| 72367 | atrevidilla | 1 |
| 72368 | atreverte | 1 |
| 72369 | atreverán | 1 |
| 72370 | atrevas | 1 |
| 72371 | atreuo | 1 |
| 72372 | atreuio | 1 |
| 72373 | atreuimientos | 1 |
| 72374 | atreuido | 1 |
| 72375 | atreues | 1 |
| 72376 | atreuer | 1 |
| 72377 | atreua | 1 |
| 72378 | atraviesen | 1 |
| 72379 | atraviese | 1 |
| 72380 | atravesósele | 1 |
| 72381 | atravesósel | 1 |
| 72382 | atravesós | 1 |
| 72383 | atravesole | 1 |
| 72384 | atravesé | 1 |
| 72385 | atravesaste | 1 |
| 72386 | atravesasen | 1 |
| 72387 | atravesase | 1 |
| 72388 | atravesarlo | 1 |
| 72389 | atravesarla | 1 |
| 72390 | atravesándolo | 1 |
| 72391 | atravesándole | 1 |
| 72392 | atravesamos | 1 |
| 72393 | atravesadas | 1 |
| 72394 | atrasando | 1 |
| 72395 | atrasaditos | 1 |
| 72396 | atrasa | 1 |
| 72397 | atrapo | 1 |
| 72398 | atraparle | 1 |
| 72399 | atrapado | 1 |
| 72400 | atrancar | 1 |
| 72401 | atraerse | 1 |
| 72402 | atraernos | 1 |
| 72403 | atraería | 1 |
| 72404 | atraerán | 1 |
| 72405 | atraen | 1 |
| 72406 | atractiva | 1 |
| 72407 | atracciones | 1 |
| 72408 | atrácate | 1 |
| 72409 | atracarse | 1 |
| 72410 | atracaban | 1 |
| 72411 | atracaba | 1 |
| 72412 | atque | 1 |
| 72413 | atosigó | 1 |
| 72414 | atosigaba | 1 |
| 72415 | atormentó | 1 |
| 72416 | atormentaron | 1 |
| 72417 | atormentaría | 1 |
| 72418 | atormentándole | 1 |
| 72419 | atormentadores | 1 |
| 72420 | atordidos | 1 |
| 72421 | atordida | 1 |
| 72422 | atora | 1 |
| 72423 | atontoneleada | 1 |
| 72424 | atontonelados | 1 |
| 72425 | atontarse | 1 |
| 72426 | atomístico | 1 |
| 72427 | atolondrada | 1 |
| 72428 | atmosférico | 1 |
| 72429 | atletas | 1 |
| 72430 | atizóle | 1 |
| 72431 | atizé | 1 |
| 72432 | atizarse | 1 |
| 72433 | atizaron | 1 |
| 72434 | atizándose | 1 |
| 72435 | atizándole | 1 |
| 72436 | atizan | 1 |
| 72437 | atizado | 1 |
| 72438 | atisbos | 1 |
| 72439 | atisbó | 1 |
| 72440 | atisbar | 1 |
| 72441 | atisbadora | 1 |
| 72442 | atisbaba | 1 |
| 72443 | atinado | 1 |
| 72444 | atinadísima | 1 |
| 72445 | atinada | 1 |
| 72446 | atilde | 1 |
| 72447 | atildadura | 1 |
| 72448 | atildado | 1 |
| 72449 | atila | 1 |
| 72450 | atiéntame | 1 |
| 72451 | atiéndense | 1 |
| 72452 | ático | 1 |
| 72453 | atiborrar | 1 |
| 72454 | atiborrados | 1 |
| 72455 | athenienses | 1 |
| 72456 | athenas | 1 |
| 72457 | atezado | 1 |
| 72458 | atestiguó | 1 |
| 72459 | atestiguase | 1 |
| 72460 | atestiguar | 1 |
| 72461 | atestiguaban | 1 |
| 72462 | atestiguaba | 1 |
| 72463 | atestaba | 1 |
| 72464 | atesores | 1 |
| 72465 | aterrorizarla | 1 |
| 72466 | aterrorizado | 1 |
| 72467 | aterrorizada | 1 |
| 72468 | aterró | 1 |
| 72469 | aterre | 1 |
| 72470 | aterradoras | 1 |
| 72471 | ateridos | 1 |
| 72472 | aterido | 1 |
| 72473 | aterida | 1 |
| 72474 | atenuase | 1 |
| 72475 | atenuaron | 1 |
| 72476 | atenuarlo | 1 |
| 72477 | atenuarían | 1 |
| 72478 | atenuaciones | 1 |
| 72479 | atenúa | 1 |
| 72480 | atentísimos | 1 |
| 72481 | atentar | 1 |
| 72482 | atentados | 1 |
| 72483 | atentadamente | 1 |
| 72484 | atentaba | 1 |
| 72485 | ateniéndose | 1 |
| 72486 | ateniéndome | 1 |
| 72487 | atenida | 1 |
| 72488 | aténgase | 1 |
| 72489 | atenernos | 1 |
| 72490 | atenea | 1 |
| 72491 | atendióle | 1 |
| 72492 | atendiól | 1 |
| 72493 | atendimos | 1 |
| 72494 | atendiésemos | 1 |
| 72495 | atendieron | 1 |
| 72496 | atendieran | 1 |
| 72497 | atendiera | 1 |
| 72498 | atendido | 1 |
| 72499 | atendí | 1 |
| 72500 | atendemos | 1 |
| 72501 | atenazó | 1 |
| 72502 | atenazado | 1 |
| 72503 | atenazaba | 1 |
| 72504 | atenácenme | 1 |
| 72505 | atemorizan | 1 |
| 72506 | atemorizados | 1 |
| 72507 | atemorizado | 1 |
| 72508 | atemoriza | 1 |
| 72509 | atemoricen | 1 |
| 72510 | atemorice | 1 |
| 72511 | ateas | 1 |
| 72512 | atea | 1 |
| 72513 | até | 1 |
| 72514 | atchuria | 1 |
| 72515 | atavíen | 1 |
| 72516 | atávicas | 1 |
| 72517 | ataviarse | 1 |
| 72518 | ataun | 1 |
| 72519 | atauio | 1 |
| 72520 | atase | 1 |
| 72521 | atascó | 1 |
| 72522 | atasco | 1 |
| 72523 | atascan | 1 |
| 72524 | atascaban | 1 |
| 72525 | atas | 1 |
| 72526 | atarugándolo | 1 |
| 72527 | atarugamiento | 1 |
| 72528 | atarugaba | 1 |
| 72529 | ataros | 1 |
| 72530 | atáronlos | 1 |
| 72531 | atármela | 1 |
| 72532 | atarjea | 1 |
| 72533 | atarés | 1 |
| 72534 | atareados | 1 |
| 72535 | atarazaba | 1 |
| 72536 | ataras | 1 |
| 72537 | atapárselos | 1 |
| 72538 | atapábale | 1 |
| 72539 | atapa | 1 |
| 72540 | ataos | 1 |
| 72541 | atañía | 1 |
| 72542 | atañederos | 1 |
| 72543 | atañederas | 1 |
| 72544 | ataña | 1 |
| 72545 | atantos | 1 |
| 72546 | atándose | 1 |
| 72547 | atán | 1 |
| 72548 | atamientos | 1 |
| 72549 | atamaña | 1 |
| 72550 | atama | 1 |
| 72551 | atalvina | 1 |
| 72552 | atalegar | 1 |
| 72553 | atalanta | 1 |
| 72554 | atajóse | 1 |
| 72555 | atajos | 1 |
| 72556 | ataje | 1 |
| 72557 | atajasolazes | 1 |
| 72558 | atajase | 1 |
| 72559 | atajas | 1 |
| 72560 | atajarle | 1 |
| 72561 | atajándole | 1 |
| 72562 | atajando | 1 |
| 72563 | atajalla | 1 |
| 72564 | atajador | 1 |
| 72565 | atáis | 1 |
| 72566 | atahona | 1 |
| 72567 | ataguylaco | 1 |
| 72568 | atadura | 1 |
| 72569 | atadlos | 1 |
| 72570 | atadillo | 1 |
| 72571 | atadijos | 1 |
| 72572 | atadijo | 1 |
| 72573 | atacóse | 1 |
| 72574 | ataco | 1 |
| 72575 | atacarte | 1 |
| 72576 | atacarles | 1 |
| 72577 | atacarle | 1 |
| 72578 | atacándonos | 1 |
| 72579 | atacándolas | 1 |
| 72580 | atabores | 1 |
| 72581 | atabor | 1 |
| 72582 | atábase | 1 |
| 72583 | asustose | 1 |
| 72584 | asustemos | 1 |
| 72585 | asustasen | 1 |
| 72586 | asustas | 1 |
| 72587 | asustarte | 1 |
| 72588 | asustarme | 1 |
| 72589 | asustaré | 1 |
| 72590 | asustaran | 1 |
| 72591 | asustábase | 1 |
| 72592 | asustaban | 1 |
| 72593 | asuramos | 1 |
| 72594 | asumptos | 1 |
| 72595 | asueto | 1 |
| 72596 | asueta | 1 |
| 72597 | asuero | 1 |
| 72598 | asuelvo | 1 |
| 72599 | asuelto | 1 |
| 72600 | asuelta | 1 |
| 72601 | asuela | 1 |
| 72602 | astutos | 1 |
| 72603 | astur | 1 |
| 72604 | astrosya | 1 |
| 72605 | astrosa | 1 |
| 72606 | astronómicos | 1 |
| 72607 | astrológicas | 1 |
| 72608 | astrolabio | 1 |
| 72609 | astri | 1 |
| 72610 | astrea | 1 |
| 72611 | astralabio | 1 |
| 72612 | astragas | 1 |
| 72613 | astragarvos | 1 |
| 72614 | astragaríe | 1 |
| 72615 | astragando | 1 |
| 72616 | astragallo | 1 |
| 72617 | astracanadas | 1 |
| 72618 | astra | 1 |
| 72619 | astolfo | 1 |
| 72620 | astilla | 1 |
| 72621 | asté | 1 |
| 72622 | assonados | 1 |
| 72623 | assoma | 1 |
| 72624 | assistentiam | 1 |
| 72625 | assimismo | 1 |
| 72626 | assimesmo | 1 |
| 72627 | assiento | 1 |
| 72628 | assienta | 1 |
| 72629 | asseverar | 1 |
| 72630 | asseo | 1 |
| 72631 | assentó | 1 |
| 72632 | assentemonos | 1 |
| 72633 | assente | 1 |
| 72634 | assentauan | 1 |
| 72635 | assentaua | 1 |
| 72636 | assentarnos | 1 |
| 72637 | assentaos | 1 |
| 72638 | assentadas | 1 |
| 72639 | assentada | 1 |
| 72640 | asseguro | 1 |
| 72641 | assegurar | 1 |
| 72642 | assegura | 1 |
| 72643 | assañóse | 1 |
| 72644 | assaño | 1 |
| 72645 | assaduras | 1 |
| 72646 | assador | 1 |
| 72647 | assadero | 1 |
| 72648 | assadas | 1 |
| 72649 | asquerosísimas | 1 |
| 72650 | asquerosidades | 1 |
| 72651 | aspires | 1 |
| 72652 | aspire | 1 |
| 72653 | aspiraste | 1 |
| 72654 | aspirales | 1 |
| 72655 | aspiradores | 1 |
| 72656 | aspirado | 1 |
| 72657 | aspiradas | 1 |
| 72658 | aspetatores | 1 |
| 72659 | asperísima | 1 |
| 72660 | asperece | 1 |
| 72661 | asperas | 1 |
| 72662 | aspeado | 1 |
| 72663 | aspaviento | 1 |
| 72664 | aspasia | 1 |
| 72665 | aspar | 1 |
| 72666 | asotiles | 1 |
| 72667 | asosegadamente | 1 |
| 72668 | asonbra | 1 |
| 72669 | asonantes | 1 |
| 72670 | asonante | 1 |
| 72671 | asonantado | 1 |
| 72672 | asonada | 1 |
| 72673 | asomes | 1 |
| 72674 | asomen | 1 |
| 72675 | asome | 1 |
| 72676 | asombrosas | 1 |
| 72677 | asombrosamente | 1 |
| 72678 | asombros | 1 |
| 72679 | asómbrese | 1 |
| 72680 | asombren | 1 |
| 72681 | asombréis | 1 |
| 72682 | asómbrate | 1 |
| 72683 | asombras | 1 |
| 72684 | asombráronse | 1 |
| 72685 | asombraron | 1 |
| 72686 | asombrarme | 1 |
| 72687 | asombrarías | 1 |
| 72688 | asombrarás | 1 |
| 72689 | asombraran | 1 |
| 72690 | asombrara | 1 |
| 72691 | asombrándose | 1 |
| 72692 | asombradiza | 1 |
| 72693 | asombraban | 1 |
| 72694 | asombrábamos | 1 |
| 72695 | asómate | 1 |
| 72696 | asomasen | 1 |
| 72697 | asómase | 1 |
| 72698 | asomarnos | 1 |
| 72699 | asomaré | 1 |
| 72700 | asomaran | 1 |
| 72701 | asomándole | 1 |
| 72702 | asoman | 1 |
| 72703 | asomábase | 1 |
| 72704 | asolvióle | 1 |
| 72705 | asolvet | 1 |
| 72706 | asolverlos | 1 |
| 72707 | asolverle | 1 |
| 72708 | asolved | 1 |
| 72709 | asolvades | 1 |
| 72710 | asolución | 1 |
| 72711 | asoleado | 1 |
| 72712 | asolaste | 1 |
| 72713 | asolase | 1 |
| 72714 | asolaron | 1 |
| 72715 | asolando | 1 |
| 72716 | asolados | 1 |
| 72717 | asoladora | 1 |
| 72718 | asolaba | 1 |
| 72719 | asociarla | 1 |
| 72720 | asociándolos | 1 |
| 72721 | asnillo | 1 |
| 72722 | asnería | 1 |
| 72723 | asnalmente | 1 |
| 72724 | asnales | 1 |
| 72725 | asna | 1 |
| 72726 | asmó | 1 |
| 72727 | asmático | 1 |
| 72728 | asmar | 1 |
| 72729 | asistirlos | 1 |
| 72730 | asistiría | 1 |
| 72731 | asistile | 1 |
| 72732 | asistiese | 1 |
| 72733 | asistidos | 1 |
| 72734 | asistida | 1 |
| 72735 | asistíamos | 1 |
| 72736 | asirte | 1 |
| 72737 | asirme | 1 |
| 72738 | asióme | 1 |
| 72739 | asintieron | 1 |
| 72740 | asinóles | 1 |
| 72741 | asinase | 1 |
| 72742 | asinado | 1 |
| 72743 | asín | 1 |
| 72744 | asimilándole | 1 |
| 72745 | asimilando | 1 |
| 72746 | asimilan | 1 |
| 72747 | asimiladas | 1 |
| 72748 | asimilaba | 1 |
| 72749 | asilla | 1 |
| 72750 | asilde | 1 |
| 72751 | asilados | 1 |
| 72752 | asigno | 1 |
| 72753 | asignatura | 1 |
| 72754 | asignarle | 1 |
| 72755 | asignara | 1 |
| 72756 | asignado | 1 |
| 72757 | asignaba | 1 |
| 72758 | asiesten | 1 |
| 72759 | asiéronse | 1 |
| 72760 | asiéronme | 1 |
| 72761 | asiéronle | 1 |
| 72762 | asiera | 1 |
| 72763 | asienten | 1 |
| 72764 | asiéndose | 1 |
| 72765 | asiéndolos | 1 |
| 72766 | asidero | 1 |
| 72767 | asiática | 1 |
| 72768 | asía | 1 |
| 72769 | asfixiarse | 1 |
| 72770 | asfixiantes | 1 |
| 72771 | asfixiado | 1 |
| 72772 | aseveró | 1 |
| 72773 | aseveraciones | 1 |
| 72774 | aseveraba | 1 |
| 72775 | asestó | 1 |
| 72776 | asestara | 1 |
| 72777 | asestar | 1 |
| 72778 | asestando | 1 |
| 72779 | asestan | 1 |
| 72780 | asestado | 1 |
| 72781 | asesta | 1 |
| 72782 | asesorado | 1 |
| 72783 | asesinó | 1 |
| 72784 | asesinarla | 1 |
| 72785 | asesinando | 1 |
| 72786 | asesinan | 1 |
| 72787 | asesinados | 1 |
| 72788 | asesinadas | 1 |
| 72789 | asesina | 1 |
| 72790 | ases | 1 |
| 72791 | aserrar | 1 |
| 72792 | asequible | 1 |
| 72793 | aseñorado | 1 |
| 72794 | asentóseme | 1 |
| 72795 | asentósele | 1 |
| 72796 | asentóme | 1 |
| 72797 | asento | 1 |
| 72798 | asentir | 1 |
| 72799 | asentía | 1 |
| 72800 | asentarse | 1 |
| 72801 | asentarlos | 1 |
| 72802 | asentaría | 1 |
| 72803 | asentados | 1 |
| 72804 | asentaderas | 1 |
| 72805 | asenderado | 1 |
| 72806 | asen | 1 |
| 72807 | asemeje | 1 |
| 72808 | asemejarse | 1 |
| 72809 | asemejándose | 1 |
| 72810 | asemejan | 1 |
| 72811 | asemejaba | 1 |
| 72812 | asemeja | 1 |
| 72813 | asegurome | 1 |
| 72814 | aseguremos | 1 |
| 72815 | asegúrelo | 1 |
| 72816 | asegúrate | 1 |
| 72817 | aseguras | 1 |
| 72818 | aseguraros | 1 |
| 72819 | asegurarme | 1 |
| 72820 | asegurarla | 1 |
| 72821 | aseguraríamos | 1 |
| 72822 | aseguraré | 1 |
| 72823 | asegurará | 1 |
| 72824 | asegúrante | 1 |
| 72825 | aseguramos | 1 |
| 72826 | asegúrame | 1 |
| 72827 | asegúrala | 1 |
| 72828 | asegurábamos | 1 |
| 72829 | asegunda | 1 |
| 72830 | asedos | 1 |
| 72831 | asediado | 1 |
| 72832 | asediaba | 1 |
| 72833 | asedía | 1 |
| 72834 | asedia | 1 |
| 72835 | asechanza | 1 |
| 72836 | aseadísima | 1 |
| 72837 | aseada | 1 |
| 72838 | ascut | 1 |
| 72839 | ascuso | 1 |
| 72840 | ascuchad | 1 |
| 72841 | ascucha | 1 |
| 72842 | ascondes | 1 |
| 72843 | asconderme | 1 |
| 72844 | asconder | 1 |
| 72845 | asconden | 1 |
| 72846 | ascondéis | 1 |
| 72847 | asconde | 1 |
| 72848 | asciendes | 1 |
| 72849 | ascienden | 1 |
| 72850 | asciende | 1 |
| 72851 | ascética | 1 |
| 72852 | ascensos | 1 |
| 72853 | ascendió | 1 |
| 72854 | ascendieron | 1 |
| 72855 | ascendían | 1 |
| 72856 | ascenderunt | 1 |
| 72857 | asçendente | 1 |
| 72858 | ascanica | 1 |
| 72859 | asáz | 1 |
| 72860 | asava | 1 |
| 72861 | asase | 1 |
| 72862 | asas | 1 |
| 72863 | asarás | 1 |
| 72864 | asará | 1 |
| 72865 | asañe | 1 |
| 72866 | asañastes | 1 |
| 72867 | asan | 1 |
| 72868 | asalten | 1 |
| 72869 | asaltásemos | 1 |
| 72870 | asaltáronle | 1 |
| 72871 | asafétida | 1 |
| 72872 | asaetee | 1 |
| 72873 | asaetearan | 1 |
| 72874 | asaetear | 1 |
| 72875 | asaduras | 1 |
| 72876 | asadura | 1 |
| 72877 | asacristanado | 1 |
| 72878 | asaban | 1 |
| 72879 | asábamonos | 1 |
| 72880 | arzobispales | 1 |
| 72881 | arzobispal | 1 |
| 72882 | arveja | 1 |
| 72883 | arúspice | 1 |
| 72884 | arufianada | 1 |
| 72885 | aruejas | 1 |
| 72886 | artzen | 1 |
| 72887 | arto | 1 |
| 72888 | artísticamente | 1 |
| 72889 | artillado | 1 |
| 72890 | artificiosos | 1 |
| 72891 | artificiosas | 1 |
| 72892 | artificiosamente | 1 |
| 72893 | artificialmente | 1 |
| 72894 | artifice | 1 |
| 72895 | artieda | 1 |
| 72896 | articuza | 1 |
| 72897 | articuló | 1 |
| 72898 | articulillo | 1 |
| 72899 | articulazo | 1 |
| 72900 | articularse | 1 |
| 72901 | articularon | 1 |
| 72902 | articulando | 1 |
| 72903 | articulaciones | 1 |
| 72904 | articulación | 1 |
| 72905 | árticas | 1 |
| 72906 | artesoncillo | 1 |
| 72907 | artesianos | 1 |
| 72908 | artesiano | 1 |
| 72909 | arteros | 1 |
| 72910 | arterías | 1 |
| 72911 | artería | 1 |
| 72912 | arteras | 1 |
| 72913 | artemisa | 1 |
| 72914 | artela | 1 |
| 72915 | artefactos | 1 |
| 72916 | arsenioso | 1 |
| 72917 | arsenales | 1 |
| 72918 | ars | 1 |
| 72919 | arrumbadas | 1 |
| 72920 | arrullas | 1 |
| 72921 | arrullarla | 1 |
| 72922 | arrullar | 1 |
| 72923 | arrullándose | 1 |
| 72924 | arrullando | 1 |
| 72925 | arrullan | 1 |
| 72926 | arrullador | 1 |
| 72927 | arruinen | 1 |
| 72928 | arruine | 1 |
| 72929 | arruinaron | 1 |
| 72930 | arruinarle | 1 |
| 72931 | arruinar | 1 |
| 72932 | arruinamos | 1 |
| 72933 | arruinados | 1 |
| 72934 | arrugase | 1 |
| 72935 | arrugarse | 1 |
| 72936 | arrugaditos | 1 |
| 72937 | arrugadas | 1 |
| 72938 | arruga | 1 |
| 72939 | arrufastes | 1 |
| 72940 | arrópese | 1 |
| 72941 | arropasen | 1 |
| 72942 | arroparon | 1 |
| 72943 | arroparme | 1 |
| 72944 | arropándose | 1 |
| 72945 | arropándole | 1 |
| 72946 | arropada | 1 |
| 72947 | arrolló | 1 |
| 72948 | arrollada | 1 |
| 72949 | arrolla | 1 |
| 72950 | arrojóse | 1 |
| 72951 | arrojóme | 1 |
| 72952 | arrojóla | 1 |
| 72953 | arrójese | 1 |
| 72954 | arrojemos | 1 |
| 72955 | arrójeme | 1 |
| 72956 | arrójate | 1 |
| 72957 | arrójase | 1 |
| 72958 | arrojárselo | 1 |
| 72959 | arrojarlos | 1 |
| 72960 | arrojarles | 1 |
| 72961 | arrojarás | 1 |
| 72962 | arrojaras | 1 |
| 72963 | arrojaran | 1 |
| 72964 | arrojará | 1 |
| 72965 | arrojándote | 1 |
| 72966 | arrojándome | 1 |
| 72967 | arrojándola | 1 |
| 72968 | arrojábase | 1 |
| 72969 | arrojábala | 1 |
| 72970 | arrogantillo | 1 |
| 72971 | arrogan | 1 |
| 72972 | arrodillóse | 1 |
| 72973 | arrodillose | 1 |
| 72974 | arrodilló | 1 |
| 72975 | arrodillé | 1 |
| 72976 | arrodillaste | 1 |
| 72977 | arrodillándome | 1 |
| 72978 | arrodillamiento | 1 |
| 72979 | arrodillado | 1 |
| 72980 | arrocadas | 1 |
| 72981 | arrobos | 1 |
| 72982 | arrobo | 1 |
| 72983 | arrobamientos | 1 |
| 72984 | arrobado | 1 |
| 72985 | arrobada | 1 |
| 72986 | arrizuri | 1 |
| 72987 | arrinconadas | 1 |
| 72988 | arrincona | 1 |
| 72989 | arrimose | 1 |
| 72990 | arrimos | 1 |
| 72991 | arrimes | 1 |
| 72992 | arrime | 1 |
| 72993 | arrimaron | 1 |
| 72994 | arrimarle | 1 |
| 72995 | arrimara | 1 |
| 72996 | arrimar | 1 |
| 72997 | arrimándonos | 1 |
| 72998 | arrimando | 1 |
| 72999 | arrimaditas | 1 |
| 73000 | arrimadita | 1 |
| 73001 | arrimábase | 1 |
| 73002 | arrimaban | 1 |
| 73003 | arriglar | 1 |
| 73004 | arriesgué | 1 |
| 73005 | arriesgue | 1 |
| 73006 | arriesgas | 1 |
| 73007 | arriesgáronse | 1 |
| 73008 | arriesgándose | 1 |
| 73009 | arriesgábase | 1 |
| 73010 | arriesgaba | 1 |
| 73011 | arriedro | 1 |
| 73012 | arribó | 1 |
| 73013 | arriado | 1 |
| 73014 | arriada | 1 |
| 73015 | arriaban | 1 |
| 73016 | arri | 1 |
| 73017 | arrezio | 1 |
| 73018 | arreziate | 1 |
| 73019 | arreziando | 1 |
| 73020 | arresto | 1 |
| 73021 | arrestado | 1 |
| 73022 | arresido | 1 |
| 73023 | arrequives | 1 |
| 73024 | arrepintiose | 1 |
| 73025 | arrepintiese | 1 |
| 73026 | arrepintiera | 1 |
| 73027 | arrepintiendo | 1 |
| 73028 | arrepintajas | 1 |
| 73029 | arrepintades | 1 |
| 73030 | arrepienten | 1 |
| 73031 | arrepientas | 1 |
| 73032 | arrepenty | 1 |
| 73033 | arrepentudo | 1 |
| 73034 | arrepentirte | 1 |
| 73035 | arrepentirme | 1 |
| 73036 | arrepentíos | 1 |
| 73037 | arrepentiera | 1 |
| 73038 | arrepentí | 1 |
| 73039 | arrepentemiento | 1 |
| 73040 | arreparen | 1 |
| 73041 | arrendamientos | 1 |
| 73042 | arrendajo | 1 |
| 73043 | arrendado | 1 |
| 73044 | arrendada | 1 |
| 73045 | arrendaba | 1 |
| 73046 | arremolinó | 1 |
| 73047 | arremolinado | 1 |
| 73048 | arremolinaban | 1 |
| 73049 | arremetiésemos | 1 |
| 73050 | arremetido | 1 |
| 73051 | arremetía | 1 |
| 73052 | arremetas | 1 |
| 73053 | arremeta | 1 |
| 73054 | arremendando | 1 |
| 73055 | arremediando | 1 |
| 73056 | arremedar | 1 |
| 73057 | arremedando | 1 |
| 73058 | arremedábamos | 1 |
| 73059 | arremedaba | 1 |
| 73060 | arremangóse | 1 |
| 73061 | arremango | 1 |
| 73062 | arremangados | 1 |
| 73063 | arremangadas | 1 |
| 73064 | arremanga | 1 |
| 73065 | arrellanados | 1 |
| 73066 | arrellanaba | 1 |
| 73067 | arreligiones | 1 |
| 73068 | arreglose | 1 |
| 73069 | arreglole | 1 |
| 73070 | arreglen | 1 |
| 73071 | arregléis | 1 |
| 73072 | arréglatelas | 1 |
| 73073 | arreglase | 1 |
| 73074 | arreglas | 1 |
| 73075 | arreglarte | 1 |
| 73076 | arreglarla | 1 |
| 73077 | arreglarás | 1 |
| 73078 | arreglamos | 1 |
| 73079 | arréglame | 1 |
| 73080 | arregladitas | 1 |
| 73081 | arregladita | 1 |
| 73082 | arregistrao | 1 |
| 73083 | arregimiento | 1 |
| 73084 | arredróse | 1 |
| 73085 | arredrávanse | 1 |
| 73086 | arredraron | 1 |
| 73087 | arredrará | 1 |
| 73088 | arrecomendada | 1 |
| 73089 | arrecogimiento | 1 |
| 73090 | arrecogidas | 1 |
| 73091 | arreçido | 1 |
| 73092 | arreciar | 1 |
| 73093 | arreciado | 1 |
| 73094 | arrecia | 1 |
| 73095 | arrechuchos | 1 |
| 73096 | arrebozo | 1 |
| 73097 | arreboza | 1 |
| 73098 | arreboles | 1 |
| 73099 | arrebolado | 1 |
| 73100 | arrebol | 1 |
| 73101 | arrebatome | 1 |
| 73102 | arrebatarle | 1 |
| 73103 | arrebatara | 1 |
| 73104 | arrebatándole | 1 |
| 73105 | arrebatándola | 1 |
| 73106 | arrebatados | 1 |
| 73107 | arrebatadamente | 1 |
| 73108 | arrebataba | 1 |
| 73109 | arrebañan | 1 |
| 73110 | arreas | 1 |
| 73111 | arrear | 1 |
| 73112 | arreándolos | 1 |
| 73113 | arreando | 1 |
| 73114 | arrean | 1 |
| 73115 | arreada | 1 |
| 73116 | arreaba | 1 |
| 73117 | arrea | 1 |
| 73118 | arraygar | 1 |
| 73119 | arraval | 1 |
| 73120 | arratzean | 1 |
| 73121 | arrastres | 1 |
| 73122 | arrastré | 1 |
| 73123 | arrastras | 1 |
| 73124 | arrastráronme | 1 |
| 73125 | arrastraron | 1 |
| 73126 | arrastrarán | 1 |
| 73127 | arrastrándote | 1 |
| 73128 | arrastrándole | 1 |
| 73129 | arrastramiento | 1 |
| 73130 | arrasó | 1 |
| 73131 | arrasarían | 1 |
| 73132 | arrasan | 1 |
| 73133 | arrasado | 1 |
| 73134 | arrapiezos | 1 |
| 73135 | arrapiezas | 1 |
| 73136 | arrapa | 1 |
| 73137 | arranquen | 1 |
| 73138 | arranquemos | 1 |
| 73139 | arranqué | 1 |
| 73140 | arrancasen | 1 |
| 73141 | arrancase | 1 |
| 73142 | arrancarlo | 1 |
| 73143 | arrancaría | 1 |
| 73144 | arrancaremos | 1 |
| 73145 | arrancaré | 1 |
| 73146 | arrancarán | 1 |
| 73147 | arrancaran | 1 |
| 73148 | arrancándosele | 1 |
| 73149 | arrancándose | 1 |
| 73150 | arrancándolos | 1 |
| 73151 | arrancándoles | 1 |
| 73152 | arrancándola | 1 |
| 73153 | arráncame | 1 |
| 73154 | arrancábase | 1 |
| 73155 | arramblaron | 1 |
| 73156 | arramblar | 1 |
| 73157 | arramblaban | 1 |
| 73158 | arramblaba | 1 |
| 73159 | arraigó | 1 |
| 73160 | arracadas | 1 |
| 73161 | arrabotza | 1 |
| 73162 | arra | 1 |
| 73163 | arquitetura | 1 |
| 73164 | arquetón | 1 |
| 73165 | arqueta | 1 |
| 73166 | arqueos | 1 |
| 73167 | arqueológicos | 1 |
| 73168 | arqueo | 1 |
| 73169 | arquear | 1 |
| 73170 | arqueada | 1 |
| 73171 | arpenas | 1 |
| 73172 | arpas | 1 |
| 73173 | arpadas | 1 |
| 73174 | arpada | 1 |
| 73175 | arouet | 1 |
| 73176 | aromatizaba | 1 |
| 73177 | arneses | 1 |
| 73178 | armose | 1 |
| 73179 | armonizando | 1 |
| 73180 | armonizadas | 1 |
| 73181 | armonizaban | 1 |
| 73182 | armonizaba | 1 |
| 73183 | armonïoso | 1 |
| 73184 | armonías | 1 |
| 73185 | armole | 1 |
| 73186 | armisticios | 1 |
| 73187 | armís | 1 |
| 73188 | armiños | 1 |
| 73189 | armés | 1 |
| 73190 | ármenme | 1 |
| 73191 | armenia | 1 |
| 73192 | armejas | 1 |
| 73193 | arme | 1 |
| 73194 | ármate | 1 |
| 73195 | armasen | 1 |
| 73196 | armarme | 1 |
| 73197 | armarías | 1 |
| 73198 | armaría | 1 |
| 73199 | armaré | 1 |
| 73200 | armaos | 1 |
| 73201 | ármanse | 1 |
| 73202 | armándose | 1 |
| 73203 | armándole | 1 |
| 73204 | armamentos | 1 |
| 73205 | armalle | 1 |
| 73206 | armale | 1 |
| 73207 | armadores | 1 |
| 73208 | armábase | 1 |
| 73209 | arlotes | 1 |
| 73210 | arlotas | 1 |
| 73211 | arlincourt | 1 |
| 73212 | arlanza | 1 |
| 73213 | aritméticos | 1 |
| 73214 | aritméticas | 1 |
| 73215 | aristótiles | 1 |
| 73216 | aristotiles | 1 |
| 73217 | aristofanesco | 1 |
| 73218 | aristas | 1 |
| 73219 | aristarco | 1 |
| 73220 | ariscas | 1 |
| 73221 | arïón | 1 |
| 73222 | arigotes | 1 |
| 73223 | árido | 1 |
| 73224 | aridiana | 1 |
| 73225 | áridas | 1 |
| 73226 | árida | 1 |
| 73227 | ariadna | 1 |
| 73228 | arhamus | 1 |
| 73229 | arguyo | 1 |
| 73230 | arguyéndose | 1 |
| 73231 | argumentó | 1 |
| 73232 | argumentillo | 1 |
| 73233 | argumente | 1 |
| 73234 | argumentaren | 1 |
| 73235 | argumentar | 1 |
| 73236 | argumentaciones | 1 |
| 73237 | arguiric | 1 |
| 73238 | argüir | 1 |
| 73239 | argu | 1 |
| 73240 | argote | 1 |
| 73241 | argonaute | 1 |
| 73242 | argollitas | 1 |
| 73243 | argólico | 1 |
| 73244 | argentería | 1 |
| 73245 | argentando | 1 |
| 73246 | argentados | 1 |
| 73247 | argentadas | 1 |
| 73248 | argensola | 1 |
| 73249 | argelinos | 1 |
| 73250 | argelia | 1 |
| 73251 | arganda | 1 |
| 73252 | argamasillesco | 1 |
| 73253 | argamasillesca | 1 |
| 73254 | arévalo | 1 |
| 73255 | aretes | 1 |
| 73256 | aresido | 1 |
| 73257 | arepiso | 1 |
| 73258 | arenosos | 1 |
| 73259 | arenoso | 1 |
| 73260 | arengar | 1 |
| 73261 | arengando | 1 |
| 73262 | arenales | 1 |
| 73263 | are | 1 |
| 73264 | ardura | 1 |
| 73265 | ardorosos | 1 |
| 73266 | ardilla | 1 |
| 73267 | ardiesse | 1 |
| 73268 | ardieron | 1 |
| 73269 | ardiera | 1 |
| 73270 | ardido | 1 |
| 73271 | ardideza | 1 |
| 73272 | ardidamente | 1 |
| 73273 | ardia | 1 |
| 73274 | ardería | 1 |
| 73275 | ardedes | 1 |
| 73276 | arda | 1 |
| 73277 | arcola | 1 |
| 73278 | arçiprestes | 1 |
| 73279 | arcillosa | 1 |
| 73280 | arçidianos | 1 |
| 73281 | archipobre | 1 |
| 73282 | archipiela | 1 |
| 73283 | archipe | 1 |
| 73284 | archipámpano | 1 |
| 73285 | archimonástica | 1 |
| 73286 | archiduque | 1 |
| 73287 | archidignísimo | 1 |
| 73288 | arcedianos | 1 |
| 73289 | arcar | 1 |
| 73290 | arcanos | 1 |
| 73291 | arcaísmos | 1 |
| 73292 | arcadores | 1 |
| 73293 | arcadias | 1 |
| 73294 | arcabuzazos | 1 |
| 73295 | arcabucería | 1 |
| 73296 | arbusto | 1 |
| 73297 | arboricultor | 1 |
| 73298 | arborescentes | 1 |
| 73299 | árbores | 1 |
| 73300 | arbórbola | 1 |
| 73301 | arbolitos | 1 |
| 73302 | arbolando | 1 |
| 73303 | arbol | 1 |
| 73304 | arbitrista | 1 |
| 73305 | arbitrar | 1 |
| 73306 | arbitrante | 1 |
| 73307 | arbitrando | 1 |
| 73308 | árbitra | 1 |
| 73309 | arbil | 1 |
| 73310 | arbea | 1 |
| 73311 | aravaca | 1 |
| 73312 | arase | 1 |
| 73313 | araquil | 1 |
| 73314 | arapiles | 1 |
| 73315 | arañó | 1 |
| 73316 | arañé | 1 |
| 73317 | arañazo | 1 |
| 73318 | arañarle | 1 |
| 73319 | arañar | 1 |
| 73320 | arañando | 1 |
| 73321 | arañaban | 1 |
| 73322 | arañaba | 1 |
| 73323 | aranjüez | 1 |
| 73324 | arango | 1 |
| 73325 | aranea | 1 |
| 73326 | arancelarios | 1 |
| 73327 | arancelarias | 1 |
| 73328 | arancelaria | 1 |
| 73329 | arancel | 1 |
| 73330 | arambre | 1 |
| 73331 | arambeles | 1 |
| 73332 | aralar | 1 |
| 73333 | araguiarrapatzallia | 1 |
| 73334 | aragonesismos | 1 |
| 73335 | aragonesas | 1 |
| 73336 | aradores | 1 |
| 73337 | arador | 1 |
| 73338 | aracnes | 1 |
| 73339 | arabista | 1 |
| 73340 | arabias | 1 |
| 73341 | arabesco | 1 |
| 73342 | arabes | 1 |
| 73343 | aquista | 1 |
| 73344 | aquis | 1 |
| 73345 | aquiriendo | 1 |
| 73346 | aquilatar | 1 |
| 73347 | aquilata | 1 |
| 73348 | aquexes | 1 |
| 73349 | aquexe | 1 |
| 73350 | aquexas | 1 |
| 73351 | aquexarles | 1 |
| 73352 | aquexandole | 1 |
| 73353 | aquexamiento | 1 |
| 73354 | aquexale | 1 |
| 73355 | aquexada | 1 |
| 73356 | aquéstas | 1 |
| 73357 | aquest | 1 |
| 73358 | aquesse | 1 |
| 73359 | aquesos | 1 |
| 73360 | aques | 1 |
| 73361 | aquellotro | 1 |
| 73362 | aqueje | 1 |
| 73363 | aquejaba | 1 |
| 73364 | aqueja | 1 |
| 73365 | apuróla | 1 |
| 73366 | apurillos | 1 |
| 73367 | apuremos | 1 |
| 73368 | apurasen | 1 |
| 73369 | apurarle | 1 |
| 73370 | apuradísima | 1 |
| 73371 | apuraba | 1 |
| 73372 | apuntóme | 1 |
| 73373 | apuntárselas | 1 |
| 73374 | apuntarme | 1 |
| 73375 | apuntarle | 1 |
| 73376 | apuntaremos | 1 |
| 73377 | apuntarán | 1 |
| 73378 | apúntanse | 1 |
| 73379 | apuntándome | 1 |
| 73380 | apuntándole | 1 |
| 73381 | apuntados | 1 |
| 73382 | apuntaban | 1 |
| 73383 | apuneauamos | 1 |
| 73384 | apuleyo | 1 |
| 73385 | apuestita | 1 |
| 73386 | apuestan | 1 |
| 73387 | apuerte | 1 |
| 73388 | apta | 1 |
| 73389 | aprueva | 1 |
| 73390 | aprueuo | 1 |
| 73391 | aprueuelo | 1 |
| 73392 | aprueuas | 1 |
| 73393 | aprueua | 1 |
| 73394 | apruebo | 1 |
| 73395 | aprueben | 1 |
| 73396 | apruebe | 1 |
| 73397 | aproximase | 1 |
| 73398 | aproximáronse | 1 |
| 73399 | aproximarme | 1 |
| 73400 | aproximaría | 1 |
| 73401 | aproximar | 1 |
| 73402 | aproximándose | 1 |
| 73403 | aproxima | 1 |
| 73404 | aprovechéme | 1 |
| 73405 | aproveché | 1 |
| 73406 | aproveche | 1 |
| 73407 | aprovechas | 1 |
| 73408 | aprovecharos | 1 |
| 73409 | aprovecharon | 1 |
| 73410 | aprovecharlo | 1 |
| 73411 | aprovecharlas | 1 |
| 73412 | aprovecharla | 1 |
| 73413 | aprovecháis | 1 |
| 73414 | aprovechábase | 1 |
| 73415 | aprouechemos | 1 |
| 73416 | aprouechemonos | 1 |
| 73417 | aprouecharas | 1 |
| 73418 | aprouechara | 1 |
| 73419 | aprouechandose | 1 |
| 73420 | aprouechan | 1 |
| 73421 | aprouechado | 1 |
| 73422 | aprouarlo | 1 |
| 73423 | aprouados | 1 |
| 73424 | aprouado | 1 |
| 73425 | apropriados | 1 |
| 73426 | apropósito | 1 |
| 73427 | apropiarnos | 1 |
| 73428 | apropiados | 1 |
| 73429 | apropiación | 1 |
| 73430 | apropia | 1 |
| 73431 | aprobase | 1 |
| 73432 | aprobaron | 1 |
| 73433 | aprobará | 1 |
| 73434 | aprobara | 1 |
| 73435 | aprobando | 1 |
| 73436 | aprobáis | 1 |
| 73437 | aprobado | 1 |
| 73438 | aprobada | 1 |
| 73439 | aprobaciones | 1 |
| 73440 | aprobaban | 1 |
| 73441 | aprisionar | 1 |
| 73442 | aprisionadas | 1 |
| 73443 | aprisionaba | 1 |
| 73444 | aprisca | 1 |
| 73445 | aprieten | 1 |
| 73446 | apriétame | 1 |
| 73447 | aprietale | 1 |
| 73448 | apriessa | 1 |
| 73449 | apretura | 1 |
| 73450 | apretósele | 1 |
| 73451 | apretóme | 1 |
| 73452 | apretóle | 1 |
| 73453 | apretemos | 1 |
| 73454 | apretauas | 1 |
| 73455 | apretársele | 1 |
| 73456 | apretáronle | 1 |
| 73457 | apretarlo | 1 |
| 73458 | apretándote | 1 |
| 73459 | apretándoselo | 1 |
| 73460 | apretándolo | 1 |
| 73461 | apretándolas | 1 |
| 73462 | apretándola | 1 |
| 73463 | apretamos | 1 |
| 73464 | apretadísimo | 1 |
| 73465 | apretadillos | 1 |
| 73466 | apretábale | 1 |
| 73467 | apresurose | 1 |
| 73468 | apresuro | 1 |
| 73469 | apresuréis | 1 |
| 73470 | apresuré | 1 |
| 73471 | apresúrate | 1 |
| 73472 | apresurate | 1 |
| 73473 | apresurase | 1 |
| 73474 | apresurarte | 1 |
| 73475 | apresurarse | 1 |
| 73476 | apresurara | 1 |
| 73477 | apresuran | 1 |
| 73478 | apresuramiento | 1 |
| 73479 | apresurada | 1 |
| 73480 | aprestos | 1 |
| 73481 | aprestando | 1 |
| 73482 | apresta | 1 |
| 73483 | apresarnos | 1 |
| 73484 | apresar | 1 |
| 73485 | apresando | 1 |
| 73486 | apresaban | 1 |
| 73487 | aprendieses | 1 |
| 73488 | aprendida | 1 |
| 73489 | aprendi | 1 |
| 73490 | apréndetelo | 1 |
| 73491 | apréndete | 1 |
| 73492 | aprendes | 1 |
| 73493 | aprenderlo | 1 |
| 73494 | aprenderlas | 1 |
| 73495 | aprenderemos | 1 |
| 73496 | aprenderé | 1 |
| 73497 | aprendé | 1 |
| 73498 | apremios | 1 |
| 73499 | apremidos | 1 |
| 73500 | apremiaua | 1 |
| 73501 | apremiaron | 1 |
| 73502 | apremiarla | 1 |
| 73503 | apremiare | 1 |
| 73504 | apremiar | 1 |
| 73505 | aprémiame | 1 |
| 73506 | apremïado | 1 |
| 73507 | apremiaban | 1 |
| 73508 | apremiaba | 1 |
| 73509 | apremia | 1 |
| 73510 | aprehendió | 1 |
| 73511 | aprehender | 1 |
| 73512 | apregonallos | 1 |
| 73513 | aprecie | 1 |
| 73514 | apreciarlos | 1 |
| 73515 | apreciarlo | 1 |
| 73516 | apreciarlas | 1 |
| 73517 | apreciarán | 1 |
| 73518 | apreciara | 1 |
| 73519 | aprecian | 1 |
| 73520 | apreciados | 1 |
| 73521 | apreciadores | 1 |
| 73522 | apreciado | 1 |
| 73523 | apreciables | 1 |
| 73524 | apreciabilísimo | 1 |
| 73525 | apreciabilísima | 1 |
| 73526 | apreçia | 1 |
| 73527 | apreçebido | 1 |
| 73528 | aprecebido | 1 |
| 73529 | approbante | 1 |
| 73530 | appellaron | 1 |
| 73531 | appellaciones | 1 |
| 73532 | appartement | 1 |
| 73533 | apoyos | 1 |
| 73534 | apoyé | 1 |
| 73535 | apoye | 1 |
| 73536 | apoyaturas | 1 |
| 73537 | apóyate | 1 |
| 73538 | apoyarla | 1 |
| 73539 | apoyaré | 1 |
| 73540 | apostrofó | 1 |
| 73541 | apóstrofo | 1 |
| 73542 | apóstrofe | 1 |
| 73543 | apostrofando | 1 |
| 73544 | apostrofaba | 1 |
| 73545 | apostólica | 1 |
| 73546 | apostolica | 1 |
| 73547 | apostoles | 1 |
| 73548 | apostó | 1 |
| 73549 | apostizo | 1 |
| 73550 | apostisos | 1 |
| 73551 | apostatar | 1 |
| 73552 | apostatáis | 1 |
| 73553 | apostaran | 1 |
| 73554 | apostará | 1 |
| 73555 | apostando | 1 |
| 73556 | apost | 1 |
| 73557 | aposentillo | 1 |
| 73558 | aposentador | 1 |
| 73559 | aposentada | 1 |
| 73560 | aposentaba | 1 |
| 73561 | aposenta | 1 |
| 73562 | aportaste | 1 |
| 73563 | aportaría | 1 |
| 73564 | aportares | 1 |
| 73565 | aportar | 1 |
| 73566 | aportaban | 1 |
| 73567 | aportaba | 1 |
| 73568 | aporreo | 1 |
| 73569 | aporrees | 1 |
| 73570 | aporrearse | 1 |
| 73571 | aporrearon | 1 |
| 73572 | aporreantes | 1 |
| 73573 | aporreando | 1 |
| 73574 | aporreada | 1 |
| 73575 | aporreaba | 1 |
| 73576 | apoques | 1 |
| 73577 | apoplejía | 1 |
| 73578 | aponiendo | 1 |
| 73579 | aponía | 1 |
| 73580 | apongo | 1 |
| 73581 | apone | 1 |
| 73582 | apoltronado | 1 |
| 73583 | apolonio | 1 |
| 73584 | apólogo | 1 |
| 73585 | apologías | 1 |
| 73586 | apología | 1 |
| 73587 | apólogas | 1 |
| 73588 | apollo | 1 |
| 73589 | apolille | 1 |
| 73590 | apolillado | 1 |
| 73591 | apódosis | 1 |
| 73592 | apoderes | 1 |
| 73593 | apoderara | 1 |
| 73594 | apoderar | 1 |
| 73595 | apoderando | 1 |
| 73596 | apoderan | 1 |
| 73597 | apoderada | 1 |
| 73598 | apodera | 1 |
| 73599 | apodas | 1 |
| 73600 | apodaba | 1 |
| 73601 | apócrifos | 1 |
| 73602 | apócrifas | 1 |
| 73603 | apocando | 1 |
| 73604 | apocalisi | 1 |
| 73605 | apocalípticas | 1 |
| 73606 | apocalipsi | 1 |
| 73607 | apocábase | 1 |
| 73608 | apliquen | 1 |
| 73609 | apliquélas | 1 |
| 73610 | apliqué | 1 |
| 73611 | aplico | 1 |
| 73612 | aplicas | 1 |
| 73613 | aplicarlo | 1 |
| 73614 | aplicarle | 1 |
| 73615 | aplicará | 1 |
| 73616 | aplicándoselas | 1 |
| 73617 | aplicándolos | 1 |
| 73618 | aplicaditos | 1 |
| 73619 | aplicadísimo | 1 |
| 73620 | aplicadísima | 1 |
| 73621 | aplicadas | 1 |
| 73622 | aplicable | 1 |
| 73623 | aplazarlo | 1 |
| 73624 | aplazando | 1 |
| 73625 | aplazado | 1 |
| 73626 | aplazaba | 1 |
| 73627 | aplaudirse | 1 |
| 73628 | aplaudirlos | 1 |
| 73629 | aplaudirla | 1 |
| 73630 | aplaudiesen | 1 |
| 73631 | aplaudiese | 1 |
| 73632 | aplaudiéndose | 1 |
| 73633 | aplaudiendo | 1 |
| 73634 | aplaudido | 1 |
| 73635 | aplaudida | 1 |
| 73636 | aplastemos | 1 |
| 73637 | aplastarlos | 1 |
| 73638 | aplastarla | 1 |
| 73639 | aplastarían | 1 |
| 73640 | aplastando | 1 |
| 73641 | aplastamiento | 1 |
| 73642 | aplastados | 1 |
| 73643 | aplasta | 1 |
| 73644 | aplanándose | 1 |
| 73645 | aplanamiento | 1 |
| 73646 | aplanada | 1 |
| 73647 | aplacarse | 1 |
| 73648 | aplacaron | 1 |
| 73649 | aplacaría | 1 |
| 73650 | aplacaré | 1 |
| 73651 | aplacará | 1 |
| 73652 | aplacándose | 1 |
| 73653 | aplacando | 1 |
| 73654 | aplacan | 1 |
| 73655 | aplacadas | 1 |
| 73656 | aplacaban | 1 |
| 73657 | aplacaba | 1 |
| 73658 | aplaca | 1 |
| 73659 | apisonara | 1 |
| 73660 | apisonar | 1 |
| 73661 | apisonado | 1 |
| 73662 | apio | 1 |
| 73663 | apiñemos | 1 |
| 73664 | apiñado | 1 |
| 73665 | apiñada | 1 |
| 73666 | apiñábase | 1 |
| 73667 | apiña | 1 |
| 73668 | apimplaba | 1 |
| 73669 | apilongados | 1 |
| 73670 | apilada | 1 |
| 73671 | apilaba | 1 |
| 73672 | apición | 1 |
| 73673 | apicarados | 1 |
| 73674 | apianándose | 1 |
| 73675 | apiade | 1 |
| 73676 | apiadarse | 1 |
| 73677 | apiadaron | 1 |
| 73678 | apiadaba | 1 |
| 73679 | apetites | 1 |
| 73680 | apetezco | 1 |
| 73681 | apetezca | 1 |
| 73682 | apeteciendo | 1 |
| 73683 | apetecidos | 1 |
| 73684 | apetecibles | 1 |
| 73685 | apetecían | 1 |
| 73686 | apetecerlo | 1 |
| 73687 | apetecen | 1 |
| 73688 | apestosa | 1 |
| 73689 | apesto | 1 |
| 73690 | apestada | 1 |
| 73691 | apesgado | 1 |
| 73692 | apesarado | 1 |
| 73693 | apesadumbrados | 1 |
| 73694 | apertar | 1 |
| 73695 | apertando | 1 |
| 73696 | aperreada | 1 |
| 73697 | aperos | 1 |
| 73698 | aperitivos | 1 |
| 73699 | aperitivo | 1 |
| 73700 | apergaminaba | 1 |
| 73701 | apercibo | 1 |
| 73702 | apercibiendo | 1 |
| 73703 | aperçibes | 1 |
| 73704 | apercibense | 1 |
| 73705 | aperciban | 1 |
| 73706 | aperciba | 1 |
| 73707 | aperçebydos | 1 |
| 73708 | aperçebydo | 1 |
| 73709 | apercebidos | 1 |
| 73710 | apeose | 1 |
| 73711 | apenino | 1 |
| 73712 | apencó | 1 |
| 73713 | apenados | 1 |
| 73714 | apeló | 1 |
| 73715 | apelmazándose | 1 |
| 73716 | apelmazada | 1 |
| 73717 | apelmazaban | 1 |
| 73718 | apellydo | 1 |
| 73719 | apello | 1 |
| 73720 | apellidarían | 1 |
| 73721 | apellidar | 1 |
| 73722 | apellidaban | 1 |
| 73723 | apellidaba | 1 |
| 73724 | apellida | 1 |
| 73725 | apellásemos | 1 |
| 73726 | apelaron | 1 |
| 73727 | apegado | 1 |
| 73728 | apega | 1 |
| 73729 | apéense | 1 |
| 73730 | apedreo | 1 |
| 73731 | apedreaste | 1 |
| 73732 | apedreado | 1 |
| 73733 | apedernaladas | 1 |
| 73734 | apechuguemos | 1 |
| 73735 | apechugue | 1 |
| 73736 | apechugó | 1 |
| 73737 | apechugadas | 1 |
| 73738 | apearnos | 1 |
| 73739 | apearla | 1 |
| 73740 | apeándole | 1 |
| 73741 | apean | 1 |
| 73742 | apeamiento | 1 |
| 73743 | apeados | 1 |
| 73744 | apeaba | 1 |
| 73745 | apaziguó | 1 |
| 73746 | apaziguado | 1 |
| 73747 | apáticos | 1 |
| 73748 | apáticamente | 1 |
| 73749 | apasionamiento | 1 |
| 73750 | apasionáis | 1 |
| 73751 | apartola | 1 |
| 73752 | aparten | 1 |
| 73753 | apartemos | 1 |
| 73754 | apartéme | 1 |
| 73755 | apartaua | 1 |
| 73756 | apartateme | 1 |
| 73757 | apartarte | 1 |
| 73758 | apartarlo | 1 |
| 73759 | apartarla | 1 |
| 73760 | apartaría | 1 |
| 73761 | apartaran | 1 |
| 73762 | apartándoles | 1 |
| 73763 | apartándolas | 1 |
| 73764 | apartándola | 1 |
| 73765 | apartamos | 1 |
| 73766 | apartamientos | 1 |
| 73767 | apártame | 1 |
| 73768 | apartalle | 1 |
| 73769 | apartáis | 1 |
| 73770 | apartadijo | 1 |
| 73771 | aparrochada | 1 |
| 73772 | aparicio | 1 |
| 73773 | aparezco | 1 |
| 73774 | aparesçió | 1 |
| 73775 | aparesçençia | 1 |
| 73776 | aparentaste | 1 |
| 73777 | aparentase | 1 |
| 73778 | aparentarlos | 1 |
| 73779 | aparentan | 1 |
| 73780 | aparenta | 1 |
| 73781 | aparencia | 1 |
| 73782 | aparejó | 1 |
| 73783 | aparejemos | 1 |
| 73784 | apareje | 1 |
| 73785 | aparejate | 1 |
| 73786 | aparejastes | 1 |
| 73787 | aparejasen | 1 |
| 73788 | aparejarnos | 1 |
| 73789 | aparejando | 1 |
| 73790 | aparejan | 1 |
| 73791 | aparejamiento | 1 |
| 73792 | aparejadísimos | 1 |
| 73793 | aparejaban | 1 |
| 73794 | aparecióse | 1 |
| 73795 | apareciose | 1 |
| 73796 | aparecimiento | 1 |
| 73797 | apareciese | 1 |
| 73798 | aparecidos | 1 |
| 73799 | aparecerse | 1 |
| 73800 | aparecerán | 1 |
| 73801 | aparecerá | 1 |
| 73802 | apareceos | 1 |
| 73803 | aparearse | 1 |
| 73804 | aparcería | 1 |
| 73805 | aparatoso | 1 |
| 73806 | aparado | 1 |
| 73807 | apañarían | 1 |
| 73808 | apañaré | 1 |
| 73809 | apañados | 1 |
| 73810 | apañador | 1 |
| 73811 | apañadito | 1 |
| 73812 | apañadita | 1 |
| 73813 | apaña | 1 |
| 73814 | apanes | 1 |
| 73815 | apande | 1 |
| 73816 | apandar | 1 |
| 73817 | apandando | 1 |
| 73818 | apandado | 1 |
| 73819 | apandaba | 1 |
| 73820 | apaleó | 1 |
| 73821 | apaleen | 1 |
| 73822 | apalee | 1 |
| 73823 | apalearle | 1 |
| 73824 | apaleando | 1 |
| 73825 | apalean | 1 |
| 73826 | apaleados | 1 |
| 73827 | apaleadas | 1 |
| 73828 | apalea | 1 |
| 73829 | apalabradas | 1 |
| 73830 | apaisada | 1 |
| 73831 | apagolo | 1 |
| 73832 | apago | 1 |
| 73833 | apagaste | 1 |
| 73834 | apagase | 1 |
| 73835 | apagarlas | 1 |
| 73836 | apagaría | 1 |
| 73837 | apagaran | 1 |
| 73838 | apagara | 1 |
| 73839 | apagábase | 1 |
| 73840 | apadrinen | 1 |
| 73841 | apadrináronle | 1 |
| 73842 | apaciguólo | 1 |
| 73843 | apaciguarse | 1 |
| 73844 | apaciguar | 1 |
| 73845 | apaciguanse | 1 |
| 73846 | apaciguámoslos | 1 |
| 73847 | apaciguado | 1 |
| 73848 | apacientan | 1 |
| 73849 | apacibilidad | 1 |
| 73850 | apacentando | 1 |
| 73851 | apacentados | 1 |
| 73852 | apabullarte | 1 |
| 73853 | apabullar | 1 |
| 73854 | aosadas | 1 |
| 73855 | aorta | 1 |
| 73856 | aora | 1 |
| 73857 | aonde | 1 |
| 73858 | aojando | 1 |
| 73859 | aojado | 1 |
| 73860 | aojadas | 1 |
| 73861 | añudemos | 1 |
| 73862 | añudarme | 1 |
| 73863 | añudar | 1 |
| 73864 | añudando | 1 |
| 73865 | añudado | 1 |
| 73866 | añudadas | 1 |
| 73867 | añudada | 1 |
| 73868 | añosos | 1 |
| 73869 | añitos | 1 |
| 73870 | añicos | 1 |
| 73871 | añedir | 1 |
| 73872 | añafyl | 1 |
| 73873 | añafiles | 1 |
| 73874 | añadís | 1 |
| 73875 | añadirse | 1 |
| 73876 | añadirles | 1 |
| 73877 | añadiósele | 1 |
| 73878 | añadiesen | 1 |
| 73879 | añadiese | 1 |
| 73880 | añadieres | 1 |
| 73881 | añadiéndole | 1 |
| 73882 | añadidos | 1 |
| 73883 | añadid | 1 |
| 73884 | añadíanse | 1 |
| 73885 | añaden | 1 |
| 73886 | añádele | 1 |
| 73887 | añádase | 1 |
| 73888 | añadas | 1 |
| 73889 | anzuelos | 1 |
| 73890 | anuncita | 1 |
| 73891 | anuncié | 1 |
| 73892 | anuncias | 1 |
| 73893 | anunciarte | 1 |
| 73894 | anunciara | 1 |
| 73895 | anunciantes | 1 |
| 73896 | anunciándose | 1 |
| 73897 | anunciándonos | 1 |
| 73898 | anunciándoles | 1 |
| 73899 | anunciadoras | 1 |
| 73900 | anularse | 1 |
| 73901 | anular | 1 |
| 73902 | anulando | 1 |
| 73903 | anulado | 1 |
| 73904 | anula | 1 |
| 73905 | anudar | 1 |
| 73906 | anudando | 1 |
| 73907 | anudados | 1 |
| 73908 | anuda | 1 |
| 73909 | anublar | 1 |
| 73910 | anualmente | 1 |
| 73911 | anual | 1 |
| 73912 | antygo | 1 |
| 73913 | antropófagos | 1 |
| 73914 | antre | 1 |
| 73915 | antoño | 1 |
| 73916 | antoñita | 1 |
| 73917 | antonios | 1 |
| 73918 | antonieta | 1 |
| 73919 | antonelli | 1 |
| 73920 | antolínez | 1 |
| 73921 | antojuna | 1 |
| 73922 | antojitos | 1 |
| 73923 | antojito | 1 |
| 73924 | antojen | 1 |
| 73925 | antójaseme | 1 |
| 73926 | antojársele | 1 |
| 73927 | antojaría | 1 |
| 73928 | antojara | 1 |
| 73929 | antojadizos | 1 |
| 73930 | antojada | 1 |
| 73931 | antojábasele | 1 |
| 73932 | antítesis | 1 |
| 73933 | antireligiosas | 1 |
| 73934 | antireligiosa | 1 |
| 73935 | antiquísimos | 1 |
| 73936 | antipatriótico | 1 |
| 73937 | antipatriótica | 1 |
| 73938 | antipáticas | 1 |
| 73939 | antipater | 1 |
| 73940 | antipara | 1 |
| 73941 | antioquía | 1 |
| 73942 | antilógica | 1 |
| 73943 | antiguedat | 1 |
| 73944 | antigualla | 1 |
| 73945 | antigramatical | 1 |
| 73946 | antiespasmódicos | 1 |
| 73947 | antiespasmódico | 1 |
| 73948 | antieconómico | 1 |
| 73949 | antídoto | 1 |
| 73950 | antidinásticas | 1 |
| 73951 | anticuados | 1 |
| 73952 | anticuadas | 1 |
| 73953 | anticuada | 1 |
| 73954 | anticonstitucional | 1 |
| 73955 | antico | 1 |
| 73956 | anticipó | 1 |
| 73957 | anticipándose | 1 |
| 73958 | anticipándome | 1 |
| 73959 | anticipando | 1 |
| 73960 | anticipaban | 1 |
| 73961 | anticipa | 1 |
| 73962 | anticanónica | 1 |
| 73963 | anteviendo | 1 |
| 73964 | antesalas | 1 |
| 73965 | anteponía | 1 |
| 73966 | anteponerse | 1 |
| 73967 | anteponen | 1 |
| 73968 | antepone | 1 |
| 73969 | antepechos | 1 |
| 73970 | antepasado | 1 |
| 73971 | anteojazo | 1 |
| 73972 | antediluvianos | 1 |
| 73973 | antediluviana | 1 |
| 73974 | antedichas | 1 |
| 73975 | antecristos | 1 |
| 73976 | antecristo | 1 |
| 73977 | antecogidos | 1 |
| 73978 | antecoger | 1 |
| 73979 | anteceden | 1 |
| 73980 | antecede | 1 |
| 73981 | antecámara | 1 |
| 73982 | antebrazo | 1 |
| 73983 | antárticas | 1 |
| 73984 | antagonismos | 1 |
| 73985 | anssarones | 1 |
| 73986 | ánssares | 1 |
| 73987 | ansiando | 1 |
| 73988 | ansiados | 1 |
| 73989 | ansiaban | 1 |
| 73990 | ansía | 1 |
| 73991 | ansi | 1 |
| 73992 | ánsares | 1 |
| 73993 | anparança | 1 |
| 73994 | anotó | 1 |
| 73995 | anormal | 1 |
| 73996 | anónimas | 1 |
| 73997 | anónima | 1 |
| 73998 | anonaden | 1 |
| 73999 | anonadar | 1 |
| 74000 | anonadando | 1 |
| 74001 | anonadaba | 1 |
| 74002 | anomalía | 1 |
| 74003 | anómala | 1 |
| 74004 | anochecidas | 1 |
| 74005 | anochecen | 1 |
| 74006 | anochece | 1 |
| 74007 | annis | 1 |
| 74008 | anni | 1 |
| 74009 | années | 1 |
| 74010 | aniversarios | 1 |
| 74011 | aniquiló | 1 |
| 74012 | aniquiléis | 1 |
| 74013 | aniquilarme | 1 |
| 74014 | aniquilarle | 1 |
| 74015 | aniquilarlas | 1 |
| 74016 | aniquilados | 1 |
| 74017 | aniquila | 1 |
| 74018 | aniñados | 1 |
| 74019 | animosísimo | 1 |
| 74020 | animose | 1 |
| 74021 | animosa | 1 |
| 74022 | animos | 1 |
| 74023 | animóle | 1 |
| 74024 | animólas | 1 |
| 74025 | animero | 1 |
| 74026 | animen | 1 |
| 74027 | animé | 1 |
| 74028 | animarse | 1 |
| 74029 | animáronme | 1 |
| 74030 | animaron | 1 |
| 74031 | animarme | 1 |
| 74032 | animarle | 1 |
| 74033 | animarla | 1 |
| 74034 | animará | 1 |
| 74035 | animándoles | 1 |
| 74036 | animándole | 1 |
| 74037 | animan | 1 |
| 74038 | animalyas | 1 |
| 74039 | animalucho | 1 |
| 74040 | animalia | 1 |
| 74041 | animalejos | 1 |
| 74042 | animadísimo | 1 |
| 74043 | animadas | 1 |
| 74044 | animábame | 1 |
| 74045 | animábale | 1 |
| 74046 | anillas | 1 |
| 74047 | aniellos | 1 |
| 74048 | anidara | 1 |
| 74049 | anida | 1 |
| 74050 | aniceto | 1 |
| 74051 | anica | 1 |
| 74052 | anhélito | 1 |
| 74053 | anhelan | 1 |
| 74054 | anhelado | 1 |
| 74055 | angustura | 1 |
| 74056 | angustió | 1 |
| 74057 | angustiéme | 1 |
| 74058 | angustiados | 1 |
| 74059 | angustiaba | 1 |
| 74060 | angulosas | 1 |
| 74061 | angulo | 1 |
| 74062 | anguarina | 1 |
| 74063 | angostísima | 1 |
| 74064 | angostillos | 1 |
| 74065 | angola | 1 |
| 74066 | anglómano | 1 |
| 74067 | anglo | 1 |
| 74068 | anglicanizados | 1 |
| 74069 | angiellas | 1 |
| 74070 | ángelus | 1 |
| 74071 | angelorios | 1 |
| 74072 | angelita | 1 |
| 74073 | angelesco | 1 |
| 74074 | angarillas | 1 |
| 74075 | anfitriones | 1 |
| 74076 | anfibológico | 1 |
| 74077 | anfibios | 1 |
| 74078 | anfibio | 1 |
| 74079 | anexo | 1 |
| 74080 | anexado | 1 |
| 74081 | anestésico | 1 |
| 74082 | anémicos | 1 |
| 74083 | anémicas | 1 |
| 74084 | anelito | 1 |
| 74085 | anejos | 1 |
| 74086 | anegase | 1 |
| 74087 | anegarse | 1 |
| 74088 | anegaron | 1 |
| 74089 | anegara | 1 |
| 74090 | anegándose | 1 |
| 74091 | anegamos | 1 |
| 74092 | anegados | 1 |
| 74093 | anegadas | 1 |
| 74094 | anegaban | 1 |
| 74095 | anegábamos | 1 |
| 74096 | anegaba | 1 |
| 74097 | anea | 1 |
| 74098 | anduvistes | 1 |
| 74099 | anduviste | 1 |
| 74100 | anduviéremos | 1 |
| 74101 | anduviere | 1 |
| 74102 | anduuieren | 1 |
| 74103 | andut | 1 |
| 74104 | andudiese | 1 |
| 74105 | andudiere | 1 |
| 74106 | andude | 1 |
| 74107 | andronico | 1 |
| 74108 | andrina | 1 |
| 74109 | andresí | 1 |
| 74110 | andrajoso | 1 |
| 74111 | andrajosas | 1 |
| 74112 | andradilla | 1 |
| 74113 | andrade | 1 |
| 74114 | andouiera | 1 |
| 74115 | andit | 1 |
| 74116 | andía | 1 |
| 74117 | andés | 1 |
| 74118 | ander | 1 |
| 74119 | andémoslo | 1 |
| 74120 | andéis | 1 |
| 74121 | anday | 1 |
| 74122 | andávanse | 1 |
| 74123 | andauan | 1 |
| 74124 | andate | 1 |
| 74125 | ándase | 1 |
| 74126 | andaros | 1 |
| 74127 | andarlas | 1 |
| 74128 | andarín | 1 |
| 74129 | andariegos | 1 |
| 74130 | andariegas | 1 |
| 74131 | andaremos | 1 |
| 74132 | andaredes | 1 |
| 74133 | andarás | 1 |
| 74134 | andaras | 1 |
| 74135 | andanzas | 1 |
| 74136 | andantescas | 1 |
| 74137 | ándanla | 1 |
| 74138 | andandona | 1 |
| 74139 | andança | 1 |
| 74140 | andamios | 1 |
| 74141 | andamiajes | 1 |
| 74142 | ándame | 1 |
| 74143 | andalúz | 1 |
| 74144 | andalusía | 1 |
| 74145 | andados | 1 |
| 74146 | andador | 1 |
| 74147 | andadera | 1 |
| 74148 | andaca | 1 |
| 74149 | andábase | 1 |
| 74150 | andabas | 1 |
| 74151 | andábanse | 1 |
| 74152 | andábanle | 1 |
| 74153 | andábame | 1 |
| 74154 | ancor | 1 |
| 74155 | ancón | 1 |
| 74156 | anclados | 1 |
| 74157 | ancladas | 1 |
| 74158 | anciens | 1 |
| 74159 | ançiano | 1 |
| 74160 | ancianitas | 1 |
| 74161 | anchurosa | 1 |
| 74162 | anchoba | 1 |
| 74163 | anchoas | 1 |
| 74164 | anca | 1 |
| 74165 | anbiçia | 1 |
| 74166 | anbas | 1 |
| 74167 | anaxagoras | 1 |
| 74168 | anatómico | 1 |
| 74169 | anatomías | 1 |
| 74170 | anathema | 1 |
| 74171 | anascotes | 1 |
| 74172 | anás | 1 |
| 74173 | anarda | 1 |
| 74174 | analogías | 1 |
| 74175 | analizó | 1 |
| 74176 | analizarla | 1 |
| 74177 | analizaremos | 1 |
| 74178 | analizara | 1 |
| 74179 | analizado | 1 |
| 74180 | analiza | 1 |
| 74181 | analítico | 1 |
| 74182 | analítica | 1 |
| 74183 | anagnórisis | 1 |
| 74184 | anafrodíticos | 1 |
| 74185 | anafrodítico | 1 |
| 74186 | anafroditas | 1 |
| 74187 | anafres | 1 |
| 74188 | anafre | 1 |
| 74189 | anadones | 1 |
| 74190 | anaden | 1 |
| 74191 | anacrónico | 1 |
| 74192 | anacoluto | 1 |
| 74193 | anacletus | 1 |
| 74194 | anabaptista | 1 |
| 74195 | án | 1 |
| 74196 | amugronadores | 1 |
| 74197 | amuerço | 1 |
| 74198 | amueblados | 1 |
| 74199 | amuebladas | 1 |
| 74200 | amputarlos | 1 |
| 74201 | amputación | 1 |
| 74202 | ampulosamente | 1 |
| 74203 | ampollas | 1 |
| 74204 | ampo | 1 |
| 74205 | amplísima | 1 |
| 74206 | amplias | 1 |
| 74207 | ampliar | 1 |
| 74208 | amparó | 1 |
| 74209 | amparen | 1 |
| 74210 | amparemos | 1 |
| 74211 | amparase | 1 |
| 74212 | amparas | 1 |
| 74213 | ampararles | 1 |
| 74214 | ampararán | 1 |
| 74215 | ampáranse | 1 |
| 74216 | amparándote | 1 |
| 74217 | amparándose | 1 |
| 74218 | amparan | 1 |
| 74219 | amparamos | 1 |
| 74220 | amparados | 1 |
| 74221 | amparador | 1 |
| 74222 | amparaba | 1 |
| 74223 | ámovos | 1 |
| 74224 | amotinose | 1 |
| 74225 | amotinó | 1 |
| 74226 | amotinados | 1 |
| 74227 | amostazado | 1 |
| 74228 | amoscose | 1 |
| 74229 | amoscando | 1 |
| 74230 | amoscado | 1 |
| 74231 | amortiguó | 1 |
| 74232 | amortiguado | 1 |
| 74233 | amortigua | 1 |
| 74234 | amortezcas | 1 |
| 74235 | amortescimientos | 1 |
| 74236 | amortescida | 1 |
| 74237 | amortesçer | 1 |
| 74238 | amortecido | 1 |
| 74239 | amortajaron | 1 |
| 74240 | amortajado | 1 |
| 74241 | amortajada | 1 |
| 74242 | amorraba | 1 |
| 74243 | amorosísimos | 1 |
| 74244 | amorem | 1 |
| 74245 | amorcito | 1 |
| 74246 | amorcillo | 1 |
| 74247 | amontones | 1 |
| 74248 | amontone | 1 |
| 74249 | amontonaron | 1 |
| 74250 | amontonado | 1 |
| 74251 | amontonaba | 1 |
| 74252 | amontona | 1 |
| 74253 | amontillado | 1 |
| 74254 | amoniaco | 1 |
| 74255 | amonestó | 1 |
| 74256 | amonestándole | 1 |
| 74257 | amonestacion | 1 |
| 74258 | amondongado | 1 |
| 74259 | amoldarse | 1 |
| 74260 | amoldarlas | 1 |
| 74261 | amoldara | 1 |
| 74262 | amoldar | 1 |
| 74263 | amoldada | 1 |
| 74264 | amolados | 1 |
| 74265 | amolada | 1 |
| 74266 | amohinóse | 1 |
| 74267 | amohinarse | 1 |
| 74268 | amohinábase | 1 |
| 74269 | amodorridos | 1 |
| 74270 | amodorrida | 1 |
| 74271 | amodorrado | 1 |
| 74272 | amnón | 1 |
| 74273 | amistat | 1 |
| 74274 | amistança | 1 |
| 74275 | amisión | 1 |
| 74276 | amira | 1 |
| 74277 | aminoró | 1 |
| 74278 | aminoraba | 1 |
| 74279 | amilanarse | 1 |
| 74280 | amilana | 1 |
| 74281 | amigota | 1 |
| 74282 | amigables | 1 |
| 74283 | amiens | 1 |
| 74284 | amicus | 1 |
| 74285 | amics | 1 |
| 74286 | amicos | 1 |
| 74287 | amicísimo | 1 |
| 74288 | amica | 1 |
| 74289 | amezquetanos | 1 |
| 74290 | ametrallarlos | 1 |
| 74291 | américos | 1 |
| 74292 | américo | 1 |
| 74293 | americanilla | 1 |
| 74294 | amerengado | 1 |
| 74295 | amenudo | 1 |
| 74296 | amenizó | 1 |
| 74297 | amenizaba | 1 |
| 74298 | ameniza | 1 |
| 74299 | amenísimos | 1 |
| 74300 | amenidades | 1 |
| 74301 | amengues | 1 |
| 74302 | amengüe | 1 |
| 74303 | amengue | 1 |
| 74304 | amenguas | 1 |
| 74305 | amenguársele | 1 |
| 74306 | amenguaron | 1 |
| 74307 | amenguar | 1 |
| 74308 | amenguado | 1 |
| 74309 | amenguadas | 1 |
| 74310 | amenguada | 1 |
| 74311 | amenguaba | 1 |
| 74312 | amenazóle | 1 |
| 74313 | amenazola | 1 |
| 74314 | amenaze | 1 |
| 74315 | amenazarla | 1 |
| 74316 | amenazándome | 1 |
| 74317 | amenazándolos | 1 |
| 74318 | amenazándoles | 1 |
| 74319 | amenazados | 1 |
| 74320 | amenazadores | 1 |
| 74321 | amenasava | 1 |
| 74322 | amenasas | 1 |
| 74323 | amenasar | 1 |
| 74324 | amenasan | 1 |
| 74325 | amenaces | 1 |
| 74326 | amenace | 1 |
| 74327 | améla | 1 |
| 74328 | améis | 1 |
| 74329 | amedrentando | 1 |
| 74330 | amedrentan | 1 |
| 74331 | amebeo | 1 |
| 74332 | ambulancias | 1 |
| 74333 | ambiláteras | 1 |
| 74334 | ambiguo | 1 |
| 74335 | ambigú | 1 |
| 74336 | ambiciosas | 1 |
| 74337 | ambicioncilla | 1 |
| 74338 | ambicionaría | 1 |
| 74339 | ámbares | 1 |
| 74340 | ambar | 1 |
| 74341 | amazónica | 1 |
| 74342 | amazacotada | 1 |
| 74343 | amaviturrieta | 1 |
| 74344 | amaurosis | 1 |
| 74345 | amatorio | 1 |
| 74346 | amatávase | 1 |
| 74347 | amatada | 1 |
| 74348 | amasteis | 1 |
| 74349 | amasses | 1 |
| 74350 | amassadas | 1 |
| 74351 | amasar | 1 |
| 74352 | amasan | 1 |
| 74353 | amasados | 1 |
| 74354 | amasada | 1 |
| 74355 | amasábanlo | 1 |
| 74356 | amasábalo | 1 |
| 74357 | amasa | 1 |
| 74358 | amarteló | 1 |
| 74359 | amartelamiento | 1 |
| 74360 | amarte | 1 |
| 74361 | amarre | 1 |
| 74362 | amarras | 1 |
| 74363 | amarraros | 1 |
| 74364 | amarrará | 1 |
| 74365 | amarrara | 1 |
| 74366 | amarrar | 1 |
| 74367 | amarrados | 1 |
| 74368 | amarrado | 1 |
| 74369 | amarraban | 1 |
| 74370 | amaros | 1 |
| 74371 | amarnos | 1 |
| 74372 | amarillentos | 1 |
| 74373 | amarilleaba | 1 |
| 74374 | amariles | 1 |
| 74375 | amariellos | 1 |
| 74376 | amarias | 1 |
| 74377 | amaría | 1 |
| 74378 | amarguísima | 1 |
| 74379 | amargues | 1 |
| 74380 | amargó | 1 |
| 74381 | amargarán | 1 |
| 74382 | amargaba | 1 |
| 74383 | amares | 1 |
| 74384 | amaren | 1 |
| 74385 | amaremos | 1 |
| 74386 | amarán | 1 |
| 74387 | amaños | 1 |
| 74388 | amaño | 1 |
| 74389 | amañar | 1 |
| 74390 | amañada | 1 |
| 74391 | amantísima | 1 |
| 74392 | amantillos | 1 |
| 74393 | amantado | 1 |
| 74394 | amanssar | 1 |
| 74395 | amanssa | 1 |
| 74396 | amanse | 1 |
| 74397 | amansaste | 1 |
| 74398 | amansarla | 1 |
| 74399 | amansaria | 1 |
| 74400 | amansará | 1 |
| 74401 | amansando | 1 |
| 74402 | amansan | 1 |
| 74403 | amansaban | 1 |
| 74404 | amanojada | 1 |
| 74405 | amanezco | 1 |
| 74406 | amanezcas | 1 |
| 74407 | amanezcamos | 1 |
| 74408 | amanescio | 1 |
| 74409 | amanesciesse | 1 |
| 74410 | amanesceria | 1 |
| 74411 | amanescer | 1 |
| 74412 | amaneramientos | 1 |
| 74413 | amaneciesse | 1 |
| 74414 | amaneciendo | 1 |
| 74415 | amanecida | 1 |
| 74416 | amanecían | 1 |
| 74417 | amanecí | 1 |
| 74418 | amanecen | 1 |
| 74419 | amándote | 1 |
| 74420 | amándola | 1 |
| 74421 | amandi | 1 |
| 74422 | amancillada | 1 |
| 74423 | amancebar | 1 |
| 74424 | amancebado | 1 |
| 74425 | amamantado | 1 |
| 74426 | amalde | 1 |
| 74427 | amala | 1 |
| 74428 | amainásemos | 1 |
| 74429 | amainaron | 1 |
| 74430 | amainamos | 1 |
| 74431 | amainado | 1 |
| 74432 | amagotes | 1 |
| 74433 | amagó | 1 |
| 74434 | amaga | 1 |
| 74435 | amaestrados | 1 |
| 74436 | amabilísimas | 1 |
| 74437 | amabilidades | 1 |
| 74438 | amábalos | 1 |
| 74439 | amábale | 1 |
| 74440 | amábades | 1 |
| 74441 | alzose | 1 |
| 74442 | alzo | 1 |
| 74443 | alzauamos | 1 |
| 74444 | alzasse | 1 |
| 74445 | alzasen | 1 |
| 74446 | alzaros | 1 |
| 74447 | alzáronse | 1 |
| 74448 | alzaremos | 1 |
| 74449 | alzaran | 1 |
| 74450 | alzándote | 1 |
| 74451 | alzándolos | 1 |
| 74452 | alzándole | 1 |
| 74453 | alzándola | 1 |
| 74454 | alzan | 1 |
| 74455 | alzamos | 1 |
| 74456 | alzámonos | 1 |
| 74457 | alzádole | 1 |
| 74458 | alynpiat | 1 |
| 74459 | aly | 1 |
| 74460 | alvum | 1 |
| 74461 | alvillo | 1 |
| 74462 | alvéolo | 1 |
| 74463 | álveo | 1 |
| 74464 | alvarico | 1 |
| 74465 | alvardanes | 1 |
| 74466 | alvardana | 1 |
| 74467 | alvañares | 1 |
| 74468 | alvalá | 1 |
| 74469 | aluvión | 1 |
| 74470 | alusiva | 1 |
| 74471 | alunbrava | 1 |
| 74472 | alúnbrase | 1 |
| 74473 | alunbrando | 1 |
| 74474 | alumno | 1 |
| 74475 | alumbró | 1 |
| 74476 | alúmbresele | 1 |
| 74477 | alumbres | 1 |
| 74478 | alumbré | 1 |
| 74479 | alumbrarme | 1 |
| 74480 | alumbrará | 1 |
| 74481 | alumbrándose | 1 |
| 74482 | alumbrándoles | 1 |
| 74483 | alumbrando | 1 |
| 74484 | alumbramientos | 1 |
| 74485 | alumbramiento | 1 |
| 74486 | aluengan | 1 |
| 74487 | aluego | 1 |
| 74488 | aludidos | 1 |
| 74489 | aludían | 1 |
| 74490 | alucinas | 1 |
| 74491 | alucinado | 1 |
| 74492 | alucinada | 1 |
| 74493 | alucinaciones | 1 |
| 74494 | alualinos | 1 |
| 74495 | altybajo | 1 |
| 74496 | altruistas | 1 |
| 74497 | altro | 1 |
| 74498 | altramuzes | 1 |
| 74499 | altozano | 1 |
| 74500 | altona | 1 |
| 74501 | altiuo | 1 |
| 74502 | altito | 1 |
| 74503 | altisonantes | 1 |
| 74504 | altisidorilla | 1 |
| 74505 | altillo | 1 |
| 74506 | altibajo | 1 |
| 74507 | altezas | 1 |
| 74508 | altesa | 1 |
| 74509 | alteróse | 1 |
| 74510 | alternen | 1 |
| 74511 | alternativos | 1 |
| 74512 | alternativa | 1 |
| 74513 | alternantes | 1 |
| 74514 | alternan | 1 |
| 74515 | alternadamente | 1 |
| 74516 | alternaba | 1 |
| 74517 | altercaciones | 1 |
| 74518 | alteraua | 1 |
| 74519 | alterasete | 1 |
| 74520 | alterasen | 1 |
| 74521 | alterase | 1 |
| 74522 | alteraron | 1 |
| 74523 | alterarlo | 1 |
| 74524 | alter | 1 |
| 74525 | altarucho | 1 |
| 74526 | altaneras | 1 |
| 74527 | altaneramente | 1 |
| 74528 | altaba | 1 |
| 74529 | alsacia | 1 |
| 74530 | alquitara | 1 |
| 74531 | alquimista | 1 |
| 74532 | alquilón | 1 |
| 74533 | alquilómele | 1 |
| 74534 | alquile | 1 |
| 74535 | alquilarla | 1 |
| 74536 | alquilando | 1 |
| 74537 | alquilan | 1 |
| 74538 | alquiladores | 1 |
| 74539 | alquilada | 1 |
| 74540 | alquilables | 1 |
| 74541 | alquilable | 1 |
| 74542 | alquilaban | 1 |
| 74543 | alquiceles | 1 |
| 74544 | alquicel | 1 |
| 74545 | alquería | 1 |
| 74546 | alpestres | 1 |
| 74547 | alpargatitas | 1 |
| 74548 | alpargates | 1 |
| 74549 | alpargata | 1 |
| 74550 | álora | 1 |
| 74551 | aloques | 1 |
| 74552 | alonzo | 1 |
| 74553 | alonsete | 1 |
| 74554 | alonguemos | 1 |
| 74555 | alongados | 1 |
| 74556 | along | 1 |
| 74557 | alondras | 1 |
| 74558 | aloncito | 1 |
| 74559 | alojó | 1 |
| 74560 | alojemos | 1 |
| 74561 | alojáronle | 1 |
| 74562 | alojarnos | 1 |
| 74563 | alojarle | 1 |
| 74564 | alojando | 1 |
| 74565 | alojan | 1 |
| 74566 | alojamientos | 1 |
| 74567 | alojados | 1 |
| 74568 | alojada | 1 |
| 74569 | alojaban | 1 |
| 74570 | aloja | 1 |
| 74571 | almuerza | 1 |
| 74572 | almuerças | 1 |
| 74573 | almuerça | 1 |
| 74574 | almueças | 1 |
| 74575 | almudes | 1 |
| 74576 | almotacén | 1 |
| 74577 | almosar | 1 |
| 74578 | almorzó | 1 |
| 74579 | almorzase | 1 |
| 74580 | almorzaría | 1 |
| 74581 | almorzaré | 1 |
| 74582 | almorzarás | 1 |
| 74583 | almorzaran | 1 |
| 74584 | almorzará | 1 |
| 74585 | almorzamos | 1 |
| 74586 | almorzados | 1 |
| 74587 | almorzadas | 1 |
| 74588 | almorzaban | 1 |
| 74589 | almorranas | 1 |
| 74590 | almorox | 1 |
| 74591 | almorçava | 1 |
| 74592 | almoradíes | 1 |
| 74593 | almohazas | 1 |
| 74594 | almohadillado | 1 |
| 74595 | almohadillada | 1 |
| 74596 | almohácenme | 1 |
| 74597 | almohaça | 1 |
| 74598 | almofalla | 1 |
| 74599 | almodrote | 1 |
| 74600 | almizque | 1 |
| 74601 | almizcles | 1 |
| 74602 | almizcladas | 1 |
| 74603 | almireces | 1 |
| 74604 | almilla | 1 |
| 74605 | almidonar | 1 |
| 74606 | almidonado | 1 |
| 74607 | almidonadas | 1 |
| 74608 | almería | 1 |
| 74609 | almendrugo | 1 |
| 74610 | almendros | 1 |
| 74611 | almendrita | 1 |
| 74612 | almendrado | 1 |
| 74613 | almendrada | 1 |
| 74614 | almenadas | 1 |
| 74615 | almeida | 1 |
| 74616 | almazenes | 1 |
| 74617 | almazarrón | 1 |
| 74618 | almatea | 1 |
| 74619 | almario | 1 |
| 74620 | almansa | 1 |
| 74621 | almalafas | 1 |
| 74622 | almajares | 1 |
| 74623 | almaizales | 1 |
| 74624 | almagra | 1 |
| 74625 | almadanas | 1 |
| 74626 | almadana | 1 |
| 74627 | almacenó | 1 |
| 74628 | almacenista | 1 |
| 74629 | allombre | 1 |
| 74630 | aller | 1 |
| 74631 | allento | 1 |
| 74632 | alleluyah | 1 |
| 74633 | alleluya | 1 |
| 74634 | alleluia | 1 |
| 74635 | allegro | 1 |
| 74636 | allegasse | 1 |
| 74637 | allegarse | 1 |
| 74638 | allegamiento | 1 |
| 74639 | allegadizo | 1 |
| 74640 | allegaban | 1 |
| 74641 | allegaba | 1 |
| 74642 | allano | 1 |
| 74643 | allane | 1 |
| 74644 | allanarlo | 1 |
| 74645 | allanaría | 1 |
| 74646 | allanando | 1 |
| 74647 | allanamiento | 1 |
| 74648 | allana | 1 |
| 74649 | allan | 1 |
| 74650 | aljofifa | 1 |
| 74651 | aljofar | 1 |
| 74652 | aljavas | 1 |
| 74653 | aljamiado | 1 |
| 74654 | aljamiada | 1 |
| 74655 | aljafería | 1 |
| 74656 | alivios | 1 |
| 74657 | aliviarse | 1 |
| 74658 | aliviarle | 1 |
| 74659 | aliviaría | 1 |
| 74660 | aliviará | 1 |
| 74661 | aliviadísimo | 1 |
| 74662 | aliviada | 1 |
| 74663 | aliviaban | 1 |
| 74664 | aliviaba | 1 |
| 74665 | aliuiar | 1 |
| 74666 | aliuiadora | 1 |
| 74667 | aliuia | 1 |
| 74668 | alistar | 1 |
| 74669 | alistados | 1 |
| 74670 | alistaba | 1 |
| 74671 | alisos | 1 |
| 74672 | aliscans | 1 |
| 74673 | alisarse | 1 |
| 74674 | alisandría | 1 |
| 74675 | alisandre | 1 |
| 74676 | alisada | 1 |
| 74677 | aliquando | 1 |
| 74678 | aliñarlas | 1 |
| 74679 | aliñándose | 1 |
| 74680 | aliñada | 1 |
| 74681 | alinearon | 1 |
| 74682 | alineado | 1 |
| 74683 | alinde | 1 |
| 74684 | alindado | 1 |
| 74685 | alinda | 1 |
| 74686 | alimpiarla | 1 |
| 74687 | alimpiando | 1 |
| 74688 | alimentó | 1 |
| 74689 | alimenten | 1 |
| 74690 | alimente | 1 |
| 74691 | aliméntate | 1 |
| 74692 | alimentas | 1 |
| 74693 | alimentarme | 1 |
| 74694 | alimentarlo | 1 |
| 74695 | alimentando | 1 |
| 74696 | alilao | 1 |
| 74697 | alígero | 1 |
| 74698 | aligerándole | 1 |
| 74699 | aligerando | 1 |
| 74700 | alifonso | 1 |
| 74701 | alifanfuón | 1 |
| 74702 | alifanfarón | 1 |
| 74703 | alifafes | 1 |
| 74704 | alienum | 1 |
| 74705 | alientes | 1 |
| 74706 | aliéntate | 1 |
| 74707 | alientan | 1 |
| 74708 | alienta | 1 |
| 74709 | alidas | 1 |
| 74710 | alicientes | 1 |
| 74711 | aliar | 1 |
| 74712 | aliadas | 1 |
| 74713 | alhucema | 1 |
| 74714 | alhoz | 1 |
| 74715 | alhorre | 1 |
| 74716 | alhombras | 1 |
| 74717 | alholis | 1 |
| 74718 | alhiara | 1 |
| 74719 | alheleles | 1 |
| 74720 | alharaca | 1 |
| 74721 | alhaonedes | 1 |
| 74722 | alhajó | 1 |
| 74723 | alhajita | 1 |
| 74724 | alhajada | 1 |
| 74725 | alguaziles | 1 |
| 74726 | algu | 1 |
| 74727 | álgido | 1 |
| 74728 | álgebra | 1 |
| 74729 | algazaras | 1 |
| 74730 | algarrobas | 1 |
| 74731 | algarroba | 1 |
| 74732 | algarea | 1 |
| 74733 | algarbe | 1 |
| 74734 | algaradas | 1 |
| 74735 | algarabías | 1 |
| 74736 | alforzadas | 1 |
| 74737 | alforza | 1 |
| 74738 | alfonsos | 1 |
| 74739 | alfonsinos | 1 |
| 74740 | alfonsina | 1 |
| 74741 | alfombrita | 1 |
| 74742 | alfombradas | 1 |
| 74743 | alfocigos | 1 |
| 74744 | alfiletero | 1 |
| 74745 | alfiles | 1 |
| 74746 | alfilerazo | 1 |
| 74747 | alfierez | 1 |
| 74748 | alffonsus | 1 |
| 74749 | alferez | 1 |
| 74750 | alferes | 1 |
| 74751 | alferecía | 1 |
| 74752 | alfeñiquén | 1 |
| 74753 | alfargías | 1 |
| 74754 | alfarache | 1 |
| 74755 | alfaquíes | 1 |
| 74756 | alfamares | 1 |
| 74757 | alfajores | 1 |
| 74758 | alfajeme | 1 |
| 74759 | alfajas | 1 |
| 74760 | alfaja | 1 |
| 74761 | alexar | 1 |
| 74762 | alexandría | 1 |
| 74763 | alexa | 1 |
| 74764 | alevosos | 1 |
| 74765 | alevosas | 1 |
| 74766 | aleuosos | 1 |
| 74767 | aleteos | 1 |
| 74768 | aletean | 1 |
| 74769 | aletargó | 1 |
| 74770 | aletargarse | 1 |
| 74771 | aletargadas | 1 |
| 74772 | aleta | 1 |
| 74773 | alerto | 1 |
| 74774 | alentarse | 1 |
| 74775 | alentarme | 1 |
| 74776 | alentándole | 1 |
| 74777 | alentaban | 1 |
| 74778 | alencastros | 1 |
| 74779 | alemañas | 1 |
| 74780 | alemaña | 1 |
| 74781 | alemanas | 1 |
| 74782 | alelí | 1 |
| 74783 | alelado | 1 |
| 74784 | alejo | 1 |
| 74785 | alejes | 1 |
| 74786 | alejéme | 1 |
| 74787 | alejéis | 1 |
| 74788 | alejasen | 1 |
| 74789 | alejase | 1 |
| 74790 | alejaran | 1 |
| 74791 | alejandrías | 1 |
| 74792 | alejandra | 1 |
| 74793 | alejándolo | 1 |
| 74794 | alejándole | 1 |
| 74795 | alejados | 1 |
| 74796 | alejada | 1 |
| 74797 | alejábamos | 1 |
| 74798 | alegues | 1 |
| 74799 | alegué | 1 |
| 74800 | alegrones | 1 |
| 74801 | alegrón | 1 |
| 74802 | alegróles | 1 |
| 74803 | alegrísimo | 1 |
| 74804 | alégrese | 1 |
| 74805 | alégrenos | 1 |
| 74806 | alegren | 1 |
| 74807 | alegréme | 1 |
| 74808 | alegrava | 1 |
| 74809 | alegraua | 1 |
| 74810 | alegrate | 1 |
| 74811 | alégrase | 1 |
| 74812 | alegrarles | 1 |
| 74813 | alegrarla | 1 |
| 74814 | alegraríamos | 1 |
| 74815 | alegraras | 1 |
| 74816 | alegrarán | 1 |
| 74817 | alegraran | 1 |
| 74818 | alegrara | 1 |
| 74819 | alégranse | 1 |
| 74820 | alegrándose | 1 |
| 74821 | alegrança | 1 |
| 74822 | alegramela | 1 |
| 74823 | alegrada | 1 |
| 74824 | alegó | 1 |
| 74825 | alegan | 1 |
| 74826 | alegado | 1 |
| 74827 | alegada | 1 |
| 74828 | aleccionado | 1 |
| 74829 | aleatorio | 1 |
| 74830 | ale | 1 |
| 74831 | alderredores | 1 |
| 74832 | alderredor | 1 |
| 74833 | aldeota | 1 |
| 74834 | aldegüela | 1 |
| 74835 | aldeco | 1 |
| 74836 | aldebarán | 1 |
| 74837 | aldaua | 1 |
| 74838 | aldas | 1 |
| 74839 | aldabonazo | 1 |
| 74840 | aldabonada | 1 |
| 74841 | aldabazos | 1 |
| 74842 | aldabas | 1 |
| 74843 | alda | 1 |
| 74844 | alcurniado | 1 |
| 74845 | alcurniadas | 1 |
| 74846 | alcudia | 1 |
| 74847 | alcubilla | 1 |
| 74848 | alcranes | 1 |
| 74849 | alcorzas | 1 |
| 74850 | alcorzada | 1 |
| 74851 | alcorza | 1 |
| 74852 | alcorrunz | 1 |
| 74853 | alcornoqueñas | 1 |
| 74854 | alcorcón | 1 |
| 74855 | alcoholizada | 1 |
| 74856 | alcohólicos | 1 |
| 74857 | alcohólicas | 1 |
| 74858 | alcoholeras | 1 |
| 74859 | alcohole | 1 |
| 74860 | alcoholatos | 1 |
| 74861 | alcoholada | 1 |
| 74862 | alcohola | 1 |
| 74863 | alcocer | 1 |
| 74864 | alcobendas | 1 |
| 74865 | alçó | 1 |
| 74866 | alcira | 1 |
| 74867 | alcïón | 1 |
| 74868 | alcimedón | 1 |
| 74869 | alcibiades | 1 |
| 74870 | alcese | 1 |
| 74871 | álcense | 1 |
| 74872 | alcéis | 1 |
| 74873 | alcayueta | 1 |
| 74874 | alcatifas | 1 |
| 74875 | alcarren | 1 |
| 74876 | alcarías | 1 |
| 74877 | alcarez | 1 |
| 74878 | alcarauan | 1 |
| 74879 | alçarás | 1 |
| 74880 | alçar | 1 |
| 74881 | alcaparrón | 1 |
| 74882 | alcañices | 1 |
| 74883 | alcanzólo | 1 |
| 74884 | alcanzauamos | 1 |
| 74885 | alcanzasse | 1 |
| 74886 | alcanzásedes | 1 |
| 74887 | alcanzárseme | 1 |
| 74888 | alcanzaros | 1 |
| 74889 | alcanzarlo | 1 |
| 74890 | alcanzarlas | 1 |
| 74891 | alcanzaremos | 1 |
| 74892 | alcanzáredes | 1 |
| 74893 | alcanzaré | 1 |
| 74894 | alcanzaras | 1 |
| 74895 | alcanzarán | 1 |
| 74896 | alcanzaran | 1 |
| 74897 | alcanzándoles | 1 |
| 74898 | alcanzandola | 1 |
| 74899 | alcánzala | 1 |
| 74900 | alcanzadas | 1 |
| 74901 | álçanse | 1 |
| 74902 | alcanfor | 1 |
| 74903 | alcandora | 1 |
| 74904 | alcándara | 1 |
| 74905 | alcandara | 1 |
| 74906 | alcanço | 1 |
| 74907 | alcancemos | 1 |
| 74908 | alcánceme | 1 |
| 74909 | alcançe | 1 |
| 74910 | alcançara | 1 |
| 74911 | alcançar | 1 |
| 74912 | alcançan | 1 |
| 74913 | alcaná | 1 |
| 74914 | alçan | 1 |
| 74915 | alcaloide | 1 |
| 74916 | alcalles | 1 |
| 74917 | alcaller | 1 |
| 74918 | alcaldito | 1 |
| 74919 | alcaldía | 1 |
| 74920 | alcahuetería | 1 |
| 74921 | alcahueteria | 1 |
| 74922 | alcaduzes | 1 |
| 74923 | alcachofa | 1 |
| 74924 | alcacer | 1 |
| 74925 | alcacel | 1 |
| 74926 | alcabaleros | 1 |
| 74927 | alcabalero | 1 |
| 74928 | alça | 1 |
| 74929 | albures | 1 |
| 74930 | album | 1 |
| 74931 | albuérbola | 1 |
| 74932 | albos | 1 |
| 74933 | alborózase | 1 |
| 74934 | alborozados | 1 |
| 74935 | alborozada | 1 |
| 74936 | alboroza | 1 |
| 74937 | alborotos | 1 |
| 74938 | alborotemos | 1 |
| 74939 | alboroté | 1 |
| 74940 | alborotaron | 1 |
| 74941 | alborotarían | 1 |
| 74942 | alborótanse | 1 |
| 74943 | alborotador | 1 |
| 74944 | alborotadito | 1 |
| 74945 | alborotadamente | 1 |
| 74946 | alboroque | 1 |
| 74947 | alboroçó | 1 |
| 74948 | alborocen | 1 |
| 74949 | alboroçaron | 1 |
| 74950 | albornoces | 1 |
| 74951 | albores | 1 |
| 74952 | alboradas | 1 |
| 74953 | albondiguillas | 1 |
| 74954 | albogón | 1 |
| 74955 | albión | 1 |
| 74956 | alberguen | 1 |
| 74957 | albergasen | 1 |
| 74958 | albergase | 1 |
| 74959 | albergaron | 1 |
| 74960 | albergara | 1 |
| 74961 | albergando | 1 |
| 74962 | albergan | 1 |
| 74963 | albergado | 1 |
| 74964 | albergaban | 1 |
| 74965 | albergaba | 1 |
| 74966 | alberga | 1 |
| 74967 | alberche | 1 |
| 74968 | alberca | 1 |
| 74969 | albéitar | 1 |
| 74970 | albas | 1 |
| 74971 | albarrazadas | 1 |
| 74972 | albarrana | 1 |
| 74973 | albaricoque | 1 |
| 74974 | albardería | 1 |
| 74975 | albarde | 1 |
| 74976 | albarazados | 1 |
| 74977 | albar | 1 |
| 74978 | albañir | 1 |
| 74979 | albañal | 1 |
| 74980 | albanega | 1 |
| 74981 | albandos | 1 |
| 74982 | albahaca | 1 |
| 74983 | alazanes | 1 |
| 74984 | alavés | 1 |
| 74985 | alaút | 1 |
| 74986 | alastrajareas | 1 |
| 74987 | alarzes | 1 |
| 74988 | alarmasen | 1 |
| 74989 | alarmaron | 1 |
| 74990 | alarmará | 1 |
| 74991 | alarmándose | 1 |
| 74992 | alarmados | 1 |
| 74993 | alarmadas | 1 |
| 74994 | alargues | 1 |
| 74995 | alarguen | 1 |
| 74996 | alarguemos | 1 |
| 74997 | alargué | 1 |
| 74998 | alargasse | 1 |
| 74999 | alargasen | 1 |
| 75000 | alargase | 1 |
| 75001 | alargarse | 1 |
| 75002 | alargaron | 1 |
| 75003 | alargarme | 1 |
| 75004 | alargarían | 1 |
| 75005 | alargándoselo | 1 |
| 75006 | alargándosela | 1 |
| 75007 | alargamos | 1 |
| 75008 | alargamiento | 1 |
| 75009 | alargado | 1 |
| 75010 | alargabas | 1 |
| 75011 | alargábalo | 1 |
| 75012 | alardeando | 1 |
| 75013 | alardea | 1 |
| 75014 | alarcos | 1 |
| 75015 | alanes | 1 |
| 75016 | alanceara | 1 |
| 75017 | alanceallas | 1 |
| 75018 | alance | 1 |
| 75019 | alancardan | 1 |
| 75020 | alanas | 1 |
| 75021 | alamo | 1 |
| 75022 | alamedas | 1 |
| 75023 | alambiques | 1 |
| 75024 | alagones | 1 |
| 75025 | alacranes | 1 |
| 75026 | alacrán | 1 |
| 75027 | alacran | 1 |
| 75028 | alacenas | 1 |
| 75029 | alacena | 1 |
| 75030 | alabéle | 1 |
| 75031 | alábele | 1 |
| 75032 | alábate | 1 |
| 75033 | alabastrina | 1 |
| 75034 | alabase | 1 |
| 75035 | alabas | 1 |
| 75036 | alabártelo | 1 |
| 75037 | alabarse | 1 |
| 75038 | alabaros | 1 |
| 75039 | alabáronsela | 1 |
| 75040 | alabarme | 1 |
| 75041 | alabarlo | 1 |
| 75042 | alabaré | 1 |
| 75043 | alabarderos | 1 |
| 75044 | alabarda | 1 |
| 75045 | alabarás | 1 |
| 75046 | alabaran | 1 |
| 75047 | alabándote | 1 |
| 75048 | alabándomela | 1 |
| 75049 | alabame | 1 |
| 75050 | alabadas | 1 |
| 75051 | akos | 1 |
| 75052 | ajutorium | 1 |
| 75053 | ajusticiados | 1 |
| 75054 | ajusticiado | 1 |
| 75055 | ajústese | 1 |
| 75056 | ajustarlas | 1 |
| 75057 | ajustaremos | 1 |
| 75058 | ajustaré | 1 |
| 75059 | ajustarán | 1 |
| 75060 | ajustará | 1 |
| 75061 | ajustara | 1 |
| 75062 | ajustándolos | 1 |
| 75063 | ajustándola | 1 |
| 75064 | ajustan | 1 |
| 75065 | ajustados | 1 |
| 75066 | ajustadas | 1 |
| 75067 | ajustábase | 1 |
| 75068 | ajustaba | 1 |
| 75069 | ajuntaron | 1 |
| 75070 | ajumarse | 1 |
| 75071 | ajumaíto | 1 |
| 75072 | ajuares | 1 |
| 75073 | ajosa | 1 |
| 75074 | ajogar | 1 |
| 75075 | ajobo | 1 |
| 75076 | ajoba | 1 |
| 75077 | ajito | 1 |
| 75078 | ajetreada | 1 |
| 75079 | ajeños | 1 |
| 75080 | ajenjos | 1 |
| 75081 | ajenjo | 1 |
| 75082 | aje | 1 |
| 75083 | ajardinados | 1 |
| 75084 | ajan | 1 |
| 75085 | ajados | 1 |
| 75086 | ajada | 1 |
| 75087 | aizarnazabal | 1 |
| 75088 | aiuntamientos | 1 |
| 75089 | aislarse | 1 |
| 75090 | aislarla | 1 |
| 75091 | aislar | 1 |
| 75092 | aislador | 1 |
| 75093 | aisladamente | 1 |
| 75094 | aislada | 1 |
| 75095 | airote | 1 |
| 75096 | airear | 1 |
| 75097 | airarse | 1 |
| 75098 | ainda | 1 |
| 75099 | aínas | 1 |
| 75100 | aigle | 1 |
| 75101 | aidant | 1 |
| 75102 | aicearen | 1 |
| 75103 | aibenzaides | 1 |
| 75104 | aiam | 1 |
| 75105 | ahuyentase | 1 |
| 75106 | ahuyentar | 1 |
| 75107 | ahuyentan | 1 |
| 75108 | ahuyentado | 1 |
| 75109 | ahuyentaba | 1 |
| 75110 | ahumados | 1 |
| 75111 | ahumada | 1 |
| 75112 | ahuma | 1 |
| 75113 | ahuecaré | 1 |
| 75114 | ahuecaditos | 1 |
| 75115 | ahuecadas | 1 |
| 75116 | ahuchados | 1 |
| 75117 | ahorrillos | 1 |
| 75118 | ahorré | 1 |
| 75119 | ahorre | 1 |
| 75120 | ahorrativo | 1 |
| 75121 | ahorrarte | 1 |
| 75122 | ahorraron | 1 |
| 75123 | ahorrarlos | 1 |
| 75124 | ahorraría | 1 |
| 75125 | ahorraréme | 1 |
| 75126 | ahorraran | 1 |
| 75127 | ahorrará | 1 |
| 75128 | ahorrara | 1 |
| 75129 | ahorrada | 1 |
| 75130 | ahorrad | 1 |
| 75131 | ahorraban | 1 |
| 75132 | ahorqué | 1 |
| 75133 | ahorque | 1 |
| 75134 | ahormasen | 1 |
| 75135 | ahorco | 1 |
| 75136 | ahorcase | 1 |
| 75137 | ahorcaran | 1 |
| 75138 | ahorcara | 1 |
| 75139 | ahorcamos | 1 |
| 75140 | ahorcaban | 1 |
| 75141 | ahorcábamos | 1 |
| 75142 | ahorcaba | 1 |
| 75143 | ahorca | 1 |
| 75144 | ahondaren | 1 |
| 75145 | ahondar | 1 |
| 75146 | ahondando | 1 |
| 75147 | ahondamos | 1 |
| 75148 | ahola | 1 |
| 75149 | ahoguillo | 1 |
| 75150 | ahoguen | 1 |
| 75151 | ahogose | 1 |
| 75152 | ahogaste | 1 |
| 75153 | ahogarte | 1 |
| 75154 | ahogaros | 1 |
| 75155 | ahogarlos | 1 |
| 75156 | ahogarlo | 1 |
| 75157 | ahogarla | 1 |
| 75158 | ahogaría | 1 |
| 75159 | ahogaré | 1 |
| 75160 | ahogaran | 1 |
| 75161 | ahogándome | 1 |
| 75162 | ahogándole | 1 |
| 75163 | ahogándola | 1 |
| 75164 | ahogamos | 1 |
| 75165 | ahogallos | 1 |
| 75166 | ahogalle | 1 |
| 75167 | ahogadas | 1 |
| 75168 | ahogadamente | 1 |
| 75169 | aho | 1 |
| 75170 | ahítos | 1 |
| 75171 | ahíto | 1 |
| 75172 | ahito | 1 |
| 75173 | ahítas | 1 |
| 75174 | ahitarse | 1 |
| 75175 | ahirmar | 1 |
| 75176 | ahíncos | 1 |
| 75177 | ahincadas | 1 |
| 75178 | ahincadamente | 1 |
| 75179 | ahilado | 1 |
| 75180 | ahijársele | 1 |
| 75181 | ahijar | 1 |
| 75182 | ahijándolos | 1 |
| 75183 | ahijada | 1 |
| 75184 | ahigadado | 1 |
| 75185 | ahi | 1 |
| 75186 | ahevos | 1 |
| 75187 | aherrojaron | 1 |
| 75188 | aherrojado | 1 |
| 75189 | ahembrados | 1 |
| 75190 | ahecho | 1 |
| 75191 | ahechar | 1 |
| 75192 | ahechándole | 1 |
| 75193 | ahechado | 1 |
| 75194 | ahechaba | 1 |
| 75195 | ahaje | 1 |
| 75196 | aguzase | 1 |
| 75197 | aguzadores | 1 |
| 75198 | aguzaban | 1 |
| 75199 | aguzaba | 1 |
| 75200 | agustinito | 1 |
| 75201 | agusadera | 1 |
| 75202 | agusa | 1 |
| 75203 | agurero | 1 |
| 75204 | agur | 1 |
| 75205 | aguó | 1 |
| 75206 | agujeritos | 1 |
| 75207 | agujereados | 1 |
| 75208 | agujerada | 1 |
| 75209 | aguinaldo | 1 |
| 75210 | aguilucho | 1 |
| 75211 | agüilla | 1 |
| 75212 | aguileño | 1 |
| 75213 | aguila | 1 |
| 75214 | aguijonearle | 1 |
| 75215 | aguijon | 1 |
| 75216 | aguijemos | 1 |
| 75217 | aguije | 1 |
| 75218 | aguijase | 1 |
| 75219 | aguijas | 1 |
| 75220 | aguijado | 1 |
| 75221 | agues | 1 |
| 75222 | aguerrida | 1 |
| 75223 | aguero | 1 |
| 75224 | agüelos | 1 |
| 75225 | agudísimos | 1 |
| 75226 | agudísimas | 1 |
| 75227 | agudísima | 1 |
| 75228 | agudillos | 1 |
| 75229 | aguase | 1 |
| 75230 | aguaron | 1 |
| 75231 | aguardientito | 1 |
| 75232 | aguardientazo | 1 |
| 75233 | aguardes | 1 |
| 75234 | aguárdense | 1 |
| 75235 | aguarden | 1 |
| 75236 | aguardemos | 1 |
| 75237 | aguárdeme | 1 |
| 75238 | aguardaua | 1 |
| 75239 | aguardarte | 1 |
| 75240 | aguardaría | 1 |
| 75241 | aguardaré | 1 |
| 75242 | aguardaras | 1 |
| 75243 | aguardándonos | 1 |
| 75244 | aguardándolos | 1 |
| 75245 | aguardándola | 1 |
| 75246 | aguárdame | 1 |
| 75247 | aguardáis | 1 |
| 75248 | aguardador | 1 |
| 75249 | aguardadas | 1 |
| 75250 | aguardábamos | 1 |
| 75251 | aguardábades | 1 |
| 75252 | aguanten | 1 |
| 75253 | aguánteme | 1 |
| 75254 | aguantas | 1 |
| 75255 | aguantarte | 1 |
| 75256 | aguantarme | 1 |
| 75257 | aguantarle | 1 |
| 75258 | aguantarían | 1 |
| 75259 | aguantaría | 1 |
| 75260 | aguantamos | 1 |
| 75261 | aguantado | 1 |
| 75262 | aguamaniles | 1 |
| 75263 | aguaduchos | 1 |
| 75264 | aguaducho | 1 |
| 75265 | aguados | 1 |
| 75266 | aguaçil | 1 |
| 75267 | aguacil | 1 |
| 75268 | aguachirle | 1 |
| 75269 | aguaba | 1 |
| 75270 | agu | 1 |
| 75271 | agruparon | 1 |
| 75272 | agrupar | 1 |
| 75273 | agrupados | 1 |
| 75274 | agrupadas | 1 |
| 75275 | agrupaciones | 1 |
| 75276 | agrupación | 1 |
| 75277 | agrupa | 1 |
| 75278 | agronomía | 1 |
| 75279 | agripina | 1 |
| 75280 | agrillo | 1 |
| 75281 | agrillados | 1 |
| 75282 | agrietadas | 1 |
| 75283 | agricultores | 1 |
| 75284 | agriamente | 1 |
| 75285 | agriaba | 1 |
| 75286 | agreste | 1 |
| 75287 | agresiva | 1 |
| 75288 | agregue | 1 |
| 75289 | agregando | 1 |
| 75290 | agregan | 1 |
| 75291 | agregados | 1 |
| 75292 | agregadas | 1 |
| 75293 | agregábansele | 1 |
| 75294 | agregaba | 1 |
| 75295 | agredida | 1 |
| 75296 | agraviando | 1 |
| 75297 | agraviados | 1 |
| 75298 | agraviadas | 1 |
| 75299 | agraviada | 1 |
| 75300 | agraviaba | 1 |
| 75301 | agravia | 1 |
| 75302 | agravaron | 1 |
| 75303 | agravaré | 1 |
| 75304 | agravante | 1 |
| 75305 | agravado | 1 |
| 75306 | agravación | 1 |
| 75307 | agrava | 1 |
| 75308 | agrauando | 1 |
| 75309 | agranizar | 1 |
| 75310 | agrandar | 1 |
| 75311 | agrandándolas | 1 |
| 75312 | agrandando | 1 |
| 75313 | agrandado | 1 |
| 75314 | agrandada | 1 |
| 75315 | agranda | 1 |
| 75316 | agrajes | 1 |
| 75317 | agradóse | 1 |
| 75318 | agradóles | 1 |
| 75319 | agradézcoos | 1 |
| 75320 | agradézcaselo | 1 |
| 75321 | agradezcamos | 1 |
| 75322 | agradezcáis | 1 |
| 75323 | agradesco | 1 |
| 75324 | agradescer | 1 |
| 75325 | agradescemos | 1 |
| 75326 | agradeciólo | 1 |
| 75327 | agradecióle | 1 |
| 75328 | agradecíles | 1 |
| 75329 | agradeciese | 1 |
| 75330 | agradeciéronselo | 1 |
| 75331 | agradeciéronmelo | 1 |
| 75332 | agradeciera | 1 |
| 75333 | agradeciéndoselo | 1 |
| 75334 | agradecidamente | 1 |
| 75335 | agradecíamos | 1 |
| 75336 | agradecéroslo | 1 |
| 75337 | agradecéroslas | 1 |
| 75338 | agradeceros | 1 |
| 75339 | agradecerme | 1 |
| 75340 | agradecerles | 1 |
| 75341 | agradecerían | 1 |
| 75342 | agradeceremos | 1 |
| 75343 | agradecerá | 1 |
| 75344 | agradéceme | 1 |
| 75345 | agradauan | 1 |
| 75346 | agradaua | 1 |
| 75347 | agradas | 1 |
| 75348 | agradaron | 1 |
| 75349 | agradándolo | 1 |
| 75350 | agradalle | 1 |
| 75351 | agradabilísimo | 1 |
| 75352 | agradábanle | 1 |
| 75353 | agració | 1 |
| 75354 | agraciarle | 1 |
| 75355 | agraciadas | 1 |
| 75356 | agra | 1 |
| 75357 | agoten | 1 |
| 75358 | agote | 1 |
| 75359 | agotarse | 1 |
| 75360 | agotar | 1 |
| 75361 | agotando | 1 |
| 75362 | agotados | 1 |
| 75363 | agostynes | 1 |
| 75364 | agostos | 1 |
| 75365 | agostarse | 1 |
| 75366 | agostada | 1 |
| 75367 | agostaba | 1 |
| 75368 | agoreros | 1 |
| 75369 | agoreras | 1 |
| 75370 | agonizar | 1 |
| 75371 | agonizada | 1 |
| 75372 | agonizaban | 1 |
| 75373 | agoniza | 1 |
| 75374 | agonioso | 1 |
| 75375 | agolpándose | 1 |
| 75376 | agobie | 1 |
| 75377 | agobiaran | 1 |
| 75378 | agobiándola | 1 |
| 75379 | agobian | 1 |
| 75380 | agobiados | 1 |
| 75381 | agobiaba | 1 |
| 75382 | agnus | 1 |
| 75383 | aglomeraron | 1 |
| 75384 | aglomerados | 1 |
| 75385 | aglomeración | 1 |
| 75386 | agitato | 1 |
| 75387 | agitarlos | 1 |
| 75388 | agitara | 1 |
| 75389 | agitar | 1 |
| 75390 | agitante | 1 |
| 75391 | agitándolas | 1 |
| 75392 | agitanada | 1 |
| 75393 | agitados | 1 |
| 75394 | agio | 1 |
| 75395 | agilítanse | 1 |
| 75396 | agigantado | 1 |
| 75397 | agible | 1 |
| 75398 | agencias | 1 |
| 75399 | agenciaron | 1 |
| 75400 | agenciándose | 1 |
| 75401 | agenciado | 1 |
| 75402 | agenciaba | 1 |
| 75403 | agazapó | 1 |
| 75404 | agazapasen | 1 |
| 75405 | agazapar | 1 |
| 75406 | agazapa | 1 |
| 75407 | agasajos | 1 |
| 75408 | agasajarlos | 1 |
| 75409 | agasajarle | 1 |
| 75410 | agasajándola | 1 |
| 75411 | agasajando | 1 |
| 75412 | agasajan | 1 |
| 75413 | agasajamos | 1 |
| 75414 | agasajador | 1 |
| 75415 | agarrotes | 1 |
| 75416 | agarrose | 1 |
| 75417 | agarro | 1 |
| 75418 | agarréme | 1 |
| 75419 | agarre | 1 |
| 75420 | agarrase | 1 |
| 75421 | agarras | 1 |
| 75422 | agarráronme | 1 |
| 75423 | agarrarle | 1 |
| 75424 | agarráramos | 1 |
| 75425 | agarrándola | 1 |
| 75426 | agárrale | 1 |
| 75427 | agarradito | 1 |
| 75428 | agarradas | 1 |
| 75429 | agarena | 1 |
| 75430 | aganipe | 1 |
| 75431 | agamenón | 1 |
| 75432 | agalla | 1 |
| 75433 | agácheme | 1 |
| 75434 | agachaban | 1 |
| 75435 | agá | 1 |
| 75436 | afynquela | 1 |
| 75437 | afyncovos | 1 |
| 75438 | afynco | 1 |
| 75439 | afyncava | 1 |
| 75440 | afyncáronle | 1 |
| 75441 | afyncándole | 1 |
| 75442 | afyncando | 1 |
| 75443 | afyncamiento | 1 |
| 75444 | afyncado | 1 |
| 75445 | afylada | 1 |
| 75446 | afusiavan | 1 |
| 75447 | afusiada | 1 |
| 75448 | afrontara | 1 |
| 75449 | afrontando | 1 |
| 75450 | afrodisíaco | 1 |
| 75451 | afrentes | 1 |
| 75452 | afrentarme | 1 |
| 75453 | afrentarlos | 1 |
| 75454 | afrentara | 1 |
| 75455 | afrentándolos | 1 |
| 75456 | afrentan | 1 |
| 75457 | afrentaba | 1 |
| 75458 | afrecho | 1 |
| 75459 | afortunadas | 1 |
| 75460 | aforre | 1 |
| 75461 | aforrasen | 1 |
| 75462 | aforrados | 1 |
| 75463 | aforquen | 1 |
| 75464 | afónico | 1 |
| 75465 | afogóse | 1 |
| 75466 | afogóla | 1 |
| 75467 | afógate | 1 |
| 75468 | afogarse | 1 |
| 75469 | afogaría | 1 |
| 75470 | afogado | 1 |
| 75471 | afluían | 1 |
| 75472 | afluente | 1 |
| 75473 | afloxo | 1 |
| 75474 | afloxar | 1 |
| 75475 | aflojé | 1 |
| 75476 | afloje | 1 |
| 75477 | aflojarle | 1 |
| 75478 | aflojara | 1 |
| 75479 | aflojar | 1 |
| 75480 | aflojando | 1 |
| 75481 | aflojaban | 1 |
| 75482 | afligirte | 1 |
| 75483 | afligirme | 1 |
| 75484 | afligirla | 1 |
| 75485 | afligiósele | 1 |
| 75486 | afligimos | 1 |
| 75487 | afligiéramos | 1 |
| 75488 | afligidísimo | 1 |
| 75489 | afligidísima | 1 |
| 75490 | afliges | 1 |
| 75491 | afligen | 1 |
| 75492 | aflictivas | 1 |
| 75493 | afliciones | 1 |
| 75494 | aflicciones | 1 |
| 75495 | aflamencado | 1 |
| 75496 | aflacar | 1 |
| 75497 | afiyncamiento | 1 |
| 75498 | afistoles | 1 |
| 75499 | afirmose | 1 |
| 75500 | afirmes | 1 |
| 75501 | afirmélo | 1 |
| 75502 | afirme | 1 |
| 75503 | afirmativos | 1 |
| 75504 | afirmase | 1 |
| 75505 | afirmaron | 1 |
| 75506 | afirmarla | 1 |
| 75507 | afirmándome | 1 |
| 75508 | afirmando | 1 |
| 75509 | afinques | 1 |
| 75510 | afinojó | 1 |
| 75511 | afinó | 1 |
| 75512 | afinidades | 1 |
| 75513 | afínese | 1 |
| 75514 | afine | 1 |
| 75515 | afincado | 1 |
| 75516 | afinca | 1 |
| 75517 | afinarte | 1 |
| 75518 | afinarme | 1 |
| 75519 | afinándola | 1 |
| 75520 | afinado | 1 |
| 75521 | afinadas | 1 |
| 75522 | afinada | 1 |
| 75523 | afinación | 1 |
| 75524 | afinaba | 1 |
| 75525 | afiliarse | 1 |
| 75526 | afilándolas | 1 |
| 75527 | afilando | 1 |
| 75528 | afilador | 1 |
| 75529 | afilaban | 1 |
| 75530 | aficionóseme | 1 |
| 75531 | aficionarse | 1 |
| 75532 | aficionáronse | 1 |
| 75533 | aficionaron | 1 |
| 75534 | aficionara | 1 |
| 75535 | aficionando | 1 |
| 75536 | aficionadísimos | 1 |
| 75537 | aficionadísimo | 1 |
| 75538 | aficionaba | 1 |
| 75539 | aficiona | 1 |
| 75540 | afianzaría | 1 |
| 75541 | afianzando | 1 |
| 75542 | afianzaba | 1 |
| 75543 | afianza | 1 |
| 75544 | affyncada | 1 |
| 75545 | affrenta | 1 |
| 75546 | affma | 1 |
| 75547 | affligida | 1 |
| 75548 | affirmaremos | 1 |
| 75549 | affirman | 1 |
| 75550 | affectos | 1 |
| 75551 | afeyte | 1 |
| 75552 | afeytadas | 1 |
| 75553 | aferró | 1 |
| 75554 | aférrate | 1 |
| 75555 | aferraron | 1 |
| 75556 | aferrados | 1 |
| 75557 | aferrada | 1 |
| 75558 | aferraba | 1 |
| 75559 | afeminas | 1 |
| 75560 | afeminada | 1 |
| 75561 | afeitéme | 1 |
| 75562 | afeitando | 1 |
| 75563 | afeitadito | 1 |
| 75564 | afeitaban | 1 |
| 75565 | afectüoso | 1 |
| 75566 | afectivo | 1 |
| 75567 | afectase | 1 |
| 75568 | afectarte | 1 |
| 75569 | afectaron | 1 |
| 75570 | afectarlos | 1 |
| 75571 | afectar | 1 |
| 75572 | afectamos | 1 |
| 75573 | afectadísimo | 1 |
| 75574 | afectadamente | 1 |
| 75575 | afearlo | 1 |
| 75576 | afeara | 1 |
| 75577 | afeado | 1 |
| 75578 | afanosos | 1 |
| 75579 | afanoso | 1 |
| 75580 | afanarse | 1 |
| 75581 | afanaran | 1 |
| 75582 | afanándose | 1 |
| 75583 | afanando | 1 |
| 75584 | afanados | 1 |
| 75585 | afanadora | 1 |
| 75586 | afanada | 1 |
| 75587 | afamados | 1 |
| 75588 | afamado | 1 |
| 75589 | afablemente | 1 |
| 75590 | aeternam | 1 |
| 75591 | aes | 1 |
| 75592 | aeroterapia | 1 |
| 75593 | aeronauta | 1 |
| 75594 | aéreas | 1 |
| 75595 | aereación | 1 |
| 75596 | aer | 1 |
| 75597 | aequo | 1 |
| 75598 | adyvas | 1 |
| 75599 | adyacentes | 1 |
| 75600 | advocaron | 1 |
| 75601 | advirtióle | 1 |
| 75602 | advirtiera | 1 |
| 75603 | advirtiéndome | 1 |
| 75604 | advirtiéndola | 1 |
| 75605 | adviniese | 1 |
| 75606 | adviértele | 1 |
| 75607 | adviértase | 1 |
| 75608 | adviertan | 1 |
| 75609 | adviértale | 1 |
| 75610 | advertírselo | 1 |
| 75611 | advertirse | 1 |
| 75612 | advertirme | 1 |
| 75613 | advertiréis | 1 |
| 75614 | advertirás | 1 |
| 75615 | advertimos | 1 |
| 75616 | advertimento | 1 |
| 75617 | advertían | 1 |
| 75618 | adverso | 1 |
| 75619 | adversas | 1 |
| 75620 | adversarios | 1 |
| 75621 | adversae | 1 |
| 75622 | adverbio | 1 |
| 75623 | adverbializada | 1 |
| 75624 | adventicia | 1 |
| 75625 | adúz | 1 |
| 75626 | aduxeronle | 1 |
| 75627 | adustos | 1 |
| 75628 | adustez | 1 |
| 75629 | adunia | 1 |
| 75630 | adunco | 1 |
| 75631 | adultero | 1 |
| 75632 | adulteraste | 1 |
| 75633 | adúlteras | 1 |
| 75634 | adulteraba | 1 |
| 75635 | adultera | 1 |
| 75636 | adulas | 1 |
| 75637 | adulando | 1 |
| 75638 | aduladores | 1 |
| 75639 | aduladoras | 1 |
| 75640 | adulado | 1 |
| 75641 | adulaciones | 1 |
| 75642 | adujo | 1 |
| 75643 | adugo | 1 |
| 75644 | aduersos | 1 |
| 75645 | aduersas | 1 |
| 75646 | aduersarios | 1 |
| 75647 | aduersario | 1 |
| 75648 | aducho | 1 |
| 75649 | aducha | 1 |
| 75650 | aduce | 1 |
| 75651 | adrezado | 1 |
| 75652 | adragea | 1 |
| 75653 | adquirirlo | 1 |
| 75654 | adquiriría | 1 |
| 75655 | adquiriré | 1 |
| 75656 | adquirían | 1 |
| 75657 | adquiri | 1 |
| 75658 | adquiero | 1 |
| 75659 | adquieren | 1 |
| 75660 | adquieras | 1 |
| 75661 | adquieran | 1 |
| 75662 | adquerido | 1 |
| 75663 | adotiuo | 1 |
| 75664 | adornome | 1 |
| 75665 | adornista | 1 |
| 75666 | adornen | 1 |
| 75667 | adornarte | 1 |
| 75668 | adornáronle | 1 |
| 75669 | adornaron | 1 |
| 75670 | adornarla | 1 |
| 75671 | adornaren | 1 |
| 75672 | adornara | 1 |
| 75673 | adormilado | 1 |
| 75674 | adormiéronse | 1 |
| 75675 | adormiendo | 1 |
| 75676 | adormido | 1 |
| 75677 | adormidera | 1 |
| 75678 | adormida | 1 |
| 75679 | adormeciera | 1 |
| 75680 | adormecía | 1 |
| 75681 | adormecerse | 1 |
| 75682 | adormecerla | 1 |
| 75683 | adormecer | 1 |
| 75684 | adormecen | 1 |
| 75685 | adoré | 1 |
| 75686 | adorava | 1 |
| 75687 | adorarse | 1 |
| 75688 | adorarme | 1 |
| 75689 | adorarle | 1 |
| 75690 | adorarlas | 1 |
| 75691 | adoraría | 1 |
| 75692 | adoraré | 1 |
| 75693 | adoraran | 1 |
| 75694 | adorara | 1 |
| 75695 | adorándote | 1 |
| 75696 | adorallo | 1 |
| 75697 | adoralle | 1 |
| 75698 | adorados | 1 |
| 75699 | adorable | 1 |
| 75700 | adoquinando | 1 |
| 75701 | adoquinadas | 1 |
| 75702 | adoquiera | 1 |
| 75703 | adoptó | 1 |
| 75704 | adoptela | 1 |
| 75705 | adopte | 1 |
| 75706 | adoptarlo | 1 |
| 75707 | adoptarla | 1 |
| 75708 | adoptaría | 1 |
| 75709 | adoptando | 1 |
| 75710 | adoptan | 1 |
| 75711 | adoptadas | 1 |
| 75712 | adoptada | 1 |
| 75713 | adonada | 1 |
| 75714 | adona | 1 |
| 75715 | adoloriar | 1 |
| 75716 | adolo | 1 |
| 75717 | adolesçer | 1 |
| 75718 | adolescentes | 1 |
| 75719 | adolecieran | 1 |
| 75720 | adocenado | 1 |
| 75721 | adocenada | 1 |
| 75722 | adobos | 1 |
| 75723 | adobcion | 1 |
| 75724 | adobarlo | 1 |
| 75725 | adobarla | 1 |
| 75726 | adobaría | 1 |
| 75727 | adobándoseme | 1 |
| 75728 | adóbame | 1 |
| 75729 | adobado | 1 |
| 75730 | adoba | 1 |
| 75731 | admitirlas | 1 |
| 75732 | admitirá | 1 |
| 75733 | admitiesen | 1 |
| 75734 | admitiere | 1 |
| 75735 | admitiéndole | 1 |
| 75736 | admíteme | 1 |
| 75737 | admitamos | 1 |
| 75738 | admirose | 1 |
| 75739 | admiróme | 1 |
| 75740 | admirole | 1 |
| 75741 | admires | 1 |
| 75742 | admiréme | 1 |
| 75743 | admireme | 1 |
| 75744 | admirativa | 1 |
| 75745 | admirasen | 1 |
| 75746 | admirase | 1 |
| 75747 | admiraros | 1 |
| 75748 | admirarlas | 1 |
| 75749 | admirarás | 1 |
| 75750 | admirarán | 1 |
| 75751 | admiraran | 1 |
| 75752 | admirara | 1 |
| 75753 | admirándole | 1 |
| 75754 | admirándolas | 1 |
| 75755 | admiradora | 1 |
| 75756 | admirador | 1 |
| 75757 | admirábame | 1 |
| 75758 | admirábala | 1 |
| 75759 | administré | 1 |
| 75760 | administrativas | 1 |
| 75761 | administrándole | 1 |
| 75762 | administradas | 1 |
| 75763 | adminículos | 1 |
| 75764 | adminícula | 1 |
| 75765 | adláteres | 1 |
| 75766 | adjuntos | 1 |
| 75767 | adjunto | 1 |
| 75768 | adjudicas | 1 |
| 75769 | adjudicamos | 1 |
| 75770 | adjetivos | 1 |
| 75771 | adivinos | 1 |
| 75772 | adivinen | 1 |
| 75773 | adivinéle | 1 |
| 75774 | adiviné | 1 |
| 75775 | adivine | 1 |
| 75776 | adivinase | 1 |
| 75777 | adivinarlo | 1 |
| 75778 | adivinanza | 1 |
| 75779 | adivinándole | 1 |
| 75780 | adivinan | 1 |
| 75781 | adivinabas | 1 |
| 75782 | adivinaban | 1 |
| 75783 | adivas | 1 |
| 75784 | aditutzendet | 1 |
| 75785 | aditamentos | 1 |
| 75786 | aditamento | 1 |
| 75787 | adiosito | 1 |
| 75788 | adinerado | 1 |
| 75789 | adicto | 1 |
| 75790 | adicion | 1 |
| 75791 | adi | 1 |
| 75792 | adhiriéndose | 1 |
| 75793 | adhieren | 1 |
| 75794 | adherirse | 1 |
| 75795 | adheridos | 1 |
| 75796 | adherido | 1 |
| 75797 | adherente | 1 |
| 75798 | adherencia | 1 |
| 75799 | adevinaron | 1 |
| 75800 | adevinando | 1 |
| 75801 | adevina | 1 |
| 75802 | adeuinos | 1 |
| 75803 | adeuinen | 1 |
| 75804 | adeuine | 1 |
| 75805 | adeuinas | 1 |
| 75806 | adeudaba | 1 |
| 75807 | adestró | 1 |
| 75808 | adestrar | 1 |
| 75809 | adestralle | 1 |
| 75810 | adestrador | 1 |
| 75811 | aderezólas | 1 |
| 75812 | aderezaste | 1 |
| 75813 | aderezase | 1 |
| 75814 | aderezas | 1 |
| 75815 | aderezáronse | 1 |
| 75816 | aderezarles | 1 |
| 75817 | aderezarle | 1 |
| 75818 | aderezarla | 1 |
| 75819 | aderezaría | 1 |
| 75820 | aderezaré | 1 |
| 75821 | aderézame | 1 |
| 75822 | aderezadas | 1 |
| 75823 | aderescen | 1 |
| 75824 | aderecéme | 1 |
| 75825 | adepto | 1 |
| 75826 | adelyñas | 1 |
| 75827 | adeliñó | 1 |
| 75828 | adeliño | 1 |
| 75829 | adeliñase | 1 |
| 75830 | adelgazaua | 1 |
| 75831 | adelgazadas | 1 |
| 75832 | adelgazada | 1 |
| 75833 | adelfa | 1 |
| 75834 | adeleta | 1 |
| 75835 | adelantóse | 1 |
| 75836 | adelanté | 1 |
| 75837 | adelantasen | 1 |
| 75838 | adelantarme | 1 |
| 75839 | adelantarlo | 1 |
| 75840 | adelantarle | 1 |
| 75841 | adelantarían | 1 |
| 75842 | adelantando | 1 |
| 75843 | adelantamos | 1 |
| 75844 | adelantaban | 1 |
| 75845 | adefinas | 1 |
| 75846 | adecuadas | 1 |
| 75847 | adecentase | 1 |
| 75848 | adecentarse | 1 |
| 75849 | adecentaras | 1 |
| 75850 | adecentar | 1 |
| 75851 | adecentado | 1 |
| 75852 | addicion | 1 |
| 75853 | adarva | 1 |
| 75854 | adaragas | 1 |
| 75855 | adaptarse | 1 |
| 75856 | adáptanse | 1 |
| 75857 | adaptándola | 1 |
| 75858 | adaptando | 1 |
| 75859 | adaptadas | 1 |
| 75860 | adaptaban | 1 |
| 75861 | adaptaba | 1 |
| 75862 | adapta | 1 |
| 75863 | adan | 1 |
| 75864 | adamo | 1 |
| 75865 | adamascado | 1 |
| 75866 | adamares | 1 |
| 75867 | adamada | 1 |
| 75868 | adamaba | 1 |
| 75869 | adama | 1 |
| 75870 | adahala | 1 |
| 75871 | acutos | 1 |
| 75872 | acutángulos | 1 |
| 75873 | acústico | 1 |
| 75874 | acussado | 1 |
| 75875 | acusó | 1 |
| 75876 | acusiossos | 1 |
| 75877 | acusemos | 1 |
| 75878 | acusavito | 1 |
| 75879 | acusava | 1 |
| 75880 | acusativo | 1 |
| 75881 | acusaron | 1 |
| 75882 | acusaré | 1 |
| 75883 | acusarás | 1 |
| 75884 | acusara | 1 |
| 75885 | acusándose | 1 |
| 75886 | acusándoles | 1 |
| 75887 | acusándole | 1 |
| 75888 | acusan | 1 |
| 75889 | acusádose | 1 |
| 75890 | acusada | 1 |
| 75891 | acurrucado | 1 |
| 75892 | acurrucada | 1 |
| 75893 | acurrucaba | 1 |
| 75894 | acuñar | 1 |
| 75895 | acuñados | 1 |
| 75896 | acuñable | 1 |
| 75897 | acuña | 1 |
| 75898 | açunbre | 1 |
| 75899 | acumulándolos | 1 |
| 75900 | acumulan | 1 |
| 75901 | acumulada | 1 |
| 75902 | acumula | 1 |
| 75903 | acuitéis | 1 |
| 75904 | acuitedes | 1 |
| 75905 | acuitaráse | 1 |
| 75906 | acuitar | 1 |
| 75907 | acueste | 1 |
| 75908 | acuestate | 1 |
| 75909 | acuéstanse | 1 |
| 75910 | acuestan | 1 |
| 75911 | acuerdes | 1 |
| 75912 | acuerden | 1 |
| 75913 | acuerdaste | 1 |
| 75914 | acueductos | 1 |
| 75915 | acueducto | 1 |
| 75916 | acudo | 1 |
| 75917 | acudiría | 1 |
| 75918 | acudiremos | 1 |
| 75919 | acudiré | 1 |
| 75920 | acudirás | 1 |
| 75921 | acudiese | 1 |
| 75922 | acudiéronme | 1 |
| 75923 | acudieren | 1 |
| 75924 | acudieran | 1 |
| 75925 | acudiera | 1 |
| 75926 | acucies | 1 |
| 75927 | acuciéis | 1 |
| 75928 | acuchíllase | 1 |
| 75929 | acuchilladas | 1 |
| 75930 | acuchillada | 1 |
| 75931 | acubilla | 1 |
| 75932 | acuáticos | 1 |
| 75933 | acuario | 1 |
| 75934 | actuar | 1 |
| 75935 | actuando | 1 |
| 75936 | actuaba | 1 |
| 75937 | activas | 1 |
| 75938 | activaba | 1 |
| 75939 | actiuo | 1 |
| 75940 | acti | 1 |
| 75941 | acteón | 1 |
| 75942 | acrobáticos | 1 |
| 75943 | acróbatas | 1 |
| 75944 | acróbata | 1 |
| 75945 | acrisole | 1 |
| 75946 | acrisolaron | 1 |
| 75947 | acrisolado | 1 |
| 75948 | acrisoladas | 1 |
| 75949 | acrisolada | 1 |
| 75950 | acrisola | 1 |
| 75951 | acriminar | 1 |
| 75952 | acribilló | 1 |
| 75953 | acribillaron | 1 |
| 75954 | acribillarlas | 1 |
| 75955 | acribillada | 1 |
| 75956 | acribillaban | 1 |
| 75957 | acribarme | 1 |
| 75958 | acribar | 1 |
| 75959 | acribado | 1 |
| 75960 | acribada | 1 |
| 75961 | acrescentaste | 1 |
| 75962 | acreditasen | 1 |
| 75963 | acreditarte | 1 |
| 75964 | acreditarse | 1 |
| 75965 | acreditarme | 1 |
| 75966 | acreditaré | 1 |
| 75967 | acreditándole | 1 |
| 75968 | acreditan | 1 |
| 75969 | acreditadísimo | 1 |
| 75970 | acreditábamos | 1 |
| 75971 | acrecientame | 1 |
| 75972 | acrecía | 1 |
| 75973 | acrecentóseles | 1 |
| 75974 | acrecentase | 1 |
| 75975 | acrecentarse | 1 |
| 75976 | acrecentarla | 1 |
| 75977 | acrecentará | 1 |
| 75978 | acrecentando | 1 |
| 75979 | acrecentamiento | 1 |
| 75980 | acrecentado | 1 |
| 75981 | acrecentaban | 1 |
| 75982 | acrecentábamos | 1 |
| 75983 | acrebillaron | 1 |
| 75984 | acrebillado | 1 |
| 75985 | acote | 1 |
| 75986 | acotáronme | 1 |
| 75987 | açotar | 1 |
| 75988 | acotar | 1 |
| 75989 | acotán | 1 |
| 75990 | acotación | 1 |
| 75991 | acostunbrado | 1 |
| 75992 | acostunbrada | 1 |
| 75993 | acostumbré | 1 |
| 75994 | acostúmbrate | 1 |
| 75995 | acostumbras | 1 |
| 75996 | acostumbraran | 1 |
| 75997 | acostumbrar | 1 |
| 75998 | acostumbrándome | 1 |
| 75999 | acostumbramos | 1 |
| 76000 | acostemos | 1 |
| 76001 | acostemonos | 1 |
| 76002 | acoste | 1 |
| 76003 | acostaua | 1 |
| 76004 | acostasen | 1 |
| 76005 | acostásemos | 1 |
| 76006 | acostáronme | 1 |
| 76007 | acostáronle | 1 |
| 76008 | acostarnos | 1 |
| 76009 | acostarla | 1 |
| 76010 | acostaremos | 1 |
| 76011 | acostaráse | 1 |
| 76012 | acostando | 1 |
| 76013 | acostabas | 1 |
| 76014 | acosó | 1 |
| 76015 | acosen | 1 |
| 76016 | acosarla | 1 |
| 76017 | acosándoles | 1 |
| 76018 | acosando | 1 |
| 76019 | acosáis | 1 |
| 76020 | acosaban | 1 |
| 76021 | acórtola | 1 |
| 76022 | acortes | 1 |
| 76023 | acorte | 1 |
| 76024 | acórtase | 1 |
| 76025 | acortaron | 1 |
| 76026 | acortaban | 1 |
| 76027 | acortaba | 1 |
| 76028 | acorta | 1 |
| 76029 | acorrió | 1 |
| 76030 | acorriesen | 1 |
| 76031 | acorrieron | 1 |
| 76032 | acorrerme | 1 |
| 76033 | acórrenos | 1 |
| 76034 | acorrednos | 1 |
| 76035 | acorredme | 1 |
| 76036 | acorredes | 1 |
| 76037 | acorralándola | 1 |
| 76038 | acorralan | 1 |
| 76039 | acorralados | 1 |
| 76040 | acorra | 1 |
| 76041 | acordóse | 1 |
| 76042 | acordonadas | 1 |
| 76043 | acordeones | 1 |
| 76044 | acordeme | 1 |
| 76045 | acordele | 1 |
| 76046 | acordays | 1 |
| 76047 | acordavos | 1 |
| 76048 | acordatvos | 1 |
| 76049 | acordastes | 1 |
| 76050 | acordarnos | 1 |
| 76051 | acordarle | 1 |
| 76052 | acordaré | 1 |
| 76053 | acordare | 1 |
| 76054 | acordarán | 1 |
| 76055 | acordaran | 1 |
| 76056 | acordándonos | 1 |
| 76057 | acordandome | 1 |
| 76058 | acordáisos | 1 |
| 76059 | acordadas | 1 |
| 76060 | acordabas | 1 |
| 76061 | acordábamos | 1 |
| 76062 | acorazó | 1 |
| 76063 | açor | 1 |
| 76064 | acopio | 1 |
| 76065 | acopiando | 1 |
| 76066 | acopiada | 1 |
| 76067 | acopiaba | 1 |
| 76068 | acontezca | 1 |
| 76069 | acontesçió | 1 |
| 76070 | acontescimiento | 1 |
| 76071 | acontescido | 1 |
| 76072 | acontencido | 1 |
| 76073 | acontecio | 1 |
| 76074 | aconteciese | 1 |
| 76075 | acontecieran | 1 |
| 76076 | aconteciera | 1 |
| 76077 | aconteciendo | 1 |
| 76078 | acontecemos | 1 |
| 76079 | aconséjoos | 1 |
| 76080 | aconséjole | 1 |
| 76081 | aconsejéles | 1 |
| 76082 | aconséjele | 1 |
| 76083 | aconsejéis | 1 |
| 76084 | aconséjate | 1 |
| 76085 | aconsejaste | 1 |
| 76086 | aconsejármelas | 1 |
| 76087 | aconsejarla | 1 |
| 76088 | aconsejaríale | 1 |
| 76089 | aconsejárale | 1 |
| 76090 | aconsejándonos | 1 |
| 76091 | aconsejándole | 1 |
| 76092 | aconsejamos | 1 |
| 76093 | aconséjame | 1 |
| 76094 | aconsejábale | 1 |
| 76095 | aconpañar | 1 |
| 76096 | aconpañados | 1 |
| 76097 | aconpañado | 1 |
| 76098 | aconpañada | 1 |
| 76099 | acónito | 1 |
| 76100 | acongojado | 1 |
| 76101 | acongojadas | 1 |
| 76102 | acongojaba | 1 |
| 76103 | acondicionados | 1 |
| 76104 | acompasado | 1 |
| 76105 | acompañome | 1 |
| 76106 | acompañolas | 1 |
| 76107 | acompañes | 1 |
| 76108 | acompáñenos | 1 |
| 76109 | acompañen | 1 |
| 76110 | acompáñeme | 1 |
| 76111 | acompañarte | 1 |
| 76112 | acompañarlos | 1 |
| 76113 | acompañarlas | 1 |
| 76114 | acompañaremos | 1 |
| 76115 | acompañarás | 1 |
| 76116 | acompañáramos | 1 |
| 76117 | acompañándome | 1 |
| 76118 | acompañándolas | 1 |
| 76119 | acompañámosla | 1 |
| 76120 | acompañador | 1 |
| 76121 | acompañad | 1 |
| 76122 | acompañábanle | 1 |
| 76123 | acompañábanla | 1 |
| 76124 | acompañábale | 1 |
| 76125 | acompaneos | 1 |
| 76126 | acompanenos | 1 |
| 76127 | acompanen | 1 |
| 76128 | acompane | 1 |
| 76129 | acompanauala | 1 |
| 76130 | acompanassen | 1 |
| 76131 | acompanaron | 1 |
| 76132 | acompanara | 1 |
| 76133 | acompanan | 1 |
| 76134 | acompanadas | 1 |
| 76135 | acomodose | 1 |
| 76136 | acomodos | 1 |
| 76137 | acomodóle | 1 |
| 76138 | acomodéme | 1 |
| 76139 | acomodaticios | 1 |
| 76140 | acomodaticia | 1 |
| 76141 | acomódate | 1 |
| 76142 | acomodase | 1 |
| 76143 | acomodársele | 1 |
| 76144 | acomodáronse | 1 |
| 76145 | acomodáremos | 1 |
| 76146 | acomodarán | 1 |
| 76147 | acomodándoos | 1 |
| 76148 | acomodan | 1 |
| 76149 | acomodamos | 1 |
| 76150 | acomodamientos | 1 |
| 76151 | acomodamiento | 1 |
| 76152 | acomódale | 1 |
| 76153 | acomodádose | 1 |
| 76154 | acomodádolas | 1 |
| 76155 | acometividad | 1 |
| 76156 | acometiéronnos | 1 |
| 76157 | acometiera | 1 |
| 76158 | acometiéndoos | 1 |
| 76159 | acometían | 1 |
| 76160 | acometerse | 1 |
| 76161 | acometerlas | 1 |
| 76162 | acometemos | 1 |
| 76163 | acometelle | 1 |
| 76164 | acometellas | 1 |
| 76165 | acometella | 1 |
| 76166 | acometedores | 1 |
| 76167 | acometas | 1 |
| 76168 | acometáis | 1 |
| 76169 | acojer | 1 |
| 76170 | acojámonos | 1 |
| 76171 | acogotar | 1 |
| 76172 | acogotamos | 1 |
| 76173 | acogistes | 1 |
| 76174 | acogimos | 1 |
| 76175 | acogímonos | 1 |
| 76176 | acogimientos | 1 |
| 76177 | acogiesen | 1 |
| 76178 | acogieron | 1 |
| 76179 | acogiera | 1 |
| 76180 | acogidos | 1 |
| 76181 | acogíase | 1 |
| 76182 | acogía | 1 |
| 76183 | acogí | 1 |
| 76184 | acogen | 1 |
| 76185 | acogedos | 1 |
| 76186 | acogednos | 1 |
| 76187 | acoged | 1 |
| 76188 | acogamonos | 1 |
| 76189 | açófar | 1 |
| 76190 | acocotaron | 1 |
| 76191 | acocear | 1 |
| 76192 | acoceado | 1 |
| 76193 | acobardóse | 1 |
| 76194 | acobarde | 1 |
| 76195 | acobardarse | 1 |
| 76196 | acobardaron | 1 |
| 76197 | acobardarme | 1 |
| 76198 | acobardarás | 1 |
| 76199 | acobardará | 1 |
| 76200 | acobardar | 1 |
| 76201 | acobardan | 1 |
| 76202 | acobardada | 1 |
| 76203 | acobardaban | 1 |
| 76204 | acobardaba | 1 |
| 76205 | aclimató | 1 |
| 76206 | aclimataba | 1 |
| 76207 | aclaróseme | 1 |
| 76208 | aclárate | 1 |
| 76209 | aclarate | 1 |
| 76210 | aclarase | 1 |
| 76211 | aclararnos | 1 |
| 76212 | aclararlo | 1 |
| 76213 | aclarando | 1 |
| 76214 | aclaran | 1 |
| 76215 | aclaraciones | 1 |
| 76216 | aclamó | 1 |
| 76217 | aclamaron | 1 |
| 76218 | aclamación | 1 |
| 76219 | aclamaban | 1 |
| 76220 | acipreste | 1 |
| 76221 | aciones | 1 |
| 76222 | acion | 1 |
| 76223 | aciertos | 1 |
| 76224 | aciertes | 1 |
| 76225 | acierten | 1 |
| 76226 | açiertas | 1 |
| 76227 | aciértanme | 1 |
| 76228 | açidya | 1 |
| 76229 | acídula | 1 |
| 76230 | acidia | 1 |
| 76231 | acidez | 1 |
| 76232 | acidentes | 1 |
| 76233 | açidente | 1 |
| 76234 | ácidas | 1 |
| 76235 | acidalia | 1 |
| 76236 | acicate | 1 |
| 76237 | acicaló | 1 |
| 76238 | acicalarse | 1 |
| 76239 | acicalarme | 1 |
| 76240 | acicalándose | 1 |
| 76241 | acicalado | 1 |
| 76242 | acicalada | 1 |
| 76243 | acicalaba | 1 |
| 76244 | aciaga | 1 |
| 76245 | achulado | 1 |
| 76246 | achuchones | 1 |
| 76247 | achucarro | 1 |
| 76248 | achocolatado | 1 |
| 76249 | achicó | 1 |
| 76250 | achicharrándome | 1 |
| 76251 | achicharrados | 1 |
| 76252 | achicharradito | 1 |
| 76253 | achicarte | 1 |
| 76254 | achicarse | 1 |
| 76255 | achicar | 1 |
| 76256 | achican | 1 |
| 76257 | achicaba | 1 |
| 76258 | achevait | 1 |
| 76259 | achatada | 1 |
| 76260 | acharnement | 1 |
| 76261 | achares | 1 |
| 76262 | achaparrado | 1 |
| 76263 | achaparrada | 1 |
| 76264 | achantarse | 1 |
| 76265 | achantado | 1 |
| 76266 | achantaditos | 1 |
| 76267 | achantada | 1 |
| 76268 | achacó | 1 |
| 76269 | achacarse | 1 |
| 76270 | achacaron | 1 |
| 76271 | achacar | 1 |
| 76272 | achaca | 1 |
| 76273 | acevedo | 1 |
| 76274 | aceto | 1 |
| 76275 | acetemos | 1 |
| 76276 | acetéle | 1 |
| 76277 | acete | 1 |
| 76278 | acetato | 1 |
| 76279 | acetaros | 1 |
| 76280 | acetáronle | 1 |
| 76281 | acetaron | 1 |
| 76282 | acetarlos | 1 |
| 76283 | acetación | 1 |
| 76284 | acetaban | 1 |
| 76285 | acetaba | 1 |
| 76286 | açes | 1 |
| 76287 | acervo | 1 |
| 76288 | acertijos | 1 |
| 76289 | acertijo | 1 |
| 76290 | açerté | 1 |
| 76291 | acertastes | 1 |
| 76292 | acertasen | 1 |
| 76293 | acertase | 1 |
| 76294 | acertaría | 1 |
| 76295 | acertares | 1 |
| 76296 | acertaréis | 1 |
| 76297 | acertáredes | 1 |
| 76298 | acertaran | 1 |
| 76299 | acertáramos | 1 |
| 76300 | acertándole | 1 |
| 76301 | acertáis | 1 |
| 76302 | acertadísimo | 1 |
| 76303 | açertad | 1 |
| 76304 | acerquen | 1 |
| 76305 | acercaste | 1 |
| 76306 | açércase | 1 |
| 76307 | acercáronse | 1 |
| 76308 | acercáronme | 1 |
| 76309 | acercará | 1 |
| 76310 | acercanos | 1 |
| 76311 | açercándosse | 1 |
| 76312 | acercándolas | 1 |
| 76313 | acercábamos | 1 |
| 76314 | açerca | 1 |
| 76315 | acerbos | 1 |
| 76316 | acerbo | 1 |
| 76317 | acerbísimo | 1 |
| 76318 | acerbísimas | 1 |
| 76319 | acerbamente | 1 |
| 76320 | acerado | 1 |
| 76321 | acequias | 1 |
| 76322 | aceptólo | 1 |
| 76323 | acéptelo | 1 |
| 76324 | aceptéla | 1 |
| 76325 | acepte | 1 |
| 76326 | aceptaste | 1 |
| 76327 | aceptase | 1 |
| 76328 | aceptaros | 1 |
| 76329 | aceptarme | 1 |
| 76330 | aceptarla | 1 |
| 76331 | aceptaré | 1 |
| 76332 | aceptarán | 1 |
| 76333 | aceptan | 1 |
| 76334 | aceptámosla | 1 |
| 76335 | aceptamos | 1 |
| 76336 | acéptalo | 1 |
| 76337 | açeña | 1 |
| 76338 | acentuole | 1 |
| 76339 | acentuar | 1 |
| 76340 | acentúan | 1 |
| 76341 | acentuación | 1 |
| 76342 | acentillo | 1 |
| 76343 | açenia | 1 |
| 76344 | acendrados | 1 |
| 76345 | acendradísimo | 1 |
| 76346 | acemilero | 1 |
| 76347 | acelero | 1 |
| 76348 | acelere | 1 |
| 76349 | acelerase | 1 |
| 76350 | acelerar | 1 |
| 76351 | acelerando | 1 |
| 76352 | aceleramientos | 1 |
| 76353 | aceleramiento | 1 |
| 76354 | aceleradas | 1 |
| 76355 | aceleraba | 1 |
| 76356 | aceitosa | 1 |
| 76357 | aceites | 1 |
| 76358 | acéfalo | 1 |
| 76359 | acechaua | 1 |
| 76360 | acechas | 1 |
| 76361 | acecharse | 1 |
| 76362 | acecharlas | 1 |
| 76363 | acecharan | 1 |
| 76364 | acechanzas | 1 |
| 76365 | acechándola | 1 |
| 76366 | acechan | 1 |
| 76367 | acechaban | 1 |
| 76368 | açebyn | 1 |
| 76369 | acebuche | 1 |
| 76370 | accionar | 1 |
| 76371 | accionaba | 1 |
| 76372 | accidentados | 1 |
| 76373 | accidens | 1 |
| 76374 | accèsit | 1 |
| 76375 | accedieron | 1 |
| 76376 | accedido | 1 |
| 76377 | accedería | 1 |
| 76378 | acceder | 1 |
| 76379 | acaya | 1 |
| 76380 | acaudillaron | 1 |
| 76381 | acaudilla | 1 |
| 76382 | acaudaladas | 1 |
| 76383 | acaudalada | 1 |
| 76384 | acato | 1 |
| 76385 | acatemos | 1 |
| 76386 | acatarrada | 1 |
| 76387 | acatarla | 1 |
| 76388 | acatando | 1 |
| 76389 | acatada | 1 |
| 76390 | acartonaditas | 1 |
| 76391 | acartonada | 1 |
| 76392 | acarreo | 1 |
| 76393 | acarree | 1 |
| 76394 | acarrearnos | 1 |
| 76395 | acarreará | 1 |
| 76396 | acarreara | 1 |
| 76397 | acarrear | 1 |
| 76398 | acarreaba | 1 |
| 76399 | acaricio | 1 |
| 76400 | acaricie | 1 |
| 76401 | acariciase | 1 |
| 76402 | acariciarte | 1 |
| 76403 | acariciarme | 1 |
| 76404 | acariciarlo | 1 |
| 76405 | acariciándoselo | 1 |
| 76406 | acariciándolas | 1 |
| 76407 | acariciándola | 1 |
| 76408 | acaríciale | 1 |
| 76409 | acariciadores | 1 |
| 76410 | acariciado | 1 |
| 76411 | acariciada | 1 |
| 76412 | acardenalarme | 1 |
| 76413 | acardenalado | 1 |
| 76414 | acaparó | 1 |
| 76415 | acaparamientos | 1 |
| 76416 | acaparadores | 1 |
| 76417 | acaparada | 1 |
| 76418 | acantos | 1 |
| 76419 | acantonar | 1 |
| 76420 | acanto | 1 |
| 76421 | acantilados | 1 |
| 76422 | acamparon | 1 |
| 76423 | acampan | 1 |
| 76424 | acampaba | 1 |
| 76425 | acalores | 1 |
| 76426 | acalorar | 1 |
| 76427 | acalorándose | 1 |
| 76428 | acalorándole | 1 |
| 76429 | acaloran | 1 |
| 76430 | acalorado | 1 |
| 76431 | acaloñarnos | 1 |
| 76432 | acalló | 1 |
| 76433 | acallarla | 1 |
| 76434 | acallaban | 1 |
| 76435 | açafrán | 1 |
| 76436 | acaesçimientos | 1 |
| 76437 | acaescieron | 1 |
| 76438 | acaescida | 1 |
| 76439 | acaesçer | 1 |
| 76440 | acaeciónos | 1 |
| 76441 | acaecimiento | 1 |
| 76442 | acaecía | 1 |
| 76443 | acaecen | 1 |
| 76444 | acabesçí | 1 |
| 76445 | acabéis | 1 |
| 76446 | acabáys | 1 |
| 76447 | acabaua | 1 |
| 76448 | acabárseme | 1 |
| 76449 | acabáronse | 1 |
| 76450 | acabarme | 1 |
| 76451 | acabarían | 1 |
| 76452 | acabaríamos | 1 |
| 76453 | acabare | 1 |
| 76454 | acabáramos | 1 |
| 76455 | acábanlos | 1 |
| 76456 | acabándonoslas | 1 |
| 76457 | acabándolos | 1 |
| 76458 | acaballe | 1 |
| 76459 | acabala | 1 |
| 76460 | acabáis | 1 |
| 76461 | acabadme | 1 |
| 76462 | acabable | 1 |
| 76463 | acabábamos | 1 |
| 76464 | ac | 1 |
| 76465 | abyva | 1 |
| 76466 | abyertas | 1 |
| 76467 | abyecto | 1 |
| 76468 | abuses | 1 |
| 76469 | abusarse | 1 |
| 76470 | aburro | 1 |
| 76471 | aburriste | 1 |
| 76472 | aburrir | 1 |
| 76473 | aburrimos | 1 |
| 76474 | aburrieran | 1 |
| 76475 | aburriera | 1 |
| 76476 | aburriendo | 1 |
| 76477 | aburriditas | 1 |
| 76478 | aburridísima | 1 |
| 76479 | aburríale | 1 |
| 76480 | aburras | 1 |
| 76481 | abundasen | 1 |
| 76482 | abundar | 1 |
| 76483 | abundantísimo | 1 |
| 76484 | abundantísima | 1 |
| 76485 | abundando | 1 |
| 76486 | abundado | 1 |
| 76487 | abulte | 1 |
| 76488 | abultase | 1 |
| 76489 | abultan | 1 |
| 76490 | abultada | 1 |
| 76491 | abuelas | 1 |
| 76492 | absuelva | 1 |
| 76493 | absueltos | 1 |
| 76494 | absuelto | 1 |
| 76495 | abstuvo | 1 |
| 76496 | abstuviese | 1 |
| 76497 | abstuviera | 1 |
| 76498 | abstrusas | 1 |
| 76499 | abstraída | 1 |
| 76500 | abstraerse | 1 |
| 76501 | abstractos | 1 |
| 76502 | abstinencias | 1 |
| 76503 | abstiene | 1 |
| 76504 | absteniéndote | 1 |
| 76505 | absteniéndose | 1 |
| 76506 | abstengas | 1 |
| 76507 | abstenerse | 1 |
| 76508 | abstenerme | 1 |
| 76509 | abstener | 1 |
| 76510 | abstendría | 1 |
| 76511 | abstención | 1 |
| 76512 | absortos | 1 |
| 76513 | absortar | 1 |
| 76514 | absorción | 1 |
| 76515 | absorbió | 1 |
| 76516 | absorben | 1 |
| 76517 | absorbederos | 1 |
| 76518 | absolvería | 1 |
| 76519 | absolverás | 1 |
| 76520 | absolver | 1 |
| 76521 | absolvello | 1 |
| 76522 | absolutos | 1 |
| 76523 | absolutistas | 1 |
| 76524 | absolutista | 1 |
| 76525 | absit | 1 |
| 76526 | absentarse | 1 |
| 76527 | abryl | 1 |
| 76528 | abrumara | 1 |
| 76529 | abrumándole | 1 |
| 76530 | abrumando | 1 |
| 76531 | abruman | 1 |
| 76532 | abrumadores | 1 |
| 76533 | abrumadoras | 1 |
| 76534 | abroquelado | 1 |
| 76535 | abroñigal | 1 |
| 76536 | abrocharte | 1 |
| 76537 | abrochar | 1 |
| 76538 | abrochando | 1 |
| 76539 | abrochados | 1 |
| 76540 | abrochada | 1 |
| 76541 | abrit | 1 |
| 76542 | abriste | 1 |
| 76543 | abrís | 1 |
| 76544 | abrirte | 1 |
| 76545 | abrirlos | 1 |
| 76546 | abrirlas | 1 |
| 76547 | abrióme | 1 |
| 76548 | abriolo | 1 |
| 76549 | abriole | 1 |
| 76550 | abrióla | 1 |
| 76551 | abriol | 1 |
| 76552 | abríla | 1 |
| 76553 | abríguese | 1 |
| 76554 | abrigó | 1 |
| 76555 | abrigasse | 1 |
| 76556 | abrigase | 1 |
| 76557 | abrigas | 1 |
| 76558 | abrigarte | 1 |
| 76559 | abrigarse | 1 |
| 76560 | abrigarla | 1 |
| 76561 | abrigándose | 1 |
| 76562 | abrigándole | 1 |
| 76563 | abrigan | 1 |
| 76564 | abrigamos | 1 |
| 76565 | abrigaditos | 1 |
| 76566 | abrigaditas | 1 |
| 76567 | abrigábamos | 1 |
| 76568 | abrigábala | 1 |
| 76569 | abrigaba | 1 |
| 76570 | abriéronse | 1 |
| 76571 | abriéndolas | 1 |
| 76572 | abríela | 1 |
| 76573 | abrie | 1 |
| 76574 | abríanse | 1 |
| 76575 | abríame | 1 |
| 76576 | abríala | 1 |
| 76577 | abri | 1 |
| 76578 | abrevió | 1 |
| 76579 | abrevies | 1 |
| 76580 | abreviemos | 1 |
| 76581 | abrevie | 1 |
| 76582 | abreviatura | 1 |
| 76583 | abreviarvos | 1 |
| 76584 | abreviarte | 1 |
| 76585 | abreviarlos | 1 |
| 76586 | abreviarlo | 1 |
| 76587 | abrevïara | 1 |
| 76588 | abrevian | 1 |
| 76589 | abréviame | 1 |
| 76590 | abrevïada | 1 |
| 76591 | abreviada | 1 |
| 76592 | abreviaba | 1 |
| 76593 | abrevadero | 1 |
| 76594 | ábrete | 1 |
| 76595 | abrenuncio | 1 |
| 76596 | ábrense | 1 |
| 76597 | ábreme | 1 |
| 76598 | ábrela | 1 |
| 76599 | abrela | 1 |
| 76600 | abrebaron | 1 |
| 76601 | abré | 1 |
| 76602 | abrazóme | 1 |
| 76603 | abrazole | 1 |
| 76604 | abrazóla | 1 |
| 76605 | abrazola | 1 |
| 76606 | abrazárselos | 1 |
| 76607 | abrazarse | 1 |
| 76608 | abrazaros | 1 |
| 76609 | abrazáronle | 1 |
| 76610 | abrazaré | 1 |
| 76611 | abrazare | 1 |
| 76612 | abrazarán | 1 |
| 76613 | abrazará | 1 |
| 76614 | abrazaos | 1 |
| 76615 | abrazándote | 1 |
| 76616 | abrazándonos | 1 |
| 76617 | abrazamiento | 1 |
| 76618 | abrazadora | 1 |
| 76619 | abrazaditos | 1 |
| 76620 | abrazadera | 1 |
| 76621 | abrazad | 1 |
| 76622 | abrazaban | 1 |
| 76623 | abrásense | 1 |
| 76624 | abrasemos | 1 |
| 76625 | ábrase | 1 |
| 76626 | abrasasen | 1 |
| 76627 | abrasarnos | 1 |
| 76628 | abrasarla | 1 |
| 76629 | abrasándote | 1 |
| 76630 | abrasando | 1 |
| 76631 | abrásame | 1 |
| 76632 | abrasaban | 1 |
| 76633 | abráis | 1 |
| 76634 | abrahán | 1 |
| 76635 | abraçóse | 1 |
| 76636 | abraçólo | 1 |
| 76637 | abraço | 1 |
| 76638 | abracitos | 1 |
| 76639 | abraçemos | 1 |
| 76640 | abraçar | 1 |
| 76641 | abovedada | 1 |
| 76642 | abotonándose | 1 |
| 76643 | aborto | 1 |
| 76644 | abortaron | 1 |
| 76645 | abortada | 1 |
| 76646 | aborta | 1 |
| 76647 | aborridos | 1 |
| 76648 | aborrezcas | 1 |
| 76649 | aborrezca | 1 |
| 76650 | aborresçes | 1 |
| 76651 | aborresçerán | 1 |
| 76652 | aborrésçenle | 1 |
| 76653 | aborresçen | 1 |
| 76654 | aborresçe | 1 |
| 76655 | aborrescas | 1 |
| 76656 | aborrençia | 1 |
| 76657 | aborregado | 1 |
| 76658 | aborrecieron | 1 |
| 76659 | aborreciera | 1 |
| 76660 | aborrecidas | 1 |
| 76661 | aborrecibles | 1 |
| 76662 | aborrecible | 1 |
| 76663 | aborrecí | 1 |
| 76664 | aborreçes | 1 |
| 76665 | aborrecerlo | 1 |
| 76666 | aborrecerle | 1 |
| 76667 | aborrecería | 1 |
| 76668 | aborrascadas | 1 |
| 76669 | abordase | 1 |
| 76670 | abordarse | 1 |
| 76671 | abordajes | 1 |
| 76672 | aboque | 1 |
| 76673 | abonos | 1 |
| 76674 | abone | 1 |
| 76675 | abondo | 1 |
| 76676 | abondas | 1 |
| 76677 | abonasen | 1 |
| 76678 | abonarían | 1 |
| 76679 | abonar | 1 |
| 76680 | abominar | 1 |
| 76681 | abominando | 1 |
| 76682 | abominación | 1 |
| 76683 | abominables | 1 |
| 76684 | abominábamos | 1 |
| 76685 | abominaba | 1 |
| 76686 | abollé | 1 |
| 76687 | abollados | 1 |
| 76688 | abolieron | 1 |
| 76689 | abolido | 1 |
| 76690 | abogadote | 1 |
| 76691 | abogadillos | 1 |
| 76692 | abogadetes | 1 |
| 76693 | abogadejo | 1 |
| 76694 | abogaba | 1 |
| 76695 | abocose | 1 |
| 76696 | aboco | 1 |
| 76697 | abochornado | 1 |
| 76698 | abochornada | 1 |
| 76699 | aboca | 1 |
| 76700 | abobado | 1 |
| 76701 | abnegaciones | 1 |
| 76702 | abluciones | 1 |
| 76703 | ablativo | 1 |
| 76704 | ablandó | 1 |
| 76705 | ablándate | 1 |
| 76706 | ablandase | 1 |
| 76707 | ablandarte | 1 |
| 76708 | ablandaron | 1 |
| 76709 | ablandarme | 1 |
| 76710 | ablandaría | 1 |
| 76711 | ablandan | 1 |
| 76712 | ablandalle | 1 |
| 76713 | ablandáis | 1 |
| 76714 | ablandad | 1 |
| 76715 | ablandaban | 1 |
| 76716 | ablandaba | 1 |
| 76717 | abivo | 1 |
| 76718 | abive | 1 |
| 76719 | abivádvos | 1 |
| 76720 | abiuate | 1 |
| 76721 | abiuaron | 1 |
| 76722 | abiuan | 1 |
| 76723 | ábitos | 1 |
| 76724 | ábito | 1 |
| 76725 | abismado | 1 |
| 76726 | abismada | 1 |
| 76727 | abin | 1 |
| 76728 | abigotado | 1 |
| 76729 | abigarrara | 1 |
| 76730 | abezo | 1 |
| 76731 | abezar | 1 |
| 76732 | abezado | 1 |
| 76733 | abeyte | 1 |
| 76734 | aberné | 1 |
| 76735 | aberenjenado | 1 |
| 76736 | abentó | 1 |
| 76737 | abenidvos | 1 |
| 76738 | abengo | 1 |
| 76739 | abengas | 1 |
| 76740 | abenencia | 1 |
| 76741 | abendarraxe | 1 |
| 76742 | abenabos | 1 |
| 76743 | abenabo | 1 |
| 76744 | abelardo | 1 |
| 76745 | abel | 1 |
| 76746 | abejorro | 1 |
| 76747 | abdicando | 1 |
| 76748 | abcesos | 1 |
| 76749 | abbeville | 1 |
| 76750 | abbatis | 1 |
| 76751 | abbades | 1 |
| 76752 | abaxes | 1 |
| 76753 | abaxé | 1 |
| 76754 | abaxe | 1 |
| 76755 | abaxasse | 1 |
| 76756 | abaxarse | 1 |
| 76757 | abaxada | 1 |
| 76758 | abatyda | 1 |
| 76759 | abatióse | 1 |
| 76760 | abatiose | 1 |
| 76761 | abatieres | 1 |
| 76762 | abatidos | 1 |
| 76763 | abatidísimo | 1 |
| 76764 | abatanar | 1 |
| 76765 | abat | 1 |
| 76766 | abastecían | 1 |
| 76767 | abastar | 1 |
| 76768 | abastada | 1 |
| 76769 | abarzuza | 1 |
| 76770 | abarredera | 1 |
| 76771 | abarraganados | 1 |
| 76772 | abarraganada | 1 |
| 76773 | abarcaron | 1 |
| 76774 | abarcándolo | 1 |
| 76775 | abarcándola | 1 |
| 76776 | abarcado | 1 |
| 76777 | abarcaban | 1 |
| 76778 | abarcaba | 1 |
| 76779 | abaniquera | 1 |
| 76780 | abanicón | 1 |
| 76781 | abanicarse | 1 |
| 76782 | abanicándose | 1 |
| 76783 | abanicaba | 1 |
| 76784 | abandoné | 1 |
| 76785 | abandonarte | 1 |
| 76786 | abandonaros | 1 |
| 76787 | abandonaría | 1 |
| 76788 | abandonaremos | 1 |
| 76789 | abandonaré | 1 |
| 76790 | abandonándola | 1 |
| 76791 | abandonamos | 1 |
| 76792 | abandonalo | 1 |
| 76793 | abalorio | 1 |
| 76794 | aballar | 1 |
| 76795 | abalánzase | 1 |
| 76796 | abalanzarse | 1 |
| 76797 | abalanzan | 1 |
| 76798 | abalanzamos | 1 |
| 76799 | abalanzado | 1 |
| 76800 | abalanzaban | 1 |
| 76801 | abalanza | 1 |
| 76802 | abalance | 1 |
| 76803 | abajito | 1 |
| 76804 | abajen | 1 |
| 76805 | abajas | 1 |
| 76806 | abajara | 1 |
| 76807 | abajan | 1 |
| 76808 | abaja | 1 |
| 76809 | abaixo | 1 |
| 76810 | abadejos | 1 |
|
| Rank | Palabra | Frec |
|---|
| 1 | the | 48446 |
| 2 | and | 43194 |
| 3 | to | 33183 |
| 4 | of | 30002 |
| 5 | i | 29174 |
| 6 | a | 21469 |
| 7 | that | 19023 |
| 8 | in | 17975 |
| 9 | you | 16129 |
| 10 | my | 15292 |
| 11 | it | 13119 |
| 12 | is | 12940 |
| 13 | for | 12647 |
| 14 | he | 12560 |
| 15 | not | 12031 |
| 16 | with | 11384 |
| 17 | his | 11237 |
| 18 | me | 10273 |
| 19 | be | 10109 |
| 20 | as | 10043 |
| 21 | s | 9362 |
| 22 | this | 9279 |
| 23 | d | 9012 |
| 24 | him | 8633 |
| 25 | but | 8430 |
| 26 | have | 8407 |
| 27 | your | 8015 |
| 28 | so | 7424 |
| 29 | thou | 6778 |
| 30 | what | 6726 |
| 31 | will | 6649 |
| 32 | all | 6598 |
| 33 | her | 5967 |
| 34 | by | 5891 |
| 35 | was | 5639 |
| 36 | on | 5511 |
| 37 | if | 5291 |
| 38 | they | 5206 |
| 39 | no | 5036 |
| 40 | are | 4782 |
| 41 | do | 4687 |
| 42 | thy | 4571 |
| 43 | we | 4554 |
| 44 | or | 4533 |
| 45 | at | 4488 |
| 46 | which | 4219 |
| 47 | from | 4153 |
| 48 | shall | 4024 |
| 49 | thee | 3945 |
| 50 | good | 3706 |
| 51 | them | 3697 |
| 52 | she | 3632 |
| 53 | our | 3589 |
| 54 | had | 3581 |
| 55 | now | 3549 |
| 56 | there | 3520 |
| 57 | would | 3507 |
| 58 | one | 3397 |
| 59 | more | 3372 |
| 60 | lord | 3234 |
| 61 | who | 3193 |
| 62 | o | 3183 |
| 63 | king | 3178 |
| 64 | come | 3162 |
| 65 | their | 3046 |
| 66 | when | 3020 |
| 67 | let | 3020 |
| 68 | said | 2998 |
| 69 | well | 2941 |
| 70 | don | 2922 |
| 71 | am | 2910 |
| 72 | then | 2894 |
| 73 | were | 2887 |
| 74 | sir | 2862 |
| 75 | than | 2816 |
| 76 | here | 2801 |
| 77 | how | 2691 |
| 78 | an | 2680 |
| 79 | say | 2652 |
| 80 | ll | 2598 |
| 81 | love | 2523 |
| 82 | man | 2492 |
| 83 | know | 2449 |
| 84 | may | 2446 |
| 85 | upon | 2408 |
| 86 | enter | 2396 |
| 87 | out | 2380 |
| 88 | like | 2346 |
| 89 | us | 2321 |
| 90 | go | 2284 |
| 91 | did | 2238 |
| 92 | see | 2219 |
| 93 | make | 2217 |
| 94 | should | 2203 |
| 95 | such | 2194 |
| 96 | quixote | 2193 |
| 97 | sancho | 2169 |
| 98 | some | 2143 |
| 99 | must | 1987 |
| 100 | hath | 1971 |
| 101 | these | 1925 |
| 102 | up | 1913 |
| 103 | give | 1905 |
| 104 | where | 1876 |
| 105 | can | 1774 |
| 106 | take | 1764 |
| 107 | time | 1746 |
| 108 | yet | 1681 |
| 109 | why | 1587 |
| 110 | t | 1583 |
| 111 | great | 1556 |
| 112 | any | 1552 |
| 113 | tell | 1550 |
| 114 | been | 1521 |
| 115 | most | 1504 |
| 116 | made | 1494 |
| 117 | first | 1468 |
| 118 | much | 1466 |
| 119 | god | 1453 |
| 120 | too | 1444 |
| 121 | master | 1443 |
| 122 | tis | 1411 |
| 123 | very | 1407 |
| 124 | mine | 1403 |
| 125 | nor | 1399 |
| 126 | never | 1377 |
| 127 | heart | 1375 |
| 128 | duke | 1374 |
| 129 | lady | 1364 |
| 130 | other | 1343 |
| 131 | father | 1341 |
| 132 | speak | 1315 |
| 133 | has | 1285 |
| 134 | could | 1277 |
| 135 | think | 1273 |
| 136 | before | 1272 |
| 137 | day | 1259 |
| 138 | himself | 1244 |
| 139 | life | 1236 |
| 140 | two | 1217 |
| 141 | own | 1217 |
| 142 | into | 1207 |
| 143 | those | 1204 |
| 144 | art | 1199 |
| 145 | though | 1195 |
| 146 | th | 1178 |
| 147 | hand | 1168 |
| 148 | look | 1144 |
| 149 | men | 1135 |
| 150 | being | 1135 |
| 151 | st | 1078 |
| 152 | away | 1071 |
| 153 | without | 1067 |
| 154 | world | 1063 |
| 155 | death | 1063 |
| 156 | night | 1047 |
| 157 | way | 1045 |
| 158 | true | 1043 |
| 159 | queen | 1037 |
| 160 | exeunt | 1036 |
| 161 | hear | 1005 |
| 162 | exit | 984 |
| 163 | eyes | 976 |
| 164 | cannot | 973 |
| 165 | down | 962 |
| 166 | about | 962 |
| 167 | again | 961 |
| 168 | fair | 954 |
| 169 | doth | 953 |
| 170 | many | 944 |
| 171 | name | 943 |
| 172 | nothing | 923 |
| 173 | myself | 921 |
| 174 | call | 904 |
| 175 | leave | 901 |
| 176 | might | 900 |
| 177 | even | 899 |
| 178 | thus | 895 |
| 179 | heaven | 890 |
| 180 | done | 882 |
| 181 | off | 877 |
| 182 | sweet | 853 |
| 183 | ever | 842 |
| 184 | head | 834 |
| 185 | came | 827 |
| 186 | son | 821 |
| 187 | old | 819 |
| 188 | better | 819 |
| 189 | house | 818 |
| 190 | little | 813 |
| 191 | fear | 810 |
| 192 | scene | 804 |
| 193 | put | 804 |
| 194 | another | 793 |
| 195 | against | 792 |
| 196 | prince | 790 |
| 197 | still | 789 |
| 198 | pray | 781 |
| 199 | ay | 777 |
| 200 | find | 776 |
| 201 | poor | 769 |
| 202 | both | 769 |
| 203 | knight | 760 |
| 204 | honour | 758 |
| 205 | brother | 756 |
| 206 | blood | 748 |
| 207 | whose | 744 |
| 208 | once | 744 |
| 209 | hast | 739 |
| 210 | comes | 739 |
| 211 | whom | 738 |
| 212 | long | 722 |
| 213 | wife | 714 |
| 214 | after | 714 |
| 215 | therefore | 713 |
| 216 | only | 710 |
| 217 | gentleman | 698 |
| 218 | friend | 693 |
| 219 | word | 684 |
| 220 | part | 683 |
| 221 | words | 675 |
| 222 | set | 673 |
| 223 | place | 670 |
| 224 | till | 668 |
| 225 | three | 665 |
| 226 | every | 665 |
| 227 | show | 660 |
| 228 | heard | 659 |
| 229 | keep | 657 |
| 230 | same | 656 |
| 231 | noble | 656 |
| 232 | nay | 654 |
| 233 | second | 653 |
| 234 | stand | 650 |
| 235 | bear | 639 |
| 236 | er | 638 |
| 237 | dead | 637 |
| 238 | grace | 634 |
| 239 | peace | 631 |
| 240 | answer | 627 |
| 241 | worship | 626 |
| 242 | hold | 620 |
| 243 | caesar | 617 |
| 244 | mind | 616 |
| 245 | over | 614 |
| 246 | saw | 613 |
| 247 | henry | 612 |
| 248 | end | 612 |
| 249 | live | 609 |
| 250 | best | 609 |
| 251 | gloucester | 608 |
| 252 | daughter | 604 |
| 253 | truth | 603 |
| 254 | back | 603 |
| 255 | full | 601 |
| 256 | things | 580 |
| 257 | soul | 576 |
| 258 | bring | 576 |
| 259 | since | 571 |
| 260 | john | 567 |
| 261 | thought | 565 |
| 262 | gone | 565 |
| 263 | face | 558 |
| 264 | france | 553 |
| 265 | right | 551 |
| 266 | left | 551 |
| 267 | indeed | 551 |
| 268 | young | 549 |
| 269 | die | 545 |
| 270 | told | 544 |
| 271 | seen | 543 |
| 272 | friends | 542 |
| 273 | does | 542 |
| 274 | thine | 541 |
| 275 | none | 539 |
| 276 | thing | 538 |
| 277 | within | 537 |
| 278 | fool | 537 |
| 279 | found | 533 |
| 280 | dost | 530 |
| 281 | woman | 529 |
| 282 | while | 527 |
| 283 | else | 526 |
| 284 | richard | 520 |
| 285 | antony | 520 |
| 286 | aside | 518 |
| 287 | mother | 517 |
| 288 | gave | 514 |
| 289 | hands | 512 |
| 290 | stay | 511 |
| 291 | senor | 510 |
| 292 | mistress | 510 |
| 293 | madam | 509 |
| 294 | fortune | 509 |
| 295 | enough | 506 |
| 296 | matter | 500 |
| 297 | faith | 499 |
| 298 | dear | 499 |
| 299 | york | 495 |
| 300 | tongue | 492 |
| 301 | because | 489 |
| 302 | page | 487 |
| 303 | servant | 486 |
| 304 | having | 486 |
| 305 | turn | 484 |
| 306 | brutus | 483 |
| 307 | rest | 481 |
| 308 | lords | 479 |
| 309 | help | 477 |
| 310 | sword | 476 |
| 311 | under | 474 |
| 312 | eye | 472 |
| 313 | fall | 471 |
| 314 | boy | 467 |
| 315 | took | 466 |
| 316 | thousand | 464 |
| 317 | rather | 462 |
| 318 | arms | 460 |
| 319 | through | 458 |
| 320 | get | 458 |
| 321 | please | 456 |
| 322 | husband | 456 |
| 323 | reason | 455 |
| 324 | far | 455 |
| 325 | mean | 453 |
| 326 | forth | 453 |
| 327 | nature | 452 |
| 328 | falstaff | 452 |
| 329 | earth | 452 |
| 330 | home | 450 |
| 331 | present | 440 |
| 332 | unto | 434 |
| 333 | beauty | 432 |
| 334 | makes | 430 |
| 335 | hope | 428 |
| 336 | wilt | 427 |
| 337 | between | 427 |
| 338 | warwick | 424 |
| 339 | replied | 424 |
| 340 | ill | 423 |
| 341 | marry | 422 |
| 342 | days | 416 |
| 343 | gentle | 415 |
| 344 | lay | 413 |
| 345 | follow | 412 |
| 346 | cause | 412 |
| 347 | tears | 411 |
| 348 | act | 409 |
| 349 | body | 406 |
| 350 | together | 405 |
| 351 | play | 400 |
| 352 | ye | 399 |
| 353 | believe | 397 |
| 354 | welcome | 395 |
| 355 | last | 394 |
| 356 | going | 394 |
| 357 | read | 393 |
| 358 | lie | 393 |
| 359 | given | 393 |
| 360 | bed | 393 |
| 361 | return | 391 |
| 362 | power | 390 |
| 363 | use | 387 |
| 364 | kind | 387 |
| 365 | hence | 387 |
| 366 | ere | 387 |
| 367 | alone | 386 |
| 368 | brought | 384 |
| 369 | went | 383 |
| 370 | people | 381 |
| 371 | clown | 380 |
| 372 | sure | 379 |
| 373 | says | 378 |
| 374 | hour | 377 |
| 375 | means | 376 |
| 376 | high | 375 |
| 377 | half | 374 |
| 378 | edward | 373 |
| 379 | yourself | 372 |
| 380 | morrow | 371 |
| 381 | less | 371 |
| 382 | light | 370 |
| 383 | meet | 369 |
| 384 | farewell | 369 |
| 385 | new | 368 |
| 386 | duchess | 368 |
| 387 | sleep | 367 |
| 388 | devil | 367 |
| 389 | rome | 366 |
| 390 | horse | 366 |
| 391 | fellow | 366 |
| 392 | others | 365 |
| 393 | state | 363 |
| 394 | news | 362 |
| 395 | iago | 362 |
| 396 | themselves | 360 |
| 397 | itself | 360 |
| 398 | ham | 359 |
| 399 | just | 358 |
| 400 | kill | 357 |
| 401 | each | 357 |
| 402 | wrong | 356 |
| 403 | bid | 356 |
| 404 | youth | 355 |
| 405 | letter | 354 |
| 406 | worthy | 353 |
| 407 | doubt | 351 |
| 408 | care | 349 |
| 409 | timon | 348 |
| 410 | near | 348 |
| 411 | wish | 345 |
| 412 | already | 344 |
| 413 | lost | 339 |
| 414 | shalt | 338 |
| 415 | england | 338 |
| 416 | strange | 337 |
| 417 | shame | 337 |
| 418 | sent | 335 |
| 419 | othello | 335 |
| 420 | pardon | 334 |
| 421 | side | 333 |
| 422 | swear | 332 |
| 423 | soon | 332 |
| 424 | court | 332 |
| 425 | send | 331 |
| 426 | mad | 331 |
| 427 | false | 330 |
| 428 | desire | 330 |
| 429 | ring | 328 |
| 430 | crown | 327 |
| 431 | antonio | 327 |
| 432 | thoughts | 325 |
| 433 | red | 323 |
| 434 | something | 322 |
| 435 | ground | 322 |
| 436 | re | 320 |
| 437 | ask | 320 |
| 438 | whole | 319 |
| 439 | honest | 318 |
| 440 | cousin | 317 |
| 441 | wit | 316 |
| 442 | voice | 315 |
| 443 | fire | 315 |
| 444 | foot | 314 |
| 445 | pass | 313 |
| 446 | neither | 312 |
| 447 | gold | 312 |
| 448 | thank | 311 |
| 449 | saying | 311 |
| 450 | times | 310 |
| 451 | soldier | 310 |
| 452 | prove | 309 |
| 453 | fight | 309 |
| 454 | lies | 308 |
| 455 | curate | 308 |
| 456 | coming | 308 |
| 457 | war | 307 |
| 458 | sea | 307 |
| 459 | messenger | 307 |
| 460 | talk | 306 |
| 461 | knows | 306 |
| 462 | anything | 305 |
| 463 | four | 304 |
| 464 | yours | 302 |
| 465 | hither | 302 |
| 466 | business | 302 |
| 467 | sun | 301 |
| 468 | known | 301 |
| 469 | knew | 301 |
| 470 | spirit | 300 |
| 471 | service | 300 |
| 472 | sound | 299 |
| 473 | purpose | 299 |
| 474 | want | 298 |
| 475 | seek | 298 |
| 476 | need | 298 |
| 477 | thyself | 297 |
| 478 | majesty | 296 |
| 479 | got | 296 |
| 480 | break | 296 |
| 481 | errant | 294 |
| 482 | arm | 293 |
| 483 | years | 292 |
| 484 | money | 292 |
| 485 | seeing | 291 |
| 486 | macbeth | 291 |
| 487 | ford | 291 |
| 488 | justice | 290 |
| 489 | gods | 289 |
| 490 | virtue | 288 |
| 491 | pleasure | 286 |
| 492 | knights | 285 |
| 493 | dulcinea | 285 |
| 494 | sight | 284 |
| 495 | happy | 284 |
| 496 | hard | 283 |
| 497 | gentlemen | 281 |
| 498 | free | 280 |
| 499 | cleopatra | 280 |
| 500 | certain | 280 |
| 501 | ass | 280 |
| 502 | point | 279 |
| 503 | whether | 278 |
| 504 | third | 278 |
| 505 | seem | 278 |
| 506 | rich | 278 |
| 507 | panza | 278 |
| 508 | mark | 278 |
| 509 | fly | 278 |
| 510 | either | 278 |
| 511 | company | 276 |
| 512 | asked | 276 |
| 513 | speed | 275 |
| 514 | open | 274 |
| 515 | country | 273 |
| 516 | child | 273 |
| 517 | bound | 273 |
| 518 | worth | 271 |
| 519 | work | 271 |
| 520 | save | 271 |
| 521 | remember | 271 |
| 522 | its | 271 |
| 523 | hot | 271 |
| 524 | called | 271 |
| 525 | course | 270 |
| 526 | valiant | 269 |
| 527 | taken | 269 |
| 528 | air | 269 |
| 529 | short | 268 |
| 530 | until | 267 |
| 531 | serve | 267 |
| 532 | born | 267 |
| 533 | villain | 266 |
| 534 | law | 266 |
| 535 | holy | 265 |
| 536 | rosalind | 264 |
| 537 | age | 263 |
| 538 | run | 262 |
| 539 | next | 261 |
| 540 | lucius | 261 |
| 541 | suffolk | 259 |
| 542 | shallow | 258 |
| 543 | buckingham | 258 |
| 544 | land | 257 |
| 545 | squire | 256 |
| 546 | castle | 255 |
| 547 | princess | 254 |
| 548 | looks | 253 |
| 549 | cassio | 253 |
| 550 | above | 253 |
| 551 | troilus | 251 |
| 552 | hang | 251 |
| 553 | general | 251 |
| 554 | further | 251 |
| 555 | among | 251 |
| 556 | lose | 250 |
| 557 | la | 250 |
| 558 | beat | 250 |
| 559 | kiss | 249 |
| 560 | fell | 249 |
| 561 | pedro | 248 |
| 562 | order | 248 |
| 563 | grief | 248 |
| 564 | breath | 248 |
| 565 | goes | 246 |
| 566 | foul | 246 |
| 567 | enemy | 246 |
| 568 | de | 246 |
| 569 | cut | 246 |
| 570 | pity | 244 |
| 571 | case | 244 |
| 572 | city | 243 |
| 573 | yes | 241 |
| 574 | women | 241 |
| 575 | person | 240 |
| 576 | field | 240 |
| 577 | cold | 240 |
| 578 | white | 239 |
| 579 | uncle | 239 |
| 580 | lives | 239 |
| 581 | eat | 239 |
| 582 | syracuse | 238 |
| 583 | dare | 238 |
| 584 | unless | 236 |
| 585 | soldiers | 236 |
| 586 | draw | 236 |
| 587 | thanks | 235 |
| 588 | sit | 235 |
| 589 | french | 234 |
| 590 | charge | 234 |
| 591 | almost | 234 |
| 592 | valentine | 233 |
| 593 | lear | 233 |
| 594 | hundred | 233 |
| 595 | ear | 233 |
| 596 | bloody | 233 |
| 597 | watch | 232 |
| 598 | stood | 232 |
| 599 | sorrow | 232 |
| 600 | ha | 232 |
| 601 | loves | 231 |
| 602 | bad | 231 |
| 603 | alas | 231 |
| 604 | titus | 230 |
| 605 | herself | 230 |
| 606 | fit | 230 |
| 607 | dog | 230 |
| 608 | become | 230 |
| 609 | wear | 229 |
| 610 | strong | 229 |
| 611 | royal | 229 |
| 612 | quickly | 229 |
| 613 | desdemona | 229 |
| 614 | cassius | 229 |
| 615 | story | 228 |
| 616 | seems | 228 |
| 617 | music | 228 |
| 618 | making | 228 |
| 619 | ladies | 228 |
| 620 | however | 228 |
| 621 | worse | 227 |
| 622 | ne | 227 |
| 623 | mouth | 227 |
| 624 | chapter | 227 |
| 625 | black | 227 |
| 626 | sake | 226 |
| 627 | grave | 226 |
| 628 | self | 225 |
| 629 | late | 225 |
| 630 | hector | 225 |
| 631 | beseech | 225 |
| 632 | proud | 224 |
| 633 | least | 224 |
| 634 | highness | 224 |
| 635 | cry | 224 |
| 636 | water | 223 |
| 637 | question | 223 |
| 638 | praise | 223 |
| 639 | patience | 223 |
| 640 | dromio | 223 |
| 641 | door | 223 |
| 642 | captain | 222 |
| 643 | proteus | 221 |
| 644 | pay | 221 |
| 645 | haste | 221 |
| 646 | joy | 220 |
| 647 | antipholus | 220 |
| 648 | wise | 219 |
| 649 | town | 219 |
| 650 | prithee | 219 |
| 651 | ready | 218 |
| 652 | ho | 218 |
| 653 | didst | 218 |
| 654 | comfort | 217 |
| 655 | angelo | 217 |
| 656 | sort | 216 |
| 657 | sister | 216 |
| 658 | petruchio | 216 |
| 659 | mrs | 216 |
| 660 | book | 216 |
| 661 | wind | 215 |
| 662 | coriolanus | 215 |
| 663 | canst | 215 |
| 664 | feel | 214 |
| 665 | ah | 214 |
| 666 | write | 213 |
| 667 | twenty | 213 |
| 668 | ears | 213 |
| 669 | always | 213 |
| 670 | began | 212 |
| 671 | pompey | 211 |
| 672 | deep | 211 |
| 673 | clarence | 211 |
| 674 | bastard | 211 |
| 675 | rocinante | 210 |
| 676 | margaret | 210 |
| 677 | hell | 210 |
| 678 | favour | 210 |
| 679 | nurse | 209 |
| 680 | maid | 209 |
| 681 | governor | 209 |
| 682 | fault | 209 |
| 683 | behind | 209 |
| 684 | letters | 208 |
| 685 | trust | 207 |
| 686 | toby | 207 |
| 687 | mercy | 206 |
| 688 | lest | 206 |
| 689 | gracious | 206 |
| 690 | common | 206 |
| 691 | host | 205 |
| 692 | close | 205 |
| 693 | command | 204 |
| 694 | touch | 203 |
| 695 | sad | 203 |
| 696 | hearts | 203 |
| 697 | wonder | 202 |
| 698 | plain | 202 |
| 699 | lead | 200 |
| 700 | carry | 200 |
| 701 | promise | 199 |
| 702 | past | 199 |
| 703 | weep | 198 |
| 704 | truly | 198 |
| 705 | history | 198 |
| 706 | content | 198 |
| 707 | christian | 198 |
| 708 | taking | 197 |
| 709 | round | 197 |
| 710 | berowne | 197 |
| 711 | menenius | 196 |
| 712 | held | 196 |
| 713 | wherein | 194 |
| 714 | sons | 194 |
| 715 | servants | 194 |
| 716 | helena | 194 |
| 717 | friar | 194 |
| 718 | yea | 193 |
| 719 | won | 193 |
| 720 | gives | 193 |
| 721 | bardolph | 193 |
| 722 | kent | 192 |
| 723 | battle | 192 |
| 724 | village | 191 |
| 725 | ten | 191 |
| 726 | spoke | 191 |
| 727 | sick | 191 |
| 728 | change | 191 |
| 729 | silence | 190 |
| 730 | shepherd | 190 |
| 731 | room | 190 |
| 732 | heavy | 190 |
| 733 | five | 189 |
| 734 | drink | 189 |
| 735 | deeds | 189 |
| 736 | citizen | 189 |
| 737 | along | 189 |
| 738 | pandarus | 188 |
| 739 | pistol | 187 |
| 740 | married | 187 |
| 741 | adventure | 187 |
| 742 | returned | 186 |
| 743 | portia | 186 |
| 744 | palace | 185 |
| 745 | hate | 185 |
| 746 | green | 185 |
| 747 | flesh | 185 |
| 748 | tender | 184 |
| 749 | morning | 184 |
| 750 | hearing | 184 |
| 751 | brave | 183 |
| 752 | base | 183 |
| 753 | warrant | 182 |
| 754 | suit | 182 |
| 755 | duty | 182 |
| 756 | often | 181 |
| 757 | mighty | 181 |
| 758 | knave | 181 |
| 759 | barber | 181 |
| 760 | wouldst | 180 |
| 761 | sin | 180 |
| 762 | force | 180 |
| 763 | cressida | 180 |
| 764 | count | 180 |
| 765 | claudio | 180 |
| 766 | children | 180 |
| 767 | books | 180 |
| 768 | bolingbroke | 180 |
| 769 | oath | 179 |
| 770 | merry | 179 |
| 771 | kept | 179 |
| 772 | ii | 179 |
| 773 | behold | 179 |
| 774 | revenge | 178 |
| 775 | feet | 178 |
| 776 | anne | 178 |
| 777 | sense | 177 |
| 778 | moment | 177 |
| 779 | moon | 176 |
| 780 | greater | 176 |
| 781 | confess | 176 |
| 782 | parolles | 175 |
| 783 | grant | 175 |
| 784 | deliver | 175 |
| 785 | understand | 174 |
| 786 | kingdom | 174 |
| 787 | hours | 174 |
| 788 | hair | 174 |
| 789 | yield | 173 |
| 790 | laid | 173 |
| 791 | instant | 173 |
| 792 | besides | 173 |
| 793 | talbot | 172 |
| 794 | lips | 172 |
| 795 | em | 172 |
| 796 | appear | 172 |
| 797 | straight | 171 |
| 798 | orlando | 171 |
| 799 | fashion | 171 |
| 800 | sing | 170 |
| 801 | note | 170 |
| 802 | met | 170 |
| 803 | bosom | 170 |
| 804 | glad | 169 |
| 805 | chance | 169 |
| 806 | achilles | 169 |
| 807 | strength | 168 |
| 808 | seemed | 168 |
| 809 | fast | 168 |
| 810 | chamber | 168 |
| 811 | beard | 168 |
| 812 | ephesus | 167 |
| 813 | doing | 167 |
| 814 | try | 166 |
| 815 | strike | 166 |
| 816 | stands | 166 |
| 817 | report | 166 |
| 818 | offer | 166 |
| 819 | imogen | 166 |
| 820 | english | 166 |
| 821 | demetrius | 166 |
| 822 | account | 166 |
| 823 | small | 165 |
| 824 | lov | 165 |
| 825 | inn | 165 |
| 826 | famous | 165 |
| 827 | carried | 165 |
| 828 | cardinal | 165 |
| 829 | twas | 164 |
| 830 | everything | 164 |
| 831 | bold | 164 |
| 832 | able | 164 |
| 833 | rom | 163 |
| 834 | office | 163 |
| 835 | judge | 163 |
| 836 | giving | 163 |
| 837 | deed | 162 |
| 838 | conscience | 162 |
| 839 | olivia | 161 |
| 840 | fine | 161 |
| 841 | emperor | 161 |
| 842 | island | 160 |
| 843 | isabella | 160 |
| 844 | heavens | 160 |
| 845 | sovereign | 159 |
| 846 | noise | 159 |
| 847 | n | 159 |
| 848 | longer | 159 |
| 849 | answered | 159 |
| 850 | trouble | 158 |
| 851 | ourselves | 158 |
| 852 | marriage | 158 |
| 853 | low | 158 |
| 854 | woe | 157 |
| 855 | saint | 157 |
| 856 | presently | 157 |
| 857 | toboso | 156 |
| 858 | romeo | 156 |
| 859 | needs | 156 |
| 860 | methinks | 156 |
| 861 | doctor | 156 |
| 862 | mancha | 155 |
| 863 | living | 155 |
| 864 | earl | 155 |
| 865 | countess | 155 |
| 866 | fie | 154 |
| 867 | enobarbus | 154 |
| 868 | road | 153 |
| 869 | julia | 153 |
| 870 | deny | 153 |
| 871 | witness | 152 |
| 872 | opinion | 152 |
| 873 | oft | 152 |
| 874 | northumberland | 152 |
| 875 | entreat | 152 |
| 876 | enemies | 152 |
| 877 | counsel | 152 |
| 878 | presence | 151 |
| 879 | pluck | 151 |
| 880 | fal | 151 |
| 881 | wherefore | 150 |
| 882 | leontes | 150 |
| 883 | attendants | 150 |
| 884 | wine | 149 |
| 885 | slave | 149 |
| 886 | simple | 149 |
| 887 | hastings | 149 |
| 888 | hark | 149 |
| 889 | grow | 149 |
| 890 | felt | 149 |
| 891 | fare | 149 |
| 892 | emilia | 149 |
| 893 | sirrah | 148 |
| 894 | rage | 148 |
| 895 | iii | 148 |
| 896 | forward | 148 |
| 897 | danger | 148 |
| 898 | year | 147 |
| 899 | walk | 147 |
| 900 | traitor | 147 |
| 901 | speaks | 147 |
| 902 | somerset | 147 |
| 903 | guard | 147 |
| 904 | en | 147 |
| 905 | win | 146 |
| 906 | salisbury | 146 |
| 907 | passion | 146 |
| 908 | moor | 146 |
| 909 | hide | 146 |
| 910 | chivalry | 146 |
| 911 | tale | 145 |
| 912 | sworn | 145 |
| 913 | soft | 145 |
| 914 | prospero | 145 |
| 915 | kings | 145 |
| 916 | begin | 145 |
| 917 | valour | 144 |
| 918 | spirits | 144 |
| 919 | receive | 144 |
| 920 | parts | 144 |
| 921 | march | 144 |
| 922 | loss | 144 |
| 923 | london | 144 |
| 924 | few | 144 |
| 925 | slain | 143 |
| 926 | quite | 143 |
| 927 | perhaps | 143 |
| 928 | paris | 143 |
| 929 | pale | 143 |
| 930 | marcius | 143 |
| 931 | government | 143 |
| 932 | fetch | 143 |
| 933 | excellent | 143 |
| 934 | dream | 143 |
| 935 | withal | 142 |
| 936 | viola | 142 |
| 937 | speech | 142 |
| 938 | paper | 142 |
| 939 | liege | 142 |
| 940 | large | 142 |
| 941 | form | 142 |
| 942 | flourish | 142 |
| 943 | attend | 142 |
| 944 | takes | 141 |
| 945 | fame | 141 |
| 946 | wars | 140 |
| 947 | sebastian | 140 |
| 948 | lordship | 140 |
| 949 | countenance | 140 |
| 950 | camilla | 140 |
| 951 | breast | 140 |
| 952 | virtuous | 139 |
| 953 | turned | 139 |
| 954 | tranio | 139 |
| 955 | subject | 139 |
| 956 | respect | 139 |
| 957 | learn | 139 |
| 958 | glory | 139 |
| 959 | cross | 139 |
| 960 | clifford | 139 |
| 961 | also | 139 |
| 962 | towards | 138 |
| 963 | suffer | 138 |
| 964 | stop | 138 |
| 965 | six | 138 |
| 966 | sicinius | 138 |
| 967 | roman | 138 |
| 968 | pain | 138 |
| 969 | marcus | 138 |
| 970 | evil | 138 |
| 971 | birth | 138 |
| 972 | lothario | 137 |
| 973 | died | 137 |
| 974 | bless | 137 |
| 975 | bene | 137 |
| 976 | anselmo | 137 |
| 977 | wait | 136 |
| 978 | looking | 136 |
| 979 | lion | 136 |
| 980 | fancy | 136 |
| 981 | easy | 136 |
| 982 | bertram | 136 |
| 983 | throw | 135 |
| 984 | signior | 135 |
| 985 | memory | 135 |
| 986 | madness | 135 |
| 987 | issue | 135 |
| 988 | health | 135 |
| 989 | fresh | 135 |
| 990 | beyond | 135 |
| 991 | bachelor | 135 |
| 992 | vile | 134 |
| 993 | shows | 134 |
| 994 | measure | 134 |
| 995 | lucio | 134 |
| 996 | choose | 134 |
| 997 | banish | 134 |
| 998 | widow | 133 |
| 999 | harm | 133 |
| 1000 | fernando | 133 |
| 1001 | caius | 133 |
| 1002 | armour | 133 |
| 1003 | apemantus | 133 |
| 1004 | alive | 133 |
| 1005 | silvia | 132 |
| 1006 | honourable | 132 |
| 1007 | perceive | 131 |
| 1008 | passed | 131 |
| 1009 | lucentio | 131 |
| 1010 | clear | 131 |
| 1011 | bears | 131 |
| 1012 | sport | 130 |
| 1013 | rise | 130 |
| 1014 | norfolk | 130 |
| 1015 | move | 130 |
| 1016 | dinner | 130 |
| 1017 | weak | 129 |
| 1018 | posthumus | 129 |
| 1019 | ought | 129 |
| 1020 | malvolio | 129 |
| 1021 | laugh | 129 |
| 1022 | hero | 129 |
| 1023 | happened | 129 |
| 1024 | anon | 129 |
| 1025 | spite | 128 |
| 1026 | safe | 128 |
| 1027 | possible | 128 |
| 1028 | judgment | 128 |
| 1029 | heads | 128 |
| 1030 | dull | 128 |
| 1031 | cap | 128 |
| 1032 | beg | 128 |
| 1033 | ajax | 128 |
| 1034 | title | 127 |
| 1035 | pride | 127 |
| 1036 | offence | 127 |
| 1037 | charles | 127 |
| 1038 | bassanio | 127 |
| 1039 | saddle | 126 |
| 1040 | quick | 126 |
| 1041 | princes | 126 |
| 1042 | masters | 126 |
| 1043 | loving | 126 |
| 1044 | leon | 126 |
| 1045 | led | 126 |
| 1046 | effect | 126 |
| 1047 | chief | 126 |
| 1048 | celia | 126 |
| 1049 | camillo | 126 |
| 1050 | wits | 125 |
| 1051 | twere | 125 |
| 1052 | thersites | 125 |
| 1053 | scorn | 125 |
| 1054 | pretty | 125 |
| 1055 | niece | 125 |
| 1056 | lack | 125 |
| 1057 | fortunes | 125 |
| 1058 | except | 125 |
| 1059 | claud | 125 |
| 1060 | aid | 125 |
| 1061 | wert | 124 |
| 1062 | souls | 124 |
| 1063 | several | 124 |
| 1064 | mock | 124 |
| 1065 | iv | 124 |
| 1066 | forget | 124 |
| 1067 | armado | 124 |
| 1068 | action | 124 |
| 1069 | william | 123 |
| 1070 | struck | 123 |
| 1071 | piece | 123 |
| 1072 | paid | 123 |
| 1073 | occasion | 123 |
| 1074 | maria | 123 |
| 1075 | poet | 122 |
| 1076 | calls | 122 |
| 1077 | worst | 121 |
| 1078 | labour | 121 |
| 1079 | dapple | 121 |
| 1080 | cymbeline | 121 |
| 1081 | consent | 121 |
| 1082 | enchanted | 120 |
| 1083 | e | 120 |
| 1084 | del | 120 |
| 1085 | costard | 120 |
| 1086 | bade | 120 |
| 1087 | sorry | 119 |
| 1088 | proper | 119 |
| 1089 | hostess | 119 |
| 1090 | heir | 119 |
| 1091 | fools | 119 |
| 1092 | elizabeth | 119 |
| 1093 | cast | 119 |
| 1094 | bottom | 119 |
| 1095 | wisdom | 118 |
| 1096 | teach | 118 |
| 1097 | lafeu | 118 |
| 1098 | hortensio | 118 |
| 1099 | hamlet | 118 |
| 1100 | glou | 118 |
| 1101 | baptista | 118 |
| 1102 | ulysses | 117 |
| 1103 | remain | 117 |
| 1104 | officers | 117 |
| 1105 | match | 117 |
| 1106 | loud | 117 |
| 1107 | jul | 117 |
| 1108 | jest | 117 |
| 1109 | greatest | 117 |
| 1110 | dress | 117 |
| 1111 | bianca | 117 |
| 1112 | allow | 117 |
| 1113 | whilst | 116 |
| 1114 | quarrel | 116 |
| 1115 | provost | 116 |
| 1116 | m | 116 |
| 1117 | foolish | 116 |
| 1118 | fill | 116 |
| 1119 | buy | 116 |
| 1120 | adventures | 116 |
| 1121 | stir | 115 |
| 1122 | shut | 115 |
| 1123 | quiet | 115 |
| 1124 | harry | 115 |
| 1125 | folly | 115 |
| 1126 | crowns | 115 |
| 1127 | condition | 115 |
| 1128 | broken | 115 |
| 1129 | wounds | 114 |
| 1130 | wild | 114 |
| 1131 | table | 114 |
| 1132 | shape | 114 |
| 1133 | pains | 114 |
| 1134 | ours | 114 |
| 1135 | mortal | 114 |
| 1136 | humour | 114 |
| 1137 | blow | 114 |
| 1138 | beast | 114 |
| 1139 | bearing | 114 |
| 1140 | proof | 113 |
| 1141 | object | 113 |
| 1142 | grey | 113 |
| 1143 | gates | 113 |
| 1144 | drum | 113 |
| 1145 | dies | 113 |
| 1146 | dauphin | 113 |
| 1147 | although | 113 |
| 1148 | waiting | 112 |
| 1149 | received | 112 |
| 1150 | officer | 112 |
| 1151 | neck | 112 |
| 1152 | meant | 112 |
| 1153 | knowing | 112 |
| 1154 | due | 112 |
| 1155 | colour | 112 |
| 1156 | calling | 112 |
| 1157 | wealth | 111 |
| 1158 | slender | 111 |
| 1159 | reply | 111 |
| 1160 | ones | 111 |
| 1161 | lorenzo | 111 |
| 1162 | katherina | 111 |
| 1163 | hadst | 111 |
| 1164 | following | 111 |
| 1165 | finding | 111 |
| 1166 | dorothea | 111 |
| 1167 | deal | 111 |
| 1168 | consider | 111 |
| 1169 | blind | 111 |
| 1170 | taste | 110 |
| 1171 | shylock | 110 |
| 1172 | obey | 110 |
| 1173 | number | 110 |
| 1174 | manner | 110 |
| 1175 | macduff | 110 |
| 1176 | liberty | 110 |
| 1177 | impossible | 110 |
| 1178 | drawn | 110 |
| 1179 | curse | 110 |
| 1180 | courtesy | 110 |
| 1181 | commend | 110 |
| 1182 | cloten | 110 |
| 1183 | woo | 109 |
| 1184 | speaking | 109 |
| 1185 | senses | 109 |
| 1186 | proceed | 109 |
| 1187 | knowledge | 109 |
| 1188 | katharine | 109 |
| 1189 | hor | 109 |
| 1190 | dark | 109 |
| 1191 | boys | 109 |
| 1192 | advice | 109 |
| 1193 | stone | 108 |
| 1194 | kate | 108 |
| 1195 | fail | 108 |
| 1196 | desires | 108 |
| 1197 | cried | 108 |
| 1198 | army | 108 |
| 1199 | anyone | 108 |
| 1200 | whither | 107 |
| 1201 | tree | 107 |
| 1202 | secret | 107 |
| 1203 | roderigo | 107 |
| 1204 | rate | 107 |
| 1205 | ran | 107 |
| 1206 | pure | 107 |
| 1207 | prison | 107 |
| 1208 | natural | 107 |
| 1209 | lover | 107 |
| 1210 | golden | 107 |
| 1211 | evans | 107 |
| 1212 | cruel | 107 |
| 1213 | angry | 107 |
| 1214 | whatever | 106 |
| 1215 | wall | 106 |
| 1216 | troth | 106 |
| 1217 | thence | 106 |
| 1218 | shake | 106 |
| 1219 | purse | 106 |
| 1220 | learned | 106 |
| 1221 | teeth | 105 |
| 1222 | feast | 105 |
| 1223 | faults | 105 |
| 1224 | deserve | 105 |
| 1225 | broke | 105 |
| 1226 | ancient | 105 |
| 1227 | advantage | 105 |
| 1228 | written | 104 |
| 1229 | whence | 104 |
| 1230 | vow | 104 |
| 1231 | v | 104 |
| 1232 | summer | 104 |
| 1233 | pisanio | 104 |
| 1234 | leaves | 104 |
| 1235 | hermia | 104 |
| 1236 | dangerous | 104 |
| 1237 | contrary | 104 |
| 1238 | cominius | 104 |
| 1239 | charmian | 104 |
| 1240 | burn | 104 |
| 1241 | awake | 104 |
| 1242 | adieu | 104 |
| 1243 | wound | 103 |
| 1244 | view | 103 |
| 1245 | toward | 103 |
| 1246 | street | 103 |
| 1247 | sometimes | 103 |
| 1248 | poins | 103 |
| 1249 | moth | 103 |
| 1250 | lysander | 103 |
| 1251 | hurt | 103 |
| 1252 | girl | 103 |
| 1253 | followed | 103 |
| 1254 | church | 103 |
| 1255 | brief | 103 |
| 1256 | awhile | 103 |
| 1257 | according | 103 |
| 1258 | wicked | 102 |
| 1259 | weary | 102 |
| 1260 | sign | 102 |
| 1261 | mounted | 102 |
| 1262 | length | 102 |
| 1263 | language | 102 |
| 1264 | join | 102 |
| 1265 | forgive | 102 |
| 1266 | fled | 102 |
| 1267 | courage | 102 |
| 1268 | brain | 102 |
| 1269 | blessed | 102 |
| 1270 | blame | 102 |
| 1271 | wolsey | 101 |
| 1272 | vain | 101 |
| 1273 | troy | 101 |
| 1274 | reads | 101 |
| 1275 | prayers | 101 |
| 1276 | nose | 101 |
| 1277 | lend | 101 |
| 1278 | leaving | 101 |
| 1279 | gainst | 101 |
| 1280 | double | 101 |
| 1281 | boyet | 101 |
| 1282 | borne | 101 |
| 1283 | asleep | 101 |
| 1284 | writ | 100 |
| 1285 | wood | 100 |
| 1286 | sings | 100 |
| 1287 | seven | 100 |
| 1288 | seal | 100 |
| 1289 | satisfied | 100 |
| 1290 | precious | 100 |
| 1291 | plague | 100 |
| 1292 | patient | 100 |
| 1293 | happiness | 100 |
| 1294 | gratiano | 100 |
| 1295 | forgot | 100 |
| 1296 | drop | 100 |
| 1297 | cardenio | 100 |
| 1298 | blows | 100 |
| 1299 | author | 100 |
| 1300 | agamemnon | 100 |
| 1301 | walls | 99 |
| 1302 | telling | 99 |
| 1303 | remedy | 99 |
| 1304 | rank | 99 |
| 1305 | poison | 99 |
| 1306 | luck | 99 |
| 1307 | humble | 99 |
| 1308 | holds | 99 |
| 1309 | exclaimed | 99 |
| 1310 | edg | 99 |
| 1311 | bright | 99 |
| 1312 | trumpet | 98 |
| 1313 | shouldst | 98 |
| 1314 | rose | 98 |
| 1315 | r | 98 |
| 1316 | perceived | 98 |
| 1317 | legs | 98 |
| 1318 | exeter | 98 |
| 1319 | escalus | 98 |
| 1320 | cade | 98 |
| 1321 | anger | 98 |
| 1322 | witch | 97 |
| 1323 | trumpets | 97 |
| 1324 | tent | 97 |
| 1325 | song | 97 |
| 1326 | single | 97 |
| 1327 | matters | 97 |
| 1328 | landlord | 97 |
| 1329 | feed | 97 |
| 1330 | falls | 97 |
| 1331 | aufidius | 97 |
| 1332 | affection | 97 |
| 1333 | aaron | 97 |
| 1334 | treason | 96 |
| 1335 | tear | 96 |
| 1336 | ta | 96 |
| 1337 | reached | 96 |
| 1338 | promised | 96 |
| 1339 | melancholy | 96 |
| 1340 | looked | 96 |
| 1341 | idle | 96 |
| 1342 | iachimo | 96 |
| 1343 | hubert | 96 |
| 1344 | grumio | 96 |
| 1345 | gate | 96 |
| 1346 | gallant | 96 |
| 1347 | damsel | 96 |
| 1348 | corn | 96 |
| 1349 | choice | 96 |
| 1350 | cheer | 96 |
| 1351 | brothers | 96 |
| 1352 | brook | 96 |
| 1353 | afterwards | 96 |
| 1354 | ways | 95 |
| 1355 | thief | 95 |
| 1356 | supper | 95 |
| 1357 | search | 95 |
| 1358 | murderer | 95 |
| 1359 | luscinda | 95 |
| 1360 | journey | 95 |
| 1361 | follows | 95 |
| 1362 | fate | 95 |
| 1363 | appearance | 95 |
| 1364 | wrongs | 94 |
| 1365 | westmoreland | 94 |
| 1366 | used | 94 |
| 1367 | thither | 94 |
| 1368 | senora | 94 |
| 1369 | rosaline | 94 |
| 1370 | rogue | 94 |
| 1371 | excuse | 94 |
| 1372 | endure | 94 |
| 1373 | delight | 94 |
| 1374 | bones | 94 |
| 1375 | yonder | 93 |
| 1376 | tower | 93 |
| 1377 | sudden | 93 |
| 1378 | spoken | 93 |
| 1379 | spent | 93 |
| 1380 | safety | 93 |
| 1381 | knock | 93 |
| 1382 | greatness | 93 |
| 1383 | dry | 93 |
| 1384 | ariel | 93 |
| 1385 | approach | 93 |
| 1386 | aguecheek | 93 |
| 1387 | affairs | 93 |
| 1388 | aeneas | 93 |
| 1389 | turning | 92 |
| 1390 | thinking | 92 |
| 1391 | stars | 92 |
| 1392 | prisoner | 92 |
| 1393 | peter | 92 |
| 1394 | owe | 92 |
| 1395 | observed | 92 |
| 1396 | gremio | 92 |
| 1397 | dispatch | 92 |
| 1398 | clock | 92 |
| 1399 | buried | 92 |
| 1400 | yourselves | 91 |
| 1401 | top | 91 |
| 1402 | teresa | 91 |
| 1403 | sirs | 91 |
| 1404 | shadow | 91 |
| 1405 | senator | 91 |
| 1406 | seat | 91 |
| 1407 | putting | 91 |
| 1408 | priest | 91 |
| 1409 | monster | 91 |
| 1410 | lovers | 91 |
| 1411 | jack | 91 |
| 1412 | fearful | 91 |
| 1413 | drown | 91 |
| 1414 | dread | 91 |
| 1415 | cure | 91 |
| 1416 | bitter | 91 |
| 1417 | adriana | 91 |
| 1418 | tamora | 90 |
| 1419 | stephano | 90 |
| 1420 | pack | 90 |
| 1421 | helen | 90 |
| 1422 | figure | 90 |
| 1423 | embrace | 90 |
| 1424 | coward | 90 |
| 1425 | catch | 90 |
| 1426 | archbishop | 90 |
| 1427 | wretched | 89 |
| 1428 | touchstone | 89 |
| 1429 | tongues | 89 |
| 1430 | resolved | 89 |
| 1431 | rare | 89 |
| 1432 | quality | 89 |
| 1433 | lance | 89 |
| 1434 | keeps | 89 |
| 1435 | hers | 89 |
| 1436 | fluellen | 89 |
| 1437 | fellows | 89 |
| 1438 | defend | 89 |
| 1439 | venice | 88 |
| 1440 | thrice | 88 |
| 1441 | swords | 88 |
| 1442 | steal | 88 |
| 1443 | silver | 88 |
| 1444 | sighs | 88 |
| 1445 | rough | 88 |
| 1446 | request | 88 |
| 1447 | possess | 88 |
| 1448 | perform | 88 |
| 1449 | malice | 88 |
| 1450 | lewis | 88 |
| 1451 | lawful | 88 |
| 1452 | jove | 88 |
| 1453 | jaques | 88 |
| 1454 | ghost | 88 |
| 1455 | former | 88 |
| 1456 | ease | 88 |
| 1457 | cries | 88 |
| 1458 | chain | 88 |
| 1459 | bestow | 88 |
| 1460 | beginning | 88 |
| 1461 | beautiful | 88 |
| 1462 | alarum | 88 |
| 1463 | whereof | 87 |
| 1464 | terms | 87 |
| 1465 | sharp | 87 |
| 1466 | percy | 87 |
| 1467 | opportunity | 87 |
| 1468 | hopes | 87 |
| 1469 | honesty | 87 |
| 1470 | heels | 87 |
| 1471 | heat | 87 |
| 1472 | guilty | 87 |
| 1473 | garden | 87 |
| 1474 | forest | 87 |
| 1475 | food | 87 |
| 1476 | fears | 87 |
| 1477 | equal | 87 |
| 1478 | diomedes | 87 |
| 1479 | demand | 87 |
| 1480 | constable | 87 |
| 1481 | cave | 87 |
| 1482 | bow | 87 |
| 1483 | window | 86 |
| 1484 | twice | 86 |
| 1485 | train | 86 |
| 1486 | spot | 86 |
| 1487 | shoulders | 86 |
| 1488 | satisfaction | 86 |
| 1489 | samson | 86 |
| 1490 | pol | 86 |
| 1491 | paulina | 86 |
| 1492 | finger | 86 |
| 1493 | creature | 86 |
| 1494 | amen | 86 |
| 1495 | wide | 85 |
| 1496 | wench | 85 |
| 1497 | wash | 85 |
| 1498 | unable | 85 |
| 1499 | standing | 85 |
| 1500 | spain | 85 |
| 1501 | pleased | 85 |
| 1502 | pair | 85 |
| 1503 | motion | 85 |
| 1504 | knees | 85 |
| 1505 | horses | 85 |
| 1506 | gain | 85 |
| 1507 | damn | 85 |
| 1508 | cunning | 85 |
| 1509 | cheek | 85 |
| 1510 | winter | 84 |
| 1511 | unhappy | 84 |
| 1512 | stones | 84 |
| 1513 | reach | 84 |
| 1514 | polixenes | 84 |
| 1515 | misfortune | 84 |
| 1516 | gift | 84 |
| 1517 | forbid | 84 |
| 1518 | dance | 84 |
| 1519 | bred | 84 |
| 1520 | bread | 84 |
| 1521 | trees | 83 |
| 1522 | talking | 83 |
| 1523 | steel | 83 |
| 1524 | post | 83 |
| 1525 | particular | 83 |
| 1526 | modesty | 83 |
| 1527 | meaning | 83 |
| 1528 | launcelot | 83 |
| 1529 | juliet | 83 |
| 1530 | fat | 83 |
| 1531 | enjoy | 83 |
| 1532 | citizens | 83 |
| 1533 | beggar | 83 |
| 1534 | weeping | 82 |
| 1535 | wast | 82 |
| 1536 | spare | 82 |
| 1537 | persons | 82 |
| 1538 | madman | 82 |
| 1539 | launce | 82 |
| 1540 | hit | 82 |
| 1541 | goodness | 82 |
| 1542 | friendship | 82 |
| 1543 | envy | 82 |
| 1544 | easily | 82 |
| 1545 | camp | 82 |
| 1546 | burgundy | 82 |
| 1547 | belarius | 82 |
| 1548 | bare | 82 |
| 1549 | aught | 82 |
| 1550 | vessel | 81 |
| 1551 | vengeance | 81 |
| 1552 | twelve | 81 |
| 1553 | sooner | 81 |
| 1554 | rude | 81 |
| 1555 | regard | 81 |
| 1556 | rain | 81 |
| 1557 | public | 81 |
| 1558 | private | 81 |
| 1559 | placed | 81 |
| 1560 | naked | 81 |
| 1561 | lancaster | 81 |
| 1562 | hardly | 81 |
| 1563 | fury | 81 |
| 1564 | fond | 81 |
| 1565 | pucelle | 80 |
| 1566 | princely | 80 |
| 1567 | keeper | 80 |
| 1568 | fixed | 80 |
| 1569 | discourse | 80 |
| 1570 | conversation | 80 |
| 1571 | abroad | 80 |
| 1572 | wounded | 79 |
| 1573 | whiles | 79 |
| 1574 | spring | 79 |
| 1575 | sigh | 79 |
| 1576 | reasons | 79 |
| 1577 | raise | 79 |
| 1578 | names | 79 |
| 1579 | mere | 79 |
| 1580 | manners | 79 |
| 1581 | liv | 79 |
| 1582 | helmet | 79 |
| 1583 | edm | 79 |
| 1584 | drew | 79 |
| 1585 | cheeks | 79 |
| 1586 | utter | 78 |
| 1587 | treasure | 78 |
| 1588 | tied | 78 |
| 1589 | step | 78 |
| 1590 | smile | 78 |
| 1591 | reading | 78 |
| 1592 | lo | 78 |
| 1593 | line | 78 |
| 1594 | lieutenant | 78 |
| 1595 | kneel | 78 |
| 1596 | jew | 78 |
| 1597 | grows | 78 |
| 1598 | goodly | 78 |
| 1599 | escape | 78 |
| 1600 | dying | 78 |
| 1601 | cost | 78 |
| 1602 | brings | 78 |
| 1603 | argument | 78 |
| 1604 | alack | 78 |
| 1605 | wrath | 77 |
| 1606 | stuff | 77 |
| 1607 | study | 77 |
| 1608 | sometime | 77 |
| 1609 | sleeping | 77 |
| 1610 | shown | 77 |
| 1611 | sheep | 77 |
| 1612 | ransom | 77 |
| 1613 | plantagenet | 77 |
| 1614 | oaths | 77 |
| 1615 | nine | 77 |
| 1616 | murder | 77 |
| 1617 | loose | 77 |
| 1618 | kindness | 77 |
| 1619 | ignorant | 77 |
| 1620 | hail | 77 |
| 1621 | drunk | 77 |
| 1622 | diana | 77 |
| 1623 | depart | 77 |
| 1624 | colours | 77 |
| 1625 | big | 77 |
| 1626 | absence | 77 |
| 1627 | zoraida | 76 |
| 1628 | wales | 76 |
| 1629 | thomas | 76 |
| 1630 | swift | 76 |
| 1631 | spend | 76 |
| 1632 | signs | 76 |
| 1633 | serv | 76 |
| 1634 | scarce | 76 |
| 1635 | raised | 76 |
| 1636 | parents | 76 |
| 1637 | painted | 76 |
| 1638 | mount | 76 |
| 1639 | middle | 76 |
| 1640 | meat | 76 |
| 1641 | laws | 76 |
| 1642 | guiderius | 76 |
| 1643 | govern | 76 |
| 1644 | giant | 76 |
| 1645 | george | 76 |
| 1646 | fought | 76 |
| 1647 | dumain | 76 |
| 1648 | despair | 76 |
| 1649 | authority | 76 |
| 1650 | arthur | 76 |
| 1651 | twixt | 75 |
| 1652 | throne | 75 |
| 1653 | shore | 75 |
| 1654 | pieces | 75 |
| 1655 | neighbour | 75 |
| 1656 | moreover | 75 |
| 1657 | lavinia | 75 |
| 1658 | honours | 75 |
| 1659 | glass | 75 |
| 1660 | gaunt | 75 |
| 1661 | flow | 75 |
| 1662 | especially | 75 |
| 1663 | custom | 75 |
| 1664 | cloth | 75 |
| 1665 | bond | 75 |
| 1666 | banquo | 75 |
| 1667 | autolycus | 75 |
| 1668 | wives | 74 |
| 1669 | trick | 74 |
| 1670 | mischief | 74 |
| 1671 | merchant | 74 |
| 1672 | maiden | 74 |
| 1673 | loved | 74 |
| 1674 | leisure | 74 |
| 1675 | gifts | 74 |
| 1676 | foe | 74 |
| 1677 | filled | 74 |
| 1678 | feeling | 74 |
| 1679 | fabian | 74 |
| 1680 | distressed | 74 |
| 1681 | distance | 74 |
| 1682 | degree | 74 |
| 1683 | continued | 74 |
| 1684 | brow | 74 |
| 1685 | becomes | 74 |
| 1686 | thunder | 73 |
| 1687 | suddenly | 73 |
| 1688 | reg | 73 |
| 1689 | philip | 73 |
| 1690 | patroclus | 73 |
| 1691 | otherwise | 73 |
| 1692 | montague | 73 |
| 1693 | monstrous | 73 |
| 1694 | miranda | 73 |
| 1695 | mend | 73 |
| 1696 | gonzalo | 73 |
| 1697 | foes | 73 |
| 1698 | flight | 73 |
| 1699 | dona | 73 |
| 1700 | claim | 73 |
| 1701 | casca | 73 |
| 1702 | blessing | 73 |
| 1703 | biondello | 73 |
| 1704 | athens | 73 |
| 1705 | wings | 72 |
| 1706 | wants | 72 |
| 1707 | verses | 72 |
| 1708 | thurio | 72 |
| 1709 | sack | 72 |
| 1710 | ross | 72 |
| 1711 | provided | 72 |
| 1712 | orleans | 72 |
| 1713 | offered | 72 |
| 1714 | observe | 72 |
| 1715 | moved | 72 |
| 1716 | faces | 72 |
| 1717 | edmund | 72 |
| 1718 | dust | 72 |
| 1719 | ducats | 72 |
| 1720 | divine | 72 |
| 1721 | catesby | 72 |
| 1722 | caliban | 72 |
| 1723 | burning | 72 |
| 1724 | bore | 72 |
| 1725 | begged | 72 |
| 1726 | victory | 71 |
| 1727 | trial | 71 |
| 1728 | thrust | 71 |
| 1729 | theseus | 71 |
| 1730 | streets | 71 |
| 1731 | star | 71 |
| 1732 | sore | 71 |
| 1733 | smell | 71 |
| 1734 | seest | 71 |
| 1735 | richmond | 71 |
| 1736 | places | 71 |
| 1737 | party | 71 |
| 1738 | lovely | 71 |
| 1739 | knee | 71 |
| 1740 | jewel | 71 |
| 1741 | humphrey | 71 |
| 1742 | fain | 71 |
| 1743 | fact | 71 |
| 1744 | duenna | 71 |
| 1745 | below | 71 |
| 1746 | aumerle | 71 |
| 1747 | attempt | 71 |
| 1748 | ape | 71 |
| 1749 | vows | 70 |
| 1750 | turns | 70 |
| 1751 | throat | 70 |
| 1752 | therein | 70 |
| 1753 | squires | 70 |
| 1754 | shed | 70 |
| 1755 | reputation | 70 |
| 1756 | lepidus | 70 |
| 1757 | knowest | 70 |
| 1758 | gentlewoman | 70 |
| 1759 | flower | 70 |
| 1760 | farther | 70 |
| 1761 | entertain | 70 |
| 1762 | delay | 70 |
| 1763 | couple | 70 |
| 1764 | conduct | 70 |
| 1765 | clouds | 70 |
| 1766 | visit | 69 |
| 1767 | somewhat | 69 |
| 1768 | showed | 69 |
| 1769 | ship | 69 |
| 1770 | prepare | 69 |
| 1771 | pleas | 69 |
| 1772 | perfect | 69 |
| 1773 | nestor | 69 |
| 1774 | maintain | 69 |
| 1775 | lying | 69 |
| 1776 | housekeeper | 69 |
| 1777 | grown | 69 |
| 1778 | doors | 69 |
| 1779 | deserves | 69 |
| 1780 | breathe | 69 |
| 1781 | blunt | 69 |
| 1782 | benedick | 69 |
| 1783 | bark | 69 |
| 1784 | wont | 68 |
| 1785 | weight | 68 |
| 1786 | wanton | 68 |
| 1787 | volumnia | 68 |
| 1788 | swore | 68 |
| 1789 | sum | 68 |
| 1790 | stain | 68 |
| 1791 | staff | 68 |
| 1792 | remembrance | 68 |
| 1793 | quit | 68 |
| 1794 | prize | 68 |
| 1795 | possession | 68 |
| 1796 | plainly | 68 |
| 1797 | mountain | 68 |
| 1798 | mayst | 68 |
| 1799 | heed | 68 |
| 1800 | freely | 68 |
| 1801 | fingers | 68 |
| 1802 | expect | 68 |
| 1803 | empty | 68 |
| 1804 | eight | 68 |
| 1805 | disposition | 68 |
| 1806 | daughters | 68 |
| 1807 | dagger | 68 |
| 1808 | clothes | 68 |
| 1809 | chamberlain | 68 |
| 1810 | ben | 68 |
| 1811 | angel | 68 |
| 1812 | tribunes | 67 |
| 1813 | suspect | 67 |
| 1814 | storm | 67 |
| 1815 | stomach | 67 |
| 1816 | slow | 67 |
| 1817 | shortly | 67 |
| 1818 | rule | 67 |
| 1819 | reward | 67 |
| 1820 | pace | 67 |
| 1821 | keeping | 67 |
| 1822 | katherine | 67 |
| 1823 | instead | 67 |
| 1824 | image | 67 |
| 1825 | human | 67 |
| 1826 | fiend | 67 |
| 1827 | encounter | 67 |
| 1828 | departure | 67 |
| 1829 | charity | 67 |
| 1830 | captive | 67 |
| 1831 | winchester | 66 |
| 1832 | tomb | 66 |
| 1833 | thinks | 66 |
| 1834 | subjects | 66 |
| 1835 | style | 66 |
| 1836 | ruin | 66 |
| 1837 | quoth | 66 |
| 1838 | promises | 66 |
| 1839 | nerissa | 66 |
| 1840 | mowbray | 66 |
| 1841 | minds | 66 |
| 1842 | laughter | 66 |
| 1843 | grove | 66 |
| 1844 | gown | 66 |
| 1845 | flies | 66 |
| 1846 | favours | 66 |
| 1847 | fairly | 66 |
| 1848 | entered | 66 |
| 1849 | afraid | 66 |
| 1850 | added | 66 |
| 1851 | wretch | 65 |
| 1852 | wishes | 65 |
| 1853 | willing | 65 |
| 1854 | warlike | 65 |
| 1855 | voices | 65 |
| 1856 | tybalt | 65 |
| 1857 | stick | 65 |
| 1858 | sides | 65 |
| 1859 | sees | 65 |
| 1860 | saturninus | 65 |
| 1861 | render | 65 |
| 1862 | rascal | 65 |
| 1863 | press | 65 |
| 1864 | powers | 65 |
| 1865 | pow | 65 |
| 1866 | perchance | 65 |
| 1867 | peasant | 65 |
| 1868 | mortimer | 65 |
| 1869 | meeting | 65 |
| 1870 | list | 65 |
| 1871 | hanging | 65 |
| 1872 | execution | 65 |
| 1873 | ends | 65 |
| 1874 | earnest | 65 |
| 1875 | dozen | 65 |
| 1876 | dishonour | 65 |
| 1877 | device | 65 |
| 1878 | delivered | 65 |
| 1879 | covered | 65 |
| 1880 | cover | 65 |
| 1881 | combat | 65 |
| 1882 | behalf | 65 |
| 1883 | appears | 65 |
| 1884 | weigh | 64 |
| 1885 | vanquished | 64 |
| 1886 | smooth | 64 |
| 1887 | slaves | 64 |
| 1888 | skill | 64 |
| 1889 | seeming | 64 |
| 1890 | sail | 64 |
| 1891 | pleasant | 64 |
| 1892 | peril | 64 |
| 1893 | mistake | 64 |
| 1894 | miserable | 64 |
| 1895 | lucetta | 64 |
| 1896 | ladyship | 64 |
| 1897 | iron | 64 |
| 1898 | hunger | 64 |
| 1899 | horns | 64 |
| 1900 | garments | 64 |
| 1901 | faint | 64 |
| 1902 | eros | 64 |
| 1903 | dignity | 64 |
| 1904 | challenge | 64 |
| 1905 | bought | 64 |
| 1906 | bids | 64 |
| 1907 | altisidora | 64 |
| 1908 | vice | 63 |
| 1909 | twill | 63 |
| 1910 | tune | 63 |
| 1911 | repent | 63 |
| 1912 | remained | 63 |
| 1913 | pyramus | 63 |
| 1914 | protector | 63 |
| 1915 | proclaim | 63 |
| 1916 | persuade | 63 |
| 1917 | offend | 63 |
| 1918 | nym | 63 |
| 1919 | nobody | 63 |
| 1920 | necessary | 63 |
| 1921 | leonato | 63 |
| 1922 | league | 63 |
| 1923 | le | 63 |
| 1924 | intelligence | 63 |
| 1925 | humbly | 63 |
| 1926 | hermione | 63 |
| 1927 | fourth | 63 |
| 1928 | forsworn | 63 |
| 1929 | flowers | 63 |
| 1930 | falling | 63 |
| 1931 | errantry | 63 |
| 1932 | early | 63 |
| 1933 | difference | 63 |
| 1934 | devils | 63 |
| 1935 | cupid | 63 |
| 1936 | credit | 63 |
| 1937 | chair | 63 |
| 1938 | cart | 63 |
| 1939 | carrasco | 63 |
| 1940 | burden | 63 |
| 1941 | arviragus | 63 |
| 1942 | aim | 63 |
| 1943 | add | 63 |
| 1944 | abuse | 63 |
| 1945 | virtues | 62 |
| 1946 | tyrant | 62 |
| 1947 | trinculo | 62 |
| 1948 | traitors | 62 |
| 1949 | taught | 62 |
| 1950 | success | 62 |
| 1951 | sought | 62 |
| 1952 | silent | 62 |
| 1953 | resolution | 62 |
| 1954 | renegade | 62 |
| 1955 | quarter | 62 |
| 1956 | orders | 62 |
| 1957 | merit | 62 |
| 1958 | merely | 62 |
| 1959 | mer | 62 |
| 1960 | likely | 62 |
| 1961 | lean | 62 |
| 1962 | laer | 62 |
| 1963 | holofernes | 62 |
| 1964 | flavius | 62 |
| 1965 | enchanters | 62 |
| 1966 | dogs | 62 |
| 1967 | bent | 62 |
| 1968 | beaten | 62 |
| 1969 | tidings | 61 |
| 1970 | suppose | 61 |
| 1971 | share | 61 |
| 1972 | ride | 61 |
| 1973 | removed | 61 |
| 1974 | mountains | 61 |
| 1975 | month | 61 |
| 1976 | mar | 61 |
| 1977 | jealous | 61 |
| 1978 | elbow | 61 |
| 1979 | dreadful | 61 |
| 1980 | different | 61 |
| 1981 | constant | 61 |
| 1982 | commanded | 61 |
| 1983 | caught | 61 |
| 1984 | cat | 61 |
| 1985 | beside | 61 |
| 1986 | begins | 61 |
| 1987 | avoid | 61 |
| 1988 | alcibiades | 61 |
| 1989 | agreed | 61 |
| 1990 | venture | 60 |
| 1991 | suspicion | 60 |
| 1992 | strikes | 60 |
| 1993 | stol | 60 |
| 1994 | sits | 60 |
| 1995 | served | 60 |
| 1996 | season | 60 |
| 1997 | ry | 60 |
| 1998 | rivers | 60 |
| 1999 | remove | 60 |
| 2000 | receiv | 60 |
| 2001 | puts | 60 |
| 2002 | plot | 60 |
| 2003 | persuaded | 60 |
| 2004 | passing | 60 |
| 2005 | nought | 60 |
| 2006 | ned | 60 |
| 2007 | minute | 60 |
| 2008 | mayor | 60 |
| 2009 | malcolm | 60 |
| 2010 | main | 60 |
| 2011 | longaville | 60 |
| 2012 | hollow | 60 |
| 2013 | herald | 60 |
| 2014 | freedom | 60 |
| 2015 | florizel | 60 |
| 2016 | discover | 60 |
| 2017 | christians | 60 |
| 2018 | carrying | 60 |
| 2019 | brains | 60 |
| 2020 | attention | 60 |
| 2021 | attended | 60 |
| 2022 | undone | 59 |
| 2023 | thick | 59 |
| 2024 | tailor | 59 |
| 2025 | sweat | 59 |
| 2026 | stanley | 59 |
| 2027 | senators | 59 |
| 2028 | running | 59 |
| 2029 | rs | 59 |
| 2030 | retire | 59 |
| 2031 | realm | 59 |
| 2032 | practice | 59 |
| 2033 | murther | 59 |
| 2034 | modest | 59 |
| 2035 | lions | 59 |
| 2036 | likewise | 59 |
| 2037 | lands | 59 |
| 2038 | jessica | 59 |
| 2039 | jealousy | 59 |
| 2040 | hearted | 59 |
| 2041 | guess | 59 |
| 2042 | breed | 59 |
| 2043 | blush | 59 |
| 2044 | betray | 59 |
| 2045 | beasts | 59 |
| 2046 | andronicus | 59 |
| 2047 | affair | 59 |
| 2048 | womb | 58 |
| 2049 | warm | 58 |
| 2050 | wanted | 58 |
| 2051 | thieves | 58 |
| 2052 | special | 58 |
| 2053 | sleeps | 58 |
| 2054 | shot | 58 |
| 2055 | sends | 58 |
| 2056 | rob | 58 |
| 2057 | remains | 58 |
| 2058 | presented | 58 |
| 2059 | pound | 58 |
| 2060 | oph | 58 |
| 2061 | months | 58 |
| 2062 | intend | 58 |
| 2063 | guest | 58 |
| 2064 | forbear | 58 |
| 2065 | followers | 58 |
| 2066 | firm | 58 |
| 2067 | falsehood | 58 |
| 2068 | fairy | 58 |
| 2069 | fairest | 58 |
| 2070 | el | 58 |
| 2071 | defence | 58 |
| 2072 | britain | 58 |
| 2073 | assure | 58 |
| 2074 | ambition | 58 |
| 2075 | alonso | 58 |
| 2076 | alb | 58 |
| 2077 | tells | 57 |
| 2078 | sky | 57 |
| 2079 | rock | 57 |
| 2080 | reverend | 57 |
| 2081 | protest | 57 |
| 2082 | plays | 57 |
| 2083 | opposite | 57 |
| 2084 | oliver | 57 |
| 2085 | luciana | 57 |
| 2086 | knife | 57 |
| 2087 | houses | 57 |
| 2088 | honey | 57 |
| 2089 | gross | 57 |
| 2090 | fruit | 57 |
| 2091 | flatter | 57 |
| 2092 | fish | 57 |
| 2093 | fallen | 57 |
| 2094 | drops | 57 |
| 2095 | distress | 57 |
| 2096 | desperate | 57 |
| 2097 | desert | 57 |
| 2098 | denied | 57 |
| 2099 | dearest | 57 |
| 2100 | counterfeit | 57 |
| 2101 | conclusion | 57 |
| 2102 | cease | 57 |
| 2103 | calm | 57 |
| 2104 | bodies | 57 |
| 2105 | blest | 57 |
| 2106 | bell | 57 |
| 2107 | beatrice | 57 |
| 2108 | amazed | 57 |
| 2109 | agrippa | 57 |
| 2110 | y | 56 |
| 2111 | winds | 56 |
| 2112 | understanding | 56 |
| 2113 | thrive | 56 |
| 2114 | temper | 56 |
| 2115 | stranger | 56 |
| 2116 | sins | 56 |
| 2117 | salt | 56 |
| 2118 | quest | 56 |
| 2119 | oxford | 56 |
| 2120 | obedience | 56 |
| 2121 | misery | 56 |
| 2122 | licentiate | 56 |
| 2123 | height | 56 |
| 2124 | heavenly | 56 |
| 2125 | griefs | 56 |
| 2126 | fields | 56 |
| 2127 | feeble | 56 |
| 2128 | estate | 56 |
| 2129 | ended | 56 |
| 2130 | employ | 56 |
| 2131 | drums | 56 |
| 2132 | doom | 56 |
| 2133 | despite | 56 |
| 2134 | darkness | 56 |
| 2135 | confusion | 56 |
| 2136 | companion | 56 |
| 2137 | chide | 56 |
| 2138 | betwixt | 56 |
| 2139 | aloud | 56 |
| 2140 | writing | 55 |
| 2141 | whip | 55 |
| 2142 | undertake | 55 |
| 2143 | triumph | 55 |
| 2144 | task | 55 |
| 2145 | singing | 55 |
| 2146 | sickness | 55 |
| 2147 | seeking | 55 |
| 2148 | seated | 55 |
| 2149 | sage | 55 |
| 2150 | romans | 55 |
| 2151 | quince | 55 |
| 2152 | punish | 55 |
| 2153 | puck | 55 |
| 2154 | perforce | 55 |
| 2155 | ordered | 55 |
| 2156 | listening | 55 |
| 2157 | innocent | 55 |
| 2158 | horn | 55 |
| 2159 | higher | 55 |
| 2160 | habit | 55 |
| 2161 | graces | 55 |
| 2162 | fiery | 55 |
| 2163 | fierce | 55 |
| 2164 | experience | 55 |
| 2165 | duennas | 55 |
| 2166 | damsels | 55 |
| 2167 | council | 55 |
| 2168 | civil | 55 |
| 2169 | bringing | 55 |
| 2170 | beheld | 55 |
| 2171 | became | 55 |
| 2172 | wanting | 54 |
| 2173 | wake | 54 |
| 2174 | thisby | 54 |
| 2175 | tall | 54 |
| 2176 | sorrows | 54 |
| 2177 | slander | 54 |
| 2178 | settled | 54 |
| 2179 | services | 54 |
| 2180 | profession | 54 |
| 2181 | prisoners | 54 |
| 2182 | prevent | 54 |
| 2183 | perfection | 54 |
| 2184 | pen | 54 |
| 2185 | painter | 54 |
| 2186 | numbers | 54 |
| 2187 | mirth | 54 |
| 2188 | ignorance | 54 |
| 2189 | grew | 54 |
| 2190 | finds | 54 |
| 2191 | express | 54 |
| 2192 | disgrace | 54 |
| 2193 | direct | 54 |
| 2194 | devise | 54 |
| 2195 | deadly | 54 |
| 2196 | wore | 53 |
| 2197 | vouchsafe | 53 |
| 2198 | unknown | 53 |
| 2199 | travel | 53 |
| 2200 | stroke | 53 |
| 2201 | store | 53 |
| 2202 | slept | 53 |
| 2203 | sentence | 53 |
| 2204 | sell | 53 |
| 2205 | sacred | 53 |
| 2206 | ripe | 53 |
| 2207 | promis | 53 |
| 2208 | native | 53 |
| 2209 | montesinos | 53 |
| 2210 | menas | 53 |
| 2211 | kindly | 53 |
| 2212 | immediately | 53 |
| 2213 | horseback | 53 |
| 2214 | holding | 53 |
| 2215 | hill | 53 |
| 2216 | gower | 53 |
| 2217 | gon | 53 |
| 2218 | furnish | 53 |
| 2219 | francis | 53 |
| 2220 | ferdinand | 53 |
| 2221 | expected | 53 |
| 2222 | example | 53 |
| 2223 | dearly | 53 |
| 2224 | clean | 53 |
| 2225 | basilio | 53 |
| 2226 | acquainted | 53 |
| 2227 | achievements | 53 |
| 2228 | woes | 52 |
| 2229 | trade | 52 |
| 2230 | tide | 52 |
| 2231 | support | 52 |
| 2232 | stretched | 52 |
| 2233 | steps | 52 |
| 2234 | snow | 52 |
| 2235 | runs | 52 |
| 2236 | punishment | 52 |
| 2237 | poverty | 52 |
| 2238 | pick | 52 |
| 2239 | north | 52 |
| 2240 | marvellous | 52 |
| 2241 | listen | 52 |
| 2242 | limbs | 52 |
| 2243 | inform | 52 |
| 2244 | hung | 52 |
| 2245 | frown | 52 |
| 2246 | egypt | 52 |
| 2247 | described | 52 |
| 2248 | cup | 52 |
| 2249 | cool | 52 |
| 2250 | condemn | 52 |
| 2251 | chiron | 52 |
| 2252 | bury | 52 |
| 2253 | ago | 52 |
| 2254 | whoreson | 51 |
| 2255 | wedding | 51 |
| 2256 | waste | 51 |
| 2257 | troubled | 51 |
| 2258 | tonight | 51 |
| 2259 | thirty | 51 |
| 2260 | surely | 51 |
| 2261 | satisfy | 51 |
| 2262 | reverence | 51 |
| 2263 | repair | 51 |
| 2264 | reign | 51 |
| 2265 | proved | 51 |
| 2266 | profit | 51 |
| 2267 | prey | 51 |
| 2268 | points | 51 |
| 2269 | plead | 51 |
| 2270 | pitch | 51 |
| 2271 | picture | 51 |
| 2272 | outward | 51 |
| 2273 | oh | 51 |
| 2274 | necessity | 51 |
| 2275 | mentioned | 51 |
| 2276 | lust | 51 |
| 2277 | lock | 51 |
| 2278 | lines | 51 |
| 2279 | kisses | 51 |
| 2280 | kinsman | 51 |
| 2281 | interest | 51 |
| 2282 | intent | 51 |
| 2283 | imagine | 51 |
| 2284 | haply | 51 |
| 2285 | front | 51 |
| 2286 | fathers | 51 |
| 2287 | eternal | 51 |
| 2288 | esteem | 51 |
| 2289 | entertainment | 51 |
| 2290 | durst | 51 |
| 2291 | dreams | 51 |
| 2292 | doll | 51 |
| 2293 | dar | 51 |
| 2294 | courteous | 51 |
| 2295 | convey | 51 |
| 2296 | contempt | 51 |
| 2297 | chaste | 51 |
| 2298 | burst | 51 |
| 2299 | bind | 51 |
| 2300 | armed | 51 |
| 2301 | appetite | 51 |
| 2302 | terror | 50 |
| 2303 | sway | 50 |
| 2304 | surrey | 50 |
| 2305 | substance | 50 |
| 2306 | strive | 50 |
| 2307 | steward | 50 |
| 2308 | sounds | 50 |
| 2309 | rueful | 50 |
| 2310 | recover | 50 |
| 2311 | rash | 50 |
| 2312 | prick | 50 |
| 2313 | parted | 50 |
| 2314 | oak | 50 |
| 2315 | mule | 50 |
| 2316 | midnight | 50 |
| 2317 | instrument | 50 |
| 2318 | hid | 50 |
| 2319 | hereafter | 50 |
| 2320 | frame | 50 |
| 2321 | faithful | 50 |
| 2322 | enchantment | 50 |
| 2323 | edge | 50 |
| 2324 | drive | 50 |
| 2325 | draws | 50 |
| 2326 | crying | 50 |
| 2327 | changed | 50 |
| 2328 | breaking | 50 |
| 2329 | board | 50 |
| 2330 | bishop | 50 |
| 2331 | birds | 50 |
| 2332 | bend | 50 |
| 2333 | belly | 50 |
| 2334 | apt | 50 |
| 2335 | amazement | 50 |
| 2336 | alencon | 50 |
| 2337 | advanced | 50 |
| 2338 | yesterday | 49 |
| 2339 | works | 49 |
| 2340 | willingly | 49 |
| 2341 | vincentio | 49 |
| 2342 | villains | 49 |
| 2343 | unlucky | 49 |
| 2344 | threw | 49 |
| 2345 | stretch | 49 |
| 2346 | spake | 49 |
| 2347 | skin | 49 |
| 2348 | showing | 49 |
| 2349 | shield | 49 |
| 2350 | shepherds | 49 |
| 2351 | safely | 49 |
| 2352 | relief | 49 |
| 2353 | reignier | 49 |
| 2354 | proceeded | 49 |
| 2355 | pour | 49 |
| 2356 | porter | 49 |
| 2357 | peers | 49 |
| 2358 | nights | 49 |
| 2359 | mars | 49 |
| 2360 | leg | 49 |
| 2361 | learning | 49 |
| 2362 | infinite | 49 |
| 2363 | happen | 49 |
| 2364 | granted | 49 |
| 2365 | forsooth | 49 |
| 2366 | forces | 49 |
| 2367 | flood | 49 |
| 2368 | fatal | 49 |
| 2369 | entirely | 49 |
| 2370 | empress | 49 |
| 2371 | dwell | 49 |
| 2372 | dumb | 49 |
| 2373 | disdain | 49 |
| 2374 | dares | 49 |
| 2375 | crack | 49 |
| 2376 | complexion | 49 |
| 2377 | committed | 49 |
| 2378 | commission | 49 |
| 2379 | charm | 49 |
| 2380 | bride | 49 |
| 2381 | believed | 49 |
| 2382 | befall | 49 |
| 2383 | bedford | 49 |
| 2384 | alike | 49 |
| 2385 | whore | 48 |
| 2386 | value | 48 |
| 2387 | urge | 48 |
| 2388 | tail | 48 |
| 2389 | shoulder | 48 |
| 2390 | score | 48 |
| 2391 | salerio | 48 |
| 2392 | prayer | 48 |
| 2393 | penance | 48 |
| 2394 | odds | 48 |
| 2395 | notice | 48 |
| 2396 | mariana | 48 |
| 2397 | liest | 48 |
| 2398 | leagues | 48 |
| 2399 | invention | 48 |
| 2400 | heartily | 48 |
| 2401 | galley | 48 |
| 2402 | fully | 48 |
| 2403 | error | 48 |
| 2404 | east | 48 |
| 2405 | debt | 48 |
| 2406 | constance | 48 |
| 2407 | confirm | 48 |
| 2408 | car | 48 |
| 2409 | brows | 48 |
| 2410 | banished | 48 |
| 2411 | apart | 48 |
| 2412 | unworthy | 47 |
| 2413 | unfortunate | 47 |
| 2414 | tricks | 47 |
| 2415 | touching | 47 |
| 2416 | strain | 47 |
| 2417 | spur | 47 |
| 2418 | shrewd | 47 |
| 2419 | root | 47 |
| 2420 | reals | 47 |
| 2421 | prevail | 47 |
| 2422 | phebe | 47 |
| 2423 | octavius | 47 |
| 2424 | nonsense | 47 |
| 2425 | nobility | 47 |
| 2426 | mov | 47 |
| 2427 | moors | 47 |
| 2428 | miracle | 47 |
| 2429 | messala | 47 |
| 2430 | maids | 47 |
| 2431 | loyal | 47 |
| 2432 | lived | 47 |
| 2433 | leading | 47 |
| 2434 | laertes | 47 |
| 2435 | injury | 47 |
| 2436 | horatio | 47 |
| 2437 | hole | 47 |
| 2438 | highest | 47 |
| 2439 | hall | 47 |
| 2440 | guide | 47 |
| 2441 | goatherd | 47 |
| 2442 | glorious | 47 |
| 2443 | fits | 47 |
| 2444 | elder | 47 |
| 2445 | discretion | 47 |
| 2446 | certainly | 47 |
| 2447 | bounty | 47 |
| 2448 | beloved | 47 |
| 2449 | affections | 47 |
| 2450 | accept | 47 |
| 2451 | yard | 46 |
| 2452 | wrought | 46 |
| 2453 | worn | 46 |
| 2454 | wished | 46 |
| 2455 | west | 46 |
| 2456 | wears | 46 |
| 2457 | weapons | 46 |
| 2458 | violent | 46 |
| 2459 | verse | 46 |
| 2460 | tread | 46 |
| 2461 | tom | 46 |
| 2462 | thrown | 46 |
| 2463 | terrible | 46 |
| 2464 | tempest | 46 |
| 2465 | tedious | 46 |
| 2466 | spread | 46 |
| 2467 | sorts | 46 |
| 2468 | solemn | 46 |
| 2469 | sold | 46 |
| 2470 | smiles | 46 |
| 2471 | slaughter | 46 |
| 2472 | shine | 46 |
| 2473 | seas | 46 |
| 2474 | ros | 46 |
| 2475 | roque | 46 |
| 2476 | restore | 46 |
| 2477 | refuse | 46 |
| 2478 | reasonable | 46 |
| 2479 | ratcliff | 46 |
| 2480 | quarters | 46 |
| 2481 | pursue | 46 |
| 2482 | purposes | 46 |
| 2483 | policy | 46 |
| 2484 | owner | 46 |
| 2485 | offended | 46 |
| 2486 | needful | 46 |
| 2487 | hie | 46 |
| 2488 | grass | 46 |
| 2489 | fifty | 46 |
| 2490 | fenton | 46 |
| 2491 | excellence | 46 |
| 2492 | envious | 46 |
| 2493 | dressed | 46 |
| 2494 | displeasure | 46 |
| 2495 | davy | 46 |
| 2496 | cursed | 46 |
| 2497 | courtier | 46 |
| 2498 | commit | 46 |
| 2499 | cloak | 46 |
| 2500 | canon | 46 |
| 2501 | brabantio | 46 |
| 2502 | bowels | 46 |
| 2503 | bird | 46 |
| 2504 | benefit | 46 |
| 2505 | beauteous | 46 |
| 2506 | barren | 46 |
| 2507 | amadis | 46 |
| 2508 | afternoon | 46 |
| 2509 | advise | 46 |
| 2510 | adam | 46 |
| 2511 | wing | 45 |
| 2512 | weeds | 45 |
| 2513 | waters | 45 |
| 2514 | understood | 45 |
| 2515 | theirs | 45 |
| 2516 | tarry | 45 |
| 2517 | stronger | 45 |
| 2518 | stage | 45 |
| 2519 | space | 45 |
| 2520 | sooth | 45 |
| 2521 | sole | 45 |
| 2522 | sly | 45 |
| 2523 | serves | 45 |
| 2524 | school | 45 |
| 2525 | sat | 45 |
| 2526 | rodriguez | 45 |
| 2527 | renowned | 45 |
| 2528 | recognised | 45 |
| 2529 | real | 45 |
| 2530 | questions | 45 |
| 2531 | provide | 45 |
| 2532 | property | 45 |
| 2533 | priam | 45 |
| 2534 | preserve | 45 |
| 2535 | pinch | 45 |
| 2536 | pearls | 45 |
| 2537 | octavia | 45 |
| 2538 | oberon | 45 |
| 2539 | mouths | 45 |
| 2540 | miss | 45 |
| 2541 | knaves | 45 |
| 2542 | henceforth | 45 |
| 2543 | hal | 45 |
| 2544 | growing | 45 |
| 2545 | grieve | 45 |
| 2546 | greek | 45 |
| 2547 | enterprise | 45 |
| 2548 | drawing | 45 |
| 2549 | damned | 45 |
| 2550 | dame | 45 |
| 2551 | cur | 45 |
| 2552 | county | 45 |
| 2553 | continue | 45 |
| 2554 | cock | 45 |
| 2555 | cares | 45 |
| 2556 | capulet | 45 |
| 2557 | breeding | 45 |
| 2558 | bassianus | 45 |
| 2559 | attending | 45 |
| 2560 | apparel | 45 |
| 2561 | amiss | 45 |
| 2562 | alexander | 45 |
| 2563 | across | 45 |
| 2564 | yond | 44 |
| 2565 | uttered | 44 |
| 2566 | tame | 44 |
| 2567 | silvius | 44 |
| 2568 | silk | 44 |
| 2569 | robert | 44 |
| 2570 | river | 44 |
| 2571 | rid | 44 |
| 2572 | related | 44 |
| 2573 | profess | 44 |
| 2574 | praises | 44 |
| 2575 | pit | 44 |
| 2576 | pause | 44 |
| 2577 | passage | 44 |
| 2578 | partly | 44 |
| 2579 | odd | 44 |
| 2580 | nobles | 44 |
| 2581 | misfortunes | 44 |
| 2582 | market | 44 |
| 2583 | losing | 44 |
| 2584 | lodovico | 44 |
| 2585 | leonela | 44 |
| 2586 | lashes | 44 |
| 2587 | lad | 44 |
| 2588 | knocking | 44 |
| 2589 | imagination | 44 |
| 2590 | handkerchief | 44 |
| 2591 | getting | 44 |
| 2592 | fright | 44 |
| 2593 | fore | 44 |
| 2594 | figures | 44 |
| 2595 | fac | 44 |
| 2596 | engaged | 44 |
| 2597 | cromwell | 44 |
| 2598 | compass | 44 |
| 2599 | coat | 44 |
| 2600 | bestowed | 44 |
| 2601 | banishment | 44 |
| 2602 | absent | 44 |
| 2603 | virgin | 43 |
| 2604 | toil | 43 |
| 2605 | suffering | 43 |
| 2606 | soothsayer | 43 |
| 2607 | slew | 43 |
| 2608 | shade | 43 |
| 2609 | setting | 43 |
| 2610 | senate | 43 |
| 2611 | rotten | 43 |
| 2612 | revolt | 43 |
| 2613 | palm | 43 |
| 2614 | milan | 43 |
| 2615 | methought | 43 |
| 2616 | message | 43 |
| 2617 | mass | 43 |
| 2618 | manage | 43 |
| 2619 | lofty | 43 |
| 2620 | lent | 43 |
| 2621 | jewels | 43 |
| 2622 | isle | 43 |
| 2623 | iras | 43 |
| 2624 | huge | 43 |
| 2625 | hazard | 43 |
| 2626 | greet | 43 |
| 2627 | greatly | 43 |
| 2628 | grand | 43 |
| 2629 | gent | 43 |
| 2630 | gaoler | 43 |
| 2631 | galleys | 43 |
| 2632 | finished | 43 |
| 2633 | fairer | 43 |
| 2634 | deer | 43 |
| 2635 | deceive | 43 |
| 2636 | crave | 43 |
| 2637 | conceit | 43 |
| 2638 | cell | 43 |
| 2639 | capitol | 43 |
| 2640 | broad | 43 |
| 2641 | bite | 43 |
| 2642 | basin | 43 |
| 2643 | appeared | 43 |
| 2644 | angels | 43 |
| 2645 | yellow | 42 |
| 2646 | withdraw | 42 |
| 2647 | villainy | 42 |
| 2648 | usual | 42 |
| 2649 | simplicity | 42 |
| 2650 | sensible | 42 |
| 2651 | renown | 42 |
| 2652 | players | 42 |
| 2653 | perdita | 42 |
| 2654 | peerless | 42 |
| 2655 | ning | 42 |
| 2656 | nice | 42 |
| 2657 | meantime | 42 |
| 2658 | leads | 42 |
| 2659 | lamb | 42 |
| 2660 | joke | 42 |
| 2661 | humours | 42 |
| 2662 | hugh | 42 |
| 2663 | hercules | 42 |
| 2664 | hat | 42 |
| 2665 | farmer | 42 |
| 2666 | fairies | 42 |
| 2667 | during | 42 |
| 2668 | dish | 42 |
| 2669 | discovered | 42 |
| 2670 | directed | 42 |
| 2671 | dew | 42 |
| 2672 | deserv | 42 |
| 2673 | cruelty | 42 |
| 2674 | countrymen | 42 |
| 2675 | consequence | 42 |
| 2676 | charms | 42 |
| 2677 | ceremony | 42 |
| 2678 | brass | 42 |
| 2679 | blown | 42 |
| 2680 | bidding | 42 |
| 2681 | belike | 42 |
| 2682 | bar | 42 |
| 2683 | allowed | 42 |
| 2684 | advance | 42 |
| 2685 | wolf | 41 |
| 2686 | wept | 41 |
| 2687 | wax | 41 |
| 2688 | viceroy | 41 |
| 2689 | unnatural | 41 |
| 2690 | twain | 41 |
| 2691 | troop | 41 |
| 2692 | tried | 41 |
| 2693 | titania | 41 |
| 2694 | stout | 41 |
| 2695 | shoes | 41 |
| 2696 | roar | 41 |
| 2697 | required | 41 |
| 2698 | pocket | 41 |
| 2699 | pembroke | 41 |
| 2700 | padua | 41 |
| 2701 | naples | 41 |
| 2702 | murtherer | 41 |
| 2703 | monsieur | 41 |
| 2704 | moe | 41 |
| 2705 | midst | 41 |
| 2706 | mayest | 41 |
| 2707 | marks | 41 |
| 2708 | lovell | 41 |
| 2709 | likes | 41 |
| 2710 | lartius | 41 |
| 2711 | jupiter | 41 |
| 2712 | italy | 41 |
| 2713 | intention | 41 |
| 2714 | hunt | 41 |
| 2715 | honor | 41 |
| 2716 | hateful | 41 |
| 2717 | forced | 41 |
| 2718 | familiar | 41 |
| 2719 | douglas | 41 |
| 2720 | diego | 41 |
| 2721 | deceiv | 41 |
| 2722 | conditions | 41 |
| 2723 | complete | 41 |
| 2724 | cloud | 41 |
| 2725 | circumstance | 41 |
| 2726 | canterbury | 41 |
| 2727 | begun | 41 |
| 2728 | band | 41 |
| 2729 | acquaintance | 41 |
| 2730 | zeal | 40 |
| 2731 | worm | 40 |
| 2732 | whisper | 40 |
| 2733 | vantage | 40 |
| 2734 | trifle | 40 |
| 2735 | thereof | 40 |
| 2736 | stoop | 40 |
| 2737 | spanish | 40 |
| 2738 | soil | 40 |
| 2739 | serpent | 40 |
| 2740 | seize | 40 |
| 2741 | scarcely | 40 |
| 2742 | rous | 40 |
| 2743 | rescue | 40 |
| 2744 | redress | 40 |
| 2745 | prologue | 40 |
| 2746 | physician | 40 |
| 2747 | newly | 40 |
| 2748 | nephew | 40 |
| 2749 | nation | 40 |
| 2750 | marvel | 40 |
| 2751 | kissing | 40 |
| 2752 | kingdoms | 40 |
| 2753 | instruments | 40 |
| 2754 | hated | 40 |
| 2755 | hack | 40 |
| 2756 | gossip | 40 |
| 2757 | glove | 40 |
| 2758 | generous | 40 |
| 2759 | garter | 40 |
| 2760 | game | 40 |
| 2761 | future | 40 |
| 2762 | friendly | 40 |
| 2763 | flying | 40 |
| 2764 | fix | 40 |
| 2765 | fearing | 40 |
| 2766 | duncan | 40 |
| 2767 | drinking | 40 |
| 2768 | destruction | 40 |
| 2769 | contents | 40 |
| 2770 | concluded | 40 |
| 2771 | conclude | 40 |
| 2772 | commands | 40 |
| 2773 | coach | 40 |
| 2774 | cinna | 40 |
| 2775 | check | 40 |
| 2776 | chase | 40 |
| 2777 | cage | 40 |
| 2778 | brotherhood | 40 |
| 2779 | boast | 40 |
| 2780 | basket | 40 |
| 2781 | babe | 40 |
| 2782 | attendant | 40 |
| 2783 | appointed | 40 |
| 2784 | altogether | 40 |
| 2785 | ages | 40 |
| 2786 | accompany | 40 |
| 2787 | wreck | 39 |
| 2788 | windsor | 39 |
| 2789 | whoever | 39 |
| 2790 | varro | 39 |
| 2791 | tut | 39 |
| 2792 | torture | 39 |
| 2793 | token | 39 |
| 2794 | threat | 39 |
| 2795 | suits | 39 |
| 2796 | strokes | 39 |
| 2797 | stock | 39 |
| 2798 | spoil | 39 |
| 2799 | slight | 39 |
| 2800 | sitting | 39 |
| 2801 | sink | 39 |
| 2802 | seldom | 39 |
| 2803 | sceptre | 39 |
| 2804 | rocks | 39 |
| 2805 | rightly | 39 |
| 2806 | rail | 39 |
| 2807 | quiteria | 39 |
| 2808 | proverbs | 39 |
| 2809 | price | 39 |
| 2810 | pleasures | 39 |
| 2811 | permit | 39 |
| 2812 | neighbours | 39 |
| 2813 | morn | 39 |
| 2814 | milk | 39 |
| 2815 | marble | 39 |
| 2816 | lusty | 39 |
| 2817 | lip | 39 |
| 2818 | leap | 39 |
| 2819 | lately | 39 |
| 2820 | killing | 39 |
| 2821 | hangs | 39 |
| 2822 | hamete | 39 |
| 2823 | hairs | 39 |
| 2824 | groans | 39 |
| 2825 | gently | 39 |
| 2826 | fifth | 39 |
| 2827 | fed | 39 |
| 2828 | exchange | 39 |
| 2829 | entrance | 39 |
| 2830 | dolabella | 39 |
| 2831 | discharge | 39 |
| 2832 | destroy | 39 |
| 2833 | curses | 39 |
| 2834 | creatures | 39 |
| 2835 | confound | 39 |
| 2836 | compare | 39 |
| 2837 | cide | 39 |
| 2838 | bravely | 39 |
| 2839 | bit | 39 |
| 2840 | bawd | 39 |
| 2841 | asking | 39 |
| 2842 | arise | 39 |
| 2843 | answers | 39 |
| 2844 | ambitious | 39 |
| 2845 | abide | 39 |
| 2846 | younger | 38 |
| 2847 | yoke | 38 |
| 2848 | yielded | 38 |
| 2849 | writes | 38 |
| 2850 | weather | 38 |
| 2851 | virgilia | 38 |
| 2852 | tremble | 38 |
| 2853 | treacherous | 38 |
| 2854 | suck | 38 |
| 2855 | sonnet | 38 |
| 2856 | shapes | 38 |
| 2857 | serving | 38 |
| 2858 | rush | 38 |
| 2859 | rode | 38 |
| 2860 | robin | 38 |
| 2861 | release | 38 |
| 2862 | prevented | 38 |
| 2863 | position | 38 |
| 2864 | plan | 38 |
| 2865 | perish | 38 |
| 2866 | osw | 38 |
| 2867 | observing | 38 |
| 2868 | nobly | 38 |
| 2869 | monument | 38 |
| 2870 | minister | 38 |
| 2871 | mess | 38 |
| 2872 | marshal | 38 |
| 2873 | importance | 38 |
| 2874 | hereford | 38 |
| 2875 | gall | 38 |
| 2876 | fox | 38 |
| 2877 | forty | 38 |
| 2878 | forgotten | 38 |
| 2879 | doublet | 38 |
| 2880 | determined | 38 |
| 2881 | desired | 38 |
| 2882 | delicate | 38 |
| 2883 | crowned | 38 |
| 2884 | cressid | 38 |
| 2885 | commonly | 38 |
| 2886 | captains | 38 |
| 2887 | buckler | 38 |
| 2888 | becoming | 38 |
| 2889 | ballad | 38 |
| 2890 | athenian | 38 |
| 2891 | anybody | 38 |
| 2892 | amongst | 38 |
| 2893 | afford | 38 |
| 2894 | addressed | 38 |
| 2895 | accuse | 38 |
| 2896 | wondrous | 37 |
| 2897 | wonderful | 37 |
| 2898 | wisely | 37 |
| 2899 | wheel | 37 |
| 2900 | weakness | 37 |
| 2901 | watching | 37 |
| 2902 | waited | 37 |
| 2903 | verona | 37 |
| 2904 | tyranny | 37 |
| 2905 | titinius | 37 |
| 2906 | thin | 37 |
| 2907 | tend | 37 |
| 2908 | supposed | 37 |
| 2909 | supply | 37 |
| 2910 | stream | 37 |
| 2911 | stays | 37 |
| 2912 | start | 37 |
| 2913 | sour | 37 |
| 2914 | slay | 37 |
| 2915 | shakespeare | 37 |
| 2916 | sets | 37 |
| 2917 | senior | 37 |
| 2918 | scape | 37 |
| 2919 | sayest | 37 |
| 2920 | saucy | 37 |
| 2921 | rope | 37 |
| 2922 | rhyme | 37 |
| 2923 | repose | 37 |
| 2924 | qualities | 37 |
| 2925 | proceeding | 37 |
| 2926 | pomp | 37 |
| 2927 | permission | 37 |
| 2928 | pawn | 37 |
| 2929 | park | 37 |
| 2930 | offers | 37 |
| 2931 | nathaniel | 37 |
| 2932 | majordomo | 37 |
| 2933 | laughing | 37 |
| 2934 | knot | 37 |
| 2935 | joyful | 37 |
| 2936 | groan | 37 |
| 2937 | graves | 37 |
| 2938 | goths | 37 |
| 2939 | gladly | 37 |
| 2940 | gaze | 37 |
| 2941 | gather | 37 |
| 2942 | gait | 37 |
| 2943 | fleet | 37 |
| 2944 | edgar | 37 |
| 2945 | eating | 37 |
| 2946 | eaten | 37 |
| 2947 | divers | 37 |
| 2948 | direction | 37 |
| 2949 | daylight | 37 |
| 2950 | corner | 37 |
| 2951 | considered | 37 |
| 2952 | chosen | 37 |
| 2953 | character | 37 |
| 2954 | breaks | 37 |
| 2955 | breach | 37 |
| 2956 | bora | 37 |
| 2957 | bleed | 37 |
| 2958 | belief | 37 |
| 2959 | behaviour | 37 |
| 2960 | assur | 37 |
| 2961 | wrote | 36 |
| 2962 | wor | 36 |
| 2963 | vex | 36 |
| 2964 | usurp | 36 |
| 2965 | treachery | 36 |
| 2966 | towns | 36 |
| 2967 | torment | 36 |
| 2968 | strife | 36 |
| 2969 | stern | 36 |
| 2970 | steed | 36 |
| 2971 | society | 36 |
| 2972 | smiling | 36 |
| 2973 | siege | 36 |
| 2974 | serious | 36 |
| 2975 | secure | 36 |
| 2976 | scotland | 36 |
| 2977 | savage | 36 |
| 2978 | roses | 36 |
| 2979 | rising | 36 |
| 2980 | retreat | 36 |
| 2981 | resolve | 36 |
| 2982 | require | 36 |
| 2983 | raising | 36 |
| 2984 | ragged | 36 |
| 2985 | purchase | 36 |
| 2986 | proverb | 36 |
| 2987 | polonius | 36 |
| 2988 | pin | 36 |
| 2989 | phrase | 36 |
| 2990 | personae | 36 |
| 2991 | pedant | 36 |
| 2992 | opened | 36 |
| 2993 | notes | 36 |
| 2994 | nails | 36 |
| 2995 | moving | 36 |
| 2996 | montano | 36 |
| 2997 | lights | 36 |
| 2998 | liberal | 36 |
| 2999 | key | 36 |
| 3000 | item | 36 |
| 3001 | idea | 36 |
| 3002 | happily | 36 |
| 3003 | forthwith | 36 |
| 3004 | et | 36 |
| 3005 | earthly | 36 |
| 3006 | eager | 36 |
| 3007 | dst | 36 |
| 3008 | dramatis | 36 |
| 3009 | diomed | 36 |
| 3010 | dine | 36 |
| 3011 | cranmer | 36 |
| 3012 | coz | 36 |
| 3013 | contented | 36 |
| 3014 | complain | 36 |
| 3015 | belong | 36 |
| 3016 | befell | 36 |
| 3017 | addition | 36 |
| 3018 | acted | 36 |
| 3019 | week | 35 |
| 3020 | wages | 35 |
| 3021 | visage | 35 |
| 3022 | ugly | 35 |
| 3023 | turk | 35 |
| 3024 | trunk | 35 |
| 3025 | troyan | 35 |
| 3026 | touched | 35 |
| 3027 | temple | 35 |
| 3028 | stamp | 35 |
| 3029 | shook | 35 |
| 3030 | rouse | 35 |
| 3031 | ricote | 35 |
| 3032 | ribs | 35 |
| 3033 | protection | 35 |
| 3034 | proportion | 35 |
| 3035 | privilege | 35 |
| 3036 | print | 35 |
| 3037 | presents | 35 |
| 3038 | poets | 35 |
| 3039 | plenty | 35 |
| 3040 | pierce | 35 |
| 3041 | pate | 35 |
| 3042 | offices | 35 |
| 3043 | narrow | 35 |
| 3044 | messengers | 35 |
| 3045 | luis | 35 |
| 3046 | lucilius | 35 |
| 3047 | loyalty | 35 |
| 3048 | lower | 35 |
| 3049 | longing | 35 |
| 3050 | listened | 35 |
| 3051 | lennox | 35 |
| 3052 | knit | 35 |
| 3053 | kindred | 35 |
| 3054 | kin | 35 |
| 3055 | increase | 35 |
| 3056 | illustrious | 35 |
| 3057 | histories | 35 |
| 3058 | harsh | 35 |
| 3059 | giants | 35 |
| 3060 | frederick | 35 |
| 3061 | fortunate | 35 |
| 3062 | finish | 35 |
| 3063 | fighting | 35 |
| 3064 | fee | 35 |
| 3065 | entreated | 35 |
| 3066 | enforce | 35 |
| 3067 | declare | 35 |
| 3068 | cuckold | 35 |
| 3069 | corin | 35 |
| 3070 | conjure | 35 |
| 3071 | commons | 35 |
| 3072 | camacho | 35 |
| 3073 | busy | 35 |
| 3074 | boot | 35 |
| 3075 | bleeding | 35 |
| 3076 | battles | 35 |
| 3077 | banquet | 35 |
| 3078 | audience | 35 |
| 3079 | assurance | 35 |
| 3080 | address | 35 |
| 3081 | worships | 34 |
| 3082 | working | 34 |
| 3083 | wither | 34 |
| 3084 | weeps | 34 |
| 3085 | weapon | 34 |
| 3086 | utmost | 34 |
| 3087 | troops | 34 |
| 3088 | tempt | 34 |
| 3089 | sufficient | 34 |
| 3090 | subtle | 34 |
| 3091 | strongly | 34 |
| 3092 | silly | 34 |
| 3093 | shines | 34 |
| 3094 | sheets | 34 |
| 3095 | sc | 34 |
| 3096 | sadness | 34 |
| 3097 | robe | 34 |
| 3098 | reveng | 34 |
| 3099 | rememb | 34 |
| 3100 | regarded | 34 |
| 3101 | push | 34 |
| 3102 | pleases | 34 |
| 3103 | playing | 34 |
| 3104 | parley | 34 |
| 3105 | obtain | 34 |
| 3106 | musicians | 34 |
| 3107 | mile | 34 |
| 3108 | menelaus | 34 |
| 3109 | mantua | 34 |
| 3110 | islands | 34 |
| 3111 | invisible | 34 |
| 3112 | household | 34 |
| 3113 | hears | 34 |
| 3114 | gardiner | 34 |
| 3115 | foreign | 34 |
| 3116 | forehead | 34 |
| 3117 | family | 34 |
| 3118 | expedition | 34 |
| 3119 | exactly | 34 |
| 3120 | droll | 34 |
| 3121 | dismiss | 34 |
| 3122 | directly | 34 |
| 3123 | dick | 34 |
| 3124 | deaf | 34 |
| 3125 | daily | 34 |
| 3126 | crow | 34 |
| 3127 | countless | 34 |
| 3128 | compassion | 34 |
| 3129 | companions | 34 |
| 3130 | coast | 34 |
| 3131 | chose | 34 |
| 3132 | chang | 34 |
| 3133 | bohemia | 34 |
| 3134 | belonging | 34 |
| 3135 | beards | 34 |
| 3136 | attack | 34 |
| 3137 | aspect | 34 |
| 3138 | arguments | 34 |
| 3139 | approaching | 34 |
| 3140 | alexas | 34 |
| 3141 | advised | 34 |
| 3142 | youthful | 33 |
| 3143 | wipe | 33 |
| 3144 | wink | 33 |
| 3145 | wed | 33 |
| 3146 | vulgar | 33 |
| 3147 | verily | 33 |
| 3148 | undo | 33 |
| 3149 | torch | 33 |
| 3150 | thread | 33 |
| 3151 | tales | 33 |
| 3152 | sixth | 33 |
| 3153 | shift | 33 |
| 3154 | secrets | 33 |
| 3155 | rugby | 33 |
| 3156 | returning | 33 |
| 3157 | resolv | 33 |
| 3158 | repeat | 33 |
| 3159 | relieve | 33 |
| 3160 | rapier | 33 |
| 3161 | protect | 33 |
| 3162 | produce | 33 |
| 3163 | portion | 33 |
| 3164 | pleasing | 33 |
| 3165 | physic | 33 |
| 3166 | payment | 33 |
| 3167 | outlaw | 33 |
| 3168 | ocean | 33 |
| 3169 | obedient | 33 |
| 3170 | muse | 33 |
| 3171 | multitude | 33 |
| 3172 | mourn | 33 |
| 3173 | minded | 33 |
| 3174 | loath | 33 |
| 3175 | lift | 33 |
| 3176 | level | 33 |
| 3177 | lays | 33 |
| 3178 | latter | 33 |
| 3179 | justly | 33 |
| 3180 | isabel | 33 |
| 3181 | intended | 33 |
| 3182 | ink | 33 |
| 3183 | hunting | 33 |
| 3184 | hungry | 33 |
| 3185 | guarded | 33 |
| 3186 | greeks | 33 |
| 3187 | grecian | 33 |
| 3188 | goose | 33 |
| 3189 | goats | 33 |
| 3190 | girls | 33 |
| 3191 | flung | 33 |
| 3192 | everyone | 33 |
| 3193 | engage | 33 |
| 3194 | eldest | 33 |
| 3195 | drove | 33 |
| 3196 | drinks | 33 |
| 3197 | disease | 33 |
| 3198 | design | 33 |
| 3199 | craft | 33 |
| 3200 | conceive | 33 |
| 3201 | clearly | 33 |
| 3202 | carefully | 33 |
| 3203 | bounds | 33 |
| 3204 | bone | 33 |
| 3205 | boar | 33 |
| 3206 | beams | 33 |
| 3207 | assured | 33 |
| 3208 | arrived | 33 |
| 3209 | apollo | 33 |
| 3210 | alter | 33 |
| 3211 | agree | 33 |
| 3212 | wot | 32 |
| 3213 | woods | 32 |
| 3214 | wills | 32 |
| 3215 | williams | 32 |
| 3216 | wholesome | 32 |
| 3217 | whereon | 32 |
| 3218 | wager | 32 |
| 3219 | vi | 32 |
| 3220 | vernon | 32 |
| 3221 | vast | 32 |
| 3222 | trembling | 32 |
| 3223 | traveller | 32 |
| 3224 | tooth | 32 |
| 3225 | thereby | 32 |
| 3226 | term | 32 |
| 3227 | shirt | 32 |
| 3228 | regan | 32 |
| 3229 | record | 32 |
| 3230 | reckon | 32 |
| 3231 | rebels | 32 |
| 3232 | rebellion | 32 |
| 3233 | quench | 32 |
| 3234 | pursuit | 32 |
| 3235 | publius | 32 |
| 3236 | pitiful | 32 |
| 3237 | piteous | 32 |
| 3238 | penalty | 32 |
| 3239 | pearl | 32 |
| 3240 | parting | 32 |
| 3241 | particularly | 32 |
| 3242 | par | 32 |
| 3243 | papers | 32 |
| 3244 | orchard | 32 |
| 3245 | notwithstanding | 32 |
| 3246 | mirrors | 32 |
| 3247 | mettle | 32 |
| 3248 | liking | 32 |
| 3249 | kills | 32 |
| 3250 | highly | 32 |
| 3251 | hideous | 32 |
| 3252 | handed | 32 |
| 3253 | guilt | 32 |
| 3254 | guests | 32 |
| 3255 | goneril | 32 |
| 3256 | giddy | 32 |
| 3257 | furious | 32 |
| 3258 | flat | 32 |
| 3259 | firmly | 32 |
| 3260 | expectation | 32 |
| 3261 | exalted | 32 |
| 3262 | event | 32 |
| 3263 | embraced | 32 |
| 3264 | dorset | 32 |
| 3265 | divide | 32 |
| 3266 | din | 32 |
| 3267 | difficulty | 32 |
| 3268 | derby | 32 |
| 3269 | defy | 32 |
| 3270 | daring | 32 |
| 3271 | dainty | 32 |
| 3272 | cowards | 32 |
| 3273 | cor | 32 |
| 3274 | consul | 32 |
| 3275 | conquest | 32 |
| 3276 | conference | 32 |
| 3277 | con | 32 |
| 3278 | cheese | 32 |
| 3279 | carries | 32 |
| 3280 | capable | 32 |
| 3281 | bottle | 32 |
| 3282 | beshrew | 32 |
| 3283 | begot | 32 |
| 3284 | beats | 32 |
| 3285 | audrey | 32 |
| 3286 | antigonus | 32 |
| 3287 | acts | 32 |
| 3288 | abundance | 32 |
| 3289 | absolute | 32 |
| 3290 | voyage | 31 |
| 3291 | velvet | 31 |
| 3292 | unfold | 31 |
| 3293 | strumpet | 31 |
| 3294 | straw | 31 |
| 3295 | sinner | 31 |
| 3296 | shout | 31 |
| 3297 | seeks | 31 |
| 3298 | scroop | 31 |
| 3299 | rend | 31 |
| 3300 | rejoice | 31 |
| 3301 | redeem | 31 |
| 3302 | rais | 31 |
| 3303 | pronounce | 31 |
| 3304 | profound | 31 |
| 3305 | petty | 31 |
| 3306 | owes | 31 |
| 3307 | obeyed | 31 |
| 3308 | nicholas | 31 |
| 3309 | nevertheless | 31 |
| 3310 | musician | 31 |
| 3311 | mourning | 31 |
| 3312 | mild | 31 |
| 3313 | melt | 31 |
| 3314 | lesser | 31 |
| 3315 | ireland | 31 |
| 3316 | injuries | 31 |
| 3317 | hush | 31 |
| 3318 | husbands | 31 |
| 3319 | goddess | 31 |
| 3320 | gar | 31 |
| 3321 | fourteen | 31 |
| 3322 | forfeit | 31 |
| 3323 | flock | 31 |
| 3324 | extreme | 31 |
| 3325 | estimation | 31 |
| 3326 | entreaties | 31 |
| 3327 | doubtful | 31 |
| 3328 | disposed | 31 |
| 3329 | disguised | 31 |
| 3330 | deserved | 31 |
| 3331 | deeply | 31 |
| 3332 | cyprus | 31 |
| 3333 | current | 31 |
| 3334 | counsels | 31 |
| 3335 | corse | 31 |
| 3336 | corrupt | 31 |
| 3337 | cordelia | 31 |
| 3338 | conceal | 31 |
| 3339 | closet | 31 |
| 3340 | burial | 31 |
| 3341 | briefly | 31 |
| 3342 | box | 31 |
| 3343 | borrow | 31 |
| 3344 | boat | 31 |
| 3345 | beware | 31 |
| 3346 | bethink | 31 |
| 3347 | belov | 31 |
| 3348 | beds | 31 |
| 3349 | arrest | 31 |
| 3350 | approve | 31 |
| 3351 | approached | 31 |
| 3352 | ambassador | 31 |
| 3353 | accompanied | 31 |
| 3354 | accident | 31 |
| 3355 | wheat | 30 |
| 3356 | whate | 30 |
| 3357 | warning | 30 |
| 3358 | violence | 30 |
| 3359 | trim | 30 |
| 3360 | trifaldi | 30 |
| 3361 | treats | 30 |
| 3362 | tomorrow | 30 |
| 3363 | swell | 30 |
| 3364 | sweetest | 30 |
| 3365 | swears | 30 |
| 3366 | sting | 30 |
| 3367 | spurs | 30 |
| 3368 | sounded | 30 |
| 3369 | softly | 30 |
| 3370 | slip | 30 |
| 3371 | sisters | 30 |
| 3372 | shoe | 30 |
| 3373 | shadows | 30 |
| 3374 | senseless | 30 |
| 3375 | seized | 30 |
| 3376 | scurvy | 30 |
| 3377 | remorse | 30 |
| 3378 | recompense | 30 |
| 3379 | prepared | 30 |
| 3380 | prepar | 30 |
| 3381 | perilous | 30 |
| 3382 | pandulph | 30 |
| 3383 | painting | 30 |
| 3384 | ophelia | 30 |
| 3385 | occasions | 30 |
| 3386 | mention | 30 |
| 3387 | marquis | 30 |
| 3388 | maritornes | 30 |
| 3389 | lot | 30 |
| 3390 | lodging | 30 |
| 3391 | linen | 30 |
| 3392 | lightning | 30 |
| 3393 | knocks | 30 |
| 3394 | killed | 30 |
| 3395 | keen | 30 |
| 3396 | jaquenetta | 30 |
| 3397 | instruct | 30 |
| 3398 | ingratitude | 30 |
| 3399 | hare | 30 |
| 3400 | guildenstern | 30 |
| 3401 | grievous | 30 |
| 3402 | grandam | 30 |
| 3403 | gobbo | 30 |
| 3404 | forswear | 30 |
| 3405 | fifteen | 30 |
| 3406 | feather | 30 |
| 3407 | effects | 30 |
| 3408 | dam | 30 |
| 3409 | curs | 30 |
| 3410 | curiosity | 30 |
| 3411 | couch | 30 |
| 3412 | coin | 30 |
| 3413 | charged | 30 |
| 3414 | careful | 30 |
| 3415 | candle | 30 |
| 3416 | calf | 30 |
| 3417 | bush | 30 |
| 3418 | bosoms | 30 |
| 3419 | boots | 30 |
| 3420 | blue | 30 |
| 3421 | bells | 30 |
| 3422 | bay | 30 |
| 3423 | bargain | 30 |
| 3424 | apace | 30 |
| 3425 | andrew | 30 |
| 3426 | alice | 30 |
| 3427 | alforjas | 30 |
| 3428 | afeard | 30 |
| 3429 | wander | 29 |
| 3430 | walks | 29 |
| 3431 | waking | 29 |
| 3432 | waist | 29 |
| 3433 | victorious | 29 |
| 3434 | veins | 29 |
| 3435 | ungrateful | 29 |
| 3436 | turks | 29 |
| 3437 | tribute | 29 |
| 3438 | treated | 29 |
| 3439 | tie | 29 |
| 3440 | sup | 29 |
| 3441 | suffice | 29 |
| 3442 | strove | 29 |
| 3443 | stole | 29 |
| 3444 | stale | 29 |
| 3445 | stable | 29 |
| 3446 | spy | 29 |
| 3447 | spoils | 29 |
| 3448 | spit | 29 |
| 3449 | smoke | 29 |
| 3450 | sierra | 29 |
| 3451 | shoot | 29 |
| 3452 | scope | 29 |
| 3453 | saved | 29 |
| 3454 | saints | 29 |
| 3455 | roof | 29 |
| 3456 | retired | 29 |
| 3457 | requite | 29 |
| 3458 | relish | 29 |
| 3459 | quitted | 29 |
| 3460 | perceiving | 29 |
| 3461 | path | 29 |
| 3462 | ox | 29 |
| 3463 | oracle | 29 |
| 3464 | murd | 29 |
| 3465 | mistaken | 29 |
| 3466 | mightst | 29 |
| 3467 | metal | 29 |
| 3468 | manifest | 29 |
| 3469 | lowly | 29 |
| 3470 | lament | 29 |
| 3471 | kneels | 29 |
| 3472 | joys | 29 |
| 3473 | je | 29 |
| 3474 | inward | 29 |
| 3475 | instance | 29 |
| 3476 | innkeeper | 29 |
| 3477 | happier | 29 |
| 3478 | guil | 29 |
| 3479 | greece | 29 |
| 3480 | gaul | 29 |
| 3481 | gallows | 29 |
| 3482 | fold | 29 |
| 3483 | flattery | 29 |
| 3484 | flame | 29 |
| 3485 | fever | 29 |
| 3486 | fares | 29 |
| 3487 | exceeding | 29 |
| 3488 | evils | 29 |
| 3489 | everybody | 29 |
| 3490 | evermore | 29 |
| 3491 | evening | 29 |
| 3492 | ely | 29 |
| 3493 | dote | 29 |
| 3494 | distinction | 29 |
| 3495 | deserving | 29 |
| 3496 | describe | 29 |
| 3497 | declared | 29 |
| 3498 | deceived | 29 |
| 3499 | curtis | 29 |
| 3500 | curious | 29 |
| 3501 | couldst | 29 |
| 3502 | convinced | 29 |
| 3503 | conquer | 29 |
| 3504 | confidence | 29 |
| 3505 | compel | 29 |
| 3506 | commonwealth | 29 |
| 3507 | chrysostom | 29 |
| 3508 | cherish | 29 |
| 3509 | censure | 29 |
| 3510 | cam | 29 |
| 3511 | burns | 29 |
| 3512 | burned | 29 |
| 3513 | bridle | 29 |
| 3514 | breathing | 29 |
| 3515 | boon | 29 |
| 3516 | biscayan | 29 |
| 3517 | belongs | 29 |
| 3518 | beating | 29 |
| 3519 | arranged | 29 |
| 3520 | amaz | 29 |
| 3521 | advis | 29 |
| 3522 | admit | 29 |
| 3523 | admiration | 29 |
| 3524 | accursed | 29 |
| 3525 | abus | 29 |
| 3526 | worcester | 28 |
| 3527 | welsh | 28 |
| 3528 | wand | 28 |
| 3529 | uttering | 28 |
| 3530 | touches | 28 |
| 3531 | tosilos | 28 |
| 3532 | torches | 28 |
| 3533 | today | 28 |
| 3534 | titles | 28 |
| 3535 | tired | 28 |
| 3536 | theme | 28 |
| 3537 | thane | 28 |
| 3538 | sweetly | 28 |
| 3539 | swallow | 28 |
| 3540 | strangely | 28 |
| 3541 | stocks | 28 |
| 3542 | stockings | 28 |
| 3543 | stafford | 28 |
| 3544 | spurn | 28 |
| 3545 | spleen | 28 |
| 3546 | south | 28 |
| 3547 | solanio | 28 |
| 3548 | slowly | 28 |
| 3549 | sicilia | 28 |
| 3550 | shouting | 28 |
| 3551 | shepherdess | 28 |
| 3552 | secretary | 28 |
| 3553 | scratch | 28 |
| 3554 | saving | 28 |
| 3555 | rul | 28 |
| 3556 | rousillon | 28 |
| 3557 | risk | 28 |
| 3558 | rights | 28 |
| 3559 | reckoning | 28 |
| 3560 | race | 28 |
| 3561 | quietly | 28 |
| 3562 | quarrels | 28 |
| 3563 | preparation | 28 |
| 3564 | praised | 28 |
| 3565 | practise | 28 |
| 3566 | poetry | 28 |
| 3567 | pledge | 28 |
| 3568 | plant | 28 |
| 3569 | perpetual | 28 |
| 3570 | peevish | 28 |
| 3571 | pays | 28 |
| 3572 | paint | 28 |
| 3573 | ordinary | 28 |
| 3574 | opening | 28 |
| 3575 | nimble | 28 |
| 3576 | nigh | 28 |
| 3577 | moorish | 28 |
| 3578 | merlin | 28 |
| 3579 | meddle | 28 |
| 3580 | marrying | 28 |
| 3581 | mantle | 28 |
| 3582 | maecenas | 28 |
| 3583 | lively | 28 |
| 3584 | lifted | 28 |
| 3585 | latin | 28 |
| 3586 | kingly | 28 |
| 3587 | important | 28 |
| 3588 | hotspur | 28 |
| 3589 | herein | 28 |
| 3590 | haven | 28 |
| 3591 | hastened | 28 |
| 3592 | harmony | 28 |
| 3593 | halter | 28 |
| 3594 | gay | 28 |
| 3595 | gathered | 28 |
| 3596 | florence | 28 |
| 3597 | extremity | 28 |
| 3598 | extraordinary | 28 |
| 3599 | execute | 28 |
| 3600 | everlasting | 28 |
| 3601 | ev | 28 |
| 3602 | ent | 28 |
| 3603 | enchantments | 28 |
| 3604 | elinor | 28 |
| 3605 | eleven | 28 |
| 3606 | eats | 28 |
| 3607 | eagle | 28 |
| 3608 | driven | 28 |
| 3609 | converse | 28 |
| 3610 | concerns | 28 |
| 3611 | climb | 28 |
| 3612 | clerk | 28 |
| 3613 | clad | 28 |
| 3614 | changes | 28 |
| 3615 | carrier | 28 |
| 3616 | bushy | 28 |
| 3617 | brown | 28 |
| 3618 | bigger | 28 |
| 3619 | beneath | 28 |
| 3620 | beholding | 28 |
| 3621 | barbary | 28 |
| 3622 | austria | 28 |
| 3623 | ant | 28 |
| 3624 | allegiance | 28 |
| 3625 | actions | 28 |
| 3626 | aboard | 28 |
| 3627 | wooing | 27 |
| 3628 | woeful | 27 |
| 3629 | windows | 27 |
| 3630 | wherever | 27 |
| 3631 | wag | 27 |
| 3632 | vous | 27 |
| 3633 | upright | 27 |
| 3634 | unseen | 27 |
| 3635 | uneasy | 27 |
| 3636 | troubles | 27 |
| 3637 | throats | 27 |
| 3638 | swearing | 27 |
| 3639 | sue | 27 |
| 3640 | succour | 27 |
| 3641 | stubborn | 27 |
| 3642 | shouts | 27 |
| 3643 | shelter | 27 |
| 3644 | riches | 27 |
| 3645 | restrain | 27 |
| 3646 | relate | 27 |
| 3647 | quantity | 27 |
| 3648 | prov | 27 |
| 3649 | plight | 27 |
| 3650 | ope | 27 |
| 3651 | oblivion | 27 |
| 3652 | notable | 27 |
| 3653 | nearly | 27 |
| 3654 | naught | 27 |
| 3655 | mood | 27 |
| 3656 | mirror | 27 |
| 3657 | ministers | 27 |
| 3658 | miles | 27 |
| 3659 | mankind | 27 |
| 3660 | lodge | 27 |
| 3661 | locks | 27 |
| 3662 | liked | 27 |
| 3663 | knighthood | 27 |
| 3664 | joan | 27 |
| 3665 | instantly | 27 |
| 3666 | innocence | 27 |
| 3667 | ingenious | 27 |
| 3668 | incidents | 27 |
| 3669 | imagined | 27 |
| 3670 | hue | 27 |
| 3671 | hose | 27 |
| 3672 | horrible | 27 |
| 3673 | hidden | 27 |
| 3674 | heirs | 27 |
| 3675 | hap | 27 |
| 3676 | grandsire | 27 |
| 3677 | garland | 27 |
| 3678 | fort | 27 |
| 3679 | forsake | 27 |
| 3680 | forc | 27 |
| 3681 | folk | 27 |
| 3682 | fancied | 27 |
| 3683 | duties | 27 |
| 3684 | dove | 27 |
| 3685 | dispose | 27 |
| 3686 | destiny | 27 |
| 3687 | deserts | 27 |
| 3688 | denmark | 27 |
| 3689 | decay | 27 |
| 3690 | deaths | 27 |
| 3691 | curst | 27 |
| 3692 | crystal | 27 |
| 3693 | contract | 27 |
| 3694 | constancy | 27 |
| 3695 | comforts | 27 |
| 3696 | closely | 27 |
| 3697 | chin | 27 |
| 3698 | c | 27 |
| 3699 | butcher | 27 |
| 3700 | bull | 27 |
| 3701 | breeches | 27 |
| 3702 | badly | 27 |
| 3703 | aware | 27 |
| 3704 | aunt | 27 |
| 3705 | attire | 27 |
| 3706 | astonishment | 27 |
| 3707 | apparent | 27 |
| 3708 | anxious | 27 |
| 3709 | amorous | 27 |
| 3710 | aged | 27 |
| 3711 | affliction | 27 |
| 3712 | affect | 27 |
| 3713 | adopted | 27 |
| 3714 | ado | 27 |
| 3715 | acknowledge | 27 |
| 3716 | abbess | 27 |
| 3717 | yielding | 26 |
| 3718 | willow | 26 |
| 3719 | whit | 26 |
| 3720 | wherewith | 26 |
| 3721 | wenches | 26 |
| 3722 | walter | 26 |
| 3723 | walking | 26 |
| 3724 | wail | 26 |
| 3725 | virginity | 26 |
| 3726 | veil | 26 |
| 3727 | urg | 26 |
| 3728 | unwilling | 26 |
| 3729 | unkind | 26 |
| 3730 | travelling | 26 |
| 3731 | transformed | 26 |
| 3732 | threats | 26 |
| 3733 | sung | 26 |
| 3734 | student | 26 |
| 3735 | stuck | 26 |
| 3736 | stirring | 26 |
| 3737 | stabs | 26 |
| 3738 | speeches | 26 |
| 3739 | ships | 26 |
| 3740 | scourge | 26 |
| 3741 | rutland | 26 |
| 3742 | royalty | 26 |
| 3743 | rosencrantz | 26 |
| 3744 | rings | 26 |
| 3745 | richly | 26 |
| 3746 | resign | 26 |
| 3747 | reproach | 26 |
| 3748 | region | 26 |
| 3749 | really | 26 |
| 3750 | raven | 26 |
| 3751 | rabble | 26 |
| 3752 | prosperous | 26 |
| 3753 | prosper | 26 |
| 3754 | pressed | 26 |
| 3755 | prais | 26 |
| 3756 | powerful | 26 |
| 3757 | port | 26 |
| 3758 | pope | 26 |
| 3759 | pole | 26 |
| 3760 | plebeians | 26 |
| 3761 | owl | 26 |
| 3762 | overdone | 26 |
| 3763 | oil | 26 |
| 3764 | offences | 26 |
| 3765 | nobleman | 26 |
| 3766 | neglect | 26 |
| 3767 | nearer | 26 |
| 3768 | natures | 26 |
| 3769 | mystery | 26 |
| 3770 | moral | 26 |
| 3771 | monarch | 26 |
| 3772 | miseries | 26 |
| 3773 | michael | 26 |
| 3774 | mercutio | 26 |
| 3775 | marg | 26 |
| 3776 | marcela | 26 |
| 3777 | manhood | 26 |
| 3778 | maidens | 26 |
| 3779 | load | 26 |
| 3780 | livery | 26 |
| 3781 | likeness | 26 |
| 3782 | laughed | 26 |
| 3783 | lark | 26 |
| 3784 | landlady | 26 |
| 3785 | lads | 26 |
| 3786 | lacquey | 26 |
| 3787 | l | 26 |
| 3788 | insult | 26 |
| 3789 | imperial | 26 |
| 3790 | immortal | 26 |
| 3791 | imitate | 26 |
| 3792 | hippolyta | 26 |
| 3793 | hey | 26 |
| 3794 | herbs | 26 |
| 3795 | helped | 26 |
| 3796 | hasty | 26 |
| 3797 | governors | 26 |
| 3798 | glendower | 26 |
| 3799 | froth | 26 |
| 3800 | features | 26 |
| 3801 | fancies | 26 |
| 3802 | expense | 26 |
| 3803 | exercise | 26 |
| 3804 | enjoyment | 26 |
| 3805 | enchanter | 26 |
| 3806 | employment | 26 |
| 3807 | dukes | 26 |
| 3808 | divided | 26 |
| 3809 | desir | 26 |
| 3810 | demands | 26 |
| 3811 | demanded | 26 |
| 3812 | decius | 26 |
| 3813 | cured | 26 |
| 3814 | creep | 26 |
| 3815 | corioli | 26 |
| 3816 | cook | 26 |
| 3817 | contain | 26 |
| 3818 | confession | 26 |
| 3819 | cities | 26 |
| 3820 | circumstances | 26 |
| 3821 | choler | 26 |
| 3822 | charg | 26 |
| 3823 | catholic | 26 |
| 3824 | caps | 26 |
| 3825 | cannon | 26 |
| 3826 | boldness | 26 |
| 3827 | betimes | 26 |
| 3828 | beguile | 26 |
| 3829 | begg | 26 |
| 3830 | beads | 26 |
| 3831 | barnardine | 26 |
| 3832 | awe | 26 |
| 3833 | astonished | 26 |
| 3834 | ashes | 26 |
| 3835 | asham | 26 |
| 3836 | arrival | 26 |
| 3837 | apprehension | 26 |
| 3838 | answering | 26 |
| 3839 | amends | 26 |
| 3840 | aegeon | 26 |
| 3841 | access | 26 |
| 3842 | wonders | 25 |
| 3843 | wolves | 25 |
| 3844 | whereto | 25 |
| 3845 | wandering | 25 |
| 3846 | visor | 25 |
| 3847 | ventidius | 25 |
| 3848 | vent | 25 |
| 3849 | tragedy | 25 |
| 3850 | torn | 25 |
| 3851 | throwing | 25 |
| 3852 | thanked | 25 |
| 3853 | swain | 25 |
| 3854 | suitor | 25 |
| 3855 | strangers | 25 |
| 3856 | stopped | 25 |
| 3857 | stopp | 25 |
| 3858 | sovereignty | 25 |
| 3859 | soundly | 25 |
| 3860 | size | 25 |
| 3861 | siward | 25 |
| 3862 | signify | 25 |
| 3863 | sheriff | 25 |
| 3864 | sex | 25 |
| 3865 | sending | 25 |
| 3866 | sandys | 25 |
| 3867 | salute | 25 |
| 3868 | robbed | 25 |
| 3869 | roaring | 25 |
| 3870 | rises | 25 |
| 3871 | respects | 25 |
| 3872 | religion | 25 |
| 3873 | rebel | 25 |
| 3874 | rashness | 25 |
| 3875 | purity | 25 |
| 3876 | pull | 25 |
| 3877 | properly | 25 |
| 3878 | prodigal | 25 |
| 3879 | pressing | 25 |
| 3880 | persuasion | 25 |
| 3881 | pernicious | 25 |
| 3882 | paying | 25 |
| 3883 | patch | 25 |
| 3884 | passes | 25 |
| 3885 | parliament | 25 |
| 3886 | osr | 25 |
| 3887 | occurred | 25 |
| 3888 | noted | 25 |
| 3889 | needed | 25 |
| 3890 | neat | 25 |
| 3891 | mules | 25 |
| 3892 | mask | 25 |
| 3893 | magic | 25 |
| 3894 | liquor | 25 |
| 3895 | limit | 25 |
| 3896 | lass | 25 |
| 3897 | joint | 25 |
| 3898 | humility | 25 |
| 3899 | hounds | 25 |
| 3900 | honoured | 25 |
| 3901 | harbour | 25 |
| 3902 | grieves | 25 |
| 3903 | gratify | 25 |
| 3904 | grain | 25 |
| 3905 | goods | 25 |
| 3906 | goat | 25 |
| 3907 | gentleness | 25 |
| 3908 | gazing | 25 |
| 3909 | frenchman | 25 |
| 3910 | forms | 25 |
| 3911 | fling | 25 |
| 3912 | female | 25 |
| 3913 | exile | 25 |
| 3914 | everywhere | 25 |
| 3915 | events | 25 |
| 3916 | est | 25 |
| 3917 | enjoyed | 25 |
| 3918 | earnestly | 25 |
| 3919 | disturb | 25 |
| 3920 | disenchantment | 25 |
| 3921 | diet | 25 |
| 3922 | devotion | 25 |
| 3923 | determine | 25 |
| 3924 | descend | 25 |
| 3925 | deputy | 25 |
| 3926 | dangers | 25 |
| 3927 | dancing | 25 |
| 3928 | crazy | 25 |
| 3929 | convenient | 25 |
| 3930 | control | 25 |
| 3931 | conqueror | 25 |
| 3932 | confident | 25 |
| 3933 | comrades | 25 |
| 3934 | completely | 25 |
| 3935 | chastity | 25 |
| 3936 | charitable | 25 |
| 3937 | capital | 25 |
| 3938 | burnt | 25 |
| 3939 | bliss | 25 |
| 3940 | blessings | 25 |
| 3941 | banks | 25 |
| 3942 | bag | 25 |
| 3943 | backs | 25 |
| 3944 | attain | 25 |
| 3945 | articles | 25 |
| 3946 | aloft | 25 |
| 3947 | alexandria | 25 |
| 3948 | zounds | 24 |
| 3949 | youngest | 24 |
| 3950 | worms | 24 |
| 3951 | whipping | 24 |
| 3952 | whereby | 24 |
| 3953 | whenever | 24 |
| 3954 | venom | 24 |
| 3955 | vassal | 24 |
| 3956 | vanquish | 24 |
| 3957 | vanity | 24 |
| 3958 | trying | 24 |
| 3959 | trifles | 24 |
| 3960 | throws | 24 |
| 3961 | thoroughly | 24 |
| 3962 | thirst | 24 |
| 3963 | tables | 24 |
| 3964 | swoon | 24 |
| 3965 | surprised | 24 |
| 3966 | summon | 24 |
| 3967 | stripped | 24 |
| 3968 | strip | 24 |
| 3969 | strew | 24 |
| 3970 | stories | 24 |
| 3971 | spacious | 24 |
| 3972 | sorely | 24 |
| 3973 | skull | 24 |
| 3974 | skins | 24 |
| 3975 | shining | 24 |
| 3976 | severally | 24 |
| 3977 | servingman | 24 |
| 3978 | semblance | 24 |
| 3979 | scruple | 24 |
| 3980 | sally | 24 |
| 3981 | sacrifice | 24 |
| 3982 | rules | 24 |
| 3983 | richer | 24 |
| 3984 | requisite | 24 |
| 3985 | religious | 24 |
| 3986 | released | 24 |
| 3987 | recorded | 24 |
| 3988 | recognise | 24 |
| 3989 | rear | 24 |
| 3990 | process | 24 |
| 3991 | played | 24 |
| 3992 | paces | 24 |
| 3993 | outside | 24 |
| 3994 | ourself | 24 |
| 3995 | nest | 24 |
| 3996 | neighbourhood | 24 |
| 3997 | moves | 24 |
| 3998 | missing | 24 |
| 3999 | marching | 24 |
| 4000 | liver | 24 |
| 4001 | lap | 24 |
| 4002 | juno | 24 |
| 4003 | julius | 24 |
| 4004 | intentions | 24 |
| 4005 | inclination | 24 |
| 4006 | impatience | 24 |
| 4007 | hiding | 24 |
| 4008 | herd | 24 |
| 4009 | guards | 24 |
| 4010 | griffith | 24 |
| 4011 | glend | 24 |
| 4012 | gets | 24 |
| 4013 | frenchmen | 24 |
| 4014 | filthy | 24 |
| 4015 | exclaiming | 24 |
| 4016 | examine | 24 |
| 4017 | esteemed | 24 |
| 4018 | endeavour | 24 |
| 4019 | elements | 24 |
| 4020 | dukedom | 24 |
| 4021 | dried | 24 |
| 4022 | dowry | 24 |
| 4023 | doubts | 24 |
| 4024 | display | 24 |
| 4025 | dismal | 24 |
| 4026 | disguise | 24 |
| 4027 | discord | 24 |
| 4028 | diest | 24 |
| 4029 | depend | 24 |
| 4030 | den | 24 |
| 4031 | defiance | 24 |
| 4032 | dearer | 24 |
| 4033 | date | 24 |
| 4034 | dat | 24 |
| 4035 | contains | 24 |
| 4036 | changing | 24 |
| 4037 | chains | 24 |
| 4038 | cassandra | 24 |
| 4039 | captives | 24 |
| 4040 | built | 24 |
| 4041 | build | 24 |
| 4042 | bridge | 24 |
| 4043 | breeds | 24 |
| 4044 | branches | 24 |
| 4045 | bonds | 24 |
| 4046 | bondage | 24 |
| 4047 | blanch | 24 |
| 4048 | bereft | 24 |
| 4049 | beggars | 24 |
| 4050 | beget | 24 |
| 4051 | befallen | 24 |
| 4052 | barbarous | 24 |
| 4053 | attacked | 24 |
| 4054 | astonish | 24 |
| 4055 | assistance | 24 |
| 4056 | arrows | 24 |
| 4057 | arch | 24 |
| 4058 | appeal | 24 |
| 4059 | amusement | 24 |
| 4060 | alarums | 24 |
| 4061 | adding | 24 |
| 4062 | whipt | 23 |
| 4063 | wearing | 23 |
| 4064 | wak | 23 |
| 4065 | vii | 23 |
| 4066 | venus | 23 |
| 4067 | varlet | 23 |
| 4068 | valeria | 23 |
| 4069 | unkindness | 23 |
| 4070 | unjust | 23 |
| 4071 | undergo | 23 |
| 4072 | twould | 23 |
| 4073 | travellers | 23 |
| 4074 | thousands | 23 |
| 4075 | tents | 23 |
| 4076 | tempted | 23 |
| 4077 | surprise | 23 |
| 4078 | surety | 23 |
| 4079 | sufferings | 23 |
| 4080 | sufferance | 23 |
| 4081 | studied | 23 |
| 4082 | striving | 23 |
| 4083 | string | 23 |
| 4084 | strict | 23 |
| 4085 | steep | 23 |
| 4086 | sleeve | 23 |
| 4087 | sinews | 23 |
| 4088 | simpcox | 23 |
| 4089 | security | 23 |
| 4090 | scholar | 23 |
| 4091 | sails | 23 |
| 4092 | robes | 23 |
| 4093 | robb | 23 |
| 4094 | roads | 23 |
| 4095 | returns | 23 |
| 4096 | result | 23 |
| 4097 | repeated | 23 |
| 4098 | regent | 23 |
| 4099 | purge | 23 |
| 4100 | prudent | 23 |
| 4101 | procure | 23 |
| 4102 | proclamation | 23 |
| 4103 | printed | 23 |
| 4104 | presume | 23 |
| 4105 | prefer | 23 |
| 4106 | pox | 23 |
| 4107 | phoebus | 23 |
| 4108 | philario | 23 |
| 4109 | perjur | 23 |
| 4110 | penny | 23 |
| 4111 | peer | 23 |
| 4112 | pages | 23 |
| 4113 | ornament | 23 |
| 4114 | oppose | 23 |
| 4115 | nuptial | 23 |
| 4116 | neptune | 23 |
| 4117 | mutiny | 23 |
| 4118 | muster | 23 |
| 4119 | moan | 23 |
| 4120 | mills | 23 |
| 4121 | merrily | 23 |
| 4122 | medicine | 23 |
| 4123 | meadow | 23 |
| 4124 | limb | 23 |
| 4125 | lighted | 23 |
| 4126 | lets | 23 |
| 4127 | leather | 23 |
| 4128 | leaning | 23 |
| 4129 | lastly | 23 |
| 4130 | kinsmen | 23 |
| 4131 | italian | 23 |
| 4132 | infant | 23 |
| 4133 | inch | 23 |
| 4134 | hides | 23 |
| 4135 | halt | 23 |
| 4136 | groom | 23 |
| 4137 | gregorio | 23 |
| 4138 | greeting | 23 |
| 4139 | gilded | 23 |
| 4140 | funeral | 23 |
| 4141 | fray | 23 |
| 4142 | flint | 23 |
| 4143 | flaminius | 23 |
| 4144 | feats | 23 |
| 4145 | favoured | 23 |
| 4146 | fainting | 23 |
| 4147 | faction | 23 |
| 4148 | ey | 23 |
| 4149 | extend | 23 |
| 4150 | executed | 23 |
| 4151 | etc | 23 |
| 4152 | enmity | 23 |
| 4153 | elsinore | 23 |
| 4154 | drunken | 23 |
| 4155 | dismounted | 23 |
| 4156 | diseases | 23 |
| 4157 | descended | 23 |
| 4158 | depths | 23 |
| 4159 | cuts | 23 |
| 4160 | craves | 23 |
| 4161 | cowardly | 23 |
| 4162 | cornwall | 23 |
| 4163 | confer | 23 |
| 4164 | complaint | 23 |
| 4165 | coats | 23 |
| 4166 | closed | 23 |
| 4167 | cheerful | 23 |
| 4168 | caused | 23 |
| 4169 | carver | 23 |
| 4170 | bona | 23 |
| 4171 | blot | 23 |
| 4172 | babes | 23 |
| 4173 | axe | 23 |
| 4174 | assault | 23 |
| 4175 | apply | 23 |
| 4176 | anywhere | 23 |
| 4177 | anxiety | 23 |
| 4178 | amity | 23 |
| 4179 | alms | 23 |
| 4180 | afoot | 23 |
| 4181 | afar | 23 |
| 4182 | admitted | 23 |
| 4183 | abused | 23 |
| 4184 | wronged | 22 |
| 4185 | ward | 22 |
| 4186 | volsces | 22 |
| 4187 | vexation | 22 |
| 4188 | vanish | 22 |
| 4189 | usage | 22 |
| 4190 | untimely | 22 |
| 4191 | underneath | 22 |
| 4192 | tutor | 22 |
| 4193 | tush | 22 |
| 4194 | trusty | 22 |
| 4195 | thankful | 22 |
| 4196 | tenderness | 22 |
| 4197 | sustain | 22 |
| 4198 | suitors | 22 |
| 4199 | statue | 22 |
| 4200 | stake | 22 |
| 4201 | split | 22 |
| 4202 | speedy | 22 |
| 4203 | sober | 22 |
| 4204 | simply | 22 |
| 4205 | shun | 22 |
| 4206 | shrewsbury | 22 |
| 4207 | shaking | 22 |
| 4208 | sergeant | 22 |
| 4209 | scorns | 22 |
| 4210 | sanchica | 22 |
| 4211 | roland | 22 |
| 4212 | rogues | 22 |
| 4213 | revenue | 22 |
| 4214 | resist | 22 |
| 4215 | requires | 22 |
| 4216 | reported | 22 |
| 4217 | relieved | 22 |
| 4218 | reed | 22 |
| 4219 | recovered | 22 |
| 4220 | rack | 22 |
| 4221 | provoke | 22 |
| 4222 | prosperity | 22 |
| 4223 | proposed | 22 |
| 4224 | proofs | 22 |
| 4225 | priests | 22 |
| 4226 | planted | 22 |
| 4227 | plains | 22 |
| 4228 | petticoat | 22 |
| 4229 | peto | 22 |
| 4230 | petition | 22 |
| 4231 | patricians | 22 |
| 4232 | panthino | 22 |
| 4233 | overcome | 22 |
| 4234 | original | 22 |
| 4235 | novel | 22 |
| 4236 | nobler | 22 |
| 4237 | nightly | 22 |
| 4238 | nail | 22 |
| 4239 | mouldy | 22 |
| 4240 | mothers | 22 |
| 4241 | monsters | 22 |
| 4242 | mischance | 22 |
| 4243 | merciful | 22 |
| 4244 | maker | 22 |
| 4245 | mak | 22 |
| 4246 | lucy | 22 |
| 4247 | letting | 22 |
| 4248 | laying | 22 |
| 4249 | laurence | 22 |
| 4250 | judges | 22 |
| 4251 | judas | 22 |
| 4252 | jot | 22 |
| 4253 | jests | 22 |
| 4254 | inclined | 22 |
| 4255 | import | 22 |
| 4256 | impediment | 22 |
| 4257 | impatient | 22 |
| 4258 | idleness | 22 |
| 4259 | hourly | 22 |
| 4260 | hind | 22 |
| 4261 | heap | 22 |
| 4262 | haughty | 22 |
| 4263 | handsome | 22 |
| 4264 | grieved | 22 |
| 4265 | gravity | 22 |
| 4266 | grateful | 22 |
| 4267 | grandfather | 22 |
| 4268 | gloss | 22 |
| 4269 | gained | 22 |
| 4270 | fran | 22 |
| 4271 | flout | 22 |
| 4272 | fellowship | 22 |
| 4273 | faulconbridge | 22 |
| 4274 | falsely | 22 |
| 4275 | exploit | 22 |
| 4276 | ending | 22 |
| 4277 | eglamour | 22 |
| 4278 | egg | 22 |
| 4279 | drift | 22 |
| 4280 | dreamt | 22 |
| 4281 | dismay | 22 |
| 4282 | discreet | 22 |
| 4283 | discovery | 22 |
| 4284 | directions | 22 |
| 4285 | despise | 22 |
| 4286 | description | 22 |
| 4287 | delightful | 22 |
| 4288 | degrees | 22 |
| 4289 | defeat | 22 |
| 4290 | deceit | 22 |
| 4291 | cuckoo | 22 |
| 4292 | crimes | 22 |
| 4293 | crest | 22 |
| 4294 | create | 22 |
| 4295 | crafty | 22 |
| 4296 | corporal | 22 |
| 4297 | cornelius | 22 |
| 4298 | conquered | 22 |
| 4299 | composition | 22 |
| 4300 | chorus | 22 |
| 4301 | cawdor | 22 |
| 4302 | causes | 22 |
| 4303 | carriage | 22 |
| 4304 | careless | 22 |
| 4305 | campeius | 22 |
| 4306 | bridegroom | 22 |
| 4307 | breadth | 22 |
| 4308 | borrowed | 22 |
| 4309 | boatswain | 22 |
| 4310 | bending | 22 |
| 4311 | beaufort | 22 |
| 4312 | beau | 22 |
| 4313 | attentively | 22 |
| 4314 | asunder | 22 |
| 4315 | armies | 22 |
| 4316 | apparently | 22 |
| 4317 | ancestors | 22 |
| 4318 | afflicted | 22 |
| 4319 | affected | 22 |
| 4320 | acquaint | 22 |
| 4321 | absurdities | 22 |
| 4322 | witted | 21 |
| 4323 | withdrew | 21 |
| 4324 | wedded | 21 |
| 4325 | vision | 21 |
| 4326 | uses | 21 |
| 4327 | uncertain | 21 |
| 4328 | tyrrel | 21 |
| 4329 | trifling | 21 |
| 4330 | treat | 21 |
| 4331 | tokens | 21 |
| 4332 | tiger | 21 |
| 4333 | tavern | 21 |
| 4334 | studies | 21 |
| 4335 | strait | 21 |
| 4336 | stab | 21 |
| 4337 | speedily | 21 |
| 4338 | sickly | 21 |
| 4339 | servilius | 21 |
| 4340 | saragossa | 21 |
| 4341 | rumour | 21 |
| 4342 | rt | 21 |
| 4343 | rites | 21 |
| 4344 | receives | 21 |
| 4345 | reap | 21 |
| 4346 | readiness | 21 |
| 4347 | raging | 21 |
| 4348 | pursued | 21 |
| 4349 | profane | 21 |
| 4350 | prodigious | 21 |
| 4351 | proculeius | 21 |
| 4352 | proceedings | 21 |
| 4353 | potent | 21 |
| 4354 | pot | 21 |
| 4355 | possessed | 21 |
| 4356 | pine | 21 |
| 4357 | perplexity | 21 |
| 4358 | particulars | 21 |
| 4359 | opposed | 21 |
| 4360 | nymphs | 21 |
| 4361 | mounting | 21 |
| 4362 | moonshine | 21 |
| 4363 | montjoy | 21 |
| 4364 | mongst | 21 |
| 4365 | mishap | 21 |
| 4366 | miracles | 21 |
| 4367 | mightily | 21 |
| 4368 | mamillius | 21 |
| 4369 | lute | 21 |
| 4370 | lists | 21 |
| 4371 | les | 21 |
| 4372 | landed | 21 |
| 4373 | kneeling | 21 |
| 4374 | kissed | 21 |
| 4375 | jesu | 21 |
| 4376 | invite | 21 |
| 4377 | intents | 21 |
| 4378 | integrity | 21 |
| 4379 | instruction | 21 |
| 4380 | inquire | 21 |
| 4381 | infected | 21 |
| 4382 | impudent | 21 |
| 4383 | impression | 21 |
| 4384 | ice | 21 |
| 4385 | hume | 21 |
| 4386 | headed | 21 |
| 4387 | hatred | 21 |
| 4388 | harvest | 21 |
| 4389 | harmless | 21 |
| 4390 | grim | 21 |
| 4391 | gratitude | 21 |
| 4392 | gines | 21 |
| 4393 | fountain | 21 |
| 4394 | forlorn | 21 |
| 4395 | flattering | 21 |
| 4396 | fitted | 21 |
| 4397 | finest | 21 |
| 4398 | finally | 21 |
| 4399 | fertile | 21 |
| 4400 | feeding | 21 |
| 4401 | faster | 21 |
| 4402 | excursions | 21 |
| 4403 | enrich | 21 |
| 4404 | election | 21 |
| 4405 | divorce | 21 |
| 4406 | division | 21 |
| 4407 | dispos | 21 |
| 4408 | diamond | 21 |
| 4409 | dealing | 21 |
| 4410 | crush | 21 |
| 4411 | crew | 21 |
| 4412 | created | 21 |
| 4413 | cowardice | 21 |
| 4414 | correction | 21 |
| 4415 | correct | 21 |
| 4416 | coronation | 21 |
| 4417 | contrived | 21 |
| 4418 | compound | 21 |
| 4419 | composed | 21 |
| 4420 | commended | 21 |
| 4421 | com | 21 |
| 4422 | clay | 21 |
| 4423 | clara | 21 |
| 4424 | characters | 21 |
| 4425 | cases | 21 |
| 4426 | bully | 21 |
| 4427 | brethren | 21 |
| 4428 | braying | 21 |
| 4429 | brakenbury | 21 |
| 4430 | beastly | 21 |
| 4431 | bands | 21 |
| 4432 | ball | 21 |
| 4433 | avaunt | 21 |
| 4434 | avail | 21 |
| 4435 | authors | 21 |
| 4436 | attach | 21 |
| 4437 | asses | 21 |
| 4438 | article | 21 |
| 4439 | approaches | 21 |
| 4440 | ample | 21 |
| 4441 | accus | 21 |
| 4442 | accomplished | 21 |
| 4443 | accidents | 21 |
| 4444 | abhorson | 21 |
| 4445 | witnesses | 20 |
| 4446 | wholly | 20 |
| 4447 | whereat | 20 |
| 4448 | wet | 20 |
| 4449 | wasted | 20 |
| 4450 | vassals | 20 |
| 4451 | valued | 20 |
| 4452 | unlike | 20 |
| 4453 | universal | 20 |
| 4454 | treasons | 20 |
| 4455 | thyreus | 20 |
| 4456 | succeed | 20 |
| 4457 | submit | 20 |
| 4458 | states | 20 |
| 4459 | snatch | 20 |
| 4460 | smallest | 20 |
| 4461 | sixty | 20 |
| 4462 | sixteen | 20 |
| 4463 | sith | 20 |
| 4464 | signal | 20 |
| 4465 | sights | 20 |
| 4466 | sheet | 20 |
| 4467 | seizing | 20 |
| 4468 | scarus | 20 |
| 4469 | sands | 20 |
| 4470 | samp | 20 |
| 4471 | rot | 20 |
| 4472 | respected | 20 |
| 4473 | reproof | 20 |
| 4474 | rein | 20 |
| 4475 | regards | 20 |
| 4476 | ravish | 20 |
| 4477 | quintus | 20 |
| 4478 | preserved | 20 |
| 4479 | precedent | 20 |
| 4480 | pounds | 20 |
| 4481 | posted | 20 |
| 4482 | pitied | 20 |
| 4483 | pindarus | 20 |
| 4484 | pilgrim | 20 |
| 4485 | perjury | 20 |
| 4486 | performance | 20 |
| 4487 | perfectly | 20 |
| 4488 | peep | 20 |
| 4489 | peaceful | 20 |
| 4490 | patiently | 20 |
| 4491 | parties | 20 |
| 4492 | palaces | 20 |
| 4493 | opinions | 20 |
| 4494 | offering | 20 |
| 4495 | obligation | 20 |
| 4496 | noblest | 20 |
| 4497 | morisco | 20 |
| 4498 | mocks | 20 |
| 4499 | mistook | 20 |
| 4500 | mingled | 20 |
| 4501 | mate | 20 |
| 4502 | manly | 20 |
| 4503 | male | 20 |
| 4504 | limits | 20 |
| 4505 | leonatus | 20 |
| 4506 | legions | 20 |
| 4507 | ld | 20 |
| 4508 | lances | 20 |
| 4509 | lame | 20 |
| 4510 | ladder | 20 |
| 4511 | keys | 20 |
| 4512 | judgments | 20 |
| 4513 | joined | 20 |
| 4514 | instinct | 20 |
| 4515 | injurious | 20 |
| 4516 | influence | 20 |
| 4517 | infection | 20 |
| 4518 | immediate | 20 |
| 4519 | images | 20 |
| 4520 | idly | 20 |
| 4521 | homage | 20 |
| 4522 | hangman | 20 |
| 4523 | guiltless | 20 |
| 4524 | gilt | 20 |
| 4525 | generosity | 20 |
| 4526 | flute | 20 |
| 4527 | flames | 20 |
| 4528 | fitting | 20 |
| 4529 | fires | 20 |
| 4530 | evidence | 20 |
| 4531 | errand | 20 |
| 4532 | epilogue | 20 |
| 4533 | dwells | 20 |
| 4534 | dubbed | 20 |
| 4535 | dian | 20 |
| 4536 | devilish | 20 |
| 4537 | descent | 20 |
| 4538 | delights | 20 |
| 4539 | dejected | 20 |
| 4540 | deck | 20 |
| 4541 | decided | 20 |
| 4542 | dash | 20 |
| 4543 | cudgel | 20 |
| 4544 | crows | 20 |
| 4545 | crossed | 20 |
| 4546 | copy | 20 |
| 4547 | consideration | 20 |
| 4548 | concern | 20 |
| 4549 | concealed | 20 |
| 4550 | compared | 20 |
| 4551 | comfortable | 20 |
| 4552 | christendom | 20 |
| 4553 | cato | 20 |
| 4554 | castilian | 20 |
| 4555 | canker | 20 |
| 4556 | cambridge | 20 |
| 4557 | butt | 20 |
| 4558 | branch | 20 |
| 4559 | bootless | 20 |
| 4560 | blushing | 20 |
| 4561 | blowing | 20 |
| 4562 | blanket | 20 |
| 4563 | ber | 20 |
| 4564 | bench | 20 |
| 4565 | bars | 20 |
| 4566 | balsam | 20 |
| 4567 | bald | 20 |
| 4568 | backward | 20 |
| 4569 | avenge | 20 |
| 4570 | assist | 20 |
| 4571 | arts | 20 |
| 4572 | apprehend | 20 |
| 4573 | anointed | 20 |
| 4574 | ambassadors | 20 |
| 4575 | alvaro | 20 |
| 4576 | aloof | 20 |
| 4577 | albany | 20 |
| 4578 | adore | 20 |
| 4579 | absurd | 20 |
| 4580 | abhor | 20 |
| 4581 | abbey | 20 |
| 4582 | worthless | 19 |
| 4583 | wool | 19 |
| 4584 | wondering | 19 |
| 4585 | witty | 19 |
| 4586 | witchcraft | 19 |
| 4587 | wisest | 19 |
| 4588 | wheels | 19 |
| 4589 | westminster | 19 |
| 4590 | weed | 19 |
| 4591 | wealthy | 19 |
| 4592 | waves | 19 |
| 4593 | victor | 19 |
| 4594 | valise | 19 |
| 4595 | urs | 19 |
| 4596 | tubal | 19 |
| 4597 | truer | 19 |
| 4598 | tribune | 19 |
| 4599 | trespass | 19 |
| 4600 | toe | 19 |
| 4601 | thorns | 19 |
| 4602 | tawny | 19 |
| 4603 | talks | 19 |
| 4604 | surpris | 19 |
| 4605 | sugar | 19 |
| 4606 | succession | 19 |
| 4607 | successful | 19 |
| 4608 | stealing | 19 |
| 4609 | stabb | 19 |
| 4610 | springs | 19 |
| 4611 | songs | 19 |
| 4612 | shop | 19 |
| 4613 | seville | 19 |
| 4614 | settle | 19 |
| 4615 | scot | 19 |
| 4616 | scheme | 19 |
| 4617 | scandal | 19 |
| 4618 | sav | 19 |
| 4619 | rue | 19 |
| 4620 | retires | 19 |
| 4621 | reserved | 19 |
| 4622 | reports | 19 |
| 4623 | remainder | 19 |
| 4624 | relent | 19 |
| 4625 | reflection | 19 |
| 4626 | reduced | 19 |
| 4627 | reaching | 19 |
| 4628 | rated | 19 |
| 4629 | queens | 19 |
| 4630 | proves | 19 |
| 4631 | prophet | 19 |
| 4632 | prophesy | 19 |
| 4633 | prime | 19 |
| 4634 | pretence | 19 |
| 4635 | polished | 19 |
| 4636 | pointed | 19 |
| 4637 | pipe | 19 |
| 4638 | pillow | 19 |
| 4639 | pike | 19 |
| 4640 | peasants | 19 |
| 4641 | partner | 19 |
| 4642 | parson | 19 |
| 4643 | noon | 19 |
| 4644 | non | 19 |
| 4645 | nod | 19 |
| 4646 | naturally | 19 |
| 4647 | named | 19 |
| 4648 | modern | 19 |
| 4649 | milford | 19 |
| 4650 | metellus | 19 |
| 4651 | maybe | 19 |
| 4652 | martius | 19 |
| 4653 | mardian | 19 |
| 4654 | maine | 19 |
| 4655 | lungs | 19 |
| 4656 | lily | 19 |
| 4657 | lazy | 19 |
| 4658 | lamp | 19 |
| 4659 | labouring | 19 |
| 4660 | knavery | 19 |
| 4661 | juan | 19 |
| 4662 | joints | 19 |
| 4663 | insolence | 19 |
| 4664 | infirmity | 19 |
| 4665 | infect | 19 |
| 4666 | implore | 19 |
| 4667 | howl | 19 |
| 4668 | honorable | 19 |
| 4669 | holp | 19 |
| 4670 | holiday | 19 |
| 4671 | hire | 19 |
| 4672 | helm | 19 |
| 4673 | heel | 19 |
| 4674 | hearers | 19 |
| 4675 | haunt | 19 |
| 4676 | hates | 19 |
| 4677 | harder | 19 |
| 4678 | hanged | 19 |
| 4679 | handle | 19 |
| 4680 | grossly | 19 |
| 4681 | garment | 19 |
| 4682 | frowns | 19 |
| 4683 | frail | 19 |
| 4684 | footing | 19 |
| 4685 | follies | 19 |
| 4686 | feature | 19 |
| 4687 | extremes | 19 |
| 4688 | exceed | 19 |
| 4689 | established | 19 |
| 4690 | escaped | 19 |
| 4691 | empire | 19 |
| 4692 | eloquence | 19 |
| 4693 | easier | 19 |
| 4694 | drowsy | 19 |
| 4695 | doug | 19 |
| 4696 | distant | 19 |
| 4697 | displayed | 19 |
| 4698 | devoted | 19 |
| 4699 | despised | 19 |
| 4700 | designs | 19 |
| 4701 | depos | 19 |
| 4702 | debts | 19 |
| 4703 | crooked | 19 |
| 4704 | coxcomb | 19 |
| 4705 | covetous | 19 |
| 4706 | courtezan | 19 |
| 4707 | countryman | 19 |
| 4708 | confine | 19 |
| 4709 | compact | 19 |
| 4710 | commodity | 19 |
| 4711 | commends | 19 |
| 4712 | commending | 19 |
| 4713 | clavileno | 19 |
| 4714 | claudia | 19 |
| 4715 | cicero | 19 |
| 4716 | chid | 19 |
| 4717 | cheap | 19 |
| 4718 | certainty | 19 |
| 4719 | castles | 19 |
| 4720 | caphis | 19 |
| 4721 | canidius | 19 |
| 4722 | buck | 19 |
| 4723 | bill | 19 |
| 4724 | bearded | 19 |
| 4725 | bank | 19 |
| 4726 | balthasar | 19 |
| 4727 | bagot | 19 |
| 4728 | b | 19 |
| 4729 | attends | 19 |
| 4730 | array | 19 |
| 4731 | april | 19 |
| 4732 | approbation | 19 |
| 4733 | algiers | 19 |
| 4734 | ale | 19 |
| 4735 | albans | 19 |
| 4736 | addressing | 19 |
| 4737 | achieved | 19 |
| 4738 | accord | 19 |
| 4739 | welkin | 18 |
| 4740 | wart | 18 |
| 4741 | warrior | 18 |
| 4742 | vouch | 18 |
| 4743 | villages | 18 |
| 4744 | vicente | 18 |
| 4745 | verg | 18 |
| 4746 | vein | 18 |
| 4747 | turkish | 18 |
| 4748 | triumphant | 18 |
| 4749 | toad | 18 |
| 4750 | thursday | 18 |
| 4751 | throng | 18 |
| 4752 | testimony | 18 |
| 4753 | talents | 18 |
| 4754 | swelling | 18 |
| 4755 | survey | 18 |
| 4756 | surfeit | 18 |
| 4757 | sums | 18 |
| 4758 | sullen | 18 |
| 4759 | suffers | 18 |
| 4760 | suffered | 18 |
| 4761 | stops | 18 |
| 4762 | stool | 18 |
| 4763 | stirred | 18 |
| 4764 | steeds | 18 |
| 4765 | spectacle | 18 |
| 4766 | sow | 18 |
| 4767 | slumber | 18 |
| 4768 | sire | 18 |
| 4769 | shores | 18 |
| 4770 | shames | 18 |
| 4771 | sham | 18 |
| 4772 | severe | 18 |
| 4773 | sennet | 18 |
| 4774 | seed | 18 |
| 4775 | secrecy | 18 |
| 4776 | saturnine | 18 |
| 4777 | safer | 18 |
| 4778 | sadly | 18 |
| 4779 | ruffian | 18 |
| 4780 | riding | 18 |
| 4781 | rewards | 18 |
| 4782 | revive | 18 |
| 4783 | restored | 18 |
| 4784 | renew | 18 |
| 4785 | remote | 18 |
| 4786 | refused | 18 |
| 4787 | recourse | 18 |
| 4788 | recollect | 18 |
| 4789 | rebuke | 18 |
| 4790 | rascals | 18 |
| 4791 | rascally | 18 |
| 4792 | range | 18 |
| 4793 | puppet | 18 |
| 4794 | produced | 18 |
| 4795 | procession | 18 |
| 4796 | privy | 18 |
| 4797 | prays | 18 |
| 4798 | pomfret | 18 |
| 4799 | plots | 18 |
| 4800 | phoenix | 18 |
| 4801 | philosophy | 18 |
| 4802 | persecute | 18 |
| 4803 | pattern | 18 |
| 4804 | passions | 18 |
| 4805 | parchment | 18 |
| 4806 | overthrow | 18 |
| 4807 | oswald | 18 |
| 4808 | oars | 18 |
| 4809 | nearest | 18 |
| 4810 | murderers | 18 |
| 4811 | motive | 18 |
| 4812 | mort | 18 |
| 4813 | mopsa | 18 |
| 4814 | mocking | 18 |
| 4815 | minion | 18 |
| 4816 | merits | 18 |
| 4817 | melted | 18 |
| 4818 | melisendra | 18 |
| 4819 | mart | 18 |
| 4820 | mare | 18 |
| 4821 | malambruno | 18 |
| 4822 | lustre | 18 |
| 4823 | lightly | 18 |
| 4824 | lechery | 18 |
| 4825 | leandra | 18 |
| 4826 | leaden | 18 |
| 4827 | lasting | 18 |
| 4828 | labours | 18 |
| 4829 | jade | 18 |
| 4830 | intends | 18 |
| 4831 | inside | 18 |
| 4832 | indignation | 18 |
| 4833 | imprisonment | 18 |
| 4834 | il | 18 |
| 4835 | iden | 18 |
| 4836 | horsemen | 18 |
| 4837 | hook | 18 |
| 4838 | hood | 18 |
| 4839 | homely | 18 |
| 4840 | hitherto | 18 |
| 4841 | helps | 18 |
| 4842 | hedge | 18 |
| 4843 | heal | 18 |
| 4844 | hatch | 18 |
| 4845 | growth | 18 |
| 4846 | graceful | 18 |
| 4847 | ghosts | 18 |
| 4848 | fulvia | 18 |
| 4849 | file | 18 |
| 4850 | fife | 18 |
| 4851 | fates | 18 |
| 4852 | fasting | 18 |
| 4853 | farthing | 18 |
| 4854 | famish | 18 |
| 4855 | exploits | 18 |
| 4856 | explain | 18 |
| 4857 | eve | 18 |
| 4858 | errors | 18 |
| 4859 | err | 18 |
| 4860 | epitaph | 18 |
| 4861 | entreaty | 18 |
| 4862 | entire | 18 |
| 4863 | enforced | 18 |
| 4864 | embracing | 18 |
| 4865 | earn | 18 |
| 4866 | dwelling | 18 |
| 4867 | doleful | 18 |
| 4868 | dismounting | 18 |
| 4869 | dismount | 18 |
| 4870 | dire | 18 |
| 4871 | determination | 18 |
| 4872 | denies | 18 |
| 4873 | delighted | 18 |
| 4874 | cushion | 18 |
| 4875 | curtain | 18 |
| 4876 | cozen | 18 |
| 4877 | courses | 18 |
| 4878 | corruption | 18 |
| 4879 | cork | 18 |
| 4880 | cord | 18 |
| 4881 | charges | 18 |
| 4882 | cesario | 18 |
| 4883 | ceremonies | 18 |
| 4884 | celestial | 18 |
| 4885 | capacity | 18 |
| 4886 | bounteous | 18 |
| 4887 | block | 18 |
| 4888 | bitterly | 18 |
| 4889 | bide | 18 |
| 4890 | bard | 18 |
| 4891 | bait | 18 |
| 4892 | bail | 18 |
| 4893 | aye | 18 |
| 4894 | assay | 18 |
| 4895 | arriv | 18 |
| 4896 | approved | 18 |
| 4897 | anjou | 18 |
| 4898 | angiers | 18 |
| 4899 | andres | 18 |
| 4900 | amend | 18 |
| 4901 | albeit | 18 |
| 4902 | actors | 18 |
| 4903 | actor | 18 |
| 4904 | acting | 18 |
| 4905 | abode | 18 |
| 4906 | yon | 17 |
| 4907 | yields | 17 |
| 4908 | wretches | 17 |
| 4909 | worthies | 17 |
| 4910 | worser | 17 |
| 4911 | worldly | 17 |
| 4912 | wooden | 17 |
| 4913 | wiser | 17 |
| 4914 | winning | 17 |
| 4915 | widows | 17 |
| 4916 | whispers | 17 |
| 4917 | whipp | 17 |
| 4918 | whereupon | 17 |
| 4919 | watchman | 17 |
| 4920 | warriors | 17 |
| 4921 | visitation | 17 |
| 4922 | vigour | 17 |
| 4923 | venerable | 17 |
| 4924 | various | 17 |
| 4925 | tyb | 17 |
| 4926 | truce | 17 |
| 4927 | trebonius | 17 |
| 4928 | topas | 17 |
| 4929 | tire | 17 |
| 4930 | threaten | 17 |
| 4931 | thereto | 17 |
| 4932 | theft | 17 |
| 4933 | test | 17 |
| 4934 | tax | 17 |
| 4935 | talked | 17 |
| 4936 | tainted | 17 |
| 4937 | supreme | 17 |
| 4938 | submission | 17 |
| 4939 | streams | 17 |
| 4940 | strangest | 17 |
| 4941 | stirs | 17 |
| 4942 | sticks | 17 |
| 4943 | square | 17 |
| 4944 | spies | 17 |
| 4945 | speaker | 17 |
| 4946 | snout | 17 |
| 4947 | skirts | 17 |
| 4948 | silken | 17 |
| 4949 | sighing | 17 |
| 4950 | scars | 17 |
| 4951 | scarlet | 17 |
| 4952 | sauce | 17 |
| 4953 | rod | 17 |
| 4954 | revenges | 17 |
| 4955 | revels | 17 |
| 4956 | restraint | 17 |
| 4957 | remaining | 17 |
| 4958 | rejected | 17 |
| 4959 | recovery | 17 |
| 4960 | recio | 17 |
| 4961 | receipt | 17 |
| 4962 | reality | 17 |
| 4963 | rape | 17 |
| 4964 | ranks | 17 |
| 4965 | que | 17 |
| 4966 | purple | 17 |
| 4967 | pulse | 17 |
| 4968 | praying | 17 |
| 4969 | plac | 17 |
| 4970 | personal | 17 |
| 4971 | period | 17 |
| 4972 | pastoral | 17 |
| 4973 | pasamonte | 17 |
| 4974 | oxen | 17 |
| 4975 | overthrown | 17 |
| 4976 | outlive | 17 |
| 4977 | orsino | 17 |
| 4978 | oppos | 17 |
| 4979 | omit | 17 |
| 4980 | occupation | 17 |
| 4981 | observance | 17 |
| 4982 | objects | 17 |
| 4983 | nuncle | 17 |
| 4984 | nobleness | 17 |
| 4985 | neglected | 17 |
| 4986 | nations | 17 |
| 4987 | nam | 17 |
| 4988 | mute | 17 |
| 4989 | mouse | 17 |
| 4990 | moody | 17 |
| 4991 | monmouth | 17 |
| 4992 | million | 17 |
| 4993 | mercury | 17 |
| 4994 | members | 17 |
| 4995 | meed | 17 |
| 4996 | meanwhile | 17 |
| 4997 | meanest | 17 |
| 4998 | mast | 17 |
| 4999 | lucky | 17 |
| 5000 | losses | 17 |
| 5001 | loins | 17 |
| 5002 | loathsome | 17 |
| 5003 | lief | 17 |
| 5004 | liar | 17 |
| 5005 | latest | 17 |
| 5006 | later | 17 |
| 5007 | knocked | 17 |
| 5008 | jaws | 17 |
| 5009 | inherit | 17 |
| 5010 | informed | 17 |
| 5011 | impossibility | 17 |
| 5012 | horror | 17 |
| 5013 | horrid | 17 |
| 5014 | holiness | 17 |
| 5015 | heinous | 17 |
| 5016 | heaviness | 17 |
| 5017 | heav | 17 |
| 5018 | handled | 17 |
| 5019 | guts | 17 |
| 5020 | goatherds | 17 |
| 5021 | gloves | 17 |
| 5022 | glance | 17 |
| 5023 | gads | 17 |
| 5024 | function | 17 |
| 5025 | fortress | 17 |
| 5026 | foil | 17 |
| 5027 | fills | 17 |
| 5028 | festival | 17 |
| 5029 | felix | 17 |
| 5030 | feeds | 17 |
| 5031 | feasts | 17 |
| 5032 | farm | 17 |
| 5033 | fan | 17 |
| 5034 | extremely | 17 |
| 5035 | executioner | 17 |
| 5036 | examples | 17 |
| 5037 | enters | 17 |
| 5038 | entering | 17 |
| 5039 | enjoying | 17 |
| 5040 | encount | 17 |
| 5041 | eggs | 17 |
| 5042 | egeus | 17 |
| 5043 | ebb | 17 |
| 5044 | drunkard | 17 |
| 5045 | drives | 17 |
| 5046 | dover | 17 |
| 5047 | distracted | 17 |
| 5048 | distinguish | 17 |
| 5049 | dislike | 17 |
| 5050 | dishes | 17 |
| 5051 | dim | 17 |
| 5052 | devour | 17 |
| 5053 | detested | 17 |
| 5054 | deception | 17 |
| 5055 | cutting | 17 |
| 5056 | crime | 17 |
| 5057 | crept | 17 |
| 5058 | cradle | 17 |
| 5059 | cousins | 17 |
| 5060 | corrupted | 17 |
| 5061 | coral | 17 |
| 5062 | condemned | 17 |
| 5063 | compassionate | 17 |
| 5064 | cleomenes | 17 |
| 5065 | choke | 17 |
| 5066 | chances | 17 |
| 5067 | champion | 17 |
| 5068 | ceased | 17 |
| 5069 | catching | 17 |
| 5070 | caparison | 17 |
| 5071 | calpurnia | 17 |
| 5072 | calchas | 17 |
| 5073 | bulk | 17 |
| 5074 | buds | 17 |
| 5075 | britaine | 17 |
| 5076 | breathless | 17 |
| 5077 | brawl | 17 |
| 5078 | boldly | 17 |
| 5079 | bodily | 17 |
| 5080 | blockhead | 17 |
| 5081 | benvolio | 17 |
| 5082 | begging | 17 |
| 5083 | beef | 17 |
| 5084 | bearer | 17 |
| 5085 | beadle | 17 |
| 5086 | baseness | 17 |
| 5087 | barcelona | 17 |
| 5088 | balm | 17 |
| 5089 | baby | 17 |
| 5090 | awoke | 17 |
| 5091 | avoided | 17 |
| 5092 | arrant | 17 |
| 5093 | antenor | 17 |
| 5094 | afresh | 17 |
| 5095 | aedile | 17 |
| 5096 | adverse | 17 |
| 5097 | admirable | 17 |
| 5098 | achieve | 17 |
| 5099 | accordance | 17 |
| 5100 | accomplish | 17 |
| 5101 | wrathful | 16 |
| 5102 | worthiness | 16 |
| 5103 | whatsoever | 16 |
| 5104 | web | 16 |
| 5105 | watched | 16 |
| 5106 | washing | 16 |
| 5107 | warn | 16 |
| 5108 | wakes | 16 |
| 5109 | volume | 16 |
| 5110 | villainous | 16 |
| 5111 | vices | 16 |
| 5112 | vexed | 16 |
| 5113 | vault | 16 |
| 5114 | valley | 16 |
| 5115 | usurping | 16 |
| 5116 | ursula | 16 |
| 5117 | urging | 16 |
| 5118 | twelvemonth | 16 |
| 5119 | trot | 16 |
| 5120 | trip | 16 |
| 5121 | tone | 16 |
| 5122 | throughout | 16 |
| 5123 | thinkest | 16 |
| 5124 | tapers | 16 |
| 5125 | taper | 16 |
| 5126 | taint | 16 |
| 5127 | sweets | 16 |
| 5128 | sweeter | 16 |
| 5129 | surveyor | 16 |
| 5130 | surgeon | 16 |
| 5131 | suppos | 16 |
| 5132 | storms | 16 |
| 5133 | stopping | 16 |
| 5134 | stomachs | 16 |
| 5135 | stiff | 16 |
| 5136 | station | 16 |
| 5137 | starve | 16 |
| 5138 | started | 16 |
| 5139 | sobs | 16 |
| 5140 | smith | 16 |
| 5141 | slanders | 16 |
| 5142 | shrew | 16 |
| 5143 | shameful | 16 |
| 5144 | shakes | 16 |
| 5145 | secretly | 16 |
| 5146 | seasons | 16 |
| 5147 | searching | 16 |
| 5148 | schoolmaster | 16 |
| 5149 | scar | 16 |
| 5150 | sans | 16 |
| 5151 | sailors | 16 |
| 5152 | roots | 16 |
| 5153 | rival | 16 |
| 5154 | risen | 16 |
| 5155 | ridiculous | 16 |
| 5156 | revel | 16 |
| 5157 | rests | 16 |
| 5158 | resolute | 16 |
| 5159 | reserve | 16 |
| 5160 | requests | 16 |
| 5161 | reigns | 16 |
| 5162 | regions | 16 |
| 5163 | rags | 16 |
| 5164 | publish | 16 |
| 5165 | prophecy | 16 |
| 5166 | prompt | 16 |
| 5167 | project | 16 |
| 5168 | progress | 16 |
| 5169 | prejudice | 16 |
| 5170 | prate | 16 |
| 5171 | politic | 16 |
| 5172 | pleaseth | 16 |
| 5173 | player | 16 |
| 5174 | plate | 16 |
| 5175 | plagues | 16 |
| 5176 | pilgrimage | 16 |
| 5177 | pigeons | 16 |
| 5178 | piercing | 16 |
| 5179 | philippi | 16 |
| 5180 | paths | 16 |
| 5181 | pasture | 16 |
| 5182 | pastime | 16 |
| 5183 | parcel | 16 |
| 5184 | pangs | 16 |
| 5185 | overheard | 16 |
| 5186 | oppression | 16 |
| 5187 | opposition | 16 |
| 5188 | opens | 16 |
| 5189 | offender | 16 |
| 5190 | notorious | 16 |
| 5191 | noses | 16 |
| 5192 | negligence | 16 |
| 5193 | needy | 16 |
| 5194 | necessities | 16 |
| 5195 | naughty | 16 |
| 5196 | napkin | 16 |
| 5197 | mutual | 16 |
| 5198 | morsel | 16 |
| 5199 | morena | 16 |
| 5200 | moiety | 16 |
| 5201 | model | 16 |
| 5202 | mistresses | 16 |
| 5203 | minutes | 16 |
| 5204 | mill | 16 |
| 5205 | micomicona | 16 |
| 5206 | mended | 16 |
| 5207 | measures | 16 |
| 5208 | marien | 16 |
| 5209 | mansion | 16 |
| 5210 | manchegan | 16 |
| 5211 | malignant | 16 |
| 5212 | malady | 16 |
| 5213 | magician | 16 |
| 5214 | madmen | 16 |
| 5215 | lucullus | 16 |
| 5216 | luce | 16 |
| 5217 | lt | 16 |
| 5218 | link | 16 |
| 5219 | leaf | 16 |
| 5220 | leader | 16 |
| 5221 | lamentation | 16 |
| 5222 | lacks | 16 |
| 5223 | labourer | 16 |
| 5224 | judgement | 16 |
| 5225 | jerkin | 16 |
| 5226 | instructed | 16 |
| 5227 | induced | 16 |
| 5228 | indifferent | 16 |
| 5229 | inclin | 16 |
| 5230 | inasmuch | 16 |
| 5231 | hurts | 16 |
| 5232 | huntsman | 16 |
| 5233 | hum | 16 |
| 5234 | hop | 16 |
| 5235 | hinder | 16 |
| 5236 | heavier | 16 |
| 5237 | hearty | 16 |
| 5238 | hastily | 16 |
| 5239 | harms | 16 |
| 5240 | grudge | 16 |
| 5241 | goest | 16 |
| 5242 | girdle | 16 |
| 5243 | gentry | 16 |
| 5244 | geese | 16 |
| 5245 | gaiferos | 16 |
| 5246 | gage | 16 |
| 5247 | fulling | 16 |
| 5248 | fruitful | 16 |
| 5249 | friars | 16 |
| 5250 | frantic | 16 |
| 5251 | fleance | 16 |
| 5252 | flatterer | 16 |
| 5253 | fist | 16 |
| 5254 | fights | 16 |
| 5255 | fig | 16 |
| 5256 | fence | 16 |
| 5257 | feared | 16 |
| 5258 | fantasy | 16 |
| 5259 | faithfully | 16 |
| 5260 | failed | 16 |
| 5261 | exposed | 16 |
| 5262 | excited | 16 |
| 5263 | excess | 16 |
| 5264 | ewes | 16 |
| 5265 | esquire | 16 |
| 5266 | envoy | 16 |
| 5267 | endless | 16 |
| 5268 | enamoured | 16 |
| 5269 | enable | 16 |
| 5270 | effected | 16 |
| 5271 | driving | 16 |
| 5272 | drawer | 16 |
| 5273 | dram | 16 |
| 5274 | doubtless | 16 |
| 5275 | donalbain | 16 |
| 5276 | distinctly | 16 |
| 5277 | distemper | 16 |
| 5278 | disorder | 16 |
| 5279 | disguis | 16 |
| 5280 | discontent | 16 |
| 5281 | discipline | 16 |
| 5282 | diligence | 16 |
| 5283 | dignities | 16 |
| 5284 | dido | 16 |
| 5285 | devis | 16 |
| 5286 | determin | 16 |
| 5287 | declaration | 16 |
| 5288 | customary | 16 |
| 5289 | curtsy | 16 |
| 5290 | crimson | 16 |
| 5291 | counted | 16 |
| 5292 | cords | 16 |
| 5293 | contrive | 16 |
| 5294 | contend | 16 |
| 5295 | consort | 16 |
| 5296 | considering | 16 |
| 5297 | confin | 16 |
| 5298 | comply | 16 |
| 5299 | complaints | 16 |
| 5300 | compell | 16 |
| 5301 | colville | 16 |
| 5302 | coldly | 16 |
| 5303 | coffin | 16 |
| 5304 | clapp | 16 |
| 5305 | circle | 16 |
| 5306 | churlish | 16 |
| 5307 | christ | 16 |
| 5308 | chiefly | 16 |
| 5309 | chatillon | 16 |
| 5310 | chambers | 16 |
| 5311 | bystanders | 16 |
| 5312 | building | 16 |
| 5313 | bruised | 16 |
| 5314 | brooks | 16 |
| 5315 | breakfast | 16 |
| 5316 | bray | 16 |
| 5317 | brace | 16 |
| 5318 | bolt | 16 |
| 5319 | bigot | 16 |
| 5320 | benengeli | 16 |
| 5321 | belmont | 16 |
| 5322 | believing | 16 |
| 5323 | beguil | 16 |
| 5324 | beauties | 16 |
| 5325 | bate | 16 |
| 5326 | bastards | 16 |
| 5327 | balls | 16 |
| 5328 | bags | 16 |
| 5329 | assail | 16 |
| 5330 | ashore | 16 |
| 5331 | around | 16 |
| 5332 | apple | 16 |
| 5333 | apes | 16 |
| 5334 | animal | 16 |
| 5335 | ana | 16 |
| 5336 | amount | 16 |
| 5337 | amiens | 16 |
| 5338 | alliance | 16 |
| 5339 | afflict | 16 |
| 5340 | adversary | 16 |
| 5341 | adrian | 16 |
| 5342 | accent | 16 |
| 5343 | abate | 16 |
| 5344 | worthier | 15 |
| 5345 | wond | 15 |
| 5346 | witches | 15 |
| 5347 | wins | 15 |
| 5348 | winged | 15 |
| 5349 | willoughby | 15 |
| 5350 | wilful | 15 |
| 5351 | weighty | 15 |
| 5352 | wednesday | 15 |
| 5353 | wearied | 15 |
| 5354 | weal | 15 |
| 5355 | waits | 15 |
| 5356 | visited | 15 |
| 5357 | vilely | 15 |
| 5358 | vicious | 15 |
| 5359 | ver | 15 |
| 5360 | variety | 15 |
| 5361 | tween | 15 |
| 5362 | trow | 15 |
| 5363 | transformation | 15 |
| 5364 | toys | 15 |
| 5365 | towers | 15 |
| 5366 | toledo | 15 |
| 5367 | tight | 15 |
| 5368 | temples | 15 |
| 5369 | tapster | 15 |
| 5370 | swifter | 15 |
| 5371 | sweep | 15 |
| 5372 | superfluous | 15 |
| 5373 | sumptuous | 15 |
| 5374 | suited | 15 |
| 5375 | suggested | 15 |
| 5376 | suff | 15 |
| 5377 | strings | 15 |
| 5378 | stray | 15 |
| 5379 | steals | 15 |
| 5380 | stead | 15 |
| 5381 | starts | 15 |
| 5382 | stakes | 15 |
| 5383 | spotted | 15 |
| 5384 | spell | 15 |
| 5385 | sounding | 15 |
| 5386 | solemnity | 15 |
| 5387 | smells | 15 |
| 5388 | singer | 15 |
| 5389 | shirts | 15 |
| 5390 | separated | 15 |
| 5391 | seiz | 15 |
| 5392 | science | 15 |
| 5393 | scale | 15 |
| 5394 | sand | 15 |
| 5395 | salamanca | 15 |
| 5396 | ruthless | 15 |
| 5397 | rouen | 15 |
| 5398 | riot | 15 |
| 5399 | rheum | 15 |
| 5400 | retirement | 15 |
| 5401 | retain | 15 |
| 5402 | repay | 15 |
| 5403 | rendered | 15 |
| 5404 | relates | 15 |
| 5405 | reflect | 15 |
| 5406 | reckoned | 15 |
| 5407 | readily | 15 |
| 5408 | raw | 15 |
| 5409 | purpos | 15 |
| 5410 | pregnant | 15 |
| 5411 | praising | 15 |
| 5412 | practices | 15 |
| 5413 | posts | 15 |
| 5414 | plunge | 15 |
| 5415 | pisa | 15 |
| 5416 | pile | 15 |
| 5417 | pig | 15 |
| 5418 | philosopher | 15 |
| 5419 | peradventure | 15 |
| 5420 | penitent | 15 |
| 5421 | paltry | 15 |
| 5422 | outrage | 15 |
| 5423 | orphans | 15 |
| 5424 | ornaments | 15 |
| 5425 | origin | 15 |
| 5426 | opportunities | 15 |
| 5427 | obscure | 15 |
| 5428 | nymph | 15 |
| 5429 | notary | 15 |
| 5430 | norway | 15 |
| 5431 | nell | 15 |
| 5432 | needless | 15 |
| 5433 | mutius | 15 |
| 5434 | mus | 15 |
| 5435 | motley | 15 |
| 5436 | motions | 15 |
| 5437 | mon | 15 |
| 5438 | mole | 15 |
| 5439 | mistrust | 15 |
| 5440 | mid | 15 |
| 5441 | merriment | 15 |
| 5442 | meadows | 15 |
| 5443 | mates | 15 |
| 5444 | mambrino | 15 |
| 5445 | madly | 15 |
| 5446 | longed | 15 |
| 5447 | litter | 15 |
| 5448 | ligarius | 15 |
| 5449 | lends | 15 |
| 5450 | lascivious | 15 |
| 5451 | lamentable | 15 |
| 5452 | lake | 15 |
| 5453 | jump | 15 |
| 5454 | jealousies | 15 |
| 5455 | invited | 15 |
| 5456 | intelligent | 15 |
| 5457 | instructions | 15 |
| 5458 | imperious | 15 |
| 5459 | imaginary | 15 |
| 5460 | hurry | 15 |
| 5461 | howling | 15 |
| 5462 | hound | 15 |
| 5463 | hills | 15 |
| 5464 | heigh | 15 |
| 5465 | hay | 15 |
| 5466 | habits | 15 |
| 5467 | greg | 15 |
| 5468 | globe | 15 |
| 5469 | generally | 15 |
| 5470 | frowning | 15 |
| 5471 | frank | 15 |
| 5472 | fortinbras | 15 |
| 5473 | forgetting | 15 |
| 5474 | follower | 15 |
| 5475 | fitter | 15 |
| 5476 | fiends | 15 |
| 5477 | fickle | 15 |
| 5478 | fantastical | 15 |
| 5479 | fang | 15 |
| 5480 | eyelids | 15 |
| 5481 | enforc | 15 |
| 5482 | embassy | 15 |
| 5483 | egyptian | 15 |
| 5484 | eastcheap | 15 |
| 5485 | dunsinane | 15 |
| 5486 | draught | 15 |
| 5487 | dragon | 15 |
| 5488 | dorcas | 15 |
| 5489 | doctors | 15 |
| 5490 | dispute | 15 |
| 5491 | dishonoured | 15 |
| 5492 | discharged | 15 |
| 5493 | devices | 15 |
| 5494 | deliberately | 15 |
| 5495 | defect | 15 |
| 5496 | deepest | 15 |
| 5497 | dealt | 15 |
| 5498 | dared | 15 |
| 5499 | dances | 15 |
| 5500 | curb | 15 |
| 5501 | cow | 15 |
| 5502 | courtiers | 15 |
| 5503 | contained | 15 |
| 5504 | conspirator | 15 |
| 5505 | consolation | 15 |
| 5506 | concerning | 15 |
| 5507 | comrade | 15 |
| 5508 | commandment | 15 |
| 5509 | commander | 15 |
| 5510 | comedy | 15 |
| 5511 | coloured | 15 |
| 5512 | coal | 15 |
| 5513 | clitus | 15 |
| 5514 | clap | 15 |
| 5515 | clamour | 15 |
| 5516 | chaplain | 15 |
| 5517 | chanced | 15 |
| 5518 | carlisle | 15 |
| 5519 | captivity | 15 |
| 5520 | bullcalf | 15 |
| 5521 | bowl | 15 |
| 5522 | blast | 15 |
| 5523 | blade | 15 |
| 5524 | bitterness | 15 |
| 5525 | bishops | 15 |
| 5526 | bills | 15 |
| 5527 | betide | 15 |
| 5528 | bernardo | 15 |
| 5529 | bathed | 15 |
| 5530 | barley | 15 |
| 5531 | badge | 15 |
| 5532 | awak | 15 |
| 5533 | attendance | 15 |
| 5534 | attained | 15 |
| 5535 | assume | 15 |
| 5536 | assembly | 15 |
| 5537 | assailed | 15 |
| 5538 | ashamed | 15 |
| 5539 | arrested | 15 |
| 5540 | arras | 15 |
| 5541 | applause | 15 |
| 5542 | apparition | 15 |
| 5543 | antique | 15 |
| 5544 | animals | 15 |
| 5545 | amused | 15 |
| 5546 | amuse | 15 |
| 5547 | airy | 15 |
| 5548 | advancing | 15 |
| 5549 | ad | 15 |
| 5550 | acorns | 15 |
| 5551 | ache | 15 |
| 5552 | accepted | 15 |
| 5553 | abominable | 15 |
| 5554 | abandon | 15 |
| 5555 | wrinkles | 14 |
| 5556 | worthiest | 14 |
| 5557 | whitmore | 14 |
| 5558 | wat | 14 |
| 5559 | voluntary | 14 |
| 5560 | veracious | 14 |
| 5561 | vale | 14 |
| 5562 | urged | 14 |
| 5563 | upward | 14 |
| 5564 | unruly | 14 |
| 5565 | unmannerly | 14 |
| 5566 | unheard | 14 |
| 5567 | unarm | 14 |
| 5568 | truant | 14 |
| 5569 | trod | 14 |
| 5570 | travels | 14 |
| 5571 | transform | 14 |
| 5572 | trace | 14 |
| 5573 | tow | 14 |
| 5574 | thumb | 14 |
| 5575 | thorough | 14 |
| 5576 | thicket | 14 |
| 5577 | teaching | 14 |
| 5578 | tardy | 14 |
| 5579 | swim | 14 |
| 5580 | suspected | 14 |
| 5581 | summit | 14 |
| 5582 | subscribe | 14 |
| 5583 | subdu | 14 |
| 5584 | stratagem | 14 |
| 5585 | staying | 14 |
| 5586 | stately | 14 |
| 5587 | starveling | 14 |
| 5588 | stark | 14 |
| 5589 | stare | 14 |
| 5590 | sprang | 14 |
| 5591 | spectacles | 14 |
| 5592 | sonnets | 14 |
| 5593 | solitudes | 14 |
| 5594 | solitude | 14 |
| 5595 | snare | 14 |
| 5596 | smote | 14 |
| 5597 | smitten | 14 |
| 5598 | smart | 14 |
| 5599 | skies | 14 |
| 5600 | sincerity | 14 |
| 5601 | shroud | 14 |
| 5602 | sepulchre | 14 |
| 5603 | separate | 14 |
| 5604 | scattered | 14 |
| 5605 | roll | 14 |
| 5606 | rightful | 14 |
| 5607 | repute | 14 |
| 5608 | repeal | 14 |
| 5609 | rent | 14 |
| 5610 | remov | 14 |
| 5611 | rehearse | 14 |
| 5612 | refuge | 14 |
| 5613 | recount | 14 |
| 5614 | reception | 14 |
| 5615 | reader | 14 |
| 5616 | rational | 14 |
| 5617 | rarest | 14 |
| 5618 | ransomed | 14 |
| 5619 | pupil | 14 |
| 5620 | puff | 14 |
| 5621 | provok | 14 |
| 5622 | proudest | 14 |
| 5623 | pretended | 14 |
| 5624 | possibility | 14 |
| 5625 | ports | 14 |
| 5626 | plucks | 14 |
| 5627 | plants | 14 |
| 5628 | pious | 14 |
| 5629 | pierced | 14 |
| 5630 | philostrate | 14 |
| 5631 | pestilence | 14 |
| 5632 | peruse | 14 |
| 5633 | peck | 14 |
| 5634 | paradise | 14 |
| 5635 | pagan | 14 |
| 5636 | owed | 14 |
| 5637 | overcame | 14 |
| 5638 | odious | 14 |
| 5639 | obliged | 14 |
| 5640 | nourish | 14 |
| 5641 | notion | 14 |
| 5642 | nativity | 14 |
| 5643 | mustardseed | 14 |
| 5644 | mortality | 14 |
| 5645 | morocco | 14 |
| 5646 | moist | 14 |
| 5647 | moderate | 14 |
| 5648 | mingle | 14 |
| 5649 | messina | 14 |
| 5650 | member | 14 |
| 5651 | meets | 14 |
| 5652 | meal | 14 |
| 5653 | malicious | 14 |
| 5654 | louder | 14 |
| 5655 | locked | 14 |
| 5656 | linger | 14 |
| 5657 | ling | 14 |
| 5658 | lime | 14 |
| 5659 | liable | 14 |
| 5660 | lewd | 14 |
| 5661 | levied | 14 |
| 5662 | lela | 14 |
| 5663 | lasts | 14 |
| 5664 | lane | 14 |
| 5665 | lace | 14 |
| 5666 | kitchen | 14 |
| 5667 | jars | 14 |
| 5668 | james | 14 |
| 5669 | issues | 14 |
| 5670 | invincible | 14 |
| 5671 | interpreter | 14 |
| 5672 | injustice | 14 |
| 5673 | inheritance | 14 |
| 5674 | infamy | 14 |
| 5675 | indies | 14 |
| 5676 | incomparable | 14 |
| 5677 | imitation | 14 |
| 5678 | husbandry | 14 |
| 5679 | holes | 14 |
| 5680 | hermit | 14 |
| 5681 | henceforward | 14 |
| 5682 | hecate | 14 |
| 5683 | heavily | 14 |
| 5684 | hautboys | 14 |
| 5685 | harp | 14 |
| 5686 | harness | 14 |
| 5687 | grating | 14 |
| 5688 | grasp | 14 |
| 5689 | governing | 14 |
| 5690 | goodman | 14 |
| 5691 | gertrude | 14 |
| 5692 | german | 14 |
| 5693 | gav | 14 |
| 5694 | gallop | 14 |
| 5695 | gaiety | 14 |
| 5696 | fruits | 14 |
| 5697 | frightened | 14 |
| 5698 | frighted | 14 |
| 5699 | fram | 14 |
| 5700 | forever | 14 |
| 5701 | flowing | 14 |
| 5702 | fixing | 14 |
| 5703 | fidelity | 14 |
| 5704 | fawn | 14 |
| 5705 | farthest | 14 |
| 5706 | exton | 14 |
| 5707 | extent | 14 |
| 5708 | expecting | 14 |
| 5709 | excellency | 14 |
| 5710 | examined | 14 |
| 5711 | eunuch | 14 |
| 5712 | engag | 14 |
| 5713 | endur | 14 |
| 5714 | encounters | 14 |
| 5715 | encountered | 14 |
| 5716 | employed | 14 |
| 5717 | emperors | 14 |
| 5718 | eleanor | 14 |
| 5719 | ecstasy | 14 |
| 5720 | dropped | 14 |
| 5721 | dropp | 14 |
| 5722 | drooping | 14 |
| 5723 | drag | 14 |
| 5724 | doings | 14 |
| 5725 | distraction | 14 |
| 5726 | dissuade | 14 |
| 5727 | dissembling | 14 |
| 5728 | discontented | 14 |
| 5729 | discomfort | 14 |
| 5730 | disclosed | 14 |
| 5731 | digest | 14 |
| 5732 | difficulties | 14 |
| 5733 | difficult | 14 |
| 5734 | dice | 14 |
| 5735 | devout | 14 |
| 5736 | derive | 14 |
| 5737 | depends | 14 |
| 5738 | deformed | 14 |
| 5739 | deem | 14 |
| 5740 | decree | 14 |
| 5741 | decision | 14 |
| 5742 | debate | 14 |
| 5743 | daybreak | 14 |
| 5744 | dawn | 14 |
| 5745 | damnation | 14 |
| 5746 | daggers | 14 |
| 5747 | crossing | 14 |
| 5748 | crab | 14 |
| 5749 | covering | 14 |
| 5750 | courier | 14 |
| 5751 | counsellor | 14 |
| 5752 | cornets | 14 |
| 5753 | controversy | 14 |
| 5754 | consented | 14 |
| 5755 | confused | 14 |
| 5756 | conceived | 14 |
| 5757 | compelled | 14 |
| 5758 | comparison | 14 |
| 5759 | companies | 14 |
| 5760 | commanding | 14 |
| 5761 | comest | 14 |
| 5762 | collected | 14 |
| 5763 | coil | 14 |
| 5764 | childish | 14 |
| 5765 | chiefest | 14 |
| 5766 | chest | 14 |
| 5767 | chastisement | 14 |
| 5768 | chastise | 14 |
| 5769 | chapel | 14 |
| 5770 | channel | 14 |
| 5771 | centre | 14 |
| 5772 | cecial | 14 |
| 5773 | caution | 14 |
| 5774 | cattle | 14 |
| 5775 | carter | 14 |
| 5776 | carriers | 14 |
| 5777 | card | 14 |
| 5778 | cambio | 14 |
| 5779 | calamity | 14 |
| 5780 | butter | 14 |
| 5781 | bulls | 14 |
| 5782 | bud | 14 |
| 5783 | buckram | 14 |
| 5784 | brazen | 14 |
| 5785 | brand | 14 |
| 5786 | bows | 14 |
| 5787 | boughs | 14 |
| 5788 | bloods | 14 |
| 5789 | blemish | 14 |
| 5790 | blank | 14 |
| 5791 | berkeley | 14 |
| 5792 | believ | 14 |
| 5793 | beam | 14 |
| 5794 | balance | 14 |
| 5795 | attempted | 14 |
| 5796 | ate | 14 |
| 5797 | appoint | 14 |
| 5798 | apothecary | 14 |
| 5799 | anchor | 14 |
| 5800 | amain | 14 |
| 5801 | allay | 14 |
| 5802 | ague | 14 |
| 5803 | affords | 14 |
| 5804 | aemilius | 14 |
| 5805 | advanc | 14 |
| 5806 | adopt | 14 |
| 5807 | adder | 14 |
| 5808 | active | 14 |
| 5809 | abundant | 14 |
| 5810 | ability | 14 |
| 5811 | abbot | 14 |
| 5812 | yards | 13 |
| 5813 | wrinkled | 13 |
| 5814 | worthily | 13 |
| 5815 | withhold | 13 |
| 5816 | wickedness | 13 |
| 5817 | watchful | 13 |
| 5818 | viii | 13 |
| 5819 | venetian | 13 |
| 5820 | uncles | 13 |
| 5821 | tullus | 13 |
| 5822 | trusted | 13 |
| 5823 | triumphs | 13 |
| 5824 | treasures | 13 |
| 5825 | travelled | 13 |
| 5826 | translate | 13 |
| 5827 | toy | 13 |
| 5828 | torments | 13 |
| 5829 | tickle | 13 |
| 5830 | thorn | 13 |
| 5831 | thigh | 13 |
| 5832 | text | 13 |
| 5833 | tenour | 13 |
| 5834 | sweating | 13 |
| 5835 | swallowed | 13 |
| 5836 | surrender | 13 |
| 5837 | supposing | 13 |
| 5838 | suns | 13 |
| 5839 | sunday | 13 |
| 5840 | suggest | 13 |
| 5841 | subdue | 13 |
| 5842 | stupid | 13 |
| 5843 | stumbling | 13 |
| 5844 | stumble | 13 |
| 5845 | struggle | 13 |
| 5846 | strives | 13 |
| 5847 | striking | 13 |
| 5848 | stricken | 13 |
| 5849 | strato | 13 |
| 5850 | stirr | 13 |
| 5851 | staves | 13 |
| 5852 | stature | 13 |
| 5853 | staring | 13 |
| 5854 | sprightly | 13 |
| 5855 | speechless | 13 |
| 5856 | sparrow | 13 |
| 5857 | smother | 13 |
| 5858 | slightly | 13 |
| 5859 | sleeves | 13 |
| 5860 | sinful | 13 |
| 5861 | showers | 13 |
| 5862 | seyton | 13 |
| 5863 | sever | 13 |
| 5864 | scroll | 13 |
| 5865 | scraps | 13 |
| 5866 | scoundrel | 13 |
| 5867 | scales | 13 |
| 5868 | savour | 13 |
| 5869 | sap | 13 |
| 5870 | sang | 13 |
| 5871 | sanctuary | 13 |
| 5872 | salve | 13 |
| 5873 | sailor | 13 |
| 5874 | rustic | 13 |
| 5875 | rub | 13 |
| 5876 | roughly | 13 |
| 5877 | righteous | 13 |
| 5878 | rey | 13 |
| 5879 | revenged | 13 |
| 5880 | reveal | 13 |
| 5881 | resort | 13 |
| 5882 | repentance | 13 |
| 5883 | rely | 13 |
| 5884 | relating | 13 |
| 5885 | regarding | 13 |
| 5886 | recreant | 13 |
| 5887 | recall | 13 |
| 5888 | rat | 13 |
| 5889 | quote | 13 |
| 5890 | quake | 13 |
| 5891 | pushed | 13 |
| 5892 | purses | 13 |
| 5893 | propriety | 13 |
| 5894 | propose | 13 |
| 5895 | promising | 13 |
| 5896 | principal | 13 |
| 5897 | pricks | 13 |
| 5898 | pots | 13 |
| 5899 | posterity | 13 |
| 5900 | polite | 13 |
| 5901 | pointing | 13 |
| 5902 | plough | 13 |
| 5903 | pledges | 13 |
| 5904 | pins | 13 |
| 5905 | pinches | 13 |
| 5906 | pilgrims | 13 |
| 5907 | phantoms | 13 |
| 5908 | personage | 13 |
| 5909 | pat | 13 |
| 5910 | outcry | 13 |
| 5911 | observation | 13 |
| 5912 | needle | 13 |
| 5913 | necks | 13 |
| 5914 | navarre | 13 |
| 5915 | mould | 13 |
| 5916 | morton | 13 |
| 5917 | mode | 13 |
| 5918 | mischievous | 13 |
| 5919 | miscarry | 13 |
| 5920 | memorable | 13 |
| 5921 | meaner | 13 |
| 5922 | mary | 13 |
| 5923 | marcellus | 13 |
| 5924 | map | 13 |
| 5925 | mangled | 13 |
| 5926 | longs | 13 |
| 5927 | liveries | 13 |
| 5928 | liquid | 13 |
| 5929 | likelihood | 13 |
| 5930 | legitimate | 13 |
| 5931 | leek | 13 |
| 5932 | lawyer | 13 |
| 5933 | lamenting | 13 |
| 5934 | lamentations | 13 |
| 5935 | lambs | 13 |
| 5936 | justices | 13 |
| 5937 | invent | 13 |
| 5938 | intending | 13 |
| 5939 | insolent | 13 |
| 5940 | ingrateful | 13 |
| 5941 | increasing | 13 |
| 5942 | imprison | 13 |
| 5943 | importune | 13 |
| 5944 | illyria | 13 |
| 5945 | hymen | 13 |
| 5946 | hurried | 13 |
| 5947 | hurl | 13 |
| 5948 | hoped | 13 |
| 5949 | hoarse | 13 |
| 5950 | hen | 13 |
| 5951 | helenus | 13 |
| 5952 | hecuba | 13 |
| 5953 | hasten | 13 |
| 5954 | happens | 13 |
| 5955 | guise | 13 |
| 5956 | guided | 13 |
| 5957 | grounds | 13 |
| 5958 | gorgeous | 13 |
| 5959 | gnaw | 13 |
| 5960 | glittering | 13 |
| 5961 | gild | 13 |
| 5962 | gentlewomen | 13 |
| 5963 | gear | 13 |
| 5964 | garlands | 13 |
| 5965 | gallia | 13 |
| 5966 | gallants | 13 |
| 5967 | gadshill | 13 |
| 5968 | furnished | 13 |
| 5969 | fro | 13 |
| 5970 | fowl | 13 |
| 5971 | fourscore | 13 |
| 5972 | foundation | 13 |
| 5973 | fortnight | 13 |
| 5974 | foolery | 13 |
| 5975 | florentine | 13 |
| 5976 | floor | 13 |
| 5977 | fiction | 13 |
| 5978 | feathers | 13 |
| 5979 | famine | 13 |
| 5980 | exquisite | 13 |
| 5981 | expose | 13 |
| 5982 | exchanged | 13 |
| 5983 | exceedingly | 13 |
| 5984 | establish | 13 |
| 5985 | entreats | 13 |
| 5986 | ensue | 13 |
| 5987 | endeavours | 13 |
| 5988 | embark | 13 |
| 5989 | elegant | 13 |
| 5990 | eighteen | 13 |
| 5991 | eagerness | 13 |
| 5992 | dunghill | 13 |
| 5993 | duly | 13 |
| 5994 | dreaming | 13 |
| 5995 | downright | 13 |
| 5996 | doting | 13 |
| 5997 | distinguished | 13 |
| 5998 | disloyal | 13 |
| 5999 | disgrac | 13 |
| 6000 | discharg | 13 |
| 6001 | dirty | 13 |
| 6002 | dig | 13 |
| 6003 | diadem | 13 |
| 6004 | despis | 13 |
| 6005 | deriv | 13 |
| 6006 | delivers | 13 |
| 6007 | deeper | 13 |
| 6008 | deceiving | 13 |
| 6009 | debtor | 13 |
| 6010 | dames | 13 |
| 6011 | damage | 13 |
| 6012 | curio | 13 |
| 6013 | curds | 13 |
| 6014 | cue | 13 |
| 6015 | cream | 13 |
| 6016 | coventry | 13 |
| 6017 | courteously | 13 |
| 6018 | costs | 13 |
| 6019 | corners | 13 |
| 6020 | convince | 13 |
| 6021 | continual | 13 |
| 6022 | contemplation | 13 |
| 6023 | construction | 13 |
| 6024 | conspiracy | 13 |
| 6025 | concord | 13 |
| 6026 | comment | 13 |
| 6027 | commendations | 13 |
| 6028 | colts | 13 |
| 6029 | cobweb | 13 |
| 6030 | cleared | 13 |
| 6031 | claws | 13 |
| 6032 | churchyard | 13 |
| 6033 | churchman | 13 |
| 6034 | cheerly | 13 |
| 6035 | chancellor | 13 |
| 6036 | ceres | 13 |
| 6037 | cats | 13 |
| 6038 | casket | 13 |
| 6039 | carrion | 13 |
| 6040 | caitiff | 13 |
| 6041 | brandon | 13 |
| 6042 | brag | 13 |
| 6043 | betters | 13 |
| 6044 | bet | 13 |
| 6045 | belaboured | 13 |
| 6046 | bees | 13 |
| 6047 | bawdy | 13 |
| 6048 | bath | 13 |
| 6049 | basest | 13 |
| 6050 | awful | 13 |
| 6051 | astray | 13 |
| 6052 | assembled | 13 |
| 6053 | arrow | 13 |
| 6054 | argues | 13 |
| 6055 | apprehended | 13 |
| 6056 | appearing | 13 |
| 6057 | anew | 13 |
| 6058 | amber | 13 |
| 6059 | allah | 13 |
| 6060 | afore | 13 |
| 6061 | afforded | 13 |
| 6062 | affects | 13 |
| 6063 | adversity | 13 |
| 6064 | adorned | 13 |
| 6065 | admired | 13 |
| 6066 | accusation | 13 |
| 6067 | accurs | 13 |
| 6068 | accordingly | 13 |
| 6069 | abject | 13 |
| 6070 | yore | 12 |
| 6071 | yesternight | 12 |
| 6072 | writings | 12 |
| 6073 | wring | 12 |
| 6074 | wonted | 12 |
| 6075 | winding | 12 |
| 6076 | wi | 12 |
| 6077 | whistle | 12 |
| 6078 | wayward | 12 |
| 6079 | wave | 12 |
| 6080 | wary | 12 |
| 6081 | waken | 12 |
| 6082 | volumnius | 12 |
| 6083 | volsce | 12 |
| 6084 | void | 12 |
| 6085 | virgins | 12 |
| 6086 | ventured | 12 |
| 6087 | vaughan | 12 |
| 6088 | vat | 12 |
| 6089 | vagabond | 12 |
| 6090 | utterance | 12 |
| 6091 | usually | 12 |
| 6092 | using | 12 |
| 6093 | untie | 12 |
| 6094 | unexampled | 12 |
| 6095 | uneasiness | 12 |
| 6096 | tyrannous | 12 |
| 6097 | tunis | 12 |
| 6098 | trivial | 12 |
| 6099 | treble | 12 |
| 6100 | trappings | 12 |
| 6101 | translated | 12 |
| 6102 | transgression | 12 |
| 6103 | traffic | 12 |
| 6104 | tore | 12 |
| 6105 | throughly | 12 |
| 6106 | thrift | 12 |
| 6107 | tearing | 12 |
| 6108 | tak | 12 |
| 6109 | tabor | 12 |
| 6110 | sympathy | 12 |
| 6111 | succeeded | 12 |
| 6112 | substitute | 12 |
| 6113 | strangeness | 12 |
| 6114 | stinking | 12 |
| 6115 | stew | 12 |
| 6116 | sports | 12 |
| 6117 | sphere | 12 |
| 6118 | spear | 12 |
| 6119 | source | 12 |
| 6120 | sorrowful | 12 |
| 6121 | solicit | 12 |
| 6122 | snake | 12 |
| 6123 | smock | 12 |
| 6124 | smil | 12 |
| 6125 | smelt | 12 |
| 6126 | sleepy | 12 |
| 6127 | sixpence | 12 |
| 6128 | shower | 12 |
| 6129 | shock | 12 |
| 6130 | shepherdesses | 12 |
| 6131 | shaken | 12 |
| 6132 | shaft | 12 |
| 6133 | seventh | 12 |
| 6134 | separation | 12 |
| 6135 | seclusion | 12 |
| 6136 | scrupulous | 12 |
| 6137 | scarf | 12 |
| 6138 | satan | 12 |
| 6139 | rust | 12 |
| 6140 | rushes | 12 |
| 6141 | rugged | 12 |
| 6142 | rowland | 12 |
| 6143 | roundly | 12 |
| 6144 | richest | 12 |
| 6145 | revolted | 12 |
| 6146 | resting | 12 |
| 6147 | reserv | 12 |
| 6148 | remuneration | 12 |
| 6149 | relics | 12 |
| 6150 | regal | 12 |
| 6151 | reflections | 12 |
| 6152 | reflecting | 12 |
| 6153 | recreation | 12 |
| 6154 | receiving | 12 |
| 6155 | rays | 12 |
| 6156 | rages | 12 |
| 6157 | pursues | 12 |
| 6158 | pursu | 12 |
| 6159 | purest | 12 |
| 6160 | purchas | 12 |
| 6161 | pulpit | 12 |
| 6162 | pulled | 12 |
| 6163 | prudence | 12 |
| 6164 | provoked | 12 |
| 6165 | province | 12 |
| 6166 | proudly | 12 |
| 6167 | prostrate | 12 |
| 6168 | professes | 12 |
| 6169 | probable | 12 |
| 6170 | pranks | 12 |
| 6171 | polydore | 12 |
| 6172 | poisonous | 12 |
| 6173 | plume | 12 |
| 6174 | plucked | 12 |
| 6175 | plotted | 12 |
| 6176 | plenteous | 12 |
| 6177 | planet | 12 |
| 6178 | plainness | 12 |
| 6179 | pictures | 12 |
| 6180 | perils | 12 |
| 6181 | perfume | 12 |
| 6182 | performed | 12 |
| 6183 | peremptory | 12 |
| 6184 | pent | 12 |
| 6185 | pence | 12 |
| 6186 | peaseblossom | 12 |
| 6187 | paul | 12 |
| 6188 | passages | 12 |
| 6189 | parle | 12 |
| 6190 | palate | 12 |
| 6191 | overtake | 12 |
| 6192 | orb | 12 |
| 6193 | oppress | 12 |
| 6194 | openly | 12 |
| 6195 | offense | 12 |
| 6196 | offenders | 12 |
| 6197 | occupied | 12 |
| 6198 | obstinate | 12 |
| 6199 | numb | 12 |
| 6200 | mutton | 12 |
| 6201 | mustard | 12 |
| 6202 | murdered | 12 |
| 6203 | mum | 12 |
| 6204 | muddy | 12 |
| 6205 | mounsieur | 12 |
| 6206 | mockery | 12 |
| 6207 | mire | 12 |
| 6208 | measured | 12 |
| 6209 | martial | 12 |
| 6210 | marr | 12 |
| 6211 | maravedis | 12 |
| 6212 | macmorris | 12 |
| 6213 | luxury | 12 |
| 6214 | lunatic | 12 |
| 6215 | livest | 12 |
| 6216 | lik | 12 |
| 6217 | lightness | 12 |
| 6218 | licence | 12 |
| 6219 | lawless | 12 |
| 6220 | knives | 12 |
| 6221 | kinds | 12 |
| 6222 | jokes | 12 |
| 6223 | jeweller | 12 |
| 6224 | jerusalem | 12 |
| 6225 | jades | 12 |
| 6226 | irons | 12 |
| 6227 | intolerable | 12 |
| 6228 | inferior | 12 |
| 6229 | infancy | 12 |
| 6230 | industry | 12 |
| 6231 | incens | 12 |
| 6232 | impose | 12 |
| 6233 | impart | 12 |
| 6234 | ills | 12 |
| 6235 | hunter | 12 |
| 6236 | humorous | 12 |
| 6237 | howe | 12 |
| 6238 | holla | 12 |
| 6239 | hits | 12 |
| 6240 | hint | 12 |
| 6241 | hic | 12 |
| 6242 | hew | 12 |
| 6243 | heralds | 12 |
| 6244 | heave | 12 |
| 6245 | harfleur | 12 |
| 6246 | grinders | 12 |
| 6247 | grapes | 12 |
| 6248 | grac | 12 |
| 6249 | governments | 12 |
| 6250 | goletta | 12 |
| 6251 | glories | 12 |
| 6252 | gentles | 12 |
| 6253 | genius | 12 |
| 6254 | generation | 12 |
| 6255 | gazed | 12 |
| 6256 | garters | 12 |
| 6257 | gaping | 12 |
| 6258 | gape | 12 |
| 6259 | gap | 12 |
| 6260 | gaol | 12 |
| 6261 | frozen | 12 |
| 6262 | froward | 12 |
| 6263 | frost | 12 |
| 6264 | friday | 12 |
| 6265 | fret | 12 |
| 6266 | frenzy | 12 |
| 6267 | frailty | 12 |
| 6268 | formerly | 12 |
| 6269 | formed | 12 |
| 6270 | forester | 12 |
| 6271 | footed | 12 |
| 6272 | folks | 12 |
| 6273 | flinty | 12 |
| 6274 | flew | 12 |
| 6275 | flatterers | 12 |
| 6276 | fitzwater | 12 |
| 6277 | filling | 12 |
| 6278 | feign | 12 |
| 6279 | feels | 12 |
| 6280 | favor | 12 |
| 6281 | fared | 12 |
| 6282 | fancying | 12 |
| 6283 | falcon | 12 |
| 6284 | fails | 12 |
| 6285 | failing | 12 |
| 6286 | expressed | 12 |
| 6287 | exclaim | 12 |
| 6288 | exact | 12 |
| 6289 | evident | 12 |
| 6290 | europe | 12 |
| 6291 | erpingham | 12 |
| 6292 | equally | 12 |
| 6293 | envied | 12 |
| 6294 | endured | 12 |
| 6295 | elsewhere | 12 |
| 6296 | element | 12 |
| 6297 | echo | 12 |
| 6298 | dower | 12 |
| 6299 | dissemble | 12 |
| 6300 | disenchanted | 12 |
| 6301 | discuss | 12 |
| 6302 | disclose | 12 |
| 6303 | dirt | 12 |
| 6304 | dion | 12 |
| 6305 | dieu | 12 |
| 6306 | dial | 12 |
| 6307 | detain | 12 |
| 6308 | despatch | 12 |
| 6309 | desirous | 12 |
| 6310 | derived | 12 |
| 6311 | deliverance | 12 |
| 6312 | deliberate | 12 |
| 6313 | decrees | 12 |
| 6314 | decreed | 12 |
| 6315 | dally | 12 |
| 6316 | cursing | 12 |
| 6317 | cull | 12 |
| 6318 | crowd | 12 |
| 6319 | croup | 12 |
| 6320 | crosses | 12 |
| 6321 | crop | 12 |
| 6322 | craze | 12 |
| 6323 | courts | 12 |
| 6324 | courtly | 12 |
| 6325 | countries | 12 |
| 6326 | costume | 12 |
| 6327 | costly | 12 |
| 6328 | contracted | 12 |
| 6329 | continent | 12 |
| 6330 | constraint | 12 |
| 6331 | constantinople | 12 |
| 6332 | confines | 12 |
| 6333 | confessor | 12 |
| 6334 | conducted | 12 |
| 6335 | compulsion | 12 |
| 6336 | composure | 12 |
| 6337 | comparisons | 12 |
| 6338 | comforted | 12 |
| 6339 | combatants | 12 |
| 6340 | comb | 12 |
| 6341 | coffers | 12 |
| 6342 | cloudy | 12 |
| 6343 | cleft | 12 |
| 6344 | cleave | 12 |
| 6345 | claims | 12 |
| 6346 | cimber | 12 |
| 6347 | cheerfully | 12 |
| 6348 | chat | 12 |
| 6349 | charmed | 12 |
| 6350 | carve | 12 |
| 6351 | capt | 12 |
| 6352 | canopy | 12 |
| 6353 | calais | 12 |
| 6354 | cakes | 12 |
| 6355 | bundle | 12 |
| 6356 | brute | 12 |
| 6357 | broils | 12 |
| 6358 | broach | 12 |
| 6359 | bridal | 12 |
| 6360 | breasts | 12 |
| 6361 | borachio | 12 |
| 6362 | bon | 12 |
| 6363 | blushes | 12 |
| 6364 | blaze | 12 |
| 6365 | bier | 12 |
| 6366 | bias | 12 |
| 6367 | belonged | 12 |
| 6368 | belch | 12 |
| 6369 | beggary | 12 |
| 6370 | beest | 12 |
| 6371 | beach | 12 |
| 6372 | barataria | 12 |
| 6373 | bankrupt | 12 |
| 6374 | bandit | 12 |
| 6375 | balthazar | 12 |
| 6376 | avenged | 12 |
| 6377 | audacity | 12 |
| 6378 | attempts | 12 |
| 6379 | ascertain | 12 |
| 6380 | ascend | 12 |
| 6381 | arrogance | 12 |
| 6382 | appointment | 12 |
| 6383 | angus | 12 |
| 6384 | anguish | 12 |
| 6385 | andromache | 12 |
| 6386 | amaze | 12 |
| 6387 | alteration | 12 |
| 6388 | altar | 12 |
| 6389 | agent | 12 |
| 6390 | advantages | 12 |
| 6391 | advancement | 12 |
| 6392 | acquired | 12 |
| 6393 | abuses | 12 |
| 6394 | abhorr | 12 |
| 6395 | wrestling | 11 |
| 6396 | wounding | 11 |
| 6397 | withered | 11 |
| 6398 | wishing | 11 |
| 6399 | wildly | 11 |
| 6400 | wilderness | 11 |
| 6401 | widower | 11 |
| 6402 | whoe | 11 |
| 6403 | whelp | 11 |
| 6404 | whe | 11 |
| 6405 | weaker | 11 |
| 6406 | washed | 11 |
| 6407 | ware | 11 |
| 6408 | vivaldo | 11 |
| 6409 | visible | 11 |
| 6410 | villany | 11 |
| 6411 | villanous | 11 |
| 6412 | vienna | 11 |
| 6413 | veiled | 11 |
| 6414 | valleys | 11 |
| 6415 | vainly | 11 |
| 6416 | utterly | 11 |
| 6417 | usurer | 11 |
| 6418 | urgent | 11 |
| 6419 | unusual | 11 |
| 6420 | unparalleled | 11 |
| 6421 | unlawful | 11 |
| 6422 | ungentle | 11 |
| 6423 | twinkling | 11 |
| 6424 | truthful | 11 |
| 6425 | trusting | 11 |
| 6426 | truest | 11 |
| 6427 | troyans | 11 |
| 6428 | trophy | 11 |
| 6429 | trimm | 11 |
| 6430 | treads | 11 |
| 6431 | transparent | 11 |
| 6432 | tragic | 11 |
| 6433 | toss | 11 |
| 6434 | toads | 11 |
| 6435 | timandra | 11 |
| 6436 | thereupon | 11 |
| 6437 | territories | 11 |
| 6438 | terrified | 11 |
| 6439 | tenth | 11 |
| 6440 | tends | 11 |
| 6441 | temperate | 11 |
| 6442 | sweetheart | 11 |
| 6443 | suspicions | 11 |
| 6444 | suspense | 11 |
| 6445 | surly | 11 |
| 6446 | supplied | 11 |
| 6447 | supped | 11 |
| 6448 | sufficiently | 11 |
| 6449 | succeeding | 11 |
| 6450 | stirrups | 11 |
| 6451 | stirrup | 11 |
| 6452 | stealth | 11 |
| 6453 | stayed | 11 |
| 6454 | statutes | 11 |
| 6455 | stairs | 11 |
| 6456 | stained | 11 |
| 6457 | sprung | 11 |
| 6458 | spots | 11 |
| 6459 | spider | 11 |
| 6460 | spheres | 11 |
| 6461 | sped | 11 |
| 6462 | solus | 11 |
| 6463 | solely | 11 |
| 6464 | soften | 11 |
| 6465 | snail | 11 |
| 6466 | slipp | 11 |
| 6467 | sifting | 11 |
| 6468 | shrink | 11 |
| 6469 | shriek | 11 |
| 6470 | shave | 11 |
| 6471 | shameless | 11 |
| 6472 | sexton | 11 |
| 6473 | sentences | 11 |
| 6474 | seleucus | 11 |
| 6475 | seats | 11 |
| 6476 | scatter | 11 |
| 6477 | sblood | 11 |
| 6478 | sayings | 11 |
| 6479 | satin | 11 |
| 6480 | sale | 11 |
| 6481 | row | 11 |
| 6482 | rout | 11 |
| 6483 | rosalinde | 11 |
| 6484 | robbing | 11 |
| 6485 | robbery | 11 |
| 6486 | robbers | 11 |
| 6487 | roasted | 11 |
| 6488 | rigour | 11 |
| 6489 | rider | 11 |
| 6490 | rhetoric | 11 |
| 6491 | retiring | 11 |
| 6492 | restor | 11 |
| 6493 | restless | 11 |
| 6494 | reputed | 11 |
| 6495 | replies | 11 |
| 6496 | redemption | 11 |
| 6497 | realms | 11 |
| 6498 | reaches | 11 |
| 6499 | rambures | 11 |
| 6500 | raiment | 11 |
| 6501 | qualified | 11 |
| 6502 | quaint | 11 |
| 6503 | pyrrhus | 11 |
| 6504 | puzzled | 11 |
| 6505 | puissant | 11 |
| 6506 | publicly | 11 |
| 6507 | provision | 11 |
| 6508 | pronounc | 11 |
| 6509 | proclaimed | 11 |
| 6510 | probably | 11 |
| 6511 | preferr | 11 |
| 6512 | preferment | 11 |
| 6513 | precisely | 11 |
| 6514 | precise | 11 |
| 6515 | precepts | 11 |
| 6516 | prating | 11 |
| 6517 | practis | 11 |
| 6518 | powder | 11 |
| 6519 | possibly | 11 |
| 6520 | possesses | 11 |
| 6521 | positively | 11 |
| 6522 | politeness | 11 |
| 6523 | poisons | 11 |
| 6524 | plunged | 11 |
| 6525 | placing | 11 |
| 6526 | pilot | 11 |
| 6527 | pigs | 11 |
| 6528 | pet | 11 |
| 6529 | permitted | 11 |
| 6530 | perfections | 11 |
| 6531 | perdition | 11 |
| 6532 | patron | 11 |
| 6533 | partake | 11 |
| 6534 | packet | 11 |
| 6535 | owest | 11 |
| 6536 | orator | 11 |
| 6537 | ominous | 11 |
| 6538 | oman | 11 |
| 6539 | offensive | 11 |
| 6540 | offending | 11 |
| 6541 | obtaining | 11 |
| 6542 | nut | 11 |
| 6543 | nan | 11 |
| 6544 | mud | 11 |
| 6545 | mishaps | 11 |
| 6546 | midwife | 11 |
| 6547 | mew | 11 |
| 6548 | melun | 11 |
| 6549 | melting | 11 |
| 6550 | meek | 11 |
| 6551 | med | 11 |
| 6552 | maskers | 11 |
| 6553 | lovel | 11 |
| 6554 | loathed | 11 |
| 6555 | lesson | 11 |
| 6556 | legate | 11 |
| 6557 | lash | 11 |
| 6558 | lantern | 11 |
| 6559 | lamps | 11 |
| 6560 | knots | 11 |
| 6561 | knell | 11 |
| 6562 | kites | 11 |
| 6563 | justify | 11 |
| 6564 | jet | 11 |
| 6565 | invented | 11 |
| 6566 | interrupt | 11 |
| 6567 | interim | 11 |
| 6568 | insulting | 11 |
| 6569 | instances | 11 |
| 6570 | inhuman | 11 |
| 6571 | infer | 11 |
| 6572 | induce | 11 |
| 6573 | inconstant | 11 |
| 6574 | incident | 11 |
| 6575 | inches | 11 |
| 6576 | incapable | 11 |
| 6577 | impress | 11 |
| 6578 | impeach | 11 |
| 6579 | imminent | 11 |
| 6580 | idiot | 11 |
| 6581 | humanity | 11 |
| 6582 | horner | 11 |
| 6583 | hoping | 11 |
| 6584 | hopeless | 11 |
| 6585 | honors | 11 |
| 6586 | honestly | 11 |
| 6587 | holland | 11 |
| 6588 | historian | 11 |
| 6589 | hiss | 11 |
| 6590 | hermitage | 11 |
| 6591 | heath | 11 |
| 6592 | haunches | 11 |
| 6593 | handmaid | 11 |
| 6594 | hag | 11 |
| 6595 | gulf | 11 |
| 6596 | guinart | 11 |
| 6597 | griev | 11 |
| 6598 | greyhounds | 11 |
| 6599 | greets | 11 |
| 6600 | greedy | 11 |
| 6601 | greasy | 11 |
| 6602 | goth | 11 |
| 6603 | goldsmith | 11 |
| 6604 | glow | 11 |
| 6605 | gloucestershire | 11 |
| 6606 | glasses | 11 |
| 6607 | germany | 11 |
| 6608 | garb | 11 |
| 6609 | frequently | 11 |
| 6610 | formal | 11 |
| 6611 | fondly | 11 |
| 6612 | folded | 11 |
| 6613 | foils | 11 |
| 6614 | floods | 11 |
| 6615 | fishes | 11 |
| 6616 | finely | 11 |
| 6617 | faculties | 11 |
| 6618 | exceeds | 11 |
| 6619 | euphronius | 11 |
| 6620 | eternity | 11 |
| 6621 | entrails | 11 |
| 6622 | enrag | 11 |
| 6623 | enjoin | 11 |
| 6624 | englishman | 11 |
| 6625 | emulation | 11 |
| 6626 | embrac | 11 |
| 6627 | efforts | 11 |
| 6628 | earned | 11 |
| 6629 | earls | 11 |
| 6630 | eagles | 11 |
| 6631 | duteous | 11 |
| 6632 | durandarte | 11 |
| 6633 | drugs | 11 |
| 6634 | drowned | 11 |
| 6635 | dressing | 11 |
| 6636 | dreaded | 11 |
| 6637 | doomsday | 11 |
| 6638 | divinity | 11 |
| 6639 | disperse | 11 |
| 6640 | dispers | 11 |
| 6641 | dishonest | 11 |
| 6642 | diamonds | 11 |
| 6643 | detestable | 11 |
| 6644 | desp | 11 |
| 6645 | depth | 11 |
| 6646 | deprive | 11 |
| 6647 | demi | 11 |
| 6648 | demeanour | 11 |
| 6649 | deign | 11 |
| 6650 | degenerate | 11 |
| 6651 | defending | 11 |
| 6652 | deals | 11 |
| 6653 | damnable | 11 |
| 6654 | cushions | 11 |
| 6655 | curtains | 11 |
| 6656 | crutch | 11 |
| 6657 | coy | 11 |
| 6658 | corpse | 11 |
| 6659 | cordial | 11 |
| 6660 | corchuelo | 11 |
| 6661 | continues | 11 |
| 6662 | containing | 11 |
| 6663 | contagious | 11 |
| 6664 | construe | 11 |
| 6665 | constantly | 11 |
| 6666 | conspirators | 11 |
| 6667 | consists | 11 |
| 6668 | confounds | 11 |
| 6669 | conflict | 11 |
| 6670 | confirmed | 11 |
| 6671 | compliment | 11 |
| 6672 | commotion | 11 |
| 6673 | commissary | 11 |
| 6674 | comely | 11 |
| 6675 | clubs | 11 |
| 6676 | clamorous | 11 |
| 6677 | chooseth | 11 |
| 6678 | chiding | 11 |
| 6679 | chariot | 11 |
| 6680 | career | 11 |
| 6681 | candles | 11 |
| 6682 | cabin | 11 |
| 6683 | buzz | 11 |
| 6684 | buys | 11 |
| 6685 | butts | 11 |
| 6686 | burdens | 11 |
| 6687 | budge | 11 |
| 6688 | britons | 11 |
| 6689 | british | 11 |
| 6690 | bribe | 11 |
| 6691 | breathes | 11 |
| 6692 | braggart | 11 |
| 6693 | bout | 11 |
| 6694 | blossom | 11 |
| 6695 | biting | 11 |
| 6696 | bites | 11 |
| 6697 | bitch | 11 |
| 6698 | birnam | 11 |
| 6699 | beseeming | 11 |
| 6700 | bequeath | 11 |
| 6701 | behave | 11 |
| 6702 | bee | 11 |
| 6703 | battered | 11 |
| 6704 | bates | 11 |
| 6705 | basset | 11 |
| 6706 | baser | 11 |
| 6707 | barr | 11 |
| 6708 | bano | 11 |
| 6709 | await | 11 |
| 6710 | avouch | 11 |
| 6711 | autumn | 11 |
| 6712 | attempting | 11 |
| 6713 | aragon | 11 |
| 6714 | arabic | 11 |
| 6715 | applaud | 11 |
| 6716 | antic | 11 |
| 6717 | ambrosio | 11 |
| 6718 | almighty | 11 |
| 6719 | allowance | 11 |
| 6720 | alarm | 11 |
| 6721 | agreement | 11 |
| 6722 | agitated | 11 |
| 6723 | aforesaid | 11 |
| 6724 | affright | 11 |
| 6725 | adversaries | 11 |
| 6726 | admittance | 11 |
| 6727 | accomplishments | 11 |
| 6728 | abhorred | 11 |
| 6729 | yeoman | 10 |
| 6730 | yare | 10 |
| 6731 | writers | 10 |
| 6732 | wrangle | 10 |
| 6733 | wooed | 10 |
| 6734 | wiped | 10 |
| 6735 | winters | 10 |
| 6736 | winking | 10 |
| 6737 | windmills | 10 |
| 6738 | wilds | 10 |
| 6739 | whet | 10 |
| 6740 | wheeled | 10 |
| 6741 | western | 10 |
| 6742 | weighs | 10 |
| 6743 | wedlock | 10 |
| 6744 | weaver | 10 |
| 6745 | volscian | 10 |
| 6746 | vial | 10 |
| 6747 | verity | 10 |
| 6748 | verges | 10 |
| 6749 | vanished | 10 |
| 6750 | upset | 10 |
| 6751 | upper | 10 |
| 6752 | uplifted | 10 |
| 6753 | unfit | 10 |
| 6754 | unexpected | 10 |
| 6755 | unequal | 10 |
| 6756 | uncover | 10 |
| 6757 | tyrants | 10 |
| 6758 | tumult | 10 |
| 6759 | tucket | 10 |
| 6760 | tribe | 10 |
| 6761 | trencher | 10 |
| 6762 | trash | 10 |
| 6763 | transported | 10 |
| 6764 | tradition | 10 |
| 6765 | tops | 10 |
| 6766 | tip | 10 |
| 6767 | tigers | 10 |
| 6768 | tides | 10 |
| 6769 | thrusts | 10 |
| 6770 | testament | 10 |
| 6771 | tearsheet | 10 |
| 6772 | syllable | 10 |
| 6773 | swine | 10 |
| 6774 | swiftly | 10 |
| 6775 | swarm | 10 |
| 6776 | swan | 10 |
| 6777 | survive | 10 |
| 6778 | sunshine | 10 |
| 6779 | summons | 10 |
| 6780 | suggestion | 10 |
| 6781 | sturdy | 10 |
| 6782 | stoutly | 10 |
| 6783 | stolen | 10 |
| 6784 | stings | 10 |
| 6785 | steer | 10 |
| 6786 | starting | 10 |
| 6787 | standard | 10 |
| 6788 | squadron | 10 |
| 6789 | spreading | 10 |
| 6790 | speakest | 10 |
| 6791 | spaniard | 10 |
| 6792 | spade | 10 |
| 6793 | somebody | 10 |
| 6794 | solid | 10 |
| 6795 | sola | 10 |
| 6796 | snug | 10 |
| 6797 | smack | 10 |
| 6798 | sloth | 10 |
| 6799 | slaught | 10 |
| 6800 | slack | 10 |
| 6801 | sicilius | 10 |
| 6802 | shrill | 10 |
| 6803 | shrift | 10 |
| 6804 | shrewdly | 10 |
| 6805 | shouted | 10 |
| 6806 | shone | 10 |
| 6807 | shillings | 10 |
| 6808 | sheathe | 10 |
| 6809 | sheath | 10 |
| 6810 | serpents | 10 |
| 6811 | seriously | 10 |
| 6812 | sequel | 10 |
| 6813 | sempronius | 10 |
| 6814 | secured | 10 |
| 6815 | seals | 10 |
| 6816 | sealed | 10 |
| 6817 | scour | 10 |
| 6818 | sciences | 10 |
| 6819 | sceptres | 10 |
| 6820 | scant | 10 |
| 6821 | scald | 10 |
| 6822 | salvation | 10 |
| 6823 | sacrament | 10 |
| 6824 | rushing | 10 |
| 6825 | rosemary | 10 |
| 6826 | rooted | 10 |
| 6827 | roaming | 10 |
| 6828 | rite | 10 |
| 6829 | riotous | 10 |
| 6830 | rides | 10 |
| 6831 | riddle | 10 |
| 6832 | repast | 10 |
| 6833 | relation | 10 |
| 6834 | reins | 10 |
| 6835 | recollection | 10 |
| 6836 | reckless | 10 |
| 6837 | rats | 10 |
| 6838 | rarely | 10 |
| 6839 | quitting | 10 |
| 6840 | quicken | 10 |
| 6841 | purposely | 10 |
| 6842 | purgatory | 10 |
| 6843 | prowess | 10 |
| 6844 | provokes | 10 |
| 6845 | provinces | 10 |
| 6846 | profitable | 10 |
| 6847 | proclaims | 10 |
| 6848 | pretend | 10 |
| 6849 | presenting | 10 |
| 6850 | plucking | 10 |
| 6851 | plentiful | 10 |
| 6852 | plea | 10 |
| 6853 | plaster | 10 |
| 6854 | pitcher | 10 |
| 6855 | pipes | 10 |
| 6856 | pierres | 10 |
| 6857 | phrases | 10 |
| 6858 | petitioner | 10 |
| 6859 | performing | 10 |
| 6860 | perceiv | 10 |
| 6861 | peg | 10 |
| 6862 | peculiar | 10 |
| 6863 | pebbles | 10 |
| 6864 | passionate | 10 |
| 6865 | parentage | 10 |
| 6866 | palfrey | 10 |
| 6867 | painful | 10 |
| 6868 | pageant | 10 |
| 6869 | pad | 10 |
| 6870 | owen | 10 |
| 6871 | ordain | 10 |
| 6872 | omitted | 10 |
| 6873 | observ | 10 |
| 6874 | obdurate | 10 |
| 6875 | nun | 10 |
| 6876 | numerous | 10 |
| 6877 | nowhere | 10 |
| 6878 | northern | 10 |
| 6879 | noontide | 10 |
| 6880 | nightingale | 10 |
| 6881 | niggard | 10 |
| 6882 | nicely | 10 |
| 6883 | neigh | 10 |
| 6884 | navy | 10 |
| 6885 | musical | 10 |
| 6886 | murtherers | 10 |
| 6887 | muleteers | 10 |
| 6888 | mournful | 10 |
| 6889 | moulded | 10 |
| 6890 | mortals | 10 |
| 6891 | montgomery | 10 |
| 6892 | monkey | 10 |
| 6893 | monday | 10 |
| 6894 | moans | 10 |
| 6895 | mixture | 10 |
| 6896 | mistaking | 10 |
| 6897 | miscarried | 10 |
| 6898 | mines | 10 |
| 6899 | military | 10 |
| 6900 | method | 10 |
| 6901 | merited | 10 |
| 6902 | merchants | 10 |
| 6903 | maxims | 10 |
| 6904 | mariners | 10 |
| 6905 | mares | 10 |
| 6906 | maintained | 10 |
| 6907 | maidenhead | 10 |
| 6908 | magnanimous | 10 |
| 6909 | madonna | 10 |
| 6910 | madame | 10 |
| 6911 | lowered | 10 |
| 6912 | loses | 10 |
| 6913 | lodged | 10 |
| 6914 | lodg | 10 |
| 6915 | lineage | 10 |
| 6916 | lieu | 10 |
| 6917 | liberality | 10 |
| 6918 | levy | 10 |
| 6919 | leaped | 10 |
| 6920 | lasted | 10 |
| 6921 | lank | 10 |
| 6922 | lackey | 10 |
| 6923 | labyrinth | 10 |
| 6924 | labor | 10 |
| 6925 | kandy | 10 |
| 6926 | jumps | 10 |
| 6927 | jester | 10 |
| 6928 | irish | 10 |
| 6929 | iris | 10 |
| 6930 | inviting | 10 |
| 6931 | intellect | 10 |
| 6932 | inhabitants | 10 |
| 6933 | inhabit | 10 |
| 6934 | ingenuity | 10 |
| 6935 | inflict | 10 |
| 6936 | infants | 10 |
| 6937 | increased | 10 |
| 6938 | incline | 10 |
| 6939 | incensed | 10 |
| 6940 | incense | 10 |
| 6941 | impossibilities | 10 |
| 6942 | hypocrite | 10 |
| 6943 | humor | 10 |
| 6944 | humbled | 10 |
| 6945 | hosts | 10 |
| 6946 | hem | 10 |
| 6947 | helping | 10 |
| 6948 | heedless | 10 |
| 6949 | healthful | 10 |
| 6950 | headstrong | 10 |
| 6951 | havoc | 10 |
| 6952 | haunts | 10 |
| 6953 | hapless | 10 |
| 6954 | hammer | 10 |
| 6955 | halting | 10 |
| 6956 | halberds | 10 |
| 6957 | gull | 10 |
| 6958 | guides | 10 |
| 6959 | grooms | 10 |
| 6960 | grievances | 10 |
| 6961 | grievance | 10 |
| 6962 | greyhound | 10 |
| 6963 | gregory | 10 |
| 6964 | gratis | 10 |
| 6965 | glutton | 10 |
| 6966 | glowing | 10 |
| 6967 | giver | 10 |
| 6968 | geffrey | 10 |
| 6969 | gathering | 10 |
| 6970 | garlic | 10 |
| 6971 | gaban | 10 |
| 6972 | fulfill | 10 |
| 6973 | fresher | 10 |
| 6974 | freeze | 10 |
| 6975 | fraught | 10 |
| 6976 | frankly | 10 |
| 6977 | francisco | 10 |
| 6978 | founded | 10 |
| 6979 | fortify | 10 |
| 6980 | forfend | 10 |
| 6981 | fooling | 10 |
| 6982 | flowed | 10 |
| 6983 | flocks | 10 |
| 6984 | flea | 10 |
| 6985 | flask | 10 |
| 6986 | flag | 10 |
| 6987 | fishermen | 10 |
| 6988 | fidele | 10 |
| 6989 | feigned | 10 |
| 6990 | feat | 10 |
| 6991 | feasting | 10 |
| 6992 | favourable | 10 |
| 6993 | fastolfe | 10 |
| 6994 | faintly | 10 |
| 6995 | factious | 10 |
| 6996 | extremest | 10 |
| 6997 | expressly | 10 |
| 6998 | explained | 10 |
| 6999 | expedient | 10 |
| 7000 | expects | 10 |
| 7001 | excus | 10 |
| 7002 | escapes | 10 |
| 7003 | entreating | 10 |
| 7004 | entitled | 10 |
| 7005 | enow | 10 |
| 7006 | energy | 10 |
| 7007 | endowed | 10 |
| 7008 | eminence | 10 |
| 7009 | eke | 10 |
| 7010 | edict | 10 |
| 7011 | earnestness | 10 |
| 7012 | dwarf | 10 |
| 7013 | durance | 10 |
| 7014 | dungeon | 10 |
| 7015 | dues | 10 |
| 7016 | duck | 10 |
| 7017 | dropping | 10 |
| 7018 | dragons | 10 |
| 7019 | dragged | 10 |
| 7020 | dotage | 10 |
| 7021 | dominions | 10 |
| 7022 | divert | 10 |
| 7023 | ditch | 10 |
| 7024 | distract | 10 |
| 7025 | dispraise | 10 |
| 7026 | disposal | 10 |
| 7027 | discussing | 10 |
| 7028 | disaster | 10 |
| 7029 | dined | 10 |
| 7030 | digging | 10 |
| 7031 | dexterity | 10 |
| 7032 | devised | 10 |
| 7033 | destroyed | 10 |
| 7034 | despairing | 10 |
| 7035 | desolation | 10 |
| 7036 | descried | 10 |
| 7037 | descends | 10 |
| 7038 | dercetas | 10 |
| 7039 | depose | 10 |
| 7040 | delivering | 10 |
| 7041 | delectable | 10 |
| 7042 | deiphobus | 10 |
| 7043 | defects | 10 |
| 7044 | decline | 10 |
| 7045 | dearth | 10 |
| 7046 | darkly | 10 |
| 7047 | damask | 10 |
| 7048 | cuff | 10 |
| 7049 | credulous | 10 |
| 7050 | creation | 10 |
| 7051 | cramm | 10 |
| 7052 | covetousness | 10 |
| 7053 | courtyard | 10 |
| 7054 | courtesies | 10 |
| 7055 | courageous | 10 |
| 7056 | counts | 10 |
| 7057 | countenances | 10 |
| 7058 | coronet | 10 |
| 7059 | convent | 10 |
| 7060 | constrain | 10 |
| 7061 | conjecture | 10 |
| 7062 | confounded | 10 |
| 7063 | confessed | 10 |
| 7064 | confederates | 10 |
| 7065 | conceits | 10 |
| 7066 | conceited | 10 |
| 7067 | compounded | 10 |
| 7068 | compose | 10 |
| 7069 | commonweal | 10 |
| 7070 | commoner | 10 |
| 7071 | commendation | 10 |
| 7072 | coarse | 10 |
| 7073 | clothe | 10 |
| 7074 | clever | 10 |
| 7075 | clarions | 10 |
| 7076 | chooses | 10 |
| 7077 | chok | 10 |
| 7078 | chimney | 10 |
| 7079 | chides | 10 |
| 7080 | checked | 10 |
| 7081 | charter | 10 |
| 7082 | challeng | 10 |
| 7083 | chairs | 10 |
| 7084 | chaff | 10 |
| 7085 | celebrated | 10 |
| 7086 | cedar | 10 |
| 7087 | caus | 10 |
| 7088 | carved | 10 |
| 7089 | cargo | 10 |
| 7090 | capon | 10 |
| 7091 | capers | 10 |
| 7092 | bullen | 10 |
| 7093 | broker | 10 |
| 7094 | brine | 10 |
| 7095 | breeze | 10 |
| 7096 | brayed | 10 |
| 7097 | bravest | 10 |
| 7098 | braver | 10 |
| 7099 | bragging | 10 |
| 7100 | bourbon | 10 |
| 7101 | bountiful | 10 |
| 7102 | bordeaux | 10 |
| 7103 | bondman | 10 |
| 7104 | boist | 10 |
| 7105 | boil | 10 |
| 7106 | bits | 10 |
| 7107 | betrayed | 10 |
| 7108 | betook | 10 |
| 7109 | betake | 10 |
| 7110 | besiege | 10 |
| 7111 | benefits | 10 |
| 7112 | belie | 10 |
| 7113 | belerma | 10 |
| 7114 | behaved | 10 |
| 7115 | begone | 10 |
| 7116 | beggarly | 10 |
| 7117 | bedfellow | 10 |
| 7118 | barefoot | 10 |
| 7119 | balth | 10 |
| 7120 | aweary | 10 |
| 7121 | authorities | 10 |
| 7122 | audacious | 10 |
| 7123 | attached | 10 |
| 7124 | assuredly | 10 |
| 7125 | assigned | 10 |
| 7126 | asks | 10 |
| 7127 | arrogant | 10 |
| 7128 | arrayed | 10 |
| 7129 | arrange | 10 |
| 7130 | arragon | 10 |
| 7131 | applied | 10 |
| 7132 | antonomasia | 10 |
| 7133 | antium | 10 |
| 7134 | annoy | 10 |
| 7135 | angelica | 10 |
| 7136 | andalusia | 10 |
| 7137 | amiable | 10 |
| 7138 | airs | 10 |
| 7139 | agitation | 10 |
| 7140 | adventurers | 10 |
| 7141 | adventurer | 10 |
| 7142 | admits | 10 |
| 7143 | abound | 10 |
| 7144 | youths | 9 |
| 7145 | x | 9 |
| 7146 | wrist | 9 |
| 7147 | wretchedness | 9 |
| 7148 | wrestler | 9 |
| 7149 | wrangling | 9 |
| 7150 | wooer | 9 |
| 7151 | woke | 9 |
| 7152 | withheld | 9 |
| 7153 | wip | 9 |
| 7154 | wildness | 9 |
| 7155 | wight | 9 |
| 7156 | whipped | 9 |
| 7157 | welfare | 9 |
| 7158 | weariness | 9 |
| 7159 | waving | 9 |
| 7160 | wasteful | 9 |
| 7161 | wantonness | 9 |
| 7162 | votre | 9 |
| 7163 | vomit | 9 |
| 7164 | verified | 9 |
| 7165 | verge | 9 |
| 7166 | ve | 9 |
| 7167 | vaux | 9 |
| 7168 | varrius | 9 |
| 7169 | values | 9 |
| 7170 | valorous | 9 |
| 7171 | utt | 9 |
| 7172 | usurper | 9 |
| 7173 | usher | 9 |
| 7174 | useless | 9 |
| 7175 | upwards | 9 |
| 7176 | uphold | 9 |
| 7177 | upbraid | 9 |
| 7178 | untrue | 9 |
| 7179 | unjustly | 9 |
| 7180 | unexpectedly | 9 |
| 7181 | undertook | 9 |
| 7182 | uncovered | 9 |
| 7183 | unborn | 9 |
| 7184 | tun | 9 |
| 7185 | tu | 9 |
| 7186 | trough | 9 |
| 7187 | tripping | 9 |
| 7188 | trice | 9 |
| 7189 | trenches | 9 |
| 7190 | trembled | 9 |
| 7191 | travail | 9 |
| 7192 | tranquil | 9 |
| 7193 | trail | 9 |
| 7194 | tombs | 9 |
| 7195 | tirteafuera | 9 |
| 7196 | tiber | 9 |
| 7197 | thunders | 9 |
| 7198 | threatens | 9 |
| 7199 | thirsty | 9 |
| 7200 | thickest | 9 |
| 7201 | therewithal | 9 |
| 7202 | tending | 9 |
| 7203 | tenderly | 9 |
| 7204 | temptation | 9 |
| 7205 | temperance | 9 |
| 7206 | team | 9 |
| 7207 | taurus | 9 |
| 7208 | tastes | 9 |
| 7209 | tasted | 9 |
| 7210 | tartar | 9 |
| 7211 | tarquin | 9 |
| 7212 | swoons | 9 |
| 7213 | swiftness | 9 |
| 7214 | swells | 9 |
| 7215 | surname | 9 |
| 7216 | surge | 9 |
| 7217 | suppress | 9 |
| 7218 | supported | 9 |
| 7219 | sucking | 9 |
| 7220 | struggling | 9 |
| 7221 | strangled | 9 |
| 7222 | strains | 9 |
| 7223 | stony | 9 |
| 7224 | sticking | 9 |
| 7225 | starv | 9 |
| 7226 | stains | 9 |
| 7227 | sprites | 9 |
| 7228 | spirited | 9 |
| 7229 | spilt | 9 |
| 7230 | spied | 9 |
| 7231 | sparks | 9 |
| 7232 | spark | 9 |
| 7233 | sparing | 9 |
| 7234 | spaniel | 9 |
| 7235 | solemnly | 9 |
| 7236 | sojourn | 9 |
| 7237 | snuff | 9 |
| 7238 | smelling | 9 |
| 7239 | slips | 9 |
| 7240 | slippery | 9 |
| 7241 | slashing | 9 |
| 7242 | skirmish | 9 |
| 7243 | skilful | 9 |
| 7244 | singular | 9 |
| 7245 | signed | 9 |
| 7246 | sicily | 9 |
| 7247 | shunn | 9 |
| 7248 | shorter | 9 |
| 7249 | shin | 9 |
| 7250 | shares | 9 |
| 7251 | sew | 9 |
| 7252 | seventeen | 9 |
| 7253 | servile | 9 |
| 7254 | sequent | 9 |
| 7255 | sentinels | 9 |
| 7256 | seemeth | 9 |
| 7257 | scolding | 9 |
| 7258 | scold | 9 |
| 7259 | scap | 9 |
| 7260 | savours | 9 |
| 7261 | salutation | 9 |
| 7262 | sallied | 9 |
| 7263 | salique | 9 |
| 7264 | saith | 9 |
| 7265 | safest | 9 |
| 7266 | rudeness | 9 |
| 7267 | royally | 9 |
| 7268 | rounds | 9 |
| 7269 | roncesvalles | 9 |
| 7270 | robs | 9 |
| 7271 | robber | 9 |
| 7272 | roam | 9 |
| 7273 | rhymes | 9 |
| 7274 | revengeful | 9 |
| 7275 | retir | 9 |
| 7276 | respectable | 9 |
| 7277 | residence | 9 |
| 7278 | resemble | 9 |
| 7279 | represent | 9 |
| 7280 | replying | 9 |
| 7281 | replete | 9 |
| 7282 | repaired | 9 |
| 7283 | repaid | 9 |
| 7284 | renewed | 9 |
| 7285 | remembered | 9 |
| 7286 | remedies | 9 |
| 7287 | remarked | 9 |
| 7288 | relations | 9 |
| 7289 | regular | 9 |
| 7290 | reck | 9 |
| 7291 | rebellious | 9 |
| 7292 | ravenspurgh | 9 |
| 7293 | random | 9 |
| 7294 | rance | 9 |
| 7295 | radiant | 9 |
| 7296 | quietness | 9 |
| 7297 | quarrelling | 9 |
| 7298 | qualify | 9 |
| 7299 | pursuing | 9 |
| 7300 | puissance | 9 |
| 7301 | pry | 9 |
| 7302 | provocation | 9 |
| 7303 | prop | 9 |
| 7304 | pronounced | 9 |
| 7305 | profits | 9 |
| 7306 | proffer | 9 |
| 7307 | professions | 9 |
| 7308 | proceeds | 9 |
| 7309 | priz | 9 |
| 7310 | privileges | 9 |
| 7311 | privately | 9 |
| 7312 | prettiest | 9 |
| 7313 | presses | 9 |
| 7314 | preserv | 9 |
| 7315 | prelate | 9 |
| 7316 | preface | 9 |
| 7317 | preach | 9 |
| 7318 | poll | 9 |
| 7319 | plaza | 9 |
| 7320 | planets | 9 |
| 7321 | plainer | 9 |
| 7322 | pikes | 9 |
| 7323 | pie | 9 |
| 7324 | picked | 9 |
| 7325 | physicians | 9 |
| 7326 | philotus | 9 |
| 7327 | philomel | 9 |
| 7328 | penury | 9 |
| 7329 | pedlar | 9 |
| 7330 | paste | 9 |
| 7331 | parish | 9 |
| 7332 | parcels | 9 |
| 7333 | paragon | 9 |
| 7334 | pander | 9 |
| 7335 | packing | 9 |
| 7336 | pacing | 9 |
| 7337 | pacified | 9 |
| 7338 | p | 9 |
| 7339 | ow | 9 |
| 7340 | ovid | 9 |
| 7341 | ounce | 9 |
| 7342 | ostentation | 9 |
| 7343 | ordinance | 9 |
| 7344 | oration | 9 |
| 7345 | oppressed | 9 |
| 7346 | olive | 9 |
| 7347 | older | 9 |
| 7348 | obsequies | 9 |
| 7349 | obeisance | 9 |
| 7350 | nuts | 9 |
| 7351 | noticed | 9 |
| 7352 | nightgown | 9 |
| 7353 | nick | 9 |
| 7354 | nets | 9 |
| 7355 | neighing | 9 |
| 7356 | negligent | 9 |
| 7357 | nakedness | 9 |
| 7358 | muskets | 9 |
| 7359 | musket | 9 |
| 7360 | murmur | 9 |
| 7361 | murders | 9 |
| 7362 | murderous | 9 |
| 7363 | muleteer | 9 |
| 7364 | muffled | 9 |
| 7365 | movement | 9 |
| 7366 | mostly | 9 |
| 7367 | moons | 9 |
| 7368 | moisture | 9 |
| 7369 | moi | 9 |
| 7370 | mixed | 9 |
| 7371 | mix | 9 |
| 7372 | misled | 9 |
| 7373 | mildly | 9 |
| 7374 | menteith | 9 |
| 7375 | melody | 9 |
| 7376 | medicines | 9 |
| 7377 | measur | 9 |
| 7378 | mature | 9 |
| 7379 | masque | 9 |
| 7380 | marullus | 9 |
| 7381 | margery | 9 |
| 7382 | mannerly | 9 |
| 7383 | maledictions | 9 |
| 7384 | madrid | 9 |
| 7385 | lovest | 9 |
| 7386 | lonely | 9 |
| 7387 | loan | 9 |
| 7388 | loaf | 9 |
| 7389 | livers | 9 |
| 7390 | lick | 9 |
| 7391 | licio | 9 |
| 7392 | leisurely | 9 |
| 7393 | lease | 9 |
| 7394 | learnt | 9 |
| 7395 | leaps | 9 |
| 7396 | larger | 9 |
| 7397 | languages | 9 |
| 7398 | laments | 9 |
| 7399 | lakes | 9 |
| 7400 | kindle | 9 |
| 7401 | juice | 9 |
| 7402 | jug | 9 |
| 7403 | jousts | 9 |
| 7404 | jolly | 9 |
| 7405 | jamy | 9 |
| 7406 | ix | 9 |
| 7407 | issued | 9 |
| 7408 | islanders | 9 |
| 7409 | isidore | 9 |
| 7410 | irritation | 9 |
| 7411 | invest | 9 |
| 7412 | interview | 9 |
| 7413 | inspired | 9 |
| 7414 | insert | 9 |
| 7415 | innumerable | 9 |
| 7416 | inns | 9 |
| 7417 | iniquity | 9 |
| 7418 | ingrate | 9 |
| 7419 | inflicted | 9 |
| 7420 | indirect | 9 |
| 7421 | indignity | 9 |
| 7422 | indian | 9 |
| 7423 | incorporate | 9 |
| 7424 | imposition | 9 |
| 7425 | imports | 9 |
| 7426 | imploring | 9 |
| 7427 | impediments | 9 |
| 7428 | ignoble | 9 |
| 7429 | ideas | 9 |
| 7430 | huntsmen | 9 |
| 7431 | howsoever | 9 |
| 7432 | hovel | 9 |
| 7433 | hortensius | 9 |
| 7434 | hopeful | 9 |
| 7435 | highnesses | 9 |
| 7436 | heretic | 9 |
| 7437 | herb | 9 |
| 7438 | hens | 9 |
| 7439 | hearer | 9 |
| 7440 | headlong | 9 |
| 7441 | hawk | 9 |
| 7442 | hart | 9 |
| 7443 | harmful | 9 |
| 7444 | harlot | 9 |
| 7445 | hardy | 9 |
| 7446 | hardness | 9 |
| 7447 | hale | 9 |
| 7448 | guiltiness | 9 |
| 7449 | groaning | 9 |
| 7450 | grind | 9 |
| 7451 | greetings | 9 |
| 7452 | greekish | 9 |
| 7453 | grapple | 9 |
| 7454 | gowns | 9 |
| 7455 | gossips | 9 |
| 7456 | gorge | 9 |
| 7457 | gore | 9 |
| 7458 | glorify | 9 |
| 7459 | glamis | 9 |
| 7460 | girths | 9 |
| 7461 | gesture | 9 |
| 7462 | gentler | 9 |
| 7463 | ganymede | 9 |
| 7464 | galls | 9 |
| 7465 | gallery | 9 |
| 7466 | gains | 9 |
| 7467 | functions | 9 |
| 7468 | fun | 9 |
| 7469 | fulfil | 9 |
| 7470 | frosty | 9 |
| 7471 | freshly | 9 |
| 7472 | fraud | 9 |
| 7473 | fortitude | 9 |
| 7474 | forswore | 9 |
| 7475 | forgiveness | 9 |
| 7476 | foretold | 9 |
| 7477 | forestall | 9 |
| 7478 | flows | 9 |
| 7479 | flown | 9 |
| 7480 | fleece | 9 |
| 7481 | flax | 9 |
| 7482 | flaw | 9 |
| 7483 | fitness | 9 |
| 7484 | fineness | 9 |
| 7485 | fashions | 9 |
| 7486 | fam | 9 |
| 7487 | fable | 9 |
| 7488 | eyne | 9 |
| 7489 | eyebrows | 9 |
| 7490 | exempt | 9 |
| 7491 | executioners | 9 |
| 7492 | excuses | 9 |
| 7493 | exception | 9 |
| 7494 | excels | 9 |
| 7495 | essential | 9 |
| 7496 | equals | 9 |
| 7497 | ensuing | 9 |
| 7498 | ensign | 9 |
| 7499 | enjoys | 9 |
| 7500 | engine | 9 |
| 7501 | encouraged | 9 |
| 7502 | encourage | 9 |
| 7503 | enchant | 9 |
| 7504 | embarrassment | 9 |
| 7505 | dulcet | 9 |
| 7506 | dug | 9 |
| 7507 | drowning | 9 |
| 7508 | drolleries | 9 |
| 7509 | drench | 9 |
| 7510 | drank | 9 |
| 7511 | doves | 9 |
| 7512 | doubled | 9 |
| 7513 | dole | 9 |
| 7514 | divining | 9 |
| 7515 | dissolve | 9 |
| 7516 | dissension | 9 |
| 7517 | disdainful | 9 |
| 7518 | discredit | 9 |
| 7519 | discern | 9 |
| 7520 | dialogue | 9 |
| 7521 | detest | 9 |
| 7522 | despatched | 9 |
| 7523 | denny | 9 |
| 7524 | denial | 9 |
| 7525 | delays | 9 |
| 7526 | defended | 9 |
| 7527 | dedicate | 9 |
| 7528 | deceased | 9 |
| 7529 | deceas | 9 |
| 7530 | dauntless | 9 |
| 7531 | dane | 9 |
| 7532 | cypress | 9 |
| 7533 | cups | 9 |
| 7534 | cuffs | 9 |
| 7535 | crushed | 9 |
| 7536 | crook | 9 |
| 7537 | creeping | 9 |
| 7538 | covers | 9 |
| 7539 | counter | 9 |
| 7540 | cordova | 9 |
| 7541 | copper | 9 |
| 7542 | copied | 9 |
| 7543 | cope | 9 |
| 7544 | convert | 9 |
| 7545 | conveniently | 9 |
| 7546 | continuance | 9 |
| 7547 | constructed | 9 |
| 7548 | consecrate | 9 |
| 7549 | conrade | 9 |
| 7550 | connected | 9 |
| 7551 | conjured | 9 |
| 7552 | conjunction | 9 |
| 7553 | confirmation | 9 |
| 7554 | conditioned | 9 |
| 7555 | conception | 9 |
| 7556 | compos | 9 |
| 7557 | complied | 9 |
| 7558 | complaining | 9 |
| 7559 | commendable | 9 |
| 7560 | coals | 9 |
| 7561 | closer | 9 |
| 7562 | cloaks | 9 |
| 7563 | clip | 9 |
| 7564 | climate | 9 |
| 7565 | civility | 9 |
| 7566 | churl | 9 |
| 7567 | chronicle | 9 |
| 7568 | chop | 9 |
| 7569 | choosing | 9 |
| 7570 | choleric | 9 |
| 7571 | checks | 9 |
| 7572 | charming | 9 |
| 7573 | charlemagne | 9 |
| 7574 | charging | 9 |
| 7575 | cauldron | 9 |
| 7576 | casting | 9 |
| 7577 | castile | 9 |
| 7578 | casildea | 9 |
| 7579 | casement | 9 |
| 7580 | carthage | 9 |
| 7581 | cars | 9 |
| 7582 | carelessness | 9 |
| 7583 | bullets | 9 |
| 7584 | bucket | 9 |
| 7585 | bruise | 9 |
| 7586 | brood | 9 |
| 7587 | brigantine | 9 |
| 7588 | brat | 9 |
| 7589 | brake | 9 |
| 7590 | boundless | 9 |
| 7591 | boorish | 9 |
| 7592 | bolts | 9 |
| 7593 | blasted | 9 |
| 7594 | blanketed | 9 |
| 7595 | blamed | 9 |
| 7596 | bladders | 9 |
| 7597 | bestride | 9 |
| 7598 | bestowing | 9 |
| 7599 | beset | 9 |
| 7600 | benediction | 9 |
| 7601 | bellario | 9 |
| 7602 | believes | 9 |
| 7603 | begs | 9 |
| 7604 | begotten | 9 |
| 7605 | befits | 9 |
| 7606 | beaver | 9 |
| 7607 | battlements | 9 |
| 7608 | batt | 9 |
| 7609 | bated | 9 |
| 7610 | basely | 9 |
| 7611 | barely | 9 |
| 7612 | banners | 9 |
| 7613 | ballads | 9 |
| 7614 | bal | 9 |
| 7615 | baggage | 9 |
| 7616 | bacon | 9 |
| 7617 | audit | 9 |
| 7618 | attribute | 9 |
| 7619 | attorney | 9 |
| 7620 | athwart | 9 |
| 7621 | ascertained | 9 |
| 7622 | arrangement | 9 |
| 7623 | aright | 9 |
| 7624 | argue | 9 |
| 7625 | arduous | 9 |
| 7626 | archidamus | 9 |
| 7627 | aptly | 9 |
| 7628 | apocryphal | 9 |
| 7629 | antiquity | 9 |
| 7630 | annoyance | 9 |
| 7631 | alehouse | 9 |
| 7632 | alcalde | 9 |
| 7633 | advocate | 9 |
| 7634 | adorn | 9 |
| 7635 | admire | 9 |
| 7636 | adders | 9 |
| 7637 | acute | 9 |
| 7638 | aches | 9 |
| 7639 | ace | 9 |
| 7640 | accounted | 9 |
| 7641 | acceptance | 9 |
| 7642 | accents | 9 |
| 7643 | absorbed | 9 |
| 7644 | aback | 9 |
| 7645 | yanguesans | 8 |
| 7646 | wrung | 8 |
| 7647 | wrongfully | 8 |
| 7648 | wrestle | 8 |
| 7649 | wrapped | 8 |
| 7650 | worshipp | 8 |
| 7651 | woful | 8 |
| 7652 | withdrawn | 8 |
| 7653 | wisdoms | 8 |
| 7654 | wiltshire | 8 |
| 7655 | wiles | 8 |
| 7656 | whores | 8 |
| 7657 | whiteness | 8 |
| 7658 | whips | 8 |
| 7659 | weeks | 8 |
| 7660 | waxen | 8 |
| 7661 | watches | 8 |
| 7662 | wastes | 8 |
| 7663 | warned | 8 |
| 7664 | walked | 8 |
| 7665 | wailing | 8 |
| 7666 | vulture | 8 |
| 7667 | vowed | 8 |
| 7668 | volumes | 8 |
| 7669 | visits | 8 |
| 7670 | violets | 8 |
| 7671 | violet | 8 |
| 7672 | vineyard | 8 |
| 7673 | vine | 8 |
| 7674 | vill | 8 |
| 7675 | victors | 8 |
| 7676 | victim | 8 |
| 7677 | vicar | 8 |
| 7678 | verdict | 8 |
| 7679 | valor | 8 |
| 7680 | uttermost | 8 |
| 7681 | unwelcome | 8 |
| 7682 | untied | 8 |
| 7683 | unrest | 8 |
| 7684 | unlook | 8 |
| 7685 | united | 8 |
| 7686 | ungracious | 8 |
| 7687 | undertaking | 8 |
| 7688 | undertaken | 8 |
| 7689 | understands | 8 |
| 7690 | uncivil | 8 |
| 7691 | tunes | 8 |
| 7692 | tuned | 8 |
| 7693 | tumble | 8 |
| 7694 | tuesday | 8 |
| 7695 | truths | 8 |
| 7696 | troublesome | 8 |
| 7697 | trodden | 8 |
| 7698 | trifaldin | 8 |
| 7699 | trembles | 8 |
| 7700 | treating | 8 |
| 7701 | treasury | 8 |
| 7702 | transport | 8 |
| 7703 | traitorous | 8 |
| 7704 | trains | 8 |
| 7705 | tough | 8 |
| 7706 | tortures | 8 |
| 7707 | toils | 8 |
| 7708 | tinker | 8 |
| 7709 | timeless | 8 |
| 7710 | tightly | 8 |
| 7711 | thunderbolt | 8 |
| 7712 | thump | 8 |
| 7713 | threshold | 8 |
| 7714 | threefold | 8 |
| 7715 | threatened | 8 |
| 7716 | thereon | 8 |
| 7717 | tewksbury | 8 |
| 7718 | testify | 8 |
| 7719 | terrors | 8 |
| 7720 | territory | 8 |
| 7721 | te | 8 |
| 7722 | target | 8 |
| 7723 | tails | 8 |
| 7724 | tailors | 8 |
| 7725 | tagus | 8 |
| 7726 | tackle | 8 |
| 7727 | swing | 8 |
| 7728 | swept | 8 |
| 7729 | sweetness | 8 |
| 7730 | sweeten | 8 |
| 7731 | sways | 8 |
| 7732 | swallowing | 8 |
| 7733 | swaggering | 8 |
| 7734 | swagger | 8 |
| 7735 | surface | 8 |
| 7736 | sups | 8 |
| 7737 | sunset | 8 |
| 7738 | sunk | 8 |
| 7739 | sunder | 8 |
| 7740 | sumpter | 8 |
| 7741 | suburbs | 8 |
| 7742 | suborn | 8 |
| 7743 | submissive | 8 |
| 7744 | subdued | 8 |
| 7745 | stumbled | 8 |
| 7746 | studying | 8 |
| 7747 | strucken | 8 |
| 7748 | stripes | 8 |
| 7749 | strengthen | 8 |
| 7750 | stratagems | 8 |
| 7751 | strand | 8 |
| 7752 | straightway | 8 |
| 7753 | stem | 8 |
| 7754 | starved | 8 |
| 7755 | startled | 8 |
| 7756 | spurring | 8 |
| 7757 | spiteful | 8 |
| 7758 | spill | 8 |
| 7759 | spices | 8 |
| 7760 | sparkling | 8 |
| 7761 | sounder | 8 |
| 7762 | somewhere | 8 |
| 7763 | soldiership | 8 |
| 7764 | soar | 8 |
| 7765 | snakes | 8 |
| 7766 | smacks | 8 |
| 7767 | slumbers | 8 |
| 7768 | slope | 8 |
| 7769 | skipping | 8 |
| 7770 | sinners | 8 |
| 7771 | silius | 8 |
| 7772 | sicken | 8 |
| 7773 | shrunk | 8 |
| 7774 | showman | 8 |
| 7775 | shorten | 8 |
| 7776 | shipp | 8 |
| 7777 | shell | 8 |
| 7778 | sharper | 8 |
| 7779 | shak | 8 |
| 7780 | seventy | 8 |
| 7781 | seigneur | 8 |
| 7782 | scythe | 8 |
| 7783 | scout | 8 |
| 7784 | scoundrels | 8 |
| 7785 | scots | 8 |
| 7786 | scornful | 8 |
| 7787 | scorned | 8 |
| 7788 | scimitar | 8 |
| 7789 | schools | 8 |
| 7790 | sawest | 8 |
| 7791 | satire | 8 |
| 7792 | sandy | 8 |
| 7793 | saluted | 8 |
| 7794 | safeguard | 8 |
| 7795 | ruminate | 8 |
| 7796 | ruler | 8 |
| 7797 | ruidera | 8 |
| 7798 | rowers | 8 |
| 7799 | rolling | 8 |
| 7800 | roguery | 8 |
| 7801 | rodrigo | 8 |
| 7802 | roast | 8 |
| 7803 | rivals | 8 |
| 7804 | reverse | 8 |
| 7805 | reverent | 8 |
| 7806 | resumed | 8 |
| 7807 | rested | 8 |
| 7808 | requir | 8 |
| 7809 | requested | 8 |
| 7810 | rents | 8 |
| 7811 | renounce | 8 |
| 7812 | removing | 8 |
| 7813 | reminded | 8 |
| 7814 | remarkable | 8 |
| 7815 | reliev | 8 |
| 7816 | rejoiced | 8 |
| 7817 | reinaldos | 8 |
| 7818 | regiment | 8 |
| 7819 | refresh | 8 |
| 7820 | refrain | 8 |
| 7821 | reform | 8 |
| 7822 | reference | 8 |
| 7823 | reconcile | 8 |
| 7824 | recommended | 8 |
| 7825 | reasoning | 8 |
| 7826 | rapt | 8 |
| 7827 | ram | 8 |
| 7828 | railing | 8 |
| 7829 | rag | 8 |
| 7830 | quill | 8 |
| 7831 | quartered | 8 |
| 7832 | pursuivant | 8 |
| 7833 | purg | 8 |
| 7834 | punished | 8 |
| 7835 | providence | 8 |
| 7836 | prouder | 8 |
| 7837 | protects | 8 |
| 7838 | prophecies | 8 |
| 7839 | progeny | 8 |
| 7840 | probation | 8 |
| 7841 | printing | 8 |
| 7842 | pretending | 8 |
| 7843 | presumption | 8 |
| 7844 | preserving | 8 |
| 7845 | preservation | 8 |
| 7846 | prerogative | 8 |
| 7847 | prattle | 8 |
| 7848 | potion | 8 |
| 7849 | portugal | 8 |
| 7850 | portrait | 8 |
| 7851 | porridge | 8 |
| 7852 | porpentine | 8 |
| 7853 | popular | 8 |
| 7854 | popilius | 8 |
| 7855 | poorly | 8 |
| 7856 | poorest | 8 |
| 7857 | poisoned | 8 |
| 7858 | poesy | 8 |
| 7859 | ply | 8 |
| 7860 | pluto | 8 |
| 7861 | plumes | 8 |
| 7862 | pless | 8 |
| 7863 | plans | 8 |
| 7864 | plaintive | 8 |
| 7865 | pith | 8 |
| 7866 | pillars | 8 |
| 7867 | petitions | 8 |
| 7868 | pestilent | 8 |
| 7869 | persuading | 8 |
| 7870 | personages | 8 |
| 7871 | persever | 8 |
| 7872 | persecuted | 8 |
| 7873 | perplexed | 8 |
| 7874 | perplex | 8 |
| 7875 | perfumes | 8 |
| 7876 | perfumed | 8 |
| 7877 | perez | 8 |
| 7878 | penitents | 8 |
| 7879 | pedigree | 8 |
| 7880 | pears | 8 |
| 7881 | peal | 8 |
| 7882 | pavilion | 8 |
| 7883 | partial | 8 |
| 7884 | panzas | 8 |
| 7885 | paced | 8 |
| 7886 | oyster | 8 |
| 7887 | owners | 8 |
| 7888 | overtook | 8 |
| 7889 | outrun | 8 |
| 7890 | outrages | 8 |
| 7891 | outlaws | 8 |
| 7892 | organ | 8 |
| 7893 | orderly | 8 |
| 7894 | onions | 8 |
| 7895 | omens | 8 |
| 7896 | omen | 8 |
| 7897 | offends | 8 |
| 7898 | odour | 8 |
| 7899 | occurrence | 8 |
| 7900 | obsequious | 8 |
| 7901 | obeying | 8 |
| 7902 | novice | 8 |
| 7903 | noting | 8 |
| 7904 | nightfall | 8 |
| 7905 | nerves | 8 |
| 7906 | namely | 8 |
| 7907 | mutinous | 8 |
| 7908 | musty | 8 |
| 7909 | murmuring | 8 |
| 7910 | multitudes | 8 |
| 7911 | mow | 8 |
| 7912 | moonlight | 8 |
| 7913 | monk | 8 |
| 7914 | moneys | 8 |
| 7915 | monastery | 8 |
| 7916 | mitre | 8 |
| 7917 | misuse | 8 |
| 7918 | mischiefs | 8 |
| 7919 | millions | 8 |
| 7920 | millers | 8 |
| 7921 | mightiness | 8 |
| 7922 | mightiest | 8 |
| 7923 | mightier | 8 |
| 7924 | micomicon | 8 |
| 7925 | merrier | 8 |
| 7926 | mercies | 8 |
| 7927 | merchandise | 8 |
| 7928 | meditating | 8 |
| 7929 | material | 8 |
| 7930 | martext | 8 |
| 7931 | marches | 8 |
| 7932 | managed | 8 |
| 7933 | majestical | 8 |
| 7934 | maim | 8 |
| 7935 | mace | 8 |
| 7936 | lump | 8 |
| 7937 | lowest | 8 |
| 7938 | lousy | 8 |
| 7939 | lordly | 8 |
| 7940 | lopp | 8 |
| 7941 | loaded | 8 |
| 7942 | lit | 8 |
| 7943 | lineal | 8 |
| 7944 | lightens | 8 |
| 7945 | lifting | 8 |
| 7946 | lied | 8 |
| 7947 | license | 8 |
| 7948 | liberties | 8 |
| 7949 | lenity | 8 |
| 7950 | laughs | 8 |
| 7951 | lattice | 8 |
| 7952 | lanthorn | 8 |
| 7953 | languish | 8 |
| 7954 | lancelot | 8 |
| 7955 | lacking | 8 |
| 7956 | knightly | 8 |
| 7957 | kite | 8 |
| 7958 | kindled | 8 |
| 7959 | kinder | 8 |
| 7960 | kicks | 8 |
| 7961 | kick | 8 |
| 7962 | kerchiefs | 8 |
| 7963 | keepers | 8 |
| 7964 | juvenal | 8 |
| 7965 | judicious | 8 |
| 7966 | judging | 8 |
| 7967 | jocund | 8 |
| 7968 | jig | 8 |
| 7969 | jesus | 8 |
| 7970 | jacob | 8 |
| 7971 | jacket | 8 |
| 7972 | ivy | 8 |
| 7973 | itch | 8 |
| 7974 | issuing | 8 |
| 7975 | isis | 8 |
| 7976 | inter | 8 |
| 7977 | inscription | 8 |
| 7978 | information | 8 |
| 7979 | indolence | 8 |
| 7980 | indirectly | 8 |
| 7981 | india | 8 |
| 7982 | incur | 8 |
| 7983 | inclinations | 8 |
| 7984 | imputation | 8 |
| 7985 | impulse | 8 |
| 7986 | imposed | 8 |
| 7987 | importing | 8 |
| 7988 | imagin | 8 |
| 7989 | illusions | 8 |
| 7990 | idol | 8 |
| 7991 | hypocrisy | 8 |
| 7992 | huswife | 8 |
| 7993 | hoop | 8 |
| 7994 | hoard | 8 |
| 7995 | hip | 8 |
| 7996 | hinds | 8 |
| 7997 | highway | 8 |
| 7998 | heroic | 8 |
| 7999 | herod | 8 |
| 8000 | hereditary | 8 |
| 8001 | hellish | 8 |
| 8002 | heathen | 8 |
| 8003 | heaps | 8 |
| 8004 | hazel | 8 |
| 8005 | haunted | 8 |
| 8006 | hats | 8 |
| 8007 | hardships | 8 |
| 8008 | happiest | 8 |
| 8009 | hammers | 8 |
| 8010 | habitation | 8 |
| 8011 | gun | 8 |
| 8012 | guessed | 8 |
| 8013 | gripe | 8 |
| 8014 | grin | 8 |
| 8015 | graze | 8 |
| 8016 | grasping | 8 |
| 8017 | grasped | 8 |
| 8018 | governed | 8 |
| 8019 | givest | 8 |
| 8020 | gipsy | 8 |
| 8021 | ginger | 8 |
| 8022 | genoa | 8 |
| 8023 | generals | 8 |
| 8024 | gasp | 8 |
| 8025 | gardener | 8 |
| 8026 | gallantry | 8 |
| 8027 | gaining | 8 |
| 8028 | fountains | 8 |
| 8029 | fouler | 8 |
| 8030 | forsook | 8 |
| 8031 | forged | 8 |
| 8032 | forg | 8 |
| 8033 | forfeiture | 8 |
| 8034 | forests | 8 |
| 8035 | forbidden | 8 |
| 8036 | fooleries | 8 |
| 8037 | foh | 8 |
| 8038 | flaming | 8 |
| 8039 | flags | 8 |
| 8040 | finishing | 8 |
| 8041 | fin | 8 |
| 8042 | filth | 8 |
| 8043 | favourites | 8 |
| 8044 | fatigue | 8 |
| 8045 | fathom | 8 |
| 8046 | fated | 8 |
| 8047 | fantastic | 8 |
| 8048 | famed | 8 |
| 8049 | fables | 8 |
| 8050 | extolled | 8 |
| 8051 | expression | 8 |
| 8052 | experiment | 8 |
| 8053 | exist | 8 |
| 8054 | exhibition | 8 |
| 8055 | ewe | 8 |
| 8056 | estimate | 8 |
| 8057 | estates | 8 |
| 8058 | ertake | 8 |
| 8059 | erlook | 8 |
| 8060 | entertained | 8 |
| 8061 | enquire | 8 |
| 8062 | enormous | 8 |
| 8063 | enlarge | 8 |
| 8064 | emperess | 8 |
| 8065 | eminent | 8 |
| 8066 | elves | 8 |
| 8067 | elm | 8 |
| 8068 | education | 8 |
| 8069 | dukedoms | 8 |
| 8070 | drudge | 8 |
| 8071 | drab | 8 |
| 8072 | doubted | 8 |
| 8073 | doubly | 8 |
| 8074 | dotes | 8 |
| 8075 | domestic | 8 |
| 8076 | dolphin | 8 |
| 8077 | doit | 8 |
| 8078 | dogberry | 8 |
| 8079 | doctrine | 8 |
| 8080 | doct | 8 |
| 8081 | distrust | 8 |
| 8082 | distresses | 8 |
| 8083 | distill | 8 |
| 8084 | displeas | 8 |
| 8085 | dispense | 8 |
| 8086 | disobedience | 8 |
| 8087 | discovers | 8 |
| 8088 | dignified | 8 |
| 8089 | digg | 8 |
| 8090 | desolate | 8 |
| 8091 | deprived | 8 |
| 8092 | depending | 8 |
| 8093 | departed | 8 |
| 8094 | denying | 8 |
| 8095 | delayed | 8 |
| 8096 | decorum | 8 |
| 8097 | declined | 8 |
| 8098 | decide | 8 |
| 8099 | deceitful | 8 |
| 8100 | dawning | 8 |
| 8101 | dart | 8 |
| 8102 | dardanius | 8 |
| 8103 | dancers | 8 |
| 8104 | dalliance | 8 |
| 8105 | dale | 8 |
| 8106 | dainties | 8 |
| 8107 | custody | 8 |
| 8108 | cures | 8 |
| 8109 | crier | 8 |
| 8110 | creditors | 8 |
| 8111 | craving | 8 |
| 8112 | covert | 8 |
| 8113 | courtship | 8 |
| 8114 | coupled | 8 |
| 8115 | counting | 8 |
| 8116 | contention | 8 |
| 8117 | consume | 8 |
| 8118 | constrained | 8 |
| 8119 | conspire | 8 |
| 8120 | consign | 8 |
| 8121 | conquering | 8 |
| 8122 | confined | 8 |
| 8123 | confederate | 8 |
| 8124 | conclusions | 8 |
| 8125 | compliments | 8 |
| 8126 | committing | 8 |
| 8127 | commanders | 8 |
| 8128 | combined | 8 |
| 8129 | colt | 8 |
| 8130 | club | 8 |
| 8131 | cloy | 8 |
| 8132 | closing | 8 |
| 8133 | cloister | 8 |
| 8134 | clime | 8 |
| 8135 | climbing | 8 |
| 8136 | cleanly | 8 |
| 8137 | circuit | 8 |
| 8138 | cid | 8 |
| 8139 | churchmen | 8 |
| 8140 | christopher | 8 |
| 8141 | chloris | 8 |
| 8142 | chink | 8 |
| 8143 | chill | 8 |
| 8144 | childhood | 8 |
| 8145 | cherry | 8 |
| 8146 | cheat | 8 |
| 8147 | chas | 8 |
| 8148 | challenger | 8 |
| 8149 | ceremonious | 8 |
| 8150 | ceaseless | 8 |
| 8151 | cavern | 8 |
| 8152 | catafalque | 8 |
| 8153 | castellan | 8 |
| 8154 | caring | 8 |
| 8155 | cards | 8 |
| 8156 | capucius | 8 |
| 8157 | caper | 8 |
| 8158 | calmness | 8 |
| 8159 | calmly | 8 |
| 8160 | calendar | 8 |
| 8161 | cadwal | 8 |
| 8162 | butchers | 8 |
| 8163 | burying | 8 |
| 8164 | bucklers | 8 |
| 8165 | bubble | 8 |
| 8166 | broil | 8 |
| 8167 | briskly | 8 |
| 8168 | briers | 8 |
| 8169 | bribes | 8 |
| 8170 | brew | 8 |
| 8171 | breaths | 8 |
| 8172 | bravery | 8 |
| 8173 | brav | 8 |
| 8174 | brands | 8 |
| 8175 | bower | 8 |
| 8176 | bowed | 8 |
| 8177 | booby | 8 |
| 8178 | bonny | 8 |
| 8179 | boiling | 8 |
| 8180 | boarded | 8 |
| 8181 | blots | 8 |
| 8182 | blindness | 8 |
| 8183 | blasts | 8 |
| 8184 | bitten | 8 |
| 8185 | binds | 8 |
| 8186 | bewitch | 8 |
| 8187 | bewildered | 8 |
| 8188 | bewail | 8 |
| 8189 | betrothal | 8 |
| 8190 | betroth | 8 |
| 8191 | beings | 8 |
| 8192 | bedlam | 8 |
| 8193 | bedchamber | 8 |
| 8194 | bearest | 8 |
| 8195 | bauble | 8 |
| 8196 | bastardy | 8 |
| 8197 | ban | 8 |
| 8198 | awaiting | 8 |
| 8199 | ave | 8 |
| 8200 | austere | 8 |
| 8201 | aunchient | 8 |
| 8202 | attired | 8 |
| 8203 | attentive | 8 |
| 8204 | assign | 8 |
| 8205 | assemble | 8 |
| 8206 | aspiring | 8 |
| 8207 | armourer | 8 |
| 8208 | aquitaine | 8 |
| 8209 | apiece | 8 |
| 8210 | anxiously | 8 |
| 8211 | angle | 8 |
| 8212 | amusing | 8 |
| 8213 | amid | 8 |
| 8214 | ambush | 8 |
| 8215 | allows | 8 |
| 8216 | aims | 8 |
| 8217 | agony | 8 |
| 8218 | afterward | 8 |
| 8219 | africa | 8 |
| 8220 | affable | 8 |
| 8221 | aediles | 8 |
| 8222 | additions | 8 |
| 8223 | acquit | 8 |
| 8224 | achiev | 8 |
| 8225 | accustomed | 8 |
| 8226 | accompanying | 8 |
| 8227 | accommodated | 8 |
| 8228 | abides | 8 |
| 8229 | abergavenny | 8 |
| 8230 | abed | 8 |
| 8231 | zealous | 7 |
| 8232 | yew | 7 |
| 8233 | writer | 7 |
| 8234 | wrest | 7 |
| 8235 | wren | 7 |
| 8236 | workman | 7 |
| 8237 | wooers | 7 |
| 8238 | woodville | 7 |
| 8239 | woodcock | 7 |
| 8240 | womanish | 7 |
| 8241 | winner | 7 |
| 8242 | windy | 7 |
| 8243 | whitest | 7 |
| 8244 | whiter | 7 |
| 8245 | whelps | 7 |
| 8246 | whale | 7 |
| 8247 | welcomes | 7 |
| 8248 | welcomed | 7 |
| 8249 | watery | 7 |
| 8250 | washes | 7 |
| 8251 | warp | 7 |
| 8252 | warder | 7 |
| 8253 | wage | 7 |
| 8254 | volscians | 7 |
| 8255 | vizards | 7 |
| 8256 | visiting | 7 |
| 8257 | violently | 7 |
| 8258 | vie | 7 |
| 8259 | viands | 7 |
| 8260 | via | 7 |
| 8261 | vessels | 7 |
| 8262 | ventures | 7 |
| 8263 | venge | 7 |
| 8264 | varied | 7 |
| 8265 | vapours | 7 |
| 8266 | vapour | 7 |
| 8267 | valencia | 7 |
| 8268 | vagaries | 7 |
| 8269 | utters | 7 |
| 8270 | useful | 7 |
| 8271 | unwillingly | 7 |
| 8272 | unwholesome | 7 |
| 8273 | untoward | 7 |
| 8274 | unsatisfied | 7 |
| 8275 | unreasonable | 7 |
| 8276 | unquiet | 7 |
| 8277 | unnecessary | 7 |
| 8278 | unluckily | 7 |
| 8279 | unity | 7 |
| 8280 | uneven | 7 |
| 8281 | unclean | 7 |
| 8282 | unceasingly | 7 |
| 8283 | unbound | 7 |
| 8284 | tying | 7 |
| 8285 | twin | 7 |
| 8286 | troubling | 7 |
| 8287 | trophies | 7 |
| 8288 | trinkets | 7 |
| 8289 | treatment | 7 |
| 8290 | traverse | 7 |
| 8291 | travers | 7 |
| 8292 | travell | 7 |
| 8293 | translation | 7 |
| 8294 | transformations | 7 |
| 8295 | tranquilly | 7 |
| 8296 | trampling | 7 |
| 8297 | tragical | 7 |
| 8298 | traders | 7 |
| 8299 | tractable | 7 |
| 8300 | torralva | 7 |
| 8301 | tithe | 7 |
| 8302 | tires | 7 |
| 8303 | tir | 7 |
| 8304 | timorous | 7 |
| 8305 | threatening | 7 |
| 8306 | threads | 7 |
| 8307 | thorny | 7 |
| 8308 | thighs | 7 |
| 8309 | theatre | 7 |
| 8310 | thaw | 7 |
| 8311 | thankfully | 7 |
| 8312 | thames | 7 |
| 8313 | termination | 7 |
| 8314 | tennis | 7 |
| 8315 | temporal | 7 |
| 8316 | tempests | 7 |
| 8317 | teaches | 7 |
| 8318 | taunts | 7 |
| 8319 | taunt | 7 |
| 8320 | tarfe | 7 |
| 8321 | tapestry | 7 |
| 8322 | tam | 7 |
| 8323 | tallow | 7 |
| 8324 | syracusian | 7 |
| 8325 | sycorax | 7 |
| 8326 | swerve | 7 |
| 8327 | surrounded | 7 |
| 8328 | surpassed | 7 |
| 8329 | surmise | 7 |
| 8330 | supple | 7 |
| 8331 | supp | 7 |
| 8332 | summoned | 7 |
| 8333 | summers | 7 |
| 8334 | sufficeth | 7 |
| 8335 | sued | 7 |
| 8336 | successfully | 7 |
| 8337 | substantial | 7 |
| 8338 | students | 7 |
| 8339 | strung | 7 |
| 8340 | strongest | 7 |
| 8341 | stripping | 7 |
| 8342 | stringing | 7 |
| 8343 | strengths | 7 |
| 8344 | strengthened | 7 |
| 8345 | strangle | 7 |
| 8346 | straining | 7 |
| 8347 | stores | 7 |
| 8348 | stooping | 7 |
| 8349 | stillness | 7 |
| 8350 | stepp | 7 |
| 8351 | stamps | 7 |
| 8352 | stalk | 7 |
| 8353 | spurns | 7 |
| 8354 | spotless | 7 |
| 8355 | splendour | 7 |
| 8356 | spending | 7 |
| 8357 | spared | 7 |
| 8358 | southwell | 7 |
| 8359 | sot | 7 |
| 8360 | sores | 7 |
| 8361 | solace | 7 |
| 8362 | softer | 7 |
| 8363 | snatching | 7 |
| 8364 | snatches | 7 |
| 8365 | slightest | 7 |
| 8366 | slanderous | 7 |
| 8367 | skirt | 7 |
| 8368 | skimmings | 7 |
| 8369 | sinks | 7 |
| 8370 | sinking | 7 |
| 8371 | sinister | 7 |
| 8372 | sighted | 7 |
| 8373 | sighed | 7 |
| 8374 | sieve | 7 |
| 8375 | shuts | 7 |
| 8376 | shooting | 7 |
| 8377 | shifts | 7 |
| 8378 | shedding | 7 |
| 8379 | settling | 7 |
| 8380 | session | 7 |
| 8381 | servingmen | 7 |
| 8382 | serviceable | 7 |
| 8383 | sentinel | 7 |
| 8384 | selfsame | 7 |
| 8385 | segovia | 7 |
| 8386 | securely | 7 |
| 8387 | sear | 7 |
| 8388 | scruples | 7 |
| 8389 | scripture | 7 |
| 8390 | scrap | 7 |
| 8391 | sconce | 7 |
| 8392 | schemes | 7 |
| 8393 | scared | 7 |
| 8394 | scanty | 7 |
| 8395 | saves | 7 |
| 8396 | sauciness | 7 |
| 8397 | satisfying | 7 |
| 8398 | satisfactory | 7 |
| 8399 | sanctified | 7 |
| 8400 | salad | 7 |
| 8401 | saddled | 7 |
| 8402 | rusty | 7 |
| 8403 | rudely | 7 |
| 8404 | rubies | 7 |
| 8405 | roused | 7 |
| 8406 | ropes | 7 |
| 8407 | rook | 7 |
| 8408 | rib | 7 |
| 8409 | revolts | 7 |
| 8410 | revenues | 7 |
| 8411 | resume | 7 |
| 8412 | restoring | 7 |
| 8413 | requited | 7 |
| 8414 | requital | 7 |
| 8415 | reprieve | 7 |
| 8416 | represented | 7 |
| 8417 | repetition | 7 |
| 8418 | repeating | 7 |
| 8419 | religiously | 7 |
| 8420 | releasing | 7 |
| 8421 | rejoicing | 7 |
| 8422 | regardless | 7 |
| 8423 | refusing | 7 |
| 8424 | refus | 7 |
| 8425 | refer | 7 |
| 8426 | recovering | 7 |
| 8427 | recognising | 7 |
| 8428 | reasonably | 7 |
| 8429 | rap | 7 |
| 8430 | rang | 7 |
| 8431 | rancour | 7 |
| 8432 | rails | 7 |
| 8433 | quoted | 7 |
| 8434 | quiver | 7 |
| 8435 | quickness | 7 |
| 8436 | questioned | 7 |
| 8437 | purposed | 7 |
| 8438 | puppy | 7 |
| 8439 | puny | 7 |
| 8440 | prunes | 7 |
| 8441 | provisions | 7 |
| 8442 | promotion | 7 |
| 8443 | promontory | 7 |
| 8444 | prolong | 7 |
| 8445 | profuse | 7 |
| 8446 | professed | 7 |
| 8447 | proclamations | 7 |
| 8448 | prizes | 7 |
| 8449 | princesses | 7 |
| 8450 | pressure | 7 |
| 8451 | presage | 7 |
| 8452 | preferred | 7 |
| 8453 | precautions | 7 |
| 8454 | pre | 7 |
| 8455 | poured | 7 |
| 8456 | possessions | 7 |
| 8457 | possessing | 7 |
| 8458 | positive | 7 |
| 8459 | poise | 7 |
| 8460 | poetical | 7 |
| 8461 | pockets | 7 |
| 8462 | plighted | 7 |
| 8463 | pledged | 7 |
| 8464 | pleading | 7 |
| 8465 | plates | 7 |
| 8466 | plasters | 7 |
| 8467 | pirates | 7 |
| 8468 | pirate | 7 |
| 8469 | piety | 7 |
| 8470 | phrynia | 7 |
| 8471 | perfidious | 7 |
| 8472 | perceives | 7 |
| 8473 | pennyworth | 7 |
| 8474 | peacefully | 7 |
| 8475 | patches | 7 |
| 8476 | parthia | 7 |
| 8477 | parrot | 7 |
| 8478 | pardons | 7 |
| 8479 | parallel | 7 |
| 8480 | pandar | 7 |
| 8481 | palpable | 7 |
| 8482 | palms | 7 |
| 8483 | owing | 7 |
| 8484 | overwhelmed | 7 |
| 8485 | outwardly | 7 |
| 8486 | outright | 7 |
| 8487 | outrageous | 7 |
| 8488 | osuna | 7 |
| 8489 | ostler | 7 |
| 8490 | osric | 7 |
| 8491 | orphan | 7 |
| 8492 | orient | 7 |
| 8493 | organs | 7 |
| 8494 | ordnance | 7 |
| 8495 | orators | 7 |
| 8496 | orange | 7 |
| 8497 | opposing | 7 |
| 8498 | onward | 7 |
| 8499 | onset | 7 |
| 8500 | olympus | 7 |
| 8501 | oftentimes | 7 |
| 8502 | offspring | 7 |
| 8503 | officious | 7 |
| 8504 | od | 7 |
| 8505 | obstacle | 7 |
| 8506 | observations | 7 |
| 8507 | obscur | 7 |
| 8508 | obligations | 7 |
| 8509 | oaks | 7 |
| 8510 | normandy | 7 |
| 8511 | noblemen | 7 |
| 8512 | ninth | 7 |
| 8513 | nimbly | 7 |
| 8514 | nile | 7 |
| 8515 | nether | 7 |
| 8516 | net | 7 |
| 8517 | neapolitan | 7 |
| 8518 | naming | 7 |
| 8519 | muses | 7 |
| 8520 | mote | 7 |
| 8521 | mortified | 7 |
| 8522 | moreno | 7 |
| 8523 | morato | 7 |
| 8524 | montera | 7 |
| 8525 | monarchy | 7 |
| 8526 | monarchs | 7 |
| 8527 | moles | 7 |
| 8528 | modestly | 7 |
| 8529 | misprision | 7 |
| 8530 | misadventure | 7 |
| 8531 | miraculous | 7 |
| 8532 | minola | 7 |
| 8533 | mildness | 7 |
| 8534 | mi | 7 |
| 8535 | messages | 7 |
| 8536 | melodious | 7 |
| 8537 | mellow | 7 |
| 8538 | meditation | 7 |
| 8539 | meddling | 7 |
| 8540 | meals | 7 |
| 8541 | masks | 7 |
| 8542 | martyr | 7 |
| 8543 | marsilio | 7 |
| 8544 | margin | 7 |
| 8545 | manifold | 7 |
| 8546 | mandate | 7 |
| 8547 | manacles | 7 |
| 8548 | maintains | 7 |
| 8549 | magnificence | 7 |
| 8550 | ma | 7 |
| 8551 | luxurious | 7 |
| 8552 | lurk | 7 |
| 8553 | lullaby | 7 |
| 8554 | lucifer | 7 |
| 8555 | lout | 7 |
| 8556 | lordships | 7 |
| 8557 | logs | 7 |
| 8558 | loathe | 7 |
| 8559 | loaden | 7 |
| 8560 | lioness | 7 |
| 8561 | lint | 7 |
| 8562 | limited | 7 |
| 8563 | lighten | 7 |
| 8564 | liars | 7 |
| 8565 | levelled | 7 |
| 8566 | lethe | 7 |
| 8567 | leaping | 7 |
| 8568 | leans | 7 |
| 8569 | leanness | 7 |
| 8570 | lawyers | 7 |
| 8571 | lavish | 7 |
| 8572 | lamented | 7 |
| 8573 | laden | 7 |
| 8574 | knavish | 7 |
| 8575 | kerns | 7 |
| 8576 | ken | 7 |
| 8577 | jurisdiction | 7 |
| 8578 | judg | 7 |
| 8579 | jovial | 7 |
| 8580 | jollity | 7 |
| 8581 | jewry | 7 |
| 8582 | jar | 7 |
| 8583 | jacks | 7 |
| 8584 | ish | 7 |
| 8585 | invitation | 7 |
| 8586 | invested | 7 |
| 8587 | interpret | 7 |
| 8588 | insensible | 7 |
| 8589 | injunction | 7 |
| 8590 | inferred | 7 |
| 8591 | infectious | 7 |
| 8592 | indicate | 7 |
| 8593 | inclining | 7 |
| 8594 | impudence | 7 |
| 8595 | importun | 7 |
| 8596 | impious | 7 |
| 8597 | imperfect | 7 |
| 8598 | impelled | 7 |
| 8599 | immodest | 7 |
| 8600 | immaculate | 7 |
| 8601 | imitating | 7 |
| 8602 | ides | 7 |
| 8603 | hunters | 7 |
| 8604 | hunted | 7 |
| 8605 | humbleness | 7 |
| 8606 | housewife | 7 |
| 8607 | horribly | 7 |
| 8608 | hoo | 7 |
| 8609 | homer | 7 |
| 8610 | hoisted | 7 |
| 8611 | hog | 7 |
| 8612 | hobby | 7 |
| 8613 | hoar | 7 |
| 8614 | hive | 7 |
| 8615 | historians | 7 |
| 8616 | hired | 7 |
| 8617 | hircania | 7 |
| 8618 | hilts | 7 |
| 8619 | hilt | 7 |
| 8620 | heme | 7 |
| 8621 | heiress | 7 |
| 8622 | heifer | 7 |
| 8623 | heaviest | 7 |
| 8624 | hatches | 7 |
| 8625 | harshly | 7 |
| 8626 | hares | 7 |
| 8627 | handling | 7 |
| 8628 | halted | 7 |
| 8629 | hairy | 7 |
| 8630 | hadji | 7 |
| 8631 | gusts | 7 |
| 8632 | guns | 7 |
| 8633 | gunner | 7 |
| 8634 | guitar | 7 |
| 8635 | guerdon | 7 |
| 8636 | guardian | 7 |
| 8637 | guadiana | 7 |
| 8638 | groves | 7 |
| 8639 | grievously | 7 |
| 8640 | grecians | 7 |
| 8641 | grease | 7 |
| 8642 | graver | 7 |
| 8643 | grants | 7 |
| 8644 | granting | 7 |
| 8645 | grandmother | 7 |
| 8646 | gotten | 7 |
| 8647 | goal | 7 |
| 8648 | giv | 7 |
| 8649 | ghostly | 7 |
| 8650 | genuine | 7 |
| 8651 | gavest | 7 |
| 8652 | gaudy | 7 |
| 8653 | gargrave | 7 |
| 8654 | gaolers | 7 |
| 8655 | gan | 7 |
| 8656 | gamester | 7 |
| 8657 | gallus | 7 |
| 8658 | furniture | 7 |
| 8659 | frights | 7 |
| 8660 | frets | 7 |
| 8661 | frequent | 7 |
| 8662 | francisca | 7 |
| 8663 | fragrant | 7 |
| 8664 | fragments | 7 |
| 8665 | fortified | 7 |
| 8666 | forsaken | 7 |
| 8667 | forked | 7 |
| 8668 | fork | 7 |
| 8669 | forgo | 7 |
| 8670 | forgetfulness | 7 |
| 8671 | forfeited | 7 |
| 8672 | foremost | 7 |
| 8673 | forcible | 7 |
| 8674 | fog | 7 |
| 8675 | flay | 7 |
| 8676 | flash | 7 |
| 8677 | flap | 7 |
| 8678 | flanders | 7 |
| 8679 | fitly | 7 |
| 8680 | finer | 7 |
| 8681 | fetter | 7 |
| 8682 | fetched | 7 |
| 8683 | feelings | 7 |
| 8684 | fearless | 7 |
| 8685 | fearfully | 7 |
| 8686 | fealty | 7 |
| 8687 | favouring | 7 |
| 8688 | fathoms | 7 |
| 8689 | fasten | 7 |
| 8690 | fardel | 7 |
| 8691 | faints | 7 |
| 8692 | fading | 7 |
| 8693 | fade | 7 |
| 8694 | factions | 7 |
| 8695 | faced | 7 |
| 8696 | fa | 7 |
| 8697 | eyesight | 7 |
| 8698 | eyed | 7 |
| 8699 | extremities | 7 |
| 8700 | external | 7 |
| 8701 | extended | 7 |
| 8702 | expire | 7 |
| 8703 | existence | 7 |
| 8704 | exertion | 7 |
| 8705 | excused | 7 |
| 8706 | exclamation | 7 |
| 8707 | excite | 7 |
| 8708 | exchequer | 7 |
| 8709 | excepting | 7 |
| 8710 | excel | 7 |
| 8711 | examination | 7 |
| 8712 | escap | 7 |
| 8713 | erst | 7 |
| 8714 | erring | 7 |
| 8715 | ergo | 7 |
| 8716 | erected | 7 |
| 8717 | epidamnum | 7 |
| 8718 | entrusted | 7 |
| 8719 | engines | 7 |
| 8720 | enforcement | 7 |
| 8721 | elephant | 7 |
| 8722 | elegance | 7 |
| 8723 | eighth | 7 |
| 8724 | effeminate | 7 |
| 8725 | eel | 7 |
| 8726 | eclipse | 7 |
| 8727 | ecclesiastic | 7 |
| 8728 | eagerly | 7 |
| 8729 | dusky | 7 |
| 8730 | droop | 7 |
| 8731 | dregs | 7 |
| 8732 | downfall | 7 |
| 8733 | dow | 7 |
| 8734 | doubting | 7 |
| 8735 | doe | 7 |
| 8736 | dive | 7 |
| 8737 | distilled | 7 |
| 8738 | dispositions | 7 |
| 8739 | dismissed | 7 |
| 8740 | disenchant | 7 |
| 8741 | discontents | 7 |
| 8742 | disciplines | 7 |
| 8743 | discarded | 7 |
| 8744 | dis | 7 |
| 8745 | direful | 7 |
| 8746 | ding | 7 |
| 8747 | diligent | 7 |
| 8748 | digestion | 7 |
| 8749 | differences | 7 |
| 8750 | dews | 7 |
| 8751 | devouring | 7 |
| 8752 | devoured | 7 |
| 8753 | despiteful | 7 |
| 8754 | desperation | 7 |
| 8755 | describing | 7 |
| 8756 | describes | 7 |
| 8757 | dennis | 7 |
| 8758 | deity | 7 |
| 8759 | defensive | 7 |
| 8760 | dedicated | 7 |
| 8761 | declining | 7 |
| 8762 | december | 7 |
| 8763 | decease | 7 |
| 8764 | dealer | 7 |
| 8765 | darts | 7 |
| 8766 | darling | 7 |
| 8767 | darest | 7 |
| 8768 | customs | 7 |
| 8769 | cruelly | 7 |
| 8770 | cropp | 7 |
| 8771 | creditor | 7 |
| 8772 | credence | 7 |
| 8773 | counties | 7 |
| 8774 | cotton | 7 |
| 8775 | cottage | 7 |
| 8776 | corinth | 7 |
| 8777 | core | 7 |
| 8778 | cools | 7 |
| 8779 | cooling | 7 |
| 8780 | convoy | 7 |
| 8781 | conveyance | 7 |
| 8782 | converted | 7 |
| 8783 | contrivance | 7 |
| 8784 | contagion | 7 |
| 8785 | consuming | 7 |
| 8786 | consum | 7 |
| 8787 | consorted | 7 |
| 8788 | consoled | 7 |
| 8789 | console | 7 |
| 8790 | conjectures | 7 |
| 8791 | congeal | 7 |
| 8792 | confessing | 7 |
| 8793 | concerned | 7 |
| 8794 | concealment | 7 |
| 8795 | concealing | 7 |
| 8796 | comprehend | 7 |
| 8797 | completed | 7 |
| 8798 | commits | 7 |
| 8799 | comeliness | 7 |
| 8800 | combine | 7 |
| 8801 | cog | 7 |
| 8802 | coffer | 7 |
| 8803 | codpiece | 7 |
| 8804 | clout | 7 |
| 8805 | cleaving | 7 |
| 8806 | clamours | 7 |
| 8807 | citadel | 7 |
| 8808 | cine | 7 |
| 8809 | chuck | 7 |
| 8810 | chronicles | 7 |
| 8811 | chaps | 7 |
| 8812 | changeling | 7 |
| 8813 | cham | 7 |
| 8814 | centaur | 7 |
| 8815 | celerity | 7 |
| 8816 | catastrophe | 7 |
| 8817 | caskets | 7 |
| 8818 | carriages | 7 |
| 8819 | carpet | 7 |
| 8820 | carpenter | 7 |
| 8821 | cardinals | 7 |
| 8822 | capering | 7 |
| 8823 | cape | 7 |
| 8824 | canary | 7 |
| 8825 | camps | 7 |
| 8826 | campo | 7 |
| 8827 | cake | 7 |
| 8828 | cain | 7 |
| 8829 | bushes | 7 |
| 8830 | buffets | 7 |
| 8831 | buckled | 7 |
| 8832 | buckle | 7 |
| 8833 | briton | 7 |
| 8834 | brisk | 7 |
| 8835 | brim | 7 |
| 8836 | brightness | 7 |
| 8837 | brawling | 7 |
| 8838 | brandish | 7 |
| 8839 | bran | 7 |
| 8840 | brambles | 7 |
| 8841 | brags | 7 |
| 8842 | bracelet | 7 |
| 8843 | bourn | 7 |
| 8844 | bounded | 7 |
| 8845 | bough | 7 |
| 8846 | bottomless | 7 |
| 8847 | bota | 7 |
| 8848 | boor | 7 |
| 8849 | bonnet | 7 |
| 8850 | bolder | 7 |
| 8851 | boding | 7 |
| 8852 | bode | 7 |
| 8853 | boards | 7 |
| 8854 | blocks | 7 |
| 8855 | blister | 7 |
| 8856 | blinded | 7 |
| 8857 | blew | 7 |
| 8858 | bleeds | 7 |
| 8859 | blazon | 7 |
| 8860 | blasphemy | 7 |
| 8861 | bewray | 7 |
| 8862 | bestows | 7 |
| 8863 | bended | 7 |
| 8864 | belied | 7 |
| 8865 | belianis | 7 |
| 8866 | beholders | 7 |
| 8867 | beforehand | 7 |
| 8868 | beetle | 7 |
| 8869 | beck | 7 |
| 8870 | bearers | 7 |
| 8871 | beacon | 7 |
| 8872 | battery | 7 |
| 8873 | bathing | 7 |
| 8874 | bathe | 7 |
| 8875 | bat | 7 |
| 8876 | basis | 7 |
| 8877 | basilisk | 7 |
| 8878 | bashful | 7 |
| 8879 | baptism | 7 |
| 8880 | bandy | 7 |
| 8881 | baleful | 7 |
| 8882 | baldric | 7 |
| 8883 | balcony | 7 |
| 8884 | bak | 7 |
| 8885 | awry | 7 |
| 8886 | authentic | 7 |
| 8887 | augustus | 7 |
| 8888 | attaint | 7 |
| 8889 | atone | 7 |
| 8890 | asturian | 7 |
| 8891 | astounded | 7 |
| 8892 | artemidorus | 7 |
| 8893 | arrive | 7 |
| 8894 | argamasilla | 7 |
| 8895 | ardour | 7 |
| 8896 | arden | 7 |
| 8897 | arabia | 7 |
| 8898 | appeased | 7 |
| 8899 | apparell | 7 |
| 8900 | apology | 7 |
| 8901 | antipodes | 7 |
| 8902 | angrily | 7 |
| 8903 | ancestry | 7 |
| 8904 | amendment | 7 |
| 8905 | aliena | 7 |
| 8906 | aldonza | 7 |
| 8907 | aldermen | 7 |
| 8908 | alcides | 7 |
| 8909 | alcaide | 7 |
| 8910 | alacrity | 7 |
| 8911 | agrees | 7 |
| 8912 | affront | 7 |
| 8913 | affrighted | 7 |
| 8914 | afflictions | 7 |
| 8915 | adultery | 7 |
| 8916 | admiring | 7 |
| 8917 | admiral | 7 |
| 8918 | admir | 7 |
| 8919 | activity | 7 |
| 8920 | achievement | 7 |
| 8921 | accounts | 7 |
| 8922 | absolutely | 7 |
| 8923 | yorkshire | 6 |
| 8924 | yearly | 6 |
| 8925 | yawn | 6 |
| 8926 | xi | 6 |
| 8927 | wrench | 6 |
| 8928 | wreak | 6 |
| 8929 | wrapp | 6 |
| 8930 | wrap | 6 |
| 8931 | worshipful | 6 |
| 8932 | worked | 6 |
| 8933 | womanhood | 6 |
| 8934 | wive | 6 |
| 8935 | winded | 6 |
| 8936 | willed | 6 |
| 8937 | wilfully | 6 |
| 8938 | wield | 6 |
| 8939 | whistling | 6 |
| 8940 | whispering | 6 |
| 8941 | wheresoe | 6 |
| 8942 | whereabouts | 6 |
| 8943 | wheeling | 6 |
| 8944 | welshmen | 6 |
| 8945 | welshman | 6 |
| 8946 | weird | 6 |
| 8947 | weighing | 6 |
| 8948 | weasel | 6 |
| 8949 | wearisome | 6 |
| 8950 | wavering | 6 |
| 8951 | watchmen | 6 |
| 8952 | wasting | 6 |
| 8953 | warmth | 6 |
| 8954 | wards | 6 |
| 8955 | waning | 6 |
| 8956 | wandered | 6 |
| 8957 | waft | 6 |
| 8958 | vulcan | 6 |
| 8959 | voltemand | 6 |
| 8960 | vogue | 6 |
| 8961 | virgil | 6 |
| 8962 | viper | 6 |
| 8963 | violate | 6 |
| 8964 | victuals | 6 |
| 8965 | victories | 6 |
| 8966 | venturous | 6 |
| 8967 | venison | 6 |
| 8968 | vehement | 6 |
| 8969 | veal | 6 |
| 8970 | varying | 6 |
| 8971 | varnish | 6 |
| 8972 | variable | 6 |
| 8973 | vanities | 6 |
| 8974 | vandalia | 6 |
| 8975 | vail | 6 |
| 8976 | vacant | 6 |
| 8977 | upside | 6 |
| 8978 | upshot | 6 |
| 8979 | uproar | 6 |
| 8980 | unused | 6 |
| 8981 | unsure | 6 |
| 8982 | unsettled | 6 |
| 8983 | unseasonable | 6 |
| 8984 | unprovided | 6 |
| 8985 | unpleasing | 6 |
| 8986 | unmeet | 6 |
| 8987 | unkindly | 6 |
| 8988 | universe | 6 |
| 8989 | unite | 6 |
| 8990 | union | 6 |
| 8991 | unholy | 6 |
| 8992 | unhallowed | 6 |
| 8993 | unfurnish | 6 |
| 8994 | unconquered | 6 |
| 8995 | unchaste | 6 |
| 8996 | unawares | 6 |
| 8997 | un | 6 |
| 8998 | uchali | 6 |
| 8999 | ubeda | 6 |
| 9000 | twigs | 6 |
| 9001 | turf | 6 |
| 9002 | tumbling | 6 |
| 9003 | tumbled | 6 |
| 9004 | tub | 6 |
| 9005 | trunks | 6 |
| 9006 | truncheon | 6 |
| 9007 | trump | 6 |
| 9008 | trudge | 6 |
| 9009 | troublous | 6 |
| 9010 | trimming | 6 |
| 9011 | tributary | 6 |
| 9012 | tresses | 6 |
| 9013 | trenchant | 6 |
| 9014 | treaty | 6 |
| 9015 | treading | 6 |
| 9016 | transferred | 6 |
| 9017 | trample | 6 |
| 9018 | trades | 6 |
| 9019 | townsman | 6 |
| 9020 | toothache | 6 |
| 9021 | tongu | 6 |
| 9022 | titan | 6 |
| 9023 | timely | 6 |
| 9024 | timber | 6 |
| 9025 | tilt | 6 |
| 9026 | tickling | 6 |
| 9027 | thrusting | 6 |
| 9028 | throngs | 6 |
| 9029 | threescore | 6 |
| 9030 | thrall | 6 |
| 9031 | thracian | 6 |
| 9032 | thanes | 6 |
| 9033 | testy | 6 |
| 9034 | tended | 6 |
| 9035 | tempting | 6 |
| 9036 | temp | 6 |
| 9037 | tattling | 6 |
| 9038 | tarpeian | 6 |
| 9039 | tapestries | 6 |
| 9040 | taffeta | 6 |
| 9041 | tabors | 6 |
| 9042 | tablecloth | 6 |
| 9043 | syria | 6 |
| 9044 | swimming | 6 |
| 9045 | swiftest | 6 |
| 9046 | sweats | 6 |
| 9047 | swallows | 6 |
| 9048 | swagg | 6 |
| 9049 | suspicious | 6 |
| 9050 | surpasses | 6 |
| 9051 | surpass | 6 |
| 9052 | supporting | 6 |
| 9053 | supplication | 6 |
| 9054 | supplant | 6 |
| 9055 | superior | 6 |
| 9056 | succeeds | 6 |
| 9057 | subscrib | 6 |
| 9058 | subjection | 6 |
| 9059 | stung | 6 |
| 9060 | stride | 6 |
| 9061 | straits | 6 |
| 9062 | stowed | 6 |
| 9063 | stormy | 6 |
| 9064 | stitches | 6 |
| 9065 | sterile | 6 |
| 9066 | stephen | 6 |
| 9067 | steeled | 6 |
| 9068 | stated | 6 |
| 9069 | stanzas | 6 |
| 9070 | stalls | 6 |
| 9071 | stall | 6 |
| 9072 | squirely | 6 |
| 9073 | squeezed | 6 |
| 9074 | squadrons | 6 |
| 9075 | sprightliness | 6 |
| 9076 | spout | 6 |
| 9077 | spouse | 6 |
| 9078 | spoon | 6 |
| 9079 | spits | 6 |
| 9080 | spiritual | 6 |
| 9081 | spinning | 6 |
| 9082 | spin | 6 |
| 9083 | speeds | 6 |
| 9084 | specially | 6 |
| 9085 | spar | 6 |
| 9086 | spaniards | 6 |
| 9087 | span | 6 |
| 9088 | soonest | 6 |
| 9089 | somerville | 6 |
| 9090 | solitary | 6 |
| 9091 | softest | 6 |
| 9092 | soe | 6 |
| 9093 | sociable | 6 |
| 9094 | smocks | 6 |
| 9095 | smithfield | 6 |
| 9096 | smear | 6 |
| 9097 | smaller | 6 |
| 9098 | slung | 6 |
| 9099 | sluggish | 6 |
| 9100 | slily | 6 |
| 9101 | slide | 6 |
| 9102 | slaughtered | 6 |
| 9103 | slaps | 6 |
| 9104 | slap | 6 |
| 9105 | slanderer | 6 |
| 9106 | sland | 6 |
| 9107 | skip | 6 |
| 9108 | singly | 6 |
| 9109 | sincere | 6 |
| 9110 | silently | 6 |
| 9111 | signature | 6 |
| 9112 | signals | 6 |
| 9113 | sightless | 6 |
| 9114 | si | 6 |
| 9115 | shy | 6 |
| 9116 | shrine | 6 |
| 9117 | shrewdness | 6 |
| 9118 | shorn | 6 |
| 9119 | shoots | 6 |
| 9120 | shields | 6 |
| 9121 | sheer | 6 |
| 9122 | shearing | 6 |
| 9123 | shaved | 6 |
| 9124 | sharpness | 6 |
| 9125 | shamefully | 6 |
| 9126 | severn | 6 |
| 9127 | severity | 6 |
| 9128 | sentenc | 6 |
| 9129 | selves | 6 |
| 9130 | selling | 6 |
| 9131 | seizes | 6 |
| 9132 | seekest | 6 |
| 9133 | seconds | 6 |
| 9134 | scouts | 6 |
| 9135 | scouring | 6 |
| 9136 | scarcity | 6 |
| 9137 | scabbard | 6 |
| 9138 | saturn | 6 |
| 9139 | sanctity | 6 |
| 9140 | sancha | 6 |
| 9141 | sallet | 6 |
| 9142 | sall | 6 |
| 9143 | sainted | 6 |
| 9144 | sailing | 6 |
| 9145 | saddles | 6 |
| 9146 | sacristan | 6 |
| 9147 | sacrifices | 6 |
| 9148 | sa | 6 |
| 9149 | rushed | 6 |
| 9150 | rung | 6 |
| 9151 | ruled | 6 |
| 9152 | ruins | 6 |
| 9153 | ruinous | 6 |
| 9154 | royalties | 6 |
| 9155 | rowing | 6 |
| 9156 | rosary | 6 |
| 9157 | roofs | 6 |
| 9158 | rood | 6 |
| 9159 | rolls | 6 |
| 9160 | roger | 6 |
| 9161 | rocky | 6 |
| 9162 | roars | 6 |
| 9163 | rive | 6 |
| 9164 | riots | 6 |
| 9165 | ringing | 6 |
| 9166 | rhodes | 6 |
| 9167 | rhadamanthus | 6 |
| 9168 | reynaldo | 6 |
| 9169 | rewarded | 6 |
| 9170 | reviving | 6 |
| 9171 | reviv | 6 |
| 9172 | retreated | 6 |
| 9173 | retort | 6 |
| 9174 | restrained | 6 |
| 9175 | restitution | 6 |
| 9176 | respite | 6 |
| 9177 | resisted | 6 |
| 9178 | resides | 6 |
| 9179 | resembling | 6 |
| 9180 | resembled | 6 |
| 9181 | rescu | 6 |
| 9182 | reprove | 6 |
| 9183 | repented | 6 |
| 9184 | remembrances | 6 |
| 9185 | remarks | 6 |
| 9186 | relieving | 6 |
| 9187 | register | 6 |
| 9188 | regidors | 6 |
| 9189 | reformation | 6 |
| 9190 | refined | 6 |
| 9191 | reeking | 6 |
| 9192 | reek | 6 |
| 9193 | reduce | 6 |
| 9194 | rectify | 6 |
| 9195 | records | 6 |
| 9196 | recoil | 6 |
| 9197 | readiest | 6 |
| 9198 | raze | 6 |
| 9199 | ray | 6 |
| 9200 | ravens | 6 |
| 9201 | ravenous | 6 |
| 9202 | rattling | 6 |
| 9203 | rashly | 6 |
| 9204 | rabbit | 6 |
| 9205 | quondam | 6 |
| 9206 | quittance | 6 |
| 9207 | quits | 6 |
| 9208 | quillets | 6 |
| 9209 | qui | 6 |
| 9210 | questioning | 6 |
| 9211 | quell | 6 |
| 9212 | quail | 6 |
| 9213 | putter | 6 |
| 9214 | pursuits | 6 |
| 9215 | puritan | 6 |
| 9216 | purgation | 6 |
| 9217 | pudding | 6 |
| 9218 | ptolemy | 6 |
| 9219 | provender | 6 |
| 9220 | protestation | 6 |
| 9221 | protected | 6 |
| 9222 | prospect | 6 |
| 9223 | prose | 6 |
| 9224 | proportions | 6 |
| 9225 | prophetic | 6 |
| 9226 | prophesied | 6 |
| 9227 | properties | 6 |
| 9228 | promptly | 6 |
| 9229 | prized | 6 |
| 9230 | pricket | 6 |
| 9231 | prevents | 6 |
| 9232 | prevention | 6 |
| 9233 | prevails | 6 |
| 9234 | presumptuous | 6 |
| 9235 | preposterous | 6 |
| 9236 | preparations | 6 |
| 9237 | preaching | 6 |
| 9238 | praiseworthy | 6 |
| 9239 | practising | 6 |
| 9240 | practised | 6 |
| 9241 | pours | 6 |
| 9242 | pouch | 6 |
| 9243 | pottle | 6 |
| 9244 | potions | 6 |
| 9245 | potency | 6 |
| 9246 | posture | 6 |
| 9247 | portly | 6 |
| 9248 | plumed | 6 |
| 9249 | playfellow | 6 |
| 9250 | pitiless | 6 |
| 9251 | pities | 6 |
| 9252 | pines | 6 |
| 9253 | pinched | 6 |
| 9254 | pillar | 6 |
| 9255 | pillage | 6 |
| 9256 | pil | 6 |
| 9257 | pierc | 6 |
| 9258 | picking | 6 |
| 9259 | pervert | 6 |
| 9260 | perus | 6 |
| 9261 | perturbation | 6 |
| 9262 | persuades | 6 |
| 9263 | perjured | 6 |
| 9264 | pepin | 6 |
| 9265 | pense | 6 |
| 9266 | penitence | 6 |
| 9267 | penetrate | 6 |
| 9268 | penalties | 6 |
| 9269 | pena | 6 |
| 9270 | pelting | 6 |
| 9271 | pedestal | 6 |
| 9272 | pauca | 6 |
| 9273 | patent | 6 |
| 9274 | pated | 6 |
| 9275 | partners | 6 |
| 9276 | partition | 6 |
| 9277 | partisans | 6 |
| 9278 | paramour | 6 |
| 9279 | pang | 6 |
| 9280 | pamphlets | 6 |
| 9281 | pageants | 6 |
| 9282 | owls | 6 |
| 9283 | overture | 6 |
| 9284 | overtaken | 6 |
| 9285 | overborne | 6 |
| 9286 | outface | 6 |
| 9287 | oui | 6 |
| 9288 | opponent | 6 |
| 9289 | operation | 6 |
| 9290 | odours | 6 |
| 9291 | occurrences | 6 |
| 9292 | occupy | 6 |
| 9293 | obstacles | 6 |
| 9294 | obscured | 6 |
| 9295 | objection | 6 |
| 9296 | nunnery | 6 |
| 9297 | numberless | 6 |
| 9298 | nook | 6 |
| 9299 | nimbleness | 6 |
| 9300 | nilus | 6 |
| 9301 | newer | 6 |
| 9302 | nettles | 6 |
| 9303 | nettle | 6 |
| 9304 | nero | 6 |
| 9305 | necessaries | 6 |
| 9306 | nap | 6 |
| 9307 | nance | 6 |
| 9308 | myrmidons | 6 |
| 9309 | murtherous | 6 |
| 9310 | mummy | 6 |
| 9311 | mounts | 6 |
| 9312 | motives | 6 |
| 9313 | mortar | 6 |
| 9314 | morion | 6 |
| 9315 | moods | 6 |
| 9316 | monuments | 6 |
| 9317 | montalvan | 6 |
| 9318 | momentary | 6 |
| 9319 | missed | 6 |
| 9320 | miser | 6 |
| 9321 | misdoubt | 6 |
| 9322 | minist | 6 |
| 9323 | midsummer | 6 |
| 9324 | meteors | 6 |
| 9325 | mermaid | 6 |
| 9326 | merciless | 6 |
| 9327 | mell | 6 |
| 9328 | medlar | 6 |
| 9329 | measuring | 6 |
| 9330 | meagre | 6 |
| 9331 | maw | 6 |
| 9332 | matron | 6 |
| 9333 | mated | 6 |
| 9334 | matches | 6 |
| 9335 | massy | 6 |
| 9336 | massacre | 6 |
| 9337 | masked | 6 |
| 9338 | marvelled | 6 |
| 9339 | marked | 6 |
| 9340 | mariner | 6 |
| 9341 | marian | 6 |
| 9342 | mari | 6 |
| 9343 | margent | 6 |
| 9344 | margarelon | 6 |
| 9345 | marched | 6 |
| 9346 | marcade | 6 |
| 9347 | mann | 6 |
| 9348 | makest | 6 |
| 9349 | makers | 6 |
| 9350 | maintaining | 6 |
| 9351 | mail | 6 |
| 9352 | magistrates | 6 |
| 9353 | magicians | 6 |
| 9354 | magalona | 6 |
| 9355 | lurking | 6 |
| 9356 | lure | 6 |
| 9357 | lucrece | 6 |
| 9358 | loser | 6 |
| 9359 | loo | 6 |
| 9360 | longest | 6 |
| 9361 | lodges | 6 |
| 9362 | loathing | 6 |
| 9363 | lizards | 6 |
| 9364 | listeners | 6 |
| 9365 | lineaments | 6 |
| 9366 | lineages | 6 |
| 9367 | lincoln | 6 |
| 9368 | limp | 6 |
| 9369 | lim | 6 |
| 9370 | libertine | 6 |
| 9371 | levity | 6 |
| 9372 | lessen | 6 |
| 9373 | legion | 6 |
| 9374 | legg | 6 |
| 9375 | leapt | 6 |
| 9376 | lawfully | 6 |
| 9377 | laurel | 6 |
| 9378 | largess | 6 |
| 9379 | larder | 6 |
| 9380 | lag | 6 |
| 9381 | ladyships | 6 |
| 9382 | laboured | 6 |
| 9383 | kindnesses | 6 |
| 9384 | kennel | 6 |
| 9385 | juggling | 6 |
| 9386 | journeys | 6 |
| 9387 | jourdain | 6 |
| 9388 | jesting | 6 |
| 9389 | jeronimo | 6 |
| 9390 | jasper | 6 |
| 9391 | invites | 6 |
| 9392 | inventory | 6 |
| 9393 | inventor | 6 |
| 9394 | introduced | 6 |
| 9395 | interpretation | 6 |
| 9396 | interesting | 6 |
| 9397 | interchange | 6 |
| 9398 | intercession | 6 |
| 9399 | insisted | 6 |
| 9400 | inscribed | 6 |
| 9401 | inquisitive | 6 |
| 9402 | innocents | 6 |
| 9403 | infused | 6 |
| 9404 | inflame | 6 |
| 9405 | inevitable | 6 |
| 9406 | induction | 6 |
| 9407 | indignities | 6 |
| 9408 | incontinent | 6 |
| 9409 | inconstancy | 6 |
| 9410 | incision | 6 |
| 9411 | incessant | 6 |
| 9412 | incertain | 6 |
| 9413 | imprisoned | 6 |
| 9414 | impregnable | 6 |
| 9415 | importunate | 6 |
| 9416 | impiety | 6 |
| 9417 | immured | 6 |
| 9418 | ilion | 6 |
| 9419 | idolatry | 6 |
| 9420 | icy | 6 |
| 9421 | hyperion | 6 |
| 9422 | hymn | 6 |
| 9423 | huts | 6 |
| 9424 | humane | 6 |
| 9425 | hug | 6 |
| 9426 | howsoe | 6 |
| 9427 | hostile | 6 |
| 9428 | hospitality | 6 |
| 9429 | horace | 6 |
| 9430 | hoodwink | 6 |
| 9431 | honourably | 6 |
| 9432 | homicide | 6 |
| 9433 | highwayman | 6 |
| 9434 | hesitation | 6 |
| 9435 | herring | 6 |
| 9436 | heresy | 6 |
| 9437 | hemp | 6 |
| 9438 | helpless | 6 |
| 9439 | heedful | 6 |
| 9440 | hearth | 6 |
| 9441 | hearken | 6 |
| 9442 | hawthorn | 6 |
| 9443 | hawks | 6 |
| 9444 | hawking | 6 |
| 9445 | haviour | 6 |
| 9446 | harangue | 6 |
| 9447 | hannibal | 6 |
| 9448 | hangings | 6 |
| 9449 | hangers | 6 |
| 9450 | hallow | 6 |
| 9451 | halfpenny | 6 |
| 9452 | gust | 6 |
| 9453 | gud | 6 |
| 9454 | guardsman | 6 |
| 9455 | grossness | 6 |
| 9456 | groat | 6 |
| 9457 | grate | 6 |
| 9458 | grandpre | 6 |
| 9459 | graciously | 6 |
| 9460 | graceless | 6 |
| 9461 | governs | 6 |
| 9462 | gout | 6 |
| 9463 | goot | 6 |
| 9464 | gloomy | 6 |
| 9465 | glean | 6 |
| 9466 | girt | 6 |
| 9467 | ginesillo | 6 |
| 9468 | gibbet | 6 |
| 9469 | ghastly | 6 |
| 9470 | gentlefolk | 6 |
| 9471 | gems | 6 |
| 9472 | garret | 6 |
| 9473 | gardens | 6 |
| 9474 | garcia | 6 |
| 9475 | gangway | 6 |
| 9476 | galled | 6 |
| 9477 | gainsay | 6 |
| 9478 | gaily | 6 |
| 9479 | fuel | 6 |
| 9480 | fry | 6 |
| 9481 | fruitless | 6 |
| 9482 | frosts | 6 |
| 9483 | freed | 6 |
| 9484 | framed | 6 |
| 9485 | founder | 6 |
| 9486 | forwardness | 6 |
| 9487 | forgetful | 6 |
| 9488 | forge | 6 |
| 9489 | foresee | 6 |
| 9490 | foresaid | 6 |
| 9491 | forbids | 6 |
| 9492 | forbearance | 6 |
| 9493 | footsteps | 6 |
| 9494 | foolishly | 6 |
| 9495 | foam | 6 |
| 9496 | flights | 6 |
| 9497 | fleeting | 6 |
| 9498 | flee | 6 |
| 9499 | flavour | 6 |
| 9500 | flatteries | 6 |
| 9501 | fisticuffs | 6 |
| 9502 | firmament | 6 |
| 9503 | fired | 6 |
| 9504 | finder | 6 |
| 9505 | files | 6 |
| 9506 | figs | 6 |
| 9507 | fierceness | 6 |
| 9508 | fewer | 6 |
| 9509 | fery | 6 |
| 9510 | fencing | 6 |
| 9511 | felixmarte | 6 |
| 9512 | feeder | 6 |
| 9513 | feasted | 6 |
| 9514 | fawning | 6 |
| 9515 | farthings | 6 |
| 9516 | families | 6 |
| 9517 | familiarity | 6 |
| 9518 | faiths | 6 |
| 9519 | faithless | 6 |
| 9520 | fairness | 6 |
| 9521 | fabric | 6 |
| 9522 | eyeless | 6 |
| 9523 | extol | 6 |
| 9524 | extant | 6 |
| 9525 | expos | 6 |
| 9526 | expert | 6 |
| 9527 | expenses | 6 |
| 9528 | exil | 6 |
| 9529 | exhibit | 6 |
| 9530 | exertions | 6 |
| 9531 | exercises | 6 |
| 9532 | executors | 6 |
| 9533 | exclaims | 6 |
| 9534 | excessive | 6 |
| 9535 | exceptions | 6 |
| 9536 | excepted | 6 |
| 9537 | excellently | 6 |
| 9538 | examining | 6 |
| 9539 | essence | 6 |
| 9540 | escaping | 6 |
| 9541 | erwhelm | 6 |
| 9542 | erudition | 6 |
| 9543 | eruct | 6 |
| 9544 | erthrown | 6 |
| 9545 | environ | 6 |
| 9546 | enveloped | 6 |
| 9547 | entertaining | 6 |
| 9548 | enterprises | 6 |
| 9549 | ensconced | 6 |
| 9550 | enrolled | 6 |
| 9551 | englishmen | 6 |
| 9552 | engenders | 6 |
| 9553 | enfranchisement | 6 |
| 9554 | endeavouring | 6 |
| 9555 | enclosed | 6 |
| 9556 | enchanting | 6 |
| 9557 | enacted | 6 |
| 9558 | empery | 6 |
| 9559 | emotion | 6 |
| 9560 | embassage | 6 |
| 9561 | elysium | 6 |
| 9562 | eloquent | 6 |
| 9563 | eighty | 6 |
| 9564 | eastern | 6 |
| 9565 | earthy | 6 |
| 9566 | earthquake | 6 |
| 9567 | earliest | 6 |
| 9568 | dutchman | 6 |
| 9569 | ducat | 6 |
| 9570 | drunkards | 6 |
| 9571 | drug | 6 |
| 9572 | drollest | 6 |
| 9573 | drawers | 6 |
| 9574 | dowager | 6 |
| 9575 | doff | 6 |
| 9576 | doers | 6 |
| 9577 | divines | 6 |
| 9578 | diverting | 6 |
| 9579 | disturbed | 6 |
| 9580 | disturbance | 6 |
| 9581 | distinct | 6 |
| 9582 | dishonourable | 6 |
| 9583 | dishonesty | 6 |
| 9584 | disgraced | 6 |
| 9585 | disdains | 6 |
| 9586 | discussed | 6 |
| 9587 | discourteous | 6 |
| 9588 | discourses | 6 |
| 9589 | disclos | 6 |
| 9590 | discard | 6 |
| 9591 | disappointed | 6 |
| 9592 | disabled | 6 |
| 9593 | dint | 6 |
| 9594 | dimm | 6 |
| 9595 | digested | 6 |
| 9596 | dieted | 6 |
| 9597 | devote | 6 |
| 9598 | detect | 6 |
| 9599 | destroying | 6 |
| 9600 | desiring | 6 |
| 9601 | deservings | 6 |
| 9602 | deserting | 6 |
| 9603 | descry | 6 |
| 9604 | descendants | 6 |
| 9605 | derives | 6 |
| 9606 | depriv | 6 |
| 9607 | departing | 6 |
| 9608 | demonstrate | 6 |
| 9609 | demon | 6 |
| 9610 | demean | 6 |
| 9611 | delusion | 6 |
| 9612 | delivery | 6 |
| 9613 | defil | 6 |
| 9614 | defied | 6 |
| 9615 | defective | 6 |
| 9616 | dedication | 6 |
| 9617 | declaring | 6 |
| 9618 | daws | 6 |
| 9619 | dates | 6 |
| 9620 | dastard | 6 |
| 9621 | danish | 6 |
| 9622 | daniel | 6 |
| 9623 | danc | 6 |
| 9624 | currents | 6 |
| 9625 | crutches | 6 |
| 9626 | crocodile | 6 |
| 9627 | cripple | 6 |
| 9628 | crete | 6 |
| 9629 | credo | 6 |
| 9630 | cram | 6 |
| 9631 | cracking | 6 |
| 9632 | coverlet | 6 |
| 9633 | couples | 6 |
| 9634 | counterpoise | 6 |
| 9635 | counsellors | 6 |
| 9636 | cough | 6 |
| 9637 | couched | 6 |
| 9638 | cooled | 6 |
| 9639 | contriv | 6 |
| 9640 | contradiction | 6 |
| 9641 | contradict | 6 |
| 9642 | contentment | 6 |
| 9643 | contemn | 6 |
| 9644 | consuls | 6 |
| 9645 | consequently | 6 |
| 9646 | consequences | 6 |
| 9647 | consents | 6 |
| 9648 | consciences | 6 |
| 9649 | conquers | 6 |
| 9650 | conquerors | 6 |
| 9651 | conjurer | 6 |
| 9652 | conferred | 6 |
| 9653 | conducting | 6 |
| 9654 | concludes | 6 |
| 9655 | conceiving | 6 |
| 9656 | conceiv | 6 |
| 9657 | compounds | 6 |
| 9658 | complexions | 6 |
| 9659 | complained | 6 |
| 9660 | commoners | 6 |
| 9661 | commence | 6 |
| 9662 | comforting | 6 |
| 9663 | comfortably | 6 |
| 9664 | colors | 6 |
| 9665 | colloquy | 6 |
| 9666 | colder | 6 |
| 9667 | coeur | 6 |
| 9668 | cobbler | 6 |
| 9669 | co | 6 |
| 9670 | cloven | 6 |
| 9671 | clog | 6 |
| 9672 | clement | 6 |
| 9673 | clears | 6 |
| 9674 | clearer | 6 |
| 9675 | claw | 6 |
| 9676 | clavijo | 6 |
| 9677 | clasped | 6 |
| 9678 | clapper | 6 |
| 9679 | civilly | 6 |
| 9680 | civilities | 6 |
| 9681 | civet | 6 |
| 9682 | churches | 6 |
| 9683 | chronicler | 6 |
| 9684 | chrish | 6 |
| 9685 | choughs | 6 |
| 9686 | chickens | 6 |
| 9687 | chew | 6 |
| 9688 | chests | 6 |
| 9689 | cheers | 6 |
| 9690 | cheater | 6 |
| 9691 | chaos | 6 |
| 9692 | chamois | 6 |
| 9693 | centurion | 6 |
| 9694 | celebration | 6 |
| 9695 | caves | 6 |
| 9696 | carelessly | 6 |
| 9697 | carcass | 6 |
| 9698 | capulets | 6 |
| 9699 | cank | 6 |
| 9700 | cane | 6 |
| 9701 | cancel | 6 |
| 9702 | camel | 6 |
| 9703 | calves | 6 |
| 9704 | calumny | 6 |
| 9705 | caithness | 6 |
| 9706 | caged | 6 |
| 9707 | buttons | 6 |
| 9708 | button | 6 |
| 9709 | burthen | 6 |
| 9710 | bunch | 6 |
| 9711 | builds | 6 |
| 9712 | buildings | 6 |
| 9713 | brutish | 6 |
| 9714 | bruising | 6 |
| 9715 | bruises | 6 |
| 9716 | broom | 6 |
| 9717 | brooch | 6 |
| 9718 | brocade | 6 |
| 9719 | brightest | 6 |
| 9720 | brier | 6 |
| 9721 | breeder | 6 |
| 9722 | breathed | 6 |
| 9723 | breaker | 6 |
| 9724 | brawls | 6 |
| 9725 | brainford | 6 |
| 9726 | brach | 6 |
| 9727 | braced | 6 |
| 9728 | bowls | 6 |
| 9729 | bowing | 6 |
| 9730 | bordered | 6 |
| 9731 | bonfires | 6 |
| 9732 | bolted | 6 |
| 9733 | boldest | 6 |
| 9734 | bodes | 6 |
| 9735 | boats | 6 |
| 9736 | boasting | 6 |
| 9737 | blossoms | 6 |
| 9738 | bloodless | 6 |
| 9739 | blemishes | 6 |
| 9740 | blanketing | 6 |
| 9741 | births | 6 |
| 9742 | binding | 6 |
| 9743 | billows | 6 |
| 9744 | bewailing | 6 |
| 9745 | betrothed | 6 |
| 9746 | bestrid | 6 |
| 9747 | bespeak | 6 |
| 9748 | beseem | 6 |
| 9749 | berries | 6 |
| 9750 | bellows | 6 |
| 9751 | beheaded | 6 |
| 9752 | behaviours | 6 |
| 9753 | beer | 6 |
| 9754 | beech | 6 |
| 9755 | bawds | 6 |
| 9756 | bass | 6 |
| 9757 | bartholomew | 6 |
| 9758 | barons | 6 |
| 9759 | barks | 6 |
| 9760 | bareheaded | 6 |
| 9761 | barabbas | 6 |
| 9762 | banner | 6 |
| 9763 | bane | 6 |
| 9764 | baldwin | 6 |
| 9765 | baited | 6 |
| 9766 | bagpipe | 6 |
| 9767 | babbling | 6 |
| 9768 | awkward | 6 |
| 9769 | awaking | 6 |
| 9770 | austerity | 6 |
| 9771 | auspicious | 6 |
| 9772 | aurora | 6 |
| 9773 | attentions | 6 |
| 9774 | assuring | 6 |
| 9775 | assails | 6 |
| 9776 | asia | 6 |
| 9777 | ascends | 6 |
| 9778 | artillery | 6 |
| 9779 | artificial | 6 |
| 9780 | arraign | 6 |
| 9781 | arose | 6 |
| 9782 | armoury | 6 |
| 9783 | arming | 6 |
| 9784 | arithmetic | 6 |
| 9785 | aristotle | 6 |
| 9786 | arbour | 6 |
| 9787 | arbitrement | 6 |
| 9788 | aqua | 6 |
| 9789 | approval | 6 |
| 9790 | apprehensive | 6 |
| 9791 | applying | 6 |
| 9792 | appellant | 6 |
| 9793 | aphorisms | 6 |
| 9794 | amour | 6 |
| 9795 | altered | 6 |
| 9796 | alt | 6 |
| 9797 | alongside | 6 |
| 9798 | allies | 6 |
| 9799 | allied | 6 |
| 9800 | alisander | 6 |
| 9801 | alias | 6 |
| 9802 | alcaldes | 6 |
| 9803 | albion | 6 |
| 9804 | alabaster | 6 |
| 9805 | aiming | 6 |
| 9806 | agramante | 6 |
| 9807 | agincourt | 6 |
| 9808 | aggravate | 6 |
| 9809 | advisable | 6 |
| 9810 | advances | 6 |
| 9811 | adds | 6 |
| 9812 | acquire | 6 |
| 9813 | acknowledged | 6 |
| 9814 | accusers | 6 |
| 9815 | accusations | 6 |
| 9816 | accost | 6 |
| 9817 | accomplishment | 6 |
| 9818 | academician | 6 |
| 9819 | abyss | 6 |
| 9820 | abstract | 6 |
| 9821 | abilities | 6 |
| 9822 | yoked | 5 |
| 9823 | yell | 5 |
| 9824 | xiii | 5 |
| 9825 | xii | 5 |
| 9826 | wrinkle | 5 |
| 9827 | wringing | 5 |
| 9828 | wrack | 5 |
| 9829 | wouldn | 5 |
| 9830 | wormwood | 5 |
| 9831 | woos | 5 |
| 9832 | wizards | 5 |
| 9833 | wizard | 5 |
| 9834 | withering | 5 |
| 9835 | winnowed | 5 |
| 9836 | widowed | 5 |
| 9837 | whosoever | 5 |
| 9838 | whoso | 5 |
| 9839 | whoop | 5 |
| 9840 | whithersoever | 5 |
| 9841 | whirl | 5 |
| 9842 | whey | 5 |
| 9843 | whatsoe | 5 |
| 9844 | whacks | 5 |
| 9845 | westward | 5 |
| 9846 | wean | 5 |
| 9847 | weakest | 5 |
| 9848 | wasp | 5 |
| 9849 | wasn | 5 |
| 9850 | warrants | 5 |
| 9851 | warranted | 5 |
| 9852 | wardrobe | 5 |
| 9853 | walled | 5 |
| 9854 | wagging | 5 |
| 9855 | volley | 5 |
| 9856 | vocation | 5 |
| 9857 | vizard | 5 |
| 9858 | vitae | 5 |
| 9859 | visions | 5 |
| 9860 | virtuously | 5 |
| 9861 | vinegar | 5 |
| 9862 | vilest | 5 |
| 9863 | vigilance | 5 |
| 9864 | viewing | 5 |
| 9865 | vesture | 5 |
| 9866 | vestal | 5 |
| 9867 | versed | 5 |
| 9868 | venturing | 5 |
| 9869 | ventur | 5 |
| 9870 | venomous | 5 |
| 9871 | veils | 5 |
| 9872 | vehemence | 5 |
| 9873 | vaward | 5 |
| 9874 | vasty | 5 |
| 9875 | variance | 5 |
| 9876 | vantages | 5 |
| 9877 | validity | 5 |
| 9878 | valiantly | 5 |
| 9879 | usurped | 5 |
| 9880 | usurers | 5 |
| 9881 | usest | 5 |
| 9882 | upbraided | 5 |
| 9883 | unworthiness | 5 |
| 9884 | unthrifty | 5 |
| 9885 | untaught | 5 |
| 9886 | untainted | 5 |
| 9887 | unspeakable | 5 |
| 9888 | unseal | 5 |
| 9889 | unnumbered | 5 |
| 9890 | unloose | 5 |
| 9891 | unlock | 5 |
| 9892 | university | 5 |
| 9893 | unhappily | 5 |
| 9894 | ungovern | 5 |
| 9895 | unequalled | 5 |
| 9896 | undoubtedly | 5 |
| 9897 | undoubted | 5 |
| 9898 | undoing | 5 |
| 9899 | undergoing | 5 |
| 9900 | undaunted | 5 |
| 9901 | uncleanly | 5 |
| 9902 | unclasp | 5 |
| 9903 | uncertainty | 5 |
| 9904 | unavailing | 5 |
| 9905 | unaccustom | 5 |
| 9906 | type | 5 |
| 9907 | twofold | 5 |
| 9908 | twisted | 5 |
| 9909 | tutors | 5 |
| 9910 | turtles | 5 |
| 9911 | turtle | 5 |
| 9912 | turrets | 5 |
| 9913 | tuft | 5 |
| 9914 | tube | 5 |
| 9915 | trusts | 5 |
| 9916 | triumphing | 5 |
| 9917 | tripp | 5 |
| 9918 | triple | 5 |
| 9919 | trimmed | 5 |
| 9920 | tremendous | 5 |
| 9921 | translator | 5 |
| 9922 | transgress | 5 |
| 9923 | towering | 5 |
| 9924 | touraine | 5 |
| 9925 | toucheth | 5 |
| 9926 | tortured | 5 |
| 9927 | tormented | 5 |
| 9928 | toll | 5 |
| 9929 | tiring | 5 |
| 9930 | tirante | 5 |
| 9931 | tin | 5 |
| 9932 | tilting | 5 |
| 9933 | tickled | 5 |
| 9934 | thwack | 5 |
| 9935 | thunderstruck | 5 |
| 9936 | thrifty | 5 |
| 9937 | thrashed | 5 |
| 9938 | thirteen | 5 |
| 9939 | thievish | 5 |
| 9940 | thereat | 5 |
| 9941 | thereabouts | 5 |
| 9942 | thatch | 5 |
| 9943 | thanking | 5 |
| 9944 | thankfulness | 5 |
| 9945 | terrace | 5 |
| 9946 | terra | 5 |
| 9947 | tenants | 5 |
| 9948 | tempts | 5 |
| 9949 | teen | 5 |
| 9950 | teeming | 5 |
| 9951 | teachest | 5 |
| 9952 | teacher | 5 |
| 9953 | taxes | 5 |
| 9954 | taxation | 5 |
| 9955 | tattered | 5 |
| 9956 | taming | 5 |
| 9957 | talkest | 5 |
| 9958 | taints | 5 |
| 9959 | synod | 5 |
| 9960 | sympathise | 5 |
| 9961 | swooned | 5 |
| 9962 | swol | 5 |
| 9963 | sweeting | 5 |
| 9964 | sweeping | 5 |
| 9965 | suspended | 5 |
| 9966 | suspects | 5 |
| 9967 | surpassing | 5 |
| 9968 | surnames | 5 |
| 9969 | surnamed | 5 |
| 9970 | surgery | 5 |
| 9971 | surfeited | 5 |
| 9972 | surer | 5 |
| 9973 | supremacy | 5 |
| 9974 | supposition | 5 |
| 9975 | supplications | 5 |
| 9976 | suppliant | 5 |
| 9977 | superstitious | 5 |
| 9978 | superiority | 5 |
| 9979 | sundry | 5 |
| 9980 | sulphur | 5 |
| 9981 | sues | 5 |
| 9982 | sucks | 5 |
| 9983 | succours | 5 |
| 9984 | successive | 5 |
| 9985 | subdues | 5 |
| 9986 | sty | 5 |
| 9987 | stumps | 5 |
| 9988 | stroll | 5 |
| 9989 | straws | 5 |
| 9990 | storehouse | 5 |
| 9991 | stools | 5 |
| 9992 | stockfish | 5 |
| 9993 | stint | 5 |
| 9994 | stink | 5 |
| 9995 | steadily | 5 |
| 9996 | statute | 5 |
| 9997 | statues | 5 |
| 9998 | stared | 5 |
| 9999 | standers | 5 |
| 10000 | stamped | 5 |
| 10001 | staggers | 5 |
| 10002 | stag | 5 |
| 10003 | stabbing | 5 |
| 10004 | sprite | 5 |
| 10005 | sprinkle | 5 |
| 10006 | springing | 5 |
| 10007 | sportive | 5 |
| 10008 | spongy | 5 |
| 10009 | sponge | 5 |
| 10010 | splitting | 5 |
| 10011 | spice | 5 |
| 10012 | spends | 5 |
| 10013 | spells | 5 |
| 10014 | spectators | 5 |
| 10015 | specify | 5 |
| 10016 | sparingly | 5 |
| 10017 | southern | 5 |
| 10018 | southampton | 5 |
| 10019 | sourest | 5 |
| 10020 | sorted | 5 |
| 10021 | soothe | 5 |
| 10022 | sol | 5 |
| 10023 | soever | 5 |
| 10024 | sociably | 5 |
| 10025 | sneak | 5 |
| 10026 | snares | 5 |
| 10027 | smoky | 5 |
| 10028 | smoking | 5 |
| 10029 | smiled | 5 |
| 10030 | slough | 5 |
| 10031 | slipper | 5 |
| 10032 | slime | 5 |
| 10033 | slighted | 5 |
| 10034 | sleepest | 5 |
| 10035 | sleepers | 5 |
| 10036 | sleek | 5 |
| 10037 | slays | 5 |
| 10038 | slaying | 5 |
| 10039 | slavish | 5 |
| 10040 | slavery | 5 |
| 10041 | slash | 5 |
| 10042 | sisterhood | 5 |
| 10043 | sinn | 5 |
| 10044 | sinewy | 5 |
| 10045 | sinew | 5 |
| 10046 | simples | 5 |
| 10047 | simpleness | 5 |
| 10048 | similes | 5 |
| 10049 | signor | 5 |
| 10050 | signieur | 5 |
| 10051 | shuns | 5 |
| 10052 | shuffle | 5 |
| 10053 | shrug | 5 |
| 10054 | shod | 5 |
| 10055 | shipping | 5 |
| 10056 | shilling | 5 |
| 10057 | shifted | 5 |
| 10058 | sherris | 5 |
| 10059 | sher | 5 |
| 10060 | shent | 5 |
| 10061 | sheepskins | 5 |
| 10062 | shears | 5 |
| 10063 | shear | 5 |
| 10064 | sharply | 5 |
| 10065 | shap | 5 |
| 10066 | shady | 5 |
| 10067 | shades | 5 |
| 10068 | setter | 5 |
| 10069 | serge | 5 |
| 10070 | sequence | 5 |
| 10071 | sensibly | 5 |
| 10072 | semblable | 5 |
| 10073 | select | 5 |
| 10074 | seemly | 5 |
| 10075 | seeds | 5 |
| 10076 | seduced | 5 |
| 10077 | sect | 5 |
| 10078 | se | 5 |
| 10079 | scum | 5 |
| 10080 | scriptures | 5 |
| 10081 | scribes | 5 |
| 10082 | screech | 5 |
| 10083 | scratching | 5 |
| 10084 | scourging | 5 |
| 10085 | scorning | 5 |
| 10086 | scholars | 5 |
| 10087 | schedule | 5 |
| 10088 | scented | 5 |
| 10089 | scent | 5 |
| 10090 | scatt | 5 |
| 10091 | scarfs | 5 |
| 10092 | scapes | 5 |
| 10093 | scaped | 5 |
| 10094 | scanted | 5 |
| 10095 | saws | 5 |
| 10096 | savoury | 5 |
| 10097 | sauf | 5 |
| 10098 | santiago | 5 |
| 10099 | santa | 5 |
| 10100 | sanguine | 5 |
| 10101 | sampson | 5 |
| 10102 | salutations | 5 |
| 10103 | saidst | 5 |
| 10104 | sages | 5 |
| 10105 | sackcloth | 5 |
| 10106 | sable | 5 |
| 10107 | russian | 5 |
| 10108 | ruffle | 5 |
| 10109 | rubs | 5 |
| 10110 | rubbed | 5 |
| 10111 | roughness | 5 |
| 10112 | rote | 5 |
| 10113 | rosy | 5 |
| 10114 | rooms | 5 |
| 10115 | roamed | 5 |
| 10116 | riseth | 5 |
| 10117 | ripened | 5 |
| 10118 | rip | 5 |
| 10119 | righting | 5 |
| 10120 | riddles | 5 |
| 10121 | ricardo | 5 |
| 10122 | ribbons | 5 |
| 10123 | rialto | 5 |
| 10124 | rful | 5 |
| 10125 | revoke | 5 |
| 10126 | revived | 5 |
| 10127 | restoration | 5 |
| 10128 | respecting | 5 |
| 10129 | resolutely | 5 |
| 10130 | reservation | 5 |
| 10131 | resemblance | 5 |
| 10132 | rescued | 5 |
| 10133 | requirements | 5 |
| 10134 | repulse | 5 |
| 10135 | repel | 5 |
| 10136 | renegades | 5 |
| 10137 | renders | 5 |
| 10138 | remorseful | 5 |
| 10139 | remnant | 5 |
| 10140 | remission | 5 |
| 10141 | remiss | 5 |
| 10142 | remind | 5 |
| 10143 | reigned | 5 |
| 10144 | regret | 5 |
| 10145 | regidor | 5 |
| 10146 | regained | 5 |
| 10147 | reflected | 5 |
| 10148 | reeds | 5 |
| 10149 | redoubted | 5 |
| 10150 | redoubled | 5 |
| 10151 | rectitude | 5 |
| 10152 | reconciled | 5 |
| 10153 | reconcil | 5 |
| 10154 | recommend | 5 |
| 10155 | reckonings | 5 |
| 10156 | rebukes | 5 |
| 10157 | rebeck | 5 |
| 10158 | rearward | 5 |
| 10159 | reapers | 5 |
| 10160 | raz | 5 |
| 10161 | raught | 5 |
| 10162 | rates | 5 |
| 10163 | rapidly | 5 |
| 10164 | rapidity | 5 |
| 10165 | rancorous | 5 |
| 10166 | rams | 5 |
| 10167 | raineth | 5 |
| 10168 | quixotes | 5 |
| 10169 | quixano | 5 |
| 10170 | quixada | 5 |
| 10171 | quis | 5 |
| 10172 | quintanona | 5 |
| 10173 | quean | 5 |
| 10174 | quart | 5 |
| 10175 | quaintly | 5 |
| 10176 | pyramid | 5 |
| 10177 | purer | 5 |
| 10178 | purchased | 5 |
| 10179 | purblind | 5 |
| 10180 | pummelled | 5 |
| 10181 | pulls | 5 |
| 10182 | pulling | 5 |
| 10183 | published | 5 |
| 10184 | propos | 5 |
| 10185 | prophetess | 5 |
| 10186 | prone | 5 |
| 10187 | prompts | 5 |
| 10188 | prompted | 5 |
| 10189 | primrose | 5 |
| 10190 | pridge | 5 |
| 10191 | pricking | 5 |
| 10192 | previously | 5 |
| 10193 | prettily | 5 |
| 10194 | preparing | 5 |
| 10195 | prentice | 5 |
| 10196 | predominant | 5 |
| 10197 | prat | 5 |
| 10198 | powerless | 5 |
| 10199 | posting | 5 |
| 10200 | possessor | 5 |
| 10201 | populous | 5 |
| 10202 | poorer | 5 |
| 10203 | poop | 5 |
| 10204 | poniard | 5 |
| 10205 | pomegranate | 5 |
| 10206 | poles | 5 |
| 10207 | poland | 5 |
| 10208 | poictiers | 5 |
| 10209 | pobre | 5 |
| 10210 | plum | 5 |
| 10211 | plies | 5 |
| 10212 | plentifully | 5 |
| 10213 | platform | 5 |
| 10214 | plantain | 5 |
| 10215 | pitying | 5 |
| 10216 | pitched | 5 |
| 10217 | pink | 5 |
| 10218 | pinion | 5 |
| 10219 | pigeon | 5 |
| 10220 | pied | 5 |
| 10221 | philosophers | 5 |
| 10222 | phantom | 5 |
| 10223 | perverse | 5 |
| 10224 | persist | 5 |
| 10225 | perpetually | 5 |
| 10226 | perpend | 5 |
| 10227 | perfum | 5 |
| 10228 | pepper | 5 |
| 10229 | pentapolin | 5 |
| 10230 | pension | 5 |
| 10231 | pens | 5 |
| 10232 | penn | 5 |
| 10233 | pell | 5 |
| 10234 | pegs | 5 |
| 10235 | pegasus | 5 |
| 10236 | peering | 5 |
| 10237 | pebble | 5 |
| 10238 | peascod | 5 |
| 10239 | pear | 5 |
| 10240 | payer | 5 |
| 10241 | paw | 5 |
| 10242 | paved | 5 |
| 10243 | paunch | 5 |
| 10244 | patterns | 5 |
| 10245 | patrimony | 5 |
| 10246 | partridge | 5 |
| 10247 | particle | 5 |
| 10248 | parti | 5 |
| 10249 | pardoned | 5 |
| 10250 | parched | 5 |
| 10251 | parallels | 5 |
| 10252 | panting | 5 |
| 10253 | pallas | 5 |
| 10254 | packed | 5 |
| 10255 | owned | 5 |
| 10256 | overlook | 5 |
| 10257 | outlet | 5 |
| 10258 | outburst | 5 |
| 10259 | orisons | 5 |
| 10260 | ordinances | 5 |
| 10261 | ordering | 5 |
| 10262 | orbs | 5 |
| 10263 | oratory | 5 |
| 10264 | opposites | 5 |
| 10265 | ooze | 5 |
| 10266 | onion | 5 |
| 10267 | oneself | 5 |
| 10268 | olla | 5 |
| 10269 | offerings | 5 |
| 10270 | ofephesus | 5 |
| 10271 | occurs | 5 |
| 10272 | occur | 5 |
| 10273 | oblige | 5 |
| 10274 | oats | 5 |
| 10275 | oar | 5 |
| 10276 | nursery | 5 |
| 10277 | nurs | 5 |
| 10278 | nuns | 5 |
| 10279 | novels | 5 |
| 10280 | nous | 5 |
| 10281 | nourished | 5 |
| 10282 | notions | 5 |
| 10283 | nonpareil | 5 |
| 10284 | noisome | 5 |
| 10285 | noises | 5 |
| 10286 | noiseless | 5 |
| 10287 | nods | 5 |
| 10288 | newest | 5 |
| 10289 | nevils | 5 |
| 10290 | nephews | 5 |
| 10291 | neighbouring | 5 |
| 10292 | needst | 5 |
| 10293 | neatly | 5 |
| 10294 | narvaez | 5 |
| 10295 | napkins | 5 |
| 10296 | mysteries | 5 |
| 10297 | mutually | 5 |
| 10298 | muttering | 5 |
| 10299 | mutinies | 5 |
| 10300 | musters | 5 |
| 10301 | musk | 5 |
| 10302 | musing | 5 |
| 10303 | murthers | 5 |
| 10304 | mulberry | 5 |
| 10305 | moustaches | 5 |
| 10306 | mourners | 5 |
| 10307 | mots | 5 |
| 10308 | montiel | 5 |
| 10309 | montagues | 5 |
| 10310 | monkeys | 5 |
| 10311 | mongrel | 5 |
| 10312 | misshapen | 5 |
| 10313 | minions | 5 |
| 10314 | mingling | 5 |
| 10315 | minding | 5 |
| 10316 | mince | 5 |
| 10317 | midway | 5 |
| 10318 | mickle | 5 |
| 10319 | mice | 5 |
| 10320 | methoughts | 5 |
| 10321 | mercer | 5 |
| 10322 | menecrates | 5 |
| 10323 | meg | 5 |
| 10324 | meekness | 5 |
| 10325 | meditations | 5 |
| 10326 | meanly | 5 |
| 10327 | meads | 5 |
| 10328 | mead | 5 |
| 10329 | matrons | 5 |
| 10330 | matching | 5 |
| 10331 | matched | 5 |
| 10332 | marseilles | 5 |
| 10333 | marketplace | 5 |
| 10334 | marjoram | 5 |
| 10335 | marias | 5 |
| 10336 | manifested | 5 |
| 10337 | manent | 5 |
| 10338 | malaga | 5 |
| 10339 | maketh | 5 |
| 10340 | majesties | 5 |
| 10341 | mainly | 5 |
| 10342 | madcap | 5 |
| 10343 | madasima | 5 |
| 10344 | macedon | 5 |
| 10345 | maccabaeus | 5 |
| 10346 | lustily | 5 |
| 10347 | lunacy | 5 |
| 10348 | lukewarm | 5 |
| 10349 | luggage | 5 |
| 10350 | lubber | 5 |
| 10351 | lowliness | 5 |
| 10352 | lovingly | 5 |
| 10353 | loudly | 5 |
| 10354 | losers | 5 |
| 10355 | los | 5 |
| 10356 | lolling | 5 |
| 10357 | log | 5 |
| 10358 | lodowick | 5 |
| 10359 | loathes | 5 |
| 10360 | loam | 5 |
| 10361 | lizard | 5 |
| 10362 | lionel | 5 |
| 10363 | linked | 5 |
| 10364 | lin | 5 |
| 10365 | limping | 5 |
| 10366 | lighter | 5 |
| 10367 | lifts | 5 |
| 10368 | lifeless | 5 |
| 10369 | licentious | 5 |
| 10370 | libya | 5 |
| 10371 | lethargy | 5 |
| 10372 | leonardo | 5 |
| 10373 | legacy | 5 |
| 10374 | leer | 5 |
| 10375 | leeks | 5 |
| 10376 | lecture | 5 |
| 10377 | leathern | 5 |
| 10378 | laughable | 5 |
| 10379 | laud | 5 |
| 10380 | lath | 5 |
| 10381 | lain | 5 |
| 10382 | lackeys | 5 |
| 10383 | lac | 5 |
| 10384 | knotty | 5 |
| 10385 | knighted | 5 |
| 10386 | knelt | 5 |
| 10387 | knaveries | 5 |
| 10388 | kicked | 5 |
| 10389 | keepest | 5 |
| 10390 | jumped | 5 |
| 10391 | july | 5 |
| 10392 | joking | 5 |
| 10393 | jointure | 5 |
| 10394 | joiner | 5 |
| 10395 | jelly | 5 |
| 10396 | ivory | 5 |
| 10397 | irregular | 5 |
| 10398 | invulnerable | 5 |
| 10399 | involved | 5 |
| 10400 | intricate | 5 |
| 10401 | intimate | 5 |
| 10402 | intervals | 5 |
| 10403 | interr | 5 |
| 10404 | interpose | 5 |
| 10405 | intermission | 5 |
| 10406 | interlude | 5 |
| 10407 | intercourse | 5 |
| 10408 | insurrection | 5 |
| 10409 | instructs | 5 |
| 10410 | inspiration | 5 |
| 10411 | inspir | 5 |
| 10412 | insinuate | 5 |
| 10413 | inserted | 5 |
| 10414 | inquiring | 5 |
| 10415 | innocency | 5 |
| 10416 | inland | 5 |
| 10417 | infuse | 5 |
| 10418 | infringe | 5 |
| 10419 | infinitely | 5 |
| 10420 | infects | 5 |
| 10421 | infantry | 5 |
| 10422 | infamous | 5 |
| 10423 | infallible | 5 |
| 10424 | industrious | 5 |
| 10425 | indifferently | 5 |
| 10426 | incurable | 5 |
| 10427 | inconvenience | 5 |
| 10428 | included | 5 |
| 10429 | incite | 5 |
| 10430 | incestuous | 5 |
| 10431 | imprudence | 5 |
| 10432 | imposing | 5 |
| 10433 | importunity | 5 |
| 10434 | importunities | 5 |
| 10435 | impair | 5 |
| 10436 | imp | 5 |
| 10437 | ilium | 5 |
| 10438 | hydra | 5 |
| 10439 | husks | 5 |
| 10440 | humh | 5 |
| 10441 | hover | 5 |
| 10442 | hotter | 5 |
| 10443 | horseman | 5 |
| 10444 | horned | 5 |
| 10445 | hoofs | 5 |
| 10446 | honneur | 5 |
| 10447 | honester | 5 |
| 10448 | homeward | 5 |
| 10449 | holmedon | 5 |
| 10450 | holidays | 5 |
| 10451 | hoist | 5 |
| 10452 | hoa | 5 |
| 10453 | hitting | 5 |
| 10454 | hitherward | 5 |
| 10455 | hir | 5 |
| 10456 | hips | 5 |
| 10457 | hilding | 5 |
| 10458 | highways | 5 |
| 10459 | hight | 5 |
| 10460 | hermits | 5 |
| 10461 | hereof | 5 |
| 10462 | herdsmen | 5 |
| 10463 | herbert | 5 |
| 10464 | heraldry | 5 |
| 10465 | helpful | 5 |
| 10466 | helmets | 5 |
| 10467 | hedges | 5 |
| 10468 | heartless | 5 |
| 10469 | hearsay | 5 |
| 10470 | headless | 5 |
| 10471 | hazards | 5 |
| 10472 | harassed | 5 |
| 10473 | happening | 5 |
| 10474 | handsomely | 5 |
| 10475 | hammering | 5 |
| 10476 | halts | 5 |
| 10477 | hallowed | 5 |
| 10478 | haggard | 5 |
| 10479 | hackney | 5 |
| 10480 | habited | 5 |
| 10481 | haberdasher | 5 |
| 10482 | gyves | 5 |
| 10483 | gurney | 5 |
| 10484 | gunpowder | 5 |
| 10485 | guinevere | 5 |
| 10486 | guile | 5 |
| 10487 | guildford | 5 |
| 10488 | guiding | 5 |
| 10489 | grounded | 5 |
| 10490 | grosser | 5 |
| 10491 | groats | 5 |
| 10492 | grip | 5 |
| 10493 | grieving | 5 |
| 10494 | greediness | 5 |
| 10495 | greed | 5 |
| 10496 | grated | 5 |
| 10497 | gramercy | 5 |
| 10498 | grains | 5 |
| 10499 | grafted | 5 |
| 10500 | graduate | 5 |
| 10501 | graced | 5 |
| 10502 | gothic | 5 |
| 10503 | gor | 5 |
| 10504 | goblins | 5 |
| 10505 | gnats | 5 |
| 10506 | glimpse | 5 |
| 10507 | glances | 5 |
| 10508 | glanced | 5 |
| 10509 | gladness | 5 |
| 10510 | gird | 5 |
| 10511 | gins | 5 |
| 10512 | gibes | 5 |
| 10513 | gestures | 5 |
| 10514 | germans | 5 |
| 10515 | gem | 5 |
| 10516 | geld | 5 |
| 10517 | gazes | 5 |
| 10518 | gaspar | 5 |
| 10519 | gashes | 5 |
| 10520 | gash | 5 |
| 10521 | garnish | 5 |
| 10522 | gamut | 5 |
| 10523 | games | 5 |
| 10524 | gallops | 5 |
| 10525 | galen | 5 |
| 10526 | galaor | 5 |
| 10527 | fustian | 5 |
| 10528 | furr | 5 |
| 10529 | furnace | 5 |
| 10530 | furies | 5 |
| 10531 | fulsome | 5 |
| 10532 | fulness | 5 |
| 10533 | fulfillment | 5 |
| 10534 | fulfilling | 5 |
| 10535 | fugitive | 5 |
| 10536 | frustrate | 5 |
| 10537 | fretting | 5 |
| 10538 | fretted | 5 |
| 10539 | freer | 5 |
| 10540 | fraternity | 5 |
| 10541 | fragrance | 5 |
| 10542 | fowls | 5 |
| 10543 | foundations | 5 |
| 10544 | foulness | 5 |
| 10545 | foster | 5 |
| 10546 | forthcoming | 5 |
| 10547 | forres | 5 |
| 10548 | forgiven | 5 |
| 10549 | forcibly | 5 |
| 10550 | footman | 5 |
| 10551 | foison | 5 |
| 10552 | foaming | 5 |
| 10553 | flutes | 5 |
| 10554 | flourishing | 5 |
| 10555 | flaws | 5 |
| 10556 | flattered | 5 |
| 10557 | flatt | 5 |
| 10558 | flats | 5 |
| 10559 | fines | 5 |
| 10560 | final | 5 |
| 10561 | filed | 5 |
| 10562 | fervour | 5 |
| 10563 | ferret | 5 |
| 10564 | fer | 5 |
| 10565 | feigning | 5 |
| 10566 | fees | 5 |
| 10567 | feelingly | 5 |
| 10568 | favourite | 5 |
| 10569 | fantasies | 5 |
| 10570 | fanciful | 5 |
| 10571 | falsehoods | 5 |
| 10572 | falconbridge | 5 |
| 10573 | fairs | 5 |
| 10574 | faintness | 5 |
| 10575 | fainted | 5 |
| 10576 | factor | 5 |
| 10577 | eyeballs | 5 |
| 10578 | extravagant | 5 |
| 10579 | extort | 5 |
| 10580 | extenuate | 5 |
| 10581 | extends | 5 |
| 10582 | extempore | 5 |
| 10583 | expressions | 5 |
| 10584 | expressing | 5 |
| 10585 | expound | 5 |
| 10586 | expostulate | 5 |
| 10587 | expel | 5 |
| 10588 | excrement | 5 |
| 10589 | exclamations | 5 |
| 10590 | exceeded | 5 |
| 10591 | exalt | 5 |
| 10592 | eulogies | 5 |
| 10593 | ethiope | 5 |
| 10594 | estremadura | 5 |
| 10595 | estimable | 5 |
| 10596 | esteems | 5 |
| 10597 | ermine | 5 |
| 10598 | equity | 5 |
| 10599 | equality | 5 |
| 10600 | epitaphs | 5 |
| 10601 | entrap | 5 |
| 10602 | entitle | 5 |
| 10603 | enslaved | 5 |
| 10604 | enraged | 5 |
| 10605 | enlargement | 5 |
| 10606 | engender | 5 |
| 10607 | engaging | 5 |
| 10608 | endeavoured | 5 |
| 10609 | encountering | 5 |
| 10610 | encompass | 5 |
| 10611 | encamp | 5 |
| 10612 | encamisados | 5 |
| 10613 | emprise | 5 |
| 10614 | empresses | 5 |
| 10615 | embracements | 5 |
| 10616 | elected | 5 |
| 10617 | elect | 5 |
| 10618 | elders | 5 |
| 10619 | elbows | 5 |
| 10620 | effectual | 5 |
| 10621 | effecting | 5 |
| 10622 | edified | 5 |
| 10623 | eclipses | 5 |
| 10624 | earldom | 5 |
| 10625 | dye | 5 |
| 10626 | dy | 5 |
| 10627 | dwelt | 5 |
| 10628 | dwarfish | 5 |
| 10629 | dun | 5 |
| 10630 | dumbness | 5 |
| 10631 | duller | 5 |
| 10632 | dub | 5 |
| 10633 | drowns | 5 |
| 10634 | droves | 5 |
| 10635 | dross | 5 |
| 10636 | drollery | 5 |
| 10637 | dreary | 5 |
| 10638 | dreading | 5 |
| 10639 | drama | 5 |
| 10640 | downwards | 5 |
| 10641 | downward | 5 |
| 10642 | downcast | 5 |
| 10643 | doughty | 5 |
| 10644 | doublets | 5 |
| 10645 | dolour | 5 |
| 10646 | doigts | 5 |
| 10647 | dogg | 5 |
| 10648 | doer | 5 |
| 10649 | diverted | 5 |
| 10650 | dit | 5 |
| 10651 | distaff | 5 |
| 10652 | dissolute | 5 |
| 10653 | disputes | 5 |
| 10654 | dispossess | 5 |
| 10655 | disposing | 5 |
| 10656 | displease | 5 |
| 10657 | disordered | 5 |
| 10658 | disgraces | 5 |
| 10659 | disfigured | 5 |
| 10660 | disfigure | 5 |
| 10661 | diseas | 5 |
| 10662 | discussion | 5 |
| 10663 | discovering | 5 |
| 10664 | discords | 5 |
| 10665 | disconsolate | 5 |
| 10666 | disastrous | 5 |
| 10667 | disappeared | 5 |
| 10668 | dimmed | 5 |
| 10669 | dimensions | 5 |
| 10670 | differ | 5 |
| 10671 | didn | 5 |
| 10672 | devoutly | 5 |
| 10673 | devising | 5 |
| 10674 | determinate | 5 |
| 10675 | desk | 5 |
| 10676 | deserted | 5 |
| 10677 | descending | 5 |
| 10678 | derision | 5 |
| 10679 | deputation | 5 |
| 10680 | depended | 5 |
| 10681 | denote | 5 |
| 10682 | deliverer | 5 |
| 10683 | dejection | 5 |
| 10684 | deities | 5 |
| 10685 | deformity | 5 |
| 10686 | deform | 5 |
| 10687 | define | 5 |
| 10688 | defile | 5 |
| 10689 | defer | 5 |
| 10690 | defendant | 5 |
| 10691 | defeated | 5 |
| 10692 | deemed | 5 |
| 10693 | declin | 5 |
| 10694 | declares | 5 |
| 10695 | deceives | 5 |
| 10696 | decayed | 5 |
| 10697 | debating | 5 |
| 10698 | debase | 5 |
| 10699 | dealings | 5 |
| 10700 | daub | 5 |
| 10701 | dank | 5 |
| 10702 | curtsies | 5 |
| 10703 | currish | 5 |
| 10704 | curl | 5 |
| 10705 | curiously | 5 |
| 10706 | curer | 5 |
| 10707 | cunningly | 5 |
| 10708 | cudgellings | 5 |
| 10709 | cudgelled | 5 |
| 10710 | cudgell | 5 |
| 10711 | crowding | 5 |
| 10712 | crispian | 5 |
| 10713 | crippled | 5 |
| 10714 | crickets | 5 |
| 10715 | creeps | 5 |
| 10716 | creating | 5 |
| 10717 | craven | 5 |
| 10718 | cracks | 5 |
| 10719 | cracked | 5 |
| 10720 | cowslip | 5 |
| 10721 | countesses | 5 |
| 10722 | counterfeiting | 5 |
| 10723 | counterfeited | 5 |
| 10724 | cote | 5 |
| 10725 | correcting | 5 |
| 10726 | cordovan | 5 |
| 10727 | copies | 5 |
| 10728 | cop | 5 |
| 10729 | cooks | 5 |
| 10730 | cony | 5 |
| 10731 | convenience | 5 |
| 10732 | controlling | 5 |
| 10733 | contriving | 5 |
| 10734 | contraries | 5 |
| 10735 | continuing | 5 |
| 10736 | contest | 5 |
| 10737 | contending | 5 |
| 10738 | contemptible | 5 |
| 10739 | contemplated | 5 |
| 10740 | contaminated | 5 |
| 10741 | consumption | 5 |
| 10742 | consummate | 5 |
| 10743 | consumed | 5 |
| 10744 | consigned | 5 |
| 10745 | considerations | 5 |
| 10746 | considerable | 5 |
| 10747 | conn | 5 |
| 10748 | conjuration | 5 |
| 10749 | conjoin | 5 |
| 10750 | confiscate | 5 |
| 10751 | confide | 5 |
| 10752 | confidante | 5 |
| 10753 | confederacy | 5 |
| 10754 | condemns | 5 |
| 10755 | condemning | 5 |
| 10756 | composing | 5 |
| 10757 | complices | 5 |
| 10758 | complicated | 5 |
| 10759 | complains | 5 |
| 10760 | competitors | 5 |
| 10761 | communication | 5 |
| 10762 | communicate | 5 |
| 10763 | commune | 5 |
| 10764 | commerce | 5 |
| 10765 | commandant | 5 |
| 10766 | comfortless | 5 |
| 10767 | comforter | 5 |
| 10768 | cometh | 5 |
| 10769 | college | 5 |
| 10770 | collecting | 5 |
| 10771 | collars | 5 |
| 10772 | collar | 5 |
| 10773 | coldness | 5 |
| 10774 | cocks | 5 |
| 10775 | coaches | 5 |
| 10776 | clutch | 5 |
| 10777 | clownish | 5 |
| 10778 | clouded | 5 |
| 10779 | clothed | 5 |
| 10780 | closes | 5 |
| 10781 | clos | 5 |
| 10782 | clocks | 5 |
| 10783 | clinging | 5 |
| 10784 | cling | 5 |
| 10785 | cleverness | 5 |
| 10786 | clerks | 5 |
| 10787 | clergy | 5 |
| 10788 | claps | 5 |
| 10789 | cited | 5 |
| 10790 | cirongilio | 5 |
| 10791 | cinque | 5 |
| 10792 | christen | 5 |
| 10793 | chins | 5 |
| 10794 | chinks | 5 |
| 10795 | cherubin | 5 |
| 10796 | chatterer | 5 |
| 10797 | chatter | 5 |
| 10798 | chants | 5 |
| 10799 | changeable | 5 |
| 10800 | chafed | 5 |
| 10801 | chafe | 5 |
| 10802 | chaf | 5 |
| 10803 | cervantes | 5 |
| 10804 | certes | 5 |
| 10805 | censured | 5 |
| 10806 | celebrate | 5 |
| 10807 | ceasing | 5 |
| 10808 | ceases | 5 |
| 10809 | cavil | 5 |
| 10810 | cavalier | 5 |
| 10811 | cautiously | 5 |
| 10812 | caterpillars | 5 |
| 10813 | catalogue | 5 |
| 10814 | casts | 5 |
| 10815 | cask | 5 |
| 10816 | cashier | 5 |
| 10817 | carts | 5 |
| 10818 | carpio | 5 |
| 10819 | cared | 5 |
| 10820 | carbonado | 5 |
| 10821 | capture | 5 |
| 10822 | cannons | 5 |
| 10823 | cannibals | 5 |
| 10824 | cages | 5 |
| 10825 | caesars | 5 |
| 10826 | buzzing | 5 |
| 10827 | buttock | 5 |
| 10828 | butler | 5 |
| 10829 | bustle | 5 |
| 10830 | businesses | 5 |
| 10831 | bushels | 5 |
| 10832 | bursting | 5 |
| 10833 | bur | 5 |
| 10834 | bulwark | 5 |
| 10835 | bullet | 5 |
| 10836 | buff | 5 |
| 10837 | budget | 5 |
| 10838 | brush | 5 |
| 10839 | bruis | 5 |
| 10840 | brothel | 5 |
| 10841 | bronze | 5 |
| 10842 | brays | 5 |
| 10843 | brawn | 5 |
| 10844 | braving | 5 |
| 10845 | bracing | 5 |
| 10846 | brabant | 5 |
| 10847 | bowshot | 5 |
| 10848 | bounden | 5 |
| 10849 | booty | 5 |
| 10850 | blunted | 5 |
| 10851 | blooded | 5 |
| 10852 | blench | 5 |
| 10853 | bleak | 5 |
| 10854 | blasting | 5 |
| 10855 | blanks | 5 |
| 10856 | blanco | 5 |
| 10857 | blades | 5 |
| 10858 | birding | 5 |
| 10859 | bewitched | 5 |
| 10860 | bethought | 5 |
| 10861 | bespoke | 5 |
| 10862 | besmear | 5 |
| 10863 | beneficial | 5 |
| 10864 | beguiles | 5 |
| 10865 | beguiled | 5 |
| 10866 | begets | 5 |
| 10867 | befriend | 5 |
| 10868 | befitting | 5 |
| 10869 | beckons | 5 |
| 10870 | barge | 5 |
| 10871 | bang | 5 |
| 10872 | banditti | 5 |
| 10873 | bandaged | 5 |
| 10874 | bake | 5 |
| 10875 | badness | 5 |
| 10876 | badges | 5 |
| 10877 | backside | 5 |
| 10878 | azure | 5 |
| 10879 | awaits | 5 |
| 10880 | awaited | 5 |
| 10881 | august | 5 |
| 10882 | attributes | 5 |
| 10883 | assumed | 5 |
| 10884 | assiduity | 5 |
| 10885 | assert | 5 |
| 10886 | aspire | 5 |
| 10887 | ascension | 5 |
| 10888 | ascended | 5 |
| 10889 | argosy | 5 |
| 10890 | arcade | 5 |
| 10891 | arbitrate | 5 |
| 10892 | aprons | 5 |
| 10893 | approves | 5 |
| 10894 | approv | 5 |
| 10895 | apprehensions | 5 |
| 10896 | applies | 5 |
| 10897 | apples | 5 |
| 10898 | applauded | 5 |
| 10899 | appetites | 5 |
| 10900 | appease | 5 |
| 10901 | appearances | 5 |
| 10902 | apparitions | 5 |
| 10903 | apish | 5 |
| 10904 | anticipated | 5 |
| 10905 | anthony | 5 |
| 10906 | anglais | 5 |
| 10907 | ang | 5 |
| 10908 | anchors | 5 |
| 10909 | ancestor | 5 |
| 10910 | anatomy | 5 |
| 10911 | amply | 5 |
| 10912 | ambrosia | 5 |
| 10913 | amadises | 5 |
| 10914 | altitude | 5 |
| 10915 | altercation | 5 |
| 10916 | altars | 5 |
| 10917 | alleys | 5 |
| 10918 | alarmed | 5 |
| 10919 | alarbus | 5 |
| 10920 | ailment | 5 |
| 10921 | aided | 5 |
| 10922 | ahead | 5 |
| 10923 | agile | 5 |
| 10924 | agate | 5 |
| 10925 | afield | 5 |
| 10926 | affrights | 5 |
| 10927 | affirm | 5 |
| 10928 | affecting | 5 |
| 10929 | affability | 5 |
| 10930 | advising | 5 |
| 10931 | adulterate | 5 |
| 10932 | adores | 5 |
| 10933 | adored | 5 |
| 10934 | administered | 5 |
| 10935 | additional | 5 |
| 10936 | actually | 5 |
| 10937 | acres | 5 |
| 10938 | acquaintances | 5 |
| 10939 | acorn | 5 |
| 10940 | acold | 5 |
| 10941 | acknowledgment | 5 |
| 10942 | accords | 5 |
| 10943 | accompaniment | 5 |
| 10944 | accommodation | 5 |
| 10945 | abram | 5 |
| 10946 | abr | 5 |
| 10947 | abjure | 5 |
| 10948 | abhors | 5 |
| 10949 | abandoned | 5 |
| 10950 | zamora | 4 |
| 10951 | yeomen | 4 |
| 10952 | xv | 4 |
| 10953 | xiv | 4 |
| 10954 | wronging | 4 |
| 10955 | wrings | 4 |
| 10956 | wrested | 4 |
| 10957 | wreath | 4 |
| 10958 | woven | 4 |
| 10959 | worlds | 4 |
| 10960 | workmen | 4 |
| 10961 | wooes | 4 |
| 10962 | wondered | 4 |
| 10963 | wittingly | 4 |
| 10964 | wittenberg | 4 |
| 10965 | witnessed | 4 |
| 10966 | withholds | 4 |
| 10967 | withdrawing | 4 |
| 10968 | winners | 4 |
| 10969 | wildest | 4 |
| 10970 | whoremaster | 4 |
| 10971 | whining | 4 |
| 10972 | whim | 4 |
| 10973 | whetstone | 4 |
| 10974 | wherewithal | 4 |
| 10975 | whereas | 4 |
| 10976 | wether | 4 |
| 10977 | weights | 4 |
| 10978 | weighed | 4 |
| 10979 | weening | 4 |
| 10980 | ween | 4 |
| 10981 | weathercock | 4 |
| 10982 | wasps | 4 |
| 10983 | waspish | 4 |
| 10984 | warwickshire | 4 |
| 10985 | warr | 4 |
| 10986 | warnings | 4 |
| 10987 | warms | 4 |
| 10988 | warmed | 4 |
| 10989 | warkworth | 4 |
| 10990 | wares | 4 |
| 10991 | wanderings | 4 |
| 10992 | wanderer | 4 |
| 10993 | wan | 4 |
| 10994 | waggon | 4 |
| 10995 | votary | 4 |
| 10996 | vital | 4 |
| 10997 | visionary | 4 |
| 10998 | visages | 4 |
| 10999 | visag | 4 |
| 11000 | violation | 4 |
| 11001 | vines | 4 |
| 11002 | villainies | 4 |
| 11003 | vigorously | 4 |
| 11004 | viedma | 4 |
| 11005 | vied | 4 |
| 11006 | videlicet | 4 |
| 11007 | veriest | 4 |
| 11008 | vere | 4 |
| 11009 | vaulting | 4 |
| 11010 | vary | 4 |
| 11011 | varlets | 4 |
| 11012 | valencian | 4 |
| 11013 | vacancy | 4 |
| 11014 | usury | 4 |
| 11015 | usurps | 4 |
| 11016 | useth | 4 |
| 11017 | urges | 4 |
| 11018 | urganda | 4 |
| 11019 | urchins | 4 |
| 11020 | upstairs | 4 |
| 11021 | upholds | 4 |
| 11022 | unyoke | 4 |
| 11023 | unwillingness | 4 |
| 11024 | untruths | 4 |
| 11025 | untold | 4 |
| 11026 | unstained | 4 |
| 11027 | unspotted | 4 |
| 11028 | unsought | 4 |
| 11029 | unsheathed | 4 |
| 11030 | unsettle | 4 |
| 11031 | unseasonably | 4 |
| 11032 | unsay | 4 |
| 11033 | unsafe | 4 |
| 11034 | unrelenting | 4 |
| 11035 | unprofitable | 4 |
| 11036 | unprepared | 4 |
| 11037 | unpitied | 4 |
| 11038 | unpeople | 4 |
| 11039 | unpaid | 4 |
| 11040 | unmatchable | 4 |
| 11041 | unmask | 4 |
| 11042 | unmanly | 4 |
| 11043 | unlooked | 4 |
| 11044 | unknit | 4 |
| 11045 | unkindest | 4 |
| 11046 | unhappiness | 4 |
| 11047 | unhandsome | 4 |
| 11048 | unfolded | 4 |
| 11049 | unfirm | 4 |
| 11050 | unfeeling | 4 |
| 11051 | undressed | 4 |
| 11052 | undoer | 4 |
| 11053 | undeserved | 4 |
| 11054 | undermine | 4 |
| 11055 | underground | 4 |
| 11056 | undergone | 4 |
| 11057 | undeceive | 4 |
| 11058 | unconstant | 4 |
| 11059 | unbridled | 4 |
| 11060 | unavoided | 4 |
| 11061 | unattended | 4 |
| 11062 | unapt | 4 |
| 11063 | unadvis | 4 |
| 11064 | ugliness | 4 |
| 11065 | twins | 4 |
| 11066 | twinn | 4 |
| 11067 | tus | 4 |
| 11068 | turpin | 4 |
| 11069 | turkey | 4 |
| 11070 | tumultuous | 4 |
| 11071 | tumbler | 4 |
| 11072 | tug | 4 |
| 11073 | trull | 4 |
| 11074 | trout | 4 |
| 11075 | trojan | 4 |
| 11076 | triumphantly | 4 |
| 11077 | tripes | 4 |
| 11078 | trickery | 4 |
| 11079 | tribunal | 4 |
| 11080 | tribes | 4 |
| 11081 | trib | 4 |
| 11082 | trials | 4 |
| 11083 | tres | 4 |
| 11084 | trepidation | 4 |
| 11085 | trent | 4 |
| 11086 | traversed | 4 |
| 11087 | trap | 4 |
| 11088 | transfer | 4 |
| 11089 | transcends | 4 |
| 11090 | tranquillity | 4 |
| 11091 | trampled | 4 |
| 11092 | tramping | 4 |
| 11093 | traitorously | 4 |
| 11094 | trained | 4 |
| 11095 | traduc | 4 |
| 11096 | tract | 4 |
| 11097 | tracing | 4 |
| 11098 | towels | 4 |
| 11099 | tournament | 4 |
| 11100 | totally | 4 |
| 11101 | total | 4 |
| 11102 | tossing | 4 |
| 11103 | tortur | 4 |
| 11104 | tordesillas | 4 |
| 11105 | tongueless | 4 |
| 11106 | tones | 4 |
| 11107 | ton | 4 |
| 11108 | tolerable | 4 |
| 11109 | tish | 4 |
| 11110 | tiny | 4 |
| 11111 | tinct | 4 |
| 11112 | ties | 4 |
| 11113 | thwarted | 4 |
| 11114 | thwart | 4 |
| 11115 | throned | 4 |
| 11116 | thron | 4 |
| 11117 | throes | 4 |
| 11118 | thrives | 4 |
| 11119 | thriftless | 4 |
| 11120 | threshing | 4 |
| 11121 | threes | 4 |
| 11122 | threadbare | 4 |
| 11123 | thrace | 4 |
| 11124 | thickly | 4 |
| 11125 | thicker | 4 |
| 11126 | thetis | 4 |
| 11127 | thankless | 4 |
| 11128 | terribly | 4 |
| 11129 | tereus | 4 |
| 11130 | tenders | 4 |
| 11131 | tendance | 4 |
| 11132 | tempestuous | 4 |
| 11133 | tempers | 4 |
| 11134 | temerity | 4 |
| 11135 | tellus | 4 |
| 11136 | tediousness | 4 |
| 11137 | tearful | 4 |
| 11138 | taverns | 4 |
| 11139 | tasks | 4 |
| 11140 | tarrying | 4 |
| 11141 | tarried | 4 |
| 11142 | tap | 4 |
| 11143 | tangle | 4 |
| 11144 | talkative | 4 |
| 11145 | talent | 4 |
| 11146 | swinstead | 4 |
| 11147 | swarthy | 4 |
| 11148 | swart | 4 |
| 11149 | suspecting | 4 |
| 11150 | surveyed | 4 |
| 11151 | surrendered | 4 |
| 11152 | surmises | 4 |
| 11153 | surges | 4 |
| 11154 | surfeits | 4 |
| 11155 | surfeiting | 4 |
| 11156 | sur | 4 |
| 11157 | suppressed | 4 |
| 11158 | supposes | 4 |
| 11159 | supplies | 4 |
| 11160 | superscription | 4 |
| 11161 | superfluity | 4 |
| 11162 | sundays | 4 |
| 11163 | sully | 4 |
| 11164 | suitable | 4 |
| 11165 | suis | 4 |
| 11166 | suggestions | 4 |
| 11167 | sug | 4 |
| 11168 | sufficiency | 4 |
| 11169 | sufficed | 4 |
| 11170 | subtly | 4 |
| 11171 | substitutes | 4 |
| 11172 | submitting | 4 |
| 11173 | submitted | 4 |
| 11174 | stuffs | 4 |
| 11175 | stuffed | 4 |
| 11176 | studious | 4 |
| 11177 | strut | 4 |
| 11178 | struggles | 4 |
| 11179 | struggled | 4 |
| 11180 | stronghold | 4 |
| 11181 | stripp | 4 |
| 11182 | strictly | 4 |
| 11183 | stretching | 4 |
| 11184 | stretches | 4 |
| 11185 | streaks | 4 |
| 11186 | straying | 4 |
| 11187 | stow | 4 |
| 11188 | stoutness | 4 |
| 11189 | stor | 4 |
| 11190 | stinging | 4 |
| 11191 | stifle | 4 |
| 11192 | stealer | 4 |
| 11193 | steady | 4 |
| 11194 | steads | 4 |
| 11195 | stanch | 4 |
| 11196 | stages | 4 |
| 11197 | stables | 4 |
| 11198 | stabbed | 4 |
| 11199 | spurred | 4 |
| 11200 | spurr | 4 |
| 11201 | spun | 4 |
| 11202 | spritely | 4 |
| 11203 | sportful | 4 |
| 11204 | spoons | 4 |
| 11205 | spoiled | 4 |
| 11206 | splitted | 4 |
| 11207 | splinter | 4 |
| 11208 | splendid | 4 |
| 11209 | spiders | 4 |
| 11210 | sparrows | 4 |
| 11211 | sparkle | 4 |
| 11212 | soud | 4 |
| 11213 | sorceress | 4 |
| 11214 | sop | 4 |
| 11215 | soliciting | 4 |
| 11216 | solicited | 4 |
| 11217 | soles | 4 |
| 11218 | solemniz | 4 |
| 11219 | softness | 4 |
| 11220 | softened | 4 |
| 11221 | societies | 4 |
| 11222 | soaring | 4 |
| 11223 | soap | 4 |
| 11224 | snores | 4 |
| 11225 | smoothness | 4 |
| 11226 | smoothly | 4 |
| 11227 | smoothed | 4 |
| 11228 | smashed | 4 |
| 11229 | sluttish | 4 |
| 11230 | sliver | 4 |
| 11231 | slippers | 4 |
| 11232 | slaughters | 4 |
| 11233 | slashes | 4 |
| 11234 | slackness | 4 |
| 11235 | skulls | 4 |
| 11236 | skirted | 4 |
| 11237 | skilless | 4 |
| 11238 | skiff | 4 |
| 11239 | sized | 4 |
| 11240 | sinon | 4 |
| 11241 | sincerely | 4 |
| 11242 | simpleton | 4 |
| 11243 | simon | 4 |
| 11244 | similar | 4 |
| 11245 | silks | 4 |
| 11246 | signum | 4 |
| 11247 | signifies | 4 |
| 11248 | significant | 4 |
| 11249 | sift | 4 |
| 11250 | shrubs | 4 |
| 11251 | shrieks | 4 |
| 11252 | shrieking | 4 |
| 11253 | shovel | 4 |
| 11254 | shortness | 4 |
| 11255 | shops | 4 |
| 11256 | shins | 4 |
| 11257 | sheen | 4 |
| 11258 | sheds | 4 |
| 11259 | shaving | 4 |
| 11260 | sharing | 4 |
| 11261 | shared | 4 |
| 11262 | shapeless | 4 |
| 11263 | shanks | 4 |
| 11264 | shan | 4 |
| 11265 | shamed | 4 |
| 11266 | sextus | 4 |
| 11267 | sewing | 4 |
| 11268 | sevenfold | 4 |
| 11269 | servitors | 4 |
| 11270 | servitor | 4 |
| 11271 | sermon | 4 |
| 11272 | sensual | 4 |
| 11273 | seneschal | 4 |
| 11274 | sender | 4 |
| 11275 | seizure | 4 |
| 11276 | seduc | 4 |
| 11277 | sects | 4 |
| 11278 | secondly | 4 |
| 11279 | seasoned | 4 |
| 11280 | scrutiny | 4 |
| 11281 | scrivener | 4 |
| 11282 | scribe | 4 |
| 11283 | screen | 4 |
| 11284 | scrape | 4 |
| 11285 | scowl | 4 |
| 11286 | scoured | 4 |
| 11287 | scottish | 4 |
| 11288 | scotch | 4 |
| 11289 | scornfully | 4 |
| 11290 | scatters | 4 |
| 11291 | scattering | 4 |
| 11292 | scathe | 4 |
| 11293 | scarecrow | 4 |
| 11294 | scare | 4 |
| 11295 | scaly | 4 |
| 11296 | scab | 4 |
| 11297 | savages | 4 |
| 11298 | satiety | 4 |
| 11299 | sarna | 4 |
| 11300 | sardis | 4 |
| 11301 | sane | 4 |
| 11302 | sandal | 4 |
| 11303 | sanctify | 4 |
| 11304 | san | 4 |
| 11305 | salutes | 4 |
| 11306 | sallies | 4 |
| 11307 | salary | 4 |
| 11308 | sagacious | 4 |
| 11309 | saffron | 4 |
| 11310 | saddest | 4 |
| 11311 | sacripante | 4 |
| 11312 | sables | 4 |
| 11313 | ruy | 4 |
| 11314 | ruth | 4 |
| 11315 | russians | 4 |
| 11316 | rumours | 4 |
| 11317 | ruining | 4 |
| 11318 | ruined | 4 |
| 11319 | ruffians | 4 |
| 11320 | ruddy | 4 |
| 11321 | rubbish | 4 |
| 11322 | rubbing | 4 |
| 11323 | rowed | 4 |
| 11324 | routed | 4 |
| 11325 | rounded | 4 |
| 11326 | rods | 4 |
| 11327 | roan | 4 |
| 11328 | ripen | 4 |
| 11329 | rice | 4 |
| 11330 | rheumatic | 4 |
| 11331 | rhenish | 4 |
| 11332 | revolve | 4 |
| 11333 | revolution | 4 |
| 11334 | revolting | 4 |
| 11335 | revives | 4 |
| 11336 | reversion | 4 |
| 11337 | reverses | 4 |
| 11338 | revealed | 4 |
| 11339 | retinue | 4 |
| 11340 | retention | 4 |
| 11341 | respective | 4 |
| 11342 | resolutions | 4 |
| 11343 | resistance | 4 |
| 11344 | resignation | 4 |
| 11345 | resembles | 4 |
| 11346 | research | 4 |
| 11347 | requiring | 4 |
| 11348 | reproved | 4 |
| 11349 | reproaches | 4 |
| 11350 | repossess | 4 |
| 11351 | reposing | 4 |
| 11352 | replication | 4 |
| 11353 | repentant | 4 |
| 11354 | repeats | 4 |
| 11355 | repairing | 4 |
| 11356 | rendezvous | 4 |
| 11357 | removes | 4 |
| 11358 | remit | 4 |
| 11359 | remembers | 4 |
| 11360 | relying | 4 |
| 11361 | relished | 4 |
| 11362 | relatives | 4 |
| 11363 | regreet | 4 |
| 11364 | reft | 4 |
| 11365 | referred | 4 |
| 11366 | reeling | 4 |
| 11367 | reel | 4 |
| 11368 | redound | 4 |
| 11369 | recounted | 4 |
| 11370 | recompensed | 4 |
| 11371 | recite | 4 |
| 11372 | rebuked | 4 |
| 11373 | reared | 4 |
| 11374 | reaping | 4 |
| 11375 | readers | 4 |
| 11376 | razor | 4 |
| 11377 | ravin | 4 |
| 11378 | ravel | 4 |
| 11379 | rave | 4 |
| 11380 | ratify | 4 |
| 11381 | ratified | 4 |
| 11382 | rarity | 4 |
| 11383 | rarer | 4 |
| 11384 | ransack | 4 |
| 11385 | rake | 4 |
| 11386 | raises | 4 |
| 11387 | rainy | 4 |
| 11388 | rained | 4 |
| 11389 | quips | 4 |
| 11390 | quinones | 4 |
| 11391 | quarrelsome | 4 |
| 11392 | qualm | 4 |
| 11393 | pythagoras | 4 |
| 11394 | puzzling | 4 |
| 11395 | puppies | 4 |
| 11396 | punk | 4 |
| 11397 | puling | 4 |
| 11398 | puffing | 4 |
| 11399 | prudish | 4 |
| 11400 | proving | 4 |
| 11401 | protracted | 4 |
| 11402 | prosecute | 4 |
| 11403 | profan | 4 |
| 11404 | prodigy | 4 |
| 11405 | prodigies | 4 |
| 11406 | privily | 4 |
| 11407 | privileg | 4 |
| 11408 | privacy | 4 |
| 11409 | pristine | 4 |
| 11410 | prisons | 4 |
| 11411 | prints | 4 |
| 11412 | preys | 4 |
| 11413 | prevailed | 4 |
| 11414 | presenteth | 4 |
| 11415 | prescription | 4 |
| 11416 | prescribe | 4 |
| 11417 | presages | 4 |
| 11418 | preposterously | 4 |
| 11419 | predecessors | 4 |
| 11420 | preceding | 4 |
| 11421 | prave | 4 |
| 11422 | prabbles | 4 |
| 11423 | pounded | 4 |
| 11424 | postern | 4 |
| 11425 | portents | 4 |
| 11426 | portend | 4 |
| 11427 | porch | 4 |
| 11428 | pool | 4 |
| 11429 | ponderous | 4 |
| 11430 | pond | 4 |
| 11431 | pompeius | 4 |
| 11432 | polo | 4 |
| 11433 | politician | 4 |
| 11434 | polestar | 4 |
| 11435 | polack | 4 |
| 11436 | plump | 4 |
| 11437 | plod | 4 |
| 11438 | pleasantest | 4 |
| 11439 | pleaded | 4 |
| 11440 | placard | 4 |
| 11441 | piteously | 4 |
| 11442 | pistols | 4 |
| 11443 | pish | 4 |
| 11444 | pint | 4 |
| 11445 | pining | 4 |
| 11446 | pimp | 4 |
| 11447 | pill | 4 |
| 11448 | pickle | 4 |
| 11449 | phrygian | 4 |
| 11450 | philo | 4 |
| 11451 | phaethon | 4 |
| 11452 | petter | 4 |
| 11453 | petitioners | 4 |
| 11454 | pestiferous | 4 |
| 11455 | pertains | 4 |
| 11456 | persuasions | 4 |
| 11457 | perseus | 4 |
| 11458 | persecutes | 4 |
| 11459 | perpetuity | 4 |
| 11460 | performers | 4 |
| 11461 | perdy | 4 |
| 11462 | per | 4 |
| 11463 | peopled | 4 |
| 11464 | pencil | 4 |
| 11465 | penances | 4 |
| 11466 | peacock | 4 |
| 11467 | peaceably | 4 |
| 11468 | patrick | 4 |
| 11469 | pathetic | 4 |
| 11470 | pates | 4 |
| 11471 | pasty | 4 |
| 11472 | pasteboard | 4 |
| 11473 | passengers | 4 |
| 11474 | partridges | 4 |
| 11475 | parthian | 4 |
| 11476 | parent | 4 |
| 11477 | paredes | 4 |
| 11478 | pare | 4 |
| 11479 | pard | 4 |
| 11480 | parapilla | 4 |
| 11481 | pap | 4 |
| 11482 | pan | 4 |
| 11483 | palter | 4 |
| 11484 | palmerin | 4 |
| 11485 | palfreys | 4 |
| 11486 | pales | 4 |
| 11487 | palates | 4 |
| 11488 | pairs | 4 |
| 11489 | painfully | 4 |
| 11490 | pac | 4 |
| 11491 | overwhelm | 4 |
| 11492 | overweening | 4 |
| 11493 | overtures | 4 |
| 11494 | overhear | 4 |
| 11495 | outcast | 4 |
| 11496 | oublie | 4 |
| 11497 | ottoman | 4 |
| 11498 | ostrich | 4 |
| 11499 | ornamented | 4 |
| 11500 | oriental | 4 |
| 11501 | oriana | 4 |
| 11502 | ordains | 4 |
| 11503 | ordained | 4 |
| 11504 | ord | 4 |
| 11505 | oran | 4 |
| 11506 | op | 4 |
| 11507 | omnipotent | 4 |
| 11508 | omitting | 4 |
| 11509 | olives | 4 |
| 11510 | oldest | 4 |
| 11511 | ointment | 4 |
| 11512 | oily | 4 |
| 11513 | oddly | 4 |
| 11514 | obtained | 4 |
| 11515 | obstruction | 4 |
| 11516 | obstinacy | 4 |
| 11517 | obscene | 4 |
| 11518 | objections | 4 |
| 11519 | objected | 4 |
| 11520 | obeys | 4 |
| 11521 | nursing | 4 |
| 11522 | novelty | 4 |
| 11523 | nourishment | 4 |
| 11524 | noticing | 4 |
| 11525 | nothings | 4 |
| 11526 | nostrils | 4 |
| 11527 | nosed | 4 |
| 11528 | noonday | 4 |
| 11529 | nonino | 4 |
| 11530 | ninny | 4 |
| 11531 | nineteen | 4 |
| 11532 | niggardly | 4 |
| 11533 | nieces | 4 |
| 11534 | niceties | 4 |
| 11535 | nests | 4 |
| 11536 | ner | 4 |
| 11537 | neglecting | 4 |
| 11538 | needles | 4 |
| 11539 | muttered | 4 |
| 11540 | mutter | 4 |
| 11541 | multiplying | 4 |
| 11542 | muffler | 4 |
| 11543 | movements | 4 |
| 11544 | mouthed | 4 |
| 11545 | moss | 4 |
| 11546 | morrows | 4 |
| 11547 | morris | 4 |
| 11548 | morgan | 4 |
| 11549 | mordake | 4 |
| 11550 | monthly | 4 |
| 11551 | mong | 4 |
| 11552 | modes | 4 |
| 11553 | moderation | 4 |
| 11554 | mocker | 4 |
| 11555 | mixing | 4 |
| 11556 | mitigate | 4 |
| 11557 | misus | 4 |
| 11558 | misty | 4 |
| 11559 | mislike | 4 |
| 11560 | mislead | 4 |
| 11561 | miscreants | 4 |
| 11562 | miscreant | 4 |
| 11563 | misbegotten | 4 |
| 11564 | misadventures | 4 |
| 11565 | minutely | 4 |
| 11566 | mint | 4 |
| 11567 | minstrels | 4 |
| 11568 | minors | 4 |
| 11569 | minority | 4 |
| 11570 | mincing | 4 |
| 11571 | milder | 4 |
| 11572 | miguelturra | 4 |
| 11573 | miguel | 4 |
| 11574 | mien | 4 |
| 11575 | mettled | 4 |
| 11576 | meteor | 4 |
| 11577 | metaphor | 4 |
| 11578 | messes | 4 |
| 11579 | mending | 4 |
| 11580 | mender | 4 |
| 11581 | memories | 4 |
| 11582 | memorial | 4 |
| 11583 | melts | 4 |
| 11584 | mechanical | 4 |
| 11585 | meanings | 4 |
| 11586 | maze | 4 |
| 11587 | maxim | 4 |
| 11588 | mattock | 4 |
| 11589 | matrimony | 4 |
| 11590 | mathematics | 4 |
| 11591 | materials | 4 |
| 11592 | matchless | 4 |
| 11593 | mat | 4 |
| 11594 | mastiffs | 4 |
| 11595 | masterly | 4 |
| 11596 | masses | 4 |
| 11597 | masham | 4 |
| 11598 | masculine | 4 |
| 11599 | marvels | 4 |
| 11600 | marrow | 4 |
| 11601 | marring | 4 |
| 11602 | marries | 4 |
| 11603 | marriages | 4 |
| 11604 | marking | 4 |
| 11605 | marchioness | 4 |
| 11606 | mantuan | 4 |
| 11607 | mane | 4 |
| 11608 | malt | 4 |
| 11609 | malmsey | 4 |
| 11610 | malign | 4 |
| 11611 | malevolent | 4 |
| 11612 | malapert | 4 |
| 11613 | majorca | 4 |
| 11614 | major | 4 |
| 11615 | mainland | 4 |
| 11616 | maidenheads | 4 |
| 11617 | mahomet | 4 |
| 11618 | maguncia | 4 |
| 11619 | magnificoes | 4 |
| 11620 | magnificent | 4 |
| 11621 | magistrate | 4 |
| 11622 | madding | 4 |
| 11623 | madder | 4 |
| 11624 | lye | 4 |
| 11625 | lusts | 4 |
| 11626 | lustful | 4 |
| 11627 | lurcher | 4 |
| 11628 | lulla | 4 |
| 11629 | ludicrous | 4 |
| 11630 | lud | 4 |
| 11631 | lowering | 4 |
| 11632 | loveth | 4 |
| 11633 | lour | 4 |
| 11634 | lott | 4 |
| 11635 | lots | 4 |
| 11636 | lope | 4 |
| 11637 | loosed | 4 |
| 11638 | looker | 4 |
| 11639 | loft | 4 |
| 11640 | lobby | 4 |
| 11641 | listens | 4 |
| 11642 | lining | 4 |
| 11643 | lingers | 4 |
| 11644 | limpid | 4 |
| 11645 | limbo | 4 |
| 11646 | likelihoods | 4 |
| 11647 | lifetime | 4 |
| 11648 | lids | 4 |
| 11649 | library | 4 |
| 11650 | lewdness | 4 |
| 11651 | leprosy | 4 |
| 11652 | lenient | 4 |
| 11653 | lengths | 4 |
| 11654 | lecherous | 4 |
| 11655 | lecher | 4 |
| 11656 | leash | 4 |
| 11657 | leas | 4 |
| 11658 | leant | 4 |
| 11659 | leander | 4 |
| 11660 | leak | 4 |
| 11661 | laur | 4 |
| 11662 | lasses | 4 |
| 11663 | largely | 4 |
| 11664 | larded | 4 |
| 11665 | lapwing | 4 |
| 11666 | lanterns | 4 |
| 11667 | langley | 4 |
| 11668 | landing | 4 |
| 11669 | lamely | 4 |
| 11670 | ladders | 4 |
| 11671 | laced | 4 |
| 11672 | labourers | 4 |
| 11673 | knotted | 4 |
| 11674 | knits | 4 |
| 11675 | kindling | 4 |
| 11676 | kid | 4 |
| 11677 | justified | 4 |
| 11678 | junius | 4 |
| 11679 | jointly | 4 |
| 11680 | jay | 4 |
| 11681 | jarring | 4 |
| 11682 | j | 4 |
| 11683 | isn | 4 |
| 11684 | isles | 4 |
| 11685 | ireful | 4 |
| 11686 | ire | 4 |
| 11687 | invocation | 4 |
| 11688 | inveterate | 4 |
| 11689 | inundation | 4 |
| 11690 | intrusion | 4 |
| 11691 | introduce | 4 |
| 11692 | intrepidity | 4 |
| 11693 | intrepid | 4 |
| 11694 | interruption | 4 |
| 11695 | interrupted | 4 |
| 11696 | interred | 4 |
| 11697 | interfere | 4 |
| 11698 | interchangeably | 4 |
| 11699 | intercepted | 4 |
| 11700 | intercept | 4 |
| 11701 | intelligible | 4 |
| 11702 | int | 4 |
| 11703 | insults | 4 |
| 11704 | install | 4 |
| 11705 | insinuating | 4 |
| 11706 | inseparable | 4 |
| 11707 | insatiate | 4 |
| 11708 | inmost | 4 |
| 11709 | inly | 4 |
| 11710 | injured | 4 |
| 11711 | injure | 4 |
| 11712 | injur | 4 |
| 11713 | inheritor | 4 |
| 11714 | inherited | 4 |
| 11715 | inhabits | 4 |
| 11716 | infirmities | 4 |
| 11717 | infirm | 4 |
| 11718 | infinity | 4 |
| 11719 | infernal | 4 |
| 11720 | inexorable | 4 |
| 11721 | inducement | 4 |
| 11722 | indistinct | 4 |
| 11723 | indignant | 4 |
| 11724 | indictment | 4 |
| 11725 | index | 4 |
| 11726 | indentures | 4 |
| 11727 | incredible | 4 |
| 11728 | inconsistent | 4 |
| 11729 | inclemency | 4 |
| 11730 | inclemencies | 4 |
| 11731 | impute | 4 |
| 11732 | impulses | 4 |
| 11733 | impotent | 4 |
| 11734 | impostor | 4 |
| 11735 | importunes | 4 |
| 11736 | implored | 4 |
| 11737 | impertinent | 4 |
| 11738 | impertinence | 4 |
| 11739 | imperfections | 4 |
| 11740 | impatiently | 4 |
| 11741 | impartial | 4 |
| 11742 | immortality | 4 |
| 11743 | imitated | 4 |
| 11744 | imaginations | 4 |
| 11745 | illusion | 4 |
| 11746 | ignobly | 4 |
| 11747 | idlers | 4 |
| 11748 | hyperboles | 4 |
| 11749 | hymns | 4 |
| 11750 | husbanded | 4 |
| 11751 | hurting | 4 |
| 11752 | hurly | 4 |
| 11753 | huntress | 4 |
| 11754 | hundreds | 4 |
| 11755 | humbler | 4 |
| 11756 | hous | 4 |
| 11757 | hotly | 4 |
| 11758 | hostility | 4 |
| 11759 | hostelry | 4 |
| 11760 | hostages | 4 |
| 11761 | horrors | 4 |
| 11762 | hoops | 4 |
| 11763 | hooks | 4 |
| 11764 | hogshead | 4 |
| 11765 | historical | 4 |
| 11766 | hinges | 4 |
| 11767 | hindrance | 4 |
| 11768 | hies | 4 |
| 11769 | hidalgos | 4 |
| 11770 | heroical | 4 |
| 11771 | heroes | 4 |
| 11772 | herne | 4 |
| 11773 | heretics | 4 |
| 11774 | hereby | 4 |
| 11775 | hereabout | 4 |
| 11776 | herdsman | 4 |
| 11777 | herds | 4 |
| 11778 | hempen | 4 |
| 11779 | helms | 4 |
| 11780 | hellespont | 4 |
| 11781 | hebrew | 4 |
| 11782 | heaved | 4 |
| 11783 | heated | 4 |
| 11784 | hearse | 4 |
| 11785 | healths | 4 |
| 11786 | healing | 4 |
| 11787 | heady | 4 |
| 11788 | haunting | 4 |
| 11789 | haud | 4 |
| 11790 | hating | 4 |
| 11791 | hateth | 4 |
| 11792 | harmonious | 4 |
| 11793 | harlotry | 4 |
| 11794 | hardship | 4 |
| 11795 | hardest | 4 |
| 11796 | haps | 4 |
| 11797 | handwriting | 4 |
| 11798 | handful | 4 |
| 11799 | hallowmas | 4 |
| 11800 | hailed | 4 |
| 11801 | hags | 4 |
| 11802 | hacks | 4 |
| 11803 | habiliments | 4 |
| 11804 | gutierrez | 4 |
| 11805 | gurapas | 4 |
| 11806 | gum | 4 |
| 11807 | guessing | 4 |
| 11808 | griffin | 4 |
| 11809 | greeted | 4 |
| 11810 | gravel | 4 |
| 11811 | gratulate | 4 |
| 11812 | gratified | 4 |
| 11813 | grape | 4 |
| 11814 | grange | 4 |
| 11815 | grandchildren | 4 |
| 11816 | granada | 4 |
| 11817 | grammar | 4 |
| 11818 | grained | 4 |
| 11819 | gorg | 4 |
| 11820 | gordian | 4 |
| 11821 | gonzago | 4 |
| 11822 | goliath | 4 |
| 11823 | godly | 4 |
| 11824 | godfather | 4 |
| 11825 | goddesses | 4 |
| 11826 | gnawing | 4 |
| 11827 | gnat | 4 |
| 11828 | gluttony | 4 |
| 11829 | gloom | 4 |
| 11830 | glib | 4 |
| 11831 | glansdale | 4 |
| 11832 | gin | 4 |
| 11833 | gender | 4 |
| 11834 | gelding | 4 |
| 11835 | gawds | 4 |
| 11836 | gauntlet | 4 |
| 11837 | gardon | 4 |
| 11838 | gardeners | 4 |
| 11839 | gambling | 4 |
| 11840 | galliard | 4 |
| 11841 | gallantly | 4 |
| 11842 | gale | 4 |
| 11843 | gaeta | 4 |
| 11844 | gad | 4 |
| 11845 | g | 4 |
| 11846 | furthest | 4 |
| 11847 | furrow | 4 |
| 11848 | furiously | 4 |
| 11849 | funerals | 4 |
| 11850 | fuming | 4 |
| 11851 | fume | 4 |
| 11852 | fullest | 4 |
| 11853 | fuller | 4 |
| 11854 | fulfilled | 4 |
| 11855 | fubb | 4 |
| 11856 | fronts | 4 |
| 11857 | frontiers | 4 |
| 11858 | frogmore | 4 |
| 11859 | frog | 4 |
| 11860 | frivolous | 4 |
| 11861 | frightful | 4 |
| 11862 | frieze | 4 |
| 11863 | fridays | 4 |
| 11864 | fretful | 4 |
| 11865 | frailties | 4 |
| 11866 | foxes | 4 |
| 11867 | foully | 4 |
| 11868 | fortunately | 4 |
| 11869 | fornication | 4 |
| 11870 | forming | 4 |
| 11871 | forgets | 4 |
| 11872 | forges | 4 |
| 11873 | forfeits | 4 |
| 11874 | foretell | 4 |
| 11875 | foresters | 4 |
| 11876 | forerun | 4 |
| 11877 | forefathers | 4 |
| 11878 | forcing | 4 |
| 11879 | foeman | 4 |
| 11880 | foals | 4 |
| 11881 | fo | 4 |
| 11882 | flouted | 4 |
| 11883 | flourishes | 4 |
| 11884 | flogging | 4 |
| 11885 | flocked | 4 |
| 11886 | flings | 4 |
| 11887 | flinging | 4 |
| 11888 | flighty | 4 |
| 11889 | fliers | 4 |
| 11890 | flemish | 4 |
| 11891 | fleas | 4 |
| 11892 | flatly | 4 |
| 11893 | fittest | 4 |
| 11894 | fisherman | 4 |
| 11895 | firmness | 4 |
| 11896 | fingres | 4 |
| 11897 | filial | 4 |
| 11898 | figur | 4 |
| 11899 | fighter | 4 |
| 11900 | fictitious | 4 |
| 11901 | feverous | 4 |
| 11902 | fetters | 4 |
| 11903 | fetching | 4 |
| 11904 | fetches | 4 |
| 11905 | fet | 4 |
| 11906 | festivals | 4 |
| 11907 | fen | 4 |
| 11908 | felicity | 4 |
| 11909 | feebleness | 4 |
| 11910 | fe | 4 |
| 11911 | favouredly | 4 |
| 11912 | faulty | 4 |
| 11913 | fatherly | 4 |
| 11914 | fasts | 4 |
| 11915 | fastened | 4 |
| 11916 | farewells | 4 |
| 11917 | fangs | 4 |
| 11918 | fangled | 4 |
| 11919 | familiarly | 4 |
| 11920 | falchion | 4 |
| 11921 | faded | 4 |
| 11922 | facts | 4 |
| 11923 | facility | 4 |
| 11924 | extinguished | 4 |
| 11925 | exterior | 4 |
| 11926 | expulsion | 4 |
| 11927 | exposition | 4 |
| 11928 | exposing | 4 |
| 11929 | expiration | 4 |
| 11930 | experiments | 4 |
| 11931 | experienc | 4 |
| 11932 | expedience | 4 |
| 11933 | exhausted | 4 |
| 11934 | executing | 4 |
| 11935 | excitement | 4 |
| 11936 | excessively | 4 |
| 11937 | excellences | 4 |
| 11938 | evidently | 4 |
| 11939 | everlastingly | 4 |
| 11940 | evenly | 4 |
| 11941 | evasion | 4 |
| 11942 | euriphile | 4 |
| 11943 | eton | 4 |
| 11944 | essex | 4 |
| 11945 | espouse | 4 |
| 11946 | esperance | 4 |
| 11947 | errs | 4 |
| 11948 | erewhile | 4 |
| 11949 | erect | 4 |
| 11950 | envying | 4 |
| 11951 | envenom | 4 |
| 11952 | entrust | 4 |
| 11953 | entomb | 4 |
| 11954 | entice | 4 |
| 11955 | enthroned | 4 |
| 11956 | enthralled | 4 |
| 11957 | entanglement | 4 |
| 11958 | entangled | 4 |
| 11959 | entail | 4 |
| 11960 | ensues | 4 |
| 11961 | enkindled | 4 |
| 11962 | engross | 4 |
| 11963 | engagement | 4 |
| 11964 | enfranchise | 4 |
| 11965 | enfranchis | 4 |
| 11966 | endures | 4 |
| 11967 | endow | 4 |
| 11968 | endeared | 4 |
| 11969 | encouragement | 4 |
| 11970 | enchants | 4 |
| 11971 | emulous | 4 |
| 11972 | emptying | 4 |
| 11973 | employments | 4 |
| 11974 | embroidered | 4 |
| 11975 | embraces | 4 |
| 11976 | embracement | 4 |
| 11977 | embowell | 4 |
| 11978 | emboss | 4 |
| 11979 | elysian | 4 |
| 11980 | elisabad | 4 |
| 11981 | elegies | 4 |
| 11982 | elegantly | 4 |
| 11983 | eld | 4 |
| 11984 | egregious | 4 |
| 11985 | egad | 4 |
| 11986 | effusion | 4 |
| 11987 | echoes | 4 |
| 11988 | ebony | 4 |
| 11989 | eaves | 4 |
| 11990 | easter | 4 |
| 11991 | easing | 4 |
| 11992 | easiest | 4 |
| 11993 | eas | 4 |
| 11994 | dyed | 4 |
| 11995 | dusty | 4 |
| 11996 | dungeons | 4 |
| 11997 | dumps | 4 |
| 11998 | dullness | 4 |
| 11999 | ducdame | 4 |
| 12000 | dubb | 4 |
| 12001 | drunkenness | 4 |
| 12002 | drubbings | 4 |
| 12003 | dresses | 4 |
| 12004 | drave | 4 |
| 12005 | draped | 4 |
| 12006 | drained | 4 |
| 12007 | drain | 4 |
| 12008 | dragging | 4 |
| 12009 | downy | 4 |
| 12010 | doubtfully | 4 |
| 12011 | doricles | 4 |
| 12012 | dons | 4 |
| 12013 | dong | 4 |
| 12014 | donation | 4 |
| 12015 | dolt | 4 |
| 12016 | dolours | 4 |
| 12017 | divorc | 4 |
| 12018 | divisions | 4 |
| 12019 | divinations | 4 |
| 12020 | divest | 4 |
| 12021 | ditty | 4 |
| 12022 | district | 4 |
| 12023 | distressful | 4 |
| 12024 | distinctive | 4 |
| 12025 | distil | 4 |
| 12026 | distempered | 4 |
| 12027 | distemp | 4 |
| 12028 | distaste | 4 |
| 12029 | dissolv | 4 |
| 12030 | dissentious | 4 |
| 12031 | disquiet | 4 |
| 12032 | disprove | 4 |
| 12033 | disproportion | 4 |
| 12034 | disparagement | 4 |
| 12035 | disobedient | 4 |
| 12036 | dismayed | 4 |
| 12037 | disinherited | 4 |
| 12038 | disguises | 4 |
| 12039 | disgorge | 4 |
| 12040 | diseased | 4 |
| 12041 | disdaining | 4 |
| 12042 | discomfited | 4 |
| 12043 | disclaim | 4 |
| 12044 | disasters | 4 |
| 12045 | disagreeable | 4 |
| 12046 | disabused | 4 |
| 12047 | directs | 4 |
| 12048 | directing | 4 |
| 12049 | diminish | 4 |
| 12050 | differs | 4 |
| 12051 | dictated | 4 |
| 12052 | diable | 4 |
| 12053 | devours | 4 |
| 12054 | devoid | 4 |
| 12055 | detriment | 4 |
| 12056 | destinies | 4 |
| 12057 | destination | 4 |
| 12058 | destin | 4 |
| 12059 | despising | 4 |
| 12060 | desperately | 4 |
| 12061 | desist | 4 |
| 12062 | depriving | 4 |
| 12063 | depicted | 4 |
| 12064 | dependent | 4 |
| 12065 | denis | 4 |
| 12066 | demure | 4 |
| 12067 | delicious | 4 |
| 12068 | defunct | 4 |
| 12069 | deficiency | 4 |
| 12070 | defense | 4 |
| 12071 | defender | 4 |
| 12072 | defences | 4 |
| 12073 | default | 4 |
| 12074 | deface | 4 |
| 12075 | defac | 4 |
| 12076 | declines | 4 |
| 12077 | decked | 4 |
| 12078 | decays | 4 |
| 12079 | debated | 4 |
| 12080 | debarred | 4 |
| 12081 | dazzle | 4 |
| 12082 | daunted | 4 |
| 12083 | daunt | 4 |
| 12084 | dateless | 4 |
| 12085 | datchet | 4 |
| 12086 | dashing | 4 |
| 12087 | daff | 4 |
| 12088 | cutlass | 4 |
| 12089 | curtsey | 4 |
| 12090 | curls | 4 |
| 12091 | curing | 4 |
| 12092 | curfew | 4 |
| 12093 | curbs | 4 |
| 12094 | cumberland | 4 |
| 12095 | cuckolds | 4 |
| 12096 | cuckoldly | 4 |
| 12097 | cuadrillero | 4 |
| 12098 | crust | 4 |
| 12099 | crumbs | 4 |
| 12100 | crotchets | 4 |
| 12101 | croak | 4 |
| 12102 | critical | 4 |
| 12103 | crests | 4 |
| 12104 | crescent | 4 |
| 12105 | credent | 4 |
| 12106 | creaking | 4 |
| 12107 | crazed | 4 |
| 12108 | cramps | 4 |
| 12109 | crags | 4 |
| 12110 | crafts | 4 |
| 12111 | cozening | 4 |
| 12112 | coxcombs | 4 |
| 12113 | covenants | 4 |
| 12114 | coursers | 4 |
| 12115 | courser | 4 |
| 12116 | counters | 4 |
| 12117 | councils | 4 |
| 12118 | cortes | 4 |
| 12119 | corrupting | 4 |
| 12120 | correctly | 4 |
| 12121 | cormorant | 4 |
| 12122 | conversing | 4 |
| 12123 | conversed | 4 |
| 12124 | convers | 4 |
| 12125 | controlment | 4 |
| 12126 | contriver | 4 |
| 12127 | continence | 4 |
| 12128 | contemplating | 4 |
| 12129 | contemplate | 4 |
| 12130 | consult | 4 |
| 12131 | constitution | 4 |
| 12132 | conspir | 4 |
| 12133 | consistory | 4 |
| 12134 | consist | 4 |
| 12135 | considers | 4 |
| 12136 | conserve | 4 |
| 12137 | consenting | 4 |
| 12138 | consecrated | 4 |
| 12139 | conjur | 4 |
| 12140 | confus | 4 |
| 12141 | confronted | 4 |
| 12142 | confounding | 4 |
| 12143 | confirms | 4 |
| 12144 | confinement | 4 |
| 12145 | confided | 4 |
| 12146 | conduit | 4 |
| 12147 | condole | 4 |
| 12148 | condescend | 4 |
| 12149 | condensed | 4 |
| 12150 | condemnation | 4 |
| 12151 | conceals | 4 |
| 12152 | compt | 4 |
| 12153 | comprehension | 4 |
| 12154 | complot | 4 |
| 12155 | complication | 4 |
| 12156 | compliance | 4 |
| 12157 | competitor | 4 |
| 12158 | compensation | 4 |
| 12159 | compelling | 4 |
| 12160 | comparing | 4 |
| 12161 | community | 4 |
| 12162 | commiseration | 4 |
| 12163 | comments | 4 |
| 12164 | color | 4 |
| 12165 | coldest | 4 |
| 12166 | coins | 4 |
| 12167 | cockle | 4 |
| 12168 | cobham | 4 |
| 12169 | clue | 4 |
| 12170 | clowns | 4 |
| 12171 | cloths | 4 |
| 12172 | clothing | 4 |
| 12173 | clipp | 4 |
| 12174 | clink | 4 |
| 12175 | cliff | 4 |
| 12176 | cleverest | 4 |
| 12177 | clerkly | 4 |
| 12178 | clemency | 4 |
| 12179 | clearness | 4 |
| 12180 | cleanliness | 4 |
| 12181 | clasps | 4 |
| 12182 | clasp | 4 |
| 12183 | claribel | 4 |
| 12184 | cite | 4 |
| 12185 | circumspect | 4 |
| 12186 | circled | 4 |
| 12187 | cipher | 4 |
| 12188 | cinders | 4 |
| 12189 | cinable | 4 |
| 12190 | christmas | 4 |
| 12191 | christening | 4 |
| 12192 | choir | 4 |
| 12193 | chidden | 4 |
| 12194 | cherubins | 4 |
| 12195 | cheered | 4 |
| 12196 | cheating | 4 |
| 12197 | cheated | 4 |
| 12198 | champions | 4 |
| 12199 | chameleon | 4 |
| 12200 | challenges | 4 |
| 12201 | challenged | 4 |
| 12202 | chafes | 4 |
| 12203 | certainties | 4 |
| 12204 | cerberus | 4 |
| 12205 | censures | 4 |
| 12206 | caverns | 4 |
| 12207 | cavaliers | 4 |
| 12208 | cavaleiro | 4 |
| 12209 | cava | 4 |
| 12210 | catches | 4 |
| 12211 | cassock | 4 |
| 12212 | cassibelan | 4 |
| 12213 | cascajo | 4 |
| 12214 | carving | 4 |
| 12215 | carters | 4 |
| 12216 | carpets | 4 |
| 12217 | carp | 4 |
| 12218 | carnal | 4 |
| 12219 | carded | 4 |
| 12220 | cankers | 4 |
| 12221 | caitiffs | 4 |
| 12222 | cacus | 4 |
| 12223 | cable | 4 |
| 12224 | caballero | 4 |
| 12225 | buzzard | 4 |
| 12226 | buttocks | 4 |
| 12227 | butterflies | 4 |
| 12228 | busines | 4 |
| 12229 | busied | 4 |
| 12230 | bursts | 4 |
| 12231 | burs | 4 |
| 12232 | burnished | 4 |
| 12233 | burgonet | 4 |
| 12234 | bum | 4 |
| 12235 | bulwarks | 4 |
| 12236 | bugle | 4 |
| 12237 | buffet | 4 |
| 12238 | budding | 4 |
| 12239 | buckles | 4 |
| 12240 | buckets | 4 |
| 12241 | bruit | 4 |
| 12242 | brotherly | 4 |
| 12243 | broth | 4 |
| 12244 | brooding | 4 |
| 12245 | brokers | 4 |
| 12246 | broached | 4 |
| 12247 | brittle | 4 |
| 12248 | brittany | 4 |
| 12249 | bristow | 4 |
| 12250 | bristle | 4 |
| 12251 | brink | 4 |
| 12252 | brimstone | 4 |
| 12253 | brighter | 4 |
| 12254 | bridled | 4 |
| 12255 | brick | 4 |
| 12256 | brevity | 4 |
| 12257 | braves | 4 |
| 12258 | bracelets | 4 |
| 12259 | bove | 4 |
| 12260 | bounties | 4 |
| 12261 | botch | 4 |
| 12262 | borrows | 4 |
| 12263 | borrowing | 4 |
| 12264 | border | 4 |
| 12265 | bonfire | 4 |
| 12266 | bondmen | 4 |
| 12267 | boisterous | 4 |
| 12268 | boiled | 4 |
| 12269 | bodkin | 4 |
| 12270 | bodied | 4 |
| 12271 | bloom | 4 |
| 12272 | bloodily | 4 |
| 12273 | blithe | 4 |
| 12274 | blindfold | 4 |
| 12275 | bled | 4 |
| 12276 | bleat | 4 |
| 12277 | blasphemies | 4 |
| 12278 | blacks | 4 |
| 12279 | blackheath | 4 |
| 12280 | blacker | 4 |
| 12281 | bitterest | 4 |
| 12282 | biscuit | 4 |
| 12283 | birthright | 4 |
| 12284 | bireno | 4 |
| 12285 | biding | 4 |
| 12286 | bides | 4 |
| 12287 | bewilderment | 4 |
| 12288 | beweep | 4 |
| 12289 | bevis | 4 |
| 12290 | betime | 4 |
| 12291 | besieg | 4 |
| 12292 | beseems | 4 |
| 12293 | beseeching | 4 |
| 12294 | bequeathed | 4 |
| 12295 | benevolence | 4 |
| 12296 | benefactors | 4 |
| 12297 | benedictus | 4 |
| 12298 | benches | 4 |
| 12299 | belt | 4 |
| 12300 | bellowing | 4 |
| 12301 | bellied | 4 |
| 12302 | behoves | 4 |
| 12303 | beguiling | 4 |
| 12304 | beginnings | 4 |
| 12305 | befalls | 4 |
| 12306 | beetles | 4 |
| 12307 | becom | 4 |
| 12308 | beadles | 4 |
| 12309 | bawcock | 4 |
| 12310 | bats | 4 |
| 12311 | basilisks | 4 |
| 12312 | barking | 4 |
| 12313 | bareness | 4 |
| 12314 | bared | 4 |
| 12315 | barbarism | 4 |
| 12316 | banquets | 4 |
| 12317 | bandage | 4 |
| 12318 | balmy | 4 |
| 12319 | balconies | 4 |
| 12320 | baiting | 4 |
| 12321 | backwards | 4 |
| 12322 | bachelors | 4 |
| 12323 | baboon | 4 |
| 12324 | babieca | 4 |
| 12325 | awakes | 4 |
| 12326 | awakened | 4 |
| 12327 | avez | 4 |
| 12328 | avails | 4 |
| 12329 | availing | 4 |
| 12330 | augment | 4 |
| 12331 | attracts | 4 |
| 12332 | attraction | 4 |
| 12333 | attracted | 4 |
| 12334 | attitude | 4 |
| 12335 | attest | 4 |
| 12336 | attainted | 4 |
| 12337 | attaining | 4 |
| 12338 | attainder | 4 |
| 12339 | attacks | 4 |
| 12340 | atom | 4 |
| 12341 | athenians | 4 |
| 12342 | assistant | 4 |
| 12343 | assent | 4 |
| 12344 | assaults | 4 |
| 12345 | assaulted | 4 |
| 12346 | assailant | 4 |
| 12347 | aspects | 4 |
| 12348 | askance | 4 |
| 12349 | ascribe | 4 |
| 12350 | arrives | 4 |
| 12351 | arrangements | 4 |
| 12352 | arising | 4 |
| 12353 | arises | 4 |
| 12354 | argus | 4 |
| 12355 | arguing | 4 |
| 12356 | argued | 4 |
| 12357 | archives | 4 |
| 12358 | arcadia | 4 |
| 12359 | aragonese | 4 |
| 12360 | arabs | 4 |
| 12361 | approof | 4 |
| 12362 | approacheth | 4 |
| 12363 | appertaining | 4 |
| 12364 | appelez | 4 |
| 12365 | appeas | 4 |
| 12366 | apoth | 4 |
| 12367 | apoplexy | 4 |
| 12368 | apartment | 4 |
| 12369 | antonius | 4 |
| 12370 | antiates | 4 |
| 12371 | antagonist | 4 |
| 12372 | answerable | 4 |
| 12373 | annual | 4 |
| 12374 | announced | 4 |
| 12375 | annals | 4 |
| 12376 | angleterre | 4 |
| 12377 | angers | 4 |
| 12378 | andronici | 4 |
| 12379 | ancients | 4 |
| 12380 | anchored | 4 |
| 12381 | amounts | 4 |
| 12382 | amended | 4 |
| 12383 | ambling | 4 |
| 12384 | ambles | 4 |
| 12385 | amazons | 4 |
| 12386 | amazon | 4 |
| 12387 | amazes | 4 |
| 12388 | amazedly | 4 |
| 12389 | alters | 4 |
| 12390 | altering | 4 |
| 12391 | alps | 4 |
| 12392 | alphabet | 4 |
| 12393 | almond | 4 |
| 12394 | almodovar | 4 |
| 12395 | allowing | 4 |
| 12396 | allons | 4 |
| 12397 | alighted | 4 |
| 12398 | alifanfaron | 4 |
| 12399 | alguacils | 4 |
| 12400 | alchemy | 4 |
| 12401 | albogues | 4 |
| 12402 | alban | 4 |
| 12403 | ailed | 4 |
| 12404 | aids | 4 |
| 12405 | aiding | 4 |
| 12406 | agents | 4 |
| 12407 | afric | 4 |
| 12408 | affectation | 4 |
| 12409 | aery | 4 |
| 12410 | aemilia | 4 |
| 12411 | advises | 4 |
| 12412 | advertisement | 4 |
| 12413 | advantageous | 4 |
| 12414 | adultress | 4 |
| 12415 | adroitly | 4 |
| 12416 | adriano | 4 |
| 12417 | adornment | 4 |
| 12418 | adoption | 4 |
| 12419 | admission | 4 |
| 12420 | administer | 4 |
| 12421 | adjunct | 4 |
| 12422 | adjudg | 4 |
| 12423 | actaeon | 4 |
| 12424 | acre | 4 |
| 12425 | aching | 4 |
| 12426 | accustom | 4 |
| 12427 | accusing | 4 |
| 12428 | accurst | 4 |
| 12429 | accoutrements | 4 |
| 12430 | accompt | 4 |
| 12431 | accepts | 4 |
| 12432 | abusing | 4 |
| 12433 | absurdity | 4 |
| 12434 | abstinence | 4 |
| 12435 | abridgment | 4 |
| 12436 | abraham | 4 |
| 12437 | abortive | 4 |
| 12438 | abindarraez | 4 |
| 12439 | zebra | 3 |
| 12440 | younker | 3 |
| 12441 | yokes | 3 |
| 12442 | yawning | 3 |
| 12443 | xxxviii | 3 |
| 12444 | xxxvii | 3 |
| 12445 | xxxvi | 3 |
| 12446 | xxxv | 3 |
| 12447 | xxxix | 3 |
| 12448 | xxxiv | 3 |
| 12449 | xxxiii | 3 |
| 12450 | xxxii | 3 |
| 12451 | xxxi | 3 |
| 12452 | xxx | 3 |
| 12453 | xxviii | 3 |
| 12454 | xxvii | 3 |
| 12455 | xxvi | 3 |
| 12456 | xxv | 3 |
| 12457 | xxix | 3 |
| 12458 | xxiv | 3 |
| 12459 | xxiii | 3 |
| 12460 | xxii | 3 |
| 12461 | xxi | 3 |
| 12462 | xx | 3 |
| 12463 | xviii | 3 |
| 12464 | xvii | 3 |
| 12465 | xvi | 3 |
| 12466 | xlviii | 3 |
| 12467 | xlvii | 3 |
| 12468 | xlvi | 3 |
| 12469 | xlv | 3 |
| 12470 | xlix | 3 |
| 12471 | xliv | 3 |
| 12472 | xliii | 3 |
| 12473 | xlii | 3 |
| 12474 | xli | 3 |
| 12475 | xl | 3 |
| 12476 | xix | 3 |
| 12477 | wye | 3 |
| 12478 | wroth | 3 |
| 12479 | wronger | 3 |
| 12480 | writhing | 3 |
| 12481 | wrists | 3 |
| 12482 | wrestled | 3 |
| 12483 | wrenching | 3 |
| 12484 | wreathed | 3 |
| 12485 | wort | 3 |
| 12486 | worrying | 3 |
| 12487 | worry | 3 |
| 12488 | workings | 3 |
| 12489 | woollen | 3 |
| 12490 | woodstock | 3 |
| 12491 | woodman | 3 |
| 12492 | woodbine | 3 |
| 12493 | wonderfully | 3 |
| 12494 | wombs | 3 |
| 12495 | womanly | 3 |
| 12496 | wolvish | 3 |
| 12497 | witnessing | 3 |
| 12498 | witless | 3 |
| 12499 | winnings | 3 |
| 12500 | winks | 3 |
| 12501 | windpipe | 3 |
| 12502 | willingness | 3 |
| 12503 | wider | 3 |
| 12504 | whomsoever | 3 |
| 12505 | whites | 3 |
| 12506 | whispered | 3 |
| 12507 | whisp | 3 |
| 12508 | whirlwind | 3 |
| 12509 | whirling | 3 |
| 12510 | whimsical | 3 |
| 12511 | wheresoever | 3 |
| 12512 | whereso | 3 |
| 12513 | wend | 3 |
| 12514 | wells | 3 |
| 12515 | weightier | 3 |
| 12516 | weaving | 3 |
| 12517 | weave | 3 |
| 12518 | wearies | 3 |
| 12519 | wearer | 3 |
| 12520 | weakly | 3 |
| 12521 | weakens | 3 |
| 12522 | waxes | 3 |
| 12523 | waxed | 3 |
| 12524 | waver | 3 |
| 12525 | wav | 3 |
| 12526 | watered | 3 |
| 12527 | watchtower | 3 |
| 12528 | wassail | 3 |
| 12529 | warranty | 3 |
| 12530 | warmly | 3 |
| 12531 | warming | 3 |
| 12532 | warmer | 3 |
| 12533 | warders | 3 |
| 12534 | warble | 3 |
| 12535 | wantons | 3 |
| 12536 | wanteth | 3 |
| 12537 | wanders | 3 |
| 12538 | walnut | 3 |
| 12539 | walloon | 3 |
| 12540 | wakened | 3 |
| 12541 | wakefield | 3 |
| 12542 | wags | 3 |
| 12543 | waggish | 3 |
| 12544 | wade | 3 |
| 12545 | vowing | 3 |
| 12546 | votes | 3 |
| 12547 | vomits | 3 |
| 12548 | vomiting | 3 |
| 12549 | voluntarily | 3 |
| 12550 | voluble | 3 |
| 12551 | voic | 3 |
| 12552 | vipers | 3 |
| 12553 | viperous | 3 |
| 12554 | violated | 3 |
| 12555 | viol | 3 |
| 12556 | vintner | 3 |
| 12557 | vigilant | 3 |
| 12558 | views | 3 |
| 12559 | victual | 3 |
| 12560 | vials | 3 |
| 12561 | vexes | 3 |
| 12562 | veritable | 3 |
| 12563 | verify | 3 |
| 12564 | verdure | 3 |
| 12565 | verbal | 3 |
| 12566 | venuto | 3 |
| 12567 | vented | 3 |
| 12568 | vengeful | 3 |
| 12569 | venetians | 3 |
| 12570 | velutus | 3 |
| 12571 | vellido | 3 |
| 12572 | velez | 3 |
| 12573 | vehemency | 3 |
| 12574 | vaunting | 3 |
| 12575 | vaunt | 3 |
| 12576 | vaulty | 3 |
| 12577 | variation | 3 |
| 12578 | vargas | 3 |
| 12579 | vanishing | 3 |
| 12580 | vane | 3 |
| 12581 | valuation | 3 |
| 12582 | valu | 3 |
| 12583 | valid | 3 |
| 12584 | valentinus | 3 |
| 12585 | vagabonds | 3 |
| 12586 | utensils | 3 |
| 12587 | usurpation | 3 |
| 12588 | usance | 3 |
| 12589 | urine | 3 |
| 12590 | upsetting | 3 |
| 12591 | uprear | 3 |
| 12592 | upbraids | 3 |
| 12593 | upbraiding | 3 |
| 12594 | unworthily | 3 |
| 12595 | unworthiest | 3 |
| 12596 | unwonted | 3 |
| 12597 | unwise | 3 |
| 12598 | unwieldy | 3 |
| 12599 | unwash | 3 |
| 12600 | untun | 3 |
| 12601 | unthrift | 3 |
| 12602 | unthought | 3 |
| 12603 | unthankfulness | 3 |
| 12604 | untender | 3 |
| 12605 | unswept | 3 |
| 12606 | unsuspected | 3 |
| 12607 | unstaid | 3 |
| 12608 | unstable | 3 |
| 12609 | unskilful | 3 |
| 12610 | unsheathe | 3 |
| 12611 | unshaken | 3 |
| 12612 | unsavoury | 3 |
| 12613 | unsanctified | 3 |
| 12614 | unreverent | 3 |
| 12615 | unreverend | 3 |
| 12616 | unready | 3 |
| 12617 | unquestionably | 3 |
| 12618 | unprotected | 3 |
| 12619 | unpeopled | 3 |
| 12620 | unparallel | 3 |
| 12621 | unmatched | 3 |
| 12622 | unmasks | 3 |
| 12623 | unmarried | 3 |
| 12624 | unlikely | 3 |
| 12625 | unlettered | 3 |
| 12626 | unlearned | 3 |
| 12627 | unlawfully | 3 |
| 12628 | unlacing | 3 |
| 12629 | unlace | 3 |
| 12630 | uninhabited | 3 |
| 12631 | unhurt | 3 |
| 12632 | unguarded | 3 |
| 12633 | ungently | 3 |
| 12634 | unfrequented | 3 |
| 12635 | unfolds | 3 |
| 12636 | unfolding | 3 |
| 12637 | unfledg | 3 |
| 12638 | unfix | 3 |
| 12639 | unfinished | 3 |
| 12640 | unfinish | 3 |
| 12641 | unfelt | 3 |
| 12642 | unfeignedly | 3 |
| 12643 | unfeigned | 3 |
| 12644 | une | 3 |
| 12645 | undress | 3 |
| 12646 | undreamt | 3 |
| 12647 | undiscover | 3 |
| 12648 | undid | 3 |
| 12649 | undertakings | 3 |
| 12650 | undertakes | 3 |
| 12651 | undergoes | 3 |
| 12652 | uncurrent | 3 |
| 12653 | uncouth | 3 |
| 12654 | unconstrained | 3 |
| 12655 | uncommon | 3 |
| 12656 | uncalled | 3 |
| 12657 | unbruis | 3 |
| 12658 | unblest | 3 |
| 12659 | unbind | 3 |
| 12660 | unbecoming | 3 |
| 12661 | unbated | 3 |
| 12662 | unarmed | 3 |
| 12663 | unacquainted | 3 |
| 12664 | unaccompanied | 3 |
| 12665 | umpire | 3 |
| 12666 | ulcerous | 3 |
| 12667 | u | 3 |
| 12668 | tyrannize | 3 |
| 12669 | tyrannical | 3 |
| 12670 | tuscan | 3 |
| 12671 | turret | 3 |
| 12672 | tully | 3 |
| 12673 | trustworthy | 3 |
| 12674 | trumpeter | 3 |
| 12675 | trowest | 3 |
| 12676 | troughs | 3 |
| 12677 | trots | 3 |
| 12678 | tripolis | 3 |
| 12679 | tries | 3 |
| 12680 | tressel | 3 |
| 12681 | trespasses | 3 |
| 12682 | tremblest | 3 |
| 12683 | trebizond | 3 |
| 12684 | treasonous | 3 |
| 12685 | treacherously | 3 |
| 12686 | trapobana | 3 |
| 12687 | tramp | 3 |
| 12688 | tragedies | 3 |
| 12689 | trader | 3 |
| 12690 | tout | 3 |
| 12691 | tours | 3 |
| 12692 | tott | 3 |
| 12693 | tortoise | 3 |
| 12694 | torrent | 3 |
| 12695 | torrellas | 3 |
| 12696 | toothsome | 3 |
| 12697 | toothpick | 3 |
| 12698 | tools | 3 |
| 12699 | tongued | 3 |
| 12700 | tolling | 3 |
| 12701 | toes | 3 |
| 12702 | toasted | 3 |
| 12703 | toast | 3 |
| 12704 | tittle | 3 |
| 12705 | titled | 3 |
| 12706 | tisick | 3 |
| 12707 | tinkers | 3 |
| 12708 | tinder | 3 |
| 12709 | tincture | 3 |
| 12710 | timid | 3 |
| 12711 | thyme | 3 |
| 12712 | thwacks | 3 |
| 12713 | thunderbolts | 3 |
| 12714 | thumbs | 3 |
| 12715 | thrill | 3 |
| 12716 | threepence | 3 |
| 12717 | thrashing | 3 |
| 12718 | thrash | 3 |
| 12719 | thistle | 3 |
| 12720 | thisbe | 3 |
| 12721 | thirsting | 3 |
| 12722 | thirds | 3 |
| 12723 | thinly | 3 |
| 12724 | thinkings | 3 |
| 12725 | thievery | 3 |
| 12726 | thews | 3 |
| 12727 | thessaly | 3 |
| 12728 | thereunto | 3 |
| 12729 | theoric | 3 |
| 12730 | thenceforward | 3 |
| 12731 | thefts | 3 |
| 12732 | thankings | 3 |
| 12733 | tetuan | 3 |
| 12734 | tetter | 3 |
| 12735 | tetchy | 3 |
| 12736 | tested | 3 |
| 12737 | terrific | 3 |
| 12738 | terrestrial | 3 |
| 12739 | tenure | 3 |
| 12740 | tenant | 3 |
| 12741 | temptations | 3 |
| 12742 | temporize | 3 |
| 12743 | tempered | 3 |
| 12744 | teller | 3 |
| 12745 | teems | 3 |
| 12746 | teem | 3 |
| 12747 | teacheth | 3 |
| 12748 | teachers | 3 |
| 12749 | tattle | 3 |
| 12750 | tasting | 3 |
| 12751 | tarre | 3 |
| 12752 | tar | 3 |
| 12753 | tapsters | 3 |
| 12754 | tangled | 3 |
| 12755 | tang | 3 |
| 12756 | tamely | 3 |
| 12757 | talons | 3 |
| 12758 | tallest | 3 |
| 12759 | talker | 3 |
| 12760 | taker | 3 |
| 12761 | tainting | 3 |
| 12762 | tagarin | 3 |
| 12763 | taffety | 3 |
| 12764 | tackling | 3 |
| 12765 | tack | 3 |
| 12766 | sycamore | 3 |
| 12767 | swor | 3 |
| 12768 | swinge | 3 |
| 12769 | swims | 3 |
| 12770 | swerving | 3 |
| 12771 | sweeps | 3 |
| 12772 | swaggerers | 3 |
| 12773 | swaddling | 3 |
| 12774 | suspend | 3 |
| 12775 | susan | 3 |
| 12776 | surcoat | 3 |
| 12777 | surcease | 3 |
| 12778 | supporters | 3 |
| 12779 | supporter | 3 |
| 12780 | supernatural | 3 |
| 12781 | sunrise | 3 |
| 12782 | sunny | 3 |
| 12783 | sunken | 3 |
| 12784 | sund | 3 |
| 12785 | sunburnt | 3 |
| 12786 | sunbeams | 3 |
| 12787 | sumptuously | 3 |
| 12788 | sultry | 3 |
| 12789 | sulphurous | 3 |
| 12790 | suiting | 3 |
| 12791 | suggests | 3 |
| 12792 | suffocate | 3 |
| 12793 | suffices | 3 |
| 12794 | sufferer | 3 |
| 12795 | succouring | 3 |
| 12796 | successively | 3 |
| 12797 | subscribes | 3 |
| 12798 | subornation | 3 |
| 12799 | su | 3 |
| 12800 | stupidities | 3 |
| 12801 | stupendous | 3 |
| 12802 | stupefied | 3 |
| 12803 | stubbornness | 3 |
| 12804 | stubble | 3 |
| 12805 | strips | 3 |
| 12806 | strides | 3 |
| 12807 | strewing | 3 |
| 12808 | streak | 3 |
| 12809 | strays | 3 |
| 12810 | strawberries | 3 |
| 12811 | stoup | 3 |
| 12812 | stoops | 3 |
| 12813 | stocking | 3 |
| 12814 | stile | 3 |
| 12815 | stifled | 3 |
| 12816 | steterat | 3 |
| 12817 | sterling | 3 |
| 12818 | sterility | 3 |
| 12819 | stepped | 3 |
| 12820 | stepfather | 3 |
| 12821 | stench | 3 |
| 12822 | steadfast | 3 |
| 12823 | stations | 3 |
| 12824 | stationed | 3 |
| 12825 | statesman | 3 |
| 12826 | startles | 3 |
| 12827 | starred | 3 |
| 12828 | starr | 3 |
| 12829 | standeth | 3 |
| 12830 | standards | 3 |
| 12831 | stalks | 3 |
| 12832 | stair | 3 |
| 12833 | stagger | 3 |
| 12834 | squirrel | 3 |
| 12835 | squash | 3 |
| 12836 | squares | 3 |
| 12837 | squar | 3 |
| 12838 | spruce | 3 |
| 12839 | spreads | 3 |
| 12840 | sprays | 3 |
| 12841 | spouts | 3 |
| 12842 | spotty | 3 |
| 12843 | spokes | 3 |
| 12844 | spok | 3 |
| 12845 | splits | 3 |
| 12846 | spitting | 3 |
| 12847 | spites | 3 |
| 12848 | spital | 3 |
| 12849 | spiritless | 3 |
| 12850 | spherical | 3 |
| 12851 | speeding | 3 |
| 12852 | speediest | 3 |
| 12853 | speculation | 3 |
| 12854 | spectre | 3 |
| 12855 | species | 3 |
| 12856 | spears | 3 |
| 12857 | speaketh | 3 |
| 12858 | spartan | 3 |
| 12859 | sparta | 3 |
| 12860 | southwark | 3 |
| 12861 | sourly | 3 |
| 12862 | soundness | 3 |
| 12863 | sorrowing | 3 |
| 12864 | sorrier | 3 |
| 12865 | sorel | 3 |
| 12866 | sorcery | 3 |
| 12867 | sorcerers | 3 |
| 12868 | sorcerer | 3 |
| 12869 | sops | 3 |
| 12870 | sophy | 3 |
| 12871 | sont | 3 |
| 12872 | somehow | 3 |
| 12873 | solomon | 3 |
| 12874 | solicits | 3 |
| 12875 | sodden | 3 |
| 12876 | sobrino | 3 |
| 12877 | snub | 3 |
| 12878 | snoring | 3 |
| 12879 | snore | 3 |
| 12880 | snip | 3 |
| 12881 | sneaking | 3 |
| 12882 | snatched | 3 |
| 12883 | snap | 3 |
| 12884 | smug | 3 |
| 12885 | smoothing | 3 |
| 12886 | smokes | 3 |
| 12887 | smirch | 3 |
| 12888 | smacked | 3 |
| 12889 | slut | 3 |
| 12890 | slug | 3 |
| 12891 | slower | 3 |
| 12892 | slipping | 3 |
| 12893 | slipped | 3 |
| 12894 | slink | 3 |
| 12895 | slings | 3 |
| 12896 | slid | 3 |
| 12897 | slice | 3 |
| 12898 | sleeper | 3 |
| 12899 | slashed | 3 |
| 12900 | slanderers | 3 |
| 12901 | slandered | 3 |
| 12902 | slab | 3 |
| 12903 | skylight | 3 |
| 12904 | skittish | 3 |
| 12905 | skinned | 3 |
| 12906 | skim | 3 |
| 12907 | skills | 3 |
| 12908 | skilfully | 3 |
| 12909 | skein | 3 |
| 12910 | siz | 3 |
| 12911 | situation | 3 |
| 12912 | siren | 3 |
| 12913 | sip | 3 |
| 12914 | singularity | 3 |
| 12915 | singled | 3 |
| 12916 | simplicities | 3 |
| 12917 | simpletons | 3 |
| 12918 | simois | 3 |
| 12919 | silliness | 3 |
| 12920 | silenc | 3 |
| 12921 | signories | 3 |
| 12922 | signiors | 3 |
| 12923 | signified | 3 |
| 12924 | signet | 3 |
| 12925 | sigeia | 3 |
| 12926 | sicyon | 3 |
| 12927 | sibyl | 3 |
| 12928 | shutting | 3 |
| 12929 | shunning | 3 |
| 12930 | shuffling | 3 |
| 12931 | shrouds | 3 |
| 12932 | shrouded | 3 |
| 12933 | shrinks | 3 |
| 12934 | shrinking | 3 |
| 12935 | shreds | 3 |
| 12936 | showy | 3 |
| 12937 | shotten | 3 |
| 12938 | shots | 3 |
| 12939 | shortsighted | 3 |
| 12940 | shortens | 3 |
| 12941 | shortcomings | 3 |
| 12942 | shooter | 3 |
| 12943 | shocks | 3 |
| 12944 | shivers | 3 |
| 12945 | shivered | 3 |
| 12946 | shiver | 3 |
| 12947 | shipwreck | 3 |
| 12948 | shipmaster | 3 |
| 12949 | shifting | 3 |
| 12950 | shielded | 3 |
| 12951 | shershel | 3 |
| 12952 | shelters | 3 |
| 12953 | shells | 3 |
| 12954 | sheathing | 3 |
| 12955 | shaver | 3 |
| 12956 | shattered | 3 |
| 12957 | shatter | 3 |
| 12958 | sharpers | 3 |
| 12959 | sharpened | 3 |
| 12960 | shaping | 3 |
| 12961 | shamest | 3 |
| 12962 | shafts | 3 |
| 12963 | shackles | 3 |
| 12964 | sewer | 3 |
| 12965 | seward | 3 |
| 12966 | severed | 3 |
| 12967 | severals | 3 |
| 12968 | sessions | 3 |
| 12969 | sessa | 3 |
| 12970 | servitude | 3 |
| 12971 | sermons | 3 |
| 12972 | sere | 3 |
| 12973 | sequestration | 3 |
| 12974 | sequest | 3 |
| 12975 | sepulchres | 3 |
| 12976 | separately | 3 |
| 12977 | sententious | 3 |
| 12978 | sentenced | 3 |
| 12979 | senis | 3 |
| 12980 | semiramis | 3 |
| 12981 | semblances | 3 |
| 12982 | seguidillas | 3 |
| 12983 | seel | 3 |
| 12984 | seduce | 3 |
| 12985 | sedition | 3 |
| 12986 | sedges | 3 |
| 12987 | securing | 3 |
| 12988 | seconded | 3 |
| 12989 | secluded | 3 |
| 12990 | seasonably | 3 |
| 12991 | sealing | 3 |
| 12992 | seacoal | 3 |
| 12993 | scythian | 3 |
| 12994 | scrubbing | 3 |
| 12995 | scrip | 3 |
| 12996 | screened | 3 |
| 12997 | scratches | 3 |
| 12998 | scorch | 3 |
| 12999 | scone | 3 |
| 13000 | scoffs | 3 |
| 13001 | scoffer | 3 |
| 13002 | scissors | 3 |
| 13003 | schoolmasters | 3 |
| 13004 | schoolboys | 3 |
| 13005 | scenes | 3 |
| 13006 | scarr | 3 |
| 13007 | scann | 3 |
| 13008 | scandalous | 3 |
| 13009 | scambling | 3 |
| 13010 | scaling | 3 |
| 13011 | scaffold | 3 |
| 13012 | savageness | 3 |
| 13013 | saunder | 3 |
| 13014 | sauc | 3 |
| 13015 | satyrs | 3 |
| 13016 | satyr | 3 |
| 13017 | satisfactorily | 3 |
| 13018 | satires | 3 |
| 13019 | sarra | 3 |
| 13020 | sapless | 3 |
| 13021 | sapient | 3 |
| 13022 | sansuena | 3 |
| 13023 | sanctimony | 3 |
| 13024 | sample | 3 |
| 13025 | sallowness | 3 |
| 13026 | sallets | 3 |
| 13027 | salamancan | 3 |
| 13028 | salaams | 3 |
| 13029 | sala | 3 |
| 13030 | sakes | 3 |
| 13031 | sagittary | 3 |
| 13032 | sagacity | 3 |
| 13033 | sadder | 3 |
| 13034 | sacks | 3 |
| 13035 | rye | 3 |
| 13036 | ruthful | 3 |
| 13037 | rustling | 3 |
| 13038 | russia | 3 |
| 13039 | russet | 3 |
| 13040 | rural | 3 |
| 13041 | runaways | 3 |
| 13042 | runaway | 3 |
| 13043 | runagate | 3 |
| 13044 | rumor | 3 |
| 13045 | ruffs | 3 |
| 13046 | ruff | 3 |
| 13047 | rubb | 3 |
| 13048 | route | 3 |
| 13049 | rolled | 3 |
| 13050 | roi | 3 |
| 13051 | roguish | 3 |
| 13052 | roe | 3 |
| 13053 | rochester | 3 |
| 13054 | roca | 3 |
| 13055 | robust | 3 |
| 13056 | robed | 3 |
| 13057 | riveted | 3 |
| 13058 | ripp | 3 |
| 13059 | riper | 3 |
| 13060 | ripens | 3 |
| 13061 | ripeness | 3 |
| 13062 | ringer | 3 |
| 13063 | rind | 3 |
| 13064 | rinaldo | 3 |
| 13065 | rigorous | 3 |
| 13066 | righted | 3 |
| 13067 | rigg | 3 |
| 13068 | rift | 3 |
| 13069 | ridicule | 3 |
| 13070 | riddling | 3 |
| 13071 | ricota | 3 |
| 13072 | ribb | 3 |
| 13073 | rhyming | 3 |
| 13074 | rheims | 3 |
| 13075 | reverently | 3 |
| 13076 | revenging | 3 |
| 13077 | revelling | 3 |
| 13078 | revell | 3 |
| 13079 | reveals | 3 |
| 13080 | returnest | 3 |
| 13081 | retreating | 3 |
| 13082 | retentive | 3 |
| 13083 | retentio | 3 |
| 13084 | retainers | 3 |
| 13085 | retail | 3 |
| 13086 | resuming | 3 |
| 13087 | resty | 3 |
| 13088 | resteth | 3 |
| 13089 | resolves | 3 |
| 13090 | resists | 3 |
| 13091 | residing | 3 |
| 13092 | reside | 3 |
| 13093 | resentment | 3 |
| 13094 | rer | 3 |
| 13095 | requisites | 3 |
| 13096 | repulsed | 3 |
| 13097 | reproving | 3 |
| 13098 | reproachful | 3 |
| 13099 | reprehended | 3 |
| 13100 | reprehend | 3 |
| 13101 | repents | 3 |
| 13102 | repeals | 3 |
| 13103 | repays | 3 |
| 13104 | repairs | 3 |
| 13105 | remorseless | 3 |
| 13106 | remnants | 3 |
| 13107 | remedied | 3 |
| 13108 | remark | 3 |
| 13109 | remainders | 3 |
| 13110 | relinquish | 3 |
| 13111 | relieves | 3 |
| 13112 | relic | 3 |
| 13113 | releas | 3 |
| 13114 | relative | 3 |
| 13115 | rel | 3 |
| 13116 | rehears | 3 |
| 13117 | regulated | 3 |
| 13118 | regist | 3 |
| 13119 | regia | 3 |
| 13120 | refuses | 3 |
| 13121 | reels | 3 |
| 13122 | reechy | 3 |
| 13123 | redressed | 3 |
| 13124 | redeems | 3 |
| 13125 | redeeming | 3 |
| 13126 | recovers | 3 |
| 13127 | recording | 3 |
| 13128 | recorders | 3 |
| 13129 | recompens | 3 |
| 13130 | recollecting | 3 |
| 13131 | recollected | 3 |
| 13132 | recognition | 3 |
| 13133 | recesses | 3 |
| 13134 | recess | 3 |
| 13135 | receptacle | 3 |
| 13136 | realities | 3 |
| 13137 | realised | 3 |
| 13138 | razed | 3 |
| 13139 | ravished | 3 |
| 13140 | raving | 3 |
| 13141 | ravening | 3 |
| 13142 | rav | 3 |
| 13143 | rature | 3 |
| 13144 | ratsbane | 3 |
| 13145 | rationally | 3 |
| 13146 | rating | 3 |
| 13147 | rately | 3 |
| 13148 | rascalities | 3 |
| 13149 | rareness | 3 |
| 13150 | rapine | 3 |
| 13151 | rapiers | 3 |
| 13152 | rapid | 3 |
| 13153 | rapes | 3 |
| 13154 | rankness | 3 |
| 13155 | ranker | 3 |
| 13156 | ranges | 3 |
| 13157 | ramping | 3 |
| 13158 | ralph | 3 |
| 13159 | raining | 3 |
| 13160 | rainbow | 3 |
| 13161 | ragozine | 3 |
| 13162 | radiance | 3 |
| 13163 | quotations | 3 |
| 13164 | quod | 3 |
| 13165 | quirks | 3 |
| 13166 | quintessence | 3 |
| 13167 | quicksilver | 3 |
| 13168 | querist | 3 |
| 13169 | quenching | 3 |
| 13170 | queller | 3 |
| 13171 | queasy | 3 |
| 13172 | quarts | 3 |
| 13173 | quarry | 3 |
| 13174 | qualifications | 3 |
| 13175 | quailed | 3 |
| 13176 | quaff | 3 |
| 13177 | qu | 3 |
| 13178 | puzzle | 3 |
| 13179 | pushing | 3 |
| 13180 | pushes | 3 |
| 13181 | purging | 3 |
| 13182 | purged | 3 |
| 13183 | purchasing | 3 |
| 13184 | puppets | 3 |
| 13185 | pummelling | 3 |
| 13186 | pullet | 3 |
| 13187 | puffed | 3 |
| 13188 | puerto | 3 |
| 13189 | ptolemies | 3 |
| 13190 | prying | 3 |
| 13191 | pruning | 3 |
| 13192 | prune | 3 |
| 13193 | protests | 3 |
| 13194 | protested | 3 |
| 13195 | protestations | 3 |
| 13196 | protectorship | 3 |
| 13197 | protectors | 3 |
| 13198 | proscription | 3 |
| 13199 | props | 3 |
| 13200 | proposes | 3 |
| 13201 | proposal | 3 |
| 13202 | proportioned | 3 |
| 13203 | prophets | 3 |
| 13204 | propertied | 3 |
| 13205 | properer | 3 |
| 13206 | propensity | 3 |
| 13207 | propagate | 3 |
| 13208 | pronouncing | 3 |
| 13209 | prompting | 3 |
| 13210 | promotions | 3 |
| 13211 | promoted | 3 |
| 13212 | promiseth | 3 |
| 13213 | promethean | 3 |
| 13214 | prologues | 3 |
| 13215 | prolixity | 3 |
| 13216 | projects | 3 |
| 13217 | progenitors | 3 |
| 13218 | profusion | 3 |
| 13219 | profitless | 3 |
| 13220 | professors | 3 |
| 13221 | profaned | 3 |
| 13222 | profanation | 3 |
| 13223 | producing | 3 |
| 13224 | produces | 3 |
| 13225 | prodigality | 3 |
| 13226 | prodding | 3 |
| 13227 | procured | 3 |
| 13228 | priory | 3 |
| 13229 | principles | 3 |
| 13230 | pricked | 3 |
| 13231 | priami | 3 |
| 13232 | previous | 3 |
| 13233 | prevailing | 3 |
| 13234 | prester | 3 |
| 13235 | preserver | 3 |
| 13236 | prescriptions | 3 |
| 13237 | prescience | 3 |
| 13238 | presageth | 3 |
| 13239 | prentices | 3 |
| 13240 | premises | 3 |
| 13241 | premeditated | 3 |
| 13242 | prefix | 3 |
| 13243 | preference | 3 |
| 13244 | prediction | 3 |
| 13245 | predicament | 3 |
| 13246 | precision | 3 |
| 13247 | precipitating | 3 |
| 13248 | precipice | 3 |
| 13249 | precedence | 3 |
| 13250 | precaution | 3 |
| 13251 | preacher | 3 |
| 13252 | prains | 3 |
| 13253 | pouring | 3 |
| 13254 | potential | 3 |
| 13255 | potentates | 3 |
| 13256 | posy | 3 |
| 13257 | posterns | 3 |
| 13258 | posset | 3 |
| 13259 | porters | 3 |
| 13260 | portentous | 3 |
| 13261 | portends | 3 |
| 13262 | portable | 3 |
| 13263 | porn | 3 |
| 13264 | pork | 3 |
| 13265 | poring | 3 |
| 13266 | poniards | 3 |
| 13267 | poisoner | 3 |
| 13268 | pois | 3 |
| 13269 | plying | 3 |
| 13270 | plutus | 3 |
| 13271 | plus | 3 |
| 13272 | plundered | 3 |
| 13273 | plummet | 3 |
| 13274 | ploughman | 3 |
| 13275 | plied | 3 |
| 13276 | plebeian | 3 |
| 13277 | pleasantry | 3 |
| 13278 | pleasantly | 3 |
| 13279 | pleasanter | 3 |
| 13280 | pleads | 3 |
| 13281 | plausive | 3 |
| 13282 | platonic | 3 |
| 13283 | plato | 3 |
| 13284 | plashy | 3 |
| 13285 | planks | 3 |
| 13286 | plaints | 3 |
| 13287 | plaintiff | 3 |
| 13288 | plaint | 3 |
| 13289 | placket | 3 |
| 13290 | pitifully | 3 |
| 13291 | pitchy | 3 |
| 13292 | pique | 3 |
| 13293 | piping | 3 |
| 13294 | pip | 3 |
| 13295 | pinnace | 3 |
| 13296 | pined | 3 |
| 13297 | pillows | 3 |
| 13298 | piles | 3 |
| 13299 | pight | 3 |
| 13300 | pies | 3 |
| 13301 | pierces | 3 |
| 13302 | piec | 3 |
| 13303 | pickaxes | 3 |
| 13304 | picardy | 3 |
| 13305 | pia | 3 |
| 13306 | phrygia | 3 |
| 13307 | phoebe | 3 |
| 13308 | pharamond | 3 |
| 13309 | petticoats | 3 |
| 13310 | pest | 3 |
| 13311 | pertinent | 3 |
| 13312 | perspective | 3 |
| 13313 | personally | 3 |
| 13314 | persistence | 3 |
| 13315 | persisted | 3 |
| 13316 | persiles | 3 |
| 13317 | persia | 3 |
| 13318 | perlerines | 3 |
| 13319 | periwig | 3 |
| 13320 | perishing | 3 |
| 13321 | perished | 3 |
| 13322 | perfected | 3 |
| 13323 | perdu | 3 |
| 13324 | perch | 3 |
| 13325 | penthouse | 3 |
| 13326 | pentecost | 3 |
| 13327 | penetrates | 3 |
| 13328 | pendent | 3 |
| 13329 | pelt | 3 |
| 13330 | pellets | 3 |
| 13331 | pelican | 3 |
| 13332 | peeps | 3 |
| 13333 | peat | 3 |
| 13334 | peas | 3 |
| 13335 | peak | 3 |
| 13336 | peach | 3 |
| 13337 | paws | 3 |
| 13338 | pathetical | 3 |
| 13339 | paternosters | 3 |
| 13340 | patents | 3 |
| 13341 | pastures | 3 |
| 13342 | pastor | 3 |
| 13343 | passenger | 3 |
| 13344 | passado | 3 |
| 13345 | partaker | 3 |
| 13346 | parlous | 3 |
| 13347 | parishioners | 3 |
| 13348 | parings | 3 |
| 13349 | paring | 3 |
| 13350 | pardoning | 3 |
| 13351 | parching | 3 |
| 13352 | parasite | 3 |
| 13353 | paramount | 3 |
| 13354 | paradoxes | 3 |
| 13355 | paradox | 3 |
| 13356 | pants | 3 |
| 13357 | pantler | 3 |
| 13358 | panther | 3 |
| 13359 | pantaloon | 3 |
| 13360 | pant | 3 |
| 13361 | pandafilando | 3 |
| 13362 | pancakes | 3 |
| 13363 | paly | 3 |
| 13364 | palsy | 3 |
| 13365 | palmers | 3 |
| 13366 | pall | 3 |
| 13367 | paler | 3 |
| 13368 | pail | 3 |
| 13369 | pah | 3 |
| 13370 | pagans | 3 |
| 13371 | packets | 3 |
| 13372 | overthrew | 3 |
| 13373 | overrul | 3 |
| 13374 | overpeer | 3 |
| 13375 | overmuch | 3 |
| 13376 | overjoyed | 3 |
| 13377 | overhead | 3 |
| 13378 | overflow | 3 |
| 13379 | overcharged | 3 |
| 13380 | overblown | 3 |
| 13381 | outweighs | 3 |
| 13382 | outwards | 3 |
| 13383 | outstrip | 3 |
| 13384 | outstretch | 3 |
| 13385 | outlives | 3 |
| 13386 | ottomites | 3 |
| 13387 | otter | 3 |
| 13388 | orpheus | 3 |
| 13389 | orld | 3 |
| 13390 | orbed | 3 |
| 13391 | oracles | 3 |
| 13392 | oppressor | 3 |
| 13393 | onslaught | 3 |
| 13394 | omnes | 3 |
| 13395 | omission | 3 |
| 13396 | ollas | 3 |
| 13397 | oftener | 3 |
| 13398 | official | 3 |
| 13399 | offal | 3 |
| 13400 | ods | 3 |
| 13401 | odorous | 3 |
| 13402 | oddest | 3 |
| 13403 | oceans | 3 |
| 13404 | occurring | 3 |
| 13405 | occupies | 3 |
| 13406 | obvious | 3 |
| 13407 | obscurity | 3 |
| 13408 | obloquy | 3 |
| 13409 | oblivious | 3 |
| 13410 | objurgations | 3 |
| 13411 | obduracy | 3 |
| 13412 | nutshell | 3 |
| 13413 | nursed | 3 |
| 13414 | ns | 3 |
| 13415 | nouns | 3 |
| 13416 | nostril | 3 |
| 13417 | norweyan | 3 |
| 13418 | northward | 3 |
| 13419 | northampton | 3 |
| 13420 | normans | 3 |
| 13421 | norman | 3 |
| 13422 | nony | 3 |
| 13423 | nonny | 3 |
| 13424 | nonce | 3 |
| 13425 | nomination | 3 |
| 13426 | nominated | 3 |
| 13427 | nominate | 3 |
| 13428 | noddy | 3 |
| 13429 | nodding | 3 |
| 13430 | nip | 3 |
| 13431 | nightwork | 3 |
| 13432 | nickname | 3 |
| 13433 | nicety | 3 |
| 13434 | nicanor | 3 |
| 13435 | newt | 3 |
| 13436 | newness | 3 |
| 13437 | nevil | 3 |
| 13438 | nev | 3 |
| 13439 | neutral | 3 |
| 13440 | neighs | 3 |
| 13441 | neighbourly | 3 |
| 13442 | neer | 3 |
| 13443 | necessarily | 3 |
| 13444 | nave | 3 |
| 13445 | natured | 3 |
| 13446 | narrative | 3 |
| 13447 | narbon | 3 |
| 13448 | nape | 3 |
| 13449 | nameless | 3 |
| 13450 | myrtle | 3 |
| 13451 | muzzle | 3 |
| 13452 | murrain | 3 |
| 13453 | murdering | 3 |
| 13454 | multiplied | 3 |
| 13455 | muffle | 3 |
| 13456 | muddied | 3 |
| 13457 | mows | 3 |
| 13458 | movables | 3 |
| 13459 | mourner | 3 |
| 13460 | mourned | 3 |
| 13461 | mountebank | 3 |
| 13462 | mountaineers | 3 |
| 13463 | mounch | 3 |
| 13464 | mottoes | 3 |
| 13465 | motto | 3 |
| 13466 | mosen | 3 |
| 13467 | morgante | 3 |
| 13468 | moralize | 3 |
| 13469 | monumental | 3 |
| 13470 | montemayor | 3 |
| 13471 | monks | 3 |
| 13472 | mongers | 3 |
| 13473 | moments | 3 |
| 13474 | molten | 3 |
| 13475 | molehill | 3 |
| 13476 | moderately | 3 |
| 13477 | mockeries | 3 |
| 13478 | mobled | 3 |
| 13479 | moat | 3 |
| 13480 | mitigation | 3 |
| 13481 | mistrusted | 3 |
| 13482 | mistakes | 3 |
| 13483 | mist | 3 |
| 13484 | misprizing | 3 |
| 13485 | misgives | 3 |
| 13486 | misenum | 3 |
| 13487 | misdeeds | 3 |
| 13488 | miry | 3 |
| 13489 | minx | 3 |
| 13490 | minos | 3 |
| 13491 | mingo | 3 |
| 13492 | mineral | 3 |
| 13493 | millstones | 3 |
| 13494 | miller | 3 |
| 13495 | milky | 3 |
| 13496 | mildew | 3 |
| 13497 | milch | 3 |
| 13498 | midday | 3 |
| 13499 | michaelmas | 3 |
| 13500 | mexico | 3 |
| 13501 | metre | 3 |
| 13502 | merriest | 3 |
| 13503 | meritorious | 3 |
| 13504 | mercenary | 3 |
| 13505 | mentioning | 3 |
| 13506 | mental | 3 |
| 13507 | mends | 3 |
| 13508 | menaces | 3 |
| 13509 | menace | 3 |
| 13510 | memorandum | 3 |
| 13511 | meetings | 3 |
| 13512 | medoro | 3 |
| 13513 | medley | 3 |
| 13514 | medlars | 3 |
| 13515 | medium | 3 |
| 13516 | medea | 3 |
| 13517 | meddler | 3 |
| 13518 | mechanic | 3 |
| 13519 | meats | 3 |
| 13520 | maugre | 3 |
| 13521 | mattress | 3 |
| 13522 | matthew | 3 |
| 13523 | mater | 3 |
| 13524 | mastership | 3 |
| 13525 | masques | 3 |
| 13526 | mason | 3 |
| 13527 | marvellously | 3 |
| 13528 | marvell | 3 |
| 13529 | markets | 3 |
| 13530 | marcheth | 3 |
| 13531 | maravedi | 3 |
| 13532 | mansions | 3 |
| 13533 | manors | 3 |
| 13534 | manor | 3 |
| 13535 | mannish | 3 |
| 13536 | manes | 3 |
| 13537 | mandrake | 3 |
| 13538 | manager | 3 |
| 13539 | manacle | 3 |
| 13540 | mall | 3 |
| 13541 | maliciously | 3 |
| 13542 | malcontent | 3 |
| 13543 | maladies | 3 |
| 13544 | majestic | 3 |
| 13545 | maintenance | 3 |
| 13546 | maimed | 3 |
| 13547 | maidenly | 3 |
| 13548 | maidenhood | 3 |
| 13549 | magnanimity | 3 |
| 13550 | madded | 3 |
| 13551 | machine | 3 |
| 13552 | machinations | 3 |
| 13553 | machiavel | 3 |
| 13554 | mab | 3 |
| 13555 | lutes | 3 |
| 13556 | lustier | 3 |
| 13557 | lurks | 3 |
| 13558 | lurch | 3 |
| 13559 | lunes | 3 |
| 13560 | lunatics | 3 |
| 13561 | lull | 3 |
| 13562 | luke | 3 |
| 13563 | ludlow | 3 |
| 13564 | lucretia | 3 |
| 13565 | luckless | 3 |
| 13566 | lucid | 3 |
| 13567 | luces | 3 |
| 13568 | lowness | 3 |
| 13569 | loveliness | 3 |
| 13570 | lovelier | 3 |
| 13571 | lottery | 3 |
| 13572 | losest | 3 |
| 13573 | lore | 3 |
| 13574 | lopez | 3 |
| 13575 | lop | 3 |
| 13576 | loosely | 3 |
| 13577 | loos | 3 |
| 13578 | loop | 3 |
| 13579 | longings | 3 |
| 13580 | loneliness | 3 |
| 13581 | lone | 3 |
| 13582 | loftiness | 3 |
| 13583 | loftiest | 3 |
| 13584 | loftier | 3 |
| 13585 | lodgers | 3 |
| 13586 | locking | 3 |
| 13587 | local | 3 |
| 13588 | loathness | 3 |
| 13589 | loathly | 3 |
| 13590 | loads | 3 |
| 13591 | llana | 3 |
| 13592 | liveth | 3 |
| 13593 | livelong | 3 |
| 13594 | livelihood | 3 |
| 13595 | lisping | 3 |
| 13596 | lisp | 3 |
| 13597 | lipp | 3 |
| 13598 | linguist | 3 |
| 13599 | lined | 3 |
| 13600 | limed | 3 |
| 13601 | lilies | 3 |
| 13602 | liker | 3 |
| 13603 | lii | 3 |
| 13604 | lightest | 3 |
| 13605 | lictors | 3 |
| 13606 | licked | 3 |
| 13607 | liberally | 3 |
| 13608 | li | 3 |
| 13609 | levying | 3 |
| 13610 | levies | 3 |
| 13611 | leven | 3 |
| 13612 | levels | 3 |
| 13613 | levell | 3 |
| 13614 | lessons | 3 |
| 13615 | leopard | 3 |
| 13616 | leonati | 3 |
| 13617 | lenten | 3 |
| 13618 | lengthens | 3 |
| 13619 | lengthen | 3 |
| 13620 | lending | 3 |
| 13621 | lender | 3 |
| 13622 | lena | 3 |
| 13623 | lemos | 3 |
| 13624 | leman | 3 |
| 13625 | leisures | 3 |
| 13626 | leicester | 3 |
| 13627 | lectures | 3 |
| 13628 | leaven | 3 |
| 13629 | learns | 3 |
| 13630 | learnedly | 3 |
| 13631 | leaders | 3 |
| 13632 | ldst | 3 |
| 13633 | lazar | 3 |
| 13634 | layest | 3 |
| 13635 | lawn | 3 |
| 13636 | lave | 3 |
| 13637 | laurels | 3 |
| 13638 | laudable | 3 |
| 13639 | latch | 3 |
| 13640 | larum | 3 |
| 13641 | larks | 3 |
| 13642 | largest | 3 |
| 13643 | lapse | 3 |
| 13644 | laps | 3 |
| 13645 | lapp | 3 |
| 13646 | lapis | 3 |
| 13647 | lapice | 3 |
| 13648 | languishing | 3 |
| 13649 | laissez | 3 |
| 13650 | lacked | 3 |
| 13651 | label | 3 |
| 13652 | knoll | 3 |
| 13653 | knog | 3 |
| 13654 | kneading | 3 |
| 13655 | knack | 3 |
| 13656 | kinswoman | 3 |
| 13657 | kine | 3 |
| 13658 | kindest | 3 |
| 13659 | kimbolton | 3 |
| 13660 | kiln | 3 |
| 13661 | killer | 3 |
| 13662 | kersey | 3 |
| 13663 | kernel | 3 |
| 13664 | kerchief | 3 |
| 13665 | kentish | 3 |
| 13666 | keel | 3 |
| 13667 | justicer | 3 |
| 13668 | june | 3 |
| 13669 | jumping | 3 |
| 13670 | jule | 3 |
| 13671 | juggler | 3 |
| 13672 | judged | 3 |
| 13673 | joyous | 3 |
| 13674 | joyfully | 3 |
| 13675 | jour | 3 |
| 13676 | jointed | 3 |
| 13677 | joining | 3 |
| 13678 | johns | 3 |
| 13679 | jineta | 3 |
| 13680 | jesters | 3 |
| 13681 | jeronima | 3 |
| 13682 | jerkins | 3 |
| 13683 | jephthah | 3 |
| 13684 | jeopardy | 3 |
| 13685 | jarteer | 3 |
| 13686 | jail | 3 |
| 13687 | jaded | 3 |
| 13688 | jackasses | 3 |
| 13689 | iwis | 3 |
| 13690 | iteration | 3 |
| 13691 | isbel | 3 |
| 13692 | irritated | 3 |
| 13693 | irrevocable | 3 |
| 13694 | irresistible | 3 |
| 13695 | irreparable | 3 |
| 13696 | irreligious | 3 |
| 13697 | irrelevant | 3 |
| 13698 | irksome | 3 |
| 13699 | irks | 3 |
| 13700 | inwardly | 3 |
| 13701 | involving | 3 |
| 13702 | involve | 3 |
| 13703 | invoked | 3 |
| 13704 | invocate | 3 |
| 13705 | inviolable | 3 |
| 13706 | investments | 3 |
| 13707 | inverness | 3 |
| 13708 | invade | 3 |
| 13709 | intruder | 3 |
| 13710 | intimation | 3 |
| 13711 | interpreted | 3 |
| 13712 | interior | 3 |
| 13713 | interests | 3 |
| 13714 | intendment | 3 |
| 13715 | intemperance | 3 |
| 13716 | insupportable | 3 |
| 13717 | insulted | 3 |
| 13718 | instituted | 3 |
| 13719 | instigation | 3 |
| 13720 | insomuch | 3 |
| 13721 | insinuation | 3 |
| 13722 | inscrutable | 3 |
| 13723 | insane | 3 |
| 13724 | inquisition | 3 |
| 13725 | inquiry | 3 |
| 13726 | inquired | 3 |
| 13727 | innovation | 3 |
| 13728 | inky | 3 |
| 13729 | inkhorn | 3 |
| 13730 | inherits | 3 |
| 13731 | infold | 3 |
| 13732 | inflicting | 3 |
| 13733 | inflexible | 3 |
| 13734 | inflaming | 3 |
| 13735 | inflam | 3 |
| 13736 | infidel | 3 |
| 13737 | inferr | 3 |
| 13738 | infatuation | 3 |
| 13739 | inestimable | 3 |
| 13740 | indulgence | 3 |
| 13741 | indulged | 3 |
| 13742 | indued | 3 |
| 13743 | induc | 3 |
| 13744 | individuals | 3 |
| 13745 | individual | 3 |
| 13746 | indisposed | 3 |
| 13747 | indigest | 3 |
| 13748 | indicates | 3 |
| 13749 | independent | 3 |
| 13750 | incurred | 3 |
| 13751 | incurr | 3 |
| 13752 | incontinency | 3 |
| 13753 | inconsiderate | 3 |
| 13754 | incomprehensible | 3 |
| 13755 | includes | 3 |
| 13756 | include | 3 |
| 13757 | inaccessible | 3 |
| 13758 | improvement | 3 |
| 13759 | improve | 3 |
| 13760 | imprimis | 3 |
| 13761 | impressure | 3 |
| 13762 | impressed | 3 |
| 13763 | impostors | 3 |
| 13764 | implements | 3 |
| 13765 | impetuous | 3 |
| 13766 | impetuosity | 3 |
| 13767 | imperilled | 3 |
| 13768 | impawn | 3 |
| 13769 | impaled | 3 |
| 13770 | immense | 3 |
| 13771 | imagining | 3 |
| 13772 | ignominy | 3 |
| 13773 | ignominious | 3 |
| 13774 | idiots | 3 |
| 13775 | icicles | 3 |
| 13776 | icarus | 3 |
| 13777 | ibat | 3 |
| 13778 | hyperbolical | 3 |
| 13779 | hut | 3 |
| 13780 | hurled | 3 |
| 13781 | hunts | 3 |
| 13782 | hungerly | 3 |
| 13783 | hulk | 3 |
| 13784 | hu | 3 |
| 13785 | howbeit | 3 |
| 13786 | hottest | 3 |
| 13787 | hostel | 3 |
| 13788 | hospital | 3 |
| 13789 | hospitable | 3 |
| 13790 | horum | 3 |
| 13791 | hors | 3 |
| 13792 | horizon | 3 |
| 13793 | hoods | 3 |
| 13794 | hooded | 3 |
| 13795 | honeysuckle | 3 |
| 13796 | holly | 3 |
| 13797 | hollowness | 3 |
| 13798 | holily | 3 |
| 13799 | hogs | 3 |
| 13800 | hoc | 3 |
| 13801 | hobgoblin | 3 |
| 13802 | hobble | 3 |
| 13803 | hissing | 3 |
| 13804 | hindmost | 3 |
| 13805 | highborn | 3 |
| 13806 | hews | 3 |
| 13807 | hest | 3 |
| 13808 | hesitated | 3 |
| 13809 | hernandez | 3 |
| 13810 | hereupon | 3 |
| 13811 | hent | 3 |
| 13812 | hemm | 3 |
| 13813 | hemlock | 3 |
| 13814 | helper | 3 |
| 13815 | heighten | 3 |
| 13816 | heedfully | 3 |
| 13817 | hectors | 3 |
| 13818 | heaving | 3 |
| 13819 | heats | 3 |
| 13820 | heathens | 3 |
| 13821 | hearest | 3 |
| 13822 | healthy | 3 |
| 13823 | healed | 3 |
| 13824 | headsman | 3 |
| 13825 | headpiece | 3 |
| 13826 | haughtiness | 3 |
| 13827 | haught | 3 |
| 13828 | hatchet | 3 |
| 13829 | harshness | 3 |
| 13830 | harpy | 3 |
| 13831 | harlots | 3 |
| 13832 | hardiness | 3 |
| 13833 | hardiment | 3 |
| 13834 | harcourt | 3 |
| 13835 | harbours | 3 |
| 13836 | harbinger | 3 |
| 13837 | harass | 3 |
| 13838 | haphazard | 3 |
| 13839 | handkercher | 3 |
| 13840 | handiwork | 3 |
| 13841 | handing | 3 |
| 13842 | halters | 3 |
| 13843 | halfpence | 3 |
| 13844 | hales | 3 |
| 13845 | hackneys | 3 |
| 13846 | gules | 3 |
| 13847 | guisando | 3 |
| 13848 | guinea | 3 |
| 13849 | guillermo | 3 |
| 13850 | grunting | 3 |
| 13851 | grumbling | 3 |
| 13852 | grumble | 3 |
| 13853 | grudging | 3 |
| 13854 | grub | 3 |
| 13855 | grovelling | 3 |
| 13856 | grizzled | 3 |
| 13857 | grisly | 3 |
| 13858 | gripes | 3 |
| 13859 | grinning | 3 |
| 13860 | grinding | 3 |
| 13861 | grazing | 3 |
| 13862 | gray | 3 |
| 13863 | graven | 3 |
| 13864 | grappling | 3 |
| 13865 | gramercies | 3 |
| 13866 | graft | 3 |
| 13867 | gradually | 3 |
| 13868 | gouty | 3 |
| 13869 | gourd | 3 |
| 13870 | gory | 3 |
| 13871 | gorging | 3 |
| 13872 | goodwill | 3 |
| 13873 | goodliest | 3 |
| 13874 | goffe | 3 |
| 13875 | goers | 3 |
| 13876 | godliness | 3 |
| 13877 | godlike | 3 |
| 13878 | godhead | 3 |
| 13879 | godfathers | 3 |
| 13880 | glorified | 3 |
| 13881 | glist | 3 |
| 13882 | glimmering | 3 |
| 13883 | glide | 3 |
| 13884 | glee | 3 |
| 13885 | glazed | 3 |
| 13886 | glassy | 3 |
| 13887 | girthed | 3 |
| 13888 | girdling | 3 |
| 13889 | girdles | 3 |
| 13890 | giralda | 3 |
| 13891 | gilbert | 3 |
| 13892 | gigantic | 3 |
| 13893 | gig | 3 |
| 13894 | gifted | 3 |
| 13895 | gibbets | 3 |
| 13896 | giantess | 3 |
| 13897 | germane | 3 |
| 13898 | gerfalcon | 3 |
| 13899 | gerard | 3 |
| 13900 | genitive | 3 |
| 13901 | gelded | 3 |
| 13902 | gasping | 3 |
| 13903 | gascon | 3 |
| 13904 | garrison | 3 |
| 13905 | ganelon | 3 |
| 13906 | gaming | 3 |
| 13907 | gamesome | 3 |
| 13908 | gambols | 3 |
| 13909 | gambol | 3 |
| 13910 | galloping | 3 |
| 13911 | gallons | 3 |
| 13912 | gaited | 3 |
| 13913 | gag | 3 |
| 13914 | gaberdine | 3 |
| 13915 | gabble | 3 |
| 13916 | fusty | 3 |
| 13917 | fuss | 3 |
| 13918 | furthermore | 3 |
| 13919 | furnishing | 3 |
| 13920 | furioso | 3 |
| 13921 | fur | 3 |
| 13922 | fumes | 3 |
| 13923 | fugitives | 3 |
| 13924 | frying | 3 |
| 13925 | froze | 3 |
| 13926 | fritters | 3 |
| 13927 | friston | 3 |
| 13928 | frighting | 3 |
| 13929 | friendships | 3 |
| 13930 | friended | 3 |
| 13931 | fried | 3 |
| 13932 | freshness | 3 |
| 13933 | freshest | 3 |
| 13934 | freebooters | 3 |
| 13935 | freaks | 3 |
| 13936 | frays | 3 |
| 13937 | frankness | 3 |
| 13938 | franciscan | 3 |
| 13939 | frames | 3 |
| 13940 | fragment | 3 |
| 13941 | fours | 3 |
| 13942 | fount | 3 |
| 13943 | founders | 3 |
| 13944 | foulest | 3 |
| 13945 | fostered | 3 |
| 13946 | forum | 3 |
| 13947 | forts | 3 |
| 13948 | forrest | 3 |
| 13949 | formally | 3 |
| 13950 | formalities | 3 |
| 13951 | forewarned | 3 |
| 13952 | foretells | 3 |
| 13953 | foreseeing | 3 |
| 13954 | foresaw | 3 |
| 13955 | forerunner | 3 |
| 13956 | forelock | 3 |
| 13957 | foreigners | 3 |
| 13958 | forehand | 3 |
| 13959 | foregone | 3 |
| 13960 | forego | 3 |
| 13961 | forefinger | 3 |
| 13962 | forage | 3 |
| 13963 | foppery | 3 |
| 13964 | footpads | 3 |
| 13965 | fondness | 3 |
| 13966 | folds | 3 |
| 13967 | foi | 3 |
| 13968 | fogs | 3 |
| 13969 | foggy | 3 |
| 13970 | foemen | 3 |
| 13971 | focile | 3 |
| 13972 | foams | 3 |
| 13973 | foal | 3 |
| 13974 | flush | 3 |
| 13975 | flurried | 3 |
| 13976 | flouting | 3 |
| 13977 | flogged | 3 |
| 13978 | flitches | 3 |
| 13979 | flit | 3 |
| 13980 | flexible | 3 |
| 13981 | fleer | 3 |
| 13982 | flatters | 3 |
| 13983 | flashes | 3 |
| 13984 | flanks | 3 |
| 13985 | fixture | 3 |
| 13986 | fixes | 3 |
| 13987 | fitteth | 3 |
| 13988 | fitchew | 3 |
| 13989 | fists | 3 |
| 13990 | fishing | 3 |
| 13991 | firstlings | 3 |
| 13992 | firebrand | 3 |
| 13993 | fingre | 3 |
| 13994 | fingering | 3 |
| 13995 | findest | 3 |
| 13996 | fillip | 3 |
| 13997 | filching | 3 |
| 13998 | filberts | 3 |
| 13999 | fil | 3 |
| 14000 | fike | 3 |
| 14001 | figuring | 3 |
| 14002 | fierabras | 3 |
| 14003 | fiddler | 3 |
| 14004 | fickleness | 3 |
| 14005 | fester | 3 |
| 14006 | feste | 3 |
| 14007 | fest | 3 |
| 14008 | ferry | 3 |
| 14009 | females | 3 |
| 14010 | feeders | 3 |
| 14011 | featured | 3 |
| 14012 | fay | 3 |
| 14013 | favourably | 3 |
| 14014 | faultless | 3 |
| 14015 | fatherless | 3 |
| 14016 | fastest | 3 |
| 14017 | fashionable | 3 |
| 14018 | fascinated | 3 |
| 14019 | farthingale | 3 |
| 14020 | fantastically | 3 |
| 14021 | fanning | 3 |
| 14022 | fann | 3 |
| 14023 | famishing | 3 |
| 14024 | falter | 3 |
| 14025 | fallow | 3 |
| 14026 | falconers | 3 |
| 14027 | faithlessness | 3 |
| 14028 | failure | 3 |
| 14029 | fadom | 3 |
| 14030 | faculty | 3 |
| 14031 | facing | 3 |
| 14032 | facetious | 3 |
| 14033 | fabulous | 3 |
| 14034 | exult | 3 |
| 14035 | extracted | 3 |
| 14036 | extra | 3 |
| 14037 | extensive | 3 |
| 14038 | extemporal | 3 |
| 14039 | expressure | 3 |
| 14040 | explore | 3 |
| 14041 | explanations | 3 |
| 14042 | explaining | 3 |
| 14043 | expiate | 3 |
| 14044 | experienced | 3 |
| 14045 | expend | 3 |
| 14046 | exists | 3 |
| 14047 | existed | 3 |
| 14048 | exigent | 3 |
| 14049 | exhalations | 3 |
| 14050 | exhalation | 3 |
| 14051 | exert | 3 |
| 14052 | execrations | 3 |
| 14053 | excursion | 3 |
| 14054 | excites | 3 |
| 14055 | exchanging | 3 |
| 14056 | exasperate | 3 |
| 14057 | exactitude | 3 |
| 14058 | exactions | 3 |
| 14059 | exaction | 3 |
| 14060 | ewer | 3 |
| 14061 | europa | 3 |
| 14062 | etes | 3 |
| 14063 | essentially | 3 |
| 14064 | esquires | 3 |
| 14065 | espy | 3 |
| 14066 | espous | 3 |
| 14067 | esplandian | 3 |
| 14068 | espied | 3 |
| 14069 | espials | 3 |
| 14070 | especial | 3 |
| 14071 | eruptions | 3 |
| 14072 | erthrow | 3 |
| 14073 | erswell | 3 |
| 14074 | errule | 3 |
| 14075 | errands | 3 |
| 14076 | ernight | 3 |
| 14077 | erheard | 3 |
| 14078 | ergrown | 3 |
| 14079 | erflows | 3 |
| 14080 | erection | 3 |
| 14081 | erebus | 3 |
| 14082 | erbear | 3 |
| 14083 | equivocator | 3 |
| 14084 | equivalent | 3 |
| 14085 | equinoctial | 3 |
| 14086 | epithet | 3 |
| 14087 | episodes | 3 |
| 14088 | environed | 3 |
| 14089 | enthron | 3 |
| 14090 | enthrall | 3 |
| 14091 | ensconce | 3 |
| 14092 | enriched | 3 |
| 14093 | enliven | 3 |
| 14094 | enlighten | 3 |
| 14095 | enjoined | 3 |
| 14096 | engrossed | 3 |
| 14097 | engendered | 3 |
| 14098 | engend | 3 |
| 14099 | enfeebled | 3 |
| 14100 | enduring | 3 |
| 14101 | endowments | 3 |
| 14102 | enamour | 3 |
| 14103 | enact | 3 |
| 14104 | emptiness | 3 |
| 14105 | emeralds | 3 |
| 14106 | embroidery | 3 |
| 14107 | embossed | 3 |
| 14108 | embarked | 3 |
| 14109 | eltham | 3 |
| 14110 | ell | 3 |
| 14111 | elf | 3 |
| 14112 | egyptians | 3 |
| 14113 | effrontery | 3 |
| 14114 | effort | 3 |
| 14115 | efface | 3 |
| 14116 | edmundsbury | 3 |
| 14117 | edifice | 3 |
| 14118 | edicts | 3 |
| 14119 | edges | 3 |
| 14120 | edged | 3 |
| 14121 | ecoutez | 3 |
| 14122 | eclogues | 3 |
| 14123 | ecclesiastics | 3 |
| 14124 | ebro | 3 |
| 14125 | ebbs | 3 |
| 14126 | ebbing | 3 |
| 14127 | eater | 3 |
| 14128 | easiness | 3 |
| 14129 | dwellers | 3 |
| 14130 | dutiful | 3 |
| 14131 | dutch | 3 |
| 14132 | dung | 3 |
| 14133 | dump | 3 |
| 14134 | dully | 3 |
| 14135 | dullest | 3 |
| 14136 | dullard | 3 |
| 14137 | dugs | 3 |
| 14138 | ducks | 3 |
| 14139 | du | 3 |
| 14140 | drubbing | 3 |
| 14141 | drubbed | 3 |
| 14142 | droops | 3 |
| 14143 | drones | 3 |
| 14144 | drone | 3 |
| 14145 | dromedaries | 3 |
| 14146 | dries | 3 |
| 14147 | drier | 3 |
| 14148 | dreamer | 3 |
| 14149 | drawbridge | 3 |
| 14150 | draughts | 3 |
| 14151 | dout | 3 |
| 14152 | dough | 3 |
| 14153 | doubloons | 3 |
| 14154 | doubling | 3 |
| 14155 | dotard | 3 |
| 14156 | dorothy | 3 |
| 14157 | doomed | 3 |
| 14158 | domitius | 3 |
| 14159 | dominator | 3 |
| 14160 | dogged | 3 |
| 14161 | dizzy | 3 |
| 14162 | divinely | 3 |
| 14163 | divined | 3 |
| 14164 | divination | 3 |
| 14165 | dividing | 3 |
| 14166 | divides | 3 |
| 14167 | diversion | 3 |
| 14168 | ditties | 3 |
| 14169 | ditches | 3 |
| 14170 | distributive | 3 |
| 14171 | distribution | 3 |
| 14172 | distributed | 3 |
| 14173 | distribute | 3 |
| 14174 | distractedly | 3 |
| 14175 | distinguishes | 3 |
| 14176 | dissolved | 3 |
| 14177 | dissolution | 3 |
| 14178 | dissolutely | 3 |
| 14179 | dissever | 3 |
| 14180 | disrobe | 3 |
| 14181 | disprais | 3 |
| 14182 | disposer | 3 |
| 14183 | disport | 3 |
| 14184 | displeasing | 3 |
| 14185 | displeased | 3 |
| 14186 | displays | 3 |
| 14187 | displaying | 3 |
| 14188 | dispersed | 3 |
| 14189 | dispensation | 3 |
| 14190 | disorders | 3 |
| 14191 | disobey | 3 |
| 14192 | dismissing | 3 |
| 14193 | dismantle | 3 |
| 14194 | dislikes | 3 |
| 14195 | disinherit | 3 |
| 14196 | disgusted | 3 |
| 14197 | disguising | 3 |
| 14198 | disenchanting | 3 |
| 14199 | discrimination | 3 |
| 14200 | discretions | 3 |
| 14201 | discoveries | 3 |
| 14202 | discoursed | 3 |
| 14203 | discordant | 3 |
| 14204 | discontentedly | 3 |
| 14205 | discloses | 3 |
| 14206 | discharging | 3 |
| 14207 | discernment | 3 |
| 14208 | disbursed | 3 |
| 14209 | disarms | 3 |
| 14210 | disarm | 3 |
| 14211 | disadvantage | 3 |
| 14212 | dip | 3 |
| 14213 | dinners | 3 |
| 14214 | dining | 3 |
| 14215 | dimpled | 3 |
| 14216 | diminutive | 3 |
| 14217 | dilated | 3 |
| 14218 | digressions | 3 |
| 14219 | dignifies | 3 |
| 14220 | dighton | 3 |
| 14221 | diffidence | 3 |
| 14222 | diff | 3 |
| 14223 | dictynna | 3 |
| 14224 | diaz | 3 |
| 14225 | dialect | 3 |
| 14226 | di | 3 |
| 14227 | devotional | 3 |
| 14228 | deum | 3 |
| 14229 | detraction | 3 |
| 14230 | determines | 3 |
| 14231 | detected | 3 |
| 14232 | details | 3 |
| 14233 | detail | 3 |
| 14234 | destitute | 3 |
| 14235 | desdemon | 3 |
| 14236 | descant | 3 |
| 14237 | des | 3 |
| 14238 | derogate | 3 |
| 14239 | dere | 3 |
| 14240 | depraved | 3 |
| 14241 | deposing | 3 |
| 14242 | deposed | 3 |
| 14243 | deplore | 3 |
| 14244 | depict | 3 |
| 14245 | dependency | 3 |
| 14246 | dependants | 3 |
| 14247 | deo | 3 |
| 14248 | deniest | 3 |
| 14249 | denier | 3 |
| 14250 | demosthenian | 3 |
| 14251 | demonstrations | 3 |
| 14252 | demonstration | 3 |
| 14253 | demesnes | 3 |
| 14254 | demerits | 3 |
| 14255 | deluge | 3 |
| 14256 | deluding | 3 |
| 14257 | deluded | 3 |
| 14258 | delphos | 3 |
| 14259 | delicacy | 3 |
| 14260 | delaying | 3 |
| 14261 | deject | 3 |
| 14262 | degrade | 3 |
| 14263 | defrauding | 3 |
| 14264 | deflower | 3 |
| 14265 | defiles | 3 |
| 14266 | defends | 3 |
| 14267 | defenders | 3 |
| 14268 | decrepit | 3 |
| 14269 | deciphered | 3 |
| 14270 | decipher | 3 |
| 14271 | decent | 3 |
| 14272 | deceiver | 3 |
| 14273 | deceits | 3 |
| 14274 | deathbed | 3 |
| 14275 | deafened | 3 |
| 14276 | dazed | 3 |
| 14277 | darting | 3 |
| 14278 | darted | 3 |
| 14279 | darnel | 3 |
| 14280 | darkling | 3 |
| 14281 | darkest | 3 |
| 14282 | darken | 3 |
| 14283 | daphne | 3 |
| 14284 | dangerously | 3 |
| 14285 | dancer | 3 |
| 14286 | damaged | 3 |
| 14287 | dallying | 3 |
| 14288 | daintily | 3 |
| 14289 | dad | 3 |
| 14290 | cytherea | 3 |
| 14291 | cynosure | 3 |
| 14292 | cydnus | 3 |
| 14293 | cutpurse | 3 |
| 14294 | customers | 3 |
| 14295 | curtly | 3 |
| 14296 | curtal | 3 |
| 14297 | cursy | 3 |
| 14298 | curled | 3 |
| 14299 | cureless | 3 |
| 14300 | curan | 3 |
| 14301 | cupbearer | 3 |
| 14302 | cum | 3 |
| 14303 | cudgels | 3 |
| 14304 | crupper | 3 |
| 14305 | crowning | 3 |
| 14306 | crowner | 3 |
| 14307 | crouching | 3 |
| 14308 | crouch | 3 |
| 14309 | crossbows | 3 |
| 14310 | crossbow | 3 |
| 14311 | crosby | 3 |
| 14312 | critic | 3 |
| 14313 | crispin | 3 |
| 14314 | crisp | 3 |
| 14315 | crisis | 3 |
| 14316 | criminal | 3 |
| 14317 | cricket | 3 |
| 14318 | credos | 3 |
| 14319 | creditable | 3 |
| 14320 | credible | 3 |
| 14321 | creator | 3 |
| 14322 | crazes | 3 |
| 14323 | craz | 3 |
| 14324 | crawl | 3 |
| 14325 | crassus | 3 |
| 14326 | crash | 3 |
| 14327 | cramp | 3 |
| 14328 | craftily | 3 |
| 14329 | crabbed | 3 |
| 14330 | cozeners | 3 |
| 14331 | cozened | 3 |
| 14332 | cozenage | 3 |
| 14333 | coyness | 3 |
| 14334 | covet | 3 |
| 14335 | covenant | 3 |
| 14336 | courtesan | 3 |
| 14337 | courted | 3 |
| 14338 | coursing | 3 |
| 14339 | courbash | 3 |
| 14340 | counterpois | 3 |
| 14341 | countermand | 3 |
| 14342 | counterfeits | 3 |
| 14343 | countercheck | 3 |
| 14344 | countenanc | 3 |
| 14345 | councillor | 3 |
| 14346 | coughing | 3 |
| 14347 | couching | 3 |
| 14348 | costumes | 3 |
| 14349 | cosmographer | 3 |
| 14350 | corsair | 3 |
| 14351 | corrupter | 3 |
| 14352 | corridors | 3 |
| 14353 | corridor | 3 |
| 14354 | corresponding | 3 |
| 14355 | correspondence | 3 |
| 14356 | coronets | 3 |
| 14357 | corns | 3 |
| 14358 | cordially | 3 |
| 14359 | coragio | 3 |
| 14360 | cophetua | 3 |
| 14361 | cooked | 3 |
| 14362 | convulsions | 3 |
| 14363 | conviction | 3 |
| 14364 | converting | 3 |
| 14365 | conversion | 3 |
| 14366 | convented | 3 |
| 14367 | contumelious | 3 |
| 14368 | controll | 3 |
| 14369 | continually | 3 |
| 14370 | continents | 3 |
| 14371 | contempts | 3 |
| 14372 | contemplative | 3 |
| 14373 | contemning | 3 |
| 14374 | consummation | 3 |
| 14375 | consultation | 3 |
| 14376 | constrains | 3 |
| 14377 | constables | 3 |
| 14378 | consisting | 3 |
| 14379 | considerate | 3 |
| 14380 | conserves | 3 |
| 14381 | consciousness | 3 |
| 14382 | congregation | 3 |
| 14383 | congregated | 3 |
| 14384 | congealed | 3 |
| 14385 | confront | 3 |
| 14386 | conform | 3 |
| 14387 | conflicting | 3 |
| 14388 | confiscated | 3 |
| 14389 | confessions | 3 |
| 14390 | conferring | 3 |
| 14391 | conferr | 3 |
| 14392 | conde | 3 |
| 14393 | conceives | 3 |
| 14394 | concave | 3 |
| 14395 | compromise | 3 |
| 14396 | comprehends | 3 |
| 14397 | comprehended | 3 |
| 14398 | complots | 3 |
| 14399 | complement | 3 |
| 14400 | compels | 3 |
| 14401 | comparative | 3 |
| 14402 | companionship | 3 |
| 14403 | commodities | 3 |
| 14404 | commissions | 3 |
| 14405 | commenting | 3 |
| 14406 | comical | 3 |
| 14407 | comic | 3 |
| 14408 | comet | 3 |
| 14409 | comers | 3 |
| 14410 | combination | 3 |
| 14411 | combats | 3 |
| 14412 | combating | 3 |
| 14413 | combatant | 3 |
| 14414 | colossus | 3 |
| 14415 | colleges | 3 |
| 14416 | collection | 3 |
| 14417 | collect | 3 |
| 14418 | colic | 3 |
| 14419 | coherent | 3 |
| 14420 | cognizance | 3 |
| 14421 | cogitations | 3 |
| 14422 | cogging | 3 |
| 14423 | codicil | 3 |
| 14424 | coated | 3 |
| 14425 | coasts | 3 |
| 14426 | clyster | 3 |
| 14427 | clusters | 3 |
| 14428 | clust | 3 |
| 14429 | clung | 3 |
| 14430 | clumsy | 3 |
| 14431 | clouts | 3 |
| 14432 | closure | 3 |
| 14433 | clogs | 3 |
| 14434 | clod | 3 |
| 14435 | clipped | 3 |
| 14436 | climbed | 3 |
| 14437 | clifton | 3 |
| 14438 | clergymen | 3 |
| 14439 | cleanse | 3 |
| 14440 | clatter | 3 |
| 14441 | class | 3 |
| 14442 | clapping | 3 |
| 14443 | clamor | 3 |
| 14444 | circumstantial | 3 |
| 14445 | circumference | 3 |
| 14446 | circe | 3 |
| 14447 | cicatrice | 3 |
| 14448 | churls | 3 |
| 14449 | chronicled | 3 |
| 14450 | chopt | 3 |
| 14451 | chopp | 3 |
| 14452 | chivalrous | 3 |
| 14453 | china | 3 |
| 14454 | childishness | 3 |
| 14455 | chick | 3 |
| 14456 | chewed | 3 |
| 14457 | chestnut | 3 |
| 14458 | chess | 3 |
| 14459 | cheshu | 3 |
| 14460 | chertsey | 3 |
| 14461 | cherishing | 3 |
| 14462 | cheering | 3 |
| 14463 | checking | 3 |
| 14464 | cheats | 3 |
| 14465 | cheaply | 3 |
| 14466 | chattels | 3 |
| 14467 | chatham | 3 |
| 14468 | chastised | 3 |
| 14469 | chastis | 3 |
| 14470 | chastely | 3 |
| 14471 | charters | 3 |
| 14472 | charmingly | 3 |
| 14473 | chariots | 3 |
| 14474 | chapters | 3 |
| 14475 | chapels | 3 |
| 14476 | chant | 3 |
| 14477 | chalky | 3 |
| 14478 | certificates | 3 |
| 14479 | certificate | 3 |
| 14480 | ceremonial | 3 |
| 14481 | century | 3 |
| 14482 | centaurs | 3 |
| 14483 | censur | 3 |
| 14484 | cement | 3 |
| 14485 | celsa | 3 |
| 14486 | ceas | 3 |
| 14487 | ce | 3 |
| 14488 | cautions | 3 |
| 14489 | causer | 3 |
| 14490 | causeless | 3 |
| 14491 | caudle | 3 |
| 14492 | cathedral | 3 |
| 14493 | cates | 3 |
| 14494 | catechize | 3 |
| 14495 | cataracts | 3 |
| 14496 | casque | 3 |
| 14497 | cash | 3 |
| 14498 | casements | 3 |
| 14499 | carv | 3 |
| 14500 | carriest | 3 |
| 14501 | carrascon | 3 |
| 14502 | carping | 3 |
| 14503 | carouses | 3 |
| 14504 | careers | 3 |
| 14505 | carbuncles | 3 |
| 14506 | carbuncle | 3 |
| 14507 | captivate | 3 |
| 14508 | capons | 3 |
| 14509 | capilet | 3 |
| 14510 | capet | 3 |
| 14511 | canvas | 3 |
| 14512 | cantle | 3 |
| 14513 | canopied | 3 |
| 14514 | canons | 3 |
| 14515 | candy | 3 |
| 14516 | candlesticks | 3 |
| 14517 | candied | 3 |
| 14518 | camest | 3 |
| 14519 | calumnious | 3 |
| 14520 | calmer | 3 |
| 14521 | callet | 3 |
| 14522 | caliver | 3 |
| 14523 | buying | 3 |
| 14524 | butterfly | 3 |
| 14525 | butchery | 3 |
| 14526 | butchered | 3 |
| 14527 | buskins | 3 |
| 14528 | busily | 3 |
| 14529 | burlesque | 3 |
| 14530 | bunting | 3 |
| 14531 | bunches | 3 |
| 14532 | bullocks | 3 |
| 14533 | buildeth | 3 |
| 14534 | builded | 3 |
| 14535 | bugs | 3 |
| 14536 | bug | 3 |
| 14537 | bubbles | 3 |
| 14538 | bruited | 3 |
| 14539 | browner | 3 |
| 14540 | broader | 3 |
| 14541 | bristly | 3 |
| 14542 | bristles | 3 |
| 14543 | brinish | 3 |
| 14544 | bringest | 3 |
| 14545 | bringer | 3 |
| 14546 | brilliantly | 3 |
| 14547 | brilliant | 3 |
| 14548 | brightly | 3 |
| 14549 | bridget | 3 |
| 14550 | brides | 3 |
| 14551 | brib | 3 |
| 14552 | breech | 3 |
| 14553 | breather | 3 |
| 14554 | breastplate | 3 |
| 14555 | brats | 3 |
| 14556 | branded | 3 |
| 14557 | brakes | 3 |
| 14558 | brainsick | 3 |
| 14559 | bounding | 3 |
| 14560 | bottles | 3 |
| 14561 | botcher | 3 |
| 14562 | botas | 3 |
| 14563 | boskos | 3 |
| 14564 | borrower | 3 |
| 14565 | borough | 3 |
| 14566 | bores | 3 |
| 14567 | borders | 3 |
| 14568 | bor | 3 |
| 14569 | bookish | 3 |
| 14570 | bolting | 3 |
| 14571 | boils | 3 |
| 14572 | bogs | 3 |
| 14573 | bodice | 3 |
| 14574 | bobb | 3 |
| 14575 | bob | 3 |
| 14576 | blunts | 3 |
| 14577 | bluntly | 3 |
| 14578 | blunders | 3 |
| 14579 | blotted | 3 |
| 14580 | bloodshed | 3 |
| 14581 | blinding | 3 |
| 14582 | blessedness | 3 |
| 14583 | blear | 3 |
| 14584 | blaspheme | 3 |
| 14585 | blandishments | 3 |
| 14586 | blameful | 3 |
| 14587 | blam | 3 |
| 14588 | blackness | 3 |
| 14589 | blab | 3 |
| 14590 | bin | 3 |
| 14591 | bien | 3 |
| 14592 | bewept | 3 |
| 14593 | bevy | 3 |
| 14594 | bettered | 3 |
| 14595 | bett | 3 |
| 14596 | betid | 3 |
| 14597 | bestrew | 3 |
| 14598 | bestir | 3 |
| 14599 | bestial | 3 |
| 14600 | berwick | 3 |
| 14601 | berri | 3 |
| 14602 | bereave | 3 |
| 14603 | benison | 3 |
| 14604 | benefice | 3 |
| 14605 | benedict | 3 |
| 14606 | bends | 3 |
| 14607 | bemoaning | 3 |
| 14608 | belzebub | 3 |
| 14609 | beltenebros | 3 |
| 14610 | belongings | 3 |
| 14611 | bellyful | 3 |
| 14612 | bellow | 3 |
| 14613 | believest | 3 |
| 14614 | belianises | 3 |
| 14615 | behove | 3 |
| 14616 | begetting | 3 |
| 14617 | befriends | 3 |
| 14618 | befooled | 3 |
| 14619 | bedew | 3 |
| 14620 | bedded | 3 |
| 14621 | becomingly | 3 |
| 14622 | beautify | 3 |
| 14623 | beautified | 3 |
| 14624 | beans | 3 |
| 14625 | bean | 3 |
| 14626 | beamed | 3 |
| 14627 | beak | 3 |
| 14628 | baynard | 3 |
| 14629 | bawdry | 3 |
| 14630 | batters | 3 |
| 14631 | batter | 3 |
| 14632 | bastinado | 3 |
| 14633 | baskets | 3 |
| 14634 | bashfulness | 3 |
| 14635 | based | 3 |
| 14636 | bas | 3 |
| 14637 | barnet | 3 |
| 14638 | bargains | 3 |
| 14639 | barefaced | 3 |
| 14640 | barbarians | 3 |
| 14641 | barbarian | 3 |
| 14642 | bans | 3 |
| 14643 | banqueting | 3 |
| 14644 | bandying | 3 |
| 14645 | baize | 3 |
| 14646 | baits | 3 |
| 14647 | bagatelle | 3 |
| 14648 | backing | 3 |
| 14649 | backed | 3 |
| 14650 | backbone | 3 |
| 14651 | babies | 3 |
| 14652 | babble | 3 |
| 14653 | awl | 3 |
| 14654 | awards | 3 |
| 14655 | awarded | 3 |
| 14656 | awaken | 3 |
| 14657 | avoiding | 3 |
| 14658 | avis | 3 |
| 14659 | aveng | 3 |
| 14660 | auvergne | 3 |
| 14661 | augury | 3 |
| 14662 | augurers | 3 |
| 14663 | augmented | 3 |
| 14664 | audible | 3 |
| 14665 | auburn | 3 |
| 14666 | attributed | 3 |
| 14667 | attractions | 3 |
| 14668 | attract | 3 |
| 14669 | attorneys | 3 |
| 14670 | attires | 3 |
| 14671 | attir | 3 |
| 14672 | attachment | 3 |
| 14673 | atomies | 3 |
| 14674 | athversary | 3 |
| 14675 | astronomer | 3 |
| 14676 | astrology | 3 |
| 14677 | astrologer | 3 |
| 14678 | assures | 3 |
| 14679 | assisted | 3 |
| 14680 | asserted | 3 |
| 14681 | assays | 3 |
| 14682 | assailants | 3 |
| 14683 | aspic | 3 |
| 14684 | asp | 3 |
| 14685 | ash | 3 |
| 14686 | artifice | 3 |
| 14687 | arranging | 3 |
| 14688 | aroused | 3 |
| 14689 | aroint | 3 |
| 14690 | arnaut | 3 |
| 14691 | arn | 3 |
| 14692 | armours | 3 |
| 14693 | armor | 3 |
| 14694 | armenia | 3 |
| 14695 | armagnac | 3 |
| 14696 | ariosto | 3 |
| 14697 | ariadne | 3 |
| 14698 | argosies | 3 |
| 14699 | argal | 3 |
| 14700 | ardent | 3 |
| 14701 | archery | 3 |
| 14702 | archers | 3 |
| 14703 | archer | 3 |
| 14704 | arc | 3 |
| 14705 | arabian | 3 |
| 14706 | arab | 3 |
| 14707 | aptness | 3 |
| 14708 | apron | 3 |
| 14709 | appropriate | 3 |
| 14710 | apprehends | 3 |
| 14711 | appointments | 3 |
| 14712 | appliances | 3 |
| 14713 | appliance | 3 |
| 14714 | appeareth | 3 |
| 14715 | appeals | 3 |
| 14716 | appeach | 3 |
| 14717 | apollonia | 3 |
| 14718 | anxieties | 3 |
| 14719 | anvil | 3 |
| 14720 | antonia | 3 |
| 14721 | antequera | 3 |
| 14722 | ante | 3 |
| 14723 | answerest | 3 |
| 14724 | annotations | 3 |
| 14725 | angling | 3 |
| 14726 | anchises | 3 |
| 14727 | anatomize | 3 |
| 14728 | amplify | 3 |
| 14729 | amours | 3 |
| 14730 | althaea | 3 |
| 14731 | ally | 3 |
| 14732 | allusion | 3 |
| 14733 | allowable | 3 |
| 14734 | alley | 3 |
| 14735 | alien | 3 |
| 14736 | alguacil | 3 |
| 14737 | alexanders | 3 |
| 14738 | alert | 3 |
| 14739 | al | 3 |
| 14740 | aimed | 3 |
| 14741 | ails | 3 |
| 14742 | ailments | 3 |
| 14743 | ail | 3 |
| 14744 | ai | 3 |
| 14745 | aha | 3 |
| 14746 | aguilar | 3 |
| 14747 | agues | 3 |
| 14748 | agreeing | 3 |
| 14749 | agility | 3 |
| 14750 | aghast | 3 |
| 14751 | aggrieved | 3 |
| 14752 | ag | 3 |
| 14753 | afloat | 3 |
| 14754 | afire | 3 |
| 14755 | affiance | 3 |
| 14756 | affectionately | 3 |
| 14757 | affectionate | 3 |
| 14758 | afear | 3 |
| 14759 | advertised | 3 |
| 14760 | advertis | 3 |
| 14761 | adulterous | 3 |
| 14762 | adroitness | 3 |
| 14763 | adoration | 3 |
| 14764 | ador | 3 |
| 14765 | adopting | 3 |
| 14766 | adonis | 3 |
| 14767 | admonition | 3 |
| 14768 | adjusted | 3 |
| 14769 | adjoining | 3 |
| 14770 | adheres | 3 |
| 14771 | addle | 3 |
| 14772 | adamant | 3 |
| 14773 | actual | 3 |
| 14774 | actium | 3 |
| 14775 | acquitted | 3 |
| 14776 | acquittance | 3 |
| 14777 | acquisition | 3 |
| 14778 | acknowledg | 3 |
| 14779 | achieving | 3 |
| 14780 | acheron | 3 |
| 14781 | accuser | 3 |
| 14782 | accused | 3 |
| 14783 | accurately | 3 |
| 14784 | accoutred | 3 |
| 14785 | accountant | 3 |
| 14786 | accountable | 3 |
| 14787 | accorded | 3 |
| 14788 | accompaniments | 3 |
| 14789 | accommodate | 3 |
| 14790 | acclamations | 3 |
| 14791 | accidentally | 3 |
| 14792 | accidental | 3 |
| 14793 | accessories | 3 |
| 14794 | accessary | 3 |
| 14795 | abysm | 3 |
| 14796 | absolv | 3 |
| 14797 | abruptly | 3 |
| 14798 | abroach | 3 |
| 14799 | abreast | 3 |
| 14800 | abatement | 3 |
| 14801 | abated | 3 |
| 14802 | zodiacs | 2 |
| 14803 | zocodover | 2 |
| 14804 | zir | 2 |
| 14805 | zancas | 2 |
| 14806 | z | 2 |
| 14807 | youngly | 2 |
| 14808 | youngling | 2 |
| 14809 | yorkists | 2 |
| 14810 | yorick | 2 |
| 14811 | yok | 2 |
| 14812 | yielder | 2 |
| 14813 | yesty | 2 |
| 14814 | yerk | 2 |
| 14815 | yeas | 2 |
| 14816 | yearns | 2 |
| 14817 | yearn | 2 |
| 14818 | yarn | 2 |
| 14819 | yarely | 2 |
| 14820 | wry | 2 |
| 14821 | wrongful | 2 |
| 14822 | wrecked | 2 |
| 14823 | wreaths | 2 |
| 14824 | wreakful | 2 |
| 14825 | wraths | 2 |
| 14826 | wow | 2 |
| 14827 | wove | 2 |
| 14828 | wots | 2 |
| 14829 | worts | 2 |
| 14830 | worths | 2 |
| 14831 | worshippers | 2 |
| 14832 | worries | 2 |
| 14833 | worldlings | 2 |
| 14834 | workmanship | 2 |
| 14835 | woolly | 2 |
| 14836 | woodcocks | 2 |
| 14837 | woefull | 2 |
| 14838 | woebegone | 2 |
| 14839 | wiving | 2 |
| 14840 | wiv | 2 |
| 14841 | witnesseth | 2 |
| 14842 | withstand | 2 |
| 14843 | withers | 2 |
| 14844 | witb | 2 |
| 14845 | wishest | 2 |
| 14846 | wiry | 2 |
| 14847 | wires | 2 |
| 14848 | wire | 2 |
| 14849 | wiping | 2 |
| 14850 | wipes | 2 |
| 14851 | winnowing | 2 |
| 14852 | winnow | 2 |
| 14853 | wines | 2 |
| 14854 | windmill | 2 |
| 14855 | willows | 2 |
| 14856 | wilfull | 2 |
| 14857 | wilder | 2 |
| 14858 | wights | 2 |
| 14859 | width | 2 |
| 14860 | widely | 2 |
| 14861 | whosoe | 2 |
| 14862 | whoa | 2 |
| 14863 | whitsun | 2 |
| 14864 | whisperings | 2 |
| 14865 | whirlwinds | 2 |
| 14866 | whirls | 2 |
| 14867 | whirled | 2 |
| 14868 | whine | 2 |
| 14869 | whiff | 2 |
| 14870 | whetted | 2 |
| 14871 | wherin | 2 |
| 14872 | whereunto | 2 |
| 14873 | whereuntil | 2 |
| 14874 | whereabout | 2 |
| 14875 | whensoever | 2 |
| 14876 | whene | 2 |
| 14877 | wheals | 2 |
| 14878 | weraday | 2 |
| 14879 | welcom | 2 |
| 14880 | weeke | 2 |
| 14881 | weeded | 2 |
| 14882 | wedges | 2 |
| 14883 | wedg | 2 |
| 14884 | weddings | 2 |
| 14885 | weaves | 2 |
| 14886 | weav | 2 |
| 14887 | wearying | 2 |
| 14888 | wearisomeness | 2 |
| 14889 | weariest | 2 |
| 14890 | wearers | 2 |
| 14891 | wealthily | 2 |
| 14892 | weals | 2 |
| 14893 | weaken | 2 |
| 14894 | watchers | 2 |
| 14895 | wassails | 2 |
| 14896 | warts | 2 |
| 14897 | warily | 2 |
| 14898 | warden | 2 |
| 14899 | warded | 2 |
| 14900 | warbling | 2 |
| 14901 | wantonly | 2 |
| 14902 | wane | 2 |
| 14903 | wands | 2 |
| 14904 | wanderers | 2 |
| 14905 | wamba | 2 |
| 14906 | walnuts | 2 |
| 14907 | wallow | 2 |
| 14908 | wakener | 2 |
| 14909 | waked | 2 |
| 14910 | wails | 2 |
| 14911 | wagoner | 2 |
| 14912 | wagon | 2 |
| 14913 | wagers | 2 |
| 14914 | wafts | 2 |
| 14915 | waftage | 2 |
| 14916 | wafer | 2 |
| 14917 | waded | 2 |
| 14918 | w | 2 |
| 14919 | vultures | 2 |
| 14920 | vraiment | 2 |
| 14921 | voyages | 2 |
| 14922 | vouchsafed | 2 |
| 14923 | vouchsaf | 2 |
| 14924 | vouches | 2 |
| 14925 | vouchers | 2 |
| 14926 | votarist | 2 |
| 14927 | votaries | 2 |
| 14928 | vot | 2 |
| 14929 | voracity | 2 |
| 14930 | vor | 2 |
| 14931 | voluptuousness | 2 |
| 14932 | volubility | 2 |
| 14933 | volt | 2 |
| 14934 | voided | 2 |
| 14935 | vlouting | 2 |
| 14936 | vizarded | 2 |
| 14937 | vividly | 2 |
| 14938 | vitals | 2 |
| 14939 | visitors | 2 |
| 14940 | virginius | 2 |
| 14941 | virginal | 2 |
| 14942 | violenta | 2 |
| 14943 | vineyards | 2 |
| 14944 | vindictive | 2 |
| 14945 | vindicate | 2 |
| 14946 | villian | 2 |
| 14947 | villanies | 2 |
| 14948 | villainously | 2 |
| 14949 | vileness | 2 |
| 14950 | vigorous | 2 |
| 14951 | vigils | 2 |
| 14952 | vigil | 2 |
| 14953 | viewest | 2 |
| 14954 | victims | 2 |
| 14955 | viceroys | 2 |
| 14956 | vicentio | 2 |
| 14957 | vexing | 2 |
| 14958 | vexations | 2 |
| 14959 | vestments | 2 |
| 14960 | vert | 2 |
| 14961 | vermin | 2 |
| 14962 | vermilion | 2 |
| 14963 | verier | 2 |
| 14964 | vergil | 2 |
| 14965 | verbis | 2 |
| 14966 | verba | 2 |
| 14967 | vents | 2 |
| 14968 | venetia | 2 |
| 14969 | vendible | 2 |
| 14970 | vell | 2 |
| 14971 | velasco | 2 |
| 14972 | vaunts | 2 |
| 14973 | vaunted | 2 |
| 14974 | vaults | 2 |
| 14975 | vaulted | 2 |
| 14976 | vaudemont | 2 |
| 14977 | vassalage | 2 |
| 14978 | varnished | 2 |
| 14979 | vaporous | 2 |
| 14980 | vanquishing | 2 |
| 14981 | vanquisher | 2 |
| 14982 | vanishest | 2 |
| 14983 | vanishes | 2 |
| 14984 | valuable | 2 |
| 14985 | vair | 2 |
| 14986 | vainness | 2 |
| 14987 | vainglory | 2 |
| 14988 | vainglorious | 2 |
| 14989 | vailing | 2 |
| 14990 | vaguely | 2 |
| 14991 | vague | 2 |
| 14992 | utility | 2 |
| 14993 | ut | 2 |
| 14994 | usurpers | 2 |
| 14995 | usuring | 2 |
| 14996 | usuries | 2 |
| 14997 | ushers | 2 |
| 14998 | ushered | 2 |
| 14999 | user | 2 |
| 15000 | urswick | 2 |
| 15001 | urn | 2 |
| 15002 | urinals | 2 |
| 15003 | urinal | 2 |
| 15004 | urgest | 2 |
| 15005 | urchin | 2 |
| 15006 | upstart | 2 |
| 15007 | uproars | 2 |
| 15008 | uprise | 2 |
| 15009 | uplift | 2 |
| 15010 | upbraidings | 2 |
| 15011 | unyoked | 2 |
| 15012 | unyok | 2 |
| 15013 | unwittingly | 2 |
| 15014 | unwind | 2 |
| 15015 | unveiling | 2 |
| 15016 | unveil | 2 |
| 15017 | unvalued | 2 |
| 15018 | unurg | 2 |
| 15019 | untying | 2 |
| 15020 | untwine | 2 |
| 15021 | untutored | 2 |
| 15022 | untutor | 2 |
| 15023 | untuneable | 2 |
| 15024 | untruth | 2 |
| 15025 | untrussing | 2 |
| 15026 | untroubled | 2 |
| 15027 | untrimmed | 2 |
| 15028 | untried | 2 |
| 15029 | untread | 2 |
| 15030 | untouch | 2 |
| 15031 | unthrifts | 2 |
| 15032 | untamed | 2 |
| 15033 | unswear | 2 |
| 15034 | unsuitable | 2 |
| 15035 | unsubstantial | 2 |
| 15036 | unstate | 2 |
| 15037 | unstanched | 2 |
| 15038 | unstain | 2 |
| 15039 | unsounded | 2 |
| 15040 | unsolicited | 2 |
| 15041 | unseeing | 2 |
| 15042 | unseason | 2 |
| 15043 | unschool | 2 |
| 15044 | unscarr | 2 |
| 15045 | unsatisfactory | 2 |
| 15046 | unroll | 2 |
| 15047 | unrivalled | 2 |
| 15048 | unripe | 2 |
| 15049 | unreveng | 2 |
| 15050 | unrestrained | 2 |
| 15051 | unrespective | 2 |
| 15052 | unrespected | 2 |
| 15053 | unreasonably | 2 |
| 15054 | unreal | 2 |
| 15055 | unquietness | 2 |
| 15056 | unquestion | 2 |
| 15057 | unpruned | 2 |
| 15058 | unprizable | 2 |
| 15059 | unprepar | 2 |
| 15060 | unpregnant | 2 |
| 15061 | unpractis | 2 |
| 15062 | unpolish | 2 |
| 15063 | unpin | 2 |
| 15064 | unparagon | 2 |
| 15065 | unpack | 2 |
| 15066 | unoccupied | 2 |
| 15067 | unnoticed | 2 |
| 15068 | unnoted | 2 |
| 15069 | unmuffling | 2 |
| 15070 | unmoved | 2 |
| 15071 | unmingled | 2 |
| 15072 | unmeritable | 2 |
| 15073 | unmeasurable | 2 |
| 15074 | unmatch | 2 |
| 15075 | unmann | 2 |
| 15076 | unmake | 2 |
| 15077 | unmade | 2 |
| 15078 | unlov | 2 |
| 15079 | unloading | 2 |
| 15080 | unloaded | 2 |
| 15081 | unload | 2 |
| 15082 | unlearn | 2 |
| 15083 | unkiss | 2 |
| 15084 | unking | 2 |
| 15085 | unkept | 2 |
| 15086 | unkennel | 2 |
| 15087 | universities | 2 |
| 15088 | unintelligible | 2 |
| 15089 | unimpeachable | 2 |
| 15090 | uniform | 2 |
| 15091 | unicorns | 2 |
| 15092 | unicorn | 2 |
| 15093 | unhoused | 2 |
| 15094 | unhindered | 2 |
| 15095 | unheedful | 2 |
| 15096 | unhatch | 2 |
| 15097 | unhandled | 2 |
| 15098 | unhallow | 2 |
| 15099 | unhair | 2 |
| 15100 | unhack | 2 |
| 15101 | unguided | 2 |
| 15102 | ungirt | 2 |
| 15103 | ungarter | 2 |
| 15104 | ungalled | 2 |
| 15105 | ungain | 2 |
| 15106 | unfriended | 2 |
| 15107 | unfortunately | 2 |
| 15108 | unforeseen | 2 |
| 15109 | unforced | 2 |
| 15110 | unfill | 2 |
| 15111 | unfettered | 2 |
| 15112 | unfathered | 2 |
| 15113 | unfair | 2 |
| 15114 | unearthly | 2 |
| 15115 | undrown | 2 |
| 15116 | undoes | 2 |
| 15117 | undivulged | 2 |
| 15118 | undisturbed | 2 |
| 15119 | undistinguishable | 2 |
| 15120 | undeserving | 2 |
| 15121 | undeserver | 2 |
| 15122 | undescribed | 2 |
| 15123 | underwent | 2 |
| 15124 | undervalued | 2 |
| 15125 | undervalue | 2 |
| 15126 | undertaker | 2 |
| 15127 | underprop | 2 |
| 15128 | underlings | 2 |
| 15129 | underhand | 2 |
| 15130 | underfoot | 2 |
| 15131 | undecided | 2 |
| 15132 | undeceived | 2 |
| 15133 | uncurable | 2 |
| 15134 | unction | 2 |
| 15135 | uncrown | 2 |
| 15136 | uncouple | 2 |
| 15137 | unconsidered | 2 |
| 15138 | unconscious | 2 |
| 15139 | unconcern | 2 |
| 15140 | uncommonly | 2 |
| 15141 | uncomfortable | 2 |
| 15142 | unclouded | 2 |
| 15143 | uncleanness | 2 |
| 15144 | uncheck | 2 |
| 15145 | unceasing | 2 |
| 15146 | uncaught | 2 |
| 15147 | uncapable | 2 |
| 15148 | unbutton | 2 |
| 15149 | unburied | 2 |
| 15150 | unbuckle | 2 |
| 15151 | unbruised | 2 |
| 15152 | unbraced | 2 |
| 15153 | unbosom | 2 |
| 15154 | unbonneted | 2 |
| 15155 | unbolt | 2 |
| 15156 | unbiassed | 2 |
| 15157 | unbar | 2 |
| 15158 | unaffected | 2 |
| 15159 | unadvisedly | 2 |
| 15160 | unadvised | 2 |
| 15161 | umber | 2 |
| 15162 | ulcer | 2 |
| 15163 | uglier | 2 |
| 15164 | tyrian | 2 |
| 15165 | typhon | 2 |
| 15166 | twos | 2 |
| 15167 | twit | 2 |
| 15168 | twist | 2 |
| 15169 | twink | 2 |
| 15170 | twine | 2 |
| 15171 | twilight | 2 |
| 15172 | twig | 2 |
| 15173 | twentieth | 2 |
| 15174 | twelfth | 2 |
| 15175 | twangling | 2 |
| 15176 | tussock | 2 |
| 15177 | turpitude | 2 |
| 15178 | turnips | 2 |
| 15179 | turkeys | 2 |
| 15180 | turbulent | 2 |
| 15181 | turbans | 2 |
| 15182 | turban | 2 |
| 15183 | tuns | 2 |
| 15184 | tuning | 2 |
| 15185 | tuneable | 2 |
| 15186 | tugging | 2 |
| 15187 | tugg | 2 |
| 15188 | tuck | 2 |
| 15189 | truss | 2 |
| 15190 | trumpeters | 2 |
| 15191 | trumpeted | 2 |
| 15192 | trumpery | 2 |
| 15193 | truckle | 2 |
| 15194 | troutlets | 2 |
| 15195 | troutlet | 2 |
| 15196 | troubadours | 2 |
| 15197 | trotting | 2 |
| 15198 | tronchon | 2 |
| 15199 | troll | 2 |
| 15200 | trojans | 2 |
| 15201 | triumvirate | 2 |
| 15202 | triumvir | 2 |
| 15203 | triumphal | 2 |
| 15204 | tristful | 2 |
| 15205 | trips | 2 |
| 15206 | trippingly | 2 |
| 15207 | tripe | 2 |
| 15208 | trinity | 2 |
| 15209 | trifled | 2 |
| 15210 | trident | 2 |
| 15211 | tricksy | 2 |
| 15212 | trickling | 2 |
| 15213 | tributaries | 2 |
| 15214 | tribulation | 2 |
| 15215 | trenched | 2 |
| 15216 | tremor | 2 |
| 15217 | trebles | 2 |
| 15218 | treatise | 2 |
| 15219 | treasurer | 2 |
| 15220 | tray | 2 |
| 15221 | traversing | 2 |
| 15222 | traps | 2 |
| 15223 | trapp | 2 |
| 15224 | transpose | 2 |
| 15225 | transports | 2 |
| 15226 | transporting | 2 |
| 15227 | translating | 2 |
| 15228 | transitory | 2 |
| 15229 | transgressing | 2 |
| 15230 | transactions | 2 |
| 15231 | transact | 2 |
| 15232 | trance | 2 |
| 15233 | traitress | 2 |
| 15234 | trailed | 2 |
| 15235 | tragedians | 2 |
| 15236 | tradesmen | 2 |
| 15237 | tradesman | 2 |
| 15238 | traded | 2 |
| 15239 | track | 2 |
| 15240 | townsmen | 2 |
| 15241 | towel | 2 |
| 15242 | tourney | 2 |
| 15243 | tournaments | 2 |
| 15244 | tottering | 2 |
| 15245 | tot | 2 |
| 15246 | toryne | 2 |
| 15247 | torturing | 2 |
| 15248 | torturer | 2 |
| 15249 | tormentors | 2 |
| 15250 | tormenting | 2 |
| 15251 | torchbearers | 2 |
| 15252 | topples | 2 |
| 15253 | topple | 2 |
| 15254 | topping | 2 |
| 15255 | topp | 2 |
| 15256 | topmast | 2 |
| 15257 | tool | 2 |
| 15258 | tolosa | 2 |
| 15259 | tolerably | 2 |
| 15260 | toledans | 2 |
| 15261 | toilsome | 2 |
| 15262 | tofore | 2 |
| 15263 | tocho | 2 |
| 15264 | tobosan | 2 |
| 15265 | toasts | 2 |
| 15266 | tithing | 2 |
| 15267 | tissue | 2 |
| 15268 | tipstaffs | 2 |
| 15269 | tinacrio | 2 |
| 15270 | timbrels | 2 |
| 15271 | tilts | 2 |
| 15272 | tilth | 2 |
| 15273 | tilter | 2 |
| 15274 | tilly | 2 |
| 15275 | tillage | 2 |
| 15276 | tightening | 2 |
| 15277 | tighten | 2 |
| 15278 | tickles | 2 |
| 15279 | tick | 2 |
| 15280 | ti | 2 |
| 15281 | thwarting | 2 |
| 15282 | thunderer | 2 |
| 15283 | thund | 2 |
| 15284 | thrower | 2 |
| 15285 | throstle | 2 |
| 15286 | thronging | 2 |
| 15287 | thrones | 2 |
| 15288 | throbbing | 2 |
| 15289 | thriving | 2 |
| 15290 | thrilling | 2 |
| 15291 | threading | 2 |
| 15292 | threaden | 2 |
| 15293 | thrasonical | 2 |
| 15294 | thraldom | 2 |
| 15295 | thoughtless | 2 |
| 15296 | thoughtful | 2 |
| 15297 | thistles | 2 |
| 15298 | thisne | 2 |
| 15299 | thirties | 2 |
| 15300 | thirdly | 2 |
| 15301 | thimble | 2 |
| 15302 | thickets | 2 |
| 15303 | thickens | 2 |
| 15304 | therewith | 2 |
| 15305 | theology | 2 |
| 15306 | thenceforth | 2 |
| 15307 | themes | 2 |
| 15308 | thanksgiving | 2 |
| 15309 | thanklessly | 2 |
| 15310 | texture | 2 |
| 15311 | tether | 2 |
| 15312 | testimonies | 2 |
| 15313 | tester | 2 |
| 15314 | terrify | 2 |
| 15315 | termed | 2 |
| 15316 | termagant | 2 |
| 15317 | tenfold | 2 |
| 15318 | tench | 2 |
| 15319 | tenantless | 2 |
| 15320 | tenantius | 2 |
| 15321 | tempters | 2 |
| 15322 | tempter | 2 |
| 15323 | temperately | 2 |
| 15324 | temperament | 2 |
| 15325 | tembleque | 2 |
| 15326 | tediously | 2 |
| 15327 | teat | 2 |
| 15328 | taxing | 2 |
| 15329 | taxations | 2 |
| 15330 | tasty | 2 |
| 15331 | tasters | 2 |
| 15332 | taster | 2 |
| 15333 | tassel | 2 |
| 15334 | tasking | 2 |
| 15335 | tartness | 2 |
| 15336 | tart | 2 |
| 15337 | tarries | 2 |
| 15338 | targets | 2 |
| 15339 | targes | 2 |
| 15340 | tape | 2 |
| 15341 | tanner | 2 |
| 15342 | tanned | 2 |
| 15343 | tamworth | 2 |
| 15344 | tameness | 2 |
| 15345 | tameji | 2 |
| 15346 | tally | 2 |
| 15347 | taller | 2 |
| 15348 | talbots | 2 |
| 15349 | takest | 2 |
| 15350 | tah | 2 |
| 15351 | taciturnity | 2 |
| 15352 | tablets | 2 |
| 15353 | syrups | 2 |
| 15354 | synagogue | 2 |
| 15355 | sympathized | 2 |
| 15356 | sympathize | 2 |
| 15357 | syllables | 2 |
| 15358 | sylla | 2 |
| 15359 | sy | 2 |
| 15360 | swum | 2 |
| 15361 | swounds | 2 |
| 15362 | swounded | 2 |
| 15363 | sworder | 2 |
| 15364 | swoop | 2 |
| 15365 | swoonings | 2 |
| 15366 | swooning | 2 |
| 15367 | swoln | 2 |
| 15368 | swits | 2 |
| 15369 | swinish | 2 |
| 15370 | sweetmeats | 2 |
| 15371 | sweepers | 2 |
| 15372 | sweaty | 2 |
| 15373 | swearings | 2 |
| 15374 | swearers | 2 |
| 15375 | swaying | 2 |
| 15376 | swathing | 2 |
| 15377 | swath | 2 |
| 15378 | swashing | 2 |
| 15379 | swashbuckler | 2 |
| 15380 | swarming | 2 |
| 15381 | sware | 2 |
| 15382 | swam | 2 |
| 15383 | swains | 2 |
| 15384 | swabber | 2 |
| 15385 | suum | 2 |
| 15386 | sustains | 2 |
| 15387 | sustaining | 2 |
| 15388 | suspire | 2 |
| 15389 | survivor | 2 |
| 15390 | survives | 2 |
| 15391 | surround | 2 |
| 15392 | surprises | 2 |
| 15393 | surplus | 2 |
| 15394 | surnam | 2 |
| 15395 | surmounted | 2 |
| 15396 | surmount | 2 |
| 15397 | surgeons | 2 |
| 15398 | sureties | 2 |
| 15399 | surest | 2 |
| 15400 | supremely | 2 |
| 15401 | supports | 2 |
| 15402 | supportance | 2 |
| 15403 | supplying | 2 |
| 15404 | supplie | 2 |
| 15405 | suppler | 2 |
| 15406 | supplement | 2 |
| 15407 | supping | 2 |
| 15408 | suppers | 2 |
| 15409 | supervise | 2 |
| 15410 | superhuman | 2 |
| 15411 | superficially | 2 |
| 15412 | superficial | 2 |
| 15413 | superabundance | 2 |
| 15414 | sunshades | 2 |
| 15415 | sunbeam | 2 |
| 15416 | summed | 2 |
| 15417 | summary | 2 |
| 15418 | sulph | 2 |
| 15419 | sullied | 2 |
| 15420 | suffrages | 2 |
| 15421 | suffic | 2 |
| 15422 | sufferers | 2 |
| 15423 | suckle | 2 |
| 15424 | sucker | 2 |
| 15425 | succoured | 2 |
| 15426 | successors | 2 |
| 15427 | successes | 2 |
| 15428 | succeeders | 2 |
| 15429 | subtlety | 2 |
| 15430 | subtleties | 2 |
| 15431 | subterfuge | 2 |
| 15432 | substituted | 2 |
| 15433 | substances | 2 |
| 15434 | suborned | 2 |
| 15435 | subjected | 2 |
| 15436 | subduing | 2 |
| 15437 | sub | 2 |
| 15438 | styx | 2 |
| 15439 | stygian | 2 |
| 15440 | sturdily | 2 |
| 15441 | stupidity | 2 |
| 15442 | stupefy | 2 |
| 15443 | stunned | 2 |
| 15444 | stump | 2 |
| 15445 | stuffing | 2 |
| 15446 | studded | 2 |
| 15447 | strutting | 2 |
| 15448 | strumpets | 2 |
| 15449 | strumpeted | 2 |
| 15450 | structure | 2 |
| 15451 | strolling | 2 |
| 15452 | stripling | 2 |
| 15453 | strikest | 2 |
| 15454 | strik | 2 |
| 15455 | strifes | 2 |
| 15456 | stricter | 2 |
| 15457 | strenuously | 2 |
| 15458 | strengthless | 2 |
| 15459 | streamers | 2 |
| 15460 | straps | 2 |
| 15461 | strappado | 2 |
| 15462 | strangling | 2 |
| 15463 | strangles | 2 |
| 15464 | straitness | 2 |
| 15465 | strained | 2 |
| 15466 | stove | 2 |
| 15467 | stoutest | 2 |
| 15468 | storming | 2 |
| 15469 | ston | 2 |
| 15470 | stomachers | 2 |
| 15471 | stocked | 2 |
| 15472 | stinted | 2 |
| 15473 | stimulate | 2 |
| 15474 | stigmatic | 2 |
| 15475 | stiffly | 2 |
| 15476 | stews | 2 |
| 15477 | stewed | 2 |
| 15478 | stewardship | 2 |
| 15479 | sternness | 2 |
| 15480 | sternly | 2 |
| 15481 | sterner | 2 |
| 15482 | steers | 2 |
| 15483 | steering | 2 |
| 15484 | steepy | 2 |
| 15485 | steeples | 2 |
| 15486 | steely | 2 |
| 15487 | stealthy | 2 |
| 15488 | stealthily | 2 |
| 15489 | startle | 2 |
| 15490 | starry | 2 |
| 15491 | starlight | 2 |
| 15492 | stares | 2 |
| 15493 | starch | 2 |
| 15494 | stanza | 2 |
| 15495 | standest | 2 |
| 15496 | staircase | 2 |
| 15497 | stainless | 2 |
| 15498 | stags | 2 |
| 15499 | staffords | 2 |
| 15500 | squier | 2 |
| 15501 | squeezing | 2 |
| 15502 | squeeze | 2 |
| 15503 | squeamish | 2 |
| 15504 | squeak | 2 |
| 15505 | squand | 2 |
| 15506 | spying | 2 |
| 15507 | spurio | 2 |
| 15508 | sprout | 2 |
| 15509 | springe | 2 |
| 15510 | sprigs | 2 |
| 15511 | spray | 2 |
| 15512 | sprawl | 2 |
| 15513 | spousal | 2 |
| 15514 | sportsmen | 2 |
| 15515 | spokesman | 2 |
| 15516 | splinters | 2 |
| 15517 | splendidly | 2 |
| 15518 | spleens | 2 |
| 15519 | spleenful | 2 |
| 15520 | spitted | 2 |
| 15521 | spinsters | 2 |
| 15522 | spinners | 2 |
| 15523 | spindle | 2 |
| 15524 | spills | 2 |
| 15525 | spilling | 2 |
| 15526 | spike | 2 |
| 15527 | spiced | 2 |
| 15528 | spero | 2 |
| 15529 | spendthrift | 2 |
| 15530 | speedier | 2 |
| 15531 | speeded | 2 |
| 15532 | speculative | 2 |
| 15533 | spectacled | 2 |
| 15534 | speciously | 2 |
| 15535 | spawn | 2 |
| 15536 | spares | 2 |
| 15537 | spangled | 2 |
| 15538 | spak | 2 |
| 15539 | sowing | 2 |
| 15540 | sov | 2 |
| 15541 | southward | 2 |
| 15542 | southam | 2 |
| 15543 | soundless | 2 |
| 15544 | soundest | 2 |
| 15545 | soulless | 2 |
| 15546 | sorrowed | 2 |
| 15547 | sorer | 2 |
| 15548 | soreness | 2 |
| 15549 | sorceries | 2 |
| 15550 | sophisticated | 2 |
| 15551 | soothing | 2 |
| 15552 | soothes | 2 |
| 15553 | sonorous | 2 |
| 15554 | somersaults | 2 |
| 15555 | solve | 2 |
| 15556 | solon | 2 |
| 15557 | solinus | 2 |
| 15558 | soliloquy | 2 |
| 15559 | solicitor | 2 |
| 15560 | solemnized | 2 |
| 15561 | solemnize | 2 |
| 15562 | solder | 2 |
| 15563 | sojourned | 2 |
| 15564 | soiled | 2 |
| 15565 | softens | 2 |
| 15566 | softening | 2 |
| 15567 | socks | 2 |
| 15568 | sobriety | 2 |
| 15569 | sobbing | 2 |
| 15570 | sob | 2 |
| 15571 | soaking | 2 |
| 15572 | soak | 2 |
| 15573 | snowy | 2 |
| 15574 | snorting | 2 |
| 15575 | sneeze | 2 |
| 15576 | sneaping | 2 |
| 15577 | snarling | 2 |
| 15578 | snar | 2 |
| 15579 | snapper | 2 |
| 15580 | smothered | 2 |
| 15581 | smites | 2 |
| 15582 | smite | 2 |
| 15583 | smilingly | 2 |
| 15584 | smartness | 2 |
| 15585 | smartly | 2 |
| 15586 | smarting | 2 |
| 15587 | sluttery | 2 |
| 15588 | sluts | 2 |
| 15589 | sluic | 2 |
| 15590 | slubber | 2 |
| 15591 | slowness | 2 |
| 15592 | slothful | 2 |
| 15593 | slops | 2 |
| 15594 | slop | 2 |
| 15595 | slit | 2 |
| 15596 | slimy | 2 |
| 15597 | slides | 2 |
| 15598 | sliced | 2 |
| 15599 | sleepless | 2 |
| 15600 | slaughtermen | 2 |
| 15601 | slaughterman | 2 |
| 15602 | slandering | 2 |
| 15603 | slackly | 2 |
| 15604 | slacken | 2 |
| 15605 | skirr | 2 |
| 15606 | skimming | 2 |
| 15607 | skillful | 2 |
| 15608 | skilled | 2 |
| 15609 | sizes | 2 |
| 15610 | situations | 2 |
| 15611 | situate | 2 |
| 15612 | sithence | 2 |
| 15613 | sinning | 2 |
| 15614 | singleness | 2 |
| 15615 | singed | 2 |
| 15616 | singe | 2 |
| 15617 | sinfully | 2 |
| 15618 | simular | 2 |
| 15619 | simpler | 2 |
| 15620 | simp | 2 |
| 15621 | silva | 2 |
| 15622 | silenced | 2 |
| 15623 | signing | 2 |
| 15624 | sifted | 2 |
| 15625 | sideways | 2 |
| 15626 | sicut | 2 |
| 15627 | sickle | 2 |
| 15628 | sickens | 2 |
| 15629 | sicils | 2 |
| 15630 | shrugged | 2 |
| 15631 | shrub | 2 |
| 15632 | shrove | 2 |
| 15633 | shriving | 2 |
| 15634 | shrive | 2 |
| 15635 | shrines | 2 |
| 15636 | shrimp | 2 |
| 15637 | shrilly | 2 |
| 15638 | shrieve | 2 |
| 15639 | shred | 2 |
| 15640 | showest | 2 |
| 15641 | shovels | 2 |
| 15642 | shove | 2 |
| 15643 | shov | 2 |
| 15644 | shoon | 2 |
| 15645 | shog | 2 |
| 15646 | shoeing | 2 |
| 15647 | shivering | 2 |
| 15648 | shipwright | 2 |
| 15649 | shipboard | 2 |
| 15650 | shes | 2 |
| 15651 | shelves | 2 |
| 15652 | sheltered | 2 |
| 15653 | shelf | 2 |
| 15654 | sheeted | 2 |
| 15655 | sheepskin | 2 |
| 15656 | sheathes | 2 |
| 15657 | sheathed | 2 |
| 15658 | shearers | 2 |
| 15659 | sheaf | 2 |
| 15660 | sharpest | 2 |
| 15661 | shark | 2 |
| 15662 | shards | 2 |
| 15663 | shar | 2 |
| 15664 | shaped | 2 |
| 15665 | shaming | 2 |
| 15666 | shambles | 2 |
| 15667 | shallows | 2 |
| 15668 | shallowest | 2 |
| 15669 | shag | 2 |
| 15670 | shafalus | 2 |
| 15671 | shadowy | 2 |
| 15672 | shadowing | 2 |
| 15673 | shadowed | 2 |
| 15674 | severing | 2 |
| 15675 | severely | 2 |
| 15676 | sev | 2 |
| 15677 | setebos | 2 |
| 15678 | serviteur | 2 |
| 15679 | serpigo | 2 |
| 15680 | serene | 2 |
| 15681 | separating | 2 |
| 15682 | sensuality | 2 |
| 15683 | sendeth | 2 |
| 15684 | sendal | 2 |
| 15685 | seller | 2 |
| 15686 | seld | 2 |
| 15687 | seese | 2 |
| 15688 | seeker | 2 |
| 15689 | seducing | 2 |
| 15690 | seditious | 2 |
| 15691 | secular | 2 |
| 15692 | sectary | 2 |
| 15693 | secretaries | 2 |
| 15694 | secondary | 2 |
| 15695 | seating | 2 |
| 15696 | seaside | 2 |
| 15697 | searched | 2 |
| 15698 | seaport | 2 |
| 15699 | seam | 2 |
| 15700 | scythians | 2 |
| 15701 | scythia | 2 |
| 15702 | scutcheon | 2 |
| 15703 | scuse | 2 |
| 15704 | scurrilous | 2 |
| 15705 | scurrility | 2 |
| 15706 | scullion | 2 |
| 15707 | scuffles | 2 |
| 15708 | scrupulously | 2 |
| 15709 | scrubbed | 2 |
| 15710 | screw | 2 |
| 15711 | scream | 2 |
| 15712 | scratched | 2 |
| 15713 | scourg | 2 |
| 15714 | scorpion | 2 |
| 15715 | scores | 2 |
| 15716 | scolds | 2 |
| 15717 | scoff | 2 |
| 15718 | scion | 2 |
| 15719 | sciatica | 2 |
| 15720 | schooled | 2 |
| 15721 | schemers | 2 |
| 15722 | schedules | 2 |
| 15723 | sceptred | 2 |
| 15724 | scept | 2 |
| 15725 | scandaliz | 2 |
| 15726 | scalp | 2 |
| 15727 | scaled | 2 |
| 15728 | scalding | 2 |
| 15729 | scabby | 2 |
| 15730 | sayas | 2 |
| 15731 | sayago | 2 |
| 15732 | saxons | 2 |
| 15733 | savagery | 2 |
| 15734 | saucily | 2 |
| 15735 | saturdays | 2 |
| 15736 | saturday | 2 |
| 15737 | saturated | 2 |
| 15738 | satisfies | 2 |
| 15739 | satirical | 2 |
| 15740 | sated | 2 |
| 15741 | sate | 2 |
| 15742 | sard | 2 |
| 15743 | sarcenet | 2 |
| 15744 | sapphire | 2 |
| 15745 | sapling | 2 |
| 15746 | sanity | 2 |
| 15747 | sanction | 2 |
| 15748 | sanctimonious | 2 |
| 15749 | sancta | 2 |
| 15750 | sampler | 2 |
| 15751 | saluting | 2 |
| 15752 | saluteth | 2 |
| 15753 | salted | 2 |
| 15754 | sallying | 2 |
| 15755 | sallow | 2 |
| 15756 | salamander | 2 |
| 15757 | saddling | 2 |
| 15758 | saddler | 2 |
| 15759 | sacrilegious | 2 |
| 15760 | sacrificing | 2 |
| 15761 | sacrific | 2 |
| 15762 | sabbath | 2 |
| 15763 | saavedra | 2 |
| 15764 | rustle | 2 |
| 15765 | rustics | 2 |
| 15766 | runners | 2 |
| 15767 | runagates | 2 |
| 15768 | rump | 2 |
| 15769 | ruminated | 2 |
| 15770 | rumia | 2 |
| 15771 | ruling | 2 |
| 15772 | rulers | 2 |
| 15773 | ruiz | 2 |
| 15774 | ruinate | 2 |
| 15775 | ruggiero | 2 |
| 15776 | rudiments | 2 |
| 15777 | rudesby | 2 |
| 15778 | ruder | 2 |
| 15779 | rudder | 2 |
| 15780 | rud | 2 |
| 15781 | ruby | 2 |
| 15782 | roy | 2 |
| 15783 | rowel | 2 |
| 15784 | roving | 2 |
| 15785 | rove | 2 |
| 15786 | routs | 2 |
| 15787 | roussi | 2 |
| 15788 | roundabout | 2 |
| 15789 | roughest | 2 |
| 15790 | rougher | 2 |
| 15791 | rotting | 2 |
| 15792 | rottenness | 2 |
| 15793 | rotted | 2 |
| 15794 | rotolando | 2 |
| 15795 | roscius | 2 |
| 15796 | roping | 2 |
| 15797 | rooks | 2 |
| 15798 | ronyon | 2 |
| 15799 | roderick | 2 |
| 15800 | robustious | 2 |
| 15801 | roared | 2 |
| 15802 | roadside | 2 |
| 15803 | rivets | 2 |
| 15804 | rivet | 2 |
| 15805 | rived | 2 |
| 15806 | rivall | 2 |
| 15807 | risks | 2 |
| 15808 | ripest | 2 |
| 15809 | ripening | 2 |
| 15810 | ringlets | 2 |
| 15811 | rim | 2 |
| 15812 | righter | 2 |
| 15813 | rigging | 2 |
| 15814 | rig | 2 |
| 15815 | rifle | 2 |
| 15816 | rids | 2 |
| 15817 | ridges | 2 |
| 15818 | ridge | 2 |
| 15819 | ridest | 2 |
| 15820 | ridden | 2 |
| 15821 | riddance | 2 |
| 15822 | ribbon | 2 |
| 15823 | ribbed | 2 |
| 15824 | riband | 2 |
| 15825 | ribald | 2 |
| 15826 | rhymers | 2 |
| 15827 | rhubarb | 2 |
| 15828 | rfull | 2 |
| 15829 | rex | 2 |
| 15830 | revolving | 2 |
| 15831 | revolved | 2 |
| 15832 | revil | 2 |
| 15833 | reverted | 2 |
| 15834 | reverenc | 2 |
| 15835 | reverberate | 2 |
| 15836 | revellers | 2 |
| 15837 | revealing | 2 |
| 15838 | returneth | 2 |
| 15839 | retrograde | 2 |
| 15840 | retorts | 2 |
| 15841 | retold | 2 |
| 15842 | reticent | 2 |
| 15843 | resurrection | 2 |
| 15844 | restrictions | 2 |
| 15845 | restricted | 2 |
| 15846 | restraining | 2 |
| 15847 | restful | 2 |
| 15848 | ress | 2 |
| 15849 | responsible | 2 |
| 15850 | responsibilities | 2 |
| 15851 | respectfully | 2 |
| 15852 | resounds | 2 |
| 15853 | resounding | 2 |
| 15854 | resounded | 2 |
| 15855 | resisting | 2 |
| 15856 | resident | 2 |
| 15857 | reserving | 2 |
| 15858 | rescuing | 2 |
| 15859 | rescues | 2 |
| 15860 | rers | 2 |
| 15861 | requites | 2 |
| 15862 | requirest | 2 |
| 15863 | requesting | 2 |
| 15864 | reputes | 2 |
| 15865 | reprobate | 2 |
| 15866 | reprieves | 2 |
| 15867 | represents | 2 |
| 15868 | representing | 2 |
| 15869 | representations | 2 |
| 15870 | reporting | 2 |
| 15871 | repletion | 2 |
| 15872 | replenished | 2 |
| 15873 | repenting | 2 |
| 15874 | reparation | 2 |
| 15875 | renouncing | 2 |
| 15876 | renewal | 2 |
| 15877 | rence | 2 |
| 15878 | remotion | 2 |
| 15879 | remonstrance | 2 |
| 15880 | remissness | 2 |
| 15881 | reminds | 2 |
| 15882 | reminding | 2 |
| 15883 | remembrancer | 2 |
| 15884 | rememberest | 2 |
| 15885 | remaineth | 2 |
| 15886 | reluctantly | 2 |
| 15887 | relishing | 2 |
| 15888 | relentless | 2 |
| 15889 | relenting | 2 |
| 15890 | rejoined | 2 |
| 15891 | rejoices | 2 |
| 15892 | reining | 2 |
| 15893 | reigning | 2 |
| 15894 | rehearsal | 2 |
| 15895 | reguerdon | 2 |
| 15896 | regain | 2 |
| 15897 | refusal | 2 |
| 15898 | refrained | 2 |
| 15899 | reformed | 2 |
| 15900 | reflex | 2 |
| 15901 | refers | 2 |
| 15902 | referring | 2 |
| 15903 | references | 2 |
| 15904 | redressing | 2 |
| 15905 | redresses | 2 |
| 15906 | redeliver | 2 |
| 15907 | redeemer | 2 |
| 15908 | redbreast | 2 |
| 15909 | rector | 2 |
| 15910 | recreants | 2 |
| 15911 | recoveries | 2 |
| 15912 | recounting | 2 |
| 15913 | recorder | 2 |
| 15914 | recordation | 2 |
| 15915 | reconsider | 2 |
| 15916 | reconciles | 2 |
| 15917 | recommends | 2 |
| 15918 | recommendation | 2 |
| 15919 | recollections | 2 |
| 15920 | reclaim | 2 |
| 15921 | recks | 2 |
| 15922 | recklessly | 2 |
| 15923 | reciterai | 2 |
| 15924 | recital | 2 |
| 15925 | reciprocal | 2 |
| 15926 | receivest | 2 |
| 15927 | recanting | 2 |
| 15928 | recantation | 2 |
| 15929 | recalling | 2 |
| 15930 | recalled | 2 |
| 15931 | rebuilt | 2 |
| 15932 | rebell | 2 |
| 15933 | reave | 2 |
| 15934 | reasonless | 2 |
| 15935 | reasoned | 2 |
| 15936 | reaps | 2 |
| 15937 | realise | 2 |
| 15938 | rawness | 2 |
| 15939 | ravishing | 2 |
| 15940 | ravisher | 2 |
| 15941 | ravings | 2 |
| 15942 | ravine | 2 |
| 15943 | raves | 2 |
| 15944 | rattled | 2 |
| 15945 | rattle | 2 |
| 15946 | rasher | 2 |
| 15947 | rarities | 2 |
| 15948 | rapture | 2 |
| 15949 | raps | 2 |
| 15950 | ransoms | 2 |
| 15951 | ransomless | 2 |
| 15952 | ransacked | 2 |
| 15953 | rankle | 2 |
| 15954 | rankest | 2 |
| 15955 | ranging | 2 |
| 15956 | ranged | 2 |
| 15957 | ramon | 2 |
| 15958 | ramm | 2 |
| 15959 | rambling | 2 |
| 15960 | rald | 2 |
| 15961 | ral | 2 |
| 15962 | raisins | 2 |
| 15963 | rains | 2 |
| 15964 | rainbows | 2 |
| 15965 | railest | 2 |
| 15966 | railed | 2 |
| 15967 | radish | 2 |
| 15968 | racks | 2 |
| 15969 | rackets | 2 |
| 15970 | racked | 2 |
| 15971 | rabblement | 2 |
| 15972 | rabbits | 2 |
| 15973 | quotidian | 2 |
| 15974 | quotes | 2 |
| 15975 | quoit | 2 |
| 15976 | quixotize | 2 |
| 15977 | quixana | 2 |
| 15978 | quire | 2 |
| 15979 | quip | 2 |
| 15980 | quintanar | 2 |
| 15981 | quinces | 2 |
| 15982 | quilt | 2 |
| 15983 | quietus | 2 |
| 15984 | quieter | 2 |
| 15985 | quickwitted | 2 |
| 15986 | quicker | 2 |
| 15987 | quickens | 2 |
| 15988 | questionable | 2 |
| 15989 | quesada | 2 |
| 15990 | quenched | 2 |
| 15991 | quando | 2 |
| 15992 | quand | 2 |
| 15993 | quak | 2 |
| 15994 | quails | 2 |
| 15995 | quailing | 2 |
| 15996 | quagmire | 2 |
| 15997 | quae | 2 |
| 15998 | pyramids | 2 |
| 15999 | puzzles | 2 |
| 16000 | puttock | 2 |
| 16001 | pusillanimity | 2 |
| 16002 | purveyor | 2 |
| 16003 | pursy | 2 |
| 16004 | pursuivants | 2 |
| 16005 | pursuest | 2 |
| 16006 | pursuance | 2 |
| 16007 | purposeth | 2 |
| 16008 | purport | 2 |
| 16009 | purpled | 2 |
| 16010 | pups | 2 |
| 16011 | pup | 2 |
| 16012 | punto | 2 |
| 16013 | punishments | 2 |
| 16014 | punctilious | 2 |
| 16015 | punches | 2 |
| 16016 | punched | 2 |
| 16017 | pumps | 2 |
| 16018 | pump | 2 |
| 16019 | pulpits | 2 |
| 16020 | pullets | 2 |
| 16021 | puddled | 2 |
| 16022 | puddle | 2 |
| 16023 | puddings | 2 |
| 16024 | publishing | 2 |
| 16025 | publisher | 2 |
| 16026 | publicola | 2 |
| 16027 | psalteries | 2 |
| 16028 | psalms | 2 |
| 16029 | prudery | 2 |
| 16030 | provoking | 2 |
| 16031 | provocative | 2 |
| 16032 | provincial | 2 |
| 16033 | providing | 2 |
| 16034 | provides | 2 |
| 16035 | provident | 2 |
| 16036 | proveth | 2 |
| 16037 | protract | 2 |
| 16038 | protesting | 2 |
| 16039 | protecting | 2 |
| 16040 | prosperously | 2 |
| 16041 | prosp | 2 |
| 16042 | proserpina | 2 |
| 16043 | prosecution | 2 |
| 16044 | prorogue | 2 |
| 16045 | prophetically | 2 |
| 16046 | prophesying | 2 |
| 16047 | promptitude | 2 |
| 16048 | prompter | 2 |
| 16049 | prolix | 2 |
| 16050 | prognostication | 2 |
| 16051 | prog | 2 |
| 16052 | profiting | 2 |
| 16053 | profited | 2 |
| 16054 | profitably | 2 |
| 16055 | proficient | 2 |
| 16056 | proffers | 2 |
| 16057 | produc | 2 |
| 16058 | prodigiously | 2 |
| 16059 | procures | 2 |
| 16060 | procur | 2 |
| 16061 | procrus | 2 |
| 16062 | proclaiming | 2 |
| 16063 | probability | 2 |
| 16064 | pro | 2 |
| 16065 | prizer | 2 |
| 16066 | privity | 2 |
| 16067 | privilegio | 2 |
| 16068 | privileged | 2 |
| 16069 | privates | 2 |
| 16070 | priority | 2 |
| 16071 | prioress | 2 |
| 16072 | printers | 2 |
| 16073 | prings | 2 |
| 16074 | principle | 2 |
| 16075 | primroses | 2 |
| 16076 | primero | 2 |
| 16077 | primal | 2 |
| 16078 | prig | 2 |
| 16079 | priesthood | 2 |
| 16080 | prided | 2 |
| 16081 | prices | 2 |
| 16082 | pribbles | 2 |
| 16083 | priamus | 2 |
| 16084 | preventing | 2 |
| 16085 | pretext | 2 |
| 16086 | presuming | 2 |
| 16087 | prest | 2 |
| 16088 | presonages | 2 |
| 16089 | presentment | 2 |
| 16090 | presentation | 2 |
| 16091 | prescript | 2 |
| 16092 | prescribed | 2 |
| 16093 | prepost | 2 |
| 16094 | prenominate | 2 |
| 16095 | preliminaries | 2 |
| 16096 | prejudicial | 2 |
| 16097 | preferments | 2 |
| 16098 | preeminence | 2 |
| 16099 | predominate | 2 |
| 16100 | predominance | 2 |
| 16101 | precipitation | 2 |
| 16102 | precinct | 2 |
| 16103 | precept | 2 |
| 16104 | prebendary | 2 |
| 16105 | preamble | 2 |
| 16106 | preaches | 2 |
| 16107 | preachers | 2 |
| 16108 | preached | 2 |
| 16109 | prattling | 2 |
| 16110 | prank | 2 |
| 16111 | prain | 2 |
| 16112 | powerfully | 2 |
| 16113 | pout | 2 |
| 16114 | pourquoi | 2 |
| 16115 | pourest | 2 |
| 16116 | pounced | 2 |
| 16117 | potter | 2 |
| 16118 | potpan | 2 |
| 16119 | potosi | 2 |
| 16120 | pothouse | 2 |
| 16121 | potently | 2 |
| 16122 | potations | 2 |
| 16123 | postures | 2 |
| 16124 | postscript | 2 |
| 16125 | postmaster | 2 |
| 16126 | posterior | 2 |
| 16127 | possesseth | 2 |
| 16128 | positions | 2 |
| 16129 | posies | 2 |
| 16130 | portrayed | 2 |
| 16131 | portray | 2 |
| 16132 | portmanteau | 2 |
| 16133 | portcullis | 2 |
| 16134 | portance | 2 |
| 16135 | portals | 2 |
| 16136 | portal | 2 |
| 16137 | porringer | 2 |
| 16138 | pore | 2 |
| 16139 | popularity | 2 |
| 16140 | popp | 2 |
| 16141 | poplar | 2 |
| 16142 | poole | 2 |
| 16143 | pontifical | 2 |
| 16144 | ponies | 2 |
| 16145 | pondering | 2 |
| 16146 | pompous | 2 |
| 16147 | pommel | 2 |
| 16148 | poltroon | 2 |
| 16149 | pollution | 2 |
| 16150 | polluted | 2 |
| 16151 | politicly | 2 |
| 16152 | polish | 2 |
| 16153 | polecats | 2 |
| 16154 | poetic | 2 |
| 16155 | poems | 2 |
| 16156 | poem | 2 |
| 16157 | pody | 2 |
| 16158 | podridas | 2 |
| 16159 | podrida | 2 |
| 16160 | plural | 2 |
| 16161 | plunging | 2 |
| 16162 | plunges | 2 |
| 16163 | plung | 2 |
| 16164 | plunder | 2 |
| 16165 | plumage | 2 |
| 16166 | ploughed | 2 |
| 16167 | plotting | 2 |
| 16168 | plodding | 2 |
| 16169 | plodded | 2 |
| 16170 | pliancy | 2 |
| 16171 | pledging | 2 |
| 16172 | pleasest | 2 |
| 16173 | pleadings | 2 |
| 16174 | pleached | 2 |
| 16175 | pleach | 2 |
| 16176 | playfellows | 2 |
| 16177 | platir | 2 |
| 16178 | plated | 2 |
| 16179 | plastered | 2 |
| 16180 | planting | 2 |
| 16181 | plantagenets | 2 |
| 16182 | planned | 2 |
| 16183 | plank | 2 |
| 16184 | planetary | 2 |
| 16185 | plainest | 2 |
| 16186 | plagued | 2 |
| 16187 | plagu | 2 |
| 16188 | plackets | 2 |
| 16189 | placeth | 2 |
| 16190 | pius | 2 |
| 16191 | pits | 2 |
| 16192 | pitfall | 2 |
| 16193 | pitchers | 2 |
| 16194 | pissing | 2 |
| 16195 | piss | 2 |
| 16196 | pioneers | 2 |
| 16197 | pinfold | 2 |
| 16198 | pinching | 2 |
| 16199 | pincers | 2 |
| 16200 | pills | 2 |
| 16201 | pillory | 2 |
| 16202 | pillicock | 2 |
| 16203 | pilate | 2 |
| 16204 | pigskin | 2 |
| 16205 | pictured | 2 |
| 16206 | picks | 2 |
| 16207 | pickaxe | 2 |
| 16208 | physiognomy | 2 |
| 16209 | physics | 2 |
| 16210 | physical | 2 |
| 16211 | phraseology | 2 |
| 16212 | philistine | 2 |
| 16213 | philippe | 2 |
| 16214 | pheeze | 2 |
| 16215 | pheasant | 2 |
| 16216 | pharaoh | 2 |
| 16217 | pewter | 2 |
| 16218 | pew | 2 |
| 16219 | peu | 2 |
| 16220 | petitionary | 2 |
| 16221 | pester | 2 |
| 16222 | perverted | 2 |
| 16223 | perverseness | 2 |
| 16224 | perusing | 2 |
| 16225 | perused | 2 |
| 16226 | perusal | 2 |
| 16227 | pertly | 2 |
| 16228 | pertinacity | 2 |
| 16229 | pertaining | 2 |
| 16230 | pertain | 2 |
| 16231 | pert | 2 |
| 16232 | personable | 2 |
| 16233 | persists | 2 |
| 16234 | persians | 2 |
| 16235 | persian | 2 |
| 16236 | persevering | 2 |
| 16237 | persevere | 2 |
| 16238 | perseverance | 2 |
| 16239 | persecuting | 2 |
| 16240 | perpetrated | 2 |
| 16241 | permitting | 2 |
| 16242 | perjure | 2 |
| 16243 | periods | 2 |
| 16244 | perge | 2 |
| 16245 | performs | 2 |
| 16246 | performances | 2 |
| 16247 | perfidy | 2 |
| 16248 | perfectness | 2 |
| 16249 | perfectest | 2 |
| 16250 | perdurable | 2 |
| 16251 | pensive | 2 |
| 16252 | pensioners | 2 |
| 16253 | pennyworths | 2 |
| 16254 | pennons | 2 |
| 16255 | penned | 2 |
| 16256 | penetrated | 2 |
| 16257 | penetrable | 2 |
| 16258 | penelope | 2 |
| 16259 | pendant | 2 |
| 16260 | pencils | 2 |
| 16261 | pelleted | 2 |
| 16262 | pelion | 2 |
| 16263 | peeping | 2 |
| 16264 | peel | 2 |
| 16265 | pede | 2 |
| 16266 | pease | 2 |
| 16267 | peard | 2 |
| 16268 | peacemakers | 2 |
| 16269 | pe | 2 |
| 16270 | pax | 2 |
| 16271 | pavement | 2 |
| 16272 | pausing | 2 |
| 16273 | paused | 2 |
| 16274 | pauper | 2 |
| 16275 | patroness | 2 |
| 16276 | patronage | 2 |
| 16277 | patrician | 2 |
| 16278 | patio | 2 |
| 16279 | patchery | 2 |
| 16280 | patched | 2 |
| 16281 | pastimes | 2 |
| 16282 | passport | 2 |
| 16283 | passeth | 2 |
| 16284 | passable | 2 |
| 16285 | pash | 2 |
| 16286 | pas | 2 |
| 16287 | partlet | 2 |
| 16288 | particularities | 2 |
| 16289 | participation | 2 |
| 16290 | participate | 2 |
| 16291 | partially | 2 |
| 16292 | parthians | 2 |
| 16293 | parrots | 2 |
| 16294 | parlour | 2 |
| 16295 | parks | 2 |
| 16296 | pardonnez | 2 |
| 16297 | pardonner | 2 |
| 16298 | parch | 2 |
| 16299 | pantheon | 2 |
| 16300 | pantaloons | 2 |
| 16301 | pans | 2 |
| 16302 | panoply | 2 |
| 16303 | pannonians | 2 |
| 16304 | panders | 2 |
| 16305 | pandars | 2 |
| 16306 | pamper | 2 |
| 16307 | palsied | 2 |
| 16308 | palmer | 2 |
| 16309 | palestine | 2 |
| 16310 | paleness | 2 |
| 16311 | palatine | 2 |
| 16312 | paints | 2 |
| 16313 | paintings | 2 |
| 16314 | painstaking | 2 |
| 16315 | pained | 2 |
| 16316 | padlock | 2 |
| 16317 | paddock | 2 |
| 16318 | paddling | 2 |
| 16319 | pacorus | 2 |
| 16320 | oyes | 2 |
| 16321 | oxlips | 2 |
| 16322 | owns | 2 |
| 16323 | overturn | 2 |
| 16324 | overta | 2 |
| 16325 | overspread | 2 |
| 16326 | overshine | 2 |
| 16327 | overrun | 2 |
| 16328 | overplus | 2 |
| 16329 | overpass | 2 |
| 16330 | overnight | 2 |
| 16331 | overlooks | 2 |
| 16332 | overgrown | 2 |
| 16333 | overflowing | 2 |
| 16334 | overcomes | 2 |
| 16335 | overboard | 2 |
| 16336 | overbear | 2 |
| 16337 | overawed | 2 |
| 16338 | oven | 2 |
| 16339 | outworn | 2 |
| 16340 | outwear | 2 |
| 16341 | outstretched | 2 |
| 16342 | outstare | 2 |
| 16343 | outset | 2 |
| 16344 | outlets | 2 |
| 16345 | outfacing | 2 |
| 16346 | outfac | 2 |
| 16347 | outdone | 2 |
| 16348 | ousel | 2 |
| 16349 | ouphes | 2 |
| 16350 | ounces | 2 |
| 16351 | otherwhere | 2 |
| 16352 | ostent | 2 |
| 16353 | ossa | 2 |
| 16354 | osiers | 2 |
| 16355 | orthography | 2 |
| 16356 | ort | 2 |
| 16357 | ork | 2 |
| 16358 | originals | 2 |
| 16359 | ore | 2 |
| 16360 | orchards | 2 |
| 16361 | orbaneja | 2 |
| 16362 | opulent | 2 |
| 16363 | oppressive | 2 |
| 16364 | oppressing | 2 |
| 16365 | opposers | 2 |
| 16366 | opposer | 2 |
| 16367 | opportune | 2 |
| 16368 | opes | 2 |
| 16369 | operibus | 2 |
| 16370 | operate | 2 |
| 16371 | operant | 2 |
| 16372 | opal | 2 |
| 16373 | ongles | 2 |
| 16374 | omne | 2 |
| 16375 | omissions | 2 |
| 16376 | olympian | 2 |
| 16377 | oleander | 2 |
| 16378 | olalla | 2 |
| 16379 | officials | 2 |
| 16380 | offic | 2 |
| 16381 | offhand | 2 |
| 16382 | odoriferous | 2 |
| 16383 | occupations | 2 |
| 16384 | occident | 2 |
| 16385 | obstructions | 2 |
| 16386 | observes | 2 |
| 16387 | observer | 2 |
| 16388 | observant | 2 |
| 16389 | observances | 2 |
| 16390 | obscuring | 2 |
| 16391 | obscenely | 2 |
| 16392 | oblique | 2 |
| 16393 | oared | 2 |
| 16394 | oaken | 2 |
| 16395 | ny | 2 |
| 16396 | nutmeg | 2 |
| 16397 | nurture | 2 |
| 16398 | nuncio | 2 |
| 16399 | numskull | 2 |
| 16400 | numbered | 2 |
| 16401 | novices | 2 |
| 16402 | novelties | 2 |
| 16403 | nourishing | 2 |
| 16404 | nourisheth | 2 |
| 16405 | notre | 2 |
| 16406 | notoriously | 2 |
| 16407 | notoriety | 2 |
| 16408 | notify | 2 |
| 16409 | notaries | 2 |
| 16410 | noseless | 2 |
| 16411 | nosegays | 2 |
| 16412 | northgate | 2 |
| 16413 | noose | 2 |
| 16414 | nominativo | 2 |
| 16415 | noised | 2 |
| 16416 | nois | 2 |
| 16417 | nointed | 2 |
| 16418 | nodded | 2 |
| 16419 | nobis | 2 |
| 16420 | nob | 2 |
| 16421 | noah | 2 |
| 16422 | nnight | 2 |
| 16423 | nit | 2 |
| 16424 | nips | 2 |
| 16425 | nipple | 2 |
| 16426 | nipping | 2 |
| 16427 | ninus | 2 |
| 16428 | ninety | 2 |
| 16429 | nimbler | 2 |
| 16430 | nill | 2 |
| 16431 | nightmare | 2 |
| 16432 | nightingales | 2 |
| 16433 | nighted | 2 |
| 16434 | niggardliness | 2 |
| 16435 | nibbling | 2 |
| 16436 | nettled | 2 |
| 16437 | nessus | 2 |
| 16438 | nerve | 2 |
| 16439 | nemean | 2 |
| 16440 | negotiations | 2 |
| 16441 | negotiation | 2 |
| 16442 | negotiate | 2 |
| 16443 | neglection | 2 |
| 16444 | needn | 2 |
| 16445 | needing | 2 |
| 16446 | nedar | 2 |
| 16447 | nectar | 2 |
| 16448 | necklace | 2 |
| 16449 | neatness | 2 |
| 16450 | nearness | 2 |
| 16451 | neaf | 2 |
| 16452 | navarino | 2 |
| 16453 | naturalists | 2 |
| 16454 | natur | 2 |
| 16455 | nasty | 2 |
| 16456 | naso | 2 |
| 16457 | narrowly | 2 |
| 16458 | napping | 2 |
| 16459 | nag | 2 |
| 16460 | mystification | 2 |
| 16461 | mysterious | 2 |
| 16462 | myrmidon | 2 |
| 16463 | muttons | 2 |
| 16464 | mutes | 2 |
| 16465 | mutability | 2 |
| 16466 | mustachio | 2 |
| 16467 | mussel | 2 |
| 16468 | musketry | 2 |
| 16469 | musics | 2 |
| 16470 | muscovites | 2 |
| 16471 | murky | 2 |
| 16472 | murcia | 2 |
| 16473 | munition | 2 |
| 16474 | municipality | 2 |
| 16475 | munching | 2 |
| 16476 | mummers | 2 |
| 16477 | mumbling | 2 |
| 16478 | multitudinous | 2 |
| 16479 | mulmutius | 2 |
| 16480 | mulier | 2 |
| 16481 | muley | 2 |
| 16482 | muffling | 2 |
| 16483 | mudejars | 2 |
| 16484 | mudded | 2 |
| 16485 | moys | 2 |
| 16486 | moy | 2 |
| 16487 | mowing | 2 |
| 16488 | movers | 2 |
| 16489 | moveables | 2 |
| 16490 | moveable | 2 |
| 16491 | mouthfuls | 2 |
| 16492 | moustache | 2 |
| 16493 | mousing | 2 |
| 16494 | mourns | 2 |
| 16495 | mountebanks | 2 |
| 16496 | mountainous | 2 |
| 16497 | mountaineer | 2 |
| 16498 | mottled | 2 |
| 16499 | motionless | 2 |
| 16500 | mortifying | 2 |
| 16501 | mortifications | 2 |
| 16502 | mortgaged | 2 |
| 16503 | mortally | 2 |
| 16504 | morsels | 2 |
| 16505 | mornings | 2 |
| 16506 | morals | 2 |
| 16507 | morality | 2 |
| 16508 | mope | 2 |
| 16509 | moorslayer | 2 |
| 16510 | montalban | 2 |
| 16511 | monger | 2 |
| 16512 | monde | 2 |
| 16513 | monarchies | 2 |
| 16514 | monachum | 2 |
| 16515 | mollis | 2 |
| 16516 | mollify | 2 |
| 16517 | molinera | 2 |
| 16518 | molest | 2 |
| 16519 | moisten | 2 |
| 16520 | module | 2 |
| 16521 | modo | 2 |
| 16522 | modesties | 2 |
| 16523 | mockwater | 2 |
| 16524 | mockers | 2 |
| 16525 | moated | 2 |
| 16526 | moaned | 2 |
| 16527 | mists | 2 |
| 16528 | mistak | 2 |
| 16529 | mista | 2 |
| 16530 | mission | 2 |
| 16531 | misprised | 2 |
| 16532 | misplaced | 2 |
| 16533 | misplac | 2 |
| 16534 | misleader | 2 |
| 16535 | misgiving | 2 |
| 16536 | misers | 2 |
| 16537 | miserably | 2 |
| 16538 | misdoubts | 2 |
| 16539 | misdeed | 2 |
| 16540 | misconstrued | 2 |
| 16541 | misconster | 2 |
| 16542 | mischances | 2 |
| 16543 | miscall | 2 |
| 16544 | misbehaved | 2 |
| 16545 | minstrelsy | 2 |
| 16546 | minstrel | 2 |
| 16547 | minor | 2 |
| 16548 | minerva | 2 |
| 16549 | mindless | 2 |
| 16550 | mindful | 2 |
| 16551 | millstone | 2 |
| 16552 | milliner | 2 |
| 16553 | milled | 2 |
| 16554 | milksops | 2 |
| 16555 | milks | 2 |
| 16556 | milkmaid | 2 |
| 16557 | milking | 2 |
| 16558 | mildest | 2 |
| 16559 | milanese | 2 |
| 16560 | midges | 2 |
| 16561 | mewed | 2 |
| 16562 | methuselah | 2 |
| 16563 | methods | 2 |
| 16564 | methodical | 2 |
| 16565 | mete | 2 |
| 16566 | metaphysical | 2 |
| 16567 | metamorphoses | 2 |
| 16568 | metamorphis | 2 |
| 16569 | metals | 2 |
| 16570 | messaline | 2 |
| 16571 | mesh | 2 |
| 16572 | menton | 2 |
| 16573 | menacing | 2 |
| 16574 | menac | 2 |
| 16575 | memento | 2 |
| 16576 | melteth | 2 |
| 16577 | mellifluous | 2 |
| 16578 | meiny | 2 |
| 16579 | meetest | 2 |
| 16580 | meeter | 2 |
| 16581 | meekly | 2 |
| 16582 | mediterranean | 2 |
| 16583 | meditate | 2 |
| 16584 | medicinal | 2 |
| 16585 | mediation | 2 |
| 16586 | media | 2 |
| 16587 | medes | 2 |
| 16588 | meddlesome | 2 |
| 16589 | meddled | 2 |
| 16590 | measureless | 2 |
| 16591 | mealy | 2 |
| 16592 | mazzard | 2 |
| 16593 | maz | 2 |
| 16594 | maws | 2 |
| 16595 | maul | 2 |
| 16596 | maturity | 2 |
| 16597 | mathematical | 2 |
| 16598 | masts | 2 |
| 16599 | mastiff | 2 |
| 16600 | mastery | 2 |
| 16601 | masterless | 2 |
| 16602 | massacres | 2 |
| 16603 | masquing | 2 |
| 16604 | masquers | 2 |
| 16605 | masquerade | 2 |
| 16606 | masonry | 2 |
| 16607 | mas | 2 |
| 16608 | marvelling | 2 |
| 16609 | marv | 2 |
| 16610 | martlet | 2 |
| 16611 | martino | 2 |
| 16612 | martin | 2 |
| 16613 | marrows | 2 |
| 16614 | marquess | 2 |
| 16615 | marketable | 2 |
| 16616 | marigold | 2 |
| 16617 | maries | 2 |
| 16618 | marica | 2 |
| 16619 | maps | 2 |
| 16620 | mapp | 2 |
| 16621 | manuscripts | 2 |
| 16622 | manuscript | 2 |
| 16623 | manured | 2 |
| 16624 | manure | 2 |
| 16625 | manuel | 2 |
| 16626 | mantles | 2 |
| 16627 | mantled | 2 |
| 16628 | mans | 2 |
| 16629 | mannered | 2 |
| 16630 | manned | 2 |
| 16631 | manna | 2 |
| 16632 | manifests | 2 |
| 16633 | manhoods | 2 |
| 16634 | mangle | 2 |
| 16635 | manger | 2 |
| 16636 | manfully | 2 |
| 16637 | mandragora | 2 |
| 16638 | managing | 2 |
| 16639 | mami | 2 |
| 16640 | malum | 2 |
| 16641 | maltreat | 2 |
| 16642 | malta | 2 |
| 16643 | malevolence | 2 |
| 16644 | males | 2 |
| 16645 | malefactors | 2 |
| 16646 | malefactor | 2 |
| 16647 | malcontents | 2 |
| 16648 | mala | 2 |
| 16649 | majority | 2 |
| 16650 | majestee | 2 |
| 16651 | maidhood | 2 |
| 16652 | mahu | 2 |
| 16653 | magnitude | 2 |
| 16654 | magnify | 2 |
| 16655 | magical | 2 |
| 16656 | maggots | 2 |
| 16657 | maggot | 2 |
| 16658 | mads | 2 |
| 16659 | madrigals | 2 |
| 16660 | madhouse | 2 |
| 16661 | madams | 2 |
| 16662 | machuca | 2 |
| 16663 | lynx | 2 |
| 16664 | lymoges | 2 |
| 16665 | lydia | 2 |
| 16666 | lycurgus | 2 |
| 16667 | ly | 2 |
| 16668 | lxxiv | 2 |
| 16669 | lxxiii | 2 |
| 16670 | lxxii | 2 |
| 16671 | lxxi | 2 |
| 16672 | lxx | 2 |
| 16673 | lxviii | 2 |
| 16674 | lxvii | 2 |
| 16675 | lxvi | 2 |
| 16676 | lxv | 2 |
| 16677 | lxix | 2 |
| 16678 | lxiv | 2 |
| 16679 | lxiii | 2 |
| 16680 | lxii | 2 |
| 16681 | lxi | 2 |
| 16682 | lx | 2 |
| 16683 | lviii | 2 |
| 16684 | lvii | 2 |
| 16685 | lvi | 2 |
| 16686 | lv | 2 |
| 16687 | luxuries | 2 |
| 16688 | lustrous | 2 |
| 16689 | lustihood | 2 |
| 16690 | lustiest | 2 |
| 16691 | luscious | 2 |
| 16692 | lupercal | 2 |
| 16693 | lunacies | 2 |
| 16694 | luna | 2 |
| 16695 | lulls | 2 |
| 16696 | lugg | 2 |
| 16697 | lug | 2 |
| 16698 | lucre | 2 |
| 16699 | luckily | 2 |
| 16700 | lucianus | 2 |
| 16701 | lucia | 2 |
| 16702 | lucar | 2 |
| 16703 | loyally | 2 |
| 16704 | lowing | 2 |
| 16705 | lovedst | 2 |
| 16706 | louvre | 2 |
| 16707 | louse | 2 |
| 16708 | louring | 2 |
| 16709 | loseth | 2 |
| 16710 | lorraine | 2 |
| 16711 | lordings | 2 |
| 16712 | loquacity | 2 |
| 16713 | lookers | 2 |
| 16714 | longinquous | 2 |
| 16715 | longeth | 2 |
| 16716 | lombardy | 2 |
| 16717 | logic | 2 |
| 16718 | loggerheads | 2 |
| 16719 | loggerhead | 2 |
| 16720 | lodgings | 2 |
| 16721 | lobuna | 2 |
| 16722 | lob | 2 |
| 16723 | loaves | 2 |
| 16724 | llous | 2 |
| 16725 | lix | 2 |
| 16726 | livia | 2 |
| 16727 | literature | 2 |
| 16728 | litany | 2 |
| 16729 | lisbon | 2 |
| 16730 | lirgandeo | 2 |
| 16731 | liquors | 2 |
| 16732 | linstock | 2 |
| 16733 | links | 2 |
| 16734 | lineament | 2 |
| 16735 | limps | 2 |
| 16736 | limitation | 2 |
| 16737 | likings | 2 |
| 16738 | likest | 2 |
| 16739 | liii | 2 |
| 16740 | lightnings | 2 |
| 16741 | lighting | 2 |
| 16742 | lieve | 2 |
| 16743 | lieutenantry | 2 |
| 16744 | lieth | 2 |
| 16745 | liegemen | 2 |
| 16746 | liegeman | 2 |
| 16747 | liefest | 2 |
| 16748 | lid | 2 |
| 16749 | lichas | 2 |
| 16750 | lice | 2 |
| 16751 | liberation | 2 |
| 16752 | libels | 2 |
| 16753 | lewdly | 2 |
| 16754 | leviathan | 2 |
| 16755 | lettings | 2 |
| 16756 | lestrake | 2 |
| 16757 | lessens | 2 |
| 16758 | lentus | 2 |
| 16759 | lengthy | 2 |
| 16760 | lendings | 2 |
| 16761 | lelilies | 2 |
| 16762 | legged | 2 |
| 16763 | lees | 2 |
| 16764 | leda | 2 |
| 16765 | leavy | 2 |
| 16766 | leavening | 2 |
| 16767 | leasing | 2 |
| 16768 | leases | 2 |
| 16769 | leaner | 2 |
| 16770 | leaky | 2 |
| 16771 | leafy | 2 |
| 16772 | laziness | 2 |
| 16773 | lazars | 2 |
| 16774 | lawrence | 2 |
| 16775 | lavender | 2 |
| 16776 | lavache | 2 |
| 16777 | laura | 2 |
| 16778 | laundress | 2 |
| 16779 | laund | 2 |
| 16780 | laugher | 2 |
| 16781 | lather | 2 |
| 16782 | lated | 2 |
| 16783 | larums | 2 |
| 16784 | largeness | 2 |
| 16785 | lards | 2 |
| 16786 | languishings | 2 |
| 16787 | languishes | 2 |
| 16788 | lanes | 2 |
| 16789 | lammas | 2 |
| 16790 | lamentably | 2 |
| 16791 | lameness | 2 |
| 16792 | lam | 2 |
| 16793 | lakin | 2 |
| 16794 | lading | 2 |
| 16795 | lachrymose | 2 |
| 16796 | lacedaemon | 2 |
| 16797 | laboursome | 2 |
| 16798 | laborious | 2 |
| 16799 | laboring | 2 |
| 16800 | laban | 2 |
| 16801 | knowingly | 2 |
| 16802 | knower | 2 |
| 16803 | knewest | 2 |
| 16804 | knapp | 2 |
| 16805 | knacks | 2 |
| 16806 | kitten | 2 |
| 16807 | kitchens | 2 |
| 16808 | killingworth | 2 |
| 16809 | killeth | 2 |
| 16810 | kidney | 2 |
| 16811 | kibes | 2 |
| 16812 | kibe | 2 |
| 16813 | keyhole | 2 |
| 16814 | kettledrums | 2 |
| 16815 | kettle | 2 |
| 16816 | kernels | 2 |
| 16817 | kern | 2 |
| 16818 | kendal | 2 |
| 16819 | keenly | 2 |
| 16820 | keech | 2 |
| 16821 | kates | 2 |
| 16822 | jutty | 2 |
| 16823 | justle | 2 |
| 16824 | jury | 2 |
| 16825 | jurist | 2 |
| 16826 | juma | 2 |
| 16827 | julietta | 2 |
| 16828 | jugs | 2 |
| 16829 | judgest | 2 |
| 16830 | jude | 2 |
| 16831 | joyless | 2 |
| 16832 | jowl | 2 |
| 16833 | joustings | 2 |
| 16834 | journeyman | 2 |
| 16835 | journal | 2 |
| 16836 | joseph | 2 |
| 16837 | jorge | 2 |
| 16838 | jordan | 2 |
| 16839 | jokers | 2 |
| 16840 | joins | 2 |
| 16841 | jogged | 2 |
| 16842 | jog | 2 |
| 16843 | job | 2 |
| 16844 | jingling | 2 |
| 16845 | jill | 2 |
| 16846 | jews | 2 |
| 16847 | jewish | 2 |
| 16848 | jewellery | 2 |
| 16849 | jerk | 2 |
| 16850 | jerez | 2 |
| 16851 | jeer | 2 |
| 16852 | jaw | 2 |
| 16853 | javelins | 2 |
| 16854 | javelin | 2 |
| 16855 | jauncing | 2 |
| 16856 | jasons | 2 |
| 16857 | jarama | 2 |
| 16858 | janus | 2 |
| 16859 | january | 2 |
| 16860 | jangling | 2 |
| 16861 | jane | 2 |
| 16862 | ithaca | 2 |
| 16863 | items | 2 |
| 16864 | itching | 2 |
| 16865 | itches | 2 |
| 16866 | issueless | 2 |
| 16867 | israel | 2 |
| 16868 | isbels | 2 |
| 16869 | irremediable | 2 |
| 16870 | irishman | 2 |
| 16871 | ipswich | 2 |
| 16872 | ipse | 2 |
| 16873 | inwards | 2 |
| 16874 | involves | 2 |
| 16875 | invoke | 2 |
| 16876 | invert | 2 |
| 16877 | inventions | 2 |
| 16878 | invariably | 2 |
| 16879 | invades | 2 |
| 16880 | intrude | 2 |
| 16881 | intrigue | 2 |
| 16882 | intestine | 2 |
| 16883 | interval | 2 |
| 16884 | interrogatories | 2 |
| 16885 | interprets | 2 |
| 16886 | interpreters | 2 |
| 16887 | interposing | 2 |
| 16888 | interposed | 2 |
| 16889 | intermingle | 2 |
| 16890 | interminable | 2 |
| 16891 | interested | 2 |
| 16892 | interchanging | 2 |
| 16893 | intense | 2 |
| 16894 | intemperate | 2 |
| 16895 | intelligencer | 2 |
| 16896 | intellectual | 2 |
| 16897 | intellects | 2 |
| 16898 | insula | 2 |
| 16899 | insufficiency | 2 |
| 16900 | instructor | 2 |
| 16901 | institute | 2 |
| 16902 | instinctively | 2 |
| 16903 | instigated | 2 |
| 16904 | instalment | 2 |
| 16905 | inspiring | 2 |
| 16906 | inspire | 2 |
| 16907 | insociable | 2 |
| 16908 | insists | 2 |
| 16909 | insisting | 2 |
| 16910 | insides | 2 |
| 16911 | inscriptions | 2 |
| 16912 | insanities | 2 |
| 16913 | inquir | 2 |
| 16914 | inprimis | 2 |
| 16915 | inordinate | 2 |
| 16916 | inkling | 2 |
| 16917 | injustices | 2 |
| 16918 | injuring | 2 |
| 16919 | injunctions | 2 |
| 16920 | inhibited | 2 |
| 16921 | inheritors | 2 |
| 16922 | inheriting | 2 |
| 16923 | ingredients | 2 |
| 16924 | ingredient | 2 |
| 16925 | infusion | 2 |
| 16926 | infus | 2 |
| 16927 | infortunate | 2 |
| 16928 | informs | 2 |
| 16929 | influences | 2 |
| 16930 | influenced | 2 |
| 16931 | inflicts | 2 |
| 16932 | infliction | 2 |
| 16933 | inflamed | 2 |
| 16934 | infidels | 2 |
| 16935 | inferiors | 2 |
| 16936 | inference | 2 |
| 16937 | infanta | 2 |
| 16938 | infallibly | 2 |
| 16939 | inextricable | 2 |
| 16940 | inequality | 2 |
| 16941 | indulge | 2 |
| 16942 | inducing | 2 |
| 16943 | indited | 2 |
| 16944 | indisposition | 2 |
| 16945 | indispensable | 2 |
| 16946 | indiscretion | 2 |
| 16947 | indiscreet | 2 |
| 16948 | indirection | 2 |
| 16949 | indifferency | 2 |
| 16950 | indications | 2 |
| 16951 | independence | 2 |
| 16952 | indenture | 2 |
| 16953 | indent | 2 |
| 16954 | indefatigable | 2 |
| 16955 | indecorous | 2 |
| 16956 | indebted | 2 |
| 16957 | inde | 2 |
| 16958 | incursions | 2 |
| 16959 | incurring | 2 |
| 16960 | incumbent | 2 |
| 16961 | incredulous | 2 |
| 16962 | increaseth | 2 |
| 16963 | incony | 2 |
| 16964 | inconvenient | 2 |
| 16965 | incomparably | 2 |
| 16966 | income | 2 |
| 16967 | inclusive | 2 |
| 16968 | incivility | 2 |
| 16969 | incest | 2 |
| 16970 | incertainties | 2 |
| 16971 | incarnate | 2 |
| 16972 | incapacitated | 2 |
| 16973 | incaged | 2 |
| 16974 | inadvertence | 2 |
| 16975 | inaccuracies | 2 |
| 16976 | improvident | 2 |
| 16977 | impropriety | 2 |
| 16978 | imposthume | 2 |
| 16979 | impos | 2 |
| 16980 | importuned | 2 |
| 16981 | importunacy | 2 |
| 16982 | importeth | 2 |
| 16983 | impon | 2 |
| 16984 | imperilling | 2 |
| 16985 | imperfection | 2 |
| 16986 | imperative | 2 |
| 16987 | impenetrable | 2 |
| 16988 | impending | 2 |
| 16989 | impeachment | 2 |
| 16990 | immur | 2 |
| 16991 | immodesty | 2 |
| 16992 | imbrue | 2 |
| 16993 | imbibed | 2 |
| 16994 | ils | 2 |
| 16995 | illustrate | 2 |
| 16996 | illness | 2 |
| 16997 | illegitimate | 2 |
| 16998 | icicle | 2 |
| 16999 | iceland | 2 |
| 17000 | iberia | 2 |
| 17001 | hyrcanian | 2 |
| 17002 | hybla | 2 |
| 17003 | husk | 2 |
| 17004 | husbandman | 2 |
| 17005 | hurries | 2 |
| 17006 | hurlyburly | 2 |
| 17007 | hurling | 2 |
| 17008 | hungerford | 2 |
| 17009 | hungary | 2 |
| 17010 | hums | 2 |
| 17011 | humors | 2 |
| 17012 | humidity | 2 |
| 17013 | humblest | 2 |
| 17014 | humbles | 2 |
| 17015 | humanely | 2 |
| 17016 | hull | 2 |
| 17017 | hugg | 2 |
| 17018 | hugely | 2 |
| 17019 | huff | 2 |
| 17020 | hued | 2 |
| 17021 | huddled | 2 |
| 17022 | howsome | 2 |
| 17023 | housings | 2 |
| 17024 | housewives | 2 |
| 17025 | housewifery | 2 |
| 17026 | houseless | 2 |
| 17027 | housekeeping | 2 |
| 17028 | households | 2 |
| 17029 | hostilius | 2 |
| 17030 | hostelries | 2 |
| 17031 | hostage | 2 |
| 17032 | horsemanship | 2 |
| 17033 | horridly | 2 |
| 17034 | hopkins | 2 |
| 17035 | hopelessly | 2 |
| 17036 | hooting | 2 |
| 17037 | hooted | 2 |
| 17038 | hooped | 2 |
| 17039 | hooked | 2 |
| 17040 | hoof | 2 |
| 17041 | hoodwinked | 2 |
| 17042 | hoodman | 2 |
| 17043 | homicides | 2 |
| 17044 | homespun | 2 |
| 17045 | homes | 2 |
| 17046 | hollowly | 2 |
| 17047 | holloa | 2 |
| 17048 | hollander | 2 |
| 17049 | holier | 2 |
| 17050 | holidame | 2 |
| 17051 | holdeth | 2 |
| 17052 | holdest | 2 |
| 17053 | holder | 2 |
| 17054 | hogsheads | 2 |
| 17055 | hoces | 2 |
| 17056 | hobnails | 2 |
| 17057 | hob | 2 |
| 17058 | hoarding | 2 |
| 17059 | hoarded | 2 |
| 17060 | hitherwards | 2 |
| 17061 | hitch | 2 |
| 17062 | hist | 2 |
| 17063 | hiren | 2 |
| 17064 | hippogriff | 2 |
| 17065 | hippocrates | 2 |
| 17066 | hipp | 2 |
| 17067 | hints | 2 |
| 17068 | hinting | 2 |
| 17069 | hinge | 2 |
| 17070 | hindering | 2 |
| 17071 | highwaymen | 2 |
| 17072 | highmost | 2 |
| 17073 | hiems | 2 |
| 17074 | hidalgo | 2 |
| 17075 | hewn | 2 |
| 17076 | hewing | 2 |
| 17077 | hests | 2 |
| 17078 | hesitating | 2 |
| 17079 | hesitate | 2 |
| 17080 | herrings | 2 |
| 17081 | heresies | 2 |
| 17082 | herefordshire | 2 |
| 17083 | hereabouts | 2 |
| 17084 | henton | 2 |
| 17085 | henares | 2 |
| 17086 | hems | 2 |
| 17087 | heights | 2 |
| 17088 | heedlessness | 2 |
| 17089 | heeding | 2 |
| 17090 | heeded | 2 |
| 17091 | hedgehogs | 2 |
| 17092 | hedg | 2 |
| 17093 | heaves | 2 |
| 17094 | heartstrings | 2 |
| 17095 | heartly | 2 |
| 17096 | hearkens | 2 |
| 17097 | heark | 2 |
| 17098 | heaping | 2 |
| 17099 | headstall | 2 |
| 17100 | headborough | 2 |
| 17101 | hazardous | 2 |
| 17102 | hazarded | 2 |
| 17103 | havings | 2 |
| 17104 | haves | 2 |
| 17105 | haunch | 2 |
| 17106 | hatfield | 2 |
| 17107 | hater | 2 |
| 17108 | hasting | 2 |
| 17109 | hasn | 2 |
| 17110 | harts | 2 |
| 17111 | harrow | 2 |
| 17112 | harping | 2 |
| 17113 | harmonies | 2 |
| 17114 | harming | 2 |
| 17115 | harmed | 2 |
| 17116 | hardened | 2 |
| 17117 | harboured | 2 |
| 17118 | harbor | 2 |
| 17119 | harbingers | 2 |
| 17120 | harasses | 2 |
| 17121 | happ | 2 |
| 17122 | hangmen | 2 |
| 17123 | hangeth | 2 |
| 17124 | handsomest | 2 |
| 17125 | handsaw | 2 |
| 17126 | handless | 2 |
| 17127 | handles | 2 |
| 17128 | handkerchers | 2 |
| 17129 | hams | 2 |
| 17130 | hampton | 2 |
| 17131 | hamlets | 2 |
| 17132 | halves | 2 |
| 17133 | hallooing | 2 |
| 17134 | halloo | 2 |
| 17135 | halloing | 2 |
| 17136 | halloa | 2 |
| 17137 | halfway | 2 |
| 17138 | halcyon | 2 |
| 17139 | hackling | 2 |
| 17140 | hacket | 2 |
| 17141 | h | 2 |
| 17142 | gypsy | 2 |
| 17143 | guy | 2 |
| 17144 | gulls | 2 |
| 17145 | guiomar | 2 |
| 17146 | guiltier | 2 |
| 17147 | guileful | 2 |
| 17148 | guildhall | 2 |
| 17149 | guilders | 2 |
| 17150 | guardant | 2 |
| 17151 | gualtier | 2 |
| 17152 | guadalajara | 2 |
| 17153 | grunt | 2 |
| 17154 | grubs | 2 |
| 17155 | grovel | 2 |
| 17156 | gros | 2 |
| 17157 | grise | 2 |
| 17158 | grips | 2 |
| 17159 | griping | 2 |
| 17160 | grimly | 2 |
| 17161 | grime | 2 |
| 17162 | greybeards | 2 |
| 17163 | greybeard | 2 |
| 17164 | greenwood | 2 |
| 17165 | greensleeves | 2 |
| 17166 | greenly | 2 |
| 17167 | grazier | 2 |
| 17168 | gravy | 2 |
| 17169 | gravestone | 2 |
| 17170 | gravest | 2 |
| 17171 | gravely | 2 |
| 17172 | gravelling | 2 |
| 17173 | graved | 2 |
| 17174 | grav | 2 |
| 17175 | gratifying | 2 |
| 17176 | grasps | 2 |
| 17177 | grapples | 2 |
| 17178 | grandson | 2 |
| 17179 | grandsires | 2 |
| 17180 | grandeur | 2 |
| 17181 | grandest | 2 |
| 17182 | grandees | 2 |
| 17183 | grandee | 2 |
| 17184 | graff | 2 |
| 17185 | gradation | 2 |
| 17186 | gracefulness | 2 |
| 17187 | governest | 2 |
| 17188 | governess | 2 |
| 17189 | gossiping | 2 |
| 17190 | gossamer | 2 |
| 17191 | gospels | 2 |
| 17192 | gospel | 2 |
| 17193 | gorgon | 2 |
| 17194 | gorget | 2 |
| 17195 | gored | 2 |
| 17196 | goodwin | 2 |
| 17197 | goodlier | 2 |
| 17198 | goodfellow | 2 |
| 17199 | gonzalez | 2 |
| 17200 | gondola | 2 |
| 17201 | golgotha | 2 |
| 17202 | godson | 2 |
| 17203 | godmother | 2 |
| 17204 | goblin | 2 |
| 17205 | goblet | 2 |
| 17206 | gobbets | 2 |
| 17207 | goaded | 2 |
| 17208 | goad | 2 |
| 17209 | gnaws | 2 |
| 17210 | gnawn | 2 |
| 17211 | gnawed | 2 |
| 17212 | gnarling | 2 |
| 17213 | gloze | 2 |
| 17214 | glowed | 2 |
| 17215 | glover | 2 |
| 17216 | glosses | 2 |
| 17217 | glossed | 2 |
| 17218 | glitters | 2 |
| 17219 | glitter | 2 |
| 17220 | glisters | 2 |
| 17221 | glistering | 2 |
| 17222 | glimpses | 2 |
| 17223 | glimmer | 2 |
| 17224 | gliding | 2 |
| 17225 | glides | 2 |
| 17226 | gleek | 2 |
| 17227 | gleaned | 2 |
| 17228 | glares | 2 |
| 17229 | gladden | 2 |
| 17230 | giveth | 2 |
| 17231 | girth | 2 |
| 17232 | girdled | 2 |
| 17233 | girding | 2 |
| 17234 | girded | 2 |
| 17235 | gillyvors | 2 |
| 17236 | gills | 2 |
| 17237 | gilding | 2 |
| 17238 | gil | 2 |
| 17239 | giglot | 2 |
| 17240 | giddiness | 2 |
| 17241 | giddily | 2 |
| 17242 | gibing | 2 |
| 17243 | gibe | 2 |
| 17244 | gib | 2 |
| 17245 | gerfalcons | 2 |
| 17246 | geometrical | 2 |
| 17247 | gentility | 2 |
| 17248 | gentilhomme | 2 |
| 17249 | gens | 2 |
| 17250 | genoese | 2 |
| 17251 | genil | 2 |
| 17252 | generously | 2 |
| 17253 | generations | 2 |
| 17254 | geck | 2 |
| 17255 | gazers | 2 |
| 17256 | gaz | 2 |
| 17257 | gayest | 2 |
| 17258 | gawsey | 2 |
| 17259 | gauntlets | 2 |
| 17260 | gaultree | 2 |
| 17261 | gatories | 2 |
| 17262 | gateway | 2 |
| 17263 | gascony | 2 |
| 17264 | garnished | 2 |
| 17265 | garner | 2 |
| 17266 | garish | 2 |
| 17267 | gard | 2 |
| 17268 | garcilasso | 2 |
| 17269 | garcilaso | 2 |
| 17270 | garboils | 2 |
| 17271 | garbage | 2 |
| 17272 | gapes | 2 |
| 17273 | gaols | 2 |
| 17274 | gandalin | 2 |
| 17275 | gallowglasses | 2 |
| 17276 | galliot | 2 |
| 17277 | galling | 2 |
| 17278 | gallimaufry | 2 |
| 17279 | gallian | 2 |
| 17280 | galateas | 2 |
| 17281 | galatea | 2 |
| 17282 | gala | 2 |
| 17283 | gaiters | 2 |
| 17284 | gainer | 2 |
| 17285 | gagg | 2 |
| 17286 | gadding | 2 |
| 17287 | furze | 2 |
| 17288 | furtherance | 2 |
| 17289 | furrows | 2 |
| 17290 | furrowed | 2 |
| 17291 | furlongs | 2 |
| 17292 | furbish | 2 |
| 17293 | fundamental | 2 |
| 17294 | fumble | 2 |
| 17295 | fulfilment | 2 |
| 17296 | frustrates | 2 |
| 17297 | fruitfully | 2 |
| 17298 | frugal | 2 |
| 17299 | frontino | 2 |
| 17300 | fronting | 2 |
| 17301 | frontier | 2 |
| 17302 | fronted | 2 |
| 17303 | frolic | 2 |
| 17304 | frock | 2 |
| 17305 | frivolity | 2 |
| 17306 | frighten | 2 |
| 17307 | frequents | 2 |
| 17308 | frequented | 2 |
| 17309 | frenchwoman | 2 |
| 17310 | freezes | 2 |
| 17311 | frees | 2 |
| 17312 | freak | 2 |
| 17313 | fraughtage | 2 |
| 17314 | franklin | 2 |
| 17315 | fractions | 2 |
| 17316 | fracted | 2 |
| 17317 | foutra | 2 |
| 17318 | forwards | 2 |
| 17319 | fortuna | 2 |
| 17320 | fortresses | 2 |
| 17321 | fortifications | 2 |
| 17322 | forswearing | 2 |
| 17323 | forspent | 2 |
| 17324 | formless | 2 |
| 17325 | forgery | 2 |
| 17326 | forgeries | 2 |
| 17327 | forgave | 2 |
| 17328 | forfeiting | 2 |
| 17329 | forewarn | 2 |
| 17330 | forestalled | 2 |
| 17331 | forespent | 2 |
| 17332 | foresight | 2 |
| 17333 | forenoon | 2 |
| 17334 | foreknowing | 2 |
| 17335 | fordone | 2 |
| 17336 | fordoes | 2 |
| 17337 | forbidding | 2 |
| 17338 | forbade | 2 |
| 17339 | footpath | 2 |
| 17340 | footboy | 2 |
| 17341 | football | 2 |
| 17342 | foolhardy | 2 |
| 17343 | font | 2 |
| 17344 | fonseca | 2 |
| 17345 | followest | 2 |
| 17346 | foix | 2 |
| 17347 | fois | 2 |
| 17348 | foining | 2 |
| 17349 | foin | 2 |
| 17350 | focative | 2 |
| 17351 | flux | 2 |
| 17352 | flutter | 2 |
| 17353 | flowery | 2 |
| 17354 | flouts | 2 |
| 17355 | flourished | 2 |
| 17356 | flour | 2 |
| 17357 | florismarte | 2 |
| 17358 | florentines | 2 |
| 17359 | flora | 2 |
| 17360 | flog | 2 |
| 17361 | floating | 2 |
| 17362 | float | 2 |
| 17363 | flinch | 2 |
| 17364 | flieth | 2 |
| 17365 | flibbertigibbet | 2 |
| 17366 | flexure | 2 |
| 17367 | fletches | 2 |
| 17368 | fleshless | 2 |
| 17369 | fleeter | 2 |
| 17370 | fledged | 2 |
| 17371 | flaying | 2 |
| 17372 | flannel | 2 |
| 17373 | flam | 2 |
| 17374 | flakes | 2 |
| 17375 | flagrant | 2 |
| 17376 | flagging | 2 |
| 17377 | flagellation | 2 |
| 17378 | fives | 2 |
| 17379 | fitment | 2 |
| 17380 | fishmonger | 2 |
| 17381 | firme | 2 |
| 17382 | firk | 2 |
| 17383 | fir | 2 |
| 17384 | fins | 2 |
| 17385 | finery | 2 |
| 17386 | finch | 2 |
| 17387 | filths | 2 |
| 17388 | film | 2 |
| 17389 | fillet | 2 |
| 17390 | filidas | 2 |
| 17391 | filch | 2 |
| 17392 | figo | 2 |
| 17393 | figments | 2 |
| 17394 | fighteth | 2 |
| 17395 | fightest | 2 |
| 17396 | fifes | 2 |
| 17397 | fiercest | 2 |
| 17398 | fidelicet | 2 |
| 17399 | fiddlestick | 2 |
| 17400 | fiddle | 2 |
| 17401 | fictions | 2 |
| 17402 | fewest | 2 |
| 17403 | feu | 2 |
| 17404 | fett | 2 |
| 17405 | fetlocks | 2 |
| 17406 | fervent | 2 |
| 17407 | fertility | 2 |
| 17408 | ferrara | 2 |
| 17409 | fernseed | 2 |
| 17410 | fernandez | 2 |
| 17411 | fens | 2 |
| 17412 | fennel | 2 |
| 17413 | fencer | 2 |
| 17414 | felony | 2 |
| 17415 | felon | 2 |
| 17416 | fells | 2 |
| 17417 | fellest | 2 |
| 17418 | fedary | 2 |
| 17419 | featly | 2 |
| 17420 | feathered | 2 |
| 17421 | fearest | 2 |
| 17422 | fawns | 2 |
| 17423 | favourer | 2 |
| 17424 | fauconbridge | 2 |
| 17425 | fattest | 2 |
| 17426 | fatted | 2 |
| 17427 | fatherland | 2 |
| 17428 | fashioning | 2 |
| 17429 | farthingales | 2 |
| 17430 | faring | 2 |
| 17431 | fans | 2 |
| 17432 | famously | 2 |
| 17433 | familiars | 2 |
| 17434 | falstaffs | 2 |
| 17435 | falsify | 2 |
| 17436 | falsest | 2 |
| 17437 | falser | 2 |
| 17438 | falseness | 2 |
| 17439 | fadge | 2 |
| 17440 | facit | 2 |
| 17441 | fabricated | 2 |
| 17442 | eyelid | 2 |
| 17443 | extricate | 2 |
| 17444 | extraordinarily | 2 |
| 17445 | extracting | 2 |
| 17446 | extract | 2 |
| 17447 | extorted | 2 |
| 17448 | extinct | 2 |
| 17449 | extern | 2 |
| 17450 | extending | 2 |
| 17451 | expressive | 2 |
| 17452 | exposure | 2 |
| 17453 | explication | 2 |
| 17454 | explanation | 2 |
| 17455 | expir | 2 |
| 17456 | expertness | 2 |
| 17457 | expenditure | 2 |
| 17458 | expeditious | 2 |
| 17459 | expeditions | 2 |
| 17460 | expectations | 2 |
| 17461 | expectancy | 2 |
| 17462 | expanse | 2 |
| 17463 | exorcist | 2 |
| 17464 | exhortation | 2 |
| 17465 | exhort | 2 |
| 17466 | exhales | 2 |
| 17467 | exhale | 2 |
| 17468 | exhal | 2 |
| 17469 | exerting | 2 |
| 17470 | executor | 2 |
| 17471 | excusing | 2 |
| 17472 | excusez | 2 |
| 17473 | excrements | 2 |
| 17474 | excommunication | 2 |
| 17475 | excommunicated | 2 |
| 17476 | excommunicate | 2 |
| 17477 | excitements | 2 |
| 17478 | exchang | 2 |
| 17479 | excelling | 2 |
| 17480 | excelled | 2 |
| 17481 | exampled | 2 |
| 17482 | examin | 2 |
| 17483 | exalts | 2 |
| 17484 | exactness | 2 |
| 17485 | exacting | 2 |
| 17486 | evilly | 2 |
| 17487 | everyday | 2 |
| 17488 | euryalus | 2 |
| 17489 | eunuchs | 2 |
| 17490 | eugenio | 2 |
| 17491 | ethiopian | 2 |
| 17492 | ethiopia | 2 |
| 17493 | eterne | 2 |
| 17494 | estranged | 2 |
| 17495 | estility | 2 |
| 17496 | esses | 2 |
| 17497 | essay | 2 |
| 17498 | espies | 2 |
| 17499 | erwatch | 2 |
| 17500 | erturn | 2 |
| 17501 | ertop | 2 |
| 17502 | ertook | 2 |
| 17503 | ersways | 2 |
| 17504 | ersway | 2 |
| 17505 | ershot | 2 |
| 17506 | ershades | 2 |
| 17507 | errun | 2 |
| 17508 | erroneous | 2 |
| 17509 | erraught | 2 |
| 17510 | erpow | 2 |
| 17511 | erpast | 2 |
| 17512 | erleap | 2 |
| 17513 | eris | 2 |
| 17514 | erflow | 2 |
| 17515 | erecting | 2 |
| 17516 | ercome | 2 |
| 17517 | ercles | 2 |
| 17518 | ercharg | 2 |
| 17519 | ercast | 2 |
| 17520 | erborne | 2 |
| 17521 | erboard | 2 |
| 17522 | erbears | 2 |
| 17523 | erbearing | 2 |
| 17524 | erat | 2 |
| 17525 | equivocation | 2 |
| 17526 | equivocal | 2 |
| 17527 | equipped | 2 |
| 17528 | equipage | 2 |
| 17529 | equerry | 2 |
| 17530 | equerries | 2 |
| 17531 | equalled | 2 |
| 17532 | equall | 2 |
| 17533 | epithets | 2 |
| 17534 | epistles | 2 |
| 17535 | epigrams | 2 |
| 17536 | epigram | 2 |
| 17537 | epicurean | 2 |
| 17538 | epic | 2 |
| 17539 | envenomed | 2 |
| 17540 | envelop | 2 |
| 17541 | entrenchments | 2 |
| 17542 | entrances | 2 |
| 17543 | enticing | 2 |
| 17544 | entertainments | 2 |
| 17545 | entanglements | 2 |
| 17546 | ensnare | 2 |
| 17547 | ensigns | 2 |
| 17548 | enroll | 2 |
| 17549 | enrage | 2 |
| 17550 | enquired | 2 |
| 17551 | enormity | 2 |
| 17552 | enlivened | 2 |
| 17553 | enlightenment | 2 |
| 17554 | enlarged | 2 |
| 17555 | enlarg | 2 |
| 17556 | enkindle | 2 |
| 17557 | enjoyments | 2 |
| 17558 | enigma | 2 |
| 17559 | engrav | 2 |
| 17560 | englutted | 2 |
| 17561 | engirt | 2 |
| 17562 | engineer | 2 |
| 17563 | engagements | 2 |
| 17564 | enforces | 2 |
| 17565 | endurance | 2 |
| 17566 | endue | 2 |
| 17567 | endings | 2 |
| 17568 | endear | 2 |
| 17569 | endanger | 2 |
| 17570 | endamage | 2 |
| 17571 | enclose | 2 |
| 17572 | encamped | 2 |
| 17573 | enamell | 2 |
| 17574 | enacts | 2 |
| 17575 | enabling | 2 |
| 17576 | enabled | 2 |
| 17577 | emulate | 2 |
| 17578 | empties | 2 |
| 17579 | emptier | 2 |
| 17580 | emptied | 2 |
| 17581 | empoison | 2 |
| 17582 | employs | 2 |
| 17583 | employing | 2 |
| 17584 | empires | 2 |
| 17585 | emphasis | 2 |
| 17586 | emnity | 2 |
| 17587 | emergency | 2 |
| 17588 | emergencies | 2 |
| 17589 | emerged | 2 |
| 17590 | emerencia | 2 |
| 17591 | embroider | 2 |
| 17592 | emblems | 2 |
| 17593 | emblem | 2 |
| 17594 | embers | 2 |
| 17595 | embellish | 2 |
| 17596 | embattl | 2 |
| 17597 | embassies | 2 |
| 17598 | embarrassments | 2 |
| 17599 | embarrassed | 2 |
| 17600 | embarking | 2 |
| 17601 | eleventh | 2 |
| 17602 | elevation | 2 |
| 17603 | elbe | 2 |
| 17604 | elated | 2 |
| 17605 | elaborate | 2 |
| 17606 | ego | 2 |
| 17607 | eglantine | 2 |
| 17608 | effectually | 2 |
| 17609 | educed | 2 |
| 17610 | edmunds | 2 |
| 17611 | edition | 2 |
| 17612 | edgeless | 2 |
| 17613 | ecus | 2 |
| 17614 | eclips | 2 |
| 17615 | ebon | 2 |
| 17616 | eaters | 2 |
| 17617 | eastward | 2 |
| 17618 | eased | 2 |
| 17619 | earns | 2 |
| 17620 | earlier | 2 |
| 17621 | dyes | 2 |
| 17622 | dyer | 2 |
| 17623 | dwindle | 2 |
| 17624 | dwarfs | 2 |
| 17625 | dungy | 2 |
| 17626 | dunghills | 2 |
| 17627 | dumbly | 2 |
| 17628 | dumbfoundered | 2 |
| 17629 | dulness | 2 |
| 17630 | dulling | 2 |
| 17631 | dulcineas | 2 |
| 17632 | duello | 2 |
| 17633 | duellist | 2 |
| 17634 | duel | 2 |
| 17635 | ducking | 2 |
| 17636 | ducked | 2 |
| 17637 | duchy | 2 |
| 17638 | duchesses | 2 |
| 17639 | dryness | 2 |
| 17640 | drunkenly | 2 |
| 17641 | drudgery | 2 |
| 17642 | drowsiness | 2 |
| 17643 | dropsy | 2 |
| 17644 | droller | 2 |
| 17645 | drizzled | 2 |
| 17646 | driveth | 2 |
| 17647 | drinkings | 2 |
| 17648 | drinketh | 2 |
| 17649 | drest | 2 |
| 17650 | dressings | 2 |
| 17651 | drenched | 2 |
| 17652 | dreads | 2 |
| 17653 | dreadfully | 2 |
| 17654 | draweth | 2 |
| 17655 | drains | 2 |
| 17656 | dragg | 2 |
| 17657 | draff | 2 |
| 17658 | drachmas | 2 |
| 17659 | dozed | 2 |
| 17660 | doxy | 2 |
| 17661 | downs | 2 |
| 17662 | dowlas | 2 |
| 17663 | dowers | 2 |
| 17664 | dovehouse | 2 |
| 17665 | dosed | 2 |
| 17666 | dormouse | 2 |
| 17667 | doria | 2 |
| 17668 | donn | 2 |
| 17669 | donkey | 2 |
| 17670 | doncaster | 2 |
| 17671 | donas | 2 |
| 17672 | domineering | 2 |
| 17673 | domine | 2 |
| 17674 | dolefully | 2 |
| 17675 | doesn | 2 |
| 17676 | documents | 2 |
| 17677 | document | 2 |
| 17678 | docks | 2 |
| 17679 | dock | 2 |
| 17680 | dobbin | 2 |
| 17681 | divulged | 2 |
| 17682 | divorced | 2 |
| 17683 | divinest | 2 |
| 17684 | dives | 2 |
| 17685 | diversity | 2 |
| 17686 | dites | 2 |
| 17687 | disturbing | 2 |
| 17688 | disturbers | 2 |
| 17689 | distrustful | 2 |
| 17690 | distributing | 2 |
| 17691 | distraught | 2 |
| 17692 | distrain | 2 |
| 17693 | distractions | 2 |
| 17694 | distillation | 2 |
| 17695 | distasteful | 2 |
| 17696 | dissuaded | 2 |
| 17697 | dissolves | 2 |
| 17698 | dissensions | 2 |
| 17699 | dissembler | 2 |
| 17700 | dissembled | 2 |
| 17701 | dissatisfied | 2 |
| 17702 | disputed | 2 |
| 17703 | disproportioned | 2 |
| 17704 | dispraising | 2 |
| 17705 | disposes | 2 |
| 17706 | displeasures | 2 |
| 17707 | displeases | 2 |
| 17708 | displace | 2 |
| 17709 | displac | 2 |
| 17710 | dispersedly | 2 |
| 17711 | dispensed | 2 |
| 17712 | disparaged | 2 |
| 17713 | disparage | 2 |
| 17714 | disown | 2 |
| 17715 | disorderly | 2 |
| 17716 | dismission | 2 |
| 17717 | dismember | 2 |
| 17718 | disloyalty | 2 |
| 17719 | disliked | 2 |
| 17720 | dislik | 2 |
| 17721 | disjoint | 2 |
| 17722 | disjoin | 2 |
| 17723 | dishonours | 2 |
| 17724 | dishonestly | 2 |
| 17725 | dishclout | 2 |
| 17726 | disgust | 2 |
| 17727 | disgracious | 2 |
| 17728 | disfurnish | 2 |
| 17729 | disembark | 2 |
| 17730 | disdaineth | 2 |
| 17731 | discussions | 2 |
| 17732 | discreetly | 2 |
| 17733 | discredited | 2 |
| 17734 | discourtesy | 2 |
| 17735 | disconcerted | 2 |
| 17736 | discomfiture | 2 |
| 17737 | discoloured | 2 |
| 17738 | discolour | 2 |
| 17739 | disclaiming | 2 |
| 17740 | disciplin | 2 |
| 17741 | disciples | 2 |
| 17742 | discerning | 2 |
| 17743 | discase | 2 |
| 17744 | disburse | 2 |
| 17745 | disappearance | 2 |
| 17746 | disabuse | 2 |
| 17747 | disable | 2 |
| 17748 | dirges | 2 |
| 17749 | dirge | 2 |
| 17750 | directitude | 2 |
| 17751 | dinted | 2 |
| 17752 | dingy | 2 |
| 17753 | dines | 2 |
| 17754 | diners | 2 |
| 17755 | diminutives | 2 |
| 17756 | diminution | 2 |
| 17757 | diminishing | 2 |
| 17758 | dimension | 2 |
| 17759 | dilatory | 2 |
| 17760 | dilate | 2 |
| 17761 | digression | 2 |
| 17762 | digressing | 2 |
| 17763 | digress | 2 |
| 17764 | dignify | 2 |
| 17765 | digestions | 2 |
| 17766 | diffus | 2 |
| 17767 | differing | 2 |
| 17768 | differently | 2 |
| 17769 | diction | 2 |
| 17770 | dianas | 2 |
| 17771 | dials | 2 |
| 17772 | diabolical | 2 |
| 17773 | devourer | 2 |
| 17774 | devant | 2 |
| 17775 | deux | 2 |
| 17776 | deuce | 2 |
| 17777 | deucalion | 2 |
| 17778 | detract | 2 |
| 17779 | detests | 2 |
| 17780 | detestation | 2 |
| 17781 | detects | 2 |
| 17782 | detecting | 2 |
| 17783 | detach | 2 |
| 17784 | destroys | 2 |
| 17785 | destroyer | 2 |
| 17786 | destined | 2 |
| 17787 | despoiled | 2 |
| 17788 | despiseth | 2 |
| 17789 | despairs | 2 |
| 17790 | despaired | 2 |
| 17791 | desirest | 2 |
| 17792 | deservest | 2 |
| 17793 | deserver | 2 |
| 17794 | deracinate | 2 |
| 17795 | depravity | 2 |
| 17796 | deposited | 2 |
| 17797 | dependence | 2 |
| 17798 | dens | 2 |
| 17799 | denounced | 2 |
| 17800 | denounce | 2 |
| 17801 | denounc | 2 |
| 17802 | denials | 2 |
| 17803 | denay | 2 |
| 17804 | demurely | 2 |
| 17805 | demons | 2 |
| 17806 | demolishing | 2 |
| 17807 | demolish | 2 |
| 17808 | demise | 2 |
| 17809 | demigod | 2 |
| 17810 | demanding | 2 |
| 17811 | demandest | 2 |
| 17812 | delve | 2 |
| 17813 | delusive | 2 |
| 17814 | delusions | 2 |
| 17815 | delude | 2 |
| 17816 | delinquents | 2 |
| 17817 | deliberation | 2 |
| 17818 | delabreth | 2 |
| 17819 | degrading | 2 |
| 17820 | degraded | 2 |
| 17821 | defying | 2 |
| 17822 | defter | 2 |
| 17823 | deflowered | 2 |
| 17824 | defies | 2 |
| 17825 | deficient | 2 |
| 17826 | deferred | 2 |
| 17827 | deference | 2 |
| 17828 | defensible | 2 |
| 17829 | defeatures | 2 |
| 17830 | deeps | 2 |
| 17831 | deducted | 2 |
| 17832 | dedicates | 2 |
| 17833 | decrease | 2 |
| 17834 | decorous | 2 |
| 17835 | declension | 2 |
| 17836 | decking | 2 |
| 17837 | deceptions | 2 |
| 17838 | deceivable | 2 |
| 17839 | debtors | 2 |
| 17840 | debosh | 2 |
| 17841 | debitor | 2 |
| 17842 | debile | 2 |
| 17843 | debauch | 2 |
| 17844 | debatement | 2 |
| 17845 | deathsman | 2 |
| 17846 | dears | 2 |
| 17847 | dean | 2 |
| 17848 | deafness | 2 |
| 17849 | dazzling | 2 |
| 17850 | dazzled | 2 |
| 17851 | dawned | 2 |
| 17852 | daw | 2 |
| 17853 | dastards | 2 |
| 17854 | dashes | 2 |
| 17855 | dashed | 2 |
| 17856 | darker | 2 |
| 17857 | darkening | 2 |
| 17858 | darius | 2 |
| 17859 | darinel | 2 |
| 17860 | dareth | 2 |
| 17861 | dardan | 2 |
| 17862 | dappled | 2 |
| 17863 | dandle | 2 |
| 17864 | damp | 2 |
| 17865 | damm | 2 |
| 17866 | damascus | 2 |
| 17867 | dalmatians | 2 |
| 17868 | dallies | 2 |
| 17869 | dallied | 2 |
| 17870 | daisies | 2 |
| 17871 | daintiest | 2 |
| 17872 | daffodils | 2 |
| 17873 | cygnet | 2 |
| 17874 | cyclops | 2 |
| 17875 | cutter | 2 |
| 17876 | customer | 2 |
| 17877 | custard | 2 |
| 17878 | curtle | 2 |
| 17879 | curtail | 2 |
| 17880 | cursies | 2 |
| 17881 | curry | 2 |
| 17882 | curly | 2 |
| 17883 | curiambro | 2 |
| 17884 | curd | 2 |
| 17885 | curbed | 2 |
| 17886 | cupids | 2 |
| 17887 | cumber | 2 |
| 17888 | culprit | 2 |
| 17889 | cullions | 2 |
| 17890 | culling | 2 |
| 17891 | cuenca | 2 |
| 17892 | cucullus | 2 |
| 17893 | cub | 2 |
| 17894 | crusts | 2 |
| 17895 | crushing | 2 |
| 17896 | cruelest | 2 |
| 17897 | crownets | 2 |
| 17898 | crowing | 2 |
| 17899 | crowds | 2 |
| 17900 | cristiano | 2 |
| 17901 | cris | 2 |
| 17902 | crimped | 2 |
| 17903 | criest | 2 |
| 17904 | criedst | 2 |
| 17905 | cribs | 2 |
| 17906 | crib | 2 |
| 17907 | crews | 2 |
| 17908 | crestfall | 2 |
| 17909 | creek | 2 |
| 17910 | creed | 2 |
| 17911 | credite | 2 |
| 17912 | crawling | 2 |
| 17913 | crav | 2 |
| 17914 | cranny | 2 |
| 17915 | craftiness | 2 |
| 17916 | cradles | 2 |
| 17917 | cradled | 2 |
| 17918 | crackers | 2 |
| 17919 | crabs | 2 |
| 17920 | cox | 2 |
| 17921 | cowslips | 2 |
| 17922 | cowed | 2 |
| 17923 | coveted | 2 |
| 17924 | coverture | 2 |
| 17925 | covent | 2 |
| 17926 | courtezans | 2 |
| 17927 | couriers | 2 |
| 17928 | courageously | 2 |
| 17929 | couplement | 2 |
| 17930 | counsell | 2 |
| 17931 | cotus | 2 |
| 17932 | cottages | 2 |
| 17933 | cot | 2 |
| 17934 | costing | 2 |
| 17935 | cosmography | 2 |
| 17936 | cosmetics | 2 |
| 17937 | corses | 2 |
| 17938 | corsairs | 2 |
| 17939 | corrosive | 2 |
| 17940 | corrigible | 2 |
| 17941 | corresponds | 2 |
| 17942 | corrects | 2 |
| 17943 | corrected | 2 |
| 17944 | corpus | 2 |
| 17945 | corporate | 2 |
| 17946 | coronal | 2 |
| 17947 | cornish | 2 |
| 17948 | cornelia | 2 |
| 17949 | corded | 2 |
| 17950 | coranto | 2 |
| 17951 | copyright | 2 |
| 17952 | copulation | 2 |
| 17953 | coolness | 2 |
| 17954 | coolly | 2 |
| 17955 | cookery | 2 |
| 17956 | convocation | 2 |
| 17957 | conveying | 2 |
| 17958 | conveyances | 2 |
| 17959 | converts | 2 |
| 17960 | converses | 2 |
| 17961 | conversant | 2 |
| 17962 | conveniency | 2 |
| 17963 | conveniences | 2 |
| 17964 | controller | 2 |
| 17965 | contrives | 2 |
| 17966 | contribution | 2 |
| 17967 | contravene | 2 |
| 17968 | contrarious | 2 |
| 17969 | contradicted | 2 |
| 17970 | continuate | 2 |
| 17971 | continency | 2 |
| 17972 | contentious | 2 |
| 17973 | contended | 2 |
| 17974 | contemptuous | 2 |
| 17975 | contaminate | 2 |
| 17976 | consumes | 2 |
| 17977 | consternation | 2 |
| 17978 | conspired | 2 |
| 17979 | conspicuously | 2 |
| 17980 | consonancy | 2 |
| 17981 | consistent | 2 |
| 17982 | consisted | 2 |
| 17983 | conscious | 2 |
| 17984 | connection | 2 |
| 17985 | conjuring | 2 |
| 17986 | conjures | 2 |
| 17987 | conjurers | 2 |
| 17988 | conjunctive | 2 |
| 17989 | conjunct | 2 |
| 17990 | conjointly | 2 |
| 17991 | conjectural | 2 |
| 17992 | congruent | 2 |
| 17993 | congratulated | 2 |
| 17994 | conger | 2 |
| 17995 | confutes | 2 |
| 17996 | confusions | 2 |
| 17997 | conformity | 2 |
| 17998 | conformable | 2 |
| 17999 | confirmations | 2 |
| 18000 | confining | 2 |
| 18001 | confiding | 2 |
| 18002 | confidently | 2 |
| 18003 | confesses | 2 |
| 18004 | confers | 2 |
| 18005 | conduits | 2 |
| 18006 | conductor | 2 |
| 18007 | conduce | 2 |
| 18008 | condolence | 2 |
| 18009 | condign | 2 |
| 18010 | concocters | 2 |
| 18011 | conclusive | 2 |
| 18012 | conclave | 2 |
| 18013 | conciseness | 2 |
| 18014 | concernings | 2 |
| 18015 | conceptions | 2 |
| 18016 | computed | 2 |
| 18017 | computation | 2 |
| 18018 | compulsive | 2 |
| 18019 | compressing | 2 |
| 18020 | comport | 2 |
| 18021 | complexioned | 2 |
| 18022 | completing | 2 |
| 18023 | complements | 2 |
| 18024 | compiled | 2 |
| 18025 | compile | 2 |
| 18026 | competent | 2 |
| 18027 | competency | 2 |
| 18028 | compensate | 2 |
| 18029 | compeers | 2 |
| 18030 | compassing | 2 |
| 18031 | compano | 2 |
| 18032 | communities | 2 |
| 18033 | commonalty | 2 |
| 18034 | commixture | 2 |
| 18035 | commingled | 2 |
| 18036 | commentaries | 2 |
| 18037 | commencement | 2 |
| 18038 | commenced | 2 |
| 18039 | commenc | 2 |
| 18040 | commandments | 2 |
| 18041 | comma | 2 |
| 18042 | comings | 2 |
| 18043 | comets | 2 |
| 18044 | comedies | 2 |
| 18045 | combustion | 2 |
| 18046 | combin | 2 |
| 18047 | colted | 2 |
| 18048 | collop | 2 |
| 18049 | colliers | 2 |
| 18050 | collied | 2 |
| 18051 | collateral | 2 |
| 18052 | colbrand | 2 |
| 18053 | col | 2 |
| 18054 | coinage | 2 |
| 18055 | coign | 2 |
| 18056 | coif | 2 |
| 18057 | cogitation | 2 |
| 18058 | coffins | 2 |
| 18059 | cockney | 2 |
| 18060 | cockatrice | 2 |
| 18061 | cobwebs | 2 |
| 18062 | coax | 2 |
| 18063 | coasting | 2 |
| 18064 | coachman | 2 |
| 18065 | clustered | 2 |
| 18066 | cloyed | 2 |
| 18067 | clouted | 2 |
| 18068 | clotpoll | 2 |
| 18069 | clothier | 2 |
| 18070 | closeness | 2 |
| 18071 | cloisters | 2 |
| 18072 | clipt | 2 |
| 18073 | climbs | 2 |
| 18074 | cliffs | 2 |
| 18075 | cleverly | 2 |
| 18076 | clerical | 2 |
| 18077 | cleitus | 2 |
| 18078 | cleansed | 2 |
| 18079 | cleaner | 2 |
| 18080 | clawed | 2 |
| 18081 | claudius | 2 |
| 18082 | clasping | 2 |
| 18083 | clapped | 2 |
| 18084 | clangor | 2 |
| 18085 | clamors | 2 |
| 18086 | clamb | 2 |
| 18087 | ciudad | 2 |
| 18088 | cites | 2 |
| 18089 | cistern | 2 |
| 18090 | circumvention | 2 |
| 18091 | circumstanced | 2 |
| 18092 | circumspection | 2 |
| 18093 | circuitous | 2 |
| 18094 | circling | 2 |
| 18095 | circles | 2 |
| 18096 | ciphers | 2 |
| 18097 | ciceronian | 2 |
| 18098 | cicely | 2 |
| 18099 | cianis | 2 |
| 18100 | churchyards | 2 |
| 18101 | christina | 2 |
| 18102 | christi | 2 |
| 18103 | chough | 2 |
| 18104 | chor | 2 |
| 18105 | chops | 2 |
| 18106 | choking | 2 |
| 18107 | choked | 2 |
| 18108 | choicest | 2 |
| 18109 | choicely | 2 |
| 18110 | chloe | 2 |
| 18111 | chivalries | 2 |
| 18112 | chirrah | 2 |
| 18113 | chipp | 2 |
| 18114 | chine | 2 |
| 18115 | chimneys | 2 |
| 18116 | childlike | 2 |
| 18117 | chicken | 2 |
| 18118 | chewing | 2 |
| 18119 | cheveril | 2 |
| 18120 | chevalier | 2 |
| 18121 | cheval | 2 |
| 18122 | chestnuts | 2 |
| 18123 | cherries | 2 |
| 18124 | cherished | 2 |
| 18125 | cher | 2 |
| 18126 | cheerfulness | 2 |
| 18127 | cheaters | 2 |
| 18128 | cheapside | 2 |
| 18129 | cheaper | 2 |
| 18130 | chattering | 2 |
| 18131 | chasing | 2 |
| 18132 | chased | 2 |
| 18133 | chartreux | 2 |
| 18134 | charon | 2 |
| 18135 | charnel | 2 |
| 18136 | charlemain | 2 |
| 18137 | charger | 2 |
| 18138 | charactery | 2 |
| 18139 | chapmen | 2 |
| 18140 | chaplet | 2 |
| 18141 | chapless | 2 |
| 18142 | chaplains | 2 |
| 18143 | chanting | 2 |
| 18144 | chanticleer | 2 |
| 18145 | channels | 2 |
| 18146 | chanc | 2 |
| 18147 | chambermaids | 2 |
| 18148 | chalice | 2 |
| 18149 | chafing | 2 |
| 18150 | cetera | 2 |
| 18151 | cesse | 2 |
| 18152 | certified | 2 |
| 18153 | censurer | 2 |
| 18154 | censer | 2 |
| 18155 | cellar | 2 |
| 18156 | ceiling | 2 |
| 18157 | cedars | 2 |
| 18158 | cavity | 2 |
| 18159 | cavilling | 2 |
| 18160 | cautious | 2 |
| 18161 | cautelous | 2 |
| 18162 | causing | 2 |
| 18163 | cauldrons | 2 |
| 18164 | caucasus | 2 |
| 18165 | cathay | 2 |
| 18166 | caterwauling | 2 |
| 18167 | caterer | 2 |
| 18168 | catechism | 2 |
| 18169 | catcher | 2 |
| 18170 | catalan | 2 |
| 18171 | cataian | 2 |
| 18172 | casually | 2 |
| 18173 | casual | 2 |
| 18174 | castigation | 2 |
| 18175 | casilda | 2 |
| 18176 | casa | 2 |
| 18177 | cas | 2 |
| 18178 | carthusian | 2 |
| 18179 | carrions | 2 |
| 18180 | carousing | 2 |
| 18181 | carouse | 2 |
| 18182 | carous | 2 |
| 18183 | carol | 2 |
| 18184 | carnation | 2 |
| 18185 | caret | 2 |
| 18186 | caressing | 2 |
| 18187 | cardecue | 2 |
| 18188 | carcasses | 2 |
| 18189 | carcase | 2 |
| 18190 | carcanet | 2 |
| 18191 | carat | 2 |
| 18192 | caracuel | 2 |
| 18193 | captivated | 2 |
| 18194 | captainship | 2 |
| 18195 | capricious | 2 |
| 18196 | capp | 2 |
| 18197 | capitulate | 2 |
| 18198 | caparisoned | 2 |
| 18199 | capacious | 2 |
| 18200 | canvass | 2 |
| 18201 | canopies | 2 |
| 18202 | canonized | 2 |
| 18203 | canoniz | 2 |
| 18204 | cannoneer | 2 |
| 18205 | candour | 2 |
| 18206 | cancell | 2 |
| 18207 | canaries | 2 |
| 18208 | canakin | 2 |
| 18209 | camlet | 2 |
| 18210 | cambria | 2 |
| 18211 | calumnies | 2 |
| 18212 | calculate | 2 |
| 18213 | calamities | 2 |
| 18214 | cager | 2 |
| 18215 | caesarion | 2 |
| 18216 | cadiz | 2 |
| 18217 | cackneys | 2 |
| 18218 | cackling | 2 |
| 18219 | cabins | 2 |
| 18220 | caballeros | 2 |
| 18221 | ca | 2 |
| 18222 | byways | 2 |
| 18223 | bye | 2 |
| 18224 | buyer | 2 |
| 18225 | buxom | 2 |
| 18226 | butcheries | 2 |
| 18227 | bust | 2 |
| 18228 | buss | 2 |
| 18229 | bushel | 2 |
| 18230 | burton | 2 |
| 18231 | burr | 2 |
| 18232 | burnish | 2 |
| 18233 | burneth | 2 |
| 18234 | burly | 2 |
| 18235 | burghers | 2 |
| 18236 | burdening | 2 |
| 18237 | buoy | 2 |
| 18238 | bumpkin | 2 |
| 18239 | bullies | 2 |
| 18240 | bullens | 2 |
| 18241 | bulky | 2 |
| 18242 | bugles | 2 |
| 18243 | bugbear | 2 |
| 18244 | buffoon | 2 |
| 18245 | bucephalus | 2 |
| 18246 | bubbling | 2 |
| 18247 | brushes | 2 |
| 18248 | brunello | 2 |
| 18249 | browsing | 2 |
| 18250 | brotherhoods | 2 |
| 18251 | broaches | 2 |
| 18252 | britaines | 2 |
| 18253 | bristol | 2 |
| 18254 | bristled | 2 |
| 18255 | bringeth | 2 |
| 18256 | brimful | 2 |
| 18257 | brilliancy | 2 |
| 18258 | briefness | 2 |
| 18259 | bridles | 2 |
| 18260 | bridges | 2 |
| 18261 | bridgenorth | 2 |
| 18262 | bricklayer | 2 |
| 18263 | briars | 2 |
| 18264 | briareus | 2 |
| 18265 | brewing | 2 |
| 18266 | brewer | 2 |
| 18267 | bretheren | 2 |
| 18268 | breeders | 2 |
| 18269 | breasted | 2 |
| 18270 | breaches | 2 |
| 18271 | brazier | 2 |
| 18272 | braz | 2 |
| 18273 | braved | 2 |
| 18274 | bravado | 2 |
| 18275 | bras | 2 |
| 18276 | brained | 2 |
| 18277 | braided | 2 |
| 18278 | braggarts | 2 |
| 18279 | bragg | 2 |
| 18280 | brabbler | 2 |
| 18281 | brabble | 2 |
| 18282 | boyish | 2 |
| 18283 | boxes | 2 |
| 18284 | bouts | 2 |
| 18285 | bourchier | 2 |
| 18286 | bounce | 2 |
| 18287 | bouciqualt | 2 |
| 18288 | bottoms | 2 |
| 18289 | bottled | 2 |
| 18290 | bots | 2 |
| 18291 | bosworth | 2 |
| 18292 | boors | 2 |
| 18293 | bookseller | 2 |
| 18294 | bonne | 2 |
| 18295 | bonelace | 2 |
| 18296 | bombast | 2 |
| 18297 | bombard | 2 |
| 18298 | bolster | 2 |
| 18299 | bohemian | 2 |
| 18300 | bog | 2 |
| 18301 | bodykins | 2 |
| 18302 | bodements | 2 |
| 18303 | boded | 2 |
| 18304 | bobbins | 2 |
| 18305 | boasts | 2 |
| 18306 | boasted | 2 |
| 18307 | boars | 2 |
| 18308 | blust | 2 |
| 18309 | blunting | 2 |
| 18310 | blunter | 2 |
| 18311 | blundering | 2 |
| 18312 | blunder | 2 |
| 18313 | blubbering | 2 |
| 18314 | blubber | 2 |
| 18315 | blossoming | 2 |
| 18316 | blooming | 2 |
| 18317 | bloodstained | 2 |
| 18318 | bloodied | 2 |
| 18319 | blisters | 2 |
| 18320 | blinking | 2 |
| 18321 | blesses | 2 |
| 18322 | blessedly | 2 |
| 18323 | blent | 2 |
| 18324 | blended | 2 |
| 18325 | bleared | 2 |
| 18326 | bleaching | 2 |
| 18327 | blazoning | 2 |
| 18328 | blazing | 2 |
| 18329 | blaz | 2 |
| 18330 | blasphemous | 2 |
| 18331 | blaspheming | 2 |
| 18332 | blanketings | 2 |
| 18333 | blames | 2 |
| 18334 | blameless | 2 |
| 18335 | bladed | 2 |
| 18336 | blackfriars | 2 |
| 18337 | blackest | 2 |
| 18338 | blackberries | 2 |
| 18339 | blackamoors | 2 |
| 18340 | blackamoor | 2 |
| 18341 | blabb | 2 |
| 18342 | bitt | 2 |
| 18343 | bisson | 2 |
| 18344 | biscay | 2 |
| 18345 | birthplace | 2 |
| 18346 | birthday | 2 |
| 18347 | billow | 2 |
| 18348 | billing | 2 |
| 18349 | billiards | 2 |
| 18350 | billeted | 2 |
| 18351 | bilbo | 2 |
| 18352 | bib | 2 |
| 18353 | bewails | 2 |
| 18354 | bewailed | 2 |
| 18355 | beverage | 2 |
| 18356 | betting | 2 |
| 18357 | bettering | 2 |
| 18358 | betraying | 2 |
| 18359 | betis | 2 |
| 18360 | betideth | 2 |
| 18361 | beteem | 2 |
| 18362 | betakes | 2 |
| 18363 | bestowal | 2 |
| 18364 | bestirr | 2 |
| 18365 | bespake | 2 |
| 18366 | besort | 2 |
| 18367 | besmirch | 2 |
| 18368 | berth | 2 |
| 18369 | bernardino | 2 |
| 18370 | bergomask | 2 |
| 18371 | bereaved | 2 |
| 18372 | berard | 2 |
| 18373 | bequests | 2 |
| 18374 | bequeathing | 2 |
| 18375 | benumbed | 2 |
| 18376 | bennet | 2 |
| 18377 | beneficiary | 2 |
| 18378 | benedicite | 2 |
| 18379 | bemock | 2 |
| 18380 | bellowed | 2 |
| 18381 | bellona | 2 |
| 18382 | bellies | 2 |
| 18383 | belgia | 2 |
| 18384 | beldams | 2 |
| 18385 | belabouring | 2 |
| 18386 | bejar | 2 |
| 18387 | behoof | 2 |
| 18388 | beholds | 2 |
| 18389 | beholdest | 2 |
| 18390 | beholder | 2 |
| 18391 | behaving | 2 |
| 18392 | beginners | 2 |
| 18393 | befriended | 2 |
| 18394 | befitted | 2 |
| 18395 | beeves | 2 |
| 18396 | beehives | 2 |
| 18397 | bedtime | 2 |
| 18398 | bedrid | 2 |
| 18399 | bedevilled | 2 |
| 18400 | bedecking | 2 |
| 18401 | bedeck | 2 |
| 18402 | bedclothes | 2 |
| 18403 | becks | 2 |
| 18404 | beaumont | 2 |
| 18405 | beatified | 2 |
| 18406 | beardless | 2 |
| 18407 | bead | 2 |
| 18408 | beached | 2 |
| 18409 | bays | 2 |
| 18410 | baying | 2 |
| 18411 | bayard | 2 |
| 18412 | battlefield | 2 |
| 18413 | battering | 2 |
| 18414 | batten | 2 |
| 18415 | bating | 2 |
| 18416 | basting | 2 |
| 18417 | basted | 2 |
| 18418 | baste | 2 |
| 18419 | basins | 2 |
| 18420 | bases | 2 |
| 18421 | barricado | 2 |
| 18422 | barns | 2 |
| 18423 | barnes | 2 |
| 18424 | barne | 2 |
| 18425 | barn | 2 |
| 18426 | barefooted | 2 |
| 18427 | barbers | 2 |
| 18428 | barbed | 2 |
| 18429 | barbason | 2 |
| 18430 | barbarossa | 2 |
| 18431 | baptised | 2 |
| 18432 | baptise | 2 |
| 18433 | banns | 2 |
| 18434 | banes | 2 |
| 18435 | bandages | 2 |
| 18436 | balk | 2 |
| 18437 | balanced | 2 |
| 18438 | bakes | 2 |
| 18439 | baffle | 2 |
| 18440 | baffl | 2 |
| 18441 | baeza | 2 |
| 18442 | baes | 2 |
| 18443 | backpiece | 2 |
| 18444 | backbiters | 2 |
| 18445 | bacchus | 2 |
| 18446 | bacchanals | 2 |
| 18447 | babylon | 2 |
| 18448 | ba | 2 |
| 18449 | azur | 2 |
| 18450 | awork | 2 |
| 18451 | awnings | 2 |
| 18452 | awning | 2 |
| 18453 | aweless | 2 |
| 18454 | awaked | 2 |
| 18455 | avow | 2 |
| 18456 | avouches | 2 |
| 18457 | avocations | 2 |
| 18458 | avert | 2 |
| 18459 | avenging | 2 |
| 18460 | avarice | 2 |
| 18461 | availed | 2 |
| 18462 | available | 2 |
| 18463 | authorized | 2 |
| 18464 | autem | 2 |
| 18465 | austerely | 2 |
| 18466 | aussi | 2 |
| 18467 | augurer | 2 |
| 18468 | augmenting | 2 |
| 18469 | auger | 2 |
| 18470 | auditor | 2 |
| 18471 | au | 2 |
| 18472 | atwain | 2 |
| 18473 | attributing | 2 |
| 18474 | attractive | 2 |
| 18475 | attendeth | 2 |
| 18476 | attendents | 2 |
| 18477 | attains | 2 |
| 18478 | attacking | 2 |
| 18479 | atonement | 2 |
| 18480 | atlas | 2 |
| 18481 | ates | 2 |
| 18482 | atalanta | 2 |
| 18483 | astride | 2 |
| 18484 | assyrian | 2 |
| 18485 | assumes | 2 |
| 18486 | assuage | 2 |
| 18487 | associated | 2 |
| 18488 | associate | 2 |
| 18489 | assistants | 2 |
| 18490 | assigns | 2 |
| 18491 | assertion | 2 |
| 18492 | assemblies | 2 |
| 18493 | assassins | 2 |
| 18494 | assailing | 2 |
| 18495 | asquint | 2 |
| 18496 | aspir | 2 |
| 18497 | aspen | 2 |
| 18498 | asketh | 2 |
| 18499 | ashford | 2 |
| 18500 | ascribed | 2 |
| 18501 | ascent | 2 |
| 18502 | ascending | 2 |
| 18503 | artus | 2 |
| 18504 | artless | 2 |
| 18505 | artistic | 2 |
| 18506 | artifices | 2 |
| 18507 | articulate | 2 |
| 18508 | arrests | 2 |
| 18509 | arraigned | 2 |
| 18510 | aromatic | 2 |
| 18511 | armourers | 2 |
| 18512 | armipotent | 2 |
| 18513 | armigero | 2 |
| 18514 | arme | 2 |
| 18515 | arithmetician | 2 |
| 18516 | ariseth | 2 |
| 18517 | argier | 2 |
| 18518 | archibald | 2 |
| 18519 | archelaus | 2 |
| 18520 | arched | 2 |
| 18521 | archdeacon | 2 |
| 18522 | archbishops | 2 |
| 18523 | arbitrators | 2 |
| 18524 | arbitrator | 2 |
| 18525 | arbitrary | 2 |
| 18526 | aranjuez | 2 |
| 18527 | araby | 2 |
| 18528 | aquiline | 2 |
| 18529 | apter | 2 |
| 18530 | apricocks | 2 |
| 18531 | appurtenance | 2 |
| 18532 | applauding | 2 |
| 18533 | appertinent | 2 |
| 18534 | appertains | 2 |
| 18535 | appertainings | 2 |
| 18536 | appertain | 2 |
| 18537 | apparelled | 2 |
| 18538 | appals | 2 |
| 18539 | appal | 2 |
| 18540 | apelles | 2 |
| 18541 | apartments | 2 |
| 18542 | anyhow | 2 |
| 18543 | antidote | 2 |
| 18544 | antics | 2 |
| 18545 | anticipation | 2 |
| 18546 | antechamber | 2 |
| 18547 | antaeus | 2 |
| 18548 | anoint | 2 |
| 18549 | annoyed | 2 |
| 18550 | announcing | 2 |
| 18551 | anklets | 2 |
| 18552 | ankles | 2 |
| 18553 | ankle | 2 |
| 18554 | angles | 2 |
| 18555 | angerly | 2 |
| 18556 | angered | 2 |
| 18557 | andrea | 2 |
| 18558 | andalusian | 2 |
| 18559 | ancientry | 2 |
| 18560 | anchoring | 2 |
| 18561 | anatomiz | 2 |
| 18562 | amurath | 2 |
| 18563 | amplest | 2 |
| 18564 | amort | 2 |
| 18565 | amities | 2 |
| 18566 | amis | 2 |
| 18567 | america | 2 |
| 18568 | ameji | 2 |
| 18569 | ambitiously | 2 |
| 18570 | ambitions | 2 |
| 18571 | ambergris | 2 |
| 18572 | amazonian | 2 |
| 18573 | amazedness | 2 |
| 18574 | alway | 2 |
| 18575 | alva | 2 |
| 18576 | alquife | 2 |
| 18577 | alonzo | 2 |
| 18578 | aloes | 2 |
| 18579 | almanac | 2 |
| 18580 | almacen | 2 |
| 18581 | allure | 2 |
| 18582 | allotted | 2 |
| 18583 | alleviate | 2 |
| 18584 | alleged | 2 |
| 18585 | allege | 2 |
| 18586 | allaying | 2 |
| 18587 | alla | 2 |
| 18588 | alicante | 2 |
| 18589 | alexandrian | 2 |
| 18590 | ales | 2 |
| 18591 | aleppo | 2 |
| 18592 | alderman | 2 |
| 18593 | alchemist | 2 |
| 18594 | albracca | 2 |
| 18595 | akin | 2 |
| 18596 | airily | 2 |
| 18597 | ainsi | 2 |
| 18598 | agone | 2 |
| 18599 | affy | 2 |
| 18600 | affray | 2 |
| 18601 | affording | 2 |
| 18602 | afflicts | 2 |
| 18603 | affined | 2 |
| 18604 | affectations | 2 |
| 18605 | aer | 2 |
| 18606 | advisedly | 2 |
| 18607 | advertise | 2 |
| 18608 | adventurous | 2 |
| 18609 | adulation | 2 |
| 18610 | adramadio | 2 |
| 18611 | adorns | 2 |
| 18612 | adoring | 2 |
| 18613 | adopts | 2 |
| 18614 | admitting | 2 |
| 18615 | admiringly | 2 |
| 18616 | admirer | 2 |
| 18617 | admirably | 2 |
| 18618 | administration | 2 |
| 18619 | adjourn | 2 |
| 18620 | adjacent | 2 |
| 18621 | adieus | 2 |
| 18622 | adhere | 2 |
| 18623 | addrest | 2 |
| 18624 | addresses | 2 |
| 18625 | addled | 2 |
| 18626 | addiction | 2 |
| 18627 | addicted | 2 |
| 18628 | adapted | 2 |
| 18629 | adapt | 2 |
| 18630 | adage | 2 |
| 18631 | acutely | 2 |
| 18632 | acquir | 2 |
| 18633 | acolyte | 2 |
| 18634 | accuses | 2 |
| 18635 | accusativo | 2 |
| 18636 | accumulate | 2 |
| 18637 | accrue | 2 |
| 18638 | accoutrement | 2 |
| 18639 | accepting | 2 |
| 18640 | academicians | 2 |
| 18641 | academes | 2 |
| 18642 | aby | 2 |
| 18643 | abstraction | 2 |
| 18644 | abridge | 2 |
| 18645 | abounds | 2 |
| 18646 | abounding | 2 |
| 18647 | abodes | 2 |
| 18648 | abjur | 2 |
| 18649 | abjects | 2 |
| 18650 | abhorring | 2 |
| 18651 | abhorrence | 2 |
| 18652 | abernuncio | 2 |
| 18653 | aberga | 2 |
| 18654 | abel | 2 |
| 18655 | abase | 2 |
| 18656 | zwagger | 1 |
| 18657 | zulema | 1 |
| 18658 | zorruna | 1 |
| 18659 | zoroastric | 1 |
| 18660 | zoroaster | 1 |
| 18661 | zopyrus | 1 |
| 18662 | zonzorino | 1 |
| 18663 | zone | 1 |
| 18664 | zoltanis | 1 |
| 18665 | zoilus | 1 |
| 18666 | zodiac | 1 |
| 18667 | zo | 1 |
| 18668 | zeuxis | 1 |
| 18669 | zerbino | 1 |
| 18670 | zephyrs | 1 |
| 18671 | zenith | 1 |
| 18672 | zenelophon | 1 |
| 18673 | zed | 1 |
| 18674 | zeca | 1 |
| 18675 | zeals | 1 |
| 18676 | zaquizami | 1 |
| 18677 | zany | 1 |
| 18678 | zanoguera | 1 |
| 18679 | zanies | 1 |
| 18680 | zagals | 1 |
| 18681 | yseult | 1 |
| 18682 | youtli | 1 |
| 18683 | younglings | 1 |
| 18684 | yorks | 1 |
| 18685 | yongrey | 1 |
| 18686 | yoketh | 1 |
| 18687 | yokefellow | 1 |
| 18688 | yieldeth | 1 |
| 18689 | yielders | 1 |
| 18690 | yicld | 1 |
| 18691 | yesterdays | 1 |
| 18692 | yelping | 1 |
| 18693 | yells | 1 |
| 18694 | yellows | 1 |
| 18695 | yellowness | 1 |
| 18696 | yellowing | 1 |
| 18697 | yellowed | 1 |
| 18698 | yedward | 1 |
| 18699 | yeast | 1 |
| 18700 | yearning | 1 |
| 18701 | yead | 1 |
| 18702 | ycliped | 1 |
| 18703 | ycleped | 1 |
| 18704 | yawned | 1 |
| 18705 | yaw | 1 |
| 18706 | yaughan | 1 |
| 18707 | yanguesan | 1 |
| 18708 | xenophon | 1 |
| 18709 | xarifa | 1 |
| 18710 | xanthus | 1 |
| 18711 | xanthippe | 1 |
| 18712 | wul | 1 |
| 18713 | wrying | 1 |
| 18714 | wronk | 1 |
| 18715 | wrongly | 1 |
| 18716 | writs | 1 |
| 18717 | writhled | 1 |
| 18718 | wristbands | 1 |
| 18719 | wringer | 1 |
| 18720 | wretchedly | 1 |
| 18721 | wretcheder | 1 |
| 18722 | wretchcd | 1 |
| 18723 | wresting | 1 |
| 18724 | wrens | 1 |
| 18725 | wrecks | 1 |
| 18726 | wrecking | 1 |
| 18727 | wreathen | 1 |
| 18728 | wreaks | 1 |
| 18729 | wrathfully | 1 |
| 18730 | wrapt | 1 |
| 18731 | wraps | 1 |
| 18732 | wrapper | 1 |
| 18733 | wranglers | 1 |
| 18734 | wrangler | 1 |
| 18735 | wrackful | 1 |
| 18736 | wouns | 1 |
| 18737 | woundless | 1 |
| 18738 | woundings | 1 |
| 18739 | wouldest | 1 |
| 18740 | wouid | 1 |
| 18741 | wotting | 1 |
| 18742 | worthied | 1 |
| 18743 | worsted | 1 |
| 18744 | worshippest | 1 |
| 18745 | worshipper | 1 |
| 18746 | worshipped | 1 |
| 18747 | worshipfully | 1 |
| 18748 | worried | 1 |
| 18749 | wormy | 1 |
| 18750 | worky | 1 |
| 18751 | workshop | 1 |
| 18752 | workmanly | 1 |
| 18753 | workers | 1 |
| 18754 | worins | 1 |
| 18755 | woolward | 1 |
| 18756 | woolsey | 1 |
| 18757 | woolsack | 1 |
| 18758 | woolcarders | 1 |
| 18759 | wooings | 1 |
| 18760 | wooingly | 1 |
| 18761 | woof | 1 |
| 18762 | woody | 1 |
| 18763 | woodmonger | 1 |
| 18764 | woodland | 1 |
| 18765 | wooded | 1 |
| 18766 | wondrously | 1 |
| 18767 | wonderstruck | 1 |
| 18768 | woncot | 1 |
| 18769 | womby | 1 |
| 18770 | womankind | 1 |
| 18771 | wolfish | 1 |
| 18772 | wolds | 1 |
| 18773 | woefullest | 1 |
| 18774 | wobble | 1 |
| 18775 | woa | 1 |
| 18776 | wo | 1 |
| 18777 | wived | 1 |
| 18778 | wittolly | 1 |
| 18779 | wittol | 1 |
| 18780 | witting | 1 |
| 18781 | wittily | 1 |
| 18782 | wittiest | 1 |
| 18783 | witticisms | 1 |
| 18784 | withstood | 1 |
| 18785 | withstanding | 1 |
| 18786 | withouten | 1 |
| 18787 | withold | 1 |
| 18788 | withdrawal | 1 |
| 18789 | witching | 1 |
| 18790 | wist | 1 |
| 18791 | wisp | 1 |
| 18792 | wishtly | 1 |
| 18793 | wishful | 1 |
| 18794 | wisheth | 1 |
| 18795 | wishers | 1 |
| 18796 | wisher | 1 |
| 18797 | wiselier | 1 |
| 18798 | wis | 1 |
| 18799 | winterly | 1 |
| 18800 | winsome | 1 |
| 18801 | winnows | 1 |
| 18802 | wingham | 1 |
| 18803 | wingfield | 1 |
| 18804 | windlasses | 1 |
| 18805 | windgalls | 1 |
| 18806 | wincot | 1 |
| 18807 | winch | 1 |
| 18808 | wince | 1 |
| 18809 | wimpled | 1 |
| 18810 | wily | 1 |
| 18811 | willissimus | 1 |
| 18812 | willeth | 1 |
| 18813 | willers | 1 |
| 18814 | wilfulness | 1 |
| 18815 | wilfulnes | 1 |
| 18816 | wildfowl | 1 |
| 18817 | wildfire | 1 |
| 18818 | wildcats | 1 |
| 18819 | wig | 1 |
| 18820 | widowhood | 1 |
| 18821 | widest | 1 |
| 18822 | widespread | 1 |
| 18823 | widens | 1 |
| 18824 | widened | 1 |
| 18825 | wid | 1 |
| 18826 | wicky | 1 |
| 18827 | wicket | 1 |
| 18828 | wickednes | 1 |
| 18829 | wickeder | 1 |
| 18830 | wick | 1 |
| 18831 | whorish | 1 |
| 18832 | whoring | 1 |
| 18833 | whoresons | 1 |
| 18834 | whoremonger | 1 |
| 18835 | whoremasterly | 1 |
| 18836 | whored | 1 |
| 18837 | whor | 1 |
| 18838 | whooping | 1 |
| 18839 | whoobub | 1 |
| 18840 | wholesom | 1 |
| 18841 | whizzing | 1 |
| 18842 | whittle | 1 |
| 18843 | whitsters | 1 |
| 18844 | whiting | 1 |
| 18845 | whitely | 1 |
| 18846 | whitehall | 1 |
| 18847 | whistles | 1 |
| 18848 | whist | 1 |
| 18849 | whirlpool | 1 |
| 18850 | whirligig | 1 |
| 18851 | whipstock | 1 |
| 18852 | whipster | 1 |
| 18853 | whippings | 1 |
| 18854 | whippers | 1 |
| 18855 | whinid | 1 |
| 18856 | whined | 1 |
| 18857 | whin | 1 |
| 18858 | whiffler | 1 |
| 18859 | whichever | 1 |
| 18860 | whew | 1 |
| 18861 | wheresome | 1 |
| 18862 | whereout | 1 |
| 18863 | whereinto | 1 |
| 18864 | wherefrom | 1 |
| 18865 | whereer | 1 |
| 18866 | whencesoever | 1 |
| 18867 | whenas | 1 |
| 18868 | whelped | 1 |
| 18869 | whelm | 1 |
| 18870 | whelks | 1 |
| 18871 | whelk | 1 |
| 18872 | wheezing | 1 |
| 18873 | wheeson | 1 |
| 18874 | wheer | 1 |
| 18875 | wheaten | 1 |
| 18876 | whatsome | 1 |
| 18877 | wharfs | 1 |
| 18878 | wharf | 1 |
| 18879 | whales | 1 |
| 18880 | whalebone | 1 |
| 18881 | wezand | 1 |
| 18882 | wetting | 1 |
| 18883 | wenching | 1 |
| 18884 | welshwomen | 1 |
| 18885 | welcoming | 1 |
| 18886 | welcomest | 1 |
| 18887 | welcomer | 1 |
| 18888 | weightless | 1 |
| 18889 | weighable | 1 |
| 18890 | weet | 1 |
| 18891 | weepings | 1 |
| 18892 | weepingly | 1 |
| 18893 | weeper | 1 |
| 18894 | weekly | 1 |
| 18895 | weedy | 1 |
| 18896 | weeding | 1 |
| 18897 | weeder | 1 |
| 18898 | wedged | 1 |
| 18899 | weavers | 1 |
| 18900 | weathers | 1 |
| 18901 | wearily | 1 |
| 18902 | wealtlly | 1 |
| 18903 | wealthiest | 1 |
| 18904 | wealsmen | 1 |
| 18905 | weaklings | 1 |
| 18906 | weakling | 1 |
| 18907 | weakened | 1 |
| 18908 | waywardness | 1 |
| 18909 | waywarder | 1 |
| 18910 | wayside | 1 |
| 18911 | waylaying | 1 |
| 18912 | waylay | 1 |
| 18913 | waylaid | 1 |
| 18914 | wayfarers | 1 |
| 18915 | waxing | 1 |
| 18916 | wawl | 1 |
| 18917 | waw | 1 |
| 18918 | waverer | 1 |
| 18919 | waved | 1 |
| 18920 | waterton | 1 |
| 18921 | waterrugs | 1 |
| 18922 | waterpots | 1 |
| 18923 | waterish | 1 |
| 18924 | watering | 1 |
| 18925 | waterford | 1 |
| 18926 | waterfly | 1 |
| 18927 | waterdrops | 1 |
| 18928 | watchword | 1 |
| 18929 | watchings | 1 |
| 18930 | watchfulness | 1 |
| 18931 | wasters | 1 |
| 18932 | washford | 1 |
| 18933 | washerwoman | 1 |
| 18934 | washer | 1 |
| 18935 | warring | 1 |
| 18936 | warrener | 1 |
| 18937 | warren | 1 |
| 18938 | warrantize | 1 |
| 18939 | warrantise | 1 |
| 18940 | warranteth | 1 |
| 18941 | warped | 1 |
| 18942 | warns | 1 |
| 18943 | warfare | 1 |
| 18944 | wardrop | 1 |
| 18945 | wardrobes | 1 |
| 18946 | wappen | 1 |
| 18947 | wann | 1 |
| 18948 | wanes | 1 |
| 18949 | waned | 1 |
| 18950 | wallon | 1 |
| 18951 | wallets | 1 |
| 18952 | wallet | 1 |
| 18953 | walker | 1 |
| 18954 | wakest | 1 |
| 18955 | wakens | 1 |
| 18956 | waive | 1 |
| 18957 | waiteth | 1 |
| 18958 | waiter | 1 |
| 18959 | waistcoat | 1 |
| 18960 | wainscot | 1 |
| 18961 | wainropes | 1 |
| 18962 | wain | 1 |
| 18963 | wailful | 1 |
| 18964 | wah | 1 |
| 18965 | wagtail | 1 |
| 18966 | waggoner | 1 |
| 18967 | waggling | 1 |
| 18968 | wafting | 1 |
| 18969 | waddled | 1 |
| 18970 | wad | 1 |
| 18971 | vying | 1 |
| 18972 | vurther | 1 |
| 18973 | vulnerable | 1 |
| 18974 | vulgo | 1 |
| 18975 | vulgars | 1 |
| 18976 | vulgarly | 1 |
| 18977 | vulgarity | 1 |
| 18978 | vulgarities | 1 |
| 18979 | vox | 1 |
| 18980 | vowels | 1 |
| 18981 | vowel | 1 |
| 18982 | voutsafe | 1 |
| 18983 | vour | 1 |
| 18984 | voudrais | 1 |
| 18985 | vouchsafing | 1 |
| 18986 | vouchsafes | 1 |
| 18987 | vouching | 1 |
| 18988 | voucher | 1 |
| 18989 | vote | 1 |
| 18990 | votarists | 1 |
| 18991 | vortnight | 1 |
| 18992 | vore | 1 |
| 18993 | voracious | 1 |
| 18994 | vomited | 1 |
| 18995 | vomissement | 1 |
| 18996 | voluptuously | 1 |
| 18997 | volunteered | 1 |
| 18998 | volunteer | 1 |
| 18999 | voluntaries | 1 |
| 19000 | volquessen | 1 |
| 19001 | volivorco | 1 |
| 19002 | volente | 1 |
| 19003 | volant | 1 |
| 19004 | volable | 1 |
| 19005 | voke | 1 |
| 19006 | voiding | 1 |
| 19007 | voce | 1 |
| 19008 | vocatur | 1 |
| 19009 | vocativo | 1 |
| 19010 | vobis | 1 |
| 19011 | vizor | 1 |
| 19012 | vizaments | 1 |
| 19013 | viz | 1 |
| 19014 | vixen | 1 |
| 19015 | vive | 1 |
| 19016 | vivar | 1 |
| 19017 | vivant | 1 |
| 19018 | vivacity | 1 |
| 19019 | viva | 1 |
| 19020 | vitx | 1 |
| 19021 | vitruvio | 1 |
| 19022 | vitement | 1 |
| 19023 | vita | 1 |
| 19024 | viso | 1 |
| 19025 | visitor | 1 |
| 19026 | visitings | 1 |
| 19027 | visitations | 1 |
| 19028 | visibly | 1 |
| 19029 | viscount | 1 |
| 19030 | visard | 1 |
| 19031 | virues | 1 |
| 19032 | virtually | 1 |
| 19033 | viriatus | 1 |
| 19034 | virgo | 1 |
| 19035 | virginalling | 1 |
| 19036 | vir | 1 |
| 19037 | violenteth | 1 |
| 19038 | violator | 1 |
| 19039 | violates | 1 |
| 19040 | vint | 1 |
| 19041 | vinedressing | 1 |
| 19042 | vindicative | 1 |
| 19043 | vindicated | 1 |
| 19044 | vincere | 1 |
| 19045 | vinaigre | 1 |
| 19046 | villians | 1 |
| 19047 | villianda | 1 |
| 19048 | villiago | 1 |
| 19049 | villanovas | 1 |
| 19050 | villalpando | 1 |
| 19051 | villagery | 1 |
| 19052 | villagers | 1 |
| 19053 | villager | 1 |
| 19054 | villadiego | 1 |
| 19055 | viler | 1 |
| 19056 | vigitant | 1 |
| 19057 | viewless | 1 |
| 19058 | vieweth | 1 |
| 19059 | vidi | 1 |
| 19060 | videsne | 1 |
| 19061 | vides | 1 |
| 19062 | video | 1 |
| 19063 | victuall | 1 |
| 19064 | victoriously | 1 |
| 19065 | victoress | 1 |
| 19066 | vict | 1 |
| 19067 | viciousness | 1 |
| 19068 | vici | 1 |
| 19069 | vicegerent | 1 |
| 19070 | vicecount | 1 |
| 19071 | vicaria | 1 |
| 19072 | vic | 1 |
| 19073 | viand | 1 |
| 19074 | vexeth | 1 |
| 19075 | vexest | 1 |
| 19076 | veux | 1 |
| 19077 | vetches | 1 |
| 19078 | vetch | 1 |
| 19079 | vestros | 1 |
| 19080 | vespers | 1 |
| 19081 | vesper | 1 |
| 19082 | versing | 1 |
| 19083 | versification | 1 |
| 19084 | versal | 1 |
| 19085 | veronesa | 1 |
| 19086 | verities | 1 |
| 19087 | verite | 1 |
| 19088 | veritas | 1 |
| 19089 | verisimilitude | 1 |
| 19090 | verino | 1 |
| 19091 | vergers | 1 |
| 19092 | verefore | 1 |
| 19093 | verdun | 1 |
| 19094 | verdant | 1 |
| 19095 | verbs | 1 |
| 19096 | verbosity | 1 |
| 19097 | verbiage | 1 |
| 19098 | verbatim | 1 |
| 19099 | verb | 1 |
| 19100 | venue | 1 |
| 19101 | venturesome | 1 |
| 19102 | ventricle | 1 |
| 19103 | ventages | 1 |
| 19104 | venomously | 1 |
| 19105 | venit | 1 |
| 19106 | venial | 1 |
| 19107 | veni | 1 |
| 19108 | vengeances | 1 |
| 19109 | veneys | 1 |
| 19110 | venereal | 1 |
| 19111 | veneration | 1 |
| 19112 | venditur | 1 |
| 19113 | velure | 1 |
| 19114 | veintiquatro | 1 |
| 19115 | veiling | 1 |
| 19116 | vehor | 1 |
| 19117 | vede | 1 |
| 19118 | vecinguerra | 1 |
| 19119 | vauvado | 1 |
| 19120 | vauntingly | 1 |
| 19121 | vaunter | 1 |
| 19122 | vaumond | 1 |
| 19123 | vaultages | 1 |
| 19124 | vates | 1 |
| 19125 | vater | 1 |
| 19126 | vastly | 1 |
| 19127 | vastidity | 1 |
| 19128 | varletto | 1 |
| 19129 | varletry | 1 |
| 19130 | varld | 1 |
| 19131 | variest | 1 |
| 19132 | variations | 1 |
| 19133 | vara | 1 |
| 19134 | vapor | 1 |
| 19135 | vapians | 1 |
| 19136 | vantbrace | 1 |
| 19137 | vant | 1 |
| 19138 | vanquisheth | 1 |
| 19139 | vanquishest | 1 |
| 19140 | van | 1 |
| 19141 | valuing | 1 |
| 19142 | valueless | 1 |
| 19143 | valorously | 1 |
| 19144 | vally | 1 |
| 19145 | vallant | 1 |
| 19146 | valladolid | 1 |
| 19147 | valiantness | 1 |
| 19148 | vales | 1 |
| 19149 | valerius | 1 |
| 19150 | valentio | 1 |
| 19151 | valence | 1 |
| 19152 | valance | 1 |
| 19153 | valanc | 1 |
| 19154 | vais | 1 |
| 19155 | vainer | 1 |
| 19156 | vaillant | 1 |
| 19157 | vailed | 1 |
| 19158 | vagrom | 1 |
| 19159 | vagram | 1 |
| 19160 | vagary | 1 |
| 19161 | vade | 1 |
| 19162 | vacation | 1 |
| 19163 | vacating | 1 |
| 19164 | va | 1 |
| 19165 | uy | 1 |
| 19166 | uttereth | 1 |
| 19167 | utrique | 1 |
| 19168 | utensil | 1 |
| 19169 | usurpingly | 1 |
| 19170 | usque | 1 |
| 19171 | ushering | 1 |
| 19172 | usances | 1 |
| 19173 | usages | 1 |
| 19174 | ursley | 1 |
| 19175 | ursa | 1 |
| 19176 | urreas | 1 |
| 19177 | urraca | 1 |
| 19178 | urns | 1 |
| 19179 | urinary | 1 |
| 19180 | urchinfield | 1 |
| 19181 | urbina | 1 |
| 19182 | urbanity | 1 |
| 19183 | upturned | 1 |
| 19184 | upspring | 1 |
| 19185 | upshoot | 1 |
| 19186 | ups | 1 |
| 19187 | uprous | 1 |
| 19188 | uprising | 1 |
| 19189 | uprightness | 1 |
| 19190 | uprighteously | 1 |
| 19191 | upreared | 1 |
| 19192 | upraised | 1 |
| 19193 | upmost | 1 |
| 19194 | upholding | 1 |
| 19195 | upholdeth | 1 |
| 19196 | upholder | 1 |
| 19197 | uphoarded | 1 |
| 19198 | upborne | 1 |
| 19199 | unwrung | 1 |
| 19200 | unwounded | 1 |
| 19201 | unworthier | 1 |
| 19202 | unwooed | 1 |
| 19203 | unwitted | 1 |
| 19204 | unwished | 1 |
| 19205 | unwish | 1 |
| 19206 | unwisely | 1 |
| 19207 | unwiped | 1 |
| 19208 | unwhipp | 1 |
| 19209 | unwept | 1 |
| 19210 | unweighing | 1 |
| 19211 | unweighed | 1 |
| 19212 | unweeded | 1 |
| 19213 | unwedgeable | 1 |
| 19214 | unwed | 1 |
| 19215 | unwearied | 1 |
| 19216 | unwatch | 1 |
| 19217 | unwary | 1 |
| 19218 | unwarily | 1 |
| 19219 | unwares | 1 |
| 19220 | unwalletted | 1 |
| 19221 | unvulnerable | 1 |
| 19222 | unvisited | 1 |
| 19223 | unvirtuous | 1 |
| 19224 | unviolated | 1 |
| 19225 | unvex | 1 |
| 19226 | unvenerable | 1 |
| 19227 | unveiled | 1 |
| 19228 | unvarnish | 1 |
| 19229 | unvanquished | 1 |
| 19230 | unvanquish | 1 |
| 19231 | unutterable | 1 |
| 19232 | unus | 1 |
| 19233 | untune | 1 |
| 19234 | untucked | 1 |
| 19235 | untruss | 1 |
| 19236 | untrodden | 1 |
| 19237 | untrod | 1 |
| 19238 | untreasur | 1 |
| 19239 | untranslated | 1 |
| 19240 | untrained | 1 |
| 19241 | untrain | 1 |
| 19242 | untraded | 1 |
| 19243 | untowardly | 1 |
| 19244 | untitled | 1 |
| 19245 | untiring | 1 |
| 19246 | untired | 1 |
| 19247 | untirable | 1 |
| 19248 | untir | 1 |
| 19249 | untimber | 1 |
| 19250 | unthread | 1 |
| 19251 | unthink | 1 |
| 19252 | unthankful | 1 |
| 19253 | untented | 1 |
| 19254 | untent | 1 |
| 19255 | untempering | 1 |
| 19256 | untasted | 1 |
| 19257 | untangled | 1 |
| 19258 | untangle | 1 |
| 19259 | untalk | 1 |
| 19260 | unsworn | 1 |
| 19261 | unswerving | 1 |
| 19262 | unswayed | 1 |
| 19263 | unswayable | 1 |
| 19264 | unsway | 1 |
| 19265 | unsustained | 1 |
| 19266 | unsuspiciously | 1 |
| 19267 | unsuspicious | 1 |
| 19268 | unsuspectingly | 1 |
| 19269 | unsurpassable | 1 |
| 19270 | unsur | 1 |
| 19271 | unsunn | 1 |
| 19272 | unsullied | 1 |
| 19273 | unsuiting | 1 |
| 19274 | unstuff | 1 |
| 19275 | unstringed | 1 |
| 19276 | unstooping | 1 |
| 19277 | unstinting | 1 |
| 19278 | unsteadfast | 1 |
| 19279 | unsquar | 1 |
| 19280 | unspoken | 1 |
| 19281 | unspoke | 1 |
| 19282 | unsphere | 1 |
| 19283 | unspeaking | 1 |
| 19284 | unspeak | 1 |
| 19285 | unsound | 1 |
| 19286 | unsorted | 1 |
| 19287 | unsoil | 1 |
| 19288 | unsmirched | 1 |
| 19289 | unslipping | 1 |
| 19290 | unskillful | 1 |
| 19291 | unskilfully | 1 |
| 19292 | unsisting | 1 |
| 19293 | unsinew | 1 |
| 19294 | unsightly | 1 |
| 19295 | unsifted | 1 |
| 19296 | unshunnable | 1 |
| 19297 | unshunn | 1 |
| 19298 | unshrubb | 1 |
| 19299 | unshrinking | 1 |
| 19300 | unshown | 1 |
| 19301 | unshout | 1 |
| 19302 | unshorn | 1 |
| 19303 | unsheath | 1 |
| 19304 | unshared | 1 |
| 19305 | unshapes | 1 |
| 19306 | unshaped | 1 |
| 19307 | unshaked | 1 |
| 19308 | unshak | 1 |
| 19309 | unsex | 1 |
| 19310 | unsever | 1 |
| 19311 | unset | 1 |
| 19312 | unserviceable | 1 |
| 19313 | unseparable | 1 |
| 19314 | unseminar | 1 |
| 19315 | unseemly | 1 |
| 19316 | unseeming | 1 |
| 19317 | unseduc | 1 |
| 19318 | unsecret | 1 |
| 19319 | unseconded | 1 |
| 19320 | unseasoned | 1 |
| 19321 | unsearch | 1 |
| 19322 | unseam | 1 |
| 19323 | unscratch | 1 |
| 19324 | unscour | 1 |
| 19325 | unscorch | 1 |
| 19326 | unscann | 1 |
| 19327 | unscalable | 1 |
| 19328 | unsated | 1 |
| 19329 | unsaluted | 1 |
| 19330 | unsaid | 1 |
| 19331 | unsaddled | 1 |
| 19332 | unrough | 1 |
| 19333 | unroot | 1 |
| 19334 | unroosted | 1 |
| 19335 | unroof | 1 |
| 19336 | unrivall | 1 |
| 19337 | unripp | 1 |
| 19338 | unrightful | 1 |
| 19339 | unrighteous | 1 |
| 19340 | unrewarded | 1 |
| 19341 | unrevers | 1 |
| 19342 | unrestricted | 1 |
| 19343 | unrestrainedly | 1 |
| 19344 | unrestor | 1 |
| 19345 | unresolv | 1 |
| 19346 | unreservedly | 1 |
| 19347 | unreprievable | 1 |
| 19348 | unremovably | 1 |
| 19349 | unremovable | 1 |
| 19350 | unregist | 1 |
| 19351 | unregarded | 1 |
| 19352 | unrecuring | 1 |
| 19353 | unrecounted | 1 |
| 19354 | unreconciliable | 1 |
| 19355 | unreconciled | 1 |
| 19356 | unrecognised | 1 |
| 19357 | unreclaimed | 1 |
| 19358 | unreasoning | 1 |
| 19359 | unreason | 1 |
| 19360 | unread | 1 |
| 19361 | unreached | 1 |
| 19362 | unrak | 1 |
| 19363 | unraised | 1 |
| 19364 | unquietly | 1 |
| 19365 | unquestionable | 1 |
| 19366 | unqueen | 1 |
| 19367 | unqualitied | 1 |
| 19368 | unpurpos | 1 |
| 19369 | unpurged | 1 |
| 19370 | unpublish | 1 |
| 19371 | unprun | 1 |
| 19372 | unprovokes | 1 |
| 19373 | unprovident | 1 |
| 19374 | unprovide | 1 |
| 19375 | unproportion | 1 |
| 19376 | unproperly | 1 |
| 19377 | unproper | 1 |
| 19378 | unpromising | 1 |
| 19379 | unprofited | 1 |
| 19380 | unpriz | 1 |
| 19381 | unprevented | 1 |
| 19382 | unprevailing | 1 |
| 19383 | unpretending | 1 |
| 19384 | unpress | 1 |
| 19385 | unpremeditated | 1 |
| 19386 | unpossible | 1 |
| 19387 | unpossessing | 1 |
| 19388 | unpossess | 1 |
| 19389 | unpolluted | 1 |
| 19390 | unpolite | 1 |
| 19391 | unpolished | 1 |
| 19392 | unpolicied | 1 |
| 19393 | unpleasant | 1 |
| 19394 | unpleas | 1 |
| 19395 | unplausive | 1 |
| 19396 | unplagu | 1 |
| 19397 | unpitifully | 1 |
| 19398 | unpink | 1 |
| 19399 | unpick | 1 |
| 19400 | unperfectness | 1 |
| 19401 | unperfect | 1 |
| 19402 | unpeg | 1 |
| 19403 | unpeaceable | 1 |
| 19404 | unpay | 1 |
| 19405 | unpaved | 1 |
| 19406 | unpath | 1 |
| 19407 | unpartial | 1 |
| 19408 | unparagoned | 1 |
| 19409 | unowed | 1 |
| 19410 | unobserved | 1 |
| 19411 | uno | 1 |
| 19412 | unnumber | 1 |
| 19413 | unnumb | 1 |
| 19414 | unnosed | 1 |
| 19415 | unnoble | 1 |
| 19416 | unnerved | 1 |
| 19417 | unneighbourly | 1 |
| 19418 | unnecessarily | 1 |
| 19419 | unnaturalness | 1 |
| 19420 | unnaturally | 1 |
| 19421 | unnapped | 1 |
| 19422 | unnamed | 1 |
| 19423 | unmuzzled | 1 |
| 19424 | unmuzzle | 1 |
| 19425 | unmusical | 1 |
| 19426 | unmuffles | 1 |
| 19427 | unmoving | 1 |
| 19428 | unmov | 1 |
| 19429 | unmoan | 1 |
| 19430 | unmixed | 1 |
| 19431 | unmix | 1 |
| 19432 | unmitigated | 1 |
| 19433 | unmitigable | 1 |
| 19434 | unmindfull | 1 |
| 19435 | unminded | 1 |
| 19436 | unmeriting | 1 |
| 19437 | unmercifully | 1 |
| 19438 | unmerciful | 1 |
| 19439 | unmentioned | 1 |
| 19440 | unmellowed | 1 |
| 19441 | unmast | 1 |
| 19442 | unmasking | 1 |
| 19443 | unmasked | 1 |
| 19444 | unmannerd | 1 |
| 19445 | unmanner | 1 |
| 19446 | unloving | 1 |
| 19447 | unloosing | 1 |
| 19448 | unloos | 1 |
| 19449 | unlocks | 1 |
| 19450 | unloads | 1 |
| 19451 | unlink | 1 |
| 19452 | unlineal | 1 |
| 19453 | unlimited | 1 |
| 19454 | unlick | 1 |
| 19455 | unletter | 1 |
| 19456 | unlesson | 1 |
| 19457 | unlaid | 1 |
| 19458 | unknowing | 1 |
| 19459 | unkinglike | 1 |
| 19460 | unkempt | 1 |
| 19461 | unjustice | 1 |
| 19462 | unjointed | 1 |
| 19463 | universally | 1 |
| 19464 | uniting | 1 |
| 19465 | unison | 1 |
| 19466 | unions | 1 |
| 19467 | unintelligent | 1 |
| 19468 | uninjured | 1 |
| 19469 | uninhabitable | 1 |
| 19470 | unimproved | 1 |
| 19471 | unhurtful | 1 |
| 19472 | unhous | 1 |
| 19473 | unhospitable | 1 |
| 19474 | unhorsed | 1 |
| 19475 | unhorse | 1 |
| 19476 | unhopefullest | 1 |
| 19477 | unhop | 1 |
| 19478 | unhooked | 1 |
| 19479 | unhinge | 1 |
| 19480 | unhidden | 1 |
| 19481 | unhesitatingly | 1 |
| 19482 | unhelpful | 1 |
| 19483 | unheedy | 1 |
| 19484 | unheedfully | 1 |
| 19485 | unhearts | 1 |
| 19486 | unharm | 1 |
| 19487 | unhardened | 1 |
| 19488 | unharassed | 1 |
| 19489 | unhappied | 1 |
| 19490 | unhang | 1 |
| 19491 | unhand | 1 |
| 19492 | unguents | 1 |
| 19493 | unguem | 1 |
| 19494 | ungrudgingly | 1 |
| 19495 | ungrown | 1 |
| 19496 | ungravely | 1 |
| 19497 | ungratefully | 1 |
| 19498 | ungoverned | 1 |
| 19499 | ungotten | 1 |
| 19500 | ungot | 1 |
| 19501 | ungor | 1 |
| 19502 | ungodly | 1 |
| 19503 | ungird | 1 |
| 19504 | ungentleness | 1 |
| 19505 | ungenitur | 1 |
| 19506 | ungart | 1 |
| 19507 | ungainly | 1 |
| 19508 | unfought | 1 |
| 19509 | unfortunates | 1 |
| 19510 | unfortified | 1 |
| 19511 | unforfeited | 1 |
| 19512 | unforc | 1 |
| 19513 | unfool | 1 |
| 19514 | unfoldeth | 1 |
| 19515 | unfitness | 1 |
| 19516 | unfilial | 1 |
| 19517 | unfenced | 1 |
| 19518 | unfellowed | 1 |
| 19519 | unfeed | 1 |
| 19520 | unfed | 1 |
| 19521 | unfavourable | 1 |
| 19522 | unfather | 1 |
| 19523 | unfasten | 1 |
| 19524 | unfashionable | 1 |
| 19525 | unfam | 1 |
| 19526 | unfallible | 1 |
| 19527 | unfaithful | 1 |
| 19528 | unfairly | 1 |
| 19529 | unexpressive | 1 |
| 19530 | unexperient | 1 |
| 19531 | unexperienc | 1 |
| 19532 | unexecuted | 1 |
| 19533 | unexamined | 1 |
| 19534 | unexamin | 1 |
| 19535 | unenforced | 1 |
| 19536 | unelected | 1 |
| 19537 | uneffectual | 1 |
| 19538 | uneducated | 1 |
| 19539 | uneath | 1 |
| 19540 | uneasines | 1 |
| 19541 | uneasily | 1 |
| 19542 | unearned | 1 |
| 19543 | uneared | 1 |
| 19544 | undutiful | 1 |
| 19545 | unduteous | 1 |
| 19546 | undressing | 1 |
| 19547 | undream | 1 |
| 19548 | undivided | 1 |
| 19549 | undividable | 1 |
| 19550 | undistinguished | 1 |
| 19551 | undispos | 1 |
| 19552 | undismayed | 1 |
| 19553 | undishonoured | 1 |
| 19554 | undisguised | 1 |
| 19555 | undiscerning | 1 |
| 19556 | undiscernible | 1 |
| 19557 | undinted | 1 |
| 19558 | undimmed | 1 |
| 19559 | undiminished | 1 |
| 19560 | undetermin | 1 |
| 19561 | undeservers | 1 |
| 19562 | undescried | 1 |
| 19563 | underwrite | 1 |
| 19564 | underwrit | 1 |
| 19565 | undervalu | 1 |
| 19566 | undertakeing | 1 |
| 19567 | underta | 1 |
| 19568 | understandings | 1 |
| 19569 | understandeth | 1 |
| 19570 | understander | 1 |
| 19571 | underprizing | 1 |
| 19572 | underminers | 1 |
| 19573 | undermined | 1 |
| 19574 | underfed | 1 |
| 19575 | undercrest | 1 |
| 19576 | underborne | 1 |
| 19577 | underbearing | 1 |
| 19578 | undelightful | 1 |
| 19579 | undeeded | 1 |
| 19580 | undeck | 1 |
| 19581 | undeaf | 1 |
| 19582 | uncurse | 1 |
| 19583 | uncurls | 1 |
| 19584 | uncurbed | 1 |
| 19585 | uncurbable | 1 |
| 19586 | uncultured | 1 |
| 19587 | uncuckolded | 1 |
| 19588 | unctuous | 1 |
| 19589 | uncross | 1 |
| 19590 | uncropped | 1 |
| 19591 | uncovering | 1 |
| 19592 | uncourteous | 1 |
| 19593 | uncounted | 1 |
| 19594 | uncountable | 1 |
| 19595 | uncorrected | 1 |
| 19596 | uncontroll | 1 |
| 19597 | uncontemn | 1 |
| 19598 | unconstrain | 1 |
| 19599 | unconscionable | 1 |
| 19600 | unconquer | 1 |
| 19601 | unconfirmed | 1 |
| 19602 | unconfirm | 1 |
| 19603 | unconfinable | 1 |
| 19604 | unconcernedly | 1 |
| 19605 | uncomprehensive | 1 |
| 19606 | uncompassionate | 1 |
| 19607 | uncomeliness | 1 |
| 19608 | uncolted | 1 |
| 19609 | uncoined | 1 |
| 19610 | unclog | 1 |
| 19611 | unclew | 1 |
| 19612 | uncleanliness | 1 |
| 19613 | unclasped | 1 |
| 19614 | unclaim | 1 |
| 19615 | unclad | 1 |
| 19616 | unchilded | 1 |
| 19617 | unchary | 1 |
| 19618 | uncharitably | 1 |
| 19619 | uncharitable | 1 |
| 19620 | uncharged | 1 |
| 19621 | uncharge | 1 |
| 19622 | unchanging | 1 |
| 19623 | unchain | 1 |
| 19624 | uncertified | 1 |
| 19625 | uncasing | 1 |
| 19626 | uncase | 1 |
| 19627 | uncape | 1 |
| 19628 | unbuttoning | 1 |
| 19629 | unburthen | 1 |
| 19630 | unburnt | 1 |
| 19631 | unburdens | 1 |
| 19632 | unburden | 1 |
| 19633 | unbuild | 1 |
| 19634 | unbuckling | 1 |
| 19635 | unbuckles | 1 |
| 19636 | unbroken | 1 |
| 19637 | unbroke | 1 |
| 19638 | unbreech | 1 |
| 19639 | unbred | 1 |
| 19640 | unbreathed | 1 |
| 19641 | unbraided | 1 |
| 19642 | unbrac | 1 |
| 19643 | unbowed | 1 |
| 19644 | unbow | 1 |
| 19645 | unbounded | 1 |
| 19646 | unbookish | 1 |
| 19647 | unbolted | 1 |
| 19648 | unbodied | 1 |
| 19649 | unblown | 1 |
| 19650 | unbloodied | 1 |
| 19651 | unbless | 1 |
| 19652 | unbitted | 1 |
| 19653 | unbinds | 1 |
| 19654 | unbidden | 1 |
| 19655 | unbid | 1 |
| 19656 | unbewail | 1 |
| 19657 | unbent | 1 |
| 19658 | unbend | 1 |
| 19659 | unbelieving | 1 |
| 19660 | unbelieved | 1 |
| 19661 | unbelaboured | 1 |
| 19662 | unbegotten | 1 |
| 19663 | unbegot | 1 |
| 19664 | unbefitting | 1 |
| 19665 | unbatter | 1 |
| 19666 | unbashful | 1 |
| 19667 | unbarb | 1 |
| 19668 | unbanded | 1 |
| 19669 | unbak | 1 |
| 19670 | unback | 1 |
| 19671 | unavoidable | 1 |
| 19672 | unauthorized | 1 |
| 19673 | unauspicious | 1 |
| 19674 | unattempted | 1 |
| 19675 | unattainted | 1 |
| 19676 | unattained | 1 |
| 19677 | unassuming | 1 |
| 19678 | unassailed | 1 |
| 19679 | unassailable | 1 |
| 19680 | unassail | 1 |
| 19681 | unarms | 1 |
| 19682 | unaptness | 1 |
| 19683 | unapproved | 1 |
| 19684 | unapproached | 1 |
| 19685 | unappeas | 1 |
| 19686 | unanswer | 1 |
| 19687 | unanimous | 1 |
| 19688 | unanel | 1 |
| 19689 | unagreeable | 1 |
| 19690 | unadorned | 1 |
| 19691 | unactive | 1 |
| 19692 | unaching | 1 |
| 19693 | unaccommodated | 1 |
| 19694 | umpires | 1 |
| 19695 | umfrevile | 1 |
| 19696 | umbrella | 1 |
| 19697 | umbrage | 1 |
| 19698 | umbra | 1 |
| 19699 | um | 1 |
| 19700 | ugliest | 1 |
| 19701 | uds | 1 |
| 19702 | udge | 1 |
| 19703 | udders | 1 |
| 19704 | ubique | 1 |
| 19705 | tyrians | 1 |
| 19706 | tyrannically | 1 |
| 19707 | types | 1 |
| 19708 | tymbria | 1 |
| 19709 | tyke | 1 |
| 19710 | tyburn | 1 |
| 19711 | tybalts | 1 |
| 19712 | twopences | 1 |
| 19713 | twopence | 1 |
| 19714 | twitting | 1 |
| 19715 | twitted | 1 |
| 19716 | twits | 1 |
| 19717 | twire | 1 |
| 19718 | twinkled | 1 |
| 19719 | twinkle | 1 |
| 19720 | twinges | 1 |
| 19721 | twined | 1 |
| 19722 | twilled | 1 |
| 19723 | twiggen | 1 |
| 19724 | twenties | 1 |
| 19725 | tweaks | 1 |
| 19726 | tway | 1 |
| 19727 | twang | 1 |
| 19728 | tutto | 1 |
| 19729 | tutored | 1 |
| 19730 | tuto | 1 |
| 19731 | tusks | 1 |
| 19732 | tusked | 1 |
| 19733 | tusk | 1 |
| 19734 | tuscany | 1 |
| 19735 | turvy | 1 |
| 19736 | turres | 1 |
| 19737 | turquoise | 1 |
| 19738 | turquesco | 1 |
| 19739 | turph | 1 |
| 19740 | turnip | 1 |
| 19741 | turneth | 1 |
| 19742 | turncoats | 1 |
| 19743 | turncoat | 1 |
| 19744 | turnbull | 1 |
| 19745 | turmoiled | 1 |
| 19746 | turmoil | 1 |
| 19747 | turlygod | 1 |
| 19748 | turfy | 1 |
| 19749 | turd | 1 |
| 19750 | turbulence | 1 |
| 19751 | tupping | 1 |
| 19752 | tunics | 1 |
| 19753 | tunic | 1 |
| 19754 | tuners | 1 |
| 19755 | tuition | 1 |
| 19756 | tugged | 1 |
| 19757 | tufts | 1 |
| 19758 | tudesqui | 1 |
| 19759 | tubs | 1 |
| 19760 | tuae | 1 |
| 19761 | ts | 1 |
| 19762 | truthfully | 1 |
| 19763 | trustfulness | 1 |
| 19764 | trusters | 1 |
| 19765 | truster | 1 |
| 19766 | trundle | 1 |
| 19767 | truncheoners | 1 |
| 19768 | trumped | 1 |
| 19769 | trulls | 1 |
| 19770 | trujillo | 1 |
| 19771 | truie | 1 |
| 19772 | truepenny | 1 |
| 19773 | trueborn | 1 |
| 19774 | trowel | 1 |
| 19775 | trove | 1 |
| 19776 | trovato | 1 |
| 19777 | trouts | 1 |
| 19778 | troublest | 1 |
| 19779 | troubler | 1 |
| 19780 | troths | 1 |
| 19781 | trothed | 1 |
| 19782 | tropically | 1 |
| 19783 | trop | 1 |
| 19784 | trooping | 1 |
| 19785 | trompet | 1 |
| 19786 | tromperies | 1 |
| 19787 | trombones | 1 |
| 19788 | troiluses | 1 |
| 19789 | troien | 1 |
| 19790 | troiant | 1 |
| 19791 | troglodytes | 1 |
| 19792 | troat | 1 |
| 19793 | triumviry | 1 |
| 19794 | triumvirs | 1 |
| 19795 | triumphers | 1 |
| 19796 | triumpher | 1 |
| 19797 | triumphed | 1 |
| 19798 | triton | 1 |
| 19799 | tristram | 1 |
| 19800 | tripped | 1 |
| 19801 | tripoli | 1 |
| 19802 | triplex | 1 |
| 19803 | tripartite | 1 |
| 19804 | trinculos | 1 |
| 19805 | trims | 1 |
| 19806 | trimmings | 1 |
| 19807 | trimly | 1 |
| 19808 | trill | 1 |
| 19809 | trigon | 1 |
| 19810 | trifler | 1 |
| 19811 | trier | 1 |
| 19812 | tricky | 1 |
| 19813 | trickster | 1 |
| 19814 | tricking | 1 |
| 19815 | tricked | 1 |
| 19816 | tributes | 1 |
| 19817 | treys | 1 |
| 19818 | trestles | 1 |
| 19819 | trespassing | 1 |
| 19820 | trespassed | 1 |
| 19821 | trenching | 1 |
| 19822 | trenchers | 1 |
| 19823 | trencherman | 1 |
| 19824 | trenchering | 1 |
| 19825 | trench | 1 |
| 19826 | trempling | 1 |
| 19827 | tremblingly | 1 |
| 19828 | trebled | 1 |
| 19829 | treaties | 1 |
| 19830 | treasuries | 1 |
| 19831 | treasonable | 1 |
| 19832 | treachers | 1 |
| 19833 | traverses | 1 |
| 19834 | travellest | 1 |
| 19835 | traveling | 1 |
| 19836 | traveler | 1 |
| 19837 | travails | 1 |
| 19838 | trashy | 1 |
| 19839 | transshape | 1 |
| 19840 | transportance | 1 |
| 19841 | transmutation | 1 |
| 19842 | transmogrified | 1 |
| 19843 | transmigrates | 1 |
| 19844 | translators | 1 |
| 19845 | translates | 1 |
| 19846 | transient | 1 |
| 19847 | transgresses | 1 |
| 19848 | transgressed | 1 |
| 19849 | transforms | 1 |
| 19850 | transforming | 1 |
| 19851 | transfixing | 1 |
| 19852 | transfixed | 1 |
| 19853 | transfix | 1 |
| 19854 | transfigur | 1 |
| 19855 | transcribing | 1 |
| 19856 | transcendence | 1 |
| 19857 | transaction | 1 |
| 19858 | tranquillised | 1 |
| 19859 | tranc | 1 |
| 19860 | tramped | 1 |
| 19861 | tramontana | 1 |
| 19862 | trammel | 1 |
| 19863 | traject | 1 |
| 19864 | trajan | 1 |
| 19865 | traitorly | 1 |
| 19866 | trait | 1 |
| 19867 | training | 1 |
| 19868 | trailing | 1 |
| 19869 | tragedian | 1 |
| 19870 | traffics | 1 |
| 19871 | traffickers | 1 |
| 19872 | traducement | 1 |
| 19873 | traduced | 1 |
| 19874 | traditional | 1 |
| 19875 | trading | 1 |
| 19876 | tracks | 1 |
| 19877 | trackless | 1 |
| 19878 | traces | 1 |
| 19879 | traced | 1 |
| 19880 | trabajos | 1 |
| 19881 | towton | 1 |
| 19882 | township | 1 |
| 19883 | townsfolk | 1 |
| 19884 | towardly | 1 |
| 19885 | touze | 1 |
| 19886 | tous | 1 |
| 19887 | toughness | 1 |
| 19888 | toughest | 1 |
| 19889 | tougher | 1 |
| 19890 | touchy | 1 |
| 19891 | tou | 1 |
| 19892 | totters | 1 |
| 19893 | tottered | 1 |
| 19894 | toto | 1 |
| 19895 | tostado | 1 |
| 19896 | tosseth | 1 |
| 19897 | tossed | 1 |
| 19898 | torturest | 1 |
| 19899 | torturers | 1 |
| 19900 | tortolites | 1 |
| 19901 | tortive | 1 |
| 19902 | torre | 1 |
| 19903 | torpid | 1 |
| 19904 | tormes | 1 |
| 19905 | tormente | 1 |
| 19906 | tormenta | 1 |
| 19907 | tordesillesque | 1 |
| 19908 | torchlight | 1 |
| 19909 | torcher | 1 |
| 19910 | torchbearer | 1 |
| 19911 | toraquis | 1 |
| 19912 | topsy | 1 |
| 19913 | topsail | 1 |
| 19914 | toppling | 1 |
| 19915 | topmost | 1 |
| 19916 | topless | 1 |
| 19917 | topgallant | 1 |
| 19918 | topful | 1 |
| 19919 | topazes | 1 |
| 19920 | toothpicker | 1 |
| 19921 | tonsure | 1 |
| 19922 | tongs | 1 |
| 19923 | toned | 1 |
| 19924 | tomyris | 1 |
| 19925 | tomillas | 1 |
| 19926 | tomboys | 1 |
| 19927 | tomboy | 1 |
| 19928 | tombless | 1 |
| 19929 | tombed | 1 |
| 19930 | tombe | 1 |
| 19931 | tomasillo | 1 |
| 19932 | tologian | 1 |
| 19933 | toleration | 1 |
| 19934 | toledan | 1 |
| 19935 | toiling | 1 |
| 19936 | toiled | 1 |
| 19937 | toged | 1 |
| 19938 | toge | 1 |
| 19939 | toed | 1 |
| 19940 | tods | 1 |
| 19941 | todpole | 1 |
| 19942 | tod | 1 |
| 19943 | tock | 1 |
| 19944 | toaze | 1 |
| 19945 | toasting | 1 |
| 19946 | toadstool | 1 |
| 19947 | tizona | 1 |
| 19948 | tityus | 1 |
| 19949 | titular | 1 |
| 19950 | tittles | 1 |
| 19951 | titleless | 1 |
| 19952 | tithed | 1 |
| 19953 | tissues | 1 |
| 19954 | tirrits | 1 |
| 19955 | tirra | 1 |
| 19956 | tirest | 1 |
| 19957 | tiresome | 1 |
| 19958 | tirantes | 1 |
| 19959 | tiquitoc | 1 |
| 19960 | tiptoe | 1 |
| 19961 | tipsy | 1 |
| 19962 | tipstaff | 1 |
| 19963 | tips | 1 |
| 19964 | tippling | 1 |
| 19965 | tipp | 1 |
| 19966 | tiopieyo | 1 |
| 19967 | tints | 1 |
| 19968 | tinted | 1 |
| 19969 | tinsel | 1 |
| 19970 | tingling | 1 |
| 19971 | tinctures | 1 |
| 19972 | timorously | 1 |
| 19973 | timor | 1 |
| 19974 | timonel | 1 |
| 19975 | timelier | 1 |
| 19976 | timed | 1 |
| 19977 | timantes | 1 |
| 19978 | tim | 1 |
| 19979 | tiltyard | 1 |
| 19980 | tillageland | 1 |
| 19981 | tile | 1 |
| 19982 | til | 1 |
| 19983 | tike | 1 |
| 19984 | tights | 1 |
| 19985 | tiff | 1 |
| 19986 | tidy | 1 |
| 19987 | tiddle | 1 |
| 19988 | ticklish | 1 |
| 19989 | tickl | 1 |
| 19990 | ticed | 1 |
| 19991 | tibullus | 1 |
| 19992 | tibey | 1 |
| 19993 | tiberio | 1 |
| 19994 | tibar | 1 |
| 19995 | tib | 1 |
| 19996 | thymus | 1 |
| 19997 | thwartings | 1 |
| 19998 | thunderstroke | 1 |
| 19999 | thunderstone | 1 |
| 20000 | thumps | 1 |
| 20001 | thumbed | 1 |
| 20002 | thrusteth | 1 |
| 20003 | thrush | 1 |
| 20004 | thrumming | 1 |
| 20005 | thrumm | 1 |
| 20006 | thrum | 1 |
| 20007 | throwest | 1 |
| 20008 | throughfares | 1 |
| 20009 | throughfare | 1 |
| 20010 | throttling | 1 |
| 20011 | throttled | 1 |
| 20012 | throttle | 1 |
| 20013 | thromuldo | 1 |
| 20014 | throe | 1 |
| 20015 | throca | 1 |
| 20016 | throbs | 1 |
| 20017 | thrivers | 1 |
| 20018 | thrived | 1 |
| 20019 | thrills | 1 |
| 20020 | thrifts | 1 |
| 20021 | thresholds | 1 |
| 20022 | thresher | 1 |
| 20023 | threepile | 1 |
| 20024 | threatest | 1 |
| 20025 | thralls | 1 |
| 20026 | thralled | 1 |
| 20027 | thoughtlessness | 1 |
| 20028 | thoughtfully | 1 |
| 20029 | thoroughfare | 1 |
| 20030 | thoroughbred | 1 |
| 20031 | thong | 1 |
| 20032 | thomases | 1 |
| 20033 | thoas | 1 |
| 20034 | thitherward | 1 |
| 20035 | thirtieth | 1 |
| 20036 | thirsts | 1 |
| 20037 | thirstiest | 1 |
| 20038 | thirstier | 1 |
| 20039 | thinness | 1 |
| 20040 | thinkst | 1 |
| 20041 | thinker | 1 |
| 20042 | thimbraeus | 1 |
| 20043 | thimbles | 1 |
| 20044 | thickskin | 1 |
| 20045 | thickheaded | 1 |
| 20046 | thicken | 1 |
| 20047 | thessalian | 1 |
| 20048 | thermodon | 1 |
| 20049 | therefrom | 1 |
| 20050 | thereafter | 1 |
| 20051 | thereabout | 1 |
| 20052 | theory | 1 |
| 20053 | theological | 1 |
| 20054 | theologian | 1 |
| 20055 | theise | 1 |
| 20056 | thein | 1 |
| 20057 | thebes | 1 |
| 20058 | theban | 1 |
| 20059 | theatres | 1 |
| 20060 | thaws | 1 |
| 20061 | thawing | 1 |
| 20062 | thasos | 1 |
| 20063 | thanksgivings | 1 |
| 20064 | thaes | 1 |
| 20065 | tevil | 1 |
| 20066 | testril | 1 |
| 20067 | testing | 1 |
| 20068 | testiness | 1 |
| 20069 | testimonied | 1 |
| 20070 | testimonials | 1 |
| 20071 | testily | 1 |
| 20072 | testifying | 1 |
| 20073 | testified | 1 |
| 20074 | testern | 1 |
| 20075 | tertio | 1 |
| 20076 | tertian | 1 |
| 20077 | tersely | 1 |
| 20078 | terriers | 1 |
| 20079 | terrene | 1 |
| 20080 | terre | 1 |
| 20081 | terras | 1 |
| 20082 | terraqueous | 1 |
| 20083 | terram | 1 |
| 20084 | termless | 1 |
| 20085 | terminations | 1 |
| 20086 | teresona | 1 |
| 20087 | teresaina | 1 |
| 20088 | terence | 1 |
| 20089 | terebinth | 1 |
| 20090 | tercel | 1 |
| 20091 | tenures | 1 |
| 20092 | tenths | 1 |
| 20093 | tented | 1 |
| 20094 | tens | 1 |
| 20095 | tenours | 1 |
| 20096 | tenorio | 1 |
| 20097 | tenements | 1 |
| 20098 | tenement | 1 |
| 20099 | tenedos | 1 |
| 20100 | tenebras | 1 |
| 20101 | tenderest | 1 |
| 20102 | tenderer | 1 |
| 20103 | tendered | 1 |
| 20104 | tendency | 1 |
| 20105 | tenable | 1 |
| 20106 | temptingly | 1 |
| 20107 | tempteth | 1 |
| 20108 | temps | 1 |
| 20109 | temporizer | 1 |
| 20110 | temporiz | 1 |
| 20111 | temporary | 1 |
| 20112 | tempora | 1 |
| 20113 | temperet | 1 |
| 20114 | temperality | 1 |
| 20115 | tellest | 1 |
| 20116 | tellers | 1 |
| 20117 | telamonius | 1 |
| 20118 | telamon | 1 |
| 20119 | teipsum | 1 |
| 20120 | teens | 1 |
| 20121 | tearfully | 1 |
| 20122 | teams | 1 |
| 20123 | tawdry | 1 |
| 20124 | tavy | 1 |
| 20125 | tauntingly | 1 |
| 20126 | taunting | 1 |
| 20127 | taunted | 1 |
| 20128 | tattlings | 1 |
| 20129 | tatters | 1 |
| 20130 | tatter | 1 |
| 20131 | tatt | 1 |
| 20132 | tasteless | 1 |
| 20133 | tasker | 1 |
| 20134 | tartly | 1 |
| 20135 | tartesians | 1 |
| 20136 | tartesian | 1 |
| 20137 | tartars | 1 |
| 20138 | tarriance | 1 |
| 20139 | tarragona | 1 |
| 20140 | tarr | 1 |
| 20141 | tarquins | 1 |
| 20142 | tarnished | 1 |
| 20143 | tariff | 1 |
| 20144 | targe | 1 |
| 20145 | tarentum | 1 |
| 20146 | tardiness | 1 |
| 20147 | tardily | 1 |
| 20148 | tardied | 1 |
| 20149 | tapping | 1 |
| 20150 | tapp | 1 |
| 20151 | taphouse | 1 |
| 20152 | tantum | 1 |
| 20153 | tantalus | 1 |
| 20154 | tantaene | 1 |
| 20155 | tanta | 1 |
| 20156 | tansillo | 1 |
| 20157 | tanquam | 1 |
| 20158 | tanneries | 1 |
| 20159 | tann | 1 |
| 20160 | tanlings | 1 |
| 20161 | tank | 1 |
| 20162 | tan | 1 |
| 20163 | tamper | 1 |
| 20164 | tames | 1 |
| 20165 | tamer | 1 |
| 20166 | tamed | 1 |
| 20167 | tambourines | 1 |
| 20168 | tambourine | 1 |
| 20169 | tallies | 1 |
| 20170 | tallied | 1 |
| 20171 | talkers | 1 |
| 20172 | talia | 1 |
| 20173 | taleporter | 1 |
| 20174 | talbotites | 1 |
| 20175 | tal | 1 |
| 20176 | taketh | 1 |
| 20177 | tainture | 1 |
| 20178 | tailing | 1 |
| 20179 | tags | 1 |
| 20180 | tagrag | 1 |
| 20181 | tagarins | 1 |
| 20182 | tag | 1 |
| 20183 | tadpoles | 1 |
| 20184 | tadpole | 1 |
| 20185 | taddle | 1 |
| 20186 | tacklings | 1 |
| 20187 | tackles | 1 |
| 20188 | tackled | 1 |
| 20189 | tacked | 1 |
| 20190 | tacit | 1 |
| 20191 | tabourines | 1 |
| 20192 | taborer | 1 |
| 20193 | tablet | 1 |
| 20194 | tabled | 1 |
| 20195 | tablantes | 1 |
| 20196 | tablante | 1 |
| 20197 | tabernas | 1 |
| 20198 | taber | 1 |
| 20199 | tabby | 1 |
| 20200 | tabarca | 1 |
| 20201 | systems | 1 |
| 20202 | syrup | 1 |
| 20203 | syrtes | 1 |
| 20204 | syriac | 1 |
| 20205 | syracusians | 1 |
| 20206 | synods | 1 |
| 20207 | sympathiz | 1 |
| 20208 | symbols | 1 |
| 20209 | sylvias | 1 |
| 20210 | syllogism | 1 |
| 20211 | swung | 1 |
| 20212 | swordsmanship | 1 |
| 20213 | swoopstake | 1 |
| 20214 | swollen | 1 |
| 20215 | swoll | 1 |
| 20216 | switzers | 1 |
| 20217 | switches | 1 |
| 20218 | swish | 1 |
| 20219 | swineherds | 1 |
| 20220 | swineherd | 1 |
| 20221 | swindling | 1 |
| 20222 | swindles | 1 |
| 20223 | swindler | 1 |
| 20224 | swimmers | 1 |
| 20225 | swimmer | 1 |
| 20226 | swills | 1 |
| 20227 | swill | 1 |
| 20228 | swifts | 1 |
| 20229 | swerver | 1 |
| 20230 | sweno | 1 |
| 20231 | swelter | 1 |
| 20232 | swellings | 1 |
| 20233 | sweetens | 1 |
| 20234 | sweaten | 1 |
| 20235 | sweated | 1 |
| 20236 | swearest | 1 |
| 20237 | swearer | 1 |
| 20238 | swathling | 1 |
| 20239 | swathed | 1 |
| 20240 | swashers | 1 |
| 20241 | swarths | 1 |
| 20242 | swarth | 1 |
| 20243 | swarms | 1 |
| 20244 | sward | 1 |
| 20245 | swap | 1 |
| 20246 | swans | 1 |
| 20247 | swaggerer | 1 |
| 20248 | swag | 1 |
| 20249 | sutton | 1 |
| 20250 | sutler | 1 |
| 20251 | sustained | 1 |
| 20252 | sust | 1 |
| 20253 | suspiration | 1 |
| 20254 | suspension | 1 |
| 20255 | surveys | 1 |
| 20256 | surveyors | 1 |
| 20257 | surveying | 1 |
| 20258 | surveyest | 1 |
| 20259 | surrounds | 1 |
| 20260 | surrounding | 1 |
| 20261 | surreys | 1 |
| 20262 | surrendering | 1 |
| 20263 | surprising | 1 |
| 20264 | surplices | 1 |
| 20265 | surplice | 1 |
| 20266 | surpassingly | 1 |
| 20267 | surpasseth | 1 |
| 20268 | surmounts | 1 |
| 20269 | surmised | 1 |
| 20270 | surmis | 1 |
| 20271 | surging | 1 |
| 20272 | surgere | 1 |
| 20273 | surfeiter | 1 |
| 20274 | surecard | 1 |
| 20275 | surd | 1 |
| 20276 | surance | 1 |
| 20277 | suppressing | 1 |
| 20278 | suppresseth | 1 |
| 20279 | supposest | 1 |
| 20280 | supposal | 1 |
| 20281 | supportor | 1 |
| 20282 | supportable | 1 |
| 20283 | supplyment | 1 |
| 20284 | supplyant | 1 |
| 20285 | suppliest | 1 |
| 20286 | supplicant | 1 |
| 20287 | suppliants | 1 |
| 20288 | suppliance | 1 |
| 20289 | suppertime | 1 |
| 20290 | supervisor | 1 |
| 20291 | supersubtle | 1 |
| 20292 | superstitiously | 1 |
| 20293 | superstition | 1 |
| 20294 | superserviceable | 1 |
| 20295 | superscript | 1 |
| 20296 | superpraise | 1 |
| 20297 | supernal | 1 |
| 20298 | superflux | 1 |
| 20299 | superfluously | 1 |
| 20300 | super | 1 |
| 20301 | sunshade | 1 |
| 20302 | sunrising | 1 |
| 20303 | sunlight | 1 |
| 20304 | sunders | 1 |
| 20305 | sunburning | 1 |
| 20306 | summum | 1 |
| 20307 | summoning | 1 |
| 20308 | summoners | 1 |
| 20309 | summa | 1 |
| 20310 | summ | 1 |
| 20311 | sumless | 1 |
| 20312 | sultan | 1 |
| 20313 | sulpherous | 1 |
| 20314 | sullies | 1 |
| 20315 | sullens | 1 |
| 20316 | sulkily | 1 |
| 20317 | suivez | 1 |
| 20318 | suite | 1 |
| 20319 | suggesting | 1 |
| 20320 | sugarsop | 1 |
| 20321 | suffrage | 1 |
| 20322 | suffocation | 1 |
| 20323 | suffocating | 1 |
| 20324 | suffigance | 1 |
| 20325 | sufficit | 1 |
| 20326 | sufficing | 1 |
| 20327 | suffereth | 1 |
| 20328 | sufferances | 1 |
| 20329 | sueth | 1 |
| 20330 | suerte | 1 |
| 20331 | suero | 1 |
| 20332 | suerly | 1 |
| 20333 | sueldos | 1 |
| 20334 | suckers | 1 |
| 20335 | sucked | 1 |
| 20336 | suchlike | 1 |
| 20337 | successor | 1 |
| 20338 | successantly | 1 |
| 20339 | succedant | 1 |
| 20340 | subverts | 1 |
| 20341 | subversion | 1 |
| 20342 | subtractors | 1 |
| 20343 | subtilly | 1 |
| 20344 | subtile | 1 |
| 20345 | subterfuges | 1 |
| 20346 | substitution | 1 |
| 20347 | subsisting | 1 |
| 20348 | subsisted | 1 |
| 20349 | subsist | 1 |
| 20350 | subsidy | 1 |
| 20351 | subsidies | 1 |
| 20352 | subsided | 1 |
| 20353 | subsequent | 1 |
| 20354 | subscription | 1 |
| 20355 | subscribed | 1 |
| 20356 | submits | 1 |
| 20357 | submissively | 1 |
| 20358 | submerg | 1 |
| 20359 | sublime | 1 |
| 20360 | sublimated | 1 |
| 20361 | subduements | 1 |
| 20362 | subcontracted | 1 |
| 20363 | suavity | 1 |
| 20364 | suadente | 1 |
| 20365 | styl | 1 |
| 20366 | styga | 1 |
| 20367 | stuprum | 1 |
| 20368 | stupified | 1 |
| 20369 | stumblest | 1 |
| 20370 | stultorum | 1 |
| 20371 | studs | 1 |
| 20372 | studiously | 1 |
| 20373 | stubbornly | 1 |
| 20374 | stubbornest | 1 |
| 20375 | stubbles | 1 |
| 20376 | strutted | 1 |
| 20377 | struts | 1 |
| 20378 | stroy | 1 |
| 20379 | strown | 1 |
| 20380 | strossers | 1 |
| 20381 | strooke | 1 |
| 20382 | stronds | 1 |
| 20383 | strond | 1 |
| 20384 | stroked | 1 |
| 20385 | strok | 1 |
| 20386 | striv | 1 |
| 20387 | stript | 1 |
| 20388 | striplings | 1 |
| 20389 | stringless | 1 |
| 20390 | stringers | 1 |
| 20391 | strikers | 1 |
| 20392 | striding | 1 |
| 20393 | stricture | 1 |
| 20394 | strictest | 1 |
| 20395 | strewments | 1 |
| 20396 | strewings | 1 |
| 20397 | strewed | 1 |
| 20398 | strenuous | 1 |
| 20399 | strengthens | 1 |
| 20400 | streching | 1 |
| 20401 | streaming | 1 |
| 20402 | streamed | 1 |
| 20403 | strayed | 1 |
| 20404 | strawy | 1 |
| 20405 | strawberry | 1 |
| 20406 | stratford | 1 |
| 20407 | strapping | 1 |
| 20408 | strap | 1 |
| 20409 | strangler | 1 |
| 20410 | stranded | 1 |
| 20411 | straitly | 1 |
| 20412 | straiter | 1 |
| 20413 | straited | 1 |
| 20414 | straightforwardly | 1 |
| 20415 | straightest | 1 |
| 20416 | straighter | 1 |
| 20417 | straighten | 1 |
| 20418 | straggling | 1 |
| 20419 | stragglers | 1 |
| 20420 | strachy | 1 |
| 20421 | stowing | 1 |
| 20422 | stowage | 1 |
| 20423 | stover | 1 |
| 20424 | stouter | 1 |
| 20425 | stoups | 1 |
| 20426 | stormed | 1 |
| 20427 | stork | 1 |
| 20428 | storehouses | 1 |
| 20429 | stored | 1 |
| 20430 | stope | 1 |
| 20431 | stooped | 1 |
| 20432 | stoodst | 1 |
| 20433 | stonish | 1 |
| 20434 | stoning | 1 |
| 20435 | stonecutter | 1 |
| 20436 | stomaching | 1 |
| 20437 | stolid | 1 |
| 20438 | stolest | 1 |
| 20439 | stokesly | 1 |
| 20440 | stoics | 1 |
| 20441 | stogs | 1 |
| 20442 | stog | 1 |
| 20443 | stockish | 1 |
| 20444 | stoccata | 1 |
| 20445 | stoccadoes | 1 |
| 20446 | stithy | 1 |
| 20447 | stithied | 1 |
| 20448 | stitching | 1 |
| 20449 | stitchery | 1 |
| 20450 | stitched | 1 |
| 20451 | stirreth | 1 |
| 20452 | stirrers | 1 |
| 20453 | stirrer | 1 |
| 20454 | stipulation | 1 |
| 20455 | stipulated | 1 |
| 20456 | stints | 1 |
| 20457 | stinks | 1 |
| 20458 | stinkingly | 1 |
| 20459 | stingless | 1 |
| 20460 | stimulator | 1 |
| 20461 | stimulant | 1 |
| 20462 | stilly | 1 |
| 20463 | stillest | 1 |
| 20464 | stiller | 1 |
| 20465 | stilled | 1 |
| 20466 | stigmatised | 1 |
| 20467 | stigmatical | 1 |
| 20468 | stifles | 1 |
| 20469 | stiffness | 1 |
| 20470 | stiffest | 1 |
| 20471 | stiffen | 1 |
| 20472 | stickler | 1 |
| 20473 | stewpots | 1 |
| 20474 | stewards | 1 |
| 20475 | sternest | 1 |
| 20476 | sternage | 1 |
| 20477 | stepping | 1 |
| 20478 | stepmothers | 1 |
| 20479 | stepmother | 1 |
| 20480 | stepdame | 1 |
| 20481 | stemming | 1 |
| 20482 | stelled | 1 |
| 20483 | steered | 1 |
| 20484 | steerage | 1 |
| 20485 | steeps | 1 |
| 20486 | steeple | 1 |
| 20487 | steeped | 1 |
| 20488 | steam | 1 |
| 20489 | stealest | 1 |
| 20490 | stealers | 1 |
| 20491 | steadier | 1 |
| 20492 | steaded | 1 |
| 20493 | stayest | 1 |
| 20494 | staving | 1 |
| 20495 | stave | 1 |
| 20496 | staunch | 1 |
| 20497 | statures | 1 |
| 20498 | statists | 1 |
| 20499 | statist | 1 |
| 20500 | statilius | 1 |
| 20501 | statesmen | 1 |
| 20502 | statements | 1 |
| 20503 | statement | 1 |
| 20504 | stateliness | 1 |
| 20505 | statelier | 1 |
| 20506 | starving | 1 |
| 20507 | starveth | 1 |
| 20508 | starvelackey | 1 |
| 20509 | starvation | 1 |
| 20510 | startling | 1 |
| 20511 | startingly | 1 |
| 20512 | starling | 1 |
| 20513 | starkly | 1 |
| 20514 | starings | 1 |
| 20515 | starching | 1 |
| 20516 | starboard | 1 |
| 20517 | staples | 1 |
| 20518 | staple | 1 |
| 20519 | stanzos | 1 |
| 20520 | stanzo | 1 |
| 20521 | stanze | 1 |
| 20522 | staniel | 1 |
| 20523 | standstill | 1 |
| 20524 | stander | 1 |
| 20525 | stanchless | 1 |
| 20526 | stanched | 1 |
| 20527 | stammering | 1 |
| 20528 | stammer | 1 |
| 20529 | stamford | 1 |
| 20530 | stalwart | 1 |
| 20531 | stalling | 1 |
| 20532 | stalking | 1 |
| 20533 | staled | 1 |
| 20534 | staking | 1 |
| 20535 | staining | 1 |
| 20536 | staineth | 1 |
| 20537 | staines | 1 |
| 20538 | staidness | 1 |
| 20539 | staider | 1 |
| 20540 | staid | 1 |
| 20541 | staggering | 1 |
| 20542 | staggered | 1 |
| 20543 | staffordshire | 1 |
| 20544 | stacks | 1 |
| 20545 | stablishment | 1 |
| 20546 | stablish | 1 |
| 20547 | stableness | 1 |
| 20548 | squirissimus | 1 |
| 20549 | squirings | 1 |
| 20550 | squiny | 1 |
| 20551 | squints | 1 |
| 20552 | squinted | 1 |
| 20553 | squibs | 1 |
| 20554 | squele | 1 |
| 20555 | squeezes | 1 |
| 20556 | squeamishly | 1 |
| 20557 | squealing | 1 |
| 20558 | squeal | 1 |
| 20559 | squeaking | 1 |
| 20560 | squat | 1 |
| 20561 | squarer | 1 |
| 20562 | squalls | 1 |
| 20563 | squalling | 1 |
| 20564 | squabble | 1 |
| 20565 | spurrer | 1 |
| 20566 | spurning | 1 |
| 20567 | spurned | 1 |
| 20568 | spriting | 1 |
| 20569 | sprited | 1 |
| 20570 | sprinkles | 1 |
| 20571 | sprinkler | 1 |
| 20572 | sprinkled | 1 |
| 20573 | springtime | 1 |
| 20574 | springhalt | 1 |
| 20575 | springeth | 1 |
| 20576 | springes | 1 |
| 20577 | sprightful | 1 |
| 20578 | sprighted | 1 |
| 20579 | sprig | 1 |
| 20580 | sprat | 1 |
| 20581 | sprag | 1 |
| 20582 | spouting | 1 |
| 20583 | sportsman | 1 |
| 20584 | sporting | 1 |
| 20585 | splenitive | 1 |
| 20586 | spleeny | 1 |
| 20587 | splay | 1 |
| 20588 | spittle | 1 |
| 20589 | spited | 1 |
| 20590 | spirt | 1 |
| 20591 | spiritualty | 1 |
| 20592 | spire | 1 |
| 20593 | spiral | 1 |
| 20594 | spinster | 1 |
| 20595 | spinii | 1 |
| 20596 | spilth | 1 |
| 20597 | spilorceria | 1 |
| 20598 | spikes | 1 |
| 20599 | spiked | 1 |
| 20600 | spigot | 1 |
| 20601 | spightfully | 1 |
| 20602 | spieth | 1 |
| 20603 | spicery | 1 |
| 20604 | sphinx | 1 |
| 20605 | sphery | 1 |
| 20606 | sphered | 1 |
| 20607 | spher | 1 |
| 20608 | sperr | 1 |
| 20609 | sperm | 1 |
| 20610 | sperato | 1 |
| 20611 | spendest | 1 |
| 20612 | spencer | 1 |
| 20613 | spelt | 1 |
| 20614 | spelling | 1 |
| 20615 | spellbound | 1 |
| 20616 | speens | 1 |
| 20617 | speediness | 1 |
| 20618 | speechifying | 1 |
| 20619 | speculations | 1 |
| 20620 | spectres | 1 |
| 20621 | spectatorship | 1 |
| 20622 | spectator | 1 |
| 20623 | specified | 1 |
| 20624 | specialty | 1 |
| 20625 | specialties | 1 |
| 20626 | specialities | 1 |
| 20627 | spearing | 1 |
| 20628 | speargrass | 1 |
| 20629 | speakers | 1 |
| 20630 | spavins | 1 |
| 20631 | spavin | 1 |
| 20632 | spat | 1 |
| 20633 | spasms | 1 |
| 20634 | spasm | 1 |
| 20635 | sparse | 1 |
| 20636 | sparkles | 1 |
| 20637 | spareness | 1 |
| 20638 | spans | 1 |
| 20639 | spann | 1 |
| 20640 | spank | 1 |
| 20641 | spaniels | 1 |
| 20642 | spangles | 1 |
| 20643 | spangle | 1 |
| 20644 | spakest | 1 |
| 20645 | spains | 1 |
| 20646 | spades | 1 |
| 20647 | spaces | 1 |
| 20648 | sowter | 1 |
| 20649 | sown | 1 |
| 20650 | sowl | 1 |
| 20651 | sowgelder | 1 |
| 20652 | sovereignvours | 1 |
| 20653 | sovereignly | 1 |
| 20654 | sovereignest | 1 |
| 20655 | souviendrai | 1 |
| 20656 | southerly | 1 |
| 20657 | souse | 1 |
| 20658 | sous | 1 |
| 20659 | sours | 1 |
| 20660 | sources | 1 |
| 20661 | soup | 1 |
| 20662 | soundpost | 1 |
| 20663 | souled | 1 |
| 20664 | sould | 1 |
| 20665 | sottish | 1 |
| 20666 | sots | 1 |
| 20667 | soto | 1 |
| 20668 | sossius | 1 |
| 20669 | sorting | 1 |
| 20670 | sortance | 1 |
| 20671 | sorrowest | 1 |
| 20672 | sorriest | 1 |
| 20673 | sorrento | 1 |
| 20674 | sorest | 1 |
| 20675 | sophistry | 1 |
| 20676 | sophister | 1 |
| 20677 | sooty | 1 |
| 20678 | soothsay | 1 |
| 20679 | soothers | 1 |
| 20680 | soothed | 1 |
| 20681 | sonties | 1 |
| 20682 | sonneting | 1 |
| 20683 | songster | 1 |
| 20684 | sonance | 1 |
| 20685 | somme | 1 |
| 20686 | somewhither | 1 |
| 20687 | somever | 1 |
| 20688 | someone | 1 |
| 20689 | sombreness | 1 |
| 20690 | sombre | 1 |
| 20691 | solyman | 1 |
| 20692 | solution | 1 |
| 20693 | solum | 1 |
| 20694 | solstices | 1 |
| 20695 | solisdan | 1 |
| 20696 | soliloquising | 1 |
| 20697 | soliloquise | 1 |
| 20698 | solidity | 1 |
| 20699 | solidares | 1 |
| 20700 | solicitous | 1 |
| 20701 | solicitings | 1 |
| 20702 | solicitations | 1 |
| 20703 | solicitation | 1 |
| 20704 | solemnities | 1 |
| 20705 | solemness | 1 |
| 20706 | solem | 1 |
| 20707 | soldiering | 1 |
| 20708 | soldest | 1 |
| 20709 | soldat | 1 |
| 20710 | solaces | 1 |
| 20711 | solaced | 1 |
| 20712 | soit | 1 |
| 20713 | soilure | 1 |
| 20714 | sod | 1 |
| 20715 | socrates | 1 |
| 20716 | sockets | 1 |
| 20717 | sobradisa | 1 |
| 20718 | soberly | 1 |
| 20719 | soars | 1 |
| 20720 | soapings | 1 |
| 20721 | soaping | 1 |
| 20722 | soaped | 1 |
| 20723 | soaks | 1 |
| 20724 | soaked | 1 |
| 20725 | snuffs | 1 |
| 20726 | snuffled | 1 |
| 20727 | snuffing | 1 |
| 20728 | snows | 1 |
| 20729 | snowed | 1 |
| 20730 | snowballs | 1 |
| 20731 | snipt | 1 |
| 20732 | snipe | 1 |
| 20733 | sniffing | 1 |
| 20734 | sniffed | 1 |
| 20735 | sneers | 1 |
| 20736 | sneering | 1 |
| 20737 | sneered | 1 |
| 20738 | sneck | 1 |
| 20739 | sneap | 1 |
| 20740 | sneakingly | 1 |
| 20741 | snatchers | 1 |
| 20742 | snarleth | 1 |
| 20743 | snarled | 1 |
| 20744 | snarl | 1 |
| 20745 | snapp | 1 |
| 20746 | snaky | 1 |
| 20747 | snails | 1 |
| 20748 | snaffle | 1 |
| 20749 | smutch | 1 |
| 20750 | smulkin | 1 |
| 20751 | smuggle | 1 |
| 20752 | smothering | 1 |
| 20753 | smoth | 1 |
| 20754 | smooths | 1 |
| 20755 | smoother | 1 |
| 20756 | smoked | 1 |
| 20757 | smok | 1 |
| 20758 | smiting | 1 |
| 20759 | smithies | 1 |
| 20760 | smit | 1 |
| 20761 | smirched | 1 |
| 20762 | smilets | 1 |
| 20763 | smilest | 1 |
| 20764 | smellest | 1 |
| 20765 | smattering | 1 |
| 20766 | smatter | 1 |
| 20767 | smatch | 1 |
| 20768 | smashing | 1 |
| 20769 | smarter | 1 |
| 20770 | smarten | 1 |
| 20771 | smalus | 1 |
| 20772 | smallness | 1 |
| 20773 | smacking | 1 |
| 20774 | slys | 1 |
| 20775 | slyly | 1 |
| 20776 | sluttishness | 1 |
| 20777 | slur | 1 |
| 20778 | slunk | 1 |
| 20779 | slumbery | 1 |
| 20780 | slumbering | 1 |
| 20781 | slumb | 1 |
| 20782 | sluggardiz | 1 |
| 20783 | sluggard | 1 |
| 20784 | slovenry | 1 |
| 20785 | slovenly | 1 |
| 20786 | slovenliness | 1 |
| 20787 | slothfully | 1 |
| 20788 | slomber | 1 |
| 20789 | slobb | 1 |
| 20790 | slitting | 1 |
| 20791 | slish | 1 |
| 20792 | sling | 1 |
| 20793 | slim | 1 |
| 20794 | slights | 1 |
| 20795 | slightness | 1 |
| 20796 | sliding | 1 |
| 20797 | slices | 1 |
| 20798 | slewest | 1 |
| 20799 | slenderly | 1 |
| 20800 | slenderer | 1 |
| 20801 | sleights | 1 |
| 20802 | sleight | 1 |
| 20803 | sleided | 1 |
| 20804 | sleid | 1 |
| 20805 | sleeplessness | 1 |
| 20806 | sleekly | 1 |
| 20807 | sledded | 1 |
| 20808 | sleave | 1 |
| 20809 | slayeth | 1 |
| 20810 | slayest | 1 |
| 20811 | slaver | 1 |
| 20812 | slaughterous | 1 |
| 20813 | slaughtering | 1 |
| 20814 | slaughterer | 1 |
| 20815 | slants | 1 |
| 20816 | slake | 1 |
| 20817 | slackened | 1 |
| 20818 | skyish | 1 |
| 20819 | skyey | 1 |
| 20820 | skulking | 1 |
| 20821 | skirmishes | 1 |
| 20822 | skipper | 1 |
| 20823 | skipped | 1 |
| 20824 | skipp | 1 |
| 20825 | skinny | 1 |
| 20826 | skinker | 1 |
| 20827 | skimmed | 1 |
| 20828 | skimble | 1 |
| 20829 | skillet | 1 |
| 20830 | sketch | 1 |
| 20831 | skelter | 1 |
| 20832 | skeleton | 1 |
| 20833 | skamble | 1 |
| 20834 | skains | 1 |
| 20835 | sizzle | 1 |
| 20836 | sixteenth | 1 |
| 20837 | sixpenny | 1 |
| 20838 | sixpences | 1 |
| 20839 | sixes | 1 |
| 20840 | situated | 1 |
| 20841 | sittest | 1 |
| 20842 | site | 1 |
| 20843 | sisyphus | 1 |
| 20844 | sisterly | 1 |
| 20845 | sist | 1 |
| 20846 | sipping | 1 |
| 20847 | singuled | 1 |
| 20848 | singularities | 1 |
| 20849 | singulariter | 1 |
| 20850 | singeth | 1 |
| 20851 | singest | 1 |
| 20852 | singes | 1 |
| 20853 | singers | 1 |
| 20854 | singeing | 1 |
| 20855 | sinewed | 1 |
| 20856 | sinel | 1 |
| 20857 | simulation | 1 |
| 20858 | simony | 1 |
| 20859 | simmering | 1 |
| 20860 | similitude | 1 |
| 20861 | simile | 1 |
| 20862 | sima | 1 |
| 20863 | silverly | 1 |
| 20864 | silvered | 1 |
| 20865 | silvato | 1 |
| 20866 | silling | 1 |
| 20867 | sillinesses | 1 |
| 20868 | silliest | 1 |
| 20869 | sillier | 1 |
| 20870 | silkman | 1 |
| 20871 | silenus | 1 |
| 20872 | silencing | 1 |
| 20873 | siguenza | 1 |
| 20874 | signiory | 1 |
| 20875 | signiories | 1 |
| 20876 | signifying | 1 |
| 20877 | significants | 1 |
| 20878 | sigismunda | 1 |
| 20879 | sightly | 1 |
| 20880 | siestas | 1 |
| 20881 | siesta | 1 |
| 20882 | sies | 1 |
| 20883 | sienna | 1 |
| 20884 | sieges | 1 |
| 20885 | sided | 1 |
| 20886 | sicles | 1 |
| 20887 | sickliness | 1 |
| 20888 | sicklied | 1 |
| 20889 | sicklemen | 1 |
| 20890 | sicker | 1 |
| 20891 | sicilian | 1 |
| 20892 | sicil | 1 |
| 20893 | sibyls | 1 |
| 20894 | sibylla | 1 |
| 20895 | shylands | 1 |
| 20896 | shuttle | 1 |
| 20897 | shunned | 1 |
| 20898 | shunless | 1 |
| 20899 | shuffled | 1 |
| 20900 | shuffl | 1 |
| 20901 | shudders | 1 |
| 20902 | shudd | 1 |
| 20903 | shrugs | 1 |
| 20904 | shrows | 1 |
| 20905 | shrow | 1 |
| 20906 | shrovetide | 1 |
| 20907 | shrouding | 1 |
| 20908 | shrives | 1 |
| 20909 | shriver | 1 |
| 20910 | shrivelled | 1 |
| 20911 | shriv | 1 |
| 20912 | shrills | 1 |
| 20913 | shriller | 1 |
| 20914 | shrews | 1 |
| 20915 | shrewishness | 1 |
| 20916 | shrewishly | 1 |
| 20917 | shrewish | 1 |
| 20918 | showered | 1 |
| 20919 | shouldering | 1 |
| 20920 | shouldered | 1 |
| 20921 | shoughs | 1 |
| 20922 | shortened | 1 |
| 20923 | shortcoming | 1 |
| 20924 | shortcake | 1 |
| 20925 | shopkeeper | 1 |
| 20926 | shootie | 1 |
| 20927 | shoemaker | 1 |
| 20928 | shoals | 1 |
| 20929 | shoal | 1 |
| 20930 | shive | 1 |
| 20931 | shirley | 1 |
| 20932 | shirk | 1 |
| 20933 | shire | 1 |
| 20934 | shipwrights | 1 |
| 20935 | shipwrecks | 1 |
| 20936 | shipwrecking | 1 |
| 20937 | shipt | 1 |
| 20938 | shipped | 1 |
| 20939 | shipmen | 1 |
| 20940 | shipman | 1 |
| 20941 | shiny | 1 |
| 20942 | shineth | 1 |
| 20943 | sheweth | 1 |
| 20944 | shepherdes | 1 |
| 20945 | shelvy | 1 |
| 20946 | shelving | 1 |
| 20947 | shelt | 1 |
| 20948 | sheffield | 1 |
| 20949 | sheering | 1 |
| 20950 | sheeps | 1 |
| 20951 | sheepfold | 1 |
| 20952 | sheepcotes | 1 |
| 20953 | sheepcote | 1 |
| 20954 | sheaves | 1 |
| 20955 | sheaved | 1 |
| 20956 | shearman | 1 |
| 20957 | sheal | 1 |
| 20958 | shaw | 1 |
| 20959 | shaven | 1 |
| 20960 | shav | 1 |
| 20961 | sharps | 1 |
| 20962 | sharpens | 1 |
| 20963 | sharpen | 1 |
| 20964 | sharers | 1 |
| 20965 | sharded | 1 |
| 20966 | shard | 1 |
| 20967 | shapen | 1 |
| 20968 | shanty | 1 |
| 20969 | shanties | 1 |
| 20970 | shank | 1 |
| 20971 | shamelessness | 1 |
| 20972 | shallowness | 1 |
| 20973 | shallowly | 1 |
| 20974 | shallenge | 1 |
| 20975 | shales | 1 |
| 20976 | shaked | 1 |
| 20977 | shaded | 1 |
| 20978 | shad | 1 |
| 20979 | shackle | 1 |
| 20980 | shabbiness | 1 |
| 20981 | sh | 1 |
| 20982 | sfoot | 1 |
| 20983 | seymour | 1 |
| 20984 | sexes | 1 |
| 20985 | sewn | 1 |
| 20986 | sevillian | 1 |
| 20987 | severs | 1 |
| 20988 | severities | 1 |
| 20989 | severest | 1 |
| 20990 | sevennight | 1 |
| 20991 | settlest | 1 |
| 20992 | settles | 1 |
| 20993 | settest | 1 |
| 20994 | setoff | 1 |
| 20995 | sestos | 1 |
| 20996 | servissimus | 1 |
| 20997 | servility | 1 |
| 20998 | serveth | 1 |
| 20999 | server | 1 |
| 21000 | servanted | 1 |
| 21001 | serpentine | 1 |
| 21002 | seriousness | 1 |
| 21003 | sergas | 1 |
| 21004 | serenity | 1 |
| 21005 | serenis | 1 |
| 21006 | serenades | 1 |
| 21007 | seraglio | 1 |
| 21008 | sequester | 1 |
| 21009 | sepulchring | 1 |
| 21010 | septentrion | 1 |
| 21011 | separates | 1 |
| 21012 | separable | 1 |
| 21013 | sentiments | 1 |
| 21014 | senoys | 1 |
| 21015 | seniory | 1 |
| 21016 | seneca | 1 |
| 21017 | semper | 1 |
| 21018 | seminary | 1 |
| 21019 | semicircle | 1 |
| 21020 | semi | 1 |
| 21021 | semblative | 1 |
| 21022 | semblably | 1 |
| 21023 | sells | 1 |
| 21024 | selim | 1 |
| 21025 | seizeth | 1 |
| 21026 | seigniory | 1 |
| 21027 | seigniories | 1 |
| 21028 | seigneurs | 1 |
| 21029 | segregation | 1 |
| 21030 | seeting | 1 |
| 21031 | seething | 1 |
| 21032 | seethes | 1 |
| 21033 | seethe | 1 |
| 21034 | seer | 1 |
| 21035 | seemingly | 1 |
| 21036 | seemest | 1 |
| 21037 | seemers | 1 |
| 21038 | seely | 1 |
| 21039 | seeling | 1 |
| 21040 | seein | 1 |
| 21041 | seedsman | 1 |
| 21042 | seedness | 1 |
| 21043 | seeded | 1 |
| 21044 | seductive | 1 |
| 21045 | seducer | 1 |
| 21046 | sedgy | 1 |
| 21047 | sedge | 1 |
| 21048 | sedg | 1 |
| 21049 | sed | 1 |
| 21050 | secundo | 1 |
| 21051 | secondarily | 1 |
| 21052 | seasoning | 1 |
| 21053 | seasonable | 1 |
| 21054 | seasick | 1 |
| 21055 | seashore | 1 |
| 21056 | seared | 1 |
| 21057 | searcheth | 1 |
| 21058 | searches | 1 |
| 21059 | searchers | 1 |
| 21060 | searce | 1 |
| 21061 | seaports | 1 |
| 21062 | seamy | 1 |
| 21063 | seamstress | 1 |
| 21064 | seams | 1 |
| 21065 | seamen | 1 |
| 21066 | seafaring | 1 |
| 21067 | seacoast | 1 |
| 21068 | sdeath | 1 |
| 21069 | scythed | 1 |
| 21070 | scyllas | 1 |
| 21071 | scylla | 1 |
| 21072 | scuttled | 1 |
| 21073 | scutcheons | 1 |
| 21074 | scut | 1 |
| 21075 | scurril | 1 |
| 21076 | sculls | 1 |
| 21077 | scuffling | 1 |
| 21078 | scud | 1 |
| 21079 | scrutinized | 1 |
| 21080 | scrutinised | 1 |
| 21081 | scroyles | 1 |
| 21082 | scrowl | 1 |
| 21083 | scrolls | 1 |
| 21084 | scripserunt | 1 |
| 21085 | scrippage | 1 |
| 21086 | scrimmage | 1 |
| 21087 | scrimers | 1 |
| 21088 | scribbled | 1 |
| 21089 | scribbl | 1 |
| 21090 | screws | 1 |
| 21091 | screens | 1 |
| 21092 | screeching | 1 |
| 21093 | screams | 1 |
| 21094 | screaming | 1 |
| 21095 | scrawl | 1 |
| 21096 | scraping | 1 |
| 21097 | scourges | 1 |
| 21098 | scotches | 1 |
| 21099 | scotched | 1 |
| 21100 | scorpions | 1 |
| 21101 | scornest | 1 |
| 21102 | scoring | 1 |
| 21103 | scored | 1 |
| 21104 | scorched | 1 |
| 21105 | scopes | 1 |
| 21106 | scoldings | 1 |
| 21107 | scoggin | 1 |
| 21108 | scoffing | 1 |
| 21109 | scoffers | 1 |
| 21110 | scoffed | 1 |
| 21111 | scipios | 1 |
| 21112 | scipio | 1 |
| 21113 | scions | 1 |
| 21114 | sciaticas | 1 |
| 21115 | schooling | 1 |
| 21116 | schoolfellows | 1 |
| 21117 | schoolboy | 1 |
| 21118 | scholastic | 1 |
| 21119 | scholarly | 1 |
| 21120 | schismatics | 1 |
| 21121 | scepter | 1 |
| 21122 | scelerisque | 1 |
| 21123 | scelera | 1 |
| 21124 | scatterest | 1 |
| 21125 | scatterbrain | 1 |
| 21126 | scathful | 1 |
| 21127 | scath | 1 |
| 21128 | scarre | 1 |
| 21129 | scaring | 1 |
| 21130 | scarifying | 1 |
| 21131 | scarify | 1 |
| 21132 | scarfed | 1 |
| 21133 | scares | 1 |
| 21134 | scarecrows | 1 |
| 21135 | scapeth | 1 |
| 21136 | scapegraces | 1 |
| 21137 | scapegrace | 1 |
| 21138 | scants | 1 |
| 21139 | scantling | 1 |
| 21140 | scanting | 1 |
| 21141 | scanter | 1 |
| 21142 | scanned | 1 |
| 21143 | scandy | 1 |
| 21144 | scandals | 1 |
| 21145 | scandalised | 1 |
| 21146 | scan | 1 |
| 21147 | scamels | 1 |
| 21148 | scamble | 1 |
| 21149 | scalps | 1 |
| 21150 | scall | 1 |
| 21151 | scalded | 1 |
| 21152 | scal | 1 |
| 21153 | scaffoldage | 1 |
| 21154 | scabs | 1 |
| 21155 | sayst | 1 |
| 21156 | saxton | 1 |
| 21157 | saxony | 1 |
| 21158 | sawyer | 1 |
| 21159 | sawpit | 1 |
| 21160 | sawn | 1 |
| 21161 | sawed | 1 |
| 21162 | savoy | 1 |
| 21163 | savouring | 1 |
| 21164 | savoured | 1 |
| 21165 | savory | 1 |
| 21166 | saviour | 1 |
| 21167 | savagely | 1 |
| 21168 | sauces | 1 |
| 21169 | saucers | 1 |
| 21170 | saucer | 1 |
| 21171 | sauced | 1 |
| 21172 | saturatio | 1 |
| 21173 | satis | 1 |
| 21174 | satiate | 1 |
| 21175 | satchel | 1 |
| 21176 | sarum | 1 |
| 21177 | sardinian | 1 |
| 21178 | sardinia | 1 |
| 21179 | sardines | 1 |
| 21180 | sardians | 1 |
| 21181 | saracens | 1 |
| 21182 | sapping | 1 |
| 21183 | sapphires | 1 |
| 21184 | sapit | 1 |
| 21185 | santrailles | 1 |
| 21186 | sannazaro | 1 |
| 21187 | sank | 1 |
| 21188 | sanguis | 1 |
| 21189 | sandoval | 1 |
| 21190 | sanded | 1 |
| 21191 | sandbags | 1 |
| 21192 | sandbag | 1 |
| 21193 | sandals | 1 |
| 21194 | sanctuarize | 1 |
| 21195 | sanctities | 1 |
| 21196 | sanctioning | 1 |
| 21197 | sanctimonies | 1 |
| 21198 | sanctifies | 1 |
| 21199 | sanchos | 1 |
| 21200 | sanchobienaya | 1 |
| 21201 | sanchico | 1 |
| 21202 | samsons | 1 |
| 21203 | samsonino | 1 |
| 21204 | sampire | 1 |
| 21205 | samingo | 1 |
| 21206 | sambenito | 1 |
| 21207 | salving | 1 |
| 21208 | salves | 1 |
| 21209 | salv | 1 |
| 21210 | salutiferous | 1 |
| 21211 | salutary | 1 |
| 21212 | saltpetre | 1 |
| 21213 | saltness | 1 |
| 21214 | salting | 1 |
| 21215 | saltiers | 1 |
| 21216 | salter | 1 |
| 21217 | salmons | 1 |
| 21218 | salmon | 1 |
| 21219 | salivation | 1 |
| 21220 | salicam | 1 |
| 21221 | salazar | 1 |
| 21222 | salable | 1 |
| 21223 | saker | 1 |
| 21224 | saintlike | 1 |
| 21225 | sain | 1 |
| 21226 | sailmaker | 1 |
| 21227 | sailed | 1 |
| 21228 | sagittarius | 1 |
| 21229 | sag | 1 |
| 21230 | safeties | 1 |
| 21231 | saf | 1 |
| 21232 | sacristans | 1 |
| 21233 | sacring | 1 |
| 21234 | sacrilege | 1 |
| 21235 | sacrificial | 1 |
| 21236 | sacrificers | 1 |
| 21237 | sacraments | 1 |
| 21238 | sackful | 1 |
| 21239 | sackerson | 1 |
| 21240 | sacked | 1 |
| 21241 | sackbuts | 1 |
| 21242 | sabaean | 1 |
| 21243 | saba | 1 |
| 21244 | rything | 1 |
| 21245 | ruttish | 1 |
| 21246 | rut | 1 |
| 21247 | rusts | 1 |
| 21248 | rusting | 1 |
| 21249 | rusticity | 1 |
| 21250 | rustically | 1 |
| 21251 | rusted | 1 |
| 21252 | rushy | 1 |
| 21253 | rushling | 1 |
| 21254 | ruptures | 1 |
| 21255 | rupture | 1 |
| 21256 | runner | 1 |
| 21257 | runn | 1 |
| 21258 | rumourer | 1 |
| 21259 | rumoured | 1 |
| 21260 | rumination | 1 |
| 21261 | ruminating | 1 |
| 21262 | ruminates | 1 |
| 21263 | ruminat | 1 |
| 21264 | ruminaies | 1 |
| 21265 | rumbling | 1 |
| 21266 | rumble | 1 |
| 21267 | rugemount | 1 |
| 21268 | rugel | 1 |
| 21269 | rug | 1 |
| 21270 | rufo | 1 |
| 21271 | ruffling | 1 |
| 21272 | ruffles | 1 |
| 21273 | ruffled | 1 |
| 21274 | rued | 1 |
| 21275 | rudest | 1 |
| 21276 | ruddock | 1 |
| 21277 | ruddle | 1 |
| 21278 | ruddiness | 1 |
| 21279 | rudand | 1 |
| 21280 | rubious | 1 |
| 21281 | rubicund | 1 |
| 21282 | rubicon | 1 |
| 21283 | roynish | 1 |
| 21284 | royalize | 1 |
| 21285 | rowlands | 1 |
| 21286 | rower | 1 |
| 21287 | rover | 1 |
| 21288 | routing | 1 |
| 21289 | rously | 1 |
| 21290 | rousing | 1 |
| 21291 | roundure | 1 |
| 21292 | rounding | 1 |
| 21293 | roundest | 1 |
| 21294 | rounder | 1 |
| 21295 | roundel | 1 |
| 21296 | rotundity | 1 |
| 21297 | rotunda | 1 |
| 21298 | rottener | 1 |
| 21299 | rots | 1 |
| 21300 | rotherham | 1 |
| 21301 | rother | 1 |
| 21302 | roted | 1 |
| 21303 | rosed | 1 |
| 21304 | rosalinda | 1 |
| 21305 | ropy | 1 |
| 21306 | ropery | 1 |
| 21307 | rooting | 1 |
| 21308 | rooteth | 1 |
| 21309 | rootedly | 1 |
| 21310 | roomy | 1 |
| 21311 | rooky | 1 |
| 21312 | rondure | 1 |
| 21313 | rondilla | 1 |
| 21314 | romish | 1 |
| 21315 | romanos | 1 |
| 21316 | romano | 1 |
| 21317 | romage | 1 |
| 21318 | rolands | 1 |
| 21319 | rojas | 1 |
| 21320 | roisting | 1 |
| 21321 | roguishly | 1 |
| 21322 | rogero | 1 |
| 21323 | rogations | 1 |
| 21324 | roes | 1 |
| 21325 | rodamonte | 1 |
| 21326 | rochford | 1 |
| 21327 | rochelle | 1 |
| 21328 | rocabertis | 1 |
| 21329 | robas | 1 |
| 21330 | roba | 1 |
| 21331 | roarings | 1 |
| 21332 | roarers | 1 |
| 21333 | rless | 1 |
| 21334 | rivulets | 1 |
| 21335 | rivulet | 1 |
| 21336 | rivo | 1 |
| 21337 | rivelled | 1 |
| 21338 | rivalry | 1 |
| 21339 | rivalries | 1 |
| 21340 | rivality | 1 |
| 21341 | rivage | 1 |
| 21342 | risking | 1 |
| 21343 | rish | 1 |
| 21344 | risest | 1 |
| 21345 | riser | 1 |
| 21346 | ripple | 1 |
| 21347 | ripping | 1 |
| 21348 | riping | 1 |
| 21349 | riphaean | 1 |
| 21350 | ripely | 1 |
| 21351 | rioting | 1 |
| 21352 | rioter | 1 |
| 21353 | rinsings | 1 |
| 21354 | rinsed | 1 |
| 21355 | ringwood | 1 |
| 21356 | ringleader | 1 |
| 21357 | rinconete | 1 |
| 21358 | rin | 1 |
| 21359 | rills | 1 |
| 21360 | ril | 1 |
| 21361 | rigorously | 1 |
| 21362 | rigol | 1 |
| 21363 | rigmarole | 1 |
| 21364 | rigid | 1 |
| 21365 | rightfully | 1 |
| 21366 | righteously | 1 |
| 21367 | riggish | 1 |
| 21368 | rigged | 1 |
| 21369 | rifted | 1 |
| 21370 | rifled | 1 |
| 21371 | ries | 1 |
| 21372 | rien | 1 |
| 21373 | rideth | 1 |
| 21374 | riders | 1 |
| 21375 | rickety | 1 |
| 21376 | richmonds | 1 |
| 21377 | ricamonte | 1 |
| 21378 | ribaudred | 1 |
| 21379 | ribands | 1 |
| 21380 | riaran | 1 |
| 21381 | rhym | 1 |
| 21382 | rhodope | 1 |
| 21383 | rhinoceros | 1 |
| 21384 | rheumy | 1 |
| 21385 | rheums | 1 |
| 21386 | rhesus | 1 |
| 21387 | rhapsody | 1 |
| 21388 | rford | 1 |
| 21389 | reworded | 1 |
| 21390 | reword | 1 |
| 21391 | rewarding | 1 |
| 21392 | rewarder | 1 |
| 21393 | revulgo | 1 |
| 21394 | revolutions | 1 |
| 21395 | revokement | 1 |
| 21396 | revoked | 1 |
| 21397 | revok | 1 |
| 21398 | reviver | 1 |
| 21399 | revival | 1 |
| 21400 | revisits | 1 |
| 21401 | revising | 1 |
| 21402 | reviles | 1 |
| 21403 | revile | 1 |
| 21404 | reviewest | 1 |
| 21405 | reviewed | 1 |
| 21406 | review | 1 |
| 21407 | revers | 1 |
| 21408 | reverie | 1 |
| 21409 | revere | 1 |
| 21410 | reverbs | 1 |
| 21411 | reverb | 1 |
| 21412 | revengingly | 1 |
| 21413 | revengers | 1 |
| 21414 | revenger | 1 |
| 21415 | revengement | 1 |
| 21416 | revelry | 1 |
| 21417 | reveller | 1 |
| 21418 | revelled | 1 |
| 21419 | reveler | 1 |
| 21420 | revania | 1 |
| 21421 | rets | 1 |
| 21422 | retreats | 1 |
| 21423 | retracted | 1 |
| 21424 | retract | 1 |
| 21425 | retourne | 1 |
| 21426 | retorted | 1 |
| 21427 | reti | 1 |
| 21428 | rethoric | 1 |
| 21429 | retell | 1 |
| 21430 | retchings | 1 |
| 21431 | retaliation | 1 |
| 21432 | retaining | 1 |
| 21433 | retails | 1 |
| 21434 | retablo | 1 |
| 21435 | resuscitation | 1 |
| 21436 | resurrections | 1 |
| 21437 | resumes | 1 |
| 21438 | resum | 1 |
| 21439 | restricts | 1 |
| 21440 | restraints | 1 |
| 21441 | restrains | 1 |
| 21442 | restoreth | 1 |
| 21443 | restores | 1 |
| 21444 | restorative | 1 |
| 21445 | restive | 1 |
| 21446 | respose | 1 |
| 21447 | responsive | 1 |
| 21448 | responsibility | 1 |
| 21449 | response | 1 |
| 21450 | responded | 1 |
| 21451 | respites | 1 |
| 21452 | respice | 1 |
| 21453 | respectively | 1 |
| 21454 | respectful | 1 |
| 21455 | respeaking | 1 |
| 21456 | resorted | 1 |
| 21457 | resolving | 1 |
| 21458 | resolveth | 1 |
| 21459 | resolvedly | 1 |
| 21460 | resolutes | 1 |
| 21461 | resistless | 1 |
| 21462 | resin | 1 |
| 21463 | residue | 1 |
| 21464 | reserves | 1 |
| 21465 | resent | 1 |
| 21466 | resembleth | 1 |
| 21467 | rere | 1 |
| 21468 | requit | 1 |
| 21469 | requisition | 1 |
| 21470 | requireth | 1 |
| 21471 | requiem | 1 |
| 21472 | requesenes | 1 |
| 21473 | reputing | 1 |
| 21474 | reputeless | 1 |
| 21475 | reputable | 1 |
| 21476 | repured | 1 |
| 21477 | repurchas | 1 |
| 21478 | repulsive | 1 |
| 21479 | repugnant | 1 |
| 21480 | repugnancy | 1 |
| 21481 | repugnance | 1 |
| 21482 | repugn | 1 |
| 21483 | republic | 1 |
| 21484 | reproves | 1 |
| 21485 | reproveable | 1 |
| 21486 | reprov | 1 |
| 21487 | reproduce | 1 |
| 21488 | reprobation | 1 |
| 21489 | reproachfully | 1 |
| 21490 | reprisal | 1 |
| 21491 | repress | 1 |
| 21492 | reprehending | 1 |
| 21493 | reposeth | 1 |
| 21494 | reposed | 1 |
| 21495 | reposal | 1 |
| 21496 | reposada | 1 |
| 21497 | reportingly | 1 |
| 21498 | reportest | 1 |
| 21499 | reporter | 1 |
| 21500 | repliest | 1 |
| 21501 | replenish | 1 |
| 21502 | replant | 1 |
| 21503 | repining | 1 |
| 21504 | repine | 1 |
| 21505 | repin | 1 |
| 21506 | repetitions | 1 |
| 21507 | repentest | 1 |
| 21508 | repelling | 1 |
| 21509 | repelled | 1 |
| 21510 | repeatedly | 1 |
| 21511 | repealing | 1 |
| 21512 | repaying | 1 |
| 21513 | repasture | 1 |
| 21514 | repass | 1 |
| 21515 | reopening | 1 |
| 21516 | renowmed | 1 |
| 21517 | renouncement | 1 |
| 21518 | renounced | 1 |
| 21519 | renews | 1 |
| 21520 | renewing | 1 |
| 21521 | renewest | 1 |
| 21522 | reneges | 1 |
| 21523 | renege | 1 |
| 21524 | renegado | 1 |
| 21525 | rending | 1 |
| 21526 | remunerated | 1 |
| 21527 | remunerate | 1 |
| 21528 | remover | 1 |
| 21529 | removedness | 1 |
| 21530 | removal | 1 |
| 21531 | remounted | 1 |
| 21532 | remotest | 1 |
| 21533 | remonstrated | 1 |
| 21534 | remodel | 1 |
| 21535 | remitted | 1 |
| 21536 | remesten | 1 |
| 21537 | remercimens | 1 |
| 21538 | remembering | 1 |
| 21539 | remedying | 1 |
| 21540 | remediate | 1 |
| 21541 | remarkably | 1 |
| 21542 | remands | 1 |
| 21543 | remade | 1 |
| 21544 | relume | 1 |
| 21545 | reluctance | 1 |
| 21546 | reliquit | 1 |
| 21547 | reliques | 1 |
| 21548 | religions | 1 |
| 21549 | reliances | 1 |
| 21550 | reliance | 1 |
| 21551 | relents | 1 |
| 21552 | relaxing | 1 |
| 21553 | relax | 1 |
| 21554 | relatively | 1 |
| 21555 | relapsed | 1 |
| 21556 | relapse | 1 |
| 21557 | rejourn | 1 |
| 21558 | rejoindure | 1 |
| 21559 | rejoicingly | 1 |
| 21560 | rejoiceth | 1 |
| 21561 | rejoic | 1 |
| 21562 | rejections | 1 |
| 21563 | rejection | 1 |
| 21564 | rejecting | 1 |
| 21565 | reject | 1 |
| 21566 | reiterate | 1 |
| 21567 | reinstate | 1 |
| 21568 | reinforcement | 1 |
| 21569 | reinforce | 1 |
| 21570 | reinforc | 1 |
| 21571 | reined | 1 |
| 21572 | regumque | 1 |
| 21573 | regulate | 1 |
| 21574 | regrets | 1 |
| 21575 | regress | 1 |
| 21576 | regreets | 1 |
| 21577 | registries | 1 |
| 21578 | registers | 1 |
| 21579 | regina | 1 |
| 21580 | regiments | 1 |
| 21581 | regentship | 1 |
| 21582 | regenerate | 1 |
| 21583 | regardfully | 1 |
| 21584 | regardest | 1 |
| 21585 | regardance | 1 |
| 21586 | regaling | 1 |
| 21587 | regalia | 1 |
| 21588 | refutations | 1 |
| 21589 | refusest | 1 |
| 21590 | refulgence | 1 |
| 21591 | refts | 1 |
| 21592 | refreshment | 1 |
| 21593 | refreshing | 1 |
| 21594 | refreshed | 1 |
| 21595 | refrains | 1 |
| 21596 | refractory | 1 |
| 21597 | reforming | 1 |
| 21598 | refinements | 1 |
| 21599 | refinement | 1 |
| 21600 | refin | 1 |
| 21601 | refigured | 1 |
| 21602 | referr | 1 |
| 21603 | refell | 1 |
| 21604 | refectory | 1 |
| 21605 | reeleth | 1 |
| 21606 | reeled | 1 |
| 21607 | reeky | 1 |
| 21608 | reeks | 1 |
| 21609 | reduction | 1 |
| 21610 | reducing | 1 |
| 21611 | reduces | 1 |
| 21612 | redondillas | 1 |
| 21613 | redolence | 1 |
| 21614 | redness | 1 |
| 21615 | redime | 1 |
| 21616 | redeemed | 1 |
| 21617 | rede | 1 |
| 21618 | reddest | 1 |
| 21619 | redder | 1 |
| 21620 | recured | 1 |
| 21621 | recure | 1 |
| 21622 | rectorships | 1 |
| 21623 | rectorship | 1 |
| 21624 | rectors | 1 |
| 21625 | recreations | 1 |
| 21626 | recreate | 1 |
| 21627 | recoverable | 1 |
| 21628 | recov | 1 |
| 21629 | recounts | 1 |
| 21630 | recountments | 1 |
| 21631 | reconsidered | 1 |
| 21632 | recondite | 1 |
| 21633 | reconciling | 1 |
| 21634 | reconciliation | 1 |
| 21635 | reconciler | 1 |
| 21636 | reconcilement | 1 |
| 21637 | recommending | 1 |
| 21638 | recomforture | 1 |
| 21639 | recomforted | 1 |
| 21640 | recoils | 1 |
| 21641 | recoiling | 1 |
| 21642 | recognizances | 1 |
| 21643 | recognizance | 1 |
| 21644 | recognises | 1 |
| 21645 | reclusive | 1 |
| 21646 | recline | 1 |
| 21647 | reclaims | 1 |
| 21648 | recking | 1 |
| 21649 | reciting | 1 |
| 21650 | recited | 1 |
| 21651 | reciprocally | 1 |
| 21652 | rechate | 1 |
| 21653 | recently | 1 |
| 21654 | receiveth | 1 |
| 21655 | receiver | 1 |
| 21656 | receipts | 1 |
| 21657 | recanter | 1 |
| 21658 | recant | 1 |
| 21659 | recalls | 1 |
| 21660 | rebus | 1 |
| 21661 | rebukeable | 1 |
| 21662 | rebuk | 1 |
| 21663 | rebound | 1 |
| 21664 | rebelling | 1 |
| 21665 | rebellas | 1 |
| 21666 | rebecks | 1 |
| 21667 | rebato | 1 |
| 21668 | rebate | 1 |
| 21669 | rears | 1 |
| 21670 | rearing | 1 |
| 21671 | reappearance | 1 |
| 21672 | reaper | 1 |
| 21673 | reaped | 1 |
| 21674 | readmission | 1 |
| 21675 | readjusted | 1 |
| 21676 | readissimus | 1 |
| 21677 | readins | 1 |
| 21678 | reacheth | 1 |
| 21679 | razure | 1 |
| 21680 | razors | 1 |
| 21681 | razorable | 1 |
| 21682 | razing | 1 |
| 21683 | razeth | 1 |
| 21684 | razes | 1 |
| 21685 | rayed | 1 |
| 21686 | rawly | 1 |
| 21687 | rawest | 1 |
| 21688 | rawer | 1 |
| 21689 | ravishments | 1 |
| 21690 | ravishers | 1 |
| 21691 | ravena | 1 |
| 21692 | ravelin | 1 |
| 21693 | rattles | 1 |
| 21694 | ratolorum | 1 |
| 21695 | rationality | 1 |
| 21696 | ratifiers | 1 |
| 21697 | ratherest | 1 |
| 21698 | ratcatcher | 1 |
| 21699 | rastrea | 1 |
| 21700 | rashers | 1 |
| 21701 | rased | 1 |
| 21702 | rascalliest | 1 |
| 21703 | rascality | 1 |
| 21704 | rar | 1 |
| 21705 | rapturous | 1 |
| 21706 | raptures | 1 |
| 21707 | rapped | 1 |
| 21708 | ranting | 1 |
| 21709 | rant | 1 |
| 21710 | ransoming | 1 |
| 21711 | ransacking | 1 |
| 21712 | rankly | 1 |
| 21713 | ranking | 1 |
| 21714 | rangers | 1 |
| 21715 | rancors | 1 |
| 21716 | ramston | 1 |
| 21717 | ramsey | 1 |
| 21718 | ramps | 1 |
| 21719 | rampir | 1 |
| 21720 | rampant | 1 |
| 21721 | rampallian | 1 |
| 21722 | ramble | 1 |
| 21723 | rakes | 1 |
| 21724 | rakers | 1 |
| 21725 | rak | 1 |
| 21726 | rainold | 1 |
| 21727 | raileth | 1 |
| 21728 | railer | 1 |
| 21729 | rah | 1 |
| 21730 | raggedness | 1 |
| 21731 | raggeder | 1 |
| 21732 | ragg | 1 |
| 21733 | rageth | 1 |
| 21734 | raft | 1 |
| 21735 | rafe | 1 |
| 21736 | radical | 1 |
| 21737 | radiating | 1 |
| 21738 | racking | 1 |
| 21739 | racket | 1 |
| 21740 | rackers | 1 |
| 21741 | racing | 1 |
| 21742 | quoniam | 1 |
| 21743 | quoits | 1 |
| 21744 | quoint | 1 |
| 21745 | quoifs | 1 |
| 21746 | quo | 1 |
| 21747 | quixotissimus | 1 |
| 21748 | quixotades | 1 |
| 21749 | quivers | 1 |
| 21750 | quivering | 1 |
| 21751 | quittest | 1 |
| 21752 | quirocia | 1 |
| 21753 | quirk | 1 |
| 21754 | quiring | 1 |
| 21755 | quintain | 1 |
| 21756 | quinapalus | 1 |
| 21757 | quilted | 1 |
| 21758 | quills | 1 |
| 21759 | quieting | 1 |
| 21760 | quietest | 1 |
| 21761 | quier | 1 |
| 21762 | quidem | 1 |
| 21763 | quiddits | 1 |
| 21764 | quiddities | 1 |
| 21765 | quid | 1 |
| 21766 | quicksilverr | 1 |
| 21767 | quicksands | 1 |
| 21768 | quicksand | 1 |
| 21769 | quicklier | 1 |
| 21770 | quickening | 1 |
| 21771 | quickened | 1 |
| 21772 | quexana | 1 |
| 21773 | queubus | 1 |
| 21774 | quests | 1 |
| 21775 | questrists | 1 |
| 21776 | questionless | 1 |
| 21777 | questioners | 1 |
| 21778 | questioner | 1 |
| 21779 | questant | 1 |
| 21780 | query | 1 |
| 21781 | quern | 1 |
| 21782 | quenchless | 1 |
| 21783 | queasiness | 1 |
| 21784 | queas | 1 |
| 21785 | quay | 1 |
| 21786 | quatch | 1 |
| 21787 | quat | 1 |
| 21788 | quasi | 1 |
| 21789 | quartos | 1 |
| 21790 | quartering | 1 |
| 21791 | quartan | 1 |
| 21792 | quarries | 1 |
| 21793 | quarrelous | 1 |
| 21794 | quarreller | 1 |
| 21795 | quarrell | 1 |
| 21796 | quare | 1 |
| 21797 | quantities | 1 |
| 21798 | quandary | 1 |
| 21799 | quam | 1 |
| 21800 | qualms | 1 |
| 21801 | qualmish | 1 |
| 21802 | qualite | 1 |
| 21803 | qualifying | 1 |
| 21804 | qualifies | 1 |
| 21805 | qualification | 1 |
| 21806 | quakes | 1 |
| 21807 | quaffing | 1 |
| 21808 | quadrangle | 1 |
| 21809 | quacks | 1 |
| 21810 | quack | 1 |
| 21811 | pyrenees | 1 |
| 21812 | pyrenean | 1 |
| 21813 | pyramises | 1 |
| 21814 | pyramis | 1 |
| 21815 | pyramides | 1 |
| 21816 | pylades | 1 |
| 21817 | pygmy | 1 |
| 21818 | pygmies | 1 |
| 21819 | pygmalion | 1 |
| 21820 | py | 1 |
| 21821 | puzzel | 1 |
| 21822 | putrified | 1 |
| 21823 | putrid | 1 |
| 21824 | putrefy | 1 |
| 21825 | purus | 1 |
| 21826 | pursueth | 1 |
| 21827 | pursuers | 1 |
| 21828 | pursuer | 1 |
| 21829 | pursents | 1 |
| 21830 | purs | 1 |
| 21831 | purr | 1 |
| 21832 | purposing | 1 |
| 21833 | purples | 1 |
| 21834 | purlieus | 1 |
| 21835 | purifying | 1 |
| 21836 | purifies | 1 |
| 21837 | purgers | 1 |
| 21838 | purgative | 1 |
| 21839 | purely | 1 |
| 21840 | purchaseth | 1 |
| 21841 | purchases | 1 |
| 21842 | pur | 1 |
| 21843 | pupils | 1 |
| 21844 | punishing | 1 |
| 21845 | punishes | 1 |
| 21846 | punctiliousness | 1 |
| 21847 | punch | 1 |
| 21848 | pun | 1 |
| 21849 | pumpion | 1 |
| 21850 | pummel | 1 |
| 21851 | pulsidge | 1 |
| 21852 | pulsat | 1 |
| 21853 | pulpiter | 1 |
| 21854 | puller | 1 |
| 21855 | pulcher | 1 |
| 21856 | puking | 1 |
| 21857 | puke | 1 |
| 21858 | puis | 1 |
| 21859 | pugging | 1 |
| 21860 | puffs | 1 |
| 21861 | puertocarrero | 1 |
| 21862 | pueritia | 1 |
| 21863 | puebla | 1 |
| 21864 | pudency | 1 |
| 21865 | pudder | 1 |
| 21866 | puckered | 1 |
| 21867 | publication | 1 |
| 21868 | publican | 1 |
| 21869 | psalmist | 1 |
| 21870 | psalm | 1 |
| 21871 | prun | 1 |
| 21872 | prowling | 1 |
| 21873 | prow | 1 |
| 21874 | provoketh | 1 |
| 21875 | provoker | 1 |
| 21876 | proviso | 1 |
| 21877 | provisioned | 1 |
| 21878 | provider | 1 |
| 21879 | providently | 1 |
| 21880 | proven | 1 |
| 21881 | provant | 1 |
| 21882 | provand | 1 |
| 21883 | prouds | 1 |
| 21884 | proudlier | 1 |
| 21885 | protrude | 1 |
| 21886 | protractive | 1 |
| 21887 | protheus | 1 |
| 21888 | protester | 1 |
| 21889 | protectress | 1 |
| 21890 | prostration | 1 |
| 21891 | prostitute | 1 |
| 21892 | prospers | 1 |
| 21893 | prospects | 1 |
| 21894 | proselytes | 1 |
| 21895 | proscriptions | 1 |
| 21896 | prorogued | 1 |
| 21897 | propugnation | 1 |
| 21898 | propre | 1 |
| 21899 | propping | 1 |
| 21900 | propped | 1 |
| 21901 | propp | 1 |
| 21902 | propounded | 1 |
| 21903 | propositions | 1 |
| 21904 | proposition | 1 |
| 21905 | proposing | 1 |
| 21906 | proposer | 1 |
| 21907 | proposals | 1 |
| 21908 | proportionable | 1 |
| 21909 | propontic | 1 |
| 21910 | propinquity | 1 |
| 21911 | prophesier | 1 |
| 21912 | propensities | 1 |
| 21913 | propension | 1 |
| 21914 | propend | 1 |
| 21915 | propagation | 1 |
| 21916 | pronouns | 1 |
| 21917 | pronoun | 1 |
| 21918 | prononcez | 1 |
| 21919 | prononcer | 1 |
| 21920 | promulgate | 1 |
| 21921 | prompture | 1 |
| 21922 | promptement | 1 |
| 21923 | promoters | 1 |
| 21924 | prominent | 1 |
| 21925 | prometheus | 1 |
| 21926 | prolongs | 1 |
| 21927 | prolonging | 1 |
| 21928 | prolonged | 1 |
| 21929 | prolixious | 1 |
| 21930 | projector | 1 |
| 21931 | projections | 1 |
| 21932 | projection | 1 |
| 21933 | projecting | 1 |
| 21934 | prohibits | 1 |
| 21935 | prohibition | 1 |
| 21936 | prohibit | 1 |
| 21937 | progression | 1 |
| 21938 | prognosticate | 1 |
| 21939 | progne | 1 |
| 21940 | profundities | 1 |
| 21941 | profoundly | 1 |
| 21942 | profoundest | 1 |
| 21943 | profferer | 1 |
| 21944 | proffered | 1 |
| 21945 | professor | 1 |
| 21946 | professing | 1 |
| 21947 | profanity | 1 |
| 21948 | profaning | 1 |
| 21949 | profaners | 1 |
| 21950 | profaneness | 1 |
| 21951 | profanely | 1 |
| 21952 | proface | 1 |
| 21953 | productions | 1 |
| 21954 | product | 1 |
| 21955 | proditor | 1 |
| 21956 | prodigals | 1 |
| 21957 | prodigally | 1 |
| 21958 | proddings | 1 |
| 21959 | procuring | 1 |
| 21960 | procurator | 1 |
| 21961 | procreation | 1 |
| 21962 | procreants | 1 |
| 21963 | procreant | 1 |
| 21964 | procrastinate | 1 |
| 21965 | proconsul | 1 |
| 21966 | proclaimeth | 1 |
| 21967 | processions | 1 |
| 21968 | processionists | 1 |
| 21969 | proceeders | 1 |
| 21970 | probal | 1 |
| 21971 | prizing | 1 |
| 21972 | prizest | 1 |
| 21973 | privilage | 1 |
| 21974 | privet | 1 |
| 21975 | prithe | 1 |
| 21976 | prisonnier | 1 |
| 21977 | prisonment | 1 |
| 21978 | priscian | 1 |
| 21979 | priories | 1 |
| 21980 | priora | 1 |
| 21981 | printless | 1 |
| 21982 | printer | 1 |
| 21983 | princox | 1 |
| 21984 | principled | 1 |
| 21985 | principio | 1 |
| 21986 | principals | 1 |
| 21987 | principality | 1 |
| 21988 | principalities | 1 |
| 21989 | primy | 1 |
| 21990 | primogenity | 1 |
| 21991 | primo | 1 |
| 21992 | primitive | 1 |
| 21993 | primeval | 1 |
| 21994 | primest | 1 |
| 21995 | primera | 1 |
| 21996 | primer | 1 |
| 21997 | primed | 1 |
| 21998 | primaeval | 1 |
| 21999 | pries | 1 |
| 22000 | prief | 1 |
| 22001 | pried | 1 |
| 22002 | prie | 1 |
| 22003 | prides | 1 |
| 22004 | pricksong | 1 |
| 22005 | preyful | 1 |
| 22006 | preventions | 1 |
| 22007 | prevaricator | 1 |
| 22008 | prevailment | 1 |
| 22009 | prevaileth | 1 |
| 22010 | prettiness | 1 |
| 22011 | prettier | 1 |
| 22012 | pretia | 1 |
| 22013 | pretense | 1 |
| 22014 | pretends | 1 |
| 22015 | pretences | 1 |
| 22016 | pret | 1 |
| 22017 | presuppos | 1 |
| 22018 | presumes | 1 |
| 22019 | presumed | 1 |
| 22020 | pressures | 1 |
| 22021 | pressingly | 1 |
| 22022 | presser | 1 |
| 22023 | president | 1 |
| 22024 | preservers | 1 |
| 22025 | preservative | 1 |
| 22026 | presenters | 1 |
| 22027 | presenter | 1 |
| 22028 | presences | 1 |
| 22029 | prescripts | 1 |
| 22030 | prescribes | 1 |
| 22031 | presaging | 1 |
| 22032 | presagers | 1 |
| 22033 | prerogatived | 1 |
| 22034 | prerogatifes | 1 |
| 22035 | prepossessing | 1 |
| 22036 | prepares | 1 |
| 22037 | preparedly | 1 |
| 22038 | preordination | 1 |
| 22039 | preordinance | 1 |
| 22040 | prenez | 1 |
| 22041 | premised | 1 |
| 22042 | premeditation | 1 |
| 22043 | prematurely | 1 |
| 22044 | prelude | 1 |
| 22045 | preliminary | 1 |
| 22046 | prejudiced | 1 |
| 22047 | prejudicates | 1 |
| 22048 | pregnantly | 1 |
| 22049 | pregnancy | 1 |
| 22050 | preformed | 1 |
| 22051 | prefixed | 1 |
| 22052 | prefiguring | 1 |
| 22053 | prefers | 1 |
| 22054 | preferring | 1 |
| 22055 | preferreth | 1 |
| 22056 | preeches | 1 |
| 22057 | predictions | 1 |
| 22058 | predicted | 1 |
| 22059 | predict | 1 |
| 22060 | predestinate | 1 |
| 22061 | predecessor | 1 |
| 22062 | predeceased | 1 |
| 22063 | precursors | 1 |
| 22064 | precurse | 1 |
| 22065 | precor | 1 |
| 22066 | precisian | 1 |
| 22067 | preciseness | 1 |
| 22068 | precipitately | 1 |
| 22069 | precipitate | 1 |
| 22070 | preciously | 1 |
| 22071 | preceptial | 1 |
| 22072 | preceeding | 1 |
| 22073 | prearranged | 1 |
| 22074 | preambulate | 1 |
| 22075 | preambles | 1 |
| 22076 | pread | 1 |
| 22077 | preachment | 1 |
| 22078 | prayed | 1 |
| 22079 | prawns | 1 |
| 22080 | prawls | 1 |
| 22081 | prattler | 1 |
| 22082 | prater | 1 |
| 22083 | prated | 1 |
| 22084 | prancing | 1 |
| 22085 | praisest | 1 |
| 22086 | prague | 1 |
| 22087 | pragging | 1 |
| 22088 | praetors | 1 |
| 22089 | praetor | 1 |
| 22090 | praemunire | 1 |
| 22091 | praeclarissimus | 1 |
| 22092 | practises | 1 |
| 22093 | practisers | 1 |
| 22094 | practiser | 1 |
| 22095 | practisants | 1 |
| 22096 | practicing | 1 |
| 22097 | practicer | 1 |
| 22098 | practiced | 1 |
| 22099 | practical | 1 |
| 22100 | practicable | 1 |
| 22101 | practic | 1 |
| 22102 | poysam | 1 |
| 22103 | poys | 1 |
| 22104 | powd | 1 |
| 22105 | pouncet | 1 |
| 22106 | pounces | 1 |
| 22107 | poultry | 1 |
| 22108 | poultney | 1 |
| 22109 | poultice | 1 |
| 22110 | poulter | 1 |
| 22111 | potting | 1 |
| 22112 | pother | 1 |
| 22113 | pothecary | 1 |
| 22114 | potful | 1 |
| 22115 | potents | 1 |
| 22116 | potch | 1 |
| 22117 | potatoes | 1 |
| 22118 | potato | 1 |
| 22119 | potable | 1 |
| 22120 | postillion | 1 |
| 22121 | posthorses | 1 |
| 22122 | posthorse | 1 |
| 22123 | posters | 1 |
| 22124 | posteriors | 1 |
| 22125 | poste | 1 |
| 22126 | postage | 1 |
| 22127 | possitable | 1 |
| 22128 | possibilities | 1 |
| 22129 | possets | 1 |
| 22130 | possessors | 1 |
| 22131 | posse | 1 |
| 22132 | posied | 1 |
| 22133 | pose | 1 |
| 22134 | posadas | 1 |
| 22135 | posada | 1 |
| 22136 | portuguese | 1 |
| 22137 | portrays | 1 |
| 22138 | portraying | 1 |
| 22139 | portraiture | 1 |
| 22140 | portotartarossa | 1 |
| 22141 | portions | 1 |
| 22142 | portioned | 1 |
| 22143 | portico | 1 |
| 22144 | portent | 1 |
| 22145 | portage | 1 |
| 22146 | pores | 1 |
| 22147 | porches | 1 |
| 22148 | pops | 1 |
| 22149 | poppy | 1 |
| 22150 | popish | 1 |
| 22151 | popingay | 1 |
| 22152 | popes | 1 |
| 22153 | popedom | 1 |
| 22154 | pop | 1 |
| 22155 | pooh | 1 |
| 22156 | pontus | 1 |
| 22157 | ponton | 1 |
| 22158 | pontiffs | 1 |
| 22159 | pontic | 1 |
| 22160 | pont | 1 |
| 22161 | ponds | 1 |
| 22162 | ponder | 1 |
| 22163 | pomps | 1 |
| 22164 | pompion | 1 |
| 22165 | pommelled | 1 |
| 22166 | pomgarnet | 1 |
| 22167 | pomewater | 1 |
| 22168 | pomander | 1 |
| 22169 | polyxena | 1 |
| 22170 | polyphemes | 1 |
| 22171 | polydamus | 1 |
| 22172 | polusion | 1 |
| 22173 | poltroons | 1 |
| 22174 | pollux | 1 |
| 22175 | politicians | 1 |
| 22176 | politely | 1 |
| 22177 | policies | 1 |
| 22178 | poli | 1 |
| 22179 | polemon | 1 |
| 22180 | polecat | 1 |
| 22181 | poleaxe | 1 |
| 22182 | pold | 1 |
| 22183 | polacks | 1 |
| 22184 | poking | 1 |
| 22185 | poke | 1 |
| 22186 | poisoning | 1 |
| 22187 | poising | 1 |
| 22188 | poises | 1 |
| 22189 | poised | 1 |
| 22190 | pointblank | 1 |
| 22191 | poinards | 1 |
| 22192 | pods | 1 |
| 22193 | pocky | 1 |
| 22194 | pocketing | 1 |
| 22195 | pocketed | 1 |
| 22196 | po | 1 |
| 22197 | plutarch | 1 |
| 22198 | plurisy | 1 |
| 22199 | plums | 1 |
| 22200 | plumpy | 1 |
| 22201 | plumaged | 1 |
| 22202 | plugs | 1 |
| 22203 | plue | 1 |
| 22204 | plucker | 1 |
| 22205 | plows | 1 |
| 22206 | plow | 1 |
| 22207 | ploughs | 1 |
| 22208 | ploughmen | 1 |
| 22209 | ploughing | 1 |
| 22210 | plotter | 1 |
| 22211 | ploody | 1 |
| 22212 | plood | 1 |
| 22213 | plods | 1 |
| 22214 | plodders | 1 |
| 22215 | plighter | 1 |
| 22216 | pliant | 1 |
| 22217 | plessing | 1 |
| 22218 | plessed | 1 |
| 22219 | plenties | 1 |
| 22220 | plenteously | 1 |
| 22221 | plenitude | 1 |
| 22222 | plenary | 1 |
| 22223 | pleines | 1 |
| 22224 | plectro | 1 |
| 22225 | plebs | 1 |
| 22226 | plebeii | 1 |
| 22227 | pleasurable | 1 |
| 22228 | pleasers | 1 |
| 22229 | pleaser | 1 |
| 22230 | pleasance | 1 |
| 22231 | pleaders | 1 |
| 22232 | pleader | 1 |
| 22233 | plazas | 1 |
| 22234 | plaything | 1 |
| 22235 | playhouse | 1 |
| 22236 | playful | 1 |
| 22237 | playeth | 1 |
| 22238 | playest | 1 |
| 22239 | plautus | 1 |
| 22240 | plausible | 1 |
| 22241 | platter | 1 |
| 22242 | platted | 1 |
| 22243 | plats | 1 |
| 22244 | platirs | 1 |
| 22245 | platforms | 1 |
| 22246 | plat | 1 |
| 22247 | plastering | 1 |
| 22248 | plasterer | 1 |
| 22249 | plast | 1 |
| 22250 | plash | 1 |
| 22251 | planteth | 1 |
| 22252 | plantation | 1 |
| 22253 | plantage | 1 |
| 22254 | planched | 1 |
| 22255 | plaisance | 1 |
| 22256 | plaintiffs | 1 |
| 22257 | plaintful | 1 |
| 22258 | plainsong | 1 |
| 22259 | plainings | 1 |
| 22260 | plaining | 1 |
| 22261 | plaguy | 1 |
| 22262 | plaguing | 1 |
| 22263 | plack | 1 |
| 22264 | placid | 1 |
| 22265 | placerdemivida | 1 |
| 22266 | placentio | 1 |
| 22267 | piu | 1 |
| 22268 | pittikins | 1 |
| 22269 | pittie | 1 |
| 22270 | pitted | 1 |
| 22271 | pittance | 1 |
| 22272 | pitie | 1 |
| 22273 | pithy | 1 |
| 22274 | pithless | 1 |
| 22275 | pisuerga | 1 |
| 22276 | pismires | 1 |
| 22277 | pips | 1 |
| 22278 | pippins | 1 |
| 22279 | pippin | 1 |
| 22280 | pipkinful | 1 |
| 22281 | pipers | 1 |
| 22282 | piper | 1 |
| 22283 | piped | 1 |
| 22284 | pioners | 1 |
| 22285 | pioner | 1 |
| 22286 | pioned | 1 |
| 22287 | piojo | 1 |
| 22288 | pintpot | 1 |
| 22289 | pintiquiniestra | 1 |
| 22290 | pinse | 1 |
| 22291 | pinproddings | 1 |
| 22292 | pinprodding | 1 |
| 22293 | pinnacles | 1 |
| 22294 | pinn | 1 |
| 22295 | pinked | 1 |
| 22296 | pineclad | 1 |
| 22297 | pinchbeck | 1 |
| 22298 | pimping | 1 |
| 22299 | pimpernell | 1 |
| 22300 | pilots | 1 |
| 22301 | pillagers | 1 |
| 22302 | pillaged | 1 |
| 22303 | pilfering | 1 |
| 22304 | pilfer | 1 |
| 22305 | pilf | 1 |
| 22306 | piled | 1 |
| 22307 | pilchers | 1 |
| 22308 | pilchards | 1 |
| 22309 | pilates | 1 |
| 22310 | pigrogromitus | 1 |
| 22311 | pignatta | 1 |
| 22312 | pigmy | 1 |
| 22313 | pigments | 1 |
| 22314 | piers | 1 |
| 22315 | piercy | 1 |
| 22316 | pierceth | 1 |
| 22317 | pier | 1 |
| 22318 | piedrahita | 1 |
| 22319 | piedness | 1 |
| 22320 | piedmont | 1 |
| 22321 | piecing | 1 |
| 22322 | piecemeal | 1 |
| 22323 | piebald | 1 |
| 22324 | pid | 1 |
| 22325 | picturing | 1 |
| 22326 | pictur | 1 |
| 22327 | pickthanks | 1 |
| 22328 | pickt | 1 |
| 22329 | pickpurse | 1 |
| 22330 | picklock | 1 |
| 22331 | pickles | 1 |
| 22332 | pickled | 1 |
| 22333 | pickers | 1 |
| 22334 | pickbone | 1 |
| 22335 | pible | 1 |
| 22336 | pibble | 1 |
| 22337 | piace | 1 |
| 22338 | phyllis | 1 |
| 22339 | phraseless | 1 |
| 22340 | photinus | 1 |
| 22341 | phorbus | 1 |
| 22342 | phoenicians | 1 |
| 22343 | phoenicia | 1 |
| 22344 | phoebuses | 1 |
| 22345 | phlegmaties | 1 |
| 22346 | phlegmatics | 1 |
| 22347 | phlegmatically | 1 |
| 22348 | phlegmatic | 1 |
| 22349 | philosophies | 1 |
| 22350 | philosophical | 1 |
| 22351 | philomela | 1 |
| 22352 | phillises | 1 |
| 22353 | phillida | 1 |
| 22354 | philippan | 1 |
| 22355 | philemon | 1 |
| 22356 | philarmonus | 1 |
| 22357 | philadelphos | 1 |
| 22358 | phibbus | 1 |
| 22359 | pheebus | 1 |
| 22360 | phebes | 1 |
| 22361 | pheazar | 1 |
| 22362 | pheasants | 1 |
| 22363 | pharsalia | 1 |
| 22364 | pharaohs | 1 |
| 22365 | phantasma | 1 |
| 22366 | phantasimes | 1 |
| 22367 | phantasime | 1 |
| 22368 | phaeton | 1 |
| 22369 | pewterer | 1 |
| 22370 | pettitoes | 1 |
| 22371 | pettish | 1 |
| 22372 | pettiness | 1 |
| 22373 | petronels | 1 |
| 22374 | petrarch | 1 |
| 22375 | petrals | 1 |
| 22376 | petit | 1 |
| 22377 | petar | 1 |
| 22378 | pessima | 1 |
| 22379 | peseech | 1 |
| 22380 | perverter | 1 |
| 22381 | perversity | 1 |
| 22382 | perversely | 1 |
| 22383 | pervaded | 1 |
| 22384 | pervade | 1 |
| 22385 | peru | 1 |
| 22386 | perturbed | 1 |
| 22387 | perturbations | 1 |
| 22388 | perturb | 1 |
| 22389 | pertaunt | 1 |
| 22390 | persuasive | 1 |
| 22391 | perspiring | 1 |
| 22392 | perspired | 1 |
| 22393 | perspicuous | 1 |
| 22394 | perspectives | 1 |
| 22395 | perspectively | 1 |
| 22396 | personified | 1 |
| 22397 | personating | 1 |
| 22398 | personates | 1 |
| 22399 | personated | 1 |
| 22400 | personate | 1 |
| 22401 | persistive | 1 |
| 22402 | persistent | 1 |
| 22403 | persistency | 1 |
| 22404 | persevers | 1 |
| 22405 | persecutors | 1 |
| 22406 | persecutor | 1 |
| 22407 | persecutions | 1 |
| 22408 | pers | 1 |
| 22409 | perrillo | 1 |
| 22410 | perplexities | 1 |
| 22411 | perpendicularly | 1 |
| 22412 | perpendicular | 1 |
| 22413 | peroration | 1 |
| 22414 | perogrullo | 1 |
| 22415 | pero | 1 |
| 22416 | perniciously | 1 |
| 22417 | permittest | 1 |
| 22418 | permits | 1 |
| 22419 | permissive | 1 |
| 22420 | permanent | 1 |
| 22421 | permafoy | 1 |
| 22422 | perlerino | 1 |
| 22423 | perlerina | 1 |
| 22424 | perkes | 1 |
| 22425 | perk | 1 |
| 22426 | perjuries | 1 |
| 22427 | peritoa | 1 |
| 22428 | perisheth | 1 |
| 22429 | perishest | 1 |
| 22430 | perishes | 1 |
| 22431 | periquillo | 1 |
| 22432 | perion | 1 |
| 22433 | periodical | 1 |
| 22434 | perigouna | 1 |
| 22435 | perigort | 1 |
| 22436 | periapts | 1 |
| 22437 | perfumery | 1 |
| 22438 | perfumer | 1 |
| 22439 | performer | 1 |
| 22440 | perfidiously | 1 |
| 22441 | perfecter | 1 |
| 22442 | perendenga | 1 |
| 22443 | peremptorily | 1 |
| 22444 | peregrination | 1 |
| 22445 | peregrinate | 1 |
| 22446 | pere | 1 |
| 22447 | perdurably | 1 |
| 22448 | perdonato | 1 |
| 22449 | perdie | 1 |
| 22450 | perdicis | 1 |
| 22451 | percussion | 1 |
| 22452 | percies | 1 |
| 22453 | perched | 1 |
| 22454 | perception | 1 |
| 22455 | perceiveth | 1 |
| 22456 | perceivest | 1 |
| 22457 | peralvillo | 1 |
| 22458 | peradventures | 1 |
| 22459 | peppery | 1 |
| 22460 | peppered | 1 |
| 22461 | peppercorn | 1 |
| 22462 | peoples | 1 |
| 22463 | peopl | 1 |
| 22464 | penurious | 1 |
| 22465 | penthesilea | 1 |
| 22466 | pensively | 1 |
| 22467 | pensived | 1 |
| 22468 | penning | 1 |
| 22469 | penman | 1 |
| 22470 | penknife | 1 |
| 22471 | penker | 1 |
| 22472 | penitently | 1 |
| 22473 | penitential | 1 |
| 22474 | peneus | 1 |
| 22475 | penetrative | 1 |
| 22476 | pendulous | 1 |
| 22477 | pendragon | 1 |
| 22478 | pending | 1 |
| 22479 | pencill | 1 |
| 22480 | peloponnesus | 1 |
| 22481 | pellis | 1 |
| 22482 | pella | 1 |
| 22483 | pelf | 1 |
| 22484 | peize | 1 |
| 22485 | peised | 1 |
| 22486 | peise | 1 |
| 22487 | peflur | 1 |
| 22488 | peevishly | 1 |
| 22489 | peesel | 1 |
| 22490 | peereth | 1 |
| 22491 | peered | 1 |
| 22492 | peeped | 1 |
| 22493 | peeled | 1 |
| 22494 | peds | 1 |
| 22495 | pedlars | 1 |
| 22496 | pedigrees | 1 |
| 22497 | pedascule | 1 |
| 22498 | pedants | 1 |
| 22499 | pedantical | 1 |
| 22500 | pecus | 1 |
| 22501 | peculiarities | 1 |
| 22502 | pecks | 1 |
| 22503 | peckish | 1 |
| 22504 | pecked | 1 |
| 22505 | pebbled | 1 |
| 22506 | peating | 1 |
| 22507 | peaten | 1 |
| 22508 | peasantry | 1 |
| 22509 | pearly | 1 |
| 22510 | peals | 1 |
| 22511 | pealing | 1 |
| 22512 | peaking | 1 |
| 22513 | peaked | 1 |
| 22514 | peacocks | 1 |
| 22515 | peaches | 1 |
| 22516 | peaces | 1 |
| 22517 | peaceable | 1 |
| 22518 | paysans | 1 |
| 22519 | paysan | 1 |
| 22520 | payments | 1 |
| 22521 | payest | 1 |
| 22522 | pawns | 1 |
| 22523 | pawning | 1 |
| 22524 | pawing | 1 |
| 22525 | pavin | 1 |
| 22526 | pavilions | 1 |
| 22527 | pav | 1 |
| 22528 | pauvres | 1 |
| 22529 | pausingly | 1 |
| 22530 | pauses | 1 |
| 22531 | pauser | 1 |
| 22532 | pauperum | 1 |
| 22533 | paunches | 1 |
| 22534 | paucas | 1 |
| 22535 | pattle | 1 |
| 22536 | patter | 1 |
| 22537 | patrum | 1 |
| 22538 | patrons | 1 |
| 22539 | patrimonial | 1 |
| 22540 | patriarch | 1 |
| 22541 | patines | 1 |
| 22542 | patients | 1 |
| 22543 | pathways | 1 |
| 22544 | pathway | 1 |
| 22545 | pathetically | 1 |
| 22546 | paternity | 1 |
| 22547 | paternal | 1 |
| 22548 | patena | 1 |
| 22549 | patay | 1 |
| 22550 | pata | 1 |
| 22551 | pastry | 1 |
| 22552 | pastors | 1 |
| 22553 | pastorals | 1 |
| 22554 | pasties | 1 |
| 22555 | pasterns | 1 |
| 22556 | passy | 1 |
| 22557 | passive | 1 |
| 22558 | passioning | 1 |
| 22559 | passio | 1 |
| 22560 | passant | 1 |
| 22561 | paso | 1 |
| 22562 | pashful | 1 |
| 22563 | pashed | 1 |
| 22564 | pasamaques | 1 |
| 22565 | partizan | 1 |
| 22566 | partisan | 1 |
| 22567 | particularize | 1 |
| 22568 | partialize | 1 |
| 22569 | partes | 1 |
| 22570 | partakers | 1 |
| 22571 | partaken | 1 |
| 22572 | parsley | 1 |
| 22573 | parsimonious | 1 |
| 22574 | parricides | 1 |
| 22575 | parricide | 1 |
| 22576 | parrhasius | 1 |
| 22577 | paroxysms | 1 |
| 22578 | paroxysm | 1 |
| 22579 | paropillo | 1 |
| 22580 | parmacity | 1 |
| 22581 | parlors | 1 |
| 22582 | parlez | 1 |
| 22583 | parles | 1 |
| 22584 | parler | 1 |
| 22585 | paritors | 1 |
| 22586 | parisians | 1 |
| 22587 | parfect | 1 |
| 22588 | parenthesis | 1 |
| 22589 | parel | 1 |
| 22590 | pared | 1 |
| 22591 | pardonne | 1 |
| 22592 | pardoner | 1 |
| 22593 | pardona | 1 |
| 22594 | parcell | 1 |
| 22595 | parca | 1 |
| 22596 | parasites | 1 |
| 22597 | paraquito | 1 |
| 22598 | parapets | 1 |
| 22599 | paramours | 1 |
| 22600 | paralytics | 1 |
| 22601 | paralyses | 1 |
| 22602 | paralysed | 1 |
| 22603 | paralipomenon | 1 |
| 22604 | paragons | 1 |
| 22605 | parading | 1 |
| 22606 | paracelsus | 1 |
| 22607 | parable | 1 |
| 22608 | paps | 1 |
| 22609 | papist | 1 |
| 22610 | papin | 1 |
| 22611 | paphos | 1 |
| 22612 | paphlagonia | 1 |
| 22613 | papal | 1 |
| 22614 | panzino | 1 |
| 22615 | pantry | 1 |
| 22616 | pantingly | 1 |
| 22617 | panted | 1 |
| 22618 | pansies | 1 |
| 22619 | pansa | 1 |
| 22620 | pannier | 1 |
| 22621 | pannel | 1 |
| 22622 | panics | 1 |
| 22623 | panic | 1 |
| 22624 | paniaguado | 1 |
| 22625 | panging | 1 |
| 22626 | panel | 1 |
| 22627 | pane | 1 |
| 22628 | panderly | 1 |
| 22629 | pandahilado | 1 |
| 22630 | pancino | 1 |
| 22631 | panchaia | 1 |
| 22632 | pancake | 1 |
| 22633 | pancackes | 1 |
| 22634 | pamphlet | 1 |
| 22635 | pamp | 1 |
| 22636 | palt | 1 |
| 22637 | palsies | 1 |
| 22638 | palomeque | 1 |
| 22639 | palmy | 1 |
| 22640 | pallida | 1 |
| 22641 | pallets | 1 |
| 22642 | palladium | 1 |
| 22643 | pallabris | 1 |
| 22644 | palisadoes | 1 |
| 22645 | palinurus | 1 |
| 22646 | paled | 1 |
| 22647 | palaver | 1 |
| 22648 | palating | 1 |
| 22649 | palamedes | 1 |
| 22650 | palafoxes | 1 |
| 22651 | paladin | 1 |
| 22652 | palabras | 1 |
| 22653 | pal | 1 |
| 22654 | pajock | 1 |
| 22655 | paired | 1 |
| 22656 | painters | 1 |
| 22657 | pails | 1 |
| 22658 | pailfuls | 1 |
| 22659 | paglia | 1 |
| 22660 | pageantry | 1 |
| 22661 | pagano | 1 |
| 22662 | paganism | 1 |
| 22663 | pads | 1 |
| 22664 | padre | 1 |
| 22665 | paddle | 1 |
| 22666 | pactolus | 1 |
| 22667 | paction | 1 |
| 22668 | pact | 1 |
| 22669 | packthread | 1 |
| 22670 | packs | 1 |
| 22671 | packings | 1 |
| 22672 | packhorses | 1 |
| 22673 | pacify | 1 |
| 22674 | pabylon | 1 |
| 22675 | pabble | 1 |
| 22676 | oxfordshire | 1 |
| 22677 | oxcart | 1 |
| 22678 | owy | 1 |
| 22679 | owning | 1 |
| 22680 | ownership | 1 |
| 22681 | oweth | 1 |
| 22682 | owedst | 1 |
| 22683 | oviedo | 1 |
| 22684 | ovidius | 1 |
| 22685 | overworn | 1 |
| 22686 | overwork | 1 |
| 22687 | overwhelming | 1 |
| 22688 | overweighted | 1 |
| 22689 | overweigh | 1 |
| 22690 | overween | 1 |
| 22691 | overwatch | 1 |
| 22692 | overturns | 1 |
| 22693 | overtops | 1 |
| 22694 | overtopp | 1 |
| 22695 | overtop | 1 |
| 22696 | overthrows | 1 |
| 22697 | overthrowing | 1 |
| 22698 | overtaketh | 1 |
| 22699 | overt | 1 |
| 22700 | overswear | 1 |
| 22701 | overstain | 1 |
| 22702 | oversights | 1 |
| 22703 | overshot | 1 |
| 22704 | overshines | 1 |
| 22705 | overshadowed | 1 |
| 22706 | overshades | 1 |
| 22707 | overset | 1 |
| 22708 | overseers | 1 |
| 22709 | overseer | 1 |
| 22710 | overscutch | 1 |
| 22711 | overpeering | 1 |
| 22712 | overpast | 1 |
| 22713 | overmounting | 1 |
| 22714 | overmasters | 1 |
| 22715 | overmastered | 1 |
| 22716 | overmaster | 1 |
| 22717 | overlooking | 1 |
| 22718 | overlooked | 1 |
| 22719 | overload | 1 |
| 22720 | overlive | 1 |
| 22721 | overleather | 1 |
| 22722 | overland | 1 |
| 22723 | overkind | 1 |
| 22724 | overhold | 1 |
| 22725 | overhauled | 1 |
| 22726 | overhanging | 1 |
| 22727 | overgorg | 1 |
| 22728 | overgone | 1 |
| 22729 | overgo | 1 |
| 22730 | overglance | 1 |
| 22731 | overflown | 1 |
| 22732 | overflowings | 1 |
| 22733 | overfar | 1 |
| 22734 | overearnest | 1 |
| 22735 | overcoming | 1 |
| 22736 | overcharg | 1 |
| 22737 | overcast | 1 |
| 22738 | overbuys | 1 |
| 22739 | overbulk | 1 |
| 22740 | overbold | 1 |
| 22741 | overawe | 1 |
| 22742 | outworths | 1 |
| 22743 | outwent | 1 |
| 22744 | outvenoms | 1 |
| 22745 | outswear | 1 |
| 22746 | outstripped | 1 |
| 22747 | outstrike | 1 |
| 22748 | outstood | 1 |
| 22749 | outstay | 1 |
| 22750 | outsport | 1 |
| 22751 | outspeaks | 1 |
| 22752 | outsides | 1 |
| 22753 | outsells | 1 |
| 22754 | outsell | 1 |
| 22755 | outscorn | 1 |
| 22756 | outscold | 1 |
| 22757 | outs | 1 |
| 22758 | outruns | 1 |
| 22759 | outrunning | 1 |
| 22760 | outroar | 1 |
| 22761 | outran | 1 |
| 22762 | outpriz | 1 |
| 22763 | outlustres | 1 |
| 22764 | outlook | 1 |
| 22765 | outliving | 1 |
| 22766 | outliv | 1 |
| 22767 | outline | 1 |
| 22768 | outlawry | 1 |
| 22769 | outlasted | 1 |
| 22770 | outlast | 1 |
| 22771 | outlandish | 1 |
| 22772 | outjest | 1 |
| 22773 | outgrown | 1 |
| 22774 | outgoes | 1 |
| 22775 | outgo | 1 |
| 22776 | outfrown | 1 |
| 22777 | outfly | 1 |
| 22778 | outfaced | 1 |
| 22779 | outdares | 1 |
| 22780 | outdare | 1 |
| 22781 | outdar | 1 |
| 22782 | outcries | 1 |
| 22783 | outbreak | 1 |
| 22784 | outbraves | 1 |
| 22785 | outbrave | 1 |
| 22786 | outbids | 1 |
| 22787 | ouches | 1 |
| 22788 | otherwhiles | 1 |
| 22789 | othergates | 1 |
| 22790 | ostlers | 1 |
| 22791 | ostents | 1 |
| 22792 | ostentare | 1 |
| 22793 | ost | 1 |
| 22794 | osprey | 1 |
| 22795 | osier | 1 |
| 22796 | oscorbidulchos | 1 |
| 22797 | orts | 1 |
| 22798 | orsini | 1 |
| 22799 | orodes | 1 |
| 22800 | ormsby | 1 |
| 22801 | orifex | 1 |
| 22802 | orianas | 1 |
| 22803 | orgillous | 1 |
| 22804 | organising | 1 |
| 22805 | orestes | 1 |
| 22806 | orelia | 1 |
| 22807 | ordure | 1 |
| 22808 | ords | 1 |
| 22809 | ordonez | 1 |
| 22810 | ordinaries | 1 |
| 22811 | ordinant | 1 |
| 22812 | orderless | 1 |
| 22813 | ordaining | 1 |
| 22814 | oratories | 1 |
| 22815 | opulency | 1 |
| 22816 | oppugnancy | 1 |
| 22817 | opprobriously | 1 |
| 22818 | opprest | 1 |
| 22819 | oppressors | 1 |
| 22820 | oppressively | 1 |
| 22821 | oppresseth | 1 |
| 22822 | oppresses | 1 |
| 22823 | oppositions | 1 |
| 22824 | opposes | 1 |
| 22825 | opposeless | 1 |
| 22826 | opin | 1 |
| 22827 | operative | 1 |
| 22828 | operations | 1 |
| 22829 | openness | 1 |
| 22830 | openings | 1 |
| 22831 | opener | 1 |
| 22832 | oozy | 1 |
| 22833 | oozes | 1 |
| 22834 | oo | 1 |
| 22835 | onwards | 1 |
| 22836 | oneyers | 1 |
| 22837 | onerous | 1 |
| 22838 | omnis | 1 |
| 22839 | omittance | 1 |
| 22840 | omecils | 1 |
| 22841 | omans | 1 |
| 22842 | olivers | 1 |
| 22843 | olivera | 1 |
| 22844 | olivantes | 1 |
| 22845 | olivante | 1 |
| 22846 | oliva | 1 |
| 22847 | oldness | 1 |
| 22848 | olden | 1 |
| 22849 | oldcastle | 1 |
| 22850 | ointments | 1 |
| 22851 | oils | 1 |
| 22852 | ohs | 1 |
| 22853 | officed | 1 |
| 22854 | offert | 1 |
| 22855 | offenses | 1 |
| 22856 | offenseless | 1 |
| 22857 | offendress | 1 |
| 22858 | offendeth | 1 |
| 22859 | offendendo | 1 |
| 22860 | offenceful | 1 |
| 22861 | oeuvres | 1 |
| 22862 | oes | 1 |
| 22863 | oeillades | 1 |
| 22864 | odes | 1 |
| 22865 | ode | 1 |
| 22866 | ocular | 1 |
| 22867 | october | 1 |
| 22868 | octavianus | 1 |
| 22869 | octave | 1 |
| 22870 | occurrents | 1 |
| 22871 | occupying | 1 |
| 22872 | occupat | 1 |
| 22873 | occupant | 1 |
| 22874 | occulted | 1 |
| 22875 | occult | 1 |
| 22876 | occiput | 1 |
| 22877 | occidit | 1 |
| 22878 | occidental | 1 |
| 22879 | occasionally | 1 |
| 22880 | obtuse | 1 |
| 22881 | obstruct | 1 |
| 22882 | obstinately | 1 |
| 22883 | obsque | 1 |
| 22884 | observingly | 1 |
| 22885 | observers | 1 |
| 22886 | observants | 1 |
| 22887 | observancy | 1 |
| 22888 | obsequiously | 1 |
| 22889 | obscures | 1 |
| 22890 | obscurely | 1 |
| 22891 | obliquely | 1 |
| 22892 | obliging | 1 |
| 22893 | obliges | 1 |
| 22894 | oblations | 1 |
| 22895 | oblation | 1 |
| 22896 | objectionable | 1 |
| 22897 | obidicut | 1 |
| 22898 | obeisances | 1 |
| 22899 | ob | 1 |
| 22900 | oathable | 1 |
| 22901 | oaten | 1 |
| 22902 | oatcake | 1 |
| 22903 | nuzas | 1 |
| 22904 | nutriment | 1 |
| 22905 | nutmegs | 1 |
| 22906 | nuthook | 1 |
| 22907 | nurtur | 1 |
| 22908 | nursh | 1 |
| 22909 | nurseth | 1 |
| 22910 | nurses | 1 |
| 22911 | nurser | 1 |
| 22912 | nuntius | 1 |
| 22913 | numidians | 1 |
| 22914 | numerus | 1 |
| 22915 | numerabis | 1 |
| 22916 | numbness | 1 |
| 22917 | numbering | 1 |
| 22918 | numantia | 1 |
| 22919 | numa | 1 |
| 22920 | num | 1 |
| 22921 | nulla | 1 |
| 22922 | nuisance | 1 |
| 22923 | nubila | 1 |
| 22924 | nubibus | 1 |
| 22925 | nt | 1 |
| 22926 | noyance | 1 |
| 22927 | noxious | 1 |
| 22928 | nowise | 1 |
| 22929 | novum | 1 |
| 22930 | novitiate | 1 |
| 22931 | novi | 1 |
| 22932 | noverbs | 1 |
| 22933 | nourishes | 1 |
| 22934 | nourisher | 1 |
| 22935 | noun | 1 |
| 22936 | noteworthy | 1 |
| 22937 | notest | 1 |
| 22938 | notedly | 1 |
| 22939 | notebooks | 1 |
| 22940 | notebook | 1 |
| 22941 | notch | 1 |
| 22942 | notably | 1 |
| 22943 | nosy | 1 |
| 22944 | nostra | 1 |
| 22945 | noster | 1 |
| 22946 | nos | 1 |
| 22947 | norwegian | 1 |
| 22948 | norways | 1 |
| 22949 | northumberlands | 1 |
| 22950 | northerly | 1 |
| 22951 | northamptonshire | 1 |
| 22952 | noriz | 1 |
| 22953 | norbery | 1 |
| 22954 | nooks | 1 |
| 22955 | noodle | 1 |
| 22956 | nonsuits | 1 |
| 22957 | nonsensical | 1 |
| 22958 | nonage | 1 |
| 22959 | nona | 1 |
| 22960 | nomenclature | 1 |
| 22961 | nole | 1 |
| 22962 | noisemaker | 1 |
| 22963 | nogales | 1 |
| 22964 | noes | 1 |
| 22965 | noddles | 1 |
| 22966 | noddle | 1 |
| 22967 | noddies | 1 |
| 22968 | noces | 1 |
| 22969 | noblesse | 1 |
| 22970 | nnights | 1 |
| 22971 | nly | 1 |
| 22972 | nizarani | 1 |
| 22973 | nisus | 1 |
| 22974 | nipp | 1 |
| 22975 | niobes | 1 |
| 22976 | niobe | 1 |
| 22977 | ningly | 1 |
| 22978 | nines | 1 |
| 22979 | nimrod | 1 |
| 22980 | nil | 1 |
| 22981 | nihil | 1 |
| 22982 | nightcaps | 1 |
| 22983 | nightcap | 1 |
| 22984 | niggarding | 1 |
| 22985 | niculoso | 1 |
| 22986 | nicolao | 1 |
| 22987 | nicks | 1 |
| 22988 | nicer | 1 |
| 22989 | niceness | 1 |
| 22990 | niarros | 1 |
| 22991 | newts | 1 |
| 22992 | newsmongers | 1 |
| 22993 | newgate | 1 |
| 22994 | newborn | 1 |
| 22995 | neuter | 1 |
| 22996 | network | 1 |
| 22997 | netherlands | 1 |
| 22998 | nervy | 1 |
| 22999 | nervous | 1 |
| 23000 | nervii | 1 |
| 23001 | nerved | 1 |
| 23002 | ners | 1 |
| 23003 | neroes | 1 |
| 23004 | nereides | 1 |
| 23005 | nerbia | 1 |
| 23006 | neoptolemus | 1 |
| 23007 | nemoroso | 1 |
| 23008 | nemesis | 1 |
| 23009 | neighings | 1 |
| 23010 | neighbors | 1 |
| 23011 | neigbbour | 1 |
| 23012 | negro | 1 |
| 23013 | negotiator | 1 |
| 23014 | neglectingly | 1 |
| 23015 | negatives | 1 |
| 23016 | negative | 1 |
| 23017 | negation | 1 |
| 23018 | nefas | 1 |
| 23019 | neeze | 1 |
| 23020 | needly | 1 |
| 23021 | needlework | 1 |
| 23022 | needlewoman | 1 |
| 23023 | needfull | 1 |
| 23024 | needer | 1 |
| 23025 | necked | 1 |
| 23026 | necessitied | 1 |
| 23027 | nec | 1 |
| 23028 | nebuchadnezzar | 1 |
| 23029 | nebour | 1 |
| 23030 | neb | 1 |
| 23031 | neath | 1 |
| 23032 | neapolitans | 1 |
| 23033 | neanmoins | 1 |
| 23034 | neamnoins | 1 |
| 23035 | nazarite | 1 |
| 23036 | nayword | 1 |
| 23037 | nayward | 1 |
| 23038 | navigation | 1 |
| 23039 | navel | 1 |
| 23040 | naval | 1 |
| 23041 | nauseous | 1 |
| 23042 | naughtily | 1 |
| 23043 | natus | 1 |
| 23044 | naturalize | 1 |
| 23045 | natives | 1 |
| 23046 | natifs | 1 |
| 23047 | nastiness | 1 |
| 23048 | narrowness | 1 |
| 23049 | narrower | 1 |
| 23050 | narration | 1 |
| 23051 | narrated | 1 |
| 23052 | narines | 1 |
| 23053 | narcissus | 1 |
| 23054 | naps | 1 |
| 23055 | napless | 1 |
| 23056 | napes | 1 |
| 23057 | namest | 1 |
| 23058 | nal | 1 |
| 23059 | nak | 1 |
| 23060 | nailed | 1 |
| 23061 | naiads | 1 |
| 23062 | nags | 1 |
| 23063 | nagging | 1 |
| 23064 | nage | 1 |
| 23065 | mystic | 1 |
| 23066 | myst | 1 |
| 23067 | mynheers | 1 |
| 23068 | muzzled | 1 |
| 23069 | muzzl | 1 |
| 23070 | muzaraque | 1 |
| 23071 | mutualities | 1 |
| 23072 | mutines | 1 |
| 23073 | mutineers | 1 |
| 23074 | mutineer | 1 |
| 23075 | mutine | 1 |
| 23076 | mutilated | 1 |
| 23077 | mutest | 1 |
| 23078 | mutations | 1 |
| 23079 | mutation | 1 |
| 23080 | mutatio | 1 |
| 23081 | mutable | 1 |
| 23082 | mustering | 1 |
| 23083 | mussels | 1 |
| 23084 | muss | 1 |
| 23085 | muskos | 1 |
| 23086 | musketoon | 1 |
| 23087 | musketeers | 1 |
| 23088 | musings | 1 |
| 23089 | musically | 1 |
| 23090 | mushrooms | 1 |
| 23091 | mush | 1 |
| 23092 | muscovy | 1 |
| 23093 | muscovits | 1 |
| 23094 | muscles | 1 |
| 23095 | muscadel | 1 |
| 23096 | murthering | 1 |
| 23097 | murrion | 1 |
| 23098 | murray | 1 |
| 23099 | murmurers | 1 |
| 23100 | murkiest | 1 |
| 23101 | murk | 1 |
| 23102 | mure | 1 |
| 23103 | murderously | 1 |
| 23104 | munitions | 1 |
| 23105 | muniments | 1 |
| 23106 | muniment | 1 |
| 23107 | munch | 1 |
| 23108 | munaton | 1 |
| 23109 | mun | 1 |
| 23110 | mummied | 1 |
| 23111 | mummer | 1 |
| 23112 | mumble | 1 |
| 23113 | multos | 1 |
| 23114 | multipotent | 1 |
| 23115 | multiply | 1 |
| 23116 | mull | 1 |
| 23117 | muliteus | 1 |
| 23118 | mulieres | 1 |
| 23119 | mulct | 1 |
| 23120 | mulberries | 1 |
| 23121 | mugs | 1 |
| 23122 | mugger | 1 |
| 23123 | muffl | 1 |
| 23124 | muffins | 1 |
| 23125 | muddled | 1 |
| 23126 | muddle | 1 |
| 23127 | muck | 1 |
| 23128 | moyses | 1 |
| 23129 | mower | 1 |
| 23130 | movousus | 1 |
| 23131 | movingly | 1 |
| 23132 | moveth | 1 |
| 23133 | mover | 1 |
| 23134 | moustached | 1 |
| 23135 | mousetrap | 1 |
| 23136 | mous | 1 |
| 23137 | mournings | 1 |
| 23138 | mourningly | 1 |
| 23139 | mournfully | 1 |
| 23140 | mounteth | 1 |
| 23141 | mountanto | 1 |
| 23142 | mountant | 1 |
| 23143 | mounseur | 1 |
| 23144 | moulten | 1 |
| 23145 | moult | 1 |
| 23146 | moulds | 1 |
| 23147 | mouldeth | 1 |
| 23148 | mouldering | 1 |
| 23149 | mought | 1 |
| 23150 | moths | 1 |
| 23151 | motherless | 1 |
| 23152 | motes | 1 |
| 23153 | mossgrown | 1 |
| 23154 | mosques | 1 |
| 23155 | mose | 1 |
| 23156 | mortise | 1 |
| 23157 | mortis | 1 |
| 23158 | mortimers | 1 |
| 23159 | mortify | 1 |
| 23160 | mortification | 1 |
| 23161 | mors | 1 |
| 23162 | moron | 1 |
| 23163 | moriscoes | 1 |
| 23164 | mori | 1 |
| 23165 | mores | 1 |
| 23166 | morally | 1 |
| 23167 | moraler | 1 |
| 23168 | mopping | 1 |
| 23169 | moping | 1 |
| 23170 | mop | 1 |
| 23171 | moorship | 1 |
| 23172 | moorings | 1 |
| 23173 | moorfields | 1 |
| 23174 | moonshines | 1 |
| 23175 | moonish | 1 |
| 23176 | moonbeams | 1 |
| 23177 | moodily | 1 |
| 23178 | montserrate | 1 |
| 23179 | montferrat | 1 |
| 23180 | montez | 1 |
| 23181 | montant | 1 |
| 23182 | montage | 1 |
| 23183 | montacute | 1 |
| 23184 | monstruosity | 1 |
| 23185 | monstrousness | 1 |
| 23186 | monstrously | 1 |
| 23187 | monsieurs | 1 |
| 23188 | mons | 1 |
| 23189 | monotonous | 1 |
| 23190 | monopoly | 1 |
| 23191 | monjui | 1 |
| 23192 | monicongo | 1 |
| 23193 | mongrels | 1 |
| 23194 | monging | 1 |
| 23195 | moneybox | 1 |
| 23196 | mondonedo | 1 |
| 23197 | moncadas | 1 |
| 23198 | monastic | 1 |
| 23199 | monast | 1 |
| 23200 | monarcho | 1 |
| 23201 | monarchize | 1 |
| 23202 | moming | 1 |
| 23203 | mome | 1 |
| 23204 | molto | 1 |
| 23205 | mollification | 1 |
| 23206 | molests | 1 |
| 23207 | molestation | 1 |
| 23208 | moldwarp | 1 |
| 23209 | mohammed | 1 |
| 23210 | modon | 1 |
| 23211 | modicums | 1 |
| 23212 | moderns | 1 |
| 23213 | modena | 1 |
| 23214 | models | 1 |
| 23215 | mockvater | 1 |
| 23216 | mockingly | 1 |
| 23217 | mocked | 1 |
| 23218 | mockable | 1 |
| 23219 | moanings | 1 |
| 23220 | mixtures | 1 |
| 23221 | mixes | 1 |
| 23222 | mitres | 1 |
| 23223 | mithridates | 1 |
| 23224 | mites | 1 |
| 23225 | misventures | 1 |
| 23226 | misuses | 1 |
| 23227 | misused | 1 |
| 23228 | mistrusting | 1 |
| 23229 | mistrustful | 1 |
| 23230 | mistriship | 1 |
| 23231 | mistresss | 1 |
| 23232 | mistreadings | 1 |
| 23233 | mistletoe | 1 |
| 23234 | misthought | 1 |
| 23235 | misthink | 1 |
| 23236 | mistful | 1 |
| 23237 | misterm | 1 |
| 23238 | mistempered | 1 |
| 23239 | mistemp | 1 |
| 23240 | mistakings | 1 |
| 23241 | mistaketh | 1 |
| 23242 | misspoke | 1 |
| 23243 | missives | 1 |
| 23244 | missive | 1 |
| 23245 | missions | 1 |
| 23246 | missingly | 1 |
| 23247 | missheathed | 1 |
| 23248 | misshap | 1 |
| 23249 | misses | 1 |
| 23250 | misreport | 1 |
| 23251 | misquote | 1 |
| 23252 | misproud | 1 |
| 23253 | mispris | 1 |
| 23254 | misplaces | 1 |
| 23255 | misord | 1 |
| 23256 | misleading | 1 |
| 23257 | misleaders | 1 |
| 23258 | misinterpret | 1 |
| 23259 | misheard | 1 |
| 23260 | misguided | 1 |
| 23261 | misguide | 1 |
| 23262 | misgraffed | 1 |
| 23263 | misgovernment | 1 |
| 23264 | misgoverned | 1 |
| 23265 | misgivings | 1 |
| 23266 | misgive | 1 |
| 23267 | miserly | 1 |
| 23268 | misericorde | 1 |
| 23269 | misdoubteth | 1 |
| 23270 | misdemeanours | 1 |
| 23271 | misdemeanour | 1 |
| 23272 | misdemean | 1 |
| 23273 | miscreate | 1 |
| 23274 | misconstrues | 1 |
| 23275 | misconstruction | 1 |
| 23276 | misconst | 1 |
| 23277 | misconduct | 1 |
| 23278 | misconceived | 1 |
| 23279 | miscarrying | 1 |
| 23280 | miscarries | 1 |
| 23281 | miscalled | 1 |
| 23282 | misbhav | 1 |
| 23283 | misbelieving | 1 |
| 23284 | misbeliever | 1 |
| 23285 | misbehaviour | 1 |
| 23286 | misbegot | 1 |
| 23287 | misbecome | 1 |
| 23288 | misbecom | 1 |
| 23289 | misbecame | 1 |
| 23290 | misapplied | 1 |
| 23291 | misanthropos | 1 |
| 23292 | misadventur | 1 |
| 23293 | mis | 1 |
| 23294 | mirthful | 1 |
| 23295 | miraguarda | 1 |
| 23296 | miraflores | 1 |
| 23297 | mirable | 1 |
| 23298 | mir | 1 |
| 23299 | mio | 1 |
| 23300 | minuteness | 1 |
| 23301 | mints | 1 |
| 23302 | minotaurs | 1 |
| 23303 | minnows | 1 |
| 23304 | minnow | 1 |
| 23305 | ministration | 1 |
| 23306 | mining | 1 |
| 23307 | minimus | 1 |
| 23308 | minimo | 1 |
| 23309 | minime | 1 |
| 23310 | minim | 1 |
| 23311 | minikin | 1 |
| 23312 | minguilla | 1 |
| 23313 | mingles | 1 |
| 23314 | minerals | 1 |
| 23315 | mined | 1 |
| 23316 | minces | 1 |
| 23317 | minc | 1 |
| 23318 | mimic | 1 |
| 23319 | milo | 1 |
| 23320 | millioned | 1 |
| 23321 | mille | 1 |
| 23322 | militarist | 1 |
| 23323 | milesian | 1 |
| 23324 | mildews | 1 |
| 23325 | miglior | 1 |
| 23326 | mightful | 1 |
| 23327 | mienne | 1 |
| 23328 | midwives | 1 |
| 23329 | midstream | 1 |
| 23330 | midriff | 1 |
| 23331 | middling | 1 |
| 23332 | middleham | 1 |
| 23333 | middest | 1 |
| 23334 | midas | 1 |
| 23335 | microcosm | 1 |
| 23336 | micocolembo | 1 |
| 23337 | miching | 1 |
| 23338 | micher | 1 |
| 23339 | micer | 1 |
| 23340 | miaulina | 1 |
| 23341 | miau | 1 |
| 23342 | mezquino | 1 |
| 23343 | mexican | 1 |
| 23344 | mewling | 1 |
| 23345 | meus | 1 |
| 23346 | mettlesome | 1 |
| 23347 | mette | 1 |
| 23348 | metropolis | 1 |
| 23349 | metres | 1 |
| 23350 | methink | 1 |
| 23351 | metheglins | 1 |
| 23352 | metheglin | 1 |
| 23353 | meteyard | 1 |
| 23354 | meted | 1 |
| 23355 | metaphysics | 1 |
| 23356 | metaphors | 1 |
| 23357 | metamorphosis | 1 |
| 23358 | mesopotamia | 1 |
| 23359 | meshes | 1 |
| 23360 | mes | 1 |
| 23361 | mervailous | 1 |
| 23362 | merrymaking | 1 |
| 23363 | merriness | 1 |
| 23364 | merriments | 1 |
| 23365 | merriman | 1 |
| 23366 | merops | 1 |
| 23367 | mermaids | 1 |
| 23368 | merlo | 1 |
| 23369 | meridian | 1 |
| 23370 | merest | 1 |
| 23371 | mered | 1 |
| 23372 | mercuries | 1 |
| 23373 | mercurial | 1 |
| 23374 | mercifully | 1 |
| 23375 | merchandized | 1 |
| 23376 | mercenaries | 1 |
| 23377 | mercatio | 1 |
| 23378 | mercatante | 1 |
| 23379 | mephostophilus | 1 |
| 23380 | meotides | 1 |
| 23381 | meona | 1 |
| 23382 | mentis | 1 |
| 23383 | mentironiana | 1 |
| 23384 | mentions | 1 |
| 23385 | meneses | 1 |
| 23386 | mendozas | 1 |
| 23387 | mendoza | 1 |
| 23388 | mencia | 1 |
| 23389 | menaphon | 1 |
| 23390 | menaced | 1 |
| 23391 | memphis | 1 |
| 23392 | memorize | 1 |
| 23393 | memoriz | 1 |
| 23394 | memorials | 1 |
| 23395 | memorandums | 1 |
| 23396 | melons | 1 |
| 23397 | melon | 1 |
| 23398 | mellowing | 1 |
| 23399 | melisandra | 1 |
| 23400 | melford | 1 |
| 23401 | melancholies | 1 |
| 23402 | meisen | 1 |
| 23403 | meilleur | 1 |
| 23404 | mehercle | 1 |
| 23405 | meetness | 1 |
| 23406 | meetly | 1 |
| 23407 | meeds | 1 |
| 23408 | medusa | 1 |
| 23409 | mediterraneum | 1 |
| 23410 | meditates | 1 |
| 23411 | meditated | 1 |
| 23412 | medina | 1 |
| 23413 | medice | 1 |
| 23414 | mediators | 1 |
| 23415 | mede | 1 |
| 23416 | medal | 1 |
| 23417 | mechante | 1 |
| 23418 | mechanism | 1 |
| 23419 | mechanics | 1 |
| 23420 | mechanicals | 1 |
| 23421 | mecca | 1 |
| 23422 | measurements | 1 |
| 23423 | measurable | 1 |
| 23424 | measles | 1 |
| 23425 | meanness | 1 |
| 23426 | meaneth | 1 |
| 23427 | meanders | 1 |
| 23428 | meacock | 1 |
| 23429 | mazorca | 1 |
| 23430 | mazes | 1 |
| 23431 | mazed | 1 |
| 23432 | maypole | 1 |
| 23433 | mayday | 1 |
| 23434 | mauvais | 1 |
| 23435 | mausolus | 1 |
| 23436 | mauritania | 1 |
| 23437 | mauri | 1 |
| 23438 | maundering | 1 |
| 23439 | maund | 1 |
| 23440 | mauling | 1 |
| 23441 | mauleon | 1 |
| 23442 | mauled | 1 |
| 23443 | maudlin | 1 |
| 23444 | maud | 1 |
| 23445 | mattresses | 1 |
| 23446 | matteo | 1 |
| 23447 | matted | 1 |
| 23448 | matrimonial | 1 |
| 23449 | matin | 1 |
| 23450 | matchmaking | 1 |
| 23451 | matcheth | 1 |
| 23452 | mastic | 1 |
| 23453 | masterpiece | 1 |
| 23454 | masterest | 1 |
| 23455 | masterdom | 1 |
| 23456 | mastcr | 1 |
| 23457 | massive | 1 |
| 23458 | massilian | 1 |
| 23459 | masquerading | 1 |
| 23460 | masons | 1 |
| 23461 | masking | 1 |
| 23462 | masker | 1 |
| 23463 | mash | 1 |
| 23464 | martyrs | 1 |
| 23465 | martyrdom | 1 |
| 23466 | marts | 1 |
| 23467 | martos | 1 |
| 23468 | martlemas | 1 |
| 23469 | martinmas | 1 |
| 23470 | martinez | 1 |
| 23471 | martha | 1 |
| 23472 | marten | 1 |
| 23473 | martem | 1 |
| 23474 | marted | 1 |
| 23475 | marshalship | 1 |
| 23476 | marshalsea | 1 |
| 23477 | marshalled | 1 |
| 23478 | marsh | 1 |
| 23479 | marrowless | 1 |
| 23480 | marred | 1 |
| 23481 | marquises | 1 |
| 23482 | marmoset | 1 |
| 23483 | marle | 1 |
| 23484 | marl | 1 |
| 23485 | markman | 1 |
| 23486 | marius | 1 |
| 23487 | maritime | 1 |
| 23488 | marines | 1 |
| 23489 | margins | 1 |
| 23490 | marge | 1 |
| 23491 | marco | 1 |
| 23492 | marcians | 1 |
| 23493 | marchpane | 1 |
| 23494 | marchionesses | 1 |
| 23495 | marbled | 1 |
| 23496 | maranon | 1 |
| 23497 | manzanares | 1 |
| 23498 | manus | 1 |
| 23499 | manual | 1 |
| 23500 | mantible | 1 |
| 23501 | manslaughter | 1 |
| 23502 | mansionry | 1 |
| 23503 | manriques | 1 |
| 23504 | manoeuvre | 1 |
| 23505 | manningtree | 1 |
| 23506 | manlike | 1 |
| 23507 | manka | 1 |
| 23508 | manjar | 1 |
| 23509 | manifoldly | 1 |
| 23510 | manifestly | 1 |
| 23511 | manifestations | 1 |
| 23512 | manifestation | 1 |
| 23513 | maniac | 1 |
| 23514 | mangy | 1 |
| 23515 | mangling | 1 |
| 23516 | mangles | 1 |
| 23517 | manet | 1 |
| 23518 | mandrakes | 1 |
| 23519 | manchus | 1 |
| 23520 | manchissima | 1 |
| 23521 | manchegans | 1 |
| 23522 | manakin | 1 |
| 23523 | management | 1 |
| 23524 | mammock | 1 |
| 23525 | mammets | 1 |
| 23526 | mammet | 1 |
| 23527 | mammering | 1 |
| 23528 | mameluke | 1 |
| 23529 | mambrine | 1 |
| 23530 | maltworms | 1 |
| 23531 | maltreating | 1 |
| 23532 | maltese | 1 |
| 23533 | malo | 1 |
| 23534 | mallows | 1 |
| 23535 | mallets | 1 |
| 23536 | mallet | 1 |
| 23537 | mallard | 1 |
| 23538 | malkin | 1 |
| 23539 | malindrania | 1 |
| 23540 | malignity | 1 |
| 23541 | malignantly | 1 |
| 23542 | malignancy | 1 |
| 23543 | malhecho | 1 |
| 23544 | malfeasance | 1 |
| 23545 | malefactions | 1 |
| 23546 | maldonado | 1 |
| 23547 | malandrino | 1 |
| 23548 | malaguero | 1 |
| 23549 | malae | 1 |
| 23550 | mal | 1 |
| 23551 | makings | 1 |
| 23552 | makeless | 1 |
| 23553 | majimasa | 1 |
| 23554 | majestically | 1 |
| 23555 | majestas | 1 |
| 23556 | majalahonda | 1 |
| 23557 | maison | 1 |
| 23558 | mais | 1 |
| 23559 | mainstay | 1 |
| 23560 | mains | 1 |
| 23561 | mainmast | 1 |
| 23562 | maincourse | 1 |
| 23563 | maims | 1 |
| 23564 | maiming | 1 |
| 23565 | mails | 1 |
| 23566 | mailed | 1 |
| 23567 | maidenliest | 1 |
| 23568 | maidenhoods | 1 |
| 23569 | mahometan | 1 |
| 23570 | magnus | 1 |
| 23571 | magnum | 1 |
| 23572 | magnified | 1 |
| 23573 | magnifico | 1 |
| 23574 | magnificently | 1 |
| 23575 | magnifi | 1 |
| 23576 | magni | 1 |
| 23577 | magnates | 1 |
| 23578 | magistracy | 1 |
| 23579 | magisterial | 1 |
| 23580 | magis | 1 |
| 23581 | magdalena | 1 |
| 23582 | magallanes | 1 |
| 23583 | madrigal | 1 |
| 23584 | madnesses | 1 |
| 23585 | madeira | 1 |
| 23586 | madasimas | 1 |
| 23587 | maculation | 1 |
| 23588 | maculate | 1 |
| 23589 | mack | 1 |
| 23590 | machination | 1 |
| 23591 | maces | 1 |
| 23592 | macdonwald | 1 |
| 23593 | maccabees | 1 |
| 23594 | macange | 1 |
| 23595 | lysippus | 1 |
| 23596 | lyric | 1 |
| 23597 | lynxes | 1 |
| 23598 | lynn | 1 |
| 23599 | lym | 1 |
| 23600 | lyen | 1 |
| 23601 | lycurguses | 1 |
| 23602 | lycaonia | 1 |
| 23603 | luxuriously | 1 |
| 23604 | luxuriant | 1 |
| 23605 | lutheran | 1 |
| 23606 | lutestring | 1 |
| 23607 | lustig | 1 |
| 23608 | luster | 1 |
| 23609 | lusted | 1 |
| 23610 | lusitanian | 1 |
| 23611 | lusitania | 1 |
| 23612 | lush | 1 |
| 23613 | lurketh | 1 |
| 23614 | lures | 1 |
| 23615 | lurchers | 1 |
| 23616 | luncheon | 1 |
| 23617 | lunched | 1 |
| 23618 | lunas | 1 |
| 23619 | lumps | 1 |
| 23620 | lumpish | 1 |
| 23621 | luminary | 1 |
| 23622 | luminaries | 1 |
| 23623 | lumbert | 1 |
| 23624 | lukewarmly | 1 |
| 23625 | luigi | 1 |
| 23626 | luffing | 1 |
| 23627 | ludovico | 1 |
| 23628 | lucullius | 1 |
| 23629 | lucrando | 1 |
| 23630 | luckiest | 1 |
| 23631 | luckier | 1 |
| 23632 | lucinda | 1 |
| 23633 | lucina | 1 |
| 23634 | lucifier | 1 |
| 23635 | lucidity | 1 |
| 23636 | lucem | 1 |
| 23637 | luccicos | 1 |
| 23638 | luc | 1 |
| 23639 | lubberly | 1 |
| 23640 | lozel | 1 |
| 23641 | loyalties | 1 |
| 23642 | lown | 1 |
| 23643 | lowers | 1 |
| 23644 | lowe | 1 |
| 23645 | lovered | 1 |
| 23646 | lovemakings | 1 |
| 23647 | lovemaking | 1 |
| 23648 | lovelorn | 1 |
| 23649 | loveletter | 1 |
| 23650 | louts | 1 |
| 23651 | loutish | 1 |
| 23652 | louted | 1 |
| 23653 | lousier | 1 |
| 23654 | louses | 1 |
| 23655 | loureth | 1 |
| 23656 | loudest | 1 |
| 23657 | lorship | 1 |
| 23658 | lorn | 1 |
| 23659 | lordlings | 1 |
| 23660 | lordliness | 1 |
| 23661 | lording | 1 |
| 23662 | lorded | 1 |
| 23663 | loquitur | 1 |
| 23664 | loosing | 1 |
| 23665 | loosening | 1 |
| 23666 | looseness | 1 |
| 23667 | loosener | 1 |
| 23668 | loosen | 1 |
| 23669 | loopholes | 1 |
| 23670 | loophole | 1 |
| 23671 | looped | 1 |
| 23672 | loon | 1 |
| 23673 | lookout | 1 |
| 23674 | lookest | 1 |
| 23675 | loof | 1 |
| 23676 | longtail | 1 |
| 23677 | longly | 1 |
| 23678 | longboat | 1 |
| 23679 | londoners | 1 |
| 23680 | lolls | 1 |
| 23681 | loitering | 1 |
| 23682 | loiterers | 1 |
| 23683 | loiterer | 1 |
| 23684 | loitered | 1 |
| 23685 | loiter | 1 |
| 23686 | logiquous | 1 |
| 23687 | loggets | 1 |
| 23688 | logger | 1 |
| 23689 | lofraso | 1 |
| 23690 | lode | 1 |
| 23691 | locusts | 1 |
| 23692 | lockram | 1 |
| 23693 | lochaber | 1 |
| 23694 | lobo | 1 |
| 23695 | lobbies | 1 |
| 23696 | loathsomest | 1 |
| 23697 | loathsomeness | 1 |
| 23698 | loather | 1 |
| 23699 | loading | 1 |
| 23700 | loach | 1 |
| 23701 | loa | 1 |
| 23702 | lnd | 1 |
| 23703 | lladres | 1 |
| 23704 | livings | 1 |
| 23705 | liveliness | 1 |
| 23706 | livelier | 1 |
| 23707 | littlest | 1 |
| 23708 | littles | 1 |
| 23709 | littleness | 1 |
| 23710 | litters | 1 |
| 23711 | lither | 1 |
| 23712 | literatured | 1 |
| 23713 | literally | 1 |
| 23714 | lisuarte | 1 |
| 23715 | listener | 1 |
| 23716 | lirra | 1 |
| 23717 | liquorish | 1 |
| 23718 | lipsbury | 1 |
| 23719 | linta | 1 |
| 23720 | linsey | 1 |
| 23721 | lingered | 1 |
| 23722 | lingare | 1 |
| 23723 | linens | 1 |
| 23724 | lineally | 1 |
| 23725 | lincolnshire | 1 |
| 23726 | limned | 1 |
| 23727 | limn | 1 |
| 23728 | limitations | 1 |
| 23729 | limekilns | 1 |
| 23730 | limehouse | 1 |
| 23731 | limber | 1 |
| 23732 | limbecks | 1 |
| 23733 | limbeck | 1 |
| 23734 | limander | 1 |
| 23735 | likened | 1 |
| 23736 | likeliest | 1 |
| 23737 | liggens | 1 |
| 23738 | lig | 1 |
| 23739 | lifteth | 1 |
| 23740 | lifter | 1 |
| 23741 | lifelings | 1 |
| 23742 | lifelike | 1 |
| 23743 | lifeblood | 1 |
| 23744 | lieutenants | 1 |
| 23745 | lien | 1 |
| 23746 | licks | 1 |
| 23747 | licker | 1 |
| 23748 | licens | 1 |
| 23749 | libertines | 1 |
| 23750 | liberte | 1 |
| 23751 | libertas | 1 |
| 23752 | liberator | 1 |
| 23753 | liberating | 1 |
| 23754 | liberated | 1 |
| 23755 | libelling | 1 |
| 23756 | libbard | 1 |
| 23757 | lewdsters | 1 |
| 23758 | leviathans | 1 |
| 23759 | levers | 1 |
| 23760 | levelling | 1 |
| 23761 | leve | 1 |
| 23762 | leur | 1 |
| 23763 | lettuce | 1 |
| 23764 | lettered | 1 |
| 23765 | lett | 1 |
| 23766 | lethargies | 1 |
| 23767 | lethargied | 1 |
| 23768 | lessoned | 1 |
| 23769 | lessened | 1 |
| 23770 | lese | 1 |
| 23771 | lers | 1 |
| 23772 | lequel | 1 |
| 23773 | leperous | 1 |
| 23774 | leper | 1 |
| 23775 | lepanto | 1 |
| 23776 | leopards | 1 |
| 23777 | leonora | 1 |
| 23778 | leonese | 1 |
| 23779 | leo | 1 |
| 23780 | lentils | 1 |
| 23781 | lemon | 1 |
| 23782 | leigers | 1 |
| 23783 | leiger | 1 |
| 23784 | leicestershire | 1 |
| 23785 | legitimation | 1 |
| 23786 | legislator | 1 |
| 23787 | legible | 1 |
| 23788 | leges | 1 |
| 23789 | legerity | 1 |
| 23790 | legends | 1 |
| 23791 | legend | 1 |
| 23792 | lege | 1 |
| 23793 | legatine | 1 |
| 23794 | leganitos | 1 |
| 23795 | legal | 1 |
| 23796 | legacies | 1 |
| 23797 | leeward | 1 |
| 23798 | leets | 1 |
| 23799 | leet | 1 |
| 23800 | leese | 1 |
| 23801 | leers | 1 |
| 23802 | leeches | 1 |
| 23803 | leech | 1 |
| 23804 | lecon | 1 |
| 23805 | lechers | 1 |
| 23806 | leavings | 1 |
| 23807 | leaver | 1 |
| 23808 | leav | 1 |
| 23809 | learnings | 1 |
| 23810 | lealest | 1 |
| 23811 | leaked | 1 |
| 23812 | leah | 1 |
| 23813 | leaguer | 1 |
| 23814 | leagued | 1 |
| 23815 | leagu | 1 |
| 23816 | leadest | 1 |
| 23817 | lazarus | 1 |
| 23818 | lazarillo | 1 |
| 23819 | lazaril | 1 |
| 23820 | layman | 1 |
| 23821 | layer | 1 |
| 23822 | laxities | 1 |
| 23823 | laxative | 1 |
| 23824 | lawns | 1 |
| 23825 | lawlessness | 1 |
| 23826 | lawlessly | 1 |
| 23827 | lawgiver | 1 |
| 23828 | lavoltas | 1 |
| 23829 | lavolt | 1 |
| 23830 | lavishness | 1 |
| 23831 | lavishly | 1 |
| 23832 | lavished | 1 |
| 23833 | lavina | 1 |
| 23834 | lavee | 1 |
| 23835 | lavapies | 1 |
| 23836 | lavajos | 1 |
| 23837 | lautrec | 1 |
| 23838 | laus | 1 |
| 23839 | laureate | 1 |
| 23840 | laurcalco | 1 |
| 23841 | laundry | 1 |
| 23842 | launched | 1 |
| 23843 | launch | 1 |
| 23844 | launces | 1 |
| 23845 | laughest | 1 |
| 23846 | laudis | 1 |
| 23847 | lauding | 1 |
| 23848 | laudem | 1 |
| 23849 | lauded | 1 |
| 23850 | laudation | 1 |
| 23851 | latten | 1 |
| 23852 | latino | 1 |
| 23853 | lateness | 1 |
| 23854 | latches | 1 |
| 23855 | lashings | 1 |
| 23856 | lashing | 1 |
| 23857 | lashed | 1 |
| 23858 | las | 1 |
| 23859 | larron | 1 |
| 23860 | laredo | 1 |
| 23861 | larding | 1 |
| 23862 | larders | 1 |
| 23863 | lara | 1 |
| 23864 | laquais | 1 |
| 23865 | lapsing | 1 |
| 23866 | lapsed | 1 |
| 23867 | lapland | 1 |
| 23868 | lapidaries | 1 |
| 23869 | lanner | 1 |
| 23870 | lanky | 1 |
| 23871 | lankness | 1 |
| 23872 | languor | 1 |
| 23873 | languishment | 1 |
| 23874 | languished | 1 |
| 23875 | langues | 1 |
| 23876 | languageless | 1 |
| 23877 | langton | 1 |
| 23878 | langage | 1 |
| 23879 | landmen | 1 |
| 23880 | landmarks | 1 |
| 23881 | landless | 1 |
| 23882 | lanch | 1 |
| 23883 | lanceth | 1 |
| 23884 | lancers | 1 |
| 23885 | lanc | 1 |
| 23886 | lampass | 1 |
| 23887 | lamound | 1 |
| 23888 | lammastide | 1 |
| 23889 | laming | 1 |
| 23890 | lamia | 1 |
| 23891 | lames | 1 |
| 23892 | lamentings | 1 |
| 23893 | lambkins | 1 |
| 23894 | lambkin | 1 |
| 23895 | lambert | 1 |
| 23896 | lair | 1 |
| 23897 | laida | 1 |
| 23898 | laguna | 1 |
| 23899 | lagoon | 1 |
| 23900 | lagging | 1 |
| 23901 | ladylove | 1 |
| 23902 | ladybird | 1 |
| 23903 | ladle | 1 |
| 23904 | lade | 1 |
| 23905 | lacqueys | 1 |
| 23906 | lacquered | 1 |
| 23907 | lackeying | 1 |
| 23908 | lackbeard | 1 |
| 23909 | lacies | 1 |
| 23910 | lachrymis | 1 |
| 23911 | laces | 1 |
| 23912 | lacerated | 1 |
| 23913 | lacedemonians | 1 |
| 23914 | labyrinths | 1 |
| 23915 | labras | 1 |
| 23916 | labourest | 1 |
| 23917 | labors | 1 |
| 23918 | labio | 1 |
| 23919 | labienus | 1 |
| 23920 | labell | 1 |
| 23921 | kyrieleison | 1 |
| 23922 | knowings | 1 |
| 23923 | knoweth | 1 |
| 23924 | knobs | 1 |
| 23925 | knitteth | 1 |
| 23926 | knitters | 1 |
| 23927 | knitted | 1 |
| 23928 | knighting | 1 |
| 23929 | knighthoods | 1 |
| 23930 | knickknack | 1 |
| 23931 | kneads | 1 |
| 23932 | kneaded | 1 |
| 23933 | knead | 1 |
| 23934 | knav | 1 |
| 23935 | klll | 1 |
| 23936 | kits | 1 |
| 23937 | kirtles | 1 |
| 23938 | kirtle | 1 |
| 23939 | kinsfolk | 1 |
| 23940 | kins | 1 |
| 23941 | kinred | 1 |
| 23942 | kindreds | 1 |
| 23943 | kindliness | 1 |
| 23944 | kindlier | 1 |
| 23945 | kindless | 1 |
| 23946 | kindles | 1 |
| 23947 | kildare | 1 |
| 23948 | kikely | 1 |
| 23949 | kidneys | 1 |
| 23950 | kicky | 1 |
| 23951 | kickshawses | 1 |
| 23952 | kickshaws | 1 |
| 23953 | kicking | 1 |
| 23954 | kettles | 1 |
| 23955 | kettledrum | 1 |
| 23956 | kestrel | 1 |
| 23957 | kernal | 1 |
| 23958 | kerely | 1 |
| 23959 | kentishmen | 1 |
| 23960 | kentishman | 1 |
| 23961 | keiser | 1 |
| 23962 | kegs | 1 |
| 23963 | keepdown | 1 |
| 23964 | keenness | 1 |
| 23965 | keels | 1 |
| 23966 | kecksies | 1 |
| 23967 | kated | 1 |
| 23968 | kandian | 1 |
| 23969 | kam | 1 |
| 23970 | juxta | 1 |
| 23971 | jutting | 1 |
| 23972 | justs | 1 |
| 23973 | justness | 1 |
| 23974 | justling | 1 |
| 23975 | justles | 1 |
| 23976 | justled | 1 |
| 23977 | justification | 1 |
| 23978 | justifiable | 1 |
| 23979 | justicers | 1 |
| 23980 | justest | 1 |
| 23981 | justeius | 1 |
| 23982 | jurymen | 1 |
| 23983 | jurors | 1 |
| 23984 | juror | 1 |
| 23985 | jurists | 1 |
| 23986 | jurisdictions | 1 |
| 23987 | jurement | 1 |
| 23988 | jure | 1 |
| 23989 | jur | 1 |
| 23990 | junkets | 1 |
| 23991 | junior | 1 |
| 23992 | junes | 1 |
| 23993 | juncture | 1 |
| 23994 | jumpeth | 1 |
| 23995 | jumbled | 1 |
| 23996 | jumble | 1 |
| 23997 | julys | 1 |
| 23998 | julio | 1 |
| 23999 | julian | 1 |
| 24000 | juiced | 1 |
| 24001 | juguetes | 1 |
| 24002 | jugglery | 1 |
| 24003 | jugglers | 1 |
| 24004 | juggled | 1 |
| 24005 | juggle | 1 |
| 24006 | judiciary | 1 |
| 24007 | judicial | 1 |
| 24008 | judgeships | 1 |
| 24009 | judases | 1 |
| 24010 | jud | 1 |
| 24011 | jubilant | 1 |
| 24012 | juana | 1 |
| 24013 | joyed | 1 |
| 24014 | jowls | 1 |
| 24015 | jovem | 1 |
| 24016 | journeymen | 1 |
| 24017 | journeying | 1 |
| 24018 | journeyed | 1 |
| 24019 | joshua | 1 |
| 24020 | joltheads | 1 |
| 24021 | jolt | 1 |
| 24022 | jointress | 1 |
| 24023 | jointing | 1 |
| 24024 | joineth | 1 |
| 24025 | joinder | 1 |
| 24026 | jogging | 1 |
| 24027 | jockey | 1 |
| 24028 | jingle | 1 |
| 24029 | jilted | 1 |
| 24030 | jills | 1 |
| 24031 | jigging | 1 |
| 24032 | jezebel | 1 |
| 24033 | jewess | 1 |
| 24034 | jets | 1 |
| 24035 | jested | 1 |
| 24036 | jesses | 1 |
| 24037 | jessamine | 1 |
| 24038 | jeshu | 1 |
| 24039 | jeronimy | 1 |
| 24040 | jerks | 1 |
| 24041 | jerking | 1 |
| 24042 | jephtha | 1 |
| 24043 | jennyasses | 1 |
| 24044 | jenny | 1 |
| 24045 | jeering | 1 |
| 24046 | jeered | 1 |
| 24047 | jays | 1 |
| 24048 | jawbone | 1 |
| 24049 | jauregui | 1 |
| 24050 | jaundies | 1 |
| 24051 | jaundice | 1 |
| 24052 | jaunce | 1 |
| 24053 | jason | 1 |
| 24054 | jargon | 1 |
| 24055 | jaramilla | 1 |
| 24056 | japhet | 1 |
| 24057 | janizzaries | 1 |
| 24058 | jangled | 1 |
| 24059 | jamany | 1 |
| 24060 | jakes | 1 |
| 24061 | jackslave | 1 |
| 24062 | jacksauce | 1 |
| 24063 | jackdaws | 1 |
| 24064 | jackass | 1 |
| 24065 | jackanapes | 1 |
| 24066 | jackals | 1 |
| 24067 | jacinth | 1 |
| 24068 | jacet | 1 |
| 24069 | jaca | 1 |
| 24070 | jaboneros | 1 |
| 24071 | ixion | 1 |
| 24072 | itshall | 1 |
| 24073 | ista | 1 |
| 24074 | ist | 1 |
| 24075 | issu | 1 |
| 24076 | isolated | 1 |
| 24077 | islander | 1 |
| 24078 | ise | 1 |
| 24079 | iscariot | 1 |
| 24080 | irritate | 1 |
| 24081 | irritable | 1 |
| 24082 | irretrievable | 1 |
| 24083 | irresolute | 1 |
| 24084 | irrepressible | 1 |
| 24085 | irremovable | 1 |
| 24086 | irregulous | 1 |
| 24087 | irrecoverable | 1 |
| 24088 | irreconcil | 1 |
| 24089 | irrationally | 1 |
| 24090 | irishmen | 1 |
| 24091 | irae | 1 |
| 24092 | ira | 1 |
| 24093 | ionian | 1 |
| 24094 | ionia | 1 |
| 24095 | inwardness | 1 |
| 24096 | invoking | 1 |
| 24097 | invitis | 1 |
| 24098 | invised | 1 |
| 24099 | invigorated | 1 |
| 24100 | investing | 1 |
| 24101 | investigator | 1 |
| 24102 | investigation | 1 |
| 24103 | investigated | 1 |
| 24104 | investigate | 1 |
| 24105 | inventors | 1 |
| 24106 | inventoried | 1 |
| 24107 | inventorially | 1 |
| 24108 | inveigled | 1 |
| 24109 | inveighing | 1 |
| 24110 | invectives | 1 |
| 24111 | invectively | 1 |
| 24112 | invasive | 1 |
| 24113 | invasion | 1 |
| 24114 | invariable | 1 |
| 24115 | inurn | 1 |
| 24116 | inure | 1 |
| 24117 | intruding | 1 |
| 24118 | introducing | 1 |
| 24119 | intrinsicate | 1 |
| 24120 | intrinse | 1 |
| 24121 | intrigues | 1 |
| 24122 | intrenchant | 1 |
| 24123 | intrench | 1 |
| 24124 | intreat | 1 |
| 24125 | intreasured | 1 |
| 24126 | intoxicates | 1 |
| 24127 | intituled | 1 |
| 24128 | intitled | 1 |
| 24129 | intimidate | 1 |
| 24130 | intil | 1 |
| 24131 | intestate | 1 |
| 24132 | interwoven | 1 |
| 24133 | intervention | 1 |
| 24134 | intervallums | 1 |
| 24135 | intertissued | 1 |
| 24136 | interrupts | 1 |
| 24137 | interruptest | 1 |
| 24138 | interrupter | 1 |
| 24139 | interrogations | 1 |
| 24140 | interposes | 1 |
| 24141 | interposer | 1 |
| 24142 | intermixed | 1 |
| 24143 | intermix | 1 |
| 24144 | intermit | 1 |
| 24145 | intermissive | 1 |
| 24146 | interlacing | 1 |
| 24147 | interjoin | 1 |
| 24148 | interjections | 1 |
| 24149 | interims | 1 |
| 24150 | interfering | 1 |
| 24151 | interferes | 1 |
| 24152 | interferences | 1 |
| 24153 | interference | 1 |
| 24154 | interfered | 1 |
| 24155 | interdiction | 1 |
| 24156 | interdict | 1 |
| 24157 | interchangement | 1 |
| 24158 | interchang | 1 |
| 24159 | interchained | 1 |
| 24160 | intercessory | 1 |
| 24161 | intercessors | 1 |
| 24162 | intercessor | 1 |
| 24163 | intercepts | 1 |
| 24164 | interception | 1 |
| 24165 | intercepter | 1 |
| 24166 | intently | 1 |
| 24167 | intentively | 1 |
| 24168 | intentionally | 1 |
| 24169 | intenible | 1 |
| 24170 | intendeth | 1 |
| 24171 | intelligo | 1 |
| 24172 | intelligis | 1 |
| 24173 | intelligibly | 1 |
| 24174 | intelligencing | 1 |
| 24175 | integritas | 1 |
| 24176 | integer | 1 |
| 24177 | intact | 1 |
| 24178 | insurrections | 1 |
| 24179 | insuring | 1 |
| 24180 | insure | 1 |
| 24181 | insuppressive | 1 |
| 24182 | insuperable | 1 |
| 24183 | insultment | 1 |
| 24184 | insufficient | 1 |
| 24185 | insufficience | 1 |
| 24186 | insufferable | 1 |
| 24187 | insubstantial | 1 |
| 24188 | instrumental | 1 |
| 24189 | instructive | 1 |
| 24190 | instructing | 1 |
| 24191 | institutions | 1 |
| 24192 | instincts | 1 |
| 24193 | instilleth | 1 |
| 24194 | instil | 1 |
| 24195 | instigator | 1 |
| 24196 | instigations | 1 |
| 24197 | instigate | 1 |
| 24198 | insteeped | 1 |
| 24199 | instate | 1 |
| 24200 | installed | 1 |
| 24201 | instability | 1 |
| 24202 | inspires | 1 |
| 24203 | inspirations | 1 |
| 24204 | inspectors | 1 |
| 24205 | inspector | 1 |
| 24206 | inspect | 1 |
| 24207 | insolences | 1 |
| 24208 | insisture | 1 |
| 24209 | insist | 1 |
| 24210 | insinuateth | 1 |
| 24211 | insinewed | 1 |
| 24212 | insignificant | 1 |
| 24213 | inshipp | 1 |
| 24214 | inshell | 1 |
| 24215 | inset | 1 |
| 24216 | inserts | 1 |
| 24217 | inserting | 1 |
| 24218 | inseparate | 1 |
| 24219 | insensibility | 1 |
| 24220 | insculpture | 1 |
| 24221 | insculp | 1 |
| 24222 | inscroll | 1 |
| 24223 | inscrib | 1 |
| 24224 | insconce | 1 |
| 24225 | insatiable | 1 |
| 24226 | insanity | 1 |
| 24227 | insanie | 1 |
| 24228 | ins | 1 |
| 24229 | inroads | 1 |
| 24230 | inquisitors | 1 |
| 24231 | inquisitiveness | 1 |
| 24232 | inquiries | 1 |
| 24233 | inopportune | 1 |
| 24234 | inoculate | 1 |
| 24235 | innovator | 1 |
| 24236 | innocently | 1 |
| 24237 | inner | 1 |
| 24238 | innamorato | 1 |
| 24239 | inlay | 1 |
| 24240 | inlaid | 1 |
| 24241 | inkstand | 1 |
| 24242 | inkles | 1 |
| 24243 | inkle | 1 |
| 24244 | injurer | 1 |
| 24245 | injointed | 1 |
| 24246 | initiate | 1 |
| 24247 | iniquitous | 1 |
| 24248 | iniquities | 1 |
| 24249 | inimicos | 1 |
| 24250 | inhoop | 1 |
| 24251 | inhibition | 1 |
| 24252 | inheritrix | 1 |
| 24253 | inherent | 1 |
| 24254 | inhearsed | 1 |
| 24255 | inhearse | 1 |
| 24256 | inhabited | 1 |
| 24257 | inhabitable | 1 |
| 24258 | ingulf | 1 |
| 24259 | ingross | 1 |
| 24260 | ingratitudes | 1 |
| 24261 | ingrates | 1 |
| 24262 | ingrated | 1 |
| 24263 | ingraft | 1 |
| 24264 | ingraffed | 1 |
| 24265 | ingots | 1 |
| 24266 | inglorious | 1 |
| 24267 | ingeniously | 1 |
| 24268 | ingener | 1 |
| 24269 | infusing | 1 |
| 24270 | infuses | 1 |
| 24271 | infringed | 1 |
| 24272 | infring | 1 |
| 24273 | informer | 1 |
| 24274 | informations | 1 |
| 24275 | informal | 1 |
| 24276 | inflammation | 1 |
| 24277 | infixing | 1 |
| 24278 | infixed | 1 |
| 24279 | infinitum | 1 |
| 24280 | infinitive | 1 |
| 24281 | infest | 1 |
| 24282 | infers | 1 |
| 24283 | inferring | 1 |
| 24284 | inferreth | 1 |
| 24285 | inferences | 1 |
| 24286 | infectiously | 1 |
| 24287 | infections | 1 |
| 24288 | infecting | 1 |
| 24289 | infantes | 1 |
| 24290 | infante | 1 |
| 24291 | infamonize | 1 |
| 24292 | inexplicable | 1 |
| 24293 | inexorably | 1 |
| 24294 | inexecrable | 1 |
| 24295 | inexcusable | 1 |
| 24296 | inevitably | 1 |
| 24297 | ineffectual | 1 |
| 24298 | industriously | 1 |
| 24299 | indurance | 1 |
| 24300 | indulging | 1 |
| 24301 | indulgent | 1 |
| 24302 | indulgences | 1 |
| 24303 | indues | 1 |
| 24304 | indue | 1 |
| 24305 | inductions | 1 |
| 24306 | inducements | 1 |
| 24307 | indubitate | 1 |
| 24308 | indu | 1 |
| 24309 | indrench | 1 |
| 24310 | indoors | 1 |
| 24311 | indoor | 1 |
| 24312 | indomitable | 1 |
| 24313 | indolent | 1 |
| 24314 | indivisible | 1 |
| 24315 | individable | 1 |
| 24316 | indites | 1 |
| 24317 | indistinguishable | 1 |
| 24318 | indistinguish | 1 |
| 24319 | indissoluble | 1 |
| 24320 | indispos | 1 |
| 24321 | indirections | 1 |
| 24322 | indigne | 1 |
| 24323 | indignations | 1 |
| 24324 | indign | 1 |
| 24325 | indigestions | 1 |
| 24326 | indigested | 1 |
| 24327 | indigent | 1 |
| 24328 | indifference | 1 |
| 24329 | indictments | 1 |
| 24330 | indicted | 1 |
| 24331 | indict | 1 |
| 24332 | indication | 1 |
| 24333 | indicated | 1 |
| 24334 | indexes | 1 |
| 24335 | indented | 1 |
| 24336 | indemnified | 1 |
| 24337 | indelible | 1 |
| 24338 | indecent | 1 |
| 24339 | ind | 1 |
| 24340 | incurs | 1 |
| 24341 | incredulity | 1 |
| 24342 | increases | 1 |
| 24343 | increas | 1 |
| 24344 | incorrigible | 1 |
| 24345 | incorrect | 1 |
| 24346 | incorps | 1 |
| 24347 | inconveniences | 1 |
| 24348 | incontinently | 1 |
| 24349 | incontinence | 1 |
| 24350 | incoherent | 1 |
| 24351 | including | 1 |
| 24352 | inclosed | 1 |
| 24353 | inclips | 1 |
| 24354 | inclines | 1 |
| 24355 | inclinable | 1 |
| 24356 | incivil | 1 |
| 24357 | incites | 1 |
| 24358 | incidentally | 1 |
| 24359 | incidental | 1 |
| 24360 | incidency | 1 |
| 24361 | incharitable | 1 |
| 24362 | incessantly | 1 |
| 24363 | incertainty | 1 |
| 24364 | incentives | 1 |
| 24365 | incentive | 1 |
| 24366 | incensing | 1 |
| 24367 | incenses | 1 |
| 24368 | incensement | 1 |
| 24369 | incarnation | 1 |
| 24370 | incarnadine | 1 |
| 24371 | incardinate | 1 |
| 24372 | incantations | 1 |
| 24373 | inauspicious | 1 |
| 24374 | inaudible | 1 |
| 24375 | inarticulate | 1 |
| 24376 | inaidable | 1 |
| 24377 | inactivity | 1 |
| 24378 | inactive | 1 |
| 24379 | inaction | 1 |
| 24380 | inaccurate | 1 |
| 24381 | impurity | 1 |
| 24382 | impure | 1 |
| 24383 | impulsive | 1 |
| 24384 | impugns | 1 |
| 24385 | impugn | 1 |
| 24386 | impudique | 1 |
| 24387 | impudently | 1 |
| 24388 | impudency | 1 |
| 24389 | imprudences | 1 |
| 24390 | improvised | 1 |
| 24391 | improvidence | 1 |
| 24392 | improves | 1 |
| 24393 | improved | 1 |
| 24394 | improper | 1 |
| 24395 | improbable | 1 |
| 24396 | imprisonments | 1 |
| 24397 | imprisoning | 1 |
| 24398 | imprinted | 1 |
| 24399 | imprint | 1 |
| 24400 | imprimendum | 1 |
| 24401 | imprest | 1 |
| 24402 | impressing | 1 |
| 24403 | impressest | 1 |
| 24404 | imprese | 1 |
| 24405 | impounded | 1 |
| 24406 | impotence | 1 |
| 24407 | imposture | 1 |
| 24408 | impositions | 1 |
| 24409 | importless | 1 |
| 24410 | imported | 1 |
| 24411 | importantly | 1 |
| 24412 | importancy | 1 |
| 24413 | implorators | 1 |
| 24414 | implor | 1 |
| 24415 | implies | 1 |
| 24416 | implied | 1 |
| 24417 | implicit | 1 |
| 24418 | implement | 1 |
| 24419 | implacable | 1 |
| 24420 | impieties | 1 |
| 24421 | impeticos | 1 |
| 24422 | imperturbable | 1 |
| 24423 | impertinency | 1 |
| 24424 | impertinences | 1 |
| 24425 | imperishable | 1 |
| 24426 | imperiously | 1 |
| 24427 | imperil | 1 |
| 24428 | imperfectly | 1 |
| 24429 | imperceiverant | 1 |
| 24430 | imperator | 1 |
| 24431 | impels | 1 |
| 24432 | impel | 1 |
| 24433 | impedes | 1 |
| 24434 | impede | 1 |
| 24435 | impeachments | 1 |
| 24436 | impeached | 1 |
| 24437 | impasted | 1 |
| 24438 | imparts | 1 |
| 24439 | impartment | 1 |
| 24440 | imparted | 1 |
| 24441 | impanelled | 1 |
| 24442 | impale | 1 |
| 24443 | impairing | 1 |
| 24444 | impaint | 1 |
| 24445 | immures | 1 |
| 24446 | immortally | 1 |
| 24447 | immortaliz | 1 |
| 24448 | immortalising | 1 |
| 24449 | immortalise | 1 |
| 24450 | immoment | 1 |
| 24451 | immoderately | 1 |
| 24452 | immoderate | 1 |
| 24453 | imminence | 1 |
| 24454 | immemorial | 1 |
| 24455 | immediacy | 1 |
| 24456 | immaterial | 1 |
| 24457 | immask | 1 |
| 24458 | immanity | 1 |
| 24459 | immaculatissimus | 1 |
| 24460 | imitator | 1 |
| 24461 | imitations | 1 |
| 24462 | imitari | 1 |
| 24463 | imbecility | 1 |
| 24464 | imbar | 1 |
| 24465 | imaginings | 1 |
| 24466 | imagines | 1 |
| 24467 | imaginative | 1 |
| 24468 | imaginable | 1 |
| 24469 | imagery | 1 |
| 24470 | imaged | 1 |
| 24471 | im | 1 |
| 24472 | illyrian | 1 |
| 24473 | illustrated | 1 |
| 24474 | illusory | 1 |
| 24475 | illumineth | 1 |
| 24476 | illuminate | 1 |
| 24477 | illumin | 1 |
| 24478 | illume | 1 |
| 24479 | illud | 1 |
| 24480 | illtilled | 1 |
| 24481 | illo | 1 |
| 24482 | illiterate | 1 |
| 24483 | illiberal | 1 |
| 24484 | iliad | 1 |
| 24485 | ild | 1 |
| 24486 | ilbow | 1 |
| 24487 | iiii | 1 |
| 24488 | ignoramus | 1 |
| 24489 | ignomy | 1 |
| 24490 | ignis | 1 |
| 24491 | ifs | 1 |
| 24492 | ield | 1 |
| 24493 | idolatrous | 1 |
| 24494 | idles | 1 |
| 24495 | identify | 1 |
| 24496 | identical | 1 |
| 24497 | idem | 1 |
| 24498 | ideal | 1 |
| 24499 | ici | 1 |
| 24500 | iament | 1 |
| 24501 | iaculis | 1 |
| 24502 | hysterica | 1 |
| 24503 | hyssop | 1 |
| 24504 | hyrcania | 1 |
| 24505 | hyrcan | 1 |
| 24506 | hypocrites | 1 |
| 24507 | hymenaeus | 1 |
| 24508 | hyen | 1 |
| 24509 | hutch | 1 |
| 24510 | huswifes | 1 |
| 24511 | hussy | 1 |
| 24512 | husht | 1 |
| 24513 | hushes | 1 |
| 24514 | husbandless | 1 |
| 24515 | hurtling | 1 |
| 24516 | hurtless | 1 |
| 24517 | hurtled | 1 |
| 24518 | hurriedly | 1 |
| 24519 | hurricanoes | 1 |
| 24520 | hurricano | 1 |
| 24521 | hurls | 1 |
| 24522 | hurgada | 1 |
| 24523 | hurdle | 1 |
| 24524 | huntington | 1 |
| 24525 | huntings | 1 |
| 24526 | huntingcoat | 1 |
| 24527 | hunteth | 1 |
| 24528 | hungrily | 1 |
| 24529 | hungrier | 1 |
| 24530 | hungarian | 1 |
| 24531 | hundredth | 1 |
| 24532 | humphry | 1 |
| 24533 | humpbacked | 1 |
| 24534 | humourists | 1 |
| 24535 | humming | 1 |
| 24536 | humiliation | 1 |
| 24537 | humbling | 1 |
| 24538 | humbleth | 1 |
| 24539 | humanist | 1 |
| 24540 | hullo | 1 |
| 24541 | hulling | 1 |
| 24542 | hulks | 1 |
| 24543 | hujus | 1 |
| 24544 | hugs | 1 |
| 24545 | hugging | 1 |
| 24546 | hugger | 1 |
| 24547 | hugest | 1 |
| 24548 | hugeness | 1 |
| 24549 | hues | 1 |
| 24550 | huddling | 1 |
| 24551 | hucksters | 1 |
| 24552 | hubbub | 1 |
| 24553 | hoyday | 1 |
| 24554 | hoy | 1 |
| 24555 | hoxes | 1 |
| 24556 | howls | 1 |
| 24557 | howlings | 1 |
| 24558 | howlet | 1 |
| 24559 | howled | 1 |
| 24560 | howeer | 1 |
| 24561 | hovers | 1 |
| 24562 | hovering | 1 |
| 24563 | hovered | 1 |
| 24564 | housekeepers | 1 |
| 24565 | householders | 1 |
| 24566 | householder | 1 |
| 24567 | housed | 1 |
| 24568 | hospitably | 1 |
| 24569 | horsing | 1 |
| 24570 | horseway | 1 |
| 24571 | horsehairs | 1 |
| 24572 | horsed | 1 |
| 24573 | horrider | 1 |
| 24574 | horologe | 1 |
| 24575 | hornpipes | 1 |
| 24576 | horning | 1 |
| 24577 | hornbook | 1 |
| 24578 | horatius | 1 |
| 24579 | hops | 1 |
| 24580 | hoppedance | 1 |
| 24581 | hopest | 1 |
| 24582 | hoots | 1 |
| 24583 | hoot | 1 |
| 24584 | hooking | 1 |
| 24585 | honouring | 1 |
| 24586 | honourible | 1 |
| 24587 | honourest | 1 |
| 24588 | honorificabilitudinitatibus | 1 |
| 24589 | honorato | 1 |
| 24590 | honorably | 1 |
| 24591 | honi | 1 |
| 24592 | honeysuckles | 1 |
| 24593 | honeyless | 1 |
| 24594 | honeying | 1 |
| 24595 | honeyed | 1 |
| 24596 | honeycomb | 1 |
| 24597 | honestest | 1 |
| 24598 | homo | 1 |
| 24599 | hommes | 1 |
| 24600 | hominem | 1 |
| 24601 | homily | 1 |
| 24602 | homewards | 1 |
| 24603 | homespuns | 1 |
| 24604 | homerus | 1 |
| 24605 | homager | 1 |
| 24606 | hollows | 1 |
| 24607 | holloaing | 1 |
| 24608 | hollanders | 1 |
| 24609 | holiest | 1 |
| 24610 | holidam | 1 |
| 24611 | holdfast | 1 |
| 24612 | holden | 1 |
| 24613 | holborn | 1 |
| 24614 | hoists | 1 |
| 24615 | hoisting | 1 |
| 24616 | hoise | 1 |
| 24617 | hois | 1 |
| 24618 | hodge | 1 |
| 24619 | hod | 1 |
| 24620 | hobbyhorse | 1 |
| 24621 | hobbididence | 1 |
| 24622 | hoary | 1 |
| 24623 | hoarser | 1 |
| 24624 | hoars | 1 |
| 24625 | hizzing | 1 |
| 24626 | hives | 1 |
| 24627 | hitched | 1 |
| 24628 | hissings | 1 |
| 24629 | hisses | 1 |
| 24630 | hissed | 1 |
| 24631 | hisperia | 1 |
| 24632 | hirtius | 1 |
| 24633 | hipparchus | 1 |
| 24634 | hipolito | 1 |
| 24635 | hing | 1 |
| 24636 | hinders | 1 |
| 24637 | hindered | 1 |
| 24638 | hinckley | 1 |
| 24639 | hinc | 1 |
| 24640 | hily | 1 |
| 24641 | hillside | 1 |
| 24642 | hillock | 1 |
| 24643 | hilloa | 1 |
| 24644 | hillo | 1 |
| 24645 | hildings | 1 |
| 24646 | highbred | 1 |
| 24647 | hig | 1 |
| 24648 | hied | 1 |
| 24649 | hidest | 1 |
| 24650 | hideousness | 1 |
| 24651 | hideously | 1 |
| 24652 | hick | 1 |
| 24653 | hiccups | 1 |
| 24654 | hibocrates | 1 |
| 24655 | heyday | 1 |
| 24656 | hewgh | 1 |
| 24657 | heureux | 1 |
| 24658 | heure | 1 |
| 24659 | hesperus | 1 |
| 24660 | hesperides | 1 |
| 24661 | herradura | 1 |
| 24662 | heron | 1 |
| 24663 | herods | 1 |
| 24664 | hermes | 1 |
| 24665 | heritier | 1 |
| 24666 | heritage | 1 |
| 24667 | herewith | 1 |
| 24668 | heretofore | 1 |
| 24669 | hereto | 1 |
| 24670 | herculean | 1 |
| 24671 | herblets | 1 |
| 24672 | herbalist | 1 |
| 24673 | heraclius | 1 |
| 24674 | henricus | 1 |
| 24675 | henri | 1 |
| 24676 | henchman | 1 |
| 24677 | hemming | 1 |
| 24678 | helter | 1 |
| 24679 | helpmate | 1 |
| 24680 | helpers | 1 |
| 24681 | helmed | 1 |
| 24682 | hellfire | 1 |
| 24683 | helicons | 1 |
| 24684 | helias | 1 |
| 24685 | heirless | 1 |
| 24686 | heinously | 1 |
| 24687 | heightened | 1 |
| 24688 | heifers | 1 |
| 24689 | hefts | 1 |
| 24690 | hefted | 1 |
| 24691 | heeled | 1 |
| 24692 | heedfull | 1 |
| 24693 | hedgehog | 1 |
| 24694 | hectic | 1 |
| 24695 | hebona | 1 |
| 24696 | heavings | 1 |
| 24697 | heavenward | 1 |
| 24698 | heauties | 1 |
| 24699 | heating | 1 |
| 24700 | heaths | 1 |
| 24701 | heathenism | 1 |
| 24702 | heathenish | 1 |
| 24703 | heartsick | 1 |
| 24704 | heartrending | 1 |
| 24705 | heartlings | 1 |
| 24706 | heartiness | 1 |
| 24707 | hearths | 1 |
| 24708 | heartfelt | 1 |
| 24709 | hearten | 1 |
| 24710 | heartbreaking | 1 |
| 24711 | heartbreak | 1 |
| 24712 | heartache | 1 |
| 24713 | hearst | 1 |
| 24714 | hearsed | 1 |
| 24715 | hearings | 1 |
| 24716 | heareth | 1 |
| 24717 | healthsome | 1 |
| 24718 | healthiest | 1 |
| 24719 | heals | 1 |
| 24720 | headland | 1 |
| 24721 | heading | 1 |
| 24722 | headier | 1 |
| 24723 | headforemost | 1 |
| 24724 | headaches | 1 |
| 24725 | hazelnut | 1 |
| 24726 | haze | 1 |
| 24727 | hawthorns | 1 |
| 24728 | havior | 1 |
| 24729 | haver | 1 |
| 24730 | havens | 1 |
| 24731 | hautboy | 1 |
| 24732 | hauled | 1 |
| 24733 | haul | 1 |
| 24734 | hauf | 1 |
| 24735 | hauberk | 1 |
| 24736 | haters | 1 |
| 24737 | hatchment | 1 |
| 24738 | hatching | 1 |
| 24739 | hastes | 1 |
| 24740 | hasted | 1 |
| 24741 | hassan | 1 |
| 24742 | hash | 1 |
| 24743 | harvests | 1 |
| 24744 | harum | 1 |
| 24745 | harrows | 1 |
| 24746 | harried | 1 |
| 24747 | harquebusses | 1 |
| 24748 | harquebuss | 1 |
| 24749 | harps | 1 |
| 24750 | harpier | 1 |
| 24751 | harper | 1 |
| 24752 | harnessing | 1 |
| 24753 | harmlessness | 1 |
| 24754 | harelip | 1 |
| 24755 | hardocks | 1 |
| 24756 | hardiest | 1 |
| 24757 | hardhearted | 1 |
| 24758 | harbouring | 1 |
| 24759 | harbourage | 1 |
| 24760 | happies | 1 |
| 24761 | hankering | 1 |
| 24762 | hanker | 1 |
| 24763 | handy | 1 |
| 24764 | handsomeness | 1 |
| 24765 | handselled | 1 |
| 24766 | handmaids | 1 |
| 24767 | handmaidens | 1 |
| 24768 | handmaiden | 1 |
| 24769 | handlest | 1 |
| 24770 | handkerchiefs | 1 |
| 24771 | handicraftsmen | 1 |
| 24772 | handicraft | 1 |
| 24773 | handfuls | 1 |
| 24774 | hamstring | 1 |
| 24775 | hamper | 1 |
| 24776 | hammered | 1 |
| 24777 | hamida | 1 |
| 24778 | hamet | 1 |
| 24779 | hames | 1 |
| 24780 | hals | 1 |
| 24781 | halls | 1 |
| 24782 | hallown | 1 |
| 24783 | hallond | 1 |
| 24784 | halidom | 1 |
| 24785 | halfpennyworth | 1 |
| 24786 | halfcan | 1 |
| 24787 | haled | 1 |
| 24788 | haldudos | 1 |
| 24789 | haldudo | 1 |
| 24790 | halberd | 1 |
| 24791 | hairless | 1 |
| 24792 | hailstorm | 1 |
| 24793 | hailstones | 1 |
| 24794 | hailstone | 1 |
| 24795 | haggling | 1 |
| 24796 | haggled | 1 |
| 24797 | haggish | 1 |
| 24798 | haggards | 1 |
| 24799 | hagarene | 1 |
| 24800 | hagar | 1 |
| 24801 | haeres | 1 |
| 24802 | haec | 1 |
| 24803 | hadrian | 1 |
| 24804 | hacked | 1 |
| 24805 | habitude | 1 |
| 24806 | habiliment | 1 |
| 24807 | gyved | 1 |
| 24808 | gyve | 1 |
| 24809 | gymnosophists | 1 |
| 24810 | guzmans | 1 |
| 24811 | guzman | 1 |
| 24812 | guysors | 1 |
| 24813 | guynes | 1 |
| 24814 | gutter | 1 |
| 24815 | gutierre | 1 |
| 24816 | gusty | 1 |
| 24817 | gushed | 1 |
| 24818 | gurreas | 1 |
| 24819 | gurnet | 1 |
| 24820 | gunshot | 1 |
| 24821 | gums | 1 |
| 24822 | gumption | 1 |
| 24823 | gumm | 1 |
| 24824 | gulping | 1 |
| 24825 | gulped | 1 |
| 24826 | gulfs | 1 |
| 24827 | gul | 1 |
| 24828 | guisopete | 1 |
| 24829 | guinever | 1 |
| 24830 | guilts | 1 |
| 24831 | guiltily | 1 |
| 24832 | guiltian | 1 |
| 24833 | guilfords | 1 |
| 24834 | guiled | 1 |
| 24835 | guienne | 1 |
| 24836 | guidon | 1 |
| 24837 | guider | 1 |
| 24838 | guidance | 1 |
| 24839 | guichard | 1 |
| 24840 | guiana | 1 |
| 24841 | guevara | 1 |
| 24842 | guesswork | 1 |
| 24843 | guessingly | 1 |
| 24844 | guesses | 1 |
| 24845 | guerra | 1 |
| 24846 | gudgeon | 1 |
| 24847 | guarino | 1 |
| 24848 | guarding | 1 |
| 24849 | guardians | 1 |
| 24850 | guardage | 1 |
| 24851 | guarantee | 1 |
| 24852 | guadarrama | 1 |
| 24853 | grunted | 1 |
| 24854 | grund | 1 |
| 24855 | grumblings | 1 |
| 24856 | grumblest | 1 |
| 24857 | gruel | 1 |
| 24858 | grudges | 1 |
| 24859 | grudged | 1 |
| 24860 | grubb | 1 |
| 24861 | growling | 1 |
| 24862 | growler | 1 |
| 24863 | groweth | 1 |
| 24864 | grouting | 1 |
| 24865 | group | 1 |
| 24866 | groundlings | 1 |
| 24867 | grotesque | 1 |
| 24868 | groping | 1 |
| 24869 | grop | 1 |
| 24870 | groomsman | 1 |
| 24871 | groin | 1 |
| 24872 | grizzle | 1 |
| 24873 | grize | 1 |
| 24874 | grissel | 1 |
| 24875 | gripped | 1 |
| 24876 | gripings | 1 |
| 24877 | grindstone | 1 |
| 24878 | grinder | 1 |
| 24879 | grijalba | 1 |
| 24880 | grievingly | 1 |
| 24881 | grievest | 1 |
| 24882 | greenwich | 1 |
| 24883 | greens | 1 |
| 24884 | greener | 1 |
| 24885 | greeing | 1 |
| 24886 | greedily | 1 |
| 24887 | gree | 1 |
| 24888 | greaves | 1 |
| 24889 | greasily | 1 |
| 24890 | greases | 1 |
| 24891 | greased | 1 |
| 24892 | grazed | 1 |
| 24893 | graz | 1 |
| 24894 | graymalkin | 1 |
| 24895 | gravities | 1 |
| 24896 | graveyard | 1 |
| 24897 | graveness | 1 |
| 24898 | gravell | 1 |
| 24899 | graveless | 1 |
| 24900 | gravediggers | 1 |
| 24901 | gratings | 1 |
| 24902 | gratillity | 1 |
| 24903 | gratii | 1 |
| 24904 | gratification | 1 |
| 24905 | grates | 1 |
| 24906 | grassy | 1 |
| 24907 | grasshoppers | 1 |
| 24908 | grappled | 1 |
| 24909 | grandsir | 1 |
| 24910 | grandjurors | 1 |
| 24911 | grandiloquent | 1 |
| 24912 | grande | 1 |
| 24913 | granddaughter | 1 |
| 24914 | grandchild | 1 |
| 24915 | grandame | 1 |
| 24916 | grammarian | 1 |
| 24917 | gram | 1 |
| 24918 | grail | 1 |
| 24919 | grafters | 1 |
| 24920 | graffing | 1 |
| 24921 | graduates | 1 |
| 24922 | graduated | 1 |
| 24923 | gracing | 1 |
| 24924 | gracefully | 1 |
| 24925 | gownsman | 1 |
| 24926 | governorship | 1 |
| 24927 | governance | 1 |
| 24928 | gouts | 1 |
| 24929 | gossiplike | 1 |
| 24930 | goss | 1 |
| 24931 | gosling | 1 |
| 24932 | gormandizing | 1 |
| 24933 | gormandize | 1 |
| 24934 | gormandiser | 1 |
| 24935 | gorboduc | 1 |
| 24936 | gorbellied | 1 |
| 24937 | goosequills | 1 |
| 24938 | gooseberry | 1 |
| 24939 | goodyears | 1 |
| 24940 | goodyear | 1 |
| 24941 | goodwins | 1 |
| 24942 | goodwife | 1 |
| 24943 | goodrig | 1 |
| 24944 | goodnight | 1 |
| 24945 | gong | 1 |
| 24946 | gonela | 1 |
| 24947 | gondolier | 1 |
| 24948 | goliases | 1 |
| 24949 | golias | 1 |
| 24950 | goldsmiths | 1 |
| 24951 | goldfinch | 1 |
| 24952 | goldenly | 1 |
| 24953 | gogs | 1 |
| 24954 | goeth | 1 |
| 24955 | goer | 1 |
| 24956 | godspeed | 1 |
| 24957 | godsons | 1 |
| 24958 | godsend | 1 |
| 24959 | godfrey | 1 |
| 24960 | goddild | 1 |
| 24961 | godden | 1 |
| 24962 | godded | 1 |
| 24963 | goblets | 1 |
| 24964 | goaty | 1 |
| 24965 | goatish | 1 |
| 24966 | goals | 1 |
| 24967 | goads | 1 |
| 24968 | gnarled | 1 |
| 24969 | gluttonous | 1 |
| 24970 | gluttoning | 1 |
| 24971 | glutted | 1 |
| 24972 | glutt | 1 |
| 24973 | glut | 1 |
| 24974 | glues | 1 |
| 24975 | glued | 1 |
| 24976 | glue | 1 |
| 24977 | glu | 1 |
| 24978 | glozes | 1 |
| 24979 | gloz | 1 |
| 24980 | glowworm | 1 |
| 24981 | glouceste | 1 |
| 24982 | glossing | 1 |
| 24983 | glose | 1 |
| 24984 | gloriously | 1 |
| 24985 | glooming | 1 |
| 24986 | globes | 1 |
| 24987 | glittered | 1 |
| 24988 | glitt | 1 |
| 24989 | glister | 1 |
| 24990 | glistening | 1 |
| 24991 | glimmers | 1 |
| 24992 | glideth | 1 |
| 24993 | glided | 1 |
| 24994 | glens | 1 |
| 24995 | gleeks | 1 |
| 24996 | gleeking | 1 |
| 24997 | gleeful | 1 |
| 24998 | gleaning | 1 |
| 24999 | gleams | 1 |
| 25000 | gleam | 1 |
| 25001 | glaz | 1 |
| 25002 | glaring | 1 |
| 25003 | glare | 1 |
| 25004 | glanders | 1 |
| 25005 | glancing | 1 |
| 25006 | glanc | 1 |
| 25007 | glamorous | 1 |
| 25008 | gladsome | 1 |
| 25009 | glade | 1 |
| 25010 | gladding | 1 |
| 25011 | gladdening | 1 |
| 25012 | gladdened | 1 |
| 25013 | gladded | 1 |
| 25014 | givings | 1 |
| 25015 | givers | 1 |
| 25016 | giu | 1 |
| 25017 | gis | 1 |
| 25018 | girds | 1 |
| 25019 | gipsies | 1 |
| 25020 | gipes | 1 |
| 25021 | giovanni | 1 |
| 25022 | gioucestershire | 1 |
| 25023 | ginn | 1 |
| 25024 | gingerly | 1 |
| 25025 | gingerbread | 1 |
| 25026 | ging | 1 |
| 25027 | gineta | 1 |
| 25028 | gimmers | 1 |
| 25029 | gimmal | 1 |
| 25030 | gillian | 1 |
| 25031 | gilliams | 1 |
| 25032 | gilds | 1 |
| 25033 | gigote | 1 |
| 25034 | giglets | 1 |
| 25035 | gibraltar | 1 |
| 25036 | gibraleon | 1 |
| 25037 | gibingly | 1 |
| 25038 | giber | 1 |
| 25039 | gibberish | 1 |
| 25040 | gibber | 1 |
| 25041 | giantlike | 1 |
| 25042 | gi | 1 |
| 25043 | ghosted | 1 |
| 25044 | getter | 1 |
| 25045 | getrude | 1 |
| 25046 | gests | 1 |
| 25047 | gest | 1 |
| 25048 | germains | 1 |
| 25049 | germaines | 1 |
| 25050 | geometry | 1 |
| 25051 | gentlest | 1 |
| 25052 | gentlemanlike | 1 |
| 25053 | gentlefolks | 1 |
| 25054 | gentiles | 1 |
| 25055 | genoux | 1 |
| 25056 | gennets | 1 |
| 25057 | geniuses | 1 |
| 25058 | genitivo | 1 |
| 25059 | generative | 1 |
| 25060 | generated | 1 |
| 25061 | genders | 1 |
| 25062 | gen | 1 |
| 25063 | geminy | 1 |
| 25064 | gelt | 1 |
| 25065 | gelidus | 1 |
| 25066 | gelida | 1 |
| 25067 | gazpacho | 1 |
| 25068 | gazeth | 1 |
| 25069 | gazer | 1 |
| 25070 | gayness | 1 |
| 25071 | gawded | 1 |
| 25072 | gauze | 1 |
| 25073 | gauge | 1 |
| 25074 | gaudeo | 1 |
| 25075 | gaudeamus | 1 |
| 25076 | gaud | 1 |
| 25077 | gatory | 1 |
| 25078 | gathers | 1 |
| 25079 | gath | 1 |
| 25080 | gated | 1 |
| 25081 | gat | 1 |
| 25082 | gastness | 1 |
| 25083 | gasted | 1 |
| 25084 | gaskins | 1 |
| 25085 | gascons | 1 |
| 25086 | gasabal | 1 |
| 25087 | gartering | 1 |
| 25088 | garterd | 1 |
| 25089 | gart | 1 |
| 25090 | garrisons | 1 |
| 25091 | garners | 1 |
| 25092 | garmet | 1 |
| 25093 | gargantua | 1 |
| 25094 | gardez | 1 |
| 25095 | garde | 1 |
| 25096 | garcon | 1 |
| 25097 | garci | 1 |
| 25098 | garaya | 1 |
| 25099 | garamantas | 1 |
| 25100 | garamanta | 1 |
| 25101 | gangren | 1 |
| 25102 | gang | 1 |
| 25103 | gammon | 1 |
| 25104 | gamers | 1 |
| 25105 | gamboys | 1 |
| 25106 | gambolling | 1 |
| 25107 | gambold | 1 |
| 25108 | gambados | 1 |
| 25109 | gam | 1 |
| 25110 | gallowses | 1 |
| 25111 | galloway | 1 |
| 25112 | gallow | 1 |
| 25113 | galloon | 1 |
| 25114 | galliots | 1 |
| 25115 | galliasses | 1 |
| 25116 | galleries | 1 |
| 25117 | galingale | 1 |
| 25118 | galician | 1 |
| 25119 | galiana | 1 |
| 25120 | gales | 1 |
| 25121 | galathe | 1 |
| 25122 | galaors | 1 |
| 25123 | gainsays | 1 |
| 25124 | gainsaying | 1 |
| 25125 | gainsaid | 1 |
| 25126 | gaingiving | 1 |
| 25127 | gagne | 1 |
| 25128 | gaging | 1 |
| 25129 | gaged | 1 |
| 25130 | gabrio | 1 |
| 25131 | gabriel | 1 |
| 25132 | futurity | 1 |
| 25133 | fut | 1 |
| 25134 | fustilarian | 1 |
| 25135 | fust | 1 |
| 25136 | furzes | 1 |
| 25137 | furtherer | 1 |
| 25138 | furth | 1 |
| 25139 | furry | 1 |
| 25140 | furor | 1 |
| 25141 | furnival | 1 |
| 25142 | furnishings | 1 |
| 25143 | furnaces | 1 |
| 25144 | furbished | 1 |
| 25145 | fumitory | 1 |
| 25146 | fumiter | 1 |
| 25147 | fumbling | 1 |
| 25148 | fumblest | 1 |
| 25149 | fumbles | 1 |
| 25150 | fum | 1 |
| 25151 | fullness | 1 |
| 25152 | fullers | 1 |
| 25153 | fullam | 1 |
| 25154 | fulfils | 1 |
| 25155 | fuit | 1 |
| 25156 | fugite | 1 |
| 25157 | fuerint | 1 |
| 25158 | fucar | 1 |
| 25159 | frutify | 1 |
| 25160 | frush | 1 |
| 25161 | fruitlessly | 1 |
| 25162 | fruition | 1 |
| 25163 | fruitfulness | 1 |
| 25164 | fruiterer | 1 |
| 25165 | fructify | 1 |
| 25166 | frowningly | 1 |
| 25167 | frontlet | 1 |
| 25168 | frolicsome | 1 |
| 25169 | froissart | 1 |
| 25170 | frogs | 1 |
| 25171 | frivolities | 1 |
| 25172 | friton | 1 |
| 25173 | frisking | 1 |
| 25174 | frisk | 1 |
| 25175 | frippery | 1 |
| 25176 | fringes | 1 |
| 25177 | fringed | 1 |
| 25178 | fringe | 1 |
| 25179 | frigate | 1 |
| 25180 | frieslander | 1 |
| 25181 | friendliness | 1 |
| 25182 | friendless | 1 |
| 25183 | friending | 1 |
| 25184 | fretten | 1 |
| 25185 | freshes | 1 |
| 25186 | freshened | 1 |
| 25187 | frequenters | 1 |
| 25188 | frequency | 1 |
| 25189 | frenzied | 1 |
| 25190 | frenchified | 1 |
| 25191 | freezings | 1 |
| 25192 | freezing | 1 |
| 25193 | freetown | 1 |
| 25194 | freestone | 1 |
| 25195 | freeness | 1 |
| 25196 | freemen | 1 |
| 25197 | freeman | 1 |
| 25198 | freelier | 1 |
| 25199 | freehearted | 1 |
| 25200 | freedoms | 1 |
| 25201 | freckles | 1 |
| 25202 | freckled | 1 |
| 25203 | freckl | 1 |
| 25204 | fraughting | 1 |
| 25205 | fraudulent | 1 |
| 25206 | fraudful | 1 |
| 25207 | fratrum | 1 |
| 25208 | fratin | 1 |
| 25209 | frateretto | 1 |
| 25210 | franticly | 1 |
| 25211 | franklins | 1 |
| 25212 | frankfort | 1 |
| 25213 | franker | 1 |
| 25214 | francolins | 1 |
| 25215 | franciae | 1 |
| 25216 | francia | 1 |
| 25217 | franchises | 1 |
| 25218 | franchisement | 1 |
| 25219 | franchised | 1 |
| 25220 | franchise | 1 |
| 25221 | frances | 1 |
| 25222 | francenia | 1 |
| 25223 | francais | 1 |
| 25224 | frampold | 1 |
| 25225 | framer | 1 |
| 25226 | frailer | 1 |
| 25227 | fragile | 1 |
| 25228 | fraction | 1 |
| 25229 | foxship | 1 |
| 25230 | fowling | 1 |
| 25231 | fowler | 1 |
| 25232 | fourfold | 1 |
| 25233 | founts | 1 |
| 25234 | foughten | 1 |
| 25235 | fost | 1 |
| 25236 | fosset | 1 |
| 25237 | forwearied | 1 |
| 25238 | forwarding | 1 |
| 25239 | fortward | 1 |
| 25240 | fortuned | 1 |
| 25241 | fortun | 1 |
| 25242 | fortifies | 1 |
| 25243 | fortification | 1 |
| 25244 | forthright | 1 |
| 25245 | forthlight | 1 |
| 25246 | forted | 1 |
| 25247 | forte | 1 |
| 25248 | forspoke | 1 |
| 25249 | forslow | 1 |
| 25250 | forse | 1 |
| 25251 | forsaketh | 1 |
| 25252 | fornicatress | 1 |
| 25253 | fornications | 1 |
| 25254 | formidable | 1 |
| 25255 | forks | 1 |
| 25256 | forgone | 1 |
| 25257 | forgoing | 1 |
| 25258 | forgettest | 1 |
| 25259 | forgetive | 1 |
| 25260 | forfended | 1 |
| 25261 | forfeitures | 1 |
| 25262 | forfeiters | 1 |
| 25263 | forewarning | 1 |
| 25264 | foreward | 1 |
| 25265 | forethought | 1 |
| 25266 | forethink | 1 |
| 25267 | foretelling | 1 |
| 25268 | foreskirt | 1 |
| 25269 | foreshow | 1 |
| 25270 | foresees | 1 |
| 25271 | foresay | 1 |
| 25272 | foreruns | 1 |
| 25273 | forerunning | 1 |
| 25274 | forenamed | 1 |
| 25275 | foreknowledge | 1 |
| 25276 | foreigner | 1 |
| 25277 | forehorse | 1 |
| 25278 | foreheads | 1 |
| 25279 | foregoing | 1 |
| 25280 | forefather | 1 |
| 25281 | forecast | 1 |
| 25282 | forebodings | 1 |
| 25283 | forebode | 1 |
| 25284 | fordo | 1 |
| 25285 | fordid | 1 |
| 25286 | forceless | 1 |
| 25287 | forceful | 1 |
| 25288 | forborne | 1 |
| 25289 | forbod | 1 |
| 25290 | forbiddenly | 1 |
| 25291 | forbears | 1 |
| 25292 | forbearing | 1 |
| 25293 | foray | 1 |
| 25294 | foragers | 1 |
| 25295 | fops | 1 |
| 25296 | foppish | 1 |
| 25297 | fopped | 1 |
| 25298 | fopp | 1 |
| 25299 | footstool | 1 |
| 25300 | footsore | 1 |
| 25301 | foots | 1 |
| 25302 | footpad | 1 |
| 25303 | footmen | 1 |
| 25304 | footfall | 1 |
| 25305 | footboys | 1 |
| 25306 | foolishness | 1 |
| 25307 | foolishest | 1 |
| 25308 | fontibell | 1 |
| 25309 | fonder | 1 |
| 25310 | folio | 1 |
| 25311 | folding | 1 |
| 25312 | foist | 1 |
| 25313 | foisons | 1 |
| 25314 | foins | 1 |
| 25315 | foiled | 1 |
| 25316 | foddering | 1 |
| 25317 | fodder | 1 |
| 25318 | foces | 1 |
| 25319 | fob | 1 |
| 25320 | foamy | 1 |
| 25321 | foamed | 1 |
| 25322 | fluxive | 1 |
| 25323 | fluttered | 1 |
| 25324 | fluster | 1 |
| 25325 | flushing | 1 |
| 25326 | flurry | 1 |
| 25327 | fluent | 1 |
| 25328 | fluctuations | 1 |
| 25329 | flowerets | 1 |
| 25330 | flourisheth | 1 |
| 25331 | floulish | 1 |
| 25332 | flote | 1 |
| 25333 | floripes | 1 |
| 25334 | florentius | 1 |
| 25335 | florentibus | 1 |
| 25336 | floors | 1 |
| 25337 | floodgates | 1 |
| 25338 | flogs | 1 |
| 25339 | floats | 1 |
| 25340 | floated | 1 |
| 25341 | flirt | 1 |
| 25342 | flints | 1 |
| 25343 | flintlocks | 1 |
| 25344 | flinched | 1 |
| 25345 | flimsy | 1 |
| 25346 | flidge | 1 |
| 25347 | flickering | 1 |
| 25348 | fleshmonger | 1 |
| 25349 | fleshment | 1 |
| 25350 | fleshly | 1 |
| 25351 | fleshes | 1 |
| 25352 | fleridas | 1 |
| 25353 | fleming | 1 |
| 25354 | fleets | 1 |
| 25355 | flees | 1 |
| 25356 | fleers | 1 |
| 25357 | fleering | 1 |
| 25358 | fleeces | 1 |
| 25359 | fleec | 1 |
| 25360 | fledge | 1 |
| 25361 | flecked | 1 |
| 25362 | flayed | 1 |
| 25363 | flaxen | 1 |
| 25364 | flavio | 1 |
| 25365 | flaunts | 1 |
| 25366 | flatterest | 1 |
| 25367 | flattened | 1 |
| 25368 | flatness | 1 |
| 25369 | flashing | 1 |
| 25370 | flashed | 1 |
| 25371 | flaring | 1 |
| 25372 | flappers | 1 |
| 25373 | flamens | 1 |
| 25374 | flamen | 1 |
| 25375 | flaky | 1 |
| 25376 | flail | 1 |
| 25377 | flagons | 1 |
| 25378 | flagon | 1 |
| 25379 | fl | 1 |
| 25380 | fixeth | 1 |
| 25381 | fixedly | 1 |
| 25382 | fivepence | 1 |
| 25383 | fittings | 1 |
| 25384 | fittingly | 1 |
| 25385 | fitful | 1 |
| 25386 | fistula | 1 |
| 25387 | fisting | 1 |
| 25388 | fisnomy | 1 |
| 25389 | fishpond | 1 |
| 25390 | fishingrod | 1 |
| 25391 | fishified | 1 |
| 25392 | fishery | 1 |
| 25393 | fishers | 1 |
| 25394 | fisher | 1 |
| 25395 | firmest | 1 |
| 25396 | firma | 1 |
| 25397 | firing | 1 |
| 25398 | fireworks | 1 |
| 25399 | firework | 1 |
| 25400 | firewood | 1 |
| 25401 | firelocks | 1 |
| 25402 | firebrands | 1 |
| 25403 | firago | 1 |
| 25404 | finsbury | 1 |
| 25405 | finn | 1 |
| 25406 | finless | 1 |
| 25407 | finisher | 1 |
| 25408 | finikin | 1 |
| 25409 | finical | 1 |
| 25410 | fing | 1 |
| 25411 | finem | 1 |
| 25412 | fineless | 1 |
| 25413 | findings | 1 |
| 25414 | findeth | 1 |
| 25415 | finders | 1 |
| 25416 | filthiest | 1 |
| 25417 | fils | 1 |
| 25418 | filly | 1 |
| 25419 | fillips | 1 |
| 25420 | fillies | 1 |
| 25421 | filius | 1 |
| 25422 | filida | 1 |
| 25423 | filches | 1 |
| 25424 | figured | 1 |
| 25425 | figueroa | 1 |
| 25426 | figged | 1 |
| 25427 | fiftyfold | 1 |
| 25428 | fifteenth | 1 |
| 25429 | fifteens | 1 |
| 25430 | fifer | 1 |
| 25431 | fiercely | 1 |
| 25432 | fielded | 1 |
| 25433 | fido | 1 |
| 25434 | fidius | 1 |
| 25435 | fidgets | 1 |
| 25436 | fico | 1 |
| 25437 | fez | 1 |
| 25438 | fewness | 1 |
| 25439 | fevers | 1 |
| 25440 | feud | 1 |
| 25441 | fettle | 1 |
| 25442 | fettering | 1 |
| 25443 | fetlock | 1 |
| 25444 | fetid | 1 |
| 25445 | festinately | 1 |
| 25446 | festinate | 1 |
| 25447 | fervently | 1 |
| 25448 | fervency | 1 |
| 25449 | fertilising | 1 |
| 25450 | fertilises | 1 |
| 25451 | ferryman | 1 |
| 25452 | ferrers | 1 |
| 25453 | ferocity | 1 |
| 25454 | ferocious | 1 |
| 25455 | fernan | 1 |
| 25456 | ferment | 1 |
| 25457 | fere | 1 |
| 25458 | fenny | 1 |
| 25459 | fends | 1 |
| 25460 | fencers | 1 |
| 25461 | fenc | 1 |
| 25462 | feminine | 1 |
| 25463 | felons | 1 |
| 25464 | felonious | 1 |
| 25465 | fellowships | 1 |
| 25466 | fellowly | 1 |
| 25467 | fellies | 1 |
| 25468 | felled | 1 |
| 25469 | felixmartes | 1 |
| 25470 | felicitate | 1 |
| 25471 | feliciano | 1 |
| 25472 | felicia | 1 |
| 25473 | feith | 1 |
| 25474 | feil | 1 |
| 25475 | fehemently | 1 |
| 25476 | feelest | 1 |
| 25477 | feeler | 1 |
| 25478 | feedeth | 1 |
| 25479 | feebly | 1 |
| 25480 | feebling | 1 |
| 25481 | feebled | 1 |
| 25482 | federary | 1 |
| 25483 | fecks | 1 |
| 25484 | february | 1 |
| 25485 | featureless | 1 |
| 25486 | featur | 1 |
| 25487 | feater | 1 |
| 25488 | feated | 1 |
| 25489 | feasible | 1 |
| 25490 | fearfulness | 1 |
| 25491 | fearfull | 1 |
| 25492 | fearer | 1 |
| 25493 | fays | 1 |
| 25494 | fawneth | 1 |
| 25495 | favout | 1 |
| 25496 | favourers | 1 |
| 25497 | favors | 1 |
| 25498 | favorably | 1 |
| 25499 | favorable | 1 |
| 25500 | favila | 1 |
| 25501 | faut | 1 |
| 25502 | faustuses | 1 |
| 25503 | fauste | 1 |
| 25504 | fausse | 1 |
| 25505 | fauns | 1 |
| 25506 | faultiness | 1 |
| 25507 | fatuus | 1 |
| 25508 | fatting | 1 |
| 25509 | fatter | 1 |
| 25510 | fats | 1 |
| 25511 | fatness | 1 |
| 25512 | fatigued | 1 |
| 25513 | fatigate | 1 |
| 25514 | fathomless | 1 |
| 25515 | fathomed | 1 |
| 25516 | fathering | 1 |
| 25517 | fathered | 1 |
| 25518 | fatally | 1 |
| 25519 | fastly | 1 |
| 25520 | fastenings | 1 |
| 25521 | fasted | 1 |
| 25522 | fashioned | 1 |
| 25523 | fascinate | 1 |
| 25524 | fas | 1 |
| 25525 | fartuous | 1 |
| 25526 | fartax | 1 |
| 25527 | farrow | 1 |
| 25528 | farre | 1 |
| 25529 | farms | 1 |
| 25530 | farmhouses | 1 |
| 25531 | farmhouse | 1 |
| 25532 | farmers | 1 |
| 25533 | fariner | 1 |
| 25534 | fardels | 1 |
| 25535 | farced | 1 |
| 25536 | farce | 1 |
| 25537 | farborough | 1 |
| 25538 | fap | 1 |
| 25539 | fantasticoes | 1 |
| 25540 | fantasied | 1 |
| 25541 | fangless | 1 |
| 25542 | fanes | 1 |
| 25543 | fane | 1 |
| 25544 | fando | 1 |
| 25545 | fanciest | 1 |
| 25546 | fanatical | 1 |
| 25547 | famoused | 1 |
| 25548 | famished | 1 |
| 25549 | falsing | 1 |
| 25550 | falsifying | 1 |
| 25551 | falorous | 1 |
| 25552 | fally | 1 |
| 25553 | fallows | 1 |
| 25554 | fallible | 1 |
| 25555 | falliable | 1 |
| 25556 | falleth | 1 |
| 25557 | fallacy | 1 |
| 25558 | falconer | 1 |
| 25559 | falces | 1 |
| 25560 | faitors | 1 |
| 25561 | faithfull | 1 |
| 25562 | faites | 1 |
| 25563 | fait | 1 |
| 25564 | fais | 1 |
| 25565 | fairwell | 1 |
| 25566 | fairings | 1 |
| 25567 | fairing | 1 |
| 25568 | fainthearted | 1 |
| 25569 | fainter | 1 |
| 25570 | fagots | 1 |
| 25571 | fagot | 1 |
| 25572 | faggots | 1 |
| 25573 | fadoms | 1 |
| 25574 | fadings | 1 |
| 25575 | fadeth | 1 |
| 25576 | factors | 1 |
| 25577 | factionary | 1 |
| 25578 | facings | 1 |
| 25579 | facinerious | 1 |
| 25580 | facilities | 1 |
| 25581 | facile | 1 |
| 25582 | faciant | 1 |
| 25583 | facere | 1 |
| 25584 | fabrication | 1 |
| 25585 | eyrie | 1 |
| 25586 | eying | 1 |
| 25587 | eyewitness | 1 |
| 25588 | eyestrings | 1 |
| 25589 | eyebrow | 1 |
| 25590 | eyeball | 1 |
| 25591 | eyases | 1 |
| 25592 | eyas | 1 |
| 25593 | exulting | 1 |
| 25594 | exultation | 1 |
| 25595 | exuent | 1 |
| 25596 | extravagantly | 1 |
| 25597 | extravagancy | 1 |
| 25598 | extraught | 1 |
| 25599 | extortions | 1 |
| 25600 | extortion | 1 |
| 25601 | extols | 1 |
| 25602 | extolment | 1 |
| 25603 | extolling | 1 |
| 25604 | extoll | 1 |
| 25605 | extirped | 1 |
| 25606 | extirpate | 1 |
| 25607 | extirp | 1 |
| 25608 | extinguishing | 1 |
| 25609 | extinguish | 1 |
| 25610 | extincture | 1 |
| 25611 | extincted | 1 |
| 25612 | extermin | 1 |
| 25613 | exteriors | 1 |
| 25614 | exteriorly | 1 |
| 25615 | extenuation | 1 |
| 25616 | extenuates | 1 |
| 25617 | extenuated | 1 |
| 25618 | extemporally | 1 |
| 25619 | exsufflicate | 1 |
| 25620 | expuls | 1 |
| 25621 | expresseth | 1 |
| 25622 | expounded | 1 |
| 25623 | exposures | 1 |
| 25624 | exposture | 1 |
| 25625 | expostulation | 1 |
| 25626 | expositor | 1 |
| 25627 | exposes | 1 |
| 25628 | explorer | 1 |
| 25629 | explode | 1 |
| 25630 | explains | 1 |
| 25631 | expiring | 1 |
| 25632 | expires | 1 |
| 25633 | expired | 1 |
| 25634 | expiation | 1 |
| 25635 | experimental | 1 |
| 25636 | experiences | 1 |
| 25637 | expels | 1 |
| 25638 | expelling | 1 |
| 25639 | expelled | 1 |
| 25640 | expell | 1 |
| 25641 | expedients | 1 |
| 25642 | expediently | 1 |
| 25643 | expecters | 1 |
| 25644 | expectant | 1 |
| 25645 | expectance | 1 |
| 25646 | expatriation | 1 |
| 25647 | expatiate | 1 |
| 25648 | expansion | 1 |
| 25649 | exorcisms | 1 |
| 25650 | exorciser | 1 |
| 25651 | exorbitant | 1 |
| 25652 | exits | 1 |
| 25653 | exion | 1 |
| 25654 | exiled | 1 |
| 25655 | exhortations | 1 |
| 25656 | exhilarated | 1 |
| 25657 | exhibits | 1 |
| 25658 | exhibiting | 1 |
| 25659 | exhibiters | 1 |
| 25660 | exhaust | 1 |
| 25661 | exerted | 1 |
| 25662 | exercised | 1 |
| 25663 | exequies | 1 |
| 25664 | exempts | 1 |
| 25665 | exemptions | 1 |
| 25666 | exempted | 1 |
| 25667 | exemplary | 1 |
| 25668 | executes | 1 |
| 25669 | execration | 1 |
| 25670 | execrable | 1 |
| 25671 | excusable | 1 |
| 25672 | excrescences | 1 |
| 25673 | excludes | 1 |
| 25674 | exchequers | 1 |
| 25675 | excesses | 1 |
| 25676 | exceptless | 1 |
| 25677 | excellencies | 1 |
| 25678 | exceedeth | 1 |
| 25679 | exasperation | 1 |
| 25680 | exasperates | 1 |
| 25681 | exasperated | 1 |
| 25682 | exampl | 1 |
| 25683 | examines | 1 |
| 25684 | examiners | 1 |
| 25685 | examiner | 1 |
| 25686 | examinations | 1 |
| 25687 | exalting | 1 |
| 25688 | exalteth | 1 |
| 25689 | exaltation | 1 |
| 25690 | exaggeration | 1 |
| 25691 | exaggerated | 1 |
| 25692 | exacts | 1 |
| 25693 | exactest | 1 |
| 25694 | exacted | 1 |
| 25695 | ewers | 1 |
| 25696 | evitate | 1 |
| 25697 | evildoing | 1 |
| 25698 | evildoer | 1 |
| 25699 | evidences | 1 |
| 25700 | eventful | 1 |
| 25701 | evens | 1 |
| 25702 | evasions | 1 |
| 25703 | evades | 1 |
| 25704 | evade | 1 |
| 25705 | euphrates | 1 |
| 25706 | eulogy | 1 |
| 25707 | etre | 1 |
| 25708 | etna | 1 |
| 25709 | ethiopians | 1 |
| 25710 | ethiopes | 1 |
| 25711 | ethiop | 1 |
| 25712 | ethereal | 1 |
| 25713 | eterniz | 1 |
| 25714 | eternally | 1 |
| 25715 | ete | 1 |
| 25716 | etceteras | 1 |
| 25717 | estridges | 1 |
| 25718 | estridge | 1 |
| 25719 | estime | 1 |
| 25720 | estimations | 1 |
| 25721 | esteeming | 1 |
| 25722 | esteemeth | 1 |
| 25723 | essays | 1 |
| 25724 | esquife | 1 |
| 25725 | esplandians | 1 |
| 25726 | espartafilardo | 1 |
| 25727 | espanoli | 1 |
| 25728 | esill | 1 |
| 25729 | escotillo | 1 |
| 25730 | escoted | 1 |
| 25731 | escort | 1 |
| 25732 | eschew | 1 |
| 25733 | es | 1 |
| 25734 | erworn | 1 |
| 25735 | erwhelmed | 1 |
| 25736 | erweighs | 1 |
| 25737 | erweigh | 1 |
| 25738 | erweens | 1 |
| 25739 | erween | 1 |
| 25740 | erwalk | 1 |
| 25741 | ervalues | 1 |
| 25742 | eruption | 1 |
| 25743 | eructations | 1 |
| 25744 | ertrip | 1 |
| 25745 | ertopping | 1 |
| 25746 | erthrows | 1 |
| 25747 | erteemed | 1 |
| 25748 | erta | 1 |
| 25749 | erstunk | 1 |
| 25750 | erstep | 1 |
| 25751 | erstare | 1 |
| 25752 | erspreads | 1 |
| 25753 | erslips | 1 |
| 25754 | erskip | 1 |
| 25755 | ersized | 1 |
| 25756 | ershine | 1 |
| 25757 | ershade | 1 |
| 25758 | erset | 1 |
| 25759 | errest | 1 |
| 25760 | erred | 1 |
| 25761 | erreaches | 1 |
| 25762 | errate | 1 |
| 25763 | errants | 1 |
| 25764 | erpressed | 1 |
| 25765 | erpress | 1 |
| 25766 | erposting | 1 |
| 25767 | erpicturing | 1 |
| 25768 | erperch | 1 |
| 25769 | erpeer | 1 |
| 25770 | erpays | 1 |
| 25771 | erparted | 1 |
| 25772 | erpaid | 1 |
| 25773 | erostratus | 1 |
| 25774 | ern | 1 |
| 25775 | ermount | 1 |
| 25776 | ermengare | 1 |
| 25777 | ermaster | 1 |
| 25778 | erlooking | 1 |
| 25779 | erleavens | 1 |
| 25780 | erleaps | 1 |
| 25781 | erjoy | 1 |
| 25782 | eringoes | 1 |
| 25783 | erhear | 1 |
| 25784 | erhasty | 1 |
| 25785 | erhanging | 1 |
| 25786 | erhang | 1 |
| 25787 | ergrowth | 1 |
| 25788 | ergrow | 1 |
| 25789 | ergone | 1 |
| 25790 | erglanced | 1 |
| 25791 | ergalled | 1 |
| 25792 | erga | 1 |
| 25793 | erfraught | 1 |
| 25794 | erflowing | 1 |
| 25795 | erflourish | 1 |
| 25796 | erects | 1 |
| 25797 | erdoing | 1 |
| 25798 | ercrows | 1 |
| 25799 | ercover | 1 |
| 25800 | ercilla | 1 |
| 25801 | ercharging | 1 |
| 25802 | ercharged | 1 |
| 25803 | ercame | 1 |
| 25804 | erblows | 1 |
| 25805 | erbeat | 1 |
| 25806 | eras | 1 |
| 25807 | equivocates | 1 |
| 25808 | equivocate | 1 |
| 25809 | equivalents | 1 |
| 25810 | equitably | 1 |
| 25811 | equitable | 1 |
| 25812 | equipment | 1 |
| 25813 | equinoxes | 1 |
| 25814 | equinox | 1 |
| 25815 | equanimity | 1 |
| 25816 | equalness | 1 |
| 25817 | equalities | 1 |
| 25818 | equalised | 1 |
| 25819 | epitome | 1 |
| 25820 | epitheton | 1 |
| 25821 | epistrophus | 1 |
| 25822 | epilogues | 1 |
| 25823 | epileptic | 1 |
| 25824 | epilepsy | 1 |
| 25825 | epidaurus | 1 |
| 25826 | epicurus | 1 |
| 25827 | epicurism | 1 |
| 25828 | epicures | 1 |
| 25829 | epicure | 1 |
| 25830 | ephesians | 1 |
| 25831 | ephesian | 1 |
| 25832 | enwraps | 1 |
| 25833 | enwombed | 1 |
| 25834 | enwheel | 1 |
| 25835 | enviously | 1 |
| 25836 | envies | 1 |
| 25837 | envenoms | 1 |
| 25838 | enveloping | 1 |
| 25839 | entwist | 1 |
| 25840 | entry | 1 |
| 25841 | entrusting | 1 |
| 25842 | entrench | 1 |
| 25843 | entreatments | 1 |
| 25844 | entre | 1 |
| 25845 | entrapp | 1 |
| 25846 | entombs | 1 |
| 25847 | entombed | 1 |
| 25848 | entitling | 1 |
| 25849 | enticements | 1 |
| 25850 | enticed | 1 |
| 25851 | enthusiasm | 1 |
| 25852 | enthrals | 1 |
| 25853 | entertainer | 1 |
| 25854 | entendre | 1 |
| 25855 | entangles | 1 |
| 25856 | entangle | 1 |
| 25857 | entame | 1 |
| 25858 | entails | 1 |
| 25859 | entailed | 1 |
| 25860 | enswathed | 1 |
| 25861 | ensued | 1 |
| 25862 | ensu | 1 |
| 25863 | ensteep | 1 |
| 25864 | ensnareth | 1 |
| 25865 | ensnared | 1 |
| 25866 | ensman | 1 |
| 25867 | enskied | 1 |
| 25868 | enshrines | 1 |
| 25869 | enshrined | 1 |
| 25870 | enshielded | 1 |
| 25871 | enshelter | 1 |
| 25872 | ensemble | 1 |
| 25873 | enseignez | 1 |
| 25874 | enseigne | 1 |
| 25875 | ensear | 1 |
| 25876 | enseamed | 1 |
| 25877 | ensconcing | 1 |
| 25878 | enschedul | 1 |
| 25879 | enrounded | 1 |
| 25880 | enrooted | 1 |
| 25881 | enrobe | 1 |
| 25882 | enrob | 1 |
| 25883 | enrique | 1 |
| 25884 | enrings | 1 |
| 25885 | enridged | 1 |
| 25886 | enriching | 1 |
| 25887 | enriches | 1 |
| 25888 | enrapt | 1 |
| 25889 | enrank | 1 |
| 25890 | enrages | 1 |
| 25891 | enquir | 1 |
| 25892 | enpierced | 1 |
| 25893 | enpatron | 1 |
| 25894 | enormously | 1 |
| 25895 | enon | 1 |
| 25896 | enobarb | 1 |
| 25897 | ennobled | 1 |
| 25898 | ennoble | 1 |
| 25899 | enmities | 1 |
| 25900 | enmeshed | 1 |
| 25901 | enmesh | 1 |
| 25902 | enlist | 1 |
| 25903 | enlink | 1 |
| 25904 | enlightened | 1 |
| 25905 | enlargeth | 1 |
| 25906 | enlard | 1 |
| 25907 | enjoyer | 1 |
| 25908 | enjoyable | 1 |
| 25909 | enjoins | 1 |
| 25910 | enigmatical | 1 |
| 25911 | enhancement | 1 |
| 25912 | enguard | 1 |
| 25913 | engrossments | 1 |
| 25914 | engrossing | 1 |
| 25915 | engrossest | 1 |
| 25916 | engrave | 1 |
| 25917 | engrafted | 1 |
| 25918 | engraft | 1 |
| 25919 | engraffed | 1 |
| 25920 | engluts | 1 |
| 25921 | enginer | 1 |
| 25922 | engilds | 1 |
| 25923 | engaol | 1 |
| 25924 | engages | 1 |
| 25925 | enfreedoming | 1 |
| 25926 | enfreed | 1 |
| 25927 | enfranchised | 1 |
| 25928 | enfranched | 1 |
| 25929 | enforcest | 1 |
| 25930 | enforcedly | 1 |
| 25931 | enfoldings | 1 |
| 25932 | enfold | 1 |
| 25933 | enfetter | 1 |
| 25934 | enfeoff | 1 |
| 25935 | enfeebles | 1 |
| 25936 | enew | 1 |
| 25937 | enernies | 1 |
| 25938 | energies | 1 |
| 25939 | eneas | 1 |
| 25940 | endymion | 1 |
| 25941 | endurer | 1 |
| 25942 | endu | 1 |
| 25943 | endows | 1 |
| 25944 | endive | 1 |
| 25945 | endite | 1 |
| 25946 | ender | 1 |
| 25947 | endart | 1 |
| 25948 | endangering | 1 |
| 25949 | endamagement | 1 |
| 25950 | encumbered | 1 |
| 25951 | encumb | 1 |
| 25952 | encroaching | 1 |
| 25953 | encrimsoned | 1 |
| 25954 | encouraging | 1 |
| 25955 | encounterer | 1 |
| 25956 | encorporal | 1 |
| 25957 | encore | 1 |
| 25958 | encompassment | 1 |
| 25959 | encompasseth | 1 |
| 25960 | encompassed | 1 |
| 25961 | enclouded | 1 |
| 25962 | enclosure | 1 |
| 25963 | enclosing | 1 |
| 25964 | encloseth | 1 |
| 25965 | encloses | 1 |
| 25966 | enclos | 1 |
| 25967 | encircling | 1 |
| 25968 | encircled | 1 |
| 25969 | encircle | 1 |
| 25970 | enchas | 1 |
| 25971 | enchantresses | 1 |
| 25972 | enchantress | 1 |
| 25973 | enchantingly | 1 |
| 25974 | enchafed | 1 |
| 25975 | enchaf | 1 |
| 25976 | enceladus | 1 |
| 25977 | encave | 1 |
| 25978 | encasing | 1 |
| 25979 | encampment | 1 |
| 25980 | encamisado | 1 |
| 25981 | enanmour | 1 |
| 25982 | enamourned | 1 |
| 25983 | enamelled | 1 |
| 25984 | enactures | 1 |
| 25985 | enactments | 1 |
| 25986 | enables | 1 |
| 25987 | emulator | 1 |
| 25988 | emulations | 1 |
| 25989 | empowered | 1 |
| 25990 | employer | 1 |
| 25991 | empleached | 1 |
| 25992 | empiricutic | 1 |
| 25993 | empirics | 1 |
| 25994 | emperial | 1 |
| 25995 | emperal | 1 |
| 25996 | empale | 1 |
| 25997 | emotions | 1 |
| 25998 | emmanuel | 1 |
| 25999 | eminently | 1 |
| 26000 | emhracing | 1 |
| 26001 | embroidering | 1 |
| 26002 | embrasures | 1 |
| 26003 | embowel | 1 |
| 26004 | embounded | 1 |
| 26005 | emboldens | 1 |
| 26006 | embold | 1 |
| 26007 | embodied | 1 |
| 26008 | emblaze | 1 |
| 26009 | embellishment | 1 |
| 26010 | embellished | 1 |
| 26011 | embay | 1 |
| 26012 | embattle | 1 |
| 26013 | embattailed | 1 |
| 26014 | embassade | 1 |
| 26015 | embarrass | 1 |
| 26016 | embarquements | 1 |
| 26017 | embarkation | 1 |
| 26018 | embalms | 1 |
| 26019 | embalm | 1 |
| 26020 | emballing | 1 |
| 26021 | elvish | 1 |
| 26022 | elucidate | 1 |
| 26023 | eloquently | 1 |
| 26024 | ellen | 1 |
| 26025 | elle | 1 |
| 26026 | eligible | 1 |
| 26027 | eliads | 1 |
| 26028 | elflocks | 1 |
| 26029 | elevated | 1 |
| 26030 | elephants | 1 |
| 26031 | elegancy | 1 |
| 26032 | elderly | 1 |
| 26033 | elches | 1 |
| 26034 | elapsed | 1 |
| 26035 | elaborately | 1 |
| 26036 | eject | 1 |
| 26037 | eisel | 1 |
| 26038 | eightpenny | 1 |
| 26039 | eie | 1 |
| 26040 | egress | 1 |
| 26041 | egregiously | 1 |
| 26042 | egmont | 1 |
| 26043 | egma | 1 |
| 26044 | eggshell | 1 |
| 26045 | eget | 1 |
| 26046 | egally | 1 |
| 26047 | egal | 1 |
| 26048 | eftest | 1 |
| 26049 | effuse | 1 |
| 26050 | effus | 1 |
| 26051 | effigy | 1 |
| 26052 | effigies | 1 |
| 26053 | efficacy | 1 |
| 26054 | effectless | 1 |
| 26055 | effective | 1 |
| 26056 | effacing | 1 |
| 26057 | eels | 1 |
| 26058 | educated | 1 |
| 26059 | educate | 1 |
| 26060 | edifies | 1 |
| 26061 | edifices | 1 |
| 26062 | edging | 1 |
| 26063 | eden | 1 |
| 26064 | ecstasies | 1 |
| 26065 | ecstacy | 1 |
| 26066 | economy | 1 |
| 26067 | economical | 1 |
| 26068 | ecolier | 1 |
| 26069 | eclogue | 1 |
| 26070 | ecliptics | 1 |
| 26071 | eclipsed | 1 |
| 26072 | echapper | 1 |
| 26073 | ecce | 1 |
| 26074 | ebrew | 1 |
| 26075 | eave | 1 |
| 26076 | eaux | 1 |
| 26077 | eatables | 1 |
| 26078 | eastertime | 1 |
| 26079 | easiliest | 1 |
| 26080 | eases | 1 |
| 26081 | easeful | 1 |
| 26082 | earthquakes | 1 |
| 26083 | earthlier | 1 |
| 26084 | earthen | 1 |
| 26085 | earliness | 1 |
| 26086 | earing | 1 |
| 26087 | eanlings | 1 |
| 26088 | eaning | 1 |
| 26089 | dwellings | 1 |
| 26090 | dusted | 1 |
| 26091 | durindana | 1 |
| 26092 | duration | 1 |
| 26093 | dupp | 1 |
| 26094 | duped | 1 |
| 26095 | dunstable | 1 |
| 26096 | dunsmore | 1 |
| 26097 | dunnest | 1 |
| 26098 | dunderhead | 1 |
| 26099 | dummy | 1 |
| 26100 | dumbe | 1 |
| 26101 | dulls | 1 |
| 26102 | dulcineae | 1 |
| 26103 | dulche | 1 |
| 26104 | duff | 1 |
| 26105 | duero | 1 |
| 26106 | duer | 1 |
| 26107 | duenissima | 1 |
| 26108 | dudgeon | 1 |
| 26109 | duchies | 1 |
| 26110 | dubitat | 1 |
| 26111 | dubbing | 1 |
| 26112 | dryshod | 1 |
| 26113 | dryads | 1 |
| 26114 | drumming | 1 |
| 26115 | drummers | 1 |
| 26116 | drummer | 1 |
| 26117 | drumble | 1 |
| 26118 | drugg | 1 |
| 26119 | drudges | 1 |
| 26120 | drowsily | 1 |
| 26121 | drowse | 1 |
| 26122 | drows | 1 |
| 26123 | drovier | 1 |
| 26124 | drovers | 1 |
| 26125 | droven | 1 |
| 26126 | drought | 1 |
| 26127 | drossy | 1 |
| 26128 | dropt | 1 |
| 26129 | dropsies | 1 |
| 26130 | dropsied | 1 |
| 26131 | droppings | 1 |
| 26132 | droppeth | 1 |
| 26133 | droppest | 1 |
| 26134 | dropper | 1 |
| 26135 | droplets | 1 |
| 26136 | dropheir | 1 |
| 26137 | droopeth | 1 |
| 26138 | drooped | 1 |
| 26139 | dromios | 1 |
| 26140 | droit | 1 |
| 26141 | drizzles | 1 |
| 26142 | drizzle | 1 |
| 26143 | drivelling | 1 |
| 26144 | driv | 1 |
| 26145 | drinker | 1 |
| 26146 | drily | 1 |
| 26147 | drifting | 1 |
| 26148 | dribbling | 1 |
| 26149 | dribble | 1 |
| 26150 | dresser | 1 |
| 26151 | dreg | 1 |
| 26152 | drearning | 1 |
| 26153 | dreamers | 1 |
| 26154 | dreadest | 1 |
| 26155 | draymen | 1 |
| 26156 | drayman | 1 |
| 26157 | drawling | 1 |
| 26158 | drawest | 1 |
| 26159 | drapery | 1 |
| 26160 | draperies | 1 |
| 26161 | dramas | 1 |
| 26162 | drake | 1 |
| 26163 | dragonish | 1 |
| 26164 | drafted | 1 |
| 26165 | draft | 1 |
| 26166 | drachma | 1 |
| 26167 | drachm | 1 |
| 26168 | drabs | 1 |
| 26169 | drabbing | 1 |
| 26170 | dozy | 1 |
| 26171 | dozens | 1 |
| 26172 | dowsabel | 1 |
| 26173 | dowries | 1 |
| 26174 | downtrodden | 1 |
| 26175 | downtrod | 1 |
| 26176 | downstrokes | 1 |
| 26177 | downstairs | 1 |
| 26178 | dowle | 1 |
| 26179 | dowerless | 1 |
| 26180 | dowdy | 1 |
| 26181 | douts | 1 |
| 26182 | doute | 1 |
| 26183 | doughy | 1 |
| 26184 | doubles | 1 |
| 26185 | doubler | 1 |
| 26186 | doubleness | 1 |
| 26187 | doteth | 1 |
| 26188 | doters | 1 |
| 26189 | doted | 1 |
| 26190 | dotards | 1 |
| 26191 | dotant | 1 |
| 26192 | dorsetshire | 1 |
| 26193 | dormitat | 1 |
| 26194 | doreus | 1 |
| 26195 | dorado | 1 |
| 26196 | doorkeeper | 1 |
| 26197 | donoso | 1 |
| 26198 | donnerai | 1 |
| 26199 | donner | 1 |
| 26200 | donned | 1 |
| 26201 | donne | 1 |
| 26202 | donec | 1 |
| 26203 | donde | 1 |
| 26204 | donc | 1 |
| 26205 | dommelton | 1 |
| 26206 | dominion | 1 |
| 26207 | dominical | 1 |
| 26208 | domineer | 1 |
| 26209 | dominations | 1 |
| 26210 | dominant | 1 |
| 26211 | dominance | 1 |
| 26212 | domestics | 1 |
| 26213 | domain | 1 |
| 26214 | dolts | 1 |
| 26215 | doltish | 1 |
| 26216 | dolorous | 1 |
| 26217 | dolor | 1 |
| 26218 | dolly | 1 |
| 26219 | dollars | 1 |
| 26220 | dollar | 1 |
| 26221 | dolfos | 1 |
| 26222 | dolet | 1 |
| 26223 | doits | 1 |
| 26224 | dogmatism | 1 |
| 26225 | dogfish | 1 |
| 26226 | doest | 1 |
| 26227 | dodging | 1 |
| 26228 | dodged | 1 |
| 26229 | dodge | 1 |
| 26230 | doctored | 1 |
| 26231 | docile | 1 |
| 26232 | doating | 1 |
| 26233 | dizy | 1 |
| 26234 | divulging | 1 |
| 26235 | divulge | 1 |
| 26236 | divulg | 1 |
| 26237 | divorcing | 1 |
| 26238 | divorcement | 1 |
| 26239 | diviners | 1 |
| 26240 | diviner | 1 |
| 26241 | divineness | 1 |
| 26242 | divin | 1 |
| 26243 | divideth | 1 |
| 26244 | dividant | 1 |
| 26245 | dividable | 1 |
| 26246 | divested | 1 |
| 26247 | diverts | 1 |
| 26248 | diversely | 1 |
| 26249 | diverse | 1 |
| 26250 | diver | 1 |
| 26251 | div | 1 |
| 26252 | diurnal | 1 |
| 26253 | ditchers | 1 |
| 26254 | disvouch | 1 |
| 26255 | disvalued | 1 |
| 26256 | disunite | 1 |
| 26257 | disturber | 1 |
| 26258 | disturbances | 1 |
| 26259 | distrusted | 1 |
| 26260 | districts | 1 |
| 26261 | distributes | 1 |
| 26262 | distressing | 1 |
| 26263 | distressedest | 1 |
| 26264 | distracts | 1 |
| 26265 | distinguishment | 1 |
| 26266 | distingue | 1 |
| 26267 | distils | 1 |
| 26268 | distilment | 1 |
| 26269 | distills | 1 |
| 26270 | distilling | 1 |
| 26271 | distich | 1 |
| 26272 | distempering | 1 |
| 26273 | distemperatures | 1 |
| 26274 | distemperature | 1 |
| 26275 | distasted | 1 |
| 26276 | distains | 1 |
| 26277 | distain | 1 |
| 26278 | distaffs | 1 |
| 26279 | dissolutions | 1 |
| 26280 | dissipation | 1 |
| 26281 | dissembly | 1 |
| 26282 | dissemblers | 1 |
| 26283 | disseat | 1 |
| 26284 | disrespectfully | 1 |
| 26285 | disrespect | 1 |
| 26286 | disreputable | 1 |
| 26287 | disrelish | 1 |
| 26288 | disregarding | 1 |
| 26289 | disregarded | 1 |
| 26290 | disquietude | 1 |
| 26291 | disquiets | 1 |
| 26292 | disquietly | 1 |
| 26293 | disquantity | 1 |
| 26294 | disputing | 1 |
| 26295 | disputations | 1 |
| 26296 | disputation | 1 |
| 26297 | disputable | 1 |
| 26298 | dispursed | 1 |
| 26299 | disproved | 1 |
| 26300 | disprov | 1 |
| 26301 | dispropertied | 1 |
| 26302 | dispraisingly | 1 |
| 26303 | dispossessing | 1 |
| 26304 | disports | 1 |
| 26305 | disponge | 1 |
| 26306 | displanting | 1 |
| 26307 | displant | 1 |
| 26308 | displaced | 1 |
| 26309 | dispiteous | 1 |
| 26310 | dispersing | 1 |
| 26311 | dispenses | 1 |
| 26312 | dispensations | 1 |
| 26313 | dispel | 1 |
| 26314 | dispassionate | 1 |
| 26315 | dispark | 1 |
| 26316 | disparity | 1 |
| 26317 | disparaging | 1 |
| 26318 | disparagements | 1 |
| 26319 | disorb | 1 |
| 26320 | disobeys | 1 |
| 26321 | disobeying | 1 |
| 26322 | disnatur | 1 |
| 26323 | dismissal | 1 |
| 26324 | dismes | 1 |
| 26325 | dismemb | 1 |
| 26326 | dismask | 1 |
| 26327 | dismantled | 1 |
| 26328 | dislodg | 1 |
| 26329 | dislocate | 1 |
| 26330 | dislimns | 1 |
| 26331 | disliken | 1 |
| 26332 | disjunction | 1 |
| 26333 | disjointed | 1 |
| 26334 | disjoins | 1 |
| 26335 | disjoining | 1 |
| 26336 | disillusion | 1 |
| 26337 | dishwater | 1 |
| 26338 | dishonourably | 1 |
| 26339 | dishonors | 1 |
| 26340 | dishonorable | 1 |
| 26341 | dishonor | 1 |
| 26342 | dishevelled | 1 |
| 26343 | disheartens | 1 |
| 26344 | disheartened | 1 |
| 26345 | dishearten | 1 |
| 26346 | dishclouts | 1 |
| 26347 | dishabited | 1 |
| 26348 | disgusting | 1 |
| 26349 | disguiser | 1 |
| 26350 | disgracing | 1 |
| 26351 | disgraceful | 1 |
| 26352 | disgoverned | 1 |
| 26353 | disedg | 1 |
| 26354 | disdnguish | 1 |
| 26355 | disdainfully | 1 |
| 26356 | disdained | 1 |
| 26357 | discredits | 1 |
| 26358 | discoverest | 1 |
| 26359 | discoverers | 1 |
| 26360 | discoverer | 1 |
| 26361 | discov | 1 |
| 26362 | discoursive | 1 |
| 26363 | discoursing | 1 |
| 26364 | discourser | 1 |
| 26365 | discouraged | 1 |
| 26366 | discourage | 1 |
| 26367 | discontinued | 1 |
| 26368 | discontinue | 1 |
| 26369 | discontenting | 1 |
| 26370 | disconsolately | 1 |
| 26371 | discommend | 1 |
| 26372 | discomforts | 1 |
| 26373 | discomfortable | 1 |
| 26374 | discomfitures | 1 |
| 26375 | discomfit | 1 |
| 26376 | discolours | 1 |
| 26377 | disclaims | 1 |
| 26378 | disciplined | 1 |
| 26379 | disciplinants | 1 |
| 26380 | discipled | 1 |
| 26381 | discerns | 1 |
| 26382 | discernings | 1 |
| 26383 | discerner | 1 |
| 26384 | discased | 1 |
| 26385 | discandying | 1 |
| 26386 | discandy | 1 |
| 26387 | disbursement | 1 |
| 26388 | disburs | 1 |
| 26389 | disburdened | 1 |
| 26390 | disbranch | 1 |
| 26391 | disbench | 1 |
| 26392 | disbelieve | 1 |
| 26393 | disarranged | 1 |
| 26394 | disarmeth | 1 |
| 26395 | disarmed | 1 |
| 26396 | disapprove | 1 |
| 26397 | disannuls | 1 |
| 26398 | disannul | 1 |
| 26399 | disanimates | 1 |
| 26400 | disallow | 1 |
| 26401 | disagree | 1 |
| 26402 | disabusing | 1 |
| 26403 | disabling | 1 |
| 26404 | disability | 1 |
| 26405 | dirlos | 1 |
| 26406 | direst | 1 |
| 26407 | direness | 1 |
| 26408 | director | 1 |
| 26409 | directive | 1 |
| 26410 | dir | 1 |
| 26411 | dips | 1 |
| 26412 | dipping | 1 |
| 26413 | dipp | 1 |
| 26414 | dioscorides | 1 |
| 26415 | diomede | 1 |
| 26416 | dinnertime | 1 |
| 26417 | diner | 1 |
| 26418 | dims | 1 |
| 26419 | dimples | 1 |
| 26420 | dimming | 1 |
| 26421 | dimity | 1 |
| 26422 | diminished | 1 |
| 26423 | diluculo | 1 |
| 26424 | diligite | 1 |
| 26425 | dilemmas | 1 |
| 26426 | dilemma | 1 |
| 26427 | dildos | 1 |
| 26428 | dild | 1 |
| 26429 | dilations | 1 |
| 26430 | dilapidated | 1 |
| 26431 | digt | 1 |
| 26432 | digs | 1 |
| 26433 | dignitary | 1 |
| 26434 | diffusest | 1 |
| 26435 | diffused | 1 |
| 26436 | diffuse | 1 |
| 26437 | diffidences | 1 |
| 26438 | difficile | 1 |
| 26439 | differency | 1 |
| 26440 | differed | 1 |
| 26441 | dieter | 1 |
| 26442 | diere | 1 |
| 26443 | diedst | 1 |
| 26444 | didest | 1 |
| 26445 | diddle | 1 |
| 26446 | dictator | 1 |
| 26447 | dico | 1 |
| 26448 | dicky | 1 |
| 26449 | dickon | 1 |
| 26450 | dickens | 1 |
| 26451 | dich | 1 |
| 26452 | dicers | 1 |
| 26453 | dic | 1 |
| 26454 | dibble | 1 |
| 26455 | diaper | 1 |
| 26456 | diameter | 1 |
| 26457 | diamantine | 1 |
| 26458 | dialogued | 1 |
| 26459 | diabolo | 1 |
| 26460 | diablo | 1 |
| 26461 | dexterously | 1 |
| 26462 | dexteriously | 1 |
| 26463 | dexter | 1 |
| 26464 | dewy | 1 |
| 26465 | dewlapp | 1 |
| 26466 | dewlap | 1 |
| 26467 | dewdrops | 1 |
| 26468 | dewberries | 1 |
| 26469 | devourers | 1 |
| 26470 | devotes | 1 |
| 26471 | devonshire | 1 |
| 26472 | devoir | 1 |
| 26473 | devises | 1 |
| 26474 | devesting | 1 |
| 26475 | deus | 1 |
| 26476 | detractions | 1 |
| 26477 | detesting | 1 |
| 26478 | determinations | 1 |
| 26479 | detention | 1 |
| 26480 | detector | 1 |
| 26481 | detection | 1 |
| 26482 | detains | 1 |
| 26483 | detained | 1 |
| 26484 | detailed | 1 |
| 26485 | detached | 1 |
| 26486 | det | 1 |
| 26487 | desultory | 1 |
| 26488 | destructive | 1 |
| 26489 | destructions | 1 |
| 26490 | destroyers | 1 |
| 26491 | dest | 1 |
| 26492 | dessert | 1 |
| 26493 | despondency | 1 |
| 26494 | despises | 1 |
| 26495 | despiser | 1 |
| 26496 | desperado | 1 |
| 26497 | desirers | 1 |
| 26498 | designments | 1 |
| 26499 | designment | 1 |
| 26500 | designing | 1 |
| 26501 | designedly | 1 |
| 26502 | designations | 1 |
| 26503 | deservers | 1 |
| 26504 | deservedly | 1 |
| 26505 | descriptions | 1 |
| 26506 | descents | 1 |
| 26507 | descension | 1 |
| 26508 | desartless | 1 |
| 26509 | derogatory | 1 |
| 26510 | derogation | 1 |
| 26511 | derogately | 1 |
| 26512 | deriving | 1 |
| 26513 | derivative | 1 |
| 26514 | derivation | 1 |
| 26515 | derides | 1 |
| 26516 | deranged | 1 |
| 26517 | derange | 1 |
| 26518 | deputing | 1 |
| 26519 | deputies | 1 |
| 26520 | deputed | 1 |
| 26521 | depute | 1 |
| 26522 | depression | 1 |
| 26523 | depressed | 1 |
| 26524 | depress | 1 |
| 26525 | depreciation | 1 |
| 26526 | depravities | 1 |
| 26527 | depraves | 1 |
| 26528 | deprave | 1 |
| 26529 | depravation | 1 |
| 26530 | deprav | 1 |
| 26531 | depository | 1 |
| 26532 | depositary | 1 |
| 26533 | depositaries | 1 |
| 26534 | deposit | 1 |
| 26535 | deportment | 1 |
| 26536 | depopulate | 1 |
| 26537 | deploring | 1 |
| 26538 | deplorable | 1 |
| 26539 | depender | 1 |
| 26540 | dependents | 1 |
| 26541 | dependences | 1 |
| 26542 | dependant | 1 |
| 26543 | depeche | 1 |
| 26544 | departures | 1 |
| 26545 | departs | 1 |
| 26546 | departest | 1 |
| 26547 | denunciation | 1 |
| 26548 | denouncing | 1 |
| 26549 | denotement | 1 |
| 26550 | denoted | 1 |
| 26551 | deni | 1 |
| 26552 | demuring | 1 |
| 26553 | demur | 1 |
| 26554 | demosthenes | 1 |
| 26555 | demonstrative | 1 |
| 26556 | demonstrating | 1 |
| 26557 | demonstrated | 1 |
| 26558 | demonstrable | 1 |
| 26559 | demoiselles | 1 |
| 26560 | demeanor | 1 |
| 26561 | delves | 1 |
| 26562 | delver | 1 |
| 26563 | della | 1 |
| 26564 | deliv | 1 |
| 26565 | deliciousness | 1 |
| 26566 | delicates | 1 |
| 26567 | delegated | 1 |
| 26568 | deja | 1 |
| 26569 | deigned | 1 |
| 26570 | deifying | 1 |
| 26571 | deified | 1 |
| 26572 | defuse | 1 |
| 26573 | defunction | 1 |
| 26574 | deftly | 1 |
| 26575 | defrauded | 1 |
| 26576 | defraud | 1 |
| 26577 | deformities | 1 |
| 26578 | deflow | 1 |
| 26579 | definitively | 1 |
| 26580 | definitive | 1 |
| 26581 | definite | 1 |
| 26582 | definement | 1 |
| 26583 | defiling | 1 |
| 26584 | defiler | 1 |
| 26585 | deficiencies | 1 |
| 26586 | defiances | 1 |
| 26587 | deferr | 1 |
| 26588 | defenceless | 1 |
| 26589 | defeats | 1 |
| 26590 | defamatory | 1 |
| 26591 | defam | 1 |
| 26592 | defacing | 1 |
| 26593 | defacers | 1 |
| 26594 | defacer | 1 |
| 26595 | defaced | 1 |
| 26596 | deesse | 1 |
| 26597 | deepvow | 1 |
| 26598 | deeming | 1 |
| 26599 | deedless | 1 |
| 26600 | deduce | 1 |
| 26601 | decreasing | 1 |
| 26602 | decreas | 1 |
| 26603 | decoy | 1 |
| 26604 | decoration | 1 |
| 26605 | decorated | 1 |
| 26606 | decoct | 1 |
| 26607 | declensions | 1 |
| 26608 | declarations | 1 |
| 26609 | declar | 1 |
| 26610 | deckt | 1 |
| 26611 | decks | 1 |
| 26612 | deciphers | 1 |
| 26613 | decimation | 1 |
| 26614 | decimas | 1 |
| 26615 | deciding | 1 |
| 26616 | decides | 1 |
| 26617 | decerns | 1 |
| 26618 | deceptive | 1 |
| 26619 | deceptious | 1 |
| 26620 | decency | 1 |
| 26621 | deceiveth | 1 |
| 26622 | deceivest | 1 |
| 26623 | deceivers | 1 |
| 26624 | decaying | 1 |
| 26625 | decayer | 1 |
| 26626 | decapitating | 1 |
| 26627 | decapitated | 1 |
| 26628 | decanted | 1 |
| 26629 | debuty | 1 |
| 26630 | debted | 1 |
| 26631 | deborah | 1 |
| 26632 | debonair | 1 |
| 26633 | debits | 1 |
| 26634 | debility | 1 |
| 26635 | debateth | 1 |
| 26636 | debaseth | 1 |
| 26637 | deathsmen | 1 |
| 26638 | deathful | 1 |
| 26639 | dearths | 1 |
| 26640 | dearness | 1 |
| 26641 | deanery | 1 |
| 26642 | dealest | 1 |
| 26643 | dealers | 1 |
| 26644 | deafs | 1 |
| 26645 | deafing | 1 |
| 26646 | deadened | 1 |
| 26647 | daytime | 1 |
| 26648 | david | 1 |
| 26649 | daventry | 1 |
| 26650 | dauntlessly | 1 |
| 26651 | dated | 1 |
| 26652 | data | 1 |
| 26653 | dartford | 1 |
| 26654 | darter | 1 |
| 26655 | darraign | 1 |
| 26656 | darn | 1 |
| 26657 | darlings | 1 |
| 26658 | darkish | 1 |
| 26659 | darkens | 1 |
| 26660 | darkened | 1 |
| 26661 | daresay | 1 |
| 26662 | dareful | 1 |
| 26663 | dardanian | 1 |
| 26664 | daraida | 1 |
| 26665 | dapples | 1 |
| 26666 | danskers | 1 |
| 26667 | dankish | 1 |
| 26668 | dangling | 1 |
| 26669 | dang | 1 |
| 26670 | dandy | 1 |
| 26671 | danced | 1 |
| 26672 | danaes | 1 |
| 26673 | dan | 1 |
| 26674 | damsons | 1 |
| 26675 | dams | 1 |
| 26676 | dampness | 1 |
| 26677 | damosella | 1 |
| 26678 | damon | 1 |
| 26679 | damoiselle | 1 |
| 26680 | damns | 1 |
| 26681 | damnably | 1 |
| 26682 | damasked | 1 |
| 26683 | damages | 1 |
| 26684 | daisy | 1 |
| 26685 | daisied | 1 |
| 26686 | dais | 1 |
| 26687 | daintry | 1 |
| 26688 | daintiness | 1 |
| 26689 | daintier | 1 |
| 26690 | dagonet | 1 |
| 26691 | daffest | 1 |
| 26692 | daffed | 1 |
| 26693 | daemon | 1 |
| 26694 | daedalus | 1 |
| 26695 | dace | 1 |
| 26696 | dabbled | 1 |
| 26697 | cyrus | 1 |
| 26698 | cypriot | 1 |
| 26699 | cynthia | 1 |
| 26700 | cynic | 1 |
| 26701 | cyme | 1 |
| 26702 | cymbals | 1 |
| 26703 | cygnets | 1 |
| 26704 | cxsar | 1 |
| 26705 | cuttlefish | 1 |
| 26706 | cuttle | 1 |
| 26707 | cutpurses | 1 |
| 26708 | cutler | 1 |
| 26709 | custure | 1 |
| 26710 | customed | 1 |
| 26711 | custalorum | 1 |
| 26712 | cushes | 1 |
| 26713 | curvetting | 1 |
| 26714 | curvets | 1 |
| 26715 | curvet | 1 |
| 26716 | curves | 1 |
| 26717 | curtsied | 1 |
| 26718 | curtius | 1 |
| 26719 | curtii | 1 |
| 26720 | curtailing | 1 |
| 26721 | curstness | 1 |
| 26722 | curstest | 1 |
| 26723 | curster | 1 |
| 26724 | cursorary | 1 |
| 26725 | currants | 1 |
| 26726 | currance | 1 |
| 26727 | curling | 1 |
| 26728 | curiel | 1 |
| 26729 | curdled | 1 |
| 26730 | curdied | 1 |
| 26731 | curbing | 1 |
| 26732 | curambro | 1 |
| 26733 | curadillo | 1 |
| 26734 | cuppele | 1 |
| 26735 | cupboarding | 1 |
| 26736 | cuore | 1 |
| 26737 | cunnings | 1 |
| 26738 | culverin | 1 |
| 26739 | culture | 1 |
| 26740 | cultivate | 1 |
| 26741 | culprits | 1 |
| 26742 | culpable | 1 |
| 26743 | cullionly | 1 |
| 26744 | cullion | 1 |
| 26745 | cuique | 1 |
| 26746 | cues | 1 |
| 26747 | cudgelling | 1 |
| 26748 | cudgeled | 1 |
| 26749 | cubs | 1 |
| 26750 | cubits | 1 |
| 26751 | cubit | 1 |
| 26752 | cubiculo | 1 |
| 26753 | cubbert | 1 |
| 26754 | cuatrero | 1 |
| 26755 | cuartos | 1 |
| 26756 | cuartillos | 1 |
| 26757 | crystals | 1 |
| 26758 | crystalline | 1 |
| 26759 | cruzadoes | 1 |
| 26760 | cruz | 1 |
| 26761 | crusty | 1 |
| 26762 | crushest | 1 |
| 26763 | crushes | 1 |
| 26764 | crusadoes | 1 |
| 26765 | crumbling | 1 |
| 26766 | crumble | 1 |
| 26767 | crumb | 1 |
| 26768 | crum | 1 |
| 26769 | cruisers | 1 |
| 26770 | cruiser | 1 |
| 26771 | cruise | 1 |
| 26772 | cruelties | 1 |
| 26773 | cruels | 1 |
| 26774 | crueller | 1 |
| 26775 | cruell | 1 |
| 26776 | crudy | 1 |
| 26777 | crucis | 1 |
| 26778 | crucifix | 1 |
| 26779 | crownet | 1 |
| 26780 | crowkeeper | 1 |
| 26781 | crowflowers | 1 |
| 26782 | crowed | 1 |
| 26783 | crowded | 1 |
| 26784 | crowbar | 1 |
| 26785 | crost | 1 |
| 26786 | crossness | 1 |
| 26787 | crossly | 1 |
| 26788 | crossings | 1 |
| 26789 | crossest | 1 |
| 26790 | crooking | 1 |
| 26791 | crookback | 1 |
| 26792 | crone | 1 |
| 26793 | cromer | 1 |
| 26794 | croaks | 1 |
| 26795 | croaking | 1 |
| 26796 | critics | 1 |
| 26797 | criticising | 1 |
| 26798 | criticise | 1 |
| 26799 | cristobal | 1 |
| 26800 | crispianus | 1 |
| 26801 | crisped | 1 |
| 26802 | cripples | 1 |
| 26803 | crinkled | 1 |
| 26804 | cringe | 1 |
| 26805 | crimping | 1 |
| 26806 | crimeless | 1 |
| 26807 | crimeful | 1 |
| 26808 | crieth | 1 |
| 26809 | criers | 1 |
| 26810 | cribbings | 1 |
| 26811 | cribb | 1 |
| 26812 | crevices | 1 |
| 26813 | crevice | 1 |
| 26814 | cretan | 1 |
| 26815 | crestless | 1 |
| 26816 | crestfallen | 1 |
| 26817 | crested | 1 |
| 26818 | cressy | 1 |
| 26819 | cressids | 1 |
| 26820 | cressets | 1 |
| 26821 | crescive | 1 |
| 26822 | creeks | 1 |
| 26823 | credulity | 1 |
| 26824 | credits | 1 |
| 26825 | creates | 1 |
| 26826 | creams | 1 |
| 26827 | craziness | 1 |
| 26828 | crawls | 1 |
| 26829 | cravings | 1 |
| 26830 | craveth | 1 |
| 26831 | cravens | 1 |
| 26832 | craved | 1 |
| 26833 | crare | 1 |
| 26834 | crants | 1 |
| 26835 | crannies | 1 |
| 26836 | crannied | 1 |
| 26837 | cranks | 1 |
| 26838 | cranking | 1 |
| 26839 | crane | 1 |
| 26840 | crams | 1 |
| 26841 | cramped | 1 |
| 26842 | craftsmen | 1 |
| 26843 | craftsman | 1 |
| 26844 | craftier | 1 |
| 26845 | craftied | 1 |
| 26846 | crafted | 1 |
| 26847 | cracker | 1 |
| 26848 | coziers | 1 |
| 26849 | cozener | 1 |
| 26850 | coystrill | 1 |
| 26851 | cowl | 1 |
| 26852 | cowish | 1 |
| 26853 | cowhide | 1 |
| 26854 | cowheels | 1 |
| 26855 | cowardship | 1 |
| 26856 | cowarded | 1 |
| 26857 | covets | 1 |
| 26858 | covetously | 1 |
| 26859 | covetings | 1 |
| 26860 | coveting | 1 |
| 26861 | covertly | 1 |
| 26862 | cove | 1 |
| 26863 | coutume | 1 |
| 26864 | couterfeit | 1 |
| 26865 | courtships | 1 |
| 26866 | courtney | 1 |
| 26867 | courtliness | 1 |
| 26868 | courtlike | 1 |
| 26869 | coursed | 1 |
| 26870 | cours | 1 |
| 26871 | couronne | 1 |
| 26872 | courages | 1 |
| 26873 | cour | 1 |
| 26874 | couplets | 1 |
| 26875 | couplet | 1 |
| 26876 | couper | 1 |
| 26877 | countrv | 1 |
| 26878 | countervail | 1 |
| 26879 | countersign | 1 |
| 26880 | counterpoints | 1 |
| 26881 | counterpart | 1 |
| 26882 | counterpane | 1 |
| 26883 | countermines | 1 |
| 26884 | countermands | 1 |
| 26885 | counterfeitly | 1 |
| 26886 | counterchange | 1 |
| 26887 | counterbalanced | 1 |
| 26888 | counteract | 1 |
| 26889 | countenace | 1 |
| 26890 | counselors | 1 |
| 26891 | counselor | 1 |
| 26892 | counselled | 1 |
| 26893 | coulter | 1 |
| 26894 | coughed | 1 |
| 26895 | coude | 1 |
| 26896 | couchings | 1 |
| 26897 | cotswold | 1 |
| 26898 | cotsole | 1 |
| 26899 | cotsall | 1 |
| 26900 | coted | 1 |
| 26901 | costlier | 1 |
| 26902 | costeth | 1 |
| 26903 | costermongers | 1 |
| 26904 | cosmo | 1 |
| 26905 | cortadillo | 1 |
| 26906 | corslet | 1 |
| 26907 | corselet | 1 |
| 26908 | corrupts | 1 |
| 26909 | corruptly | 1 |
| 26910 | corruptibly | 1 |
| 26911 | corruptible | 1 |
| 26912 | corrupters | 1 |
| 26913 | corroborate | 1 |
| 26914 | corrivals | 1 |
| 26915 | corrival | 1 |
| 26916 | corresponsive | 1 |
| 26917 | correspondent | 1 |
| 26918 | corresponded | 1 |
| 26919 | correspond | 1 |
| 26920 | correctioner | 1 |
| 26921 | corpulent | 1 |
| 26922 | corps | 1 |
| 26923 | corporals | 1 |
| 26924 | corollary | 1 |
| 26925 | cornuto | 1 |
| 26926 | cornerstone | 1 |
| 26927 | corky | 1 |
| 26928 | corking | 1 |
| 26929 | corinthian | 1 |
| 26930 | corellas | 1 |
| 26931 | cordis | 1 |
| 26932 | cordiality | 1 |
| 26933 | corde | 1 |
| 26934 | corbo | 1 |
| 26935 | corantos | 1 |
| 26936 | corambus | 1 |
| 26937 | coram | 1 |
| 26938 | copying | 1 |
| 26939 | copulatives | 1 |
| 26940 | coppice | 1 |
| 26941 | copperspur | 1 |
| 26942 | copious | 1 |
| 26943 | copatain | 1 |
| 26944 | coops | 1 |
| 26945 | coop | 1 |
| 26946 | coolers | 1 |
| 26947 | cooler | 1 |
| 26948 | cooking | 1 |
| 26949 | cooings | 1 |
| 26950 | cooing | 1 |
| 26951 | convive | 1 |
| 26952 | convincing | 1 |
| 26953 | convinces | 1 |
| 26954 | convicted | 1 |
| 26955 | convict | 1 |
| 26956 | conveyers | 1 |
| 26957 | conveyed | 1 |
| 26958 | convertites | 1 |
| 26959 | convertite | 1 |
| 26960 | convertest | 1 |
| 26961 | conversations | 1 |
| 26962 | convents | 1 |
| 26963 | conventicles | 1 |
| 26964 | contusions | 1 |
| 26965 | contumely | 1 |
| 26966 | contumeliously | 1 |
| 26967 | contumacy | 1 |
| 26968 | controls | 1 |
| 26969 | contrivers | 1 |
| 26970 | contrivances | 1 |
| 26971 | contrite | 1 |
| 26972 | contributors | 1 |
| 26973 | contributed | 1 |
| 26974 | contre | 1 |
| 26975 | contravention | 1 |
| 26976 | contravened | 1 |
| 26977 | contrasted | 1 |
| 26978 | contrariously | 1 |
| 26979 | contrariety | 1 |
| 26980 | contrarieties | 1 |
| 26981 | contradicts | 1 |
| 26982 | contraction | 1 |
| 26983 | contracting | 1 |
| 26984 | continuous | 1 |
| 26985 | continuer | 1 |
| 26986 | continuantly | 1 |
| 26987 | continu | 1 |
| 26988 | contexture | 1 |
| 26989 | contests | 1 |
| 26990 | contestation | 1 |
| 26991 | contento | 1 |
| 26992 | contentless | 1 |
| 26993 | contenting | 1 |
| 26994 | contenteth | 1 |
| 26995 | contentedly | 1 |
| 26996 | contenta | 1 |
| 26997 | contendon | 1 |
| 26998 | contemptuously | 1 |
| 26999 | contemplates | 1 |
| 27000 | contemns | 1 |
| 27001 | contemned | 1 |
| 27002 | contact | 1 |
| 27003 | consumptions | 1 |
| 27004 | consults | 1 |
| 27005 | consulting | 1 |
| 27006 | consulships | 1 |
| 27007 | consulship | 1 |
| 27008 | construct | 1 |
| 27009 | constring | 1 |
| 27010 | constraineth | 1 |
| 27011 | constitutions | 1 |
| 27012 | constitutes | 1 |
| 27013 | constituted | 1 |
| 27014 | constellations | 1 |
| 27015 | constellation | 1 |
| 27016 | constantine | 1 |
| 27017 | constancies | 1 |
| 27018 | conspiring | 1 |
| 27019 | conspires | 1 |
| 27020 | conspirers | 1 |
| 27021 | conspirant | 1 |
| 27022 | conspectuities | 1 |
| 27023 | consortest | 1 |
| 27024 | consonant | 1 |
| 27025 | consolate | 1 |
| 27026 | consisteth | 1 |
| 27027 | consistency | 1 |
| 27028 | consigning | 1 |
| 27029 | considerings | 1 |
| 27030 | considerance | 1 |
| 27031 | conserved | 1 |
| 27032 | consecrations | 1 |
| 27033 | conscionable | 1 |
| 27034 | conscientious | 1 |
| 27035 | conscienc | 1 |
| 27036 | consanguinity | 1 |
| 27037 | consanguineous | 1 |
| 27038 | cons | 1 |
| 27039 | conquring | 1 |
| 27040 | conquests | 1 |
| 27041 | conqu | 1 |
| 27042 | connoisseur | 1 |
| 27043 | connive | 1 |
| 27044 | conjuro | 1 |
| 27045 | conjurations | 1 |
| 27046 | conjoins | 1 |
| 27047 | conjoined | 1 |
| 27048 | conjecturing | 1 |
| 27049 | conjecturally | 1 |
| 27050 | conies | 1 |
| 27051 | congruing | 1 |
| 27052 | congregations | 1 |
| 27053 | congregate | 1 |
| 27054 | congreeted | 1 |
| 27055 | congreeing | 1 |
| 27056 | congratulations | 1 |
| 27057 | congratulate | 1 |
| 27058 | congied | 1 |
| 27059 | congest | 1 |
| 27060 | congee | 1 |
| 27061 | congealment | 1 |
| 27062 | confutation | 1 |
| 27063 | confusing | 1 |
| 27064 | confusedly | 1 |
| 27065 | conflux | 1 |
| 27066 | confluence | 1 |
| 27067 | conflicts | 1 |
| 27068 | confixed | 1 |
| 27069 | confiscation | 1 |
| 27070 | confirmities | 1 |
| 27071 | confirming | 1 |
| 27072 | confirmers | 1 |
| 27073 | confirmer | 1 |
| 27074 | confirmatory | 1 |
| 27075 | confiners | 1 |
| 27076 | confineless | 1 |
| 27077 | confesseth | 1 |
| 27078 | confections | 1 |
| 27079 | confectionary | 1 |
| 27080 | confection | 1 |
| 27081 | coney | 1 |
| 27082 | conected | 1 |
| 27083 | conductors | 1 |
| 27084 | condoling | 1 |
| 27085 | condolent | 1 |
| 27086 | condolement | 1 |
| 27087 | conditionally | 1 |
| 27088 | concurs | 1 |
| 27089 | concurring | 1 |
| 27090 | concur | 1 |
| 27091 | concupy | 1 |
| 27092 | concupiscible | 1 |
| 27093 | concubine | 1 |
| 27094 | concolinel | 1 |
| 27095 | concoctor | 1 |
| 27096 | concocter | 1 |
| 27097 | concocted | 1 |
| 27098 | concoct | 1 |
| 27099 | concluding | 1 |
| 27100 | conclud | 1 |
| 27101 | concert | 1 |
| 27102 | concerneth | 1 |
| 27103 | concernancy | 1 |
| 27104 | conceptious | 1 |
| 27105 | concentrated | 1 |
| 27106 | conceivable | 1 |
| 27107 | conceitless | 1 |
| 27108 | concealments | 1 |
| 27109 | concavities | 1 |
| 27110 | comutual | 1 |
| 27111 | compunctious | 1 |
| 27112 | compunction | 1 |
| 27113 | compulsatory | 1 |
| 27114 | comptrollers | 1 |
| 27115 | comptible | 1 |
| 27116 | compromis | 1 |
| 27117 | comprising | 1 |
| 27118 | compris | 1 |
| 27119 | compremises | 1 |
| 27120 | comprehending | 1 |
| 27121 | compounding | 1 |
| 27122 | composture | 1 |
| 27123 | compost | 1 |
| 27124 | complying | 1 |
| 27125 | complutum | 1 |
| 27126 | complotted | 1 |
| 27127 | complimented | 1 |
| 27128 | complimentary | 1 |
| 27129 | complimental | 1 |
| 27130 | complies | 1 |
| 27131 | complicity | 1 |
| 27132 | completion | 1 |
| 27133 | completes | 1 |
| 27134 | complaisance | 1 |
| 27135 | complainings | 1 |
| 27136 | complainest | 1 |
| 27137 | complainer | 1 |
| 27138 | complainant | 1 |
| 27139 | complacency | 1 |
| 27140 | compil | 1 |
| 27141 | competence | 1 |
| 27142 | compete | 1 |
| 27143 | compatriot | 1 |
| 27144 | compasses | 1 |
| 27145 | compartner | 1 |
| 27146 | compares | 1 |
| 27147 | compar | 1 |
| 27148 | comorin | 1 |
| 27149 | comonty | 1 |
| 27150 | commute | 1 |
| 27151 | communing | 1 |
| 27152 | communications | 1 |
| 27153 | communicating | 1 |
| 27154 | communicated | 1 |
| 27155 | communicat | 1 |
| 27156 | commotions | 1 |
| 27157 | commodious | 1 |
| 27158 | commixtion | 1 |
| 27159 | commixed | 1 |
| 27160 | commix | 1 |
| 27161 | committ | 1 |
| 27162 | commissioners | 1 |
| 27163 | commissioned | 1 |
| 27164 | commissariat | 1 |
| 27165 | commentary | 1 |
| 27166 | commendatory | 1 |
| 27167 | commencing | 1 |
| 27168 | commences | 1 |
| 27169 | comme | 1 |
| 27170 | commande | 1 |
| 27171 | comfits | 1 |
| 27172 | comfit | 1 |
| 27173 | comfect | 1 |
| 27174 | comer | 1 |
| 27175 | comeliest | 1 |
| 27176 | comedians | 1 |
| 27177 | comedian | 1 |
| 27178 | combless | 1 |
| 27179 | combings | 1 |
| 27180 | combing | 1 |
| 27181 | combinations | 1 |
| 27182 | combinate | 1 |
| 27183 | combed | 1 |
| 27184 | combated | 1 |
| 27185 | comart | 1 |
| 27186 | comagene | 1 |
| 27187 | colures | 1 |
| 27188 | columbines | 1 |
| 27189 | columbine | 1 |
| 27190 | colouring | 1 |
| 27191 | colourable | 1 |
| 27192 | coloquintida | 1 |
| 27193 | colonnas | 1 |
| 27194 | colocynth | 1 |
| 27195 | colmekill | 1 |
| 27196 | colme | 1 |
| 27197 | collusion | 1 |
| 27198 | collier | 1 |
| 27199 | collegiate | 1 |
| 27200 | collector | 1 |
| 27201 | collectively | 1 |
| 27202 | colleagued | 1 |
| 27203 | collapse | 1 |
| 27204 | colebrook | 1 |
| 27205 | coldspur | 1 |
| 27206 | colds | 1 |
| 27207 | colchos | 1 |
| 27208 | coining | 1 |
| 27209 | coiner | 1 |
| 27210 | cohorts | 1 |
| 27211 | coherence | 1 |
| 27212 | cohere | 1 |
| 27213 | coher | 1 |
| 27214 | cohabitants | 1 |
| 27215 | cogscomb | 1 |
| 27216 | cognition | 1 |
| 27217 | cogitationes | 1 |
| 27218 | coesar | 1 |
| 27219 | coelestibus | 1 |
| 27220 | cods | 1 |
| 27221 | codpieces | 1 |
| 27222 | codling | 1 |
| 27223 | codding | 1 |
| 27224 | cod | 1 |
| 27225 | cocytus | 1 |
| 27226 | coctus | 1 |
| 27227 | cocksure | 1 |
| 27228 | cockpit | 1 |
| 27229 | cockled | 1 |
| 27230 | cockering | 1 |
| 27231 | cockatrices | 1 |
| 27232 | cobloaf | 1 |
| 27233 | cobbled | 1 |
| 27234 | cobble | 1 |
| 27235 | coarsely | 1 |
| 27236 | coagulate | 1 |
| 27237 | coactive | 1 |
| 27238 | coact | 1 |
| 27239 | coachmakers | 1 |
| 27240 | cnemies | 1 |
| 27241 | cneius | 1 |
| 27242 | clysters | 1 |
| 27243 | clustering | 1 |
| 27244 | clumsily | 1 |
| 27245 | cluck | 1 |
| 27246 | cloys | 1 |
| 27247 | cloyment | 1 |
| 27248 | cloyless | 1 |
| 27249 | cloying | 1 |
| 27250 | clowder | 1 |
| 27251 | clovest | 1 |
| 27252 | cloves | 1 |
| 27253 | clover | 1 |
| 27254 | cloudiness | 1 |
| 27255 | clotpoles | 1 |
| 27256 | clothiers | 1 |
| 27257 | clotharius | 1 |
| 27258 | clothair | 1 |
| 27259 | clotens | 1 |
| 27260 | closets | 1 |
| 27261 | closeted | 1 |
| 27262 | closest | 1 |
| 27263 | cloquence | 1 |
| 27264 | cloistress | 1 |
| 27265 | clogging | 1 |
| 27266 | clods | 1 |
| 27267 | clodpole | 1 |
| 27268 | clodhopper | 1 |
| 27269 | cloddy | 1 |
| 27270 | clodcrusher | 1 |
| 27271 | cloakbag | 1 |
| 27272 | clo | 1 |
| 27273 | clipping | 1 |
| 27274 | clippeth | 1 |
| 27275 | clipper | 1 |
| 27276 | clinquant | 1 |
| 27277 | clinking | 1 |
| 27278 | climbeth | 1 |
| 27279 | climber | 1 |
| 27280 | climature | 1 |
| 27281 | climates | 1 |
| 27282 | cliffords | 1 |
| 27283 | clients | 1 |
| 27284 | client | 1 |
| 27285 | clew | 1 |
| 27286 | cleverer | 1 |
| 27287 | clergyman | 1 |
| 27288 | clerestories | 1 |
| 27289 | clept | 1 |
| 27290 | clepeth | 1 |
| 27291 | cleopatpa | 1 |
| 27292 | clenched | 1 |
| 27293 | clenardo | 1 |
| 27294 | clefts | 1 |
| 27295 | clef | 1 |
| 27296 | cleaves | 1 |
| 27297 | cleavage | 1 |
| 27298 | clearing | 1 |
| 27299 | clearest | 1 |
| 27300 | cleansing | 1 |
| 27301 | cleans | 1 |
| 27302 | cleanliest | 1 |
| 27303 | cleaning | 1 |
| 27304 | clays | 1 |
| 27305 | clawing | 1 |
| 27306 | clause | 1 |
| 27307 | clauquel | 1 |
| 27308 | clashing | 1 |
| 27309 | clarion | 1 |
| 27310 | claridiana | 1 |
| 27311 | claret | 1 |
| 27312 | clare | 1 |
| 27313 | clang | 1 |
| 27314 | clammer | 1 |
| 27315 | clamber | 1 |
| 27316 | claiming | 1 |
| 27317 | claimed | 1 |
| 27318 | clack | 1 |
| 27319 | civilised | 1 |
| 27320 | cittern | 1 |
| 27321 | citing | 1 |
| 27322 | citest | 1 |
| 27323 | cital | 1 |
| 27324 | cirimony | 1 |
| 27325 | cirimonies | 1 |
| 27326 | circumvent | 1 |
| 27327 | circumspectly | 1 |
| 27328 | circumscription | 1 |
| 27329 | circumscribed | 1 |
| 27330 | circumscrib | 1 |
| 27331 | circummur | 1 |
| 27332 | circumcised | 1 |
| 27333 | circum | 1 |
| 27334 | circulated | 1 |
| 27335 | circlets | 1 |
| 27336 | circa | 1 |
| 27337 | cincture | 1 |
| 27338 | cimmerian | 1 |
| 27339 | cilicia | 1 |
| 27340 | ciitzens | 1 |
| 27341 | ciel | 1 |
| 27342 | ciceter | 1 |
| 27343 | cicatrices | 1 |
| 27344 | chus | 1 |
| 27345 | churned | 1 |
| 27346 | churn | 1 |
| 27347 | churlishly | 1 |
| 27348 | chuffs | 1 |
| 27349 | chud | 1 |
| 27350 | chucks | 1 |
| 27351 | chrysolite | 1 |
| 27352 | chroniclers | 1 |
| 27353 | christus | 1 |
| 27354 | christophero | 1 |
| 27355 | christom | 1 |
| 27356 | christobal | 1 |
| 27357 | christianlike | 1 |
| 27358 | christianity | 1 |
| 27359 | christenings | 1 |
| 27360 | christened | 1 |
| 27361 | christendoms | 1 |
| 27362 | choristers | 1 |
| 27363 | choppy | 1 |
| 27364 | chopping | 1 |
| 27365 | chopped | 1 |
| 27366 | choplogic | 1 |
| 27367 | chopine | 1 |
| 27368 | chooser | 1 |
| 27369 | chollors | 1 |
| 27370 | cholers | 1 |
| 27371 | chokes | 1 |
| 27372 | choirs | 1 |
| 27373 | chitopher | 1 |
| 27374 | chisels | 1 |
| 27375 | chisel | 1 |
| 27376 | chirurgeonly | 1 |
| 27377 | chirping | 1 |
| 27378 | chips | 1 |
| 27379 | chipper | 1 |
| 27380 | chinese | 1 |
| 27381 | chines | 1 |
| 27382 | chimurcho | 1 |
| 27383 | chimneypiece | 1 |
| 27384 | chimes | 1 |
| 27385 | chimeras | 1 |
| 27386 | chimera | 1 |
| 27387 | chime | 1 |
| 27388 | chills | 1 |
| 27389 | chilling | 1 |
| 27390 | childness | 1 |
| 27391 | childing | 1 |
| 27392 | childhoods | 1 |
| 27393 | childeric | 1 |
| 27394 | childed | 1 |
| 27395 | childbirth | 1 |
| 27396 | chien | 1 |
| 27397 | chiders | 1 |
| 27398 | chicurmurco | 1 |
| 27399 | chicory | 1 |
| 27400 | chickpea | 1 |
| 27401 | chi | 1 |
| 27402 | chez | 1 |
| 27403 | chews | 1 |
| 27404 | chewet | 1 |
| 27405 | chevaliers | 1 |
| 27406 | chev | 1 |
| 27407 | chetas | 1 |
| 27408 | chester | 1 |
| 27409 | cherubims | 1 |
| 27410 | cherub | 1 |
| 27411 | cherrypit | 1 |
| 27412 | cherishes | 1 |
| 27413 | cherisher | 1 |
| 27414 | chequer | 1 |
| 27415 | cheeses | 1 |
| 27416 | cheery | 1 |
| 27417 | cheerless | 1 |
| 27418 | cheerer | 1 |
| 27419 | checker | 1 |
| 27420 | cheapest | 1 |
| 27421 | cheapen | 1 |
| 27422 | che | 1 |
| 27423 | chawdron | 1 |
| 27424 | chaw | 1 |
| 27425 | chaunted | 1 |
| 27426 | chaud | 1 |
| 27427 | chattles | 1 |
| 27428 | chattered | 1 |
| 27429 | chatterbox | 1 |
| 27430 | chatt | 1 |
| 27431 | chats | 1 |
| 27432 | chastising | 1 |
| 27433 | chastest | 1 |
| 27434 | chaseth | 1 |
| 27435 | chaser | 1 |
| 27436 | charybdises | 1 |
| 27437 | charybdis | 1 |
| 27438 | chary | 1 |
| 27439 | charolois | 1 |
| 27440 | charny | 1 |
| 27441 | charneco | 1 |
| 27442 | charmeth | 1 |
| 27443 | charmer | 1 |
| 27444 | charities | 1 |
| 27445 | charitably | 1 |
| 27446 | charing | 1 |
| 27447 | chariness | 1 |
| 27448 | chariest | 1 |
| 27449 | chargeth | 1 |
| 27450 | chargeful | 1 |
| 27451 | chares | 1 |
| 27452 | chare | 1 |
| 27453 | charcoal | 1 |
| 27454 | charbon | 1 |
| 27455 | characts | 1 |
| 27456 | characterless | 1 |
| 27457 | charactered | 1 |
| 27458 | chapfallen | 1 |
| 27459 | chapeless | 1 |
| 27460 | chape | 1 |
| 27461 | chap | 1 |
| 27462 | chantry | 1 |
| 27463 | chantries | 1 |
| 27464 | chanted | 1 |
| 27465 | chanson | 1 |
| 27466 | changest | 1 |
| 27467 | changer | 1 |
| 27468 | changelings | 1 |
| 27469 | changeful | 1 |
| 27470 | chandler | 1 |
| 27471 | champains | 1 |
| 27472 | champain | 1 |
| 27473 | champaign | 1 |
| 27474 | champagne | 1 |
| 27475 | champ | 1 |
| 27476 | chambermaid | 1 |
| 27477 | chamberlains | 1 |
| 27478 | chamberers | 1 |
| 27479 | challengers | 1 |
| 27480 | chalks | 1 |
| 27481 | chalk | 1 |
| 27482 | chalices | 1 |
| 27483 | chalic | 1 |
| 27484 | chaldee | 1 |
| 27485 | chaldeans | 1 |
| 27486 | chagrin | 1 |
| 27487 | chaffless | 1 |
| 27488 | chaces | 1 |
| 27489 | cette | 1 |
| 27490 | cestern | 1 |
| 27491 | cessation | 1 |
| 27492 | cess | 1 |
| 27493 | ces | 1 |
| 27494 | certify | 1 |
| 27495 | certifies | 1 |
| 27496 | certainer | 1 |
| 27497 | cerns | 1 |
| 27498 | ceremoniousness | 1 |
| 27499 | ceremoniously | 1 |
| 27500 | cerements | 1 |
| 27501 | cerecloth | 1 |
| 27502 | cerdas | 1 |
| 27503 | cerbellon | 1 |
| 27504 | centurions | 1 |
| 27505 | centuries | 1 |
| 27506 | cents | 1 |
| 27507 | centred | 1 |
| 27508 | censuring | 1 |
| 27509 | censurers | 1 |
| 27510 | censorious | 1 |
| 27511 | censorinus | 1 |
| 27512 | censor | 1 |
| 27513 | cells | 1 |
| 27514 | cellarage | 1 |
| 27515 | celesti | 1 |
| 27516 | celebrates | 1 |
| 27517 | ceilings | 1 |
| 27518 | cedius | 1 |
| 27519 | ceaseth | 1 |
| 27520 | cazoleros | 1 |
| 27521 | cawing | 1 |
| 27522 | cawdron | 1 |
| 27523 | caviary | 1 |
| 27524 | caviar | 1 |
| 27525 | caveto | 1 |
| 27526 | cavalry | 1 |
| 27527 | cavalery | 1 |
| 27528 | cautiousness | 1 |
| 27529 | cautery | 1 |
| 27530 | cauterizing | 1 |
| 27531 | cautels | 1 |
| 27532 | cautel | 1 |
| 27533 | causeth | 1 |
| 27534 | causest | 1 |
| 27535 | cauf | 1 |
| 27536 | caudrillero | 1 |
| 27537 | catonian | 1 |
| 27538 | catlings | 1 |
| 27539 | catling | 1 |
| 27540 | catlike | 1 |
| 27541 | catiline | 1 |
| 27542 | caters | 1 |
| 27543 | cater | 1 |
| 27544 | catechising | 1 |
| 27545 | cate | 1 |
| 27546 | catarrhs | 1 |
| 27547 | catapult | 1 |
| 27548 | cataplasm | 1 |
| 27549 | catalonia | 1 |
| 27550 | casualty | 1 |
| 27551 | casualties | 1 |
| 27552 | castor | 1 |
| 27553 | castilians | 1 |
| 27554 | castiliano | 1 |
| 27555 | castigate | 1 |
| 27556 | caster | 1 |
| 27557 | casted | 1 |
| 27558 | castaways | 1 |
| 27559 | castaway | 1 |
| 27560 | castalion | 1 |
| 27561 | cassocks | 1 |
| 27562 | cassado | 1 |
| 27563 | casques | 1 |
| 27564 | casketed | 1 |
| 27565 | casing | 1 |
| 27566 | cased | 1 |
| 27567 | casaer | 1 |
| 27568 | carves | 1 |
| 27569 | carthagena | 1 |
| 27570 | cartels | 1 |
| 27571 | cartagena | 1 |
| 27572 | carrots | 1 |
| 27573 | carper | 1 |
| 27574 | carped | 1 |
| 27575 | caroused | 1 |
| 27576 | carols | 1 |
| 27577 | carolea | 1 |
| 27578 | carobs | 1 |
| 27579 | carnations | 1 |
| 27580 | carnarvonshire | 1 |
| 27581 | carnally | 1 |
| 27582 | carmine | 1 |
| 27583 | carmen | 1 |
| 27584 | carman | 1 |
| 27585 | carloto | 1 |
| 27586 | carlot | 1 |
| 27587 | carl | 1 |
| 27588 | caressed | 1 |
| 27589 | careered | 1 |
| 27590 | carduus | 1 |
| 27591 | cardmaker | 1 |
| 27592 | cardinally | 1 |
| 27593 | carders | 1 |
| 27594 | carcases | 1 |
| 27595 | carcajona | 1 |
| 27596 | carcajes | 1 |
| 27597 | carbuncled | 1 |
| 27598 | caraways | 1 |
| 27599 | caraculiambro | 1 |
| 27600 | caracks | 1 |
| 27601 | carack | 1 |
| 27602 | caput | 1 |
| 27603 | capturing | 1 |
| 27604 | captum | 1 |
| 27605 | captors | 1 |
| 27606 | captivates | 1 |
| 27607 | captious | 1 |
| 27608 | caprichoso | 1 |
| 27609 | caprices | 1 |
| 27610 | caprice | 1 |
| 27611 | capriccio | 1 |
| 27612 | capparum | 1 |
| 27613 | cappadocia | 1 |
| 27614 | capocchia | 1 |
| 27615 | capitulated | 1 |
| 27616 | capite | 1 |
| 27617 | capitaine | 1 |
| 27618 | capilla | 1 |
| 27619 | capels | 1 |
| 27620 | capel | 1 |
| 27621 | capdv | 1 |
| 27622 | capacities | 1 |
| 27623 | capability | 1 |
| 27624 | canzonet | 1 |
| 27625 | canus | 1 |
| 27626 | cantons | 1 |
| 27627 | cantillana | 1 |
| 27628 | cantera | 1 |
| 27629 | canter | 1 |
| 27630 | canstick | 1 |
| 27631 | canonry | 1 |
| 27632 | canonize | 1 |
| 27633 | canonised | 1 |
| 27634 | cano | 1 |
| 27635 | cannonade | 1 |
| 27636 | cannibally | 1 |
| 27637 | cankerworm | 1 |
| 27638 | cankerblossom | 1 |
| 27639 | canine | 1 |
| 27640 | candidatus | 1 |
| 27641 | cancionero | 1 |
| 27642 | cancer | 1 |
| 27643 | cancels | 1 |
| 27644 | cancelling | 1 |
| 27645 | cancelled | 1 |
| 27646 | camping | 1 |
| 27647 | campeador | 1 |
| 27648 | campaigns | 1 |
| 27649 | campaign | 1 |
| 27650 | camomile | 1 |
| 27651 | camoens | 1 |
| 27652 | camels | 1 |
| 27653 | camelot | 1 |
| 27654 | cambyses | 1 |
| 27655 | cambrics | 1 |
| 27656 | cambric | 1 |
| 27657 | calypso | 1 |
| 27658 | calydon | 1 |
| 27659 | calveskins | 1 |
| 27660 | calved | 1 |
| 27661 | calve | 1 |
| 27662 | calumniating | 1 |
| 27663 | calumniated | 1 |
| 27664 | calumniate | 1 |
| 27665 | calms | 1 |
| 27666 | calmest | 1 |
| 27667 | calmed | 1 |
| 27668 | callow | 1 |
| 27669 | callings | 1 |
| 27670 | callest | 1 |
| 27671 | calle | 1 |
| 27672 | callat | 1 |
| 27673 | cality | 1 |
| 27674 | calipolis | 1 |
| 27675 | calibans | 1 |
| 27676 | calendars | 1 |
| 27677 | calen | 1 |
| 27678 | calculation | 1 |
| 27679 | calculated | 1 |
| 27680 | calatrava | 1 |
| 27681 | calainos | 1 |
| 27682 | calabrian | 1 |
| 27683 | calaber | 1 |
| 27684 | cak | 1 |
| 27685 | caii | 1 |
| 27686 | cagion | 1 |
| 27687 | caelo | 1 |
| 27688 | caelius | 1 |
| 27689 | cadwallader | 1 |
| 27690 | caduceus | 1 |
| 27691 | cadmus | 1 |
| 27692 | cades | 1 |
| 27693 | cadent | 1 |
| 27694 | cadence | 1 |
| 27695 | cadells | 1 |
| 27696 | caddisses | 1 |
| 27697 | caddis | 1 |
| 27698 | cacodemon | 1 |
| 27699 | cackney | 1 |
| 27700 | cacique | 1 |
| 27701 | cachopins | 1 |
| 27702 | cachidiablo | 1 |
| 27703 | cabra | 1 |
| 27704 | cables | 1 |
| 27705 | cabileros | 1 |
| 27706 | cabbages | 1 |
| 27707 | cabbage | 1 |
| 27708 | byzantium | 1 |
| 27709 | bygone | 1 |
| 27710 | buzzers | 1 |
| 27711 | buzzards | 1 |
| 27712 | buttry | 1 |
| 27713 | buttress | 1 |
| 27714 | buttonhole | 1 |
| 27715 | buttery | 1 |
| 27716 | butterwoman | 1 |
| 27717 | buttered | 1 |
| 27718 | butron | 1 |
| 27719 | butcherly | 1 |
| 27720 | butcheed | 1 |
| 27721 | busybodies | 1 |
| 27722 | busts | 1 |
| 27723 | bustling | 1 |
| 27724 | bustamante | 1 |
| 27725 | bussing | 1 |
| 27726 | busses | 1 |
| 27727 | busky | 1 |
| 27728 | buskin | 1 |
| 27729 | busiris | 1 |
| 27730 | busiest | 1 |
| 27731 | burthens | 1 |
| 27732 | burrows | 1 |
| 27733 | burnet | 1 |
| 27734 | burlador | 1 |
| 27735 | buriest | 1 |
| 27736 | burier | 1 |
| 27737 | burguillos | 1 |
| 27738 | burgomasters | 1 |
| 27739 | burglary | 1 |
| 27740 | burgher | 1 |
| 27741 | burgh | 1 |
| 27742 | burdenous | 1 |
| 27743 | burdened | 1 |
| 27744 | burd | 1 |
| 27745 | burbolt | 1 |
| 27746 | bungle | 1 |
| 27747 | bunghole | 1 |
| 27748 | bung | 1 |
| 27749 | bundred | 1 |
| 27750 | bums | 1 |
| 27751 | bumper | 1 |
| 27752 | bump | 1 |
| 27753 | bumbast | 1 |
| 27754 | bulmer | 1 |
| 27755 | bulks | 1 |
| 27756 | bulkier | 1 |
| 27757 | buffoons | 1 |
| 27758 | buffeting | 1 |
| 27759 | budging | 1 |
| 27760 | budger | 1 |
| 27761 | budded | 1 |
| 27762 | bucolics | 1 |
| 27763 | bucks | 1 |
| 27764 | bucklersbury | 1 |
| 27765 | bucking | 1 |
| 27766 | bucketful | 1 |
| 27767 | bubukles | 1 |
| 27768 | brushwood | 1 |
| 27769 | brushing | 1 |
| 27770 | brunt | 1 |
| 27771 | brundusium | 1 |
| 27772 | bruisers | 1 |
| 27773 | browse | 1 |
| 27774 | browny | 1 |
| 27775 | brownist | 1 |
| 27776 | broths | 1 |
| 27777 | broomstaff | 1 |
| 27778 | brooksides | 1 |
| 27779 | brookside | 1 |
| 27780 | brooded | 1 |
| 27781 | brooches | 1 |
| 27782 | broking | 1 |
| 27783 | brokes | 1 |
| 27784 | brokenly | 1 |
| 27785 | broiling | 1 |
| 27786 | brogues | 1 |
| 27787 | brock | 1 |
| 27788 | brocas | 1 |
| 27789 | brocades | 1 |
| 27790 | brocaded | 1 |
| 27791 | brocabruno | 1 |
| 27792 | broadsides | 1 |
| 27793 | broadest | 1 |
| 27794 | broadcast | 1 |
| 27795 | brittleness | 1 |
| 27796 | bristling | 1 |
| 27797 | brisky | 1 |
| 27798 | briskness | 1 |
| 27799 | briskish | 1 |
| 27800 | bringings | 1 |
| 27801 | brindled | 1 |
| 27802 | brinded | 1 |
| 27803 | brims | 1 |
| 27804 | brimming | 1 |
| 27805 | brillador | 1 |
| 27806 | brigliador | 1 |
| 27807 | brighten | 1 |
| 27808 | brigands | 1 |
| 27809 | brigandine | 1 |
| 27810 | brigand | 1 |
| 27811 | briefest | 1 |
| 27812 | briefer | 1 |
| 27813 | bridegrooms | 1 |
| 27814 | bricks | 1 |
| 27815 | bricklayers | 1 |
| 27816 | brickbats | 1 |
| 27817 | bribery | 1 |
| 27818 | briber | 1 |
| 27819 | bribed | 1 |
| 27820 | briareuses | 1 |
| 27821 | brews | 1 |
| 27822 | brewers | 1 |
| 27823 | brewage | 1 |
| 27824 | brevis | 1 |
| 27825 | breviaries | 1 |
| 27826 | bretons | 1 |
| 27827 | brethen | 1 |
| 27828 | bretagne | 1 |
| 27829 | breff | 1 |
| 27830 | breezes | 1 |
| 27831 | breese | 1 |
| 27832 | breeching | 1 |
| 27833 | brecknock | 1 |
| 27834 | breathest | 1 |
| 27835 | breathers | 1 |
| 27836 | breasting | 1 |
| 27837 | bream | 1 |
| 27838 | breakfasted | 1 |
| 27839 | brayers | 1 |
| 27840 | brayer | 1 |
| 27841 | brawns | 1 |
| 27842 | brawler | 1 |
| 27843 | bravo | 1 |
| 27844 | braveries | 1 |
| 27845 | brassy | 1 |
| 27846 | brandishing | 1 |
| 27847 | brandished | 1 |
| 27848 | brandabarbaran | 1 |
| 27849 | branchless | 1 |
| 27850 | branching | 1 |
| 27851 | branched | 1 |
| 27852 | brainsickly | 1 |
| 27853 | brainless | 1 |
| 27854 | brainish | 1 |
| 27855 | braids | 1 |
| 27856 | braid | 1 |
| 27857 | brahmans | 1 |
| 27858 | bragless | 1 |
| 27859 | bragged | 1 |
| 27860 | braggards | 1 |
| 27861 | braggardism | 1 |
| 27862 | bradamante | 1 |
| 27863 | bracy | 1 |
| 27864 | brac | 1 |
| 27865 | bowstring | 1 |
| 27866 | bowsprit | 1 |
| 27867 | bowshots | 1 |
| 27868 | bowling | 1 |
| 27869 | bowler | 1 |
| 27870 | bowcase | 1 |
| 27871 | bourdeaux | 1 |
| 27872 | bourbier | 1 |
| 27873 | bountifully | 1 |
| 27874 | bounteously | 1 |
| 27875 | boundeth | 1 |
| 27876 | bouncing | 1 |
| 27877 | bouillon | 1 |
| 27878 | bouge | 1 |
| 27879 | botchy | 1 |
| 27880 | botches | 1 |
| 27881 | boss | 1 |
| 27882 | bosque | 1 |
| 27883 | boson | 1 |
| 27884 | bosomed | 1 |
| 27885 | bosky | 1 |
| 27886 | bosko | 1 |
| 27887 | boscan | 1 |
| 27888 | boroughs | 1 |
| 27889 | boring | 1 |
| 27890 | bored | 1 |
| 27891 | boreas | 1 |
| 27892 | bordering | 1 |
| 27893 | borderers | 1 |
| 27894 | borcegui | 1 |
| 27895 | booties | 1 |
| 27896 | bootes | 1 |
| 27897 | booted | 1 |
| 27898 | boons | 1 |
| 27899 | bood | 1 |
| 27900 | bonville | 1 |
| 27901 | bonus | 1 |
| 27902 | bonum | 1 |
| 27903 | bonto | 1 |
| 27904 | bonos | 1 |
| 27905 | bonneted | 1 |
| 27906 | bonjour | 1 |
| 27907 | boneless | 1 |
| 27908 | bondslave | 1 |
| 27909 | bondmaid | 1 |
| 27910 | bonded | 1 |
| 27911 | bombazine | 1 |
| 27912 | bombards | 1 |
| 27913 | bolters | 1 |
| 27914 | bolter | 1 |
| 27915 | bologna | 1 |
| 27916 | boliche | 1 |
| 27917 | bolds | 1 |
| 27918 | bolden | 1 |
| 27919 | boitier | 1 |
| 27920 | boisterously | 1 |
| 27921 | boiardo | 1 |
| 27922 | bohun | 1 |
| 27923 | boggler | 1 |
| 27924 | boggle | 1 |
| 27925 | bodiless | 1 |
| 27926 | bodg | 1 |
| 27927 | bocchus | 1 |
| 27928 | bobtail | 1 |
| 27929 | boblibindo | 1 |
| 27930 | boastful | 1 |
| 27931 | boarish | 1 |
| 27932 | boarding | 1 |
| 27933 | bo | 1 |
| 27934 | blusters | 1 |
| 27935 | blustering | 1 |
| 27936 | blusterer | 1 |
| 27937 | bluster | 1 |
| 27938 | blushest | 1 |
| 27939 | blurt | 1 |
| 27940 | blurs | 1 |
| 27941 | blurred | 1 |
| 27942 | blurr | 1 |
| 27943 | blur | 1 |
| 27944 | bluntness | 1 |
| 27945 | bluntest | 1 |
| 27946 | bluest | 1 |
| 27947 | bluecaps | 1 |
| 27948 | blubb | 1 |
| 27949 | blowse | 1 |
| 27950 | blowest | 1 |
| 27951 | blowers | 1 |
| 27952 | blowed | 1 |
| 27953 | blount | 1 |
| 27954 | blotting | 1 |
| 27955 | blooms | 1 |
| 27956 | bloodshedding | 1 |
| 27957 | bloodiest | 1 |
| 27958 | bloodier | 1 |
| 27959 | bloodhound | 1 |
| 27960 | blois | 1 |
| 27961 | blockish | 1 |
| 27962 | blockheads | 1 |
| 27963 | bloat | 1 |
| 27964 | blits | 1 |
| 27965 | blithild | 1 |
| 27966 | blist | 1 |
| 27967 | blink | 1 |
| 27968 | blinds | 1 |
| 27969 | blindly | 1 |
| 27970 | blindfolds | 1 |
| 27971 | blindfolded | 1 |
| 27972 | blesseth | 1 |
| 27973 | blend | 1 |
| 27974 | blenches | 1 |
| 27975 | bleedeth | 1 |
| 27976 | bleedest | 1 |
| 27977 | bleats | 1 |
| 27978 | bleating | 1 |
| 27979 | bleated | 1 |
| 27980 | bleach | 1 |
| 27981 | blazoned | 1 |
| 27982 | blazes | 1 |
| 27983 | blastments | 1 |
| 27984 | blas | 1 |
| 27985 | blankets | 1 |
| 27986 | blanketers | 1 |
| 27987 | blanketeers | 1 |
| 27988 | blanca | 1 |
| 27989 | blanc | 1 |
| 27990 | blains | 1 |
| 27991 | bladder | 1 |
| 27992 | blacksmiths | 1 |
| 27993 | blacksmith | 1 |
| 27994 | blackmere | 1 |
| 27995 | blackbreech | 1 |
| 27996 | blackberry | 1 |
| 27997 | blabs | 1 |
| 27998 | blabbing | 1 |
| 27999 | biter | 1 |
| 28000 | bis | 1 |
| 28001 | birthrights | 1 |
| 28002 | birthdom | 1 |
| 28003 | birdlime | 1 |
| 28004 | birdcages | 1 |
| 28005 | birch | 1 |
| 28006 | bindeth | 1 |
| 28007 | billings | 1 |
| 28008 | billets | 1 |
| 28009 | bile | 1 |
| 28010 | bilbow | 1 |
| 28011 | bilboes | 1 |
| 28012 | bilberry | 1 |
| 28013 | bigness | 1 |
| 28014 | biggest | 1 |
| 28015 | biggen | 1 |
| 28016 | bigamy | 1 |
| 28017 | bifold | 1 |
| 28018 | biddy | 1 |
| 28019 | biddings | 1 |
| 28020 | bidden | 1 |
| 28021 | bickerings | 1 |
| 28022 | bibble | 1 |
| 28023 | bianco | 1 |
| 28024 | bezonians | 1 |
| 28025 | bezonian | 1 |
| 28026 | bewitchment | 1 |
| 28027 | bewhored | 1 |
| 28028 | bewet | 1 |
| 28029 | bewasted | 1 |
| 28030 | beverages | 1 |
| 28031 | bevel | 1 |
| 28032 | bettre | 1 |
| 28033 | betted | 1 |
| 28034 | betroths | 1 |
| 28035 | betrims | 1 |
| 28036 | betrays | 1 |
| 28037 | betossed | 1 |
| 28038 | betoken | 1 |
| 28039 | bethump | 1 |
| 28040 | bethrothed | 1 |
| 28041 | betaking | 1 |
| 28042 | bestrides | 1 |
| 28043 | bestraught | 1 |
| 28044 | bested | 1 |
| 28045 | bestained | 1 |
| 28046 | bessy | 1 |
| 28047 | bess | 1 |
| 28048 | bespotted | 1 |
| 28049 | bespice | 1 |
| 28050 | bespangled | 1 |
| 28051 | besought | 1 |
| 28052 | besotted | 1 |
| 28053 | besom | 1 |
| 28054 | besmeared | 1 |
| 28055 | beslubber | 1 |
| 28056 | besieged | 1 |
| 28057 | beseemeth | 1 |
| 28058 | beseek | 1 |
| 28059 | beseechers | 1 |
| 28060 | beseeched | 1 |
| 28061 | bescreen | 1 |
| 28062 | berry | 1 |
| 28063 | berrueca | 1 |
| 28064 | berrord | 1 |
| 28065 | berod | 1 |
| 28066 | bermoothes | 1 |
| 28067 | berhyme | 1 |
| 28068 | berhym | 1 |
| 28069 | bergamo | 1 |
| 28070 | berengeneros | 1 |
| 28071 | berengenas | 1 |
| 28072 | berengena | 1 |
| 28073 | bereaves | 1 |
| 28074 | bere | 1 |
| 28075 | beray | 1 |
| 28076 | berattle | 1 |
| 28077 | bequest | 1 |
| 28078 | bepray | 1 |
| 28079 | bepaint | 1 |
| 28080 | bents | 1 |
| 28081 | bentivolii | 1 |
| 28082 | bentii | 1 |
| 28083 | benign | 1 |
| 28084 | benied | 1 |
| 28085 | benevolent | 1 |
| 28086 | benevolences | 1 |
| 28087 | benetted | 1 |
| 28088 | benefited | 1 |
| 28089 | beneficently | 1 |
| 28090 | beneficent | 1 |
| 28091 | benedictions | 1 |
| 28092 | benedictine | 1 |
| 28093 | bencher | 1 |
| 28094 | benalcazar | 1 |
| 28095 | bemused | 1 |
| 28096 | bemonster | 1 |
| 28097 | bemoil | 1 |
| 28098 | bemoaned | 1 |
| 28099 | bemoan | 1 |
| 28100 | bemete | 1 |
| 28101 | bemet | 1 |
| 28102 | bemadding | 1 |
| 28103 | belying | 1 |
| 28104 | beloving | 1 |
| 28105 | belock | 1 |
| 28106 | belman | 1 |
| 28107 | bellowings | 1 |
| 28108 | bellman | 1 |
| 28109 | bellerophon | 1 |
| 28110 | belle | 1 |
| 28111 | belisardas | 1 |
| 28112 | believers | 1 |
| 28113 | believer | 1 |
| 28114 | beliest | 1 |
| 28115 | belfry | 1 |
| 28116 | belee | 1 |
| 28117 | beleaguered | 1 |
| 28118 | beldame | 1 |
| 28119 | beldam | 1 |
| 28120 | belching | 1 |
| 28121 | belches | 1 |
| 28122 | belabour | 1 |
| 28123 | bel | 1 |
| 28124 | behowls | 1 |
| 28125 | behooves | 1 |
| 28126 | behooffull | 1 |
| 28127 | beholden | 1 |
| 28128 | behests | 1 |
| 28129 | behest | 1 |
| 28130 | behead | 1 |
| 28131 | behaviors | 1 |
| 28132 | behavior | 1 |
| 28133 | behavedst | 1 |
| 28134 | behav | 1 |
| 28135 | behalfs | 1 |
| 28136 | begrudges | 1 |
| 28137 | begrimed | 1 |
| 28138 | begnawn | 1 |
| 28139 | beginnest | 1 |
| 28140 | beggarman | 1 |
| 28141 | beggared | 1 |
| 28142 | begetteth | 1 |
| 28143 | befortune | 1 |
| 28144 | befor | 1 |
| 28145 | befit | 1 |
| 28146 | befalling | 1 |
| 28147 | beefs | 1 |
| 28148 | beeches | 1 |
| 28149 | bedward | 1 |
| 28150 | bedside | 1 |
| 28151 | bedrench | 1 |
| 28152 | bedfellows | 1 |
| 28153 | bedazzled | 1 |
| 28154 | bedaub | 1 |
| 28155 | bedash | 1 |
| 28156 | bedabbled | 1 |
| 28157 | becomings | 1 |
| 28158 | becomed | 1 |
| 28159 | beckon | 1 |
| 28160 | bechanced | 1 |
| 28161 | bechance | 1 |
| 28162 | bechanc | 1 |
| 28163 | beavers | 1 |
| 28164 | beautifully | 1 |
| 28165 | beautied | 1 |
| 28166 | beaumond | 1 |
| 28167 | beaters | 1 |
| 28168 | beated | 1 |
| 28169 | beastliness | 1 |
| 28170 | beastliest | 1 |
| 28171 | bearings | 1 |
| 28172 | beareth | 1 |
| 28173 | bearding | 1 |
| 28174 | beamest | 1 |
| 28175 | beaks | 1 |
| 28176 | beagles | 1 |
| 28177 | beagle | 1 |
| 28178 | beadsmen | 1 |
| 28179 | beaded | 1 |
| 28180 | beachy | 1 |
| 28181 | bazan | 1 |
| 28182 | bayonne | 1 |
| 28183 | bawling | 1 |
| 28184 | bawl | 1 |
| 28185 | bavin | 1 |
| 28186 | baulked | 1 |
| 28187 | baulk | 1 |
| 28188 | baubling | 1 |
| 28189 | baubles | 1 |
| 28190 | batty | 1 |
| 28191 | battled | 1 |
| 28192 | batteries | 1 |
| 28193 | battalions | 1 |
| 28194 | battalia | 1 |
| 28195 | batler | 1 |
| 28196 | baths | 1 |
| 28197 | bathes | 1 |
| 28198 | batches | 1 |
| 28199 | batch | 1 |
| 28200 | batailles | 1 |
| 28201 | bastes | 1 |
| 28202 | bastardly | 1 |
| 28203 | bastardizing | 1 |
| 28204 | basta | 1 |
| 28205 | basle | 1 |
| 28206 | bask | 1 |
| 28207 | basingstoke | 1 |
| 28208 | basimecu | 1 |
| 28209 | basilisco | 1 |
| 28210 | basil | 1 |
| 28211 | baseless | 1 |
| 28212 | basan | 1 |
| 28213 | bartered | 1 |
| 28214 | barter | 1 |
| 28215 | barson | 1 |
| 28216 | barrow | 1 |
| 28217 | barrier | 1 |
| 28218 | barricadoes | 1 |
| 28219 | barricade | 1 |
| 28220 | barrenness | 1 |
| 28221 | barrenly | 1 |
| 28222 | barrels | 1 |
| 28223 | barrel | 1 |
| 28224 | barrabas | 1 |
| 28225 | barony | 1 |
| 28226 | baronies | 1 |
| 28227 | baron | 1 |
| 28228 | barnacles | 1 |
| 28229 | barm | 1 |
| 28230 | barky | 1 |
| 28231 | barkloughly | 1 |
| 28232 | baring | 1 |
| 28233 | bargulus | 1 |
| 28234 | bargaining | 1 |
| 28235 | barful | 1 |
| 28236 | barefac | 1 |
| 28237 | bards | 1 |
| 28238 | barcino | 1 |
| 28239 | barbermonger | 1 |
| 28240 | barba | 1 |
| 28241 | baratario | 1 |
| 28242 | baptiz | 1 |
| 28243 | baptist | 1 |
| 28244 | banqueted | 1 |
| 28245 | banos | 1 |
| 28246 | banning | 1 |
| 28247 | bannerets | 1 |
| 28248 | bankrupts | 1 |
| 28249 | bankrout | 1 |
| 28250 | banister | 1 |
| 28251 | banishing | 1 |
| 28252 | banishers | 1 |
| 28253 | bangor | 1 |
| 28254 | banging | 1 |
| 28255 | banditto | 1 |
| 28256 | banding | 1 |
| 28257 | bandied | 1 |
| 28258 | banbury | 1 |
| 28259 | banares | 1 |
| 28260 | bames | 1 |
| 28261 | balvastro | 1 |
| 28262 | balsamum | 1 |
| 28263 | balms | 1 |
| 28264 | ballow | 1 |
| 28265 | ballet | 1 |
| 28266 | ballenatos | 1 |
| 28267 | ballasting | 1 |
| 28268 | ballast | 1 |
| 28269 | bales | 1 |
| 28270 | bale | 1 |
| 28271 | baldrick | 1 |
| 28272 | balbastro | 1 |
| 28273 | balanc | 1 |
| 28274 | baking | 1 |
| 28275 | bakers | 1 |
| 28276 | baker | 1 |
| 28277 | baked | 1 |
| 28278 | bajazet | 1 |
| 28279 | baitings | 1 |
| 28280 | baiser | 1 |
| 28281 | baisees | 1 |
| 28282 | baisant | 1 |
| 28283 | baily | 1 |
| 28284 | baillez | 1 |
| 28285 | bailiff | 1 |
| 28286 | bagpipes | 1 |
| 28287 | baggages | 1 |
| 28288 | baffled | 1 |
| 28289 | badged | 1 |
| 28290 | bacons | 1 |
| 28291 | backwardly | 1 |
| 28292 | backstrokes | 1 |
| 28293 | backstroke | 1 |
| 28294 | backbitten | 1 |
| 28295 | backbiter | 1 |
| 28296 | backbite | 1 |
| 28297 | bach | 1 |
| 28298 | bacare | 1 |
| 28299 | bacallao | 1 |
| 28300 | baboons | 1 |
| 28301 | babie | 1 |
| 28302 | babbled | 1 |
| 28303 | babbl | 1 |
| 28304 | babazon | 1 |
| 28305 | baa | 1 |
| 28306 | azpeitia | 1 |
| 28307 | azote | 1 |
| 28308 | ayez | 1 |
| 28309 | axletree | 1 |
| 28310 | axle | 1 |
| 28311 | awooing | 1 |
| 28312 | awesome | 1 |
| 28313 | awasy | 1 |
| 28314 | award | 1 |
| 28315 | awakens | 1 |
| 28316 | aw | 1 |
| 28317 | avowal | 1 |
| 28318 | avouchment | 1 |
| 28319 | avouched | 1 |
| 28320 | avoirdupois | 1 |
| 28321 | avoids | 1 |
| 28322 | avila | 1 |
| 28323 | avidity | 1 |
| 28324 | aves | 1 |
| 28325 | averted | 1 |
| 28326 | aversions | 1 |
| 28327 | avers | 1 |
| 28328 | averring | 1 |
| 28329 | averred | 1 |
| 28330 | average | 1 |
| 28331 | avellaneda | 1 |
| 28332 | avaricious | 1 |
| 28333 | autre | 1 |
| 28334 | authorizing | 1 |
| 28335 | authorised | 1 |
| 28336 | aut | 1 |
| 28337 | austriada | 1 |
| 28338 | austereness | 1 |
| 28339 | auro | 1 |
| 28340 | auricular | 1 |
| 28341 | aunts | 1 |
| 28342 | auld | 1 |
| 28343 | augusts | 1 |
| 28344 | augustinus | 1 |
| 28345 | augurs | 1 |
| 28346 | auguring | 1 |
| 28347 | augures | 1 |
| 28348 | augsburg | 1 |
| 28349 | augmentation | 1 |
| 28350 | aughts | 1 |
| 28351 | aufidiuses | 1 |
| 28352 | audre | 1 |
| 28353 | auditory | 1 |
| 28354 | auditors | 1 |
| 28355 | audis | 1 |
| 28356 | audaciously | 1 |
| 28357 | aucun | 1 |
| 28358 | aubrey | 1 |
| 28359 | attuned | 1 |
| 28360 | attributive | 1 |
| 28361 | attribution | 1 |
| 28362 | attorneyship | 1 |
| 28363 | attorneyed | 1 |
| 28364 | attested | 1 |
| 28365 | attentivenes | 1 |
| 28366 | attent | 1 |
| 28367 | attemptable | 1 |
| 28368 | attainture | 1 |
| 28369 | attainment | 1 |
| 28370 | attaching | 1 |
| 28371 | attaches | 1 |
| 28372 | atropos | 1 |
| 28373 | atrociously | 1 |
| 28374 | atonements | 1 |
| 28375 | atoned | 1 |
| 28376 | atomy | 1 |
| 28377 | athol | 1 |
| 28378 | athirst | 1 |
| 28379 | asylum | 1 |
| 28380 | astute | 1 |
| 28381 | asturias | 1 |
| 28382 | astronomy | 1 |
| 28383 | astronomical | 1 |
| 28384 | astronomers | 1 |
| 28385 | astrolabe | 1 |
| 28386 | astrea | 1 |
| 28387 | astraea | 1 |
| 28388 | astraddle | 1 |
| 28389 | astound | 1 |
| 28390 | astonishing | 1 |
| 28391 | astolfo | 1 |
| 28392 | astern | 1 |
| 28393 | assyrians | 1 |
| 28394 | assumption | 1 |
| 28395 | assum | 1 |
| 28396 | assubjugate | 1 |
| 28397 | associates | 1 |
| 28398 | assisting | 1 |
| 28399 | assistances | 1 |
| 28400 | assinico | 1 |
| 28401 | assez | 1 |
| 28402 | asseverations | 1 |
| 28403 | assessor | 1 |
| 28404 | assessed | 1 |
| 28405 | asserts | 1 |
| 28406 | assemblance | 1 |
| 28407 | assaying | 1 |
| 28408 | assassination | 1 |
| 28409 | assaileth | 1 |
| 28410 | assailable | 1 |
| 28411 | aspirations | 1 |
| 28412 | aspiration | 1 |
| 28413 | aspics | 1 |
| 28414 | aspicious | 1 |
| 28415 | aspersion | 1 |
| 28416 | asperity | 1 |
| 28417 | asparagus | 1 |
| 28418 | asmath | 1 |
| 28419 | aslant | 1 |
| 28420 | askew | 1 |
| 28421 | asker | 1 |
| 28422 | ashy | 1 |
| 28423 | ashouting | 1 |
| 28424 | asher | 1 |
| 28425 | ascribes | 1 |
| 28426 | asceticism | 1 |
| 28427 | ascertaining | 1 |
| 28428 | ascendeth | 1 |
| 28429 | ascanius | 1 |
| 28430 | asaph | 1 |
| 28431 | artois | 1 |
| 28432 | artists | 1 |
| 28433 | artist | 1 |
| 28434 | artire | 1 |
| 28435 | artificer | 1 |
| 28436 | artfully | 1 |
| 28437 | arteries | 1 |
| 28438 | artemisia | 1 |
| 28439 | arrogancy | 1 |
| 28440 | arrobas | 1 |
| 28441 | arriving | 1 |
| 28442 | arrivance | 1 |
| 28443 | arriba | 1 |
| 28444 | arrearages | 1 |
| 28445 | arranges | 1 |
| 28446 | arraignment | 1 |
| 28447 | arraigning | 1 |
| 28448 | arouse | 1 |
| 28449 | armament | 1 |
| 28450 | armadoes | 1 |
| 28451 | arma | 1 |
| 28452 | arlanza | 1 |
| 28453 | ark | 1 |
| 28454 | aristode | 1 |
| 28455 | arisen | 1 |
| 28456 | arion | 1 |
| 28457 | arinies | 1 |
| 28458 | arinado | 1 |
| 28459 | aries | 1 |
| 28460 | arid | 1 |
| 28461 | ariachne | 1 |
| 28462 | argu | 1 |
| 28463 | argo | 1 |
| 28464 | argent | 1 |
| 28465 | arevalo | 1 |
| 28466 | arde | 1 |
| 28467 | arcu | 1 |
| 28468 | architecture | 1 |
| 28469 | architect | 1 |
| 28470 | archipiela | 1 |
| 28471 | archduke | 1 |
| 28472 | archbishopric | 1 |
| 28473 | arcalaus | 1 |
| 28474 | arbors | 1 |
| 28475 | arbitration | 1 |
| 28476 | arbitrating | 1 |
| 28477 | araucana | 1 |
| 28478 | aras | 1 |
| 28479 | araise | 1 |
| 28480 | arabias | 1 |
| 28481 | aquilon | 1 |
| 28482 | aptitude | 1 |
| 28483 | aptest | 1 |
| 28484 | appurtenances | 1 |
| 28485 | approvers | 1 |
| 28486 | appropriation | 1 |
| 28487 | appropriating | 1 |
| 28488 | approachers | 1 |
| 28489 | appris | 1 |
| 28490 | apprenticehood | 1 |
| 28491 | apprentice | 1 |
| 28492 | apprenne | 1 |
| 28493 | apprendre | 1 |
| 28494 | appreciation | 1 |
| 28495 | appreciating | 1 |
| 28496 | appraisers | 1 |
| 28497 | apportioned | 1 |
| 28498 | appoints | 1 |
| 28499 | applications | 1 |
| 28500 | applicants | 1 |
| 28501 | applicant | 1 |
| 28502 | appletart | 1 |
| 28503 | applauses | 1 |
| 28504 | appertinents | 1 |
| 28505 | apperil | 1 |
| 28506 | appendix | 1 |
| 28507 | appelons | 1 |
| 28508 | appellants | 1 |
| 28509 | appeles | 1 |
| 28510 | appelee | 1 |
| 28511 | appele | 1 |
| 28512 | appelant | 1 |
| 28513 | appeasing | 1 |
| 28514 | appealing | 1 |
| 28515 | appealed | 1 |
| 28516 | appalled | 1 |
| 28517 | appall | 1 |
| 28518 | apothecaries | 1 |
| 28519 | apostrophas | 1 |
| 28520 | apostles | 1 |
| 28521 | apostle | 1 |
| 28522 | apostasy | 1 |
| 28523 | apoplex | 1 |
| 28524 | apologue | 1 |
| 28525 | apologised | 1 |
| 28526 | apollodorus | 1 |
| 28527 | apollinem | 1 |
| 28528 | apennines | 1 |
| 28529 | apennine | 1 |
| 28530 | ap | 1 |
| 28531 | antwerp | 1 |
| 28532 | antres | 1 |
| 28533 | antoniad | 1 |
| 28534 | antiquities | 1 |
| 28535 | antiquary | 1 |
| 28536 | antipholuses | 1 |
| 28537 | antipathy | 1 |
| 28538 | antiopa | 1 |
| 28539 | antidotes | 1 |
| 28540 | anticly | 1 |
| 28541 | antick | 1 |
| 28542 | anticipating | 1 |
| 28543 | anticipatest | 1 |
| 28544 | anticipates | 1 |
| 28545 | anticipate | 1 |
| 28546 | anthropophaginian | 1 |
| 28547 | anthropophagi | 1 |
| 28548 | anthems | 1 |
| 28549 | anthem | 1 |
| 28550 | anteroom | 1 |
| 28551 | antenorides | 1 |
| 28552 | antechambers | 1 |
| 28553 | antagonists | 1 |
| 28554 | answerer | 1 |
| 28555 | anoints | 1 |
| 28556 | annoying | 1 |
| 28557 | annoyances | 1 |
| 28558 | announces | 1 |
| 28559 | announce | 1 |
| 28560 | annothanize | 1 |
| 28561 | annotation | 1 |
| 28562 | annis | 1 |
| 28563 | annihilated | 1 |
| 28564 | annihilate | 1 |
| 28565 | annexment | 1 |
| 28566 | annexions | 1 |
| 28567 | annexed | 1 |
| 28568 | annex | 1 |
| 28569 | anna | 1 |
| 28570 | animis | 1 |
| 28571 | animate | 1 |
| 28572 | angulo | 1 |
| 28573 | anglish | 1 |
| 28574 | angliae | 1 |
| 28575 | angler | 1 |
| 28576 | angl | 1 |
| 28577 | anges | 1 |
| 28578 | angelical | 1 |
| 28579 | andren | 1 |
| 28580 | andradilla | 1 |
| 28581 | andpholus | 1 |
| 28582 | andirons | 1 |
| 28583 | andandona | 1 |
| 28584 | ancus | 1 |
| 28585 | anchovies | 1 |
| 28586 | anchorage | 1 |
| 28587 | anarda | 1 |
| 28588 | amyntas | 1 |
| 28589 | amusements | 1 |
| 28590 | ampthill | 1 |
| 28591 | amplified | 1 |
| 28592 | ampler | 1 |
| 28593 | amphimacus | 1 |
| 28594 | amounted | 1 |
| 28595 | amorously | 1 |
| 28596 | amnipotent | 1 |
| 28597 | aminta | 1 |
| 28598 | amidst | 1 |
| 28599 | amidships | 1 |
| 28600 | amicus | 1 |
| 28601 | amicos | 1 |
| 28602 | amicably | 1 |
| 28603 | amica | 1 |
| 28604 | ames | 1 |
| 28605 | amerce | 1 |
| 28606 | ambushes | 1 |
| 28607 | ambuscadoes | 1 |
| 28608 | ambo | 1 |
| 28609 | amblers | 1 |
| 28610 | ambled | 1 |
| 28611 | amble | 1 |
| 28612 | ambiguous | 1 |
| 28613 | ambiguities | 1 |
| 28614 | ambiguides | 1 |
| 28615 | amazing | 1 |
| 28616 | amazeth | 1 |
| 28617 | amatory | 1 |
| 28618 | amarillises | 1 |
| 28619 | amarilises | 1 |
| 28620 | amaranth | 1 |
| 28621 | amamon | 1 |
| 28622 | amaking | 1 |
| 28623 | amaimon | 1 |
| 28624 | altro | 1 |
| 28625 | alton | 1 |
| 28626 | alternative | 1 |
| 28627 | alternate | 1 |
| 28628 | alphonso | 1 |
| 28629 | alphabetical | 1 |
| 28630 | almsman | 1 |
| 28631 | almorzar | 1 |
| 28632 | almonds | 1 |
| 28633 | almohaza | 1 |
| 28634 | almohades | 1 |
| 28635 | almanacs | 1 |
| 28636 | almanack | 1 |
| 28637 | almain | 1 |
| 28638 | allycholly | 1 |
| 28639 | alluring | 1 |
| 28640 | allurement | 1 |
| 28641 | allur | 1 |
| 28642 | alluding | 1 |
| 28643 | alludes | 1 |
| 28644 | allude | 1 |
| 28645 | alls | 1 |
| 28646 | alloy | 1 |
| 28647 | allottery | 1 |
| 28648 | allots | 1 |
| 28649 | allot | 1 |
| 28650 | alligator | 1 |
| 28651 | alligant | 1 |
| 28652 | allicholy | 1 |
| 28653 | allhallowmas | 1 |
| 28654 | allen | 1 |
| 28655 | allegories | 1 |
| 28656 | allegiant | 1 |
| 28657 | allegations | 1 |
| 28658 | allegation | 1 |
| 28659 | allays | 1 |
| 28660 | allayments | 1 |
| 28661 | allayment | 1 |
| 28662 | allayed | 1 |
| 28663 | aljaferia | 1 |
| 28664 | aliquando | 1 |
| 28665 | aliis | 1 |
| 28666 | alights | 1 |
| 28667 | alighting | 1 |
| 28668 | alight | 1 |
| 28669 | alienated | 1 |
| 28670 | alhucema | 1 |
| 28671 | alhombra | 1 |
| 28672 | alheli | 1 |
| 28673 | algerine | 1 |
| 28674 | algarve | 1 |
| 28675 | alforias | 1 |
| 28676 | alfeniquen | 1 |
| 28677 | alfaqui | 1 |
| 28678 | alexandra | 1 |
| 28679 | alewife | 1 |
| 28680 | alessandria | 1 |
| 28681 | alengon | 1 |
| 28682 | alencastros | 1 |
| 28683 | alehouses | 1 |
| 28684 | alecto | 1 |
| 28685 | alder | 1 |
| 28686 | alcocer | 1 |
| 28687 | alcobendas | 1 |
| 28688 | alcazar | 1 |
| 28689 | alcarria | 1 |
| 28690 | alcantara | 1 |
| 28691 | alcancia | 1 |
| 28692 | alcana | 1 |
| 28693 | alcala | 1 |
| 28694 | albraca | 1 |
| 28695 | albogue | 1 |
| 28696 | alastrajareas | 1 |
| 28697 | alarms | 1 |
| 28698 | alamos | 1 |
| 28699 | alagones | 1 |
| 28700 | akilling | 1 |
| 28701 | airless | 1 |
| 28702 | aired | 1 |
| 28703 | aio | 1 |
| 28704 | aimest | 1 |
| 28705 | aidless | 1 |
| 28706 | aidant | 1 |
| 28707 | aidance | 1 |
| 28708 | aiaria | 1 |
| 28709 | aialvolio | 1 |
| 28710 | ahungry | 1 |
| 28711 | aguero | 1 |
| 28712 | agueface | 1 |
| 28713 | agued | 1 |
| 28714 | aground | 1 |
| 28715 | agreeably | 1 |
| 28716 | agrajes | 1 |
| 28717 | agonies | 1 |
| 28718 | agnize | 1 |
| 28719 | aglow | 1 |
| 28720 | aglet | 1 |
| 28721 | agilers | 1 |
| 28722 | aggrief | 1 |
| 28723 | agenor | 1 |
| 28724 | agaz | 1 |
| 28725 | agape | 1 |
| 28726 | agamemmon | 1 |
| 28727 | aga | 1 |
| 28728 | aftermost | 1 |
| 28729 | afront | 1 |
| 28730 | african | 1 |
| 28731 | aforehand | 1 |
| 28732 | affronted | 1 |
| 28733 | affordeth | 1 |
| 28734 | affirming | 1 |
| 28735 | affirmed | 1 |
| 28736 | affirmatives | 1 |
| 28737 | affirmation | 1 |
| 28738 | affinity | 1 |
| 28739 | affin | 1 |
| 28740 | affied | 1 |
| 28741 | affidavit | 1 |
| 28742 | affianced | 1 |
| 28743 | affianc | 1 |
| 28744 | affeer | 1 |
| 28745 | affecteth | 1 |
| 28746 | affectedly | 1 |
| 28747 | affaire | 1 |
| 28748 | aetna | 1 |
| 28749 | aesop | 1 |
| 28750 | aeson | 1 |
| 28751 | aesculapius | 1 |
| 28752 | aerial | 1 |
| 28753 | aequo | 1 |
| 28754 | aeolus | 1 |
| 28755 | aemelia | 1 |
| 28756 | aegles | 1 |
| 28757 | aegion | 1 |
| 28758 | aeacides | 1 |
| 28759 | aeacida | 1 |
| 28760 | advocation | 1 |
| 28761 | advocacy | 1 |
| 28762 | advisings | 1 |
| 28763 | adviser | 1 |
| 28764 | advices | 1 |
| 28765 | advertising | 1 |
| 28766 | adversities | 1 |
| 28767 | adversely | 1 |
| 28768 | adversae | 1 |
| 28769 | adventurously | 1 |
| 28770 | adventuring | 1 |
| 28771 | adventur | 1 |
| 28772 | advent | 1 |
| 28773 | advantaging | 1 |
| 28774 | advantaged | 1 |
| 28775 | advantageable | 1 |
| 28776 | advancements | 1 |
| 28777 | adulteries | 1 |
| 28778 | adulteress | 1 |
| 28779 | adulterers | 1 |
| 28780 | adulterates | 1 |
| 28781 | adsum | 1 |
| 28782 | adriatic | 1 |
| 28783 | adriani | 1 |
| 28784 | adown | 1 |
| 28785 | adornments | 1 |
| 28786 | adornings | 1 |
| 28787 | adorning | 1 |
| 28788 | adoreth | 1 |
| 28789 | adorest | 1 |
| 28790 | adorer | 1 |
| 28791 | adorations | 1 |
| 28792 | adoptious | 1 |
| 28793 | adoptedly | 1 |
| 28794 | admonishments | 1 |
| 28795 | admonishment | 1 |
| 28796 | admonishing | 1 |
| 28797 | admonished | 1 |
| 28798 | admonish | 1 |
| 28799 | adjured | 1 |
| 28800 | adjuncts | 1 |
| 28801 | adjudged | 1 |
| 28802 | adjoin | 1 |
| 28803 | addict | 1 |
| 28804 | addeth | 1 |
| 28805 | adapting | 1 |
| 28806 | adaptation | 1 |
| 28807 | adamantine | 1 |
| 28808 | adallas | 1 |
| 28809 | acture | 1 |
| 28810 | actively | 1 |
| 28811 | acquittances | 1 |
| 28812 | acquiring | 1 |
| 28813 | acquires | 1 |
| 28814 | acquiesced | 1 |
| 28815 | acquaints | 1 |
| 28816 | acordo | 1 |
| 28817 | aconitum | 1 |
| 28818 | acknown | 1 |
| 28819 | achitophel | 1 |
| 28820 | achilleses | 1 |
| 28821 | achieves | 1 |
| 28822 | achiever | 1 |
| 28823 | acerb | 1 |
| 28824 | accuseth | 1 |
| 28825 | accusative | 1 |
| 28826 | accurate | 1 |
| 28827 | accuracy | 1 |
| 28828 | accumulation | 1 |
| 28829 | accumulated | 1 |
| 28830 | accosted | 1 |
| 28831 | accordeth | 1 |
| 28832 | accordant | 1 |
| 28833 | accomplishing | 1 |
| 28834 | accomplices | 1 |
| 28835 | accompanies | 1 |
| 28836 | accommodo | 1 |
| 28837 | accommodations | 1 |
| 28838 | accommodating | 1 |
| 28839 | accolade | 1 |
| 28840 | accites | 1 |
| 28841 | accited | 1 |
| 28842 | accite | 1 |
| 28843 | accidence | 1 |
| 28844 | accessible | 1 |
| 28845 | acceptable | 1 |
| 28846 | academies | 1 |
| 28847 | academe | 1 |
| 28848 | abutting | 1 |
| 28849 | abusive | 1 |
| 28850 | abuser | 1 |
| 28851 | abundantly | 1 |
| 28852 | absyrtus | 1 |
| 28853 | abstracted | 1 |
| 28854 | abstemious | 1 |
| 28855 | abstains | 1 |
| 28856 | abstaining | 1 |
| 28857 | abstain | 1 |
| 28858 | absorbing | 1 |
| 28859 | absolving | 1 |
| 28860 | absolves | 1 |
| 28861 | absolver | 1 |
| 28862 | absolved | 1 |
| 28863 | absit | 1 |
| 28864 | absey | 1 |
| 28865 | absenting | 1 |
| 28866 | abscond | 1 |
| 28867 | abruption | 1 |
| 28868 | abrupt | 1 |
| 28869 | abrook | 1 |
| 28870 | abrogate | 1 |
| 28871 | abridged | 1 |
| 28872 | abridg | 1 |
| 28873 | abrenuncio | 1 |
| 28874 | abounded | 1 |
| 28875 | abortives | 1 |
| 28876 | abominations | 1 |
| 28877 | abominate | 1 |
| 28878 | abominably | 1 |
| 28879 | abolishing | 1 |
| 28880 | abolished | 1 |
| 28881 | aboding | 1 |
| 28882 | abodements | 1 |
| 28883 | aboded | 1 |
| 28884 | abler | 1 |
| 28885 | ablaze | 1 |
| 28886 | abjectly | 1 |
| 28887 | abideth | 1 |
| 28888 | abhominable | 1 |
| 28889 | abetting | 1 |
| 28890 | abet | 1 |
| 28891 | abbreviated | 1 |
| 28892 | abbots | 1 |
| 28893 | abbominable | 1 |
| 28894 | abbeys | 1 |
| 28895 | abates | 1 |
| 28896 | abatements | 1 |
| 28897 | abash | 1 |
| 28898 | abasement | 1 |
| 28899 | abandons | 1 |
| 28900 | abandoning | 1 |
| 28901 | abajo | 1 |
| 28902 | abaissiez | 1 |
| 28903 | abadejo | 1 |
|
|
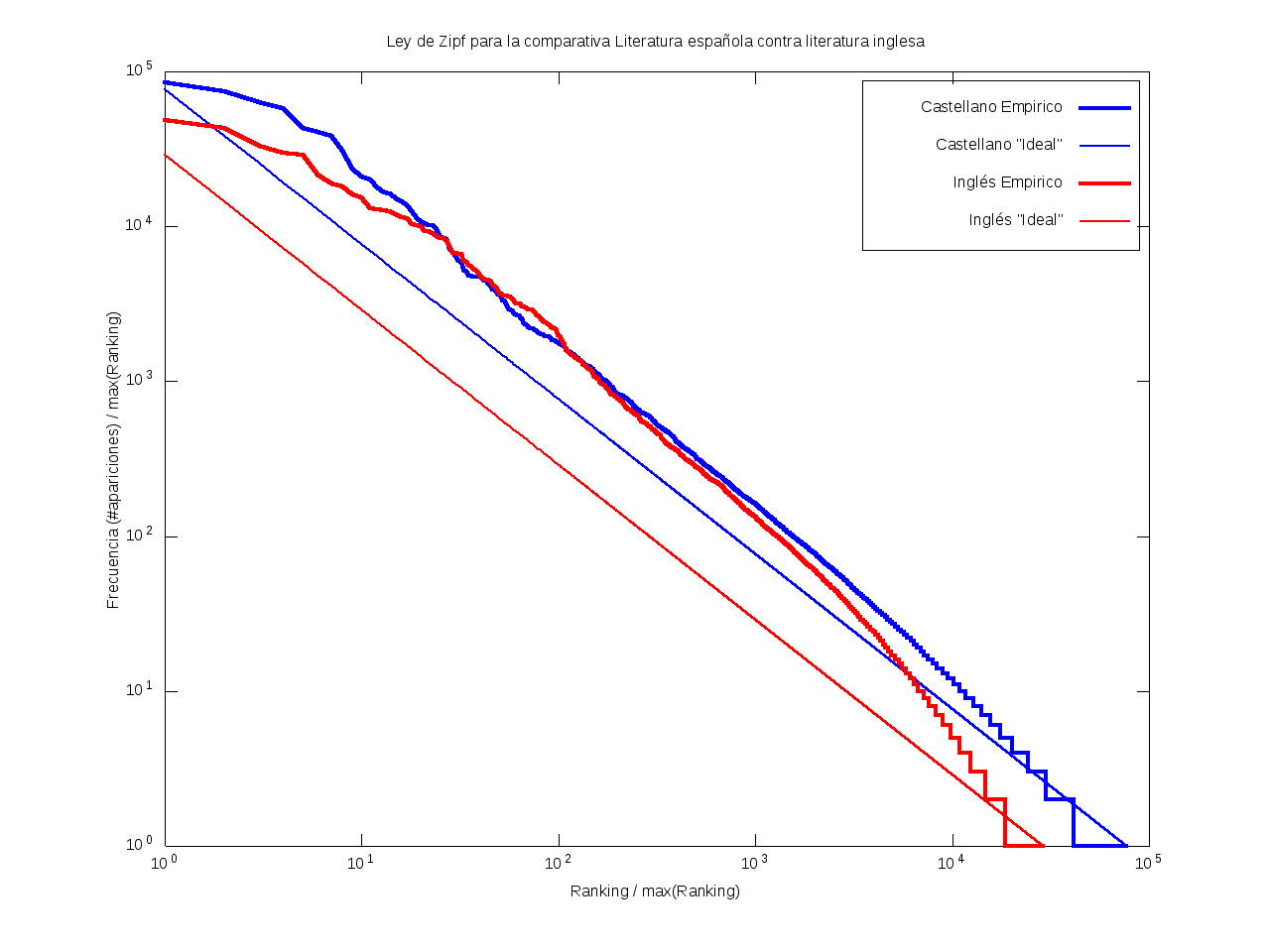
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará un conjunto (Castellano) (conjunto 1)
contra el otro (Inglés) (conjunto 2) y viceversa.
A continuación se muestra una lista de todas las palabras presentes en los textos,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
En este caso no tiene sentido aplicar el test de Dunning ya que los textos están en idiomas distintos.


