Comparativa: La Regenta lematizada contra Fortunata y Jacinta lematizada
Índice
Información General
| Título: | La Regenta (lematizado) |
|---|
| Autor: | Leopoldo Alas Clarín (lematizado) |
|---|
| Idioma: | Castellano (lematizado) |
|---|
| #Palabras total: | 308922 |
|---|
| #Palabras distintas: | 11595 |
|---|
| Type-Token ratio: | 3.75% |
|---|
|
| Título: | Fortunata y Jacinta (lematizado) |
|---|
| Autor: | Benito Pérez Galdós (lematizado) |
|---|
| Idioma: | Castellano (lematizado) |
|---|
| #Palabras total: | 393844 |
|---|
| #Palabras distintas: | 13855 |
|---|
| Type-Token ratio: | 3.52% |
|---|
|
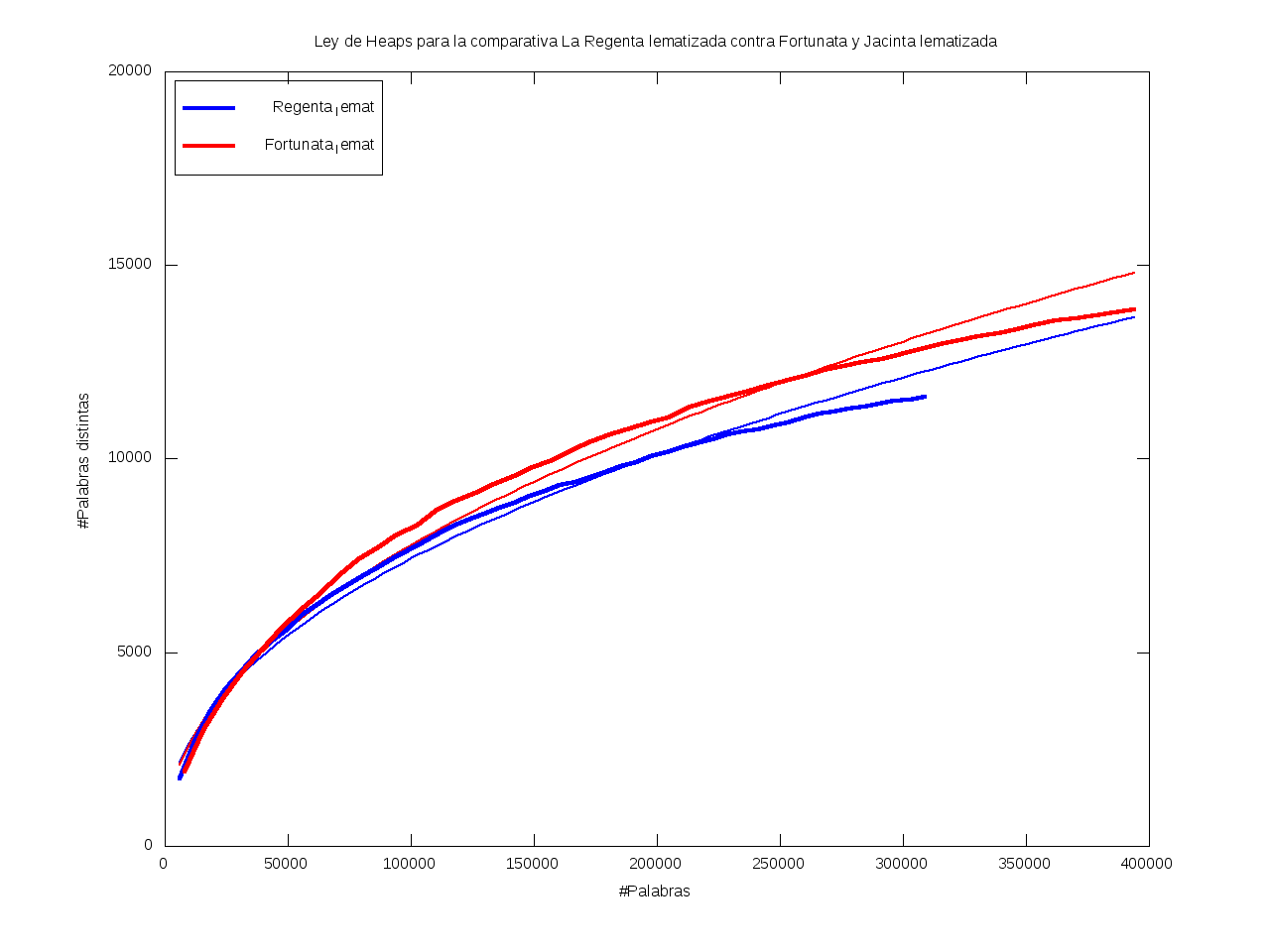
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| Regenta_lemat | Fortunata_lemat |
|---|
| #Palabras: | #Palabras distintas: |
|---|
| 6178 | 1747 |
| 12356 | 2775 |
| 18534 | 3494 |
| 24712 | 4048 |
| 30890 | 4515 |
| 37068 | 4931 |
| 43246 | 5286 |
| 49424 | 5581 |
| 55602 | 5962 |
| 61780 | 6210 |
| 67958 | 6492 |
| 74136 | 6739 |
| 80314 | 6963 |
| 86492 | 7199 |
| 92670 | 7426 |
| 98848 | 7629 |
| 105026 | 7847 |
| 111204 | 8069 |
| 117382 | 8260 |
| 123560 | 8429 |
| 129738 | 8588 |
| 135916 | 8723 |
| 142094 | 8860 |
| 148272 | 9028 |
| 154450 | 9169 |
| 160628 | 9310 |
| 166806 | 9392 |
| 172984 | 9533 |
| 179162 | 9645 |
| 185340 | 9797 |
| 191518 | 9922 |
| 197696 | 10067 |
| 203874 | 10173 |
| 210052 | 10285 |
| 216230 | 10397 |
| 222408 | 10487 |
| 228586 | 10622 |
| 234764 | 10697 |
| 240942 | 10756 |
| 247120 | 10858 |
| 253298 | 10945 |
| 259476 | 11053 |
| 265654 | 11159 |
| 271832 | 11223 |
| 278010 | 11294 |
| 284188 | 11353 |
| 290366 | 11429 |
| 296544 | 11490 |
| 302722 | 11534 |
| 308900 | 11595 |
| 308922 | 11595 |
|
| #Palabras: | #Palabras distintas: |
|---|
| 7876 | 1911 |
| 15752 | 2998 |
| 23628 | 3820 |
| 31504 | 4491 |
| 39380 | 5072 |
| 47256 | 5620 |
| 55132 | 6092 |
| 63008 | 6505 |
| 70884 | 6989 |
| 78760 | 7392 |
| 86636 | 7702 |
| 94512 | 8036 |
| 102388 | 8274 |
| 110264 | 8653 |
| 118140 | 8908 |
| 126016 | 9125 |
| 133892 | 9345 |
| 141768 | 9564 |
| 149644 | 9783 |
| 157520 | 9971 |
| 165396 | 10223 |
| 173272 | 10448 |
| 181148 | 10618 |
| 189024 | 10785 |
| 196900 | 10922 |
| 204776 | 11069 |
| 212652 | 11308 |
| 220528 | 11473 |
| 228404 | 11609 |
| 236280 | 11731 |
| 244156 | 11888 |
| 252032 | 12012 |
| 259908 | 12145 |
| 267784 | 12285 |
| 275660 | 12398 |
| 283536 | 12488 |
| 291412 | 12586 |
| 299288 | 12702 |
| 307164 | 12841 |
| 315040 | 12946 |
| 322916 | 13054 |
| 330792 | 13174 |
| 338668 | 13252 |
| 346544 | 13345 |
| 354420 | 13476 |
| 362296 | 13560 |
| 370172 | 13626 |
| 378048 | 13709 |
| 385924 | 13770 |
| 393800 | 13854 |
| 393844 | 13855 |
|
|
Ajuste por mínimos cuadrados de los datos a K*n^b: |
| Regenta_lemat |
|
Fortunata_lemat |
| K = 43.718 |
|
K = 34.438 |
| b = 0.446 |
|
b = 0.471 |
|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Regenta_lemat | Fortunata_lemat |
Ilustración del principio de mínimo esfuerzo: |
| Rank | Palabra | Frec |
|---|
| 1 | el | 29227 |
| 2 | de | 19493 |
| 3 | que | 9866 |
| 4 | a | 9542 |
| 5 | y | 9435 |
| 6 | lo | 7613 |
| 7 | en | 7123 |
| 8 | se | 6093 |
| 9 | un | 5272 |
| 10 | no | 4979 |
| 11 | ser | 4157 |
| 12 | su | 4081 |
| 13 | haber | 3872 |
| 14 | con | 3199 |
| 15 | por | 2872 |
| 16 | pero | 1908 |
| 17 | aquel | 1882 |
| 18 | don | 1791 |
| 19 | todo | 1770 |
| 20 | como | 1751 |
| 21 | más | 1725 |
| 22 | estar | 1438 |
| 23 | tener | 1431 |
| 24 | decir | 1398 |
| 25 | para | 1365 |
| 26 | si | 1165 |
| 27 | él | 1112 |
| 28 | qué | 1109 |
| 29 | sin | 1096 |
| 30 | poder | 1039 |
| 31 | ella | 1007 |
| 32 | hacer | 999 |
| 33 | otro | 944 |
| 34 | ver | 920 |
| 35 | ya | 902 |
| 36 | ana | 896 |
| 37 | saber | 867 |
| 38 | querer | 865 |
| 39 | usted | 806 |
| 40 | ir | 781 |
| 41 | me | 774 |
| 42 | magistral | 769 |
| 43 | este | 745 |
| 44 | yo | 696 |
| 45 | dar | 693 |
| 46 | sí | 671 |
| 47 | ni | 671 |
| 48 | era | 669 |
| 49 | mucho | 659 |
| 50 | hablar | 636 |
| 51 | o | 634 |
| 52 | la | 631 |
| 53 | vez | 608 |
| 54 | poco | 594 |
| 55 | éste | 590 |
| 56 | pensar | 570 |
| 57 | parecer | 563 |
| 58 | muy | 555 |
| 59 | señor | 529 |
| 60 | volver | 514 |
| 61 | sobre | 506 |
| 62 | cuando | 494 |
| 63 | víctor | 490 |
| 64 | casa | 488 |
| 65 | mismo | 485 |
| 66 | regenta | 468 |
| 67 | sentir | 453 |
| 68 | allí | 446 |
| 69 | bueno | 445 |
| 70 | día | 444 |
| 71 | vetusta | 443 |
| 72 | dejar | 440 |
| 73 | nada | 416 |
| 74 | después | 416 |
| 75 | doña | 414 |
| 76 | llegar | 410 |
| 77 | porque | 396 |
| 78 | creer | 393 |
| 79 | algún | 381 |
| 80 | hombre | 378 |
| 81 | grande | 378 |
| 82 | salir | 376 |
| 83 | también | 374 |
| 84 | mesía | 372 |
| 85 | oír | 363 |
| 86 | ahora | 361 |
| 87 | entre | 360 |
| 88 | bien | 358 |
| 89 | ojo | 355 |
| 90 | hasta | 352 |
| 91 | mi | 350 |
| 92 | mujer | 349 |
| 93 | llamar | 349 |
| 94 | fermín | 349 |
| 95 | cosa | 348 |
| 96 | pasar | 347 |
| 97 | dios | 346 |
| 98 | dos | 333 |
| 99 | ése | 331 |
| 100 | siempre | 330 |
| 101 | tan | 327 |
| 102 | menos | 325 |
| 103 | así | 325 |
| 104 | deber | 324 |
| 105 | vida | 319 |
| 106 | algo | 318 |
| 107 | amor | 314 |
| 108 | mirar | 306 |
| 109 | tiempo | 304 |
| 110 | quintanar | 304 |
| 111 | ese | 304 |
| 112 | amigo | 303 |
| 113 | venir | 301 |
| 114 | señora | 301 |
| 115 | hijo | 296 |
| 116 | tanto | 294 |
| 117 | mundo | 292 |
| 118 | alma | 292 |
| 119 | te | 286 |
| 120 | mano | 286 |
| 121 | hora | 283 |
| 122 | poner | 280 |
| 123 | noche | 270 |
| 124 | voz | 266 |
| 125 | comer | 262 |
| 126 | mal | 258 |
| 127 | mejor | 253 |
| 128 | madre | 252 |
| 129 | desde | 251 |
| 130 | aquél | 251 |
| 131 | pues | 249 |
| 132 | cabeza | 248 |
| 133 | tal | 245 |
| 134 | petra | 241 |
| 135 | año | 238 |
| 136 | quien | 231 |
| 137 | quedar | 231 |
| 138 | entrar | 230 |
| 139 | seguir | 220 |
| 140 | aunque | 219 |
| 141 | cuanto | 212 |
| 142 | tarde | 209 |
| 143 | llevar | 208 |
| 144 | frígilis | 207 |
| 145 | tomar | 205 |
| 146 | cierto | 205 |
| 147 | además | 205 |
| 148 | es | 202 |
| 149 | encontrar | 202 |
| 150 | pie | 200 |
| 151 | nuevo | 200 |
| 152 | solo | 199 |
| 153 | palabra | 199 |
| 154 | nadie | 199 |
| 155 | leer | 197 |
| 156 | caer | 197 |
| 157 | obdulia | 194 |
| 158 | los | 194 |
| 159 | buscar | 194 |
| 160 | casi | 192 |
| 161 | según | 191 |
| 162 | morir | 190 |
| 163 | entonces | 190 |
| 164 | anita | 189 |
| 165 | antes | 187 |
| 166 | donde | 186 |
| 167 | cómo | 186 |
| 168 | quién | 183 |
| 169 | idea | 183 |
| 170 | mientras | 182 |
| 171 | entender | 182 |
| 172 | conocer | 182 |
| 173 | vivir | 181 |
| 174 | visita | 179 |
| 175 | recordar | 178 |
| 176 | perder | 178 |
| 177 | cuerpo | 175 |
| 178 | cada | 174 |
| 179 | paula | 173 |
| 180 | sólo | 172 |
| 181 | paco | 171 |
| 182 | aquí | 171 |
| 183 | pas | 170 |
| 184 | esperar | 170 |
| 185 | dentro | 167 |
| 186 | luz | 166 |
| 187 | fin | 166 |
| 188 | allá | 166 |
| 189 | nunca | 164 |
| 190 | paso | 162 |
| 191 | pobre | 159 |
| 192 | correr | 159 |
| 193 | tratar | 158 |
| 194 | fuera | 158 |
| 195 | puerta | 157 |
| 196 | momento | 157 |
| 197 | verdad | 155 |
| 198 | provisor | 155 |
| 199 | subir | 154 |
| 200 | modo | 153 |
| 201 | mayor | 153 |
| 202 | atrever | 149 |
| 203 | negro | 146 |
| 204 | demás | 145 |
| 205 | brazo | 144 |
| 206 | al | 143 |
| 207 | abrir | 143 |
| 208 | una | 142 |
| 209 | parte | 142 |
| 210 | iglesia | 142 |
| 211 | marquesa | 141 |
| 212 | tú | 140 |
| 213 | sonreír | 140 |
| 214 | necesitar | 140 |
| 215 | padre | 139 |
| 216 | contar | 139 |
| 217 | comprender | 139 |
| 218 | santo | 138 |
| 219 | pedir | 138 |
| 220 | miedo | 138 |
| 221 | hecho | 138 |
| 222 | echar | 138 |
| 223 | nos | 137 |
| 224 | malo | 137 |
| 225 | marqués | 136 |
| 226 | alto | 134 |
| 227 | confesar | 133 |
| 228 | vegallana | 132 |
| 229 | lado | 132 |
| 230 | calle | 132 |
| 231 | sino | 131 |
| 232 | ellos | 131 |
| 233 | tres | 130 |
| 234 | ronzal | 130 |
| 235 | callar | 130 |
| 236 | oh | 129 |
| 237 | seguro | 128 |
| 238 | medio | 128 |
| 239 | fuerza | 128 |
| 240 | uno | 127 |
| 241 | frío | 127 |
| 242 | marido | 126 |
| 243 | levantar | 126 |
| 244 | fuerte | 126 |
| 245 | acabar | 126 |
| 246 | pompeyo | 125 |
| 247 | obispo | 125 |
| 248 | espíritu | 125 |
| 249 | llenar | 124 |
| 250 | aire | 123 |
| 251 | figurar | 122 |
| 252 | dormir | 122 |
| 253 | suyo | 121 |
| 254 | servir | 121 |
| 255 | pueblo | 121 |
| 256 | ozores | 121 |
| 257 | catedral | 121 |
| 258 | blanco | 120 |
| 259 | mí | 119 |
| 260 | pasión | 118 |
| 261 | casino | 118 |
| 262 | balcón | 118 |
| 263 | triste | 117 |
| 264 | loco | 117 |
| 265 | lejos | 117 |
| 266 | acercar | 117 |
| 267 | faltar | 116 |
| 268 | pesar | 115 |
| 269 | eso | 115 |
| 270 | pronto | 114 |
| 271 | mañana | 114 |
| 272 | ante | 114 |
| 273 | corazón | 112 |
| 274 | soler | 111 |
| 275 | claro | 111 |
| 276 | vestir | 110 |
| 277 | mío | 110 |
| 278 | libro | 110 |
| 279 | empezar | 110 |
| 280 | paseo | 108 |
| 281 | agua | 108 |
| 282 | último | 107 |
| 283 | ruido | 107 |
| 284 | junto | 107 |
| 285 | cual | 107 |
| 286 | santos | 106 |
| 287 | bajo | 106 |
| 288 | propio | 104 |
| 289 | placer | 104 |
| 290 | dulce | 104 |
| 291 | contra | 104 |
| 292 | sentar | 103 |
| 293 | san | 103 |
| 294 | notar | 103 |
| 295 | escribir | 103 |
| 296 | cura | 103 |
| 297 | visitación | 102 |
| 298 | tocar | 102 |
| 299 | rostro | 102 |
| 300 | dama | 102 |
| 301 | cantar | 102 |
| 302 | teatro | 101 |
| 303 | salón | 101 |
| 304 | puro | 101 |
| 305 | cielo | 101 |
| 306 | traer | 100 |
| 307 | temer | 100 |
| 308 | presentar | 100 |
| 309 | canónigo | 100 |
| 310 | sol | 99 |
| 311 | silencio | 99 |
| 312 | cerca | 98 |
| 313 | ripamilán | 97 |
| 314 | ridículo | 97 |
| 315 | mesa | 97 |
| 316 | enemigo | 97 |
| 317 | olvidar | 96 |
| 318 | procurar | 95 |
| 319 | preguntar | 95 |
| 320 | camino | 95 |
| 321 | mover | 94 |
| 322 | importar | 94 |
| 323 | hacia | 94 |
| 324 | detrás | 94 |
| 325 | andar | 94 |
| 326 | virtud | 93 |
| 327 | matar | 93 |
| 328 | mandar | 93 |
| 329 | las | 93 |
| 330 | foja | 93 |
| 331 | casar | 93 |
| 332 | boca | 93 |
| 333 | amo | 93 |
| 334 | obscuro | 92 |
| 335 | hermoso | 92 |
| 336 | caso | 92 |
| 337 | cualquier | 91 |
| 338 | todavía | 90 |
| 339 | sacar | 90 |
| 340 | piedad | 90 |
| 341 | pensamiento | 90 |
| 342 | llorar | 90 |
| 343 | jamás | 90 |
| 344 | fe | 90 |
| 345 | explicar | 90 |
| 346 | alegría | 90 |
| 347 | sombra | 89 |
| 348 | reír | 89 |
| 349 | glocester | 89 |
| 350 | delante | 89 |
| 351 | veces | 88 |
| 352 | religión | 88 |
| 353 | razón | 88 |
| 354 | enamorar | 88 |
| 355 | cerrar | 88 |
| 356 | único | 87 |
| 357 | tierra | 87 |
| 358 | vuelta | 86 |
| 359 | ello | 86 |
| 360 | amar | 86 |
| 361 | acordar | 86 |
| 362 | nuestro | 85 |
| 363 | general | 85 |
| 364 | contestar | 85 |
| 365 | color | 85 |
| 366 | ningún | 84 |
| 367 | gritar | 84 |
| 368 | gozar | 84 |
| 369 | cara | 84 |
| 370 | orgaz | 83 |
| 371 | médico | 83 |
| 372 | tales | 82 |
| 373 | preferir | 82 |
| 374 | persona | 82 |
| 375 | pasado | 82 |
| 376 | largo | 82 |
| 377 | guimarán | 82 |
| 378 | clérigo | 82 |
| 379 | arte | 82 |
| 380 | viejo | 81 |
| 381 | noble | 81 |
| 382 | negar | 81 |
| 383 | siquiera | 80 |
| 384 | pálido | 80 |
| 385 | muerte | 80 |
| 386 | mirada | 80 |
| 387 | media | 80 |
| 388 | gabinete | 80 |
| 389 | frente | 80 |
| 390 | natural | 79 |
| 391 | dónde | 79 |
| 392 | conciencia | 79 |
| 393 | ustedes | 78 |
| 394 | ocasión | 78 |
| 395 | miserable | 78 |
| 396 | efecto | 78 |
| 397 | asustar | 78 |
| 398 | vivero | 77 |
| 399 | obra | 77 |
| 400 | ellas | 77 |
| 401 | carne | 77 |
| 402 | tu | 76 |
| 403 | gracia | 76 |
| 404 | dijo | 76 |
| 405 | conversación | 76 |
| 406 | capilla | 76 |
| 407 | campo | 76 |
| 408 | lecho | 75 |
| 409 | hombro | 75 |
| 410 | engañar | 75 |
| 411 | deseo | 75 |
| 412 | debajo | 75 |
| 413 | bajar | 75 |
| 414 | joven | 74 |
| 415 | cuatro | 74 |
| 416 | cuarto | 74 |
| 417 | coger | 74 |
| 418 | bermúdez | 74 |
| 419 | arrojar | 74 |
| 420 | religioso | 73 |
| 421 | pagar | 73 |
| 422 | ocultar | 73 |
| 423 | niño | 73 |
| 424 | madrid | 73 |
| 425 | enfermo | 73 |
| 426 | despertar | 73 |
| 427 | abajo | 73 |
| 428 | vencer | 72 |
| 429 | repente | 72 |
| 430 | punto | 72 |
| 431 | preparar | 72 |
| 432 | papel | 72 |
| 433 | tono | 71 |
| 434 | secreto | 71 |
| 435 | piedra | 71 |
| 436 | manera | 71 |
| 437 | dolor | 71 |
| 438 | convertir | 71 |
| 439 | antiguo | 71 |
| 440 | sueño | 70 |
| 441 | mil | 70 |
| 442 | fuego | 70 |
| 443 | esposo | 70 |
| 444 | despreciar | 70 |
| 445 | ahí | 70 |
| 446 | puesto | 69 |
| 447 | público | 69 |
| 448 | meter | 69 |
| 449 | huir | 69 |
| 450 | hoy | 69 |
| 451 | despacho | 69 |
| 452 | serio | 68 |
| 453 | saltar | 68 |
| 454 | primero | 68 |
| 455 | lágrima | 68 |
| 456 | costumbre | 68 |
| 457 | comenzar | 68 |
| 458 | tristeza | 67 |
| 459 | tampoco | 67 |
| 460 | sonar | 67 |
| 461 | saludar | 67 |
| 462 | primera | 67 |
| 463 | nombre | 67 |
| 464 | jesús | 67 |
| 465 | fingir | 67 |
| 466 | conseguir | 67 |
| 467 | carta | 67 |
| 468 | ayudar | 67 |
| 469 | asunto | 67 |
| 470 | temblar | 66 |
| 471 | salud | 66 |
| 472 | recibir | 66 |
| 473 | petronila | 66 |
| 474 | ofrecer | 66 |
| 475 | honor | 66 |
| 476 | fondo | 66 |
| 477 | despedir | 66 |
| 478 | confesión | 66 |
| 479 | cama | 66 |
| 480 | sentido | 65 |
| 481 | santa | 65 |
| 482 | pasear | 65 |
| 483 | exigir | 65 |
| 484 | demasiado | 65 |
| 485 | dignar | 64 |
| 486 | derecho | 64 |
| 487 | caserón | 64 |
| 488 | verde | 63 |
| 489 | valer | 63 |
| 490 | señorita | 63 |
| 491 | dedo | 63 |
| 492 | tranquilo | 62 |
| 493 | presencia | 62 |
| 494 | moral | 62 |
| 495 | gusto | 62 |
| 496 | gustar | 62 |
| 497 | entregar | 62 |
| 498 | duda | 62 |
| 499 | culpa | 62 |
| 500 | coche | 62 |
| 501 | carlos | 62 |
| 502 | ocho | 61 |
| 503 | inclinar | 61 |
| 504 | historia | 61 |
| 505 | atrás | 61 |
| 506 | arcipreste | 61 |
| 507 | verso | 60 |
| 508 | sangre | 60 |
| 509 | peor | 60 |
| 510 | hermano | 60 |
| 511 | espiritual | 60 |
| 512 | cerebro | 60 |
| 513 | bastar | 60 |
| 514 | banco | 60 |
| 515 | arriba | 60 |
| 516 | alegrar | 60 |
| 517 | acompañar | 60 |
| 518 | sé | 59 |
| 519 | satisfacer | 59 |
| 520 | peligro | 59 |
| 521 | labio | 59 |
| 522 | frase | 59 |
| 523 | espolón | 59 |
| 524 | elegante | 59 |
| 525 | aparecer | 59 |
| 526 | admirar | 59 |
| 527 | vergüenza | 58 |
| 528 | primer | 58 |
| 529 | pared | 58 |
| 530 | gesto | 58 |
| 531 | detener | 58 |
| 532 | clase | 58 |
| 533 | alcoba | 58 |
| 534 | tío | 57 |
| 535 | separar | 57 |
| 536 | principal | 57 |
| 537 | plaza | 57 |
| 538 | escándalo | 57 |
| 539 | criar | 57 |
| 540 | barinaga | 57 |
| 541 | voluntad | 56 |
| 542 | pecado | 56 |
| 543 | libre | 56 |
| 544 | entero | 56 |
| 545 | disimular | 56 |
| 546 | calor | 56 |
| 547 | aventura | 56 |
| 548 | apretar | 56 |
| 549 | apoyar | 56 |
| 550 | valor | 55 |
| 551 | teresina | 55 |
| 552 | rodear | 55 |
| 553 | obligar | 55 |
| 554 | mozo | 55 |
| 555 | jurar | 55 |
| 556 | joaquín | 55 |
| 557 | íntimo | 55 |
| 558 | ganar | 55 |
| 559 | curar | 55 |
| 560 | cubrir | 55 |
| 561 | caballero | 55 |
| 562 | verdadero | 54 |
| 563 | tentación | 54 |
| 564 | rincón | 54 |
| 565 | repetir | 54 |
| 566 | remordimiento | 54 |
| 567 | reconocer | 54 |
| 568 | oro | 54 |
| 569 | mar | 54 |
| 570 | gritó | 54 |
| 571 | escena | 54 |
| 572 | embargo | 54 |
| 573 | coro | 54 |
| 574 | bastante | 54 |
| 575 | absurdo | 54 |
| 576 | traje | 53 |
| 577 | nube | 53 |
| 578 | materia | 53 |
| 579 | juventud | 53 |
| 580 | edelmira | 53 |
| 581 | disponer | 53 |
| 582 | cuyo | 53 |
| 583 | culto | 53 |
| 584 | continuar | 53 |
| 585 | árbol | 53 |
| 586 | aldea | 53 |
| 587 | sotana | 52 |
| 588 | rico | 52 |
| 589 | propósito | 52 |
| 590 | luna | 52 |
| 591 | forma | 52 |
| 592 | estrecho | 52 |
| 593 | cruz | 52 |
| 594 | convenir | 52 |
| 595 | contener | 52 |
| 596 | adelantar | 52 |
| 597 | acudir | 52 |
| 598 | respetar | 51 |
| 599 | oído | 51 |
| 600 | mejilla | 51 |
| 601 | liberal | 51 |
| 602 | huerta | 51 |
| 603 | doncella | 51 |
| 604 | costar | 51 |
| 605 | confianza | 51 |
| 606 | clavar | 51 |
| 607 | son | 50 |
| 608 | somoza | 50 |
| 609 | siglo | 50 |
| 610 | representar | 50 |
| 611 | palacio | 50 |
| 612 | necesario | 50 |
| 613 | mes | 50 |
| 614 | humor | 50 |
| 615 | etcétera | 50 |
| 616 | especie | 50 |
| 617 | cristal | 50 |
| 618 | contemplar | 50 |
| 619 | atención | 50 |
| 620 | antojar | 50 |
| 621 | ánimo | 50 |
| 622 | teresa | 49 |
| 623 | sospechar | 49 |
| 624 | proponer | 49 |
| 625 | prometer | 49 |
| 626 | perdonar | 49 |
| 627 | pedro | 49 |
| 628 | espalda | 49 |
| 629 | enfermedad | 49 |
| 630 | declarar | 49 |
| 631 | custodio | 49 |
| 632 | carcajada | 49 |
| 633 | ancho | 49 |
| 634 | visitar | 48 |
| 635 | ventana | 48 |
| 636 | usar | 48 |
| 637 | suerte | 48 |
| 638 | soñar | 48 |
| 639 | sonrisa | 48 |
| 640 | preguntó | 48 |
| 641 | permitir | 48 |
| 642 | ocurrir | 48 |
| 643 | motivo | 48 |
| 644 | jugar | 48 |
| 645 | guardar | 48 |
| 646 | dinero | 48 |
| 647 | cuestión | 48 |
| 648 | cuadro | 48 |
| 649 | cayetano | 48 |
| 650 | broma | 48 |
| 651 | bosque | 48 |
| 652 | arrancar | 48 |
| 653 | arcediano | 48 |
| 654 | templo | 47 |
| 655 | suelo | 47 |
| 656 | segundo | 47 |
| 657 | salvar | 47 |
| 658 | romántico | 47 |
| 659 | resolver | 47 |
| 660 | polvo | 47 |
| 661 | perro | 47 |
| 662 | naturaleza | 47 |
| 663 | música | 47 |
| 664 | mezclar | 47 |
| 665 | fijo | 47 |
| 666 | d | 47 |
| 667 | contentar | 47 |
| 668 | clero | 47 |
| 669 | chico | 47 |
| 670 | caballo | 47 |
| 671 | baile | 47 |
| 672 | anuncia | 47 |
| 673 | adelante | 47 |
| 674 | vulgar | 46 |
| 675 | verano | 46 |
| 676 | trabajo | 46 |
| 677 | suave | 46 |
| 678 | prohibir | 46 |
| 679 | profundo | 46 |
| 680 | partido | 46 |
| 681 | parque | 46 |
| 682 | místico | 46 |
| 683 | locura | 46 |
| 684 | ley | 46 |
| 685 | hoja | 46 |
| 686 | hermosura | 46 |
| 687 | eterno | 46 |
| 688 | esconder | 46 |
| 689 | e | 46 |
| 690 | ciudad | 46 |
| 691 | ciencia | 46 |
| 692 | carraspique | 46 |
| 693 | cargar | 46 |
| 694 | asomar | 46 |
| 695 | añadir | 46 |
| 696 | vamos | 45 |
| 697 | silla | 45 |
| 698 | señorito | 45 |
| 699 | recuerdo | 45 |
| 700 | piadoso | 45 |
| 701 | parar | 45 |
| 702 | páez | 45 |
| 703 | letra | 45 |
| 704 | juan | 45 |
| 705 | frutos | 45 |
| 706 | diez | 45 |
| 707 | descubrir | 45 |
| 708 | decía | 45 |
| 709 | dado | 45 |
| 710 | cinco | 45 |
| 711 | aborrecer | 45 |
| 712 | volar | 44 |
| 713 | semejante | 44 |
| 714 | seguida | 44 |
| 715 | periódico | 44 |
| 716 | ocupar | 44 |
| 717 | murmurar | 44 |
| 718 | lugar | 44 |
| 719 | hija | 44 |
| 720 | grosero | 44 |
| 721 | estilo | 44 |
| 722 | esperanza | 44 |
| 723 | encoger | 44 |
| 724 | devoto | 44 |
| 725 | cumplir | 44 |
| 726 | crimen | 44 |
| 727 | caridad | 44 |
| 728 | benítez | 44 |
| 729 | amistad | 44 |
| 730 | alegre | 44 |
| 731 | acaso | 44 |
| 732 | siguiente | 43 |
| 733 | saturnino | 43 |
| 734 | sala | 43 |
| 735 | sacerdote | 43 |
| 736 | sabio | 43 |
| 737 | quejar | 43 |
| 738 | minuto | 43 |
| 739 | marquesito | 43 |
| 740 | le | 43 |
| 741 | esfuerzo | 43 |
| 742 | del | 43 |
| 743 | confesor | 43 |
| 744 | comedor | 43 |
| 745 | cocina | 43 |
| 746 | beber | 43 |
| 747 | aprensión | 43 |
| 748 | vengar | 42 |
| 749 | sociedad | 42 |
| 750 | político | 42 |
| 751 | nosotros | 42 |
| 752 | molestar | 42 |
| 753 | merecer | 42 |
| 754 | interés | 42 |
| 755 | imagen | 42 |
| 756 | ideal | 42 |
| 757 | hierro | 42 |
| 758 | familia | 42 |
| 759 | falda | 42 |
| 760 | enterar | 42 |
| 761 | dominar | 42 |
| 762 | aún | 42 |
| 763 | tardar | 41 |
| 764 | soledad | 41 |
| 765 | señalar | 41 |
| 766 | recoger | 41 |
| 767 | protestar | 41 |
| 768 | orgullo | 41 |
| 769 | nervioso | 41 |
| 770 | movimiento | 41 |
| 771 | expresión | 41 |
| 772 | ex | 41 |
| 773 | envidiar | 41 |
| 774 | ejemplo | 41 |
| 775 | diablo | 41 |
| 776 | desear | 41 |
| 777 | crespo | 41 |
| 778 | celo | 41 |
| 779 | virgen | 40 |
| 780 | romper | 40 |
| 781 | respirar | 40 |
| 782 | quitar | 40 |
| 783 | probar | 40 |
| 784 | paz | 40 |
| 785 | opinión | 40 |
| 786 | necesidad | 40 |
| 787 | muerto | 40 |
| 788 | monte | 40 |
| 789 | memoria | 40 |
| 790 | lleno | 40 |
| 791 | lengua | 40 |
| 792 | lástima | 40 |
| 793 | juego | 40 |
| 794 | irritar | 40 |
| 795 | hambre | 40 |
| 796 | grito | 40 |
| 797 | energía | 40 |
| 798 | emplear | 40 |
| 799 | emoción | 40 |
| 800 | cortar | 40 |
| 801 | cabo | 40 |
| 802 | asegurar | 40 |
| 803 | suspirar | 39 |
| 804 | remedio | 39 |
| 805 | referir | 39 |
| 806 | perseguir | 39 |
| 807 | marchar | 39 |
| 808 | luego | 39 |
| 809 | lucir | 39 |
| 810 | lejano | 39 |
| 811 | ira | 39 |
| 812 | imponer | 39 |
| 813 | imaginación | 39 |
| 814 | cuánto | 39 |
| 815 | cristiano | 39 |
| 816 | calumnia | 39 |
| 817 | café | 39 |
| 818 | aprovechar | 39 |
| 819 | apenas | 39 |
| 820 | amante | 39 |
| 821 | vanidad | 38 |
| 822 | trabuco | 38 |
| 823 | temprano | 38 |
| 824 | saturno | 38 |
| 825 | ropa | 38 |
| 826 | rayo | 38 |
| 827 | provincia | 38 |
| 828 | principio | 38 |
| 829 | orden | 38 |
| 830 | objeto | 38 |
| 831 | menudo | 38 |
| 832 | llave | 38 |
| 833 | humilde | 38 |
| 834 | furioso | 38 |
| 835 | fresco | 38 |
| 836 | figura | 38 |
| 837 | estado | 38 |
| 838 | escalera | 38 |
| 839 | delicia | 38 |
| 840 | defender | 38 |
| 841 | convencer | 38 |
| 842 | cenar | 38 |
| 843 | camila | 38 |
| 844 | arrastrar | 38 |
| 845 | acostar | 38 |
| 846 | abandonar | 38 |
| 847 | vista | 37 |
| 848 | trabajar | 37 |
| 849 | torre | 37 |
| 850 | terreno | 37 |
| 851 | sombrero | 37 |
| 852 | resistir | 37 |
| 853 | realidad | 37 |
| 854 | querido | 37 |
| 855 | piso | 37 |
| 856 | pecho | 37 |
| 857 | observar | 37 |
| 858 | nacer | 37 |
| 859 | madera | 37 |
| 860 | librar | 37 |
| 861 | invierno | 37 |
| 862 | imposible | 37 |
| 863 | extremo | 37 |
| 864 | encerrar | 37 |
| 865 | durar | 37 |
| 866 | dudar | 37 |
| 867 | cuidado | 37 |
| 868 | cuello | 37 |
| 869 | comprar | 37 |
| 870 | cansar | 37 |
| 871 | borracho | 37 |
| 872 | venganza | 36 |
| 873 | vano | 36 |
| 874 | suponer | 36 |
| 875 | solemne | 36 |
| 876 | socio | 36 |
| 877 | servicio | 36 |
| 878 | presidente | 36 |
| 879 | luchar | 36 |
| 880 | inútil | 36 |
| 881 | imitar | 36 |
| 882 | gato | 36 |
| 883 | flor | 36 |
| 884 | falta | 36 |
| 885 | escapar | 36 |
| 886 | enfrente | 36 |
| 887 | edad | 36 |
| 888 | divertir | 36 |
| 889 | desgracia | 36 |
| 890 | decidir | 36 |
| 891 | cruzar | 36 |
| 892 | criada | 36 |
| 893 | convento | 36 |
| 894 | consentir | 36 |
| 895 | comedia | 36 |
| 896 | bailar | 36 |
| 897 | ay | 36 |
| 898 | anselmo | 36 |
| 899 | vino | 35 |
| 900 | triunfo | 35 |
| 901 | ti | 35 |
| 902 | rojo | 35 |
| 903 | rezar | 35 |
| 904 | olor | 35 |
| 905 | misa | 35 |
| 906 | mía | 35 |
| 907 | máquina | 35 |
| 908 | gente | 35 |
| 909 | fijar | 35 |
| 910 | feliz | 35 |
| 911 | envidia | 35 |
| 912 | desaparecer | 35 |
| 913 | coser | 35 |
| 914 | corriente | 35 |
| 915 | contento | 35 |
| 916 | considerar | 35 |
| 917 | compañía | 35 |
| 918 | brillar | 35 |
| 919 | aun | 35 |
| 920 | asistir | 35 |
| 921 | anterior | 35 |
| 922 | acto | 35 |
| 923 | viento | 34 |
| 924 | viaje | 34 |
| 925 | tropezar | 34 |
| 926 | tomás | 34 |
| 927 | terminar | 34 |
| 928 | supuesto | 34 |
| 929 | sorprender | 34 |
| 930 | solas | 34 |
| 931 | rumor | 34 |
| 932 | robustiano | 34 |
| 933 | rama | 34 |
| 934 | prado | 34 |
| 935 | pepe | 34 |
| 936 | mostrar | 34 |
| 937 | manteo | 34 |
| 938 | joaquinito | 34 |
| 939 | género | 34 |
| 940 | falso | 34 |
| 941 | extender | 34 |
| 942 | estrépito | 34 |
| 943 | contrario | 34 |
| 944 | cien | 34 |
| 945 | burlar | 34 |
| 946 | azul | 34 |
| 947 | apagar | 34 |
| 948 | aburrir | 34 |
| 949 | tender | 33 |
| 950 | sucio | 33 |
| 951 | suceder | 33 |
| 952 | sacrificio | 33 |
| 953 | reloj | 33 |
| 954 | prueba | 33 |
| 955 | presente | 33 |
| 956 | personaje | 33 |
| 957 | pequeño | 33 |
| 958 | pena | 33 |
| 959 | pecar | 33 |
| 960 | palomares | 33 |
| 961 | padecer | 33 |
| 962 | novela | 33 |
| 963 | nervio | 33 |
| 964 | instante | 33 |
| 965 | había | 33 |
| 966 | formar | 33 |
| 967 | fiel | 33 |
| 968 | exponer | 33 |
| 969 | entusiasmo | 33 |
| 970 | entraña | 33 |
| 971 | eclesiástico | 33 |
| 972 | duelo | 33 |
| 973 | discutir | 33 |
| 974 | dirigir | 33 |
| 975 | diente | 33 |
| 976 | cuidar | 33 |
| 977 | cuenta | 33 |
| 978 | causa | 33 |
| 979 | beata | 33 |
| 980 | viuda | 32 |
| 981 | vago | 32 |
| 982 | terror | 32 |
| 983 | sacudir | 32 |
| 984 | posible | 32 |
| 985 | poesía | 32 |
| 986 | pisar | 32 |
| 987 | piel | 32 |
| 988 | patio | 32 |
| 989 | pan | 32 |
| 990 | pájaro | 32 |
| 991 | morder | 32 |
| 992 | meditar | 32 |
| 993 | maría | 32 |
| 994 | libertad | 32 |
| 995 | fino | 32 |
| 996 | fermo | 32 |
| 997 | enseñar | 32 |
| 998 | encimada | 32 |
| 999 | encender | 32 |
| 1000 | durante | 32 |
| 1001 | digno | 32 |
| 1002 | desafiar | 32 |
| 1003 | cariño | 32 |
| 1004 | beso | 32 |
| 1005 | ateo | 32 |
| 1006 | ataque | 32 |
| 1007 | agradecer | 32 |
| 1008 | admitir | 32 |
| 1009 | víctima | 31 |
| 1010 | tormento | 31 |
| 1011 | terrible | 31 |
| 1012 | risa | 31 |
| 1013 | relación | 31 |
| 1014 | redondo | 31 |
| 1015 | plata | 31 |
| 1016 | pasillo | 31 |
| 1017 | jefe | 31 |
| 1018 | interrumpir | 31 |
| 1019 | insistir | 31 |
| 1020 | hogar | 31 |
| 1021 | grave | 31 |
| 1022 | filósofo | 31 |
| 1023 | farol | 31 |
| 1024 | fama | 31 |
| 1025 | evitar | 31 |
| 1026 | esto | 31 |
| 1027 | encima | 31 |
| 1028 | empeñar | 31 |
| 1029 | consolar | 31 |
| 1030 | comparar | 31 |
| 1031 | cómico | 31 |
| 1032 | citar | 31 |
| 1033 | cesar | 31 |
| 1034 | cazador | 31 |
| 1035 | capaz | 31 |
| 1036 | besar | 31 |
| 1037 | altar | 31 |
| 1038 | vicio | 30 |
| 1039 | vecino | 30 |
| 1040 | varias | 30 |
| 1041 | todas | 30 |
| 1042 | tienda | 30 |
| 1043 | robar | 30 |
| 1044 | río | 30 |
| 1045 | respeto | 30 |
| 1046 | producir | 30 |
| 1047 | poeta | 30 |
| 1048 | noticia | 30 |
| 1049 | nobleza | 30 |
| 1050 | lectura | 30 |
| 1051 | instinto | 30 |
| 1052 | fortunato | 30 |
| 1053 | fortuna | 30 |
| 1054 | fiebre | 30 |
| 1055 | envolver | 30 |
| 1056 | devoción | 30 |
| 1057 | derecha | 30 |
| 1058 | condenar | 30 |
| 1059 | colocar | 30 |
| 1060 | colgar | 30 |
| 1061 | causar | 30 |
| 1062 | ayer | 30 |
| 1063 | adiós | 30 |
| 1064 | yerba | 29 |
| 1065 | vivo | 29 |
| 1066 | tirar | 29 |
| 1067 | susto | 29 |
| 1068 | sujetar | 29 |
| 1069 | social | 29 |
| 1070 | sermón | 29 |
| 1071 | sentimiento | 29 |
| 1072 | rufina | 29 |
| 1073 | rosa | 29 |
| 1074 | respetable | 29 |
| 1075 | regente | 29 |
| 1076 | portal | 29 |
| 1077 | poderoso | 29 |
| 1078 | pasa | 29 |
| 1079 | misterioso | 29 |
| 1080 | juntar | 29 |
| 1081 | humano | 29 |
| 1082 | honrar | 29 |
| 1083 | grandeza | 29 |
| 1084 | galería | 29 |
| 1085 | distraer | 29 |
| 1086 | discreto | 29 |
| 1087 | débil | 29 |
| 1088 | cristo | 29 |
| 1089 | consuelo | 29 |
| 1090 | conservar | 29 |
| 1091 | carretera | 29 |
| 1092 | anunciar | 29 |
| 1093 | animar | 29 |
| 1094 | veras | 28 |
| 1095 | unir | 28 |
| 1096 | tonto | 28 |
| 1097 | talento | 28 |
| 1098 | sitio | 28 |
| 1099 | semana | 28 |
| 1100 | sagrado | 28 |
| 1101 | retirar | 28 |
| 1102 | púlpito | 28 |
| 1103 | plan | 28 |
| 1104 | pintar | 28 |
| 1105 | milagro | 28 |
| 1106 | infierno | 28 |
| 1107 | gracioso | 28 |
| 1108 | gloria | 28 |
| 1109 | exclamar | 28 |
| 1110 | estudiar | 28 |
| 1111 | estrechar | 28 |
| 1112 | desierto | 28 |
| 1113 | copa | 28 |
| 1114 | celebrar | 28 |
| 1115 | animal | 28 |
| 1116 | ambición | 28 |
| 1117 | ala | 28 |
| 1118 | adivinar | 28 |
| 1119 | versar | 27 |
| 1120 | veinte | 27 |
| 1121 | superior | 27 |
| 1122 | soltar | 27 |
| 1123 | señores | 27 |
| 1124 | saborear | 27 |
| 1125 | oreja | 27 |
| 1126 | necio | 27 |
| 1127 | mourelo | 27 |
| 1128 | monja | 27 |
| 1129 | maestro | 27 |
| 1130 | loreto | 27 |
| 1131 | llover | 27 |
| 1132 | interior | 27 |
| 1133 | inocente | 27 |
| 1134 | humedad | 27 |
| 1135 | guante | 27 |
| 1136 | gobierno | 27 |
| 1137 | francisco | 27 |
| 1138 | favor | 27 |
| 1139 | fantasía | 27 |
| 1140 | familiar | 27 |
| 1141 | fácil | 27 |
| 1142 | extrañar | 27 |
| 1143 | excitar | 27 |
| 1144 | encanto | 27 |
| 1145 | emprender | 27 |
| 1146 | elocuencia | 27 |
| 1147 | doce | 27 |
| 1148 | disputar | 27 |
| 1149 | cuándo | 27 |
| 1150 | comercio | 27 |
| 1151 | chispa | 27 |
| 1152 | capricho | 27 |
| 1153 | aya | 27 |
| 1154 | atravesar | 27 |
| 1155 | adorar | 27 |
| 1156 | abierto | 27 |
| 1157 | turbar | 26 |
| 1158 | tenorio | 26 |
| 1159 | techo | 26 |
| 1160 | tabla | 26 |
| 1161 | sencillo | 26 |
| 1162 | seis | 26 |
| 1163 | satisfecho | 26 |
| 1164 | responder | 26 |
| 1165 | primavera | 26 |
| 1166 | poético | 26 |
| 1167 | pies | 26 |
| 1168 | pereza | 26 |
| 1169 | palco | 26 |
| 1170 | olvido | 26 |
| 1171 | oficio | 26 |
| 1172 | obedecer | 26 |
| 1173 | ministro | 26 |
| 1174 | lucha | 26 |
| 1175 | ladrón | 26 |
| 1176 | infame | 26 |
| 1177 | grupo | 26 |
| 1178 | flaco | 26 |
| 1179 | escuchar | 26 |
| 1180 | drama | 26 |
| 1181 | desnudo | 26 |
| 1182 | debilidad | 26 |
| 1183 | costa | 26 |
| 1184 | condición | 26 |
| 1185 | compañero | 26 |
| 1186 | cena | 26 |
| 1187 | celedonio | 26 |
| 1188 | católico | 26 |
| 1189 | cármenes | 26 |
| 1190 | carácter | 26 |
| 1191 | cambio | 26 |
| 1192 | calumniar | 26 |
| 1193 | aturdir | 26 |
| 1194 | asco | 26 |
| 1195 | aprender | 26 |
| 1196 | amoroso | 26 |
| 1197 | amenazar | 26 |
| 1198 | alabar | 26 |
| 1199 | afición | 26 |
| 1200 | admiración | 26 |
| 1201 | torcer | 25 |
| 1202 | sufrir | 25 |
| 1203 | solitario | 25 |
| 1204 | situación | 25 |
| 1205 | sacristía | 25 |
| 1206 | robusto | 25 |
| 1207 | resolución | 25 |
| 1208 | preocupar | 25 |
| 1209 | preciso | 25 |
| 1210 | perfectamente | 25 |
| 1211 | perezoso | 25 |
| 1212 | oprimir | 25 |
| 1213 | oponer | 25 |
| 1214 | opinar | 25 |
| 1215 | montar | 25 |
| 1216 | miseria | 25 |
| 1217 | mire | 25 |
| 1218 | mantener | 25 |
| 1219 | limpiar | 25 |
| 1220 | justicia | 25 |
| 1221 | influencia | 25 |
| 1222 | infinito | 25 |
| 1223 | indignar | 25 |
| 1224 | importante | 25 |
| 1225 | hueso | 25 |
| 1226 | forzar | 25 |
| 1227 | filosofía | 25 |
| 1228 | duro | 25 |
| 1229 | dueño | 25 |
| 1230 | dogma | 25 |
| 1231 | distraído | 25 |
| 1232 | delicado | 25 |
| 1233 | convidar | 25 |
| 1234 | cólera | 25 |
| 1235 | cambiar | 25 |
| 1236 | bedoya | 25 |
| 1237 | barón | 25 |
| 1238 | barca | 25 |
| 1239 | ah | 25 |
| 1240 | adentros | 25 |
| 1241 | aceptar | 25 |
| 1242 | victoria | 24 |
| 1243 | suplicar | 24 |
| 1244 | seco | 24 |
| 1245 | rey | 24 |
| 1246 | rendir | 24 |
| 1247 | rato | 24 |
| 1248 | pormenor | 24 |
| 1249 | pariente | 24 |
| 1250 | oración | 24 |
| 1251 | oler | 24 |
| 1252 | nave | 24 |
| 1253 | malicia | 24 |
| 1254 | lodo | 24 |
| 1255 | intención | 24 |
| 1256 | húmedo | 24 |
| 1257 | golpe | 24 |
| 1258 | fiesta | 24 |
| 1259 | exclamó | 24 |
| 1260 | esquina | 24 |
| 1261 | español | 24 |
| 1262 | época | 24 |
| 1263 | crecer | 24 |
| 1264 | consagrar | 24 |
| 1265 | cobarde | 24 |
| 1266 | ciego | 24 |
| 1267 | cera | 24 |
| 1268 | ceñir | 24 |
| 1269 | cazar | 24 |
| 1270 | bóveda | 24 |
| 1271 | beneficiar | 24 |
| 1272 | belleza | 24 |
| 1273 | bah | 24 |
| 1274 | avisar | 24 |
| 1275 | autoridad | 24 |
| 1276 | ambiente | 24 |
| 1277 | amarillo | 24 |
| 1278 | agradar | 24 |
| 1279 | trato | 23 |
| 1280 | tras | 23 |
| 1281 | traición | 23 |
| 1282 | tiniebla | 23 |
| 1283 | suficiente | 23 |
| 1284 | sostener | 23 |
| 1285 | siete | 23 |
| 1286 | rigor | 23 |
| 1287 | repugnante | 23 |
| 1288 | remediar | 23 |
| 1289 | puño | 23 |
| 1290 | pluma | 23 |
| 1291 | perdón | 23 |
| 1292 | partir | 23 |
| 1293 | pañuelo | 23 |
| 1294 | obscurecer | 23 |
| 1295 | nueva | 23 |
| 1296 | niebla | 23 |
| 1297 | material | 23 |
| 1298 | honra | 23 |
| 1299 | hipócrita | 23 |
| 1300 | habilidad | 23 |
| 1301 | guapo | 23 |
| 1302 | gris | 23 |
| 1303 | grado | 23 |
| 1304 | gracias | 23 |
| 1305 | fuente | 23 |
| 1306 | felicidad | 23 |
| 1307 | experiencia | 23 |
| 1308 | espectáculo | 23 |
| 1309 | disgusto | 23 |
| 1310 | desprecio | 23 |
| 1311 | demostrar | 23 |
| 1312 | delgado | 23 |
| 1313 | curiosidad | 23 |
| 1314 | compasión | 23 |
| 1315 | circunstancia | 23 |
| 1316 | caza | 23 |
| 1317 | carrera | 23 |
| 1318 | caber | 23 |
| 1319 | avergonzar | 23 |
| 1320 | autor | 23 |
| 1321 | aludir | 23 |
| 1322 | alejar | 23 |
| 1323 | aldeano | 23 |
| 1324 | ahogar | 23 |
| 1325 | trifón | 22 |
| 1326 | tren | 22 |
| 1327 | treinta | 22 |
| 1328 | tocador | 22 |
| 1329 | tapar | 22 |
| 1330 | seda | 22 |
| 1331 | secar | 22 |
| 1332 | rubio | 22 |
| 1333 | rodar | 22 |
| 1334 | raro | 22 |
| 1335 | próximo | 22 |
| 1336 | pegar | 22 |
| 1337 | pardo | 22 |
| 1338 | par | 22 |
| 1339 | oye | 22 |
| 1340 | nariz | 22 |
| 1341 | moda | 22 |
| 1342 | melancólico | 22 |
| 1343 | marcha | 22 |
| 1344 | mamá | 22 |
| 1345 | junta | 22 |
| 1346 | impulso | 22 |
| 1347 | idiota | 22 |
| 1348 | humillar | 22 |
| 1349 | fandiño | 22 |
| 1350 | estimar | 22 |
| 1351 | educación | 22 |
| 1352 | doler | 22 |
| 1353 | difícil | 22 |
| 1354 | devorar | 22 |
| 1355 | desconocido | 22 |
| 1356 | contacto | 22 |
| 1357 | confundir | 22 |
| 1358 | concluir | 22 |
| 1359 | completo | 22 |
| 1360 | columna | 22 |
| 1361 | civil | 22 |
| 1362 | cabildo | 22 |
| 1363 | buen | 22 |
| 1364 | baño | 22 |
| 1365 | atormentar | 22 |
| 1366 | aquella | 22 |
| 1367 | aplicar | 22 |
| 1368 | alcalde | 22 |
| 1369 | absoluto | 22 |
| 1370 | voluptuoso | 21 |
| 1371 | vinagre | 21 |
| 1372 | supremo | 21 |
| 1373 | seña | 21 |
| 1374 | seno | 21 |
| 1375 | sea | 21 |
| 1376 | sanar | 21 |
| 1377 | rodillas | 21 |
| 1378 | rival | 21 |
| 1379 | revelar | 21 |
| 1380 | repartir | 21 |
| 1381 | reflejar | 21 |
| 1382 | real | 21 |
| 1383 | promesa | 21 |
| 1384 | prisa | 21 |
| 1385 | pretender | 21 |
| 1386 | paquito | 21 |
| 1387 | orilla | 21 |
| 1388 | ordinario | 21 |
| 1389 | oportuno | 21 |
| 1390 | mueble | 21 |
| 1391 | mitad | 21 |
| 1392 | manchar | 21 |
| 1393 | magistrado | 21 |
| 1394 | lección | 21 |
| 1395 | justo | 21 |
| 1396 | ja | 21 |
| 1397 | inventar | 21 |
| 1398 | imaginar | 21 |
| 1399 | horror | 21 |
| 1400 | halagar | 21 |
| 1401 | fortaleza | 21 |
| 1402 | extraño | 21 |
| 1403 | espiar | 21 |
| 1404 | espejo | 21 |
| 1405 | espada | 21 |
| 1406 | escoger | 21 |
| 1407 | esbelto | 21 |
| 1408 | entierro | 21 |
| 1409 | disimulo | 21 |
| 1410 | deshacer | 21 |
| 1411 | consistir | 21 |
| 1412 | consejo | 21 |
| 1413 | comida | 21 |
| 1414 | cocinero | 21 |
| 1415 | capa | 21 |
| 1416 | camisa | 21 |
| 1417 | atar | 21 |
| 1418 | aquello | 21 |
| 1419 | apariencia | 21 |
| 1420 | ángel | 21 |
| 1421 | amable | 21 |
| 1422 | agujero | 21 |
| 1423 | advertir | 21 |
| 1424 | actividad | 21 |
| 1425 | virtuoso | 20 |
| 1426 | tresillo | 20 |
| 1427 | tertuliar | 20 |
| 1428 | sospecha | 20 |
| 1429 | sordo | 20 |
| 1430 | seducir | 20 |
| 1431 | salvación | 20 |
| 1432 | salar | 20 |
| 1433 | respecto | 20 |
| 1434 | regalar | 20 |
| 1435 | raíz | 20 |
| 1436 | quinta | 20 |
| 1437 | prosaico | 20 |
| 1438 | preocupación | 20 |
| 1439 | papá | 20 |
| 1440 | país | 20 |
| 1441 | órgano | 20 |
| 1442 | novio | 20 |
| 1443 | necedad | 20 |
| 1444 | mudar | 20 |
| 1445 | montón | 20 |
| 1446 | malicioso | 20 |
| 1447 | lluvia | 20 |
| 1448 | levita | 20 |
| 1449 | león | 20 |
| 1450 | lavar | 20 |
| 1451 | jardín | 20 |
| 1452 | gobernador | 20 |
| 1453 | gastar | 20 |
| 1454 | garganta | 20 |
| 1455 | formidable | 20 |
| 1456 | fábrica | 20 |
| 1457 | estrella | 20 |
| 1458 | estallar | 20 |
| 1459 | escrúpulo | 20 |
| 1460 | escandaloso | 20 |
| 1461 | escalofrío | 20 |
| 1462 | doblar | 20 |
| 1463 | distinguir | 20 |
| 1464 | dignidad | 20 |
| 1465 | desdén | 20 |
| 1466 | colorar | 20 |
| 1467 | claridad | 20 |
| 1468 | capital | 20 |
| 1469 | cajón | 20 |
| 1470 | buenas | 20 |
| 1471 | bravo | 20 |
| 1472 | aristocracia | 20 |
| 1473 | argumento | 20 |
| 1474 | ardiente | 20 |
| 1475 | alta | 20 |
| 1476 | acusar | 20 |
| 1477 | acostumbrar | 20 |
| 1478 | voluptuosidad | 19 |
| 1479 | verja | 19 |
| 1480 | vaya | 19 |
| 1481 | varios | 19 |
| 1482 | trasladar | 19 |
| 1483 | tolerar | 19 |
| 1484 | tierno | 19 |
| 1485 | testigo | 19 |
| 1486 | sistema | 19 |
| 1487 | sexo | 19 |
| 1488 | sereno | 19 |
| 1489 | santidad | 19 |
| 1490 | región | 19 |
| 1491 | recorrer | 19 |
| 1492 | recitar | 19 |
| 1493 | rápido | 19 |
| 1494 | punta | 19 |
| 1495 | prudente | 19 |
| 1496 | proyecto | 19 |
| 1497 | profanar | 19 |
| 1498 | primo | 19 |
| 1499 | precisamente | 19 |
| 1500 | positivo | 19 |
| 1501 | plato | 19 |
| 1502 | plantar | 19 |
| 1503 | pistola | 19 |
| 1504 | pesado | 19 |
| 1505 | pelo | 19 |
| 1506 | peligroso | 19 |
| 1507 | particular | 19 |
| 1508 | mérito | 19 |
| 1509 | menor | 19 |
| 1510 | matrimonio | 19 |
| 1511 | marear | 19 |
| 1512 | manía | 19 |
| 1513 | manejar | 19 |
| 1514 | lujo | 19 |
| 1515 | interesar | 19 |
| 1516 | inspirar | 19 |
| 1517 | insignificante | 19 |
| 1518 | impaciencia | 19 |
| 1519 | iluminar | 19 |
| 1520 | humo | 19 |
| 1521 | humildad | 19 |
| 1522 | hola | 19 |
| 1523 | habitación | 19 |
| 1524 | gorro | 19 |
| 1525 | germán | 19 |
| 1526 | frialdad | 19 |
| 1527 | flaqueza | 19 |
| 1528 | firmar | 19 |
| 1529 | fiar | 19 |
| 1530 | exaltación | 19 |
| 1531 | estudiante | 19 |
| 1532 | estirar | 19 |
| 1533 | estaba | 19 |
| 1534 | está | 19 |
| 1535 | esposar | 19 |
| 1536 | espesar | 19 |
| 1537 | elemento | 19 |
| 1538 | dorar | 19 |
| 1539 | doméstico | 19 |
| 1540 | desnudar | 19 |
| 1541 | delito | 19 |
| 1542 | conquistar | 19 |
| 1543 | confuso | 19 |
| 1544 | comulgar | 19 |
| 1545 | colonia | 19 |
| 1546 | ceder | 19 |
| 1547 | casualidad | 19 |
| 1548 | calma | 19 |
| 1549 | brillante | 19 |
| 1550 | bismarck | 19 |
| 1551 | batir | 19 |
| 1552 | barba | 19 |
| 1553 | atacar | 19 |
| 1554 | arreglar | 19 |
| 1555 | apuntar | 19 |
| 1556 | anda | 19 |
| 1557 | ambos | 19 |
| 1558 | ajeno | 19 |
| 1559 | vieja | 18 |
| 1560 | vejez | 18 |
| 1561 | tragar | 18 |
| 1562 | término | 18 |
| 1563 | tela | 18 |
| 1564 | sus | 18 |
| 1565 | sudor | 18 |
| 1566 | sobrino | 18 |
| 1567 | simpático | 18 |
| 1568 | silencioso | 18 |
| 1569 | seductor | 18 |
| 1570 | sacrificar | 18 |
| 1571 | rodilla | 18 |
| 1572 | resultar | 18 |
| 1573 | pozo | 18 |
| 1574 | parroquia | 18 |
| 1575 | paciencia | 18 |
| 1576 | ostentar | 18 |
| 1577 | orar | 18 |
| 1578 | novena | 18 |
| 1579 | muchacho | 18 |
| 1580 | monótono | 18 |
| 1581 | moderno | 18 |
| 1582 | medir | 18 |
| 1583 | largar | 18 |
| 1584 | lámpara | 18 |
| 1585 | jesuita | 18 |
| 1586 | invisible | 18 |
| 1587 | intenso | 18 |
| 1588 | ingrato | 18 |
| 1589 | inglés | 18 |
| 1590 | inefable | 18 |
| 1591 | igual | 18 |
| 1592 | hundir | 18 |
| 1593 | gritos | 18 |
| 1594 | fonda | 18 |
| 1595 | existencia | 18 |
| 1596 | exaltar | 18 |
| 1597 | esclavo | 18 |
| 1598 | escaso | 18 |
| 1599 | esa | 18 |
| 1600 | ensueño | 18 |
| 1601 | elocuente | 18 |
| 1602 | ejercicio | 18 |
| 1603 | egoísmo | 18 |
| 1604 | disgustar | 18 |
| 1605 | cursi | 18 |
| 1606 | consultar | 18 |
| 1607 | constantino | 18 |
| 1608 | conducta | 18 |
| 1609 | común | 18 |
| 1610 | complacer | 18 |
| 1611 | codo | 18 |
| 1612 | círculo | 18 |
| 1613 | chiquillo | 18 |
| 1614 | cariñoso | 18 |
| 1615 | caricia | 18 |
| 1616 | calleja | 18 |
| 1617 | caja | 18 |
| 1618 | butaca | 18 |
| 1619 | barrio | 18 |
| 1620 | azotar | 18 |
| 1621 | aventurar | 18 |
| 1622 | audiencia | 18 |
| 1623 | asiento | 18 |
| 1624 | americano | 18 |
| 1625 | alborotar | 18 |
| 1626 | afán | 18 |
| 1627 | aconsejar | 18 |
| 1628 | acera | 18 |
| 1629 | visión | 17 |
| 1630 | vender | 17 |
| 1631 | tus | 17 |
| 1632 | trapo | 17 |
| 1633 | ternura | 17 |
| 1634 | talar | 17 |
| 1635 | sudar | 17 |
| 1636 | sublime | 17 |
| 1637 | sonriente | 17 |
| 1638 | solemnidad | 17 |
| 1639 | sofá | 17 |
| 1640 | salvaje | 17 |
| 1641 | romanticismo | 17 |
| 1642 | resto | 17 |
| 1643 | renunciar | 17 |
| 1644 | recobrar | 17 |
| 1645 | quince | 17 |
| 1646 | prudencia | 17 |
| 1647 | procesión | 17 |
| 1648 | probable | 17 |
| 1649 | predicar | 17 |
| 1650 | pícaro | 17 |
| 1651 | picante | 17 |
| 1652 | penetrar | 17 |
| 1653 | pedazo | 17 |
| 1654 | párroco | 17 |
| 1655 | pareja | 17 |
| 1656 | paraguas | 17 |
| 1657 | obrar | 17 |
| 1658 | murmuración | 17 |
| 1659 | mísero | 17 |
| 1660 | mentira | 17 |
| 1661 | mentir | 17 |
| 1662 | manifestar | 17 |
| 1663 | manga | 17 |
| 1664 | limosna | 17 |
| 1665 | insultar | 17 |
| 1666 | inmóvil | 17 |
| 1667 | influenciar | 17 |
| 1668 | ilusión | 17 |
| 1669 | hipocresía | 17 |
| 1670 | ha | 17 |
| 1671 | gritaba | 17 |
| 1672 | gran | 17 |
| 1673 | gas | 17 |
| 1674 | fresca | 17 |
| 1675 | frecuentar | 17 |
| 1676 | finar | 17 |
| 1677 | feo | 17 |
| 1678 | fanatismo | 17 |
| 1679 | estúpido | 17 |
| 1680 | estación | 17 |
| 1681 | especial | 17 |
| 1682 | escuela | 17 |
| 1683 | enternecer | 17 |
| 1684 | dulzura | 17 |
| 1685 | divino | 17 |
| 1686 | disparatar | 17 |
| 1687 | discurso | 17 |
| 1688 | diócesis | 17 |
| 1689 | dificultad | 17 |
| 1690 | descargar | 17 |
| 1691 | desaire | 17 |
| 1692 | demonio | 17 |
| 1693 | cuerda | 17 |
| 1694 | corte | 17 |
| 1695 | concepto | 17 |
| 1696 | completamente | 17 |
| 1697 | cigarro | 17 |
| 1698 | cercar | 17 |
| 1699 | castaño | 17 |
| 1700 | bolsillo | 17 |
| 1701 | atribuir | 17 |
| 1702 | atraer | 17 |
| 1703 | arder | 17 |
| 1704 | apetito | 17 |
| 1705 | acariciar | 17 |
| 1706 | velar | 16 |
| 1707 | vagamente | 16 |
| 1708 | trueno | 16 |
| 1709 | tronco | 16 |
| 1710 | todos | 16 |
| 1711 | tiro | 16 |
| 1712 | sutil | 16 |
| 1713 | solicitar | 16 |
| 1714 | singular | 16 |
| 1715 | respectivo | 16 |
| 1716 | rasgar | 16 |
| 1717 | prosa | 16 |
| 1718 | primeros | 16 |
| 1719 | pretensión | 16 |
| 1720 | presidir | 16 |
| 1721 | poema | 16 |
| 1722 | picar | 16 |
| 1723 | peso | 16 |
| 1724 | permiso | 16 |
| 1725 | perfume | 16 |
| 1726 | perdiz | 16 |
| 1727 | perales | 16 |
| 1728 | partes | 16 |
| 1729 | padrino | 16 |
| 1730 | os | 16 |
| 1731 | orador | 16 |
| 1732 | ola | 16 |
| 1733 | ofender | 16 |
| 1734 | ocupación | 16 |
| 1735 | novedad | 16 |
| 1736 | muro | 16 |
| 1737 | multitud | 16 |
| 1738 | moralidad | 16 |
| 1739 | montaña | 16 |
| 1740 | melancolía | 16 |
| 1741 | marqueses | 16 |
| 1742 | ligero | 16 |
| 1743 | legua | 16 |
| 1744 | infeliz | 16 |
| 1745 | indignación | 16 |
| 1746 | impío | 16 |
| 1747 | horrorizar | 16 |
| 1748 | horizonte | 16 |
| 1749 | hábito | 16 |
| 1750 | fila | 16 |
| 1751 | fatigar | 16 |
| 1752 | fantasma | 16 |
| 1753 | excursión | 16 |
| 1754 | estudio | 16 |
| 1755 | estatua | 16 |
| 1756 | esta | 16 |
| 1757 | espina | 16 |
| 1758 | equivocar | 16 |
| 1759 | enérgico | 16 |
| 1760 | elegancia | 16 |
| 1761 | disparar | 16 |
| 1762 | desvanecer | 16 |
| 1763 | descansar | 16 |
| 1764 | cuento | 16 |
| 1765 | convidado | 16 |
| 1766 | contiguo | 16 |
| 1767 | confidencia | 16 |
| 1768 | conferencia | 16 |
| 1769 | cometer | 16 |
| 1770 | cobrar | 16 |
| 1771 | cita | 16 |
| 1772 | chato | 16 |
| 1773 | cenador | 16 |
| 1774 | cementerio | 16 |
| 1775 | castigar | 16 |
| 1776 | cabello | 16 |
| 1777 | blando | 16 |
| 1778 | ausencia | 16 |
| 1779 | arrogante | 16 |
| 1780 | armario | 16 |
| 1781 | aristócrata | 16 |
| 1782 | aplastar | 16 |
| 1783 | apartar | 16 |
| 1784 | almo | 16 |
| 1785 | alimento | 16 |
| 1786 | alcohol | 16 |
| 1787 | agradable | 16 |
| 1788 | adornar | 16 |
| 1789 | acción | 16 |
| 1790 | abusar | 16 |
| 1791 | abismo | 16 |
| 1792 | vuelo | 15 |
| 1793 | vicario | 15 |
| 1794 | venerable | 15 |
| 1795 | vela | 15 |
| 1796 | vaso | 15 |
| 1797 | vacilar | 15 |
| 1798 | universal | 15 |
| 1799 | triunfante | 15 |
| 1800 | torpe | 15 |
| 1801 | tigre | 15 |
| 1802 | tertulia | 15 |
| 1803 | teología | 15 |
| 1804 | temperamento | 15 |
| 1805 | tembloroso | 15 |
| 1806 | taberna | 15 |
| 1807 | suspender | 15 |
| 1808 | subterráneo | 15 |
| 1809 | soplar | 15 |
| 1810 | sofisma | 15 |
| 1811 | símbolo | 15 |
| 1812 | serenar | 15 |
| 1813 | señal | 15 |
| 1814 | satisfacción | 15 |
| 1815 | salto | 15 |
| 1816 | sábana | 15 |
| 1817 | rianzares | 15 |
| 1818 | retumbar | 15 |
| 1819 | repentino | 15 |
| 1820 | raza | 15 |
| 1821 | querida | 15 |
| 1822 | pudor | 15 |
| 1823 | provocar | 15 |
| 1824 | primeras | 15 |
| 1825 | prestar | 15 |
| 1826 | pollo | 15 |
| 1827 | pierna | 15 |
| 1828 | pico | 15 |
| 1829 | peligrar | 15 |
| 1830 | palo | 15 |
| 1831 | osar | 15 |
| 1832 | norte | 15 |
| 1833 | negocio | 15 |
| 1834 | mira | 15 |
| 1835 | medida | 15 |
| 1836 | matalerejo | 15 |
| 1837 | mármol | 15 |
| 1838 | juzgar | 15 |
| 1839 | juicio | 15 |
| 1840 | injusticia | 15 |
| 1841 | infamar | 15 |
| 1842 | inconveniente | 15 |
| 1843 | impresión | 15 |
| 1844 | ilustre | 15 |
| 1845 | ilustrar | 15 |
| 1846 | ignorar | 15 |
| 1847 | helar | 15 |
| 1848 | hastío | 15 |
| 1849 | futuro | 15 |
| 1850 | fumar | 15 |
| 1851 | fruto | 15 |
| 1852 | excepción | 15 |
| 1853 | españa | 15 |
| 1854 | enterrar | 15 |
| 1855 | encantar | 15 |
| 1856 | eh | 15 |
| 1857 | difunto | 15 |
| 1858 | deshonra | 15 |
| 1859 | describir | 15 |
| 1860 | dedicar | 15 |
| 1861 | culpar | 15 |
| 1862 | corredor | 15 |
| 1863 | contemplación | 15 |
| 1864 | comprometer | 15 |
| 1865 | compadecer | 15 |
| 1866 | coincidir | 15 |
| 1867 | chiste | 15 |
| 1868 | chimenea | 15 |
| 1869 | cerrado | 15 |
| 1870 | celestina | 15 |
| 1871 | canción | 15 |
| 1872 | camoirán | 15 |
| 1873 | bulto | 15 |
| 1874 | aspirar | 15 |
| 1875 | arqueólogo | 15 |
| 1876 | apenar | 15 |
| 1877 | ansia | 15 |
| 1878 | alrededor | 15 |
| 1879 | almohada | 15 |
| 1880 | adquirir | 15 |
| 1881 | acero | 15 |
| 1882 | zapato | 14 |
| 1883 | yacer | 14 |
| 1884 | vergonzoso | 14 |
| 1885 | ventaja | 14 |
| 1886 | varón | 14 |
| 1887 | trampa | 14 |
| 1888 | tordo | 14 |
| 1889 | tesoro | 14 |
| 1890 | terciopelo | 14 |
| 1891 | temor | 14 |
| 1892 | tejado | 14 |
| 1893 | supersticioso | 14 |
| 1894 | sumir | 14 |
| 1895 | suceso | 14 |
| 1896 | sublevar | 14 |
| 1897 | silenciar | 14 |
| 1898 | significar | 14 |
| 1899 | seducción | 14 |
| 1900 | ruina | 14 |
| 1901 | rubia | 14 |
| 1902 | rotar | 14 |
| 1903 | rinconada | 14 |
| 1904 | revolución | 14 |
| 1905 | revelación | 14 |
| 1906 | repugnancia | 14 |
| 1907 | reinar | 14 |
| 1908 | recinto | 14 |
| 1909 | pulcro | 14 |
| 1910 | profanación | 14 |
| 1911 | prestigio | 14 |
| 1912 | postura | 14 |
| 1913 | pliegue | 14 |
| 1914 | patria | 14 |
| 1915 | pastor | 14 |
| 1916 | pantalón | 14 |
| 1917 | obrero | 14 |
| 1918 | misterio | 14 |
| 1919 | millón | 14 |
| 1920 | militar | 14 |
| 1921 | miel | 14 |
| 1922 | medias | 14 |
| 1923 | llanto | 14 |
| 1924 | literata | 14 |
| 1925 | literario | 14 |
| 1926 | liga | 14 |
| 1927 | lenguaje | 14 |
| 1928 | latín | 14 |
| 1929 | intentar | 14 |
| 1930 | inocencia | 14 |
| 1931 | inmenso | 14 |
| 1932 | infanzón | 14 |
| 1933 | indispensable | 14 |
| 1934 | improvisar | 14 |
| 1935 | humanidad | 14 |
| 1936 | hondo | 14 |
| 1937 | herir | 14 |
| 1938 | gravar | 14 |
| 1939 | gordo | 14 |
| 1940 | expansivo | 14 |
| 1941 | exagerar | 14 |
| 1942 | estorbar | 14 |
| 1943 | estómago | 14 |
| 1944 | esparcir | 14 |
| 1945 | dominio | 14 |
| 1946 | doloroso | 14 |
| 1947 | disimulado | 14 |
| 1948 | discretamente | 14 |
| 1949 | disciplina | 14 |
| 1950 | diferente | 14 |
| 1951 | diálogo | 14 |
| 1952 | destino | 14 |
| 1953 | desafío | 14 |
| 1954 | deje | 14 |
| 1955 | criminal | 14 |
| 1956 | criado | 14 |
| 1957 | coronel | 14 |
| 1958 | convicción | 14 |
| 1959 | constante | 14 |
| 1960 | conocimiento | 14 |
| 1961 | columpio | 14 |
| 1962 | charco | 14 |
| 1963 | centro | 14 |
| 1964 | celosía | 14 |
| 1965 | cegar | 14 |
| 1966 | castidad | 14 |
| 1967 | casero | 14 |
| 1968 | cargo | 14 |
| 1969 | calzar | 14 |
| 1970 | calderón | 14 |
| 1971 | cadena | 14 |
| 1972 | buena | 14 |
| 1973 | brotar | 14 |
| 1974 | bolsa | 14 |
| 1975 | bofetada | 14 |
| 1976 | batalla | 14 |
| 1977 | bañar | 14 |
| 1978 | auditorio | 14 |
| 1979 | atender | 14 |
| 1980 | aspecto | 14 |
| 1981 | asir | 14 |
| 1982 | artístico | 14 |
| 1983 | artista | 14 |
| 1984 | arrugar | 14 |
| 1985 | arena | 14 |
| 1986 | apurar | 14 |
| 1987 | apreciar | 14 |
| 1988 | alumbrar | 14 |
| 1989 | agustín | 14 |
| 1990 | ademán | 14 |
| 1991 | vocación | 13 |
| 1992 | violín | 13 |
| 1993 | viernes | 13 |
| 1994 | vacío | 13 |
| 1995 | uso | 13 |
| 1996 | tranquilidad | 13 |
| 1997 | tarea | 13 |
| 1998 | soso | 13 |
| 1999 | sorpresa | 13 |
| 2000 | sincero | 13 |
| 2001 | severo | 13 |
| 2002 | salida | 13 |
| 2003 | sabiduría | 13 |
| 2004 | risueño | 13 |
| 2005 | revolver | 13 |
| 2006 | retórica | 13 |
| 2007 | reparar | 13 |
| 2008 | reñir | 13 |
| 2009 | relámpago | 13 |
| 2010 | reflejo | 13 |
| 2011 | reconciliar | 13 |
| 2012 | recomendar | 13 |
| 2013 | reclamar | 13 |
| 2014 | quemar | 13 |
| 2015 | pulso | 13 |
| 2016 | puesta | 13 |
| 2017 | proceder | 13 |
| 2018 | prenda | 13 |
| 2019 | porvenir | 13 |
| 2020 | plebeyo | 13 |
| 2021 | pino | 13 |
| 2022 | piano | 13 |
| 2023 | pernueces | 13 |
| 2024 | penitente | 13 |
| 2025 | pendiente | 13 |
| 2026 | pavimento | 13 |
| 2027 | pausa | 13 |
| 2028 | pasmar | 13 |
| 2029 | partidario | 13 |
| 2030 | página | 13 |
| 2031 | orgulloso | 13 |
| 2032 | ópera | 13 |
| 2033 | músculo | 13 |
| 2034 | murmullo | 13 |
| 2035 | muralla | 13 |
| 2036 | mundano | 13 |
| 2037 | moribundo | 13 |
| 2038 | moneda | 13 |
| 2039 | medicina | 13 |
| 2040 | mártir | 13 |
| 2041 | maneras | 13 |
| 2042 | maldecir | 13 |
| 2043 | libertino | 13 |
| 2044 | lazo | 13 |
| 2045 | jugador | 13 |
| 2046 | ironía | 13 |
| 2047 | intimidad | 13 |
| 2048 | interesante | 13 |
| 2049 | inteligente | 13 |
| 2050 | infancia | 13 |
| 2051 | indicar | 13 |
| 2052 | imprudencia | 13 |
| 2053 | ignorancia | 13 |
| 2054 | ídolo | 13 |
| 2055 | horroroso | 13 |
| 2056 | honrado | 13 |
| 2057 | hermosísimo | 13 |
| 2058 | heredar | 13 |
| 2059 | guerra | 13 |
| 2060 | grano | 13 |
| 2061 | gota | 13 |
| 2062 | freír | 13 |
| 2063 | flotar | 13 |
| 2064 | flamenco | 13 |
| 2065 | fanático | 13 |
| 2066 | famoso | 13 |
| 2067 | explicación | 13 |
| 2068 | excelente | 13 |
| 2069 | escopeta | 13 |
| 2070 | error | 13 |
| 2071 | entusiasmar | 13 |
| 2072 | entrada | 13 |
| 2073 | engaño | 13 |
| 2074 | empleado | 13 |
| 2075 | elevar | 13 |
| 2076 | egoísta | 13 |
| 2077 | dorado | 13 |
| 2078 | doctor | 13 |
| 2079 | distancia | 13 |
| 2080 | disparate | 13 |
| 2081 | dicho | 13 |
| 2082 | deslumbrar | 13 |
| 2083 | desgraciado | 13 |
| 2084 | desesperar | 13 |
| 2085 | descanso | 13 |
| 2086 | delicioso | 13 |
| 2087 | deleite | 13 |
| 2088 | decente | 13 |
| 2089 | daño | 13 |
| 2090 | cuervo | 13 |
| 2091 | cuarenta | 13 |
| 2092 | corto | 13 |
| 2093 | corfín | 13 |
| 2094 | coquetería | 13 |
| 2095 | contraste | 13 |
| 2096 | contestó | 13 |
| 2097 | construir | 13 |
| 2098 | conquista | 13 |
| 2099 | cómplice | 13 |
| 2100 | chocar | 13 |
| 2101 | castigo | 13 |
| 2102 | caro | 13 |
| 2103 | capitán | 13 |
| 2104 | cansado | 13 |
| 2105 | campana | 13 |
| 2106 | caliente | 13 |
| 2107 | calidad | 13 |
| 2108 | calentar | 13 |
| 2109 | brazos | 13 |
| 2110 | bendito | 13 |
| 2111 | bello | 13 |
| 2112 | atmósfera | 13 |
| 2113 | asqueroso | 13 |
| 2114 | artículo | 13 |
| 2115 | arruinar | 13 |
| 2116 | armonía | 13 |
| 2117 | aprobar | 13 |
| 2118 | amanecer | 13 |
| 2119 | altura | 13 |
| 2120 | aliento | 13 |
| 2121 | algazara | 13 |
| 2122 | alcanzar | 13 |
| 2123 | acá | 13 |
| 2124 | abrazar | 13 |
| 2125 | vulgo | 12 |
| 2126 | violentar | 12 |
| 2127 | vetusto | 12 |
| 2128 | triunfar | 12 |
| 2129 | tipo | 12 |
| 2130 | tila | 12 |
| 2131 | suma | 12 |
| 2132 | sugerir | 12 |
| 2133 | sofocar | 12 |
| 2134 | sobrenatural | 12 |
| 2135 | sería | 12 |
| 2136 | sensación | 12 |
| 2137 | sendos | 12 |
| 2138 | sendero | 12 |
| 2139 | seminario | 12 |
| 2140 | secular | 12 |
| 2141 | sastre | 12 |
| 2142 | sarcasmo | 12 |
| 2143 | salesas | 12 |
| 2144 | sacrílego | 12 |
| 2145 | restituir | 12 |
| 2146 | reservar | 12 |
| 2147 | repasar | 12 |
| 2148 | reluciente | 12 |
| 2149 | religiosidad | 12 |
| 2150 | recurso | 12 |
| 2151 | recado | 12 |
| 2152 | rasar | 12 |
| 2153 | quedo | 12 |
| 2154 | puramente | 12 |
| 2155 | publicar | 12 |
| 2156 | propasar | 12 |
| 2157 | profano | 12 |
| 2158 | probablemente | 12 |
| 2159 | preguntaba | 12 |
| 2160 | pregunta | 12 |
| 2161 | pobreza | 12 |
| 2162 | pilar | 12 |
| 2163 | parís | 12 |
| 2164 | parecido | 12 |
| 2165 | otoño | 12 |
| 2166 | original | 12 |
| 2167 | odio | 12 |
| 2168 | obstáculo | 12 |
| 2169 | observación | 12 |
| 2170 | moza | 12 |
| 2171 | mortal | 12 |
| 2172 | moreno | 12 |
| 2173 | morar | 12 |
| 2174 | mojar | 12 |
| 2175 | mina | 12 |
| 2176 | majestuoso | 12 |
| 2177 | madrugar | 12 |
| 2178 | lugareño | 12 |
| 2179 | lontananza | 12 |
| 2180 | loma | 12 |
| 2181 | limpieza | 12 |
| 2182 | levitar | 12 |
| 2183 | lector | 12 |
| 2184 | latigazo | 12 |
| 2185 | lascivo | 12 |
| 2186 | lascivia | 12 |
| 2187 | lamentar | 12 |
| 2188 | italiano | 12 |
| 2189 | invitar | 12 |
| 2190 | invencible | 12 |
| 2191 | inundar | 12 |
| 2192 | indiferencia | 12 |
| 2193 | incapaz | 12 |
| 2194 | imprudente | 12 |
| 2195 | impacientar | 12 |
| 2196 | hueco | 12 |
| 2197 | histórico | 12 |
| 2198 | hilo | 12 |
| 2199 | gallo | 12 |
| 2200 | furor | 12 |
| 2201 | frescura | 12 |
| 2202 | francés | 12 |
| 2203 | florar | 12 |
| 2204 | firme | 12 |
| 2205 | fiera | 12 |
| 2206 | fervor | 12 |
| 2207 | farsa | 12 |
| 2208 | fantástico | 12 |
| 2209 | exquisito | 12 |
| 2210 | expediente | 12 |
| 2211 | exageración | 12 |
| 2212 | estridente | 12 |
| 2213 | especialmente | 12 |
| 2214 | escenario | 12 |
| 2215 | escape | 12 |
| 2216 | enfermar | 12 |
| 2217 | encargar | 12 |
| 2218 | embozar | 12 |
| 2219 | educar | 12 |
| 2220 | edificio | 12 |
| 2221 | distracción | 12 |
| 2222 | discreción | 12 |
| 2223 | diputado | 12 |
| 2224 | deuda | 12 |
| 2225 | delirio | 12 |
| 2226 | defecto | 12 |
| 2227 | crítico | 12 |
| 2228 | coronar | 12 |
| 2229 | comunicar | 12 |
| 2230 | comerciante | 12 |
| 2231 | colchón | 12 |
| 2232 | codiciar | 12 |
| 2233 | clásico | 12 |
| 2234 | claramente | 12 |
| 2235 | cereza | 12 |
| 2236 | célebre | 12 |
| 2237 | casado | 12 |
| 2238 | cántico | 12 |
| 2239 | bullicioso | 12 |
| 2240 | breve | 12 |
| 2241 | baronesa | 12 |
| 2242 | ayuntamiento | 12 |
| 2243 | averiguar | 12 |
| 2244 | aragonés | 12 |
| 2245 | apresurar | 12 |
| 2246 | antigüedad | 12 |
| 2247 | amarillento | 12 |
| 2248 | amabilidad | 12 |
| 2249 | alarmar | 12 |
| 2250 | alarde | 12 |
| 2251 | aguardiente | 12 |
| 2252 | afirmar | 12 |
| 2253 | aficionado | 12 |
| 2254 | adulterio | 12 |
| 2255 | activo | 12 |
| 2256 | acólito | 12 |
| 2257 | abnegación | 12 |
| 2258 | vientre | 11 |
| 2259 | ves | 11 |
| 2260 | valiente | 11 |
| 2261 | universo | 11 |
| 2262 | tronar | 11 |
| 2263 | tribunal | 11 |
| 2264 | transformar | 11 |
| 2265 | traidor | 11 |
| 2266 | tirano | 11 |
| 2267 | terso | 11 |
| 2268 | tenía | 11 |
| 2269 | tambor | 11 |
| 2270 | suspiro | 11 |
| 2271 | sublimar | 11 |
| 2272 | suavidad | 11 |
| 2273 | sopa | 11 |
| 2274 | sillón | 11 |
| 2275 | silbar | 11 |
| 2276 | sierra | 11 |
| 2277 | servidumbre | 11 |
| 2278 | seriedad | 11 |
| 2279 | será | 11 |
| 2280 | sentimental | 11 |
| 2281 | secretar | 11 |
| 2282 | saludo | 11 |
| 2283 | roncar | 11 |
| 2284 | roce | 11 |
| 2285 | roble | 11 |
| 2286 | riqueza | 11 |
| 2287 | reunir | 11 |
| 2288 | retorcer | 11 |
| 2289 | reja | 11 |
| 2290 | reina | 11 |
| 2291 | reflexión | 11 |
| 2292 | recrear | 11 |
| 2293 | ratos | 11 |
| 2294 | pupila | 11 |
| 2295 | puntillas | 11 |
| 2296 | puerto | 11 |
| 2297 | prójimo | 11 |
| 2298 | progreso | 11 |
| 2299 | prodigar | 11 |
| 2300 | presenciar | 11 |
| 2301 | precisar | 11 |
| 2302 | precioso | 11 |
| 2303 | plomo | 11 |
| 2304 | plazuela | 11 |
| 2305 | pinchar | 11 |
| 2306 | pesadilla | 11 |
| 2307 | pertenecer | 11 |
| 2308 | perfecto | 11 |
| 2309 | perdido | 11 |
| 2310 | percal | 11 |
| 2311 | peinar | 11 |
| 2312 | pegajoso | 11 |
| 2313 | partida | 11 |
| 2314 | párpado | 11 |
| 2315 | parece | 11 |
| 2316 | paño | 11 |
| 2317 | palidez | 11 |
| 2318 | oriente | 11 |
| 2319 | once | 11 |
| 2320 | oiga | 11 |
| 2321 | náusea | 11 |
| 2322 | museo | 11 |
| 2323 | mortificar | 11 |
| 2324 | molino | 11 |
| 2325 | modelo | 11 |
| 2326 | metálico | 11 |
| 2327 | mayo | 11 |
| 2328 | marisma | 11 |
| 2329 | maldito | 11 |
| 2330 | majadero | 11 |
| 2331 | maíz | 11 |
| 2332 | magnífico | 11 |
| 2333 | limpio | 11 |
| 2334 | jaqueca | 11 |
| 2335 | izquierda | 11 |
| 2336 | irresistible | 11 |
| 2337 | inmediatamente | 11 |
| 2338 | importancia | 11 |
| 2339 | impedir | 11 |
| 2340 | héroe | 11 |
| 2341 | grueso | 11 |
| 2342 | golosina | 11 |
| 2343 | fúnebre | 11 |
| 2344 | formalidad | 11 |
| 2345 | fácilmente | 11 |
| 2346 | expresar | 11 |
| 2347 | exposición | 11 |
| 2348 | excesivo | 11 |
| 2349 | evidente | 11 |
| 2350 | eucaliptus | 11 |
| 2351 | estoy | 11 |
| 2352 | espeso | 11 |
| 2353 | espantar | 11 |
| 2354 | entretener | 11 |
| 2355 | engordar | 11 |
| 2356 | enamorado | 11 |
| 2357 | empresa | 11 |
| 2358 | embozo | 11 |
| 2359 | elogio | 11 |
| 2360 | dramático | 11 |
| 2361 | dividir | 11 |
| 2362 | distinto | 11 |
| 2363 | dispensar | 11 |
| 2364 | dichoso | 11 |
| 2365 | devolver | 11 |
| 2366 | desmayar | 11 |
| 2367 | desfachatez | 11 |
| 2368 | descalzar | 11 |
| 2369 | depositar | 11 |
| 2370 | delantero | 11 |
| 2371 | dejado | 11 |
| 2372 | dañar | 11 |
| 2373 | crujir | 11 |
| 2374 | cruel | 11 |
| 2375 | cristianar | 11 |
| 2376 | crear | 11 |
| 2377 | correcto | 11 |
| 2378 | conversión | 11 |
| 2379 | continuo | 11 |
| 2380 | consiguiente | 11 |
| 2381 | conducir | 11 |
| 2382 | comisión | 11 |
| 2383 | comentario | 11 |
| 2384 | combatir | 11 |
| 2385 | brutal | 11 |
| 2386 | bronce | 11 |
| 2387 | borrar | 11 |
| 2388 | bondad | 11 |
| 2389 | biblioteca | 11 |
| 2390 | berlina | 11 |
| 2391 | basta | 11 |
| 2392 | barrer | 11 |
| 2393 | arranque | 11 |
| 2394 | armar | 11 |
| 2395 | arco | 11 |
| 2396 | apóstol | 11 |
| 2397 | aplaudir | 11 |
| 2398 | aparte | 11 |
| 2399 | apagado | 11 |
| 2400 | ansiedad | 11 |
| 2401 | anhelo | 11 |
| 2402 | almunia | 11 |
| 2403 | alfombra | 11 |
| 2404 | agudo | 11 |
| 2405 | acendrado | 11 |
| 2406 | aburrimiento | 11 |
| 2407 | abrazo | 11 |
| 2408 | abanico | 11 |
| 2409 | visto | 10 |
| 2410 | vigor | 10 |
| 2411 | vigilia | 10 |
| 2412 | vencedor | 10 |
| 2413 | vehemente | 10 |
| 2414 | útil | 10 |
| 2415 | trébol | 10 |
| 2416 | tranquilizar | 10 |
| 2417 | trágico | 10 |
| 2418 | tercera | 10 |
| 2419 | temible | 10 |
| 2420 | temblor | 10 |
| 2421 | taza | 10 |
| 2422 | tapia | 10 |
| 2423 | tamaño | 10 |
| 2424 | taciturno | 10 |
| 2425 | sor | 10 |
| 2426 | soñador | 10 |
| 2427 | solemnemente | 10 |
| 2428 | soberbio | 10 |
| 2429 | so | 10 |
| 2430 | sien | 10 |
| 2431 | servanda | 10 |
| 2432 | seriar | 10 |
| 2433 | sequedad | 10 |
| 2434 | semilla | 10 |
| 2435 | seguridad | 10 |
| 2436 | sano | 10 |
| 2437 | romería | 10 |
| 2438 | retroceder | 10 |
| 2439 | respuesta | 10 |
| 2440 | resorte | 10 |
| 2441 | resistencia | 10 |
| 2442 | resbalar | 10 |
| 2443 | repugnar | 10 |
| 2444 | regular | 10 |
| 2445 | regla | 10 |
| 2446 | recreo | 10 |
| 2447 | rebelión | 10 |
| 2448 | puñetazo | 10 |
| 2449 | proposición | 10 |
| 2450 | propiedad | 10 |
| 2451 | propaganda | 10 |
| 2452 | pronunciar | 10 |
| 2453 | profesar | 10 |
| 2454 | pretexto | 10 |
| 2455 | predicador | 10 |
| 2456 | precio | 10 |
| 2457 | posición | 10 |
| 2458 | platónico | 10 |
| 2459 | pintura | 10 |
| 2460 | personal | 10 |
| 2461 | perfección | 10 |
| 2462 | pellizco | 10 |
| 2463 | pechera | 10 |
| 2464 | paraíso | 10 |
| 2465 | pantorrilla | 10 |
| 2466 | paisano | 10 |
| 2467 | pacífico | 10 |
| 2468 | olfatear | 10 |
| 2469 | oficina | 10 |
| 2470 | oculto | 10 |
| 2471 | nueve | 10 |
| 2472 | nosotras | 10 |
| 2473 | náufrago | 10 |
| 2474 | merienda | 10 |
| 2475 | materialismo | 10 |
| 2476 | masa | 10 |
| 2477 | maldad | 10 |
| 2478 | luis | 10 |
| 2479 | lógica | 10 |
| 2480 | leyenda | 10 |
| 2481 | jinete | 10 |
| 2482 | instrumento | 10 |
| 2483 | insolente | 10 |
| 2484 | inferior | 10 |
| 2485 | inés | 10 |
| 2486 | indudablemente | 10 |
| 2487 | indiscreto | 10 |
| 2488 | i | 10 |
| 2489 | huérfano | 10 |
| 2490 | higiene | 10 |
| 2491 | heroico | 10 |
| 2492 | hereje | 10 |
| 2493 | haz | 10 |
| 2494 | hay | 10 |
| 2495 | hallar | 10 |
| 2496 | grotesco | 10 |
| 2497 | griego | 10 |
| 2498 | ganancia | 10 |
| 2499 | galantería | 10 |
| 2500 | fundar | 10 |
| 2501 | fulgosio | 10 |
| 2502 | franco | 10 |
| 2503 | fraile | 10 |
| 2504 | forastero | 10 |
| 2505 | florido | 10 |
| 2506 | fingido | 10 |
| 2507 | filosófico | 10 |
| 2508 | fidelidad | 10 |
| 2509 | facultad | 10 |
| 2510 | exterior | 10 |
| 2511 | expansión | 10 |
| 2512 | estrado | 10 |
| 2513 | estante | 10 |
| 2514 | estancia | 10 |
| 2515 | espacio | 10 |
| 2516 | escupir | 10 |
| 2517 | escandalizar | 10 |
| 2518 | erótico | 10 |
| 2519 | erizar | 10 |
| 2520 | emborrachar | 10 |
| 2521 | elección | 10 |
| 2522 | edificar | 10 |
| 2523 | economía | 10 |
| 2524 | ea | 10 |
| 2525 | divinidad | 10 |
| 2526 | disposición | 10 |
| 2527 | disfrazar | 10 |
| 2528 | discusión | 10 |
| 2529 | disculpar | 10 |
| 2530 | diccionario | 10 |
| 2531 | deshonrar | 10 |
| 2532 | desgraciar | 10 |
| 2533 | descuido | 10 |
| 2534 | desahogar | 10 |
| 2535 | curia | 10 |
| 2536 | cuchillo | 10 |
| 2537 | cuál | 10 |
| 2538 | crucero | 10 |
| 2539 | criterio | 10 |
| 2540 | crisis | 10 |
| 2541 | criatura | 10 |
| 2542 | creo | 10 |
| 2543 | corresponder | 10 |
| 2544 | constancia | 10 |
| 2545 | conservador | 10 |
| 2546 | complicado | 10 |
| 2547 | comentar | 10 |
| 2548 | cofradía | 10 |
| 2549 | cintura | 10 |
| 2550 | cincuenta | 10 |
| 2551 | ceja | 10 |
| 2552 | catecismo | 10 |
| 2553 | carlista | 10 |
| 2554 | capellán | 10 |
| 2555 | campanario | 10 |
| 2556 | caminar | 10 |
| 2557 | bocado | 10 |
| 2558 | billar | 10 |
| 2559 | bando | 10 |
| 2560 | ausente | 10 |
| 2561 | atener | 10 |
| 2562 | arroyo | 10 |
| 2563 | arrimar | 10 |
| 2564 | arribar | 10 |
| 2565 | arrepentir | 10 |
| 2566 | arma | 10 |
| 2567 | aristocrático | 10 |
| 2568 | apear | 10 |
| 2569 | aparente | 10 |
| 2570 | anegar | 10 |
| 2571 | anciano | 10 |
| 2572 | amargura | 10 |
| 2573 | amantar | 10 |
| 2574 | alguien | 10 |
| 2575 | alabanza | 10 |
| 2576 | agarrar | 10 |
| 2577 | afortunadamente | 10 |
| 2578 | actual | 10 |
| 2579 | abrochar | 10 |
| 2580 | zorrilla | 9 |
| 2581 | zarzuela | 9 |
| 2582 | zapatilla | 9 |
| 2583 | violencia | 9 |
| 2584 | vestido | 9 |
| 2585 | vara | 9 |
| 2586 | valle | 9 |
| 2587 | vagar | 9 |
| 2588 | utilidad | 9 |
| 2589 | tributar | 9 |
| 2590 | trecho | 9 |
| 2591 | través | 9 |
| 2592 | trascoro | 9 |
| 2593 | trance | 9 |
| 2594 | toser | 9 |
| 2595 | título | 9 |
| 2596 | tienes | 9 |
| 2597 | tiene | 9 |
| 2598 | teoría | 9 |
| 2599 | tenue | 9 |
| 2600 | sur | 9 |
| 2601 | suavemente | 9 |
| 2602 | soslayar | 9 |
| 2603 | sombrío | 9 |
| 2604 | sólido | 9 |
| 2605 | solícito | 9 |
| 2606 | sobrar | 9 |
| 2607 | síntoma | 9 |
| 2608 | silbido | 9 |
| 2609 | sed | 9 |
| 2610 | saludable | 9 |
| 2611 | sable | 9 |
| 2612 | sabes | 9 |
| 2613 | rueda | 9 |
| 2614 | roma | 9 |
| 2615 | responsabilidad | 9 |
| 2616 | resignar | 9 |
| 2617 | repitió | 9 |
| 2618 | reducir | 9 |
| 2619 | recurrir | 9 |
| 2620 | reaccionario | 9 |
| 2621 | reacción | 9 |
| 2622 | quería | 9 |
| 2623 | quejido | 9 |
| 2624 | pureza | 9 |
| 2625 | punzante | 9 |
| 2626 | pulcritud | 9 |
| 2627 | provecho | 9 |
| 2628 | protesta | 9 |
| 2629 | prisión | 9 |
| 2630 | principalmente | 9 |
| 2631 | prescindir | 9 |
| 2632 | precaución | 9 |
| 2633 | portar | 9 |
| 2634 | población | 9 |
| 2635 | pesimismo | 9 |
| 2636 | perfumar | 9 |
| 2637 | penitencia | 9 |
| 2638 | peláez | 9 |
| 2639 | pecador | 9 |
| 2640 | ojos | 9 |
| 2641 | odioso | 9 |
| 2642 | novelar | 9 |
| 2643 | nombrar | 9 |
| 2644 | nadar | 9 |
| 2645 | nacimiento | 9 |
| 2646 | motivar | 9 |
| 2647 | materialista | 9 |
| 2648 | marinero | 9 |
| 2649 | lujuria | 9 |
| 2650 | lograr | 9 |
| 2651 | línea | 9 |
| 2652 | límite | 9 |
| 2653 | lance | 9 |
| 2654 | kempis | 9 |
| 2655 | juez | 9 |
| 2656 | isidro | 9 |
| 2657 | intensar | 9 |
| 2658 | inteligencia | 9 |
| 2659 | insustancial | 9 |
| 2660 | infalibilidad | 9 |
| 2661 | industria | 9 |
| 2662 | indiano | 9 |
| 2663 | incienso | 9 |
| 2664 | importuno | 9 |
| 2665 | ilustrado | 9 |
| 2666 | idear | 9 |
| 2667 | idealismo | 9 |
| 2668 | ida | 9 |
| 2669 | honesto | 9 |
| 2670 | hembra | 9 |
| 2671 | habitar | 9 |
| 2672 | hábil | 9 |
| 2673 | guiar | 9 |
| 2674 | guardia | 9 |
| 2675 | gravedad | 9 |
| 2676 | gratitud | 9 |
| 2677 | grandísimo | 9 |
| 2678 | granada | 9 |
| 2679 | glorioso | 9 |
| 2680 | glorieta | 9 |
| 2681 | gárrulo | 9 |
| 2682 | gallina | 9 |
| 2683 | gallardo | 9 |
| 2684 | galán | 9 |
| 2685 | función | 9 |
| 2686 | frotar | 9 |
| 2687 | froilán | 9 |
| 2688 | frecuente | 9 |
| 2689 | franqueza | 9 |
| 2690 | frac | 9 |
| 2691 | forrar | 9 |
| 2692 | físico | 9 |
| 2693 | fatiga | 9 |
| 2694 | existir | 9 |
| 2695 | exigencia | 9 |
| 2696 | examen | 9 |
| 2697 | etiqueta | 9 |
| 2698 | estremecer | 9 |
| 2699 | espontáneo | 9 |
| 2700 | espera | 9 |
| 2701 | espanto | 9 |
| 2702 | escocés | 9 |
| 2703 | entrañar | 9 |
| 2704 | enseñanza | 9 |
| 2705 | enfrentar | 9 |
| 2706 | encuentro | 9 |
| 2707 | empujar | 9 |
| 2708 | eficaz | 9 |
| 2709 | dominó | 9 |
| 2710 | disolver | 9 |
| 2711 | disfrutar | 9 |
| 2712 | dirección | 9 |
| 2713 | dinástico | 9 |
| 2714 | diabólico | 9 |
| 2715 | desesperación | 9 |
| 2716 | descuidar | 9 |
| 2717 | delatar | 9 |
| 2718 | declaración | 9 |
| 2719 | deán | 9 |
| 2720 | dato | 9 |
| 2721 | damasco | 9 |
| 2722 | curva | 9 |
| 2723 | cuchicheo | 9 |
| 2724 | cuales | 9 |
| 2725 | corro | 9 |
| 2726 | conversar | 9 |
| 2727 | convalecencia | 9 |
| 2728 | continente | 9 |
| 2729 | conmigo | 9 |
| 2730 | componer | 9 |
| 2731 | comparación | 9 |
| 2732 | colorado | 9 |
| 2733 | colección | 9 |
| 2734 | clavo | 9 |
| 2735 | ciento | 9 |
| 2736 | chorrear | 9 |
| 2737 | choque | 9 |
| 2738 | chillón | 9 |
| 2739 | chateaubriand | 9 |
| 2740 | ceniza | 9 |
| 2741 | catalejo | 9 |
| 2742 | casto | 9 |
| 2743 | cascabel | 9 |
| 2744 | carro | 9 |
| 2745 | carnal | 9 |
| 2746 | carga | 9 |
| 2747 | capítulo | 9 |
| 2748 | campanada | 9 |
| 2749 | calvario | 9 |
| 2750 | caldo | 9 |
| 2751 | cadáver | 9 |
| 2752 | cabaña | 9 |
| 2753 | busca | 9 |
| 2754 | burla | 9 |
| 2755 | bruto | 9 |
| 2756 | brisa | 9 |
| 2757 | bostezar | 9 |
| 2758 | bonito | 9 |
| 2759 | bola | 9 |
| 2760 | blanquecino | 9 |
| 2761 | blandura | 9 |
| 2762 | beato | 9 |
| 2763 | bailarín | 9 |
| 2764 | azular | 9 |
| 2765 | auténtico | 9 |
| 2766 | aureola | 9 |
| 2767 | aumentar | 9 |
| 2768 | audacia | 9 |
| 2769 | atrocidad | 9 |
| 2770 | atrevimiento | 9 |
| 2771 | aspaviento | 9 |
| 2772 | asesinar | 9 |
| 2773 | arduo | 9 |
| 2774 | apasionar | 9 |
| 2775 | añadió | 9 |
| 2776 | antipático | 9 |
| 2777 | anchas | 9 |
| 2778 | amontonar | 9 |
| 2779 | alusión | 9 |
| 2780 | alimentar | 9 |
| 2781 | ajustar | 9 |
| 2782 | ajedrez | 9 |
| 2783 | airoso | 9 |
| 2784 | aguja | 9 |
| 2785 | agradecimiento | 9 |
| 2786 | afectar | 9 |
| 2787 | acoger | 9 |
| 2788 | acertar | 9 |
| 2789 | accidente | 9 |
| 2790 | abundante | 9 |
| 2791 | abrumar | 9 |
| 2792 | abrasar | 9 |
| 2793 | abandono | 9 |
| 2794 | voto | 8 |
| 2795 | vil | 8 |
| 2796 | vía | 8 |
| 2797 | vetar | 8 |
| 2798 | verdura | 8 |
| 2799 | veneno | 8 |
| 2800 | vena | 8 |
| 2801 | velo | 8 |
| 2802 | vapor | 8 |
| 2803 | ultrajar | 8 |
| 2804 | trémulo | 8 |
| 2805 | traza | 8 |
| 2806 | trasnochador | 8 |
| 2807 | trasaltar | 8 |
| 2808 | transigir | 8 |
| 2809 | torpeza | 8 |
| 2810 | tormenta | 8 |
| 2811 | tolerancia | 8 |
| 2812 | toda | 8 |
| 2813 | tinta | 8 |
| 2814 | timbre | 8 |
| 2815 | tibio | 8 |
| 2816 | teólogo | 8 |
| 2817 | tentador | 8 |
| 2818 | temporada | 8 |
| 2819 | tema | 8 |
| 2820 | teja | 8 |
| 2821 | tajada | 8 |
| 2822 | superioridad | 8 |
| 2823 | sumo | 8 |
| 2824 | suelto | 8 |
| 2825 | soplo | 8 |
| 2826 | sonoro | 8 |
| 2827 | solución | 8 |
| 2828 | siesta | 8 |
| 2829 | seglar | 8 |
| 2830 | sapo | 8 |
| 2831 | salvo | 8 |
| 2832 | sacramento | 8 |
| 2833 | saciar | 8 |
| 2834 | sabroso | 8 |
| 2835 | sabe | 8 |
| 2836 | s | 8 |
| 2837 | roja | 8 |
| 2838 | rogar | 8 |
| 2839 | respondió | 8 |
| 2840 | reputar | 8 |
| 2841 | repetía | 8 |
| 2842 | renegar | 8 |
| 2843 | rencor | 8 |
| 2844 | remontar | 8 |
| 2845 | relativo | 8 |
| 2846 | reflexionar | 8 |
| 2847 | rasgo | 8 |
| 2848 | ráfaga | 8 |
| 2849 | racional | 8 |
| 2850 | provocativo | 8 |
| 2851 | proporción | 8 |
| 2852 | prolongar | 8 |
| 2853 | programa | 8 |
| 2854 | pretextar | 8 |
| 2855 | presumir | 8 |
| 2856 | preparativo | 8 |
| 2857 | prensa | 8 |
| 2858 | premio | 8 |
| 2859 | práctica | 8 |
| 2860 | poseer | 8 |
| 2861 | podredumbre | 8 |
| 2862 | pintor | 8 |
| 2863 | picaresco | 8 |
| 2864 | peseta | 8 |
| 2865 | persecución | 8 |
| 2866 | permanecer | 8 |
| 2867 | perfil | 8 |
| 2868 | pepa | 8 |
| 2869 | pender | 8 |
| 2870 | pecaminoso | 8 |
| 2871 | paternal | 8 |
| 2872 | participar | 8 |
| 2873 | papa | 8 |
| 2874 | paloma | 8 |
| 2875 | palmo | 8 |
| 2876 | palique | 8 |
| 2877 | paja | 8 |
| 2878 | ostentoso | 8 |
| 2879 | onda | 8 |
| 2880 | oleaje | 8 |
| 2881 | oficial | 8 |
| 2882 | ocurrencia | 8 |
| 2883 | ocioso | 8 |
| 2884 | obispado | 8 |
| 2885 | notable | 8 |
| 2886 | nocturno | 8 |
| 2887 | niñez | 8 |
| 2888 | nieve | 8 |
| 2889 | nazareno | 8 |
| 2890 | naturalismo | 8 |
| 2891 | muchedumbre | 8 |
| 2892 | moro | 8 |
| 2893 | morada | 8 |
| 2894 | montañés | 8 |
| 2895 | mono | 8 |
| 2896 | monaguillo | 8 |
| 2897 | mojado | 8 |
| 2898 | mitología | 8 |
| 2899 | minar | 8 |
| 2900 | millonario | 8 |
| 2901 | mercado | 8 |
| 2902 | mediar | 8 |
| 2903 | mediante | 8 |
| 2904 | mecedora | 8 |
| 2905 | mate | 8 |
| 2906 | marfil | 8 |
| 2907 | maravilla | 8 |
| 2908 | manzana | 8 |
| 2909 | manos | 8 |
| 2910 | macho | 8 |
| 2911 | lumbre | 8 |
| 2912 | lujuriar | 8 |
| 2913 | lúbrico | 8 |
| 2914 | lomo | 8 |
| 2915 | literatura | 8 |
| 2916 | líquido | 8 |
| 2917 | licenciar | 8 |
| 2918 | leve | 8 |
| 2919 | lento | 8 |
| 2920 | lana | 8 |
| 2921 | ladrar | 8 |
| 2922 | jesucristo | 8 |
| 2923 | jaula | 8 |
| 2924 | inverosímil | 8 |
| 2925 | intriga | 8 |
| 2926 | intervenir | 8 |
| 2927 | institución | 8 |
| 2928 | instalar | 8 |
| 2929 | inquieto | 8 |
| 2930 | inmundicia | 8 |
| 2931 | incorporar | 8 |
| 2932 | incidente | 8 |
| 2933 | impertinente | 8 |
| 2934 | horrible | 8 |
| 2935 | hojarasca | 8 |
| 2936 | hierba | 8 |
| 2937 | heredero | 8 |
| 2938 | hablador | 8 |
| 2939 | gruñir | 8 |
| 2940 | gritaron | 8 |
| 2941 | grabar | 8 |
| 2942 | godino | 8 |
| 2943 | gobernar | 8 |
| 2944 | formal | 8 |
| 2945 | fatuo | 8 |
| 2946 | fabricar | 8 |
| 2947 | extraordinario | 8 |
| 2948 | exacto | 8 |
| 2949 | estupidez | 8 |
| 2950 | estribo | 8 |
| 2951 | estrepitoso | 8 |
| 2952 | esplendor | 8 |
| 2953 | esencia | 8 |
| 2954 | escéptico | 8 |
| 2955 | eran | 8 |
| 2956 | equilibrio | 8 |
| 2957 | enredar | 8 |
| 2958 | enorme | 8 |
| 2959 | encendido | 8 |
| 2960 | encarnar | 8 |
| 2961 | encaramar | 8 |
| 2962 | enagua | 8 |
| 2963 | empuñar | 8 |
| 2964 | ejercer | 8 |
| 2965 | efímero | 8 |
| 2966 | dolores | 8 |
| 2967 | docena | 8 |
| 2968 | distinguido | 8 |
| 2969 | dibujar | 8 |
| 2970 | destinar | 8 |
| 2971 | destacar | 8 |
| 2972 | desesperado | 8 |
| 2973 | desdeñar | 8 |
| 2974 | desconfiar | 8 |
| 2975 | desconfianza | 8 |
| 2976 | descender | 8 |
| 2977 | descalzo | 8 |
| 2978 | desairar | 8 |
| 2979 | desacreditar | 8 |
| 2980 | desabrido | 8 |
| 2981 | derribar | 8 |
| 2982 | deprisa | 8 |
| 2983 | defensa | 8 |
| 2984 | cualidad | 8 |
| 2985 | cuadrado | 8 |
| 2986 | crianza | 8 |
| 2987 | creencia | 8 |
| 2988 | cortés | 8 |
| 2989 | correo | 8 |
| 2990 | corbata | 8 |
| 2991 | corazonada | 8 |
| 2992 | copiar | 8 |
| 2993 | contradecir | 8 |
| 2994 | contracayes | 8 |
| 2995 | contorno | 8 |
| 2996 | consideración | 8 |
| 2997 | consecuencia | 8 |
| 2998 | conocido | 8 |
| 2999 | conformar | 8 |
| 3000 | colmo | 8 |
| 3001 | colgadura | 8 |
| 3002 | cola | 8 |
| 3003 | cochero | 8 |
| 3004 | claustro | 8 |
| 3005 | cirio | 8 |
| 3006 | churrigueresco | 8 |
| 3007 | chupar | 8 |
| 3008 | champaña | 8 |
| 3009 | ceremonia | 8 |
| 3010 | celestial | 8 |
| 3011 | celda | 8 |
| 3012 | catástrofe | 8 |
| 3013 | castilla | 8 |
| 3014 | carnaval | 8 |
| 3015 | cárcel | 8 |
| 3016 | carbón | 8 |
| 3017 | caprichoso | 8 |
| 3018 | cañón | 8 |
| 3019 | canto | 8 |
| 3020 | canónico | 8 |
| 3021 | canon | 8 |
| 3022 | cana | 8 |
| 3023 | campaña | 8 |
| 3024 | calmar | 8 |
| 3025 | caído | 8 |
| 3026 | brusco | 8 |
| 3027 | brigadiera | 8 |
| 3028 | botón | 8 |
| 3029 | bota | 8 |
| 3030 | bordar | 8 |
| 3031 | bigote | 8 |
| 3032 | batallar | 8 |
| 3033 | barquilla | 8 |
| 3034 | barato | 8 |
| 3035 | azúcar | 8 |
| 3036 | asombrar | 8 |
| 3037 | arrodillar | 8 |
| 3038 | arquitectura | 8 |
| 3039 | arqueológico | 8 |
| 3040 | aridez | 8 |
| 3041 | apuro | 8 |
| 3042 | apretón | 8 |
| 3043 | aparición | 8 |
| 3044 | aparentar | 8 |
| 3045 | angustia | 8 |
| 3046 | andadas | 8 |
| 3047 | análogo | 8 |
| 3048 | amparo | 8 |
| 3049 | américa | 8 |
| 3050 | amargar | 8 |
| 3051 | almíbar | 8 |
| 3052 | alas | 8 |
| 3053 | agosto | 8 |
| 3054 | afirmación | 8 |
| 3055 | aficionar | 8 |
| 3056 | acuerdo | 8 |
| 3057 | acontecimiento | 8 |
| 3058 | acerca | 8 |
| 3059 | abstener | 8 |
| 3060 | abril | 8 |
| 3061 | abrigo | 8 |
| 3062 | abrigar | 8 |
| 3063 | zaragoza | 7 |
| 3064 | zapatero | 7 |
| 3065 | yeso | 7 |
| 3066 | voltaire | 7 |
| 3067 | vigoroso | 7 |
| 3068 | vigilar | 7 |
| 3069 | vicente | 7 |
| 3070 | ven | 7 |
| 3071 | vegetar | 7 |
| 3072 | v | 7 |
| 3073 | usurero | 7 |
| 3074 | urgente | 7 |
| 3075 | unción | 7 |
| 3076 | umbral | 7 |
| 3077 | trepar | 7 |
| 3078 | tremendo | 7 |
| 3079 | trazar | 7 |
| 3080 | transeúnte | 7 |
| 3081 | tranquilamente | 7 |
| 3082 | tradición | 7 |
| 3083 | tórtola | 7 |
| 3084 | tornear | 7 |
| 3085 | toldo | 7 |
| 3086 | terco | 7 |
| 3087 | teñir | 7 |
| 3088 | técnico | 7 |
| 3089 | té | 7 |
| 3090 | taller | 7 |
| 3091 | sujeto | 7 |
| 3092 | suculento | 7 |
| 3093 | soy | 7 |
| 3094 | sórdido | 7 |
| 3095 | somnolencia | 7 |
| 3096 | solterona | 7 |
| 3097 | solitaria | 7 |
| 3098 | soberbia | 7 |
| 3099 | simpatía | 7 |
| 3100 | sigilo | 7 |
| 3101 | severidad | 7 |
| 3102 | seso | 7 |
| 3103 | septiembre | 7 |
| 3104 | seguido | 7 |
| 3105 | santiguar | 7 |
| 3106 | sangrar | 7 |
| 3107 | sabor | 7 |
| 3108 | ruborizar | 7 |
| 3109 | rozar | 7 |
| 3110 | rosita | 7 |
| 3111 | rizo | 7 |
| 3112 | rítmico | 7 |
| 3113 | rita | 7 |
| 3114 | reyerta | 7 |
| 3115 | resucitar | 7 |
| 3116 | resplandor | 7 |
| 3117 | resonar | 7 |
| 3118 | resignación | 7 |
| 3119 | reserva | 7 |
| 3120 | reprender | 7 |
| 3121 | renta | 7 |
| 3122 | renacer | 7 |
| 3123 | remoto | 7 |
| 3124 | relucir | 7 |
| 3125 | regencia | 7 |
| 3126 | realizar | 7 |
| 3127 | rabiar | 7 |
| 3128 | rabia | 7 |
| 3129 | quiere | 7 |
| 3130 | quebrar | 7 |
| 3131 | puede | 7 |
| 3132 | pudrir | 7 |
| 3133 | providencia | 7 |
| 3134 | proseguir | 7 |
| 3135 | progresista | 7 |
| 3136 | principiar | 7 |
| 3137 | pretendiente | 7 |
| 3138 | prender | 7 |
| 3139 | prelado | 7 |
| 3140 | precipitar | 7 |
| 3141 | prebendado | 7 |
| 3142 | postigo | 7 |
| 3143 | popular | 7 |
| 3144 | plática | 7 |
| 3145 | plástico | 7 |
| 3146 | pillar | 7 |
| 3147 | picardía | 7 |
| 3148 | pescar | 7 |
| 3149 | perspectiva | 7 |
| 3150 | pequeñez | 7 |
| 3151 | pensó | 7 |
| 3152 | pasajero | 7 |
| 3153 | pasaje | 7 |
| 3154 | párrafo | 7 |
| 3155 | parir | 7 |
| 3156 | parche | 7 |
| 3157 | paraje | 7 |
| 3158 | paraguay | 7 |
| 3159 | pánico | 7 |
| 3160 | palidecer | 7 |
| 3161 | paisaje | 7 |
| 3162 | pagano | 7 |
| 3163 | p | 7 |
| 3164 | otorgar | 7 |
| 3165 | origen | 7 |
| 3166 | ordenar | 7 |
| 3167 | oratorio | 7 |
| 3168 | oposición | 7 |
| 3169 | oía | 7 |
| 3170 | odiar | 7 |
| 3171 | octubre | 7 |
| 3172 | obligación | 7 |
| 3173 | nota | 7 |
| 3174 | negra | 7 |
| 3175 | nata | 7 |
| 3176 | na | 7 |
| 3177 | mudo | 7 |
| 3178 | mosca | 7 |
| 3179 | modos | 7 |
| 3180 | modestia | 7 |
| 3181 | mística | 7 |
| 3182 | misión | 7 |
| 3183 | metido | 7 |
| 3184 | merendar | 7 |
| 3185 | merced | 7 |
| 3186 | mejorar | 7 |
| 3187 | mecánico | 7 |
| 3188 | mayoría | 7 |
| 3189 | mata | 7 |
| 3190 | martirio | 7 |
| 3191 | mantel | 7 |
| 3192 | maliciar | 7 |
| 3193 | maledicencia | 7 |
| 3194 | maestra | 7 |
| 3195 | madrileño | 7 |
| 3196 | luminoso | 7 |
| 3197 | leche | 7 |
| 3198 | lastimar | 7 |
| 3199 | larga | 7 |
| 3200 | lanzar | 7 |
| 3201 | lamer | 7 |
| 3202 | juramento | 7 |
| 3203 | junio | 7 |
| 3204 | jilguero | 7 |
| 3205 | isla | 7 |
| 3206 | inveterado | 7 |
| 3207 | interlocutor | 7 |
| 3208 | insulto | 7 |
| 3209 | insufrible | 7 |
| 3210 | insinuación | 7 |
| 3211 | inmortal | 7 |
| 3212 | injusto | 7 |
| 3213 | injuria | 7 |
| 3214 | ingenio | 7 |
| 3215 | infiel | 7 |
| 3216 | infantil | 7 |
| 3217 | infalible | 7 |
| 3218 | indiferente | 7 |
| 3219 | indecoroso | 7 |
| 3220 | inclusive | 7 |
| 3221 | inclinación | 7 |
| 3222 | incierto | 7 |
| 3223 | imitación | 7 |
| 3224 | idolatría | 7 |
| 3225 | ido | 7 |
| 3226 | honradez | 7 |
| 3227 | heroína | 7 |
| 3228 | herencia | 7 |
| 3229 | hacienda | 7 |
| 3230 | guiñar | 7 |
| 3231 | globo | 7 |
| 3232 | gaita | 7 |
| 3233 | frecuencia | 7 |
| 3234 | fórmula | 7 |
| 3235 | folletín | 7 |
| 3236 | follaje | 7 |
| 3237 | favorecer | 7 |
| 3238 | facción | 7 |
| 3239 | extravío | 7 |
| 3240 | éxtasis | 7 |
| 3241 | exceso | 7 |
| 3242 | exaltado | 7 |
| 3243 | estrago | 7 |
| 3244 | estos | 7 |
| 3245 | están | 7 |
| 3246 | establecer | 7 |
| 3247 | esquivar | 7 |
| 3248 | espectador | 7 |
| 3249 | esforzar | 7 |
| 3250 | escribano | 7 |
| 3251 | escondite | 7 |
| 3252 | erudito | 7 |
| 3253 | erguir | 7 |
| 3254 | envidioso | 7 |
| 3255 | enfadar | 7 |
| 3256 | encarnado | 7 |
| 3257 | empeño | 7 |
| 3258 | eléctrico | 7 |
| 3259 | edificante | 7 |
| 3260 | dote | 7 |
| 3261 | divertido | 7 |
| 3262 | dispersar | 7 |
| 3263 | discurrir | 7 |
| 3264 | diferencia | 7 |
| 3265 | diestro | 7 |
| 3266 | despierto | 7 |
| 3267 | despedazar | 7 |
| 3268 | despachar | 7 |
| 3269 | desorden | 7 |
| 3270 | desmoronar | 7 |
| 3271 | desechar | 7 |
| 3272 | descubrimiento | 7 |
| 3273 | delicadeza | 7 |
| 3274 | deleitar | 7 |
| 3275 | decidor | 7 |
| 3276 | debe | 7 |
| 3277 | cumbre | 7 |
| 3278 | cueva | 7 |
| 3279 | cuaresma | 7 |
| 3280 | crueldad | 7 |
| 3281 | cortesía | 7 |
| 3282 | corral | 7 |
| 3283 | cordel | 7 |
| 3284 | conyugal | 7 |
| 3285 | contribuir | 7 |
| 3286 | constar | 7 |
| 3287 | conserje | 7 |
| 3288 | conjunto | 7 |
| 3289 | confidente | 7 |
| 3290 | cómodo | 7 |
| 3291 | comodidad | 7 |
| 3292 | combinación | 7 |
| 3293 | colega | 7 |
| 3294 | casulla | 7 |
| 3295 | cartucho | 7 |
| 3296 | capar | 7 |
| 3297 | caña | 7 |
| 3298 | cansancio | 7 |
| 3299 | campanero | 7 |
| 3300 | callado | 7 |
| 3301 | calificar | 7 |
| 3302 | cal | 7 |
| 3303 | bucólico | 7 |
| 3304 | brinco | 7 |
| 3305 | brecha | 7 |
| 3306 | brasa | 7 |
| 3307 | borbotones | 7 |
| 3308 | bonachón | 7 |
| 3309 | blasfemar | 7 |
| 3310 | blas | 7 |
| 3311 | barco | 7 |
| 3312 | avaricia | 7 |
| 3313 | avanzar | 7 |
| 3314 | auxilio | 7 |
| 3315 | atractivo | 7 |
| 3316 | atentar | 7 |
| 3317 | áspero | 7 |
| 3318 | aspereza | 7 |
| 3319 | asesino | 7 |
| 3320 | artillero | 7 |
| 3321 | ara | 7 |
| 3322 | apretado | 7 |
| 3323 | apoderar | 7 |
| 3324 | aparato | 7 |
| 3325 | anticuario | 7 |
| 3326 | ángulo | 7 |
| 3327 | amiguito | 7 |
| 3328 | alvarito | 7 |
| 3329 | alentar | 7 |
| 3330 | álamo | 7 |
| 3331 | aguantar | 7 |
| 3332 | actitud | 7 |
| 3333 | achacar | 7 |
| 3334 | abuso | 7 |
| 3335 | abonar | 7 |
| 3336 | abdicación | 7 |
| 3337 | zumbar | 6 |
| 3338 | zorro | 6 |
| 3339 | vulgaridad | 6 |
| 3340 | vinculete | 6 |
| 3341 | verá | 6 |
| 3342 | vecindario | 6 |
| 3343 | variedad | 6 |
| 3344 | varar | 6 |
| 3345 | valladolid | 6 |
| 3346 | vaguedad | 6 |
| 3347 | vacilante | 6 |
| 3348 | va | 6 |
| 3349 | urraca | 6 |
| 3350 | turgente | 6 |
| 3351 | traslacerca | 6 |
| 3352 | tostar | 6 |
| 3353 | torbellino | 6 |
| 3354 | tontería | 6 |
| 3355 | tomo | 6 |
| 3356 | tísico | 6 |
| 3357 | tinte | 6 |
| 3358 | tímido | 6 |
| 3359 | tientas | 6 |
| 3360 | tesis | 6 |
| 3361 | telón | 6 |
| 3362 | tacto | 6 |
| 3363 | subrepticio | 6 |
| 3364 | sopor | 6 |
| 3365 | someter | 6 |
| 3366 | soltero | 6 |
| 3367 | sollozo | 6 |
| 3368 | solar | 6 |
| 3369 | socarrón | 6 |
| 3370 | sobresalto | 6 |
| 3371 | sinceramente | 6 |
| 3372 | silueta | 6 |
| 3373 | seto | 6 |
| 3374 | sesión | 6 |
| 3375 | sesenta | 6 |
| 3376 | servilleta | 6 |
| 3377 | seriamente | 6 |
| 3378 | señorón | 6 |
| 3379 | sal | 6 |
| 3380 | saco | 6 |
| 3381 | sabía | 6 |
| 3382 | rutina | 6 |
| 3383 | ruin | 6 |
| 3384 | rubor | 6 |
| 3385 | rozagante | 6 |
| 3386 | rosario | 6 |
| 3387 | ronco | 6 |
| 3388 | rocío | 6 |
| 3389 | roca | 6 |
| 3390 | rizar | 6 |
| 3391 | retrasar | 6 |
| 3392 | resumen | 6 |
| 3393 | resultado | 6 |
| 3394 | restituto | 6 |
| 3395 | respiración | 6 |
| 3396 | resonancia | 6 |
| 3397 | remorder | 6 |
| 3398 | relieve | 6 |
| 3399 | régimen | 6 |
| 3400 | redimir | 6 |
| 3401 | red | 6 |
| 3402 | recto | 6 |
| 3403 | recomendación | 6 |
| 3404 | reciente | 6 |
| 3405 | rechinar | 6 |
| 3406 | rechazar | 6 |
| 3407 | rebaño | 6 |
| 3408 | rapidez | 6 |
| 3409 | ramona | 6 |
| 3410 | quieto | 6 |
| 3411 | queja | 6 |
| 3412 | puntiagudo | 6 |
| 3413 | pulla | 6 |
| 3414 | pueril | 6 |
| 3415 | ps | 6 |
| 3416 | proximidad | 6 |
| 3417 | provincial | 6 |
| 3418 | proteger | 6 |
| 3419 | profundamente | 6 |
| 3420 | príncipe | 6 |
| 3421 | predominar | 6 |
| 3422 | predilecto | 6 |
| 3423 | pórtico | 6 |
| 3424 | portero | 6 |
| 3425 | policía | 6 |
| 3426 | poblar | 6 |
| 3427 | plateresco | 6 |
| 3428 | plataforma | 6 |
| 3429 | planta | 6 |
| 3430 | pío | 6 |
| 3431 | pimienta | 6 |
| 3432 | pieza | 6 |
| 3433 | pez | 6 |
| 3434 | petróleo | 6 |
| 3435 | peste | 6 |
| 3436 | perversión | 6 |
| 3437 | persuadir | 6 |
| 3438 | perpetuo | 6 |
| 3439 | perjuicio | 6 |
| 3440 | perfumado | 6 |
| 3441 | pensador | 6 |
| 3442 | pécora | 6 |
| 3443 | pavor | 6 |
| 3444 | paulinas | 6 |
| 3445 | palmadita | 6 |
| 3446 | palmada | 6 |
| 3447 | palma | 6 |
| 3448 | pablo | 6 |
| 3449 | oso | 6 |
| 3450 | orgía | 6 |
| 3451 | oportunidad | 6 |
| 3452 | ondulante | 6 |
| 3453 | oeste | 6 |
| 3454 | océano | 6 |
| 3455 | obstinar | 6 |
| 3456 | obsequiar | 6 |
| 3457 | número | 6 |
| 3458 | noticiar | 6 |
| 3459 | notario | 6 |
| 3460 | noches | 6 |
| 3461 | naranja | 6 |
| 3462 | muelle | 6 |
| 3463 | muceta | 6 |
| 3464 | morado | 6 |
| 3465 | monotonía | 6 |
| 3466 | molestia | 6 |
| 3467 | mismísimo | 6 |
| 3468 | milagroso | 6 |
| 3469 | miembro | 6 |
| 3470 | metal | 6 |
| 3471 | metáfora | 6 |
| 3472 | mesilla | 6 |
| 3473 | mesar | 6 |
| 3474 | melifluo | 6 |
| 3475 | meditación | 6 |
| 3476 | mediquillo | 6 |
| 3477 | matiz | 6 |
| 3478 | mas | 6 |
| 3479 | martillazo | 6 |
| 3480 | mantón | 6 |
| 3481 | mantilla | 6 |
| 3482 | manosear | 6 |
| 3483 | manifestación | 6 |
| 3484 | mancebo | 6 |
| 3485 | malvado | 6 |
| 3486 | luto | 6 |
| 3487 | lujoso | 6 |
| 3488 | lucía | 6 |
| 3489 | lope | 6 |
| 3490 | listo | 6 |
| 3491 | licor | 6 |
| 3492 | lícito | 6 |
| 3493 | laurel | 6 |
| 3494 | ladrido | 6 |
| 3495 | lacayo | 6 |
| 3496 | juguete | 6 |
| 3497 | juanito | 6 |
| 3498 | juana | 6 |
| 3499 | joya | 6 |
| 3500 | invocar | 6 |
| 3501 | invención | 6 |
| 3502 | invadir | 6 |
| 3503 | intimar | 6 |
| 3504 | interpretar | 6 |
| 3505 | interminable | 6 |
| 3506 | intensidad | 6 |
| 3507 | intelectual | 6 |
| 3508 | inspiración | 6 |
| 3509 | insoportable | 6 |
| 3510 | insolencia | 6 |
| 3511 | insinuar | 6 |
| 3512 | inquietud | 6 |
| 3513 | inofensivo | 6 |
| 3514 | inmaculado | 6 |
| 3515 | injertar | 6 |
| 3516 | iniciativa | 6 |
| 3517 | influir | 6 |
| 3518 | infidelidad | 6 |
| 3519 | infernal | 6 |
| 3520 | inesperado | 6 |
| 3521 | inerte | 6 |
| 3522 | indigno | 6 |
| 3523 | incomodar | 6 |
| 3524 | inclinado | 6 |
| 3525 | impropio | 6 |
| 3526 | importunar | 6 |
| 3527 | impiedad | 6 |
| 3528 | imperioso | 6 |
| 3529 | imperio | 6 |
| 3530 | ilustrísimo | 6 |
| 3531 | igualdad | 6 |
| 3532 | humanar | 6 |
| 3533 | horno | 6 |
| 3534 | hito | 6 |
| 3535 | himno | 6 |
| 3536 | higiénico | 6 |
| 3537 | hermandad | 6 |
| 3538 | herida | 6 |
| 3539 | herejía | 6 |
| 3540 | helado | 6 |
| 3541 | hechizo | 6 |
| 3542 | hastiar | 6 |
| 3543 | hallazgo | 6 |
| 3544 | gutural | 6 |
| 3545 | grillo | 6 |
| 3546 | gloriar | 6 |
| 3547 | gesticular | 6 |
| 3548 | genio | 6 |
| 3549 | gabán | 6 |
| 3550 | fusil | 6 |
| 3551 | fray | 6 |
| 3552 | franja | 6 |
| 3553 | francamente | 6 |
| 3554 | fornido | 6 |
| 3555 | flotante | 6 |
| 3556 | flojo | 6 |
| 3557 | favorito | 6 |
| 3558 | fatal | 6 |
| 3559 | fango | 6 |
| 3560 | fanatizar | 6 |
| 3561 | facilitar | 6 |
| 3562 | fachada | 6 |
| 3563 | exuberante | 6 |
| 3564 | extraviar | 6 |
| 3565 | excitación | 6 |
| 3566 | evangelio | 6 |
| 3567 | eternamente | 6 |
| 3568 | estéril | 6 |
| 3569 | espaldas | 6 |
| 3570 | esmero | 6 |
| 3571 | escudriñar | 6 |
| 3572 | escoba | 6 |
| 3573 | escandalosa | 6 |
| 3574 | envidiable | 6 |
| 3575 | envenenar | 6 |
| 3576 | entrega | 6 |
| 3577 | entablar | 6 |
| 3578 | ensayar | 6 |
| 3579 | enroscar | 6 |
| 3580 | enfriar | 6 |
| 3581 | endiablado | 6 |
| 3582 | encina | 6 |
| 3583 | embustero | 6 |
| 3584 | elegía | 6 |
| 3585 | ejemplar | 6 |
| 3586 | eficacia | 6 |
| 3587 | económico | 6 |
| 3588 | eco | 6 |
| 3589 | dotar | 6 |
| 3590 | domingo | 6 |
| 3591 | distinción | 6 |
| 3592 | disputa | 6 |
| 3593 | director | 6 |
| 3594 | diputar | 6 |
| 3595 | diplomático | 6 |
| 3596 | diplomacia | 6 |
| 3597 | determinar | 6 |
| 3598 | desvergonzar | 6 |
| 3599 | destrozar | 6 |
| 3600 | despotismo | 6 |
| 3601 | despojar | 6 |
| 3602 | despensa | 6 |
| 3603 | despacio | 6 |
| 3604 | desinteresado | 6 |
| 3605 | desengaño | 6 |
| 3606 | desengañar | 6 |
| 3607 | desconocer | 6 |
| 3608 | descomponer | 6 |
| 3609 | derrotar | 6 |
| 3610 | deliberar | 6 |
| 3611 | dejo | 6 |
| 3612 | decoroso | 6 |
| 3613 | cutis | 6 |
| 3614 | cuna | 6 |
| 3615 | cultivar | 6 |
| 3616 | culinario | 6 |
| 3617 | crónica | 6 |
| 3618 | crítica | 6 |
| 3619 | crepúsculo | 6 |
| 3620 | creía | 6 |
| 3621 | costurero | 6 |
| 3622 | cosquillar | 6 |
| 3623 | cortina | 6 |
| 3624 | corrillo | 6 |
| 3625 | corregir | 6 |
| 3626 | corrección | 6 |
| 3627 | corporal | 6 |
| 3628 | corona | 6 |
| 3629 | cordial | 6 |
| 3630 | conveniencia | 6 |
| 3631 | convaleciente | 6 |
| 3632 | contenido | 6 |
| 3633 | consola | 6 |
| 3634 | congoja | 6 |
| 3635 | confusión | 6 |
| 3636 | confiar | 6 |
| 3637 | concierto | 6 |
| 3638 | concejal | 6 |
| 3639 | conceder | 6 |
| 3640 | compromiso | 6 |
| 3641 | complicar | 6 |
| 3642 | compás | 6 |
| 3643 | comezón | 6 |
| 3644 | comediar | 6 |
| 3645 | colondres | 6 |
| 3646 | colmar | 6 |
| 3647 | colina | 6 |
| 3648 | colcha | 6 |
| 3649 | cogote | 6 |
| 3650 | codear | 6 |
| 3651 | chusco | 6 |
| 3652 | chorro | 6 |
| 3653 | chocolate | 6 |
| 3654 | chillido | 6 |
| 3655 | chaleco | 6 |
| 3656 | cerebrar | 6 |
| 3657 | ceño | 6 |
| 3658 | cejar | 6 |
| 3659 | cavilación | 6 |
| 3660 | catorce | 6 |
| 3661 | catequista | 6 |
| 3662 | catarata | 6 |
| 3663 | castillo | 6 |
| 3664 | carruaje | 6 |
| 3665 | cárdeno | 6 |
| 3666 | campestre | 6 |
| 3667 | callejón | 6 |
| 3668 | cabecero | 6 |
| 3669 | bobo | 6 |
| 3670 | blasfemia | 6 |
| 3671 | blancura | 6 |
| 3672 | beneficio | 6 |
| 3673 | bautista | 6 |
| 3674 | bata | 6 |
| 3675 | basílica | 6 |
| 3676 | barquero | 6 |
| 3677 | bárbaro | 6 |
| 3678 | barandilla | 6 |
| 3679 | balandrán | 6 |
| 3680 | bacante | 6 |
| 3681 | baba | 6 |
| 3682 | ayuda | 6 |
| 3683 | avenir | 6 |
| 3684 | ave | 6 |
| 3685 | aturdimiento | 6 |
| 3686 | ateísmo | 6 |
| 3687 | asomo | 6 |
| 3688 | asombro | 6 |
| 3689 | asfixiar | 6 |
| 3690 | ascender | 6 |
| 3691 | arriesgar | 6 |
| 3692 | arrebato | 6 |
| 3693 | armonioso | 6 |
| 3694 | armiño | 6 |
| 3695 | arca | 6 |
| 3696 | arañar | 6 |
| 3697 | aproximar | 6 |
| 3698 | aplazar | 6 |
| 3699 | antepecho | 6 |
| 3700 | amorío | 6 |
| 3701 | amores | 6 |
| 3702 | amistar | 6 |
| 3703 | amenaza | 6 |
| 3704 | ambas | 6 |
| 3705 | alzar | 6 |
| 3706 | alzacuello | 6 |
| 3707 | alcance | 6 |
| 3708 | alba | 6 |
| 3709 | ahorrar | 6 |
| 3710 | aguardar | 6 |
| 3711 | afable | 6 |
| 3712 | adúltero | 6 |
| 3713 | adorno | 6 |
| 3714 | adorador | 6 |
| 3715 | administración | 6 |
| 3716 | acento | 6 |
| 3717 | acechar | 6 |
| 3718 | acceso | 6 |
| 3719 | acabado | 6 |
| 3720 | aburrido | 6 |
| 3721 | abstracto | 6 |
| 3722 | abstracción | 6 |
| 3723 | absolver | 6 |
| 3724 | absolutamente | 6 |
| 3725 | abandonado | 6 |
| 3726 | zarza | 5 |
| 3727 | zapico | 5 |
| 3728 | zaguán | 5 |
| 3729 | xv | 5 |
| 3730 | votar | 5 |
| 3731 | volvió | 5 |
| 3732 | vociferar | 5 |
| 3733 | vivienda | 5 |
| 3734 | vivaracho | 5 |
| 3735 | viudo | 5 |
| 3736 | víspera | 5 |
| 3737 | visionar | 5 |
| 3738 | viscoso | 5 |
| 3739 | villano | 5 |
| 3740 | vigilancia | 5 |
| 3741 | vidrio | 5 |
| 3742 | viciar | 5 |
| 3743 | vibrar | 5 |
| 3744 | vibrante | 5 |
| 3745 | vibración | 5 |
| 3746 | vestíbulo | 5 |
| 3747 | vericueto | 5 |
| 3748 | vencido | 5 |
| 3749 | veinticinco | 5 |
| 3750 | varonil | 5 |
| 3751 | valía | 5 |
| 3752 | vacante | 5 |
| 3753 | vaca | 5 |
| 3754 | utilizar | 5 |
| 3755 | tuyo | 5 |
| 3756 | túnica | 5 |
| 3757 | trucha | 5 |
| 3758 | trote | 5 |
| 3759 | tripa | 5 |
| 3760 | tradicional | 5 |
| 3761 | total | 5 |
| 3762 | tosco | 5 |
| 3763 | tomate | 5 |
| 3764 | tiranía | 5 |
| 3765 | tijera | 5 |
| 3766 | texto | 5 |
| 3767 | testamento | 5 |
| 3768 | terciar | 5 |
| 3769 | teológico | 5 |
| 3770 | tentar | 5 |
| 3771 | temporal | 5 |
| 3772 | templar | 5 |
| 3773 | tempestad | 5 |
| 3774 | temeroso | 5 |
| 3775 | temerario | 5 |
| 3776 | temblón | 5 |
| 3777 | telégrafo | 5 |
| 3778 | telaraña | 5 |
| 3779 | tejar | 5 |
| 3780 | tarima | 5 |
| 3781 | tapiz | 5 |
| 3782 | tapiar | 5 |
| 3783 | talle | 5 |
| 3784 | taco | 5 |
| 3785 | tácito | 5 |
| 3786 | ta | 5 |
| 3787 | súplica | 5 |
| 3788 | superstición | 5 |
| 3789 | superficie | 5 |
| 3790 | sumisión | 5 |
| 3791 | sucumbir | 5 |
| 3792 | suavizar | 5 |
| 3793 | soto | 5 |
| 3794 | sospechoso | 5 |
| 3795 | soporífero | 5 |
| 3796 | soñoliento | 5 |
| 3797 | sonrosado | 5 |
| 3798 | soldado | 5 |
| 3799 | socialista | 5 |
| 3800 | sinceridad | 5 |
| 3801 | sincerar | 5 |
| 3802 | simétrico | 5 |
| 3803 | simbólico | 5 |
| 3804 | sesgo | 5 |
| 3805 | señas | 5 |
| 3806 | seminarista | 5 |
| 3807 | semejar | 5 |
| 3808 | semejanza | 5 |
| 3809 | sembrar | 5 |
| 3810 | segunda | 5 |
| 3811 | santuario | 5 |
| 3812 | santianes | 5 |
| 3813 | salmón | 5 |
| 3814 | salido | 5 |
| 3815 | sacramentos | 5 |
| 3816 | ruego | 5 |
| 3817 | rúa | 5 |
| 3818 | rosado | 5 |
| 3819 | rondar | 5 |
| 3820 | ronca | 5 |
| 3821 | roblar | 5 |
| 3822 | ritmo | 5 |
| 3823 | rienda | 5 |
| 3824 | revoltoso | 5 |
| 3825 | reunión | 5 |
| 3826 | retoño | 5 |
| 3827 | responsable | 5 |
| 3828 | remover | 5 |
| 3829 | relato | 5 |
| 3830 | rejuvenecer | 5 |
| 3831 | reino | 5 |
| 3832 | registro | 5 |
| 3833 | regentar | 5 |
| 3834 | regazo | 5 |
| 3835 | regalo | 5 |
| 3836 | refugio | 5 |
| 3837 | refinar | 5 |
| 3838 | redacción | 5 |
| 3839 | rectoral | 5 |
| 3840 | rector | 5 |
| 3841 | rectificar | 5 |
| 3842 | recetar | 5 |
| 3843 | rebajar | 5 |
| 3844 | rara | 5 |
| 3845 | quiero | 5 |
| 3846 | puñalada | 5 |
| 3847 | puñal | 5 |
| 3848 | pulmón | 5 |
| 3849 | pudo | 5 |
| 3850 | próximamente | 5 |
| 3851 | provinciano | 5 |
| 3852 | protestante | 5 |
| 3853 | protector | 5 |
| 3854 | propinar | 5 |
| 3855 | problema | 5 |
| 3856 | privilegio | 5 |
| 3857 | prisionero | 5 |
| 3858 | princesa | 5 |
| 3859 | presupuesto | 5 |
| 3860 | prestado | 5 |
| 3861 | presidio | 5 |
| 3862 | presentimiento | 5 |
| 3863 | preparado | 5 |
| 3864 | premiar | 5 |
| 3865 | pregonar | 5 |
| 3866 | preciar | 5 |
| 3867 | práctico | 5 |
| 3868 | porción | 5 |
| 3869 | poética | 5 |
| 3870 | podrido | 5 |
| 3871 | pliego | 5 |
| 3872 | platear | 5 |
| 3873 | pizca | 5 |
| 3874 | pinche | 5 |
| 3875 | pillete | 5 |
| 3876 | pillastre | 5 |
| 3877 | perdición | 5 |
| 3878 | pensativo | 5 |
| 3879 | pensaba | 5 |
| 3880 | penoso | 5 |
| 3881 | penitenciar | 5 |
| 3882 | pavo | 5 |
| 3883 | pato | 5 |
| 3884 | patético | 5 |
| 3885 | patena | 5 |
| 3886 | patada | 5 |
| 3887 | pascua | 5 |
| 3888 | pasatiempo | 5 |
| 3889 | pasadizo | 5 |
| 3890 | pasada | 5 |
| 3891 | parroquiano | 5 |
| 3892 | parroquial | 5 |
| 3893 | parentesco | 5 |
| 3894 | panza | 5 |
| 3895 | panera | 5 |
| 3896 | palmatoria | 5 |
| 3897 | palmar | 5 |
| 3898 | ostensible | 5 |
| 3899 | orlar | 5 |
| 3900 | originar | 5 |
| 3901 | organista | 5 |
| 3902 | ordinariamente | 5 |
| 3903 | operación | 5 |
| 3904 | olla | 5 |
| 3905 | olías | 5 |
| 3906 | ochavo | 5 |
| 3907 | ocaso | 5 |
| 3908 | obsesión | 5 |
| 3909 | observador | 5 |
| 3910 | obdulita | 5 |
| 3911 | numeroso | 5 |
| 3912 | nudo | 5 |
| 3913 | nuca | 5 |
| 3914 | nogal | 5 |
| 3915 | negruzco | 5 |
| 3916 | negativo | 5 |
| 3917 | nauplia | 5 |
| 3918 | naturalista | 5 |
| 3919 | nacido | 5 |
| 3920 | murmurador | 5 |
| 3921 | murciélago | 5 |
| 3922 | muñeca | 5 |
| 3923 | multiplicar | 5 |
| 3924 | mujercita | 5 |
| 3925 | muestra | 5 |
| 3926 | monumento | 5 |
| 3927 | monstruo | 5 |
| 3928 | modesto | 5 |
| 3929 | miramiento | 5 |
| 3930 | miércoles | 5 |
| 3931 | metro | 5 |
| 3932 | meretriz | 5 |
| 3933 | mercader | 5 |
| 3934 | medrar | 5 |
| 3935 | mediodía | 5 |
| 3936 | matutino | 5 |
| 3937 | máscara | 5 |
| 3938 | mascar | 5 |
| 3939 | martillo | 5 |
| 3940 | marquetería | 5 |
| 3941 | mariposa | 5 |
| 3942 | marina | 5 |
| 3943 | manso | 5 |
| 3944 | mandil | 5 |
| 3945 | manantial | 5 |
| 3946 | majestad | 5 |
| 3947 | local | 5 |
| 3948 | llaga | 5 |
| 3949 | lista | 5 |
| 3950 | linajudo | 5 |
| 3951 | ligar | 5 |
| 3952 | lienzo | 5 |
| 3953 | lid | 5 |
| 3954 | licenciado | 5 |
| 3955 | levemente | 5 |
| 3956 | leopoldo | 5 |
| 3957 | leñador | 5 |
| 3958 | lentamente | 5 |
| 3959 | lechuguino | 5 |
| 3960 | latir | 5 |
| 3961 | látigo | 5 |
| 3962 | lateral | 5 |
| 3963 | lápiz | 5 |
| 3964 | lánguido | 5 |
| 3965 | languidez | 5 |
| 3966 | laico | 5 |
| 3967 | labor | 5 |
| 3968 | judío | 5 |
| 3969 | júbilo | 5 |
| 3970 | jergón | 5 |
| 3971 | jamona | 5 |
| 3972 | jactar | 5 |
| 3973 | izquierdo | 5 |
| 3974 | irreverente | 5 |
| 3975 | irónico | 5 |
| 3976 | introducir | 5 |
| 3977 | intervalo | 5 |
| 3978 | interrumpió | 5 |
| 3979 | intachable | 5 |
| 3980 | insinuante | 5 |
| 3981 | inmediato | 5 |
| 3982 | ingratitud | 5 |
| 3983 | inexpugnable | 5 |
| 3984 | inercia | 5 |
| 3985 | inconsciente | 5 |
| 3986 | implacable | 5 |
| 3987 | ilustrísima | 5 |
| 3988 | ii | 5 |
| 3989 | ignorante | 5 |
| 3990 | iconoclasta | 5 |
| 3991 | huracán | 5 |
| 3992 | huevo | 5 |
| 3993 | huerto | 5 |
| 3994 | hospital | 5 |
| 3995 | hortaliza | 5 |
| 3996 | hielo | 5 |
| 3997 | hermanar | 5 |
| 3998 | heno | 5 |
| 3999 | he | 5 |
| 4000 | hazaña | 5 |
| 4001 | habla | 5 |
| 4002 | habitual | 5 |
| 4003 | gusano | 5 |
| 4004 | groseramente | 5 |
| 4005 | gótico | 5 |
| 4006 | gorrión | 5 |
| 4007 | goce | 5 |
| 4008 | genuflexión | 5 |
| 4009 | generación | 5 |
| 4010 | garantía | 5 |
| 4011 | ganoso | 5 |
| 4012 | ganado | 5 |
| 4013 | ganadero | 5 |
| 4014 | gana | 5 |
| 4015 | gala | 5 |
| 4016 | gacetillero | 5 |
| 4017 | gacetilla | 5 |
| 4018 | fundamento | 5 |
| 4019 | fragua | 5 |
| 4020 | fragmento | 5 |
| 4021 | frágil | 5 |
| 4022 | forzoso | 5 |
| 4023 | fogón | 5 |
| 4024 | firmemente | 5 |
| 4025 | filosofar | 5 |
| 4026 | fibra | 5 |
| 4027 | fiambre | 5 |
| 4028 | feria | 5 |
| 4029 | fecha | 5 |
| 4030 | extranjero | 5 |
| 4031 | explotar | 5 |
| 4032 | experto | 5 |
| 4033 | expedición | 5 |
| 4034 | excusar | 5 |
| 4035 | excomulgar | 5 |
| 4036 | examinar | 5 |
| 4037 | exactitud | 5 |
| 4038 | evocar | 5 |
| 4039 | evidenciar | 5 |
| 4040 | eufemismo | 5 |
| 4041 | estuco | 5 |
| 4042 | estrujar | 5 |
| 4043 | estrechez | 5 |
| 4044 | estatura | 5 |
| 4045 | estanquillo | 5 |
| 4046 | estallido | 5 |
| 4047 | espuma | 5 |
| 4048 | esperanzar | 5 |
| 4049 | esclavitud | 5 |
| 4050 | escaparate | 5 |
| 4051 | escalar | 5 |
| 4052 | escala | 5 |
| 4053 | entrecejo | 5 |
| 4054 | entornar | 5 |
| 4055 | ennegrecer | 5 |
| 4056 | enjugar | 5 |
| 4057 | enganchar | 5 |
| 4058 | empecatado | 5 |
| 4059 | empapar | 5 |
| 4060 | emma | 5 |
| 4061 | embargar | 5 |
| 4062 | electoral | 5 |
| 4063 | ejército | 5 |
| 4064 | egipcio | 5 |
| 4065 | efectivamente | 5 |
| 4066 | dulcemente | 5 |
| 4067 | dolorosa | 5 |
| 4068 | documento | 5 |
| 4069 | doctrinar | 5 |
| 4070 | dócil | 5 |
| 4071 | diversión | 5 |
| 4072 | displicente | 5 |
| 4073 | disparatado | 5 |
| 4074 | disolvente | 5 |
| 4075 | disimuladamente | 5 |
| 4076 | disculpa | 5 |
| 4077 | directo | 5 |
| 4078 | directamente | 5 |
| 4079 | digestión | 5 |
| 4080 | dificultar | 5 |
| 4081 | dictador | 5 |
| 4082 | diablura | 5 |
| 4083 | devocionario | 5 |
| 4084 | desplomar | 5 |
| 4085 | despertador | 5 |
| 4086 | despellejar | 5 |
| 4087 | desnudez | 5 |
| 4088 | deslumbrante | 5 |
| 4089 | desgarrar | 5 |
| 4090 | derretir | 5 |
| 4091 | depender | 5 |
| 4092 | demasía | 5 |
| 4093 | decoro | 5 |
| 4094 | debido | 5 |
| 4095 | curso | 5 |
| 4096 | curioso | 5 |
| 4097 | cumplido | 5 |
| 4098 | culpable | 5 |
| 4099 | cuerno | 5 |
| 4100 | cuclillas | 5 |
| 4101 | cuchichear | 5 |
| 4102 | cubierto | 5 |
| 4103 | cuartel | 5 |
| 4104 | cuántas | 5 |
| 4105 | crucificar | 5 |
| 4106 | creyente | 5 |
| 4107 | cree | 5 |
| 4108 | crédito | 5 |
| 4109 | correligionario | 5 |
| 4110 | copia | 5 |
| 4111 | convite | 5 |
| 4112 | contradicción | 5 |
| 4113 | contigo | 5 |
| 4114 | consumir | 5 |
| 4115 | conspirar | 5 |
| 4116 | conjurar | 5 |
| 4117 | confirmar | 5 |
| 4118 | condicional | 5 |
| 4119 | concurso | 5 |
| 4120 | concurrir | 5 |
| 4121 | concilio | 5 |
| 4122 | concienciar | 5 |
| 4123 | concepción | 5 |
| 4124 | conato | 5 |
| 4125 | comprimir | 5 |
| 4126 | complicación | 5 |
| 4127 | complacencia | 5 |
| 4128 | compensar | 5 |
| 4129 | comerciar | 5 |
| 4130 | colectivo | 5 |
| 4131 | colás | 5 |
| 4132 | cohete | 5 |
| 4133 | circular | 5 |
| 4134 | circo | 5 |
| 4135 | cinta | 5 |
| 4136 | cínico | 5 |
| 4137 | ciertamente | 5 |
| 4138 | científico | 5 |
| 4139 | chocho | 5 |
| 4140 | chaparrón | 5 |
| 4141 | cháchara | 5 |
| 4142 | cesta | 5 |
| 4143 | cerdo | 5 |
| 4144 | cerco | 5 |
| 4145 | cercano | 5 |
| 4146 | censura | 5 |
| 4147 | ceniciento | 5 |
| 4148 | cenceño | 5 |
| 4149 | ceguera | 5 |
| 4150 | cautela | 5 |
| 4151 | cátedra | 5 |
| 4152 | catalán | 5 |
| 4153 | castellano | 5 |
| 4154 | casco | 5 |
| 4155 | carmesí | 5 |
| 4156 | careta | 5 |
| 4157 | cardenal | 5 |
| 4158 | caracol | 5 |
| 4159 | canario | 5 |
| 4160 | campiña | 5 |
| 4161 | calzado | 5 |
| 4162 | cálculo | 5 |
| 4163 | calcular | 5 |
| 4164 | caballeresco | 5 |
| 4165 | burlesco | 5 |
| 4166 | burdeos | 5 |
| 4167 | bruces | 5 |
| 4168 | brindar | 5 |
| 4169 | brincar | 5 |
| 4170 | brillo | 5 |
| 4171 | boulevard | 5 |
| 4172 | botella | 5 |
| 4173 | botánico | 5 |
| 4174 | borrachera | 5 |
| 4175 | bobalicón | 5 |
| 4176 | bilis | 5 |
| 4177 | biblia | 5 |
| 4178 | besugo | 5 |
| 4179 | bestia | 5 |
| 4180 | belén | 5 |
| 4181 | bayeta | 5 |
| 4182 | basilio | 5 |
| 4183 | barro | 5 |
| 4184 | barra | 5 |
| 4185 | barcaza | 5 |
| 4186 | banquete | 5 |
| 4187 | balmes | 5 |
| 4188 | balar | 5 |
| 4189 | azar | 5 |
| 4190 | aviso | 5 |
| 4191 | avanzado | 5 |
| 4192 | autorizar | 5 |
| 4193 | atrevido | 5 |
| 4194 | atrasado | 5 |
| 4195 | astro | 5 |
| 4196 | aspiración | 5 |
| 4197 | asís | 5 |
| 4198 | asediar | 5 |
| 4199 | asalto | 5 |
| 4200 | ardor | 5 |
| 4201 | araña | 5 |
| 4202 | aprobación | 5 |
| 4203 | aprensivo | 5 |
| 4204 | apostar | 5 |
| 4205 | aplauso | 5 |
| 4206 | apiñar | 5 |
| 4207 | apetecible | 5 |
| 4208 | anunciación | 5 |
| 4209 | anticipar | 5 |
| 4210 | anteojo | 5 |
| 4211 | antaño | 5 |
| 4212 | ansiar | 5 |
| 4213 | anónimo | 5 |
| 4214 | anochecer | 5 |
| 4215 | anoche | 5 |
| 4216 | anís | 5 |
| 4217 | anhelar | 5 |
| 4218 | anguloso | 5 |
| 4219 | ampuloso | 5 |
| 4220 | amparar | 5 |
| 4221 | ameno | 5 |
| 4222 | amargo | 5 |
| 4223 | amanerado | 5 |
| 4224 | amado | 5 |
| 4225 | alusivo | 5 |
| 4226 | alias | 5 |
| 4227 | alargar | 5 |
| 4228 | alambicar | 5 |
| 4229 | águila | 5 |
| 4230 | agolpar | 5 |
| 4231 | adversario | 5 |
| 4232 | adoración | 5 |
| 4233 | adónde | 5 |
| 4234 | adolescente | 5 |
| 4235 | admirable | 5 |
| 4236 | acostumbrado | 5 |
| 4237 | aclarar | 5 |
| 4238 | acceder | 5 |
| 4239 | académico | 5 |
| 4240 | acacia | 5 |
| 4241 | abundar | 5 |
| 4242 | abuelo | 5 |
| 4243 | absolución | 5 |
| 4244 | abismar | 5 |
| 4245 | aberración | 5 |
| 4246 | vocinglero | 4 |
| 4247 | viva | 4 |
| 4248 | viudedad | 4 |
| 4249 | violento | 4 |
| 4250 | viene | 4 |
| 4251 | verosimilitud | 4 |
| 4252 | verosímil | 4 |
| 4253 | venus | 4 |
| 4254 | ventura | 4 |
| 4255 | ventanilla | 4 |
| 4256 | venga | 4 |
| 4257 | veintisiete | 4 |
| 4258 | vecindad | 4 |
| 4259 | valla | 4 |
| 4260 | vale | 4 |
| 4261 | vacación | 4 |
| 4262 | usía | 4 |
| 4263 | uña | 4 |
| 4264 | universidad | 4 |
| 4265 | uniforme | 4 |
| 4266 | únicamente | 4 |
| 4267 | ultraje | 4 |
| 4268 | últimamente | 4 |
| 4269 | turno | 4 |
| 4270 | turgencia | 4 |
| 4271 | tubo | 4 |
| 4272 | tropezón | 4 |
| 4273 | tronado | 4 |
| 4274 | trompeta | 4 |
| 4275 | tributo | 4 |
| 4276 | trechos | 4 |
| 4277 | trasto | 4 |
| 4278 | trabajador | 4 |
| 4279 | tos | 4 |
| 4280 | toro | 4 |
| 4281 | torcido | 4 |
| 4282 | tomillo | 4 |
| 4283 | tolerable | 4 |
| 4284 | toga | 4 |
| 4285 | tisis | 4 |
| 4286 | timorato | 4 |
| 4287 | timidez | 4 |
| 4288 | tímidamente | 4 |
| 4289 | tieso | 4 |
| 4290 | tibieza | 4 |
| 4291 | tibiar | 4 |
| 4292 | terrón | 4 |
| 4293 | territorial | 4 |
| 4294 | terminante | 4 |
| 4295 | tercer | 4 |
| 4296 | tentativa | 4 |
| 4297 | tenor | 4 |
| 4298 | tendido | 4 |
| 4299 | tenaza | 4 |
| 4300 | tenacidad | 4 |
| 4301 | tedio | 4 |
| 4302 | tarsila | 4 |
| 4303 | tambalear | 4 |
| 4304 | tamaña | 4 |
| 4305 | talón | 4 |
| 4306 | taburete | 4 |
| 4307 | tablado | 4 |
| 4308 | tabique | 4 |
| 4309 | tabaco | 4 |
| 4310 | sustituto | 4 |
| 4311 | suplir | 4 |
| 4312 | supino | 4 |
| 4313 | sueños | 4 |
| 4314 | suela | 4 |
| 4315 | sucesor | 4 |
| 4316 | sucesión | 4 |
| 4317 | sótano | 4 |
| 4318 | soportal | 4 |
| 4319 | sollozar | 4 |
| 4320 | solicitud | 4 |
| 4321 | sócrates | 4 |
| 4322 | sobrecoger | 4 |
| 4323 | soberano | 4 |
| 4324 | sobado | 4 |
| 4325 | sinuoso | 4 |
| 4326 | siniestro | 4 |
| 4327 | singularmente | 4 |
| 4328 | simonía | 4 |
| 4329 | significativo | 4 |
| 4330 | sietemesino | 4 |
| 4331 | sepultura | 4 |
| 4332 | señorío | 4 |
| 4333 | sentimentalismo | 4 |
| 4334 | sentada | 4 |
| 4335 | sensual | 4 |
| 4336 | sencillez | 4 |
| 4337 | secularizar | 4 |
| 4338 | sebo | 4 |
| 4339 | santísima | 4 |
| 4340 | salvador | 4 |
| 4341 | salpicar | 4 |
| 4342 | salga | 4 |
| 4343 | sagaz | 4 |
| 4344 | sacudida | 4 |
| 4345 | sabiamente | 4 |
| 4346 | rutinario | 4 |
| 4347 | rústico | 4 |
| 4348 | rural | 4 |
| 4349 | rumiar | 4 |
| 4350 | rugió | 4 |
| 4351 | romano | 4 |
| 4352 | rollizo | 4 |
| 4353 | rodeo | 4 |
| 4354 | rizado | 4 |
| 4355 | riesgo | 4 |
| 4356 | retozón | 4 |
| 4357 | retorcido | 4 |
| 4358 | retirado | 4 |
| 4359 | retablo | 4 |
| 4360 | restauración | 4 |
| 4361 | respetuoso | 4 |
| 4362 | resonante | 4 |
| 4363 | resbaladizo | 4 |
| 4364 | republicano | 4 |
| 4365 | representación | 4 |
| 4366 | reprensión | 4 |
| 4367 | reposo | 4 |
| 4368 | reponer | 4 |
| 4369 | replicar | 4 |
| 4370 | reparto | 4 |
| 4371 | reparación | 4 |
| 4372 | reliquia | 4 |
| 4373 | registrar | 4 |
| 4374 | regir | 4 |
| 4375 | refugiar | 4 |
| 4376 | refuerzo | 4 |
| 4377 | refresco | 4 |
| 4378 | recortar | 4 |
| 4379 | recóndito | 4 |
| 4380 | recio | 4 |
| 4381 | raya | 4 |
| 4382 | ratón | 4 |
| 4383 | ras | 4 |
| 4384 | ramos | 4 |
| 4385 | raíces | 4 |
| 4386 | radical | 4 |
| 4387 | racimo | 4 |
| 4388 | rabillo | 4 |
| 4389 | quizás | 4 |
| 4390 | quintilla | 4 |
| 4391 | quehacer | 4 |
| 4392 | quebrantar | 4 |
| 4393 | quebradero | 4 |
| 4394 | púrpura | 4 |
| 4395 | purísimo | 4 |
| 4396 | puñada | 4 |
| 4397 | pulquérrimo | 4 |
| 4398 | pulmonía | 4 |
| 4399 | puente | 4 |
| 4400 | puchero | 4 |
| 4401 | psicológico | 4 |
| 4402 | psicología | 4 |
| 4403 | prurito | 4 |
| 4404 | provisión | 4 |
| 4405 | protección | 4 |
| 4406 | propalar | 4 |
| 4407 | producto | 4 |
| 4408 | pródigo | 4 |
| 4409 | procurador | 4 |
| 4410 | probabilidad | 4 |
| 4411 | primitivo | 4 |
| 4412 | presbítero | 4 |
| 4413 | preparación | 4 |
| 4414 | preocupado | 4 |
| 4415 | prematuro | 4 |
| 4416 | preferencia | 4 |
| 4417 | predilección | 4 |
| 4418 | postizo | 4 |
| 4419 | posesión | 4 |
| 4420 | portento | 4 |
| 4421 | pontífice | 4 |
| 4422 | pongo | 4 |
| 4423 | podrir | 4 |
| 4424 | podía | 4 |
| 4425 | podar | 4 |
| 4426 | pocilga | 4 |
| 4427 | plomizo | 4 |
| 4428 | pleito | 4 |
| 4429 | plegar | 4 |
| 4430 | plebe | 4 |
| 4431 | pitillo | 4 |
| 4432 | pipa | 4 |
| 4433 | pintoresco | 4 |
| 4434 | pillo | 4 |
| 4435 | piar | 4 |
| 4436 | personar | 4 |
| 4437 | permanente | 4 |
| 4438 | perjudicar | 4 |
| 4439 | perilla | 4 |
| 4440 | peral | 4 |
| 4441 | pellizcar | 4 |
| 4442 | pellejo | 4 |
| 4443 | peculiar | 4 |
| 4444 | pausar | 4 |
| 4445 | pausadamente | 4 |
| 4446 | pátina | 4 |
| 4447 | patata | 4 |
| 4448 | patadas | 4 |
| 4449 | pata | 4 |
| 4450 | pasmo | 4 |
| 4451 | parterre | 4 |
| 4452 | parcerisa | 4 |
| 4453 | parábola | 4 |
| 4454 | panteísmo | 4 |
| 4455 | panorama | 4 |
| 4456 | pana | 4 |
| 4457 | palpar | 4 |
| 4458 | pajarera | 4 |
| 4459 | pacto | 4 |
| 4460 | pábulo | 4 |
| 4461 | otra | 4 |
| 4462 | ortodoxo | 4 |
| 4463 | orquesta | 4 |
| 4464 | orillas | 4 |
| 4465 | optimismo | 4 |
| 4466 | occidente | 4 |
| 4467 | obsequio | 4 |
| 4468 | objetar | 4 |
| 4469 | objeción | 4 |
| 4470 | nuestra | 4 |
| 4471 | nublado | 4 |
| 4472 | noviembre | 4 |
| 4473 | novicio | 4 |
| 4474 | nostalgia | 4 |
| 4475 | noroeste | 4 |
| 4476 | noé | 4 |
| 4477 | niñería | 4 |
| 4478 | negación | 4 |
| 4479 | navidad | 4 |
| 4480 | navegar | 4 |
| 4481 | naturalidad | 4 |
| 4482 | narrar | 4 |
| 4483 | napoleón | 4 |
| 4484 | nácar | 4 |
| 4485 | mutuo | 4 |
| 4486 | mustio | 4 |
| 4487 | municipio | 4 |
| 4488 | mundanal | 4 |
| 4489 | mula | 4 |
| 4490 | muda | 4 |
| 4491 | mostrador | 4 |
| 4492 | mosquito | 4 |
| 4493 | monumental | 4 |
| 4494 | montaraz | 4 |
| 4495 | monosílabo | 4 |
| 4496 | mondar | 4 |
| 4497 | molinero | 4 |
| 4498 | modificar | 4 |
| 4499 | moderar | 4 |
| 4500 | modelar | 4 |
| 4501 | mitra | 4 |
| 4502 | minero | 4 |
| 4503 | mimar | 4 |
| 4504 | mia | 4 |
| 4505 | mezquino | 4 |
| 4506 | metafísica | 4 |
| 4507 | meseta | 4 |
| 4508 | mental | 4 |
| 4509 | mensual | 4 |
| 4510 | menester | 4 |
| 4511 | menear | 4 |
| 4512 | meloso | 4 |
| 4513 | medicinar | 4 |
| 4514 | mecánica | 4 |
| 4515 | maza | 4 |
| 4516 | maternal | 4 |
| 4517 | masculino | 4 |
| 4518 | marzo | 4 |
| 4519 | marcial | 4 |
| 4520 | maravillar | 4 |
| 4521 | marasmo | 4 |
| 4522 | manto | 4 |
| 4523 | manta | 4 |
| 4524 | mandilón | 4 |
| 4525 | mandato | 4 |
| 4526 | mancha | 4 |
| 4527 | malva | 4 |
| 4528 | maltratar | 4 |
| 4529 | malsano | 4 |
| 4530 | maldición | 4 |
| 4531 | maldiciente | 4 |
| 4532 | magnate | 4 |
| 4533 | madrugador | 4 |
| 4534 | madero | 4 |
| 4535 | lúgubre | 4 |
| 4536 | luciente | 4 |
| 4537 | llegó | 4 |
| 4538 | llano | 4 |
| 4539 | llamarada | 4 |
| 4540 | lisonjero | 4 |
| 4541 | linterna | 4 |
| 4542 | ligeramente | 4 |
| 4543 | libremente | 4 |
| 4544 | liberalismo | 4 |
| 4545 | leña | 4 |
| 4546 | lego | 4 |
| 4547 | legítimo | 4 |
| 4548 | lechar | 4 |
| 4549 | latino | 4 |
| 4550 | larva | 4 |
| 4551 | jubilado | 4 |
| 4552 | jesuitas | 4 |
| 4553 | jerarquía | 4 |
| 4554 | jadeante | 4 |
| 4555 | irrespetuoso | 4 |
| 4556 | irracional | 4 |
| 4557 | iriarte | 4 |
| 4558 | intersticio | 4 |
| 4559 | insípido | 4 |
| 4560 | inquisidor | 4 |
| 4561 | inoportuno | 4 |
| 4562 | inmundo | 4 |
| 4563 | inminente | 4 |
| 4564 | iniciar | 4 |
| 4565 | ingenuo | 4 |
| 4566 | ingeniero | 4 |
| 4567 | infundir | 4 |
| 4568 | influyente | 4 |
| 4569 | influjo | 4 |
| 4570 | inflar | 4 |
| 4571 | infamia | 4 |
| 4572 | indumentaria | 4 |
| 4573 | indiscreción | 4 |
| 4574 | índice | 4 |
| 4575 | incurable | 4 |
| 4576 | incrustar | 4 |
| 4577 | incluso | 4 |
| 4578 | incertidumbre | 4 |
| 4579 | incensar | 4 |
| 4580 | inaugurar | 4 |
| 4581 | inagotable | 4 |
| 4582 | impuro | 4 |
| 4583 | impulsar | 4 |
| 4584 | impresionar | 4 |
| 4585 | imposición | 4 |
| 4586 | ímpetu | 4 |
| 4587 | ilegítimo | 4 |
| 4588 | idealista | 4 |
| 4589 | huella | 4 |
| 4590 | homenaje | 4 |
| 4591 | hoguera | 4 |
| 4592 | hinchar | 4 |
| 4593 | hilar | 4 |
| 4594 | hierático | 4 |
| 4595 | herrar | 4 |
| 4596 | hacha | 4 |
| 4597 | hace | 4 |
| 4598 | hablilla | 4 |
| 4599 | habana | 4 |
| 4600 | guisar | 4 |
| 4601 | gruñido | 4 |
| 4602 | gregorio | 4 |
| 4603 | granate | 4 |
| 4604 | gozoso | 4 |
| 4605 | gorra | 4 |
| 4606 | golpecito | 4 |
| 4607 | girar | 4 |
| 4608 | gimnasia | 4 |
| 4609 | gemelo | 4 |
| 4610 | gata | 4 |
| 4611 | gasto | 4 |
| 4612 | gastado | 4 |
| 4613 | garra | 4 |
| 4614 | fundador | 4 |
| 4615 | funciones | 4 |
| 4616 | fruta | 4 |
| 4617 | francisca | 4 |
| 4618 | francia | 4 |
| 4619 | flexible | 4 |
| 4620 | flauta | 4 |
| 4621 | fisiológico | 4 |
| 4622 | finura | 4 |
| 4623 | final | 4 |
| 4624 | filtrar | 4 |
| 4625 | filial | 4 |
| 4626 | figurín | 4 |
| 4627 | femenino | 4 |
| 4628 | femenil | 4 |
| 4629 | felicitar | 4 |
| 4630 | favorable | 4 |
| 4631 | fatalidad | 4 |
| 4632 | fascinar | 4 |
| 4633 | falsedad | 4 |
| 4634 | factor | 4 |
| 4635 | extremar | 4 |
| 4636 | extraviado | 4 |
| 4637 | extinguir | 4 |
| 4638 | externo | 4 |
| 4639 | éxito | 4 |
| 4640 | excepcional | 4 |
| 4641 | excelentísimo | 4 |
| 4642 | evangélico | 4 |
| 4643 | eternidad | 4 |
| 4644 | estupefacto | 4 |
| 4645 | estufa | 4 |
| 4646 | estímulo | 4 |
| 4647 | estameña | 4 |
| 4648 | esponja | 4 |
| 4649 | esplendoroso | 4 |
| 4650 | espléndido | 4 |
| 4651 | espantado | 4 |
| 4652 | esfera | 4 |
| 4653 | esencial | 4 |
| 4654 | escrupuloso | 4 |
| 4655 | escarabajo | 4 |
| 4656 | equivocación | 4 |
| 4657 | epigrama | 4 |
| 4658 | enseñorear | 4 |
| 4659 | ensanchar | 4 |
| 4660 | enramada | 4 |
| 4661 | enojo | 4 |
| 4662 | engendrar | 4 |
| 4663 | énfasis | 4 |
| 4664 | encomendar | 4 |
| 4665 | encimar | 4 |
| 4666 | encierro | 4 |
| 4667 | encerrona | 4 |
| 4668 | encaje | 4 |
| 4669 | empleo | 4 |
| 4670 | embutir | 4 |
| 4671 | embriaguez | 4 |
| 4672 | embriagar | 4 |
| 4673 | embarazoso | 4 |
| 4674 | emanación | 4 |
| 4675 | elogiar | 4 |
| 4676 | elegir | 4 |
| 4677 | eclipsar | 4 |
| 4678 | duradero | 4 |
| 4679 | dormitar | 4 |
| 4680 | doctrina | 4 |
| 4681 | doctora | 4 |
| 4682 | doble | 4 |
| 4683 | distingo | 4 |
| 4684 | disminuir | 4 |
| 4685 | dimisión | 4 |
| 4686 | diluvio | 4 |
| 4687 | diligenciar | 4 |
| 4688 | diligencia | 4 |
| 4689 | digo | 4 |
| 4690 | dignísimo | 4 |
| 4691 | diario | 4 |
| 4692 | devaneo | 4 |
| 4693 | determinado | 4 |
| 4694 | desvencijado | 4 |
| 4695 | despojo | 4 |
| 4696 | despejar | 4 |
| 4697 | despedida | 4 |
| 4698 | despecho | 4 |
| 4699 | deslizar | 4 |
| 4700 | desigualdad | 4 |
| 4701 | desigual | 4 |
| 4702 | desfallecimiento | 4 |
| 4703 | desfallecer | 4 |
| 4704 | desempeñar | 4 |
| 4705 | descuidado | 4 |
| 4706 | descripción | 4 |
| 4707 | descrédito | 4 |
| 4708 | desconsuelo | 4 |
| 4709 | descendiente | 4 |
| 4710 | desatar | 4 |
| 4711 | desaliento | 4 |
| 4712 | derramar | 4 |
| 4713 | degradar | 4 |
| 4714 | degradación | 4 |
| 4715 | definir | 4 |
| 4716 | decoración | 4 |
| 4717 | declamar | 4 |
| 4718 | decisivo | 4 |
| 4719 | debo | 4 |
| 4720 | danza | 4 |
| 4721 | culebra | 4 |
| 4722 | cuestas | 4 |
| 4723 | cuántos | 4 |
| 4724 | cruzado | 4 |
| 4725 | cruzada | 4 |
| 4726 | crudo | 4 |
| 4727 | crucificado | 4 |
| 4728 | cristianismo | 4 |
| 4729 | crispar | 4 |
| 4730 | cresta | 4 |
| 4731 | cráneo | 4 |
| 4732 | cosas | 4 |
| 4733 | corujedo | 4 |
| 4734 | cortesano | 4 |
| 4735 | corrupción | 4 |
| 4736 | corrosivo | 4 |
| 4737 | corromper | 4 |
| 4738 | correspondiente | 4 |
| 4739 | cordón | 4 |
| 4740 | convencional | 4 |
| 4741 | controversia | 4 |
| 4742 | contratiempo | 4 |
| 4743 | contrarrestar | 4 |
| 4744 | contrariedad | 4 |
| 4745 | contradictorio | 4 |
| 4746 | contemporáneo | 4 |
| 4747 | consunción | 4 |
| 4748 | conspirador | 4 |
| 4749 | considerable | 4 |
| 4750 | conquistador | 4 |
| 4751 | conforme | 4 |
| 4752 | conflicto | 4 |
| 4753 | confitería | 4 |
| 4754 | confidencial | 4 |
| 4755 | conde | 4 |
| 4756 | conciudadano | 4 |
| 4757 | conciliábulo | 4 |
| 4758 | comunión | 4 |
| 4759 | composición | 4 |
| 4760 | complot | 4 |
| 4761 | compatible | 4 |
| 4762 | comendador | 4 |
| 4763 | comedir | 4 |
| 4764 | combinar | 4 |
| 4765 | colono | 4 |
| 4766 | colegio | 4 |
| 4767 | codicia | 4 |
| 4768 | cobre | 4 |
| 4769 | clerical | 4 |
| 4770 | clara | 4 |
| 4771 | ciudadano | 4 |
| 4772 | cilicio | 4 |
| 4773 | cieno | 4 |
| 4774 | chubasco | 4 |
| 4775 | chorizo | 4 |
| 4776 | charlar | 4 |
| 4777 | charada | 4 |
| 4778 | césped | 4 |
| 4779 | cerveza | 4 |
| 4780 | ceremonioso | 4 |
| 4781 | cepillar | 4 |
| 4782 | censurar | 4 |
| 4783 | caviloso | 4 |
| 4784 | catedrático | 4 |
| 4785 | casilla | 4 |
| 4786 | casera | 4 |
| 4787 | cascada | 4 |
| 4788 | casadero | 4 |
| 4789 | cartón | 4 |
| 4790 | carmen | 4 |
| 4791 | carbonero | 4 |
| 4792 | capellanía | 4 |
| 4793 | cantero | 4 |
| 4794 | candoroso | 4 |
| 4795 | calvo | 4 |
| 4796 | calavera | 4 |
| 4797 | calar | 4 |
| 4798 | calabaza | 4 |
| 4799 | cabizbajo | 4 |
| 4800 | busto | 4 |
| 4801 | burlón | 4 |
| 4802 | brasero | 4 |
| 4803 | brasar | 4 |
| 4804 | borla | 4 |
| 4805 | bordada | 4 |
| 4806 | boquirroto | 4 |
| 4807 | bondadoso | 4 |
| 4808 | boj | 4 |
| 4809 | bendecir | 4 |
| 4810 | beltrand | 4 |
| 4811 | baúl | 4 |
| 4812 | barniz | 4 |
| 4813 | barítono | 4 |
| 4814 | bandada | 4 |
| 4815 | bancarrota | 4 |
| 4816 | balde | 4 |
| 4817 | babilonia | 4 |
| 4818 | azafrán | 4 |
| 4819 | ayuno | 4 |
| 4820 | avergonzado | 4 |
| 4821 | aurora | 4 |
| 4822 | audaz | 4 |
| 4823 | atleta | 4 |
| 4824 | aterrar | 4 |
| 4825 | atento | 4 |
| 4826 | asaltar | 4 |
| 4827 | artillería | 4 |
| 4828 | artefacto | 4 |
| 4829 | arrullo | 4 |
| 4830 | arrullar | 4 |
| 4831 | arrepentimiento | 4 |
| 4832 | arrebatar | 4 |
| 4833 | arraigar | 4 |
| 4834 | arraigado | 4 |
| 4835 | arqueología | 4 |
| 4836 | arcángel | 4 |
| 4837 | aquellas | 4 |
| 4838 | apostólico | 4 |
| 4839 | apetitoso | 4 |
| 4840 | apacible | 4 |
| 4841 | antojo | 4 |
| 4842 | antero | 4 |
| 4843 | animación | 4 |
| 4844 | angosto | 4 |
| 4845 | andaluz | 4 |
| 4846 | análisis | 4 |
| 4847 | anales | 4 |
| 4848 | ambicionar | 4 |
| 4849 | amapola | 4 |
| 4850 | alterar | 4 |
| 4851 | altanero | 4 |
| 4852 | alpaca | 4 |
| 4853 | almohadón | 4 |
| 4854 | alegoría | 4 |
| 4855 | albañil | 4 |
| 4856 | alarmante | 4 |
| 4857 | ajo | 4 |
| 4858 | aislar | 4 |
| 4859 | airar | 4 |
| 4860 | ahumado | 4 |
| 4861 | ahorro | 4 |
| 4862 | agrio | 4 |
| 4863 | agregar | 4 |
| 4864 | aflojar | 4 |
| 4865 | afecto | 4 |
| 4866 | afectación | 4 |
| 4867 | adular | 4 |
| 4868 | adolescencia | 4 |
| 4869 | adentrar | 4 |
| 4870 | actor | 4 |
| 4871 | acompañamiento | 4 |
| 4872 | acierto | 4 |
| 4873 | aceite | 4 |
| 4874 | acecho | 4 |
| 4875 | acalorar | 4 |
| 4876 | abominable | 4 |
| 4877 | abalorio | 4 |
| 4878 | zángano | 3 |
| 4879 | xiv | 3 |
| 4880 | wamba | 3 |
| 4881 | voy | 3 |
| 4882 | viudez | 3 |
| 4883 | vistoso | 3 |
| 4884 | vislumbrar | 3 |
| 4885 | visible | 3 |
| 4886 | viril | 3 |
| 4887 | villanía | 3 |
| 4888 | vicisitud | 3 |
| 4889 | vicioso | 3 |
| 4890 | viajar | 3 |
| 4891 | vestigio | 3 |
| 4892 | vertical | 3 |
| 4893 | verter | 3 |
| 4894 | verdugo | 3 |
| 4895 | verdor | 3 |
| 4896 | veranear | 3 |
| 4897 | ventilar | 3 |
| 4898 | veleidad | 3 |
| 4899 | velador | 3 |
| 4900 | vejiga | 3 |
| 4901 | vejar | 3 |
| 4902 | veinticuatro | 3 |
| 4903 | ve | 3 |
| 4904 | varilla | 3 |
| 4905 | vaporoso | 3 |
| 4906 | vaciar | 3 |
| 4907 | utilitario | 3 |
| 4908 | urna | 3 |
| 4909 | uñir | 3 |
| 4910 | unión | 3 |
| 4911 | unidad | 3 |
| 4912 | unanimidad | 3 |
| 4913 | unánime | 3 |
| 4914 | última | 3 |
| 4915 | u | 3 |
| 4916 | turnar | 3 |
| 4917 | turba | 3 |
| 4918 | tunante | 3 |
| 4919 | trovador | 3 |
| 4920 | tristón | 3 |
| 4921 | trigo | 3 |
| 4922 | tregua | 3 |
| 4923 | trece | 3 |
| 4924 | travesaño | 3 |
| 4925 | traspasar | 3 |
| 4926 | trasnochar | 3 |
| 4927 | transparentar | 3 |
| 4928 | transformación | 3 |
| 4929 | transacción | 3 |
| 4930 | tramar | 3 |
| 4931 | trago | 3 |
| 4932 | tragedia | 3 |
| 4933 | tráfico | 3 |
| 4934 | traducir | 3 |
| 4935 | tostado | 3 |
| 4936 | tortuoso | 3 |
| 4937 | tortuga | 3 |
| 4938 | torrente | 3 |
| 4939 | torno | 3 |
| 4940 | tornillo | 3 |
| 4941 | tornasol | 3 |
| 4942 | torero | 3 |
| 4943 | toma | 3 |
| 4944 | toledo | 3 |
| 4945 | todd | 3 |
| 4946 | tocante | 3 |
| 4947 | titular | 3 |
| 4948 | tirso | 3 |
| 4949 | tiesto | 3 |
| 4950 | tibia | 3 |
| 4951 | testimonio | 3 |
| 4952 | testero | 3 |
| 4953 | tesón | 3 |
| 4954 | terremoto | 3 |
| 4955 | termasaltas | 3 |
| 4956 | teórico | 3 |
| 4957 | tensión | 3 |
| 4958 | tendero | 3 |
| 4959 | telar | 3 |
| 4960 | tardío | 3 |
| 4961 | tapaboca | 3 |
| 4962 | tañer | 3 |
| 4963 | tajar | 3 |
| 4964 | tacón | 3 |
| 4965 | tablero | 3 |
| 4966 | tabernero | 3 |
| 4967 | susurro | 3 |
| 4968 | surgir | 3 |
| 4969 | suprimir | 3 |
| 4970 | suplicante | 3 |
| 4971 | supersticiosamente | 3 |
| 4972 | suicidio | 3 |
| 4973 | sugestión | 3 |
| 4974 | sueldo | 3 |
| 4975 | subrayar | 3 |
| 4976 | sonido | 3 |
| 4977 | sondear | 3 |
| 4978 | sonámbulo | 3 |
| 4979 | solidez | 3 |
| 4980 | solicitante | 3 |
| 4981 | soldar | 3 |
| 4982 | sojuzgar | 3 |
| 4983 | socorro | 3 |
| 4984 | sobriedad | 3 |
| 4985 | situar | 3 |
| 4986 | sinodal | 3 |
| 4987 | simulacro | 3 |
| 4988 | sílaba | 3 |
| 4989 | signo | 3 |
| 4990 | sidra | 3 |
| 4991 | sevilla | 3 |
| 4992 | setenta | 3 |
| 4993 | serpear | 3 |
| 4994 | serenidad | 3 |
| 4995 | seráfico | 3 |
| 4996 | sepultar | 3 |
| 4997 | sepulcro | 3 |
| 4998 | separación | 3 |
| 4999 | sentenciar | 3 |
| 5000 | sentencia | 3 |
| 5001 | sensible | 3 |
| 5002 | senda | 3 |
| 5003 | seguía | 3 |
| 5004 | segismundo | 3 |
| 5005 | segar | 3 |
| 5006 | sectario | 3 |
| 5007 | saya | 3 |
| 5008 | savia | 3 |
| 5009 | sardina | 3 |
| 5010 | sandez | 3 |
| 5011 | saliva | 3 |
| 5012 | sagacidad | 3 |
| 5013 | sacristán | 3 |
| 5014 | sacerdocio | 3 |
| 5015 | sábado | 3 |
| 5016 | rusia | 3 |
| 5017 | ruiseñor | 3 |
| 5018 | ruinoso | 3 |
| 5019 | rugir | 3 |
| 5020 | roto | 3 |
| 5021 | rosina | 3 |
| 5022 | rosetón | 3 |
| 5023 | roque | 3 |
| 5024 | rompimiento | 3 |
| 5025 | romero | 3 |
| 5026 | románico | 3 |
| 5027 | rojizo | 3 |
| 5028 | roer | 3 |
| 5029 | rodrigo | 3 |
| 5030 | rocín | 3 |
| 5031 | risum | 3 |
| 5032 | revolucionario | 3 |
| 5033 | retraer | 3 |
| 5034 | retiro | 3 |
| 5035 | retirada | 3 |
| 5036 | reticencia | 3 |
| 5037 | resumidas | 3 |
| 5038 | restaurar | 3 |
| 5039 | resquicio | 3 |
| 5040 | respaldo | 3 |
| 5041 | resignado | 3 |
| 5042 | reseco | 3 |
| 5043 | requerir | 3 |
| 5044 | reprensible | 3 |
| 5045 | repleto | 3 |
| 5046 | repetido | 3 |
| 5047 | reparo | 3 |
| 5048 | rentar | 3 |
| 5049 | renovar | 3 |
| 5050 | renglón | 3 |
| 5051 | rendición | 3 |
| 5052 | rencoroso | 3 |
| 5053 | renan | 3 |
| 5054 | remolino | 3 |
| 5055 | remiendo | 3 |
| 5056 | remendar | 3 |
| 5057 | relacionar | 3 |
| 5058 | reglar | 3 |
| 5059 | regar | 3 |
| 5060 | regañadientes | 3 |
| 5061 | refinado | 3 |
| 5062 | reemplazar | 3 |
| 5063 | redonda | 3 |
| 5064 | redomado | 3 |
| 5065 | redactor | 3 |
| 5066 | reconciliación | 3 |
| 5067 | recompensar | 3 |
| 5068 | recluta | 3 |
| 5069 | reclamo | 3 |
| 5070 | recato | 3 |
| 5071 | recatado | 3 |
| 5072 | recargar | 3 |
| 5073 | recaer | 3 |
| 5074 | rebosar | 3 |
| 5075 | rebelde | 3 |
| 5076 | rebelar | 3 |
| 5077 | razonar | 3 |
| 5078 | razonable | 3 |
| 5079 | rayar | 3 |
| 5080 | rastro | 3 |
| 5081 | rasero | 3 |
| 5082 | rascar | 3 |
| 5083 | raquítico | 3 |
| 5084 | rana | 3 |
| 5085 | ramo | 3 |
| 5086 | raído | 3 |
| 5087 | raciocinio | 3 |
| 5088 | quinqué | 3 |
| 5089 | quincalla | 3 |
| 5090 | quieres | 3 |
| 5091 | querrá | 3 |
| 5092 | quejumbroso | 3 |
| 5093 | purgatorio | 3 |
| 5094 | pupitre | 3 |
| 5095 | puntería | 3 |
| 5096 | pulsar | 3 |
| 5097 | puf | 3 |
| 5098 | puertas | 3 |
| 5099 | proyectar | 3 |
| 5100 | providencial | 3 |
| 5101 | provechoso | 3 |
| 5102 | proscenio | 3 |
| 5103 | proporcionar | 3 |
| 5104 | propina | 3 |
| 5105 | propietario | 3 |
| 5106 | prólogo | 3 |
| 5107 | prohibición | 3 |
| 5108 | prodigio | 3 |
| 5109 | proclamar | 3 |
| 5110 | privar | 3 |
| 5111 | primor | 3 |
| 5112 | primogénito | 3 |
| 5113 | prever | 3 |
| 5114 | prevenir | 3 |
| 5115 | préstamo | 3 |
| 5116 | presentir | 3 |
| 5117 | preliminar | 3 |
| 5118 | precoz | 3 |
| 5119 | preclaro | 3 |
| 5120 | preceder | 3 |
| 5121 | praxíteles | 3 |
| 5122 | pradera | 3 |
| 5123 | practicar | 3 |
| 5124 | potencia | 3 |
| 5125 | postre | 3 |
| 5126 | posta | 3 |
| 5127 | positivismo | 3 |
| 5128 | positivamente | 3 |
| 5129 | posar | 3 |
| 5130 | pos | 3 |
| 5131 | portátil | 3 |
| 5132 | pordiosero | 3 |
| 5133 | poquito | 3 |
| 5134 | poniente | 3 |
| 5135 | pompadour | 3 |
| 5136 | pólvora | 3 |
| 5137 | polémica | 3 |
| 5138 | poetisa | 3 |
| 5139 | poderío | 3 |
| 5140 | pobrecita | 3 |
| 5141 | pluvial | 3 |
| 5142 | plumero | 3 |
| 5143 | pleno | 3 |
| 5144 | playa | 3 |
| 5145 | platea | 3 |
| 5146 | plantón | 3 |
| 5147 | plácido | 3 |
| 5148 | placa | 3 |
| 5149 | pisotear | 3 |
| 5150 | pirueta | 3 |
| 5151 | pinturas | 3 |
| 5152 | pintada | 3 |
| 5153 | petimetre | 3 |
| 5154 | pestillo | 3 |
| 5155 | pese | 3 |
| 5156 | pescuezo | 3 |
| 5157 | pesca | 3 |
| 5158 | pesadumbre | 3 |
| 5159 | perspicacia | 3 |
| 5160 | personalidad | 3 |
| 5161 | perseverancia | 3 |
| 5162 | perpendicular | 3 |
| 5163 | perlas | 3 |
| 5164 | perífrasis | 3 |
| 5165 | pergamino | 3 |
| 5166 | perenne | 3 |
| 5167 | pepita | 3 |
| 5168 | penetrante | 3 |
| 5169 | penas | 3 |
| 5170 | pelota | 3 |
| 5171 | pelado | 3 |
| 5172 | pedante | 3 |
| 5173 | pedagógico | 3 |
| 5174 | patrón | 3 |
| 5175 | patriotismo | 3 |
| 5176 | patas | 3 |
| 5177 | pasta | 3 |
| 5178 | pasmoso | 3 |
| 5179 | pasivo | 3 |
| 5180 | pase | 3 |
| 5181 | pascuas | 3 |
| 5182 | partícula | 3 |
| 5183 | paroxismo | 3 |
| 5184 | parodiar | 3 |
| 5185 | parecía | 3 |
| 5186 | paralela | 3 |
| 5187 | panurgo | 3 |
| 5188 | panteón | 3 |
| 5189 | paniaguado | 3 |
| 5190 | palpitar | 3 |
| 5191 | palpable | 3 |
| 5192 | palmera | 3 |
| 5193 | palabreja | 3 |
| 5194 | paca | 3 |
| 5195 | pabellón | 3 |
| 5196 | otras | 3 |
| 5197 | ortografía | 3 |
| 5198 | orillar | 3 |
| 5199 | originalidad | 3 |
| 5200 | oriental | 3 |
| 5201 | oratoria | 3 |
| 5202 | opio | 3 |
| 5203 | opaco | 3 |
| 5204 | ondear | 3 |
| 5205 | olvidito | 3 |
| 5206 | ojuelos | 3 |
| 5207 | ojeriza | 3 |
| 5208 | ojalá | 3 |
| 5209 | oidor | 3 |
| 5210 | oda | 3 |
| 5211 | ocio | 3 |
| 5212 | ocasionar | 3 |
| 5213 | oblicuo | 3 |
| 5214 | obediencia | 3 |
| 5215 | nuez | 3 |
| 5216 | núcleo | 3 |
| 5217 | nubes | 3 |
| 5218 | novelesco | 3 |
| 5219 | notaba | 3 |
| 5220 | nono | 3 |
| 5221 | nimiedad | 3 |
| 5222 | nilo | 3 |
| 5223 | nido | 3 |
| 5224 | nevar | 3 |
| 5225 | neutral | 3 |
| 5226 | negrura | 3 |
| 5227 | necesariamente | 3 |
| 5228 | navaja | 3 |
| 5229 | naturalmente | 3 |
| 5230 | narrativo | 3 |
| 5231 | narración | 3 |
| 5232 | nacional | 3 |
| 5233 | mutuamente | 3 |
| 5234 | mustiar | 3 |
| 5235 | muslo | 3 |
| 5236 | musical | 3 |
| 5237 | muera | 3 |
| 5238 | mueca | 3 |
| 5239 | muchísimo | 3 |
| 5240 | muchas | 3 |
| 5241 | mozalbete | 3 |
| 5242 | montico | 3 |
| 5243 | montera | 3 |
| 5244 | monstruoso | 3 |
| 5245 | monopolio | 3 |
| 5246 | molde | 3 |
| 5247 | modal | 3 |
| 5248 | mitrado | 3 |
| 5249 | misteriosamente | 3 |
| 5250 | mis | 3 |
| 5251 | miren | 3 |
| 5252 | mimo | 3 |
| 5253 | millar | 3 |
| 5254 | miga | 3 |
| 5255 | miente | 3 |
| 5256 | miedoso | 3 |
| 5257 | miasma | 3 |
| 5258 | metrópoli | 3 |
| 5259 | metafísico | 3 |
| 5260 | mercantil | 3 |
| 5261 | mente | 3 |
| 5262 | memorable | 3 |
| 5263 | mejoría | 3 |
| 5264 | mejía | 3 |
| 5265 | meditabundo | 3 |
| 5266 | mediano | 3 |
| 5267 | medalla | 3 |
| 5268 | máxima | 3 |
| 5269 | matrona | 3 |
| 5270 | matorral | 3 |
| 5271 | masón | 3 |
| 5272 | martínez | 3 |
| 5273 | martín | 3 |
| 5274 | maridar | 3 |
| 5275 | mari | 3 |
| 5276 | margen | 3 |
| 5277 | mareo | 3 |
| 5278 | marea | 3 |
| 5279 | marcos | 3 |
| 5280 | marco | 3 |
| 5281 | manolillo | 3 |
| 5282 | manjar | 3 |
| 5283 | manirroto | 3 |
| 5284 | maniquí | 3 |
| 5285 | maniqueo | 3 |
| 5286 | maniático | 3 |
| 5287 | maligno | 3 |
| 5288 | maldita | 3 |
| 5289 | magullar | 3 |
| 5290 | magnético | 3 |
| 5291 | maestría | 3 |
| 5292 | maduro | 3 |
| 5293 | madrugón | 3 |
| 5294 | madrugada | 3 |
| 5295 | madreselva | 3 |
| 5296 | macizo | 3 |
| 5297 | lunar | 3 |
| 5298 | lumbrera | 3 |
| 5299 | ludibrio | 3 |
| 5300 | lozano | 3 |
| 5301 | lola | 3 |
| 5302 | locuaz | 3 |
| 5303 | llenas | 3 |
| 5304 | llegada | 3 |
| 5305 | lívido | 3 |
| 5306 | liviandad | 3 |
| 5307 | liebre | 3 |
| 5308 | librería | 3 |
| 5309 | libación | 3 |
| 5310 | levar | 3 |
| 5311 | lealtad | 3 |
| 5312 | lavabo | 3 |
| 5313 | latido | 3 |
| 5314 | lamento | 3 |
| 5315 | ladrones | 3 |
| 5316 | ladera | 3 |
| 5317 | lacónico | 3 |
| 5318 | labrar | 3 |
| 5319 | kilómetro | 3 |
| 5320 | justamente | 3 |
| 5321 | jurado | 3 |
| 5322 | julio | 3 |
| 5323 | jubilar | 3 |
| 5324 | jubilación | 3 |
| 5325 | jovial | 3 |
| 5326 | josé | 3 |
| 5327 | job | 3 |
| 5328 | jipijapa | 3 |
| 5329 | irrupción | 3 |
| 5330 | irrevocable | 3 |
| 5331 | irreverencia | 3 |
| 5332 | irreprochable | 3 |
| 5333 | irreflexivo | 3 |
| 5334 | iris | 3 |
| 5335 | iría | 3 |
| 5336 | inventor | 3 |
| 5337 | invento | 3 |
| 5338 | invasión | 3 |
| 5339 | intrigar | 3 |
| 5340 | intratable | 3 |
| 5341 | interesado | 3 |
| 5342 | intento | 3 |
| 5343 | intempestivo | 3 |
| 5344 | intemperie | 3 |
| 5345 | insulso | 3 |
| 5346 | instrucción | 3 |
| 5347 | inquietar | 3 |
| 5348 | inquebrantable | 3 |
| 5349 | inodoro | 3 |
| 5350 | inmortalidad | 3 |
| 5351 | inmoral | 3 |
| 5352 | inflexible | 3 |
| 5353 | infinitamente | 3 |
| 5354 | infelices | 3 |
| 5355 | infames | 3 |
| 5356 | inexorable | 3 |
| 5357 | inepto | 3 |
| 5358 | indulgente | 3 |
| 5359 | indudable | 3 |
| 5360 | índole | 3 |
| 5361 | individuo | 3 |
| 5362 | indirecta | 3 |
| 5363 | indio | 3 |
| 5364 | indias | 3 |
| 5365 | independencia | 3 |
| 5366 | indecente | 3 |
| 5367 | incorrecto | 3 |
| 5368 | incompatible | 3 |
| 5369 | incomparable | 3 |
| 5370 | incómodo | 3 |
| 5371 | incipiente | 3 |
| 5372 | incentivar | 3 |
| 5373 | incansable | 3 |
| 5374 | incalificable | 3 |
| 5375 | impureza | 3 |
| 5376 | impúdico | 3 |
| 5377 | impresionable | 3 |
| 5378 | imponente | 3 |
| 5379 | impertinencia | 3 |
| 5380 | imperdonable | 3 |
| 5381 | impasible | 3 |
| 5382 | impaciente | 3 |
| 5383 | ilustración | 3 |
| 5384 | ignominioso | 3 |
| 5385 | ignominia | 3 |
| 5386 | idioma | 3 |
| 5387 | huraño | 3 |
| 5388 | humorístico | 3 |
| 5389 | humorismo | 3 |
| 5390 | humildemente | 3 |
| 5391 | huésped | 3 |
| 5392 | hotel | 3 |
| 5393 | hostia | 3 |
| 5394 | hortera | 3 |
| 5395 | hondonada | 3 |
| 5396 | honda | 3 |
| 5397 | holocausto | 3 |
| 5398 | hojuela | 3 |
| 5399 | hipótesis | 3 |
| 5400 | hipócrates | 3 |
| 5401 | hermanito | 3 |
| 5402 | hermanitas | 3 |
| 5403 | herido | 3 |
| 5404 | helecho | 3 |
| 5405 | hebilla | 3 |
| 5406 | has | 3 |
| 5407 | han | 3 |
| 5408 | hambriento | 3 |
| 5409 | halago | 3 |
| 5410 | habría | 3 |
| 5411 | habitante | 3 |
| 5412 | guijarro | 3 |
| 5413 | guía | 3 |
| 5414 | grosería | 3 |
| 5415 | grana | 3 |
| 5416 | gotera | 3 |
| 5417 | goma | 3 |
| 5418 | goberna | 3 |
| 5419 | gigante | 3 |
| 5420 | geométrico | 3 |
| 5421 | gentil | 3 |
| 5422 | genial | 3 |
| 5423 | generalizado | 3 |
| 5424 | gemir | 3 |
| 5425 | gatillo | 3 |
| 5426 | garbo | 3 |
| 5427 | garbanzo | 3 |
| 5428 | gangoso | 3 |
| 5429 | gancho | 3 |
| 5430 | galante | 3 |
| 5431 | gafa | 3 |
| 5432 | funda | 3 |
| 5433 | fulgencia | 3 |
| 5434 | frutar | 3 |
| 5435 | frisar | 3 |
| 5436 | frenesí | 3 |
| 5437 | fraternidad | 3 |
| 5438 | frasco | 3 |
| 5439 | franela | 3 |
| 5440 | fósforo | 3 |
| 5441 | fortificar | 3 |
| 5442 | formalmente | 3 |
| 5443 | forcejear | 3 |
| 5444 | fogoso | 3 |
| 5445 | flojedad | 3 |
| 5446 | flato | 3 |
| 5447 | flanquear | 3 |
| 5448 | fisonomía | 3 |
| 5449 | finito | 3 |
| 5450 | fingimiento | 3 |
| 5451 | figúrate | 3 |
| 5452 | fiero | 3 |
| 5453 | fidias | 3 |
| 5454 | feuillet | 3 |
| 5455 | ferviente | 3 |
| 5456 | feriar | 3 |
| 5457 | febril | 3 |
| 5458 | fauna | 3 |
| 5459 | fatigoso | 3 |
| 5460 | fangoso | 3 |
| 5461 | falsificar | 3 |
| 5462 | faena | 3 |
| 5463 | extremoso | 3 |
| 5464 | extravagante | 3 |
| 5465 | extenso | 3 |
| 5466 | experimentar | 3 |
| 5467 | exhibición | 3 |
| 5468 | excomunión | 3 |
| 5469 | exclusivamente | 3 |
| 5470 | exclamaba | 3 |
| 5471 | exagerado | 3 |
| 5472 | europa | 3 |
| 5473 | estucar | 3 |
| 5474 | estribillo | 3 |
| 5475 | estrellar | 3 |
| 5476 | estío | 3 |
| 5477 | estercolero | 3 |
| 5478 | estás | 3 |
| 5479 | estaría | 3 |
| 5480 | establecimiento | 3 |
| 5481 | estaban | 3 |
| 5482 | esqueleto | 3 |
| 5483 | espumar | 3 |
| 5484 | espontáneamente | 3 |
| 5485 | espiritualidad | 3 |
| 5486 | espiritista | 3 |
| 5487 | espionaje | 3 |
| 5488 | espinoso | 3 |
| 5489 | espía | 3 |
| 5490 | esperma | 3 |
| 5491 | espantoso | 3 |
| 5492 | espantada | 3 |
| 5493 | espaldar | 3 |
| 5494 | espacioso | 3 |
| 5495 | espaciar | 3 |
| 5496 | esmerar | 3 |
| 5497 | escudo | 3 |
| 5498 | escuálido | 3 |
| 5499 | escritor | 3 |
| 5500 | escrito | 3 |
| 5501 | esclavina | 3 |
| 5502 | escarlata | 3 |
| 5503 | escarcha | 3 |
| 5504 | escapatoria | 3 |
| 5505 | esbeltez | 3 |
| 5506 | epístola | 3 |
| 5507 | envejecer | 3 |
| 5508 | entró | 3 |
| 5509 | entretanto | 3 |
| 5510 | entremés | 3 |
| 5511 | ensimismar | 3 |
| 5512 | ensayo | 3 |
| 5513 | ensalada | 3 |
| 5514 | enrique | 3 |
| 5515 | ennoblecer | 3 |
| 5516 | enlutar | 3 |
| 5517 | enguantar | 3 |
| 5518 | engomar | 3 |
| 5519 | enfrascar | 3 |
| 5520 | encubridor | 3 |
| 5521 | encenagar | 3 |
| 5522 | encarar | 3 |
| 5523 | encajar | 3 |
| 5524 | empedrar | 3 |
| 5525 | emparejar | 3 |
| 5526 | empapelar | 3 |
| 5527 | eminente | 3 |
| 5528 | emigración | 3 |
| 5529 | embutido | 3 |
| 5530 | embalsamar | 3 |
| 5531 | electricidad | 3 |
| 5532 | ebrio | 3 |
| 5533 | duras | 3 |
| 5534 | dudoso | 3 |
| 5535 | dormido | 3 |
| 5536 | dogmático | 3 |
| 5537 | divisa | 3 |
| 5538 | diván | 3 |
| 5539 | distrito | 3 |
| 5540 | distante | 3 |
| 5541 | disfrazado | 3 |
| 5542 | discordia | 3 |
| 5543 | discípulo | 3 |
| 5544 | disciplinar | 3 |
| 5545 | directivo | 3 |
| 5546 | dirá | 3 |
| 5547 | dictar | 3 |
| 5548 | dicen | 3 |
| 5549 | dice | 3 |
| 5550 | dibujo | 3 |
| 5551 | diamante | 3 |
| 5552 | diagonal | 3 |
| 5553 | desván | 3 |
| 5554 | desterrar | 3 |
| 5555 | destello | 3 |
| 5556 | despilfarro | 3 |
| 5557 | desperdiciar | 3 |
| 5558 | desocupar | 3 |
| 5559 | deslumbrador | 3 |
| 5560 | descriptivo | 3 |
| 5561 | descompuesto | 3 |
| 5562 | descolgar | 3 |
| 5563 | descarnar | 3 |
| 5564 | descabellado | 3 |
| 5565 | desanimar | 3 |
| 5566 | desairado | 3 |
| 5567 | desagravio | 3 |
| 5568 | desagradable | 3 |
| 5569 | derribo | 3 |
| 5570 | depósito | 3 |
| 5571 | dependiente | 3 |
| 5572 | demonche | 3 |
| 5573 | demócrata | 3 |
| 5574 | delirar | 3 |
| 5575 | delirante | 3 |
| 5576 | deletéreo | 3 |
| 5577 | delantal | 3 |
| 5578 | déjame | 3 |
| 5579 | degenerar | 3 |
| 5580 | defensor | 3 |
| 5581 | decretar | 3 |
| 5582 | décima | 3 |
| 5583 | decían | 3 |
| 5584 | decaimiento | 3 |
| 5585 | decadencia | 3 |
| 5586 | debía | 3 |
| 5587 | curación | 3 |
| 5588 | cundir | 3 |
| 5589 | cuero | 3 |
| 5590 | cuentas | 3 |
| 5591 | cubo | 3 |
| 5592 | cubierta | 3 |
| 5593 | cuarteto | 3 |
| 5594 | cuánta | 3 |
| 5595 | cuadrar | 3 |
| 5596 | cuaderno | 3 |
| 5597 | crujiente | 3 |
| 5598 | crujía | 3 |
| 5599 | crónico | 3 |
| 5600 | cromo | 3 |
| 5601 | cristalino | 3 |
| 5602 | crees | 3 |
| 5603 | creador | 3 |
| 5604 | creación | 3 |
| 5605 | corteza | 3 |
| 5606 | cortejo | 3 |
| 5607 | corrido | 3 |
| 5608 | correspondencia | 3 |
| 5609 | corralada | 3 |
| 5610 | corpulento | 3 |
| 5611 | corporación | 3 |
| 5612 | coraza | 3 |
| 5613 | coquetear | 3 |
| 5614 | copón | 3 |
| 5615 | convocar | 3 |
| 5616 | conveniente | 3 |
| 5617 | contrahacer | 3 |
| 5618 | contorsión | 3 |
| 5619 | contestación | 3 |
| 5620 | contera | 3 |
| 5621 | contagio | 3 |
| 5622 | consumar | 3 |
| 5623 | consolador | 3 |
| 5624 | conservación | 3 |
| 5625 | consejero | 3 |
| 5626 | conformidad | 3 |
| 5627 | conferenciar | 3 |
| 5628 | conejo | 3 |
| 5629 | conducto | 3 |
| 5630 | concretar | 3 |
| 5631 | cónclave | 3 |
| 5632 | concertar | 3 |
| 5633 | concentrar | 3 |
| 5634 | concebir | 3 |
| 5635 | compungir | 3 |
| 5636 | compuesto | 3 |
| 5637 | comprimido | 3 |
| 5638 | complejo | 3 |
| 5639 | competencia | 3 |
| 5640 | comitiva | 3 |
| 5641 | comidilla | 3 |
| 5642 | comestible | 3 |
| 5643 | comarca | 3 |
| 5644 | comandante | 3 |
| 5645 | columbrar | 3 |
| 5646 | colocación | 3 |
| 5647 | colmena | 3 |
| 5648 | colgado | 3 |
| 5649 | codorniz | 3 |
| 5650 | código | 3 |
| 5651 | codiciado | 3 |
| 5652 | codazo | 3 |
| 5653 | cochera | 3 |
| 5654 | cobijar | 3 |
| 5655 | club | 3 |
| 5656 | cloaca | 3 |
| 5657 | clementina | 3 |
| 5658 | clamar | 3 |
| 5659 | civilización | 3 |
| 5660 | cirial | 3 |
| 5661 | circunspecto | 3 |
| 5662 | circunloquio | 3 |
| 5663 | cima | 3 |
| 5664 | cid | 3 |
| 5665 | chuzo | 3 |
| 5666 | chistar | 3 |
| 5667 | chisme | 3 |
| 5668 | chirrido | 3 |
| 5669 | chino | 3 |
| 5670 | charol | 3 |
| 5671 | chal | 3 |
| 5672 | cesto | 3 |
| 5673 | cesantía | 3 |
| 5674 | cerrazón | 3 |
| 5675 | cerradura | 3 |
| 5676 | cerilla | 3 |
| 5677 | cerero | 3 |
| 5678 | ceñido | 3 |
| 5679 | centinela | 3 |
| 5680 | celeste | 3 |
| 5681 | cejijunto | 3 |
| 5682 | cebolleta | 3 |
| 5683 | cavar | 3 |
| 5684 | caudillo | 3 |
| 5685 | cauce | 3 |
| 5686 | católica | 3 |
| 5687 | categórico | 3 |
| 5688 | castor | 3 |
| 5689 | casta | 3 |
| 5690 | carrillo | 3 |
| 5691 | carpintero | 3 |
| 5692 | carnero | 3 |
| 5693 | carbonera | 3 |
| 5694 | característica | 3 |
| 5695 | capullo | 3 |
| 5696 | cañada | 3 |
| 5697 | cantidad | 3 |
| 5698 | canónigos | 3 |
| 5699 | candidato | 3 |
| 5700 | candelero | 3 |
| 5701 | candelas | 3 |
| 5702 | cancel | 3 |
| 5703 | canastillo | 3 |
| 5704 | campillo | 3 |
| 5705 | campanilla | 3 |
| 5706 | camarada | 3 |
| 5707 | calvicie | 3 |
| 5708 | cáliz | 3 |
| 5709 | cajero | 3 |
| 5710 | cadete | 3 |
| 5711 | cadera | 3 |
| 5712 | cacho | 3 |
| 5713 | cabezada | 3 |
| 5714 | cábala | 3 |
| 5715 | burbuja | 3 |
| 5716 | bullanguero | 3 |
| 5717 | bujía | 3 |
| 5718 | buenos | 3 |
| 5719 | brutalidad | 3 |
| 5720 | brujo | 3 |
| 5721 | bramar | 3 |
| 5722 | borroso | 3 |
| 5723 | borrico | 3 |
| 5724 | bolo | 3 |
| 5725 | bofetón | 3 |
| 5726 | boda | 3 |
| 5727 | blusa | 3 |
| 5728 | bizarro | 3 |
| 5729 | bienestar | 3 |
| 5730 | bíblico | 3 |
| 5731 | benevolencia | 3 |
| 5732 | benemérito | 3 |
| 5733 | benéfico | 3 |
| 5734 | bendición | 3 |
| 5735 | belisario | 3 |
| 5736 | batín | 3 |
| 5737 | batería | 3 |
| 5738 | basura | 3 |
| 5739 | basto | 3 |
| 5740 | barriada | 3 |
| 5741 | barbero | 3 |
| 5742 | banquero | 3 |
| 5743 | bandido | 3 |
| 5744 | banda | 3 |
| 5745 | baladí | 3 |
| 5746 | bala | 3 |
| 5747 | badajo | 3 |
| 5748 | bactriana | 3 |
| 5749 | azote | 3 |
| 5750 | azahar | 3 |
| 5751 | avenar | 3 |
| 5752 | avena | 3 |
| 5753 | avellanar | 3 |
| 5754 | ausentar | 3 |
| 5755 | aura | 3 |
| 5756 | augusto | 3 |
| 5757 | atronar | 3 |
| 5758 | atrio | 3 |
| 5759 | atributo | 3 |
| 5760 | atragantar | 3 |
| 5761 | astuto | 3 |
| 5762 | astucia | 3 |
| 5763 | astorga | 3 |
| 5764 | asiduo | 3 |
| 5765 | asechanza | 3 |
| 5766 | ascensión | 3 |
| 5767 | artificial | 3 |
| 5768 | artesano | 3 |
| 5769 | arrinconar | 3 |
| 5770 | arreo | 3 |
| 5771 | aroma | 3 |
| 5772 | armonizar | 3 |
| 5773 | armónico | 3 |
| 5774 | armero | 3 |
| 5775 | armazón | 3 |
| 5776 | arenga | 3 |
| 5777 | arbusto | 3 |
| 5778 | aragón | 3 |
| 5779 | aquelarre | 3 |
| 5780 | apoyo | 3 |
| 5781 | apodo | 3 |
| 5782 | aplicación | 3 |
| 5783 | aplacar | 3 |
| 5784 | apestar | 3 |
| 5785 | apasionado | 3 |
| 5786 | aparatoso | 3 |
| 5787 | antipatía | 3 |
| 5788 | antigua | 3 |
| 5789 | anticipo | 3 |
| 5790 | antesala | 3 |
| 5791 | aniquilar | 3 |
| 5792 | animado | 3 |
| 5793 | angustiar | 3 |
| 5794 | anémico | 3 |
| 5795 | anemia | 3 |
| 5796 | andrajoso | 3 |
| 5797 | andaría | 3 |
| 5798 | anca | 3 |
| 5799 | anarquía | 3 |
| 5800 | anaquel | 3 |
| 5801 | analizar | 3 |
| 5802 | anacronismo | 3 |
| 5803 | anacleto | 3 |
| 5804 | amplio | 3 |
| 5805 | amonestación | 3 |
| 5806 | amigote | 3 |
| 5807 | americana | 3 |
| 5808 | amén | 3 |
| 5809 | ambicioso | 3 |
| 5810 | amanerar | 3 |
| 5811 | amadeo | 3 |
| 5812 | altozano | 3 |
| 5813 | altivo | 3 |
| 5814 | altivar | 3 |
| 5815 | alternar | 3 |
| 5816 | alteración | 3 |
| 5817 | alrededores | 3 |
| 5818 | almorzar | 3 |
| 5819 | aliviar | 3 |
| 5820 | alfonso | 3 |
| 5821 | alfombrar | 3 |
| 5822 | aleteo | 3 |
| 5823 | alertar | 3 |
| 5824 | alegar | 3 |
| 5825 | alcázar | 3 |
| 5826 | alcaraván | 3 |
| 5827 | alcantarilla | 3 |
| 5828 | albergue | 3 |
| 5829 | alarido | 3 |
| 5830 | ajustado | 3 |
| 5831 | ajuar | 3 |
| 5832 | ahorcar | 3 |
| 5833 | ahínco | 3 |
| 5834 | aguacero | 3 |
| 5835 | agravio | 3 |
| 5836 | agravar | 3 |
| 5837 | agradecido | 3 |
| 5838 | agapita | 3 |
| 5839 | agachar | 3 |
| 5840 | afortunar | 3 |
| 5841 | afligir | 3 |
| 5842 | afilado | 3 |
| 5843 | afectado | 3 |
| 5844 | adusto | 3 |
| 5845 | adquirido | 3 |
| 5846 | adonde | 3 |
| 5847 | adivinación | 3 |
| 5848 | adelantado | 3 |
| 5849 | acusación | 3 |
| 5850 | acumular | 3 |
| 5851 | acreditado | 3 |
| 5852 | acosar | 3 |
| 5853 | aclimatación | 3 |
| 5854 | achaque | 3 |
| 5855 | acendrar | 3 |
| 5856 | aceituna | 3 |
| 5857 | acatar | 3 |
| 5858 | abundancia | 3 |
| 5859 | abultado | 3 |
| 5860 | absorto | 3 |
| 5861 | ábside | 3 |
| 5862 | abrumador | 3 |
| 5863 | abordar | 3 |
| 5864 | abono | 3 |
| 5865 | abolengo | 3 |
| 5866 | zurriagar | 2 |
| 5867 | zurriágame | 2 |
| 5868 | zumbido | 2 |
| 5869 | zueco | 2 |
| 5870 | zarzamora | 2 |
| 5871 | zarandear | 2 |
| 5872 | zagal | 2 |
| 5873 | yugo | 2 |
| 5874 | york | 2 |
| 5875 | x | 2 |
| 5876 | werther | 2 |
| 5877 | vuestro | 2 |
| 5878 | vuelve | 2 |
| 5879 | votación | 2 |
| 5880 | vos | 2 |
| 5881 | voluptuosamente | 2 |
| 5882 | voluntariamente | 2 |
| 5883 | vocabulario | 2 |
| 5884 | viviente | 2 |
| 5885 | viveza | 2 |
| 5886 | visual | 2 |
| 5887 | vistazo | 2 |
| 5888 | vistas | 2 |
| 5889 | vistalegre | 2 |
| 5890 | viso | 2 |
| 5891 | virginal | 2 |
| 5892 | violeta | 2 |
| 5893 | viña | 2 |
| 5894 | villegas | 2 |
| 5895 | viii | 2 |
| 5896 | vii | 2 |
| 5897 | viga | 2 |
| 5898 | veterano | 2 |
| 5899 | vestidura | 2 |
| 5900 | vertiginoso | 2 |
| 5901 | vergonzante | 2 |
| 5902 | verdaderamente | 2 |
| 5903 | vera | 2 |
| 5904 | ventorrillo | 2 |
| 5905 | venial | 2 |
| 5906 | venía | 2 |
| 5907 | venia | 2 |
| 5908 | venciste | 2 |
| 5909 | velludo | 2 |
| 5910 | vello | 2 |
| 5911 | veintiséis | 2 |
| 5912 | vega | 2 |
| 5913 | vastísimo | 2 |
| 5914 | variar | 2 |
| 5915 | variado | 2 |
| 5916 | vaquero | 2 |
| 5917 | vanidoso | 2 |
| 5918 | vanamente | 2 |
| 5919 | vanagloriar | 2 |
| 5920 | vanagloria | 2 |
| 5921 | van | 2 |
| 5922 | valeroso | 2 |
| 5923 | valentía | 2 |
| 5924 | valdés | 2 |
| 5925 | vajilla | 2 |
| 5926 | vade | 2 |
| 5927 | vacilación | 2 |
| 5928 | urbano | 2 |
| 5929 | untar | 2 |
| 5930 | unidos | 2 |
| 5931 | uf | 2 |
| 5932 | tutear | 2 |
| 5933 | turco | 2 |
| 5934 | turbio | 2 |
| 5935 | turbado | 2 |
| 5936 | turbación | 2 |
| 5937 | tupir | 2 |
| 5938 | tupido | 2 |
| 5939 | tumbar | 2 |
| 5940 | tul | 2 |
| 5941 | tubinga | 2 |
| 5942 | tropa | 2 |
| 5943 | trochar | 2 |
| 5944 | trocar | 2 |
| 5945 | triunfador | 2 |
| 5946 | tripular | 2 |
| 5947 | trenza | 2 |
| 5948 | traviesa | 2 |
| 5949 | traviata | 2 |
| 5950 | tratamiento | 2 |
| 5951 | tratado | 2 |
| 5952 | trastienda | 2 |
| 5953 | trasplantar | 2 |
| 5954 | trapillo | 2 |
| 5955 | trapicheo | 2 |
| 5956 | transparente | 2 |
| 5957 | transfusión | 2 |
| 5958 | trama | 2 |
| 5959 | traducción | 2 |
| 5960 | trabucar | 2 |
| 5961 | tortura | 2 |
| 5962 | tortilla | 2 |
| 5963 | torso | 2 |
| 5964 | torquemada | 2 |
| 5965 | torcida | 2 |
| 5966 | topo | 2 |
| 5967 | tópico | 2 |
| 5968 | topar | 2 |
| 5969 | tonsurar | 2 |
| 5970 | tonel | 2 |
| 5971 | toalla | 2 |
| 5972 | tiznar | 2 |
| 5973 | titán | 2 |
| 5974 | tiros | 2 |
| 5975 | tirón | 2 |
| 5976 | tirantez | 2 |
| 5977 | tirante | 2 |
| 5978 | tirador | 2 |
| 5979 | tinto | 2 |
| 5980 | tintero | 2 |
| 5981 | tino | 2 |
| 5982 | tez | 2 |
| 5983 | testarudo | 2 |
| 5984 | tesorero | 2 |
| 5985 | terrado | 2 |
| 5986 | terquedad | 2 |
| 5987 | tenorios | 2 |
| 5988 | tenia | 2 |
| 5989 | tendría | 2 |
| 5990 | tendrá | 2 |
| 5991 | tendencia | 2 |
| 5992 | temple | 2 |
| 5993 | templado | 2 |
| 5994 | temperatura | 2 |
| 5995 | temeridad | 2 |
| 5996 | tarsa | 2 |
| 5997 | tarjeta | 2 |
| 5998 | tapizar | 2 |
| 5999 | tapete | 2 |
| 6000 | tangible | 2 |
| 6001 | tamaza | 2 |
| 6002 | talla | 2 |
| 6003 | talía | 2 |
| 6004 | talante | 2 |
| 6005 | tálamo | 2 |
| 6006 | taimado | 2 |
| 6007 | tachar | 2 |
| 6008 | sutilmente | 2 |
| 6009 | sutileza | 2 |
| 6010 | sustituir | 2 |
| 6011 | sustentar | 2 |
| 6012 | sustancial | 2 |
| 6013 | suscitar | 2 |
| 6014 | susceptibilidad | 2 |
| 6015 | surtidor | 2 |
| 6016 | surcar | 2 |
| 6017 | superlativo | 2 |
| 6018 | superar | 2 |
| 6019 | supeditar | 2 |
| 6020 | sumergir | 2 |
| 6021 | sufrimiento | 2 |
| 6022 | suficientemente | 2 |
| 6023 | sueco | 2 |
| 6024 | sudeste | 2 |
| 6025 | suciedad | 2 |
| 6026 | sucesivo | 2 |
| 6027 | sucedáneo | 2 |
| 6028 | subversivo | 2 |
| 6029 | subsiguiente | 2 |
| 6030 | subrepticiamente | 2 |
| 6031 | submarino | 2 |
| 6032 | subasta | 2 |
| 6033 | sr | 2 |
| 6034 | sosegar | 2 |
| 6035 | sortija | 2 |
| 6036 | sordidez | 2 |
| 6037 | soñaba | 2 |
| 6038 | sonsonete | 2 |
| 6039 | sonrosar | 2 |
| 6040 | sonante | 2 |
| 6041 | sonaja | 2 |
| 6042 | somos | 2 |
| 6043 | somero | 2 |
| 6044 | sombrilla | 2 |
| 6045 | soltura | 2 |
| 6046 | solariego | 2 |
| 6047 | solapar | 2 |
| 6048 | sois | 2 |
| 6049 | sofocado | 2 |
| 6050 | socorrer | 2 |
| 6051 | socarronería | 2 |
| 6052 | sobrio | 2 |
| 6053 | sobrevivir | 2 |
| 6054 | sobresaltar | 2 |
| 6055 | sobra | 2 |
| 6056 | sitiar | 2 |
| 6057 | sistemático | 2 |
| 6058 | sistemáticamente | 2 |
| 6059 | sirena | 2 |
| 6060 | síncope | 2 |
| 6061 | simultáneo | 2 |
| 6062 | simón | 2 |
| 6063 | similor | 2 |
| 6064 | sigue | 2 |
| 6065 | significado | 2 |
| 6066 | siglos | 2 |
| 6067 | siervo | 2 |
| 6068 | sicilia | 2 |
| 6069 | sexto | 2 |
| 6070 | setentón | 2 |
| 6071 | sesudo | 2 |
| 6072 | servidor | 2 |
| 6073 | serrar | 2 |
| 6074 | serían | 2 |
| 6075 | serenata | 2 |
| 6076 | señuelo | 2 |
| 6077 | señalado | 2 |
| 6078 | sensibilidad | 2 |
| 6079 | sensato | 2 |
| 6080 | semblante | 2 |
| 6081 | sello | 2 |
| 6082 | seguramente | 2 |
| 6083 | segundón | 2 |
| 6084 | sedentario | 2 |
| 6085 | sedar | 2 |
| 6086 | secundaria | 2 |
| 6087 | secundar | 2 |
| 6088 | secas | 2 |
| 6089 | seca | 2 |
| 6090 | sazón | 2 |
| 6091 | sauce | 2 |
| 6092 | santurrón | 2 |
| 6093 | santísimo | 2 |
| 6094 | sangría | 2 |
| 6095 | sancionar | 2 |
| 6096 | salvedad | 2 |
| 6097 | salve | 2 |
| 6098 | salvarme | 2 |
| 6099 | salva | 2 |
| 6100 | salsa | 2 |
| 6101 | salía | 2 |
| 6102 | salero | 2 |
| 6103 | sajón | 2 |
| 6104 | sacramental | 2 |
| 6105 | saborcillo | 2 |
| 6106 | rumboso | 2 |
| 6107 | rumbo | 2 |
| 6108 | ruidoso | 2 |
| 6109 | ruegos | 2 |
| 6110 | ruedo | 2 |
| 6111 | ruboroso | 2 |
| 6112 | rubí | 2 |
| 6113 | rousseau | 2 |
| 6114 | rossini | 2 |
| 6115 | rollo | 2 |
| 6116 | rodrigón | 2 |
| 6117 | rociar | 2 |
| 6118 | robustez | 2 |
| 6119 | robo | 2 |
| 6120 | rito | 2 |
| 6121 | riquísimo | 2 |
| 6122 | riñón | 2 |
| 6123 | riego | 2 |
| 6124 | ribete | 2 |
| 6125 | rezo | 2 |
| 6126 | rezagar | 2 |
| 6127 | revuelta | 2 |
| 6128 | revista | 2 |
| 6129 | revestir | 2 |
| 6130 | revés | 2 |
| 6131 | reventar | 2 |
| 6132 | retrospectivo | 2 |
| 6133 | retractar | 2 |
| 6134 | retórico | 2 |
| 6135 | retardar | 2 |
| 6136 | retar | 2 |
| 6137 | respondía | 2 |
| 6138 | respetabilidad | 2 |
| 6139 | resaltar | 2 |
| 6140 | resabio | 2 |
| 6141 | res | 2 |
| 6142 | requisito | 2 |
| 6143 | reputación | 2 |
| 6144 | republicanismo | 2 |
| 6145 | reposar | 2 |
| 6146 | reportar | 2 |
| 6147 | repletar | 2 |
| 6148 | repetición | 2 |
| 6149 | repatriación | 2 |
| 6150 | rendija | 2 |
| 6151 | remitir | 2 |
| 6152 | remilgo | 2 |
| 6153 | rematar | 2 |
| 6154 | relajar | 2 |
| 6155 | reguero | 2 |
| 6156 | regocijar | 2 |
| 6157 | regatear | 2 |
| 6158 | regata | 2 |
| 6159 | reformista | 2 |
| 6160 | reforma | 2 |
| 6161 | redoblar | 2 |
| 6162 | redivivo | 2 |
| 6163 | redil | 2 |
| 6164 | rectángulo | 2 |
| 6165 | recostar | 2 |
| 6166 | recordaba | 2 |
| 6167 | reconcentrar | 2 |
| 6168 | recoletas | 2 |
| 6169 | recolección | 2 |
| 6170 | recogimiento | 2 |
| 6171 | recodo | 2 |
| 6172 | reclutar | 2 |
| 6173 | recipiente | 2 |
| 6174 | receloso | 2 |
| 6175 | recelo | 2 |
| 6176 | recatar | 2 |
| 6177 | recargado | 2 |
| 6178 | rebuscar | 2 |
| 6179 | rebozar | 2 |
| 6180 | rebeldía | 2 |
| 6181 | rebasar | 2 |
| 6182 | reata | 2 |
| 6183 | reaparecer | 2 |
| 6184 | reanudar | 2 |
| 6185 | realmente | 2 |
| 6186 | realismo | 2 |
| 6187 | realar | 2 |
| 6188 | rayos | 2 |
| 6189 | raudal | 2 |
| 6190 | rastrero | 2 |
| 6191 | raso | 2 |
| 6192 | rasguño | 2 |
| 6193 | rápidamente | 2 |
| 6194 | rapé | 2 |
| 6195 | ramillete | 2 |
| 6196 | raer | 2 |
| 6197 | radicalmente | 2 |
| 6198 | radiante | 2 |
| 6199 | quintar | 2 |
| 6200 | química | 2 |
| 6201 | quimera | 2 |
| 6202 | quijote | 2 |
| 6203 | quiá | 2 |
| 6204 | quevedo | 2 |
| 6205 | queso | 2 |
| 6206 | purgar | 2 |
| 6207 | punzada | 2 |
| 6208 | puntapiés | 2 |
| 6209 | puntapié | 2 |
| 6210 | puntal | 2 |
| 6211 | pundonoroso | 2 |
| 6212 | pun | 2 |
| 6213 | pulverizar | 2 |
| 6214 | pulular | 2 |
| 6215 | pulgar | 2 |
| 6216 | pulgada | 2 |
| 6217 | pugnar | 2 |
| 6218 | puerro | 2 |
| 6219 | puerilidad | 2 |
| 6220 | provocación | 2 |
| 6221 | provisorato | 2 |
| 6222 | provisional | 2 |
| 6223 | provincialismo | 2 |
| 6224 | protesto | 2 |
| 6225 | protagonista | 2 |
| 6226 | prostituir | 2 |
| 6227 | prostitución | 2 |
| 6228 | prosperar | 2 |
| 6229 | prosiguió | 2 |
| 6230 | prorrumpir | 2 |
| 6231 | prórroga | 2 |
| 6232 | propiciar | 2 |
| 6233 | propagar | 2 |
| 6234 | propagandista | 2 |
| 6235 | proletario | 2 |
| 6236 | progresar | 2 |
| 6237 | profusión | 2 |
| 6238 | profesor | 2 |
| 6239 | profesión | 2 |
| 6240 | prodigioso | 2 |
| 6241 | proceso | 2 |
| 6242 | procedimiento | 2 |
| 6243 | procedente | 2 |
| 6244 | procaz | 2 |
| 6245 | privilegiado | 2 |
| 6246 | privado | 2 |
| 6247 | pringue | 2 |
| 6248 | primitiva | 2 |
| 6249 | primerizo | 2 |
| 6250 | pretérito | 2 |
| 6251 | presuntuoso | 2 |
| 6252 | preso | 2 |
| 6253 | presea | 2 |
| 6254 | prescripción | 2 |
| 6255 | prensar | 2 |
| 6256 | premioso | 2 |
| 6257 | predio | 2 |
| 6258 | precocidad | 2 |
| 6259 | precoces | 2 |
| 6260 | precipitado | 2 |
| 6261 | pp | 2 |
| 6262 | postrado | 2 |
| 6263 | posterior | 2 |
| 6264 | postergar | 2 |
| 6265 | positivar | 2 |
| 6266 | posibilidad | 2 |
| 6267 | portugués | 2 |
| 6268 | porquería | 2 |
| 6269 | porqué | 2 |
| 6270 | porcelana | 2 |
| 6271 | popularidad | 2 |
| 6272 | populacho | 2 |
| 6273 | pontificio | 2 |
| 6274 | pontifical | 2 |
| 6275 | pompa | 2 |
| 6276 | polvoriento | 2 |
| 6277 | polichinela | 2 |
| 6278 | pobres | 2 |
| 6279 | plegaria | 2 |
| 6280 | plazo | 2 |
| 6281 | platónicamente | 2 |
| 6282 | platillo | 2 |
| 6283 | plano | 2 |
| 6284 | planchar | 2 |
| 6285 | pistoletazo | 2 |
| 6286 | pisotón | 2 |
| 6287 | piropo | 2 |
| 6288 | pirámide | 2 |
| 6289 | pintado | 2 |
| 6290 | pinchazo | 2 |
| 6291 | pimiento | 2 |
| 6292 | pilón | 2 |
| 6293 | pilluelo | 2 |
| 6294 | pílades | 2 |
| 6295 | pila | 2 |
| 6296 | pienso | 2 |
| 6297 | picaresca | 2 |
| 6298 | petrica | 2 |
| 6299 | petitorio | 2 |
| 6300 | petaca | 2 |
| 6301 | pestañear | 2 |
| 6302 | pestaña | 2 |
| 6303 | pésimo | 2 |
| 6304 | pesimista | 2 |
| 6305 | pesebre | 2 |
| 6306 | pésame | 2 |
| 6307 | pervertir | 2 |
| 6308 | perspicaz | 2 |
| 6309 | personificar | 2 |
| 6310 | perol | 2 |
| 6311 | pernicioso | 2 |
| 6312 | perla | 2 |
| 6313 | período | 2 |
| 6314 | perfeccionar | 2 |
| 6315 | perdigón | 2 |
| 6316 | pérdida | 2 |
| 6317 | percha | 2 |
| 6318 | pequeñísimo | 2 |
| 6319 | peón | 2 |
| 6320 | peñón | 2 |
| 6321 | peña | 2 |
| 6322 | penúltimo | 2 |
| 6323 | pendón | 2 |
| 6324 | penacho | 2 |
| 6325 | peluca | 2 |
| 6326 | pelear | 2 |
| 6327 | pedrada | 2 |
| 6328 | pechuga | 2 |
| 6329 | pausado | 2 |
| 6330 | paúl | 2 |
| 6331 | patriótico | 2 |
| 6332 | patriota | 2 |
| 6333 | patrio | 2 |
| 6334 | patrimonio | 2 |
| 6335 | patentar | 2 |
| 6336 | pastoril | 2 |
| 6337 | pastoral | 2 |
| 6338 | pastar | 2 |
| 6339 | pasmado | 2 |
| 6340 | parsimonia | 2 |
| 6341 | parodia | 2 |
| 6342 | parejo | 2 |
| 6343 | parecíale | 2 |
| 6344 | pardiez | 2 |
| 6345 | parchar | 2 |
| 6346 | páramo | 2 |
| 6347 | paralelo | 2 |
| 6348 | paquita | 2 |
| 6349 | papanatas | 2 |
| 6350 | pantoja | 2 |
| 6351 | panegírico | 2 |
| 6352 | palomo | 2 |
| 6353 | palomar | 2 |
| 6354 | palaciego | 2 |
| 6355 | palabras | 2 |
| 6356 | pajarita | 2 |
| 6357 | pago | 2 |
| 6358 | pagadero | 2 |
| 6359 | padrenuestros | 2 |
| 6360 | oyente | 2 |
| 6361 | osa | 2 |
| 6362 | ortiga | 2 |
| 6363 | ornitólogo | 2 |
| 6364 | orla | 2 |
| 6365 | orientar | 2 |
| 6366 | orfandad | 2 |
| 6367 | ordenanza | 2 |
| 6368 | opuesto | 2 |
| 6369 | optimista | 2 |
| 6370 | opresión | 2 |
| 6371 | ondulación | 2 |
| 6372 | ominoso | 2 |
| 6373 | olvidado | 2 |
| 6374 | oloroso | 2 |
| 6375 | ojival | 2 |
| 6376 | ojeroso | 2 |
| 6377 | oficialmente | 2 |
| 6378 | ofensa | 2 |
| 6379 | ofendido | 2 |
| 6380 | ociosidad | 2 |
| 6381 | ochocientos | 2 |
| 6382 | obtener | 2 |
| 6383 | obstinado | 2 |
| 6384 | observó | 2 |
| 6385 | observatorio | 2 |
| 6386 | obscenidad | 2 |
| 6387 | obligado | 2 |
| 6388 | obispos | 2 |
| 6389 | obediente | 2 |
| 6390 | nupcial | 2 |
| 6391 | nulo | 2 |
| 6392 | notorio | 2 |
| 6393 | nombramiento | 2 |
| 6394 | ninguno | 2 |
| 6395 | nicho | 2 |
| 6396 | nevado | 2 |
| 6397 | neuralgia | 2 |
| 6398 | nebuloso | 2 |
| 6399 | neblina | 2 |
| 6400 | nauseabundo | 2 |
| 6401 | natillas | 2 |
| 6402 | narrador | 2 |
| 6403 | naipe | 2 |
| 6404 | nación | 2 |
| 6405 | músico | 2 |
| 6406 | muscular | 2 |
| 6407 | musa | 2 |
| 6408 | murió | 2 |
| 6409 | murillo | 2 |
| 6410 | muñeco | 2 |
| 6411 | municipal | 2 |
| 6412 | muerta | 2 |
| 6413 | mudéjar | 2 |
| 6414 | motín | 2 |
| 6415 | mote | 2 |
| 6416 | mostrenco | 2 |
| 6417 | mortificación | 2 |
| 6418 | mortífero | 2 |
| 6419 | morirá | 2 |
| 6420 | moreto | 2 |
| 6421 | mórbido | 2 |
| 6422 | moratín | 2 |
| 6423 | moralizar | 2 |
| 6424 | moqueta | 2 |
| 6425 | monje | 2 |
| 6426 | monedero | 2 |
| 6427 | molina | 2 |
| 6428 | molière | 2 |
| 6429 | molicie | 2 |
| 6430 | molesto | 2 |
| 6431 | molécula | 2 |
| 6432 | mole | 2 |
| 6433 | mojigato | 2 |
| 6434 | mojadura | 2 |
| 6435 | mohín | 2 |
| 6436 | mochuelo | 2 |
| 6437 | mitigar | 2 |
| 6438 | mister | 2 |
| 6439 | misioneros | 2 |
| 6440 | misionero | 2 |
| 6441 | misericordioso | 2 |
| 6442 | miserables | 2 |
| 6443 | mirado | 2 |
| 6444 | minutar | 2 |
| 6445 | minucioso | 2 |
| 6446 | minoría | 2 |
| 6447 | ministerio | 2 |
| 6448 | mínimo | 2 |
| 6449 | mínguez | 2 |
| 6450 | minerva | 2 |
| 6451 | mimoso | 2 |
| 6452 | mimosa | 2 |
| 6453 | mímico | 2 |
| 6454 | militante | 2 |
| 6455 | miliciano | 2 |
| 6456 | miles | 2 |
| 6457 | migaja | 2 |
| 6458 | midas | 2 |
| 6459 | microscopio | 2 |
| 6460 | mezclado | 2 |
| 6461 | mezcla | 2 |
| 6462 | meticuloso | 2 |
| 6463 | meritorio | 2 |
| 6464 | mercancía | 2 |
| 6465 | mequetrefe | 2 |
| 6466 | menudencia | 2 |
| 6467 | menudear | 2 |
| 6468 | mentecato | 2 |
| 6469 | mentar | 2 |
| 6470 | menoscabo | 2 |
| 6471 | menguar | 2 |
| 6472 | mendrugo | 2 |
| 6473 | melódico | 2 |
| 6474 | meléndez | 2 |
| 6475 | mefistófeles | 2 |
| 6476 | mediados | 2 |
| 6477 | medallón | 2 |
| 6478 | mechón | 2 |
| 6479 | mecer | 2 |
| 6480 | mazorca | 2 |
| 6481 | máximo | 2 |
| 6482 | matricular | 2 |
| 6483 | matilde | 2 |
| 6484 | matemático | 2 |
| 6485 | matanzas | 2 |
| 6486 | mástil | 2 |
| 6487 | marrullero | 2 |
| 6488 | maroto | 2 |
| 6489 | marino | 2 |
| 6490 | margarita | 2 |
| 6491 | marejada | 2 |
| 6492 | marcar | 2 |
| 6493 | marar | 2 |
| 6494 | maquinación | 2 |
| 6495 | maquiavelo | 2 |
| 6496 | maquiavélico | 2 |
| 6497 | maña | 2 |
| 6498 | manzano | 2 |
| 6499 | manuel | 2 |
| 6500 | manteca | 2 |
| 6501 | mansión | 2 |
| 6502 | mansedumbre | 2 |
| 6503 | manrique | 2 |
| 6504 | manotada | 2 |
| 6505 | manolé | 2 |
| 6506 | mangar | 2 |
| 6507 | mando | 2 |
| 6508 | mandamiento | 2 |
| 6509 | mampara | 2 |
| 6510 | maltratado | 2 |
| 6511 | malhumorado | 2 |
| 6512 | malhaya | 2 |
| 6513 | malgastar | 2 |
| 6514 | malagueño | 2 |
| 6515 | majestuosamente | 2 |
| 6516 | magnetismo | 2 |
| 6517 | mágico | 2 |
| 6518 | magia | 2 |
| 6519 | magdalena | 2 |
| 6520 | madurar | 2 |
| 6521 | madres | 2 |
| 6522 | machacar | 2 |
| 6523 | lutero | 2 |
| 6524 | lunes | 2 |
| 6525 | lugarteniente | 2 |
| 6526 | lucas | 2 |
| 6527 | lotería | 2 |
| 6528 | lona | 2 |
| 6529 | locuacidad | 2 |
| 6530 | llavín | 2 |
| 6531 | llanura | 2 |
| 6532 | llamativo | 2 |
| 6533 | llamada | 2 |
| 6534 | liturgia | 2 |
| 6535 | lisonjear | 2 |
| 6536 | lisonja | 2 |
| 6537 | lírico | 2 |
| 6538 | lira | 2 |
| 6539 | liquidación | 2 |
| 6540 | linaje | 2 |
| 6541 | límpido | 2 |
| 6542 | limpia | 2 |
| 6543 | limón | 2 |
| 6544 | limitar | 2 |
| 6545 | ligorio | 2 |
| 6546 | licencia | 2 |
| 6547 | librote | 2 |
| 6548 | librepensador | 2 |
| 6549 | libertar | 2 |
| 6550 | letrina | 2 |
| 6551 | letrero | 2 |
| 6552 | lesa | 2 |
| 6553 | leñar | 2 |
| 6554 | lentitud | 2 |
| 6555 | lengüeta | 2 |
| 6556 | leguas | 2 |
| 6557 | legitimidad | 2 |
| 6558 | lechoso | 2 |
| 6559 | lear | 2 |
| 6560 | leandro | 2 |
| 6561 | latón | 2 |
| 6562 | latamente | 2 |
| 6563 | lacónicamente | 2 |
| 6564 | labrador | 2 |
| 6565 | juvenil | 2 |
| 6566 | justar | 2 |
| 6567 | júpiter | 2 |
| 6568 | juguetear | 2 |
| 6569 | jueves | 2 |
| 6570 | judicial | 2 |
| 6571 | judía | 2 |
| 6572 | jubón | 2 |
| 6573 | jornada | 2 |
| 6574 | jirón | 2 |
| 6575 | jaspe | 2 |
| 6576 | jarrón | 2 |
| 6577 | jarro | 2 |
| 6578 | jarras | 2 |
| 6579 | jardinero | 2 |
| 6580 | jamón | 2 |
| 6581 | jactancioso | 2 |
| 6582 | jactancia | 2 |
| 6583 | italia | 2 |
| 6584 | isabel | 2 |
| 6585 | irritante | 2 |
| 6586 | irrisorio | 2 |
| 6587 | irresponsable | 2 |
| 6588 | irreparable | 2 |
| 6589 | irremediable | 2 |
| 6590 | involuntario | 2 |
| 6591 | invasor | 2 |
| 6592 | invariable | 2 |
| 6593 | inválido | 2 |
| 6594 | inútilmente | 2 |
| 6595 | inutilidad | 2 |
| 6596 | intuición | 2 |
| 6597 | intruso | 2 |
| 6598 | intransigencia | 2 |
| 6599 | intranquilo | 2 |
| 6600 | intolerancia | 2 |
| 6601 | intolerable | 2 |
| 6602 | intervención | 2 |
| 6603 | interrupción | 2 |
| 6604 | interrogatorio | 2 |
| 6605 | intermedio | 2 |
| 6606 | interinar | 2 |
| 6607 | interceptar | 2 |
| 6608 | inteligible | 2 |
| 6609 | integridad | 2 |
| 6610 | insultante | 2 |
| 6611 | insuficiente | 2 |
| 6612 | instruir | 2 |
| 6613 | instituciones | 2 |
| 6614 | instintivo | 2 |
| 6615 | instantáneo | 2 |
| 6616 | inspección | 2 |
| 6617 | insomnio | 2 |
| 6618 | insistente | 2 |
| 6619 | insistencia | 2 |
| 6620 | insigne | 2 |
| 6621 | inseparable | 2 |
| 6622 | insensiblemente | 2 |
| 6623 | insecto | 2 |
| 6624 | inscripción | 2 |
| 6625 | insano | 2 |
| 6626 | inquina | 2 |
| 6627 | inmemorial | 2 |
| 6628 | injerto | 2 |
| 6629 | iniquidad | 2 |
| 6630 | inimitable | 2 |
| 6631 | inicial | 2 |
| 6632 | inhibir | 2 |
| 6633 | inhabitable | 2 |
| 6634 | inglaterra | 2 |
| 6635 | ingénito | 2 |
| 6636 | ingenioso | 2 |
| 6637 | ingeniar | 2 |
| 6638 | ínfula | 2 |
| 6639 | informe | 2 |
| 6640 | inflamar | 2 |
| 6641 | infiltrar | 2 |
| 6642 | infestar | 2 |
| 6643 | infanzones | 2 |
| 6644 | infaliblemente | 2 |
| 6645 | inexperto | 2 |
| 6646 | industrial | 2 |
| 6647 | indiscutible | 2 |
| 6648 | indignidad | 2 |
| 6649 | indicio | 2 |
| 6650 | india | 2 |
| 6651 | indescriptible | 2 |
| 6652 | independiente | 2 |
| 6653 | indefinidamente | 2 |
| 6654 | indefectiblemente | 2 |
| 6655 | indecencia | 2 |
| 6656 | incurrir | 2 |
| 6657 | incruento | 2 |
| 6658 | incomodidad | 2 |
| 6659 | incólume | 2 |
| 6660 | incoherente | 2 |
| 6661 | incógnito | 2 |
| 6662 | incitante | 2 |
| 6663 | incentivo | 2 |
| 6664 | inaugural | 2 |
| 6665 | inaudito | 2 |
| 6666 | impunemente | 2 |
| 6667 | improvisado | 2 |
| 6668 | impreso | 2 |
| 6669 | imprenta | 2 |
| 6670 | importación | 2 |
| 6671 | implícito | 2 |
| 6672 | implícitamente | 2 |
| 6673 | imperturbable | 2 |
| 6674 | imparcialmente | 2 |
| 6675 | imitador | 2 |
| 6676 | imán | 2 |
| 6677 | imaginario | 2 |
| 6678 | igualar | 2 |
| 6679 | idólatra | 2 |
| 6680 | idiotas | 2 |
| 6681 | idéntico | 2 |
| 6682 | iban | 2 |
| 6683 | hurto | 2 |
| 6684 | hurtar | 2 |
| 6685 | hurtadillas | 2 |
| 6686 | humillación | 2 |
| 6687 | humedecer | 2 |
| 6688 | huida | 2 |
| 6689 | huesudo | 2 |
| 6690 | hubiera | 2 |
| 6691 | hoyo | 2 |
| 6692 | hornacina | 2 |
| 6693 | hormiga | 2 |
| 6694 | horizontal | 2 |
| 6695 | horcar | 2 |
| 6696 | hongo | 2 |
| 6697 | hombruno | 2 |
| 6698 | hojear | 2 |
| 6699 | hojalata | 2 |
| 6700 | hizo | 2 |
| 6701 | hisopo | 2 |
| 6702 | hiponax | 2 |
| 6703 | hiperbólico | 2 |
| 6704 | hiel | 2 |
| 6705 | híbrido | 2 |
| 6706 | herodes | 2 |
| 6707 | hermosísima | 2 |
| 6708 | hermosear | 2 |
| 6709 | hermosa | 2 |
| 6710 | herético | 2 |
| 6711 | hércules | 2 |
| 6712 | herbario | 2 |
| 6713 | hechizar | 2 |
| 6714 | hebdomadario | 2 |
| 6715 | hartazgo | 2 |
| 6716 | hartar | 2 |
| 6717 | harina | 2 |
| 6718 | harapo | 2 |
| 6719 | hacinar | 2 |
| 6720 | hachazo | 2 |
| 6721 | hachar | 2 |
| 6722 | habían | 2 |
| 6723 | habano | 2 |
| 6724 | gula | 2 |
| 6725 | guitarra | 2 |
| 6726 | guisa | 2 |
| 6727 | guirnalda | 2 |
| 6728 | guarnición | 2 |
| 6729 | guarda | 2 |
| 6730 | gruta | 2 |
| 6731 | grillete | 2 |
| 6732 | grillera | 2 |
| 6733 | grietar | 2 |
| 6734 | graznar | 2 |
| 6735 | gratuito | 2 |
| 6736 | grasiento | 2 |
| 6737 | grasa | 2 |
| 6738 | granizo | 2 |
| 6739 | grandioso | 2 |
| 6740 | gramática | 2 |
| 6741 | grada | 2 |
| 6742 | gracejo | 2 |
| 6743 | götinga | 2 |
| 6744 | golpear | 2 |
| 6745 | goloso | 2 |
| 6746 | gitano | 2 |
| 6747 | gigantón | 2 |
| 6748 | gigantesco | 2 |
| 6749 | gestar | 2 |
| 6750 | gertrudis | 2 |
| 6751 | geografía | 2 |
| 6752 | generalmente | 2 |
| 6753 | generalizar | 2 |
| 6754 | generalife | 2 |
| 6755 | generalidad | 2 |
| 6756 | gavilán | 2 |
| 6757 | gastrónomo | 2 |
| 6758 | gastronómico | 2 |
| 6759 | gasa | 2 |
| 6760 | garza | 2 |
| 6761 | garrote | 2 |
| 6762 | gañán | 2 |
| 6763 | galón | 2 |
| 6764 | gallego | 2 |
| 6765 | gallardía | 2 |
| 6766 | galápago | 2 |
| 6767 | galanteo | 2 |
| 6768 | furtivo | 2 |
| 6769 | fundir | 2 |
| 6770 | fundación | 2 |
| 6771 | funcionar | 2 |
| 6772 | fulano | 2 |
| 6773 | fugitivo | 2 |
| 6774 | fuero | 2 |
| 6775 | frívolo | 2 |
| 6776 | frenético | 2 |
| 6777 | fragilidad | 2 |
| 6778 | fragancia | 2 |
| 6779 | fortísimo | 2 |
| 6780 | fomento | 2 |
| 6781 | fofo | 2 |
| 6782 | floricultura | 2 |
| 6783 | florete | 2 |
| 6784 | floreciente | 2 |
| 6785 | flora | 2 |
| 6786 | flan | 2 |
| 6787 | flammarion | 2 |
| 6788 | flamante | 2 |
| 6789 | física | 2 |
| 6790 | fiscal | 2 |
| 6791 | firma | 2 |
| 6792 | finísimo | 2 |
| 6793 | filosóficamente | 2 |
| 6794 | filo | 2 |
| 6795 | filípica | 2 |
| 6796 | filigrana | 2 |
| 6797 | filar | 2 |
| 6798 | filantrópico | 2 |
| 6799 | fijeza | 2 |
| 6800 | figurémonos | 2 |
| 6801 | fígaro | 2 |
| 6802 | fieltro | 2 |
| 6803 | ficción | 2 |
| 6804 | feudal | 2 |
| 6805 | festivo | 2 |
| 6806 | fervorosamente | 2 |
| 6807 | férula | 2 |
| 6808 | ferrocarril | 2 |
| 6809 | fernando | 2 |
| 6810 | féretro | 2 |
| 6811 | fenómeno | 2 |
| 6812 | felonía | 2 |
| 6813 | felizmente | 2 |
| 6814 | felipe | 2 |
| 6815 | felino | 2 |
| 6816 | fealdad | 2 |
| 6817 | fé | 2 |
| 6818 | fausto | 2 |
| 6819 | fauces | 2 |
| 6820 | farolero | 2 |
| 6821 | faro | 2 |
| 6822 | fariseo | 2 |
| 6823 | familiarmente | 2 |
| 6824 | faldero | 2 |
| 6825 | faja | 2 |
| 6826 | facultativo | 2 |
| 6827 | facha | 2 |
| 6828 | fabuloso | 2 |
| 6829 | fa | 2 |
| 6830 | extensión | 2 |
| 6831 | extasiar | 2 |
| 6832 | explíquese | 2 |
| 6833 | explícito | 2 |
| 6834 | experimento | 2 |
| 6835 | exótico | 2 |
| 6836 | exordio | 2 |
| 6837 | exorbitante | 2 |
| 6838 | exijo | 2 |
| 6839 | execrable | 2 |
| 6840 | exclusivo | 2 |
| 6841 | excluir | 2 |
| 6842 | excitante | 2 |
| 6843 | excelencia | 2 |
| 6844 | exageradamente | 2 |
| 6845 | evidencia | 2 |
| 6846 | evaporar | 2 |
| 6847 | europeo | 2 |
| 6848 | eunuco | 2 |
| 6849 | eudoro | 2 |
| 6850 | estreno | 2 |
| 6851 | estrenar | 2 |
| 6852 | estrellado | 2 |
| 6853 | estrangular | 2 |
| 6854 | estrada | 2 |
| 6855 | estorbo | 2 |
| 6856 | estimación | 2 |
| 6857 | estima | 2 |
| 6858 | estético | 2 |
| 6859 | estertor | 2 |
| 6860 | estela | 2 |
| 6861 | estas | 2 |
| 6862 | estandarte | 2 |
| 6863 | estancar | 2 |
| 6864 | estampar | 2 |
| 6865 | estampa | 2 |
| 6866 | estamos | 2 |
| 6867 | estambre | 2 |
| 6868 | estados | 2 |
| 6869 | estadística | 2 |
| 6870 | establo | 2 |
| 6871 | esputar | 2 |
| 6872 | esponjar | 2 |
| 6873 | espirar | 2 |
| 6874 | espiga | 2 |
| 6875 | espere | 2 |
| 6876 | esperaba | 2 |
| 6877 | especulación | 2 |
| 6878 | especialista | 2 |
| 6879 | especia | 2 |
| 6880 | esparto | 2 |
| 6881 | espadachín | 2 |
| 6882 | esgrimir | 2 |
| 6883 | esgrima | 2 |
| 6884 | escultural | 2 |
| 6885 | escultura | 2 |
| 6886 | escueto | 2 |
| 6887 | escuelas | 2 |
| 6888 | escudar | 2 |
| 6889 | escritorio | 2 |
| 6890 | escote | 2 |
| 6891 | escotar | 2 |
| 6892 | escobazo | 2 |
| 6893 | escasez | 2 |
| 6894 | escasear | 2 |
| 6895 | escarnio | 2 |
| 6896 | escarceos | 2 |
| 6897 | escandalosamente | 2 |
| 6898 | escalonar | 2 |
| 6899 | escalinata | 2 |
| 6900 | esbirro | 2 |
| 6901 | esas | 2 |
| 6902 | erre | 2 |
| 6903 | eres | 2 |
| 6904 | erard | 2 |
| 6905 | equipaje | 2 |
| 6906 | episodio | 2 |
| 6907 | épico | 2 |
| 6908 | envalentonar | 2 |
| 6909 | enumeración | 2 |
| 6910 | entusiástico | 2 |
| 6911 | entumecido | 2 |
| 6912 | entumecer | 2 |
| 6913 | entrometido | 2 |
| 6914 | entristecer | 2 |
| 6915 | entrevista | 2 |
| 6916 | entrever | 2 |
| 6917 | entremeter | 2 |
| 6918 | entregarla | 2 |
| 6919 | entreacto | 2 |
| 6920 | entreabrir | 2 |
| 6921 | entreabierto | 2 |
| 6922 | entrañable | 2 |
| 6923 | entornado | 2 |
| 6924 | entallado | 2 |
| 6925 | enredo | 2 |
| 6926 | enredadera | 2 |
| 6927 | enlazar | 2 |
| 6928 | enjaular | 2 |
| 6929 | enjambrar | 2 |
| 6930 | enhorabuena | 2 |
| 6931 | engrandecer | 2 |
| 6932 | enfermizo | 2 |
| 6933 | enfático | 2 |
| 6934 | enero | 2 |
| 6935 | energúmeno | 2 |
| 6936 | enérgicamente | 2 |
| 6937 | endiosar | 2 |
| 6938 | encargado | 2 |
| 6939 | encaprichar | 2 |
| 6940 | empresario | 2 |
| 6941 | empotrar | 2 |
| 6942 | emporio | 2 |
| 6943 | empolvar | 2 |
| 6944 | empirismo | 2 |
| 6945 | empezaba | 2 |
| 6946 | empalagar | 2 |
| 6947 | empadronamiento | 2 |
| 6948 | emisario | 2 |
| 6949 | emigrar | 2 |
| 6950 | embrutecer | 2 |
| 6951 | embrollar | 2 |
| 6952 | embozadamente | 2 |
| 6953 | embocadura | 2 |
| 6954 | emancipar | 2 |
| 6955 | elevación | 2 |
| 6956 | elemental | 2 |
| 6957 | elector | 2 |
| 6958 | égida | 2 |
| 6959 | efusión | 2 |
| 6960 | educando | 2 |
| 6961 | educado | 2 |
| 6962 | editor | 2 |
| 6963 | ecbátana | 2 |
| 6964 | dureza | 2 |
| 6965 | dulzón | 2 |
| 6966 | dufour | 2 |
| 6967 | dominicales | 2 |
| 6968 | dominante | 2 |
| 6969 | domicilio | 2 |
| 6970 | domador | 2 |
| 6971 | divulgar | 2 |
| 6972 | divisar | 2 |
| 6973 | disuadir | 2 |
| 6974 | distender | 2 |
| 6975 | dispuesto | 2 |
| 6976 | dispénseme | 2 |
| 6977 | dispensa | 2 |
| 6978 | disimulan | 2 |
| 6979 | disertación | 2 |
| 6980 | disecar | 2 |
| 6981 | discrecional | 2 |
| 6982 | discordante | 2 |
| 6983 | diosa | 2 |
| 6984 | dinamita | 2 |
| 6985 | diminutivo | 2 |
| 6986 | dimensión | 2 |
| 6987 | dime | 2 |
| 6988 | diligente | 2 |
| 6989 | difuso | 2 |
| 6990 | difundir | 2 |
| 6991 | difícilmente | 2 |
| 6992 | diego | 2 |
| 6993 | dieciséis | 2 |
| 6994 | dieciocho | 2 |
| 6995 | diciembre | 2 |
| 6996 | dicharacho | 2 |
| 6997 | dicha | 2 |
| 6998 | diariamente | 2 |
| 6999 | diablillo | 2 |
| 7000 | di | 2 |
| 7001 | detenimiento | 2 |
| 7002 | desvergonzado | 2 |
| 7003 | destruir | 2 |
| 7004 | destierro | 2 |
| 7005 | destemplado | 2 |
| 7006 | desquite | 2 |
| 7007 | despreocupación | 2 |
| 7008 | desprendimiento | 2 |
| 7009 | desprender | 2 |
| 7010 | despreciable | 2 |
| 7011 | déspota | 2 |
| 7012 | desplumar | 2 |
| 7013 | desparramar | 2 |
| 7014 | desparpajo | 2 |
| 7015 | desmenuzar | 2 |
| 7016 | desmejorar | 2 |
| 7017 | desmayo | 2 |
| 7018 | desmadejar | 2 |
| 7019 | deslucir | 2 |
| 7020 | desliz | 2 |
| 7021 | deslenguado | 2 |
| 7022 | desistir | 2 |
| 7023 | designio | 2 |
| 7024 | desfachatado | 2 |
| 7025 | desentonar | 2 |
| 7026 | desengañado | 2 |
| 7027 | desenganchar | 2 |
| 7028 | desenfrenar | 2 |
| 7029 | desencajado | 2 |
| 7030 | desdicha | 2 |
| 7031 | desdeñoso | 2 |
| 7032 | descuento | 2 |
| 7033 | descreer | 2 |
| 7034 | desconsolador | 2 |
| 7035 | desconfiado | 2 |
| 7036 | descomunal | 2 |
| 7037 | descollar | 2 |
| 7038 | descifrar | 2 |
| 7039 | desceñir | 2 |
| 7040 | descaro | 2 |
| 7041 | descarnado | 2 |
| 7042 | descarar | 2 |
| 7043 | descalza | 2 |
| 7044 | desbancar | 2 |
| 7045 | desatino | 2 |
| 7046 | desarrollo | 2 |
| 7047 | desarrollar | 2 |
| 7048 | desahuciar | 2 |
| 7049 | desahogo | 2 |
| 7050 | desafinado | 2 |
| 7051 | derrumbar | 2 |
| 7052 | derredor | 2 |
| 7053 | deplorar | 2 |
| 7054 | departamento | 2 |
| 7055 | demagogo | 2 |
| 7056 | deliquio | 2 |
| 7057 | delincuente | 2 |
| 7058 | delicadísimo | 2 |
| 7059 | deleznable | 2 |
| 7060 | delator | 2 |
| 7061 | déjese | 2 |
| 7062 | déjela | 2 |
| 7063 | déjate | 2 |
| 7064 | dejadme | 2 |
| 7065 | deja | 2 |
| 7066 | degollar | 2 |
| 7067 | definitiva | 2 |
| 7068 | definido | 2 |
| 7069 | definición | 2 |
| 7070 | decreto | 2 |
| 7071 | decorosamente | 2 |
| 7072 | decidido | 2 |
| 7073 | decencia | 2 |
| 7074 | decaer | 2 |
| 7075 | decadente | 2 |
| 7076 | deben | 2 |
| 7077 | debate | 2 |
| 7078 | dardo | 2 |
| 7079 | da | 2 |
| 7080 | curtido | 2 |
| 7081 | cuñado | 2 |
| 7082 | cumplimiento | 2 |
| 7083 | cultura | 2 |
| 7084 | cultivo | 2 |
| 7085 | culminante | 2 |
| 7086 | cuidadosamente | 2 |
| 7087 | cucurucho | 2 |
| 7088 | cuba | 2 |
| 7089 | cuarta | 2 |
| 7090 | cuantía | 2 |
| 7091 | cuán | 2 |
| 7092 | cualquiera | 2 |
| 7093 | cruelmente | 2 |
| 7094 | crucifijo | 2 |
| 7095 | criticar | 2 |
| 7096 | crisóstomo | 2 |
| 7097 | cripta | 2 |
| 7098 | creíase | 2 |
| 7099 | crédulo | 2 |
| 7100 | credulidad | 2 |
| 7101 | crecimiento | 2 |
| 7102 | creciente | 2 |
| 7103 | crasitud | 2 |
| 7104 | costura | 2 |
| 7105 | cosquillas | 2 |
| 7106 | corujedos | 2 |
| 7107 | cortésmente | 2 |
| 7108 | cortaplumas | 2 |
| 7109 | cortado | 2 |
| 7110 | corroborar | 2 |
| 7111 | corresponsal | 2 |
| 7112 | cornucopia | 2 |
| 7113 | cornisa | 2 |
| 7114 | corista | 2 |
| 7115 | cordillera | 2 |
| 7116 | cordialidad | 2 |
| 7117 | coqueta | 2 |
| 7118 | copo | 2 |
| 7119 | copla | 2 |
| 7120 | copioso | 2 |
| 7121 | convenio | 2 |
| 7122 | contraventana | 2 |
| 7123 | contrastar | 2 |
| 7124 | contraer | 2 |
| 7125 | continuó | 2 |
| 7126 | contingentar | 2 |
| 7127 | contertulio | 2 |
| 7128 | contendiente | 2 |
| 7129 | contagiar | 2 |
| 7130 | consumo | 2 |
| 7131 | consulta | 2 |
| 7132 | constituir | 2 |
| 7133 | constipar | 2 |
| 7134 | constelación | 2 |
| 7135 | conste | 2 |
| 7136 | constantemente | 2 |
| 7137 | conspiración | 2 |
| 7138 | consistente | 2 |
| 7139 | consistencia | 2 |
| 7140 | conserva | 2 |
| 7141 | consentimiento | 2 |
| 7142 | consagrado | 2 |
| 7143 | consagración | 2 |
| 7144 | consabido | 2 |
| 7145 | conjeturar | 2 |
| 7146 | conjetura | 2 |
| 7147 | congreso | 2 |
| 7148 | congregar | 2 |
| 7149 | congojar | 2 |
| 7150 | congénere | 2 |
| 7151 | condescendencia | 2 |
| 7152 | concubina | 2 |
| 7153 | concreto | 2 |
| 7154 | concordia | 2 |
| 7155 | conclusión | 2 |
| 7156 | concha | 2 |
| 7157 | comunicativo | 2 |
| 7158 | comte | 2 |
| 7159 | compromisario | 2 |
| 7160 | comprobar | 2 |
| 7161 | comprende | 2 |
| 7162 | complexión | 2 |
| 7163 | completar | 2 |
| 7164 | compartir | 2 |
| 7165 | comparecer | 2 |
| 7166 | comparable | 2 |
| 7167 | compadre | 2 |
| 7168 | cómodamente | 2 |
| 7169 | cometido | 2 |
| 7170 | comensal | 2 |
| 7171 | combate | 2 |
| 7172 | comadrona | 2 |
| 7173 | columpiar | 2 |
| 7174 | coloso | 2 |
| 7175 | coloquio | 2 |
| 7176 | colón | 2 |
| 7177 | coliseo | 2 |
| 7178 | colegial | 2 |
| 7179 | coleccionador | 2 |
| 7180 | colapso | 2 |
| 7181 | colación | 2 |
| 7182 | coincidencia | 2 |
| 7183 | cohecho | 2 |
| 7184 | coetáneo | 2 |
| 7185 | codillo | 2 |
| 7186 | cocinar | 2 |
| 7187 | cobardía | 2 |
| 7188 | cliente | 2 |
| 7189 | clavel | 2 |
| 7190 | clasificar | 2 |
| 7191 | clarisas | 2 |
| 7192 | clarinete | 2 |
| 7193 | clarín | 2 |
| 7194 | clandestino | 2 |
| 7195 | clac | 2 |
| 7196 | cirino | 2 |
| 7197 | circulante | 2 |
| 7198 | circulación | 2 |
| 7199 | cinto | 2 |
| 7200 | cinismo | 2 |
| 7201 | cinegético | 2 |
| 7202 | cigarra | 2 |
| 7203 | cierre | 2 |
| 7204 | cielos | 2 |
| 7205 | ciegamente | 2 |
| 7206 | chusma | 2 |
| 7207 | chulo | 2 |
| 7208 | chito | 2 |
| 7209 | chisporrotear | 2 |
| 7210 | chiripa | 2 |
| 7211 | chiquito | 2 |
| 7212 | chinto | 2 |
| 7213 | chinesco | 2 |
| 7214 | chica | 2 |
| 7215 | chasquido | 2 |
| 7216 | chascarrillo | 2 |
| 7217 | chaquetar | 2 |
| 7218 | chaqueta | 2 |
| 7219 | césar | 2 |
| 7220 | cerril | 2 |
| 7221 | cerrados | 2 |
| 7222 | cerebral | 2 |
| 7223 | cerbatana | 2 |
| 7224 | cepillo | 2 |
| 7225 | ceñudo | 2 |
| 7226 | central | 2 |
| 7227 | céntimo | 2 |
| 7228 | censor | 2 |
| 7229 | celoso | 2 |
| 7230 | celibato | 2 |
| 7231 | cédula | 2 |
| 7232 | cebo | 2 |
| 7233 | cavador | 2 |
| 7234 | cauterio | 2 |
| 7235 | caudal | 2 |
| 7236 | catolicismo | 2 |
| 7237 | categoría | 2 |
| 7238 | catar | 2 |
| 7239 | catafalco | 2 |
| 7240 | cataclismo | 2 |
| 7241 | casual | 2 |
| 7242 | castañuelo | 2 |
| 7243 | castaña | 2 |
| 7244 | casos | 2 |
| 7245 | caserío | 2 |
| 7246 | casería | 2 |
| 7247 | carvajal | 2 |
| 7248 | carretero | 2 |
| 7249 | carnoso | 2 |
| 7250 | carnaza | 2 |
| 7251 | carita | 2 |
| 7252 | caricatura | 2 |
| 7253 | cargante | 2 |
| 7254 | cargamento | 2 |
| 7255 | cargado | 2 |
| 7256 | carecer | 2 |
| 7257 | cardo | 2 |
| 7258 | caramelo | 2 |
| 7259 | carámbano | 2 |
| 7260 | carabinar | 2 |
| 7261 | capón | 2 |
| 7262 | cañonazo | 2 |
| 7263 | cántaro | 2 |
| 7264 | cándido | 2 |
| 7265 | candelabro | 2 |
| 7266 | canal | 2 |
| 7267 | campesino | 2 |
| 7268 | campechano | 2 |
| 7269 | camarero | 2 |
| 7270 | cámara | 2 |
| 7271 | calzón | 2 |
| 7272 | calumnioso | 2 |
| 7273 | callejero | 2 |
| 7274 | califa | 2 |
| 7275 | calenturiento | 2 |
| 7276 | calderoniano | 2 |
| 7277 | calatayud | 2 |
| 7278 | cacique | 2 |
| 7279 | cachete | 2 |
| 7280 | cachazudo | 2 |
| 7281 | cacharro | 2 |
| 7282 | cabra | 2 |
| 7283 | cabellera | 2 |
| 7284 | cabe | 2 |
| 7285 | caballeroso | 2 |
| 7286 | caballerito | 2 |
| 7287 | cabal | 2 |
| 7288 | buscaba | 2 |
| 7289 | burlador | 2 |
| 7290 | buque | 2 |
| 7291 | bum | 2 |
| 7292 | bula | 2 |
| 7293 | bufanda | 2 |
| 7294 | bucólica | 2 |
| 7295 | bruscamente | 2 |
| 7296 | brindis | 2 |
| 7297 | brigadier | 2 |
| 7298 | brevedad | 2 |
| 7299 | breña | 2 |
| 7300 | bramido | 2 |
| 7301 | botonar | 2 |
| 7302 | bote | 2 |
| 7303 | botar | 2 |
| 7304 | bostezo | 2 |
| 7305 | borrego | 2 |
| 7306 | borrasca | 2 |
| 7307 | borde | 2 |
| 7308 | boquiabierto | 2 |
| 7309 | bonete | 2 |
| 7310 | bombo | 2 |
| 7311 | bomba | 2 |
| 7312 | bodega | 2 |
| 7313 | bochornoso | 2 |
| 7314 | bochorno | 2 |
| 7315 | blandir | 2 |
| 7316 | blanca | 2 |
| 7317 | biografía | 2 |
| 7318 | billete | 2 |
| 7319 | bienquistar | 2 |
| 7320 | bernesga | 2 |
| 7321 | benito | 2 |
| 7322 | benavides | 2 |
| 7323 | beatífico | 2 |
| 7324 | bazar | 2 |
| 7325 | batista | 2 |
| 7326 | batallón | 2 |
| 7327 | batacazo | 2 |
| 7328 | bastear | 2 |
| 7329 | base | 2 |
| 7330 | barroco | 2 |
| 7331 | barrenar | 2 |
| 7332 | barragana | 2 |
| 7333 | barnizar | 2 |
| 7334 | barbilindo | 2 |
| 7335 | barbaridad | 2 |
| 7336 | bandeja | 2 |
| 7337 | balduque | 2 |
| 7338 | baldar | 2 |
| 7339 | balbucear | 2 |
| 7340 | balanceo | 2 |
| 7341 | bajeza | 2 |
| 7342 | bajero | 2 |
| 7343 | bailé | 2 |
| 7344 | báculo | 2 |
| 7345 | baco | 2 |
| 7346 | babucha | 2 |
| 7347 | babilónico | 2 |
| 7348 | b | 2 |
| 7349 | azor | 2 |
| 7350 | azafranado | 2 |
| 7351 | axioma | 2 |
| 7352 | avizor | 2 |
| 7353 | averiar | 2 |
| 7354 | aventurado | 2 |
| 7355 | avaro | 2 |
| 7356 | autonomía | 2 |
| 7357 | automático | 2 |
| 7358 | auricular | 2 |
| 7359 | aunar | 2 |
| 7360 | atusar | 2 |
| 7361 | atropello | 2 |
| 7362 | atribulado | 2 |
| 7363 | atónito | 2 |
| 7364 | átomo | 2 |
| 7365 | atolondramiento | 2 |
| 7366 | atizar | 2 |
| 7367 | atestar | 2 |
| 7368 | atesorar | 2 |
| 7369 | atentado | 2 |
| 7370 | atañer | 2 |
| 7371 | atado | 2 |
| 7372 | asustadizo | 2 |
| 7373 | asfixia | 2 |
| 7374 | aserto | 2 |
| 7375 | ascua | 2 |
| 7376 | asceta | 2 |
| 7377 | asar | 2 |
| 7378 | artificio | 2 |
| 7379 | artífice | 2 |
| 7380 | articulista | 2 |
| 7381 | artesonar | 2 |
| 7382 | artesón | 2 |
| 7383 | arrugado | 2 |
| 7384 | arruga | 2 |
| 7385 | arrogancia | 2 |
| 7386 | arroba | 2 |
| 7387 | arrinconado | 2 |
| 7388 | arremolinar | 2 |
| 7389 | arrellanar | 2 |
| 7390 | arreglo | 2 |
| 7391 | aromático | 2 |
| 7392 | árnica | 2 |
| 7393 | armónica | 2 |
| 7394 | armisticio | 2 |
| 7395 | armería | 2 |
| 7396 | armatoste | 2 |
| 7397 | arisco | 2 |
| 7398 | ariscar | 2 |
| 7399 | argentino | 2 |
| 7400 | areo | 2 |
| 7401 | arenar | 2 |
| 7402 | arenal | 2 |
| 7403 | área | 2 |
| 7404 | arcadia | 2 |
| 7405 | arboricultura | 2 |
| 7406 | arboleda | 2 |
| 7407 | árbitro | 2 |
| 7408 | arañazo | 2 |
| 7409 | arabesco | 2 |
| 7410 | aquiles | 2 |
| 7411 | aquellos | 2 |
| 7412 | apurado | 2 |
| 7413 | apuesto | 2 |
| 7414 | apuesta | 2 |
| 7415 | aprisionar | 2 |
| 7416 | aprendiz | 2 |
| 7417 | aprecio | 2 |
| 7418 | apoteosis | 2 |
| 7419 | apóstata | 2 |
| 7420 | apostasía | 2 |
| 7421 | aplomo | 2 |
| 7422 | apiñado | 2 |
| 7423 | apiadar | 2 |
| 7424 | apellidar | 2 |
| 7425 | aparentemente | 2 |
| 7426 | añadía | 2 |
| 7427 | anzuelo | 2 |
| 7428 | anuncio | 2 |
| 7429 | antonomasia | 2 |
| 7430 | antonio | 2 |
| 7431 | antitético | 2 |
| 7432 | antinomia | 2 |
| 7433 | anticuar | 2 |
| 7434 | antecesor | 2 |
| 7435 | annatas | 2 |
| 7436 | aniversario | 2 |
| 7437 | aniquilamiento | 2 |
| 7438 | animador | 2 |
| 7439 | angelina | 2 |
| 7440 | angelical | 2 |
| 7441 | anfiteatro | 2 |
| 7442 | anfibio | 2 |
| 7443 | andrajo | 2 |
| 7444 | andén | 2 |
| 7445 | andamiaje | 2 |
| 7446 | anchura | 2 |
| 7447 | anatomía | 2 |
| 7448 | analogía | 2 |
| 7449 | amorosamente | 2 |
| 7450 | amoratar | 2 |
| 7451 | ambrosio | 2 |
| 7452 | ámbito | 2 |
| 7453 | ambientar | 2 |
| 7454 | amazona | 2 |
| 7455 | amargor | 2 |
| 7456 | amago | 2 |
| 7457 | amagar | 2 |
| 7458 | amador | 2 |
| 7459 | álvaro | 2 |
| 7460 | alvarín | 2 |
| 7461 | alucinación | 2 |
| 7462 | alternativamente | 2 |
| 7463 | altercar | 2 |
| 7464 | alquiler | 2 |
| 7465 | almohadillado | 2 |
| 7466 | almohadilla | 2 |
| 7467 | almidonar | 2 |
| 7468 | almacenar | 2 |
| 7469 | almacén | 2 |
| 7470 | alinear | 2 |
| 7471 | alhambra | 2 |
| 7472 | alhaja | 2 |
| 7473 | alguna | 2 |
| 7474 | alemán | 2 |
| 7475 | aleluya | 2 |
| 7476 | alejandro | 2 |
| 7477 | alejandría | 2 |
| 7478 | aleación | 2 |
| 7479 | aldabonazo | 2 |
| 7480 | aldabón | 2 |
| 7481 | alcoholismo | 2 |
| 7482 | alborotador | 2 |
| 7483 | alambre | 2 |
| 7484 | alambicado | 2 |
| 7485 | alacena | 2 |
| 7486 | ajar | 2 |
| 7487 | aislamiento | 2 |
| 7488 | ahondar | 2 |
| 7489 | aguzar | 2 |
| 7490 | agudeza | 2 |
| 7491 | agrietado | 2 |
| 7492 | agridulce | 2 |
| 7493 | agregado | 2 |
| 7494 | agitar | 2 |
| 7495 | agitado | 2 |
| 7496 | agente | 2 |
| 7497 | aforismo | 2 |
| 7498 | afligido | 2 |
| 7499 | afeminar | 2 |
| 7500 | afeminamiento | 2 |
| 7501 | afeminado | 2 |
| 7502 | afeitar | 2 |
| 7503 | afectuoso | 2 |
| 7504 | afabilidad | 2 |
| 7505 | advirtió | 2 |
| 7506 | advertencia | 2 |
| 7507 | adulación | 2 |
| 7508 | adormecer | 2 |
| 7509 | adoptar | 2 |
| 7510 | adocenado | 2 |
| 7511 | admirador | 2 |
| 7512 | administrar | 2 |
| 7513 | adentro | 2 |
| 7514 | adaptación | 2 |
| 7515 | adán | 2 |
| 7516 | actualmente | 2 |
| 7517 | actualidad | 2 |
| 7518 | activar | 2 |
| 7519 | acreditar | 2 |
| 7520 | acorde | 2 |
| 7521 | acontecer | 2 |
| 7522 | acompasar | 2 |
| 7523 | acomodo | 2 |
| 7524 | acomodar | 2 |
| 7525 | aclimatar | 2 |
| 7526 | achicar | 2 |
| 7527 | achaparrar | 2 |
| 7528 | achacoso | 2 |
| 7529 | acequia | 2 |
| 7530 | acelerar | 2 |
| 7531 | acallar | 2 |
| 7532 | aburren | 2 |
| 7533 | abstinencia | 2 |
| 7534 | absorber | 2 |
| 7535 | absorbente | 2 |
| 7536 | abroño | 2 |
| 7537 | abrió | 2 |
| 7538 | abominar | 2 |
| 7539 | abogado | 2 |
| 7540 | abdomen | 2 |
| 7541 | abdicar | 2 |
| 7542 | abarcar | 2 |
| 7543 | abanicar | 2 |
| 7544 | zurriago | 1 |
| 7545 | zurriagazo | 1 |
| 7546 | zurcir | 1 |
| 7547 | zurcido | 1 |
| 7548 | zurbarán | 1 |
| 7549 | zumarri | 1 |
| 7550 | zuavo | 1 |
| 7551 | zozobra | 1 |
| 7552 | zoológico | 1 |
| 7553 | zona | 1 |
| 7554 | zodiaco | 1 |
| 7555 | zascandil | 1 |
| 7556 | zas | 1 |
| 7557 | zarzaparrilla | 1 |
| 7558 | zarpar | 1 |
| 7559 | zarandaja | 1 |
| 7560 | zaquizamí | 1 |
| 7561 | zancadilla | 1 |
| 7562 | zambullir | 1 |
| 7563 | zamarra | 1 |
| 7564 | zamacois | 1 |
| 7565 | zafio | 1 |
| 7566 | yodo | 1 |
| 7567 | yema | 1 |
| 7568 | xxx | 1 |
| 7569 | xxviii | 1 |
| 7570 | xxvii | 1 |
| 7571 | xxvi | 1 |
| 7572 | xxv | 1 |
| 7573 | xxix | 1 |
| 7574 | xxiv | 1 |
| 7575 | xxiii | 1 |
| 7576 | xxii | 1 |
| 7577 | xxi | 1 |
| 7578 | xx | 1 |
| 7579 | xviii | 1 |
| 7580 | xvii | 1 |
| 7581 | xvi | 1 |
| 7582 | xix | 1 |
| 7583 | xiii | 1 |
| 7584 | xii | 1 |
| 7585 | xi | 1 |
| 7586 | wisseman | 1 |
| 7587 | wieland | 1 |
| 7588 | vulgarmente | 1 |
| 7589 | vuélvete | 1 |
| 7590 | vox | 1 |
| 7591 | vosotros | 1 |
| 7592 | vosotras | 1 |
| 7593 | volvía | 1 |
| 7594 | volveré | 1 |
| 7595 | voluta | 1 |
| 7596 | voluntario | 1 |
| 7597 | voluminoso | 1 |
| 7598 | vogt | 1 |
| 7599 | voces | 1 |
| 7600 | vocal | 1 |
| 7601 | vocablo | 1 |
| 7602 | vizconde | 1 |
| 7603 | vivirá | 1 |
| 7604 | vivimos | 1 |
| 7605 | vividor | 1 |
| 7606 | vive | 1 |
| 7607 | vituperar | 1 |
| 7608 | vitriolo | 1 |
| 7609 | vitrina | 1 |
| 7610 | vitando | 1 |
| 7611 | vitalidad | 1 |
| 7612 | vitalicio | 1 |
| 7613 | vislumbre | 1 |
| 7614 | visitaciones | 1 |
| 7615 | visionario | 1 |
| 7616 | visiblemente | 1 |
| 7617 | visera | 1 |
| 7618 | viseo | 1 |
| 7619 | vis | 1 |
| 7620 | viruela | 1 |
| 7621 | virilidad | 1 |
| 7622 | virchov | 1 |
| 7623 | viola | 1 |
| 7624 | vinader | 1 |
| 7625 | villavieja | 1 |
| 7626 | villancico | 1 |
| 7627 | villafranca | 1 |
| 7628 | villa | 1 |
| 7629 | vigorizar | 1 |
| 7630 | vigente | 1 |
| 7631 | vientecillo | 1 |
| 7632 | vienes | 1 |
| 7633 | viena | 1 |
| 7634 | vidrioso | 1 |
| 7635 | vidente | 1 |
| 7636 | victis | 1 |
| 7637 | vicepresidente | 1 |
| 7638 | víbora | 1 |
| 7639 | viático | 1 |
| 7640 | viable | 1 |
| 7641 | vi | 1 |
| 7642 | vestusta | 1 |
| 7643 | vestuario | 1 |
| 7644 | vestimenta | 1 |
| 7645 | vespucios | 1 |
| 7646 | vértigo | 1 |
| 7647 | vertiente | 1 |
| 7648 | vertedero | 1 |
| 7649 | versión | 1 |
| 7650 | versículo | 1 |
| 7651 | versalles | 1 |
| 7652 | veritas | 1 |
| 7653 | verificar | 1 |
| 7654 | veríamos | 1 |
| 7655 | veremundo | 1 |
| 7656 | verdulera | 1 |
| 7657 | verdoso | 1 |
| 7658 | verdinegro | 1 |
| 7659 | verbosidad | 1 |
| 7660 | verbo | 1 |
| 7661 | verbigracia | 1 |
| 7662 | veranillo | 1 |
| 7663 | veraniego | 1 |
| 7664 | veraneo | 1 |
| 7665 | veo | 1 |
| 7666 | ventrílocuo | 1 |
| 7667 | ventero | 1 |
| 7668 | ventar | 1 |
| 7669 | ventanillo | 1 |
| 7670 | venta | 1 |
| 7671 | venidero | 1 |
| 7672 | vengo | 1 |
| 7673 | vengábase | 1 |
| 7674 | venerar | 1 |
| 7675 | venerando | 1 |
| 7676 | veneciano | 1 |
| 7677 | venecia | 1 |
| 7678 | vendrás | 1 |
| 7679 | vendrán | 1 |
| 7680 | vendrá | 1 |
| 7681 | venal | 1 |
| 7682 | velón | 1 |
| 7683 | vellón | 1 |
| 7684 | veleidoso | 1 |
| 7685 | veleidades | 1 |
| 7686 | velado | 1 |
| 7687 | vejamen | 1 |
| 7688 | veintitrés | 1 |
| 7689 | veíalo | 1 |
| 7690 | veíala | 1 |
| 7691 | veía | 1 |
| 7692 | vehículo | 1 |
| 7693 | vehemencia | 1 |
| 7694 | veguellinas | 1 |
| 7695 | vegetación | 1 |
| 7696 | vegallanas | 1 |
| 7697 | vedado | 1 |
| 7698 | véase | 1 |
| 7699 | veamos | 1 |
| 7700 | vea | 1 |
| 7701 | váyase | 1 |
| 7702 | vauban | 1 |
| 7703 | vate | 1 |
| 7704 | vasto | 1 |
| 7705 | vástago | 1 |
| 7706 | vasar | 1 |
| 7707 | vas | 1 |
| 7708 | variante | 1 |
| 7709 | variación | 1 |
| 7710 | vampiro | 1 |
| 7711 | vallar | 1 |
| 7712 | valetudinario | 1 |
| 7713 | valera | 1 |
| 7714 | valdiñón | 1 |
| 7715 | vaivén | 1 |
| 7716 | vaina | 1 |
| 7717 | vae | 1 |
| 7718 | uva | 1 |
| 7719 | utrecht | 1 |
| 7720 | utensilio | 1 |
| 7721 | usurpador | 1 |
| 7722 | usura | 1 |
| 7723 | usual | 1 |
| 7724 | usado | 1 |
| 7725 | urdir | 1 |
| 7726 | urbanidad | 1 |
| 7727 | unto | 1 |
| 7728 | unos | 1 |
| 7729 | universidades | 1 |
| 7730 | unísono | 1 |
| 7731 | uniformar | 1 |
| 7732 | unido | 1 |
| 7733 | uníase | 1 |
| 7734 | unas | 1 |
| 7735 | ultratelúrica | 1 |
| 7736 | ultramontanismo | 1 |
| 7737 | ulloa | 1 |
| 7738 | ujier | 1 |
| 7739 | tuy | 1 |
| 7740 | tuvo | 1 |
| 7741 | tutor | 1 |
| 7742 | tutela | 1 |
| 7743 | tute | 1 |
| 7744 | turquía | 1 |
| 7745 | turbante | 1 |
| 7746 | turbamulta | 1 |
| 7747 | túnel | 1 |
| 7748 | tumba | 1 |
| 7749 | tugurio | 1 |
| 7750 | tufillo | 1 |
| 7751 | tuerca | 1 |
| 7752 | tuberculosis | 1 |
| 7753 | truncado | 1 |
| 7754 | trozo | 1 |
| 7755 | troya | 1 |
| 7756 | trovadores | 1 |
| 7757 | trotaconventos | 1 |
| 7758 | tropo | 1 |
| 7759 | tropezones | 1 |
| 7760 | tropel | 1 |
| 7761 | trono | 1 |
| 7762 | tronada | 1 |
| 7763 | trompetear | 1 |
| 7764 | trompa | 1 |
| 7765 | trocito | 1 |
| 7766 | triunfal | 1 |
| 7767 | tristemente | 1 |
| 7768 | triple | 1 |
| 7769 | trinchera | 1 |
| 7770 | trinchante | 1 |
| 7771 | trimestre | 1 |
| 7772 | trifoncito | 1 |
| 7773 | trifoncillo | 1 |
| 7774 | tridentino | 1 |
| 7775 | tribu | 1 |
| 7776 | triángulo | 1 |
| 7777 | trepidación | 1 |
| 7778 | trenzar | 1 |
| 7779 | trena | 1 |
| 7780 | tratable | 1 |
| 7781 | trasvolar | 1 |
| 7782 | trasunto | 1 |
| 7783 | traslucir | 1 |
| 7784 | trascender | 1 |
| 7785 | trascendencia | 1 |
| 7786 | traquetear | 1 |
| 7787 | trapacero | 1 |
| 7788 | tranvía | 1 |
| 7789 | transportar | 1 |
| 7790 | transmitir | 1 |
| 7791 | tránsito | 1 |
| 7792 | transición | 1 |
| 7793 | transformismo | 1 |
| 7794 | transcurrir | 1 |
| 7795 | tranquilícese | 1 |
| 7796 | tramposo | 1 |
| 7797 | tramo | 1 |
| 7798 | tralla | 1 |
| 7799 | tragarse | 1 |
| 7800 | tragaluz | 1 |
| 7801 | traerlos | 1 |
| 7802 | tráeme | 1 |
| 7803 | traductor | 1 |
| 7804 | tradicionalmente | 1 |
| 7805 | trabilla | 1 |
| 7806 | torvo | 1 |
| 7807 | torturar | 1 |
| 7808 | torrentes | 1 |
| 7809 | torpemente | 1 |
| 7810 | tornasolar | 1 |
| 7811 | tornar | 1 |
| 7812 | tornadizo | 1 |
| 7813 | torcuato | 1 |
| 7814 | torcedor | 1 |
| 7815 | toral | 1 |
| 7816 | toraces | 1 |
| 7817 | toque | 1 |
| 7818 | topetazo | 1 |
| 7819 | tontunas | 1 |
| 7820 | tontina | 1 |
| 7821 | tonta | 1 |
| 7822 | tonillo | 1 |
| 7823 | ton | 1 |
| 7824 | tole | 1 |
| 7825 | tocado | 1 |
| 7826 | toca | 1 |
| 7827 | tobillo | 1 |
| 7828 | tizne | 1 |
| 7829 | titulado | 1 |
| 7830 | titubear | 1 |
| 7831 | tito | 1 |
| 7832 | titilar | 1 |
| 7833 | títere | 1 |
| 7834 | tirotear | 1 |
| 7835 | tiritar | 1 |
| 7836 | tirilla | 1 |
| 7837 | tiránico | 1 |
| 7838 | tirada | 1 |
| 7839 | tira | 1 |
| 7840 | tiple | 1 |
| 7841 | tímpano | 1 |
| 7842 | tiempos | 1 |
| 7843 | tiemblan | 1 |
| 7844 | tiburón | 1 |
| 7845 | thackeray | 1 |
| 7846 | tétrico | 1 |
| 7847 | tetrarca | 1 |
| 7848 | testimoniar | 1 |
| 7849 | tesar | 1 |
| 7850 | terruño | 1 |
| 7851 | terrorista | 1 |
| 7852 | territorio | 1 |
| 7853 | terpsícore | 1 |
| 7854 | terneza | 1 |
| 7855 | termómetro | 1 |
| 7856 | términos | 1 |
| 7857 | terminantemente | 1 |
| 7858 | terminación | 1 |
| 7859 | tergiversar | 1 |
| 7860 | terceto | 1 |
| 7861 | tercero | 1 |
| 7862 | terapéutica | 1 |
| 7863 | teócrito | 1 |
| 7864 | teocrático | 1 |
| 7865 | tentáculo | 1 |
| 7866 | teniente | 1 |
| 7867 | tenían | 1 |
| 7868 | tengo | 1 |
| 7869 | tenebroso | 1 |
| 7870 | tendré | 1 |
| 7871 | tenaz | 1 |
| 7872 | templete | 1 |
| 7873 | templanza | 1 |
| 7874 | tempé | 1 |
| 7875 | temo | 1 |
| 7876 | temía | 1 |
| 7877 | temerón | 1 |
| 7878 | temblábale | 1 |
| 7879 | telescopio | 1 |
| 7880 | telegrama | 1 |
| 7881 | tejido | 1 |
| 7882 | tejer | 1 |
| 7883 | tejadillo | 1 |
| 7884 | tecnicismo | 1 |
| 7885 | tecla | 1 |
| 7886 | techar | 1 |
| 7887 | teatral | 1 |
| 7888 | taurina | 1 |
| 7889 | tasso | 1 |
| 7890 | tascar | 1 |
| 7891 | tartana | 1 |
| 7892 | tarso | 1 |
| 7893 | tarsilita | 1 |
| 7894 | tarascar | 1 |
| 7895 | taparelli | 1 |
| 7896 | tapado | 1 |
| 7897 | tapa | 1 |
| 7898 | tañido | 1 |
| 7899 | tantas | 1 |
| 7900 | tamizar | 1 |
| 7901 | tamiz | 1 |
| 7902 | tamboril | 1 |
| 7903 | tamañitos | 1 |
| 7904 | tallo | 1 |
| 7905 | tallar | 1 |
| 7906 | tallado | 1 |
| 7907 | talismán | 1 |
| 7908 | talega | 1 |
| 7909 | tajo | 1 |
| 7910 | taigeto | 1 |
| 7911 | tahúr | 1 |
| 7912 | tagarnina | 1 |
| 7913 | tafetán | 1 |
| 7914 | taconeo | 1 |
| 7915 | tácitamente | 1 |
| 7916 | tacita | 1 |
| 7917 | tacha | 1 |
| 7918 | tacaño | 1 |
| 7919 | tablilla | 1 |
| 7920 | tabicar | 1 |
| 7921 | tabernáculo | 1 |
| 7922 | suya | 1 |
| 7923 | sutilísimo | 1 |
| 7924 | sustraer | 1 |
| 7925 | sustancia | 1 |
| 7926 | suspira | 1 |
| 7927 | suspicacia | 1 |
| 7928 | suspensión | 1 |
| 7929 | susodicho | 1 |
| 7930 | suscripción | 1 |
| 7931 | supremacía | 1 |
| 7932 | suposición | 1 |
| 7933 | suponiendo | 1 |
| 7934 | suplicio | 1 |
| 7935 | superfino | 1 |
| 7936 | superficialidad | 1 |
| 7937 | superficial | 1 |
| 7938 | suntuoso | 1 |
| 7939 | suministrar | 1 |
| 7940 | sumergido | 1 |
| 7941 | sumar | 1 |
| 7942 | sulfurar | 1 |
| 7943 | suizo | 1 |
| 7944 | suicidar | 1 |
| 7945 | suicida | 1 |
| 7946 | sufrido | 1 |
| 7947 | sufre | 1 |
| 7948 | sufragio | 1 |
| 7949 | suegro | 1 |
| 7950 | suecia | 1 |
| 7951 | sudario | 1 |
| 7952 | sucursal | 1 |
| 7953 | sucumbiría | 1 |
| 7954 | sucesivamente | 1 |
| 7955 | subvencionar | 1 |
| 7956 | suburbio | 1 |
| 7957 | subterfugio | 1 |
| 7958 | subteniente | 1 |
| 7959 | subsuelo | 1 |
| 7960 | subsistir | 1 |
| 7961 | subjetivar | 1 |
| 7962 | súbito | 1 |
| 7963 | subió | 1 |
| 7964 | subido | 1 |
| 7965 | subida | 1 |
| 7966 | súbdito | 1 |
| 7967 | subalterno | 1 |
| 7968 | strauss | 1 |
| 7969 | stoa | 1 |
| 7970 | sport | 1 |
| 7971 | spirto | 1 |
| 7972 | spínolas | 1 |
| 7973 | sousa | 1 |
| 7974 | sostenido | 1 |
| 7975 | sosiego | 1 |
| 7976 | sortear | 1 |
| 7977 | sordomudo | 1 |
| 7978 | sordina | 1 |
| 7979 | sorbo | 1 |
| 7980 | sorbete | 1 |
| 7981 | soportar | 1 |
| 7982 | soportable | 1 |
| 7983 | sopar | 1 |
| 7984 | soñado | 1 |
| 7985 | sonrojar | 1 |
| 7986 | soneto | 1 |
| 7987 | sonda | 1 |
| 7988 | sonado | 1 |
| 7989 | somieda | 1 |
| 7990 | solterón | 1 |
| 7991 | soltera | 1 |
| 7992 | soliviantar | 1 |
| 7993 | solideo | 1 |
| 7994 | solidaridad | 1 |
| 7995 | solicitación | 1 |
| 7996 | solía | 1 |
| 7997 | solfear | 1 |
| 7998 | solecismo | 1 |
| 7999 | solazar | 1 |
| 8000 | solapado | 1 |
| 8001 | solamente | 1 |
| 8002 | soga | 1 |
| 8003 | sofocación | 1 |
| 8004 | sofión | 1 |
| 8005 | socorrido | 1 |
| 8006 | socialismo | 1 |
| 8007 | sociable | 1 |
| 8008 | sochantre | 1 |
| 8009 | sobrón | 1 |
| 8010 | sobrevenir | 1 |
| 8011 | sobrenadar | 1 |
| 8012 | sobremesa | 1 |
| 8013 | sobrehumano | 1 |
| 8014 | sobradamente | 1 |
| 8015 | soberanía | 1 |
| 8016 | sobar | 1 |
| 8017 | sobaco | 1 |
| 8018 | sixto | 1 |
| 8019 | sitial | 1 |
| 8020 | sistemática | 1 |
| 8021 | sisar | 1 |
| 8022 | sisa | 1 |
| 8023 | siria | 1 |
| 8024 | sinuosidad | 1 |
| 8025 | sintió | 1 |
| 8026 | sintetizar | 1 |
| 8027 | síntesis | 1 |
| 8028 | sinrazón | 1 |
| 8029 | sinónimo | 1 |
| 8030 | singularísimo | 1 |
| 8031 | sinapismo | 1 |
| 8032 | simular | 1 |
| 8033 | simplicidad | 1 |
| 8034 | simplemente | 1 |
| 8035 | símil | 1 |
| 8036 | simiente | 1 |
| 8037 | simetría | 1 |
| 8038 | simeón | 1 |
| 8039 | simbolismo | 1 |
| 8040 | simancas | 1 |
| 8041 | sima | 1 |
| 8042 | silva | 1 |
| 8043 | sillería | 1 |
| 8044 | sillar | 1 |
| 8045 | sigiloso | 1 |
| 8046 | sierpe | 1 |
| 8047 | siendo | 1 |
| 8048 | shakespeare | 1 |
| 8049 | sexta | 1 |
| 8050 | sevillano | 1 |
| 8051 | sesgar | 1 |
| 8052 | sesentón | 1 |
| 8053 | servilmente | 1 |
| 8054 | servilletero | 1 |
| 8055 | servil | 1 |
| 8056 | servicial | 1 |
| 8057 | serrallo | 1 |
| 8058 | serpiente | 1 |
| 8059 | serón | 1 |
| 8060 | sermones | 1 |
| 8061 | serie | 1 |
| 8062 | serán | 1 |
| 8063 | sepárese | 1 |
| 8064 | separado | 1 |
| 8065 | señorial | 1 |
| 8066 | sentía | 1 |
| 8067 | sentado | 1 |
| 8068 | sensualista | 1 |
| 8069 | sensualismo | 1 |
| 8070 | sensualidad | 1 |
| 8071 | sensiblería | 1 |
| 8072 | sensatamente | 1 |
| 8073 | senil | 1 |
| 8074 | sempiterno | 1 |
| 8075 | semillero | 1 |
| 8076 | semicírculo | 1 |
| 8077 | semicientífico | 1 |
| 8078 | semental | 1 |
| 8079 | sembrado | 1 |
| 8080 | selvático | 1 |
| 8081 | selva | 1 |
| 8082 | segura | 1 |
| 8083 | segadora | 1 |
| 8084 | sedoso | 1 |
| 8085 | sediento | 1 |
| 8086 | sedentarismo | 1 |
| 8087 | secundario | 1 |
| 8088 | secularización | 1 |
| 8089 | secuestrar | 1 |
| 8090 | secuestrador | 1 |
| 8091 | secuentia | 1 |
| 8092 | secretario | 1 |
| 8093 | secretaría | 1 |
| 8094 | secretamente | 1 |
| 8095 | sección | 1 |
| 8096 | secchi | 1 |
| 8097 | sebastopol | 1 |
| 8098 | sebastián | 1 |
| 8099 | sazonar | 1 |
| 8100 | sayón | 1 |
| 8101 | saturnillo | 1 |
| 8102 | saturación | 1 |
| 8103 | satírico | 1 |
| 8104 | sátira | 1 |
| 8105 | satinado | 1 |
| 8106 | satín | 1 |
| 8107 | satén | 1 |
| 8108 | satánico | 1 |
| 8109 | satán | 1 |
| 8110 | sastrería | 1 |
| 8111 | sarraceno | 1 |
| 8112 | sardou | 1 |
| 8113 | sardónico | 1 |
| 8114 | sarcástico | 1 |
| 8115 | saquear | 1 |
| 8116 | sansón | 1 |
| 8117 | sanitario | 1 |
| 8118 | sanguinolento | 1 |
| 8119 | sanguinario | 1 |
| 8120 | sanguijuela | 1 |
| 8121 | sangriento | 1 |
| 8122 | sangrientamente | 1 |
| 8123 | sandunga | 1 |
| 8124 | sandio | 1 |
| 8125 | sandalia | 1 |
| 8126 | sancti | 1 |
| 8127 | sancionado | 1 |
| 8128 | sanción | 1 |
| 8129 | sancho | 1 |
| 8130 | sálvense | 1 |
| 8131 | sálvamelo | 1 |
| 8132 | saludó | 1 |
| 8133 | saltarín | 1 |
| 8134 | salpimentar | 1 |
| 8135 | salomónico | 1 |
| 8136 | salomón | 1 |
| 8137 | salmista | 1 |
| 8138 | salió | 1 |
| 8139 | saliente | 1 |
| 8140 | salid | 1 |
| 8141 | saldar | 1 |
| 8142 | salchichón | 1 |
| 8143 | sahumar | 1 |
| 8144 | sagunto | 1 |
| 8145 | sagrario | 1 |
| 8146 | sacudido | 1 |
| 8147 | sacrosanto | 1 |
| 8148 | sacro | 1 |
| 8149 | sacrilegio | 1 |
| 8150 | sacrificándose | 1 |
| 8151 | sacramentar | 1 |
| 8152 | sacerdotisa | 1 |
| 8153 | sacerdotal | 1 |
| 8154 | sacada | 1 |
| 8155 | sabría | 1 |
| 8156 | sablazo | 1 |
| 8157 | sabihondo | 1 |
| 8158 | sabandija | 1 |
| 8159 | sabana | 1 |
| 8160 | ruso | 1 |
| 8161 | rumoroso | 1 |
| 8162 | ruleta | 1 |
| 8163 | rugido | 1 |
| 8164 | rufinita | 1 |
| 8165 | rudo | 1 |
| 8166 | rudesinda | 1 |
| 8167 | rúbrica | 1 |
| 8168 | ruborizarse | 1 |
| 8169 | rubito | 1 |
| 8170 | rozado | 1 |
| 8171 | rotundo | 1 |
| 8172 | rótulo | 1 |
| 8173 | rosendo | 1 |
| 8174 | rosal | 1 |
| 8175 | rorro | 1 |
| 8176 | roquero | 1 |
| 8177 | ropón | 1 |
| 8178 | ronzalillo | 1 |
| 8179 | ronquido | 1 |
| 8180 | ronda | 1 |
| 8181 | ron | 1 |
| 8182 | rompecabezas | 1 |
| 8183 | romo | 1 |
| 8184 | romea | 1 |
| 8185 | romancero | 1 |
| 8186 | romana | 1 |
| 8187 | rojas | 1 |
| 8188 | rogativa | 1 |
| 8189 | roedor | 1 |
| 8190 | rodríguez | 1 |
| 8191 | rococó | 1 |
| 8192 | robledo | 1 |
| 8193 | robledal | 1 |
| 8194 | rivalizar | 1 |
| 8195 | ristre | 1 |
| 8196 | riña | 1 |
| 8197 | rima | 1 |
| 8198 | riguroso | 1 |
| 8199 | rigolade | 1 |
| 8200 | rígido | 1 |
| 8201 | rigidez | 1 |
| 8202 | rifa | 1 |
| 8203 | ricacho | 1 |
| 8204 | ribera | 1 |
| 8205 | ríase | 1 |
| 8206 | rezumar | 1 |
| 8207 | rezando | 1 |
| 8208 | reyes | 1 |
| 8209 | revuelto | 1 |
| 8210 | revolucionar | 1 |
| 8211 | revolar | 1 |
| 8212 | reverso | 1 |
| 8213 | reverencia | 1 |
| 8214 | reverbero | 1 |
| 8215 | reverberar | 1 |
| 8216 | revelaciones | 1 |
| 8217 | retumbante | 1 |
| 8218 | retroceso | 1 |
| 8219 | retrato | 1 |
| 8220 | retratar | 1 |
| 8221 | retraso | 1 |
| 8222 | retractación | 1 |
| 8223 | retozar | 1 |
| 8224 | retorta | 1 |
| 8225 | retocar | 1 |
| 8226 | retintín | 1 |
| 8227 | retina | 1 |
| 8228 | resurrección | 1 |
| 8229 | resumir | 1 |
| 8230 | resultas | 1 |
| 8231 | resuelto | 1 |
| 8232 | resuello | 1 |
| 8233 | restringido | 1 |
| 8234 | restañar | 1 |
| 8235 | restablecer | 1 |
| 8236 | responso | 1 |
| 8237 | responde | 1 |
| 8238 | resplandeciente | 1 |
| 8239 | respiró | 1 |
| 8240 | respiro | 1 |
| 8241 | respectivamente | 1 |
| 8242 | respecta | 1 |
| 8243 | residir | 1 |
| 8244 | residencia | 1 |
| 8245 | reservado | 1 |
| 8246 | reseñar | 1 |
| 8247 | resentido | 1 |
| 8248 | rescatar | 1 |
| 8249 | requebrar | 1 |
| 8250 | repuso | 1 |
| 8251 | reproducir | 1 |
| 8252 | reprimir | 1 |
| 8253 | representativo | 1 |
| 8254 | representante | 1 |
| 8255 | representaba | 1 |
| 8256 | reposado | 1 |
| 8257 | repliegue | 1 |
| 8258 | replicaba | 1 |
| 8259 | repiqueteo | 1 |
| 8260 | repique | 1 |
| 8261 | repicar | 1 |
| 8262 | repertorio | 1 |
| 8263 | repercutir | 1 |
| 8264 | repechar | 1 |
| 8265 | reo | 1 |
| 8266 | renuncia | 1 |
| 8267 | rentístico | 1 |
| 8268 | renovado | 1 |
| 8269 | renovación | 1 |
| 8270 | rendimiento | 1 |
| 8271 | rendido | 1 |
| 8272 | renacimiento | 1 |
| 8273 | remolque | 1 |
| 8274 | remolón | 1 |
| 8275 | remolacha | 1 |
| 8276 | remiso | 1 |
| 8277 | remendón | 1 |
| 8278 | remedar | 1 |
| 8279 | remanso | 1 |
| 8280 | relojero | 1 |
| 8281 | rellenar | 1 |
| 8282 | relevar | 1 |
| 8283 | relator | 1 |
| 8284 | relativos | 1 |
| 8285 | relativamente | 1 |
| 8286 | relamer | 1 |
| 8287 | relajación | 1 |
| 8288 | reivindicar | 1 |
| 8289 | reivindicación | 1 |
| 8290 | reiterado | 1 |
| 8291 | reintegrar | 1 |
| 8292 | reíanse | 1 |
| 8293 | rehusar | 1 |
| 8294 | rehuir | 1 |
| 8295 | rehuía | 1 |
| 8296 | rehabilitar | 1 |
| 8297 | regularmente | 1 |
| 8298 | regresar | 1 |
| 8299 | regocijo | 1 |
| 8300 | reglamento | 1 |
| 8301 | reglamentario | 1 |
| 8302 | registrándole | 1 |
| 8303 | regeneración | 1 |
| 8304 | regateo | 1 |
| 8305 | refutar | 1 |
| 8306 | refugiábanse | 1 |
| 8307 | refrigerar | 1 |
| 8308 | refriega | 1 |
| 8309 | refrescar | 1 |
| 8310 | refrenar | 1 |
| 8311 | refrán | 1 |
| 8312 | refractar | 1 |
| 8313 | reforzar | 1 |
| 8314 | reflexivo | 1 |
| 8315 | refinamiento | 1 |
| 8316 | referente | 1 |
| 8317 | reencarnación | 1 |
| 8318 | reedificar | 1 |
| 8319 | reduplicar | 1 |
| 8320 | redundante | 1 |
| 8321 | redundancia | 1 |
| 8322 | reducto | 1 |
| 8323 | redondilla | 1 |
| 8324 | redondear | 1 |
| 8325 | redoma | 1 |
| 8326 | redoble | 1 |
| 8327 | rédito | 1 |
| 8328 | rediós | 1 |
| 8329 | redentor | 1 |
| 8330 | redención | 1 |
| 8331 | redactar | 1 |
| 8332 | recular | 1 |
| 8333 | recuerda | 1 |
| 8334 | recuento | 1 |
| 8335 | rectificaba | 1 |
| 8336 | rectangular | 1 |
| 8337 | recta | 1 |
| 8338 | recorte | 1 |
| 8339 | recortado | 1 |
| 8340 | recorrido | 1 |
| 8341 | recopilación | 1 |
| 8342 | reconvención | 1 |
| 8343 | recontar | 1 |
| 8344 | reconquista | 1 |
| 8345 | reconozco | 1 |
| 8346 | reconciliarás | 1 |
| 8347 | recompensa | 1 |
| 8348 | recoletos | 1 |
| 8349 | recogida | 1 |
| 8350 | recobraste | 1 |
| 8351 | reclinar | 1 |
| 8352 | recíproca | 1 |
| 8353 | recibimiento | 1 |
| 8354 | recelar | 1 |
| 8355 | recaudar | 1 |
| 8356 | recatadamente | 1 |
| 8357 | recalcitrante | 1 |
| 8358 | recaída | 1 |
| 8359 | rebullir | 1 |
| 8360 | rebozo | 1 |
| 8361 | rebotar | 1 |
| 8362 | reblandecer | 1 |
| 8363 | rebeca | 1 |
| 8364 | reanimar | 1 |
| 8365 | reacio | 1 |
| 8366 | re | 1 |
| 8367 | ratificar | 1 |
| 8368 | raspar | 1 |
| 8369 | rarísimo | 1 |
| 8370 | rapto | 1 |
| 8371 | rapsodia | 1 |
| 8372 | rapidísimo | 1 |
| 8373 | rapar | 1 |
| 8374 | rancio | 1 |
| 8375 | ramificación | 1 |
| 8376 | ramayana | 1 |
| 8377 | ralea | 1 |
| 8378 | raja | 1 |
| 8379 | racionalmente | 1 |
| 8380 | racionalismo | 1 |
| 8381 | racionales | 1 |
| 8382 | ración | 1 |
| 8383 | rachir | 1 |
| 8384 | rabo | 1 |
| 8385 | rabioso | 1 |
| 8386 | rábano | 1 |
| 8387 | r | 1 |
| 8388 | quizá | 1 |
| 8389 | quítese | 1 |
| 8390 | quisquilloso | 1 |
| 8391 | quisque | 1 |
| 8392 | quisicosa | 1 |
| 8393 | quise | 1 |
| 8394 | quintana | 1 |
| 8395 | quintal | 1 |
| 8396 | quinientas | 1 |
| 8397 | químico | 1 |
| 8398 | quijotesco | 1 |
| 8399 | quijotada | 1 |
| 8400 | quijada | 1 |
| 8401 | quietud | 1 |
| 8402 | quietismo | 1 |
| 8403 | quieren | 1 |
| 8404 | quiera | 1 |
| 8405 | quiénes | 1 |
| 8406 | quid | 1 |
| 8407 | querrían | 1 |
| 8408 | querría | 1 |
| 8409 | querían | 1 |
| 8410 | queremos | 1 |
| 8411 | querella | 1 |
| 8412 | quemadura | 1 |
| 8413 | quemado | 1 |
| 8414 | quema | 1 |
| 8415 | quedó | 1 |
| 8416 | queda | 1 |
| 8417 | quando | 1 |
| 8418 | pústula | 1 |
| 8419 | pusilánime | 1 |
| 8420 | purulento | 1 |
| 8421 | purificar | 1 |
| 8422 | puridad | 1 |
| 8423 | purga | 1 |
| 8424 | pupilo | 1 |
| 8425 | puños | 1 |
| 8426 | puñetazos | 1 |
| 8427 | puñados | 1 |
| 8428 | puñado | 1 |
| 8429 | punzar | 1 |
| 8430 | puntuación | 1 |
| 8431 | puntillo | 1 |
| 8432 | puntada | 1 |
| 8433 | pundonor | 1 |
| 8434 | pumarada | 1 |
| 8435 | pum | 1 |
| 8436 | pulvisés | 1 |
| 8437 | pulir | 1 |
| 8438 | pulga | 1 |
| 8439 | pujanza | 1 |
| 8440 | pugna | 1 |
| 8441 | pugilato | 1 |
| 8442 | puertos | 1 |
| 8443 | puerperio | 1 |
| 8444 | puerperal | 1 |
| 8445 | puerco | 1 |
| 8446 | pudoroso | 1 |
| 8447 | pudiente | 1 |
| 8448 | pudibundo | 1 |
| 8449 | publicidad | 1 |
| 8450 | públicamente | 1 |
| 8451 | publicación | 1 |
| 8452 | puar | 1 |
| 8453 | púa | 1 |
| 8454 | psíquico | 1 |
| 8455 | psicológicamente | 1 |
| 8456 | pseudoclásico | 1 |
| 8457 | prudentemente | 1 |
| 8458 | proyectil | 1 |
| 8459 | provocador | 1 |
| 8460 | provisto | 1 |
| 8461 | provisionalmente | 1 |
| 8462 | proverbial | 1 |
| 8463 | provenir | 1 |
| 8464 | proveer | 1 |
| 8465 | protoplasma | 1 |
| 8466 | protejo | 1 |
| 8467 | protegido | 1 |
| 8468 | prostituto | 1 |
| 8469 | prosternar | 1 |
| 8470 | próspero | 1 |
| 8471 | prosperidad | 1 |
| 8472 | prosopopeya | 1 |
| 8473 | prosélito | 1 |
| 8474 | propuesta | 1 |
| 8475 | proporcionado | 1 |
| 8476 | propongo | 1 |
| 8477 | pronunciado | 1 |
| 8478 | pronóstico | 1 |
| 8479 | pronosticar | 1 |
| 8480 | promulgar | 1 |
| 8481 | prominencia | 1 |
| 8482 | prolongado | 1 |
| 8483 | prolijo | 1 |
| 8484 | prole | 1 |
| 8485 | prohibían | 1 |
| 8486 | programar | 1 |
| 8487 | profundísima | 1 |
| 8488 | profeso | 1 |
| 8489 | proferir | 1 |
| 8490 | proeza | 1 |
| 8491 | prodigiosamente | 1 |
| 8492 | prodigalidad | 1 |
| 8493 | procedencia | 1 |
| 8494 | probo | 1 |
| 8495 | probidad | 1 |
| 8496 | probecicos | 1 |
| 8497 | pro | 1 |
| 8498 | privilegiar | 1 |
| 8499 | privación | 1 |
| 8500 | prístino | 1 |
| 8501 | prismático | 1 |
| 8502 | principado | 1 |
| 8503 | primoroso | 1 |
| 8504 | primordial | 1 |
| 8505 | primicia | 1 |
| 8506 | primeramente | 1 |
| 8507 | primar | 1 |
| 8508 | prez | 1 |
| 8509 | previo | 1 |
| 8510 | previamente | 1 |
| 8511 | prevenido | 1 |
| 8512 | prevención | 1 |
| 8513 | prevaricación | 1 |
| 8514 | prevaler | 1 |
| 8515 | prevalecer | 1 |
| 8516 | pretil | 1 |
| 8517 | pretendido | 1 |
| 8518 | presuroso | 1 |
| 8519 | presto | 1 |
| 8520 | prestigiar | 1 |
| 8521 | prestidigitador | 1 |
| 8522 | preste | 1 |
| 8523 | prestamista | 1 |
| 8524 | presión | 1 |
| 8525 | presilla | 1 |
| 8526 | presidiario | 1 |
| 8527 | presidenta | 1 |
| 8528 | presidencia | 1 |
| 8529 | presentación | 1 |
| 8530 | prescribir | 1 |
| 8531 | prescindamos | 1 |
| 8532 | presbiterio | 1 |
| 8533 | prerrogativa | 1 |
| 8534 | preñar | 1 |
| 8535 | prensado | 1 |
| 8536 | premeditado | 1 |
| 8537 | pregúntaselo | 1 |
| 8538 | preguntaron | 1 |
| 8539 | pregonero | 1 |
| 8540 | preferible | 1 |
| 8541 | preeminente | 1 |
| 8542 | predisposición | 1 |
| 8543 | precursor | 1 |
| 8544 | precisión | 1 |
| 8545 | precipitadamente | 1 |
| 8546 | precipicio | 1 |
| 8547 | preciosa | 1 |
| 8548 | preces | 1 |
| 8549 | precepto | 1 |
| 8550 | precaver | 1 |
| 8551 | prebenda | 1 |
| 8552 | pragmática | 1 |
| 8553 | poussin | 1 |
| 8554 | potro | 1 |
| 8555 | potente | 1 |
| 8556 | potentado | 1 |
| 8557 | póstumo | 1 |
| 8558 | postdata | 1 |
| 8559 | posponer | 1 |
| 8560 | posada | 1 |
| 8561 | portocarrero | 1 |
| 8562 | portezuela | 1 |
| 8563 | portería | 1 |
| 8564 | portentoso | 1 |
| 8565 | portador | 1 |
| 8566 | porrazo | 1 |
| 8567 | porra | 1 |
| 8568 | porfiado | 1 |
| 8569 | porfía | 1 |
| 8570 | porche | 1 |
| 8571 | poquísimo | 1 |
| 8572 | populoso | 1 |
| 8573 | pontificii | 1 |
| 8574 | pontificado | 1 |
| 8575 | pomposo | 1 |
| 8576 | pomares | 1 |
| 8577 | polvareda | 1 |
| 8578 | polo | 1 |
| 8579 | polea | 1 |
| 8580 | polaina | 1 |
| 8581 | polaco | 1 |
| 8582 | poetizar | 1 |
| 8583 | poe | 1 |
| 8584 | podría | 1 |
| 8585 | podrá | 1 |
| 8586 | pocas | 1 |
| 8587 | poca | 1 |
| 8588 | pobretería | 1 |
| 8589 | poblado | 1 |
| 8590 | pluralidad | 1 |
| 8591 | plomar | 1 |
| 8592 | plenamente | 1 |
| 8593 | plegadera | 1 |
| 8594 | platón | 1 |
| 8595 | platicar | 1 |
| 8596 | plasticidad | 1 |
| 8597 | plástica | 1 |
| 8598 | plantado | 1 |
| 8599 | planicie | 1 |
| 8600 | planeta | 1 |
| 8601 | plancha | 1 |
| 8602 | pizpireto | 1 |
| 8603 | pizpireta | 1 |
| 8604 | pizcar | 1 |
| 8605 | pizarro | 1 |
| 8606 | pitonisa | 1 |
| 8607 | pitar | 1 |
| 8608 | pitágoras | 1 |
| 8609 | pistilo | 1 |
| 8610 | pista | 1 |
| 8611 | pisci | 1 |
| 8612 | pisada | 1 |
| 8613 | pirata | 1 |
| 8614 | piña | 1 |
| 8615 | pinzón | 1 |
| 8616 | pinón | 1 |
| 8617 | pingüe | 1 |
| 8618 | pinar | 1 |
| 8619 | pin | 1 |
| 8620 | pimpollo | 1 |
| 8621 | píldora | 1 |
| 8622 | pigault | 1 |
| 8623 | pietista | 1 |
| 8624 | piensa | 1 |
| 8625 | picotear | 1 |
| 8626 | picota | 1 |
| 8627 | pichón | 1 |
| 8628 | picazón | 1 |
| 8629 | pican | 1 |
| 8630 | picador | 1 |
| 8631 | picado | 1 |
| 8632 | picacho | 1 |
| 8633 | piara | 1 |
| 8634 | piafar | 1 |
| 8635 | petrificar | 1 |
| 8636 | petirrojo | 1 |
| 8637 | petardo | 1 |
| 8638 | pétalo | 1 |
| 8639 | pespuntear | 1 |
| 8640 | pesetero | 1 |
| 8641 | pescaremos | 1 |
| 8642 | pescante | 1 |
| 8643 | pescador | 1 |
| 8644 | pesadez | 1 |
| 8645 | pervertido | 1 |
| 8646 | perverso | 1 |
| 8647 | perú | 1 |
| 8648 | perturbar | 1 |
| 8649 | perturbador | 1 |
| 8650 | pertinente | 1 |
| 8651 | pertinaz | 1 |
| 8652 | persuasión | 1 |
| 8653 | personificación | 1 |
| 8654 | persistir | 1 |
| 8655 | persistente | 1 |
| 8656 | persignar | 1 |
| 8657 | perseguidor | 1 |
| 8658 | perrería | 1 |
| 8659 | perpetua | 1 |
| 8660 | perorar | 1 |
| 8661 | permítame | 1 |
| 8662 | peritonitis | 1 |
| 8663 | peritar | 1 |
| 8664 | periodista | 1 |
| 8665 | periódicos | 1 |
| 8666 | perifollo | 1 |
| 8667 | pergeño | 1 |
| 8668 | pergeñar | 1 |
| 8669 | perfumería | 1 |
| 8670 | perfidia | 1 |
| 8671 | perfecta | 1 |
| 8672 | perezosos | 1 |
| 8673 | perezosamente | 1 |
| 8674 | pérez | 1 |
| 8675 | perentorio | 1 |
| 8676 | peregrinación | 1 |
| 8677 | pereda | 1 |
| 8678 | perecedero | 1 |
| 8679 | perdulario | 1 |
| 8680 | perdóneme | 1 |
| 8681 | perdonarla | 1 |
| 8682 | perdonadle | 1 |
| 8683 | perdida | 1 |
| 8684 | perceptivo | 1 |
| 8685 | peraltado | 1 |
| 8686 | pera | 1 |
| 8687 | pepinillo | 1 |
| 8688 | peonza | 1 |
| 8689 | peonar | 1 |
| 8690 | peñasco | 1 |
| 8691 | penuria | 1 |
| 8692 | penumbra | 1 |
| 8693 | pentagrama | 1 |
| 8694 | pensaban | 1 |
| 8695 | penitenciario | 1 |
| 8696 | péndulo | 1 |
| 8697 | pendencia | 1 |
| 8698 | penar | 1 |
| 8699 | peluquería | 1 |
| 8700 | pelucón | 1 |
| 8701 | peleo | 1 |
| 8702 | peldaño | 1 |
| 8703 | pelayo | 1 |
| 8704 | pelar | 1 |
| 8705 | peinador | 1 |
| 8706 | peinado | 1 |
| 8707 | pegado | 1 |
| 8708 | pegada | 1 |
| 8709 | pega | 1 |
| 8710 | pedirla | 1 |
| 8711 | pedigüeño | 1 |
| 8712 | pedestre | 1 |
| 8713 | pedestal | 1 |
| 8714 | pedantesco | 1 |
| 8715 | pedantería | 1 |
| 8716 | pechina | 1 |
| 8717 | pechar | 1 |
| 8718 | pebetero | 1 |
| 8719 | pche | 1 |
| 8720 | pavoroso | 1 |
| 8721 | paulo | 1 |
| 8722 | paulatino | 1 |
| 8723 | paulatinamente | 1 |
| 8724 | paul | 1 |
| 8725 | patronato | 1 |
| 8726 | patrocinar | 1 |
| 8727 | patris | 1 |
| 8728 | patriarca | 1 |
| 8729 | patraña | 1 |
| 8730 | patitas | 1 |
| 8731 | patíbulo | 1 |
| 8732 | patear | 1 |
| 8733 | patarata | 1 |
| 8734 | pataleo | 1 |
| 8735 | pastoreo | 1 |
| 8736 | pastora | 1 |
| 8737 | pastilla | 1 |
| 8738 | pasteur | 1 |
| 8739 | pastelero | 1 |
| 8740 | pastel | 1 |
| 8741 | pasó | 1 |
| 8742 | pásmese | 1 |
| 8743 | pasmábase | 1 |
| 8744 | paseíto | 1 |
| 8745 | pascal | 1 |
| 8746 | pasará | 1 |
| 8747 | parves | 1 |
| 8748 | parvedad | 1 |
| 8749 | particularmente | 1 |
| 8750 | parrilla | 1 |
| 8751 | parisiense | 1 |
| 8752 | parejita | 1 |
| 8753 | paredón | 1 |
| 8754 | parecen | 1 |
| 8755 | pardal | 1 |
| 8756 | parcial | 1 |
| 8757 | parca | 1 |
| 8758 | pararrayos | 1 |
| 8759 | parangón | 1 |
| 8760 | paradoja | 1 |
| 8761 | parado | 1 |
| 8762 | paquete | 1 |
| 8763 | papista | 1 |
| 8764 | papas | 1 |
| 8765 | pañales | 1 |
| 8766 | pañal | 1 |
| 8767 | panteísta | 1 |
| 8768 | pantalla | 1 |
| 8769 | panoplia | 1 |
| 8770 | panecillo | 1 |
| 8771 | pandereta | 1 |
| 8772 | pamplinas | 1 |
| 8773 | palúdico | 1 |
| 8774 | palpitación | 1 |
| 8775 | palmito | 1 |
| 8776 | palmario | 1 |
| 8777 | palmado | 1 |
| 8778 | pallavicini | 1 |
| 8779 | palio | 1 |
| 8780 | palinodia | 1 |
| 8781 | palillo | 1 |
| 8782 | pálida | 1 |
| 8783 | palas | 1 |
| 8784 | palafrén | 1 |
| 8785 | palabrota | 1 |
| 8786 | paje | 1 |
| 8787 | pajas | 1 |
| 8788 | pajarraco | 1 |
| 8789 | pájara | 1 |
| 8790 | pajar | 1 |
| 8791 | paix | 1 |
| 8792 | paginar | 1 |
| 8793 | paganismo | 1 |
| 8794 | padrinos | 1 |
| 8795 | padres | 1 |
| 8796 | padrenuestro | 1 |
| 8797 | padrazo | 1 |
| 8798 | padecimiento | 1 |
| 8799 | pactar | 1 |
| 8800 | pacos | 1 |
| 8801 | pacíficamente | 1 |
| 8802 | paciente | 1 |
| 8803 | oxígeno | 1 |
| 8804 | oxidado | 1 |
| 8805 | ovillo | 1 |
| 8806 | oveja | 1 |
| 8807 | ovalado | 1 |
| 8808 | oval | 1 |
| 8809 | ovación | 1 |
| 8810 | otrosí | 1 |
| 8811 | otros | 1 |
| 8812 | otoñada | 1 |
| 8813 | osuna | 1 |
| 8814 | ostracismo | 1 |
| 8815 | ostensiblemente | 1 |
| 8816 | oscilar | 1 |
| 8817 | osado | 1 |
| 8818 | osadía | 1 |
| 8819 | orza | 1 |
| 8820 | orto | 1 |
| 8821 | ortiz | 1 |
| 8822 | orsini | 1 |
| 8823 | orquestar | 1 |
| 8824 | oropel | 1 |
| 8825 | ornato | 1 |
| 8826 | ornamento | 1 |
| 8827 | ornamentar | 1 |
| 8828 | orientalista | 1 |
| 8829 | orgullosa | 1 |
| 8830 | orgasmo | 1 |
| 8831 | organismo | 1 |
| 8832 | organdí | 1 |
| 8833 | orejera | 1 |
| 8834 | ordenó | 1 |
| 8835 | ordenado | 1 |
| 8836 | órbita | 1 |
| 8837 | orangután | 1 |
| 8838 | oráculo | 1 |
| 8839 | opulento | 1 |
| 8840 | opulencia | 1 |
| 8841 | óptimo | 1 |
| 8842 | óptico | 1 |
| 8843 | opresor | 1 |
| 8844 | oppert | 1 |
| 8845 | opositor | 1 |
| 8846 | oportunísimo | 1 |
| 8847 | oportunamente | 1 |
| 8848 | opinaba | 1 |
| 8849 | onza | 1 |
| 8850 | omnipotencia | 1 |
| 8851 | olivo | 1 |
| 8852 | olimpo | 1 |
| 8853 | olfato | 1 |
| 8854 | olé | 1 |
| 8855 | ojiva | 1 |
| 8856 | ojazos | 1 |
| 8857 | oirá | 1 |
| 8858 | oigámoslo | 1 |
| 8859 | ofrendar | 1 |
| 8860 | ofrenda | 1 |
| 8861 | oficiar | 1 |
| 8862 | ofensiva | 1 |
| 8863 | ocupaciones | 1 |
| 8864 | ocupábase | 1 |
| 8865 | octava | 1 |
| 8866 | ochentón | 1 |
| 8867 | occidental | 1 |
| 8868 | ocasional | 1 |
| 8869 | obstante | 1 |
| 8870 | obseso | 1 |
| 8871 | observe | 1 |
| 8872 | obscuridad | 1 |
| 8873 | obreros | 1 |
| 8874 | oblongo | 1 |
| 8875 | obligatorio | 1 |
| 8876 | objetó | 1 |
| 8877 | objetivo | 1 |
| 8878 | obdulias | 1 |
| 8879 | obcecar | 1 |
| 8880 | nutrir | 1 |
| 8881 | nuncio | 1 |
| 8882 | nuevas | 1 |
| 8883 | nuestras | 1 |
| 8884 | nublar | 1 |
| 8885 | nubarrón | 1 |
| 8886 | novísimo | 1 |
| 8887 | noviazgo | 1 |
| 8888 | novenas | 1 |
| 8889 | novelista | 1 |
| 8890 | novedades | 1 |
| 8891 | notó | 1 |
| 8892 | noten | 1 |
| 8893 | notabilidad | 1 |
| 8894 | noruega | 1 |
| 8895 | normandos | 1 |
| 8896 | normal | 1 |
| 8897 | nordeste | 1 |
| 8898 | non | 1 |
| 8899 | nominar | 1 |
| 8900 | nodriza | 1 |
| 8901 | nocivo | 1 |
| 8902 | noción | 1 |
| 8903 | nocedal | 1 |
| 8904 | noblemente | 1 |
| 8905 | nivelar | 1 |
| 8906 | niños | 1 |
| 8907 | niñas | 1 |
| 8908 | ninon | 1 |
| 8909 | nínive | 1 |
| 8910 | ninfa | 1 |
| 8911 | nimbo | 1 |
| 8912 | nieto | 1 |
| 8913 | niega | 1 |
| 8914 | nevada | 1 |
| 8915 | neutro | 1 |
| 8916 | nene | 1 |
| 8917 | nemrod | 1 |
| 8918 | negligencia | 1 |
| 8919 | nefasto | 1 |
| 8920 | nefando | 1 |
| 8921 | necia | 1 |
| 8922 | necesito | 1 |
| 8923 | necesitaba | 1 |
| 8924 | necedades | 1 |
| 8925 | nay | 1 |
| 8926 | navío | 1 |
| 8927 | navegación | 1 |
| 8928 | naval | 1 |
| 8929 | náutico | 1 |
| 8930 | natividad | 1 |
| 8931 | natalicio | 1 |
| 8932 | natalia | 1 |
| 8933 | narigudo | 1 |
| 8934 | narices | 1 |
| 8935 | narciso | 1 |
| 8936 | naranjo | 1 |
| 8937 | naranjas | 1 |
| 8938 | nació | 1 |
| 8939 | naciente | 1 |
| 8940 | musgoso | 1 |
| 8941 | musgo | 1 |
| 8942 | musculoso | 1 |
| 8943 | murmuró | 1 |
| 8944 | murmuraban | 1 |
| 8945 | murmuraba | 1 |
| 8946 | muñoz | 1 |
| 8947 | muñón | 1 |
| 8948 | munificencia | 1 |
| 8949 | munda | 1 |
| 8950 | múltiple | 1 |
| 8951 | multar | 1 |
| 8952 | mullir | 1 |
| 8953 | mulato | 1 |
| 8954 | mujerzuela | 1 |
| 8955 | mujeril | 1 |
| 8956 | mugre | 1 |
| 8957 | múdese | 1 |
| 8958 | mu | 1 |
| 8959 | mr | 1 |
| 8960 | movible | 1 |
| 8961 | movedizo | 1 |
| 8962 | mostaza | 1 |
| 8963 | mosco | 1 |
| 8964 | mortuorio | 1 |
| 8965 | morro | 1 |
| 8966 | moroso | 1 |
| 8967 | morigerar | 1 |
| 8968 | morfina | 1 |
| 8969 | morería | 1 |
| 8970 | morena | 1 |
| 8971 | mordedura | 1 |
| 8972 | morcillo | 1 |
| 8973 | morcilla | 1 |
| 8974 | morboso | 1 |
| 8975 | morbidez | 1 |
| 8976 | moño | 1 |
| 8977 | moña | 1 |
| 8978 | montes | 1 |
| 8979 | montecristo | 1 |
| 8980 | monólogo | 1 |
| 8981 | monolito | 1 |
| 8982 | monocromo | 1 |
| 8983 | mónica | 1 |
| 8984 | monescillo | 1 |
| 8985 | móndame | 1 |
| 8986 | monástico | 1 |
| 8987 | monago | 1 |
| 8988 | mona | 1 |
| 8989 | momentáneo | 1 |
| 8990 | mollera | 1 |
| 8991 | moleschott | 1 |
| 8992 | moler | 1 |
| 8993 | moldura | 1 |
| 8994 | mojigata | 1 |
| 8995 | mojiganga | 1 |
| 8996 | modismo | 1 |
| 8997 | modificación | 1 |
| 8998 | mocoso | 1 |
| 8999 | mobiliario | 1 |
| 9000 | mixto | 1 |
| 9001 | mitológico | 1 |
| 9002 | místicos | 1 |
| 9003 | místicamente | 1 |
| 9004 | misterios | 1 |
| 9005 | misiva | 1 |
| 9006 | misérrimo | 1 |
| 9007 | miserere | 1 |
| 9008 | miserablemente | 1 |
| 9009 | misántropo | 1 |
| 9010 | mirón | 1 |
| 9011 | mirlar | 1 |
| 9012 | mírele | 1 |
| 9013 | mirábala | 1 |
| 9014 | míos | 1 |
| 9015 | miope | 1 |
| 9016 | minué | 1 |
| 9017 | minuciosamente | 1 |
| 9018 | miniatura | 1 |
| 9019 | mineral | 1 |
| 9020 | mimado | 1 |
| 9021 | milo | 1 |
| 9022 | militaba | 1 |
| 9023 | milano | 1 |
| 9024 | milagrosamente | 1 |
| 9025 | miguel | 1 |
| 9026 | migar | 1 |
| 9027 | mezquita | 1 |
| 9028 | mezquinar | 1 |
| 9029 | metz | 1 |
| 9030 | metropolitano | 1 |
| 9031 | metralla | 1 |
| 9032 | método | 1 |
| 9033 | metodista | 1 |
| 9034 | metida | 1 |
| 9035 | meteorológico | 1 |
| 9036 | meteorología | 1 |
| 9037 | metafóricamente | 1 |
| 9038 | meta | 1 |
| 9039 | meses | 1 |
| 9040 | mero | 1 |
| 9041 | mermar | 1 |
| 9042 | merino | 1 |
| 9043 | meridional | 1 |
| 9044 | merecimiento | 1 |
| 9045 | merecido | 1 |
| 9046 | merecidísimo | 1 |
| 9047 | mentor | 1 |
| 9048 | mentón | 1 |
| 9049 | mentís | 1 |
| 9050 | mentalmente | 1 |
| 9051 | mengua | 1 |
| 9052 | menestral | 1 |
| 9053 | meneses | 1 |
| 9054 | meneo | 1 |
| 9055 | méndez | 1 |
| 9056 | mencionar | 1 |
| 9057 | memorias | 1 |
| 9058 | memento | 1 |
| 9059 | membibres | 1 |
| 9060 | melodioso | 1 |
| 9061 | melodía | 1 |
| 9062 | melocotón | 1 |
| 9063 | melancólicamente | 1 |
| 9064 | mejorcito | 1 |
| 9065 | méjico | 1 |
| 9066 | médula | 1 |
| 9067 | medro | 1 |
| 9068 | medrados | 1 |
| 9069 | meditaba | 1 |
| 9070 | médicis | 1 |
| 9071 | medianoche | 1 |
| 9072 | medianero | 1 |
| 9073 | mechero | 1 |
| 9074 | mecha | 1 |
| 9075 | mecedor | 1 |
| 9076 | mecanismo | 1 |
| 9077 | mecánicamente | 1 |
| 9078 | mazar | 1 |
| 9079 | mayúsculo | 1 |
| 9080 | mayorazgo | 1 |
| 9081 | mayoral | 1 |
| 9082 | maudsley | 1 |
| 9083 | matrícula | 1 |
| 9084 | matizar | 1 |
| 9085 | matiella | 1 |
| 9086 | matías | 1 |
| 9087 | maternidad | 1 |
| 9088 | mateo | 1 |
| 9089 | matemáticamente | 1 |
| 9090 | matarla | 1 |
| 9091 | matadero | 1 |
| 9092 | masini | 1 |
| 9093 | martirizar | 1 |
| 9094 | marte | 1 |
| 9095 | marsilla | 1 |
| 9096 | marrón | 1 |
| 9097 | marquesina | 1 |
| 9098 | marmitón | 1 |
| 9099 | maritornes | 1 |
| 9100 | marismas | 1 |
| 9101 | mares | 1 |
| 9102 | mareantes | 1 |
| 9103 | mareado | 1 |
| 9104 | marchito | 1 |
| 9105 | marchitar | 1 |
| 9106 | maravilloso | 1 |
| 9107 | maquinilla | 1 |
| 9108 | maquinalmente | 1 |
| 9109 | maquinal | 1 |
| 9110 | mapa | 1 |
| 9111 | maño | 1 |
| 9112 | manuscribir | 1 |
| 9113 | mantillas | 1 |
| 9114 | manterola | 1 |
| 9115 | mantear | 1 |
| 9116 | manriques | 1 |
| 9117 | manoseado | 1 |
| 9118 | manolito | 1 |
| 9119 | manola | 1 |
| 9120 | manojo | 1 |
| 9121 | manir | 1 |
| 9122 | maniobra | 1 |
| 9123 | manifestó | 1 |
| 9124 | manejo | 1 |
| 9125 | mandria | 1 |
| 9126 | mandoble | 1 |
| 9127 | mandamos | 1 |
| 9128 | mandaba | 1 |
| 9129 | manar | 1 |
| 9130 | maná | 1 |
| 9131 | mampostería | 1 |
| 9132 | mamar | 1 |
| 9133 | maltrecho | 1 |
| 9134 | malquistar | 1 |
| 9135 | malla | 1 |
| 9136 | malhechor | 1 |
| 9137 | malévolo | 1 |
| 9138 | malestar | 1 |
| 9139 | malbaratar | 1 |
| 9140 | malamente | 1 |
| 9141 | malabar | 1 |
| 9142 | mala | 1 |
| 9143 | majo | 1 |
| 9144 | majar | 1 |
| 9145 | majaderos | 1 |
| 9146 | majadería | 1 |
| 9147 | maizal | 1 |
| 9148 | maitines | 1 |
| 9149 | mahoma | 1 |
| 9150 | mago | 1 |
| 9151 | magno | 1 |
| 9152 | magnífica | 1 |
| 9153 | magnanimidad | 1 |
| 9154 | magistratura | 1 |
| 9155 | magistrales | 1 |
| 9156 | madriguera | 1 |
| 9157 | madrigal | 1 |
| 9158 | madrejón | 1 |
| 9159 | madrastra | 1 |
| 9160 | madeja | 1 |
| 9161 | macizar | 1 |
| 9162 | macilento | 1 |
| 9163 | machacón | 1 |
| 9164 | maceta | 1 |
| 9165 | macabro | 1 |
| 9166 | macabeos | 1 |
| 9167 | m | 1 |
| 9168 | luzbel | 1 |
| 9169 | luys | 1 |
| 9170 | lustroso | 1 |
| 9171 | lustre | 1 |
| 9172 | lusitano | 1 |
| 9173 | luján | 1 |
| 9174 | lugarejo | 1 |
| 9175 | luengo | 1 |
| 9176 | lucubración | 1 |
| 9177 | lucro | 1 |
| 9178 | lucrecio | 1 |
| 9179 | lucrativo | 1 |
| 9180 | lucrar | 1 |
| 9181 | luciría | 1 |
| 9182 | lucifer | 1 |
| 9183 | lucido | 1 |
| 9184 | lucharía | 1 |
| 9185 | luchador | 1 |
| 9186 | lucero | 1 |
| 9187 | lucerna | 1 |
| 9188 | lucaaam | 1 |
| 9189 | lubricidad | 1 |
| 9190 | lozoya | 1 |
| 9191 | lozanía | 1 |
| 9192 | loza | 1 |
| 9193 | lovelace | 1 |
| 9194 | lot | 1 |
| 9195 | losa | 1 |
| 9196 | lonja | 1 |
| 9197 | longevidad | 1 |
| 9198 | longaniza | 1 |
| 9199 | locuras | 1 |
| 9200 | locos | 1 |
| 9201 | loca | 1 |
| 9202 | lóbrego | 1 |
| 9203 | lobezno | 1 |
| 9204 | loable | 1 |
| 9205 | llueve | 1 |
| 9206 | llovía | 1 |
| 9207 | llovería | 1 |
| 9208 | llorón | 1 |
| 9209 | lloro | 1 |
| 9210 | lloriquear | 1 |
| 9211 | llévame | 1 |
| 9212 | lleva | 1 |
| 9213 | llegaron | 1 |
| 9214 | llegará | 1 |
| 9215 | llegamos | 1 |
| 9216 | llaneza | 1 |
| 9217 | llana | 1 |
| 9218 | llamé | 1 |
| 9219 | llame | 1 |
| 9220 | llamado | 1 |
| 9221 | llamaba | 1 |
| 9222 | liviano | 1 |
| 9223 | litigante | 1 |
| 9224 | literato | 1 |
| 9225 | listillo | 1 |
| 9226 | listar | 1 |
| 9227 | listado | 1 |
| 9228 | liso | 1 |
| 9229 | líricamente | 1 |
| 9230 | liquen | 1 |
| 9231 | lío | 1 |
| 9232 | linfa | 1 |
| 9233 | lindoro | 1 |
| 9234 | limítrofe | 1 |
| 9235 | limitado | 1 |
| 9236 | limbo | 1 |
| 9237 | ligereza | 1 |
| 9238 | ligera | 1 |
| 9239 | ligadura | 1 |
| 9240 | lidiar | 1 |
| 9241 | librepensamiento | 1 |
| 9242 | libraco | 1 |
| 9243 | libra | 1 |
| 9244 | libelo | 1 |
| 9245 | levantisco | 1 |
| 9246 | levántate | 1 |
| 9247 | leva | 1 |
| 9248 | letargo | 1 |
| 9249 | letanía | 1 |
| 9250 | lesionar | 1 |
| 9251 | lesión | 1 |
| 9252 | lesbos | 1 |
| 9253 | les | 1 |
| 9254 | leproso | 1 |
| 9255 | leonor | 1 |
| 9256 | lenteja | 1 |
| 9257 | lenidad | 1 |
| 9258 | lenclós | 1 |
| 9259 | lema | 1 |
| 9260 | legislación | 1 |
| 9261 | legendario | 1 |
| 9262 | legar | 1 |
| 9263 | legalmente | 1 |
| 9264 | lechuga | 1 |
| 9265 | lebrun | 1 |
| 9266 | leal | 1 |
| 9267 | laxitud | 1 |
| 9268 | laurent | 1 |
| 9269 | latorre | 1 |
| 9270 | lastimoso | 1 |
| 9271 | lastimero | 1 |
| 9272 | lasciami | 1 |
| 9273 | larguísimo | 1 |
| 9274 | largos | 1 |
| 9275 | largamente | 1 |
| 9276 | lapsus | 1 |
| 9277 | languidecer | 1 |
| 9278 | lánguidamente | 1 |
| 9279 | landó | 1 |
| 9280 | lanchar | 1 |
| 9281 | lancha | 1 |
| 9282 | lanas | 1 |
| 9283 | lampiño | 1 |
| 9284 | lamparilla | 1 |
| 9285 | laminar | 1 |
| 9286 | lamentable | 1 |
| 9287 | lamego | 1 |
| 9288 | lamartine | 1 |
| 9289 | lagarto | 1 |
| 9290 | lagar | 1 |
| 9291 | lacrimoso | 1 |
| 9292 | labriego | 1 |
| 9293 | labranza | 1 |
| 9294 | laborioso | 1 |
| 9295 | laborar | 1 |
| 9296 | laberinto | 1 |
| 9297 | l | 1 |
| 9298 | kock | 1 |
| 9299 | justillo | 1 |
| 9300 | justificar | 1 |
| 9301 | justificable | 1 |
| 9302 | justa | 1 |
| 9303 | jurídico | 1 |
| 9304 | juremos | 1 |
| 9305 | juntura | 1 |
| 9306 | junco | 1 |
| 9307 | juguetón | 1 |
| 9308 | jugo | 1 |
| 9309 | judit | 1 |
| 9310 | jubileo | 1 |
| 9311 | joyero | 1 |
| 9312 | jovialidad | 1 |
| 9313 | jovellanos | 1 |
| 9314 | jota | 1 |
| 9315 | jorobar | 1 |
| 9316 | jornalero | 1 |
| 9317 | jornal | 1 |
| 9318 | jorge | 1 |
| 9319 | jónico | 1 |
| 9320 | jofaina | 1 |
| 9321 | jocoso | 1 |
| 9322 | jinojo | 1 |
| 9323 | jícara | 1 |
| 9324 | jesuitismo | 1 |
| 9325 | jesuítico | 1 |
| 9326 | jerusalén | 1 |
| 9327 | jerusalem | 1 |
| 9328 | jeroma | 1 |
| 9329 | jericó | 1 |
| 9330 | jerga | 1 |
| 9331 | jeremías | 1 |
| 9332 | jerárquico | 1 |
| 9333 | jehová | 1 |
| 9334 | je | 1 |
| 9335 | jazmín | 1 |
| 9336 | jardinera | 1 |
| 9337 | jarana | 1 |
| 9338 | japón | 1 |
| 9339 | jaime | 1 |
| 9340 | jaco | 1 |
| 9341 | jaccoud | 1 |
| 9342 | jacas | 1 |
| 9343 | j | 1 |
| 9344 | ix | 1 |
| 9345 | iv | 1 |
| 9346 | ítem | 1 |
| 9347 | israelita | 1 |
| 9348 | israel | 1 |
| 9349 | islote | 1 |
| 9350 | isis | 1 |
| 9351 | irritarse | 1 |
| 9352 | irritación | 1 |
| 9353 | irritabilidad | 1 |
| 9354 | irrisión | 1 |
| 9355 | irresponsabilidad | 1 |
| 9356 | irremisiblemente | 1 |
| 9357 | irregularidad | 1 |
| 9358 | irreflexivamente | 1 |
| 9359 | irradiar | 1 |
| 9360 | ironías | 1 |
| 9361 | irisar | 1 |
| 9362 | iria | 1 |
| 9363 | iremos | 1 |
| 9364 | iré | 1 |
| 9365 | irá | 1 |
| 9366 | invulnerable | 1 |
| 9367 | involucrar | 1 |
| 9368 | investigar | 1 |
| 9369 | invertir | 1 |
| 9370 | invernante | 1 |
| 9371 | invernadero | 1 |
| 9372 | invernáculo | 1 |
| 9373 | inventario | 1 |
| 9374 | invariablemente | 1 |
| 9375 | inusitado | 1 |
| 9376 | intrincado | 1 |
| 9377 | intrigante | 1 |
| 9378 | intrépido | 1 |
| 9379 | intransigente | 1 |
| 9380 | intestinal | 1 |
| 9381 | interrogar | 1 |
| 9382 | interrogante | 1 |
| 9383 | intérprete | 1 |
| 9384 | interpretación | 1 |
| 9385 | interponer | 1 |
| 9386 | interno | 1 |
| 9387 | intermitente | 1 |
| 9388 | interjección | 1 |
| 9389 | interioridad | 1 |
| 9390 | interino | 1 |
| 9391 | interinamente | 1 |
| 9392 | intentona | 1 |
| 9393 | intensamente | 1 |
| 9394 | intendente | 1 |
| 9395 | íntegro | 1 |
| 9396 | integrar | 1 |
| 9397 | integrante | 1 |
| 9398 | integral | 1 |
| 9399 | intacto | 1 |
| 9400 | insurrecto | 1 |
| 9401 | insulsez | 1 |
| 9402 | instrumentista | 1 |
| 9403 | instrumentar | 1 |
| 9404 | instruido | 1 |
| 9405 | instituto | 1 |
| 9406 | instigar | 1 |
| 9407 | instar | 1 |
| 9408 | instancia | 1 |
| 9409 | insólito | 1 |
| 9410 | insolenta | 1 |
| 9411 | insinuó | 1 |
| 9412 | insignificancia | 1 |
| 9413 | insidioso | 1 |
| 9414 | inservible | 1 |
| 9415 | insertar | 1 |
| 9416 | insensato | 1 |
| 9417 | inquisición | 1 |
| 9418 | inquirir | 1 |
| 9419 | inquilino | 1 |
| 9420 | inoportunamente | 1 |
| 9421 | inopinado | 1 |
| 9422 | inocentada | 1 |
| 9423 | innumerable | 1 |
| 9424 | innovador | 1 |
| 9425 | innovación | 1 |
| 9426 | innominado | 1 |
| 9427 | innato | 1 |
| 9428 | inmovilidad | 1 |
| 9429 | inmoralidad | 1 |
| 9430 | inmodestia | 1 |
| 9431 | inmediaciones | 1 |
| 9432 | inmaculada | 1 |
| 9433 | injurioso | 1 |
| 9434 | injerencia | 1 |
| 9435 | iniciación | 1 |
| 9436 | ingreso | 1 |
| 9437 | ingresar | 1 |
| 9438 | ingenuidad | 1 |
| 9439 | ingenuamente | 1 |
| 9440 | infructuoso | 1 |
| 9441 | infringir | 1 |
| 9442 | infraganti | 1 |
| 9443 | infracción | 1 |
| 9444 | inflexión | 1 |
| 9445 | inflamable | 1 |
| 9446 | infecundo | 1 |
| 9447 | infausto | 1 |
| 9448 | infatigable | 1 |
| 9449 | infante | 1 |
| 9450 | infamatorio | 1 |
| 9451 | inextinguible | 1 |
| 9452 | inexplicable | 1 |
| 9453 | inescrutable | 1 |
| 9454 | inequívoco | 1 |
| 9455 | ineludible | 1 |
| 9456 | industriar | 1 |
| 9457 | indumentario | 1 |
| 9458 | indómito | 1 |
| 9459 | indomable | 1 |
| 9460 | indisciplinar | 1 |
| 9461 | indirecto | 1 |
| 9462 | indino | 1 |
| 9463 | indignamente | 1 |
| 9464 | indígena | 1 |
| 9465 | indicó | 1 |
| 9466 | indicado | 1 |
| 9467 | indescifrable | 1 |
| 9468 | indemnización | 1 |
| 9469 | indefinido | 1 |
| 9470 | indefenso | 1 |
| 9471 | indeciso | 1 |
| 9472 | indecible | 1 |
| 9473 | indagar | 1 |
| 9474 | incuria | 1 |
| 9475 | incumbencia | 1 |
| 9476 | inculcar | 1 |
| 9477 | increíble | 1 |
| 9478 | incredulidad | 1 |
| 9479 | incorruptible | 1 |
| 9480 | incorregible | 1 |
| 9481 | inconveniencia | 1 |
| 9482 | incontrastable | 1 |
| 9483 | inconstancia | 1 |
| 9484 | inconsolable | 1 |
| 9485 | inconexo | 1 |
| 9486 | incompleto | 1 |
| 9487 | incompatibilidad | 1 |
| 9488 | incomparablemente | 1 |
| 9489 | incombustible | 1 |
| 9490 | incoherencia | 1 |
| 9491 | inciso | 1 |
| 9492 | incendio | 1 |
| 9493 | incendiar | 1 |
| 9494 | incauto | 1 |
| 9495 | incautar | 1 |
| 9496 | incasable | 1 |
| 9497 | incalculable | 1 |
| 9498 | inarticulado | 1 |
| 9499 | inarco | 1 |
| 9500 | inapreciable | 1 |
| 9501 | inapetencia | 1 |
| 9502 | inanimado | 1 |
| 9503 | inanición | 1 |
| 9504 | inalienable | 1 |
| 9505 | inaguantable | 1 |
| 9506 | inadvertencia | 1 |
| 9507 | inacabable | 1 |
| 9508 | in | 1 |
| 9509 | imputar | 1 |
| 9510 | impune | 1 |
| 9511 | improvisación | 1 |
| 9512 | impropiamente | 1 |
| 9513 | improperio | 1 |
| 9514 | improper | 1 |
| 9515 | ímprobo | 1 |
| 9516 | imprimir | 1 |
| 9517 | imprescindible | 1 |
| 9518 | imprentar | 1 |
| 9519 | impregnar | 1 |
| 9520 | imprecar | 1 |
| 9521 | imprecación | 1 |
| 9522 | impotente | 1 |
| 9523 | impotencia | 1 |
| 9524 | impostura | 1 |
| 9525 | imposibilidad | 1 |
| 9526 | importantísimo | 1 |
| 9527 | importador | 1 |
| 9528 | implorar | 1 |
| 9529 | impermeable | 1 |
| 9530 | impericia | 1 |
| 9531 | imperial | 1 |
| 9532 | imperceptible | 1 |
| 9533 | imperativo | 1 |
| 9534 | imperar | 1 |
| 9535 | impecable | 1 |
| 9536 | imbuir | 1 |
| 9537 | imbécil | 1 |
| 9538 | imantar | 1 |
| 9539 | imagínole | 1 |
| 9540 | imaginativo | 1 |
| 9541 | imaginaria | 1 |
| 9542 | ilusorio | 1 |
| 9543 | iluso | 1 |
| 9544 | ilusionar | 1 |
| 9545 | iluminado | 1 |
| 9546 | ilmo | 1 |
| 9547 | iliterato | 1 |
| 9548 | ilíada | 1 |
| 9549 | ilegible | 1 |
| 9550 | ilegal | 1 |
| 9551 | iii | 1 |
| 9552 | ignoraba | 1 |
| 9553 | idilio | 1 |
| 9554 | idealizar | 1 |
| 9555 | ictericia | 1 |
| 9556 | ibérico | 1 |
| 9557 | iba | 1 |
| 9558 | huyo | 1 |
| 9559 | hurgar | 1 |
| 9560 | humorado | 1 |
| 9561 | humíllate | 1 |
| 9562 | humillante | 1 |
| 9563 | humeante | 1 |
| 9564 | humanizar | 1 |
| 9565 | humanitario | 1 |
| 9566 | huiría | 1 |
| 9567 | huiré | 1 |
| 9568 | hugonotes | 1 |
| 9569 | hugo | 1 |
| 9570 | hueste | 1 |
| 9571 | huesca | 1 |
| 9572 | hubo | 1 |
| 9573 | hoz | 1 |
| 9574 | hostilidad | 1 |
| 9575 | hospitalidad | 1 |
| 9576 | hospicio | 1 |
| 9577 | hospiciano | 1 |
| 9578 | horticultura | 1 |
| 9579 | hortelano | 1 |
| 9580 | horriblemente | 1 |
| 9581 | hormigueo | 1 |
| 9582 | horchatería | 1 |
| 9583 | horchata | 1 |
| 9584 | horas | 1 |
| 9585 | horadar | 1 |
| 9586 | honroso | 1 |
| 9587 | honradamente | 1 |
| 9588 | honores | 1 |
| 9589 | honorario | 1 |
| 9590 | honni | 1 |
| 9591 | honestidad | 1 |
| 9592 | honestamente | 1 |
| 9593 | hondura | 1 |
| 9594 | hondamente | 1 |
| 9595 | homo | 1 |
| 9596 | homero | 1 |
| 9597 | hombrear | 1 |
| 9598 | hollar | 1 |
| 9599 | holgazanería | 1 |
| 9600 | holgazán | 1 |
| 9601 | holgado | 1 |
| 9602 | holgadamente | 1 |
| 9603 | holanda | 1 |
| 9604 | hocico | 1 |
| 9605 | hita | 1 |
| 9606 | histerismo | 1 |
| 9607 | histérico | 1 |
| 9608 | hipotético | 1 |
| 9609 | hipotérmico | 1 |
| 9610 | hipotecar | 1 |
| 9611 | hipopótamo | 1 |
| 9612 | hipógrifo | 1 |
| 9613 | hipódromo | 1 |
| 9614 | hiperbólicamente | 1 |
| 9615 | hinojos | 1 |
| 9616 | hinchazón | 1 |
| 9617 | hinchado | 1 |
| 9618 | hincar | 1 |
| 9619 | hijuelo | 1 |
| 9620 | hijos | 1 |
| 9621 | hijita | 1 |
| 9622 | higuera | 1 |
| 9623 | hígado | 1 |
| 9624 | hidra | 1 |
| 9625 | hidalgo | 1 |
| 9626 | hicieron | 1 |
| 9627 | heterogéneo | 1 |
| 9628 | hervir | 1 |
| 9629 | herreros | 1 |
| 9630 | herradura | 1 |
| 9631 | heroísmo | 1 |
| 9632 | heroicidad | 1 |
| 9633 | herodías | 1 |
| 9634 | heresiarca | 1 |
| 9635 | heredad | 1 |
| 9636 | herborizar | 1 |
| 9637 | heráldica | 1 |
| 9638 | hepatitis | 1 |
| 9639 | henao | 1 |
| 9640 | helada | 1 |
| 9641 | hegemonía | 1 |
| 9642 | hedor | 1 |
| 9643 | hediondo | 1 |
| 9644 | hechura | 1 |
| 9645 | hechos | 1 |
| 9646 | haraposo | 1 |
| 9647 | hará | 1 |
| 9648 | hamlet | 1 |
| 9649 | hame | 1 |
| 9650 | hamaca | 1 |
| 9651 | halagüeño | 1 |
| 9652 | hagámonos | 1 |
| 9653 | haga | 1 |
| 9654 | hacía | 1 |
| 9655 | hachón | 1 |
| 9656 | hacerse | 1 |
| 9657 | hacerla | 1 |
| 9658 | habrán | 1 |
| 9659 | habrá | 1 |
| 9660 | habló | 1 |
| 9661 | hablo | 1 |
| 9662 | hablemos | 1 |
| 9663 | hablé | 1 |
| 9664 | hable | 1 |
| 9665 | hablas | 1 |
| 9666 | hablarme | 1 |
| 9667 | hablarle | 1 |
| 9668 | habitado | 1 |
| 9669 | hábilmente | 1 |
| 9670 | habéis | 1 |
| 9671 | haba | 1 |
| 9672 | gutierre | 1 |
| 9673 | gustoso | 1 |
| 9674 | gustazo | 1 |
| 9675 | guillotinar | 1 |
| 9676 | guillotina | 1 |
| 9677 | guerrero | 1 |
| 9678 | guedeja | 1 |
| 9679 | guasa | 1 |
| 9680 | guarecer | 1 |
| 9681 | guardilla | 1 |
| 9682 | guarden | 1 |
| 9683 | guardador | 1 |
| 9684 | guapetón | 1 |
| 9685 | guadalquivir | 1 |
| 9686 | gruyer | 1 |
| 9687 | grupa | 1 |
| 9688 | grijalte | 1 |
| 9689 | grifo | 1 |
| 9690 | grieta | 1 |
| 9691 | grecia | 1 |
| 9692 | gravísimo | 1 |
| 9693 | gravemente | 1 |
| 9694 | grato | 1 |
| 9695 | gratis | 1 |
| 9696 | grata | 1 |
| 9697 | granuja | 1 |
| 9698 | granizada | 1 |
| 9699 | granear | 1 |
| 9700 | grandilocuente | 1 |
| 9701 | granar | 1 |
| 9702 | gráfico | 1 |
| 9703 | graciosamente | 1 |
| 9704 | grabado | 1 |
| 9705 | gozo | 1 |
| 9706 | gozando | 1 |
| 9707 | gotear | 1 |
| 9708 | gorjeo | 1 |
| 9709 | gorjear | 1 |
| 9710 | gordas | 1 |
| 9711 | gonzález | 1 |
| 9712 | gongorino | 1 |
| 9713 | góngora | 1 |
| 9714 | góndola | 1 |
| 9715 | golondrina | 1 |
| 9716 | gollería | 1 |
| 9717 | golfo | 1 |
| 9718 | gobernadora | 1 |
| 9719 | gloriosamente | 1 |
| 9720 | giro | 1 |
| 9721 | giraldi | 1 |
| 9722 | gira | 1 |
| 9723 | gimnástico | 1 |
| 9724 | gimnasio | 1 |
| 9725 | gimió | 1 |
| 9726 | gil | 1 |
| 9727 | gestación | 1 |
| 9728 | gerundio | 1 |
| 9729 | geológico | 1 |
| 9730 | geográfico | 1 |
| 9731 | genuinamente | 1 |
| 9732 | gentío | 1 |
| 9733 | gentileza | 1 |
| 9734 | genil | 1 |
| 9735 | generoso | 1 |
| 9736 | generosidad | 1 |
| 9737 | gayo | 1 |
| 9738 | gayarre | 1 |
| 9739 | gauthier | 1 |
| 9740 | gatito | 1 |
| 9741 | gatillar | 1 |
| 9742 | gatazo | 1 |
| 9743 | gatas | 1 |
| 9744 | gastroenteritis | 1 |
| 9745 | gástrico | 1 |
| 9746 | gaseoso | 1 |
| 9747 | garzo | 1 |
| 9748 | garden | 1 |
| 9749 | garcilaso | 1 |
| 9750 | garcía | 1 |
| 9751 | garabato | 1 |
| 9752 | ganzúa | 1 |
| 9753 | ganas | 1 |
| 9754 | ganancial | 1 |
| 9755 | gamo | 1 |
| 9756 | galope | 1 |
| 9757 | gallinero | 1 |
| 9758 | gallardete | 1 |
| 9759 | gallardamente | 1 |
| 9760 | galileo | 1 |
| 9761 | galicismo | 1 |
| 9762 | galgo | 1 |
| 9763 | galera | 1 |
| 9764 | galdós | 1 |
| 9765 | galardonar | 1 |
| 9766 | galantear | 1 |
| 9767 | gaitero | 1 |
| 9768 | gacho | 1 |
| 9769 | futura | 1 |
| 9770 | fútil | 1 |
| 9771 | furibundo | 1 |
| 9772 | fungoso | 1 |
| 9773 | funesto | 1 |
| 9774 | fundición | 1 |
| 9775 | fundamentar | 1 |
| 9776 | funcionario | 1 |
| 9777 | fumador | 1 |
| 9778 | fulminar | 1 |
| 9779 | fulminante | 1 |
| 9780 | fulgor | 1 |
| 9781 | fulanito | 1 |
| 9782 | fulanita | 1 |
| 9783 | fuguillas | 1 |
| 9784 | fuga | 1 |
| 9785 | fuese | 1 |
| 9786 | fuertemente | 1 |
| 9787 | fuer | 1 |
| 9788 | fuelle | 1 |
| 9789 | fue | 1 |
| 9790 | frutal | 1 |
| 9791 | frustrar | 1 |
| 9792 | fruncir | 1 |
| 9793 | fruela | 1 |
| 9794 | frontón | 1 |
| 9795 | frontispicio | 1 |
| 9796 | frontero | 1 |
| 9797 | frontal | 1 |
| 9798 | frondoso | 1 |
| 9799 | frivolidad | 1 |
| 9800 | frito | 1 |
| 9801 | frigorífico | 1 |
| 9802 | fríamente | 1 |
| 9803 | fría | 1 |
| 9804 | freno | 1 |
| 9805 | frenéticos | 1 |
| 9806 | frenar | 1 |
| 9807 | fraternizar | 1 |
| 9808 | fraternal | 1 |
| 9809 | frascueeeelo | 1 |
| 9810 | francklin | 1 |
| 9811 | franciscos | 1 |
| 9812 | franciscas | 1 |
| 9813 | francesa | 1 |
| 9814 | fraigerundio | 1 |
| 9815 | fr | 1 |
| 9816 | fosforera | 1 |
| 9817 | fosco | 1 |
| 9818 | forzado | 1 |
| 9819 | fortuito | 1 |
| 9820 | fortalecer | 1 |
| 9821 | foro | 1 |
| 9822 | fornos | 1 |
| 9823 | formulismo | 1 |
| 9824 | formular | 1 |
| 9825 | formado | 1 |
| 9826 | forjar | 1 |
| 9827 | forajido | 1 |
| 9828 | fontanero | 1 |
| 9829 | follar | 1 |
| 9830 | fogonazo | 1 |
| 9831 | foco | 1 |
| 9832 | fluir | 1 |
| 9833 | floricultor | 1 |
| 9834 | flórez | 1 |
| 9835 | flores | 1 |
| 9836 | florero | 1 |
| 9837 | flema | 1 |
| 9838 | fleco | 1 |
| 9839 | flammarión | 1 |
| 9840 | flamígero | 1 |
| 9841 | flagrante | 1 |
| 9842 | fisiólogo | 1 |
| 9843 | fisiológicamente | 1 |
| 9844 | fiscalía | 1 |
| 9845 | firmeza | 1 |
| 9846 | firmaba | 1 |
| 9847 | finge | 1 |
| 9848 | fineza | 1 |
| 9849 | fincar | 1 |
| 9850 | finca | 1 |
| 9851 | filtro | 1 |
| 9852 | filtración | 1 |
| 9853 | filón | 1 |
| 9854 | filius | 1 |
| 9855 | filis | 1 |
| 9856 | filete | 1 |
| 9857 | filarmónico | 1 |
| 9858 | filantropía | 1 |
| 9859 | fijamente | 1 |
| 9860 | figurilla | 1 |
| 9861 | figúrese | 1 |
| 9862 | fierabrás | 1 |
| 9863 | fielding | 1 |
| 9864 | fidelísimo | 1 |
| 9865 | fichar | 1 |
| 9866 | feudalismo | 1 |
| 9867 | fétido | 1 |
| 9868 | fervoroso | 1 |
| 9869 | fertilidad | 1 |
| 9870 | fértil | 1 |
| 9871 | feroz | 1 |
| 9872 | fermento | 1 |
| 9873 | fermentar | 1 |
| 9874 | felpudo | 1 |
| 9875 | felices | 1 |
| 9876 | feijóo | 1 |
| 9877 | federación | 1 |
| 9878 | fecundo | 1 |
| 9879 | fecundar | 1 |
| 9880 | febrero | 1 |
| 9881 | faz | 1 |
| 9882 | fatalista | 1 |
| 9883 | fastidioso | 1 |
| 9884 | fastidiar | 1 |
| 9885 | farnesios | 1 |
| 9886 | faringe | 1 |
| 9887 | faraones | 1 |
| 9888 | fantásticamente | 1 |
| 9889 | fantasear | 1 |
| 9890 | fanfarrón | 1 |
| 9891 | fanal | 1 |
| 9892 | famosísimo | 1 |
| 9893 | familiaridad | 1 |
| 9894 | faltriquera | 1 |
| 9895 | fallo | 1 |
| 9896 | fallido | 1 |
| 9897 | fallecer | 1 |
| 9898 | fallar | 1 |
| 9899 | falange | 1 |
| 9900 | faisán | 1 |
| 9901 | facistol | 1 |
| 9902 | facilidad | 1 |
| 9903 | facial | 1 |
| 9904 | fachenda | 1 |
| 9905 | fábula | 1 |
| 9906 | fabricante | 1 |
| 9907 | fabiolita | 1 |
| 9908 | f | 1 |
| 9909 | extremidad | 1 |
| 9910 | extremeño | 1 |
| 9911 | extremado | 1 |
| 9912 | extraer | 1 |
| 9913 | extenuado | 1 |
| 9914 | extendido | 1 |
| 9915 | extático | 1 |
| 9916 | expropiación | 1 |
| 9917 | exprofeso | 1 |
| 9918 | exprimir | 1 |
| 9919 | expreso | 1 |
| 9920 | expresivo | 1 |
| 9921 | expositio | 1 |
| 9922 | exportar | 1 |
| 9923 | explotación | 1 |
| 9924 | explosivo | 1 |
| 9925 | explosión | 1 |
| 9926 | explorar | 1 |
| 9927 | exploración | 1 |
| 9928 | expirar | 1 |
| 9929 | expeditar | 1 |
| 9930 | expedientar | 1 |
| 9931 | expedicionario | 1 |
| 9932 | expectación | 1 |
| 9933 | existente | 1 |
| 9934 | exíjase | 1 |
| 9935 | exiguo | 1 |
| 9936 | exhausto | 1 |
| 9937 | exhalar | 1 |
| 9938 | exentar | 1 |
| 9939 | exegético | 1 |
| 9940 | excusa | 1 |
| 9941 | excursionar | 1 |
| 9942 | exclamación | 1 |
| 9943 | excesivamente | 1 |
| 9944 | exceptuar | 1 |
| 9945 | exceder | 1 |
| 9946 | excavación | 1 |
| 9947 | evidentemente | 1 |
| 9948 | evangelii | 1 |
| 9949 | eucalipto | 1 |
| 9950 | etrusco | 1 |
| 9951 | ética | 1 |
| 9952 | eternizar | 1 |
| 9953 | estupro | 1 |
| 9954 | estupor | 1 |
| 9955 | estupendo | 1 |
| 9956 | estupefacción | 1 |
| 9957 | estudioso | 1 |
| 9958 | estudia | 1 |
| 9959 | estuche | 1 |
| 9960 | estricto | 1 |
| 9961 | estribor | 1 |
| 9962 | estrepitosos | 1 |
| 9963 | estremecimiento | 1 |
| 9964 | estrangulado | 1 |
| 9965 | estrangulación | 1 |
| 9966 | estragado | 1 |
| 9967 | estornino | 1 |
| 9968 | estorbaré | 1 |
| 9969 | estola | 1 |
| 9970 | estofa | 1 |
| 9971 | estocada | 1 |
| 9972 | estirpe | 1 |
| 9973 | estirado | 1 |
| 9974 | estimular | 1 |
| 9975 | estilita | 1 |
| 9976 | estética | 1 |
| 9977 | estereotipar | 1 |
| 9978 | esterar | 1 |
| 9979 | ester | 1 |
| 9980 | estepa | 1 |
| 9981 | esté | 1 |
| 9982 | estatuto | 1 |
| 9983 | estate | 1 |
| 9984 | estarían | 1 |
| 9985 | estará | 1 |
| 9986 | estaño | 1 |
| 9987 | estañar | 1 |
| 9988 | estanquero | 1 |
| 9989 | estanque | 1 |
| 9990 | estancamiento | 1 |
| 9991 | estancado | 1 |
| 9992 | estampilla | 1 |
| 9993 | estaciones | 1 |
| 9994 | estacar | 1 |
| 9995 | estable | 1 |
| 9996 | esquilache | 1 |
| 9997 | esquila | 1 |
| 9998 | esquela | 1 |
| 9999 | espuela | 1 |
| 10000 | esponjoso | 1 |
| 10001 | espliego | 1 |
| 10002 | espíritus | 1 |
| 10003 | espirituoso | 1 |
| 10004 | espiritualista | 1 |
| 10005 | espino | 1 |
| 10006 | espinazo | 1 |
| 10007 | espigar | 1 |
| 10008 | espesura | 1 |
| 10009 | esperaría | 1 |
| 10010 | esperará | 1 |
| 10011 | espejismo | 1 |
| 10012 | especificar | 1 |
| 10013 | especialísimo | 1 |
| 10014 | espartero | 1 |
| 10015 | española | 1 |
| 10016 | espantajo | 1 |
| 10017 | espantadizo | 1 |
| 10018 | espaldera | 1 |
| 10019 | esotérico | 1 |
| 10020 | esos | 1 |
| 10021 | esmerado | 1 |
| 10022 | escupió | 1 |
| 10023 | escultórico | 1 |
| 10024 | escultor | 1 |
| 10025 | escuadrar | 1 |
| 10026 | escrupulosidad | 1 |
| 10027 | escrupulosamente | 1 |
| 10028 | escritura | 1 |
| 10029 | escribió | 1 |
| 10030 | escríbame | 1 |
| 10031 | escriba | 1 |
| 10032 | escozor | 1 |
| 10033 | escotillón | 1 |
| 10034 | escosura | 1 |
| 10035 | escoria | 1 |
| 10036 | escondrijo | 1 |
| 10037 | escondidos | 1 |
| 10038 | escombro | 1 |
| 10039 | escolta | 1 |
| 10040 | escolástica | 1 |
| 10041 | escogido | 1 |
| 10042 | esclarecer | 1 |
| 10043 | escepticismo | 1 |
| 10044 | escénico | 1 |
| 10045 | escayola | 1 |
| 10046 | escatimar | 1 |
| 10047 | escarnecer | 1 |
| 10048 | escarmentar | 1 |
| 10049 | escapulario | 1 |
| 10050 | escandalizarse | 1 |
| 10051 | escamar | 1 |
| 10052 | escamandro | 1 |
| 10053 | escalpelo | 1 |
| 10054 | escalón | 1 |
| 10055 | escalofriar | 1 |
| 10056 | escabroso | 1 |
| 10057 | eruditamente | 1 |
| 10058 | erudición | 1 |
| 10059 | eructar | 1 |
| 10060 | erróneo | 1 |
| 10061 | errante | 1 |
| 10062 | erradamente | 1 |
| 10063 | erotismo | 1 |
| 10064 | ermitaño | 1 |
| 10065 | erizado | 1 |
| 10066 | erario | 1 |
| 10067 | equívoco | 1 |
| 10068 | equivocado | 1 |
| 10069 | equivaler | 1 |
| 10070 | equitativo | 1 |
| 10071 | equinoccio | 1 |
| 10072 | equilibrar | 1 |
| 10073 | epopeya | 1 |
| 10074 | episcopal | 1 |
| 10075 | epílogo | 1 |
| 10076 | epigramático | 1 |
| 10077 | epidemia | 1 |
| 10078 | epicuro | 1 |
| 10079 | epicureísmo | 1 |
| 10080 | epiceno | 1 |
| 10081 | envuelto | 1 |
| 10082 | envoltorio | 1 |
| 10083 | enviar | 1 |
| 10084 | enviado | 1 |
| 10085 | envejecido | 1 |
| 10086 | envanecer | 1 |
| 10087 | enumerar | 1 |
| 10088 | entusiasta | 1 |
| 10089 | entumecimiento | 1 |
| 10090 | entrometer | 1 |
| 10091 | entreverar | 1 |
| 10092 | entretenimiento | 1 |
| 10093 | entresuelo | 1 |
| 10094 | entregarme | 1 |
| 10095 | entraré | 1 |
| 10096 | entra | 1 |
| 10097 | entorpecimiento | 1 |
| 10098 | entonar | 1 |
| 10099 | entonado | 1 |
| 10100 | entomólogo | 1 |
| 10101 | entidad | 1 |
| 10102 | entibiar | 1 |
| 10103 | enterrador | 1 |
| 10104 | enterado | 1 |
| 10105 | entendimiento | 1 |
| 10106 | entendido | 1 |
| 10107 | entendedor | 1 |
| 10108 | entendámonos | 1 |
| 10109 | ente | 1 |
| 10110 | entallar | 1 |
| 10111 | ensuciar | 1 |
| 10112 | ensortijar | 1 |
| 10113 | ensoñador | 1 |
| 10114 | ensoñación | 1 |
| 10115 | ensartar | 1 |
| 10116 | ensanche | 1 |
| 10117 | enrevesado | 1 |
| 10118 | enramar | 1 |
| 10119 | enojar | 1 |
| 10120 | enmudecer | 1 |
| 10121 | enmendar | 1 |
| 10122 | enmascarar | 1 |
| 10123 | enlutado | 1 |
| 10124 | enloquecer | 1 |
| 10125 | enjuto | 1 |
| 10126 | enjambre | 1 |
| 10127 | enigma | 1 |
| 10128 | enhestar | 1 |
| 10129 | engolfar | 1 |
| 10130 | englobar | 1 |
| 10131 | engalanar | 1 |
| 10132 | enfurecer | 1 |
| 10133 | enfundar | 1 |
| 10134 | enfrenar | 1 |
| 10135 | enfilar | 1 |
| 10136 | enfermero | 1 |
| 10137 | enervar | 1 |
| 10138 | enemistad | 1 |
| 10139 | enderezar | 1 |
| 10140 | endemoniado | 1 |
| 10141 | endémico | 1 |
| 10142 | encorvada | 1 |
| 10143 | encopetar | 1 |
| 10144 | encontrado | 1 |
| 10145 | encontrábase | 1 |
| 10146 | encomienda | 1 |
| 10147 | encogimiento | 1 |
| 10148 | encogido | 1 |
| 10149 | encinta | 1 |
| 10150 | enciende | 1 |
| 10151 | encienda | 1 |
| 10152 | enchufar | 1 |
| 10153 | encharcado | 1 |
| 10154 | encerar | 1 |
| 10155 | encauzar | 1 |
| 10156 | encarnizado | 1 |
| 10157 | encarnación | 1 |
| 10158 | encarecer | 1 |
| 10159 | encarcelar | 1 |
| 10160 | encapotado | 1 |
| 10161 | encantador | 1 |
| 10162 | encantado | 1 |
| 10163 | enano | 1 |
| 10164 | enamoramiento | 1 |
| 10165 | enaltecer | 1 |
| 10166 | enajenación | 1 |
| 10167 | emulación | 1 |
| 10168 | empujón | 1 |
| 10169 | empuje | 1 |
| 10170 | emprendedor | 1 |
| 10171 | empleara | 1 |
| 10172 | emplazamiento | 1 |
| 10173 | emplasto | 1 |
| 10174 | empinar | 1 |
| 10175 | empinado | 1 |
| 10176 | empieza | 1 |
| 10177 | empezó | 1 |
| 10178 | emperifollar | 1 |
| 10179 | emperador | 1 |
| 10180 | empequeñecer | 1 |
| 10181 | empeorar | 1 |
| 10182 | empeñarse | 1 |
| 10183 | empedernir | 1 |
| 10184 | emparejarse | 1 |
| 10185 | emparedar | 1 |
| 10186 | emparedado | 1 |
| 10187 | empanar | 1 |
| 10188 | empanada | 1 |
| 10189 | empalmar | 1 |
| 10190 | empalagoso | 1 |
| 10191 | empadronar | 1 |
| 10192 | emocionar | 1 |
| 10193 | eminentemente | 1 |
| 10194 | emigró | 1 |
| 10195 | embuste | 1 |
| 10196 | embrutecimiento | 1 |
| 10197 | embrujar | 1 |
| 10198 | embrollo | 1 |
| 10199 | embrión | 1 |
| 10200 | embozado | 1 |
| 10201 | embotar | 1 |
| 10202 | emboscar | 1 |
| 10203 | embobar | 1 |
| 10204 | embellecer | 1 |
| 10205 | embeleso | 1 |
| 10206 | embebecer | 1 |
| 10207 | embarcar | 1 |
| 10208 | embajada | 1 |
| 10209 | emancipación | 1 |
| 10210 | eludir | 1 |
| 10211 | eloïm | 1 |
| 10212 | elevado | 1 |
| 10213 | elegantemente | 1 |
| 10214 | elefante | 1 |
| 10215 | elástico | 1 |
| 10216 | elaboración | 1 |
| 10217 | ejercitar | 1 |
| 10218 | ejecutor | 1 |
| 10219 | ejecutivo | 1 |
| 10220 | ejecución | 1 |
| 10221 | ego | 1 |
| 10222 | égloga | 1 |
| 10223 | egeria | 1 |
| 10224 | efusivo | 1 |
| 10225 | efluvio | 1 |
| 10226 | efímera | 1 |
| 10227 | efectivo | 1 |
| 10228 | eduardo | 1 |
| 10229 | edicto | 1 |
| 10230 | edgar | 1 |
| 10231 | ecuestre | 1 |
| 10232 | economizar | 1 |
| 10233 | economista | 1 |
| 10234 | economato | 1 |
| 10235 | eclipse | 1 |
| 10236 | échele | 1 |
| 10237 | echarla | 1 |
| 10238 | echada | 1 |
| 10239 | ebro | 1 |
| 10240 | ébano | 1 |
| 10241 | ebanista | 1 |
| 10242 | duración | 1 |
| 10243 | dupanloup | 1 |
| 10244 | dúo | 1 |
| 10245 | dumio | 1 |
| 10246 | dumas | 1 |
| 10247 | duerme | 1 |
| 10248 | dudó | 1 |
| 10249 | dúctil | 1 |
| 10250 | ducha | 1 |
| 10251 | dualista | 1 |
| 10252 | dramaturgo | 1 |
| 10253 | doy | 1 |
| 10254 | dovela | 1 |
| 10255 | dosis | 1 |
| 10256 | dorso | 1 |
| 10257 | dormitorio | 1 |
| 10258 | donoso | 1 |
| 10259 | donar | 1 |
| 10260 | dominus | 1 |
| 10261 | dómine | 1 |
| 10262 | domiciliar | 1 |
| 10263 | domesticar | 1 |
| 10264 | domar | 1 |
| 10265 | döllinger | 1 |
| 10266 | docente | 1 |
| 10267 | doblado | 1 |
| 10268 | divisible | 1 |
| 10269 | divina | 1 |
| 10270 | divertirme | 1 |
| 10271 | divertidísimo | 1 |
| 10272 | distributivo | 1 |
| 10273 | distribución | 1 |
| 10274 | distintivo | 1 |
| 10275 | distintamente | 1 |
| 10276 | distanciar | 1 |
| 10277 | displicencia | 1 |
| 10278 | disperso | 1 |
| 10279 | dispersión | 1 |
| 10280 | disparo | 1 |
| 10281 | disoluto | 1 |
| 10282 | dislocar | 1 |
| 10283 | dislocado | 1 |
| 10284 | dislate | 1 |
| 10285 | disipar | 1 |
| 10286 | disimulaba | 1 |
| 10287 | disimula | 1 |
| 10288 | disertar | 1 |
| 10289 | disculpas | 1 |
| 10290 | disculpable | 1 |
| 10291 | discretear | 1 |
| 10292 | disciplinario | 1 |
| 10293 | discernir | 1 |
| 10294 | dirían | 1 |
| 10295 | diretes | 1 |
| 10296 | diré | 1 |
| 10297 | diputación | 1 |
| 10298 | dionisíaco | 1 |
| 10299 | dintel | 1 |
| 10300 | dinastía | 1 |
| 10301 | dinamitar | 1 |
| 10302 | dimisionario | 1 |
| 10303 | diminuto | 1 |
| 10304 | dimes | 1 |
| 10305 | dilucidar | 1 |
| 10306 | dilatación | 1 |
| 10307 | díjolo | 1 |
| 10308 | dijeron | 1 |
| 10309 | dije | 1 |
| 10310 | dignificar | 1 |
| 10311 | dignatario | 1 |
| 10312 | dignamente | 1 |
| 10313 | digestivo | 1 |
| 10314 | digerir | 1 |
| 10315 | dígase | 1 |
| 10316 | díganme | 1 |
| 10317 | dígame | 1 |
| 10318 | dígalo | 1 |
| 10319 | difuntos | 1 |
| 10320 | dificilísimo | 1 |
| 10321 | diferenciar | 1 |
| 10322 | diezmo | 1 |
| 10323 | dieta | 1 |
| 10324 | diestra | 1 |
| 10325 | diecisiete | 1 |
| 10326 | dictatorial | 1 |
| 10327 | dictamen | 1 |
| 10328 | dictadura | 1 |
| 10329 | dickens | 1 |
| 10330 | dichas | 1 |
| 10331 | dicharachero | 1 |
| 10332 | dibujado | 1 |
| 10333 | días | 1 |
| 10334 | diapasón | 1 |
| 10335 | diana | 1 |
| 10336 | diáfano | 1 |
| 10337 | diácono | 1 |
| 10338 | diabluras | 1 |
| 10339 | diablos | 1 |
| 10340 | devastación | 1 |
| 10341 | devanadera | 1 |
| 10342 | deudo | 1 |
| 10343 | detonación | 1 |
| 10344 | determinación | 1 |
| 10345 | deteriorar | 1 |
| 10346 | detenidamente | 1 |
| 10347 | detalle | 1 |
| 10348 | desvivir | 1 |
| 10349 | desviar | 1 |
| 10350 | desventurado | 1 |
| 10351 | desvencijar | 1 |
| 10352 | desvelo | 1 |
| 10353 | desvelar | 1 |
| 10354 | desvarío | 1 |
| 10355 | desvanecimiento | 1 |
| 10356 | desvanecido | 1 |
| 10357 | desvalijar | 1 |
| 10358 | desuso | 1 |
| 10359 | destrucción | 1 |
| 10360 | destrozado | 1 |
| 10361 | destreza | 1 |
| 10362 | desteñir | 1 |
| 10363 | destartalado | 1 |
| 10364 | destajo | 1 |
| 10365 | desquitar | 1 |
| 10366 | despuntar | 1 |
| 10367 | desprovisto | 1 |
| 10368 | despropósito | 1 |
| 10369 | desproporcionado | 1 |
| 10370 | desprestigio | 1 |
| 10371 | despreocupado | 1 |
| 10372 | despoblar | 1 |
| 10373 | desplegar | 1 |
| 10374 | despídame | 1 |
| 10375 | desperezar | 1 |
| 10376 | desperdicio | 1 |
| 10377 | despeñar | 1 |
| 10378 | despeluznar | 1 |
| 10379 | despejado | 1 |
| 10380 | despeinar | 1 |
| 10381 | despego | 1 |
| 10382 | despear | 1 |
| 10383 | despeado | 1 |
| 10384 | despavorido | 1 |
| 10385 | desparpajar | 1 |
| 10386 | despabilar | 1 |
| 10387 | desorientar | 1 |
| 10388 | desollar | 1 |
| 10389 | desolación | 1 |
| 10390 | desocupado | 1 |
| 10391 | desmesurar | 1 |
| 10392 | desmentir | 1 |
| 10393 | desmedido | 1 |
| 10394 | desmayado | 1 |
| 10395 | desmañado | 1 |
| 10396 | desmantelar | 1 |
| 10397 | desmán | 1 |
| 10398 | desleír | 1 |
| 10399 | desidia | 1 |
| 10400 | deshora | 1 |
| 10401 | deshonesto | 1 |
| 10402 | deshojar | 1 |
| 10403 | deshilachar | 1 |
| 10404 | desheredar | 1 |
| 10405 | desgarrador | 1 |
| 10406 | desgajar | 1 |
| 10407 | desfiladero | 1 |
| 10408 | desfigurar | 1 |
| 10409 | desfigurado | 1 |
| 10410 | desfavorable | 1 |
| 10411 | deseoso | 1 |
| 10412 | desenvoltura | 1 |
| 10413 | desenterrar | 1 |
| 10414 | desentender | 1 |
| 10415 | desenlazar | 1 |
| 10416 | desenfreno | 1 |
| 10417 | desenfadar | 1 |
| 10418 | desencanto | 1 |
| 10419 | desencajar | 1 |
| 10420 | desencadenar | 1 |
| 10421 | desembolso | 1 |
| 10422 | desembarco | 1 |
| 10423 | desecho | 1 |
| 10424 | desdoro | 1 |
| 10425 | desdentado | 1 |
| 10426 | desdecir | 1 |
| 10427 | descuide | 1 |
| 10428 | descubridor | 1 |
| 10429 | descuartizar | 1 |
| 10430 | descreimiento | 1 |
| 10431 | descotado | 1 |
| 10432 | descoser | 1 |
| 10433 | descontentar | 1 |
| 10434 | desconcierto | 1 |
| 10435 | descompasar | 1 |
| 10436 | descoco | 1 |
| 10437 | descenso | 1 |
| 10438 | descendimiento | 1 |
| 10439 | descastado | 1 |
| 10440 | descarado | 1 |
| 10441 | descaminado | 1 |
| 10442 | descalzas | 1 |
| 10443 | desbordar | 1 |
| 10444 | desbordado | 1 |
| 10445 | desazonar | 1 |
| 10446 | desayuno | 1 |
| 10447 | desatinar | 1 |
| 10448 | desasosiego | 1 |
| 10449 | desasir | 1 |
| 10450 | desarróllase | 1 |
| 10451 | desarrollado | 1 |
| 10452 | desarreglo | 1 |
| 10453 | desaprobación | 1 |
| 10454 | desapasionado | 1 |
| 10455 | desaparición | 1 |
| 10456 | desapacible | 1 |
| 10457 | desanimado | 1 |
| 10458 | desandar | 1 |
| 10459 | desamparado | 1 |
| 10460 | desaliño | 1 |
| 10461 | desalentar | 1 |
| 10462 | desalar | 1 |
| 10463 | desagradecido | 1 |
| 10464 | desacierto | 1 |
| 10465 | desabrochar | 1 |
| 10466 | desabrimiento | 1 |
| 10467 | derrotado | 1 |
| 10468 | derrota | 1 |
| 10469 | derrochar | 1 |
| 10470 | derrengar | 1 |
| 10471 | derrame | 1 |
| 10472 | derramamiento | 1 |
| 10473 | derivado | 1 |
| 10474 | derivación | 1 |
| 10475 | depositario | 1 |
| 10476 | dentera | 1 |
| 10477 | dentadura | 1 |
| 10478 | denso | 1 |
| 10479 | densidad | 1 |
| 10480 | demontre | 1 |
| 10481 | demoler | 1 |
| 10482 | demodoco | 1 |
| 10483 | demanda | 1 |
| 10484 | deleitábale | 1 |
| 10485 | delegar | 1 |
| 10486 | delegación | 1 |
| 10487 | delantera | 1 |
| 10488 | dejen | 1 |
| 10489 | déjeme | 1 |
| 10490 | dejaría | 1 |
| 10491 | dejará | 1 |
| 10492 | dejando | 1 |
| 10493 | déjale | 1 |
| 10494 | déjala | 1 |
| 10495 | deísmo | 1 |
| 10496 | degollado | 1 |
| 10497 | defraudar | 1 |
| 10498 | deforme | 1 |
| 10499 | definitivo | 1 |
| 10500 | definitivamente | 1 |
| 10501 | deficiencia | 1 |
| 10502 | defensivo | 1 |
| 10503 | deducir | 1 |
| 10504 | decorar | 1 |
| 10505 | declive | 1 |
| 10506 | declamador | 1 |
| 10507 | declamación | 1 |
| 10508 | decisión | 1 |
| 10509 | decirle | 1 |
| 10510 | decimal | 1 |
| 10511 | decentemente | 1 |
| 10512 | decantar | 1 |
| 10513 | decálogo | 1 |
| 10514 | decaído | 1 |
| 10515 | débilmente | 1 |
| 10516 | debilitar | 1 |
| 10517 | debatir | 1 |
| 10518 | dativo | 1 |
| 10519 | date | 1 |
| 10520 | datar | 1 |
| 10521 | darwin | 1 |
| 10522 | darro | 1 |
| 10523 | daría | 1 |
| 10524 | danzar | 1 |
| 10525 | dante | 1 |
| 10526 | dandy | 1 |
| 10527 | dan | 1 |
| 10528 | damisela | 1 |
| 10529 | dame | 1 |
| 10530 | dalila | 1 |
| 10531 | daga | 1 |
| 10532 | dadme | 1 |
| 10533 | daba | 1 |
| 10534 | cúspide | 1 |
| 10535 | curvo | 1 |
| 10536 | cursilón | 1 |
| 10537 | curita | 1 |
| 10538 | curiosón | 1 |
| 10539 | cúpula | 1 |
| 10540 | cuota | 1 |
| 10541 | cuneta | 1 |
| 10542 | cumplidamente | 1 |
| 10543 | cumpleaños | 1 |
| 10544 | culata | 1 |
| 10545 | cuestor | 1 |
| 10546 | cuesta | 1 |
| 10547 | cuerdamente | 1 |
| 10548 | cuchufleta | 1 |
| 10549 | cucharilla | 1 |
| 10550 | cucharada | 1 |
| 10551 | cubríale | 1 |
| 10552 | cubilete | 1 |
| 10553 | cúbico | 1 |
| 10554 | cuartucho | 1 |
| 10555 | cuartilla | 1 |
| 10556 | cuajar | 1 |
| 10557 | cuadricular | 1 |
| 10558 | crusología | 1 |
| 10559 | crudeza | 1 |
| 10560 | crucifixión | 1 |
| 10561 | cromático | 1 |
| 10562 | cristos | 1 |
| 10563 | cristóbal | 1 |
| 10564 | cristiana | 1 |
| 10565 | cristalería | 1 |
| 10566 | crispado | 1 |
| 10567 | crisol | 1 |
| 10568 | crisálida | 1 |
| 10569 | crin | 1 |
| 10570 | criminalmente | 1 |
| 10571 | cría | 1 |
| 10572 | creyó | 1 |
| 10573 | creyendo | 1 |
| 10574 | crema | 1 |
| 10575 | creíale | 1 |
| 10576 | creería | 1 |
| 10577 | créanlo | 1 |
| 10578 | créame | 1 |
| 10579 | coz | 1 |
| 10580 | coyuntura | 1 |
| 10581 | covent | 1 |
| 10582 | covadonga | 1 |
| 10583 | cotorra | 1 |
| 10584 | coto | 1 |
| 10585 | cotización | 1 |
| 10586 | cotidiano | 1 |
| 10587 | cotarro | 1 |
| 10588 | cota | 1 |
| 10589 | costoso | 1 |
| 10590 | costera | 1 |
| 10591 | cosquilleo | 1 |
| 10592 | cosmético | 1 |
| 10593 | cosechero | 1 |
| 10594 | cosechar | 1 |
| 10595 | cosecha | 1 |
| 10596 | corzo | 1 |
| 10597 | corvo | 1 |
| 10598 | corva | 1 |
| 10599 | cortinilla | 1 |
| 10600 | cortes | 1 |
| 10601 | corsé | 1 |
| 10602 | corruptela | 1 |
| 10603 | corroboraba | 1 |
| 10604 | corrió | 1 |
| 10605 | corrigió | 1 |
| 10606 | correveidile | 1 |
| 10607 | correría | 1 |
| 10608 | correctamente | 1 |
| 10609 | correa | 1 |
| 10610 | corre | 1 |
| 10611 | corralón | 1 |
| 10612 | corpiño | 1 |
| 10613 | coronilla | 1 |
| 10614 | corolario | 1 |
| 10615 | corneta | 1 |
| 10616 | cornamenta | 1 |
| 10617 | corintio | 1 |
| 10618 | córdoba | 1 |
| 10619 | cordialmente | 1 |
| 10620 | cordero | 1 |
| 10621 | corcovar | 1 |
| 10622 | corchete | 1 |
| 10623 | corbatín | 1 |
| 10624 | corazoncito | 1 |
| 10625 | coral | 1 |
| 10626 | copiosamente | 1 |
| 10627 | copar | 1 |
| 10628 | coordinar | 1 |
| 10629 | convulso | 1 |
| 10630 | convivencia | 1 |
| 10631 | convídesele | 1 |
| 10632 | converso | 1 |
| 10633 | convergencia | 1 |
| 10634 | conventual | 1 |
| 10635 | convencido | 1 |
| 10636 | contumaz | 1 |
| 10637 | contrincante | 1 |
| 10638 | contrición | 1 |
| 10639 | contribuyente | 1 |
| 10640 | contribución | 1 |
| 10641 | contratar | 1 |
| 10642 | contratante | 1 |
| 10643 | contrasentido | 1 |
| 10644 | contrariar | 1 |
| 10645 | contrabandista | 1 |
| 10646 | contorsionar | 1 |
| 10647 | contoneo | 1 |
| 10648 | contestaron | 1 |
| 10649 | contestaban | 1 |
| 10650 | contestaba | 1 |
| 10651 | contentadizo | 1 |
| 10652 | contender | 1 |
| 10653 | contemplativo | 1 |
| 10654 | contarían | 1 |
| 10655 | contado | 1 |
| 10656 | consumidor | 1 |
| 10657 | consumado | 1 |
| 10658 | consultado | 1 |
| 10659 | consuetudinario | 1 |
| 10660 | construcción | 1 |
| 10661 | constituían | 1 |
| 10662 | constitución | 1 |
| 10663 | constipado | 1 |
| 10664 | consternar | 1 |
| 10665 | constantinopla | 1 |
| 10666 | consorte | 1 |
| 10667 | consonante | 1 |
| 10668 | consolidar | 1 |
| 10669 | consistorios | 1 |
| 10670 | consigo | 1 |
| 10671 | consigna | 1 |
| 10672 | conserjería | 1 |
| 10673 | consentido | 1 |
| 10674 | conocía | 1 |
| 10675 | conoce | 1 |
| 10676 | cono | 1 |
| 10677 | conmutar | 1 |
| 10678 | conmover | 1 |
| 10679 | conmiseración | 1 |
| 10680 | conmemorar | 1 |
| 10681 | conjuro | 1 |
| 10682 | conjurado | 1 |
| 10683 | conjuntar | 1 |
| 10684 | cónico | 1 |
| 10685 | congraciar | 1 |
| 10686 | congestión | 1 |
| 10687 | congeniar | 1 |
| 10688 | confusamente | 1 |
| 10689 | confortante | 1 |
| 10690 | confortable | 1 |
| 10691 | confitero | 1 |
| 10692 | confirmó | 1 |
| 10693 | confirmación | 1 |
| 10694 | confirmábase | 1 |
| 10695 | confiado | 1 |
| 10696 | conferencias | 1 |
| 10697 | confeccionar | 1 |
| 10698 | condiscípulo | 1 |
| 10699 | condimento | 1 |
| 10700 | condiciones | 1 |
| 10701 | condescendiente | 1 |
| 10702 | condensar | 1 |
| 10703 | condecoración | 1 |
| 10704 | concurrido | 1 |
| 10705 | concupiscente | 1 |
| 10706 | concupiscencia | 1 |
| 10707 | concretamente | 1 |
| 10708 | concordato | 1 |
| 10709 | concluyó | 1 |
| 10710 | concluía | 1 |
| 10711 | conciso | 1 |
| 10712 | conciliar | 1 |
| 10713 | concesión | 1 |
| 10714 | conceptuoso | 1 |
| 10715 | cóncavo | 1 |
| 10716 | comúnmente | 1 |
| 10717 | comunidad | 1 |
| 10718 | comunicación | 1 |
| 10719 | compunción | 1 |
| 10720 | compuerta | 1 |
| 10721 | comprendió | 1 |
| 10722 | comprendía | 1 |
| 10723 | compre | 1 |
| 10724 | comprador | 1 |
| 10725 | compostura | 1 |
| 10726 | componenda | 1 |
| 10727 | complicidad | 1 |
| 10728 | complemento | 1 |
| 10729 | complaciente | 1 |
| 10730 | competente | 1 |
| 10731 | compenetrar | 1 |
| 10732 | compasivo | 1 |
| 10733 | comparado | 1 |
| 10734 | compacto | 1 |
| 10735 | comisura | 1 |
| 10736 | comistrajo | 1 |
| 10737 | comisionista | 1 |
| 10738 | comisionar | 1 |
| 10739 | comisionado | 1 |
| 10740 | comisario | 1 |
| 10741 | comino | 1 |
| 10742 | cominero | 1 |
| 10743 | comilona | 1 |
| 10744 | comienzo | 1 |
| 10745 | comido | 1 |
| 10746 | cómetela | 1 |
| 10747 | comería | 1 |
| 10748 | comercial | 1 |
| 10749 | comehostias | 1 |
| 10750 | comedimiento | 1 |
| 10751 | combustión | 1 |
| 10752 | comarcano | 1 |
| 10753 | coma | 1 |
| 10754 | colosal | 1 |
| 10755 | colorín | 1 |
| 10756 | colorete | 1 |
| 10757 | colmillo | 1 |
| 10758 | collar | 1 |
| 10759 | collado | 1 |
| 10760 | colgadizo | 1 |
| 10761 | colérico | 1 |
| 10762 | colegiala | 1 |
| 10763 | colectividad | 1 |
| 10764 | colectivamente | 1 |
| 10765 | coleccionar | 1 |
| 10766 | colasa | 1 |
| 10767 | colaborar | 1 |
| 10768 | coimbra | 1 |
| 10769 | cofre | 1 |
| 10770 | coercitivo | 1 |
| 10771 | codicioso | 1 |
| 10772 | cocido | 1 |
| 10773 | cocer | 1 |
| 10774 | cobos | 1 |
| 10775 | cobertizo | 1 |
| 10776 | coadjutor | 1 |
| 10777 | climatológico | 1 |
| 10778 | clavija | 1 |
| 10779 | clavetear | 1 |
| 10780 | clave | 1 |
| 10781 | clavada | 1 |
| 10782 | cláusula | 1 |
| 10783 | claudio | 1 |
| 10784 | claraboya | 1 |
| 10785 | clandestinamente | 1 |
| 10786 | clamor | 1 |
| 10787 | civis | 1 |
| 10788 | civilizar | 1 |
| 10789 | civilizado | 1 |
| 10790 | ciutti | 1 |
| 10791 | citado | 1 |
| 10792 | cisterna | 1 |
| 10793 | ciruelo | 1 |
| 10794 | circunstancias | 1 |
| 10795 | circunstancial | 1 |
| 10796 | circunspección | 1 |
| 10797 | ciprés | 1 |
| 10798 | cinturón | 1 |
| 10799 | cínicamente | 1 |
| 10800 | cincel | 1 |
| 10801 | cimodocea | 1 |
| 10802 | cimiento | 1 |
| 10803 | cilíndrico | 1 |
| 10804 | cigüeña | 1 |
| 10805 | cigarrera | 1 |
| 10806 | cifra | 1 |
| 10807 | cierzo | 1 |
| 10808 | ciervo | 1 |
| 10809 | cierta | 1 |
| 10810 | cierra | 1 |
| 10811 | cierne | 1 |
| 10812 | cientos | 1 |
| 10813 | cicuta | 1 |
| 10814 | ciclópeo | 1 |
| 10815 | cíclope | 1 |
| 10816 | ciclón | 1 |
| 10817 | ciclo | 1 |
| 10818 | cíclades | 1 |
| 10819 | chusquin | 1 |
| 10820 | chorrito | 1 |
| 10821 | chorretada | 1 |
| 10822 | chomel | 1 |
| 10823 | chocha | 1 |
| 10824 | chitón | 1 |
| 10825 | chipre | 1 |
| 10826 | chinita | 1 |
| 10827 | china | 1 |
| 10828 | chin | 1 |
| 10829 | chiflado | 1 |
| 10830 | chevrière | 1 |
| 10831 | chasquir | 1 |
| 10832 | chasco | 1 |
| 10833 | charlatán | 1 |
| 10834 | charanga | 1 |
| 10835 | chaquetón | 1 |
| 10836 | chapa | 1 |
| 10837 | chanza | 1 |
| 10838 | chantre | 1 |
| 10839 | chantal | 1 |
| 10840 | chambra | 1 |
| 10841 | chambón | 1 |
| 10842 | chambergo | 1 |
| 10843 | chalet | 1 |
| 10844 | cetro | 1 |
| 10845 | cerviz | 1 |
| 10846 | cervantes | 1 |
| 10847 | certamen | 1 |
| 10848 | cerro | 1 |
| 10849 | ceremonial | 1 |
| 10850 | cerda | 1 |
| 10851 | cerciorar | 1 |
| 10852 | cercenar | 1 |
| 10853 | cepo | 1 |
| 10854 | centuria | 1 |
| 10855 | centímetro | 1 |
| 10856 | centésima | 1 |
| 10857 | centellear | 1 |
| 10858 | cenarás | 1 |
| 10859 | celta | 1 |
| 10860 | celonio | 1 |
| 10861 | celestinas | 1 |
| 10862 | celesta | 1 |
| 10863 | celeres | 1 |
| 10864 | celenio | 1 |
| 10865 | celar | 1 |
| 10866 | celaje | 1 |
| 10867 | ceguedad | 1 |
| 10868 | cefiso | 1 |
| 10869 | céfiro | 1 |
| 10870 | cedro | 1 |
| 10871 | cebolla | 1 |
| 10872 | cazurro | 1 |
| 10873 | cazadero | 1 |
| 10874 | cavilar | 1 |
| 10875 | caverna | 1 |
| 10876 | caveant | 1 |
| 10877 | cauto | 1 |
| 10878 | cautiverio | 1 |
| 10879 | cautivar | 1 |
| 10880 | cautelar | 1 |
| 10881 | catarro | 1 |
| 10882 | catálogo | 1 |
| 10883 | catacumbas | 1 |
| 10884 | castelar | 1 |
| 10885 | castañeteo | 1 |
| 10886 | castañar | 1 |
| 10887 | casquivano | 1 |
| 10888 | caseta | 1 |
| 10889 | caseoso | 1 |
| 10890 | cascarón | 1 |
| 10891 | cáscara | 1 |
| 10892 | casamata | 1 |
| 10893 | cartulina | 1 |
| 10894 | cartujo | 1 |
| 10895 | cartela | 1 |
| 10896 | cartel | 1 |
| 10897 | cartapacio | 1 |
| 10898 | carraspiques | 1 |
| 10899 | carraca | 1 |
| 10900 | carolina | 1 |
| 10901 | carmín | 1 |
| 10902 | caritativo | 1 |
| 10903 | caricaturar | 1 |
| 10904 | carestía | 1 |
| 10905 | cardona | 1 |
| 10906 | cardiopatía | 1 |
| 10907 | cardíaco | 1 |
| 10908 | cardan | 1 |
| 10909 | carcomido | 1 |
| 10910 | carcamal | 1 |
| 10911 | carca | 1 |
| 10912 | carbonizar | 1 |
| 10913 | carbayeda | 1 |
| 10914 | carátula | 1 |
| 10915 | carambola | 1 |
| 10916 | caramba | 1 |
| 10917 | característico | 1 |
| 10918 | caracolear | 1 |
| 10919 | capua | 1 |
| 10920 | capota | 1 |
| 10921 | capitular | 1 |
| 10922 | capitel | 1 |
| 10923 | capitanear | 1 |
| 10924 | capitalista | 1 |
| 10925 | capirote | 1 |
| 10926 | capelo | 1 |
| 10927 | capellanías | 1 |
| 10928 | capcioso | 1 |
| 10929 | capalleja | 1 |
| 10930 | capacidad | 1 |
| 10931 | caótico | 1 |
| 10932 | caos | 1 |
| 10933 | cañedo | 1 |
| 10934 | cañamón | 1 |
| 10935 | cantera | 1 |
| 10936 | cántaros | 1 |
| 10937 | cantante | 1 |
| 10938 | cantando | 1 |
| 10939 | cantábrico | 1 |
| 10940 | cansarse | 1 |
| 10941 | canonjía | 1 |
| 10942 | canonista | 1 |
| 10943 | canela | 1 |
| 10944 | candil | 1 |
| 10945 | candidatura | 1 |
| 10946 | candente | 1 |
| 10947 | candelillar | 1 |
| 10948 | candado | 1 |
| 10949 | canciones | 1 |
| 10950 | cancerbero | 1 |
| 10951 | camposanto | 1 |
| 10952 | campbell | 1 |
| 10953 | campar | 1 |
| 10954 | campanillazo | 1 |
| 10955 | campanillas | 1 |
| 10956 | campamento | 1 |
| 10957 | camisolín | 1 |
| 10958 | camisola | 1 |
| 10959 | camilla | 1 |
| 10960 | camarote | 1 |
| 10961 | camarín | 1 |
| 10962 | calzonazos | 1 |
| 10963 | calzada | 1 |
| 10964 | calza | 1 |
| 10965 | calva | 1 |
| 10966 | calumniador | 1 |
| 10967 | calomarde | 1 |
| 10968 | callo | 1 |
| 10969 | callejuela | 1 |
| 10970 | callaba | 1 |
| 10971 | calizo | 1 |
| 10972 | caliza | 1 |
| 10973 | caliginoso | 1 |
| 10974 | cálidas | 1 |
| 10975 | calibre | 1 |
| 10976 | calepino | 1 |
| 10977 | calentura | 1 |
| 10978 | calefacción | 1 |
| 10979 | caldear | 1 |
| 10980 | calculador | 1 |
| 10981 | calculaba | 1 |
| 10982 | calcetín | 1 |
| 10983 | calcetar | 1 |
| 10984 | calatravas | 1 |
| 10985 | calado | 1 |
| 10986 | calada | 1 |
| 10987 | calabozo | 1 |
| 10988 | cajista | 1 |
| 10989 | caín | 1 |
| 10990 | caída | 1 |
| 10991 | cafetera | 1 |
| 10992 | caería | 1 |
| 10993 | cadenilla | 1 |
| 10994 | cadencioso | 1 |
| 10995 | cacofónico | 1 |
| 10996 | cachivache | 1 |
| 10997 | cachaza | 1 |
| 10998 | cacerola | 1 |
| 10999 | cacería | 1 |
| 11000 | cabotaje | 1 |
| 11001 | cable | 1 |
| 11002 | cabezota | 1 |
| 11003 | cabellar | 1 |
| 11004 | cabalmente | 1 |
| 11005 | caballeriza | 1 |
| 11006 | caballería | 1 |
| 11007 | caballerete | 1 |
| 11008 | cabalístico | 1 |
| 11009 | ca | 1 |
| 11010 | byron | 1 |
| 11011 | búsquelo | 1 |
| 11012 | buscada | 1 |
| 11013 | burlándose | 1 |
| 11014 | burgués | 1 |
| 11015 | burdo | 1 |
| 11016 | bullir | 1 |
| 11017 | bullicio | 1 |
| 11018 | buitre | 1 |
| 11019 | buhonero | 1 |
| 11020 | bufos | 1 |
| 11021 | bufar | 1 |
| 11022 | buey | 1 |
| 11023 | buchner | 1 |
| 11024 | buche | 1 |
| 11025 | brooke | 1 |
| 11026 | bromista | 1 |
| 11027 | brochada | 1 |
| 11028 | brocado | 1 |
| 11029 | brioso | 1 |
| 11030 | brígida | 1 |
| 11031 | bribón | 1 |
| 11032 | brevísimo | 1 |
| 11033 | brevemente | 1 |
| 11034 | bretón | 1 |
| 11035 | brechar | 1 |
| 11036 | brea | 1 |
| 11037 | bramante | 1 |
| 11038 | braga | 1 |
| 11039 | bracear | 1 |
| 11040 | bozal | 1 |
| 11041 | boto | 1 |
| 11042 | boticario | 1 |
| 11043 | botica | 1 |
| 11044 | botarate | 1 |
| 11045 | botánica | 1 |
| 11046 | borrón | 1 |
| 11047 | borrador | 1 |
| 11048 | borona | 1 |
| 11049 | bordear | 1 |
| 11050 | bordado | 1 |
| 11051 | bonitos | 1 |
| 11052 | bombardeo | 1 |
| 11053 | bolsón | 1 |
| 11054 | bolsista | 1 |
| 11055 | bolera | 1 |
| 11056 | bogar | 1 |
| 11057 | bodegón | 1 |
| 11058 | bocacalle | 1 |
| 11059 | bobadas | 1 |
| 11060 | bobada | 1 |
| 11061 | bloqueo | 1 |
| 11062 | bloquear | 1 |
| 11063 | bloque | 1 |
| 11064 | blindar | 1 |
| 11065 | blindaje | 1 |
| 11066 | blindado | 1 |
| 11067 | blasfemo | 1 |
| 11068 | blanquear | 1 |
| 11069 | blandón | 1 |
| 11070 | blandamente | 1 |
| 11071 | bizcocho | 1 |
| 11072 | bizcochar | 1 |
| 11073 | bizcar | 1 |
| 11074 | bizantino | 1 |
| 11075 | birrete | 1 |
| 11076 | bípedo | 1 |
| 11077 | bion | 1 |
| 11078 | bilioso | 1 |
| 11079 | bílbilis | 1 |
| 11080 | bilbao | 1 |
| 11081 | bilateral | 1 |
| 11082 | bienhechor | 1 |
| 11083 | bibliófilo | 1 |
| 11084 | betún | 1 |
| 11085 | bethlehem | 1 |
| 11086 | bestial | 1 |
| 11087 | berruguete | 1 |
| 11088 | bernardo | 1 |
| 11089 | bernard | 1 |
| 11090 | bermudo | 1 |
| 11091 | berlín | 1 |
| 11092 | bengala | 1 |
| 11093 | benévolo | 1 |
| 11094 | beneplácito | 1 |
| 11095 | beneficioso | 1 |
| 11096 | benedicto | 1 |
| 11097 | belvedere | 1 |
| 11098 | belo | 1 |
| 11099 | bellaquería | 1 |
| 11100 | bellaco | 1 |
| 11101 | belem | 1 |
| 11102 | begonia | 1 |
| 11103 | becerro | 1 |
| 11104 | bebida | 1 |
| 11105 | bebedor | 1 |
| 11106 | beatería | 1 |
| 11107 | be | 1 |
| 11108 | bayonetazo | 1 |
| 11109 | bautizar | 1 |
| 11110 | battistini | 1 |
| 11111 | bastonazo | 1 |
| 11112 | bastón | 1 |
| 11113 | bastidores | 1 |
| 11114 | bastidor | 1 |
| 11115 | bastiat | 1 |
| 11116 | basquiña | 1 |
| 11117 | basilisco | 1 |
| 11118 | barroquismo | 1 |
| 11119 | barrera | 1 |
| 11120 | barbas | 1 |
| 11121 | bárbaros | 1 |
| 11122 | bárbara | 1 |
| 11123 | barbar | 1 |
| 11124 | barata | 1 |
| 11125 | barajar | 1 |
| 11126 | báquico | 1 |
| 11127 | banqueta | 1 |
| 11128 | bandolero | 1 |
| 11129 | bambolear | 1 |
| 11130 | bambalina | 1 |
| 11131 | balzac | 1 |
| 11132 | baltasar | 1 |
| 11133 | balbuciente | 1 |
| 11134 | balbuceó | 1 |
| 11135 | balaustre | 1 |
| 11136 | balaustrar | 1 |
| 11137 | balaustrada | 1 |
| 11138 | balancear | 1 |
| 11139 | bájese | 1 |
| 11140 | bajada | 1 |
| 11141 | baglivio | 1 |
| 11142 | badulaque | 1 |
| 11143 | bachiller | 1 |
| 11144 | bacantes | 1 |
| 11145 | bacalao | 1 |
| 11146 | baboso | 1 |
| 11147 | babor | 1 |
| 11148 | azuzar | 1 |
| 11149 | azulado | 1 |
| 11150 | azufre | 1 |
| 11151 | azucarero | 1 |
| 11152 | azucarado | 1 |
| 11153 | azotacalles | 1 |
| 11154 | azogar | 1 |
| 11155 | ayunar | 1 |
| 11156 | ayúdeme | 1 |
| 11157 | ayudante | 1 |
| 11158 | ayudábala | 1 |
| 11159 | axis | 1 |
| 11160 | avinagrar | 1 |
| 11161 | avinagrado | 1 |
| 11162 | averiguación | 1 |
| 11163 | aventurero | 1 |
| 11164 | aventado | 1 |
| 11165 | avenida | 1 |
| 11166 | avellanado | 1 |
| 11167 | avellana | 1 |
| 11168 | avasallar | 1 |
| 11169 | avasallador | 1 |
| 11170 | avanzada | 1 |
| 11171 | avalorar | 1 |
| 11172 | auxiliar | 1 |
| 11173 | autoridades | 1 |
| 11174 | autómata | 1 |
| 11175 | auto | 1 |
| 11176 | aúpa | 1 |
| 11177 | aumento | 1 |
| 11178 | aulló | 1 |
| 11179 | aullido | 1 |
| 11180 | audiencias | 1 |
| 11181 | atropellar | 1 |
| 11182 | atronador | 1 |
| 11183 | atril | 1 |
| 11184 | atribular | 1 |
| 11185 | atribución | 1 |
| 11186 | atrévete | 1 |
| 11187 | atravesado | 1 |
| 11188 | atracón | 1 |
| 11189 | atracción | 1 |
| 11190 | atonía | 1 |
| 11191 | aterir | 1 |
| 11192 | atenuar | 1 |
| 11193 | atenea | 1 |
| 11194 | atemorizar | 1 |
| 11195 | atávico | 1 |
| 11196 | ataúd | 1 |
| 11197 | atareado | 1 |
| 11198 | atalayar | 1 |
| 11199 | atajo | 1 |
| 11200 | atajar | 1 |
| 11201 | asueto | 1 |
| 11202 | asturias | 1 |
| 11203 | asturiano | 1 |
| 11204 | astronomía | 1 |
| 11205 | astillar | 1 |
| 11206 | aspirado | 1 |
| 11207 | aspar | 1 |
| 11208 | aspa | 1 |
| 11209 | asombrosamente | 1 |
| 11210 | asolar | 1 |
| 11211 | asociar | 1 |
| 11212 | asociación | 1 |
| 11213 | asimilar | 1 |
| 11214 | asilo | 1 |
| 11215 | asilar | 1 |
| 11216 | asignatura | 1 |
| 11217 | asia | 1 |
| 11218 | asestar | 1 |
| 11219 | asesorar | 1 |
| 11220 | asesinato | 1 |
| 11221 | asentar | 1 |
| 11222 | asegurado | 1 |
| 11223 | asedio | 1 |
| 11224 | asear | 1 |
| 11225 | ascetismo | 1 |
| 11226 | ascético | 1 |
| 11227 | asamblea | 1 |
| 11228 | as | 1 |
| 11229 | artesonado | 1 |
| 11230 | artela | 1 |
| 11231 | arruinado | 1 |
| 11232 | arroz | 1 |
| 11233 | arropar | 1 |
| 11234 | arrollar | 1 |
| 11235 | arrobar | 1 |
| 11236 | arriesgado | 1 |
| 11237 | arriero | 1 |
| 11238 | arresto | 1 |
| 11239 | arrendamiento | 1 |
| 11240 | arremetida | 1 |
| 11241 | arregla | 1 |
| 11242 | arrasar | 1 |
| 11243 | arras | 1 |
| 11244 | arraigo | 1 |
| 11245 | arrabal | 1 |
| 11246 | arquitecto | 1 |
| 11247 | arouet | 1 |
| 11248 | aromar | 1 |
| 11249 | aro | 1 |
| 11250 | armas | 1 |
| 11251 | armando | 1 |
| 11252 | armadura | 1 |
| 11253 | árido | 1 |
| 11254 | argumosa | 1 |
| 11255 | argucia | 1 |
| 11256 | argos | 1 |
| 11257 | arengar | 1 |
| 11258 | ardilla | 1 |
| 11259 | arcón | 1 |
| 11260 | arciprestazgo | 1 |
| 11261 | arcilla | 1 |
| 11262 | archivo | 1 |
| 11263 | archimonástica | 1 |
| 11264 | arcar | 1 |
| 11265 | arcadias | 1 |
| 11266 | arboricultor | 1 |
| 11267 | arbolado | 1 |
| 11268 | arbitrista | 1 |
| 11269 | arbitrar | 1 |
| 11270 | aragonesa | 1 |
| 11271 | árabe | 1 |
| 11272 | aquilatar | 1 |
| 11273 | apuntando | 1 |
| 11274 | aproximadamente | 1 |
| 11275 | apropósito | 1 |
| 11276 | aprobado | 1 |
| 11277 | aprieto | 1 |
| 11278 | apremiante | 1 |
| 11279 | apreciación | 1 |
| 11280 | apóstrofe | 1 |
| 11281 | apóstoles | 1 |
| 11282 | apostatar | 1 |
| 11283 | apostaría | 1 |
| 11284 | apostaba | 1 |
| 11285 | aposento | 1 |
| 11286 | aportar | 1 |
| 11287 | apoplético | 1 |
| 11288 | apoplejía | 1 |
| 11289 | apólogo | 1 |
| 11290 | apología | 1 |
| 11291 | apoderado | 1 |
| 11292 | apodar | 1 |
| 11293 | apocalíptico | 1 |
| 11294 | apocado | 1 |
| 11295 | aplicable | 1 |
| 11296 | aplausos | 1 |
| 11297 | aplaude | 1 |
| 11298 | apiñábase | 1 |
| 11299 | ápice | 1 |
| 11300 | apetecer | 1 |
| 11301 | aperitivo | 1 |
| 11302 | apéndice | 1 |
| 11303 | apelmazar | 1 |
| 11304 | apegar | 1 |
| 11305 | apatía | 1 |
| 11306 | apasionamiento | 1 |
| 11307 | apartamiento | 1 |
| 11308 | apartado | 1 |
| 11309 | apareció | 1 |
| 11310 | aparador | 1 |
| 11311 | apañar | 1 |
| 11312 | apalear | 1 |
| 11313 | apagó | 1 |
| 11314 | apacentar | 1 |
| 11315 | añoso | 1 |
| 11316 | años | 1 |
| 11317 | añicos | 1 |
| 11318 | anuncita | 1 |
| 11319 | anular | 1 |
| 11320 | anual | 1 |
| 11321 | antro | 1 |
| 11322 | antonelli | 1 |
| 11323 | antón | 1 |
| 11324 | antolínez | 1 |
| 11325 | antojadizo | 1 |
| 11326 | antojábasele | 1 |
| 11327 | antigüedades | 1 |
| 11328 | antiguamente | 1 |
| 11329 | antiespasmódicos | 1 |
| 11330 | anticuado | 1 |
| 11331 | anticipado | 1 |
| 11332 | antepasado | 1 |
| 11333 | antecedentes | 1 |
| 11334 | anónimos | 1 |
| 11335 | animalucho | 1 |
| 11336 | animalejo | 1 |
| 11337 | aniceto | 1 |
| 11338 | anhelante | 1 |
| 11339 | angustioso | 1 |
| 11340 | anguila | 1 |
| 11341 | angostar | 1 |
| 11342 | angola | 1 |
| 11343 | angelito | 1 |
| 11344 | angelino | 1 |
| 11345 | angélico | 1 |
| 11346 | angarillas | 1 |
| 11347 | anfibológico | 1 |
| 11348 | andrómaca | 1 |
| 11349 | anden | 1 |
| 11350 | andarín | 1 |
| 11351 | andalucía | 1 |
| 11352 | analítico | 1 |
| 11353 | amplitud | 1 |
| 11354 | ampliar | 1 |
| 11355 | amotinado | 1 |
| 11356 | amostazar | 1 |
| 11357 | amortajar | 1 |
| 11358 | amorcillo | 1 |
| 11359 | amoratado | 1 |
| 11360 | amontonado | 1 |
| 11361 | amoldar | 1 |
| 11362 | amnistiar | 1 |
| 11363 | amistoso | 1 |
| 11364 | amistades | 1 |
| 11365 | américo | 1 |
| 11366 | américas | 1 |
| 11367 | amenizar | 1 |
| 11368 | amenidad | 1 |
| 11369 | amenguar | 1 |
| 11370 | amenazador | 1 |
| 11371 | ambulante | 1 |
| 11372 | amazacotar | 1 |
| 11373 | amasijo | 1 |
| 11374 | amasar | 1 |
| 11375 | amarrar | 1 |
| 11376 | amarillez | 1 |
| 11377 | amarillear | 1 |
| 11378 | amarilla | 1 |
| 11379 | amarilis | 1 |
| 11380 | amaré | 1 |
| 11381 | amaño | 1 |
| 11382 | amansar | 1 |
| 11383 | amaneramiento | 1 |
| 11384 | amaba | 1 |
| 11385 | alvarico | 1 |
| 11386 | aluvión | 1 |
| 11387 | alumbramiento | 1 |
| 11388 | aludido | 1 |
| 11389 | alucinar | 1 |
| 11390 | alturas | 1 |
| 11391 | altivez | 1 |
| 11392 | altisonante | 1 |
| 11393 | altísimo | 1 |
| 11394 | altanería | 1 |
| 11395 | alquilar | 1 |
| 11396 | alpiste | 1 |
| 11397 | alondra | 1 |
| 11398 | almuerzo | 1 |
| 11399 | almidonado | 1 |
| 11400 | almidón | 1 |
| 11401 | almibarar | 1 |
| 11402 | almibarado | 1 |
| 11403 | almena | 1 |
| 11404 | alleluia | 1 |
| 11405 | allanar | 1 |
| 11406 | alimentación | 1 |
| 11407 | alimaña | 1 |
| 11408 | aliciente | 1 |
| 11409 | alianza | 1 |
| 11410 | alharaca | 1 |
| 11411 | alguno | 1 |
| 11412 | algunas | 1 |
| 11413 | algodones | 1 |
| 11414 | algodón | 1 |
| 11415 | alforja | 1 |
| 11416 | alfonsos | 1 |
| 11417 | alfiletero | 1 |
| 11418 | alfilerar | 1 |
| 11419 | alfiler | 1 |
| 11420 | aletear | 1 |
| 11421 | aletargar | 1 |
| 11422 | alero | 1 |
| 11423 | alemania | 1 |
| 11424 | alegremente | 1 |
| 11425 | alegórico | 1 |
| 11426 | aleccionar | 1 |
| 11427 | aleatorio | 1 |
| 11428 | aldebarán | 1 |
| 11429 | alcurnia | 1 |
| 11430 | alcubilla | 1 |
| 11431 | alcornoque | 1 |
| 11432 | alcohólico | 1 |
| 11433 | alcides | 1 |
| 11434 | alcaldesa | 1 |
| 11435 | alcaide | 1 |
| 11436 | álbum | 1 |
| 11437 | alboroto | 1 |
| 11438 | alborada | 1 |
| 11439 | albión | 1 |
| 11440 | albergar | 1 |
| 11441 | alberca | 1 |
| 11442 | albéitar | 1 |
| 11443 | albedrío | 1 |
| 11444 | albañal | 1 |
| 11445 | albaicín | 1 |
| 11446 | alarmado | 1 |
| 11447 | alarma | 1 |
| 11448 | alarcón | 1 |
| 11449 | alambrar | 1 |
| 11450 | alabado | 1 |
| 11451 | ajustábase | 1 |
| 11452 | ajenjo | 1 |
| 11453 | aislador | 1 |
| 11454 | airado | 1 |
| 11455 | ahuyentar | 1 |
| 11456 | ahumar | 1 |
| 11457 | ahorita | 1 |
| 11458 | ahogado | 1 |
| 11459 | ahíto | 1 |
| 11460 | ahitar | 1 |
| 11461 | ahincar | 1 |
| 11462 | agustinito | 1 |
| 11463 | agujerito | 1 |
| 11464 | aguijonear | 1 |
| 11465 | aguijón | 1 |
| 11466 | aguerrido | 1 |
| 11467 | aguas | 1 |
| 11468 | aguar | 1 |
| 11469 | agrónomo | 1 |
| 11470 | agrícola | 1 |
| 11471 | agriar | 1 |
| 11472 | agreste | 1 |
| 11473 | agravante | 1 |
| 11474 | agradézcaselo | 1 |
| 11475 | agradablemente | 1 |
| 11476 | agradábale | 1 |
| 11477 | agotar | 1 |
| 11478 | agorero | 1 |
| 11479 | agorar | 1 |
| 11480 | agonizar | 1 |
| 11481 | agonía | 1 |
| 11482 | agobiar | 1 |
| 11483 | aglomerar | 1 |
| 11484 | aglomeración | 1 |
| 11485 | agilidad | 1 |
| 11486 | ágil | 1 |
| 11487 | agenciar | 1 |
| 11488 | agencia | 1 |
| 11489 | agazapar | 1 |
| 11490 | agasajo | 1 |
| 11491 | agasajar | 1 |
| 11492 | agarrada | 1 |
| 11493 | afueras | 1 |
| 11494 | africano | 1 |
| 11495 | afrentar | 1 |
| 11496 | afrenta | 1 |
| 11497 | afirmó | 1 |
| 11498 | afirmativo | 1 |
| 11499 | afilar | 1 |
| 11500 | afilador | 1 |
| 11501 | afianzar | 1 |
| 11502 | aferrar | 1 |
| 11503 | afeitado | 1 |
| 11504 | afectivo | 1 |
| 11505 | afectísimo | 1 |
| 11506 | afear | 1 |
| 11507 | afanar | 1 |
| 11508 | afablemente | 1 |
| 11509 | aeroterapia | 1 |
| 11510 | aéreo | 1 |
| 11511 | adverso | 1 |
| 11512 | adulterado | 1 |
| 11513 | adulador | 1 |
| 11514 | aducir | 1 |
| 11515 | aduana | 1 |
| 11516 | adquisición | 1 |
| 11517 | adocenar | 1 |
| 11518 | adobar | 1 |
| 11519 | admitido | 1 |
| 11520 | adjunto | 1 |
| 11521 | adjetivo | 1 |
| 11522 | adiosito | 1 |
| 11523 | adición | 1 |
| 11524 | adhesión | 1 |
| 11525 | adherir | 1 |
| 11526 | aderezo | 1 |
| 11527 | adelanto | 1 |
| 11528 | adefesio | 1 |
| 11529 | adecuar | 1 |
| 11530 | adaptarse | 1 |
| 11531 | adamascado | 1 |
| 11532 | adamado | 1 |
| 11533 | acústico | 1 |
| 11534 | acusador | 1 |
| 11535 | acudió | 1 |
| 11536 | acuarela | 1 |
| 11537 | actriz | 1 |
| 11538 | acta | 1 |
| 11539 | acróbata | 1 |
| 11540 | acritud | 1 |
| 11541 | acribillar | 1 |
| 11542 | acreedor | 1 |
| 11543 | acortar | 1 |
| 11544 | acongojar | 1 |
| 11545 | acompasado | 1 |
| 11546 | acomodamiento | 1 |
| 11547 | aclamación | 1 |
| 11548 | acíbar | 1 |
| 11549 | achantar | 1 |
| 11550 | acervo | 1 |
| 11551 | acertado | 1 |
| 11552 | acerico | 1 |
| 11553 | acerado | 1 |
| 11554 | aceptó | 1 |
| 11555 | aceitar | 1 |
| 11556 | accionista | 1 |
| 11557 | accionar | 1 |
| 11558 | accesorio | 1 |
| 11559 | acatarrar | 1 |
| 11560 | acartonado | 1 |
| 11561 | acarrear | 1 |
| 11562 | acariciador | 1 |
| 11563 | acaparar | 1 |
| 11564 | acaparador | 1 |
| 11565 | acantos | 1 |
| 11566 | acantilado | 1 |
| 11567 | acampar | 1 |
| 11568 | acalorado | 1 |
| 11569 | academia | 1 |
| 11570 | abyección | 1 |
| 11571 | abur | 1 |
| 11572 | abundantemente | 1 |
| 11573 | abultar | 1 |
| 11574 | abstraer | 1 |
| 11575 | abstractar | 1 |
| 11576 | abstención | 1 |
| 11577 | abroquelado | 1 |
| 11578 | abrigado | 1 |
| 11579 | abreviatura | 1 |
| 11580 | abreviar | 1 |
| 11581 | abreviado | 1 |
| 11582 | abrasador | 1 |
| 11583 | abra | 1 |
| 11584 | aborrecido | 1 |
| 11585 | aborrecía | 1 |
| 11586 | abonado | 1 |
| 11587 | abominación | 1 |
| 11588 | abogar | 1 |
| 11589 | abofetear | 1 |
| 11590 | ablución | 1 |
| 11591 | ablativo | 1 |
| 11592 | ablandar | 1 |
| 11593 | abertura | 1 |
| 11594 | abelardo | 1 |
| 11595 | abeja | 1 |
|
| Rank | Palabra | Frec |
|---|
| 1 | el | 31365 |
| 2 | de | 20458 |
| 3 | que | 15596 |
| 4 | y | 13273 |
| 5 | lo | 12622 |
| 6 | a | 11998 |
| 7 | se | 8317 |
| 8 | no | 7621 |
| 9 | en | 7593 |
| 10 | un | 6609 |
| 11 | ser | 5091 |
| 12 | su | 5028 |
| 13 | con | 4631 |
| 14 | haber | 4571 |
| 15 | me | 3613 |
| 16 | por | 3599 |
| 17 | decir | 2850 |
| 18 | tener | 2726 |
| 19 | estar | 2658 |
| 20 | más | 2309 |
| 21 | para | 2266 |
| 22 | como | 2162 |
| 23 | pero | 2096 |
| 24 | si | 2030 |
| 25 | hacer | 1936 |
| 26 | ver | 1932 |
| 27 | todo | 1905 |
| 28 | te | 1792 |
| 29 | qué | 1791 |
| 30 | yo | 1697 |
| 31 | aquel | 1674 |
| 32 | usted | 1584 |
| 33 | dar | 1551 |
| 34 | ir | 1528 |
| 35 | este | 1454 |
| 36 | otro | 1374 |
| 37 | querer | 1334 |
| 38 | poder | 1276 |
| 39 | muy | 1215 |
| 40 | éste | 1195 |
| 41 | ya | 1175 |
| 42 | porque | 1094 |
| 43 | cuando | 1083 |
| 44 | ella | 1046 |
| 45 | tan | 1028 |
| 46 | saber | 999 |
| 47 | o | 986 |
| 48 | poner | 954 |
| 49 | pues | 903 |
| 50 | mi | 903 |
| 51 | casa | 884 |
| 52 | bien | 874 |
| 53 | fortunata | 869 |
| 54 | sin | 862 |
| 55 | mucho | 831 |
| 56 | parecer | 829 |
| 57 | él | 796 |
| 58 | día | 759 |
| 59 | la | 754 |
| 60 | ni | 735 |
| 61 | cosa | 735 |
| 62 | sí | 730 |
| 63 | doña | 714 |
| 64 | volver | 681 |
| 65 | bueno | 670 |
| 66 | mujer | 658 |
| 67 | dos | 652 |
| 68 | nada | 642 |
| 69 | mirar | 637 |
| 70 | después | 620 |
| 71 | ese | 613 |
| 72 | poco | 609 |
| 73 | mismo | 603 |
| 74 | salir | 593 |
| 75 | algún | 576 |
| 76 | jacinta | 571 |
| 77 | entrar | 562 |
| 78 | pasar | 561 |
| 79 | tú | 560 |
| 80 | hombre | 558 |
| 81 | hablar | 553 |
| 82 | venir | 552 |
| 83 | grande | 547 |
| 84 | señora | 533 |
| 85 | tanto | 526 |
| 86 | lupe | 520 |
| 87 | aquí | 512 |
| 88 | dios | 508 |
| 89 | llevar | 506 |
| 90 | vez | 504 |
| 91 | mano | 494 |
| 92 | sobre | 489 |
| 93 | dejar | 485 |
| 94 | amigo | 484 |
| 95 | tomar | 483 |
| 96 | hijo | 479 |
| 97 | mí | 475 |
| 98 | ahora | 471 |
| 99 | era | 463 |
| 100 | también | 453 |
| 101 | echar | 446 |
| 102 | algo | 444 |
| 103 | idea | 441 |
| 104 | hasta | 441 |
| 105 | cabeza | 438 |
| 106 | calle | 430 |
| 107 | noche | 426 |
| 108 | oír | 421 |
| 109 | tal | 413 |
| 110 | siempre | 412 |
| 111 | ése | 411 |
| 112 | fin | 409 |
| 113 | tiempo | 406 |
| 114 | vida | 402 |
| 115 | es | 402 |
| 116 | d | 401 |
| 117 | así | 400 |
| 118 | pensar | 397 |
| 119 | llegar | 384 |
| 120 | nos | 380 |
| 121 | comer | 371 |
| 122 | sentir | 361 |
| 123 | allí | 358 |
| 124 | ojo | 356 |
| 125 | quien | 355 |
| 126 | creer | 351 |
| 127 | cómo | 351 |
| 128 | deber | 350 |
| 129 | llamar | 348 |
| 130 | quedar | 340 |
| 131 | tío | 336 |
| 132 | palabra | 336 |
| 133 | cara | 334 |
| 134 | sacar | 332 |
| 135 | malo | 331 |
| 136 | entre | 322 |
| 137 | guillermina | 320 |
| 138 | coger | 319 |
| 139 | persona | 315 |
| 140 | chico | 315 |
| 141 | traer | 314 |
| 142 | cierto | 314 |
| 143 | rubín | 313 |
| 144 | vivir | 311 |
| 145 | alma | 310 |
| 146 | juan | 309 |
| 147 | marido | 308 |
| 148 | maxi | 304 |
| 149 | puerta | 302 |
| 150 | mejor | 298 |
| 151 | cual | 298 |
| 152 | maximiliano | 294 |
| 153 | mal | 294 |
| 154 | tu | 289 |
| 155 | verdad | 284 |
| 156 | contar | 284 |
| 157 | caer | 284 |
| 158 | señor | 277 |
| 159 | mundo | 276 |
| 160 | aunque | 276 |
| 161 | mañana | 275 |
| 162 | cruz | 273 |
| 163 | uno | 267 |
| 164 | empezar | 267 |
| 165 | santa | 266 |
| 166 | pobre | 266 |
| 167 | menos | 266 |
| 168 | desde | 264 |
| 169 | conocer | 263 |
| 170 | encontrar | 259 |
| 171 | seguir | 253 |
| 172 | hecho | 252 |
| 173 | año | 251 |
| 174 | meter | 250 |
| 175 | quitar | 244 |
| 176 | al | 242 |
| 177 | pronto | 238 |
| 178 | luego | 230 |
| 179 | casar | 230 |
| 180 | voz | 228 |
| 181 | reír | 228 |
| 182 | tres | 227 |
| 183 | sino | 227 |
| 184 | hora | 227 |
| 185 | fuera | 224 |
| 186 | ningún | 221 |
| 187 | nunca | 220 |
| 188 | parte | 219 |
| 189 | hermano | 219 |
| 190 | allá | 219 |
| 191 | antes | 217 |
| 192 | donde | 216 |
| 193 | caso | 212 |
| 194 | solo | 211 |
| 195 | mío | 211 |
| 196 | sólo | 202 |
| 197 | cada | 201 |
| 198 | los | 199 |
| 199 | boca | 199 |
| 200 | niño | 198 |
| 201 | morir | 198 |
| 202 | vaya | 196 |
| 203 | tratar | 196 |
| 204 | santo | 195 |
| 205 | faltar | 195 |
| 206 | sentar | 194 |
| 207 | gustar | 194 |
| 208 | pedir | 190 |
| 209 | mauricia | 190 |
| 210 | barbarita | 190 |
| 211 | abrir | 190 |
| 212 | propio | 189 |
| 213 | familia | 189 |
| 214 | perder | 188 |
| 215 | medio | 187 |
| 216 | dormir | 187 |
| 217 | modo | 183 |
| 218 | paso | 182 |
| 219 | ay | 182 |
| 220 | ah | 182 |
| 221 | tarde | 181 |
| 222 | cuarto | 181 |
| 223 | brazo | 180 |
| 224 | mayor | 179 |
| 225 | dijo | 178 |
| 226 | quién | 177 |
| 227 | joven | 177 |
| 228 | corazón | 177 |
| 229 | rato | 176 |
| 230 | hacia | 176 |
| 231 | mandar | 175 |
| 232 | hoy | 173 |
| 233 | una | 170 |
| 234 | madre | 170 |
| 235 | andar | 170 |
| 236 | amor | 166 |
| 237 | ti | 164 |
| 238 | subir | 164 |
| 239 | dónde | 164 |
| 240 | tocar | 163 |
| 241 | nuevo | 161 |
| 242 | izquierdo | 161 |
| 243 | entonces | 161 |
| 244 | cuanto | 161 |
| 245 | preguntar | 160 |
| 246 | levantar | 160 |
| 247 | moreno | 158 |
| 248 | manera | 158 |
| 249 | dentro | 158 |
| 250 | mesa | 157 |
| 251 | ocurrir | 156 |
| 252 | mil | 155 |
| 253 | buscar | 155 |
| 254 | nadie | 154 |
| 255 | lado | 154 |
| 256 | esperar | 154 |
| 257 | cuerpo | 151 |
| 258 | sé | 150 |
| 259 | madrid | 149 |
| 260 | correr | 149 |
| 261 | sobrino | 148 |
| 262 | momento | 146 |
| 263 | punto | 144 |
| 264 | puesto | 144 |
| 265 | pablo | 144 |
| 266 | eso | 143 |
| 267 | dinero | 142 |
| 268 | acabar | 141 |
| 269 | vamos | 140 |
| 270 | delante | 140 |
| 271 | cuatro | 140 |
| 272 | entender | 139 |
| 273 | bajar | 139 |
| 274 | café | 138 |
| 275 | último | 136 |
| 276 | razón | 134 |
| 277 | comprar | 134 |
| 278 | ballester | 134 |
| 279 | gracia | 133 |
| 280 | suyo | 132 |
| 281 | mientras | 132 |
| 282 | gente | 132 |
| 283 | ellos | 132 |
| 284 | contra | 132 |
| 285 | casi | 130 |
| 286 | aquél | 130 |
| 287 | tirar | 129 |
| 288 | negro | 127 |
| 289 | ganar | 127 |
| 290 | pensamiento | 126 |
| 291 | matar | 126 |
| 292 | vuelta | 125 |
| 293 | duda | 124 |
| 294 | mira | 123 |
| 295 | estupiñá | 123 |
| 296 | claro | 123 |
| 297 | aún | 123 |
| 298 | vestir | 122 |
| 299 | padre | 122 |
| 300 | tonto | 121 |
| 301 | ropa | 121 |
| 302 | junto | 121 |
| 303 | ahí | 120 |
| 304 | acordar | 120 |
| 305 | pegar | 119 |
| 306 | miedo | 119 |
| 307 | feijoo | 119 |
| 308 | baldomero | 119 |
| 309 | pasado | 118 |
| 310 | dado | 118 |
| 311 | recibir | 117 |
| 312 | agua | 117 |
| 313 | soltar | 116 |
| 314 | instante | 116 |
| 315 | expresar | 115 |
| 316 | desear | 115 |
| 317 | callar | 115 |
| 318 | bonito | 115 |
| 319 | tienda | 114 |
| 320 | papitos | 114 |
| 321 | cualquier | 114 |
| 322 | sala | 113 |
| 323 | nicolás | 112 |
| 324 | las | 112 |
| 325 | san | 111 |
| 326 | obra | 111 |
| 327 | fuerte | 111 |
| 328 | comprender | 111 |
| 329 | gusto | 110 |
| 330 | valer | 109 |
| 331 | primero | 109 |
| 332 | pie | 109 |
| 333 | trabajo | 108 |
| 334 | servir | 108 |
| 335 | verdadero | 107 |
| 336 | plácido | 107 |
| 337 | luz | 107 |
| 338 | guardar | 107 |
| 339 | mirada | 106 |
| 340 | real | 105 |
| 341 | nuestro | 105 |
| 342 | cuenta | 105 |
| 343 | cama | 105 |
| 344 | trabajar | 104 |
| 345 | cuyo | 104 |
| 346 | aire | 103 |
| 347 | mamá | 102 |
| 348 | evaristo | 102 |
| 349 | ante | 102 |
| 350 | primera | 101 |
| 351 | mes | 101 |
| 352 | siguiente | 100 |
| 353 | papel | 100 |
| 354 | necesitar | 100 |
| 355 | leer | 100 |
| 356 | le | 100 |
| 357 | cielo | 100 |
| 358 | aun | 100 |
| 359 | llenar | 99 |
| 360 | espíritu | 99 |
| 361 | conversación | 99 |
| 362 | salar | 98 |
| 363 | conciencia | 98 |
| 364 | fuerza | 97 |
| 365 | ellas | 97 |
| 366 | diez | 97 |
| 367 | alcoba | 97 |
| 368 | mostrar | 96 |
| 369 | loco | 96 |
| 370 | escalera | 96 |
| 371 | enterar | 96 |
| 372 | único | 95 |
| 373 | vengar | 94 |
| 374 | todavía | 94 |
| 375 | romper | 94 |
| 376 | observar | 94 |
| 377 | juanito | 94 |
| 378 | sentimiento | 93 |
| 379 | segundo | 93 |
| 380 | llorar | 93 |
| 381 | enfermo | 93 |
| 382 | bajo | 93 |
| 383 | pueblo | 92 |
| 384 | delfín | 92 |
| 385 | chiquillo | 92 |
| 386 | presentar | 91 |
| 387 | infeliz | 91 |
| 388 | demás | 91 |
| 389 | retirar | 90 |
| 390 | importar | 90 |
| 391 | gana | 90 |
| 392 | esposo | 90 |
| 393 | nombre | 89 |
| 394 | bastante | 89 |
| 395 | ofrecer | 88 |
| 396 | largo | 88 |
| 397 | humano | 88 |
| 398 | figurar | 88 |
| 399 | permitir | 87 |
| 400 | tono | 86 |
| 401 | suelo | 86 |
| 402 | convenir | 86 |
| 403 | sueño | 85 |
| 404 | responder | 85 |
| 405 | remedio | 85 |
| 406 | precisar | 85 |
| 407 | pañuelo | 85 |
| 408 | josé | 85 |
| 409 | duro | 85 |
| 410 | visita | 84 |
| 411 | rico | 84 |
| 412 | posible | 84 |
| 413 | mover | 84 |
| 414 | dedo | 84 |
| 415 | recoger | 83 |
| 416 | puro | 83 |
| 417 | olvidar | 83 |
| 418 | dama | 83 |
| 419 | cuidar | 83 |
| 420 | tampoco | 82 |
| 421 | lástima | 82 |
| 422 | arreglar | 82 |
| 423 | son | 81 |
| 424 | soler | 81 |
| 425 | quizás | 81 |
| 426 | ido | 81 |
| 427 | enseñar | 81 |
| 428 | despertar | 81 |
| 429 | deseo | 81 |
| 430 | criar | 81 |
| 431 | contestar | 81 |
| 432 | cinco | 81 |
| 433 | perdonar | 80 |
| 434 | muerte | 80 |
| 435 | historia | 80 |
| 436 | engañar | 80 |
| 437 | disponer | 80 |
| 438 | ángel | 80 |
| 439 | silla | 79 |
| 440 | notar | 79 |
| 441 | mente | 79 |
| 442 | conmigo | 79 |
| 443 | cargar | 79 |
| 444 | camino | 79 |
| 445 | atrever | 79 |
| 446 | sostener | 78 |
| 447 | repetir | 78 |
| 448 | peor | 78 |
| 449 | merecer | 78 |
| 450 | expresión | 78 |
| 451 | ello | 78 |
| 452 | carne | 78 |
| 453 | blanco | 78 |
| 454 | armar | 78 |
| 455 | tras | 77 |
| 456 | cumplir | 77 |
| 457 | aurora | 77 |
| 458 | pelo | 76 |
| 459 | media | 76 |
| 460 | jáuregui | 76 |
| 461 | frente | 76 |
| 462 | estado | 76 |
| 463 | aparecer | 76 |
| 464 | abajo | 76 |
| 465 | semejante | 75 |
| 466 | ley | 75 |
| 467 | iglesia | 75 |
| 468 | don | 75 |
| 469 | cortar | 75 |
| 470 | viuda | 74 |
| 471 | pesar | 74 |
| 472 | pagar | 74 |
| 473 | orden | 74 |
| 474 | moral | 74 |
| 475 | escribir | 74 |
| 476 | cuánto | 74 |
| 477 | cariño | 74 |
| 478 | amar | 74 |
| 479 | villalonga | 73 |
| 480 | severiana | 73 |
| 481 | probar | 73 |
| 482 | labio | 73 |
| 483 | durante | 73 |
| 484 | cocina | 73 |
| 485 | acercar | 73 |
| 486 | ustedes | 72 |
| 487 | coser | 72 |
| 488 | aprender | 72 |
| 489 | acompañar | 72 |
| 490 | señorita | 71 |
| 491 | marchar | 71 |
| 492 | concluir | 71 |
| 493 | color | 71 |
| 494 | tontería | 70 |
| 495 | situación | 70 |
| 496 | segunda | 70 |
| 497 | samaniego | 70 |
| 498 | nacer | 70 |
| 499 | frío | 70 |
| 500 | derecho | 70 |
| 501 | curiosidad | 70 |
| 502 | cerrar | 70 |
| 503 | casta | 70 |
| 504 | broma | 70 |
| 505 | seguro | 69 |
| 506 | pasa | 69 |
| 507 | nariz | 69 |
| 508 | exclamó | 69 |
| 509 | descubrir | 69 |
| 510 | balcón | 69 |
| 511 | ayudar | 69 |
| 512 | atención | 69 |
| 513 | alto | 69 |
| 514 | fijar | 68 |
| 515 | cura | 68 |
| 516 | coche | 68 |
| 517 | apenas | 68 |
| 518 | acostar | 68 |
| 519 | sonreír | 67 |
| 520 | risa | 67 |
| 521 | público | 67 |
| 522 | pecho | 67 |
| 523 | falta | 67 |
| 524 | clase | 67 |
| 525 | arriba | 67 |
| 526 | veces | 66 |
| 527 | unir | 66 |
| 528 | plaza | 66 |
| 529 | partir | 66 |
| 530 | honrar | 66 |
| 531 | arrojar | 66 |
| 532 | arnaiz | 66 |
| 533 | apartar | 66 |
| 534 | temer | 65 |
| 535 | sangre | 65 |
| 536 | recordar | 65 |
| 537 | ocasión | 65 |
| 538 | e | 65 |
| 539 | próximo | 64 |
| 540 | pieza | 64 |
| 541 | pena | 64 |
| 542 | paseo | 64 |
| 543 | parar | 64 |
| 544 | monja | 64 |
| 545 | hermoso | 64 |
| 546 | asegurar | 64 |
| 547 | ambos | 64 |
| 548 | alegría | 64 |
| 549 | alegrar | 64 |
| 550 | sor | 63 |
| 551 | según | 63 |
| 552 | preparar | 63 |
| 553 | ocupar | 63 |
| 554 | misa | 63 |
| 555 | memoria | 63 |
| 556 | juicio | 63 |
| 557 | formar | 63 |
| 558 | despedir | 63 |
| 559 | cuidado | 63 |
| 560 | sonar | 62 |
| 561 | sociedad | 62 |
| 562 | primer | 62 |
| 563 | efecto | 62 |
| 564 | repente | 61 |
| 565 | conseguir | 61 |
| 566 | usar | 60 |
| 567 | triste | 60 |
| 568 | tranquilo | 60 |
| 569 | siquiera | 60 |
| 570 | oh | 60 |
| 571 | naturaleza | 60 |
| 572 | jugar | 60 |
| 573 | hija | 60 |
| 574 | del | 60 |
| 575 | clavar | 60 |
| 576 | cerca | 60 |
| 577 | ayer | 60 |
| 578 | apretar | 60 |
| 579 | acá | 60 |
| 580 | virgen | 59 |
| 581 | saltar | 59 |
| 582 | producir | 59 |
| 583 | limpiar | 59 |
| 584 | golpe | 59 |
| 585 | encender | 59 |
| 586 | dolor | 59 |
| 587 | detener | 59 |
| 588 | costumbre | 59 |
| 589 | corredor | 59 |
| 590 | viejo | 58 |
| 591 | sr | 58 |
| 592 | ruido | 58 |
| 593 | mentira | 58 |
| 594 | gordo | 58 |
| 595 | contener | 58 |
| 596 | tristeza | 57 |
| 597 | reconocer | 57 |
| 598 | hombro | 57 |
| 599 | encima | 57 |
| 600 | carácter | 57 |
| 601 | anoche | 57 |
| 602 | vecino | 56 |
| 603 | tus | 56 |
| 604 | sabes | 56 |
| 605 | resultar | 56 |
| 606 | político | 56 |
| 607 | ii | 56 |
| 608 | diferente | 56 |
| 609 | detrás | 56 |
| 610 | asunto | 56 |
| 611 | arte | 56 |
| 612 | vista | 55 |
| 613 | principio | 55 |
| 614 | médico | 55 |
| 615 | maldito | 55 |
| 616 | dudar | 55 |
| 617 | tardar | 54 |
| 618 | tales | 54 |
| 619 | sombrero | 54 |
| 620 | sol | 54 |
| 621 | noticia | 54 |
| 622 | negar | 54 |
| 623 | natural | 54 |
| 624 | frase | 54 |
| 625 | culpa | 54 |
| 626 | asustar | 54 |
| 627 | vivo | 53 |
| 628 | proponer | 53 |
| 629 | padecer | 53 |
| 630 | forma | 53 |
| 631 | difícil | 53 |
| 632 | demonio | 53 |
| 633 | cerebro | 53 |
| 634 | caballero | 53 |
| 635 | botica | 53 |
| 636 | arrancar | 53 |
| 637 | talento | 52 |
| 638 | soñar | 52 |
| 639 | serio | 52 |
| 640 | principal | 52 |
| 641 | pasión | 52 |
| 642 | paciencia | 52 |
| 643 | lengua | 52 |
| 644 | interés | 52 |
| 645 | feo | 52 |
| 646 | feliz | 52 |
| 647 | explicar | 52 |
| 648 | español | 52 |
| 649 | encargar | 52 |
| 650 | emplear | 52 |
| 651 | doce | 52 |
| 652 | confianza | 52 |
| 653 | ánimo | 52 |
| 654 | amo | 52 |
| 655 | alzar | 52 |
| 656 | además | 52 |
| 657 | acción | 52 |
| 658 | sofá | 51 |
| 659 | sitio | 51 |
| 660 | pasillo | 51 |
| 661 | particular | 51 |
| 662 | lógica | 51 |
| 663 | llave | 51 |
| 664 | libro | 51 |
| 665 | habitación | 51 |
| 666 | existir | 51 |
| 667 | disparate | 51 |
| 668 | basilio | 51 |
| 669 | acto | 51 |
| 670 | sentido | 50 |
| 671 | realidad | 50 |
| 672 | pecar | 50 |
| 673 | paz | 50 |
| 674 | pared | 50 |
| 675 | os | 50 |
| 676 | lejos | 50 |
| 677 | i | 50 |
| 678 | horrible | 50 |
| 679 | gabinete | 50 |
| 680 | escapar | 50 |
| 681 | contrario | 50 |
| 682 | compañero | 50 |
| 683 | calor | 50 |
| 684 | atrás | 50 |
| 685 | rostro | 49 |
| 686 | respeto | 49 |
| 687 | honor | 49 |
| 688 | gastar | 49 |
| 689 | fundador | 49 |
| 690 | fe | 49 |
| 691 | defender | 49 |
| 692 | decidir | 49 |
| 693 | cuales | 49 |
| 694 | cantar | 49 |
| 695 | valor | 48 |
| 696 | pintar | 48 |
| 697 | novio | 48 |
| 698 | movimiento | 48 |
| 699 | interior | 48 |
| 700 | ilusión | 48 |
| 701 | hallar | 48 |
| 702 | edad | 48 |
| 703 | convento | 48 |
| 704 | continuar | 48 |
| 705 | causa | 48 |
| 706 | vino | 47 |
| 707 | revolver | 47 |
| 708 | lavar | 47 |
| 709 | inspirar | 47 |
| 710 | gozar | 47 |
| 711 | examinar | 47 |
| 712 | durar | 47 |
| 713 | curar | 47 |
| 714 | considerar | 47 |
| 715 | ambas | 47 |
| 716 | abandonar | 47 |
| 717 | torquemada | 46 |
| 718 | social | 46 |
| 719 | par | 46 |
| 720 | maría | 46 |
| 721 | envolver | 46 |
| 722 | beber | 46 |
| 723 | antiguo | 46 |
| 724 | vergüenza | 45 |
| 725 | ventana | 45 |
| 726 | tierra | 45 |
| 727 | salvar | 45 |
| 728 | religioso | 45 |
| 729 | negocio | 45 |
| 730 | matrimonio | 45 |
| 731 | mantón | 45 |
| 732 | guapo | 45 |
| 733 | esto | 45 |
| 734 | diente | 45 |
| 735 | cristo | 45 |
| 736 | contigo | 45 |
| 737 | visitar | 44 |
| 738 | siete | 44 |
| 739 | rezar | 44 |
| 740 | replicó | 44 |
| 741 | religión | 44 |
| 742 | piedra | 44 |
| 743 | patio | 44 |
| 744 | necesidad | 44 |
| 745 | mar | 44 |
| 746 | lanzar | 44 |
| 747 | impresión | 44 |
| 748 | fondo | 44 |
| 749 | fácil | 44 |
| 750 | divertir | 44 |
| 751 | carta | 44 |
| 752 | bastar | 44 |
| 753 | apoyar | 44 |
| 754 | señorito | 43 |
| 755 | segismundo | 43 |
| 756 | música | 43 |
| 757 | muerto | 43 |
| 758 | jurar | 43 |
| 759 | inclinar | 43 |
| 760 | empeñar | 43 |
| 761 | derecha | 43 |
| 762 | debajo | 43 |
| 763 | comedor | 43 |
| 764 | cambiar | 43 |
| 765 | bota | 43 |
| 766 | bárbara | 43 |
| 767 | aparisi | 43 |
| 768 | víctima | 42 |
| 769 | suerte | 42 |
| 770 | silencio | 42 |
| 771 | seis | 42 |
| 772 | revelar | 42 |
| 773 | portar | 42 |
| 774 | portal | 42 |
| 775 | pan | 42 |
| 776 | objeto | 42 |
| 777 | mona | 42 |
| 778 | micaelas | 42 |
| 779 | jaqueca | 42 |
| 780 | género | 42 |
| 781 | fresco | 42 |
| 782 | establecimiento | 42 |
| 783 | discurrir | 42 |
| 784 | decente | 42 |
| 785 | confesar | 42 |
| 786 | beso | 42 |
| 787 | banco | 42 |
| 788 | apreciar | 42 |
| 789 | anunciar | 42 |
| 790 | adelantar | 42 |
| 791 | tremendo | 41 |
| 792 | temblar | 41 |
| 793 | relación | 41 |
| 794 | perdón | 41 |
| 795 | pedazo | 41 |
| 796 | opinión | 41 |
| 797 | mitad | 41 |
| 798 | lleno | 41 |
| 799 | lenguaje | 41 |
| 800 | lección | 41 |
| 801 | lágrima | 41 |
| 802 | justicia | 41 |
| 803 | ja | 41 |
| 804 | imagen | 41 |
| 805 | esconder | 41 |
| 806 | entregar | 41 |
| 807 | dueño | 41 |
| 808 | disimular | 41 |
| 809 | conservar | 41 |
| 810 | cansar | 41 |
| 811 | azul | 41 |
| 812 | alguien | 41 |
| 813 | agradecer | 41 |
| 814 | absolutamente | 41 |
| 815 | tema | 40 |
| 816 | profundo | 40 |
| 817 | número | 40 |
| 818 | muchacho | 40 |
| 819 | leche | 40 |
| 820 | imposible | 40 |
| 821 | imaginar | 40 |
| 822 | fino | 40 |
| 823 | dirigir | 40 |
| 824 | cuento | 40 |
| 825 | convencer | 40 |
| 826 | contemplar | 40 |
| 827 | colocar | 40 |
| 828 | caña | 40 |
| 829 | averiguar | 40 |
| 830 | asomar | 40 |
| 831 | apetito | 40 |
| 832 | almorzar | 40 |
| 833 | alborotar | 40 |
| 834 | voluntad | 39 |
| 835 | virtud | 39 |
| 836 | temor | 39 |
| 837 | suponer | 39 |
| 838 | simpático | 39 |
| 839 | secreto | 39 |
| 840 | robar | 39 |
| 841 | resistir | 39 |
| 842 | punta | 39 |
| 843 | papá | 39 |
| 844 | muñoz | 39 |
| 845 | mire | 39 |
| 846 | marqués | 39 |
| 847 | igual | 39 |
| 848 | figura | 39 |
| 849 | favor | 39 |
| 850 | esposar | 39 |
| 851 | entretener | 39 |
| 852 | enteramente | 39 |
| 853 | disposición | 39 |
| 854 | criatura | 39 |
| 855 | costar | 39 |
| 856 | contento | 39 |
| 857 | colgar | 39 |
| 858 | capa | 39 |
| 859 | cantidad | 39 |
| 860 | adquirir | 39 |
| 861 | verde | 38 |
| 862 | pico | 38 |
| 863 | pequeño | 38 |
| 864 | pepe | 38 |
| 865 | pasear | 38 |
| 866 | nervioso | 38 |
| 867 | nene | 38 |
| 868 | libertad | 38 |
| 869 | ira | 38 |
| 870 | grito | 38 |
| 871 | flor | 38 |
| 872 | extrañar | 38 |
| 873 | enfadar | 38 |
| 874 | ejemplo | 38 |
| 875 | dulce | 38 |
| 876 | declarar | 38 |
| 877 | completo | 38 |
| 878 | vender | 37 |
| 879 | saludar | 37 |
| 880 | salida | 37 |
| 881 | quevedo | 37 |
| 882 | prestar | 37 |
| 883 | plantar | 37 |
| 884 | oído | 37 |
| 885 | nosotros | 37 |
| 886 | manifestar | 37 |
| 887 | jamás | 37 |
| 888 | disparatar | 37 |
| 889 | determinar | 37 |
| 890 | bendito | 37 |
| 891 | amistad | 37 |
| 892 | aguantar | 37 |
| 893 | acudir | 37 |
| 894 | tragar | 36 |
| 895 | suspiro | 36 |
| 896 | salvaje | 36 |
| 897 | raro | 36 |
| 898 | práctico | 36 |
| 899 | polvo | 36 |
| 900 | plato | 36 |
| 901 | piso | 36 |
| 902 | pasmar | 36 |
| 903 | miseria | 36 |
| 904 | manía | 36 |
| 905 | juanín | 36 |
| 906 | inglés | 36 |
| 907 | iii | 36 |
| 908 | estudiar | 36 |
| 909 | doler | 36 |
| 910 | demasiado | 36 |
| 911 | cuál | 36 |
| 912 | crecer | 36 |
| 913 | convertir | 36 |
| 914 | comunicar | 36 |
| 915 | causar | 36 |
| 916 | campo | 36 |
| 917 | barrio | 36 |
| 918 | amante | 36 |
| 919 | advertir | 36 |
| 920 | admirable | 36 |
| 921 | superior | 35 |
| 922 | suceso | 35 |
| 923 | sospechar | 35 |
| 924 | secar | 35 |
| 925 | pronunciar | 35 |
| 926 | preguntó | 35 |
| 927 | picar | 35 |
| 928 | país | 35 |
| 929 | motivo | 35 |
| 930 | molestar | 35 |
| 931 | lugar | 35 |
| 932 | genio | 35 |
| 933 | falda | 35 |
| 934 | espiritual | 35 |
| 935 | enemigo | 35 |
| 936 | distinto | 35 |
| 937 | chocolate | 35 |
| 938 | ves | 34 |
| 939 | vencer | 34 |
| 940 | separar | 34 |
| 941 | ruiz | 34 |
| 942 | rojo | 34 |
| 943 | querido | 34 |
| 944 | prometer | 34 |
| 945 | pregunta | 34 |
| 946 | plan | 34 |
| 947 | letra | 34 |
| 948 | largar | 34 |
| 949 | ji | 34 |
| 950 | inmenso | 34 |
| 951 | hierro | 34 |
| 952 | gritar | 34 |
| 953 | gracioso | 34 |
| 954 | gobierno | 34 |
| 955 | fuego | 34 |
| 956 | farmacéutico | 34 |
| 957 | delicado | 34 |
| 958 | crear | 34 |
| 959 | consejo | 34 |
| 960 | cesar | 34 |
| 961 | caridad | 34 |
| 962 | cabo | 34 |
| 963 | caber | 34 |
| 964 | bolsillo | 34 |
| 965 | atar | 34 |
| 966 | aceptar | 34 |
| 967 | veras | 33 |
| 968 | velar | 33 |
| 969 | treinta | 33 |
| 970 | teatro | 33 |
| 971 | sonrisa | 33 |
| 972 | señal | 33 |
| 973 | salud | 33 |
| 974 | sacudir | 33 |
| 975 | respecto | 33 |
| 976 | primeros | 33 |
| 977 | poquito | 33 |
| 978 | perro | 33 |
| 979 | pareja | 33 |
| 980 | palo | 33 |
| 981 | olmedo | 33 |
| 982 | ocultar | 33 |
| 983 | intentar | 33 |
| 984 | inocente | 33 |
| 985 | gracias | 33 |
| 986 | gato | 33 |
| 987 | francamente | 33 |
| 988 | extender | 33 |
| 989 | estómago | 33 |
| 990 | escena | 33 |
| 991 | equivocar | 33 |
| 992 | domingo | 33 |
| 993 | distinguir | 33 |
| 994 | dignidad | 33 |
| 995 | cuello | 33 |
| 996 | comercio | 33 |
| 997 | cambio | 33 |
| 998 | caja | 33 |
| 999 | ave | 33 |
| 1000 | aumentar | 33 |
| 1001 | apurar | 33 |
| 1002 | veinte | 32 |
| 1003 | tuyo | 32 |
| 1004 | trato | 32 |
| 1005 | tapar | 32 |
| 1006 | reventar | 32 |
| 1007 | respuesta | 32 |
| 1008 | ratito | 32 |
| 1009 | prisa | 32 |
| 1010 | prenda | 32 |
| 1011 | oscuro | 32 |
| 1012 | oro | 32 |
| 1013 | nueve | 32 |
| 1014 | libre | 32 |
| 1015 | hermosura | 32 |
| 1016 | existencia | 32 |
| 1017 | estilo | 32 |
| 1018 | esta | 32 |
| 1019 | educación | 32 |
| 1020 | dichoso | 32 |
| 1021 | desgraciar | 32 |
| 1022 | desgracia | 32 |
| 1023 | delfina | 32 |
| 1024 | cuestión | 32 |
| 1025 | consolar | 32 |
| 1026 | consentir | 32 |
| 1027 | concepto | 32 |
| 1028 | completamente | 32 |
| 1029 | compañía | 32 |
| 1030 | charlar | 32 |
| 1031 | barbaridad | 32 |
| 1032 | asilo | 32 |
| 1033 | arrastrar | 32 |
| 1034 | añadir | 32 |
| 1035 | alargar | 32 |
| 1036 | actitud | 32 |
| 1037 | versar | 31 |
| 1038 | tertuliar | 31 |
| 1039 | término | 31 |
| 1040 | tela | 31 |
| 1041 | superiora | 31 |
| 1042 | sucio | 31 |
| 1043 | suceder | 31 |
| 1044 | semana | 31 |
| 1045 | rodear | 31 |
| 1046 | rey | 31 |
| 1047 | reloj | 31 |
| 1048 | recomendar | 31 |
| 1049 | preciso | 31 |
| 1050 | oye | 31 |
| 1051 | mueble | 31 |
| 1052 | grave | 31 |
| 1053 | general | 31 |
| 1054 | esfuerzo | 31 |
| 1055 | enfermedad | 31 |
| 1056 | encerrar | 31 |
| 1057 | elegante | 31 |
| 1058 | descomponer | 31 |
| 1059 | cómodo | 31 |
| 1060 | cava | 31 |
| 1061 | breve | 31 |
| 1062 | billete | 31 |
| 1063 | belén | 31 |
| 1064 | autoridad | 31 |
| 1065 | adorar | 31 |
| 1066 | vicio | 30 |
| 1067 | toledo | 30 |
| 1068 | terror | 30 |
| 1069 | terreno | 30 |
| 1070 | sombra | 30 |
| 1071 | rincón | 30 |
| 1072 | representar | 30 |
| 1073 | referir | 30 |
| 1074 | poseer | 30 |
| 1075 | pez | 30 |
| 1076 | penetrar | 30 |
| 1077 | mía | 30 |
| 1078 | librar | 30 |
| 1079 | ladrillo | 30 |
| 1080 | isla | 30 |
| 1081 | impulso | 30 |
| 1082 | imaginación | 30 |
| 1083 | hucha | 30 |
| 1084 | honradez | 30 |
| 1085 | grupo | 30 |
| 1086 | finar | 30 |
| 1087 | fatigar | 30 |
| 1088 | excelente | 30 |
| 1089 | evitar | 30 |
| 1090 | dura | 30 |
| 1091 | desaparecer | 30 |
| 1092 | clérigo | 30 |
| 1093 | ciego | 30 |
| 1094 | cariñoso | 30 |
| 1095 | acento | 30 |
| 1096 | viento | 29 |
| 1097 | trasto | 29 |
| 1098 | tiro | 29 |
| 1099 | techo | 29 |
| 1100 | sujetar | 29 |
| 1101 | siglo | 29 |
| 1102 | servicio | 29 |
| 1103 | respirar | 29 |
| 1104 | resolver | 29 |
| 1105 | quejar | 29 |
| 1106 | puesta | 29 |
| 1107 | proteger | 29 |
| 1108 | periódico | 29 |
| 1109 | pecado | 29 |
| 1110 | nadar | 29 |
| 1111 | menudo | 29 |
| 1112 | ladrón | 29 |
| 1113 | inventar | 29 |
| 1114 | individuo | 29 |
| 1115 | fijo | 29 |
| 1116 | feliciana | 29 |
| 1117 | espejo | 29 |
| 1118 | españa | 29 |
| 1119 | dominar | 29 |
| 1120 | destino | 29 |
| 1121 | cubrir | 29 |
| 1122 | bestia | 29 |
| 1123 | benigna | 29 |
| 1124 | argumento | 29 |
| 1125 | anterior | 29 |
| 1126 | altar | 29 |
| 1127 | volar | 28 |
| 1128 | vacilar | 28 |
| 1129 | tren | 28 |
| 1130 | tender | 28 |
| 1131 | sustancia | 28 |
| 1132 | prueba | 28 |
| 1133 | problema | 28 |
| 1134 | pecador | 28 |
| 1135 | pariente | 28 |
| 1136 | ocho | 28 |
| 1137 | obligar | 28 |
| 1138 | obedecer | 28 |
| 1139 | moda | 28 |
| 1140 | máquina | 28 |
| 1141 | juego | 28 |
| 1142 | iv | 28 |
| 1143 | hoja | 28 |
| 1144 | fundar | 28 |
| 1145 | extremo | 28 |
| 1146 | estúpido | 28 |
| 1147 | esquina | 28 |
| 1148 | época | 28 |
| 1149 | edificio | 28 |
| 1150 | dirección | 28 |
| 1151 | conque | 28 |
| 1152 | componer | 28 |
| 1153 | claridad | 28 |
| 1154 | circunstancia | 28 |
| 1155 | capellán | 28 |
| 1156 | capaz | 28 |
| 1157 | besar | 28 |
| 1158 | atender | 28 |
| 1159 | apuntar | 28 |
| 1160 | aplicar | 28 |
| 1161 | anda | 28 |
| 1162 | acertar | 28 |
| 1163 | vecindad | 27 |
| 1164 | varias | 27 |
| 1165 | valiente | 27 |
| 1166 | v | 27 |
| 1167 | trastornar | 27 |
| 1168 | traje | 27 |
| 1169 | timidez | 27 |
| 1170 | seso | 27 |
| 1171 | serenidad | 27 |
| 1172 | semblante | 27 |
| 1173 | seguramente | 27 |
| 1174 | reñir | 27 |
| 1175 | rabia | 27 |
| 1176 | propósito | 27 |
| 1177 | prójima | 27 |
| 1178 | primo | 27 |
| 1179 | pertenecer | 27 |
| 1180 | parir | 27 |
| 1181 | obligación | 27 |
| 1182 | noble | 27 |
| 1183 | mozo | 27 |
| 1184 | minuto | 27 |
| 1185 | mérito | 27 |
| 1186 | medicina | 27 |
| 1187 | león | 27 |
| 1188 | iluminar | 27 |
| 1189 | huevo | 27 |
| 1190 | guerra | 27 |
| 1191 | falso | 27 |
| 1192 | extranjero | 27 |
| 1193 | encarnación | 27 |
| 1194 | dicho | 27 |
| 1195 | convicción | 27 |
| 1196 | conformar | 27 |
| 1197 | cobrar | 27 |
| 1198 | ciencia | 27 |
| 1199 | celo | 27 |
| 1200 | carrera | 27 |
| 1201 | árbol | 27 |
| 1202 | agarrar | 27 |
| 1203 | admirar | 27 |
| 1204 | adiós | 27 |
| 1205 | aburrir | 27 |
| 1206 | viaje | 26 |
| 1207 | vela | 26 |
| 1208 | variar | 26 |
| 1209 | trapo | 26 |
| 1210 | tranquilizar | 26 |
| 1211 | total | 26 |
| 1212 | tertulia | 26 |
| 1213 | satisfacer | 26 |
| 1214 | satisfacción | 26 |
| 1215 | sabe | 26 |
| 1216 | ratos | 26 |
| 1217 | plata | 26 |
| 1218 | permanecer | 26 |
| 1219 | perfecto | 26 |
| 1220 | parroquiano | 26 |
| 1221 | oreja | 26 |
| 1222 | oler | 26 |
| 1223 | oficio | 26 |
| 1224 | obtener | 26 |
| 1225 | observación | 26 |
| 1226 | mosca | 26 |
| 1227 | madera | 26 |
| 1228 | lucir | 26 |
| 1229 | lecho | 26 |
| 1230 | interesar | 26 |
| 1231 | indecente | 26 |
| 1232 | increíble | 26 |
| 1233 | imponer | 26 |
| 1234 | humor | 26 |
| 1235 | hueco | 26 |
| 1236 | gesto | 26 |
| 1237 | filosofía | 26 |
| 1238 | excitar | 26 |
| 1239 | estudio | 26 |
| 1240 | entusiasmar | 26 |
| 1241 | entendimiento | 26 |
| 1242 | diferencia | 26 |
| 1243 | cuerda | 26 |
| 1244 | cuándo | 26 |
| 1245 | corriente | 26 |
| 1246 | contentar | 26 |
| 1247 | condenar | 26 |
| 1248 | compra | 26 |
| 1249 | comida | 26 |
| 1250 | caballo | 26 |
| 1251 | boda | 26 |
| 1252 | atravesar | 26 |
| 1253 | asiento | 26 |
| 1254 | absoluto | 26 |
| 1255 | villuendas | 25 |
| 1256 | vaso | 25 |
| 1257 | tiene | 25 |
| 1258 | sorprender | 25 |
| 1259 | soledad | 25 |
| 1260 | significar | 25 |
| 1261 | seno | 25 |
| 1262 | rodilla | 25 |
| 1263 | retrato | 25 |
| 1264 | recado | 25 |
| 1265 | ramo | 25 |
| 1266 | piedad | 25 |
| 1267 | perfectamente | 25 |
| 1268 | parís | 25 |
| 1269 | olor | 25 |
| 1270 | novedad | 25 |
| 1271 | nicanora | 25 |
| 1272 | menor | 25 |
| 1273 | mantener | 25 |
| 1274 | limosna | 25 |
| 1275 | lectura | 25 |
| 1276 | intención | 25 |
| 1277 | incomodar | 25 |
| 1278 | hostia | 25 |
| 1279 | haz | 25 |
| 1280 | hartar | 25 |
| 1281 | hambre | 25 |
| 1282 | físico | 25 |
| 1283 | farmacia | 25 |
| 1284 | entusiasmo | 25 |
| 1285 | doblar | 25 |
| 1286 | cruzar | 25 |
| 1287 | criada | 25 |
| 1288 | convidar | 25 |
| 1289 | condición | 25 |
| 1290 | cincuenta | 25 |
| 1291 | calmar | 25 |
| 1292 | arrepentir | 25 |
| 1293 | acostumbrar | 25 |
| 1294 | terrible | 24 |
| 1295 | sufrir | 24 |
| 1296 | suegro | 24 |
| 1297 | sorpresa | 24 |
| 1298 | sofocar | 24 |
| 1299 | síntoma | 24 |
| 1300 | señalar | 24 |
| 1301 | seda | 24 |
| 1302 | santidad | 24 |
| 1303 | resultado | 24 |
| 1304 | recobrar | 24 |
| 1305 | rafaela | 24 |
| 1306 | quiere | 24 |
| 1307 | puño | 24 |
| 1308 | presencia | 24 |
| 1309 | personal | 24 |
| 1310 | peinar | 24 |
| 1311 | pálido | 24 |
| 1312 | pájaro | 24 |
| 1313 | pacheco | 24 |
| 1314 | muchísimo | 24 |
| 1315 | misterioso | 24 |
| 1316 | manta | 24 |
| 1317 | maestro | 24 |
| 1318 | lujo | 24 |
| 1319 | juntar | 24 |
| 1320 | indicar | 24 |
| 1321 | impedir | 24 |
| 1322 | hueso | 24 |
| 1323 | herencia | 24 |
| 1324 | grado | 24 |
| 1325 | gloria | 24 |
| 1326 | furioso | 24 |
| 1327 | extraordinario | 24 |
| 1328 | espalda | 24 |
| 1329 | escuela | 24 |
| 1330 | desconocer | 24 |
| 1331 | descansar | 24 |
| 1332 | demostrar | 24 |
| 1333 | decía | 24 |
| 1334 | debilidad | 24 |
| 1335 | corto | 24 |
| 1336 | compasión | 24 |
| 1337 | comedia | 24 |
| 1338 | círculo | 24 |
| 1339 | anciano | 24 |
| 1340 | alcanzar | 24 |
| 1341 | ahogar | 24 |
| 1342 | agradar | 24 |
| 1343 | adoración | 24 |
| 1344 | uso | 23 |
| 1345 | toda | 23 |
| 1346 | tipo | 23 |
| 1347 | temeroso | 23 |
| 1348 | sosegar | 23 |
| 1349 | severidad | 23 |
| 1350 | sabio | 23 |
| 1351 | respetar | 23 |
| 1352 | reparar | 23 |
| 1353 | remediar | 23 |
| 1354 | rápidamente | 23 |
| 1355 | rama | 23 |
| 1356 | procurar | 23 |
| 1357 | podrir | 23 |
| 1358 | pícaro | 23 |
| 1359 | periodo | 23 |
| 1360 | pata | 23 |
| 1361 | orgullo | 23 |
| 1362 | ordinario | 23 |
| 1363 | oponer | 23 |
| 1364 | olimpia | 23 |
| 1365 | nombrar | 23 |
| 1366 | mudar | 23 |
| 1367 | moneda | 23 |
| 1368 | marcela | 23 |
| 1369 | marcar | 23 |
| 1370 | manto | 23 |
| 1371 | ligero | 23 |
| 1372 | jesús | 23 |
| 1373 | isabel | 23 |
| 1374 | infame | 23 |
| 1375 | humanidad | 23 |
| 1376 | huir | 23 |
| 1377 | honrado | 23 |
| 1378 | hábito | 23 |
| 1379 | gobernar | 23 |
| 1380 | facultad | 23 |
| 1381 | energía | 23 |
| 1382 | enamorar | 23 |
| 1383 | difunto | 23 |
| 1384 | cristiano | 23 |
| 1385 | cometer | 23 |
| 1386 | bruto | 23 |
| 1387 | avanzar | 23 |
| 1388 | artículo | 23 |
| 1389 | animar | 23 |
| 1390 | amarillo | 23 |
| 1391 | ajeno | 23 |
| 1392 | abrazar | 23 |
| 1393 | aborrecer | 23 |
| 1394 | vi | 22 |
| 1395 | temprano | 22 |
| 1396 | sinceridad | 22 |
| 1397 | serenar | 22 |
| 1398 | seguridad | 22 |
| 1399 | santísimo | 22 |
| 1400 | sano | 22 |
| 1401 | salón | 22 |
| 1402 | sacerdote | 22 |
| 1403 | rodar | 22 |
| 1404 | río | 22 |
| 1405 | recorrer | 22 |
| 1406 | realizar | 22 |
| 1407 | rabiar | 22 |
| 1408 | quedose | 22 |
| 1409 | peso | 22 |
| 1410 | peseta | 22 |
| 1411 | peligro | 22 |
| 1412 | paquete | 22 |
| 1413 | paño | 22 |
| 1414 | nosotras | 22 |
| 1415 | norte | 22 |
| 1416 | miserable | 22 |
| 1417 | manuel | 22 |
| 1418 | línea | 22 |
| 1419 | inquietud | 22 |
| 1420 | importancia | 22 |
| 1421 | hay | 22 |
| 1422 | fortuna | 22 |
| 1423 | formalidad | 22 |
| 1424 | fingir | 22 |
| 1425 | felicidad | 22 |
| 1426 | estás | 22 |
| 1427 | escándalo | 22 |
| 1428 | empujar | 22 |
| 1429 | emoción | 22 |
| 1430 | eh | 22 |
| 1431 | echado | 22 |
| 1432 | doméstico | 22 |
| 1433 | distraer | 22 |
| 1434 | dificultad | 22 |
| 1435 | dedicar | 22 |
| 1436 | cuadro | 22 |
| 1437 | cristal | 22 |
| 1438 | copa | 22 |
| 1439 | consultar | 22 |
| 1440 | consecuencia | 22 |
| 1441 | cintura | 22 |
| 1442 | célebre | 22 |
| 1443 | ceja | 22 |
| 1444 | castigar | 22 |
| 1445 | cargo | 22 |
| 1446 | capital | 22 |
| 1447 | camisa | 22 |
| 1448 | calma | 22 |
| 1449 | buen | 22 |
| 1450 | barba | 22 |
| 1451 | bailar | 22 |
| 1452 | asombrar | 22 |
| 1453 | apariencia | 22 |
| 1454 | alejar | 22 |
| 1455 | agujero | 22 |
| 1456 | afectar | 22 |
| 1457 | acometer | 22 |
| 1458 | acera | 22 |
| 1459 | verdaderamente | 21 |
| 1460 | tranquilidad | 21 |
| 1461 | trampa | 21 |
| 1462 | sujeto | 21 |
| 1463 | suelto | 21 |
| 1464 | simpatía | 21 |
| 1465 | sillón | 21 |
| 1466 | santísima | 21 |
| 1467 | risueño | 21 |
| 1468 | repartir | 21 |
| 1469 | quieres | 21 |
| 1470 | querida | 21 |
| 1471 | presente | 21 |
| 1472 | plazuela | 21 |
| 1473 | partido | 21 |
| 1474 | oscuridad | 21 |
| 1475 | ordenar | 21 |
| 1476 | ofender | 21 |
| 1477 | nones | 21 |
| 1478 | nacimiento | 21 |
| 1479 | montón | 21 |
| 1480 | meditar | 21 |
| 1481 | mas | 21 |
| 1482 | local | 21 |
| 1483 | limpio | 21 |
| 1484 | judío | 21 |
| 1485 | íntimo | 21 |
| 1486 | inteligencia | 21 |
| 1487 | inmediato | 21 |
| 1488 | idear | 21 |
| 1489 | horror | 21 |
| 1490 | ha | 21 |
| 1491 | gravar | 21 |
| 1492 | explicación | 21 |
| 1493 | está | 21 |
| 1494 | entero | 21 |
| 1495 | enorme | 21 |
| 1496 | distancia | 21 |
| 1497 | disgusto | 21 |
| 1498 | discutir | 21 |
| 1499 | discreto | 21 |
| 1500 | desdén | 21 |
| 1501 | cordero | 21 |
| 1502 | consistir | 21 |
| 1503 | conocimiento | 21 |
| 1504 | confundir | 21 |
| 1505 | cajón | 21 |
| 1506 | bribón | 21 |
| 1507 | bola | 21 |
| 1508 | bofetada | 21 |
| 1509 | asco | 21 |
| 1510 | antonio | 21 |
| 1511 | animal | 21 |
| 1512 | admiración | 21 |
| 1513 | ademán | 21 |
| 1514 | adelante | 21 |
| 1515 | acerca | 21 |
| 1516 | acentuar | 21 |
| 1517 | zalamero | 20 |
| 1518 | vera | 20 |
| 1519 | varios | 20 |
| 1520 | vanidad | 20 |
| 1521 | tunante | 20 |
| 1522 | tropa | 20 |
| 1523 | tía | 20 |
| 1524 | tarascar | 20 |
| 1525 | socorro | 20 |
| 1526 | sistema | 20 |
| 1527 | seco | 20 |
| 1528 | sagrario | 20 |
| 1529 | sagrado | 20 |
| 1530 | sábana | 20 |
| 1531 | resto | 20 |
| 1532 | reservar | 20 |
| 1533 | referente | 20 |
| 1534 | quieto | 20 |
| 1535 | quemar | 20 |
| 1536 | pretender | 20 |
| 1537 | pintado | 20 |
| 1538 | pesado | 20 |
| 1539 | patricia | 20 |
| 1540 | pase | 20 |
| 1541 | orar | 20 |
| 1542 | naturalmente | 20 |
| 1543 | modelo | 20 |
| 1544 | magnífico | 20 |
| 1545 | maestra | 20 |
| 1546 | jueves | 20 |
| 1547 | insignificante | 20 |
| 1548 | huerta | 20 |
| 1549 | gozoso | 20 |
| 1550 | ginés | 20 |
| 1551 | función | 20 |
| 1552 | franqueza | 20 |
| 1553 | francisco | 20 |
| 1554 | firmar | 20 |
| 1555 | fiera | 20 |
| 1556 | fiel | 20 |
| 1557 | fenómeno | 20 |
| 1558 | establecer | 20 |
| 1559 | esperanza | 20 |
| 1560 | espacio | 20 |
| 1561 | embargo | 20 |
| 1562 | económico | 20 |
| 1563 | divino | 20 |
| 1564 | desplegar | 20 |
| 1565 | despachar | 20 |
| 1566 | deshacer | 20 |
| 1567 | desempeñar | 20 |
| 1568 | dependiente | 20 |
| 1569 | dato | 20 |
| 1570 | consuelo | 20 |
| 1571 | confusión | 20 |
| 1572 | conducta | 20 |
| 1573 | combinar | 20 |
| 1574 | capilla | 20 |
| 1575 | campanilla | 20 |
| 1576 | buena | 20 |
| 1577 | bobo | 20 |
| 1578 | bah | 20 |
| 1579 | avisar | 20 |
| 1580 | aspecto | 20 |
| 1581 | aproximar | 20 |
| 1582 | amenazar | 20 |
| 1583 | admitir | 20 |
| 1584 | abrigo | 20 |
| 1585 | vestido | 19 |
| 1586 | venga | 19 |
| 1587 | solar | 19 |
| 1588 | simple | 19 |
| 1589 | seriedad | 19 |
| 1590 | seguida | 19 |
| 1591 | ridículo | 19 |
| 1592 | revólver | 19 |
| 1593 | rendir | 19 |
| 1594 | rencor | 19 |
| 1595 | reja | 19 |
| 1596 | rápido | 19 |
| 1597 | prudente | 19 |
| 1598 | protección | 19 |
| 1599 | proceder | 19 |
| 1600 | pretexto | 19 |
| 1601 | presunción | 19 |
| 1602 | préstamo | 19 |
| 1603 | pozo | 19 |
| 1604 | personar | 19 |
| 1605 | nube | 19 |
| 1606 | novela | 19 |
| 1607 | nota | 19 |
| 1608 | natividad | 19 |
| 1609 | murmuró | 19 |
| 1610 | medida | 19 |
| 1611 | limpieza | 19 |
| 1612 | instinto | 19 |
| 1613 | infierno | 19 |
| 1614 | importante | 19 |
| 1615 | hacienda | 19 |
| 1616 | gumersindo | 19 |
| 1617 | fórmula | 19 |
| 1618 | facha | 19 |
| 1619 | extraño | 19 |
| 1620 | estirar | 19 |
| 1621 | estación | 19 |
| 1622 | especie | 19 |
| 1623 | espantar | 19 |
| 1624 | escalón | 19 |
| 1625 | encargo | 19 |
| 1626 | educar | 19 |
| 1627 | duque | 19 |
| 1628 | despacho | 19 |
| 1629 | deshonrar | 19 |
| 1630 | cuerdo | 19 |
| 1631 | crimen | 19 |
| 1632 | comparar | 19 |
| 1633 | celebrar | 19 |
| 1634 | busca | 19 |
| 1635 | botón | 19 |
| 1636 | borrar | 19 |
| 1637 | bondad | 19 |
| 1638 | belleza | 19 |
| 1639 | bastón | 19 |
| 1640 | artista | 19 |
| 1641 | aplacar | 19 |
| 1642 | antipático | 19 |
| 1643 | alta | 19 |
| 1644 | almuerzo | 19 |
| 1645 | afecto | 19 |
| 1646 | adentrar | 19 |
| 1647 | acaso | 19 |
| 1648 | vulgar | 18 |
| 1649 | veinticinco | 18 |
| 1650 | vale | 18 |
| 1651 | turbar | 18 |
| 1652 | trujillo | 18 |
| 1653 | tropezar | 18 |
| 1654 | tercera | 18 |
| 1655 | suavemente | 18 |
| 1656 | socorrer | 18 |
| 1657 | sermón | 18 |
| 1658 | sencillo | 18 |
| 1659 | satisfecho | 18 |
| 1660 | repitió | 18 |
| 1661 | regular | 18 |
| 1662 | profesor | 18 |
| 1663 | primeras | 18 |
| 1664 | precisamente | 18 |
| 1665 | partida | 18 |
| 1666 | pantalón | 18 |
| 1667 | once | 18 |
| 1668 | noticiar | 18 |
| 1669 | misterio | 18 |
| 1670 | militar | 18 |
| 1671 | mental | 18 |
| 1672 | mejilla | 18 |
| 1673 | marcha | 18 |
| 1674 | lograr | 18 |
| 1675 | locura | 18 |
| 1676 | lance | 18 |
| 1677 | juzgar | 18 |
| 1678 | inútil | 18 |
| 1679 | infantil | 18 |
| 1680 | indicó | 18 |
| 1681 | improvisar | 18 |
| 1682 | hilo | 18 |
| 1683 | herir | 18 |
| 1684 | hablador | 18 |
| 1685 | guardia | 18 |
| 1686 | guante | 18 |
| 1687 | gritó | 18 |
| 1688 | furor | 18 |
| 1689 | frotar | 18 |
| 1690 | fenelón | 18 |
| 1691 | federico | 18 |
| 1692 | eterno | 18 |
| 1693 | estremecer | 18 |
| 1694 | estrellar | 18 |
| 1695 | entierro | 18 |
| 1696 | ejercicio | 18 |
| 1697 | disputar | 18 |
| 1698 | dignar | 18 |
| 1699 | devoción | 18 |
| 1700 | desorden | 18 |
| 1701 | delirio | 18 |
| 1702 | corte | 18 |
| 1703 | conveniente | 18 |
| 1704 | consideración | 18 |
| 1705 | conforme | 18 |
| 1706 | confiar | 18 |
| 1707 | común | 18 |
| 1708 | claramente | 18 |
| 1709 | chillido | 18 |
| 1710 | centro | 18 |
| 1711 | ceder | 18 |
| 1712 | carcajada | 18 |
| 1713 | burlar | 18 |
| 1714 | arreglo | 18 |
| 1715 | arma | 18 |
| 1716 | apresurar | 18 |
| 1717 | aparentar | 18 |
| 1718 | amiguito | 18 |
| 1719 | aguardar | 18 |
| 1720 | adivinar | 18 |
| 1721 | vii | 17 |
| 1722 | vigilar | 17 |
| 1723 | vara | 17 |
| 1724 | trocar | 17 |
| 1725 | trance | 17 |
| 1726 | toma | 17 |
| 1727 | tocayo | 17 |
| 1728 | tierno | 17 |
| 1729 | tantísimo | 17 |
| 1730 | tamaño | 17 |
| 1731 | taller | 17 |
| 1732 | soy | 17 |
| 1733 | sobrar | 17 |
| 1734 | sea | 17 |
| 1735 | retiro | 17 |
| 1736 | reducir | 17 |
| 1737 | ramón | 17 |
| 1738 | provincia | 17 |
| 1739 | providencia | 17 |
| 1740 | preferir | 17 |
| 1741 | precioso | 17 |
| 1742 | pongo | 17 |
| 1743 | pluma | 17 |
| 1744 | píldora | 17 |
| 1745 | pescar | 17 |
| 1746 | perdido | 17 |
| 1747 | patria | 17 |
| 1748 | parecido | 17 |
| 1749 | parece | 17 |
| 1750 | pardo | 17 |
| 1751 | necesario | 17 |
| 1752 | montes | 17 |
| 1753 | modal | 17 |
| 1754 | masa | 17 |
| 1755 | marear | 17 |
| 1756 | manolo | 17 |
| 1757 | maldad | 17 |
| 1758 | liberal | 17 |
| 1759 | invitar | 17 |
| 1760 | infundir | 17 |
| 1761 | indignar | 17 |
| 1762 | impertinente | 17 |
| 1763 | humo | 17 |
| 1764 | heredar | 17 |
| 1765 | grueso | 17 |
| 1766 | grandísimo | 17 |
| 1767 | francia | 17 |
| 1768 | finísimo | 17 |
| 1769 | febril | 17 |
| 1770 | fábrica | 17 |
| 1771 | extraordinariamente | 17 |
| 1772 | estudiante | 17 |
| 1773 | entrada | 17 |
| 1774 | ea | 17 |
| 1775 | diverso | 17 |
| 1776 | devolver | 17 |
| 1777 | despreciar | 17 |
| 1778 | desarrollar | 17 |
| 1779 | defensa | 17 |
| 1780 | decoro | 17 |
| 1781 | débil | 17 |
| 1782 | cristianar | 17 |
| 1783 | corresponder | 17 |
| 1784 | comentario | 17 |
| 1785 | codo | 17 |
| 1786 | ciento | 17 |
| 1787 | cien | 17 |
| 1788 | chupar | 17 |
| 1789 | cegar | 17 |
| 1790 | carro | 17 |
| 1791 | cárcel | 17 |
| 1792 | calentar | 17 |
| 1793 | cálculo | 17 |
| 1794 | cabello | 17 |
| 1795 | bulto | 17 |
| 1796 | bruscamente | 17 |
| 1797 | botella | 17 |
| 1798 | baúl | 17 |
| 1799 | azúcar | 17 |
| 1800 | autor | 17 |
| 1801 | asombro | 17 |
| 1802 | ardor | 17 |
| 1803 | aprovechar | 17 |
| 1804 | apagar | 17 |
| 1805 | alumno | 17 |
| 1806 | aguja | 17 |
| 1807 | afán | 17 |
| 1808 | acariciar | 17 |
| 1809 | vetar | 16 |
| 1810 | verano | 16 |
| 1811 | verá | 16 |
| 1812 | toro | 16 |
| 1813 | tendero | 16 |
| 1814 | será | 16 |
| 1815 | sensación | 16 |
| 1816 | sanar | 16 |
| 1817 | salita | 16 |
| 1818 | rumor | 16 |
| 1819 | reunir | 16 |
| 1820 | refugio | 16 |
| 1821 | quince | 16 |
| 1822 | principiar | 16 |
| 1823 | pillo | 16 |
| 1824 | pierna | 16 |
| 1825 | perseguir | 16 |
| 1826 | pensó | 16 |
| 1827 | pedro | 16 |
| 1828 | parentesco | 16 |
| 1829 | nuera | 16 |
| 1830 | monte | 16 |
| 1831 | ministro | 16 |
| 1832 | machacar | 16 |
| 1833 | lotería | 16 |
| 1834 | lío | 16 |
| 1835 | lejano | 16 |
| 1836 | inspiración | 16 |
| 1837 | insistir | 16 |
| 1838 | inferior | 16 |
| 1839 | histórico | 16 |
| 1840 | he | 16 |
| 1841 | gota | 16 |
| 1842 | gas | 16 |
| 1843 | fisonomía | 16 |
| 1844 | fiebre | 16 |
| 1845 | fecha | 16 |
| 1846 | favorecer | 16 |
| 1847 | facción | 16 |
| 1848 | extensión | 16 |
| 1849 | exponer | 16 |
| 1850 | escoger | 16 |
| 1851 | error | 16 |
| 1852 | envidiar | 16 |
| 1853 | enfrente | 16 |
| 1854 | domicilio | 16 |
| 1855 | doctrina | 16 |
| 1856 | diablo | 16 |
| 1857 | descargar | 16 |
| 1858 | desagradable | 16 |
| 1859 | deje | 16 |
| 1860 | cuarenta | 16 |
| 1861 | crítico | 16 |
| 1862 | crisis | 16 |
| 1863 | cortesía | 16 |
| 1864 | constituir | 16 |
| 1865 | conferencia | 16 |
| 1866 | conducir | 16 |
| 1867 | completar | 16 |
| 1868 | chillar | 16 |
| 1869 | catar | 16 |
| 1870 | castelar | 16 |
| 1871 | casamiento | 16 |
| 1872 | caro | 16 |
| 1873 | ataque | 16 |
| 1874 | asistir | 16 |
| 1875 | arroz | 16 |
| 1876 | ardiente | 16 |
| 1877 | ansiedad | 16 |
| 1878 | almohada | 16 |
| 1879 | actividad | 16 |
| 1880 | abrigar | 16 |
| 1881 | abierto | 16 |
| 1882 | vicioso | 15 |
| 1883 | vía | 15 |
| 1884 | velo | 15 |
| 1885 | uña | 15 |
| 1886 | turbación | 15 |
| 1887 | tesoro | 15 |
| 1888 | té | 15 |
| 1889 | suspender | 15 |
| 1890 | seguido | 15 |
| 1891 | seductor | 15 |
| 1892 | salto | 15 |
| 1893 | salido | 15 |
| 1894 | rubio | 15 |
| 1895 | rosario | 15 |
| 1896 | rigor | 15 |
| 1897 | replicar | 15 |
| 1898 | relacionar | 15 |
| 1899 | redondo | 15 |
| 1900 | rebajar | 15 |
| 1901 | proyecto | 15 |
| 1902 | pontejos | 15 |
| 1903 | poeta | 15 |
| 1904 | pintura | 15 |
| 1905 | piel | 15 |
| 1906 | pensaba | 15 |
| 1907 | peldaño | 15 |
| 1908 | párpado | 15 |
| 1909 | papa | 15 |
| 1910 | paloma | 15 |
| 1911 | paca | 15 |
| 1912 | oscuras | 15 |
| 1913 | orgulloso | 15 |
| 1914 | operación | 15 |
| 1915 | oiga | 15 |
| 1916 | niñez | 15 |
| 1917 | nervio | 15 |
| 1918 | morenos | 15 |
| 1919 | montar | 15 |
| 1920 | ministerio | 15 |
| 1921 | mejorar | 15 |
| 1922 | meditación | 15 |
| 1923 | maña | 15 |
| 1924 | levita | 15 |
| 1925 | lentamente | 15 |
| 1926 | insigne | 15 |
| 1927 | ideal | 15 |
| 1928 | goce | 15 |
| 1929 | fresca | 15 |
| 1930 | final | 15 |
| 1931 | fiar | 15 |
| 1932 | favorable | 15 |
| 1933 | éxito | 15 |
| 1934 | exigir | 15 |
| 1935 | estoy | 15 |
| 1936 | espectáculo | 15 |
| 1937 | esparcir | 15 |
| 1938 | esforzar | 15 |
| 1939 | distracción | 15 |
| 1940 | deuda | 15 |
| 1941 | desvanecer | 15 |
| 1942 | descuidar | 15 |
| 1943 | cuchillo | 15 |
| 1944 | cruel | 15 |
| 1945 | crees | 15 |
| 1946 | constar | 15 |
| 1947 | consagrar | 15 |
| 1948 | comprometer | 15 |
| 1949 | clavo | 15 |
| 1950 | cigarro | 15 |
| 1951 | chuleta | 15 |
| 1952 | chistar | 15 |
| 1953 | chamberí | 15 |
| 1954 | cerebral | 15 |
| 1955 | cavilación | 15 |
| 1956 | casualidad | 15 |
| 1957 | candelaria | 15 |
| 1958 | calcular | 15 |
| 1959 | buenas | 15 |
| 1960 | brillar | 15 |
| 1961 | atormentar | 15 |
| 1962 | aterrar | 15 |
| 1963 | aspirar | 15 |
| 1964 | aplicación | 15 |
| 1965 | angelical | 15 |
| 1966 | acechar | 15 |
| 1967 | venganza | 14 |
| 1968 | valencia | 14 |
| 1969 | vago | 14 |
| 1970 | vagar | 14 |
| 1971 | trastorno | 14 |
| 1972 | toquilla | 14 |
| 1973 | susto | 14 |
| 1974 | solución | 14 |
| 1975 | soberbio | 14 |
| 1976 | silvia | 14 |
| 1977 | sal | 14 |
| 1978 | riqueza | 14 |
| 1979 | reproducir | 14 |
| 1980 | relativo | 14 |
| 1981 | reinar | 14 |
| 1982 | regalo | 14 |
| 1983 | recogida | 14 |
| 1984 | razonable | 14 |
| 1985 | rayo | 14 |
| 1986 | quia | 14 |
| 1987 | protestante | 14 |
| 1988 | profundamente | 14 |
| 1989 | procesión | 14 |
| 1990 | pretensión | 14 |
| 1991 | porvenir | 14 |
| 1992 | popular | 14 |
| 1993 | pobreza | 14 |
| 1994 | pensativo | 14 |
| 1995 | penoso | 14 |
| 1996 | peine | 14 |
| 1997 | mortificar | 14 |
| 1998 | monstruo | 14 |
| 1999 | modestia | 14 |
| 2000 | milagro | 14 |
| 2001 | metal | 14 |
| 2002 | menester | 14 |
| 2003 | marzo | 14 |
| 2004 | londres | 14 |
| 2005 | jefe | 14 |
| 2006 | introducir | 14 |
| 2007 | inteligente | 14 |
| 2008 | inquietar | 14 |
| 2009 | iniciar | 14 |
| 2010 | infalible | 14 |
| 2011 | inexplicable | 14 |
| 2012 | inconveniente | 14 |
| 2013 | grosero | 14 |
| 2014 | gorro | 14 |
| 2015 | gloriar | 14 |
| 2016 | garganta | 14 |
| 2017 | gallo | 14 |
| 2018 | finca | 14 |
| 2019 | fácilmente | 14 |
| 2020 | extravagancia | 14 |
| 2021 | examen | 14 |
| 2022 | estancia | 14 |
| 2023 | enredar | 14 |
| 2024 | encendido | 14 |
| 2025 | disgustar | 14 |
| 2026 | discurso | 14 |
| 2027 | dice | 14 |
| 2028 | determinación | 14 |
| 2029 | despacio | 14 |
| 2030 | desazón | 14 |
| 2031 | derramar | 14 |
| 2032 | déjame | 14 |
| 2033 | defecto | 14 |
| 2034 | crudo | 14 |
| 2035 | criminal | 14 |
| 2036 | corregir | 14 |
| 2037 | condenado | 14 |
| 2038 | compromiso | 14 |
| 2039 | comercial | 14 |
| 2040 | comandanta | 14 |
| 2041 | cólera | 14 |
| 2042 | cerrado | 14 |
| 2043 | cementerio | 14 |
| 2044 | caricia | 14 |
| 2045 | borde | 14 |
| 2046 | aventura | 14 |
| 2047 | ausencia | 14 |
| 2048 | atraer | 14 |
| 2049 | arrullar | 14 |
| 2050 | aprobar | 14 |
| 2051 | antojar | 14 |
| 2052 | alegre | 14 |
| 2053 | afirmar | 14 |
| 2054 | aconsejar | 14 |
| 2055 | absurdo | 14 |
| 2056 | vivísimo | 13 |
| 2057 | villa | 13 |
| 2058 | ventaja | 13 |
| 2059 | varón | 13 |
| 2060 | vacío | 13 |
| 2061 | trazar | 13 |
| 2062 | torcer | 13 |
| 2063 | tocante | 13 |
| 2064 | terminar | 13 |
| 2065 | temporada | 13 |
| 2066 | tarea | 13 |
| 2067 | taberna | 13 |
| 2068 | surgir | 13 |
| 2069 | sudar | 13 |
| 2070 | súbito | 13 |
| 2071 | someter | 13 |
| 2072 | solitario | 13 |
| 2073 | seña | 13 |
| 2074 | rotar | 13 |
| 2075 | rosa | 13 |
| 2076 | respiración | 13 |
| 2077 | respetable | 13 |
| 2078 | república | 13 |
| 2079 | renegar | 13 |
| 2080 | remoto | 13 |
| 2081 | regla | 13 |
| 2082 | registro | 13 |
| 2083 | regalar | 13 |
| 2084 | raza | 13 |
| 2085 | rascar | 13 |
| 2086 | puramente | 13 |
| 2087 | proposición | 13 |
| 2088 | promesa | 13 |
| 2089 | príncipe | 13 |
| 2090 | primitivo | 13 |
| 2091 | pollo | 13 |
| 2092 | placero | 13 |
| 2093 | pescuezo | 13 |
| 2094 | pedernero | 13 |
| 2095 | pausa | 13 |
| 2096 | patata | 13 |
| 2097 | paja | 13 |
| 2098 | otra | 13 |
| 2099 | oprimir | 13 |
| 2100 | ochoa | 13 |
| 2101 | obrar | 13 |
| 2102 | nieto | 13 |
| 2103 | nacional | 13 |
| 2104 | músculo | 13 |
| 2105 | murmurar | 13 |
| 2106 | multitud | 13 |
| 2107 | muestra | 13 |
| 2108 | motivar | 13 |
| 2109 | mostrador | 13 |
| 2110 | morder | 13 |
| 2111 | molestia | 13 |
| 2112 | moderno | 13 |
| 2113 | mimar | 13 |
| 2114 | mesías | 13 |
| 2115 | medir | 13 |
| 2116 | marrar | 13 |
| 2117 | manolita | 13 |
| 2118 | manejar | 13 |
| 2119 | manchar | 13 |
| 2120 | majestad | 13 |
| 2121 | madrugada | 13 |
| 2122 | lumbre | 13 |
| 2123 | lista | 13 |
| 2124 | liar | 13 |
| 2125 | legua | 13 |
| 2126 | justo | 13 |
| 2127 | juicioso | 13 |
| 2128 | juez | 13 |
| 2129 | intervenir | 13 |
| 2130 | infinito | 13 |
| 2131 | infancia | 13 |
| 2132 | indulgencia | 13 |
| 2133 | indecible | 13 |
| 2134 | impresionar | 13 |
| 2135 | imitar | 13 |
| 2136 | humildad | 13 |
| 2137 | hogar | 13 |
| 2138 | hembra | 13 |
| 2139 | grosería | 13 |
| 2140 | gratitud | 13 |
| 2141 | gorra | 13 |
| 2142 | garbanzo | 13 |
| 2143 | fruncir | 13 |
| 2144 | frialdad | 13 |
| 2145 | frescura | 13 |
| 2146 | franco | 13 |
| 2147 | francés | 13 |
| 2148 | formal | 13 |
| 2149 | florar | 13 |
| 2150 | filosófico | 13 |
| 2151 | facunda | 13 |
| 2152 | exaltar | 13 |
| 2153 | estorbar | 13 |
| 2154 | espantoso | 13 |
| 2155 | escuchar | 13 |
| 2156 | envidia | 13 |
| 2157 | enfermar | 13 |
| 2158 | enderezar | 13 |
| 2159 | emprender | 13 |
| 2160 | ejercer | 13 |
| 2161 | director | 13 |
| 2162 | desnudar | 13 |
| 2163 | deslizar | 13 |
| 2164 | desenvolver | 13 |
| 2165 | desdémona | 13 |
| 2166 | desconsuelo | 13 |
| 2167 | desconocido | 13 |
| 2168 | desconcertar | 13 |
| 2169 | descender | 13 |
| 2170 | delantal | 13 |
| 2171 | dañar | 13 |
| 2172 | creerás | 13 |
| 2173 | corrección | 13 |
| 2174 | coronel | 13 |
| 2175 | concepción | 13 |
| 2176 | compadecer | 13 |
| 2177 | comerciante | 13 |
| 2178 | colegio | 13 |
| 2179 | chasco | 13 |
| 2180 | cavilar | 13 |
| 2181 | católico | 13 |
| 2182 | benevolencia | 13 |
| 2183 | bendición | 13 |
| 2184 | bárbaro | 13 |
| 2185 | atroz | 13 |
| 2186 | arder | 13 |
| 2187 | añadió | 13 |
| 2188 | alarmar | 13 |
| 2189 | agitar | 13 |
| 2190 | admirablemente | 13 |
| 2191 | zapato | 12 |
| 2192 | vuestro | 12 |
| 2193 | viii | 12 |
| 2194 | verificar | 12 |
| 2195 | varonil | 12 |
| 2196 | únicamente | 12 |
| 2197 | trincar | 12 |
| 2198 | transigir | 12 |
| 2199 | tiesto | 12 |
| 2200 | tienes | 12 |
| 2201 | terciopelo | 12 |
| 2202 | talle | 12 |
| 2203 | talar | 12 |
| 2204 | sublimar | 12 |
| 2205 | sospecha | 12 |
| 2206 | sordo | 12 |
| 2207 | soltero | 12 |
| 2208 | solas | 12 |
| 2209 | sesenta | 12 |
| 2210 | sencillez | 12 |
| 2211 | sazón | 12 |
| 2212 | sacristán | 12 |
| 2213 | sacrificio | 12 |
| 2214 | sacrificar | 12 |
| 2215 | sabroso | 12 |
| 2216 | rudo | 12 |
| 2217 | revolucionario | 12 |
| 2218 | resolución | 12 |
| 2219 | reserva | 12 |
| 2220 | región | 12 |
| 2221 | recibimiento | 12 |
| 2222 | raya | 12 |
| 2223 | ratón | 12 |
| 2224 | púsose | 12 |
| 2225 | provenir | 12 |
| 2226 | protector | 12 |
| 2227 | propiedad | 12 |
| 2228 | progreso | 12 |
| 2229 | principalmente | 12 |
| 2230 | presteza | 12 |
| 2231 | presenciar | 12 |
| 2232 | postura | 12 |
| 2233 | posición | 12 |
| 2234 | pormenor | 12 |
| 2235 | policía | 12 |
| 2236 | pobrecito | 12 |
| 2237 | planta | 12 |
| 2238 | pisar | 12 |
| 2239 | pillar | 12 |
| 2240 | personalidad | 12 |
| 2241 | perfil | 12 |
| 2242 | penar | 12 |
| 2243 | pavos | 12 |
| 2244 | pavo | 12 |
| 2245 | patada | 12 |
| 2246 | pandereta | 12 |
| 2247 | palillo | 12 |
| 2248 | onda | 12 |
| 2249 | oficina | 12 |
| 2250 | odio | 12 |
| 2251 | obstante | 12 |
| 2252 | observó | 12 |
| 2253 | municipal | 12 |
| 2254 | moza | 12 |
| 2255 | miguel | 12 |
| 2256 | miel | 12 |
| 2257 | mezclar | 12 |
| 2258 | mercado | 12 |
| 2259 | máscara | 12 |
| 2260 | manila | 12 |
| 2261 | mando | 12 |
| 2262 | maldita | 12 |
| 2263 | lindo | 12 |
| 2264 | levantose | 12 |
| 2265 | letrero | 12 |
| 2266 | leopoldo | 12 |
| 2267 | legítimo | 12 |
| 2268 | leal | 12 |
| 2269 | labor | 12 |
| 2270 | joaquín | 12 |
| 2271 | jerónima | 12 |
| 2272 | ix | 12 |
| 2273 | interrumpir | 12 |
| 2274 | interesante | 12 |
| 2275 | inglaterra | 12 |
| 2276 | ingenioso | 12 |
| 2277 | indulgente | 12 |
| 2278 | incorporar | 12 |
| 2279 | ilustre | 12 |
| 2280 | hundir | 12 |
| 2281 | humilde | 12 |
| 2282 | humanar | 12 |
| 2283 | hortera | 12 |
| 2284 | horizonte | 12 |
| 2285 | herida | 12 |
| 2286 | hace | 12 |
| 2287 | gravedad | 12 |
| 2288 | gobernador | 12 |
| 2289 | gobernación | 12 |
| 2290 | gasto | 12 |
| 2291 | futuro | 12 |
| 2292 | forzoso | 12 |
| 2293 | firme | 12 |
| 2294 | finura | 12 |
| 2295 | fila | 12 |
| 2296 | fiesta | 12 |
| 2297 | farsa | 12 |
| 2298 | famoso | 12 |
| 2299 | etcétera | 12 |
| 2300 | estrenar | 12 |
| 2301 | estrella | 12 |
| 2302 | espléndido | 12 |
| 2303 | escupir | 12 |
| 2304 | escritorio | 12 |
| 2305 | escoba | 12 |
| 2306 | entró | 12 |
| 2307 | entraña | 12 |
| 2308 | empresa | 12 |
| 2309 | efectivo | 12 |
| 2310 | doctor | 12 |
| 2311 | dispuesto | 12 |
| 2312 | disparar | 12 |
| 2313 | digno | 12 |
| 2314 | diabla | 12 |
| 2315 | destruir | 12 |
| 2316 | destinar | 12 |
| 2317 | desprender | 12 |
| 2318 | despabilar | 12 |
| 2319 | desgraciado | 12 |
| 2320 | dejo | 12 |
| 2321 | cuñado | 12 |
| 2322 | cuba | 12 |
| 2323 | cuarta | 12 |
| 2324 | crítica | 12 |
| 2325 | criterio | 12 |
| 2326 | criado | 12 |
| 2327 | creeríase | 12 |
| 2328 | costura | 12 |
| 2329 | cortina | 12 |
| 2330 | colmo | 12 |
| 2331 | colcha | 12 |
| 2332 | cochero | 12 |
| 2333 | civilización | 12 |
| 2334 | ciudad | 12 |
| 2335 | cesta | 12 |
| 2336 | carlos | 12 |
| 2337 | capricho | 12 |
| 2338 | canto | 12 |
| 2339 | cállate | 12 |
| 2340 | brotar | 12 |
| 2341 | batir | 12 |
| 2342 | barrer | 12 |
| 2343 | atacar | 12 |
| 2344 | asir | 12 |
| 2345 | ansia | 12 |
| 2346 | anochecer | 12 |
| 2347 | amoroso | 12 |
| 2348 | altura | 12 |
| 2349 | alrededor | 12 |
| 2350 | almacén | 12 |
| 2351 | ajustar | 12 |
| 2352 | aguardiente | 12 |
| 2353 | abur | 12 |
| 2354 | yema | 11 |
| 2355 | vuelo | 11 |
| 2356 | vocablo | 11 |
| 2357 | vivienda | 11 |
| 2358 | viva | 11 |
| 2359 | viudo | 11 |
| 2360 | vergonzoso | 11 |
| 2361 | vástago | 11 |
| 2362 | tuno | 11 |
| 2363 | tronco | 11 |
| 2364 | traspasar | 11 |
| 2365 | transformar | 11 |
| 2366 | tercero | 11 |
| 2367 | teñir | 11 |
| 2368 | tenía | 11 |
| 2369 | tengo | 11 |
| 2370 | tambor | 11 |
| 2371 | suspirar | 11 |
| 2372 | sucesión | 11 |
| 2373 | sublime | 11 |
| 2374 | solemne | 11 |
| 2375 | soberbia | 11 |
| 2376 | silenciar | 11 |
| 2377 | sílaba | 11 |
| 2378 | signo | 11 |
| 2379 | sexo | 11 |
| 2380 | sereno | 11 |
| 2381 | sabiduría | 11 |
| 2382 | rossini | 11 |
| 2383 | rondar | 11 |
| 2384 | rogar | 11 |
| 2385 | revolución | 11 |
| 2386 | revés | 11 |
| 2387 | revelación | 11 |
| 2388 | retener | 11 |
| 2389 | restauración | 11 |
| 2390 | responsabilidad | 11 |
| 2391 | respectivo | 11 |
| 2392 | resistencia | 11 |
| 2393 | relucir | 11 |
| 2394 | refrescar | 11 |
| 2395 | recto | 11 |
| 2396 | reclamar | 11 |
| 2397 | realmente | 11 |
| 2398 | rastro | 11 |
| 2399 | rasgo | 11 |
| 2400 | quite | 11 |
| 2401 | quita | 11 |
| 2402 | pueril | 11 |
| 2403 | provecho | 11 |
| 2404 | prohibir | 11 |
| 2405 | presumir | 11 |
| 2406 | precio | 11 |
| 2407 | preceder | 11 |
| 2408 | practicar | 11 |
| 2409 | portero | 11 |
| 2410 | personaje | 11 |
| 2411 | perdición | 11 |
| 2412 | penitente | 11 |
| 2413 | pelota | 11 |
| 2414 | origen | 11 |
| 2415 | oportuno | 11 |
| 2416 | ojos | 11 |
| 2417 | ocupación | 11 |
| 2418 | observador | 11 |
| 2419 | obrador | 11 |
| 2420 | notable | 11 |
| 2421 | mono | 11 |
| 2422 | millón | 11 |
| 2423 | medicinar | 11 |
| 2424 | materno | 11 |
| 2425 | maternidad | 11 |
| 2426 | materia | 11 |
| 2427 | marfil | 11 |
| 2428 | luna | 11 |
| 2429 | lúgubre | 11 |
| 2430 | llover | 11 |
| 2431 | llanto | 11 |
| 2432 | liberación | 11 |
| 2433 | latín | 11 |
| 2434 | joya | 11 |
| 2435 | inundar | 11 |
| 2436 | insolente | 11 |
| 2437 | insensato | 11 |
| 2438 | inscripción | 11 |
| 2439 | insano | 11 |
| 2440 | inquilino | 11 |
| 2441 | inquieto | 11 |
| 2442 | infidelidad | 11 |
| 2443 | infernal | 11 |
| 2444 | independencia | 11 |
| 2445 | incredulidad | 11 |
| 2446 | impulsar | 11 |
| 2447 | impropio | 11 |
| 2448 | impacientar | 11 |
| 2449 | ignominia | 11 |
| 2450 | horriblemente | 11 |
| 2451 | hondo | 11 |
| 2452 | hebra | 11 |
| 2453 | guitarra | 11 |
| 2454 | generoso | 11 |
| 2455 | furia | 11 |
| 2456 | freír | 11 |
| 2457 | forzar | 11 |
| 2458 | filósofo | 11 |
| 2459 | filipinas | 11 |
| 2460 | figúrate | 11 |
| 2461 | familiar | 11 |
| 2462 | fama | 11 |
| 2463 | extravagante | 11 |
| 2464 | éxtasis | 11 |
| 2465 | exclamar | 11 |
| 2466 | exclamación | 11 |
| 2467 | excitación | 11 |
| 2468 | exaltación | 11 |
| 2469 | estrechar | 11 |
| 2470 | estimar | 11 |
| 2471 | espanto | 11 |
| 2472 | espada | 11 |
| 2473 | esencial | 11 |
| 2474 | entrever | 11 |
| 2475 | enmendar | 11 |
| 2476 | engaño | 11 |
| 2477 | encimar | 11 |
| 2478 | empleado | 11 |
| 2479 | ejército | 11 |
| 2480 | efusión | 11 |
| 2481 | dormitorio | 11 |
| 2482 | donaire | 11 |
| 2483 | dime | 11 |
| 2484 | detalle | 11 |
| 2485 | desventurado | 11 |
| 2486 | desvarío | 11 |
| 2487 | desprecio | 11 |
| 2488 | describir | 11 |
| 2489 | descanso | 11 |
| 2490 | depósito | 11 |
| 2491 | custodiar | 11 |
| 2492 | cursi | 11 |
| 2493 | cultivar | 11 |
| 2494 | cuartel | 11 |
| 2495 | crédito | 11 |
| 2496 | corbata | 11 |
| 2497 | contradecir | 11 |
| 2498 | contestación | 11 |
| 2499 | confuso | 11 |
| 2500 | combinación | 11 |
| 2501 | chiflar | 11 |
| 2502 | cera | 11 |
| 2503 | cenar | 11 |
| 2504 | celoso | 11 |
| 2505 | celestial | 11 |
| 2506 | castigo | 11 |
| 2507 | casado | 11 |
| 2508 | caminos | 11 |
| 2509 | calzar | 11 |
| 2510 | cabra | 11 |
| 2511 | burro | 11 |
| 2512 | bonifacio | 11 |
| 2513 | blando | 11 |
| 2514 | basta | 11 |
| 2515 | barcelona | 11 |
| 2516 | auxilio | 11 |
| 2517 | asesino | 11 |
| 2518 | arribar | 11 |
| 2519 | arrepentimiento | 11 |
| 2520 | aptitud | 11 |
| 2521 | apetecer | 11 |
| 2522 | amargar | 11 |
| 2523 | alterar | 11 |
| 2524 | alhajar | 11 |
| 2525 | algodón | 11 |
| 2526 | alentar | 11 |
| 2527 | afligir | 11 |
| 2528 | acostumbrado | 11 |
| 2529 | acomodar | 11 |
| 2530 | aceite | 11 |
| 2531 | aburrimiento | 11 |
| 2532 | abrazo | 11 |
| 2533 | zaragoza | 10 |
| 2534 | viveza | 10 |
| 2535 | visto | 10 |
| 2536 | visión | 10 |
| 2537 | verídico | 10 |
| 2538 | verbo | 10 |
| 2539 | verás | 10 |
| 2540 | ve | 10 |
| 2541 | variedad | 10 |
| 2542 | vaciar | 10 |
| 2543 | turrón | 10 |
| 2544 | triunfo | 10 |
| 2545 | triunfar | 10 |
| 2546 | través | 10 |
| 2547 | transeúnte | 10 |
| 2548 | tornar | 10 |
| 2549 | tolerancia | 10 |
| 2550 | tieso | 10 |
| 2551 | tesar | 10 |
| 2552 | ternura | 10 |
| 2553 | tentar | 10 |
| 2554 | tenedor | 10 |
| 2555 | tembloroso | 10 |
| 2556 | teatral | 10 |
| 2557 | sus | 10 |
| 2558 | sur | 10 |
| 2559 | sudor | 10 |
| 2560 | sopa | 10 |
| 2561 | severo | 10 |
| 2562 | seriar | 10 |
| 2563 | salvación | 10 |
| 2564 | sacramento | 10 |
| 2565 | rutina | 10 |
| 2566 | rótulo | 10 |
| 2567 | ronda | 10 |
| 2568 | roncar | 10 |
| 2569 | repugnar | 10 |
| 2570 | reposo | 10 |
| 2571 | reino | 10 |
| 2572 | regresar | 10 |
| 2573 | registrar | 10 |
| 2574 | recrear | 10 |
| 2575 | recortar | 10 |
| 2576 | realar | 10 |
| 2577 | quizá | 10 |
| 2578 | purificar | 10 |
| 2579 | puñal | 10 |
| 2580 | pulso | 10 |
| 2581 | puchero | 10 |
| 2582 | prodigio | 10 |
| 2583 | probable | 10 |
| 2584 | primogénito | 10 |
| 2585 | premio | 10 |
| 2586 | precipitar | 10 |
| 2587 | práctica | 10 |
| 2588 | posar | 10 |
| 2589 | placer | 10 |
| 2590 | pillín | 10 |
| 2591 | pesadilla | 10 |
| 2592 | perverso | 10 |
| 2593 | permiso | 10 |
| 2594 | perfección | 10 |
| 2595 | paternal | 10 |
| 2596 | patear | 10 |
| 2597 | pastor | 10 |
| 2598 | pascual | 10 |
| 2599 | participar | 10 |
| 2600 | parroquia | 10 |
| 2601 | párrafo | 10 |
| 2602 | parado | 10 |
| 2603 | palacio | 10 |
| 2604 | pago | 10 |
| 2605 | padilla | 10 |
| 2606 | pacífico | 10 |
| 2607 | ópera | 10 |
| 2608 | ola | 10 |
| 2609 | obrero | 10 |
| 2610 | nobleza | 10 |
| 2611 | navidad | 10 |
| 2612 | naranja | 10 |
| 2613 | muñeca | 10 |
| 2614 | mundano | 10 |
| 2615 | morar | 10 |
| 2616 | misión | 10 |
| 2617 | mesilla | 10 |
| 2618 | menear | 10 |
| 2619 | mayo | 10 |
| 2620 | martirio | 10 |
| 2621 | mármol | 10 |
| 2622 | maravillar | 10 |
| 2623 | mantilla | 10 |
| 2624 | manicomio | 10 |
| 2625 | mamar | 10 |
| 2626 | madrileño | 10 |
| 2627 | luminoso | 10 |
| 2628 | luchar | 10 |
| 2629 | lobo | 10 |
| 2630 | juventud | 10 |
| 2631 | jarabe | 10 |
| 2632 | isidro | 10 |
| 2633 | interrogar | 10 |
| 2634 | inocencia | 10 |
| 2635 | ingrato | 10 |
| 2636 | ingenio | 10 |
| 2637 | influenciar | 10 |
| 2638 | imperio | 10 |
| 2639 | ilustrar | 10 |
| 2640 | ignorar | 10 |
| 2641 | hule | 10 |
| 2642 | huésped | 10 |
| 2643 | heredero | 10 |
| 2644 | has | 10 |
| 2645 | habrá | 10 |
| 2646 | golosina | 10 |
| 2647 | fuertemente | 10 |
| 2648 | frenesí | 10 |
| 2649 | fregar | 10 |
| 2650 | fraternal | 10 |
| 2651 | flaco | 10 |
| 2652 | exterior | 10 |
| 2653 | expresivo | 10 |
| 2654 | experiencia | 10 |
| 2655 | eulalia | 10 |
| 2656 | estatura | 10 |
| 2657 | espectro | 10 |
| 2658 | escrúpulo | 10 |
| 2659 | envenenar | 10 |
| 2660 | enojar | 10 |
| 2661 | enérgico | 10 |
| 2662 | encarnar | 10 |
| 2663 | encantar | 10 |
| 2664 | empleo | 10 |
| 2665 | elogiar | 10 |
| 2666 | elegancia | 10 |
| 2667 | efectivamente | 10 |
| 2668 | edificar | 10 |
| 2669 | doloroso | 10 |
| 2670 | docena | 10 |
| 2671 | divertido | 10 |
| 2672 | disimulo | 10 |
| 2673 | discusión | 10 |
| 2674 | disco | 10 |
| 2675 | dictar | 10 |
| 2676 | diario | 10 |
| 2677 | desmentir | 10 |
| 2678 | desdichado | 10 |
| 2679 | deogracias | 10 |
| 2680 | demencia | 10 |
| 2681 | custodia | 10 |
| 2682 | cuchichear | 10 |
| 2683 | cree | 10 |
| 2684 | corro | 10 |
| 2685 | corrida | 10 |
| 2686 | coro | 10 |
| 2687 | construir | 10 |
| 2688 | conmover | 10 |
| 2689 | conjunto | 10 |
| 2690 | confirmar | 10 |
| 2691 | comunicación | 10 |
| 2692 | colar | 10 |
| 2693 | cola | 10 |
| 2694 | clara | 10 |
| 2695 | cinta | 10 |
| 2696 | chaleco | 10 |
| 2697 | cerrojo | 10 |
| 2698 | ceremonia | 10 |
| 2699 | cena | 10 |
| 2700 | celda | 10 |
| 2701 | castillo | 10 |
| 2702 | carlista | 10 |
| 2703 | carecer | 10 |
| 2704 | calzado | 10 |
| 2705 | burla | 10 |
| 2706 | bordar | 10 |
| 2707 | bondadoso | 10 |
| 2708 | blas | 10 |
| 2709 | bebida | 10 |
| 2710 | baba | 10 |
| 2711 | atrevimiento | 10 |
| 2712 | atónito | 10 |
| 2713 | ascua | 10 |
| 2714 | asaltar | 10 |
| 2715 | arranque | 10 |
| 2716 | armonía | 10 |
| 2717 | apuro | 10 |
| 2718 | antonia | 10 |
| 2719 | antipatía | 10 |
| 2720 | animación | 10 |
| 2721 | andrés | 10 |
| 2722 | ancho | 10 |
| 2723 | amanecer | 10 |
| 2724 | amable | 10 |
| 2725 | alumbrar | 10 |
| 2726 | aliento | 10 |
| 2727 | ala | 10 |
| 2728 | agudo | 10 |
| 2729 | aforar | 10 |
| 2730 | afición | 10 |
| 2731 | administrador | 10 |
| 2732 | administración | 10 |
| 2733 | acuerdo | 10 |
| 2734 | acecho | 10 |
| 2735 | zancudo | 9 |
| 2736 | yeso | 9 |
| 2737 | voto | 9 |
| 2738 | vivamente | 9 |
| 2739 | virtuoso | 9 |
| 2740 | violencia | 9 |
| 2741 | vieja | 9 |
| 2742 | viático | 9 |
| 2743 | verdugo | 9 |
| 2744 | veneno | 9 |
| 2745 | vallejo | 9 |
| 2746 | u | 9 |
| 2747 | tubo | 9 |
| 2748 | tronar | 9 |
| 2749 | transmitir | 9 |
| 2750 | trágico | 9 |
| 2751 | toser | 9 |
| 2752 | torre | 9 |
| 2753 | torpe | 9 |
| 2754 | tom | 9 |
| 2755 | templar | 9 |
| 2756 | tabla | 9 |
| 2757 | sutil | 9 |
| 2758 | suplicio | 9 |
| 2759 | sumergir | 9 |
| 2760 | sonido | 9 |
| 2761 | sólido | 9 |
| 2762 | sofocado | 9 |
| 2763 | sobrevenir | 9 |
| 2764 | so | 9 |
| 2765 | singular | 9 |
| 2766 | sincero | 9 |
| 2767 | setiembre | 9 |
| 2768 | rueda | 9 |
| 2769 | roto | 9 |
| 2770 | riquísimo | 9 |
| 2771 | resplandor | 9 |
| 2772 | repugnancia | 9 |
| 2773 | reprender | 9 |
| 2774 | renunciar | 9 |
| 2775 | renta | 9 |
| 2776 | renovar | 9 |
| 2777 | renglón | 9 |
| 2778 | remordimiento | 9 |
| 2779 | reflexionar | 9 |
| 2780 | redentor | 9 |
| 2781 | reconciliación | 9 |
| 2782 | recién | 9 |
| 2783 | re | 9 |
| 2784 | ráfaga | 9 |
| 2785 | quiero | 9 |
| 2786 | quedo | 9 |
| 2787 | puñalada | 9 |
| 2788 | pulmón | 9 |
| 2789 | prosiguió | 9 |
| 2790 | propiamente | 9 |
| 2791 | prolongar | 9 |
| 2792 | prim | 9 |
| 2793 | prever | 9 |
| 2794 | presuroso | 9 |
| 2795 | preso | 9 |
| 2796 | presentimiento | 9 |
| 2797 | portería | 9 |
| 2798 | porrazo | 9 |
| 2799 | porquería | 9 |
| 2800 | ponce | 9 |
| 2801 | pólvora | 9 |
| 2802 | poderoso | 9 |
| 2803 | plantón | 9 |
| 2804 | planchar | 9 |
| 2805 | pintor | 9 |
| 2806 | picardía | 9 |
| 2807 | piar | 9 |
| 2808 | pendiente | 9 |
| 2809 | peineta | 9 |
| 2810 | pastelero | 9 |
| 2811 | pasaje | 9 |
| 2812 | paraíso | 9 |
| 2813 | papeleta | 9 |
| 2814 | palmar | 9 |
| 2815 | pájara | 9 |
| 2816 | pagaré | 9 |
| 2817 | olvido | 9 |
| 2818 | oficiar | 9 |
| 2819 | oficial | 9 |
| 2820 | obispo | 9 |
| 2821 | nación | 9 |
| 2822 | molina | 9 |
| 2823 | moderar | 9 |
| 2824 | mimo | 9 |
| 2825 | metálico | 9 |
| 2826 | merluza | 9 |
| 2827 | merino | 9 |
| 2828 | menudencia | 9 |
| 2829 | melancolía | 9 |
| 2830 | medicamento | 9 |
| 2831 | materialismo | 9 |
| 2832 | material | 9 |
| 2833 | mancha | 9 |
| 2834 | magdalena | 9 |
| 2835 | listo | 9 |
| 2836 | lienzo | 9 |
| 2837 | libra | 9 |
| 2838 | lana | 9 |
| 2839 | lámpara | 9 |
| 2840 | jota | 9 |
| 2841 | jaula | 9 |
| 2842 | jacinto | 9 |
| 2843 | jabón | 9 |
| 2844 | irresistible | 9 |
| 2845 | intensísimo | 9 |
| 2846 | insoportable | 9 |
| 2847 | inmóvil | 9 |
| 2848 | infamar | 9 |
| 2849 | inefable | 9 |
| 2850 | industria | 9 |
| 2851 | indudablemente | 9 |
| 2852 | indignación | 9 |
| 2853 | indiferencia | 9 |
| 2854 | incluso | 9 |
| 2855 | inclusa | 9 |
| 2856 | implacable | 9 |
| 2857 | impaciencia | 9 |
| 2858 | ídolo | 9 |
| 2859 | idolatrar | 9 |
| 2860 | horrorizar | 9 |
| 2861 | horacio | 9 |
| 2862 | hola | 9 |
| 2863 | hipócrita | 9 |
| 2864 | héroe | 9 |
| 2865 | helar | 9 |
| 2866 | hallábase | 9 |
| 2867 | guiñar | 9 |
| 2868 | gris | 9 |
| 2869 | grato | 9 |
| 2870 | gozo | 9 |
| 2871 | goloso | 9 |
| 2872 | ganancia | 9 |
| 2873 | gallina | 9 |
| 2874 | gala | 9 |
| 2875 | furibundo | 9 |
| 2876 | funcionar | 9 |
| 2877 | fuensanta | 9 |
| 2878 | freno | 9 |
| 2879 | frecuentar | 9 |
| 2880 | frasco | 9 |
| 2881 | fíjate | 9 |
| 2882 | fiereza | 9 |
| 2883 | febrero | 9 |
| 2884 | faena | 9 |
| 2885 | externo | 9 |
| 2886 | exquisito | 9 |
| 2887 | exhalar | 9 |
| 2888 | exclusivamente | 9 |
| 2889 | exaltado | 9 |
| 2890 | ex | 9 |
| 2891 | evangelio | 9 |
| 2892 | estrépito | 9 |
| 2893 | estampar | 9 |
| 2894 | estallido | 9 |
| 2895 | escurrir | 9 |
| 2896 | escondite | 9 |
| 2897 | escape | 9 |
| 2898 | escaparate | 9 |
| 2899 | equivocación | 9 |
| 2900 | engracia | 9 |
| 2901 | encuentro | 9 |
| 2902 | embargar | 9 |
| 2903 | elevar | 9 |
| 2904 | elegir | 9 |
| 2905 | eléctrico | 9 |
| 2906 | eclesiástico | 9 |
| 2907 | dramático | 9 |
| 2908 | drama | 9 |
| 2909 | dosis | 9 |
| 2910 | disputa | 9 |
| 2911 | dispensar | 9 |
| 2912 | diciembre | 9 |
| 2913 | devorar | 9 |
| 2914 | devanar | 9 |
| 2915 | desesperación | 9 |
| 2916 | descuido | 9 |
| 2917 | desairar | 9 |
| 2918 | desahogar | 9 |
| 2919 | delito | 9 |
| 2920 | delincuente | 9 |
| 2921 | delicioso | 9 |
| 2922 | delicadeza | 9 |
| 2923 | declaración | 9 |
| 2924 | decencia | 9 |
| 2925 | curva | 9 |
| 2926 | curioso | 9 |
| 2927 | culto | 9 |
| 2928 | culebra | 9 |
| 2929 | cuchara | 9 |
| 2930 | continuo | 9 |
| 2931 | consumar | 9 |
| 2932 | consigo | 9 |
| 2933 | conocido | 9 |
| 2934 | conflicto | 9 |
| 2935 | confidencia | 9 |
| 2936 | conceder | 9 |
| 2937 | comisión | 9 |
| 2938 | colocación | 9 |
| 2939 | clarear | 9 |
| 2940 | citar | 9 |
| 2941 | ciertamente | 9 |
| 2942 | chorrear | 9 |
| 2943 | chocar | 9 |
| 2944 | charla | 9 |
| 2945 | centinela | 9 |
| 2946 | cazar | 9 |
| 2947 | casco | 9 |
| 2948 | carmen | 9 |
| 2949 | característico | 9 |
| 2950 | cansancio | 9 |
| 2951 | cana | 9 |
| 2952 | cállese | 9 |
| 2953 | calamidad | 9 |
| 2954 | cádiz | 9 |
| 2955 | butaca | 9 |
| 2956 | bulla | 9 |
| 2957 | brusco | 9 |
| 2958 | bronce | 9 |
| 2959 | borracho | 9 |
| 2960 | bolsa | 9 |
| 2961 | bocado | 9 |
| 2962 | bigote | 9 |
| 2963 | beneficencia | 9 |
| 2964 | bata | 9 |
| 2965 | barricada | 9 |
| 2966 | banca | 9 |
| 2967 | aventurar | 9 |
| 2968 | auxiliar | 9 |
| 2969 | aturdir | 9 |
| 2970 | atmósfera | 9 |
| 2971 | atizar | 9 |
| 2972 | atentar | 9 |
| 2973 | arena | 9 |
| 2974 | apretón | 9 |
| 2975 | apreciación | 9 |
| 2976 | apostar | 9 |
| 2977 | aposento | 9 |
| 2978 | apoderar | 9 |
| 2979 | aparato | 9 |
| 2980 | anticipar | 9 |
| 2981 | anhelo | 9 |
| 2982 | angustia | 9 |
| 2983 | ángulo | 9 |
| 2984 | angelito | 9 |
| 2985 | ambiente | 9 |
| 2986 | alquilar | 9 |
| 2987 | almirez | 9 |
| 2988 | algazara | 9 |
| 2989 | alfonso | 9 |
| 2990 | alcalde | 9 |
| 2991 | ahorro | 9 |
| 2992 | agasajar | 9 |
| 2993 | aflojar | 9 |
| 2994 | afable | 9 |
| 2995 | aclarar | 9 |
| 2996 | abnegación | 9 |
| 2997 | abismo | 9 |
| 2998 | abanico | 9 |
| 2999 | zapatilla | 8 |
| 3000 | zapatería | 8 |
| 3001 | zalamería | 8 |
| 3002 | x | 8 |
| 3003 | vistazo | 8 |
| 3004 | victoria | 8 |
| 3005 | vibración | 8 |
| 3006 | va | 8 |
| 3007 | unión | 8 |
| 3008 | ultrajar | 8 |
| 3009 | trujillos | 8 |
| 3010 | tristísimo | 8 |
| 3011 | tribunal | 8 |
| 3012 | trastada | 8 |
| 3013 | transformación | 8 |
| 3014 | traidor | 8 |
| 3015 | tormento | 8 |
| 3016 | toque | 8 |
| 3017 | tolerar | 8 |
| 3018 | tirón | 8 |
| 3019 | tino | 8 |
| 3020 | testigo | 8 |
| 3021 | tercer | 8 |
| 3022 | tallar | 8 |
| 3023 | sumisión | 8 |
| 3024 | subida | 8 |
| 3025 | sotana | 8 |
| 3026 | soplar | 8 |
| 3027 | sombrío | 8 |
| 3028 | soldar | 8 |
| 3029 | sobreponer | 8 |
| 3030 | sobra | 8 |
| 3031 | sinvergüenza | 8 |
| 3032 | simpleza | 8 |
| 3033 | señorío | 8 |
| 3034 | semejanza | 8 |
| 3035 | seducir | 8 |
| 3036 | saludo | 8 |
| 3037 | salmerón | 8 |
| 3038 | romántico | 8 |
| 3039 | rodillas | 8 |
| 3040 | robusto | 8 |
| 3041 | rezo | 8 |
| 3042 | revestir | 8 |
| 3043 | retorcer | 8 |
| 3044 | resplandecer | 8 |
| 3045 | réspice | 8 |
| 3046 | resoplido | 8 |
| 3047 | resignar | 8 |
| 3048 | repugnante | 8 |
| 3049 | reparación | 8 |
| 3050 | relimpio | 8 |
| 3051 | relato | 8 |
| 3052 | reina | 8 |
| 3053 | regocijar | 8 |
| 3054 | regente | 8 |
| 3055 | refunfuñar | 8 |
| 3056 | redención | 8 |
| 3057 | red | 8 |
| 3058 | rectitud | 8 |
| 3059 | recomendación | 8 |
| 3060 | recelo | 8 |
| 3061 | recaer | 8 |
| 3062 | rara | 8 |
| 3063 | rapidez | 8 |
| 3064 | rabo | 8 |
| 3065 | pulmonía | 8 |
| 3066 | prurito | 8 |
| 3067 | progresista | 8 |
| 3068 | profesar | 8 |
| 3069 | procedimiento | 8 |
| 3070 | probablemente | 8 |
| 3071 | prevenir | 8 |
| 3072 | presupuesto | 8 |
| 3073 | portamonedas | 8 |
| 3074 | poesía | 8 |
| 3075 | plenitud | 8 |
| 3076 | pleito | 8 |
| 3077 | platillo | 8 |
| 3078 | pintoresco | 8 |
| 3079 | pies | 8 |
| 3080 | picaresco | 8 |
| 3081 | picante | 8 |
| 3082 | piano | 8 |
| 3083 | pi | 8 |
| 3084 | perrería | 8 |
| 3085 | patético | 8 |
| 3086 | paseíto | 8 |
| 3087 | paréceme | 8 |
| 3088 | pantalla | 8 |
| 3089 | paisaje | 8 |
| 3090 | padrino | 8 |
| 3091 | oyose | 8 |
| 3092 | oriente | 8 |
| 3093 | oración | 8 |
| 3094 | ojalá | 8 |
| 3095 | odiar | 8 |
| 3096 | nido | 8 |
| 3097 | mortal | 8 |
| 3098 | moño | 8 |
| 3099 | molino | 8 |
| 3100 | moler | 8 |
| 3101 | místico | 8 |
| 3102 | misántropo | 8 |
| 3103 | metido | 8 |
| 3104 | mentar | 8 |
| 3105 | mediano | 8 |
| 3106 | mayormente | 8 |
| 3107 | matrimonial | 8 |
| 3108 | maternal | 8 |
| 3109 | mascar | 8 |
| 3110 | marco | 8 |
| 3111 | maravilloso | 8 |
| 3112 | manifestó | 8 |
| 3113 | malicia | 8 |
| 3114 | maldición | 8 |
| 3115 | lucha | 8 |
| 3116 | literario | 8 |
| 3117 | lazo | 8 |
| 3118 | lastimoso | 8 |
| 3119 | lámina | 8 |
| 3120 | lamentar | 8 |
| 3121 | judía | 8 |
| 3122 | joaquinito | 8 |
| 3123 | jardín | 8 |
| 3124 | izquierda | 8 |
| 3125 | irritar | 8 |
| 3126 | invisible | 8 |
| 3127 | invadir | 8 |
| 3128 | intranquilo | 8 |
| 3129 | interno | 8 |
| 3130 | instrucción | 8 |
| 3131 | institución | 8 |
| 3132 | instalar | 8 |
| 3133 | iniciativa | 8 |
| 3134 | informar | 8 |
| 3135 | infamia | 8 |
| 3136 | indudable | 8 |
| 3137 | indispensable | 8 |
| 3138 | imperial | 8 |
| 3139 | igualar | 8 |
| 3140 | humillar | 8 |
| 3141 | húmedo | 8 |
| 3142 | hospital | 8 |
| 3143 | honra | 8 |
| 3144 | hiel | 8 |
| 3145 | guiar | 8 |
| 3146 | gritos | 8 |
| 3147 | grandioso | 8 |
| 3148 | glacial | 8 |
| 3149 | gemir | 8 |
| 3150 | gemido | 8 |
| 3151 | fugaz | 8 |
| 3152 | fuente | 8 |
| 3153 | forrar | 8 |
| 3154 | flaqueza | 8 |
| 3155 | fiscal | 8 |
| 3156 | fiero | 8 |
| 3157 | fidelidad | 8 |
| 3158 | felisa | 8 |
| 3159 | farol | 8 |
| 3160 | faldón | 8 |
| 3161 | extremar | 8 |
| 3162 | exigencia | 8 |
| 3163 | exactamente | 8 |
| 3164 | estrecho | 8 |
| 3165 | estimular | 8 |
| 3166 | estimación | 8 |
| 3167 | estatua | 8 |
| 3168 | estampa | 8 |
| 3169 | escocer | 8 |
| 3170 | esclavo | 8 |
| 3171 | esclavitud | 8 |
| 3172 | escaso | 8 |
| 3173 | eres | 8 |
| 3174 | epiléptico | 8 |
| 3175 | entrecejo | 8 |
| 3176 | entereza | 8 |
| 3177 | enseñanza | 8 |
| 3178 | enojo | 8 |
| 3179 | encarar | 8 |
| 3180 | encajar | 8 |
| 3181 | embustero | 8 |
| 3182 | elemental | 8 |
| 3183 | egoísmo | 8 |
| 3184 | dulzura | 8 |
| 3185 | doscientos | 8 |
| 3186 | dorar | 8 |
| 3187 | doncella | 8 |
| 3188 | dolorido | 8 |
| 3189 | divinidad | 8 |
| 3190 | distraído | 8 |
| 3191 | disminuir | 8 |
| 3192 | disfrutar | 8 |
| 3193 | discreción | 8 |
| 3194 | dígame | 8 |
| 3195 | diálogo | 8 |
| 3196 | despejar | 8 |
| 3197 | despedida | 8 |
| 3198 | desechar | 8 |
| 3199 | descollar | 8 |
| 3200 | descolgar | 8 |
| 3201 | desbordar | 8 |
| 3202 | desatino | 8 |
| 3203 | dentadura | 8 |
| 3204 | delirante | 8 |
| 3205 | decorar | 8 |
| 3206 | declaró | 8 |
| 3207 | dátil | 8 |
| 3208 | datar | 8 |
| 3209 | curso | 8 |
| 3210 | culpable | 8 |
| 3211 | cuidadosamente | 8 |
| 3212 | cuero | 8 |
| 3213 | cuadrar | 8 |
| 3214 | crianza | 8 |
| 3215 | cráneo | 8 |
| 3216 | corrillo | 8 |
| 3217 | correspondiente | 8 |
| 3218 | cordura | 8 |
| 3219 | convulsivo | 8 |
| 3220 | contrariedad | 8 |
| 3221 | contrabando | 8 |
| 3222 | contacto | 8 |
| 3223 | construcción | 8 |
| 3224 | constante | 8 |
| 3225 | considerablemente | 8 |
| 3226 | conquistar | 8 |
| 3227 | confesión | 8 |
| 3228 | concurrir | 8 |
| 3229 | concienciar | 8 |
| 3230 | comunidad | 8 |
| 3231 | competencia | 8 |
| 3232 | compasivo | 8 |
| 3233 | combatir | 8 |
| 3234 | colorado | 8 |
| 3235 | cobre | 8 |
| 3236 | cobrador | 8 |
| 3237 | civil | 8 |
| 3238 | cirila | 8 |
| 3239 | chuchería | 8 |
| 3240 | chispa | 8 |
| 3241 | chillón | 8 |
| 3242 | chica | 8 |
| 3243 | cesto | 8 |
| 3244 | cesante | 8 |
| 3245 | cercar | 8 |
| 3246 | ceño | 8 |
| 3247 | cautivar | 8 |
| 3248 | casorio | 8 |
| 3249 | carita | 8 |
| 3250 | caramelo | 8 |
| 3251 | cañón | 8 |
| 3252 | cantón | 8 |
| 3253 | cansado | 8 |
| 3254 | calumniar | 8 |
| 3255 | cajita | 8 |
| 3256 | busto | 8 |
| 3257 | brío | 8 |
| 3258 | brillante | 8 |
| 3259 | bregar | 8 |
| 3260 | bravo | 8 |
| 3261 | botín | 8 |
| 3262 | boticario | 8 |
| 3263 | bomba | 8 |
| 3264 | base | 8 |
| 3265 | barro | 8 |
| 3266 | azotar | 8 |
| 3267 | avivar | 8 |
| 3268 | avergonzar | 8 |
| 3269 | autoritario | 8 |
| 3270 | atrevido | 8 |
| 3271 | atenuar | 8 |
| 3272 | atentamente | 8 |
| 3273 | aspaviento | 8 |
| 3274 | asesinar | 8 |
| 3275 | aseo | 8 |
| 3276 | arrogante | 8 |
| 3277 | arrimar | 8 |
| 3278 | arco | 8 |
| 3279 | aragón | 8 |
| 3280 | apretado | 8 |
| 3281 | apostamos | 8 |
| 3282 | aplaudir | 8 |
| 3283 | aparición | 8 |
| 3284 | anonadar | 8 |
| 3285 | amparar | 8 |
| 3286 | altercar | 8 |
| 3287 | alimento | 8 |
| 3288 | alcance | 8 |
| 3289 | albañil | 8 |
| 3290 | airoso | 8 |
| 3291 | agraciar | 8 |
| 3292 | agitación | 8 |
| 3293 | afligido | 8 |
| 3294 | afirmativo | 8 |
| 3295 | adornar | 8 |
| 3296 | adoptar | 8 |
| 3297 | acontecer | 8 |
| 3298 | acero | 8 |
| 3299 | acceso | 8 |
| 3300 | abuelito | 8 |
| 3301 | abatir | 8 |
| 3302 | yerba | 7 |
| 3303 | votar | 7 |
| 3304 | volvió | 7 |
| 3305 | volcar | 7 |
| 3306 | vigilancia | 7 |
| 3307 | viernes | 7 |
| 3308 | ventanilla | 7 |
| 3309 | vagamente | 7 |
| 3310 | vagabundo | 7 |
| 3311 | usurero | 7 |
| 3312 | tutear | 7 |
| 3313 | tripa | 7 |
| 3314 | tratamiento | 7 |
| 3315 | traspaso | 7 |
| 3316 | tranvía | 7 |
| 3317 | trago | 7 |
| 3318 | trabar | 7 |
| 3319 | tos | 7 |
| 3320 | torpeza | 7 |
| 3321 | torno | 7 |
| 3322 | tirria | 7 |
| 3323 | tiritar | 7 |
| 3324 | tinta | 7 |
| 3325 | texto | 7 |
| 3326 | teta | 7 |
| 3327 | testamento | 7 |
| 3328 | ternera | 7 |
| 3329 | teniente | 7 |
| 3330 | tejado | 7 |
| 3331 | supuesto | 7 |
| 3332 | suavidad | 7 |
| 3333 | soso | 7 |
| 3334 | soñador | 7 |
| 3335 | solicitar | 7 |
| 3336 | solemnidad | 7 |
| 3337 | socio | 7 |
| 3338 | sobresaltar | 7 |
| 3339 | simplemente | 7 |
| 3340 | símbolo | 7 |
| 3341 | sillar | 7 |
| 3342 | siéntese | 7 |
| 3343 | servidor | 7 |
| 3344 | sequedad | 7 |
| 3345 | sentose | 7 |
| 3346 | semejar | 7 |
| 3347 | sed | 7 |
| 3348 | secretear | 7 |
| 3349 | samaniegas | 7 |
| 3350 | salado | 7 |
| 3351 | sagunto | 7 |
| 3352 | sacristía | 7 |
| 3353 | sábado | 7 |
| 3354 | ruina | 7 |
| 3355 | rosita | 7 |
| 3356 | roer | 7 |
| 3357 | rival | 7 |
| 3358 | ricamente | 7 |
| 3359 | retumbar | 7 |
| 3360 | retratar | 7 |
| 3361 | resma | 7 |
| 3362 | reputación | 7 |
| 3363 | representación | 7 |
| 3364 | reponer | 7 |
| 3365 | repasar | 7 |
| 3366 | rehacer | 7 |
| 3367 | regentar | 7 |
| 3368 | reforma | 7 |
| 3369 | rédito | 7 |
| 3370 | recurso | 7 |
| 3371 | reconocimiento | 7 |
| 3372 | reconciliar | 7 |
| 3373 | recluso | 7 |
| 3374 | recíprocamente | 7 |
| 3375 | rechazar | 7 |
| 3376 | rebosar | 7 |
| 3377 | rasar | 7 |
| 3378 | queja | 7 |
| 3379 | purísima | 7 |
| 3380 | pulga | 7 |
| 3381 | proximidad | 7 |
| 3382 | proporcionar | 7 |
| 3383 | programa | 7 |
| 3384 | privar | 7 |
| 3385 | prensa | 7 |
| 3386 | predicar | 7 |
| 3387 | preciosidad | 7 |
| 3388 | postas | 7 |
| 3389 | poseedor | 7 |
| 3390 | portera | 7 |
| 3391 | ponderar | 7 |
| 3392 | polla | 7 |
| 3393 | poético | 7 |
| 3394 | pliegue | 7 |
| 3395 | plantear | 7 |
| 3396 | piadoso | 7 |
| 3397 | peste | 7 |
| 3398 | persecución | 7 |
| 3399 | perra | 7 |
| 3400 | perla | 7 |
| 3401 | peripecia | 7 |
| 3402 | percibir | 7 |
| 3403 | percha | 7 |
| 3404 | pensión | 7 |
| 3405 | penitenciar | 7 |
| 3406 | peligroso | 7 |
| 3407 | pechar | 7 |
| 3408 | paterno | 7 |
| 3409 | palique | 7 |
| 3410 | palco | 7 |
| 3411 | opinar | 7 |
| 3412 | odioso | 7 |
| 3413 | ocioso | 7 |
| 3414 | ocasionar | 7 |
| 3415 | obediencia | 7 |
| 3416 | nieves | 7 |
| 3417 | negativo | 7 |
| 3418 | narrador | 7 |
| 3419 | napoleón | 7 |
| 3420 | muro | 7 |
| 3421 | muñeco | 7 |
| 3422 | muleta | 7 |
| 3423 | mugido | 7 |
| 3424 | muelle | 7 |
| 3425 | mudanza | 7 |
| 3426 | muchas | 7 |
| 3427 | mota | 7 |
| 3428 | molde | 7 |
| 3429 | mojar | 7 |
| 3430 | modesto | 7 |
| 3431 | mimoso | 7 |
| 3432 | milicia | 7 |
| 3433 | mercantil | 7 |
| 3434 | mequetrefe | 7 |
| 3435 | mediodía | 7 |
| 3436 | mediar | 7 |
| 3437 | mechón | 7 |
| 3438 | mártir | 7 |
| 3439 | manotada | 7 |
| 3440 | manifestación | 7 |
| 3441 | maniático | 7 |
| 3442 | mangonear | 7 |
| 3443 | malvina | 7 |
| 3444 | maltratar | 7 |
| 3445 | malicioso | 7 |
| 3446 | majo | 7 |
| 3447 | majadero | 7 |
| 3448 | magín | 7 |
| 3449 | maduro | 7 |
| 3450 | lustre | 7 |
| 3451 | lozoya | 7 |
| 3452 | lógico | 7 |
| 3453 | lívido | 7 |
| 3454 | levitar | 7 |
| 3455 | letargo | 7 |
| 3456 | lealtad | 7 |
| 3457 | lastimar | 7 |
| 3458 | ladrar | 7 |
| 3459 | labrar | 7 |
| 3460 | juguete | 7 |
| 3461 | júbilo | 7 |
| 3462 | jarro | 7 |
| 3463 | invocar | 7 |
| 3464 | invierno | 7 |
| 3465 | intimidad | 7 |
| 3466 | inmensidad | 7 |
| 3467 | inmediatamente | 7 |
| 3468 | índole | 7 |
| 3469 | indeciso | 7 |
| 3470 | inclinación | 7 |
| 3471 | ignorancia | 7 |
| 3472 | ida | 7 |
| 3473 | huérfano | 7 |
| 3474 | honesto | 7 |
| 3475 | hocico | 7 |
| 3476 | hereje | 7 |
| 3477 | habla | 7 |
| 3478 | habilidad | 7 |
| 3479 | guisar | 7 |
| 3480 | guasa | 7 |
| 3481 | guapetón | 7 |
| 3482 | gran | 7 |
| 3483 | gonzález | 7 |
| 3484 | girar | 7 |
| 3485 | gatito | 7 |
| 3486 | ganga | 7 |
| 3487 | gafa | 7 |
| 3488 | fusil | 7 |
| 3489 | fúnebre | 7 |
| 3490 | fumar | 7 |
| 3491 | fresa | 7 |
| 3492 | ferrocarril | 7 |
| 3493 | felicitar | 7 |
| 3494 | fatal | 7 |
| 3495 | fantástico | 7 |
| 3496 | explotar | 7 |
| 3497 | excursión | 7 |
| 3498 | exagerar | 7 |
| 3499 | estupendo | 7 |
| 3500 | estaba | 7 |
| 3501 | espérate | 7 |
| 3502 | especialidad | 7 |
| 3503 | esa | 7 |
| 3504 | enzarzar | 7 |
| 3505 | ensimismar | 7 |
| 3506 | enfriar | 7 |
| 3507 | encanto | 7 |
| 3508 | encaminar | 7 |
| 3509 | empuje | 7 |
| 3510 | elección | 7 |
| 3511 | ejercitar | 7 |
| 3512 | economía | 7 |
| 3513 | dureza | 7 |
| 3514 | dote | 7 |
| 3515 | dómine | 7 |
| 3516 | dividir | 7 |
| 3517 | discípulo | 7 |
| 3518 | diligencia | 7 |
| 3519 | digo | 7 |
| 3520 | di | 7 |
| 3521 | desusado | 7 |
| 3522 | desterrar | 7 |
| 3523 | desplomar | 7 |
| 3524 | despecho | 7 |
| 3525 | desmayar | 7 |
| 3526 | desigual | 7 |
| 3527 | deseoso | 7 |
| 3528 | desdecir | 7 |
| 3529 | desconsolado | 7 |
| 3530 | desatinar | 7 |
| 3531 | desatar | 7 |
| 3532 | depender | 7 |
| 3533 | departamento | 7 |
| 3534 | demonios | 7 |
| 3535 | deleite | 7 |
| 3536 | déjeme | 7 |
| 3537 | déjate | 7 |
| 3538 | dejado | 7 |
| 3539 | debido | 7 |
| 3540 | debe | 7 |
| 3541 | cumplimiento | 7 |
| 3542 | coyuntura | 7 |
| 3543 | cortedad | 7 |
| 3544 | conquista | 7 |
| 3545 | conformidad | 7 |
| 3546 | confesor | 7 |
| 3547 | concejal | 7 |
| 3548 | comulgar | 7 |
| 3549 | complacer | 7 |
| 3550 | cómico | 7 |
| 3551 | colorar | 7 |
| 3552 | cohibir | 7 |
| 3553 | cocinero | 7 |
| 3554 | cláusula | 7 |
| 3555 | chimenea | 7 |
| 3556 | céntimo | 7 |
| 3557 | ceniza | 7 |
| 3558 | catorce | 7 |
| 3559 | catedral | 7 |
| 3560 | catarro | 7 |
| 3561 | cascote | 7 |
| 3562 | cartilla | 7 |
| 3563 | carbón | 7 |
| 3564 | caramba | 7 |
| 3565 | canonjía | 7 |
| 3566 | campaña | 7 |
| 3567 | calzón | 7 |
| 3568 | callado | 7 |
| 3569 | calentura | 7 |
| 3570 | calar | 7 |
| 3571 | caído | 7 |
| 3572 | cadáver | 7 |
| 3573 | cacharro | 7 |
| 3574 | cabezada | 7 |
| 3575 | cabecero | 7 |
| 3576 | burlesco | 7 |
| 3577 | bromuro | 7 |
| 3578 | brinco | 7 |
| 3579 | bendecir | 7 |
| 3580 | bayeta | 7 |
| 3581 | barriga | 7 |
| 3582 | baño | 7 |
| 3583 | banqueta | 7 |
| 3584 | baile | 7 |
| 3585 | bacalao | 7 |
| 3586 | atrocidad | 7 |
| 3587 | atractivo | 7 |
| 3588 | atocha | 7 |
| 3589 | asqueroso | 7 |
| 3590 | asociar | 7 |
| 3591 | asentimiento | 7 |
| 3592 | artístico | 7 |
| 3593 | articular | 7 |
| 3594 | aristocracia | 7 |
| 3595 | arañar | 7 |
| 3596 | apelar | 7 |
| 3597 | aparte | 7 |
| 3598 | anteojo | 7 |
| 3599 | anegar | 7 |
| 3600 | anarquista | 7 |
| 3601 | anarquía | 7 |
| 3602 | amparo | 7 |
| 3603 | americana | 7 |
| 3604 | ameno | 7 |
| 3605 | alternativa | 7 |
| 3606 | alimentar | 7 |
| 3607 | alhaja | 7 |
| 3608 | alfiler | 7 |
| 3609 | alburquerque | 7 |
| 3610 | alambre | 7 |
| 3611 | agregó | 7 |
| 3612 | agradecido | 7 |
| 3613 | agradable | 7 |
| 3614 | ágil | 7 |
| 3615 | aflicción | 7 |
| 3616 | afanar | 7 |
| 3617 | adoptivo | 7 |
| 3618 | adefesio | 7 |
| 3619 | acreedor | 7 |
| 3620 | acordose | 7 |
| 3621 | acobardar | 7 |
| 3622 | achuchón | 7 |
| 3623 | accionar | 7 |
| 3624 | accidente | 7 |
| 3625 | acalorar | 7 |
| 3626 | abusar | 7 |
| 3627 | abuelo | 7 |
| 3628 | abrasar | 7 |
| 3629 | zaragata | 6 |
| 3630 | xi | 6 |
| 3631 | vulgo | 6 |
| 3632 | vulgaridad | 6 |
| 3633 | voy | 6 |
| 3634 | votación | 6 |
| 3635 | vosotros | 6 |
| 3636 | visible | 6 |
| 3637 | violentar | 6 |
| 3638 | viciar | 6 |
| 3639 | viajar | 6 |
| 3640 | viajante | 6 |
| 3641 | vendedor | 6 |
| 3642 | ven | 6 |
| 3643 | veleta | 6 |
| 3644 | váyase | 6 |
| 3645 | vacilación | 6 |
| 3646 | urbanidad | 6 |
| 3647 | universal | 6 |
| 3648 | últimamente | 6 |
| 3649 | turno | 6 |
| 3650 | turco | 6 |
| 3651 | tumulto | 6 |
| 3652 | trozo | 6 |
| 3653 | tropiezo | 6 |
| 3654 | trompetilla | 6 |
| 3655 | triquiñuela | 6 |
| 3656 | trémulo | 6 |
| 3657 | travieso | 6 |
| 3658 | trasladar | 6 |
| 3659 | tránsito | 6 |
| 3660 | transición | 6 |
| 3661 | traición | 6 |
| 3662 | trabajador | 6 |
| 3663 | torcido | 6 |
| 3664 | tonillo | 6 |
| 3665 | tomás | 6 |
| 3666 | título | 6 |
| 3667 | tintoreros | 6 |
| 3668 | tiniebla | 6 |
| 3669 | timo | 6 |
| 3670 | tigre | 6 |
| 3671 | tez | 6 |
| 3672 | terminante | 6 |
| 3673 | tentación | 6 |
| 3674 | temperamento | 6 |
| 3675 | temerario | 6 |
| 3676 | tellería | 6 |
| 3677 | tardanza | 6 |
| 3678 | tablero | 6 |
| 3679 | suprimir | 6 |
| 3680 | superioridad | 6 |
| 3681 | sumamente | 6 |
| 3682 | suma | 6 |
| 3683 | sugerir | 6 |
| 3684 | suelos | 6 |
| 3685 | sueldo | 6 |
| 3686 | suela | 6 |
| 3687 | sucesor | 6 |
| 3688 | sublevar | 6 |
| 3689 | súbitamente | 6 |
| 3690 | suave | 6 |
| 3691 | sopetón | 6 |
| 3692 | sonrosar | 6 |
| 3693 | somnolencia | 6 |
| 3694 | sollozo | 6 |
| 3695 | silencioso | 6 |
| 3696 | signar | 6 |
| 3697 | sietemesino | 6 |
| 3698 | sien | 6 |
| 3699 | sevilla | 6 |
| 3700 | servidumbre | 6 |
| 3701 | serie | 6 |
| 3702 | separación | 6 |
| 3703 | sentimental | 6 |
| 3704 | sensato | 6 |
| 3705 | sayo | 6 |
| 3706 | samaritano | 6 |
| 3707 | salvo | 6 |
| 3708 | salió | 6 |
| 3709 | saladero | 6 |
| 3710 | sacudida | 6 |
| 3711 | saborear | 6 |
| 3712 | ruidoso | 6 |
| 3713 | rudeza | 6 |
| 3714 | rosquilla | 6 |
| 3715 | revolcar | 6 |
| 3716 | responsable | 6 |
| 3717 | respaldo | 6 |
| 3718 | resonar | 6 |
| 3719 | reproducción | 6 |
| 3720 | remontar | 6 |
| 3721 | relativamente | 6 |
| 3722 | relamer | 6 |
| 3723 | regreso | 6 |
| 3724 | regocijo | 6 |
| 3725 | reflexión | 6 |
| 3726 | recuerdo | 6 |
| 3727 | reciente | 6 |
| 3728 | recetar | 6 |
| 3729 | receta | 6 |
| 3730 | recelar | 6 |
| 3731 | rebelde | 6 |
| 3732 | reacción | 6 |
| 3733 | razonar | 6 |
| 3734 | razonamiento | 6 |
| 3735 | raimundo | 6 |
| 3736 | rabioso | 6 |
| 3737 | quinqué | 6 |
| 3738 | quijada | 6 |
| 3739 | queda | 6 |
| 3740 | pureza | 6 |
| 3741 | puntillas | 6 |
| 3742 | púlpito | 6 |
| 3743 | puede | 6 |
| 3744 | publicar | 6 |
| 3745 | puar | 6 |
| 3746 | provisión | 6 |
| 3747 | protestar | 6 |
| 3748 | proseguir | 6 |
| 3749 | proporción | 6 |
| 3750 | propietario | 6 |
| 3751 | propaganda | 6 |
| 3752 | privado | 6 |
| 3753 | prisión | 6 |
| 3754 | prestamista | 6 |
| 3755 | presentir | 6 |
| 3756 | precursor | 6 |
| 3757 | positivo | 6 |
| 3758 | pobrecilla | 6 |
| 3759 | pliego | 6 |
| 3760 | pleno | 6 |
| 3761 | plazo | 6 |
| 3762 | pito | 6 |
| 3763 | pisto | 6 |
| 3764 | pino | 6 |
| 3765 | pillete | 6 |
| 3766 | picador | 6 |
| 3767 | pianista | 6 |
| 3768 | petróleo | 6 |
| 3769 | pescador | 6 |
| 3770 | perversidad | 6 |
| 3771 | perturbar | 6 |
| 3772 | perdulario | 6 |
| 3773 | percal | 6 |
| 3774 | pelear | 6 |
| 3775 | pasta | 6 |
| 3776 | paréntesis | 6 |
| 3777 | papelito | 6 |
| 3778 | palpar | 6 |
| 3779 | página | 6 |
| 3780 | original | 6 |
| 3781 | oía | 6 |
| 3782 | oficiosidad | 6 |
| 3783 | ofensa | 6 |
| 3784 | nudo | 6 |
| 3785 | noria | 6 |
| 3786 | narciso | 6 |
| 3787 | napoleónico | 6 |
| 3788 | murria | 6 |
| 3789 | murmullo | 6 |
| 3790 | mula | 6 |
| 3791 | mugre | 6 |
| 3792 | muchedumbre | 6 |
| 3793 | motor | 6 |
| 3794 | mote | 6 |
| 3795 | mosquito | 6 |
| 3796 | monosílabo | 6 |
| 3797 | monarquía | 6 |
| 3798 | modelar | 6 |
| 3799 | miga | 6 |
| 3800 | mezcla | 6 |
| 3801 | memorable | 6 |
| 3802 | melancólico | 6 |
| 3803 | meditabundo | 6 |
| 3804 | mecánico | 6 |
| 3805 | mazapán | 6 |
| 3806 | mayoría | 6 |
| 3807 | maridar | 6 |
| 3808 | marca | 6 |
| 3809 | maravilla | 6 |
| 3810 | manos | 6 |
| 3811 | manguito | 6 |
| 3812 | mango | 6 |
| 3813 | manga | 6 |
| 3814 | luto | 6 |
| 3815 | lulio | 6 |
| 3816 | llavín | 6 |
| 3817 | líquido | 6 |
| 3818 | linaje | 6 |
| 3819 | limpia | 6 |
| 3820 | ligeramente | 6 |
| 3821 | leña | 6 |
| 3822 | lento | 6 |
| 3823 | leganés | 6 |
| 3824 | junta | 6 |
| 3825 | junio | 6 |
| 3826 | junco | 6 |
| 3827 | julio | 6 |
| 3828 | jovial | 6 |
| 3829 | jerez | 6 |
| 3830 | jarana | 6 |
| 3831 | ironía | 6 |
| 3832 | interlocutor | 6 |
| 3833 | intento | 6 |
| 3834 | insultar | 6 |
| 3835 | inseguro | 6 |
| 3836 | ingenuidad | 6 |
| 3837 | infaliblemente | 6 |
| 3838 | índice | 6 |
| 3839 | indicación | 6 |
| 3840 | incapaz | 6 |
| 3841 | impreso | 6 |
| 3842 | imperioso | 6 |
| 3843 | humorístico | 6 |
| 3844 | humorado | 6 |
| 3845 | hongo | 6 |
| 3846 | hito | 6 |
| 3847 | hinchar | 6 |
| 3848 | higo | 6 |
| 3849 | hermosísimo | 6 |
| 3850 | hechura | 6 |
| 3851 | habitante | 6 |
| 3852 | hábil | 6 |
| 3853 | gruñir | 6 |
| 3854 | gruñido | 6 |
| 3855 | gravelinas | 6 |
| 3856 | grata | 6 |
| 3857 | granuja | 6 |
| 3858 | grandeza | 6 |
| 3859 | glorioso | 6 |
| 3860 | gilimón | 6 |
| 3861 | generosidad | 6 |
| 3862 | gatillo | 6 |
| 3863 | gallego | 6 |
| 3864 | galán | 6 |
| 3865 | gabán | 6 |
| 3866 | fusilar | 6 |
| 3867 | frito | 6 |
| 3868 | fósforo | 6 |
| 3869 | formidable | 6 |
| 3870 | forastero | 6 |
| 3871 | fonda | 6 |
| 3872 | firma | 6 |
| 3873 | finalmente | 6 |
| 3874 | figurábase | 6 |
| 3875 | festivo | 6 |
| 3876 | feroz | 6 |
| 3877 | felipe | 6 |
| 3878 | faz | 6 |
| 3879 | fárrago | 6 |
| 3880 | facilidad | 6 |
| 3881 | extraviar | 6 |
| 3882 | extinguir | 6 |
| 3883 | expirar | 6 |
| 3884 | experimentar | 6 |
| 3885 | excepción | 6 |
| 3886 | exactitud | 6 |
| 3887 | etiqueta | 6 |
| 3888 | estropear | 6 |
| 3889 | estrechez | 6 |
| 3890 | estos | 6 |
| 3891 | estirón | 6 |
| 3892 | estallar | 6 |
| 3893 | espinazo | 6 |
| 3894 | espetar | 6 |
| 3895 | escritura | 6 |
| 3896 | escarola | 6 |
| 3897 | escandalizar | 6 |
| 3898 | escalofrío | 6 |
| 3899 | esas | 6 |
| 3900 | equivaler | 6 |
| 3901 | equilibrio | 6 |
| 3902 | enviar | 6 |
| 3903 | envalentonar | 6 |
| 3904 | entrole | 6 |
| 3905 | entresuelo | 6 |
| 3906 | entornar | 6 |
| 3907 | enredo | 6 |
| 3908 | enhorabuena | 6 |
| 3909 | engatusar | 6 |
| 3910 | enero | 6 |
| 3911 | encogimiento | 6 |
| 3912 | encarnado | 6 |
| 3913 | enamorado | 6 |
| 3914 | empalagoso | 6 |
| 3915 | emigración | 6 |
| 3916 | embriagar | 6 |
| 3917 | ejemplar | 6 |
| 3918 | ejecución | 6 |
| 3919 | eco | 6 |
| 3920 | echose | 6 |
| 3921 | duquesa | 6 |
| 3922 | dulcemente | 6 |
| 3923 | dudoso | 6 |
| 3924 | ducha | 6 |
| 3925 | droguería | 6 |
| 3926 | droga | 6 |
| 3927 | dominio | 6 |
| 3928 | dominante | 6 |
| 3929 | domar | 6 |
| 3930 | diván | 6 |
| 3931 | distribuir | 6 |
| 3932 | distribución | 6 |
| 3933 | disipar | 6 |
| 3934 | díjole | 6 |
| 3935 | digerir | 6 |
| 3936 | dígale | 6 |
| 3937 | dices | 6 |
| 3938 | dibujo | 6 |
| 3939 | dialéctico | 6 |
| 3940 | diablura | 6 |
| 3941 | devaneo | 6 |
| 3942 | deudor | 6 |
| 3943 | determinado | 6 |
| 3944 | destrozar | 6 |
| 3945 | destacar | 6 |
| 3946 | despejado | 6 |
| 3947 | desnudo | 6 |
| 3948 | desfilar | 6 |
| 3949 | desdeñoso | 6 |
| 3950 | desconsolar | 6 |
| 3951 | descompuesto | 6 |
| 3952 | descalzar | 6 |
| 3953 | derribar | 6 |
| 3954 | derivar | 6 |
| 3955 | demostración | 6 |
| 3956 | delirar | 6 |
| 3957 | delgado | 6 |
| 3958 | daño | 6 |
| 3959 | dale | 6 |
| 3960 | curiosear | 6 |
| 3961 | cuña | 6 |
| 3962 | cuentas | 6 |
| 3963 | cucharada | 6 |
| 3964 | cuartito | 6 |
| 3965 | cretona | 6 |
| 3966 | creo | 6 |
| 3967 | créetelo | 6 |
| 3968 | credencial | 6 |
| 3969 | cotorra | 6 |
| 3970 | cosquillar | 6 |
| 3971 | cortado | 6 |
| 3972 | corsé | 6 |
| 3973 | correo | 6 |
| 3974 | copar | 6 |
| 3975 | contrabandista | 6 |
| 3976 | consumir | 6 |
| 3977 | constantemente | 6 |
| 3978 | consorte | 6 |
| 3979 | conocedor | 6 |
| 3980 | concebir | 6 |
| 3981 | compostura | 6 |
| 3982 | comparación | 6 |
| 3983 | comandante | 6 |
| 3984 | coco | 6 |
| 3985 | cocido | 6 |
| 3986 | cocer | 6 |
| 3987 | cobarde | 6 |
| 3988 | clavetear | 6 |
| 3989 | citado | 6 |
| 3990 | cifra | 6 |
| 3991 | chocho | 6 |
| 3992 | chiquito | 6 |
| 3993 | chiquitín | 6 |
| 3994 | chafar | 6 |
| 3995 | cerilla | 6 |
| 3996 | cerebrar | 6 |
| 3997 | cerdo | 6 |
| 3998 | central | 6 |
| 3999 | cazador | 6 |
| 4000 | caza | 6 |
| 4001 | cavidad | 6 |
| 4002 | caudal | 6 |
| 4003 | caserío | 6 |
| 4004 | cascarón | 6 |
| 4005 | cartagena | 6 |
| 4006 | caritativo | 6 |
| 4007 | capirote | 6 |
| 4008 | canutar | 6 |
| 4009 | cantero | 6 |
| 4010 | canónigo | 6 |
| 4011 | canela | 6 |
| 4012 | cándido | 6 |
| 4013 | campanada | 6 |
| 4014 | caliente | 6 |
| 4015 | caldear | 6 |
| 4016 | calaverada | 6 |
| 4017 | cabellera | 6 |
| 4018 | caballería | 6 |
| 4019 | bullicio | 6 |
| 4020 | buenos | 6 |
| 4021 | brutal | 6 |
| 4022 | botar | 6 |
| 4023 | bonita | 6 |
| 4024 | bonilla | 6 |
| 4025 | bloque | 6 |
| 4026 | berrido | 6 |
| 4027 | benéfico | 6 |
| 4028 | bello | 6 |
| 4029 | bayona | 6 |
| 4030 | bautizo | 6 |
| 4031 | basura | 6 |
| 4032 | barullo | 6 |
| 4033 | barco | 6 |
| 4034 | barato | 6 |
| 4035 | bandera | 6 |
| 4036 | bandeja | 6 |
| 4037 | babero | 6 |
| 4038 | ayún | 6 |
| 4039 | ayuda | 6 |
| 4040 | atropellar | 6 |
| 4041 | atrasar | 6 |
| 4042 | atracción | 6 |
| 4043 | atontar | 6 |
| 4044 | aterrador | 6 |
| 4045 | ateo | 6 |
| 4046 | aspereza | 6 |
| 4047 | artesa | 6 |
| 4048 | arruinar | 6 |
| 4049 | arrugar | 6 |
| 4050 | arroyo | 6 |
| 4051 | arquitectura | 6 |
| 4052 | arca | 6 |
| 4053 | apunte | 6 |
| 4054 | aprensión | 6 |
| 4055 | apreciable | 6 |
| 4056 | apartado | 6 |
| 4057 | ansioso | 6 |
| 4058 | amarrar | 6 |
| 4059 | amantar | 6 |
| 4060 | amalia | 6 |
| 4061 | amado | 6 |
| 4062 | alivio | 6 |
| 4063 | aliviar | 6 |
| 4064 | aletargar | 6 |
| 4065 | alboroto | 6 |
| 4066 | albert | 6 |
| 4067 | alarmado | 6 |
| 4068 | alarde | 6 |
| 4069 | alabar | 6 |
| 4070 | ajar | 6 |
| 4071 | airar | 6 |
| 4072 | agudeza | 6 |
| 4073 | aguar | 6 |
| 4074 | agrandar | 6 |
| 4075 | agente | 6 |
| 4076 | afinar | 6 |
| 4077 | afilar | 6 |
| 4078 | adúltero | 6 |
| 4079 | adormecer | 6 |
| 4080 | administrativo | 6 |
| 4081 | administrar | 6 |
| 4082 | acusar | 6 |
| 4083 | acosar | 6 |
| 4084 | abundar | 6 |
| 4085 | abundante | 6 |
| 4086 | abatimiento | 6 |
| 4087 | abandono | 6 |
| 4088 | zozobra | 5 |
| 4089 | zona | 5 |
| 4090 | zarzuela | 5 |
| 4091 | vosotras | 5 |
| 4092 | visitación | 5 |
| 4093 | visaje | 5 |
| 4094 | viruela | 5 |
| 4095 | violín | 5 |
| 4096 | violentamente | 5 |
| 4097 | villaamil | 5 |
| 4098 | viga | 5 |
| 4099 | vientre | 5 |
| 4100 | vidrio | 5 |
| 4101 | vicario | 5 |
| 4102 | víbora | 5 |
| 4103 | venta | 5 |
| 4104 | vengo | 5 |
| 4105 | venerable | 5 |
| 4106 | vena | 5 |
| 4107 | vecindario | 5 |
| 4108 | variedades | 5 |
| 4109 | vapor | 5 |
| 4110 | vano | 5 |
| 4111 | valía | 5 |
| 4112 | valeroso | 5 |
| 4113 | vaca | 5 |
| 4114 | útil | 5 |
| 4115 | uniforme | 5 |
| 4116 | turquesa | 5 |
| 4117 | trompeta | 5 |
| 4118 | trivial | 5 |
| 4119 | trinar | 5 |
| 4120 | trecho | 5 |
| 4121 | trayecto | 5 |
| 4122 | travesura | 5 |
| 4123 | transparentar | 5 |
| 4124 | transfigurar | 5 |
| 4125 | transcurrir | 5 |
| 4126 | transacción | 5 |
| 4127 | tramo | 5 |
| 4128 | traicionero | 5 |
| 4129 | tragedia | 5 |
| 4130 | tradición | 5 |
| 4131 | tostar | 5 |
| 4132 | torero | 5 |
| 4133 | tontaina | 5 |
| 4134 | todos | 5 |
| 4135 | toalla | 5 |
| 4136 | tintero | 5 |
| 4137 | tímidamente | 5 |
| 4138 | tilín | 5 |
| 4139 | tientas | 5 |
| 4140 | tétrico | 5 |
| 4141 | testimonio | 5 |
| 4142 | terrón | 5 |
| 4143 | tendré | 5 |
| 4144 | tenaza | 5 |
| 4145 | templo | 5 |
| 4146 | telégrafo | 5 |
| 4147 | tecla | 5 |
| 4148 | taza | 5 |
| 4149 | tapujo | 5 |
| 4150 | tapiar | 5 |
| 4151 | tamañito | 5 |
| 4152 | tacón | 5 |
| 4153 | tabernillas | 5 |
| 4154 | surtir | 5 |
| 4155 | suplicar | 5 |
| 4156 | supersticioso | 5 |
| 4157 | suizo | 5 |
| 4158 | suicidio | 5 |
| 4159 | suficiencia | 5 |
| 4160 | sucesivo | 5 |
| 4161 | sospechoso | 5 |
| 4162 | soportar | 5 |
| 4163 | sopor | 5 |
| 4164 | solutamente | 5 |
| 4165 | solito | 5 |
| 4166 | soliloquio | 5 |
| 4167 | soldado | 5 |
| 4168 | sobrenatural | 5 |
| 4169 | sobrante | 5 |
| 4170 | siniestro | 5 |
| 4171 | sinceramente | 5 |
| 4172 | silbar | 5 |
| 4173 | serrano | 5 |
| 4174 | sería | 5 |
| 4175 | serafín | 5 |
| 4176 | sentíase | 5 |
| 4177 | sensible | 5 |
| 4178 | senquá | 5 |
| 4179 | sembrar | 5 |
| 4180 | sedación | 5 |
| 4181 | secta | 5 |
| 4182 | satánico | 5 |
| 4183 | sarcasmo | 5 |
| 4184 | saliva | 5 |
| 4185 | salamanca | 5 |
| 4186 | saco | 5 |
| 4187 | sablazo | 5 |
| 4188 | rutinario | 5 |
| 4189 | rumbo | 5 |
| 4190 | rufinita | 5 |
| 4191 | rúbrica | 5 |
| 4192 | ronquido | 5 |
| 4193 | rompimiento | 5 |
| 4194 | romano | 5 |
| 4195 | robustez | 5 |
| 4196 | revivir | 5 |
| 4197 | revisar | 5 |
| 4198 | reverdecer | 5 |
| 4199 | reunión | 5 |
| 4200 | retroceder | 5 |
| 4201 | reticencia | 5 |
| 4202 | restregar | 5 |
| 4203 | resbalar | 5 |
| 4204 | resabio | 5 |
| 4205 | requemar | 5 |
| 4206 | repóblica | 5 |
| 4207 | repetición | 5 |
| 4208 | reparador | 5 |
| 4209 | remiendo | 5 |
| 4210 | remedar | 5 |
| 4211 | relatar | 5 |
| 4212 | reinado | 5 |
| 4213 | refajo | 5 |
| 4214 | reducido | 5 |
| 4215 | reclinar | 5 |
| 4216 | rechinar | 5 |
| 4217 | receloso | 5 |
| 4218 | recatar | 5 |
| 4219 | rayar | 5 |
| 4220 | rasguear | 5 |
| 4221 | raquítico | 5 |
| 4222 | ramsés | 5 |
| 4223 | racimo | 5 |
| 4224 | quítate | 5 |
| 4225 | quintos | 5 |
| 4226 | quinto | 5 |
| 4227 | quinientos | 5 |
| 4228 | quietud | 5 |
| 4229 | quicio | 5 |
| 4230 | quejumbroso | 5 |
| 4231 | quebrantar | 5 |
| 4232 | puñado | 5 |
| 4233 | pum | 5 |
| 4234 | proyectar | 5 |
| 4235 | provocar | 5 |
| 4236 | prosperidad | 5 |
| 4237 | prójimo | 5 |
| 4238 | prodigar | 5 |
| 4239 | procedencia | 5 |
| 4240 | privación | 5 |
| 4241 | prisionero | 5 |
| 4242 | primor | 5 |
| 4243 | primar | 5 |
| 4244 | prevención | 5 |
| 4245 | prevalecer | 5 |
| 4246 | presidio | 5 |
| 4247 | preocupar | 5 |
| 4248 | preocupación | 5 |
| 4249 | prender | 5 |
| 4250 | prendar | 5 |
| 4251 | pregonar | 5 |
| 4252 | pregón | 5 |
| 4253 | preciosísimo | 5 |
| 4254 | preciar | 5 |
| 4255 | precaución | 5 |
| 4256 | postre | 5 |
| 4257 | posesión | 5 |
| 4258 | portillo | 5 |
| 4259 | poquillo | 5 |
| 4260 | poníase | 5 |
| 4261 | podrido | 5 |
| 4262 | población | 5 |
| 4263 | plomo | 5 |
| 4264 | pizcar | 5 |
| 4265 | pizca | 5 |
| 4266 | pisotear | 5 |
| 4267 | pirrar | 5 |
| 4268 | pinchar | 5 |
| 4269 | pillería | 5 |
| 4270 | piensa | 5 |
| 4271 | picor | 5 |
| 4272 | pesadumbre | 5 |
| 4273 | perteneciente | 5 |
| 4274 | persistir | 5 |
| 4275 | perezoso | 5 |
| 4276 | peregrinar | 5 |
| 4277 | perdone | 5 |
| 4278 | pelotera | 5 |
| 4279 | pellizco | 5 |
| 4280 | pellejo | 5 |
| 4281 | pelagatos | 5 |
| 4282 | pegado | 5 |
| 4283 | pedernal | 5 |
| 4284 | pavero | 5 |
| 4285 | patrocinio | 5 |
| 4286 | pastilla | 5 |
| 4287 | pasmado | 5 |
| 4288 | pascua | 5 |
| 4289 | pasajero | 5 |
| 4290 | particularmente | 5 |
| 4291 | particularidad | 5 |
| 4292 | paquetito | 5 |
| 4293 | pánico | 5 |
| 4294 | panadería | 5 |
| 4295 | pana | 5 |
| 4296 | palotada | 5 |
| 4297 | palmito | 5 |
| 4298 | palidez | 5 |
| 4299 | paleto | 5 |
| 4300 | oveja | 5 |
| 4301 | ostentar | 5 |
| 4302 | opulento | 5 |
| 4303 | oposición | 5 |
| 4304 | onza | 5 |
| 4305 | olivo | 5 |
| 4306 | olfato | 5 |
| 4307 | ofrecimiento | 5 |
| 4308 | nueva | 5 |
| 4309 | novelar | 5 |
| 4310 | noción | 5 |
| 4311 | ninguna | 5 |
| 4312 | nieve | 5 |
| 4313 | neto | 5 |
| 4314 | nefando | 5 |
| 4315 | nave | 5 |
| 4316 | na | 5 |
| 4317 | músico | 5 |
| 4318 | muestrario | 5 |
| 4319 | mudo | 5 |
| 4320 | móvil | 5 |
| 4321 | mortuorio | 5 |
| 4322 | moro | 5 |
| 4323 | moña | 5 |
| 4324 | montera | 5 |
| 4325 | mitón | 5 |
| 4326 | mismamente | 5 |
| 4327 | misericordia | 5 |
| 4328 | miren | 5 |
| 4329 | mirador | 5 |
| 4330 | miquis | 5 |
| 4331 | mico | 5 |
| 4332 | metro | 5 |
| 4333 | metamorfosis | 5 |
| 4334 | mesar | 5 |
| 4335 | menudillos | 5 |
| 4336 | mendigo | 5 |
| 4337 | memo | 5 |
| 4338 | melitona | 5 |
| 4339 | mecanismo | 5 |
| 4340 | mecánica | 5 |
| 4341 | materialista | 5 |
| 4342 | mata | 5 |
| 4343 | martillo | 5 |
| 4344 | mantillo | 5 |
| 4345 | manifiesto | 5 |
| 4346 | mama | 5 |
| 4347 | malito | 5 |
| 4348 | madurar | 5 |
| 4349 | lunes | 5 |
| 4350 | luis | 5 |
| 4351 | lozanía | 5 |
| 4352 | lomo | 5 |
| 4353 | llegada | 5 |
| 4354 | lisonjero | 5 |
| 4355 | límite | 5 |
| 4356 | limitar | 5 |
| 4357 | licor | 5 |
| 4358 | licencia | 5 |
| 4359 | leve | 5 |
| 4360 | leñar | 5 |
| 4361 | legal | 5 |
| 4362 | lata | 5 |
| 4363 | largamente | 5 |
| 4364 | lápiz | 5 |
| 4365 | lápida | 5 |
| 4366 | lanilla | 5 |
| 4367 | laboratorio | 5 |
| 4368 | labia | 5 |
| 4369 | jorobar | 5 |
| 4370 | jeta | 5 |
| 4371 | jesucristo | 5 |
| 4372 | japonés | 5 |
| 4373 | inverosímil | 5 |
| 4374 | invención | 5 |
| 4375 | interpretar | 5 |
| 4376 | intermitente | 5 |
| 4377 | instrumento | 5 |
| 4378 | instruir | 5 |
| 4379 | inspección | 5 |
| 4380 | insensible | 5 |
| 4381 | injuria | 5 |
| 4382 | ínfula | 5 |
| 4383 | industrial | 5 |
| 4384 | individual | 5 |
| 4385 | indiferente | 5 |
| 4386 | indicio | 5 |
| 4387 | incrédulo | 5 |
| 4388 | inconstante | 5 |
| 4389 | incierto | 5 |
| 4390 | inaudito | 5 |
| 4391 | imprimir | 5 |
| 4392 | imitación | 5 |
| 4393 | ilustrado | 5 |
| 4394 | ilusionar | 5 |
| 4395 | idiota | 5 |
| 4396 | humedad | 5 |
| 4397 | hospicio | 5 |
| 4398 | horripilar | 5 |
| 4399 | hormiga | 5 |
| 4400 | honrada | 5 |
| 4401 | hipotecar | 5 |
| 4402 | himno | 5 |
| 4403 | hígado | 5 |
| 4404 | hervir | 5 |
| 4405 | herrero | 5 |
| 4406 | hastío | 5 |
| 4407 | hambriento | 5 |
| 4408 | había | 5 |
| 4409 | greña | 5 |
| 4410 | gravemente | 5 |
| 4411 | gratis | 5 |
| 4412 | grano | 5 |
| 4413 | gradualmente | 5 |
| 4414 | gentío | 5 |
| 4415 | gata | 5 |
| 4416 | garra | 5 |
| 4417 | garabato | 5 |
| 4418 | gallardamente | 5 |
| 4419 | galera | 5 |
| 4420 | futura | 5 |
| 4421 | funesto | 5 |
| 4422 | fulgor | 5 |
| 4423 | fuero | 5 |
| 4424 | fruto | 5 |
| 4425 | fruta | 5 |
| 4426 | friolera | 5 |
| 4427 | frenético | 5 |
| 4428 | frecuencia | 5 |
| 4429 | fragancia | 5 |
| 4430 | fortaleza | 5 |
| 4431 | formular | 5 |
| 4432 | follaje | 5 |
| 4433 | flojo | 5 |
| 4434 | fineza | 5 |
| 4435 | financiero | 5 |
| 4436 | fijamente | 5 |
| 4437 | figurín | 5 |
| 4438 | ferocidad | 5 |
| 4439 | feria | 5 |
| 4440 | femenino | 5 |
| 4441 | fascinación | 5 |
| 4442 | fardo | 5 |
| 4443 | fango | 5 |
| 4444 | familiarizar | 5 |
| 4445 | familiaridad | 5 |
| 4446 | fajar | 5 |
| 4447 | facilitar | 5 |
| 4448 | fabricar | 5 |
| 4449 | extrañeza | 5 |
| 4450 | extraer | 5 |
| 4451 | expulsar | 5 |
| 4452 | expectación | 5 |
| 4453 | exacto | 5 |
| 4454 | evocar | 5 |
| 4455 | estupefacción | 5 |
| 4456 | estribillo | 5 |
| 4457 | estas | 5 |
| 4458 | esqueleto | 5 |
| 4459 | espiritista | 5 |
| 4460 | esperanzar | 5 |
| 4461 | espera | 5 |
| 4462 | espaldas | 5 |
| 4463 | esmerar | 5 |
| 4464 | escorial | 5 |
| 4465 | escoltar | 5 |
| 4466 | erudición | 5 |
| 4467 | equipaje | 5 |
| 4468 | envoltorio | 5 |
| 4469 | envejecer | 5 |
| 4470 | entusiasta | 5 |
| 4471 | entristecer | 5 |
| 4472 | entrevista | 5 |
| 4473 | entrañar | 5 |
| 4474 | entonar | 5 |
| 4475 | entidad | 5 |
| 4476 | entablar | 5 |
| 4477 | ensalada | 5 |
| 4478 | enroscar | 5 |
| 4479 | enredadera | 5 |
| 4480 | ennoblecer | 5 |
| 4481 | enfurruñar | 5 |
| 4482 | enfrentar | 5 |
| 4483 | enfático | 5 |
| 4484 | énfasis | 5 |
| 4485 | endeble | 5 |
| 4486 | encierro | 5 |
| 4487 | encasquetar | 5 |
| 4488 | embuste | 5 |
| 4489 | embrutecer | 5 |
| 4490 | embozar | 5 |
| 4491 | emborrachar | 5 |
| 4492 | embebecer | 5 |
| 4493 | emanar | 5 |
| 4494 | elogio | 5 |
| 4495 | elocuente | 5 |
| 4496 | elemento | 5 |
| 4497 | eje | 5 |
| 4498 | eficaz | 5 |
| 4499 | eclipsar | 5 |
| 4500 | dorado | 5 |
| 4501 | donativo | 5 |
| 4502 | divina | 5 |
| 4503 | displicente | 5 |
| 4504 | disolver | 5 |
| 4505 | disculpar | 5 |
| 4506 | directamente | 5 |
| 4507 | diplomático | 5 |
| 4508 | diligenciar | 5 |
| 4509 | dicha | 5 |
| 4510 | diamante | 5 |
| 4511 | desvelar | 5 |
| 4512 | despidiose | 5 |
| 4513 | despensa | 5 |
| 4514 | desmayado | 5 |
| 4515 | desigualdad | 5 |
| 4516 | desierto | 5 |
| 4517 | deshonra | 5 |
| 4518 | desesperar | 5 |
| 4519 | descuidado | 5 |
| 4520 | descalzo | 5 |
| 4521 | descabezar | 5 |
| 4522 | desbaratar | 5 |
| 4523 | desayuno | 5 |
| 4524 | desasosiego | 5 |
| 4525 | desagradar | 5 |
| 4526 | desabrido | 5 |
| 4527 | depositar | 5 |
| 4528 | denunciar | 5 |
| 4529 | delantera | 5 |
| 4530 | definitivo | 5 |
| 4531 | dedillo | 5 |
| 4532 | decoración | 5 |
| 4533 | décimo | 5 |
| 4534 | decidido | 5 |
| 4535 | dame | 5 |
| 4536 | cuna | 5 |
| 4537 | cuerno | 5 |
| 4538 | cucharilla | 5 |
| 4539 | cubil | 5 |
| 4540 | cúbico | 5 |
| 4541 | cualidad | 5 |
| 4542 | cuajar | 5 |
| 4543 | cruzado | 5 |
| 4544 | crujir | 5 |
| 4545 | cristóbal | 5 |
| 4546 | cría | 5 |
| 4547 | crespón | 5 |
| 4548 | creencia | 5 |
| 4549 | costra | 5 |
| 4550 | costear | 5 |
| 4551 | cosquillas | 5 |
| 4552 | coscorrón | 5 |
| 4553 | cortés | 5 |
| 4554 | cortes | 5 |
| 4555 | correspondencia | 5 |
| 4556 | coronar | 5 |
| 4557 | corona | 5 |
| 4558 | coraje | 5 |
| 4559 | convencimiento | 5 |
| 4560 | contraste | 5 |
| 4561 | contraer | 5 |
| 4562 | contestó | 5 |
| 4563 | contenido | 5 |
| 4564 | constitución | 5 |
| 4565 | constancia | 5 |
| 4566 | consiguiente | 5 |
| 4567 | considerable | 5 |
| 4568 | congreso | 5 |
| 4569 | conducto | 5 |
| 4570 | condensar | 5 |
| 4571 | concordia | 5 |
| 4572 | concertar | 5 |
| 4573 | concerniente | 5 |
| 4574 | compinche | 5 |
| 4575 | compás | 5 |
| 4576 | comodidad | 5 |
| 4577 | comezón | 5 |
| 4578 | comerciar | 5 |
| 4579 | columna | 5 |
| 4580 | colega | 5 |
| 4581 | colchón | 5 |
| 4582 | cofre | 5 |
| 4583 | clerical | 5 |
| 4584 | cita | 5 |
| 4585 | circunstante | 5 |
| 4586 | cimiento | 5 |
| 4587 | cigarrillo | 5 |
| 4588 | cifrar | 5 |
| 4589 | chorro | 5 |
| 4590 | choque | 5 |
| 4591 | chiste | 5 |
| 4592 | chino | 5 |
| 4593 | china | 5 |
| 4594 | chapa | 5 |
| 4595 | chalán | 5 |
| 4596 | cerveza | 5 |
| 4597 | cayetano | 5 |
| 4598 | categoría | 5 |
| 4599 | catástrofe | 5 |
| 4600 | casita | 5 |
| 4601 | casera | 5 |
| 4602 | cáscara | 5 |
| 4603 | carnicería | 5 |
| 4604 | cariñosamente | 5 |
| 4605 | careta | 5 |
| 4606 | carcelero | 5 |
| 4607 | cánovas | 5 |
| 4608 | canción | 5 |
| 4609 | canario | 5 |
| 4610 | cambiazo | 5 |
| 4611 | calva | 5 |
| 4612 | callejón | 5 |
| 4613 | caletre | 5 |
| 4614 | burlón | 5 |
| 4615 | burgos | 5 |
| 4616 | bufanda | 5 |
| 4617 | brujo | 5 |
| 4618 | bronco | 5 |
| 4619 | bromear | 5 |
| 4620 | bodegón | 5 |
| 4621 | bicerra | 5 |
| 4622 | betún | 5 |
| 4623 | benigno | 5 |
| 4624 | benévolo | 5 |
| 4625 | bazar | 5 |
| 4626 | batalla | 5 |
| 4627 | bastero | 5 |
| 4628 | barrendero | 5 |
| 4629 | barra | 5 |
| 4630 | balbució | 5 |
| 4631 | balancear | 5 |
| 4632 | bajón | 5 |
| 4633 | baja | 5 |
| 4634 | azuzar | 5 |
| 4635 | azorar | 5 |
| 4636 | ayuntamiento | 5 |
| 4637 | aviar | 5 |
| 4638 | avenir | 5 |
| 4639 | autorizar | 5 |
| 4640 | ausentar | 5 |
| 4641 | aula | 5 |
| 4642 | atufar | 5 |
| 4643 | atributo | 5 |
| 4644 | atrasado | 5 |
| 4645 | atajar | 5 |
| 4646 | áspero | 5 |
| 4647 | asno | 5 |
| 4648 | asimilar | 5 |
| 4649 | asilar | 5 |
| 4650 | asiático | 5 |
| 4651 | ascender | 5 |
| 4652 | arsénico | 5 |
| 4653 | arrodillar | 5 |
| 4654 | arroba | 5 |
| 4655 | arrebatado | 5 |
| 4656 | armario | 5 |
| 4657 | aritmético | 5 |
| 4658 | aristocrático | 5 |
| 4659 | aprisa | 5 |
| 4660 | apremiar | 5 |
| 4661 | aprecio | 5 |
| 4662 | apóstol | 5 |
| 4663 | aplastar | 5 |
| 4664 | apestar | 5 |
| 4665 | apenar | 5 |
| 4666 | apechugar | 5 |
| 4667 | antiespasmódica | 5 |
| 4668 | anhelar | 5 |
| 4669 | angustioso | 5 |
| 4670 | andaluz | 5 |
| 4671 | amasar | 5 |
| 4672 | amargura | 5 |
| 4673 | amargo | 5 |
| 4674 | amabilidad | 5 |
| 4675 | alternar | 5 |
| 4676 | alquiler | 5 |
| 4677 | almo | 5 |
| 4678 | alfombrar | 5 |
| 4679 | alcalá | 5 |
| 4680 | alborotado | 5 |
| 4681 | alarmante | 5 |
| 4682 | agregar | 5 |
| 4683 | agradecimiento | 5 |
| 4684 | agotar | 5 |
| 4685 | agonía | 5 |
| 4686 | agachar | 5 |
| 4687 | afrenta | 5 |
| 4688 | afirmativamente | 5 |
| 4689 | afirmación | 5 |
| 4690 | aficionar | 5 |
| 4691 | aficionado | 5 |
| 4692 | afeitar | 5 |
| 4693 | afectuoso | 5 |
| 4694 | adecentar | 5 |
| 4695 | acusación | 5 |
| 4696 | acumular | 5 |
| 4697 | actriz | 5 |
| 4698 | activar | 5 |
| 4699 | acortar | 5 |
| 4700 | acertado | 5 |
| 4701 | acentuado | 5 |
| 4702 | aburrido | 5 |
| 4703 | abultar | 5 |
| 4704 | abstracción | 5 |
| 4705 | abreviar | 5 |
| 4706 | zarandear | 4 |
| 4707 | zapatero | 4 |
| 4708 | yerto | 4 |
| 4709 | xii | 4 |
| 4710 | vómito | 4 |
| 4711 | volcán | 4 |
| 4712 | viviente | 4 |
| 4713 | vistoso | 4 |
| 4714 | visionario | 4 |
| 4715 | visionar | 4 |
| 4716 | violento | 4 |
| 4717 | violar | 4 |
| 4718 | viña | 4 |
| 4719 | vil | 4 |
| 4720 | viene | 4 |
| 4721 | viéndole | 4 |
| 4722 | vete | 4 |
| 4723 | vestíbulo | 4 |
| 4724 | verter | 4 |
| 4725 | veremos | 4 |
| 4726 | venus | 4 |
| 4727 | venturoso | 4 |
| 4728 | ventura | 4 |
| 4729 | ventanillo | 4 |
| 4730 | veneración | 4 |
| 4731 | vencedor | 4 |
| 4732 | velocidad | 4 |
| 4733 | velador | 4 |
| 4734 | vejez | 4 |
| 4735 | vehemente | 4 |
| 4736 | vaticinar | 4 |
| 4737 | vastísimo | 4 |
| 4738 | van | 4 |
| 4739 | valle | 4 |
| 4740 | vaguedad | 4 |
| 4741 | uva | 4 |
| 4742 | urna | 4 |
| 4743 | uniformar | 4 |
| 4744 | unción | 4 |
| 4745 | ultramar | 4 |
| 4746 | tute | 4 |
| 4747 | túnel | 4 |
| 4748 | tufo | 4 |
| 4749 | trombón | 4 |
| 4750 | triunfante | 4 |
| 4751 | tristemente | 4 |
| 4752 | trenza | 4 |
| 4753 | traza | 4 |
| 4754 | trastamara | 4 |
| 4755 | trapito | 4 |
| 4756 | trapisonda | 4 |
| 4757 | trajín | 4 |
| 4758 | tradicional | 4 |
| 4759 | tosco | 4 |
| 4760 | tortuoso | 4 |
| 4761 | todas | 4 |
| 4762 | tocata | 4 |
| 4763 | toca | 4 |
| 4764 | tirano | 4 |
| 4765 | tímido | 4 |
| 4766 | timar | 4 |
| 4767 | tesón | 4 |
| 4768 | terso | 4 |
| 4769 | terneza | 4 |
| 4770 | términos | 4 |
| 4771 | terminantemente | 4 |
| 4772 | terciar | 4 |
| 4773 | teoría | 4 |
| 4774 | tenue | 4 |
| 4775 | tentativa | 4 |
| 4776 | tenemos | 4 |
| 4777 | tendencia | 4 |
| 4778 | tenaz | 4 |
| 4779 | temple | 4 |
| 4780 | tempestad | 4 |
| 4781 | temblor | 4 |
| 4782 | telón | 4 |
| 4783 | tarjeta | 4 |
| 4784 | tararí | 4 |
| 4785 | tapia | 4 |
| 4786 | talonario | 4 |
| 4787 | tagarote | 4 |
| 4788 | tacto | 4 |
| 4789 | tabique | 4 |
| 4790 | susurro | 4 |
| 4791 | sustraer | 4 |
| 4792 | suspicaz | 4 |
| 4793 | superficie | 4 |
| 4794 | superar | 4 |
| 4795 | sumo | 4 |
| 4796 | sufrimiento | 4 |
| 4797 | subsecretario | 4 |
| 4798 | sosegado | 4 |
| 4799 | sortear | 4 |
| 4800 | sorber | 4 |
| 4801 | sonoro | 4 |
| 4802 | soltura | 4 |
| 4803 | solterón | 4 |
| 4804 | solfa | 4 |
| 4805 | sofía | 4 |
| 4806 | sodio | 4 |
| 4807 | sócrates | 4 |
| 4808 | sobremesa | 4 |
| 4809 | sobón | 4 |
| 4810 | soberano | 4 |
| 4811 | situar | 4 |
| 4812 | sirviente | 4 |
| 4813 | singularísimo | 4 |
| 4814 | sincerar | 4 |
| 4815 | simpatizar | 4 |
| 4816 | sigue | 4 |
| 4817 | significación | 4 |
| 4818 | sierra | 4 |
| 4819 | severamente | 4 |
| 4820 | setenta | 4 |
| 4821 | sesión | 4 |
| 4822 | servilleta | 4 |
| 4823 | sermonear | 4 |
| 4824 | seriamente | 4 |
| 4825 | sepulcro | 4 |
| 4826 | sendero | 4 |
| 4827 | sello | 4 |
| 4828 | sedar | 4 |
| 4829 | secretario | 4 |
| 4830 | secretar | 4 |
| 4831 | sebastián | 4 |
| 4832 | satanás | 4 |
| 4833 | sastre | 4 |
| 4834 | sardina | 4 |
| 4835 | sangrar | 4 |
| 4836 | samaniegos | 4 |
| 4837 | salivar | 4 |
| 4838 | sahumar | 4 |
| 4839 | sagaz | 4 |
| 4840 | sacrílego | 4 |
| 4841 | sabedor | 4 |
| 4842 | ronco | 4 |
| 4843 | romanticismo | 4 |
| 4844 | rodeo | 4 |
| 4845 | rito | 4 |
| 4846 | riñón | 4 |
| 4847 | rinconada | 4 |
| 4848 | rígido | 4 |
| 4849 | ridiculez | 4 |
| 4850 | ribete | 4 |
| 4851 | reyerta | 4 |
| 4852 | revuelta | 4 |
| 4853 | retroceso | 4 |
| 4854 | retozar | 4 |
| 4855 | retintín | 4 |
| 4856 | resumidas | 4 |
| 4857 | resucitar | 4 |
| 4858 | respetabilidad | 4 |
| 4859 | residir | 4 |
| 4860 | resentimiento | 4 |
| 4861 | reposado | 4 |
| 4862 | repentino | 4 |
| 4863 | renovación | 4 |
| 4864 | rematar | 4 |
| 4865 | religiosamente | 4 |
| 4866 | relámpago | 4 |
| 4867 | relajación | 4 |
| 4868 | rehuir | 4 |
| 4869 | regularidad | 4 |
| 4870 | refrenar | 4 |
| 4871 | refregar | 4 |
| 4872 | reformar | 4 |
| 4873 | reflejar | 4 |
| 4874 | redonda | 4 |
| 4875 | redimir | 4 |
| 4876 | redacción | 4 |
| 4877 | recurrir | 4 |
| 4878 | rectificar | 4 |
| 4879 | recóndito | 4 |
| 4880 | reclamo | 4 |
| 4881 | rechazo | 4 |
| 4882 | rebaño | 4 |
| 4883 | reaparecer | 4 |
| 4884 | raudal | 4 |
| 4885 | rasguñar | 4 |
| 4886 | ras | 4 |
| 4887 | rancio | 4 |
| 4888 | radiante | 4 |
| 4889 | raciocinio | 4 |
| 4890 | quitose | 4 |
| 4891 | querencia | 4 |
| 4892 | quejido | 4 |
| 4893 | quehacer | 4 |
| 4894 | purísimo | 4 |
| 4895 | purificación | 4 |
| 4896 | puntualidad | 4 |
| 4897 | puntual | 4 |
| 4898 | puntilla | 4 |
| 4899 | pulgas | 4 |
| 4900 | publicación | 4 |
| 4901 | prudencia | 4 |
| 4902 | prorrumpir | 4 |
| 4903 | propuso | 4 |
| 4904 | pronunciación | 4 |
| 4905 | prontitud | 4 |
| 4906 | prontamente | 4 |
| 4907 | profesión | 4 |
| 4908 | profecía | 4 |
| 4909 | producto | 4 |
| 4910 | prodigioso | 4 |
| 4911 | previo | 4 |
| 4912 | pretendiente | 4 |
| 4913 | presbítero | 4 |
| 4914 | preparativo | 4 |
| 4915 | predilecto | 4 |
| 4916 | precoz | 4 |
| 4917 | prado | 4 |
| 4918 | practicante | 4 |
| 4919 | prácticamente | 4 |
| 4920 | plencia | 4 |
| 4921 | plegar | 4 |
| 4922 | platicar | 4 |
| 4923 | plática | 4 |
| 4924 | plancha | 4 |
| 4925 | placidez | 4 |
| 4926 | placentero | 4 |
| 4927 | pláceme | 4 |
| 4928 | pisada | 4 |
| 4929 | pirámide | 4 |
| 4930 | pintada | 4 |
| 4931 | pingo | 4 |
| 4932 | pingajo | 4 |
| 4933 | pila | 4 |
| 4934 | pienso | 4 |
| 4935 | picotear | 4 |
| 4936 | picarón | 4 |
| 4937 | petitorio | 4 |
| 4938 | pestañear | 4 |
| 4939 | pesimismo | 4 |
| 4940 | pescado | 4 |
| 4941 | perspicaz | 4 |
| 4942 | perros | 4 |
| 4943 | perplejidad | 4 |
| 4944 | permanente | 4 |
| 4945 | perecer | 4 |
| 4946 | perdiz | 4 |
| 4947 | pérdida | 4 |
| 4948 | pepito | 4 |
| 4949 | pepa | 4 |
| 4950 | peña | 4 |
| 4951 | penitencia | 4 |
| 4952 | penetrante | 4 |
| 4953 | peludo | 4 |
| 4954 | pellizcar | 4 |
| 4955 | pelar | 4 |
| 4956 | peinador | 4 |
| 4957 | pedrada | 4 |
| 4958 | pedido | 4 |
| 4959 | patriotismo | 4 |
| 4960 | patricio | 4 |
| 4961 | patraña | 4 |
| 4962 | patita | 4 |
| 4963 | patilla | 4 |
| 4964 | patíbulo | 4 |
| 4965 | patas | 4 |
| 4966 | pasmoso | 4 |
| 4967 | pasada | 4 |
| 4968 | partidario | 4 |
| 4969 | participación | 4 |
| 4970 | papelera | 4 |
| 4971 | palpitar | 4 |
| 4972 | palpitación | 4 |
| 4973 | palmo | 4 |
| 4974 | palmetazo | 4 |
| 4975 | palma | 4 |
| 4976 | palidecer | 4 |
| 4977 | paco | 4 |
| 4978 | pachorra | 4 |
| 4979 | otros | 4 |
| 4980 | otorgar | 4 |
| 4981 | osar | 4 |
| 4982 | orillo | 4 |
| 4983 | orilla | 4 |
| 4984 | órgano | 4 |
| 4985 | organizar | 4 |
| 4986 | orador | 4 |
| 4987 | opresión | 4 |
| 4988 | omitir | 4 |
| 4989 | óleo | 4 |
| 4990 | olé | 4 |
| 4991 | ojuelos | 4 |
| 4992 | oíase | 4 |
| 4993 | ofuscar | 4 |
| 4994 | ofendido | 4 |
| 4995 | octubre | 4 |
| 4996 | obstinar | 4 |
| 4997 | obstáculo | 4 |
| 4998 | obsequiar | 4 |
| 4999 | nuez | 4 |
| 5000 | nuevamente | 4 |
| 5001 | normal | 4 |
| 5002 | nodriza | 4 |
| 5003 | niñería | 4 |
| 5004 | niebla | 4 |
| 5005 | neófito | 4 |
| 5006 | negra | 4 |
| 5007 | náusea | 4 |
| 5008 | naturalidad | 4 |
| 5009 | nardo | 4 |
| 5010 | musical | 4 |
| 5011 | muscular | 4 |
| 5012 | mus | 4 |
| 5013 | muletilla | 4 |
| 5014 | mugriento | 4 |
| 5015 | muela | 4 |
| 5016 | mueca | 4 |
| 5017 | mudéjar | 4 |
| 5018 | mu | 4 |
| 5019 | mortificación | 4 |
| 5020 | moribundo | 4 |
| 5021 | moralmente | 4 |
| 5022 | moralidad | 4 |
| 5023 | montaña | 4 |
| 5024 | molinillo | 4 |
| 5025 | mohín | 4 |
| 5026 | mocoso | 4 |
| 5027 | mísero | 4 |
| 5028 | miles | 4 |
| 5029 | miembro | 4 |
| 5030 | mezquino | 4 |
| 5031 | metiose | 4 |
| 5032 | meta | 4 |
| 5033 | merced | 4 |
| 5034 | mentalmente | 4 |
| 5035 | mensual | 4 |
| 5036 | mejoría | 4 |
| 5037 | medias | 4 |
| 5038 | matute | 4 |
| 5039 | masticar | 4 |
| 5040 | marrullería | 4 |
| 5041 | marimorena | 4 |
| 5042 | marea | 4 |
| 5043 | maquinalmente | 4 |
| 5044 | maquinal | 4 |
| 5045 | mañoso | 4 |
| 5046 | mañanita | 4 |
| 5047 | manzana | 4 |
| 5048 | mangar | 4 |
| 5049 | maná | 4 |
| 5050 | mampara | 4 |
| 5051 | maliciar | 4 |
| 5052 | madrugar | 4 |
| 5053 | madero | 4 |
| 5054 | lustroso | 4 |
| 5055 | lucido | 4 |
| 5056 | loza | 4 |
| 5057 | lodo | 4 |
| 5058 | lóbrego | 4 |
| 5059 | llorente | 4 |
| 5060 | llano | 4 |
| 5061 | llamada | 4 |
| 5062 | llamábase | 4 |
| 5063 | liviano | 4 |
| 5064 | libremente | 4 |
| 5065 | liberar | 4 |
| 5066 | les | 4 |
| 5067 | lente | 4 |
| 5068 | lengüetazo | 4 |
| 5069 | legítima | 4 |
| 5070 | lector | 4 |
| 5071 | lechar | 4 |
| 5072 | lavapiés | 4 |
| 5073 | lastimero | 4 |
| 5074 | larga | 4 |
| 5075 | lago | 4 |
| 5076 | juntamente | 4 |
| 5077 | juárez | 4 |
| 5078 | jinete | 4 |
| 5079 | invencible | 4 |
| 5080 | intriga | 4 |
| 5081 | intimar | 4 |
| 5082 | interponer | 4 |
| 5083 | interiormente | 4 |
| 5084 | intenso | 4 |
| 5085 | instar | 4 |
| 5086 | instantáneo | 4 |
| 5087 | insistencia | 4 |
| 5088 | inofensivo | 4 |
| 5089 | ingratitud | 4 |
| 5090 | ingenuo | 4 |
| 5091 | influir | 4 |
| 5092 | inflexión | 4 |
| 5093 | inflar | 4 |
| 5094 | infiel | 4 |
| 5095 | inexperto | 4 |
| 5096 | inerte | 4 |
| 5097 | indigestar | 4 |
| 5098 | independiente | 4 |
| 5099 | indecoroso | 4 |
| 5100 | indagar | 4 |
| 5101 | inconsolable | 4 |
| 5102 | inciso | 4 |
| 5103 | incertidumbre | 4 |
| 5104 | inauguración | 4 |
| 5105 | imperturbable | 4 |
| 5106 | impertinencia | 4 |
| 5107 | imparcialidad | 4 |
| 5108 | igualmente | 4 |
| 5109 | humedecer | 4 |
| 5110 | hortaleza | 4 |
| 5111 | horizontal | 4 |
| 5112 | honradamente | 4 |
| 5113 | homicidio | 4 |
| 5114 | hoguera | 4 |
| 5115 | hipocresía | 4 |
| 5116 | hilaridad | 4 |
| 5117 | hilar | 4 |
| 5118 | hielo | 4 |
| 5119 | hez | 4 |
| 5120 | hermanito | 4 |
| 5121 | hazte | 4 |
| 5122 | hazme | 4 |
| 5123 | haya | 4 |
| 5124 | harto | 4 |
| 5125 | hallazgo | 4 |
| 5126 | halar | 4 |
| 5127 | hágame | 4 |
| 5128 | habíale | 4 |
| 5129 | gusanillo | 4 |
| 5130 | guindilla | 4 |
| 5131 | guardias | 4 |
| 5132 | guardarropa | 4 |
| 5133 | guarda | 4 |
| 5134 | gresca | 4 |
| 5135 | grecia | 4 |
| 5136 | grasa | 4 |
| 5137 | gradar | 4 |
| 5138 | golpear | 4 |
| 5139 | giro | 4 |
| 5140 | gimnasia | 4 |
| 5141 | gesticular | 4 |
| 5142 | gatas | 4 |
| 5143 | garfio | 4 |
| 5144 | ganas | 4 |
| 5145 | galón | 4 |
| 5146 | gallardo | 4 |
| 5147 | galante | 4 |
| 5148 | fugitivo | 4 |
| 5149 | fue | 4 |
| 5150 | frontera | 4 |
| 5151 | fritanga | 4 |
| 5152 | frecuente | 4 |
| 5153 | fraternidad | 4 |
| 5154 | franquear | 4 |
| 5155 | fraile | 4 |
| 5156 | frágil | 4 |
| 5157 | fracaso | 4 |
| 5158 | forro | 4 |
| 5159 | fleco | 4 |
| 5160 | flandes | 4 |
| 5161 | filo | 4 |
| 5162 | fideo | 4 |
| 5163 | ficción | 4 |
| 5164 | fibra | 4 |
| 5165 | fétido | 4 |
| 5166 | ferrolana | 4 |
| 5167 | fernando | 4 |
| 5168 | fermentar | 4 |
| 5169 | felpudo | 4 |
| 5170 | fealdad | 4 |
| 5171 | fatigoso | 4 |
| 5172 | fatiga | 4 |
| 5173 | fatalidad | 4 |
| 5174 | fastidiar | 4 |
| 5175 | fase | 4 |
| 5176 | fantasmón | 4 |
| 5177 | famélico | 4 |
| 5178 | fábula | 4 |
| 5179 | extravío | 4 |
| 5180 | extracto | 4 |
| 5181 | explosión | 4 |
| 5182 | explanar | 4 |
| 5183 | exhalación | 4 |
| 5184 | excusar | 4 |
| 5185 | excluir | 4 |
| 5186 | excelso | 4 |
| 5187 | evidente | 4 |
| 5188 | europeo | 4 |
| 5189 | etapa | 4 |
| 5190 | estrujar | 4 |
| 5191 | estruendo | 4 |
| 5192 | estrepitoso | 4 |
| 5193 | estremecimiento | 4 |
| 5194 | estrafalario | 4 |
| 5195 | estético | 4 |
| 5196 | estanque | 4 |
| 5197 | estamos | 4 |
| 5198 | estafar | 4 |
| 5199 | espontaneidad | 4 |
| 5200 | espeso | 4 |
| 5201 | espesar | 4 |
| 5202 | específico | 4 |
| 5203 | especial | 4 |
| 5204 | espasmódico | 4 |
| 5205 | espartero | 4 |
| 5206 | espacioso | 4 |
| 5207 | esmero | 4 |
| 5208 | esgrimir | 4 |
| 5209 | escultura | 4 |
| 5210 | escrupuloso | 4 |
| 5211 | escritor | 4 |
| 5212 | escondrijo | 4 |
| 5213 | escéptico | 4 |
| 5214 | escarnecer | 4 |
| 5215 | escandaloso | 4 |
| 5216 | escalonar | 4 |
| 5217 | escala | 4 |
| 5218 | escabullir | 4 |
| 5219 | equilibrar | 4 |
| 5220 | entretenimiento | 4 |
| 5221 | entretenido | 4 |
| 5222 | entretanto | 4 |
| 5223 | entremezclar | 4 |
| 5224 | entrega | 4 |
| 5225 | entrecano | 4 |
| 5226 | enternecer | 4 |
| 5227 | ensuciar | 4 |
| 5228 | ensayo | 4 |
| 5229 | enojoso | 4 |
| 5230 | enmienda | 4 |
| 5231 | enlazar | 4 |
| 5232 | engranar | 4 |
| 5233 | engordar | 4 |
| 5234 | engolosinar | 4 |
| 5235 | enfrenar | 4 |
| 5236 | endiablado | 4 |
| 5237 | encubridor | 4 |
| 5238 | encariñar | 4 |
| 5239 | encaje | 4 |
| 5240 | enano | 4 |
| 5241 | empuñar | 4 |
| 5242 | emperador | 4 |
| 5243 | empeñado | 4 |
| 5244 | embriaguez | 4 |
| 5245 | embozo | 4 |
| 5246 | embestir | 4 |
| 5247 | embarullar | 4 |
| 5248 | embarazar | 4 |
| 5249 | durmiente | 4 |
| 5250 | dotar | 4 |
| 5251 | dorotea | 4 |
| 5252 | donnell | 4 |
| 5253 | documento | 4 |
| 5254 | doctrinar | 4 |
| 5255 | doble | 4 |
| 5256 | divorcio | 4 |
| 5257 | diversión | 4 |
| 5258 | distante | 4 |
| 5259 | displicencia | 4 |
| 5260 | disfrazar | 4 |
| 5261 | discretamente | 4 |
| 5262 | disciplinar | 4 |
| 5263 | directo | 4 |
| 5264 | diplomacia | 4 |
| 5265 | diligente | 4 |
| 5266 | dicen | 4 |
| 5267 | dialéctica | 4 |
| 5268 | diabólico | 4 |
| 5269 | detúvose | 4 |
| 5270 | desvelado | 4 |
| 5271 | destapar | 4 |
| 5272 | despropósito | 4 |
| 5273 | desplumar | 4 |
| 5274 | despierto | 4 |
| 5275 | despechar | 4 |
| 5276 | despavorir | 4 |
| 5277 | desordenado | 4 |
| 5278 | desmejorar | 4 |
| 5279 | desmedrar | 4 |
| 5280 | desmedido | 4 |
| 5281 | desmandar | 4 |
| 5282 | designar | 4 |
| 5283 | deshora | 4 |
| 5284 | deshilachar | 4 |
| 5285 | desgraciadamente | 4 |
| 5286 | desgarrar | 4 |
| 5287 | desembuchar | 4 |
| 5288 | desdicha | 4 |
| 5289 | descuide | 4 |
| 5290 | descuartizar | 4 |
| 5291 | descontentar | 4 |
| 5292 | desconfiar | 4 |
| 5293 | desconfianza | 4 |
| 5294 | desconcierto | 4 |
| 5295 | descarriar | 4 |
| 5296 | descarado | 4 |
| 5297 | desarrollo | 4 |
| 5298 | desarmar | 4 |
| 5299 | desanimar | 4 |
| 5300 | desalentar | 4 |
| 5301 | desairado | 4 |
| 5302 | derivativo | 4 |
| 5303 | dengoso | 4 |
| 5304 | demente | 4 |
| 5305 | dementar | 4 |
| 5306 | dejose | 4 |
| 5307 | dejarla | 4 |
| 5308 | deducir | 4 |
| 5309 | decoroso | 4 |
| 5310 | decaer | 4 |
| 5311 | debate | 4 |
| 5312 | danzante | 4 |
| 5313 | dámaso | 4 |
| 5314 | dábale | 4 |
| 5315 | curita | 4 |
| 5316 | cuestionar | 4 |
| 5317 | cuchufleta | 4 |
| 5318 | cuchilleros | 4 |
| 5319 | cuchicheo | 4 |
| 5320 | cuadrito | 4 |
| 5321 | crueldad | 4 |
| 5322 | crucificar | 4 |
| 5323 | crónico | 4 |
| 5324 | crin | 4 |
| 5325 | cotorrear | 4 |
| 5326 | costado | 4 |
| 5327 | costa | 4 |
| 5328 | corteza | 4 |
| 5329 | corrido | 4 |
| 5330 | correos | 4 |
| 5331 | corpus | 4 |
| 5332 | corazonada | 4 |
| 5333 | copla | 4 |
| 5334 | coñac | 4 |
| 5335 | conyugal | 4 |
| 5336 | contundente | 4 |
| 5337 | contratar | 4 |
| 5338 | contrastar | 4 |
| 5339 | contrariar | 4 |
| 5340 | contracción | 4 |
| 5341 | contemplación | 4 |
| 5342 | contante | 4 |
| 5343 | contado | 4 |
| 5344 | consumado | 4 |
| 5345 | consternar | 4 |
| 5346 | consternación | 4 |
| 5347 | consolidar | 4 |
| 5348 | consejero | 4 |
| 5349 | consecuente | 4 |
| 5350 | conjunción | 4 |
| 5351 | confianzudo | 4 |
| 5352 | confeccionar | 4 |
| 5353 | conejo | 4 |
| 5354 | conclusión | 4 |
| 5355 | concierto | 4 |
| 5356 | complicado | 4 |
| 5357 | compensar | 4 |
| 5358 | compaginar | 4 |
| 5359 | comestible | 4 |
| 5360 | comensal | 4 |
| 5361 | coma | 4 |
| 5362 | colosal | 4 |
| 5363 | coloquio | 4 |
| 5364 | colonia | 4 |
| 5365 | coleta | 4 |
| 5366 | col | 4 |
| 5367 | cojín | 4 |
| 5368 | cochinada | 4 |
| 5369 | cobranza | 4 |
| 5370 | clero | 4 |
| 5371 | clamar | 4 |
| 5372 | chistera | 4 |
| 5373 | chisme | 4 |
| 5374 | chiquillada | 4 |
| 5375 | chiquilla | 4 |
| 5376 | chinita | 4 |
| 5377 | chicos | 4 |
| 5378 | charco | 4 |
| 5379 | chal | 4 |
| 5380 | chacota | 4 |
| 5381 | cerrada | 4 |
| 5382 | cerciorar | 4 |
| 5383 | cercano | 4 |
| 5384 | cejar | 4 |
| 5385 | cebada | 4 |
| 5386 | cavernoso | 4 |
| 5387 | caverna | 4 |
| 5388 | cautela | 4 |
| 5389 | cátedra | 4 |
| 5390 | catecismo | 4 |
| 5391 | catalán | 4 |
| 5392 | casero | 4 |
| 5393 | cascar | 4 |
| 5394 | casarse | 4 |
| 5395 | casarredonda | 4 |
| 5396 | carretilla | 4 |
| 5397 | carnero | 4 |
| 5398 | carga | 4 |
| 5399 | carbonero | 4 |
| 5400 | caracol | 4 |
| 5401 | capcioso | 4 |
| 5402 | cañizares | 4 |
| 5403 | cantor | 4 |
| 5404 | cantinela | 4 |
| 5405 | cantería | 4 |
| 5406 | cantera | 4 |
| 5407 | canonizar | 4 |
| 5408 | candoroso | 4 |
| 5409 | canalla | 4 |
| 5410 | campechano | 4 |
| 5411 | camorra | 4 |
| 5412 | caminar | 4 |
| 5413 | callosar | 4 |
| 5414 | callejero | 4 |
| 5415 | calixta | 4 |
| 5416 | calavera | 4 |
| 5417 | cal | 4 |
| 5418 | cadena | 4 |
| 5419 | burrada | 4 |
| 5420 | bromazo | 4 |
| 5421 | bringas | 4 |
| 5422 | botonar | 4 |
| 5423 | botijo | 4 |
| 5424 | bostezo | 4 |
| 5425 | borroso | 4 |
| 5426 | bolsín | 4 |
| 5427 | blanquear | 4 |
| 5428 | bizcar | 4 |
| 5429 | bilis | 4 |
| 5430 | bicho | 4 |
| 5431 | biberón | 4 |
| 5432 | biarritz | 4 |
| 5433 | besugo | 4 |
| 5434 | bazo | 4 |
| 5435 | bautismo | 4 |
| 5436 | barreño | 4 |
| 5437 | baratija | 4 |
| 5438 | banda | 4 |
| 5439 | azahar | 4 |
| 5440 | ayunas | 4 |
| 5441 | ayunar | 4 |
| 5442 | aviado | 4 |
| 5443 | aversión | 4 |
| 5444 | avaricia | 4 |
| 5445 | austria | 4 |
| 5446 | augusto | 4 |
| 5447 | auditorio | 4 |
| 5448 | audacia | 4 |
| 5449 | aturdido | 4 |
| 5450 | atrozmente | 4 |
| 5451 | atavío | 4 |
| 5452 | ataúd | 4 |
| 5453 | aspiración | 4 |
| 5454 | asimilación | 4 |
| 5455 | asentir | 4 |
| 5456 | ascendiente | 4 |
| 5457 | artificial | 4 |
| 5458 | arrepentido | 4 |
| 5459 | arrechucho | 4 |
| 5460 | arrebato | 4 |
| 5461 | arrebatar | 4 |
| 5462 | arrastrado | 4 |
| 5463 | armonizar | 4 |
| 5464 | argumentar | 4 |
| 5465 | argumentación | 4 |
| 5466 | arenal | 4 |
| 5467 | apurado | 4 |
| 5468 | apuntó | 4 |
| 5469 | aproximación | 4 |
| 5470 | apropiar | 4 |
| 5471 | apoyo | 4 |
| 5472 | apostolado | 4 |
| 5473 | aportar | 4 |
| 5474 | aporrear | 4 |
| 5475 | apatía | 4 |
| 5476 | apacible | 4 |
| 5477 | añadidura | 4 |
| 5478 | anuncio | 4 |
| 5479 | anular | 4 |
| 5480 | antón | 4 |
| 5481 | angustiar | 4 |
| 5482 | angostar | 4 |
| 5483 | anécdota | 4 |
| 5484 | andrajo | 4 |
| 5485 | anchas | 4 |
| 5486 | anatema | 4 |
| 5487 | anaquelería | 4 |
| 5488 | amplitud | 4 |
| 5489 | amonestación | 4 |
| 5490 | americano | 4 |
| 5491 | ambulante | 4 |
| 5492 | ambición | 4 |
| 5493 | amansar | 4 |
| 5494 | amaneramiento | 4 |
| 5495 | amadeo | 4 |
| 5496 | alucinación | 4 |
| 5497 | almendra | 4 |
| 5498 | alabardero | 4 |
| 5499 | ajustado | 4 |
| 5500 | ajuar | 4 |
| 5501 | ajo | 4 |
| 5502 | ajetreo | 4 |
| 5503 | ahumar | 4 |
| 5504 | ahuecar | 4 |
| 5505 | ahorrar | 4 |
| 5506 | ahínco | 4 |
| 5507 | aguzar | 4 |
| 5508 | agujerito | 4 |
| 5509 | aguador | 4 |
| 5510 | agravio | 4 |
| 5511 | afrentar | 4 |
| 5512 | afirmó | 4 |
| 5513 | afabilidad | 4 |
| 5514 | adusto | 4 |
| 5515 | adulterar | 4 |
| 5516 | aduana | 4 |
| 5517 | adrede | 4 |
| 5518 | adorno | 4 |
| 5519 | actor | 4 |
| 5520 | activo | 4 |
| 5521 | aciago | 4 |
| 5522 | acantonar | 4 |
| 5523 | acalorado | 4 |
| 5524 | acallar | 4 |
| 5525 | absorto | 4 |
| 5526 | absorber | 4 |
| 5527 | abrumador | 4 |
| 5528 | abril | 4 |
| 5529 | abandonado | 4 |
| 5530 | abalanzar | 4 |
| 5531 | zarpa | 3 |
| 5532 | zapatón | 3 |
| 5533 | zángano | 3 |
| 5534 | zanca | 3 |
| 5535 | vulgarmente | 3 |
| 5536 | vuestra | 3 |
| 5537 | volviose | 3 |
| 5538 | volveré | 3 |
| 5539 | volumen | 3 |
| 5540 | vive | 3 |
| 5541 | vivaracho | 3 |
| 5542 | vitoria | 3 |
| 5543 | víspera | 3 |
| 5544 | viso | 3 |
| 5545 | visiblemente | 3 |
| 5546 | vio | 3 |
| 5547 | vínculo | 3 |
| 5548 | vinagre | 3 |
| 5549 | vigoroso | 3 |
| 5550 | vigorizar | 3 |
| 5551 | vigor | 3 |
| 5552 | vibrar | 3 |
| 5553 | viajero | 3 |
| 5554 | veterano | 3 |
| 5555 | vestigio | 3 |
| 5556 | verla | 3 |
| 5557 | verídicamente | 3 |
| 5558 | vereda | 3 |
| 5559 | vente | 3 |
| 5560 | ventar | 3 |
| 5561 | venida | 3 |
| 5562 | venerar | 3 |
| 5563 | vencido | 3 |
| 5564 | velón | 3 |
| 5565 | vello | 3 |
| 5566 | veis | 3 |
| 5567 | veintitrés | 3 |
| 5568 | veintisiete | 3 |
| 5569 | veinticuatro | 3 |
| 5570 | vehículo | 3 |
| 5571 | vehemencia | 3 |
| 5572 | véase | 3 |
| 5573 | vea | 3 |
| 5574 | varar | 3 |
| 5575 | valioso | 3 |
| 5576 | valientes | 3 |
| 5577 | valeriano | 3 |
| 5578 | vagón | 3 |
| 5579 | vacante | 3 |
| 5580 | uy | 3 |
| 5581 | usual | 3 |
| 5582 | usado | 3 |
| 5583 | universo | 3 |
| 5584 | universidad | 3 |
| 5585 | tumbar | 3 |
| 5586 | tufillo | 3 |
| 5587 | trote | 3 |
| 5588 | trono | 3 |
| 5589 | trofeo | 3 |
| 5590 | triunfal | 3 |
| 5591 | trinidad | 3 |
| 5592 | trimestre | 3 |
| 5593 | tributar | 3 |
| 5594 | tribulación | 3 |
| 5595 | tresillo | 3 |
| 5596 | trepidación | 3 |
| 5597 | tratante | 3 |
| 5598 | trastornado | 3 |
| 5599 | trastienda | 3 |
| 5600 | trastear | 3 |
| 5601 | trapisondista | 3 |
| 5602 | transparencia | 3 |
| 5603 | trámite | 3 |
| 5604 | tramar | 3 |
| 5605 | tragaderas | 3 |
| 5606 | tráfico | 3 |
| 5607 | tráete | 3 |
| 5608 | traducir | 3 |
| 5609 | trabajillo | 3 |
| 5610 | tortilla | 3 |
| 5611 | toros | 3 |
| 5612 | tome | 3 |
| 5613 | tomate | 3 |
| 5614 | toledano | 3 |
| 5615 | tiznar | 3 |
| 5616 | tisis | 3 |
| 5617 | tinte | 3 |
| 5618 | timbre | 3 |
| 5619 | tila | 3 |
| 5620 | tijera | 3 |
| 5621 | tifus | 3 |
| 5622 | tie | 3 |
| 5623 | tetuán | 3 |
| 5624 | tesis | 3 |
| 5625 | terrorífico | 3 |
| 5626 | terquedad | 3 |
| 5627 | terno | 3 |
| 5628 | terco | 3 |
| 5629 | tenducho | 3 |
| 5630 | tenacidad | 3 |
| 5631 | ten | 3 |
| 5632 | temporal | 3 |
| 5633 | tempestuoso | 3 |
| 5634 | telegrafiar | 3 |
| 5635 | tejido | 3 |
| 5636 | teja | 3 |
| 5637 | teclear | 3 |
| 5638 | tasar | 3 |
| 5639 | tasa | 3 |
| 5640 | tartán | 3 |
| 5641 | tantear | 3 |
| 5642 | talco | 3 |
| 5643 | talante | 3 |
| 5644 | tácito | 3 |
| 5645 | tabaco | 3 |
| 5646 | t | 3 |
| 5647 | susurrar | 3 |
| 5648 | sustituir | 3 |
| 5649 | suspenso | 3 |
| 5650 | supremo | 3 |
| 5651 | suposición | 3 |
| 5652 | suficiente | 3 |
| 5653 | suéltame | 3 |
| 5654 | subsistir | 3 |
| 5655 | subordinación | 3 |
| 5656 | subasta | 3 |
| 5657 | subalterno | 3 |
| 5658 | sótano | 3 |
| 5659 | sosiego | 3 |
| 5660 | sosiégate | 3 |
| 5661 | sortija | 3 |
| 5662 | soportal | 3 |
| 5663 | soplo | 3 |
| 5664 | sopar | 3 |
| 5665 | soñoliento | 3 |
| 5666 | sonrosado | 3 |
| 5667 | sondear | 3 |
| 5668 | sonda | 3 |
| 5669 | soltera | 3 |
| 5670 | solomillo | 3 |
| 5671 | sollozar | 3 |
| 5672 | solitaria | 3 |
| 5673 | soga | 3 |
| 5674 | sofisma | 3 |
| 5675 | socorrido | 3 |
| 5676 | socarrón | 3 |
| 5677 | sobriedad | 3 |
| 5678 | sobresalto | 3 |
| 5679 | sobar | 3 |
| 5680 | sintético | 3 |
| 5681 | singularmente | 3 |
| 5682 | singapore | 3 |
| 5683 | sigüenza | 3 |
| 5684 | sesudo | 3 |
| 5685 | serpiente | 3 |
| 5686 | sepultura | 3 |
| 5687 | septiembre | 3 |
| 5688 | señores | 3 |
| 5689 | señá | 3 |
| 5690 | sentencia | 3 |
| 5691 | sellar | 3 |
| 5692 | selecto | 3 |
| 5693 | seguimiento | 3 |
| 5694 | segar | 3 |
| 5695 | seducción | 3 |
| 5696 | secuestrador | 3 |
| 5697 | savia | 3 |
| 5698 | sartén | 3 |
| 5699 | sarcástico | 3 |
| 5700 | sarao | 3 |
| 5701 | sarampión | 3 |
| 5702 | saña | 3 |
| 5703 | sandez | 3 |
| 5704 | sándalo | 3 |
| 5705 | sánchez | 3 |
| 5706 | samaniega | 3 |
| 5707 | salvador | 3 |
| 5708 | saludable | 3 |
| 5709 | salpicar | 3 |
| 5710 | saldar | 3 |
| 5711 | saeta | 3 |
| 5712 | sacramentos | 3 |
| 5713 | saben | 3 |
| 5714 | rústico | 3 |
| 5715 | rusia | 3 |
| 5716 | rugir | 3 |
| 5717 | ruda | 3 |
| 5718 | rozar | 3 |
| 5719 | roñoso | 3 |
| 5720 | ron | 3 |
| 5721 | romero | 3 |
| 5722 | roma | 3 |
| 5723 | roca | 3 |
| 5724 | rizar | 3 |
| 5725 | rivalidad | 3 |
| 5726 | ritmo | 3 |
| 5727 | riguroso | 3 |
| 5728 | rifar | 3 |
| 5729 | riego | 3 |
| 5730 | ridiculizar | 3 |
| 5731 | rezongar | 3 |
| 5732 | revolotear | 3 |
| 5733 | rever | 3 |
| 5734 | reventón | 3 |
| 5735 | revancha | 3 |
| 5736 | reuma | 3 |
| 5737 | retórica | 3 |
| 5738 | retirado | 3 |
| 5739 | resurrección | 3 |
| 5740 | resueltamente | 3 |
| 5741 | restaurar | 3 |
| 5742 | resquicio | 3 |
| 5743 | respondía | 3 |
| 5744 | resplandeciente | 3 |
| 5745 | respiro | 3 |
| 5746 | resollar | 3 |
| 5747 | resobar | 3 |
| 5748 | resignación | 3 |
| 5749 | resguardar | 3 |
| 5750 | reputar | 3 |
| 5751 | reprimenda | 3 |
| 5752 | reposar | 3 |
| 5753 | repito | 3 |
| 5754 | repicar | 3 |
| 5755 | repetido | 3 |
| 5756 | reoyos | 3 |
| 5757 | remover | 3 |
| 5758 | remojo | 3 |
| 5759 | remitir | 3 |
| 5760 | remilgo | 3 |
| 5761 | remate | 3 |
| 5762 | relieve | 3 |
| 5763 | rejilla | 3 |
| 5764 | reiterar | 3 |
| 5765 | rehusar | 3 |
| 5766 | regularmente | 3 |
| 5767 | reglar | 3 |
| 5768 | reglamento | 3 |
| 5769 | regimiento | 3 |
| 5770 | regeneración | 3 |
| 5771 | regar | 3 |
| 5772 | regañón | 3 |
| 5773 | regaliz | 3 |
| 5774 | refrán | 3 |
| 5775 | refinar | 3 |
| 5776 | redoblar | 3 |
| 5777 | recreo | 3 |
| 5778 | reconcentrar | 3 |
| 5779 | recogimiento | 3 |
| 5780 | recinto | 3 |
| 5781 | recato | 3 |
| 5782 | rebuscar | 3 |
| 5783 | rebotica | 3 |
| 5784 | rebelar | 3 |
| 5785 | reanudar | 3 |
| 5786 | rata | 3 |
| 5787 | raso | 3 |
| 5788 | rareza | 3 |
| 5789 | rapar | 3 |
| 5790 | ramoncita | 3 |
| 5791 | ramaje | 3 |
| 5792 | ralo | 3 |
| 5793 | racionar | 3 |
| 5794 | racional | 3 |
| 5795 | ración | 3 |
| 5796 | quítese | 3 |
| 5797 | quintal | 3 |
| 5798 | quinta | 3 |
| 5799 | quijote | 3 |
| 5800 | quiebro | 3 |
| 5801 | queso | 3 |
| 5802 | quelo | 3 |
| 5803 | quédate | 3 |
| 5804 | quedamos | 3 |
| 5805 | quedábase | 3 |
| 5806 | pupila | 3 |
| 5807 | puñetazo | 3 |
| 5808 | puñados | 3 |
| 5809 | puntualmente | 3 |
| 5810 | puntapié | 3 |
| 5811 | pulverizar | 3 |
| 5812 | pulsar | 3 |
| 5813 | pulir | 3 |
| 5814 | pulcritud | 3 |
| 5815 | puerco | 3 |
| 5816 | puente | 3 |
| 5817 | pudor | 3 |
| 5818 | púa | 3 |
| 5819 | prusiano | 3 |
| 5820 | proyectil | 3 |
| 5821 | provisto | 3 |
| 5822 | proveer | 3 |
| 5823 | prórroga | 3 |
| 5824 | propagandista | 3 |
| 5825 | pronunciamiento | 3 |
| 5826 | profetizar | 3 |
| 5827 | proceso | 3 |
| 5828 | probabilidad | 3 |
| 5829 | pringar | 3 |
| 5830 | principios | 3 |
| 5831 | primoroso | 3 |
| 5832 | previsión | 3 |
| 5833 | pretextar | 3 |
| 5834 | presumido | 3 |
| 5835 | presidir | 3 |
| 5836 | presentose | 3 |
| 5837 | preferencia | 3 |
| 5838 | precipitadamente | 3 |
| 5839 | postración | 3 |
| 5840 | postizo | 3 |
| 5841 | posibilidad | 3 |
| 5842 | posesionar | 3 |
| 5843 | portezuela | 3 |
| 5844 | poro | 3 |
| 5845 | porción | 3 |
| 5846 | ponte | 3 |
| 5847 | polvoriento | 3 |
| 5848 | polémica | 3 |
| 5849 | podría | 3 |
| 5850 | podrá | 3 |
| 5851 | podar | 3 |
| 5852 | pobrecillo | 3 |
| 5853 | platerías | 3 |
| 5854 | plañidero | 3 |
| 5855 | pitar | 3 |
| 5856 | pistola | 3 |
| 5857 | pío | 3 |
| 5858 | pesimista | 3 |
| 5859 | pervertir | 3 |
| 5860 | persuasión | 3 |
| 5861 | perspicacia | 3 |
| 5862 | persignar | 3 |
| 5863 | perrito | 3 |
| 5864 | perrera | 3 |
| 5865 | perpetuo | 3 |
| 5866 | perjuicio | 3 |
| 5867 | periodista | 3 |
| 5868 | perfume | 3 |
| 5869 | pérfido | 3 |
| 5870 | perfeccionar | 3 |
| 5871 | peregrino | 3 |
| 5872 | perdónala | 3 |
| 5873 | perdona | 3 |
| 5874 | pera | 3 |
| 5875 | pentecostés | 3 |
| 5876 | penitenciario | 3 |
| 5877 | penales | 3 |
| 5878 | peluquería | 3 |
| 5879 | peluca | 3 |
| 5880 | pelmazo | 3 |
| 5881 | peligrar | 3 |
| 5882 | peines | 3 |
| 5883 | peinado | 3 |
| 5884 | pegote | 3 |
| 5885 | pegadizo | 3 |
| 5886 | pechuga | 3 |
| 5887 | pavía | 3 |
| 5888 | pausar | 3 |
| 5889 | pausadamente | 3 |
| 5890 | patrona | 3 |
| 5891 | patrón | 3 |
| 5892 | patochada | 3 |
| 5893 | pataleo | 3 |
| 5894 | patalear | 3 |
| 5895 | pastel | 3 |
| 5896 | pastar | 3 |
| 5897 | pasmarote | 3 |
| 5898 | pascuas | 3 |
| 5899 | pasaba | 3 |
| 5900 | parto | 3 |
| 5901 | parisiense | 3 |
| 5902 | parentela | 3 |
| 5903 | pareciole | 3 |
| 5904 | paralela | 3 |
| 5905 | paraguas | 3 |
| 5906 | paradójico | 3 |
| 5907 | papelista | 3 |
| 5908 | palmotear | 3 |
| 5909 | palmada | 3 |
| 5910 | palanca | 3 |
| 5911 | paladar | 3 |
| 5912 | ovillo | 3 |
| 5913 | ostra | 3 |
| 5914 | ostentación | 3 |
| 5915 | oscurecer | 3 |
| 5916 | orquesta | 3 |
| 5917 | oriundo | 3 |
| 5918 | orgía | 3 |
| 5919 | organización | 3 |
| 5920 | orgánico | 3 |
| 5921 | optimismo | 3 |
| 5922 | oloroso | 3 |
| 5923 | olorcillo | 3 |
| 5924 | olfatorio | 3 |
| 5925 | ojeroso | 3 |
| 5926 | ojera | 3 |
| 5927 | ojal | 3 |
| 5928 | oficioso | 3 |
| 5929 | oferta | 3 |
| 5930 | ocurriósele | 3 |
| 5931 | ocurriole | 3 |
| 5932 | ociosidad | 3 |
| 5933 | ochavo | 3 |
| 5934 | obstrucción | 3 |
| 5935 | objetar | 3 |
| 5936 | nudillo | 3 |
| 5937 | nubes | 3 |
| 5938 | noviembre | 3 |
| 5939 | novena | 3 |
| 5940 | novelesco | 3 |
| 5941 | novelda | 3 |
| 5942 | notorio | 3 |
| 5943 | non | 3 |
| 5944 | nocturno | 3 |
| 5945 | niña | 3 |
| 5946 | nicolasa | 3 |
| 5947 | neurosis | 3 |
| 5948 | negrito | 3 |
| 5949 | negociar | 3 |
| 5950 | negociante | 3 |
| 5951 | necio | 3 |
| 5952 | náufrago | 3 |
| 5953 | naturalista | 3 |
| 5954 | nativo | 3 |
| 5955 | nasal | 3 |
| 5956 | narrar | 3 |
| 5957 | naranjo | 3 |
| 5958 | nacido | 3 |
| 5959 | mutuo | 3 |
| 5960 | muslo | 3 |
| 5961 | musgo | 3 |
| 5962 | museo | 3 |
| 5963 | murillo | 3 |
| 5964 | multiplicar | 3 |
| 5965 | muladar | 3 |
| 5966 | movida | 3 |
| 5967 | morros | 3 |
| 5968 | morro | 3 |
| 5969 | morrión | 3 |
| 5970 | moros | 3 |
| 5971 | morisqueta | 3 |
| 5972 | moriones | 3 |
| 5973 | morejón | 3 |
| 5974 | morado | 3 |
| 5975 | morada | 3 |
| 5976 | monstruosidad | 3 |
| 5977 | monserga | 3 |
| 5978 | monopolizar | 3 |
| 5979 | momia | 3 |
| 5980 | momentito | 3 |
| 5981 | molido | 3 |
| 5982 | mocedad | 3 |
| 5983 | misterios | 3 |
| 5984 | mismísimo | 3 |
| 5985 | mis | 3 |
| 5986 | miramiento | 3 |
| 5987 | mírame | 3 |
| 5988 | minutar | 3 |
| 5989 | minucioso | 3 |
| 5990 | minuciosamente | 3 |
| 5991 | miente | 3 |
| 5992 | método | 3 |
| 5993 | metódico | 3 |
| 5994 | metida | 3 |
| 5995 | mermar | 3 |
| 5996 | mercurio | 3 |
| 5997 | mercachifle | 3 |
| 5998 | menudear | 3 |
| 5999 | mentiroso | 3 |
| 6000 | mensaje | 3 |
| 6001 | menestral | 3 |
| 6002 | meneo | 3 |
| 6003 | mendicidad | 3 |
| 6004 | melindre | 3 |
| 6005 | melchor | 3 |
| 6006 | médicis | 3 |
| 6007 | mediante | 3 |
| 6008 | mechero | 3 |
| 6009 | mazar | 3 |
| 6010 | matritense | 3 |
| 6011 | matorral | 3 |
| 6012 | matadero | 3 |
| 6013 | masón | 3 |
| 6014 | martirizar | 3 |
| 6015 | martín | 3 |
| 6016 | marianas | 3 |
| 6017 | mareo | 3 |
| 6018 | mareado | 3 |
| 6019 | marcial | 3 |
| 6020 | marcado | 3 |
| 6021 | manzanares | 3 |
| 6022 | manubrio | 3 |
| 6023 | manteca | 3 |
| 6024 | mansedumbre | 3 |
| 6025 | manotear | 3 |
| 6026 | manotazo | 3 |
| 6027 | maniquí | 3 |
| 6028 | mandil | 3 |
| 6029 | mandarín | 3 |
| 6030 | mancebo | 3 |
| 6031 | manceba | 3 |
| 6032 | malsano | 3 |
| 6033 | malograr | 3 |
| 6034 | malísimo | 3 |
| 6035 | maligno | 3 |
| 6036 | maleza | 3 |
| 6037 | majestuoso | 3 |
| 6038 | maja | 3 |
| 6039 | magra | 3 |
| 6040 | mágico | 3 |
| 6041 | madriz | 3 |
| 6042 | madriguera | 3 |
| 6043 | madeja | 3 |
| 6044 | macho | 3 |
| 6045 | lujoso | 3 |
| 6046 | locuaz | 3 |
| 6047 | lluvia | 3 |
| 6048 | lloro | 3 |
| 6049 | lloriquear | 3 |
| 6050 | llegó | 3 |
| 6051 | llamole | 3 |
| 6052 | literatura | 3 |
| 6053 | listar | 3 |
| 6054 | lisonja | 3 |
| 6055 | lindar | 3 |
| 6056 | ligereza | 3 |
| 6057 | ligar | 3 |
| 6058 | librería | 3 |
| 6059 | libertino | 3 |
| 6060 | libertar | 3 |
| 6061 | leyenda | 3 |
| 6062 | leopardi | 3 |
| 6063 | legalidad | 3 |
| 6064 | lazar | 3 |
| 6065 | láudano | 3 |
| 6066 | latitud | 3 |
| 6067 | latir | 3 |
| 6068 | lárgate | 3 |
| 6069 | lamento | 3 |
| 6070 | lacayo | 3 |
| 6071 | labrado | 3 |
| 6072 | jurisdicción | 3 |
| 6073 | juramento | 3 |
| 6074 | jugador | 3 |
| 6075 | judas | 3 |
| 6076 | jubilar | 3 |
| 6077 | juana | 3 |
| 6078 | jovialidad | 3 |
| 6079 | jergón | 3 |
| 6080 | jarras | 3 |
| 6081 | jamón | 3 |
| 6082 | jaime | 3 |
| 6083 | jadeante | 3 |
| 6084 | jacintilla | 3 |
| 6085 | italiano | 3 |
| 6086 | isabelita | 3 |
| 6087 | irritación | 3 |
| 6088 | irregularidad | 3 |
| 6089 | irregular | 3 |
| 6090 | iré | 3 |
| 6091 | invitación | 3 |
| 6092 | inválido | 3 |
| 6093 | intranquilidad | 3 |
| 6094 | íntimamente | 3 |
| 6095 | interrupción | 3 |
| 6096 | interminable | 3 |
| 6097 | interesantísimo | 3 |
| 6098 | interceder | 3 |
| 6099 | intelectual | 3 |
| 6100 | intacto | 3 |
| 6101 | intachable | 3 |
| 6102 | insufrible | 3 |
| 6103 | insubordinar | 3 |
| 6104 | instructivo | 3 |
| 6105 | institutriz | 3 |
| 6106 | instituto | 3 |
| 6107 | instintivamente | 3 |
| 6108 | insomnio | 3 |
| 6109 | insignia | 3 |
| 6110 | insensiblemente | 3 |
| 6111 | inocentón | 3 |
| 6112 | innato | 3 |
| 6113 | inmutar | 3 |
| 6114 | inmundo | 3 |
| 6115 | inmundicia | 3 |
| 6116 | inmueble | 3 |
| 6117 | inmemorial | 3 |
| 6118 | injusticia | 3 |
| 6119 | injuriar | 3 |
| 6120 | ininteligible | 3 |
| 6121 | ingeniero | 3 |
| 6122 | infracción | 3 |
| 6123 | infortunado | 3 |
| 6124 | informe | 3 |
| 6125 | influencia | 3 |
| 6126 | inflexible | 3 |
| 6127 | inflamar | 3 |
| 6128 | infinitamente | 3 |
| 6129 | inferioridad | 3 |
| 6130 | inevitable | 3 |
| 6131 | inesperadamente | 3 |
| 6132 | inequívoco | 3 |
| 6133 | inducir | 3 |
| 6134 | indolencia | 3 |
| 6135 | indino | 3 |
| 6136 | indefinible | 3 |
| 6137 | incurrir | 3 |
| 6138 | incumbencia | 3 |
| 6139 | incorporose | 3 |
| 6140 | incomprensible | 3 |
| 6141 | incomparable | 3 |
| 6142 | inclinose | 3 |
| 6143 | incitar | 3 |
| 6144 | incautar | 3 |
| 6145 | inapreciable | 3 |
| 6146 | imprudente | 3 |
| 6147 | impotente | 3 |
| 6148 | imposibilitar | 3 |
| 6149 | imposibilidad | 3 |
| 6150 | impetuoso | 3 |
| 6151 | imperdible | 3 |
| 6152 | imbécil | 3 |
| 6153 | iluminado | 3 |
| 6154 | ildefonso | 3 |
| 6155 | ignorante | 3 |
| 6156 | iglesias | 3 |
| 6157 | idolatría | 3 |
| 6158 | idioma | 3 |
| 6159 | iba | 3 |
| 6160 | humillación | 3 |
| 6161 | huella | 3 |
| 6162 | horrendo | 3 |
| 6163 | honda | 3 |
| 6164 | hombruno | 3 |
| 6165 | hízolo | 3 |
| 6166 | hinchazón | 3 |
| 6167 | hijos | 3 |
| 6168 | hijas | 3 |
| 6169 | herramienta | 3 |
| 6170 | heroísmo | 3 |
| 6171 | herido | 3 |
| 6172 | helada | 3 |
| 6173 | hebilla | 3 |
| 6174 | hato | 3 |
| 6175 | hastiar | 3 |
| 6176 | haragán | 3 |
| 6177 | hágase | 3 |
| 6178 | habría | 3 |
| 6179 | habló | 3 |
| 6180 | hablando | 3 |
| 6181 | habladuría | 3 |
| 6182 | habitual | 3 |
| 6183 | habana | 3 |
| 6184 | gustoso | 3 |
| 6185 | gustavito | 3 |
| 6186 | guisante | 3 |
| 6187 | guijarro | 3 |
| 6188 | guedeja | 3 |
| 6189 | gritería | 3 |
| 6190 | grillete | 3 |
| 6191 | grifo | 3 |
| 6192 | granito | 3 |
| 6193 | grandón | 3 |
| 6194 | granar | 3 |
| 6195 | grabar | 3 |
| 6196 | gotita | 3 |
| 6197 | golpecito | 3 |
| 6198 | globo | 3 |
| 6199 | geografía | 3 |
| 6200 | generalmente | 3 |
| 6201 | generala | 3 |
| 6202 | generación | 3 |
| 6203 | gatera | 3 |
| 6204 | garrotillo | 3 |
| 6205 | gargarismo | 3 |
| 6206 | garcía | 3 |
| 6207 | fundamento | 3 |
| 6208 | fundamental | 3 |
| 6209 | funciones | 3 |
| 6210 | fulano | 3 |
| 6211 | fuga | 3 |
| 6212 | frutar | 3 |
| 6213 | fruncido | 3 |
| 6214 | frugal | 3 |
| 6215 | fraude | 3 |
| 6216 | fragua | 3 |
| 6217 | fraga | 3 |
| 6218 | fotografía | 3 |
| 6219 | forzado | 3 |
| 6220 | fogoso | 3 |
| 6221 | flexible | 3 |
| 6222 | flechar | 3 |
| 6223 | flecha | 3 |
| 6224 | flaquear | 3 |
| 6225 | flamante | 3 |
| 6226 | físicamente | 3 |
| 6227 | firmeza | 3 |
| 6228 | fingido | 3 |
| 6229 | filtrar | 3 |
| 6230 | filípica | 3 |
| 6231 | filantrópico | 3 |
| 6232 | figuración | 3 |
| 6233 | figueras | 3 |
| 6234 | fervor | 3 |
| 6235 | felizmente | 3 |
| 6236 | fecundo | 3 |
| 6237 | fatuidad | 3 |
| 6238 | fastidio | 3 |
| 6239 | farsante | 3 |
| 6240 | fantasía | 3 |
| 6241 | fanático | 3 |
| 6242 | falsete | 3 |
| 6243 | fallecer | 3 |
| 6244 | facundia | 3 |
| 6245 | fachada | 3 |
| 6246 | fabricante | 3 |
| 6247 | extremidad | 3 |
| 6248 | expresó | 3 |
| 6249 | explosivo | 3 |
| 6250 | explorar | 3 |
| 6251 | expectativa | 3 |
| 6252 | expectante | 3 |
| 6253 | expansivo | 3 |
| 6254 | expansión | 3 |
| 6255 | excitante | 3 |
| 6256 | exceso | 3 |
| 6257 | excesivo | 3 |
| 6258 | exageración | 3 |
| 6259 | evolución | 3 |
| 6260 | evasivamente | 3 |
| 6261 | evasiva | 3 |
| 6262 | evasión | 3 |
| 6263 | evangélico | 3 |
| 6264 | europa | 3 |
| 6265 | eternidad | 3 |
| 6266 | estupor | 3 |
| 6267 | estupidez | 3 |
| 6268 | estudiado | 3 |
| 6269 | estuche | 3 |
| 6270 | estucar | 3 |
| 6271 | estrujón | 3 |
| 6272 | estrofa | 3 |
| 6273 | estridente | 3 |
| 6274 | estrechamente | 3 |
| 6275 | estipendio | 3 |
| 6276 | estilar | 3 |
| 6277 | estaría | 3 |
| 6278 | espumar | 3 |
| 6279 | espuma | 3 |
| 6280 | esperpento | 3 |
| 6281 | esparto | 3 |
| 6282 | esparcimiento | 3 |
| 6283 | espantajo | 3 |
| 6284 | espantada | 3 |
| 6285 | esfinge | 3 |
| 6286 | esencia | 3 |
| 6287 | escudriñar | 3 |
| 6288 | escudo | 3 |
| 6289 | escocés | 3 |
| 6290 | escobillón | 3 |
| 6291 | escarmiento | 3 |
| 6292 | escarmentar | 3 |
| 6293 | escapatoria | 3 |
| 6294 | escanciar | 3 |
| 6295 | escalerilla | 3 |
| 6296 | escabeche | 3 |
| 6297 | errante | 3 |
| 6298 | erizar | 3 |
| 6299 | erguir | 3 |
| 6300 | equívoco | 3 |
| 6301 | equivocado | 3 |
| 6302 | episodio | 3 |
| 6303 | enviudar | 3 |
| 6304 | envidioso | 3 |
| 6305 | envenenamiento | 3 |
| 6306 | entrometido | 3 |
| 6307 | entrometer | 3 |
| 6308 | entrañablemente | 3 |
| 6309 | entorpecer | 3 |
| 6310 | entornado | 3 |
| 6311 | enterose | 3 |
| 6312 | enterado | 3 |
| 6313 | enrevesado | 3 |
| 6314 | enrejar | 3 |
| 6315 | enloquecer | 3 |
| 6316 | enlace | 3 |
| 6317 | enjuto | 3 |
| 6318 | enigma | 3 |
| 6319 | enfurecer | 3 |
| 6320 | enfermizo | 3 |
| 6321 | endilgar | 3 |
| 6322 | encorvar | 3 |
| 6323 | encontronazo | 3 |
| 6324 | encoger | 3 |
| 6325 | encinas | 3 |
| 6326 | encerrarme | 3 |
| 6327 | encargado | 3 |
| 6328 | encaramar | 3 |
| 6329 | encantado | 3 |
| 6330 | encalabrinar | 3 |
| 6331 | enaltecer | 3 |
| 6332 | enagua | 3 |
| 6333 | emulación | 3 |
| 6334 | empolvar | 3 |
| 6335 | empinar | 3 |
| 6336 | empezó | 3 |
| 6337 | empeño | 3 |
| 6338 | empaquetar | 3 |
| 6339 | empaque | 3 |
| 6340 | empapar | 3 |
| 6341 | empañado | 3 |
| 6342 | eminencia | 3 |
| 6343 | emblema | 3 |
| 6344 | embellecer | 3 |
| 6345 | embelesar | 3 |
| 6346 | embaucar | 3 |
| 6347 | emancipar | 3 |
| 6348 | emanación | 3 |
| 6349 | elocuencia | 3 |
| 6350 | eliminar | 3 |
| 6351 | electrizar | 3 |
| 6352 | egipcio | 3 |
| 6353 | efectuar | 3 |
| 6354 | educativo | 3 |
| 6355 | edificación | 3 |
| 6356 | durmiose | 3 |
| 6357 | dulzón | 3 |
| 6358 | dulcificar | 3 |
| 6359 | dragón | 3 |
| 6360 | dormitar | 3 |
| 6361 | dominguero | 3 |
| 6362 | domiciliario | 3 |
| 6363 | dolores | 3 |
| 6364 | dogma | 3 |
| 6365 | divisar | 3 |
| 6366 | distrito | 3 |
| 6367 | distinguido | 3 |
| 6368 | distar | 3 |
| 6369 | dispensa | 3 |
| 6370 | disolvente | 3 |
| 6371 | disoluto | 3 |
| 6372 | dislocar | 3 |
| 6373 | disimulado | 3 |
| 6374 | disciplina | 3 |
| 6375 | diputar | 3 |
| 6376 | diole | 3 |
| 6377 | dímelo | 3 |
| 6378 | dilo | 3 |
| 6379 | dile | 3 |
| 6380 | dilatar | 3 |
| 6381 | dígase | 3 |
| 6382 | dificultar | 3 |
| 6383 | difícilmente | 3 |
| 6384 | diferenciar | 3 |
| 6385 | dieciocho | 3 |
| 6386 | dictamen | 3 |
| 6387 | dichosos | 3 |
| 6388 | dibujar | 3 |
| 6389 | devoto | 3 |
| 6390 | devolución | 3 |
| 6391 | desviar | 3 |
| 6392 | desvelo | 3 |
| 6393 | desvariar | 3 |
| 6394 | desvanecimiento | 3 |
| 6395 | destrozado | 3 |
| 6396 | desproporción | 3 |
| 6397 | desprendimiento | 3 |
| 6398 | despotismo | 3 |
| 6399 | despojo | 3 |
| 6400 | despintar | 3 |
| 6401 | despacito | 3 |
| 6402 | despabilado | 3 |
| 6403 | desolado | 3 |
| 6404 | desmerecer | 3 |
| 6405 | desmenuzar | 3 |
| 6406 | desmejorado | 3 |
| 6407 | desilusionar | 3 |
| 6408 | deshilachado | 3 |
| 6409 | desflorar | 3 |
| 6410 | desfigurar | 3 |
| 6411 | desfavorable | 3 |
| 6412 | desesperado | 3 |
| 6413 | desengañar | 3 |
| 6414 | desenfado | 3 |
| 6415 | descuida | 3 |
| 6416 | descubrimiento | 3 |
| 6417 | descifrar | 3 |
| 6418 | descarar | 3 |
| 6419 | descalabrar | 3 |
| 6420 | desbastar | 3 |
| 6421 | desasosegar | 3 |
| 6422 | desasir | 3 |
| 6423 | desaparición | 3 |
| 6424 | desaliento | 3 |
| 6425 | desalar | 3 |
| 6426 | desaire | 3 |
| 6427 | desahogo | 3 |
| 6428 | desabrigar | 3 |
| 6429 | derroche | 3 |
| 6430 | depravación | 3 |
| 6431 | deplorable | 3 |
| 6432 | deparar | 3 |
| 6433 | demonche | 3 |
| 6434 | democrático | 3 |
| 6435 | delicia | 3 |
| 6436 | déjese | 3 |
| 6437 | definir | 3 |
| 6438 | decisión | 3 |
| 6439 | decíale | 3 |
| 6440 | debo | 3 |
| 6441 | debilitar | 3 |
| 6442 | damasco | 3 |
| 6443 | cúpula | 3 |
| 6444 | cundir | 3 |
| 6445 | culpar | 3 |
| 6446 | cuita | 3 |
| 6447 | cuestas | 3 |
| 6448 | cuesta | 3 |
| 6449 | cuchitril | 3 |
| 6450 | cuatrocientos | 3 |
| 6451 | cuarterón | 3 |
| 6452 | cuántos | 3 |
| 6453 | cuántas | 3 |
| 6454 | crujía | 3 |
| 6455 | crucifijo | 3 |
| 6456 | cromo | 3 |
| 6457 | criticar | 3 |
| 6458 | cristiandad | 3 |
| 6459 | crío | 3 |
| 6460 | crepúsculo | 3 |
| 6461 | créete | 3 |
| 6462 | créelo | 3 |
| 6463 | crecimiento | 3 |
| 6464 | créame | 3 |
| 6465 | creador | 3 |
| 6466 | coz | 3 |
| 6467 | cosas | 3 |
| 6468 | corruptor | 3 |
| 6469 | corromper | 3 |
| 6470 | corroborar | 3 |
| 6471 | corretaje | 3 |
| 6472 | correcto | 3 |
| 6473 | coronilla | 3 |
| 6474 | corneta | 3 |
| 6475 | corista | 3 |
| 6476 | corinto | 3 |
| 6477 | cordial | 3 |
| 6478 | coral | 3 |
| 6479 | coquetería | 3 |
| 6480 | copiar | 3 |
| 6481 | conveniencia | 3 |
| 6482 | convencional | 3 |
| 6483 | contrato | 3 |
| 6484 | contratiempo | 3 |
| 6485 | continuidad | 3 |
| 6486 | contingencia | 3 |
| 6487 | continente | 3 |
| 6488 | contemporizar | 3 |
| 6489 | contemporáneo | 3 |
| 6490 | consumo | 3 |
| 6491 | consternado | 3 |
| 6492 | conspirar | 3 |
| 6493 | conspirador | 3 |
| 6494 | consolador | 3 |
| 6495 | consignar | 3 |
| 6496 | conservación | 3 |
| 6497 | consabido | 3 |
| 6498 | confín | 3 |
| 6499 | confabular | 3 |
| 6500 | conde | 3 |
| 6501 | concurso | 3 |
| 6502 | concurrencia | 3 |
| 6503 | conciliar | 3 |
| 6504 | conciliador | 3 |
| 6505 | concha | 3 |
| 6506 | conceptuar | 3 |
| 6507 | comúnmente | 3 |
| 6508 | comunión | 3 |
| 6509 | comunicativo | 3 |
| 6510 | comprendo | 3 |
| 6511 | comprador | 3 |
| 6512 | compota | 3 |
| 6513 | composición | 3 |
| 6514 | comportamiento | 3 |
| 6515 | cómplice | 3 |
| 6516 | complicación | 3 |
| 6517 | complexión | 3 |
| 6518 | complacencia | 3 |
| 6519 | comitiva | 3 |
| 6520 | comediar | 3 |
| 6521 | combatiente | 3 |
| 6522 | colorín | 3 |
| 6523 | coloquiar | 3 |
| 6524 | colmena | 3 |
| 6525 | colérico | 3 |
| 6526 | colegial | 3 |
| 6527 | colección | 3 |
| 6528 | colación | 3 |
| 6529 | codos | 3 |
| 6530 | club | 3 |
| 6531 | clavado | 3 |
| 6532 | claustro | 3 |
| 6533 | ciudadano | 3 |
| 6534 | cisco | 3 |
| 6535 | circular | 3 |
| 6536 | circulación | 3 |
| 6537 | ciprés | 3 |
| 6538 | cierta | 3 |
| 6539 | cicatero | 3 |
| 6540 | chusco | 3 |
| 6541 | chuscada | 3 |
| 6542 | chulo | 3 |
| 6543 | chulita | 3 |
| 6544 | chula | 3 |
| 6545 | chinesco | 3 |
| 6546 | chí | 3 |
| 6547 | chaveta | 3 |
| 6548 | chato | 3 |
| 6549 | chaqueta | 3 |
| 6550 | chanza | 3 |
| 6551 | chambra | 3 |
| 6552 | ceñudo | 3 |
| 6553 | ceñir | 3 |
| 6554 | celar | 3 |
| 6555 | cebolla | 3 |
| 6556 | cebar | 3 |
| 6557 | cautiverio | 3 |
| 6558 | cauteloso | 3 |
| 6559 | cautelosamente | 3 |
| 6560 | categórico | 3 |
| 6561 | catedrático | 3 |
| 6562 | catecúmeno | 3 |
| 6563 | cataclismo | 3 |
| 6564 | castrense | 3 |
| 6565 | castita | 3 |
| 6566 | castañetazo | 3 |
| 6567 | castaña | 3 |
| 6568 | caserón | 3 |
| 6569 | casaca | 3 |
| 6570 | cartón | 3 |
| 6571 | cartel | 3 |
| 6572 | cartear | 3 |
| 6573 | carruaje | 3 |
| 6574 | carretero | 3 |
| 6575 | carnicero | 3 |
| 6576 | carmín | 3 |
| 6577 | carca | 3 |
| 6578 | carbonería | 3 |
| 6579 | carambita | 3 |
| 6580 | capotar | 3 |
| 6581 | capota | 3 |
| 6582 | capítulo | 3 |
| 6583 | capar | 3 |
| 6584 | cáñamo | 3 |
| 6585 | cántaro | 3 |
| 6586 | canastilla | 3 |
| 6587 | camps | 3 |
| 6588 | campanario | 3 |
| 6589 | campana | 3 |
| 6590 | camello | 3 |
| 6591 | camastro | 3 |
| 6592 | cámara | 3 |
| 6593 | calvo | 3 |
| 6594 | calmo | 3 |
| 6595 | callejuela | 3 |
| 6596 | calla | 3 |
| 6597 | calidad | 3 |
| 6598 | calentito | 3 |
| 6599 | calderilla | 3 |
| 6600 | calabaza | 3 |
| 6601 | caimán | 3 |
| 6602 | cafetero | 3 |
| 6603 | cadera | 3 |
| 6604 | cachivache | 3 |
| 6605 | cachete | 3 |
| 6606 | caca | 3 |
| 6607 | cabizbajo | 3 |
| 6608 | cabellar | 3 |
| 6609 | burra | 3 |
| 6610 | burdeos | 3 |
| 6611 | bufar | 3 |
| 6612 | buenazo | 3 |
| 6613 | brujería | 3 |
| 6614 | bruces | 3 |
| 6615 | brocha | 3 |
| 6616 | brindar | 3 |
| 6617 | breva | 3 |
| 6618 | brea | 3 |
| 6619 | brasero | 3 |
| 6620 | bramido | 3 |
| 6621 | bóveda | 3 |
| 6622 | bostezar | 3 |
| 6623 | borrasca | 3 |
| 6624 | bonaparte | 3 |
| 6625 | blandura | 3 |
| 6626 | blancura | 3 |
| 6627 | birlar | 3 |
| 6628 | biblioteca | 3 |
| 6629 | biblia | 3 |
| 6630 | besuqueo | 3 |
| 6631 | berrear | 3 |
| 6632 | beneficio | 3 |
| 6633 | belga | 3 |
| 6634 | beata | 3 |
| 6635 | baza | 3 |
| 6636 | bautizar | 3 |
| 6637 | batista | 3 |
| 6638 | barruntar | 3 |
| 6639 | barril | 3 |
| 6640 | barbar | 3 |
| 6641 | baratura | 3 |
| 6642 | baratar | 3 |
| 6643 | barandal | 3 |
| 6644 | barajar | 3 |
| 6645 | baqueta | 3 |
| 6646 | banquete | 3 |
| 6647 | bálsamo | 3 |
| 6648 | baldomerito | 3 |
| 6649 | balbucir | 3 |
| 6650 | balance | 3 |
| 6651 | bala | 3 |
| 6652 | baboso | 3 |
| 6653 | azoramiento | 3 |
| 6654 | avispado | 3 |
| 6655 | aviso | 3 |
| 6656 | autócrata | 3 |
| 6657 | auténtico | 3 |
| 6658 | aureola | 3 |
| 6659 | aullido | 3 |
| 6660 | audiencia | 3 |
| 6661 | atusar | 3 |
| 6662 | atropelladamente | 3 |
| 6663 | atracón | 3 |
| 6664 | atontado | 3 |
| 6665 | aterrada | 3 |
| 6666 | atenazar | 3 |
| 6667 | asunción | 3 |
| 6668 | astuto | 3 |
| 6669 | asociación | 3 |
| 6670 | asistencia | 3 |
| 6671 | asimismo | 3 |
| 6672 | asfixia | 3 |
| 6673 | asesinato | 3 |
| 6674 | asado | 3 |
| 6675 | artesón | 3 |
| 6676 | arsenal | 3 |
| 6677 | arrogancia | 3 |
| 6678 | arrendar | 3 |
| 6679 | arraigar | 3 |
| 6680 | arrabal | 3 |
| 6681 | arquear | 3 |
| 6682 | aro | 3 |
| 6683 | árnica | 3 |
| 6684 | aritmética | 3 |
| 6685 | arenar | 3 |
| 6686 | ardientemente | 3 |
| 6687 | arcano | 3 |
| 6688 | arbusto | 3 |
| 6689 | arancelario | 3 |
| 6690 | apóstrofe | 3 |
| 6691 | apellido | 3 |
| 6692 | apellidar | 3 |
| 6693 | apático | 3 |
| 6694 | apasionado | 3 |
| 6695 | aparente | 3 |
| 6696 | apañar | 3 |
| 6697 | apañadito | 3 |
| 6698 | apalear | 3 |
| 6699 | anulación | 3 |
| 6700 | antemano | 3 |
| 6701 | antagonismo | 3 |
| 6702 | animado | 3 |
| 6703 | angosto | 3 |
| 6704 | andalucía | 3 |
| 6705 | andadas | 3 |
| 6706 | analizar | 3 |
| 6707 | amoratar | 3 |
| 6708 | amontonar | 3 |
| 6709 | amonestar | 3 |
| 6710 | amoldar | 3 |
| 6711 | amigote | 3 |
| 6712 | amiga | 3 |
| 6713 | amenaza | 3 |
| 6714 | alusión | 3 |
| 6715 | alucinar | 3 |
| 6716 | altísimo | 3 |
| 6717 | alpiste | 3 |
| 6718 | almacenista | 3 |
| 6719 | aligerar | 3 |
| 6720 | alfonsino | 3 |
| 6721 | alevoso | 3 |
| 6722 | aldea | 3 |
| 6723 | alcohol | 3 |
| 6724 | albergar | 3 |
| 6725 | alba | 3 |
| 6726 | alardear | 3 |
| 6727 | alambique | 3 |
| 6728 | alabado | 3 |
| 6729 | ajedrez | 3 |
| 6730 | ahuyentar | 3 |
| 6731 | ahogo | 3 |
| 6732 | ahilar | 3 |
| 6733 | agujereado | 3 |
| 6734 | agrio | 3 |
| 6735 | agresor | 3 |
| 6736 | agradecidísimo | 3 |
| 6737 | agilidad | 3 |
| 6738 | afrontar | 3 |
| 6739 | afinidad | 3 |
| 6740 | aferrar | 3 |
| 6741 | afear | 3 |
| 6742 | advertencia | 3 |
| 6743 | adulterio | 3 |
| 6744 | adquisición | 3 |
| 6745 | adoquín | 3 |
| 6746 | adónde | 3 |
| 6747 | adivinación | 3 |
| 6748 | adentro | 3 |
| 6749 | adarme | 3 |
| 6750 | adaptar | 3 |
| 6751 | acusón | 3 |
| 6752 | acusador | 3 |
| 6753 | acuéstate | 3 |
| 6754 | actual | 3 |
| 6755 | acritud | 3 |
| 6756 | acreditado | 3 |
| 6757 | acordábase | 3 |
| 6758 | acopiar | 3 |
| 6759 | acompañamiento | 3 |
| 6760 | acoger | 3 |
| 6761 | ácido | 3 |
| 6762 | achaque | 3 |
| 6763 | achacar | 3 |
| 6764 | acercose | 3 |
| 6765 | aceituna | 3 |
| 6766 | aceitoso | 3 |
| 6767 | accesible | 3 |
| 6768 | acceder | 3 |
| 6769 | académico | 3 |
| 6770 | acabado | 3 |
| 6771 | abundancia | 3 |
| 6772 | absolutismo | 3 |
| 6773 | abrumar | 3 |
| 6774 | abonar | 3 |
| 6775 | abollar | 3 |
| 6776 | abocar | 3 |
| 6777 | ablandar | 3 |
| 6778 | abarcar | 3 |
| 6779 | zurrón | 2 |
| 6780 | zurita | 2 |
| 6781 | zurcir | 2 |
| 6782 | zumbido | 2 |
| 6783 | zorro | 2 |
| 6784 | zócalo | 2 |
| 6785 | zipizape | 2 |
| 6786 | zarpar | 2 |
| 6787 | zampar | 2 |
| 6788 | zambullir | 2 |
| 6789 | zalea | 2 |
| 6790 | zafio | 2 |
| 6791 | yacer | 2 |
| 6792 | yacente | 2 |
| 6793 | xvi | 2 |
| 6794 | wagner | 2 |
| 6795 | voraz | 2 |
| 6796 | voracidad | 2 |
| 6797 | vomitar | 2 |
| 6798 | volviéndose | 2 |
| 6799 | voluminoso | 2 |
| 6800 | voltereta | 2 |
| 6801 | voltear | 2 |
| 6802 | volcado | 2 |
| 6803 | vocación | 2 |
| 6804 | vizcaíno | 2 |
| 6805 | víveres | 2 |
| 6806 | vivacidad | 2 |
| 6807 | vivaaaa | 2 |
| 6808 | vislumbrar | 2 |
| 6809 | visera | 2 |
| 6810 | virar | 2 |
| 6811 | violado | 2 |
| 6812 | vilo | 2 |
| 6813 | vigilante | 2 |
| 6814 | vienes | 2 |
| 6815 | viena | 2 |
| 6816 | vidrioso | 2 |
| 6817 | vicente | 2 |
| 6818 | viaducto | 2 |
| 6819 | vértigo | 2 |
| 6820 | verso | 2 |
| 6821 | verdura | 2 |
| 6822 | verdulera | 2 |
| 6823 | verdoso | 2 |
| 6824 | verbigracia | 2 |
| 6825 | veo | 2 |
| 6826 | ventilar | 2 |
| 6827 | ventilación | 2 |
| 6828 | vengan | 2 |
| 6829 | venenoso | 2 |
| 6830 | venecia | 2 |
| 6831 | vellón | 2 |
| 6832 | veintiséis | 2 |
| 6833 | vega | 2 |
| 6834 | ved | 2 |
| 6835 | vean | 2 |
| 6836 | veamos | 2 |
| 6837 | vasto | 2 |
| 6838 | vascular | 2 |
| 6839 | varita | 2 |
| 6840 | variadísimo | 2 |
| 6841 | vanidoso | 2 |
| 6842 | vanagloriar | 2 |
| 6843 | vámonos | 2 |
| 6844 | valenciano | 2 |
| 6845 | vajilla | 2 |
| 6846 | vaciado | 2 |
| 6847 | utilidad | 2 |
| 6848 | usurpar | 2 |
| 6849 | usurario | 2 |
| 6850 | usura | 2 |
| 6851 | urgente | 2 |
| 6852 | uñir | 2 |
| 6853 | untar | 2 |
| 6854 | unánimemente | 2 |
| 6855 | tutelar | 2 |
| 6856 | turulato | 2 |
| 6857 | turbio | 2 |
| 6858 | tumor | 2 |
| 6859 | tul | 2 |
| 6860 | truncar | 2 |
| 6861 | tropical | 2 |
| 6862 | tropel | 2 |
| 6863 | triquitraque | 2 |
| 6864 | trinquetada | 2 |
| 6865 | trino | 2 |
| 6866 | trigo | 2 |
| 6867 | trifulca | 2 |
| 6868 | triangular | 2 |
| 6869 | tremolina | 2 |
| 6870 | tremenda | 2 |
| 6871 | tregua | 2 |
| 6872 | trechos | 2 |
| 6873 | trece | 2 |
| 6874 | tratado | 2 |
| 6875 | traspié | 2 |
| 6876 | trasero | 2 |
| 6877 | trapicheo | 2 |
| 6878 | transmigrar | 2 |
| 6879 | tranquilízate | 2 |
| 6880 | tranquilizador | 2 |
| 6881 | tranco | 2 |
| 6882 | tramposo | 2 |
| 6883 | trajear | 2 |
| 6884 | tráiganme | 2 |
| 6885 | tráigame | 2 |
| 6886 | tragaluz | 2 |
| 6887 | tragaldabas | 2 |
| 6888 | tráfago | 2 |
| 6889 | tradicionalista | 2 |
| 6890 | totalidad | 2 |
| 6891 | toscamente | 2 |
| 6892 | torvo | 2 |
| 6893 | tórtola | 2 |
| 6894 | torta | 2 |
| 6895 | torpemente | 2 |
| 6896 | tornillo | 2 |
| 6897 | tornear | 2 |
| 6898 | tormenta | 2 |
| 6899 | torear | 2 |
| 6900 | torbellino | 2 |
| 6901 | topete | 2 |
| 6902 | tontear | 2 |
| 6903 | tontamente | 2 |
| 6904 | tonta | 2 |
| 6905 | tonadilla | 2 |
| 6906 | tole | 2 |
| 6907 | toldo | 2 |
| 6908 | tocino | 2 |
| 6909 | tocador | 2 |
| 6910 | tizne | 2 |
| 6911 | titular | 2 |
| 6912 | titubear | 2 |
| 6913 | tisú | 2 |
| 6914 | tirotear | 2 |
| 6915 | tirante | 2 |
| 6916 | tiranía | 2 |
| 6917 | tirador | 2 |
| 6918 | tira | 2 |
| 6919 | tiñoso | 2 |
| 6920 | tinglado | 2 |
| 6921 | timbrar | 2 |
| 6922 | tiita | 2 |
| 6923 | tibio | 2 |
| 6924 | testero | 2 |
| 6925 | ternero | 2 |
| 6926 | terapéutico | 2 |
| 6927 | teólogo | 2 |
| 6928 | teología | 2 |
| 6929 | tenuemente | 2 |
| 6930 | tenlo | 2 |
| 6931 | tenebroso | 2 |
| 6932 | tendido | 2 |
| 6933 | templado | 2 |
| 6934 | telegráfico | 2 |
| 6935 | telaraña | 2 |
| 6936 | tejer | 2 |
| 6937 | tedioso | 2 |
| 6938 | techumbre | 2 |
| 6939 | tate | 2 |
| 6940 | tarumba | 2 |
| 6941 | tartamudear | 2 |
| 6942 | tarro | 2 |
| 6943 | tarambana | 2 |
| 6944 | tapizar | 2 |
| 6945 | tapiz | 2 |
| 6946 | tapa | 2 |
| 6947 | tañer | 2 |
| 6948 | tanda | 2 |
| 6949 | talón | 2 |
| 6950 | talludito | 2 |
| 6951 | tallo | 2 |
| 6952 | talla | 2 |
| 6953 | tálamo | 2 |
| 6954 | tajada | 2 |
| 6955 | taimado | 2 |
| 6956 | táctico | 2 |
| 6957 | taciturno | 2 |
| 6958 | tácitamente | 2 |
| 6959 | tablear | 2 |
| 6960 | tabicar | 2 |
| 6961 | sutilizar | 2 |
| 6962 | sutileza | 2 |
| 6963 | sustitución | 2 |
| 6964 | sustentar | 2 |
| 6965 | sustancioso | 2 |
| 6966 | suspensión | 2 |
| 6967 | susceptible | 2 |
| 6968 | susceptibilidad | 2 |
| 6969 | susana | 2 |
| 6970 | surco | 2 |
| 6971 | surcar | 2 |
| 6972 | supremacía | 2 |
| 6973 | suplicante | 2 |
| 6974 | superstición | 2 |
| 6975 | superficial | 2 |
| 6976 | superchería | 2 |
| 6977 | sulfato | 2 |
| 6978 | sujeción | 2 |
| 6979 | suiza | 2 |
| 6980 | suicidar | 2 |
| 6981 | suicida | 2 |
| 6982 | sugestivo | 2 |
| 6983 | sugestión | 2 |
| 6984 | suficientemente | 2 |
| 6985 | suez | 2 |
| 6986 | suculento | 2 |
| 6987 | suciedad | 2 |
| 6988 | sucesivamente | 2 |
| 6989 | subyugar | 2 |
| 6990 | subterráneo | 2 |
| 6991 | subterfugio | 2 |
| 6992 | sublimemente | 2 |
| 6993 | subió | 2 |
| 6994 | suavizar | 2 |
| 6995 | soslayar | 2 |
| 6996 | sorprendente | 2 |
| 6997 | sordera | 2 |
| 6998 | soporífero | 2 |
| 6999 | sonsonete | 2 |
| 7000 | sonsacar | 2 |
| 7001 | sonrojo | 2 |
| 7002 | sonriente | 2 |
| 7003 | sonata | 2 |
| 7004 | somos | 2 |
| 7005 | sombrilla | 2 |
| 7006 | solidificar | 2 |
| 7007 | solidaridad | 2 |
| 7008 | solicitud | 2 |
| 7009 | solemnemente | 2 |
| 7010 | solapar | 2 |
| 7011 | sola | 2 |
| 7012 | sofocante | 2 |
| 7013 | socialista | 2 |
| 7014 | socialismo | 2 |
| 7015 | sobresalir | 2 |
| 7016 | sobrecoger | 2 |
| 7017 | soberanamente | 2 |
| 7018 | sinrazón | 2 |
| 7019 | sinfonía | 2 |
| 7020 | simetría | 2 |
| 7021 | simbolizar | 2 |
| 7022 | sillero | 2 |
| 7023 | sillería | 2 |
| 7024 | silenciosamente | 2 |
| 7025 | silbido | 2 |
| 7026 | siguió | 2 |
| 7027 | sigilo | 2 |
| 7028 | siesta | 2 |
| 7029 | siéntate | 2 |
| 7030 | shakespeare | 2 |
| 7031 | serrana | 2 |
| 7032 | seré | 2 |
| 7033 | sepultar | 2 |
| 7034 | sepulcral | 2 |
| 7035 | sepa | 2 |
| 7036 | señorón | 2 |
| 7037 | señoras | 2 |
| 7038 | señas | 2 |
| 7039 | señalado | 2 |
| 7040 | sentía | 2 |
| 7041 | sentado | 2 |
| 7042 | sensatez | 2 |
| 7043 | seminario | 2 |
| 7044 | semestre | 2 |
| 7045 | segovia | 2 |
| 7046 | sediento | 2 |
| 7047 | secular | 2 |
| 7048 | secretaría | 2 |
| 7049 | sección | 2 |
| 7050 | secadero | 2 |
| 7051 | seamos | 2 |
| 7052 | sazonar | 2 |
| 7053 | satén | 2 |
| 7054 | sarta | 2 |
| 7055 | sargento | 2 |
| 7056 | saquito | 2 |
| 7057 | sáqueme | 2 |
| 7058 | santurrón | 2 |
| 7059 | santiago | 2 |
| 7060 | santamente | 2 |
| 7061 | sanidad | 2 |
| 7062 | sangriento | 2 |
| 7063 | samaritana | 2 |
| 7064 | salvajismo | 2 |
| 7065 | salmón | 2 |
| 7066 | salivazo | 2 |
| 7067 | salero | 2 |
| 7068 | saldo | 2 |
| 7069 | sagasta | 2 |
| 7070 | sacrilegio | 2 |
| 7071 | saciar | 2 |
| 7072 | sacerdotal | 2 |
| 7073 | sabiendo | 2 |
| 7074 | ruptura | 2 |
| 7075 | rumiar | 2 |
| 7076 | ruinoso | 2 |
| 7077 | rugido | 2 |
| 7078 | rufina | 2 |
| 7079 | royan | 2 |
| 7080 | rosado | 2 |
| 7081 | rondón | 2 |
| 7082 | rondas | 2 |
| 7083 | rollo | 2 |
| 7084 | rojizo | 2 |
| 7085 | rodrigo | 2 |
| 7086 | rodillera | 2 |
| 7087 | roce | 2 |
| 7088 | robo | 2 |
| 7089 | roble | 2 |
| 7090 | rivero | 2 |
| 7091 | risilla | 2 |
| 7092 | risible | 2 |
| 7093 | riñonada | 2 |
| 7094 | ríete | 2 |
| 7095 | rienda | 2 |
| 7096 | rezonas | 2 |
| 7097 | rezagar | 2 |
| 7098 | reyes | 2 |
| 7099 | revuelto | 2 |
| 7100 | revolucionar | 2 |
| 7101 | revoltijo | 2 |
| 7102 | reverencia | 2 |
| 7103 | retrospectivo | 2 |
| 7104 | retrasar | 2 |
| 7105 | retrasado | 2 |
| 7106 | retozón | 2 |
| 7107 | retírate | 2 |
| 7108 | retiráronse | 2 |
| 7109 | retar | 2 |
| 7110 | retahíla | 2 |
| 7111 | restar | 2 |
| 7112 | restallido | 2 |
| 7113 | restablecer | 2 |
| 7114 | respingado | 2 |
| 7115 | resolviose | 2 |
| 7116 | residente | 2 |
| 7117 | residencia | 2 |
| 7118 | reservado | 2 |
| 7119 | requetefinos | 2 |
| 7120 | requerir | 2 |
| 7121 | repuso | 2 |
| 7122 | repuesto | 2 |
| 7123 | republicano | 2 |
| 7124 | representante | 2 |
| 7125 | réplica | 2 |
| 7126 | repletar | 2 |
| 7127 | repique | 2 |
| 7128 | repetía | 2 |
| 7129 | repelón | 2 |
| 7130 | repecho | 2 |
| 7131 | repaso | 2 |
| 7132 | reparo | 2 |
| 7133 | reo | 2 |
| 7134 | reñido | 2 |
| 7135 | renquear | 2 |
| 7136 | renovado | 2 |
| 7137 | rendido | 2 |
| 7138 | rencoroso | 2 |
| 7139 | remesa | 2 |
| 7140 | remendar | 2 |
| 7141 | rematado | 2 |
| 7142 | relumbrón | 2 |
| 7143 | relumbrar | 2 |
| 7144 | relumbrante | 2 |
| 7145 | religiosidad | 2 |
| 7146 | relevar | 2 |
| 7147 | relatores | 2 |
| 7148 | reintegro | 2 |
| 7149 | regurgitación | 2 |
| 7150 | reguapo | 2 |
| 7151 | régimen | 2 |
| 7152 | regenerar | 2 |
| 7153 | regazo | 2 |
| 7154 | regatear | 2 |
| 7155 | regaño | 2 |
| 7156 | regañar | 2 |
| 7157 | refundir | 2 |
| 7158 | refugiose | 2 |
| 7159 | refugiar | 2 |
| 7160 | reflexivo | 2 |
| 7161 | reflejo | 2 |
| 7162 | referido | 2 |
| 7163 | referencia | 2 |
| 7164 | redondear | 2 |
| 7165 | redactar | 2 |
| 7166 | recta | 2 |
| 7167 | recostar | 2 |
| 7168 | reclusión | 2 |
| 7169 | reclamación | 2 |
| 7170 | recio | 2 |
| 7171 | recientemente | 2 |
| 7172 | recibo | 2 |
| 7173 | recibido | 2 |
| 7174 | receptividad | 2 |
| 7175 | recepción | 2 |
| 7176 | rebullir | 2 |
| 7177 | rebasar | 2 |
| 7178 | rebañar | 2 |
| 7179 | ratero | 2 |
| 7180 | rastras | 2 |
| 7181 | raspar | 2 |
| 7182 | rasguño | 2 |
| 7183 | rarísimo | 2 |
| 7184 | rapaza | 2 |
| 7185 | rapaz | 2 |
| 7186 | randa | 2 |
| 7187 | ramos | 2 |
| 7188 | raíz | 2 |
| 7189 | raigón | 2 |
| 7190 | rábano | 2 |
| 7191 | ra | 2 |
| 7192 | quitarvos | 2 |
| 7193 | quiso | 2 |
| 7194 | quisiera | 2 |
| 7195 | quintar | 2 |
| 7196 | química | 2 |
| 7197 | quimera | 2 |
| 7198 | querindango | 2 |
| 7199 | quercus | 2 |
| 7200 | quédese | 2 |
| 7201 | quedamente | 2 |
| 7202 | quebradero | 2 |
| 7203 | puso | 2 |
| 7204 | purgatorio | 2 |
| 7205 | pupitre | 2 |
| 7206 | punzar | 2 |
| 7207 | puntería | 2 |
| 7208 | puntear | 2 |
| 7209 | puntal | 2 |
| 7210 | puntada | 2 |
| 7211 | pulsación | 2 |
| 7212 | pulgar | 2 |
| 7213 | puerto | 2 |
| 7214 | puedo | 2 |
| 7215 | puedes | 2 |
| 7216 | pudiente | 2 |
| 7217 | publicidad | 2 |
| 7218 | pública | 2 |
| 7219 | próximamente | 2 |
| 7220 | provisionar | 2 |
| 7221 | provisional | 2 |
| 7222 | provechoso | 2 |
| 7223 | protegida | 2 |
| 7224 | prostitución | 2 |
| 7225 | propuesta | 2 |
| 7226 | propinar | 2 |
| 7227 | propicio | 2 |
| 7228 | propenso | 2 |
| 7229 | propagar | 2 |
| 7230 | promulgar | 2 |
| 7231 | prométeme | 2 |
| 7232 | prolongación | 2 |
| 7233 | prohibición | 2 |
| 7234 | profanar | 2 |
| 7235 | profanación | 2 |
| 7236 | probado | 2 |
| 7237 | princesa | 2 |
| 7238 | primitiva | 2 |
| 7239 | previsor | 2 |
| 7240 | presión | 2 |
| 7241 | presidiario | 2 |
| 7242 | presidente | 2 |
| 7243 | presentable | 2 |
| 7244 | presentábase | 2 |
| 7245 | presagio | 2 |
| 7246 | preparémonos | 2 |
| 7247 | preparación | 2 |
| 7248 | preocupado | 2 |
| 7249 | premiar | 2 |
| 7250 | premeditación | 2 |
| 7251 | prehistórico | 2 |
| 7252 | pregúntaselo | 2 |
| 7253 | pregúntale | 2 |
| 7254 | predominio | 2 |
| 7255 | predecesor | 2 |
| 7256 | precoces | 2 |
| 7257 | precipitación | 2 |
| 7258 | preciados | 2 |
| 7259 | potro | 2 |
| 7260 | potingue | 2 |
| 7261 | potencia | 2 |
| 7262 | potaje | 2 |
| 7263 | posterior | 2 |
| 7264 | pórtico | 2 |
| 7265 | portazo | 2 |
| 7266 | portante | 2 |
| 7267 | porfiar | 2 |
| 7268 | porcelana | 2 |
| 7269 | poquísimo | 2 |
| 7270 | póngase | 2 |
| 7271 | ponferrada | 2 |
| 7272 | ponerse | 2 |
| 7273 | pompadour | 2 |
| 7274 | pompa | 2 |
| 7275 | poética | 2 |
| 7276 | pobretín | 2 |
| 7277 | pobretería | 2 |
| 7278 | pobrecita | 2 |
| 7279 | pluralidad | 2 |
| 7280 | plumaje | 2 |
| 7281 | plebeyo | 2 |
| 7282 | plebe | 2 |
| 7283 | plazoleta | 2 |
| 7284 | playa | 2 |
| 7285 | platón | 2 |
| 7286 | platito | 2 |
| 7287 | platería | 2 |
| 7288 | platear | 2 |
| 7289 | plasencia | 2 |
| 7290 | plano | 2 |
| 7291 | plancheta | 2 |
| 7292 | pla | 2 |
| 7293 | pizarra | 2 |
| 7294 | pivote | 2 |
| 7295 | pistoletazo | 2 |
| 7296 | pisotón | 2 |
| 7297 | piñón | 2 |
| 7298 | pinturero | 2 |
| 7299 | pinchazo | 2 |
| 7300 | pincel | 2 |
| 7301 | piltrafa | 2 |
| 7302 | pildorita | 2 |
| 7303 | pilar | 2 |
| 7304 | pignorar | 2 |
| 7305 | pifiar | 2 |
| 7306 | piénselo | 2 |
| 7307 | piensas | 2 |
| 7308 | picos | 2 |
| 7309 | picado | 2 |
| 7310 | pezón | 2 |
| 7311 | petrolero | 2 |
| 7312 | petra | 2 |
| 7313 | petaca | 2 |
| 7314 | pestaña | 2 |
| 7315 | pescadero | 2 |
| 7316 | pesadez | 2 |
| 7317 | pesadamente | 2 |
| 7318 | perversión | 2 |
| 7319 | pertinente | 2 |
| 7320 | persuasiva | 2 |
| 7321 | persuadir | 2 |
| 7322 | personificar | 2 |
| 7323 | personalmente | 2 |
| 7324 | personalizar | 2 |
| 7325 | perseverancia | 2 |
| 7326 | perrillo | 2 |
| 7327 | perrada | 2 |
| 7328 | perpetuar | 2 |
| 7329 | perorata | 2 |
| 7330 | perol | 2 |
| 7331 | periodismo | 2 |
| 7332 | periódicamente | 2 |
| 7333 | perilla | 2 |
| 7334 | perfumar | 2 |
| 7335 | perfilar | 2 |
| 7336 | pereza | 2 |
| 7337 | perdurable | 2 |
| 7338 | perdóneme | 2 |
| 7339 | perdóname | 2 |
| 7340 | perchero | 2 |
| 7341 | pequeñez | 2 |
| 7342 | pepita | 2 |
| 7343 | penumbra | 2 |
| 7344 | penique | 2 |
| 7345 | península | 2 |
| 7346 | peneque | 2 |
| 7347 | pelotazo | 2 |
| 7348 | pella | 2 |
| 7349 | peletería | 2 |
| 7350 | pelayo | 2 |
| 7351 | peces | 2 |
| 7352 | pavoroso | 2 |
| 7353 | pavor | 2 |
| 7354 | pava | 2 |
| 7355 | paul | 2 |
| 7356 | patriótico | 2 |
| 7357 | patrio | 2 |
| 7358 | patriarcal | 2 |
| 7359 | patológico | 2 |
| 7360 | pataleta | 2 |
| 7361 | pastoral | 2 |
| 7362 | pastora | 2 |
| 7363 | pastelería | 2 |
| 7364 | pasos | 2 |
| 7365 | pasó | 2 |
| 7366 | pasivo | 2 |
| 7367 | pasamanos | 2 |
| 7368 | partícipe | 2 |
| 7369 | partición | 2 |
| 7370 | partes | 2 |
| 7371 | parson | 2 |
| 7372 | parrilla | 2 |
| 7373 | parral | 2 |
| 7374 | parque | 2 |
| 7375 | parose | 2 |
| 7376 | parlamento | 2 |
| 7377 | parejo | 2 |
| 7378 | parecíame | 2 |
| 7379 | parecía | 2 |
| 7380 | pardos | 2 |
| 7381 | pararrayos | 2 |
| 7382 | paralizar | 2 |
| 7383 | paralítico | 2 |
| 7384 | paradoja | 2 |
| 7385 | paradero | 2 |
| 7386 | parábola | 2 |
| 7387 | parabién | 2 |
| 7388 | paparrucha | 2 |
| 7389 | papamoscas | 2 |
| 7390 | pañolón | 2 |
| 7391 | pañería | 2 |
| 7392 | panza | 2 |
| 7393 | panorama | 2 |
| 7394 | panecillo | 2 |
| 7395 | pamplina | 2 |
| 7396 | pamema | 2 |
| 7397 | palote | 2 |
| 7398 | palmita | 2 |
| 7399 | palmatoria | 2 |
| 7400 | palmario | 2 |
| 7401 | paliza | 2 |
| 7402 | palio | 2 |
| 7403 | paletada | 2 |
| 7404 | palabrería | 2 |
| 7405 | pala | 2 |
| 7406 | pajel | 2 |
| 7407 | pajarito | 2 |
| 7408 | pajarita | 2 |
| 7409 | pajarete | 2 |
| 7410 | paisano | 2 |
| 7411 | paices | 2 |
| 7412 | pae | 2 |
| 7413 | padillita | 2 |
| 7414 | paciente | 2 |
| 7415 | pacer | 2 |
| 7416 | pa | 2 |
| 7417 | oyéronse | 2 |
| 7418 | oyente | 2 |
| 7419 | osuna | 2 |
| 7420 | oscilar | 2 |
| 7421 | osadía | 2 |
| 7422 | ortografía | 2 |
| 7423 | ortiz | 2 |
| 7424 | originalidad | 2 |
| 7425 | oriental | 2 |
| 7426 | organismo | 2 |
| 7427 | orfila | 2 |
| 7428 | orejita | 2 |
| 7429 | orear | 2 |
| 7430 | ordinariamente | 2 |
| 7431 | ordenanza | 2 |
| 7432 | ordenada | 2 |
| 7433 | órdago | 2 |
| 7434 | oratorio | 2 |
| 7435 | oratoria | 2 |
| 7436 | orán | 2 |
| 7437 | opuesto | 2 |
| 7438 | optimista | 2 |
| 7439 | oportunidad | 2 |
| 7440 | opaco | 2 |
| 7441 | olfatear | 2 |
| 7442 | ojival | 2 |
| 7443 | ojazos | 2 |
| 7444 | oída | 2 |
| 7445 | oíanse | 2 |
| 7446 | oí | 2 |
| 7447 | ochocientos | 2 |
| 7448 | occidente | 2 |
| 7449 | occidental | 2 |
| 7450 | obstruccionar | 2 |
| 7451 | observancia | 2 |
| 7452 | objetivo | 2 |
| 7453 | nupcial | 2 |
| 7454 | núñez | 2 |
| 7455 | numerar | 2 |
| 7456 | numen | 2 |
| 7457 | nuestra | 2 |
| 7458 | nuca | 2 |
| 7459 | nublar | 2 |
| 7460 | novísimo | 2 |
| 7461 | novillo | 2 |
| 7462 | noviazgo | 2 |
| 7463 | noventa | 2 |
| 7464 | novelista | 2 |
| 7465 | novelero | 2 |
| 7466 | novar | 2 |
| 7467 | normalmente | 2 |
| 7468 | nombramiento | 2 |
| 7469 | noé | 2 |
| 7470 | noches | 2 |
| 7471 | niñera | 2 |
| 7472 | ninguno | 2 |
| 7473 | nicho | 2 |
| 7474 | nicarona | 2 |
| 7475 | neri | 2 |
| 7476 | nena | 2 |
| 7477 | negose | 2 |
| 7478 | necesariamente | 2 |
| 7479 | nebulosa | 2 |
| 7480 | nazareno | 2 |
| 7481 | navegar | 2 |
| 7482 | navaja | 2 |
| 7483 | naufragio | 2 |
| 7484 | naturalismo | 2 |
| 7485 | narices | 2 |
| 7486 | nápoles | 2 |
| 7487 | nalga | 2 |
| 7488 | naciente | 2 |
| 7489 | nabucodonosor | 2 |
| 7490 | mujerzuela | 2 |
| 7491 | mujeril | 2 |
| 7492 | mugir | 2 |
| 7493 | muerta | 2 |
| 7494 | muda | 2 |
| 7495 | movilidad | 2 |
| 7496 | movible | 2 |
| 7497 | motejar | 2 |
| 7498 | mostaza | 2 |
| 7499 | morriña | 2 |
| 7500 | morrazo | 2 |
| 7501 | mormón | 2 |
| 7502 | morisco | 2 |
| 7503 | morfina | 2 |
| 7504 | morcilla | 2 |
| 7505 | morboso | 2 |
| 7506 | moralista | 2 |
| 7507 | moraleja | 2 |
| 7508 | monstruoso | 2 |
| 7509 | monomaniaco | 2 |
| 7510 | monólogo | 2 |
| 7511 | monjil | 2 |
| 7512 | monería | 2 |
| 7513 | mondongo | 2 |
| 7514 | monaguillo | 2 |
| 7515 | molinete | 2 |
| 7516 | mojado | 2 |
| 7517 | mohoso | 2 |
| 7518 | modoso | 2 |
| 7519 | modificar | 2 |
| 7520 | moco | 2 |
| 7521 | mitra | 2 |
| 7522 | mitología | 2 |
| 7523 | misericordioso | 2 |
| 7524 | misantropía | 2 |
| 7525 | mirolo | 2 |
| 7526 | mírela | 2 |
| 7527 | míralos | 2 |
| 7528 | mírala | 2 |
| 7529 | mirado | 2 |
| 7530 | mirábale | 2 |
| 7531 | mirábalas | 2 |
| 7532 | minio | 2 |
| 7533 | mínimo | 2 |
| 7534 | mineral | 2 |
| 7535 | mímica | 2 |
| 7536 | mimbre | 2 |
| 7537 | miliciano | 2 |
| 7538 | mías | 2 |
| 7539 | mia | 2 |
| 7540 | metafísico | 2 |
| 7541 | metafísica | 2 |
| 7542 | merienda | 2 |
| 7543 | merengar | 2 |
| 7544 | merendar | 2 |
| 7545 | merecido | 2 |
| 7546 | mercurial | 2 |
| 7547 | mercader | 2 |
| 7548 | meñique | 2 |
| 7549 | mentirijilla | 2 |
| 7550 | mensajero | 2 |
| 7551 | menosprecio | 2 |
| 7552 | menestra | 2 |
| 7553 | menesteroso | 2 |
| 7554 | mendizábal | 2 |
| 7555 | mendigar | 2 |
| 7556 | mencionar | 2 |
| 7557 | mención | 2 |
| 7558 | mena | 2 |
| 7559 | memorial | 2 |
| 7560 | melómano | 2 |
| 7561 | melodramático | 2 |
| 7562 | melodrama | 2 |
| 7563 | melenudo | 2 |
| 7564 | mejorcito | 2 |
| 7565 | médula | 2 |
| 7566 | medroso | 2 |
| 7567 | mediterráneo | 2 |
| 7568 | medianamente | 2 |
| 7569 | mediados | 2 |
| 7570 | mediación | 2 |
| 7571 | mecha | 2 |
| 7572 | mecer | 2 |
| 7573 | meca | 2 |
| 7574 | maza | 2 |
| 7575 | mausoleo | 2 |
| 7576 | matrona | 2 |
| 7577 | matriz | 2 |
| 7578 | matiz | 2 |
| 7579 | matinal | 2 |
| 7580 | matilde | 2 |
| 7581 | materialidad | 2 |
| 7582 | matemático | 2 |
| 7583 | matarme | 2 |
| 7584 | mastín | 2 |
| 7585 | masticación | 2 |
| 7586 | masónico | 2 |
| 7587 | martos | 2 |
| 7588 | martínez | 2 |
| 7589 | martillar | 2 |
| 7590 | marrano | 2 |
| 7591 | marranada | 2 |
| 7592 | marino | 2 |
| 7593 | marinero | 2 |
| 7594 | marina | 2 |
| 7595 | marchitar | 2 |
| 7596 | márchese | 2 |
| 7597 | maravillosamente | 2 |
| 7598 | maraña | 2 |
| 7599 | maquinaria | 2 |
| 7600 | maño | 2 |
| 7601 | manteo | 2 |
| 7602 | mantelería | 2 |
| 7603 | manso | 2 |
| 7604 | manosear | 2 |
| 7605 | manojo | 2 |
| 7606 | manjavacas | 2 |
| 7607 | manjar | 2 |
| 7608 | manirroto | 2 |
| 7609 | manir | 2 |
| 7610 | maneras | 2 |
| 7611 | manejo | 2 |
| 7612 | mandamiento | 2 |
| 7613 | manda | 2 |
| 7614 | manchego | 2 |
| 7615 | manaza | 2 |
| 7616 | manada | 2 |
| 7617 | mamotreto | 2 |
| 7618 | mamón | 2 |
| 7619 | maltrecho | 2 |
| 7620 | maltratado | 2 |
| 7621 | malla | 2 |
| 7622 | malestar | 2 |
| 7623 | maleante | 2 |
| 7624 | maldecir | 2 |
| 7625 | majadería | 2 |
| 7626 | magistral | 2 |
| 7627 | magia | 2 |
| 7628 | madrugón | 2 |
| 7629 | madrugador | 2 |
| 7630 | madrina | 2 |
| 7631 | mácula | 2 |
| 7632 | machacón | 2 |
| 7633 | luterano | 2 |
| 7634 | lunático | 2 |
| 7635 | luengo | 2 |
| 7636 | lucrativo | 2 |
| 7637 | lucimiento | 2 |
| 7638 | lucero | 2 |
| 7639 | lote | 2 |
| 7640 | lópez | 2 |
| 7641 | lontananza | 2 |
| 7642 | lonja | 2 |
| 7643 | lombarda | 2 |
| 7644 | locomotora | 2 |
| 7645 | llorón | 2 |
| 7646 | llevándose | 2 |
| 7647 | llevadero | 2 |
| 7648 | llegaría | 2 |
| 7649 | llamarme | 2 |
| 7650 | llamarada | 2 |
| 7651 | llamador | 2 |
| 7652 | llamábanla | 2 |
| 7653 | llama | 2 |
| 7654 | llaga | 2 |
| 7655 | liviandad | 2 |
| 7656 | litro | 2 |
| 7657 | liquidar | 2 |
| 7658 | liquidación | 2 |
| 7659 | linterna | 2 |
| 7660 | lince | 2 |
| 7661 | limpión | 2 |
| 7662 | limón | 2 |
| 7663 | liebre | 2 |
| 7664 | licenciar | 2 |
| 7665 | librote | 2 |
| 7666 | lía | 2 |
| 7667 | levemente | 2 |
| 7668 | levar | 2 |
| 7669 | levante | 2 |
| 7670 | letras | 2 |
| 7671 | leonés | 2 |
| 7672 | lentitud | 2 |
| 7673 | lema | 2 |
| 7674 | lebrel | 2 |
| 7675 | lazareto | 2 |
| 7676 | lava | 2 |
| 7677 | lastrar | 2 |
| 7678 | larguísimo | 2 |
| 7679 | laredo | 2 |
| 7680 | lamer | 2 |
| 7681 | lamentable | 2 |
| 7682 | lagarto | 2 |
| 7683 | lagarta | 2 |
| 7684 | ladino | 2 |
| 7685 | laciar | 2 |
| 7686 | labrador | 2 |
| 7687 | laborioso | 2 |
| 7688 | laberinto | 2 |
| 7689 | laberíntico | 2 |
| 7690 | kock | 2 |
| 7691 | king | 2 |
| 7692 | juvenil | 2 |
| 7693 | justificar | 2 |
| 7694 | justiciero | 2 |
| 7695 | juramentar | 2 |
| 7696 | jura | 2 |
| 7697 | judicial | 2 |
| 7698 | jornal | 2 |
| 7699 | jicarazo | 2 |
| 7700 | jeroglífico | 2 |
| 7701 | jerarquía | 2 |
| 7702 | jayán | 2 |
| 7703 | javiera | 2 |
| 7704 | jaleo | 2 |
| 7705 | jactar | 2 |
| 7706 | jactábase | 2 |
| 7707 | italia | 2 |
| 7708 | irún | 2 |
| 7709 | irresponsable | 2 |
| 7710 | irreparable | 2 |
| 7711 | irradiación | 2 |
| 7712 | irónico | 2 |
| 7713 | iremos | 2 |
| 7714 | inyectar | 2 |
| 7715 | invocación | 2 |
| 7716 | invento | 2 |
| 7717 | inventario | 2 |
| 7718 | invasión | 2 |
| 7719 | invariablemente | 2 |
| 7720 | invariable | 2 |
| 7721 | inútilmente | 2 |
| 7722 | inutilidad | 2 |
| 7723 | intervalo | 2 |
| 7724 | interrogación | 2 |
| 7725 | interpretación | 2 |
| 7726 | intermediario | 2 |
| 7727 | interceptar | 2 |
| 7728 | intelectualmente | 2 |
| 7729 | insustancial | 2 |
| 7730 | insurgente | 2 |
| 7731 | ínsula | 2 |
| 7732 | instintivo | 2 |
| 7733 | instantáneamente | 2 |
| 7734 | instaláronse | 2 |
| 7735 | instalación | 2 |
| 7736 | inspector | 2 |
| 7737 | inspeccionar | 2 |
| 7738 | insolvencia | 2 |
| 7739 | insolencia | 2 |
| 7740 | insinuar | 2 |
| 7741 | inservible | 2 |
| 7742 | inseguridad | 2 |
| 7743 | inquisición | 2 |
| 7744 | inquirir | 2 |
| 7745 | inquina | 2 |
| 7746 | inmortalidad | 2 |
| 7747 | inmortal | 2 |
| 7748 | inmoral | 2 |
| 7749 | injusto | 2 |
| 7750 | inicial | 2 |
| 7751 | iniciador | 2 |
| 7752 | inhábil | 2 |
| 7753 | ingresar | 2 |
| 7754 | ingrediente | 2 |
| 7755 | ingenuamente | 2 |
| 7756 | infernar | 2 |
| 7757 | infausto | 2 |
| 7758 | infatigable | 2 |
| 7759 | infamante | 2 |
| 7760 | inestimable | 2 |
| 7761 | inesperado | 2 |
| 7762 | inepto | 2 |
| 7763 | ineficacia | 2 |
| 7764 | ineducado | 2 |
| 7765 | indulto | 2 |
| 7766 | indiscutible | 2 |
| 7767 | indiscreto | 2 |
| 7768 | indiscreción | 2 |
| 7769 | indirecto | 2 |
| 7770 | indirecta | 2 |
| 7771 | indicado | 2 |
| 7772 | indemnizar | 2 |
| 7773 | indemnización | 2 |
| 7774 | indefinidamente | 2 |
| 7775 | indecencia | 2 |
| 7776 | inculto | 2 |
| 7777 | increpar | 2 |
| 7778 | inconscientemente | 2 |
| 7779 | inconmensurable | 2 |
| 7780 | incompleto | 2 |
| 7781 | incoherente | 2 |
| 7782 | incluir | 2 |
| 7783 | incidente | 2 |
| 7784 | incendiar | 2 |
| 7785 | incansable | 2 |
| 7786 | inapetencia | 2 |
| 7787 | inacabable | 2 |
| 7788 | improvisado | 2 |
| 7789 | impresionable | 2 |
| 7790 | imprentar | 2 |
| 7791 | imprenta | 2 |
| 7792 | importador | 2 |
| 7793 | imponente | 2 |
| 7794 | implorar | 2 |
| 7795 | imperceptible | 2 |
| 7796 | impavidez | 2 |
| 7797 | ilusorio | 2 |
| 7798 | igualdad | 2 |
| 7799 | idilio | 2 |
| 7800 | idéntico | 2 |
| 7801 | ideación | 2 |
| 7802 | hurtadillas | 2 |
| 7803 | huraño | 2 |
| 7804 | hundido | 2 |
| 7805 | humildemente | 2 |
| 7806 | húmera | 2 |
| 7807 | huéspeda | 2 |
| 7808 | hubiérase | 2 |
| 7809 | hubiera | 2 |
| 7810 | hostilidad | 2 |
| 7811 | hostil | 2 |
| 7812 | hostigar | 2 |
| 7813 | hortaliza | 2 |
| 7814 | horroroso | 2 |
| 7815 | hornillo | 2 |
| 7816 | hormigueo | 2 |
| 7817 | horchata | 2 |
| 7818 | horcar | 2 |
| 7819 | honroso | 2 |
| 7820 | hondura | 2 |
| 7821 | hondamente | 2 |
| 7822 | homicida | 2 |
| 7823 | holgura | 2 |
| 7824 | holgazán | 2 |
| 7825 | hocicudo | 2 |
| 7826 | hocicar | 2 |
| 7827 | hízose | 2 |
| 7828 | hízole | 2 |
| 7829 | historiar | 2 |
| 7830 | hipoteca | 2 |
| 7831 | hipocrático | 2 |
| 7832 | hiperbólico | 2 |
| 7833 | hincar | 2 |
| 7834 | hincapié | 2 |
| 7835 | hilada | 2 |
| 7836 | hidalguía | 2 |
| 7837 | hidalgo | 2 |
| 7838 | heterogeneidad | 2 |
| 7839 | hervidero | 2 |
| 7840 | heroína | 2 |
| 7841 | heroico | 2 |
| 7842 | hernán | 2 |
| 7843 | herméticamente | 2 |
| 7844 | herejía | 2 |
| 7845 | hemos | 2 |
| 7846 | hazaña | 2 |
| 7847 | haré | 2 |
| 7848 | han | 2 |
| 7849 | hallábanse | 2 |
| 7850 | hacha | 2 |
| 7851 | hablose | 2 |
| 7852 | hablilla | 2 |
| 7853 | habitar | 2 |
| 7854 | habilidoso | 2 |
| 7855 | habíase | 2 |
| 7856 | habéis | 2 |
| 7857 | gutural | 2 |
| 7858 | gustábale | 2 |
| 7859 | gusano | 2 |
| 7860 | guitarrear | 2 |
| 7861 | guisa | 2 |
| 7862 | guiño | 2 |
| 7863 | guillotinar | 2 |
| 7864 | gubernamental | 2 |
| 7865 | guarida | 2 |
| 7866 | guapeza | 2 |
| 7867 | groseramente | 2 |
| 7868 | gro | 2 |
| 7869 | gritaba | 2 |
| 7870 | grillera | 2 |
| 7871 | greda | 2 |
| 7872 | granuloso | 2 |
| 7873 | granujería | 2 |
| 7874 | grandes | 2 |
| 7875 | granada | 2 |
| 7876 | grana | 2 |
| 7877 | gramo | 2 |
| 7878 | gramática | 2 |
| 7879 | gradual | 2 |
| 7880 | goma | 2 |
| 7881 | glóbulo | 2 |
| 7882 | gitano | 2 |
| 7883 | gitanesco | 2 |
| 7884 | gibraltar | 2 |
| 7885 | getafe | 2 |
| 7886 | gestar | 2 |
| 7887 | genial | 2 |
| 7888 | gelatinoso | 2 |
| 7889 | gaveta | 2 |
| 7890 | gatuperio | 2 |
| 7891 | gatería | 2 |
| 7892 | gárrulo | 2 |
| 7893 | garrote | 2 |
| 7894 | garrafal | 2 |
| 7895 | garbo | 2 |
| 7896 | garantía | 2 |
| 7897 | gancho | 2 |
| 7898 | ganado | 2 |
| 7899 | gama | 2 |
| 7900 | gallardía | 2 |
| 7901 | galápago | 2 |
| 7902 | galantería | 2 |
| 7903 | gaita | 2 |
| 7904 | gabacho | 2 |
| 7905 | funeral | 2 |
| 7906 | fundir | 2 |
| 7907 | fundamentar | 2 |
| 7908 | fundación | 2 |
| 7909 | fugar | 2 |
| 7910 | fuertecillo | 2 |
| 7911 | fuer | 2 |
| 7912 | fuelle | 2 |
| 7913 | frustrar | 2 |
| 7914 | fruncimiento | 2 |
| 7915 | frontal | 2 |
| 7916 | friega | 2 |
| 7917 | frescachón | 2 |
| 7918 | fresar | 2 |
| 7919 | fray | 2 |
| 7920 | francesilla | 2 |
| 7921 | frac | 2 |
| 7922 | fotografiar | 2 |
| 7923 | fosfato | 2 |
| 7924 | forzosamente | 2 |
| 7925 | fortísimo | 2 |
| 7926 | forraje | 2 |
| 7927 | fornos | 2 |
| 7928 | fornido | 2 |
| 7929 | formalito | 2 |
| 7930 | forjar | 2 |
| 7931 | forcejear | 2 |
| 7932 | foco | 2 |
| 7933 | fluir | 2 |
| 7934 | fluctuar | 2 |
| 7935 | flotante | 2 |
| 7936 | florín | 2 |
| 7937 | florear | 2 |
| 7938 | flojilla | 2 |
| 7939 | flequillo | 2 |
| 7940 | flamenco | 2 |
| 7941 | fisiológico | 2 |
| 7942 | física | 2 |
| 7943 | fisgón | 2 |
| 7944 | firmemente | 2 |
| 7945 | finito | 2 |
| 7946 | filigrana | 2 |
| 7947 | filar | 2 |
| 7948 | fijose | 2 |
| 7949 | fijeza | 2 |
| 7950 | figurita | 2 |
| 7951 | figúrese | 2 |
| 7952 | fieltro | 2 |
| 7953 | feudal | 2 |
| 7954 | festín | 2 |
| 7955 | ferretero | 2 |
| 7956 | felicitación | 2 |
| 7957 | felicísimo | 2 |
| 7958 | fecundidad | 2 |
| 7959 | favorecido | 2 |
| 7960 | fatuo | 2 |
| 7961 | fatídico | 2 |
| 7962 | fastidioso | 2 |
| 7963 | fascinar | 2 |
| 7964 | faro | 2 |
| 7965 | fanfarronada | 2 |
| 7966 | fandango | 2 |
| 7967 | familiarmente | 2 |
| 7968 | faltábale | 2 |
| 7969 | fallir | 2 |
| 7970 | faja | 2 |
| 7971 | facturar | 2 |
| 7972 | faceta | 2 |
| 7973 | fabulista | 2 |
| 7974 | fabricación | 2 |
| 7975 | extremeño | 2 |
| 7976 | extremado | 2 |
| 7977 | extraviado | 2 |
| 7978 | extinguido | 2 |
| 7979 | exterminio | 2 |
| 7980 | extenso | 2 |
| 7981 | expulsión | 2 |
| 7982 | exposición | 2 |
| 7983 | explotación | 2 |
| 7984 | explayar | 2 |
| 7985 | expiar | 2 |
| 7986 | experto | 2 |
| 7987 | experimento | 2 |
| 7988 | expeditivo | 2 |
| 7989 | expedir | 2 |
| 7990 | expedición | 2 |
| 7991 | eximio | 2 |
| 7992 | exhortación | 2 |
| 7993 | exhibir | 2 |
| 7994 | execrable | 2 |
| 7995 | excusa | 2 |
| 7996 | excursionar | 2 |
| 7997 | exclamaba | 2 |
| 7998 | excepcional | 2 |
| 7999 | excelencia | 2 |
| 8000 | eucaristía | 2 |
| 8001 | etiquetar | 2 |
| 8002 | etéreo | 2 |
| 8003 | estúpidamente | 2 |
| 8004 | estropajoso | 2 |
| 8005 | estricnina | 2 |
| 8006 | estribo | 2 |
| 8007 | estrangular | 2 |
| 8008 | estrago | 2 |
| 8009 | estragado | 2 |
| 8010 | estornudo | 2 |
| 8011 | estoico | 2 |
| 8012 | estocada | 2 |
| 8013 | estirpe | 2 |
| 8014 | estirado | 2 |
| 8015 | estímulo | 2 |
| 8016 | estima | 2 |
| 8017 | estiércol | 2 |
| 8018 | estertor | 2 |
| 8019 | estéril | 2 |
| 8020 | estático | 2 |
| 8021 | estate | 2 |
| 8022 | estarcido | 2 |
| 8023 | estarás | 2 |
| 8024 | estará | 2 |
| 8025 | estafa | 2 |
| 8026 | estacionar | 2 |
| 8027 | espumarajo | 2 |
| 8028 | espliego | 2 |
| 8029 | espiritualmente | 2 |
| 8030 | espiral | 2 |
| 8031 | espionaje | 2 |
| 8032 | espina | 2 |
| 8033 | espichar | 2 |
| 8034 | esperaré | 2 |
| 8035 | espasmo | 2 |
| 8036 | esparteros | 2 |
| 8037 | espantable | 2 |
| 8038 | eslabón | 2 |
| 8039 | esférico | 2 |
| 8040 | esfera | 2 |
| 8041 | esencialmente | 2 |
| 8042 | escueto | 2 |
| 8043 | escudar | 2 |
| 8044 | escrutinio | 2 |
| 8045 | escrutador | 2 |
| 8046 | escondidos | 2 |
| 8047 | escombro | 2 |
| 8048 | escolta | 2 |
| 8049 | esclavizar | 2 |
| 8050 | esclavina | 2 |
| 8051 | escepticismo | 2 |
| 8052 | escenario | 2 |
| 8053 | escayola | 2 |
| 8054 | escasear | 2 |
| 8055 | escarbar | 2 |
| 8056 | escapada | 2 |
| 8057 | escandalosa | 2 |
| 8058 | escamotear | 2 |
| 8059 | escamar | 2 |
| 8060 | escabechar | 2 |
| 8061 | esbelto | 2 |
| 8062 | erizado | 2 |
| 8063 | eran | 2 |
| 8064 | equipo | 2 |
| 8065 | equidad | 2 |
| 8066 | epístola | 2 |
| 8067 | epidermis | 2 |
| 8068 | enviciar | 2 |
| 8069 | entrecortar | 2 |
| 8070 | entráronle | 2 |
| 8071 | entrabar | 2 |
| 8072 | entonación | 2 |
| 8073 | ensueño | 2 |
| 8074 | ensordecer | 2 |
| 8075 | ensoberbecer | 2 |
| 8076 | ensayar | 2 |
| 8077 | ensalzar | 2 |
| 8078 | ensalmo | 2 |
| 8079 | ensaladera | 2 |
| 8080 | enrojecer | 2 |
| 8081 | enriquecer | 2 |
| 8082 | enorgullecer | 2 |
| 8083 | enojado | 2 |
| 8084 | enmudecer | 2 |
| 8085 | enlutar | 2 |
| 8086 | enjambre | 2 |
| 8087 | enhebrar | 2 |
| 8088 | engrudo | 2 |
| 8089 | engrosar | 2 |
| 8090 | engolfar | 2 |
| 8091 | engendrar | 2 |
| 8092 | enganchar | 2 |
| 8093 | engalanar | 2 |
| 8094 | enfado | 2 |
| 8095 | enea | 2 |
| 8096 | endurecido | 2 |
| 8097 | endulzar | 2 |
| 8098 | endemoniar | 2 |
| 8099 | encopetado | 2 |
| 8100 | encontradizo | 2 |
| 8101 | encomendar | 2 |
| 8102 | encogido | 2 |
| 8103 | encharcar | 2 |
| 8104 | encerrose | 2 |
| 8105 | encarecer | 2 |
| 8106 | encaprichar | 2 |
| 8107 | encantador | 2 |
| 8108 | encanijar | 2 |
| 8109 | encanallar | 2 |
| 8110 | encamar | 2 |
| 8111 | encadenamiento | 2 |
| 8112 | empujón | 2 |
| 8113 | empréstito | 2 |
| 8114 | emprendedor | 2 |
| 8115 | empobrecer | 2 |
| 8116 | emplastar | 2 |
| 8117 | emperejilar | 2 |
| 8118 | empeorar | 2 |
| 8119 | empedrar | 2 |
| 8120 | empedrado | 2 |
| 8121 | empedernir | 2 |
| 8122 | empalmar | 2 |
| 8123 | emitir | 2 |
| 8124 | emético | 2 |
| 8125 | embrutecimiento | 2 |
| 8126 | embrujar | 2 |
| 8127 | embocar | 2 |
| 8128 | embobar | 2 |
| 8129 | embestida | 2 |
| 8130 | embeleso | 2 |
| 8131 | embelesado | 2 |
| 8132 | embarcación | 2 |
| 8133 | embajada | 2 |
| 8134 | embadurnar | 2 |
| 8135 | elevado | 2 |
| 8136 | electoral | 2 |
| 8137 | elástico | 2 |
| 8138 | elaborar | 2 |
| 8139 | ejemplaridad | 2 |
| 8140 | ejecutivo | 2 |
| 8141 | ejecutar | 2 |
| 8142 | egoistón | 2 |
| 8143 | egoísta | 2 |
| 8144 | egipto | 2 |
| 8145 | efigie | 2 |
| 8146 | eficacia | 2 |
| 8147 | edredón | 2 |
| 8148 | editor | 2 |
| 8149 | economista | 2 |
| 8150 | echábaselas | 2 |
| 8151 | duramente | 2 |
| 8152 | duérmete | 2 |
| 8153 | duchar | 2 |
| 8154 | doscientas | 2 |
| 8155 | dorregaray | 2 |
| 8156 | dormilón | 2 |
| 8157 | domesticar | 2 |
| 8158 | docto | 2 |
| 8159 | docilidad | 2 |
| 8160 | dócil | 2 |
| 8161 | doceno | 2 |
| 8162 | doblez | 2 |
| 8163 | divorciar | 2 |
| 8164 | dividendo | 2 |
| 8165 | disuadir | 2 |
| 8166 | distintivo | 2 |
| 8167 | dispersar | 2 |
| 8168 | dispepsia | 2 |
| 8169 | disparidad | 2 |
| 8170 | disparado | 2 |
| 8171 | disparadero | 2 |
| 8172 | disfavor | 2 |
| 8173 | discrepar | 2 |
| 8174 | disciplinario | 2 |
| 8175 | diríale | 2 |
| 8176 | diretes | 2 |
| 8177 | dirá | 2 |
| 8178 | dimisión | 2 |
| 8179 | diminutivo | 2 |
| 8180 | dimes | 2 |
| 8181 | dilema | 2 |
| 8182 | díjome | 2 |
| 8183 | dígole | 2 |
| 8184 | difuso | 2 |
| 8185 | diego | 2 |
| 8186 | diciéndolo | 2 |
| 8187 | diapasón | 2 |
| 8188 | deudo | 2 |
| 8189 | detuviéronse | 2 |
| 8190 | detenidamente | 2 |
| 8191 | detallar | 2 |
| 8192 | desvergonzar | 2 |
| 8193 | desventaja | 2 |
| 8194 | desvalido | 2 |
| 8195 | destreza | 2 |
| 8196 | destilar | 2 |
| 8197 | desquiciar | 2 |
| 8198 | despuntar | 2 |
| 8199 | desprestigiar | 2 |
| 8200 | despreciable | 2 |
| 8201 | despótico | 2 |
| 8202 | déspota | 2 |
| 8203 | desposar | 2 |
| 8204 | despojar | 2 |
| 8205 | despidiéronse | 2 |
| 8206 | desperezar | 2 |
| 8207 | desperdicio | 2 |
| 8208 | despejo | 2 |
| 8209 | despeinado | 2 |
| 8210 | despego | 2 |
| 8211 | despegar | 2 |
| 8212 | despedazar | 2 |
| 8213 | desparpajar | 2 |
| 8214 | desorientar | 2 |
| 8215 | desolación | 2 |
| 8216 | desocupar | 2 |
| 8217 | desmañado | 2 |
| 8218 | deslumbrar | 2 |
| 8219 | deslomar | 2 |
| 8220 | desligar | 2 |
| 8221 | desliar | 2 |
| 8222 | desleír | 2 |
| 8223 | deslealtad | 2 |
| 8224 | desinteresado | 2 |
| 8225 | desilusión | 2 |
| 8226 | deshonroso | 2 |
| 8227 | desgastar | 2 |
| 8228 | desgarrado | 2 |
| 8229 | desgarbado | 2 |
| 8230 | desgajar | 2 |
| 8231 | desgaire | 2 |
| 8232 | desentumecer | 2 |
| 8233 | desenroscar | 2 |
| 8234 | desenojar | 2 |
| 8235 | desengaño | 2 |
| 8236 | desecho | 2 |
| 8237 | desdoblar | 2 |
| 8238 | descrédito | 2 |
| 8239 | descortés | 2 |
| 8240 | descorrer | 2 |
| 8241 | descorazonar | 2 |
| 8242 | descontar | 2 |
| 8243 | desconcertado | 2 |
| 8244 | descomunal | 2 |
| 8245 | descolorido | 2 |
| 8246 | descendiente | 2 |
| 8247 | descendencia | 2 |
| 8248 | descaro | 2 |
| 8249 | descarga | 2 |
| 8250 | descaradamente | 2 |
| 8251 | desbordamiento | 2 |
| 8252 | desbarrar | 2 |
| 8253 | desbandar | 2 |
| 8254 | desavenencia | 2 |
| 8255 | desastroso | 2 |
| 8256 | desastre | 2 |
| 8257 | desasosegado | 2 |
| 8258 | desarreglar | 2 |
| 8259 | desamparado | 2 |
| 8260 | desafinar | 2 |
| 8261 | desacreditar | 2 |
| 8262 | derrumbar | 2 |
| 8263 | derrotar | 2 |
| 8264 | derrota | 2 |
| 8265 | derribo | 2 |
| 8266 | derretir | 2 |
| 8267 | derredor | 2 |
| 8268 | derogar | 2 |
| 8269 | depresión | 2 |
| 8270 | depreciación | 2 |
| 8271 | deplorar | 2 |
| 8272 | denuncia | 2 |
| 8273 | denso | 2 |
| 8274 | denominación | 2 |
| 8275 | demudar | 2 |
| 8276 | deme | 2 |
| 8277 | demagogia | 2 |
| 8278 | delineante | 2 |
| 8279 | delicadísimo | 2 |
| 8280 | dejándose | 2 |
| 8281 | déjale | 2 |
| 8282 | degradación | 2 |
| 8283 | degollar | 2 |
| 8284 | deformar | 2 |
| 8285 | definitivamente | 2 |
| 8286 | definición | 2 |
| 8287 | decretar | 2 |
| 8288 | dechado | 2 |
| 8289 | decálogo | 2 |
| 8290 | decaimiento | 2 |
| 8291 | decadencia | 2 |
| 8292 | debió | 2 |
| 8293 | debí | 2 |
| 8294 | dardo | 2 |
| 8295 | dañado | 2 |
| 8296 | danzar | 2 |
| 8297 | danza | 2 |
| 8298 | dámele | 2 |
| 8299 | dádiva | 2 |
| 8300 | da | 2 |
| 8301 | cutis | 2 |
| 8302 | curtis | 2 |
| 8303 | curtido | 2 |
| 8304 | cuota | 2 |
| 8305 | cúmulo | 2 |
| 8306 | cultura | 2 |
| 8307 | cuervo | 2 |
| 8308 | cuéntame | 2 |
| 8309 | cucurucho | 2 |
| 8310 | cubo | 2 |
| 8311 | cubilete | 2 |
| 8312 | cubierta | 2 |
| 8313 | cuarentena | 2 |
| 8314 | cuánta | 2 |
| 8315 | cuajarón | 2 |
| 8316 | cuadrilátero | 2 |
| 8317 | cuadernillo | 2 |
| 8318 | cruzada | 2 |
| 8319 | crucero | 2 |
| 8320 | cristina | 2 |
| 8321 | creyó | 2 |
| 8322 | créeme | 2 |
| 8323 | creciente | 2 |
| 8324 | créalo | 2 |
| 8325 | creación | 2 |
| 8326 | crea | 2 |
| 8327 | craso | 2 |
| 8328 | cotarro | 2 |
| 8329 | costurero | 2 |
| 8330 | corvo | 2 |
| 8331 | cortadillo | 2 |
| 8332 | corrupción | 2 |
| 8333 | corretear | 2 |
| 8334 | corredera | 2 |
| 8335 | correctamente | 2 |
| 8336 | correccional | 2 |
| 8337 | corporación | 2 |
| 8338 | corpacho | 2 |
| 8339 | cornisa | 2 |
| 8340 | cornezuelo | 2 |
| 8341 | cordón | 2 |
| 8342 | córdoba | 2 |
| 8343 | cordel | 2 |
| 8344 | corcho | 2 |
| 8345 | copita | 2 |
| 8346 | copioso | 2 |
| 8347 | cónyuge | 2 |
| 8348 | conviene | 2 |
| 8349 | conveníale | 2 |
| 8350 | convencido | 2 |
| 8351 | convaleciente | 2 |
| 8352 | convalecencia | 2 |
| 8353 | contusionar | 2 |
| 8354 | contusión | 2 |
| 8355 | controversia | 2 |
| 8356 | contrincante | 2 |
| 8357 | contrición | 2 |
| 8358 | contribuir | 2 |
| 8359 | contrata | 2 |
| 8360 | contrasentido | 2 |
| 8361 | contorsionar | 2 |
| 8362 | contorsión | 2 |
| 8363 | contole | 2 |
| 8364 | contemplativo | 2 |
| 8365 | contagio | 2 |
| 8366 | contador | 2 |
| 8367 | contabilidad | 2 |
| 8368 | consulta | 2 |
| 8369 | constructivo | 2 |
| 8370 | constitutivo | 2 |
| 8371 | constipar | 2 |
| 8372 | conspiración | 2 |
| 8373 | conservatorio | 2 |
| 8374 | conservarse | 2 |
| 8375 | consagración | 2 |
| 8376 | conozco | 2 |
| 8377 | conmovedor | 2 |
| 8378 | conmoción | 2 |
| 8379 | conmiseración | 2 |
| 8380 | conllevar | 2 |
| 8381 | congregar | 2 |
| 8382 | congojar | 2 |
| 8383 | confrontar | 2 |
| 8384 | confortar | 2 |
| 8385 | configuración | 2 |
| 8386 | confidente | 2 |
| 8387 | conductor | 2 |
| 8388 | condiciones | 2 |
| 8389 | condescendencia | 2 |
| 8390 | concubinato | 2 |
| 8391 | concreto | 2 |
| 8392 | concretar | 2 |
| 8393 | concordar | 2 |
| 8394 | conciliación | 2 |
| 8395 | concentrar | 2 |
| 8396 | cóncavo | 2 |
| 8397 | concavidad | 2 |
| 8398 | conato | 2 |
| 8399 | compungir | 2 |
| 8400 | comprimir | 2 |
| 8401 | componenda | 2 |
| 8402 | complicidad | 2 |
| 8403 | complaciente | 2 |
| 8404 | compinchar | 2 |
| 8405 | compenetrar | 2 |
| 8406 | comparsa | 2 |
| 8407 | comparativo | 2 |
| 8408 | cómoda | 2 |
| 8409 | comisionar | 2 |
| 8410 | comienzo | 2 |
| 8411 | cometido | 2 |
| 8412 | cometa | 2 |
| 8413 | comenzar | 2 |
| 8414 | comentar | 2 |
| 8415 | comediante | 2 |
| 8416 | comedero | 2 |
| 8417 | columbrar | 2 |
| 8418 | colorista | 2 |
| 8419 | colina | 2 |
| 8420 | colgado | 2 |
| 8421 | coleto | 2 |
| 8422 | colegir | 2 |
| 8423 | cojo | 2 |
| 8424 | cojita | 2 |
| 8425 | cojear | 2 |
| 8426 | coincidir | 2 |
| 8427 | cohonestar | 2 |
| 8428 | cohibido | 2 |
| 8429 | codear | 2 |
| 8430 | cocinilla | 2 |
| 8431 | cochino | 2 |
| 8432 | clínica | 2 |
| 8433 | claustral | 2 |
| 8434 | claraboya | 2 |
| 8435 | clamó | 2 |
| 8436 | civilizar | 2 |
| 8437 | civilizado | 2 |
| 8438 | cisterna | 2 |
| 8439 | cirio | 2 |
| 8440 | cinismo | 2 |
| 8441 | cielos | 2 |
| 8442 | ciegamente | 2 |
| 8443 | chusma | 2 |
| 8444 | chumbo | 2 |
| 8445 | chufa | 2 |
| 8446 | chubasco | 2 |
| 8447 | chocolatera | 2 |
| 8448 | chocante | 2 |
| 8449 | chispita | 2 |
| 8450 | chispeante | 2 |
| 8451 | chinito | 2 |
| 8452 | chilló | 2 |
| 8453 | chillería | 2 |
| 8454 | chiflado | 2 |
| 8455 | chi | 2 |
| 8456 | cheong | 2 |
| 8457 | chasquear | 2 |
| 8458 | charol | 2 |
| 8459 | charlatán | 2 |
| 8460 | charca | 2 |
| 8461 | chaqué | 2 |
| 8462 | chapuzar | 2 |
| 8463 | chanchullo | 2 |
| 8464 | chamusquina | 2 |
| 8465 | chalana | 2 |
| 8466 | cháchara | 2 |
| 8467 | cevil | 2 |
| 8468 | ceuta | 2 |
| 8469 | cesantía | 2 |
| 8470 | cervantes | 2 |
| 8471 | certidumbre | 2 |
| 8472 | certeza | 2 |
| 8473 | cerradura | 2 |
| 8474 | cerrados | 2 |
| 8475 | ceremonioso | 2 |
| 8476 | cerco | 2 |
| 8477 | cepillo | 2 |
| 8478 | centigramo | 2 |
| 8479 | centeno | 2 |
| 8480 | cencerrada | 2 |
| 8481 | celeste | 2 |
| 8482 | celebridad | 2 |
| 8483 | celaje | 2 |
| 8484 | celador | 2 |
| 8485 | cejijunto | 2 |
| 8486 | ceca | 2 |
| 8487 | caviloso | 2 |
| 8488 | cavador | 2 |
| 8489 | cautelar | 2 |
| 8490 | causante | 2 |
| 8491 | caudillo | 2 |
| 8492 | caudaloso | 2 |
| 8493 | categóricamente | 2 |
| 8494 | catarroso | 2 |
| 8495 | catálogo | 2 |
| 8496 | catadura | 2 |
| 8497 | castidad | 2 |
| 8498 | castellano | 2 |
| 8499 | castaño | 2 |
| 8500 | casino | 2 |
| 8501 | casillero | 2 |
| 8502 | casilla | 2 |
| 8503 | cascabel | 2 |
| 8504 | casarme | 2 |
| 8505 | casada | 2 |
| 8506 | cartucho | 2 |
| 8507 | cartero | 2 |
| 8508 | carros | 2 |
| 8509 | carretas | 2 |
| 8510 | carpintero | 2 |
| 8511 | carpeta | 2 |
| 8512 | carpanta | 2 |
| 8513 | carlismo | 2 |
| 8514 | cariz | 2 |
| 8515 | caricaturar | 2 |
| 8516 | caribe | 2 |
| 8517 | cargante | 2 |
| 8518 | cargamento | 2 |
| 8519 | cardo | 2 |
| 8520 | cárdenas | 2 |
| 8521 | cardenal | 2 |
| 8522 | carbonera | 2 |
| 8523 | carátula | 2 |
| 8524 | carantoña | 2 |
| 8525 | caracterizar | 2 |
| 8526 | cápsula | 2 |
| 8527 | caprichoso | 2 |
| 8528 | capón | 2 |
| 8529 | capitana | 2 |
| 8530 | capitán | 2 |
| 8531 | capitalista | 2 |
| 8532 | capacidad | 2 |
| 8533 | caoba | 2 |
| 8534 | cañamón | 2 |
| 8535 | cantante | 2 |
| 8536 | candorosamente | 2 |
| 8537 | candidez | 2 |
| 8538 | candelero | 2 |
| 8539 | candelabro | 2 |
| 8540 | canciller | 2 |
| 8541 | canal | 2 |
| 8542 | campar | 2 |
| 8543 | campante | 2 |
| 8544 | campanillazo | 2 |
| 8545 | camisería | 2 |
| 8546 | camelia | 2 |
| 8547 | cambiante | 2 |
| 8548 | camarero | 2 |
| 8549 | camarada | 2 |
| 8550 | calzonazos | 2 |
| 8551 | calza | 2 |
| 8552 | calvario | 2 |
| 8553 | caluroso | 2 |
| 8554 | calumniador | 2 |
| 8555 | calumnia | 2 |
| 8556 | callosa | 2 |
| 8557 | calificar | 2 |
| 8558 | calandria | 2 |
| 8559 | calambre | 2 |
| 8560 | calabozo | 2 |
| 8561 | caín | 2 |
| 8562 | cafre | 2 |
| 8563 | cachorro | 2 |
| 8564 | cacerola | 2 |
| 8565 | cacarear | 2 |
| 8566 | cabildo | 2 |
| 8567 | caballete | 2 |
| 8568 | caballerosidad | 2 |
| 8569 | cabal | 2 |
| 8570 | buscón | 2 |
| 8571 | burocrático | 2 |
| 8572 | burdo | 2 |
| 8573 | bullicioso | 2 |
| 8574 | bullanga | 2 |
| 8575 | bular | 2 |
| 8576 | bujía | 2 |
| 8577 | buey | 2 |
| 8578 | buenavista | 2 |
| 8579 | budista | 2 |
| 8580 | buche | 2 |
| 8581 | búcaro | 2 |
| 8582 | brutalidad | 2 |
| 8583 | bronca | 2 |
| 8584 | brocal | 2 |
| 8585 | brocado | 2 |
| 8586 | brindis | 2 |
| 8587 | brincar | 2 |
| 8588 | brígida | 2 |
| 8589 | bribona | 2 |
| 8590 | brevemente | 2 |
| 8591 | brazos | 2 |
| 8592 | bravura | 2 |
| 8593 | bozo | 2 |
| 8594 | botonadura | 2 |
| 8595 | botarate | 2 |
| 8596 | botaratada | 2 |
| 8597 | borrego | 2 |
| 8598 | borrachera | 2 |
| 8599 | borla | 2 |
| 8600 | bordado | 2 |
| 8601 | boquete | 2 |
| 8602 | boquear | 2 |
| 8603 | bono | 2 |
| 8604 | bonísimo | 2 |
| 8605 | bombo | 2 |
| 8606 | bolsista | 2 |
| 8607 | bollo | 2 |
| 8608 | bojío | 2 |
| 8609 | bofe | 2 |
| 8610 | bocaza | 2 |
| 8611 | bobería | 2 |
| 8612 | bobalicón | 2 |
| 8613 | bizma | 2 |
| 8614 | bizcocho | 2 |
| 8615 | biografía | 2 |
| 8616 | billar | 2 |
| 8617 | bierzo | 2 |
| 8618 | bienestar | 2 |
| 8619 | bienaventurado | 2 |
| 8620 | bienandanza | 2 |
| 8621 | besuquear | 2 |
| 8622 | berrinche | 2 |
| 8623 | bernardino | 2 |
| 8624 | bermellón | 2 |
| 8625 | bermejo | 2 |
| 8626 | berlina | 2 |
| 8627 | bellota | 2 |
| 8628 | bellísimo | 2 |
| 8629 | béjar | 2 |
| 8630 | beethoven | 2 |
| 8631 | bedmar | 2 |
| 8632 | beatriz | 2 |
| 8633 | beato | 2 |
| 8634 | bazofia | 2 |
| 8635 | batidor | 2 |
| 8636 | batería | 2 |
| 8637 | batallar | 2 |
| 8638 | basurero | 2 |
| 8639 | bastidor | 2 |
| 8640 | basilisco | 2 |
| 8641 | basar | 2 |
| 8642 | barrionuevo | 2 |
| 8643 | barrabás | 2 |
| 8644 | barbarie | 2 |
| 8645 | bando | 2 |
| 8646 | banderilla | 2 |
| 8647 | bandada | 2 |
| 8648 | banasta | 2 |
| 8649 | baldosa | 2 |
| 8650 | baldar | 2 |
| 8651 | balbuciente | 2 |
| 8652 | balar | 2 |
| 8653 | balanza | 2 |
| 8654 | balandrán | 2 |
| 8655 | balancín | 2 |
| 8656 | bajó | 2 |
| 8657 | bajeza | 2 |
| 8658 | badulaque | 2 |
| 8659 | babilla | 2 |
| 8660 | azulear | 2 |
| 8661 | azular | 2 |
| 8662 | azucarado | 2 |
| 8663 | azorado | 2 |
| 8664 | ayudante | 2 |
| 8665 | ayúdame | 2 |
| 8666 | avisado | 2 |
| 8667 | avío | 2 |
| 8668 | ávido | 2 |
| 8669 | averiguador | 2 |
| 8670 | averiguación | 2 |
| 8671 | avergonzado | 2 |
| 8672 | aventurero | 2 |
| 8673 | aventajar | 2 |
| 8674 | autocrático | 2 |
| 8675 | auscultar | 2 |
| 8676 | aumento | 2 |
| 8677 | aturdimiento | 2 |
| 8678 | atropello | 2 |
| 8679 | atropellado | 2 |
| 8680 | atrio | 2 |
| 8681 | atribuir | 2 |
| 8682 | atrapar | 2 |
| 8683 | atracar | 2 |
| 8684 | atolladero | 2 |
| 8685 | atinado | 2 |
| 8686 | atildar | 2 |
| 8687 | atestiguar | 2 |
| 8688 | aterrorizar | 2 |
| 8689 | atenuación | 2 |
| 8690 | atento | 2 |
| 8691 | atentado | 2 |
| 8692 | atemperar | 2 |
| 8693 | ataviar | 2 |
| 8694 | atascar | 2 |
| 8695 | atarugar | 2 |
| 8696 | atarear | 2 |
| 8697 | atadero | 2 |
| 8698 | asturiano | 2 |
| 8699 | astucia | 2 |
| 8700 | astro | 2 |
| 8701 | astorga | 2 |
| 8702 | aspar | 2 |
| 8703 | asomo | 2 |
| 8704 | asomáronse | 2 |
| 8705 | asignar | 2 |
| 8706 | asiduo | 2 |
| 8707 | aseveración | 2 |
| 8708 | asentador | 2 |
| 8709 | asemejar | 2 |
| 8710 | asechanza | 2 |
| 8711 | ascenso | 2 |
| 8712 | asar | 2 |
| 8713 | articulación | 2 |
| 8714 | arruga | 2 |
| 8715 | arrope | 2 |
| 8716 | arropar | 2 |
| 8717 | arrollar | 2 |
| 8718 | arrobamiento | 2 |
| 8719 | arriero | 2 |
| 8720 | arrepiéntete | 2 |
| 8721 | arreo | 2 |
| 8722 | arreglador | 2 |
| 8723 | arreglado | 2 |
| 8724 | arramblar | 2 |
| 8725 | arquitectónico | 2 |
| 8726 | arqueo | 2 |
| 8727 | armonioso | 2 |
| 8728 | armatoste | 2 |
| 8729 | armadura | 2 |
| 8730 | armado | 2 |
| 8731 | armada | 2 |
| 8732 | aristócrata | 2 |
| 8733 | argentino | 2 |
| 8734 | arganzuela | 2 |
| 8735 | arengar | 2 |
| 8736 | ardid | 2 |
| 8737 | arcón | 2 |
| 8738 | árbitro | 2 |
| 8739 | arbitrio | 2 |
| 8740 | ara | 2 |
| 8741 | aquiescencia | 2 |
| 8742 | aquello | 2 |
| 8743 | aquella | 2 |
| 8744 | apuntalar | 2 |
| 8745 | apuesta | 2 |
| 8746 | aprisita | 2 |
| 8747 | aprisionar | 2 |
| 8748 | aprensivo | 2 |
| 8749 | apodo | 2 |
| 8750 | aplomo | 2 |
| 8751 | aplomar | 2 |
| 8752 | aplazar | 2 |
| 8753 | aplanar | 2 |
| 8754 | apilado | 2 |
| 8755 | apelmazar | 2 |
| 8756 | apear | 2 |
| 8757 | apasionar | 2 |
| 8758 | apartamiento | 2 |
| 8759 | aparejo | 2 |
| 8760 | aparador | 2 |
| 8761 | apagado | 2 |
| 8762 | añejo | 2 |
| 8763 | anzuelo | 2 |
| 8764 | anticuado | 2 |
| 8765 | anticipado | 2 |
| 8766 | antepecho | 2 |
| 8767 | antecesor | 2 |
| 8768 | antecedente | 2 |
| 8769 | anteayer | 2 |
| 8770 | ansiar | 2 |
| 8771 | anís | 2 |
| 8772 | aniquilar | 2 |
| 8773 | ánima | 2 |
| 8774 | anillo | 2 |
| 8775 | anidar | 2 |
| 8776 | anhelante | 2 |
| 8777 | angustias | 2 |
| 8778 | anguloso | 2 |
| 8779 | angelote | 2 |
| 8780 | angelón | 2 |
| 8781 | anémico | 2 |
| 8782 | andrómina | 2 |
| 8783 | andrea | 2 |
| 8784 | andrajoso | 2 |
| 8785 | ande | 2 |
| 8786 | andanada | 2 |
| 8787 | andana | 2 |
| 8788 | andamiaje | 2 |
| 8789 | andado | 2 |
| 8790 | anatomía | 2 |
| 8791 | anacoreta | 2 |
| 8792 | amueblar | 2 |
| 8793 | ampliación | 2 |
| 8794 | amortajar | 2 |
| 8795 | amilanar | 2 |
| 8796 | amiguita | 2 |
| 8797 | américa | 2 |
| 8798 | amenizar | 2 |
| 8799 | amenguar | 2 |
| 8800 | ambicioso | 2 |
| 8801 | amazona | 2 |
| 8802 | amancebamiento | 2 |
| 8803 | aludir | 2 |
| 8804 | alpargata | 2 |
| 8805 | almendrar | 2 |
| 8806 | almacenes | 2 |
| 8807 | alinear | 2 |
| 8808 | alimaña | 2 |
| 8809 | algunas | 2 |
| 8810 | alguna | 2 |
| 8811 | algarrobo | 2 |
| 8812 | alfombra | 2 |
| 8813 | aletargado | 2 |
| 8814 | alero | 2 |
| 8815 | alejandro | 2 |
| 8816 | alegar | 2 |
| 8817 | alcoy | 2 |
| 8818 | alcázar | 2 |
| 8819 | alcantarilla | 2 |
| 8820 | albricias | 2 |
| 8821 | alborozo | 2 |
| 8822 | albo | 2 |
| 8823 | albergue | 2 |
| 8824 | alarma | 2 |
| 8825 | alarido | 2 |
| 8826 | ajusticiar | 2 |
| 8827 | ajajá | 2 |
| 8828 | aislar | 2 |
| 8829 | aislamiento | 2 |
| 8830 | airado | 2 |
| 8831 | ahorita | 2 |
| 8832 | ahorcar | 2 |
| 8833 | águila | 2 |
| 8834 | aguas | 2 |
| 8835 | agrícola | 2 |
| 8836 | agriar | 2 |
| 8837 | agresión | 2 |
| 8838 | agradábale | 2 |
| 8839 | agosto | 2 |
| 8840 | agonizante | 2 |
| 8841 | agitado | 2 |
| 8842 | afueras | 2 |
| 8843 | afortunadamente | 2 |
| 8844 | aflictivo | 2 |
| 8845 | afianzar | 2 |
| 8846 | afeitado | 2 |
| 8847 | afectado | 2 |
| 8848 | afectación | 2 |
| 8849 | adular | 2 |
| 8850 | adoquinar | 2 |
| 8851 | adjudicar | 2 |
| 8852 | adherir | 2 |
| 8853 | adelgazar | 2 |
| 8854 | adelanto | 2 |
| 8855 | adecuar | 2 |
| 8856 | adecuado | 2 |
| 8857 | acusado | 2 |
| 8858 | acurrucar | 2 |
| 8859 | acuarela | 2 |
| 8860 | actuar | 2 |
| 8861 | acribillar | 2 |
| 8862 | acostose | 2 |
| 8863 | acostáronse | 2 |
| 8864 | acorralar | 2 |
| 8865 | acordeón | 2 |
| 8866 | acorde | 2 |
| 8867 | acoquinar | 2 |
| 8868 | acompañante | 2 |
| 8869 | acólito | 2 |
| 8870 | acogotar | 2 |
| 8871 | acierto | 2 |
| 8872 | acíbar | 2 |
| 8873 | achantar | 2 |
| 8874 | acerté | 2 |
| 8875 | acercábase | 2 |
| 8876 | aceptable | 2 |
| 8877 | accidental | 2 |
| 8878 | accidentado | 2 |
| 8879 | acatar | 2 |
| 8880 | academia | 2 |
| 8881 | acabamiento | 2 |
| 8882 | abyección | 2 |
| 8883 | abuso | 2 |
| 8884 | abundamiento | 2 |
| 8885 | abstraído | 2 |
| 8886 | absolver | 2 |
| 8887 | abrochar | 2 |
| 8888 | abriose | 2 |
| 8889 | abrígate | 2 |
| 8890 | abra | 2 |
| 8891 | abordar | 2 |
| 8892 | abolir | 2 |
| 8893 | abolición | 2 |
| 8894 | abogado | 2 |
| 8895 | zurriago | 1 |
| 8896 | zurcido | 1 |
| 8897 | zumo | 1 |
| 8898 | zumbón | 1 |
| 8899 | zumbar | 1 |
| 8900 | zozobrar | 1 |
| 8901 | zote | 1 |
| 8902 | zoquetes | 1 |
| 8903 | zoquete | 1 |
| 8904 | zopenco | 1 |
| 8905 | zascandil | 1 |
| 8906 | zarzal | 1 |
| 8907 | zarandaja | 1 |
| 8908 | zapateado | 1 |
| 8909 | zapata | 1 |
| 8910 | zancadilla | 1 |
| 8911 | zanahoria | 1 |
| 8912 | zampa | 1 |
| 8913 | zamorano | 1 |
| 8914 | zambullida | 1 |
| 8915 | zambombazo | 1 |
| 8916 | zamarra | 1 |
| 8917 | zahorí | 1 |
| 8918 | zagalón | 1 |
| 8919 | zafar | 1 |
| 8920 | zacarías | 1 |
| 8921 | yesería | 1 |
| 8922 | yerno | 1 |
| 8923 | yermar | 1 |
| 8924 | xv | 1 |
| 8925 | xix | 1 |
| 8926 | xiv | 1 |
| 8927 | xiii | 1 |
| 8928 | wellington | 1 |
| 8929 | wamba | 1 |
| 8930 | vusté | 1 |
| 8931 | vuelvo | 1 |
| 8932 | vuélvete | 1 |
| 8933 | vuelve | 1 |
| 8934 | vuelva | 1 |
| 8935 | vuelco | 1 |
| 8936 | votante | 1 |
| 8937 | vomitivo | 1 |
| 8938 | volvía | 1 |
| 8939 | volvería | 1 |
| 8940 | volvemos | 1 |
| 8941 | volvámonos | 1 |
| 8942 | voluntarioso | 1 |
| 8943 | voluntario | 1 |
| 8944 | voluble | 1 |
| 8945 | volatín | 1 |
| 8946 | volátil | 1 |
| 8947 | volador | 1 |
| 8948 | vocear | 1 |
| 8949 | vocal | 1 |
| 8950 | vocabulario | 1 |
| 8951 | vivito | 1 |
| 8952 | vivirá | 1 |
| 8953 | vivía | 1 |
| 8954 | viveros | 1 |
| 8955 | vivaaa | 1 |
| 8956 | vitrina | 1 |
| 8957 | vitalicio | 1 |
| 8958 | visual | 1 |
| 8959 | vistiose | 1 |
| 8960 | vistillas | 1 |
| 8961 | viste | 1 |
| 8962 | vísperas | 1 |
| 8963 | visitante | 1 |
| 8964 | visiones | 1 |
| 8965 | visillo | 1 |
| 8966 | virus | 1 |
| 8967 | virtuosa | 1 |
| 8968 | virtudes | 1 |
| 8969 | viril | 1 |
| 8970 | vírgenes | 1 |
| 8971 | vira | 1 |
| 8972 | viose | 1 |
| 8973 | viole | 1 |
| 8974 | vinoso | 1 |
| 8975 | vinazo | 1 |
| 8976 | vinatero | 1 |
| 8977 | villaviciosa | 1 |
| 8978 | villarreal | 1 |
| 8979 | villanía | 1 |
| 8980 | villancico | 1 |
| 8981 | villahermosa | 1 |
| 8982 | vigorización | 1 |
| 8983 | vigilia | 1 |
| 8984 | vigía | 1 |
| 8985 | vigente | 1 |
| 8986 | viéronle | 1 |
| 8987 | vientos | 1 |
| 8988 | viéndote | 1 |
| 8989 | viéndome | 1 |
| 8990 | viéndola | 1 |
| 8991 | viendo | 1 |
| 8992 | victorioso | 1 |
| 8993 | vicisitud | 1 |
| 8994 | viciado | 1 |
| 8995 | vicaría | 1 |
| 8996 | vibratorio | 1 |
| 8997 | vibrante | 1 |
| 8998 | viana | 1 |
| 8999 | viabilidad | 1 |
| 9000 | vetusto | 1 |
| 9001 | vestuario | 1 |
| 9002 | vestimenta | 1 |
| 9003 | vertiente | 1 |
| 9004 | vértice | 1 |
| 9005 | vertical | 1 |
| 9006 | versionar | 1 |
| 9007 | versión | 1 |
| 9008 | verosímil | 1 |
| 9009 | vernet | 1 |
| 9010 | verle | 1 |
| 9011 | verja | 1 |
| 9012 | verificábase | 1 |
| 9013 | vericueto | 1 |
| 9014 | vergonzante | 1 |
| 9015 | verdor | 1 |
| 9016 | verdades | 1 |
| 9017 | verbal | 1 |
| 9018 | verba | 1 |
| 9019 | veraz | 1 |
| 9020 | veranear | 1 |
| 9021 | verán | 1 |
| 9022 | veracidad | 1 |
| 9023 | ventosa | 1 |
| 9024 | ventorrillo | 1 |
| 9025 | ventajoso | 1 |
| 9026 | venidero | 1 |
| 9027 | venialmente | 1 |
| 9028 | venia | 1 |
| 9029 | vengativo | 1 |
| 9030 | vengarse | 1 |
| 9031 | venerando | 1 |
| 9032 | vendrás | 1 |
| 9033 | vendrá | 1 |
| 9034 | vendiendo | 1 |
| 9035 | vendida | 1 |
| 9036 | vencimiento | 1 |
| 9037 | velas | 1 |
| 9038 | vejiga | 1 |
| 9039 | veintiuno | 1 |
| 9040 | veintiocho | 1 |
| 9041 | veíase | 1 |
| 9042 | veíanse | 1 |
| 9043 | vegetativo | 1 |
| 9044 | vegetal | 1 |
| 9045 | vegetación | 1 |
| 9046 | vedar | 1 |
| 9047 | vecinas | 1 |
| 9048 | veámoslo | 1 |
| 9049 | véalo | 1 |
| 9050 | váyanse | 1 |
| 9051 | vayan | 1 |
| 9052 | vaticinio | 1 |
| 9053 | vasija | 1 |
| 9054 | vascongadas | 1 |
| 9055 | vasco | 1 |
| 9056 | vas | 1 |
| 9057 | varilla | 1 |
| 9058 | variante | 1 |
| 9059 | variado | 1 |
| 9060 | variación | 1 |
| 9061 | varear | 1 |
| 9062 | varas | 1 |
| 9063 | vaqueta | 1 |
| 9064 | vapulear | 1 |
| 9065 | vampiro | 1 |
| 9066 | valoraciones | 1 |
| 9067 | vallehermoso | 1 |
| 9068 | valledor | 1 |
| 9069 | vallecas | 1 |
| 9070 | valimiento | 1 |
| 9071 | valiéndose | 1 |
| 9072 | válido | 1 |
| 9073 | válganos | 1 |
| 9074 | valentía | 1 |
| 9075 | vaivén | 1 |
| 9076 | vais | 1 |
| 9077 | vaho | 1 |
| 9078 | vagancia | 1 |
| 9079 | vacuno | 1 |
| 9080 | vacía | 1 |
| 9081 | vacar | 1 |
| 9082 | vacación | 1 |
| 9083 | utilitario | 1 |
| 9084 | utilísimo | 1 |
| 9085 | usurpación | 1 |
| 9086 | usufructuario | 1 |
| 9087 | usufructo | 1 |
| 9088 | ustés | 1 |
| 9089 | usté | 1 |
| 9090 | uribe | 1 |
| 9091 | urgir | 1 |
| 9092 | urgencia | 1 |
| 9093 | urdir | 1 |
| 9094 | urdimbre | 1 |
| 9095 | urbano | 1 |
| 9096 | unos | 1 |
| 9097 | universitario | 1 |
| 9098 | uniformidad | 1 |
| 9099 | unidos | 1 |
| 9100 | unicornio | 1 |
| 9101 | ungüento | 1 |
| 9102 | ungir | 1 |
| 9103 | unanimidad | 1 |
| 9104 | unánime | 1 |
| 9105 | umbral | 1 |
| 9106 | ultratumba | 1 |
| 9107 | ultramarino | 1 |
| 9108 | ultraje | 1 |
| 9109 | úlcera | 1 |
| 9110 | ubre | 1 |
| 9111 | tuvo | 1 |
| 9112 | tuviéronla | 1 |
| 9113 | tuve | 1 |
| 9114 | tutora | 1 |
| 9115 | tutor | 1 |
| 9116 | tutela | 1 |
| 9117 | turgente | 1 |
| 9118 | turégano | 1 |
| 9119 | turbulento | 1 |
| 9120 | turbose | 1 |
| 9121 | turbante | 1 |
| 9122 | turbado | 1 |
| 9123 | turbábala | 1 |
| 9124 | tupé | 1 |
| 9125 | túnica | 1 |
| 9126 | tundir | 1 |
| 9127 | tunantería | 1 |
| 9128 | tunantas | 1 |
| 9129 | tun | 1 |
| 9130 | tumultuoso | 1 |
| 9131 | tugurio | 1 |
| 9132 | tuétano | 1 |
| 9133 | tubería | 1 |
| 9134 | tuberculosis | 1 |
| 9135 | trujillas | 1 |
| 9136 | truhán | 1 |
| 9137 | trufar | 1 |
| 9138 | trueno | 1 |
| 9139 | truchimán | 1 |
| 9140 | trovador | 1 |
| 9141 | tropezones | 1 |
| 9142 | tropezón | 1 |
| 9143 | tronado | 1 |
| 9144 | trompo | 1 |
| 9145 | trompicones | 1 |
| 9146 | trompicón | 1 |
| 9147 | trompada | 1 |
| 9148 | trizar | 1 |
| 9149 | triturar | 1 |
| 9150 | tris | 1 |
| 9151 | tripudo | 1 |
| 9152 | trípode | 1 |
| 9153 | triple | 1 |
| 9154 | trinca | 1 |
| 9155 | tributo | 1 |
| 9156 | tribuna | 1 |
| 9157 | triana | 1 |
| 9158 | treta | 1 |
| 9159 | trescientos | 1 |
| 9160 | trescientas | 1 |
| 9161 | trepar | 1 |
| 9162 | trepador | 1 |
| 9163 | trencilla | 1 |
| 9164 | trebejos | 1 |
| 9165 | trazado | 1 |
| 9166 | travesía | 1 |
| 9167 | traté | 1 |
| 9168 | tratadista | 1 |
| 9169 | tratábase | 1 |
| 9170 | trasunto | 1 |
| 9171 | trasuntar | 1 |
| 9172 | trastocar | 1 |
| 9173 | trastazo | 1 |
| 9174 | trasquilar | 1 |
| 9175 | trasnochar | 1 |
| 9176 | trasnochador | 1 |
| 9177 | trasmitir | 1 |
| 9178 | trasluz | 1 |
| 9179 | traslucir | 1 |
| 9180 | traslación | 1 |
| 9181 | trasegar | 1 |
| 9182 | trascender | 1 |
| 9183 | trascendencia | 1 |
| 9184 | traqueteo | 1 |
| 9185 | traquetear | 1 |
| 9186 | trapillo | 1 |
| 9187 | trap | 1 |
| 9188 | transporte | 1 |
| 9189 | transportar | 1 |
| 9190 | transparente | 1 |
| 9191 | transformismo | 1 |
| 9192 | transfiguración | 1 |
| 9193 | transferencia | 1 |
| 9194 | transcurso | 1 |
| 9195 | tranquilamente | 1 |
| 9196 | trancazo | 1 |
| 9197 | trancar | 1 |
| 9198 | tramposa | 1 |
| 9199 | tráiganos | 1 |
| 9200 | traían | 1 |
| 9201 | traía | 1 |
| 9202 | tragón | 1 |
| 9203 | tragicómico | 1 |
| 9204 | tragadero | 1 |
| 9205 | traficante | 1 |
| 9206 | trafalgar | 1 |
| 9207 | traería | 1 |
| 9208 | tráeme | 1 |
| 9209 | trae | 1 |
| 9210 | tradújose | 1 |
| 9211 | traducción | 1 |
| 9212 | trabucar | 1 |
| 9213 | trabilla | 1 |
| 9214 | trabajosamente | 1 |
| 9215 | tóxico | 1 |
| 9216 | totalmente | 1 |
| 9217 | tosquedad | 1 |
| 9218 | torzal | 1 |
| 9219 | torvamente | 1 |
| 9220 | tortuga | 1 |
| 9221 | tórtolo | 1 |
| 9222 | tortoleo | 1 |
| 9223 | tortillita | 1 |
| 9224 | torrero | 1 |
| 9225 | torreón | 1 |
| 9226 | torrellas | 1 |
| 9227 | torniquete | 1 |
| 9228 | torneo | 1 |
| 9229 | torneado | 1 |
| 9230 | tornasol | 1 |
| 9231 | torna | 1 |
| 9232 | toril | 1 |
| 9233 | torcedura | 1 |
| 9234 | tórax | 1 |
| 9235 | torácico | 1 |
| 9236 | tópico | 1 |
| 9237 | topetazo | 1 |
| 9238 | topar | 1 |
| 9239 | topacio | 1 |
| 9240 | tontín | 1 |
| 9241 | tontada | 1 |
| 9242 | tonsurar | 1 |
| 9243 | tónico | 1 |
| 9244 | tónica | 1 |
| 9245 | tonel | 1 |
| 9246 | tomola | 1 |
| 9247 | tomó | 1 |
| 9248 | tomo | 1 |
| 9249 | tomarla | 1 |
| 9250 | tomaremos | 1 |
| 9251 | tomándole | 1 |
| 9252 | tomad | 1 |
| 9253 | tomaba | 1 |
| 9254 | tolú | 1 |
| 9255 | tollina | 1 |
| 9256 | tolerable | 1 |
| 9257 | tocaya | 1 |
| 9258 | tocándole | 1 |
| 9259 | tocado | 1 |
| 9260 | titubeaba | 1 |
| 9261 | tísico | 1 |
| 9262 | tirantez | 1 |
| 9263 | tiránico | 1 |
| 9264 | tirabuzón | 1 |
| 9265 | tiorras | 1 |
| 9266 | tiologías | 1 |
| 9267 | tinturar | 1 |
| 9268 | tinto | 1 |
| 9269 | tinieblas | 1 |
| 9270 | tinaja | 1 |
| 9271 | tina | 1 |
| 9272 | tímpano | 1 |
| 9273 | timonear | 1 |
| 9274 | timbal | 1 |
| 9275 | timador | 1 |
| 9276 | tijeretazo | 1 |
| 9277 | tijeretas | 1 |
| 9278 | tijereta | 1 |
| 9279 | tiento | 1 |
| 9280 | tiembla | 1 |
| 9281 | tic | 1 |
| 9282 | tiburón | 1 |
| 9283 | tibidabo | 1 |
| 9284 | tibia | 1 |
| 9285 | thinville | 1 |
| 9286 | textualmente | 1 |
| 9287 | tetera | 1 |
| 9288 | testuz | 1 |
| 9289 | testimoniar | 1 |
| 9290 | testera | 1 |
| 9291 | testar | 1 |
| 9292 | tesorería | 1 |
| 9293 | teruel | 1 |
| 9294 | terruño | 1 |
| 9295 | territorio | 1 |
| 9296 | terrestre | 1 |
| 9297 | terrenal | 1 |
| 9298 | terraza | 1 |
| 9299 | terráqueo | 1 |
| 9300 | terranova | 1 |
| 9301 | ternerito | 1 |
| 9302 | terne | 1 |
| 9303 | tercio | 1 |
| 9304 | teórico | 1 |
| 9305 | teológico | 1 |
| 9306 | tenuidad | 1 |
| 9307 | tentativo | 1 |
| 9308 | tentador | 1 |
| 9309 | tenla | 1 |
| 9310 | teníase | 1 |
| 9311 | teníanle | 1 |
| 9312 | teníale | 1 |
| 9313 | tengamos | 1 |
| 9314 | téngalo | 1 |
| 9315 | tened | 1 |
| 9316 | tendrías | 1 |
| 9317 | tendría | 1 |
| 9318 | tendremos | 1 |
| 9319 | tendrán | 1 |
| 9320 | tendralos | 1 |
| 9321 | tendrá | 1 |
| 9322 | tendón | 1 |
| 9323 | tenderete | 1 |
| 9324 | tenacilla | 1 |
| 9325 | temperatura | 1 |
| 9326 | temible | 1 |
| 9327 | temía | 1 |
| 9328 | teméis | 1 |
| 9329 | teme | 1 |
| 9330 | telar | 1 |
| 9331 | tejavana | 1 |
| 9332 | tejar | 1 |
| 9333 | tedio | 1 |
| 9334 | tea | 1 |
| 9335 | tazón | 1 |
| 9336 | tauromaquia | 1 |
| 9337 | taurómaco | 1 |
| 9338 | tartana | 1 |
| 9339 | tarima | 1 |
| 9340 | tardío | 1 |
| 9341 | tardecillo | 1 |
| 9342 | tarancón | 1 |
| 9343 | tarabilla | 1 |
| 9344 | tapón | 1 |
| 9345 | tapete | 1 |
| 9346 | tapadera | 1 |
| 9347 | tangible | 1 |
| 9348 | tangente | 1 |
| 9349 | tamizar | 1 |
| 9350 | tamiz | 1 |
| 9351 | tamboril | 1 |
| 9352 | talud | 1 |
| 9353 | tallado | 1 |
| 9354 | talega | 1 |
| 9355 | talavera | 1 |
| 9356 | taladrar | 1 |
| 9357 | tahona | 1 |
| 9358 | tafetán | 1 |
| 9359 | táctica | 1 |
| 9360 | tacita | 1 |
| 9361 | tachuela | 1 |
| 9362 | tacaño | 1 |
| 9363 | tabernero | 1 |
| 9364 | tabacos | 1 |
| 9365 | ta | 1 |
| 9366 | sutilísimo | 1 |
| 9367 | sustancial | 1 |
| 9368 | suspiraba | 1 |
| 9369 | suspicacia | 1 |
| 9370 | susodicho | 1 |
| 9371 | suscripción | 1 |
| 9372 | suscribir | 1 |
| 9373 | suscitar | 1 |
| 9374 | surtidor | 1 |
| 9375 | súpose | 1 |
| 9376 | suponiendo | 1 |
| 9377 | suponíales | 1 |
| 9378 | suponía | 1 |
| 9379 | supongo | 1 |
| 9380 | supongamos | 1 |
| 9381 | suplir | 1 |
| 9382 | súplica | 1 |
| 9383 | suplemento | 1 |
| 9384 | suplementario | 1 |
| 9385 | súpito | 1 |
| 9386 | supe | 1 |
| 9387 | sumiso | 1 |
| 9388 | sumir | 1 |
| 9389 | suministrar | 1 |
| 9390 | sulfurar | 1 |
| 9391 | sujetose | 1 |
| 9392 | sufragio | 1 |
| 9393 | sueños | 1 |
| 9394 | suéltese | 1 |
| 9395 | suéltela | 1 |
| 9396 | sucumbir | 1 |
| 9397 | subteniente | 1 |
| 9398 | subsistencia | 1 |
| 9399 | subsiguiente | 1 |
| 9400 | subsidio | 1 |
| 9401 | subrepticiamente | 1 |
| 9402 | sublimidad | 1 |
| 9403 | subiría | 1 |
| 9404 | subiré | 1 |
| 9405 | subiéronle | 1 |
| 9406 | subiéndose | 1 |
| 9407 | subido | 1 |
| 9408 | súbdito | 1 |
| 9409 | suba | 1 |
| 9410 | suárez | 1 |
| 9411 | sotabanco | 1 |
| 9412 | sostenimiento | 1 |
| 9413 | sostenía | 1 |
| 9414 | sosería | 1 |
| 9415 | sosegadamente | 1 |
| 9416 | sosamente | 1 |
| 9417 | sortilegio | 1 |
| 9418 | sorpresita | 1 |
| 9419 | sorna | 1 |
| 9420 | sordina | 1 |
| 9421 | sordidez | 1 |
| 9422 | sordamente | 1 |
| 9423 | sorbo | 1 |
| 9424 | sopesar | 1 |
| 9425 | sopero | 1 |
| 9426 | sopera | 1 |
| 9427 | sonreía | 1 |
| 9428 | sonoridad | 1 |
| 9429 | sonámbulo | 1 |
| 9430 | somero | 1 |
| 9431 | sombrerero | 1 |
| 9432 | sombrear | 1 |
| 9433 | soltería | 1 |
| 9434 | solos | 1 |
| 9435 | solidificación | 1 |
| 9436 | solidez | 1 |
| 9437 | sólidamente | 1 |
| 9438 | solfeo | 1 |
| 9439 | soleta | 1 |
| 9440 | solecismo | 1 |
| 9441 | soldevilla | 1 |
| 9442 | soldados | 1 |
| 9443 | soldadito | 1 |
| 9444 | solaz | 1 |
| 9445 | solapa | 1 |
| 9446 | solana | 1 |
| 9447 | solamente | 1 |
| 9448 | sojuzgar | 1 |
| 9449 | sofocón | 1 |
| 9450 | sofoco | 1 |
| 9451 | sofistería | 1 |
| 9452 | soez | 1 |
| 9453 | socorriome | 1 |
| 9454 | socórrale | 1 |
| 9455 | sociedades | 1 |
| 9456 | socavar | 1 |
| 9457 | sobrio | 1 |
| 9458 | sobrevivir | 1 |
| 9459 | sobrestante | 1 |
| 9460 | sobresaliente | 1 |
| 9461 | sobrepujar | 1 |
| 9462 | sobreparto | 1 |
| 9463 | sobredorar | 1 |
| 9464 | sobado | 1 |
| 9465 | sobaco | 1 |
| 9466 | sito | 1 |
| 9467 | sistematizar | 1 |
| 9468 | sirven | 1 |
| 9469 | sinvergüenzonas | 1 |
| 9470 | síntomas | 1 |
| 9471 | sintiole | 1 |
| 9472 | sinónimo | 1 |
| 9473 | singularidad | 1 |
| 9474 | singer | 1 |
| 9475 | síncope | 1 |
| 9476 | síncopa | 1 |
| 9477 | simultáneo | 1 |
| 9478 | simultáneamente | 1 |
| 9479 | simular | 1 |
| 9480 | simulacro | 1 |
| 9481 | simpson | 1 |
| 9482 | simplón | 1 |
| 9483 | simón | 1 |
| 9484 | similar | 1 |
| 9485 | símil | 1 |
| 9486 | simiente | 1 |
| 9487 | simbolismo | 1 |
| 9488 | silueta | 1 |
| 9489 | silogismo | 1 |
| 9490 | silleta | 1 |
| 9491 | sílfide | 1 |
| 9492 | silabeo | 1 |
| 9493 | sigunda | 1 |
| 9494 | siguiole | 1 |
| 9495 | siguiéndoles | 1 |
| 9496 | significativo | 1 |
| 9497 | significado | 1 |
| 9498 | sicilianas | 1 |
| 9499 | sicario | 1 |
| 9500 | sibila | 1 |
| 9501 | sibarita | 1 |
| 9502 | shangai | 1 |
| 9503 | sexto | 1 |
| 9504 | sexta | 1 |
| 9505 | severísimamente | 1 |
| 9506 | severiano | 1 |
| 9507 | seto | 1 |
| 9508 | setecientas | 1 |
| 9509 | sesera | 1 |
| 9510 | servil | 1 |
| 9511 | servíale | 1 |
| 9512 | sert | 1 |
| 9513 | seroso | 1 |
| 9514 | serón | 1 |
| 9515 | serénate | 1 |
| 9516 | seráfico | 1 |
| 9517 | séquito | 1 |
| 9518 | séptimo | 1 |
| 9519 | separáronse | 1 |
| 9520 | separado | 1 |
| 9521 | seo | 1 |
| 9522 | sentina | 1 |
| 9523 | sentíala | 1 |
| 9524 | sentenciar | 1 |
| 9525 | sentáronse | 1 |
| 9526 | sentándose | 1 |
| 9527 | sentada | 1 |
| 9528 | sensiblemente | 1 |
| 9529 | senil | 1 |
| 9530 | senador | 1 |
| 9531 | semioscura | 1 |
| 9532 | semilla | 1 |
| 9533 | seiscientos | 1 |
| 9534 | segura | 1 |
| 9535 | segundón | 1 |
| 9536 | seguíales | 1 |
| 9537 | segoviano | 1 |
| 9538 | seglar | 1 |
| 9539 | sedimentar | 1 |
| 9540 | sedeño | 1 |
| 9541 | sede | 1 |
| 9542 | sedante | 1 |
| 9543 | sedanes | 1 |
| 9544 | sedán | 1 |
| 9545 | secuestrar | 1 |
| 9546 | seccionar | 1 |
| 9547 | seboso | 1 |
| 9548 | schiller | 1 |
| 9549 | sazonado | 1 |
| 9550 | sayón | 1 |
| 9551 | saya | 1 |
| 9552 | saturar | 1 |
| 9553 | satisfactorio | 1 |
| 9554 | satírico | 1 |
| 9555 | sastrería | 1 |
| 9556 | sastra | 1 |
| 9557 | sarna | 1 |
| 9558 | saquear | 1 |
| 9559 | sapo | 1 |
| 9560 | sañudamente | 1 |
| 9561 | santuario | 1 |
| 9562 | santificar | 1 |
| 9563 | santificación | 1 |
| 9564 | santander | 1 |
| 9565 | sanguinolento | 1 |
| 9566 | sanguíneo | 1 |
| 9567 | sanguinario | 1 |
| 9568 | sangría | 1 |
| 9569 | sandía | 1 |
| 9570 | sancho | 1 |
| 9571 | salvedad | 1 |
| 9572 | salvamento | 1 |
| 9573 | salvajada | 1 |
| 9574 | salva | 1 |
| 9575 | saludáronse | 1 |
| 9576 | saludador | 1 |
| 9577 | saltó | 1 |
| 9578 | saltimbanqui | 1 |
| 9579 | saltear | 1 |
| 9580 | salteado | 1 |
| 9581 | saltamontes | 1 |
| 9582 | salta | 1 |
| 9583 | salsa | 1 |
| 9584 | salomón | 1 |
| 9585 | salobre | 1 |
| 9586 | salmuera | 1 |
| 9587 | salí | 1 |
| 9588 | salgo | 1 |
| 9589 | salesas | 1 |
| 9590 | sales | 1 |
| 9591 | sajón | 1 |
| 9592 | saint | 1 |
| 9593 | sahumerio | 1 |
| 9594 | sagrados | 1 |
| 9595 | sagrada | 1 |
| 9596 | sagra | 1 |
| 9597 | sagacidad | 1 |
| 9598 | sacudido | 1 |
| 9599 | sacramentar | 1 |
| 9600 | sacramentado | 1 |
| 9601 | sacola | 1 |
| 9602 | sacó | 1 |
| 9603 | saciedad | 1 |
| 9604 | sacáronla | 1 |
| 9605 | sácalos | 1 |
| 9606 | sabusté | 1 |
| 9607 | sabor | 1 |
| 9608 | sable | 1 |
| 9609 | sabiéndolas | 1 |
| 9610 | sabéis | 1 |
| 9611 | sabañón | 1 |
| 9612 | s | 1 |
| 9613 | ruso | 1 |
| 9614 | rupertito | 1 |
| 9615 | rumboso | 1 |
| 9616 | rumbar | 1 |
| 9617 | ruin | 1 |
| 9618 | ruego | 1 |
| 9619 | ruedo | 1 |
| 9620 | rudimentario | 1 |
| 9621 | ruborizar | 1 |
| 9622 | ruborizado | 1 |
| 9623 | rubor | 1 |
| 9624 | rubines | 1 |
| 9625 | rubia | 1 |
| 9626 | rozamiento | 1 |
| 9627 | rozadura | 1 |
| 9628 | rotura | 1 |
| 9629 | rothschild | 1 |
| 9630 | rostchild | 1 |
| 9631 | rosicler | 1 |
| 9632 | rosca | 1 |
| 9633 | roque | 1 |
| 9634 | ropaje | 1 |
| 9635 | roña | 1 |
| 9636 | ronca | 1 |
| 9637 | rompí | 1 |
| 9638 | rompelanzas | 1 |
| 9639 | romo | 1 |
| 9640 | romería | 1 |
| 9641 | rombo | 1 |
| 9642 | romanza | 1 |
| 9643 | romanos | 1 |
| 9644 | románico | 1 |
| 9645 | romadizo | 1 |
| 9646 | roger | 1 |
| 9647 | roedor | 1 |
| 9648 | rodríguez | 1 |
| 9649 | rodil | 1 |
| 9650 | rocío | 1 |
| 9651 | rociada | 1 |
| 9652 | robustecer | 1 |
| 9653 | robledo | 1 |
| 9654 | rizado | 1 |
| 9655 | ritual | 1 |
| 9656 | rítmico | 1 |
| 9657 | rita | 1 |
| 9658 | risas | 1 |
| 9659 | ripio | 1 |
| 9660 | riose | 1 |
| 9661 | rioja | 1 |
| 9662 | ringorrango | 1 |
| 9663 | rimero | 1 |
| 9664 | rimar | 1 |
| 9665 | rija | 1 |
| 9666 | rigorista | 1 |
| 9667 | rígidamente | 1 |
| 9668 | rifle | 1 |
| 9669 | riesgo | 1 |
| 9670 | ridículamente | 1 |
| 9671 | ricardo | 1 |
| 9672 | ricacho | 1 |
| 9673 | rica | 1 |
| 9674 | ribetear | 1 |
| 9675 | ribera | 1 |
| 9676 | ríase | 1 |
| 9677 | rezumos | 1 |
| 9678 | rezumar | 1 |
| 9679 | rezongó | 1 |
| 9680 | revuelco | 1 |
| 9681 | revolvió | 1 |
| 9682 | revoltoso | 1 |
| 9683 | revolcose | 1 |
| 9684 | revoco | 1 |
| 9685 | revocar | 1 |
| 9686 | revista | 1 |
| 9687 | revisión | 1 |
| 9688 | revirar | 1 |
| 9689 | revertir | 1 |
| 9690 | reversión | 1 |
| 9691 | reverente | 1 |
| 9692 | reverbero | 1 |
| 9693 | reverberar | 1 |
| 9694 | reventa | 1 |
| 9695 | revenir | 1 |
| 9696 | revelarte | 1 |
| 9697 | revelado | 1 |
| 9698 | reumático | 1 |
| 9699 | retumbante | 1 |
| 9700 | retraimiento | 1 |
| 9701 | retraer | 1 |
| 9702 | retortero | 1 |
| 9703 | retorta | 1 |
| 9704 | retórico | 1 |
| 9705 | retorcido | 1 |
| 9706 | retorcedura | 1 |
| 9707 | retoñar | 1 |
| 9708 | retocar | 1 |
| 9709 | retirose | 1 |
| 9710 | retiradamente | 1 |
| 9711 | retirábase | 1 |
| 9712 | retina | 1 |
| 9713 | reteniéndole | 1 |
| 9714 | retención | 1 |
| 9715 | retemblar | 1 |
| 9716 | retazo | 1 |
| 9717 | retardar | 1 |
| 9718 | resurgir | 1 |
| 9719 | resumir | 1 |
| 9720 | resumen | 1 |
| 9721 | resultas | 1 |
| 9722 | resulta | 1 |
| 9723 | resuelto | 1 |
| 9724 | resuello | 1 |
| 9725 | restañar | 1 |
| 9726 | restante | 1 |
| 9727 | restallar | 1 |
| 9728 | restablecimiento | 1 |
| 9729 | resquebrajar | 1 |
| 9730 | responso | 1 |
| 9731 | respondón | 1 |
| 9732 | respondió | 1 |
| 9733 | responderme | 1 |
| 9734 | respóndeme | 1 |
| 9735 | respóndame | 1 |
| 9736 | respiradero | 1 |
| 9737 | respirable | 1 |
| 9738 | respingar | 1 |
| 9739 | respetuoso | 1 |
| 9740 | respetuosamente | 1 |
| 9741 | resorte | 1 |
| 9742 | resonante | 1 |
| 9743 | resolvió | 1 |
| 9744 | resolvíase | 1 |
| 9745 | resistente | 1 |
| 9746 | resina | 1 |
| 9747 | resguardo | 1 |
| 9748 | resentir | 1 |
| 9749 | resellar | 1 |
| 9750 | resecar | 1 |
| 9751 | rescoldo | 1 |
| 9752 | resbalón | 1 |
| 9753 | resbaladizo | 1 |
| 9754 | resaltar | 1 |
| 9755 | res | 1 |
| 9756 | requisito | 1 |
| 9757 | requetefinas | 1 |
| 9758 | requemado | 1 |
| 9759 | requejo | 1 |
| 9760 | reputado | 1 |
| 9761 | repuntar | 1 |
| 9762 | repulsión | 1 |
| 9763 | repulgo | 1 |
| 9764 | repulgar | 1 |
| 9765 | republicanismo | 1 |
| 9766 | reprobación | 1 |
| 9767 | reprobable | 1 |
| 9768 | reprimir | 1 |
| 9769 | reprensión | 1 |
| 9770 | repreciosa | 1 |
| 9771 | repostero | 1 |
| 9772 | repoblicanos | 1 |
| 9773 | repliegue | 1 |
| 9774 | replegar | 1 |
| 9775 | repartió | 1 |
| 9776 | reparón | 1 |
| 9777 | repantigar | 1 |
| 9778 | renacimiento | 1 |
| 9779 | renacer | 1 |
| 9780 | remotamente | 1 |
| 9781 | remorder | 1 |
| 9782 | remolque | 1 |
| 9783 | remolcar | 1 |
| 9784 | remojar | 1 |
| 9785 | remo | 1 |
| 9786 | remite | 1 |
| 9787 | reminiscencia | 1 |
| 9788 | remilgar | 1 |
| 9789 | remilgado | 1 |
| 9790 | remesar | 1 |
| 9791 | remedo | 1 |
| 9792 | remala | 1 |
| 9793 | remadera | 1 |
| 9794 | remachar | 1 |
| 9795 | relojero | 1 |
| 9796 | relojería | 1 |
| 9797 | reliquia | 1 |
| 9798 | relamido | 1 |
| 9799 | relajado | 1 |
| 9800 | relacionado | 1 |
| 9801 | rejuvenecer | 1 |
| 9802 | reírme | 1 |
| 9803 | reintegrar | 1 |
| 9804 | reincidir | 1 |
| 9805 | reincidente | 1 |
| 9806 | reguapa | 1 |
| 9807 | regrande | 1 |
| 9808 | regordete | 1 |
| 9809 | regocijado | 1 |
| 9810 | reglamentario | 1 |
| 9811 | regio | 1 |
| 9812 | regenerado | 1 |
| 9813 | regalón | 1 |
| 9814 | regadera | 1 |
| 9815 | refutar | 1 |
| 9816 | refunfuñó | 1 |
| 9817 | refunfuño | 1 |
| 9818 | refulgente | 1 |
| 9819 | refuerzo | 1 |
| 9820 | refregón | 1 |
| 9821 | refractario | 1 |
| 9822 | refinamiento | 1 |
| 9823 | refiérome | 1 |
| 9824 | refiere | 1 |
| 9825 | referirle | 1 |
| 9826 | refeos | 1 |
| 9827 | refectorio | 1 |
| 9828 | reducto | 1 |
| 9829 | redondel | 1 |
| 9830 | redaño | 1 |
| 9831 | recuento | 1 |
| 9832 | rectilíneo | 1 |
| 9833 | rectificó | 1 |
| 9834 | recrudecimiento | 1 |
| 9835 | recreábase | 1 |
| 9836 | recortándolo | 1 |
| 9837 | recortado | 1 |
| 9838 | recorrido | 1 |
| 9839 | reconstruir | 1 |
| 9840 | reconstituyente | 1 |
| 9841 | reconozco | 1 |
| 9842 | reconociendo | 1 |
| 9843 | reconocido | 1 |
| 9844 | reconocería | 1 |
| 9845 | recondenada | 1 |
| 9846 | recomponer | 1 |
| 9847 | recompensar | 1 |
| 9848 | recompensa | 1 |
| 9849 | recomendado | 1 |
| 9850 | recomendable | 1 |
| 9851 | recoletos | 1 |
| 9852 | recógete | 1 |
| 9853 | recoba | 1 |
| 9854 | reclinatorio | 1 |
| 9855 | recibiome | 1 |
| 9856 | recibió | 1 |
| 9857 | rechupete | 1 |
| 9858 | rechupado | 1 |
| 9859 | rechacemos | 1 |
| 9860 | recaudar | 1 |
| 9861 | recaudador | 1 |
| 9862 | recaudación | 1 |
| 9863 | recargar | 1 |
| 9864 | recapacitar | 1 |
| 9865 | recalentar | 1 |
| 9866 | recalcar | 1 |
| 9867 | recaída | 1 |
| 9868 | rebuznó | 1 |
| 9869 | rebuznar | 1 |
| 9870 | rebuscado | 1 |
| 9871 | rebullicio | 1 |
| 9872 | reblandecimiento | 1 |
| 9873 | reblandecer | 1 |
| 9874 | rebeca | 1 |
| 9875 | rebanada | 1 |
| 9876 | rebaja | 1 |
| 9877 | reapertura | 1 |
| 9878 | reanimar | 1 |
| 9879 | realización | 1 |
| 9880 | realista | 1 |
| 9881 | reales | 1 |
| 9882 | rayuela | 1 |
| 9883 | rayano | 1 |
| 9884 | rayado | 1 |
| 9885 | raudo | 1 |
| 9886 | ratificar | 1 |
| 9887 | ratera | 1 |
| 9888 | rastrear | 1 |
| 9889 | rasgueo | 1 |
| 9890 | rasgos | 1 |
| 9891 | rasgar | 1 |
| 9892 | raquitismo | 1 |
| 9893 | rapé | 1 |
| 9894 | rapacidad | 1 |
| 9895 | ranero | 1 |
| 9896 | rana | 1 |
| 9897 | ramplón | 1 |
| 9898 | rampa | 1 |
| 9899 | ramona | 1 |
| 9900 | ramojo | 1 |
| 9901 | ramillete | 1 |
| 9902 | rameaditas | 1 |
| 9903 | ramalazo | 1 |
| 9904 | rallar | 1 |
| 9905 | ralea | 1 |
| 9906 | rajar | 1 |
| 9907 | raja | 1 |
| 9908 | raído | 1 |
| 9909 | radio | 1 |
| 9910 | radicar | 1 |
| 9911 | radicalmente | 1 |
| 9912 | radical | 1 |
| 9913 | racionalista | 1 |
| 9914 | rachir | 1 |
| 9915 | racha | 1 |
| 9916 | rabillo | 1 |
| 9917 | rabadilla | 1 |
| 9918 | r | 1 |
| 9919 | quitole | 1 |
| 9920 | quitándose | 1 |
| 9921 | quítale | 1 |
| 9922 | quisto | 1 |
| 9923 | quisquilloso | 1 |
| 9924 | quirúrgicamente | 1 |
| 9925 | quintín | 1 |
| 9926 | quintilla | 1 |
| 9927 | quintero | 1 |
| 9928 | quinina | 1 |
| 9929 | quinientas | 1 |
| 9930 | quinceno | 1 |
| 9931 | quincena | 1 |
| 9932 | quincalla | 1 |
| 9933 | quina | 1 |
| 9934 | químico | 1 |
| 9935 | quilo | 1 |
| 9936 | quijotesco | 1 |
| 9937 | quiéreme | 1 |
| 9938 | quiera | 1 |
| 9939 | quiénes | 1 |
| 9940 | quiebra | 1 |
| 9941 | quid | 1 |
| 9942 | quevedos | 1 |
| 9943 | quesada | 1 |
| 9944 | queriéndome | 1 |
| 9945 | quería | 1 |
| 9946 | quererte | 1 |
| 9947 | quemado | 1 |
| 9948 | quedeme | 1 |
| 9949 | quedarse | 1 |
| 9950 | quedábanse | 1 |
| 9951 | quebrar | 1 |
| 9952 | putrefacción | 1 |
| 9953 | putona | 1 |
| 9954 | putativo | 1 |
| 9955 | pusiéronle | 1 |
| 9956 | púseme | 1 |
| 9957 | purgar | 1 |
| 9958 | puré | 1 |
| 9959 | pura | 1 |
| 9960 | punzón | 1 |
| 9961 | punzante | 1 |
| 9962 | punzada | 1 |
| 9963 | puntilloso | 1 |
| 9964 | puntiagudo | 1 |
| 9965 | puntero | 1 |
| 9966 | puntera | 1 |
| 9967 | pundonoroso | 1 |
| 9968 | pulsera | 1 |
| 9969 | pulpejo | 1 |
| 9970 | pulpa | 1 |
| 9971 | pulimentar | 1 |
| 9972 | pulgada | 1 |
| 9973 | pulcro | 1 |
| 9974 | pujanza | 1 |
| 9975 | pujante | 1 |
| 9976 | pugilato | 1 |
| 9977 | puertas | 1 |
| 9978 | puerilidad | 1 |
| 9979 | puerca | 1 |
| 9980 | pueden | 1 |
| 9981 | pueblecito | 1 |
| 9982 | pudrir | 1 |
| 9983 | pucheta | 1 |
| 9984 | publicista | 1 |
| 9985 | pseudo | 1 |
| 9986 | psch | 1 |
| 9987 | pruuun | 1 |
| 9988 | pruebe | 1 |
| 9989 | prudencial | 1 |
| 9990 | proyección | 1 |
| 9991 | provincias | 1 |
| 9992 | provinciano | 1 |
| 9993 | provincial | 1 |
| 9994 | protesta | 1 |
| 9995 | proteccionista | 1 |
| 9996 | prostituir | 1 |
| 9997 | prosternar | 1 |
| 9998 | prosperar | 1 |
| 9999 | prospecto | 1 |
| 10000 | prosélito | 1 |
| 10001 | proscenio | 1 |
| 10002 | prosa | 1 |
| 10003 | proporcional | 1 |
| 10004 | proporcionadamente | 1 |
| 10005 | proporcionábale | 1 |
| 10006 | propónense | 1 |
| 10007 | propina | 1 |
| 10008 | propender | 1 |
| 10009 | propalar | 1 |
| 10010 | pronóstico | 1 |
| 10011 | pronosticar | 1 |
| 10012 | promontorio | 1 |
| 10013 | prominente | 1 |
| 10014 | prometida | 1 |
| 10015 | prometíaselas | 1 |
| 10016 | prolijidad | 1 |
| 10017 | prolijamente | 1 |
| 10018 | prolífico | 1 |
| 10019 | prohijar | 1 |
| 10020 | progresivo | 1 |
| 10021 | progresar | 1 |
| 10022 | progenie | 1 |
| 10023 | profundísimamente | 1 |
| 10024 | profundísima | 1 |
| 10025 | profundidad | 1 |
| 10026 | profético | 1 |
| 10027 | profeta | 1 |
| 10028 | profesional | 1 |
| 10029 | profano | 1 |
| 10030 | proeza | 1 |
| 10031 | productor | 1 |
| 10032 | pródigo | 1 |
| 10033 | procurarle | 1 |
| 10034 | procura | 1 |
| 10035 | proclamar | 1 |
| 10036 | prócida | 1 |
| 10037 | procesionalmente | 1 |
| 10038 | proceroso | 1 |
| 10039 | procedente | 1 |
| 10040 | procaz | 1 |
| 10041 | procacidad | 1 |
| 10042 | probrecilla | 1 |
| 10043 | probes | 1 |
| 10044 | probe | 1 |
| 10045 | pro | 1 |
| 10046 | prismático | 1 |
| 10047 | prisma | 1 |
| 10048 | pringue | 1 |
| 10049 | primordial | 1 |
| 10050 | primeramente | 1 |
| 10051 | primario | 1 |
| 10052 | primaria | 1 |
| 10053 | prima | 1 |
| 10054 | price | 1 |
| 10055 | preventivo | 1 |
| 10056 | prevaricar | 1 |
| 10057 | pretextos | 1 |
| 10058 | pretérito | 1 |
| 10059 | presunto | 1 |
| 10060 | presumida | 1 |
| 10061 | prestigio | 1 |
| 10062 | prestidigitador | 1 |
| 10063 | prestidigitación | 1 |
| 10064 | presidencial | 1 |
| 10065 | presidencia | 1 |
| 10066 | preservativo | 1 |
| 10067 | preséntate | 1 |
| 10068 | prescribir | 1 |
| 10069 | prescindir | 1 |
| 10070 | presbiterio | 1 |
| 10071 | presagiar | 1 |
| 10072 | prepárese | 1 |
| 10073 | preparatorio | 1 |
| 10074 | prepárate | 1 |
| 10075 | preparando | 1 |
| 10076 | preparado | 1 |
| 10077 | preparábase | 1 |
| 10078 | premiado | 1 |
| 10079 | preliminar | 1 |
| 10080 | prejuicio | 1 |
| 10081 | preguntón | 1 |
| 10082 | preguntome | 1 |
| 10083 | preguntole | 1 |
| 10084 | prefieres | 1 |
| 10085 | preferiremos | 1 |
| 10086 | preferible | 1 |
| 10087 | prefería | 1 |
| 10088 | predisposición | 1 |
| 10089 | predicador | 1 |
| 10090 | predestinar | 1 |
| 10091 | precozmente | 1 |
| 10092 | precocidad | 1 |
| 10093 | precisión | 1 |
| 10094 | precipicio | 1 |
| 10095 | precepto | 1 |
| 10096 | precedente | 1 |
| 10097 | práxedes | 1 |
| 10098 | pragmático | 1 |
| 10099 | pragmática | 1 |
| 10100 | praga | 1 |
| 10101 | pradoluengo | 1 |
| 10102 | pradera | 1 |
| 10103 | practicable | 1 |
| 10104 | pozos | 1 |
| 10105 | potestad | 1 |
| 10106 | potente | 1 |
| 10107 | pote | 1 |
| 10108 | potasio | 1 |
| 10109 | póstumo | 1 |
| 10110 | postrimerías | 1 |
| 10111 | postrado | 1 |
| 10112 | poste | 1 |
| 10113 | postal | 1 |
| 10114 | posta | 1 |
| 10115 | positivar | 1 |
| 10116 | positivamente | 1 |
| 10117 | posada | 1 |
| 10118 | portugal | 1 |
| 10119 | portento | 1 |
| 10120 | portear | 1 |
| 10121 | porra | 1 |
| 10122 | pordiosero | 1 |
| 10123 | pordiosear | 1 |
| 10124 | popularidad | 1 |
| 10125 | ponzoñoso | 1 |
| 10126 | pontevedra | 1 |
| 10127 | ponlo | 1 |
| 10128 | ponle | 1 |
| 10129 | ponía | 1 |
| 10130 | pongámosle | 1 |
| 10131 | pongamos | 1 |
| 10132 | ponderación | 1 |
| 10133 | poncio | 1 |
| 10134 | pollino | 1 |
| 10135 | política | 1 |
| 10136 | polinesia | 1 |
| 10137 | policíaco | 1 |
| 10138 | policiaco | 1 |
| 10139 | polichinela | 1 |
| 10140 | polemista | 1 |
| 10141 | poema | 1 |
| 10142 | podrías | 1 |
| 10143 | podredumbre | 1 |
| 10144 | podrás | 1 |
| 10145 | podías | 1 |
| 10146 | pócima | 1 |
| 10147 | pocillo | 1 |
| 10148 | pocilga | 1 |
| 10149 | pobrete | 1 |
| 10150 | pobres | 1 |
| 10151 | poblar | 1 |
| 10152 | plomizo | 1 |
| 10153 | pléyade | 1 |
| 10154 | plenipotenciario | 1 |
| 10155 | plazos | 1 |
| 10156 | platero | 1 |
| 10157 | plateado | 1 |
| 10158 | plataforma | 1 |
| 10159 | plasta | 1 |
| 10160 | plantose | 1 |
| 10161 | plantilla | 1 |
| 10162 | plantificar | 1 |
| 10163 | planicie | 1 |
| 10164 | planeta | 1 |
| 10165 | plana | 1 |
| 10166 | plagar | 1 |
| 10167 | placita | 1 |
| 10168 | placidito | 1 |
| 10169 | placar | 1 |
| 10170 | pituitario | 1 |
| 10171 | pitón | 1 |
| 10172 | pitita | 1 |
| 10173 | pitillo | 1 |
| 10174 | pitido | 1 |
| 10175 | pitágoras | 1 |
| 10176 | piscicultura | 1 |
| 10177 | pirineo | 1 |
| 10178 | piratería | 1 |
| 10179 | pirata | 1 |
| 10180 | pirar | 1 |
| 10181 | piojoso | 1 |
| 10182 | pinto | 1 |
| 10183 | pintiparar | 1 |
| 10184 | pinitos | 1 |
| 10185 | pingüe | 1 |
| 10186 | pindonga | 1 |
| 10187 | pincelada | 1 |
| 10188 | pinar | 1 |
| 10189 | pináculo | 1 |
| 10190 | pin | 1 |
| 10191 | pimpollo | 1 |
| 10192 | pimiento | 1 |
| 10193 | piloso | 1 |
| 10194 | pilluelo | 1 |
| 10195 | pillinadas | 1 |
| 10196 | pillastre | 1 |
| 10197 | pilatos | 1 |
| 10198 | pidiole | 1 |
| 10199 | pidiéronle | 1 |
| 10200 | pídeselo | 1 |
| 10201 | pidámosle | 1 |
| 10202 | pichón | 1 |
| 10203 | picazón | 1 |
| 10204 | picaresca | 1 |
| 10205 | picardías | 1 |
| 10206 | picaporte | 1 |
| 10207 | picapedrero | 1 |
| 10208 | picadura | 1 |
| 10209 | picadilly | 1 |
| 10210 | picadillo | 1 |
| 10211 | picada | 1 |
| 10212 | pica | 1 |
| 10213 | pía | 1 |
| 10214 | petrificado | 1 |
| 10215 | petrarca | 1 |
| 10216 | petimetre | 1 |
| 10217 | pestilencia | 1 |
| 10218 | pestífero | 1 |
| 10219 | pestañar | 1 |
| 10220 | pesquisa | 1 |
| 10221 | pesebre | 1 |
| 10222 | pescadilla | 1 |
| 10223 | pesca | 1 |
| 10224 | pesares | 1 |
| 10225 | pesa | 1 |
| 10226 | perturbación | 1 |
| 10227 | pertinencia | 1 |
| 10228 | persuasivo | 1 |
| 10229 | perspectiva | 1 |
| 10230 | personas | 1 |
| 10231 | persistente | 1 |
| 10232 | perseverar | 1 |
| 10233 | persépolis | 1 |
| 10234 | perseguidor | 1 |
| 10235 | persecutorio | 1 |
| 10236 | persecuciones | 1 |
| 10237 | persa | 1 |
| 10238 | perruna | 1 |
| 10239 | perplejo | 1 |
| 10240 | perpiñá | 1 |
| 10241 | perpetuidad | 1 |
| 10242 | pernoctar | 1 |
| 10243 | perneta | 1 |
| 10244 | permuta | 1 |
| 10245 | perjudicial | 1 |
| 10246 | periquito | 1 |
| 10247 | periquillo | 1 |
| 10248 | perifollo | 1 |
| 10249 | perico | 1 |
| 10250 | pericial | 1 |
| 10251 | peri | 1 |
| 10252 | pergeñar | 1 |
| 10253 | pergenio | 1 |
| 10254 | pergamino | 1 |
| 10255 | perfumado | 1 |
| 10256 | perfec | 1 |
| 10257 | pérez | 1 |
| 10258 | perenne | 1 |
| 10259 | perendengue | 1 |
| 10260 | perejil | 1 |
| 10261 | perdidamente | 1 |
| 10262 | perdida | 1 |
| 10263 | percusión | 1 |
| 10264 | perchel | 1 |
| 10265 | peptona | 1 |
| 10266 | pepes | 1 |
| 10267 | peón | 1 |
| 10268 | peñuelas | 1 |
| 10269 | peñascal | 1 |
| 10270 | pentagrama | 1 |
| 10271 | pensionar | 1 |
| 10272 | pensaste | 1 |
| 10273 | pensará | 1 |
| 10274 | pensando | 1 |
| 10275 | pensador | 1 |
| 10276 | pensad | 1 |
| 10277 | penosamente | 1 |
| 10278 | penetración | 1 |
| 10279 | péndulo | 1 |
| 10280 | pendolista | 1 |
| 10281 | pender | 1 |
| 10282 | penca | 1 |
| 10283 | penalidad | 1 |
| 10284 | penal | 1 |
| 10285 | pelusa | 1 |
| 10286 | pelotón | 1 |
| 10287 | pelotilla | 1 |
| 10288 | pelliza | 1 |
| 10289 | pelleja | 1 |
| 10290 | pelinegro | 1 |
| 10291 | peligros | 1 |
| 10292 | pelea | 1 |
| 10293 | pelaje | 1 |
| 10294 | pelafustán | 1 |
| 10295 | peladilla | 1 |
| 10296 | peinada | 1 |
| 10297 | pégueme | 1 |
| 10298 | pégame | 1 |
| 10299 | pegajoso | 1 |
| 10300 | pegada | 1 |
| 10301 | pedrisco | 1 |
| 10302 | pedirme | 1 |
| 10303 | pedigüeño | 1 |
| 10304 | pedantería | 1 |
| 10305 | pedal | 1 |
| 10306 | pecoso | 1 |
| 10307 | pechugón | 1 |
| 10308 | pechera | 1 |
| 10309 | pececillos | 1 |
| 10310 | pecaminoso | 1 |
| 10311 | pe | 1 |
| 10312 | payo | 1 |
| 10313 | payaso | 1 |
| 10314 | payar | 1 |
| 10315 | pavimento | 1 |
| 10316 | paúl | 1 |
| 10317 | patulea | 1 |
| 10318 | patriota | 1 |
| 10319 | patrimonial | 1 |
| 10320 | patriarca | 1 |
| 10321 | patoso | 1 |
| 10322 | pato | 1 |
| 10323 | patito | 1 |
| 10324 | patitas | 1 |
| 10325 | patinar | 1 |
| 10326 | patinador | 1 |
| 10327 | pátina | 1 |
| 10328 | pateta | 1 |
| 10329 | paternidad | 1 |
| 10330 | paternalmente | 1 |
| 10331 | patentar | 1 |
| 10332 | patena | 1 |
| 10333 | pastorear | 1 |
| 10334 | pastelón | 1 |
| 10335 | pasmo | 1 |
| 10336 | pásmense | 1 |
| 10337 | pasmábase | 1 |
| 10338 | pasividad | 1 |
| 10339 | pasivas | 1 |
| 10340 | pasen | 1 |
| 10341 | paseante | 1 |
| 10342 | pasáronle | 1 |
| 10343 | pasaría | 1 |
| 10344 | pasaporte | 1 |
| 10345 | pasábanse | 1 |
| 10346 | partirle | 1 |
| 10347 | parra | 1 |
| 10348 | parola | 1 |
| 10349 | parlanchín | 1 |
| 10350 | parlamentar | 1 |
| 10351 | parienta | 1 |
| 10352 | parido | 1 |
| 10353 | parida | 1 |
| 10354 | paria | 1 |
| 10355 | párese | 1 |
| 10356 | pareciéronle | 1 |
| 10357 | parecían | 1 |
| 10358 | pardillo | 1 |
| 10359 | parche | 1 |
| 10360 | parca | 1 |
| 10361 | párate | 1 |
| 10362 | parásito | 1 |
| 10363 | parasitario | 1 |
| 10364 | pararse | 1 |
| 10365 | parándose | 1 |
| 10366 | paramento | 1 |
| 10367 | parálisis | 1 |
| 10368 | paralelamente | 1 |
| 10369 | parada | 1 |
| 10370 | paquito | 1 |
| 10371 | paquita | 1 |
| 10372 | pápiro | 1 |
| 10373 | papelillo | 1 |
| 10374 | papal | 1 |
| 10375 | papagayo | 1 |
| 10376 | paños | 1 |
| 10377 | pañero | 1 |
| 10378 | pantufla | 1 |
| 10379 | panteísta | 1 |
| 10380 | pantaleón | 1 |
| 10381 | pánfilo | 1 |
| 10382 | panegírico | 1 |
| 10383 | pandilla | 1 |
| 10384 | pancorvo | 1 |
| 10385 | panadero | 1 |
| 10386 | panacea | 1 |
| 10387 | pamplinas | 1 |
| 10388 | pámpano | 1 |
| 10389 | paludismo | 1 |
| 10390 | palpitante | 1 |
| 10391 | palpable | 1 |
| 10392 | palomar | 1 |
| 10393 | palmera | 1 |
| 10394 | palmado | 1 |
| 10395 | palmadita | 1 |
| 10396 | paliativo | 1 |
| 10397 | paletilla | 1 |
| 10398 | palatino | 1 |
| 10399 | palabrota | 1 |
| 10400 | palabrero | 1 |
| 10401 | palabreja | 1 |
| 10402 | pajita | 1 |
| 10403 | paje | 1 |
| 10404 | pajarraco | 1 |
| 10405 | pájaros | 1 |
| 10406 | pajarero | 1 |
| 10407 | paisajista | 1 |
| 10408 | paicen | 1 |
| 10409 | pagarle | 1 |
| 10410 | pagano | 1 |
| 10411 | paganismo | 1 |
| 10412 | paella | 1 |
| 10413 | padrenuestros | 1 |
| 10414 | padecimiento | 1 |
| 10415 | padecía | 1 |
| 10416 | pacto | 1 |
| 10417 | pacificar | 1 |
| 10418 | pacíficamente | 1 |
| 10419 | pacificador | 1 |
| 10420 | pabellón | 1 |
| 10421 | p | 1 |
| 10422 | oyoles | 1 |
| 10423 | oyola | 1 |
| 10424 | oyó | 1 |
| 10425 | oyen | 1 |
| 10426 | óvalo | 1 |
| 10427 | otras | 1 |
| 10428 | otero | 1 |
| 10429 | otelo | 1 |
| 10430 | oso | 1 |
| 10431 | orza | 1 |
| 10432 | oropel | 1 |
| 10433 | ornitológico | 1 |
| 10434 | ornato | 1 |
| 10435 | orlar | 1 |
| 10436 | orinar | 1 |
| 10437 | orillas | 1 |
| 10438 | orihuela | 1 |
| 10439 | orígenes | 1 |
| 10440 | orientar | 1 |
| 10441 | orgullosamente | 1 |
| 10442 | organizador | 1 |
| 10443 | organillo | 1 |
| 10444 | orfandad | 1 |
| 10445 | ordinariez | 1 |
| 10446 | ordenó | 1 |
| 10447 | ordenanzas | 1 |
| 10448 | ordenador | 1 |
| 10449 | ordenación | 1 |
| 10450 | orbe | 1 |
| 10451 | orate | 1 |
| 10452 | orangután | 1 |
| 10453 | oráculo | 1 |
| 10454 | opusiéronse | 1 |
| 10455 | opulencia | 1 |
| 10456 | optar | 1 |
| 10457 | oportunista | 1 |
| 10458 | opóngase | 1 |
| 10459 | opio | 1 |
| 10460 | opinó | 1 |
| 10461 | opiáceo | 1 |
| 10462 | ópalo | 1 |
| 10463 | opacidad | 1 |
| 10464 | ooooh | 1 |
| 10465 | onofre | 1 |
| 10466 | ondular | 1 |
| 10467 | ondear | 1 |
| 10468 | onde | 1 |
| 10469 | omoplato | 1 |
| 10470 | omnipotente | 1 |
| 10471 | omnipotencia | 1 |
| 10472 | omnímodo | 1 |
| 10473 | ómnibus | 1 |
| 10474 | omisión | 1 |
| 10475 | ombligo | 1 |
| 10476 | olvídate | 1 |
| 10477 | olvidadizo | 1 |
| 10478 | olózaga | 1 |
| 10479 | olmos | 1 |
| 10480 | olla | 1 |
| 10481 | olivares | 1 |
| 10482 | olivar | 1 |
| 10483 | oliva | 1 |
| 10484 | olimpa | 1 |
| 10485 | oleada | 1 |
| 10486 | ojiva | 1 |
| 10487 | ojeriza | 1 |
| 10488 | ojeador | 1 |
| 10489 | ojeada | 1 |
| 10490 | oímos | 1 |
| 10491 | óigame | 1 |
| 10492 | oíale | 1 |
| 10493 | ofreció | 1 |
| 10494 | ofrecíase | 1 |
| 10495 | oficialmente | 1 |
| 10496 | ofensor | 1 |
| 10497 | ofensivo | 1 |
| 10498 | ocurrírseme | 1 |
| 10499 | ocurrirle | 1 |
| 10500 | ocurrente | 1 |
| 10501 | ocurrencia | 1 |
| 10502 | ocupado | 1 |
| 10503 | oculto | 1 |
| 10504 | ocultáronse | 1 |
| 10505 | ocultamente | 1 |
| 10506 | ocular | 1 |
| 10507 | octava | 1 |
| 10508 | ocre | 1 |
| 10509 | océano | 1 |
| 10510 | ocasional | 1 |
| 10511 | obstruir | 1 |
| 10512 | obstinación | 1 |
| 10513 | obstetricia | 1 |
| 10514 | observo | 1 |
| 10515 | observándola | 1 |
| 10516 | obsérvale | 1 |
| 10517 | observábale | 1 |
| 10518 | observábala | 1 |
| 10519 | observa | 1 |
| 10520 | obsequio | 1 |
| 10521 | obligada | 1 |
| 10522 | oblicuidad | 1 |
| 10523 | oblicuar | 1 |
| 10524 | obeso | 1 |
| 10525 | obesidad | 1 |
| 10526 | obediente | 1 |
| 10527 | ñoño | 1 |
| 10528 | nutrir | 1 |
| 10529 | nuncio | 1 |
| 10530 | numismático | 1 |
| 10531 | numeroso | 1 |
| 10532 | numérico | 1 |
| 10533 | nulo | 1 |
| 10534 | nulidad | 1 |
| 10535 | nuevecito | 1 |
| 10536 | nuevas | 1 |
| 10537 | nudoso | 1 |
| 10538 | nublado | 1 |
| 10539 | noviciado | 1 |
| 10540 | novel | 1 |
| 10541 | novecientos | 1 |
| 10542 | noticiero | 1 |
| 10543 | notario | 1 |
| 10544 | notabilísimo | 1 |
| 10545 | notabilidad | 1 |
| 10546 | notábase | 1 |
| 10547 | nostri | 1 |
| 10548 | nostalgia | 1 |
| 10549 | normalizar | 1 |
| 10550 | norma | 1 |
| 10551 | nominativo | 1 |
| 10552 | nominal | 1 |
| 10553 | nómina | 1 |
| 10554 | nomenclatura | 1 |
| 10555 | nomenclátor | 1 |
| 10556 | nombrábase | 1 |
| 10557 | nogal | 1 |
| 10558 | nocivo | 1 |
| 10559 | nochecita | 1 |
| 10560 | nobiliario | 1 |
| 10561 | nizán | 1 |
| 10562 | nitro | 1 |
| 10563 | níquel | 1 |
| 10564 | niños | 1 |
| 10565 | niñero | 1 |
| 10566 | niñas | 1 |
| 10567 | nimiedad | 1 |
| 10568 | nilo | 1 |
| 10569 | nieva | 1 |
| 10570 | newton | 1 |
| 10571 | nevar | 1 |
| 10572 | nevado | 1 |
| 10573 | nevada | 1 |
| 10574 | neutralizar | 1 |
| 10575 | neptuno | 1 |
| 10576 | negrura | 1 |
| 10577 | negligente | 1 |
| 10578 | negativa | 1 |
| 10579 | negarle | 1 |
| 10580 | negación | 1 |
| 10581 | necios | 1 |
| 10582 | necesito | 1 |
| 10583 | necesitas | 1 |
| 10584 | necesitaré | 1 |
| 10585 | navío | 1 |
| 10586 | navidades | 1 |
| 10587 | navarra | 1 |
| 10588 | nauseabundo | 1 |
| 10589 | nato | 1 |
| 10590 | narración | 1 |
| 10591 | narigudo | 1 |
| 10592 | narcótico | 1 |
| 10593 | narcisus | 1 |
| 10594 | naranjeros | 1 |
| 10595 | naranjado | 1 |
| 10596 | najar | 1 |
| 10597 | nació | 1 |
| 10598 | mutuamente | 1 |
| 10599 | mutismo | 1 |
| 10600 | mutación | 1 |
| 10601 | mustiar | 1 |
| 10602 | musotros | 1 |
| 10603 | musas | 1 |
| 10604 | murmuración | 1 |
| 10605 | murga | 1 |
| 10606 | muralla | 1 |
| 10607 | muñón | 1 |
| 10608 | munificencia | 1 |
| 10609 | municipio | 1 |
| 10610 | múltiple | 1 |
| 10611 | multar | 1 |
| 10612 | mulo | 1 |
| 10613 | mujeriego | 1 |
| 10614 | mujeres | 1 |
| 10615 | mujercita | 1 |
| 10616 | mujeraza | 1 |
| 10617 | muellemente | 1 |
| 10618 | mudos | 1 |
| 10619 | mucosa | 1 |
| 10620 | mucílago | 1 |
| 10621 | muchísimas | 1 |
| 10622 | mozuela | 1 |
| 10623 | mozart | 1 |
| 10624 | mozárabe | 1 |
| 10625 | mozalbete | 1 |
| 10626 | moyano | 1 |
| 10627 | motín | 1 |
| 10628 | mostrándose | 1 |
| 10629 | mosquitero | 1 |
| 10630 | mosquita | 1 |
| 10631 | moscón | 1 |
| 10632 | mortecino | 1 |
| 10633 | mortalmente | 1 |
| 10634 | mortaja | 1 |
| 10635 | morrón | 1 |
| 10636 | morris | 1 |
| 10637 | morralla | 1 |
| 10638 | morral | 1 |
| 10639 | morosidad | 1 |
| 10640 | morirme | 1 |
| 10641 | morenito | 1 |
| 10642 | mordisco | 1 |
| 10643 | mordiscar | 1 |
| 10644 | moralizar | 1 |
| 10645 | mora | 1 |
| 10646 | moquillo | 1 |
| 10647 | moqueta | 1 |
| 10648 | moñuca | 1 |
| 10649 | monumento | 1 |
| 10650 | monumentalidad | 1 |
| 10651 | monumental | 1 |
| 10652 | montpensier | 1 |
| 10653 | montesinos | 1 |
| 10654 | montesa | 1 |
| 10655 | montés | 1 |
| 10656 | montemuru | 1 |
| 10657 | monteleón | 1 |
| 10658 | monotonía | 1 |
| 10659 | monje | 1 |
| 10660 | monigote | 1 |
| 10661 | mongólico | 1 |
| 10662 | monetario | 1 |
| 10663 | monear | 1 |
| 10664 | moncloa | 1 |
| 10665 | monasterio | 1 |
| 10666 | monamente | 1 |
| 10667 | mon | 1 |
| 10668 | momentáneamente | 1 |
| 10669 | molusco | 1 |
| 10670 | mollera | 1 |
| 10671 | molleja | 1 |
| 10672 | molesto | 1 |
| 10673 | molestábale | 1 |
| 10674 | mole | 1 |
| 10675 | moldear | 1 |
| 10676 | molar | 1 |
| 10677 | mojicón | 1 |
| 10678 | mojama | 1 |
| 10679 | modulación | 1 |
| 10680 | modos | 1 |
| 10681 | modorra | 1 |
| 10682 | modisto | 1 |
| 10683 | modistilla | 1 |
| 10684 | modismo | 1 |
| 10685 | modificación | 1 |
| 10686 | modestamente | 1 |
| 10687 | moderado | 1 |
| 10688 | moderación | 1 |
| 10689 | mochuelo | 1 |
| 10690 | mochila | 1 |
| 10691 | mocetón | 1 |
| 10692 | mixtura | 1 |
| 10693 | mitológico | 1 |
| 10694 | mito | 1 |
| 10695 | mitchell | 1 |
| 10696 | míseramente | 1 |
| 10697 | misal | 1 |
| 10698 | mirosté | 1 |
| 10699 | mirón | 1 |
| 10700 | mirola | 1 |
| 10701 | miró | 1 |
| 10702 | mirlo | 1 |
| 10703 | miriñaque | 1 |
| 10704 | mírenlo | 1 |
| 10705 | míreme | 1 |
| 10706 | mírelos | 1 |
| 10707 | mírele | 1 |
| 10708 | miráronla | 1 |
| 10709 | miraron | 1 |
| 10710 | miraría | 1 |
| 10711 | miraré | 1 |
| 10712 | míranse | 1 |
| 10713 | miranda | 1 |
| 10714 | mirad | 1 |
| 10715 | mirábase | 1 |
| 10716 | mirábales | 1 |
| 10717 | miope | 1 |
| 10718 | minino | 1 |
| 10719 | minas | 1 |
| 10720 | mina | 1 |
| 10721 | mímico | 1 |
| 10722 | mimado | 1 |
| 10723 | millonario | 1 |
| 10724 | milla | 1 |
| 10725 | militante | 1 |
| 10726 | milaneses | 1 |
| 10727 | milagroso | 1 |
| 10728 | migar | 1 |
| 10729 | mies | 1 |
| 10730 | miércoles | 1 |
| 10731 | miedoso | 1 |
| 10732 | miaja | 1 |
| 10733 | mezquita | 1 |
| 10734 | mezquinar | 1 |
| 10735 | mezclado | 1 |
| 10736 | metz | 1 |
| 10737 | metrópoli | 1 |
| 10738 | metodizar | 1 |
| 10739 | mételes | 1 |
| 10740 | mete | 1 |
| 10741 | metálicamente | 1 |
| 10742 | mesonero | 1 |
| 10743 | mesón | 1 |
| 10744 | meseta | 1 |
| 10745 | mero | 1 |
| 10746 | merendero | 1 |
| 10747 | merecimiento | 1 |
| 10748 | merecedor | 1 |
| 10749 | mercenario | 1 |
| 10750 | mercancía | 1 |
| 10751 | mentís | 1 |
| 10752 | mentirilla | 1 |
| 10753 | mentir | 1 |
| 10754 | menospreciar | 1 |
| 10755 | menoscabo | 1 |
| 10756 | mengue | 1 |
| 10757 | menguar | 1 |
| 10758 | mendiry | 1 |
| 10759 | mendicante | 1 |
| 10760 | méndez | 1 |
| 10761 | mencionado | 1 |
| 10762 | menaje | 1 |
| 10763 | membrillo | 1 |
| 10764 | melón | 1 |
| 10765 | melena | 1 |
| 10766 | melancólicamente | 1 |
| 10767 | mela | 1 |
| 10768 | mejores | 1 |
| 10769 | mejora | 1 |
| 10770 | meditemos | 1 |
| 10771 | medidor | 1 |
| 10772 | medicinal | 1 |
| 10773 | medianero | 1 |
| 10774 | mediana | 1 |
| 10775 | medalla | 1 |
| 10776 | mécele | 1 |
| 10777 | mazmorra | 1 |
| 10778 | maximiliana | 1 |
| 10779 | mauro | 1 |
| 10780 | maula | 1 |
| 10781 | matrimoniar | 1 |
| 10782 | matricular | 1 |
| 10783 | matías | 1 |
| 10784 | materialmente | 1 |
| 10785 | mateo | 1 |
| 10786 | mate | 1 |
| 10787 | mátate | 1 |
| 10788 | matarle | 1 |
| 10789 | matanza | 1 |
| 10790 | mátameles | 1 |
| 10791 | matador | 1 |
| 10792 | matachín | 1 |
| 10793 | massarnau | 1 |
| 10794 | massanielo | 1 |
| 10795 | mascullar | 1 |
| 10796 | masarnau | 1 |
| 10797 | masar | 1 |
| 10798 | martillazo | 1 |
| 10799 | martes | 1 |
| 10800 | marte | 1 |
| 10801 | marsella | 1 |
| 10802 | marítimo | 1 |
| 10803 | marisma | 1 |
| 10804 | marisabidilla | 1 |
| 10805 | mariquita | 1 |
| 10806 | mariposa | 1 |
| 10807 | marinar | 1 |
| 10808 | marica | 1 |
| 10809 | mariana | 1 |
| 10810 | margarita | 1 |
| 10811 | marcos | 1 |
| 10812 | marchose | 1 |
| 10813 | marchito | 1 |
| 10814 | márchate | 1 |
| 10815 | marcharse | 1 |
| 10816 | marchante | 1 |
| 10817 | marcador | 1 |
| 10818 | marcadamente | 1 |
| 10819 | maravillas | 1 |
| 10820 | maravillábase | 1 |
| 10821 | marar | 1 |
| 10822 | maquinar | 1 |
| 10823 | maquinación | 1 |
| 10824 | manzanilla | 1 |
| 10825 | manueles | 1 |
| 10826 | mantillas | 1 |
| 10827 | mantel | 1 |
| 10828 | mantecada | 1 |
| 10829 | mansión | 1 |
| 10830 | manolitos | 1 |
| 10831 | manolito | 1 |
| 10832 | maniobrar | 1 |
| 10833 | manglar | 1 |
| 10834 | mandria | 1 |
| 10835 | mandola | 1 |
| 10836 | mandó | 1 |
| 10837 | mandinga | 1 |
| 10838 | mandíbula | 1 |
| 10839 | mándeme | 1 |
| 10840 | mandato | 1 |
| 10841 | mándale | 1 |
| 10842 | mandado | 1 |
| 10843 | mancillar | 1 |
| 10844 | manchado | 1 |
| 10845 | mameluco | 1 |
| 10846 | malva | 1 |
| 10847 | malsonante | 1 |
| 10848 | malquerencia | 1 |
| 10849 | malhumorado | 1 |
| 10850 | maleta | 1 |
| 10851 | maleficiar | 1 |
| 10852 | maledicencia | 1 |
| 10853 | maleado | 1 |
| 10854 | maldonadas | 1 |
| 10855 | malditos | 1 |
| 10856 | malditamente | 1 |
| 10857 | maldiciente | 1 |
| 10858 | malayo | 1 |
| 10859 | malaventurado | 1 |
| 10860 | malagueño | 1 |
| 10861 | málaga | 1 |
| 10862 | mala | 1 |
| 10863 | majagranzas | 1 |
| 10864 | maíz | 1 |
| 10865 | magullar | 1 |
| 10866 | mago | 1 |
| 10867 | magnitud | 1 |
| 10868 | magnético | 1 |
| 10869 | magnánimo | 1 |
| 10870 | magistratura | 1 |
| 10871 | magistrado | 1 |
| 10872 | magisterio | 1 |
| 10873 | maestría | 1 |
| 10874 | madurez | 1 |
| 10875 | madroño | 1 |
| 10876 | madrigal | 1 |
| 10877 | madrastra | 1 |
| 10878 | madrás | 1 |
| 10879 | madoz | 1 |
| 10880 | macilento | 1 |
| 10881 | machito | 1 |
| 10882 | machete | 1 |
| 10883 | machetazo | 1 |
| 10884 | machamartillo | 1 |
| 10885 | machacárselo | 1 |
| 10886 | machacante | 1 |
| 10887 | maceta | 1 |
| 10888 | m | 1 |
| 10889 | lustro | 1 |
| 10890 | lustrar | 1 |
| 10891 | lunar | 1 |
| 10892 | lúgubremente | 1 |
| 10893 | lucio | 1 |
| 10894 | lúcido | 1 |
| 10895 | lucidez | 1 |
| 10896 | lucida | 1 |
| 10897 | luchana | 1 |
| 10898 | lozano | 1 |
| 10899 | lourdes | 1 |
| 10900 | lotero | 1 |
| 10901 | loterías | 1 |
| 10902 | losa | 1 |
| 10903 | lorito | 1 |
| 10904 | lorenzo | 1 |
| 10905 | lorenzana | 1 |
| 10906 | loquito | 1 |
| 10907 | longaniza | 1 |
| 10908 | lola | 1 |
| 10909 | lógicamente | 1 |
| 10910 | logia | 1 |
| 10911 | locamente | 1 |
| 10912 | lóbulo | 1 |
| 10913 | lluvioso | 1 |
| 10914 | llovido | 1 |
| 10915 | lloroso | 1 |
| 10916 | lloriqueo | 1 |
| 10917 | llevose | 1 |
| 10918 | llevola | 1 |
| 10919 | lléveselo | 1 |
| 10920 | llévate | 1 |
| 10921 | llevándola | 1 |
| 10922 | llévalos | 1 |
| 10923 | llevábase | 1 |
| 10924 | llevaba | 1 |
| 10925 | lleva | 1 |
| 10926 | llénese | 1 |
| 10927 | llegose | 1 |
| 10928 | llegaron | 1 |
| 10929 | llaneza | 1 |
| 10930 | llana | 1 |
| 10931 | llamola | 1 |
| 10932 | llamó | 1 |
| 10933 | llame | 1 |
| 10934 | llamáronle | 1 |
| 10935 | llamaré | 1 |
| 10936 | llámanse | 1 |
| 10937 | llaman | 1 |
| 10938 | llámame | 1 |
| 10939 | llamado | 1 |
| 10940 | liverpool | 1 |
| 10941 | liturgia | 1 |
| 10942 | listón | 1 |
| 10943 | lisonjear | 1 |
| 10944 | liso | 1 |
| 10945 | lisiar | 1 |
| 10946 | liquen | 1 |
| 10947 | linneo | 1 |
| 10948 | linfático | 1 |
| 10949 | lindeza | 1 |
| 10950 | lindero | 1 |
| 10951 | limpió | 1 |
| 10952 | limítrofe | 1 |
| 10953 | limitose | 1 |
| 10954 | limitado | 1 |
| 10955 | limbo | 1 |
| 10956 | lija | 1 |
| 10957 | ligera | 1 |
| 10958 | ligadura | 1 |
| 10959 | liga | 1 |
| 10960 | lidiar | 1 |
| 10961 | licencioso | 1 |
| 10962 | licenciatura | 1 |
| 10963 | licenciado | 1 |
| 10964 | libreta | 1 |
| 10965 | librepensador | 1 |
| 10966 | librecambista | 1 |
| 10967 | liado | 1 |
| 10968 | levántate | 1 |
| 10969 | levantamiento | 1 |
| 10970 | levantábase | 1 |
| 10971 | levanta | 1 |
| 10972 | levadura | 1 |
| 10973 | lesa | 1 |
| 10974 | lérida | 1 |
| 10975 | lepanto | 1 |
| 10976 | leopardo | 1 |
| 10977 | leo | 1 |
| 10978 | leñera | 1 |
| 10979 | leñador | 1 |
| 10980 | lentejuela | 1 |
| 10981 | lenteja | 1 |
| 10982 | lengüeta | 1 |
| 10983 | lenguado | 1 |
| 10984 | lelo | 1 |
| 10985 | legitimidad | 1 |
| 10986 | legalizar | 1 |
| 10987 | legación | 1 |
| 10988 | lee | 1 |
| 10989 | lechuzo | 1 |
| 10990 | lechuza | 1 |
| 10991 | lechuga | 1 |
| 10992 | lazada | 1 |
| 10993 | lavatorio | 1 |
| 10994 | lavandero | 1 |
| 10995 | lavadura | 1 |
| 10996 | lavado | 1 |
| 10997 | lavadero | 1 |
| 10998 | lavabo | 1 |
| 10999 | laura | 1 |
| 11000 | laudatorio | 1 |
| 11001 | laudable | 1 |
| 11002 | latino | 1 |
| 11003 | latina | 1 |
| 11004 | latigazo | 1 |
| 11005 | latido | 1 |
| 11006 | latente | 1 |
| 11007 | laringe | 1 |
| 11008 | lara | 1 |
| 11009 | lapso | 1 |
| 11010 | lanza | 1 |
| 11011 | lanuza | 1 |
| 11012 | lantigua | 1 |
| 11013 | langosta | 1 |
| 11014 | landó | 1 |
| 11015 | lanceta | 1 |
| 11016 | lamparilla | 1 |
| 11017 | lamido | 1 |
| 11018 | lamentación | 1 |
| 11019 | laico | 1 |
| 11020 | lagartijo | 1 |
| 11021 | laganitos | 1 |
| 11022 | ladronas | 1 |
| 11023 | ladrona | 1 |
| 11024 | ladinamente | 1 |
| 11025 | ladear | 1 |
| 11026 | lacrimoso | 1 |
| 11027 | lacio | 1 |
| 11028 | laceria | 1 |
| 11029 | lacerante | 1 |
| 11030 | laborar | 1 |
| 11031 | labiano | 1 |
| 11032 | juzgábase | 1 |
| 11033 | justificación | 1 |
| 11034 | justar | 1 |
| 11035 | justamente | 1 |
| 11036 | juro | 1 |
| 11037 | jurídico | 1 |
| 11038 | juraría | 1 |
| 11039 | júramelo | 1 |
| 11040 | júpiter | 1 |
| 11041 | juntose | 1 |
| 11042 | juntas | 1 |
| 11043 | juntáronse | 1 |
| 11044 | juliana | 1 |
| 11045 | jugoso | 1 |
| 11046 | jugarreta | 1 |
| 11047 | judaísmo | 1 |
| 11048 | júcar | 1 |
| 11049 | jubileo | 1 |
| 11050 | jubilación | 1 |
| 11051 | jovencito | 1 |
| 11052 | jovellar | 1 |
| 11053 | jovellanos | 1 |
| 11054 | joto | 1 |
| 11055 | josés | 1 |
| 11056 | josef | 1 |
| 11057 | jornada | 1 |
| 11058 | jordán | 1 |
| 11059 | jofaina | 1 |
| 11060 | job | 1 |
| 11061 | joaquina | 1 |
| 11062 | jilguero | 1 |
| 11063 | jícara | 1 |
| 11064 | jesuítico | 1 |
| 11065 | jesuíticamente | 1 |
| 11066 | jesuita | 1 |
| 11067 | jericó | 1 |
| 11068 | jena | 1 |
| 11069 | jaulones | 1 |
| 11070 | játiva | 1 |
| 11071 | jardinería | 1 |
| 11072 | jardinera | 1 |
| 11073 | jáquima | 1 |
| 11074 | jamona | 1 |
| 11075 | jalear | 1 |
| 11076 | jaez | 1 |
| 11077 | jactancia | 1 |
| 11078 | jacquard | 1 |
| 11079 | jacintillo | 1 |
| 11080 | jabonadura | 1 |
| 11081 | itinerario | 1 |
| 11082 | istmo | 1 |
| 11083 | israelita | 1 |
| 11084 | iscariote | 1 |
| 11085 | irujo | 1 |
| 11086 | irritabilidad | 1 |
| 11087 | irrevocable | 1 |
| 11088 | irreverentemente | 1 |
| 11089 | irreverente | 1 |
| 11090 | irreverencia | 1 |
| 11091 | irrespetuoso | 1 |
| 11092 | irremediable | 1 |
| 11093 | irme | 1 |
| 11094 | irisar | 1 |
| 11095 | irascibilidad | 1 |
| 11096 | irás | 1 |
| 11097 | iracundo | 1 |
| 11098 | irá | 1 |
| 11099 | inza | 1 |
| 11100 | involuntario | 1 |
| 11101 | involución | 1 |
| 11102 | invitado | 1 |
| 11103 | investigar | 1 |
| 11104 | investigador | 1 |
| 11105 | investigación | 1 |
| 11106 | inventor | 1 |
| 11107 | inventiva | 1 |
| 11108 | inventariar | 1 |
| 11109 | inusitado | 1 |
| 11110 | inundación | 1 |
| 11111 | intuitivo | 1 |
| 11112 | intruso | 1 |
| 11113 | introductor | 1 |
| 11114 | intríngulis | 1 |
| 11115 | intrigar | 1 |
| 11116 | intrigante | 1 |
| 11117 | intransitable | 1 |
| 11118 | intranquilizar | 1 |
| 11119 | intolerante | 1 |
| 11120 | intolerable | 1 |
| 11121 | interrumpió | 1 |
| 11122 | interrogó | 1 |
| 11123 | interrogador | 1 |
| 11124 | intérprete | 1 |
| 11125 | internar | 1 |
| 11126 | intermedio | 1 |
| 11127 | interjección | 1 |
| 11128 | interioridad | 1 |
| 11129 | interino | 1 |
| 11130 | interesado | 1 |
| 11131 | intensidad | 1 |
| 11132 | intensar | 1 |
| 11133 | intendente | 1 |
| 11134 | intencionado | 1 |
| 11135 | intempestivo | 1 |
| 11136 | intemperie | 1 |
| 11137 | inteligible | 1 |
| 11138 | insurreccionar | 1 |
| 11139 | insurrección | 1 |
| 11140 | insulto | 1 |
| 11141 | insuficiente | 1 |
| 11142 | instrumentar | 1 |
| 11143 | instruido | 1 |
| 11144 | instintos | 1 |
| 11145 | instancias | 1 |
| 11146 | instancia | 1 |
| 11147 | instalose | 1 |
| 11148 | inspirábale | 1 |
| 11149 | insolvente | 1 |
| 11150 | insoluble | 1 |
| 11151 | insistió | 1 |
| 11152 | insistente | 1 |
| 11153 | insípido | 1 |
| 11154 | insinuó | 1 |
| 11155 | insinuación | 1 |
| 11156 | insepulto | 1 |
| 11157 | inseparable | 1 |
| 11158 | insensatez | 1 |
| 11159 | insecto | 1 |
| 11160 | inquietamente | 1 |
| 11161 | inoportuno | 1 |
| 11162 | inopinadamente | 1 |
| 11163 | inocentes | 1 |
| 11164 | inocentada | 1 |
| 11165 | innumerable | 1 |
| 11166 | innovador | 1 |
| 11167 | innoble | 1 |
| 11168 | innegable | 1 |
| 11169 | inmutable | 1 |
| 11170 | inmunidad | 1 |
| 11171 | inmovilidad | 1 |
| 11172 | inmoralidad | 1 |
| 11173 | inmodestia | 1 |
| 11174 | inmensamente | 1 |
| 11175 | inmediaciones | 1 |
| 11176 | injurioso | 1 |
| 11177 | injurias | 1 |
| 11178 | injertar | 1 |
| 11179 | iniciación | 1 |
| 11180 | iniciábasele | 1 |
| 11181 | iniciábase | 1 |
| 11182 | inhumano | 1 |
| 11183 | inhabitable | 1 |
| 11184 | ingreso | 1 |
| 11185 | ingrata | 1 |
| 11186 | ingestión | 1 |
| 11187 | ingente | 1 |
| 11188 | ingénito | 1 |
| 11189 | infructuoso | 1 |
| 11190 | infranqueable | 1 |
| 11191 | informador | 1 |
| 11192 | influjo | 1 |
| 11193 | infligir | 1 |
| 11194 | inflexibilidad | 1 |
| 11195 | inflamación | 1 |
| 11196 | infinitivo | 1 |
| 11197 | infestar | 1 |
| 11198 | infantería | 1 |
| 11199 | infante | 1 |
| 11200 | infames | 1 |
| 11201 | infalibilidad | 1 |
| 11202 | inexpugnable | 1 |
| 11203 | inexpresivo | 1 |
| 11204 | inercia | 1 |
| 11205 | ineficaz | 1 |
| 11206 | industrioso | 1 |
| 11207 | indolente | 1 |
| 11208 | individualizar | 1 |
| 11209 | individualidad | 1 |
| 11210 | indisponer | 1 |
| 11211 | indisoluble | 1 |
| 11212 | indisciplinar | 1 |
| 11213 | indirectamente | 1 |
| 11214 | indio | 1 |
| 11215 | indigno | 1 |
| 11216 | indigesto | 1 |
| 11217 | indigente | 1 |
| 11218 | indicáronle | 1 |
| 11219 | indias | 1 |
| 11220 | indiano | 1 |
| 11221 | indiana | 1 |
| 11222 | indeterminado | 1 |
| 11223 | indestructible | 1 |
| 11224 | indefinido | 1 |
| 11225 | indefenso | 1 |
| 11226 | indecentes | 1 |
| 11227 | indagatorio | 1 |
| 11228 | indagador | 1 |
| 11229 | indagación | 1 |
| 11230 | incumbir | 1 |
| 11231 | incultura | 1 |
| 11232 | inculpabilidad | 1 |
| 11233 | incrustar | 1 |
| 11234 | incorruptible | 1 |
| 11235 | incorrecto | 1 |
| 11236 | incorrección | 1 |
| 11237 | incontrastable | 1 |
| 11238 | inconstancia | 1 |
| 11239 | inconsecuencia | 1 |
| 11240 | inconcuso | 1 |
| 11241 | incompatible | 1 |
| 11242 | incómodo | 1 |
| 11243 | incomodidad | 1 |
| 11244 | incoloro | 1 |
| 11245 | inclusive | 1 |
| 11246 | inclusero | 1 |
| 11247 | inclinábase | 1 |
| 11248 | incitante | 1 |
| 11249 | incipiente | 1 |
| 11250 | incienso | 1 |
| 11251 | incidencia | 1 |
| 11252 | incentivo | 1 |
| 11253 | incensario | 1 |
| 11254 | incendio | 1 |
| 11255 | incauto | 1 |
| 11256 | incautación | 1 |
| 11257 | incapacidad | 1 |
| 11258 | inaugurar | 1 |
| 11259 | inarmónico | 1 |
| 11260 | inapetente | 1 |
| 11261 | inanición | 1 |
| 11262 | inamovible | 1 |
| 11263 | inalterado | 1 |
| 11264 | inalterable | 1 |
| 11265 | inaguantable | 1 |
| 11266 | inagotable | 1 |
| 11267 | inactivo | 1 |
| 11268 | inactividad | 1 |
| 11269 | inaccesible | 1 |
| 11270 | imputar | 1 |
| 11271 | impuro | 1 |
| 11272 | impureza | 1 |
| 11273 | impulsión | 1 |
| 11274 | impúber | 1 |
| 11275 | improviso | 1 |
| 11276 | improvisación | 1 |
| 11277 | improbable | 1 |
| 11278 | impresiones | 1 |
| 11279 | impregnar | 1 |
| 11280 | imprecación | 1 |
| 11281 | imposición | 1 |
| 11282 | importunar | 1 |
| 11283 | importe | 1 |
| 11284 | importación | 1 |
| 11285 | implantar | 1 |
| 11286 | impiedad | 1 |
| 11287 | impíamente | 1 |
| 11288 | ímpetu | 1 |
| 11289 | impetrar | 1 |
| 11290 | impersonal | 1 |
| 11291 | imperfección | 1 |
| 11292 | imperativo | 1 |
| 11293 | imperar | 1 |
| 11294 | impenetrabilidad | 1 |
| 11295 | impávido | 1 |
| 11296 | impasible | 1 |
| 11297 | imparcialmente | 1 |
| 11298 | imparcial | 1 |
| 11299 | impar | 1 |
| 11300 | impalpable | 1 |
| 11301 | impaciente | 1 |
| 11302 | imítela | 1 |
| 11303 | imitativo | 1 |
| 11304 | imbuir | 1 |
| 11305 | imbecilidad | 1 |
| 11306 | imagínese | 1 |
| 11307 | imaginativo | 1 |
| 11308 | imaginario | 1 |
| 11309 | imaginándose | 1 |
| 11310 | ilustrísimo | 1 |
| 11311 | ilusionarse | 1 |
| 11312 | iluminación | 1 |
| 11313 | ilimitado | 1 |
| 11314 | ilegal | 1 |
| 11315 | ignorantes | 1 |
| 11316 | ignorado | 1 |
| 11317 | ignominioso | 1 |
| 11318 | ignominiosamente | 1 |
| 11319 | idumeo | 1 |
| 11320 | idos | 1 |
| 11321 | idólatra | 1 |
| 11322 | idealista | 1 |
| 11323 | idealismo | 1 |
| 11324 | iconografía | 1 |
| 11325 | hurgar | 1 |
| 11326 | huracán | 1 |
| 11327 | hundiose | 1 |
| 11328 | hundiéronse | 1 |
| 11329 | humorismo | 1 |
| 11330 | humillante | 1 |
| 11331 | humeante | 1 |
| 11332 | humanitario | 1 |
| 11333 | humanamente | 1 |
| 11334 | huelva | 1 |
| 11335 | huelgas | 1 |
| 11336 | huelga | 1 |
| 11337 | hoz | 1 |
| 11338 | hoyo | 1 |
| 11339 | hoyar | 1 |
| 11340 | hotel | 1 |
| 11341 | hosanna | 1 |
| 11342 | horquilla | 1 |
| 11343 | hormiguero | 1 |
| 11344 | horita | 1 |
| 11345 | horda | 1 |
| 11346 | horca | 1 |
| 11347 | horadar | 1 |
| 11348 | honorario | 1 |
| 11349 | honorabilidad | 1 |
| 11350 | honestidad | 1 |
| 11351 | homenaje | 1 |
| 11352 | hombros | 1 |
| 11353 | hombría | 1 |
| 11354 | hombres | 1 |
| 11355 | hombrada | 1 |
| 11356 | hollín | 1 |
| 11357 | hollar | 1 |
| 11358 | holgazanería | 1 |
| 11359 | holgar | 1 |
| 11360 | holgadamente | 1 |
| 11361 | hojuela | 1 |
| 11362 | hojita | 1 |
| 11363 | hojarasca | 1 |
| 11364 | hociquear | 1 |
| 11365 | hocicada | 1 |
| 11366 | hízome | 1 |
| 11367 | histrionismo | 1 |
| 11368 | historiador | 1 |
| 11369 | hispanófilo | 1 |
| 11370 | hispano | 1 |
| 11371 | hipotéticamente | 1 |
| 11372 | hipótesis | 1 |
| 11373 | hipódromo | 1 |
| 11374 | hipócrates | 1 |
| 11375 | hipo | 1 |
| 11376 | hiperbólicamente | 1 |
| 11377 | hipérbole | 1 |
| 11378 | hindostán | 1 |
| 11379 | hincósele | 1 |
| 11380 | hinchado | 1 |
| 11381 | hinchada | 1 |
| 11382 | hilvanar | 1 |
| 11383 | hileras | 1 |
| 11384 | hildebrando | 1 |
| 11385 | hijita | 1 |
| 11386 | hijastro | 1 |
| 11387 | higiénico | 1 |
| 11388 | higiene | 1 |
| 11389 | higa | 1 |
| 11390 | hierba | 1 |
| 11391 | hidropesía | 1 |
| 11392 | hiciéronle | 1 |
| 11393 | híceme | 1 |
| 11394 | heterogéneo | 1 |
| 11395 | heterodoxo | 1 |
| 11396 | hervor | 1 |
| 11397 | herrería | 1 |
| 11398 | herrar | 1 |
| 11399 | herraje | 1 |
| 11400 | hermosamente | 1 |
| 11401 | hermanas | 1 |
| 11402 | hermanar | 1 |
| 11403 | hermana | 1 |
| 11404 | hereditario | 1 |
| 11405 | heráldico | 1 |
| 11406 | hepático | 1 |
| 11407 | hendidura | 1 |
| 11408 | henchir | 1 |
| 11409 | hemorragia | 1 |
| 11410 | heliotropo | 1 |
| 11411 | helénico | 1 |
| 11412 | helena | 1 |
| 11413 | helecho | 1 |
| 11414 | helado | 1 |
| 11415 | heine | 1 |
| 11416 | hediondo | 1 |
| 11417 | hechicero | 1 |
| 11418 | hazlo | 1 |
| 11419 | hazle | 1 |
| 11420 | haymarket | 1 |
| 11421 | harta | 1 |
| 11422 | harina | 1 |
| 11423 | harías | 1 |
| 11424 | haría | 1 |
| 11425 | hamos | 1 |
| 11426 | hamo | 1 |
| 11427 | hamlet | 1 |
| 11428 | hamburgo | 1 |
| 11429 | hállase | 1 |
| 11430 | halláronse | 1 |
| 11431 | hallándose | 1 |
| 11432 | hálito | 1 |
| 11433 | halcón | 1 |
| 11434 | halagar | 1 |
| 11435 | hala | 1 |
| 11436 | hágolo | 1 |
| 11437 | hágalo | 1 |
| 11438 | haga | 1 |
| 11439 | haeckel | 1 |
| 11440 | hacinar | 1 |
| 11441 | haciendo | 1 |
| 11442 | hacíala | 1 |
| 11443 | hache | 1 |
| 11444 | haces | 1 |
| 11445 | hacendoso | 1 |
| 11446 | hacendista | 1 |
| 11447 | haced | 1 |
| 11448 | habríale | 1 |
| 11449 | habrase | 1 |
| 11450 | hablo | 1 |
| 11451 | hablan | 1 |
| 11452 | háblame | 1 |
| 11453 | habitado | 1 |
| 11454 | habilísimo | 1 |
| 11455 | habanero | 1 |
| 11456 | habanera | 1 |
| 11457 | haba | 1 |
| 11458 | guttenberg | 1 |
| 11459 | gustosamente | 1 |
| 11460 | gusanera | 1 |
| 11461 | guitarrista | 1 |
| 11462 | guita | 1 |
| 11463 | guisote | 1 |
| 11464 | guiso | 1 |
| 11465 | guirnalda | 1 |
| 11466 | guirigay | 1 |
| 11467 | guiñada | 1 |
| 11468 | guindalera | 1 |
| 11469 | guillermo | 1 |
| 11470 | guía | 1 |
| 11471 | guetaria | 1 |
| 11472 | guerrillero | 1 |
| 11473 | guerrero | 1 |
| 11474 | güeno | 1 |
| 11475 | guelbenzu | 1 |
| 11476 | gubernativo | 1 |
| 11477 | gubernación | 1 |
| 11478 | guasón | 1 |
| 11479 | guasear | 1 |
| 11480 | guarismo | 1 |
| 11481 | guardés | 1 |
| 11482 | guárdate | 1 |
| 11483 | guardando | 1 |
| 11484 | guardador | 1 |
| 11485 | guardacantón | 1 |
| 11486 | guardábalo | 1 |
| 11487 | guapetona | 1 |
| 11488 | guapamente | 1 |
| 11489 | guadalupe | 1 |
| 11490 | gruñó | 1 |
| 11491 | gruesa | 1 |
| 11492 | grúa | 1 |
| 11493 | grotesco | 1 |
| 11494 | gros | 1 |
| 11495 | grietar | 1 |
| 11496 | grieta | 1 |
| 11497 | griego | 1 |
| 11498 | gremios | 1 |
| 11499 | gremio | 1 |
| 11500 | gravitar | 1 |
| 11501 | gravísimo | 1 |
| 11502 | grasiento | 1 |
| 11503 | granulación | 1 |
| 11504 | grandullón | 1 |
| 11505 | grandísimas | 1 |
| 11506 | grandemente | 1 |
| 11507 | granadino | 1 |
| 11508 | gramatical | 1 |
| 11509 | grajear | 1 |
| 11510 | gráficamente | 1 |
| 11511 | graduar | 1 |
| 11512 | graduación | 1 |
| 11513 | gradación | 1 |
| 11514 | gracejo | 1 |
| 11515 | gozne | 1 |
| 11516 | gótico | 1 |
| 11517 | goterón | 1 |
| 11518 | gotear | 1 |
| 11519 | gorritas | 1 |
| 11520 | gorrino | 1 |
| 11521 | gorrina | 1 |
| 11522 | gorjear | 1 |
| 11523 | gordura | 1 |
| 11524 | gordito | 1 |
| 11525 | gorda | 1 |
| 11526 | golpes | 1 |
| 11527 | golondrina | 1 |
| 11528 | gollería | 1 |
| 11529 | gola | 1 |
| 11530 | goiri | 1 |
| 11531 | gobiernos | 1 |
| 11532 | gobernaor | 1 |
| 11533 | gobernable | 1 |
| 11534 | gobernábala | 1 |
| 11535 | glotón | 1 |
| 11536 | girasol | 1 |
| 11537 | gimnástica | 1 |
| 11538 | gigantón | 1 |
| 11539 | gigantesco | 1 |
| 11540 | gestión | 1 |
| 11541 | gestación | 1 |
| 11542 | germen | 1 |
| 11543 | germán | 1 |
| 11544 | genuino | 1 |
| 11545 | genuflexión | 1 |
| 11546 | gentualla | 1 |
| 11547 | gentileza | 1 |
| 11548 | generalización | 1 |
| 11549 | generador | 1 |
| 11550 | genealógico | 1 |
| 11551 | gemelo | 1 |
| 11552 | gaznate | 1 |
| 11553 | gaznápiro | 1 |
| 11554 | gatuno | 1 |
| 11555 | gatitos | 1 |
| 11556 | gaseosa | 1 |
| 11557 | gasa | 1 |
| 11558 | garrulería | 1 |
| 11559 | garrotazo | 1 |
| 11560 | garrapato | 1 |
| 11561 | garrafa | 1 |
| 11562 | garita | 1 |
| 11563 | garboso | 1 |
| 11564 | garantíceme | 1 |
| 11565 | garabito | 1 |
| 11566 | ganzúa | 1 |
| 11567 | ganso | 1 |
| 11568 | gangrenar | 1 |
| 11569 | gandía | 1 |
| 11570 | gande | 1 |
| 11571 | ganarás | 1 |
| 11572 | ganapán | 1 |
| 11573 | galo | 1 |
| 11574 | galleta | 1 |
| 11575 | gallardear | 1 |
| 11576 | galindo | 1 |
| 11577 | galimatías | 1 |
| 11578 | galileo | 1 |
| 11579 | galgo | 1 |
| 11580 | galería | 1 |
| 11581 | galdós | 1 |
| 11582 | gaeta | 1 |
| 11583 | gacha | 1 |
| 11584 | gacetilla | 1 |
| 11585 | gaceta | 1 |
| 11586 | fuste | 1 |
| 11587 | furtivo | 1 |
| 11588 | furiosamente | 1 |
| 11589 | fundado | 1 |
| 11590 | fundábase | 1 |
| 11591 | funcionario | 1 |
| 11592 | fumada | 1 |
| 11593 | fulminar | 1 |
| 11594 | fulminante | 1 |
| 11595 | fulastre | 1 |
| 11596 | fui | 1 |
| 11597 | fuguilla | 1 |
| 11598 | fuencarral | 1 |
| 11599 | fruslería | 1 |
| 11600 | fruición | 1 |
| 11601 | frugalidad | 1 |
| 11602 | frote | 1 |
| 11603 | frontero | 1 |
| 11604 | frondoso | 1 |
| 11605 | frívolo | 1 |
| 11606 | frivolidad | 1 |
| 11607 | frisar | 1 |
| 11608 | friolero | 1 |
| 11609 | fríamente | 1 |
| 11610 | fresno | 1 |
| 11611 | frecuentemente | 1 |
| 11612 | frascuelo | 1 |
| 11613 | franja | 1 |
| 11614 | franela | 1 |
| 11615 | francisca | 1 |
| 11616 | francesa | 1 |
| 11617 | francachela | 1 |
| 11618 | fragmento | 1 |
| 11619 | fouquier | 1 |
| 11620 | fotográfico | 1 |
| 11621 | fortunatita | 1 |
| 11622 | fortunatas | 1 |
| 11623 | fortunaaá | 1 |
| 11624 | fortificar | 1 |
| 11625 | fortalecimiento | 1 |
| 11626 | fortalecer | 1 |
| 11627 | foro | 1 |
| 11628 | formose | 1 |
| 11629 | fórmico | 1 |
| 11630 | formalmente | 1 |
| 11631 | formación | 1 |
| 11632 | forajido | 1 |
| 11633 | for | 1 |
| 11634 | fomentar | 1 |
| 11635 | folleto | 1 |
| 11636 | folletit | 1 |
| 11637 | fogón | 1 |
| 11638 | fofo | 1 |
| 11639 | flote | 1 |
| 11640 | flotar | 1 |
| 11641 | florido | 1 |
| 11642 | floreo | 1 |
| 11643 | florecer | 1 |
| 11644 | flojita | 1 |
| 11645 | flexión | 1 |
| 11646 | flexibilidad | 1 |
| 11647 | flema | 1 |
| 11648 | flechazo | 1 |
| 11649 | flatulento | 1 |
| 11650 | flanco | 1 |
| 11651 | flamear | 1 |
| 11652 | fláccido | 1 |
| 11653 | fiscalizar | 1 |
| 11654 | firmamento | 1 |
| 11655 | finiquito | 1 |
| 11656 | fingimiento | 1 |
| 11657 | fingidamente | 1 |
| 11658 | fincar | 1 |
| 11659 | finamente | 1 |
| 11660 | finalizar | 1 |
| 11661 | filosófica | 1 |
| 11662 | filipino | 1 |
| 11663 | filibustero | 1 |
| 11664 | filiación | 1 |
| 11665 | filete | 1 |
| 11666 | filantropía | 1 |
| 11667 | fíjese | 1 |
| 11668 | fijarse | 1 |
| 11669 | fijándose | 1 |
| 11670 | fija | 1 |
| 11671 | figurose | 1 |
| 11672 | figurón | 1 |
| 11673 | figurado | 1 |
| 11674 | figuerola | 1 |
| 11675 | fíese | 1 |
| 11676 | fierecilla | 1 |
| 11677 | fielmente | 1 |
| 11678 | fidedigno | 1 |
| 11679 | fichar | 1 |
| 11680 | ficha | 1 |
| 11681 | fiasco | 1 |
| 11682 | fiambrera | 1 |
| 11683 | feúcho | 1 |
| 11684 | fetiche | 1 |
| 11685 | festonear | 1 |
| 11686 | fervoroso | 1 |
| 11687 | ferviente | 1 |
| 11688 | férula | 1 |
| 11689 | fértil | 1 |
| 11690 | ferretería | 1 |
| 11691 | fernández | 1 |
| 11692 | fernán | 1 |
| 11693 | feote | 1 |
| 11694 | fénico | 1 |
| 11695 | fenicio | 1 |
| 11696 | fenelona | 1 |
| 11697 | femenil | 1 |
| 11698 | felpilla | 1 |
| 11699 | felpar | 1 |
| 11700 | felicíteme | 1 |
| 11701 | feíto | 1 |
| 11702 | fedro | 1 |
| 11703 | federal | 1 |
| 11704 | fecundísimo | 1 |
| 11705 | fecundar | 1 |
| 11706 | feculento | 1 |
| 11707 | fechar | 1 |
| 11708 | favorablemente | 1 |
| 11709 | fausto | 1 |
| 11710 | fauces | 1 |
| 11711 | fascinador | 1 |
| 11712 | fariseo | 1 |
| 11713 | fardar | 1 |
| 11714 | fantásticamente | 1 |
| 11715 | fantasmagórico | 1 |
| 11716 | fantasmagoría | 1 |
| 11717 | fantasma | 1 |
| 11718 | fanfarronería | 1 |
| 11719 | fanega | 1 |
| 11720 | faltón | 1 |
| 11721 | falsificar | 1 |
| 11722 | falsificación | 1 |
| 11723 | falsedad | 1 |
| 11724 | falsario | 1 |
| 11725 | falleció | 1 |
| 11726 | fallecimiento | 1 |
| 11727 | fallar | 1 |
| 11728 | faenar | 1 |
| 11729 | factura | 1 |
| 11730 | facilillo | 1 |
| 11731 | fabuloso | 1 |
| 11732 | f | 1 |
| 11733 | ezquerdo | 1 |
| 11734 | eylau | 1 |
| 11735 | exuberante | 1 |
| 11736 | extrañísimo | 1 |
| 11737 | extranjerizar | 1 |
| 11738 | extranjerismo | 1 |
| 11739 | extractor | 1 |
| 11740 | extracción | 1 |
| 11741 | extirpación | 1 |
| 11742 | exteriorizar | 1 |
| 11743 | extenuación | 1 |
| 11744 | extendido | 1 |
| 11745 | extático | 1 |
| 11746 | expuso | 1 |
| 11747 | expurgación | 1 |
| 11748 | exprisiones | 1 |
| 11749 | exprimir | 1 |
| 11750 | expresábase | 1 |
| 11751 | explícito | 1 |
| 11752 | explícitamente | 1 |
| 11753 | explícate | 1 |
| 11754 | explícame | 1 |
| 11755 | experimental | 1 |
| 11756 | experimentado | 1 |
| 11757 | expensas | 1 |
| 11758 | expender | 1 |
| 11759 | expediente | 1 |
| 11760 | exótico | 1 |
| 11761 | exordio | 1 |
| 11762 | exitazo | 1 |
| 11763 | exigente | 1 |
| 11764 | exhortar | 1 |
| 11765 | exhibición | 1 |
| 11766 | exhausto | 1 |
| 11767 | exentar | 1 |
| 11768 | exclusiva | 1 |
| 11769 | exclusión | 1 |
| 11770 | exclaustrado | 1 |
| 11771 | excesivamente | 1 |
| 11772 | excéntrico | 1 |
| 11773 | excentricidad | 1 |
| 11774 | excelentísimo | 1 |
| 11775 | exasperar | 1 |
| 11776 | examínalo | 1 |
| 11777 | exagerado | 1 |
| 11778 | exabrupto | 1 |
| 11779 | evocación | 1 |
| 11780 | evidenciar | 1 |
| 11781 | evidencia | 1 |
| 11782 | eventual | 1 |
| 11783 | evasivo | 1 |
| 11784 | evaporar | 1 |
| 11785 | evangelistas | 1 |
| 11786 | evangelios | 1 |
| 11787 | eugenio | 1 |
| 11788 | eton | 1 |
| 11789 | estúpidos | 1 |
| 11790 | estupefacto | 1 |
| 11791 | estudioso | 1 |
| 11792 | estudiantil | 1 |
| 11793 | estropicio | 1 |
| 11794 | estropajo | 1 |
| 11795 | estro | 1 |
| 11796 | estricto | 1 |
| 11797 | estrictamente | 1 |
| 11798 | estribación | 1 |
| 11799 | estreno | 1 |
| 11800 | estraza | 1 |
| 11801 | estratégico | 1 |
| 11802 | estrabismo | 1 |
| 11803 | estorbo | 1 |
| 11804 | estómagos | 1 |
| 11805 | estólido | 1 |
| 11806 | estolidez | 1 |
| 11807 | estoicismo | 1 |
| 11808 | estofar | 1 |
| 11809 | estofado | 1 |
| 11810 | estofa | 1 |
| 11811 | estimulante | 1 |
| 11812 | estigma | 1 |
| 11813 | estese | 1 |
| 11814 | esternón | 1 |
| 11815 | esterlina | 1 |
| 11816 | esterilidad | 1 |
| 11817 | esterar | 1 |
| 11818 | estera | 1 |
| 11819 | estepa | 1 |
| 11820 | estentóreo | 1 |
| 11821 | estela | 1 |
| 11822 | estatuario | 1 |
| 11823 | estarse | 1 |
| 11824 | estaribel | 1 |
| 11825 | estaré | 1 |
| 11826 | estantigua | 1 |
| 11827 | estantería | 1 |
| 11828 | estancar | 1 |
| 11829 | están | 1 |
| 11830 | estampita | 1 |
| 11831 | estampido | 1 |
| 11832 | estafeta | 1 |
| 11833 | estados | 1 |
| 11834 | estadística | 1 |
| 11835 | estacar | 1 |
| 11836 | estaca | 1 |
| 11837 | estable | 1 |
| 11838 | estábamos | 1 |
| 11839 | esquivar | 1 |
| 11840 | esquinazo | 1 |
| 11841 | esquela | 1 |
| 11842 | espuela | 1 |
| 11843 | espotrica | 1 |
| 11844 | espontáneo | 1 |
| 11845 | espontanear | 1 |
| 11846 | espontáneamente | 1 |
| 11847 | esponjar | 1 |
| 11848 | esponja | 1 |
| 11849 | espolvorear | 1 |
| 11850 | esplendor | 1 |
| 11851 | esplendidez | 1 |
| 11852 | espléndidamente | 1 |
| 11853 | espirituoso | 1 |
| 11854 | espiritui | 1 |
| 11855 | espiritualizar | 1 |
| 11856 | espiritualista | 1 |
| 11857 | espiritualidad | 1 |
| 11858 | espinoso | 1 |
| 11859 | espiar | 1 |
| 11860 | espía | 1 |
| 11861 | espérese | 1 |
| 11862 | espeluznante | 1 |
| 11863 | espejuelo | 1 |
| 11864 | especulativo | 1 |
| 11865 | especulación | 1 |
| 11866 | espectador | 1 |
| 11867 | especiar | 1 |
| 11868 | especia | 1 |
| 11869 | espátula | 1 |
| 11870 | espatarrar | 1 |
| 11871 | espárrago | 1 |
| 11872 | esparcido | 1 |
| 11873 | españolizar | 1 |
| 11874 | españita | 1 |
| 11875 | espantado | 1 |
| 11876 | espaldilla | 1 |
| 11877 | espaldarazo | 1 |
| 11878 | espaciar | 1 |
| 11879 | esos | 1 |
| 11880 | esmerose | 1 |
| 11881 | esmaltar | 1 |
| 11882 | eslabonar | 1 |
| 11883 | esforzábase | 1 |
| 11884 | escurridizo | 1 |
| 11885 | escupidera | 1 |
| 11886 | escultor | 1 |
| 11887 | esculapio | 1 |
| 11888 | escuerzo | 1 |
| 11889 | escudilla | 1 |
| 11890 | escudero | 1 |
| 11891 | escucha | 1 |
| 11892 | escuálido | 1 |
| 11893 | escualidez | 1 |
| 11894 | escuadrón | 1 |
| 11895 | escriturar | 1 |
| 11896 | escribirle | 1 |
| 11897 | escribiente | 1 |
| 11898 | escribiéndole | 1 |
| 11899 | escribe | 1 |
| 11900 | escorzo | 1 |
| 11901 | escoplo | 1 |
| 11902 | escopeta | 1 |
| 11903 | escollo | 1 |
| 11904 | escolástico | 1 |
| 11905 | escolar | 1 |
| 11906 | escogido | 1 |
| 11907 | escocia | 1 |
| 11908 | escobón | 1 |
| 11909 | esclarecer | 1 |
| 11910 | escénico | 1 |
| 11911 | escayolar | 1 |
| 11912 | escasez | 1 |
| 11913 | escarolar | 1 |
| 11914 | escarlatina | 1 |
| 11915 | escaray | 1 |
| 11916 | escaño | 1 |
| 11917 | escamoteo | 1 |
| 11918 | escamoso | 1 |
| 11919 | escama | 1 |
| 11920 | escaldar | 1 |
| 11921 | escalar | 1 |
| 11922 | escalafón | 1 |
| 11923 | esbozar | 1 |
| 11924 | erudito | 1 |
| 11925 | erre | 1 |
| 11926 | errar | 1 |
| 11927 | erizo | 1 |
| 11928 | erigir | 1 |
| 11929 | erección | 1 |
| 11930 | equivocadamente | 1 |
| 11931 | equilibrado | 1 |
| 11932 | equi | 1 |
| 11933 | epopeya | 1 |
| 11934 | epitafio | 1 |
| 11935 | episcopal | 1 |
| 11936 | epígrafe | 1 |
| 11937 | epidérmico | 1 |
| 11938 | epaminondas | 1 |
| 11939 | envolvíase | 1 |
| 11940 | envolverse | 1 |
| 11941 | envilecer | 1 |
| 11942 | envidiosa | 1 |
| 11943 | envidar | 1 |
| 11944 | envejecido | 1 |
| 11945 | envainar | 1 |
| 11946 | enturbiar | 1 |
| 11947 | entrevía | 1 |
| 11948 | entreverar | 1 |
| 11949 | entretenida | 1 |
| 11950 | entresacar | 1 |
| 11951 | entreabrir | 1 |
| 11952 | entreabierto | 1 |
| 11953 | entraré | 1 |
| 11954 | entrañas | 1 |
| 11955 | entrañable | 1 |
| 11956 | entramado | 1 |
| 11957 | entrábale | 1 |
| 11958 | entorpecimiento | 1 |
| 11959 | entonado | 1 |
| 11960 | entiendo | 1 |
| 11961 | entiéndete | 1 |
| 11962 | entiende | 1 |
| 11963 | enterrar | 1 |
| 11964 | entenebrecer | 1 |
| 11965 | entendía | 1 |
| 11966 | entendedor | 1 |
| 11967 | entendederas | 1 |
| 11968 | entarimado | 1 |
| 11969 | entablose | 1 |
| 11970 | ensordecedor | 1 |
| 11971 | enseñorear | 1 |
| 11972 | enséñemela | 1 |
| 11973 | ensartar | 1 |
| 11974 | ensarriá | 1 |
| 11975 | ensañar | 1 |
| 11976 | ensangrentado | 1 |
| 11977 | enronquecer | 1 |
| 11978 | enrejado | 1 |
| 11979 | enredador | 1 |
| 11980 | enranciar | 1 |
| 11981 | enramar | 1 |
| 11982 | enramada | 1 |
| 11983 | ennegrecer | 1 |
| 11984 | enmohecer | 1 |
| 11985 | enmascarar | 1 |
| 11986 | enjugar | 1 |
| 11987 | enjaretar | 1 |
| 11988 | enjabonáronle | 1 |
| 11989 | engullir | 1 |
| 11990 | engrasar | 1 |
| 11991 | engrandecer | 1 |
| 11992 | engranaje | 1 |
| 11993 | engomar | 1 |
| 11994 | engendro | 1 |
| 11995 | engastar | 1 |
| 11996 | engarzar | 1 |
| 11997 | engañoso | 1 |
| 11998 | engañarme | 1 |
| 11999 | engañador | 1 |
| 12000 | enfrascar | 1 |
| 12001 | enflaquecer | 1 |
| 12002 | enfermero | 1 |
| 12003 | enérgicamente | 1 |
| 12004 | enemistar | 1 |
| 12005 | eneas | 1 |
| 12006 | endurecimiento | 1 |
| 12007 | endurecer | 1 |
| 12008 | endiablar | 1 |
| 12009 | endemoniado | 1 |
| 12010 | encubrir | 1 |
| 12011 | encontrola | 1 |
| 12012 | encontrémela | 1 |
| 12013 | encontrarse | 1 |
| 12014 | encontrábase | 1 |
| 12015 | encono | 1 |
| 12016 | encomienda | 1 |
| 12017 | encomiar | 1 |
| 12018 | encinta | 1 |
| 12019 | enciclopédico | 1 |
| 12020 | encía | 1 |
| 12021 | encharcado | 1 |
| 12022 | encerrona | 1 |
| 12023 | encerrarse | 1 |
| 12024 | encerrarla | 1 |
| 12025 | encenagar | 1 |
| 12026 | encauzar | 1 |
| 12027 | encastillar | 1 |
| 12028 | encargábase | 1 |
| 12029 | encarecimiento | 1 |
| 12030 | encarcelar | 1 |
| 12031 | encanecer | 1 |
| 12032 | encandilar | 1 |
| 12033 | encandilado | 1 |
| 12034 | encajero | 1 |
| 12035 | encadenar | 1 |
| 12036 | enardecer | 1 |
| 12037 | enanito | 1 |
| 12038 | enamoriscar | 1 |
| 12039 | enamoramiento | 1 |
| 12040 | enajenación | 1 |
| 12041 | empujones | 1 |
| 12042 | empujole | 1 |
| 12043 | empujola | 1 |
| 12044 | empresario | 1 |
| 12045 | empozar | 1 |
| 12046 | emporcar | 1 |
| 12047 | empolvado | 1 |
| 12048 | empollar | 1 |
| 12049 | emplomar | 1 |
| 12050 | emplasto | 1 |
| 12051 | empinado | 1 |
| 12052 | empezamos | 1 |
| 12053 | emperifollar | 1 |
| 12054 | empequeñecer | 1 |
| 12055 | empeñadamente | 1 |
| 12056 | empeñábase | 1 |
| 12057 | empenachado | 1 |
| 12058 | emparrado | 1 |
| 12059 | emparentar | 1 |
| 12060 | emparejar | 1 |
| 12061 | empapelar | 1 |
| 12062 | empalme | 1 |
| 12063 | emolumento | 1 |
| 12064 | emoliente | 1 |
| 12065 | emocionar | 1 |
| 12066 | emisión | 1 |
| 12067 | eminentemente | 1 |
| 12068 | eminente | 1 |
| 12069 | emilion | 1 |
| 12070 | emilio | 1 |
| 12071 | emigrar | 1 |
| 12072 | embudo | 1 |
| 12073 | embrionario | 1 |
| 12074 | embotar | 1 |
| 12075 | emboscada | 1 |
| 12076 | embetunar | 1 |
| 12077 | embeber | 1 |
| 12078 | embebecimiento | 1 |
| 12079 | embaular | 1 |
| 12080 | embarcar | 1 |
| 12081 | embarazo | 1 |
| 12082 | embaldosar | 1 |
| 12083 | embalaje | 1 |
| 12084 | embajador | 1 |
| 12085 | eludir | 1 |
| 12086 | elevación | 1 |
| 12087 | electricidad | 1 |
| 12088 | elduayen | 1 |
| 12089 | elasticidad | 1 |
| 12090 | elaboración | 1 |
| 12091 | ejido | 1 |
| 12092 | ejercía | 1 |
| 12093 | ejemplos | 1 |
| 12094 | efeméride | 1 |
| 12095 | efectos | 1 |
| 12096 | efectividad | 1 |
| 12097 | edificante | 1 |
| 12098 | edecán | 1 |
| 12099 | ecuménico | 1 |
| 12100 | ecónomo | 1 |
| 12101 | economizar | 1 |
| 12102 | económicas | 1 |
| 12103 | eclipse | 1 |
| 12104 | echándose | 1 |
| 12105 | echamos | 1 |
| 12106 | echábalas | 1 |
| 12107 | echa | 1 |
| 12108 | ebro | 1 |
| 12109 | durmió | 1 |
| 12110 | durísimo | 1 |
| 12111 | duración | 1 |
| 12112 | duermes | 1 |
| 12113 | duerme | 1 |
| 12114 | duelos | 1 |
| 12115 | dudas | 1 |
| 12116 | dubitativo | 1 |
| 12117 | dubarry | 1 |
| 12118 | dualismo | 1 |
| 12119 | dromedario | 1 |
| 12120 | droguista | 1 |
| 12121 | drástico | 1 |
| 12122 | dramón | 1 |
| 12123 | doy | 1 |
| 12124 | dover | 1 |
| 12125 | dormirlas | 1 |
| 12126 | dormido | 1 |
| 12127 | dominó | 1 |
| 12128 | domini | 1 |
| 12129 | domiciliaria | 1 |
| 12130 | domiciliar | 1 |
| 12131 | domesticidad | 1 |
| 12132 | dolorosa | 1 |
| 12133 | doliente | 1 |
| 12134 | dolencia | 1 |
| 12135 | dogal | 1 |
| 12136 | doctrinario | 1 |
| 12137 | doctorar | 1 |
| 12138 | doctoral | 1 |
| 12139 | doblón | 1 |
| 12140 | doblegar | 1 |
| 12141 | doblado | 1 |
| 12142 | dobladillar | 1 |
| 12143 | do | 1 |
| 12144 | divulgar | 1 |
| 12145 | divisorio | 1 |
| 12146 | divinidades | 1 |
| 12147 | divertirse | 1 |
| 12148 | divertimiento | 1 |
| 12149 | diversidad | 1 |
| 12150 | diurno | 1 |
| 12151 | diurético | 1 |
| 12152 | distráete | 1 |
| 12153 | distraerme | 1 |
| 12154 | distingo | 1 |
| 12155 | distanciar | 1 |
| 12156 | disputábanse | 1 |
| 12157 | disponible | 1 |
| 12158 | dispone | 1 |
| 12159 | disperso | 1 |
| 12160 | dispersión | 1 |
| 12161 | dispénseme | 1 |
| 12162 | dispense | 1 |
| 12163 | dispensador | 1 |
| 12164 | disparo | 1 |
| 12165 | disparatadamente | 1 |
| 12166 | disolución | 1 |
| 12167 | dislocado | 1 |
| 12168 | disipación | 1 |
| 12169 | disimuladamente | 1 |
| 12170 | disfrute | 1 |
| 12171 | disfrazado | 1 |
| 12172 | disertar | 1 |
| 12173 | disertación | 1 |
| 12174 | diseño | 1 |
| 12175 | disentimiento | 1 |
| 12176 | disensión | 1 |
| 12177 | diseminar | 1 |
| 12178 | disección | 1 |
| 12179 | discutiose | 1 |
| 12180 | discurrió | 1 |
| 12181 | disculpose | 1 |
| 12182 | disculpa | 1 |
| 12183 | discernir | 1 |
| 12184 | dirigiose | 1 |
| 12185 | dirigiéndose | 1 |
| 12186 | diríase | 1 |
| 12187 | diré | 1 |
| 12188 | diranle | 1 |
| 12189 | diputación | 1 |
| 12190 | dipósito | 1 |
| 12191 | diploma | 1 |
| 12192 | dioses | 1 |
| 12193 | diosecito | 1 |
| 12194 | diosa | 1 |
| 12195 | díos | 1 |
| 12196 | diome | 1 |
| 12197 | diócesis | 1 |
| 12198 | dio | 1 |
| 12199 | dintel | 1 |
| 12200 | dinos | 1 |
| 12201 | dinastía | 1 |
| 12202 | dinamita | 1 |
| 12203 | dimpués | 1 |
| 12204 | diminuto | 1 |
| 12205 | dimetria | 1 |
| 12206 | dimensión | 1 |
| 12207 | dímelas | 1 |
| 12208 | diluvio | 1 |
| 12209 | diluviar | 1 |
| 12210 | dilucidar | 1 |
| 12211 | dilatado | 1 |
| 12212 | digresión | 1 |
| 12213 | dígolo | 1 |
| 12214 | dignísimo | 1 |
| 12215 | dignamente | 1 |
| 12216 | digital | 1 |
| 12217 | digestivo | 1 |
| 12218 | digestión | 1 |
| 12219 | digan | 1 |
| 12220 | dígamelo | 1 |
| 12221 | diga | 1 |
| 12222 | difundir | 1 |
| 12223 | dificilillo | 1 |
| 12224 | diferir | 1 |
| 12225 | difamatorio | 1 |
| 12226 | diestro | 1 |
| 12227 | diéronle | 1 |
| 12228 | diéranle | 1 |
| 12229 | diera | 1 |
| 12230 | dieciséis | 1 |
| 12231 | dictador | 1 |
| 12232 | diciendo | 1 |
| 12233 | dicharacho | 1 |
| 12234 | dicharachero | 1 |
| 12235 | diccionario | 1 |
| 12236 | díaz | 1 |
| 12237 | días | 1 |
| 12238 | diariamente | 1 |
| 12239 | diantre | 1 |
| 12240 | diamantino | 1 |
| 12241 | diagnóstico | 1 |
| 12242 | diáfano | 1 |
| 12243 | diafanidad | 1 |
| 12244 | diablos | 1 |
| 12245 | diablillo | 1 |
| 12246 | devolverle | 1 |
| 12247 | devocionario | 1 |
| 12248 | devastar | 1 |
| 12249 | devastador | 1 |
| 12250 | detiénese | 1 |
| 12251 | detestable | 1 |
| 12252 | determinose | 1 |
| 12253 | deteriorar | 1 |
| 12254 | detenimiento | 1 |
| 12255 | detallista | 1 |
| 12256 | desvivir | 1 |
| 12257 | desvergüenza | 1 |
| 12258 | desvergonzado | 1 |
| 12259 | desventura | 1 |
| 12260 | desventajoso | 1 |
| 12261 | desván | 1 |
| 12262 | desusar | 1 |
| 12263 | destructor | 1 |
| 12264 | destrución | 1 |
| 12265 | destinósele | 1 |
| 12266 | destinatario | 1 |
| 12267 | destiladera | 1 |
| 12268 | destierro | 1 |
| 12269 | desternillar | 1 |
| 12270 | destemplar | 1 |
| 12271 | destemplado | 1 |
| 12272 | destajo | 1 |
| 12273 | desquite | 1 |
| 12274 | desquiciamiento | 1 |
| 12275 | desprovisto | 1 |
| 12276 | desproporcionadamente | 1 |
| 12277 | desprevenido | 1 |
| 12278 | despreocupación | 1 |
| 12279 | despotricar | 1 |
| 12280 | despóticamente | 1 |
| 12281 | desplante | 1 |
| 12282 | despilfarro | 1 |
| 12283 | despilfarrar | 1 |
| 12284 | despidiéronla | 1 |
| 12285 | despidiéndose | 1 |
| 12286 | despídase | 1 |
| 12287 | despiadado | 1 |
| 12288 | desperezo | 1 |
| 12289 | despercudir | 1 |
| 12290 | despepitar | 1 |
| 12291 | despeñar | 1 |
| 12292 | despeñaperros | 1 |
| 12293 | desparramado | 1 |
| 12294 | desparpajo | 1 |
| 12295 | desorganización | 1 |
| 12296 | desollar | 1 |
| 12297 | desojar | 1 |
| 12298 | desobediente | 1 |
| 12299 | desobediencia | 1 |
| 12300 | desobedecer | 1 |
| 12301 | desnudez | 1 |
| 12302 | desmoralizar | 1 |
| 12303 | desmontar | 1 |
| 12304 | desmemoriar | 1 |
| 12305 | desmejorada | 1 |
| 12306 | desmedrado | 1 |
| 12307 | desmedir | 1 |
| 12308 | desmedidamente | 1 |
| 12309 | desmayo | 1 |
| 12310 | desmadejar | 1 |
| 12311 | deslucir | 1 |
| 12312 | deslizose | 1 |
| 12313 | desistir | 1 |
| 12314 | deshonor | 1 |
| 12315 | deshojar | 1 |
| 12316 | deshelar | 1 |
| 12317 | deshabitado | 1 |
| 12318 | desgranar | 1 |
| 12319 | desgobernar | 1 |
| 12320 | desgaste | 1 |
| 12321 | desgañitar | 1 |
| 12322 | desganar | 1 |
| 12323 | desfile | 1 |
| 12324 | desfavorecer | 1 |
| 12325 | desfavorablemente | 1 |
| 12326 | desfallecimiento | 1 |
| 12327 | desesperante | 1 |
| 12328 | desesperadamente | 1 |
| 12329 | desertar | 1 |
| 12330 | deserción | 1 |
| 12331 | desequilibrio | 1 |
| 12332 | desequilibrar | 1 |
| 12333 | desenvuelto | 1 |
| 12334 | desentrañar | 1 |
| 12335 | desentonar | 1 |
| 12336 | desentonado | 1 |
| 12337 | desenlace | 1 |
| 12338 | desengáñese | 1 |
| 12339 | desengañado | 1 |
| 12340 | desenfundar | 1 |
| 12341 | desenfadar | 1 |
| 12342 | desencajado | 1 |
| 12343 | desembozar | 1 |
| 12344 | desembozándose | 1 |
| 12345 | desembocar | 1 |
| 12346 | desembarco | 1 |
| 12347 | desembarcar | 1 |
| 12348 | desellar | 1 |
| 12349 | desdoro | 1 |
| 12350 | desdeñar | 1 |
| 12351 | desdentado | 1 |
| 12352 | descuidero | 1 |
| 12353 | descuento | 1 |
| 12354 | descubriolo | 1 |
| 12355 | descubierta | 1 |
| 12356 | descrismar | 1 |
| 12357 | descriptivo | 1 |
| 12358 | descosido | 1 |
| 12359 | descoser | 1 |
| 12360 | descorazonamiento | 1 |
| 12361 | descontento | 1 |
| 12362 | desconsolador | 1 |
| 12363 | desconsideradamente | 1 |
| 12364 | descompostura | 1 |
| 12365 | descomposición | 1 |
| 12366 | descomedir | 1 |
| 12367 | desclavar | 1 |
| 12368 | descastado | 1 |
| 12369 | descascarar | 1 |
| 12370 | descartar | 1 |
| 12371 | descarnar | 1 |
| 12372 | descargo | 1 |
| 12373 | descansado | 1 |
| 12374 | descamisar | 1 |
| 12375 | desbravar | 1 |
| 12376 | desbarajuste | 1 |
| 12377 | desbarajustar | 1 |
| 12378 | desbandada | 1 |
| 12379 | desazonar | 1 |
| 12380 | desayunar | 1 |
| 12381 | desaviar | 1 |
| 12382 | desavenido | 1 |
| 12383 | desaseo | 1 |
| 12384 | desasear | 1 |
| 12385 | desarraigar | 1 |
| 12386 | desaprobar | 1 |
| 12387 | desapacible | 1 |
| 12388 | desanimado | 1 |
| 12389 | desamparar | 1 |
| 12390 | desamortización | 1 |
| 12391 | desamor | 1 |
| 12392 | desalquilar | 1 |
| 12393 | desalmado | 1 |
| 12394 | desahucio | 1 |
| 12395 | desahogado | 1 |
| 12396 | desahogadamente | 1 |
| 12397 | desaguisado | 1 |
| 12398 | desagradablemente | 1 |
| 12399 | desafuero | 1 |
| 12400 | desaforadamente | 1 |
| 12401 | desafío | 1 |
| 12402 | desafiar | 1 |
| 12403 | desacorde | 1 |
| 12404 | desacertar | 1 |
| 12405 | desacato | 1 |
| 12406 | desacatar | 1 |
| 12407 | desabrochar | 1 |
| 12408 | desabrimiento | 1 |
| 12409 | desabrigado | 1 |
| 12410 | desabotonar | 1 |
| 12411 | derrotero | 1 |
| 12412 | derrochador | 1 |
| 12413 | derrengar | 1 |
| 12414 | derrame | 1 |
| 12415 | derramamiento | 1 |
| 12416 | derivación | 1 |
| 12417 | derechamente | 1 |
| 12418 | depurar | 1 |
| 12419 | deprisa | 1 |
| 12420 | depravar | 1 |
| 12421 | depravado | 1 |
| 12422 | depende | 1 |
| 12423 | departir | 1 |
| 12424 | denuesto | 1 |
| 12425 | dentición | 1 |
| 12426 | dentellar | 1 |
| 12427 | denotar | 1 |
| 12428 | denominar | 1 |
| 12429 | denme | 1 |
| 12430 | denle | 1 |
| 12431 | denegación | 1 |
| 12432 | demolición | 1 |
| 12433 | demoler | 1 |
| 12434 | demócrata | 1 |
| 12435 | demetria | 1 |
| 12436 | demanda | 1 |
| 12437 | demagogo | 1 |
| 12438 | demagógico | 1 |
| 12439 | delta | 1 |
| 12440 | delicias | 1 |
| 12441 | deliberar | 1 |
| 12442 | deliberadamente | 1 |
| 12443 | delfines | 1 |
| 12444 | deleznable | 1 |
| 12445 | deleitar | 1 |
| 12446 | delegar | 1 |
| 12447 | dele | 1 |
| 12448 | delatar | 1 |
| 12449 | delación | 1 |
| 12450 | dejoles | 1 |
| 12451 | dejémonos | 1 |
| 12452 | déjele | 1 |
| 12453 | déjase | 1 |
| 12454 | déjamele | 1 |
| 12455 | déjalo | 1 |
| 12456 | dejadez | 1 |
| 12457 | dejada | 1 |
| 12458 | dejábase | 1 |
| 12459 | dehesa | 1 |
| 12460 | degüello | 1 |
| 12461 | degradar | 1 |
| 12462 | degeneración | 1 |
| 12463 | defraudación | 1 |
| 12464 | definitiva | 1 |
| 12465 | déficit | 1 |
| 12466 | deficiencia | 1 |
| 12467 | defensor | 1 |
| 12468 | defensivo | 1 |
| 12469 | defendemos | 1 |
| 12470 | dédalo | 1 |
| 12471 | dedal | 1 |
| 12472 | decreto | 1 |
| 12473 | decorativo | 1 |
| 12474 | decorativamente | 1 |
| 12475 | declive | 1 |
| 12476 | declinación | 1 |
| 12477 | declaraba | 1 |
| 12478 | declamatorio | 1 |
| 12479 | declamación | 1 |
| 12480 | decisivo | 1 |
| 12481 | decirme | 1 |
| 12482 | décima | 1 |
| 12483 | decidor | 1 |
| 12484 | decidirse | 1 |
| 12485 | decididamente | 1 |
| 12486 | decible | 1 |
| 12487 | decíase | 1 |
| 12488 | decías | 1 |
| 12489 | decadente | 1 |
| 12490 | débito | 1 |
| 12491 | débilmente | 1 |
| 12492 | debes | 1 |
| 12493 | debatir | 1 |
| 12494 | deán | 1 |
| 12495 | davidson | 1 |
| 12496 | david | 1 |
| 12497 | dátiles | 1 |
| 12498 | darwin | 1 |
| 12499 | daría | 1 |
| 12500 | dañino | 1 |
| 12501 | dante | 1 |
| 12502 | danme | 1 |
| 12503 | daniel | 1 |
| 12504 | dándosela | 1 |
| 12505 | dándose | 1 |
| 12506 | dándole | 1 |
| 12507 | dámelo | 1 |
| 12508 | daganzo | 1 |
| 12509 | dadivoso | 1 |
| 12510 | dábase | 1 |
| 12511 | dabas | 1 |
| 12512 | curvo | 1 |
| 12513 | cursilería | 1 |
| 12514 | cursar | 1 |
| 12515 | curiosona | 1 |
| 12516 | curiosísimo | 1 |
| 12517 | curia | 1 |
| 12518 | curado | 1 |
| 12519 | cuneta | 1 |
| 12520 | cumplidamente | 1 |
| 12521 | cúmplase | 1 |
| 12522 | culpabilidad | 1 |
| 12523 | culminante | 1 |
| 12524 | culinario | 1 |
| 12525 | cuitado | 1 |
| 12526 | cuiste | 1 |
| 12527 | cuidarse | 1 |
| 12528 | cuidadoso | 1 |
| 12529 | cuidadito | 1 |
| 12530 | cuevas | 1 |
| 12531 | cueva | 1 |
| 12532 | cuentero | 1 |
| 12533 | cuente | 1 |
| 12534 | cuentan | 1 |
| 12535 | cuéntala | 1 |
| 12536 | cuco | 1 |
| 12537 | cuchillada | 1 |
| 12538 | cucaracha | 1 |
| 12539 | cubierto | 1 |
| 12540 | cuartos | 1 |
| 12541 | cuartilla | 1 |
| 12542 | cuarteto | 1 |
| 12543 | cuaresma | 1 |
| 12544 | cuantioso | 1 |
| 12545 | cuanta | 1 |
| 12546 | cuajo | 1 |
| 12547 | cuajado | 1 |
| 12548 | cuajada | 1 |
| 12549 | cuadrilongo | 1 |
| 12550 | cuadrilla | 1 |
| 12551 | cuadratura | 1 |
| 12552 | cuadra | 1 |
| 12553 | cuaderno | 1 |
| 12554 | cruzamiento | 1 |
| 12555 | cruelmente | 1 |
| 12556 | crudeza | 1 |
| 12557 | cruceta | 1 |
| 12558 | crónica | 1 |
| 12559 | cristianamente | 1 |
| 12560 | criáronle | 1 |
| 12561 | creyolo | 1 |
| 12562 | creyérase | 1 |
| 12563 | creyente | 1 |
| 12564 | crencha | 1 |
| 12565 | creíase | 1 |
| 12566 | creía | 1 |
| 12567 | creería | 1 |
| 12568 | creerá | 1 |
| 12569 | créemelo | 1 |
| 12570 | credulidad | 1 |
| 12571 | credo | 1 |
| 12572 | creció | 1 |
| 12573 | crecido | 1 |
| 12574 | creánmelo | 1 |
| 12575 | covacha | 1 |
| 12576 | courtray | 1 |
| 12577 | cotizar | 1 |
| 12578 | cotización | 1 |
| 12579 | cotidiano | 1 |
| 12580 | costera | 1 |
| 12581 | costados | 1 |
| 12582 | cósmico | 1 |
| 12583 | cosechero | 1 |
| 12584 | cosechar | 1 |
| 12585 | cosecha | 1 |
| 12586 | coruñas | 1 |
| 12587 | cortinilla | 1 |
| 12588 | cortésmente | 1 |
| 12589 | cortesano | 1 |
| 12590 | cortante | 1 |
| 12591 | cortada | 1 |
| 12592 | corsario | 1 |
| 12593 | corrompido | 1 |
| 12594 | corriole | 1 |
| 12595 | corrió | 1 |
| 12596 | corrígete | 1 |
| 12597 | corriéndose | 1 |
| 12598 | corríase | 1 |
| 12599 | corría | 1 |
| 12600 | correría | 1 |
| 12601 | correctivo | 1 |
| 12602 | correctísimo | 1 |
| 12603 | correa | 1 |
| 12604 | corral | 1 |
| 12605 | corpulento | 1 |
| 12606 | corpulencia | 1 |
| 12607 | corpóreo | 1 |
| 12608 | corporal | 1 |
| 12609 | coronado | 1 |
| 12610 | cornudo | 1 |
| 12611 | corifeo | 1 |
| 12612 | coria | 1 |
| 12613 | cordialidad | 1 |
| 12614 | cordelero | 1 |
| 12615 | cordelería | 1 |
| 12616 | corchete | 1 |
| 12617 | corbatín | 1 |
| 12618 | corazones | 1 |
| 12619 | corazoncito | 1 |
| 12620 | coraza | 1 |
| 12621 | corambre | 1 |
| 12622 | coquetear | 1 |
| 12623 | copulativo | 1 |
| 12624 | copudo | 1 |
| 12625 | copón | 1 |
| 12626 | copo | 1 |
| 12627 | copiosamente | 1 |
| 12628 | copiador | 1 |
| 12629 | copete | 1 |
| 12630 | convulsionar | 1 |
| 12631 | convulsión | 1 |
| 12632 | convocar | 1 |
| 12633 | convite | 1 |
| 12634 | convidado | 1 |
| 12635 | convexidad | 1 |
| 12636 | converso | 1 |
| 12637 | conversión | 1 |
| 12638 | conversar | 1 |
| 12639 | convénzase | 1 |
| 12640 | convenio | 1 |
| 12641 | convencionalismo | 1 |
| 12642 | convéncete | 1 |
| 12643 | contuso | 1 |
| 12644 | contristar | 1 |
| 12645 | contribución | 1 |
| 12646 | contreras | 1 |
| 12647 | contravenir | 1 |
| 12648 | contratista | 1 |
| 12649 | contratante | 1 |
| 12650 | contratación | 1 |
| 12651 | contrariábala | 1 |
| 12652 | contrahacer | 1 |
| 12653 | contradictorio | 1 |
| 12654 | contradicción | 1 |
| 12655 | contorno | 1 |
| 12656 | contonear | 1 |
| 12657 | contó | 1 |
| 12658 | continuadamente | 1 |
| 12659 | continuación | 1 |
| 12660 | continencia | 1 |
| 12661 | contiguo | 1 |
| 12662 | contienda | 1 |
| 12663 | contestole | 1 |
| 12664 | contera | 1 |
| 12665 | contentábase | 1 |
| 12666 | contenta | 1 |
| 12667 | contendiente | 1 |
| 12668 | contender | 1 |
| 12669 | contemporizador | 1 |
| 12670 | contempló | 1 |
| 12671 | contarle | 1 |
| 12672 | contándote | 1 |
| 12673 | contagioso | 1 |
| 12674 | contagiar | 1 |
| 12675 | contaduría | 1 |
| 12676 | contábale | 1 |
| 12677 | consunción | 1 |
| 12678 | consumidor | 1 |
| 12679 | consúltalo | 1 |
| 12680 | cónsul | 1 |
| 12681 | consuetudinario | 1 |
| 12682 | constipado | 1 |
| 12683 | constantino | 1 |
| 12684 | conspicuo | 1 |
| 12685 | consonante | 1 |
| 12686 | consonancia | 1 |
| 12687 | consolarse | 1 |
| 12688 | consolábase | 1 |
| 12689 | consola | 1 |
| 12690 | consistente | 1 |
| 12691 | considerándose | 1 |
| 12692 | considéralo | 1 |
| 12693 | considerábase | 1 |
| 12694 | considerábanla | 1 |
| 12695 | conservador | 1 |
| 12696 | conserva | 1 |
| 12697 | consecutivo | 1 |
| 12698 | consciente | 1 |
| 12699 | conociole | 1 |
| 12700 | conocía | 1 |
| 12701 | connivencia | 1 |
| 12702 | conminación | 1 |
| 12703 | conjurar | 1 |
| 12704 | conjeturar | 1 |
| 12705 | congrio | 1 |
| 12706 | congratular | 1 |
| 12707 | congestionar | 1 |
| 12708 | congestión | 1 |
| 12709 | confusamente | 1 |
| 12710 | confitería | 1 |
| 12711 | confitar | 1 |
| 12712 | confiésame | 1 |
| 12713 | confiado | 1 |
| 12714 | confesionario | 1 |
| 12715 | confección | 1 |
| 12716 | confabulación | 1 |
| 12717 | condújola | 1 |
| 12718 | condoler | 1 |
| 12719 | condiscípulo | 1 |
| 12720 | condimento | 1 |
| 12721 | condimentar | 1 |
| 12722 | condicional | 1 |
| 12723 | condenación | 1 |
| 12724 | condena | 1 |
| 12725 | concurrido | 1 |
| 12726 | concurrente | 1 |
| 12727 | conculcar | 1 |
| 12728 | concretamente | 1 |
| 12729 | concluyó | 1 |
| 12730 | concluyente | 1 |
| 12731 | concisión | 1 |
| 12732 | concilio | 1 |
| 12733 | concibe | 1 |
| 12734 | concesión | 1 |
| 12735 | concertado | 1 |
| 12736 | concernir | 1 |
| 12737 | concentración | 1 |
| 12738 | concatenación | 1 |
| 12739 | comunícase | 1 |
| 12740 | compuesto | 1 |
| 12741 | compuerta | 1 |
| 12742 | comprometido | 1 |
| 12743 | comprobar | 1 |
| 12744 | comprobación | 1 |
| 12745 | comprimiéndose | 1 |
| 12746 | compresión | 1 |
| 12747 | comprensible | 1 |
| 12748 | comprendiolo | 1 |
| 12749 | comprendió | 1 |
| 12750 | comprendiendo | 1 |
| 12751 | comprendido | 1 |
| 12752 | compras | 1 |
| 12753 | compositor | 1 |
| 12754 | complicar | 1 |
| 12755 | complemento | 1 |
| 12756 | complejo | 1 |
| 12757 | competir | 1 |
| 12758 | competidor | 1 |
| 12759 | compatible | 1 |
| 12760 | compatibilidad | 1 |
| 12761 | compasar | 1 |
| 12762 | comparó | 1 |
| 12763 | compañías | 1 |
| 12764 | compañerismo | 1 |
| 12765 | compadre | 1 |
| 12766 | compadécete | 1 |
| 12767 | compacto | 1 |
| 12768 | comisura | 1 |
| 12769 | comistrajo | 1 |
| 12770 | comió | 1 |
| 12771 | comino | 1 |
| 12772 | comilona | 1 |
| 12773 | comerías | 1 |
| 12774 | comento | 1 |
| 12775 | cómeme | 1 |
| 12776 | comedir | 1 |
| 12777 | come | 1 |
| 12778 | combustión | 1 |
| 12779 | combustible | 1 |
| 12780 | combate | 1 |
| 12781 | comanditario | 1 |
| 12782 | comadre | 1 |
| 12783 | colorete | 1 |
| 12784 | colón | 1 |
| 12785 | colocado | 1 |
| 12786 | colmillo | 1 |
| 12787 | colmar | 1 |
| 12788 | colmado | 1 |
| 12789 | collarín | 1 |
| 12790 | colisión | 1 |
| 12791 | coliflor | 1 |
| 12792 | colgajo | 1 |
| 12793 | colgadura | 1 |
| 12794 | coletazo | 1 |
| 12795 | colegiata | 1 |
| 12796 | colectivo | 1 |
| 12797 | colecta | 1 |
| 12798 | coleccionista | 1 |
| 12799 | coleccionar | 1 |
| 12800 | colapso | 1 |
| 12801 | cojera | 1 |
| 12802 | coja | 1 |
| 12803 | coincidencia | 1 |
| 12804 | cohete | 1 |
| 12805 | cogiola | 1 |
| 12806 | cogiéronse | 1 |
| 12807 | cogiditos | 1 |
| 12808 | cogida | 1 |
| 12809 | cógelo | 1 |
| 12810 | cofradía | 1 |
| 12811 | cofrade | 1 |
| 12812 | codorniz | 1 |
| 12813 | codillo | 1 |
| 12814 | código | 1 |
| 12815 | codificación | 1 |
| 12816 | codicioso | 1 |
| 12817 | codiciado | 1 |
| 12818 | codicia | 1 |
| 12819 | cochina | 1 |
| 12820 | cochecillo | 1 |
| 12821 | coca | 1 |
| 12822 | cobrábale | 1 |
| 12823 | cobardía | 1 |
| 12824 | cobalto | 1 |
| 12825 | clorhidrato | 1 |
| 12826 | cloral | 1 |
| 12827 | clima | 1 |
| 12828 | clientela | 1 |
| 12829 | clavel | 1 |
| 12830 | clave | 1 |
| 12831 | claudio | 1 |
| 12832 | clasificar | 1 |
| 12833 | clásico | 1 |
| 12834 | clases | 1 |
| 12835 | clarísimo | 1 |
| 12836 | clarín | 1 |
| 12837 | clarificar | 1 |
| 12838 | claridades | 1 |
| 12839 | claréate | 1 |
| 12840 | clandestino | 1 |
| 12841 | clamor | 1 |
| 12842 | cisne | 1 |
| 12843 | cirugía | 1 |
| 12844 | ciruela | 1 |
| 12845 | cirineo | 1 |
| 12846 | cirilo | 1 |
| 12847 | circunstancias | 1 |
| 12848 | circunspecto | 1 |
| 12849 | circunspección | 1 |
| 12850 | circunscribir | 1 |
| 12851 | circunloquio | 1 |
| 12852 | circunferencia | 1 |
| 12853 | circundar | 1 |
| 12854 | circo | 1 |
| 12855 | cinturón | 1 |
| 12856 | cincuentón | 1 |
| 12857 | cimarra | 1 |
| 12858 | cima | 1 |
| 12859 | cilindrar | 1 |
| 12860 | cilicio | 1 |
| 12861 | cigüeña | 1 |
| 12862 | cierro | 1 |
| 12863 | cierras | 1 |
| 12864 | cieno | 1 |
| 12865 | cienfuegos | 1 |
| 12866 | ciclón | 1 |
| 12867 | cicerone | 1 |
| 12868 | cicerón | 1 |
| 12869 | cicatriz | 1 |
| 12870 | cibeles | 1 |
| 12871 | chuzo | 1 |
| 12872 | churruca | 1 |
| 12873 | chupa | 1 |
| 12874 | chuletas | 1 |
| 12875 | chulesco | 1 |
| 12876 | chorrera | 1 |
| 12877 | choquezuela | 1 |
| 12878 | chopo | 1 |
| 12879 | chocolatero | 1 |
| 12880 | chochear | 1 |
| 12881 | chocarrero | 1 |
| 12882 | chitito | 1 |
| 12883 | chispazo | 1 |
| 12884 | chismoso | 1 |
| 12885 | chismorreo | 1 |
| 12886 | chismorrear | 1 |
| 12887 | chisgarabís | 1 |
| 12888 | chirrido | 1 |
| 12889 | chirimbolo | 1 |
| 12890 | chirigota | 1 |
| 12891 | chiquititas | 1 |
| 12892 | chiquillería | 1 |
| 12893 | chinchoso | 1 |
| 12894 | chinchón | 1 |
| 12895 | chinchilla | 1 |
| 12896 | chinar | 1 |
| 12897 | chillaba | 1 |
| 12898 | chilla | 1 |
| 12899 | chifladura | 1 |
| 12900 | chicooo | 1 |
| 12901 | chichón | 1 |
| 12902 | chicha | 1 |
| 12903 | chavo | 1 |
| 12904 | chavala | 1 |
| 12905 | chasquido | 1 |
| 12906 | charrán | 1 |
| 12907 | charolar | 1 |
| 12908 | chaquetar | 1 |
| 12909 | chapuzón | 1 |
| 12910 | chapoteo | 1 |
| 12911 | chapotear | 1 |
| 12912 | chanfaina | 1 |
| 12913 | chancleta | 1 |
| 12914 | champagne | 1 |
| 12915 | chambelán | 1 |
| 12916 | chalar | 1 |
| 12917 | chafarrinón | 1 |
| 12918 | chabacano | 1 |
| 12919 | cetro | 1 |
| 12920 | cetrería | 1 |
| 12921 | céspedes | 1 |
| 12922 | césar | 1 |
| 12923 | cerril | 1 |
| 12924 | cero | 1 |
| 12925 | cereza | 1 |
| 12926 | ceremoniosamente | 1 |
| 12927 | cerdear | 1 |
| 12928 | cerda | 1 |
| 12929 | cerciorose | 1 |
| 12930 | cerámica | 1 |
| 12931 | cepa | 1 |
| 12932 | ceñido | 1 |
| 12933 | centuplicar | 1 |
| 12934 | centrípeto | 1 |
| 12935 | centrífugo | 1 |
| 12936 | centímetro | 1 |
| 12937 | centenar | 1 |
| 12938 | centelleo | 1 |
| 12939 | cenital | 1 |
| 12940 | cenefa | 1 |
| 12941 | cencerro | 1 |
| 12942 | cenagoso | 1 |
| 12943 | celos | 1 |
| 12944 | célibe | 1 |
| 12945 | celibato | 1 |
| 12946 | celestina | 1 |
| 12947 | celeridad | 1 |
| 12948 | celebro | 1 |
| 12949 | celada | 1 |
| 12950 | ceguera | 1 |
| 12951 | cédula | 1 |
| 12952 | cedazo | 1 |
| 12953 | ceceoso | 1 |
| 12954 | ceceo | 1 |
| 12955 | cebón | 1 |
| 12956 | cebollino | 1 |
| 12957 | cazuela | 1 |
| 12958 | cazo | 1 |
| 12959 | cayose | 1 |
| 12960 | cavour | 1 |
| 12961 | cautivábale | 1 |
| 12962 | catre | 1 |
| 12963 | catolicismo | 1 |
| 12964 | católicamente | 1 |
| 12965 | caterva | 1 |
| 12966 | catequizar | 1 |
| 12967 | catarral | 1 |
| 12968 | catarata | 1 |
| 12969 | cataplasma | 1 |
| 12970 | catafalco | 1 |
| 12971 | catador | 1 |
| 12972 | casulla | 1 |
| 12973 | casualmente | 1 |
| 12974 | castro | 1 |
| 12975 | casto | 1 |
| 12976 | castizo | 1 |
| 12977 | castilla | 1 |
| 12978 | castellana | 1 |
| 12979 | castañuelo | 1 |
| 12980 | castañeteo | 1 |
| 12981 | castamente | 1 |
| 12982 | casquillo | 1 |
| 12983 | casquería | 1 |
| 12984 | caspitina | 1 |
| 12985 | caspa | 1 |
| 12986 | casose | 1 |
| 12987 | caseta | 1 |
| 12988 | cascajo | 1 |
| 12989 | cascado | 1 |
| 12990 | cásale | 1 |
| 12991 | casadita | 1 |
| 12992 | cartuja | 1 |
| 12993 | cartelón | 1 |
| 12994 | carroza | 1 |
| 12995 | carromato | 1 |
| 12996 | carrillera | 1 |
| 12997 | carrillar | 1 |
| 12998 | carrete | 1 |
| 12999 | carraspear | 1 |
| 13000 | carrasca | 1 |
| 13001 | carpetazo | 1 |
| 13002 | carnavales | 1 |
| 13003 | carnaval | 1 |
| 13004 | carmesí | 1 |
| 13005 | caricatura | 1 |
| 13006 | cariacontecido | 1 |
| 13007 | cargado | 1 |
| 13008 | cargábanle | 1 |
| 13009 | careto | 1 |
| 13010 | cardiaco | 1 |
| 13011 | cárdeno | 1 |
| 13012 | cardar | 1 |
| 13013 | carcomido | 1 |
| 13014 | caracoles | 1 |
| 13015 | carabanchel | 1 |
| 13016 | captura | 1 |
| 13017 | cápsulas | 1 |
| 13018 | capote | 1 |
| 13019 | capitanear | 1 |
| 13020 | capitalizar | 1 |
| 13021 | capitación | 1 |
| 13022 | capear | 1 |
| 13023 | caño | 1 |
| 13024 | cañamazo | 1 |
| 13025 | cantonal | 1 |
| 13026 | cantina | 1 |
| 13027 | canterac | 1 |
| 13028 | cantábrico | 1 |
| 13029 | canon | 1 |
| 13030 | cano | 1 |
| 13031 | canino | 1 |
| 13032 | canilla | 1 |
| 13033 | canijo | 1 |
| 13034 | caníbal | 1 |
| 13035 | canelo | 1 |
| 13036 | candil | 1 |
| 13037 | candidatura | 1 |
| 13038 | candidato | 1 |
| 13039 | candela | 1 |
| 13040 | candado | 1 |
| 13041 | cancillería | 1 |
| 13042 | cancelación | 1 |
| 13043 | cancel | 1 |
| 13044 | cancamurria | 1 |
| 13045 | canasto | 1 |
| 13046 | canasta | 1 |
| 13047 | canapé | 1 |
| 13048 | canallas | 1 |
| 13049 | canallada | 1 |
| 13050 | camús | 1 |
| 13051 | camuesa | 1 |
| 13052 | camposanto | 1 |
| 13053 | campos | 1 |
| 13054 | campestre | 1 |
| 13055 | campesino | 1 |
| 13056 | campanillas | 1 |
| 13057 | campaneo | 1 |
| 13058 | camita | 1 |
| 13059 | camisola | 1 |
| 13060 | camión | 1 |
| 13061 | caminata | 1 |
| 13062 | camilla | 1 |
| 13063 | cambrí | 1 |
| 13064 | camarín | 1 |
| 13065 | camarilla | 1 |
| 13066 | camaleón | 1 |
| 13067 | calzoncillos | 1 |
| 13068 | calvinista | 1 |
| 13069 | cálmese | 1 |
| 13070 | cálmate | 1 |
| 13071 | callémonos | 1 |
| 13072 | calleja | 1 |
| 13073 | cállatela | 1 |
| 13074 | callao | 1 |
| 13075 | cáliz | 1 |
| 13076 | caligráfico | 1 |
| 13077 | caligrafía | 1 |
| 13078 | calificado | 1 |
| 13079 | calibre | 1 |
| 13080 | calibrar | 1 |
| 13081 | calenturiento | 1 |
| 13082 | calendario | 1 |
| 13083 | caldo | 1 |
| 13084 | calderón | 1 |
| 13085 | calcula | 1 |
| 13086 | calco | 1 |
| 13087 | calcetín | 1 |
| 13088 | calcetar | 1 |
| 13089 | calcáreo | 1 |
| 13090 | calatravas | 1 |
| 13091 | calatrava | 1 |
| 13092 | calaínos | 1 |
| 13093 | calainos | 1 |
| 13094 | calado | 1 |
| 13095 | cajista | 1 |
| 13096 | cae | 1 |
| 13097 | caduco | 1 |
| 13098 | cadmio | 1 |
| 13099 | cadencioso | 1 |
| 13100 | cadencia | 1 |
| 13101 | cadavérico | 1 |
| 13102 | cacumen | 1 |
| 13103 | caciquismo | 1 |
| 13104 | cachucha | 1 |
| 13105 | cacharrería | 1 |
| 13106 | cacao | 1 |
| 13107 | cacahuete | 1 |
| 13108 | cabrón | 1 |
| 13109 | cabrito | 1 |
| 13110 | cabriolar | 1 |
| 13111 | cable | 1 |
| 13112 | cabestrillo | 1 |
| 13113 | cabecilla | 1 |
| 13114 | cabaña | 1 |
| 13115 | caballista | 1 |
| 13116 | caballeriza | 1 |
| 13117 | caballerete | 1 |
| 13118 | caballeresco | 1 |
| 13119 | buscarle | 1 |
| 13120 | buscaba | 1 |
| 13121 | burocracia | 1 |
| 13122 | búrlate | 1 |
| 13123 | burlador | 1 |
| 13124 | burguesía | 1 |
| 13125 | burgués | 1 |
| 13126 | burbujear | 1 |
| 13127 | buque | 1 |
| 13128 | buñuelo | 1 |
| 13129 | bufón | 1 |
| 13130 | bufido | 1 |
| 13131 | bruñir | 1 |
| 13132 | bruñido | 1 |
| 13133 | brr | 1 |
| 13134 | broza | 1 |
| 13135 | brote | 1 |
| 13136 | bromista | 1 |
| 13137 | brochazo | 1 |
| 13138 | brindose | 1 |
| 13139 | brillo | 1 |
| 13140 | brillantísimo | 1 |
| 13141 | brillantez | 1 |
| 13142 | brihuega | 1 |
| 13143 | bribonaza | 1 |
| 13144 | bribonada | 1 |
| 13145 | breviario | 1 |
| 13146 | brevedad | 1 |
| 13147 | brega | 1 |
| 13148 | brebaje | 1 |
| 13149 | brazada | 1 |
| 13150 | braveza | 1 |
| 13151 | brasa | 1 |
| 13152 | bramante | 1 |
| 13153 | bramaba | 1 |
| 13154 | bracero | 1 |
| 13155 | bracear | 1 |
| 13156 | bozal | 1 |
| 13157 | boya | 1 |
| 13158 | botoneras | 1 |
| 13159 | boteros | 1 |
| 13160 | botellazo | 1 |
| 13161 | bote | 1 |
| 13162 | botánica | 1 |
| 13163 | bosquejar | 1 |
| 13164 | borricada | 1 |
| 13165 | borrascoso | 1 |
| 13166 | borgias | 1 |
| 13167 | bordadores | 1 |
| 13168 | bordador | 1 |
| 13169 | borbotones | 1 |
| 13170 | borbones | 1 |
| 13171 | bonitamente | 1 |
| 13172 | bonillas | 1 |
| 13173 | bondadosamente | 1 |
| 13174 | bonancible | 1 |
| 13175 | bomberos | 1 |
| 13176 | bombero | 1 |
| 13177 | bolo | 1 |
| 13178 | bollero | 1 |
| 13179 | bollería | 1 |
| 13180 | bólido | 1 |
| 13181 | bohardilla | 1 |
| 13182 | bofes | 1 |
| 13183 | bocón | 1 |
| 13184 | bochorno | 1 |
| 13185 | bocanada | 1 |
| 13186 | bobada | 1 |
| 13187 | blonda | 1 |
| 13188 | blasonar | 1 |
| 13189 | blasfemo | 1 |
| 13190 | blasfemar | 1 |
| 13191 | blanquecino | 1 |
| 13192 | blandamente | 1 |
| 13193 | bizcochar | 1 |
| 13194 | bizantino | 1 |
| 13195 | bisoño | 1 |
| 13196 | bismark | 1 |
| 13197 | bismarck | 1 |
| 13198 | birmingham | 1 |
| 13199 | biombo | 1 |
| 13200 | bilbao | 1 |
| 13201 | bigotera | 1 |
| 13202 | bifurcación | 1 |
| 13203 | bienhechor | 1 |
| 13204 | bienaventuranza | 1 |
| 13205 | bienaventurados | 1 |
| 13206 | bicoca | 1 |
| 13207 | bichito | 1 |
| 13208 | bíblico | 1 |
| 13209 | betsabée | 1 |
| 13210 | besamanos | 1 |
| 13211 | berza | 1 |
| 13212 | berro | 1 |
| 13213 | bergante | 1 |
| 13214 | berdan | 1 |
| 13215 | benignita | 1 |
| 13216 | benignidad | 1 |
| 13217 | benévolamente | 1 |
| 13218 | bendita | 1 |
| 13219 | belladona | 1 |
| 13220 | belicoso | 1 |
| 13221 | belfort | 1 |
| 13222 | belencita | 1 |
| 13223 | beldar | 1 |
| 13224 | begonia | 1 |
| 13225 | befa | 1 |
| 13226 | becerrada | 1 |
| 13227 | bebedor | 1 |
| 13228 | bebe | 1 |
| 13229 | baztán | 1 |
| 13230 | batuta | 1 |
| 13231 | batlló | 1 |
| 13232 | batido | 1 |
| 13233 | batallita | 1 |
| 13234 | batahola | 1 |
| 13235 | batacazo | 1 |
| 13236 | basto | 1 |
| 13237 | bastión | 1 |
| 13238 | bastimento | 1 |
| 13239 | bastiat | 1 |
| 13240 | bastardo | 1 |
| 13241 | bastábale | 1 |
| 13242 | basílica | 1 |
| 13243 | basilea | 1 |
| 13244 | báscula | 1 |
| 13245 | basca | 1 |
| 13246 | basamento | 1 |
| 13247 | bártulo | 1 |
| 13248 | barroquismo | 1 |
| 13249 | barrigón | 1 |
| 13250 | barreno | 1 |
| 13251 | barredura | 1 |
| 13252 | barranco | 1 |
| 13253 | barranca | 1 |
| 13254 | barquinazo | 1 |
| 13255 | baronesa | 1 |
| 13256 | barón | 1 |
| 13257 | barnizar | 1 |
| 13258 | barniz | 1 |
| 13259 | bargueño | 1 |
| 13260 | bardal | 1 |
| 13261 | barcia | 1 |
| 13262 | barca | 1 |
| 13263 | barbilla | 1 |
| 13264 | barbería | 1 |
| 13265 | baratillo | 1 |
| 13266 | barástolis | 1 |
| 13267 | baraja | 1 |
| 13268 | bar | 1 |
| 13269 | baquetear | 1 |
| 13270 | bañar | 1 |
| 13271 | bañado | 1 |
| 13272 | banquero | 1 |
| 13273 | bandido | 1 |
| 13274 | banderita | 1 |
| 13275 | banderillero | 1 |
| 13276 | baluarte | 1 |
| 13277 | balsain | 1 |
| 13278 | balsa | 1 |
| 13279 | ballesta | 1 |
| 13280 | baldón | 1 |
| 13281 | baldío | 1 |
| 13282 | balanceo | 1 |
| 13283 | baladronada | 1 |
| 13284 | bajarlo | 1 |
| 13285 | bajáis | 1 |
| 13286 | bailotear | 1 |
| 13287 | bailly | 1 |
| 13288 | baillière | 1 |
| 13289 | bagaje | 1 |
| 13290 | badila | 1 |
| 13291 | bachillería | 1 |
| 13292 | bachiller | 1 |
| 13293 | bache | 1 |
| 13294 | babosa | 1 |
| 13295 | babilonia | 1 |
| 13296 | babieca | 1 |
| 13297 | babia | 1 |
| 13298 | babel | 1 |
| 13299 | b | 1 |
| 13300 | azulejo | 1 |
| 13301 | azulado | 1 |
| 13302 | azufre | 1 |
| 13303 | azucena | 1 |
| 13304 | azotaina | 1 |
| 13305 | azar | 1 |
| 13306 | azalea | 1 |
| 13307 | azada | 1 |
| 13308 | avieso | 1 |
| 13309 | avidez | 1 |
| 13310 | aventurábase | 1 |
| 13311 | avenida | 1 |
| 13312 | avenencia | 1 |
| 13313 | avellana | 1 |
| 13314 | avasallador | 1 |
| 13315 | avaro | 1 |
| 13316 | autorizado | 1 |
| 13317 | autenticidad | 1 |
| 13318 | austerlitz | 1 |
| 13319 | austeridad | 1 |
| 13320 | auspicios | 1 |
| 13321 | aurorita | 1 |
| 13322 | aureolar | 1 |
| 13323 | augurio | 1 |
| 13324 | audición | 1 |
| 13325 | atril | 1 |
| 13326 | atreviose | 1 |
| 13327 | atrevidilla | 1 |
| 13328 | atrayéndola | 1 |
| 13329 | atravesósele | 1 |
| 13330 | atragantar | 1 |
| 13331 | atosigar | 1 |
| 13332 | atonía | 1 |
| 13333 | atmosférico | 1 |
| 13334 | atleta | 1 |
| 13335 | atlas | 1 |
| 13336 | atiza | 1 |
| 13337 | atisbo | 1 |
| 13338 | atisbar | 1 |
| 13339 | atisbador | 1 |
| 13340 | atienda | 1 |
| 13341 | atestar | 1 |
| 13342 | atentísimamente | 1 |
| 13343 | atener | 1 |
| 13344 | ateneo | 1 |
| 13345 | ateísmo | 1 |
| 13346 | atavismo | 1 |
| 13347 | atarés | 1 |
| 13348 | atareado | 1 |
| 13349 | atañer | 1 |
| 13350 | atadijo | 1 |
| 13351 | asustose | 1 |
| 13352 | asustábase | 1 |
| 13353 | asturias | 1 |
| 13354 | astronomía | 1 |
| 13355 | astilla | 1 |
| 13356 | asquerosidad | 1 |
| 13357 | aspirador | 1 |
| 13358 | aspaventar | 1 |
| 13359 | aspasia | 1 |
| 13360 | asomose | 1 |
| 13361 | asombroso | 1 |
| 13362 | asolear | 1 |
| 13363 | asmático | 1 |
| 13364 | asistente | 1 |
| 13365 | asilado | 1 |
| 13366 | asia | 1 |
| 13367 | aserrar | 1 |
| 13368 | aseñorado | 1 |
| 13369 | asensio | 1 |
| 13370 | asegurado | 1 |
| 13371 | asear | 1 |
| 13372 | aseado | 1 |
| 13373 | ascetismo | 1 |
| 13374 | ascensión | 1 |
| 13375 | asamblea | 1 |
| 13376 | asaltáronle | 1 |
| 13377 | asadura | 1 |
| 13378 | asador | 1 |
| 13379 | asa | 1 |
| 13380 | artimaña | 1 |
| 13381 | artillero | 1 |
| 13382 | artillería | 1 |
| 13383 | artificioso | 1 |
| 13384 | artificio | 1 |
| 13385 | artesiano | 1 |
| 13386 | artesano | 1 |
| 13387 | artes | 1 |
| 13388 | arrumaco | 1 |
| 13389 | arrojo | 1 |
| 13390 | arrodillose | 1 |
| 13391 | arrobo | 1 |
| 13392 | arrimo | 1 |
| 13393 | arriesgar | 1 |
| 13394 | arrepentidas | 1 |
| 13395 | arremangar | 1 |
| 13396 | arremangado | 1 |
| 13397 | arreglole | 1 |
| 13398 | arréglame | 1 |
| 13399 | arredrar | 1 |
| 13400 | arreciar | 1 |
| 13401 | arrebolar | 1 |
| 13402 | arrear | 1 |
| 13403 | arrasar | 1 |
| 13404 | arrancose | 1 |
| 13405 | arquitecto | 1 |
| 13406 | arqueólogo | 1 |
| 13407 | arqueológico | 1 |
| 13408 | arqueología | 1 |
| 13409 | aroma | 1 |
| 13410 | arnés | 1 |
| 13411 | armónico | 1 |
| 13412 | armiño | 1 |
| 13413 | armería | 1 |
| 13414 | armador | 1 |
| 13415 | aristarco | 1 |
| 13416 | arisco | 1 |
| 13417 | arias | 1 |
| 13418 | arguyó | 1 |
| 13419 | argüir | 1 |
| 13420 | argüía | 1 |
| 13421 | argucia | 1 |
| 13422 | argolla | 1 |
| 13423 | arganda | 1 |
| 13424 | argamasillesca | 1 |
| 13425 | ardoroso | 1 |
| 13426 | arcola | 1 |
| 13427 | archivo | 1 |
| 13428 | archipámpano | 1 |
| 13429 | arcar | 1 |
| 13430 | arcada | 1 |
| 13431 | arboleda | 1 |
| 13432 | arbitrar | 1 |
| 13433 | aravaca | 1 |
| 13434 | arañazo | 1 |
| 13435 | araña | 1 |
| 13436 | arango | 1 |
| 13437 | aranceles | 1 |
| 13438 | arancel | 1 |
| 13439 | aragonés | 1 |
| 13440 | arábigo | 1 |
| 13441 | arabesco | 1 |
| 13442 | aquellas | 1 |
| 13443 | apuesto | 1 |
| 13444 | apuestas | 1 |
| 13445 | aprovechamiento | 1 |
| 13446 | apropiación | 1 |
| 13447 | aprobación | 1 |
| 13448 | apretura | 1 |
| 13449 | apresúrate | 1 |
| 13450 | apresurado | 1 |
| 13451 | apresuradamente | 1 |
| 13452 | aprendizaje | 1 |
| 13453 | aprendiz | 1 |
| 13454 | apréndete | 1 |
| 13455 | aprended | 1 |
| 13456 | apremiante | 1 |
| 13457 | apoyó | 1 |
| 13458 | apoyatura | 1 |
| 13459 | apóyate | 1 |
| 13460 | apostólico | 1 |
| 13461 | apóstoles | 1 |
| 13462 | aposentar | 1 |
| 13463 | aporreado | 1 |
| 13464 | apología | 1 |
| 13465 | apoderarse | 1 |
| 13466 | apócrifo | 1 |
| 13467 | apocamiento | 1 |
| 13468 | apocado | 1 |
| 13469 | aplauso | 1 |
| 13470 | apio | 1 |
| 13471 | apilar | 1 |
| 13472 | apetitoso | 1 |
| 13473 | aperrear | 1 |
| 13474 | apergaminar | 1 |
| 13475 | apercibir | 1 |
| 13476 | apeose | 1 |
| 13477 | apéndice | 1 |
| 13478 | apencar | 1 |
| 13479 | apegar | 1 |
| 13480 | apegado | 1 |
| 13481 | apáticamente | 1 |
| 13482 | apartola | 1 |
| 13483 | aparentemente | 1 |
| 13484 | aparejar | 1 |
| 13485 | aparatoso | 1 |
| 13486 | apandar | 1 |
| 13487 | apalabrar | 1 |
| 13488 | apaisado | 1 |
| 13489 | apacentar | 1 |
| 13490 | apabullar | 1 |
| 13491 | aorta | 1 |
| 13492 | años | 1 |
| 13493 | añada | 1 |
| 13494 | anudar | 1 |
| 13495 | anualmente | 1 |
| 13496 | antorcha | 1 |
| 13497 | antoñita | 1 |
| 13498 | antonieta | 1 |
| 13499 | antojo | 1 |
| 13500 | antojitos | 1 |
| 13501 | antípodas | 1 |
| 13502 | antipatriótico | 1 |
| 13503 | antioquía | 1 |
| 13504 | antigüedad | 1 |
| 13505 | antiguamente | 1 |
| 13506 | antigualla | 1 |
| 13507 | antiespasmódico | 1 |
| 13508 | antieconómico | 1 |
| 13509 | antidinásticas | 1 |
| 13510 | anticonstitucional | 1 |
| 13511 | anticipo | 1 |
| 13512 | anticipándome | 1 |
| 13513 | antequera | 1 |
| 13514 | anteponer | 1 |
| 13515 | antecedentes | 1 |
| 13516 | anteanoche | 1 |
| 13517 | antaño | 1 |
| 13518 | antagonista | 1 |
| 13519 | ansiado | 1 |
| 13520 | anotación | 1 |
| 13521 | anormal | 1 |
| 13522 | anómalo | 1 |
| 13523 | anomalía | 1 |
| 13524 | aniversario | 1 |
| 13525 | anisar | 1 |
| 13526 | aniquilamiento | 1 |
| 13527 | anímese | 1 |
| 13528 | animales | 1 |
| 13529 | anilla | 1 |
| 13530 | angustiado | 1 |
| 13531 | angulema | 1 |
| 13532 | anguila | 1 |
| 13533 | angostura | 1 |
| 13534 | angélico | 1 |
| 13535 | angélica | 1 |
| 13536 | anestésico | 1 |
| 13537 | andurrial | 1 |
| 13538 | andante | 1 |
| 13539 | andando | 1 |
| 13540 | andamiar | 1 |
| 13541 | andábanle | 1 |
| 13542 | anclar | 1 |
| 13543 | anchura | 1 |
| 13544 | anchoa | 1 |
| 13545 | análogo | 1 |
| 13546 | anacronismo | 1 |
| 13547 | anacleto | 1 |
| 13548 | anabaptista | 1 |
| 13549 | amputación | 1 |
| 13550 | ampolla | 1 |
| 13551 | amplísimo | 1 |
| 13552 | amplio | 1 |
| 13553 | amotinar | 1 |
| 13554 | amorrar | 1 |
| 13555 | amorosamente | 1 |
| 13556 | amorío | 1 |
| 13557 | amoniaco | 1 |
| 13558 | amodorrar | 1 |
| 13559 | amito | 1 |
| 13560 | amistoso | 1 |
| 13561 | amistosamente | 1 |
| 13562 | amistar | 1 |
| 13563 | amigos | 1 |
| 13564 | amigas | 1 |
| 13565 | amigablemente | 1 |
| 13566 | amenazador | 1 |
| 13567 | ambientar | 1 |
| 13568 | ambicionar | 1 |
| 13569 | ámbar | 1 |
| 13570 | amazónico | 1 |
| 13571 | amasábanlo | 1 |
| 13572 | amasábalo | 1 |
| 13573 | amas | 1 |
| 13574 | amartelamiento | 1 |
| 13575 | amarillento | 1 |
| 13576 | amargor | 1 |
| 13577 | amañar | 1 |
| 13578 | amanerado | 1 |
| 13579 | amancebar | 1 |
| 13580 | amalgamar | 1 |
| 13581 | amago | 1 |
| 13582 | amagar | 1 |
| 13583 | amaestrado | 1 |
| 13584 | amábale | 1 |
| 13585 | ama | 1 |
| 13586 | alzamiento | 1 |
| 13587 | alza | 1 |
| 13588 | alumbramiento | 1 |
| 13589 | aludido | 1 |
| 13590 | alucinado | 1 |
| 13591 | altozano | 1 |
| 13592 | altivez | 1 |
| 13593 | alteza | 1 |
| 13594 | alternativamente | 1 |
| 13595 | alternadamente | 1 |
| 13596 | altanería | 1 |
| 13597 | altaneramente | 1 |
| 13598 | alsacia | 1 |
| 13599 | alonar | 1 |
| 13600 | alojar | 1 |
| 13601 | alojamiento | 1 |
| 13602 | almuerzas | 1 |
| 13603 | almorzaré | 1 |
| 13604 | almoneda | 1 |
| 13605 | almohadón | 1 |
| 13606 | almidón | 1 |
| 13607 | almería | 1 |
| 13608 | almeja | 1 |
| 13609 | almansa | 1 |
| 13610 | almanaque | 1 |
| 13611 | almagre | 1 |
| 13612 | allego | 1 |
| 13613 | allegar | 1 |
| 13614 | allegado | 1 |
| 13615 | allegadizo | 1 |
| 13616 | allanamiento | 1 |
| 13617 | aliñar | 1 |
| 13618 | alijo | 1 |
| 13619 | alijar | 1 |
| 13620 | alifonso | 1 |
| 13621 | alicante | 1 |
| 13622 | alias | 1 |
| 13623 | aliar | 1 |
| 13624 | alianza | 1 |
| 13625 | alhambra | 1 |
| 13626 | álgido | 1 |
| 13627 | algeciras | 1 |
| 13628 | algarroba | 1 |
| 13629 | alga | 1 |
| 13630 | alfilerazo | 1 |
| 13631 | aleluya | 1 |
| 13632 | alelí | 1 |
| 13633 | alejose | 1 |
| 13634 | alejándose | 1 |
| 13635 | alegrose | 1 |
| 13636 | alegremente | 1 |
| 13637 | alegrarse | 1 |
| 13638 | alegórico | 1 |
| 13639 | alegoría | 1 |
| 13640 | aldeano | 1 |
| 13641 | alcorcón | 1 |
| 13642 | alcoholismo | 1 |
| 13643 | alcohólico | 1 |
| 13644 | alcira | 1 |
| 13645 | alcé | 1 |
| 13646 | alcarria | 1 |
| 13647 | alcarreño | 1 |
| 13648 | alcaraz | 1 |
| 13649 | alcantarillar | 1 |
| 13650 | alcanfor | 1 |
| 13651 | alcánceme | 1 |
| 13652 | alcaloide | 1 |
| 13653 | alcaldía | 1 |
| 13654 | alcahuete | 1 |
| 13655 | alcachofa | 1 |
| 13656 | alborozar | 1 |
| 13657 | alborotadamente | 1 |
| 13658 | albillo | 1 |
| 13659 | albedrío | 1 |
| 13660 | albaricoque | 1 |
| 13661 | albaicín | 1 |
| 13662 | albahaca | 1 |
| 13663 | alas | 1 |
| 13664 | alargamiento | 1 |
| 13665 | alameda | 1 |
| 13666 | alambrar | 1 |
| 13667 | alambicar | 1 |
| 13668 | alado | 1 |
| 13669 | alabarderos | 1 |
| 13670 | alabanza | 1 |
| 13671 | ajuste | 1 |
| 13672 | ajuntar | 1 |
| 13673 | ajardinar | 1 |
| 13674 | airear | 1 |
| 13675 | ahumado | 1 |
| 13676 | ahondar | 1 |
| 13677 | ahola | 1 |
| 13678 | ahitar | 1 |
| 13679 | ahijar | 1 |
| 13680 | agujerear | 1 |
| 13681 | aguirre | 1 |
| 13682 | aguinaldo | 1 |
| 13683 | aguileño | 1 |
| 13684 | agüero | 1 |
| 13685 | aguárdese | 1 |
| 13686 | aguárdate | 1 |
| 13687 | aguarda | 1 |
| 13688 | aguántate | 1 |
| 13689 | aguanta | 1 |
| 13690 | aguacero | 1 |
| 13691 | agrupar | 1 |
| 13692 | agricultura | 1 |
| 13693 | agregábansele | 1 |
| 13694 | agredir | 1 |
| 13695 | agraviar | 1 |
| 13696 | agravación | 1 |
| 13697 | agrado | 1 |
| 13698 | agradablemente | 1 |
| 13699 | agradabilísimo | 1 |
| 13700 | agotado | 1 |
| 13701 | agorar | 1 |
| 13702 | agonizar | 1 |
| 13703 | agobiar | 1 |
| 13704 | agitanar | 1 |
| 13705 | agenciar | 1 |
| 13706 | agarrotar | 1 |
| 13707 | agalla | 1 |
| 13708 | afortunar | 1 |
| 13709 | aforismo | 1 |
| 13710 | afluir | 1 |
| 13711 | afinado | 1 |
| 13712 | afiliar | 1 |
| 13713 | afilado | 1 |
| 13714 | afeite | 1 |
| 13715 | afeitada | 1 |
| 13716 | afección | 1 |
| 13717 | afanador | 1 |
| 13718 | adviértale | 1 |
| 13719 | advertía | 1 |
| 13720 | adversidad | 1 |
| 13721 | adventicio | 1 |
| 13722 | adúuultera | 1 |
| 13723 | adustez | 1 |
| 13724 | adúlteros | 1 |
| 13725 | adulón | 1 |
| 13726 | adulación | 1 |
| 13727 | adquirido | 1 |
| 13728 | adormilar | 1 |
| 13729 | adormidera | 1 |
| 13730 | adormecido | 1 |
| 13731 | adoptado | 1 |
| 13732 | adonis | 1 |
| 13733 | adonde | 1 |
| 13734 | adolecer | 1 |
| 13735 | adobar | 1 |
| 13736 | admisión | 1 |
| 13737 | admirábala | 1 |
| 13738 | adjetivo | 1 |
| 13739 | adivinanza | 1 |
| 13740 | adictoo | 1 |
| 13741 | adición | 1 |
| 13742 | adherido | 1 |
| 13743 | adeudar | 1 |
| 13744 | aderezo | 1 |
| 13745 | aderezar | 1 |
| 13746 | aderezado | 1 |
| 13747 | adepto | 1 |
| 13748 | adentros | 1 |
| 13749 | adela | 1 |
| 13750 | adán | 1 |
| 13751 | adamar | 1 |
| 13752 | ad | 1 |
| 13753 | acuñar | 1 |
| 13754 | acuéstese | 1 |
| 13755 | acuérdate | 1 |
| 13756 | acueducto | 1 |
| 13757 | acudimos | 1 |
| 13758 | acubilla | 1 |
| 13759 | actualmente | 1 |
| 13760 | activamente | 1 |
| 13761 | acta | 1 |
| 13762 | acrisolar | 1 |
| 13763 | acreditar | 1 |
| 13764 | acrecer | 1 |
| 13765 | acostumbrada | 1 |
| 13766 | acostáronle | 1 |
| 13767 | acostarme | 1 |
| 13768 | acostado | 1 |
| 13769 | acorazar | 1 |
| 13770 | acontecimiento | 1 |
| 13771 | aconséjele | 1 |
| 13772 | aconséjate | 1 |
| 13773 | acompañábanle | 1 |
| 13774 | acomodo | 1 |
| 13775 | acomodaticio | 1 |
| 13776 | acomodado | 1 |
| 13777 | acometida | 1 |
| 13778 | acometería | 1 |
| 13779 | acobardarme | 1 |
| 13780 | aclimatación | 1 |
| 13781 | aclaración | 1 |
| 13782 | aclamación | 1 |
| 13783 | acídulo | 1 |
| 13784 | acidez | 1 |
| 13785 | acicalar | 1 |
| 13786 | achicharrar | 1 |
| 13787 | achicar | 1 |
| 13788 | acetato | 1 |
| 13789 | acertijo | 1 |
| 13790 | acerqueme | 1 |
| 13791 | acerico | 1 |
| 13792 | acercósele | 1 |
| 13793 | acerado | 1 |
| 13794 | acéptelo | 1 |
| 13795 | acéptalo | 1 |
| 13796 | aceptación | 1 |
| 13797 | acentuación | 1 |
| 13798 | acémila | 1 |
| 13799 | acelerar | 1 |
| 13800 | acelerado | 1 |
| 13801 | aceitar | 1 |
| 13802 | acechador | 1 |
| 13803 | acebuche | 1 |
| 13804 | accionista | 1 |
| 13805 | accidentar | 1 |
| 13806 | acaudalado | 1 |
| 13807 | acatemos | 1 |
| 13808 | acatarrar | 1 |
| 13809 | acaparamiento | 1 |
| 13810 | acampar | 1 |
| 13811 | acaloradamente | 1 |
| 13812 | acaecer | 1 |
| 13813 | acacia | 1 |
| 13814 | acabose | 1 |
| 13815 | aburridísimo | 1 |
| 13816 | abstruso | 1 |
| 13817 | abstraerse | 1 |
| 13818 | abstraer | 1 |
| 13819 | abstinencia | 1 |
| 13820 | abstener | 1 |
| 13821 | absorción | 1 |
| 13822 | absolutista | 1 |
| 13823 | absoluta | 1 |
| 13824 | absolución | 1 |
| 13825 | abroñigal | 1 |
| 13826 | abriolo | 1 |
| 13827 | abriole | 1 |
| 13828 | abrigado | 1 |
| 13829 | abrevie | 1 |
| 13830 | abreviatura | 1 |
| 13831 | abre | 1 |
| 13832 | abovedado | 1 |
| 13833 | abotonar | 1 |
| 13834 | aborregado | 1 |
| 13835 | aborrecimiento | 1 |
| 13836 | aborrecido | 1 |
| 13837 | abonos | 1 |
| 13838 | abono | 1 |
| 13839 | abominar | 1 |
| 13840 | abolladura | 1 |
| 13841 | abogar | 1 |
| 13842 | abocose | 1 |
| 13843 | abochornar | 1 |
| 13844 | abigarrar | 1 |
| 13845 | abigarrado | 1 |
| 13846 | abiertamente | 1 |
| 13847 | aberración | 1 |
| 13848 | abejorro | 1 |
| 13849 | abejón | 1 |
| 13850 | abeja | 1 |
| 13851 | abdicar | 1 |
| 13852 | abatido | 1 |
| 13853 | abanicar | 1 |
| 13854 | abalorio | 1 |
| 13855 | abadesa | 1 |
|
|
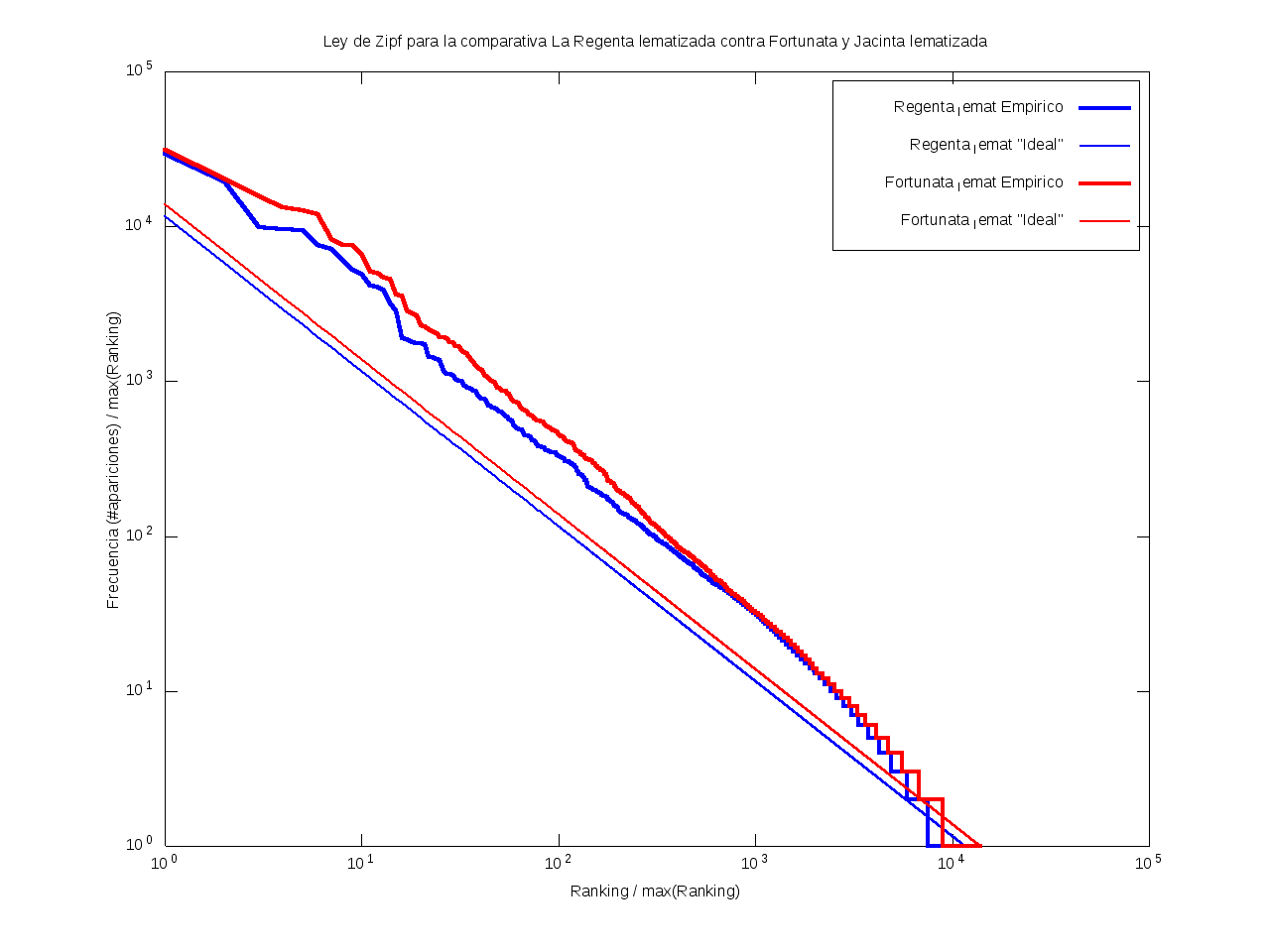
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará un conjunto (Regenta_lemat) (conjunto 1)
contra el otro (Fortunata_lemat) (conjunto 2) y viceversa.
A continuación se muestra una lista de todas las palabras presentes en los textos,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
Mostrar todo
Recoger


