Comparativa: La Regenta contra Fortunata y Jacinta

Índice

Información General
Ley de Heaps - Saturación léxica
Ley de Zipf
Test de Dunning

Información General

Título:	La Regenta
Autor:	Leopoldo Alas Clarín
Idioma:	Castellano
#Palabras total:	308254
#Palabras distintas:	22907
Type-Token ratio:	7.43%

Título:	Fortunata y Jacinta
Autor:	Benito Pérez Galdós
Idioma:	Castellano
#Palabras total:	394672
#Palabras distintas:	29367
Type-Token ratio:	7.44%

Ley de Heaps - Saturación léxica

La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto. Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto, según la fórmula

v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6) y K es una cierta constante, habitualmente entre 10 y 100.

En particular, mayores valores de b se corresponden con vocabularios más grandes, en el sentido de que aumentan rápidamente; mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).

Regenta

Fortunata

#Palabras:	#Palabras distintas:
6165	2271
12330	3791
18495	4953
24660	5904
30825	6760
36990	7547
43155	8247
49320	8872
55485	9606
61650	10139
67815	10711
73980	11235
80145	11782
86310	12283
92475	12770
98640	13211
104805	13627
110970	14110
117135	14532
123300	14951
129465	15322
135630	15644
141795	15987
147960	16358
154125	16712
160290	17052
166455	17290
172620	17613
178785	17904
184950	18254
191115	18547
197280	18859
203445	19141
209610	19458
215775	19748
221940	19993
228105	20309
234270	20503
240435	20676
246600	20921
252765	21135
258930	21405
265095	21645
271260	21842
277425	22023
283590	22213
289755	22389
295920	22595
302085	22760
308250	22907
308254	22907

#Palabras:	#Palabras distintas:
7893	2565
15786	4264
23679	5618
31572	6883
39465	8003
47358	9041
55251	10012
63144	10853
71037	11795
78930	12676
86823	13361
94716	14081
102609	14711
110502	15429
118395	16060
126288	16619
134181	17131
142074	17675
149967	18208
157860	18684
165753	19289
173646	19816
181539	20285
189432	20724
197325	21105
205218	21491
213111	21983
221004	22443
228897	22823
236790	23160
244683	23592
252576	23966
260469	24316
268362	24700
276255	25017
284148	25313
292041	25575
299934	25919
307827	26259
315720	26604
323613	26910
331506	27234
339399	27507
347292	27816
355185	28142
363078	28404
370971	28671
378864	28907
386757	29093
394650	29367
394672	29367

Ajuste por mínimos cuadrados de los datos a K*n^b:

Regenta

Fortunata

K = 20.142

K = 14.613

b = 0.561

b = 0.595

Ley de Zipf

La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo. Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia, mientras que hay un gran número de palabras son poco empleadas.

Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera es inversamente proporcional a su ranking, entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente, unas tres veces más que la tercera palabra más frecuente, etc.

Gráficamente, cuando una curva se encuentra por encima de la recta "ideal" quiere decir que el texto emplea recurrentemente un número de palabras muy reducido, habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal", el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.

Regenta

Fortunata

Ilustración del principio de mínimo esfuerzo:

Rank	Palabra	Frec
1	de	16580
2	la	11489
3	que	9901
4	y	9457
5	el	8268
6	a	7535
7	en	7137
8	no	4999
9	se	4779
10	los	4033
11	con	3202
12	un	3121
13	su	3084
14	del	3016
15	las	2939
16	por	2879
17	le	2436
18	lo	2335
19	era	2301
20	había	2212
21	una	2206
22	al	2168
23	pero	1914
24	como	1866
25	don	1798
26	más	1733
27	para	1377
28	él	1208
29	es	1193
30	si	1173
31	sin	1097
32	qué	1097
33	ella	1021
34	sus	1018
35	todo	917
36	ya	906
37	ana	898
38	usted	822
39	magistral	769
40	aquella	764
41	aquel	735
42	estaba	731
43	yo	712
44	sí	677
45	ni	672
46	me	638
47	o	635
48	tenía	610
49	muy	555
50	sobre	508
51	cuando	494
52	víctor	490
53	álvaro	490
54	casa	487
55	regenta	478
56	vetusta	471
57	esto	468
58	señor	460
59	poco	459
60	allí	450
61	ser	437
62	nada	434
63	todos	427
64	después	418
65	doña	414
66	decía	414
67	porque	401
68	eso	400
69	vez	392
70	también	378
71	mesía	373
72	entre	372
73	podía	369
74	ahora	364
75	bien	355
76	hasta	352
77	esta	351
78	fermín	350
79	ojos	347
80	así	347
81	ha	343
82	mucho	342
83	dos	334
84	iba	333
85	eran	333
86	siempre	332
87	tan	328
88	quería	328
89	menos	328
90	vida	326
91	dijo	326
92	otra	324
93	algo	321
94	mismo	320
95	hombre	318
96	este	314
97	dios	311
98	veces	307
99	quintanar	306
100	otro	303
101	mundo	303
102	habían	302
103	mi	291
104	mujer	286
105	alma	285
106	todas	284
107	tiempo	284
108	ver	280
109	sabía	279
110	día	272
111	amor	268
112	parecía	267
113	madre	267
114	aquello	266
115	decir	259
116	mal	252
117	desde	251
118	tal	249
119	pues	249
120	cabeza	247
121	hay	245
122	petra	241
123	fue	237
124	voz	235
125	hacía	234
126	aquellos	232
127	mejor	231
128	cosa	231
129	noche	230
130	está	230
131	señora	229
132	quien	229
133	te	225
134	antes	223
135	toda	221
136	aunque	219
137	gran	216
138	sido	214
139	frígilis	211
140	tarde	208
141	además	206
142	buen	205
143	pensaba	203
144	nadie	202
145	creía	200
146	obdulia	195
147	según	194
148	entonces	194
149	otros	192
150	casi	192
151	aquellas	190
152	anita	190
153	hacer	187
154	cuanto	187
155	hubiera	186
156	donde	186
157	cómo	186
158	años	186
159	fuera	185
160	quién	183
161	tiene	182
162	mientras	182
163	días	179
164	hecho	178
165	aquí	178
166	sentía	176
167	dicho	175
168	daba	175
169	cada	175
170	cuerpo	174
171	paula	173
172	sólo	172
173	mano	172
174	pas	171
175	paco	171
176	dentro	170
177	allá	167
178	tanto	166
179	nunca	165
180	ese	165
181	visto	163
182	verdad	162
183	otras	162
184	hora	162
185	fin	162
186	hablaba	161
187	visita	159
188	marquesa	159
189	cosas	159
190	vio	157
191	veía	156
192	les	156
193	provisor	155
194	estas	155
195	volvió	154
196	debía	152
197	demás	150
198	sé	147
199	modo	147
200	luz	147
201	amigo	147
202	son	145
203	sintió	145
204	hija	144
205	puerta	143
206	tú	141
207	parte	139
208	padre	138
209	hijo	138
210	momento	137
211	misma	137
212	ellos	137
213	he	135
214	iglesia	134
215	muchos	133
216	miedo	133
217	hablar	133
218	vegallana	132
219	fuerza	132
220	sino	131
221	santos	131
222	tres	130
223	ronzal	130
224	oh	130
225	lado	129
226	obispo	128
227	manos	128
228	pobre	127
229	muchas	127
230	mayor	127
231	pensar	126
232	horas	126
233	esa	126
234	pompeyo	125
235	ozores	124
236	saber	123
237	sabe	123
238	marqués	123
239	algunos	123
240	medio	122
241	haber	122
242	dar	121
243	catedral	121
244	pie	120
245	mí	120
246	marido	120
247	espíritu	118
248	casino	118
249	buena	118
250	palabras	117
251	llamaba	117
252	lejos	117
253	estaban	117
254	pronto	116
255	cerca	115
256	calle	115
257	tuvo	113
258	puede	113
259	pies	113
260	silencio	112
261	señores	112
262	sería	111
263	corazón	111
264	uno	110
265	soy	110
266	paso	109
267	aire	109
268	pudo	108
269	cual	108
270	santa	107
271	san	107
272	hizo	107
273	pueblo	106
274	mañana	106
275	llegó	106
276	fuerte	106
277	parece	105
278	idea	104
279	estos	104
280	contra	104
281	agua	104
282	salió	103
283	ir	103
284	visitación	102
285	nos	102
286	grandes	102
287	cielo	102
288	volvía	101
289	pasión	101
290	media	101
291	rostro	100
292	quiere	100
293	cura	100
294	tener	98
295	pensó	98
296	sol	97
297	salón	97
298	ripamilán	97
299	dio	97
300	creo	97
301	bueno	97
302	quiero	96
303	pasar	96
304	cierto	96
305	venía	95
306	triste	95
307	poder	95
308	unos	94
309	tales	94
310	mesa	94
311	hacia	94
312	gritó	94
313	estoy	94
314	detrás	94
315	salir	93
316	foja	93
317	claro	93
318	caso	93
319	boca	93
320	todavía	92
321	ruido	92
322	pesar	92
323	balcón	92
324	nuevo	91
325	nueva	91
326	fe	91
327	camino	91
328	piedad	90
329	oía	90
330	jamás	90
331	ideas	90
332	glocester	90
333	entró	90
334	brazos	90
335	alegría	90
336	tenían	89
337	teatro	89
338	seguro	89
339	frío	89
340	delante	89
341	virtud	88
342	solo	88
343	placer	87
344	palabra	87
345	niña	87
346	grande	87
347	ello	87
348	dice	87
349	tierra	86
350	tengo	86
351	sea	86
352	religión	86
353	razón	86
354	va	85
355	puso	85
356	dejaba	85
357	cara	84
358	ustedes	83
359	solía	83
360	seguía	83
361	orgaz	83
362	general	83
363	canónigo	83
364	algunas	83
365	señoras	82
366	negro	82
367	llegaba	82
368	guimarán	82
369	alto	82
370	pasaba	81
371	mía	81
372	conciencia	81
373	siquiera	80
374	parecían	80
375	frente	80
376	libre	79
377	lecho	79
378	dulce	79
379	dónde	79
380	algún	79
381	paseo	78
382	miraba	78
383	joven	78
384	gabinete	78
385	ellas	78
386	ante	78
387	vivero	77
388	tu	77
389	oído	77
390	muerte	77
391	hace	77
392	pasado	76
393	fuese	76
394	estar	76
395	carne	76
396	arte	76
397	unas	75
398	debajo	75
399	bajo	75
400	amigos	75
401	pocas	74
402	cuatro	74
403	caer	74
404	bermúdez	74
405	arriba	74
406	alguna	74
407	volver	73
408	sola	73
409	mujeres	73
410	médico	73
411	madrid	73
412	despacho	73
413	abajo	73
414	repente	72
415	primero	71
416	falta	71
417	efecto	71
418	dejó	71
419	amiga	71
420	ahí	71
421	querido	70
422	preguntó	70
423	mil	70
424	entrar	70
425	trataba	69
426	puesto	69
427	miró	69
428	hoy	69
429	cuarto	69
430	único	68
431	recordaba	68
432	oír	68
433	mío	68
434	llegar	68
435	hombres	68
436	han	68
437	vetustenses	67
438	tampoco	67
439	sombra	67
440	salía	67
441	punto	67
442	pensando	67
443	obra	67
444	jesús	67
445	fuego	67
446	campo	67
447	cama	67
448	brazo	67
449	tono	66
450	santo	66
451	salud	66
452	petronila	66
453	estado	66
454	demasiado	66
455	cruz	66
456	cerebro	66
457	capilla	66
458	adelante	66
459	mala	65
460	honor	65
461	gracia	65
462	vetustense	64
463	ridículo	64
464	presencia	64
465	oro	64
466	ocasión	64
467	mucha	64
468	lágrimas	64
469	culpa	64
470	comer	64
471	vivir	63
472	sangre	63
473	mis	63
474	hubo	63
475	historia	63
476	fondo	63
477	vuelta	62
478	primera	62
479	manera	62
480	libros	62
481	clérigo	62
482	carlos	62
483	atrás	62
484	vamos	61
485	sentir	61
486	peor	61
487	pasó	61
488	ocho	61
489	natural	61
490	llegado	61
491	junto	61
492	duda	61
493	dejar	61
494	cuenta	61
495	conversación	61
496	arcipreste	61
497	vergüenza	60
498	quiso	59
499	peligro	59
500	parque	59
501	nombre	59
502	iban	59
503	espolón	59
504	esperaba	59
505	encontraba	59
506	dolor	59
507	cualquier	59
508	conocía	59
509	caserón	59
510	sentido	58
511	pudiera	58
512	primer	58
513	papel	58
514	miserable	58
515	diciendo	58
516	amo	58
517	alcoba	58
518	viejo	57
519	sueño	57
520	pensamiento	57
521	gritaba	57
522	enemigo	57
523	embargo	57
524	barinaga	57
525	suya	56
526	quedaba	56
527	puedo	56
528	pasos	56
529	leer	56
530	labios	56
531	decían	56
532	damas	56
533	calor	56
534	año	56
535	amores	56
536	ama	56
537	valor	55
538	teresina	55
539	temía	55
540	tantas	55
541	será	55
542	plaza	55
543	joaquín	55
544	confesonario	55
545	voluntad	54
546	vino	54
547	querer	54
548	quedó	54
549	mirada	54
550	juventud	54
551	frutos	54
552	espiritual	54
553	coro	54
554	confesión	54
555	carta	54
556	buscar	54
557	bastante	54
558	apenas	54
559	podían	53
560	noches	53
561	llevaba	53
562	juan	53
563	gusto	53
564	escándalo	53
565	entraba	53
566	edelmira	53
567	contestó	53
568	color	53
569	alegre	53
570	voy	52
571	versos	52
572	teresa	52
573	necesitaba	52
574	mar	52
575	luna	52
576	loca	52
577	hablaban	52
578	dado	52
579	blanco	52
580	traje	51
581	secreto	51
582	público	51
583	noble	51
584	libro	51
585	hombros	51
586	hermosa	51
587	hablado	51
588	d	51
589	buenas	51
590	anuncia	51
591	suelo	50
592	somoza	50
593	principal	50
594	ponía	50
595	niño	50
596	moral	50
597	exclamó	50
598	ex	50
599	esposa	50
600	esas	50
601	dedos	50
602	banco	50
603	tristeza	49
604	sabes	49
605	pocos	49
606	pedro	49
607	oyó	49
608	muerto	49
609	loco	49
610	ido	49
611	hacían	49
612	etc	49
613	digo	49
614	custodio	49
615	confianza	49
616	confesar	49
617	coche	49
618	clase	49
619	tomar	48
620	perder	48
621	pecado	48
622	naturaleza	48
623	música	48
624	humor	48
625	especie	48
626	dinero	48
627	curas	48
628	cuestión	48
629	creyó	48
630	clero	48
631	cayetano	48
632	atención	48
633	arcediano	48
634	ánimo	48
635	alta	48
636	acababa	48
637	templo	47
638	podría	47
639	persona	47
640	mozo	47
641	largo	47
642	huerta	47
643	hermosura	47
644	gritos	47
645	figuraba	47
646	figura	47
647	estilo	47
648	enfrente	47
649	doncella	47
650	digno	47
651	dama	47
652	ciertas	47
653	atrevió	47
654	pura	46
655	polvo	46
656	piedra	46
657	páez	46
658	morir	46
659	e	46
660	deseo	46
661	derecho	46
662	cierta	46
663	carraspique	46
664	amistad	46
665	verde	45
666	verano	45
667	sotana	45
668	solas	45
669	señorito	45
670	seguida	45
671	nubes	45
672	motivo	45
673	materia	45
674	influencia	45
675	importaba	45
676	habló	45
677	diez	45
678	cinco	45
679	ciencia	45
680	caridad	45
681	añadió	45
682	trabajo	44
683	tías	44
684	tenido	44
685	tantos	44
686	quiera	44
687	puro	44
688	personas	44
689	palacio	44
690	mejillas	44
691	marquesito	44
692	hierro	44
693	gesto	44
694	están	44
695	encontró	44
696	enamorado	44
697	daban	44
698	ciudad	44
699	benítez	44
700	aldea	44
701	acaso	44
702	última	43
703	segura	43
704	saturnino	43
705	sala	43
706	remedio	43
707	perdido	43
708	partido	43
709	llama	43
710	lástima	43
711	eres	43
712	entero	43
713	entendía	43
714	dando	43
715	culto	43
716	comedor	43
717	absurdo	43
718	pálido	42
719	nosotros	42
720	ningún	42
721	miradas	42
722	haciendo	42
723	entender	42
724	energía	42
725	debe	42
726	crimen	42
727	costumbre	42
728	blanca	42
729	aún	42
730	vista	41
731	último	41
732	tentación	41
733	sociedad	41
734	siguió	41
735	siguiente	41
736	monte	41
737	liberal	41
738	juntos	41
739	hijas	41
740	hablando	41
741	fueron	41
742	expresión	41
743	entrañas	41
744	empezaba	41
745	ejemplo	41
746	da	41
747	crespo	41
748	confesor	41
749	asunto	41
750	vivía	40
751	virgen	40
752	verle	40
753	trabuco	40
754	tomó	40
755	tienen	40
756	siendo	40
757	propósito	40
758	orgullo	40
759	luego	40
760	llena	40
761	hambre	40
762	faltaba	40
763	espalda	40
764	enfermo	40
765	enferma	40
766	dicen	40
767	cocina	40
768	cabo	40
769	baile	40
770	árboles	40
771	tienes	39
772	subía	39
773	sonreía	39
774	respeto	39
775	propia	39
776	principio	39
777	podido	39
778	partes	39
779	obscuro	39
780	obscuridad	39
781	ira	39
782	importa	39
783	imaginación	39
784	frase	39
785	esposo	39
786	esos	39
787	escena	39
788	enfermedad	39
789	enemigos	39
790	criada	39
791	correr	39
792	carcajadas	39
793	buenos	39
794	ve	38
795	soledad	38
796	serio	38
797	saturno	38
798	regente	38
799	realidad	38
800	pedía	38
801	pecho	38
802	paz	38
803	pasaban	38
804	orden	38
805	necesidad	38
806	levantó	38
807	leía	38
808	invierno	38
809	honra	38
810	esperanza	38
811	desgracia	38
812	debo	38
813	camila	38
814	café	38
815	basta	38
816	amante	38
817	vuelto	37
818	venir	37
819	ropa	37
820	rincón	37
821	procuraba	37
822	poner	37
823	meses	37
824	lleno	37
825	hojas	37
826	hermano	37
827	envidia	37
828	elegante	37
829	criados	37
830	causa	37
831	caballo	37
832	bosque	37
833	aventuras	37
834	acercó	37
835	viuda	36
836	vanidad	36
837	ti	36
838	temprano	36
839	tanta	36
840	supuesto	36
841	subir	36
842	propio	36
843	pobres	36
844	opinión	36
845	mirar	36
846	locura	36
847	habla	36
848	gracias	36
849	feliz	36
850	familia	36
851	entusiasmo	36
852	encima	36
853	cuello	36
854	creer	36
855	comprendió	36
856	colores	36
857	ay	36
858	anselmo	36
859	venganza	35
860	valía	35
861	tomaba	35
862	terreno	35
863	suyo	35
864	solemne	35
865	servía	35
866	recuerdos	35
867	recuerdo	35
868	provincia	35
869	presidente	35
870	piso	35
871	perro	35
872	paseos	35
873	niñas	35
874	minutos	35
875	memoria	35
876	malo	35
877	madera	35
878	lengua	35
879	imposible	35
880	ideal	35
881	hermoso	35
882	fría	35
883	fijo	35
884	escalera	35
885	encimada	35
886	duelo	35
887	darle	35
888	calles	35
889	aun	35
890	ateo	35
891	alas	35
892	abrió	35
893	torre	34
894	tomás	34
895	sonrisa	34
896	solos	34
897	señoritas	34
898	sabio	34
899	sabían	34
900	rodillas	34
901	robustiano	34
902	repetía	34
903	prefería	34
904	pepe	34
905	palomares	34
906	nuestro	34
907	nervios	34
908	necesario	34
909	llamaban	34
910	leído	34
911	joaquinito	34
912	infame	34
913	estrépito	34
914	cualquiera	34
915	cien	34
916	buscaba	34
917	baja	34
918	atrevía	34
919	voces	33
920	ventana	33
921	triunfo	33
922	suerte	33
923	sombrero	33
924	sentó	33
925	satisfecho	33
926	sacerdote	33
927	río	33
928	reloj	33
929	preciso	33
930	piernas	33
931	pensamientos	33
932	pedir	33
933	nuestra	33
934	misa	33
935	maría	33
936	hubiese	33
937	hogar	33
938	has	33
939	estuvo	33
940	edad	33
941	dormir	33
942	diría	33
943	dejado	33
944	deber	33
945	caballero	33
946	ataque	33
947	anda	33
948	visitas	32
949	viene	32
950	veras	32
951	supo	32
952	suave	32
953	religioso	32
954	pareció	32
955	negra	32
956	movía	32
957	menudo	32
958	lugar	32
959	llevar	32
960	levita	32
961	larga	32
962	inútil	32
963	instante	32
964	gozaba	32
965	gloria	32
966	género	32
967	fermo	32
968	esperar	32
969	durante	32
970	detuvo	32
971	derecha	32
972	cristales	32
973	corría	32
974	comprendía	32
975	compañía	32
976	celos	32
977	caza	32
978	calumnia	32
979	caía	32
980	abierto	32
981	terror	31
982	tenorio	31
983	sonrió	31
984	silla	31
985	salían	31
986	querida	31
987	querían	31
988	preguntaba	31
989	plata	31
990	patio	31
991	notó	31
992	nobleza	31
993	mire	31
994	libertad	31
995	juego	31
996	gato	31
997	fiebre	31
998	fama	31
999	deseos	31
1000	darse	31
1001	cariño	31
1002	capaz	31
1003	viento	30
1004	venido	30
1005	venían	30
1006	veían	30
1007	varias	30
1008	van	30
1009	traía	30
1010	socios	30
1011	segundo	30
1012	roja	30
1013	relaciones	30
1014	presente	30
1015	posible	30
1016	poesía	30
1017	piel	30
1018	pasa	30
1019	pan	30
1020	nobles	30
1021	negros	30
1022	mayores	30
1023	marqueses	30
1024	leyó	30
1025	jefe	30
1026	humilde	30
1027	hemos	30
1028	fortunato	30
1029	flores	30
1030	cristo	30
1031	cree	30
1032	corriente	30
1033	consuelo	30
1034	comía	30
1035	ayer	30
1036	anterior	30
1037	adiós	30
1038	viaje	29
1039	vestido	29
1040	talento	29
1041	sonriendo	29
1042	siglo	29
1043	servicio	29
1044	señorita	29
1045	seguir	29
1046	rufina	29
1047	remordimiento	29
1048	religiosa	29
1049	portal	29
1050	periódicos	29
1051	paredes	29
1052	pared	29
1053	olor	29
1054	nuevas	29
1055	necesito	29
1056	manteo	29
1057	letras	29
1058	huir	29
1059	habría	29
1060	gustaba	29
1061	grave	29
1062	gente	29
1063	fortuna	29
1064	formas	29
1065	forma	29
1066	echar	29
1067	dormía	29
1068	desprecio	29
1069	delicia	29
1070	decirle	29
1071	corrió	29
1072	contestaba	29
1073	broma	29
1074	almas	29
1075	alcalde	29
1076	vicio	28
1077	tertulia	28
1078	supiera	28
1079	sentidos	28
1080	semejante	28
1081	romántico	28
1082	quisiera	28
1083	prueba	28
1084	pecados	28
1085	oye	28
1086	olvido	28
1087	malicia	28
1088	llamó	28
1089	infierno	28
1090	humedad	28
1091	hacen	28
1092	habrá	28
1093	gobierno	28
1094	furioso	28
1095	extremo	28
1096	devoción	28
1097	cristiano	28
1098	costumbres	28
1099	costa	28
1100	contento	28
1101	comercio	28
1102	callaba	28
1103	balcones	28
1104	azul	28
1105	altar	28
1106	águeda	28
1107	abría	28
1108	aborrecía	28
1109	veinte	27
1110	vaya	27
1111	vano	27
1112	salido	27
1113	quedaban	27
1114	perfectamente	27
1115	olvidado	27
1116	obras	27
1117	ninguna	27
1118	mourelo	27
1119	máquina	27
1120	loreto	27
1121	llamar	27
1122	lábaro	27
1123	justicia	27
1124	jóvenes	27
1125	interés	27
1126	imagen	27
1127	hubieran	27
1128	haría	27
1129	francisco	27
1130	escribir	27
1131	elocuencia	27
1132	doce	27
1133	dejaban	27
1134	deja	27
1135	cuándo	27
1136	convento	27
1137	comprender	27
1138	casas	27
1139	buscó	27
1140	aya	27
1141	aventura	27
1142	añadía	27
1143	antojaba	27
1144	ambición	27
1145	alguno	27
1146	alegres	27
1147	vulgar	26
1148	vueltas	26
1149	trato	26
1150	trata	26
1151	tranquilo	26
1152	terrible	26
1153	tendría	26
1154	techo	26
1155	superior	26
1156	sueños	26
1157	seis	26
1158	sacristía	26
1159	recordó	26
1160	rayos	26
1161	ramas	26
1162	púlpito	26
1163	primavera	26
1164	prados	26
1165	objeto	26
1166	mejores	26
1167	maneras	26
1168	junta	26
1169	hacerse	26
1170	fuerzas	26
1171	fueran	26
1172	fantasía	26
1173	exigía	26
1174	eterna	26
1175	dulces	26
1176	digna	26
1177	dientes	26
1178	cuidado	26
1179	creído	26
1180	cenar	26
1181	celedonio	26
1182	carretera	26
1183	cármenes	26
1184	cansado	26
1185	borracho	26
1186	barón	26
1187	asuntos	26
1188	andar	26
1189	ambiente	26
1190	víctima	25
1191	verdadero	25
1192	ven	25
1193	tranquila	25
1194	tormento	25
1195	tiempos	25
1196	suyos	25
1197	sublime	25
1198	situación	25
1199	sitio	25
1200	siglos	25
1201	remordimientos	25
1202	presentó	25
1203	piedras	25
1204	pereza	25
1205	novelas	25
1206	niños	25
1207	necesita	25
1208	moría	25
1209	miserables	25
1210	marcha	25
1211	llave	25
1212	idiota	25
1213	hombro	25
1214	filósofo	25
1215	falda	25
1216	fácil	25
1217	emoción	25
1218	diablo	25
1219	despreciaba	25
1220	cuánto	25
1221	cuadros	25
1222	cuadro	25
1223	contrario	25
1224	continuó	25
1225	contar	25
1226	confesaba	25
1227	cólera	25
1228	cambio	25
1229	bedoya	25
1230	barca	25
1231	antiguo	25
1232	ah	25
1233	adentros	25
1234	vieja	24
1235	verse	24
1236	verdadera	24
1237	tinieblas	24
1238	siete	24
1239	sereno	24
1240	seda	24
1241	resolución	24
1242	parecer	24
1243	pálida	24
1244	pájaros	24
1245	oficio	24
1246	obscuras	24
1247	notar	24
1248	muerta	24
1249	malos	24
1250	maestro	24
1251	lodo	24
1252	llorar	24
1253	llenos	24
1254	ley	24
1255	fresco	24
1256	filosofía	24
1257	estrecha	24
1258	echaba	24
1259	dispuesto	24
1260	cuya	24
1261	comenzó	24
1262	chispas	24
1263	cera	24
1264	capa	24
1265	bah	24
1266	asco	24
1267	admiración	24
1268	yerba	23
1269	volvían	23
1270	ves	23
1271	vencer	23
1272	usaba	23
1273	tren	23
1274	tras	23
1275	tocador	23
1276	temblaba	23
1277	subió	23
1278	sonaba	23
1279	solían	23
1280	seria	23
1281	resistir	23
1282	quedado	23
1283	profunda	23
1284	poeta	23
1285	ojo	23
1286	oídos	23
1287	mística	23
1288	mirando	23
1289	ilustre	23
1290	hijos	23
1291	felicidad	23
1292	explicaba	23
1293	evitar	23
1294	estaría	23
1295	esfuerzo	23
1296	escrito	23
1297	elegantes	23
1298	dogma	23
1299	devota	23
1300	debilidad	23
1301	débil	23
1302	curiosidad	23
1303	conocido	23
1304	compasión	23
1305	colonia	23
1306	circunstancias	23
1307	carácter	23
1308	calma	23
1309	calló	23
1310	callar	23
1311	caballeros	23
1312	acto	23
1313	acordaba	23
1314	vulgares	22
1315	verla	22
1316	tuviera	22
1317	tristes	22
1318	trifón	22
1319	treinta	22
1320	tienda	22
1321	susto	22
1322	sombras	22
1323	serían	22
1324	salvación	22
1325	sacrificio	22
1326	saberlo	22
1327	saben	22
1328	risa	22
1329	ridícula	22
1330	respetable	22
1331	redondo	22
1332	rato	22
1333	pueden	22
1334	presentaba	22
1335	pormenores	22
1336	perdía	22
1337	pena	22
1338	pañuelo	22
1339	miseria	22
1340	metido	22
1341	mandaba	22
1342	llegaban	22
1343	leyes	22
1344	lectura	22
1345	galería	22
1346	firme	22
1347	fandiño	22
1348	familiar	22
1349	experiencia	22
1350	estrecho	22
1351	estás	22
1352	entierro	22
1353	encontrar	22
1354	encogió	22
1355	educación	22
1356	contacto	22
1357	contaba	22
1358	comedias	22
1359	cena	22
1360	cazador	22
1361	cantaba	22
1362	cabildo	22
1363	belleza	22
1364	beatas	22
1365	beata	22
1366	autoridad	22
1367	aprensiones	22
1368	afición	22
1369	acercaba	22
1370	acabó	22
1371	viva	21
1372	vinagre	21
1373	traición	21
1374	seno	21
1375	saludó	21
1376	rumor	21
1377	rubia	21
1378	rojo	21
1379	rival	21
1380	recordar	21
1381	quieren	21
1382	prisa	21
1383	primeras	21
1384	política	21
1385	perdón	21
1386	paquito	21
1387	papá	21
1388	paciencia	21
1389	oyendo	21
1390	oreja	21
1391	nerviosa	21
1392	movimiento	21
1393	momentos	21
1394	mitad	21
1395	mismos	21
1396	material	21
1397	luchar	21
1398	llevaban	21
1399	llegaron	21
1400	levantaba	21
1401	ja	21
1402	interior	21
1403	intención	21
1404	hola	21
1405	haya	21
1406	gozar	21
1407	fuertes	21
1408	fresca	21
1409	extraño	21
1410	esquina	21
1411	esfuerzos	21
1412	enamorada	21
1413	dormido	21
1414	dolores	21
1415	criadas	21
1416	copa	21
1417	convenía	21
1418	comedia	21
1419	cobarde	21
1420	civil	21
1421	ciertos	21
1422	cerró	21
1423	casos	21
1424	casada	21
1425	cantar	21
1426	camisa	21
1427	beneficiado	21
1428	aprensión	21
1429	antigua	21
1430	animal	21
1431	anchas	21
1432	amaba	21
1433	admiraba	21
1434	actividad	21
1435	victoria	20
1436	vestidos	20
1437	vestía	20
1438	venga	20
1439	tristezas	20
1440	tresillo	20
1441	tocaba	20
1442	suficiente	20
1443	sonreír	20
1444	siento	20
1445	servir	20
1446	secretos	20
1447	sacar	20
1448	respondía	20
1449	respecto	20
1450	reía	20
1451	protesta	20
1452	profundo	20
1453	perales	20
1454	pensado	20
1455	ocultar	20
1456	obscura	20
1457	nuevos	20
1458	movimientos	20
1459	mira	20
1460	matar	20
1461	lucha	20
1462	luces	20
1463	locos	20
1464	interrumpió	20
1465	habilidad	20
1466	grandeza	20
1467	germán	20
1468	garganta	20
1469	frases	20
1470	fortaleza	20
1471	fingía	20
1472	fiel	20
1473	faldas	20
1474	esperaban	20
1475	espada	20
1476	época	20
1477	empezó	20
1478	diócesis	20
1479	dignidad	20
1480	despertar	20
1481	dejando	20
1482	daño	20
1483	comida	20
1484	clérigos	20
1485	claridad	20
1486	chica	20
1487	carrera	20
1488	canónigos	20
1489	bromas	20
1490	bismarck	20
1491	asustada	20
1492	aristocracia	20
1493	acercarse	20
1494	voluptuosidad	19
1495	visiones	19
1496	viendo	19
1497	verá	19
1498	varios	19
1499	única	19
1500	soñaba	19
1501	somos	19
1502	sintiendo	19
1503	segunda	19
1504	satisfacer	19
1505	sabido	19
1506	rigor	19
1507	rey	19
1508	quinta	19
1509	quieres	19
1510	propuso	19
1511	primo	19
1512	precisamente	19
1513	político	19
1514	placeres	19
1515	piadosa	19
1516	pasiones	19
1517	pasillos	19
1518	par	19
1519	palco	19
1520	noticia	19
1521	notaba	19
1522	niebla	19
1523	montes	19
1524	moda	19
1525	manda	19
1526	mamá	19
1527	lujo	19
1528	lucía	19
1529	lloró	19
1530	levantarse	19
1531	león	19
1532	iría	19
1533	íntimo	19
1534	instinto	19
1535	impaciencia	19
1536	humo	19
1537	humildad	19
1538	habido	19
1539	guante	19
1540	grado	19
1541	frialdad	19
1542	fonda	19
1543	flor	19
1544	favor	19
1545	existencia	19
1546	espera	19
1547	entraban	19
1548	encontrado	19
1549	eclesiástico	19
1550	dueño	19
1551	drama	19
1552	distraído	19
1553	disgusto	19
1554	desdén	19
1555	cristiana	19
1556	conozco	19
1557	común	19
1558	cita	19
1559	ciego	19
1560	cesar	19
1561	calumnias	19
1562	asustado	19
1563	ambos	19
1564	volvieron	18
1565	verdes	18
1566	veo	18
1567	vejez	18
1568	v	18
1569	ta	18
1570	sonaban	18
1571	social	18
1572	sexo	18
1573	sermones	18
1574	señas	18
1575	sentada	18
1576	sabría	18
1577	rosa	18
1578	romanticismo	18
1579	puertas	18
1580	pueblos	18
1581	pública	18
1582	prudencia	18
1583	propios	18
1584	prohibido	18
1585	presentes	18
1586	poca	18
1587	pidió	18
1588	pasando	18
1589	pagaba	18
1590	orilla	18
1591	obscurecer	18
1592	novio	18
1593	novela	18
1594	noticias	18
1595	notado	18
1596	negaba	18
1597	naturales	18
1598	nacido	18
1599	muere	18
1600	muchacha	18
1601	ministro	18
1602	milagro	18
1603	matrimonio	18
1604	llamado	18
1605	irritaba	18
1606	hermana	18
1607	hastío	18
1608	hago	18
1609	grosero	18
1610	gorro	18
1611	fino	18
1612	fingiendo	18
1613	fanatismo	18
1614	fábrica	18
1615	exaltación	18
1616	estrellas	18
1617	estará	18
1618	espectáculo	18
1619	envidiaba	18
1620	egoísmo	18
1621	ea	18
1622	disimulo	18
1623	deshonra	18
1624	deseaba	18
1625	deje	18
1626	cuerda	18
1627	cristal	18
1628	creían	18
1629	corte	18
1630	convidados	18
1631	continuaba	18
1632	constantino	18
1633	conducta	18
1634	cogió	18
1635	chico	18
1636	cerrado	18
1637	casualidad	18
1638	capital	18
1639	bravo	18
1640	bóveda	18
1641	blancos	18
1642	bastaba	18
1643	barba	18
1644	audiencia	18
1645	antiguas	18
1646	andaba	18
1647	amarillo	18
1648	amable	18
1649	advirtió	18
1650	acordó	18
1651	vivos	17
1652	verja	17
1653	tus	17
1654	tiro	17
1655	tenemos	17
1656	sonriente	17
1657	sofá	17
1658	sistema	17
1659	sentimiento	17
1660	semana	17
1661	santidad	17
1662	rincones	17
1663	rico	17
1664	respondió	17
1665	repugnante	17
1666	reían	17
1667	real	17
1668	quince	17
1669	prima	17
1670	pretexto	17
1671	preparaba	17
1672	pozo	17
1673	ponerse	17
1674	personal	17
1675	personaje	17
1676	permitía	17
1677	paseaba	17
1678	paraguas	17
1679	pagar	17
1680	órgano	17
1681	ninguno	17
1682	montón	17
1683	misticismo	17
1684	miraban	17
1685	menor	17
1686	medias	17
1687	magistrado	17
1688	lujuria	17
1689	lluvia	17
1690	lloraba	17
1691	lleva	17
1692	levantar	17
1693	letra	17
1694	lejanos	17
1695	largos	17
1696	justo	17
1697	íntima	17
1698	inocente	17
1699	indignación	17
1700	in	17
1701	horror	17
1702	hipócrita	17
1703	hipocresía	17
1704	hechos	17
1705	hable	17
1706	gris	17
1707	gestos	17
1708	gas	17
1709	fuesen	17
1710	formidable	17
1711	fina	17
1712	farol	17
1713	estuviera	17
1714	espejo	17
1715	escuela	17
1716	escrúpulos	17
1717	empezado	17
1718	elemento	17
1719	diga	17
1720	difícil	17
1721	diablos	17
1722	descubierto	17
1723	delito	17
1724	creyendo	17
1725	contenerse	17
1726	contemplaba	17
1727	completamente	17
1728	coger	17
1729	caricias	17
1730	capricho	17
1731	caído	17
1732	busca	17
1733	brillaban	17
1734	besos	17
1735	bajaba	17
1736	ancho	17
1737	afán	17
1738	acudía	17
1739	abierta	17
1740	virtuosa	16
1741	vagamente	16
1742	trueno	16
1743	tomado	16
1744	ternura	16
1745	tenga	16
1746	tela	16
1747	tablas	16
1748	suertes	16
1749	subían	16
1750	sermón	16
1751	semejantes	16
1752	saltar	16
1753	sacaba	16
1754	ricos	16
1755	recibía	16
1756	rara	16
1757	quejaba	16
1758	quedarse	16
1759	pulso	16
1760	prudente	16
1761	prosa	16
1762	prometido	16
1763	procuró	16
1764	primeros	16
1765	preocupaciones	16
1766	pone	16
1767	personajes	16
1768	permiso	16
1769	penas	16
1770	pelo	16
1771	patria	16
1772	particular	16
1773	párroco	16
1774	parecido	16
1775	parar	16
1776	país	16
1777	ocasiones	16
1778	observó	16
1779	obligaba	16
1780	norte	16
1781	murmuraba	16
1782	multitud	16
1783	moralidad	16
1784	monjas	16
1785	mes	16
1786	mérito	16
1787	merecía	16
1788	melancolía	16
1789	mata	16
1790	malas	16
1791	llorando	16
1792	ladrón	16
1793	kempis	16
1794	juegos	16
1795	izquierda	16
1796	íntimos	16
1797	intereses	16
1798	infeliz	16
1799	humana	16
1800	fieles	16
1801	falso	16
1802	eterno	16
1803	estudiante	16
1804	especial	16
1805	escenas	16
1806	escalofríos	16
1807	entiende	16
1808	ensueños	16
1809	engañaba	16
1810	empezar	16
1811	emociones	16
1812	ejercicio	16
1813	dirá	16
1814	desierto	16
1815	derechos	16
1816	deleite	16
1817	cuidados	16
1818	cuesta	16
1819	conoce	16
1820	completo	16
1821	cómico	16
1822	colorado	16
1823	círculo	16
1824	cenador	16
1825	cayó	16
1826	cantando	16
1827	buscando	16
1828	bolsa	16
1829	beber	16
1830	asomaba	16
1831	asiento	16
1832	arena	16
1833	ardiente	16
1834	apareció	16
1835	aparecía	16
1836	alcohol	16
1837	agustín	16
1838	abiertos	16
1839	volviéndose	15
1840	volar	15
1841	viera	15
1842	vienen	15
1843	viejos	15
1844	vestida	15
1845	verso	15
1846	ventanas	15
1847	vale	15
1848	universal	15
1849	traído	15
1850	toma	15
1851	temer	15
1852	suspiró	15
1853	suaves	15
1854	solitario	15
1855	sobrina	15
1856	singular	15
1857	simpático	15
1858	sillas	15
1859	servían	15
1860	seco	15
1861	satisfecha	15
1862	satisfacción	15
1863	salieron	15
1864	saliendo	15
1865	ruidos	15
1866	rianzares	15
1867	revolución	15
1868	retórica	15
1869	raza	15
1870	rayo	15
1871	raíces	15
1872	puramente	15
1873	pudor	15
1874	procesión	15
1875	prestigio	15
1876	pluma	15
1877	pistola	15
1878	pierna	15
1879	periódico	15
1880	pensador	15
1881	pasaron	15
1882	pariente	15
1883	papeles	15
1884	oían	15
1885	ofrecía	15
1886	ocurrido	15
1887	nave	15
1888	muchachas	15
1889	moverse	15
1890	místico	15
1891	matarla	15
1892	matalerejo	15
1893	manía	15
1894	llega	15
1895	lenguaje	15
1896	intenso	15
1897	inocencia	15
1898	inmóvil	15
1899	infinito	15
1900	inclinó	15
1901	importante	15
1902	imitar	15
1903	imágenes	15
1904	ilusiones	15
1905	humanidad	15
1906	huesos	15
1907	hacerlo	15
1908	hacerle	15
1909	hablo	15
1910	hablaron	15
1911	fiesta	15
1912	estómago	15
1913	estación	15
1914	espeso	15
1915	españa	15
1916	espaldas	15
1917	escape	15
1918	entera	15
1919	elegancia	15
1920	eh	15
1921	dudaba	15
1922	diputado	15
1923	despidió	15
1924	desaire	15
1925	cuyo	15
1926	cumplido	15
1927	cuentas	15
1928	cubierta	15
1929	costaba	15
1930	conversaciones	15
1931	contenta	15
1932	consistía	15
1933	comían	15
1934	coches	15
1935	clases	15
1936	chato	15
1937	cerrar	15
1938	cementerio	15
1939	celestina	15
1940	cartas	15
1941	camoirán	15
1942	caían	15
1943	bolsillo	15
1944	beso	15
1945	batalla	15
1946	barrio	15
1947	ausencia	15
1948	aseguraba	15
1949	arrogante	15
1950	arqueólogo	15
1951	ángel	15
1952	amigas	15
1953	altas	15
1954	alrededor	15
1955	aires	15
1956	adelantado	15
1957	vulgo	14
1958	vicario	14
1959	vago	14
1960	uso	14
1961	últimos	14
1962	triunfante	14
1963	trabajar	14
1964	tonto	14
1965	tigre	14
1966	terminar	14
1967	terciopelo	14
1968	ten	14
1969	tapia	14
1970	suponía	14
1971	suma	14
1972	sucia	14
1973	sonrisas	14
1974	sincera	14
1975	símbolo	14
1976	seguían	14
1977	seducción	14
1978	sed	14
1979	seca	14
1980	salvaje	14
1981	saludaba	14
1982	salto	14
1983	ronca	14
1984	robado	14
1985	resuelto	14
1986	representaba	14
1987	reina	14
1988	refería	14
1989	recordando	14
1990	recibió	14
1991	raso	14
1992	puños	14
1993	procurar	14
1994	preguntar	14
1995	podrá	14
1996	pliegues	14
1997	planes	14
1998	plan	14
1999	piensa	14
2000	picante	14
2001	piadosas	14
2002	peso	14
2003	perdida	14
2004	pensaban	14
2005	peligros	14
2006	paseaban	14
2007	órdenes	14
2008	oración	14
2009	oportuno	14
2010	olvidó	14
2011	olía	14
2012	oiga	14
2013	objetos	14
2014	modos	14
2015	misteriosa	14
2016	mármol	14
2017	llevado	14
2018	llenas	14
2019	leyendo	14
2020	juraba	14
2021	juicio	14
2022	jesuitas	14
2023	jardín	14
2024	infanzón	14
2025	inefable	14
2026	incienso	14
2027	huía	14
2028	horizonte	14
2029	honrado	14
2030	hermanas	14
2031	hablarle	14
2032	hábito	14
2033	grupo	14
2034	grosera	14
2035	graves	14
2036	gobernador	14
2037	figuró	14
2038	fatiga	14
2039	faroles	14
2040	falsa	14
2041	extraña	14
2042	espinas	14
2043	española	14
2044	escribió	14
2045	entiendo	14
2046	encanto	14
2047	elocuente	14
2048	divertirse	14
2049	disparates	14
2050	disimular	14
2051	discretamente	14
2052	discreta	14
2053	despertó	14
2054	despedirse	14
2055	desnudos	14
2056	desnudo	14
2057	descanso	14
2058	dejarle	14
2059	dedo	14
2060	decírselo	14
2061	debían	14
2062	deben	14
2063	cuantos	14
2064	corrían	14
2065	coronel	14
2066	contraste	14
2067	contemplación	14
2068	constante	14
2069	consejos	14
2070	confidencias	14
2071	confesiones	14
2072	condiciones	14
2073	condición	14
2074	concepto	14
2075	comprar	14
2076	comenzaba	14
2077	columpio	14
2078	cocinero	14
2079	castidad	14
2080	calderón	14
2081	caja	14
2082	cabía	14
2083	baños	14
2084	bailar	14
2085	ayuda	14
2086	auditorio	14
2087	atrevido	14
2088	aspecto	14
2089	árbol	14
2090	apretaba	14
2091	apoyó	14
2092	apariencias	14
2093	ancha	14
2094	americano	14
2095	aliento	14
2096	alfombra	14
2097	agujero	14
2098	agradable	14
2099	acudir	14
2100	acostarse	14
2101	acero	14
2102	vuelo	13
2103	vocación	13
2104	vivían	13
2105	viernes	13
2106	vencido	13
2107	vaga	13
2108	tronco	13
2109	tranquilidad	13
2110	tocar	13
2111	tocado	13
2112	toca	13
2113	tía	13
2114	teología	13
2115	tentaciones	13
2116	temblorosa	13
2117	temblar	13
2118	tejados	13
2119	teatros	13
2120	tardes	13
2121	taberna	13
2122	suspiraba	13
2123	sudor	13
2124	sospechaba	13
2125	sopa	13
2126	sepa	13
2127	sentimientos	13
2128	sentado	13
2129	sentaba	13
2130	sencilla	13
2131	seminario	13
2132	sagrado	13
2133	sacrificios	13
2134	sacerdotes	13
2135	sabiduría	13
2136	rumores	13
2137	rubio	13
2138	rinconada	13
2139	rica	13
2140	repugnancia	13
2141	remediarlo	13
2142	reconocía	13
2143	recinto	13
2144	ratos	13
2145	queda	13
2146	puño	13
2147	puedes	13
2148	próxima	13
2149	probable	13
2150	pregunta	13
2151	porvenir	13
2152	poética	13
2153	poema	13
2154	pico	13
2155	piano	13
2156	perros	13
2157	pernueces	13
2158	pendiente	13
2159	pavimento	13
2160	pausa	13
2161	pasillo	13
2162	parroquia	13
2163	padrinos	13
2164	ofreció	13
2165	obreros	13
2166	nuestras	13
2167	novena	13
2168	negar	13
2169	narices	13
2170	muebles	13
2171	molestaba	13
2172	modista	13
2173	modelo	13
2174	místicas	13
2175	mismas	13
2176	millones	13
2177	medicina	13
2178	mas	13
2179	mártir	13
2180	mangas	13
2181	lugares	13
2182	locuras	13
2183	llevó	13
2184	llaves	13
2185	liberales	13
2186	lejano	13
2187	largas	13
2188	jugar	13
2189	ironía	13
2190	inteligente	13
2191	infancia	13
2192	indispensable	13
2193	inclinaba	13
2194	impulso	13
2195	ignorancia	13
2196	i	13
2197	hermosísima	13
2198	gustos	13
2199	guerra	13
2200	guardaba	13
2201	grupos	13
2202	golpe	13
2203	estimaba	13
2204	esperando	13
2205	escribía	13
2206	escondido	13
2207	escenario	13
2208	entrada	13
2209	engañado	13
2210	encogía	13
2211	encantos	13
2212	egoísta	13
2213	discurso	13
2214	devoto	13
2215	destino	13
2216	desconocido	13
2217	descalza	13
2218	desafío	13
2219	dejaron	13
2220	defendía	13
2221	cumplir	13
2222	cuarenta	13
2223	corro	13
2224	corriendo	13
2225	corre	13
2226	corfín	13
2227	conseguido	13
2228	conoció	13
2229	conocer	13
2230	comulgar	13
2231	comprendido	13
2232	clara	13
2233	chicos	13
2234	cerraba	13
2235	centro	13
2236	castigo	13
2237	casarse	13
2238	carretela	13
2239	carga	13
2240	cantaban	13
2241	calleja	13
2242	caliente	13
2243	cajón	13
2244	bajos	13
2245	azules	13
2246	autor	13
2247	atmósfera	13
2248	arrojaba	13
2249	apoyaba	13
2250	aparte	13
2251	apagados	13
2252	amar	13
2253	amado	13
2254	amabilidad	13
2255	altura	13
2256	algazara	13
2257	aldeana	13
2258	adulterio	13
2259	acompañaba	13
2260	acera	13
2261	acá	13
2262	vuelve	12
2263	volvería	12
2264	vivo	12
2265	visitar	12
2266	últimas	12
2267	tratándose	12
2268	traer	12
2269	tila	12
2270	temperamento	12
2271	tarea	12
2272	sucio	12
2273	sospechas	12
2274	sospechar	12
2275	solemnidad	12
2276	sociales	12
2277	sentarse	12
2278	sana	12
2279	salvo	12
2280	saltaba	12
2281	salida	12
2282	salesas	12
2283	sacó	12
2284	rum	12
2285	roto	12
2286	romántica	12
2287	respirar	12
2288	repitió	12
2289	religiosos	12
2290	religiosidad	12
2291	regiones	12
2292	reflejos	12
2293	razones	12
2294	punta	12
2295	puesta	12
2296	prosiguió	12
2297	propósitos	12
2298	promesa	12
2299	probablemente	12
2300	pretensiones	12
2301	pollos	12
2302	poético	12
2303	poderosa	12
2304	pobreza	12
2305	pobrecita	12
2306	plomo	12
2307	pienso	12
2308	pequeña	12
2309	penitencia	12
2310	parís	12
2311	pareja	12
2312	parecida	12
2313	paraba	12
2314	original	12
2315	oriente	12
2316	orador	12
2317	olvidar	12
2318	odio	12
2319	ocurrió	12
2320	ocupaciones	12
2321	observaba	12
2322	nuestros	12
2323	nervioso	12
2324	necios	12
2325	músculos	12
2326	murió	12
2327	muertos	12
2328	muda	12
2329	muchacho	12
2330	motivos	12
2331	morales	12
2332	mísero	12
2333	mirado	12
2334	miel	12
2335	merienda	12
2336	mentira	12
2337	meditaba	12
2338	materias	12
2339	marismas	12
2340	lontananza	12
2341	llanto	12
2342	literata	12
2343	limpieza	12
2344	liga	12
2345	leguas	12
2346	lecciones	12
2347	latín	12
2348	lascivia	12
2349	lámpara	12
2350	ladrones	12
2351	intimidad	12
2352	instintos	12
2353	indigno	12
2354	indiferencia	12
2355	inconveniente	12
2356	incapaz	12
2357	impulsos	12
2358	importancia	12
2359	húmeda	12
2360	hermandad	12
2361	hecha	12
2362	haga	12
2363	hacerla	12
2364	hablemos	12
2365	habitación	12
2366	gritar	12
2367	graciosa	12
2368	fuentes	12
2369	frescura	12
2370	fervor	12
2371	exige	12
2372	excepción	12
2373	excelente	12
2374	exaltada	12
2375	estrechas	12
2376	estatua	12
2377	espíritus	12
2378	especialmente	12
2379	escopeta	12
2380	entraron	12
2381	entrando	12
2382	entendido	12
2383	engaño	12
2384	engañar	12
2385	enérgico	12
2386	encuentro	12
2387	empleaba	12
2388	echado	12
2389	dulzura	12
2390	dominó	12
2391	dominaba	12
2392	distraída	12
2393	distancia	12
2394	discutía	12
2395	discreción	12
2396	dijera	12
2397	dificultades	12
2398	devoraba	12
2399	despreciar	12
2400	despertaba	12
2401	desgraciado	12
2402	desesperado	12
2403	demonio	12
2404	delirio	12
2405	dejarse	12
2406	declaró	12
2407	decirlo	12
2408	daría	12
2409	dan	12
2410	cuentos	12
2411	cubierto	12
2412	criminal	12
2413	crea	12
2414	corredor	12
2415	contestar	12
2416	contemplar	12
2417	consiguió	12
2418	consideraba	12
2419	conseguir	12
2420	conquista	12
2421	comido	12
2422	columnas	12
2423	codicia	12
2424	claramente	12
2425	cigarro	12
2426	ciega	12
2427	chimenea	12
2428	catecismo	12
2429	casero	12
2430	cargo	12
2431	cargados	12
2432	capitán	12
2433	brillantes	12
2434	boulevard	12
2435	biblioteca	12
2436	berlina	12
2437	bailes	12
2438	ayuntamiento	12
2439	atreverse	12
2440	ataques	12
2441	asesino	12
2442	artista	12
2443	armonía	12
2444	aragonés	12
2445	apretó	12
2446	apetito	12
2447	aparecer	12
2448	altos	12
2449	alimento	12
2450	aguardiente	12
2451	acuerdo	12
2452	actos	12
2453	acercándose	12
2454	acababan	12
2455	aburría	12
2456	abnegación	12
2457	abandono	12
2458	volverse	11
2459	vivido	11
2460	vive	11
2461	vientre	11
2462	vaso	11
2463	vas	11
2464	universo	11
2465	tuviese	11
2466	tratar	11
2467	tonta	11
2468	tirano	11
2469	tierna	11
2470	testigo	11
2471	términos	11
2472	temor	11
2473	temblando	11
2474	sufrir	11
2475	suavidad	11
2476	soñado	11
2477	so	11
2478	sierra	11
2479	siente	11
2480	servidumbre	11
2481	serios	11
2482	seriedad	11
2483	señoritos	11
2484	semanas	11
2485	seductor	11
2486	secas	11
2487	santas	11
2488	rosas	11
2489	rodeada	11
2490	robusto	11
2491	robusta	11
2492	rezaba	11
2493	representa	11
2494	regla	11
2495	recibir	11
2496	recado	11
2497	queriendo	11
2498	quedo	11
2499	puntillas	11
2500	pruebas	11
2501	proyecto	11
2502	proponía	11
2503	propias	11
2504	prójimo	11
2505	profanación	11
2506	presa	11
2507	preocupado	11
2508	prendas	11
2509	preguntas	11
2510	platos	11
2511	perseguía	11
2512	perfección	11
2513	perezosa	11
2514	pensarlo	11
2515	pedazos	11
2516	párpados	11
2517	paraíso	11
2518	palidez	11
2519	p	11
2520	otoño	11
2521	orgullosa	11
2522	oraciones	11
2523	once	11
2524	olas	11
2525	oculto	11
2526	nube	11
2527	novedad	11
2528	nombres	11
2529	negocio	11
2530	necedades	11
2531	náuseas	11
2532	nariz	11
2533	museo	11
2534	murmurar	11
2535	murmullo	11
2536	movían	11
2537	mostraba	11
2538	morada	11
2539	montaña	11
2540	monja	11
2541	mezclado	11
2542	medida	11
2543	mayo	11
2544	mate	11
2545	maridos	11
2546	maíz	11
2547	magnífico	11
2548	llenaban	11
2549	libres	11
2550	libertino	11
2551	leyenda	11
2552	latigazos	11
2553	juró	11
2554	jurado	11
2555	juntas	11
2556	jaqueca	11
2557	italiana	11
2558	irresistible	11
2559	interesante	11
2560	instrumento	11
2561	insignificante	11
2562	inmensa	11
2563	inmediatamente	11
2564	injusticia	11
2565	inglés	11
2566	infames	11
2567	imprudencia	11
2568	impresión	11
2569	iglesias	11
2570	humano	11
2571	higiene	11
2572	gusta	11
2573	guapa	11
2574	grito	11
2575	gracioso	11
2576	gozando	11
2577	golpes	11
2578	ganar	11
2579	gana	11
2580	fuente	11
2581	formalidad	11
2582	flaqueza	11
2583	flamenco	11
2584	filas	11
2585	fijos	11
2586	fija	11
2587	feo	11
2588	farsa	11
2589	faltaban	11
2590	fácilmente	11
2591	extremos	11
2592	extendía	11
2593	exposición	11
2594	explicó	11
2595	excursiones	11
2596	evidente	11
2597	eucaliptus	11
2598	estúpido	11
2599	estridente	11
2600	esté	11
2601	estamos	11
2602	espirituales	11
2603	esperanzas	11
2604	espanto	11
2605	escasa	11
2606	entrado	11
2607	entra	11
2608	enterado	11
2609	enfermedades	11
2610	encontraban	11
2611	empleado	11
2612	empeño	11
2613	eclesiástica	11
2614	echó	11
2615	duro	11
2616	dura	11
2617	dudar	11
2618	doctor	11
2619	discreto	11
2620	disciplina	11
2621	dirigió	11
2622	diré	11
2623	diente	11
2624	dicha	11
2625	diccionario	11
2626	diálogo	11
2627	desnuda	11
2628	desfachatez	11
2629	desaparecía	11
2630	decidió	11
2631	deberes	11
2632	cuyos	11
2633	cubría	11
2634	cubiertos	11
2635	cuartos	11
2636	cuantas	11
2637	creerse	11
2638	coquetería	11
2639	convencido	11
2640	continuar	11
2641	contigua	11
2642	contener	11
2643	contemplando	11
2644	conocían	11
2645	compañero	11
2646	comisión	11
2647	colocaba	11
2648	cogido	11
2649	chistes	11
2650	celosía	11
2651	cayendo	11
2652	católico	11
2653	católica	11
2654	cargado	11
2655	caprichos	11
2656	canciones	11
2657	calidad	11
2658	butacas	11
2659	bosques	11
2660	bondad	11
2661	blancas	11
2662	bajó	11
2663	asustaba	11
2664	arrastraba	11
2665	argumento	11
2666	apóstol	11
2667	antiguos	11
2668	ansias	11
2669	amparo	11
2670	amantes	11
2671	almunia	11
2672	aldeas	11
2673	agradecía	11
2674	acerca	11
2675	aceptó	11
2676	aburrimiento	11
2677	absoluta	11
2678	zorrilla	10
2679	zas	10
2680	zapatos	10
2681	vuelven	10
2682	volviendo	10
2683	voluptuoso	10
2684	voluptuosa	10
2685	volaba	10
2686	vigor	10
2687	vestir	10
2688	vería	10
2689	ventajas	10
2690	vecinos	10
2691	varón	10
2692	varas	10
2693	valiente	10
2694	tuvieron	10
2695	tribunal	10
2696	trébol	10
2697	trazas	10
2698	tomo	10
2699	tipo	10
2700	tersa	10
2701	tercera	10
2702	temo	10
2703	teja	10
2704	tardó	10
2705	tambor	10
2706	tabla	10
2707	suyas	10
2708	supremo	10
2709	supersticioso	10
2710	sujetaba	10
2711	suelta	10
2712	subido	10
2713	sube	10
2714	sospecha	10
2715	sorprendido	10
2716	sor	10
2717	solemnemente	10
2718	sofismas	10
2719	sobrenatural	10
2720	servanda	10
2721	serena	10
2722	sentimental	10
2723	senderos	10
2724	seguido	10
2725	sarcasmo	10
2726	sano	10
2727	salvar	10
2728	saludar	10
2729	sale	10
2730	sábanas	10
2731	s	10
2732	ruina	10
2733	rodeado	10
2734	roce	10
2735	rezar	10
2736	resto	10
2737	resistencia	10
2738	repetir	10
2739	recreo	10
2740	reconoció	10
2741	recoger	10
2742	pupilas	10
2743	propiedad	10
2744	propaganda	10
2745	prometió	10
2746	profanos	10
2747	probar	10
2748	preparar	10
2749	posición	10
2750	plantas	10
2751	pisar	10
2752	pícaro	10
2753	pesaba	10
2754	perfumes	10
2755	perfecta	10
2756	perdonaba	10
2757	percal	10
2758	pechera	10
2759	parientes	10
2760	parecen	10
2761	palomo	10
2762	pálidos	10
2763	padres	10
2764	padecía	10
2765	ordinaria	10
2766	olvidaba	10
2767	oírle	10
2768	obscuros	10
2769	nueve	10
2770	nosotras	10
2771	necedad	10
2772	muro	10
2773	murmuración	10
2774	moribundo	10
2775	mordía	10
2776	molino	10
2777	minuto	10
2778	ministra	10
2779	milagros	10
2780	metió	10
2781	metía	10
2782	mato	10
2783	materialismo	10
2784	masa	10
2785	marchaba	10
2786	mandado	10
2787	maldad	10
2788	majadero	10
2789	luis	10
2790	lógica	10
2791	llovía	10
2792	llenaba	10
2793	llamarse	10
2794	llaman	10
2795	limosna	10
2796	lección	10
2797	jugaba	10
2798	iré	10
2799	invencible	10
2800	insistió	10
2801	inocentes	10
2802	inglesa	10
2803	inés	10
2804	indudablemente	10
2805	importantes	10
2806	iguales	10
2807	igual	10
2808	ignoraba	10
2809	ídolo	10
2810	hueso	10
2811	hueco	10
2812	hondo	10
2813	hoja	10
2814	hierba	10
2815	hicieron	10
2816	hiciera	10
2817	hembra	10
2818	haberlo	10
2819	gritaron	10
2820	gr	10
2821	ganado	10
2822	gallo	10
2823	furor	10
2824	fulgosio	10
2825	frías	10
2826	francés	10
2827	flaca	10
2828	físico	10
2829	finos	10
2830	fingió	10
2831	figuras	10
2832	figurarse	10
2833	fiestas	10
2834	fiera	10
2835	fidelidad	10
2836	familias	10
2837	explicar	10
2838	expedientes	10
2839	expansiva	10
2840	estuviese	10
2841	estancia	10
2842	espesa	10
2843	escandaloso	10
2844	escandalosa	10
2845	entregado	10
2846	entregaba	10
2847	entendían	10
2848	echaban	10
2849	dormirse	10
2850	dorada	10
2851	doloroso	10
2852	dispense	10
2853	dignos	10
2854	despedía	10
2855	desconocida	10
2856	delgada	10
2857	delantero	10
2858	dejo	10
2859	declarar	10
2860	decidido	10
2861	dé	10
2862	cursis	10
2863	cursi	10
2864	curia	10
2865	cuchillo	10
2866	cuántas	10
2867	cuales	10
2868	cruel	10
2869	crucero	10
2870	crítica	10
2871	criterio	10
2872	crisis	10
2873	creí	10
2874	costó	10
2875	cortar	10
2876	convidado	10
2877	convertido	10
2878	conversión	10
2879	convalecencia	10
2880	constancia	10
2881	consiguiente	10
2882	conservar	10
2883	conseguía	10
2884	conmigo	10
2885	conferencia	10
2886	comentarios	10
2887	come	10
2888	columna	10
2889	colorada	10
2890	clarín	10
2891	cintura	10
2892	cincuenta	10
2893	cerrando	10
2894	cerrados	10
2895	célebre	10
2896	castaño	10
2897	casta	10
2898	carcajada	10
2899	capillas	10
2900	cánticos	10
2901	campos	10
2902	cabello	10
2903	caballos	10
2904	burla	10
2905	bronce	10
2906	brillaba	10
2907	botas	10
2908	borrachos	10
2909	bienes	10
2910	baronesa	10
2911	bancos	10
2912	ayudaba	10
2913	aviso	10
2914	atender	10
2915	atado	10
2916	arroyo	10
2917	arma	10
2918	argumentos	10
2919	arco	10
2920	aprovechaba	10
2921	apoyada	10
2922	aparente	10
2923	antigüedades	10
2924	amorosa	10
2925	amargura	10
2926	amanecer	10
2927	almohadas	10
2928	alguien	10
2929	alerta	10
2930	ajedrez	10
2931	afortunadamente	10
2932	aficionado	10
2933	adoraba	10
2934	adivinar	10
2935	acendrada	10
2936	acaba	10
2937	absoluto	10
2938	abrigo	10
2939	abismo	10
2940	volviera	9
2941	vistió	9
2942	visitaba	9
2943	violín	9
2944	violento	9
2945	vete	9
2946	vengo	9
2947	vencedor	9
2948	vela	9
2949	vecino	9
2950	vaciló	9
2951	útil	9
2952	tropezar	9
2953	trecho	9
2954	través	9
2955	trascoro	9
2956	trapo	9
2957	torpe	9
2958	tomaban	9
2959	tolerancia	9
2960	tocaban	9
2961	tesoro	9
2962	término	9
2963	tenerla	9
2964	taza	9
2965	tamaño	9
2966	sur	9
2967	suplicó	9
2968	sujeto	9
2969	sudaba	9
2970	suavemente	9
2971	soslayo	9
2972	sorpresa	9
2973	sonreían	9
2974	soberbia	9
2975	sillón	9
2976	sienes	9
2977	servido	9
2978	serlo	9
2979	seré	9
2980	sequedad	9
2981	separado	9
2982	señales	9
2983	señal	9
2984	sentirse	9
2985	sencillo	9
2986	seguridad	9
2987	salvarse	9
2988	saltaban	9
2989	sacudir	9
2990	sabrá	9
2991	saborear	9
2992	saboreaba	9
2993	rompía	9
2994	romper	9
2995	romería	9
2996	roma	9
2997	rodeaban	9
2998	rodar	9
2999	risas	9
3000	riqueza	9
3001	resultaba	9
3002	respuesta	9
3003	responsabilidad	9
3004	respiró	9
3005	respiraba	9
3006	respetar	9
3007	respetaba	9
3008	reflexiones	9
3009	redonda	9
3010	recursos	9
3011	recogió	9
3012	rebelión	9
3013	reacción	9
3014	rápida	9
3015	raíz	9
3016	quedaron	9
3017	puñetazo	9
3018	pulcritud	9
3019	pueda	9
3020	provecho	9
3021	propuesto	9
3022	proposición	9
3023	promesas	9
3024	programa	9
3025	producía	9
3026	principalmente	9
3027	presentarse	9
3028	prensa	9
3029	prenda	9
3030	preferido	9
3031	precio	9
3032	poniendo	9
3033	polka	9
3034	podemos	9
3035	población	9
3036	plato	9
3037	pierde	9
3038	pide	9
3039	pesimismo	9
3040	perfume	9
3041	perezoso	9
3042	perdió	9
3043	peláez	9
3044	pastor	9
3045	paseando	9
3046	partidario	9
3047	partida	9
3048	palos	9
3049	páginas	9
3050	ostentaba	9
3051	orillas	9
3052	oprimía	9
3053	opinaba	9
3054	ópera	9
3055	ocupaba	9
3056	ocultaba	9
3057	observación	9
3058	obligó	9
3059	nieve	9
3060	negras	9
3061	negó	9
3062	necesaria	9
3063	naves	9
3064	naturalismo	9
3065	nacimiento	9
3066	muralla	9
3067	muera	9
3068	moza	9
3069	morado	9
3070	místicos	9
3071	misterioso	9
3072	mirarle	9
3073	militar	9
3074	mezclaban	9
3075	merece	9
3076	materialista	9
3077	mañanas	9
3078	mandó	9
3079	loma	9
3080	líneas	9
3081	limpia	9
3082	ligero	9
3083	leve	9
3084	lance	9
3085	juez	9
3086	jesuita	9
3087	jesucristo	9
3088	isidro	9
3089	invisibles	9
3090	invisible	9
3091	inteligencia	9
3092	insignificantes	9
3093	ingrata	9
3094	ingleses	9
3095	inferior	9
3096	infalibilidad	9
3097	inclinándose	9
3098	inclinada	9
3099	imprudente	9
3100	impaciente	9
3101	ilustrada	9
3102	idealismo	9
3103	huyendo	9
3104	huérfana	9
3105	honrada	9
3106	hielo	9
3107	gravedad	9
3108	gratitud	9
3109	grandezas	9
3110	granada	9
3111	gordo	9
3112	glorieta	9
3113	froilán	9
3114	fríos	9
3115	frescas	9
3116	frecuentes	9
3117	franqueza	9
3118	frac	9
3119	flaco	9
3120	felices	9
3121	facultades	9
3122	explicaciones	9
3123	examen	9
3124	etiqueta	9
3125	estudio	9
3126	estrechos	9
3127	estrado	9
3128	esperó	9
3129	espacio	9
3130	esclavo	9
3131	enseñaba	9
3132	encerraba	9
3133	encantaba	9
3134	emprender	9
3135	empieza	9
3136	embozo	9
3137	eficaz	9
3138	efectos	9
3139	echando	9
3140	dormían	9
3141	dorado	9
3142	doradas	9
3143	dominio	9
3144	dominar	9
3145	doméstica	9
3146	divina	9
3147	divertido	9
3148	dispuesta	9
3149	disposición	9
3150	disimulada	9
3151	dirán	9
3152	dinástico	9
3153	dificultad	9
3154	desesperación	9
3155	descuido	9
3156	deprisa	9
3157	delicias	9
3158	delicado	9
3159	declaración	9
3160	decirse	9
3161	debió	9
3162	debes	9
3163	deán	9
3164	dándole	9
3165	damasco	9
3166	culpas	9
3167	cuervo	9
3168	cuánta	9
3169	crecía	9
3170	corto	9
3171	corrido	9
3172	convertía	9
3173	conventos	9
3174	contraria	9
3175	continuo	9
3176	contentarse	9
3177	contentaba	9
3178	consultar	9
3179	consigo	9
3180	conserje	9
3181	consentía	9
3182	conquistar	9
3183	conferencias	9
3184	comparación	9
3185	codos	9
3186	codo	9
3187	cochero	9
3188	clavados	9
3189	citas	9
3190	choque	9
3191	chateaubriand	9
3192	cerrada	9
3193	ceñida	9
3194	ceniza	9
3195	celo	9
3196	celebraba	9
3197	causaba	9
3198	católicos	9
3199	catalejo	9
3200	caro	9
3201	cariñosa	9
3202	cargada	9
3203	capellán	9
3204	cantó	9
3205	calvario	9
3206	caída	9
3207	cadáver	9
3208	burlaba	9
3209	brisa	9
3210	bofetadas	9
3211	blanda	9
3212	bendito	9
3213	bajar	9
3214	b	9
3215	autores	9
3216	aureola	9
3217	audacia	9
3218	aturdido	9
3219	atrevían	9
3220	atormentaba	9
3221	atento	9
3222	aspavientos	9
3223	asomó	9
3224	asombro	9
3225	asistir	9
3226	artes	9
3227	arrojó	9
3228	arquitectura	9
3229	armas	9
3230	armario	9
3231	aristócrata	9
3232	aprendido	9
3233	apagado	9
3234	antojaban	9
3235	amenazaba	9
3236	ahogaba	9
3237	agradecimiento	9
3238	admirado	9
3239	ademán	9
3240	acuerdas	9
3241	activa	9
3242	acostumbrado	9
3243	acólito	9
3244	acción	9
3245	abandonado	9
3246	zarzuela	8
3247	zapatillas	8
3248	vigilia	8
3249	viese	8
3250	vieron	8
3251	vicente	8
3252	verdura	8
3253	venerables	8
3254	venerable	8
3255	veneno	8
3256	vencida	8
3257	velas	8
3258	vea	8
3259	utilidad	8
3260	trémula	8
3261	trasnochadores	8
3262	trasaltar	8
3263	trapos	8
3264	trance	8
3265	trabajaba	8
3266	tordo	8
3267	torcido	8
3268	timbre	8
3269	tiendas	8
3270	testigos	8
3271	teoría	8
3272	tenue	8
3273	tendió	8
3274	tendida	8
3275	temible	8
3276	temblor	8
3277	tembló	8
3278	tajada	8
3279	sutiles	8
3280	sutil	8
3281	suprema	8
3282	superioridad	8
3283	sucesos	8
3284	sucedido	8
3285	sordo	8
3286	sorda	8
3287	solución	8
3288	solitaria	8
3289	sirvió	8
3290	sirve	8
3291	siguieron	8
3292	sigue	8
3293	siesta	8
3294	servicios	8
3295	serias	8
3296	señalando	8
3297	seña	8
3298	sensación	8
3299	sendas	8
3300	seducir	8
3301	secular	8
3302	saludo	8
3303	saludable	8
3304	salones	8
3305	sagrada	8
3306	sacudió	8
3307	sacramentos	8
3308	sabemos	8
3309	roquete	8
3310	románticas	8
3311	robles	8
3312	roble	8
3313	ridículas	8
3314	reyes	8
3315	revelaciones	8
3316	retirado	8
3317	resumen	8
3318	relámpago	8
3319	reír	8
3320	reinaba	8
3321	regular	8
3322	reconocer	8
3323	reconciliar	8
3324	recibido	8
3325	reaccionario	8
3326	rama	8
3327	racional	8
3328	rabia	8
3329	quitaba	8
3330	querrá	8
3331	pureza	8
3332	pudiese	8
3333	proyectos	8
3334	prosaica	8
3335	prometía	8
3336	principales	8
3337	preparativos	8
3338	prefiero	8
3339	preferían	8
3340	predicador	8
3341	precauciones	8
3342	prado	8
3343	positiva	8
3344	poniéndose	8
3345	pongo	8
3346	poéticas	8
3347	podrida	8
3348	plumas	8
3349	plazuela	8
3350	platónico	8
3351	pintada	8
3352	pinos	8
3353	pillo	8
3354	piadoso	8
3355	pesadilla	8
3356	perseguir	8
3357	perdiz	8
3358	perdiendo	8
3359	perdices	8
3360	pequeños	8
3361	pepa	8
3362	pasear	8
3363	parches	8
3364	papa	8
3365	pantorrilla	8
3366	pantalones	8
3367	palmo	8
3368	palique	8
3369	palacios	8
3370	pájaro	8
3371	paisano	8
3372	os	8
3373	orejas	8
3374	ordinario	8
3375	oratorio	8
3376	ora	8
3377	oleaje	8
3378	oigo	8
3379	ocurría	8
3380	ocupaban	8
3381	obstáculos	8
3382	obispado	8
3383	novedades	8
3384	niñez	8
3385	niego	8
3386	necesitó	8
3387	nazareno	8
3388	muero	8
3389	mueble	8
3390	mozos	8
3391	movió	8
3392	mortal	8
3393	monedas	8
3394	mitología	8
3395	misterio	8
3396	minas	8
3397	mercado	8
3398	mentir	8
3399	melancólico	8
3400	melancólica	8
3401	mejilla	8
3402	médicos	8
3403	mediante	8
3404	martirio	8
3405	marfil	8
3406	máquinas	8
3407	mantener	8
3408	manejaba	8
3409	mandar	8
3410	maldito	8
3411	majestuoso	8
3412	macho	8
3413	lumbre	8
3414	llegaría	8
3415	llamas	8
3416	literatura	8
3417	licenciado	8
3418	levantado	8
3419	lecturas	8
3420	lazo	8
3421	juramento	8
3422	jugadores	8
3423	jugaban	8
3424	jinete	8
3425	irse	8
3426	inverosímil	8
3427	interrumpía	8
3428	ingrato	8
3429	infinita	8
3430	industria	8
3431	indigna	8
3432	incapaces	8
3433	impertinente	8
3434	imaginar	8
3435	hundida	8
3436	humildes	8
3437	humanas	8
3438	hojarasca	8
3439	hilos	8
3440	halagaba	8
3441	habitaciones	8
3442	hábil	8
3443	gustan	8
3444	guardia	8
3445	guantes	8
3446	groseras	8
3447	grano	8
3448	gotas	8
3449	godino	8
3450	gobernadora	8
3451	gentes	8
3452	galantería	8
3453	galán	8
3454	furiosa	8
3455	funciones	8
3456	fruto	8
3457	fraile	8
3458	forastero	8
3459	flotante	8
3460	flaquezas	8
3461	fingida	8
3462	figuraban	8
3463	favores	8
3464	fantasmas	8
3465	fantasma	8
3466	exterior	8
3467	exigir	8
3468	exigían	8
3469	exigencias	8
3470	exclamaba	8
3471	estupidez	8
3472	estúpida	8
3473	estudios	8
3474	estudiar	8
3475	estudiaba	8
3476	espiaba	8
3477	espere	8
3478	esmero	8
3479	escocesa	8
3480	escapar	8
3481	escapaba	8
3482	escándalos	8
3483	esbelta	8
3484	entregada	8
3485	entiendes	8
3486	enseñanza	8
3487	engaña	8
3488	encuentra	8
3489	encontraron	8
3490	encendido	8
3491	enaguas	8
3492	emplear	8
3493	empleados	8
3494	economía	8
3495	dulcísima	8
3496	duerme	8
3497	dudas	8
3498	dolorosa	8
3499	divinidad	8
3500	distracciones	8
3501	disponía	8
3502	disparate	8
3503	disimulados	8
3504	disimulado	8
3505	disimulaba	8
3506	dirección	8
3507	diligencia	8
3508	dijeron	8
3509	dignas	8
3510	diferente	8
3511	dieron	8
3512	despreciado	8
3513	despierto	8
3514	despertado	8
3515	desgraciada	8
3516	desconfianza	8
3517	desafiar	8
3518	delgado	8
3519	déjame	8
3520	defensa	8
3521	declaraba	8
3522	decentes	8
3523	curvas	8
3524	cuidar	8
3525	cuántos	8
3526	cualidades	8
3527	cuál	8
3528	crianza	8
3529	criado	8
3530	cosquillas	8
3531	cortés	8
3532	correo	8
3533	copas	8
3534	convicción	8
3535	convertir	8
3536	contuvo	8
3537	contracayes	8
3538	continente	8
3539	contentó	8
3540	contado	8
3541	conocimiento	8
3542	conjunto	8
3543	confuso	8
3544	concluía	8
3545	comprende	8
3546	cómplice	8
3547	compañeros	8
3548	comió	8
3549	cómicos	8
3550	comerciante	8
3551	colmo	8
3552	colchón	8
3553	claustro	8
3554	ciento	8
3555	chiquillos	8
3556	charcos	8
3557	champaña	8
3558	ceja	8
3559	catástrofe	8
3560	castilla	8
3561	casado	8
3562	carnaval	8
3563	cárcel	8
3564	carbón	8
3565	canto	8
3566	campaña	8
3567	campanadas	8
3568	cambiar	8
3569	calzado	8
3570	callaban	8
3571	calla	8
3572	cadena	8
3573	cabellos	8
3574	cabaña	8
3575	buscaban	8
3576	bulto	8
3577	bruto	8
3578	brigadiera	8
3579	breve	8
3580	brasas	8
3581	botón	8
3582	billar	8
3583	bigote	8
3584	besó	8
3585	barro	8
3586	barquilla	8
3587	baño	8
3588	bajando	8
3589	azúcar	8
3590	atribuía	8
3591	atrevimiento	8
3592	atravesó	8
3593	atenerse	8
3594	asustó	8
3595	aspiraba	8
3596	asegurar	8
3597	arrojar	8
3598	arrancar	8
3599	aridez	8
3600	aprovechar	8
3601	apreciar	8
3602	antojó	8
3603	animales	8
3604	anhelos	8
3605	anduvo	8
3606	andadas	8
3607	amos	8
3608	américa	8
3609	alumbraba	8
3610	aludía	8
3611	alejaba	8
3612	alegraba	8
3613	agosto	8
3614	adornaban	8
3615	admirar	8
3616	adivinaba	8
3617	actual	8
3618	acostó	8
3619	acabar	8
3620	acabado	8
3621	abrir	8
3622	abrían	8
3623	abandonada	8
3624	zaragoza	7
3625	yeso	7
3626	yacían	7
3627	yacía	7
3628	voltaire	7
3629	viven	7
3630	violencia	7
3631	víctimas	7
3632	vicios	7
3633	vía	7
3634	vi	7
3635	vergonzoso	7
3636	veremos	7
3637	verás	7
3638	venidas	7
3639	vengarse	7
3640	vendría	7
3641	venas	7
3642	velo	7
3643	velaba	7
3644	valle	7
3645	vacío	7
3646	usurero	7
3647	urgente	7
3648	unción	7
3649	umbral	7
3650	tuve	7
3651	tranquilamente	7
3652	trampas	7
3653	trampa	7
3654	trabajos	7
3655	torpeza	7
3656	tormenta	7
3657	torcida	7
3658	tonos	7
3659	tome	7
3660	toldo	7
3661	tocó	7
3662	tocando	7
3663	tibia	7
3664	tertulios	7
3665	teólogo	7
3666	temporada	7
3667	té	7
3668	tapaba	7
3669	sustos	7
3670	suspiros	7
3671	suceder	7
3672	sublevaba	7
3673	sotanas	7
3674	sostener	7
3675	soplo	7
3676	somnolencia	7
3677	soltó	7
3678	socio	7
3679	síntomas	7
3680	silenciosa	7
3681	significaba	7
3682	sigilo	7
3683	severidad	7
3684	severa	7
3685	septiembre	7
3686	separarse	7
3687	separaba	7
3688	señalado	7
3689	semillas	7
3690	secreta	7
3691	sastre	7
3692	saciar	7
3693	sacado	7
3694	sabré	7
3695	sabor	7
3696	ruedas	7
3697	rosita	7
3698	rizos	7
3699	rita	7
3700	ricas	7
3701	revelación	7
3702	retumbaban	7
3703	retiró	7
3704	resultado	7
3705	resuelta	7
3706	restos	7
3707	respetables	7
3708	resolvió	7
3709	resolver	7
3710	resignación	7
3711	replicó	7
3712	repentina	7
3713	repasaba	7
3714	repartía	7
3715	reluciente	7
3716	religiosas	7
3717	región	7
3718	regencia	7
3719	reflexionar	7
3720	recordaban	7
3721	reales	7
3722	rápidas	7
3723	quejas	7
3724	queja	7
3725	puntas	7
3726	pulcro	7
3727	puerto	7
3728	providencia	7
3729	protestas	7
3730	protestaba	7
3731	prohibía	7
3732	progreso	7
3733	procurado	7
3734	proceder	7
3735	principios	7
3736	preparada	7
3737	prelado	7
3738	prefirió	7
3739	precioso	7
3740	posturas	7
3741	postura	7
3742	positivas	7
3743	ponían	7
3744	pollo	7
3745	poetas	7
3746	podrían	7
3747	podredumbre	7
3748	poderosos	7
3749	poderoso	7
3750	plebeyos	7
3751	pisando	7
3752	pintura	7
3753	pesado	7
3754	pesadas	7
3755	persecución	7
3756	perfumado	7
3757	perdonar	7
3758	pequeño	7
3759	pensaría	7
3760	penitentes	7
3761	pellizco	7
3762	peligrosos	7
3763	pedido	7
3764	pedían	7
3765	paulinas	7
3766	paternal	7
3767	patadas	7
3768	parejas	7
3769	pardo	7
3770	pardas	7
3771	parda	7
3772	paraguay	7
3773	paño	7
3774	pantalón	7
3775	pánico	7
3776	palomas	7
3777	palmadas	7
3778	palcos	7
3779	paja	7
3780	paisaje	7
3781	padecer	7
3782	pacífico	7
3783	oyera	7
3784	oposición	7
3785	ondas	7
3786	ofrecer	7
3787	ofrece	7
3788	ocultando	7
3789	oculta	7
3790	octubre	7
3791	obligación	7
3792	notas	7
3793	nerviosas	7
3794	negocios	7
3795	negarse	7
3796	necio	7
3797	necia	7
3798	náufrago	7
3799	nata	7
3800	na	7
3801	murmuraciones	7
3802	mudo	7
3803	muchachos	7
3804	moscas	7
3805	monótono	7
3806	molestar	7
3807	modestia	7
3808	moderna	7
3809	misterios	7
3810	mezclaba	7
3811	merced	7
3812	memorias	7
3813	mecedora	7
3814	mecánica	7
3815	mayoría	7
3816	matarle	7
3817	mareaba	7
3818	marchar	7
3819	maravillas	7
3820	manteos	7
3821	manchas	7
3822	maliciosos	7
3823	maledicencia	7
3824	maestra	7
3825	luto	7
3826	llenó	7
3827	limpias	7
3828	limosnas	7
3829	legua	7
3830	leche	7
3831	lasciva	7
3832	juro	7
3833	junio	7
3834	irritatio	7
3835	irritado	7
3836	intrigas	7
3837	íntimas	7
3838	intentar	7
3839	intensa	7
3840	intelectual	7
3841	insustancial	7
3842	insultos	7
3843	inspiraba	7
3844	insolente	7
3845	inmortal	7
3846	ingenio	7
3847	infalible	7
3848	inclusive	7
3849	inclinación	7
3850	impíos	7
3851	impío	7
3852	imperio	7
3853	imitación	7
3854	imitaban	7
3855	imitaba	7
3856	idolatría	7
3857	ideales	7
3858	idas	7
3859	humillaba	7
3860	hubiesen	7
3861	honradez	7
3862	hilo	7
3863	hermosas	7
3864	hermanos	7
3865	herido	7
3866	herencia	7
3867	haces	7
3868	hablan	7
3869	haberle	7
3870	gritando	7
3871	gozado	7
3872	gloriosa	7
3873	globo	7
3874	gatos	7
3875	ganaba	7
3876	galerías	7
3877	futura	7
3878	fúnebre	7
3879	frecuente	7
3880	frecuencia	7
3881	formal	7
3882	formado	7
3883	fingían	7
3884	figurado	7
3885	fanático	7
3886	facciones	7
3887	éxtasis	7
3888	explicarse	7
3889	exageraciones	7
3890	evidencia	7
3891	evangelio	7
3892	estragos	7
3893	estirar	7
3894	estarían	7
3895	est	7
3896	espuma	7
3897	esbelto	7
3898	errores	7
3899	equivocado	7
3900	equilibrio	7
3901	entregarse	7
3902	entrega	7
3903	encerrado	7
3904	encendidas	7
3905	elogios	7
3906	edificio	7
3907	duros	7
3908	duró	7
3909	dramas	7
3910	dormida	7
3911	dolía	7
3912	doble	7
3913	divino	7
3914	distraídos	7
3915	distinguía	7
3916	distinción	7
3917	discutir	7
3918	discutió	7
3919	discusión	7
3920	disculpa	7
3921	dirigía	7
3922	diestro	7
3923	dices	7
3924	deudas	7
3925	deuda	7
3926	detenerse	7
3927	despedida	7
3928	despacio	7
3929	desorden	7
3930	deseado	7
3931	descubrir	7
3932	descubrimiento	7
3933	describía	7
3934	desapareció	7
3935	desafiando	7
3936	delicioso	7
3937	delicadeza	7
3938	delicada	7
3939	dejarla	7
3940	defender	7
3941	decente	7
3942	datos	7
3943	cuidaba	7
3944	cuento	7
3945	cuaresma	7
3946	cuadrado	7
3947	crueldad	7
3948	crítico	7
3949	cristianos	7
3950	crees	7
3951	creerá	7
3952	cortesía	7
3953	corta	7
3954	cordel	7
3955	corbata	7
3956	corazonada	7
3957	conviene	7
3958	contestaban	7
3959	contenía	7
3960	contando	7
3961	contaban	7
3962	conservador	7
3963	consentido	7
3964	consejo	7
3965	consagrada	7
3966	conforme	7
3967	confiesa	7
3968	confesarse	7
3969	confesarlo	7
3970	confesado	7
3971	comprado	7
3972	complacía	7
3973	comparar	7
3974	comenzaron	7
3975	comenzar	7
3976	comenzado	7
3977	comen	7
3978	colgado	7
3979	colcha	7
3980	cola	7
3981	cofradías	7
3982	clavaba	7
3983	cirios	7
3984	chocolate	7
3985	chiquillo	7
3986	cesaron	7
3987	cereza	7
3988	cazar	7
3989	castigar	7
3990	castaños	7
3991	cascabeles	7
3992	casadas	7
3993	carro	7
3994	carnal	7
3995	cariñoso	7
3996	cargadas	7
3997	cansancio	7
3998	cánones	7
3999	canas	7
4000	campanario	7
4001	campana	7
4002	cambiado	7
4003	calumniado	7
4004	callaron	7
4005	callada	7
4006	caldo	7
4007	cal	7
4008	cajones	7
4009	caería	7
4010	cabecera	7
4011	butaca	7
4012	buscado	7
4013	bultos	7
4014	bulliciosa	7
4015	brutal	7
4016	brillante	7
4017	brecha	7
4018	borbotones	7
4019	bofetada	7
4020	blas	7
4021	blandura	7
4022	bebía	7
4023	batallas	7
4024	bala	7
4025	ayudar	7
4026	avergonzado	7
4027	avergonzada	7
4028	avaricia	7
4029	ausente	7
4030	atraía	7
4031	atractivo	7
4032	artillero	7
4033	artículos	7
4034	arruinado	7
4035	arrojarse	7
4036	arroja	7
4037	arrastrando	7
4038	arranques	7
4039	armarios	7
4040	aristócratas	7
4041	aras	7
4042	apretado	7
4043	apresuró	7
4044	aplicaba	7
4045	apariencia	7
4046	aparición	7
4047	aparecían	7
4048	ansiedad	7
4049	animó	7
4050	ángeles	7
4051	andando	7
4052	americanos	7
4053	amenazó	7
4054	alvarito	7
4055	alborotar	7
4056	alarde	7
4057	álamos	7
4058	ajena	7
4059	airoso	7
4060	agujeros	7
4061	aguda	7
4062	aguas	7
4063	agradar	7
4064	agradaba	7
4065	aficionados	7
4066	admite	7
4067	acordado	7
4068	acontecimientos	7
4069	acompañaban	7
4070	acercaban	7
4071	acciones	7
4072	absurdos	7
4073	abril	7
4074	abrazo	7
4075	abismos	7
4076	abdicación	7
4077	abanico	7
4078	zorros	6
4079	yerbas	6
4080	volviese	6
4081	volaban	6
4082	vistas	6
4083	visitaban	6
4084	virtudes	6
4085	vírgenes	6
4086	vinculete	6
4087	vil	6
4088	vientos	6
4089	viejas	6
4090	vidrieras	6
4091	viajes	6
4092	verlo	6
4093	vendrá	6
4094	vende	6
4095	venció	6
4096	vehemente	6
4097	vecindario	6
4098	vecinas	6
4099	varonil	6
4100	variedad	6
4101	vara	6
4102	vapores	6
4103	valladolid	6
4104	vagos	6
4105	vacía	6
4106	usía	6
4107	urraca	6
4108	ubi	6
4109	turno	6
4110	truenos	6
4111	tropezó	6
4112	tropezando	6
4113	tresillistas	6
4114	tratara	6
4115	trataban	6
4116	traslacerca	6
4117	tranquilos	6
4118	trajes	6
4119	traían	6
4120	torpes	6
4121	tormentos	6
4122	tordos	6
4123	torbellino	6
4124	tonterías	6
4125	tomando	6
4126	tolerar	6
4127	tirar	6
4128	tinte	6
4129	tinta	6
4130	tientas	6
4131	tesis	6
4132	terribles	6
4133	terminó	6
4134	tercer	6
4135	tentador	6
4136	tenerle	6
4137	tendido	6
4138	tendía	6
4139	temiendo	6
4140	telón	6
4141	tejado	6
4142	tardar	6
4143	talle	6
4144	talar	6
4145	tacto	6
4146	suplicaba	6
4147	suceso	6
4148	sucedía	6
4149	subterráneos	6
4150	subiendo	6
4151	sopor	6
4152	soñar	6
4153	soñador	6
4154	solteronas	6
4155	solícita	6
4156	sofocaba	6
4157	sinceramente	6
4158	simpatía	6
4159	silencioso	6
4160	silbidos	6
4161	silbaba	6
4162	sesión	6
4163	sesenta	6
4164	servirle	6
4165	seriamente	6
4166	separar	6
4167	separando	6
4168	señorío	6
4169	señaló	6
4170	señalaba	6
4171	sentían	6
4172	segundos	6
4173	seguirle	6
4174	seglar	6
4175	seductores	6
4176	satisfechos	6
4177	sapo	6
4178	salve	6
4179	saludando	6
4180	saltó	6
4181	saliese	6
4182	saliera	6
4183	salga	6
4184	salas	6
4185	sal	6
4186	sacudiendo	6
4187	sacramento	6
4188	sábana	6
4189	ruegos	6
4190	rubor	6
4191	rosario	6
4192	ronda	6
4193	rompo	6
4194	rodeaba	6
4195	rocío	6
4196	roca	6
4197	rizada	6
4198	rítmico	6
4199	risueña	6
4200	restituto	6
4201	restaurant	6
4202	respirando	6
4203	respiración	6
4204	respectivos	6
4205	resistía	6
4206	reserva	6
4207	repugnantes	6
4208	representar	6
4209	rentas	6
4210	rendida	6
4211	rencores	6
4212	relámpagos	6
4213	rejas	6
4214	reino	6
4215	régimen	6
4216	regalado	6
4217	reflejaban	6
4218	recuerda	6
4219	recobraba	6
4220	recitaba	6
4221	recibieron	6
4222	ras	6
4223	raro	6
4224	rapidez	6
4225	ramos	6
4226	ramona	6
4227	quisieron	6
4228	quisieran	6
4229	queridas	6
4230	quejarse	6
4231	pusieron	6
4232	puros	6
4233	puntos	6
4234	pudieron	6
4235	pudieran	6
4236	pudiendo	6
4237	ps	6
4238	próximo	6
4239	proximidad	6
4240	prosaico	6
4241	proporciones	6
4242	profundamente	6
4243	procurando	6
4244	probaban	6
4245	príncipe	6
4246	pretendiente	6
4247	pretendían	6
4248	pretendía	6
4249	prestado	6
4250	preparándose	6
4251	preparando	6
4252	preparado	6
4253	preferir	6
4254	práctica	6
4255	positivo	6
4256	popular	6
4257	plataforma	6
4258	pizca	6
4259	pinturas	6
4260	pintado	6
4261	pino	6
4262	pinche	6
4263	pimienta	6
4264	pilares	6
4265	pilar	6
4266	picaresca	6
4267	pícara	6
4268	petróleo	6
4269	perversión	6
4270	perspectiva	6
4271	perfumada	6
4272	perfil	6
4273	perdono	6
4274	perdición	6
4275	pequeñas	6
4276	penitente	6
4277	penetraba	6
4278	pegajosa	6
4279	pegado	6
4280	pedazo	6
4281	pécora	6
4282	pecar	6
4283	pavor	6
4284	pataditas	6
4285	pasará	6
4286	pasara	6
4287	pasan	6
4288	pasaje	6
4289	pasada	6
4290	palo	6
4291	padecido	6
4292	pablo	6
4293	oyes	6
4294	oyeran	6
4295	origen	6
4296	orgía	6
4297	oportunidad	6
4298	opina	6
4299	olvidada	6
4300	olores	6
4301	ofrecían	6
4302	oeste	6
4303	ocurrencia	6
4304	ocupada	6
4305	ocultos	6
4306	océano	6
4307	observar	6
4308	obedecía	6
4309	novenas	6
4310	notario	6
4311	muros	6
4312	mundano	6
4313	muchedumbre	6
4314	moviendo	6
4315	morirse	6
4316	morena	6
4317	montañés	6
4318	montañas	6
4319	monotonía	6
4320	monótona	6
4321	monaguillo	6
4322	modernos	6
4323	misión	6
4324	míos	6
4325	mina	6
4326	millonario	6
4327	miedos	6
4328	mia	6
4329	mezcla	6
4330	metida	6
4331	metían	6
4332	meterse	6
4333	metal	6
4334	metáforas	6
4335	mesilla	6
4336	mesas	6
4337	mentía	6
4338	meditando	6
4339	mediquillo	6
4340	medios	6
4341	médica	6
4342	mecánico	6
4343	materiales	6
4344	mataba	6
4345	marinero	6
4346	marina	6
4347	marcharse	6
4348	mantón	6
4349	mantilla	6
4350	mantel	6
4351	manifestación	6
4352	manga	6
4353	malicioso	6
4354	maliciosa	6
4355	males	6
4356	luchas	6
4357	luchaba	6
4358	lúbrica	6
4359	lope	6
4360	lomo	6
4361	llueve	6
4362	llover	6
4363	llevarla	6
4364	llevando	6
4365	llegue	6
4366	llegase	6
4367	llamarle	6
4368	llamarla	6
4369	llamaría	6
4370	limpio	6
4371	límites	6
4372	ligas	6
4373	leña	6
4374	lenta	6
4375	lejana	6
4376	leían	6
4377	lector	6
4378	lana	6
4379	lámparas	6
4380	ladridos	6
4381	lados	6
4382	juanito	6
4383	juana	6
4384	jaula	6
4385	jardines	6
4386	isla	6
4387	inútiles	6
4388	interlocutor	6
4389	interiores	6
4390	interesaba	6
4391	intensidad	6
4392	insultar	6
4393	instituciones	6
4394	insistir	6
4395	insistía	6
4396	iniciativa	6
4397	infidelidad	6
4398	infelices	6
4399	inerte	6
4400	inercia	6
4401	indiferentes	6
4402	indianos	6
4403	indecoroso	6
4404	inclinarse	6
4405	impuso	6
4406	impresiones	6
4407	importuno	6
4408	imponía	6
4409	impone	6
4410	impiedad	6
4411	ilustrísima	6
4412	ilustres	6
4413	ii	6
4414	igualdad	6
4415	ídem	6
4416	idealidad	6
4417	húmedas	6
4418	horrorizaba	6
4419	horrísono	6
4420	horrible	6
4421	hito	6
4422	hipócritas	6
4423	hiciesen	6
4424	héroes	6
4425	héroe	6
4426	hereje	6
4427	heredado	6
4428	haz	6
4429	haré	6
4430	hallazgo	6
4431	halagado	6
4432	h	6
4433	guardaban	6
4434	guapo	6
4435	guapas	6
4436	gritaban	6
4437	grises	6
4438	golosina	6
4439	genio	6
4440	ganancia	6
4441	gallinas	6
4442	gallardo	6
4443	gabán	6
4444	futuro	6
4445	función	6
4446	fray	6
4447	franco	6
4448	francamente	6
4449	follaje	6
4450	flacas	6
4451	filósofos	6
4452	fila	6
4453	fijaba	6
4454	fiaba	6
4455	fantástico	6
4456	fango	6
4457	familiares	6
4458	faltó	6
4459	faltar	6
4460	extravíos	6
4461	expuso	6
4462	exponerse	6
4463	expansión	6
4464	excursión	6
4465	excitada	6
4466	eternamente	6
4467	estuvieran	6
4468	estremeció	6
4469	estorbaba	6
4470	estalló	6
4471	estados	6
4472	espiar	6
4473	espectáculos	6
4474	español	6
4475	esencia	6
4476	escuchar	6
4477	escondida	6
4478	escoger	6
4479	escoba	6
4480	esclava	6
4481	escéptico	6
4482	escalofrío	6
4483	escala	6
4484	error	6
4485	envuelto	6
4486	envolvía	6
4487	enterarse	6
4488	enorme	6
4489	engordar	6
4490	engañó	6
4491	encontrarse	6
4492	encarnado	6
4493	enamorarse	6
4494	enamorar	6
4495	enamora	6
4496	empresas	6
4497	emprendía	6
4498	empeñado	6
4499	elecciones	6
4500	eficacia	6
4501	educado	6
4502	duraba	6
4503	duele	6
4504	dote	6
4505	doncellas	6
4506	dominios	6
4507	doctrina	6
4508	divertía	6
4509	distinguidas	6
4510	disputando	6
4511	disputaba	6
4512	disparar	6
4513	disimulando	6
4514	disgustos	6
4515	disgustaba	6
4516	director	6
4517	diplomacia	6
4518	digámoslo	6
4519	difunto	6
4520	diferentes	6
4521	diferencia	6
4522	devotas	6
4523	despotismo	6
4524	despensa	6
4525	desiertos	6
4526	descalzos	6
4527	desaparecer	6
4528	derrotado	6
4529	delicadas	6
4530	dejasen	6
4531	dejándose	6
4532	defectos	6
4533	defecto	6
4534	decoro	6
4535	decidor	6
4536	débiles	6
4537	debido	6
4538	cutis	6
4539	cuna	6
4540	culta	6
4541	cuartel	6
4542	cruzadas	6
4543	cruzaban	6
4544	crujir	6
4545	crucificado	6
4546	crepúsculo	6
4547	creencias	6
4548	coser	6
4549	corrieron	6
4550	corrección	6
4551	corral	6
4552	cordial	6
4553	conyugal	6
4554	convidaba	6
4555	convicciones	6
4556	convertirse	6
4557	conveniencia	6
4558	convaleciente	6
4559	contó	6
4560	contestado	6
4561	contentos	6
4562	contenida	6
4563	considerar	6
4564	conservaba	6
4565	conserva	6
4566	conocimientos	6
4567	confidente	6
4568	confesó	6
4569	confesaban	6
4570	conducía	6
4571	concluyó	6
4572	comunes	6
4573	comprendían	6
4574	complicada	6
4575	completa	6
4576	compás	6
4577	comparaba	6
4578	compadecía	6
4579	cometido	6
4580	combinaciones	6
4581	colondres	6
4582	colgaduras	6
4583	colecciones	6
4584	cogote	6
4585	cognac	6
4586	clerical	6
4587	clavo	6
4588	claras	6
4589	citaba	6
4590	chusco	6
4591	chocar	6
4592	chiste	6
4593	charco	6
4594	ceremonias	6
4595	ceñido	6
4596	celestial	6
4597	celebrar	6
4598	celda	6
4599	cejas	6
4600	ceguera	6
4601	cavilaciones	6
4602	cautela	6
4603	catorce	6
4604	catequistas	6
4605	cátedra	6
4606	casullas	6
4607	carnes	6
4608	carlistas	6
4609	capítulo	6
4610	capas	6
4611	cañón	6
4612	cansarse	6
4613	cansada	6
4614	canónico	6
4615	campanas	6
4616	caminos	6
4617	callado	6
4618	cadenas	6
4619	cabezas	6
4620	burlado	6
4621	bóvedas	6
4622	bocado	6
4623	blando	6
4624	blancura	6
4625	beneficio	6
4626	bebió	6
4627	bebido	6
4628	bautista	6
4629	batirse	6
4630	bata	6
4631	basílica	6
4632	barquero	6
4633	barco	6
4634	barandilla	6
4635	bando	6
4636	balandrán	6
4637	baba	6
4638	averiguar	6
4639	avena	6
4640	avanzados	6
4641	auxilio	6
4642	auténticos	6
4643	aturdimiento	6
4644	aturdida	6
4645	atrevidos	6
4646	atrevería	6
4647	ateísmo	6
4648	asqueroso	6
4649	asperezas	6
4650	asistía	6
4651	asalto	6
4652	artículo	6
4653	arrugado	6
4654	arrimado	6
4655	arrastrar	6
4656	arranque	6
4657	arrancarle	6
4658	arrancaba	6
4659	aristocrático	6
4660	ardían	6
4661	araña	6
4662	apuntaba	6
4663	aprobaba	6
4664	apretados	6
4665	apretada	6
4666	apetitos	6
4667	apearse	6
4668	anticuario	6
4669	antepecho	6
4670	antaño	6
4671	animado	6
4672	animaba	6
4673	ángulo	6
4674	anciano	6
4675	anchos	6
4676	amorosos	6
4677	amoríos	6
4678	amenaza	6
4679	ambas	6
4680	amargo	6
4681	alzacuello	6
4682	aludiendo	6
4683	alabar	6
4684	alabanzas	6
4685	águila	6
4686	agradeció	6
4687	afirmaba	6
4688	aficiones	6
4689	administración	6
4690	adentro	6
4691	adelantar	6
4692	acudió	6
4693	acudían	6
4694	actitud	6
4695	acordarse	6
4696	acompañado	6
4697	aceptar	6
4698	accidentes	6
4699	aburrido	6
4700	abundante	6
4701	absolutamente	6
4702	abriendo	6
4703	abrazó	6
4704	abonados	6
4705	abiertas	6
4706	zapico	5
4707	zapateros	5
4708	zaguán	5
4709	xv	5
4710	vulgaridades	5
4711	vuelva	5
4712	volando	5
4713	vivió	5
4714	viste	5
4715	vigilancia	5
4716	victorias	5
4717	vibraciones	5
4718	vestirse	5
4719	vestidas	5
4720	vestíbulo	5
4721	vericuetos	5
4722	ventaja	5
4723	vendido	5
4724	vencía	5
4725	veinticinco	5
4726	vegetar	5
4727	vecina	5
4728	valga	5
4729	vaguedad	5
4730	vagas	5
4731	uñas	5
4732	uniforme	5
4733	turbó	5
4734	turbar	5
4735	turbado	5
4736	truchas	5
4737	tropezones	5
4738	tropezaba	5
4739	triunfos	5
4740	tricot	5
4741	trató	5
4742	tratado	5
4743	transigir	5
4744	transeúntes	5
4745	tranquilas	5
4746	traidores	5
4747	tradición	5
4748	total	5
4749	torcía	5
4750	tontos	5
4751	tomate	5
4752	tocarle	5
4753	título	5
4754	tísica	5
4755	tiranía	5
4756	tijeras	5
4757	tierras	5
4758	tierno	5
4759	testamento	5
4760	tesoros	5
4761	tertulias	5
4762	tenerse	5
4763	tendrá	5
4764	temían	5
4765	temblaban	5
4766	telarañas	5
4767	tarima	5
4768	tardaba	5
4769	tapar	5
4770	taciturno	5
4771	tabique	5
4772	suponiendo	5
4773	superstición	5
4774	superficie	5
4775	sumo	5
4776	sumisión	5
4777	sujetó	5
4778	sujeta	5
4779	sufría	5
4780	suena	5
4781	suelto	5
4782	suele	5
4783	sudores	5
4784	sucede	5
4785	subterráneo	5
4786	soto	5
4787	soso	5
4788	sosa	5
4789	sorprendía	5
4790	sorprender	5
4791	soplaba	5
4792	sonó	5
4793	sombrío	5
4794	soltera	5
4795	sollozos	5
4796	solitarios	5
4797	solicitar	5
4798	solemnidades	5
4799	sois	5
4800	sofisma	5
4801	sobrinas	5
4802	sobresaltos	5
4803	sirvo	5
4804	sinceridad	5
4805	siguiendo	5
4806	sesos	5
4807	sesgo	5
4808	serviría	5
4809	servilleta	5
4810	seres	5
4811	señorona	5
4812	señoril	5
4813	sensaciones	5
4814	sendos	5
4815	semi	5
4816	sastres	5
4817	santuario	5
4818	santianes	5
4819	sanar	5
4820	saltos	5
4821	saltando	5
4822	salgo	5
4823	salen	5
4824	saldría	5
4825	sacrificarse	5
4826	sacaban	5
4827	sable	5
4828	rutina	5
4829	ruinas	5
4830	rugió	5
4831	rueda	5
4832	rúa	5
4833	rozagante	5
4834	rompió	5
4835	rojas	5
4836	rodilla	5
4837	robaba	5
4838	ritmo	5
4839	rió	5
4840	rindió	5
4841	rigodón	5
4842	ríe	5
4843	ría	5
4844	retirada	5
4845	restauración	5
4846	responsable	5
4847	responder	5
4848	respetado	5
4849	resortes	5
4850	resorte	5
4851	resistió	5
4852	reputaba	5
4853	repugnaba	5
4854	representando	5
4855	representan	5
4856	reposo	5
4857	repetidas	5
4858	renunciar	5
4859	remordía	5
4860	relucientes	5
4861	relato	5
4862	relación	5
4863	reja	5
4864	regazo	5
4865	regalo	5
4866	refugio	5
4867	refirió	5
4868	redacción	5
4869	rectoral	5
4870	rector	5
4871	recorriendo	5
4872	recorría	5
4873	recomendaciones	5
4874	recogiendo	5
4875	reciente	5
4876	ráfaga	5
4877	quo	5
4878	quita	5
4879	quejó	5
4880	quejidos	5
4881	quedar	5
4882	quedándose	5
4883	puras	5
4884	puñal	5
4885	punzantes	5
4886	pulcra	5
4887	puertos	5
4888	pueril	5
4889	pude	5
4890	próximamente	5
4891	provocativa	5
4892	provincial	5
4893	protectrices	5
4894	prostitución	5
4895	proporción	5
4896	propasaba	5
4897	progresos	5
4898	producido	5
4899	probado	5
4900	prisión	5
4901	presupuesto	5
4902	presta	5
4903	presidio	5
4904	presentimiento	5
4905	presentaban	5
4906	preparó	5
4907	preparaban	5
4908	preocupaba	5
4909	premio	5
4910	preguntaban	5
4911	prefiere	5
4912	predicaba	5
4913	prebendado	5
4914	postigo	5
4915	portado	5
4916	porción	5
4917	policía	5
4918	podré	5
4919	plantar	5
4920	pisaba	5
4921	pillos	5
4922	pilletes	5
4923	pez	5
4924	pesetas	5
4925	peseta	5
4926	perseguido	5
4927	permitido	5
4928	permite	5
4929	perjuicio	5
4930	perdonado	5
4931	perdona	5
4932	perderse	5
4933	perderla	5
4934	pequeñez	5
4935	penetrar	5
4936	pendían	5
4937	peligrosas	5
4938	peinado	5
4939	pegada	5
4940	pedirle	5
4941	pavo	5
4942	patenas	5
4943	patas	5
4944	pastores	5
4945	pasmado	5
4946	pascua	5
4947	parroquias	5
4948	párrafos	5
4949	parentesco	5
4950	pareciera	5
4951	parecidos	5
4952	parajes	5
4953	panza	5
4954	panera	5
4955	palmatoria	5
4956	palma	5
4957	pálidas	5
4958	países	5
4959	pago	5
4960	pagaban	5
4961	paga	5
4962	padrino	5
4963	pa	5
4964	oyese	5
4965	oyeron	5
4966	ostensible	5
4967	oso	5
4968	osado	5
4969	orquesta	5
4970	orgulloso	5
4971	organista	5
4972	ordinariamente	5
4973	opuso	5
4974	oprimían	5
4975	oportuna	5
4976	oponerse	5
4977	opinó	5
4978	óperas	5
4979	olla	5
4980	olías	5
4981	ola	5
4982	oírse	5
4983	oficinas	5
4984	oficina	5
4985	ofendido	5
4986	ofender	5
4987	ocupar	5
4988	ocupación	5
4989	ocultaban	5
4990	ocaso	5
4991	obsesión	5
4992	observado	5
4993	obedecían	5
4994	obedecer	5
4995	obdulita	5
4996	nuca	5
4997	notable	5
4998	notaban	5
4999	noroeste	5
5000	non	5
5001	niega	5
5002	negativa	5
5003	necesitan	5
5004	nauplia	5
5005	naranjas	5
5006	nacía	5
5007	nacer	5
5008	murmurando	5
5009	murmuraban	5
5010	muriendo	5
5011	murciélago	5
5012	mundos	5
5013	mujercita	5
5014	muertas	5
5015	muelle	5
5016	muceta	5
5017	mover	5
5018	mostrando	5
5019	mostraban	5
5020	moros	5
5021	moriría	5
5022	morían	5
5023	moreno	5
5024	mordió	5
5025	mono	5
5026	moneda	5
5027	molesta	5
5028	mojarse	5
5029	mojado	5
5030	modesto	5
5031	misteriosos	5
5032	mismísimo	5
5033	miserias	5
5034	misas	5
5035	miraron	5
5036	mirarla	5
5037	miércoles	5
5038	mientes	5
5039	mezclada	5
5040	metros	5
5041	metafísica	5
5042	merecer	5
5043	mentiras	5
5044	meliflua	5
5045	meditar	5
5046	mediodía	5
5047	medidas	5
5048	matices	5
5049	maternal	5
5050	matando	5
5051	martillo	5
5052	martillazos	5
5053	marquetería	5
5054	mariposas	5
5055	mares	5
5056	mareo	5
5057	marchado	5
5058	manzana	5
5059	manías	5
5060	mandil	5
5061	mandaban	5
5062	mancha	5
5063	manantial	5
5064	maldita	5
5065	maldecir	5
5066	majestad	5
5067	magistrados	5
5068	madrugar	5
5069	lugareño	5
5070	luciendo	5
5071	local	5
5072	llevase	5
5073	llenando	5
5074	llenado	5
5075	llano	5
5076	literarias	5
5077	literaria	5
5078	limpiar	5
5079	lienzo	5
5080	libremente	5
5081	librea	5
5082	librar	5
5083	levemente	5
5084	levantando	5
5085	levantaban	5
5086	leopoldo	5
5087	leñador	5
5088	lentamente	5
5089	lenguas	5
5090	lectores	5
5091	lazos	5
5092	látigo	5
5093	lápiz	5
5094	languidez	5
5095	jugador	5
5096	júbilo	5
5097	jilgueros	5
5098	jergón	5
5099	inveterada	5
5100	inventar	5
5101	invención	5
5102	inundaba	5
5103	interrumpido	5
5104	interesantes	5
5105	interesado	5
5106	insufrible	5
5107	inspiración	5
5108	insoportable	5
5109	insolencia	5
5110	insinuante	5
5111	insinuaciones	5
5112	inmundicias	5
5113	inmaculada	5
5114	injusta	5
5115	ingratitud	5
5116	infiel	5
5117	infantil	5
5118	inexpugnable	5
5119	indiscreta	5
5120	indignado	5
5121	índice	5
5122	inconsciente	5
5123	inclinando	5
5124	incierto	5
5125	incidente	5
5126	inagotable	5
5127	impuesto	5
5128	importaban	5
5129	imaginaba	5
5130	ilustrísimo	5
5131	iconoclasta	5
5132	ibi	5
5133	huido	5
5134	huertas	5
5135	hospital	5
5136	horroroso	5
5137	horrorosa	5
5138	horrorizada	5
5139	histórico	5
5140	himno	5
5141	hermosos	5
5142	heno	5
5143	heladas	5
5144	hechizos	5
5145	hechas	5
5146	hará	5
5147	hacienda	5
5148	hacerme	5
5149	hacemos	5
5150	habrán	5
5151	hablaría	5
5152	hablaremos	5
5153	hablaré	5
5154	gutural	5
5155	guardó	5
5156	guarda	5
5157	groseros	5
5158	groseramente	5
5159	grillos	5
5160	griego	5
5161	granos	5
5162	grabados	5
5163	gota	5
5164	golosinas	5
5165	gentil	5
5166	gastadas	5
5167	ganas	5
5168	ganarse	5
5169	gallos	5
5170	gaita	5
5171	fusil	5
5172	fúnebres	5
5173	fundamento	5
5174	fumaba	5
5175	fuí	5
5176	fragua	5
5177	fornido	5
5178	fórmula	5
5179	fogón	5
5180	fluxus	5
5181	flexible	5
5182	firmemente	5
5183	fingirse	5
5184	fines	5
5185	finas	5
5186	fijarse	5
5187	figurándose	5
5188	fieras	5
5189	ferias	5
5190	favorito	5
5191	fatuos	5
5192	fatal	5
5193	famoso	5
5194	famosa	5
5195	faltan	5
5196	fachada	5
5197	extrañas	5
5198	extendiendo	5
5199	exquisita	5
5200	exponía	5
5201	explicación	5
5202	explica	5
5203	existía	5
5204	exijo	5
5205	excitado	5
5206	excesos	5
5207	excesiva	5
5208	exaltado	5
5209	exagerada	5
5210	exageración	5
5211	exacto	5
5212	exactitud	5
5213	eternas	5
5214	et	5
5215	estuvieron	5
5216	estuco	5
5217	estrella	5
5218	estrechez	5
5219	estiró	5
5220	estéril	5
5221	estatura	5
5222	estantes	5
5223	estante	5
5224	estando	5
5225	estallaban	5
5226	espontánea	5
5227	esplendor	5
5228	esperaría	5
5229	espectadores	5
5230	esparcidos	5
5231	españoles	5
5232	espantada	5
5233	escudo	5
5234	escuchaba	5
5235	escribo	5
5236	escribano	5
5237	escondite	5
5238	escondió	5
5239	esclavitud	5
5240	escandalosas	5
5241	erudito	5
5242	envueltos	5
5243	envuelta	5
5244	envidiaban	5
5245	entusiasmado	5
5246	entrecejo	5
5247	entendió	5
5248	enseñado	5
5249	enfermos	5
5250	énfasis	5
5251	encinas	5
5252	encerró	5
5253	encerrarse	5
5254	encargó	5
5255	empresa	5
5256	empezaron	5
5257	emma	5
5258	embustero	5
5259	elogio	5
5260	elementos	5
5261	elegía	5
5262	eléctrica	5
5263	efectivamente	5
5264	edificios	5
5265	edificante	5
5266	económico	5
5267	eco	5
5268	echarse	5
5269	echarlo	5
5270	echarle	5
5271	echan	5
5272	echada	5
5273	echa	5
5274	durar	5
5275	dulzuras	5
5276	dulcemente	5
5277	dueños	5
5278	dramática	5
5279	doy	5
5280	domingo	5
5281	dominado	5
5282	domésticos	5
5283	doméstico	5
5284	doctora	5
5285	dócil	5
5286	dobló	5
5287	doblar	5
5288	disputar	5
5289	displicente	5
5290	disimulos	5
5291	disimuladamente	5
5292	disfrutaba	5
5293	disfrazado	5
5294	discursos	5
5295	dirían	5
5296	directamente	5
5297	diplomático	5
5298	difuntos	5
5299	difíciles	5
5300	dictador	5
5301	diciéndole	5
5302	dichoso	5
5303	dichosa	5
5304	devorar	5
5305	destrozar	5
5306	despertador	5
5307	desnudez	5
5308	desierta	5
5309	desesperada	5
5310	desengaño	5
5311	deseando	5
5312	descubrió	5
5313	describir	5
5314	descompuesto	5
5315	descargó	5
5316	descansaba	5
5317	desaparecido	5
5318	desabrida	5
5319	demostraba	5
5320	demonios	5
5321	deliciosa	5
5322	dejan	5
5323	debiera	5
5324	darles	5
5325	danza	5
5326	curso	5
5327	curar	5
5328	curaba	5
5329	cumplía	5
5330	cuevas	5
5331	cuestiones	5
5332	cuestas	5
5333	cuervos	5
5334	cuclillas	5
5335	cuchicheos	5
5336	cruzó	5
5337	cruzando	5
5338	cruzados	5
5339	cruzado	5
5340	crujía	5
5341	cristianismo	5
5342	crímenes	5
5343	criaturas	5
5344	criatura	5
5345	creyera	5
5346	cortado	5
5347	cortada	5
5348	corrientes	5
5349	correspondencia	5
5350	corona	5
5351	convite	5
5352	convirtió	5
5353	convertían	5
5354	convenido	5
5355	convencer	5
5356	contornos	5
5357	contiguo	5
5358	contigo	5
5359	contarse	5
5360	consolaba	5
5361	consintió	5
5362	considerando	5
5363	consideraciones	5
5364	consideraban	5
5365	consecuencias	5
5366	consagró	5
5367	conquistador	5
5368	conocerlo	5
5369	confusa	5
5370	confianzas	5
5371	concurso	5
5372	concluido	5
5373	conciencias	5
5374	concepción	5
5375	compró	5
5376	comprendiendo	5
5377	compra	5
5378	complot	5
5379	cómplices	5
5380	comiendo	5
5381	comezón	5
5382	combatir	5
5383	colocar	5
5384	colgando	5
5385	colgada	5
5386	colegas	5
5387	colás	5
5388	cobrar	5
5389	clerigalla	5
5390	claros	5
5391	cigarros	5
5392	ciertamente	5
5393	chocho	5
5394	chin	5
5395	chalequeras	5
5396	cháchara	5
5397	cerraban	5
5398	cerezas	5
5399	ceño	5
5400	ceñía	5
5401	cenceño	5
5402	cenas	5
5403	cedido	5
5404	cazadora	5
5405	caserones	5
5406	cartuchos	5
5407	carruaje	5
5408	carmesí	5
5409	careta	5
5410	caracteres	5
5411	capellanías	5
5412	capaces	5
5413	cantares	5
5414	canción	5
5415	campiña	5
5416	campestres	5
5417	callejón	5
5418	callejas	5
5419	cachet	5
5420	cabe	5
5421	burdeos	5
5422	bruces	5
5423	brinco	5
5424	brillo	5
5425	bordadas	5
5426	bola	5
5427	bocados	5
5428	blasfemias	5
5429	blanquecino	5
5430	bilis	5
5431	biblia	5
5432	besugo	5
5433	bello	5
5434	bellas	5
5435	belén	5
5436	bayeta	5
5437	bastó	5
5438	basilio	5
5439	barcaza	5
5440	balmes	5
5441	bajas	5
5442	bajaban	5
5443	bailarinas	5
5444	bailarina	5
5445	azotar	5
5446	ayudarle	5
5447	ayudado	5
5448	avisar	5
5449	ávila	5
5450	aves	5
5451	ausentes	5
5452	atrocidad	5
5453	atreve	5
5454	astros	5
5455	aspirar	5
5456	asomar	5
5457	asís	5
5458	aseguró	5
5459	artístico	5
5460	artística	5
5461	arrojado	5
5462	arreglar	5
5463	arranca	5
5464	arqueológico	5
5465	armónica	5
5466	armiño	5
5467	ardía	5
5468	arañas	5
5469	apuro	5
5470	apuntando	5
5471	aprobación	5
5472	apretón	5
5473	apretar	5
5474	aprender	5
5475	apoyarse	5
5476	aplicar	5
5477	aplausos	5
5478	aparato	5
5479	anunciación	5
5480	anunciaba	5
5481	antipática	5
5482	antigüedad	5
5483	anteriores	5
5484	anteojo	5
5485	anoche	5
5486	anís	5
5487	anhelo	5
5488	angustia	5
5489	andaban	5
5490	ampuloso	5
5491	amoroso	5
5492	amorosas	5
5493	amistades	5
5494	amarillento	5
5495	amarillenta	5
5496	amarilla	5
5497	amarga	5
5498	amaban	5
5499	alusiones	5
5500	almohada	5
5501	almíbar	5
5502	alias	5
5503	alejó	5
5504	alcanza	5
5505	alcance	5
5506	alba	5
5507	alardes	5
5508	alababan	5
5509	alababa	5
5510	ajo	5
5511	ajenas	5
5512	agujas	5
5513	agradecido	5
5514	afirmación	5
5515	afable	5
5516	adversario	5
5517	adquirido	5
5518	adornos	5
5519	adoración	5
5520	adoraban	5
5521	adónde	5
5522	admitió	5
5523	admitía	5
5524	admiró	5
5525	ademanes	5
5526	activo	5
5527	acostumbrada	5
5528	acordándose	5
5529	acercado	5
5530	aceras	5
5531	aceptaba	5
5532	acento	5
5533	aceite	5
5534	accesos	5
5535	acariciando	5
5536	acacias	5
5537	abusos	5
5538	aburrirse	5
5539	absolución	5
5540	abominable	5
5541	abandonar	5
5542	zarzas	4
5543	zapato	4
5544	wamba	4
5545	wals	4
5546	votos	4
5547	voto	4
5548	volverían	4
5549	vivienda	4
5550	vivas	4
5551	viudita	4
5552	viudedad	4
5553	víspera	4
5554	violines	4
5555	viniese	4
5556	viniera	4
5557	villano	4
5558	vigorosa	4
5559	vigilaba	4
5560	vidrios	4
5561	vestían	4
5562	verosimilitud	4
5563	verosímil	4
5564	verían	4
5565	verán	4
5566	venus	4
5567	ventura	4
5568	vengar	4
5569	vemos	4
5570	veleidades	4
5571	veintisiete	4
5572	vehementes	4
5573	vecindad	4
5574	vean	4
5575	vasos	4
5576	varones	4
5577	valla	4
5578	vacilante	4
5579	vacante	4
5580	vacaciones	4
5581	usar	4
5582	usando	4
5583	universidad	4
5584	unidos	4
5585	únicamente	4
5586	ultrajado	4
5587	últimamente	4
5588	tuya	4
5589	turbaba	4
5590	túnica	4
5591	trovador	4
5592	trote	4
5593	trotaconventos	4
5594	tropezado	4
5595	troncos	4
5596	tripas	4
5597	tributo	4
5598	tributaba	4
5599	trechos	4
5600	traviata	4
5601	tratase	4
5602	trasladó	4
5603	trajo	4
5604	traigo	4
5605	traigan	4
5606	trágico	4
5607	tragar	4
5608	tostada	4
5609	tórtola	4
5610	tornasoles	4
5611	tomillo	4
5612	tolerable	4
5613	toga	4
5614	tocarla	4
5615	títulos	4
5616	tisis	4
5617	tiros	4
5618	timidez	4
5619	tímidamente	4
5620	tímida	4
5621	tibieza	4
5622	tibias	4
5623	testimonio	4
5624	tertulín	4
5625	territorial	4
5626	terrenos	4
5627	terremoto	4
5628	terminante	4
5629	terminada	4
5630	tenor	4
5631	tendidos	4
5632	tenazas	4
5633	tenacidad	4
5634	tempore	4
5635	temporal	4
5636	tempestad	4
5637	temeroso	4
5638	temas	4
5639	tema	4
5640	telégrafo	4
5641	tedio	4
5642	técnicos	4
5643	tarsila	4
5644	tardaría	4
5645	tapices	4
5646	talleres	4
5647	tácito	4
5648	tablado	4
5649	tabaco	4
5650	sustituto	4
5651	suspiro	4
5652	supongo	4
5653	suponer	4
5654	súplicas	4
5655	supina	4
5656	sumido	4
5657	sueltas	4
5658	suela	4
5659	sudando	4
5660	suculento	4
5661	sucias	4
5662	sucesión	4
5663	subo	4
5664	sublimes	4
5665	sótanos	4
5666	sostenía	4
5667	sorpresas	4
5668	sorprendió	4
5669	sórdido	4
5670	soportales	4
5671	soplar	4
5672	soñando	4
5673	sonreído	4
5674	sonoras	4
5675	sonar	4
5676	sombreros	4
5677	sollozando	4
5678	solitarias	4
5679	sólidos	4
5680	sólida	4
5681	solicitud	4
5682	solicitaba	4
5683	sofocada	4
5684	sócrates	4
5685	socarrón	4
5686	sobrinita	4
5687	soberbios	4
5688	soberbio	4
5689	sobado	4
5690	sirven	4
5691	sintiera	4
5692	siniestro	4
5693	singularmente	4
5694	simonía	4
5695	simbólico	4
5696	silenciosos	4
5697	severo	4
5698	seto	4
5699	serán	4
5700	sepultura	4
5701	señalar	4
5702	señalada	4
5703	sentirlo	4
5704	sentimentalismo	4
5705	sentaban	4
5706	sencillez	4
5707	semejanza	4
5708	seguidos	4
5709	seculares	4
5710	secretas	4
5711	secos	4
5712	sebo	4
5713	seas	4
5714	seamos	4
5715	santísima	4
5716	sangrando	4
5717	salvarme	4
5718	salvador	4
5719	salvado	4
5720	salva	4
5721	saludaban	4
5722	saltado	4
5723	salmón	4
5724	saldré	4
5725	sagradas	4
5726	sagaz	4
5727	sacudida	4
5728	sacudía	4
5729	sacrílego	4
5730	saco	4
5731	sacerdocio	4
5732	sacarle	4
5733	saca	4
5734	saboreado	4
5735	sables	4
5736	sabios	4
5737	sabiendo	4
5738	sabiamente	4
5739	sabia	4
5740	ruso	4
5741	run	4
5742	ronco	4
5743	rojos	4
5744	rodeos	4
5745	rodando	4
5746	robo	4
5747	rizado	4
5748	rigores	4
5749	riendo	4
5750	rienda	4
5751	ríen	4
5752	ridículos	4
5753	rezando	4
5754	reyertas	4
5755	revista	4
5756	revela	4
5757	retorcidos	4
5758	retiro	4
5759	retirarse	4
5760	retablo	4
5761	responde	4
5762	resplandor	4
5763	respetaban	4
5764	respeta	4
5765	respectivo	4
5766	respectivas	4
5767	resonancias	4
5768	representación	4
5769	representaban	4
5770	reprensión	4
5771	repetían	4
5772	reparto	4
5773	reparaba	4
5774	renunciaba	4
5775	renta	4
5776	rendido	4
5777	remediar	4
5778	religiones	4
5779	relieves	4
5780	rejuvenecido	4
5781	regaló	4
5782	refresco	4
5783	reflejaba	4
5784	refinada	4
5785	referir	4
5786	reducido	4
5787	recto	4
5788	recorrer	4
5789	reconozco	4
5790	reconoce	4
5791	recomendaba	4
5792	recogido	4
5793	recobrar	4
5794	reclamo	4
5795	reclamaban	4
5796	recitar	4
5797	recitando	4
5798	recargado	4
5799	rebaño	4
5800	raya	4
5801	ratón	4
5802	rasgos	4
5803	rasgo	4
5804	rasgaba	4
5805	rápido	4
5806	rapavelas	4
5807	radical	4
5808	rabillo	4
5809	quizás	4
5810	quitar	4
5811	quitaban	4
5812	quintillas	4
5813	quinqué	4
5814	quieran	4
5815	quiá	4
5816	querría	4
5817	queremos	4
5818	quemaba	4
5819	quema	4
5820	quejido	4
5821	quehaceres	4
5822	quedan	4
5823	quebraderos	4
5824	q	4
5825	púrpura	4
5826	puñaladas	4
5827	punzante	4
5828	pulvisés	4
5829	pulquérrimo	4
5830	pulmonía	4
5831	pulla	4
5832	puente	4
5833	pudiesen	4
5834	publicaba	4
5835	psicología	4
5836	pseudo	4
5837	prurito	4
5838	provisiones	4
5839	provincias	4
5840	protestó	4
5841	protesto	4
5842	protestantes	4
5843	protección	4
5844	prosaicas	4
5845	propinas	4
5846	propina	4
5847	prometiendo	4
5848	prometer	4
5849	prohibidos	4
5850	prohibida	4
5851	prohíbe	4
5852	progresistas	4
5853	profano	4
5854	producto	4
5855	producir	4
5856	prodigaba	4
5857	procuraban	4
5858	problema	4
5859	probables	4
5860	prisiones	4
5861	princesa	4
5862	pretensión	4
5863	pretendiendo	4
5864	presentaron	4
5865	presentar	4
5866	presentado	4
5867	presenta	4
5868	prescindir	4
5869	presbítero	4
5870	preparación	4
5871	preocupación	4
5872	preocupaban	4
5873	premios	4
5874	preguntarle	4
5875	preciosa	4
5876	prácticas	4
5877	pórtico	4
5878	pontífice	4
5879	ponerle	4
5880	ponerla	4
5881	pómulos	4
5882	plebeyo	4
5883	plebe	4
5884	plática	4
5885	platea	4
5886	plásticas	4
5887	planta	4
5888	pistolas	4
5889	pipa	4
5890	pío	4
5891	pintores	4
5892	pintor	4
5893	pintar	4
5894	pinchaban	4
5895	pillastre	4
5896	piden	4
5897	picardías	4
5898	picaba	4
5899	pica	4
5900	piadosos	4
5901	pescuezo	4
5902	pesados	4
5903	pesadillas	4
5904	pesada	4
5905	perseguían	4
5906	perpetua	4
5907	permitían	4
5908	permanente	4
5909	perilla	4
5910	perfecto	4
5911	perdidos	4
5912	perdidas	4
5913	perdería	4
5914	pensadores	4
5915	peligroso	4
5916	peligrosa	4
5917	peguetas	4
5918	pecadora	4
5919	pausadamente	4
5920	pátina	4
5921	paseó	4
5922	pase	4
5923	partidarios	4
5924	particulares	4
5925	parroquial	4
5926	paró	4
5927	parezca	4
5928	pares	4
5929	parecieron	4
5930	parecíale	4
5931	parecerse	4
5932	parecerle	4
5933	parcerisa	4
5934	paños	4
5935	panorama	4
5936	pana	4
5937	palmada	4
5938	pajarillo	4
5939	pajarera	4
5940	página	4
5941	pacto	4
5942	pábulo	4
5943	ostentaban	4
5944	osaba	4
5945	ordinarios	4
5946	optimismo	4
5947	opiniones	4
5948	olvidé	4
5949	ofrecido	4
5950	oficios	4
5951	oficiales	4
5952	oficial	4
5953	ochavo	4
5954	occidente	4
5955	obstáculo	4
5956	observador	4
5957	obscurantista	4
5958	obligado	4
5959	obliga	4
5960	obispos	4
5961	número	4
5962	nudo	4
5963	nublado	4
5964	nubecillas	4
5965	noviembre	4
5966	novicia	4
5967	nostalgia	4
5968	nogal	4
5969	noé	4
5970	niñerías	4
5971	nimiedades	4
5972	nieblas	4
5973	nerviosos	4
5974	negarlo	4
5975	necesarias	4
5976	navidad	4
5977	náufragos	4
5978	naturalista	4
5979	naturalidad	4
5980	napoleón	4
5981	nació	4
5982	nacían	4
5983	nácar	4
5984	mustio	4
5985	murmuró	4
5986	murmuradores	4
5987	muriese	4
5988	murallas	4
5989	municipio	4
5990	mundanas	4
5991	muertes	4
5992	mozas	4
5993	mostrar	4
5994	mostrador	4
5995	mortales	4
5996	morirá	4
5997	moradas	4
5998	montaraz	4
5999	monos	4
6000	molestia	4
6001	molestarle	4
6002	mitra	4
6003	misioneros	4
6004	mísera	4
6005	miramientos	4
6006	mimado	4
6007	militares	4
6008	metiendo	4
6009	meterle	4
6010	metálico	4
6011	metálica	4
6012	meretrices	4
6013	merecido	4
6014	mente	4
6015	meditó	4
6016	meditación	4
6017	medicinas	4
6018	maza	4
6019	mató	4
6020	mataría	4
6021	matan	4
6022	máscara	4
6023	masas	4
6024	marzo	4
6025	margen	4
6026	marea	4
6027	marco	4
6028	marcial	4
6029	maravilla	4
6030	marasmo	4
6031	maquiavelismo	4
6032	manto	4
6033	mantenía	4
6034	mansos	4
6035	manifestó	4
6036	manifestar	4
6037	manifestaba	4
6038	mando	4
6039	mandilón	4
6040	mancebo	4
6041	mamás	4
6042	malvados	4
6043	malva	4
6044	mainate	4
6045	madrugador	4
6046	madrugaba	4
6047	madrileño	4
6048	lugareña	4
6049	lucirse	4
6050	luchó	4
6051	locas	4
6052	llevaron	4
6053	llegara	4
6054	llegando	4
6055	llegan	4
6056	llame	4
6057	llamase	4
6058	llamaradas	4
6059	llamada	4
6060	llagas	4
6061	listo	4
6062	lista	4
6063	líquido	4
6064	linterna	4
6065	limpiando	4
6066	ligeramente	4
6067	ligera	4
6068	licor	4
6069	lícito	4
6070	librarse	4
6071	liberalismo	4
6072	levanto	4
6073	legos	4
6074	lechuguino	4
6075	lavaba	4
6076	laureles	4
6077	latidos	4
6078	laterales	4
6079	larvas	4
6080	lamentaba	4
6081	laico	4
6082	lágrima	4
6083	ladraba	4
6084	lacayos	4
6085	labor	4
6086	labio	4
6087	juzgar	4
6088	juzgaba	4
6089	justa	4
6090	jurar	4
6091	juntar	4
6092	juntando	4
6093	juntaban	4
6094	judío	4
6095	jubilado	4
6096	joya	4
6097	jerarquía	4
6098	je	4
6099	irritada	4
6100	irreverente	4
6101	iriarte	4
6102	irían	4
6103	iremos	4
6104	invocaba	4
6105	invitado	4
6106	inventado	4
6107	intensos	4
6108	intenciones	4
6109	intachable	4
6110	insultaba	4
6111	institución	4
6112	instaló	4
6113	inquietud	4
6114	inofensivo	4
6115	inodoro	4
6116	inmundo	4
6117	inminente	4
6118	injusticias	4
6119	injurias	4
6120	injertaba	4
6121	influjo	4
6122	infernal	4
6123	inefables	4
6124	indumentaria	4
6125	indiscreción	4
6126	indirectas	4
6127	india	4
6128	inconvenientes	4
6129	incluso	4
6130	inclinado	4
6131	incertidumbre	4
6132	incentivo	4
6133	improvisó	4
6134	implacable	4
6135	iluminar	4
6136	iluminada	4
6137	illo	4
6138	il	4
6139	ignorante	4
6140	idealista	4
6141	huyó	4
6142	humillados	4
6143	humillado	4
6144	huevos	4
6145	huerto	4
6146	hortalizas	4
6147	horrores	4
6148	horno	4
6149	honestas	4
6150	hondas	4
6151	homenaje	4
6152	hoguera	4
6153	histórica	4
6154	hipótesis	4
6155	hice	4
6156	heroína	4
6157	heroico	4
6158	heroica	4
6159	hermanitas	4
6160	herida	4
6161	herejía	4
6162	herejes	4
6163	helado	4
6164	hazañas	4
6165	hayan	4
6166	haciéndose	4
6167	hachas	4
6168	hablillas	4
6169	hablé	4
6170	hablase	4
6171	hablas	4
6172	hablara	4
6173	hablador	4
6174	habíamos	4
6175	haberse	4
6176	habéis	4
6177	habana	4
6178	gustado	4
6179	guisa	4
6180	guiñaba	4
6181	gruñido	4
6182	gruesos	4
6183	gruesa	4
6184	grotesca	4
6185	gregorio	4
6186	grandísimo	4
6187	grandísima	4
6188	granate	4
6189	grana	4
6190	grados	4
6191	graciosos	4
6192	grabado	4
6193	gozo	4
6194	gozan	4
6195	gorriones	4
6196	gorra	4
6197	glorias	4
6198	gimnasia	4
6199	generales	4
6200	gemelos	4
6201	gatillo	4
6202	gastado	4
6203	ganancias	4
6204	gala	4
6205	gacetilla	4
6206	fundar	4
6207	fumar	4
6208	fuere	4
6209	fuegos	4
6210	fruta	4
6211	frotaba	4
6212	frescos	4
6213	francisca	4
6214	francia	4
6215	francesa	4
6216	franca	4
6217	fragmentos	4
6218	formada	4
6219	formaban	4
6220	fondos	4
6221	folletines	4
6222	flotaban	4
6223	floridos	4
6224	florida	4
6225	flora	4
6226	física	4
6227	fío	4
6228	finura	4
6229	final	4
6230	filosófico	4
6231	filial	4
6232	fijó	4
6233	figúrate	4
6234	fibras	4
6235	fecha	4
6236	febril	4
6237	fausto	4
6238	fatalidad	4
6239	fantásticos	4
6240	falsedad	4
6241	factor	4
6242	exuberante	4
6243	extraviado	4
6244	extraordinario	4
6245	extranjero	4
6246	externo	4
6247	extendió	4
6248	extendían	4
6249	exquisito	4
6250	expresar	4
6251	explicarlo	4
6252	expedición	4
6253	expansiones	4
6254	éxito	4
6255	excomulgar	4
6256	exclamar	4
6257	excitación	4
6258	excitaba	4
6259	excesivo	4
6260	excepcional	4
6261	evangélica	4
6262	eufemismos	4
6263	estufa	4
6264	estudia	4
6265	estribos	4
6266	estribo	4
6267	estreno	4
6268	estrechar	4
6269	estirado	4
6270	estimaban	4
6271	éste	4
6272	estatuas	4
6273	estameña	4
6274	estallar	4
6275	estallaba	4
6276	estábamos	4
6277	esquivaba	4
6278	espléndida	4
6279	espiando	4
6280	espero	4
6281	esperase	4
6282	espejos	4
6283	espacios	4
6284	eses	4
6285	esencial	4
6286	escuelas	4
6287	escuchó	4
6288	escuchaban	4
6289	escrúpulo	4
6290	escribe	4
6291	escondidas	4
6292	escondía	4
6293	escaso	4
6294	escapó	4
6295	escaparate	4
6296	escapado	4
6297	escandalosos	4
6298	esbeltos	4
6299	eróticas	4
6300	erguía	4
6301	épocas	4
6302	epigramas	4
6303	envidió	4
6304	envidias	4
6305	envidiable	4
6306	entregar	4
6307	enterrar	4
6308	enteros	4
6309	enternecido	4
6310	enternecida	4
6311	enternecía	4
6312	enterase	4
6313	entenderse	4
6314	entendemos	4
6315	entendámonos	4
6316	enseñando	4
6317	enojo	4
6318	engañarse	4
6319	engañada	4
6320	endiablado	4
6321	encontrando	4
6322	encendían	4
6323	encendía	4
6324	encarnada	4
6325	enamorados	4
6326	emprendió	4
6327	empleó	4
6328	empleaban	4
6329	empezaban	4
6330	empeñó	4
6331	empeñaba	4
6332	empeña	4
6333	embriaguez	4
6334	embriagado	4
6335	emanaciones	4
6336	elocuentes	4
6337	elevarse	4
6338	elevar	4
6339	elección	4
6340	ejemplar	4
6341	egipcios	4
6342	efímero	4
6343	duras	4
6344	duran	4
6345	dramático	4
6346	dotes	4
6347	dorados	4
6348	dominicales	4
6349	dominarse	4
6350	documentos	4
6351	docenas	4
6352	docena	4
6353	divertían	4
6354	distracción	4
6355	distinto	4
6356	distinguido	4
6357	distingo	4
6358	disputaban	4
6359	disponer	4
6360	disparatada	4
6361	disparado	4
6362	disimuló	4
6363	disgustado	4
6364	discusiones	4
6365	disculpaba	4
6366	discretos	4
6367	disciplinas	4
6368	dirigiéndose	4
6369	directa	4
6370	dineral	4
6371	dimisión	4
6372	diluvio	4
6373	dije	4
6374	dignísimo	4
6375	digan	4
6376	difunta	4
6377	diera	4
6378	diario	4
6379	diabólica	4
6380	devotos	4
6381	devociones	4
6382	devocionario	4
6383	determinado	4
6384	detenía	4
6385	desvanecerse	4
6386	destacándose	4
6387	despreciaban	4
6388	despedían	4
6389	despecho	4
6390	desmoronaba	4
6391	desmayada	4
6392	deslumbrar	4
6393	desinteresada	4
6394	desigual	4
6395	deshecho	4
6396	deshacía	4
6397	desesperaba	4
6398	desear	4
6399	desdeñar	4
6400	descubierta	4
6401	descrédito	4
6402	desconsuelo	4
6403	descendiente	4
6404	descender	4
6405	descargaba	4
6406	descansar	4
6407	desaires	4
6408	desahogaba	4
6409	desafía	4
6410	depósito	4
6411	depositar	4
6412	demostrar	4
6413	demasías	4
6414	delicados	4
6415	dejes	4
6416	dejen	4
6417	déjate	4
6418	dejaría	4
6419	dejará	4
6420	dejamos	4
6421	degradación	4
6422	defendían	4
6423	decorosa	4
6424	declara	4
6425	decirla	4
6426	decidida	4
6427	decide	4
6428	debilidades	4
6429	debí	4
6430	dandy	4
6431	cuyas	4
6432	cumbre	4
6433	cultos	4
6434	culpable	4
6435	cuerpos	4
6436	cuerno	4
6437	cuchicheo	4
6438	cubiertas	4
6439	cuán	4
6440	cruces	4
6441	crónica	4
6442	crecer	4
6443	creación	4
6444	cráneo	4
6445	corujedo	4
6446	cortina	4
6447	corteses	4
6448	corrillos	4
6449	correcto	4
6450	corporal	4
6451	cordón	4
6452	copia	4
6453	convirtiera	4
6454	convino	4
6455	convierte	4
6456	convidar	4
6457	convertidos	4
6458	convenían	4
6459	convenció	4
6460	convencidos	4
6461	contrarrestar	4
6462	contradicción	4
6463	contorsiones	4
6464	continuaban	4
6465	contestación	4
6466	contenido	4
6467	consunción	4
6468	consumía	4
6469	consuela	4
6470	consolarle	4
6471	consiste	4
6472	consiente	4
6473	considerable	4
6474	conservado	4
6475	consentir	4
6476	conseguirlo	4
6477	consagrar	4
6478	consagraba	4
6479	congojas	4
6480	congoja	4
6481	confusión	4
6482	confundían	4
6483	conflicto	4
6484	confidencial	4
6485	confesárselo	4
6486	confesando	4
6487	condenada	4
6488	condenaba	4
6489	condena	4
6490	cónclave	4
6491	conciudadanos	4
6492	concilio	4
6493	conciertos	4
6494	concejales	4
6495	comunión	4
6496	compuesto	4
6497	comprendo	4
6498	complicados	4
6499	complicaciones	4
6500	complacencia	4
6501	comparando	4
6502	comparado	4
6503	compañera	4
6504	cómodo	4
6505	comodidad	4
6506	cómica	4
6507	cometer	4
6508	comerciantes	4
6509	comenzaban	4
6510	comendador	4
6511	colocada	4
6512	colinas	4
6513	colgar	4
6514	colección	4
6515	colchones	4
6516	coincidiendo	4
6517	coincidía	4
6518	cohetes	4
6519	cogía	4
6520	cocinera	4
6521	cocinas	4
6522	cobre	4
6523	clavado	4
6524	clavaban	4
6525	clava	4
6526	clásicos	4
6527	clásico	4
6528	clásica	4
6529	civiles	4
6530	cieno	4
6531	ciegos	4
6532	chusma	4
6533	churrigueresco	4
6534	chorreando	4
6535	chorizos	4
6536	chimeneas	4
6537	chillona	4
6538	chicas	4
6539	charadas	4
6540	chaqueta	4
6541	chaleco	4
6542	césped	4
6543	cerveza	4
6544	cerero	4
6545	ceder	4
6546	cazadores	4
6547	cayera	4
6548	cavilosa	4
6549	causado	4
6550	catarata	4
6551	catalán	4
6552	casto	4
6553	castillo	4
6554	castellano	4
6555	casó	4
6556	caseros	4
6557	casera	4
6558	cascos	4
6559	cascada	4
6560	casaban	4
6561	casaba	4
6562	cartón	4
6563	carmen	4
6564	carlista	4
6565	cardenal	4
6566	carca	4
6567	característica	4
6568	caracol	4
6569	cañas	4
6570	cantan	4
6571	canta	4
6572	cansó	4
6573	canarios	4
6574	campanero	4
6575	caminar	4
6576	calzaba	4
6577	calvo	4
6578	calorcillo	4
6579	callando	4
6580	calificar	4
6581	calientes	4
6582	calentaba	4
6583	cálculos	4
6584	calculaba	4
6585	calada	4
6586	calabazas	4
6587	cajas	4
6588	caiga	4
6589	caerse	4
6590	busque	4
6591	buscarme	4
6592	burlas	4
6593	burlándose	4
6594	burlaban	4
6595	brutales	4
6596	brotar	4
6597	breves	4
6598	brasero	4
6599	botánico	4
6600	borrachera	4
6601	borla	4
6602	boquirroto	4
6603	bonita	4
6604	bonachón	4
6605	bolas	4
6606	boj	4
6607	besarle	4
6608	besar	4
6609	besaba	4
6610	bendita	4
6611	beltrand	4
6612	basura	4
6613	barría	4
6614	barrer	4
6615	barniz	4
6616	barítono	4
6617	barbero	4
6618	barato	4
6619	bandos	4
6620	bancarrota	4
6621	balde	4
6622	bailado	4
6623	bacantes	4
6624	babilonia	4
6625	azar	4
6626	azafrán	4
6627	ayes	4
6628	aventurado	4
6629	autoridades	4
6630	aurora	4
6631	aumentaba	4
6632	audaz	4
6633	atrocidades	4
6634	atribuían	4
6635	atrevieron	4
6636	atravesaba	4
6637	atrasado	4
6638	atormentaban	4
6639	atleta	4
6640	atacaba	4
6641	asquerosas	4
6642	asomo	4
6643	asistido	4
6644	asistían	4
6645	asfixia	4
6646	artillería	4
6647	arrojaban	4
6648	arrodillada	4
6649	arrepentimiento	4
6650	arrepentida	4
6651	arregla	4
6652	arrastrado	4
6653	arraigadas	4
6654	arqueología	4
6655	ardua	4
6656	ardientes	4
6657	arcas	4
6658	arcángel	4
6659	aquél	4
6660	apuros	4
6661	apurada	4
6662	apuraban	4
6663	apuntó	4
6664	aprovechó	4
6665	aprovechase	4
6666	aprovechan	4
6667	aprobó	4
6668	apretadas	4
6669	apresuraba	4
6670	aprensiva	4
6671	apoyándose	4
6672	apoyando	4
6673	apostólico	4
6674	aplicó	4
6675	aplaudía	4
6676	aplastaba	4
6677	apiñados	4
6678	apetecible	4
6679	apasionado	4
6680	apasionada	4
6681	apagó	4
6682	apagada	4
6683	apagaba	4
6684	apacible	4
6685	anunciar	4
6686	antiquísima	4
6687	antero	4
6688	ansiedades	4
6689	ansia	4
6690	anochecer	4
6691	animación	4
6692	animaban	4
6693	angustias	4
6694	ancianos	4
6695	análisis	4
6696	anales	4
6697	amiguita	4
6698	amapola	4
6699	amaneradas	4
6700	alusión	4
6701	aludir	4
6702	altivo	4
6703	alpaca	4
6704	alimentos	4
6705	alemanes	4
6706	alejaban	4
6707	alegro	4
6708	aldeanos	4
6709	aldeano	4
6710	alabanza	4
6711	ajustado	4
6712	ajustada	4
6713	ajenos	4
6714	airado	4
6715	ahumado	4
6716	ahorros	4
6717	ahínco	4
6718	aguja	4
6719	águilas	4
6720	agudos	4
6721	agrada	4
6722	afectación	4
6723	adolescente	4
6724	adolescencia	4
6725	admirada	4
6726	admiraban	4
6727	adivinó	4
6728	ad	4
6729	acusado	4
6730	acusaba	4
6731	acusa	4
6732	acostaba	4
6733	acompañaron	4
6734	acompañarla	4
6735	acompañar	4
6736	acompañamiento	4
6737	acompañada	4
6738	aceptado	4
6739	acecho	4
6740	acarició	4
6741	acabase	4
6742	abusando	4
6743	aburrida	4
6744	aburren	4
6745	absurdas	4
6746	absurda	4
6747	abstracción	4
6748	abrumaba	4
6749	abrirle	4
6750	abrigado	4
6751	abrazos	4
6752	aborrecido	4
6753	aborrecer	4
6754	aborrece	4
6755	abanicos	4
6756	abandonaba	4
6757	abalorios	4
6758	zurriágame	3
6759	zumbaron	3
6760	xiv	3
6761	vuelvo	3
6762	vuelos	3
6763	votó	3
6764	volverme	3
6765	volveré	3
6766	vocinglero	3
6767	vivimos	3
6768	viviera	3
6769	viudez	3
6770	visitarla	3
6771	visión	3
6772	visible	3
6773	virtuoso	3
6774	vinieron	3
6775	villanía	3
6776	vieran	3
6777	viéndole	3
6778	vidriera	3
6779	vicisitudes	3
6780	viceversa	3
6781	vibrante	3
6782	vibraban	3
6783	vestigios	3
6784	veríamos	3
6785	vergonzosos	3
6786	vergonzosa	3
6787	verdugos	3
6788	verdores	3
6789	verdades	3
6790	verdaderos	3
6791	ventanilla	3
6792	venimos	3
6793	vendía	3
6794	vencerle	3
6795	vencerla	3
6796	velos	3
6797	velar	3
6798	velador	3
6799	vejiga	3
6800	vejete	3
6801	veinticuatro	3
6802	varillas	3
6803	vanos	3
6804	vanidades	3
6805	vanas	3
6806	vana	3
6807	valles	3
6808	valen	3
6809	vacíos	3
6810	vacilaba	3
6811	vacas	3
6812	utilizar	3
6813	usan	3
6814	urna	3
6815	unión	3
6816	unidad	3
6817	unida	3
6818	unanimidad	3
6819	unánime	3
6820	u	3
6821	turgentes	3
6822	turgente	3
6823	turgencias	3
6824	turbarse	3
6825	turbada	3
6826	tupido	3
6827	tubo	3
6828	tronado	3
6829	tronada	3
6830	trompa	3
6831	tristón	3
6832	trigo	3
6833	tremenda	3
6834	trece	3
6835	traza	3
6836	trasladarse	3
6837	trasladar	3
6838	trasladado	3
6839	transtiberina	3
6840	transparentes	3
6841	transformó	3
6842	transformada	3
6843	transformaba	3
6844	tranquilizarse	3
6845	tralla	3
6846	trajeron	3
6847	traidor	3
6848	traiciones	3
6849	tragó	3
6850	trágicas	3
6851	tragaba	3
6852	tráfico	3
6853	traen	3
6854	tradicional	3
6855	trabajando	3
6856	trabajado	3
6857	trabaja	3
6858	tosía	3
6859	toses	3
6860	tosco	3
6861	tos	3
6862	tortura	3
6863	tortuga	3
6864	tórtolas	3
6865	torres	3
6866	torrentes	3
6867	toros	3
6868	torno	3
6869	torneado	3
6870	torcer	3
6871	tomarse	3
6872	tomaron	3
6873	tomaría	3
6874	toman	3
6875	toleraba	3
6876	toledo	3
6877	todd	3
6878	tocante	3
6879	tocan	3
6880	tirso	3
6881	tires	3
6882	tirando	3
6883	tiran	3
6884	tirada	3
6885	tiraba	3
6886	tira	3
6887	tiestos	3
6888	tieso	3
6889	tiernos	3
6890	tibio	3
6891	tiara	3
6892	texto	3
6893	testero	3
6894	tesón	3
6895	terrones	3
6896	terminado	3
6897	termasaltas	3
6898	terco	3
6899	terciando	3
6900	teológico	3
6901	teñía	3
6902	tentativas	3
6903	tensión	3
6904	tenerlo	3
6905	teneatis	3
6906	tendré	3
6907	tendero	3
6908	temperamentos	3
6909	temores	3
6910	teme	3
6911	temblona	3
6912	telar	3
6913	tejas	3
6914	tapada	3
6915	tapabocas	3
6916	tapa	3
6917	tambaleaba	3
6918	taller	3
6919	tálamo	3
6920	tajadas	3
6921	tacos	3
6922	taciturna	3
6923	taburetes	3
6924	taberneros	3
6925	suspirar	3
6926	suspiraban	3
6927	suspira	3
6928	suspendió	3
6929	suspendieron	3
6930	suspender	3
6931	supuestos	3
6932	supremos	3
6933	suplicante	3
6934	supieran	3
6935	supersticiosamente	3
6936	supersticiosa	3
6937	superiores	3
6938	sumida	3
6939	suicidio	3
6940	sugerido	3
6941	suficientes	3
6942	suelas	3
6943	sudaban	3
6944	sucumbir	3
6945	sucios	3
6946	sucesor	3
6947	sucedió	3
6948	subrepticia	3
6949	subieron	3
6950	stabat	3
6951	spirto	3
6952	sostenida	3
6953	sostenían	3
6954	sospechosas	3
6955	sospeche	3
6956	sospechase	3
6957	sospecharlo	3
6958	sospechara	3
6959	sospechaban	3
6960	sosos	3
6961	sordos	3
6962	soporífero	3
6963	soplando	3
6964	soñó	3
6965	soñadora	3
6966	sonrosado	3
6967	sonrosada	3
6968	sonrieron	3
6969	sonríe	3
6970	sonora	3
6971	sonado	3
6972	sombría	3
6973	solidez	3
6974	soles	3
6975	soledades	3
6976	soldados	3
6977	soldado	3
6978	sojuzgada	3
6979	socorro	3
6980	sociedades	3
6981	socialista	3
6982	sobriedad	3
6983	sobra	3
6984	sitios	3
6985	sinodal	3
6986	sine	3
6987	sincero	3
6988	simpática	3
6989	siluetas	3
6990	silueta	3
6991	silbido	3
6992	sílabas	3
6993	sigo	3
6994	sietemesino	3
6995	sidra	3
6996	sexos	3
6997	sevilla	3
6998	setenta	3
6999	serenidad	3
7000	sepulcro	3
7001	separaron	3
7002	separarnos	3
7003	separándose	3
7004	separada	3
7005	separación	3
7006	separa	3
7007	sentiría	3
7008	sentencias	3
7009	sentencia	3
7010	sentaron	3
7011	sentar	3
7012	sentados	3
7013	sensual	3
7014	sensible	3
7015	sencillas	3
7016	seminarista	3
7017	semilla	3
7018	semejaba	3
7019	seguros	3
7020	seguidas	3
7021	segismundo	3
7022	seducirle	3
7023	secularizar	3
7024	sectario	3
7025	sean	3
7026	saya	3
7027	savia	3
7028	satisfechas	3
7029	satisfacía	3
7030	sardinas	3
7031	santiguarse	3
7032	sandio	3
7033	sandeces	3
7034	salvajes	3
7035	saludos	3
7036	salta	3
7037	salpicaba	3
7038	saliva	3
7039	salacia	3
7040	sagrados	3
7041	sagacidad	3
7042	sacrílegos	3
7043	sacrílega	3
7044	sacrificado	3
7045	sacarla	3
7046	sacando	3
7047	sacan	3
7048	sabrosos	3
7049	sabrosa	3
7050	sábado	3
7051	rústica	3
7052	rusia	3
7053	rurales	3
7054	rumbo	3
7055	ruiseñor	3
7056	ruines	3
7057	ruin	3
7058	ruborizó	3
7059	ruborizarse	3
7060	rubios	3
7061	rota	3
7062	rossini	3
7063	rosina	3
7064	rosetones	3
7065	rosada	3
7066	roque	3
7067	rompimiento	3
7068	rompiendo	3
7069	romero	3
7070	románticos	3
7071	romano	3
7072	rodrigo	3
7073	rodearon	3
7074	rodean	3
7075	rodea	3
7076	rocín	3
7077	roba	3
7078	risum	3
7079	risueño	3
7080	ríos	3
7081	riñón	3
7082	riéndose	3
7083	ribeteadoras	3
7084	ríase	3
7085	rezó	3
7086	reyerta	3
7087	revolver	3
7088	revelar	3
7089	revelaban	3
7090	revelaba	3
7091	reunir	3
7092	reuniones	3
7093	reunido	3
7094	retumbar	3
7095	retrocedía	3
7096	retorcía	3
7097	retoños	3
7098	retiraba	3
7099	reticencias	3
7100	resumidas	3
7101	resultó	3
7102	resulta	3
7103	resuelve	3
7104	resucitar	3
7105	resquicios	3
7106	respondo	3
7107	resplandores	3
7108	respiro	3
7109	respetando	3
7110	respetada	3
7111	resonantes	3
7112	resignado	3
7113	resignada	3
7114	reservas	3
7115	reservaba	3
7116	reseco	3
7117	resbalar	3
7118	resbalando	3
7119	reputó	3
7120	repuso	3
7121	republicano	3
7122	reprensible	3
7123	repleto	3
7124	repito	3
7125	repite	3
7126	repetidos	3
7127	repentino	3
7128	repentinas	3
7129	repasando	3
7130	reparte	3
7131	reparo	3
7132	reparado	3
7133	reparación	3
7134	renegaba	3
7135	rendición	3
7136	rendía	3
7137	renan	3
7138	renacía	3
7139	remontaba	3
7140	remolinos	3
7141	remiendos	3
7142	relucir	3
7143	relucía	3
7144	reliquias	3
7145	relieve	3
7146	relativas	3
7147	relativa	3
7148	reído	3
7149	registros	3
7150	regañadientes	3
7151	regalista	3
7152	regalar	3
7153	refuerzo	3
7154	reflejo	3
7155	reflejando	3
7156	refleja	3
7157	refinado	3
7158	referían	3
7159	redomado	3
7160	rediós	3
7161	redes	3
7162	red	3
7163	recurso	3
7164	recurrir	3
7165	recurría	3
7166	recorrido	3
7167	recordándole	3
7168	reconocían	3
7169	reconocerlo	3
7170	recompensa	3
7171	recogerla	3
7172	recobrado	3
7173	recluta	3
7174	reclamar	3
7175	reclamaba	3
7176	recios	3
7177	rechazaba	3
7178	recato	3
7179	reasumiendo	3
7180	realizado	3
7181	rayas	3
7182	ratones	3
7183	rastro	3
7184	rasgó	3
7185	rasgar	3
7186	rasgaban	3
7187	rasero	3
7188	raras	3
7189	ráfagas	3
7190	racimo	3
7191	quitó	3
7192	quitarle	3
7193	quisiese	3
7194	quise	3
7195	quintana	3
7196	quincalla	3
7197	quieras	3
7198	quererla	3
7199	quemar	3
7200	quedaría	3
7201	quedamos	3
7202	quebrantada	3
7203	pusiera	3
7204	purgatorio	3
7205	purga	3
7206	pupitre	3
7207	puñadas	3
7208	punzadas	3
7209	puntería	3
7210	puntapiés	3
7211	pulmones	3
7212	pullas	3
7213	puf	3
7214	puestos	3
7215	puedan	3
7216	publicó	3
7217	públicas	3
7218	prudentes	3
7219	provocada	3
7220	provinciano	3
7221	providencial	3
7222	protestar	3
7223	protectora	3
7224	proscenio	3
7225	propasarse	3
7226	prolongaba	3
7227	prólogo	3
7228	prohibir	3
7229	prohibición	3
7230	progresista	3
7231	profundas	3
7232	profanar	3
7233	profanado	3
7234	profanaciones	3
7235	profana	3
7236	produjo	3
7237	pródigo	3
7238	prodigio	3
7239	prodigar	3
7240	procurase	3
7241	procurador	3
7242	procedía	3
7243	probó	3
7244	probaba	3
7245	privilegio	3
7246	primores	3
7247	primogénito	3
7248	primitivo	3
7249	presumir	3
7250	presumía	3
7251	presidir	3
7252	presidiendo	3
7253	presidida	3
7254	presidía	3
7255	presenciar	3
7256	prepararle	3
7257	preocupados	3
7258	prender	3
7259	prematura	3
7260	preliminares	3
7261	preguntaron	3
7262	preguntado	3
7263	predominaba	3
7264	predilecto	3
7265	predilección	3
7266	predicar	3
7267	precoz	3
7268	praxíteles	3
7269	praderas	3
7270	práctico	3
7271	postres	3
7272	postergado	3
7273	positivismo	3
7274	positivamente	3
7275	posibles	3
7276	posesión	3
7277	pos	3
7278	porteros	3
7279	portero	3
7280	portentos	3
7281	pordiosero	3
7282	poquito	3
7283	poniente	3
7284	pones	3
7285	ponen	3
7286	pondría	3
7287	pompadour	3
7288	pomaradas	3
7289	pólvora	3
7290	pollastres	3
7291	políticos	3
7292	poetisa	3
7293	poesías	3
7294	poemas	3
7295	podremos	3
7296	poderosas	3
7297	poderío	3
7298	pocilga	3
7299	pobrecitos	3
7300	poblados	3
7301	pluviales	3
7302	plumero	3
7303	pliegos	3
7304	pliego	3
7305	plazuelas	3
7306	playa	3
7307	pláticas	3
7308	plateresco	3
7309	plateas	3
7310	plantado	3
7311	planchadora	3
7312	plácida	3
7313	pitillo	3
7314	pisos	3
7315	pisadas	3
7316	pintó	3
7317	pinta	3
7318	piezas	3
7319	pieza	3
7320	pierden	3
7321	piense	3
7322	pidiendo	3
7323	picardía	3
7324	picantes	3
7325	petit	3
7326	petimetre	3
7327	pestillo	3
7328	pestes	3
7329	peste	3
7330	pesebre	3
7331	pese	3
7332	pescar	3
7333	pesca	3
7334	pesadumbre	3
7335	pesa	3
7336	pertenecía	3
7337	perspicacia	3
7338	perseverancia	3
7339	perrero	3
7340	perpendicular	3
7341	perniciosa	3
7342	permitirle	3
7343	permitió	3
7344	permaneció	3
7345	perlas	3
7346	perífrasis	3
7347	perezosos	3
7348	perezosas	3
7349	perenne	3
7350	perdonó	3
7351	perdone	3
7352	perderme	3
7353	pequeñeces	3
7354	pepita	3
7355	pensativo	3
7356	pensará	3
7357	pensara	3
7358	penosa	3
7359	penetraban	3
7360	pelos	3
7361	pellizcos	3
7362	pellizcaba	3
7363	pellejos	3
7364	pelado	3
7365	pegajoso	3
7366	pegaba	3
7367	pedacitos	3
7368	peculiar	3
7369	pecaminosa	3
7370	pecadillos	3
7371	pecaba	3
7372	paúl	3
7373	patriotismo	3
7374	patos	3
7375	patéticos	3
7376	pasta	3
7377	pasmosa	3
7378	pasmados	3
7379	paseándose	3
7380	paseado	3
7381	pasatiempo	3
7382	pasase	3
7383	pasarse	3
7384	pasajera	3
7385	pasados	3
7386	pasadizo	3
7387	pasadas	3
7388	partidos	3
7389	partidas	3
7390	participaban	3
7391	parterres	3
7392	parroquiano	3
7393	parecidas	3
7394	paralelas	3
7395	parada	3
7396	parábolas	3
7397	panurgo	3
7398	panteón	3
7399	panteísmo	3
7400	palpitaba	3
7401	palmas	3
7402	palmaditas	3
7403	palmadita	3
7404	palidecía	3
7405	palabreja	3
7406	pague	3
7407	pagarle	3
7408	pagaría	3
7409	pagano	3
7410	pagana	3
7411	paces	3
7412	paca	3
7413	pabellón	3
7414	otorgó	3
7415	ostentoso	3
7416	ostentosa	3
7417	ostentar	3
7418	ortografía	3
7419	orla	3
7420	originalidad	3
7421	órganos	3
7422	ordalías	3
7423	oratoria	3
7424	oradores	3
7425	oprimió	3
7426	oponía	3
7427	oponer	3
7428	opone	3
7429	opio	3
7430	opinaban	3
7431	operación	3
7432	ondulantes	3
7433	ondulante	3
7434	olvidito	3
7435	olvidando	3
7436	olvidados	3
7437	olvidaban	3
7438	oliendo	3
7439	olfatear	3
7440	olfateaba	3
7441	oler	3
7442	ojuelos	3
7443	ojeriza	3
7444	ojalá	3
7445	oidor	3
7446	ofreciendo	3
7447	odiosos	3
7448	odioso	3
7449	odiosa	3
7450	ocurrían	3
7451	ocurre	3
7452	ocupó	3
7453	ocupado	3
7454	ocultó	3
7455	ocultándose	3
7456	ociosas	3
7457	ocio	3
7458	obstina	3
7459	observaciones	3
7460	obscurecía	3
7461	obrar	3
7462	obligar	3
7463	obligados	3
7464	obligada	3
7465	obligaban	3
7466	objeciones	3
7467	obediencia	3
7468	obedezco	3
7469	numerosos	3
7470	números	3
7471	núcleo	3
7472	notarlo	3
7473	notables	3
7474	nota	3
7475	nono	3
7476	nombraba	3
7477	nocturnos	3
7478	nocturna	3
7479	nilo	3
7480	neutral	3
7481	negaban	3
7482	necesitas	3
7483	necesitar	3
7484	necesitamos	3
7485	necesidades	3
7486	necesarios	3
7487	necesariamente	3
7488	navajas	3
7489	naturalmente	3
7490	narrativa	3
7491	narración	3
7492	narraba	3
7493	nacionales	3
7494	nace	3
7495	mutuamente	3
7496	musical	3
7497	muñecas	3
7498	municipal	3
7499	mundanal	3
7500	multiplicaba	3
7501	mula	3
7502	mueve	3
7503	mueva	3
7504	muestras	3
7505	mudos	3
7506	mortuoria	3
7507	mortificaban	3
7508	mortificaba	3
7509	moribunda	3
7510	mordido	3
7511	morder	3
7512	monumentos	3
7513	monumento	3
7514	monumentales	3
7515	montones	3
7516	montico	3
7517	montera	3
7518	montaraces	3
7519	monstruos	3
7520	monstruo	3
7521	monótonas	3
7522	monosílabos	3
7523	monopolio	3
7524	móndame	3
7525	monaguillos	3
7526	molinero	3
7527	molesto	3
7528	mojada	3
7529	mojaba	3
7530	moderno	3
7531	modas	3
7532	modales	3
7533	mitrado	3
7534	misteriosamente	3
7535	miserere	3
7536	miren	3
7537	mirase	3
7538	miras	3
7539	mirarse	3
7540	miran	3
7541	ministros	3
7542	mineros	3
7543	millares	3
7544	milagroso	3
7545	milagrosa	3
7546	migas	3
7547	miga	3
7548	miembros	3
7549	miembro	3
7550	midió	3
7551	miasmas	3
7552	mezquino	3
7553	mezclando	3
7554	mezcladas	3
7555	metrópoli	3
7556	meter	3
7557	meseta	3
7558	méritos	3
7559	mereciera	3
7560	merecían	3
7561	mercantil	3
7562	mercader	3
7563	menudos	3
7564	mental	3
7565	mensuales	3
7566	menester	3
7567	memorable	3
7568	melunga	3
7569	melancólicos	3
7570	melancólicas	3
7571	mejoría	3
7572	mejía	3
7573	medir	3
7574	mediocritas	3
7575	medían	3
7576	mediaba	3
7577	máxima	3
7578	matorral	3
7579	mater	3
7580	matemáticas	3
7581	masón	3
7582	martínez	3
7583	martín	3
7584	marineros	3
7585	mari	3
7586	marear	3
7587	marcos	3
7588	marchó	3
7589	maña	3
7590	manzanas	3
7591	mantenían	3
7592	mantenerse	3
7593	manta	3
7594	manosear	3
7595	manoseadas	3
7596	manolillo	3
7597	manjares	3
7598	maniquí	3
7599	manejar	3
7600	mande	3
7601	mandarle	3
7602	mandaría	3
7603	manchaba	3
7604	malvado	3
7605	maligna	3
7606	malhaya	3
7607	malagueñas	3
7608	majestuosa	3
7609	majaderos	3
7610	magnate	3
7611	maestros	3
7612	maestría	3
7613	maduro	3
7614	madrugada	3
7615	madreselva	3
7616	madres	3
7617	madero	3
7618	maderas	3
7619	m	3
7620	luminosa	3
7621	lumbrera	3
7622	lujosa	3
7623	lúgubre	3
7624	ludibrio	3
7625	lucir	3
7626	lucido	3
7627	lucían	3
7628	luchando	3
7629	lozana	3
7630	lomas	3
7631	lola	3
7632	logró	3
7633	lodazal	3
7634	locuaz	3
7635	lluvias	3
7636	lloro	3
7637	llorado	3
7638	lloraban	3
7639	lleven	3
7640	llevársela	3
7641	llenarse	3
7642	llenan	3
7643	llegada	3
7644	llamasen	3
7645	llamándole	3
7646	llamando	3
7647	lívido	3
7648	liviandad	3
7649	literario	3
7650	lisonjeras	3
7651	líquidos	3
7652	límite	3
7653	ligeras	3
7654	lid	3
7655	licencias	3
7656	libaciones	3
7657	leyera	3
7658	lejanas	3
7659	lealtad	3
7660	lavar	3
7661	lavándose	3
7662	lavado	3
7663	lavabo	3
7664	latina	3
7665	lascivo	3
7666	lasciami	3
7667	lapsus	3
7668	lanas	3
7669	lamentos	3
7670	laderas	3
7671	l	3
7672	juzga	3
7673	justos	3
7674	justamente	3
7675	jurisconsulto	3
7676	juntarse	3
7677	julio	3
7678	juguetes	3
7679	juguete	3
7680	juega	3
7681	jubilación	3
7682	jovial	3
7683	josé	3
7684	jorge	3
7685	job	3
7686	jipijapa	3
7687	jamona	3
7688	jadeante	3
7689	jactarse	3
7690	irritaban	3
7691	irreverencia	3
7692	irracional	3
7693	irónica	3
7694	irme	3
7695	iris	3
7696	inventos	3
7697	intriga	3
7698	intratable	3
7699	intervenir	3
7700	intervalos	3
7701	intersticio	3
7702	intermitencias	3
7703	interminables	3
7704	interminable	3
7705	interesa	3
7706	intento	3
7707	intemperie	3
7708	instalado	3
7709	inspirado	3
7710	insolentes	3
7711	insisto	3
7712	inquisidor	3
7713	inquietos	3
7714	inquieto	3
7715	inquebrantable	3
7716	inoportuno	3
7717	innominada	3
7718	inmundicia	3
7719	inmortalidad	3
7720	inmoral	3
7721	inmenso	3
7722	inmediata	3
7723	injuria	3
7724	ingeniero	3
7725	infinitamente	3
7726	infamia	3
7727	inexorable	3
7728	inepto	3
7729	indulgente	3
7730	indudable	3
7731	índole	3
7732	indiscreto	3
7733	indignidad	3
7734	indiferente	3
7735	indicar	3
7736	indicaba	3
7737	indias	3
7738	indiano	3
7739	independencia	3
7740	incurable	3
7741	incorporarse	3
7742	incómoda	3
7743	incipiente	3
7744	incidentes	3
7745	incansable	3
7746	impuro	3
7747	imprudentes	3
7748	impropio	3
7749	improper	3
7750	imprenta	3
7751	imposiciones	3
7752	imposibles	3
7753	importunos	3
7754	importuna	3
7755	ímpetu	3
7756	imperiosa	3
7757	imperdonable	3
7758	impasible	3
7759	impacientaba	3
7760	imitando	3
7761	imitaciones	3
7762	imaginaria	3
7763	ilustrado	3
7764	ilustraciones	3
7765	ilustración	3
7766	ilusión	3
7767	ilegítimos	3
7768	ignominioso	3
7769	ignominia	3
7770	ídolos	3
7771	idioma	3
7772	huraña	3
7773	huracanes	3
7774	hundir	3
7775	humorismo	3
7776	humores	3
7777	humillarse	3
7778	humildemente	3
7779	húmedos	3
7780	húmedo	3
7781	huellas	3
7782	hotel	3
7783	horrorizado	3
7784	horca	3
7785	honrados	3
7786	honesta	3
7787	hondonada	3
7788	holocausto	3
7789	hojuelas	3
7790	hipógrifo	3
7791	hipocritona	3
7792	hipócrates	3
7793	hijita	3
7794	higiénico	3
7795	higiénicas	3
7796	hiciese	3
7797	híbrido	3
7798	heroínas	3
7799	herir	3
7800	heredada	3
7801	helechos	3
7802	helada	3
7803	hebilla	3
7804	harían	3
7805	halló	3
7806	halagos	3
7807	hagas	3
7808	hagan	3
7809	hagamos	3
7810	haciéndole	3
7811	hacerles	3
7812	habrían	3
7813	habrás	3
7814	hablarla	3
7815	hablará	3
7816	habituales	3
7817	habitual	3
7818	habitantes	3
7819	habilidades	3
7820	habías	3
7821	habíale	3
7822	gusanos	3
7823	guijarros	3
7824	guiaba	3
7825	guardar	3
7826	guapísima	3
7827	gruñir	3
7828	gruñía	3
7829	grueso	3
7830	grotesco	3
7831	grietas	3
7832	gramática	3
7833	gozoso	3
7834	gótica	3
7835	goteras	3
7836	gorda	3
7837	góndola	3
7838	goma	3
7839	golpecitos	3
7840	goce	3
7841	gobernar	3
7842	goberna	3
7843	glorioso	3
7844	globulus	3
7845	genuflexión	3
7846	géneros	3
7847	generalizada	3
7848	generación	3
7849	gaudeamus	3
7850	gata	3
7851	gastos	3
7852	gárrulo	3
7853	garbo	3
7854	garbanzos	3
7855	garantía	3
7856	ganó	3
7857	gangosa	3
7858	ganando	3
7859	ganan	3
7860	gallina	3
7861	gallarda	3
7862	gafas	3
7863	gacetillero	3
7864	gabinetes	3
7865	fundado	3
7866	funda	3
7867	fulgencia	3
7868	fueras	3
7869	frívolo	3
7870	frenesí	3
7871	frecuentar	3
7872	fraternidad	3
7873	frasco	3
7874	franjas	3
7875	franja	3
7876	franela	3
7877	franceses	3
7878	frágil	3
7879	forzosa	3
7880	formidables	3
7881	formar	3
7882	formalmente	3
7883	forasteros	3
7884	folletín	3
7885	fogoso	3
7886	flotar	3
7887	flotando	3
7888	florido	3
7889	flojedad	3
7890	floja	3
7891	flato	3
7892	fisiológico	3
7893	firmes	3
7894	firmar	3
7895	finge	3
7896	filosóficas	3
7897	filosófica	3
7898	filosofar	3
7899	filo	3
7900	fijaron	3
7901	figurín	3
7902	figúrese	3
7903	fíes	3
7904	fidias	3
7905	fiambres	3
7906	feuillet	3
7907	feudal	3
7908	feria	3
7909	feos	3
7910	femenino	3
7911	femenil	3
7912	favorecer	3
7913	favorable	3
7914	fauna	3
7915	fanatizado	3
7916	fanáticos	3
7917	faltas	3
7918	falsos	3
7919	falsas	3
7920	faena	3
7921	fáciles	3
7922	fabricaba	3
7923	extremosa	3
7924	extravagante	3
7925	extraordinaria	3
7926	extraños	3
7927	extensos	3
7928	expuesto	3
7929	explíquese	3
7930	explique	3
7931	experto	3
7932	expediente	3
7933	expansivo	3
7934	exigido	3
7935	exhibición	3
7936	excomunión	3
7937	exclusivamente	3
7938	excitar	3
7939	excitaban	3
7940	excepciones	3
7941	excelentísimo	3
7942	exaltaba	3
7943	exagerar	3
7944	europeo	3
7945	europa	3
7946	estudiantes	3
7947	estribillo	3
7948	estrepitosos	3
7949	estrepitosas	3
7950	estrechó	3
7951	estrechaba	3
7952	estío	3
7953	estímulos	3
7954	estima	3
7955	estercolero	3
7956	estarán	3
7957	estanquillo	3
7958	estampa	3
7959	estallido	3
7960	estaciones	3
7961	establecimiento	3
7962	establecía	3
7963	esquinas	3
7964	esposas	3
7965	espontáneo	3
7966	espontáneamente	3
7967	esponjas	3
7968	esplendoroso	3
7969	esplendores	3
7970	espiritualidad	3
7971	espiritista	3
7972	espionaje	3
7973	espiga	3
7974	espesas	3
7975	esperma	3
7976	esperado	3
7977	esparcido	3
7978	esparcidas	3
7979	espantaba	3
7980	espaldar	3
7981	espadas	3
7982	esgrima	3
7983	esforzaba	3
7984	esfera	3
7985	escupió	3
7986	escupía	3
7987	escritos	3
7988	escritorio	3
7989	escritores	3
7990	escrita	3
7991	escribirle	3
7992	esconderse	3
7993	escogido	3
7994	escogía	3
7995	esclavina	3
7996	escasas	3
7997	escarlata	3
7998	escarabajos	3
7999	escaleras	3
8000	esbeltez	3
8001	ésa	3
8002	epístola	3
8003	envidiosos	3
8004	envidiada	3
8005	entretenerse	3
8006	entretanto	3
8007	entremeses	3
8008	entregó	3
8009	entregaban	3
8010	entiendan	3
8011	enterrado	3
8012	enternecimientos	3
8013	entendiese	3
8014	entenderlo	3
8015	entablar	3
8016	enseñaban	3
8017	ensalada	3
8018	enrique	3
8019	enredaba	3
8020	enramada	3
8021	enguantada	3
8022	engañarle	3
8023	engañan	3
8024	engañaban	3
8025	enfriaba	3
8026	enérgica	3
8027	encogido	3
8028	encierro	3
8029	encerronas	3
8030	encerrada	3
8031	encendió	3
8032	encendida	3
8033	encarnadas	3
8034	encaramarse	3
8035	encaramado	3
8036	encantado	3
8037	encantada	3
8038	encajes	3
8039	enamoró	3
8040	empuñaba	3
8041	empujaba	3
8042	empleo	3
8043	empeñaban	3
8044	empecatada	3
8045	empapado	3
8046	emigración	3
8047	embozado	3
8048	embalsamado	3
8049	elevación	3
8050	elevaba	3
8051	electricidad	3
8052	electoral	3
8053	ejércitos	3
8054	ejercía	3
8055	efímeras	3
8056	educada	3
8057	edificar	3
8058	edades	3
8059	eclipsado	3
8060	echase	3
8061	durmió	3
8062	duraría	3
8063	durado	3
8064	duradera	3
8065	dudó	3
8066	dogmas	3
8067	dividían	3
8068	dividía	3
8069	divertir	3
8070	diversiones	3
8071	diván	3
8072	diva	3
8073	distrito	3
8074	distraerse	3
8075	distintas	3
8076	distinta	3
8077	distinguían	3
8078	distante	3
8079	disputas	3
8080	disputa	3
8081	dispuestos	3
8082	dispersaron	3
8083	disparó	3
8084	disparatar	3
8085	disparatados	3
8086	disparaba	3
8087	disolvente	3
8088	disimularlo	3
8089	disimulan	3
8090	disimulaban	3
8091	discutían	3
8092	discurría	3
8093	discordia	3
8094	dirigido	3
8095	directiva	3
8096	diputados	3
8097	dioses	3
8098	dinamita	3
8099	dijese	3
8100	dignó	3
8101	digestión	3
8102	dígase	3
8103	diese	3
8104	dieran	3
8105	diciéndose	3
8106	diamantes	3
8107	diálogos	3
8108	diagonales	3
8109	diabólicos	3
8110	diabluras	3
8111	diablura	3
8112	devolver	3
8113	devaneos	3
8114	deteniéndose	3
8115	desvencijada	3
8116	destierro	3
8117	destellos	3
8118	destacaba	3
8119	desprecia	3
8120	déspota	3
8121	despojos	3
8122	desplomado	3
8123	despierta	3
8124	despidieron	3
8125	despertando	3
8126	despedirme	3
8127	despedirla	3
8128	desparpajo	3
8129	desnudas	3
8130	desnudaba	3
8131	desmejorado	3
8132	deslumbrante	3
8133	desigualdad	3
8134	deshonrar	3
8135	deshonrado	3
8136	desgracias	3
8137	desfallecimientos	3
8138	deseó	3
8139	desengañado	3
8140	desencajado	3
8141	desechar	3
8142	deseaban	3
8143	descuide	3
8144	descripción	3
8145	desconfiar	3
8146	desconfiada	3
8147	descargar	3
8148	desaparecían	3
8149	desaliento	3
8150	desairado	3
8151	desahogo	3
8152	desagradable	3
8153	desafíos	3
8154	desafiaba	3
8155	derribo	3
8156	derribar	3
8157	demostró	3
8158	demasiada	3
8159	delirante	3
8160	delgadas	3
8161	deletérea	3
8162	delantal	3
8163	déjeme	3
8164	déjela	3
8165	dejé	3
8166	dejase	3
8167	dejaran	3
8168	dejara	3
8169	déjale	3
8170	dejadme	3
8171	defenderse	3
8172	dedicó	3
8173	dedicaba	3
8174	decoroso	3
8175	decoraciones	3
8176	declarado	3
8177	declamando	3
8178	decisivo	3
8179	decirme	3
8180	decidirse	3
8181	debemos	3
8182	debate	3
8183	darte	3
8184	darme	3
8185	darían	3
8186	dará	3
8187	dándose	3
8188	dame	3
8189	dada	3
8190	curioso	3
8191	curación	3
8192	cumplió	3
8193	cumbres	3
8194	cultivo	3
8195	culinario	3
8196	cuidarse	3
8197	cuidando	3
8198	cuero	3
8199	cuente	3
8200	cubrió	3
8201	cubo	3
8202	cuaderno	3
8203	cruzaba	3
8204	crujientes	3
8205	crónicas	3
8206	crochet	3
8207	cristianas	3
8208	creyese	3
8209	creyentes	3
8210	creyente	3
8211	creyéndose	3
8212	creyéndome	3
8213	creencia	3
8214	creen	3
8215	crédito	3
8216	crecido	3
8217	crear	3
8218	creador	3
8219	costureras	3
8220	costado	3
8221	cortos	3
8222	cortinaje	3
8223	corteza	3
8224	cortesana	3
8225	cortejo	3
8226	cortadas	3
8227	corrupción	3
8228	corrosiva	3
8229	corresponsal	3
8230	correspondía	3
8231	corresponde	3
8232	corregía	3
8233	corredores	3
8234	correctas	3
8235	correcta	3
8236	corralada	3
8237	coronados	3
8238	corazones	3
8239	coraza	3
8240	convirtiendo	3
8241	convinieron	3
8242	convertirlos	3
8243	convertirle	3
8244	conversar	3
8245	conversando	3
8246	conveniente	3
8247	convencida	3
8248	convence	3
8249	controversia	3
8250	contratiempo	3
8251	contrariedades	3
8252	contorno	3
8253	continuando	3
8254	contera	3
8255	contemporáneos	3
8256	contempló	3
8257	contagio	3
8258	consumados	3
8259	construía	3
8260	conste	3
8261	constaba	3
8262	conspirador	3
8263	consolas	3
8264	consolarla	3
8265	consolar	3
8266	consola	3
8267	consienten	3
8268	consideración	3
8269	conservación	3
8270	consecuencia	3
8271	conquistas	3
8272	conquistado	3
8273	conociese	3
8274	conocidos	3
8275	conocida	3
8276	conocerse	3
8277	conocemos	3
8278	conjeturas	3
8279	confusos	3
8280	confusas	3
8281	confundir	3
8282	confundía	3
8283	conformidad	3
8284	conformes	3
8285	confitería	3
8286	confirmó	3
8287	confieso	3
8288	confiese	3
8289	confesonarios	3
8290	conejos	3
8291	conducto	3
8292	condicionales	3
8293	condenaban	3
8294	concluyendo	3
8295	concluían	3
8296	conceptos	3
8297	concentrada	3
8298	conatos	3
8299	comunicaba	3
8300	compungido	3
8301	compromisos	3
8302	compromiso	3
8303	comprometía	3
8304	comprometer	3
8305	compromete	3
8306	comprimidos	3
8307	comprendes	3
8308	compraba	3
8309	composición	3
8310	complicado	3
8311	complicadas	3
8312	complacer	3
8313	competencia	3
8314	compatible	3
8315	compañías	3
8316	compañeras	3
8317	comodidades	3
8318	comitiva	3
8319	comité	3
8320	comidilla	3
8321	cómicas	3
8322	cometía	3
8323	comestibles	3
8324	comería	3
8325	comarca	3
8326	comandante	3
8327	coma	3
8328	colonos	3
8329	colocó	3
8330	colocación	3
8331	colmena	3
8332	colegio	3
8333	colectiva	3
8334	cojo	3
8335	coincidido	3
8336	cogida	3
8337	cogerla	3
8338	coge	3
8339	cofradía	3
8340	código	3
8341	codiciado	3
8342	codiciada	3
8343	cobrando	3
8344	cobardía	3
8345	cobardes	3
8346	club	3
8347	clementina	3
8348	clavos	3
8349	clavó	3
8350	clavar	3
8351	clavando	3
8352	clavadas	3
8353	civilización	3
8354	ciriales	3
8355	circunspecto	3
8356	circunloquios	3
8357	círculos	3
8358	circular	3
8359	circo	3
8360	cintas	3
8361	cilicios	3
8362	científicas	3
8363	cielos	3
8364	cid	3
8365	chuzo	3
8366	churrigueresca	3
8367	chubasco	3
8368	chorros	3
8369	chorro	3
8370	chispa	3
8371	chismes	3
8372	chiquilla	3
8373	china	3
8374	chillones	3
8375	chillidos	3
8376	chillido	3
8377	chiflado	3
8378	chic	3
8379	chasco	3
8380	charol	3
8381	chaparrón	3
8382	chal	3
8383	cesto	3
8384	cesta	3
8385	cerrazón	3
8386	ceremonia	3
8387	cerdos	3
8388	cerco	3
8389	cepillo	3
8390	ceñir	3
8391	centinela	3
8392	censurar	3
8393	censura	3
8394	cenicienta	3
8395	cenaba	3
8396	celosías	3
8397	celebraban	3
8398	cedió	3
8399	cebolletas	3
8400	cazaba	3
8401	cayeron	3
8402	causarle	3
8403	caudillo	3
8404	cauce	3
8405	catedrático	3
8406	castor	3
8407	casillas	3
8408	cascaciruelas	3
8409	casaderas	3
8410	carrillos	3
8411	carreteras	3
8412	carreras	3
8413	caros	3
8414	carneros	3
8415	cargos	3
8416	cargar	3
8417	carbonero	3
8418	caras	3
8419	caramelo	3
8420	caprichosas	3
8421	caprichosa	3
8422	capítulos	3
8423	capitales	3
8424	cañada	3
8425	caña	3
8426	cantidad	3
8427	canteros	3
8428	cantara	3
8429	candoroso	3
8430	candidato	3
8431	candeleros	3
8432	candelas	3
8433	canastillo	3
8434	campillo	3
8435	campanilla	3
8436	campaneros	3
8437	campanarios	3
8438	caminaba	3
8439	calzados	3
8440	calumniar	3
8441	cálices	3
8442	calavera	3
8443	cajero	3
8444	caigo	3
8445	cae	3
8446	cadete	3
8447	cachipote	3
8448	cabizbajo	3
8449	cabían	3
8450	caballerito	3
8451	cábalas	3
8452	busto	3
8453	buscase	3
8454	buscarte	3
8455	buscarlos	3
8456	buscarlo	3
8457	buscarle	3
8458	buscan	3
8459	burlona	3
8460	burlesca	3
8461	burlarse	3
8462	burbujas	3
8463	bulliciosos	3
8464	bucólico	3
8465	bucólica	3
8466	brutalidad	3
8467	bruscos	3
8468	brusco	3
8469	brotaban	3
8470	brotaba	3
8471	bromitas	3
8472	brindando	3
8473	brincos	3
8474	brasa	3
8475	botones	3
8476	botella	3
8477	bostezó	3
8478	borrico	3
8479	borrar	3
8480	bordada	3
8481	bonito	3
8482	bondadosa	3
8483	bonachona	3
8484	bomba	3
8485	bom	3
8486	bolsas	3
8487	bolos	3
8488	bofetón	3
8489	boda	3
8490	bobo	3
8491	bobalicones	3
8492	boba	3
8493	blusa	3
8494	blanquecina	3
8495	bienestar	3
8496	bíblico	3
8497	bestias	3
8498	benevolencia	3
8499	beneficiados	3
8500	bellezas	3
8501	bella	3
8502	belisario	3
8503	bebían	3
8504	be	3
8505	baúl	3
8506	batín	3
8507	batiendo	3
8508	basto	3
8509	barrios	3
8510	barras	3
8511	barragana	3
8512	baroncito	3
8513	barbas	3
8514	bárbaro	3
8515	bárbara	3
8516	bañaba	3
8517	banquete	3
8518	bandadas	3
8519	baladí	3
8520	bajaron	3
8521	bailando	3
8522	bailaba	3
8523	baila	3
8524	badajo	3
8525	bactriana	3
8526	bacante	3
8527	azulada	3
8528	azotó	3
8529	azahar	3
8530	ayudarla	3
8531	ayudara	3
8532	ayudaban	3
8533	avisado	3
8534	avergonzó	3
8535	avergonzaba	3
8536	aventuró	3
8537	aventurar	3
8538	aumentó	3
8539	audaces	3
8540	aturdían	3
8541	aturde	3
8542	atrio	3
8543	atributos	3
8544	atrevo	3
8545	atreviéndose	3
8546	atravesar	3
8547	atravesando	3
8548	atacar	3
8549	asustarle	3
8550	asustan	3
8551	asustados	3
8552	astuta	3
8553	astucia	3
8554	astorga	3
8555	aspiración	3
8556	áspero	3
8557	asomos	3
8558	asistiendo	3
8559	asilo	3
8560	asientos	3
8561	aseguro	3
8562	asegurarse	3
8563	asechanzas	3
8564	ascensión	3
8565	ascender	3
8566	artísticos	3
8567	artistas	3
8568	artesones	3
8569	artefacto	3
8570	arrugada	3
8571	arrugaba	3
8572	arrojase	3
8573	arrodillarse	3
8574	arriesgar	3
8575	arreos	3
8576	arregló	3
8577	arreglado	3
8578	arrebatos	3
8579	arrebato	3
8580	arrastraban	3
8581	arrancando	3
8582	arrancaban	3
8583	aromas	3
8584	armonizar	3
8585	armoniosa	3
8586	armeros	3
8587	armazón	3
8588	aristocrática	3
8589	ardor	3
8590	arca	3
8591	arbustos	3
8592	aragón	3
8593	aquelarre	3
8594	apurado	3
8595	apuntar	3
8596	apuesto	3
8597	apretones	3
8598	apretando	3
8599	aprendiendo	3
8600	aprecio	3
8601	apodo	3
8602	aplazar	3
8603	apasionados	3
8604	apartó	3
8605	apartar	3
8606	aparecido	3
8607	apagar	3
8608	apagaban	3
8609	apaga	3
8610	añadir	3
8611	anunciado	3
8612	antojo	3
8613	antiquísimas	3
8614	antipático	3
8615	antipatía	3
8616	anti	3
8617	antesala	3
8618	ansiaba	3
8619	anguloso	3
8620	angelina	3
8621	anémico	3
8622	anemia	3
8623	anegada	3
8624	andaría	3
8625	andan	3
8626	andaluz	3
8627	andado	3
8628	ancas	3
8629	anarquía	3
8630	anaqueles	3
8631	análogos	3
8632	análogas	3
8633	anacronismos	3
8634	anacleto	3
8635	amontonados	3
8636	amontonada	3
8637	amonestaciones	3
8638	amigotes	3
8639	americana	3
8640	amenazado	3
8641	amena	3
8642	amén	3
8643	ambicioso	3
8644	ambicionar	3
8645	amarle	3
8646	amadeo	3
8647	amada	3
8648	amables	3
8649	altares	3
8650	alrededores	3
8651	almohadones	3
8652	almíbares	3
8653	alfonso	3
8654	aleteo	3
8655	alentar	3
8656	alemana	3
8657	alejado	3
8658	alegró	3
8659	alegrarse	3
8660	alegorías	3
8661	alcázar	3
8662	alcaravanes	3
8663	alcantarillas	3
8664	alborotaba	3
8665	albergue	3
8666	alarmarse	3
8667	alarmante	3
8668	alarma	3
8669	alaridos	3
8670	ajustar	3
8671	ajuar	3
8672	ajeno	3
8673	aguardaba	3
8674	aguantar	3
8675	agria	3
8676	agregada	3
8677	agradecida	3
8678	agolpaban	3
8679	agarrada	3
8680	agapita	3
8681	afirmaciones	3
8682	afilados	3
8683	afeminado	3
8684	afectos	3
8685	afecto	3
8686	afectada	3
8687	afectaba	3
8688	advertir	3
8689	advertido	3
8690	advertía	3
8691	adúltero	3
8692	adulaba	3
8693	adquirir	3
8694	adorno	3
8695	adoradores	3
8696	adorador	3
8697	adorado	3
8698	adora	3
8699	adonde	3
8700	admitir	3
8701	admitido	3
8702	admirable	3
8703	adivinado	3
8704	adelantaba	3
8705	acuérdate	3
8706	acudieron	3
8707	acudido	3
8708	actores	3
8709	acostumbraba	3
8710	acompañara	3
8711	acompañando	3
8712	acólitos	3
8713	acogió	3
8714	aclimatación	3
8715	acierto	3
8716	achaques	3
8717	achacaba	3
8718	acercaron	3
8719	acendrado	3
8720	acechaba	3
8721	accidente	3
8722	acataba	3
8723	acabaron	3
8724	abuso	3
8725	abundantes	3
8726	abundancia	3
8727	abstracto	3
8728	abstracta	3
8729	absorbente	3
8730	ábside	3
8731	abrochó	3
8732	abrasaba	3
8733	abra	3
8734	abono	3
8735	abolengo	3
8736	aberraciones	3
8737	abandonarle	3
8738	abandonaban	3
8739	zurriago	2
8740	zumbido	2
8741	zumbaba	2
8742	zig	2
8743	zarzamora	2
8744	zapatero	2
8745	zánganos	2
8746	zagal	2
8747	yugo	2
8748	york	2
8749	yendo	2
8750	x	2
8751	werther	2
8752	vulgarmente	2
8753	vulgarísima	2
8754	vuelvan	2
8755	vos	2
8756	volviose	2
8757	volví	2
8758	volveremos	2
8759	volverán	2
8760	volverá	2
8761	volvemos	2
8762	voluptuosamente	2
8763	voluntariamente	2
8764	voluntades	2
8765	volaría	2
8766	volado	2
8767	vociferó	2
8768	vocabulario	2
8769	viviese	2
8770	vivieron	2
8771	viviente	2
8772	viviendo	2
8773	viveza	2
8774	vives	2
8775	vivaracho	2
8776	vivaracha	2
8777	visual	2
8778	vistazo	2
8779	vistalegre	2
8780	viso	2
8781	vislumbraba	2
8782	visitó	2
8783	visitado	2
8784	viscoso	2
8785	viscosa	2
8786	virtuosísima	2
8787	viril	2
8788	virginal	2
8789	violeta	2
8790	violentas	2
8791	violentar	2
8792	violenta	2
8793	violencias	2
8794	vinos	2
8795	viniesen	2
8796	vinajeras	2
8797	villegas	2
8798	viles	2
8799	viii	2
8800	vii	2
8801	vigorosas	2
8802	vigilias	2
8803	viga	2
8804	viesen	2
8805	vieras	2
8806	vienes	2
8807	viéndose	2
8808	viejecillo	2
8809	viciosa	2
8810	vibrantes	2
8811	vestiduras	2
8812	vespucios	2
8813	vespucio	2
8814	vertiginosas	2
8815	verticales	2
8816	verme	2
8817	verlos	2
8818	verjas	2
8819	veritas	2
8820	vergonzante	2
8821	veré	2
8822	verdaderas	2
8823	verdaderamente	2
8824	veranos	2
8825	veranillo	2
8826	ventorrillos	2
8827	venirse	2
8828	veniales	2
8829	venganzas	2
8830	vengan	2
8831	vengábase	2
8832	vengaba	2
8833	vendré	2
8834	vendrán	2
8835	vendió	2
8836	vendían	2
8837	vendemos	2
8838	venciste	2
8839	vencieron	2
8840	vencidas	2
8841	vencían	2
8842	vencerían	2
8843	vencerás	2
8844	vence	2
8845	vello	2
8846	veintiséis	2
8847	vega	2
8848	véase	2
8849	vayan	2
8850	vayamos	2
8851	vapor	2
8852	vanamente	2
8853	vanagloria	2
8854	vámonos	2
8855	valientes	2
8856	valido	2
8857	valerse	2
8858	valer	2
8859	valdrá	2
8860	valdés	2
8861	vajilla	2
8862	vagando	2
8863	vade	2
8864	vacilar	2
8865	vacilantes	2
8866	vacilaciones	2
8867	vaca	2
8868	utilitaria	2
8869	usado	2
8870	usaban	2
8871	usa	2
8872	úrsula	2
8873	uña	2
8874	unido	2
8875	ultramontanos	2
8876	ultrajes	2
8877	ultraje	2
8878	ultrajados	2
8879	ultra	2
8880	uf	2
8881	tuviesen	2
8882	tuvieran	2
8883	tutti	2
8884	tuteaba	2
8885	turcos	2
8886	turbas	2
8887	turba	2
8888	tuo	2
8889	tunante	2
8890	tumba	2
8891	tul	2
8892	tubinga	2
8893	truquage	2
8894	trovadores	2
8895	tropezaban	2
8896	tropa	2
8897	trompetas	2
8898	trompeta	2
8899	triunfó	2
8900	triunfador	2
8901	triunfado	2
8902	triunfaba	2
8903	tributando	2
8904	trepar	2
8905	trepaban	2
8906	trenzas	2
8907	tremendos	2
8908	tremendo	2
8909	tregua	2
8910	trayendo	2
8911	traviesa	2
8912	travesaño	2
8913	trataron	2
8914	tratándole	2
8915	tratamos	2
8916	tratamiento	2
8917	trastos	2
8918	trasto	2
8919	trastienda	2
8920	traspasaba	2
8921	trapillo	2
8922	trapicheos	2
8923	transformarse	2
8924	transformaciones	2
8925	transeúnte	2
8926	transacciones	2
8927	tranquilizó	2
8928	tranquilizar	2
8929	tranquilícese	2
8930	tramo	2
8931	trama	2
8932	traidora	2
8933	traídas	2
8934	tragos	2
8935	trágica	2
8936	tragedia	2
8937	tragarse	2
8938	tragando	2
8939	traeré	2
8940	tráeme	2
8941	trae	2
8942	traducir	2
8943	traducción	2
8944	tradiciones	2
8945	tradicionales	2
8946	trabajadores	2
8947	trabajador	2
8948	trabajaban	2
8949	tostados	2
8950	tosió	2
8951	tosca	2
8952	tortuosas	2
8953	torso	2
8954	torrecilla	2
8955	torquemada	2
8956	torpezas	2
8957	tornillo	2
8958	torneados	2
8959	torneada	2
8960	torero	2
8961	torcidas	2
8962	toques	2
8963	topó	2
8964	topo	2
8965	toos	2
8966	tontiloco	2
8967	tontería	2
8968	tonsurado	2
8969	tonel	2
8970	tomillares	2
8971	tomas	2
8972	tomarle	2
8973	tomándola	2
8974	tolerarlas	2
8975	tocadas	2
8976	toalla	2
8977	to	2
8978	titulaba	2
8979	tirón	2
8980	tirarse	2
8981	tirantez	2
8982	tirantes	2
8983	tirador	2
8984	tirado	2
8985	tipos	2
8986	tíos	2
8987	tinto	2
8988	tintas	2
8989	tino	2
8990	timorato	2
8991	times	2
8992	tiesa	2
8993	tiemblo	2
8994	tiemblan	2
8995	tié	2
8996	tic	2
8997	thorum	2
8998	the	2
8999	tez	2
9000	textos	2
9001	testarudo	2
9002	tesorera	2
9003	tertulio	2
9004	terquedad	2
9005	terminaba	2
9006	tercero	2
9007	terca	2
9008	teóricos	2
9009	teológica	2
9010	teologías	2
9011	teñían	2
9012	tente	2
9013	tentada	2
9014	tenorios	2
9015	teníamos	2
9016	tendremos	2
9017	tendrás	2
9018	tendencias	2
9019	temporales	2
9020	templos	2
9021	temple	2
9022	templado	2
9023	templada	2
9024	temperatura	2
9025	temió	2
9026	temibles	2
9027	temerarias	2
9028	temen	2
9029	temblorosas	2
9030	temblores	2
9031	temblonas	2
9032	telas	2
9033	teje	2
9034	técnicas	2
9035	tarsa	2
9036	tarjeta	2
9037	tardía	2
9038	tardase	2
9039	tapiz	2
9040	tapicero	2
9041	tapete	2
9042	tapadillo	2
9043	tañidos	2
9044	tangible	2
9045	tamaza	2
9046	tamañas	2
9047	tamaña	2
9048	talones	2
9049	talón	2
9050	talla	2
9051	talía	2
9052	talante	2
9053	tacones	2
9054	taco	2
9055	tacaño	2
9056	tac	2
9057	tablero	2
9058	tabernas	2
9059	sutilmente	2
9060	susurro	2
9061	sustituir	2
9062	suspirando	2
9063	suspendida	2
9064	susceptibilidad	2
9065	surtidores	2
9066	supongamos	2
9067	supone	2
9068	suplicando	2
9069	suplicado	2
9070	supiese	2
9071	supieron	2
9072	superlativos	2
9073	sumidos	2
9074	sumidas	2
9075	sumía	2
9076	sumergido	2
9077	sujetar	2
9078	sujetaban	2
9079	sugestiones	2
9080	sugería	2
9081	sufrido	2
9082	sufre	2
9083	suficientemente	2
9084	sueña	2
9085	sueltos	2
9086	suelen	2
9087	sueldo	2
9088	sudeste	2
9089	sucumbiría	2
9090	suculentos	2
9091	suciedad	2
9092	sucedáneos	2
9093	subterráneas	2
9094	subterránea	2
9095	subrepticio	2
9096	subrepticiamente	2
9097	submarina	2
9098	subiera	2
9099	subida	2
9100	subasta	2
9101	subamos	2
9102	suavizar	2
9103	suavizaba	2
9104	sr	2
9105	sostuvo	2
9106	sostengo	2
9107	sospechosa	2
9108	sospechando	2
9109	sospechado	2
9110	sortijas	2
9111	sorprendidas	2
9112	sorprendida	2
9113	sordidez	2
9114	soplos	2
9115	soñolienta	2
9116	soñada	2
9117	sonsonete	2
9118	sonrisita	2
9119	sonido	2
9120	sonaron	2
9121	sonámbulo	2
9122	sonajas	2
9123	sombrillas	2
9124	soltura	2
9125	soltando	2
9126	solícito	2
9127	solicitantes	2
9128	solicitante	2
9129	solicitadas	2
9130	soldada	2
9131	solariegas	2
9132	solapada	2
9133	sofocados	2
9134	socorrido	2
9135	socialistas	2
9136	socarronería	2
9137	socarrona	2
9138	sobro	2
9139	sobrinilla	2
9140	sobrenaturales	2
9141	sobrado	2
9142	soberana	2
9143	situado	2
9144	sistemático	2
9145	sistemáticamente	2
9146	sistemas	2
9147	sirviendo	2
9148	sinuosas	2
9149	síntoma	2
9150	síntesis	2
9151	simulacro	2
9152	simoníaco	2
9153	simoniaco	2
9154	simón	2
9155	similor	2
9156	simétricos	2
9157	simétrico	2
9158	sillones	2
9159	silbantes	2
9160	silbaban	2
9161	siguientes	2
9162	siguen	2
9163	signum	2
9164	signos	2
9165	significativa	2
9166	significar	2
9167	significado	2
9168	significaban	2
9169	significa	2
9170	sierva	2
9171	sienta	2
9172	sicilia	2
9173	sexto	2
9174	setos	2
9175	setentón	2
9176	sesudos	2
9177	seso	2
9178	servidor	2
9179	serre	2
9180	serrar	2
9181	seremos	2
9182	serás	2
9183	seráfico	2
9184	sepultados	2
9185	separó	2
9186	seor	2
9187	señuelo	2
9188	señoronas	2
9189	señorial	2
9190	sentirla	2
9191	sentimentales	2
9192	sentí	2
9193	sentarme	2
9194	sentadas	2
9195	sensuales	2
9196	sensibilidad	2
9197	sendero	2
9198	senda	2
9199	seminaristas	2
9200	semejaban	2
9201	sembrado	2
9202	semblante	2
9203	seguras	2
9204	seguramente	2
9205	segundón	2
9206	seguirla	2
9207	seguiría	2
9208	seglares	2
9209	segada	2
9210	seducido	2
9211	seducía	2
9212	secretaría	2
9213	secaba	2
9214	scortum	2
9215	sazón	2
9216	satisface	2
9217	satín	2
9218	sarcasmos	2
9219	saqué	2
9220	saque	2
9221	sapos	2
9222	santísimo	2
9223	santiguó	2
9224	santidades	2
9225	sans	2
9226	sangría	2
9227	sancionado	2
9228	salvedades	2
9229	salvarle	2
9230	salvarla	2
9231	salvaría	2
9232	sálvamelo	2
9233	salvaban	2
9234	saludaron	2
9235	saludarla	2
9236	saltaron	2
9237	saltaría	2
9238	salsa	2
9239	salí	2
9240	salero	2
9241	saldremos	2
9242	saldrá	2
9243	sajón	2
9244	sacudidas	2
9245	sacro	2
9246	sacristanes	2
9247	sacrílegas	2
9248	sacrificarme	2
9249	sacrificaban	2
9250	sacos	2
9251	sacándole	2
9252	sabrían	2
9253	saborearle	2
9254	saborea	2
9255	saborcillo	2
9256	sabías	2
9257	sabias	2
9258	saberse	2
9259	rutinario	2
9260	rumiar	2
9261	ruega	2
9262	ruborosa	2
9263	rubí	2
9264	rozaban	2
9265	rousseau	2
9266	rotas	2
9267	rostros	2
9268	rosal	2
9269	rosadas	2
9270	rondar	2
9271	roncos	2
9272	rompieron	2
9273	rompe	2
9274	románico	2
9275	romana	2
9276	rollo	2
9277	rolliza	2
9278	rojizos	2
9279	rogar	2
9280	rogado	2
9281	roedores	2
9282	rodrigón	2
9283	rodeo	2
9284	rodeando	2
9285	rodeados	2
9286	rodeadas	2
9287	rodamos	2
9288	rodaba	2
9289	roces	2
9290	robustos	2
9291	robustez	2
9292	robar	2
9293	rizoso	2
9294	rito	2
9295	risueños	2
9296	risueñas	2
9297	riquísima	2
9298	riquezas	2
9299	riñe	2
9300	rinden	2
9301	rigoroso	2
9302	rigorosa	2
9303	rige	2
9304	riesgos	2
9305	riesgo	2
9306	rieron	2
9307	riego	2
9308	ribetes	2
9309	rezo	2
9310	rezan	2
9311	reza	2
9312	revueltos	2
9313	revueltas	2
9314	revuelta	2
9315	revolviendo	2
9316	revolvía	2
9317	revolucionaria	2
9318	revoltosos	2
9319	revistas	2
9320	revés	2
9321	revelado	2
9322	reunión	2
9323	reunían	2
9324	retumbó	2
9325	retumbaba	2
9326	retrocedió	2
9327	retrocedido	2
9328	retroceder	2
9329	retro	2
9330	retraso	2
9331	retrasar	2
9332	retraía	2
9333	retozonas	2
9334	retozona	2
9335	retorcían	2
9336	retorcer	2
9337	retoño	2
9338	retirar	2
9339	resultados	2
9340	resuelva	2
9341	resucitado	2
9342	restituyó	2
9343	restituiría	2
9344	restituido	2
9345	respetuoso	2
9346	respete	2
9347	respetabilidad	2
9348	respectiva	2
9349	respaldo	2
9350	resonó	2
9351	resonar	2
9352	resonancia	2
9353	resolverán	2
9354	resignaban	2
9355	reses	2
9356	reservado	2
9357	reservada	2
9358	resbaladizo	2
9359	resbaladiza	2
9360	resaltando	2
9361	resabios	2
9362	rerum	2
9363	requisitos	2
9364	requiescat	2
9365	repugnaban	2
9366	republicanismo	2
9367	reps	2
9368	representada	2
9369	reprendió	2
9370	repitieron	2
9371	repetido	2
9372	repetición	2
9373	repentinos	2
9374	repatriación	2
9375	repasar	2
9376	repartir	2
9377	reparó	2
9378	reñido	2
9379	reñían	2
9380	renunció	2
9381	renunciara	2
9382	renglones	2
9383	renegado	2
9384	renegaban	2
9385	rendir	2
9386	rendijas	2
9387	rencor	2
9388	renacer	2
9389	remotos	2
9390	remotas	2
9391	remota	2
9392	remontarse	2
9393	remontándose	2
9394	remilgos	2
9395	remedios	2
9396	relativo	2
9397	relativamente	2
9398	rejuvenecía	2
9399	reiría	2
9400	regulares	2
9401	regueros	2
9402	regordeta	2
9403	regocijo	2
9404	reglas	2
9405	registró	2
9406	registro	2
9407	regía	2
9408	regatas	2
9409	regalaban	2
9410	reforma	2
9411	reflexión	2
9412	refiriendo	2
9413	referirse	2
9414	referirlos	2
9415	referido	2
9416	reemplazar	2
9417	reducía	2
9418	redondas	2
9419	redil	2
9420	rededor	2
9421	redactores	2
9422	recurrido	2
9423	rectificó	2
9424	rectificar	2
9425	rectificaba	2
9426	recrearse	2
9427	recrear	2
9428	recreaba	2
9429	recortar	2
9430	recorren	2
9431	recordarle	2
9432	recordado	2
9433	reconocido	2
9434	recónditos	2
9435	reconciliarse	2
9436	reconciliación	2
9437	recomienda	2
9438	recomendar	2
9439	recomendado	2
9440	recoletas	2
9441	recolección	2
9442	recogimiento	2
9443	recogidas	2
9444	recogida	2
9445	recogía	2
9446	recodo	2
9447	recobró	2
9448	reclutas	2
9449	recitó	2
9450	recita	2
9451	recipiente	2
9452	recibiendo	2
9453	recibían	2
9454	recibe	2
9455	rechinar	2
9456	recetó	2
9457	recelo	2
9458	recatadas	2
9459	recargada	2
9460	recaída	2
9461	rebeldía	2
9462	rebelde	2
9463	rebelaba	2
9464	rebaños	2
9465	reata	2
9466	realmente	2
9467	realizar	2
9468	realismo	2
9469	razonables	2
9470	rayitas	2
9471	rayaba	2
9472	rasguño	2
9473	rascaba	2
9474	raros	2
9475	raquíticas	2
9476	rápidamente	2
9477	rapé	2
9478	ranas	2
9479	ramitos	2
9480	raído	2
9481	raída	2
9482	radicalmente	2
9483	radiante	2
9484	racionales	2
9485	raciocinio	2
9486	rabo	2
9487	rabió	2
9488	rabiaba	2
9489	quitarse	2
9490	quitará	2
9491	quitan	2
9492	quisiéramos	2
9493	quintas	2
9494	química	2
9495	quimeras	2
9496	quijote	2
9497	quieto	2
9498	quietas	2
9499	quieta	2
9500	quiénes	2
9501	quienes	2
9502	quiebra	2
9503	quevedo	2
9504	queso	2
9505	querrían	2
9506	queridísimo	2
9507	querías	2
9508	quererte	2
9509	quererle	2
9510	quejado	2
9511	quedé	2
9512	quede	2
9513	quedará	2
9514	quedara	2
9515	quedando	2
9516	quebraban	2
9517	pusieran	2
9518	purísimo	2
9519	puñetazos	2
9520	puntiagudos	2
9521	puntiagudo	2
9522	pundonoroso	2
9523	pun	2
9524	púlpitos	2
9525	pulmón	2
9526	pulgar	2
9527	pulgadas	2
9528	pulcras	2
9529	puestas	2
9530	puerco	2
9531	pueblecillo	2
9532	pucheros	2
9533	puchero	2
9534	publicado	2
9535	púas	2
9536	psicológicos	2
9537	prudentísimo	2
9538	próximos	2
9539	provocativos	2
9540	provocase	2
9541	provocar	2
9542	provocaciones	2
9543	provocaba	2
9544	provisorato	2
9545	provisional	2
9546	provincialismo	2
9547	provinciales	2
9548	protestado	2
9549	protestaban	2
9550	protegido	2
9551	proteger	2
9552	protector	2
9553	protagonista	2
9554	prostituida	2
9555	prosaicos	2
9556	prórroga	2
9557	propusieron	2
9558	proporcionada	2
9559	proponerle	2
9560	proponer	2
9561	propone	2
9562	propietario	2
9563	propicia	2
9564	pronunciar	2
9565	pronuncian	2
9566	pronunciado	2
9567	pronunciaba	2
9568	pronta	2
9569	prolongó	2
9570	prohibidas	2
9571	profusión	2
9572	profundos	2
9573	profesión	2
9574	profesado	2
9575	profesaba	2
9576	profesa	2
9577	profanas	2
9578	profanaba	2
9579	producían	2
9580	producen	2
9581	produce	2
9582	prodigarse	2
9583	prodigado	2
9584	procuraría	2
9585	procul	2
9586	proceso	2
9587	procesiones	2
9588	proceden	2
9589	procaz	2
9590	probarle	2
9591	probando	2
9592	probabilidades	2
9593	probabilidad	2
9594	privilegios	2
9595	privada	2
9596	prisioneros	2
9597	prisionera	2
9598	pringue	2
9599	primitiva	2
9600	primaveras	2
9601	previsto	2
9602	pretendida	2
9603	pretende	2
9604	presto	2
9605	préstamo	2
9606	prestados	2
9607	prestaba	2
9608	preso	2
9609	presidenta	2
9610	presentados	2
9611	presenciaban	2
9612	prescripciones	2
9613	prescindía	2
9614	preparase	2
9615	prepararse	2
9616	preparan	2
9617	preparados	2
9618	preocupa	2
9619	premiar	2
9620	pregunto	2
9621	pregunté	2
9622	preguntárselo	2
9623	preguntando	2
9624	pregonando	2
9625	preferencias	2
9626	preferencia	2
9627	predilecta	2
9628	predicando	2
9629	predicadores	2
9630	predica	2
9631	precocidad	2
9632	precoces	2
9633	preclaros	2
9634	precisar	2
9635	precipitar	2
9636	precipitados	2
9637	preciaba	2
9638	preces	2
9639	prebendados	2
9640	pp	2
9641	potencia	2
9642	postrada	2
9643	postiza	2
9644	postigos	2
9645	postas	2
9646	posibilidad	2
9647	poseer	2
9648	posada	2
9649	pórticos	2
9650	portátil	2
9651	porqué	2
9652	pormenor	2
9653	porcelana	2
9654	popularidad	2
9655	populacho	2
9656	pontificia	2
9657	pontifical	2
9658	ponga	2
9659	ponerme	2
9660	pomares	2
9661	polvos	2
9662	politiquilla	2
9663	políticas	2
9664	polichinela	2
9665	polémicas	2
9666	poéticos	2
9667	podridos	2
9668	podrido	2
9669	podríamos	2
9670	podrán	2
9671	poderes	2
9672	podaba	2
9673	poblaba	2
9674	plomizo	2
9675	pliegue	2
9676	plena	2
9677	pleitos	2
9678	pleito	2
9679	plegarias	2
9680	plazas	2
9681	platónicamente	2
9682	platerescos	2
9683	plastón	2
9684	plástica	2
9685	plantones	2
9686	plano	2
9687	placas	2
9688	pistoletazo	2
9689	pisotón	2
9690	pisarle	2
9691	pisaban	2
9692	piruetas	2
9693	piropo	2
9694	pirámide	2
9695	pintón	2
9696	pintas	2
9697	pintarle	2
9698	pintadas	2
9699	pintaba	2
9700	pinchazos	2
9701	pimientos	2
9702	pilón	2
9703	pilluelos	2
9704	pílades	2
9705	pila	2
9706	pierdo	2
9707	pienses	2
9708	piensas	2
9709	pieles	2
9710	pido	2
9711	pidiera	2
9712	pides	2
9713	picos	2
9714	picarescas	2
9715	picar	2
9716	pican	2
9717	picado	2
9718	picada	2
9719	pías	2
9720	petrica	2
9721	petitorio	2
9722	petaca	2
9723	pestañear	2
9724	pestañas	2
9725	pesos	2
9726	pesimista	2
9727	pésima	2
9728	pescaron	2
9729	pesando	2
9730	pésame	2
9731	pertenecían	2
9732	persuadir	2
9733	perspicaz	2
9734	personilla	2
9735	personalidad	2
9736	personales	2
9737	persigue	2
9738	perseguidas	2
9739	perseguida	2
9740	perpetuo	2
9741	permitirse	2
9742	permitiéndose	2
9743	permítame	2
9744	permanecer	2
9745	perla	2
9746	perjudica	2
9747	períodos	2
9748	pergamino	2
9749	perfiles	2
9750	perdones	2
9751	perdóneme	2
9752	perdonarla	2
9753	pérdida	2
9754	perdían	2
9755	perderlo	2
9756	perderle	2
9757	percha	2
9758	peón	2
9759	peñón	2
9760	peña	2
9761	pensativa	2
9762	pensase	2
9763	pensándolo	2
9764	penitencias	2
9765	penetrantes	2
9766	penetra	2
9767	pendón	2
9768	pendía	2
9769	peluca	2
9770	pelota	2
9771	peinaba	2
9772	pegar	2
9773	pegaban	2
9774	pega	2
9775	pedradas	2
9776	pedirla	2
9777	pediría	2
9778	pediré	2
9779	pedestre	2
9780	pedante	2
9781	pedagógico	2
9782	pechuga	2
9783	pecaminoso	2
9784	pecaminosas	2
9785	pecadores	2
9786	pecador	2
9787	pecaban	2
9788	pausas	2
9789	pausadas	2
9790	pausada	2
9791	patrón	2
9792	patrimonio	2
9793	pato	2
9794	patética	2
9795	patente	2
9796	patatas	2
9797	patata	2
9798	pataleo	2
9799	patada	2
9800	pata	2
9801	pastoril	2
9802	pastoral	2
9803	pasmos	2
9804	pasmo	2
9805	pásmese	2
9806	pasiva	2
9807	pasioncilla	2
9808	pasiegos	2
9809	pasearse	2
9810	pascuas	2
9811	pasatiempos	2
9812	pasas	2
9813	pasaría	2
9814	pasajero	2
9815	pasajeras	2
9816	pasadizos	2
9817	partir	2
9818	partículas	2
9819	participó	2
9820	participar	2
9821	partía	2
9822	parsimonia	2
9823	parroquianos	2
9824	párrocos	2
9825	párrafo	2
9826	parques	2
9827	paroxismo	2
9828	parodias	2
9829	pareciese	2
9830	parecerían	2
9831	parecería	2
9832	parecerá	2
9833	pardos	2
9834	pardiez	2
9835	parcería	2
9836	parase	2
9837	pararse	2
9838	parándose	2
9839	páramo	2
9840	paraje	2
9841	paraban	2
9842	paquita	2
9843	papas	2
9844	papando	2
9845	papanatas	2
9846	pañales	2
9847	panzudas	2
9848	pantorrillas	2
9849	pantoja	2
9850	paniaguados	2
9851	panes	2
9852	palpable	2
9853	palomar	2
9854	palmera	2
9855	palidece	2
9856	palaciegas	2
9857	paje	2
9858	pajas	2
9859	pájara	2
9860	paisanos	2
9861	pagó	2
9862	pagará	2
9863	pagada	2
9864	padrenuestros	2
9865	padeció	2
9866	padeciendo	2
9867	pacífica	2
9868	pace	2
9869	oyentes	2
9870	oyéndole	2
9871	oyen	2
9872	osos	2
9873	osaría	2
9874	osa	2
9875	ortodoxos	2
9876	ortigas	2
9877	ornitólogo	2
9878	ornamento	2
9879	orlada	2
9880	originado	2
9881	orientales	2
9882	orfandad	2
9883	ordenó	2
9884	ordenanza	2
9885	ordenados	2
9886	ordena	2
9887	or	2
9888	opuesto	2
9889	optimista	2
9890	oprimido	2
9891	oprime	2
9892	oponían	2
9893	operaciones	2
9894	opacas	2
9895	onzas	2
9896	ondulaciones	2
9897	olvidarse	2
9898	olvidaría	2
9899	olorosa	2
9900	olfateado	2
9901	ojival	2
9902	ojillos	2
9903	ojeroso	2
9904	oírlas	2
9905	oigan	2
9906	oidium	2
9907	oí	2
9908	ofrezca	2
9909	ofrenda	2
9910	ofreciera	2
9911	ofrecerle	2
9912	ofrecen	2
9913	oficialmente	2
9914	ofensa	2
9915	ofendía	2
9916	odios	2
9917	odiaba	2
9918	oda	2
9919	ocurrencias	2
9920	ocupase	2
9921	ocupados	2
9922	ocultárselo	2
9923	ocultarlo	2
9924	ociosos	2
9925	ocioso	2
9926	ociosidad	2
9927	ochocientos	2
9928	ocasionadas	2
9929	obstinó	2
9930	obstinado	2
9931	obstante	2
9932	observando	2
9933	observa	2
9934	obsequios	2
9935	obsequio	2
9936	obsequiándote	2
9937	obscenidades	2
9938	obrero	2
9939	obligo	2
9940	obligándole	2
9941	obligan	2
9942	obedeciendo	2
9943	obedecido	2
9944	nupcial	2
9945	nueces	2
9946	nubecilla	2
9947	novelesca	2
9948	notase	2
9949	nocturnas	2
9950	nobis	2
9951	niegue	2
9952	nido	2
9953	nichos	2
9954	nevada	2
9955	neuralgia	2
9956	nerviosilla	2
9957	negruzco	2
9958	negruzca	2
9959	negrura	2
9960	negarme	2
9961	negarle	2
9962	negando	2
9963	negaciones	2
9964	negación	2
9965	necias	2
9966	necesitará	2
9967	necesitado	2
9968	necesitaban	2
9969	neblina	2
9970	nazarena	2
9971	navegar	2
9972	nauseabundo	2
9973	naturalezas	2
9974	natura	2
9975	natillas	2
9976	narrador	2
9977	naranja	2
9978	nado	2
9979	nación	2
9980	mutuas	2
9981	muslo	2
9982	músico	2
9983	muscular	2
9984	murmura	2
9985	murmullos	2
9986	murillo	2
9987	muñeca	2
9988	mundanos	2
9989	mundana	2
9990	muevas	2
9991	muestra	2
9992	mueca	2
9993	mudó	2
9994	mudéjar	2
9995	mudarse	2
9996	mudar	2
9997	mudaba	2
9998	muchísimo	2
9999	muchedumbres	2
10000	mozalbete	2
10001	movile	2
10002	motín	2
10003	mostrencos	2
10004	mostrarse	2
10005	mosquitos	2
10006	mosquito	2
10007	mortificación	2
10008	mortifica	2
10009	moro	2
10010	morirás	2
10011	moreto	2
10012	mordiéndose	2
10013	mordiendo	2
10014	morderla	2
10015	moratín	2
10016	morados	2
10017	moqueta	2
10018	montañesa	2
10019	monótonos	2
10020	monísima	2
10021	molina	2
10022	molière	2
10023	molicie	2
10024	molestias	2
10025	molestas	2
10026	molestarla	2
10027	molestado	2
10028	mole	2
10029	molde	2
10030	mojigata	2
10031	mojadura	2
10032	mohín	2
10033	modificar	2
10034	modernas	2
10035	moderada	2
10036	modelada	2
10037	mister	2
10038	misiones	2
10039	misericordioso	2
10040	miro	2
10041	mírele	2
10042	mirarlo	2
10043	mirarles	2
10044	mirándose	2
10045	mirándole	2
10046	minoría	2
10047	mínimo	2
10048	mínguez	2
10049	minerva	2
10050	minarle	2
10051	minar	2
10052	minando	2
10053	mimoso	2
10054	mimosas	2
10055	mimos	2
10056	millonaria	2
10057	miliciano	2
10058	miles	2
10059	migajas	2
10060	miente	2
10061	mieles	2
10062	miedosos	2
10063	midiendo	2
10064	midas	2
10065	microscopio	2
10066	mías	2
10067	mezquina	2
10068	mezclar	2
10069	meticulosa	2
10070	meten	2
10071	mete	2
10072	metálicas	2
10073	metafísico	2
10074	meta	2
10075	mesándose	2
10076	meriendas	2
10077	meretriz	2
10078	mercancía	2
10079	mercaderes	2
10080	menudencias	2
10081	menudas	2
10082	mentecato	2
10083	menoscabo	2
10084	menores	2
10085	menear	2
10086	melosa	2
10087	melódica	2
10088	meléndez	2
10089	mejorcito	2
10090	mejorado	2
10091	mefistófeles	2
10092	medrando	2
10093	meditaría	2
10094	meditaciones	2
10095	meditabundo	2
10096	medido	2
10097	mediar	2
10098	mediana	2
10099	mediados	2
10100	medía	2
10101	medallón	2
10102	medallas	2
10103	mechones	2
10104	mecedoras	2
10105	mazorca	2
10106	matutinas	2
10107	matrona	2
10108	matrimonios	2
10109	matiz	2
10110	matilde	2
10111	matarlos	2
10112	matanzas	2
10113	matado	2
10114	mástil	2
10115	masculino	2
10116	mascar	2
10117	mascaba	2
10118	mártires	2
10119	marrullero	2
10120	marrón	2
10121	maroto	2
10122	margarita	2
10123	marejada	2
10124	marearle	2
10125	mareada	2
10126	mareaban	2
10127	marcho	2
10128	maquiavelo	2
10129	maquiavélico	2
10130	manzanos	2
10131	manuel	2
10132	manteca	2
10133	mansión	2
10134	mansedumbre	2
10135	manrique	2
10136	manotadas	2
10137	manolito	2
10138	manolé	2
10139	manirroto	2
10140	maniqueos	2
10141	maniático	2
10142	maníaco	2
10143	manejo	2
10144	maneje	2
10145	manejando	2
10146	maneja	2
10147	mandatos	2
10148	mandato	2
10149	mandan	2
10150	mancharse	2
10151	manchado	2
10152	mancebos	2
10153	mampara	2
10154	mamarracho	2
10155	maltratados	2
10156	maltratada	2
10157	malsano	2
10158	malsana	2
10159	malorum	2
10160	maliciosas	2
10161	malicias	2
10162	malhumorado	2
10163	maldiciones	2
10164	maldición	2
10165	maldicientes	2
10166	maldiciente	2
10167	maldice	2
10168	maldecían	2
10169	maldecía	2
10170	majestuosamente	2
10171	magullaba	2
10172	magnetismo	2
10173	mágica	2
10174	magia	2
10175	magdalena	2
10176	madrugón	2
10177	madrileños	2
10178	macizos	2
10179	lutero	2
10180	lunes	2
10181	lune	2
10182	lunar	2
10183	luminoso	2
10184	lujosas	2
10185	lugarteniente	2
10186	lugareños	2
10187	luciría	2
10188	lucientes	2
10189	luciente	2
10190	lucecillas	2
10191	luce	2
10192	lucas	2
10193	lotería	2
10194	lona	2
10195	lomos	2
10196	lograr	2
10197	logrado	2
10198	locuacidad	2
10199	locales	2
10200	llueva	2
10201	llovido	2
10202	llovería	2
10203	lloras	2
10204	llevo	2
10205	llevas	2
10206	llevárselo	2
10207	llevarse	2
10208	llevarle	2
10209	llevaría	2
10210	llevará	2
10211	llevándola	2
10212	llevamos	2
10213	llenaron	2
10214	llenar	2
10215	llegas	2
10216	llegaran	2
10217	llegará	2
10218	llegamos	2
10219	llavín	2
10220	llantos	2
10221	llana	2
10222	llamo	2
10223	llames	2
10224	llamémoslo	2
10225	llamaron	2
10226	llamaré	2
10227	llamamos	2
10228	llamadas	2
10229	liturgia	2
10230	literatas	2
10231	literarios	2
10232	listos	2
10233	listas	2
10234	lisonjas	2
10235	lírico	2
10236	lira	2
10237	liquidación	2
10238	linajudos	2
10239	linajudo	2
10240	linaje	2
10241	limpió	2
10242	limpiaba	2
10243	ligorio	2
10244	ligerezas	2
10245	liebres	2
10246	lides	2
10247	licores	2
10248	lícitos	2
10249	licencia	2
10250	librotes	2
10251	librería	2
10252	librepensadores	2
10253	librase	2
10254	librarla	2
10255	librándose	2
10256	libraba	2
10257	libertinos	2
10258	libertades	2
10259	liberalotes	2
10260	liberalote	2
10261	li	2
10262	levítico	2
10263	levitas	2
10264	leves	2
10265	levante	2
10266	levantaron	2
10267	levantándolo	2
10268	levantada	2
10269	letrina	2
10270	letrero	2
10271	lesa	2
10272	lentitud	2
10273	lengüeta	2
10274	leída	2
10275	legítimo	2
10276	legitimidad	2
10277	legítima	2
10278	leerlo	2
10279	leerlas	2
10280	leerla	2
10281	lee	2
10282	lear	2
10283	leandro	2
10284	lavandera	2
10285	lavan	2
10286	laurel	2
10287	latón	2
10288	latino	2
10289	latines	2
10290	latamente	2
10291	lascivas	2
10292	lanzas	2
10293	lánguida	2
10294	lamían	2
10295	lamentó	2
10296	lamentándose	2
10297	ladrona	2
10298	ladró	2
10299	lacónicamente	2
10300	lacayo	2
10301	labrar	2
10302	labrador	2
10303	labores	2
10304	kilómetros	2
10305	juvenil	2
10306	jurando	2
10307	jura	2
10308	júpiter	2
10309	juntan	2
10310	jugando	2
10311	jugado	2
10312	jueves	2
10313	judicial	2
10314	judías	2
10315	jubón	2
10316	jubiló	2
10317	joyas	2
10318	jornada	2
10319	joco	2
10320	jinetes	2
10321	jilguero	2
10322	jesuitismo	2
10323	jefes	2
10324	jaulas	2
10325	jaspe	2
10326	jarrones	2
10327	jarro	2
10328	jarras	2
10329	jaquet	2
10330	japoneses	2
10331	jamonas	2
10332	jactancia	2
10333	jactaba	2
10334	italiano	2
10335	italia	2
10336	isabel	2
10337	irrupción	2
10338	irritarse	2
10339	irritara	2
10340	irritante	2
10341	irrisoria	2
10342	irrevocables	2
10343	irrevocable	2
10344	irresponsable	2
10345	irrespetuoso	2
10346	irrespetuosas	2
10347	irreprochables	2
10348	irreparable	2
10349	irreflexiva	2
10350	irnos	2
10351	irguió	2
10352	invulnerable	2
10353	involuntario	2
10354	invocando	2
10355	invitaba	2
10356	inventores	2
10357	inventando	2
10358	inventada	2
10359	inventaba	2
10360	inventa	2
10361	invencibles	2
10362	invasión	2
10363	invariable	2
10364	invadido	2
10365	inútilmente	2
10366	inutilidad	2
10367	inundó	2
10368	inundaban	2
10369	intransigencia	2
10370	intolerancia	2
10371	intolerable	2
10372	intimar	2
10373	intervino	2
10374	intervención	2
10375	intervalo	2
10376	interrupciones	2
10377	interrumpir	2
10378	interrumpiendo	2
10379	interrumpían	2
10380	interpretado	2
10381	interpretaba	2
10382	interno	2
10383	intermedio	2
10384	interina	2
10385	interesar	2
10386	interesados	2
10387	interesada	2
10388	inter	2
10389	intentó	2
10390	intempestiva	2
10391	inteligible	2
10392	integridad	2
10393	insustanciales	2
10394	insultante	2
10395	insultaban	2
10396	insulta	2
10397	insufribles	2
10398	insuficiente	2
10399	instruido	2
10400	instrucción	2
10401	instintiva	2
10402	instantes	2
10403	inspiraban	2
10404	inspira	2
10405	inspección	2
10406	insistían	2
10407	insistente	2
10408	insistencia	2
10409	insípidos	2
10410	insípida	2
10411	insinuarle	2
10412	insinuación	2
10413	insinuaba	2
10414	insignes	2
10415	insensiblemente	2
10416	inscripciones	2
10417	insana	2
10418	inquina	2
10419	inquietudes	2
10420	inquietas	2
10421	inopinada	2
10422	inofensiva	2
10423	inmóviles	2
10424	inmemorial	2
10425	inmediato	2
10426	injusto	2
10427	injertar	2
10428	iniquidad	2
10429	inimitable	2
10430	inhabitable	2
10431	inglaterra	2
10432	ingenioso	2
10433	ingenios	2
10434	infundir	2
10435	ínfulas	2
10436	influyentes	2
10437	influyente	2
10438	influye	2
10439	influía	2
10440	inflo	2
10441	inflexible	2
10442	inflamados	2
10443	infinitos	2
10444	infiltraba	2
10445	infieles	2
10446	infernales	2
10447	infanzones	2
10448	infantiles	2
10449	infaliblemente	2
10450	inesperado	2
10451	inesperada	2
10452	industrias	2
10453	industriales	2
10454	individuo	2
10455	indignada	2
10456	indicios	2
10457	indescriptible	2
10458	independiente	2
10459	indefinidamente	2
10460	indefectiblemente	2
10461	indecente	2
10462	incrustaba	2
10463	incorporándose	2
10464	incompleta	2
10465	incompatibles	2
10466	incomparable	2
10467	incomoda	2
10468	incólume	2
10469	incógnito	2
10470	inclinaron	2
10471	inclinar	2
10472	incitante	2
10473	incalificable	2
10474	inaugural	2
10475	impurezas	2
10476	impunemente	2
10477	impuestas	2
10478	impúdica	2
10479	imprudencias	2
10480	improvisar	2
10481	improvisado	2
10482	improvisadas	2
10483	improvisaba	2
10484	impropia	2
10485	impresionable	2
10486	importunas	2
10487	importación	2
10488	imponente	2
10489	impondría	2
10490	implícitamente	2
10491	impía	2
10492	imperturbable	2
10493	impertinencia	2
10494	impedían	2
10495	imparcialmente	2
10496	impacientarse	2
10497	imitaré	2
10498	imitador	2
10499	imaginando	2
10500	imaginado	2
10501	ilumine	2
10502	iluminando	2
10503	iluminaban	2
10504	iii	2
10505	ignorarlo	2
10506	idolillo	2
10507	idólatra	2
10508	idiotas	2
10509	ida	2
10510	íbamos	2
10511	huyo	2
10512	hurto	2
10513	hurtadillas	2
10514	huracán	2
10515	hundiendo	2
10516	hunde	2
10517	humillar	2
10518	humillaciones	2
10519	humanos	2
10520	huiré	2
10521	huida	2
10522	huí	2
10523	huesuda	2
10524	huéspedes	2
10525	huella	2
10526	huecos	2
10527	hueca	2
10528	hubiéramos	2
10529	hoyo	2
10530	hostias	2
10531	hortera	2
10532	horrorosos	2
10533	horroriza	2
10534	horribles	2
10535	hornos	2
10536	hornilla	2
10537	hornacinas	2
10538	horizontes	2
10539	horizontales	2
10540	honradas	2
10541	honores	2
10542	honesto	2
10543	honda	2
10544	homo	2
10545	holanda	2
10546	hojeó	2
10547	hojalata	2
10548	hoc	2
10549	históricos	2
10550	históricas	2
10551	historias	2
10552	hisopos	2
10553	hiponax	2
10554	hinchando	2
10555	hinchados	2
10556	higienista	2
10557	hierático	2
10558	hierática	2
10559	hieran	2
10560	hiel	2
10561	hicieran	2
10562	heroicas	2
10563	herodes	2
10564	hermosísimo	2
10565	hermoseado	2
10566	hermanita	2
10567	heridas	2
10568	herejías	2
10569	herederos	2
10570	heredero	2
10571	herederas	2
10572	heredera	2
10573	heredara	2
10574	hércules	2
10575	herbario	2
10576	helados	2
10577	hechizado	2
10578	hebdomadario	2
10579	hayas	2
10580	hastiado	2
10581	harto	2
10582	hartazgo	2
10583	hambriento	2
10584	hallaba	2
10585	halagaría	2
10586	hacinados	2
10587	haciendas	2
10588	hachazos	2
10589	hacernos	2
10590	hacerlos	2
10591	hables	2
10592	hablarte	2
10593	hablarse	2
10594	hablarme	2
10595	hablarían	2
10596	habladores	2
10597	habladora	2
10598	hábitos	2
10599	habitaban	2
10600	habitaba	2
10601	habano	2
10602	gustar	2
10603	gustaban	2
10604	gusano	2
10605	gula	2
10606	guitarra	2
10607	guirnaldas	2
10608	guiñó	2
10609	guillotina	2
10610	guiarla	2
10611	guiada	2
10612	guía	2
10613	guarnición	2
10614	guardo	2
10615	guardaría	2
10616	guardado	2
10617	gruta	2
10618	grotescos	2
10619	grosería	2
10620	gritase	2
10621	gritado	2
10622	griegas	2
10623	griega	2
10624	grava	2
10625	gratuitos	2
10626	grasa	2
10627	granizo	2
10628	graciosísimo	2
10629	gracejo	2
10630	gozó	2
10631	gozándose	2
10632	götinga	2
10633	gótico	2
10634	gordas	2
10635	golosa	2
10636	goda	2
10637	goces	2
10638	gobernaba	2
10639	gitana	2
10640	giró	2
10641	gigante	2
10642	gesticulaban	2
10643	gesticulaba	2
10644	gertrudis	2
10645	geografía	2
10646	genui	2
10647	genuflexiones	2
10648	gentuza	2
10649	geniales	2
10650	generalmente	2
10651	generalizaba	2
10652	generalife	2
10653	generalidades	2
10654	generaciones	2
10655	gemía	2
10656	gazmoñería	2
10657	gavilanes	2
10658	gatas	2
10659	gastrónomo	2
10660	gastar	2
10661	gastan	2
10662	gastados	2
10663	gasta	2
10664	gasa	2
10665	garza	2
10666	gárrulos	2
10667	gárrulas	2
10668	gárrula	2
10669	garrote	2
10670	garras	2
10671	garra	2
10672	garcía	2
10673	garantías	2
10674	gañán	2
10675	ganosas	2
10676	ganchos	2
10677	ganaderos	2
10678	ganadero	2
10679	ganadas	2
10680	galones	2
10681	gallego	2
10682	gallardía	2
10683	galápago	2
10684	galanterías	2
10685	galanteo	2
10686	galante	2
10687	galanes	2
10688	gaitas	2
10689	gacetilleros	2
10690	futuros	2
10691	furores	2
10692	furiosos	2
10693	fundadores	2
10694	fumando	2
10695	fumaban	2
10696	fulano	2
10697	fui	2
10698	fugitivo	2
10699	fueros	2
10700	fuelle	2
10701	frotó	2
10702	freno	2
10703	frecuenta	2
10704	frailes	2
10705	fragilidad	2
10706	frágiles	2
10707	fósforo	2
10708	forzoso	2
10709	fortificar	2
10710	forrado	2
10711	forrada	2
10712	forraba	2
10713	fórmulas	2
10714	forminge	2
10715	formando	2
10716	formales	2
10717	formadas	2
10718	formaba	2
10719	forcejeaba	2
10720	foncé	2
10721	fomento	2
10722	fofa	2
10723	flotaba	2
10724	floricultura	2
10725	florete	2
10726	florecillas	2
10727	floreciente	2
10728	flojo	2
10729	flautas	2
10730	flauta	2
10731	flanqueada	2
10732	flammarion	2
10733	flamenca	2
10734	flacos	2
10735	fisonomía	2
10736	físicos	2
10737	fiscal	2
10738	firmaba	2
10739	firma	2
10740	finito	2
10741	finísima	2
10742	fingir	2
10743	fingimiento	2
10744	fingido	2
10745	filtraba	2
10746	filosóficos	2
10747	filosóficamente	2
10748	filosofando	2
10749	filius	2
10750	filípica	2
10751	fijeza	2
10752	fijas	2
10753	fijar	2
10754	figurémonos	2
10755	fígaro	2
10756	fieltro	2
10757	fiambre	2
10758	fía	2
10759	festivo	2
10760	fervorosamente	2
10761	ferviente	2
10762	férula	2
10763	ferrocarril	2
10764	ferreruelo	2
10765	fernando	2
10766	fermento	2
10767	féretro	2
10768	fenómenos	2
10769	femenina	2
10770	felonía	2
10771	felizmente	2
10772	felipe	2
10773	felicitaba	2
10774	fecunda	2
10775	fea	2
10776	fé	2
10777	favorita	2
10778	favorecía	2
10779	faut	2
10780	fauces	2
10781	fatuo	2
10782	fatigosa	2
10783	fatigas	2
10784	fatigados	2
10785	fatigada	2
10786	fatigaban	2
10787	fatigaba	2
10788	fascinado	2
10789	farolero	2
10790	faro	2
10791	fariseos	2
10792	fantástica	2
10793	fangosos	2
10794	fanatizados	2
10795	fanática	2
10796	famosos	2
10797	familiarmente	2
10798	faltaron	2
10799	faltarían	2
10800	faltaría	2
10801	faltado	2
10802	faldero	2
10803	faja	2
10804	facilitó	2
10805	facilitaban	2
10806	facha	2
10807	fábricas	2
10808	fabricar	2
10809	f	2
10810	exuberantes	2
10811	extremis	2
10812	extremada	2
10813	extraviados	2
10814	extrañó	2
10815	exteriores	2
10816	extensión	2
10817	extendido	2
10818	extender	2
10819	exquisitas	2
10820	expuestos	2
10821	expuestas	2
10822	expresaban	2
10823	expresaba	2
10824	exponemos	2
10825	explotar	2
10826	explícito	2
10827	explicaron	2
10828	explicarme	2
10829	explicarle	2
10830	explicaría	2
10831	explicando	2
10832	explicado	2
10833	explicaban	2
10834	experimentaba	2
10835	exordio	2
10836	exigen	2
10837	excusó	2
10838	exclusiva	2
10839	excitaciones	2
10840	excita	2
10841	exceso	2
10842	excesivos	2
10843	excelencias	2
10844	exageradas	2
10845	exageradamente	2
10846	exageraba	2
10847	exagera	2
10848	exacta	2
10849	evocaba	2
10850	evitarlo	2
10851	eunuco	2
10852	eudoro	2
10853	ética	2
10854	eternidades	2
10855	eternidad	2
10856	etelvina	2
10857	etcétera	2
10858	estuve	2
10859	estupefacto	2
10860	estudiarla	2
10861	estucada	2
10862	estrepitosa	2
10863	estrellitas	2
10864	estrellada	2
10865	estrechado	2
10866	estrangulado	2
10867	estrada	2
10868	estorbo	2
10869	estorbaré	2
10870	estorba	2
10871	estirando	2
10872	estiman	2
10873	estimación	2
10874	estética	2
10875	estertor	2
10876	estén	2
10877	estela	2
10878	estarse	2
10879	estarlo	2
10880	estaño	2
10881	estanquillos	2
10882	estanco	2
10883	estallidos	2
10884	estadística	2
10885	ésta	2
10886	esquivando	2
10887	esqueleto	2
10888	esputo	2
10889	esposos	2
10890	esponja	2
10891	espiritualismo	2
10892	espinoso	2
10893	espina	2
10894	espín	2
10895	espías	2
10896	espía	2
10897	espesos	2
10898	esperarle	2
10899	esperándole	2
10900	esperan	2
10901	especulaciones	2
10902	espectador	2
10903	especies	2
10904	especias	2
10905	esparto	2
10906	espantados	2
10907	espantado	2
10908	espadachín	2
10909	esferas	2
10910	esencias	2
10911	escupirle	2
10912	escultura	2
10913	escudriñar	2
10914	escudriñando	2
10915	escucha	2
10916	escuálida	2
10917	escrupuloso	2
10918	escribiendo	2
10919	escribían	2
10920	escriben	2
10921	escribanos	2
10922	escriba	2
10923	escote	2
10924	escotada	2
10925	escondites	2
10926	escondidos	2
10927	escondían	2
10928	esconder	2
10929	esconde	2
10930	escogió	2
10931	escoge	2
10932	esclavos	2
10933	escépticos	2
10934	escasez	2
10935	escarnio	2
10936	escarcha	2
10937	escarceos	2
10938	escapatorias	2
10939	escaparía	2
10940	escandalosamente	2
10941	escandalizó	2
10942	escandalizarse	2
10943	escandalizada	2
10944	escalo	2
10945	escalinata	2
10946	escajos	2
10947	esbeltas	2
10948	erre	2
10949	eróticos	2
10950	erótico	2
10951	erótica	2
10952	erizadas	2
10953	eriza	2
10954	erard	2
10955	éramos	2
10956	equivocó	2
10957	equivocarse	2
10958	equivocaciones	2
10959	equivocación	2
10960	equipaje	2
10961	episodios	2
10962	envuelve	2
10963	envueltas	2
10964	envidioso	2
10965	envidiosa	2
10966	envidiar	2
10967	envidiables	2
10968	envenenado	2
10969	envenenada	2
10970	envejecido	2
10971	envalentonado	2
10972	entusiástico	2
10973	entusiasmada	2
10974	entro	2
10975	entristecían	2
10976	entrevista	2
10977	entrever	2
10978	entretenido	2
10979	entretenía	2
10980	entremos	2
10981	entrego	2
10982	entregase	2
10983	entregarla	2
10984	entregadas	2
10985	entreacto	2
10986	entreabiertas	2
10987	entraría	2
10988	entraré	2
10989	entrañable	2
10990	entornados	2
10991	entierros	2
10992	enterrarle	2
10993	enterrador	2
10994	enteró	2
10995	enterneció	2
10996	enternecimiento	2
10997	entere	2
10998	enterasen	2
10999	enteras	2
11000	enterar	2
11001	enterada	2
11002	entendieron	2
11003	entendiera	2
11004	entendidos	2
11005	entenderle	2
11006	entenderla	2
11007	entallado	2
11008	entablaron	2
11009	ensueño	2
11010	ensimismada	2
11011	enseñorearse	2
11012	enseñarle	2
11013	enseñar	2
11014	enseña	2
11015	ensayos	2
11016	ensayo	2
11017	ensayar	2
11018	ensayado	2
11019	ensanchaba	2
11020	enroscaban	2
11021	enredos	2
11022	enredar	2
11023	enramadas	2
11024	enormísima	2
11025	enormes	2
11026	ennoblecía	2
11027	ennegrecida	2
11028	enlutadas	2
11029	enlutada	2
11030	enjugaba	2
11031	enjambres	2
11032	enhorabuena	2
11033	engordarla	2
11034	engomado	2
11035	engendrado	2
11036	engaños	2
11037	enfrascado	2
11038	enfermizo	2
11039	enfático	2
11040	enfadaba	2
11041	enero	2
11042	enérgicamente	2
11043	enemiga	2
11044	endiablada	2
11045	encuentran	2
11046	encubridora	2
11047	encontré	2
11048	encontrarle	2
11049	encontraría	2
11050	encomendarse	2
11051	encogiendo	2
11052	encogidos	2
11053	enciende	2
11054	encendieron	2
11055	encendidos	2
11056	encender	2
11057	encargado	2
11058	encargaba	2
11059	encarándose	2
11060	encaje	2
11061	enamoradas	2
11062	enamoraban	2
11063	empuñó	2
11064	empujó	2
11065	empresario	2
11066	emprendiese	2
11067	emprendido	2
11068	emporio	2
11069	empleada	2
11070	empirismo	2
11071	empeñarse	2
11072	empeñados	2
11073	empapelar	2
11074	empanadas	2
11075	empalagaba	2
11076	empadronamiento	2
11077	eminentes	2
11078	embutidos	2
11079	embutido	2
11080	embozos	2
11081	embozó	2
11082	embozadamente	2
11083	emborracharse	2
11084	emborracharon	2
11085	emborrachado	2
11086	embocadura	2
11087	embargado	2
11088	embarazosa	2
11089	elogiaba	2
11090	elevadas	2
11091	elemental	2
11092	elegías	2
11093	eléctrico	2
11094	electorales	2
11095	ejército	2
11096	ejercicios	2
11097	ejercer	2
11098	ejemplares	2
11099	égida	2
11100	efusión	2
11101	eficaces	2
11102	educandas	2
11103	educadas	2
11104	educaba	2
11105	edificantes	2
11106	edificado	2
11107	edificada	2
11108	edifica	2
11109	economías	2
11110	eclesiásticos	2
11111	eclesiásticas	2
11112	echo	2
11113	echarla	2
11114	echara	2
11115	echándose	2
11116	ecbátana	2
11117	ebrio	2
11118	dureza	2
11119	duraban	2
11120	dumas	2
11121	dulcísimas	2
11122	dufour	2
11123	dramáticos	2
11124	donna	2
11125	dones	2
11126	dominus	2
11127	dominante	2
11128	dominando	2
11129	domicilio	2
11130	domador	2
11131	dolió	2
11132	dolían	2
11133	doctrinas	2
11134	doctores	2
11135	doblando	2
11136	doblaba	2
11137	divisa	2
11138	divinidades	2
11139	divinas	2
11140	divierten	2
11141	divierta	2
11142	divididos	2
11143	divertida	2
11144	diversión	2
11145	distraía	2
11146	distintos	2
11147	distinguir	2
11148	distinguidos	2
11149	distinguida	2
11150	distingos	2
11151	distender	2
11152	distancias	2
11153	disputan	2
11154	dispuso	2
11155	dispuestas	2
11156	dispénseme	2
11157	dispensas	2
11158	disolventes	2
11159	disimuladas	2
11160	disimula	2
11161	disgustó	2
11162	disfruto	2
11163	disfrutar	2
11164	disfrazar	2
11165	disfrazaba	2
11166	disecado	2
11167	discutido	2
11168	discurrir	2
11169	disculpó	2
11170	disculpas	2
11171	discrecional	2
11172	discordantes	2
11173	discípulo	2
11174	disciplinadas	2
11175	dirigir	2
11176	dirigiendo	2
11177	dirige	2
11178	diosa	2
11179	diminutivos	2
11180	dimensiones	2
11181	dime	2
11182	dijeran	2
11183	dijéramos	2
11184	dignamente	2
11185	digestiones	2
11186	digas	2
11187	dígalo	2
11188	difusa	2
11189	difícilmente	2
11190	diferencias	2
11191	diego	2
11192	dieciséis	2
11193	dieciocho	2
11194	diecinueve	2
11195	diciembre	2
11196	dichas	2
11197	dicharachos	2
11198	dibujos	2
11199	dibujo	2
11200	dibujada	2
11201	diariamente	2
11202	diabólicas	2
11203	diablillos	2
11204	di	2
11205	devorando	2
11206	devolvía	2
11207	detiene	2
11208	determinada	2
11209	detenimiento	2
11210	detenerme	2
11211	desvergüenzas	2
11212	desvergonzada	2
11213	desvanes	2
11214	desvanecido	2
11215	desvanecida	2
11216	desvanecía	2
11217	desvanecer	2
11218	destinos	2
11219	destinado	2
11220	destinadas	2
11221	destinada	2
11222	desterrado	2
11223	desquite	2
11224	despreocupación	2
11225	desprendimiento	2
11226	despreciará	2
11227	desprecian	2
11228	despreciable	2
11229	despojó	2
11230	despojado	2
11231	despilfarros	2
11232	despiertos	2
11233	despide	2
11234	despertaron	2
11235	despertarla	2
11236	despertara	2
11237	despertaban	2
11238	desperdiciar	2
11239	despellejar	2
11240	despejado	2
11241	despedir	2
11242	despedidas	2
11243	despedazada	2
11244	despedazaba	2
11245	desocupada	2
11246	desmenuzar	2
11247	desmayado	2
11248	deslumbrantes	2
11249	deslumbran	2
11250	deslumbrador	2
11251	deslumbrado	2
11252	deslumbraba	2
11253	deslucían	2
11254	deslizaban	2
11255	deslenguado	2
11256	desinteresado	2
11257	designios	2
11258	deshizo	2
11259	deshacerse	2
11260	deshacerle	2
11261	desgraciados	2
11262	desfigurada	2
11263	desfallecer	2
11264	desfachatada	2
11265	desengaños	2
11266	desengañarse	2
11267	desenganchar	2
11268	desenfrenada	2
11269	desempeñaba	2
11270	desechaba	2
11271	desdichas	2
11272	desdeñoso	2
11273	desdeñando	2
11274	desdeñaba	2
11275	desdenes	2
11276	descuidados	2
11277	descuidado	2
11278	descuidadas	2
11279	descuida	2
11280	descuento	2
11281	descubriendo	2
11282	descubiertos	2
11283	descriptiva	2
11284	describiendo	2
11285	descreídos	2
11286	desconocidas	2
11287	desconfiando	2
11288	desconfía	2
11289	descomunal	2
11290	descomponía	2
11291	descendió	2
11292	descaro	2
11293	descarnado	2
11294	descarga	2
11295	descarado	2
11296	descansando	2
11297	descansa	2
11298	descalzas	2
11299	descabellada	2
11300	desató	2
11301	desarrollo	2
11302	desarrollada	2
11303	desanimado	2
11304	desairar	2
11305	desahogar	2
11306	desagravios	2
11307	desafinado	2
11308	desafiase	2
11309	desafiado	2
11310	desacreditado	2
11311	desabridos	2
11312	desabrido	2
11313	derretía	2
11314	derredor	2
11315	derramado	2
11316	depositó	2
11317	depositados	2
11318	deploraba	2
11319	dependientes	2
11320	dependía	2
11321	demuestra	2
11322	demostrarle	2
11323	demostrando	2
11324	demostrado	2
11325	demos	2
11326	demonches	2
11327	demócrata	2
11328	delitos	2
11329	deliquio	2
11330	delgados	2
11331	deleznable	2
11332	deleitaba	2
11333	delata	2
11334	dejos	2
11335	déjese	2
11336	dejas	2
11337	dejarlos	2
11338	dejarlo	2
11339	dejarán	2
11340	dejándote	2
11341	dejándole	2
11342	degenerar	2
11343	definitiva	2
11344	definido	2
11345	definida	2
11346	definición	2
11347	defiendo	2
11348	defensores	2
11349	defendido	2
11350	dedicarse	2
11351	dedican	2
11352	dedicaban	2
11353	decreto	2
11354	decorosamente	2
11355	declare	2
11356	declararse	2
11357	declararon	2
11358	declararme	2
11359	decirlas	2
11360	décimas	2
11361	decencia	2
11362	decaimiento	2
11363	decaer	2
11364	decadente	2
11365	decadencia	2
11366	debieron	2
11367	dato	2
11368	date	2
11369	darwinismo	2
11370	darnos	2
11371	dale	2
11372	curva	2
11373	curarme	2
11374	curado	2
11375	cundió	2
11376	cumplidos	2
11377	cumplida	2
11378	cultura	2
11379	cultivar	2
11380	culpaba	2
11381	culminante	2
11382	culinaria	2
11383	culebras	2
11384	culebra	2
11385	cuidarle	2
11386	cuidadosamente	2
11387	cuida	2
11388	cueva	2
11389	cuerpecito	2
11390	cuerdas	2
11391	cucuruchos	2
11392	cuchicheaban	2
11393	cuchicheaba	2
11394	cubrían	2
11395	cuba	2
11396	cuarteto	2
11397	cuarta	2
11398	cuantía	2
11399	cuáles	2
11400	crujió	2
11401	cruelmente	2
11402	cruda	2
11403	crucifijo	2
11404	crucifícale	2
11405	cronicones	2
11406	crónico	2
11407	cromos	2
11408	críticos	2
11409	cristianar	2
11410	crispaba	2
11411	crisóstomo	2
11412	cripta	2
11413	criminales	2
11414	cría	2
11415	crestas	2
11416	cresta	2
11417	creíase	2
11418	creerme	2
11419	creería	2
11420	creemos	2
11421	credulidad	2
11422	créditos	2
11423	creció	2
11424	crecimiento	2
11425	creciente	2
11426	creas	2
11427	créame	2
11428	créalo	2
11429	creado	2
11430	creaba	2
11431	crasitud	2
11432	costurera	2
11433	costura	2
11434	costar	2
11435	costaban	2
11436	corva	2
11437	corujedos	2
11438	cortó	2
11439	cortinas	2
11440	cortésmente	2
11441	cortesano	2
11442	cortes	2
11443	cortas	2
11444	cortaplumas	2
11445	cortando	2
11446	cortan	2
11447	cortaba	2
11448	corrompido	2
11449	corroborar	2
11450	corriste	2
11451	corrillo	2
11452	correspondientes	2
11453	correspondiente	2
11454	correligionario	2
11455	correligionarias	2
11456	corpulento	2
11457	corporales	2
11458	corporaciones	2
11459	coros	2
11460	coronada	2
11461	cornucopias	2
11462	coristas	2
11463	cordialidad	2
11464	corazonadas	2
11465	coquetona	2
11466	coqueterías	2
11467	coquetear	2
11468	coqueta	2
11469	copos	2
11470	copón	2
11471	copioso	2
11472	copias	2
11473	copiado	2
11474	convirtieron	2
11475	convertidas	2
11476	convertida	2
11477	converso	2
11478	conversaban	2
11479	convenio	2
11480	convendría	2
11481	convencionales	2
11482	convencional	2
11483	convencía	2
11484	convencerse	2
11485	contribuía	2
11486	contraventanas	2
11487	contraído	2
11488	contrahecha	2
11489	contradictorio	2
11490	contradictorias	2
11491	contradecir	2
11492	contradecía	2
11493	contingente	2
11494	contiene	2
11495	contestaron	2
11496	contertulios	2
11497	contentándose	2
11498	contendiente	2
11499	contemplarla	2
11500	contara	2
11501	consumo	2
11502	consuma	2
11503	consultas	2
11504	consultando	2
11505	consultado	2
11506	consultaba	2
11507	consuelos	2
11508	construida	2
11509	construían	2
11510	constitución	2
11511	constantemente	2
11512	consta	2
11513	conspirar	2
11514	conspiraba	2
11515	consonantes	2
11516	consoladora	2
11517	consolaban	2
11518	consistir	2
11519	consistente	2
11520	consistencia	2
11521	consintiera	2
11522	consiguieron	2
11523	consigue	2
11524	consideró	2
11525	considera	2
11526	conservadores	2
11527	consentirá	2
11528	consentimiento	2
11529	consejero	2
11530	conseguían	2
11531	consagrado	2
11532	consagración	2
11533	conozca	2
11534	conociendo	2
11535	conoces	2
11536	conocerle	2
11537	conocerla	2
11538	conocen	2
11539	conjurados	2
11540	conjurado	2
11541	conjuración	2
11542	congresos	2
11543	congéneres	2
11544	confusiones	2
11545	confundirse	2
11546	confundido	2
11547	confunde	2
11548	confortable	2
11549	confort	2
11550	confirmábase	2
11551	confidentes	2
11552	confidencia	2
11553	confiaban	2
11554	confiaba	2
11555	confesores	2
11556	confesata	2
11557	conducían	2
11558	conduce	2
11559	condicional	2
11560	condescendencia	2
11561	condes	2
11562	condeno	2
11563	condenar	2
11564	condenados	2
11565	condenado	2
11566	conde	2
11567	concurridos	2
11568	concurrían	2
11569	concubina	2
11570	concretas	2
11571	concordia	2
11572	conclusión	2
11573	concluir	2
11574	conciliábulos	2
11575	conciliábulo	2
11576	concierto	2
11577	concejal	2
11578	concedían	2
11579	conceder	2
11580	concebía	2
11581	conato	2
11582	comunicó	2
11583	comunicativa	2
11584	comunicar	2
11585	comulgaría	2
11586	comte	2
11587	compuesta	2
11588	compromisario	2
11589	comprometerla	2
11590	comprimida	2
11591	comprendiera	2
11592	comprendí	2
11593	comprenda	2
11594	componer	2
11595	complicación	2
11596	complexión	2
11597	compleja	2
11598	complaciéndose	2
11599	complacerle	2
11600	compensar	2
11601	compensaba	2
11602	compareció	2
11603	comparada	2
11604	comparable	2
11605	compara	2
11606	compadecían	2
11607	compadecerse	2
11608	cómodos	2
11609	cómodamente	2
11610	comm	2
11611	comiera	2
11612	comienza	2
11613	comidas	2
11614	comes	2
11615	comerse	2
11616	comenzada	2
11617	comentar	2
11618	comentaban	2
11619	comentaba	2
11620	comensales	2
11621	comedido	2
11622	combate	2
11623	comadronas	2
11624	columbrar	2
11625	coloso	2
11626	colorados	2
11627	coloquio	2
11628	colocado	2
11629	coloca	2
11630	colmar	2
11631	colmada	2
11632	coliseo	2
11633	colina	2
11634	colgó	2
11635	colgadura	2
11636	colgaba	2
11637	colegiales	2
11638	colega	2
11639	colectivo	2
11640	coleccionador	2
11641	colapso	2
11642	colación	2
11643	coja	2
11644	coincide	2
11645	cohechos	2
11646	cogiendo	2
11647	cogidos	2
11648	cogían	2
11649	codorniz	2
11650	codearse	2
11651	codeándose	2
11652	codazos	2
11653	cocineros	2
11654	cocineras	2
11655	cocido	2
11656	cocheras	2
11657	cloaca	2
11658	clavel	2
11659	clavarse	2
11660	clavarle	2
11661	clavada	2
11662	claudicante	2
11663	clarisas	2
11664	clarinetes	2
11665	clandestino	2
11666	claire	2
11667	clac	2
11668	ciudades	2
11669	ciudadanos	2
11670	citó	2
11671	cito	2
11672	citando	2
11673	citados	2
11674	citado	2
11675	citaban	2
11676	cirino	2
11677	circulante	2
11678	circulación	2
11679	circos	2
11680	cinto	2
11681	cinta	2
11682	cinismo	2
11683	cínicos	2
11684	cínico	2
11685	cima	2
11686	cilicio	2
11687	cigarras	2
11688	cierre	2
11689	cierra	2
11690	cientos	2
11691	ciencias	2
11692	ciegamente	2
11693	chupando	2
11694	chupan	2
11695	chorreaban	2
11696	chorreaba	2
11697	chocaban	2
11698	chitón	2
11699	chito	2
11700	chirridos	2
11701	chiripa	2
11702	chiquita	2
11703	chinto	2
11704	chino	2
11705	chinescas	2
11706	chasquido	2
11707	chascarrillos	2
11708	chas	2
11709	chartreuse	2
11710	charlando	2
11711	chaparrones	2
11712	chantre	2
11713	chalet	2
11714	chalecos	2
11715	cestas	2
11716	cesó	2
11717	césar	2
11718	cesantía	2
11719	cerradura	2
11720	cerillas	2
11721	ceremoniosa	2
11722	cerebral	2
11723	cerdo	2
11724	cercos	2
11725	cercanos	2
11726	cercano	2
11727	cerbatana	2
11728	cepillar	2
11729	central	2
11730	censuras	2
11731	cenó	2
11732	cenaron	2
11733	cenado	2
11734	celucos	2
11735	celibato	2
11736	celestiales	2
11737	celestes	2
11738	celebró	2
11739	célebres	2
11740	celdas	2
11741	cejijunto	2
11742	cegado	2
11743	cédula	2
11744	cediendo	2
11745	cede	2
11746	cebo	2
11747	cayeran	2
11748	cauterio	2
11749	causó	2
11750	causas	2
11751	causaban	2
11752	caudal	2
11753	catolicismo	2
11754	católicas	2
11755	categórica	2
11756	categoría	2
11757	cataratas	2
11758	casuchas	2
11759	casualidades	2
11760	casual	2
11761	castillos	2
11762	castigos	2
11763	castañuelas	2
11764	castañas	2
11765	casé	2
11766	cascabel	2
11767	casarían	2
11768	casar	2
11769	carvajal	2
11770	cartucho	2
11771	carros	2
11772	carpintero	2
11773	carnaza	2
11774	carnales	2
11775	carita	2
11776	cariñosos	2
11777	caricaturas	2
11778	cargamento	2
11779	carecía	2
11780	cardos	2
11781	cárdeno	2
11782	cárdenas	2
11783	carboneras	2
11784	carbonera	2
11785	carámbano	2
11786	carabina	2
11787	capullos	2
11788	caprichosos	2
11789	capones	2
11790	capitoné	2
11791	cañones	2
11792	cañonazos	2
11793	canturia	2
11794	cántico	2
11795	cante	2
11796	cantaron	2
11797	cántaro	2
11798	cantado	2
11799	cansar	2
11800	cansando	2
11801	canonjía	2
11802	canónicas	2
11803	cancel	2
11804	campechano	2
11805	campanada	2
11806	cambios	2
11807	cambió	2
11808	cambiando	2
11809	cambiaba	2
11810	camareros	2
11811	camarada	2
11812	cámara	2
11813	calzón	2
11814	calzar	2
11815	calvicie	2
11816	calumniaba	2
11817	calmar	2
11818	cállese	2
11819	callarse	2
11820	callarán	2
11821	caliza	2
11822	calificaba	2
11823	califas	2
11824	calidades	2
11825	calenturienta	2
11826	calentarse	2
11827	caldos	2
11828	calderonianas	2
11829	calatayud	2
11830	cafés	2
11831	caen	2
11832	caderas	2
11833	cacique	2
11834	cacho	2
11835	cacharros	2
11836	cabezadas	2
11837	cabellera	2
11838	cabecita	2
11839	caballeritos	2
11840	caballeresco	2
11841	caballerescas	2
11842	cabal	2
11843	c	2
11844	búsquela	2
11845	buscasen	2
11846	buscaron	2
11847	buscarla	2
11848	buscaría	2
11849	burlador	2
11850	burgueses	2
11851	buque	2
11852	bum	2
11853	bullicioso	2
11854	bullicio	2
11855	bullanguera	2
11856	bujía	2
11857	bufanda	2
11858	bucólicos	2
11859	bruscamente	2
11860	bruja	2
11861	brotó	2
11862	brindis	2
11863	brillar	2
11864	brilla	2
11865	brigadier	2
11866	brevedad	2
11867	breñas	2
11868	bramaba	2
11869	botellas	2
11870	bote	2
11871	bostezo	2
11872	bostezar	2
11873	borrosa	2
11874	borrego	2
11875	borradas	2
11876	borracha	2
11877	borde	2
11878	bordados	2
11879	boquiabierta	2
11880	bonitas	2
11881	bonete	2
11882	bombo	2
11883	bolsillos	2
11884	bochorno	2
11885	bobadas	2
11886	blindado	2
11887	blasfemar	2
11888	blasfemando	2
11889	blanquísimos	2
11890	blanquísimo	2
11891	blanduras	2
11892	bizcocho	2
11893	bizarro	2
11894	bis	2
11895	billete	2
11896	billares	2
11897	bijou	2
11898	bigotillo	2
11899	bestia	2
11900	besándole	2
11901	besa	2
11902	bernesga	2
11903	benito	2
11904	beneméritos	2
11905	beneficiao	2
11906	benéfica	2
11907	bendiciones	2
11908	benavides	2
11909	belvedere	2
11910	bebiendo	2
11911	bebés	2
11912	beatos	2
11913	beatífica	2
11914	beatería	2
11915	bazar	2
11916	batista	2
11917	batiéndose	2
11918	baterías	2
11919	batacazo	2
11920	bastidores	2
11921	bastaron	2
11922	base	2
11923	barroco	2
11924	barriada	2
11925	barra	2
11926	baronesas	2
11927	barbilindo	2
11928	bárbaros	2
11929	barbaridad	2
11930	baratos	2
11931	barata	2
11932	bañándose	2
11933	bañan	2
11934	bañaban	2
11935	banquetes	2
11936	banquero	2
11937	bandido	2
11938	bandeja	2
11939	banda	2
11940	balduque	2
11941	balbucear	2
11942	balaustrada	2
11943	balas	2
11944	balanceo	2
11945	bajeza	2
11946	bajera	2
11947	bajado	2
11948	bailé	2
11949	bailaban	2
11950	báculo	2
11951	baco	2
11952	babuchas	2
11953	azotes	2
11954	azote	2
11955	azotando	2
11956	azotaba	2
11957	azota	2
11958	azor	2
11959	azafranada	2
11960	ayunos	2
11961	ayuno	2
11962	ayudo	2
11963	ayúdeme	2
11964	ayude	2
11965	ayudarme	2
11966	ayudando	2
11967	ayudan	2
11968	axioma	2
11969	avizor	2
11970	avisos	2
11971	avisan	2
11972	averiguó	2
11973	averiguado	2
11974	avergonzaban	2
11975	aventurilla	2
11976	avenido	2
11977	avellanas	2
11978	avellana	2
11979	avanzó	2
11980	avanzar	2
11981	avanzada	2
11982	auxilios	2
11983	autoriza	2
11984	autonomía	2
11985	automático	2
11986	auténtica	2
11987	auricular	2
11988	aurea	2
11989	auras	2
11990	augusto	2
11991	aturdirse	2
11992	aturdía	2
11993	atronaba	2
11994	atrición	2
11995	atribulado	2
11996	atribuir	2
11997	atrevimientos	2
11998	atreviera	2
11999	atrévete	2
12000	atrever	2
12001	atreva	2
12002	atraviesa	2
12003	atravesado	2
12004	atravesaban	2
12005	atrasada	2
12006	atragantó	2
12007	atrae	2
12008	atormenten	2
12009	atormentarse	2
12010	atormentado	2
12011	atónitos	2
12012	atolondramiento	2
12013	aterraba	2
12014	ateos	2
12015	atentado	2
12016	atenta	2
12017	atendió	2
12018	atenciones	2
12019	atañe	2
12020	atadas	2
12021	atada	2
12022	asuste	2
12023	asustara	2
12024	asustar	2
12025	asustadiza	2
12026	asusta	2
12027	asquerosa	2
12028	aspiraciones	2
12029	ásperas	2
12030	asombrado	2
12031	asombrada	2
12032	asomaron	2
12033	asomara	2
12034	asomados	2
12035	asomado	2
12036	asomada	2
12037	asomaban	2
12038	asistió	2
12039	asistieron	2
12040	asistiera	2
12041	asisten	2
12042	asiduo	2
12043	asfixiaba	2
12044	asesinar	2
12045	asesinado	2
12046	aserto	2
12047	aseguraban	2
12048	asedio	2
12049	asedian	2
12050	ascuas	2
12051	ascos	2
12052	asceta	2
12053	artísticas	2
12054	artificios	2
12055	artificiales	2
12056	artífice	2
12057	articulista	2
12058	artesonado	2
12059	artesanos	2
12060	arrullos	2
12061	arrullo	2
12062	arrullaba	2
12063	arruinando	2
12064	arruina	2
12065	arrugas	2
12066	arrojo	2
12067	arrojaron	2
12068	arrojarle	2
12069	arrojara	2
12070	arrojando	2
12071	arrojada	2
12072	arrogancia	2
12073	arrobas	2
12074	arrinconado	2
12075	arrinconada	2
12076	arrimada	2
12077	arrepentido	2
12078	arrepentía	2
12079	arrastrase	2
12080	arrastrara	2
12081	arrastradas	2
12082	arrancó	2
12083	arrancado	2
12084	arraigado	2
12085	arqueológica	2
12086	árnica	2
12087	armoniosas	2
12088	armería	2
12089	armatoste	2
12090	armando	2
12091	armado	2
12092	arisca	2
12093	argentina	2
12094	areo	2
12095	arenga	2
12096	arenal	2
12097	área	2
12098	arduos	2
12099	arduo	2
12100	ardores	2
12101	ardiendo	2
12102	ardentísima	2
12103	arceas	2
12104	arcadia	2
12105	arboricultura	2
12106	arbolillos	2
12107	arboleda	2
12108	arbolado	2
12109	árbitro	2
12110	arabescos	2
12111	aquiles	2
12112	aquéllos	2
12113	aquélla	2
12114	apuesta	2
12115	aproximó	2
12116	aproximarse	2
12117	aprovechando	2
12118	aprovecha	2
12119	apretarla	2
12120	aprendió	2
12121	apreciaba	2
12122	apoyo	2
12123	apoyar	2
12124	apoyados	2
12125	apoyado	2
12126	apoteosis	2
12127	apóstoles	2
12128	apóstata	2
12129	apostasía	2
12130	apostar	2
12131	apoderó	2
12132	apoderado	2
12133	aplomo	2
12134	aplicaciones	2
12135	aplica	2
12136	aplaudió	2
12137	aplaude	2
12138	aplasto	2
12139	aplastar	2
12140	aplastado	2
12141	aplastadas	2
12142	apiñadas	2
12143	apetitosos	2
12144	apetitosa	2
12145	apencar	2
12146	aparentes	2
12147	aparentemente	2
12148	aparentar	2
12149	aparentando	2
12150	aparecieron	2
12151	apareciendo	2
12152	aparece	2
12153	aparatosa	2
12154	aparatos	2
12155	apagadas	2
12156	añadido	2
12157	anzuelo	2
12158	anunció	2
12159	anuncio	2
12160	anunciarse	2
12161	anunciando	2
12162	anuncian	2
12163	antonomasia	2
12164	antonio	2
12165	antoja	2
12166	antitéticos	2
12167	antinomia	2
12168	antífrasis	2
12169	anticuado	2
12170	anticipo	2
12171	anónimos	2
12172	anónimo	2
12173	annatas	2
12174	aniversario	2
12175	aniquilamiento	2
12176	ánimos	2
12177	animándose	2
12178	animadora	2
12179	anima	2
12180	anhelante	2
12181	anhelaba	2
12182	angulosa	2
12183	angosto	2
12184	angostas	2
12185	angelillo	2
12186	angelical	2
12187	anfiteatro	2
12188	anegado	2
12189	andrajosos	2
12190	andén	2
12191	anden	2
12192	andará	2
12193	andamiaje	2
12194	anatomía	2
12195	analizar	2
12196	anafrodita	2
12197	amorosamente	2
12198	amontonaban	2
12199	amiguitas	2
12200	amenazando	2
12201	ambrosio	2
12202	ámbitos	2
12203	amazona	2
12204	amas	2
12205	amarlas	2
12206	amarillas	2
12207	amargos	2
12208	amargor	2
12209	amaré	2
12210	amanerado	2
12211	amanerada	2
12212	amando	2
12213	aman	2
12214	amador	2
12215	alzar	2
12216	alvarín	2
12217	alusivos	2
12218	alusivo	2
12219	alumbrar	2
12220	alumbrada	2
12221	aludió	2
12222	aludido	2
12223	alude	2
12224	alucinación	2
12225	alturas	2
12226	altruista	2
12227	altozanos	2
12228	altiva	2
12229	alternativamente	2
12230	alternaban	2
12231	alteración	2
12232	altanera	2
12233	alquiler	2
12234	almorzar	2
12235	almohadillas	2
12236	almo	2
12237	almidonada	2
12238	almacén	2
12239	alimentarse	2
12240	alimentado	2
12241	alimentaba	2
12242	alhambra	2
12243	aleluya	2
12244	alejar	2
12245	alejandro	2
12246	alejandría	2
12247	alegra	2
12248	aleación	2
12249	aldeanas	2
12250	aldabón	2
12251	alcoholismo	2
12252	alcobas	2
12253	alcanzaron	2
12254	alborotadores	2
12255	alborota	2
12256	albañiles	2
12257	albañil	2
12258	alarmar	2
12259	alarmado	2
12260	alargaba	2
12261	alambre	2
12262	alambicados	2
12263	alambicado	2
12264	alambicada	2
12265	alabado	2
12266	alaba	2
12267	aislamiento	2
12268	airecillo	2
12269	ahorrarme	2
12270	ahondaba	2
12271	ahogarle	2
12272	ahogándose	2
12273	ahoga	2
12274	aguardar	2
12275	aguantaba	2
12276	aguaceros	2
12277	agridulce	2
12278	agregó	2
12279	agravó	2
12280	agravios	2
12281	agradezco	2
12282	agradecer	2
12283	agradarla	2
12284	agradables	2
12285	agitado	2
12286	agarrado	2
12287	áfrica	2
12288	afortunado	2
12289	afligidos	2
12290	afirmó	2
12291	afirman	2
12292	afeminamiento	2
12293	afeitados	2
12294	afectado	2
12295	afabilidad	2
12296	advertirle	2
12297	advertida	2
12298	advertencia	2
12299	adusto	2
12300	adulación	2
12301	adquiridas	2
12302	adquirida	2
12303	adquiría	2
12304	adornado	2
12305	adoratrices	2
12306	adocenados	2
12307	admiten	2
12308	admita	2
12309	admiraciones	2
12310	admirables	2
12311	adivinación	2
12312	adelantó	2
12313	adelantarse	2
12314	adelantada	2
12315	adelanta	2
12316	adaptación	2
12317	adán	2
12318	acusarse	2
12319	acusación	2
12320	acumulado	2
12321	acuesta	2
12322	acuerdan	2
12323	actualmente	2
12324	actualidad	2
12325	actuales	2
12326	actor	2
12327	acreditados	2
12328	acostumbró	2
12329	acostumbrados	2
12330	acostumbraban	2
12331	acostado	2
12332	acosado	2
12333	acordes	2
12334	acordarás	2
12335	acordaban	2
12336	aconsejarle	2
12337	aconsejar	2
12338	aconsejado	2
12339	aconsejaba	2
12340	aconseja	2
12341	acompasados	2
12342	acompañarle	2
12343	acomodo	2
12344	acoger	2
12345	aclaraban	2
12346	aclaraba	2
12347	achaque	2
12348	achacoso	2
12349	acertó	2
12350	acertado	2
12351	acercase	2
12352	acercando	2
12353	acequia	2
12354	aceituna	2
12355	accediendo	2
12356	acariciaba	2
12357	acaloró	2
12358	académico	2
12359	académica	2
12360	academia	2
12361	acabe	2
12362	acabarse	2
12363	acabara	2
12364	acaban	2
12365	abusar	2
12366	abusado	2
12367	abusaba	2
12368	abusa	2
12369	aburrían	2
12370	aburre	2
12371	abundaban	2
12372	abultadas	2
12373	abuelos	2
12374	abuela	2
12375	abstracciones	2
12376	abstinencia	2
12377	abstengo	2
12378	absolvía	2
12379	abrumados	2
12380	abroño	2
12381	abrochaba	2
12382	abriría	2
12383	abriera	2
12384	abrazar	2
12385	abrazado	2
12386	abrasarse	2
12387	abrasados	2
12388	aborrezco	2
12389	aborreciendo	2
12390	abordar	2
12391	abonadas	2
12392	abogados	2
12393	abismarse	2
12394	aberración	2
12395	abecedario	2
12396	abdomen	2
12397	abdicar	2
12398	abandonase	2
12399	abandonarse	2
12400	abandona	2
12401	zurriagazo	1
12402	zurcidos	1
12403	zurcido	1
12404	zurbarán	1
12405	zumbaban	1
12406	zumarri	1
12407	zuecos	1
12408	zueco	1
12409	zuavo	1
12410	zozobra	1
12411	zoológica	1
12412	zona	1
12413	zodiaco	1
12414	zascandil	1
12415	zarzuelas	1
12416	zarzaparrilla	1
12417	zarza	1
12418	zarpa	1
12419	zarandeando	1
12420	zarandeaban	1
12421	zarandajas	1
12422	zaquizamí	1
12423	zapatilla	1
12424	zángano	1
12425	zancadilla	1
12426	zambulló	1
12427	zamarra	1
12428	zamacois	1
12429	zalamea	1
12430	zag	1
12431	zafio	1
12432	yodo	1
12433	yema	1
12434	xxx	1
12435	xxviii	1
12436	xxvii	1
12437	xxvi	1
12438	xxv	1
12439	xxix	1
12440	xxiv	1
12441	xxiii	1
12442	xxii	1
12443	xxi	1
12444	xx	1
12445	xviii	1
12446	xvii	1
12447	xvi	1
12448	xix	1
12449	xiii	1
12450	xii	1
12451	xi	1
12452	wisseman	1
12453	wieland	1
12454	washingtonia	1
12455	w	1
12456	vulgarísimo	1
12457	vulgaridad	1
12458	vuestros	1
12459	vuestro	1
12460	vuélvete	1
12461	vuelves	1
12462	vuela	1
12463	vuecencia	1
12464	voyageur	1
12465	vox	1
12466	votaron	1
12467	votaciones	1
12468	votación	1
12469	votaba	1
12470	vosotros	1
12471	vosotras	1
12472	volviolos	1
12473	volvimos	1
12474	volviéramos	1
12475	volvíase	1
12476	volvernos	1
12477	volverla	1
12478	volutas	1
12479	voluptuosas	1
12480	voluntario	1
12481	voluminoso	1
12482	volteriano	1
12483	voló	1
12484	volatilizándolo	1
12485	volaré	1
12486	volara	1
12487	volada	1
12488	vogt	1
12489	vocis	1
12490	vocinglera	1
12491	vociferando	1
12492	vociferaban	1
12493	vociferaba	1
12494	vocifera	1
12495	vocales	1
12496	vocaciones	1
12497	vocablos	1
12498	vobis	1
12499	vizconde	1
12500	vivirlas	1
12501	vivirá	1
12502	viviendas	1
12503	vividos	1
12504	vividor	1
12505	viví	1
12506	vivendi	1
12507	vivarachos	1
12508	vivan	1
12509	viudo	1
12510	vituperar	1
12511	vitriolo	1
12512	vitrina	1
12513	vitandos	1
12514	vitalidad	1
12515	vitalicia	1
12516	vita	1
12517	vistosos	1
12518	vistoso	1
12519	vístose	1
12520	vistosas	1
12521	vistos	1
12522	vistieron	1
12523	vistiera	1
12524	vísperas	1
12525	visos	1
12526	vislumbres	1
12527	vislumbrar	1
12528	visitarle	1
12529	visitara	1
12530	visitamos	1
12531	visitaciones	1
12532	visionaria	1
12533	visiblemente	1
12534	visera	1
12535	viseo	1
12536	viscosos	1
12537	vis	1
12538	viruelas	1
12539	virtutis	1
12540	virtuosas	1
12541	virilidad	1
12542	viriles	1
12543	virchov	1
12544	vir	1
12545	violentando	1
12546	violas	1
12547	viñas	1
12548	viña	1
12549	viniere	1
12550	viniendo	1
12551	vinci	1
12552	vinader	1
12553	vilo	1
12554	villavieja	1
12555	villancicos	1
12556	villanas	1
12557	villafranca	1
12558	villa	1
12559	vigoroso	1
12560	vigorizar	1
12561	vigilaré	1
12562	vigilara	1
12563	vigilar	1
12564	vigentes	1
12565	vieses	1
12566	viéramos	1
12567	vientecillo	1
12568	viéndolos	1
12569	viéndolas	1
12570	viéndola	1
12571	viena	1
12572	vien	1
12573	viejecito	1
12574	vidriosa	1
12575	vidrio	1
12576	videor	1
12577	vidente	1
12578	victis	1
12579	vicioso	1
12580	vicia	1
12581	vicepresidente	1
12582	vicarios	1
12583	vibrando	1
12584	vibraba	1
12585	viborezno	1
12586	víbora	1
12587	viático	1
12588	vías	1
12589	viajado	1
12590	viajaba	1
12591	viable	1
12592	vetustente	1
12593	vetustas	1
12594	veteranos	1
12595	veterano	1
12596	vestusta	1
12597	vestuario	1
12598	vestimos	1
12599	vestimenta	1
12600	vestiglos	1
12601	vertió	1
12602	vértigo	1
12603	vertieron	1
12604	vertiente	1
12605	vertido	1
12606	vertical	1
12607	vertederos	1
12608	versión	1
12609	versículo	1
12610	versate	1
12611	versalles	1
12612	veros	1
12613	vernos	1
12614	vermis	1
12615	verles	1
12616	verificar	1
12617	vergüenzas	1
12618	vergonzosas	1
12619	veremundo	1
12620	veréis	1
12621	verduleras	1
12622	verdosas	1
12623	verdinegro	1
12624	verbum	1
12625	verbosidad	1
12626	verbo	1
12627	verbigracia	1
12628	veraniega	1
12629	veraneo	1
12630	veraneado	1
12631	veraneaban	1
12632	veraneaba	1
12633	venzo	1
12634	ventrílocuo	1
12635	ventilen	1
12636	ventilar	1
12637	ventilaba	1
12638	venteros	1
12639	ventanillo	1
12640	ventanillas	1
12641	venta	1
12642	venirle	1
12643	venideras	1
12644	venida	1
12645	venid	1
12646	venias	1
12647	venia	1
12648	vengarme	1
12649	vengándose	1
12650	vengando	1
12651	vengado	1
12652	vengaban	1
12653	venero	1
12654	venerando	1
12655	venenos	1
12656	veneciana	1
12657	venecia	1
12658	vendrían	1
12659	vendrás	1
12660	vendo	1
12661	vendiese	1
12662	vendiendo	1
12663	venderse	1
12664	venderlos	1
12665	vender	1
12666	venciendo	1
12667	vencí	1
12668	vencerme	1
12669	vencerlos	1
12670	vencerlas	1
12671	vencedora	1
12672	venales	1
12673	vena	1
12674	velón	1
12675	velocidad	1
12676	velludo	1
12677	velluda	1
12678	vellones	1
12679	velis	1
12680	veleidoso	1
12681	velarle	1
12682	velando	1
12683	velados	1
12684	velado	1
12685	vejetes	1
12686	vejamen	1
12687	veintitrés	1
12688	veíalo	1
12689	veíalas	1
12690	veíala	1
12691	vehículo	1
12692	vehemencia	1
12693	veguellinas	1
12694	vegetando	1
12695	vegetación	1
12696	vegetaba	1
12697	vegallanas	1
12698	vedado	1
12699	veamos	1
12700	veáis	1
12701	váyase	1
12702	vauban	1
12703	vate	1
12704	vastos	1
12705	vastísimos	1
12706	vastísimo	1
12707	vástago	1
12708	vasares	1
12709	variantes	1
12710	variados	1
12711	variadas	1
12712	variada	1
12713	variación	1
12714	variaba	1
12715	vaqueros	1
12716	vaquero	1
12717	vaporosos	1
12718	vaporoso	1
12719	vaporosa	1
12720	vanidosos	1
12721	vanidoso	1
12722	vanagloriarse	1
12723	vanagloriaba	1
12724	vampiro	1
12725	valió	1
12726	valieran	1
12727	valiéndose	1
12728	valían	1
12729	válgate	1
12730	valetudinario	1
12731	valerosos	1
12732	valeroso	1
12733	valera	1
12734	valentísimo	1
12735	valentías	1
12736	valentía	1
12737	valemos	1
12738	valdrían	1
12739	valdría	1
12740	valdiñón	1
12741	vaivenes	1
12742	vais	1
12743	vaina	1
12744	vaguedades	1
12745	vagaban	1
12746	vae	1
12747	vacilando	1
12748	vacías	1
12749	vacantes	1
12750	uva	1
12751	utrecht	1
12752	utilizado	1
12753	utilizaba	1
12754	utilitario	1
12755	utilidades	1
12756	útiles	1
12757	utile	1
12758	utero	1
12759	utensilios	1
12760	usurpador	1
12761	usura	1
12762	usual	1
12763	usté	1
12764	usos	1
12765	usen	1
12766	usase	1
12767	usarse	1
12768	usarlo	1
12769	usara	1
12770	usados	1
12771	usada	1
12772	us	1
12773	urgentísimo	1
12774	urdido	1
12775	urbicesorbi	1
12776	urbano	1
12777	urbanidad	1
12778	urbana	1
12779	unto	1
12780	untados	1
12781	untaba	1
12782	universidades	1
12783	universi	1
12784	unísono	1
12785	unió	1
12786	unidas	1
12787	únicos	1
12788	uníase	1
12789	unía	1
12790	uní	1
12791	une	1
12792	ultratelúrica	1
12793	ultramontano	1
12794	ultramontanismo	1
12795	ultramontanas	1
12796	ultrajando	1
12797	ultrajada	1
12798	ulloa	1
12799	ujier	1
12800	ue	1
12801	tuyo	1
12802	tuy	1
12803	tuviste	1
12804	tuviéramos	1
12805	tutor	1
12806	tutela	1
12807	tute	1
12808	turris	1
12809	turres	1
12810	turquía	1
12811	turpia	1
12812	turnaban	1
12813	turgencia	1
12814	turcas	1
12815	turbio	1
12816	turbias	1
12817	turbarle	1
12818	turbante	1
12819	turbándose	1
12820	turbamulta	1
12821	turbaciones	1
12822	turbación	1
12823	tupida	1
12824	túnicas	1
12825	túnel	1
12826	tunantes	1
12827	tunanta	1
12828	tumban	1
12829	tumbados	1
12830	tugurios	1
12831	tufillo	1
12832	tuesta	1
12833	tuerces	1
12834	tuerce	1
12835	tuerca	1
12836	tubos	1
12837	tuberculosis	1
12838	tuae	1
12839	truqueurs	1
12840	truncado	1
12841	truenan	1
12842	trozos	1
12843	troya	1
12844	trotes	1
12845	tropo	1
12846	tropiece	1
12847	tropezasen	1
12848	tropel	1
12849	trono	1
12850	tronar	1
12851	tronados	1
12852	tronaba	1
12853	trompeteada	1
12854	trompas	1
12855	trocitos	1
12856	trochas	1
12857	trocha	1
12858	trocarse	1
12859	trocados	1
12860	triunfe	1
12861	triunfantes	1
12862	triunfando	1
12863	triunfal	1
12864	triunfaban	1
12865	triunfa	1
12866	tristemente	1
12867	tripulando	1
12868	tripulaban	1
12869	triple	1
12870	tripa	1
12871	trincheras	1
12872	trinchante	1
12873	trimestre	1
12874	trifoncito	1
12875	trifoncillo	1
12876	trifona	1
12877	tridentino	1
12878	tributó	1
12879	tributar	1
12880	tributaban	1
12881	tribus	1
12882	tribunales	1
12883	triángulo	1
12884	trepidación	1
12885	trepando	1
12886	trepaba	1
12887	trepa	1
12888	trenzados	1
12889	trena	1
12890	trémolo	1
12891	treguas	1
12892	trazó	1
12893	trazaba	1
12894	travesaños	1
12895	tratos	1
12896	traté	1
12897	tratarse	1
12898	tratarlo	1
12899	tratarle	1
12900	tratarla	1
12901	tratando	1
12902	tratados	1
12903	tratable	1
12904	trasvolado	1
12905	trasunto	1
12906	trasplantada	1
12907	trasplantaba	1
12908	traspasar	1
12909	trasnochar	1
12910	trasnochado	1
12911	trasnochaban	1
12912	traslucir	1
12913	trasladaron	1
12914	trasladarle	1
12915	trasladándose	1
12916	trasladándonos	1
12917	trasladan	1
12918	trasladaba	1
12919	trascender	1
12920	trascendencia	1
12921	traqueteo	1
12922	trapicheo	1
12923	trapacero	1
12924	tranvías	1
12925	transportada	1
12926	transparente	1
12927	transparentarse	1
12928	transparentando	1
12929	transmitían	1
12930	tránsito	1
12931	transijo	1
12932	transigió	1
12933	transigía	1
12934	transición	1
12935	transfusiones	1
12936	transfusión	1
12937	transformismo	1
12938	transformase	1
12939	transformado	1
12940	transformación	1
12941	transcurrido	1
12942	transacción	1
12943	tranquilizado	1
12944	tranquilizaba	1
12945	trances	1
12946	tramposo	1
12947	tramando	1
12948	tramaban	1
12949	trajese	1
12950	traiga	1
12951	traídos	1
12952	traidoras	1
12953	traída	1
12954	tragué	1
12955	trago	1
12956	trágicos	1
12957	tragedias	1
12958	tragas	1
12959	tragármela	1
12960	tragaría	1
12961	tragaluces	1
12962	tragaban	1
12963	traerlos	1
12964	traerle	1
12965	traerla	1
12966	traería	1
12967	traerá	1
12968	traductora	1
12969	traducidos	1
12970	tradicionalmente	1
12971	trabucos	1
12972	trabillas	1
12973	trabajó	1
12974	trabajase	1
12975	tostasen	1
12976	tostado	1
12977	tostadas	1
12978	tosiendo	1
12979	tosido	1
12980	toscas	1
12981	torvo	1
12982	tortuosos	1
12983	tortillas	1
12984	tortilla	1
12985	torrente	1
12986	torpemente	1
12987	toro	1
12988	tornillos	1
12989	tornadiza	1
12990	tornaba	1
12991	tormentas	1
12992	toreros	1
12993	torcuato	1
12994	torcieron	1
12995	torciéndose	1
12996	torciendo	1
12997	torcidos	1
12998	torcedor	1
12999	toral	1
13000	toraces	1
13001	tópicos	1
13002	tópico	1
13003	topetazo	1
13004	too	1
13005	tontunas	1
13006	tontina	1
13007	tontear	1
13008	tontas	1
13009	tonillo	1
13010	ton	1
13011	tomos	1
13012	tomé	1
13013	tomase	1
13014	tomarlo	1
13015	tomarla	1
13016	tomarán	1
13017	tomará	1
13018	tomándolo	1
13019	tomándole	1
13020	tomadas	1
13021	tomada	1
13022	toleres	1
13023	toleraron	1
13024	tolerarlo	1
13025	toleraría	1
13026	toleran	1
13027	toleradas	1
13028	toleraban	1
13029	tolera	1
13030	tole	1
13031	tocase	1
13032	tocas	1
13033	tocarlos	1
13034	tocarás	1
13035	tocándole	1
13036	tocándola	1
13037	tocada	1
13038	tobillo	1
13039	tiznes	1
13040	tiznándole	1
13041	tiznado	1
13042	titulados	1
13043	titulado	1
13044	titubear	1
13045	tito	1
13046	titilar	1
13047	títeres	1
13048	titanes	1
13049	titán	1
13050	tísico	1
13051	tirsos	1
13052	tiroteo	1
13053	tiritando	1
13054	tirilla	1
13055	tiraría	1
13056	tiránico	1
13057	tiple	1
13058	tío	1
13059	tiñéndolo	1
13060	tinteros	1
13061	tintero	1
13062	tímpano	1
13063	timoratos	1
13064	timorata	1
13065	tímido	1
13066	tímidas	1
13067	timarse	1
13068	timaban	1
13069	timaba	1
13070	tigres	1
13071	tiesos	1
13072	tiernísimo	1
13073	tiernísima	1
13074	tiende	1
13075	tiemblas	1
13076	tiembla	1
13077	tiburón	1
13078	tibios	1
13079	thackeray	1
13080	tétrico	1
13081	tetrarca	1
13082	tessitura	1
13083	terso	1
13084	terruño	1
13085	terrorista	1
13086	terrores	1
13087	terrón	1
13088	territorio	1
13089	terrenas	1
13090	terranova	1
13091	terrados	1
13092	terrado	1
13093	terpsícore	1
13094	ternuras	1
13095	ternezas	1
13096	termómetro	1
13097	termine	1
13098	terminasen	1
13099	terminantemente	1
13100	terminando	1
13101	terminadas	1
13102	terminaciones	1
13103	terminaban	1
13104	tergiversemos	1
13105	tercos	1
13106	terciar	1
13107	terciado	1
13108	terciaba	1
13109	tercetos	1
13110	tercas	1
13111	terapéutica	1
13112	teórica	1
13113	teorías	1
13114	teólogos	1
13115	teológicos	1
13116	teócrito	1
13117	teocrático	1
13118	teñidas	1
13119	tenues	1
13120	tentativa	1
13121	tentarse	1
13122	tentar	1
13123	tentando	1
13124	tentadores	1
13125	tentadora	1
13126	tentáculos	1
13127	tenientes	1
13128	teniendo	1
13129	tenida	1
13130	tenias	1
13131	tenia	1
13132	tengan	1
13133	tengamos	1
13134	tenerles	1
13135	tenerlas	1
13136	tenebrosa	1
13137	tendrían	1
13138	tendríamos	1
13139	tendrán	1
13140	tendieron	1
13141	tendiendo	1
13142	tendían	1
13143	tender	1
13144	tenaz	1
13145	tenaces	1
13146	tempranos	1
13147	temprana	1
13148	temporis	1
13149	temporadas	1
13150	tempora	1
13151	templete	1
13152	templar	1
13153	templanza	1
13154	tempestades	1
13155	tempé	1
13156	temiéndolo	1
13157	temido	1
13158	temida	1
13159	temías	1
13160	temes	1
13161	temerosa	1
13162	temerones	1
13163	temeridades	1
13164	temeridad	1
13165	temerarios	1
13166	temerario	1
13167	temeraria	1
13168	temblorosos	1
13169	tembloroso	1
13170	temblorcico	1
13171	temblase	1
13172	temblaron	1
13173	temblábale	1
13174	telones	1
13175	telescopio	1
13176	telegramas	1
13177	telégrafos	1
13178	tejiendo	1
13179	tejido	1
13180	tejadillos	1
13181	tecum	1
13182	técnico	1
13183	tecnicismo	1
13184	técnica	1
13185	teclas	1
13186	techos	1
13187	teatrales	1
13188	teatral	1
13189	tazas	1
13190	taurina	1
13191	tatiste	1
13192	tasso	1
13193	tascaba	1
13194	tartana	1
13195	tarso	1
13196	tarsilita	1
13197	tareas	1
13198	tardo	1
13199	tardío	1
13200	tardé	1
13201	tardaron	1
13202	tardado	1
13203	tardaban	1
13204	tarasca	1
13205	tapó	1
13206	tapizada	1
13207	tapiceros	1
13208	tapias	1
13209	tape	1
13210	taparse	1
13211	taparle	1
13212	taparelli	1
13213	tapándose	1
13214	tapado	1
13215	tapadillos	1
13216	tañida	1
13217	tañía	1
13218	tañedor	1
13219	tantico	1
13220	tamizada	1
13221	tamiz	1
13222	tamboril	1
13223	tambores	1
13224	tambaleándose	1
13225	tamaños	1
13226	tamañitos	1
13227	tallos	1
13228	tallado	1
13229	talismán	1
13230	talegas	1
13231	talares	1
13232	tajos	1
13233	taimado	1
13234	taimada	1
13235	taigeto	1
13236	tahúr	1
13237	tagarnina	1
13238	tafurería	1
13239	tafetán	1
13240	taconeo	1
13241	tacón	1
13242	taciturnos	1
13243	taciturnas	1
13244	tácitos	1
13245	tácitamente	1
13246	tacita	1
13247	tachó	1
13248	tachado	1
13249	tacha	1
13250	taburete	1
13251	tablillas	1
13252	tableros	1
13253	tabernáculo	1
13254	suum	1
13255	sutilísimas	1
13256	sutilezas	1
13257	sutileza	1
13258	susurros	1
13259	sustraérsele	1
13260	sustentase	1
13261	sustentadas	1
13262	sustanciales	1
13263	sustancial	1
13264	sustancia	1
13265	suspirado	1
13266	suspicacias	1
13267	suspensión	1
13268	suspendo	1
13269	suspendiesen	1
13270	suspendidos	1
13271	suspende	1
13272	susodicho	1
13273	suscripción	1
13274	suscitar	1
13275	suscitaba	1
13276	surgieron	1
13277	surgiendo	1
13278	surgido	1
13279	surcadas	1
13280	surcaban	1
13281	surbicesorbi	1
13282	suprimiendo	1
13283	suprimida	1
13284	suprimían	1
13285	supremacía	1
13286	supra	1
13287	suposición	1
13288	suponiéndole	1
13289	suponíalo	1
13290	suponérseles	1
13291	suponerlo	1
13292	suplir	1
13293	suplico	1
13294	suplicio	1
13295	suplicaron	1
13296	suplicarle	1
13297	suplicar	1
13298	súplica	1
13299	suplica	1
13300	suplían	1
13301	suplía	1
13302	suple	1
13303	supersticiosas	1
13304	superfino	1
13305	superficialidades	1
13306	superficialidad	1
13307	superficial	1
13308	superan	1
13309	superaba	1
13310	supeditado	1
13311	supeditada	1
13312	supe	1
13313	suñera	1
13314	suntuosa	1
13315	sunt	1
13316	sumirlo	1
13317	suministraba	1
13318	sumergida	1
13319	sumas	1
13320	sumando	1
13321	sum	1
13322	sulfure	1
13323	sujetos	1
13324	sujetándole	1
13325	sujetando	1
13326	sujétale	1
13327	suizas	1
13328	suicidarnos	1
13329	suicida	1
13330	sugirió	1
13331	sugiriese	1
13332	sugirieron	1
13333	sugiriéndole	1
13334	sugieran	1
13335	sugestión	1
13336	sugeridas	1
13337	sugerían	1
13338	sufrirlos	1
13339	sufrirle	1
13340	sufrirlas	1
13341	sufrirá	1
13342	sufrió	1
13343	sufrimientos	1
13344	sufrimiento	1
13345	sufridos	1
13346	sufragio	1
13347	sufra	1
13348	suene	1
13349	suenan	1
13350	sueldos	1
13351	suegro	1
13352	suecos	1
13353	sueco	1
13354	suecia	1
13355	sudario	1
13356	sudar	1
13357	sucursal	1
13358	sucumbían	1
13359	suculenta	1
13360	sucesores	1
13361	sucesivas	1
13362	sucesivamente	1
13363	sucesiva	1
13364	sucedieran	1
13365	sucediéndose	1
13366	sucederse	1
13367	sucedáneo	1
13368	sucedan	1
13369	suceda	1
13370	subversivo	1
13371	subversiva	1
13372	subvenciones	1
13373	suburbios	1
13374	subterfugios	1
13375	subteniente	1
13376	subsuelo	1
13377	substituía	1
13378	subsistir	1
13379	subsiguientes	1
13380	subsiguiente	1
13381	subrepticios	1
13382	subrayó	1
13383	subrayando	1
13384	subrayadas	1
13385	subrayaba	1
13386	sublimizado	1
13387	sublimiza	1
13388	sublevó	1
13389	sublevarse	1
13390	sublevaron	1
13391	sublevado	1
13392	sublevadas	1
13393	sublevaban	1
13394	subleva	1
13395	subjetivo	1
13396	súbitas	1
13397	subirla	1
13398	subiría	1
13399	subidos	1
13400	subidas	1
13401	subes	1
13402	suben	1
13403	súbditos	1
13404	subalternos	1
13405	suba	1
13406	suavice	1
13407	stulta	1
13408	stream	1
13409	strauss	1
13410	stoa	1
13411	sprit	1
13412	sposa	1
13413	sport	1
13414	splendorum	1
13415	spiritu	1
13416	spínolas	1
13417	sousa	1
13418	sostenido	1
13419	sostenga	1
13420	sostendré	1
13421	sospechoso	1
13422	sospechó	1
13423	sospecho	1
13424	sospecharse	1
13425	sospechabas	1
13426	sosiéguese	1
13427	sosiego	1
13428	sosegado	1
13429	sorteaba	1
13430	sorprendieron	1
13431	sorprendiera	1
13432	sorprendiéndola	1
13433	sorprendían	1
13434	sorprenderle	1
13435	sorprenda	1
13436	sordomudos	1
13437	sordina	1
13438	sórdidos	1
13439	sórdidas	1
13440	sórdida	1
13441	sordas	1
13442	sorbos	1
13443	sorbete	1
13444	soportar	1
13445	soportable	1
13446	soporíferos	1
13447	soporífera	1
13448	sopló	1
13449	soplarse	1
13450	soplándose	1
13451	soñolientos	1
13452	soñoliento	1
13453	soñolientas	1
13454	soñarlo	1
13455	soñaré	1
13456	soñadores	1
13457	sonsoniche	1
13458	sonrosadas	1
13459	sonrojaba	1
13460	sonrisilla	1
13461	sonriéndoles	1
13462	sonreírse	1
13463	sonorosos	1
13464	sonoro	1
13465	sonidos	1
13466	sonetos	1
13467	sondearle	1
13468	sondear	1
13469	sondeado	1
13470	sonda	1
13471	sonasen	1
13472	sonase	1
13473	sonarían	1
13474	sonara	1
13475	sonantes	1
13476	sonante	1
13477	sonámbulos	1
13478	sonámbula	1
13479	sonados	1
13480	sonada	1
13481	somieda	1
13482	sometieron	1
13483	sometidos	1
13484	sometido	1
13485	sometida	1
13486	sometía	1
13487	somete	1
13488	someros	1
13489	somera	1
13490	sombríos	1
13491	solterona	1
13492	solterón	1
13493	soltero	1
13494	solteras	1
13495	soltarse	1
13496	soltaron	1
13497	soltarlo	1
13498	soltar	1
13499	soltaba	1
13500	sollozo	1
13501	soliviantados	1
13502	sólido	1
13503	solideo	1
13504	sólidas	1
13505	solidaridad	1
13506	solidaria	1
13507	sólidamente	1
13508	solícitos	1
13509	solicitaron	1
13510	solicitan	1
13511	solicitado	1
13512	solicitada	1
13513	solicitación	1
13514	solicita	1
13515	solfeó	1
13516	solemos	1
13517	solemnes	1
13518	solecismos	1
13519	solazarse	1
13520	solar	1
13521	solapas	1
13522	solamente	1
13523	soit	1
13524	soga	1
13525	sofocar	1
13526	sofocado	1
13527	sofocaciones	1
13528	sofiones	1
13529	socorros	1
13530	socialismo	1
13531	sociable	1
13532	socia	1
13533	sochantre	1
13534	sobrón	1
13535	sobrios	1
13536	sobrio	1
13537	sobrino	1
13538	sobrinitas	1
13539	sobrevivirían	1
13540	sobrevivirá	1
13541	sobrevenía	1
13542	sobresalto	1
13543	sobresaltadas	1
13544	sobresaltada	1
13545	sobrenadó	1
13546	sobremesa	1
13547	sobrehumano	1
13548	sobrecogió	1
13549	sobrecogían	1
13550	sobrecogía	1
13551	sobrecogería	1
13552	sobras	1
13553	sobran	1
13554	sobramos	1
13555	sobradamente	1
13556	sobrada	1
13557	soberanos	1
13558	soberano	1
13559	soberanía	1
13560	sobadas	1
13561	sobaco	1
13562	sixto	1
13563	situada	1
13564	sitial	1
13565	sitiada	1
13566	sitiaba	1
13567	sistemática	1
13568	sisas	1
13569	sisar	1
13570	sirvieron	1
13571	sirves	1
13572	sirva	1
13573	siria	1
13574	sirenas	1
13575	sirena	1
13576	sinuoso	1
13577	sinuosidades	1
13578	sinuosa	1
13579	sintiéndolo	1
13580	sintetizan	1
13581	sinrazones	1
13582	sinónimo	1
13583	singularísima	1
13584	singulares	1
13585	síncopes	1
13586	síncope	1
13587	sinceras	1
13588	sinapismos	1
13589	simultáneos	1
13590	simultáneo	1
13591	simulacros	1
13592	simulaba	1
13593	simplicidad	1
13594	simplemente	1
13595	simpatías	1
13596	simonías	1
13597	símil	1
13598	simiente	1
13599	simétricas	1
13600	simetría	1
13601	simeón	1
13602	símbolos	1
13603	simbolismos	1
13604	simbólica	1
13605	simancas	1
13606	sima	1
13607	silva	1
13608	sillería	1
13609	sillares	1
13610	silenciosas	1
13611	silencios	1
13612	silbar	1
13613	silbante	1
13614	silbándoles	1
13615	silbado	1
13616	siguiesen	1
13617	siguiera	1
13618	sígueme	1
13619	signo	1
13620	significativo	1
13621	significativas	1
13622	significada	1
13623	sigiloso	1
13624	sigas	1
13625	sigan	1
13626	siga	1
13627	sietemesinos	1
13628	sierpes	1
13629	sientes	1
13630	sienten	1
13631	siéntate	1
13632	sientas	1
13633	sien	1
13634	siemprevivas	1
13635	sic	1
13636	sibila	1
13637	shakespeare	1
13638	sexta	1
13639	sevillano	1
13640	severos	1
13641	severísima	1
13642	severas	1
13643	sesiones	1
13644	sesgaba	1
13645	sesentona	1
13646	servilmente	1
13647	servilletero	1
13648	servilletas	1
13649	serviles	1
13650	servida	1
13651	servicial	1
13652	serviam	1
13653	servíale	1
13654	serrallo	1
13655	serpiente	1
13656	serpentones	1
13657	serpeando	1
13658	serpeaba	1
13659	serpea	1
13660	serones	1
13661	sernos	1
13662	serme	1
13663	serle	1
13664	serie	1
13665	serenísimo	1
13666	serenatas	1
13667	serenata	1
13668	serenarse	1
13669	seráfica	1
13670	sequedades	1
13671	sepultadas	1
13672	sépase	1
13673	sepas	1
13674	separose	1
13675	sepárese	1
13676	separarme	1
13677	separarlo	1
13678	separarlas	1
13679	separarla	1
13680	separadas	1
13681	separaban	1
13682	sepan	1
13683	señoriles	1
13684	señoa	1
13685	señalo	1
13686	señalados	1
13687	señaladas	1
13688	señalaban	1
13689	señala	1
13690	sentirlos	1
13691	sentirle	1
13692	sentirlas	1
13693	sentimos	1
13694	sentíalo	1
13695	sentarte	1
13696	sentarnos	1
13697	sentao	1
13698	sentándose	1
13699	sensualista	1
13700	sensualismo	1
13701	sensualidad	1
13702	sensiblería	1
13703	sensatos	1
13704	sensatas	1
13705	sensatamente	1
13706	senil	1
13707	sencillos	1
13708	sencillísimo	1
13709	sempiternas	1
13710	semillero	1
13711	semicírculo	1
13712	semicientífico	1
13713	sementales	1
13714	semejanzas	1
13715	sembrara	1
13716	sembrar	1
13717	sembrados	1
13718	sembraba	1
13719	selvática	1
13720	selva	1
13721	sellos	1
13722	sello	1
13723	selecto	1
13724	seguridades	1
13725	seguirlas	1
13726	seguiremos	1
13727	seguiré	1
13728	seguirán	1
13729	seguirá	1
13730	seguí	1
13731	segadora	1
13732	segaban	1
13733	sedúzcanmela	1
13734	sedujeron	1
13735	seductoras	1
13736	seducírselo	1
13737	seducida	1
13738	seduce	1
13739	seducciones	1
13740	sedoso	1
13741	sediento	1
13742	sedentarismo	1
13743	sedentario	1
13744	sedentaria	1
13745	secundum	1
13746	secundario	1
13747	secundarias	1
13748	secundaria	1
13749	secundar	1
13750	secundaba	1
13751	secularizándose	1
13752	secularización	1
13753	secuestrarlo	1
13754	secuestramos	1
13755	secuestrador	1
13756	secuentia	1
13757	secretillo	1
13758	secretario	1
13759	secretamente	1
13760	secciones	1
13761	secchi	1
13762	secarse	1
13763	secando	1
13764	secado	1
13765	secaban	1
13766	sebastopol	1
13767	sebastián	1
13768	sazonada	1
13769	sayones	1
13770	sauces	1
13771	sauce	1
13772	saturnillo	1
13773	saturación	1
13774	satisfizo	1
13775	satisfagan	1
13776	satisfacerles	1
13777	satisfacerle	1
13778	satíricos	1
13779	sátira	1
13780	satinado	1
13781	satén	1
13782	satánico	1
13783	satán	1
13784	sastrerías	1
13785	sarraceno	1
13786	sardou	1
13787	sardónica	1
13788	sarcástica	1
13789	saquen	1
13790	saqueaban	1
13791	santurrona	1
13792	santurrón	1
13793	santina	1
13794	santiguado	1
13795	santiguaba	1
13796	santificante	1
13797	sansón	1
13798	sansimoniano	1
13799	sanos	1
13800	sanó	1
13801	sanitario	1
13802	sanguis	1
13803	sanguinolenta	1
13804	sanguinario	1
13805	sanguijuelas	1
13806	sangrientamente	1
13807	sangrienta	1
13808	sangrar	1
13809	sangraban	1
13810	sandunga	1
13811	sandalias	1
13812	sanctos	1
13813	sanctorum	1
13814	sancti	1
13815	sancionaría	1
13816	sanción	1
13817	sancho	1
13818	sanase	1
13819	sanaría	1
13820	sanaba	1
13821	salvó	1
13822	sálvense	1
13823	salvaremos	1
13824	salvara	1
13825	salvadora	1
13826	salvada	1
13827	salvaba	1
13828	salus	1
13829	salúdele	1
13830	saludarse	1
13831	saludarme	1
13832	saludarle	1
13833	saludarlas	1
13834	saludaran	1
13835	saludándola	1
13836	saludado	1
13837	saludables	1
13838	saluda	1
13839	salté	1
13840	saltase	1
13841	saltarlo	1
13842	saltarines	1
13843	saltará	1
13844	saltan	1
13845	salpimentar	1
13846	salpicar	1
13847	salomónicas	1
13848	salomón	1
13849	salmones	1
13850	salmistas	1
13851	salirle	1
13852	salimos	1
13853	salientes	1
13854	salidas	1
13855	salid	1
13856	saldaba	1
13857	salchichón	1
13858	salado	1
13859	salada	1
13860	sahumados	1
13861	sagunto	1
13862	sagrarios	1
13863	sacudirse	1
13864	sacudirles	1
13865	sacudimientos	1
13866	sacudiéndola	1
13867	sacudido	1
13868	sacrosanto	1
13869	sacristán	1
13870	sacris	1
13871	sacrilegio	1
13872	sacrifico	1
13873	sacrificase	1
13874	sacrificaría	1
13875	sacrificándose	1
13876	sacrifican	1
13877	sacrificada	1
13878	sacrificaba	1
13879	sacramentales	1
13880	sacramental	1
13881	sacias	1
13882	sacerdotisa	1
13883	sacerdotal	1
13884	sacatrapos	1
13885	sacaste	1
13886	sacarte	1
13887	sacaron	1
13888	sacarlo	1
13889	sacaran	1
13890	sacará	1
13891	sacao	1
13892	sacada	1
13893	sabroso	1
13894	sabrosas	1
13895	sabrás	1
13896	sabores	1
13897	saboreó	1
13898	saboreando	1
13899	sablazos	1
13900	sabihondo	1
13901	saberle	1
13902	saberlas	1
13903	sábelo	1
13904	sabandija	1
13905	sabanas	1
13906	rutinas	1
13907	rutinarios	1
13908	rutinaria	1
13909	rústico	1
13910	rural	1
13911	rumorosa	1
13912	rumorcillo	1
13913	rumiase	1
13914	rumiara	1
13915	rumboso	1
13916	rumbosa	1
13917	ruleta	1
13918	ruinosos	1
13919	ruinosas	1
13920	ruinosa	1
13921	ruidosos	1
13922	ruidosas	1
13923	rugir	1
13924	rugidos	1
13925	rugía	1
13926	rufinita	1
13927	ruego	1
13928	ruedos	1
13929	ruedo	1
13930	rudo	1
13931	rudesinda	1
13932	rucutucua	1
13933	rúbrica	1
13934	ruborizándose	1
13935	ruborizadas	1
13936	rubores	1
13937	rubita	1
13938	rozase	1
13939	rozarse	1
13940	rozando	1
13941	rozagantes	1
13942	rozado	1
13943	rozaba	1
13944	royéndolo	1
13945	rotundo	1
13946	rótulo	1
13947	rotos	1
13948	rotin	1
13949	rosendo	1
13950	rorro	1
13951	roquetes	1
13952	roquero	1
13953	ropón	1
13954	ropas	1
13955	ronzalillo	1
13956	ronzalesco	1
13957	ronzalesca	1
13958	ronquidos	1
13959	rondaba	1
13960	roncas	1
13961	roncando	1
13962	ron	1
13963	rompiéndose	1
13964	rompiéndome	1
13965	romperse	1
13966	romperla	1
13967	rompen	1
13968	rompecabezas	1
13969	romerías	1
13970	romea	1
13971	romas	1
13972	romanus	1
13973	romantismo	1
13974	románica	1
13975	romancero	1
13976	romanas	1
13977	rollizos	1
13978	rollizo	1
13979	rojizo	1
13980	roían	1
13981	roía	1
13982	rogativas	1
13983	rogando	1
13984	rogaba	1
13985	rodríguez	1
13986	rodó	1
13987	rodeó	1
13988	rodearte	1
13989	rodear	1
13990	rodaron	1
13991	rococó	1
13992	roció	1
13993	rociaba	1
13994	robustas	1
13995	robledo	1
13996	robledales	1
13997	robas	1
13998	robarle	1
13999	robándole	1
14000	robando	1
14001	rivalizar	1
14002	rivales	1
14003	ritos	1
14004	rítmicos	1
14005	ristre	1
14006	rire	1
14007	rio	1
14008	riñó	1
14009	riño	1
14010	riñeran	1
14011	ríñeme	1
14012	riñas	1
14013	riña	1
14014	rinconadas	1
14015	rima	1
14016	riguroso	1
14017	rigolade	1
14018	rigodones	1
14019	rigidez	1
14020	rígida	1
14021	rifas	1
14022	ríes	1
14023	riendas	1
14024	riegan	1
14025	ridente	1
14026	ricacho	1
14027	ribera	1
14028	ríanse	1
14029	rían	1
14030	rezumaba	1
14031	rezos	1
14032	rezarle	1
14033	rezaría	1
14034	rezagados	1
14035	rezagadas	1
14036	rewólver	1
14037	revuelven	1
14038	revue	1
14039	revolvió	1
14040	revolverse	1
14041	revoluciones	1
14042	revolucionarios	1
14043	revoltoso	1
14044	revoltosas	1
14045	revoltosa	1
14046	revolando	1
14047	revestido	1
14048	revestían	1
14049	reverso	1
14050	reverencias	1
14051	reverbero	1
14052	reverberada	1
14053	reventó	1
14054	reventaba	1
14055	revele	1
14056	revelase	1
14057	revelaron	1
14058	revelarle	1
14059	revelando	1
14060	reveladas	1
14061	reunidos	1
14062	reunidas	1
14063	reúna	1
14064	retumbante	1
14065	retumba	1
14066	retuerce	1
14067	retrospectivo	1
14068	retrospectiva	1
14069	retroceso	1
14070	retrocediendo	1
14071	retrato	1
14072	retrataba	1
14073	retrasó	1
14074	retrasen	1
14075	retrasaba	1
14076	retrae	1
14077	retractase	1
14078	retractarse	1
14079	retractación	1
14080	retozaba	1
14081	retour	1
14082	retorta	1
14083	retórico	1
14084	retorció	1
14085	retorcida	1
14086	retorcerse	1
14087	retocados	1
14088	retiré	1
14089	retirasen	1
14090	retirarlo	1
14091	retiran	1
14092	retira	1
14093	retintín	1
14094	retina	1
14095	retebién	1
14096	retarde	1
14097	retardaba	1
14098	retado	1
14099	retaba	1
14100	resurrección	1
14101	resumía	1
14102	resultas	1
14103	resultan	1
14104	resuelven	1
14105	resueltos	1
14106	resuello	1
14107	resucitaba	1
14108	resucita	1
14109	restriñimientos	1
14110	restringido	1
14111	restreñimientos	1
14112	restituya	1
14113	restituirse	1
14114	restituirlo	1
14115	restituir	1
14116	restituida	1
14117	restituía	1
14118	restaurar	1
14119	restaurando	1
14120	restaurado	1
14121	restañar	1
14122	restablecido	1
14123	respuestas	1
14124	responsos	1
14125	respondieron	1
14126	responda	1
14127	resplandeciente	1
14128	respiraron	1
14129	respiraban	1
14130	respira	1
14131	respetuosos	1
14132	respetuosa	1
14133	respeten	1
14134	respetaron	1
14135	respetaran	1
14136	respetadas	1
14137	respetabilísimos	1
14138	respectivamente	1
14139	respecta	1
14140	respaldos	1
14141	resonaron	1
14142	resonante	1
14143	resonaban	1
14144	resonaba	1
14145	resolvía	1
14146	resolvérsele	1
14147	resolverse	1
14148	resolvería	1
14149	resolvamos	1
14150	resoluciones	1
14151	resistiría	1
14152	resistido	1
14153	resistían	1
14154	resignó	1
14155	resignaron	1
14156	resignarnos	1
14157	resignan	1
14158	residir	1
14159	residencia	1
14160	reservarle	1
14161	reservarían	1
14162	reservados	1
14163	reservaban	1
14164	reseñada	1
14165	resentido	1
14166	rescatar	1
14167	resbaló	1
14168	resbalas	1
14169	resbalan	1
14170	resbalaban	1
14171	resbalaba	1
14172	res	1
14173	requirió	1
14174	requerido	1
14175	requerida	1
14176	requebrarla	1
14177	reputaciones	1
14178	reputación	1
14179	reputábala	1
14180	repugnándole	1
14181	repugnancias	1
14182	repugnan	1
14183	repugna	1
14184	repuesto	1
14185	republicanitos	1
14186	republicana	1
14187	reproducen	1
14188	reprimió	1
14189	represiva	1
14190	representativo	1
14191	representársela	1
14192	representarse	1
14193	representante	1
14194	representado	1
14195	representadas	1
14196	reprendo	1
14197	reprendiese	1
14198	reprendido	1
14199	reprendía	1
14200	reprenden	1
14201	reposado	1
14202	reposaba	1
14203	reportase	1
14204	reportarse	1
14205	repone	1
14206	repliegues	1
14207	replicar	1
14208	replicado	1
14209	replicaba	1
14210	repletos	1
14211	repleta	1
14212	repitiendo	1
14213	repiqueteo	1
14214	repiquen	1
14215	repique	1
14216	repetirlo	1
14217	repetiría	1
14218	repertorio	1
14219	repercutiendo	1
14220	repentista	1
14221	repecho	1
14222	repartirse	1
14223	repartiros	1
14224	repartidos	1
14225	repartido	1
14226	repartidas	1
14227	repartida	1
14228	repartían	1
14229	reparten	1
14230	repartan	1
14231	reparos	1
14232	repararon	1
14233	reparar	1
14234	reparando	1
14235	reparaciones	1
14236	reo	1
14237	reñirle	1
14238	reñir	1
14239	reñía	1
14240	renuncio	1
14241	renunciarla	1
14242	renunciando	1
14243	renunciado	1
14244	renuncia	1
14245	renueva	1
14246	rentístico	1
14247	renovar	1
14248	renovada	1
14249	renovación	1
14250	renovaban	1
14251	reniega	1
14252	renglón	1
14253	rendondilla	1
14254	rendirse	1
14255	rendirle	1
14256	rendimiento	1
14257	rendidas	1
14258	rendían	1
14259	rencoroso	1
14260	rencorosas	1
14261	rencorosa	1
14262	renacimiento	1
14263	renaciera	1
14264	renacían	1
14265	removiendo	1
14266	removida	1
14267	removían	1
14268	removía	1
14269	remover	1
14270	remoto	1
14271	remordiera	1
14272	remontar	1
14273	remonísima	1
14274	remolque	1
14275	remolones	1
14276	remolacha	1
14277	remito	1
14278	remitido	1
14279	remiso	1
14280	remendón	1
14281	remendando	1
14282	remendados	1
14283	remendado	1
14284	remedia	1
14285	remedaban	1
14286	remate	1
14287	rematados	1
14288	remanso	1
14289	relucían	1
14290	relojes	1
14291	relojero	1
14292	rellenas	1
14293	reliquia	1
14294	relevaban	1
14295	relator	1
14296	relativos	1
14297	relamida	1
14298	relajar	1
14299	relajamiento	1
14300	relajado	1
14301	relajación	1
14302	relacionaba	1
14303	rejuveneciendo	1
14304	reivindicar	1
14305	reivindicación	1
14306	reiteradas	1
14307	reírse	1
14308	reintegrado	1
14309	reinase	1
14310	reinas	1
14311	reinar	1
14312	reíanse	1
14313	rehusar	1
14314	rehuir	1
14315	rehuía	1
14316	rehabilitarse	1
14317	regumque	1
14318	regularmente	1
14319	regulam	1
14320	regresó	1
14321	regocijó	1
14322	reglamento	1
14323	reglamentarios	1
14324	registrar	1
14325	registrándole	1
14326	registrando	1
14327	regio	1
14328	regeneración	1
14329	rege	1
14330	regazados	1
14331	regateo	1
14332	regatear	1
14333	regatean	1
14334	regar	1
14335	regalen	1
14336	regalarle	1
14337	regalan	1
14338	regalados	1
14339	regaladas	1
14340	regada	1
14341	refutaría	1
14342	refugió	1
14343	refugiarse	1
14344	refugiadas	1
14345	refugiábanse	1
14346	refugiaba	1
14347	refuerzos	1
14348	refrigerado	1
14349	refriega	1
14350	refrescar	1
14351	refrenada	1
14352	refrán	1
14353	refractaban	1
14354	reforzada	1
14355	reformistas	1
14356	reformista	1
14357	reflexivo	1
14358	reflexionando	1
14359	reflejados	1
14360	reflejado	1
14361	reflejadas	1
14362	refiriéndose	1
14363	refinamiento	1
14364	refinados	1
14365	refieren	1
14366	refiere	1
14367	referírselas	1
14368	referiré	1
14369	referente	1
14370	reencarnación	1
14371	reemplazarlas	1
14372	reedificaba	1
14373	reduplicado	1
14374	redundantes	1
14375	redundancia	1
14376	redujo	1
14377	reducto	1
14378	reducirle	1
14379	reducida	1
14380	redondos	1
14381	redondillas	1
14382	redondeaban	1
14383	redoma	1
14384	redobló	1
14385	redoble	1
14386	redoblar	1
14387	redivivo	1
14388	rediviva	1
14389	réditos	1
14390	redimirse	1
14391	redimirle	1
14392	redimir	1
14393	redimido	1
14394	redimidas	1
14395	redimía	1
14396	redentor	1
14397	redención	1
14398	redactor	1
14399	redactaré	1
14400	recurrió	1
14401	reculó	1
14402	recuerden	1
14403	recuento	1
14404	rectos	1
14405	rectificando	1
14406	rectas	1
14407	rectángulos	1
14408	rectángulo	1
14409	rectangular	1
14410	rectae	1
14411	recta	1
14412	recreos	1
14413	recrearme	1
14414	recreándose	1
14415	recreándonos	1
14416	recreaban	1
14417	recostole	1
14418	recostó	1
14419	recostaba	1
14420	recortes	1
14421	recortado	1
14422	recortadas	1
14423	recortaba	1
14424	recorriese	1
14425	recorrían	1
14426	recorre	1
14427	recordasen	1
14428	recordarlo	1
14429	recordarla	1
14430	recordará	1
14431	recordara	1
14432	recordadas	1
14433	recopilación	1
14434	reconvención	1
14435	recontaba	1
14436	reconquista	1
14437	reconocieron	1
14438	reconociera	1
14439	reconociendo	1
14440	reconocidos	1
14441	reconocida	1
14442	reconocí	1
14443	reconocerle	1
14444	reconocerla	1
14445	reconocería	1
14446	recóndito	1
14447	recóndita	1
14448	reconcilió	1
14449	reconciliarme	1
14450	reconciliaría	1
14451	reconciliarás	1
14452	reconciliaciones	1
14453	reconcentradas	1
14454	reconcentrada	1
14455	recompensar	1
14456	recomendó	1
14457	recomendarle	1
14458	recomendados	1
14459	recomendación	1
14460	recoletos	1
14461	recojo	1
14462	recoja	1
14463	recogidos	1
14464	recogerlo	1
14465	recogen	1
14466	recogemos	1
14467	recobraste	1
14468	recobrará	1
14469	recobrando	1
14470	reclinada	1
14471	reclamando	1
14472	reclama	1
14473	recitados	1
14474	recíproca	1
14475	recintos	1
14476	recientes	1
14477	recibirá	1
14478	recibimos	1
14479	recibimiento	1
14480	recibiera	1
14481	recibiéndolas	1
14482	recibidas	1
14483	recibida	1
14484	recibí	1
14485	recias	1
14486	rechinasen	1
14487	rechinaran	1
14488	rechinaban	1
14489	rechinaba	1
14490	rechazar	1
14491	rechazando	1
14492	rechazadas	1
14493	recetas	1
14494	recetaba	1
14495	receta	1
14496	recentales	1
14497	recelosas	1
14498	recelosa	1
14499	recelos	1
14500	rece	1
14501	recayó	1
14502	recaudado	1
14503	recatarse	1
14504	recatados	1
14505	recatadamente	1
14506	recatada	1
14507	recalcitrantes	1
14508	recaía	1
14509	recados	1
14510	rebuscar	1
14511	rebuscaban	1
14512	rebullir	1
14513	rebrinquen	1
14514	rebozo	1
14515	rebozado	1
14516	rebozada	1
14517	rebotaron	1
14518	rebosando	1
14519	rebosaba	1
14520	rebosa	1
14521	reblandecer	1
14522	rebeliones	1
14523	rebeldes	1
14524	rebela	1
14525	rebeca	1
14526	rebasaría	1
14527	rebasara	1
14528	rebajó	1
14529	rebajarse	1
14530	rebajar	1
14531	rebajando	1
14532	rebaja	1
14533	reapareció	1
14534	reaparecía	1
14535	reanudó	1
14536	reanudados	1
14537	reanuda	1
14538	reanimó	1
14539	realizando	1
14540	realizados	1
14541	realizaban	1
14542	reacias	1
14543	reaccionarios	1
14544	re	1
14545	razonable	1
14546	razonaba	1
14547	rayó	1
14548	rayar	1
14549	raudales	1
14550	raudal	1
14551	ratoncillo	1
14552	ratificó	1
14553	rastrero	1
14554	rastrera	1
14555	raspaba	1
14556	rasgarse	1
14557	rasgara	1
14558	rasgando	1
14559	rasgadas	1
14560	rascándose	1
14561	rarísimas	1
14562	raquítica	1
14563	rapto	1
14564	rapsodias	1
14565	rápidos	1
14566	rapidísima	1
14567	rapado	1
14568	rapa	1
14569	rancios	1
14570	rana	1
14571	ramilletes	1
14572	ramillete	1
14573	ramificaciones	1
14574	ramerilla	1
14575	ramayana	1
14576	ralea	1
14577	raja	1
14578	raídas	1
14579	racionalmente	1
14580	racionalismo	1
14581	ración	1
14582	raciocinios	1
14583	racimos	1
14584	racha	1
14585	rabiosos	1
14586	rabien	1
14587	rabiar	1
14588	rabian	1
14589	rábano	1
14590	r	1
14591	quum	1
14592	quod	1
14593	quizá	1
14594	quito	1
14595	quítese	1
14596	quite	1
14597	quitaron	1
14598	quitarme	1
14599	quitando	1
14600	quítame	1
14601	quitado	1
14602	quisquilloso	1
14603	quisque	1
14604	quisiste	1
14605	quisieras	1
14606	quisicosa	1
14607	quis	1
14608	quinto	1
14609	quinti	1
14610	quintales	1
14611	quinientas	1
14612	químicos	1
14613	químico	1
14614	quijotescos	1
14615	quijotada	1
14616	quijada	1
14617	quietud	1
14618	quietismo	1
14619	quiés	1
14620	quid	1
14621	quia	1
14622	qui	1
14623	question	1
14624	querrías	1
14625	querríamos	1
14626	querrás	1
14627	querrán	1
14628	queridísima	1
14629	queríala	1
14630	quererme	1
14631	quererlos	1
14632	quererlo	1
14633	querella	1
14634	queréis	1
14635	quepa	1
14636	quemó	1
14637	quemarlo	1
14638	quemando	1
14639	quemadura	1
14640	quemado	1
14641	quejumbrosos	1
14642	quejumbroso	1
14643	quejumbrosa	1
14644	quejo	1
14645	queje	1
14646	quejaron	1
14647	quejándose	1
14648	quejabas	1
14649	quejaban	1
14650	quedase	1
14651	quedarte	1
14652	quedarían	1
14653	quedaremos	1
14654	quedaré	1
14655	quedaran	1
14656	quedaos	1
14657	quedábamos	1
14658	quebrantarse	1
14659	quebrándose	1
14660	quebrada	1
14661	quebraba	1
14662	quanti	1
14663	quando	1
14664	quam	1
14665	pústulas	1
14666	pusiste	1
14667	pusilánime	1
14668	pusiese	1
14669	puse	1
14670	purulentas	1
14671	purpurinos	1
14672	purísimas	1
14673	purísima	1
14674	purificada	1
14675	puridad	1
14676	purezas	1
14677	pupilo	1
14678	pupila	1
14679	puñalada	1
14680	puñados	1
14681	puñado	1
14682	puñada	1
14683	puntuación	1
14684	puntillo	1
14685	puntiagudas	1
14686	puntiaguda	1
14687	puntapié	1
14688	puntales	1
14689	puntal	1
14690	puntadas	1
14691	pundonor	1
14692	pumaradas	1
14693	pumarada	1
14694	pum	1
14695	pulvis	1
14696	pulverizarse	1
14697	pulverizar	1
14698	pululan	1
14699	pululáis	1
14700	pulsa	1
14701	pulidas	1
14702	pulgas	1
14703	pulgada	1
14704	pujanza	1
14705	pugnaban	1
14706	pugnaba	1
14707	pugna	1
14708	pugilato	1
14709	puéstole	1
14710	pués	1
14711	puerros	1
14712	puerro	1
14713	puerperio	1
14714	puerperales	1
14715	puerilidades	1
14716	puerilidad	1
14717	pueriles	1
14718	puercos	1
14719	pué	1
14720	pudrirse	1
14721	pudriría	1
14722	pudrirá	1
14723	pudrían	1
14724	pudren	1
14725	pudre	1
14726	pudra	1
14727	pudorosa	1
14728	pudieras	1
14729	pudiéramos	1
14730	pudientes	1
14731	pudibundo	1
14732	publicidad	1
14733	publicarlas	1
14734	publicaría	1
14735	publicar	1
14736	públicamente	1
14737	publicación	1
14738	publicaban	1
14739	psíquico	1
14740	psicológico	1
14741	psicológicas	1
14742	psicológicamente	1
14743	psicologías	1
14744	pseudoclásico	1
14745	pruebo	1
14746	pruebe	1
14747	prudentemente	1
14748	proyectiles	1
14749	proyectado	1
14750	proyectada	1
14751	proyectaba	1
14752	próximas	1
14753	provocó	1
14754	provocativo	1
14755	provocarlas	1
14756	provocan	1
14757	provocados	1
14758	provocador	1
14759	provocado	1
14760	provoca	1
14761	provisto	1
14762	provisores	1
14763	provisionalmente	1
14764	provincianos	1
14765	provinciana	1
14766	proviene	1
14767	proverbial	1
14768	proveer	1
14769	provechosos	1
14770	provechosas	1
14771	provechosa	1
14772	protoplasma	1
14773	protestase	1
14774	protestaron	1
14775	protestara	1
14776	protestante	1
14777	protestan	1
14778	protejo	1
14779	proteja	1
14780	protegió	1
14781	protegiendo	1
14782	prostituta	1
14783	prosternaban	1
14784	próspero	1
14785	prosperidad	1
14786	prosperaría	1
14787	prosperaba	1
14788	prosopopeya	1
14789	prosigue	1
14790	prosigas	1
14791	prosélito	1
14792	proseguir	1
14793	prorrumpir	1
14794	prorrumpiéramos	1
14795	propuesta	1
14796	propter	1
14797	proposiciones	1
14798	proporcionado	1
14799	proponían	1
14800	propongo	1
14801	proponga	1
14802	proponemos	1
14803	propietarios	1
14804	prophani	1
14805	propedéutica	1
14806	propasó	1
14807	propasase	1
14808	propasado	1
14809	propasa	1
14810	propalar	1
14811	propalando	1
14812	propalaba	1
14813	propala	1
14814	propagar	1
14815	propagandistas	1
14816	propagandista	1
14817	propagaban	1
14818	pronunció	1
14819	pronunciaron	1
14820	pronuncia	1
14821	pronósticos	1
14822	pronosticado	1
14823	promulgó	1
14824	prominencias	1
14825	prometo	1
14826	prometida	1
14827	prometían	1
14828	prometerse	1
14829	prometerla	1
14830	prometería	1
14831	promete	1
14832	prolongándose	1
14833	prolongadas	1
14834	prolongaban	1
14835	prolonga	1
14836	prolija	1
14837	proletarios	1
14838	proletarias	1
14839	prole	1
14840	prohibiría	1
14841	prohibió	1
14842	prohibiera	1
14843	prohibían	1
14844	prohíban	1
14845	progresa	1
14846	profundísima	1
14847	profiriese	1
14848	profesores	1
14849	profesor	1
14850	profeso	1
14851	profesaron	1
14852	profesar	1
14853	profesadas	1
14854	profesaban	1
14855	profanó	1
14856	profanarlo	1
14857	profanaran	1
14858	profanaban	1
14859	proezas	1
14860	produciendo	1
14861	producidas	1
14862	producida	1
14863	prodromos	1
14864	prodigioso	1
14865	prodigiosamente	1
14866	prodigiosa	1
14867	prodigara	1
14868	prodigando	1
14869	prodigalidad	1
14870	pródiga	1
14871	procurose	1
14872	procuro	1
14873	procurarse	1
14874	procurarla	1
14875	procurará	1
14876	procurándolo	1
14877	procuradores	1
14878	procura	1
14879	proclamarse	1
14880	proclamamos	1
14881	proclama	1
14882	procedimientos	1
14883	procedimiento	1
14884	procedentes	1
14885	procedente	1
14886	procedencia	1
14887	procede	1
14888	proboscidio	1
14889	problemas	1
14890	probidad	1
14891	probecicos	1
14892	probasen	1
14893	probarme	1
14894	probarlo	1
14895	proba	1
14896	pro	1
14897	privilegiado	1
14898	privilegiadas	1
14899	privilegiada	1
14900	privarse	1
14901	privarle	1
14902	privación	1
14903	priva	1
14904	prístina	1
14905	prismáticos	1
14906	prisionero	1
14907	principium	1
14908	principiar	1
14909	principado	1
14910	princesas	1
14911	primos	1
14912	primorosa	1
14913	primordiales	1
14914	primitivas	1
14915	primita	1
14916	primicias	1
14917	primerizos	1
14918	primerizo	1
14919	primeriza	1
14920	primeramente	1
14921	previo	1
14922	previamente	1
14923	preveo	1
14924	prevenirnos	1
14925	prevenirle	1
14926	prevenida	1
14927	prevenía	1
14928	prevención	1
14929	prevaricaciones	1
14930	prevaliéndose	1
14931	prevaleciese	1
14932	pretil	1
14933	pretexta	1
14934	pretéritos	1
14935	pretérita	1
14936	pretericiones	1
14937	pretendientes	1
14938	pretendí	1
14939	pretenda	1
14940	presurosos	1
14941	presuntuoso	1
14942	presuntuosa	1
14943	presumiese	1
14944	presumidillas	1
14945	presumían	1
14946	prestidigitador	1
14947	preste	1
14948	prestaríamos	1
14949	prestaría	1
14950	prestar	1
14951	préstamos	1
14952	prestamista	1
14953	prestada	1
14954	presión	1
14955	presillas	1
14956	presiento	1
14957	presidió	1
14958	presidiera	1
14959	presididos	1
14960	presidido	1
14961	presidiario	1
14962	presidencia	1
14963	presentimientos	1
14964	presentían	1
14965	presentía	1
14966	presenten	1
14967	presentase	1
14968	presentarlo	1
14969	presentarles	1
14970	presentaría	1
14971	presentada	1
14972	presentación	1
14973	presentable	1
14974	presenció	1
14975	presenciara	1
14976	presenciado	1
14977	presenciaba	1
14978	preseas	1
14979	presea	1
14980	prescribe	1
14981	prescindirían	1
14982	prescindiendo	1
14983	prescindido	1
14984	prescindamos	1
14985	presbiterio	1
14986	presas	1
14987	prerrogativa	1
14988	prepararme	1
14989	prepararían	1
14990	prepararía	1
14991	preparándolos	1
14992	preparadas	1
14993	prepara	1
14994	preocupó	1
14995	preocuparse	1
14996	preocupándole	1
14997	preocupan	1
14998	preñadas	1
14999	prensas	1
15000	prensados	1
15001	prendieran	1
15002	prendido	1
15003	prendían	1
15004	prenderle	1
15005	premioso	1
15006	premiosas	1
15007	premiarle	1
15008	premiaba	1
15009	premeditada	1
15010	prematuro	1
15011	preguntes	1
15012	pregunte	1
15013	pregúntaselo	1
15014	preguntase	1
15015	preguntarte	1
15016	preguntarme	1
15017	preguntaré	1
15018	preguntara	1
15019	preguntándose	1
15020	pregonero	1
15021	pregonar	1
15022	pregonaban	1
15023	pregonaba	1
15024	prefirieron	1
15025	prefiriendo	1
15026	prefieren	1
15027	prefiera	1
15028	preferiría	1
15029	preferible	1
15030	prefación	1
15031	preeminentes	1
15032	predominar	1
15033	predominaban	1
15034	predomina	1
15035	predisposición	1
15036	predique	1
15037	predios	1
15038	predio	1
15039	predilectos	1
15040	predilecciones	1
15041	predicó	1
15042	predicas	1
15043	predicado	1
15044	predicaban	1
15045	precursor	1
15046	preclara	1
15047	precisión	1
15048	precisas	1
15049	precipitó	1
15050	precipitarse	1
15051	precipitadamente	1
15052	precipitaban	1
15053	precipitaba	1
15054	precipita	1
15055	precipicios	1
15056	preciosos	1
15057	precios	1
15058	precian	1
15059	preciaban	1
15060	precia	1
15061	precepto	1
15062	precedido	1
15063	precedía	1
15064	preceden	1
15065	precavido	1
15066	precaución	1
15067	prebendas	1
15068	pragmática	1
15069	practicaron	1
15070	practican	1
15071	practicada	1
15072	pozos	1
15073	poussin	1
15074	pour	1
15075	potros	1
15076	potente	1
15077	potentado	1
15078	potencias	1
15079	póstuma	1
15080	postró	1
15081	postizos	1
15082	postizo	1
15083	posteriores	1
15084	posterior	1
15085	postdata	1
15086	posta	1
15087	post	1
15088	possumus	1
15089	posponerle	1
15090	posiciones	1
15091	posesiones	1
15092	poseo	1
15093	poseía	1
15094	poseerte	1
15095	poseerla	1
15096	poseerás	1
15097	posee	1
15098	posarse	1
15099	posaban	1
15100	posaba	1
15101	portuguesa	1
15102	portugués	1
15103	portocarrero	1
15104	portó	1
15105	portier	1
15106	portezuela	1
15107	portería	1
15108	portentosa	1
15109	portento	1
15110	porte	1
15111	portátiles	1
15112	portador	1
15113	portaban	1
15114	portaba	1
15115	porrazo	1
15116	porra	1
15117	porquerías	1
15118	porquería	1
15119	porfiado	1
15120	porfía	1
15121	porches	1
15122	poquísimo	1
15123	populoso	1
15124	populi	1
15125	populares	1
15126	pontificii	1
15127	pontificado	1
15128	ponte	1
15129	ponío	1
15130	poniéndosele	1
15131	poniéndole	1
15132	poníase	1
15133	póngase	1
15134	ponérselas	1
15135	ponérsela	1
15136	ponernos	1
15137	ponerlos	1
15138	ponerlo	1
15139	pon	1
15140	pomposo	1
15141	pompas	1
15142	pompa	1
15143	pomarada	1
15144	polvorosas	1
15145	polvorín	1
15146	polvorientas	1
15147	polvorienta	1
15148	polvareda	1
15149	polo	1
15150	pollastre	1
15151	polizontes	1
15152	pólizas	1
15153	poliuto	1
15154	pólipo	1
15155	polilla	1
15156	policías	1
15157	polémica	1
15158	poleas	1
15159	polainas	1
15160	polaco	1
15161	poetizados	1
15162	poetillas	1
15163	poetilla	1
15164	poe	1
15165	podredumbres	1
15166	podrás	1
15167	pocula	1
15168	pocilgas	1
15169	pobretes	1
15170	pobretería	1
15171	pobladas	1
15172	poblada	1
15173	poblachones	1
15174	poblachón	1
15175	pluralidad	1
15176	plun	1
15177	plomizas	1
15178	plomiza	1
15179	plenos	1
15180	plenamente	1
15181	plegadera	1
15182	plegaba	1
15183	plebeyas	1
15184	plebeya	1
15185	plazos	1
15186	plazo	1
15187	platónicos	1
15188	platónica	1
15189	platón	1
15190	platillos	1
15191	platillo	1
15192	platicar	1
15193	plateresca	1
15194	plateadas	1
15195	plásticos	1
15196	plástico	1
15197	plasticidad	1
15198	plantón	1
15199	plantó	1
15200	plantando	1
15201	plantados	1
15202	plantaba	1
15203	planicies	1
15204	planetas	1
15205	planchas	1
15206	planchar	1
15207	planchadoras	1
15208	planchado	1
15209	placa	1
15210	pizpiretas	1
15211	pizpireta	1
15212	pizarro	1
15213	pittore	1
15214	pitonisa	1
15215	pitisa	1
15216	pitillos	1
15217	pitanza	1
15218	pitando	1
15219	pitágoras	1
15220	pisto	1
15221	pistilos	1
15222	pista	1
15223	pisoteado	1
15224	pisoteadas	1
15225	pisoteada	1
15226	piscis	1
15227	pisarlas	1
15228	pisara	1
15229	pisándose	1
15230	pisado	1
15231	pirueta	1
15232	piratas	1
15233	piquillo	1
15234	piquemos	1
15235	piqué	1
15236	pionono	1
15237	piña	1
15238	pinzones	1
15239	pintorescos	1
15240	pintoresco	1
15241	pintorescas	1
15242	pintoresca	1
15243	pintarse	1
15244	pintaría	1
15245	pintao	1
15246	pinón	1
15247	pingües	1
15248	pingos	1
15249	pinchó	1
15250	pincharle	1
15251	pincharlas	1
15252	pinchándole	1
15253	pinchado	1
15254	pinchaba	1
15255	pinares	1
15256	pin	1
15257	pimpollo	1
15258	pillastres	1
15259	píldoras	1
15260	pigault	1
15261	pietista	1
15262	piensan	1
15263	pidieron	1
15264	pidiéndole	1
15265	picoteaba	1
15266	picota	1
15267	picona	1
15268	pichones	1
15269	picazón	1
15270	pícaros	1
15271	picarísima	1
15272	picarilla	1
15273	picarescos	1
15274	picaresco	1
15275	picará	1
15276	picador	1
15277	picachos	1
15278	piara	1
15279	piafar	1
15280	phorminx	1
15281	petrificada	1
15282	petirrojos	1
15283	petatur	1
15284	petardos	1
15285	pétalos	1
15286	pespunteados	1
15287	peseteros	1
15288	pescas	1
15289	pescaremos	1
15290	pescante	1
15291	pescador	1
15292	pescaba	1
15293	pesas	1
15294	pesaría	1
15295	pesara	1
15296	pesándole	1
15297	pesadísimo	1
15298	pesadez	1
15299	pesaban	1
15300	pervertido	1
15301	pervertidas	1
15302	pervertía	1
15303	perversas	1
15304	perú	1
15305	perturbadora	1
15306	perturbado	1
15307	pertinente	1
15308	pertinaz	1
15309	perteneció	1
15310	perteneciera	1
15311	perteneces	1
15312	pertenecerle	1
15313	pertenecen	1
15314	pertenece	1
15315	persuasión	1
15316	persuadirle	1
15317	persuadidos	1
15318	persuadido	1
15319	persuadida	1
15320	perspectivas	1
15321	personificar	1
15322	personifican	1
15323	personificaciones	1
15324	personalidades	1
15325	persistía	1
15326	persistente	1
15327	persiguió	1
15328	persiguiéndose	1
15329	persiguiendo	1
15330	persiguen	1
15331	persignarse	1
15332	pérsica	1
15333	perseguirla	1
15334	perseguidor	1
15335	persecuciones	1
15336	perrerías	1
15337	perpetuos	1
15338	peros	1
15339	perorando	1
15340	peroles	1
15341	perol	1
15342	permito	1
15343	permitirme	1
15344	permitir	1
15345	permitiese	1
15346	permitieron	1
15347	permitiera	1
15348	permita	1
15349	permanezca	1
15350	permanecido	1
15351	permanecía	1
15352	perladas	1
15353	perjuicios	1
15354	perjudicaría	1
15355	perjudicar	1
15356	peritonitis	1
15357	perito	1
15358	peripatético	1
15359	periodista	1
15360	periódica	1
15361	perifollo	1
15362	periféricos	1
15363	pergeño	1
15364	pergeñadas	1
15365	pergaminos	1
15366	perfumería	1
15367	perfidia	1
15368	perfeccionarse	1
15369	perfeccionando	1
15370	perezosamente	1
15371	perezas	1
15372	pérez	1
15373	perentoria	1
15374	peregrinación	1
15375	pereda	1
15376	perecedero	1
15377	perdulario	1
15378	perdonóselos	1
15379	perdonase	1
15380	perdonarlo	1
15381	perdonarle	1
15382	perdonaría	1
15383	perdonara	1
15384	perdonándoselo	1
15385	perdonando	1
15386	perdóname	1
15387	perdonadle	1
15388	perdonaban	1
15389	perdigones	1
15390	perdigonada	1
15391	perdigón	1
15392	perdiese	1
15393	perdieron	1
15394	perdiera	1
15395	perdiéndose	1
15396	perdí	1
15397	perceptivas	1
15398	percalina	1
15399	percales	1
15400	peras	1
15401	peraltados	1
15402	per	1
15403	pequeñuelos	1
15404	pequeñísimo	1
15405	pequeñísima	1
15406	pepinillos	1
15407	peores	1
15408	peonza	1
15409	peones	1
15410	peoncillo	1
15411	peñasco	1
15412	penuria	1
15413	penumbra	1
15414	penúltimo	1
15415	penúltima	1
15416	pentagrama	1
15417	pensé	1
15418	pense	1
15419	pensarse	1
15420	pensamos	1
15421	pensadorzuelo	1
15422	pensadas	1
15423	penosos	1
15424	penoso	1
15425	penitenciarias	1
15426	penetrante	1
15427	penetrando	1
15428	péndulos	1
15429	pendones	1
15430	pendientes	1
15431	pender	1
15432	pendencias	1
15433	pendebat	1
15434	penachos	1
15435	penacho	1
15436	peluquería	1
15437	peluconas	1
15438	pelotas	1
15439	pellizcaban	1
15440	pellejo	1
15441	peligró	1
15442	peligra	1
15443	peleo	1
15444	peleé	1
15445	pelear	1
15446	peldaños	1
15447	pelayo	1
15448	pelada	1
15449	pela	1
15450	peinó	1
15451	peino	1
15452	peinar	1
15453	peinamos	1
15454	peinador	1
15455	peinadas	1
15456	pegó	1
15457	pegarse	1
15458	pegarnos	1
15459	pegarle	1
15460	pegando	1
15461	pegan	1
15462	pegajosos	1
15463	pegajosas	1
15464	pegados	1
15465	pedimos	1
15466	pedigüeño	1
15467	pedestal	1
15468	pedantón	1
15469	pedantesca	1
15470	pedantes	1
15471	pedantería	1
15472	pedagógicas	1
15473	pecuniarios	1
15474	peculiares	1
15475	pechinas	1
15476	peces	1
15477	peccata	1
15478	pecará	1
15479	pecaminosos	1
15480	pecadoras	1
15481	pecadillo	1
15482	peca	1
15483	pebetero	1
15484	pche	1
15485	pavorosos	1
15486	pavés	1
15487	pausado	1
15488	pauperum	1
15489	paulo	1
15490	paulatinos	1
15491	paulatinamente	1
15492	paul	1
15493	patrones	1
15494	patronato	1
15495	patrocinado	1
15496	patris	1
15497	patrióticas	1
15498	patriótica	1
15499	patriotas	1
15500	patriota	1
15501	patriarca	1
15502	patrañas	1
15503	patitas	1
15504	patios	1
15505	patíbulo	1
15506	paternales	1
15507	patena	1
15508	patearle	1
15509	patarata	1
15510	pastoreo	1
15511	pastora	1
15512	pasto	1
15513	pastillas	1
15514	pasteur	1
15515	pasteles	1
15516	pastelero	1
15517	pastas	1
15518	pasmasen	1
15519	pasmadas	1
15520	pasmada	1
15521	pasmábase	1
15522	pasmaban	1
15523	pasmaba	1
15524	pasma	1
15525	pasivos	1
15526	pasemos	1
15527	paseíto	1
15528	pasearon	1
15529	paseándola	1
15530	pasean	1
15531	pasea	1
15532	pascal	1
15533	pasarlas	1
15534	pasarla	1
15535	pasaremos	1
15536	pasaran	1
15537	pasao	1
15538	pasándolos	1
15539	pasamano	1
15540	pasajes	1
15541	pasabas	1
15542	parves	1
15543	parvedad	1
15544	parto	1
15545	partiquino	1
15546	partió	1
15547	particularmente	1
15548	partícula	1
15549	participaba	1
15550	parterre	1
15551	parteras	1
15552	parta	1
15553	parroquiales	1
15554	parrilla	1
15555	paroxismos	1
15556	parodiar	1
15557	parodiaba	1
15558	parodia	1
15559	parnaso	1
15560	parisienses	1
15561	parisién	1
15562	parió	1
15563	parezcan	1
15564	parejita	1
15565	paredones	1
15566	pareciendo	1
15567	parecíanle	1
15568	pareces	1
15569	parecérselo	1
15570	parecernos	1
15571	parecerla	1
15572	pareceres	1
15573	parduzco	1
15574	pardeaba	1
15575	pardales	1
15576	parciales	1
15577	parche	1
15578	parca	1
15579	pararrayos	1
15580	pararía	1
15581	parangón	1
15582	paran	1
15583	paralelos	1
15584	paralelo	1
15585	paradojas	1
15586	parábola	1
15587	parábanse	1
15588	paquete	1
15589	papista	1
15590	papisa	1
15591	papelucho	1
15592	pañuelos	1
15593	panzuda	1
15594	pantorriiiilla	1
15595	panteísticos	1
15596	panteística	1
15597	panteísta	1
15598	panteísmos	1
15599	pantalla	1
15600	panoplia	1
15601	paniaguado	1
15602	panegíricos	1
15603	panegírico	1
15604	panecillo	1
15605	panderetas	1
15606	pamplinas	1
15607	palúdicas	1
15608	palpitaciones	1
15609	palparles	1
15610	palpar	1
15611	palpando	1
15612	palpables	1
15613	palpaba	1
15614	paloma	1
15615	palmito	1
15616	palmeras	1
15617	palmario	1
15618	pallavicini	1
15619	palisandro	1
15620	palio	1
15621	palinodia	1
15622	palillo	1
15623	palillero	1
15624	paliducha	1
15625	palido	1
15626	palideció	1
15627	palidecer	1
15628	palas	1
15629	palafrén	1
15630	palación	1
15631	palabrotas	1
15632	pajarracos	1
15633	pajaritas	1
15634	pajarita	1
15635	pajar	1
15636	paix	1
15637	pagina	1
15638	pagase	1
15639	pagárselo	1
15640	pagaron	1
15641	pagarlo	1
15642	pagarías	1
15643	pagaríamos	1
15644	pagarás	1
15645	pagarán	1
15646	paganos	1
15647	paganismo	1
15648	pagamos	1
15649	pagados	1
15650	pagado	1
15651	pagaderos	1
15652	pagaderas	1
15653	paece	1
15654	padrenuestro	1
15655	padrazo	1
15656	padezco	1
15657	padezcas	1
15658	padezca	1
15659	padecimientos	1
15660	padecieron	1
15661	padeces	1
15662	padecerla	1
15663	padecerá	1
15664	padece	1
15665	pactos	1
15666	pacos	1
15667	pacíficos	1
15668	pacíficamente	1
15669	pacientes	1
15670	pábilos	1
15671	oyesen	1
15672	oyéndola	1
15673	oxígeno	1
15674	oxidadas	1
15675	ovillo	1
15676	oveja	1
15677	ovaladas	1
15678	oval	1
15679	ovación	1
15680	otrosí	1
15681	otorgaría	1
15682	otorgar	1
15683	otorgado	1
15684	otorgaba	1
15685	otoños	1
15686	otoñada	1
15687	osuna	1
15688	ostracismo	1
15689	ostentosos	1
15690	ostentosas	1
15691	ostentando	1
15692	ostentan	1
15693	ostensiblemente	1
15694	osó	1
15695	oscilando	1
15696	osaron	1
15697	osar	1
15698	osados	1
15699	osadía	1
15700	osadas	1
15701	orza	1
15702	ortodoxas	1
15703	ortodoxa	1
15704	orto	1
15705	ortiz	1
15706	orsini	1
15707	oropel	1
15708	oró	1
15709	ornato	1
15710	orladas	1
15711	orlaban	1
15712	orillo	1
15713	originó	1
15714	originarse	1
15715	originales	1
15716	origina	1
15717	orígenes	1
15718	orientarse	1
15719	orientalista	1
15720	oriental	1
15721	orgullosos	1
15722	orgullos	1
15723	orgullito	1
15724	orgasmo	1
15725	organizado	1
15726	organizaba	1
15727	organismo	1
15728	organdí	1
15729	orejeras	1
15730	ordo	1
15731	ordine	1
15732	ordenase	1
15733	ordenarse	1
15734	ordenaba	1
15735	órbita	1
15736	orangutanes	1
15737	oradoras	1
15738	orado	1
15739	oráculo	1
15740	opusieron	1
15741	opusiera	1
15742	opulenta	1
15743	opulencia	1
15744	opuestas	1
15745	opuesta	1
15746	óptima	1
15747	óptico	1
15748	oprimiéndose	1
15749	oprimiendo	1
15750	oprimidos	1
15751	oprimida	1
15752	opresor	1
15753	opresiones	1
15754	opresión	1
15755	oppert	1
15756	opositor	1
15757	oportunos	1
15758	oportunísimo	1
15759	oportunas	1
15760	oportunamente	1
15761	opino	1
15762	opinar	1
15763	opinan	1
15764	opaco	1
15765	ondeado	1
15766	ondeadas	1
15767	ondeada	1
15768	onda	1
15769	omnipotencia	1
15770	omnilateral	1
15771	ominosos	1
15772	ominoso	1
15773	olvidos	1
15774	olvides	1
15775	olvidastes	1
15776	olvidase	1
15777	olvidas	1
15778	olvidarlo	1
15779	olvidarlas	1
15780	olvidarla	1
15781	olvidan	1
15782	olvidadas	1
15783	olvida	1
15784	olivo	1
15785	olimpo	1
15786	oliente	1
15787	olido	1
15788	olfato	1
15789	olfateo	1
15790	olfateando	1
15791	olé	1
15792	ojivas	1
15793	ojivales	1
15794	ojitos	1
15795	ojazos	1
15796	oírte	1
15797	oírme	1
15798	oírlos	1
15799	oírlo	1
15800	oírla	1
15801	oirían	1
15802	oirás	1
15803	oirá	1
15804	oigámoslo	1
15805	óigame	1
15806	óigalo	1
15807	oi	1
15808	ogaño	1
15809	ofrecieron	1
15810	ofreciéndole	1
15811	ofrecida	1
15812	ofidiana	1
15813	oficiando	1
15814	ofensivas	1
15815	ofendidos	1
15816	ofendida	1
15817	ofendían	1
15818	ofenderse	1
15819	ofenderle	1
15820	ofenda	1
15821	odias	1
15822	odiarme	1
15823	odiar	1
15824	odas	1
15825	ocurrírsele	1
15826	ocurriría	1
15827	ocurrir	1
15828	ocurrieron	1
15829	ocurrieran	1
15830	ocurren	1
15831	ocurra	1
15832	ocupe	1
15833	ocuparse	1
15834	ocuparé	1
15835	ocupándose	1
15836	ocupadas	1
15837	ocupábase	1
15838	ocupa	1
15839	ocultes	1
15840	ocultéis	1
15841	ocultase	1
15842	ocultas	1
15843	ocultaron	1
15844	ocultarlos	1
15845	ocultarle	1
15846	ocultarlas	1
15847	ocultado	1
15848	octavo	1
15849	octava	1
15850	ociosa	1
15851	ochentón	1
15852	ochavos	1
15853	occidental	1
15854	ocasional	1
15855	obtuvo	1
15856	obtener	1
15857	obstinada	1
15858	obstinaba	1
15859	obseso	1
15860	observo	1
15861	observe	1
15862	observatorios	1
15863	observatorio	1
15864	observarle	1
15865	observamos	1
15866	observadores	1
15867	observaban	1
15868	obsequiarle	1
15869	obsequiadas	1
15870	obsequiaban	1
15871	obsequiaba	1
15872	obscurezca	1
15873	obscurecida	1
15874	obscurantismo	1
15875	obraban	1
15876	oblonga	1
15877	obligatorio	1
15878	obligase	1
15879	obligaron	1
15880	obligarle	1
15881	obligarla	1
15882	obligaríanles	1
15883	obligara	1
15884	obligando	1
15885	oblicuos	1
15886	oblicuo	1
15887	oblicuas	1
15888	objetó	1
15889	objetivo	1
15890	objetado	1
15891	objetaba	1
15892	objeción	1
15893	obispillo	1
15894	obedientes	1
15895	obediente	1
15896	obedecí	1
15897	obedecerle	1
15898	obedece	1
15899	obdulias	1
15900	obcecado	1
15901	nutrir	1
15902	nuncio	1
15903	numeroso	1
15904	numerosa	1
15905	nulo	1
15906	nulas	1
15907	nuez	1
15908	nudos	1
15909	nublada	1
15910	nubarrones	1
15911	novísima	1
15912	novios	1
15913	noviazgos	1
15914	novia	1
15915	novenario	1
15916	novelistas	1
15917	novelescos	1
15918	noveladores	1
15919	notorio	1
15920	notoria	1
15921	noticierismo	1
15922	noten	1
15923	notasen	1
15924	notadas	1
15925	notada	1
15926	notabilidad	1
15927	not	1
15928	noruega	1
15929	normandos	1
15930	normal	1
15931	nordeste	1
15932	nomine	1
15933	nombró	1
15934	nombrando	1
15935	nombramientos	1
15936	nombramiento	1
15937	nombra	1
15938	nolis	1
15939	nogales	1
15940	nodrizas	1
15941	nocivas	1
15942	nociones	1
15943	nocedal	1
15944	noblemente	1
15945	nobilísimo	1
15946	nivelaba	1
15947	nisi	1
15948	ninon	1
15949	nínive	1
15950	ninfa	1
15951	nimbo	1
15952	nihil	1
15953	nieves	1
15954	nieto	1
15955	niegas	1
15956	nidos	1
15957	nevatilla	1
15958	nevase	1
15959	nevado	1
15960	nevaba	1
15961	neutra	1
15962	neos	1
15963	neo	1
15964	nenas	1
15965	nemrod	1
15966	nemorosos	1
15967	negruzcas	1
15968	negruras	1
15969	negrillo	1
15970	negligencia	1
15971	negase	1
15972	negarte	1
15973	negaron	1
15974	negarla	1
15975	negarán	1
15976	negándoles	1
15977	negado	1
15978	nefastos	1
15979	nefasta	1
15980	nefas	1
15981	nefando	1
15982	necesiten	1
15983	necesite	1
15984	necesitarlos	1
15985	necesitarlas	1
15986	necesitara	1
15987	necesitáis	1
15988	necesitados	1
15989	necesitábamos	1
15990	nebuloso	1
15991	nebulosa	1
15992	nazcan	1
15993	nay	1
15994	navío	1
15995	navegando	1
15996	navegados	1
15997	navegación	1
15998	naval	1
15999	náutica	1
16000	naturans	1
16001	naturalistas	1
16002	naturalísimo	1
16003	natividad	1
16004	natalicio	1
16005	natalia	1
16006	natal	1
16007	narrar	1
16008	narigudo	1
16009	narciso	1
16010	naranjos	1
16011	naipes	1
16012	naipe	1
16013	nadar	1
16014	nadando	1
16015	nacimientos	1
16016	naciera	1
16017	naciente	1
16018	naciendo	1
16019	nacida	1
16020	nací	1
16021	mutuos	1
16022	mutua	1
16023	mustios	1
16024	mustias	1
16025	mustia	1
16026	muslos	1
16027	musgosas	1
16028	musgo	1
16029	musculosa	1
16030	músculo	1
16031	musas	1
16032	musa	1
16033	murmuren	1
16034	murmurase	1
16035	murmuraría	1
16036	murmuran	1
16037	murmurador	1
16038	murmurado	1
16039	muriéndose	1
16040	muriéndonos	1
16041	muñoz	1
16042	muñón	1
16043	muñeira	1
16044	muñecos	1
16045	muñeco	1
16046	munificencia	1
16047	mundanales	1
16048	munda	1
16049	multiplicándose	1
16050	multiplicadas	1
16051	múltiples	1
16052	multas	1
16053	mullido	1
16054	mulata	1
16055	mulas	1
16056	mujerzuela	1
16057	mujerota	1
16058	mujeril	1
16059	mugre	1
16060	muévete	1
16061	mueven	1
16062	mueres	1
16063	mueren	1
16064	muerdes	1
16065	muelles	1
16066	muecas	1
16067	mueblista	1
16068	mueblaje	1
16069	múdese	1
16070	mudando	1
16071	muchísimos	1
16072	muchachuelas	1
16073	mucetas	1
16074	mu	1
16075	mr	1
16076	mozalbetes	1
16077	moviesen	1
16078	moviese	1
16079	movieron	1
16080	moviera	1
16081	moviéndose	1
16082	movido	1
16083	movibles	1
16084	moverlos	1
16085	moverla	1
16086	movediza	1
16087	motes	1
16088	mote	1
16089	mostró	1
16090	mostrase	1
16091	mostrarlo	1
16092	mostrarle	1
16093	mostrándose	1
16094	mostrándole	1
16095	mostradas	1
16096	mostaza	1
16097	mosco	1
16098	mortificarme	1
16099	mortificarla	1
16100	mortificar	1
16101	mortificado	1
16102	mortífero	1
16103	mortífera	1
16104	morro	1
16105	morosos	1
16106	morirme	1
16107	morimos	1
16108	morigerado	1
16109	morigerada	1
16110	morfina	1
16111	morería	1
16112	morenos	1
16113	morenas	1
16114	mordieron	1
16115	mordían	1
16116	morderse	1
16117	mordería	1
16118	mordedura	1
16119	morcillas	1
16120	morcilla	1
16121	morbosa	1
16122	mórbido	1
16123	morbidez	1
16124	mórbida	1
16125	moran	1
16126	moralmente	1
16127	moralizarla	1
16128	moralizar	1
16129	mora	1
16130	moño	1
16131	moña	1
16132	monumental	1
16133	monterilla	1
16134	montecristo	1
16135	montase	1
16136	montar	1
16137	montados	1
16138	montadas	1
16139	montada	1
16140	montaba	1
16141	monta	1
16142	monstruoso	1
16143	monstruosas	1
16144	monstruosa	1
16145	monosílabo	1
16146	monólogo	1
16147	monolito	1
16148	monocromos	1
16149	monjitas	1
16150	monjío	1
16151	monjes	1
16152	monje	1
16153	mónica	1
16154	monescillo	1
16155	monederos	1
16156	monedero	1
16157	mondes	1
16158	mondar	1
16159	monda	1
16160	monástica	1
16161	monagos	1
16162	mona	1
16163	momentánea	1
16164	mollera	1
16165	molinos	1
16166	molineros	1
16167	moliera	1
16168	molestos	1
16169	moleste	1
16170	molestarse	1
16171	molestándolos	1
16172	molestándoles	1
16173	molestándole	1
16174	moleslo	1
16175	moleschott	1
16176	moléculas	1
16177	molécula	1
16178	molduras	1
16179	moldes	1
16180	mojigatos	1
16181	mojigangas	1
16182	mojar	1
16183	mojando	1
16184	mojados	1
16185	mojadas	1
16186	mohicanos	1
16187	modus	1
16188	modismos	1
16189	modificado	1
16190	modificaciones	1
16191	modificaba	1
16192	moderados	1
16193	moderado	1
16194	mocosos	1
16195	mochuelos	1
16196	mochuelo	1
16197	mobiliario	1
16198	mo	1
16199	mixto	1
16200	mixtificación	1
16201	mitológicos	1
16202	mitologías	1
16203	mitigado	1
16204	mitigada	1
16205	místicamente	1
16206	misteriosas	1
16207	miss	1
16208	mismísima	1
16209	misiva	1
16210	misérrimo	1
16211	míseros	1
16212	miserablemente	1
16213	misántropo	1
16214	mirones	1
16215	mirlaba	1
16216	mirarme	1
16217	mirarían	1
16218	mirarás	1
16219	mirándoos	1
16220	mirándola	1
16221	miramiento	1
16222	mírale	1
16223	mirábala	1
16224	miope	1
16225	minuta	1
16226	minué	1
16227	minucioso	1
16228	minuciosamente	1
16229	minuciosa	1
16230	ministerios	1
16231	ministerio	1
16232	miniatura	1
16233	minero	1
16234	mineralógicas	1
16235	minerales	1
16236	mimosa	1
16237	mimo	1
16238	mímicos	1
16239	mímicas	1
16240	mimaban	1
16241	mimaba	1
16242	milo	1
16243	millón	1
16244	milito	1
16245	militantes	1
16246	militante	1
16247	militaba	1
16248	miliarias	1
16249	milano	1
16250	milagrosamente	1
16251	miguel	1
16252	miento	1
16253	mienta	1
16254	miedosa	1
16255	midiéramos	1
16256	mide	1
16257	mica	1
16258	mezquita	1
16259	mezcló	1
16260	mezclase	1
16261	mezclarse	1
16262	mezclándose	1
16263	mezclados	1
16264	meus	1
16265	meum	1
16266	metz	1
16267	metropolitano	1
16268	metralla	1
16269	método	1
16270	metodista	1
16271	metiera	1
16272	metiéndose	1
16273	metiéndole	1
16274	metiditos	1
16275	metidito	1
16276	metidas	1
16277	metérselo	1
16278	meteorológicos	1
16279	meteorología	1
16280	metamorfosis	1
16281	metalizado	1
16282	metálicos	1
16283	metafóricamente	1
16284	mesetas	1
16285	mescolanzas	1
16286	mesaba	1
16287	mero	1
16288	mermas	1
16289	meritorio	1
16290	meritoria	1
16291	merino	1
16292	meriendo	1
16293	meridionales	1
16294	merezco	1
16295	merendado	1
16296	merendaba	1
16297	merecimiento	1
16298	mereciese	1
16299	merecidísimo	1
16300	merecerles	1
16301	mera	1
16302	mequetrefes	1
16303	mequetrefe	1
16304	menudeando	1
16305	menudean	1
16306	menuda	1
16307	mentor	1
16308	mentón	1
16309	mentís	1
16310	mentido	1
16311	mentida	1
16312	mentían	1
16313	mentarle	1
16314	mentarla	1
16315	mentalmente	1
16316	mentales	1
16317	mensual	1
16318	menjurjes	1
16319	menguada	1
16320	menguaba	1
16321	mengua	1
16322	menestrales	1
16323	menesteres	1
16324	meneses	1
16325	meneó	1
16326	meneo	1
16327	meneaban	1
16328	mendrugos	1
16329	mendrugo	1
16330	méndez	1
16331	mencionaré	1
16332	memento	1
16333	membibres	1
16334	meloso	1
16335	melosas	1
16336	melodiosa	1
16337	melodías	1
16338	melocotón	1
16339	meliora	1
16340	melindrán	1
16341	melifluo	1
16342	melancólicamente	1
16343	mejorase	1
16344	mejorarán	1
16345	mejorar	1
16346	mejoraba	1
16347	méjico	1
16348	mefistofélicos	1
16349	médula	1
16350	medró	1
16351	medro	1
16352	medrar	1
16353	medran	1
16354	medrados	1
16355	medite	1
16356	meditan	1
16357	meditado	1
16358	meditabunda	1
16359	medita	1
16360	medirse	1
16361	médicis	1
16362	medianoche	1
16363	medianería	1
16364	medianeras	1
16365	medianas	1
16366	medalla	1
16367	mecida	1
16368	mecía	1
16369	mecheros	1
16370	mecha	1
16371	mecanismo	1
16372	mecánicamente	1
16373	mazas	1
16374	mayúscula	1
16375	mayorazguetes	1
16376	mayorazguete	1
16377	mayorazgo	1
16378	mayoral	1
16379	mayaba	1
16380	máximo	1
16381	máximas	1
16382	maudsley	1
16383	matutinos	1
16384	matutino	1
16385	matutina	1
16386	matronas	1
16387	matriculados	1
16388	matriculadas	1
16389	matrícula	1
16390	matinée	1
16391	matiella	1
16392	matías	1
16393	maternidad	1
16394	materialistas	1
16395	mateo	1
16396	maten	1
16397	matemáticos	1
16398	matemático	1
16399	matemáticamente	1
16400	maté	1
16401	matase	1
16402	matas	1
16403	matarse	1
16404	matara	1
16405	mátale	1
16406	matadero	1
16407	masini	1
16408	masculinos	1
16409	masculinas	1
16410	máscaras	1
16411	masca	1
16412	martirizarle	1
16413	martillazo	1
16414	marte	1
16415	marsilla	1
16416	marquilla	1
16417	marquesitas	1
16418	marquesina	1
16419	marmolillo	1
16420	mármoles	1
16421	marmitón	1
16422	maritornes	1
16423	mariscos	1
16424	mariposa	1
16425	marinos	1
16426	marino	1
16427	marimachos	1
16428	marimacho	1
16429	marearlos	1
16430	mareantes	1
16431	mareado	1
16432	mare	1
16433	marchitos	1
16434	marchitaban	1
16435	marcharte	1
16436	marcharía	1
16437	marchando	1
16438	marcando	1
16439	maravillosa	1
16440	maravillado	1
16441	maragato	1
16442	maquinillas	1
16443	maquinalmente	1
16444	maquinal	1
16445	maquinaciones	1
16446	maquinación	1
16447	mapa	1
16448	manuscrito	1
16449	manu	1
16450	mantuvo	1
16451	mantuvieron	1
16452	mantillas	1
16453	manterola	1
16454	mantenido	1
16455	mantengo	1
16456	mantengas	1
16457	mantenerlo	1
16458	mantendría	1
16459	manteleta	1
16460	manteles	1
16461	mantas	1
16462	mansa	1
16463	manriques	1
16464	manoseando	1
16465	manolesco	1
16466	manola	1
16467	manojo	1
16468	manirrota	1
16469	maniqueo	1
16470	maniobras	1
16471	manifestase	1
16472	manifestara	1
16473	manifestándose	1
16474	manifestamos	1
16475	manifestado	1
16476	manifestaciones	1
16477	manifestaban	1
16478	maniática	1
16479	manejaban	1
16480	mandria	1
16481	mandobles	1
16482	mandilona	1
16483	mandé	1
16484	mandasen	1
16485	mandase	1
16486	mandarse	1
16487	mandaron	1
16488	mandarlo	1
16489	mandarla	1
16490	mandaremos	1
16491	mandando	1
16492	mandamos	1
16493	mandamientos	1
16494	mandamiento	1
16495	manchara	1
16496	manchar	1
16497	manchándolos	1
16498	manchan	1
16499	manchadas	1
16500	manchada	1
16501	manar	1
16502	maná	1
16503	mampostería	1
16504	mamar	1
16505	maltrecho	1
16506	maltratadas	1
16507	maltrataba	1
16508	malquistarle	1
16509	malla	1
16510	maliciado	1
16511	maliciaban	1
16512	malhumor	1
16513	malhechor	1
16514	malgré	1
16515	malgastado	1
16516	malgastada	1
16517	malévolas	1
16518	malestar	1
16519	malditos	1
16520	maldiciendo	1
16521	maldecirá	1
16522	malbaratado	1
16523	malamente	1
16524	malabares	1
16525	majo	1
16526	majestuosos	1
16527	majas	1
16528	majaderías	1
16529	maizales	1
16530	maitines	1
16531	mainates	1
16532	mahoma	1
16533	magyares	1
16534	magullar	1
16535	mago	1
16536	magno	1
16537	magnitud	1
16538	magnífica	1
16539	magnético	1
16540	magnéticas	1
16541	magnética	1
16542	magnates	1
16543	magnanimidad	1
16544	magistratura	1
16545	magistrales	1
16546	maduros	1
16547	madurando	1
16548	madrugue	1
16549	madrugones	1
16550	madrugo	1
16551	madrugaría	1
16552	madrugado	1
16553	madrileñitos	1
16554	madrileñas	1
16555	madrigueras	1
16556	madrigales	1
16557	madrejón	1
16558	madrastra	1
16559	madona	1
16560	maderos	1
16561	maderita	1
16562	madeja	1
16563	macizo	1
16564	maciza	1
16565	macilento	1
16566	machacona	1
16567	machacan	1
16568	machacaba	1
16569	macetas	1
16570	macedónico	1
16571	macabra	1
16572	macabeos	1
16573	luzbel	1
16574	luys	1
16575	lustroso	1
16576	lustre	1
16577	lusitana	1
16578	lupus	1
16579	lunares	1
16580	luminosos	1
16581	luminosas	1
16582	lujosos	1
16583	luján	1
16584	lúgubres	1
16585	lugarón	1
16586	lugareñas	1
16587	lugarejo	1
16588	luenga	1
16589	lucubraciones	1
16590	lucro	1
16591	lucrecio	1
16592	lucrativa	1
16593	lucrar	1
16594	lució	1
16595	luciferum	1
16596	lucifer	1
16597	luciéramos	1
16598	luciera	1
16599	lucidos	1
16600	lucidas	1
16601	lucí	1
16602	lucho	1
16603	luché	1
16604	lucharía	1
16605	luchador	1
16606	luchaban	1
16607	lucero	1
16608	lucerna	1
16609	lucaaam	1
16610	lúbricos	1
16611	lubricidad	1
16612	lúbricas	1
16613	lozoya	1
16614	lozanías	1
16615	loza	1
16616	lovelace	1
16617	lote	1
16618	lot	1
16619	losas	1
16620	loriga	1
16621	loquitur	1
16622	loquillo	1
16623	loquillas	1
16624	loquilla	1
16625	lonjas	1
16626	longevidad	1
16627	longanizas	1
16628	logrando	1
16629	lograba	1
16630	logomaquias	1
16631	lodazales	1
16632	locus	1
16633	localidad	1
16634	lóbrega	1
16635	lobezno	1
16636	loable	1
16637	llovió	1
16638	lloviera	1
16639	lloviendo	1
16640	llorón	1
16641	lloriqueando	1
16642	lloréis	1
16643	lloraría	1
16644	lloraré	1
16645	llorará	1
16646	llora	1
16647	lleve	1
16648	llevarnos	1
16649	llevármela	1
16650	llevarlo	1
16651	llevarles	1
16652	llevaré	1
16653	llevarás	1
16654	llevarán	1
16655	llevándoselo	1
16656	llevándose	1
16657	llevan	1
16658	llévame	1
16659	llevados	1
16660	llevadas	1
16661	llevada	1
16662	llenen	1
16663	llenaría	1
16664	llenará	1
16665	llenándole	1
16666	lleguemos	1
16667	llegasen	1
16668	llegarían	1
16669	llegaremos	1
16670	llegaré	1
16671	llanuras	1
16672	llanura	1
16673	llaneza	1
16674	llamen	1
16675	llamémosle	1
16676	llámelo	1
16677	llamé	1
16678	llamativos	1
16679	llamativa	1
16680	llamárselo	1
16681	llamarnos	1
16682	llamarlo	1
16683	llamarlas	1
16684	llamaremos	1
16685	llamarán	1
16686	llamaran	1
16687	llamará	1
16688	llamara	1
16689	llamándolos	1
16690	llaga	1
16691	liviana	1
16692	litigantes	1
16693	literato	1
16694	listillas	1
16695	listado	1
16696	lisonjera	1
16697	lisonjeado	1
16698	lisonjea	1
16699	lisa	1
16700	líricamente	1
16701	lírica	1
16702	líquida	1
16703	liquen	1
16704	liquefacta	1
16705	lionense	1
16706	lío	1
16707	linfas	1
16708	línea	1
16709	lindoro	1
16710	linajudas	1
16711	limpios	1
16712	límpido	1
16713	límpida	1
16714	limpiaron	1
16715	limpiarle	1
16716	limpiándose	1
16717	limones	1
16718	limón	1
16719	limítrofe	1
16720	limitarse	1
16721	limitada	1
16722	limitaban	1
16723	limbo	1
16724	ligeros	1
16725	ligereza	1
16726	ligamen	1
16727	ligaduras	1
16728	ligados	1
16729	life	1
16730	liebre	1
16731	lidiaba	1
16732	licenciarse	1
16733	licenciados	1
16734	librerías	1
16735	librepensamiento	1
16736	librepensador	1
16737	librasen	1
16738	libras	1
16739	librara	1
16740	libraco	1
16741	liberté	1
16742	libelo	1
16743	libellus	1
16744	leyeron	1
16745	levítica	1
16746	levantisca	1
16747	levántate	1
16748	levantaría	1
16749	levantara	1
16750	levantados	1
16751	leva	1
16752	letargo	1
16753	letanía	1
16754	lesiones	1
16755	lesión	1
16756	lesbos	1
16757	leproso	1
16758	leonor	1
16759	leones	1
16760	leonardo	1
16761	lentos	1
16762	lento	1
16763	lentejas	1
16764	lenidad	1
16765	lengüetería	1
16766	lenclós	1
16767	lema	1
16768	lego	1
16769	legislación	1
16770	legendarios	1
16771	lege	1
16772	legalmente	1
16773	lees	1
16774	leerse	1
16775	leerme	1
16776	leen	1
16777	léela	1
16778	lectora	1
16779	lechuguinos	1
16780	lechuga	1
16781	lechoso	1
16782	lechosa	1
16783	leccioncita	1
16784	lebrun	1
16785	léanla	1
16786	leal	1
16787	laxitud	1
16788	lavó	1
16789	lavarse	1
16790	lavaron	1
16791	lavadas	1
16792	lavaban	1
16793	laurent	1
16794	laudes	1
16795	laudatores	1
16796	latorre	1
16797	latitudinario	1
16798	latió	1
16799	latigazo	1
16800	latieron	1
16801	latía	1
16802	lateral	1
16803	late	1
16804	lastimosa	1
16805	lastimero	1
16806	lastimarla	1
16807	lastimara	1
16808	lastimar	1
16809	lastimada	1
16810	lastimaban	1
16811	lastimaba	1
16812	lastima	1
16813	lascivos	1
16814	larguísima	1
16815	largarse	1
16816	largamente	1
16817	lanzó	1
16818	lanzándose	1
16819	lanzaba	1
16820	lanza	1
16821	lante	1
16822	lánguidos	1
16823	lánguido	1
16824	languidecer	1
16825	lánguidas	1
16826	lánguidamente	1
16827	landó	1
16828	lanchas	1
16829	lancha	1
16830	láncese	1
16831	lampiño	1
16832	lamparilla	1
16833	laminada	1
16834	lamiéndose	1
16835	lamiendo	1
16836	lamidas	1
16837	lamía	1
16838	lamería	1
16839	lamento	1
16840	lamentaron	1
16841	lamentando	1
16842	lamentamos	1
16843	lamentable	1
16844	lamenta	1
16845	lamego	1
16846	lamartine	1
16847	laicos	1
16848	lagarto	1
16849	lagar	1
16850	ladre	1
16851	ladrar	1
16852	lacrimosa	1
16853	lacrimae	1
16854	lacónico	1
16855	lacónicas	1
16856	lacónica	1
16857	lacería	1
16858	labriegos	1
16859	labranza	1
16860	labrado	1
16861	labraba	1
16862	laboriosa	1
16863	laberintos	1
16864	labe	1
16865	kock	1
16866	kirschen	1
16867	kilómetro	1
16868	juzgarse	1
16869	juzgando	1
16870	juzgada	1
16871	juzgaban	1
16872	justillo	1
16873	justificar	1
16874	justificables	1
16875	justas	1
16876	jurisconsultos	1
16877	juris	1
16878	jurídico	1
16879	juremos	1
16880	jure	1
16881	juraste	1
16882	jurarse	1
16883	jurarle	1
16884	jurándose	1
16885	júramelo	1
16886	jurados	1
16887	jurada	1
16888	juraban	1
16889	junturas	1
16890	juntaran	1
16891	juntado	1
16892	juntaba	1
16893	juncos	1
16894	juicios	1
16895	juguetona	1
16896	jugueteando	1
16897	jugueteaban	1
16898	jugo	1
16899	jugándose	1
16900	jugáis	1
16901	jugábamos	1
16902	juegan	1
16903	judit	1
16904	judíos	1
16905	jubileos	1
16906	jubilé	1
16907	joyero	1
16908	jovialidad	1
16909	jovellanos	1
16910	jota	1
16911	jorobado	1
16912	jornaleros	1
16913	jornal	1
16914	jónico	1
16915	jofaina	1
16916	jocoso	1
16917	jocoserio	1
16918	jirones	1
16919	jirón	1
16920	jinojo	1
16921	jícara	1
16922	jesuítica	1
16923	jerusalén	1
16924	jerusalem	1
16925	jeroma	1
16926	jericó	1
16927	jerga	1
16928	jeremías	1
16929	jerárquicos	1
16930	jehová	1
16931	jazmín	1
16932	jaropes	1
16933	jardineros	1
16934	jardinero	1
16935	jardineras	1
16936	jarana	1
16937	japón	1
16938	jamones	1
16939	jamón	1
16940	jaleadores	1
16941	jaime	1
16942	jadeantes	1
16943	jactancioso	1
16944	jactanciosa	1
16945	jaco	1
16946	jaccoud	1
16947	jacas	1
16948	jabalíes	1
16949	j	1
16950	izquierdo	1
16951	ix	1
16952	iv	1
16953	ítem	1
16954	israelitas	1
16955	israel	1
16956	islote	1
16957	islas	1
16958	isis	1
16959	is	1
16960	irrupciones	1
16961	irritó	1
16962	irritarla	1
16963	irritar	1
16964	irritados	1
16965	irritación	1
16966	irritabilidad	1
16967	irrita	1
16968	irrisión	1
16969	irreverentes	1
16970	irresponsabilidad	1
16971	irreprochable	1
16972	irremisiblemente	1
16973	irremediables	1
16974	irremediable	1
16975	irregularidades	1
16976	irreflexivas	1
16977	irreflexivamente	1
16978	irradiaba	1
16979	irracionales	1
16980	irónicos	1
16981	irónico	1
16982	ironías	1
16983	irisados	1
16984	iria	1
16985	irás	1
16986	irá	1
16987	ipsa	1
16988	io	1
16989	involucremos	1
16990	invitó	1
16991	invitarle	1
16992	invitarla	1
16993	invitar	1
16994	invitándole	1
16995	invitando	1
16996	invita	1
16997	invirtieron	1
16998	inveterado	1
16999	inveteradas	1
17000	investigar	1
17001	invernante	1
17002	invernadero	1
17003	invernáculo	1
17004	inventor	1
17005	inventó	1
17006	inventaron	1
17007	inventario	1
17008	inventados	1
17009	inventaban	1
17010	invenciones	1
17011	invasores	1
17012	invasor	1
17013	invasiones	1
17014	invariablemente	1
17015	inválido	1
17016	inválidas	1
17017	invadieron	1
17018	invadida	1
17019	invadían	1
17020	invadía	1
17021	inusitadas	1
17022	inundarle	1
17023	inundara	1
17024	inundar	1
17025	intuiciones	1
17026	intuición	1
17027	intrusos	1
17028	intrusa	1
17029	introduzcan	1
17030	introdujese	1
17031	introducir	1
17032	introduciendo	1
17033	introducido	1
17034	intrincados	1
17035	intrigantes	1
17036	intrigado	1
17037	intrépidas	1
17038	intransigentes	1
17039	intranquilo	1
17040	intranquila	1
17041	intimó	1
17042	intimo	1
17043	intimidades	1
17044	intimarle	1
17045	intimaba	1
17046	intestinal	1
17047	intervinieran	1
17048	intervenido	1
17049	intervenía	1
17050	intersticios	1
17051	interrumpirla	1
17052	interrumpieron	1
17053	interrumpiera	1
17054	interrumpiéndole	1
17055	interrumpida	1
17056	interrumpen	1
17057	interrumpas	1
17058	interrogatorios	1
17059	interrogatorio	1
17060	interrogarle	1
17061	interrogante	1
17062	interpretó	1
17063	intérprete	1
17064	interpretar	1
17065	interpretación	1
17066	interponiendo	1
17067	intermitentes	1
17068	interlocutores	1
17069	interjecciones	1
17070	interioridades	1
17071	interinos	1
17072	interino	1
17073	interinas	1
17074	interinamente	1
17075	interesarse	1
17076	interesarla	1
17077	intercolumnios	1
17078	intercolumnio	1
17079	interceptado	1
17080	interceptaban	1
17081	intentona	1
17082	intenté	1
17083	intentaré	1
17084	intentado	1
17085	intentaban	1
17086	intenta	1
17087	intensas	1
17088	intensamente	1
17089	intendente	1
17090	intende	1
17091	intencionados	1
17092	intempestivo	1
17093	intellectu	1
17094	inteligentes	1
17095	íntegro	1
17096	integrar	1
17097	integrante	1
17098	integral	1
17099	intacta	1
17100	intachables	1
17101	insurrectos	1
17102	insultó	1
17103	insultara	1
17104	insultando	1
17105	insulsos	1
17106	insulsez	1
17107	insulsas	1
17108	insulsa	1
17109	instrumentista	1
17110	instruidas	1
17111	instrucciones	1
17112	instó	1
17113	instituto	1
17114	instigara	1
17115	instantáneo	1
17116	instantánea	1
17117	instancia	1
17118	instalar	1
17119	inspire	1
17120	inspirarse	1
17121	inspirará	1
17122	inspiran	1
17123	inspirados	1
17124	inspiraciones	1
17125	insoportables	1
17126	insomnios	1
17127	insomnio	1
17128	insólito	1
17129	insolenta	1
17130	insolencias	1
17131	insistimos	1
17132	insistieron	1
17133	insistiendo	1
17134	insistido	1
17135	insisten	1
17136	insinuó	1
17137	insinuar	1
17138	insinuado	1
17139	insignificancia	1
17140	insidiosos	1
17141	inservible	1
17142	insertar	1
17143	inseparables	1
17144	inseparable	1
17145	insensato	1
17146	insectos	1
17147	insecto	1
17148	inquisidores	1
17149	inquisición	1
17150	inquirió	1
17151	inquilinos	1
17152	inquietarle	1
17153	inquietaban	1
17154	inquieta	1
17155	inoportunos	1
17156	inoportunamente	1
17157	inoportuna	1
17158	inopinado	1
17159	inocentadas	1
17160	innumerables	1
17161	innovador	1
17162	innovación	1
17163	innobles	1
17164	innata	1
17165	inmundas	1
17166	inmovilidad	1
17167	inmoralidad	1
17168	inmodestia	1
17169	inmediaciones	1
17170	inmaculados	1
17171	inmaculado	1
17172	injustísima	1
17173	injuriosas	1
17174	injertos	1
17175	injerto	1
17176	injerencias	1
17177	inició	1
17178	iniciarse	1
17179	iniciales	1
17180	inicial	1
17181	iniciado	1
17182	iniciadas	1
17183	iniciación	1
17184	inhibirse	1
17185	inhibía	1
17186	ingresos	1
17187	ingresamos	1
17188	ingratos	1
17189	ingenuos	1
17190	ingenuo	1
17191	ingenuidad	1
17192	ingenuas	1
17193	ingenuamente	1
17194	ingenua	1
17195	ingénitos	1
17196	ingénita	1
17197	ingenieros	1
17198	ingeniara	1
17199	infusorios	1
17200	infundía	1
17201	infundan	1
17202	infructuosa	1
17203	infringir	1
17204	infraganti	1
17205	infracción	1
17206	informes	1
17207	informe	1
17208	influyó	1
17209	influido	1
17210	influencias	1
17211	inflexiones	1
17212	inflexibles	1
17213	inflamable	1
17214	inflados	1
17215	inflaba	1
17216	infinitas	1
17217	infestarse	1
17218	infestado	1
17219	inferiores	1
17220	infecundos	1
17221	infausta	1
17222	infatigable	1
17223	infantería	1
17224	infante	1
17225	infamias	1
17226	infamatorio	1
17227	infalibidad	1
17228	infali	1
17229	inextinguible	1
17230	inexplicable	1
17231	inexpertos	1
17232	inexperto	1
17233	inesperados	1
17234	inesperadas	1
17235	inescrutables	1
17236	inertes	1
17237	inequívocas	1
17238	ineludible	1
17239	indumentario	1
17240	indómitos	1
17241	indomable	1
17242	individuos	1
17243	indispensables	1
17244	indiscutibles	1
17245	indiscutible	1
17246	indiscretos	1
17247	indiscretas	1
17248	indisciplinado	1
17249	indiqué	1
17250	indique	1
17251	indios	1
17252	indino	1
17253	indignos	1
17254	indignas	1
17255	indignaría	1
17256	indignamente	1
17257	indignaban	1
17258	indignaba	1
17259	indígena	1
17260	indicó	1
17261	indicarse	1
17262	indicaron	1
17263	indicarán	1
17264	indicando	1
17265	indicado	1
17266	indica	1
17267	indescifrable	1
17268	indemnizaciones	1
17269	indefinidos	1
17270	indefenso	1
17271	indecorosas	1
17272	indecisa	1
17273	indecible	1
17274	indecentes	1
17275	indecencias	1
17276	indecencia	1
17277	indagadas	1
17278	incurrir	1
17279	incurría	1
17280	incuria	1
17281	incurables	1
17282	incumbencia	1
17283	inculcará	1
17284	incrustadas	1
17285	incrusta	1
17286	incruentos	1
17287	incruentas	1
17288	increíble	1
17289	incredulidad	1
17290	incorruptible	1
17291	incorregible	1
17292	incorrecto	1
17293	incorrectas	1
17294	incorrecta	1
17295	incorporó	1
17296	incorporada	1
17297	incorporaban	1
17298	inconveniencia	1
17299	incontrastable	1
17300	inconstancia	1
17301	inconsolable	1
17302	inconscientes	1
17303	inconfesables	1
17304	inconexos	1
17305	incompatible	1
17306	incompatibilidades	1
17307	incomparables	1
17308	incomparablemente	1
17309	incomodo	1
17310	incomodidades	1
17311	incomodidad	1
17312	incomodarme	1
17313	incomodada	1
17314	incomodaba	1
17315	incombustible	1
17316	incoherentes	1
17317	incoherente	1
17318	incoherencia	1
17319	inclinan	1
17320	inclinados	1
17321	inclinaban	1
17322	incisos	1
17323	inciertos	1
17324	incierta	1
17325	incentivos	1
17326	incensario	1
17327	incendio	1
17328	incendiada	1
17329	incautos	1
17330	incauto	1
17331	incasables	1
17332	incalificables	1
17333	incalculable	1
17334	inauguró	1
17335	inauguren	1
17336	inaugurar	1
17337	inauguraban	1
17338	inaudito	1
17339	inaudita	1
17340	inarticulada	1
17341	inarco	1
17342	inapreciable	1
17343	inapetencias	1
17344	inanimados	1
17345	inanición	1
17346	inalienables	1
17347	inaguantable	1
17348	inadvertencia	1
17349	inacabable	1
17350	imputaban	1
17351	impusiese	1
17352	impusieron	1
17353	impusiera	1
17354	impuse	1
17355	impureza	1
17356	impura	1
17357	impune	1
17358	impulsan	1
17359	impuesta	1
17360	impúdicas	1
17361	improvisaron	1
17362	improvisados	1
17363	improvisada	1
17364	improvisación	1
17365	improvisaban	1
17366	improvisa	1
17367	impropias	1
17368	impropiamente	1
17369	improperios	1
17370	ímprobo	1
17371	imprimían	1
17372	impreso	1
17373	impresionables	1
17374	impresionaban	1
17375	impresiona	1
17376	imprescindible	1
17377	impresas	1
17378	impregnado	1
17379	imprecaciones	1
17380	imprecaba	1
17381	impotente	1
17382	impotencia	1
17383	impostura	1
17384	imposición	1
17385	imposibilidad	1
17386	importunase	1
17387	importó	1
17388	importasen	1
17389	importarle	1
17390	importará	1
17391	importantísimo	1
17392	importan	1
17393	importadores	1
17394	importado	1
17395	imponían	1
17396	impongan	1
17397	imponerse	1
17398	imponerme	1
17399	imponerle	1
17400	imponer	1
17401	imponentes	1
17402	imponen	1
17403	imploro	1
17404	implícito	1
17405	implícitas	1
17406	implacables	1
17407	impidió	1
17408	impidiesen	1
17409	impidiera	1
17410	impide	1
17411	impías	1
17412	ímpetus	1
17413	impertinencias	1
17414	impermeable	1
17415	imperiosos	1
17416	imperioso	1
17417	imperiosas	1
17418	impericia	1
17419	imperiales	1
17420	imperceptible	1
17421	imperativo	1
17422	imperando	1
17423	impedirlos	1
17424	impedirlo	1
17425	impedirle	1
17426	impedir	1
17427	impedido	1
17428	impecable	1
17429	imparcial	1
17430	impacientes	1
17431	imitarse	1
17432	imitara	1
17433	imita	1
17434	imbuirlas	1
17435	imbécil	1
17436	imantada	1
17437	imanes	1
17438	imán	1
17439	imagínole	1
17440	imaginativos	1
17441	imaginarse	1
17442	imaginarlo	1
17443	imaginarla	1
17444	imaginarios	1
17445	imaginada	1
17446	imaginaciones	1
17447	ilustrarse	1
17448	ilustradas	1
17449	ilusos	1
17450	ilusorios	1
17451	iluminó	1
17452	iluminarme	1
17453	iluminados	1
17454	iluminado	1
17455	iluminaba	1
17456	ilumina	1
17457	ilmo	1
17458	iliteratas	1
17459	ilíada	1
17460	ilegítima	1
17461	ilegibles	1
17462	ilegal	1
17463	iguale	1
17464	igualdades	1
17465	ignore	1
17466	ignoraría	1
17467	ignorantes	1
17468	ignorada	1
17469	ignora	1
17470	idilio	1
17471	idénticos	1
17472	idéntica	1
17473	idealizar	1
17474	id	1
17475	ictericia	1
17476	íberos	1
17477	ibérica	1
17478	huyes	1
17479	huyeron	1
17480	huyen	1
17481	hurtos	1
17482	hurtado	1
17483	hurgaba	1
17484	hundió	1
17485	hundimos	1
17486	hundidas	1
17487	hundíamos	1
17488	humour	1
17489	humorístico	1
17490	humorísticas	1
17491	humorística	1
17492	humorado	1
17493	humilló	1
17494	humíllate	1
17495	humillaría	1
17496	humillante	1
17497	humillación	1
17498	humedecerse	1
17499	humedecer	1
17500	humeante	1
17501	humanizada	1
17502	humanizaban	1
17503	humanitarias	1
17504	humanidades	1
17505	humani	1
17506	huiría	1
17507	huían	1
17508	hugonotes	1
17509	hugo	1
17510	huevo	1
17511	huevecillo	1
17512	huestes	1
17513	huésped	1
17514	huesca	1
17515	huertos	1
17516	huérfanas	1
17517	huelo	1
17518	hueles	1
17519	huela	1
17520	hubieras	1
17521	hoz	1
17522	hoteles	1
17523	hostilidades	1
17524	hostia	1
17525	hospitalidad	1
17526	hospicios	1
17527	hospiciano	1
17528	horticultura	1
17529	horteras	1
17530	hortelano	1
17531	hortaliza	1
17532	horrorosas	1
17533	horriblemente	1
17534	hormigueo	1
17535	hormigas	1
17536	hormiga	1
17537	horchaterías	1
17538	horchata	1
17539	horada	1
17540	honrosa	1
17541	honrar	1
17542	honrando	1
17543	honradamente	1
17544	honraba	1
17545	honorario	1
17546	honni	1
17547	hongos	1
17548	hongo	1
17549	honestidad	1
17550	honestamente	1
17551	honduras	1
17552	hondos	1
17553	hondonadas	1
17554	hondamente	1
17555	homini	1
17556	homero	1
17557	hombrunas	1
17558	hombruna	1
17559	hombreándose	1
17560	holgazanes	1
17561	holgazanería	1
17562	holgadamente	1
17563	holgada	1
17564	hojaldres	1
17565	hogares	1
17566	hodie	1
17567	hocico	1
17568	hita	1
17569	histerismo	1
17570	histérica	1
17571	hiriese	1
17572	hipotéticos	1
17573	hipotérmico	1
17574	hipotecada	1
17575	hipopótamos	1
17576	hipódromos	1
17577	hiperbólicas	1
17578	hiperbólicamente	1
17579	hiperbólica	1
17580	hinojos	1
17581	hinchó	1
17582	hinchazón	1
17583	hincaba	1
17584	himnos	1
17585	hilaba	1
17586	hijuelos	1
17587	higuera	1
17588	higiénicos	1
17589	high	1
17590	hígado	1
17591	hierros	1
17592	hierocrático	1
17593	hierbas	1
17594	hielos	1
17595	hidra	1
17596	hidalga	1
17597	hiciste	1
17598	hic	1
17599	heterogéneos	1
17600	heterogénea	1
17601	hervir	1
17602	herreros	1
17603	herrar	1
17604	herradura	1
17605	herpéticos	1
17606	heroísmo	1
17607	heroicidad	1
17608	herodías	1
17609	hermanitos	1
17610	herirle	1
17611	heridos	1
17612	herían	1
17613	hería	1
17614	heréticas	1
17615	herética	1
17616	heresiarcas	1
17617	heresiarca	1
17618	heredar	1
17619	heredan	1
17620	heredad	1
17621	herborizando	1
17622	heráldica	1
17623	hepatitis	1
17624	henao	1
17625	hemostática	1
17626	heló	1
17627	helar	1
17628	helándole	1
17629	hegemonía	1
17630	hedores	1
17631	hediondas	1
17632	hechuras	1
17633	hechizo	1
17634	hazle	1
17635	hazaña	1
17636	hastía	1
17637	harinas	1
17638	harina	1
17639	haríamos	1
17640	haremos	1
17641	haraposa	1
17642	harapos	1
17643	harapo	1
17644	harán	1
17645	hamlet	1
17646	hame	1
17647	hambrientos	1
17648	hamaca	1
17649	hallé	1
17650	hallarás	1
17651	hallará	1
17652	hallándose	1
17653	halladas	1
17654	halagüeños	1
17655	halagasen	1
17656	halagaron	1
17657	halagada	1
17658	halagaban	1
17659	halaga	1
17660	hágase	1
17661	hagámosela	1
17662	hagámonos	1
17663	hágame	1
17664	haec	1
17665	haciéndome	1
17666	haciéndoles	1
17667	hacíale	1
17668	hachones	1
17669	hache	1
17670	hacha	1
17671	hacerte	1
17672	hacérsenos	1
17673	hacérsele	1
17674	hacérsela	1
17675	hacerlas	1
17676	habrías	1
17677	habré	1
17678	hablen	1
17679	hablasteis	1
17680	hablasen	1
17681	hablaríamos	1
17682	hablaran	1
17683	habláramos	1
17684	hablándose	1
17685	hablándole	1
17686	háblame	1
17687	hablábamos	1
17688	habitaron	1
17689	habitar	1
17690	habitan	1
17691	habitados	1
17692	habitado	1
17693	habitable	1
17694	habita	1
17695	hábilmente	1
17696	hábiles	1
17697	habiendo	1
17698	habíase	1
17699	habíanle	1
17700	habet	1
17701	habérselas	1
17702	haberme	1
17703	haberlos	1
17704	haberlas	1
17705	haberla	1
17706	habas	1
17707	guturales	1
17708	gutierre	1
17709	gutapercha	1
17710	gustoso	1
17711	gustazo	1
17712	gustas	1
17713	gustaría	1
17714	gusanera	1
17715	gulf	1
17716	guisar	1
17717	guisaban	1
17718	guiñando	1
17719	guíe	1
17720	guías	1
17721	guiar	1
17722	guerrero	1
17723	guedejas	1
17724	guasa	1
17725	guarecidos	1
17726	guardolo	1
17727	guardillas	1
17728	guardias	1
17729	guárdese	1
17730	guarden	1
17731	guardé	1
17732	guarde	1
17733	guardase	1
17734	guardas	1
17735	guardarlas	1
17736	guardaré	1
17737	guardándose	1
17738	guardándonos	1
17739	guardando	1
17740	guardamalletas	1
17741	guardados	1
17742	guardador	1
17743	guardada	1
17744	guapos	1
17745	guapetona	1
17746	guadalquivir	1
17747	gruyer	1
17748	grupa	1
17749	gruñó	1
17750	gruñendo	1
17751	gruesecillo	1
17752	grotescas	1
17753	groserías	1
17754	grites	1
17755	grillo	1
17756	grilletes	1
17757	grillete	1
17758	grilleras	1
17759	grillera	1
17760	grijalte	1
17761	grifo	1
17762	griegos	1
17763	grecia	1
17764	graznar	1
17765	graznado	1
17766	gravísimo	1
17767	gravemente	1
17768	grato	1
17769	gratis	1
17770	grata	1
17771	grasiento	1
17772	grasientas	1
17773	granujas	1
17774	granizada	1
17775	graneado	1
17776	grandísimos	1
17777	grandioso	1
17778	grandiosas	1
17779	grandilocuentes	1
17780	gráficas	1
17781	gradas	1
17782	grada	1
17783	graciosas	1
17784	graciosamente	1
17785	gozquecillo	1
17786	gozose	1
17787	gozosa	1
17788	gozase	1
17789	gozarlo	1
17790	gozará	1
17791	gozamos	1
17792	goza	1
17793	goteaban	1
17794	gorros	1
17795	gorrona	1
17796	gorrión	1
17797	gorjeos	1
17798	gorjeaban	1
17799	gordos	1
17800	gonzález	1
17801	gongorino	1
17802	góngora	1
17803	gomogga	1
17804	golpeó	1
17805	golpecito	1
17806	golpeaban	1
17807	golondrinas	1
17808	gollería	1
17809	golfos	1
17810	gobiernos	1
17811	gobiernan	1
17812	gobernarse	1
17813	gloriosos	1
17814	gloriosamente	1
17815	giros	1
17816	giro	1
17817	giras	1
17818	girando	1
17819	giraldi	1
17820	ginebrino	1
17821	gimnásticos	1
17822	gimnasio	1
17823	gimió	1
17824	gil	1
17825	gigantona	1
17826	gigantón	1
17827	gigantescas	1
17828	gigantesca	1
17829	gigantes	1
17830	gesticularíamos	1
17831	gesticulando	1
17832	gestación	1
17833	gerundio	1
17834	geométricos	1
17835	geométricas	1
17836	geométrica	1
17837	geológicos	1
17838	geográficos	1
17839	genuinamente	1
17840	gentleman	1
17841	gentío	1
17842	gentileza	1
17843	gentiles	1
17844	genios	1
17845	genil	1
17846	genial	1
17847	generoso	1
17848	generosidad	1
17849	gemir	1
17850	gazmoña	1
17851	gayarre	1
17852	gaya	1
17853	gauthier	1
17854	gatito	1
17855	gatazo	1
17856	gastronómicos	1
17857	gastronómico	1
17858	gastroenteritis	1
17859	gástrico	1
17860	gastó	1
17861	gasto	1
17862	gasten	1
17863	gastase	1
17864	gastando	1
17865	gastada	1
17866	gastaban	1
17867	gastaba	1
17868	gaseosos	1
17869	garzos	1
17870	garden	1
17871	garcilaso	1
17872	garbanzo	1
17873	garante	1
17874	garabatos	1
17875	ganzúa	1
17876	ganosos	1
17877	ganoso	1
17878	ganosa	1
17879	gancho	1
17880	ganarnos	1
17881	ganaría	1
17882	ganara	1
17883	gananciales	1
17884	ganamos	1
17885	ganados	1
17886	ganadera	1
17887	ganada	1
17888	gamo	1
17889	galope	1
17890	gallineros	1
17891	galleta	1
17892	gallardísima	1
17893	gallardete	1
17894	gallardamente	1
17895	galileo	1
17896	galicismos	1
17897	galgo	1
17898	galerna	1
17899	galera	1
17900	galdós	1
17901	galas	1
17902	galardonaron	1
17903	galantes	1
17904	galantear	1
17905	gaitero	1
17906	gacha	1
17907	gacetillas	1
17908	gaceta	1
17909	futuras	1
17910	futraque	1
17911	fútiles	1
17912	fustis	1
17913	fusiles	1
17914	fusilémosle	1
17915	furtivos	1
17916	furtivo	1
17917	furiosas	1
17918	furibundos	1
17919	fungosa	1
17920	funesto	1
17921	fundó	1
17922	fundido	1
17923	fundidas	1
17924	fundición	1
17925	funde	1
17926	fundarse	1
17927	fundamentos	1
17928	fundadora	1
17929	fundador	1
17930	fundada	1
17931	fundaciones	1
17932	fundación	1
17933	funcionario	1
17934	funcionaba	1
17935	funámbula	1
17936	fuman	1
17937	fumador	1
17938	fumado	1
17939	fulminó	1
17940	fulminantes	1
17941	fulgores	1
17942	fulanito	1
17943	fulanita	1
17944	fuiste	1
17945	fuimos	1
17946	fuguillas	1
17947	fuga	1
17948	fueses	1
17949	fuertemente	1
17950	fuero	1
17951	fuéramos	1
17952	fuer	1
17953	frutas	1
17954	frutales	1
17955	frustrado	1
17956	frustó	1
17957	fruncido	1
17958	fruela	1
17959	frotar	1
17960	frotándose	1
17961	frotando	1
17962	frontones	1
17963	frontispicio	1
17964	frontera	1
17965	frontal	1
17966	frondosos	1
17967	frívolos	1
17968	frivolidad	1
17969	fritos	1
17970	frisar	1
17971	frisaban	1
17972	frisaba	1
17973	frigorífico	1
17974	fríamente	1
17975	frenéticos	1
17976	frenéticas	1
17977	frenética	1
17978	frecuentase	1
17979	frecuentan	1
17980	frecuentado	1
17981	frecuentaban	1
17982	frecuentaba	1
17983	fraternizar	1
17984	fraternal	1
17985	frascueeeelo	1
17986	francklin	1
17987	franciscos	1
17988	franciscas	1
17989	francesas	1
17990	fraigerundio	1
17991	fragmento	1
17992	fraganti	1
17993	fragancias	1
17994	fragancia	1
17995	fr	1
17996	fósforos	1
17997	fosforeras	1
17998	fosco	1
17999	forzada	1
18000	fortunas	1
18001	fortuitos	1
18002	fortísimo	1
18003	fortísima	1
18004	fortificaba	1
18005	fortifica	1
18006	fortalezas	1
18007	fortalecían	1
18008	forró	1
18009	forrados	1
18010	forradas	1
18011	foros	1
18012	fornos	1
18013	fornidos	1
18014	formulismo	1
18015	formulando	1
18016	formó	1
18017	formemos	1
18018	formaron	1
18019	forman	1
18020	forjado	1
18021	forcejeaban	1
18022	forajidos	1
18023	fontanero	1
18024	follis	1
18025	follajes	1
18026	fogonazo	1
18027	foco	1
18028	fluir	1
18029	flota	1
18030	floricultor	1
18031	flórez	1
18032	floreros	1
18033	flojas	1
18034	flema	1
18035	flegmasías	1
18036	flegmasía	1
18037	flecos	1
18038	flatus	1
18039	flanqueándola	1
18040	flanes	1
18041	flan	1
18042	flammarión	1
18043	flamígeros	1
18044	flamencos	1
18045	flamencas	1
18046	flamantes	1
18047	flamante	1
18048	flagrantes	1
18049	fisonomías	1
18050	fisiólogo	1
18051	fisiológicos	1
18052	fisiológicas	1
18053	fisiológicamente	1
18054	físicas	1
18055	fiscalías	1
18056	firmó	1
18057	firmeza	1
18058	firmado	1
18059	finitas	1
18060	fingimientos	1
18061	fingiera	1
18062	fingidos	1
18063	fingidas	1
18064	fingen	1
18065	fineza	1
18066	fincas	1
18067	finca	1
18068	finado	1
18069	filtro	1
18070	filtrando	1
18071	filtrado	1
18072	filtración	1
18073	filosofías	1
18074	filosofastros	1
18075	filosofaba	1
18076	filón	1
18077	filis	1
18078	filigranas	1
18079	filigrana	1
18080	filete	1
18081	filarmónico	1
18082	filantrópicos	1
18083	filantrópico	1
18084	filantropía	1
18085	fijara	1
18086	fijan	1
18087	fijamente	1
18088	fijado	1
18089	fijaban	1
18090	figuronas	1
18091	figuro	1
18092	figurines	1
18093	figurillas	1
18094	figúreselo	1
18095	figures	1
18096	figurársele	1
18097	figuraríamos	1
18098	figurar	1
18099	figurándoselo	1
18100	figurándosela	1
18101	figuran	1
18102	figurábase	1
18103	figaro	1
18104	fierabrás	1
18105	fielding	1
18106	fidelísimo	1
18107	fidei	1
18108	fichas	1
18109	ficciones	1
18110	ficción	1
18111	fibra	1
18112	fiarse	1
18113	fían	1
18114	fiado	1
18115	fiada	1
18116	feudalismo	1
18117	feudales	1
18118	fétido	1
18119	fervorosa	1
18120	fervientes	1
18121	fertilidad	1
18122	fértiles	1
18123	feroz	1
18124	fementida	1
18125	femeniles	1
18126	felpudo	1
18127	felinos	1
18128	felinas	1
18129	felicitó	1
18130	felicitaron	1
18131	felice	1
18132	feísima	1
18133	feijóo	1
18134	federación	1
18135	fecit	1
18136	fechas	1
18137	febrero	1
18138	feas	1
18139	fealdades	1
18140	fealdad	1
18141	faz	1
18142	favorecido	1
18143	favorecida	1
18144	favorecían	1
18145	favorecerle	1
18146	favorables	1
18147	fatua	1
18148	fatigosas	1
18149	fatigado	1
18150	fatalista	1
18151	fatales	1
18152	fastuosidad	1
18153	fastos	1
18154	fastidiosos	1
18155	fastidiarle	1
18156	fascinada	1
18157	fascinaba	1
18158	fas	1
18159	farsas	1
18160	farolón	1
18161	farnesios	1
18162	fariseas	1
18163	faringe	1
18164	faraones	1
18165	fantásticas	1
18166	fantásticamente	1
18167	fantasías	1
18168	fantaseaba	1
18169	fangoso	1
18170	fanfarrones	1
18171	fanatizada	1
18172	fanáticas	1
18173	fanal	1
18174	famosísimo	1
18175	famosas	1
18176	familiaridad	1
18177	faltriquera	1
18178	falten	1
18179	faltemos	1
18180	faltase	1
18181	faltarle	1
18182	faltaré	1
18183	faltará	1
18184	faltando	1
18185	falsísima	1
18186	falsificó	1
18187	falsificado	1
18188	falsificada	1
18189	falló	1
18190	fallo	1
18191	fallidas	1
18192	fallecido	1
18193	falange	1
18194	faisán	1
18195	facultativos	1
18196	facultativa	1
18197	facultad	1
18198	factum	1
18199	factorías	1
18200	factores	1
18201	façon	1
18202	facistol	1
18203	facimus	1
18204	facilitaba	1
18205	facilita	1
18206	facilidad	1
18207	facial	1
18208	fachenda	1
18209	fachadas	1
18210	fabuloso	1
18211	fabulosas	1
18212	fábulas	1
18213	fabricante	1
18214	fabricado	1
18215	fabricada	1
18216	fabrica	1
18217	fabiolita	1
18218	fabiola	1
18219	fa	1
18220	extremidades	1
18221	extremeño	1
18222	extrememos	1
18223	extremas	1
18224	extravió	1
18225	extravío	1
18226	extravían	1
18227	extraviada	1
18228	extraviaba	1
18229	extraordinarios	1
18230	extrañar	1
18231	extrañado	1
18232	extrañaba	1
18233	extranjera	1
18234	extraído	1
18235	extinguirse	1
18236	extinguir	1
18237	extinguiera	1
18238	extinguido	1
18239	extiende	1
18240	extenuado	1
18241	extendiera	1
18242	extendiéndome	1
18243	extendidos	1
18244	extendidas	1
18245	extendida	1
18246	extenderse	1
18247	extática	1
18248	extasiado	1
18249	extasiada	1
18250	exquisitos	1
18251	expropiación	1
18252	exprofeso	1
18253	exprimían	1
18254	expreso	1
18255	expresivas	1
18256	exprese	1
18257	expresando	1
18258	expresa	1
18259	expositio	1
18260	exportado	1
18261	exponiendo	1
18262	expones	1
18263	exponerte	1
18264	exponerla	1
18265	exponer	1
18266	expone	1
18267	expondría	1
18268	explotarlos	1
18269	explotarlo	1
18270	explotaré	1
18271	explotación	1
18272	explosiva	1
18273	explosión	1
18274	exploremos	1
18275	exploraciones	1
18276	expliques	1
18277	expliquen	1
18278	explíquemelo	1
18279	explico	1
18280	explícate	1
18281	explicase	1
18282	explicárselo	1
18283	explicárselas	1
18284	explicársela	1
18285	explicaré	1
18286	explicará	1
18287	explicara	1
18288	explican	1
18289	explicados	1
18290	expiraba	1
18291	expertos	1
18292	expertas	1
18293	experimentos	1
18294	experimento	1
18295	experimentar	1
18296	experiencias	1
18297	expedita	1
18298	expediciones	1
18299	expedicionario	1
18300	expectación	1
18301	expansivas	1
18302	exóticas	1
18303	exótica	1
18304	exorbitantes	1
18305	exorbitante	1
18306	existiese	1
18307	existieran	1
18308	existían	1
18309	existente	1
18310	existencias	1
18311	existen	1
18312	exíjase	1
18313	exigua	1
18314	exigiría	1
18315	exigió	1
18316	exigieron	1
18317	exigiendo	1
18318	exigencia	1
18319	exhaustas	1
18320	exhalaban	1
18321	exenta	1
18322	exegéticas	1
18323	execración	1
18324	execrables	1
18325	execrable	1
18326	excusar	1
18327	excusadas	1
18328	excusaba	1
18329	excusa	1
18330	excomulgado	1
18331	excluye	1
18332	excluía	1
18333	exclaustrar	1
18334	exclamado	1
18335	exclamación	1
18336	excitó	1
18337	excitarlo	1
18338	excitantes	1
18339	excitante	1
18340	excitadota	1
18341	excitados	1
18342	excitadilla	1
18343	excitadas	1
18344	excesivamente	1
18345	exceptuaba	1
18346	excepcionales	1
18347	excelentísima	1
18348	excelentes	1
18349	excedía	1
18350	excavaciones	1
18351	examino	1
18352	examinarme	1
18353	examinar	1
18354	examinaba	1
18355	examina	1
18356	exaltó	1
18357	exaltas	1
18358	exaltados	1
18359	exaltadas	1
18360	exaltaciones	1
18361	exalta	1
18362	exagerarlos	1
18363	exagerando	1
18364	exagerado	1
18365	exageradísima	1
18366	exactos	1
18367	evocarla	1
18368	evocar	1
18369	evocados	1
18370	evite	1
18371	evitarse	1
18372	evitarlos	1
18373	evitara	1
18374	evitado	1
18375	evitaba	1
18376	evidentemente	1
18377	evaporaban	1
18378	evaporaba	1
18379	evangelii	1
18380	europea	1
18381	eureka	1
18382	eufemismo	1
18383	eucologio	1
18384	eucaliptos	1
18385	etruscos	1
18386	etnógrafo	1
18387	eternizaba	1
18388	était	1
18389	estuviste	1
18390	estuvieras	1
18391	estuviéramos	1
18392	estupro	1
18393	estupor	1
18394	estúpidos	1
18395	estupenda	1
18396	estupefactos	1
18397	estupefacta	1
18398	estupefacción	1
18399	estudioso	1
18400	estudiarse	1
18401	estudiaría	1
18402	estudiando	1
18403	estudian	1
18404	estudiado	1
18405	estudiaban	1
18406	estuches	1
18407	estuche	1
18408	estucado	1
18409	estrujarse	1
18410	estrujar	1
18411	estrujándose	1
18412	estrujado	1
18413	estrujaba	1
18414	estropicio	1
18415	estridentes	1
18416	estricta	1
18417	estribor	1
18418	estrepitoso	1
18419	estremecimientos	1
18420	estremeciéndose	1
18421	estremecía	1
18422	estremecerse	1
18423	estrechaban	1
18424	estrangulada	1
18425	estrangulación	1
18426	estragados	1
18427	estrados	1
18428	estote	1
18429	estorninos	1
18430	estorbos	1
18431	estorbase	1
18432	estorbarse	1
18433	estorbarle	1
18434	estorbar	1
18435	estoraque	1
18436	estoposa	1
18437	estola	1
18438	estofa	1
18439	estocadas	1
18440	estirpe	1
18441	estirada	1
18442	estiraba	1
18443	estímulo	1
18444	estimule	1
18445	estimando	1
18446	estimado	1
18447	estilita	1
18448	estilista	1
18449	estético	1
18450	estés	1
18451	estériles	1
18452	estereotipada	1
18453	estera	1
18454	ester	1
18455	estepas	1
18456	estemos	1
18457	estatutos	1
18458	estáte	1
18459	estate	1
18460	estaré	1
18461	estarás	1
18462	estanquero	1
18463	estanque	1
18464	estandartes	1
18465	estandarte	1
18466	estancamiento	1
18467	estancadas	1
18468	estampilla	1
18469	estampada	1
18470	estambres	1
18471	estambre	1
18472	estalle	1
18473	estallaron	1
18474	estallarme	1
18475	estáis	1
18476	estacada	1
18477	establos	1
18478	establo	1
18479	establecido	1
18480	establecidas	1
18481	establecer	1
18482	establecen	1
18483	estable	1
18484	esquivar	1
18485	esquilón	1
18486	esquilas	1
18487	esquilache	1
18488	esqueletos	1
18489	esquela	1
18490	espumar	1
18491	espuela	1
18492	esprit	1
18493	espontáneos	1
18494	esponjosa	1
18495	esponjan	1
18496	espolios	1
18497	espliego	1
18498	esplendorosa	1
18499	espirituosos	1
18500	espiritualista	1
18501	espiritualísima	1
18502	espirar	1
18503	espirando	1
18504	espío	1
18505	espinosas	1
18506	espinosa	1
18507	espinos	1
18508	espinazo	1
18509	espifor	1
18510	espiarlos	1
18511	espesura	1
18512	espesísima	1
18513	esperemos	1
18514	esperé	1
18515	esperarse	1
18516	esperaron	1
18517	esperarla	1
18518	esperará	1
18519	esperándola	1
18520	espejismo	1
18521	espectación	1
18522	especificado	1
18523	especialistas	1
18524	especialista	1
18525	especialísima	1
18526	especiales	1
18527	espartero	1
18528	esparcir	1
18529	esparció	1
18530	esparcida	1
18531	españolas	1
18532	espantoso	1
18533	espantosas	1
18534	espantosa	1
18535	espantó	1
18536	espantes	1
18537	espantando	1
18538	espantajo	1
18539	espantadiza	1
18540	espanta	1
18541	espaldera	1
18542	espaciosos	1
18543	espacioso	1
18544	espaciosa	1
18545	espaciada	1
18546	esotéricos	1
18547	esmerado	1
18548	esmerada	1
18549	esgrimía	1
18550	esforzó	1
18551	esforzarse	1
18552	esforzaban	1
18553	esenciada	1
18554	escupiría	1
18555	escupirá	1
18556	escupiendo	1
18557	esculturales	1
18558	escultural	1
18559	escultóricos	1
18560	escultor	1
18561	escuetas	1
18562	escueta	1
18563	escudriñó	1
18564	escudriñado	1
18565	escuchase	1
18566	escucharle	1
18567	escuchando	1
18568	escuchado	1
18569	escuchad	1
18570	escuálido	1
18571	escuadra	1
18572	escrupulosos	1
18573	escrupulosidad	1
18574	escrupulosamente	1
18575	escrupulosa	1
18576	escrituras	1
18577	escribirlas	1
18578	escribiría	1
18579	escribiré	1
18580	escribieron	1
18581	escribiera	1
18582	escribas	1
18583	escríbame	1
18584	escozor	1
18585	escotillón	1
18586	escosura	1
18587	escorias	1
18588	escopetas	1
18589	escondrijos	1
18590	escondieron	1
18591	escondiéndose	1
18592	esconderla	1
18593	escondería	1
18594	escombros	1
18595	escolta	1
18596	escolios	1
18597	escolasticismo	1
18598	escolástica	1
18599	escoja	1
18600	escogitar	1
18601	escogieron	1
18602	escogidos	1
18603	escogidísimos	1
18604	escogidísimo	1
18605	escogidas	1
18606	escogida	1
18607	escogen	1
18608	escocias	1
18609	escocés	1
18610	escobazos	1
18611	escobazo	1
18612	esclavas	1
18613	esclarecidos	1
18614	escepticismo	1
18615	escénico	1
18616	escayola	1
18617	escatimados	1
18618	escasos	1
18619	escasearían	1
18620	escaseando	1
18621	escarnecía	1
18622	escarmiento	1
18623	escarchas	1
18624	escarabajo	1
18625	escapularios	1
18626	escapatoria	1
18627	escapase	1
18628	escapas	1
18629	escaparon	1
18630	escaparían	1
18631	escaparates	1
18632	escapan	1
18633	escapadas	1
18634	escapa	1
18635	escandalizarte	1
18636	escandalizando	1
18637	escandalizan	1
18638	escandalizado	1
18639	escandalizaba	1
18640	escame	1
18641	escamandro	1
18642	escalpelo	1
18643	escalones	1
18644	escalonada	1
18645	escalón	1
18646	escalasen	1
18647	escalar	1
18648	escabrosas	1
18649	esbirros	1
18650	esbirro	1
18651	ésas	1
18652	eruptos	1
18653	eruditos	1
18654	eruditamente	1
18655	erudita	1
18656	erudición	1
18657	eructaba	1
18658	errónea	1
18659	errante	1
18660	erradamente	1
18661	erotismo	1
18662	ermitaño	1
18663	erizó	1
18664	erizaron	1
18665	erizándose	1
18666	erizando	1
18667	erizados	1
18668	erizada	1
18669	erizaban	1
18670	erguido	1
18671	ergo	1
18672	erba	1
18673	erat	1
18674	erario	1
18675	equivoco	1
18676	equivocar	1
18677	equivocando	1
18678	equivocados	1
18679	equivocada	1
18680	equívoca	1
18681	equivoca	1
18682	equivalía	1
18683	equitativo	1
18684	equinoccio	1
18685	equilibrios	1
18686	equilibrado	1
18687	epopeya	1
18688	episcopal	1
18689	epílogo	1
18690	epigramático	1
18691	epidemia	1
18692	epicuro	1
18693	epicurista	1
18694	epicureísmo	1
18695	épico	1
18696	epiceno	1
18697	epicena	1
18698	épica	1
18699	epanadiplosis	1
18700	envuelven	1
18701	envolviole	1
18702	envolvió	1
18703	envolvían	1
18704	envolverla	1
18705	envolver	1
18706	envoltorio	1
18707	envidiando	1
18708	envidiados	1
18709	envidiado	1
18710	enviarle	1
18711	enviados	1
18712	envenenando	1
18713	envenenaban	1
18714	envejeciendo	1
18715	envejecía	1
18716	envanecían	1
18717	enumerar	1
18718	enumeraciones	1
18719	enumeración	1
18720	entusiastas	1
18721	entusiasmó	1
18722	entusiasmarse	1
18723	entusiasmaba	1
18724	enturbiar	1
18725	entumecimiento	1
18726	entumecidos	1
18727	entumecida	1
18728	entumecían	1
18729	entumecía	1
18730	entrometidos	1
18731	entrometido	1
18732	entrometidas	1
18733	entreverados	1
18734	entretienen	1
18735	entretiene	1
18736	entretenimiento	1
18737	entretenían	1
18738	entretengan	1
18739	entresuelo	1
18740	entremetidos	1
18741	entremetido	1
18742	entregárselo	1
18743	entregarme	1
18744	entregarlo	1
18745	entregarle	1
18746	entregaría	1
18747	entregara	1
18748	entregándose	1
18749	entregándole	1
18750	entregándolas	1
18751	entregan	1
18752	entregados	1
18753	entreabrió	1
18754	entreabiertos	1
18755	entrasen	1
18756	entrase	1
18757	entras	1
18758	entrarle	1
18759	entraremos	1
18760	entraras	1
18761	entrara	1
18762	entraña	1
18763	entran	1
18764	entramos	1
18765	entradas	1
18766	entorpecimientos	1
18767	entornó	1
18768	entornándolos	1
18769	entornado	1
18770	entornada	1
18771	entornaba	1
18772	entonado	1
18773	entonadas	1
18774	entomólogo	1
18775	entomológicas	1
18776	entierren	1
18777	entierre	1
18778	entienden	1
18779	entidades	1
18780	entibiaba	1
18781	enterrarán	1
18782	enterramientos	1
18783	enterraba	1
18784	enternezco	1
18785	enternecerse	1
18786	enternecer	1
18787	enteren	1
18788	enterarle	1
18789	enterados	1
18790	enteraba	1
18791	entendimiento	1
18792	entendieran	1
18793	entendiendo	1
18794	entendidas	1
18795	entendida	1
18796	entendernos	1
18797	entenderían	1
18798	entenderé	1
18799	entendedor	1
18800	ente	1
18801	entallada	1
18802	entablaba	1
18803	ensuciar	1
18804	ensortijado	1
18805	ensoñadora	1
18806	ensoñación	1
18807	ensimismado	1
18808	enseñorease	1
18809	enseñoreados	1
18810	enseñó	1
18811	enseñes	1
18812	enseñarte	1
18813	enseñaron	1
18814	enseñanzas	1
18815	enseñándole	1
18816	ensayó	1
18817	ensartadas	1
18818	ensanche	1
18819	ensancharse	1
18820	ensanchándose	1
18821	ensalzarás	1
18822	enroscarse	1
18823	enroscándose	1
18824	enroscado	1
18825	enroscadas	1
18826	enrevesados	1
18827	enredó	1
18828	enredado	1
18829	enredaderas	1
18830	enredadera	1
18831	enredada	1
18832	enredaban	1
18833	enreda	1
18834	enojosísimos	1
18835	enojaba	1
18836	ennoblecemos	1
18837	ennegrecidos	1
18838	ennegrecidas	1
18839	ennegrecían	1
18840	enmudece	1
18841	enmienda	1
18842	enmascarado	1
18843	enloquecidas	1
18844	enlazados	1
18845	enlazaba	1
18846	enjutos	1
18847	enjugó	1
18848	enjugar	1
18849	enjugando	1
18850	enjaulado	1
18851	enjaulada	1
18852	enjambre	1
18853	enigma	1
18854	enhiesto	1
18855	engrandecía	1
18856	engrandecer	1
18857	engordase	1
18858	engordando	1
18859	engordado	1
18860	engomada	1
18861	engolfarse	1
18862	englobado	1
18863	engendrar	1
18864	engendraban	1
18865	engañaste	1
18866	engañarlos	1
18867	engañándose	1
18868	engañando	1
18869	enganchó	1
18870	enganchados	1
18871	enganchado	1
18872	enganchadas	1
18873	enganchaba	1
18874	engalanadas	1
18875	enfurecía	1
18876	enfundadas	1
18877	enfriara	1
18878	enfriado	1
18879	enfriaban	1
18880	enfrenados	1
18881	enfrascarse	1
18882	enfrascados	1
18883	enfilándose	1
18884	enfermucho	1
18885	enfermero	1
18886	enfermemos	1
18887	enfermaste	1
18888	enfermar	1
18889	enfant	1
18890	enfado	1
18891	enfadarle	1
18892	enfadado	1
18893	enfadada	1
18894	enfada	1
18895	enerve	1
18896	energúmenos	1
18897	energúmeno	1
18898	enérgicos	1
18899	enemistad	1
18900	endiosas	1
18901	endiosarse	1
18902	enderezarle	1
18903	endemoniada	1
18904	endémicos	1
18905	encuentras	1
18906	encubridoras	1
18907	encorvadas	1
18908	encopetadas	1
18909	encontremos	1
18910	encontrase	1
18911	encontrársela	1
18912	encontrarla	1
18913	encontraremos	1
18914	encontrarán	1
18915	encontraran	1
18916	encontrará	1
18917	encontramos	1
18918	encontrados	1
18919	encontrábase	1
18920	encomienda	1
18921	encomendó	1
18922	encomendaron	1
18923	encogimiento	1
18924	encogiéndose	1
18925	encogida	1
18926	encogerse	1
18927	encoge	1
18928	enclenques	1
18929	encinta	1
18930	encina	1
18931	encierros	1
18932	encierras	1
18933	encierra	1
18934	encienden	1
18935	encienda	1
18936	enchufaban	1
18937	encharcados	1
18938	encerrona	1
18939	encerraron	1
18940	encerrarla	1
18941	encerrar	1
18942	encerrándose	1
18943	encerrados	1
18944	encerraban	1
18945	encerado	1
18946	encendiese	1
18947	encenderse	1
18948	encenderla	1
18949	encenagó	1
18950	encenagados	1
18951	encenagaba	1
18952	encauzada	1
18953	encaró	1
18954	encarnizada	1
18955	encarnados	1
18956	encarnación	1
18957	encarnaba	1
18958	encargarse	1
18959	encargaría	1
18960	encargadas	1
18961	encargada	1
18962	encargaban	1
18963	encareciendo	1
18964	encarcelado	1
18965	encaraman	1
18966	encaramaban	1
18967	encaprichara	1
18968	encaprichadas	1
18969	encapotado	1
18970	encantar	1
18971	encantadora	1
18972	encajarte	1
18973	encajan	1
18974	enanos	1
18975	enano	1
18976	enamoro	1
18977	enamoren	1
18978	enamorarla	1
18979	enamorándome	1
18980	enamoran	1
18981	enamoramiento	1
18982	enamoraba	1
18983	enaltecerla	1
18984	enajenación	1
18985	emulación	1
18986	empuño	1
18987	empuñar	1
18988	empuñando	1
18989	empujón	1
18990	empuje	1
18991	empujasen	1
18992	empujando	1
18993	empujado	1
18994	empujaban	1
18995	emprendieron	1
18996	emprendían	1
18997	emprenderla	1
18998	emprendemos	1
18999	emprendedor	1
19000	empotrados	1
19001	empotrado	1
19002	empolvado	1
19003	empolvada	1
19004	empleos	1
19005	emplearse	1
19006	empleará	1
19007	empleara	1
19008	empleando	1
19009	emplea	1
19010	emplazamiento	1
19011	emplastos	1
19012	empingorotados	1
19013	empingorotado	1
19014	empinados	1
19015	empinada	1
19016	empezara	1
19017	empezamos	1
19018	empero	1
19019	emperifolladas	1
19020	emperador	1
19021	empequeñecido	1
19022	empeorar	1
19023	empeñas	1
19024	empeñaron	1
19025	empeñada	1
19026	empedrado	1
19027	empedradas	1
19028	empedrada	1
19029	empedernido	1
19030	empecía	1
19031	empecemos	1
19032	empecé	1
19033	empecatado	1
19034	empecatadas	1
19035	emparejó	1
19036	emparejarse	1
19037	emparejaron	1
19038	emparejaba	1
19039	emparedados	1
19040	emparedada	1
19041	empapelado	1
19042	empapando	1
19043	empapada	1
19044	empalmándose	1
19045	empalagosa	1
19046	empadronar	1
19047	emisarios	1
19048	emisario	1
19049	eminentemente	1
19050	eminente	1
19051	emigró	1
19052	emigrar	1
19053	emigrada	1
19054	embutiendo	1
19055	embutida	1
19056	embute	1
19057	embustera	1
19058	embuste	1
19059	embrutecimiento	1
19060	embrutecían	1
19061	embrutecía	1
19062	embrujado	1
19063	embrollo	1
19064	embrollado	1
19065	embrollaba	1
19066	embrión	1
19067	embriagada	1
19068	embozarse	1
19069	embozándose	1
19070	embozando	1
19071	embozan	1
19072	embozadas	1
19073	embozada	1
19074	embozaban	1
19075	embozaba	1
19076	embotar	1
19077	emboscadas	1
19078	emborracharle	1
19079	emborrachan	1
19080	emborrachaban	1
19081	emborrachaba	1
19082	embobado	1
19083	embelleció	1
19084	embeleso	1
19085	embebecido	1
19086	embargó	1
19087	embarcarte	1
19088	embarazosos	1
19089	embarazosas	1
19090	embajada	1
19091	emanciparse	1
19092	emancipado	1
19093	emancipación	1
19094	eludiendo	1
19095	eloïm	1
19096	elogiando	1
19097	élite	1
19098	eligiesen	1
19099	elevados	1
19100	elevada	1
19101	elegido	1
19102	elegida	1
19103	elegíaca	1
19104	elegantón	1
19105	elegantemente	1
19106	elegancias	1
19107	elefante	1
19108	eléctricos	1
19109	electores	1
19110	elector	1
19111	elástico	1
19112	elaboración	1
19113	ejercitaba	1
19114	ejerció	1
19115	ejerciendo	1
19116	ejercido	1
19117	ejemplos	1
19118	ejecutor	1
19119	ejecutivo	1
19120	ejecución	1
19121	egoístas	1
19122	ego	1
19123	églogas	1
19124	égloga	1
19125	egipcias	1
19126	egida	1
19127	egeria	1
19128	efusivo	1
19129	efluvios	1
19130	efímeros	1
19131	efímera	1
19132	efectiva	1
19133	educó	1
19134	educar	1
19135	eduardo	1
19136	editores	1
19137	editor	1
19138	edificando	1
19139	edifican	1
19140	edificaba	1
19141	edicto	1
19142	edgar	1
19143	edemíaca	1
19144	ecuestre	1
19145	ecos	1
19146	economizarlo	1
19147	economista	1
19148	económica	1
19149	economato	1
19150	eclipses	1
19151	eclipsar	1
19152	eciomo	1
19153	échele	1
19154	echasen	1
19155	echas	1
19156	echarlos	1
19157	echándole	1
19158	echados	1
19159	ecco	1
19160	ebro	1
19161	ebria	1
19162	ébano	1
19163	ebanista	1
19164	è	1
19165	é	1
19166	durmiese	1
19167	durmiéndola	1
19168	durmiendo	1
19169	dure	1
19170	durase	1
19171	durará	1
19172	duraderos	1
19173	duración	1
19174	dupanloup	1
19175	dúo	1
19176	dumio	1
19177	dum	1
19178	dulzones	1
19179	dulzón	1
19180	dulcísimo	1
19181	duermes	1
19182	duerma	1
19183	dueña	1
19184	duelos	1
19185	dudoso	1
19186	dudosas	1
19187	dudosa	1
19188	dudemos	1
19189	dudase	1
19190	dudando	1
19191	dudaban	1
19192	dúctil	1
19193	duchas	1
19194	dualista	1
19195	dramaturgo	1
19196	dramáticas	1
19197	dovelas	1
19198	dotó	1
19199	dotar	1
19200	dotada	1
19201	dosis	1
19202	dosimétrico	1
19203	doseletes	1
19204	dorso	1
19205	dormitorio	1
19206	dormitar	1
19207	dormitan	1
19208	dormitaban	1
19209	dormitaba	1
19210	dormiremos	1
19211	dormidas	1
19212	dórico	1
19213	donosura	1
19214	donosa	1
19215	domini	1
19216	domingos	1
19217	dómine	1
19218	dominase	1
19219	dominarnos	1
19220	dominarla	1
19221	dominándolos	1
19222	dominándola	1
19223	dominados	1
19224	dominada	1
19225	domina	1
19226	domiciliada	1
19227	domésticas	1
19228	domesticado	1
19229	domaba	1
19230	dolorosos	1
19231	döllinger	1
19232	dolido	1
19233	dolería	1
19234	dogmáticos	1
19235	dogmático	1
19236	dogmáticas	1
19237	documento	1
19238	doctrino	1
19239	docente	1
19240	doceañista	1
19241	doblaron	1
19242	doblándose	1
19243	doblado	1
19244	dobla	1
19245	dixit	1
19246	divulgar	1
19247	divulgado	1
19248	divisó	1
19249	divisibles	1
19250	divisas	1
19251	divisar	1
19252	divirtiendo	1
19253	divinos	1
19254	divinam	1
19255	divido	1
19256	dividió	1
19257	dividido	1
19258	divertirme	1
19259	divertiría	1
19260	divertidísima	1
19261	disuelven	1
19262	disuelve	1
19263	disueltas	1
19264	disuelta	1
19265	disuadir	1
19266	disuadía	1
19267	distributiva	1
19268	distribución	1
19269	distrajo	1
19270	distrajeran	1
19271	distrajera	1
19272	distraídas	1
19273	distraían	1
19274	distraerte	1
19275	distraerle	1
19276	distraerla	1
19277	distraerían	1
19278	distraer	1
19279	distrae	1
19280	distintivo	1
19281	distintamente	1
19282	distinguirse	1
19283	distinguirlos	1
19284	distinguirlo	1
19285	distinguió	1
19286	distinguidísimo	1
19287	distingue	1
19288	distinciones	1
19289	disputó	1
19290	disputárselo	1
19291	disputaron	1
19292	disputándose	1
19293	dispusiera	1
19294	disposiciones	1
19295	disponiendo	1
19296	disponían	1
19297	disponerse	1
19298	displicencia	1
19299	dispersos	1
19300	dispersión	1
19301	dispersar	1
19302	dispersándose	1
19303	dispersado	1
19304	dispersa	1
19305	dispensase	1
19306	dispensado	1
19307	disparo	1
19308	disparitas	1
19309	disparatando	1
19310	disparatado	1
19311	disparataba	1
19312	disolvió	1
19313	disolviera	1
19314	disolvían	1
19315	disolvía	1
19316	disolverse	1
19317	disoluta	1
19318	disminuyó	1
19319	disminuyendo	1
19320	disminuían	1
19321	disminuía	1
19322	dislocado	1
19323	dislocada	1
19324	dislate	1
19325	disipar	1
19326	disimulase	1
19327	disimularon	1
19328	disimularlos	1
19329	disgustillo	1
19330	disgustarse	1
19331	disgustaron	1
19332	disgustarle	1
19333	disgustan	1
19334	disfrazasen	1
19335	disfrazase	1
19336	disfrazadas	1
19337	disfrazada	1
19338	disertaciones	1
19339	disertación	1
19340	disertaba	1
19341	discutirla	1
19342	discutiría	1
19343	discutiendo	1
19344	discursito	1
19345	discurrió	1
19346	discurrido	1
19347	disculparlo	1
19348	disculpando	1
19349	disculpables	1
19350	discretísimas	1
19351	discreteo	1
19352	discretas	1
19353	discípulos	1
19354	disciplinarias	1
19355	disciplentes	1
19356	discernir	1
19357	dirigiese	1
19358	dirigieron	1
19359	diríase	1
19360	diretes	1
19361	diremos	1
19362	directores	1
19363	directo	1
19364	direcciones	1
19365	dirás	1
19366	diputación	1
19367	diplomática	1
19368	dionisíacas	1
19369	dintel	1
19370	dinidad	1
19371	dinásticos	1
19372	dinastía	1
19373	dimisionario	1
19374	diminuto	1
19375	dimes	1
19376	dilucidar	1
19377	diligentes	1
19378	diligente	1
19379	dile	1
19380	dilatación	1
19381	dilacerar	1
19382	díjolo	1
19383	dijes	1
19384	dignificar	1
19385	dignidades	1
19386	dignatario	1
19387	dignase	1
19388	dignarse	1
19389	dignaba	1
19390	digestivas	1
19391	digería	1
19392	díganme	1
19393	digamos	1
19394	dígame	1
19395	difuntas	1
19396	difundirse	1
19397	difundían	1
19398	dificultaban	1
19399	dificultaba	1
19400	dificilísima	1
19401	diezmos	1
19402	dieta	1
19403	diestra	1
19404	diesen	1
19405	dies	1
19406	diéramos	1
19407	diecisiete	1
19408	die	1
19409	dictatorial	1
19410	dictaría	1
19411	dictando	1
19412	dictan	1
19413	dictamen	1
19414	dictadura	1
19415	dico	1
19416	dickens	1
19417	diciéndoselo	1
19418	diciéndome	1
19419	dichosos	1
19420	dichosas	1
19421	dichos	1
19422	dicharacheros	1
19423	dibujó	1
19424	dibujar	1
19425	dibujándose	1
19426	dibujando	1
19427	dibujado	1
19428	dibujaban	1
19429	dibujaba	1
19430	diapasón	1
19431	diana	1
19432	diaforético	1
19433	diáfano	1
19434	diácono	1
19435	diablesas	1
19436	diablejo	1
19437	devuelto	1
19438	devorándola	1
19439	devoran	1
19440	devora	1
19441	devolvió	1
19442	devolvieran	1
19443	devolviéndole	1
19444	devolviendo	1
19445	devolvían	1
19446	devocionarios	1
19447	devastación	1
19448	devaneo	1
19449	devanadera	1
19450	deux	1
19451	deus	1
19452	deudo	1
19453	detuvieron	1
19454	detuviera	1
19455	detractores	1
19456	detonación	1
19457	determinarse	1
19458	determinaron	1
19459	determinadas	1
19460	determinación	1
19461	determinaban	1
19462	determinaba	1
19463	deteriorando	1
19464	detenido	1
19465	detenidamente	1
19466	detenida	1
19467	detenerlo	1
19468	detenerle	1
19469	detener	1
19470	detenemos	1
19471	detalles	1
19472	desvivo	1
19473	desviadas	1
19474	desvergüenza	1
19475	desvergonzarse	1
19476	desvergonzados	1
19477	desvergonzado	1
19478	desventurada	1
19479	desvencijado	1
19480	desvencijadas	1
19481	desvelos	1
19482	desvelada	1
19483	desvaríos	1
19484	desvaneció	1
19485	desvanecimiento	1
19486	desvaneciéndose	1
19487	desvaneciendo	1
19488	desvanecidos	1
19489	desvanecidas	1
19490	desvanecíase	1
19491	desvanecen	1
19492	desván	1
19493	desvalijado	1
19494	desuso	1
19495	destruyó	1
19496	destruyeron	1
19497	destruía	1
19498	destrucción	1
19499	destrozarme	1
19500	destrozáis	1
19501	destrozado	1
19502	destreza	1
19503	destocándose	1
19504	destocado	1
19505	destinados	1
19506	destinaba	1
19507	desterrada	1
19508	desteñía	1
19509	destemplado	1
19510	destempladas	1
19511	destartalado	1
19512	destajo	1
19513	destacaban	1
19514	desquitaba	1
19515	despuntaba	1
19516	desprovistos	1
19517	despropósito	1
19518	desproporcionadas	1
19519	desprestigio	1
19520	despreocupada	1
19521	desprendido	1
19522	desprenderse	1
19523	despreció	1
19524	despreciase	1
19525	despreciarse	1
19526	despreciaros	1
19527	despreciara	1
19528	despreciándolos	1
19529	despreciándole	1
19530	despreciándolas	1
19531	despojo	1
19532	despojaban	1
19533	despojaba	1
19534	despoblado	1
19535	desplumarle	1
19536	desplumaban	1
19537	desplomarse	1
19538	desplomaba	1
19539	desplieguen	1
19540	despilfarro	1
19541	despidiéndose	1
19542	despidiendo	1
19543	despídete	1
19544	despídame	1
19545	despertarnos	1
19546	despertarle	1
19547	despertadora	1
19548	desperezarse	1
19549	desperdicios	1
19550	desperdiciado	1
19551	despeñada	1
19552	despeluznado	1
19553	despellejarse	1
19554	despellejaban	1
19555	despellejaba	1
19556	despejarse	1
19557	despejados	1
19558	despejadas	1
19559	despejada	1
19560	despeinarse	1
19561	despego	1
19562	despedirlos	1
19563	despedido	1
19564	despedazara	1
19565	despedazar	1
19566	despedazado	1
19567	despearse	1
19568	despeada	1
19569	despavorida	1
19570	desparramándose	1
19571	desparramaban	1
19572	despache	1
19573	despachar	1
19574	despachaba	1
19575	despabilaban	1
19576	desorientada	1
19577	desollar	1
19578	desolación	1
19579	desocupados	1
19580	desocupadas	1
19581	desnudó	1
19582	desnudeces	1
19583	desnudar	1
19584	desmoronarse	1
19585	desmoronar	1
19586	desmorona	1
19587	desmesurada	1
19588	desmentía	1
19589	desmedida	1
19590	desmayos	1
19591	desmayo	1
19592	desmayé	1
19593	desmayaron	1
19594	desmayados	1
19595	desmayadas	1
19596	desmayaba	1
19597	desmaya	1
19598	desmañado	1
19599	desmantelada	1
19600	desmanes	1
19601	desmadejado	1
19602	desmadejadas	1
19603	deslumbro	1
19604	deslumbradora	1
19605	deslumbrada	1
19606	deslumbraban	1
19607	deslizó	1
19608	deslizarse	1
19609	desliz	1
19610	deslices	1
19611	desleído	1
19612	desistieron	1
19613	desistido	1
19614	desiguales	1
19615	desigualdades	1
19616	desiertas	1
19617	desidia	1
19618	deshora	1
19619	deshonran	1
19620	deshonrada	1
19621	deshonesto	1
19622	deshojadas	1
19623	deshilachaban	1
19624	desheredados	1
19625	deshechas	1
19626	desharía	1
19627	deshaciéndola	1
19628	deshacían	1
19629	deshacer	1
19630	deshacen	1
19631	deshace	1
19632	desgarrarse	1
19633	desgarrando	1
19634	desgarrador	1
19635	desgarradas	1
19636	desgarrada	1
19637	desgarraban	1
19638	desgajarse	1
19639	desfiladero	1
19640	desfavorable	1
19641	desfallecimiento	1
19642	desfallecidos	1
19643	desfallecía	1
19644	desestero	1
19645	desespera	1
19646	deseoso	1
19647	desenvoltura	1
19648	desentonar	1
19649	desentona	1
19650	desenterrado	1
19651	desentendido	1
19652	desenlace	1
19653	desengañados	1
19654	desengañadas	1
19655	desenfreno	1
19656	desenfado	1
19657	desencanto	1
19658	desencadenado	1
19659	desempeñado	1
19660	desempeña	1
19661	desembolsos	1
19662	desembarco	1
19663	desecho	1
19664	desechado	1
19665	desechaban	1
19666	deseara	1
19667	dese	1
19668	desdoro	1
19669	desdiga	1
19670	desdentada	1
19671	descuidos	1
19672	descuidillo	1
19673	descuidarse	1
19674	descuidada	1
19675	descuidaba	1
19676	descubrirse	1
19677	descubrirlos	1
19678	descubrirlo	1
19679	descubrieron	1
19680	descubrieran	1
19681	descubriéndole	1
19682	descubridor	1
19683	descubría	1
19684	descubiertas	1
19685	descuartizaba	1
19686	descriptivas	1
19687	descripciones	1
19688	describe	1
19689	descreimiento	1
19690	descreídas	1
19691	descotada	1
19692	descoser	1
19693	descontenta	1
19694	desconsoladoras	1
19695	desconsolador	1
19696	desconocidos	1
19697	desconocíamos	1
19698	desconocen	1
19699	desconcierto	1
19700	descomponiéndose	1
19701	descomponerla	1
19702	descompone	1
19703	descompasado	1
19704	descollando	1
19705	descollaban	1
19706	descolgarse	1
19707	descolgarla	1
19708	descolgaba	1
19709	descoco	1
19710	desciñó	1
19711	descifró	1
19712	descifrarlas	1
19713	desceñida	1
19714	descenso	1
19715	descendimiento	1
19716	descendiendo	1
19717	descendía	1
19718	descastada	1
19719	descarnadas	1
19720	descarnada	1
19721	descarnaba	1
19722	descargaría	1
19723	descargado	1
19724	descargada	1
19725	descarada	1
19726	descanse	1
19727	descansan	1
19728	descansaban	1
19729	descaminos	1
19730	descaminada	1
19731	descalzo	1
19732	descalzaba	1
19733	descabellado	1
19734	desbordar	1
19735	desbordado	1
19736	desbanque	1
19737	desbancado	1
19738	desazones	1
19739	desayuno	1
19740	desatinos	1
19741	desatino	1
19742	desatinada	1
19743	desataron	1
19744	desataban	1
19745	desata	1
19746	desasosiego	1
19747	desasirse	1
19748	desarróllase	1
19749	desarrolla	1
19750	desarreglos	1
19751	desaprobación	1
19752	desapasionado	1
19753	desapartarse	1
19754	desaparición	1
19755	desaparecieron	1
19756	desapareciera	1
19757	desaparecíamos	1
19758	desapacible	1
19759	desanimar	1
19760	desanimaba	1
19761	desanduvo	1
19762	desandando	1
19763	desamparado	1
19764	desaliño	1
19765	desalientos	1
19766	desalentada	1
19767	desalado	1
19768	desairarlos	1
19769	desairarle	1
19770	desairarla	1
19771	desairados	1
19772	desairadas	1
19773	desairada	1
19774	desahuciarlo	1
19775	desahuciado	1
19776	desahogue	1
19777	desahogan	1
19778	desahogaban	1
19779	desagravio	1
19780	desagradecida	1
19781	desafió	1
19782	desafíe	1
19783	desafiarle	1
19784	desafiaría	1
19785	desacreditó	1
19786	desacreditarse	1
19787	desacreditar	1
19788	desacreditándote	1
19789	desacreditan	1
19790	desacredita	1
19791	desaciertos	1
19792	desabrochándose	1
19793	desabrimiento	1
19794	des	1
19795	derrumbara	1
19796	derrumbar	1
19797	derrotada	1
19798	derrota	1
19799	derrochaban	1
19800	derritiéndose	1
19801	derríbela	1
19802	derribarme	1
19803	derribarle	1
19804	derribado	1
19805	derribaba	1
19806	derretirá	1
19807	derretían	1
19808	derrengado	1
19809	derramó	1
19810	derrame	1
19811	derramarse	1
19812	derramamiento	1
19813	derivados	1
19814	derivación	1
19815	depresivo	1
19816	deprecaba	1
19817	depositario	1
19818	depositando	1
19819	depositado	1
19820	depositadas	1
19821	depositaban	1
19822	depositaba	1
19823	dependiese	1
19824	dependiente	1
19825	depender	1
19826	depende	1
19827	departamentos	1
19828	departamento	1
19829	dentera	1
19830	dentadura	1
19831	densidad	1
19832	densa	1
19833	dengue	1
19834	den	1
19835	demuestran	1
19836	demostré	1
19837	demostraban	1
19838	demontres	1
19839	demonche	1
19840	demoler	1
19841	demodoco	1
19842	demócratas	1
19843	demasía	1
19844	demanda	1
19845	demagogo	1
19846	demagoga	1
19847	deliró	1
19848	delirado	1
19849	deliraba	1
19850	delincuentes	1
19851	delincuente	1
19852	deliciosos	1
19853	delicadísimo	1
19854	delicadísima	1
19855	delicadezas	1
19856	deliberó	1
19857	deliberemos	1
19858	deliberase	1
19859	deliberaron	1
19860	deliberar	1
19861	deliberado	1
19862	delgadilla	1
19863	deletéreos	1
19864	deleites	1
19865	deleitasen	1
19866	deleitábale	1
19867	delegado	1
19868	delegación	1
19869	delatores	1
19870	delator	1
19871	delató	1
19872	delatase	1
19873	delatarse	1
19874	delataron	1
19875	delatar	1
19876	delataban	1
19877	delataba	1
19878	delanteros	1
19879	delantera	1
19880	dejose	1
19881	dejémoslo	1
19882	déjele	1
19883	dejaste	1
19884	dejarlas	1
19885	dejarían	1
19886	dejaré	1
19887	dejaras	1
19888	déjala	1
19889	déjà	1
19890	deísmo	1
19891	degradarse	1
19892	degradarla	1
19893	degradan	1
19894	degradado	1
19895	degollarla	1
19896	degollar	1
19897	degollado	1
19898	degli	1
19899	degeneraba	1
19900	defraudaba	1
19901	deforme	1
19902	definitivo	1
19903	definitivamente	1
19904	definirse	1
19905	definía	1
19906	defienden	1
19907	defiende	1
19908	deficiencias	1
19909	defensor	1
19910	defensiva	1
19911	defensas	1
19912	defendió	1
19913	defendiera	1
19914	defendiendo	1
19915	defenderle	1
19916	defenderla	1
19917	defectillo	1
19918	deducía	1
19919	dedique	1
19920	dedicar	1
19921	dedicándonos	1
19922	decurión	1
19923	decretos	1
19924	decretó	1
19925	decretado	1
19926	decoración	1
19927	declive	1
19928	declaro	1
19929	declarados	1
19930	declarada	1
19931	declaraciones	1
19932	declaraban	1
19933	declamador	1
19934	declamado	1
19935	declamaciones	1
19936	declamaba	1
19937	decisiva	1
19938	decisión	1
19939	decírtelo	1
19940	decírsele	1
19941	decirlos	1
19942	decimales	1
19943	décima	1
19944	decidores	1
19945	decidir	1
19946	decidiera	1
19947	decidiendo	1
19948	decididamente	1
19949	decidía	1
19950	decidí	1
19951	decida	1
19952	decíale	1
19953	decentemente	1
19954	decantado	1
19955	decálogo	1
19956	decaimientos	1
19957	decaído	1
19958	decadencias	1
19959	debiste	1
19960	debilucho	1
19961	débilmente	1
19962	debilitado	1
19963	debiéramos	1
19964	debiéndolo	1
19965	debida	1
19966	debíase	1
19967	debías	1
19968	debérsela	1
19969	deberían	1
19970	debería	1
19971	davídicas	1
19972	dativo	1
19973	das	1
19974	darwinista	1
19975	darwin	1
19976	dárselos	1
19977	dárselo	1
19978	dárselas	1
19979	dársela	1
19980	darro	1
19981	darlos	1
19982	darla	1
19983	dardos	1
19984	dardo	1
19985	daños	1
19986	dañaría	1
19987	dañaba	1
19988	daña	1
19989	dante	1
19990	dándola	1
19991	damos	1
19992	damiselas	1
19993	dami	1
19994	dalila	1
19995	daga	1
19996	dadme	1
19997	custodire	1
19998	cúspide	1
19999	curtidos	1
20000	curtido	1
20001	cursilona	1
20002	currente	1
20003	curita	1
20004	curiosos	1
20005	curiosón	1
20006	curiosa	1
20007	curiales	1
20008	curial	1
20009	curarse	1
20010	curaría	1
20011	curando	1
20012	curada	1
20013	cúpula	1
20014	cuota	1
20015	cuñado	1
20016	cuñada	1
20017	cuneta	1
20018	cunero	1
20019	cundiese	1
20020	cúmulus	1
20021	cumulus	1
20022	cumplirse	1
20023	cumplirlas	1
20024	cumpliría	1
20025	cumplirá	1
20026	cumplimientos	1
20027	cumplimiento	1
20028	cumplieron	1
20029	cumplieran	1
20030	cumpliendo	1
20031	cumplidamente	1
20032	cumplen	1
20033	cumpleaños	1
20034	cumple	1
20035	cumplas	1
20036	cumín	1
20037	cum	1
20038	cultus	1
20039	cultivara	1
20040	cultivando	1
20041	cultivan	1
20042	cultas	1
20043	culparle	1
20044	culpar	1
20045	culpables	1
20046	culotte	1
20047	culinarias	1
20048	culata	1
20049	cuique	1
20050	cuide	1
20051	cuidase	1
20052	cuidara	1
20053	cuidada	1
20054	cueto	1
20055	cuestores	1
20056	cuestan	1
20057	cuernos	1
20058	cuerdamente	1
20059	cuentan	1
20060	cuellos	1
20061	cuelgue	1
20062	cuelgan	1
20063	cuelga	1
20064	cuchufletas	1
20065	cuchillos	1
20066	cuchicheando	1
20067	cucharilla	1
20068	cucharada	1
20069	cubrirse	1
20070	cubriera	1
20071	cubriéndolos	1
20072	cubriéndola	1
20073	cubríale	1
20074	cubren	1
20075	cubiletes	1
20076	cúbicos	1
20077	cuartucho	1
20078	cuartilla	1
20079	cuartetos	1
20080	cuartas	1
20081	cuajados	1
20082	cuadriculado	1
20083	cuadras	1
20084	cuadradillos	1
20085	cuadradas	1
20086	cuadraban	1
20087	cruzarse	1
20088	cruzar	1
20089	cruzan	1
20090	cruzada	1
20091	cruza	1
20092	crusología	1
20093	crujieron	1
20094	cruelísimo	1
20095	crueles	1
20096	crudos	1
20097	crudezas	1
20098	crudas	1
20099	crucifixión	1
20100	crucificó	1
20101	cronométrica	1
20102	cromo	1
20103	cromáticas	1
20104	croiset	1
20105	criticaron	1
20106	criticar	1
20107	criterios	1
20108	cristos	1
20109	cristóbal	1
20110	cristinos	1
20111	cristalino	1
20112	cristalinas	1
20113	cristalina	1
20114	cristalerías	1
20115	crispan	1
20116	crispados	1
20117	crispadas	1
20118	crisol	1
20119	crisálida	1
20120	crin	1
20121	criminalmente	1
20122	criaos	1
20123	criao	1
20124	criaban	1
20125	creyesen	1
20126	creyéndolo	1
20127	creó	1
20128	crema	1
20129	creías	1
20130	creíale	1
20131	creíala	1
20132	creernos	1
20133	creerlos	1
20134	creerlo	1
20135	creerle	1
20136	creerla	1
20137	creerían	1
20138	creerás	1
20139	creerán	1
20140	crédulas	1
20141	crédula	1
20142	creciese	1
20143	creciendo	1
20144	crecían	1
20145	creces	1
20146	crecería	1
20147	crece	1
20148	crearía	1
20149	créanme	1
20150	créanlo	1
20151	crac	1
20152	coyuntura	1
20153	covent	1
20154	covadonga	1
20155	covachuelismo	1
20156	cotorrón	1
20157	cotorra	1
20158	coto	1
20159	cotización	1
20160	cotidianas	1
20161	cotarro	1
20162	cota	1
20163	costurero	1
20164	costoso	1
20165	costera	1
20166	costase	1
20167	costas	1
20168	costará	1
20169	costara	1
20170	cosquilleo	1
20171	cosméticos	1
20172	cositas	1
20173	cosido	1
20174	cosía	1
20175	cosechero	1
20176	cosechas	1
20177	cosecha	1
20178	coscorrón	1
20179	corzos	1
20180	corvetas	1
20181	cortito	1
20182	cortinillas	1
20183	cortarle	1
20184	cortados	1
20185	corsé	1
20186	corruptela	1
20187	corrupciones	1
20188	corrosivo	1
20189	corrompidas	1
20190	corrompía	1
20191	corromperla	1
20192	corromper	1
20193	corroboró	1
20194	corroboraba	1
20195	corrijan	1
20196	corrigió	1
20197	corrigiendo	1
20198	corriese	1
20199	corriéndose	1
20200	corridos	1
20201	correveidile	1
20202	correspondió	1
20203	correspondiera	1
20204	correspondían	1
20205	corresponderle	1
20206	correrías	1
20207	corren	1
20208	correligionarios	1
20209	corregir	1
20210	correctos	1
20211	correctamente	1
20212	correccionalista	1
20213	correa	1
20214	corran	1
20215	corralón	1
20216	corrales	1
20217	corra	1
20218	corpulentas	1
20219	corporación	1
20220	corpiño	1
20221	corpachón	1
20222	coronilla	1
20223	coronas	1
20224	coronarse	1
20225	coronarlo	1
20226	coronar	1
20227	coronando	1
20228	coronado	1
20229	coronadas	1
20230	coronaba	1
20231	corolario	1
20232	cornisas	1
20233	cornisa	1
20234	corneta	1
20235	cornamenta	1
20236	corintio	1
20237	córdoba	1
20238	cordilleras	1
20239	cordillera	1
20240	cordialmente	1
20241	corderos	1
20242	corcovados	1
20243	corchetes	1
20244	corbatín	1
20245	corbatas	1
20246	corazoncito	1
20247	coram	1
20248	corales	1
20249	coraceros	1
20250	coquetismo	1
20251	coqueteaban	1
20252	copones	1
20253	coplas	1
20254	copla	1
20255	copiosamente	1
20256	copiaremos	1
20257	copiar	1
20258	copiando	1
20259	copiados	1
20260	copiada	1
20261	coordinar	1
20262	coooosa	1
20263	conyugales	1
20264	convulso	1
20265	convocándole	1
20266	convocando	1
20267	convocados	1
20268	convivencia	1
20269	conviniesen	1
20270	conviniese	1
20271	conviniera	1
20272	convierten	1
20273	convídesele	1
20274	convidase	1
20275	convidarles	1
20276	convidándoles	1
20277	conversiones	1
20278	convergencia	1
20279	convenza	1
20280	conventual	1
20281	convenirle	1
20282	convenir	1
20283	convenientes	1
20284	conveniencias	1
20285	convenida	1
20286	convenciendo	1
20287	convencernos	1
20288	convencerme	1
20289	convencerle	1
20290	convenceré	1
20291	contumaz	1
20292	controversias	1
20293	contrincantes	1
20294	contrición	1
20295	contribuyo	1
20296	contribuyente	1
20297	contribuye	1
20298	contribuirá	1
20299	contribuido	1
20300	contribuían	1
20301	contribución	1
20302	contratiempos	1
20303	contratantes	1
20304	contratado	1
20305	contrastaban	1
20306	contrastaba	1
20307	contrasentidos	1
20308	contrarios	1
20309	contrariedad	1
20310	contrariar	1
20311	contrajudías	1
20312	contrahechas	1
20313	contradiciéndose	1
20314	contradiciendo	1
20315	contradicciones	1
20316	contradecirse	1
20317	contradecían	1
20318	contradanza	1
20319	contrabandista	1
20320	contoneo	1
20321	continuos	1
20322	continúo	1
20323	continuasen	1
20324	continuase	1
20325	continuado	1
20326	continua	1
20327	continentes	1
20328	contienda	1
20329	conteste	1
20330	contestarle	1
20331	contestaras	1
20332	contesta	1
20333	contentón	1
20334	contenti	1
20335	contentas	1
20336	contentaron	1
20337	contentaría	1
20338	contentar	1
20339	contentándonos	1
20340	contentado	1
20341	contentadiza	1
20342	contentaban	1
20343	conteniéndose	1
20344	conteniendo	1
20345	contenerte	1
20346	contenerlos	1
20347	contenerle	1
20348	contemporáneas	1
20349	contemplo	1
20350	contemplativo	1
20351	contemplarse	1
20352	contemplarían	1
20353	contemplado	1
20354	contemplaciones	1
20355	contemplaban	1
20356	conté	1
20357	contárselo	1
20358	contarles	1
20359	contarle	1
20360	contarla	1
20361	contarían	1
20362	contaré	1
20363	contarás	1
20364	contándoselo	1
20365	contándose	1
20366	contándome	1
20367	contándoles	1
20368	contagió	1
20369	contagiar	1
20370	contagiado	1
20371	contadas	1
20372	contada	1
20373	contactos	1
20374	consumidores	1
20375	consumían	1
20376	consumes	1
20377	consumaría	1
20378	consultó	1
20379	consultaron	1
20380	consultaría	1
20381	consulta	1
20382	consules	1
20383	consuetudinaria	1
20384	consuelan	1
20385	construyó	1
20386	construyendo	1
20387	construyan	1
20388	construir	1
20389	construido	1
20390	construidas	1
20391	construcción	1
20392	constituyen	1
20393	constituida	1
20394	constituían	1
20395	constipado	1
20396	constipada	1
20397	constipaba	1
20398	consternado	1
20399	constelaciones	1
20400	constelación	1
20401	constantinopla	1
20402	constaban	1
20403	conspirando	1
20404	conspiradores	1
20405	conspiraciones	1
20406	conspiración	1
20407	consorte	1
20408	consolidó	1
20409	consolémonos	1
20410	consolase	1
20411	consolarse	1
20412	consolarme	1
20413	consolaría	1
20414	consolará	1
20415	consolando	1
20416	consolador	1
20417	consistorios	1
20418	consiguiera	1
20419	consiguientes	1
20420	consiguiendo	1
20421	consiguen	1
20422	consigna	1
20423	considerarle	1
20424	considerado	1
20425	considerada	1
20426	considerábase	1
20427	conservo	1
20428	conserve	1
20429	conservas	1
20430	conservando	1
20431	conservaduría	1
20432	conservadoras	1
20433	conservadora	1
20434	conservada	1
20435	conserjería	1
20436	consentiría	1
20437	consentidas	1
20438	consejeros	1
20439	consejas	1
20440	consagrarse	1
20441	consagrarlos	1
20442	consagrarle	1
20443	consagrándose	1
20444	consabido	1
20445	consabida	1
20446	conquistaron	1
20447	conquistarla	1
20448	conquistando	1
20449	conquistada	1
20450	conquistaba	1
20451	conozcamos	1
20452	conocieron	1
20453	conocieran	1
20454	conociera	1
20455	conocidas	1
20456	conocí	1
20457	conocería	1
20458	conocerá	1
20459	cono	1
20460	conmutó	1
20461	conmoverse	1
20462	conmiseración	1
20463	conmemoraban	1
20464	conmemora	1
20465	conjuro	1
20466	conjurar	1
20467	conjuraban	1
20468	conjuraba	1
20469	conjetura	1
20470	cónicos	1
20471	congruas	1
20472	congregarla	1
20473	congregados	1
20474	congraciándose	1
20475	congojosa	1
20476	congestión	1
20477	congeniaban	1
20478	confusamente	1
20479	confundiéndose	1
20480	confundiendo	1
20481	confundidos	1
20482	confundidas	1
20483	confundamos	1
20484	confunda	1
20485	confortante	1
20486	conformarse	1
20487	conformaba	1
20488	confitero	1
20489	confiterías	1
20490	confirmar	1
20491	confirmación	1
20492	confirmaba	1
20493	confirma	1
20494	confiéseme	1
20495	confiaría	1
20496	confiadote	1
20497	confiado	1
20498	confiada	1
20499	confesaron	1
20500	confesarme	1
20501	confesarle	1
20502	confesarla	1
20503	confesaré	1
20504	confesados	1
20505	conferenciaban	1
20506	confectu	1
20507	confeccionar	1
20508	condujo	1
20509	condiscípulo	1
20510	condimento	1
20511	condescendiente	1
20512	condensadas	1
20513	condenó	1
20514	condene	1
20515	condenase	1
20516	condenarse	1
20517	condenarlo	1
20518	condenaría	1
20519	condenando	1
20520	condecoraciones	1
20521	concurridas	1
20522	concurrida	1
20523	concupiscente	1
20524	concupiscencias	1
20525	concreto	1
20526	concreten	1
20527	concretar	1
20528	concretamente	1
20529	concordato	1
20530	concluyen	1
20531	conciso	1
20532	concilios	1
20533	concilió	1
20534	concilia	1
20535	concibió	1
20536	conchas	1
20537	concha	1
20538	concesiones	1
20539	concertar	1
20540	concertando	1
20541	concertado	1
20542	conceptuosos	1
20543	concepta	1
20544	concedo	1
20545	concederle	1
20546	cóncava	1
20547	concausas	1
20548	comúnmente	1
20549	comunidades	1
20550	comunicárselo	1
20551	comunicará	1
20552	comunican	1
20553	comunicados	1
20554	comunicado	1
20555	comunicación	1
20556	comulgó	1
20557	comulgando	1
20558	comulgaba	1
20559	comulga	1
20560	compuso	1
20561	compunción	1
20562	compuertas	1
20563	comprometo	1
20564	comprometida	1
20565	comprometían	1
20566	comprometernos	1
20567	comprobar	1
20568	comprobados	1
20569	comprimió	1
20570	comprimidas	1
20571	comprime	1
20572	comprendida	1
20573	comprenderle	1
20574	comprenderlas	1
20575	comprenderá	1
20576	comprendan	1
20577	compre	1
20578	comprarlos	1
20579	comprarla	1
20580	compraran	1
20581	compradores	1
20582	compostura	1
20583	composiciones	1
20584	composicioncilla	1
20585	componía	1
20586	componenda	1
20587	componen	1
20588	compondría	1
20589	complicidad	1
20590	completos	1
20591	completan	1
20592	complemento	1
20593	complejas	1
20594	complazco	1
20595	complaciente	1
20596	complacíase	1
20597	complaces	1
20598	complaceros	1
20599	complacencias	1
20600	complace	1
20601	competente	1
20602	compensara	1
20603	compenetran	1
20604	compatibles	1
20605	compasivo	1
20606	compartía	1
20607	comparten	1
20608	comparó	1
20609	comparo	1
20610	compares	1
20611	comparen	1
20612	compare	1
20613	comparanza	1
20614	comparados	1
20615	comparaban	1
20616	compadres	1
20617	compadre	1
20618	compadeció	1
20619	compadeciéndose	1
20620	compadecidos	1
20621	compadecerle	1
20622	compadece	1
20623	compactas	1
20624	cómoda	1
20625	commis	1
20626	comisuras	1
20627	comistrajos	1
20628	comiste	1
20629	comisionista	1
20630	comisiones	1
20631	comisionados	1
20632	comisario	1
20633	comino	1
20634	comineros	1
20635	comilonas	1
20636	comiesen	1
20637	comienzos	1
20638	comienzan	1
20639	comías	1
20640	comezones	1
20641	cometiese	1
20642	cometiera	1
20643	cometiendo	1
20644	cometidos	1
20645	cometí	1
20646	cómetela	1
20647	comercios	1
20648	comerciando	1
20649	comercial	1
20650	comerciaban	1
20651	comercia	1
20652	comerá	1
20653	comentarlas	1
20654	comentario	1
20655	comentando	1
20656	comentado	1
20657	comentada	1
20658	comensalía	1
20659	comemos	1
20660	comehostias	1
20661	comedimiento	1
20662	comedidos	1
20663	comedidas	1
20664	comediantes	1
20665	combustión	1
20666	combinar	1
20667	combinadas	1
20668	combinación	1
20669	combinaban	1
20670	combinaba	1
20671	combatirla	1
20672	combatiré	1
20673	combatió	1
20674	combatientes	1
20675	combatiendo	1
20676	combatido	1
20677	combatida	1
20678	comarcanos	1
20679	coman	1
20680	columpiaron	1
20681	columpiar	1
20682	columbraba	1
20683	colosal	1
20684	colorines	1
20685	colorete	1
20686	coloradilla	1
20687	coloradas	1
20688	colono	1
20689	colonial	1
20690	colones	1
20691	colón	1
20692	colocarse	1
20693	colocaran	1
20694	colocando	1
20695	colmó	1
20696	colmillo	1
20697	colmaba	1
20698	collis	1
20699	collares	1
20700	collados	1
20701	colgaron	1
20702	colgarlo	1
20703	colgados	1
20704	colgadizos	1
20705	colgadas	1
20706	colgaban	1
20707	colerilla	1
20708	colérica	1
20709	colegios	1
20710	colegiala	1
20711	colectividades	1
20712	colectivamente	1
20713	colasa	1
20714	colas	1
20715	colaboraba	1
20716	cójala	1
20717	coincidir	1
20718	coincidiese	1
20719	coincidencias	1
20720	coincidencia	1
20721	coimbra	1
20722	cohonestarse	1
20723	cohete	1
20724	cogiese	1
20725	cogiera	1
20726	cogerlo	1
20727	cogerás	1
20728	cofre	1
20729	coeteris	1
20730	coetáneos	1
20731	coetáneo	1
20732	coercitivo	1
20733	codornices	1
20734	codillos	1
20735	codillo	1
20736	codiciosa	1
20737	codiciar	1
20738	codeaban	1
20739	codeaba	1
20740	codazo	1
20741	cocotte	1
20742	cocinaba	1
20743	cochera	1
20744	coces	1
20745	cobro	1
20746	cobras	1
20747	cobrárselo	1
20748	cobrarlos	1
20749	cobrarla	1
20750	cobrarían	1
20751	cobrándole	1
20752	cobran	1
20753	cobos	1
20754	cobijados	1
20755	cobijaba	1
20756	cobija	1
20757	cobertizo	1
20758	coadjutor	1
20759	cloacas	1
20760	climatológica	1
20761	clientes	1
20762	cliente	1
20763	clerófobo	1
20764	clerófoba	1
20765	clavijas	1
20766	claveteada	1
20767	clave	1
20768	clavaron	1
20769	clavarlos	1
20770	clavarás	1
20771	clavándose	1
20772	clavándole	1
20773	clavan	1
20774	cláusulas	1
20775	claudio	1
20776	clasificarla	1
20777	clasificar	1
20778	clarito	1
20779	claridades	1
20780	claraboya	1
20781	clandestinamente	1
20782	clamor	1
20783	clamó	1
20784	clamar	1
20785	clamaba	1
20786	clama	1
20787	civis	1
20788	civilizado	1
20789	civilizada	1
20790	ciutti	1
20791	ciudadano	1
20792	ciudadanas	1
20793	citarse	1
20794	citar	1
20795	citan	1
20796	cisterna	1
20797	ciruelo	1
20798	cirrus	1
20799	cirio	1
20800	circunstanciales	1
20801	circunstancia	1
20802	circunspección	1
20803	circulo	1
20804	circulillos	1
20805	circulando	1
20806	cipreses	1
20807	ciñó	1
20808	ciñendo	1
20809	ciñen	1
20810	cinturón	1
20811	cintajos	1
20812	cínicamente	1
20813	cínica	1
20814	cinegético	1
20815	cinegéticas	1
20816	cincel	1
20817	cimodocea	1
20818	cimientos	1
20819	cimas	1
20820	cilíndricos	1
20821	cigüeña	1
20822	cigarreras	1
20823	cifra	1
20824	cierzo	1
20825	ciervo	1
20826	cierro	1
20827	ciernes	1
20828	científico	1
20829	científica	1
20830	ciel	1
20831	ciegas	1
20832	cicuta	1
20833	ciclopios	1
20834	ciclópea	1
20835	cíclope	1
20836	ciclones	1
20837	ciclo	1
20838	cíclades	1
20839	cicatrices	1
20840	chusquin	1
20841	churriguerescos	1
20842	chupó	1
20843	chupar	1
20844	chupándose	1
20845	chupa	1
20846	chulos	1
20847	chulo	1
20848	chubascos	1
20849	chorritos	1
20850	chorretadas	1
20851	chorrea	1
20852	choques	1
20853	chomel	1
20854	chochas	1
20855	chocasen	1
20856	chocarían	1
20857	chocando	1
20858	chocaba	1
20859	chistera	1
20860	chistar	1
20861	chisporroteos	1
20862	chisporroteo	1
20863	chisporroteaba	1
20864	chirrido	1
20865	chipre	1
20866	chinitas	1
20867	chillonas	1
20868	chillón	1
20869	chiflao	1
20870	chicuela	1
20871	chiaror	1
20872	chevrière	1
20873	che	1
20874	chata	1
20875	chasquidos	1
20876	charlatán	1
20877	charlar	1
20878	charlado	1
20879	charanga	1
20880	chaquetón	1
20881	chaquet	1
20882	chapas	1
20883	chanza	1
20884	chantal	1
20885	chance	1
20886	chambra	1
20887	chambones	1
20888	chambergo	1
20889	chalets	1
20890	cetro	1
20891	cesantías	1
20892	cesando	1
20893	cesado	1
20894	cesa	1
20895	cerviz	1
20896	cervantesca	1
20897	cervantes	1
20898	certámenes	1
20899	cerro	1
20900	cerriles	1
20901	cerril	1
20902	cerrarlos	1
20903	cerraduras	1
20904	cerradas	1
20905	cernida	1
20906	cernía	1
20907	cerilla	1
20908	ceremoniosos	1
20909	ceremonioso	1
20910	ceremonial	1
20911	cereales	1
20912	cerdas	1
20913	cercioraba	1
20914	cercenando	1
20915	cercana	1
20916	cepo	1
20917	cepilla	1
20918	ceñudo	1
20919	ceñuda	1
20920	ceños	1
20921	ceñidas	1
20922	centuria	1
20923	centros	1
20924	céntimos	1
20925	céntimo	1
20926	centímetro	1
20927	centésima	1
20928	centelleaba	1
20929	censuró	1
20930	censuren	1
20931	censores	1
20932	censor	1
20933	ceno	1
20934	cenit	1
20935	ceniciento	1
20936	cenicientas	1
20937	cenarían	1
20938	cenarás	1
20939	cenaban	1
20940	cementerios	1
20941	celtíberos	1
20942	celtas	1
20943	celosos	1
20944	celoso	1
20945	celonio	1
20946	celestinas	1
20947	celeste	1
20948	celesta	1
20949	celeres	1
20950	celenio	1
20951	celebro	1
20952	celebraron	1
20953	celebrarlos	1
20954	celebrarla	1
20955	celebraría	1
20956	celebrara	1
20957	celebrando	1
20958	celebrado	1
20959	celajes	1
20960	celaba	1
20961	cejijuntos	1
20962	cejase	1
20963	cejaría	1
20964	ceguedad	1
20965	cegó	1
20966	cegaba	1
20967	cefiso	1
20968	céfiro	1
20969	cefalalgia	1
20970	cedros	1
20971	cedía	1
20972	cedí	1
20973	cederá	1
20974	cebollas	1
20975	cebolla	1
20976	ce	1
20977	cazurro	1
20978	cazuela	1
20979	cazas	1
20980	cazaron	1
20981	cazara	1
20982	cazando	1
20983	cazan	1
20984	cazado	1
20985	cazaderos	1
20986	cavilar	1
20987	caverna	1
20988	caveant	1
20989	cavar	1
20990	cavando	1
20991	cavadores	1
20992	cavador	1
20993	cavada	1
20994	cauto	1
20995	cautivó	1
20996	cautiverio	1
20997	causaron	1
20998	causar	1
20999	causan	1
21000	causada	1
21001	caulis	1
21002	cathedra	1
21003	categórico	1
21004	catedráticos	1
21005	catedrales	1
21006	cátate	1
21007	catarros	1
21008	catar	1
21009	catalunga	1
21010	catálogo	1
21011	catalanes	1
21012	catafalcos	1
21013	catafalco	1
21014	catacumbas	1
21015	cataclismos	1
21016	cataclismo	1
21017	casulla	1
21018	casuismo	1
21019	castos	1
21020	castigue	1
21021	castigó	1
21022	castigarlos	1
21023	castigaran	1
21024	castigaban	1
21025	castigaba	1
21026	castiga	1
21027	castellana	1
21028	castelar	1
21029	castañeteo	1
21030	castañedos	1
21031	castañares	1
21032	casquivano	1
21033	casinos	1
21034	casilla	1
21035	caseta	1
21036	caseríos	1
21037	caserío	1
21038	caserías	1
21039	casería	1
21040	caseosa	1
21041	case	1
21042	casco	1
21043	cascarón	1
21044	cáscara	1
21045	casase	1
21046	casarte	1
21047	casarme	1
21048	casaría	1
21049	casará	1
21050	casara	1
21051	casándose	1
21052	casamatas	1
21053	casados	1
21054	casadera	1
21055	cartulina	1
21056	cartujo	1
21057	cartitas	1
21058	cartera	1
21059	carteles	1
21060	cartelas	1
21061	cartapacio	1
21062	carruajes	1
21063	carrick	1
21064	carreteros	1
21065	carretero	1
21066	carraspiques	1
21067	carracas	1
21068	carpinteros	1
21069	carpanta	1
21070	carolo	1
21071	carolina	1
21072	carnoso	1
21073	carnosa	1
21074	carnavalesco	1
21075	carmín	1
21076	caritativos	1
21077	cariños	1
21078	caricia	1
21079	caricatura	1
21080	cargarse	1
21081	cargantes	1
21082	cargante	1
21083	cargan	1
21084	caretas	1
21085	carestía	1
21086	cardona	1
21087	cardiopatía	1
21088	cardíacos	1
21089	cárdenos	1
21090	cardenales	1
21091	cárdena	1
21092	cardan	1
21093	carcunda	1
21094	carcomida	1
21095	carcas	1
21096	carcamal	1
21097	carbonizaban	1
21098	carbayeda	1
21099	carátulas	1
21100	carambolas	1
21101	caramba	1
21102	característicos	1
21103	caracoles	1
21104	caracolear	1
21105	capullo	1
21106	capua	1
21107	capotón	1
21108	capota	1
21109	capitulares	1
21110	capitular	1
21111	capiteles	1
21112	capitanes	1
21113	capitaneaban	1
21114	capitalista	1
21115	capisco	1
21116	capirotes	1
21117	capelo	1
21118	capellanes	1
21119	capciosa	1
21120	capalleja	1
21121	capacidad	1
21122	caótico	1
21123	caos	1
21124	cañedo	1
21125	cañamones	1
21126	cantero	1
21127	cantera	1
21128	canten	1
21129	cantatrices	1
21130	cantarse	1
21131	cántaros	1
21132	cantaran	1
21133	cantante	1
21134	cantándole	1
21135	cantados	1
21136	cantábrico	1
21137	cansase	1
21138	cansaron	1
21139	cansados	1
21140	cansadas	1
21141	cansaba	1
21142	cansa	1
21143	canonistas	1
21144	canónigas	1
21145	canónicos	1
21146	canon	1
21147	canela	1
21148	candorosa	1
21149	candil	1
21150	cándido	1
21151	candidaturas	1
21152	cándida	1
21153	candentes	1
21154	candelillas	1
21155	candelabros	1
21156	candelabro	1
21157	candado	1
21158	cancerbero	1
21159	canceles	1
21160	canario	1
21161	canariera	1
21162	canales	1
21163	canal	1
21164	cana	1
21165	camposanto	1
21166	campestre	1
21167	campesinos	1
21168	campesinas	1
21169	campbell	1
21170	campanillazos	1
21171	campanillas	1
21172	campamento	1
21173	camisolín	1
21174	camisola	1
21175	camisas	1
21176	caminando	1
21177	caminaban	1
21178	camilla	1
21179	camelias	1
21180	cambie	1
21181	cambiaban	1
21182	cambia	1
21183	camas	1
21184	camarote	1
21185	camarín	1
21186	camaradas	1
21187	calzonazos	1
21188	calzo	1
21189	calzadas	1
21190	calzaban	1
21191	calza	1
21192	calvicies	1
21193	calva	1
21194	calumniosas	1
21195	calumniosa	1
21196	calumnian	1
21197	calumniadores	1
21198	calumniaban	1
21199	calorosa	1
21200	calores	1
21201	calomarde	1
21202	calmarse	1
21203	calmándose	1
21204	calmado	1
21205	calmaba	1
21206	callos	1
21207	callis	1
21208	callejuela	1
21209	callejones	1
21210	callejero	1
21211	callejera	1
21212	callase	1
21213	callaría	1
21214	callan	1
21215	calladas	1
21216	caliginosas	1
21217	calificada	1
21218	cálidas	1
21219	calibre	1
21220	calepino	1
21221	calentura	1
21222	calentar	1
21223	calentándose	1
21224	calentaban	1
21225	calendario	1
21226	calefacción	1
21227	caldeaba	1
21228	cálculo	1
21229	calculo	1
21230	calcular	1
21231	calculador	1
21232	calcetines	1
21233	calceta	1
21234	calaverilla	1
21235	calaveras	1
21236	calatravas	1
21237	calamo	1
21238	calados	1
21239	calado	1
21240	calabozo	1
21241	cajonería	1
21242	cajistas	1
21243	caín	1
21244	caídas	1
21245	cafetera	1
21246	caes	1
21247	cadera	1
21248	cadenillas	1
21249	cadenciosas	1
21250	cadenaaa	1
21251	cadáveres	1
21252	cacofónico	1
21253	caciquil	1
21254	cachos	1
21255	cachivaches	1
21256	cachetes	1
21257	cachete	1
21258	cachazudas	1
21259	cachazuda	1
21260	cachaza	1
21261	cacerolas	1
21262	cacería	1
21263	cabremos	1
21264	cabras	1
21265	cabra	1
21266	cabotaje	1
21267	cables	1
21268	cabizbaja	1
21269	cabida	1
21270	cabezota	1
21271	cabezada	1
21272	cabañas	1
21273	cabalmente	1
21274	caballerosos	1
21275	caballeroso	1
21276	caballeriza	1
21277	caballerías	1
21278	caballeretes	1
21279	caballeresca	1
21280	cabalística	1
21281	ca	1
21282	byroniano	1
21283	byron	1
21284	bustos	1
21285	búsquenle	1
21286	búsquelo	1
21287	busilis	1
21288	busco	1
21289	buscárselos	1
21290	buscarlas	1
21291	buscaré	1
21292	buscara	1
21293	buscándote	1
21294	buscándola	1
21295	buscadas	1
21296	buscada	1
21297	burocráticas	1
21298	burlonas	1
21299	burlescos	1
21300	burlesco	1
21301	burlasen	1
21302	burlarían	1
21303	burlando	1
21304	burlan	1
21305	burdos	1
21306	bulló	1
21307	bullían	1
21308	bullen	1
21309	bullanguero	1
21310	bulas	1
21311	bula	1
21312	bujías	1
21313	buitre	1
21314	buhoneros	1
21315	bufos	1
21316	bufando	1
21317	buey	1
21318	bucólicas	1
21319	buchner	1
21320	buche	1
21321	bruyère	1
21322	brutos	1
21323	brusquer	1
21324	bruscas	1
21325	brusca	1
21326	brujas	1
21327	brotando	1
21328	brota	1
21329	brooke	1
21330	bronces	1
21331	bromista	1
21332	brochada	1
21333	brocado	1
21334	briscada	1
21335	briosos	1
21336	brindar	1
21337	brindaba	1
21338	brincar	1
21339	brincan	1
21340	brincaban	1
21341	brincaba	1
21342	brilló	1
21343	brillaron	1
21344	brillará	1
21345	brillando	1
21346	brígida	1
21347	bribón	1
21348	brevísima	1
21349	brevemente	1
21350	bretón	1
21351	brechas	1
21352	brea	1
21353	bravos	1
21354	brava	1
21355	bramidos	1
21356	bramido	1
21357	bramar	1
21358	bramante	1
21359	brama	1
21360	braga	1
21361	braceando	1
21362	bozal	1
21363	boutade	1
21364	bouquet	1
21365	botonazos	1
21366	boticario	1
21367	botica	1
21368	botarga	1
21369	botarate	1
21370	botánicas	1
21371	botánica	1
21372	botando	1
21373	bota	1
21374	bostezos	1
21375	bostezara	1
21376	bostezado	1
21377	bostezaban	1
21378	bostezaba	1
21379	borrosos	1
21380	borrón	1
21381	borró	1
21382	borro	1
21383	borrascas	1
21384	borrasca	1
21385	borran	1
21386	borrador	1
21387	borrada	1
21388	borrachón	1
21389	borracheras	1
21390	borraban	1
21391	borraba	1
21392	borona	1
21393	bordó	1
21394	bordeando	1
21395	bordado	1
21396	borda	1
21397	boquirris	1
21398	bonus	1
21399	bonitos	1
21400	bondadoso	1
21401	bombardeo	1
21402	bolsón	1
21403	bolsistas	1
21404	bolera	1
21405	bogando	1
21406	bofetá	1
21407	bodegón	1
21408	bodegas	1
21409	bodega	1
21410	bock	1
21411	bochornosos	1
21412	bochornosa	1
21413	bocas	1
21414	bocacalle	1
21415	bobalicona	1
21416	bobalicón	1
21417	bloqueo	1
21418	bloqueadas	1
21419	bloque	1
21420	blindaje	1
21421	blasfemos	1
21422	blasfemo	1
21423	blasfemia	1
21424	blasfeme	1
21425	blasfemaba	1
21426	blanquísima	1
21427	blanquecinas	1
21428	blanquear	1
21429	blandos	1
21430	blandones	1
21431	blandiéndolo	1
21432	blandía	1
21433	blandamente	1
21434	bizco	1
21435	bizarra	1
21436	bizantina	1
21437	birrete	1
21438	bípedo	1
21439	bion	1
21440	biografías	1
21441	biografía	1
21442	bilioso	1
21443	bílbilis	1
21444	bilbao	1
21445	bilateral	1
21446	bienquisto	1
21447	bienquista	1
21448	bienhechora	1
21449	bicho	1
21450	bibliófilo	1
21451	bibelot	1
21452	bi	1
21453	betún	1
21454	bethlehem	1
21455	bestialidad	1
21456	bestial	1
21457	besas	1
21458	besaron	1
21459	besarla	1
21460	besara	1
21461	besando	1
21462	besado	1
21463	besada	1
21464	besaban	1
21465	berruguete	1
21466	berroqueño	1
21467	bernardo	1
21468	bernard	1
21469	bermudo	1
21470	berlín	1
21471	bengala	1
21472	benévolos	1
21473	beneplácito	1
21474	benemérito	1
21475	benéfico	1
21476	beneficioso	1
21477	benedicto	1
21478	bendiga	1
21479	bendición	1
21480	bendecir	1
21481	bendecían	1
21482	bendecía	1
21483	belo	1
21484	bellos	1
21485	belloritas	1
21486	bellaquerías	1
21487	bellacas	1
21488	belem	1
21489	begonia	1
21490	becerro	1
21491	bebo	1
21492	bebiese	1
21493	bebiera	1
21494	bebida	1
21495	bebería	1
21496	bebedores	1
21497	beatuela	1
21498	bayonetazos	1
21499	bautizar	1
21500	baúles	1
21501	battistini	1
21502	batrania	1
21503	bato	1
21504	batirme	1
21505	batiría	1
21506	batieran	1
21507	batido	1
21508	batía	1
21509	batería	1
21510	baten	1
21511	batas	1
21512	batallones	1
21513	batallón	1
21514	bastos	1
21515	bastonazos	1
21516	bastón	1
21517	bastiat	1
21518	basteado	1
21519	basteada	1
21520	bastase	1
21521	bastarle	1
21522	bastará	1
21523	bastan	1
21524	bastamos	1
21525	bastado	1
21526	bastaban	1
21527	basquiña	1
21528	basilisco	1
21529	barullón	1
21530	barullero	1
21531	barroquismo	1
21532	barrió	1
21533	barriera	1
21534	barriendo	1
21535	barriadas	1
21536	barreras	1
21537	barreno	1
21538	barrenaba	1
21539	barnizados	1
21540	barnizada	1
21541	barcos	1
21542	barcelona	1
21543	baratas	1
21544	baraja	1
21545	báquico	1
21546	bañarse	1
21547	bañarme	1
21548	bañando	1
21549	bañados	1
21550	bañado	1
21551	baña	1
21552	banqueta	1
21553	banqueros	1
21554	bandolero	1
21555	bandidos	1
21556	bandas	1
21557	bandada	1
21558	bamboleaban	1
21559	bambalinas	1
21560	balzac	1
21561	baltasar	1
21562	baldo	1
21563	balda	1
21564	balbuciente	1
21565	balbuceó	1
21566	balaustres	1
21567	balanceaban	1
21568	bajito	1
21569	bájese	1
21570	baje	1
21571	bajarte	1
21572	bajarme	1
21573	bajarán	1
21574	bajada	1
21575	bailasen	1
21576	bailaron	1
21577	bailarín	1
21578	bailan	1
21579	bailábamos	1
21580	baglivio	1
21581	badulaque	1
21582	bachillera	1
21583	bachiller	1
21584	bacalao	1
21585	babosa	1
21586	babor	1
21587	babilónicos	1
21588	babilónico	1
21589	azuzarlas	1
21590	azulados	1
21591	azufre	1
21592	azucarera	1
21593	azucarada	1
21594	azotarla	1
21595	azotada	1
21596	azotacalles	1
21597	azotaban	1
21598	azogue	1
21599	azares	1
21600	ayunaría	1
21601	ayudó	1
21602	ayuden	1
21603	ayudémonos	1
21604	ayudase	1
21605	ayudas	1
21606	ayudaron	1
21607	ayudarnos	1
21608	ayudarlos	1
21609	ayudaría	1
21610	ayudaremos	1
21611	ayudará	1
21612	ayudantes	1
21613	ayudados	1
21614	ayudada	1
21615	ayudábala	1
21616	axis	1
21617	avisó	1
21618	avise	1
21619	avisaría	1
21620	avisaré	1
21621	avisarán	1
21622	avisaba	1
21623	avisa	1
21624	avinagrados	1
21625	avinagrado	1
21626	aviene	1
21627	averigüé	1
21628	averiguarlo	1
21629	averiguaciones	1
21630	averiados	1
21631	averiada	1
21632	avergüence	1
21633	avergonzarme	1
21634	avergonzarla	1
21635	avergonzando	1
21636	avergonzadas	1
21637	aventurillas	1
21638	aventurero	1
21639	aventurarse	1
21640	aventurándose	1
21641	aventuradas	1
21642	aventuraba	1
21643	aventado	1
21644	avenirse	1
21645	avenidos	1
21646	avenida	1
21647	avenía	1
21648	avellanos	1
21649	avellanado	1
21650	ave	1
21651	avasallan	1
21652	avasalladores	1
21653	avaros	1
21654	avaro	1
21655	avariento	1
21656	avanzando	1
21657	avanzaba	1
21658	avalora	1
21659	autos	1
21660	autorizar	1
21661	autorizado	1
21662	autorizaba	1
21663	autora	1
21664	autómatas	1
21665	autolatría	1
21666	auténtico	1
21667	ausenta	1
21668	ausencias	1
21669	aura	1
21670	aúpa	1
21671	aunarme	1
21672	aúnan	1
21673	aumento	1
21674	aumentar	1
21675	aumentado	1
21676	aulló	1
21677	aullidos	1
21678	augustas	1
21679	audiencias	1
21680	atusando	1
21681	atusaba	1
21682	aturdiendo	1
21683	aturdidos	1
21684	atropellos	1
21685	atropello	1
21686	atropellaban	1
21687	atronando	1
21688	atronador	1
21689	atriles	1
21690	atribuyeron	1
21691	atribuyendo	1
21692	atribuye	1
21693	atribulada	1
21694	atribuciones	1
21695	atrevidísima	1
21696	atrevidas	1
21697	atreví	1
21698	atreverme	1
21699	atreverías	1
21700	atrayendo	1
21701	atravesasen	1
21702	atravesaron	1
21703	atravesadas	1
21704	atravesada	1
21705	atrajo	1
21706	atraído	1
21707	atraían	1
21708	atragantaban	1
21709	atraerle	1
21710	atraería	1
21711	atraer	1
21712	atraen	1
21713	atracón	1
21714	atracción	1
21715	atormentarle	1
21716	atormentarla	1
21717	atormentando	1
21718	atonía	1
21719	átomos	1
21720	átomo	1
21721	ató	1
21722	atizaron	1
21723	atiende	1
21724	atice	1
21725	atestados	1
21726	atestadas	1
21727	atesoraba	1
21728	atesora	1
21729	aterrados	1
21730	aterrado	1
21731	aterida	1
21732	atenuaba	1
21733	atenía	1
21734	atengo	1
21735	ateneo	1
21736	atenea	1
21737	atendía	1
21738	atemorizado	1
21739	atea	1
21740	atávicas	1
21741	ataúd	1
21742	atarse	1
21743	atarla	1
21744	atareada	1
21745	atar	1
21746	atan	1
21747	atalaya	1
21748	atajo	1
21749	atajado	1
21750	atados	1
21751	ataco	1
21752	atacarte	1
21753	atacarle	1
21754	ataca	1
21755	ataban	1
21756	ataba	1
21757	ata	1
21758	asustes	1
21759	asustemos	1
21760	asusté	1
21761	asustarte	1
21762	asustaría	1
21763	asueto	1
21764	asturias	1
21765	asturiana	1
21766	astronomía	1
21767	astro	1
21768	astri	1
21769	astillas	1
21770	assistentiam	1
21771	asquerosos	1
21772	aspirado	1
21773	aspiradas	1
21774	aspiraban	1
21775	aspira	1
21776	ásperos	1
21777	aspereza	1
21778	áspera	1
21779	aspectos	1
21780	aspas	1
21781	aspa	1
21782	asombrosamente	1
21783	asombraban	1
21784	asomasen	1
21785	asomaran	1
21786	asomando	1
21787	asolado	1
21788	asociarla	1
21789	asociación	1
21790	asistirlos	1
21791	asistirle	1
21792	asiste	1
21793	asirle	1
21794	asimilaba	1
21795	asignatura	1
21796	asiduos	1
21797	asia	1
21798	asfixiarse	1
21799	asfixiado	1
21800	aseveraba	1
21801	asestaban	1
21802	asesorado	1
21803	asesinos	1
21804	asesinato	1
21805	asesinarla	1
21806	aseo	1
21807	asentaba	1
21808	asegurarlo	1
21809	asegurarle	1
21810	asegurando	1
21811	asegurado	1
21812	asegurada	1
21813	asegura	1
21814	asediaban	1
21815	asediaba	1
21816	asedia	1
21817	ascetismo	1
21818	ascética	1
21819	ascendiendo	1
21820	ascendido	1
21821	ascendía	1
21822	asar	1
21823	asamblea	1
21824	asaltaron	1
21825	asaltar	1
21826	asaltaba	1
21827	asafétida	1
21828	asada	1
21829	as	1
21830	arúspice	1
21831	artificial	1
21832	articulillo	1
21833	articulejo	1
21834	artesano	1
21835	artela	1
21836	artefactos	1
21837	arrullado	1
21838	arrullaban	1
21839	arruine	1
21840	arruinarle	1
21841	arruinados	1
21842	arrugase	1
21843	arrugar	1
21844	arrugados	1
21845	arrugaditos	1
21846	arrugadas	1
21847	arroz	1
21848	arropada	1
21849	arrollado	1
21850	arrojasen	1
21851	arrojárselo	1
21852	arrojarme	1
21853	arrojarlo	1
21854	arrojarles	1
21855	arrojarla	1
21856	arrogantes	1
21857	arrodilladas	1
21858	arrobado	1
21859	arrinconadas	1
21860	arrimó	1
21861	arrimaron	1
21862	arriesgándose	1
21863	arriesgados	1
21864	arriesgado	1
21865	arriesgada	1
21866	arrieros	1
21867	arresto	1
21868	arrepintió	1
21869	arrepintiéndose	1
21870	arreo	1
21871	arrendamientos	1
21872	arremolinó	1
21873	arremolinaban	1
21874	arremetida	1
21875	arrellanados	1
21876	arrellanado	1
21877	arreglos	1
21878	arreglo	1
21879	arreglarlo	1
21880	arreglaría	1
21881	arreglarás	1
21882	arreglan	1
21883	arreglaba	1
21884	arrebató	1
21885	arrebatando	1
21886	arrebatado	1
21887	arrebataba	1
21888	arrastró	1
21889	arrasados	1
21890	arras	1
21891	arranco	1
21892	arrancasen	1
21893	arrancas	1
21894	arrancarse	1
21895	arrancaron	1
21896	arrancarlo	1
21897	arrancarla	1
21898	arrancaría	1
21899	arrancándoles	1
21900	arrancándola	1
21901	arrancados	1
21902	arraigo	1
21903	arraigada	1
21904	arraigaba	1
21905	arrabales	1
21906	arquitecto	1
21907	arqueológicos	1
21908	arouet	1
21909	aromático	1
21910	aromáticas	1
21911	aroma	1
21912	aro	1
21913	armonioso	1
21914	armónico	1
21915	armonías	1
21916	armisticios	1
21917	armisticio	1
21918	armiños	1
21919	armadura	1
21920	aristocráticos	1
21921	aristocráticas	1
21922	arisco	1
21923	ariscas	1
21924	áridos	1
21925	argumosa	1
21926	argucias	1
21927	argos	1
21928	arenilla	1
21929	arengas	1
21930	arengaba	1
21931	arduas	1
21932	ardió	1
21933	ardilla	1
21934	ardiera	1
21935	arder	1
21936	ardentísimo	1
21937	arde	1
21938	arcos	1
21939	arcones	1
21940	arciprestazgo	1
21941	arcilla	1
21942	archivo	1
21943	archimonástica	1
21944	arcadias	1
21945	arboricultor	1
21946	arbitrista	1
21947	arbitrar	1
21948	arañazos	1
21949	arañazo	1
21950	aragonesa	1
21951	árabes	1
21952	aquilata	1
21953	aquéllas	1
21954	apuren	1
21955	apurasen	1
21956	apuras	1
21957	apurarse	1
21958	apuran	1
21959	apuntara	1
21960	apuntado	1
21961	aproximando	1
21962	aproximadamente	1
21963	aproximaba	1
21964	aprovechemos	1
21965	aprovecharon	1
21966	aprovecharlo	1
21967	aprovecharlas	1
21968	aprovechándose	1
21969	aprovechado	1
21970	apropósito	1
21971	aprobar	1
21972	aprobando	1
21973	aprobado	1
21974	aprobadas	1
21975	aprisionados	1
21976	aprisionaba	1
21977	aprietos	1
21978	aprietan	1
21979	aprieta	1
21980	apretarse	1
21981	apretándose	1
21982	apresure	1
21983	aprensivo	1
21984	aprendiz	1
21985	aprendiera	1
21986	aprendidas	1
21987	aprendices	1
21988	aprendían	1
21989	aprendía	1
21990	aprendí	1
21991	aprenderá	1
21992	aprende	1
21993	apremiante	1
21994	apreció	1
21995	apreciarlos	1
21996	apreciaciones	1
21997	aprecia	1
21998	approbante	1
21999	apoyos	1
22000	apoyadas	1
22001	apóstrofes	1
22002	apostatar	1
22003	apostaría	1
22004	apostados	1
22005	apostado	1
22006	apostaba	1
22007	aposentos	1
22008	aportaría	1
22009	apoplético	1
22010	apoplejía	1
22011	apólogos	1
22012	apologías	1
22013	apodos	1
22014	apodere	1
22015	apoderarse	1
22016	apoderando	1
22017	apoderaba	1
22018	apocalípticas	1
22019	apocados	1
22020	aplico	1
22021	aplicarse	1
22022	aplicándose	1
22023	aplicando	1
22024	aplicación	1
22025	aplicable	1
22026	aplazando	1
22027	aplazado	1
22028	aplazaba	1
22029	aplauso	1
22030	aplaudiese	1
22031	aplaudidos	1
22032	aplaudido	1
22033	aplaudían	1
22034	aplastemos	1
22035	aplastarla	1
22036	aplastarían	1
22037	aplastada	1
22038	aplacarla	1
22039	aplacar	1
22040	aplacaban	1
22041	apiñada	1
22042	apiñábase	1
22043	ápice	1
22044	apiadarse	1
22045	apiadaba	1
22046	apetitoso	1
22047	apetecida	1
22048	apetecibles	1
22049	apesto	1
22050	apestas	1
22051	apestaba	1
22052	aperitivos	1
22053	apeó	1
22054	apéndice	1
22055	apelmazada	1
22056	apellido	1
22057	apellidaban	1
22058	apellidaba	1
22059	apego	1
22060	apearon	1
22061	apearme	1
22062	apeado	1
22063	apeaba	1
22064	apatía	1
22065	apasionamiento	1
22066	apasionadas	1
22067	aparto	1
22068	apartarle	1
22069	apartaría	1
22070	apartamiento	1
22071	apartado	1
22072	apartadas	1
22073	apartada	1
22074	apartaban	1
22075	apartaba	1
22076	aparta	1
22077	apariciones	1
22078	aparentarla	1
22079	aparentan	1
22080	aparecérsele	1
22081	aparatoso	1
22082	aparador	1
22083	apañaré	1
22084	apaleaban	1
22085	apagase	1
22086	apagarla	1
22087	apacentaba	1
22088	añosos	1
22089	añicos	1
22090	añado	1
22091	añadiría	1
22092	añadiendo	1
22093	añadían	1
22094	anuncita	1
22095	anuncios	1
22096	anuncias	1
22097	anunciarle	1
22098	anunciándoles	1
22099	anunciadas	1
22100	anulo	1
22101	anual	1
22102	antro	1
22103	antonelli	1
22104	antón	1
22105	antolínez	1
22106	antojos	1
22107	antojase	1
22108	antojársele	1
22109	antojara	1
22110	antojado	1
22111	antojadiza	1
22112	antojábasele	1
22113	antítesis	1
22114	antipáticos	1
22115	antiguamente	1
22116	antiespasmódicos	1
22117	anticuarios	1
22118	anticuada	1
22119	anticipos	1
22120	anticipar	1
22121	anticipándose	1
22122	anticipando	1
22123	anticipado	1
22124	anticipada	1
22125	anticipaba	1
22126	antepasados	1
22127	antecesores	1
22128	antecesor	1
22129	antecedentes	1
22130	ansiando	1
22131	ansiaban	1
22132	anónimas	1
22133	anónima	1
22134	anochecía	1
22135	aniquilarme	1
22136	aniquilarle	1
22137	aniquilados	1
22138	animen	1
22139	ánimas	1
22140	animaron	1
22141	animando	1
22142	animan	1
22143	animalucho	1
22144	animalitos	1
22145	animalejo	1
22146	animados	1
22147	animada	1
22148	aniceto	1
22149	anhelaban	1
22150	angustioso	1
22151	angustiado	1
22152	angustiaba	1
22153	ángulos	1
22154	anguilas	1
22155	angosta	1
22156	angola	1
22157	angelito	1
22158	angélico	1
22159	angarillas	1
22160	anfibológico	1
22161	anfibios	1
22162	anfibio	1
22163	anegó	1
22164	anegarse	1
22165	anegar	1
22166	anegamos	1
22167	anegaban	1
22168	anduviese	1
22169	anduvieron	1
22170	anduvieran	1
22171	anduviera	1
22172	andrómaca	1
22173	andrina	1
22174	andrajosa	1
22175	andrajos	1
22176	andrajo	1
22177	anday	1
22178	andas	1
22179	andarín	1
22180	andaríamos	1
22181	andamos	1
22182	andalucía	1
22183	andaluces	1
22184	andábamos	1
22185	ancor	1
22186	anchuras	1
22187	anchura	1
22188	anchísima	1
22189	anch	1
22190	análogo	1
22191	analogías	1
22192	analogía	1
22193	análoga	1
22194	analizarla	1
22195	analítica	1
22196	anagnórisis	1
22197	anafrodíticos	1
22198	anafrodítico	1
22199	anafroditas	1
22200	anacronismo	1
22201	anacreóntica	1
22202	amueblada	1
22203	amplitud	1
22204	amplios	1
22205	amplias	1
22206	ampliar	1
22207	amplia	1
22208	ampararse	1
22209	amparando	1
22210	amotinados	1
22211	amostazado	1
22212	amortajada	1
22213	amorcillo	1
22214	amoratados	1
22215	amoratado	1
22216	amoratada	1
22217	amontonado	1
22218	amontonaba	1
22219	amoldarse	1
22220	amó	1
22221	amnistía	1
22222	amistosas	1
22223	amiguito	1
22224	américo	1
22225	américas	1
22226	americanilla	1
22227	ameno	1
22228	amenizaba	1
22229	amenidad	1
22230	amengua	1
22231	amenazas	1
22232	amenazarla	1
22233	amenazar	1
22234	amenazándome	1
22235	amenazándola	1
22236	amenazador	1
22237	amenazaban	1
22238	amenas	1
22239	amen	1
22240	ambulante	1
22241	ambiciones	1
22242	ambicionaba	1
22243	amazacotada	1
22244	amasijo	1
22245	amasados	1
22246	amarrado	1
22247	amarla	1
22248	amarillez	1
22249	amarillentos	1
22250	amarillentas	1
22251	amarilleaba	1
22252	amarilis	1
22253	amaranto	1
22254	amaños	1
22255	amansando	1
22256	amaneramiento	1
22257	amaneció	1
22258	amanecido	1
22259	amanecía	1
22260	amagos	1
22261	amagó	1
22262	amago	1
22263	amaga	1
22264	amadas	1
22265	alzó	1
22266	alzasen	1
22267	alzase	1
22268	alzando	1
22269	alza	1
22270	alvarico	1
22271	aluvión	1
22272	alusiva	1
22273	alumbramiento	1
22274	alumbraban	1
22275	alumbra	1
22276	aludían	1
22277	alucinas	1
22278	altruistas	1
22279	altozano	1
22280	altivez	1
22281	altisonante	1
22282	altísimos	1
22283	alteró	1
22284	alternando	1
22285	alteres	1
22286	altercados	1
22287	altercado	1
22288	alterarse	1
22289	alterar	1
22290	alteraciones	1
22291	altaneros	1
22292	altanero	1
22293	altanería	1
22294	alquilar	1
22295	alpiste	1
22296	alondras	1
22297	almuerzo	1
22298	almorzaba	1
22299	almohadón	1
22300	almohadillado	1
22301	almohadillada	1
22302	almidonadas	1
22303	almidón	1
22304	almibarados	1
22305	almibarado	1
22306	almenas	1
22307	almacenó	1
22308	almacenes	1
22309	alleluia	1
22310	allanarlo	1
22311	alivio	1
22312	aliviada	1
22313	aliviaban	1
22314	alineado	1
22315	alineadas	1
22316	alimentan	1
22317	alimentada	1
22318	alimentación	1
22319	alimenta	1
22320	alimañas	1
22321	alientos	1
22322	alientan	1
22323	alicientes	1
22324	alianza	1
22325	alharaca	1
22326	alhajas	1
22327	alhaja	1
22328	algos	1
22329	algodones	1
22330	algodón	1
22331	algaradas	1
22332	alforjas	1
22333	alfonsos	1
22334	alfombras	1
22335	alfiletero	1
22336	alfileres	1
22337	alfiler	1
22338	alfayate	1
22339	aletean	1
22340	aletargada	1
22341	alero	1
22342	alentaba	1
22343	alemania	1
22344	alejaran	1
22345	alegué	1
22346	alegremente	1
22347	alegrase	1
22348	alegrarle	1
22349	alegrar	1
22350	alegraban	1
22351	alegórica	1
22352	alegoría	1
22353	alegando	1
22354	alegaba	1
22355	aleccionado	1
22356	aleatorio	1
22357	aldebarán	1
22358	aldabonazos	1
22359	aldabonazo	1
22360	aldabonada	1
22361	alcurnia	1
22362	alcubilla	1
22363	alcornoque	1
22364	alcohólicos	1
22365	alcides	1
22366	alcanzó	1
22367	alcanzase	1
22368	alcanzara	1
22369	alcanzamos	1
22370	alcanzados	1
22371	alcanzaban	1
22372	alcanzaba	1
22373	alcances	1
22374	alcaldito	1
22375	alcaldesa	1
22376	alcaide	1
22377	alcacer	1
22378	álbum	1
22379	alborotó	1
22380	alboroto	1
22381	alborote	1
22382	alborotando	1
22383	alborotan	1
22384	alborotado	1
22385	alborotaban	1
22386	alboroque	1
22387	alborada	1
22388	albión	1
22389	albergaba	1
22390	alberca	1
22391	albéitar	1
22392	albedrío	1
22393	albas	1
22394	albañal	1
22395	albaicín	1
22396	alarmó	1
22397	alarmasen	1
22398	alarmará	1
22399	alarmantes	1
22400	alarmada	1
22401	alargó	1
22402	alargarse	1
22403	alargando	1
22404	alarcón	1
22405	alancardan	1
22406	alambres	1
22407	alambicadas	1
22408	alacenas	1
22409	alacena	1
22410	alabó	1
22411	alabarle	1
22412	alabarla	1
22413	alabando	1
22414	alaban	1
22415	alabados	1
22416	alabada	1
22417	ala	1
22418	ajutorium	1
22419	ajustadas	1
22420	ajustábase	1
22421	ajenjo	1
22422	ajajá	1
22423	ajado	1
22424	aislarla	1
22425	aislados	1
22426	aislador	1
22427	aislado	1
22428	aislada	1
22429	airosas	1
22430	airosa	1
22431	airada	1
22432	ahuyentaba	1
22433	ahumados	1
22434	ahorró	1
22435	ahorrar	1
22436	ahorrada	1
22437	ahorraba	1
22438	ahorita	1
22439	ahorcarse	1
22440	ahorcar	1
22441	ahorcado	1
22442	ahogó	1
22443	ahogarse	1
22444	ahogaron	1
22445	ahogarlo	1
22446	ahogarla	1
22447	ahogar	1
22448	ahogando	1
22449	ahogados	1
22450	ahogaban	1
22451	ahítas	1
22452	ahíta	1
22453	aguzado	1
22454	aguzaba	1
22455	agustinito	1
22456	agujerito	1
22457	aguijones	1
22458	aguijonearle	1
22459	aguerrido	1
22460	agüero	1
22461	agudezas	1
22462	agudeza	1
22463	aguarde	1
22464	aguardando	1
22465	aguanto	1
22466	aguantado	1
22467	aguacero	1
22468	agrónomo	1
22469	agrietadas	1
22470	agrietada	1
22471	agrícola	1
22472	agrias	1
22473	agriado	1
22474	agreste	1
22475	agregarse	1
22476	agregadas	1
22477	agravio	1
22478	agravante	1
22479	agravaba	1
22480	agradézcaselo	1
22481	agradezcamos	1
22482	agradeces	1
22483	agradecerlo	1
22484	agradecerle	1
22485	agradecería	1
22486	agradeceré	1
22487	agradece	1
22488	agrade	1
22489	agradarle	1
22490	agradado	1
22491	agradablemente	1
22492	agradaban	1
22493	agradábale	1
22494	agotando	1
22495	agostado	1
22496	agostada	1
22497	agoreras	1
22498	agonizaba	1
22499	agonía	1
22500	agolpándose	1
22501	agolpaba	1
22502	agobiados	1
22503	aglomeraron	1
22504	aglomeración	1
22505	agitada	1
22506	agitaba	1
22507	agilidad	1
22508	ágil	1
22509	agentes	1
22510	agente	1
22511	agencias	1
22512	agencia	1
22513	agazapado	1
22514	agasajos	1
22515	agasajada	1
22516	agarró	1
22517	agarrarse	1
22518	agarrándose	1
22519	agarran	1
22520	agarraban	1
22521	agarraba	1
22522	agachar	1
22523	agachándose	1
22524	agachado	1
22525	afueras	1
22526	afrodisíaco	1
22527	africana	1
22528	afrento	1
22529	afrenta	1
22530	afortunados	1
22531	aforismos	1
22532	aforismo	1
22533	aflojara	1
22534	aflojando	1
22535	aflojaban	1
22536	aflojaba	1
22537	aflija	1
22538	afligió	1
22539	afligido	1
22540	afirmativa	1
22541	afirmarse	1
22542	afirmar	1
22543	afirma	1
22544	afinaban	1
22545	afiló	1
22546	afilador	1
22547	aficionara	1
22548	afianzaría	1
22549	affma	1
22550	aferradas	1
22551	afeminados	1
22552	afeitar	1
22553	afeitado	1
22554	afectuoso	1
22555	afectuosa	1
22556	afectivo	1
22557	afectísimo	1
22558	afectar	1
22559	afectando	1
22560	afearlo	1
22561	afanes	1
22562	afanaba	1
22563	afables	1
22564	afablemente	1
22565	aeroterapia	1
22566	aéreo	1
22567	aereación	1
22568	advirtieron	1
22569	advierto	1
22570	advertirse	1
22571	advertencias	1
22572	adversa	1
22573	advenediza	1
22574	adustos	1
22575	adúlteros	1
22576	adúlteras	1
22577	adulterado	1
22578	adúltera	1
22579	aduladores	1
22580	adulaban	1
22581	aducía	1
22582	aduana	1
22583	adquisición	1
22584	adquirió	1
22585	adquirieron	1
22586	adquirían	1
22587	adquirí	1
22588	adquiera	1
22589	adornó	1
22590	adornar	1
22591	adornadas	1
22592	adornada	1
22593	adormecida	1
22594	adormecerla	1
22595	adorarle	1
22596	adorarla	1
22597	adorar	1
22598	adorando	1
22599	adorados	1
22600	adorada	1
22601	adoptar	1
22602	adoptado	1
22603	adolescentes	1
22604	adocenado	1
22605	adocenada	1
22606	adobes	1
22607	admito	1
22608	admitirlos	1
22609	admitieron	1
22610	admitiera	1
22611	admitida	1
22612	admitían	1
22613	admiré	1
22614	admirarla	1
22615	admiraría	1
22616	admirándole	1
22617	admirándolas	1
22618	admirando	1
22619	admirados	1
22620	admiradora	1
22621	admirador	1
22622	admira	1
22623	administrar	1
22624	administrado	1
22625	adjuntos	1
22626	adjetivos	1
22627	adivinarle	1
22628	adivinando	1
22629	adivinaciones	1
22630	adivina	1
22631	adiosito	1
22632	adiciones	1
22633	adhesión	1
22634	adherirme	1
22635	aderezos	1
22636	adelantos	1
22637	adelantarlo	1
22638	adelantarle	1
22639	adelantándose	1
22640	adelantados	1
22641	adefesios	1
22642	adecuados	1
22643	adecuadas	1
22644	adaptarse	1
22645	adamascado	1
22646	adamado	1
22647	acústico	1
22648	acusó	1
22649	acuso	1
22650	acusemos	1
22651	acusara	1
22652	acusadora	1
22653	acusada	1
22654	acusaciones	1
22655	acusaban	1
22656	acumulando	1
22657	acuestes	1
22658	acuéstate	1
22659	acuestas	1
22660	acuérdese	1
22661	acuerda	1
22662	acudiesen	1
22663	acudiese	1
22664	acudiendo	1
22665	acuden	1
22666	acude	1
22667	acuda	1
22668	acuarelas	1
22669	actrices	1
22670	actitudes	1
22671	acti	1
22672	acta	1
22673	acróbata	1
22674	acritud	1
22675	acribillada	1
22676	acreedores	1
22677	acreditado	1
22678	acreditadas	1
22679	acreditaban	1
22680	acostumbre	1
22681	acostumbra	1
22682	acostaron	1
22683	acostarla	1
22684	acostara	1
22685	acostada	1
22686	acostabas	1
22687	acosarla	1
22688	acortaban	1
22689	acordase	1
22690	acordarte	1
22691	acordaron	1
22692	acordaría	1
22693	acontecimiento	1
22694	acontecía	1
22695	acontecer	1
22696	acontecemos	1
22697	aconsejó	1
22698	aconsejes	1
22699	aconsejarte	1
22700	aconsejaron	1
22701	aconsejaría	1
22702	aconsejan	1
22703	aconsejada	1
22704	aconsejaban	1
22705	acongojaba	1
22706	acompasado	1
22707	acompañó	1
22708	acompáñenos	1
22709	acompáñeme	1
22710	acompañe	1
22711	acompañase	1
22712	acompañarse	1
22713	acompañarlos	1
22714	acompañaré	1
22715	acompañados	1
22716	acompañadas	1
22717	acompaña	1
22718	acomodaron	1
22719	acomodamiento	1
22720	acomoda	1
22721	acogido	1
22722	acogidas	1
22723	acogida	1
22724	acogíase	1
22725	acogerse	1
22726	aclimató	1
22727	aclimataba	1
22728	aclararlo	1
22729	aclamación	1
22730	aciertos	1
22731	aciertas	1
22732	acierta	1
22733	acíbar	1
22734	achico	1
22735	achicaba	1
22736	achaparrado	1
22737	achaparrada	1
22738	achantarse	1
22739	achacó	1
22740	achacaban	1
22741	acervo	1
22742	acertaría	1
22743	acertar	1
22744	acertada	1
22745	acertaba	1
22746	acerquen	1
22747	acerque	1
22748	aceros	1
22749	acerico	1
22750	acércate	1
22751	acercará	1
22752	acercamos	1
22753	acerados	1
22754	aceptaré	1
22755	aceptámosla	1
22756	aceptables	1
22757	acentos	1
22758	acendrados	1
22759	acelerar	1
22760	aceleraba	1
22761	aceitunas	1
22762	acecharse	1
22763	acechar	1
22764	acecha	1
22765	accionistas	1
22766	accionaba	1
22767	accesorios	1
22768	acceso	1
22769	accèsit	1
22770	accedido	1
22771	accedería	1
22772	acceder	1
22773	acatarrada	1
22774	acartonada	1
22775	acarreaba	1
22776	acaricie	1
22777	acariciarte	1
22778	acariciarle	1
22779	acariciar	1
22780	acariciadores	1
22781	acariciado	1
22782	acariciaban	1
22783	acaparó	1
22784	acaparadores	1
22785	acantos	1
22786	acantilados	1
22787	acamparon	1
22788	acalorado	1
22789	acalorada	1
22790	acaloraba	1
22791	acalló	1
22792	acallar	1
22793	académicos	1
22794	acabose	1
22795	acabo	1
22796	acaben	1
22797	acabemos	1
22798	acabasen	1
22799	acabársele	1
22800	acabaría	1
22801	acabarás	1
22802	acabará	1
22803	acabando	1
22804	acabamos	1
22805	abyección	1
22806	abuse	1
22807	abusas	1
22808	abusarse	1
22809	aburro	1
22810	aburrirle	1
22811	aburrieran	1
22812	aburriéndose	1
22813	aburriendo	1
22814	aburridos	1
22815	aburridas	1
22816	abur	1
22817	abundasen	1
22818	abundantemente	1
22819	abundando	1
22820	abunda	1
22821	abultado	1
22822	abultada	1
22823	abuelo	1
22824	absueltos	1
22825	absuelto	1
22826	absuelta	1
22827	abstuviese	1
22828	abstuviera	1
22829	abstraída	1
22830	abstractos	1
22831	abstiene	1
22832	abstenerse	1
22833	abstenerme	1
22834	abstendría	1
22835	abstención	1
22836	absortos	1
22837	absorto	1
22838	absorta	1
22839	absorbía	1
22840	absorben	1
22841	absolvería	1
22842	absolutos	1
22843	abrumándole	1
22844	abrumando	1
22845	abrumadores	1
22846	abrumadora	1
22847	abrumador	1
22848	abrumada	1
22849	abroquelado	1
22850	abrochar	1
22851	abrochándose	1
22852	abrochando	1
22853	abrochado	1
22854	abrochada	1
22855	abro	1
22856	abrirse	1
22857	abrirá	1
22858	abriles	1
22859	abrigos	1
22860	abrigara	1
22861	abrigan	1
22862	abrigábala	1
22863	abrigaba	1
22864	abrieran	1
22865	abreviaturas	1
22866	abreviar	1
22867	abreviada	1
22868	abren	1
22869	ábreme	1
22870	abre	1
22871	abrazase	1
22872	abrazada	1
22873	abrazaba	1
22874	ábrase	1
22875	abrasarme	1
22876	abrasadores	1
22877	abrasa	1
22878	aborrecían	1
22879	aborrecerá	1
22880	aborrecen	1
22881	abordase	1
22882	abonado	1
22883	abomino	1
22884	abominación	1
22885	abominaba	1
22886	abogadote	1
22887	abogado	1
22888	abogadillos	1
22889	abogadetes	1
22890	abofetear	1
22891	abluciones	1
22892	ablativo	1
22893	ablandado	1
22894	abismado	1
22895	abismada	1
22896	abertura	1
22897	abelardo	1
22898	abeja	1
22899	abarcándola	1
22900	abarcaba	1
22901	abanicándose	1
22902	abanicaba	1
22903	abandonó	1
22904	abandonarme	1
22905	abandonarlo	1
22906	abandonados	1
22907	abandonadas	1

Rank	Palabra	Frec
1	de	18253
2	que	15616
3	la	14563
4	y	13277
5	a	9945
6	el	7919
7	no	7657
8	en	7609
9	se	6206
10	con	4637
11	le	4034
12	lo	4028
13	su	4000
14	los	3930
15	un	3767
16	las	3736
17	por	3617
18	me	3140
19	una	2873
20	más	2337
21	al	2312
22	del	2310
23	como	2294
24	para	2285
25	es	2263
26	pero	2097
27	si	2032
28	qué	1782
29	yo	1722
30	era	1656
31	usted	1626
32	te	1430
33	había	1393
34	muy	1215
35	ya	1180
36	porque	1094
37	cuando	1085
38	ella	1074
39	dijo	1073
40	sus	1041
41	tan	1028
42	o	989
43	todo	903
44	pues	903
45	bien	894
46	él	883
47	casa	874
48	esta	872
49	fortunata	869
50	sin	863
51	estaba	858
52	mi	801
53	ha	778
54	tenía	767
55	sí	758
56	esto	747
57	ni	736
58	doña	733
59	aquel	730
60	nada	690
61	aquella	666
62	dos	658
63	este	650
64	otra	629
65	después	622
66	tú	572
67	jacinta	571
68	fue	569
69	ver	560
70	hay	553
71	está	551
72	mujer	542
73	aquí	530
74	día	522
75	lupe	521
76	he	519
77	ser	517
78	mucho	513
79	poco	512
80	mí	499
81	sobre	488
82	hombre	486
83	ahora	480
84	señora	473
85	también	466
86	dios	461
87	otro	453
88	algo	448
89	eso	446
90	cabeza	443
91	hasta	441
92	tiene	435
93	calle	425
94	mismo	421
95	decir	420
96	así	419
97	siempre	415
98	tal	414
99	cosas	414
100	fin	408
101	vida	405
102	d	404
103	todos	398
104	cosa	396
105	santa	392
106	noche	377
107	iba	375
108	hacer	371
109	vez	365
110	allí	361
111	toda	356
112	tiempo	354
113	cómo	351
114	entre	350
115	tanto	337
116	decía	337
117	ojos	333
118	nos	333
119	quien	331
120	cara	329
121	parecía	320
122	guillermina	320
123	gran	317
124	les	316
125	tía	315
126	mano	315
127	rubín	314
128	juan	310
129	tengo	309
130	alma	309
131	idea	305
132	maxi	304
133	marido	304
134	sé	300
135	eran	297
136	parece	296
137	maximiliano	295
138	cual	295
139	todas	294
140	tu	289
141	esa	289
142	mal	287
143	mejor	284
144	podía	283
145	mundo	280
146	puerta	277
147	verdad	276
148	aunque	276
149	cruz	275
150	menos	272
151	hacía	272
152	estas	270
153	desde	264
154	mañana	263
155	digo	261
156	fuera	260
157	va	259
158	uno	259
159	hecho	255
160	señor	254
161	son	253
162	antes	251
163	días	248
164	buena	243
165	puede	242
166	hace	239
167	pobre	238
168	quiero	237
169	hija	237
170	dicho	237
171	dar	237
172	pronto	236
173	estoy	235
174	parte	232
175	luego	232
176	hijo	232
177	ese	232
178	voy	231
179	nunca	230
180	tres	228
181	sino	227
182	sabe	227
183	quería	226
184	hizo	225
185	allá	224
186	vaya	223
187	daba	221
188	donde	218
189	manos	217
190	quiere	215
191	voz	213
192	veces	211
193	tener	208
194	vio	207
195	soy	203
196	sólo	203
197	sido	201
198	cada	201
199	estos	198
200	caso	198
201	has	197
202	puso	196
203	buen	196
204	entró	195
205	boca	193
206	visto	192
207	mauricia	192
208	volvió	191
209	vamos	191
210	dio	191
211	palabras	190
212	barbarita	190
213	bueno	189
214	amigo	187
215	otras	186
216	mala	186
217	salir	185
218	han	184
219	persona	183
220	tarde	182
221	chico	182
222	ay	182
223	ah	182
224	modo	180
225	habían	180
226	sabía	178
227	joven	178
228	dice	178
229	quién	177
230	misma	177
231	hoy	176
232	hacia	176
233	ido	175
234	familia	175
235	tienes	174
236	ti	173
237	corazón	173
238	años	171
239	alguna	167
240	medio	165
241	saber	164
242	dónde	164
243	diciendo	163
244	entonces	162
245	da	162
246	sea	161
247	rato	161
248	palabra	161
249	ir	161
250	amiga	161
251	ideas	160
252	nadie	159
253	mayor	159
254	dentro	159
255	moreno	158
256	grande	156
257	aquellos	156
258	amor	156
259	tuvo	155
260	mil	155
261	manera	154
262	hablar	153
263	estaban	151
264	cuarto	151
265	mira	150
266	madrid	150
267	personas	149
268	hubiera	148
269	estuvo	148
270	entrar	148
271	salió	145
272	pablo	145
273	izquierdo	145
274	cuerpo	145
275	lado	144
276	estás	144
277	dinero	143
278	niño	142
279	mesa	141
280	delante	141
281	estar	140
282	cuatro	140
283	dando	139
284	unos	138
285	sabes	138
286	dado	138
287	cuenta	138
288	hora	137
289	algunas	137
290	madre	135
291	punto	134
292	pudo	134
293	esas	134
294	ballester	134
295	otros	133
296	gente	133
297	ellos	133
298	aquellas	133
299	mientras	132
300	habría	132
301	falta	132
302	contra	132
303	cierto	132
304	cuanto	131
305	haciendo	130
306	casi	130
307	replicó	129
308	aquello	129
309	momento	128
310	estado	128
311	algún	128
312	mujeres	126
313	mío	125
314	ahí	125
315	duda	124
316	tomar	123
317	estupiñá	123
318	aún	123
319	veía	122
320	sentía	122
321	miedo	122
322	viene	120
323	ropa	119
324	razón	119
325	quieres	119
326	puesto	119
327	feijoo	119
328	café	119
329	baldomero	119
330	unas	118
331	pasar	118
332	mía	118
333	eres	118
334	pensaba	117
335	gusto	116
336	sala	115
337	puedo	115
338	pasado	115
339	ninguna	115
340	tenían	114
341	poner	114
342	papitos	114
343	empezó	114
344	ponía	113
345	pasaba	113
346	nicolás	113
347	mucha	113
348	amigos	113
349	agua	113
350	pasó	112
351	muchos	112
352	instante	112
353	volver	111
354	san	111
355	preciso	111
356	paso	111
357	muchas	111
358	miraba	111
359	sola	110
360	primero	110
361	mis	109
362	mirando	109
363	hermano	109
364	comer	109
365	creo	108
366	algunos	108
367	segunda	107
368	debía	105
369	cama	105
370	ve	104
371	conciencia	104
372	veo	103
373	será	103
374	gracia	103
375	tienda	102
376	mamá	102
377	evaristo	102
378	están	102
379	plácido	101
380	sintió	100
381	pensamiento	100
382	diez	100
383	aun	100
384	primera	99
385	padre	99
386	luz	99
387	haber	99
388	ellas	99
389	claro	99
390	cielo	99
391	brazo	99
392	juanito	98
393	trabajo	97
394	todavía	97
395	suelo	97
396	oír	97
397	alcoba	97
398	vivir	96
399	mas	96
400	fuerte	96
401	chica	96
402	tanta	95
403	iban	94
404	espíritu	94
405	esos	94
406	miró	93
407	media	93
408	fuerza	93
409	delfín	93
410	conversación	93
411	sobrino	92
412	sería	92
413	propio	92
414	junto	92
415	horas	92
416	grandes	92
417	ganas	92
418	demás	92
419	brazos	92
420	tenido	91
421	siguiente	91
422	preguntó	91
423	llegó	91
424	infeliz	91
425	hombres	89
426	querer	88
427	debe	88
428	remedio	87
429	llevaba	87
430	cuidado	87
431	llegar	86
432	josé	86
433	aire	86
434	viendo	85
435	año	85
436	quiera	84
437	quedó	84
438	malo	84
439	venía	83
440	tampoco	83
441	señoras	83
442	posible	83
443	lástima	83
444	conmigo	83
445	cinco	83
446	vino	82
447	vi	82
448	venir	82
449	nombre	82
450	esposa	82
451	cualquier	82
452	arriba	82
453	quizás	81
454	muerte	81
455	mirar	81
456	ello	81
457	echó	81
458	bastante	81
459	verás	80
460	tono	80
461	niña	80
462	exclamó	80
463	dejó	80
464	viuda	79
465	sueño	79
466	ningún	79
467	mente	79
468	frente	79
469	escalera	79
470	entraba	79
471	don	79
472	tras	78
473	salía	78
474	pueblo	78
475	podría	78
476	pie	78
477	pasos	78
478	papel	78
479	camino	78
480	abajo	78
481	reales	77
482	quiso	77
483	pensó	77
484	obra	77
485	creía	77
486	ustedes	76
487	jáuregui	76
488	historia	76
489	cierta	76
490	aurora	76
491	orden	75
492	oído	75
493	gusta	75
494	pasa	74
495	cocina	74
496	ángel	74
497	villalonga	73
498	severiana	73
499	pensar	73
500	negro	73
501	hermana	73
502	gana	73
503	durante	73
504	van	72
505	solo	72
506	samaniego	72
507	hijos	72
508	estamos	72
509	dije	72
510	bajo	72
511	vista	71
512	verla	71
513	último	71
514	pecho	71
515	hubo	71
516	fueron	71
517	darle	71
518	ves	70
519	tienen	70
520	señorita	70
521	poder	70
522	cariño	70
523	buenas	70
524	apenas	70
525	peor	69
526	pañuelo	69
527	llevar	69
528	labios	69
529	iglesia	69
530	gracias	69
531	casta	69
532	ante	69
533	vuelta	68
534	sangre	68
535	reír	68
536	quisiera	68
537	nuevo	68
538	importa	68
539	hemos	68
540	hacen	68
541	encima	68
542	curiosidad	68
543	ciertas	68
544	atención	68
545	e	67
546	cerca	67
547	situación	66
548	semejante	66
549	santo	66
550	arnaiz	66
551	meses	65
552	honrada	65
553	expresión	65
554	tales	64
555	plaza	64
556	moral	64
557	miradas	64
558	habrá	64
559	hablaba	64
560	dama	64
561	creer	64
562	ambos	64
563	alegría	64
564	acá	64
565	sor	63
566	según	63
567	risa	63
568	niños	63
569	mirada	63
570	visita	62
571	verdadero	62
572	vas	62
573	único	62
574	siguió	62
575	primer	62
576	ponerse	62
577	largo	62
578	casas	62
579	ayer	62
580	siquiera	61
581	repente	61
582	memoria	61
583	ii	61
584	enfermo	61
585	vueltas	60
586	venga	60
587	pensando	60
588	oh	60
589	nueva	60
590	echar	60
591	chicos	60
592	cerebro	60
593	ama	60
594	virgen	59
595	viera	59
596	verle	59
597	ven	59
598	vale	59
599	pituso	59
600	pena	59
601	pelo	59
602	dedos	59
603	decirle	59
604	cura	59
605	tiempos	58
606	tenemos	58
607	sr	58
608	propia	58
609	hablando	58
610	fuese	58
611	efecto	58
612	echando	58
613	diré	58
614	dan	58
615	caer	58
616	vivo	57
617	venido	57
618	silla	57
619	sale	57
620	naturaleza	57
621	dicen	57
622	creyó	57
623	anoche	57
624	tus	56
625	suya	56
626	poniendo	56
627	paciencia	56
628	habló	56
629	detrás	56
630	derecho	56
631	dejar	56
632	color	56
633	carne	56
634	suyo	55
635	sociedad	55
636	ruido	55
637	puedes	55
638	perdido	55
639	noches	55
640	natural	55
641	disparates	55
642	público	54
643	oyó	54
644	lógica	54
645	doce	54
646	añadió	54
647	veras	53
648	vea	53
649	triste	53
650	toma	53
651	sombrero	53
652	sol	53
653	sofá	53
654	silencio	53
655	pudiera	53
656	indicó	53
657	dolor	53
658	diferentes	53
659	dejaba	53
660	culpa	53
661	cuánto	53
662	coche	53
663	clase	53
664	atrás	53
665	andar	53
666	solía	52
667	sentido	52
668	mona	52
669	llevó	52
670	feliz	52
671	cuales	52
672	botica	52
673	bonita	52
674	además	52
675	tantas	51
676	segundo	51
677	paz	51
678	parecían	51
679	mentira	51
680	ley	51
681	lejos	51
682	gabinete	51
683	frío	51
684	faltaba	51
685	cogió	51
686	calor	51
687	buenos	51
688	basilio	51
689	viejo	50
690	tonta	50
691	tantos	50
692	sentimiento	50
693	realidad	50
694	pesar	50
695	médico	50
696	i	50
697	fe	50
698	di	50
699	dé	50
700	balcón	50
701	vivía	49
702	tonto	49
703	tertulia	49
704	talento	49
705	sobrina	49
706	particular	49
707	observó	49
708	nariz	49
709	misa	49
710	mire	49
711	llamar	49
712	llaman	49
713	llama	49
714	lengua	49
715	honor	49
716	contar	49
717	arte	49
718	tomó	48
719	tomaba	48
720	seguía	48
721	sacar	48
722	respeto	48
723	principio	48
724	paseo	48
725	oro	48
726	maría	48
727	llorar	48
728	fundadora	48
729	conviene	48
730	contigo	48
731	confianza	48
732	causa	48
733	ánimo	48
734	anda	48
735	alta	48
736	adelante	48
737	vestido	47
738	valor	47
739	tuviera	47
740	tomando	47
741	tenga	47
742	suerte	47
743	rostro	47
744	ratos	47
745	pone	47
746	pies	47
747	loco	47
748	interés	47
749	gustaba	47
750	dormir	47
751	diga	47
752	difícil	47
753	carácter	47
754	bonito	47
755	baja	47
756	ambas	47
757	verá	46
758	tristeza	46
759	torquemada	46
760	tío	46
761	siete	46
762	repitió	46
763	querida	46
764	pasando	46
765	derecha	46
766	cuya	46
767	cree	46
768	cayó	46
769	asunto	46
770	vuelto	45
771	poca	45
772	par	45
773	ocasión	45
774	micaelas	45
775	juicio	45
776	interior	45
777	empezaba	45
778	duros	45
779	cristo	45
780	crees	45
781	costumbre	45
782	corredor	45
783	convento	45
784	caballero	45
785	vergüenza	44
786	sitio	44
787	sentimientos	44
788	seis	44
789	sacó	44
790	ojo	44
791	nosotros	44
792	muerto	44
793	humana	44
794	golpe	44
795	edad	44
796	diciéndole	44
797	criada	44
798	conocía	44
799	comedor	44
800	bárbara	44
801	amigas	44
802	tierra	43
803	sentir	43
804	segismundo	43
805	sacaba	43
806	real	43
807	querido	43
808	oye	43
809	mes	43
810	mar	43
811	loca	43
812	llena	43
813	llegaba	43
814	leche	43
815	lágrimas	43
816	ja	43
817	deseo	43
818	debajo	43
819	botas	43
820	aparisi	43
821	subir	42
822	pura	42
823	pongo	42
824	política	42
825	pareció	42
826	oía	42
827	monjas	42
828	mitad	42
829	ira	42
830	ilusión	42
831	haya	42
832	género	42
833	establecimiento	42
834	dices	42
835	daban	42
836	ciertos	42
837	alguien	42
838	volviendo	41
839	vive	41
840	veremos	41
841	señores	41
842	quita	41
843	principal	41
844	pepe	41
845	patio	41
846	pan	41
847	música	41
848	lenguaje	41
849	justicia	41
850	hechos	41
851	hacían	41
852	fácil	41
853	esperaba	41
854	dura	41
855	deseos	41
856	comprar	41
857	caído	41
858	alguno	41
859	absolutamente	41
860	vuelve	40
861	víctima	40
862	traía	40
863	tontería	40
864	perdón	40
865	lleva	40
866	gritó	40
867	fueran	40
868	entrado	40
869	echado	40
870	dejando	40
871	coger	40
872	busca	40
873	andaba	40
874	volvía	39
875	voluntad	39
876	traer	39
877	serio	39
878	religión	39
879	quieras	39
880	quedaba	39
881	pueden	39
882	pieza	39
883	nuestro	39
884	noticia	39
885	muñoz	39
886	meter	39
887	marqués	39
888	malas	39
889	madres	39
890	jamás	39
891	horrible	39
892	hago	39
893	hacerle	39
894	forma	39
895	figura	39
896	enteramente	39
897	duro	39
898	doy	39
899	correr	39
900	casarse	39
901	cargo	39
902	calles	39
903	bromas	39
904	azul	39
905	abrió	39
906	tendrá	38
907	supo	38
908	siento	38
909	siendo	38
910	salida	38
911	portal	38
912	perder	38
913	pedir	38
914	obras	38
915	negra	38
916	libre	38
917	libertad	38
918	genio	38
919	encontraba	38
920	deseaba	38
921	cuyo	38
922	crea	38
923	chiquilla	38
924	casos	38
925	banco	38
926	viva	37
927	quevedo	37
928	próxima	37
929	podían	37
930	opinión	37
931	matrimonio	37
932	matar	37
933	llave	37
934	haga	37
935	grave	37
936	favor	37
937	cuento	37
938	contestó	37
939	comercio	37
940	asilo	37
941	social	36
942	señorito	36
943	salido	36
944	ruiz	36
945	ratito	36
946	prosiguió	36
947	parecido	36
948	órdenes	36
949	necesidad	36
950	movimiento	36
951	mantón	36
952	mandó	36
953	llegado	36
954	juanín	36
955	iii	36
956	haces	36
957	habitación	36
958	fondo	36
959	encontró	36
960	demasiado	36
961	cuentas	36
962	contrario	36
963	campo	36
964	basta	36
965	terror	35
966	salud	35
967	puertas	35
968	pobres	35
969	piedra	35
970	pico	35
971	pasillo	35
972	malos	35
973	cuartos	35
974	conozco	35
975	virtud	34
976	verdadera	34
977	ventana	34
978	treinta	34
979	tranquilo	34
980	tema	34
981	sonriendo	34
982	sentó	34
983	seguro	34
984	rico	34
985	reía	34
986	querían	34
987	puro	34
988	pecado	34
989	país	34
990	nuestra	34
991	noticias	34
992	ninguno	34
993	murmuró	34
994	modelo	34
995	lleno	34
996	levantó	34
997	leer	34
998	ji	34
999	hermosa	34
1000	hablado	34
1001	gobierno	34
1002	francamente	34
1003	estómago	34
1004	echaba	34
1005	dientes	34
1006	criatura	34
1007	compañía	34
1008	cómoda	34
1009	chocolate	34
1010	chiquillos	34
1011	capa	34
1012	broma	34
1013	apetito	34
1014	alto	34
1015	afirmó	34
1016	veinte	33
1017	última	33
1018	trato	33
1019	trabajar	33
1020	somos	33
1021	seguir	33
1022	salían	33
1023	respecto	33
1024	queda	33
1025	primeros	33
1026	platón	33
1027	parecer	33
1028	olmedo	33
1029	objeto	33
1030	motivo	33
1031	manía	33
1032	manda	33
1033	maldita	33
1034	llamaba	33
1035	hombros	33
1036	hecha	33
1037	gordo	33
1038	gloria	33
1039	fuego	33
1040	frase	33
1041	estuviera	33
1042	entraron	33
1043	encontrar	33
1044	ejemplo	33
1045	disparate	33
1046	dignidad	33
1047	delfina	33
1048	consigo	33
1049	caridad	33
1050	caña	33
1051	cantidad	33
1052	caía	33
1053	blanco	33
1054	acciones	33
1055	vicio	32
1056	tonterías	32
1057	subió	32
1058	sonrisa	32
1059	segura	32
1060	sacando	32
1061	relaciones	32
1062	rabia	32
1063	quieren	32
1064	polvo	32
1065	pase	32
1066	pared	32
1067	papá	32
1068	os	32
1069	ocurrió	32
1070	nueve	32
1071	muchacho	32
1072	metió	32
1073	lecho	32
1074	imposible	32
1075	hierro	32
1076	hacerlo	32
1077	habla	32
1078	gritos	32
1079	flores	32
1080	estuvieron	32
1081	esposo	32
1082	entusiasmo	32
1083	educación	32
1084	demonio	32
1085	deja	32
1086	decían	32
1087	decente	32
1088	cualquiera	32
1089	cuál	32
1090	completamente	32
1091	benigna	32
1092	acuerdo	32
1093	actitud	32
1094	trataba	31
1095	toledo	31
1096	tendría	31
1097	superiora	31
1098	santísima	31
1099	salieron	31
1100	reloj	31
1101	pueda	31
1102	poquito	31
1103	piso	31
1104	pasión	31
1105	pareja	31
1106	número	31
1107	mostraba	31
1108	llevado	31
1109	libros	31
1110	juro	31
1111	hombro	31
1112	hermosura	31
1113	fino	31
1114	estilo	31
1115	dulce	31
1116	dormido	31
1117	diría	31
1118	demonios	31
1119	cuello	31
1120	corrió	31
1121	cogía	31
1122	cava	31
1123	cambio	31
1124	visitas	30
1125	única	30
1126	tomado	30
1127	teatro	30
1128	serlo	30
1129	riendo	30
1130	quedose	30
1131	punta	30
1132	puestos	30
1133	prisa	30
1134	poniéndose	30
1135	pocas	30
1136	piernas	30
1137	ocho	30
1138	negocio	30
1139	necesitaba	30
1140	morir	30
1141	miseria	30
1142	lugar	30
1143	llega	30
1144	jaqueca	30
1145	imaginación	30
1146	igual	30
1147	honradez	30
1148	espiritual	30
1149	entra	30
1150	destino	30
1151	creí	30
1152	calma	30
1153	bajó	30
1154	asiento	30
1155	acto	30
1156	vieron	29
1157	suspiro	29
1158	saca	29
1159	saben	29
1160	río	29
1161	rey	29
1162	respuesta	29
1163	primo	29
1164	pregunta	29
1165	pocos	29
1166	pobrecito	29
1167	manifestó	29
1168	llamó	29
1169	levantarse	29
1170	infame	29
1171	impresión	29
1172	humor	29
1173	general	29
1174	fresco	29
1175	feliciana	29
1176	españa	29
1177	enferma	29
1178	dormía	29
1179	disposición	29
1180	dieron	29
1181	debo	29
1182	dándole	29
1183	damas	29
1184	conforme	29
1185	cogido	29
1186	casar	29
1187	carrera	29
1188	buscar	29
1189	blanca	29
1190	belén	29
1191	autoridad	29
1192	viento	28
1193	verse	28
1194	trae	28
1195	terreno	28
1196	superior	28
1197	sombra	28
1198	rodillas	28
1199	recuerdo	28
1200	quite	28
1201	quitado	28
1202	quitaba	28
1203	piensa	28
1204	permitía	28
1205	pensamientos	28
1206	ocurre	28
1207	muebles	28
1208	miraban	28
1209	juego	28
1210	iv	28
1211	hará	28
1212	farmacia	28
1213	farmacéutico	28
1214	expresar	28
1215	esperando	28
1216	entrando	28
1217	dueño	28
1218	dedo	28
1219	curas	28
1220	creyendo	28
1221	contento	28
1222	conque	28
1223	conocer	28
1224	conoce	28
1225	compras	28
1226	claridad	28
1227	carta	28
1228	capaz	28
1229	besos	28
1230	ave	28
1231	adiós	28
1232	acento	28
1233	acababa	28
1234	voces	27
1235	varias	27
1236	v	27
1237	tren	27
1238	tranquila	27
1239	trajo	27
1240	teniendo	27
1241	temor	27
1242	soltó	27
1243	solos	27
1244	serenidad	27
1245	sepa	27
1246	sentado	27
1247	semblante	27
1248	seguramente	27
1249	seda	27
1250	salvaje	27
1251	presente	27
1252	plato	27
1253	plata	27
1254	plan	27
1255	pintado	27
1256	pez	27
1257	padres	27
1258	oficio	27
1259	ocurrido	27
1260	niñas	27
1261	nene	27
1262	maldito	27
1263	larga	27
1264	juntos	27
1265	humano	27
1266	hice	27
1267	extremo	27
1268	esté	27
1269	escribir	27
1270	entendía	27
1271	entender	27
1272	encarnación	27
1273	dispuesto	27
1274	dirección	27
1275	desgracia	27
1276	déjame	27
1277	dejado	27
1278	clérigo	27
1279	cincuenta	27
1280	barrio	27
1281	barbaridad	27
1282	apareció	27
1283	amistad	27
1284	alegre	27
1285	vuelvo	26
1286	vienen	26
1287	verde	26
1288	vengo	26
1289	vendrá	26
1290	vecindad	26
1291	total	26
1292	resultado	26
1293	respondió	26
1294	respondía	26
1295	ramo	26
1296	queriendo	26
1297	puesta	26
1298	prójima	26
1299	presencia	26
1300	piedad	26
1301	perfectamente	26
1302	pasaron	26
1303	orgullo	26
1304	ocurría	26
1305	muerta	26
1306	meterse	26
1307	medicina	26
1308	limpia	26
1309	isla	26
1310	inocente	26
1311	inglés	26
1312	hucha	26
1313	hostia	26
1314	hijas	26
1315	fina	26
1316	feo	26
1317	existencia	26
1318	estará	26
1319	época	26
1320	dicha	26
1321	cuándo	26
1322	convicción	26
1323	contaba	26
1324	ciencia	26
1325	ciego	26
1326	celos	26
1327	capellán	26
1328	cae	26
1329	cabo	26
1330	bestia	26
1331	abrir	26
1332	villuendas	25
1333	traído	25
1334	toca	25
1335	timidez	25
1336	términos	25
1337	sustancia	25
1338	soledad	25
1339	simpático	25
1340	sigue	25
1341	seriedad	25
1342	secreto	25
1343	satisfacción	25
1344	rincón	25
1345	ricos	25
1346	recibir	25
1347	rara	25
1348	quedado	25
1349	prendas	25
1350	ponen	25
1351	piezas	25
1352	pienso	25
1353	perro	25
1354	parís	25
1355	parecen	25
1356	papeles	25
1357	nuevas	25
1358	nicanora	25
1359	metido	25
1360	máquina	25
1361	maestro	25
1362	levantándose	25
1363	lección	25
1364	iré	25
1365	imagen	25
1366	hermanos	25
1367	herencia	25
1368	esquina	25
1369	espejo	25
1370	entiende	25
1371	diera	25
1372	darse	25
1373	cumplir	25
1374	compra	25
1375	completo	25
1376	compasión	25
1377	comida	25
1378	comía	25
1379	cojo	25
1380	circunstancias	25
1381	buscando	25
1382	bolsillo	25
1383	boda	25
1384	amante	25
1385	admirable	25
1386	vela	24
1387	uso	24
1388	usaba	24
1389	tuvieron	24
1390	tuve	24
1391	sorpresa	24
1392	sintiendo	24
1393	sillas	24
1394	severidad	24
1395	servicio	24
1396	seria	24
1397	sentarse	24
1398	seguida	24
1399	sabido	24
1400	recogidas	24
1401	rafaela	24
1402	quienes	24
1403	pusieron	24
1404	propios	24
1405	podrá	24
1406	pide	24
1407	pedazo	24
1408	patricia	24
1409	pacheco	24
1410	oyendo	24
1411	olor	24
1412	ocasiones	24
1413	nones	24
1414	narices	24
1415	medios	24
1416	manto	24
1417	leyes	24
1418	izquierda	24
1419	imaginar	24
1420	humanidad	24
1421	humanas	24
1422	haré	24
1423	hambre	24
1424	hacerse	24
1425	guerra	24
1426	grado	24
1427	gozo	24
1428	fiera	24
1429	falda	24
1430	esperar	24
1431	escena	24
1432	entendimiento	24
1433	empezar	24
1434	desgraciado	24
1435	decirse	24
1436	debían	24
1437	cuestión	24
1438	criado	24
1439	creerás	24
1440	contenta	24
1441	cogiendo	24
1442	chiquillo	24
1443	bendito	24
1444	ayuda	24
1445	asombro	24
1446	anterior	24
1447	adoración	24
1448	abrigo	24
1449	verte	23
1450	valiente	23
1451	tiro	23
1452	tiendas	23
1453	techo	23
1454	sinceridad	23
1455	sillón	23
1456	seré	23
1457	saliendo	23
1458	romper	23
1459	retiró	23
1460	retirarse	23
1461	religiosa	23
1462	rápidamente	23
1463	probar	23
1464	ponían	23
1465	podido	23
1466	pillo	23
1467	pasaban	23
1468	olimpia	23
1469	observando	23
1470	novia	23
1471	nosotras	23
1472	nena	23
1473	nacido	23
1474	monja	23
1475	metía	23
1476	marcela	23
1477	local	23
1478	limosna	23
1479	libro	23
1480	león	23
1481	jesús	23
1482	isabel	23
1483	hubieran	23
1484	hiciera	23
1485	guapa	23
1486	gato	23
1487	firme	23
1488	filosofía	23
1489	fijo	23
1490	felicidad	23
1491	entero	23
1492	enfermedad	23
1493	daría	23
1494	cuentos	23
1495	continuaba	23
1496	conocido	23
1497	chulita	23
1498	casada	23
1499	acerca	23
1500	acción	23
1501	verdaderamente	22
1502	vaso	22
1503	tratar	22
1504	tranquilidad	22
1505	tirar	22
1506	temprano	22
1507	temía	22
1508	siglo	22
1509	señal	22
1510	sentada	22
1511	seno	22
1512	salen	22
1513	sacerdote	22
1514	retrato	22
1515	razones	22
1516	quia	22
1517	preguntas	22
1518	práctica	22
1519	peso	22
1520	pecados	22
1521	partes	22
1522	palo	22
1523	norte	22
1524	necesito	22
1525	mérito	22
1526	mejores	22
1527	mayores	22
1528	manuel	22
1529	lujo	22
1530	llevo	22
1531	importancia	22
1532	hicieron	22
1533	haría	22
1534	hagas	22
1535	habrían	22
1536	fría	22
1537	frases	22
1538	formalidad	22
1539	figuras	22
1540	expresó	22
1541	español	22
1542	espalda	22
1543	enemigo	22
1544	encuentro	22
1545	embargo	22
1546	elegante	22
1547	eh	22
1548	ea	22
1549	dijera	22
1550	diferencia	22
1551	declaró	22
1552	casado	22
1553	carnes	22
1554	caras	22
1555	amo	22
1556	altar	22
1557	almorzar	22
1558	adentro	22
1559	acercó	22
1560	acera	22
1561	últimos	21
1562	tocar	21
1563	tira	21
1564	tendré	21
1565	tela	21
1566	sostener	21
1567	solas	21
1568	sentándose	21
1569	semana	21
1570	seguridad	21
1571	sano	21
1572	salto	21
1573	sagrario	21
1574	quitó	21
1575	prueba	21
1576	problema	21
1577	primeras	21
1578	plazuela	21
1579	pensado	21
1580	patria	21
1581	pasiones	21
1582	partido	21
1583	oscuridad	21
1584	momentos	21
1585	minutos	21
1586	mesas	21
1587	mandar	21
1588	limpio	21
1589	letras	21
1590	inteligencia	21
1591	hoja	21
1592	hablaban	21
1593	fortuna	21
1594	expresaba	21
1595	excelente	21
1596	estaría	21
1597	esposos	21
1598	escuela	21
1599	entrada	21
1600	enterarse	21
1601	enfrente	21
1602	edificio	21
1603	dudas	21
1604	dispuesta	21
1605	disimular	21
1606	deseando	21
1607	decirlo	21
1608	debilidad	21
1609	cuerda	21
1610	corría	21
1611	conoces	21
1612	conducta	21
1613	coja	21
1614	coge	21
1615	cintura	21
1616	callar	21
1617	averiguar	21
1618	aseguro	21
1619	arma	21
1620	antonio	21
1621	andando	21
1622	anciano	21
1623	admiración	21
1624	actos	21
1625	acaso	21
1626	acabó	21
1627	abur	21
1628	volvería	20
1629	verme	20
1630	varios	20
1631	vanidad	20
1632	valía	20
1633	tratando	20
1634	tocan	20
1635	subía	20
1636	socorro	20
1637	sentar	20
1638	santidad	20
1639	salón	20
1640	saco	20
1641	principios	20
1642	ponga	20
1643	pido	20
1644	pelos	20
1645	pecadora	20
1646	pasan	20
1647	partida	20
1648	nuevos	20
1649	nuestros	20
1650	noble	20
1651	nerviosa	20
1652	necesita	20
1653	naturalmente	20
1654	mozo	20
1655	mete	20
1656	menor	20
1657	marcha	20
1658	mando	20
1659	maestra	20
1660	largas	20
1661	juntas	20
1662	jueves	20
1663	inquietud	20
1664	impulso	20
1665	huerta	20
1666	ginés	20
1667	gesto	20
1668	fui	20
1669	francisco	20
1670	estuve	20
1671	envidia	20
1672	encargo	20
1673	echarle	20
1674	distancia	20
1675	dirá	20
1676	digas	20
1677	desdén	20
1678	dejo	20
1679	deje	20
1680	decoro	20
1681	creas	20
1682	corte	20
1683	corriente	20
1684	consejos	20
1685	círculo	20
1686	cafés	20
1687	breve	20
1688	bondad	20
1689	balcones	20
1690	bah	20
1691	apreciar	20
1692	amantes	20
1693	almuerzo	20
1694	agregó	20
1695	abierta	20
1696	zalamero	19
1697	volverse	19
1698	vinieron	19
1699	vete	19
1700	vengan	19
1701	veían	19
1702	vara	19
1703	trujillo	19
1704	tocaba	19
1705	tercera	19
1706	suegra	19
1707	sucesos	19
1708	sonreía	19
1709	soltar	19
1710	sesos	19
1711	satisfecho	19
1712	rompió	19
1713	revólver	19
1714	responder	19
1715	reserva	19
1716	recado	19
1717	quitar	19
1718	pudiendo	19
1719	pública	19
1720	protección	19
1721	propósito	19
1722	perros	19
1723	perdone	19
1724	pavos	19
1725	paredes	19
1726	oscuro	19
1727	once	19
1728	obligación	19
1729	nuera	19
1730	nervioso	19
1731	natividad	19
1732	moda	19
1733	miserable	19
1734	mañanas	19
1735	limpieza	19
1736	levita	19
1737	intención	19
1738	inspiraba	19
1739	indecente	19
1740	increíble	19
1741	importante	19
1742	hilo	19
1743	hacienda	19
1744	habiendo	19
1745	gumersindo	19
1746	fresca	19
1747	franqueza	19
1748	flor	19
1749	espera	19
1750	escaleras	19
1751	entraban	19
1752	energía	19
1753	encontrado	19
1754	domingos	19
1755	disgusto	19
1756	despacho	19
1757	custodia	19
1758	corta	19
1759	correspondencia	19
1760	cordero	19
1761	confusión	19
1762	condición	19
1763	común	19
1764	claramente	19
1765	clara	19
1766	casó	19
1767	cárcel	19
1768	capital	19
1769	capilla	19
1770	caminos	19
1771	cabello	19
1772	bribona	19
1773	botón	19
1774	atrevía	19
1775	aspecto	19
1776	arreglo	19
1777	antiguo	19
1778	antigua	19
1779	aires	19
1780	acabar	19
1781	viaje	18
1782	velas	18
1783	veinticinco	18
1784	vecinas	18
1785	tremendo	18
1786	traje	18
1787	terrible	18
1788	ten	18
1789	tarasca	18
1790	suelto	18
1791	suavemente	18
1792	soberbia	18
1793	sistema	18
1794	sirve	18
1795	simple	18
1796	serían	18
1797	revelaba	18
1798	rencor	18
1799	recibido	18
1800	ramas	18
1801	quieran	18
1802	quedar	18
1803	pruebas	18
1804	prudente	18
1805	providencia	18
1806	precisamente	18
1807	peligro	18
1808	patas	18
1809	pañuelos	18
1810	pájaros	18
1811	oscuras	18
1812	observación	18
1813	negocios	18
1814	murió	18
1815	montes	18
1816	modales	18
1817	menudo	18
1818	llevaron	18
1819	llamaban	18
1820	juicios	18
1821	infierno	18
1822	improviso	18
1823	impresiones	18
1824	ilustre	18
1825	honrado	18
1826	hablaron	18
1827	gustan	18
1828	graciosa	18
1829	furor	18
1830	funciones	18
1831	fuertes	18
1832	francia	18
1833	formas	18
1834	fija	18
1835	figúrate	18
1836	fenelón	18
1837	federico	18
1838	fea	18
1839	familias	18
1840	facha	18
1841	evitar	18
1842	esperanza	18
1843	especie	18
1844	española	18
1845	espanto	18
1846	esfuerzos	18
1847	emoción	18
1848	echarse	18
1849	duque	18
1850	dichoso	18
1851	despertar	18
1852	delirio	18
1853	deben	18
1854	cuarenta	18
1855	cristiano	18
1856	convenía	18
1857	contado	18
1858	consuelo	18
1859	compañero	18
1860	comedia	18
1861	come	18
1862	centro	18
1863	cayendo	18
1864	campanilla	18
1865	buscaba	18
1866	bruto	18
1867	bajar	18
1868	azúcar	18
1869	ataque	18
1870	animal	18
1871	alegro	18
1872	acuerdas	18
1873	volvieron	17
1874	vivos	17
1875	vii	17
1876	vendría	17
1877	vecino	17
1878	valen	17
1879	tropa	17
1880	trance	17
1881	trabajaba	17
1882	tontos	17
1883	tardó	17
1884	tamaño	17
1885	taller	17
1886	supiera	17
1887	suceso	17
1888	sublime	17
1889	sonaba	17
1890	simpatía	17
1891	seguido	17
1892	seca	17
1893	seas	17
1894	sean	17
1895	sacado	17
1896	sábanas	17
1897	rica	17
1898	retiro	17
1899	resulta	17
1900	repetía	17
1901	remediar	17
1902	reja	17
1903	regular	17
1904	rata	17
1905	ramón	17
1906	quince	17
1907	quedarse	17
1908	pusiera	17
1909	próximo	17
1910	propuso	17
1911	propias	17
1912	profundo	17
1913	profunda	17
1914	preguntar	17
1915	pierna	17
1916	periódicos	17
1917	perdida	17
1918	pequeña	17
1919	pedazos	17
1920	pasillos	17
1921	parar	17
1922	pa	17
1923	oyeron	17
1924	oían	17
1925	novedades	17
1926	notar	17
1927	nacimiento	17
1928	muchísimo	17
1929	morenos	17
1930	monte	17
1931	mirándola	17
1932	merece	17
1933	mental	17
1934	medida	17
1935	manolo	17
1936	madera	17
1937	lance	17
1938	jugar	17
1939	inmenso	17
1940	individuos	17
1941	imágenes	17
1942	humo	17
1943	hermoso	17
1944	grupo	17
1945	golpes	17
1946	fenómeno	17
1947	extraordinariamente	17
1948	estación	17
1949	espacio	17
1950	engañado	17
1951	empezado	17
1952	doctrina	17
1953	divina	17
1954	dime	17
1955	dígame	17
1956	desgraciada	17
1957	defensa	17
1958	débil	17
1959	das	17
1960	cuerdo	17
1961	cuantos	17
1962	crecía	17
1963	contener	17
1964	conocimiento	17
1965	concluir	17
1966	concepto	17
1967	compañera	17
1968	colores	17
1969	ciento	17
1970	cien	17
1971	célebre	17
1972	cartas	17
1973	camisa	17
1974	caja	17
1975	caían	17
1976	cabía	17
1977	caballo	17
1978	bruscamente	17
1979	bola	17
1980	billetes	17
1981	belleza	17
1982	aguas	17
1983	ademán	17
1984	vienes	16
1985	vestir	16
1986	tuyo	16
1987	tuya	16
1988	turbación	16
1989	trató	16
1990	trampa	16
1991	tocayo	16
1992	tiró	16
1993	sujeto	16
1994	sostenía	16
1995	servía	16
1996	sereno	16
1997	sentidos	16
1998	sales	16
1999	rojo	16
2000	resistir	16
2001	reían	16
2002	refugio	16
2003	recibió	16
2004	quedándose	16
2005	púsose	16
2006	profesor	16
2007	prenda	16
2008	pontejos	16
2009	pitusa	16
2010	pidió	16
2011	personal	16
2012	periodo	16
2013	perdía	16
2014	pegar	16
2015	pedro	16
2016	paseos	16
2017	pariente	16
2018	pago	16
2019	pagar	16
2020	orejas	16
2021	olvidar	16
2022	oiga	16
2023	ofrecía	16
2024	novio	16
2025	notó	16
2026	nervios	16
2027	negras	16
2028	mostrando	16
2029	montón	16
2030	misas	16
2031	mata	16
2032	masa	16
2033	lotería	16
2034	llevándose	16
2035	llevando	16
2036	llevan	16
2037	lío	16
2038	lecciones	16
2039	inspiración	16
2040	infantil	16
2041	hueco	16
2042	hubieras	16
2043	hermanas	16
2044	hallaba	16
2045	hable	16
2046	hábitos	16
2047	habías	16
2048	guapo	16
2049	graves	16
2050	fuerzas	16
2051	filomenas	16
2052	fiel	16
2053	extranjero	16
2054	estuviese	16
2055	estúpido	16
2056	estudio	16
2057	estudiar	16
2058	estaré	16
2059	entierro	16
2060	encontré	16
2061	empezaban	16
2062	echa	16
2063	duró	16
2064	domicilio	16
2065	difunto	16
2066	dificultades	16
2067	detuvo	16
2068	despertó	16
2069	desconsuelo	16
2070	desconocido	16
2071	delicado	16
2072	decirme	16
2073	debemos	16
2074	crisis	16
2075	creen	16
2076	copa	16
2077	contó	16
2078	contestar	16
2079	contemplando	16
2080	contarle	16
2081	consejo	16
2082	concluido	16
2083	comprendió	16
2084	completa	16
2085	coches	16
2086	clases	16
2087	chasco	16
2088	castelar	16
2089	casamiento	16
2090	cansado	16
2091	cajas	16
2092	botella	16
2093	barba	16
2094	ayudaba	16
2095	artista	16
2096	artículo	16
2097	arroz	16
2098	ardor	16
2099	árbol	16
2100	apariencias	16
2101	ansiedad	16
2102	amiguita	16
2103	afán	16
2104	acercaba	16
2105	absoluta	16
2106	abierto	16
2107	viven	15
2108	venían	15
2109	vengas	15
2110	velo	15
2111	tuviese	15
2112	tremenda	15
2113	trastos	15
2114	traigo	15
2115	toros	15
2116	tomo	15
2117	tocando	15
2118	tengas	15
2119	té	15
2120	susto	15
2121	suspiros	15
2122	simón	15
2123	señá	15
2124	seco	15
2125	salita	15
2126	sagrada	15
2127	rumor	15
2128	rosario	15
2129	respirar	15
2130	respiración	15
2131	representaba	15
2132	regente	15
2133	recoger	15
2134	re	15
2135	razonable	15
2136	quedaron	15
2137	quedaban	15
2138	puño	15
2139	pueblos	15
2140	pozo	15
2141	ponerle	15
2142	pescuezo	15
2143	perfecta	15
2144	pensé	15
2145	pego	15
2146	pausa	15
2147	paño	15
2148	paca	15
2149	ochoa	15
2150	observar	15
2151	nuestras	15
2152	niñez	15
2153	nació	15
2154	monstruo	15
2155	modestia	15
2156	mías	15
2157	locura	15
2158	llevarle	15
2159	llamado	15
2160	lista	15
2161	levantose	15
2162	levantar	15
2163	letra	15
2164	lentamente	15
2165	ladrón	15
2166	ladrillos	15
2167	ladrillo	15
2168	jóvenes	15
2169	insigne	15
2170	huevo	15
2171	hubiese	15
2172	horror	15
2173	herida	15
2174	haciéndole	15
2175	habitaciones	15
2176	guardia	15
2177	garganta	15
2178	formaban	15
2179	fisonomía	15
2180	faltó	15
2181	facciones	15
2182	extraña	15
2183	extensión	15
2184	expresarse	15
2185	estrellas	15
2186	escándalo	15
2187	entrañas	15
2188	encargado	15
2189	empezaron	15
2190	eclesiástica	15
2191	durmió	15
2192	díjole	15
2193	desprecio	15
2194	despidió	15
2195	desorden	15
2196	desdémona	15
2197	desagradable	15
2198	debió	15
2199	crimen	15
2200	corriendo	15
2201	conseguir	15
2202	consecuencia	15
2203	conferencia	15
2204	conceptos	15
2205	comprendo	15
2206	comprender	15
2207	cólera	15
2208	codo	15
2209	claras	15
2210	chillidos	15
2211	chamberí	15
2212	cejas	15
2213	carga	15
2214	candelaria	15
2215	cállate	15
2216	cajón	15
2217	cabezas	15
2218	bulto	15
2219	bulla	15
2220	beso	15
2221	bata	15
2222	bajaba	15
2223	armó	15
2224	armar	15
2225	argumentos	15
2226	ángeles	15
2227	amar	15
2228	alzar	15
2229	acordaba	15
2230	vuelves	14
2231	vuelva	14
2232	volví	14
2233	vía	14
2234	vestidos	14
2235	verdes	14
2236	verdades	14
2237	verano	14
2238	vayas	14
2239	valencia	14
2240	tunante	14
2241	tratado	14
2242	trata	14
2243	trasto	14
2244	trapo	14
2245	trabajos	14
2246	tenéis	14
2247	sueños	14
2248	suelta	14
2249	sonó	14
2250	solución	14
2251	soltando	14
2252	silvia	14
2253	siente	14
2254	seres	14
2255	sal	14
2256	sabiendo	14
2257	risueña	14
2258	rezar	14
2259	revés	14
2260	recibía	14
2261	raza	14
2262	querrá	14
2263	quedo	14
2264	pulso	14
2265	provincia	14
2266	progreso	14
2267	profundamente	14
2268	procesión	14
2269	presunción	14
2270	preparado	14
2271	porvenir	14
2272	pones	14
2273	podrían	14
2274	pobreza	14
2275	pobrecilla	14
2276	planta	14
2277	píldoras	14
2278	pidiendo	14
2279	perdona	14
2280	pequeño	14
2281	penas	14
2282	pegado	14
2283	pasará	14
2284	pálida	14
2285	ordinaria	14
2286	ocurren	14
2287	novedad	14
2288	notas	14
2289	notaba	14
2290	muertos	14
2291	muere	14
2292	muera	14
2293	moviendo	14
2294	moscas	14
2295	monedas	14
2296	meto	14
2297	merezco	14
2298	marzo	14
2299	maridos	14
2300	marcharse	14
2301	manta	14
2302	mandaba	14
2303	londres	14
2304	llegaron	14
2305	llegando	14
2306	llaves	14
2307	liberación	14
2308	leía	14
2309	lados	14
2310	jefe	14
2311	jaquecas	14
2312	irse	14
2313	iremos	14
2314	inmensa	14
2315	importaba	14
2316	hueso	14
2317	hallábase	14
2318	hacerme	14
2319	habrás	14
2320	hablarle	14
2321	haberse	14
2322	grito	14
2323	gorro	14
2324	gorda	14
2325	gas	14
2326	ganado	14
2327	finas	14
2328	fíjate	14
2329	fiebre	14
2330	febril	14
2331	faltado	14
2332	fácilmente	14
2333	fábrica	14
2334	extraordinario	14
2335	explicaciones	14
2336	existe	14
2337	estancia	14
2338	esfuerzo	14
2339	escape	14
2340	entiendo	14
2341	enterado	14
2342	enfermos	14
2343	enamorado	14
2344	empleado	14
2345	duele	14
2346	domingo	14
2347	divertido	14
2348	digan	14
2349	despacio	14
2350	descubrir	14
2351	dependientes	14
2352	delantal	14
2353	déjate	14
2354	deber	14
2355	dándose	14
2356	cuantas	14
2357	cristiana	14
2358	cristales	14
2359	creerlo	14
2360	creeríase	14
2361	costumbres	14
2362	cortesía	14
2363	coronel	14
2364	conveniente	14
2365	contestaba	14
2366	conocí	14
2367	comprendía	14
2368	comandanta	14
2369	clavado	14
2370	cerró	14
2371	cerrada	14
2372	casualidad	14
2373	cariñosa	14
2374	cantar	14
2375	cállese	14
2376	bonitas	14
2377	bocas	14
2378	billete	14
2379	beber	14
2380	baúl	14
2381	bastón	14
2382	atroz	14
2383	atrevió	14
2384	argumento	14
2385	aprendido	14
2386	aplicación	14
2387	apartar	14
2388	angelical	14
2389	amas	14
2390	aguantar	14
2391	actividad	14
2392	abriendo	14
2393	vulgar	13
2394	vivido	13
2395	vestirse	13
2396	vestida	13
2397	vecinos	13
2398	vean	13
2399	uñas	13
2400	tuvieran	13
2401	traían	13
2402	trabajando	13
2403	tome	13
2404	tocó	13
2405	tocante	13
2406	tirando	13
2407	tipo	13
2408	tesoro	13
2409	temores	13
2410	temo	13
2411	talle	13
2412	suponer	13
2413	suma	13
2414	sucia	13
2415	subiendo	13
2416	sube	13
2417	sosiego	13
2418	sofocada	13
2419	síntomas	13
2420	signo	13
2421	servir	13
2422	sermón	13
2423	señales	13
2424	sentirse	13
2425	rubio	13
2426	rigor	13
2427	ricas	13
2428	resto	13
2429	resolución	13
2430	regalo	13
2431	referente	13
2432	recordaba	13
2433	recogió	13
2434	quitarle	13
2435	puramente	13
2436	pude	13
2437	principalmente	13
2438	pretensiones	13
2439	presentes	13
2440	preguntaba	13
2441	práctico	13
2442	pondría	13
2443	pondré	13
2444	piedras	13
2445	pícara	13
2446	perdonar	13
2447	perdió	13
2448	pensarlo	13
2449	pedernero	13
2450	parezca	13
2451	parecíale	13
2452	paraba	13
2453	paja	13
2454	olvidado	13
2455	oigo	13
2456	ofreció	13
2457	novela	13
2458	negros	13
2459	muero	13
2460	muchacha	13
2461	mostrador	13
2462	mosca	13
2463	misterios	13
2464	mismos	13
2465	miraron	13
2466	mirarle	13
2467	mirado	13
2468	ministerio	13
2469	metal	13
2470	mesías	13
2471	matado	13
2472	marras	13
2473	manolita	13
2474	majestad	13
2475	madrugada	13
2476	lumbre	13
2477	llorando	13
2478	llamada	13
2479	liberal	13
2480	lectura	13
2481	lanzó	13
2482	justo	13
2483	juez	13
2484	judío	13
2485	interesante	13
2486	inteligente	13
2487	influencia	13
2488	infancia	13
2489	indulgencia	13
2490	iguales	13
2491	humildad	13
2492	huevos	13
2493	horriblemente	13
2494	hebra	13
2495	hablaremos	13
2496	guardar	13
2497	guardaba	13
2498	grupos	13
2499	gratitud	13
2500	gallo	13
2501	frialdad	13
2502	fórmula	13
2503	final	13
2504	felices	13
2505	fecha	13
2506	faltas	13
2507	falsa	13
2508	facunda	13
2509	facultades	13
2510	extraño	13
2511	expresiones	13
2512	éxito	13
2513	estuvieran	13
2514	enorme	13
2515	engañar	13
2516	encuentra	13
2517	encender	13
2518	ejercicio	13
2519	echo	13
2520	echaron	13
2521	echándose	13
2522	dormida	13
2523	disimulo	13
2524	discurso	13
2525	discurriendo	13
2526	dijeron	13
2527	diente	13
2528	diablo	13
2529	devoción	13
2530	deshonra	13
2531	desea	13
2532	delicada	13
2533	dejan	13
2534	dejaban	13
2535	decirte	13
2536	debes	13
2537	dale	13
2538	cuchillo	13
2539	cuántas	13
2540	crítica	13
2541	créetelo	13
2542	copas	13
2543	conservaba	13
2544	concepción	13
2545	comprendiendo	13
2546	compañeras	13
2547	colmo	13
2548	chuletas	13
2549	causaba	13
2550	carcajada	13
2551	canto	13
2552	calzado	13
2553	benevolencia	13
2554	bajando	13
2555	asuntos	13
2556	asco	13
2557	artículos	13
2558	arranque	13
2559	apretó	13
2560	apretaba	13
2561	apoyando	13
2562	aparecer	13
2563	alzando	13
2564	almas	13
2565	aguardiente	13
2566	admirablemente	13
2567	acostarse	13
2568	acordó	13
2569	abría	13
2570	abra	13
2571	vuelvas	12
2572	villa	12
2573	viii	12
2574	ventanas	12
2575	venganza	12
2576	únicamente	12
2577	últimas	12
2578	tristezas	12
2579	trapos	12
2580	traeré	12
2581	toquilla	12
2582	tomarlo	12
2583	tercero	12
2584	tendremos	12
2585	temeroso	12
2586	tardes	12
2587	suyos	12
2588	sufrir	12
2589	sucesión	12
2590	sospechaba	12
2591	soñado	12
2592	sociales	12
2593	síntoma	12
2594	siguieron	12
2595	significaba	12
2596	sesenta	12
2597	serás	12
2598	señas	12
2599	sentaba	12
2600	sencillez	12
2601	secretos	12
2602	seamos	12
2603	sazón	12
2604	santísimo	12
2605	saltó	12
2606	saliera	12
2607	saberlo	12
2608	roto	12
2609	riqueza	12
2610	república	12
2611	repito	12
2612	regla	12
2613	registro	12
2614	recibimiento	12
2615	realmente	12
2616	rasgos	12
2617	quedan	12
2618	pronunciar	12
2619	príncipe	12
2620	prima	12
2621	pretexto	12
2622	presteza	12
2623	préstamos	12
2624	presentarse	12
2625	premio	12
2626	ponerme	12
2627	pollo	12
2628	pluma	12
2629	piensas	12
2630	peseta	12
2631	personalidad	12
2632	pelota	12
2633	pedirle	12
2634	pasas	12
2635	parroquia	12
2636	parientes	12
2637	parentesco	12
2638	paquete	12
2639	pantalones	12
2640	padecía	12
2641	padecer	12
2642	oyera	12
2643	oírla	12
2644	oí	12
2645	obstante	12
2646	objetos	12
2647	nubes	12
2648	nombres	12
2649	nieto	12
2650	multitud	12
2651	movimientos	12
2652	moverse	12
2653	motivos	12
2654	morirme	12
2655	mirarla	12
2656	militares	12
2657	miguel	12
2658	medicinas	12
2659	mecánica	12
2660	manila	12
2661	malicia	12
2662	llenos	12
2663	líneas	12
2664	leopoldo	12
2665	leña	12
2666	lecturas	12
2667	jugando	12
2668	joaquín	12
2669	jerónima	12
2670	ix	12
2671	iría	12
2672	instinto	12
2673	inglaterra	12
2674	inferior	12
2675	inexplicable	12
2676	individuo	12
2677	indecible	12
2678	inclinándose	12
2679	impulsos	12
2680	impertinente	12
2681	horribles	12
2682	hogar	12
2683	guantes	12
2684	grosería	12
2685	gravedad	12
2686	gobernación	12
2687	gatos	12
2688	furioso	12
2689	furiosa	12
2690	frescura	12
2691	forzoso	12
2692	físico	12
2693	falso	12
2694	faldas	12
2695	extrañas	12
2696	exaltación	12
2697	etc	12
2698	estremecer	12
2699	espectáculo	12
2700	escritorio	12
2701	escalones	12
2702	error	12
2703	entré	12
2704	emplear	12
2705	divertirse	12
2706	distinta	12
2707	digno	12
2708	dieran	12
2709	diabla	12
2710	despierto	12
2711	deseado	12
2712	descubierto	12
2713	descompuesto	12
2714	desazón	12
2715	dejara	12
2716	cumplido	12
2717	cuesta	12
2718	cuarta	12
2719	cuadros	12
2720	cruel	12
2721	crítico	12
2722	cría	12
2723	creído	12
2724	costura	12
2725	corrido	12
2726	concluyó	12
2727	concluida	12
2728	compromiso	12
2729	comprendido	12
2730	comprado	12
2731	comían	12
2732	colegio	12
2733	colcha	12
2734	cochero	12
2735	charla	12
2736	cesta	12
2737	cerebral	12
2738	cementerio	12
2739	celestial	12
2740	cavilaciones	12
2741	casadas	12
2742	carlos	12
2743	caracteres	12
2744	aventuras	12
2745	atrevido	12
2746	asesino	12
2747	arrojar	12
2748	arrojando	12
2749	arreglar	12
2750	aparte	12
2751	añadiendo	12
2752	andan	12
2753	amores	12
2754	alrededor	12
2755	alhajas	12
2756	ajeno	12
2757	agujeros	12
2758	aguja	12
2759	advirtió	12
2760	acompañado	12
2761	aceite	12
2762	acaba	12
2763	volveré	11
2764	viveza	11
2765	visitar	11
2766	viéndole	11
2767	viciosa	11
2768	verán	11
2769	vencido	11
2770	vecina	11
2771	veas	11
2772	unidos	11
2773	tuno	11
2774	trastorno	11
2775	trajeron	11
2776	tontas	11
2777	tomándole	11
2778	tiraba	11
2779	tiestos	11
2780	terciopelo	11
2781	tengamos	11
2782	temerosa	11
2783	suyas	11
2784	supe	11
2785	sueltas	11
2786	suele	11
2787	sucio	11
2788	suceder	11
2789	subido	11
2790	sopa	11
2791	sonreír	11
2792	soltaba	11
2793	sociedades	11
2794	sobra	11
2795	simpática	11
2796	siga	11
2797	servido	11
2798	sepas	11
2799	saque	11
2800	salvación	11
2801	sacristán	11
2802	sacan	11
2803	sabemos	11
2804	rossini	11
2805	robado	11
2806	risas	11
2807	restauración	11
2808	respetable	11
2809	relato	11
2810	relativa	11
2811	relación	11
2812	reconozco	11
2813	recelo	11
2814	rayo	11
2815	raya	11
2816	rastro	11
2817	quisieran	11
2818	quieto	11
2819	querías	11
2820	puntos	11
2821	provecho	11
2822	principales	11
2823	posición	11
2824	poseía	11
2825	portero	11
2826	pormenores	11
2827	poniéndole	11
2828	policía	11
2829	podré	11
2830	podemos	11
2831	pintura	11
2832	pesetas	11
2833	pertenecía	11
2834	permitió	11
2835	perdición	11
2836	peores	11
2837	peldaños	11
2838	pega	11
2839	pavo	11
2840	parroquianos	11
2841	paréceme	11
2842	papa	11
2843	palos	11
2844	oírle	11
2845	odio	11
2846	obtener	11
2847	observaba	11
2848	obrador	11
2849	nube	11
2850	novelas	11
2851	muchachos	11
2852	moza	11
2853	movía	11
2854	miro	11
2855	ministro	11
2856	merecido	11
2857	mejilla	11
2858	maternidad	11
2859	materia	11
2860	marfil	11
2861	marchar	11
2862	mantener	11
2863	mande	11
2864	mandado	11
2865	males	11
2866	luna	11
2867	luces	11
2868	llanto	11
2869	ligero	11
2870	levantaba	11
2871	leal	11
2872	lavar	11
2873	inútil	11
2874	insignificante	11
2875	inocencia	11
2876	infidelidad	11
2877	independencia	11
2878	incredulidad	11
2879	ideal	11
2880	huesos	11
2881	hiciese	11
2882	hazte	11
2883	haz	11
2884	harto	11
2885	hallándose	11
2886	haciéndose	11
2887	hablan	11
2888	hablamos	11
2889	hablador	11
2890	gustaban	11
2891	guitarra	11
2892	gorra	11
2893	gasto	11
2894	ganaba	11
2895	furia	11
2896	formando	11
2897	filipinas	11
2898	figurarte	11
2899	favorable	11
2900	farsa	11
2901	fama	11
2902	extraordinaria	11
2903	éxtasis	11
2904	excitación	11
2905	entran	11
2906	enseñar	11
2907	enojo	11
2908	engaño	11
2909	encontraron	11
2910	encendió	11
2911	ejército	11
2912	ejemplos	11
2913	doctor	11
2914	distinguir	11
2915	dispuso	11
2916	disponer	11
2917	dichosa	11
2918	dichas	11
2919	determinó	11
2920	despedirse	11
2921	despecho	11
2922	desear	11
2923	descanso	11
2924	derechos	11
2925	den	11
2926	déjeme	11
2927	dejarla	11
2928	defender	11
2929	decentes	11
2930	decencia	11
2931	debiera	11
2932	deberes	11
2933	dato	11
2934	daré	11
2935	dará	11
2936	daño	11
2937	cuyas	11
2938	cuidar	11
2939	cuente	11
2940	cuartel	11
2941	cuadro	11
2942	criterio	11
2943	costaba	11
2944	cosquillas	11
2945	corto	11
2946	cortado	11
2947	corre	11
2948	continuó	11
2949	consiste	11
2950	considerar	11
2951	consideración	11
2952	condenada	11
2953	comprende	11
2954	comiendo	11
2955	comido	11
2956	comercial	11
2957	cola	11
2958	civilización	11
2959	charlando	11
2960	cerrado	11
2961	cera	11
2962	ceja	11
2963	caricias	11
2964	capas	11
2965	callado	11
2966	breves	11
2967	botones	11
2968	bonitos	11
2969	bonifacio	11
2970	bofetadas	11
2971	bofetada	11
2972	blancos	11
2973	blancas	11
2974	bendición	11
2975	barrios	11
2976	barcelona	11
2977	autor	11
2978	arrepentimiento	11
2979	armas	11
2980	ardiente	11
2981	árboles	11
2982	apuntó	11
2983	animación	11
2984	amistades	11
2985	aliento	11
2986	algodón	11
2987	afecto	11
2988	admirables	11
2989	acostumbrado	11
2990	acostar	11
2991	aburrimiento	11
2992	abre	11
2993	zaragoza	10
2994	zapatos	10
2995	vuelo	10
2996	volvían	10
2997	visiones	10
2998	vieja	10
2999	vestía	10
3000	verbo	10
3001	vencer	10
3002	velar	10
3003	variedad	10
3004	turrón	10
3005	tristes	10
3006	trayendo	10
3007	través	10
3008	trastornada	10
3009	toque	10
3010	tomaron	10
3011	tomaban	10
3012	tiros	10
3013	tipos	10
3014	término	10
3015	tenderos	10
3016	temblaba	10
3017	temas	10
3018	telas	10
3019	taberna	10
3020	sur	10
3021	suelen	10
3022	subían	10
3023	sospecha	10
3024	soñaba	10
3025	sobrinito	10
3026	so	10
3027	sirven	10
3028	sentose	10
3029	sentados	10
3030	sensación	10
3031	sencilla	10
3032	semanas	10
3033	satisfecha	10
3034	salvo	10
3035	salga	10
3036	sacramento	10
3037	sabrá	10
3038	sabios	10
3039	ronca	10
3040	ridículo	10
3041	responsabilidad	10
3042	resistencia	10
3043	reposo	10
3044	relucir	10
3045	religioso	10
3046	reinaba	10
3047	redonda	10
3048	ratón	10
3049	ramsés	10
3050	quizá	10
3051	quise	10
3052	queja	10
3053	puse	10
3054	puños	10
3055	puñal	10
3056	pulgas	10
3057	proyecto	10
3058	proposición	10
3059	prometió	10
3060	produjo	10
3061	producía	10
3062	primogénito	10
3063	prestaba	10
3064	presentaba	10
3065	presenta	10
3066	preguntarle	10
3067	precio	10
3068	postura	10
3069	ponte	10
3070	pobrecita	10
3071	platos	10
3072	pizca	10
3073	piel	10
3074	pesadilla	10
3075	permiso	10
3076	periódico	10
3077	perdono	10
3078	peines	10
3079	pedía	10
3080	pata	10
3081	pascual	10
3082	pareces	10
3083	paquetes	10
3084	papeletas	10
3085	paloma	10
3086	palmadas	10
3087	palillo	10
3088	paga	10
3089	padrino	10
3090	padilla	10
3091	oyose	10
3092	orgullosa	10
3093	oreja	10
3094	operación	10
3095	oídos	10
3096	ofrece	10
3097	obispo	10
3098	nota	10
3099	nobleza	10
3100	negar	10
3101	navidad	10
3102	nacional	10
3103	músculos	10
3104	municipal	10
3105	morales	10
3106	moneda	10
3107	molestia	10
3108	mismamente	10
3109	misión	10
3110	miren	10
3111	miras	10
3112	mirándole	10
3113	millones	10
3114	milagro	10
3115	miel	10
3116	mesilla	10
3117	menudencias	10
3118	menester	10
3119	mayo	10
3120	materialismo	10
3121	mármol	10
3122	mañas	10
3123	mantas	10
3124	manicomio	10
3125	mangas	10
3126	maneras	10
3127	maldad	10
3128	magnífico	10
3129	maderas	10
3130	lloraba	10
3131	lleve	10
3132	llenó	10
3133	llamaron	10
3134	listo	10
3135	línea	10
3136	leído	10
3137	juventud	10
3138	juárez	10
3139	josefinas	10
3140	isidro	10
3141	insolente	10
3142	inquieto	10
3143	inocentes	10
3144	inmediato	10
3145	inmediata	10
3146	inglesa	10
3147	infelices	10
3148	infalible	10
3149	inconveniente	10
3150	imposibles	10
3151	imponía	10
3152	imperio	10
3153	iglesias	10
3154	hola	10
3155	hojas	10
3156	hayas	10
3157	harás	10
3158	hacerla	10
3159	habrías	10
3160	hablo	10
3161	haberle	10
3162	haberla	10
3163	guardo	10
3164	grandísima	10
3165	gozosa	10
3166	fuesen	10
3167	fuertemente	10
3168	frenesí	10
3169	formal	10
3170	física	10
3171	fatiga	10
3172	facultad	10
3173	extravagancias	10
3174	experiencia	10
3175	existía	10
3176	exaltado	10
3177	ex	10
3178	eulalia	10
3179	eterno	10
3180	estudios	10
3181	estrella	10
3182	estate	10
3183	estando	10
3184	estallido	10
3185	espero	10
3186	escapó	10
3187	envuelto	10
3188	entro	10
3189	entretenía	10
3190	endivido	10
3191	encontrando	10
3192	elegantes	10
3193	elegancia	10
3194	efusión	10
3195	efectivamente	10
3196	eché	10
3197	echan	10
3198	duermo	10
3199	dudar	10
3200	dolores	10
3201	dolía	10
3202	diversos	10
3203	disputa	10
3204	disposiciones	10
3205	discurrió	10
3206	disco	10
3207	director	10
3208	dirás	10
3209	dirán	10
3210	desvaríos	10
3211	despierta	10
3212	desesperación	10
3213	descuido	10
3214	desconocida	10
3215	descompuesta	10
3216	deogracias	10
3217	dejase	10
3218	dejarse	10
3219	declaraba	10
3220	datos	10
3221	darte	10
3222	darme	10
3223	dame	10
3224	dábale	10
3225	cuestiones	10
3226	cuba	10
3227	criminal	10
3228	crédito	10
3229	corrida	10
3230	corrección	10
3231	contando	10
3232	conoció	10
3233	conocían	10
3234	conjunto	10
3235	condenado	10
3236	comunicaba	10
3237	cometido	10
3238	comerciante	10
3239	comedias	10
3240	coma	10
3241	cobre	10
3242	ciudad	10
3243	cigarro	10
3244	chaleco	10
3245	cesar	10
3246	cerrando	10
3247	ceremonia	10
3248	ceño	10
3249	catorce	10
3250	castigo	10
3251	casarme	10
3252	carro	10
3253	canas	10
3254	caballerito	10
3255	burla	10
3256	bota	10
3257	borde	10
3258	blas	10
3259	bebida	10
3260	barbas	10
3261	auxilio	10
3262	ausencia	10
3263	atreverse	10
3264	asegurar	10
3265	arreglará	10
3266	armonía	10
3267	apresuró	10
3268	aparecía	10
3269	anunciaba	10
3270	antonia	10
3271	angustia	10
3272	andrés	10
3273	amparo	10
3274	ambiente	10
3275	amada	10
3276	amable	10
3277	alumnos	10
3278	almohada	10
3279	almacén	10
3280	alargando	10
3281	agujero	10
3282	agradaba	10
3283	advertir	10
3284	adquirir	10
3285	adquirido	10
3286	administración	10
3287	acostumbrada	10
3288	acecho	10
3289	abrazo	10
3290	abandono	10
3291	zancuda	9
3292	zalamerías	9
3293	yema	9
3294	volviéndose	9
3295	vivían	9
3296	vivamente	9
3297	virtuosa	9
3298	vidas	9
3299	viático	9
3300	viajes	9
3301	verlas	9
3302	vería	9
3303	verdugo	9
3304	vendía	9
3305	veis	9
3306	ved	9
3307	varonil	9
3308	varón	9
3309	vallejo	9
3310	vacío	9
3311	vacía	9
3312	u	9
3313	tronco	9
3314	tratara	9
3315	trajes	9
3316	traiga	9
3317	tragaba	9
3318	traen	9
3319	tontín	9
3320	tom	9
3321	tolerancia	9
3322	tenedor	9
3323	tarea	9
3324	suplicio	9
3325	súbito	9
3326	sosegada	9
3327	solemne	9
3328	soldados	9
3329	sirvió	9
3330	siguientes	9
3331	setiembre	9
3332	señalando	9
3333	semejantes	9
3334	santos	9
3335	sana	9
3336	salvajes	9
3337	salva	9
3338	salta	9
3339	saliva	9
3340	salí	9
3341	saldría	9
3342	sacrificio	9
3343	sacarle	9
3344	sabían	9
3345	ronda	9
3346	ríe	9
3347	resultaba	9
3348	resuelto	9
3349	respetar	9
3350	repugnancia	9
3351	renglón	9
3352	reino	9
3353	regocijo	9
3354	redondo	9
3355	recién	9
3356	rasgo	9
3357	raro	9
3358	quitándose	9
3359	quedé	9
3360	purísima	9
3361	puntillas	9
3362	puntas	9
3363	pulmones	9
3364	puedas	9
3365	pudieran	9
3366	propiedad	9
3367	propiamente	9
3368	primitivo	9
3369	prim	9
3370	presentó	9
3371	preparaba	9
3372	precioso	9
3373	portería	9
3374	portamonedas	9
3375	popular	9
3376	ponce	9
3377	pólvora	9
3378	poeta	9
3379	plantón	9
3380	pitusín	9
3381	pillín	9
3382	piden	9
3383	picos	9
3384	pícaro	9
3385	pi	9
3386	permitían	9
3387	perfil	9
3388	perfecto	9
3389	perdiendo	9
3390	pensativo	9
3391	penitencia	9
3392	pater	9
3393	patatas	9
3394	pasara	9
3395	párpado	9
3396	pareciole	9
3397	pardo	9
3398	paraíso	9
3399	papás	9
3400	pájara	9
3401	pagaba	9
3402	ocultar	9
3403	números	9
3404	necesitas	9
3405	necesidades	9
3406	napoleón	9
3407	nación	9
3408	mundano	9
3409	mu	9
3410	mover	9
3411	mostrarse	9
3412	mostrar	9
3413	mono	9
3414	molina	9
3415	modas	9
3416	misteriosa	9
3417	misterio	9
3418	miran	9
3419	míos	9
3420	minuto	9
3421	meterle	9
3422	merluza	9
3423	merecía	9
3424	mereces	9
3425	mercado	9
3426	mentiras	9
3427	meditaciones	9
3428	matrimonios	9
3429	materna	9
3430	máscara	9
3431	martirio	9
3432	mantones	9
3433	mantilla	9
3434	magdalena	9
3435	llevaban	9
3436	llenaba	9
3437	llegue	9
3438	llamas	9
3439	llamando	9
3440	leyó	9
3441	levantado	9
3442	letrero	9
3443	largos	9
3444	lana	9
3445	lámpara	9
3446	ladrones	9
3447	ladrona	9
3448	judías	9
3449	jarabe	9
3450	jacinto	9
3451	jabón	9
3452	irá	9
3453	íntima	9
3454	intentó	9
3455	inspirado	9
3456	insistió	9
3457	insignificantes	9
3458	ingenio	9
3459	indulgente	9
3460	indudablemente	9
3461	indignación	9
3462	indiferencia	9
3463	indecentes	9
3464	incluso	9
3465	inclusa	9
3466	inclinó	9
3467	implacable	9
3468	imperial	9
3469	impaciencia	9
3470	ídolo	9
3471	humilde	9
3472	hule	9
3473	huéspedes	9
3474	huecos	9
3475	horizonte	9
3476	horacio	9
3477	honra	9
3478	heredero	9
3479	hagan	9
3480	habido	9
3481	guarda	9
3482	gruesa	9
3483	gritando	9
3484	gritaba	9
3485	gracioso	9
3486	gota	9
3487	goces	9
3488	goce	9
3489	gobernar	9
3490	gobernador	9
3491	gastaba	9
3492	gasta	9
3493	gala	9
3494	función	9
3495	fuensanta	9
3496	fresa	9
3497	freno	9
3498	finca	9
3499	filósofo	9
3500	fila	9
3501	fijó	9
3502	figurado	9
3503	figurábase	9
3504	fiesta	9
3505	fiereza	9
3506	febrero	9
3507	fatigado	9
3508	familiar	9
3509	faena	9
3510	extravagantes	9
3511	exterior	9
3512	extendió	9
3513	expresándose	9
3514	exclusivamente	9
3515	excelentes	9
3516	examinaba	9
3517	examen	9
3518	evangelio	9
3519	estúpida	9
3520	estudiante	9
3521	estrépito	9
3522	estatura	9
3523	estarse	9
3524	estábamos	9
3525	especialidad	9
3526	españoles	9
3527	espaldas	9
3528	escrito	9
3529	escenas	9
3530	escalón	9
3531	entrole	9
3532	entrecejo	9
3533	entrase	9
3534	entiendes	9
3535	entere	9
3536	engracia	9
3537	enemigos	9
3538	encendido	9
3539	encendida	9
3540	empleados	9
3541	empieza	9
3542	durmiendo	9
3543	dulzura	9
3544	dotes	9
3545	dosis	9
3546	donaire	9
3547	docena	9
3548	distracción	9
3549	distinto	9
3550	dijese	9
3551	dificultad	9
3552	diciembre	9
3553	diario	9
3554	diálogo	9
3555	dialéctica	9
3556	deuda	9
3557	determinación	9
3558	detalles	9
3559	desventurado	9
3560	descuida	9
3561	desapareció	9
3562	depósito	9
3563	demente	9
3564	demencia	9
3565	delirante	9
3566	delincuente	9
3567	déjese	9
3568	defendía	9
3569	cuyos	9
3570	cubierto	9
3571	créelo	9
3572	costó	9
3573	corredores	9
3574	coro	9
3575	corbata	9
3576	contestación	9
3577	contenerse	9
3578	consideraba	9
3579	consentir	9
3580	conseguido	9
3581	confesar	9
3582	comunes	9
3583	comentarios	9
3584	comen	9
3585	colocar	9
3586	colocación	9
3587	cogiéndola	9
3588	cobrar	9
3589	cinta	9
3590	ciertamente	9
3591	ciega	9
3592	cesaba	9
3593	cerrar	9
3594	cena	9
3595	celda	9
3596	casados	9
3597	carros	9
3598	carmen	9
3599	capricho	9
3600	cantaba	9
3601	cansancio	9
3602	cálculo	9
3603	calamidad	9
3604	cádiz	9
3605	caballos	9
3606	bronce	9
3607	bolsillos	9
3608	bocado	9
3609	boba	9
3610	beneficencia	9
3611	bendita	9
3612	bastantes	9
3613	barro	9
3614	banca	9
3615	balbució	9
3616	bailar	9
3617	atmósfera	9
3618	atentamente	9
3619	atendía	9
3620	asustada	9
3621	aseo	9
3622	ascuas	9
3623	artes	9
3624	arrojó	9
3625	arrepentida	9
3626	arreglando	9
3627	aprender	9
3628	apostamos	9
3629	apartaba	9
3630	antipático	9
3631	anteayer	9
3632	anhelo	9
3633	alzaba	9
3634	almirez	9
3635	algazara	9
3636	alfonso	9
3637	alcalde	9
3638	alargó	9
3639	afuera	9
3640	afligida	9
3641	afectos	9
3642	acuerda	9
3643	acordose	9
3644	acercarse	9
3645	acercándose	9
3646	aceptar	9
3647	aburrido	9
3648	absoluto	9
3649	abiertos	9
3650	zapatería	8
3651	yeso	8
3652	x	8
3653	volviose	8
3654	vivienda	8
3655	vivas	8
3656	vistazo	8
3657	viniese	8
3658	viese	8
3659	viejas	8
3660	victoria	8
3661	veréis	8
3662	veré	8
3663	veneno	8
3664	véase	8
3665	vámonos	8
3666	usar	8
3667	usan	8
3668	unión	8
3669	trujillos	8
3670	trataban	8
3671	traspaso	8
3672	transeúntes	8
3673	trago	8
3674	tos	8
3675	tomaría	8
3676	tirón	8
3677	tino	8
3678	tinieblas	8
3679	timo	8
3680	tilín	8
3681	teta	8
3682	tertulias	8
3683	ternura	8
3684	tercer	8
3685	temporada	8
3686	temblar	8
3687	supuesto	8
3688	superiores	8
3689	sumisión	8
3690	sujetos	8
3691	suelos	8
3692	sudor	8
3693	subida	8
3694	sordo	8
3695	sinvergüenza	8
3696	singular	8
3697	siglos	8
3698	siéntese	8
3699	sienten	8
3700	siéntate	8
3701	sienta	8
3702	seso	8
3703	señorío	8
3704	sentíase	8
3705	sentí	8
3706	semejanza	8
3707	seguían	8
3708	sed	8
3709	secar	8
3710	samaniegas	8
3711	salvar	8
3712	salmerón	8
3713	saldrá	8
3714	salado	8
3715	sacaron	8
3716	sabiduría	8
3717	rompiendo	8
3718	rompía	8
3719	rompe	8
3720	rojos	8
3721	rodando	8
3722	riéndose	8
3723	rezando	8
3724	revelación	8
3725	retirado	8
3726	resplandor	8
3727	reñir	8
3728	relimpio	8
3729	reina	8
3730	redentor	8
3731	rectitud	8
3732	recordar	8
3733	recordando	8
3734	reconocer	8
3735	reconciliación	8
3736	recogiendo	8
3737	rayas	8
3738	rápido	8
3739	rapidez	8
3740	rápida	8
3741	ramos	8
3742	rabiar	8
3743	quitaban	8
3744	queremos	8
3745	pusieran	8
3746	pulmonía	8
3747	pueril	8
3748	próximas	8
3749	protege	8
3750	propósitos	8
3751	proponía	8
3752	promesa	8
3753	procuraba	8
3754	proceder	8
3755	problemas	8
3756	probablemente	8
3757	probable	8
3758	pretextos	8
3759	presupuesto	8
3760	préstamo	8
3761	preso	8
3762	presa	8
3763	preguntando	8
3764	portarse	8
3765	poníase	8
3766	pongas	8
3767	político	8
3768	podríamos	8
3769	pliegues	8
3770	plenitud	8
3771	placer	8
3772	pintada	8
3773	picaba	8
3774	piano	8
3775	personales	8
3776	perra	8
3777	permaneció	8
3778	perdí	8
3779	percha	8
3780	pequeñuelo	8
3781	penitente	8
3782	penetrar	8
3783	peligros	8
3784	peine	8
3785	paternal	8
3786	patadas	8
3787	pastor	8
3788	pasmada	8
3789	pasaría	8
3790	pasados	8
3791	partía	8
3792	parroquiano	8
3793	pardos	8
3794	paños	8
3795	pañolería	8
3796	panderetas	8
3797	pálido	8
3798	palacio	8
3799	paisaje	8
3800	padecido	8
3801	oscura	8
3802	origen	8
3803	oriente	8
3804	ópera	8
3805	onda	8
3806	olvido	8
3807	olvidaba	8
3808	ojalá	8
3809	ofrecido	8
3810	oficina	8
3811	ofendida	8
3812	observaciones	8
3813	obligaciones	8
3814	novios	8
3815	nobles	8
3816	naranja	8
3817	muestras	8
3818	muestra	8
3819	movida	8
3820	mostró	8
3821	moría	8
3822	molino	8
3823	molestaba	8
3824	misterioso	8
3825	misántropo	8
3826	mezcla	8
3827	meta	8
3828	menuda	8
3829	melancolía	8
3830	meditación	8
3831	medir	8
3832	mediodía	8
3833	mayormente	8
3834	matrimonial	8
3835	mato	8
3836	matarme	8
3837	marchaba	8
3838	maravilla	8
3839	maña	8
3840	manifestaba	8
3841	manchas	8
3842	lustre	8
3843	lúgubre	8
3844	locos	8
3845	llevas	8
3846	llevarse	8
3847	llenas	8
3848	llamo	8
3849	llamarse	8
3850	ligera	8
3851	leyendo	8
3852	levanto	8
3853	lelo	8
3854	lela	8
3855	legua	8
3856	legítima	8
3857	latines	8
3858	labor	8
3859	junta	8
3860	juicioso	8
3861	juegos	8
3862	jota	8
3863	joaquinito	8
3864	irás	8
3865	interesaba	8
3866	instintos	8
3867	inspira	8
3868	insoportable	8
3869	insana	8
3870	inquieta	8
3871	inmóvil	8
3872	inmediatamente	8
3873	injurias	8
3874	ingleses	8
3875	infernal	8
3876	industria	8
3877	impaciente	8
3878	ilusiones	8
3879	ignominia	8
3880	hospital	8
3881	horteras	8
3882	honradas	8
3883	hízole	8
3884	hiel	8
3885	hermosas	8
3886	hazme	8
3887	harías	8
3888	hagamos	8
3889	hábito	8
3890	haberme	8
3891	guardó	8
3892	guardando	8
3893	guardado	8
3894	guapas	8
3895	gozaba	8
3896	gordos	8
3897	glacial	8
3898	gestos	8
3899	generoso	8
3900	garbanzos	8
3901	fugaz	8
3902	fruto	8
3903	fraternal	8
3904	formar	8
3905	fondos	8
3906	finísimo	8
3907	fingiendo	8
3908	felisa	8
3909	faltar	8
3910	extraños	8
3911	exactamente	8
3912	estudiantes	8
3913	estimación	8
3914	estarás	8
3915	estabas	8
3916	espectro	8
3917	espada	8
3918	esencial	8
3919	escondite	8
3920	escoba	8
3921	escapaba	8
3922	equivocado	8
3923	envuelta	8
3924	entereza	8
3925	enterando	8
3926	entendido	8
3927	enseñaba	8
3928	enseña	8
3929	enormes	8
3930	enfermedades	8
3931	enfadar	8
3932	empleo	8
3933	egoísmo	8
3934	edades	8
3935	económica	8
3936	echose	8
3937	echamos	8
3938	dulces	8
3939	dueña	8
3940	dudo	8
3941	doscientos	8
3942	dominar	8
3943	dominaba	8
3944	doméstico	8
3945	doméstica	8
3946	doble	8
3947	divinidad	8
3948	discutir	8
3949	discusión	8
3950	discurrir	8
3951	discreto	8
3952	discreta	8
3953	discreción	8
3954	diligencia	8
3955	digna	8
3956	dichosos	8
3957	determinado	8
3958	despertaba	8
3959	despedida	8
3960	desnudo	8
3961	desconcertó	8
3962	desasosiego	8
3963	desaparecido	8
3964	dentadura	8
3965	delicadeza	8
3966	dejes	8
3967	dejé	8
3968	defectos	8
3969	declaración	8
3970	decidido	8
3971	decidida	8
3972	dátiles	8
3973	curso	8
3974	culto	8
3975	cuidadosamente	8
3976	cuidados	8
3977	cuidaba	8
3978	cuerpos	8
3979	cuántos	8
3980	cuánta	8
3981	cristal	8
3982	criar	8
3983	crianza	8
3984	cráneo	8
3985	costado	8
3986	coser	8
3987	cortinas	8
3988	corrillo	8
3989	cordura	8
3990	corazones	8
3991	conversaciones	8
3992	contrabando	8
3993	contacto	8
3994	conste	8
3995	consistía	8
3996	considerablemente	8
3997	confusa	8
3998	conformidad	8
3999	conflicto	8
4000	condiciones	8
4001	competencia	8
4002	comisión	8
4003	comiéndose	8
4004	comentario	8
4005	colorada	8
4006	clavos	8
4007	clavo	8
4008	clarito	8
4009	civil	8
4010	cirila	8
4011	cesto	8
4012	cerrojo	8
4013	cerraba	8
4014	centinela	8
4015	caza	8
4016	castillo	8
4017	castiga	8
4018	casorio	8
4019	carita	8
4020	cariñoso	8
4021	cargado	8
4022	cambiado	8
4023	calló	8
4024	callaba	8
4025	calla	8
4026	cálculos	8
4027	cabra	8
4028	cabos	8
4029	cabe	8
4030	caballeros	8
4031	buscarle	8
4032	burro	8
4033	brillaban	8
4034	boticario	8
4035	bomba	8
4036	bolsa	8
4037	bigote	8
4038	basilisco	8
4039	bárbaro	8
4040	bajito	8
4041	bacalao	8
4042	aumentaba	8
4043	atrevimiento	8
4044	asusta	8
4045	aspavientos	8
4046	asomaban	8
4047	ascos	8
4048	aragón	8
4049	apuros	8
4050	apures	8
4051	aproximaba	8
4052	aprende	8
4053	apartó	8
4054	apartado	8
4055	aparato	8
4056	añadir	8
4057	antipatía	8
4058	anochecer	8
4059	ánimos	8
4060	ángulo	8
4061	anarquista	8
4062	americana	8
4063	amarillo	8
4064	alzó	8
4065	altas	8
4066	altares	8
4067	alborotada	8
4068	ahogaba	8
4069	aguanta	8
4070	agitación	8
4071	afición	8
4072	administrador	8
4073	acudió	8
4074	acostó	8
4075	acompañar	8
4076	acero	8
4077	acercose	8
4078	acabe	8
4079	acabado	8
4080	abnegación	8
4081	abandonó	8
4082	vulgaris	7
4083	vuestro	7
4084	voto	7
4085	vosotros	7
4086	volverá	7
4087	vocablos	7
4088	vivísima	7
4089	vistiendo	7
4090	viniera	7
4091	vigilar	7
4092	vigilancia	7
4093	viernes	7
4094	verídico	7
4095	verdaderas	7
4096	venus	7
4097	ventaja	7
4098	venden	7
4099	vencida	7
4100	váyase	7
4101	vástagos	7
4102	variar	7
4103	valientes	7
4104	valga	7
4105	vago	7
4106	vagamente	7
4107	vacilar	7
4108	uniforme	7
4109	tropiezo	7
4110	tremendas	7
4111	tratos	7
4112	tratamiento	7
4113	trastornado	7
4114	trampas	7
4115	traigan	7
4116	traes	7
4117	trabaja	7
4118	torpeza	7
4119	torno	7
4120	tormento	7
4121	torcido	7
4122	tonos	7
4123	tomara	7
4124	tocada	7
4125	tirria	7
4126	tiologías	7
4127	tieso	7
4128	tiesas	7
4129	tie	7
4130	testamento	7
4131	ternera	7
4132	teniente	7
4133	tenerle	7
4134	tendrían	7
4135	tendrás	7
4136	tendrán	7
4137	temple	7
4138	temiendo	7
4139	temblorosa	7
4140	temblando	7
4141	temblaban	7
4142	teatral	7
4143	tantísima	7
4144	talmente	7
4145	sueltos	7
4146	sueldo	7
4147	sublimes	7
4148	suavidad	7
4149	sostenían	7
4150	sonido	7
4151	sollozos	7
4152	solían	7
4153	solemnidad	7
4154	sobrinos	7
4155	sitios	7
4156	sintieron	7
4157	simplemente	7
4158	sigo	7
4159	serle	7
4160	serie	7
4161	seremos	7
4162	serán	7
4163	sequedad	7
4164	señoritos	7
4165	sencillo	7
4166	semos	7
4167	sarcasmo	7
4168	samaritana	7
4169	saludo	7
4170	saltando	7
4171	salgo	7
4172	sagunto	7
4173	sacudida	7
4174	sacristía	7
4175	rueda	7
4176	rubinius	7
4177	rosita	7
4178	rosas	7
4179	ropas	7
4180	rodilla	7
4181	rodeada	7
4182	rodeaba	7
4183	rival	7
4184	ricamente	7
4185	revolviendo	7
4186	revolución	7
4187	retratos	7
4188	resultó	7
4189	restos	7
4190	réspice	7
4191	respectivas	7
4192	resoplidos	7
4193	resmas	7
4194	reputación	7
4195	repuso	7
4196	repitiendo	7
4197	reparar	7
4198	renta	7
4199	rendida	7
4200	reírse	7
4201	regiones	7
4202	referentes	7
4203	redención	7
4204	recorrer	7
4205	reconocimiento	7
4206	reconociendo	7
4207	reconocía	7
4208	recogida	7
4209	recíprocamente	7
4210	recibían	7
4211	raso	7
4212	raras	7
4213	rabo	7
4214	quítate	7
4215	quisiese	7
4216	quieta	7
4217	quererle	7
4218	quedaría	7
4219	puñalada	7
4220	puñados	7
4221	proximidad	7
4222	protestantes	7
4223	protestante	7
4224	propuesto	7
4225	prontamente	7
4226	progresista	7
4227	programa	7
4228	profundísimo	7
4229	probarlo	7
4230	primerito	7
4231	preparando	7
4232	prensa	7
4233	pregunto	7
4234	preciosa	7
4235	postas	7
4236	portera	7
4237	pon	7
4238	polvos	7
4239	políticos	7
4240	poesía	7
4241	pobrecillo	7
4242	pleito	7
4243	planes	7
4244	placeras	7
4245	piojín	7
4246	pillos	7
4247	piense	7
4248	picardía	7
4249	picar	7
4250	pesado	7
4251	personaje	7
4252	perrerías	7
4253	permitido	7
4254	permanecía	7
4255	permanecer	7
4256	perla	7
4257	periodos	7
4258	perfecciones	7
4259	perfección	7
4260	perdonado	7
4261	pensión	7
4262	penosa	7
4263	penetró	7
4264	peinetas	7
4265	pegarle	7
4266	pechos	7
4267	paseíto	7
4268	paseaba	7
4269	pasada	7
4270	parta	7
4271	paró	7
4272	parándose	7
4273	parada	7
4274	pantalón	7
4275	pantalla	7
4276	palique	7
4277	pájaro	7
4278	pae	7
4279	padece	7
4280	oyen	7
4281	olas	7
4282	oírse	7
4283	oíase	7
4284	ofrecer	7
4285	ocurrían	7
4286	ocuparse	7
4287	ocupar	7
4288	ocupado	7
4289	ocupaciones	7
4290	obligado	7
4291	obediencia	7
4292	nieves	7
4293	negaba	7
4294	necesitan	7
4295	necesaria	7
4296	nacer	7
4297	murmuraba	7
4298	muriendo	7
4299	mundos	7
4300	muleta	7
4301	mozos	7
4302	mortificaba	7
4303	morada	7
4304	moño	7
4305	montado	7
4306	moderna	7
4307	mismas	7
4308	miserias	7
4309	ministra	7
4310	milicia	7
4311	migas	7
4312	metiose	7
4313	metida	7
4314	metí	7
4315	merino	7
4316	mercantil	7
4317	mejillas	7
4318	meditando	7
4319	medias	7
4320	material	7
4321	mate	7
4322	marchado	7
4323	marca	7
4324	malvina	7
4325	maldades	7
4326	magín	7
4327	lucido	7
4328	lozoya	7
4329	llevada	7
4330	llegué	7
4331	llegara	7
4332	llamamos	7
4333	limpiar	7
4334	ligeramente	7
4335	leo	7
4336	lejano	7
4337	lejana	7
4338	lealtad	7
4339	lazo	7
4340	lastimoso	7
4341	lances	7
4342	labio	7
4343	judía	7
4344	júbilo	7
4345	jarro	7
4346	irresistible	7
4347	ironía	7
4348	invierno	7
4349	inútiles	7
4350	introducir	7
4351	íntimo	7
4352	intentar	7
4353	instrumento	7
4354	inscripción	7
4355	inmensidad	7
4356	infamia	7
4357	indudable	7
4358	índole	7
4359	increíbles	7
4360	inclinando	7
4361	inclinaba	7
4362	impropio	7
4363	iluminado	7
4364	ignorancia	7
4365	hondo	7
4366	historias	7
4367	hipócrita	7
4368	hijito	7
4369	héroes	7
4370	hereje	7
4371	hembras	7
4372	hastío	7
4373	halló	7
4374	hágame	7
4375	hacerte	7
4376	hacemos	7
4377	hablándole	7
4378	habíamos	7
4379	gustos	7
4380	guardias	7
4381	guapísima	7
4382	guante	7
4383	guano	7
4384	grata	7
4385	grandeza	7
4386	gozar	7
4387	gotas	7
4388	gonzález	7
4389	generosidad	7
4390	ganando	7
4391	gafas	7
4392	futuro	7
4393	futura	7
4394	friolera	7
4395	francés	7
4396	fiscal	7
4397	firma	7
4398	finura	7
4399	finísima	7
4400	fines	7
4401	figurarse	7
4402	figuraba	7
4403	fidelidad	7
4404	feroz	7
4405	faltando	7
4406	faltaban	7
4407	faldones	7
4408	explicarse	7
4409	explicación	7
4410	exclamaciones	7
4411	excitado	7
4412	examinar	7
4413	éste	7
4414	estatua	7
4415	estampas	7
4416	estados	7
4417	espérate	7
4418	esperanzas	7
4419	espantosa	7
4420	esforzaba	7
4421	escritura	7
4422	escribe	7
4423	esclavitud	7
4424	escarola	7
4425	escándalos	7
4426	errores	7
4427	eras	7
4428	érale	7
4429	equivocación	7
4430	envolvía	7
4431	entrara	7
4432	enterada	7
4433	enseñando	7
4434	enracimaban	7
4435	enmienda	7
4436	enhorabuena	7
4437	engañas	7
4438	enfado	7
4439	energías	7
4440	encuentre	7
4441	encuentras	7
4442	encontrara	7
4443	encargó	7
4444	enamorarse	7
4445	empuje	7
4446	empresa	7
4447	empeño	7
4448	efectos	7
4449	edificios	7
4450	económico	7
4451	economía	7
4452	eche	7
4453	echándole	7
4454	echaban	7
4455	dureza	7
4456	dramas	7
4457	doncella	7
4458	dómine	7
4459	divinas	7
4460	divertía	7
4461	distraída	7
4462	distintos	7
4463	distintas	7
4464	disgustos	7
4465	dirigió	7
4466	dijeran	7
4467	dígale	7
4468	difunta	7
4469	diese	7
4470	diablos	7
4471	despedían	7
4472	desgracias	7
4473	descuide	7
4474	descansar	7
4475	desbordaba	7
4476	des	7
4477	departamento	7
4478	demostrando	7
4479	deme	7
4480	delito	7
4481	deliciosa	7
4482	delantera	7
4483	dejaron	7
4484	decidirse	7
4485	decíale	7
4486	cumplimiento	7
4487	cumple	7
4488	culpable	7
4489	cuentan	7
4490	cubierta	7
4491	cruzadas	7
4492	crudo	7
4493	crímenes	7
4494	creció	7
4495	créalo	7
4496	cosiendo	7
4497	cortos	7
4498	cortedad	7
4499	cortas	7
4500	cortar	7
4501	corro	7
4502	correo	7
4503	corona	7
4504	convulsiva	7
4505	contrariedad	7
4506	contraria	7
4507	conteniendo	7
4508	contenía	7
4509	construcción	7
4510	consideraciones	7
4511	consecuencias	7
4512	confesor	7
4513	confesión	7
4514	concejal	7
4515	comunidad	7
4516	comunicación	7
4517	compraré	7
4518	compinche	7
4519	compañeros	7
4520	cogí	7
4521	codos	7
4522	cobrador	7
4523	clavó	7
4524	cláusulas	7
4525	citas	7
4526	cifra	7
4527	chispas	7
4528	chiquitín	7
4529	china	7
4530	chilló	7
4531	chicas	7
4532	celoso	7
4533	cavilar	7
4534	causaban	7
4535	cascote	7
4536	cartilla	7
4537	cariñosas	7
4538	cargando	7
4539	caramba	7
4540	característico	7
4541	cañas	7
4542	cantón	7
4543	canela	7
4544	campaña	7
4545	cambiaría	7
4546	cambiar	7
4547	callarse	7
4548	callada	7
4549	caliente	7
4550	caiga	7
4551	cabecera	7
4552	busto	7
4553	burlesca	7
4554	bruja	7
4555	bromuro	7
4556	brillante	7
4557	bobo	7
4558	besó	7
4559	bebía	7
4560	baza	7
4561	basura	7
4562	barullo	7
4563	barriga	7
4564	bajado	7
4565	aumentar	7
4566	atrevo	7
4567	atónita	7
4568	atocha	7
4569	aterrada	7
4570	aterraba	7
4571	asentimiento	7
4572	arrastrando	7
4573	arrastrada	7
4574	arranca	7
4575	armada	7
4576	armaba	7
4577	aristocracia	7
4578	arena	7
4579	aptitud	7
4580	apretando	7
4581	aprendiendo	7
4582	apreciación	7
4583	apoyar	7
4584	apoyada	7
4585	aplicó	7
4586	aplicar	7
4587	ansia	7
4588	animales	7
4589	anarquía	7
4590	altura	7
4591	almohadas	7
4592	alhaja	7
4593	alegraba	7
4594	alburquerque	7
4595	alas	7
4596	alarmada	7
4597	agudo	7
4598	agradecido	7
4599	afable	7
4600	acudir	7
4601	acompañada	7
4602	acompañaba	7
4603	acometida	7
4604	acentuando	7
4605	acentuada	7
4606	abismo	7
4607	abiertas	7
4608	abandonado	7
4609	zaragata	6
4610	zapatillas	6
4611	xi	6
4612	vusté	6
4613	vulgo	6
4614	vuestra	6
4615	votación	6
4616	volverme	6
4617	volverlo	6
4618	voló	6
4619	viviera	6
4620	viste	6
4621	virtudes	6
4622	vieras	6
4623	viéndose	6
4624	viéndola	6
4625	vidriera	6
4626	vestidas	6
4627	verlos	6
4628	ventanilla	6
4629	ventajas	6
4630	vendiendo	6
4631	vender	6
4632	vayan	6
4633	vais	6
4634	vacilando	6
4635	vacilaba	6
4636	urbanidad	6
4637	universal	6
4638	últimamente	6
4639	ulmus	6
4640	turno	6
4641	turbada	6
4642	tunantes	6
4643	tumulto	6
4644	triunfo	6
4645	tripas	6
4646	tribunal	6
4647	trastada	6
4648	tranvía	6
4649	transformación	6
4650	tranquilizó	6
4651	traerle	6
4652	trabajado	6
4653	tonillo	6
4654	tomás	6
4655	tomas	6
4656	tomarse	6
4657	tomarle	6
4658	tocas	6
4659	tintoreros	6
4660	tintero	6
4661	tigre	6
4662	tierno	6
4663	tez	6
4664	testimonio	6
4665	terribles	6
4666	tengan	6
4667	tenerlo	6
4668	tendero	6
4669	tellería	6
4670	techos	6
4671	tardanza	6
4672	tapaba	6
4673	tapa	6
4674	tambor	6
4675	talentos	6
4676	tablero	6
4677	sylvestris	6
4678	superioridad	6
4679	sumamente	6
4680	suena	6
4681	sucesor	6
4682	súbitamente	6
4683	subieron	6
4684	sospechar	6
4685	sospechando	6
4686	sosona	6
4687	sopetón	6
4688	soñé	6
4689	sonrosada	6
4690	solutamente	6
4691	solitaria	6
4692	solar	6
4693	sofocado	6
4694	sirvo	6
4695	sintiera	6
4696	sílaba	6
4697	siguiendo	6
4698	sietemesino	6
4699	sientes	6
4700	sexos	6
4701	sevilla	6
4702	servidumbre	6
4703	servicios	6
4704	separación	6
4705	sentiré	6
4706	sentimental	6
4707	sentadas	6
4708	sensaciones	6
4709	seguirle	6
4710	saqué	6
4711	salvado	6
4712	saludar	6
4713	saludaba	6
4714	saltaba	6
4715	salimos	6
4716	saliese	6
4717	saladero	6
4718	sagrado	6
4719	sacara	6
4720	sabré	6
4721	sabio	6
4722	sábado	6
4723	rutinas	6
4724	run	6
4725	rudo	6
4726	rudeza	6
4727	rótulo	6
4728	rosquillas	6
4729	rosa	6
4730	rondaba	6
4731	rompiera	6
4732	rodar	6
4733	risueño	6
4734	ridícula	6
4735	rías	6
4736	rezo	6
4737	revolvió	6
4738	revolvía	6
4739	revoluciones	6
4740	revolucionario	6
4741	revienta	6
4742	reventaba	6
4743	retiraba	6
4744	responsable	6
4745	respaldo	6
4746	repugnante	6
4747	reproducción	6
4748	representación	6
4749	repóblica	6
4750	repetir	6
4751	repartir	6
4752	reparó	6
4753	reparación	6
4754	renunciar	6
4755	renegando	6
4756	remordimientos	6
4757	religiosos	6
4758	religiosas	6
4759	relativamente	6
4760	reírme	6
4761	reído	6
4762	regreso	6
4763	reglas	6
4764	regalos	6
4765	recta	6
4766	recomendado	6
4767	recobró	6
4768	recibe	6
4769	recados	6
4770	rebajo	6
4771	realizar	6
4772	raimundo	6
4773	rabiando	6
4774	quitárselo	6
4775	quitarse	6
4776	quinqué	6
4777	querré	6
4778	quererme	6
4779	queréis	6
4780	quede	6
4781	quedará	6
4782	quedando	6
4783	puros	6
4784	pum	6
4785	púlpito	6
4786	puestas	6
4787	prurito	6
4788	proyectos	6
4789	provisiones	6
4790	provenía	6
4791	protectora	6
4792	proporciones	6
4793	propongo	6
4794	propaganda	6
4795	pronunciando	6
4796	prometido	6
4797	prodigio	6
4798	procedimientos	6
4799	prisión	6
4800	presentimiento	6
4801	presentar	6
4802	prepararse	6
4803	preparada	6
4804	preguntado	6
4805	prácticas	6
4806	posibles	6
4807	portado	6
4808	porrazo	6
4809	porquerías	6
4810	poquitín	6
4811	pongamos	6
4812	ponerlo	6
4813	ponerla	6
4814	pondremos	6
4815	poetas	6
4816	podrás	6
4817	plantó	6
4818	plácida	6
4819	pito	6
4820	pisos	6
4821	pisando	6
4822	pierde	6
4823	picador	6
4824	pianito	6
4825	pianista	6
4826	petróleo	6
4827	pesados	6
4828	pesada	6
4829	pesaba	6
4830	perversidad	6
4831	pertenece	6
4832	persecución	6
4833	peregrino	6
4834	perdonaba	6
4835	perdidos	6
4836	pensador	6
4837	peinado	6
4838	pegó	6
4839	pegando	6
4840	pegaba	6
4841	pedido	6
4842	pedacitos	6
4843	pecar	6
4844	paterna	6
4845	pasito	6
4846	pasear	6
4847	pasé	6
4848	pascua	6
4849	párpados	6
4850	paréntesis	6
4851	parecida	6
4852	papas	6
4853	palotada	6
4854	palco	6
4855	paice	6
4856	pagarle	6
4857	pagaré	6
4858	oyéndole	6
4859	ordinario	6
4860	oponerse	6
4861	olvide	6
4862	olía	6
4863	oírte	6
4864	ofreciéndole	6
4865	oficiosidad	6
4866	ocupaban	6
4867	ocupaba	6
4868	obtuvo	6
4869	observadora	6
4870	obreros	6
4871	obligaba	6
4872	obedeciendo	6
4873	nudo	6
4874	notables	6
4875	noria	6
4876	nieve	6
4877	niegue	6
4878	narrador	6
4879	narciso	6
4880	nace	6
4881	na	6
4882	mugre	6
4883	muelas	6
4884	muda	6
4885	muchísima	6
4886	muchachas	6
4887	motor	6
4888	mortal	6
4889	morirse	6
4890	montones	6
4891	moderaos	6
4892	misteriosas	6
4893	mirarse	6
4894	mirándose	6
4895	mimos	6
4896	militar	6
4897	metieron	6
4898	meterme	6
4899	metamorfosis	6
4900	metálico	6
4901	memorable	6
4902	meditar	6
4903	médicos	6
4904	médicis	6
4905	medicamento	6
4906	mazapán	6
4907	maza	6
4908	mayoría	6
4909	matando	6
4910	martillo	6
4911	mango	6
4912	mancha	6
4913	mamarracho	6
4914	malditas	6
4915	majadero	6
4916	maja	6
4917	magnífica	6
4918	luto	6
4919	lulio	6
4920	luchando	6
4921	lógico	6
4922	llorado	6
4923	llora	6
4924	llego	6
4925	llegándose	6
4926	llavín	6
4927	llamándole	6
4928	limpios	6
4929	limpiando	6
4930	libres	6
4931	liberales	6
4932	letargo	6
4933	leguas	6
4934	legítimo	6
4935	leganés	6
4936	lavarse	6
4937	lámina	6
4938	junio	6
4939	julio	6
4940	jugado	6
4941	juega	6
4942	ju	6
4943	joya	6
4944	jovial	6
4945	jeta	6
4946	jerez	6
4947	jardín	6
4948	jarana	6
4949	irme	6
4950	invitó	6
4951	invisible	6
4952	intervenir	6
4953	intenciones	6
4954	instrucción	6
4955	insensato	6
4956	iniciativa	6
4957	ingenuidad	6
4958	infundía	6
4959	infaliblemente	6
4960	inefable	6
4961	indispensable	6
4962	indiferente	6
4963	indicaba	6
4964	incapaz	6
4965	impedir	6
4966	huyendo	6
4967	humanos	6
4968	huir	6
4969	horrores	6
4970	hongo	6
4971	hito	6
4972	histórico	6
4973	hierros	6
4974	hiciste	6
4975	hermosos	6
4976	hembra	6
4977	hechura	6
4978	haciéndola	6
4979	hables	6
4980	hablarte	6
4981	hablara	6
4982	hábil	6
4983	habéis	6
4984	gustaría	6
4985	gustar	6
4986	gustado	6
4987	groseras	6
4988	gravelinas	6
4989	grato	6
4990	grandísimo	6
4991	gozoso	6
4992	gozando	6
4993	golosina	6
4994	golosa	6
4995	gilimón	6
4996	gatitos	6
4997	garbanzo	6
4998	ganancias	6
4999	gallinas	6
5000	galán	6
5001	fusiles	6
5002	fundar	6
5003	fuente	6
5004	frotándose	6
5005	frías	6
5006	frescas	6
5007	frasco	6
5008	francesa	6
5009	fórmulas	6
5010	fonda	6
5011	fío	6
5012	finuras	6
5013	fincas	6
5014	finalmente	6
5015	filosófica	6
5016	fijas	6
5017	fijaba	6
5018	ferrocarriles	6
5019	ferocidad	6
5020	felipe	6
5021	faz	6
5022	fatigada	6
5023	fatal	6
5024	fárrago	6
5025	facilidad	6
5026	extracto	6
5027	expresando	6
5028	expresado	6
5029	existían	6
5030	existencias	6
5031	exigencias	6
5032	exclamaba	6
5033	examinó	6
5034	exactitud	6
5035	estorbaba	6
5036	estés	6
5037	estarían	6
5038	ésta	6
5039	espléndida	6
5040	espíritus	6
5041	espirituales	6
5042	espinazo	6
5043	espantoso	6
5044	escrúpulos	6
5045	escribía	6
5046	escondido	6
5047	escalofríos	6
5048	equilibrio	6
5049	entretener	6
5050	entresuelo	6
5051	entregar	6
5052	entregado	6
5053	entornada	6
5054	enteró	6
5055	enteraba	6
5056	enseñó	6
5057	enseñado	6
5058	engañan	6
5059	engaña	6
5060	énfasis	6
5061	enero	6
5062	encontrarse	6
5063	encontraban	6
5064	encierro	6
5065	encerrada	6
5066	encendidos	6
5067	encendía	6
5068	encargos	6
5069	encanto	6
5070	empiezan	6
5071	empezando	6
5072	emigración	6
5073	eléctrico	6
5074	ejecución	6
5075	efectiva	6
5076	eclesiástico	6
5077	dulcemente	6
5078	duerme	6
5079	dudaba	6
5080	droguería	6
5081	dormitorio	6
5082	dominio	6
5083	dolorosa	6
5084	dolorida	6
5085	divorcio	6
5086	diván	6
5087	distribución	6
5088	distracciones	6
5089	dispense	6
5090	diole	6
5091	dímelo	6
5092	dile	6
5093	difíciles	6
5094	diciéndose	6
5095	deudas	6
5096	determinar	6
5097	deteniéndose	6
5098	despidiose	6
5099	despedía	6
5100	desenvolverse	6
5101	desempeñar	6
5102	desdichado	6
5103	descubrió	6
5104	descollaba	6
5105	descarada	6
5106	dependiente	6
5107	depende	6
5108	dejose	6
5109	defecto	6
5110	decidió	6
5111	decide	6
5112	debido	6
5113	dárselo	6
5114	dándote	6
5115	dadas	6
5116	cursi	6
5117	cuñada	6
5118	culpas	6
5119	culebra	6
5120	cuidando	6
5121	cuerdas	6
5122	cuentes	6
5123	cuchara	6
5124	cuartito	6
5125	cruces	6
5126	criados	6
5127	creías	6
5128	créete	6
5129	creería	6
5130	creerá	6
5131	credencial	6
5132	créame	6
5133	coyuntura	6
5134	cosillas	6
5135	cortó	6
5136	cortes	6
5137	corrientes	6
5138	convenido	6
5139	contaré	6
5140	consternada	6
5141	constantemente	6
5142	constante	6
5143	consolaba	6
5144	conservaban	6
5145	conseguirlo	6
5146	conocidas	6
5147	conocida	6
5148	confesonario	6
5149	compuesta	6
5150	compró	6
5151	compré	6
5152	componía	6
5153	comió	6
5154	cómica	6
5155	comes	6
5156	combinación	6
5157	comandante	6
5158	comadrón	6
5159	coloquio	6
5160	cohibida	6
5161	cogiéndole	6
5162	coco	6
5163	cocinera	6
5164	cocido	6
5165	clavados	6
5166	clavaba	6
5167	claros	6
5168	círculos	6
5169	chucherías	6
5170	cesante	6
5171	cerrados	6
5172	ceniza	6
5173	cenar	6
5174	celo	6
5175	célebres	6
5176	ceder	6
5177	cautela	6
5178	causas	6
5179	caudal	6
5180	catarro	6
5181	casco	6
5182	casaron	6
5183	cartagena	6
5184	caro	6
5185	carlista	6
5186	cargue	6
5187	cargan	6
5188	canuto	6
5189	cantidades	6
5190	canonjía	6
5191	canónigo	6
5192	camisas	6
5193	calentura	6
5194	cajones	6
5195	cajita	6
5196	caí	6
5197	caen	6
5198	cabellera	6
5199	butaca	6
5200	buscó	6
5201	buscarme	6
5202	bullicio	6
5203	brutos	6
5204	brusca	6
5205	bronca	6
5206	brío	6
5207	brincos	6
5208	brillaba	6
5209	bordes	6
5210	bonilla	6
5211	bondadoso	6
5212	bolas	6
5213	blando	6
5214	bayona	6
5215	bautizo	6
5216	base	6
5217	barricadas	6
5218	banqueta	6
5219	bajaban	6
5220	baba	6
5221	azules	6
5222	azucenas	6
5223	ayún	6
5224	ayes	6
5225	aves	6
5226	aturdido	6
5227	aturdida	6
5228	atravesó	6
5229	atravesar	6
5230	atender	6
5231	atado	6
5232	asustó	6
5233	asustado	6
5234	asomaba	6
5235	arsénico	6
5236	arroyo	6
5237	arrojaba	6
5238	arrogante	6
5239	arreglarse	6
5240	arregla	6
5241	arranco	6
5242	arrancarle	6
5243	arquitectura	6
5244	apuntes	6
5245	apretón	6
5246	apretándole	6
5247	apretado	6
5248	aprecio	6
5249	apreciando	6
5250	apoyó	6
5251	aposento	6
5252	apetitos	6
5253	apellido	6
5254	apelar	6
5255	apariencia	6
5256	aparición	6
5257	aparentar	6
5258	anunció	6
5259	anunciar	6
5260	anunciando	6
5261	anteojos	6
5262	animado	6
5263	angelito	6
5264	andaban	6
5265	anchas	6
5266	amoroso	6
5267	amarillos	6
5268	amarilla	6
5269	amarga	6
5270	amalia	6
5271	amabilidad	6
5272	amaba	6
5273	alternativas	6
5274	altercado	6
5275	alivio	6
5276	alboroto	6
5277	albert	6
5278	alargaba	6
5279	alambre	6
5280	ajo	6
5281	ahorros	6
5282	agujas	6
5283	agradezco	6
5284	agradecida	6
5285	agradecer	6
5286	ágil	6
5287	agente	6
5288	afrenta	6
5289	aflicción	6
5290	afectando	6
5291	admiraba	6
5292	achuchón	6
5293	acertaba	6
5294	acechando	6
5295	acceso	6
5296	acabo	6
5297	acabaron	6
5298	acababan	6
5299	abundante	6
5300	abuela	6
5301	absurdo	6
5302	abatimiento	6
5303	abanicos	6
5304	abandonar	6
5305	abandonada	6
5306	zozobra	5
5307	zona	5
5308	zarpa	5
5309	yerba	5
5310	vulgares	5
5311	vuelven	5
5312	vosotras	5
5313	volverás	5
5314	volando	5
5315	volada	5
5316	viviendo	5
5317	viudo	5
5318	vistas	5
5319	visitación	5
5320	visitaba	5
5321	visión	5
5322	visible	5
5323	visajes	5
5324	violentamente	5
5325	violencia	5
5326	villaamil	5
5327	vigas	5
5328	vieran	5
5329	vientre	5
5330	viéndote	5
5331	vidrieras	5
5332	vicario	5
5333	vibración	5
5334	verlo	5
5335	verles	5
5336	verificado	5
5337	verdaderos	5
5338	venidas	5
5339	venerable	5
5340	vendré	5
5341	vende	5
5342	veleta	5
5343	vecindario	5
5344	veamos	5
5345	variedades	5
5346	vapor	5
5347	valiéndose	5
5348	valer	5
5349	vaga	5
5350	vaciló	5
5351	vacilación	5
5352	vaca	5
5353	usurero	5
5354	usado	5
5355	unirse	5
5356	turquesas	5
5357	tubos	5
5358	trompetilla	5
5359	triunfante	5
5360	triquiñuelas	5
5361	trecho	5
5362	trayecto	5
5363	travesura	5
5364	tránsito	5
5365	transigir	5
5366	transición	5
5367	tranquilizaba	5
5368	tramo	5
5369	trajera	5
5370	traigas	5
5371	trágica	5
5372	tragar	5
5373	tragando	5
5374	traerme	5
5375	trabajan	5
5376	tostada	5
5377	torres	5
5378	torpes	5
5379	tornó	5
5380	toques	5
5381	tomase	5
5382	tomarme	5
5383	tomaré	5
5384	tomándolo	5
5385	toman	5
5386	todito	5
5387	tocándole	5
5388	tocado	5
5389	título	5
5390	tiras	5
5391	tirado	5
5392	tinta	5
5393	tímidamente	5
5394	tiita	5
5395	tierna	5
5396	tientas	5
5397	tiembla	5
5398	tías	5
5399	terquedad	5
5400	tenías	5
5401	tenazas	5
5402	temporadas	5
5403	teme	5
5404	tejado	5
5405	tartera	5
5406	tarda	5
5407	tapujos	5
5408	tapia	5
5409	tambores	5
5410	tablas	5
5411	tabernillas	5
5412	sutil	5
5413	suponía	5
5414	suicidio	5
5415	suficiencia	5
5416	suelas	5
5417	sucedieron	5
5418	suba	5
5419	suaves	5
5420	sostenida	5
5421	sostengo	5
5422	sorprendió	5
5423	sorprendida	5
5424	sopor	5
5425	soplaba	5
5426	soñando	5
5427	soñadora	5
5428	sonrisilla	5
5429	sonar	5
5430	somnolencia	5
5431	sombreros	5
5432	sombras	5
5433	solteras	5
5434	solitario	5
5435	sólida	5
5436	socorrerla	5
5437	sobrinas	5
5438	sobrevino	5
5439	sobreponerse	5
5440	sobrenatural	5
5441	soberbio	5
5442	situaciones	5
5443	sincero	5
5444	sinceramente	5
5445	sincera	5
5446	simplezas	5
5447	silenciosa	5
5448	sílabas	5
5449	sierra	5
5450	sexo	5
5451	severa	5
5452	servidora	5
5453	sermones	5
5454	serias	5
5455	seriamente	5
5456	serena	5
5457	sentaban	5
5458	senquá	5
5459	seguros	5
5460	seguidos	5
5461	seductor	5
5462	sedación	5
5463	secta	5
5464	sayo	5
5465	satisfacer	5
5466	santas	5
5467	saltar	5
5468	salgas	5
5469	salamanca	5
5470	sacrificar	5
5471	sacarla	5
5472	sacaría	5
5473	sábana	5
5474	rufinita	5
5475	ruedas	5
5476	ruda	5
5477	ronquidos	5
5478	rompimiento	5
5479	rojas	5
5480	roja	5
5481	robustez	5
5482	rincones	5
5483	ríes	5
5484	reza	5
5485	reyes	5
5486	revuelto	5
5487	reviento	5
5488	reventando	5
5489	revelar	5
5490	reunión	5
5491	retirose	5
5492	resumidas	5
5493	resultando	5
5494	respondo	5
5495	resplandecía	5
5496	resistía	5
5497	repugnaba	5
5498	repetición	5
5499	repetían	5
5500	rendido	5
5501	religiones	5
5502	reinado	5
5503	región	5
5504	regalitos	5
5505	refunfuñando	5
5506	reducido	5
5507	red	5
5508	reconoció	5
5509	recomendó	5
5510	recomendación	5
5511	recobrando	5
5512	recobrado	5
5513	reclamo	5
5514	reciente	5
5515	recibo	5
5516	recadito	5
5517	reacción	5
5518	razonamiento	5
5519	rascaba	5
5520	rama	5
5521	ráfaga	5
5522	radiante	5
5523	quitose	5
5524	quitando	5
5525	quitan	5
5526	quintos	5
5527	quinto	5
5528	quinientos	5
5529	quijada	5
5530	quietud	5
5531	quicio	5
5532	quejas	5
5533	quejarse	5
5534	quédate	5
5535	quedase	5
5536	quedarme	5
5537	quedamos	5
5538	quedábase	5
5539	pureza	5
5540	puras	5
5541	pudieron	5
5542	pucheros	5
5543	puchero	5
5544	pseudo	5
5545	protector	5
5546	prosperidad	5
5547	prontito	5
5548	prometo	5
5549	promesas	5
5550	prójimo	5
5551	producían	5
5552	produce	5
5553	procurando	5
5554	procedencia	5
5555	probado	5
5556	primores	5
5557	pretendo	5
5558	pretendía	5
5559	presuroso	5
5560	presunciones	5
5561	presumida	5
5562	prestar	5
5563	prestamista	5
5564	presidio	5
5565	presentose	5
5566	presentan	5
5567	preparó	5
5568	preciosidad	5
5569	prácticos	5
5570	pozos	5
5571	postre	5
5572	posesión	5
5573	poseer	5
5574	poseen	5
5575	portillo	5
5576	porté	5
5577	portales	5
5578	poquillo	5
5579	populares	5
5580	pongan	5
5581	ponerte	5
5582	poderlo	5
5583	plumas	5
5584	plomo	5
5585	pliegos	5
5586	plazo	5
5587	platillo	5
5588	plancha	5
5589	plaf	5
5590	placera	5
5591	pisto	5
5592	pinturas	5
5593	pintoresco	5
5594	pintores	5
5595	pintados	5
5596	pintaba	5
5597	pino	5
5598	pillete	5
5599	pillería	5
5600	pierdo	5
5601	pierdes	5
5602	pierden	5
5603	pieles	5
5604	pides	5
5605	picor	5
5606	picaresca	5
5607	picante	5
5608	picada	5
5609	pesquis	5
5610	pescado	5
5611	pesca	5
5612	perteneciente	5
5613	pertenecían	5
5614	permitiéndose	5
5615	perdones	5
5616	pepa	5
5617	pensativa	5
5618	pendientes	5
5619	peldaño	5
5620	pelagatos	5
5621	pegarte	5
5622	pedían	5
5623	peces	5
5624	peca	5
5625	patrocinio	5
5626	patios	5
5627	patíbulo	5
5628	patética	5
5629	patada	5
5630	pastelera	5
5631	pasta	5
5632	pasmaron	5
5633	pasase	5
5634	pasaje	5
5635	partidario	5
5636	particularmente	5
5637	particulares	5
5638	parroquiana	5
5639	párrafos	5
5640	párrafo	5
5641	parido	5
5642	parecieron	5
5643	pareciendo	5
5644	parecerse	5
5645	papelito	5
5646	pánico	5
5647	panadería	5
5648	panacea	5
5649	pana	5
5650	palomas	5
5651	palmito	5
5652	palabritas	5
5653	palabrita	5
5654	paices	5
5655	pague	5
5656	pacífico	5
5657	paces	5
5658	oyéndola	5
5659	original	5
5660	ordenó	5
5661	oración	5
5662	ora	5
5663	oportuno	5
5664	opinó	5
5665	opiniones	5
5666	opinaba	5
5667	operaciones	5
5668	olvidó	5
5669	olían	5
5670	olfato	5
5671	oficinas	5
5672	oficial	5
5673	odoripherus	5
5674	ocurrieron	5
5675	ocupada	5
5676	ocultaba	5
5677	oculta	5
5678	observador	5
5679	observa	5
5680	obrar	5
5681	obligada	5
5682	numancia	5
5683	notaron	5
5684	notado	5
5685	notable	5
5686	nociones	5
5687	niega	5
5688	nido	5
5689	negarlo	5
5690	necesitó	5
5691	naturalidad	5
5692	napoleónica	5
5693	muñeco	5
5694	muñecas	5
5695	muñeca	5
5696	mulas	5
5697	muestrario	5
5698	muertas	5
5699	muelles	5
5700	mudarse	5
5701	muchedumbre	5
5702	movido	5
5703	mote	5
5704	mota	5
5705	mostrándose	5
5706	mostrándole	5
5707	mortuoria	5
5708	morros	5
5709	moros	5
5710	montera	5
5711	monarquía	5
5712	molde	5
5713	modos	5
5714	mismito	5
5715	mírame	5
5716	miquis	5
5717	mimoso	5
5718	milagros	5
5719	miiii	5
5720	mientes	5
5721	mia	5
5722	metiéndose	5
5723	metiendo	5
5724	metían	5
5725	méritos	5
5726	menudillos	5
5727	menudas	5
5728	menores	5
5729	melitona	5
5730	melenas	5
5731	mejorado	5
5732	mediano	5
5733	mecanismo	5
5734	maternal	5
5735	maten	5
5736	mártir	5
5737	marcos	5
5738	marco	5
5739	marchó	5
5740	marchas	5
5741	marcado	5
5742	mantillo	5
5743	manifiesto	5
5744	manías	5
5745	mandaré	5
5746	mamar	5
5747	mama	5
5748	maldición	5
5749	madura	5
5750	madrileños	5
5751	machacar	5
5752	lunes	5
5753	luis	5
5754	lugares	5
5755	lucida	5
5756	lucha	5
5757	lozanía	5
5758	lomo	5
5759	loba	5
5760	lleven	5
5761	llevarme	5
5762	llevaré	5
5763	llevaran	5
5764	llevándola	5
5765	llegase	5
5766	llegaría	5
5767	llegaré	5
5768	llegan	5
5769	llegada	5
5770	llamase	5
5771	llamaré	5
5772	llamándola	5
5773	líquido	5
5774	lindos	5
5775	limpiado	5
5776	ligeras	5
5777	lienzos	5
5778	libras	5
5779	librar	5
5780	libra	5
5781	liado	5
5782	levantaron	5
5783	levantando	5
5784	lenguas	5
5785	legal	5
5786	lee	5
5787	lavado	5
5788	largamente	5
5789	lanzado	5
5790	labores	5
5791	laboratorio	5
5792	labia	5
5793	juzgar	5
5794	joyas	5
5795	jesucristo	5
5796	jaula	5
5797	inverosímil	5
5798	inventaba	5
5799	invención	5
5800	intimidad	5
5801	interna	5
5802	intereses	5
5803	intento	5
5804	intensísimo	5
5805	inspección	5
5806	insistencia	5
5807	insensible	5
5808	inquilinos	5
5809	ingrato	5
5810	ínfulas	5
5811	infinito	5
5812	infiernos	5
5813	infalibles	5
5814	indigno	5
5815	índice	5
5816	indeciso	5
5817	incomodarse	5
5818	incomodado	5
5819	inaudita	5
5820	impresionó	5
5821	impertinentes	5
5822	imparcial	5
5823	iluminaba	5
5824	ideales	5
5825	ibas	5
5826	humorado	5
5827	humedad	5
5828	huérfanos	5
5829	hotel	5
5830	hospicio	5
5831	hormigas	5
5832	hondos	5
5833	hocicos	5
5834	hocico	5
5835	hízolo	5
5836	hipotecas	5
5837	hijita	5
5838	higos	5
5839	hígado	5
5840	hielo	5
5841	herir	5
5842	heredó	5
5843	heredado	5
5844	hechas	5
5845	hala	5
5846	hágase	5
5847	hágalo	5
5848	haciéndolo	5
5849	hablase	5
5850	hablaré	5
5851	habilidad	5
5852	haberlo	5
5853	guasa	5
5854	guapetona	5
5855	gruñido	5
5856	groseros	5
5857	gritar	5
5858	grises	5
5859	gravemente	5
5860	gratis	5
5861	gradualmente	5
5862	gordas	5
5863	glorias	5
5864	giro	5
5865	gentío	5
5866	gemido	5
5867	gatillos	5
5868	gatas	5
5869	gata	5
5870	gastos	5
5871	gastar	5
5872	garras	5
5873	ganga	5
5874	ganar	5
5875	gallardamente	5
5876	furibunda	5
5877	fúnebre	5
5878	fundamento	5
5879	fundada	5
5880	frecuencia	5
5881	franco	5
5882	franceses	5
5883	fotografías	5
5884	forzada	5
5885	fortaleza	5
5886	formado	5
5887	follaje	5
5888	flin	5
5889	flan	5
5890	filas	5
5891	fijarse	5
5892	fijamente	5
5893	figurines	5
5894	figúrese	5
5895	festivo	5
5896	feos	5
5897	feas	5
5898	fascinación	5
5899	farol	5
5900	fango	5
5901	famoso	5
5902	extrañeza	5
5903	extranjeros	5
5904	extranjera	5
5905	extendía	5
5906	explicar	5
5907	expectación	5
5908	exigía	5
5909	excursiones	5
5910	excitaba	5
5911	excepción	5
5912	examinando	5
5913	exámenes	5
5914	exaltada	5
5915	estúpidos	5
5916	estupenda	5
5917	estupefacción	5
5918	estudiaba	5
5919	estrecha	5
5920	estén	5
5921	estáis	5
5922	estaciones	5
5923	establecer	5
5924	espuma	5
5925	esperó	5
5926	espere	5
5927	esmero	5
5928	esforzándose	5
5929	escudo	5
5930	escuchaba	5
5931	escorial	5
5932	escondida	5
5933	esconde	5
5934	escoger	5
5935	escasa	5
5936	escaparates	5
5937	escapado	5
5938	escapa	5
5939	erudición	5
5940	equivocarse	5
5941	envoltorio	5
5942	entrevista	5
5943	entrever	5
5944	entretuvo	5
5945	entretenida	5
5946	entraría	5
5947	entera	5
5948	enseñarle	5
5949	enseñanza	5
5950	ensalada	5
5951	enredadera	5
5952	enemiga	5
5953	enderezar	5
5954	endeble	5
5955	encuentran	5
5956	encontrase	5
5957	encontraría	5
5958	encontramos	5
5959	encogimiento	5
5960	encerrado	5
5961	encajes	5
5962	empresas	5
5963	empeñó	5
5964	empeñadas	5
5965	empeña	5
5966	emociones	5
5967	elementales	5
5968	ejercicios	5
5969	ejercía	5
5970	eficaz	5
5971	efectivo	5
5972	económicas	5
5973	echada	5
5974	duermes	5
5975	dudoso	5
5976	duchas	5
5977	dormitorios	5
5978	dorado	5
5979	dominante	5
5980	doloroso	5
5981	documento	5
5982	doblar	5
5983	diversas	5
5984	disponiéndose	5
5985	displicente	5
5986	disparado	5
5987	disimulaba	5
5988	discurría	5
5989	disciplina	5
5990	dirigirse	5
5991	dirigir	5
5992	directamente	5
5993	dimpués	5
5994	dijiste	5
5995	dijéramos	5
5996	digamos	5
5997	diferencias	5
5998	diamante	5
5999	diabluras	5
6000	devociones	5
6001	detúvose	5
6002	determinaciones	5
6003	determinaba	5
6004	detenidamente	5
6005	detenía	5
6006	detenerse	5
6007	desvanecía	5
6008	desplegar	5
6009	despidiendo	5
6010	despertado	5
6011	despertaban	5
6012	despensa	5
6013	deslizándose	5
6014	desigual	5
6015	desierto	5
6016	deseosa	5
6017	deseara	5
6018	descuidada	5
6019	descubre	5
6020	descubierta	5
6021	descanse	5
6022	descansa	5
6023	descalza	5
6024	desayuno	5
6025	desatino	5
6026	desarrollo	5
6027	desarrollarse	5
6028	desaparecer	5
6029	desairada	5
6030	desabrido	5
6031	derramar	5
6032	deleite	5
6033	dejas	5
6034	dejarte	5
6035	dejarme	5
6036	dejarle	5
6037	dejaré	5
6038	dejándose	5
6039	dejándola	5
6040	deis	5
6041	dedillo	5
6042	dedicó	5
6043	declarar	5
6044	decírselo	5
6045	décimo	5
6046	decidir	5
6047	decías	5
6048	debilidades	5
6049	debí	5
6050	debate	5
6051	date	5
6052	darles	5
6053	darían	5
6054	curvas	5
6055	curva	5
6056	cursis	5
6057	curioso	5
6058	curiosear	5
6059	curar	5
6060	curado	5
6061	cuñado	5
6062	cuña	5
6063	cumplidos	5
6064	cuide	5
6065	cuero	5
6066	cubil	5
6067	cualidades	5
6068	cuadra	5
6069	cristóbal	5
6070	criaturas	5
6071	criadas	5
6072	creyeron	5
6073	creían	5
6074	creeré	5
6075	créeme	5
6076	cotorra	5
6077	coscorrones	5
6078	cortina	5
6079	cortés	5
6080	cortaba	5
6081	corsé	5
6082	corrieron	5
6083	correspondiente	5
6084	correspondía	5
6085	correos	5
6086	corredora	5
6087	coraje	5
6088	convino	5
6089	convierte	5
6090	convertir	5
6091	convertido	5
6092	convencimiento	5
6093	convencido	5
6094	convencer	5
6095	contuvo	5
6096	contrabandista	5
6097	continuar	5
6098	contenido	5
6099	contempló	5
6100	contara	5
6101	contadas	5
6102	consumados	5
6103	consulta	5
6104	consternación	5
6105	constancia	5
6106	consiguiente	5
6107	conservando	5
6108	conserva	5
6109	conquista	5
6110	conozca	5
6111	conocimientos	5
6112	conocidos	5
6113	conmovía	5
6114	congreso	5
6115	conformarse	5
6116	conformaba	5
6117	confidencias	5
6118	confidencia	5
6119	condenados	5
6120	concordia	5
6121	concluyendo	5
6122	conciencias	5
6123	comunicó	5
6124	comprendes	5
6125	comprenderá	5
6126	compraba	5
6127	compás	5
6128	comerse	5
6129	comería	5
6130	combinaciones	5
6131	combatir	5
6132	colgado	5
6133	cojita	5
6134	cogieron	5
6135	cogerle	5
6136	cogerla	5
6137	cofre	5
6138	cobarde	5
6139	clerical	5
6140	clareaba	5
6141	circunstantes	5
6142	cigarros	5
6143	cigarrillo	5
6144	ciegos	5
6145	choque	5
6146	chocho	5
6147	chistar	5
6148	chillando	5
6149	chillaba	5
6150	chí	5
6151	charlar	5
6152	chapa	5
6153	chalán	5
6154	cesó	5
6155	cerveza	5
6156	celosa	5
6157	cebada	5
6158	cazador	5
6159	cayetano	5
6160	cavidad	5
6161	católico	5
6162	católica	5
6163	catedral	5
6164	catástrofe	5
6165	castillos	5
6166	castigar	5
6167	cascos	5
6168	cascarón	5
6169	carteras	5
6170	cartera	5
6171	carnicería	5
6172	cariñosamente	5
6173	cariños	5
6174	cargada	5
6175	careta	5
6176	carcajadas	5
6177	cañón	5
6178	cansada	5
6179	cánovas	5
6180	cándido	5
6181	calva	5
6182	calmó	5
6183	calmarle	5
6184	callo	5
6185	callejón	5
6186	caletre	5
6187	calderilla	5
6188	caída	5
6189	cabezadas	5
6190	caballería	5
6191	busque	5
6192	burgos	5
6193	brasero	5
6194	botín	5
6195	bloque	5
6196	bilboquet	5
6197	bienes	5
6198	bicerra	5
6199	betún	5
6200	bestias	5
6201	bella	5
6202	batalla	5
6203	bastones	5
6204	bastero	5
6205	bastaba	5
6206	barbaridades	5
6207	barato	5
6208	bandeja	5
6209	bancos	5
6210	bajos	5
6211	bajón	5
6212	bajan	5
6213	baile	5
6214	ayuntamiento	5
6215	ayunas	5
6216	avisar	5
6217	avanzó	5
6218	avanzaba	5
6219	aumentó	5
6220	atributos	5
6221	atreve	5
6222	atravesaba	5
6223	atracción	5
6224	atento	5
6225	atenta	5
6226	atendiendo	5
6227	atada	5
6228	aspirar	5
6229	asomó	5
6230	asno	5
6231	aseguraba	5
6232	artesa	5
6233	arrojado	5
6234	arreglaré	5
6235	arreglada	5
6236	arrastrado	5
6237	armario	5
6238	arenas	5
6239	ardientes	5
6240	arco	5
6241	aquél	5
6242	apurar	5
6243	apurada	5
6244	apuntar	5
6245	aprisa	5
6246	apretar	5
6247	aprenden	5
6248	apreciable	5
6249	apreciaba	5
6250	apoyo	5
6251	apartando	5
6252	aparentaba	5
6253	aparecido	5
6254	apacible	5
6255	antipática	5
6256	antiespasmódica	5
6257	anteriores	5
6258	ansias	5
6259	angustias	5
6260	andado	5
6261	ancha	5
6262	amorosas	5
6263	alumnas	5
6264	alturas	5
6265	alquilar	5
6266	almacenes	5
6267	alimento	5
6268	alejó	5
6269	alejándose	5
6270	alejado	5
6271	alegres	5
6272	alcanzar	5
6273	alcance	5
6274	alcalá	5
6275	albañiles	5
6276	ajenas	5
6277	airada	5
6278	agudísimo	5
6279	agudeza	5
6280	agradeció	5
6281	agradecía	5
6282	agradable	5
6283	agonías	5
6284	afirmativamente	5
6285	afectaba	5
6286	adquiriendo	5
6287	adorno	5
6288	adorada	5
6289	adoptiva	5
6290	adivinaba	5
6291	acusaciones	5
6292	acudieron	5
6293	activo	5
6294	acostada	5
6295	acompañe	5
6296	acertó	5
6297	acerté	5
6298	acercando	5
6299	acepta	5
6300	acentuado	5
6301	acabara	5
6302	abuelito	5
6303	abstracción	5
6304	abro	5
6305	abrirle	5
6306	yerta	4
6307	yendo	4
6308	yeciones	4
6309	yeción	4
6310	xii	4
6311	vus	4
6312	vulgaridad	4
6313	volviese	4
6314	volviera	4
6315	volverla	4
6316	volcán	4
6317	vocablo	4
6318	vivirá	4
6319	vivió	4
6320	viviese	4
6321	viviente	4
6322	vistió	4
6323	vísperas	4
6324	visitado	4
6325	viruelas	4
6326	violín	4
6327	violentas	4
6328	violenta	4
6329	violencias	4
6330	viñas	4
6331	vínole	4
6332	vinieran	4
6333	viniendo	4
6334	vimos	4
6335	vientos	4
6336	vicios	4
6337	víbora	4
6338	viajar	4
6339	viajante	4
6340	vestíbulo	4
6341	verbi	4
6342	ventura	4
6343	vente	4
6344	ventanillo	4
6345	vengarse	4
6346	vengaré	4
6347	veneración	4
6348	vendrán	4
6349	vendida	4
6350	vena	4
6351	velocidad	4
6352	veinticuatro	4
6353	veíase	4
6354	vastísimo	4
6355	vástago	4
6356	varones	4
6357	valle	4
6358	valían	4
6359	vagas	4
6360	vagar	4
6361	vaciado	4
6362	uvas	4
6363	usté	4
6364	urna	4
6365	uña	4
6366	unción	4
6367	ultramar	4
6368	ultrajado	4
6369	tuvieras	4
6370	tute	4
6371	turco	4
6372	túnel	4
6373	tun	4
6374	tufo	4
6375	tubo	4
6376	trozo	4
6377	tropezó	4
6378	tropezaron	4
6379	tropas	4
6380	trono	4
6381	tronar	4
6382	trompeta	4
6383	trombón	4
6384	trocaba	4
6385	triunfos	4
6386	triunfar	4
6387	tristísima	4
6388	tristemente	4
6389	trinqué	4
6390	trenzas	4
6391	trémula	4
6392	trazas	4
6393	travieso	4
6394	tratarte	4
6395	trataron	4
6396	trataré	4
6397	tratándose	4
6398	tratan	4
6399	trastornos	4
6400	trastornaba	4
6401	trastamara	4
6402	trapitos	4
6403	trapisondas	4
6404	transijo	4
6405	transacción	4
6406	tranquilizarse	4
6407	tranquilizarla	4
6408	traidor	4
6409	traída	4
6410	traición	4
6411	tragedia	4
6412	tragaderas	4
6413	tráete	4
6414	tráeme	4
6415	tradiciones	4
6416	tradicional	4
6417	trabaje	4
6418	torre	4
6419	torpe	4
6420	toro	4
6421	torcer	4
6422	tomes	4
6423	tomé	4
6424	tomarla	4
6425	tocaya	4
6426	tocata	4
6427	tocara	4
6428	toalla	4
6429	tiran	4
6430	timbre	4
6431	tierras	4
6432	tiernas	4
6433	texto	4
6434	tétrica	4
6435	testigos	4
6436	testigo	4
6437	tesón	4
6438	terrorífica	4
6439	terrones	4
6440	terminantemente	4
6441	terminante	4
6442	teorías	4
6443	tentaciones	4
6444	tendido	4
6445	tendida	4
6446	tenaz	4
6447	tempranito	4
6448	templo	4
6449	templado	4
6450	tempestad	4
6451	temperamento	4
6452	temer	4
6453	temblor	4
6454	telón	4
6455	teje	4
6456	taza	4
6457	tarjeta	4
6458	tareas	4
6459	tardar	4
6460	tardaba	4
6461	tararí	4
6462	tapó	4
6463	tapias	4
6464	tapar	4
6465	tapándose	4
6466	tantísimos	4
6467	talonario	4
6468	talante	4
6469	tacto	4
6470	tacón	4
6471	tabla	4
6472	sutiles	4
6473	susurro	4
6474	sustancias	4
6475	suspicaz	4
6476	suspendiendo	4
6477	suponiendo	4
6478	supongo	4
6479	supongamos	4
6480	supieron	4
6481	supieran	4
6482	superficie	4
6483	sumo	4
6484	sujetó	4
6485	sujeta	4
6486	suizo	4
6487	sufría	4
6488	suegros	4
6489	sudorosa	4
6490	sudar	4
6491	sudaba	4
6492	sucias	4
6493	sucede	4
6494	sotanas	4
6495	sotana	4
6496	sostuvo	4
6497	sosteniendo	4
6498	sospechas	4
6499	soso	4
6500	sosiégate	4
6501	sosegado	4
6502	sortijillas	4
6503	soñar	4
6504	sonrió	4
6505	sonaban	4
6506	someter	4
6507	sombrío	4
6508	soltura	4
6509	soltero	4
6510	soltera	4
6511	solfa	4
6512	soldado	4
6513	sofía	4
6514	sodio	4
6515	sócrates	4
6516	socorros	4
6517	socios	4
6518	sobremesa	4
6519	sobras	4
6520	sobrante	4
6521	sirviera	4
6522	sirves	4
6523	sintiéndose	4
6524	simpatías	4
6525	símbolos	4
6526	sillita	4
6527	sillares	4
6528	siguiera	4
6529	signos	4
6530	significan	4
6531	significación	4
6532	significa	4
6533	severamente	4
6534	setenta	4
6535	servilleta	4
6536	serrano	4
6537	serrana	4
6538	serías	4
6539	seríamos	4
6540	sepulcro	4
6541	separó	4
6542	separaba	4
6543	sensible	4
6544	senderos	4
6545	seductores	4
6546	seductora	4
6547	secretario	4
6548	secretaría	4
6549	secándose	4
6550	sebastián	4
6551	satanás	4
6552	sáqueme	4
6553	santidades	4
6554	samaniegos	4
6555	salvarse	4
6556	saludó	4
6557	saltara	4
6558	sagaz	4
6559	sacudió	4
6560	sabroso	4
6561	sabrosas	4
6562	sabría	4
6563	sablazo	4
6564	sabias	4
6565	rutina	4
6566	rumbo	4
6567	ruina	4
6568	rótulos	4
6569	rotos	4
6570	rotas	4
6571	rota	4
6572	ropita	4
6573	romanticismo	4
6574	romántica	4
6575	roma	4
6576	rogar	4
6577	robo	4
6578	rió	4
6579	riñas	4
6580	ridiculez	4
6581	rezos	4
6582	rezaba	4
6583	revuelta	4
6584	revolviéndose	4
6585	revolver	4
6586	revolucionaria	4
6587	revolcándose	4
6588	revista	4
6589	reventar	4
6590	reveló	4
6591	revelado	4
6592	retroceso	4
6593	retiraron	4
6594	retirándose	4
6595	retintín	4
6596	reticencia	4
6597	resultados	4
6598	respetabilidad	4
6599	respectivos	4
6600	resolvió	4
6601	resistiéndose	4
6602	resiste	4
6603	res	4
6604	representar	4
6605	reposado	4
6606	repetidas	4
6607	repartió	4
6608	renegar	4
6609	remota	4
6610	remojo	4
6611	remilgos	4
6612	remiendos	4
6613	remedios	4
6614	remate	4
6615	religiosamente	4
6616	relámpago	4
6617	relajación	4
6618	relacionadas	4
6619	reías	4
6620	rehízo	4
6621	regularidad	4
6622	refrescaba	4
6623	reforma	4
6624	reflexión	4
6625	refirió	4
6626	refiero	4
6627	refiere	4
6628	referir	4
6629	refería	4
6630	reducida	4
6631	rédito	4
6632	redacciones	4
6633	recurso	4
6634	recurrir	4
6635	recto	4
6636	recreo	4
6637	recreándose	4
6638	recorriendo	4
6639	recomiendo	4
6640	recomendándole	4
6641	recomendaba	4
6642	recogido	4
6643	recoge	4
6644	recocho	4
6645	recobrar	4
6646	reclusa	4
6647	reclama	4
6648	recibiera	4
6649	recibí	4
6650	rechazo	4
6651	recetas	4
6652	receta	4
6653	recelosa	4
6654	rebelde	4
6655	rebaño	4
6656	ras	4
6657	raros	4
6658	ráfagas	4
6659	quitarán	4
6660	quitará	4
6661	quitara	4
6662	quisieras	4
6663	quinta	4
6664	quid	4
6665	querría	4
6666	quercus	4
6667	quejumbrosa	4
6668	quejándose	4
6669	quehaceres	4
6670	quédese	4
6671	quedara	4
6672	pusiese	4
6673	purificación	4
6674	purifica	4
6675	puntual	4
6676	puedan	4
6677	publicaciones	4
6678	púas	4
6679	prudencia	4
6680	provincias	4
6681	protesta	4
6682	proteger	4
6683	proponer	4
6684	propietario	4
6685	pronunciamiento	4
6686	pronunciación	4
6687	prontitud	4
6688	prolongar	4
6689	profundos	4
6690	profundísima	4
6691	profesión	4
6692	produzca	4
6693	produciéndole	4
6694	producido	4
6695	prodigios	4
6696	procedía	4
6697	probó	4
6698	privada	4
6699	previsto	4
6700	prevención	4
6701	pretenden	4
6702	presurosa	4
6703	prestó	4
6704	preparativos	4
6705	preparar	4
6706	preocupaciones	4
6707	preguntándole	4
6708	pregúntale	4
6709	prefiero	4
6710	precoz	4
6711	preciosísima	4
6712	prado	4
6713	prácticamente	4
6714	poseedor	4
6715	portó	4
6716	pondrán	4
6717	pondrá	4
6718	pollos	4
6719	pollas	4
6720	poéticas	4
6721	poética	4
6722	podrán	4
6723	podías	4
6724	poderosa	4
6725	pobrecitos	4
6726	población	4
6727	plencia	4
6728	plena	4
6729	platerías	4
6730	plantas	4
6731	plantado	4
6732	planchadora	4
6733	placidez	4
6734	plácemes	4
6735	pisadas	4
6736	pintor	4
6737	pinto	4
6738	pintar	4
6739	pintadas	4
6740	pierda	4
6741	pienses	4
6742	piénselo	4
6743	picoteando	4
6744	picarona	4
6745	picado	4
6746	pica	4
6747	pestes	4
6748	pestañear	4
6749	pesó	4
6750	pesimismo	4
6751	pescadores	4
6752	pesadumbre	4
6753	perverso	4
6754	perspicaz	4
6755	personajes	4
6756	perseguido	4
6757	perplejidad	4
6758	permitiera	4
6759	permite	4
6760	peripecia	4
6761	perfume	4
6762	perfiles	4
6763	perdulario	4
6764	perdónala	4
6765	perdis	4
6766	percal	4
6767	pequeños	4
6768	pequeñas	4
6769	pepito	4
6770	pensara	4
6771	penoso	4
6772	penetrante	4
6773	pendiente	4
6774	pellejo	4
6775	peligroso	4
6776	pelea	4
6777	peinarse	4
6778	pegarme	4
6779	pegándose	4
6780	pegan	4
6781	pegados	4
6782	pegada	4
6783	pediría	4
6784	pedernal	4
6785	pecadoras	4
6786	patriotismo	4
6787	patillas	4
6788	patético	4
6789	patata	4
6790	pasmado	4
6791	pasmaba	4
6792	pasearse	4
6793	pasarse	4
6794	pasajes	4
6795	partir	4
6796	parrafito	4
6797	parola	4
6798	pares	4
6799	parentescos	4
6800	parejas	4
6801	pararse	4
6802	pararon	4
6803	paquetito	4
6804	papelera	4
6805	pandereta	4
6806	palidez	4
6807	página	4
6808	pagarés	4
6809	pagado	4
6810	padeciendo	4
6811	paco	4
6812	pachorra	4
6813	oscuros	4
6814	orillo	4
6815	orilla	4
6816	orígenes	4
6817	órgano	4
6818	organización	4
6819	orgánica	4
6820	ordenaba	4
6821	opuesto	4
6822	onzas	4
6823	ondas	4
6824	olvides	4
6825	olvidarse	4
6826	olvida	4
6827	oler	4
6828	olé	4
6829	ojuelos	4
6830	oírlo	4
6831	oírlas	4
6832	ofrecimientos	4
6833	ofrecieron	4
6834	ofreciendo	4
6835	ofender	4
6836	odios	4
6837	odiaba	4
6838	ocurriole	4
6839	ocupó	4
6840	ocupación	4
6841	octubre	4
6842	obtenido	4
6843	observado	4
6844	obrera	4
6845	obedecía	4
6846	obedecer	4
6847	nuevamente	4
6848	noté	4
6849	notando	4
6850	nombró	4
6851	nodriza	4
6852	niñita	4
6853	niegues	4
6854	nidos	4
6855	neófita	4
6856	negarás	4
6857	necesarios	4
6858	necesario	4
6859	nave	4
6860	náuseas	4
6861	naturalezas	4
6862	naturales	4
6863	narcissus	4
6864	nacimientos	4
6865	nacidos	4
6866	nacen	4
6867	muslo	4
6868	músico	4
6869	muscular	4
6870	mus	4
6871	muros	4
6872	murmullo	4
6873	muriera	4
6874	mujeronas	4
6875	mugidos	4
6876	mugido	4
6877	mueren	4
6878	mudanzas	4
6879	movió	4
6880	moviéndose	4
6881	movían	4
6882	mostrábase	4
6883	moro	4
6884	moralmente	4
6885	moralidad	4
6886	moñas	4
6887	monos	4
6888	monas	4
6889	molido	4
6890	molestaban	4
6891	molesta	4
6892	mohín	4
6893	modistas	4
6894	modesto	4
6895	mocosos	4
6896	místico	4
6897	misericordia	4
6898	mírela	4
6899	miré	4
6900	mírala	4
6901	mirábale	4
6902	mimo	4
6903	miles	4
6904	mico	4
6905	metro	4
6906	metidos	4
6907	mercurio	4
6908	merced	4
6909	mequetrefe	4
6910	mentar	4
6911	mentalmente	4
6912	mensual	4
6913	menesteres	4
6914	memo	4
6915	melancólica	4
6916	mejoró	4
6917	mejoría	4
6918	meditabunda	4
6919	mechones	4
6920	matute	4
6921	materialista	4
6922	matarte	4
6923	matarle	4
6924	matarla	4
6925	marquesas	4
6926	marquesa	4
6927	marimorena	4
6928	maravillosa	4
6929	maquinalmente	4
6930	mañanita	4
6931	manotadas	4
6932	manifestarse	4
6933	manifestar	4
6934	manifestaciones	4
6935	maniática	4
6936	manguito	4
6937	mandarla	4
6938	mandando	4
6939	maná	4
6940	mampara	4
6941	malito	4
6942	maldiciones	4
6943	maldecido	4
6944	majo	4
6945	maduras	4
6946	madrecita	4
6947	machacárselo	4
6948	machacando	4
6949	luminosa	4
6950	lúgubres	4
6951	loza	4
6952	logró	4
6953	lograba	4
6954	llovía	4
6955	llorente	4
6956	llevársela	4
6957	llevarla	4
6958	llevaría	4
6959	llevaremos	4
6960	llevara	4
6961	llevándole	4
6962	llenar	4
6963	llegaban	4
6964	llano	4
6965	llamarle	4
6966	llamados	4
6967	llamábase	4
6968	lívida	4
6969	literarias	4
6970	linda	4
6971	limpiándose	4
6972	limosnas	4
6973	limón	4
6974	lienzo	4
6975	licor	4
6976	libremente	4
6977	librarse	4
6978	levitas	4
6979	leve	4
6980	leona	4
6981	lector	4
6982	lavapiés	4
6983	lavaba	4
6984	láudano	4
6985	latín	4
6986	lápiz	4
6987	lápida	4
6988	lagrimita	4
6989	lágrima	4
6990	labrado	4
6991	juntamente	4
6992	juncos	4
6993	juiciosa	4
6994	juguete	4
6995	jovialidad	4
6996	jaulas	4
6997	jamón	4
6998	islas	4
6999	irías	4
7000	invencible	4
7001	inundaba	4
7002	intranquilo	4
7003	intranquila	4
7004	interrumpió	4
7005	interlocutora	4
7006	interiormente	4
7007	intereso	4
7008	interesa	4
7009	intentaba	4
7010	instruirse	4
7011	instituciones	4
7012	institución	4
7013	instantes	4
7014	instantánea	4
7015	insinuó	4
7016	inseguro	4
7017	inscripciones	4
7018	inofensivo	4
7019	inmuebles	4
7020	ingratitud	4
7021	ingrata	4
7022	ingenua	4
7023	ingenioso	4
7024	ingeniosa	4
7025	inflexiones	4
7026	inferiores	4
7027	infames	4
7028	inerte	4
7029	inefables	4
7030	individual	4
7031	indignada	4
7032	indicación	4
7033	incorporose	4
7034	inconvenientes	4
7035	incomodada	4
7036	inclinose	4
7037	inclinada	4
7038	inclinaciones	4
7039	inciso	4
7040	inauguración	4
7041	in	4
7042	impulsaba	4
7043	imprenta	4
7044	importe	4
7045	imperturbable	4
7046	impedirlo	4
7047	imparcialidad	4
7048	imitando	4
7049	imitación	4
7050	imaginarse	4
7051	iluminados	4
7052	igualmente	4
7053	ignoraba	4
7054	ignominias	4
7055	ida	4
7056	humorístico	4
7057	humildes	4
7058	húmedos	4
7059	humedecieron	4
7060	huerfanito	4
7061	huchas	4
7062	hortera	4
7063	hortaleza	4
7064	horrorizada	4
7065	honradamente	4
7066	homicidio	4
7067	holanda	4
7068	hoguera	4
7069	históricos	4
7070	histórica	4
7071	hipocresía	4
7072	himno	4
7073	hilaridad	4
7074	hicieran	4
7075	herrero	4
7076	hermosísimo	4
7077	herido	4
7078	helada	4
7079	heces	4
7080	hartarse	4
7081	hartaba	4
7082	harta	4
7083	harían	4
7084	hambres	4
7085	hallarse	4
7086	habré	4
7087	hablemos	4
7088	hablas	4
7089	habladores	4
7090	habitual	4
7091	habíale	4
7092	gusanillo	4
7093	guisado	4
7094	guiñando	4
7095	guerras	4
7096	guarde	4
7097	guardas	4
7098	guardarropa	4
7099	guardaré	4
7100	guardan	4
7101	gruñidos	4
7102	grueso	4
7103	gris	4
7104	gresca	4
7105	greñas	4
7106	grecia	4
7107	grasa	4
7108	granuja	4
7109	grano	4
7110	grandioso	4
7111	grandiosa	4
7112	grana	4
7113	graciosas	4
7114	gozosos	4
7115	gori	4
7116	golosinas	4
7117	gobierna	4
7118	gobernaba	4
7119	gigantea	4
7120	géneros	4
7121	generala	4
7122	gemidos	4
7123	gastan	4
7124	ganó	4
7125	ganitas	4
7126	ganarse	4
7127	galera	4
7128	fundó	4
7129	fulgor	4
7130	fueras	4
7131	fuéramos	4
7132	frunció	4
7133	frunciendo	4
7134	frescos	4
7135	fraude	4
7136	fraternidad	4
7137	francos	4
7138	franca	4
7139	fragancia	4
7140	forro	4
7141	formarse	4
7142	formaba	4
7143	forastero	4
7144	flaquezas	4
7145	flaqueza	4
7146	flandes	4
7147	firmado	4
7148	fingiéndose	4
7149	filosóficas	4
7150	filo	4
7151	fijos	4
7152	fíjese	4
7153	fijando	4
7154	figuro	4
7155	figurando	4
7156	fieles	4
7157	fideos	4
7158	fiar	4
7159	ferrolana	4
7160	fernando	4
7161	fechas	4
7162	fealdad	4
7163	favorables	4
7164	fatuidad	4
7165	fatalidad	4
7166	farsante	4
7167	fardo	4
7168	famosa	4
7169	familiaridad	4
7170	faltara	4
7171	faja	4
7172	faetón	4
7173	extravagancia	4
7174	extrañaba	4
7175	extiende	4
7176	externo	4
7177	expresivo	4
7178	expresiva	4
7179	explosión	4
7180	explico	4
7181	explica	4
7182	existir	4
7183	existiera	4
7184	existen	4
7185	exige	4
7186	exhaló	4
7187	exhalación	4
7188	excusas	4
7189	excursión	4
7190	exclamación	4
7191	excitar	4
7192	excitada	4
7193	etiquetas	4
7194	etiqueta	4
7195	eternas	4
7196	eterna	4
7197	estuviste	4
7198	estruendo	4
7199	estremeció	4
7200	estrechez	4
7201	estirón	4
7202	estiró	4
7203	estipendio	4
7204	estanque	4
7205	estampía	4
7206	establecimientos	4
7207	esquelita	4
7208	esqueleto	4
7209	espontaneidad	4
7210	espiritistas	4
7211	espejos	4
7212	especial	4
7213	espartero	4
7214	españolas	4
7215	espantada	4
7216	espaciosa	4
7217	escurría	4
7218	escultura	4
7219	escrúpulo	4
7220	escritos	4
7221	escrita	4
7222	escribiendo	4
7223	escondrijo	4
7224	escondía	4
7225	escobas	4
7226	esclavo	4
7227	escaparate	4
7228	escapar	4
7229	escalerilla	4
7230	equivocó	4
7231	equivocada	4
7232	equivocaba	4
7233	equipaje	4
7234	épocas	4
7235	epiléptica	4
7236	envidio	4
7237	entusiasmos	4
7238	entretenerse	4
7239	entretanto	4
7240	entregó	4
7241	entregas	4
7242	entidad	4
7243	entendida	4
7244	entenderá	4
7245	entablar	4
7246	ensimismada	4
7247	ensayo	4
7248	enredos	4
7249	enredo	4
7250	enojada	4
7251	engañó	4
7252	engañé	4
7253	engañarme	4
7254	engañando	4
7255	engañaba	4
7256	enfadada	4
7257	enfada	4
7258	enérgico	4
7259	encubridora	4
7260	encerrarme	4
7261	encerrarle	4
7262	encaró	4
7263	encarnado	4
7264	empujándole	4
7265	emprender	4
7266	empleos	4
7267	emplearía	4
7268	empleando	4
7269	empleaba	4
7270	emperador	4
7271	empeñan	4
7272	empeñado	4
7273	empeñaba	4
7274	embustero	4
7275	embriaguez	4
7276	elogió	4
7277	elección	4
7278	ejercer	4
7279	educado	4
7280	edificar	4
7281	eco	4
7282	eches	4
7283	echas	4
7284	echarme	4
7285	echarla	4
7286	durara	4
7287	duraba	4
7288	duquesa	4
7289	duérmete	4
7290	dueños	4
7291	drogas	4
7292	dramático	4
7293	dorotea	4
7294	dormirse	4
7295	donnell	4
7296	donativos	4
7297	domésticos	4
7298	docenas	4
7299	distraído	4
7300	distinguía	4
7301	disputaban	4
7302	disponía	4
7303	dispongo	4
7304	dispone	4
7305	displicencia	4
7306	disminuir	4
7307	disimulado	4
7308	disfrutaba	4
7309	discutía	4
7310	discurro	4
7311	discretamente	4
7312	discípulo	4
7313	directora	4
7314	dioses	4
7315	dineros	4
7316	dilo	4
7317	diligencias	4
7318	dilema	4
7319	díjome	4
7320	dignos	4
7321	diciéndome	4
7322	diciéndolo	4
7323	dichos	4
7324	dibujos	4
7325	devuelve	4
7326	devolver	4
7327	devaneos	4
7328	deudor	4
7329	detenerla	4
7330	detalle	4
7331	desvelada	4
7332	desusado	4
7333	desusada	4
7334	desprendimiento	4
7335	desprenderse	4
7336	desplegaban	4
7337	desplegaba	4
7338	despierte	4
7339	despidiéndose	4
7340	despejado	4
7341	despejada	4
7342	despedidas	4
7343	despachó	4
7344	despachaba	4
7345	despabilado	4
7346	desmejorado	4
7347	desmejorada	4
7348	desmedido	4
7349	deshora	4
7350	deshonrada	4
7351	desgraciadamente	4
7352	desempeñaba	4
7353	deseamos	4
7354	desdichas	4
7355	desdichada	4
7356	desdeñoso	4
7357	descubría	4
7358	describiendo	4
7359	desconsolado	4
7360	desconsolada	4
7361	desconocidas	4
7362	desconcierto	4
7363	desconcertado	4
7364	descomponiéndose	4
7365	descomponerse	4
7366	descarga	4
7367	desatinos	4
7368	desaparecieron	4
7369	desaliento	4
7370	desairado	4
7371	desahogo	4
7372	derramado	4
7373	derivativo	4
7374	demostró	4
7375	demostrar	4
7376	demostraciones	4
7377	defiende	4
7378	defenderse	4
7379	dedicaba	4
7380	decoración	4
7381	declaro	4
7382	debieran	4
7383	darlos	4
7384	dañada	4
7385	danzante	4
7386	damos	4
7387	dámaso	4
7388	dada	4
7389	curita	4
7390	cuna	4
7391	cumplía	4
7392	cultivaba	4
7393	cuidarse	4
7394	cuidarle	4
7395	cuida	4
7396	cuerno	4
7397	cuchufletas	4
7398	cuchilleros	4
7399	cuchicheo	4
7400	cuchichearon	4
7401	cucharilla	4
7402	cucharada	4
7403	cuantito	4
7404	cuán	4
7405	cuáles	4
7406	cruzó	4
7407	cruzando	4
7408	cruzados	4
7409	crueldad	4
7410	crudos	4
7411	crónico	4
7412	cristianos	4
7413	cristianar	4
7414	crío	4
7415	crines	4
7416	criminales	4
7417	criando	4
7418	criaba	4
7419	creyera	4
7420	cretonas	4
7421	crespón	4
7422	creerse	4
7423	creerán	4
7424	crecer	4
7425	costra	4
7426	costa	4
7427	corteza	4
7428	correspondían	4
7429	corresponde	4
7430	correcciones	4
7431	corra	4
7432	corpus	4
7433	coquetería	4
7434	coplas	4
7435	coñac	4
7436	convinieron	4
7437	convido	4
7438	conventos	4
7439	convenientes	4
7440	convéncete	4
7441	convencerás	4
7442	contraste	4
7443	contrarios	4
7444	contrarias	4
7445	contorsiones	4
7446	continuo	4
7447	continuando	4
7448	contestarle	4
7449	contemplarla	4
7450	contemplaba	4
7451	contante	4
7452	contándole	4
7453	contados	4
7454	consultar	4
7455	consuelos	4
7456	constituye	4
7457	constitución	4
7458	consorte	4
7459	consolidado	4
7460	consiento	4
7461	considerando	4
7462	conservar	4
7463	consejera	4
7464	conseguía	4
7465	conocieron	4
7466	conociera	4
7467	conocen	4
7468	conocemos	4
7469	confundir	4
7470	confiese	4
7471	confianzas	4
7472	confiaba	4
7473	confesora	4
7474	conducto	4
7475	conducía	4
7476	condenar	4
7477	condenadas	4
7478	concierto	4
7479	concerniente	4
7480	comunicarle	4
7481	comunica	4
7482	comprometo	4
7483	comprarle	4
7484	comprada	4
7485	compostura	4
7486	composición	4
7487	componían	4
7488	complexión	4
7489	completar	4
7490	completaban	4
7491	compasiva	4
7492	compararse	4
7493	comodidad	4
7494	comieron	4
7495	comezón	4
7496	comestibles	4
7497	comerciantes	4
7498	comensales	4
7499	combinados	4
7500	combinado	4
7501	combinadas	4
7502	colonia	4
7503	colocado	4
7504	colgar	4
7505	colgando	4
7506	colgados	4
7507	coleta	4
7508	colchones	4
7509	col	4
7510	cogidos	4
7511	cogida	4
7512	cogían	4
7513	cogerte	4
7514	cogeré	4
7515	cobranza	4
7516	cobra	4
7517	clero	4
7518	clérigos	4
7519	clavar	4
7520	clavando	4
7521	clavada	4
7522	circunstancia	4
7523	cifras	4
7524	cierra	4
7525	chuletita	4
7526	chorreando	4
7527	chocar	4
7528	chistes	4
7529	chiquito	4
7530	chiquillas	4
7531	chino	4
7532	chimenea	4
7533	chillonas	4
7534	chiflada	4
7535	chaveta	4
7536	champagne	4
7537	chacota	4
7538	cerdo	4
7539	central	4
7540	céntimos	4
7541	celebraron	4
7542	celebraba	4
7543	cediendo	4
7544	categoría	4
7545	cátedra	4
7546	catecismo	4
7547	casita	4
7548	casero	4
7549	caserío	4
7550	casera	4
7551	casé	4
7552	casarredonda	4
7553	carretillas	4
7554	carnero	4
7555	carlistas	4
7556	cargaba	4
7557	carcelera	4
7558	carbonero	4
7559	carbón	4
7560	caramelos	4
7561	caramelo	4
7562	carambita	4
7563	capitales	4
7564	capirotes	4
7565	cañizares	4
7566	cantinela	4
7567	cantero	4
7568	cantería	4
7569	cantera	4
7570	canta	4
7571	canso	4
7572	cansaba	4
7573	canción	4
7574	canalla	4
7575	campanadas	4
7576	camorra	4
7577	camelias	4
7578	calzones	4
7579	calumnia	4
7580	callose	4
7581	callaron	4
7582	callando	4
7583	callados	4
7584	calladita	4
7585	calixta	4
7586	calcula	4
7587	calaverada	4
7588	cal	4
7589	caes	4
7590	caerse	4
7591	cadáveres	4
7592	cadáver	4
7593	cacharro	4
7594	buscas	4
7595	burlarse	4
7596	bulle	4
7597	bufanda	4
7598	brutal	4
7599	brotaba	4
7600	bromazo	4
7601	bringas	4
7602	bravo	4
7603	borrado	4
7604	borrachos	4
7605	boquita	4
7606	bondadosa	4
7607	bonaparte	4
7608	bolsín	4
7609	bilis	4
7610	bicho	4
7611	biblia	4
7612	biberón	4
7613	biarritz	4
7614	besugo	4
7615	besándola	4
7616	benévola	4
7617	bayeta	4
7618	bautismo	4
7619	barrer	4
7620	barreño	4
7621	barrenderos	4
7622	barras	4
7623	baratijas	4
7624	baños	4
7625	bandera	4
7626	bálsamo	4
7627	bala	4
7628	bajaron	4
7629	bajaré	4
7630	babero	4
7631	babas	4
7632	azorado	4
7633	ayudado	4
7634	aversión	4
7635	averiguarlo	4
7636	aventuró	4
7637	aventura	4
7638	avariento	4
7639	avaricia	4
7640	avanzando	4
7641	auxiliar	4
7642	autores	4
7643	austria	4
7644	ausencias	4
7645	aureola	4
7646	auditorio	4
7647	aturdimiento	4
7648	atrozmente	4
7649	atrocidades	4
7650	atrevida	4
7651	atractivos	4
7652	ató	4
7653	atizó	4
7654	ateo	4
7655	atavío	4
7656	ataques	4
7657	asustarse	4
7658	asquerosa	4
7659	aspirando	4
7660	aspereza	4
7661	áspera	4
7662	asista	4
7663	asimilación	4
7664	ascendiente	4
7665	artístico	4
7666	articular	4
7667	arrepentidas	4
7668	arreglos	4
7669	arrastraba	4
7670	arrancarse	4
7671	arrancar	4
7672	arrancaba	4
7673	armando	4
7674	arman	4
7675	arguyó	4
7676	argumentación	4
7677	arca	4
7678	apurado	4
7679	apunta	4
7680	apuesto	4
7681	aptitudes	4
7682	aproximarse	4
7683	aprovechando	4
7684	aprensión	4
7685	aprenderá	4
7686	aprenda	4
7687	apostolado	4
7688	apóstol	4
7689	aplomo	4
7690	apetecer	4
7691	apatía	4
7692	aparecieron	4
7693	apagada	4
7694	añadidura	4
7695	antón	4
7696	antipáticos	4
7697	antiguos	4
7698	antiguas	4
7699	anteanoche	4
7700	animalito	4
7701	animaba	4
7702	anhelaba	4
7703	angosta	4
7704	anegada	4
7705	anécdotas	4
7706	andaluz	4
7707	anaquelería	4
7708	amplitud	4
7709	amos	4
7710	amenazaba	4
7711	amena	4
7712	ambición	4
7713	amargo	4
7714	amadeo	4
7715	alfonsismo	4
7716	alfombra	4
7717	alfileres	4
7718	alegrías	4
7719	alegraría	4
7720	alcohol	4
7721	alcobas	4
7722	alcanzaba	4
7723	alborotados	4
7724	alborotado	4
7725	alborotaba	4
7726	alarde	4
7727	alabardero	4
7728	ala	4
7729	ajuar	4
7730	ajetreo	4
7731	ajenos	4
7732	ajena	4
7733	airosa	4
7734	ahínco	4
7735	agujerito	4
7736	aguárdese	4
7737	agradecimiento	4
7738	agradecidísimo	4
7739	agradar	4
7740	agitó	4
7741	áfrica	4
7742	afligido	4
7743	afirmativo	4
7744	aficiones	4
7745	aficionado	4
7746	afectuoso	4
7747	afectada	4
7748	afabilidad	4
7749	adúuultera	4
7750	adúlteros	4
7751	aduana	4
7752	adrede	4
7753	adoro	4
7754	adoraba	4
7755	administrativa	4
7756	ademanes	4
7757	adefesio	4
7758	acuesto	4
7759	actriz	4
7760	acreedor	4
7761	acostumbrando	4
7762	acostumbraba	4
7763	acostado	4
7764	acordé	4
7765	acordarse	4
7766	acordar	4
7767	acordándose	4
7768	acordábase	4
7769	acompañaré	4
7770	acompañadas	4
7771	acometido	4
7772	acometer	4
7773	achaques	4
7774	acertar	4
7775	aceptó	4
7776	acentos	4
7777	acecha	4
7778	accidentes	4
7779	accidente	4
7780	acariciándole	4
7781	acalorada	4
7782	acabaría	4
7783	acaban	4
7784	acabadita	4
7785	abusando	4
7786	aburría	4
7787	abundaba	4
7788	abuelita	4
7789	absurda	4
7790	abril	4
7791	abrían	4
7792	abren	4
7793	abrazos	4
7794	abrazó	4
7795	abrazándola	4
7796	abanico	4
7797	zas	3
7798	zarzuela	3
7799	zapatones	3
7800	zapatero	3
7801	zancas	3
7802	vulgarmente	3
7803	vueltos	3
7804	vuelca	3
7805	votos	3
7806	votar	3
7807	vómitos	3
7808	volvemos	3
7809	volumen	3
7810	volar	3
7811	vizcaína	3
7812	vivísimo	3
7813	vivimos	3
7814	viviendas	3
7815	vivan	3
7816	vitoria	3
7817	vistoso	3
7818	visitó	3
7819	visionaria	3
7820	visiblemente	3
7821	violentísimo	3
7822	vinagre	3
7823	vil	3
7824	vigor	3
7825	viejos	3
7826	vidrio	3
7827	víctimas	3
7828	vibraciones	3
7829	viajeros	3
7830	veterano	3
7831	vestirle	3
7832	vestiré	3
7833	versó	3
7834	verificose	3
7835	verificó	3
7836	verídicamente	3
7837	vergonzosos	3
7838	vergonzosas	3
7839	vergonzosa	3
7840	veredas	3
7841	venturoso	3
7842	ventas	3
7843	venta	3
7844	vengaba	3
7845	vendrás	3
7846	vendían	3
7847	vendedores	3
7848	vendedor	3
7849	venció	3
7850	vencedora	3
7851	vemos	3
7852	velos	3
7853	velón	3
7854	vello	3
7855	velador	3
7856	vejez	3
7857	veintitrés	3
7858	veintisiete	3
7859	veíanse	3
7860	vehículo	3
7861	vehementes	3
7862	vehemencia	3
7863	vayamos	3
7864	vasos	3
7865	varoniles	3
7866	variaron	3
7867	variando	3
7868	variado	3
7869	variaba	3
7870	varía	3
7871	varas	3
7872	valido	3
7873	valerosa	3
7874	valeriano	3
7875	valdría	3
7876	vagón	3
7877	vagabundo	3
7878	vagabunda	3
7879	vagaban	3
7880	uy	3
7881	útil	3
7882	usuales	3
7883	usaron	3
7884	usando	3
7885	usadas	3
7886	universo	3
7887	universidad	3
7888	unido	3
7889	unida	3
7890	uníase	3
7891	ultrajar	3
7892	tuviesen	3
7893	turbó	3
7894	turbar	3
7895	tunanta	3
7896	tufillo	3
7897	tropezando	3
7898	trocó	3
7899	triviales	3
7900	tristísimo	3
7901	triquitraque	3
7902	trinidad	3
7903	trifulca	3
7904	tributo	3
7905	tribunales	3
7906	tribulación	3
7907	tresillo	3
7908	trepidación	3
7909	trémulo	3
7910	tremendos	3
7911	trece	3
7912	trazar	3
7913	traté	3
7914	tratarse	3
7915	tratarla	3
7916	tratante	3
7917	tratándole	3
7918	trastorna	3
7919	trastienda	3
7920	trapisondista	3
7921	transparentes	3
7922	transcurrido	3
7923	tranquilízate	3
7924	tramando	3
7925	trajín	3
7926	trajeran	3
7927	trajecito	3
7928	tráiganme	3
7929	tragué	3
7930	tragos	3
7931	tragado	3
7932	tráfico	3
7933	traerla	3
7934	traería	3
7935	trabajó	3
7936	trabajadora	3
7937	toser	3
7938	tosca	3
7939	torero	3
7940	torcidas	3
7941	toquillas	3
7942	tontaina	3
7943	tomándose	3
7944	tomada	3
7945	toleraba	3
7946	toditos	3
7947	tocaban	3
7948	tisis	3
7949	tirita	3
7950	tirarlos	3
7951	tirarle	3
7952	tirándole	3
7953	tíos	3
7954	tiorras	3
7955	tiñe	3
7956	tila	3
7957	tifus	3
7958	tiesos	3
7959	tiesa	3
7960	tiernísimo	3
7961	textos	3
7962	tetuán	3
7963	tesis	3
7964	tertulios	3
7965	ternezas	3
7966	terminando	3
7967	tenue	3
7968	tentativas	3
7969	teníamos	3
7970	tenerlos	3
7971	tenducho	3
7972	tendiendo	3
7973	temió	3
7974	temido	3
7975	temerario	3
7976	tembló	3
7977	telégrafos	3
7978	tejados	3
7979	tedio	3
7980	teclas	3
7981	teatros	3
7982	teatrales	3
7983	tasa	3
7984	tartán	3
7985	tardaron	3
7986	tardado	3
7987	tarambana	3
7988	tapando	3
7989	tantísimo	3
7990	tantísimas	3
7991	talla	3
7992	talentazo	3
7993	talco	3
7994	tagarotes	3
7995	tácita	3
7996	tabiques	3
7997	tabique	3
7998	tabernas	3
7999	t	3
8000	suspirando	3
8001	suscriciones	3
8002	surgido	3
8003	suposición	3
8004	suplico	3
8005	suplicante	3
8006	sujetar	3
8007	sujetándole	3
8008	suiza	3
8009	sufrimientos	3
8010	suficiente	3
8011	sueña	3
8012	suéltame	3
8013	suela	3
8014	sudando	3
8015	sucios	3
8016	sucesivos	3
8017	subsecretario	3
8018	subordinación	3
8019	súbita	3
8020	subiéndose	3
8021	subí	3
8022	sótano	3
8023	sostiene	3
8024	sostenido	3
8025	sospechó	3
8026	sorprendido	3
8027	sorda	3
8028	soportar	3
8029	soportales	3
8030	soplo	3
8031	sopas	3
8032	soñó	3
8033	sonríe	3
8034	sonda	3
8035	sonaran	3
8036	sonada	3
8037	sombrerito	3
8038	solterón	3
8039	soltaron	3
8040	soltado	3
8041	solomillo	3
8042	solitarios	3
8043	solita	3
8044	soliloquios	3
8045	sólido	3
8046	solidaridad	3
8047	solicitaba	3
8048	solamente	3
8049	sois	3
8050	sofoques	3
8051	sofocadísima	3
8052	sofismas	3
8053	soeces	3
8054	socio	3
8055	socarronería	3
8056	sobriedad	3
8057	sobresalto	3
8058	sobresaltada	3
8059	soberano	3
8060	sirviente	3
8061	sirva	3
8062	siniestra	3
8063	singularmente	3
8064	singapore	3
8065	simpleza	3
8066	símbolo	3
8067	sillar	3
8068	sigüenza	3
8069	siguen	3
8070	significaban	3
8071	sienes	3
8072	sien	3
8073	severo	3
8074	sesión	3
8075	serpiente	3
8076	serenos	3
8077	serenó	3
8078	serenarse	3
8079	serafines	3
8080	septiembre	3
8081	separarse	3
8082	separar	3
8083	separados	3
8084	separaban	3
8085	señaló	3
8086	señalado	3
8087	seña	3
8088	sentían	3
8089	sentase	3
8090	sentara	3
8091	sensata	3
8092	senos	3
8093	semejaban	3
8094	semejaba	3
8095	sello	3
8096	segundos	3
8097	seguiría	3
8098	seguirá	3
8099	seguimos	3
8100	secreteo	3
8101	secreteándose	3
8102	secreta	3
8103	secos	3
8104	secciones	3
8105	secas	3
8106	savia	3
8107	satánica	3
8108	sastres	3
8109	sartén	3
8110	sardinas	3
8111	sarampión	3
8112	saques	3
8113	saña	3
8114	sandeces	3
8115	sándalo	3
8116	sánchez	3
8117	samaniega	3
8118	salvó	3
8119	salve	3
8120	salvarme	3
8121	saludando	3
8122	saluda	3
8123	saltaron	3
8124	saliste	3
8125	salirse	3
8126	salidita	3
8127	saldo	3
8128	sahumar	3
8129	sagaces	3
8130	sacudirse	3
8131	sacudiendo	3
8132	sacudía	3
8133	sacuden	3
8134	sacrificios	3
8135	sacramentos	3
8136	sacas	3
8137	sacada	3
8138	sabrosa	3
8139	sabidurías	3
8140	sabia	3
8141	sabéis	3
8142	sabedor	3
8143	rusia	3
8144	ruinas	3
8145	ruidosa	3
8146	ruidos	3
8147	rúbrica	3
8148	rondas	3
8149	ron	3
8150	rompo	3
8151	rompería	3
8152	romero	3
8153	románticas	3
8154	romanos	3
8155	rogó	3
8156	roe	3
8157	rodeos	3
8158	rodearon	3
8159	rodeaban	3
8160	rodea	3
8161	roce	3
8162	robusto	3
8163	robusta	3
8164	robar	3
8165	robaba	3
8166	roba	3
8167	rivalidad	3
8168	rito	3
8169	riquísimos	3
8170	riquísimo	3
8171	riquezas	3
8172	riñón	3
8173	riñendo	3
8174	rinconada	3
8175	ríete	3
8176	rieron	3
8177	riego	3
8178	ridículos	3
8179	ribetes	3
8180	ría	3
8181	revueltos	3
8182	revueltas	3
8183	revolvían	3
8184	revolucionarios	3
8185	reventones	3
8186	revelaciones	3
8187	revelaban	3
8188	revancha	3
8189	reunidos	3
8190	reunían	3
8191	reuma	3
8192	retuvo	3
8193	retrocedió	3
8194	retiráronse	3
8195	retirar	3
8196	retirada	3
8197	resurrección	3
8198	resueltamente	3
8199	resuello	3
8200	resquicio	3
8201	respuestas	3
8202	responderle	3
8203	respiró	3
8204	respirando	3
8205	respiraba	3
8206	respetos	3
8207	respetando	3
8208	respetabilísima	3
8209	resignada	3
8210	resignación	3
8211	reservada	3
8212	resentimientos	3
8213	resabio	3
8214	reproducía	3
8215	reprimenda	3
8216	representaban	3
8217	reprendía	3
8218	reprender	3
8219	reponerse	3
8220	replicaba	3
8221	repitiera	3
8222	repentino	3
8223	repaso	3
8224	repasar	3
8225	repartiendo	3
8226	reparo	3
8227	reparador	3
8228	reoyos	3
8229	rentas	3
8230	renovación	3
8231	remotos	3
8232	remoto	3
8233	remotas	3
8234	remordimiento	3
8235	relieve	3
8236	relativo	3
8237	relamía	3
8238	rejilla	3
8239	reiría	3
8240	regularmente	3
8241	regresó	3
8242	reglamento	3
8243	registrar	3
8244	regaliz	3
8245	refrescó	3
8246	refrán	3
8247	reformas	3
8248	reflexiones	3
8249	referirse	3
8250	refajo	3
8251	réditos	3
8252	redes	3
8253	recursos	3
8254	recuerdos	3
8255	recreaba	3
8256	recortar	3
8257	recorrió	3
8258	recorría	3
8259	recordó	3
8260	reconocieron	3
8261	reconocerle	3
8262	recomienda	3
8263	recomendara	3
8264	recomendaciones	3
8265	recogimiento	3
8266	recogieron	3
8267	recobraba	3
8268	reclusas	3
8269	recinto	3
8270	recibiría	3
8271	recibieron	3
8272	recibida	3
8273	rechazaba	3
8274	recato	3
8275	rebotica	3
8276	rebosando	3
8277	rayos	3
8278	rayado	3
8279	raudal	3
8280	rasguñar	3
8281	rasgueadas	3
8282	randa	3
8283	ramoncita	3
8284	ramaje	3
8285	ralo	3
8286	ración	3
8287	raciocinio	3
8288	racimo	3
8289	racha	3
8290	rabioso	3
8291	rabiosa	3
8292	quito	3
8293	quítese	3
8294	quiten	3
8295	quitaron	3
8296	quitándole	3
8297	quisieron	3
8298	quijote	3
8299	quietecito	3
8300	querrías	3
8301	quererse	3
8302	quererla	3
8303	querencia	3
8304	quepa	3
8305	quelo	3
8306	quejaba	3
8307	quedas	3
8308	quedaré	3
8309	quedábanse	3
8310	pusiéronle	3
8311	pupitre	3
8312	punzada	3
8313	puntualmente	3
8314	puntualidad	3
8315	pulcritud	3
8316	puff	3
8317	pueriles	3
8318	puerca	3
8319	puente	3
8320	pudor	3
8321	pudiese	3
8322	púa	3
8323	prusianos	3
8324	próximos	3
8325	protegida	3
8326	protegía	3
8327	proposiciones	3
8328	propiedades	3
8329	propagandista	3
8330	pronunciada	3
8331	pronunciaba	3
8332	pronta	3
8333	prometiendo	3
8334	prométeme	3
8335	productos	3
8336	producir	3
8337	producíale	3
8338	producen	3
8339	prodigiosa	3
8340	proceso	3
8341	probaré	3
8342	probando	3
8343	probabilidades	3
8344	privado	3
8345	privaciones	3
8346	prisionera	3
8347	prisas	3
8348	principia	3
8349	primorosas	3
8350	primitivos	3
8351	primitiva	3
8352	primas	3
8353	previsión	3
8354	preverlo	3
8355	prevengo	3
8356	pretextando	3
8357	presumir	3
8358	presumía	3
8359	prestan	3
8360	prestado	3
8361	presos	3
8362	presintió	3
8363	presento	3
8364	presentimientos	3
8365	presentará	3
8366	presentara	3
8367	presentado	3
8368	presenciado	3
8369	presbítero	3
8370	preparémonos	3
8371	preocupada	3
8372	premios	3
8373	preguntita	3
8374	pregunté	3
8375	pregúntaselo	3
8376	preguntaban	3
8377	pregones	3
8378	pregonar	3
8379	prefiriendo	3
8380	prefería	3
8381	preferencia	3
8382	predilecto	3
8383	predicar	3
8384	precursores	3
8385	precipitó	3
8386	precipitadamente	3
8387	precios	3
8388	preciaba	3
8389	precedieron	3
8390	precauciones	3
8391	practicante	3
8392	practicaba	3
8393	potásico	3
8394	postración	3
8395	positiva	3
8396	posibilidad	3
8397	posee	3
8398	posada	3
8399	portezuela	3
8400	portarme	3
8401	porta	3
8402	porrazos	3
8403	porquería	3
8404	poros	3
8405	porción	3
8406	poquitito	3
8407	ponme	3
8408	ponlo	3
8409	póngase	3
8410	ponérselo	3
8411	pondrás	3
8412	ponderar	3
8413	polla	3
8414	polkas	3
8415	polisón	3
8416	podremos	3
8417	poderoso	3
8418	podéis	3
8419	platillos	3
8420	planto	3
8421	plantan	3
8422	planchar	3
8423	pistola	3
8424	pío	3
8425	pintón	3
8426	pintarte	3
8427	pingajos	3
8428	pim	3
8429	píldora	3
8430	pilas	3
8431	piensan	3
8432	pidiera	3
8433	pida	3
8434	picotazos	3
8435	picaresco	3
8436	picardías	3
8437	picantes	3
8438	picando	3
8439	piar	3
8440	pianitos	3
8441	piadoso	3
8442	piadosa	3
8443	petitorios	3
8444	peste	3
8445	pestañas	3
8446	pescar	3
8447	pesara	3
8448	pesadito	3
8449	pesadas	3
8450	pesa	3
8451	perversos	3
8452	persuasión	3
8453	perspicacia	3
8454	perrito	3
8455	perrera	3
8456	peros	3
8457	permito	3
8458	permitir	3
8459	permitieron	3
8460	permanente	3
8461	perjuicio	3
8462	peripecias	3
8463	pérfido	3
8464	perdóneme	3
8465	perdonaría	3
8466	perdiz	3
8467	perdiéndose	3
8468	pérdidas	3
8469	percibió	3
8470	peras	3
8471	pequeñuelos	3
8472	peña	3
8473	pentecostés	3
8474	pensaría	3
8475	pensará	3
8476	pensamos	3
8477	penitentes	3
8478	penitenciario	3
8479	penita	3
8480	penetraba	3
8481	penando	3
8482	penales	3
8483	peluquería	3
8484	peludo	3
8485	peluca	3
8486	peloteras	3
8487	pellizcos	3
8488	pellizco	3
8489	peinar	3
8490	peinadas	3
8491	pegarse	3
8492	pegaría	3
8493	pegadizo	3
8494	pedradas	3
8495	pedidos	3
8496	peco	3
8497	pechuga	3
8498	pecador	3
8499	pavía	3
8500	pavero	3
8501	pausadamente	3
8502	patrona	3
8503	patriota	3
8504	patraña	3
8505	patochada	3
8506	patita	3
8507	pateo	3
8508	pateada	3
8509	pastillas	3
8510	pasmo	3
8511	pasmará	3
8512	pasmadas	3
8513	pasen	3
8514	paseándose	3
8515	paseando	3
8516	paseaban	3
8517	pascuas	3
8518	pasándole	3
8519	pasadas	3
8520	partos	3
8521	partieron	3
8522	particularidades	3
8523	participar	3
8524	participación	3
8525	participaba	3
8526	partición	3
8527	parose	3
8528	parentela	3
8529	pareciese	3
8530	parecerme	3
8531	parecerlo	3
8532	parecería	3
8533	paralela	3
8534	paraguas	3
8535	parados	3
8536	parado	3
8537	paraban	3
8538	papamoscas	3
8539	panecillo	3
8540	pamplinas	3
8541	palomos	3
8542	palmo	3
8543	palmada	3
8544	palma	3
8545	paliza	3
8546	palideciendo	3
8547	palanca	3
8548	pajarito	3
8549	pagos	3
8550	pagará	3
8551	padezco	3
8552	padeció	3
8553	pacífica	3
8554	oyes	3
8555	ovillo	3
8556	ovejas	3
8557	ostentación	3
8558	oscurísimo	3
8559	orquesta	3
8560	orificios	3
8561	ordinarios	3
8562	ordinarias	3
8563	ordenada	3
8564	órdago	3
8565	orador	3
8566	oraciones	3
8567	opuso	3
8568	oprimiendo	3
8569	oprimida	3
8570	oprimía	3
8571	opresión	3
8572	oposiciones	3
8573	oportuna	3
8574	oponer	3
8575	omitir	3
8576	olvidaré	3
8577	olvidara	3
8578	olorcillo	3
8579	olivo	3
8580	oliente	3
8581	oliendo	3
8582	óleo	3
8583	ola	3
8584	ojitos	3
8585	ojerosa	3
8586	ojeras	3
8587	ojazos	3
8588	oída	3
8589	oficiando	3
8590	oferta	3
8591	ofensas	3
8592	ofensa	3
8593	ofendido	3
8594	ofendería	3
8595	odioso	3
8596	odiosa	3
8597	ocurrir	3
8598	ocurriósele	3
8599	ocurriera	3
8600	ocupe	3
8601	ocuparon	3
8602	ocultó	3
8603	ociosidad	3
8604	ociosas	3
8605	obvio	3
8606	obstrucciones	3
8607	obstáculo	3
8608	obligó	3
8609	obispa	3
8610	obedezca	3
8611	obedeció	3
8612	obedece	3
8613	nuez	3
8614	nudillos	3
8615	nublaron	3
8616	noviembre	3
8617	novelda	3
8618	notoria	3
8619	normal	3
8620	nombro	3
8621	niñito	3
8622	niñería	3
8623	nieblas	3
8624	nicolasa	3
8625	neurosis	3
8626	nenito	3
8627	nenín	3
8628	negrito	3
8629	negociante	3
8630	negó	3
8631	negativo	3
8632	negativa	3
8633	nefando	3
8634	necesitaban	3
8635	náufrago	3
8636	naturalistas	3
8637	nativo	3
8638	nacionales	3
8639	nacía	3
8640	musgo	3
8641	museo	3
8642	músculo	3
8643	murrias	3
8644	murria	3
8645	muro	3
8646	murillo	3
8647	murieron	3
8648	mugrienta	3
8649	mueve	3
8650	muertes	3
8651	mueras	3
8652	muecas	3
8653	mueble	3
8654	mudos	3
8655	mudó	3
8656	mudo	3
8657	mudar	3
8658	mudanza	3
8659	móvil	3
8660	movidas	3
8661	mostrarle	3
8662	mosquitos	3
8663	mosquito	3
8664	mortificación	3
8665	morrión	3
8666	morisquetas	3
8667	moriré	3
8668	morirá	3
8669	moriones	3
8670	moribunda	3
8671	morfina	3
8672	morena	3
8673	morejón	3
8674	morder	3
8675	moraba	3
8676	montaña	3
8677	monstruosidad	3
8678	monserga	3
8679	monosílabos	3
8680	monosílabo	3
8681	monólogo	3
8682	monísimo	3
8683	monísima	3
8684	molinillos	3
8685	molesto	3
8686	molestias	3
8687	moleste	3
8688	molestar	3
8689	mojado	3
8690	modesta	3
8691	modernas	3
8692	mocedad	3
8693	mitones	3
8694	misticismo	3
8695	místicas	3
8696	mísero	3
8697	miserables	3
8698	mires	3
8699	mírenlo	3
8700	miremos	3
8701	miraré	3
8702	mirara	3
8703	mirándome	3
8704	míralos	3
8705	miradores	3
8706	mirad	3
8707	minuciosamente	3
8708	ministración	3
8709	mimosos	3
8710	mimaba	3
8711	miembros	3
8712	mezquino	3
8713	mezclando	3
8714	mezcladas	3
8715	método	3
8716	metiera	3
8717	meterla	3
8718	merecen	3
8719	merecemos	3
8720	mercados	3
8721	mequetrefes	3
8722	menudeaban	3
8723	mendigos	3
8724	mendigo	3
8725	mendicidad	3
8726	melindres	3
8727	melchor	3
8728	mejorar	3
8729	meditaba	3
8730	medita	3
8731	medidas	3
8732	medicamentos	3
8733	mediante	3
8734	mediana	3
8735	mechón	3
8736	mecheros	3
8737	mató	3
8738	maternales	3
8739	matas	3
8740	mataré	3
8741	matara	3
8742	matan	3
8743	matadero	3
8744	masticando	3
8745	máscaras	3
8746	mascando	3
8747	martín	3
8748	marrullerías	3
8749	marianas	3
8750	mares	3
8751	mareas	3
8752	marear	3
8753	marean	3
8754	mareaba	3
8755	marea	3
8756	marcial	3
8757	marcharte	3
8758	marchara	3
8759	marcando	3
8760	maravillosas	3
8761	máquinas	3
8762	maquinal	3
8763	manzanares	3
8764	manzana	3
8765	manubrio	3
8766	mantiene	3
8767	manteca	3
8768	mansedumbre	3
8769	manoteando	3
8770	manotada	3
8771	maniquís	3
8772	manifiestan	3
8773	manifestación	3
8774	manifestábase	3
8775	mangonear	3
8776	manejar	3
8777	mandil	3
8778	manden	3
8779	mandarle	3
8780	mandara	3
8781	mandaban	3
8782	manchada	3
8783	mancebo	3
8784	manceba	3
8785	mamás	3
8786	mamarrachos	3
8787	malísimo	3
8788	maliciosa	3
8789	maleza	3
8790	magras	3
8791	magníficas	3
8792	madrugar	3
8793	madriz	3
8794	luminosos	3
8795	lujosa	3
8796	lucidos	3
8797	lucía	3
8798	luchas	3
8799	lodo	3
8800	locuras	3
8801	locuaz	3
8802	lobo	3
8803	lluvia	3
8804	lloro	3
8805	lléveselo	3
8806	llévate	3
8807	llevase	3
8808	llevarte	3
8809	llevará	3
8810	llenaron	3
8811	llenan	3
8812	llenado	3
8813	llamole	3
8814	llamarme	3
8815	llamarla	3
8816	llamaran	3
8817	llamará	3
8818	lívido	3
8819	literatura	3
8820	lisonja	3
8821	liquidación	3
8822	lindo	3
8823	lindísimo	3
8824	lindas	3
8825	linajes	3
8826	linaje	3
8827	limpiaba	3
8828	límite	3
8829	ligereza	3
8830	licencias	3
8831	librarle	3
8832	libertades	3
8833	leves	3
8834	levante	3
8835	levantara	3
8836	levantada	3
8837	levanta	3
8838	letreros	3
8839	leopardi	3
8840	lento	3
8841	lengüetazos	3
8842	legalidad	3
8843	lectoral	3
8844	lazos	3
8845	lavo	3
8846	laven	3
8847	lava	3
8848	latas	3
8849	lata	3
8850	lárgate	3
8851	lanzar	3
8852	lanzada	3
8853	lanzaba	3
8854	lanilla	3
8855	lamentaba	3
8856	lago	3
8857	ladronas	3
8858	lacio	3
8859	lacayo	3
8860	jurisdicción	3
8861	juraría	3
8862	juramento	3
8863	juntar	3
8864	jui	3
8865	juguetes	3
8866	jugaban	3
8867	jugaba	3
8868	judas	3
8869	juana	3
8870	jotas	3
8871	jinete	3
8872	jarras	3
8873	japonesa	3
8874	jamases	3
8875	jaime	3
8876	jacintilla	3
8877	isabelita	3
8878	irritación	3
8879	irregular	3
8880	irían	3
8881	irán	3
8882	ioduro	3
8883	invocando	3
8884	inventó	3
8885	inundada	3
8886	intrigas	3
8887	intranquilidad	3
8888	íntimos	3
8889	íntimamente	3
8890	interrumpía	3
8891	interrogó	3
8892	interrogaba	3
8893	interponía	3
8894	intermitentes	3
8895	interiores	3
8896	interesarse	3
8897	intentaban	3
8898	intenso	3
8899	intensísima	3
8900	institutriz	3
8901	institutos	3
8902	instintivamente	3
8903	inspiran	3
8904	inspiraban	3
8905	insomnio	3
8906	insistía	3
8907	insensiblemente	3
8908	insensata	3
8909	insano	3
8910	inquisidora	3
8911	inquilina	3
8912	inocentona	3
8913	inmundicia	3
8914	inmiscuirse	3
8915	inmemorial	3
8916	injusticia	3
8917	iniciarse	3
8918	inglesas	3
8919	ingeniosas	3
8920	ingenieros	3
8921	infunde	3
8922	infracción	3
8923	inflexible	3
8924	infinitos	3
8925	infinitamente	3
8926	infinita	3
8927	infiel	3
8928	infernales	3
8929	inferioridad	3
8930	inevitable	3
8931	inesperadamente	3
8932	industriales	3
8933	industrial	3
8934	indulgentes	3
8935	indolencia	3
8936	individua	3
8937	indispensables	3
8938	indirecta	3
8939	indicio	3
8940	indefinible	3
8941	indecoroso	3
8942	incrédulo	3
8943	incorporó	3
8944	incorporado	3
8945	inconstante	3
8946	inconsolable	3
8947	incomparable	3
8948	inclinación	3
8949	incierta	3
8950	incertidumbre	3
8951	incendio	3
8952	inapreciable	3
8953	impropia	3
8954	imposibilidad	3
8955	importaría	3
8956	importará	3
8957	importan	3
8958	impone	3
8959	impetuosa	3
8960	imperiosa	3
8961	imperdible	3
8962	imitaba	3
8963	imbécil	3
8964	imaginó	3
8965	imaginaba	3
8966	ilustrado	3
8967	iluminó	3
8968	ilumina	3
8969	ildefonso	3
8970	idolatraba	3
8971	idiota	3
8972	idioma	3
8973	idas	3
8974	íbase	3
8975	íbamos	3
8976	huyó	3
8977	huye	3
8978	hundido	3
8979	humorismo	3
8980	húmeda	3
8981	humareda	3
8982	huevera	3
8983	huelen	3
8984	huele	3
8985	hubieron	3
8986	hubiéramos	3
8987	hostias	3
8988	horizontes	3
8989	horizontal	3
8990	hondísimo	3
8991	hoc	3
8992	históricas	3
8993	hinchazón	3
8994	hilos	3
8995	hervía	3
8996	herramientas	3
8997	herméticamente	3
8998	hermanitas	3
8999	heridas	3
9000	heladas	3
9001	hayan	3
9002	hato	3
9003	haremos	3
9004	hambriento	3
9005	hallazgo	3
9006	hallando	3
9007	halla	3
9008	haciéndoles	3
9009	hacernos	3
9010	habríamos	3
9011	habrán	3
9012	hablose	3
9013	hablarles	3
9014	hablaran	3
9015	hablará	3
9016	habladurías	3
9017	habitantes	3
9018	habitante	3
9019	habíase	3
9020	habíalo	3
9021	habana	3
9022	gustó	3
9023	guste	3
9024	gustavito	3
9025	gustará	3
9026	guita	3
9027	guisantes	3
9028	guindillas	3
9029	guedejas	3
9030	guardaron	3
9031	guapote	3
9032	gruñó	3
9033	gruesas	3
9034	gritería	3
9035	grillete	3
9036	granito	3
9037	graciosos	3
9038	gracejo	3
9039	gozaban	3
9040	golpeando	3
9041	golosos	3
9042	glorioso	3
9043	gimnasia	3
9044	gesticulando	3
9045	geografía	3
9046	gentuza	3
9047	generalmente	3
9048	generales	3
9049	gemir	3
9050	gases	3
9051	garrotillo	3
9052	gargarismos	3
9053	garfios	3
9054	garcía	3
9055	garatusas	3
9056	garabatos	3
9057	ganancia	3
9058	ganan	3
9059	ganaban	3
9060	gallina	3
9061	gallegos	3
9062	gallarda	3
9063	galante	3
9064	gabinetito	3
9065	gabanes	3
9066	gabán	3
9067	futuras	3
9068	funesta	3
9069	fundado	3
9070	fundaba	3
9071	fulano	3
9072	fuiste	3
9073	fuga	3
9074	fuero	3
9075	frutas	3
9076	fruncido	3
9077	frugal	3
9078	frontera	3
9079	fritos	3
9080	fritangas	3
9081	friegas	3
9082	fregar	3
9083	frecuentes	3
9084	frecuente	3
9085	frecuentaba	3
9086	frascos	3
9087	fraile	3
9088	fragua	3
9089	frágiles	3
9090	fraganti	3
9091	fraga	3
9092	fósforos	3
9093	fósforo	3
9094	fosfato	3
9095	formidables	3
9096	formidable	3
9097	formaron	3
9098	formales	3
9099	for	3
9100	flexible	3
9101	fleco	3
9102	flaco	3
9103	flaca	3
9104	físicas	3
9105	físicamente	3
9106	firmeza	3
9107	finos	3
9108	fingir	3
9109	finge	3
9110	fineza	3
9111	financieras	3
9112	filosófico	3
9113	filosofías	3
9114	filípica	3
9115	fijaron	3
9116	fijar	3
9117	fijado	3
9118	figurar	3
9119	figurándose	3
9120	figueras	3
9121	fiestas	3
9122	fieras	3
9123	ficción	3
9124	fibra	3
9125	fervor	3
9126	ferias	3
9127	fenómenos	3
9128	femenino	3
9129	felpudo	3
9130	felizmente	3
9131	fecundo	3
9132	febriles	3
9133	favores	3
9134	favorecido	3
9135	favorecía	3
9136	favorece	3
9137	favorcito	3
9138	fatigadísima	3
9139	fatigadas	3
9140	fastidio	3
9141	faroles	3
9142	farmacéuticos	3
9143	farmacéutica	3
9144	fardos	3
9145	fantástico	3
9146	fantasía	3
9147	famélico	3
9148	falte	3
9149	faltábale	3
9150	falsos	3
9151	falsete	3
9152	falleció	3
9153	facundia	3
9154	facturas	3
9155	fáciles	3
9156	fábricas	3
9157	fabricante	3
9158	fabricando	3
9159	extremos	3
9160	extremidades	3
9161	extremada	3
9162	extraviados	3
9163	extraviada	3
9164	extranjeras	3
9165	externa	3
9166	extendido	3
9167	exquisitos	3
9168	exquisito	3
9169	expuso	3
9170	expresan	3
9171	explotar	3
9172	explosiva	3
9173	explicase	3
9174	explicaré	3
9175	explicara	3
9176	explanada	3
9177	experimentaba	3
9178	expectativa	3
9179	expectante	3
9180	existido	3
9181	exhalando	3
9182	excitó	3
9183	excesivo	3
9184	examinarse	3
9185	examinándole	3
9186	exaltándose	3
9187	exageración	3
9188	exageraba	3
9189	exacta	3
9190	evolución	3
9191	evocando	3
9192	evasivamente	3
9193	evasión	3
9194	europa	3
9195	eternidad	3
9196	estuviéramos	3
9197	estudiando	3
9198	estudiado	3
9199	estrujón	3
9200	estridente	3
9201	estricnina	3
9202	estribillo	3
9203	estrepitoso	3
9204	estrechó	3
9205	estrechamente	3
9206	estrafalario	3
9207	estirar	3
9208	estima	3
9209	estéis	3
9210	estarlo	3
9211	estaremos	3
9212	estarán	3
9213	establecerse	3
9214	esquinas	3
9215	esplín	3
9216	espléndido	3
9217	espionaje	3
9218	espeso	3
9219	espesa	3
9220	esperpento	3
9221	esperase	3
9222	esperaron	3
9223	esperaremos	3
9224	esperan	3
9225	esperaban	3
9226	espectáculos	3
9227	específico	3
9228	esparto	3
9229	esparció	3
9230	espantado	3
9231	espadas	3
9232	espacios	3
9233	esfinge	3
9234	esenciales	3
9235	esencia	3
9236	escupiendo	3
9237	escuelas	3
9238	escuchar	3
9239	escucha	3
9240	escrupuloso	3
9241	escondidos	3
9242	esconder	3
9243	esconden	3
9244	escogía	3
9245	escocesa	3
9246	escobillón	3
9247	esclava	3
9248	escepticismo	3
9249	escayolas	3
9250	escarmiento	3
9251	escapatorias	3
9252	escandalosa	3
9253	escandalizar	3
9254	escala	3
9255	escabeche	3
9256	errante	3
9257	éranle	3
9258	éralo	3
9259	equivoco	3
9260	equivalía	3
9261	equivale	3
9262	epigastrio	3
9263	envueltos	3
9264	envolvían	3
9265	envolverse	3
9266	envido	3
9267	envidiosa	3
9268	envidiaba	3
9269	envenenar	3
9270	envenenamiento	3
9271	envalentonó	3
9272	entusiastas	3
9273	entusiasmarse	3
9274	entusiasmado	3
9275	entusiasmaba	3
9276	entrometida	3
9277	entretiene	3
9278	entretenimientos	3
9279	entretenido	3
9280	entres	3
9281	entren	3
9282	entrego	3
9283	entregaba	3
9284	entrecano	3
9285	entras	3
9286	entráronle	3
9287	entraré	3
9288	entrañablemente	3
9289	entrambos	3
9290	entrábale	3
9291	entienden	3
9292	enterose	3
9293	enterase	3
9294	enteraron	3
9295	enterándose	3
9296	entenderse	3
9297	enseñaron	3
9298	enseñaré	3
9299	enseñanzas	3
9300	enredar	3
9301	enojosa	3
9302	ennoblece	3
9303	enigma	3
9304	engañada	3
9305	enfadó	3
9306	enfadarse	3
9307	enérgica	3
9308	eneas	3
9309	encontrarla	3
9310	encinas	3
9311	encerrarse	3
9312	encerraba	3
9313	encendieron	3
9314	encendiendo	3
9315	encendidas	3
9316	encarnados	3
9317	encarnadas	3
9318	encarnada	3
9319	encargar	3
9320	encarga	3
9321	encandilados	3
9322	encaminó	3
9323	enana	3
9324	enaguas	3
9325	emulación	3
9326	empujó	3
9327	empujaba	3
9328	emprendió	3
9329	emplasto	3
9330	empiezo	3
9331	empezaría	3
9332	empeñas	3
9333	empeñarse	3
9334	empedrado	3
9335	empaque	3
9336	empalagosas	3
9337	embuste	3
9338	embozo	3
9339	emblema	3
9340	embargaba	3
9341	embarazo	3
9342	elogios	3
9343	elocuentes	3
9344	elocuencia	3
9345	elevando	3
9346	elemento	3
9347	elemental	3
9348	elegir	3
9349	elegida	3
9350	electrizaba	3
9351	eléctrica	3
9352	elecciones	3
9353	ejercitarse	3
9354	ejemplares	3
9355	ejemplar	3
9356	eje	3
9357	edificación	3
9358	echárselas	3
9359	echaré	3
9360	echándoselas	3
9361	durmiose	3
9362	durmieron	3
9363	durmiera	3
9364	durase	3
9365	duras	3
9366	duraría	3
9367	dulcísimos	3
9368	duerma	3
9369	duela	3
9370	ducha	3
9371	dramática	3
9372	dragón	3
9373	doradas	3
9374	domina	3
9375	domiciliaria	3
9376	dogma	3
9377	doctrinas	3
9378	doblado	3
9379	divino	3
9380	divinidades	3
9381	diversión	3
9382	distrajo	3
9383	distraía	3
9384	distraerse	3
9385	distinguió	3
9386	distinguían	3
9387	distantes	3
9388	dispensa	3
9389	disparada	3
9390	disolventes	3
9391	disminuía	3
9392	disimulando	3
9393	disgustó	3
9394	disgustada	3
9395	disgustaba	3
9396	disfrazado	3
9397	discurrido	3
9398	discretos	3
9399	discretas	3
9400	dirigiose	3
9401	dirigiéndose	3
9402	dirigiendo	3
9403	dirigían	3
9404	diplomático	3
9405	diplomacia	3
9406	dinidá	3
9407	diligentes	3
9408	dígole	3
9409	dignó	3
9410	digerir	3
9411	dígase	3
9412	difícilmente	3
9413	dificilillo	3
9414	diferente	3
9415	dieciocho	3
9416	dictando	3
9417	dictamen	3
9418	dializado	3
9419	devoto	3
9420	determinaron	3
9421	deteniendo	3
9422	detener	3
9423	desvelado	3
9424	desvanecimiento	3
9425	desvanecido	3
9426	destrozado	3
9427	destrozaba	3
9428	destempladas	3
9429	destacaba	3
9430	despropósitos	3
9431	desproporción	3
9432	despreciar	3
9433	desprecia	3
9434	despotismo	3
9435	despojos	3
9436	desplegó	3
9437	desplegando	3
9438	despertaron	3
9439	desparpajo	3
9440	despacito	3
9441	despachar	3
9442	desórdenes	3
9443	desordenada	3
9444	desolada	3
9445	desnudos	3
9446	desnudarse	3
9447	desnuda	3
9448	desmedrada	3
9449	desmayada	3
9450	desigualdades	3
9451	deshonrar	3
9452	deshizo	3
9453	deshilachada	3
9454	deshacer	3
9455	deshace	3
9456	desgraciados	3
9457	desesperados	3
9458	desenfado	3
9459	desempeñó	3
9460	descubrirse	3
9461	descubrimiento	3
9462	descubrían	3
9463	descrito	3
9464	descontento	3
9465	desconoce	3
9466	desconfianza	3
9467	descendiendo	3
9468	descendía	3
9469	descaro	3
9470	descargar	3
9471	descargaba	3
9472	descalzo	3
9473	desbarajuste	3
9474	desasirse	3
9475	desarrolló	3
9476	desaires	3
9477	desairar	3
9478	desagradaba	3
9479	desabrimiento	3
9480	derroche	3
9481	derechita	3
9482	deplorable	3
9483	denunciaba	3
9484	dengue	3
9485	delitos	3
9486	delicia	3
9487	delicados	3
9488	delicadas	3
9489	delgado	3
9490	dejen	3
9491	dejemos	3
9492	dejémonos	3
9493	déjele	3
9494	dejaría	3
9495	dejaran	3
9496	dejándole	3
9497	definitivo	3
9498	definitiva	3
9499	defenderle	3
9500	dedicarse	3
9501	dedicado	3
9502	declaraban	3
9503	declara	3
9504	decisión	3
9505	decírmelo	3
9506	decirles	3
9507	decido	3
9508	debiste	3
9509	debidos	3
9510	dársele	3
9511	dársela	3
9512	daremos	3
9513	darás	3
9514	danza	3
9515	dándome	3
9516	damasco	3
9517	curiosidades	3
9518	curarse	3
9519	curarle	3
9520	cumpliría	3
9521	cumplidas	3
9522	cumpla	3
9523	culebras	3
9524	cuitas	3
9525	cuidadito	3
9526	cuestas	3
9527	cueros	3
9528	cuéntame	3
9529	cuelga	3
9530	cuchitril	3
9531	cuchicheos	3
9532	cucharas	3
9533	cuatrocientos	3
9534	cuajados	3
9535	cuajada	3
9536	crujía	3
9537	crueles	3
9538	cruda	3
9539	crucifijo	3
9540	cristiandad	3
9541	crié	3
9542	críe	3
9543	crezca	3
9544	creyéndolo	3
9545	crepúsculo	3
9546	creerte	3
9547	creeréis	3
9548	creencia	3
9549	crecimiento	3
9550	crecido	3
9551	créanmelo	3
9552	costados	3
9553	cortada	3
9554	corros	3
9555	corrigen	3
9556	corriéndose	3
9557	corrían	3
9558	corrí	3
9559	corretaje	3
9560	correspondientes	3
9561	corresponden	3
9562	correcta	3
9563	coronilla	3
9564	corista	3
9565	corinto	3
9566	corazonada	3
9567	convidó	3
9568	convidados	3
9569	convidaba	3
9570	convenza	3
9571	convenga	3
9572	convendría	3
9573	convencional	3
9574	convencida	3
9575	convencía	3
9576	contratas	3
9577	contradecía	3
9578	contracción	3
9579	continuidad	3
9580	continuaban	3
9581	continua	3
9582	contingencia	3
9583	continente	3
9584	contesta	3
9585	contentos	3
9586	contentísima	3
9587	contentará	3
9588	contenían	3
9589	contemporizar	3
9590	contemporánea	3
9591	contemplar	3
9592	contemplación	3
9593	contemplaban	3
9594	contaste	3
9595	contarse	3
9596	contarles	3
9597	contaban	3
9598	consumado	3
9599	consultarle	3
9600	consultado	3
9601	consuele	3
9602	construir	3
9603	constituían	3
9604	constaba	3
9605	conspiradores	3
9606	consolar	3
9607	consiente	3
9608	considerado	3
9609	considerables	3
9610	conserve	3
9611	conservarse	3
9612	conservación	3
9613	consentido	3
9614	consentía	3
9615	consecuente	3
9616	consagrar	3
9617	consabida	3
9618	conquistar	3
9619	conocimos	3
9620	conociendo	3
9621	conocerle	3
9622	conocería	3
9623	conocedor	3
9624	conmovido	3
9625	conmovida	3
9626	conjunción	3
9627	confundidos	3
9628	confirmó	3
9629	confieso	3
9630	confiesa	3
9631	confiando	3
9632	confesó	3
9633	confesarse	3
9634	conducen	3
9635	conde	3
9636	concurso	3
9637	concurrir	3
9638	concurrencia	3
9639	conclusión	3
9640	concedo	3
9641	comúnmente	3
9642	comunión	3
9643	comunicativo	3
9644	comunicaciones	3
9645	comulgar	3
9646	compromisos	3
9647	comprometido	3
9648	comprendieron	3
9649	compre	3
9650	comportamiento	3
9651	componer	3
9652	cómplice	3
9653	compasivo	3
9654	comparado	3
9655	comparaciones	3
9656	comparación	3
9657	compaginar	3
9658	comitiva	3
9659	comidas	3
9660	cómico	3
9661	cometía	3
9662	comérselo	3
9663	comerciales	3
9664	comerá	3
9665	combinar	3
9666	comas	3
9667	coman	3
9668	columna	3
9669	colosal	3
9670	colorines	3
9671	colorados	3
9672	colorado	3
9673	coloradita	3
9674	coloque	3
9675	colocarse	3
9676	colmena	3
9677	colgadas	3
9678	colgaban	3
9679	colegiales	3
9680	colega	3
9681	colación	3
9682	cojín	3
9683	cogiera	3
9684	cogidas	3
9685	cogerlo	3
9686	cogería	3
9687	cochinada	3
9688	coces	3
9689	clavándole	3
9690	clavan	3
9691	claustro	3
9692	claritas	3
9693	claques	3
9694	clamó	3
9695	ciudadanos	3
9696	citada	3
9697	cita	3
9698	circulación	3
9699	cipreses	3
9700	cimiento	3
9701	cielos	3
9702	cicatero	3
9703	chupando	3
9704	chupaba	3
9705	chupa	3
9706	chulos	3
9707	chuleta	3
9708	chorros	3
9709	chistera	3
9710	chiste	3
9711	chisme	3
9712	chinitas	3
9713	chinita	3
9714	chimeneas	3
9715	chillones	3
9716	chillido	3
9717	chillar	3
9718	chilla	3
9719	charló	3
9720	charlaron	3
9721	charco	3
9722	chanza	3
9723	chal	3
9724	cese	3
9725	cesaron	3
9726	cerillas	3
9727	cerilla	3
9728	cerebrales	3
9729	cerco	3
9730	cerciorarse	3
9731	cercano	3
9732	céntimo	3
9733	cencerro	3
9734	cementerios	3
9735	celebrar	3
9736	cedía	3
9737	cebolla	3
9738	cayera	3
9739	cavilo	3
9740	cavilación	3
9741	cavernosa	3
9742	cautiverio	3
9743	cautivaba	3
9744	cautelosamente	3
9745	católicas	3
9746	catado	3
9747	castrense	3
9748	castita	3
9749	castigos	3
9750	case	3
9751	cáscara	3
9752	casarte	3
9753	casara	3
9754	casamos	3
9755	casaca	3
9756	carúnculas	3
9757	caros	3
9758	carnicero	3
9759	carmín	3
9760	caricia	3
9761	cargar	3
9762	cargados	3
9763	cargadas	3
9764	carecía	3
9765	carecer	3
9766	cárdenas	3
9767	carcas	3
9768	carbones	3
9769	carbonería	3
9770	caracoles	3
9771	cápsulas	3
9772	caprichos	3
9773	capota	3
9774	cañones	3
9775	cáñamo	3
9776	cantoras	3
9777	cantara	3
9778	cantando	3
9779	cansarse	3
9780	cansar	3
9781	cansados	3
9782	cansa	3
9783	candoroso	3
9784	canastillas	3
9785	canario	3
9786	camps	3
9787	campos	3
9788	campechano	3
9789	campanillas	3
9790	campana	3
9791	cambios	3
9792	cambió	3
9793	cambiazo	3
9794	cambian	3
9795	cambiaba	3
9796	camastro	3
9797	camaraíta	3
9798	cámara	3
9799	calzón	3
9800	calumnias	3
9801	calmar	3
9802	callejuelas	3
9803	callandito	3
9804	calladito	3
9805	calentarse	3
9806	calentando	3
9807	calculo	3
9808	calavera	3
9809	calado	3
9810	caimán	3
9811	caerá	3
9812	cadena	3
9813	cachivaches	3
9814	cacharros	3
9815	caca	3
9816	cabras	3
9817	butacas	3
9818	busqué	3
9819	buscarse	3
9820	buscarlo	3
9821	buscarla	3
9822	buscaría	3
9823	burros	3
9824	burras	3
9825	burrada	3
9826	burlona	3
9827	burlas	3
9828	burlar	3
9829	burdeos	3
9830	buenazo	3
9831	bruces	3
9832	bromitas	3
9833	brocha	3
9834	brisas	3
9835	bríos	3
9836	brea	3
9837	bravas	3
9838	bramido	3
9839	bóveda	3
9840	botines	3
9841	botijos	3
9842	botijo	3
9843	bostezos	3
9844	borró	3
9845	borrascas	3
9846	borrar	3
9847	borrachona	3
9848	borracho	3
9849	bofes	3
9850	bodegón	3
9851	bobos	3
9852	blanda	3
9853	blancura	3
9854	bizcocho	3
9855	biblioteca	3
9856	besar	3
9857	berroqueña	3
9858	berrinchín	3
9859	berridos	3
9860	berrido	3
9861	benditos	3
9862	belga	3
9863	belenes	3
9864	bebiéndose	3
9865	bebido	3
9866	bazar	3
9867	bayetas	3
9868	baúles	3
9869	bastaban	3
9870	bases	3
9871	barros	3
9872	barriles	3
9873	barricada	3
9874	barcos	3
9875	barco	3
9876	barbián	3
9877	baratura	3
9878	baratos	3
9879	barandal	3
9880	baqueta	3
9881	baño	3
9882	banquete	3
9883	banda	3
9884	baldosines	3
9885	baldomerito	3
9886	bájate	3
9887	bailes	3
9888	bailando	3
9889	baila	3
9890	babosos	3
9891	azoramiento	3
9892	azorada	3
9893	ayudará	3
9894	ayudar	3
9895	ayudando	3
9896	ayudan	3
9897	ayúdame	3
9898	avivó	3
9899	aviso	3
9900	aviado	3
9901	averigüe	3
9902	averiguado	3
9903	avergonzado	3
9904	avergonzaba	3
9905	avanzaron	3
9906	autoritario	3
9907	autoritaria	3
9908	autoridades	3
9909	autócrata	3
9910	aumento	3
9911	aumentan	3
9912	aullidos	3
9913	aula	3
9914	audiencia	3
9915	audacia	3
9916	atropellarse	3
9917	atropellado	3
9918	atropelladamente	3
9919	atrocidad	3
9920	atroces	3
9921	atreviera	3
9922	atreviéndose	3
9923	atrayéndola	3
9924	atrayendo	3
9925	atrasado	3
9926	atrasadas	3
9927	atractivo	3
9928	atormentando	3
9929	atontado	3
9930	atontada	3
9931	atolladero	3
9932	atiza	3
9933	atienda	3
9934	aterradora	3
9935	atando	3
9936	atados	3
9937	asustes	3
9938	asuste	3
9939	asustar	3
9940	asustaba	3
9941	asunción	3
9942	astuta	3
9943	astorga	3
9944	aspiraciones	3
9945	aspiraba	3
9946	asombrada	3
9947	asomáronse	3
9948	asomándose	3
9949	asomando	3
9950	asistir	3
9951	asistía	3
9952	asistencia	3
9953	asimismo	3
9954	asimilarse	3
9955	asfixia	3
9956	aseveración	3
9957	asesinato	3
9958	aseguró	3
9959	asegura	3
9960	ascendía	3
9961	asaltaron	3
9962	asado	3
9963	artistas	3
9964	artificial	3
9965	artesón	3
9966	arsenal	3
9967	arrugando	3
9968	arrojan	3
9969	arrojaban	3
9970	arroja	3
9971	arrogancia	3
9972	arrodillándose	3
9973	arrobas	3
9974	arrepiéntete	3
9975	arrepentirse	3
9976	arrepentido	3
9977	arreglaría	3
9978	arreglaremos	3
9979	arreglan	3
9980	arreglaban	3
9981	arreglaba	3
9982	arrechucho	3
9983	arrebató	3
9984	arrebatada	3
9985	arrastrar	3
9986	arranques	3
9987	arrancó	3
9988	árnica	3
9989	armado	3
9990	armaban	3
9991	aritmético	3
9992	aritmética	3
9993	arenal	3
9994	ardientemente	3
9995	ardía	3
9996	arcos	3
9997	arcas	3
9998	apuró	3
9999	apuro	3
10000	apure	3
10001	apunte	3
10002	apuntaba	3
10003	apuestas	3
10004	aprueba	3
10005	aproximó	3
10006	aprovechar	3
10007	aprobó	3
10008	aprobar	3
10009	aprisita	3
10010	aprieta	3
10011	apretones	3
10012	apretadas	3
10013	apretada	3
10014	apresurándose	3
10015	aprendía	3
10016	aprendería	3
10017	apreció	3
10018	apoyado	3
10019	apóstoles	3
10020	aposentos	3
10021	apoderarse	3
10022	apoderaba	3
10023	aplastada	3
10024	aplacar	3
10025	aplacado	3
10026	apetecía	3
10027	apático	3
10028	apasionado	3
10029	aparente	3
10030	aparentando	3
10031	apareciendo	3
10032	aparecían	3
10033	aparece	3
10034	apagaba	3
10035	anuncio	3
10036	anulación	3
10037	antojó	3
10038	antoje	3
10039	antoja	3
10040	anticipar	3
10041	anticipaba	3
10042	antemano	3
10043	antecedentes	3
10044	ansiosa	3
10045	anochecido	3
10046	ánimas	3
10047	animados	3
10048	animada	3
10049	angustiosa	3
10050	angelitos	3
10051	anduvo	3
10052	andrajos	3
10053	ándate	3
10054	andas	3
10055	andalucía	3
10056	andadas	3
10057	amenazó	3
10058	amenazándole	3
10059	amenaza	3
10060	amén	3
10061	ambulantes	3
10062	amasando	3
10063	amarillas	3
10064	amargura	3
10065	amaneramiento	3
10066	amanecer	3
10067	amado	3
10068	alusión	3
10069	alucinación	3
10070	altos	3
10071	alquiler	3
10072	alpiste	3
10073	almorzado	3
10074	almorzaba	3
10075	almendra	3
10076	alimentos	3
10077	alijo	3
10078	alientos	3
10079	algarrobos	3
10080	alfiler	3
10081	aletargaba	3
10082	alejar	3
10083	alejandro	3
10084	alegrarse	3
10085	alegrar	3
10086	alegraban	3
10087	alcanzó	3
10088	alcanza	3
10089	alcantarilla	3
10090	alcances	3
10091	alborote	3
10092	alborotando	3
10093	alborotaban	3
10094	albañil	3
10095	alba	3
10096	alarmante	3
10097	alarmadísima	3
10098	alarma	3
10099	alambique	3
10100	alabado	3
10101	ajustarle	3
10102	ajustado	3
10103	ajustada	3
10104	ajedrez	3
10105	ahumado	3
10106	ahorro	3
10107	ahogar	3
10108	agujereada	3
10109	águila	3
10110	aguardó	3
10111	aguarde	3
10112	aguarda	3
10113	aguanto	3
10114	aguantando	3
10115	aguador	3
10116	agravios	3
10117	agrandaba	3
10118	agradeciendo	3
10119	agradables	3
10120	agradaban	3
10121	agraciados	3
10122	agraciada	3
10123	agotado	3
10124	agitaba	3
10125	agilidad	3
10126	agarró	3
10127	agarrándose	3
10128	agarrada	3
10129	agachó	3
10130	afueras	3
10131	afirmar	3
10132	afirmaciones	3
10133	afectó	3
10134	afanaba	3
10135	advierto	3
10136	adusta	3
10137	adquisición	3
10138	adquirió	3
10139	adquiridos	3
10140	adornada	3
10141	adorado	3
10142	adoquines	3
10143	adoptar	3
10144	adónde	3
10145	admito	3
10146	admirando	3
10147	adivina	3
10148	adelantado	3
10149	adefesios	3
10150	adarme	3
10151	ad	3
10152	acusón	3
10153	acumulando	3
10154	acuestes	3
10155	acuéstate	3
10156	acuérdate	3
10157	acudiendo	3
10158	acudían	3
10159	actual	3
10160	activa	3
10161	acritud	3
10162	acreedores	3
10163	acostose	3
10164	acostarle	3
10165	acostaré	3
10166	acordarás	3
10167	acordara	3
10168	acontecía	3
10169	acontecer	3
10170	aconsejar	3
10171	aconsejaba	3
10172	acompañarla	3
10173	acompañando	3
10174	acompañamiento	3
10175	acompaña	3
10176	acomodaba	3
10177	acierta	3
10178	ácido	3
10179	aciago	3
10180	acertando	3
10181	acercaron	3
10182	acercar	3
10183	acercábase	3
10184	acepto	3
10185	aceptado	3
10186	aceptaba	3
10187	acentuaba	3
10188	aceitunas	3
10189	accionando	3
10190	accesible	3
10191	acariciar	3
10192	acantonamos	3
10193	acaloraba	3
10194	acabose	3
10195	acabase	3
10196	acabando	3
10197	acabados	3
10198	aburrirse	3
10199	abundancia	3
10200	absurdos	3
10201	abstraído	3
10202	absorbedero	3
10203	absolutismo	3
10204	abrumador	3
10205	abriose	3
10206	abrigado	3
10207	abriese	3
10208	abriéndose	3
10209	abreviar	3
10210	abrazando	3
10211	abrasaba	3
10212	abrasa	3
10213	aborrezco	3
10214	aborrecía	3
10215	aborrecer	3
10216	aborrecen	3
10217	abatido	3
10218	abandonará	3
10219	zurrón	2
10220	zurita	2
10221	zurcir	2
10222	zumbido	2
10223	zorro	2
10224	zócalo	2
10225	zipizape	2
10226	zascandil	2
10227	zarzuelas	2
10228	zarandearte	2
10229	zapato	2
10230	zapatilla	2
10231	zángano	2
10232	zambulló	2
10233	zagalona	2
10234	yoduro	2
10235	yio	2
10236	yia	2
10237	yerbas	2
10238	yéndose	2
10239	yemas	2
10240	yacente	2
10241	xvi	2
10242	wagner	2
10243	vulgaridades	2
10244	vuestras	2
10245	vuélvete	2
10246	voraz	2
10247	voracidad	2
10248	vomitar	2
10249	volviste	2
10250	volviéndolo	2
10251	volviéndole	2
10252	volvías	2
10253	volveríamos	2
10254	volveremos	2
10255	volverán	2
10256	volteretas	2
10257	volcados	2
10258	volarse	2
10259	volaron	2
10260	vocerrón	2
10261	vocación	2
10262	vivísimos	2
10263	viviremos	2
10264	viviré	2
10265	vives	2
10266	viveros	2
10267	víveres	2
10268	vivaracha	2
10269	vivacidad	2
10270	vivaaaa	2
10271	viudita	2
10272	viudas	2
10273	vistiéndose	2
10274	vistiéndome	2
10275	visos	2
10276	visitarte	2
10277	visitarla	2
10278	visitaban	2
10279	visera	2
10280	vira	2
10281	viose	2
10282	violentísima	2
10283	viole	2
10284	violado	2
10285	vinos	2
10286	vine	2
10287	vínculos	2
10288	vilo	2
10289	vigorosos	2
10290	vigilarla	2
10291	vigilaban	2
10292	viéronle	2
10293	viena	2
10294	vidrioso	2
10295	vidrios	2
10296	viciosos	2
10297	vicioso	2
10298	viceversa	2
10299	vicente	2
10300	vibraba	2
10301	viajantes	2
10302	viaducto	2
10303	vestigios	2
10304	vértigo	2
10305	versos	2
10306	vernos	2
10307	verídicos	2
10308	verídica	2
10309	veríamos	2
10310	vergonzoso	2
10311	verbigracia	2
10312	veranos	2
10313	ventorro	2
10314	ventilación	2
10315	venimos	2
10316	venida	2
10317	venid	2
10318	venganzas	2
10319	venenos	2
10320	venecia	2
10321	vendrían	2
10322	venderlo	2
10323	venda	2
10324	vellón	2
10325	velarla	2
10326	veintiséis	2
10327	veíais	2
10328	vegetales	2
10329	vega	2
10330	vascular	2
10331	variadísima	2
10332	vano	2
10333	vanidosa	2
10334	valiosas	2
10335	válgame	2
10336	vales	2
10337	valeroso	2
10338	valentías	2
10339	valenciana	2
10340	valemos	2
10341	valdrá	2
10342	vajilla	2
10343	vaguedades	2
10344	vaguedad	2
10345	vagos	2
10346	vagando	2
10347	vacíos	2
10348	vacilado	2
10349	vacante	2
10350	utilidad	2
10351	útiles	2
10352	usura	2
10353	uste	2
10354	usaban	2
10355	usa	2
10356	unir	2
10357	uniéndose	2
10358	uniendo	2
10359	únicos	2
10360	unía	2
10361	undécimo	2
10362	unánimemente	2
10363	ultraje	2
10364	tuyas	2
10365	tuvimos	2
10366	tutelar	2
10367	tuteaban	2
10368	turbarse	2
10369	turbado	2
10370	tupé	2
10371	tumor	2
10372	tul	2
10373	tuerce	2
10374	trun	2
10375	trozos	2
10376	trovador	2
10377	trousseaux	2
10378	trote	2
10379	tropical	2
10380	tropezones	2
10381	tropezar	2
10382	tropezaba	2
10383	tropel	2
10384	troncos	2
10385	trompicones	2
10386	trofeo	2
10387	trocándose	2
10388	trocado	2
10389	trivial	2
10390	triunfales	2
10391	triunfado	2
10392	trinquetada	2
10393	trinos	2
10394	trincó	2
10395	trincando	2
10396	trinando	2
10397	trinaba	2
10398	trimestre	2
10399	triangular	2
10400	tremolina	2
10401	tregua	2
10402	trechos	2
10403	trazada	2
10404	trazaba	2
10405	travesuras	2
10406	traten	2
10407	trate	2
10408	tratarme	2
10409	tratarlo	2
10410	tratarles	2
10411	tratarían	2
10412	trataría	2
10413	trasunto	2
10414	trastorné	2
10415	trastornase	2
10416	trastornar	2
10417	trastornan	2
10418	trasteando	2
10419	trastadas	2
10420	traspasado	2
10421	traspasaba	2
10422	trasluz	2
10423	traseros	2
10424	traqueteo	2
10425	trapicheos	2
10426	transporte	2
10427	transparencias	2
10428	transmitido	2
10429	transformó	2
10430	transformaciones	2
10431	transformaba	2
10432	transfigurado	2
10433	transfigurada	2
10434	transferencia	2
10435	transeúnte	2
10436	tranquilos	2
10437	tranquilas	2
10438	trangullones	2
10439	trancos	2
10440	tramposa	2
10441	trámite	2
10442	trajese	2
10443	trajecitos	2
10444	trajeado	2
10445	tráigame	2
10446	traidora	2
10447	traídas	2
10448	traiciones	2
10449	traicionero	2
10450	traicionera	2
10451	traías	2
10452	tragó	2
10453	trágicas	2
10454	tragaldabas	2
10455	tráfago	2
10456	traerlo	2
10457	traerá	2
10458	traemos	2
10459	tradicionalista	2
10460	trabar	2
10461	trabajillo	2
10462	trabajen	2
10463	trabajaron	2
10464	trabajaré	2
10465	trabajara	2
10466	trabajador	2
10467	trabajaban	2
10468	totalidad	2
10469	toscamente	2
10470	tosa	2
10471	torva	2
10472	tortuosa	2
10473	tórtola	2
10474	tortilla	2
10475	tortas	2
10476	torpemente	2
10477	tornillo	2
10478	torneados	2
10479	tornaron	2
10480	tornaba	2
10481	tormenta	2
10482	toreros	2
10483	torcida	2
10484	torbellino	2
10485	topete	2
10486	tontuela	2
10487	tontito	2
10488	tontamente	2
10489	tontainas	2
10490	tonadilla	2
10491	tomen	2
10492	tómelo	2
10493	tomate	2
10494	tomarlos	2
10495	tómalo	2
10496	tomad	2
10497	toleraría	2
10498	tolerar	2
10499	toledana	2
10500	tole	2
10501	toldo	2
10502	toíto	2
10503	todita	2
10504	tocino	2
10505	tocase	2
10506	tocaron	2
10507	tocará	2
10508	tocándose	2
10509	tocador	2
10510	tizne	2
10511	tiznada	2
10512	titulada	2
10513	tisú	2
10514	tirito	2
10515	tiré	2
10516	tire	2
10517	tirarte	2
10518	tirarlo	2
10519	tiraría	2
10520	tiraré	2
10521	tirantes	2
10522	tiranía	2
10523	tirana	2
10524	tiraban	2
10525	tiqui	2
10526	tinturas	2
10527	tinte	2
10528	tintas	2
10529	tinglado	2
10530	tin	2
10531	tímido	2
10532	timideces	2
10533	tijeretas	2
10534	tijeras	2
10535	tiito	2
10536	tiernos	2
10537	tienta	2
10538	tesoros	2
10539	teruel	2
10540	tertulio	2
10541	terso	2
10542	terrenos	2
10543	terrenal	2
10544	ternuras	2
10545	terno	2
10546	ternero	2
10547	terminó	2
10548	terminar	2
10549	terminantes	2
10550	terminados	2
10551	tercia	2
10552	terca	2
10553	teología	2
10554	teñir	2
10555	teñidas	2
10556	tenuemente	2
10557	tentativa	2
10558	tentando	2
10559	tentación	2
10560	tenlo	2
10561	teníase	2
10562	teníale	2
10563	teníala	2
10564	tenerte	2
10565	tenerme	2
10566	tenerla	2
10567	tendrías	2
10568	tendríamos	2
10569	tendió	2
10570	tendencias	2
10571	tendencia	2
10572	tenacidad	2
10573	tenaces	2
10574	temprana	2
10575	temporales	2
10576	templar	2
10577	templada	2
10578	tempestuoso	2
10579	temperamentos	2
10580	temiera	2
10581	temían	2
10582	temerarios	2
10583	temblorosas	2
10584	telégrafo	2
10585	telarañas	2
10586	tejidos	2
10587	tejido	2
10588	tejares	2
10589	teja	2
10590	tecla	2
10591	techumbre	2
10592	tate	2
10593	tarumba	2
10594	tarro	2
10595	tardando	2
10596	tarascas	2
10597	tapizada	2
10598	tapiz	2
10599	tapaban	2
10600	tantismo	2
10601	tantismas	2
10602	tanda	2
10603	tamañitos	2
10604	tamañita	2
10605	tallado	2
10606	tallada	2
10607	tálamo	2
10608	taimada	2
10609	tácitamente	2
10610	tableado	2
10611	tabacos	2
10612	tabaco	2
10613	susurró	2
10614	sustraerse	2
10615	sustitución	2
10616	sustentada	2
10617	suspirar	2
10618	suspiraba	2
10619	suspensión	2
10620	suspensa	2
10621	suspendió	2
10622	suspendidos	2
10623	suspendía	2
10624	suspender	2
10625	suscrición	2
10626	susceptible	2
10627	susceptibilidad	2
10628	susana	2
10629	surtían	2
10630	surgió	2
10631	surgían	2
10632	surge	2
10633	surcos	2
10634	suprimir	2
10635	supremo	2
10636	supremacía	2
10637	suponerse	2
10638	supone	2
10639	supón	2
10640	supieras	2
10641	supersticioso	2
10642	supersticiosas	2
10643	superchería	2
10644	suministrarle	2
10645	sumergirse	2
10646	sumergido	2
10647	sumergía	2
10648	sulfato	2
10649	sujetas	2
10650	sujetarle	2
10651	sujetarla	2
10652	sujeción	2
10653	suicida	2
10654	sui	2
10655	sugirió	2
10656	sugestivo	2
10657	sufrirá	2
10658	sufrió	2
10659	suficientemente	2
10660	suez	2
10661	suene	2
10662	suéltela	2
10663	sueltan	2
10664	sudores	2
10665	suciedad	2
10666	sucesivo	2
10667	sucesivamente	2
10668	sucedió	2
10669	sucedido	2
10670	suceda	2
10671	subterráneo	2
10672	subterfugios	2
10673	subo	2
10674	sublimemente	2
10675	sublevaban	2
10676	suben	2
10677	subastas	2
10678	suavizando	2
10679	sostienen	2
10680	sostenga	2
10681	sostendrá	2
10682	sospechoso	2
10683	sospechosas	2
10684	sospechará	2
10685	sosón	2
10686	soslayo	2
10687	sortija	2
10688	sorprendía	2
10689	sorprendente	2
10690	sorprende	2
10691	sordos	2
10692	sordera	2
10693	sopicaldo	2
10694	sopera	2
10695	soñador	2
10696	sonsonete	2
10697	sonriente	2
10698	sonreían	2
10699	sonora	2
10700	sonidos	2
10701	sonatas	2
10702	sonando	2
10703	sometido	2
10704	sombrilla	2
10705	sombrías	2
10706	solteros	2
10707	soltarle	2
10708	sollozaba	2
10709	solitarias	2
10710	soliloquio	2
10711	solicitud	2
10712	solemnísimo	2
10713	solemnes	2
10714	solemnemente	2
10715	solares	2
10716	solapa	2
10717	soga	2
10718	sofocó	2
10719	sofocar	2
10720	sofocante	2
10721	sofocados	2
10722	sofocaba	2
10723	socorrida	2
10724	socorrer	2
10725	socialismo	2
10726	socarrona	2
10727	sobrinitos	2
10728	sobrinita	2
10729	sobrinillo	2
10730	sobresaltado	2
10731	sobresalían	2
10732	sobres	2
10733	sobrado	2
10734	sobraba	2
10735	sobones	2
10736	sobón	2
10737	soberanamente	2
10738	soba	2
10739	sito	2
10740	sistemas	2
10741	sirvan	2
10742	sintiose	2
10743	sintéticas	2
10744	siniestro	2
10745	singularísimas	2
10746	singularísima	2
10747	sinceros	2
10748	simpatizaba	2
10749	simpáticas	2
10750	simetría	2
10751	simbolizaba	2
10752	sillero	2
10753	sillería	2
10754	silenciosamente	2
10755	silbaba	2
10756	siguiese	2
10757	significara	2
10758	sigilo	2
10759	sigamos	2
10760	siesta	2
10761	sientas	2
10762	shakespeare	2
10763	sesuda	2
10764	sesada	2
10765	servidos	2
10766	servidor	2
10767	serpentón	2
10768	seretas	2
10769	serafín	2
10770	sepultura	2
10771	sepulcral	2
10772	sépase	2
10773	separas	2
10774	separaron	2
10775	separan	2
10776	separa	2
10777	sepan	2
10778	sepamos	2
10779	sépalo	2
10780	señoronas	2
10781	señoritingo	2
10782	señalar	2
10783	sentirlo	2
10784	sentida	2
10785	sentencias	2
10786	sentencia	2
10787	sentaron	2
10788	sentándola	2
10789	sentando	2
10790	sensatez	2
10791	sensatas	2
10792	semíramis	2
10793	seminario	2
10794	sembrado	2
10795	sellada	2
10796	selectas	2
10797	segundas	2
10798	seguirla	2
10799	seguiré	2
10800	seguimiento	2
10801	seguidita	2
10802	seguidas	2
10803	segovia	2
10804	seductoras	2
10805	seducía	2
10806	seduce	2
10807	seducciones	2
10808	sedas	2
10809	seculares	2
10810	secuestrador	2
10811	secando	2
10812	seáis	2
10813	satisfizo	2
10814	satánico	2
10815	sarcástica	2
10816	saraos	2
10817	saquen	2
10818	santurrona	2
10819	santito	2
10820	santificación	2
10821	santiago	2
10822	santamente	2
10823	sanó	2
10824	sanidad	2
10825	samaritanas	2
10826	salvarnos	2
10827	salvan	2
10828	salvajismo	2
10829	saludos	2
10830	salude	2
10831	saludaron	2
10832	saludarla	2
10833	saludable	2
10834	saludaban	2
10835	salteados	2
10836	salte	2
10837	salones	2
10838	salmón	2
10839	salitas	2
10840	saliéndole	2
10841	salíamos	2
10842	salgan	2
10843	salero	2
10844	saldré	2
10845	saldrás	2
10846	salada	2
10847	saint	2
10848	sahumaremos	2
10849	sagasta	2
10850	saeta	2
10851	sacudir	2
10852	sacudiéndose	2
10853	sacudidas	2
10854	sacudían	2
10855	sacrílega	2
10856	sacrificada	2
10857	sacrifica	2
10858	sacramentado	2
10859	sacola	2
10860	sacerdotes	2
10861	sacerdocio	2
10862	sacaste	2
10863	sacase	2
10864	sacarme	2
10865	sacarlos	2
10866	sacarían	2
10867	sacaré	2
10868	sacaran	2
10869	sacándola	2
10870	sácalo	2
10871	sacaban	2
10872	sacábale	2
10873	sabrosísimo	2
10874	sabrás	2
10875	saborear	2
10876	saboreando	2
10877	sabías	2
10878	saberse	2
10879	rutinarias	2
10880	ruptura	2
10881	rumorcillo	2
10882	rum	2
10883	ruidosas	2
10884	rugido	2
10885	rufina	2
10886	rudos	2
10887	rudas	2
10888	rúbricas	2
10889	rubia	2
10890	royan	2
10891	rostros	2
10892	rosarios	2
10893	rorró	2
10894	roñoso	2
10895	rondón	2
10896	rondando	2
10897	rompieron	2
10898	rompían	2
10899	rompen	2
10900	rompa	2
10901	romano	2
10902	rodrigo	2
10903	rodilleras	2
10904	rodeado	2
10905	rodeadas	2
10906	rodaba	2
10907	roca	2
10908	robustos	2
10909	roble	2
10910	robarle	2
10911	robándome	2
10912	ro	2
10913	rizado	2
10914	rivero	2
10915	ritmo	2
10916	risueños	2
10917	risita	2
10918	risilla	2
10919	riquísimas	2
10920	riñones	2
10921	riñonadas	2
10922	rigurosa	2
10923	rigores	2
10924	rígido	2
10925	rígida	2
10926	rifa	2
10927	rienda	2
10928	ríen	2
10929	ridiculizar	2
10930	riales	2
10931	rezongando	2
10932	rezonas	2
10933	rezó	2
10934	rezaré	2
10935	reyertas	2
10936	reyerta	2
10937	revuelven	2
10938	revolverse	2
10939	revoltijo	2
10940	revoco	2
10941	revivir	2
10942	revivió	2
10943	revisó	2
10944	revisando	2
10945	reviente	2
10946	revestía	2
10947	reventara	2
10948	reventado	2
10949	revelando	2
10950	revela	2
10951	reunirse	2
10952	retumbar	2
10953	retrospectivos	2
10954	retroceder	2
10955	retratado	2
10956	retozona	2
10957	retozar	2
10958	retozaba	2
10959	retóricas	2
10960	retorciéndose	2
10961	retorcer	2
10962	retírate	2
10963	retirarme	2
10964	retiraría	2
10965	retiraré	2
10966	retirara	2
10967	retiran	2
10968	retira	2
10969	retener	2
10970	retahíla	2
10971	resulte	2
10972	resultas	2
10973	resultaría	2
10974	resultaban	2
10975	resuelve	2
10976	resuelta	2
10977	restregándose	2
10978	restallido	2
10979	respondiéndose	2
10980	respondiendo	2
10981	respondido	2
10982	respondí	2
10983	responderme	2
10984	respóndeme	2
10985	responde	2
10986	resplandeciente	2
10987	respiros	2
10988	respiro	2
10989	respira	2
10990	respeten	2
10991	respetables	2
10992	resonó	2
10993	resolviose	2
10994	resolvieron	2
10995	resolver	2
10996	resignarse	2
10997	residentes	2
10998	residencia	2
10999	resguardándose	2
11000	reservar	2
11001	reservándose	2
11002	reservados	2
11003	reservaba	2
11004	resbalando	2
11005	resabios	2
11006	requetefinos	2
11007	requemada	2
11008	requemaba	2
11009	reputado	2
11010	repugnantes	2
11011	repugnaban	2
11012	repugna	2
11013	repuesto	2
11014	republicano	2
11015	reprodujo	2
11016	reproducían	2
11017	representó	2
11018	representante	2
11019	representándose	2
11020	reposadas	2
11021	repoblicanos	2
11022	réplica	2
11023	repleto	2
11024	repite	2
11025	repicar	2
11026	repetirlo	2
11027	repetida	2
11028	repelones	2
11029	repecho	2
11030	reparten	2
11031	reparos	2
11032	reparan	2
11033	reparadora	2
11034	reparaciones	2
11035	reos	2
11036	reñirle	2
11037	reñiría	2
11038	reñido	2
11039	reñida	2
11040	reñía	2
11041	renunció	2
11042	renqueando	2
11043	renovando	2
11044	renovados	2
11045	renovado	2
11046	reniegue	2
11047	rendirse	2
11048	rendidas	2
11049	remontarse	2
11050	remesas	2
11051	remedándole	2
11052	rematado	2
11053	relumbraban	2
11054	religiosidad	2
11055	relatores	2
11056	relacionarse	2
11057	relacionados	2
11058	rejas	2
11059	reírnos	2
11060	reirá	2
11061	reintegro	2
11062	reinaban	2
11063	rehusó	2
11064	rehuía	2
11065	regurgitación	2
11066	reguapo	2
11067	regresaría	2
11068	regresaban	2
11069	regocijaba	2
11070	registros	2
11071	registrando	2
11072	registra	2
11073	regio	2
11074	regimiento	2
11075	régimen	2
11076	regeneración	2
11077	regazo	2
11078	regañón	2
11079	regalito	2
11080	regalar	2
11081	refunfuñó	2
11082	refugiose	2
11083	refrescarle	2
11084	refregándose	2
11085	reflexionó	2
11086	reflexionar	2
11087	reflexiona	2
11088	reflejos	2
11089	reflejo	2
11090	refistolera	2
11091	refiriéndole	2
11092	refiriendo	2
11093	referidos	2
11094	refajos	2
11095	reducirla	2
11096	reduciendo	2
11097	reducía	2
11098	reduce	2
11099	redobló	2
11100	redimido	2
11101	redimía	2
11102	redentora	2
11103	recuerdan	2
11104	recuerda	2
11105	rectificar	2
11106	rectifica	2
11107	rectas	2
11108	recortarlo	2
11109	recortados	2
11110	recorrido	2
11111	recorre	2
11112	recordarlo	2
11113	reconocerse	2
11114	reconocerla	2
11115	reconocería	2
11116	reconoce	2
11117	recóndito	2
11118	recónditas	2
11119	reconciliarse	2
11120	reconcentrar	2
11121	recomendar	2
11122	recogiéndose	2
11123	recogía	2
11124	recogí	2
11125	recógete	2
11126	recogen	2
11127	reclusión	2
11128	reclinar	2
11129	reclamar	2
11130	reclamación	2
11131	recientemente	2
11132	recibirlos	2
11133	recibirla	2
11134	recibes	2
11135	reciben	2
11136	reciba	2
11137	rechinar	2
11138	recetaba	2
11139	receptividad	2
11140	recepción	2
11141	receloso	2
11142	recela	2
11143	recataba	2
11144	recaer	2
11145	rebosar	2
11146	rebeldes	2
11147	rebajarme	2
11148	reanudó	2
11149	realizó	2
11150	realizarse	2
11151	realizarlo	2
11152	realizando	2
11153	realidades	2
11154	razonar	2
11155	razonaba	2
11156	rayaban	2
11157	ratones	2
11158	ratero	2
11159	ratas	2
11160	rastras	2
11161	rasguños	2
11162	rascó	2
11163	rasa	2
11164	rarísima	2
11165	rareza	2
11166	raquítico	2
11167	raquítica	2
11168	rápidas	2
11169	rapaza	2
11170	rapaz	2
11171	rancio	2
11172	rameado	2
11173	raigones	2
11174	racional	2
11175	racimos	2
11176	rabietina	2
11177	rabien	2
11178	rabie	2
11179	rábano	2
11180	rabadilla	2
11181	ra	2
11182	quitaste	2
11183	quitarvos	2
11184	quitarte	2
11185	quitársela	2
11186	quitarles	2
11187	quítame	2
11188	quisiéramos	2
11189	quintales	2
11190	quincena	2
11191	química	2
11192	quimeras	2
11193	quiéreme	2
11194	quiénes	2
11195	quiebro	2
11196	quevedos	2
11197	quesos	2
11198	querindango	2
11199	queridas	2
11200	quererte	2
11201	queráis	2
11202	quemó	2
11203	quemo	2
11204	quemas	2
11205	quemarse	2
11206	quemar	2
11207	quemado	2
11208	quemaba	2
11209	quema	2
11210	quejó	2
11211	quejidos	2
11212	quejido	2
11213	quejarte	2
11214	quedito	2
11215	quedes	2
11216	queden	2
11217	quedáronse	2
11218	quedaremos	2
11219	quedamente	2
11220	quebrantan	2
11221	quebraderos	2
11222	pusiste	2
11223	pusieras	2
11224	purificarse	2
11225	purgatorio	2
11226	pur	2
11227	pupila	2
11228	puñetazo	2
11229	puñaladas	2
11230	puntería	2
11231	puntera	2
11232	puntapié	2
11233	puntal	2
11234	puntadita	2
11235	pulpitillo	2
11236	pulga	2
11237	puéstose	2
11238	puerto	2
11239	pué	2
11240	pue	2
11241	pudiente	2
11242	publicidad	2
11243	pruritos	2
11244	pruebes	2
11245	prueben	2
11246	pruebe	2
11247	proyectil	2
11248	proyectada	2
11249	próximamente	2
11250	provocar	2
11251	provocado	2
11252	provista	2
11253	provisional	2
11254	provisión	2
11255	proveerse	2
11256	protestar	2
11257	protestanta	2
11258	protegiendo	2
11259	protegían	2
11260	prostitución	2
11261	prospectos	2
11262	prorrumpiendo	2
11263	prórroga	2
11264	propuesta	2
11265	proporción	2
11266	proponían	2
11267	proponga	2
11268	propietaria	2
11269	pronunciado	2
11270	prometía	2
11271	prometí	2
11272	prométame	2
11273	prolongación	2
11274	prohibirle	2
11275	prohibiendo	2
11276	prohibido	2
11277	profundas	2
11278	profetizando	2
11279	profético	2
11280	profesores	2
11281	profeso	2
11282	profesado	2
11283	profesaba	2
11284	profecías	2
11285	profecía	2
11286	profanaciones	2
11287	producirse	2
11288	producida	2
11289	procures	2
11290	procurarse	2
11291	procedimiento	2
11292	procedían	2
11293	procederes	2
11294	probarme	2
11295	probara	2
11296	probada	2
11297	probables	2
11298	probaba	2
11299	privados	2
11300	privación	2
11301	pringue	2
11302	principian	2
11303	principiaba	2
11304	princesa	2
11305	primitivas	2
11306	previsor	2
11307	previo	2
11308	prevenir	2
11309	prevaleció	2
11310	pretendientes	2
11311	pretendiente	2
11312	pretender	2
11313	pretende	2
11314	presumiendo	2
11315	presto	2
11316	preste	2
11317	prestase	2
11318	prestada	2
11319	presión	2
11320	presidente	2
11321	presentando	2
11322	presentable	2
11323	presentábase	2
11324	presentaban	2
11325	presenciar	2
11326	presagio	2
11327	prepárese	2
11328	prepare	2
11329	prepárate	2
11330	preparación	2
11331	prepara	2
11332	preocupaba	2
11333	prendida	2
11334	prendado	2
11335	premeditación	2
11336	prehistórica	2
11337	preguntole	2
11338	preguntes	2
11339	pregunte	2
11340	preguntarles	2
11341	preguntara	2
11342	pregón	2
11343	prefieres	2
11344	preferiré	2
11345	preferido	2
11346	predominio	2
11347	precursor	2
11348	precoces	2
11349	precisado	2
11350	precisa	2
11351	precipitemos	2
11352	precipitaste	2
11353	precipitación	2
11354	preciosidades	2
11355	preciados	2
11356	precedido	2
11357	precedidas	2
11358	precedida	2
11359	precaución	2
11360	praga	2
11361	practicar	2
11362	potro	2
11363	potencia	2
11364	potaje	2
11365	posturas	2
11366	postizo	2
11367	posterior	2
11368	positivos	2
11369	posesionarse	2
11370	poseedores	2
11371	posarse	2
11372	posados	2
11373	posado	2
11374	pórtico	2
11375	portaré	2
11376	portar	2
11377	portante	2
11378	portando	2
11379	portaba	2
11380	porcelana	2
11381	poniéndome	2
11382	poniéndolos	2
11383	poniéndoles	2
11384	poníale	2
11385	ponferrada	2
11386	ponérsele	2
11387	ponerlos	2
11388	ponemos	2
11389	pompas	2
11390	pompadour	2
11391	polvoriento	2
11392	polluelo	2
11393	pollería	2
11394	políticas	2
11395	polisones	2
11396	policías	2
11397	polémica	2
11398	podridos	2
11399	podrida	2
11400	podrías	2
11401	poderosas	2
11402	poderlas	2
11403	poderla	2
11404	poderes	2
11405	pobretín	2
11406	pobretería	2
11407	pluralidad	2
11408	plumaje	2
11409	plum	2
11410	plin	2
11411	plieguecitos	2
11412	pleno	2
11413	plegando	2
11414	plebeyo	2
11415	plebe	2
11416	plazos	2
11417	plazoleta	2
11418	plazas	2
11419	playa	2
11420	platito	2
11421	pláticas	2
11422	platicar	2
11423	plática	2
11424	plasencia	2
11425	plañidero	2
11426	plantose	2
11427	planteando	2
11428	planté	2
11429	plantarse	2
11430	plantarle	2
11431	plantar	2
11432	plancheta	2
11433	planchando	2
11434	planas	2
11435	plam	2
11436	placeres	2
11437	placentera	2
11438	pla	2
11439	pivote	2
11440	pitando	2
11441	pistoletazo	2
11442	pisotones	2
11443	pisoteando	2
11444	pirran	2
11445	pirraba	2
11446	pirámides	2
11447	pirámide	2
11448	piores	2
11449	piñón	2
11450	pinturera	2
11451	pintoresca	2
11452	pintó	2
11453	pinté	2
11454	pintas	2
11455	pintándole	2
11456	pintando	2
11457	pingos	2
11458	pingo	2
11459	pindongona	2
11460	pinchazos	2
11461	pinchas	2
11462	pincha	2
11463	pilletes	2
11464	pildoritas	2
11465	pilar	2
11466	pif	2
11467	piececita	2
11468	pidiole	2
11469	picarescos	2
11470	pezón	2
11471	petrolero	2
11472	petra	2
11473	petaca	2
11474	pesos	2
11475	pesimistas	2
11476	pescó	2
11477	pescas	2
11478	pescados	2
11479	pescador	2
11480	pescadero	2
11481	pesas	2
11482	pesares	2
11483	pesando	2
11484	pesadez	2
11485	pesadamente	2
11486	perversión	2
11487	perversa	2
11488	pertinentes	2
11489	pertenecido	2
11490	persuasiva	2
11491	personalmente	2
11492	persiguiendo	2
11493	persignándose	2
11494	persignaba	2
11495	perseverancia	2
11496	perseguir	2
11497	perseguía	2
11498	persecuciones	2
11499	persa	2
11500	perrillo	2
11501	perradas	2
11502	perpetua	2
11503	perorata	2
11504	peroles	2
11505	permitirle	2
11506	permaneciendo	2
11507	periodista	2
11508	periodismo	2
11509	periódicamente	2
11510	perilla	2
11511	peri	2
11512	perfectos	2
11513	perezoso	2
11514	perezosa	2
11515	pereza	2
11516	perdurable	2
11517	perdularios	2
11518	perdonarla	2
11519	perdonará	2
11520	perdóname	2
11521	perdiste	2
11522	perderlo	2
11523	perderle	2
11524	percibía	2
11525	percales	2
11526	pequeñito	2
11527	pequeñez	2
11528	pepitas	2
11529	pepes	2
11530	peorcito	2
11531	peón	2
11532	penumbra	2
11533	pensaron	2
11534	pensándolo	2
11535	pensada	2
11536	pensaban	2
11537	penosos	2
11538	penitencias	2
11539	peniques	2
11540	península	2
11541	penetraron	2
11542	penetrando	2
11543	peneque	2
11544	pelotera	2
11545	pelotazo	2
11546	pelmazos	2
11547	pella	2
11548	pelitos	2
11549	pelito	2
11550	peletería	2
11551	pelear	2
11552	pelayo	2
11553	pelaban	2
11554	pela	2
11555	peineta	2
11556	peinándose	2
11557	peinadoras	2
11558	peinadora	2
11559	peinada	2
11560	peinaba	2
11561	pegué	2
11562	pegotes	2
11563	pegaron	2
11564	pegadas	2
11565	pedirte	2
11566	pedirme	2
11567	pedirles	2
11568	pediremos	2
11569	pedimos	2
11570	pedí	2
11571	pedantería	2
11572	pechera	2
11573	pecas	2
11574	pecadillos	2
11575	payo	2
11576	pavorosa	2
11577	pavor	2
11578	paveros	2
11579	pava	2
11580	paul	2
11581	patrones	2
11582	patriarcal	2
11583	patitas	2
11584	paternales	2
11585	patente	2
11586	pateando	2
11587	patatín	2
11588	patatán	2
11589	pataleta	2
11590	pataleos	2
11591	pataleando	2
11592	pataditas	2
11593	patá	2
11594	pastores	2
11595	pastora	2
11596	pasto	2
11597	pastilla	2
11598	pasteles	2
11599	pastelero	2
11600	pastelería	2
11601	pasteleras	2
11602	pastas	2
11603	pasmosas	2
11604	pasmó	2
11605	pásmense	2
11606	pasmarote	2
11607	pasmaban	2
11608	pases	2
11609	pasemos	2
11610	pasee	2
11611	pasearon	2
11612	pasean	2
11613	paseamos	2
11614	pasasen	2
11615	pasarlo	2
11616	pasarle	2
11617	pasarían	2
11618	pasaré	2
11619	pasándose	2
11620	pasamos	2
11621	pasamanos	2
11622	pasajeros	2
11623	pasajera	2
11624	parto	2
11625	partiendo	2
11626	partidos	2
11627	partidas	2
11628	particularidad	2
11629	participando	2
11630	partían	2
11631	parson	2
11632	parroquianas	2
11633	parrilla	2
11634	parque	2
11635	parlamento	2
11636	parisiense	2
11637	parió	2
11638	parezco	2
11639	párese	2
11640	pareciéndose	2
11641	parecidas	2
11642	parecíame	2
11643	paré	2
11644	pardas	2
11645	parda	2
11646	pararrayos	2
11647	paradójico	2
11648	paradojas	2
11649	paradero	2
11650	paradas	2
11651	parabienes	2
11652	papelista	2
11653	paparrucha	2
11654	pañosa	2
11655	pañolón	2
11656	pañolito	2
11657	pañería	2
11658	panza	2
11659	panorama	2
11660	panfilona	2
11661	panes	2
11662	panderetazos	2
11663	pamema	2
11664	palpitaciones	2
11665	palpitación	2
11666	palpitaba	2
11667	palmotear	2
11668	palmitas	2
11669	palmetazos	2
11670	palmetazo	2
11671	palmatoria	2
11672	palitos	2
11673	palio	2
11674	palillos	2
11675	pálidas	2
11676	paletos	2
11677	paletada	2
11678	paleta	2
11679	paladar	2
11680	palacios	2
11681	palabrería	2
11682	pajeles	2
11683	pajaritas	2
11684	pajarillos	2
11685	pajarete	2
11686	países	2
11687	paisano	2
11688	paicía	2
11689	páginas	2
11690	pagarla	2
11691	pagarás	2
11692	pagan	2
11693	padillita	2
11694	pacíficos	2
11695	paciente	2
11696	oyese	2
11697	oyéronse	2
11698	oyeran	2
11699	oyentes	2
11700	oveja	2
11701	osuna	2
11702	ostras	2
11703	ostentaba	2
11704	oscurece	2
11705	osadía	2
11706	ortografía	2
11707	ortiz	2
11708	oriundo	2
11709	originalidad	2
11710	orgulloso	2
11711	orgullosas	2
11712	orgías	2
11713	organismo	2
11714	orfila	2
11715	ordinariamente	2
11716	ordenar	2
11717	ordenanzas	2
11718	ordenan	2
11719	ordenado	2
11720	ordena	2
11721	oratorias	2
11722	orán	2
11723	opulentos	2
11724	opulenta	2
11725	optimistas	2
11726	optimismo	2
11727	oprimido	2
11728	oposición	2
11729	oportunidad	2
11730	oportunas	2
11731	opone	2
11732	óperas	2
11733	olvidos	2
11734	olvidará	2
11735	olvidando	2
11736	olvidan	2
11737	olvidada	2
11738	olorosas	2
11739	olivos	2
11740	olivares	2
11741	olfatorios	2
11742	ojival	2
11743	ojal	2
11744	oírme	2
11745	oirá	2
11746	óigame	2
11747	oíanse	2
11748	oíale	2
11749	ofuscado	2
11750	ofrezca	2
11751	ofreciera	2
11752	ofrecí	2
11753	ofrecerle	2
11754	oficiosa	2
11755	oficiar	2
11756	oficialas	2
11757	oficiala	2
11758	oficiaba	2
11759	ofende	2
11760	ofenda	2
11761	ocurrírseme	2
11762	ocurriría	2
11763	ocurrirá	2
11764	ocurra	2
11765	ocupemos	2
11766	ocuparme	2
11767	ocupan	2
11768	ocupa	2
11769	oculte	2
11770	ocultado	2
11771	ocioso	2
11772	ociosa	2
11773	ochocientos	2
11774	ochavo	2
11775	occidente	2
11776	occidental	2
11777	obtenerla	2
11778	obstrucción	2
11779	observo	2
11780	observaron	2
11781	observándole	2
11782	observándola	2
11783	observancia	2
11784	obsequiar	2
11785	obliga	2
11786	obedeces	2
11787	nupcial	2
11788	núñez	2
11789	numeradas	2
11790	numen	2
11791	nuca	2
11792	novillos	2
11793	noviazgo	2
11794	noventa	2
11795	novena	2
11796	novelescos	2
11797	novelería	2
11798	novelera	2
11799	novar	2
11800	noto	2
11801	notase	2
11802	notarse	2
11803	notada	2
11804	normalmente	2
11805	nombrar	2
11806	nómbrame	2
11807	noé	2
11808	nocturna	2
11809	niñera	2
11810	nietos	2
11811	nichos	2
11812	nicarona	2
11813	nevada	2
11814	netos	2
11815	neta	2
11816	neri	2
11817	nenes	2
11818	nenas	2
11819	neísmo	2
11820	negose	2
11821	negarse	2
11822	negarle	2
11823	negarán	2
11824	necios	2
11825	necesite	2
11826	necesitara	2
11827	necesitamos	2
11828	necesarias	2
11829	necesariamente	2
11830	nebulosa	2
11831	nea	2
11832	nazcan	2
11833	nazca	2
11834	nazareno	2
11835	navegando	2
11836	naturalismo	2
11837	nasal	2
11838	narrando	2
11839	nardos	2
11840	nardo	2
11841	naranjos	2
11842	naranjas	2
11843	nápoles	2
11844	nalgas	2
11845	nadar	2
11846	nadando	2
11847	naciste	2
11848	nacieron	2
11849	naciente	2
11850	naciendo	2
11851	nabucodonosor	2
11852	mutuos	2
11853	músicas	2
11854	musicales	2
11855	musical	2
11856	murmurando	2
11857	murmullos	2
11858	muove	2
11859	muñecos	2
11860	municipales	2
11861	multiplicaba	2
11862	muletillas	2
11863	muletilla	2
11864	muladar	2
11865	mujerzuela	2
11866	mujerona	2
11867	mujeril	2
11868	muge	2
11869	muevo	2
11870	muevas	2
11871	muertecito	2
11872	muérete	2
11873	mueres	2
11874	muerdo	2
11875	mueran	2
11876	muelle	2
11877	muele	2
11878	mudéjares	2
11879	mudéjar	2
11880	mudaba	2
11881	movilidad	2
11882	móviles	2
11883	moverme	2
11884	motivada	2
11885	motas	2
11886	mostrase	2
11887	mostráronse	2
11888	mostrarlo	2
11889	mostaza	2
11890	mortificaban	2
11891	mortales	2
11892	morriña	2
11893	morrazo	2
11894	mormón	2
11895	moriría	2
11896	morimos	2
11897	morenito	2
11898	morcilla	2
11899	morboso	2
11900	moralista	2
11901	moraleja	2
11902	moradas	2
11903	moñuca	2
11904	montada	2
11905	monta	2
11906	monjil	2
11907	monerías	2
11908	mondongo	2
11909	monaguillo	2
11910	momia	2
11911	momentito	2
11912	molinete	2
11913	molestarme	2
11914	molestaran	2
11915	mole	2
11916	moldes	2
11917	modosa	2
11918	modestita	2
11919	moderno	2
11920	moderado	2
11921	modelado	2
11922	moco	2
11923	mitón	2
11924	mitología	2
11925	miss	2
11926	mismísima	2
11927	misita	2
11928	misionero	2
11929	misericordioso	2
11930	miserere	2
11931	misantropía	2
11932	mirosté	2
11933	mirolo	2
11934	míreme	2
11935	mírelos	2
11936	mírele	2
11937	miráronla	2
11938	mirarlo	2
11939	miraría	2
11940	mirará	2
11941	miramientos	2
11942	mirador	2
11943	mirábalas	2
11944	minucioso	2
11945	ministros	2
11946	ministerios	2
11947	minio	2
11948	mínimo	2
11949	mineral	2
11950	mimir	2
11951	mímica	2
11952	mimbres	2
11953	mimar	2
11954	mimando	2
11955	mimado	2
11956	mima	2
11957	miento	2
11958	mieles	2
11959	miedos	2
11960	miajita	2
11961	mezquinos	2
11962	mezclado	2
11963	mezclada	2
11964	mezclábase	2
11965	metódica	2
11966	metieran	2
11967	metiéndolo	2
11968	metiéndole	2
11969	metálica	2
11970	metafísico	2
11971	metafísica	2
11972	merinos	2
11973	merienda	2
11974	mereciera	2
11975	merecidos	2
11976	merecer	2
11977	mercaderes	2
11978	mercachifle	2
11979	meñique	2
11980	mentarle	2
11981	mensajeros	2
11982	mensaje	2
11983	menosprecio	2
11984	menestrala	2
11985	menestra	2
11986	menesterosos	2
11987	meneos	2
11988	meneó	2
11989	menéese	2
11990	menear	2
11991	meneando	2
11992	mendizábal	2
11993	mención	2
11994	mena	2
11995	memorias	2
11996	melodrama	2
11997	melancólico	2
11998	melancolías	2
11999	mejorcito	2
12000	médula	2
12001	mediterránea	2
12002	meditemos	2
12003	meditabundo	2
12004	médica	2
12005	medianería	2
12006	medianamente	2
12007	mediados	2
12008	mediación	2
12009	mecánico	2
12010	meca	2
12011	mausoleos	2
12012	matritenses	2
12013	matorral	2
12014	matinal	2
12015	matilde	2
12016	materno	2
12017	materias	2
12018	materiales	2
12019	matemático	2
12020	matemáticas	2
12021	mataron	2
12022	matarles	2
12023	mataran	2
12024	mastín	2
12025	masticación	2
12026	masónica	2
12027	masón	2
12028	mascar	2
12029	masas	2
12030	martos	2
12031	martirizaba	2
12032	mártires	2
12033	martínez	2
12034	marrasquino	2
12035	marmotona	2
12036	marmolillo	2
12037	mariposita	2
12038	marina	2
12039	maridillo	2
12040	mareos	2
12041	marees	2
12042	mareados	2
12043	mareada	2
12044	márchese	2
12045	marché	2
12046	marchase	2
12047	marcharon	2
12048	marcharme	2
12049	marcharía	2
12050	marcharé	2
12051	marcar	2
12052	marcados	2
12053	marcada	2
12054	marcaban	2
12055	marcaba	2
12056	maravillosamente	2
12057	maravillas	2
12058	maravillada	2
12059	maquinaria	2
12060	mañosa	2
12061	mantuvo	2
12062	mantillas	2
12063	manteniendo	2
12064	mantenerle	2
12065	mantelería	2
12066	mantecadas	2
12067	manotazos	2
12068	manojo	2
12069	manjavacas	2
12070	manirroto	2
12071	manifestaron	2
12072	manifestarlo	2
12073	maniáticas	2
12074	manguitos	2
12075	manejo	2
12076	maneje	2
12077	manejaba	2
12078	mandes	2
12079	mándeme	2
12080	mandé	2
12081	mandarte	2
12082	mandarines	2
12083	mandará	2
12084	mandan	2
12085	máncharras	2
12086	manchado	2
12087	manazas	2
12088	mamón	2
12089	mamando	2
12090	maltrecho	2
12091	maltrató	2
12092	maltratar	2
12093	maltratado	2
12094	malsanos	2
12095	malograse	2
12096	malla	2
12097	malita	2
12098	maligna	2
12099	malicioso	2
12100	maliciosas	2
12101	malestar	2
12102	maleante	2
12103	malditos	2
12104	majadería	2
12105	magníficos	2
12106	magistral	2
12107	mágico	2
12108	magia	2
12109	maestras	2
12110	madrugones	2
12111	madrina	2
12112	madrileño	2
12113	madrileña	2
12114	madriguera	2
12115	maderos	2
12116	madero	2
12117	madejas	2
12118	madapolanes	2
12119	máculas	2
12120	macho	2
12121	machacaba	2
12122	macana	2
12123	luteranos	2
12124	lutera	2
12125	lustroso	2
12126	lustrosa	2
12127	lunática	2
12128	luminoso	2
12129	lujos	2
12130	lúgubremente	2
12131	lucirse	2
12132	lucimiento	2
12133	lucidas	2
12134	lucían	2
12135	lucero	2
12136	lotes	2
12137	loterías	2
12138	losa	2
12139	lord	2
12140	loquinaria	2
12141	lópez	2
12142	logrado	2
12143	logra	2
12144	locomotoras	2
12145	lóbrega	2
12146	llovido	2
12147	llover	2
12148	lloriqueando	2
12149	llore	2
12150	lloraste	2
12151	lloraban	2
12152	llévese	2
12153	llevéis	2
12154	llevé	2
12155	llevárselo	2
12156	llevarían	2
12157	llevándolo	2
12158	llevamos	2
12159	llevadera	2
12160	llenarse	2
12161	llenara	2
12162	llenando	2
12163	llegarían	2
12164	llegaremos	2
12165	llegaran	2
12166	llegamos	2
12167	llamémosle	2
12168	llame	2
12169	llamarte	2
12170	llamador	2
12171	llamábanla	2
12172	liviano	2
12173	literario	2
12174	literaria	2
12175	lisonjeras	2
12176	líquidos	2
12177	lipendi	2
12178	líos	2
12179	linterna	2
12180	lindísimos	2
12181	lindísimas	2
12182	lince	2
12183	limpión	2
12184	límites	2
12185	limitado	2
12186	liga	2
12187	liebre	2
12188	lié	2
12189	licencia	2
12190	libritos	2
12191	librería	2
12192	libertino	2
12193	liberaremos	2
12194	liberar	2
12195	liada	2
12196	liaba	2
12197	lía	2
12198	leyenda	2
12199	levemente	2
12200	levantaría	2
12201	levantan	2
12202	leoneses	2
12203	lentitud	2
12204	lentes	2
12205	lente	2
12206	lenta	2
12207	lema	2
12208	leída	2
12209	legítimos	2
12210	leerás	2
12211	lebrel	2
12212	lea	2
12213	lavó	2
12214	lavadas	2
12215	lavada	2
12216	latitud	2
12217	latidos	2
12218	lastimeros	2
12219	lastimada	2
12220	largó	2
12221	largarse	2
12222	largaba	2
12223	laredo	2
12224	lanzaron	2
12225	lanzarme	2
12226	lanzarla	2
12227	lanzando	2
12228	lanza	2
12229	lanillas	2
12230	láminas	2
12231	lamentos	2
12232	lamentar	2
12233	lamentable	2
12234	laissez	2
12235	lagrimones	2
12236	lagarto	2
12237	lagarta	2
12238	ladrar	2
12239	ladrando	2
12240	ladino	2
12241	labrar	2
12242	labrador	2
12243	labrada	2
12244	laberinto	2
12245	laberíntico	2
12246	kock	2
12247	king	2
12248	juzgue	2
12249	juzgó	2
12250	juzgando	2
12251	jures	2
12252	jure	2
12253	juramentos	2
12254	juntando	2
12255	junde	2
12256	junda	2
12257	junco	2
12258	juimos	2
12259	jugador	2
12260	juegan	2
12261	judíos	2
12262	judicial	2
12263	judaísmo	2
12264	jubilar	2
12265	jorobar	2
12266	jornal	2
12267	jicarazo	2
12268	jergón	2
12269	javiera	2
12270	jardines	2
12271	jarabes	2
12272	japonés	2
12273	jaleo	2
12274	jadeante	2
12275	jactándose	2
12276	jactábase	2
12277	jaciendo	2
12278	italiano	2
12279	italia	2
12280	irún	2
12281	írsele	2
12282	irresponsable	2
12283	irresistibles	2
12284	irregularidad	2
12285	irradiación	2
12286	irónica	2
12287	irguiéndose	2
12288	involucrar	2
12289	invitados	2
12290	invitado	2
12291	invitación	2
12292	invisibles	2
12293	invento	2
12294	inventé	2
12295	invente	2
12296	inventas	2
12297	inventario	2
12298	inventar	2
12299	inventan	2
12300	inventado	2
12301	invasión	2
12302	invariablemente	2
12303	invariable	2
12304	inválida	2
12305	invadiendo	2
12306	invadía	2
12307	inútilmente	2
12308	inutilidad	2
12309	inundaron	2
12310	intriga	2
12311	intimidades	2
12312	íntimas	2
12313	intimar	2
12314	intervenía	2
12315	intervengo	2
12316	interrupción	2
12317	interrumpido	2
12318	interpretación	2
12319	interno	2
12320	intermitente	2
12321	intermitencias	2
12322	interminable	2
12323	intermediario	2
12324	interesara	2
12325	interesantísima	2
12326	interesada	2
12327	intentara	2
12328	intentando	2
12329	intellectus	2
12330	intelectualmente	2
12331	intelectuales	2
12332	intelectual	2
12333	intacto	2
12334	intachable	2
12335	insustancial	2
12336	insultado	2
12337	insufrible	2
12338	insubordinaba	2
12339	instructivo	2
12340	instrucciones	2
12341	instintivo	2
12342	instantáneamente	2
12343	instaláronse	2
12344	instalada	2
12345	instalación	2
12346	inspirábale	2
12347	inspector	2
12348	insignias	2
12349	inservibles	2
12350	insensatos	2
12351	inseguridad	2
12352	inquisición	2
12353	inquina	2
12354	inquilinas	2
12355	inquietudes	2
12356	inquietó	2
12357	inquietísima	2
12358	inquietarse	2
12359	innata	2
12360	inmortalidad	2
12361	inmortales	2
12362	inmensos	2
12363	inmediatos	2
12364	ininteligibles	2
12365	inició	2
12366	iniciativas	2
12367	inicial	2
12368	iniciada	2
12369	inicia	2
12370	ingredientes	2
12371	ingratos	2
12372	ingenuamente	2
12373	infundió	2
12374	infortunado	2
12375	informes	2
12376	informe	2
12377	inflado	2
12378	infinitas	2
12379	infausto	2
12380	infatigable	2
12381	infantiles	2
12382	infamante	2
12383	inexplicables	2
12384	inexperta	2
12385	inestimable	2
12386	inequívocas	2
12387	ineficacia	2
12388	indiscutible	2
12389	indiscreto	2
12390	indiscreción	2
12391	indisciplina	2
12392	indilugencias	2
12393	indignó	2
12394	indignado	2
12395	indignaba	2
12396	indigna	2
12397	indicios	2
12398	indicar	2
12399	indicándole	2
12400	indicada	2
12401	indicaciones	2
12402	indica	2
12403	indiano	2
12404	independientes	2
12405	independiente	2
12406	indemnización	2
12407	indefinidamente	2
12408	indecisa	2
12409	indecencias	2
12410	indagar	2
12411	incurría	2
12412	incumbencias	2
12413	inculta	2
12414	incrédula	2
12415	incorporarse	2
12416	incorporándose	2
12417	incorporada	2
12418	inconstantes	2
12419	inconscientemente	2
12420	incomprensibles	2
12421	incomodó	2
12422	incomodidad	2
12423	incomodaba	2
12424	incoherente	2
12425	inclinar	2
12426	inclinado	2
12427	incierto	2
12428	incendios	2
12429	incansable	2
12430	inapetencia	2
12431	inacabables	2
12432	impuso	2
12433	impulsada	2
12434	impuesto	2
12435	imprudente	2
12436	imprimiendo	2
12437	impreso	2
12438	impresionaron	2
12439	impresionado	2
12440	impresionables	2
12441	impresa	2
12442	impotentes	2
12443	imposibilitaban	2
12444	importantes	2
12445	imponían	2
12446	imponerse	2
12447	imponente	2
12448	impidiera	2
12449	impertinencias	2
12450	impertinencia	2
12451	imperioso	2
12452	imperceptible	2
12453	impedirme	2
12454	impedían	2
12455	impedía	2
12456	impavidez	2
12457	impacientaba	2
12458	imitar	2
12459	imita	2
12460	imaginándose	2
12461	ilustradas	2
12462	iluminen	2
12463	iluminaron	2
12464	iluminadas	2
12465	iluminada	2
12466	igualdad	2
12467	ignorantes	2
12468	ignorante	2
12469	ignorando	2
12470	íes	2
12471	idumeo	2
12472	idolatría	2
12473	idolatraré	2
12474	idolatrando	2
12475	idiotas	2
12476	idilio	2
12477	ideación	2
12478	íbanse	2
12479	huyeron	2
12480	hurtadillas	2
12481	huraño	2
12482	hundida	2
12483	hunda	2
12484	humillarse	2
12485	humillar	2
12486	humillado	2
12487	humillación	2
12488	humildemente	2
12489	húmera	2
12490	humaredas	2
12491	huéspeda	2
12492	huerfanitos	2
12493	huérfana	2
12494	huellas	2
12495	huella	2
12496	hueca	2
12497	hubiérase	2
12498	hoyo	2
12499	hostilidad	2
12500	hostil	2
12501	hosanna	2
12502	horrorosas	2
12503	horrorizado	2
12504	horripilaba	2
12505	horrendo	2
12506	hornillo	2
12507	hormigueo	2
12508	horchata	2
12509	horca	2
12510	honroso	2
12511	honras	2
12512	honrados	2
12513	honores	2
12514	honesto	2
12515	honestas	2
12516	honesta	2
12517	hondura	2
12518	hondísima	2
12519	hondamente	2
12520	honda	2
12521	homicida	2
12522	hombruna	2
12523	holgura	2
12524	hocicuda	2
12525	hízose	2
12526	hipocritona	2
12527	hipócritas	2
12528	hinchado	2
12529	hincapié	2
12530	hilada	2
12531	hijitos	2
12532	higiénico	2
12533	hidalguía	2
12534	hidalgo	2
12535	hicieras	2
12536	heterogeneidad	2
12537	hervidero	2
12538	heroísmo	2
12539	heroína	2
12540	heroico	2
12541	héroe	2
12542	hernán	2
12543	hermosuras	2
12544	hermosota	2
12545	hermanita	2
12546	heredar	2
12547	heredada	2
12548	helado	2
12549	hebilla	2
12550	hazlo	2
12551	hazle	2
12552	hayamos	2
12553	hatchisschina	2
12554	hastiaba	2
12555	harte	2
12556	hartas	2
12557	harmonium	2
12558	haraganes	2
12559	hamos	2
12560	hambrienta	2
12561	hallábanse	2
12562	hagáis	2
12563	haciéndote	2
12564	hacías	2
12565	hacíamos	2
12566	hacíalo	2
12567	hacíala	2
12568	hacha	2
12569	hacerlos	2
12570	hacerles	2
12571	hablillas	2
12572	hablé	2
12573	hablarían	2
12574	hablaría	2
12575	hablándoles	2
12576	habladora	2
12577	habitados	2
12578	habilidoso	2
12579	habilidades	2
12580	habiéndose	2
12581	habiéndole	2
12582	habíanle	2
12583	haberte	2
12584	habérselas	2
12585	habaneras	2
12586	gustase	2
12587	gustarme	2
12588	gustarle	2
12589	gustando	2
12590	gustábale	2
12591	gusanos	2
12592	guitarreo	2
12593	guisa	2
12594	guiñaba	2
12595	guillotina	2
12596	guillati	2
12597	guijarros	2
12598	guía	2
12599	guasoncita	2
12600	guasitas	2
12601	guasas	2
12602	guárdese	2
12603	guardarlos	2
12604	guardaría	2
12605	guardadito	2
12606	guardada	2
12607	guapetonas	2
12608	gruñir	2
12609	gruñía	2
12610	gruñendo	2
12611	gruesos	2
12612	grotesco	2
12613	grosero	2
12614	groseramente	2
12615	gro	2
12616	gritaron	2
12617	gritaban	2
12618	grillera	2
12619	grifo	2
12620	grietas	2
12621	greda	2
12622	gratas	2
12623	granujería	2
12624	granujas	2
12625	granos	2
12626	grandón	2
12627	grandísimas	2
12628	granada	2
12629	gramática	2
12630	gradual	2
12631	grados	2
12632	grada	2
12633	gozándose	2
12634	gotitas	2
12635	gorras	2
12636	goma	2
12637	golpecitos	2
12638	gobiernos	2
12639	gobernaor	2
12640	gobernadores	2
12641	gloriosa	2
12642	globos	2
12643	gitanesca	2
12644	giró	2
12645	gibraltar	2
12646	getafe	2
12647	gentes	2
12648	geniazo	2
12649	genial	2
12650	generosa	2
12651	generis	2
12652	generaciones	2
12653	gemía	2
12654	gelatinosas	2
12655	gaveta	2
12656	gatuperio	2
12657	gatito	2
12658	gatesca	2
12659	gateras	2
12660	gastarla	2
12661	gastando	2
12662	gastado	2
12663	gastadas	2
12664	garrote	2
12665	garrafales	2
12666	garbo	2
12667	garabato	2
12668	ganita	2
12669	gangas	2
12670	gandulones	2
12671	gande	2
12672	gancho	2
12673	ganara	2
12674	ganada	2
12675	gama	2
12676	galones	2
12677	galón	2
12678	gallardía	2
12679	galeras	2
12680	galapaguito	2
12681	galápago	2
12682	galantería	2
12683	gaita	2
12684	gaceta	2
12685	fusilen	2
12686	fusil	2
12687	furibundo	2
12688	fuoco	2
12689	fúnebres	2
12690	fundándose	2
12691	fundan	2
12692	fundamental	2
12693	fundadoras	2
12694	fundador	2
12695	fundación	2
12696	fumar	2
12697	fumando	2
12698	fuguilla	2
12699	fugó	2
12700	fugitivo	2
12701	fuertecillo	2
12702	fueros	2
12703	fuer	2
12704	fuentes	2
12705	fuelle	2
12706	fuegos	2
12707	fruta	2
12708	fruncimiento	2
12709	fruncidas	2
12710	frotó	2
12711	frotado	2
12712	frota	2
12713	frita	2
12714	fríos	2
12715	fresas	2
12716	frenéticos	2
12717	frenético	2
12718	fregado	2
12719	fray	2
12720	fraternales	2
12721	franquearon	2
12722	franqueaban	2
12723	francesota	2
12724	frailes	2
12725	fracasos	2
12726	fracaso	2
12727	frac	2
12728	forzosamente	2
12729	fortísimo	2
12730	forraje	2
12731	forrados	2
12732	forrado	2
12733	forrada	2
12734	fornos	2
12735	fornido	2
12736	formulando	2
12737	formó	2
12738	formara	2
12739	fogosa	2
12740	foco	2
12741	fluxión	2
12742	fluctuando	2
12743	flotante	2
12744	florín	2
12745	floreados	2
12746	flojos	2
12747	flojilla	2
12748	floja	2
12749	flequillo	2
12750	flechas	2
12751	flauteados	2
12752	flamantes	2
12753	flacos	2
12754	flácida	2
12755	flacas	2
12756	fisiológica	2
12757	físicos	2
12758	fisgona	2
12759	fiscalizadora	2
12760	fiscales	2
12761	firmemente	2
12762	firmas	2
12763	firmaba	2
12764	finísimas	2
12765	fingido	2
12766	fingía	2
12767	finezas	2
12768	finales	2
12769	filtrándose	2
12770	filósofos	2
12771	filosóficos	2
12772	filomena	2
12773	filigranas	2
12774	fijose	2
12775	fijeza	2
12776	fijaremos	2
12777	fijándose	2
12778	figuran	2
12779	figurada	2
12780	figuración	2
12781	fiero	2
12782	fierecita	2
12783	fieltro	2
12784	fiebres	2
12785	fichú	2
12786	fichas	2
12787	feudal	2
12788	fétida	2
12789	festín	2
12790	fernández	2
12791	feria	2
12792	fenelona	2
12793	felicitar	2
12794	felicitaciones	2
12795	felicitaban	2
12796	felicísima	2
12797	federal	2
12798	fecundidad	2
12799	favorezca	2
12800	favoreció	2
12801	fausto	2
12802	fatigoso	2
12803	fatigosa	2
12804	fatigados	2
12805	fases	2
12806	fase	2
12807	farolón	2
12808	faro	2
12809	fantásticos	2
12810	fantasmona	2
12811	fanfarronadas	2
12812	famosos	2
12813	familiarmente	2
12814	familiares	2
12815	faltarme	2
12816	faltará	2
12817	falsas	2
12818	fallido	2
12819	fallecimiento	2
12820	fallar	2
12821	falansterio	2
12822	faenas	2
12823	factible	2
12824	facilitado	2
12825	facilillo	2
12826	fachada	2
12827	facetas	2
12828	facción	2
12829	fabulista	2
12830	fábulas	2
12831	fábula	2
12832	fabricación	2
12833	f	2
12834	extremeño	2
12835	extremado	2
12836	extravíos	2
12837	extravío	2
12838	extravagante	2
12839	extinguida	2
12840	extinguían	2
12841	extienden	2
12842	externos	2
12843	extenso	2
12844	extendiendo	2
12845	extendidos	2
12846	extendidas	2
12847	extender	2
12848	exquisita	2
12849	expulsión	2
12850	expulsado	2
12851	expuestos	2
12852	expuesto	2
12853	expuesta	2
12854	exprisiones	2
12855	expresivos	2
12856	expresada	2
12857	expresa	2
12858	exponía	2
12859	exponga	2
12860	exponer	2
12861	explotan	2
12862	explotación	2
12863	expliques	2
12864	expliquemos	2
12865	explique	2
12866	explicó	2
12867	explícate	2
12868	explicarme	2
12869	explicarlo	2
12870	explicarle	2
12871	explícame	2
12872	explicaba	2
12873	expirando	2
12874	experimentaron	2
12875	expeditivo	2
12876	expedir	2
12877	expedición	2
12878	expansiva	2
12879	expansiones	2
12880	éxitos	2
12881	existió	2
12882	exigencia	2
12883	exhortación	2
12884	excluía	2
12885	exclamar	2
12886	excitantes	2
12887	excitante	2
12888	excitadísima	2
12889	exceso	2
12890	excelsa	2
12891	excelentísimo	2
12892	excelencia	2
12893	examinarle	2
12894	examinan	2
12895	examinado	2
12896	exageradas	2
12897	exacto	2
12898	evitarlo	2
12899	evitarle	2
12900	evitado	2
12901	evitaba	2
12902	evita	2
12903	evidentes	2
12904	evidente	2
12905	evidencia	2
12906	evasivas	2
12907	europea	2
12908	eucaristía	2
12909	etcétera	2
12910	etapas	2
12911	etapa	2
12912	estupor	2
12913	estupidez	2
12914	estúpidas	2
12915	estúpidamente	2
12916	estupefacta	2
12917	estudió	2
12918	estudian	2
12919	estudiadas	2
12920	estudiada	2
12921	estuche	2
12922	estucadas	2
12923	estrofa	2
12924	estribos	2
12925	estribillos	2
12926	estreno	2
12927	estrenar	2
12928	estrenada	2
12929	estremecimientos	2
12930	estremecimiento	2
12931	estremecía	2
12932	estrelló	2
12933	estrello	2
12934	estrellarse	2
12935	estrecho	2
12936	estrecheces	2
12937	estrechas	2
12938	estrechándole	2
12939	estragos	2
12940	estorbo	2
12941	estorba	2
12942	estirones	2
12943	estirándose	2
12944	estirada	2
12945	estiraba	2
12946	estimulaba	2
12947	estimula	2
12948	estimo	2
12949	estimaba	2
12950	estilos	2
12951	estiércol	2
12952	estético	2
12953	estética	2
12954	estese	2
12955	estertor	2
12956	esterilidad	2
12957	estéril	2
12958	estarla	2
12959	estaríamos	2
12960	estampada	2
12961	estampa	2
12962	estallar	2
12963	estafa	2
12964	estacazo	2
12965	estaca	2
12966	estableció	2
12967	establecido	2
12968	establece	2
12969	espumarajos	2
12970	esponja	2
12971	espliego	2
12972	espléndidos	2
12973	espiritui	2
12974	espiritualmente	2
12975	espiral	2
12976	espinas	2
12977	espinal	2
12978	esperé	2
12979	esperarle	2
12980	esperaré	2
12981	esperándote	2
12982	espectros	2
12983	especias	2
12984	espasmódico	2
12985	espasmódica	2
12986	esparteros	2
12987	esparcir	2
12988	esparcimiento	2
12989	esparcieron	2
12990	esparciendo	2
12991	esparcido	2
12992	esparcía	2
12993	esparce	2
12994	espantajo	2
12995	espantables	2
12996	espantaba	2
12997	espanta	2
12998	esmerose	2
12999	eslabón	2
13000	esgrimía	2
13001	esforzaban	2
13002	esférica	2
13003	eses	2
13004	esencialmente	2
13005	escupo	2
13006	escupió	2
13007	escupía	2
13008	escueza	2
13009	escuece	2
13010	escritores	2
13011	escritor	2
13012	escribo	2
13013	escribirle	2
13014	escribirlas	2
13015	escribió	2
13016	escribieran	2
13017	escondió	2
13018	escondiendo	2
13019	escondidas	2
13020	escombros	2
13021	escolta	2
13022	escogió	2
13023	escogiese	2
13024	escocia	2
13025	esclavina	2
13026	escéptica	2
13027	escenario	2
13028	escaso	2
13029	escarnecerle	2
13030	escapas	2
13031	escapan	2
13032	escapaban	2
13033	escandaloso	2
13034	escandalizada	2
13035	escandalera	2
13036	escanciar	2
13037	escalonados	2
13038	escabulló	2
13039	erizo	2
13040	erizadas	2
13041	ergotina	2
13042	éramos	2
13043	er	2
13044	equivocadamente	2
13045	equivocaciones	2
13046	equívoca	2
13047	equilibrado	2
13048	equidad	2
13049	epístola	2
13050	episodio	2
13051	episcopal	2
13052	epiléptico	2
13053	epidermis	2
13054	enzarzando	2
13055	envolvió	2
13056	envolviéndose	2
13057	envolviendo	2
13058	envolver	2
13059	enviudar	2
13060	envidiosona	2
13061	enviaba	2
13062	envejecido	2
13063	envalentonándose	2
13064	entusiasta	2
13065	entusiasmada	2
13066	entristeció	2
13067	entrevió	2
13068	entreveía	2
13069	entretienes	2
13070	entreteniéndose	2
13071	entretenidas	2
13072	entretenían	2
13073	entremos	2
13074	entremezclaban	2
13075	entremedio	2
13076	entregarse	2
13077	entregarás	2
13078	entregaran	2
13079	entregándole	2
13080	entregan	2
13081	entraste	2
13082	entraran	2
13083	entrará	2
13084	entrañaban	2
13085	entrábamos	2
13086	entonado	2
13087	entonación	2
13088	entona	2
13089	entierros	2
13090	entiéndete	2
13091	entiéndelo	2
13092	enteros	2
13093	enternecían	2
13094	enteras	2
13095	enterara	2
13096	entendió	2
13097	entendimientos	2
13098	entendiese	2
13099	entendieron	2
13100	entendiera	2
13101	entendernos	2
13102	entenderemos	2
13103	entendemos	2
13104	ensueños	2
13105	ensimismado	2
13106	enséñemela	2
13107	enseñarla	2
13108	enseñaría	2
13109	enseñan	2
13110	ensayándose	2
13111	ensalmo	2
13112	ensaladera	2
13113	enroscadas	2
13114	enredando	2
13115	enredan	2
13116	enorgullecía	2
13117	enojoso	2
13118	enojarse	2
13119	enmendó	2
13120	enmendado	2
13121	enmedio	2
13122	enlaces	2
13123	enlace	2
13124	enjuta	2
13125	enjambre	2
13126	enhoramala	2
13127	enhebrada	2
13128	engrudo	2
13129	engranados	2
13130	engrana	2
13131	engordado	2
13132	engolosinar	2
13133	engatusarás	2
13134	engañes	2
13135	engañarte	2
13136	engañados	2
13137	engañaban	2
13138	enfurruñaba	2
13139	enfriado	2
13140	enfrenar	2
13141	enfermiza	2
13142	enfático	2
13143	enfática	2
13144	enfadas	2
13145	enfadado	2
13146	enfadaba	2
13147	enérgicos	2
13148	endilgó	2
13149	endiablada	2
13150	enderezando	2
13151	endemoniada	2
13152	encuentres	2
13153	encorvado	2
13154	encontrose	2
13155	encontronazo	2
13156	encontreme	2
13157	encontrarle	2
13158	encontrará	2
13159	encontradizo	2
13160	encontrábamos	2
13161	encogidos	2
13162	encienden	2
13163	encerrose	2
13164	encerrar	2
13165	encerrados	2
13166	encerradita	2
13167	encerradas	2
13168	encendían	2
13169	encefalitis	2
13170	encargándole	2
13171	encargando	2
13172	encargaba	2
13173	encarar	2
13174	encarándose	2
13175	encaramándose	2
13176	encantos	2
13177	encantado	2
13178	encantada	2
13179	encantaban	2
13180	encantaba	2
13181	encaminado	2
13182	encalabrinado	2
13183	encaje	2
13184	encajado	2
13185	encadenamiento	2
13186	enamorar	2
13187	enamorados	2
13188	enamorada	2
13189	empuñó	2
13190	empuñando	2
13191	empujón	2
13192	empujaron	2
13193	empujar	2
13194	empujándola	2
13195	empujan	2
13196	empréstito	2
13197	emprendieron	2
13198	emprendedor	2
13199	empolvado	2
13200	empleomanía	2
13201	empleó	2
13202	emplee	2
13203	emplearon	2
13204	emplean	2
13205	empleada	2
13206	empinada	2
13207	empiezas	2
13208	empiece	2
13209	empezamos	2
13210	empeñe	2
13211	empeñar	2
13212	empeñada	2
13213	empecé	2
13214	empaquetado	2
13215	empapado	2
13216	empañados	2
13217	eminencia	2
13218	embustes	2
13219	embustera	2
13220	embrutecimiento	2
13221	embrujado	2
13222	embozó	2
13223	embozado	2
13224	emborrachaba	2
13225	embocó	2
13226	embistió	2
13227	embeleso	2
13228	embebecido	2
13229	embebecía	2
13230	embarazada	2
13231	embajada	2
13232	emanación	2
13233	emanaba	2
13234	emana	2
13235	elogio	2
13236	elogiaba	2
13237	elocuente	2
13238	elevarse	2
13239	elevar	2
13240	elevadas	2
13241	elementos	2
13242	elegantísima	2
13243	electricidad	2
13244	electoral	2
13245	ejes	2
13246	ejercitar	2
13247	ejercen	2
13248	ejemplaridad	2
13249	ejecutivo	2
13250	egoistón	2
13251	egoístas	2
13252	egipto	2
13253	egipcia	2
13254	efigie	2
13255	eficacísimo	2
13256	eficacia	2
13257	educatriz	2
13258	educativas	2
13259	educarla	2
13260	educar	2
13261	edredón	2
13262	editores	2
13263	ecos	2
13264	económicos	2
13265	eclipsaba	2
13266	eclesiásticas	2
13267	échate	2
13268	echaremos	2
13269	echándosela	2
13270	echados	2
13271	echábaselas	2
13272	durmientes	2
13273	durmiente	2
13274	durito	2
13275	dure	2
13276	duraron	2
13277	durar	2
13278	duramente	2
13279	duquesas	2
13280	dulzona	2
13281	duermen	2
13282	dueñas	2
13283	duelen	2
13284	dudó	2
13285	dudes	2
13286	dudarse	2
13287	dudarlo	2
13288	dudando	2
13289	droga	2
13290	dramáticos	2
13291	drama	2
13292	doscientas	2
13293	dorregaray	2
13294	dormirme	2
13295	dormidito	2
13296	dormían	2
13297	dormí	2
13298	dorada	2
13299	doncellas	2
13300	donaires	2
13301	domingueras	2
13302	dominaron	2
13303	dominarle	2
13304	dominando	2
13305	domésticas	2
13306	domada	2
13307	doler	2
13308	docto	2
13309	docilidad	2
13310	dócil	2
13311	dobleces	2
13312	doblaron	2
13313	doblándose	2
13314	doblaba	2
13315	divirtiéndote	2
13316	divierten	2
13317	divierte	2
13318	divierta	2
13319	dividieron	2
13320	divide	2
13321	divertidas	2
13322	divertida	2
13323	divertían	2
13324	distrito	2
13325	distribuir	2
13326	distraerme	2
13327	distintivo	2
13328	distinguiendo	2
13329	distinguidos	2
13330	distinguido	2
13331	distinguidas	2
13332	distinguida	2
13333	distinguen	2
13334	distancias	2
13335	disputas	2
13336	disputar	2
13337	disputaba	2
13338	dispuestos	2
13339	disponiendo	2
13340	disponga	2
13341	dispensar	2
13342	disparidad	2
13343	disparatado	2
13344	disparatadas	2
13345	disparadero	2
13346	disolviendo	2
13347	disipado	2
13348	disimularla	2
13349	disgustado	2
13350	disfrutan	2
13351	disfavor	2
13352	discutiendo	2
13353	discusiones	2
13354	discursos	2
13355	disculpando	2
13356	discípulos	2
13357	disciplinas	2
13358	dirigirlo	2
13359	dirigido	2
13360	dirigida	2
13361	dirigía	2
13362	dirigen	2
13363	dirige	2
13364	diríale	2
13365	diretes	2
13366	directo	2
13367	directa	2
13368	diputado	2
13369	diócesis	2
13370	dinerales	2
13371	dimisión	2
13372	diminutivo	2
13373	dimes	2
13374	diluvio	2
13375	dilatado	2
13376	dijimos	2
13377	dignas	2
13378	digámoslo	2
13379	difusa	2
13380	diéronle	2
13381	diego	2
13382	dieciséis	2
13383	dictadas	2
13384	dicta	2
13385	diciéndoles	2
13386	dibujo	2
13387	diapasón	2
13388	diabólico	2
13389	devoró	2
13390	devolvió	2
13391	devolvía	2
13392	devolución	2
13393	devaneo	2
13394	devane	2
13395	devanaba	2
13396	deudos	2
13397	deudores	2
13398	detuviéronse	2
13399	detuvieron	2
13400	detuvieran	2
13401	detiene	2
13402	determinose	2
13403	detenerme	2
13404	desvergüenza	2
13405	desventurada	2
13406	desvelos	2
13407	desvarío	2
13408	desvanecida	2
13409	destruyendo	2
13410	destruyen	2
13411	destruir	2
13412	destrozados	2
13413	destreza	2
13414	destinos	2
13415	destinillo	2
13416	destinados	2
13417	destinado	2
13418	destinadas	2
13419	destinada	2
13420	desterrar	2
13421	desterrado	2
13422	desprende	2
13423	despreciarle	2
13424	despreciable	2
13425	despreciaba	2
13426	déspota	2
13427	desposada	2
13428	desplomó	2
13429	desplomarse	2
13430	despintadas	2
13431	despidiéronse	2
13432	despide	2
13433	despertara	2
13434	despertando	2
13435	desperdicios	2
13436	despejo	2
13437	despejar	2
13438	despeinada	2
13439	despego	2
13440	despega	2
13441	despedirme	2
13442	despedirla	2
13443	despavorida	2
13444	despachaderas	2
13445	despabiló	2
13446	despabilo	2
13447	despabilarse	2
13448	despabilándose	2
13449	despabilada	2
13450	desolación	2
13451	desnudaba	2
13452	desmentirse	2
13453	desmentiría	2
13454	desmentir	2
13455	desmentía	2
13456	desmedrado	2
13457	desmayo	2
13458	desmayar	2
13459	desmaya	2
13460	desmañado	2
13461	desmandarse	2
13462	deslomo	2
13463	deslizaba	2
13464	desleían	2
13465	desilusionó	2
13466	desiguales	2
13467	desigualdad	2
13468	desierta	2
13469	deshonroso	2
13470	deshonre	2
13471	deshonor	2
13472	deshilachados	2
13473	deshilachado	2
13474	deshago	2
13475	deshacerse	2
13476	desgarrada	2
13477	desgarraba	2
13478	desgarbado	2
13479	desgana	2
13480	desgajaba	2
13481	desgaire	2
13482	desflorando	2
13483	desfilando	2
13484	desfilaban	2
13485	desfavorable	2
13486	desenvueltas	2
13487	desempeñara	2
13488	desembuchaba	2
13489	desembozándose	2
13490	desechos	2
13491	deseas	2
13492	deseaban	2
13493	desdigo	2
13494	desdenes	2
13495	descuidado	2
13496	descubro	2
13497	descubriese	2
13498	descubriéndose	2
13499	descubriendo	2
13500	descubra	2
13501	descubiertas	2
13502	descrédito	2
13503	descosido	2
13504	descortés	2
13505	desconsoladas	2
13506	desconocía	2
13507	desconfiaba	2
13508	desconcertada	2
13509	descomunal	2
13510	descompuso	2
13511	descomponía	2
13512	descompone	2
13513	descolgar	2
13514	descifrar	2
13515	descendió	2
13516	descendientes	2
13517	descender	2
13518	descendencia	2
13519	descendemos	2
13520	descarriada	2
13521	descargado	2
13522	descaradamente	2
13523	descansos	2
13524	descalzos	2
13525	descabezar	2
13526	desazones	2
13527	desavenencias	2
13528	desató	2
13529	desatinar	2
13530	desatinado	2
13531	desatinada	2
13532	desastroso	2
13533	desarrollar	2
13534	desarrollando	2
13535	desarmada	2
13536	desaparición	2
13537	desapacible	2
13538	desanimaba	2
13539	desalquilado	2
13540	desalentada	2
13541	desalado	2
13542	desahogar	2
13543	desaguisado	2
13544	desagradables	2
13545	desacato	2
13546	derrumbaba	2
13547	derrota	2
13548	derribo	2
13549	derribados	2
13550	derredor	2
13551	derivan	2
13552	derechito	2
13553	depresiones	2
13554	depreciación	2
13555	depravación	2
13556	depósitos	2
13557	depositaría	2
13558	deplorando	2
13559	denuncias	2
13560	dengoso	2
13561	demuestra	2
13562	demostración	2
13563	demostraba	2
13564	demos	2
13565	demonches	2
13566	democrático	2
13567	demagogia	2
13568	delirando	2
13569	deliraba	2
13570	delineantes	2
13571	delicadísimo	2
13572	delicadezas	2
13573	delgada	2
13574	deleites	2
13575	dele	2
13576	dejosas	2
13577	dejos	2
13578	dejarlas	2
13579	dejará	2
13580	dejándote	2
13581	dejándoles	2
13582	dejamos	2
13583	déjale	2
13584	dejábase	2
13585	degradación	2
13586	deforme	2
13587	definitivamente	2
13588	definir	2
13589	definición	2
13590	defendió	2
13591	defendido	2
13592	defendían	2
13593	defenderme	2
13594	defenderé	2
13595	dedito	2
13596	dedicarme	2
13597	decorosa	2
13598	declarado	2
13599	decírsela	2
13600	decidirá	2
13601	decidía	2
13602	dechado	2
13603	decálogo	2
13604	decaimiento	2
13605	decadencia	2
13606	debida	2
13607	debías	2
13608	debíamos	2
13609	deambulación	2
13610	databa	2
13611	darnos	2
13612	darla	2
13613	dardo	2
13614	daña	2
13615	dándoles	2
13616	dándolas	2
13617	dámele	2
13618	dais	2
13619	dádivas	2
13620	dábase	2
13621	cutis	2
13622	curtis	2
13623	curiosa	2
13624	curial	2
13625	cure	2
13626	curaría	2
13627	curan	2
13628	curada	2
13629	cúpula	2
13630	cundía	2
13631	cúmulo	2
13632	cumplo	2
13633	cumplió	2
13634	cumpliendo	2
13635	cumplida	2
13636	cultura	2
13637	cultivado	2
13638	cultivada	2
13639	cuidó	2
13640	cuidaban	2
13641	cuervos	2
13642	cuerdos	2
13643	cuentecita	2
13644	cuellos	2
13645	cucurucho	2
13646	cuchillos	2
13647	cucharadas	2
13648	cubrirla	2
13649	cubrir	2
13650	cubrió	2
13651	cubo	2
13652	cubiertas	2
13653	cúbico	2
13654	cubas	2
13655	cuartillo	2
13656	cuarterón	2
13657	cuarentena	2
13658	cualsiquiera	2
13659	cuajarones	2
13660	cuadrote	2
13661	cuadritos	2
13662	cuadrito	2
13663	cuadrilátero	2
13664	cuadernillos	2
13665	cruzaron	2
13666	cruzan	2
13667	cruzaba	2
13668	crujir	2
13669	crucero	2
13670	cromo	2
13671	críticos	2
13672	críticas	2
13673	cristina	2
13674	cristianas	2
13675	crió	2
13676	criaturita	2
13677	crías	2
13678	criarle	2
13679	criamos	2
13680	criadita	2
13681	cretona	2
13682	creída	2
13683	creíase	2
13684	creerle	2
13685	creencias	2
13686	creemos	2
13687	créemelo	2
13688	creciente	2
13689	creciendo	2
13690	crean	2
13691	créamelo	2
13692	creados	2
13693	creador	2
13694	crasa	2
13695	cotorrearon	2
13696	cotarro	2
13697	costurera	2
13698	costeó	2
13699	cositas	2
13700	cosita	2
13701	cosecha	2
13702	cose	2
13703	corva	2
13704	coruñas	2
13705	cortesías	2
13706	corté	2
13707	cortarse	2
13708	cortaron	2
13709	cortarle	2
13710	cortaran	2
13711	cortándole	2
13712	cortando	2
13713	cortados	2
13714	cortadillo	2
13715	cortaban	2
13716	corruptor	2
13717	corrupción	2
13718	corrompida	2
13719	corroborando	2
13720	corrigió	2
13721	corriese	2
13722	corresponder	2
13723	corren	2
13724	corregir	2
13725	corregida	2
13726	correctamente	2
13727	correccional	2
13728	corporación	2
13729	corpacho	2
13730	cornezuelo	2
13731	cornetas	2
13732	corizas	2
13733	coriza	2
13734	córdoba	2
13735	cordial	2
13736	cordera	2
13737	cordel	2
13738	corcho	2
13739	corbatas	2
13740	corazonadas	2
13741	corales	2
13742	copita	2
13743	copioso	2
13744	copiaba	2
13745	cónyuges	2
13746	conyugales	2
13747	conyugal	2
13748	convulsiones	2
13749	convirtiose	2
13750	convidaron	2
13751	convidar	2
13752	convidando	2
13753	convidado	2
13754	convicciones	2
13755	convertirla	2
13756	convertimos	2
13757	convertida	2
13758	conveniencia	2
13759	conveníale	2
13760	convengo	2
13761	convenció	2
13762	convenciera	2
13763	convenciendo	2
13764	convencerse	2
13765	convencerle	2
13766	convencerla	2
13767	convence	2
13768	convaleciente	2
13769	convalecencia	2
13770	contusiones	2
13771	contusión	2
13772	contundentes	2
13773	contundente	2
13774	controversia	2
13775	contrición	2
13776	contribuir	2
13777	contrato	2
13778	contratiempos	2
13779	contrata	2
13780	contrastes	2
13781	contrasentido	2
13782	contrariarle	2
13783	contrariaba	2
13784	contradecir	2
13785	contradecían	2
13786	contole	2
13787	continuas	2
13788	contiene	2
13789	contienda	2
13790	contestole	2
13791	contesté	2
13792	conteste	2
13793	contestaron	2
13794	contestara	2
13795	contestando	2
13796	contestado	2
13797	contestaciones	2
13798	contentas	2
13799	contentarse	2
13800	contenerle	2
13801	contenerla	2
13802	contemplativa	2
13803	contemplado	2
13804	contaron	2
13805	contarlas	2
13806	contagio	2
13807	contador	2
13808	contada	2
13809	contabilidad	2
13810	consumos	2
13811	consumo	2
13812	consumir	2
13813	consume	2
13814	consumar	2
13815	consumada	2
13816	consultara	2
13817	consultaba	2
13818	consuelan	2
13819	construida	2
13820	constituyéndose	2
13821	constituía	2
13822	constipar	2
13823	consternado	2
13824	constar	2
13825	constantes	2
13826	conspiración	2
13827	consortes	2
13828	consoló	2
13829	consolara	2
13830	consolando	2
13831	consoladora	2
13832	consolábase	2
13833	consintió	2
13834	consintiera	2
13835	consienta	2
13836	consideró	2
13837	considero	2
13838	considere	2
13839	considerándose	2
13840	considerándole	2
13841	consideran	2
13842	considerable	2
13843	considera	2
13844	conservatorio	2
13845	conservado	2
13846	consagró	2
13847	consagrados	2
13848	consagrada	2
13849	consagración	2
13850	consagraba	2
13851	conquistas	2
13852	conozcan	2
13853	conocieran	2
13854	conocerse	2
13855	conmoción	2
13856	conmiseración	2
13857	conllevar	2
13858	confuso	2
13859	confusiones	2
13860	confundidas	2
13861	confundían	2
13862	confundía	2
13863	confió	2
13864	confines	2
13865	configuración	2
13866	confidente	2
13867	confiar	2
13868	confianzudo	2
13869	confianzuda	2
13870	confiado	2
13871	confesarme	2
13872	confesado	2
13873	confesaba	2
13874	confecciones	2
13875	conejos	2
13876	conejo	2
13877	conducir	2
13878	condescendencia	2
13879	condensaba	2
13880	condenes	2
13881	condena	2
13882	concurría	2
13883	concubinato	2
13884	concreto	2
13885	concluyen	2
13886	concluía	2
13887	conciliadora	2
13888	conciliador	2
13889	conciliación	2
13890	concha	2
13891	concertando	2
13892	concertada	2
13893	conceptuaba	2
13894	concedido	2
13895	concavidad	2
13896	comunicarse	2
13897	comunicaron	2
13898	comunicando	2
13899	comunicaban	2
13900	comulgan	2
13901	compungida	2
13902	compuesto	2
13903	comprometía	2
13904	comprometer	2
13905	comprometas	2
13906	compres	2
13907	comprendida	2
13908	compradora	2
13909	compradas	2
13910	compota	2
13911	composturas	2
13912	componendas	2
13913	compone	2
13914	complicidad	2
13915	complicada	2
13916	complicación	2
13917	completaba	2
13918	complaciente	2
13919	complacencia	2
13920	compensaba	2
13921	comparó	2
13922	comparo	2
13923	compararme	2
13924	compañías	2
13925	compadezco	2
13926	compadecía	2
13927	compadecer	2
13928	compadece	2
13929	comisiones	2
13930	comiera	2
13931	comienzos	2
13932	cometiera	2
13933	cometían	2
13934	cometer	2
13935	comerías	2
13936	comedero	2
13937	combinando	2
13938	combatirle	2
13939	combatientes	2
13940	columnas	2
13941	colorista	2
13942	colonias	2
13943	colocó	2
13944	colocase	2
13945	colocaron	2
13946	colocara	2
13947	colocados	2
13948	colocadas	2
13949	colgándose	2
13950	colgada	2
13951	colgaba	2
13952	coleto	2
13953	colérica	2
13954	colegas	2
13955	colección	2
13956	coincidir	2
13957	cogiéndose	2
13958	coges	2
13959	cogerlos	2
13960	cogen	2
13961	codearse	2
13962	cocinilla	2
13963	cocinerita	2
13964	cocinas	2
13965	cociendo	2
13966	cocía	2
13967	cochina	2
13968	cobro	2
13969	cobrando	2
13970	club	2
13971	clorótica	2
13972	clorhidrato	2
13973	clínicas	2
13974	cleriguito	2
13975	claveteado	2
13976	clavelero	2
13977	clavadas	2
13978	claustral	2
13979	clarita	2
13980	clarear	2
13981	claraboyas	2
13982	claque	2
13983	ciudades	2
13984	citunas	2
13985	citado	2
13986	citaba	2
13987	cisterna	2
13988	cisco	2
13989	cirio	2
13990	circular	2
13991	cintas	2
13992	cinismo	2
13993	cimientos	2
13994	cierran	2
13995	ciencias	2
13996	ciegamente	2
13997	chusma	2
13998	chusco	2
13999	chuscadas	2
14000	churumbé	2
14001	chumbos	2
14002	chulas	2
14003	chufas	2
14004	chuchería	2
14005	chubasco	2
14006	chubasca	2
14007	choza	2
14008	chorro	2
14009	chorreaban	2
14010	chocolatito	2
14011	chocolates	2
14012	chocolatera	2
14013	chocheces	2
14014	chocando	2
14015	chitito	2
14016	chistó	2
14017	chisté	2
14018	chistaba	2
14019	chispita	2
14020	chispeantes	2
14021	chismes	2
14022	chirris	2
14023	chiquititas	2
14024	chiquilladas	2
14025	chiquillada	2
14026	chínchirri	2
14027	chinche	2
14028	chillería	2
14029	chifle	2
14030	chiflarse	2
14031	chifladura	2
14032	chiflados	2
14033	chifla	2
14034	chicuela	2
14035	chic	2
14036	chi	2
14037	cheong	2
14038	chavales	2
14039	chavala	2
14040	chata	2
14041	chascos	2
14042	charol	2
14043	charlatánicas	2
14044	charlaban	2
14045	charlaba	2
14046	charca	2
14047	chaquetas	2
14048	chaqueta	2
14049	chaqué	2
14050	chanchullos	2
14051	chamusquina	2
14052	chambras	2
14053	chales	2
14054	chalana	2
14055	chafalditas	2
14056	chafado	2
14057	chafada	2
14058	cháchara	2
14059	cevil	2
14060	ceuta	2
14061	cesantía	2
14062	cesantes	2
14063	cesaban	2
14064	cervantes	2
14065	certidumbre	2
14066	certeza	2
14067	cerrojos	2
14068	cerrase	2
14069	cerradura	2
14070	cerradas	2
14071	cerraban	2
14072	cerdos	2
14073	cerciorose	2
14074	ceñudo	2
14075	ceñidos	2
14076	centrales	2
14077	centigramo	2
14078	centeno	2
14079	cencerrada	2
14080	cenando	2
14081	celestina	2
14082	celeste	2
14083	celebró	2
14084	celador	2
14085	cejijunta	2
14086	cegó	2
14087	cedo	2
14088	cedió	2
14089	ceca	2
14090	cebollino	2
14091	cazar	2
14092	cazando	2
14093	cayese	2
14094	caviloso	2
14095	cavilaba	2
14096	cavernas	2
14097	caverna	2
14098	cavador	2
14099	cautivar	2
14100	cautivaban	2
14101	cautelosa	2
14102	causó	2
14103	causar	2
14104	causante	2
14105	causado	2
14106	caudillo	2
14107	caudaloso	2
14108	cato	2
14109	caten	2
14110	categóricas	2
14111	categóricamente	2
14112	catedrático	2
14113	catedrales	2
14114	catarroso	2
14115	catarlo	2
14116	catar	2
14117	catálogos	2
14118	catalán	2
14119	cataclismo	2
14120	castos	2
14121	castidad	2
14122	castellano	2
14123	castaño	2
14124	castañetazos	2
14125	castaña	2
14126	casillero	2
14127	cásese	2
14128	cases	2
14129	caserón	2
14130	caseríos	2
14131	cáscaras	2
14132	cascabel	2
14133	cásate	2
14134	casaría	2
14135	casaban	2
14136	casaba	2
14137	carunculosa	2
14138	cartones	2
14139	cartón	2
14140	cartitas	2
14141	carteles	2
14142	cartea	2
14143	carruaje	2
14144	carromato	2
14145	carromatero	2
14146	carreteros	2
14147	carretas	2
14148	carpanta	2
14149	carlismo	2
14150	cariz	2
14151	caritativo	2
14152	caritativas	2
14153	caritativa	2
14154	cariñosos	2
14155	caridades	2
14156	caricaturas	2
14157	cargó	2
14158	cargante	2
14159	cargamento	2
14160	cargaban	2
14161	carece	2
14162	cardenales	2
14163	carbonera	2
14164	carátula	2
14165	carantoñas	2
14166	caracol	2
14167	capotes	2
14168	capones	2
14169	capítulo	2
14170	capitana	2
14171	capitalito	2
14172	capitalista	2
14173	capirote	2
14174	capellanes	2
14175	capciosas	2
14176	capacidad	2
14177	capaces	2
14178	caoba	2
14179	cañamón	2
14180	cantos	2
14181	cantonales	2
14182	canteros	2
14183	cántaro	2
14184	cantaría	2
14185	cantan	2
14186	cansadas	2
14187	candorosamente	2
14188	candelabros	2
14189	canciller	2
14190	canaleja	2
14191	canal	2
14192	campechana	2
14193	campar	2
14194	campante	2
14195	campanillazo	2
14196	campanario	2
14197	campanada	2
14198	camisería	2
14199	camello	2
14200	cambrí	2
14201	cambiazos	2
14202	cambiaron	2
14203	cambiara	2
14204	cambiante	2
14205	cambiando	2
14206	camas	2
14207	camarada	2
14208	calzonazos	2
14209	calzados	2
14210	calzada	2
14211	calza	2
14212	calvas	2
14213	calvario	2
14214	calurosos	2
14215	calumnió	2
14216	calores	2
14217	cálmese	2
14218	calmarse	2
14219	calmaba	2
14220	callosa	2
14221	callejera	2
14222	calladas	2
14223	callaban	2
14224	calidad	2
14225	calibre	2
14226	caldo	2
14227	caldeado	2
14228	caldeada	2
14229	calcule	2
14230	calculan	2
14231	calaveradas	2
14232	calambres	2
14233	calados	2
14234	calabozo	2
14235	calabaza	2
14236	cajitas	2
14237	caín	2
14238	caigo	2
14239	cafetero	2
14240	caerle	2
14241	caerás	2
14242	caderas	2
14243	cachetes	2
14244	cachemira	2
14245	cabizbajo	2
14246	cabildo	2
14247	cabían	2
14248	cabezada	2
14249	cabellos	2
14250	cabecita	2
14251	caballete	2
14252	caballerosidad	2
14253	caballera	2
14254	cabal	2
14255	cab	2
14256	buscarlos	2
14257	buscaré	2
14258	buscara	2
14259	buscándole	2
14260	buscan	2
14261	burradas	2
14262	burocráticas	2
14263	burlaba	2
14264	burda	2
14265	bultos	2
14266	bujías	2
14267	buey	2
14268	buenavista	2
14269	buche	2
14270	búcaros	2
14271	brutalidades	2
14272	brutales	2
14273	brujería	2
14274	brotar	2
14275	bromear	2
14276	brochar	2
14277	brochado	2
14278	brocal	2
14279	brindose	2
14280	brindó	2
14281	brindis	2
14282	brinco	2
14283	brillo	2
14284	brillantes	2
14285	brígida	2
14286	bribonaza	2
14287	bribonas	2
14288	bribón	2
14289	brevemente	2
14290	breva	2
14291	bregó	2
14292	bregar	2
14293	bregando	2
14294	brecolera	2
14295	bravura	2
14296	bravos	2
14297	bozo	2
14298	botonaduras	2
14299	botitas	2
14300	boticas	2
14301	boteros	2
14302	botellita	2
14303	botellas	2
14304	botarate	2
14305	bostezar	2
14306	borroso	2
14307	borrego	2
14308	borrando	2
14309	borrachera	2
14310	borlas	2
14311	bordados	2
14312	bordado	2
14313	bordadas	2
14314	borceguíes	2
14315	boquete	2
14316	bonos	2
14317	bonitísimos	2
14318	bonitísimo	2
14319	bónibus	2
14320	bondades	2
14321	bombo	2
14322	bomberos	2
14323	bolsistas	2
14324	bojío	2
14325	bodegones	2
14326	bodas	2
14327	bocaza	2
14328	bocados	2
14329	bobito	2
14330	bóbilis	2
14331	bobas	2
14332	bobalicón	2
14333	blanquísimos	2
14334	blanduras	2
14335	blandos	2
14336	bistec	2
14337	biografía	2
14338	billar	2
14339	bierzo	2
14340	bienestar	2
14341	bienaventurados	2
14342	besuqueos	2
14343	besarme	2
14344	besándole	2
14345	besado	2
14346	berzas	2
14347	berrinche	2
14348	berreaba	2
14349	bernardino	2
14350	bermellón	2
14351	bermejos	2
14352	berlina	2
14353	benigno	2
14354	benéfico	2
14355	beneficio	2
14356	benéficas	2
14357	benditas	2
14358	bendiciones	2
14359	bendecirán	2
14360	bellísima	2
14361	bellezas	2
14362	bellas	2
14363	béjar	2
14364	beethoven	2
14365	bedmar	2
14366	bebo	2
14367	bebió	2
14368	beberemos	2
14369	bebe	2
14370	beatriz	2
14371	beatas	2
14372	bazares	2
14373	batistas	2
14374	batidor	2
14375	batería	2
14376	batallas	2
14377	basurero	2
14378	basto	2
14379	bastidor	2
14380	bastas	2
14381	bastara	2
14382	bastado	2
14383	bastábale	2
14384	barruntaba	2
14385	barrionuevo	2
14386	barrabás	2
14387	barra	2
14388	bárbaros	2
14389	barbarie	2
14390	bárbaras	2
14391	baratas	2
14392	barajar	2
14393	bando	2
14394	bandido	2
14395	banderillas	2
14396	banderas	2
14397	baldosín	2
14398	baldosa	2
14399	balbuciente	2
14400	balanza	2
14401	balances	2
14402	bajen	2
14403	bajé	2
14404	baje	2
14405	bajas	2
14406	bajarlo	2
14407	bailad	2
14408	badulaques	2
14409	babilla	2
14410	babia	2
14411	baberos	2
14412	azuzaba	2
14413	azuleaba	2
14414	azucarillos	2
14415	azucarada	2
14416	azotes	2
14417	azoten	2
14418	azotaba	2
14419	azahares	2
14420	azahar	2
14421	ayudarás	2
14422	ayudante	2
14423	ayudadas	2
14424	ayudada	2
14425	ayudaban	2
14426	avivando	2
14427	avivaba	2
14428	avisos	2
14429	avise	2
14430	avisas	2
14431	avisaré	2
14432	avisadas	2
14433	avío	2
14434	avino	2
14435	ávida	2
14436	aviada	2
14437	averiguo	2
14438	averiguando	2
14439	avergonzada	2
14440	aventurera	2
14441	avanzara	2
14442	avanza	2
14443	auxilios	2
14444	autora	2
14445	auténtico	2
14446	ausentarse	2
14447	aumentaban	2
14448	aulas	2
14449	aujeritos	2
14450	augusto	2
14451	augusta	2
14452	atufado	2
14453	atufa	2
14454	atropina	2
14455	atrio	2
14456	atreviose	2
14457	atrevimientos	2
14458	atrevidas	2
14459	atrevíase	2
14460	atrevían	2
14461	atreveré	2
14462	atreva	2
14463	atravesada	2
14464	atrasada	2
14465	atraían	2
14466	atraer	2
14467	atracones	2
14468	atormentado	2
14469	atormentaban	2
14470	atormentaba	2
14471	atontadas	2
14472	atónito	2
14473	atiendo	2
14474	aterrador	2
14475	aterra	2
14476	atenuar	2
14477	atenuado	2
14478	atentado	2
14479	atengo	2
14480	atenciones	2
14481	atemperar	2
14482	ataúdes	2
14483	ataúd	2
14484	atarlas	2
14485	atareada	2
14486	atar	2
14487	atajarla	2
14488	atadero	2
14489	ataca	2
14490	ataba	2
14491	asusto	2
14492	asustan	2
14493	asustadísimo	2
14494	asturiana	2
14495	asquerosos	2
14496	asperezas	2
14497	aspectos	2
14498	aspas	2
14499	asomose	2
14500	asomé	2
14501	asombres	2
14502	asombrarse	2
14503	asombra	2
14504	asomarse	2
14505	asomar	2
14506	asomado	2
14507	asomada	2
14508	asociar	2
14509	asociaciones	2
14510	asociaba	2
14511	asiste	2
14512	asintió	2
14513	asiáticos	2
14514	asiático	2
14515	asesinos	2
14516	asesinarme	2
14517	asesinaban	2
14518	asentadores	2
14519	asegurártelo	2
14520	asegurarte	2
14521	asegurarse	2
14522	asegurarlo	2
14523	asegurándose	2
14524	asegurando	2
14525	aseguran	2
14526	asechanzas	2
14527	ascenso	2
14528	asaltado	2
14529	asaltaba	2
14530	artísticas	2
14531	artística	2
14532	arrulló	2
14533	arrullándole	2
14534	arrullaba	2
14535	arruinado	2
14536	arrugó	2
14537	arrugas	2
14538	arropó	2
14539	arrope	2
14540	arrojé	2
14541	arrojase	2
14542	arrojándose	2
14543	arrogantísima	2
14544	arrogantes	2
14545	arroba	2
14546	arrimados	2
14547	arrimaba	2
14548	arriendo	2
14549	arribita	2
14550	arrepintiéndose	2
14551	arrepiente	2
14552	arregló	2
14553	arreglarlo	2
14554	arreglara	2
14555	arreglador	2
14556	arreglado	2
14557	arregladito	2
14558	arreció	2
14559	arrebatos	2
14560	arrebato	2
14561	arrebatado	2
14562	arrastren	2
14563	arrancose	2
14564	arrancando	2
14565	arrancado	2
14566	arrancada	2
14567	arrabal	2
14568	arqueando	2
14569	arpegios	2
14570	aro	2
14571	armatoste	2
14572	armara	2
14573	armadura	2
14574	armados	2
14575	aristocrático	2
14576	aristocrática	2
14577	aristócrata	2
14578	argumentaba	2
14579	arganzuela	2
14580	ardores	2
14581	ardiendo	2
14582	ardían	2
14583	arder	2
14584	ardentísima	2
14585	arcón	2
14586	arcano	2
14587	arbustos	2
14588	ara	2
14589	aquiescencia	2
14590	aquélla	2
14591	apuras	2
14592	apurarse	2
14593	apuradas	2
14594	apuntaron	2
14595	apuntalada	2
14596	aproximaciones	2
14597	aproximación	2
14598	aprovechó	2
14599	aprovechaba	2
14600	apropiarse	2
14601	aprobaba	2
14602	apretándosela	2
14603	apretados	2
14604	aprensiones	2
14605	aprendió	2
14606	aprendas	2
14607	aprendamos	2
14608	apreciaciones	2
14609	apreciaban	2
14610	apoyarse	2
14611	apoyándose	2
14612	apóstrofes	2
14613	apostaba	2
14614	apodo	2
14615	apoderose	2
14616	aplicara	2
14617	aplicando	2
14618	aplicaba	2
14619	aplaudo	2
14620	aplacarle	2
14621	aplacarla	2
14622	aplacara	2
14623	apilados	2
14624	apestaba	2
14625	apesta	2
14626	apenada	2
14627	apegada	2
14628	apee	2
14629	apechugar	2
14630	apasionadas	2
14631	apartarse	2
14632	apartaron	2
14633	apartara	2
14634	apartados	2
14635	apartadas	2
14636	apartada	2
14637	apariciones	2
14638	aparentó	2
14639	aparecen	2
14640	aparadores	2
14641	apañaditas	2
14642	apagar	2
14643	apagado	2
14644	añejos	2
14645	añadía	2
14646	anzuelo	2
14647	anunciándole	2
14648	anuncia	2
14649	antojo	2
14650	antojaron	2
14651	antipatías	2
14652	anti	2
14653	antagonismo	2
14654	ansiosas	2
14655	ansiaba	2
14656	anonadada	2
14657	anonada	2
14658	anises	2
14659	animó	2
14660	animar	2
14661	animándose	2
14662	anhelantes	2
14663	angustioso	2
14664	angosto	2
14665	angelote	2
14666	angelón	2
14667	angélica	2
14668	aneurisma	2
14669	anémico	2
14670	andróminas	2
14671	andrea	2
14672	ándese	2
14673	ande	2
14674	andaría	2
14675	andante	2
14676	andanada	2
14677	andana	2
14678	andamos	2
14679	ancianos	2
14680	anchos	2
14681	ancho	2
14682	anatemas	2
14683	anatema	2
14684	anacoreta	2
14685	ampliación	2
14686	amoscándose	2
14687	amoratada	2
14688	amonestando	2
14689	amonestaciones	2
14690	amonestación	2
14691	amiguitos	2
14692	amiguitas	2
14693	amigote	2
14694	americanos	2
14695	américa	2
14696	ameno	2
14697	amenazas	2
14698	amenazando	2
14699	amenazado	2
14700	ambiciosa	2
14701	amasado	2
14702	amarra	2
14703	amarguras	2
14704	amargas	2
14705	amará	2
14706	amaneció	2
14707	amanece	2
14708	amancebamiento	2
14709	alzaban	2
14710	alza	2
14711	álvarez	2
14712	alumna	2
14713	alumbrada	2
14714	alumbraba	2
14715	alucinar	2
14716	altísimo	2
14717	alteró	2
14718	alternar	2
14719	altere	2
14720	altercados	2
14721	alterar	2
14722	alteraba	2
14723	altarito	2
14724	alquiló	2
14725	alquileres	2
14726	alpargatas	2
14727	almuerzos	2
14728	almorzando	2
14729	almendras	2
14730	almejas	2
14731	almacenistas	2
14732	allegados	2
14733	alimenta	2
14734	alimaña	2
14735	alias	2
14736	algos	2
14737	algas	2
14738	alfonsino	2
14739	alevoso	2
14740	aletargado	2
14741	aletargada	2
14742	aleros	2
14743	alejose	2
14744	alejaban	2
14745	alejaba	2
14746	alegrose	2
14747	alegró	2
14748	alegrará	2
14749	aldea	2
14750	alcoy	2
14751	alcázar	2
14752	alcanzan	2
14753	alcanzado	2
14754	álbumes	2
14755	albricias	2
14756	alborozo	2
14757	alborotó	2
14758	alborotase	2
14759	alborotaría	2
14760	alborotar	2
14761	alborota	2
14762	albo	2
14763	albergue	2
14764	albardero	2
14765	alarmó	2
14766	alarmantes	2
14767	alarmaba	2
14768	alargándole	2
14769	alardes	2
14770	alambres	2
14771	alabando	2
14772	ajuste	2
14773	ajumao	2
14774	ajajá	2
14775	ajadas	2
14776	aislamiento	2
14777	airosos	2
14778	airosas	2
14779	airados	2
14780	ahumadas	2
14781	ahorraba	2
14782	ahorita	2
14783	ahogue	2
14784	ahogo	2
14785	ahogas	2
14786	ahilada	2
14787	aguzando	2
14788	agüero	2
14789	aguda	2
14790	aguárdate	2
14791	aguardar	2
14792	aguardando	2
14793	aguántate	2
14794	agrícola	2
14795	agria	2
14796	agresora	2
14797	agresión	2
14798	agrado	2
14799	agradeceré	2
14800	agradecen	2
14801	agradábale	2
14802	agrada	2
14803	agotó	2
14804	agosto	2
14805	agonizante	2
14806	agitándose	2
14807	agitado	2
14808	agitaban	2
14809	agasajado	2
14810	agasajaditos	2
14811	agasajaba	2
14812	agarrarse	2
14813	agarrando	2
14814	agarraban	2
14815	afrontar	2
14816	afortunadamente	2
14817	aflojó	2
14818	afloja	2
14819	afloencias	2
14820	afligidas	2
14821	afligía	2
14822	afirmo	2
14823	afirmativas	2
14824	afirmación	2
14825	afirmaba	2
14826	afinidad	2
14827	afinar	2
14828	afilado	2
14829	aficionados	2
14830	aficionada	2
14831	afeitarse	2
14832	afeitado	2
14833	afeitaba	2
14834	afectan	2
14835	afectación	2
14836	afeaba	2
14837	afanes	2
14838	afables	2
14839	advertía	2
14840	advertencias	2
14841	adulterio	2
14842	adulterado	2
14843	adúltera	2
14844	adulación	2
14845	adquiridas	2
14846	adquiría	2
14847	adormeció	2
14848	adorar	2
14849	adora	2
14850	adoptivo	2
14851	admitirla	2
14852	admitir	2
14853	admitía	2
14854	admite	2
14855	admiró	2
14856	admiro	2
14857	admirarla	2
14858	admirar	2
14859	admirada	2
14860	administraron	2
14861	administradora	2
14862	adivinó	2
14863	adivinación	2
14864	adelantos	2
14865	adelantó	2
14866	adelantaba	2
14867	adelanta	2
14868	adecuado	2
14869	adecuada	2
14870	acusador	2
14871	acusado	2
14872	acumular	2
14873	acuéstese	2
14874	acuestas	2
14875	acuerde	2
14876	acudido	2
14877	acude	2
14878	acuarelas	2
14879	actores	2
14880	actor	2
14881	actividades	2
14882	acreditado	2
14883	acostumbran	2
14884	acostase	2
14885	acostarte	2
14886	acostáronse	2
14887	acostados	2
14888	acostaba	2
14889	acosado	2
14890	acorralada	2
14891	acordeón	2
14892	acordarte	2
14893	acordaron	2
14894	acordando	2
14895	acoquinar	2
14896	aconsejarle	2
14897	acongojadísima	2
14898	acompañó	2
14899	acompaño	2
14900	acompañase	2
14901	acompañaría	2
14902	acompañados	2
14903	acompañaban	2
14904	acomode	2
14905	acometió	2
14906	acometiese	2
14907	acometiendo	2
14908	acólito	2
14909	acogoto	2
14910	acobardó	2
14911	aclarar	2
14912	aclaraban	2
14913	acierto	2
14914	acíbar	2
14915	acertado	2
14916	acercaban	2
14917	aceptarlo	2
14918	aceptaría	2
14919	aceptada	2
14920	aceptable	2
14921	acentuó	2
14922	aceitosas	2
14923	accidental	2
14924	accesos	2
14925	accedió	2
14926	acariciando	2
14927	acaricia	2
14928	acallarle	2
14929	academia	2
14930	acabes	2
14931	acabé	2
14932	acabamiento	2
14933	abyección	2
14934	abusos	2
14935	aburrirás	2
14936	aburre	2
14937	abundamiento	2
14938	abultado	2
14939	abultaba	2
14940	absurdas	2
14941	absorto	2
14942	absorta	2
14943	absorbiendo	2
14944	absolutas	2
14945	abrumada	2
14946	abrirse	2
14947	abrígate	2
14948	abrigadito	2
14949	abrieron	2
14950	abres	2
14951	abrazaron	2
14952	abrazarle	2
14953	abrazarla	2
14954	abrazar	2
14955	aborreciendo	2
14956	aborrecerte	2
14957	aborrecerla	2
14958	aborreceré	2
14959	abordó	2
14960	abollada	2
14961	aboliciones	2
14962	abogados	2
14963	abismos	2
14964	abatir	2
14965	abatieron	2
14966	abandone	2
14967	abandonarla	2
14968	abandonando	2
14969	abandona	2
14970	abalanzó	2
14971	zurriago	1
14972	zurcidor	1
14973	zurcido	1
14974	zumo	1
14975	zumbón	1
14976	zumban	1
14977	zozobras	1
14978	zote	1
14979	zoquetes	1
14980	zoquete	1
14981	zopencos	1
14982	zarzal	1
14983	zarandearse	1
14984	zarandean	1
14985	zarandajas	1
14986	zaragüelles	1
14987	zapatito	1
14988	zapatetas	1
14989	zapateros	1
14990	zapateado	1
14991	zapatas	1
14992	zánganos	1
14993	zancadilla	1
14994	zanahorias	1
14995	zampo	1
14996	zampado	1
14997	zampa	1
14998	zamoranos	1
14999	zambullida	1
15000	zambombazos	1
15001	zamarras	1
15002	zaleas	1
15003	zalea	1
15004	zalamera	1
15005	zahúrdas	1
15006	zahorí	1
15007	zagalote	1
15008	zagalón	1
15009	zafiote	1
15010	zafias	1
15011	zafia	1
15012	zafarme	1
15013	zacarías	1
15014	yesos	1
15015	yeserías	1
15016	yerra	1
15017	yernos	1
15018	yermo	1
15019	yéndome	1
15020	yacía	1
15021	yacen	1
15022	xv	1
15023	xix	1
15024	xiv	1
15025	xiii	1
15026	werther	1
15027	wellington	1
15028	wamba	1
15029	walses	1
15030	vulgarote	1
15031	vulgarísimo	1
15032	vuestros	1
15033	vuelvan	1
15034	vueltecita	1
15035	vuelos	1
15036	vuelco	1
15037	vuelan	1
15038	vuela	1
15039	vuecencia	1
15040	vu	1
15041	votó	1
15042	votantes	1
15043	votando	1
15044	votaba	1
15045	vómito	1
15046	vomitivos	1
15047	volviole	1
15048	volvime	1
15049	volviesen	1
15050	volviéronle	1
15051	volviéndolos	1
15052	volviéndoles	1
15053	volvíase	1
15054	volvíale	1
15055	volverte	1
15056	volverle	1
15057	volvámonos	1
15058	voluntariosa	1
15059	voluntarios	1
15060	voluntaria	1
15061	voluminoso	1
15062	voluminosa	1
15063	voluble	1
15064	volteo	1
15065	volteando	1
15066	volé	1
15067	volcó	1
15068	volcara	1
15069	volcar	1
15070	volcado	1
15071	volatines	1
15072	volátil	1
15073	volandas	1
15074	voladora	1
15075	volado	1
15076	volaba	1
15077	vocerío	1
15078	vocecilla	1
15079	vocear	1
15080	vocales	1
15081	vocabulario	1
15082	vivito	1
15083	vivísimas	1
15084	vivís	1
15085	vivirías	1
15086	vivirían	1
15087	viviría	1
15088	vivieron	1
15089	vivieras	1
15090	vivieran	1
15091	vivíamos	1
15092	vivaracho	1
15093	vivaaa	1
15094	viudos	1
15095	vitrina	1
15096	vitalicio	1
15097	visual	1
15098	vistosos	1
15099	vistos	1
15100	vistiose	1
15101	vistillas	1
15102	vistiese	1
15103	vistiéndolo	1
15104	vistiéndola	1
15105	vistes	1
15106	visten	1
15107	víspera	1
15108	viso	1
15109	vislumbran	1
15110	vislumbraba	1
15111	visito	1
15112	visítela	1
15113	visitase	1
15114	visitaron	1
15115	visitarme	1
15116	visitarle	1
15117	visitante	1
15118	visitándola	1
15119	visitando	1
15120	visitada	1
15121	visionario	1
15122	visillos	1
15123	visibles	1
15124	virutas	1
15125	virus	1
15126	viruela	1
15127	virtuosas	1
15128	virosos	1
15129	viró	1
15130	viril	1
15131	vírgulas	1
15132	vírgenes	1
15133	violo	1
15134	violines	1
15135	violentó	1
15136	violentísimas	1
15137	violentarse	1
15138	violados	1
15139	violadas	1
15140	vinosas	1
15141	viniéronle	1
15142	vinieras	1
15143	vindicta	1
15144	vínculo	1
15145	vinazo	1
15146	vinateros	1
15147	villaviciosa	1
15148	villas	1
15149	villarreal	1
15150	villanía	1
15151	villancicos	1
15152	villahermosa	1
15153	viles	1
15154	vigoroso	1
15155	vigorizó	1
15156	vigorizan	1
15157	vigorización	1
15158	vigorizaba	1
15159	vigilia	1
15160	vigilase	1
15161	vigilarlas	1
15162	vigilantes	1
15163	vigilante	1
15164	vigilando	1
15165	vigilado	1
15166	vigilada	1
15167	vigilaba	1
15168	vigía	1
15169	vigente	1
15170	viesen	1
15171	vierte	1
15172	viéronse	1
15173	vierais	1
15174	viente	1
15175	viéndoselo	1
15176	viéndome	1
15177	viéndolos	1
15178	viéndolo	1
15179	viéndoles	1
15180	viejona	1
15181	viejecillos	1
15182	vidita	1
15183	victorioso	1
15184	victorias	1
15185	vicisitudes	1
15186	viciosote	1
15187	viciosonas	1
15188	viciosas	1
15189	viciado	1
15190	vicaría	1
15191	vibró	1
15192	vibratorio	1
15193	vibrante	1
15194	víboras	1
15195	vías	1
15196	viana	1
15197	viajecito	1
15198	viajado	1
15199	viabilidad	1
15200	via	1
15201	vetustos	1
15202	veto	1
15203	vestuario	1
15204	vestimos	1
15205	vestimenta	1
15206	vestiglo	1
15207	vestigio	1
15208	vestidito	1
15209	vestidita	1
15210	vestían	1
15211	vertiente	1
15212	vertido	1
15213	vertidas	1
15214	vértice	1
15215	vertical	1
15216	verter	1
15217	versiones	1
15218	versión	1
15219	verruguita	1
15220	verosímil	1
15221	vernet	1
15222	verja	1
15223	verificaría	1
15224	verificar	1
15225	verifican	1
15226	verificada	1
15227	verificábase	1
15228	verídicas	1
15229	vericuetos	1
15230	verías	1
15231	verían	1
15232	veríais	1
15233	vergüenzas	1
15234	vergonzante	1
15235	verduras	1
15236	verdura	1
15237	verduleras	1
15238	verdulera	1
15239	verdoso	1
15240	verdosa	1
15241	verdor	1
15242	verbales	1
15243	verba	1
15244	veraz	1
15245	veranear	1
15246	veracidad	1
15247	vera	1
15248	venturosa	1
15249	ventosa	1
15250	ventorrillo	1
15251	ventilara	1
15252	ventilados	1
15253	ventanuchos	1
15254	ventanucha	1
15255	ventanillas	1
15256	ventajoso	1
15257	venís	1
15258	venirte	1
15259	venirse	1
15260	venirme	1
15261	venideros	1
15262	venialmente	1
15263	venia	1
15264	vengativos	1
15265	véngase	1
15266	vengarme	1
15267	vengado	1
15268	venerandas	1
15269	venerado	1
15270	veneradas	1
15271	venera	1
15272	venenosas	1
15273	venenosa	1
15274	vendo	1
15275	vendió	1
15276	vendiéndolos	1
15277	vendidos	1
15278	vendido	1
15279	vendíalos	1
15280	vendí	1
15281	vendes	1
15282	venderse	1
15283	venderlos	1
15284	venderle	1
15285	venderla	1
15286	venderían	1
15287	vendehumos	1
15288	vencimiento	1
15289	venciendo	1
15290	vencidas	1
15291	vencía	1
15292	vencerme	1
15293	vencerlo	1
15294	vencerá	1
15295	vencedor	1
15296	venas	1
15297	velito	1
15298	velitas	1
15299	veletas	1
15300	velaría	1
15301	velaremos	1
15302	velándosele	1
15303	veladores	1
15304	velaban	1
15305	velaba	1
15306	vejiga	1
15307	vejeces	1
15308	veintiuno	1
15309	veintiocho	1
15310	veíalos	1
15311	veíala	1
15312	vehemente	1
15313	vegetativa	1
15314	vegetación	1
15315	veee	1
15316	vedlo	1
15317	vedlas	1
15318	vedan	1
15319	vecindades	1
15320	veámoslo	1
15321	véalo	1
15322	váyanse	1
15323	vaticinó	1
15324	vaticinios	1
15325	vaticinar	1
15326	vaticinan	1
15327	vaticinaba	1
15328	vasto	1
15329	vasta	1
15330	vasito	1
15331	vasijas	1
15332	vascongadas	1
15333	vasco	1
15334	varoncitos	1
15335	varitas	1
15336	varita	1
15337	varisis	1
15338	varió	1
15339	varillas	1
15340	variarle	1
15341	variaran	1
15342	variantes	1
15343	variados	1
15344	variada	1
15345	variación	1
15346	vargueño	1
15347	vareo	1
15348	vareando	1
15349	vaqueta	1
15350	vapulean	1
15351	vapores	1
15352	vaporcito	1
15353	vanos	1
15354	vanas	1
15355	vanaglorió	1
15356	vanagloriarse	1
15357	vana	1
15358	vampiros	1
15359	valores	1
15360	valoraciones	1
15361	vallehermoso	1
15362	valledor	1
15363	vallecas	1
15364	valioso	1
15365	valimiento	1
15366	valieran	1
15367	válida	1
15368	valgo	1
15369	válganos	1
15370	valgamos	1
15371	valerte	1
15372	valerse	1
15373	valeriana	1
15374	valera	1
15375	valenciennes	1
15376	vaivenes	1
15377	vaho	1
15378	vagones	1
15379	vagancia	1
15380	vagabundos	1
15381	vagaba	1
15382	vadita	1
15383	vacuna	1
15384	vació	1
15385	vacilo	1
15386	vacilaron	1
15387	vacilará	1
15388	vacilaciones	1
15389	vacías	1
15390	vaciaba	1
15391	vacas	1
15392	vacantes	1
15393	vacaciones	1
15394	utilitaria	1
15395	utilísimas	1
15396	usurparle	1
15397	usurpan	1
15398	usurpación	1
15399	usureros	1
15400	usurera	1
15401	usurarias	1
15402	usuraria	1
15403	usufructuaria	1
15404	usufructo	1
15405	ustés	1
15406	usos	1
15407	usó	1
15408	usía	1
15409	usaré	1
15410	usara	1
15411	usada	1
15412	uribe	1
15413	urgía	1
15414	urgentes	1
15415	urgente	1
15416	urgencia	1
15417	urdimbres	1
15418	urdidas	1
15419	urbanas	1
15420	untado	1
15421	untada	1
15422	universitario	1
15423	uniste	1
15424	unirte	1
15425	unirles	1
15426	uniones	1
15427	unió	1
15428	uniformidad	1
15429	uniformes	1
15430	uniformados	1
15431	unidas	1
15432	unicornio	1
15433	únicas	1
15434	uníanse	1
15435	unían	1
15436	ungüento	1
15437	ungidas	1
15438	unen	1
15439	unanimidad	1
15440	unánime	1
15441	umbral	1
15442	ultratumba	1
15443	ultramarinos	1
15444	úlceras	1
15445	ujeros	1
15446	ujeritos	1
15447	úes	1
15448	ubre	1
15449	tuyos	1
15450	tuviste	1
15451	tuviéronle	1
15452	tuviéronla	1
15453	tutti	1
15454	tutora	1
15455	tutor	1
15456	tutela	1
15457	tutearle	1
15458	tuteándose	1
15459	tuteándola	1
15460	tuteaba	1
15461	tutea	1
15462	tururú	1
15463	turulatos	1
15464	turulato	1
15465	turrones	1
15466	turris	1
15467	turquí	1
15468	turgentes	1
15469	turégano	1
15470	turcas	1
15471	turca	1
15472	turbulenta	1
15473	turbose	1
15474	turbo	1
15475	turbio	1
15476	turbia	1
15477	turbarle	1
15478	turbante	1
15479	turbadísima	1
15480	turbaban	1
15481	turbábala	1
15482	turbaba	1
15483	túnica	1
15484	tundiéndole	1
15485	tunanterías	1
15486	tunantas	1
15487	tuna	1
15488	tumultuoso	1
15489	tumban	1
15490	tumbaba	1
15491	tumba	1
15492	tullerías	1
15493	tugurios	1
15494	tuétano	1
15495	tubería	1
15496	tuberculosis	1
15497	truncadas	1
15498	truncada	1
15499	trujillesca	1
15500	trujillas	1
15501	truhán	1
15502	trufas	1
15503	trueque	1
15504	trueno	1
15505	truena	1
15506	truchimán	1
15507	trotes	1
15508	tropiezos	1
15509	tropezado	1
15510	tronó	1
15511	tronchos	1
15512	tronaron	1
15513	tronados	1
15514	tronado	1
15515	tronada	1
15516	trompo	1
15517	trompetitas	1
15518	trompetillas	1
15519	trompetas	1
15520	trompazos	1
15521	trompadas	1
15522	trofeos	1
15523	trocase	1
15524	trocaran	1
15525	trocara	1
15526	trocar	1
15527	trocábase	1
15528	trocaban	1
15529	trizas	1
15530	triunfase	1
15531	triunfara	1
15532	triunfal	1
15533	triunfaban	1
15534	triunfaba	1
15535	trituro	1
15536	triturada	1
15537	tristísimos	1
15538	tris	1
15539	triquiñuela	1
15540	tripudas	1
15541	trípode	1
15542	triple	1
15543	tripicallero	1
15544	tripa	1
15545	trinquis	1
15546	trinquen	1
15547	trinco	1
15548	trincaron	1
15549	trincan	1
15550	trinca	1
15551	trinan	1
15552	trimestres	1
15553	trigos	1
15554	trigo	1
15555	trifulcas	1
15556	tributar	1
15557	tribuna	1
15558	triana	1
15559	treta	1
15560	tresillistas	1
15561	trescientos	1
15562	trescientas	1
15563	trepar	1
15564	trepadora	1
15565	trenes	1
15566	trencilla	1
15567	tremens	1
15568	trebejos	1
15569	trazó	1
15570	trazo	1
15571	trazáronla	1
15572	trazarle	1
15573	trazando	1
15574	trazados	1
15575	trazadas	1
15576	traza	1
15577	trayéndole	1
15578	trayéndola	1
15579	traviesos	1
15580	traviesa	1
15581	traviatta	1
15582	traviatonas	1
15583	travesía	1
15584	tratose	1
15585	trátele	1
15586	tratas	1
15587	tratáronse	1
15588	tratarnos	1
15589	tratarlos	1
15590	tratarle	1
15591	trataremos	1
15592	tratándoles	1
15593	tratándola	1
15594	tratamos	1
15595	tratamientos	1
15596	trátame	1
15597	tratados	1
15598	tratadistas	1
15599	tratadas	1
15600	tratábase	1
15601	tratábame	1
15602	tratábala	1
15603	trastornarle	1
15604	trastornadas	1
15605	trastornaban	1
15606	trastocar	1
15607	trastea	1
15608	trastazos	1
15609	trasquilase	1
15610	traspiés	1
15611	traspié	1
15612	traspasó	1
15613	traspasar	1
15614	traspasándole	1
15615	traspasando	1
15616	traspasan	1
15617	traspasaban	1
15618	trasnochar	1
15619	trasnochadores	1
15620	trasmitiendo	1
15621	traslucirse	1
15622	trasladó	1
15623	trasladándose	1
15624	trasladándola	1
15625	trasladando	1
15626	trasladado	1
15627	trasladada	1
15628	traslación	1
15629	trasegarlo	1
15630	trascienden	1
15631	trascendencia	1
15632	trapillo	1
15633	trap	1
15634	tranvías	1
15635	transparente	1
15636	transparentarse	1
15637	transparentado	1
15638	transparencia	1
15639	transmitirlo	1
15640	transmitir	1
15641	transmitió	1
15642	transmitiendo	1
15643	transmitía	1
15644	transmiten	1
15645	transmite	1
15646	transmigrar	1
15647	transmigraban	1
15648	tránsitos	1
15649	transigiendo	1
15650	transigido	1
15651	transigían	1
15652	transiciones	1
15653	transformismo	1
15654	transforme	1
15655	transformase	1
15656	transformar	1
15657	transformándose	1
15658	transformado	1
15659	transformaban	1
15660	transforma	1
15661	transfiguraciones	1
15662	transfiguraba	1
15663	transcurso	1
15664	transcurrió	1
15665	transcurrían	1
15666	transacciones	1
15667	tranquilizarle	1
15668	tranquilizaré	1
15669	tranquilizar	1
15670	tranquilizándose	1
15671	tranquilizándola	1
15672	tranquilizando	1
15673	tranquilizadora	1
15674	tranquilizador	1
15675	tranquilizado	1
15676	tranquilices	1
15677	tranquilamente	1
15678	trancazo	1
15679	tranca	1
15680	tramposos	1
15681	trámites	1
15682	trajiste	1
15683	trajines	1
15684	trajineros	1
15685	trajesen	1
15686	trajéronle	1
15687	trajerais	1
15688	tráiganos	1
15689	tráigamela	1
15690	tráigala	1
15691	traídos	1
15692	traidores	1
15693	traidoras	1
15694	traicioneros	1
15695	traíanla	1
15696	trague	1
15697	tragón	1
15698	trágicos	1
15699	tragicómicos	1
15700	trágico	1
15701	tragedias	1
15702	tragándose	1
15703	tragándole	1
15704	tragan	1
15705	tragaluz	1
15706	tragaluces	1
15707	tragadero	1
15708	tragacanto	1
15709	tragábamos	1
15710	traga	1
15711	traficante	1
15712	trafalgar	1
15713	tráetelo	1
15714	traerte	1
15715	traerse	1
15716	traérnosle	1
15717	traerlas	1
15718	traerán	1
15719	tráele	1
15720	tradújose	1
15721	traducirse	1
15722	traducirla	1
15723	traducía	1
15724	traducción	1
15725	tradición	1
15726	trabucazos	1
15727	trabucan	1
15728	trabó	1
15729	trabillas	1
15730	trabase	1
15731	trabándose	1
15732	trabajosamente	1
15733	trabajillos	1
15734	trabajes	1
15735	trabajarla	1
15736	trabajaría	1
15737	trabájalo	1
15738	trabajadores	1
15739	trabajadoras	1
15740	trabado	1
15741	trababa	1
15742	tóxicos	1
15743	toxicación	1
15744	totalmente	1
15745	tostadita	1
15746	tostaba	1
15747	tosquedad	1
15748	toso	1
15749	tosió	1
15750	tosía	1
15751	tose	1
15752	toscos	1
15753	torzales	1
15754	torvamente	1
15755	tortuosos	1
15756	tortuoso	1
15757	tortuga	1
15758	tórtolos	1
15759	tortolitos	1
15760	tortoleo	1
15761	tortillita	1
15762	tortillas	1
15763	torrero	1
15764	torreón	1
15765	torrellas	1
15766	torrecilla	1
15767	torpezas	1
15768	torniquete	1
15769	tornillándola	1
15770	torneo	1
15771	torneando	1
15772	torneadita	1
15773	tornasol	1
15774	tornas	1
15775	torna	1
15776	tormentos	1
15777	toril	1
15778	toreado	1
15779	toreaba	1
15780	torcidos	1
15781	torcerse	1
15782	torceduras	1
15783	tórax	1
15784	torácica	1
15785	toquen	1
15786	toquéis	1
15787	toquecito	1
15788	tópico	1
15789	topetazo	1
15790	topar	1
15791	topacio	1
15792	tontuna	1
15793	tontita	1
15794	tontees	1
15795	tonteando	1
15796	tontadas	1
15797	tonsurados	1
15798	tonito	1
15799	tónicos	1
15800	tónica	1
15801	tonel	1
15802	tomole	1
15803	tomola	1
15804	tomemos	1
15805	toméis	1
15806	tómbola	1
15807	tomazo	1
15808	tomates	1
15809	tomarnos	1
15810	tomarlas	1
15811	tomarían	1
15812	tomaríale	1
15813	tomaremos	1
15814	tomáramos	1
15815	tomará	1
15816	tomándola	1
15817	tomamos	1
15818	tomáis	1
15819	tomador	1
15820	tomábase	1
15821	tomábala	1
15822	tolú	1
15823	tolosa	1
15824	tolondrón	1
15825	tollina	1
15826	tolerancias	1
15827	tolerable	1
15828	tolera	1
15829	toledano	1
15830	toilette	1
15831	toco	1
15832	tocati	1
15833	tocarme	1
15834	tocarlos	1
15835	tocarlo	1
15836	tocarle	1
15837	tocarían	1
15838	tocaría	1
15839	tocaré	1
15840	tocaran	1
15841	tocándoles	1
15842	tocados	1
15843	tocábamos	1
15844	toallas	1
15845	tizona	1
15846	tiznando	1
15847	títulos	1
15848	títulas	1
15849	titubear	1
15850	titubeando	1
15851	titubeaba	1
15852	tísico	1
15853	tiroteo	1
15854	tirotearse	1
15855	tiritos	1
15856	tiritar	1
15857	tiritaba	1
15858	tiren	1
15859	tirase	1
15860	tirársela	1
15861	tiraron	1
15862	tirarás	1
15863	tirantez	1
15864	tirano	1
15865	tiranístico	1
15866	tiránica	1
15867	tirándose	1
15868	tiranas	1
15869	tiradores	1
15870	tirador	1
15871	tirádola	1
15872	tirabuzones	1
15873	tirabas	1
15874	tirábalo	1
15875	tiquitique	1
15876	tiote	1
15877	tiotas	1
15878	tiota	1
15879	tiorra	1
15880	tiona	1
15881	tiólogos	1
15882	tiñoso	1
15883	tiñosa	1
15884	tiñéndosela	1
15885	tintura	1
15886	tinto	1
15887	tintes	1
15888	tiniente	1
15889	tinajas	1
15890	tina	1
15891	tímpano	1
15892	timos	1
15893	timonear	1
15894	tímidos	1
15895	tímida	1
15896	timbrado	1
15897	timbales	1
15898	timarte	1
15899	timan	1
15900	timadora	1
15901	timaba	1
15902	tílburi	1
15903	tijeretazo	1
15904	tijera	1
15905	tigres	1
15906	tiesto	1
15907	tiernísimos	1
15908	tiernísima	1
15909	tiento	1
15910	tientes	1
15911	tienden	1
15912	tien	1
15913	tiemblo	1
15914	tic	1
15915	tiburones	1
15916	tiburonas	1
15917	tibios	1
15918	tibidabo	1
15919	tibias	1
15920	tibia	1
15921	tiara	1
15922	thinville	1
15923	textualmente	1
15924	tétrico	1
15925	tetita	1
15926	tetera	1
15927	tetánica	1
15928	testuz	1
15929	testeros	1
15930	testero	1
15931	testera	1
15932	testar	1
15933	tesorería	1
15934	tertuliantes	1
15935	tersos	1
15936	tersas	1
15937	tersa	1
15938	terruño	1
15939	terrón	1
15940	territorio	1
15941	terrestre	1
15942	terraza	1
15943	terráqueo	1
15944	terranova	1
15945	terra	1
15946	ternos	1
15947	terneza	1
15948	ternerito	1
15949	terne	1
15950	terminase	1
15951	terminarse	1
15952	terminado	1
15953	terminadas	1
15954	terminada	1
15955	terciopelos	1
15956	terció	1
15957	tercio	1
15958	terciándose	1
15959	tercas	1
15960	terapéutico	1
15961	terapéuticas	1
15962	teóricas	1
15963	teólogos	1
15964	teólogo	1
15965	teológicas	1
15966	teogonías	1
15967	teogonía	1
15968	teñirse	1
15969	teñidos	1
15970	teñida	1
15971	tenuidad	1
15972	tenues	1
15973	tentó	1
15974	tente	1
15975	tentarte	1
15976	tentarían	1
15977	tentar	1
15978	tentador	1
15979	tentaba	1
15980	tenla	1
15981	teniéndose	1
15982	teniéndole	1
15983	teniéndola	1
15984	tenidas	1
15985	teníanle	1
15986	teníalas	1
15987	téngalo	1
15988	tenerlas	1
15989	tenedores	1
15990	tened	1
15991	tenebrosos	1
15992	tenebroso	1
15993	tendréis	1
15994	tendralos	1
15995	tendones	1
15996	tendiera	1
15997	tendidos	1
15998	tendíanse	1
15999	tendían	1
16000	tenderse	1
16001	tenderil	1
16002	tenderete	1
16003	tender	1
16004	tenacillas	1
16005	tenacidades	1
16006	temporal	1
16007	temporadillas	1
16008	temporadilla	1
16009	templos	1
16010	templadita	1
16011	tempestuosos	1
16012	temperatura	1
16013	temida	1
16014	temible	1
16015	temerás	1
16016	temeraria	1
16017	teméis	1
16018	temblorosos	1
16019	tembloroso	1
16020	tembláronle	1
16021	temblara	1
16022	tembladores	1
16023	temamos	1
16024	telegráficos	1
16025	telegráfico	1
16026	telegrafías	1
16027	telegrafiarse	1
16028	telegrafía	1
16029	telares	1
16030	tejiendo	1
16031	tejavana	1
16032	tejas	1
16033	tejar	1
16034	tegel	1
16035	tediosas	1
16036	tediosa	1
16037	tecleando	1
16038	tecleaban	1
16039	tecleaba	1
16040	tea	1
16041	tazón	1
16042	tazas	1
16043	tauromaquia	1
16044	taurómacas	1
16045	tasado	1
16046	tasada	1
16047	tasaba	1
16048	tartana	1
16049	tartamudeó	1
16050	tartamudeando	1
16051	tarima	1
16052	tardo	1
16053	tardío	1
16054	tardecillo	1
16055	tardé	1
16056	tardase	1
16057	tardas	1
16058	tardaré	1
16059	tardara	1
16060	tardan	1
16061	tardamos	1
16062	tarancón	1
16063	tarabilla	1
16064	tapujo	1
16065	tapujito	1
16066	tapón	1
16067	tapete	1
16068	tapase	1
16069	tapas	1
16070	taparle	1
16071	tapándoselo	1
16072	tapan	1
16073	tapado	1
16074	tapadita	1
16075	tapadera	1
16076	tapada	1
16077	tañido	1
16078	tañer	1
16079	tantooo	1
16080	tantismos	1
16081	tantearemos	1
16082	tantear	1
16083	tanteado	1
16084	tangible	1
16085	tangente	1
16086	tamizada	1
16087	tamiz	1
16088	tamente	1
16089	tamboril	1
16090	tamborazos	1
16091	tamañitas	1
16092	taludes	1
16093	talones	1
16094	talón	1
16095	talluditos	1
16096	talludito	1
16097	tallos	1
16098	tallo	1
16099	talles	1
16100	talleres	1
16101	tallas	1
16102	tallarla	1
16103	tallando	1
16104	talegas	1
16105	talcualita	1
16106	talavera	1
16107	talar	1
16108	taladraban	1
16109	tala	1
16110	tajadas	1
16111	tajada	1
16112	tahona	1
16113	tagarote	1
16114	tafetanes	1
16115	táctico	1
16116	tácticas	1
16117	táctica	1
16118	tacones	1
16119	taciturno	1
16120	taciturna	1
16121	tacita	1
16122	tachuelas	1
16123	tacaña	1
16124	tablitas	1
16125	tablajero	1
16126	tablajera	1
16127	tabernero	1
16128	tabacazo	1
16129	ta	1
16130	sutilizaron	1
16131	sutilizado	1
16132	sutilísimo	1
16133	sutilezas	1
16134	sutileza	1
16135	susurraron	1
16136	sustraernos	1
16137	sustraer	1
16138	sustos	1
16139	sustituyeron	1
16140	sustituye	1
16141	sustituirla	1
16142	sustancioso	1
16143	sustanciosa	1
16144	sustancial	1
16145	suspirona	1
16146	suspire	1
16147	suspiras	1
16148	suspirante	1
16149	suspicacia	1
16150	suspenso	1
16151	suspendido	1
16152	suspendida	1
16153	suspenderlo	1
16154	susodichos	1
16155	suscritoras	1
16156	suscritor	1
16157	suscripciones	1
16158	suscripción	1
16159	suscricioncita	1
16160	suscribió	1
16161	suscitara	1
16162	suscepciones	1
16163	surtidos	1
16164	surtidores	1
16165	surtido	1
16166	surtía	1
16167	surgir	1
16168	surgieron	1
16169	surgieran	1
16170	surgía	1
16171	surco	1
16172	surcaban	1
16173	supuesta	1
16174	suprimo	1
16175	suprimirse	1
16176	suprimirlo	1
16177	suprimido	1
16178	suprema	1
16179	súpose	1
16180	suponiéndolo	1
16181	suponiéndoles	1
16182	suponían	1
16183	suponíales	1
16184	suponga	1
16185	suponérsela	1
16186	suponeres	1
16187	suponemos	1
16188	suplió	1
16189	suplicó	1
16190	suplicándole	1
16191	suplicando	1
16192	súplica	1
16193	suplementos	1
16194	suplementario	1
16195	súpitas	1
16196	supiste	1
16197	supiese	1
16198	supersticiosa	1
16199	supersticiones	1
16200	superstición	1
16201	superfirolíticos	1
16202	superfirolíticas	1
16203	superficiales	1
16204	superficial	1
16205	superciliar	1
16206	superávit	1
16207	superarla	1
16208	superaban	1
16209	superaba	1
16210	supera	1
16211	sumisa	1
16212	suministrado	1
16213	sumida	1
16214	sumergirla	1
16215	sumergiendo	1
16216	sumergida	1
16217	sulfurándose	1
16218	sujetose	1
16219	sujetarse	1
16220	sujetaron	1
16221	sujetarles	1
16222	sujetaran	1
16223	sujetan	1
16224	sujetada	1
16225	sujetaban	1
16226	suicido	1
16227	suicide	1
16228	sugirieron	1
16229	sugiriera	1
16230	sugestiones	1
16231	sugestionada	1
16232	sugestión	1
16233	sugeríanle	1
16234	sugerían	1
16235	sugeríale	1
16236	sugería	1
16237	sufrirte	1
16238	sufriría	1
16239	sufrimiento	1
16240	sufrieron	1
16241	sufriendo	1
16242	sufridos	1
16243	sufragios	1
16244	suertes	1
16245	sueñecito	1
16246	sueñecillo	1
16247	sueñan	1
16248	sueno	1
16249	suenen	1
16250	suéltese	1
16251	sueltecito	1
16252	suegro	1
16253	sudario	1
16254	sudadas	1
16255	suda	1
16256	sucumbió	1
16257	suculento	1
16258	suculenta	1
16259	sucediera	1
16260	sucedidos	1
16261	sucedían	1
16262	sucederme	1
16263	sucederá	1
16264	subyugando	1
16265	subyugada	1
16266	subteniente	1
16267	subsistiendo	1
16268	subsistía	1
16269	subsistencia	1
16270	subsiste	1
16271	subsiguientes	1
16272	subsidio	1
16273	subsecretarios	1
16274	subrepticiamente	1
16275	sublimidades	1
16276	sublimaban	1
16277	sublevó	1
16278	sublevo	1
16279	sublevaba	1
16280	subleva	1
16281	súbitas	1
16282	subirlas	1
16283	subiría	1
16284	subiré	1
16285	subiese	1
16286	subiéronle	1
16287	subiera	1
16288	subiéndosele	1
16289	subiéndome	1
16290	subes	1
16291	súbdito	1
16292	subasta	1
16293	subamos	1
16294	subalternos	1
16295	subalterno	1
16296	subalterna	1
16297	suave	1
16298	suárez	1
16299	sport	1
16300	sotabanco	1
16301	sostienes	1
16302	sostenimiento	1
16303	sosteniéndose	1
16304	sosteniéndola	1
16305	sostenías	1
16306	sostenerse	1
16307	sostendré	1
16308	sostén	1
16309	sospechosa	1
16310	sospecho	1
16311	sospechen	1
16312	sospechara	1
16313	sospechabas	1
16314	sosos	1
16315	sosería	1
16316	sosegó	1
16317	sosegarle	1
16318	sosegando	1
16319	sosegadamente	1
16320	sosas	1
16321	sosamente	1
16322	sosa	1
16323	sortilegio	1
16324	sortijas	1
16325	sortearlo	1
16326	sortearle	1
16327	sortear	1
16328	sorteando	1
16329	sorpresita	1
16330	sorprendo	1
16331	sorprendiese	1
16332	sorprendieron	1
16333	sorprendidos	1
16334	sorprendidas	1
16335	sorprendí	1
16336	sorprenderá	1
16337	sorprender	1
16338	sorna	1
16339	sordina	1
16340	sordidez	1
16341	sordas	1
16342	sordamente	1
16343	sorbo	1
16344	sorbió	1
16345	sorbieran	1
16346	sorber	1
16347	sorbe	1
16348	soportan	1
16349	soportado	1
16350	soporífero	1
16351	soporífera	1
16352	soplaron	1
16353	soplao	1
16354	soplándose	1
16355	soplando	1
16356	sopesarlos	1
16357	soñoliento	1
16358	soñolientas	1
16359	soñolienta	1
16360	soñaron	1
16361	soñadas	1
16362	sonsaques	1
16363	sonsacado	1
16364	sonrosados	1
16365	sonrosado	1
16366	sonrosadas	1
16367	sonrojos	1
16368	sonrojo	1
16369	sonrisas	1
16370	sonríes	1
16371	sonriéndose	1
16372	sonoro	1
16373	sonoridad	1
16374	sonoras	1
16375	sondéela	1
16376	sondear	1
16377	sondeaba	1
16378	sondaje	1
16379	sonarme	1
16380	sonara	1
16381	sonándose	1
16382	sonándola	1
16383	sonambulismo	1
16384	sonámbula	1
16385	somnolencias	1
16386	sometiera	1
16387	sometiéndose	1
16388	sometida	1
16389	sometían	1
16390	sometía	1
16391	someterlas	1
16392	someta	1
16393	someras	1
16394	sombríos	1
16395	sombrillazo	1
16396	sombría	1
16397	sombreritos	1
16398	sombrerero	1
16399	sombreo	1
16400	sombrajos	1
16401	soluciones	1
16402	soltole	1
16403	solterones	1
16404	soltería	1
16405	soltaste	1
16406	soltarse	1
16407	soltarlo	1
16408	soltarla	1
16409	soltarían	1
16410	soltara	1
16411	soltaban	1
16412	sollozar	1
16413	sollozando	1
16414	soliviantada	1
16415	solitos	1
16416	solito	1
16417	sólidos	1
16418	solidificación	1
16419	solidificaba	1
16420	solidifica	1
16421	solidez	1
16422	sólidamente	1
16423	solicito	1
16424	solicitara	1
16425	solicitar	1
16426	solicitados	1
16427	solfeo	1
16428	soleta	1
16429	soles	1
16430	solemos	1
16431	solemnidades	1
16432	solecismos	1
16433	soldevilla	1
16434	soldarla	1
16435	soldadura	1
16436	soldaditos	1
16437	solaz	1
16438	solapas	1
16439	solana	1
16440	sojuzgado	1
16441	sogas	1
16442	soforas	1
16443	sofocones	1
16444	sofoco	1
16445	sofocase	1
16446	sofocarse	1
16447	sofocaban	1
16448	sofisterías	1
16449	soez	1
16450	socorriome	1
16451	socorrió	1
16452	socorriese	1
16453	socorridas	1
16454	socorrías	1
16455	socorría	1
16456	socorrerme	1
16457	socorreremos	1
16458	socorrerá	1
16459	socorre	1
16460	socórrale	1
16461	socialistas	1
16462	socialista	1
16463	socavaban	1
16464	socarronas	1
16465	sobro	1
16466	sobrio	1
16467	sobrevive	1
16468	sobreviniese	1
16469	sobreviene	1
16470	sobrevenirle	1
16471	sobrevenido	1
16472	sobrestante	1
16473	sobresaltos	1
16474	sobresaltó	1
16475	sobresalientes	1
16476	sobrepujó	1
16477	sobreponiéndose	1
16478	sobreponían	1
16479	sobreponía	1
16480	sobreparto	1
16481	sobredorada	1
16482	sobrecogía	1
16483	sobrecoge	1
16484	sobraron	1
16485	sobrantes	1
16486	sobrando	1
16487	sobran	1
16488	sobraban	1
16489	soberbios	1
16490	soberbias	1
16491	soberana	1
16492	sobar	1
16493	sobadas	1
16494	sobaco	1
16495	situó	1
16496	situados	1
16497	situado	1
16498	situada	1
16499	sita	1
16500	sístole	1
16501	sistematizar	1
16502	sirvieron	1
16503	sirvientes	1
16504	sirviéndole	1
16505	sirviendo	1
16506	sirvas	1
16507	siquera	1
16508	sinvergüenzones	1
16509	sinvergüenzonas	1
16510	sintiole	1
16511	sintieses	1
16512	sintieran	1
16513	sintético	1
16514	sinrazones	1
16515	sinrazón	1
16516	sinónimos	1
16517	sinodales	1
16518	sinificancia	1
16519	siniestros	1
16520	singularidad	1
16521	singulares	1
16522	singer	1
16523	sinfonías	1
16524	sinfonía	1
16525	síncope	1
16526	síncopas	1
16527	sinceridades	1
16528	sinceras	1
16529	simultáneos	1
16530	simultáneamente	1
16531	simulado	1
16532	simulacro	1
16533	simpson	1
16534	simplona	1
16535	simplín	1
16536	simplicitas	1
16537	simples	1
16538	simpatizase	1
16539	simpatizado	1
16540	simpáticos	1
16541	simones	1
16542	similares	1
16543	símil	1
16544	simiente	1
16545	simbolismo	1
16546	siluetas	1
16547	silogismos	1
16548	sillones	1
16549	silleta	1
16550	silfidones	1
16551	silfidona	1
16552	sílfide	1
16553	silenciosos	1
16554	silbidos	1
16555	silbido	1
16556	silbe	1
16557	silbante	1
16558	silbándole	1
16559	silbando	1
16560	silabeo	1
16561	sigunda	1
16562	siguiole	1
16563	siguiéndoles	1
16564	sigues	1
16565	significativa	1
16566	significado	1
16567	sigan	1
16568	sietes	1
16569	siervas	1
16570	sientan	1
16571	siéndolo	1
16572	siéndole	1
16573	siego	1
16574	sicilianas	1
16575	sicario	1
16576	sibila	1
16577	sibarita	1
16578	shangai	1
16579	sexto	1
16580	sexta	1
16581	sevicia	1
16582	severos	1
16583	severísimos	1
16584	severísimamente	1
16585	severidades	1
16586	severiano	1
16587	severas	1
16588	setos	1
16589	sétimo	1
16590	setecientas	1
16591	sesudo	1
16592	sesudas	1
16593	sesiones	1
16594	sesera	1
16595	servirte	1
16596	servirles	1
16597	servirle	1
16598	serviría	1
16599	servirá	1
16600	servilón	1
16601	serviles	1
16602	servidores	1
16603	servida	1
16604	servían	1
16605	servíale	1
16606	serte	1
16607	sert	1
16608	serpentine	1
16609	serosa	1
16610	serones	1
16611	sernos	1
16612	sermoneo	1
16613	sermonearle	1
16614	sermonearé	1
16615	sermoneaba	1
16616	sermoncito	1
16617	sermonazo	1
16618	sermonarias	1
16619	serme	1
16620	serios	1
16621	seríale	1
16622	sereta	1
16623	serénese	1
16624	serene	1
16625	serénate	1
16626	serenase	1
16627	serenaron	1
16628	serenarás	1
16629	serenado	1
16630	seráfica	1
16631	séquito	1
16632	seque	1
16633	sepulturas	1
16634	sepultarse	1
16635	sepultado	1
16636	séptimo	1
16637	separose	1
16638	separes	1
16639	separáronse	1
16640	separarnos	1
16641	separaremos	1
16642	separándose	1
16643	separado	1
16644	separadas	1
16645	separada	1
16646	separábanse	1
16647	seo	1
16648	señoriticas	1
16649	señoritas	1
16650	señoril	1
16651	señorete	1
16652	señó	1
16653	señale	1
16654	señalarse	1
16655	señalándote	1
16656	señalados	1
16657	señalada	1
16658	señalaba	1
16659	señala	1
16660	sentirme	1
16661	sentirla	1
16662	sentirás	1
16663	sentirá	1
16664	sentinas	1
16665	sentimos	1
16666	sentías	1
16667	sentíalo	1
16668	sentíala	1
16669	sentenciador	1
16670	senté	1
16671	sentáronse	1
16672	sentaré	1
16673	sentándosele	1
16674	sentadita	1
16675	sentábase	1
16676	sensibles	1
16677	sensiblemente	1
16678	sensato	1
16679	senil	1
16680	sencillos	1
16681	sencillísima	1
16682	senador	1
16683	semioscura	1
16684	semilla	1
16685	semestres	1
16686	semestre	1
16687	semeja	1
16688	sembrara	1
16689	sembrar	1
16690	sembrando	1
16691	sellos	1
16692	selló	1
16693	sellaíto	1
16694	selecto	1
16695	seiscientos	1
16696	seguridades	1
16697	seguras	1
16698	segundón	1
16699	seguirlos	1
16700	seguirlas	1
16701	seguirían	1
16702	seguiríamos	1
16703	seguiremos	1
16704	seguirás	1
16705	seguío	1
16706	seguimientos	1
16707	seguíales	1
16708	seguíala	1
16709	segovianos	1
16710	seglar	1
16711	segar	1
16712	segándole	1
16713	seducir	1
16714	seducido	1
16715	seducidas	1
16716	seducida	1
16717	seducción	1
16718	sedimentado	1
16719	sedientos	1
16720	sedienta	1
16721	sedeño	1
16722	sede	1
16723	sedante	1
16724	sedanes	1
16725	sedán	1
16726	secuestradoras	1
16727	secuestrado	1
16728	secretito	1
16729	secretillo	1
16730	secreteos	1
16731	secreteó	1
16732	secretearse	1
16733	secreteara	1
16734	secretas	1
16735	secó	1
16736	secaron	1
16737	secarle	1
16738	secara	1
16739	secamente	1
16740	secado	1
16741	secaderos	1
16742	secadero	1
16743	secaban	1
16744	sebosa	1
16745	scott	1
16746	scirroso	1
16747	schiller	1
16748	sc	1
16749	sazonarla	1
16750	sazonado	1
16751	sazonada	1
16752	sayos	1
16753	sayones	1
16754	saya	1
16755	saturada	1
16756	satisfechos	1
16757	satisfechas	1
16758	satisfactoria	1
16759	satisfacían	1
16760	satisfacía	1
16761	satisfacerse	1
16762	satisfacerlos	1
16763	satisfacerlo	1
16764	satisfacerla	1
16765	satisfacciones	1
16766	satíricos	1
16767	satenes	1
16768	satén	1
16769	sastrería	1
16770	sastre	1
16771	sastra	1
16772	sartas	1
16773	sarta	1
16774	sarna	1
16775	sargentos	1
16776	sargento	1
16777	sardina	1
16778	sarcástico	1
16779	sarao	1
16780	saquitos	1
16781	saquito	1
16782	saqueaban	1
16783	sapos	1
16784	sapientísimas	1
16785	sañudamente	1
16786	sañuda	1
16787	santuario	1
16788	santona	1
16789	santisma	1
16790	santifiquísimas	1
16791	santificarnos	1
16792	santander	1
16793	sanos	1
16794	sanitarismo	1
16795	sanguinolento	1
16796	sanguínea	1
16797	sanguinaria	1
16798	sangrientos	1
16799	sangrienta	1
16800	sangría	1
16801	sangraran	1
16802	sandía	1
16803	sandez	1
16804	sancta	1
16805	sancionadora	1
16806	sancho	1
16807	sanas	1
16808	sanarte	1
16809	sanara	1
16810	sanan	1
16811	sanado	1
16812	salvedades	1
16813	salvarías	1
16814	salvaré	1
16815	salvará	1
16816	salvando	1
16817	salvamento	1
16818	salvajito	1
16819	salvajita	1
16820	salvajadas	1
16821	salvadoras	1
16822	salvadora	1
16823	salvador	1
16824	salvadera	1
16825	saludes	1
16826	saludarte	1
16827	saludáronse	1
16828	saludarles	1
16829	saludarle	1
16830	saludarlas	1
16831	saludándola	1
16832	saludadores	1
16833	saludables	1
16834	saltos	1
16835	saltimbanquis	1
16836	saltase	1
16837	saltarla	1
16838	saltaran	1
16839	saltándosele	1
16840	saltándola	1
16841	saltan	1
16842	saltamontes	1
16843	saltado	1
16844	saltaban	1
16845	salsas	1
16846	salpicaron	1
16847	salpicado	1
16848	salpicada	1
16849	salomón	1
16850	salobre	1
16851	salmuera	1
16852	salivita	1
16853	salivazos	1
16854	salivazo	1
16855	salís	1
16856	salieran	1
16857	saliditas	1
16858	salesas	1
16859	saldrían	1
16860	saldrán	1
16861	saldar	1
16862	saldan	1
16863	salas	1
16864	salaremos	1
16865	saladísimo	1
16866	saladas	1
16867	sajonas	1
16868	sahumerio	1
16869	sagrados	1
16870	sagra	1
16871	sagacidad	1
16872	saetazos	1
16873	saetas	1
16874	sacudo	1
16875	sacudirme	1
16876	sacudirlas	1
16877	sacudiré	1
16878	sacudimientos	1
16879	sacudimiento	1
16880	sacudieran	1
16881	sacudiéndoles	1
16882	sacudiéndole	1
16883	sacudiéndola	1
16884	sacudido	1
16885	sacude	1
16886	sacristanes	1
16887	sacrílegos	1
16888	sacrílego	1
16889	sacrilegios	1
16890	sacrilegio	1
16891	sacrifíquese	1
16892	sacrifique	1
16893	sacrificaba	1
16894	sacos	1
16895	saciedad	1
16896	saciar	1
16897	saciaba	1
16898	sacerdotales	1
16899	sacerdotal	1
16900	sacáronla	1
16901	sacarles	1
16902	sacarlas	1
16903	sacarán	1
16904	sacará	1
16905	sácanos	1
16906	sacándose	1
16907	sacándome	1
16908	sacándolos	1
16909	sacándole	1
16910	sacamos	1
16911	sácalos	1
16912	sacados	1
16913	sacadas	1
16914	sacábala	1
16915	sabusté	1
16916	sabrosos	1
16917	sabríais	1
16918	sabremos	1
16919	sabrán	1
16920	saboréate	1
16921	saboreaba	1
16922	sabor	1
16923	sable	1
16924	sablazos	1
16925	sabiéndolas	1
16926	sabiendas	1
16927	sabíamos	1
16928	saberlas	1
16929	sabeees	1
16930	sabedoras	1
16931	sabañones	1
16932	sábados	1
16933	s	1
16934	rutinarios	1
16935	rutinario	1
16936	rutinaria	1
16937	rústicos	1
16938	rústicas	1
16939	rusticación	1
16940	rústica	1
16941	rusos	1
16942	rupertito	1
16943	rumores	1
16944	rumiarlas	1
16945	rumiaba	1
16946	rumboso	1
16947	rumbos	1
16948	rumbeles	1
16949	ruinosos	1
16950	ruinoso	1
16951	ruin	1
16952	ruidosos	1
16953	ruidito	1
16954	rugió	1
16955	rugidos	1
16956	rugía	1
16957	ruegos	1
16958	ruego	1
16959	ruedos	1
16960	ruedita	1
16961	ruede	1
16962	rudimentarios	1
16963	ruborizarse	1
16964	ruborizada	1
16965	rubor	1
16966	rubines	1
16967	rubias	1
16968	rubén	1
16969	rropa	1
16970	rozó	1
16971	rozamiento	1
16972	rozadura	1
16973	rozaban	1
16974	royendo	1
16975	rotura	1
16976	rothschild	1
16977	roten	1
16978	rostchild	1
16979	rossiniano	1
16980	rosicler	1
16981	rosca	1
16982	rosados	1
16983	rosada	1
16984	ros	1
16985	rorrooó	1
16986	roque	1
16987	ropillas	1
16988	ropaje	1
16989	roñosas	1
16990	roña	1
16991	ronde	1
16992	rondara	1
16993	rondar	1
16994	ronco	1
16995	roncas	1
16996	roncando	1
16997	roncaban	1
16998	roncaba	1
16999	rompiéndose	1
17000	rompí	1
17001	romperte	1
17002	romperse	1
17003	romperle	1
17004	romperla	1
17005	rompemos	1
17006	rómpeme	1
17007	rompelanzas	1
17008	romos	1
17009	romerías	1
17010	rombo	1
17011	romanzas	1
17012	romántico	1
17013	románicos	1
17014	romancesco	1
17015	romancesca	1
17016	romana	1
17017	romadizo	1
17018	rollos	1
17019	rollo	1
17020	rojizo	1
17021	rojizas	1
17022	roído	1
17023	roía	1
17024	roger	1
17025	rogaron	1
17026	rogarle	1
17027	rogando	1
17028	rogado	1
17029	roer	1
17030	roedor	1
17031	rodríguez	1
17032	rodó	1
17033	rodil	1
17034	rodeó	1
17035	rodeo	1
17036	rodearse	1
17037	rodean	1
17038	rodeados	1
17039	rodadas	1
17040	rocío	1
17041	rociada	1
17042	rocas	1
17043	robustecer	1
17044	robos	1
17045	robó	1
17046	robledo	1
17047	roben	1
17048	robe	1
17049	robaste	1
17050	robaron	1
17051	robármelo	1
17052	robaré	1
17053	robaran	1
17054	robará	1
17055	robara	1
17056	robándoselo	1
17057	roban	1
17058	robaban	1
17059	road	1
17060	rizoso	1
17061	rizosa	1
17062	rizarse	1
17063	rizada	1
17064	rivalidades	1
17065	ritual	1
17066	ritos	1
17067	ritornellos	1
17068	ritmos	1
17069	rítmico	1
17070	rita	1
17071	risitas	1
17072	risibles	1
17073	risible	1
17074	riquísima	1
17075	ripio	1
17076	riose	1
17077	ríos	1
17078	rioja	1
17079	riñó	1
17080	riñan	1
17081	riña	1
17082	ringorrangos	1
17083	rindiera	1
17084	rinden	1
17085	rinde	1
17086	rinconadas	1
17087	rimpuesta	1
17088	rimero	1
17089	rimados	1
17090	rija	1
17091	rigurosas	1
17092	rigoristas	1
17093	rígidamente	1
17094	rifle	1
17095	rifarla	1
17096	riesgo	1
17097	rieras	1
17098	rieran	1
17099	riéndole	1
17100	ridiculizando	1
17101	ridículas	1
17102	ridículamente	1
17103	ricardo	1
17104	ricacho	1
17105	ricacha	1
17106	ribeteada	1
17107	ribete	1
17108	ribera	1
17109	ríase	1
17110	ríanse	1
17111	rían	1
17112	rezumos	1
17113	rezumía	1
17114	rezumados	1
17115	rezongó	1
17116	rezongar	1
17117	rezongaba	1
17118	rezarían	1
17119	rezaría	1
17120	rezándole	1
17121	rézale	1
17122	rezagadas	1
17123	rezagada	1
17124	rezado	1
17125	rezaban	1
17126	revuelve	1
17127	revuelcos	1
17128	revuelco	1
17129	revolviese	1
17130	revolvieron	1
17131	revolviéndola	1
17132	revolverlas	1
17133	revoltosa	1
17134	revoloteó	1
17135	revolotear	1
17136	revoloteaban	1
17137	revolcose	1
17138	revolcarse	1
17139	reviviendo	1
17140	revistió	1
17141	revistiéndolas	1
17142	revisten	1
17143	revisión	1
17144	revisaré	1
17145	reviradas	1
17146	revientan	1
17147	revestirse	1
17148	revestir	1
17149	revestimiento	1
17150	revestido	1
17151	revestían	1
17152	reveses	1
17153	revertida	1
17154	reversión	1
17155	reverente	1
17156	reverencias	1
17157	reverencia	1
17158	reverdeció	1
17159	reverdeciendo	1
17160	reverdecidas	1
17161	reverdecer	1
17162	reverdece	1
17163	reverberos	1
17164	reverberar	1
17165	reventó	1
17166	reventas	1
17167	reventaban	1
17168	revenidos	1
17169	revelarte	1
17170	revelaron	1
17171	revelarle	1
17172	revelara	1
17173	reveladas	1
17174	revelada	1
17175	reunir	1
17176	reunió	1
17177	reunieran	1
17178	reuniendo	1
17179	reunido	1
17180	reunidas	1
17181	reunía	1
17182	reúne	1
17183	reumáticos	1
17184	retuvieron	1
17185	retumbó	1
17186	retumbantes	1
17187	retumban	1
17188	retumbado	1
17189	retumbaban	1
17190	retumbaba	1
17191	retuerce	1
17192	retrogradaba	1
17193	retratarse	1
17194	retratar	1
17195	retratada	1
17196	retrataaar	1
17197	retrasar	1
17198	retrasados	1
17199	retrasada	1
17200	retrasaba	1
17201	retraimiento	1
17202	retraerse	1
17203	retozos	1
17204	retortijado	1
17205	retortero	1
17206	retorta	1
17207	retóricos	1
17208	retórica	1
17209	retorciendo	1
17210	retorcidos	1
17211	retorcidas	1
17212	retorcía	1
17213	retorcedura	1
17214	retor	1
17215	retoñado	1
17216	retocando	1
17217	reto	1
17218	retires	1
17219	retiré	1
17220	retire	1
17221	retirase	1
17222	retirarlos	1
17223	retirarle	1
17224	retiraran	1
17225	retirándolo	1
17226	retirando	1
17227	retiradamente	1
17228	retirábase	1
17229	retiraban	1
17230	retina	1
17231	reticencias	1
17232	reteniéndole	1
17233	reteniéndola	1
17234	retenido	1
17235	retenían	1
17236	retenerlo	1
17237	retenerle	1
17238	retención	1
17239	retemblar	1
17240	retazos	1
17241	retardaba	1
17242	retaba	1
17243	resurgía	1
17244	resumen	1
17245	resultole	1
17246	resultasen	1
17247	resultase	1
17248	resultarle	1
17249	resultará	1
17250	resultara	1
17251	resultar	1
17252	resultan	1
17253	resuelven	1
17254	resuelva	1
17255	resueltos	1
17256	resuella	1
17257	resucitara	1
17258	resucitar	1
17259	resucitan	1
17260	resucitado	1
17261	restregón	1
17262	restregó	1
17263	restregáronle	1
17264	restregado	1
17265	restregaba	1
17266	restaurar	1
17267	restaurant	1
17268	restauradas	1
17269	restauraba	1
17270	restañaba	1
17271	restantes	1
17272	restallaban	1
17273	restablecimiento	1
17274	restablecido	1
17275	restablecer	1
17276	restaba	1
17277	resta	1
17278	resquebrajaba	1
17279	responso	1
17280	responsabilidades	1
17281	respondona	1
17282	respondiome	1
17283	respondieran	1
17284	respondiera	1
17285	respondiéndome	1
17286	respondiéndole	1
17287	respondería	1
17288	respóndame	1
17289	resplandores	1
17290	resplandeció	1
17291	resplandecientes	1
17292	resplandeciendo	1
17293	resplandecían	1
17294	respirase	1
17295	respiraron	1
17296	respirado	1
17297	respiraderos	1
17298	respirable	1
17299	respingar	1
17300	respingados	1
17301	respingadas	1
17302	réspices	1
17303	respetuosos	1
17304	respetuosamente	1
17305	respetosa	1
17306	respéteme	1
17307	respete	1
17308	respetaran	1
17309	respetado	1
17310	respetad	1
17311	respetabilísimo	1
17312	respetabilísimas	1
17313	respetaba	1
17314	respeta	1
17315	resortes	1
17316	resorte	1
17317	resoplido	1
17318	resonarán	1
17319	resonar	1
17320	resonantes	1
17321	resonaban	1
17322	resonaba	1
17323	resolvimos	1
17324	resolviéndose	1
17325	resolviendo	1
17326	resolvíase	1
17327	resolvía	1
17328	resolverse	1
17329	resolverlos	1
17330	resolverlo	1
17331	resolverá	1
17332	resoluciones	1
17333	resobándose	1
17334	resobado	1
17335	resobaba	1
17336	resma	1
17337	resisto	1
17338	resistirlo	1
17339	resistió	1
17340	resistiese	1
17341	resistieras	1
17342	resistiera	1
17343	resistiendo	1
17344	resistido	1
17345	resistes	1
17346	resistente	1
17347	resistencias	1
17348	resisten	1
17349	resinas	1
17350	resigne	1
17351	resignado	1
17352	resignadas	1
17353	resido	1
17354	residían	1
17355	residía	1
17356	reside	1
17357	resguardo	1
17358	resguardar	1
17359	reses	1
17360	reservo	1
17361	reservas	1
17362	reservarse	1
17363	reservarle	1
17364	reservando	1
17365	reservadísimo	1
17366	resentirse	1
17367	resentimiento	1
17368	reselles	1
17369	resecaban	1
17370	rescoldo	1
17371	resbalón	1
17372	resbalar	1
17373	resbalan	1
17374	resbaladiza	1
17375	resbalaban	1
17376	resaltar	1
17377	resalao	1
17378	requisito	1
17379	requetefinas	1
17380	requesón	1
17381	requerido	1
17382	requería	1
17383	requemo	1
17384	requemado	1
17385	requejo	1
17386	reputados	1
17387	reputaban	1
17388	repuntaba	1
17389	repulsión	1
17390	repulgos	1
17391	repulgo	1
17392	repugnaría	1
17393	repúblicas	1
17394	republicanismo	1
17395	reprodujeron	1
17396	reprodujera	1
17397	reproducir	1
17398	reproduciéndose	1
17399	reproduciéndolo	1
17400	reproduciendo	1
17401	reproducídose	1
17402	reproducidas	1
17403	reprobación	1
17404	reprobables	1
17405	reprimir	1
17406	represente	1
17407	representaron	1
17408	representando	1
17409	representan	1
17410	representaciones	1
17411	reprensión	1
17412	reprendieran	1
17413	reprenderla	1
17414	reprenden	1
17415	repreciosa	1
17416	repostero	1
17417	reposada	1
17418	reponiéndose	1
17419	reponiendo	1
17420	reponerte	1
17421	repoblicanas	1
17422	repliegue	1
17423	repliégate	1
17424	repitiese	1
17425	repitiéndose	1
17426	repitiéndole	1
17427	repítelas	1
17428	repiques	1
17429	repique	1
17430	repicando	1
17431	repetírselo	1
17432	repetido	1
17433	repentina	1
17434	repasó	1
17435	repasando	1
17436	repasaba	1
17437	repartirse	1
17438	repartiría	1
17439	repartido	1
17440	repartidas	1
17441	repartían	1
17442	repartía	1
17443	reparta	1
17444	reparona	1
17445	repares	1
17446	reparatrices	1
17447	repararía	1
17448	reparando	1
17449	reparaba	1
17450	repara	1
17451	repantigado	1
17452	reñían	1
17453	renuncia	1
17454	rentita	1
17455	renovó	1
17456	renovase	1
17457	renovará	1
17458	renovaciones	1
17459	renovaban	1
17460	renovaba	1
17461	rengloncito	1
17462	renegó	1
17463	rendirle	1
17464	rendir	1
17465	rendidísimo	1
17466	rendidísima	1
17467	rendía	1
17468	rencoroso	1
17469	rencorosa	1
17470	rencores	1
17471	rencorcillo	1
17472	renacimiento	1
17473	renacía	1
17474	remuerde	1
17475	removió	1
17476	removieran	1
17477	removía	1
17478	remotísimo	1
17479	remotamente	1
17480	remos	1
17481	remontó	1
17482	remontarme	1
17483	remontabas	1
17484	remontaba	1
17485	remonona	1
17486	remolque	1
17487	remolcándola	1
17488	remitiese	1
17489	remitidas	1
17490	remitía	1
17491	remite	1
17492	reminiscencias	1
17493	remilgadas	1
17494	remilgada	1
17495	remiendo	1
17496	remesa	1
17497	remendarla	1
17498	remendada	1
17499	remedos	1
17500	remedo	1
17501	remedie	1
17502	remediarlo	1
17503	remediaban	1
17504	remedando	1
17505	remeda	1
17506	remataron	1
17507	rematar	1
17508	rematados	1
17509	rematadas	1
17510	remataban	1
17511	remala	1
17512	remadera	1
17513	remachando	1
17514	relumbrones	1
17515	relumbrón	1
17516	relumbrantes	1
17517	relumbrante	1
17518	relucían	1
17519	relojero	1
17520	relojería	1
17521	reliquias	1
17522	relevase	1
17523	relevado	1
17524	relatos	1
17525	relatando	1
17526	relataba	1
17527	relampagueaban	1
17528	relamiendo	1
17529	relamida	1
17530	relámete	1
17531	relamerse	1
17532	relajadas	1
17533	relacionase	1
17534	relacionara	1
17535	relacionado	1
17536	relacionaban	1
17537	relacionaba	1
17538	relaciona	1
17539	rejuvenece	1
17540	reiterándole	1
17541	reiterando	1
17542	reiteradas	1
17543	reíros	1
17544	reirías	1
17545	reirían	1
17546	reiré	1
17547	reirás	1
17548	reintegraría	1
17549	reinos	1
17550	reinó	1
17551	reincidir	1
17552	reincidente	1
17553	reinara	1
17554	reímos	1
17555	reíase	1
17556	reíanse	1
17557	reíamos	1
17558	reí	1
17559	rehusaron	1
17560	rehuir	1
17561	rehuido	1
17562	rehecho	1
17563	rehacerse	1
17564	rehacer	1
17565	regulares	1
17566	reguapa	1
17567	regresar	1
17568	regresaba	1
17569	regresa	1
17570	regrande	1
17571	regordete	1
17572	regocijar	1
17573	regocijándose	1
17574	regocijadas	1
17575	regocijada	1
17576	reglamentario	1
17577	registraremos	1
17578	registrado	1
17579	regimientos	1
17580	regenerarte	1
17581	regenerarlas	1
17582	regenerada	1
17583	regeneraciones	1
17584	regeneraba	1
17585	regateando	1
17586	regateaba	1
17587	regar	1
17588	regaños	1
17589	regañona	1
17590	regañó	1
17591	regaño	1
17592	regañar	1
17593	regando	1
17594	regalona	1
17595	regaló	1
17596	regalé	1
17597	regalarte	1
17598	regaláronle	1
17599	regaláramos	1
17600	regalado	1
17601	regalaba	1
17602	regaderas	1
17603	regaba	1
17604	refutara	1
17605	refunfuños	1
17606	refunfuñas	1
17607	refunfuñan	1
17608	refundiéndose	1
17609	refundida	1
17610	refulgentes	1
17611	refugió	1
17612	refugiarse	1
17613	refuerzo	1
17614	refrescar	1
17615	refrescan	1
17616	refrénate	1
17617	refrenase	1
17618	refrenarse	1
17619	refrenar	1
17620	refregones	1
17621	refregarte	1
17622	refregar	1
17623	refractario	1
17624	reforme	1
17625	reformase	1
17626	reformar	1
17627	reformada	1
17628	reflexivo	1
17629	reflexiva	1
17630	reflexiono	1
17631	reflexionaba	1
17632	reflejándose	1
17633	reflejábase	1
17634	reflejaba	1
17635	refiriéndose	1
17636	refirencias	1
17637	refinarlos	1
17638	refinar	1
17639	refinamientos	1
17640	refinada	1
17641	refiérome	1
17642	refiera	1
17643	referirle	1
17644	referirían	1
17645	referido	1
17646	referían	1
17647	referencias	1
17648	referencia	1
17649	refeos	1
17650	refectorio	1
17651	reductos	1
17652	reducirlo	1
17653	reduciéndose	1
17654	reducidos	1
17655	reducidas	1
17656	reducen	1
17657	redondel	1
17658	redondear	1
17659	redondeado	1
17660	redondas	1
17661	redoblar	1
17662	redentorista	1
17663	redenciones	1
17664	redaño	1
17665	redactar	1
17666	redactada	1
17667	recuento	1
17668	rectos	1
17669	rectilíneas	1
17670	rectificó	1
17671	recrudecimiento	1
17672	recreábase	1
17673	recreaban	1
17674	recrea	1
17675	recostase	1
17676	recostaba	1
17677	recortaran	1
17678	recortándolo	1
17679	recortadas	1
17680	recortaba	1
17681	recorta	1
17682	recorrieron	1
17683	recorren	1
17684	recordase	1
17685	recordarme	1
17686	recordarás	1
17687	reconstruí	1
17688	reconstituyentes	1
17689	reconozca	1
17690	reconocidos	1
17691	reconocida	1
17692	reconocían	1
17693	reconoces	1
17694	reconocerlo	1
17695	reconocerlas	1
17696	reconoceremos	1
17697	reconocerá	1
17698	reconocen	1
17699	recondenada	1
17700	reconciliémonos	1
17701	reconciliaron	1
17702	reconciliar	1
17703	reconciliado	1
17704	reconciliaciones	1
17705	reconciliábamos	1
17706	reconcilia	1
17707	reconcentrado	1
17708	recomponía	1
17709	recompensaba	1
17710	recompensa	1
17711	recomiendan	1
17712	recomendé	1
17713	recomendando	1
17714	recomendados	1
17715	recomendadas	1
17716	recomendada	1
17717	recomendables	1
17718	recoletos	1
17719	recojo	1
17720	recoja	1
17721	recogiéndolo	1
17722	recogiéndole	1
17723	recogían	1
17724	recogerlos	1
17725	recogerlo	1
17726	recogerlas	1
17727	recogeremos	1
17728	recogeré	1
17729	recogerá	1
17730	recobrada	1
17731	recoba	1
17732	reclinó	1
17733	reclinatorios	1
17734	reclinado	1
17735	reclinada	1
17736	reclamarlo	1
17737	reclamará	1
17738	reclamando	1
17739	reclamado	1
17740	reclamaba	1
17741	recios	1
17742	recio	1
17743	recientes	1
17744	recibirme	1
17745	recibirle	1
17746	recibirás	1
17747	recibiome	1
17748	recibidas	1
17749	recibías	1
17750	recíbele	1
17751	rechupidos	1
17752	rechupete	1
17753	rechupando	1
17754	rechupado	1
17755	rechinando	1
17756	rechinaba	1
17757	rechina	1
17758	rechazó	1
17759	rechazara	1
17760	rechazándola	1
17761	rechazada	1
17762	rechacemos	1
17763	recetó	1
17764	recetaría	1
17765	recetábale	1
17766	recelos	1
17767	rece	1
17768	recayó	1
17769	recayese	1
17770	recayera	1
17771	recaudados	1
17772	recaudador	1
17773	recaudación	1
17774	recatarse	1
17775	recatándose	1
17776	recatado	1
17777	recargaba	1
17778	recapacitando	1
17779	recalentaban	1
17780	recalcar	1
17781	recaída	1
17782	recaía	1
17783	recaen	1
17784	recae	1
17785	recaditos	1
17786	rebuznó	1
17787	rebuznar	1
17788	rebusque	1
17789	rebuscó	1
17790	rebuscada	1
17791	rebuscaba	1
17792	rebullir	1
17793	rebullicio	1
17794	rebulle	1
17795	rebosaban	1
17796	rebosa	1
17797	reblandeció	1
17798	reblandecimiento	1
17799	rebeló	1
17800	rebelarse	1
17801	rebelaba	1
17802	rebeca	1
17803	rebasaron	1
17804	rebasados	1
17805	rebañaba	1
17806	rebaña	1
17807	rebanada	1
17808	rebajes	1
17809	rebajase	1
17810	rebajarse	1
17811	rebajaremos	1
17812	rebajar	1
17813	rebajado	1
17814	rebajada	1
17815	rebaja	1
17816	reapertura	1
17817	reapareció	1
17818	reaparecieron	1
17819	reaparecer	1
17820	reaparecen	1
17821	reanudar	1
17822	reanimaba	1
17823	realizarlos	1
17824	realizarla	1
17825	realizaría	1
17826	realizara	1
17827	realizado	1
17828	realizadas	1
17829	realizada	1
17830	realización	1
17831	realito	1
17832	realista	1
17833	realice	1
17834	realetes	1
17835	reacciones	1
17836	razonando	1
17837	razonamientos	1
17838	razonador	1
17839	razonables	1
17840	razona	1
17841	rayuela	1
17842	rayana	1
17843	rayaditas	1
17844	rayaba	1
17845	raudo	1
17846	raudales	1
17847	ratoncillo	1
17848	ratifico	1
17849	ratera	1
17850	rastros	1
17851	rastrear	1
17852	rásquese	1
17853	rasque	1
17854	raspe	1
17855	raspándolo	1
17856	rasos	1
17857	rasguñaban	1
17858	rasgueo	1
17859	rasguear	1
17860	rasgueando	1
17861	rasgar	1
17862	rascarse	1
17863	rascándose	1
17864	rascan	1
17865	ráscame	1
17866	rarificaciones	1
17867	rarezas	1
17868	raquitismo	1
17869	raquíticos	1
17870	rápidos	1
17871	rapé	1
17872	rapazuelo	1
17873	raparte	1
17874	rapadas	1
17875	rapada	1
17876	rapacidad	1
17877	ranero	1
17878	randas	1
17879	rancios	1
17880	rancias	1
17881	ranas	1
17882	rana	1
17883	ramplona	1
17884	rampas	1
17885	rampa	1
17886	ramona	1
17887	ramojo	1
17888	ramilletes	1
17889	rameados	1
17890	rameaditas	1
17891	ramalazo	1
17892	rallando	1
17893	ralea	1
17894	rajada	1
17895	raja	1
17896	raíz	1
17897	raída	1
17898	raíces	1
17899	radio	1
17900	radicalmente	1
17901	radical	1
17902	radicaba	1
17903	racionó	1
17904	racionarse	1
17905	racionarnos	1
17906	racionalistas	1
17907	racionales	1
17908	raciocinios	1
17909	rabos	1
17910	rabito	1
17911	rabiosito	1
17912	rabiosilla	1
17913	rabillo	1
17914	rabietinas	1
17915	rabiará	1
17916	rabiaba	1
17917	rabeles	1
17918	rabel	1
17919	r	1
17920	quo	1
17921	quitósele	1
17922	quitole	1
17923	quites	1
17924	quíteme	1
17925	quité	1
17926	quitas	1
17927	quitárselas	1
17928	quitáronle	1
17929	quitármelo	1
17930	quitármela	1
17931	quitarme	1
17932	quitarlos	1
17933	quitarlo	1
17934	quitaría	1
17935	quitaré	1
17936	quitaran	1
17937	quitaos	1
17938	quitándome	1
17939	quitamos	1
17940	quítale	1
17941	quitádmelo	1
17942	quisto	1
17943	quisquilloso	1
17944	quisieren	1
17945	quisierais	1
17946	quirúrgicamente	1
17947	quiquiriquí	1
17948	quintín	1
17949	quintillas	1
17950	quintero	1
17951	quintas	1
17952	quintal	1
17953	quinina	1
17954	quinientas	1
17955	quincalla	1
17956	quina	1
17957	químicos	1
17958	químico	1
17959	quilo	1
17960	quijotesco	1
17961	quijadas	1
17962	quietos	1
17963	quietas	1
17964	quieles	1
17965	quiebros	1
17966	quiebras	1
17967	quiebran	1
17968	queso	1
17969	quesitos	1
17970	quesada	1
17971	querrás	1
17972	querrán	1
17973	queriéndome	1
17974	queriéndole	1
17975	queriéndola	1
17976	queridos	1
17977	queridísimos	1
17978	queridísimo	1
17979	querenciosa	1
17980	querencias	1
17981	queramos	1
17982	querámonos	1
17983	quepan	1
17984	queme	1
17985	quemazón	1
17986	quemasteis	1
17987	quemaron	1
17988	quemándose	1
17989	quemando	1
17990	quejumbroso	1
17991	quejo	1
17992	quejáronse	1
17993	quejarás	1
17994	quejar	1
17995	quejando	1
17996	quejamos	1
17997	quejado	1
17998	quedeme	1
17999	quedaste	1
18000	quedasen	1
18001	quedarías	1
18002	quedarás	1
18003	quedaran	1
18004	quedaos	1
18005	quedábamos	1
18006	quebrantar	1
18007	quebrantado	1
18008	quebrantadas	1
18009	qartos	1
18010	putrefacción	1
18011	putona	1
18012	putativa	1
18013	púsolos	1
18014	púsole	1
18015	pusimos	1
18016	pusiéronla	1
18017	púseme	1
18018	purito	1
18019	purísimo	1
18020	purísimas	1
18021	purificarla	1
18022	purificará	1
18023	purificado	1
18024	purificada	1
18025	purga	1
18026	purezas	1
18027	purés	1
18028	pupilas	1
18029	puñetazos	1
18030	puñales	1
18031	puñado	1
18032	punzón	1
18033	punzantes	1
18034	punzadora	1
18035	puntualísimo	1
18036	puntualidades	1
18037	puntillosa	1
18038	puntilla	1
18039	puntiagudos	1
18040	puntear	1
18041	punteados	1
18042	puntapiés	1
18043	puntadas	1
18044	puntada	1
18045	pundonorosas	1
18046	pulverizo	1
18047	pulverizado	1
18048	pulverizadas	1
18049	pulsera	1
18050	pulsaciones	1
18051	pulsación	1
18052	pulpejo	1
18053	pulpa	1
18054	pulmonías	1
18055	pulirse	1
18056	pulimentado	1
18057	puliéndola	1
18058	puliendo	1
18059	pulgares	1
18060	pulgar	1
18061	pulgada	1
18062	pulcra	1
18063	pujanza	1
18064	pujante	1
18065	pugilato	1
18066	puertecilla	1
18067	puerquísima	1
18068	puerilidad	1
18069	puercos	1
18070	puercas	1
18071	puercachones	1
18072	pueblecitos	1
18073	pudre	1
18074	pudiste	1
18075	pudimos	1
18076	pudieras	1
18077	pucheta	1
18078	pucheritos	1
18079	pucherito	1
18080	públicos	1
18081	publicó	1
18082	publicista	1
18083	publicarlos	1
18084	publicantones	1
18085	publicanos	1
18086	publicaban	1
18087	publicaba	1
18088	publica	1
18089	psch	1
18090	pruuun	1
18091	prum	1
18092	pruebo	1
18093	prueban	1
18094	prudhonianas	1
18095	prudentes	1
18096	prudencial	1
18097	proyectiles	1
18098	proyectando	1
18099	proyectan	1
18100	proyectado	1
18101	proyección	1
18102	provocó	1
18103	provocada	1
18104	provisto	1
18105	provino	1
18106	provincianos	1
18107	provincial	1
18108	provenirle	1
18109	provenir	1
18110	provenido	1
18111	provenían	1
18112	provendrá	1
18113	proveía	1
18114	provechosos	1
18115	provechosas	1
18116	protoioduro	1
18117	protestas	1
18118	protestaron	1
18119	protestamos	1
18120	protejo	1
18121	proteja	1
18122	protegiéndole	1
18123	protegidos	1
18124	protegido	1
18125	protegerte	1
18126	protegerle	1
18127	protegería	1
18128	protegeré	1
18129	protegerá	1
18130	protegen	1
18131	protectoras	1
18132	proteccionistas	1
18133	protecciones	1
18134	prostituyese	1
18135	prosterne	1
18136	prospera	1
18137	prosiguieron	1
18138	prosiguiendo	1
18139	prosélitos	1
18140	proscenio	1
18141	prosa	1
18142	prorrumpió	1
18143	prorrumpieron	1
18144	prórrogas	1
18145	propusimos	1
18146	propusieran	1
18147	propuse	1
18148	proporcionó	1
18149	proporcionase	1
18150	proporcionales	1
18151	proporcionado	1
18152	proporcionadamente	1
18153	proporcionada	1
18154	proporcionábale	1
18155	proporcionaba	1
18156	proporciona	1
18157	proponiéndose	1
18158	proponiendo	1
18159	propongámosla	1
18160	propongamos	1
18161	propones	1
18162	proponerte	1
18163	proponérselo	1
18164	proponerse	1
18165	proponerles	1
18166	proponerle	1
18167	propónense	1
18168	propinó	1
18169	propinilla	1
18170	propinas	1
18171	propina	1
18172	propicios	1
18173	propicia	1
18174	propenso	1
18175	propensa	1
18176	propendían	1
18177	propalar	1
18178	propague	1
18179	propagar	1
18180	pronunció	1
18181	pronunciaron	1
18182	pronunciarlo	1
18183	pronunciara	1
18184	pronunciándolas	1
18185	pronuncian	1
18186	pronunciadas	1
18187	pronunciaban	1
18188	pronuncia	1
18189	prontos	1
18190	prontísimo	1
18191	pronósticos	1
18192	pronosticando	1
18193	promulgando	1
18194	promulga	1
18195	promontorio	1
18196	prominentes	1
18197	prometiste	1
18198	prometiéndole	1
18199	prometida	1
18200	prometíaselas	1
18201	prometer	1
18202	promete	1
18203	prolongarse	1
18204	prolongando	1
18205	prolongado	1
18206	prolongaba	1
18207	prolonga	1
18208	prolijidad	1
18209	prolijamente	1
18210	prolífica	1
18211	prójimas	1
18212	proive	1
18213	prohijar	1
18214	prohibió	1
18215	prohibiciones	1
18216	prohibición	1
18217	prohibía	1
18218	prohibí	1
18219	prohíben	1
18220	prohíbe	1
18221	progresos	1
18222	progresivo	1
18223	progresistón	1
18224	progresistas	1
18225	progresado	1
18226	progenie	1
18227	profundísimamente	1
18228	profundidad	1
18229	profetizaron	1
18230	profeta	1
18231	profesora	1
18232	profesionales	1
18233	profesando	1
18234	profesaban	1
18235	profano	1
18236	profanidad	1
18237	profanar	1
18238	profana	1
18239	proezas	1
18240	prodújose	1
18241	produjeron	1
18242	produjera	1
18243	productores	1
18244	producto	1
18245	producirlos	1
18246	producirán	1
18247	produciéndose	1
18248	producidos	1
18249	producidas	1
18250	producíase	1
18251	prodrómico	1
18252	prodigole	1
18253	pródigo	1
18254	prodigioso	1
18255	prodigar	1
18256	prodigándole	1
18257	prodigando	1
18258	prodigaban	1
18259	prodigaba	1
18260	procuró	1
18261	procuro	1
18262	procuremos	1
18263	procure	1
18264	procurarle	1
18265	procuraré	1
18266	procurará	1
18267	procura	1
18268	proclamas	1
18269	proclamar	1
18270	prócida	1
18271	procesionalmente	1
18272	proceroso	1
18273	procediera	1
18274	procedentes	1
18275	procede	1
18276	procedamos	1
18277	procaz	1
18278	procacidad	1
18279	probrecilla	1
18280	probeza	1
18281	probes	1
18282	probe	1
18283	probártelo	1
18284	probarla	1
18285	probaría	1
18286	probaran	1
18287	probará	1
18288	probadas	1
18289	pro	1
18290	privar	1
18291	privándose	1
18292	privándole	1
18293	privadas	1
18294	prismática	1
18295	prisma	1
18296	prisiones	1
18297	prisioneros	1
18298	prisionero	1
18299	pringado	1
18300	pringadas	1
18301	principiar	1
18302	príncipes	1
18303	primos	1
18304	primordial	1
18305	primito	1
18306	primita	1
18307	primeramente	1
18308	primarias	1
18309	primaria	1
18310	price	1
18311	previstos	1
18312	previsora	1
18313	previas	1
18314	previa	1
18315	preventivo	1
18316	prevenirlo	1
18317	prevenidos	1
18318	prevenida	1
18319	prevenciones	1
18320	preveía	1
18321	prevaricaban	1
18322	prevalecido	1
18323	prevalecer	1
18324	prevalece	1
18325	pretérita	1
18326	pretensión	1
18327	pretendiera	1
18328	pretenderás	1
18329	presunta	1
18330	presumiera	1
18331	presumes	1
18332	prestigio	1
18333	prestidigitador	1
18334	prestidigitaciones	1
18335	prestaros	1
18336	prestarle	1
18337	prestara	1
18338	prestándole	1
18339	prestamistas	1
18340	prestaban	1
18341	presta	1
18342	presona	1
18343	presientes	1
18344	presienten	1
18345	presidir	1
18346	presidios	1
18347	presidieran	1
18348	presidiendo	1
18349	presidida	1
18350	presidiarios	1
18351	presidiario	1
18352	presidencial	1
18353	presidencia	1
18354	preservativo	1
18355	presentido	1
18356	preséntate	1
18357	presentársele	1
18358	presentáronse	1
18359	presentarles	1
18360	presentándose	1
18361	presentándole	1
18362	presentándola	1
18363	presentados	1
18364	presentación	1
18365	presenció	1
18366	presencié	1
18367	presenciaron	1
18368	presenciara	1
18369	presencian	1
18370	prescrito	1
18371	prescindir	1
18372	presbíteros	1
18373	presbiterio	1
18374	presagiar	1
18375	preparo	1
18376	preparen	1
18377	preparé	1
18378	preparatorias	1
18379	preparase	1
18380	prepararon	1
18381	prepararla	1
18382	prepararemos	1
18383	preparándose	1
18384	preparándole	1
18385	preparábase	1
18386	preparaban	1
18387	preocuparse	1
18388	preocupado	1
18389	preocupación	1
18390	prendió	1
18391	prendiendo	1
18392	prendidas	1
18393	prender	1
18394	prendarse	1
18395	prendara	1
18396	prendaba	1
18397	premiten	1
18398	premite	1
18399	premiso	1
18400	premiados	1
18401	prematuro	1
18402	preliminares	1
18403	prejuicios	1
18404	preguntonas	1
18405	preguntome	1
18406	preguntitas	1
18407	pregúnteselo	1
18408	pregúntenle	1
18409	pregunten	1
18410	preguntárselo	1
18411	preguntársela	1
18412	preguntaron	1
18413	preguntarme	1
18414	preguntarlo	1
18415	preguntaría	1
18416	preguntará	1
18417	preguntándose	1
18418	preguntábamos	1
18419	pregone	1
18420	pregonaba	1
18421	prefiere	1
18422	prefieras	1
18423	preferiremos	1
18424	preferir	1
18425	preferible	1
18426	predisposición	1
18427	predilecta	1
18428	predicó	1
18429	predico	1
18430	predicara	1
18431	predicador	1
18432	predicaba	1
18433	predestinados	1
18434	predecesores	1
18435	predecesoras	1
18436	precursoras	1
18437	precozmente	1
18438	precocidad	1
18439	precisos	1
18440	precisión	1
18441	precisar	1
18442	precipites	1
18443	precipitada	1
18444	precipitaba	1
18445	precipicio	1
18446	preciosísimos	1
18447	preciosas	1
18448	preciábase	1
18449	precepto	1
18450	preceder	1
18451	precedente	1
18452	precede	1
18453	práxedes	1
18454	pragmáticas	1
18455	pragmática	1
18456	pradoluengo	1
18457	praderas	1
18458	practico	1
18459	practicarla	1
18460	practicantes	1
18461	practicando	1
18462	practicado	1
18463	practicadas	1
18464	practicable	1
18465	practica	1
18466	potingues	1
18467	potingue	1
18468	potestad	1
18469	potes	1
18470	potente	1
18471	potentadas	1
18472	potentada	1
18473	potasio	1
18474	póstuma	1
18475	postrimerías	1
18476	postrado	1
18477	postizas	1
18478	poste	1
18479	postal	1
18480	posta	1
18481	positivo	1
18482	positivas	1
18483	positivamente	1
18484	posiciones	1
18485	posesionarían	1
18486	poseo	1
18487	poseído	1
18488	poseída	1
18489	poseerte	1
18490	poseerlo	1
18491	poseedora	1
18492	posea	1
18493	posarle	1
18494	posadas	1
18495	portugal	1
18496	portentos	1
18497	portear	1
18498	porte	1
18499	portazos	1
18500	portazo	1
18501	portas	1
18502	portarte	1
18503	portarnos	1
18504	portan	1
18505	portamos	1
18506	portabas	1
18507	porra	1
18508	pormenor	1
18509	porfiado	1
18510	porfiaba	1
18511	pordiosero	1
18512	pordioseaba	1
18513	porcelanescas	1
18514	poquitos	1
18515	poquita	1
18516	poquísimos	1
18517	poquísimas	1
18518	popularidad	1
18519	ponzoñoso	1
18520	pontevedra	1
18521	ponle	1
18522	poniéndoselos	1
18523	poniéndola	1
18524	poníasele	1
18525	ponías	1
18526	poníala	1
18527	pongámosle	1
18528	pongámonos	1
18529	póngalo	1
18530	ponérteme	1
18531	ponérsela	1
18532	ponérmela	1
18533	ponerles	1
18534	ponéis	1
18535	ponedla	1
18536	pondrías	1
18537	pondrían	1
18538	pondríamos	1
18539	ponderarle	1
18540	ponderando	1
18541	ponderaciones	1
18542	ponderaban	1
18543	ponderaba	1
18544	poncio	1
18545	ponchera	1
18546	pómulos	1
18547	pompones	1
18548	pómez	1
18549	pomada	1
18550	polvorosos	1
18551	polvorosa	1
18552	polvorienta	1
18553	polvillo	1
18554	polluela	1
18555	pollita	1
18556	pollino	1
18557	polleros	1
18558	pollerías	1
18559	pollera	1
18560	polka	1
18561	polizonte	1
18562	politicastros	1
18563	polinesia	1
18564	policiacos	1
18565	policíaca	1
18566	polichinela	1
18567	polemista	1
18568	polémicas	1
18569	poético	1
18570	poesías	1
18571	poemas	1
18572	podrido	1
18573	podridas	1
18574	podredumbre	1
18575	podíamos	1
18576	poderse	1
18577	poderme	1
18578	poderle	1
18579	podamos	1
18580	poción	1
18581	pócima	1
18582	pocillo	1
18583	pocilga	1
18584	pobrísima	1
18585	pobrete	1
18586	pobrecitas	1
18587	pobrecillas	1
18588	poblaciones	1
18589	poblaban	1
18590	plumonía	1
18591	plumear	1
18592	plumacho	1
18593	plomizas	1
18594	plim	1
18595	pliegue	1
18596	pliego	1
18597	pléyade	1
18598	pleticó	1
18599	pleticar	1
18600	plenipotenciario	1
18601	pleitos	1
18602	pléiticas	1
18603	pleitazo	1
18604	platónicas	1
18605	platónica	1
18606	platicando	1
18607	platica	1
18608	platero	1
18609	platería	1
18610	plateado	1
18611	plateadas	1
18612	plateada	1
18613	plataformas	1
18614	plasta	1
18615	plañidera	1
18616	plantilla	1
18617	plantifiquen	1
18618	planteo	1
18619	plantear	1
18620	planteándole	1
18621	planteado	1
18622	planteaba	1
18623	plantea	1
18624	plantársele	1
18625	plantaron	1
18626	plantarme	1
18627	plantaremos	1
18628	plantándose	1
18629	plantada	1
18630	plantaba	1
18631	planos	1
18632	planicie	1
18633	planeta	1
18634	planche	1
18635	planchas	1
18636	planchándole	1
18637	planchado	1
18638	planchaba	1
18639	plaga	1
18640	placita	1
18641	placidito	1
18642	placeros	1
18643	placenteros	1
18644	placentero	1
18645	place	1
18646	placa	1
18647	pizarras	1
18648	pizarra	1
18649	pitusiana	1
18650	pituitaria	1
18651	pitos	1
18652	pitón	1
18653	pitoja	1
18654	pitofufito	1
18655	pitita	1
18656	pítima	1
18657	pitillo	1
18658	pitidos	1
18659	pitarás	1
18660	pitanza	1
18661	pitágoras	1
18662	pita	1
18663	pistos	1
18664	pisotearla	1
18665	pisoteado	1
18666	pisotea	1
18667	piscicultura	1
18668	pisas	1
18669	pisárselas	1
18670	pisándose	1
18671	pisándoles	1
18672	pisaba	1
18673	piruétano	1
18674	pirra	1
18675	pirineo	1
18676	piratería	1
18677	piratas	1
18678	pira	1
18679	piquito	1
18680	piques	1
18681	pique	1
18682	pior	1
18683	piojosa	1
18684	piñones	1
18685	pintorescos	1
18686	pintiparada	1
18687	pintarlas	1
18688	pintándose	1
18689	pintaban	1
18690	pinta	1
18691	pinos	1
18692	pinitos	1
18693	pingües	1
18694	pingajo	1
18695	pindonga	1
18696	pinchase	1
18697	pinchamos	1
18698	pinchacitos	1
18699	pinceles	1
18700	pincelada	1
18701	pincel	1
18702	pinares	1
18703	pináculo	1
18704	pin	1
18705	pimpollos	1
18706	pimientos	1
18707	piltrafas	1
18708	piltrafa	1
18709	pilosa	1
18710	pilluelos	1
18711	pillines	1
18712	pillincito	1
18713	pillinadas	1
18714	pille	1
18715	pillastres	1
18716	pilatos	1
18717	pilastrones	1
18718	pila	1
18719	pignoró	1
18720	pignorado	1
18721	pifias	1
18722	pifia	1
18723	piernazas	1
18724	pierdas	1
18725	pierdan	1
18726	piensen	1
18727	piensasté	1
18728	piedrecita	1
18729	piececitas	1
18730	pidiéronle	1
18731	pidieron	1
18732	pidieras	1
18733	pidieran	1
18734	pidiéndole	1
18735	pídeselo	1
18736	pídele	1
18737	pidas	1
18738	pidan	1
18739	pidámosle	1
18740	picorcillo	1
18741	picó	1
18742	pichoncitos	1
18743	pichona	1
18744	picazón	1
18745	picas	1
18746	pícaros	1
18747	picaronaza	1
18748	picará	1
18749	picaporte	1
18750	picapedreros	1
18751	pican	1
18752	picadura	1
18753	picadilly	1
18754	picadillo	1
18755	piazo	1
18756	pianino	1
18757	pianillo	1
18758	pian	1
18759	piadosos	1
18760	piache	1
18761	pía	1
18762	petrificada	1
18763	petrarca	1
18764	petitorio	1
18765	petimetres	1
18766	petaba	1
18767	pestilencia	1
18768	pestífera	1
18769	pesquisas	1
18770	pespuntar	1
18771	pesimista	1
18772	pésemelo	1
18773	pesebre	1
18774	pescuezos	1
18775	pesco	1
18776	pescadilla	1
18777	pescaban	1
18778	pescaba	1
18779	pesase	1
18780	pesadumbres	1
18781	pesadita	1
18782	pesadísima	1
18783	pesaban	1
18784	pervertírsele	1
18785	pervertir	1
18786	pervertimos	1
18787	perversas	1
18788	perturbe	1
18789	perturbase	1
18790	perturbar	1
18791	perturbado	1
18792	perturbadas	1
18793	perturbaciones	1
18794	perturbaba	1
18795	pertinencia	1
18796	pertenezco	1
18797	pertenecí	1
18798	pertenecer	1
18799	pertenecen	1
18800	persuasivas	1
18801	persuadirle	1
18802	persuadí	1
18803	perspectivas	1
18804	personó	1
18805	personificado	1
18806	personificaba	1
18807	personarse	1
18808	personaron	1
18809	personalizar	1
18810	personalizando	1
18811	personalidá	1
18812	persistió	1
18813	persistieron	1
18814	persistían	1
18815	persistía	1
18816	persistentes	1
18817	persiste	1
18818	persiguió	1
18819	persiguiéndole	1
18820	persiguen	1
18821	persignó	1
18822	persiga	1
18823	perseverando	1
18824	persépolis	1
18825	perseguirte	1
18826	perseguidora	1
18827	perseguían	1
18828	persecutorio	1
18829	perruna	1
18830	perrería	1
18831	perrazo	1
18832	perras	1
18833	perpleja	1
18834	perpiñá	1
18835	perpetuo	1
18836	perpetuidad	1
18837	perpetuase	1
18838	perpetuarse	1
18839	pernoctar	1
18840	perniquiebres	1
18841	pernetas	1
18842	permuta	1
18843	permitírselo	1
18844	permitirme	1
18845	permitirlos	1
18846	permitirles	1
18847	permitiría	1
18848	permitirá	1
18849	permitiole	1
18850	permitieran	1
18851	permitiéndole	1
18852	permitiendo	1
18853	permitíale	1
18854	permiten	1
18855	permitas	1
18856	permanentes	1
18857	permanecieron	1
18858	permanecían	1
18859	perlas	1
18860	perjudicial	1
18861	periquito	1
18862	periquillo	1
18863	período	1
18864	periodistas	1
18865	periodiqueros	1
18866	periódicas	1
18867	periódica	1
18868	perifollo	1
18869	periespíritu	1
18870	pericos	1
18871	pericial	1
18872	pergeñada	1
18873	pergenio	1
18874	pergaminos	1
18875	perfumes	1
18876	perfumadas	1
18877	perfilados	1
18878	perfeccionado	1
18879	perfec	1
18880	perezosas	1
18881	perezca	1
18882	pérez	1
18883	perenne	1
18884	perendengues	1
18885	perejil	1
18886	peregrinas	1
18887	peregrina	1
18888	pereciendo	1
18889	perecemos	1
18890	perece	1
18891	perdonó	1
18892	perdoné	1
18893	perdonas	1
18894	perdonarte	1
18895	perdonárselos	1
18896	perdonarnos	1
18897	perdonaré	1
18898	perdonara	1
18899	perdonándosela	1
18900	perdonan	1
18901	perdonamos	1
18902	perdonadas	1
18903	perdiose	1
18904	perdío	1
18905	perdiese	1
18906	perdieron	1
18907	perdiera	1
18908	perdidas	1
18909	perdidamente	1
18910	pérdida	1
18911	perdices	1
18912	perderte	1
18913	perderse	1
18914	perderme	1
18915	perderles	1
18916	perderla	1
18917	perdería	1
18918	perderé	1
18919	perdemos	1
18920	percusión	1
18921	percloruro	1
18922	percibir	1
18923	percibida	1
18924	percheros	1
18925	perchero	1
18926	perchel	1
18927	peques	1
18928	pequeñuelas	1
18929	pequeñitas	1
18930	pequeñita	1
18931	pequemos	1
18932	peque	1
18933	peptona	1
18934	pepita	1
18935	peñuelas	1
18936	peñascales	1
18937	peñas	1
18938	pentagrama	1
18939	pensiono	1
18940	pensaste	1
18941	pensasen	1
18942	pensase	1
18943	pensarse	1
18944	pensaré	1
18945	pensarás	1
18946	pensarán	1
18947	pensad	1
18948	pensabas	1
18949	penosísimos	1
18950	penosas	1
18951	penosamente	1
18952	penitas	1
18953	penetres	1
18954	penetré	1
18955	penetrase	1
18956	penetrarse	1
18957	penetraras	1
18958	penetrándose	1
18959	penetrada	1
18960	penetración	1
18961	penetraban	1
18962	pene	1
18963	péndulo	1
18964	pendoncillo	1
18965	pendolista	1
18966	pendían	1
18967	pendencia	1
18968	pencas	1
18969	penates	1
18970	penar	1
18971	penalidad	1
18972	penal	1
18973	penado	1
18974	pelusa	1
18975	peluda	1
18976	peluche	1
18977	pelotones	1
18978	pelotilla	1
18979	pelotada	1
18980	pelmazo	1
18981	pellizcándole	1
18982	pellizcando	1
18983	pellizcaban	1
18984	pelliza	1
18985	pellejos	1
18986	pelleja	1
18987	pelinegra	1
18988	peligrosos	1
18989	peligrosas	1
18990	peligrosa	1
18991	peleando	1
18992	pelando	1
18993	pelaje	1
18994	pelafustán	1
18995	peladilla	1
18996	peinose	1
18997	peinó	1
18998	peinarte	1
18999	peinando	1
19000	peinados	1
19001	peina	1
19002	pégueme	1
19003	pegue	1
19004	pegote	1
19005	pegasteis	1
19006	pegase	1
19007	pegárselo	1
19008	pegársela	1
19009	pegármela	1
19010	pegaré	1
19011	pegaras	1
19012	pegándomela	1
19013	pégame	1
19014	pegajosa	1
19015	pedrisco	1
19016	pedrada	1
19017	pedís	1
19018	pediré	1
19019	pedirás	1
19020	pedigüeñas	1
19021	pedías	1
19022	pedernales	1
19023	pedal	1
19024	pedacito	1
19025	pecosa	1
19026	pecó	1
19027	pechugón	1
19028	pechona	1
19029	pececillos	1
19030	pecase	1
19031	pecara	1
19032	pecando	1
19033	pecaminosos	1
19034	pecadores	1
19035	pecaban	1
19036	pecaba	1
19037	pe	1
19038	payasa	1
19039	pavonadas	1
19040	pavisosa	1
19041	pavimento	1
19042	pausas	1
19043	pausada	1
19044	paúl	1
19045	patulea	1
19046	patrón	1
19047	patrióticos	1
19048	patrióticas	1
19049	patrimonial	1
19050	patriarcalismo	1
19051	patriarca	1
19052	patrañas	1
19053	patoso	1
19054	patológicos	1
19055	patológico	1
19056	pato	1
19057	patito	1
19058	patinar	1
19059	patinadores	1
19060	patinación	1
19061	pátina	1
19062	pateta	1
19063	paterno	1
19064	paternidad	1
19065	paternalmente	1
19066	patencures	1
19067	patena	1
19068	patee	1
19069	pateándole	1
19070	patatitas	1
19071	pataplum	1
19072	pataleo	1
19073	patalea	1
19074	patadillas	1
19075	pastoreaba	1
19076	pastorales	1
19077	pastoral	1
19078	pastelón	1
19079	pastel	1
19080	passer	1
19081	pasola	1
19082	pasmoso	1
19083	pasmose	1
19084	pasmosa	1
19085	pásmese	1
19086	pasmarte	1
19087	pasmarotes	1
19088	pasmarías	1
19089	pasmaré	1
19090	pasmaran	1
19091	pasman	1
19092	pasmados	1
19093	pasmábase	1
19094	pasma	1
19095	pasivo	1
19096	pasividad	1
19097	pasivas	1
19098	pasiva	1
19099	pasitos	1
19100	pasita	1
19101	pasiega	1
19102	paseítos	1
19103	paséese	1
19104	paséate	1
19105	pasearnos	1
19106	paseante	1
19107	paseado	1
19108	paseábanse	1
19109	pasáronle	1
19110	pasarme	1
19111	pasaríamos	1
19112	pasaremos	1
19113	pasaras	1
19114	pasaran	1
19115	pasaporte	1
19116	pasamanería	1
19117	pasajero	1
19118	pasajeras	1
19119	pasadita	1
19120	pasábanse	1
19121	párvulos	1
19122	partirse	1
19123	partirle	1
19124	partiese	1
19125	partieran	1
19126	partiéndole	1
19127	partidita	1
19128	partícipes	1
19129	partícipe	1
19130	participaste	1
19131	participaciones	1
19132	participaban	1
19133	parten	1
19134	partan	1
19135	parroquias	1
19136	parriba	1
19137	parrales	1
19138	parral	1
19139	parra	1
19140	parlanchín	1
19141	parlamentarismo	1
19142	parlamentarios	1
19143	parlamentario	1
19144	parlamentaria	1
19145	parlamentando	1
19146	park	1
19147	parisienses	1
19148	parir	1
19149	pariera	1
19150	parienta	1
19151	pariendo	1
19152	paridas	1
19153	parida	1
19154	parias	1
19155	parían	1
19156	paría	1
19157	parezcas	1
19158	pareciome	1
19159	pareciesen	1
19160	pareciéronle	1
19161	pareciéralo	1
19162	pareciéndole	1
19163	parecidos	1
19164	parecíanle	1
19165	parecérsele	1
19166	parecerían	1
19167	pareceres	1
19168	parecerá	1
19169	pare	1
19170	pardillo	1
19171	pardessus	1
19172	parche	1
19173	parca	1
19174	párate	1
19175	parásito	1
19176	parasitario	1
19177	paráronse	1
19178	pararía	1
19179	parará	1
19180	parara	1
19181	paramento	1
19182	paralizado	1
19183	paralizadas	1
19184	paralítico	1
19185	paralítica	1
19186	parálisis	1
19187	paralelamente	1
19188	paraguazo	1
19189	paradójica	1
19190	parábolas	1
19191	parábola	1
19192	parábase	1
19193	paquito	1
19194	paquita	1
19195	paquetitos	1
19196	papos	1
19197	pápiros	1
19198	papelitos	1
19199	papelistas	1
19200	papelillo	1
19201	papeletitas	1
19202	papelejos	1
19203	papelejo	1
19204	papé	1
19205	papal	1
19206	papaíto	1
19207	papagayo	1
19208	pañero	1
19209	panzudo	1
19210	pantuflas	1
19211	panteístas	1
19212	pantaloncitos	1
19213	pantallas	1
19214	pantaleón	1
19215	panoli	1
19216	panificación	1
19217	pánfila	1
19218	panegírico	1
19219	pandillas	1
19220	pancorvo	1
19221	panadero	1
19222	panaceas	1
19223	pámpano	1
19224	paludismo	1
19225	palpó	1
19226	palpitar	1
19227	palpitante	1
19228	palpitando	1
19229	palpe	1
19230	palpar	1
19231	palpando	1
19232	palpables	1
19233	palpaban	1
19234	palpaba	1
19235	palotes	1
19236	palote	1
19237	palosanto	1
19238	palomar	1
19239	palmoteándole	1
19240	palmos	1
19241	palmeras	1
19242	palmas	1
19243	palmarios	1
19244	palmaria	1
19245	palmadita	1
19246	palito	1
19247	palideció	1
19248	palidecía	1
19249	palideces	1
19250	palidecer	1
19251	paliativos	1
19252	paleto	1
19253	paletilla	1
19254	palcos	1
19255	palatino	1
19256	palastro	1
19257	palas	1
19258	palante	1
19259	paladares	1
19260	palación	1
19261	palabrotas	1
19262	palabrillas	1
19263	palabrilla	1
19264	palabrero	1
19265	palabreja	1
19266	pala	1
19267	pal	1
19268	pajita	1
19269	pajes	1
19270	pajarraco	1
19271	pajaritos	1
19272	pajarera	1
19273	paisajista	1
19274	paicían	1
19275	paicerse	1
19276	paicen	1
19277	paguen	1
19278	pagué	1
19279	paginitas	1
19280	pagarme	1
19281	pagarlo	1
19282	pagarán	1
19283	pagara	1
19284	pagano	1
19285	paganismo	1
19286	pagándole	1
19287	pagando	1
19288	pagaban	1
19289	paella	1
19290	padrenuestros	1
19291	padrenuestro	1
19292	padezcamos	1
19293	padezca	1
19294	padecimientos	1
19295	padecían	1
19296	padecí	1
19297	padecerías	1
19298	padecería	1
19299	padecen	1
19300	pactos	1
19301	pacos	1
19302	pacificar	1
19303	pacíficamente	1
19304	pacificadoras	1
19305	pábilo	1
19306	pabellones	1
19307	p	1
19308	oyoles	1
19309	oyola	1
19310	oyeras	1
19311	óyense	1
19312	oyéndose	1
19313	oyéndolo	1
19314	óyeme	1
19315	óvalo	1
19316	otorgase	1
19317	otorgarle	1
19318	otorgándose	1
19319	otorgado	1
19320	otero	1
19321	otelo	1
19322	ostra	1
19323	ostentando	1
19324	ostentan	1
19325	ostentaban	1
19326	osos	1
19327	oso	1
19328	oscurecen	1
19329	oscilando	1
19330	oscilaba	1
19331	osaría	1
19332	osara	1
19333	osar	1
19334	osados	1
19335	orza	1
19336	ortógrafo	1
19337	oropel	1
19338	ornitológicas	1
19339	ornato	1
19340	orla	1
19341	oriundos	1
19342	orinó	1
19343	orillas	1
19344	orihuela	1
19345	originalísimo	1
19346	originales	1
19347	orientándose	1
19348	orientales	1
19349	oriental	1
19350	orgullosos	1
19351	orgullosamente	1
19352	orgía	1
19353	organizó	1
19354	organizarse	1
19355	organizador	1
19356	organizadas	1
19357	organizada	1
19358	organillo	1
19359	orfandad	1
19360	orejitas	1
19361	orejita	1
19362	orearan	1
19363	orea	1
19364	ordinariotes	1
19365	ordinariota	1
19366	ordinarieces	1
19367	ordenarse	1
19368	ordenanza	1
19369	ordenados	1
19370	ordenador	1
19371	ordenadas	1
19372	ordenación	1
19373	ordenaban	1
19374	orbe	1
19375	oratorios	1
19376	oratoria	1
19377	orates	1
19378	orangutanes	1
19379	oradores	1
19380	oráculo	1
19381	oraba	1
19382	opusiéronse	1
19383	opulento	1
19384	opulencia	1
19385	opuestos	1
19386	opuestas	1
19387	opuesta	1
19388	optimismos	1
19389	opta	1
19390	oprimidos	1
19391	oprimidas	1
19392	oprimían	1
19393	opresiones	1
19394	oportunos	1
19395	oportunista	1
19396	oponiendo	1
19397	oponía	1
19398	opongo	1
19399	opóngase	1
19400	oponga	1
19401	oponen	1
19402	opio	1
19403	opinado	1
19404	opiáceo	1
19405	ópalo	1
19406	opacos	1
19407	opacidad	1
19408	opaca	1
19409	ooooh	1
19410	onza	1
19411	onofre	1
19412	onduladas	1
19413	ondeando	1
19414	onde	1
19415	omoplato	1
19416	omnipotente	1
19417	omnipotencia	1
19418	omnímodo	1
19419	ómnibus	1
19420	omitida	1
19421	omisiones	1
19422	ombligo	1
19423	olviden	1
19424	olvídate	1
19425	olvidarte	1
19426	olvidárseles	1
19427	olvidaron	1
19428	olvidarla	1
19429	olvidáramos	1
19430	olvidándose	1
19431	olvidados	1
19432	olvidadizos	1
19433	olvidaban	1
19434	olózaga	1
19435	olorosísimas	1
19436	olorosa	1
19437	olores	1
19438	olmos	1
19439	olla	1
19440	oliva	1
19441	olió	1
19442	olimpa	1
19443	olido	1
19444	olfatorias	1
19445	olfateando	1
19446	olfatea	1
19447	óleos	1
19448	oleeé	1
19449	oleadas	1
19450	ojivas	1
19451	ojeriza	1
19452	ojeador	1
19453	ojeadas	1
19454	ojales	1
19455	ojalateros	1
19456	oírnos	1
19457	oírlos	1
19458	oírles	1
19459	oiría	1
19460	oiré	1
19461	oímos	1
19462	oigas	1
19463	oigan	1
19464	oídas	1
19465	oíanle	1
19466	oíamos	1
19467	oíales	1
19468	ofuscaras	1
19469	ofuscándose	1
19470	ofrecimiento	1
19471	ofreciéndoseles	1
19472	ofreciéndose	1
19473	ofreciéndolo	1
19474	ofreciéndoles	1
19475	ofrecíase	1
19476	ofrecían	1
19477	ofrecérselo	1
19478	ofrecerse	1
19479	ofrecerme	1
19480	ofrecerles	1
19481	ofrecerla	1
19482	ofrecerá	1
19483	ofrecen	1
19484	ofrécele	1
19485	oficiosos	1
19486	oficios	1
19487	oficinalis	1
19488	oficialmente	1
19489	oficiales	1
19490	ofícialas	1
19491	ofensor	1
19492	ofensiva	1
19493	ofendió	1
19494	ofendiera	1
19495	ofendiendo	1
19496	ofendía	1
19497	ofenderse	1
19498	odisea	1
19499	odiosos	1
19500	odié	1
19501	ocurrírsele	1
19502	ocurrirle	1
19503	ocurrirían	1
19504	ocurriome	1
19505	ocurriendo	1
19506	ocurridos	1
19507	ocurrente	1
19508	ocurrencias	1
19509	ocurran	1
19510	ocupes	1
19511	ocuparte	1
19512	ocuparían	1
19513	ocuparía	1
19514	ocupándose	1
19515	ocupándola	1
19516	ocupando	1
19517	ocupador	1
19518	ocupadas	1
19519	ocultis	1
19520	ocultes	1
19521	ocultas	1
19522	ocultarte	1
19523	ocultárselo	1
19524	ocultarse	1
19525	ocultáronse	1
19526	ocultarle	1
19527	ocultarían	1
19528	ocultara	1
19529	ocultamente	1
19530	ocular	1
19531	octavo	1
19532	octava	1
19533	ocre	1
19534	ochentines	1
19535	ochavos	1
19536	ochavito	1
19537	océano	1
19538	ocasionó	1
19539	ocasionan	1
19540	ocasional	1
19541	ocasionado	1
19542	ocasionaban	1
19543	ocasiona	1
19544	obtienen	1
19545	obteniendo	1
19546	obtenidas	1
19547	obstruían	1
19548	obstino	1
19549	obstinas	1
19550	obstinación	1
19551	obstinaba	1
19552	obstina	1
19553	obstetricia	1
19554	obstáculos	1
19555	observole	1
19556	observe	1
19557	observaste	1
19558	observas	1
19559	observarse	1
19560	observarla	1
19561	obsérvale	1
19562	observados	1
19563	observada	1
19564	observábale	1
19565	observábala	1
19566	obsequiosissimus	1
19567	obsequios	1
19568	obsequio	1
19569	obsequiadas	1
19570	obrero	1
19571	obre	1
19572	obrase	1
19573	obrando	1
19574	obran	1
19575	obrado	1
19576	obraba	1
19577	obligas	1
19578	obligaron	1
19579	obligaran	1
19580	obligar	1
19581	obligándole	1
19582	obligan	1
19583	oblicuidad	1
19584	oblicuas	1
19585	objetivos	1
19586	objetiva	1
19587	obeso	1
19588	obesidad	1
19589	obedientes	1
19590	obedezco	1
19591	obedecían	1
19592	obedecen	1
19593	ñoños	1
19594	nutría	1
19595	nuncio	1
19596	numismático	1
19597	numerosa	1
19598	numérico	1
19599	nulidad	1
19600	nula	1
19601	nuevecitas	1
19602	nueces	1
19603	nudoso	1
19604	nubló	1
19605	nublado	1
19606	nublaba	1
19607	novísimo	1
19608	novísima	1
19609	noviciado	1
19610	novias	1
19611	noveno	1
19612	novenas	1
19613	novelistas	1
19614	novelista	1
19615	novelesco	1
19616	novelador	1
19617	novel	1
19618	novecientos	1
19619	noticiero	1
19620	notarios	1
19621	notándose	1
19622	notabilísima	1
19623	notabilidades	1
19624	notábase	1
19625	notaban	1
19626	nostri	1
19627	nostalgia	1
19628	normalizar	1
19629	normales	1
19630	norma	1
19631	noramala	1
19632	non	1
19633	nominativas	1
19634	nominal	1
19635	nómina	1
19636	nomenclaturas	1
19637	nomenclátor	1
19638	nombrarla	1
19639	nombrara	1
19640	nombran	1
19641	nombramientos	1
19642	nombramiento	1
19643	nombrados	1
19644	nombrado	1
19645	nombrábase	1
19646	nombraban	1
19647	nombraba	1
19648	nombra	1
19649	nogal	1
19650	nocturnos	1
19651	nocturnas	1
19652	nociva	1
19653	nochecita	1
19654	nobilísimos	1
19655	nobilísima	1
19656	nobiliarias	1
19657	nizán	1
19658	nitro	1
19659	níquel	1
19660	nipis	1
19661	niñerías	1
19662	niñeras	1
19663	nimiedades	1
19664	nilo	1
19665	nieva	1
19666	nietecito	1
19667	niego	1
19668	niegas	1
19669	niebla	1
19670	newton	1
19671	neutralizado	1
19672	neto	1
19673	nerviosos	1
19674	nerviosísima	1
19675	nerviosas	1
19676	neptuno	1
19677	neos	1
19678	neo	1
19679	nenita	1
19680	negrura	1
19681	negrazo	1
19682	negociara	1
19683	negociar	1
19684	negligente	1
19685	negativos	1
19686	negativas	1
19687	negase	1
19688	negaron	1
19689	negaran	1
19690	negándose	1
19691	negación	1
19692	negábase	1
19693	nefandos	1
19694	nefandas	1
19695	necio	1
19696	necias	1
19697	necesitaré	1
19698	necesitará	1
19699	necesitar	1
19700	necesitando	1
19701	necesitados	1
19702	neas	1
19703	navío	1
19704	navidades	1
19705	naves	1
19706	navas	1
19707	navarra	1
19708	navajas	1
19709	navaja	1
19710	nauseabundo	1
19711	naufragios	1
19712	naufragio	1
19713	náufraga	1
19714	náu	1
19715	nato	1
19716	nasales	1
19717	narradora	1
19718	narración	1
19719	narra	1
19720	narina	1
19721	narigudos	1
19722	naricillas	1
19723	narcótico	1
19724	narcisus	1
19725	naranjo	1
19726	naranjeros	1
19727	naranjado	1
19728	napoleónicas	1
19729	nansouk	1
19730	najo	1
19731	najabao	1
19732	nadasen	1
19733	nadase	1
19734	nadamos	1
19735	nadaban	1
19736	naciones	1
19737	nacida	1
19738	nací	1
19739	nacerá	1
19740	mutuo	1
19741	mutuamente	1
19742	mutismo	1
19743	mutaciones	1
19744	mustio	1
19745	musotros	1
19746	muslito	1
19747	músicos	1
19748	musas	1
19749	murmurantes	1
19750	murmuración	1
19751	muriese	1
19752	murieras	1
19753	muriéndose	1
19754	muriéndome	1
19755	murgas	1
19756	murcia	1
19757	murallas	1
19758	muñón	1
19759	munificencia	1
19760	municipio	1
19761	mundanos	1
19762	mundana	1
19763	multitudes	1
19764	multiplica	1
19765	múltiples	1
19766	multas	1
19767	mulo	1
19768	muladares	1
19769	mula	1
19770	mujeriego	1
19771	mujercita	1
19772	mujeraza	1
19773	mugrientas	1
19774	mugir	1
19775	mueven	1
19776	mueva	1
19777	muestrarios	1
19778	muerde	1
19779	muerdas	1
19780	muerda	1
19781	muellemente	1
19782	mueca	1
19783	mudemos	1
19784	mudas	1
19785	mudaron	1
19786	mudara	1
19787	mudando	1
19788	mudan	1
19789	mucosa	1
19790	mucílago	1
19791	muchísimos	1
19792	muchísimas	1
19793	muchedumbres	1
19794	muchachuelas	1
19795	muchachones	1
19796	mozuela	1
19797	mozas	1
19798	mozart	1
19799	mozárabe	1
19800	mozalbetes	1
19801	moyano	1
19802	moviese	1
19803	moviera	1
19804	moviéndola	1
19805	movibles	1
19806	movible	1
19807	movíase	1
19808	movías	1
19809	motivaran	1
19810	motivados	1
19811	motivado	1
19812	motín	1
19813	motes	1
19814	motejaban	1
19815	moteja	1
19816	mostrose	1
19817	mostraron	1
19818	mostrarla	1
19819	mostrándoselos	1
19820	mostrándoselo	1
19821	mostrándolos	1
19822	mostrándolo	1
19823	mostrándola	1
19824	mostrado	1
19825	mosquitero	1
19826	mosquita	1
19827	moscones	1
19828	mortuorio	1
19829	mortifique	1
19830	mortificó	1
19831	mortificarla	1
19832	mortificara	1
19833	mortificando	1
19834	mortificaciones	1
19835	mortero	1
19836	mortecina	1
19837	mortalmente	1
19838	mortaja	1
19839	morrones	1
19840	morro	1
19841	morritos	1
19842	morris	1
19843	morralla	1
19844	morral	1
19845	morrada	1
19846	morosidades	1
19847	moró	1
19848	morisco	1
19849	morisca	1
19850	morírseme	1
19851	morirían	1
19852	moriríamos	1
19853	moriremos	1
19854	moribundo	1
19855	morían	1
19856	morí	1
19857	mordiscos	1
19858	mordiscar	1
19859	mordió	1
19860	mordiéndose	1
19861	mordiendo	1
19862	mordida	1
19863	mordía	1
19864	mordentes	1
19865	moras	1
19866	morar	1
19867	moralizar	1
19868	morados	1
19869	moquito	1
19870	moquillo	1
19871	moqueta	1
19872	moños	1
19873	moña	1
19874	monumento	1
19875	monumentalidad	1
19876	monumental	1
19877	montpensier	1
19878	montose	1
19879	montoncitos	1
19880	montesinos	1
19881	montesa	1
19882	montés	1
19883	montemuru	1
19884	monteleón	1
19885	montarse	1
19886	montarlo	1
19887	montar	1
19888	montañas	1
19889	montaba	1
19890	monstruosos	1
19891	monstruosa	1
19892	monstrua	1
19893	monotonía	1
19894	monopolizaron	1
19895	monopolizando	1
19896	monopolizaban	1
19897	monomaniacos	1
19898	monomaniaca	1
19899	monjes	1
19900	monísimos	1
19901	monísimas	1
19902	monises	1
19903	monín	1
19904	monilla	1
19905	monigote	1
19906	mongólico	1
19907	monetaria	1
19908	monea	1
19909	monde	1
19910	moncloa	1
19911	monasterio	1
19912	monarquías	1
19913	monamente	1
19914	mon	1
19915	momias	1
19916	momentitos	1
19917	momentico	1
19918	momentáneamente	1
19919	molusco	1
19920	molto	1
19921	mollera	1
19922	molleja	1
19923	molinillo	1
19924	molida	1
19925	molía	1
19926	molestó	1
19927	molestísimas	1
19928	molestísima	1
19929	molestase	1
19930	molestas	1
19931	molestarte	1
19932	molestarle	1
19933	molestaré	1
19934	molestará	1
19935	molestan	1
19936	molestábale	1
19937	moler	1
19938	moldearla	1
19939	mojó	1
19940	mojicón	1
19941	mojaría	1
19942	mojar	1
19943	mojándole	1
19944	mojamos	1
19945	mojama	1
19946	mojaba	1
19947	mohosos	1
19948	mohosas	1
19949	modulaciones	1
19950	modosita	1
19951	modorra	1
19952	moditos	1
19953	modistos	1
19954	modistillas	1
19955	modismos	1
19956	modificó	1
19957	modificado	1
19958	modificación	1
19959	modestísimo	1
19960	modestamente	1
19961	modernos	1
19962	modere	1
19963	moderarse	1
19964	moderantismo	1
19965	moderando	1
19966	moderaísmo	1
19967	moderación	1
19968	modelito	1
19969	modele	1
19970	modelaban	1
19971	mochuelo	1
19972	mochila	1
19973	mocetón	1
19974	mixtura	1
19975	mitras	1
19976	mitra	1
19977	mitos	1
19978	mitológico	1
19979	mitchell	1
19980	mistress	1
19981	mistos	1
19982	mistiquerías	1
19983	mística	1
19984	misteriosos	1
19985	mister	1
19986	misté	1
19987	mismísimo	1
19988	misitas	1
19989	misiones	1
19990	misericordias	1
19991	míseras	1
19992	míseramente	1
19993	misales	1
19994	mironas	1
19995	mirola	1
19996	mirlo	1
19997	miriñaque	1
19998	mírelo	1
19999	mirarme	1
20000	mirarlos	1
20001	mirarlas	1
20002	mirarían	1
20003	miraran	1
20004	míranse	1
20005	miranda	1
20006	miramos	1
20007	miramiento	1
20008	míralo	1
20009	mirados	1
20010	mirábase	1
20011	mirábanse	1
20012	mirábanla	1
20013	mirábamos	1
20014	mirábales	1
20015	mirábala	1
20016	miope	1
20017	minueto	1
20018	minuciosas	1
20019	ministerialismo	1
20020	minino	1
20021	miniaturita	1
20022	minas	1
20023	mina	1
20024	mimosidad	1
20025	mimosa	1
20026	mimitos	1
20027	mímicas	1
20028	mimarle	1
20029	mimadito	1
20030	mimadita	1
20031	mimada	1
20032	mimaban	1
20033	millonarios	1
20034	millón	1
20035	millas	1
20036	militante	1
20037	milicianos	1
20038	miliciano	1
20039	milaneses	1
20040	milagroso	1
20041	miiiii	1
20042	mies	1
20043	miércoles	1
20044	miente	1
20045	miembro	1
20046	mielero	1
20047	miedosa	1
20048	midiera	1
20049	midiendo	1
20050	miden	1
20051	micos	1
20052	micho	1
20053	miajitas	1
20054	miaja	1
20055	mezquita	1
20056	mezcló	1
20057	metz	1
20058	metros	1
20059	metrópoli	1
20060	métome	1
20061	metodizando	1
20062	metódicas	1
20063	metiole	1
20064	metiese	1
20065	metiéndola	1
20066	metidita	1
20067	metíase	1
20068	métete	1
20069	metes	1
20070	meterte	1
20071	metérselo	1
20072	meterlos	1
20073	meteré	1
20074	meterá	1
20075	meten	1
20076	metempsícosis	1
20077	metemos	1
20078	mételo	1
20079	mételes	1
20080	metas	1
20081	metan	1
20082	metamos	1
20083	metálicas	1
20084	metálicamente	1
20085	metales	1
20086	metáis	1
20087	metá	1
20088	mesonero	1
20089	mesón	1
20090	mesocrático	1
20091	mesita	1
20092	mesianitis	1
20093	meseta	1
20094	mescolanza	1
20095	mero	1
20096	mermó	1
20097	mermar	1
20098	mermados	1
20099	meriendas	1
20100	meriendan	1
20101	merezcas	1
20102	merengue	1
20103	merengada	1
20104	merenderos	1
20105	mereció	1
20106	merecimientos	1
20107	mereciesen	1
20108	mereciese	1
20109	merecían	1
20110	merecerlo	1
20111	merecería	1
20112	merecéis	1
20113	merecedor	1
20114	mercuriales	1
20115	mercurial	1
20116	mercenarias	1
20117	mercancías	1
20118	mercachifles	1
20119	menudos	1
20120	menudillo	1
20121	mentó	1
20122	mentís	1
20123	mentiroso	1
20124	mentirosas	1
20125	mentirosa	1
20126	mentirilla	1
20127	mentirijillas	1
20128	mentirijilla	1
20129	mentir	1
20130	mentarlo	1
20131	mentales	1
20132	mensajes	1
20133	menospreciar	1
20134	menoscabo	1
20135	menjurje	1
20136	menistro	1
20137	meningo	1
20138	menina	1
20139	mengue	1
20140	menguaban	1
20141	menestrales	1
20142	meneo	1
20143	menease	1
20144	menearse	1
20145	meneallo	1
20146	meneada	1
20147	menea	1
20148	mendiry	1
20149	mendigas	1
20150	mendicante	1
20151	méndez	1
20152	mencionar	1
20153	mencionados	1
20154	mencionada	1
20155	menaje	1
20156	memos	1
20157	memoriales	1
20158	memorial	1
20159	membrillo	1
20160	melón	1
20161	melómanos	1
20162	melómano	1
20163	melodramáticos	1
20164	melodramática	1
20165	melicianos	1
20166	melenudos	1
20167	melenuda	1
20168	melena	1
20169	melancólicamente	1
20170	melaera	1
20171	mela	1
20172	mejoras	1
20173	mejoraré	1
20174	mejoraba	1
20175	meetings	1
20176	medroso	1
20177	medrosica	1
20178	medrosa	1
20179	meditó	1
20180	meditado	1
20181	medirse	1
20182	medió	1
20183	medidor	1
20184	medicinales	1
20185	mediasen	1
20186	mediascañas	1
20187	mediaron	1
20188	medianero	1
20189	mediando	1
20190	medianas	1
20191	medíalas	1
20192	mediaban	1
20193	medía	1
20194	medallas	1
20195	meciéndose	1
20196	mechas	1
20197	mecha	1
20198	meces	1
20199	mécele	1
20200	mecánicos	1
20201	mazmorra	1
20202	maximiliana	1
20203	mauro	1
20204	maulas	1
20205	matuteros	1
20206	matronas	1
20207	matrona	1
20208	matriz	1
20209	matritense	1
20210	matrimoñesca	1
20211	matricularse	1
20212	matrices	1
20213	matorrales	1
20214	matiz	1
20215	matitas	1
20216	matices	1
20217	matías	1
20218	materialmente	1
20219	materialistas	1
20220	materialidades	1
20221	materialidad	1
20222	mateo	1
20223	matemos	1
20224	matemática	1
20225	mátate	1
20226	matase	1
20227	matarnos	1
20228	mataría	1
20229	mataremos	1
20230	matanza	1
20231	mátameles	1
20232	matadores	1
20233	matachines	1
20234	mataba	1
20235	masticarlos	1
20236	massarnau	1
20237	massanielo	1
20238	masque	1
20239	masónico	1
20240	masones	1
20241	mascullones	1
20242	mascullando	1
20243	mascota	1
20244	mascase	1
20245	masca	1
20246	masarnau	1
20247	martirizarle	1
20248	martirios	1
20249	martillos	1
20250	martillazo	1
20251	martillase	1
20252	martes	1
20253	marte	1
20254	marsella	1
20255	marrullería	1
20256	marranos	1
20257	marrano	1
20258	marranadas	1
20259	marranada	1
20260	marquilla	1
20261	marquesito	1
20262	marítimos	1
20263	marismas	1
20264	mariscos	1
20265	marisabidilla	1
20266	mariquita	1
20267	mariposa	1
20268	marinos	1
20269	marino	1
20270	marineros	1
20271	marinero	1
20272	marinas	1
20273	marimachos	1
20274	marica	1
20275	mariana	1
20276	margaritas	1
20277	mareo	1
20278	marearse	1
20279	marearla	1
20280	marearán	1
20281	mareante	1
20282	mareando	1
20283	mareado	1
20284	marcó	1
20285	marchose	1
20286	marcho	1
20287	marchito	1
20288	marchitas	1
20289	marchitarse	1
20290	marche	1
20291	márchate	1
20292	marchasen	1
20293	marcharan	1
20294	marchante	1
20295	marchándose	1
20296	marchando	1
20297	marchan	1
20298	marchádose	1
20299	marchaban	1
20300	marcas	1
20301	marcarles	1
20302	marcándolos	1
20303	marcan	1
20304	marcador	1
20305	marcadas	1
20306	marcadamente	1
20307	maravilloso	1
20308	maravillase	1
20309	maravillarse	1
20310	maravillaron	1
20311	maravillábase	1
20312	maravillaban	1
20313	maravillaba	1
20314	marañas	1
20315	maraña	1
20316	maragatos	1
20317	maragatería	1
20318	maquinales	1
20319	maquinaciones	1
20320	maquina	1
20321	mañoso	1
20322	mañosito	1
20323	mañosas	1
20324	manzanilla	1
20325	manzanas	1
20326	manueles	1
20327	mantuviera	1
20328	manteos	1
20329	manteo	1
20330	mantenido	1
20331	mantenía	1
20332	mantenga	1
20333	mantenerse	1
20334	mantenerla	1
20335	manteleta	1
20336	manteles	1
20337	mansión	1
20338	mansas	1
20339	mansa	1
20340	manoteaba	1
20341	manotazo	1
20342	manosear	1
20343	manoseándole	1
20344	manolos	1
20345	manolitos	1
20346	manolito	1
20347	manjares	1
20348	manjar	1
20349	maniobrar	1
20350	manifiesten	1
20351	manifieste	1
20352	manifestose	1
20353	manifestárselo	1
20354	manifestarle	1
20355	manifestara	1
20356	manifestado	1
20357	manifestaban	1
20358	maniático	1
20359	mangueros	1
20360	mangonee	1
20361	mangoneando	1
20362	mangonean	1
20363	mangoneado	1
20364	manglares	1
20365	manga	1
20366	manetizan	1
20367	manejos	1
20368	manejes	1
20369	manejarte	1
20370	manejándole	1
20371	manejada	1
20372	manejaban	1
20373	maneja	1
20374	manecita	1
20375	mane	1
20376	mandria	1
20377	mandole	1
20378	mandola	1
20379	mandingas	1
20380	mandíbulas	1
20381	mándelas	1
20382	mandéis	1
20383	mandato	1
20384	mandaste	1
20385	mandasen	1
20386	mandase	1
20387	mandas	1
20388	mandaron	1
20389	mandarme	1
20390	mandarles	1
20391	mandarín	1
20392	mandaría	1
20393	mandaremos	1
20394	mandare	1
20395	mandaran	1
20396	mandándole	1
20397	mandamientos	1
20398	mandamiento	1
20399	mándale	1
20400	mandados	1
20401	mandábala	1
20402	mancilla	1
20403	manchurrones	1
20404	manchego	1
20405	manchega	1
20406	mancharse	1
20407	mancháis	1
20408	manchadas	1
20409	manchaba	1
20410	manaza	1
20411	manadas	1
20412	manada	1
20413	mamotretos	1
20414	mamotreto	1
20415	mamen	1
20416	mameluco	1
20417	mamándose	1
20418	mamaíta	1
20419	mamaba	1
20420	malva	1
20421	maltrate	1
20422	maltratada	1
20423	maltrataba	1
20424	maltrajeao	1
20425	malsonante	1
20426	malsana	1
20427	malquerencia	1
20428	malogró	1
20429	maligno	1
20430	malicias	1
20431	malhumorado	1
20432	maleta	1
20433	maleficiar	1
20434	maledicencias	1
20435	maleada	1
20436	maldonadas	1
20437	malditamente	1
20438	maldicientes	1
20439	maldice	1
20440	maldecidos	1
20441	maldecida	1
20442	malchara	1
20443	malayas	1
20444	malaventurado	1
20445	malakoff	1
20446	malagueñas	1
20447	málaga	1
20448	majestuoso	1
20449	majestuosas	1
20450	majestuosa	1
20451	majagranzas	1
20452	majadera	1
20453	maíz	1
20454	mahones	1
20455	magullada	1
20456	mago	1
20457	magnitud	1
20458	magnética	1
20459	magnánimos	1
20460	magistratura	1
20461	magistrado	1
20462	magisterio	1
20463	mágica	1
20464	maestros	1
20465	maestrita	1
20466	maestría	1
20467	madurez	1
20468	madure	1
20469	madurando	1
20470	maduran	1
20471	madrugues	1
20472	madrugadores	1
20473	madrugador	1
20474	madruga	1
20475	madroños	1
20476	madroñaje	1
20477	madrileñas	1
20478	madrigueras	1
20479	madrigales	1
20480	madrastras	1
20481	madrás	1
20482	madoz	1
20483	madeja	1
20484	macuquinas	1
20485	macilenta	1
20486	machos	1
20487	machito	1
20488	machete	1
20489	machetazos	1
20490	machaqué	1
20491	machamartillo	1
20492	machacones	1
20493	machacona	1
20494	machacarla	1
20495	machacante	1
20496	machacado	1
20497	macetas	1
20498	m	1
20499	luteras	1
20500	luterano	1
20501	lustros	1
20502	lunar	1
20503	luminosas	1
20504	lugo	1
20505	lugarón	1
20506	luengos	1
20507	luenga	1
20508	lucrativo	1
20509	lucrativa	1
20510	lucirme	1
20511	luciría	1
20512	lucir	1
20513	lució	1
20514	lucio	1
20515	luciera	1
20516	luciendo	1
20517	lúcidos	1
20518	lucidez	1
20519	lucharían	1
20520	luchar	1
20521	luchana	1
20522	luchan	1
20523	luchaban	1
20524	lucecita	1
20525	luce	1
20526	lozanas	1
20527	lourdes	1
20528	lotero	1
20529	lotérica	1
20530	lorito	1
20531	lores	1
20532	lorenzo	1
20533	lorenzana	1
20534	loquito	1
20535	loquilla	1
20536	lontananzas	1
20537	lontananza	1
20538	lonjas	1
20539	lonja	1
20540	longaniza	1
20541	londonenses	1
20542	lombardas	1
20543	lombarda	1
20544	lola	1
20545	logras	1
20546	lograrlo	1
20547	lograría	1
20548	lograr	1
20549	logrando	1
20550	logradas	1
20551	lógicos	1
20552	lógicamente	1
20553	logia	1
20554	lodos	1
20555	locurilla	1
20556	locuaces	1
20557	locas	1
20558	locamente	1
20559	lóbulos	1
20560	lóbrego	1
20561	lóbregas	1
20562	lobos	1
20563	lobas	1
20564	lluvioso	1
20565	llueven	1
20566	llueve	1
20567	lloviendo	1
20568	lloverá	1
20569	llorosa	1
20570	lloros	1
20571	llorones	1
20572	llorona	1
20573	lloró	1
20574	lloriqueo	1
20575	lloriquear	1
20576	llores	1
20577	llorase	1
20578	llorarle	1
20579	llorándome	1
20580	lloradas	1
20581	llevose	1
20582	llevola	1
20583	lleves	1
20584	llevárselos	1
20585	llevársele	1
20586	lleváronle	1
20587	llevárnoslo	1
20588	llevárnosle	1
20589	llevármelo	1
20590	llevármele	1
20591	llevarlo	1
20592	llevarlas	1
20593	llevándoselas	1
20594	llevándolos	1
20595	llévalos	1
20596	llévalo	1
20597	llevados	1
20598	llevábase	1
20599	llevabas	1
20600	llenola	1
20601	llénese	1
20602	llenéis	1
20603	llenarles	1
20604	llenarla	1
20605	llenaran	1
20606	llenándose	1
20607	llenábase	1
20608	llegues	1
20609	lleguen	1
20610	lleguemos	1
20611	llegose	1
20612	llégate	1
20613	llegas	1
20614	llegarse	1
20615	llegarás	1
20616	llegándole	1
20617	llegados	1
20618	llegadas	1
20619	llaneza	1
20620	llana	1
20621	llamola	1
20622	llamen	1
20623	llamé	1
20624	llamasen	1
20625	llamársela	1
20626	llamáronle	1
20627	llamaríamos	1
20628	llamarás	1
20629	llamarán	1
20630	llamaradas	1
20631	llamarada	1
20632	llamara	1
20633	llámanse	1
20634	llamándome	1
20635	llámame	1
20636	llámalos	1
20637	llámalo	1
20638	llamadas	1
20639	llamabas	1
20640	llamábamos	1
20641	llagas	1
20642	llaga	1
20643	lla	1
20644	livianos	1
20645	liviandades	1
20646	liviandad	1
20647	liviana	1
20648	liverpool	1
20649	liturgia	1
20650	litros	1
20651	litro	1
20652	literarios	1
20653	listos	1
20654	listones	1
20655	lisonjeros	1
20656	lisonjero	1
20657	lisonjera	1
20658	lisonjear	1
20659	liso	1
20660	lisiados	1
20661	lirón	1
20662	liquidar	1
20663	liquidada	1
20664	líquenes	1
20665	lió	1
20666	linneo	1
20667	linfática	1
20668	lindísima	1
20669	lindezas	1
20670	linderos	1
20671	lindaba	1
20672	limpió	1
20673	limpié	1
20674	limpiasen	1
20675	limpias	1
20676	limpiarte	1
20677	limpiarse	1
20678	limpiaron	1
20679	limpiarlos	1
20680	limpiarlo	1
20681	limpiarle	1
20682	limpiara	1
20683	limpiados	1
20684	limpiaban	1
20685	limosnita	1
20686	limítrofes	1
20687	limitose	1
20688	limitó	1
20689	limitados	1
20690	limitada	1
20691	limitaban	1
20692	limbo	1
20693	lija	1
20694	ligeros	1
20695	ligar	1
20696	ligaduras	1
20697	ligaba	1
20698	lidiar	1
20699	licores	1
20700	lición	1
20701	licencioso	1
20702	licenciatura	1
20703	licenciarla	1
20704	licenciados	1
20705	licenciado	1
20706	librotes	1
20707	librote	1
20708	librillos	1
20709	libreta	1
20710	librerías	1
20711	librepensadores	1
20712	librecambista	1
20713	libré	1
20714	librarlas	1
20715	librara	1
20716	librándose	1
20717	líbrame	1
20718	librado	1
20719	libertinos	1
20720	liberticidas	1
20721	liberté	1
20722	liberó	1
20723	liberalescos	1
20724	liarte	1
20725	liar	1
20726	liándose	1
20727	liados	1
20728	leyeras	1
20729	leyeran	1
20730	leyéndolas	1
20731	leyendas	1
20732	levitín	1
20733	levantes	1
20734	levanten	1
20735	levanté	1
20736	levántate	1
20737	levantase	1
20738	levantarme	1
20739	levantarles	1
20740	levantarle	1
20741	levantarlas	1
20742	levantaré	1
20743	levantará	1
20744	levantándola	1
20745	levantamiento	1
20746	levantadas	1
20747	levantábase	1
20748	levantaban	1
20749	levadura	1
20750	letargos	1
20751	lesa	1
20752	lérida	1
20753	lepanto	1
20754	leopardo	1
20755	leoncillo	1
20756	leñera	1
20757	leñador	1
20758	lentejuelas	1
20759	lentejas	1
20760	lentas	1
20761	lengüetazo	1
20762	lengüetas	1
20763	lengüecita	1
20764	lenguaza	1
20765	lenguaraces	1
20766	lenguados	1
20767	lejanos	1
20768	lejanas	1
20769	leitoral	1
20770	leían	1
20771	leí	1
20772	legitimidades	1
20773	legía	1
20774	legalizado	1
20775	legación	1
20776	lees	1
20777	leerte	1
20778	leerle	1
20779	leerla	1
20780	leen	1
20781	leemos	1
20782	lechuzos	1
20783	lechuzas	1
20784	lechuga	1
20785	lean	1
20786	leales	1
20787	lazaretos	1
20788	lazareto	1
20789	lazadas	1
20790	lazada	1
20791	lavose	1
20792	lavemos	1
20793	lave	1
20794	lavatorio	1
20795	lavas	1
20796	lavarle	1
20797	lavaría	1
20798	lavaré	1
20799	lavándose	1
20800	lavando	1
20801	lavandera	1
20802	lavan	1
20803	lavaduras	1
20804	lavadero	1
20805	lavabo	1
20806	lavaban	1
20807	laura	1
20808	laudatorio	1
20809	laudable	1
20810	latro	1
20811	latonero	1
20812	latitudes	1
20813	latinos	1
20814	latinas	1
20815	latina	1
20816	latigazo	1
20817	latía	1
20818	latente	1
20819	lastre	1
20820	lastraba	1
20821	lastimosísimo	1
20822	lastimosísima	1
20823	lastimosa	1
20824	lastimó	1
20825	lastimero	1
20826	lastimera	1
20827	lástimas	1
20828	lastimar	1
20829	lastimándose	1
20830	lastimado	1
20831	lastimaba	1
20832	laringe	1
20833	larguísimas	1
20834	larguísima	1
20835	larguilucho	1
20836	largue	1
20837	largaran	1
20838	largara	1
20839	largar	1
20840	largamos	1
20841	largado	1
20842	lara	1
20843	lapso	1
20844	lápidas	1
20845	lápices	1
20846	lañador	1
20847	lanzará	1
20848	lanzara	1
20849	lanzaban	1
20850	lanuza	1
20851	lantigua	1
20852	langostino	1
20853	langosta	1
20854	landó	1
20855	lanceta	1
20856	lamparilla	1
20857	lámparas	1
20858	laminotas	1
20859	laminitas	1
20860	lamido	1
20861	lamía	1
20862	lamento	1
20863	lamentarse	1
20864	lamentándose	1
20865	lamentaciones	1
20866	lamentábase	1
20867	lamentaban	1
20868	lamen	1
20869	laica	1
20870	lagrimitas	1
20871	lagos	1
20872	lagartijo	1
20873	laganitos	1
20874	ladronicio	1
20875	ladró	1
20876	ladrillazo	1
20877	ladrándole	1
20878	ladra	1
20879	ladinamente	1
20880	ladeando	1
20881	lacto	1
20882	lactancia	1
20883	lacrimoso	1
20884	lacerias	1
20885	lacerante	1
20886	labrando	1
20887	labrados	1
20888	labradas	1
20889	laborioso	1
20890	laboriosa	1
20891	labiano	1
20892	juzgues	1
20893	juzguéis	1
20894	juzgo	1
20895	juzgándose	1
20896	juzgan	1
20897	juzgábase	1
20898	juzgaba	1
20899	juzga	1
20900	juveniles	1
20901	juvenil	1
20902	justificar	1
20903	justificadas	1
20904	justificación	1
20905	justicieras	1
20906	justiciera	1
20907	justiciada	1
20908	justamente	1
20909	justa	1
20910	juros	1
20911	jurídica	1
20912	juras	1
20913	jurarme	1
20914	jurarlo	1
20915	jurar	1
20916	jurando	1
20917	júramelo	1
20918	jurados	1
20919	jurado	1
20920	jura	1
20921	júpiter	1
20922	juntose	1
20923	juntó	1
20924	juntitos	1
20925	juntillas	1
20926	juntarse	1
20927	juntáronse	1
20928	juntan	1
20929	juntábanse	1
20930	juntaban	1
20931	juntaba	1
20932	jumeras	1
20933	jum	1
20934	juliana	1
20935	juiciosos	1
20936	juiciosísimo	1
20937	juiciosillo	1
20938	juiciosas	1
20939	jugué	1
20940	jugosos	1
20941	jugó	1
20942	jugo	1
20943	jugasen	1
20944	jugase	1
20945	jugarreta	1
20946	jugaron	1
20947	jugarle	1
20948	jugadores	1
20949	juergas	1
20950	juegas	1
20951	jueces	1
20952	júcar	1
20953	jubileo	1
20954	jubilarte	1
20955	jubilarse	1
20956	jubilación	1
20957	jovenzuelas	1
20958	jovenzuela	1
20959	jovencito	1
20960	jovellar	1
20961	jovellanos	1
20962	josés	1
20963	josef	1
20964	jorobándonos	1
20965	jorobados	1
20966	jorobadita	1
20967	jorobada	1
20968	jornada	1
20969	jormiguita	1
20970	jordán	1
20971	jonjabaron	1
20972	joloanas	1
20973	jollines	1
20974	jofaina	1
20975	joco	1
20976	job	1
20977	joaquina	1
20978	jipíos	1
20979	jinetes	1
20980	jiménez	1
20981	jilguero	1
20982	jierros	1
20983	jierro	1
20984	jícara	1
20985	jesuítico	1
20986	jesuíticamente	1
20987	jesuita	1
20988	jeroglíficos	1
20989	jeroglífico	1
20990	jericó	1
20991	jergones	1
20992	jerarquías	1
20993	jerarquía	1
20994	jena	1
20995	jefes	1
20996	jayanes	1
20997	jayán	1
20998	javanesas	1
20999	jaulones	1
21000	játiva	1
21001	jarrito	1
21002	jarretiera	1
21003	jardinillo	1
21004	jardinería	1
21005	jardineras	1
21006	jáquima	1
21007	jaquecoso	1
21008	jamona	1
21009	james	1
21010	jaleos	1
21011	jalapa	1
21012	jaez	1
21013	jadeantes	1
21014	jactancia	1
21015	jacquard	1
21016	jacometrenzo	1
21017	jacintillo	1
21018	jabonadura	1
21019	itinerario	1
21020	italiana	1
21021	istmo	1
21022	israelita	1
21023	isprisiones	1
21024	iscariote	1
21025	irujo	1
21026	irte	1
21027	irritó	1
21028	irrites	1
21029	irritarle	1
21030	irritado	1
21031	irritadas	1
21032	irritada	1
21033	irritabilidad	1
21034	irritábase	1
21035	irritaban	1
21036	irritaba	1
21037	irrevocable	1
21038	irreverentemente	1
21039	irreverente	1
21040	irreverencia	1
21041	irrespetuosas	1
21042	irreparables	1
21043	irreparable	1
21044	irremediables	1
21045	irregularidades	1
21046	ironías	1
21047	irlos	1
21048	irlas	1
21049	irlandas	1
21050	irla	1
21051	irisados	1
21052	irascibilidad	1
21053	iracundo	1
21054	iracunda	1
21055	ipso	1
21056	inza	1
21057	inyectados	1
21058	inyectaban	1
21059	invóqueles	1
21060	involuntarios	1
21061	involucremos	1
21062	involucre	1
21063	involución	1
21064	invocó	1
21065	invocaciones	1
21066	invocación	1
21067	invocaba	1
21068	invoca	1
21069	invitole	1
21070	inviten	1
21071	invite	1
21072	invitase	1
21073	invitaron	1
21074	invitará	1
21075	invitar	1
21076	invitando	1
21077	invitaciones	1
21078	invitaba	1
21079	investigó	1
21080	investigador	1
21081	investigación	1
21082	inverosímiles	1
21083	inventos	1
21084	inventor	1
21085	inventiva	1
21086	inventéis	1
21087	inventase	1
21088	inventarlo	1
21089	inventariar	1
21090	inventará	1
21091	inventando	1
21092	inventadas	1
21093	inventada	1
21094	inventa	1
21095	inválido	1
21096	invadió	1
21097	invadido	1
21098	invadían	1
21099	invaden	1
21100	inusitada	1
21101	inundose	1
21102	inundándola	1
21103	inundación	1
21104	inundaban	1
21105	intuitiva	1
21106	intrusa	1
21107	introdujo	1
21108	introdujese	1
21109	introductora	1
21110	introducirse	1
21111	introducirlo	1
21112	introduciendo	1
21113	introducido	1
21114	introducen	1
21115	intríngulis	1
21116	intrigüelas	1
21117	intrigante	1
21118	intrigantas	1
21119	intransitable	1
21120	intranquilizó	1
21121	intolerante	1
21122	intolerable	1
21123	intimó	1
21124	intimando	1
21125	intervino	1
21126	intervinieron	1
21127	intervenían	1
21128	intervalos	1
21129	intervalo	1
21130	interrupciones	1
21131	interrumpiera	1
21132	interrumpiéndole	1
21133	interrumpida	1
21134	interrumpas	1
21135	interrumpan	1
21136	interrogar	1
21137	interrogándose	1
21138	interrogándola	1
21139	interrogando	1
21140	interrogador	1
21141	interrogada	1
21142	interrogaciones	1
21143	interrogación	1
21144	intérprete	1
21145	interprete	1
21146	interpretar	1
21147	interpretándolos	1
21148	interpretándola	1
21149	interpretabas	1
21150	interponiéndose	1
21151	internos	1
21152	internaron	1
21153	interminables	1
21154	intermedia	1
21155	interlocutores	1
21156	interlocutor	1
21157	interjecciones	1
21158	interioridad	1
21159	interino	1
21160	interesar	1
21161	interesantísimo	1
21162	interesan	1
21163	interesado	1
21164	interesaban	1
21165	interceptaron	1
21166	interceptaban	1
21167	intercedí	1
21168	intercede	1
21169	interceda	1
21170	intentos	1
21171	intenté	1
21172	intentase	1
21173	intentaron	1
21174	intentarlo	1
21175	intentaría	1
21176	intentado	1
21177	intensos	1
21178	intensísimas	1
21179	intensidad	1
21180	intensa	1
21181	intendente	1
21182	intencionada	1
21183	intempestivas	1
21184	intemperie	1
21185	inteligible	1
21186	inteligentes	1
21187	intactas	1
21188	intachables	1
21189	insurreccionó	1
21190	insurrección	1
21191	insurgentes	1
21192	insurgente	1
21193	insultos	1
21194	insulté	1
21195	insultase	1
21196	insultarle	1
21197	insultar	1
21198	ínsulas	1
21199	ínsula	1
21200	insufribles	1
21201	insuficientes	1
21202	insubordina	1
21203	instruye	1
21204	instrumentos	1
21205	instruirte	1
21206	instruido	1
21207	instructiva	1
21208	instó	1
21209	instantáneo	1
21210	instancias	1
21211	instancia	1
21212	instalose	1
21213	instaló	1
21214	instalarse	1
21215	instalándose	1
21216	instalado	1
21217	instalaban	1
21218	instalaba	1
21219	instado	1
21220	instaban	1
21221	instaba	1
21222	inspirole	1
21223	inspirarse	1
21224	inspiraron	1
21225	inspirarle	1
21226	inspirar	1
21227	inspirándome	1
21228	inspirabas	1
21229	inspeccionando	1
21230	inspecciona	1
21231	insoportables	1
21232	insolvente	1
21233	insolvencias	1
21234	insolvencia	1
21235	insoluble	1
21236	insolentes	1
21237	insolencias	1
21238	insolencia	1
21239	insistiré	1
21240	insistir	1
21241	insistiese	1
21242	insistiendo	1
21243	insistido	1
21244	insistente	1
21245	insisten	1
21246	insiste	1
21247	insípido	1
21248	insinuarse	1
21249	insinuantes	1
21250	insinuándose	1
21251	insinuaciones	1
21252	insignia	1
21253	insepulto	1
21254	inseparable	1
21255	insensatez	1
21256	inseguros	1
21257	inseguras	1
21258	insectos	1
21259	insecto	1
21260	inquirir	1
21261	inquiriendo	1
21262	inquilino	1
21263	inquietas	1
21264	inquietamente	1
21265	inquietaban	1
21266	inquietaba	1
21267	inoportuno	1
21268	inopinadamente	1
21269	inocentadas	1
21270	inocentada	1
21271	innumerables	1
21272	innovador	1
21273	innobles	1
21274	innegable	1
21275	innatas	1
21276	inmutó	1
21277	inmutarse	1
21278	inmutada	1
21279	inmutables	1
21280	inmunidad	1
21281	inmundo	1
21282	inmundas	1
21283	inmunda	1
21284	inmueble	1
21285	inmovilidad	1
21286	inmóviles	1
21287	inmoralidad	1
21288	inmorales	1
21289	inmoral	1
21290	inmodestia	1
21291	inmensas	1
21292	inmensamente	1
21293	inmediaciones	1
21294	injustos	1
21295	injusto	1
21296	injuriosas	1
21297	injuria	1
21298	injertado	1
21299	ininteligible	1
21300	iniciose	1
21301	iniciarlo	1
21302	iniciar	1
21303	iniciándole	1
21304	inician	1
21305	iniciadoras	1
21306	iniciadora	1
21307	iniciación	1
21308	iniciábasele	1
21309	iniciábase	1
21310	iniciaba	1
21311	inhumanas	1
21312	inhabitables	1
21313	inhábiles	1
21314	inhábil	1
21315	ingreso	1
21316	ingresara	1
21317	ingresar	1
21318	ingratuelo	1
21319	inglesotes	1
21320	inglesote	1
21321	inglesones	1
21322	inglesona	1
21323	ingestión	1
21324	ingente	1
21325	ingénito	1
21326	ingeniosos	1
21327	ingeniosísimos	1
21328	ingenios	1
21329	infundirte	1
21330	infundirse	1
21331	infundiéndole	1
21332	infundíanle	1
21333	infundían	1
21334	infundíale	1
21335	infundes	1
21336	infunden	1
21337	infructuoso	1
21338	infranqueables	1
21339	infortunada	1
21340	informarse	1
21341	informarlo	1
21342	informándose	1
21343	informadora	1
21344	informado	1
21345	informada	1
21346	informaba	1
21347	informa	1
21348	influyese	1
21349	influyendo	1
21350	influye	1
21351	influjo	1
21352	influir	1
21353	infló	1
21354	infligir	1
21355	inflexibilidad	1
21356	inflándose	1
21357	inflamados	1
21358	inflamado	1
21359	inflamación	1
21360	inflamaba	1
21361	inflaban	1
21362	infinitivos	1
21363	infieles	1
21364	infestada	1
21365	infelizote	1
21366	infantería	1
21367	infante	1
21368	infamias	1
21369	infamar	1
21370	infalibilidad	1
21371	inexpugnable	1
21372	inexpresiva	1
21373	inexperto	1
21374	inexpertas	1
21375	inesperadas	1
21376	inesperada	1
21377	inervación	1
21378	inercia	1
21379	inequívoca	1
21380	ineptas	1
21381	inepta	1
21382	ineficaz	1
21383	ineducado	1
21384	ineducada	1
21385	industriosa	1
21386	industrias	1
21387	indultos	1
21388	indulto	1
21389	indújole	1
21390	indujo	1
21391	indujeran	1
21392	indudables	1
21393	induce	1
21394	indolente	1
21395	indivudua	1
21396	individualizar	1
21397	individualidades	1
21398	individuales	1
21399	indispuesta	1
21400	indisoluble	1
21401	indirecto	1
21402	indirectas	1
21403	indirectamente	1
21404	indinos	1
21405	indino	1
21406	indina	1
21407	indilugencia	1
21408	indignarse	1
21409	indignarían	1
21410	indignaban	1
21411	indigestos	1
21412	indigéstate	1
21413	indigestan	1
21414	indigestada	1
21415	indigestaba	1
21416	indigente	1
21417	índices	1
21418	indicáronle	1
21419	indicaron	1
21420	indicarle	1
21421	indicara	1
21422	indicado	1
21423	indias	1
21424	indiana	1
21425	india	1
21426	indeterminado	1
21427	indestructibles	1
21428	indemnizarse	1
21429	indemnizaba	1
21430	indefinido	1
21431	indefensos	1
21432	indecorosa	1
21433	indecibles	1
21434	indecentonas	1
21435	indecentísimos	1
21436	indagatorias	1
21437	indagando	1
21438	indagador	1
21439	indagación	1
21440	indagaba	1
21441	incurrir	1
21442	incumbía	1
21443	incumbencia	1
21444	incultura	1
21445	incultivados	1
21446	inculpabilidad	1
21447	incrustando	1
21448	increpar	1
21449	increpaba	1
21450	incorruptible	1
21451	incorrecta	1
21452	incorrección	1
21453	incorporan	1
21454	incorporábase	1
21455	incontrastables	1
21456	inconstancia	1
21457	inconsolables	1
21458	inconsecuencia	1
21459	inconmensurables	1
21460	inconmensurable	1
21461	inconcuso	1
21462	incomprensible	1
21463	incompletos	1
21464	incompletas	1
21465	incompatible	1
21466	incómodo	1
21467	incomodé	1
21468	incomodase	1
21469	incomodarme	1
21470	incomodara	1
21471	incomodar	1
21472	incomodándose	1
21473	incomodan	1
21474	incomodadísima	1
21475	incomodadas	1
21476	incomoda	1
21477	incoloras	1
21478	incluyeran	1
21479	inclusive	1
21480	inclusero	1
21481	incluido	1
21482	inclino	1
21483	inclinarse	1
21484	inclinábase	1
21485	incitó	1
21486	incitar	1
21487	incitantes	1
21488	incitada	1
21489	incipiente	1
21490	incienso	1
21491	incidentes	1
21492	incidente	1
21493	incidencia	1
21494	incertidumbres	1
21495	incentivo	1
21496	incensario	1
21497	incautos	1
21498	incautas	1
21499	incautado	1
21500	incautación	1
21501	incautaba	1
21502	incapacidad	1
21503	inauguró	1
21504	inarmónica	1
21505	inapetente	1
21506	inanición	1
21507	inamovible	1
21508	inalterada	1
21509	inalterable	1
21510	inaguantable	1
21511	inagotable	1
21512	inactivo	1
21513	inactividad	1
21514	inaccesible	1
21515	imputado	1
21516	impuro	1
21517	impurezas	1
21518	impulsión	1
21519	impulsan	1
21520	impulsado	1
21521	impulsábala	1
21522	impulsa	1
21523	impuesta	1
21524	impúber	1
21525	imprudentes	1
21526	improvisar	1
21527	improvisador	1
21528	improvisado	1
21529	improvisada	1
21530	improvisación	1
21531	impropios	1
21532	impropias	1
21533	improbable	1
21534	imprimir	1
21535	imprimían	1
21536	imprimía	1
21537	imprimen	1
21538	impresos	1
21539	impresionar	1
21540	impresionable	1
21541	impresionaba	1
21542	impresas	1
21543	impregnadas	1
21544	imprecación	1
21545	impotente	1
21546	imposiciones	1
21547	imposibilitándola	1
21548	importunarla	1
21549	importarán	1
21550	importadoras	1
21551	importador	1
21552	importación	1
21553	importaban	1
21554	imponiendo	1
21555	imponíale	1
21556	imponérsele	1
21557	imponer	1
21558	imponen	1
21559	implorar	1
21560	implorando	1
21561	implantado	1
21562	impiedad	1
21563	impido	1
21564	impidió	1
21565	impidiéndose	1
21566	impíamente	1
21567	ímpetus	1
21568	impetrando	1
21569	impersonal	1
21570	imperiosos	1
21571	imperfecciones	1
21572	imperativo	1
21573	imperaba	1
21574	impenetrabilidad	1
21575	impedirle	1
21576	impedirla	1
21577	impediré	1
21578	impávida	1
21579	impasible	1
21580	impares	1
21581	imparcialmente	1
21582	impalpable	1
21583	impacientes	1
21584	impacientarse	1
21585	impacienta	1
21586	imítela	1
21587	imitativa	1
21588	imitarlo	1
21589	imitarla	1
21590	imitado	1
21591	imitaciones	1
21592	imbuyen	1
21593	imbecilidad	1
21594	imbéciles	1
21595	imagínese	1
21596	imaginativos	1
21597	imagínate	1
21598	imaginársela	1
21599	imaginarla	1
21600	imaginario	1
21601	imaginando	1
21602	imaginan	1
21603	imaginamos	1
21604	imaginacioncilla	1
21605	ilustrísimo	1
21606	ilustres	1
21607	ilustrando	1
21608	ilustran	1
21609	ilustrada	1
21610	ilusorios	1
21611	ilusorio	1
21612	ilusionó	1
21613	ilusioncita	1
21614	ilusionarse	1
21615	ilusionándose	1
21616	ilusionan	1
21617	ilusionado	1
21618	ilusionaba	1
21619	iluminarme	1
21620	iluminará	1
21621	iluminación	1
21622	ilimitado	1
21623	ilegal	1
21624	iiii	1
21625	iguale	1
21626	igualarían	1
21627	igualara	1
21628	igualada	1
21629	igualaban	1
21630	ignore	1
21631	ignoras	1
21632	ignorar	1
21633	ignoran	1
21634	ignorada	1
21635	ignominioso	1
21636	ignominiosamente	1
21637	iglesita	1
21638	idos	1
21639	idolatrías	1
21640	idolatrar	1
21641	idólatra	1
21642	idolatra	1
21643	ideó	1
21644	idéntico	1
21645	idéntica	1
21646	ídem	1
21647	ideítas	1
21648	idease	1
21649	idear	1
21650	idealista	1
21651	idealismo	1
21652	ideada	1
21653	iconografía	1
21654	ibérica	1
21655	huyas	1
21656	hurón	1
21657	hurgado	1
21658	huracán	1
21659	hundirse	1
21660	hundiose	1
21661	hundiéronse	1
21662	hundidos	1
21663	hundían	1
21664	hundía	1
21665	húndete	1
21666	hunden	1
21667	hunde	1
21668	humos	1
21669	humorísticas	1
21670	humorística	1
21671	humorada	1
21672	humillen	1
21673	humillarles	1
21674	humillante	1
21675	humillaciones	1
21676	humildísimo	1
21677	húmedo	1
21678	humeante	1
21679	humanitario	1
21680	humanamente	1
21681	hules	1
21682	huían	1
21683	huía	1
21684	huevitos	1
21685	hueverito	1
21686	huevería	1
21687	hueveras	1
21688	huésped	1
21689	huérfano	1
21690	huelva	1
21691	huelgas	1
21692	huelga	1
21693	huecas	1
21694	hubiesen	1
21695	hubiérales	1
21696	hoz	1
21697	hoteles	1
21698	hostigó	1
21699	hostigándole	1
21700	hortalizas	1
21701	hortaliza	1
21702	horroroso	1
21703	horrorizadas	1
21704	horroriza	1
21705	horrorice	1
21706	horripilé	1
21707	horripiladas	1
21708	horripila	1
21709	horrenda	1
21710	horquillas	1
21711	hornito	1
21712	hormiguilla	1
21713	hormiguero	1
21714	horizontales	1
21715	horita	1
21716	hordas	1
21717	horcas	1
21718	horada	1
21719	honrarle	1
21720	honrar	1
21721	honrando	1
21722	honradote	1
21723	honradito	1
21724	honradísimo	1
21725	honradeces	1
21726	honorarios	1
21727	honorario	1
21728	honorabilidad	1
21729	honguito	1
21730	honestos	1
21731	honestidad	1
21732	hondísimos	1
21733	hondísimas	1
21734	hondero	1
21735	hondas	1
21736	homenaje	1
21737	hombrunas	1
21738	hombrón	1
21739	hombría	1
21740	hombrada	1
21741	hombrachón	1
21742	hollín	1
21743	holgazanote	1
21744	holgazanes	1
21745	holgazanería	1
21746	holgazana	1
21747	holgados	1
21748	holgadísimas	1
21749	holgadamente	1
21750	holandas	1
21751	hojuelas	1
21752	hojitas	1
21753	hojarasca	1
21754	hogares	1
21755	hociquitos	1
21756	hociquearemos	1
21757	hocicadas	1
21758	hocicada	1
21759	hízome	1
21760	hízola	1
21761	histrionismo	1
21762	histriónica	1
21763	historiador	1
21764	hispanófilo	1
21765	hispana	1
21766	hirviendo	1
21767	hirió	1
21768	hirieran	1
21769	hiriera	1
21770	hiriendo	1
21771	hipotéticamente	1
21772	hipótesis	1
21773	hipotecan	1
21774	hipotecado	1
21775	hipoquitropíticas	1
21776	hipódromo	1
21777	hipocritón	1
21778	hipocráticos	1
21779	hipocráticas	1
21780	hipócrates	1
21781	hipo	1
21782	hiperquinesia	1
21783	hiperbólicos	1
21784	hiperbólico	1
21785	hiperbólicamente	1
21786	hipérbole	1
21787	hindostán	1
21788	hincósele	1
21789	hinchar	1
21790	hinchándose	1
21791	hinchando	1
21792	hinchados	1
21793	hinchada	1
21794	hinchaba	1
21795	hincar	1
21796	hincaba	1
21797	himnos	1
21798	hilvanarlos	1
21799	hilito	1
21800	hilillos	1
21801	hileras	1
21802	hildebrando	1
21803	hilar	1
21804	hiladito	1
21805	hilaban	1
21806	hijastra	1
21807	higuí	1
21808	higo	1
21809	higiénicos	1
21810	higiene	1
21811	higa	1
21812	hierven	1
21813	hiero	1
21814	hiere	1
21815	hierba	1
21816	hidropesía	1
21817	hidrógeno	1
21818	hidra	1
21819	hide	1
21820	hicimos	1
21821	hiciéronle	1
21822	híceme	1
21823	heterogéneo	1
21824	heterodoxa	1
21825	hervores	1
21826	herreros	1
21827	herrería	1
21828	herrar	1
21829	herraje	1
21830	heroísmos	1
21831	hermosotes	1
21832	hermosismo	1
21833	hermosísimas	1
21834	hermosísima	1
21835	hermosamente	1
21836	hermanillo	1
21837	heridos	1
21838	hería	1
21839	herejotes	1
21840	herejote	1
21841	herejías	1
21842	herejía	1
21843	hereditario	1
21844	herederos	1
21845	herede	1
21846	heredáis	1
21847	heredadas	1
21848	hereda	1
21849	heráldica	1
21850	hepáticas	1
21851	hendiduras	1
21852	henchido	1
21853	hemorragia	1
21854	hemoptisis	1
21855	hemicráneo	1
21856	heló	1
21857	heliotropo	1
21858	heliogábalo	1
21859	helénica	1
21860	helena	1
21861	helechos	1
21862	helas	1
21863	helaron	1
21864	helar	1
21865	heine	1
21866	hediondo	1
21867	hechicero	1
21868	hebillas	1
21869	hazañas	1
21870	hazaña	1
21871	haymarket	1
21872	hatchiss	1
21873	hartaran	1
21874	hartándose	1
21875	hartan	1
21876	harpías	1
21877	harpía	1
21878	harina	1
21879	haragán	1
21880	hamlet	1
21881	hamburgo	1
21882	hallole	1
21883	hallo	1
21884	hallazgos	1
21885	hállase	1
21886	halláronse	1
21887	hallaron	1
21888	hallar	1
21889	hallamos	1
21890	hallado	1
21891	hálito	1
21892	halcón	1
21893	halagarle	1
21894	hágote	1
21895	hágolo	1
21896	háganme	1
21897	hagámonos	1
21898	haeckel	1
21899	hacinadas	1
21900	haciéndosele	1
21901	haciéndomelo	1
21902	haciéndome	1
21903	hacíanla	1
21904	hacíale	1
21905	haches	1
21906	hache	1
21907	hacérselos	1
21908	hacérsele	1
21909	hacerlas	1
21910	hacendosa	1
21911	hacendista	1
21912	haced	1
21913	habríase	1
21914	habríale	1
21915	habremos	1
21916	habrase	1
21917	hablen	1
21918	háblele	1
21919	hablarse	1
21920	hablarás	1
21921	hablaras	1
21922	hablarán	1
21923	háblame	1
21924	habladoras	1
21925	hablabas	1
21926	habitaba	1
21927	habita	1
21928	habilísimas	1
21929	habiéndote	1
21930	habiéndome	1
21931	habiéndolo	1
21932	habíales	1
21933	habíalas	1
21934	habíala	1
21935	habia	1
21936	habértelo	1
21937	haberlos	1
21938	habas	1
21939	guturales	1
21940	gutural	1
21941	guttenberg	1
21942	gutapercha	1
21943	gustosos	1
21944	gustoso	1
21945	gustosamente	1
21946	gustosa	1
21947	gustes	1
21948	gustas	1
21949	gustara	1
21950	gustable	1
21951	gusanera	1
21952	guras	1
21953	gurapas	1
21954	guitarrista	1
21955	guisotes	1
21956	guiso	1
21957	guisas	1
21958	guisadas	1
21959	guisaba	1
21960	guirnaldas	1
21961	guirigay	1
21962	guiños	1
21963	guiñó	1
21964	guiño	1
21965	guiñar	1
21966	guiñados	1
21967	guiñada	1
21968	guindilla	1
21969	guindalera	1
21970	guillotinadas	1
21971	guillermo	1
21972	guillado	1
21973	guijarro	1
21974	guiase	1
21975	guiarte	1
21976	guiarse	1
21977	guiar	1
21978	guiándolas	1
21979	guiando	1
21980	guiado	1
21981	guiaba	1
21982	guetaria	1
21983	guerrillero	1
21984	guerrera	1
21985	güeno	1
21986	güelvo	1
21987	güélvete	1
21988	guelbenzu	1
21989	guealés	1
21990	gubernativo	1
21991	gubernamentales	1
21992	gubernamental	1
21993	gubernación	1
21994	guasón	1
21995	guasee	1
21996	guarismo	1
21997	guaridas	1
21998	guarida	1
21999	guardesas	1
22000	guardes	1
22001	guarden	1
22002	guárdelo	1
22003	guárdate	1
22004	guardase	1
22005	guardárselo	1
22006	guardarlo	1
22007	guardarle	1
22008	guardarlas	1
22009	guardarla	1
22010	guardarían	1
22011	guardándolo	1
22012	guardamos	1
22013	guardamalletas	1
22014	guárdalo	1
22015	guárdala	1
22016	guardados	1
22017	guardadora	1
22018	guardadas	1
22019	guardacantón	1
22020	guardabrisas	1
22021	guardaban	1
22022	guardábalo	1
22023	guapos	1
22024	guapito	1
22025	guapines	1
22026	guapín	1
22027	guapillas	1
22028	guapezas	1
22029	guapeza	1
22030	guapetones	1
22031	guapamente	1
22032	guadalupe	1
22033	grupito	1
22034	gruesísima	1
22035	grúas	1
22036	groserías	1
22037	grosera	1
22038	gros	1
22039	grite	1
22040	grita	1
22041	grifos	1
22042	griego	1
22043	greña	1
22044	gremios	1
22045	gremio	1
22046	gravitó	1
22047	gravitativo	1
22048	gravísimas	1
22049	grasiento	1
22050	granuloso	1
22051	granulosa	1
22052	granulaciones	1
22053	granujita	1
22054	grandullón	1
22055	grandones	1
22056	grandezas	1
22057	grandemente	1
22058	grandecitos	1
22059	grandecitas	1
22060	grandecita	1
22061	granadinas	1
22062	gramos	1
22063	gramo	1
22064	gramaticales	1
22065	grajeas	1
22066	gráficamente	1
22067	graduación	1
22068	graduaba	1
22069	gradaciones	1
22070	graciosísima	1
22071	grabados	1
22072	grabadas	1
22073	grababan	1
22074	gozosas	1
22075	gozón	1
22076	goznes	1
22077	gozaremos	1
22078	gozaré	1
22079	gozan	1
22080	gotita	1
22081	gótico	1
22082	goterones	1
22083	gotear	1
22084	gorritas	1
22085	gorrita	1
22086	gorrinos	1
22087	gorrina	1
22088	gorjeo	1
22089	gordura	1
22090	gordito	1
22091	gordita	1
22092	gordísimo	1
22093	golviésemos	1
22094	golver	1
22095	golpecito	1
22096	golpeaba	1
22097	golpazos	1
22098	goloso	1
22099	golondrina	1
22100	gollerías	1
22101	goled	1
22102	gola	1
22103	goiri	1
22104	goëthe	1
22105	gocen	1
22106	gocemos	1
22107	gobernarte	1
22108	gobernarse	1
22109	gobernarlo	1
22110	gobernara	1
22111	gobernando	1
22112	gobernadora	1
22113	gobernable	1
22114	gobernábala	1
22115	gluten	1
22116	glotona	1
22117	gloriosos	1
22118	gloriosas	1
22119	glóbulos	1
22120	glóbulo	1
22121	globo	1
22122	gitano	1
22123	gitani	1
22124	gitanas	1
22125	gitana	1
22126	girones	1
22127	girasoles	1
22128	girase	1
22129	girar	1
22130	girando	1
22131	giraba	1
22132	gimnástica	1
22133	gimnasias	1
22134	gimió	1
22135	gimiendo	1
22136	gilís	1
22137	gigantones	1
22138	gigantescas	1
22139	gestión	1
22140	gesticulaba	1
22141	gestación	1
22142	germen	1
22143	germán	1
22144	genuino	1
22145	genuflexión	1
22146	gentualla	1
22147	gentileza	1
22148	gentil	1
22149	generosos	1
22150	generalización	1
22151	generadora	1
22152	generación	1
22153	genealógico	1
22154	gendarme	1
22155	gemelos	1
22156	gelsemina	1
22157	gaznate	1
22158	gaznápiro	1
22159	gazmoño	1
22160	gayola	1
22161	gatuno	1
22162	gatillo	1
22163	gaterías	1
22164	gatería	1
22165	gatera	1
22166	gasté	1
22167	gaste	1
22168	gastas	1
22169	gastarse	1
22170	gastarlo	1
22171	gastarían	1
22172	gastaré	1
22173	gastarás	1
22174	gastará	1
22175	gastándolo	1
22176	gastados	1
22177	gaseosa	1
22178	gasas	1
22179	gárrulo	1
22180	garrulería	1
22181	gárrula	1
22182	garrotazo	1
22183	garró	1
22184	garrapatos	1
22185	garrafas	1
22186	garlochín	1
22187	garita	1
22188	garfio	1
22189	garfiñé	1
22190	garfiñaran	1
22191	garbosa	1
22192	garantíceme	1
22193	garantías	1
22194	garantía	1
22195	garabito	1
22196	ganzúa	1
22197	ganso	1
22198	gangrenada	1
22199	gane	1
22200	gandía	1
22201	ganarle	1
22202	ganaremos	1
22203	ganarás	1
22204	ganará	1
22205	ganapán	1
22206	ganándose	1
22207	ganamos	1
22208	ganadas	1
22209	ganábalo	1
22210	galonado	1
22211	gallos	1
22212	gallinejera	1
22213	gallineja	1
22214	gallináceas	1
22215	galletas	1
22216	galleta	1
22217	gallego	1
22218	gallegas	1
22219	gallega	1
22220	gallardo	1
22221	gallardísimo	1
22222	gallardeaba	1
22223	galindo	1
22224	galimatías	1
22225	galileo	1
22226	galgo	1
22227	galerías	1
22228	galería	1
22229	galdós	1
22230	galas	1
22231	galantes	1
22232	gaeta	1
22233	gachas	1
22234	gacetilla	1
22235	gabinetes	1
22236	gabachos	1
22237	gabachas	1
22238	fustes	1
22239	fusileros	1
22240	fusilaron	1
22241	fusilar	1
22242	fusilaba	1
22243	furtivas	1
22244	furores	1
22245	furiosos	1
22246	furiosas	1
22247	furiosamente	1
22248	furibundos	1
22249	furibundas	1
22250	funestos	1
22251	funestas	1
22252	funerales	1
22253	funeral	1
22254	fundirnos	1
22255	fundiéndose	1
22256	fundarme	1
22257	fundándonos	1
22258	fundándome	1
22259	fundando	1
22260	fundamentales	1
22261	fundamenta	1
22262	fundados	1
22263	fundábase	1
22264	fundabas	1
22265	funda	1
22266	funcionario	1
22267	funcionara	1
22268	funcionar	1
22269	funcionante	1
22270	funcionando	1
22271	funcionaban	1
22272	funcionaba	1
22273	fumarse	1
22274	fumándose	1
22275	fumada	1
22276	fumaba	1
22277	fuma	1
22278	fulminó	1
22279	fulminantes	1
22280	fulgores	1
22281	fulastre	1
22282	fuisteis	1
22283	fuimos	1
22284	fugitivos	1
22285	fugitiva	1
22286	fugaces	1
22287	fuertecilla	1
22288	fueren	1
22289	fuentecillas	1
22290	fuencarral	1
22291	fu	1
22292	frustrar	1
22293	frustrado	1
22294	fruslerías	1
22295	fruncir	1
22296	fruncidos	1
22297	fruncida	1
22298	fruición	1
22299	frugalidad	1
22300	froten	1
22301	frote	1
22302	frotasen	1
22303	frotándole	1
22304	frotándola	1
22305	frotando	1
22306	frotábase	1
22307	frotaban	1
22308	frontiles	1
22309	frontil	1
22310	frontero	1
22311	fronteras	1
22312	frontales	1
22313	frontal	1
22314	frondoso	1
22315	frivolidad	1
22316	frívola	1
22317	fritas	1
22318	fritanga	1
22319	frisaba	1
22320	frigidísimo	1
22321	fríes	1
22322	frieron	1
22323	fríamente	1
22324	fresquecito	1
22325	fresquecita	1
22326	fresno	1
22327	frescuras	1
22328	frescachona	1
22329	frescachón	1
22330	frenopático	1
22331	frenética	1
22332	freír	1
22333	freidera	1
22334	fregoteo	1
22335	fregotee	1
22336	fregaré	1
22337	fregando	1
22338	fregaban	1
22339	fregaba	1
22340	freeeesero	1
22341	frecuentemente	1
22342	frecuentar	1
22343	frecuentando	1
22344	frecuentaban	1
22345	frecuenta	1
22346	freatas	1
22347	frasecilla	1
22348	frasear	1
22349	frascuelo	1
22350	franquezas	1
22351	franja	1
22352	franela	1
22353	francisca	1
22354	francesillas	1
22355	francesilla	1
22356	francesas	1
22357	francachelas	1
22358	fragmentos	1
22359	fragmento	1
22360	frágil	1
22361	fragatonas	1
22362	fragancias	1
22363	fouquier	1
22364	fotográfico	1
22365	fortunatita	1
22366	fortunatas	1
22367	fortunas	1
22368	fortunaaá	1
22369	fortifica	1
22370	fortalecimiento	1
22371	fortalecídose	1
22372	fortalecido	1
22373	fortalecen	1
22374	fortalece	1
22375	forros	1
22376	forraría	1
22377	foro	1
22378	formuló	1
22379	formularlo	1
22380	formular	1
22381	formose	1
22382	fórmico	1
22383	forme	1
22384	formarte	1
22385	formarle	1
22386	formarlas	1
22387	formaría	1
22388	forman	1
22389	formalmente	1
22390	formalito	1
22391	formalita	1
22392	formada	1
22393	formación	1
22394	forjarse	1
22395	forjar	1
22396	forcejear	1
22397	forcejeando	1
22398	forasteros	1
22399	forasteras	1
22400	forajido	1
22401	fontainebleau	1
22402	fomento	1
22403	fomentas	1
22404	folletos	1
22405	folletito	1
22406	fogosas	1
22407	fogón	1
22408	fofa	1
22409	fluidos	1
22410	fluido	1
22411	flote	1
22412	flotar	1
22413	florilogios	1
22414	floridas	1
22415	floreos	1
22416	florecer	1
22417	flojo	1
22418	flojita	1
22419	flexiones	1
22420	flexibilidad	1
22421	flema	1
22422	flecos	1
22423	flechazo	1
22424	flecharla	1
22425	flechadas	1
22426	flechaba	1
22427	flecha	1
22428	flatulento	1
22429	flatulenta	1
22430	flaquear	1
22431	flaqueaban	1
22432	flaqueaba	1
22433	flanco	1
22434	flamencos	1
22435	flamenco	1
22436	flameando	1
22437	flamante	1
22438	fláccidas	1
22439	fisonómico	1
22440	fisonomías	1
22441	fiscalizar	1
22442	firmísima	1
22443	firmando	1
22444	firmamento	1
22445	finito	1
22446	finitas	1
22447	finiquito	1
22448	fingió	1
22449	fingimientos	1
22450	fingidos	1
22451	fingidamente	1
22452	fingida	1
22453	financiero	1
22454	financiera	1
22455	finamente	1
22456	finalizar	1
22457	filtrar	1
22458	filipina	1
22459	filibustero	1
22460	filiación	1
22461	filete	1
22462	filantrópicos	1
22463	filantrópico	1
22464	filantrópicas	1
22465	filantrópica	1
22466	filantropía	1
22467	fije	1
22468	fijáronse	1
22469	fijarlas	1
22470	fijaría	1
22471	fijan	1
22472	fijados	1
22473	figurose	1
22474	figurones	1
22475	figuró	1
22476	figuritas	1
22477	figurita	1
22478	figúrenselo	1
22479	figúrense	1
22480	figuremos	1
22481	figurémonos	1
22482	figuré	1
22483	figure	1
22484	figurarme	1
22485	figuraran	1
22486	figuraciones	1
22487	figuerola	1
22488	fíese	1
22489	fíes	1
22490	fierro	1
22491	fieros	1
22492	fierezas	1
22493	fierecilla	1
22494	fielmente	1
22495	fidelidades	1
22496	fidedignas	1
22497	ficciones	1
22498	fibras	1
22499	fíate	1
22500	fiasco	1
22501	fiara	1
22502	fiambrera	1
22503	fiado	1
22504	fiaba	1
22505	feúcha	1
22506	fétido	1
22507	fétidas	1
22508	fetiches	1
22509	festoneados	1
22510	festiva	1
22511	fervorosa	1
22512	fervientes	1
22513	férula	1
22514	fértil	1
22515	ferruje	1
22516	ferrocarril	1
22517	ferretero	1
22518	ferretería	1
22519	ferretera	1
22520	ferocidades	1
22521	feroces	1
22522	fernán	1
22523	fermentaron	1
22524	fermentando	1
22525	fermentados	1
22526	fermenta	1
22527	feotes	1
22528	feona	1
22529	feón	1
22530	fénico	1
22531	fenicias	1
22532	femeninas	1
22533	femenina	1
22534	femenil	1
22535	felpudos	1
22536	felpilla	1
22537	felpa	1
22538	felicito	1
22539	felicíteme	1
22540	felicitaron	1
22541	felicitándose	1
22542	felicidades	1
22543	feíto	1
22544	feísimo	1
22545	fedro	1
22546	fecundísimo	1
22547	fecunda	1
22548	feculentos	1
22549	fechadura	1
22550	featón	1
22551	favoreciéndoles	1
22552	favoreciendo	1
22553	favorecidos	1
22554	favorecían	1
22555	favorecen	1
22556	favorablemente	1
22557	fauces	1
22558	fatuo	1
22559	fatua	1
22560	fatigas	1
22561	fatigándose	1
22562	fatigando	1
22563	fatigadísimo	1
22564	fatigaba	1
22565	fatídicas	1
22566	fatídica	1
22567	fatales	1
22568	fastidioso	1
22569	fastidiosa	1
22570	fastídiese	1
22571	fastidien	1
22572	fastidie	1
22573	fastidiar	1
22574	fascinador	1
22575	fascinaban	1
22576	fascinaba	1
22577	farsas	1
22578	farsantuelo	1
22579	farolona	1
22580	fariseos	1
22581	farfantonas	1
22582	farfantona	1
22583	fare	1
22584	fantásticas	1
22585	fantásticamente	1
22586	fantástica	1
22587	fantasmonas	1
22588	fantasmón	1
22589	fantasmas	1
22590	fantasmagórica	1
22591	fantasmagorías	1
22592	fantasiar	1
22593	fanfarronería	1
22594	fanegas	1
22595	fandangos	1
22596	fandango	1
22597	fanáticos	1
22598	fanático	1
22599	fanática	1
22600	famosas	1
22601	familiona	1
22602	familión	1
22603	familiarizarse	1
22604	familiarizaran	1
22605	familiarizara	1
22606	familiarizado	1
22607	familiarizadas	1
22608	familiaridades	1
22609	famélicas	1
22610	faltoncito	1
22611	faltón	1
22612	faltes	1
22613	faltase	1
22614	faltaron	1
22615	faltarnos	1
22616	faltaría	1
22617	faltarás	1
22618	faltan	1
22619	falsísimo	1
22620	falsificadas	1
22621	falsificada	1
22622	falsificación	1
22623	falsedad	1
22624	falseamiento	1
22625	falsarias	1
22626	fallecido	1
22627	falle	1
22628	falla	1
22629	faldón	1
22630	fajita	1
22631	fajas	1
22632	fajarlo	1
22633	fajado	1
22634	facto	1
22635	facilitaran	1
22636	facilitan	1
22637	facilita	1
22638	fachas	1
22639	fachadas	1
22640	faccioso	1
22641	fabulosos	1
22642	fabricar	1
22643	fabrican	1
22644	fa	1
22645	ezquerdo	1
22646	eylau	1
22647	exuberante	1
22648	extremando	1
22649	extremaba	1
22650	extrema	1
22651	extrayendo	1
22652	extraviarse	1
22653	extravían	1
22654	extraviadas	1
22655	extraordinarios	1
22656	extraordinarias	1
22657	extrañó	1
22658	extrañísima	1
22659	extrañe	1
22660	extrañase	1
22661	extrañará	1
22662	extrañando	1
22663	extranjis	1
22664	extranjerote	1
22665	extranjerizado	1
22666	extranjerismo	1
22667	extraído	1
22668	extraía	1
22669	extraerle	1
22670	extraer	1
22671	extractor	1
22672	extracción	1
22673	extra	1
22674	extirpación	1
22675	extinguirse	1
22676	extinguieran	1
22677	extinguido	1
22678	extinguía	1
22679	exterminios	1
22680	exterminio	1
22681	exteriorizarse	1
22682	exteriores	1
22683	extenuación	1
22684	extensiones	1
22685	extendiéndose	1
22686	extendían	1
22687	extenderlas	1
22688	extáticos	1
22689	exquisitas	1
22690	expusiera	1
22691	expurgación	1
22692	expulsarla	1
22693	expulsados	1
22694	expulsadas	1
22695	expugnador	1
22696	exprimidas	1
22697	express	1
22698	expreso	1
22699	expresivas	1
22700	expresase	1
22701	expresarlo	1
22702	expresarle	1
22703	expresarlas	1
22704	expresándole	1
22705	expresábase	1
22706	expresaban	1
22707	expositor	1
22708	exposiciones	1
22709	exposición	1
22710	exponían	1
22711	expondré	1
22712	explotarse	1
22713	explotados	1
22714	exploró	1
22715	explore	1
22716	exploraba	1
22717	explíquese	1
22718	expliquen	1
22719	explícito	1
22720	explícitamente	1
22721	explicas	1
22722	explicártelo	1
22723	explicaran	1
22724	explicado	1
22725	explaye	1
22726	explayándose	1
22727	explanó	1
22728	expiró	1
22729	expiraron	1
22730	expirar	1
22731	expirantes	1
22732	expiraban	1
22733	expiar	1
22734	expiad	1
22735	expertos	1
22736	expertísimo	1
22737	expertas	1
22738	experimentos	1
22739	experimentó	1
22740	experimento	1
22741	experimentando	1
22742	experimentales	1
22743	experimentada	1
22744	expensas	1
22745	expenden	1
22746	expediente	1
22747	expansivo	1
22748	expansión	1
22749	exóticas	1
22750	exordio	1
22751	exitazo	1
22752	existirá	1
22753	existieran	1
22754	existan	1
22755	exista	1
22756	eximios	1
22757	eximio	1
22758	exijo	1
22759	exigüidad	1
22760	exigirle	1
22761	exigían	1
22762	exigí	1
22763	exiges	1
22764	exigente	1
22765	exigen	1
22766	exhortaba	1
22767	exhibir	1
22768	exhibición	1
22769	exhibe	1
22770	exhausta	1
22771	exhalar	1
22772	exhalaba	1
22773	exenta	1
22774	execrables	1
22775	execrable	1
22776	excusó	1
22777	excusaba	1
22778	excluyó	1
22779	exclusivo	1
22780	exclusiva	1
22781	exclusión	1
22782	excluían	1
22783	exclaustrados	1
22784	exclaustrado	1
22785	excite	1
22786	excitase	1
22787	excitadísimo	1
22788	excitaban	1
22789	excesos	1
22790	excesivamente	1
22791	excepciones	1
22792	excepcionales	1
22793	excepcional	1
22794	excentricidades	1
22795	excéntricas	1
22796	excelsos	1
22797	excelso	1
22798	exasperaba	1
22799	examinemos	1
22800	examine	1
22801	examinase	1
22802	examinarlas	1
22803	examinarla	1
22804	examínalo	1
22805	examínale	1
22806	examinadas	1
22807	examina	1
22808	exaltarse	1
22809	exaltando	1
22810	exaltados	1
22811	exaltadas	1
22812	exaltaba	1
22813	exagerar	1
22814	exagerando	1
22815	exagerada	1
22816	exageraciones	1
22817	exabrupto	1
22818	evocó	1
22819	evocadas	1
22820	evocación	1
22821	eviten	1
22822	evitarlas	1
22823	evitaban	1
22824	eventuales	1
22825	evasivos	1
22826	evasiva	1
22827	evaporado	1
22828	evangelísticos	1
22829	evangelistas	1
22830	evangelios	1
22831	evangélicos	1
22832	evangélico	1
22833	evangélica	1
22834	europeos	1
22835	europeas	1
22836	eugenio	1
22837	éufrates	1
22838	eton	1
22839	etnográfico	1
22840	eternos	1
22841	eternamente	1
22842	etéreo	1
22843	etéreas	1
22844	etalaje	1
22845	estuvimos	1
22846	estuviesen	1
22847	estupores	1
22848	estupideces	1
22849	estupendos	1
22850	estupendo	1
22851	estudiosos	1
22852	estudias	1
22853	estudiarle	1
22854	estudiaré	1
22855	estudiantillo	1
22856	estudiantiles	1
22857	estudiándole	1
22858	estudia	1
22859	estuchitos	1
22860	estuches	1
22861	estucada	1
22862	estrujaron	1
22863	estrujarla	1
22864	estrujar	1
22865	estrujaba	1
22866	estropicio	1
22867	estropearon	1
22868	estropear	1
22869	estropeándose	1
22870	estropeado	1
22871	estropeadísima	1
22872	estropeada	1
22873	estropea	1
22874	estropajosas	1
22875	estropajosa	1
22876	estropajo	1
22877	estrofas	1
22878	estro	1
22879	estrictamente	1
22880	estricta	1
22881	estribación	1
22882	estrepitosa	1
22883	estrenó	1
22884	estrenaríamos	1
22885	estrenaré	1
22886	estrenara	1
22887	estrenado	1
22888	estrenaba	1
22889	estrena	1
22890	estremecerse	1
22891	estremece	1
22892	estrellitas	1
22893	estrellarla	1
22894	estrellándolas	1
22895	estrecharle	1
22896	estrechar	1
22897	estrechándola	1
22898	estrechando	1
22899	estrechaba	1
22900	estraza	1
22901	estratégico	1
22902	estrangulándola	1
22903	estrangulado	1
22904	estrambóticas	1
22905	estrambótica	1
22906	estragados	1
22907	estragado	1
22908	estrafalarios	1
22909	estrabismo	1
22910	estotra	1
22911	estornudos	1
22912	estornudo	1
22913	estorbe	1
22914	estorbarle	1
22915	estorbar	1
22916	estorbaban	1
22917	estómagos	1
22918	estólidos	1
22919	estolidez	1
22920	estoico	1
22921	estoicismo	1
22922	estoica	1
22923	estofados	1
22924	estofadas	1
22925	estofa	1
22926	estocadas	1
22927	estocada	1
22928	estirpes	1
22929	estirpe	1
22930	estirase	1
22931	estirarse	1
22932	estirarlo	1
22933	estiraran	1
22934	estirando	1
22935	estirados	1
22936	estirado	1
22937	estiradas	1
22938	estímulos	1
22939	estimuló	1
22940	estímulo	1
22941	estimulante	1
22942	estimulándole	1
22943	estimulando	1
22944	estimulada	1
22945	estimó	1
22946	estimaran	1
22947	estiman	1
22948	estimados	1
22949	estimada	1
22950	estimaban	1
22951	estilan	1
22952	estila	1
22953	estigma	1
22954	estéticas	1
22955	esternón	1
22956	esterlinas	1
22957	esteritas	1
22958	esterita	1
22959	esteras	1
22960	estera	1
22961	esteparios	1
22962	estepa	1
22963	estentórea	1
22964	estela	1
22965	estaturas	1
22966	estatuas	1
22967	estatuario	1
22968	estático	1
22969	estática	1
22970	estarte	1
22971	estaribel	1
22972	estarcidos	1
22973	estarcido	1
22974	estantigua	1
22975	estantería	1
22976	estanco	1
22977	estancias	1
22978	estampó	1
22979	estampitas	1
22980	estampido	1
22981	estámpelo	1
22982	estampar	1
22983	estampado	1
22984	estampadas	1
22985	estampaba	1
22986	estalló	1
22987	estallo	1
22988	estalle	1
22989	estallase	1
22990	estafetas	1
22991	estafase	1
22992	estafarles	1
22993	estafar	1
22994	estafamos	1
22995	estadística	1
22996	establezcamos	1
22997	estableciendo	1
22998	establecidos	1
22999	establecía	1
23000	establecerme	1
23001	establecen	1
23002	estable	1
23003	estábase	1
23004	estábanlo	1
23005	esquivaba	1
23006	esquinazo	1
23007	esquilón	1
23008	esquelitas	1
23009	esqueletos	1
23010	esquelas	1
23011	espumas	1
23012	espuerta	1
23013	espuelas	1
23014	esprit	1
23015	espotrique	1
23016	espotricarás	1
23017	espotrica	1
23018	esposas	1
23019	espontáneas	1
23020	espontanearse	1
23021	espontáneamente	1
23022	espolvoreada	1
23023	esplines	1
23024	esplinado	1
23025	esplendor	1
23026	esplendidez	1
23027	espléndidas	1
23028	espléndidamente	1
23029	espirituosa	1
23030	espiritualizar	1
23031	espiritualista	1
23032	espiritualidad	1
23033	espiritista	1
23034	espinoso	1
23035	espigadita	1
23036	espichamos	1
23037	espichaba	1
23038	espich	1
23039	espías	1
23040	espiaba	1
23041	espetó	1
23042	espetarle	1
23043	espetaría	1
23044	espetando	1
23045	espetaba	1
23046	espeta	1
23047	espesos	1
23048	espesas	1
23049	espérese	1
23050	esperes	1
23051	esperarme	1
23052	esperarían	1
23053	esperándole	1
23054	esperándola	1
23055	esperamos	1
23056	esperado	1
23057	esperabas	1
23058	espeluznante	1
23059	espejuelos	1
23060	especulativas	1
23061	especulación	1
23062	espectador	1
23063	específicos	1
23064	especies	1
23065	espátula	1
23066	espatarrados	1
23067	espasmos	1
23068	espasmo	1
23069	espárragos	1
23070	esparcimientos	1
23071	esparcidos	1
23072	españolizada	1
23073	españita	1
23074	espante	1
23075	espantas	1
23076	espantarlo	1
23077	espantara	1
23078	espantar	1
23079	espantan	1
23080	espantajos	1
23081	espantadas	1
23082	espaldilla	1
23083	espaldarazo	1
23084	espaciosísima	1
23085	espació	1
23086	espachurrar	1
23087	esmeró	1
23088	esmerándose	1
23089	esmeradísimos	1
23090	esmerada	1
23091	esmeraba	1
23092	esmaltadas	1
23093	eslabonaba	1
23094	esgrimió	1
23095	esgrimiéndola	1
23096	esforzarte	1
23097	esforzábase	1
23098	esferas	1
23099	esfera	1
23100	eserina	1
23101	esencialísimo	1
23102	escurro	1
23103	escurriendo	1
23104	escurridiza	1
23105	escurrían	1
23106	escurrí	1
23107	escurren	1
23108	escupiría	1
23109	escupiera	1
23110	escupidera	1
23111	escupe	1
23112	escultor	1
23113	esculapio	1
23114	escuezan	1
23115	escuetos	1
23116	escueta	1
23117	escuerzo	1
23118	escuecen	1
23119	escudriñar	1
23120	escudriñando	1
23121	escudriñadoras	1
23122	escudriñaba	1
23123	escudito	1
23124	escudilla	1
23125	escudero	1
23126	escuchó	1
23127	escuchara	1
23128	escuchado	1
23129	escualidez	1
23130	escuálida	1
23131	escuadrones	1
23132	escrutinios	1
23133	escrutinio	1
23134	escrutadora	1
23135	escrutador	1
23136	escrupulosa	1
23137	escritas	1
23138	escribirse	1
23139	escribiré	1
23140	escribirás	1
23141	escribiera	1
23142	escribiente	1
23143	escribiéndole	1
23144	escribidores	1
23145	escribida	1
23146	escriben	1
23147	escríbele	1
23148	escriba	1
23149	escozorcillo	1
23150	escorzos	1
23151	escoplos	1
23152	escopetilla	1
23153	escopeta	1
23154	escondo	1
23155	escondites	1
23156	escondidísimo	1
23157	escondían	1
23158	escondí	1
23159	esconderse	1
23160	esconderme	1
23161	escondería	1
23162	esconderé	1
23163	escóndelo	1
23164	escomienzo	1
23165	escoltaron	1
23166	escoltando	1
23167	escoltado	1
23168	escoltadas	1
23169	escoltada	1
23170	escollos	1
23171	escolásticos	1
23172	escolar	1
23173	escogidos	1
23174	escogido	1
23175	escogidas	1
23176	escogida	1
23177	escoge	1
23178	escocias	1
23179	escocía	1
23180	escocer	1
23181	escobones	1
23182	esclavos	1
23183	esclavizarles	1
23184	esclavizar	1
23185	esclavitudes	1
23186	esclarecerla	1
23187	escépticos	1
23188	escéptico	1
23189	escenita	1
23190	escénico	1
23191	escaseces	1
23192	escasean	1
23193	escaseaban	1
23194	escasas	1
23195	escarnecida	1
23196	escarnecía	1
23197	escarmientos	1
23198	escarmiente	1
23199	escarmentar	1
23200	escarmentada	1
23201	escarlatina	1
23202	escarbando	1
23203	escarbaba	1
23204	escaray	1
23205	escapose	1
23206	escapo	1
23207	escapes	1
23208	escapé	1
23209	escapase	1
23210	escaparte	1
23211	escapárseme	1
23212	escaparse	1
23213	escaparon	1
23214	escapadas	1
23215	escapada	1
23216	escaños	1
23217	escandalosas	1
23218	escandalizan	1
23219	escanciaba	1
23220	escamoteos	1
23221	escamotees	1
23222	escamoteadas	1
23223	escamosa	1
23224	escamonea	1
23225	escamón	1
23226	escamo	1
23227	escamas	1
23228	escamarse	1
23229	escamaba	1
23230	escalonada	1
23231	escalo	1
23232	escaldado	1
23233	escalas	1
23234	escalafón	1
23235	escabullo	1
23236	escabullirse	1
23237	escabecharnos	1
23238	escabecharla	1
23239	escabechadas	1
23240	esbozarse	1
23241	esbelto	1
23242	esbeltísimo	1
23243	esbeltas	1
23244	ésa	1
23245	eruditos	1
23246	erres	1
23247	eroísma	1
23248	erizado	1
23249	erizaba	1
23250	erigido	1
23251	erguía	1
23252	erección	1
23253	érase	1
23254	érales	1
23255	equivoqué	1
23256	equivoque	1
23257	equívocos	1
23258	equivocas	1
23259	equivocarme	1
23260	equivocaría	1
23261	equivocan	1
23262	equivocamos	1
23263	equivoca	1
23264	equipos	1
23265	equipo	1
23266	equipajes	1
23267	equilibrarás	1
23268	equilibradas	1
23269	equilibraban	1
23270	equi	1
23271	epopeyas	1
23272	epitafios	1
23273	episodios	1
23274	epilépticos	1
23275	epilépticas	1
23276	epígrafe	1
23277	epidérmicas	1
23278	epaminondas	1
23279	enzarzó	1
23280	enzarzaran	1
23281	enzarzados	1
23282	enzarzado	1
23283	enzarzaban	1
23284	envuelven	1
23285	envuelve	1
23286	envuelvas	1
23287	envueltitos	1
23288	envueltas	1
23289	envolvíase	1
23290	envolverlos	1
23291	enviudé	1
23292	enviudaste	1
23293	enviole	1
23294	envilecen	1
23295	envidioso	1
23296	envidiarían	1
23297	envidiado	1
23298	envidiada	1
23299	enviciados	1
23300	enviciadas	1
23301	enviarle	1
23302	enviaré	1
23303	enviar	1
23304	enviado	1
23305	envenene	1
23306	envenenas	1
23307	envenenarse	1
23308	envenenara	1
23309	envenenado	1
23310	envenenada	1
23311	envenena	1
23312	envejecidas	1
23313	envejecida	1
23314	envejecer	1
23315	envejece	1
23316	envalentonaban	1
23317	envainó	1
23318	entusiasmó	1
23319	entusiasmes	1
23320	entusiasmas	1
23321	entusiasmándose	1
23322	entusiasman	1
23323	entusiasmaban	1
23324	enturbiando	1
23325	entrometimiento	1
23326	entrometidos	1
23327	entrometidas	1
23328	entrometerse	1
23329	entristeciendo	1
23330	entristecían	1
23331	entristecía	1
23332	entreviendo	1
23333	entrevía	1
23334	entreverando	1
23335	entrevé	1
23336	entretenle	1
23337	entretenimiento	1
23338	entretenidos	1
23339	entretenga	1
23340	entretendría	1
23341	entresacando	1
23342	entremezcladas	1
23343	entremezclada	1
23344	entregues	1
23345	entregue	1
23346	entregárselos	1
23347	entregarme	1
23348	entregarle	1
23349	entregaría	1
23350	entregándoselo	1
23351	entregando	1
23352	entregados	1
23353	entregábase	1
23354	entregábalos	1
23355	entrega	1
23356	entrecortadas	1
23357	entrecortaba	1
23358	entrecanos	1
23359	entreabriendo	1
23360	entreabierta	1
23361	entrarme	1
23362	entrarían	1
23363	entraremos	1
23364	entrañable	1
23365	entrañaba	1
23366	éntranle	1
23367	entramos	1
23368	entrambas	1
23369	entramado	1
23370	entortolarse	1
23371	entorpecimiento	1
23372	entorpecían	1
23373	entorpecerle	1
23374	entorpecería	1
23375	entornados	1
23376	entornadas	1
23377	entornaba	1
23378	entonan	1
23379	entonaban	1
23380	entiesaba	1
23381	entienda	1
23382	entidades	1
23383	enterrasen	1
23384	enterrarle	1
23385	enterneció	1
23386	enternecimiento	1
23387	enterneciéndose	1
23388	enternecerían	1
23389	enterita	1
23390	entérese	1
23391	enteres	1
23392	enteremos	1
23393	enteraste	1
23394	enterasen	1
23395	enteraría	1
23396	enteraré	1
23397	entenebrecidos	1
23398	entendiesen	1
23399	entendieran	1
23400	entendían	1
23401	entendí	1
23402	entenderías	1
23403	entenderé	1
23404	entendedor	1
23405	entendederas	1
23406	entendedera	1
23407	entendamos	1
23408	entendámonos	1
23409	entenada	1
23410	entarimado	1
23411	entablose	1
23412	entablaba	1
23413	ensuciarlo	1
23414	ensuciaré	1
23415	ensucian	1
23416	ensuciados	1
23417	ensuciaba	1
23418	ensordecían	1
23419	ensordecedor	1
23420	ensordece	1
23421	ensoberbecido	1
23422	ensoberbecía	1
23423	ensimisme	1
23424	enseñoreando	1
23425	enseñen	1
23426	enséñemelo	1
23427	enseñé	1
23428	enseñe	1
23429	enseñas	1
23430	enseñarte	1
23431	enseñárselo	1
23432	enseñarme	1
23433	enseñarles	1
23434	enseñará	1
23435	enseñándosela	1
23436	enseñándome	1
23437	enseñándole	1
23438	enseñándola	1
23439	enséñame	1
23440	enséñale	1
23441	enseñabas	1
23442	enseñaban	1
23443	ensartadas	1
23444	ensarriá	1
23445	ensañas	1
23446	ensangrentados	1
23447	ensalzaron	1
23448	ensalza	1
23449	enroscado	1
23450	enroscada	1
23451	enroscaba	1
23452	enronquecido	1
23453	enrojecidos	1
23454	enrojecidas	1
23455	enriquecido	1
23456	enriquecer	1
23457	enrevesado	1
23458	enrevesadas	1
23459	enrevesada	1
23460	enrejados	1
23461	enrejado	1
23462	enrejadas	1
23463	enrejada	1
23464	enredarse	1
23465	enredarme	1
23466	enredadora	1
23467	enredado	1
23468	enredada	1
23469	enredaban	1
23470	enreda	1
23471	enranciaran	1
23472	enramada	1
23473	enramaban	1
23474	enojó	1
23475	enojado	1
23476	enojábanla	1
23477	enojaba	1
23478	ennobleciendo	1
23479	ennoblecerse	1
23480	ennegrecido	1
23481	enmudecía	1
23482	enmudecer	1
23483	enmohecidas	1
23484	enmiendes	1
23485	enmendarse	1
23486	enmendar	1
23487	enmendada	1
23488	enmascarando	1
23489	enluto	1
23490	enlutados	1
23491	enloquecía	1
23492	enloquecerme	1
23493	enloquecer	1
23494	enlazan	1
23495	enlazados	1
23496	enlazadas	1
23497	enjuto	1
23498	enjutísimas	1
23499	enjugando	1
23500	enjaretarle	1
23501	enjabonáronle	1
23502	enigmas	1
23503	engullir	1
23504	engrosando	1
23505	engrosaba	1
23506	engrasado	1
23507	engrandecerte	1
23508	engranaje	1
23509	engorden	1
23510	engordas	1
23511	engomado	1
23512	engolosinaron	1
23513	engolosina	1
23514	engolfó	1
23515	engolfada	1
23516	engendros	1
23517	engendrar	1
23518	engendra	1
23519	engatusas	1
23520	engatusar	1
23521	engatusando	1
23522	engatusa	1
23523	engastado	1
23524	engarzada	1
23525	engarza	1
23526	engarnos	1
23527	engarfiñaron	1
23528	engañosa	1
23529	engañen	1
23530	engañe	1
23531	engañase	1
23532	engañarse	1
23533	engañarás	1
23534	engañara	1
23535	engañamos	1
23536	engañadores	1
23537	engañábase	1
23538	enganchadas	1
23539	engancha	1
23540	engalanó	1
23541	engalanarse	1
23542	enfurruñas	1
23543	enfurruñados	1
23544	enfurruñado	1
23545	enfureció	1
23546	enfureciendo	1
23547	enfurecía	1
23548	enfriase	1
23549	enfriarás	1
23550	enfriaran	1
23551	enfriara	1
23552	enfriar	1
23553	enfrenada	1
23554	enfrenaba	1
23555	enfrascaron	1
23556	enflaquecido	1
23557	enfermó	1
23558	enfermizo	1
23559	enfermera	1
23560	enfermara	1
23561	enfáticos	1
23562	enfáticas	1
23563	enfadosas	1
23564	enfadé	1
23565	enfade	1
23566	enfadarías	1
23567	enfadaré	1
23568	enfadará	1
23569	enfadan	1
23570	enfadadito	1
23571	enérgicas	1
23572	enérgicamente	1
23573	enemistad	1
23574	endurecimiento	1
23575	endurecidos	1
23576	endurecida	1
23577	endurecía	1
23578	endulzó	1
23579	endulzara	1
23580	endividos	1
23581	endiñarles	1
23582	endilgarle	1
23583	endiablo	1
23584	endiablados	1
23585	endiablado	1
23586	enderezó	1
23587	enderezarse	1
23588	enderezarán	1
23589	enderezaran	1
23590	enderezado	1
23591	enderezaba	1
23592	endemoniados	1
23593	encuentros	1
23594	encubra	1
23595	encorvarse	1
23596	encopetadas	1
23597	encopetada	1
23598	encontronazos	1
23599	encontrolo	1
23600	encontrole	1
23601	encontrola	1
23602	encontrémela	1
23603	encontrarte	1
23604	encontrársele	1
23605	encontrarme	1
23606	encontrarlos	1
23607	encontrarlo	1
23608	encontrarían	1
23609	encontraremos	1
23610	encontraré	1
23611	encontrábase	1
23612	enconos	1
23613	encomienda	1
23614	encomiástico	1
23615	encomiando	1
23616	encomendole	1
23617	encomendarse	1
23618	encomendaba	1
23619	encolerizado	1
23620	encogimientos	1
23621	encogido	1
23622	encogida	1
23623	encogerlo	1
23624	enclenque	1
23625	encintado	1
23626	encinta	1
23627	encierran	1
23628	enciende	1
23629	encienda	1
23630	enciclopédica	1
23631	encía	1
23632	encharcadas	1
23633	encharcada	1
23634	encharcad	1
23635	encerrona	1
23636	encerró	1
23637	encerrarla	1
23638	encerrarán	1
23639	encerrándose	1
23640	encerrando	1
23641	encerraban	1
23642	encenegándose	1
23643	encendiera	1
23644	encendiéndolas	1
23645	encenderse	1
23646	encenderlas	1
23647	encendería	1
23648	encenágate	1
23649	encefálico	1
23650	encauzarlo	1
23651	encastilló	1
23652	encasquetarme	1
23653	encasquetan	1
23654	encasquetado	1
23655	encasquetada	1
23656	encasquetaba	1
23657	encarose	1
23658	encarnarse	1
23659	encarnándose	1
23660	encarna	1
23661	encariñarte	1
23662	encariñan	1
23663	encariñada	1
23664	encariñaba	1
23665	encargue	1
23666	encárgate	1
23667	encargase	1
23668	encargarte	1
23669	encargarse	1
23670	encargarle	1
23671	encargaría	1
23672	encargaremos	1
23673	encargaras	1
23674	encargara	1
23675	encargados	1
23676	encargadas	1
23677	encargada	1
23678	encargábase	1
23679	encargaban	1
23680	encareció	1
23681	encarecimientos	1
23682	encarecer	1
23683	encarcelada	1
23684	encaramando	1
23685	encaprichó	1
23686	encapricharte	1
23687	encantando	1
23688	encantan	1
23689	encantados	1
23690	encantadora	1
23691	encantador	1
23692	encanta	1
23693	encanijado	1
23694	encanijada	1
23695	encanecido	1
23696	encanallan	1
23697	encanallamiento	1
23698	encanallado	1
23699	encaminaron	1
23700	encaminarla	1
23701	encamarme	1
23702	encamada	1
23703	encalabrinada	1
23704	encajó	1
23705	encajería	1
23706	encajera	1
23707	encajan	1
23708	encajaba	1
23709	encadenando	1
23710	enardecía	1
23711	enano	1
23712	enanita	1
23713	enamorisca	1
23714	enamoraran	1
23715	enamoramiento	1
23716	enamoradito	1
23717	enamoradas	1
23718	enamora	1
23719	enaltecido	1
23720	enaltecerlo	1
23721	enaltecer	1
23722	enajenación	1
23723	emulsión	1
23724	empujones	1
23725	empujole	1
23726	empujola	1
23727	empujaran	1
23728	empujará	1
23729	empujándose	1
23730	empujando	1
23731	empuja	1
23732	empuerca	1
23733	empresario	1
23734	emprendiera	1
23735	emprendido	1
23736	emprendía	1
23737	emprenderla	1
23738	empozado	1
23739	empolvadas	1
23740	empolva	1
23741	empollar	1
23742	empollándola	1
23743	empobreciesen	1
23744	empobrecida	1
23745	emplomadas	1
23746	empleolo	1
23747	empleíto	1
23748	empleitas	1
23749	empleasen	1
23750	emplearse	1
23751	emplearla	1
23752	empleara	1
23753	empleábale	1
23754	empingorotó	1
23755	empingorotadas	1
23756	empingorotada	1
23757	empinándose	1
23758	empina	1
23759	empieces	1
23760	empezase	1
23761	empezaremos	1
23762	empezaré	1
23763	empezarás	1
23764	empezarán	1
23765	emperifollada	1
23766	emperejilarse	1
23767	emperejilado	1
23768	empequeñecido	1
23769	empeoró	1
23770	empeoraba	1
23771	empeñemos	1
23772	empeñáronse	1
23773	empeñaron	1
23774	empeñarme	1
23775	empeñarás	1
23776	empeñará	1
23777	empeñando	1
23778	empeñadamente	1
23779	empeñábase	1
23780	empenachados	1
23781	empedrados	1
23782	empedernido	1
23783	empedernidas	1
23784	empecemos	1
23785	emparrados	1
23786	emparentada	1
23787	emparejan	1
23788	empaquetados	1
23789	empapelar	1
23790	empapada	1
23791	empañado	1
23792	empalme	1
23793	empalmaste	1
23794	empalmaba	1
23795	empalagosos	1
23796	empalagoso	1
23797	empalagosa	1
23798	emolumentos	1
23799	emoliente	1
23800	emitir	1
23801	emitía	1
23802	emisión	1
23803	eminentemente	1
23804	eminente	1
23805	eminencias	1
23806	emilion	1
23807	emilio	1
23808	emigrar	1
23809	eméticos	1
23810	emético	1
23811	emersión	1
23812	embusteros	1
23813	embusteras	1
23814	embudo	1
23815	embruteció	1
23816	embrutecido	1
23817	embrutecida	1
23818	embrutecía	1
23819	embrutecerse	1
23820	embrionario	1
23821	embriagó	1
23822	embriago	1
23823	embriagarle	1
23824	embriagado	1
23825	embriagada	1
23826	embriagaba	1
23827	embozos	1
23828	embozándose	1
23829	embozadito	1
23830	embotarse	1
23831	emboscada	1
23832	emborrachen	1
23833	emborrachado	1
23834	emborrachaban	1
23835	emboce	1
23836	embobar	1
23837	embobado	1
23838	embiste	1
23839	embetunadas	1
23840	embestirla	1
23841	embestidas	1
23842	embestida	1
23843	embelleciéndose	1
23844	embellecían	1
23845	embellecer	1
23846	embelesarse	1
23847	embelesan	1
23848	embelesado	1
23849	embelesadas	1
23850	embelesada	1
23851	embebecimiento	1
23852	embebecida	1
23853	embebe	1
23854	embaulará	1
23855	embaucara	1
23856	embaucar	1
23857	embaucando	1
23858	embarulló	1
23859	embarullarse	1
23860	embarullar	1
23861	embarullaba	1
23862	embargué	1
23863	embargaron	1
23864	embargaría	1
23865	embargado	1
23866	embarcase	1
23867	embarcaciones	1
23868	embarcación	1
23869	embaldosados	1
23870	embalajes	1
23871	embajador	1
23872	embadurnadas	1
23873	embadurnada	1
23874	emancipaste	1
23875	emanciparse	1
23876	emanciparía	1
23877	emanada	1
23878	emanaciones	1
23879	emanaban	1
23880	eludir	1
23881	elogiaron	1
23882	elogiarle	1
23883	elogiando	1
23884	elogian	1
23885	elle	1
23886	elimine	1
23887	eliminar	1
23888	eliminación	1
23889	eliminaba	1
23890	eligió	1
23891	elige	1
23892	elevado	1
23893	elevación	1
23894	elevaban	1
23895	elevaba	1
23896	elegirte	1
23897	elegantona	1
23898	elegantísimo	1
23899	electriza	1
23900	elduayen	1
23901	elástico	1
23902	elasticidad	1
23903	elástica	1
23904	elaboradas	1
23905	elaboración	1
23906	elaboraba	1
23907	ejido	1
23908	ejerzo	1
23909	ejercitando	1
23910	ejercitaban	1
23911	ejercían	1
23912	ejerce	1
23913	ejecutarla	1
23914	ejecuta	1
23915	egipcios	1
23916	efusiones	1
23917	efeméride	1
23918	efectuó	1
23919	efectuase	1
23920	efectuarse	1
23921	efectivos	1
23922	efectividad	1
23923	eduqué	1
23924	educatrices	1
23925	educativa	1
23926	educarse	1
23927	educarle	1
23928	educarlas	1
23929	educaré	1
23930	educaran	1
23931	educan	1
23932	educados	1
23933	educadito	1
23934	educadas	1
23935	educaba	1
23936	educa	1
23937	edificó	1
23938	edificársenos	1
23939	edificarse	1
23940	edificara	1
23941	edificante	1
23942	edificado	1
23943	edificadas	1
23944	edificaba	1
23945	edecán	1
23946	ecuménico	1
23947	ecónomo	1
23948	economizar	1
23949	economistas	1
23950	economista	1
23951	eclipsó	1
23952	eclipses	1
23953	eclipse	1
23954	eclipsaban	1
23955	echole	1
23956	échenme	1
23957	échenle	1
23958	echen	1
23959	echemos	1
23960	echaste	1
23961	echase	1
23962	echártela	1
23963	echárnosla	1
23964	echarnos	1
23965	echarlos	1
23966	echarlo	1
23967	echarles	1
23968	echarían	1
23969	echaría	1
23970	echarás	1
23971	echará	1
23972	echándotelas	1
23973	echándotela	1
23974	échame	1
23975	echadito	1
23976	echabas	1
23977	echábamos	1
23978	echábalo	1
23979	echábalas	1
23980	ebro	1
23981	durmiese	1
23982	durmiéndola	1
23983	duritos	1
23984	durísima	1
23985	duretes	1
23986	durete	1
23987	duración	1
23988	duraban	1
23989	durábale	1
23990	duques	1
23991	duodécimo	1
23992	dulzuras	1
23993	dulzón	1
23994	dulcísimo	1
23995	dulcificó	1
23996	dulcificarla	1
23997	dulcificando	1
23998	duerman	1
23999	duelos	1
24000	duelo	1
24001	duelitos	1
24002	dudosa	1
24003	duden	1
24004	dude	1
24005	dudara	1
24006	dudan	1
24007	dubitativo	1
24008	dubarry	1
24009	dualismos	1
24010	dromedario	1
24011	droguista	1
24012	drástico	1
24013	dramón	1
24014	dramita	1
24015	dover	1
24016	dotrina	1
24017	dotarle	1
24018	dotada	1
24019	dormitar	1
24020	dormitaban	1
24021	dormitaba	1
24022	dormiste	1
24023	dormirte	1
24024	dormirnos	1
24025	dormirlas	1
24026	dormiría	1
24027	dormiremos	1
24028	dormiré	1
24029	dormilones	1
24030	dormilón	1
24031	dormías	1
24032	dorando	1
24033	dorados	1
24034	doraba	1
24035	donativo	1
24036	dominó	1
24037	domini	1
24038	domingueros	1
24039	domine	1
24040	dominarse	1
24041	dominantes	1
24042	dominan	1
24043	dominado	1
24044	domicilios	1
24045	domiciliarios	1
24046	domestiquen	1
24047	domesticidad	1
24048	domesticaremos	1
24049	domesticar	1
24050	domarle	1
24051	domaríamos	1
24052	domar	1
24053	domado	1
24054	dolorido	1
24055	doloridas	1
24056	doliesen	1
24057	doliese	1
24058	dolieron	1
24059	doliente	1
24060	dolían	1
24061	dolerle	1
24062	dolencia	1
24063	dogal	1
24064	doctrinarios	1
24065	doctrinario	1
24066	doctores	1
24067	doctoral	1
24068	doctora	1
24069	docilota	1
24070	doblones	1
24071	dobloncito	1
24072	dobló	1
24073	doblemos	1
24074	doblegarse	1
24075	doblase	1
24076	doblarlos	1
24077	doblarlo	1
24078	doblados	1
24079	dobladitos	1
24080	dobladillar	1
24081	dobladas	1
24082	dobla	1
24083	do	1
24084	divulgasen	1
24085	divisoria	1
24086	divisara	1
24087	divisar	1
24088	divisado	1
24089	divirtió	1
24090	divirtiera	1
24091	divierto	1
24092	diviertan	1
24093	dividió	1
24094	divididos	1
24095	divididas	1
24096	dividíanse	1
24097	dividendos	1
24098	dividendo	1
24099	dividen	1
24100	divertirte	1
24101	divertirme	1
24102	divertimientos	1
24103	divertidos	1
24104	divertíanla	1
24105	divertí	1
24106	diverso	1
24107	diversiones	1
24108	diversidad	1
24109	diversa	1
24110	diurna	1
24111	diuréticos	1
24112	disuélvase	1
24113	disuelto	1
24114	disuadirle	1
24115	disuadir	1
24116	distritos	1
24117	distribuyendo	1
24118	distribuirse	1
24119	distribuidos	1
24120	distribuido	1
24121	distrayendo	1
24122	distrajeron	1
24123	distrajera	1
24124	distraigo	1
24125	distráiganme	1
24126	distraidita	1
24127	distráete	1
24128	distraerle	1
24129	distraería	1
24130	distraedme	1
24131	distrae	1
24132	disto	1
24133	distinguirle	1
24134	distinguirla	1
24135	distinguieron	1
24136	distinguiéndose	1
24137	distinguí	1
24138	distingue	1
24139	distingos	1
24140	diste	1
24141	distante	1
24142	distaba	1
24143	disputó	1
24144	disputase	1
24145	disputárselo	1
24146	disputaron	1
24147	disputara	1
24148	disputando	1
24149	disputan	1
24150	disputábanse	1
24151	dispuestilla	1
24152	dispuestas	1
24153	disponibles	1
24154	dispersión	1
24155	dispersas	1
24156	dispersado	1
24157	dispersaban	1
24158	dispepsias	1
24159	dispepsia	1
24160	dispensó	1
24161	dispénseme	1
24162	dispensarme	1
24163	dispensará	1
24164	dispensadora	1
24165	disparos	1
24166	disparó	1
24167	disparatar	1
24168	disparatadamente	1
24169	dispararlos	1
24170	disparar	1
24171	disparándole	1
24172	disparan	1
24173	disparaba	1
24174	disolvían	1
24175	disolutos	1
24176	disoluto	1
24177	disoluta	1
24178	disolución	1
24179	disminuye	1
24180	disloquemos	1
24181	dislocará	1
24182	dislocado	1
24183	dislocada	1
24184	disiparan	1
24185	disipará	1
24186	disipar	1
24187	disipación	1
24188	disipaban	1
24189	disinificantes	1
24190	disimulas	1
24191	disimularse	1
24192	disimularlo	1
24193	disimulan	1
24194	disimuladamente	1
24195	disimulada	1
24196	disimula	1
24197	disimilo	1
24198	disgustarla	1
24199	disgustar	1
24200	disgustaban	1
24201	disfrute	1
24202	disfrutar	1
24203	disfruta	1
24204	disfrazaron	1
24205	disfrazan	1
24206	disfrazados	1
24207	disfrazada	1
24208	disertaron	1
24209	disertación	1
24210	diseño	1
24211	disentimiento	1
24212	disensiones	1
24213	diseminaban	1
24214	disección	1
24215	discutiremos	1
24216	discutiré	1
24217	discutirá	1
24218	discutiose	1
24219	discutió	1
24220	discutían	1
24221	discutíamos	1
24222	discute	1
24223	discursazo	1
24224	discurriera	1
24225	discurres	1
24226	discurre	1
24227	discurras	1
24228	disculpose	1
24229	disculparse	1
24230	disculpar	1
24231	disculpan	1
24232	disculpa	1
24233	discrepando	1
24234	discrepaban	1
24235	discípula	1
24236	disciplinarias	1
24237	disciplinaria	1
24238	discernir	1
24239	discernimiento	1
24240	dirigirá	1
24241	dirigieran	1
24242	dirigiera	1
24243	diríase	1
24244	dirías	1
24245	dirían	1
24246	diremos	1
24247	direcciones	1
24248	diranle	1
24249	diquiá	1
24250	diputados	1
24251	diputación	1
24252	dipósito	1
24253	diplomáticas	1
24254	diplomática	1
24255	diplomacias	1
24256	diploma	1
24257	diósela	1
24258	diosecito	1
24259	diose	1
24260	diosa	1
24261	díos	1
24262	diome	1
24263	dintel	1
24264	dinos	1
24265	dineral	1
24266	dinastía	1
24267	dinamita	1
24268	diminuto	1
24269	dimetria	1
24270	dimensiones	1
24271	dímelas	1
24272	dímela	1
24273	diluviaba	1
24274	dilucidemos	1
24275	diligentísima	1
24276	diligente	1
24277	dilatadas	1
24278	dilatada	1
24279	díjoles	1
24280	dijesen	1
24281	digresiones	1
24282	dígolo	1
24283	dignísimo	1
24284	dignamente	1
24285	dignado	1
24286	digitalina	1
24287	digital	1
24288	digiere	1
24289	digestivo	1
24290	digestión	1
24291	digerido	1
24292	digería	1
24293	dígamelo	1
24294	dígalo	1
24295	difuntos	1
24296	difundido	1
24297	dificultara	1
24298	dificultaba	1
24299	diferir	1
24300	diferiencia	1
24301	diferencian	1
24302	diferenciaban	1
24303	difamatorios	1
24304	diestros	1
24305	diesen	1
24306	diéronse	1
24307	diéranle	1
24308	diéramos	1
24309	dierais	1
24310	dientecillos	1
24311	diecinueve	1
24312	dido	1
24313	dictó	1
24314	dictar	1
24315	dictan	1
24316	dictador	1
24317	dictaba	1
24318	diciéndote	1
24319	diciéndolas	1
24320	dicharachos	1
24321	dicharachera	1
24322	diccionario	1
24323	dibujando	1
24324	dibujan	1
24325	dibujado	1
24326	díaz	1
24327	diátesis	1
24328	diarias	1
24329	diariamente	1
24330	diaria	1
24331	diaquilón	1
24332	diantres	1
24333	dianches	1
24334	diamantinos	1
24335	dialécticas	1
24336	diagnóstico	1
24337	diafanidad	1
24338	diáfana	1
24339	diabólicos	1
24340	diabólicas	1
24341	diablura	1
24342	diablillos	1
24343	diablesca	1
24344	dextrina	1
24345	devuelves	1
24346	devorarle	1
24347	devorarla	1
24348	devorar	1
24349	devorándola	1
24350	devorando	1
24351	devorado	1
24352	devoraban	1
24353	devolviéndoselo	1
24354	devolvérselos	1
24355	devolverle	1
24356	devolverlas	1
24357	devolvería	1
24358	devoluciones	1
24359	devocionarios	1
24360	devastadores	1
24361	devastaba	1
24362	devano	1
24363	devanarse	1
24364	devanar	1
24365	devanamos	1
24366	devanábamos	1
24367	deudora	1
24368	detuviera	1
24369	detiénese	1
24370	detestable	1
24371	determino	1
24372	determiné	1
24373	determinas	1
24374	determinarse	1
24375	determináronse	1
24376	determinaremos	1
24377	determinando	1
24378	determinan	1
24379	determinados	1
24380	determinadas	1
24381	determinada	1
24382	determina	1
24383	deteriorado	1
24384	detenimiento	1
24385	deteniéndola	1
24386	detenido	1
24387	detenida	1
24388	deteníase	1
24389	detenían	1
24390	detengas	1
24391	detenga	1
24392	detenernos	1
24393	detenerlo	1
24394	detenerle	1
24395	detallistas	1
24396	desviven	1
24397	desvió	1
24398	desviar	1
24399	desviado	1
24400	desvergonzó	1
24401	desvergonzada	1
24402	desventurados	1
24403	desventura	1
24404	desventajosa	1
24405	desventajas	1
24406	desventaja	1
24407	desvelo	1
24408	desvelados	1
24409	desvela	1
24410	desvariar	1
24411	desvariando	1
24412	desvanecieron	1
24413	desvaneciéndose	1
24414	desvanecidas	1
24415	desvanecerse	1
24416	desvanecen	1
24417	desván	1
24418	desvalidos	1
24419	desvalido	1
24420	destruyo	1
24421	destruyese	1
24422	destruirlos	1
24423	destruirlo	1
24424	destruido	1
24425	destruía	1
24426	destructoras	1
24427	destrución	1
24428	destrozará	1
24429	destinósele	1
24430	destinatario	1
24431	destinaba	1
24432	destilando	1
24433	destiladera	1
24434	destilaba	1
24435	destierro	1
24436	desterrarlo	1
24437	desterrando	1
24438	desterrados	1
24439	desternillaba	1
24440	destape	1
24441	destapas	1
24442	destapar	1
24443	destapaba	1
24444	destajo	1
24445	destacose	1
24446	destacó	1
24447	destacándose	1
24448	destacaban	1
24449	desquite	1
24450	desquicien	1
24451	desquiciaron	1
24452	desquiciamiento	1
24453	despuntaban	1
24454	despuntaba	1
24455	desprovista	1
24456	despropósito	1
24457	desproporcionadamente	1
24458	desprevenida	1
24459	desprestigiaría	1
24460	desprestigiar	1
24461	despreocupación	1
24462	desprendió	1
24463	desprendiese	1
24464	desprendiendo	1
24465	desprendido	1
24466	desprendía	1
24467	desprenderme	1
24468	despreció	1
24469	desprecian	1
24470	despreciado	1
24471	despreciadas	1
24472	despotricar	1
24473	despótico	1
24474	despóticamente	1
24475	despótica	1
24476	despojaron	1
24477	despojado	1
24478	desplumó	1
24479	desplumar	1
24480	desplumados	1
24481	desplumadoras	1
24482	desplumaban	1
24483	desplomose	1
24484	desplomado	1
24485	desplomada	1
24486	desplomaban	1
24487	desplegadas	1
24488	desplantes	1
24489	despinta	1
24490	despilfarros	1
24491	despilfarro	1
24492	despiertísima	1
24493	despido	1
24494	despidiéronla	1
24495	despidiera	1
24496	despídete	1
24497	despiden	1
24498	despídase	1
24499	despiadado	1
24500	desperté	1
24501	despertase	1
24502	despertáronse	1
24503	despertarla	1
24504	despertaré	1
24505	despertándose	1
24506	desperna	1
24507	desperezos	1
24508	desperezo	1
24509	desperezara	1
24510	desperdicio	1
24511	despercudir	1
24512	despercudida	1
24513	despepita	1
24514	despeñó	1
24515	despeñaperros	1
24516	despejaría	1
24517	despejará	1
24518	despejándole	1
24519	despejadísimo	1
24520	despejaban	1
24521	despedirles	1
24522	despedirlas	1
24523	despedir	1
24524	despedido	1
24525	despedazaría	1
24526	despedazados	1
24527	despechada	1
24528	despavorido	1
24529	despavoridas	1
24530	desparramados	1
24531	despachos	1
24532	despácheme	1
24533	despaché	1
24534	despache	1
24535	despachase	1
24536	despachara	1
24537	despachando	1
24538	despachados	1
24539	despacha	1
24540	despabile	1
24541	despabilarme	1
24542	desorientados	1
24543	desorientaba	1
24544	desorganización	1
24545	desordenadas	1
24546	desollaron	1
24547	desojaban	1
24548	desocuparme	1
24549	desocupado	1
24550	desobedientes	1
24551	desobediencia	1
24552	desobedecería	1
24553	desnudez	1
24554	desnudabas	1
24555	desmoralizados	1
24556	desmontó	1
24557	desmintieran	1
24558	desmintiendo	1
24559	desmiente	1
24560	desmerecía	1
24561	desmerecer	1
24562	desmerece	1
24563	desmenuzar	1
24564	desmenuzadas	1
24565	desmenuzaba	1
24566	desmentirá	1
24567	desmentidas	1
24568	desmemoriado	1
24569	desmejorarse	1
24570	desmejoramiento	1
24571	desmejoradillo	1
24572	desmedidamente	1
24573	desmedida	1
24574	desmayó	1
24575	desmayan	1
24576	desmayados	1
24577	desmayado	1
24578	desmayaba	1
24579	desmandase	1
24580	desmanda	1
24581	desmadejada	1
24582	deslumbrado	1
24583	deslumbraba	1
24584	deslucida	1
24585	deslomar	1
24586	deslizose	1
24587	deslizó	1
24588	deslizarse	1
24589	deslizar	1
24590	deslizando	1
24591	deslizado	1
24592	desligado	1
24593	desligada	1
24594	deslicen	1
24595	desliando	1
24596	desliaba	1
24597	deslealtades	1
24598	deslealtad	1
24599	desistió	1
24600	desinteresados	1
24601	desinteresada	1
24602	desilusiones	1
24603	desilusionada	1
24604	desilusión	1
24605	designaré	1
24606	designará	1
24607	designado	1
24608	designada	1
24609	desiderátum	1
24610	deshonró	1
24611	deshonras	1
24612	deshonrarme	1
24613	deshonrarán	1
24614	deshojar	1
24615	deshelaba	1
24616	deshecho	1
24617	deshechas	1
24618	deshaciéndose	1
24619	deshaciendo	1
24620	deshacían	1
24621	deshacía	1
24622	deshacen	1
24623	deshabitada	1
24624	desgranadas	1
24625	desgraciadas	1
24626	desgobernando	1
24627	desgaste	1
24628	desgastase	1
24629	desgastará	1
24630	desgarran	1
24631	desgarrado	1
24632	desgañitarse	1
24633	desganada	1
24634	desflorar	1
24635	desfile	1
24636	desfilaron	1
24637	desfilar	1
24638	desfigurarla	1
24639	desfigurados	1
24640	desfiguraba	1
24641	desfavorecido	1
24642	desfavorables	1
24643	desfavorablemente	1
24644	desfallecimientos	1
24645	desesperarse	1
24646	desesperaría	1
24647	desesperante	1
24648	desesperado	1
24649	desesperadamente	1
24650	desesperada	1
24651	desesperaba	1
24652	desertar	1
24653	deserción	1
24654	desequilibrio	1
24655	desequilibraba	1
24656	deseoso	1
24657	deseosas	1
24658	desenvuelve	1
24659	desenvuelta	1
24660	desenvolvía	1
24661	desenvolveros	1
24662	desenvolverme	1
24663	desenvolver	1
24664	desentumecían	1
24665	desentumecía	1
24666	desentrañar	1
24667	desentono	1
24668	desentonada	1
24669	desenroscarse	1
24670	desenrosca	1
24671	desenojaría	1
24672	desenojar	1
24673	desenlace	1
24674	desengonzado	1
24675	desengaños	1
24676	desengaño	1
24677	desengáñese	1
24678	desengañarle	1
24679	desengañaos	1
24680	desengañado	1
24681	desengañadas	1
24682	desenfundan	1
24683	desenfadada	1
24684	desencuadernarse	1
24685	desencarna	1
24686	desencajados	1
24687	desempeñes	1
24688	desempeñarlo	1
24689	desempeñarla	1
24690	desempeñan	1
24691	desempeñado	1
24692	desembuchas	1
24693	desembuchando	1
24694	desembocar	1
24695	desembarcos	1
24696	desembarcar	1
24697	desellando	1
24698	deseé	1
24699	desecho	1
24700	deseché	1
24701	desecharon	1
24702	desecharla	1
24703	desechar	1
24704	desechando	1
24705	desechados	1
24706	desechadas	1
24707	desearan	1
24708	deseándolo	1
24709	deseándole	1
24710	desean	1
24711	desdoro	1
24712	desdoblado	1
24713	desdoblaba	1
24714	desdijera	1
24715	desdiciéndose	1
24716	desdicha	1
24717	desdice	1
24718	desdeñosas	1
24719	desdeñosa	1
24720	desdeñado	1
24721	desdentado	1
24722	desdecirme	1
24723	descuidos	1
24724	descuidillos	1
24725	descuidero	1
24726	descuidera	1
24727	descuidar	1
24728	descuidadas	1
24729	descuidaban	1
24730	descuentos	1
24731	descuelgue	1
24732	descuelgas	1
24733	descuelga	1
24734	descubriremos	1
24735	descubriolo	1
24736	descubrimos	1
24737	descubrieran	1
24738	descubriera	1
24739	descubrí	1
24740	descubren	1
24741	descubras	1
24742	descuartizarla	1
24743	descuartizar	1
24744	descuartizada	1
24745	descuartice	1
24746	descrita	1
24747	descrismándose	1
24748	descriptivo	1
24749	describirse	1
24750	describía	1
24751	describe	1
24752	descorrían	1
24753	descorrer	1
24754	descorazonó	1
24755	descorazonamiento	1
24756	descorazonado	1
24757	descontentos	1
24758	descontenta	1
24759	descontándole	1
24760	descontadas	1
24761	desconsuelos	1
24762	desconsoladora	1
24763	desconsoladísima	1
24764	desconsolaba	1
24765	desconsideradamente	1
24766	desconozco	1
24767	desconociendo	1
24768	desconocidos	1
24769	desconfías	1
24770	desconfianzas	1
24771	desconfía	1
24772	desconcertados	1
24773	desconcertaba	1
24774	descompusiera	1
24775	descompostura	1
24776	descomposición	1
24777	descomponiéndole	1
24778	descomponían	1
24779	descomedida	1
24780	descolorido	1
24781	descoloridas	1
24782	descollaría	1
24783	descollar	1
24784	descolgarte	1
24785	descolgarlos	1
24786	descolgándose	1
24787	desclavar	1
24788	descifraba	1
24789	descendido	1
24790	descendían	1
24791	descastada	1
24792	descascaraba	1
24793	descartaba	1
24794	descarriado	1
24795	descarriadas	1
24796	descarnada	1
24797	descargos	1
24798	descargó	1
24799	descargo	1
24800	descargasen	1
24801	descargase	1
24802	descargándosela	1
24803	descargando	1
24804	descargados	1
24805	descargada	1
24806	descarado	1
24807	descansó	1
24808	descanses	1
24809	descansen	1
24810	descansaron	1
24811	descansando	1
24812	descansado	1
24813	descansada	1
24814	descansaba	1
24815	descamisado	1
24816	descalzarle	1
24817	descalcitos	1
24818	descalabré	1
24819	descalabrado	1
24820	descalabra	1
24821	descaecimiento	1
24822	descabezando	1
24823	descabezado	1
24824	descabezaban	1
24825	descabaladas	1
24826	desbravase	1
24827	desbordarse	1
24828	desbordamientos	1
24829	desbordamiento	1
24830	desbordaban	1
24831	desbastaron	1
24832	desbastar	1
24833	desbastándola	1
24834	desbarro	1
24835	desbarraba	1
24836	desbaratarse	1
24837	desbaratar	1
24838	desbaratando	1
24839	desbarataba	1
24840	desbarata	1
24841	desbandó	1
24842	desbandan	1
24843	desbandada	1
24844	desazonaba	1
24845	desayunarse	1
24846	desavío	1
24847	desavenidos	1
24848	desatinadas	1
24849	desate	1
24850	desatar	1
24851	desatado	1
24852	desatada	1
24853	desataban	1
24854	desastres	1
24855	desastre	1
24856	desasosegado	1
24857	desasosegada	1
24858	desasosegaba	1
24859	desaseo	1
24860	desaseado	1
24861	desarrollaron	1
24862	desarrollándosele	1
24863	desarrolladas	1
24864	desarrollaban	1
24865	desarregladas	1
24866	desarreglada	1
24867	desarraigar	1
24868	desarmarle	1
24869	desarmar	1
24870	desaprobar	1
24871	desapartaísos	1
24872	desapartada	1
24873	desapariciones	1
24874	desaparezca	1
24875	desapareciendo	1
24876	desaparecida	1
24877	desaparecía	1
24878	desanimarte	1
24879	desanimándose	1
24880	desanimados	1
24881	desamparado	1
24882	desamparadas	1
24883	desamparada	1
24884	desamortización	1
24885	desamor	1
24886	desalmado	1
24887	desalentaban	1
24888	desalada	1
24889	desairaban	1
24890	desahucios	1
24891	desahogos	1
24892	desahogó	1
24893	desahógate	1
24894	desahogaran	1
24895	desahogándola	1
24896	desahogan	1
24897	desahogadamente	1
24898	desahogada	1
24899	desagrado	1
24900	desagradaron	1
24901	desagradablemente	1
24902	desafueros	1
24903	desaforadamente	1
24904	desafíos	1
24905	desafinar	1
24906	desafinamos	1
24907	desafiaban	1
24908	desacredito	1
24909	desacreditar	1
24910	desacordes	1
24911	desacierto	1
24912	desabrocharon	1
24913	desabrigues	1
24914	desabrigo	1
24915	desabrigara	1
24916	desabrigado	1
24917	desabridísimo	1
24918	desabotonar	1
24919	desaborida	1
24920	derroteros	1
24921	derrotar	1
24922	derrotados	1
24923	derrochador	1
24924	derritieran	1
24925	derritiendo	1
24926	derribarle	1
24927	derribar	1
24928	derribando	1
24929	derribada	1
24930	derrengado	1
24931	derramó	1
24932	derramo	1
24933	derrames	1
24934	derrame	1
24935	derramarse	1
24936	derramamiento	1
24937	derramaba	1
24938	derrama	1
24939	derogando	1
24940	derogada	1
24941	derivado	1
24942	derivadas	1
24943	derivaciones	1
24944	derivaba	1
24945	deriva	1
24946	derechitos	1
24947	derechas	1
24948	derechamente	1
24949	depurar	1
24950	deprisa	1
24951	depravados	1
24952	depravado	1
24953	depravaciones	1
24954	depositó	1
24955	depositar	1
24956	depositaban	1
24957	deplorar	1
24958	dependiera	1
24959	dependía	1
24960	departió	1
24961	deparó	1
24962	depare	1
24963	deparándote	1
24964	denuncies	1
24965	denunciado	1
24966	denunciaban	1
24967	denuestos	1
24968	dentición	1
24969	dentelladas	1
24970	denso	1
24971	densísimo	1
24972	densa	1
24973	denotaban	1
24974	denominó	1
24975	denominaciones	1
24976	denominación	1
24977	denme	1
24978	denle	1
24979	dengues	1
24980	dengosas	1
24981	dengosa	1
24982	denegaciones	1
24983	demuestras	1
24984	demuestran	1
24985	demudó	1
24986	demudado	1
24987	demostrarlo	1
24988	demostraré	1
24989	demostrándolo	1
24990	demonche	1
24991	demolieron	1
24992	demolición	1
24993	democráticas	1
24994	democrática	1
24995	demócratas	1
24996	demi	1
24997	demetria	1
24998	demencias	1
24999	demasiadas	1
25000	demasiada	1
25001	demanda	1
25002	demagogo	1
25003	demagógica	1
25004	delta	1
25005	delos	1
25006	delirium	1
25007	delirios	1
25008	delirara	1
25009	delirar	1
25010	delira	1
25011	deliciosos	1
25012	delicioso	1
25013	delicias	1
25014	delicadito	1
25015	deliberadamente	1
25016	deliberada	1
25017	delgadas	1
25018	delfinito	1
25019	delfines	1
25020	deleznables	1
25021	deleitaba	1
25022	delegando	1
25023	delatarla	1
25024	delantito	1
25025	delación	1
25026	dejoso	1
25027	dejolo	1
25028	dejoles	1
25029	dejola	1
25030	dejémoslo	1
25031	déjemelo	1
25032	déjela	1
25033	déjase	1
25034	dejártela	1
25035	dejárselos	1
25036	dejarnos	1
25037	dejarlo	1
25038	dejarles	1
25039	dejaremos	1
25040	dejarás	1
25041	dejarán	1
25042	déjanos	1
25043	dejándotela	1
25044	dejándonos	1
25045	dejándome	1
25046	dejándolo	1
25047	déjamele	1
25048	déjalo	1
25049	déjales	1
25050	déjala	1
25051	dejáis	1
25052	dejadez	1
25053	dejadas	1
25054	dejábalos	1
25055	deicidas	1
25056	dehesa	1
25057	degüello	1
25058	degüellan	1
25059	degrada	1
25060	degollina	1
25061	degollada	1
25062	deglutaba	1
25063	degeneración	1
25064	defraudaciones	1
25065	definiendo	1
25066	defiendo	1
25067	defiéndete	1
25068	déficit	1
25069	deficiencias	1
25070	defensor	1
25071	defensivo	1
25072	defendiera	1
25073	defendiéndose	1
25074	defendiendo	1
25075	defendidos	1
25076	defendida	1
25077	defenderlo	1
25078	defenderlas	1
25079	defendemos	1
25080	defectuosísima	1
25081	deducirse	1
25082	deduciendo	1
25083	deducía	1
25084	deduce	1
25085	deditos	1
25086	dedico	1
25087	dedicas	1
25088	dedicaría	1
25089	dedicar	1
25090	dedicaban	1
25091	dédalos	1
25092	dedal	1
25093	decretó	1
25094	decreto	1
25095	decretado	1
25096	decoroso	1
25097	decorosas	1
25098	decoró	1
25099	decorativas	1
25100	decorativamente	1
25101	decorar	1
25102	decoran	1
25103	decoraciones	1
25104	decoraban	1
25105	decoraba	1
25106	decomisura	1
25107	declive	1
25108	declinación	1
25109	declare	1
25110	declarase	1
25111	declaras	1
25112	declararse	1
25113	declararlo	1
25114	declararía	1
25115	declarando	1
25116	declaran	1
25117	declarados	1
25118	declaraciones	1
25119	declamatorio	1
25120	declamaciones	1
25121	decisivas	1
25122	decírtelo	1
25123	decírselas	1
25124	deciros	1
25125	decirnos	1
25126	decirlas	1
25127	décimos	1
25128	decimos	1
25129	décimas	1
25130	decidor	1
25131	decidirían	1
25132	decidiría	1
25133	decidiose	1
25134	decidieron	1
25135	decidiera	1
25136	decididamente	1
25137	decidí	1
25138	decídete	1
25139	deciden	1
25140	decidáis	1
25141	decible	1
25142	decíase	1
25143	decíanle	1
25144	decíame	1
25145	decíalas	1
25146	decentísimo	1
25147	decayendo	1
25148	decaída	1
25149	decaía	1
25150	decaer	1
25151	decadente	1
25152	débitos	1
25153	débilmente	1
25154	debilitarse	1
25155	debilitado	1
25156	debilitada	1
25157	débiles	1
25158	debieras	1
25159	debiendo	1
25160	deberían	1
25161	deberíamos	1
25162	debería	1
25163	deberá	1
25164	deba	1
25165	deán	1
25166	davidson	1
25167	david	1
25168	dátil	1
25169	dáselo	1
25170	darwinista	1
25171	darwin	1
25172	dártelo	1
25173	dárselas	1
25174	daros	1
25175	dármelo	1
25176	dármelas	1
25177	darlo	1
25178	darías	1
25179	darán	1
25180	daños	1
25181	dañino	1
25182	dañan	1
25183	dañados	1
25184	dañado	1
25185	danzando	1
25186	dante	1
25187	danme	1
25188	daniel	1
25189	dandys	1
25190	dándosela	1
25191	dándolo	1
25192	dámelo	1
25193	damasquería	1
25194	daganzo	1
25195	dádselo	1
25196	dados	1
25197	dadivosos	1
25198	daca	1
25199	dabas	1
25200	dábanse	1
25201	dábalo	1
25202	cutíes	1
25203	custodiarla	1
25204	custodiaba	1
25205	curtidos	1
25206	curtido	1
25207	cursilerías	1
25208	cursilería	1
25209	cursaban	1
25210	curó	1
25211	curo	1
25212	curiosos	1
25213	curiosona	1
25214	curiosísimo	1
25215	curioseo	1
25216	curiosas	1
25217	curia	1
25218	curdela	1
25219	curda	1
25220	curárselas	1
25221	curarme	1
25222	curara	1
25223	curánganos	1
25224	curadas	1
25225	curaba	1
25226	cúpulas	1
25227	cupiesen	1
25228	cuotas	1
25229	cuota	1
25230	cuñas	1
25231	cuñados	1
25232	cuñadita	1
25233	cunitas	1
25234	cunita	1
25235	cuneta	1
25236	cundiendo	1
25237	cunas	1
25238	cumplirse	1
25239	cumplirlo	1
25240	cumplirla	1
25241	cumpliré	1
25242	cumplidísima	1
25243	cumplidamente	1
25244	cumplían	1
25245	cumples	1
25246	cúmplase	1
25247	cumplas	1
25248	cumplamos	1
25249	cultos	1
25250	cultivarlo	1
25251	cultivar	1
25252	cultivando	1
25253	culpables	1
25254	culpabilidad	1
25255	culminante	1
25256	culito	1
25257	culinaria	1
25258	cuitado	1
25259	cuiste	1
25260	cuides	1
25261	cuidarme	1
25262	cuidarlos	1
25263	cuidarla	1
25264	cuidaré	1
25265	cuidará	1
25266	cuidándole	1
25267	cuidándolas	1
25268	cuidadoso	1
25269	cueza	1
25270	cuevas	1
25271	cueva	1
25272	cuestionar	1
25273	cuestionando	1
25274	cuestionaban	1
25275	cuestan	1
25276	cuernos	1
25277	cuentera	1
25278	cuéntenme	1
25279	cuéntanos	1
25280	cuéntale	1
25281	cuéntala	1
25282	cuelguen	1
25283	cuélgueme	1
25284	cuelgo	1
25285	cuela	1
25286	cuco	1
25287	cuchillote	1
25288	cuchillito	1
25289	cuchilladas	1
25290	cuchicheó	1
25291	cuchicheando	1
25292	cuchicheaban	1
25293	cucharillas	1
25294	cucharetazos	1
25295	cucaracha	1
25296	cucamonas	1
25297	cubrirse	1
25298	cubriole	1
25299	cubriéronle	1
25300	cubrieron	1
25301	cubriendo	1
25302	cubrían	1
25303	cubría	1
25304	cúbrete	1
25305	cubres	1
25306	cúbrele	1
25307	cubiletes	1
25308	cubilete	1
25309	cúbicos	1
25310	cúbicas	1
25311	cúbica	1
25312	cuatros	1
25313	cuatrillones	1
25314	cuartillas	1
25315	cuartetos	1
25316	cuarterones	1
25317	cuartelesco	1
25318	cuaresma	1
25319	cuantiosas	1
25320	cuanti	1
25321	cuanta	1
25322	cualisquiera	1
25323	cuajo	1
25324	cuaje	1
25325	cuajarse	1
25326	cuadrumana	1
25327	cuadró	1
25328	cuadrilongo	1
25329	cuadrilla	1
25330	cuadril	1
25331	cuadratura	1
25332	cuadrase	1
25333	cuadrángano	1
25334	cuadraba	1
25335	cuadernos	1
25336	cruzáronse	1
25337	cruzarnos	1
25338	cruzar	1
25339	cruzándose	1
25340	cruzamiento	1
25341	cruzaban	1
25342	crujió	1
25343	crujieron	1
25344	crujidos	1
25345	crujida	1
25346	crujías	1
25347	cruelmente	1
25348	cruelísimas	1
25349	cruelísima	1
25350	crudísimo	1
25351	crudillo	1
25352	crudezas	1
25353	crudas	1
25354	crucis	1
25355	crucifique	1
25356	crucificando	1
25357	crucificados	1
25358	crucifica	1
25359	cruceta	1
25360	croto	1
25361	croquetita	1
25362	crónicas	1
25363	cromwell	1
25364	cromos	1
25365	crochet	1
25366	criticó	1
25367	criticar	1
25368	criticando	1
25369	criterios	1
25370	cristianamente	1
25371	cristalitos	1
25372	crispamientos	1
25373	crinolinas	1
25374	criminala	1
25375	criáronle	1
25376	criaron	1
25377	criarlos	1
25378	criarlo	1
25379	criaré	1
25380	criaban	1
25381	creyolo	1
25382	creyérase	1
25383	creyeran	1
25384	creyente	1
25385	creyéndose	1
25386	crespones	1
25387	crenchas	1
25388	creímos	1
25389	creíamos	1
25390	creételo	1
25391	creérmelo	1
25392	creerlas	1
25393	creerla	1
25394	credulidad	1
25395	credo	1
25396	créditos	1
25397	credencialeja	1
25398	crecieron	1
25399	crecidos	1
25400	crecidito	1
25401	creciditas	1
25402	crecidita	1
25403	creces	1
25404	crearía	1
25405	creánmelo	1
25406	créanlo	1
25407	creamos	1
25408	créamela	1
25409	creadoras	1
25410	creado	1
25411	creaciones	1
25412	creación	1
25413	crac	1
25414	coyunturas	1
25415	covacha	1
25416	courtray	1
25417	cotta	1
25418	cotorrear	1
25419	cotorreaban	1
25420	cotorras	1
25421	cotizaciones	1
25422	cotiza	1
25423	cotidiano	1
25424	costurones	1
25425	costuras	1
25426	costras	1
25427	costera	1
25428	costeo	1
25429	costear	1
25430	costeando	1
25431	costaría	1
25432	costará	1
25433	costar	1
25434	costanilla	1
25435	cósmico	1
25436	cosidos	1
25437	cosido	1
25438	cosidas	1
25439	cosida	1
25440	cosía	1
25441	cosedoras	1
25442	cosecheros	1
25443	coscorrón	1
25444	cortísimo	1
25445	cortinones	1
25446	cortinón	1
25447	cortinilla	1
25448	cortésmente	1
25449	cortesanas	1
25450	cortesana	1
25451	corten	1
25452	cortase	1
25453	cortarte	1
25454	cortarme	1
25455	cortarían	1
25456	cortaría	1
25457	cortará	1
25458	cortante	1
25459	cortándose	1
25460	cortan	1
25461	cortadito	1
25462	cortadísima	1
25463	cortadas	1
25464	corsés	1
25465	corsario	1
25466	corruptora	1
25467	corrompido	1
25468	corrompe	1
25469	corroboró	1
25470	corriole	1
25471	corrillos	1
25472	corrigiendo	1
25473	corrígete	1
25474	corrige	1
25475	corriéndola	1
25476	corriendito	1
25477	corridas	1
25478	corríase	1
25479	corríale	1
25480	corretear	1
25481	correteando	1
25482	correspondencias	1
25483	correrse	1
25484	correrla	1
25485	correrías	1
25486	correría	1
25487	corregirte	1
25488	corregirla	1
25489	corregían	1
25490	correderas	1
25491	corredera	1
25492	correctivos	1
25493	correctísima	1
25494	correa	1
25495	corras	1
25496	corral	1
25497	corpulenta	1
25498	corpulencia	1
25499	corpórea	1
25500	corporal	1
25501	corpachón	1
25502	coros	1
25503	coronen	1
25504	coronado	1
25505	coronadas	1
25506	coronada	1
25507	cornuda	1
25508	cornisas	1
25509	cornisa	1
25510	corneta	1
25511	corito	1
25512	corifeos	1
25513	coria	1
25514	cordones	1
25515	cordón	1
25516	cordilla	1
25517	cordialidad	1
25518	cordiales	1
25519	cordelero	1
25520	cordelería	1
25521	corchetes	1
25522	corbatín	1
25523	corazoncito	1
25524	coraza	1
25525	corambres	1
25526	coral	1
25527	coqueterías	1
25528	coqueteaba	1
25529	coquera	1
25530	copulativas	1
25531	copudo	1
25532	copos	1
25533	copón	1
25534	copo	1
25535	coplitas	1
25536	copiosamente	1
25537	copio	1
25538	copiadores	1
25539	copete	1
25540	convulsivo	1
25541	convocando	1
25542	convite	1
25543	convirtió	1
25544	convirtieran	1
25545	convirtiera	1
25546	convirtiéndose	1
25547	conviniera	1
25548	convierto	1
25549	convierta	1
25550	convienen	1
25551	convide	1
25552	convidara	1
25553	convidadas	1
25554	convidaban	1
25555	convidábale	1
25556	convida	1
25557	convexidad	1
25558	convertirse	1
25559	convertirlo	1
25560	convertirle	1
25561	convertirlas	1
25562	convertiría	1
25563	convertiré	1
25564	convertidas	1
25565	convertían	1
25566	convertía	1
25567	conversos	1
25568	conversión	1
25569	conversando	1
25570	convénzase	1
25571	convenio	1
25572	convenimos	1
25573	conveniencias	1
25574	convencionalismo	1
25575	convencían	1
25576	convences	1
25577	convencerías	1
25578	convencerá	1
25579	convéncele	1
25580	contuso	1
25581	contrista	1
25582	contrincantes	1
25583	contrincante	1
25584	contribuciones	1
25585	contreras	1
25586	contraviniendo	1
25587	contraventores	1
25588	contratos	1
25589	contratista	1
25590	contratiempo	1
25591	contratar	1
25592	contratantes	1
25593	contratación	1
25594	contrastar	1
25595	contrastando	1
25596	contrastaba	1
25597	contrariedades	1
25598	contrariaron	1
25599	contrariada	1
25600	contrariábala	1
25601	contraída	1
25602	contraía	1
25603	contrahechas	1
25604	contrafalda	1
25605	contraer	1
25606	contraen	1
25607	contrae	1
25608	contradijo	1
25609	contradictorias	1
25610	contradiciéndole	1
25611	contradice	1
25612	contradicciones	1
25613	contradecirla	1
25614	contradanzas	1
25615	contracciones	1
25616	contrabandistas	1
25617	contornos	1
25618	contonean	1
25619	contome	1
25620	continuase	1
25621	continuaremos	1
25622	continuara	1
25623	continúan	1
25624	continuadamente	1
25625	continuación	1
25626	continencia	1
25627	contigua	1
25628	contesto	1
25629	contestarse	1
25630	contestarles	1
25631	contéstame	1
25632	contestábale	1
25633	conteras	1
25634	contentísimo	1
25635	contenti	1
25636	conténtate	1
25637	contentaría	1
25638	contentarás	1
25639	contentado	1
25640	contentábase	1
25641	contentaban	1
25642	contentaba	1
25643	contenidas	1
25644	contenida	1
25645	contengo	1
25646	contenga	1
25647	contenerme	1
25648	contendientes	1
25649	contemporizador	1
25650	contemplo	1
25651	contemplarse	1
25652	contemplándole	1
25653	contemplándola	1
25654	contemplaciones	1
25655	conté	1
25656	contase	1
25657	contártelo	1
25658	contarte	1
25659	contárselo	1
25660	contármelo	1
25661	contarme	1
25662	contarlos	1
25663	contaría	1
25664	contaremos	1
25665	contarás	1
25666	contará	1
25667	contándote	1
25668	contándose	1
25669	contamos	1
25670	contagiosas	1
25671	contagiada	1
25672	contaduría	1
25673	contábale	1
25674	consunción	1
25675	consumirte	1
25676	consumidor	1
25677	consumido	1
25678	consumían	1
25679	consumía	1
25680	consumen	1
25681	consumaría	1
25682	consultó	1
25683	consultarme	1
25684	consultarlo	1
25685	consultaré	1
25686	consultándose	1
25687	consúltalo	1
25688	consultada	1
25689	cónsul	1
25690	consuetudinaria	1
25691	consuela	1
25692	construiré	1
25693	construidos	1
25694	construido	1
25695	construidas	1
25696	construían	1
25697	constructivo	1
25698	constructiva	1
25699	construcciones	1
25700	constituyo	1
25701	constituyesen	1
25702	constituyen	1
25703	constitutivo	1
25704	constitutiva	1
25705	constituirse	1
25706	constituida	1
25707	constituciones	1
25708	constipase	1
25709	constipado	1
25710	consternados	1
25711	constara	1
25712	constantino	1
25713	consta	1
25714	conspirar	1
25715	conspirando	1
25716	conspiran	1
25717	conspicuo	1
25718	conspicuas	1
25719	consonante	1
25720	consonancia	1
25721	consolemos	1
25722	consolé	1
25723	consolarte	1
25724	consolarse	1
25725	consolarnos	1
25726	consolarme	1
25727	consolarla	1
25728	consolaré	1
25729	consoladoras	1
25730	consolado	1
25731	consolaban	1
25732	consola	1
25733	consistió	1
25734	consistentes	1
25735	consista	1
25736	consiguió	1
25737	consiguiendo	1
25738	consiguen	1
25739	consigue	1
25740	consignar	1
25741	consignada	1
25742	consigna	1
25743	consienten	1
25744	consideré	1
25745	considerarte	1
25746	considerarse	1
25747	considerarle	1
25748	considerara	1
25749	considéralo	1
25750	considerada	1
25751	considerábase	1
25752	considerábanla	1
25753	consideraban	1
25754	conservas	1
25755	conservarla	1
25756	conservaré	1
25757	conservadora	1
25758	conservadas	1
25759	conservada	1
25760	consentirse	1
25761	consentimos	1
25762	consentían	1
25763	consecutivos	1
25764	consecuentes	1
25765	consciente	1
25766	consagraría	1
25767	consagraremos	1
25768	consagrado	1
25769	consagra	1
25770	conquistó	1
25771	conquistara	1
25772	conquistando	1
25773	conquistado	1
25774	conquistada	1
25775	conozcas	1
25776	conozcamos	1
25777	conociole	1
25778	conociéndola	1
25779	conocías	1
25780	conocerlo	1
25781	conocerla	1
25782	conocerían	1
25783	conoceremos	1
25784	conoceré	1
25785	conocerás	1
25786	conocerá	1
25787	conocedores	1
25788	conocedoras	1
25789	conocedora	1
25790	connivencia	1
25791	conmovió	1
25792	conmovidísima	1
25793	conmovedora	1
25794	conmovedor	1
25795	conminación	1
25796	conllevando	1
25797	conjuraban	1
25798	conjunciones	1
25799	conjeturas	1
25800	congrio	1
25801	congregarse	1
25802	congregados	1
25803	congratularse	1
25804	congojas	1
25805	congoja	1
25806	congestionaba	1
25807	congestión	1
25808	congenialidad	1
25809	confusas	1
25810	confusamente	1
25811	confundo	1
25812	confundirme	1
25813	confundieran	1
25814	confundiera	1
25815	confundido	1
25816	confundida	1
25817	confunden	1
25818	confundamos	1
25819	confrontar	1
25820	confrontándolas	1
25821	confortaron	1
25822	confortado	1
25823	conformó	1
25824	confórmese	1
25825	conformes	1
25826	conformaron	1
25827	conformarnos	1
25828	conformará	1
25829	conformándose	1
25830	conformado	1
25831	conflictos	1
25832	confitó	1
25833	confitería	1
25834	confirmo	1
25835	confirmase	1
25836	confirmaron	1
25837	confirmarlo	1
25838	confirmar	1
25839	confirmándose	1
25840	confirmaba	1
25841	confín	1
25842	confiéselo	1
25843	confiesas	1
25844	confiesan	1
25845	confiésame	1
25846	confíe	1
25847	confíate	1
25848	confiase	1
25849	confiarme	1
25850	confiadas	1
25851	confía	1
25852	confesiones	1
25853	confesionario	1
25854	confesaste	1
25855	confesarte	1
25856	confesaron	1
25857	confesarlo	1
25858	confesarían	1
25859	confesándose	1
25860	confesada	1
25861	confesaban	1
25862	conferencias	1
25863	confeccionar	1
25864	confeccionados	1
25865	confeccionada	1
25866	confeccionaba	1
25867	confabulado	1
25868	confabulada	1
25869	confabulación	1
25870	confabulaban	1
25871	condújola	1
25872	condujo	1
25873	conductos	1
25874	conductores	1
25875	conductor	1
25876	conducirse	1
25877	conducidos	1
25878	conducido	1
25879	conducidas	1
25880	conducida	1
25881	conduce	1
25882	condoliéndose	1
25883	condiscípulos	1
25884	condimento	1
25885	condimentado	1
25886	condicional	1
25887	condensarse	1
25888	condensándose	1
25889	condensaban	1
25890	condeno	1
25891	condenarse	1
25892	condenarás	1
25893	condenando	1
25894	condenación	1
25895	concurriendo	1
25896	concurridos	1
25897	concurrida	1
25898	concurrentes	1
25899	concurre	1
25900	conculcar	1
25901	concretándose	1
25902	concretan	1
25903	concretamente	1
25904	concordaban	1
25905	concordaba	1
25906	concluyese	1
25907	concluyeron	1
25908	concluyera	1
25909	concluyentes	1
25910	concluye	1
25911	conclusiones	1
25912	concluirla	1
25913	concluiría	1
25914	concluimos	1
25915	concluidas	1
25916	concisión	1
25917	concilio	1
25918	conciliasen	1
25919	conciliarse	1
25920	conciliaba	1
25921	concierne	1
25922	concibió	1
25923	concibiendo	1
25924	concibe	1
25925	conchas	1
25926	concesión	1
25927	concertados	1
25928	concertado	1
25929	concernientes	1
25930	conceptuándola	1
25931	concentrándose	1
25932	concentrado	1
25933	concentración	1
25934	concejales	1
25935	concediendo	1
25936	concedía	1
25937	conceder	1
25938	concede	1
25939	concebiría	1
25940	concebir	1
25941	concebido	1
25942	concebí	1
25943	cóncavos	1
25944	cóncavo	1
25945	concatenación	1
25946	conatos	1
25947	conato	1
25948	comunidades	1
25949	comunícase	1
25950	comunicase	1
25951	comunicar	1
25952	comunicándose	1
25953	comunicado	1
25954	comunicadas	1
25955	comunicada	1
25956	comulgas	1
25957	comulgaron	1
25958	compusiera	1
25959	compuestos	1
25960	compuertas	1
25961	comprometió	1
25962	comprometerle	1
25963	comprometen	1
25964	comprobarse	1
25965	comprobación	1
25966	compro	1
25967	comprimió	1
25968	comprimiéndose	1
25969	comprimidas	1
25970	compresión	1
25971	comprensible	1
25972	comprendiolo	1
25973	comprendiera	1
25974	comprendí	1
25975	comprenderlo	1
25976	comprenderías	1
25977	comprenderían	1
25978	comprenderás	1
25979	comprenden	1
25980	comprendemos	1
25981	comprendan	1
25982	compremos	1
25983	cómpreme	1
25984	compraste	1
25985	comprasen	1
25986	comprase	1
25987	comprárselo	1
25988	compraron	1
25989	comprarme	1
25990	comprarlo	1
25991	compraría	1
25992	compraremos	1
25993	compraran	1
25994	compráramos	1
25995	comprara	1
25996	comprando	1
25997	compran	1
25998	compramos	1
25999	comprados	1
26000	compradores	1
26001	compraban	1
26002	compotas	1
26003	compositores	1
26004	composicioncita	1
26005	componiéndose	1
26006	componíase	1
26007	compones	1
26008	componen	1
26009	compondría	1
26010	compondremos	1
26011	complicar	1
26012	complicado	1
26013	complicadas	1
26014	complicaciones	1
26015	completos	1
26016	completó	1
26017	completas	1
26018	completado	1
26019	complemento	1
26020	compleja	1
26021	complaciéndose	1
26022	complacido	1
26023	complacidísima	1
26024	complacida	1
26025	complacía	1
26026	complacerle	1
26027	complacerla	1
26028	complacer	1
26029	complacencias	1
26030	complace	1
26031	competir	1
26032	competidores	1
26033	competía	1
26034	compensó	1
26035	compensar	1
26036	compenetraron	1
26037	compenetrando	1
26038	compatibles	1
26039	compatibilidad	1
26040	compasivos	1
26041	compases	1
26042	comparsas	1
26043	comparsa	1
26044	compare	1
26045	comparativos	1
26046	comparativo	1
26047	compararlo	1
26048	comparar	1
26049	comparando	1
26050	comparan	1
26051	comparaba	1
26052	compara	1
26053	compañerismo	1
26054	compaña	1
26055	compagina	1
26056	compadre	1
26057	compadeció	1
26058	compadecida	1
26059	compadécete	1
26060	compadecerte	1
26061	compadecerse	1
26062	compadecerle	1
26063	compactas	1
26064	cómodo	1
26065	comodidades	1
26066	cómodas	1
26067	comitentes	1
26068	comiteles	1
26069	comisuras	1
26070	comistrajo	1
26071	comistraje	1
26072	comisionados	1
26073	comiquito	1
26074	cominos	1
26075	comino	1
26076	comilonas	1
26077	comiéndoselo	1
26078	comiéndosele	1
26079	comiéndolo	1
26080	cómicamente	1
26081	comí	1
26082	comezones	1
26083	cometió	1
26084	cometieron	1
26085	cometiendo	1
26086	cometidos	1
26087	cometí	1
26088	cometerlas	1
26089	cometas	1
26090	cometa	1
26091	comérsele	1
26092	comérselas	1
26093	comérsela	1
26094	comerlos	1
26095	comerla	1
26096	comeré	1
26097	comercian	1
26098	comerás	1
26099	comerán	1
26100	comenzar	1
26101	comenzando	1
26102	comentos	1
26103	comentase	1
26104	comentando	1
26105	comenencias	1
26106	comenencia	1
26107	comemos	1
26108	cómeme	1
26109	comedido	1
26110	comediante	1
26111	comedianta	1
26112	combustión	1
26113	combustible	1
26114	combinada	1
26115	combinaba	1
26116	combina	1
26117	combatiente	1
26118	combatían	1
26119	combate	1
26120	comático	1
26121	comanditaria	1
26122	comadre	1
26123	columnarias	1
26124	columbró	1
26125	columbrar	1
26126	colose	1
26127	colosales	1
26128	colorete	1
26129	colorao	1
26130	coloradas	1
26131	coloquios	1
26132	colóqueme	1
26133	coloqué	1
26134	colón	1
26135	colocártelos	1
26136	colocarme	1
26137	colocarlo	1
26138	colocarle	1
26139	colocarlas	1
26140	colocao	1
26141	colocándose	1
26142	colocan	1
26143	colocaciones	1
26144	colocaban	1
26145	colocaba	1
26146	coló	1
26147	colmillo	1
26148	colmado	1
26149	collarines	1
26150	colisión	1
26151	coliseo	1
26152	colinas	1
26153	colina	1
26154	coligió	1
26155	coligieron	1
26156	coliflor	1
26157	colguemos	1
26158	colgarle	1
26159	colgaría	1
26160	colgara	1
26161	colgándosele	1
26162	colgándome	1
26163	colgajo	1
26164	colgadura	1
26165	coletazos	1
26166	coléricas	1
26167	colegios	1
26168	colegiata	1
26169	colectiva	1
26170	colectas	1
26171	coleccionistas	1
26172	coleccionista	1
26173	colecciones	1
26174	coleccionarlos	1
26175	colé	1
26176	colchón	1
26177	colarse	1
26178	colaríamos	1
26179	colaría	1
26180	colapso	1
26181	colado	1
26182	colada	1
26183	colaban	1
26184	colaba	1
26185	cojines	1
26186	cojera	1
26187	cojearás	1
26188	cojeaban	1
26189	coincidencia	1
26190	cohonestarse	1
26191	cohonestar	1
26192	cohibido	1
26193	cohibían	1
26194	cohibía	1
26195	cohete	1
26196	cogiste	1
26197	cogiola	1
26198	cogiese	1
26199	cogiéronse	1
26200	cogieran	1
26201	cogiéndolo	1
26202	cogiéndolas	1
26203	cogiditos	1
26204	cogerme	1
26205	cogerá	1
26206	cógelo	1
26207	cogéis	1
26208	cofradía	1
26209	cofrades	1
26210	codornices	1
26211	codillo	1
26212	código	1
26213	codificación	1
26214	codiciosas	1
26215	codiciado	1
26216	codicia	1
26217	coclearia	1
26218	cocinero	1
26219	cocidas	1
26220	cochino	1
26221	cochinamente	1
26222	cochinadas	1
26223	cochecillo	1
26224	coca	1
26225	cobró	1
26226	cobrase	1
26227	cobras	1
26228	cobraron	1
26229	cobraría	1
26230	cobran	1
26231	cobradores	1
26232	cobrado	1
26233	cobrábale	1
26234	cobraba	1
26235	cobardía	1
26236	cobardes	1
26237	cobalto	1
26238	co	1
26239	clubs	1
26240	cloral	1
26241	clima	1
26242	clientela	1
26243	clerofobia	1
26244	clericales	1
26245	clavetee	1
26246	claveteara	1
26247	claveteando	1
26248	claveteados	1
26249	claves	1
26250	clavel	1
26251	clave	1
26252	clavazón	1
26253	clavase	1
26254	clavársele	1
26255	clavarles	1
26256	clavarle	1
26257	clavarla	1
26258	clavándose	1
26259	clavamos	1
26260	clavaban	1
26261	claudio	1
26262	clasificar	1
26263	clásico	1
26264	clarísima	1
26265	clarines	1
26266	clarificado	1
26267	claridades	1
26268	claréate	1
26269	clareando	1
26270	clarea	1
26271	clandestinos	1
26272	clamor	1
26273	clamas	1
26274	clamaron	1
26275	clamaba	1
26276	clabos	1
26277	clabar	1
26278	civilizo	1
26279	civilizados	1
26280	civilizado	1
26281	civilizada	1
26282	civilizaciones	1
26283	civiles	1
26284	citutina	1
26285	citó	1
26286	citita	1
26287	cite	1
26288	citados	1
26289	cisne	1
26290	ciscos	1
26291	cirugía	1
26292	ciruelas	1
26293	cirineo	1
26294	cirilo	1
26295	circunspecto	1
26296	circunspección	1
26297	circunscrita	1
26298	circunloquios	1
26299	circunferencias	1
26300	circundan	1
26301	circulito	1
26302	circulaban	1
26303	circo	1
26304	cinturón	1
26305	cinturas	1
26306	cintajos	1
26307	cincuentona	1
26308	cimbros	1
26309	cimarra	1
26310	cima	1
26311	cilindro	1
26312	cilicio	1
26313	cigüeña	1
26314	cigarrillos	1
26315	cierro	1
26316	cierre	1
26317	cierras	1
26318	cieno	1
26319	cienfuegos	1
26320	cielito	1
26321	cicutina	1
26322	ciclón	1
26323	cicerone	1
26324	cicerón	1
26325	cicatriz	1
26326	cicatrices	1
26327	cicateros	1
26328	cibeles	1
26329	cianuro	1
26330	chuzo	1
26331	chuscada	1
26332	chusca	1
26333	churruca	1
26334	chupe	1
26335	chupase	1
26336	chupas	1
26337	chuparse	1
26338	chuparla	1
26339	chupar	1
26340	chupan	1
26341	chupado	1
26342	chupada	1
26343	chulito	1
26344	chulesca	1
26345	chula	1
26346	chu	1
26347	christophorus	1
26348	chovelar	1
26349	chorreras	1
26350	chorrear	1
26351	chorreaba	1
26352	chorrea	1
26353	choquezuela	1
26354	chopos	1
26355	chocolatero	1
26356	chochos	1
26357	chocheemos	1
26358	chocarrera	1
26359	chocaron	1
26360	chocantes	1
26361	chocante	1
26362	chocaba	1
26363	choca	1
26364	chistosísima	1
26365	chisto	1
26366	chisteras	1
26367	chistasen	1
26368	chistaré	1
26369	chistara	1
26370	chispos	1
26371	chispazos	1
26372	chispa	1
26373	chismosos	1
26374	chismorreo	1
26375	chismorreando	1
26376	chismográfico	1
26377	chismajos	1
26378	chisgarabís	1
26379	chis	1
26380	chirrido	1
26381	chirlata	1
26382	chiripón	1
26383	chirimbolos	1
26384	chirigotas	1
26385	chiquitos	1
26386	chiquitito	1
26387	chiquitita	1
26388	chiquita	1
26389	chiquirrininas	1
26390	chiquillín	1
26391	chiquillería	1
26392	chinos	1
26393	chinescos	1
26394	chinescas	1
26395	chinesca	1
26396	chinchoso	1
26397	chinchón	1
26398	chinchillas	1
26399	chinas	1
26400	chillona	1
26401	chillón	1
26402	chille	1
26403	chifló	1
26404	chiflado	1
26405	chiflaba	1
26406	chicooo	1
26407	chichones	1
26408	chicha	1
26409	chavo	1
26410	chauvinisme	1
26411	chato	1
26412	chasquido	1
26413	chasqueado	1
26414	chasqueada	1
26415	charrán	1
26416	charoles	1
26417	charlatana	1
26418	charlatán	1
26419	charlaría	1
26420	charlaremos	1
26421	charlado	1
26422	charcos	1
26423	chaquetillas	1
26424	chapuzón	1
26425	chapuzarse	1
26426	chapuzaba	1
26427	chapurraba	1
26428	chapoteo	1
26429	chapoteaban	1
26430	chapapote	1
26431	chanfaina	1
26432	chancleta	1
26433	champignons	1
26434	chambritas	1
26435	chambra	1
26436	chambelán	1
26437	chalanescas	1
26438	chafé	1
26439	chafarrinones	1
26440	chafarle	1
26441	chachito	1
26442	chabacana	1
26443	cetro	1
26444	cetrería	1
26445	céspedes	1
26446	cesaran	1
26447	césar	1
26448	cesando	1
26449	cesa	1
26450	cerril	1
26451	cerrarse	1
26452	cerrarle	1
26453	cerraré	1
26454	cerrándose	1
26455	cerrándolos	1
26456	cerrándoles	1
26457	ceros	1
26458	cero	1
26459	cerezas	1
26460	ceremoniosas	1
26461	ceremoniosamente	1
26462	ceremoniosa	1
26463	cerebros	1
26464	cerdea	1
26465	cerda	1
26466	cercioró	1
26467	cercana	1
26468	cerámica	1
26469	cepillos	1
26470	cepillo	1
26471	cepa	1
26472	ceñuda	1
26473	ceñidas	1
26474	ceñía	1
26475	centuplicado	1
26476	centrípeto	1
26477	centrífuga	1
26478	centinelas	1
26479	centímetros	1
26480	centenes	1
26481	centenares	1
26482	centén	1
26483	centelleo	1
26484	cenó	1
26485	cenizas	1
26486	cenital	1
26487	cenefas	1
26488	cenas	1
26489	cenarían	1
26490	cenagosa	1
26491	cenado	1
26492	celitos	1
26493	célibe	1
26494	celibato	1
26495	celibatarios	1
26496	celestiales	1
26497	celeridad	1
26498	celemín	1
26499	celebro	1
26500	celebridades	1
26501	celebridad	1
26502	celebrarse	1
26503	celebrarlo	1
26504	celebrándose	1
26505	celebrado	1
26506	celebrada	1
26507	celebraban	1
26508	celdas	1
26509	celajes	1
26510	celaje	1
26511	celadas	1
26512	cejar	1
26513	ceguezuelo	1
26514	ceguera	1
26515	cegué	1
26516	cegarse	1
26517	cegarla	1
26518	cegado	1
26519	cefalálgicos	1
26520	cefalalgia	1
26521	cédula	1
26522	cede	1
26523	cedazo	1
26524	ceceoso	1
26525	ceceo	1
26526	cebón	1
26527	cebáronse	1
26528	cebados	1
26529	cebaba	1
26530	cazuelas	1
26531	cazó	1
26532	cazo	1
26533	cazarlo	1
26534	cazadores	1
26535	cazadas	1
26536	cazable	1
26537	cazaba	1
26538	cayose	1
26539	cayeron	1
26540	cayeran	1
26541	cavour	1
26542	caviles	1
26543	cavilando	1
26544	cavidades	1
26545	cavernoso	1
26546	cautivan	1
26547	cautivábale	1
26548	cauteloso	1
26549	causo	1
26550	causarle	1
26551	causaría	1
26552	causara	1
26553	causados	1
26554	causábale	1
26555	caudalito	1
26556	catre	1
26557	catoliquísima	1
26558	catolicismo	1
26559	católicamente	1
26560	cató	1
26561	catilinario	1
26562	caterva	1
26563	catequizas	1
26564	catequizador	1
26565	categórico	1
26566	categóricarnente	1
26567	categorías	1
26568	catedrática	1
26569	cátedras	1
26570	catecúmenos	1
26571	catecúmeno	1
26572	catecúmena	1
26573	caté	1
26574	catástrofes	1
26575	catarros	1
26576	catarral	1
26577	catarían	1
26578	catarata	1
26579	cataplasma	1
26580	cátalas	1
26581	catalanes	1
26582	catalanas	1
26583	catafalco	1
26584	cataduras	1
26585	catadura	1
26586	catador	1
26587	cataclismos	1
26588	cataba	1
26589	casullas	1
26590	casucha	1
26591	casualmente	1
26592	casualidades	1
26593	castro	1
26594	castrametación	1
26595	castiza	1
26596	castilla	1
26597	castigase	1
26598	castigas	1
26599	castigarles	1
26600	castigarle	1
26601	castigara	1
26602	castigando	1
26603	castigada	1
26604	castellana	1
26605	castas	1
26606	castañuelas	1
26607	castañeteo	1
26608	castañetazo	1
26609	castañas	1
26610	castamente	1
26611	casquillo	1
26612	casquería	1
26613	caspitina	1
26614	caspa	1
26615	casose	1
26616	casitas	1
26617	casinos	1
26618	casino	1
26619	casillas	1
26620	casilla	1
26621	casetas	1
26622	caserones	1
26623	caseras	1
26624	cascarones	1
26625	cascarla	1
26626	cascajo	1
26627	cascado	1
26628	cascadas	1
26629	casase	1
26630	casarle	1
26631	casarlas	1
26632	casarías	1
26633	casaré	1
26634	casaras	1
26635	casan	1
26636	casamientos	1
26637	cásale	1
26638	casaditas	1
26639	casadita	1
26640	cartuja	1
26641	cartuchos	1
26642	cartucho	1
26643	cartita	1
26644	carteros	1
26645	cartero	1
26646	cartelón	1
26647	cartel	1
26648	carteaba	1
26649	carruajes	1
26650	carrozas	1
26651	carrilleras	1
26652	carrillera	1
26653	carrilladas	1
26654	carretes	1
26655	carretero	1
26656	carretela	1
26657	carreras	1
26658	carraspeo	1
26659	carrascales	1
26660	carrasca	1
26661	carpinteros	1
26662	carpintero	1
26663	carpetazo	1
26664	carpetas	1
26665	carpeta	1
26666	carnicerías	1
26667	carnecitas	1
26668	carnavalesca	1
26669	carnavales	1
26670	carnaval	1
26671	carminoso	1
26672	carmesí	1
26673	cariñitos	1
26674	caricatura	1
26675	caribes	1
26676	caribe	1
26677	cariacontecido	1
26678	cargos	1
26679	cargas	1
26680	cargarse	1
26681	cargarlo	1
26682	cargarás	1
26683	cargara	1
26684	cargábanle	1
26685	caretas	1
26686	careciese	1
26687	careciendo	1
26688	cardos	1
26689	cardo	1
26690	cardiaca	1
26691	cardarle	1
26692	carcundas	1
26693	carcunda	1
26694	carcomida	1
26695	cárceles	1
26696	carceleros	1
26697	carcelero	1
26698	carcajadita	1
26699	carca	1
26700	caraiter	1
26701	caracterizar	1
26702	caracterizan	1
26703	característicos	1
26704	característica	1
26705	caracolitos	1
26706	carabanchel	1
26707	capuchoncitos	1
26708	captura	1
26709	caprichosos	1
26710	caprichoso	1
26711	caprichosa	1
26712	capote	1
26713	capotas	1
26714	capítulos	1
26715	capitanes	1
26716	capitaneadas	1
26717	capitán	1
26718	capitalizaba	1
26719	capitalazo	1
26720	capitación	1
26721	capita	1
26722	capillas	1
26723	capearlo	1
26724	capcioso	1
26725	capciosa	1
26726	caño	1
26727	cañí	1
26728	cañamoncito	1
26729	cañamazo	1
26730	canturriaba	1
26731	cantorrios	1
26732	cantor	1
26733	cantones	1
26734	cantonalismo	1
26735	cantó	1
26736	cantina	1
26737	canterac	1
26738	canten	1
26739	cantazo	1
26740	cantase	1
26741	cántaros	1
26742	cantarle	1
26743	cantaré	1
26744	cantará	1
26745	cantantes	1
26746	cantante	1
26747	cántale	1
26748	cantado	1
26749	cantadas	1
26750	cantábrico	1
26751	cantabile	1
26752	cantaban	1
26753	canses	1
26754	cansemos	1
26755	cansaron	1
26756	cansarme	1
26757	cansarás	1
26758	cansará	1
26759	cansando	1
26760	cansamos	1
26761	cansadita	1
26762	cansábase	1
26763	canonjías	1
26764	canonizarlas	1
26765	canonizaremos	1
26766	canonizar	1
26767	canonizada	1
26768	canonizable	1
26769	canonizaban	1
26770	canon	1
26771	canina	1
26772	canillas	1
26773	canijo	1
26774	caníbales	1
26775	candorosa	1
26776	candilones	1
26777	candil	1
26778	candidez	1
26779	candideces	1
26780	candidatura	1
26781	candidato	1
26782	cándidas	1
26783	candeleros	1
26784	candelero	1
26785	candelas	1
26786	candados	1
26787	canciones	1
26788	cancillerías	1
26789	canceles	1
26790	cancelación	1
26791	cancamurria	1
26792	canastos	1
26793	canasto	1
26794	canastas	1
26795	canarios	1
26796	canarias	1
26797	canapé	1
26798	canallas	1
26799	canallada	1
26800	canalejas	1
26801	camús	1
26802	camuesa	1
26803	camposanto	1
26804	campestre	1
26805	campesinos	1
26806	campaneo	1
26807	campanas	1
26808	campanarios	1
26809	camita	1
26810	camisolas	1
26811	camiones	1
26812	caminatas	1
26813	caminando	1
26814	camilla	1
26815	camellos	1
26816	cambias	1
26817	cambiarte	1
26818	cambiaran	1
26819	cambiándolos	1
26820	cambiándolo	1
26821	cambiada	1
26822	camarín	1
26823	camarilla	1
26824	camarero	1
26825	camarera	1
26826	camará	1
26827	camaleones	1
26828	calzoncillos	1
26829	calzarse	1
26830	calzará	1
26831	calzan	1
26832	calzaba	1
26833	calvo	1
26834	calvinista	1
26835	calumniaste	1
26836	calumniadora	1
26837	calumniador	1
26838	calorcillo	1
26839	calo	1
26840	calme	1
26841	cálmate	1
26842	calmándose	1
26843	calmando	1
26844	calman	1
26845	calmado	1
26846	callémonos	1
26847	callejero	1
26848	callejeras	1
26849	callejas	1
26850	callé	1
26851	cállatela	1
26852	callas	1
26853	callarte	1
26854	callaría	1
26855	callaré	1
26856	callara	1
26857	callao	1
26858	callan	1
26859	callaíto	1
26860	calladitos	1
26861	cáliz	1
26862	caligráficos	1
26863	caligrafía	1
26864	calificó	1
26865	calificar	1
26866	calificado	1
26867	calientes	1
26868	calienta	1
26869	calidades	1
26870	calidá	1
26871	calenturienta	1
26872	calenturas	1
26873	calentito	1
26874	calentitas	1
26875	calentita	1
26876	calenté	1
26877	calentaste	1
26878	calentarte	1
26879	calentármela	1
26880	calentarlo	1
26881	calentarle	1
26882	calentándome	1
26883	calentándolo	1
26884	calendario	1
26885	caldito	1
26886	calderón	1
26887	calderería	1
26888	caldeos	1
26889	caldeando	1
26890	caldeaba	1
26891	calculó	1
26892	calculé	1
26893	calculas	1
26894	calcular	1
26895	calculada	1
26896	calculaba	1
26897	calco	1
26898	calcetín	1
26899	calceta	1
26900	calcárea	1
26901	calaveras	1
26902	calatravas	1
26903	calatrava	1
26904	calandrias	1
26905	calandria	1
26906	calándoselos	1
26907	calándose	1
26908	calaínos	1
26909	calainos	1
26910	calabazas	1
26911	calábase	1
26912	calaba	1
26913	cajista	1
26914	cajetilla	1
26915	caíste	1
26916	caímos	1
26917	caíme	1
26918	caídos	1
26919	cafres	1
26920	cafre	1
26921	cafeteros	1
26922	caería	1
26923	caerán	1
26924	caenas	1
26925	caemos	1
26926	caduca	1
26927	cadmio	1
26928	cadera	1
26929	cadencioso	1
26930	cadencias	1
26931	cadenas	1
26932	cadavérica	1
26933	cadávere	1
26934	cacumen	1
26935	caciquismo	1
26936	cachucha	1
26937	cachorros	1
26938	cachorro	1
26939	cachete	1
26940	cacharrería	1
26941	cacerolas	1
26942	cacerola	1
26943	cacareo	1
26944	cacarearlo	1
26945	cacao	1
26946	cacahuetes	1
26947	cabrón	1
26948	cabritos	1
26949	cabriolas	1
26950	cable	1
26951	cabizbaja	1
26952	cabida	1
26953	cabestrillo	1
26954	caben	1
26955	cabellerías	1
26956	cabecilla	1
26957	cabañas	1
26958	caballista	1
26959	caballerizas	1
26960	caballerías	1
26961	caballerete	1
26962	caballeresca	1
26963	cabalitos	1
26964	ca	1
26965	bustos	1
26966	buscona	1
26967	buscón	1
26968	buscaste	1
26969	buscase	1
26970	buscarte	1
26971	buscaron	1
26972	buscármelo	1
26973	buscaríamos	1
26974	buscaremos	1
26975	buscaran	1
26976	buscándola	1
26977	buscada	1
26978	buscaban	1
26979	burris	1
26980	burra	1
26981	burocracia	1
26982	burlones	1
26983	burlón	1
26984	burlen	1
26985	búrlate	1
26986	burlasen	1
26987	burlándose	1
26988	burlando	1
26989	burlan	1
26990	burladores	1
26991	burlado	1
26992	burlaban	1
26993	burguesía	1
26994	burgués	1
26995	burbujeaba	1
26996	buque	1
26997	buñuelo	1
26998	bulliciosos	1
26999	bulliciosa	1
27000	bullangas	1
27001	bullanga	1
27002	buleros	1
27003	bulas	1
27004	bula	1
27005	bufón	1
27006	bufidos	1
27007	bufando	1
27008	bufandas	1
27009	bufaban	1
27010	bufaba	1
27011	budistas	1
27012	budista	1
27013	bucólica	1
27014	bruta	1
27015	bruscos	1
27016	brusco	1
27017	bruscas	1
27018	bruños	1
27019	bruñido	1
27020	bruñida	1
27021	brujerías	1
27022	brrrr	1
27023	brrr	1
27024	brr	1
27025	broza	1
27026	brotó	1
27027	brotes	1
27028	brotaran	1
27029	brotando	1
27030	brotan	1
27031	brotado	1
27032	brotaban	1
27033	broncíneos	1
27034	broncas	1
27035	bromista	1
27036	bromee	1
27037	bromeas	1
27038	bromeando	1
27039	brochazos	1
27040	brochase	1
27041	brocados	1
27042	brocado	1
27043	brisca	1
27044	brindarles	1
27045	brincando	1
27046	brillantísima	1
27047	brillantez	1
27048	brihuega	1
27049	bribones	1
27050	bribonada	1
27051	breviarios	1
27052	brevedad	1
27053	brevas	1
27054	bregué	1
27055	bregaron	1
27056	brega	1
27057	brebajes	1
27058	brazadas	1
27059	braveza	1
27060	braserón	1
27061	brasas	1
27062	branco	1
27063	bramante	1
27064	bramaba	1
27065	bracmánica	1
27066	bracitos	1
27067	bracete	1
27068	bracero	1
27069	braceaban	1
27070	bozal	1
27071	boya	1
27072	boxear	1
27073	box	1
27074	botoneras	1
27075	botita	1
27076	boticarito	1
27077	boticarios	1
27078	boticarín	1
27079	botes	1
27080	botellazo	1
27081	bote	1
27082	botaratadas	1
27083	botaratada	1
27084	botánica	1
27085	bostezo	1
27086	bostezando	1
27087	bosquejada	1
27088	borrosas	1
27089	borrosa	1
27090	borro	1
27091	borriqueros	1
27092	borricales	1
27093	borricada	1
27094	borre	1
27095	borrascosos	1
27096	borrarlas	1
27097	borrara	1
27098	borran	1
27099	borrachas	1
27100	borracha	1
27101	borraban	1
27102	borraba	1
27103	borlita	1
27104	borleo	1
27105	borgias	1
27106	bordo	1
27107	bordaron	1
27108	bordar	1
27109	bordan	1
27110	bordadores	1
27111	bordador	1
27112	bordaban	1
27113	borbotones	1
27114	borbones	1
27115	boqueás	1
27116	boqueadas	1
27117	boquea	1
27118	bonitísima	1
27119	bonitamente	1
27120	bonísimo	1
27121	bonísima	1
27122	bonillas	1
27123	bonibus	1
27124	bondadosamente	1
27125	bonancibles	1
27126	bolsas	1
27127	bolos	1
27128	bollos	1
27129	bollo	1
27130	bollero	1
27131	bollería	1
27132	bólido	1
27133	boletín	1
27134	bohardillón	1
27135	bohardillas	1
27136	bocona	1
27137	bochorno	1
27138	bocanadas	1
27139	bobones	1
27140	bobona	1
27141	bobón	1
27142	boberías	1
27143	bobería	1
27144	bobadas	1
27145	bloques	1
27146	blondas	1
27147	blinco	1
27148	blasonados	1
27149	blasfemo	1
27150	blasfemando	1
27151	blanquecina	1
27152	blanqueará	1
27153	blanquear	1
27154	blanquean	1
27155	blanqueado	1
27156	blandura	1
27157	blandamente	1
27158	bizmas	1
27159	bizma	1
27160	bizcochitos	1
27161	bizcochito	1
27162	bizco	1
27163	bizcas	1
27164	bizcando	1
27165	bizca	1
27166	bizantinas	1
27167	bisteques	1
27168	bisoño	1
27169	bismark	1
27170	bismarck	1
27171	birmingham	1
27172	birló	1
27173	birlado	1
27174	birla	1
27175	biricornio	1
27176	biombo	1
27177	billetito	1
27178	bilbao	1
27179	bigotito	1
27180	bigotes	1
27181	bigotera	1
27182	bifurcación	1
27183	biftec	1
27184	bienhechora	1
27185	bienaventuranza	1
27186	bienaventurado	1
27187	bienandanzas	1
27188	bienandanza	1
27189	bicoca	1
27190	bichos	1
27191	bichito	1
27192	bíblico	1
27193	betsabée	1
27194	besuqueó	1
27195	besuqueo	1
27196	besuqueándose	1
27197	besugos	1
27198	besárselos	1
27199	besaron	1
27200	besarla	1
27201	besándose	1
27202	besando	1
27203	besan	1
27204	besamanos	1
27205	besadlas	1
27206	besadera	1
27207	besaba	1
27208	besa	1
27209	berza	1
27210	berrugones	1
27211	berroqueñas	1
27212	berro	1
27213	berreando	1
27214	bermingán	1
27215	bergantes	1
27216	bergante	1
27217	bergantas	1
27218	berganta	1
27219	berdan	1
27220	benignita	1
27221	benignidad	1
27222	benévolos	1
27223	benévolo	1
27224	benevolencias	1
27225	benévolamente	1
27226	benéficos	1
27227	beneficios	1
27228	benéfica	1
27229	bendijo	1
27230	bendigo	1
27231	bendiciendo	1
27232	bendicen	1
27233	bendecirá	1
27234	bendecidas	1
27235	bemol	1
27236	bellotes	1
27237	bellotas	1
27238	bellota	1
27239	bello	1
27240	belladona	1
27241	belicosas	1
27242	belfort	1
27243	belencita	1
27244	beldad	1
27245	begonias	1
27246	befa	1
27247	becerradas	1
27248	bebimos	1
27249	bebiese	1
27250	bebieron	1
27251	bebiera	1
27252	bebiéndola	1
27253	bebiendo	1
27254	bebí	1
27255	beberse	1
27256	beberías	1
27257	bebería	1
27258	beberé	1
27259	beben	1
27260	bebedor	1
27261	bebé	1
27262	beba	1
27263	beatos	1
27264	beato	1
27265	beata	1
27266	baztán	1
27267	bazofias	1
27268	bazofia	1
27269	bautizos	1
27270	bautizaré	1
27271	bautizan	1
27272	batuta	1
27273	batón	1
27274	batlló	1
27275	batita	1
27276	batista	1
27277	batirse	1
27278	batirme	1
27279	batiéndose	1
27280	batiéndola	1
27281	batido	1
27282	batidas	1
27283	bate	1
27284	batallitas	1
27285	batahola	1
27286	batacazo	1
27287	bastó	1
27288	bastiones	1
27289	bastimentos	1
27290	bastiat	1
27291	baste	1
27292	bastaría	1
27293	bastardos	1
27294	bastar	1
27295	bastándoles	1
27296	bastándole	1
27297	basílica	1
27298	basilea	1
27299	báscula	1
27300	bascas	1
27301	basamento	1
27302	basadas	1
27303	bártulos	1
27304	barruntó	1
27305	barroquismo	1
27306	barrilitos	1
27307	barrigón	1
27308	barrieran	1
27309	barriendo	1
27310	barrido	1
27311	barrida	1
27312	barría	1
27313	barrerme	1
27314	barrerle	1
27315	barreremos	1
27316	barrenos	1
27317	barrendero	1
27318	barreduras	1
27319	barre	1
27320	barranco	1
27321	barrancas	1
27322	barrabasadas	1
27323	barrabasada	1
27324	barquitos	1
27325	barquito	1
27326	barquinazo	1
27327	baronesa	1
27328	barón	1
27329	barniz	1
27330	barnices	1
27331	bargueño	1
27332	bardales	1
27333	barcia	1
27334	barca	1
27335	barbilla	1
27336	barbianas	1
27337	barbería	1
27338	baratillos	1
27339	barástolis	1
27340	barajaban	1
27341	baraja	1
27342	bar	1
27343	baqueteados	1
27344	bañándose	1
27345	bañado	1
27346	banquetas	1
27347	banquero	1
27348	bandoleros	1
27349	banderita	1
27350	banderillero	1
27351	bandejas	1
27352	bandas	1
27353	bandadas	1
27354	bandada	1
27355	banastas	1
27356	banasta	1
27357	baluarte	1
27358	balsain	1
27359	balsa	1
27360	ballesta	1
27361	baldón	1
27362	baldío	1
27363	baldada	1
27364	balda	1
27365	balconcillo	1
27366	balbucir	1
27367	balbucientes	1
27368	balbuciendo	1
27369	balbucía	1
27370	balas	1
27371	balandranes	1
27372	balandrán	1
27373	balancines	1
27374	balancín	1
27375	balanceos	1
27376	balanceó	1
27377	balancearse	1
27378	balanceara	1
27379	balanceándose	1
27380	balanceaban	1
27381	balance	1
27382	baladronada	1
27383	bajoncito	1
27384	bajita	1
27385	bajísimos	1
27386	bajezas	1
27387	bajeza	1
27388	bajase	1
27389	bajarla	1
27390	bajarían	1
27391	bajaría	1
27392	bajarán	1
27393	bajándola	1
27394	bajáis	1
27395	bajada	1
27396	bajábala	1
27397	bailoteando	1
27398	bailo	1
27399	bailly	1
27400	baillière	1
27401	bailara	1
27402	bailadas	1
27403	bailaban	1
27404	bailaba	1
27405	baguetilla	1
27406	bagaje	1
27407	badila	1
27408	bachillería	1
27409	bachiller	1
27410	baches	1
27411	babosa	1
27412	babilonia	1
27413	babieca	1
27414	babel	1
27415	b	1
27416	azuzándole	1
27417	azuzan	1
27418	azuzáis	1
27419	azuzado	1
27420	azulejos	1
27421	azulado	1
27422	azufre	1
27423	azucarillo	1
27424	azotando	1
27425	azotaina	1
27426	azotaban	1
27427	azota	1
27428	azares	1
27429	azalea	1
27430	azada	1
27431	aza	1
27432	ayunar	1
27433	ayunaba	1
27434	ayuna	1
27435	ayudemos	1
27436	ayúdeme	1
27437	ayudéis	1
27438	ayude	1
27439	ayudase	1
27440	ayudarte	1
27441	ayudáronla	1
27442	ayudarnos	1
27443	ayudarles	1
27444	ayudarle	1
27445	ayudarla	1
27446	ayudaría	1
27447	ayudaré	1
27448	ayudados	1
27449	avivar	1
27450	avispados	1
27451	avispado	1
27452	avispada	1
27453	avisó	1
27454	avisasteis	1
27455	avisaste	1
27456	avisaron	1
27457	avisaremos	1
27458	avisarás	1
27459	avisando	1
27460	avisado	1
27461	avisada	1
27462	avíos	1
27463	avine	1
27464	aviesa	1
27465	aviene	1
27466	avidez	1
27467	ávidas	1
27468	aviarme	1
27469	aviarla	1
27470	aviar	1
27471	averígüelo	1
27472	averiguase	1
27473	averiguarle	1
27474	averiguaría	1
27475	averiguaré	1
27476	averiguadores	1
27477	averiguador	1
27478	averiguaciones	1
27479	averiguación	1
27480	avergüenzo	1
27481	avergonzose	1
27482	avergonzó	1
27483	avergonzados	1
27484	aventurillas	1
27485	aventuremos	1
27486	aventurar	1
27487	aventurándose	1
27488	aventurábase	1
27489	aventajada	1
27490	aventaja	1
27491	avenida	1
27492	avenía	1
27493	avenencia	1
27494	avellana	1
27495	avasallador	1
27496	avaro	1
27497	avariciosa	1
27498	avanzadas	1
27499	avanzada	1
27500	auxiliase	1
27501	auxiliarse	1
27502	auxiliarla	1
27503	auxiliado	1
27504	autorizarme	1
27505	autorizan	1
27506	autorizado	1
27507	autorizada	1
27508	autoriza	1
27509	autoritarios	1
27510	autoritarias	1
27511	autoritariamente	1
27512	autorice	1
27513	autocrático	1
27514	autocrática	1
27515	autenticidad	1
27516	auténtica	1
27517	austerlitz	1
27518	austeridad	1
27519	auspicios	1
27520	ausento	1
27521	ausente	1
27522	ausentarme	1
27523	ausentándose	1
27524	ausculte	1
27525	auscultarle	1
27526	aurorita	1
27527	auroras	1
27528	aumentos	1
27529	aumente	1
27530	aumentase	1
27531	aumentaron	1
27532	aumentarlas	1
27533	aumentando	1
27534	auméntame	1
27535	aumentada	1
27536	augurios	1
27537	audición	1
27538	audacias	1
27539	atusó	1
27540	atusarte	1
27541	atusada	1
27542	aturullo	1
27543	aturullada	1
27544	aturdió	1
27545	aturdidísima	1
27546	atufo	1
27547	atropellos	1
27548	atropelló	1
27549	atropello	1
27550	atropellando	1
27551	atropellada	1
27552	atronaban	1
27553	atril	1
27554	atribuyeron	1
27555	atribuyéndole	1
27556	atrevidilla	1
27557	atreví	1
27558	atreverías	1
27559	atraviesa	1
27560	atravesósele	1
27561	atravesole	1
27562	atravesase	1
27563	atravesaron	1
27564	atravesándolo	1
27565	atravesándole	1
27566	atravesados	1
27567	atravesado	1
27568	atraso	1
27569	atrasados	1
27570	atrasaditos	1
27571	atrasa	1
27572	atrapo	1
27573	atrapado	1
27574	atrajo	1
27575	atraídos	1
27576	atraído	1
27577	atraída	1
27578	atraía	1
27579	atragantaban	1
27580	atracón	1
27581	atracciones	1
27582	atrácate	1
27583	atracaba	1
27584	atosigaba	1
27585	atormentó	1
27586	atormentarme	1
27587	atormentarle	1
27588	atormentarla	1
27589	atormentándole	1
27590	atormentada	1
27591	atormenta	1
27592	atontarse	1
27593	atónitos	1
27594	atonía	1
27595	atmosférico	1
27596	atletas	1
27597	atlas	1
27598	atizé	1
27599	atizándose	1
27600	atizado	1
27601	atisbos	1
27602	atisbando	1
27603	atisbadora	1
27604	atinado	1
27605	atinadas	1
27606	atildado	1
27607	atildada	1
27608	atiende	1
27609	atice	1
27610	atestiguó	1
27611	atestiguaban	1
27612	atestados	1
27613	aterrorizarla	1
27614	aterrorizada	1
27615	aterró	1
27616	aterrados	1
27617	aterradoras	1
27618	ateos	1
27619	atenuase	1
27620	atenuada	1
27621	atenuaciones	1
27622	atenuación	1
27623	atenuaba	1
27624	atenúa	1
27625	atentísimamente	1
27626	atentar	1
27627	ateneo	1
27628	atendió	1
27629	atendido	1
27630	atendidas	1
27631	atenazó	1
27632	atenazado	1
27633	atenazaba	1
27634	ateísmo	1
27635	ateas	1
27636	atavismo	1
27637	atavíen	1
27638	ataviarse	1
27639	atascó	1
27640	atascaban	1
27641	atarugándolo	1
27642	atarugaba	1
27643	ataros	1
27644	ataron	1
27645	atarme	1
27646	atarles	1
27647	atarla	1
27648	atarés	1
27649	atareado	1
27650	atañen	1
27651	atan	1
27652	atajarle	1
27653	atajar	1
27654	atajan	1
27655	atáis	1
27656	atadijo	1
27657	atacó	1
27658	atacar	1
27659	atacados	1
27660	atacada	1
27661	atacaba	1
27662	ata	1
27663	asustose	1
27664	asusté	1
27665	asustas	1
27666	asustarme	1
27667	asustaré	1
27668	asustaran	1
27669	asustando	1
27670	asustadísima	1
27671	asustadas	1
27672	asustábase	1
27673	asustaban	1
27674	asturias	1
27675	astucias	1
27676	astucia	1
27677	astros	1
27678	astronomía	1
27679	astro	1
27680	astilla	1
27681	asté	1
27682	asqueroso	1
27683	asquerosísimas	1
27684	asquerosidades	1
27685	aspires	1
27686	aspiradores	1
27687	aspiración	1
27688	aspiraban	1
27689	aspira	1
27690	ásperas	1
27691	aspaviento	1
27692	aspasia	1
27693	asomos	1
27694	asomo	1
27695	asomes	1
27696	asombrosa	1
27697	asombró	1
27698	asómbrese	1
27699	asombréis	1
27700	asombre	1
27701	asombráronse	1
27702	asombrarías	1
27703	asombrarás	1
27704	asombrándose	1
27705	asombrado	1
27706	asombraba	1
27707	asomase	1
27708	asomaron	1
27709	asomara	1
27710	asoma	1
27711	asoleado	1
27712	asociándolos	1
27713	asociadas	1
27714	asociada	1
27715	asociación	1
27716	asmático	1
27717	asistirle	1
27718	asistirla	1
27719	asistiría	1
27720	asistiendo	1
27721	asistido	1
27722	asistían	1
27723	asistente	1
27724	asín	1
27725	asimilan	1
27726	asimiladas	1
27727	asilados	1
27728	asignarle	1
27729	asignara	1
27730	asienta	1
27731	asiduos	1
27732	asiduo	1
27733	asida	1
27734	asiática	1
27735	asia	1
27736	aseveró	1
27737	asesinó	1
27738	asesinatos	1
27739	asesinando	1
27740	asesinado	1
27741	asesina	1
27742	aserrar	1
27743	aseñorado	1
27744	asentir	1
27745	asentía	1
27746	asensio	1
27747	asemejaban	1
27748	asemeja	1
27749	aseguremos	1
27750	asegure	1
27751	aseguraron	1
27752	asegurarla	1
27753	aseguraría	1
27754	aseguraran	1
27755	asegurándole	1
27756	asegúrame	1
27757	asegurado	1
27758	aseguradas	1
27759	aseadísima	1
27760	aseada	1
27761	ascua	1
27762	ascetismo	1
27763	ascensión	1
27764	ascendió	1
27765	ascendido	1
27766	asar	1
27767	asamblea	1
27768	asaltó	1
27769	asaltáronle	1
27770	asaltar	1
27771	asalta	1
27772	asadura	1
27773	asador	1
27774	asacristanado	1
27775	asaban	1
27776	asa	1
27777	artimañas	1
27778	artilleros	1
27779	artillería	1
27780	artificioso	1
27781	artificios	1
27782	artificiales	1
27783	articuló	1
27784	articulazo	1
27785	articularse	1
27786	articulando	1
27787	articulaciones	1
27788	articulación	1
27789	artesianos	1
27790	artesas	1
27791	artesano	1
27792	arsenioso	1
27793	arrumacos	1
27794	arrullo	1
27795	arrullas	1
27796	arrullándose	1
27797	arrullando	1
27798	arrullan	1
27799	arrullado	1
27800	arrullaban	1
27801	arrulla	1
27802	arruinen	1
27803	arruinaron	1
27804	arruinar	1
27805	arruinando	1
27806	arrugarse	1
27807	arrollado	1
27808	arrolla	1
27809	arrojo	1
27810	arroje	1
27811	arrojas	1
27812	arrojaron	1
27813	arrojarle	1
27814	arrojarla	1
27815	arrojándole	1
27816	arrojadas	1
27817	arrogantillo	1
27818	arrodillose	1
27819	arrodillaste	1
27820	arrodilladas	1
27821	arrobo	1
27822	arrobamientos	1
27823	arrobamiento	1
27824	arrimó	1
27825	arrimo	1
27826	arrimarse	1
27827	arrimándose	1
27828	arrimado	1
27829	arrimaban	1
27830	arriesgáronse	1
27831	arriesgados	1
27832	arrieros	1
27833	arriero	1
27834	arrepintiose	1
27835	arrepintiera	1
27836	arrepintiendo	1
27837	arrepiento	1
27838	arrepientes	1
27839	arrepienten	1
27840	arrepentirte	1
27841	arrepentimientos	1
27842	arreos	1
27843	arreo	1
27844	arrendaba	1
27845	arremangó	1
27846	arremangados	1
27847	arreglole	1
27848	arreglito	1
27849	arreglen	1
27850	arregléis	1
27851	arréglatelas	1
27852	arreglase	1
27853	arreglándose	1
27854	arréglame	1
27855	arreglados	1
27856	arregladitas	1
27857	arregladita	1
27858	arredraba	1
27859	arrecogidas	1
27860	arreciar	1
27861	arrechuchos	1
27862	arrebolada	1
27863	arrebatándole	1
27864	arreaba	1
27865	arrastró	1
27866	arrastrarse	1
27867	arrastraron	1
27868	arrastrarán	1
27869	arrastrándote	1
27870	arrastrándose	1
27871	arrastran	1
27872	arrastra	1
27873	arrasado	1
27874	arranqué	1
27875	arrancaron	1
27876	arrancarles	1
27877	arrancarla	1
27878	arrancándose	1
27879	arrancándolos	1
27880	arrancan	1
27881	arramblaron	1
27882	arramblaban	1
27883	arraigados	1
27884	arraigado	1
27885	arraigada	1
27886	arrabales	1
27887	arquitectónico	1
27888	arquitectónica	1
27889	arquitecto	1
27890	arqueos	1
27891	arqueólogo	1
27892	arqueológica	1
27893	arqueología	1
27894	arqueo	1
27895	arqueadas	1
27896	aros	1
27897	aroma	1
27898	arneses	1
27899	armose	1
27900	armonizar	1
27901	armonizando	1
27902	armonizadas	1
27903	armonizaba	1
27904	armoniosas	1
27905	armoniosa	1
27906	armónico	1
27907	armole	1
27908	armo	1
27909	armiño	1
27910	armería	1
27911	armejas	1
27912	armasen	1
27913	armase	1
27914	armaron	1
27915	armarme	1
27916	armarías	1
27917	armándose	1
27918	armándole	1
27919	armadores	1
27920	armadas	1
27921	aritméticos	1
27922	aritméticas	1
27923	aristocráticas	1
27924	aristarco	1
27925	arisca	1
27926	arias	1
27927	arguyéndose	1
27928	argumentar	1
27929	argumentando	1
27930	argüía	1
27931	argucias	1
27932	argollitas	1
27933	argollas	1
27934	argentino	1
27935	argentina	1
27936	arganda	1
27937	argamasillesca	1
27938	arenilla	1
27939	arengando	1
27940	arengaba	1
27941	arenales	1
27942	ardorosos	1
27943	ardió	1
27944	ardides	1
27945	ardid	1
27946	ardería	1
27947	ardentísimo	1
27948	arden	1
27949	arda	1
27950	arcola	1
27951	archivo	1
27952	archipámpano	1
27953	arcanos	1
27954	arcadas	1
27955	arbusto	1
27956	arboledas	1
27957	árbitro	1
27958	arbitrios	1
27959	arbitrio	1
27960	arbitrando	1
27961	árbitra	1
27962	aravaca	1
27963	arañó	1
27964	arañé	1
27965	arañazos	1
27966	arañas	1
27967	arañarle	1
27968	arañar	1
27969	arañando	1
27970	arañada	1
27971	arañaban	1
27972	arango	1
27973	aranceles	1
27974	arancelarios	1
27975	arancelarias	1
27976	arancelaria	1
27977	arancel	1
27978	aragonés	1
27979	arábiga	1
27980	arabesco	1
27981	apurillos	1
27982	apuren	1
27983	apuran	1
27984	apuradísima	1
27985	apura	1
27986	apuntárselas	1
27987	apuntarle	1
27988	apuntaré	1
27989	apuntándole	1
27990	apuntando	1
27991	apuntadas	1
27992	apuntaban	1
27993	apuestan	1
27994	aproximaría	1
27995	aproximar	1
27996	aproximada	1
27997	aproximaban	1
27998	aproxima	1
27999	aprovecharnos	1
28000	aprovechará	1
28001	aprovechara	1
28002	aprovechan	1
28003	aprovechamiento	1
28004	aprovecháis	1
28005	aprovechadas	1
28006	aprovechaban	1
28007	apropiado	1
28008	apropiada	1
28009	apropiación	1
28010	aprobase	1
28011	aprobadas	1
28012	aprobada	1
28013	aprobación	1
28014	aprobaban	1
28015	aprisionar	1
28016	aprisionados	1
28017	aprietes	1
28018	aprietas	1
28019	aprietan	1
28020	apretura	1
28021	apretársele	1
28022	apretándoselo	1
28023	apretándola	1
28024	apresuré	1
28025	apresúrate	1
28026	apresurase	1
28027	apresuraron	1
28028	apresurar	1
28029	apresuradamente	1
28030	apresurada	1
28031	apresuraba	1
28032	aprensivo	1
28033	aprensiva	1
28034	aprendo	1
28035	aprendizaje	1
28036	aprendiz	1
28037	aprendieron	1
28038	aprendiera	1
28039	aprendidas	1
28040	aprendían	1
28041	apréndetelo	1
28042	apréndete	1
28043	aprendes	1
28044	aprenderán	1
28045	aprendemos	1
28046	aprended	1
28047	aprendan	1
28048	apremiaron	1
28049	apremiarla	1
28050	apremiantes	1
28051	apremiante	1
28052	apremiado	1
28053	apremiaban	1
28054	apremiaba	1
28055	apreciarlas	1
28056	apreciarán	1
28057	apreciados	1
28058	apreciado	1
28059	apreciadas	1
28060	apreciables	1
28061	apreciabilísimo	1
28062	apreciabilísima	1
28063	apoye	1
28064	apoyaturas	1
28065	apóyate	1
28066	apoyaban	1
28067	apoyaba	1
28068	apoya	1
28069	apoteosis	1
28070	apóstrofe	1
28071	apostólicos	1
28072	apostaría	1
28073	apostado	1
28074	aposentados	1
28075	aportaste	1
28076	aportar	1
28077	aportaban	1
28078	aportaba	1
28079	aporreo	1
28080	aporreando	1
28081	aporrean	1
28082	aporreada	1
28083	aporrea	1
28084	apología	1
28085	apoderó	1
28086	apoderaron	1
28087	apoderada	1
28088	apoderaban	1
28089	apócrifo	1
28090	apocamiento	1
28091	apocado	1
28092	apliquen	1
28093	aplícate	1
28094	aplicarse	1
28095	aplicarlo	1
28096	aplicándose	1
28097	aplicados	1
28098	aplicado	1
28099	aplicaditos	1
28100	aplicadísimo	1
28101	aplicadísima	1
28102	aplicaciones	1
28103	aplica	1
28104	aplazó	1
28105	aplazarlo	1
28106	aplausos	1
28107	aplaudirse	1
28108	aplaudir	1
28109	aplaudiesen	1
28110	aplaudieron	1
28111	aplaudiéndose	1
28112	aplaudía	1
28113	aplaude	1
28114	aplasto	1
28115	aplastando	1
28116	aplastado	1
28117	aplanado	1
28118	aplanada	1
28119	aplacó	1
28120	aplacaría	1
28121	aplacará	1
28122	aplacando	1
28123	aplacada	1
28124	aplacaba	1
28125	aplaca	1
28126	apio	1
28127	apilaba	1
28128	apetitoso	1
28129	apetezca	1
28130	apeteciendo	1
28131	apetecido	1
28132	apetecían	1
28133	apestando	1
28134	aperreada	1
28135	apergaminaba	1
28136	apercibiendo	1
28137	apeose	1
28138	apéndice	1
28139	apencó	1
28140	apenado	1
28141	apelo	1
28142	apelmazándose	1
28143	apelmazaban	1
28144	apechuguemos	1
28145	apechugue	1
28146	apechugó	1
28147	apearme	1
28148	apáticamente	1
28149	apasionada	1
28150	apartola	1
28151	aparto	1
28152	aparté	1
28153	apartase	1
28154	apartas	1
28155	apartarte	1
28156	apartarlo	1
28157	apartarle	1
28158	apartarla	1
28159	apartándolas	1
28160	apartan	1
28161	apartamientos	1
28162	apartamiento	1
28163	apártame	1
28164	apartaban	1
28165	aparezco	1
28166	aparezca	1
28167	aparentemente	1
28168	aparentase	1
28169	aparentarla	1
28170	aparejos	1
28171	aparejo	1
28172	aparejados	1
28173	apareciese	1
28174	apareciera	1
28175	aparecerán	1
28176	aparecerá	1
28177	aparatosa	1
28178	aparatos	1
28179	apañados	1
28180	apañado	1
28181	apañaditos	1
28182	apañadita	1
28183	apaña	1
28184	apandando	1
28185	apalearle	1
28186	apalean	1
28187	apaleaban	1
28188	apalabrado	1
28189	apalabradas	1
28190	apaisada	1
28191	apagolo	1
28192	apagó	1
28193	apagaste	1
28194	apagarse	1
28195	apagarlas	1
28196	apagarla	1
28197	apagaría	1
28198	apagaran	1
28199	apagábase	1
28200	apagaban	1
28201	apaga	1
28202	apacentaba	1
28203	apabullar	1
28204	aorta	1
28205	añadirse	1
28206	añadiéndole	1
28207	añadido	1
28208	añada	1
28209	anuncios	1
28210	anuncié	1
28211	anunciarte	1
28212	anunciarse	1
28213	anunciarme	1
28214	anunciarle	1
28215	anunciará	1
28216	anunciara	1
28217	anunciándose	1
28218	anunciado	1
28219	anunciadas	1
28220	anunciaban	1
28221	anularse	1
28222	anular	1
28223	anulando	1
28224	anula	1
28225	anudado	1
28226	anualmente	1
28227	antorchas	1
28228	antoñita	1
28229	antonieta	1
28230	antojitos	1
28231	antojito	1
28232	antojaría	1
28233	antojaba	1
28234	antiquísimos	1
28235	antípodas	1
28236	antipatriótico	1
28237	antipáticas	1
28238	antioquía	1
28239	antigüedad	1
28240	antiguamente	1
28241	antigualla	1
28242	antiespasmódico	1
28243	antieconómico	1
28244	antidinásticas	1
28245	anticuados	1
28246	anticuado	1
28247	anticonstitucional	1
28248	anticipos	1
28249	anticipó	1
28250	anticiparse	1
28251	anticipándome	1
28252	anticipado	1
28253	anticipada	1
28254	anticipaban	1
28255	antequera	1
28256	anteponen	1
28257	antepechos	1
28258	antepecho	1
28259	anteojo	1
28260	anteojazo	1
28261	antediluvianos	1
28262	antediluviana	1
28263	antecesores	1
28264	antecesor	1
28265	antaño	1
28266	antagonista	1
28267	antagonismos	1
28268	ansiosos	1
28269	ansiedades	1
28270	ansiados	1
28271	anotaciones	1
28272	anormal	1
28273	anonadar	1
28274	anonadando	1
28275	anonadado	1
28276	anonadaba	1
28277	anomalías	1
28278	anómala	1
28279	anochecía	1
28280	aniversario	1
28281	anís	1
28282	aniquilar	1
28283	aniquilan	1
28284	aniquilamiento	1
28285	animose	1
28286	anímese	1
28287	animarse	1
28288	animarle	1
28289	animarla	1
28290	animándole	1
28291	animalitos	1
28292	animadísimo	1
28293	animadas	1
28294	animábale	1
28295	anillos	1
28296	anillo	1
28297	anillas	1
28298	anidara	1
28299	anida	1
28300	anhela	1
28301	angustiada	1
28302	angulosas	1
28303	angulosa	1
28304	ángulos	1
28305	angulema	1
28306	anguila	1
28307	angosturas	1
28308	angostas	1
28309	anglómano	1
28310	anglicanizados	1
28311	angelita	1
28312	angelicales	1
28313	anfitriones	1
28314	anestésico	1
28315	anegar	1
28316	anegándose	1
28317	anega	1
28318	anduvieron	1
28319	anduviera	1
28320	anduve	1
28321	andurriales	1
28322	andrajosas	1
28323	andrajosa	1
28324	andrajo	1
28325	ando	1
28326	anden	1
28327	andarse	1
28328	andarían	1
28329	andaríamos	1
28330	andarás	1
28331	andamio	1
28332	andamiajes	1
28333	andamiaje	1
28334	andaluza	1
28335	andábanle	1
28336	ancladas	1
28337	ancianas	1
28338	anchura	1
28339	anchoas	1
28340	anatomías	1
28341	anatomía	1
28342	anascotes	1
28343	análogos	1
28344	analizó	1
28345	analizara	1
28346	analizar	1
28347	anafres	1
28348	anacronismo	1
28349	anacletus	1
28350	anacleto	1
28351	anabaptista	1
28352	amueblados	1
28353	amuebladas	1
28354	amputación	1
28355	ampolla	1
28356	amplísima	1
28357	amplia	1
28358	ampare	1
28359	ampararse	1
28360	ampararles	1
28361	ampararán	1
28362	amparaba	1
28363	ampara	1
28364	amotinó	1
28365	amoscose	1
28366	amortajó	1
28367	amortajaron	1
28368	amorraba	1
28369	amorosamente	1
28370	amorosa	1
28371	amoríos	1
28372	amorcito	1
28373	amoratados	1
28374	amontones	1
28375	amontone	1
28376	amontonaron	1
28377	amoniaco	1
28378	amonestó	1
28379	amoldarlas	1
28380	amoldara	1
28381	amoldada	1
28382	amodorrado	1
28383	amito	1
28384	amistoso	1
28385	amistosamente	1
28386	amilanarse	1
28387	amilana	1
28388	amiguito	1
28389	amigotes	1
28390	amigota	1
28391	amigablemente	1
28392	americano	1
28393	amenizó	1
28394	ameniza	1
28395	amenguársele	1
28396	amenguar	1
28397	amenazar	1
28398	amenazándolos	1
28399	amenazándola	1
28400	amenazadores	1
28401	amenazador	1
28402	amenazada	1
28403	amenazaban	1
28404	amenas	1
28405	ame	1
28406	ambulante	1
28407	ambicionar	1
28408	ámbar	1
28409	amazónica	1
28410	amazonas	1
28411	amazona	1
28412	amasara	1
28413	amasábanlo	1
28414	amasábalo	1
28415	amartelamiento	1
28416	amarre	1
28417	amarrara	1
28418	amarrar	1
28419	amarrada	1
28420	amarillentas	1
28421	amargos	1
28422	amargor	1
28423	amargarán	1
28424	amargan	1
28425	amargaban	1
28426	amargaba	1
28427	amaremos	1
28428	amaranto	1
28429	amara	1
28430	amañada	1
28431	amantísima	1
28432	amanse	1
28433	amansarla	1
28434	amansará	1
28435	amansaban	1
28436	amansa	1
28437	amanezco	1
28438	amanezca	1
28439	amaneramientos	1
28440	amanerado	1
28441	amanecía	1
28442	amándola	1
28443	amando	1
28444	amancebada	1
28445	aman	1
28446	amalgama	1
28447	amago	1
28448	amagado	1
28449	amaestrados	1
28450	amables	1
28451	amábale	1
28452	alzarse	1
28453	alzándolos	1
28454	alzándole	1
28455	alzamiento	1
28456	alzada	1
28457	alumbré	1
28458	alumbrar	1
28459	alumbrándose	1
28460	alumbrando	1
28461	alumbramientos	1
28462	alumbrado	1
28463	alumbra	1
28464	aluego	1
28465	aludir	1
28466	aludiendo	1
28467	aludidos	1
28468	alucinado	1
28469	alucinada	1
28470	alucinaciones	1
28471	altozanos	1
28472	altona	1
28473	altivez	1
28474	altísima	1
28475	alteza	1
28476	alternativamente	1
28477	alternativa	1
28478	alternando	1
28479	alternadamente	1
28480	alternaban	1
28481	alterna	1
28482	alteres	1
28483	alterando	1
28484	alterada	1
28485	altarucho	1
28486	altanería	1
28487	altaneramente	1
28488	alsacia	1
28489	alquilan	1
28490	alquilado	1
28491	alquila	1
28492	alpargatitas	1
28493	alones	1
28494	alojamiento	1
28495	alojaba	1
28496	almuerzas	1
28497	almuerza	1
28498	almorzó	1
28499	almorzaron	1
28500	almorzaría	1
28501	almorzaré	1
28502	almorzarás	1
28503	almorzaran	1
28504	almorzará	1
28505	almorzaban	1
28506	almorcemos	1
28507	almonedas	1
28508	almohadón	1
28509	almireces	1
28510	almidón	1
28511	almería	1
28512	almendrita	1
28513	almendrado	1
28514	almansa	1
28515	almanaques	1
28516	almagre	1
28517	almacenista	1
28518	aller	1
28519	allegro	1
28520	allego	1
28521	allegadizo	1
28522	allanamiento	1
28523	alivió	1
28524	aliviarle	1
28525	alivian	1
28526	aliviado	1
28527	aliviaba	1
28528	alivia	1
28529	aliñada	1
28530	alinearon	1
28531	alineadas	1
28532	alimentarse	1
28533	alimentarlo	1
28534	alimentados	1
28535	alimentada	1
28536	alimentaba	1
28537	alilao	1
28538	aligerándole	1
28539	aligeraba	1
28540	aligera	1
28541	alifonso	1
28542	alicante	1
28543	aliar	1
28544	alianza	1
28545	alhambra	1
28546	alhajita	1
28547	álgido	1
28548	algeciras	1
28549	algarroba	1
28550	alfonsina	1
28551	alfombrita	1
28552	alfombras	1
28553	alfombrado	1
28554	alfombrada	1
28555	alfilerazo	1
28556	alfargías	1
28557	alevosa	1
28558	aletargarse	1
28559	alentó	1
28560	alentarme	1
28561	alentara	1
28562	alentar	1
28563	alentado	1
28564	alentada	1
28565	alentaba	1
28566	aleluya	1
28567	alelí	1
28568	alejaron	1
28569	alejándole	1
28570	alegrones	1
28571	alegremente	1
28572	alegrase	1
28573	alegras	1
28574	alegrarte	1
28575	alegrarla	1
28576	alegraríamos	1
28577	alegraran	1
28578	alegrado	1
28579	alegrábanse	1
28580	alegra	1
28581	alegórica	1
28582	alegoría	1
28583	alegar	1
28584	alegando	1
28585	aldeota	1
28586	aldeas	1
28587	aldeanos	1
28588	alcorcón	1
28589	alcoholismo	1
28590	alcohólico	1
28591	alcohólicas	1
28592	alcoholatos	1
28593	alcira	1
28594	alcé	1
28595	alcarria	1
28596	alcarreño	1
28597	alcaraz	1
28598	alcanzas	1
28599	alcanzarla	1
28600	alcanzaría	1
28601	alcanzamos	1
28602	alcanzaban	1
28603	alcantarillas	1
28604	alcanfor	1
28605	alcánceme	1
28606	alcaloide	1
28607	alcaldía	1
28608	alcahuetas	1
28609	alcachofas	1
28610	alborozada	1
28611	alborotos	1
28612	alborotes	1
28613	alborotemos	1
28614	alboroté	1
28615	alborotaron	1
28616	alborotan	1
28617	alborotadamente	1
28618	albis	1
28619	albillo	1
28620	albergarse	1
28621	albergar	1
28622	albergaban	1
28623	albedrío	1
28624	albaricoque	1
28625	albardería	1
28626	albaicín	1
28627	albahaca	1
28628	alarmas	1
28629	alarmarse	1
28630	alarmaron	1
28631	alarmar	1
28632	alarmándose	1
28633	alarmando	1
28634	alarmados	1
28635	alarmado	1
28636	alaridos	1
28637	alarido	1
28638	alargué	1
28639	alargaron	1
28640	alargarle	1
28641	alargar	1
28642	alargándosela	1
28643	alargamiento	1
28644	alargábalo	1
28645	alardeando	1
28646	alardeaba	1
28647	alardea	1
28648	alamedas	1
28649	alambicados	1
28650	alados	1
28651	alabó	1
28652	alabarderos	1
28653	alabar	1
28654	alabanzas	1
28655	alaban	1
28656	alababan	1
28657	akos	1
28658	ajusticiar	1
28659	ajusticiados	1
28660	ajustaré	1
28661	ajustarán	1
28662	ajustar	1
28663	ajustándolos	1
28664	ajustados	1
28665	ajustaba	1
28666	ajuntaron	1
28667	ajumarse	1
28668	ajumaíto	1
28669	ajuares	1
28670	ajos	1
28671	ajito	1
28672	ajenjos	1
28673	ajardinados	1
28674	ajan	1
28675	aislados	1
28676	aislado	1
28677	airote	1
28678	airear	1
28679	airado	1
28680	airadas	1
28681	ahuyentase	1
28682	ahuyentar	1
28683	ahuyentan	1
28684	ahuma	1
28685	ahuecar	1
28686	ahuecados	1
28687	ahuecadas	1
28688	ahueca	1
28689	ahorrarse	1
28690	ahorrar	1
28691	ahorcarme	1
28692	ahorcado	1
28693	ahondando	1
28694	ahola	1
28695	ahoguillo	1
28696	ahogos	1
28697	ahogarte	1
28698	ahogarse	1
28699	ahogarle	1
28700	ahogaría	1
28701	ahogaran	1
28702	ahogándose	1
28703	ahogándola	1
28704	ahogando	1
28705	ahogado	1
28706	ahogadas	1
28707	ahoga	1
28708	ahíto	1
28709	ahilado	1
28710	ahijado	1
28711	ahijada	1
28712	aguzadores	1
28713	aguzado	1
28714	aguzaban	1
28715	agujeritos	1
28716	agujereados	1
28717	aguirre	1
28718	aguinaldo	1
28719	aguileña	1
28720	águilas	1
28721	agudos	1
28722	agudísimos	1
28723	agudísima	1
28724	agudezas	1
28725	aguaron	1
28726	aguardo	1
28727	aguardientito	1
28728	aguardientazo	1
28729	aguárdense	1
28730	aguardaron	1
28731	aguardaba	1
28732	aguantó	1
28733	aguanten	1
28734	aguánteme	1
28735	aguante	1
28736	aguantas	1
28737	aguantarme	1
28738	aguantarle	1
28739	aguantaría	1
28740	aguantamos	1
28741	aguadores	1
28742	aguacero	1
28743	agrupar	1
28744	agricultura	1
28745	agrias	1
28746	agriado	1
28747	agriaba	1
28748	agresor	1
28749	agregarse	1
28750	agregando	1
28751	agregábansele	1
28752	agregaba	1
28753	agredida	1
28754	agravio	1
28755	agraviadas	1
28756	agravación	1
28757	agrandando	1
28758	agrandado	1
28759	agrandada	1
28760	agradó	1
28761	agradezcáis	1
28762	agradecimientos	1
28763	agradeces	1
28764	agradecerle	1
28765	agradecerían	1
28766	agradeceremos	1
28767	agradéceme	1
28768	agradece	1
28769	agradaron	1
28770	agradarle	1
28771	agradan	1
28772	agradablemente	1
28773	agradabilísimo	1
28774	agradábanle	1
28775	agració	1
28776	agraciadas	1
28777	agotarse	1
28778	agostaba	1
28779	agonizada	1
28780	agobia	1
28781	agitato	1
28782	agitara	1
28783	agitante	1
28784	agitanada	1
28785	agitadas	1
28786	ágiles	1
28787	agenciado	1
28788	agasajarle	1
28789	agasajar	1
28790	agasajando	1
28791	agasajan	1
28792	agasajada	1
28793	agarrotes	1
28794	agarrose	1
28795	agarré	1
28796	agarre	1
28797	agarrase	1
28798	agarras	1
28799	agarraron	1
28800	agarrarlo	1
28801	agarrándole	1
28802	agarrados	1
28803	agarrado	1
28804	agarradas	1
28805	agarraba	1
28806	agarra	1
28807	agallas	1
28808	agachaban	1
28809	agacha	1
28810	afrontando	1
28811	africana	1
28812	afrento	1
28813	afrentas	1
28814	afrentar	1
28815	afortunado	1
28816	aforismos	1
28817	afluía	1
28818	aflojé	1
28819	afloje	1
28820	aflojarse	1
28821	aflojarle	1
28822	aflojar	1
28823	aflijas	1
28824	afligidos	1
28825	afligidísimo	1
28826	aflige	1
28827	aflictivo	1
28828	aflictiva	1
28829	aflicciones	1
28830	aflamencado	1
28831	afirme	1
28832	afirmativos	1
28833	afirmativa	1
28834	afirmase	1
28835	afirmarse	1
28836	afinó	1
28837	afinidades	1
28838	afines	1
28839	afinado	1
28840	afinadas	1
28841	afinaba	1
28842	afiló	1
28843	afiliarse	1
28844	afilándolas	1
28845	afilados	1
28846	afiladas	1
28847	afilaban	1
28848	afianzando	1
28849	afianzaba	1
28850	aferradas	1
28851	aferrada	1
28852	aferraba	1
28853	afeiten	1
28854	afeite	1
28855	afeitadito	1
28856	afeitada	1
28857	afectuosos	1
28858	afectase	1
28859	afectarte	1
28860	afectaron	1
28861	afectadísimo	1
28862	afección	1
28863	afeaban	1
28864	afanándose	1
28865	afanados	1
28866	afanadora	1
28867	afanada	1
28868	advirtieron	1
28869	advirtiera	1
28870	advirtiéndole	1
28871	adviniese	1
28872	adviértele	1
28873	advierte	1
28874	adviertas	1
28875	adviértale	1
28876	advertirle	1
28877	advertido	1
28878	advertida	1
28879	advertían	1
28880	advertencia	1
28881	adversidad	1
28882	adventicia	1
28883	adustez	1
28884	adustas	1
28885	adúltero	1
28886	adultero	1
28887	adulterios	1
28888	adulteraba	1
28889	adulona	1
28890	adulando	1
28891	adulaban	1
28892	adquiriría	1
28893	adquiriré	1
28894	adquirida	1
28895	adquieren	1
28896	adquieran	1
28897	adquiera	1
28898	adornó	1
28899	adornarse	1
28900	adornar	1
28901	adornados	1
28902	adormilado	1
28903	adormidera	1
28904	adormeciera	1
28905	adormecido	1
28906	adormecida	1
28907	adormecía	1
28908	adormecerse	1
28909	adoren	1
28910	adore	1
28911	adorarte	1
28912	adorarse	1
28913	adoraron	1
28914	adorarme	1
28915	adoraría	1
28916	adoraré	1
28917	adoraran	1
28918	adorara	1
28919	adorando	1
28920	adoramos	1
28921	adorabas	1
28922	adoquinando	1
28923	adoquinadas	1
28924	adoptó	1
28925	adopte	1
28926	adoptarlo	1
28927	adoptarla	1
28928	adoptaría	1
28929	adoptado	1
28930	adonis	1
28931	adonde	1
28932	adolecieran	1
28933	adobado	1
28934	admitirlo	1
28935	admitirle	1
28936	admitió	1
28937	admitiesen	1
28938	admitiera	1
28939	admitiendo	1
28940	admitidas	1
28941	admitida	1
28942	admitamos	1
28943	admisión	1
28944	admirose	1
28945	admirase	1
28946	admiras	1
28947	admiraron	1
28948	admiraría	1
28949	admiran	1
28950	admiramos	1
28951	admiradas	1
28952	admirábala	1
28953	admira	1
28954	administre	1
28955	administrativo	1
28956	administrativas	1
28957	administrado	1
28958	administraba	1
28959	administra	1
28960	adjudicó	1
28961	adjudicado	1
28962	adjetivo	1
28963	adiviné	1
28964	adivinarlo	1
28965	adivinarle	1
28966	adivinar	1
28967	adivinanza	1
28968	adivinándole	1
28969	adivinando	1
28970	adivinado	1
28971	adivinaciones	1
28972	adivinabas	1
28973	adicto	1
28974	adiciones	1
28975	adhiriéndose	1
28976	adhiere	1
28977	adheridos	1
28978	adeudaba	1
28979	aderezo	1
28980	aderezado	1
28981	aderezada	1
28982	adepto	1
28983	adentros	1
28984	adelgazadas	1
28985	adelgazada	1
28986	adelanto	1
28987	adelantarse	1
28988	adelantarían	1
28989	adelantar	1
28990	adelantan	1
28991	adelantamos	1
28992	adela	1
28993	adecentase	1
28994	adecentarse	1
28995	adecentaras	1
28996	adecentar	1
28997	adecentado	1
28998	adaptando	1
28999	adaptada	1
29000	adaptaban	1
29001	adán	1
29002	adamado	1
29003	adagio	1
29004	acuse	1
29005	acusarse	1
29006	acusaré	1
29007	acusándose	1
29008	acusándoles	1
29009	acusádose	1
29010	acusadora	1
29011	acusaban	1
29012	acurrucó	1
29013	acurrucada	1
29014	acuñar	1
29015	acueste	1
29016	acuesta	1
29017	acuerdos	1
29018	acuérdese	1
29019	acuerden	1
29020	acuerdan	1
29021	acueducto	1
29022	acudo	1
29023	acudiremos	1
29024	acudiré	1
29025	acudimos	1
29026	acudiera	1
29027	acudía	1
29028	acuden	1
29029	acudas	1
29030	acubilla	1
29031	actuar	1
29032	actuando	1
29033	actualmente	1
29034	actrices	1
29035	activamente	1
29036	activaba	1
29037	actitudes	1
29038	acta	1
29039	acrisolada	1
29040	acribilló	1
29041	acribillarlas	1
29042	acredite	1
29043	acreditadísimo	1
29044	acreditada	1
29045	acrecía	1
29046	acostumbres	1
29047	acostumbré	1
29048	acostumbrarse	1
29049	acostumbraran	1
29050	acostumbrados	1
29051	acostumbradas	1
29052	acostumbra	1
29053	acosté	1
29054	acostáronle	1
29055	acostaron	1
29056	acostarme	1
29057	acostaría	1
29058	acostaremos	1
29059	acostara	1
29060	acostando	1
29061	acosen	1
29062	acosándoles	1
29063	acosando	1
29064	acosados	1
29065	acorte	1
29066	acortarse	1
29067	acortar	1
29068	acortando	1
29069	acortaba	1
29070	acorralan	1
29071	acordes	1
29072	acorde	1
29073	acordase	1
29074	acordarme	1
29075	acordaría	1
29076	acordaré	1
29077	acordará	1
29078	acordándome	1
29079	acordado	1
29080	acordada	1
29081	acordabas	1
29082	acordaban	1
29083	acorazó	1
29084	acopio	1
29085	acopiando	1
29086	acopiada	1
29087	acontecimientos	1
29088	aconteciendo	1
29089	acontece	1
29090	aconsejo	1
29091	aconséjele	1
29092	aconséjate	1
29093	aconsejas	1
29094	aconsejarte	1
29095	aconsejármelas	1
29096	aconsejaría	1
29097	aconseja	1
29098	acónito	1
29099	acompañolas	1
29100	acompañes	1
29101	acompañaron	1
29102	acompañara	1
29103	acompañantes	1
29104	acompañante	1
29105	acompañándola	1
29106	acompañan	1
29107	acompañamos	1
29108	acompañábanle	1
29109	acompañábanla	1
29110	acomodó	1
29111	acomodo	1
29112	acomodaticios	1
29113	acomodarse	1
29114	acomodar	1
29115	acomodándose	1
29116	acomodando	1
29117	acomodado	1
29118	acomodada	1
29119	acomoda	1
29120	acometía	1
29121	acometerla	1
29122	acometería	1
29123	acoja	1
29124	acogió	1
29125	acogida	1
29126	acobardes	1
29127	acobardarse	1
29128	acobardaron	1
29129	acobardarme	1
29130	acobardará	1
29131	acobardado	1
29132	aclimatación	1
29133	aclaró	1
29134	aclare	1
29135	aclaran	1
29136	aclaración	1
29137	aclaraba	1
29138	aclara	1
29139	aclamaciones	1
29140	aciertas	1
29141	aciertan	1
29142	acídula	1
29143	acidez	1
29144	acicaló	1
29145	aciaga	1
29146	achuchones	1
29147	achicharrados	1
29148	achicarte	1
29149	achantado	1
29150	achantada	1
29151	achacaban	1
29152	achacaba	1
29153	acetato	1
29154	acertijos	1
29155	acertaré	1
29156	acertados	1
29157	acertadas	1
29158	acertada	1
29159	acertaban	1
29160	acerqueme	1
29161	acerico	1
29162	acercósele	1
29163	acercase	1
29164	acercara	1
29165	acercan	1
29166	acerbísimo	1
29167	acerbísimas	1
29168	acerados	1
29169	acéptelo	1
29170	acepté	1
29171	acéptalo	1
29172	aceptación	1
29173	acentuole	1
29174	acentuar	1
29175	acentúan	1
29176	acentuación	1
29177	acémilas	1
29178	aceleró	1
29179	aceleradas	1
29180	aceitosa	1
29181	acechas	1
29182	acecharlas	1
29183	acecharan	1
29184	acechar	1
29185	acechándola	1
29186	acechador	1
29187	acechaban	1
29188	acechaba	1
29189	acebuche	1
29190	accionistas	1
29191	accidentados	1
29192	accidentada	1
29193	accedieron	1
29194	acaudalada	1
29195	acatemos	1
29196	acatarrado	1
29197	acatar	1
29198	acataba	1
29199	acarició	1
29200	acariciarlo	1
29201	acariciarle	1
29202	acariciándoselo	1
29203	acariciándolas	1
29204	acariciaba	1
29205	acaparamientos	1
29206	acantonar	1
29207	acampan	1
29208	acalores	1
29209	acalorándose	1
29210	acalorándole	1
29211	acaloran	1
29212	acaloradamente	1
29213	acallar	1
29214	acallaban	1
29215	acaeció	1
29216	académicos	1
29217	académico	1
29218	académica	1
29219	acacias	1
29220	acabas	1
29221	acabarás	1
29222	acabarán	1
29223	acabáramos	1
29224	abuso	1
29225	abusas	1
29226	abusar	1
29227	aburriste	1
29228	aburrirle	1
29229	aburrir	1
29230	aburrió	1
29231	aburriera	1
29232	aburriéndose	1
29233	aburridos	1
29234	aburridísima	1
29235	aburridas	1
29236	aburrida	1
29237	aburrían	1
29238	aburríale	1
29239	aburres	1
29240	aburra	1
29241	abundan	1
29242	abunda	1
29243	abulte	1
29244	abuelos	1
29245	absuelta	1
29246	abstrusas	1
29247	abstraerse	1
29248	abstracciones	1
29249	abstinencia	1
29250	absteniéndose	1
29251	absorción	1
29252	absorbió	1
29253	absorbía	1
29254	absorbederos	1
29255	absolverás	1
29256	absolutista	1
29257	absolución	1
29258	abrumara	1
29259	abrumadoras	1
29260	abrumadora	1
29261	abruma	1
29262	abroñigal	1
29263	abrocharte	1
29264	abrochándose	1
29265	abrirlos	1
29266	abrirla	1
29267	abriría	1
29268	abriremos	1
29269	abrirá	1
29270	abriolo	1
29271	abriole	1
29272	abrigos	1
29273	abrigase	1
29274	abrigas	1
29275	abrigarte	1
29276	abrigarse	1
29277	abrigara	1
29278	abrigar	1
29279	abrigándose	1
29280	abrigándole	1
29281	abrigados	1
29282	abrigaditos	1
29283	abrigaditas	1
29284	abrigábamos	1
29285	abriera	1
29286	abriéndolos	1
29287	abriéndole	1
29288	abriéndolas	1
29289	abriéndola	1
29290	abrí	1
29291	abreviemos	1
29292	abrevie	1
29293	abreviaturas	1
29294	abreviarlos	1
29295	abreviarlo	1
29296	ábrete	1
29297	abrazola	1
29298	abrazara	1
29299	abrazándose	1
29300	abrazándole	1
29301	abrazados	1
29302	abrazaba	1
29303	abrasado	1
29304	abras	1
29305	abran	1
29306	abracitos	1
29307	abovedada	1
29308	abotonándose	1
29309	aborregado	1
29310	aborrecimiento	1
29311	aborreciera	1
29312	aborrecido	1
29313	aborrecidas	1
29314	aborrecida	1
29315	aborrecerlo	1
29316	aborrecerle	1
29317	aboque	1
29318	abonos	1
29319	abono	1
29320	abonados	1
29321	abonado	1
29322	abona	1
29323	abominando	1
29324	abolladuras	1
29325	abollados	1
29326	abolieron	1
29327	abolida	1
29328	abogaba	1
29329	abocose	1
29330	aboco	1
29331	abochornada	1
29332	aboca	1
29333	abnegaciones	1
29334	ablande	1
29335	ablandaría	1
29336	ablanda	1
29337	abigarrado	1
29338	abigarradas	1
29339	abiertamente	1
29340	aberración	1
29341	abejorro	1
29342	abejón	1
29343	abejas	1
29344	abdicar	1
29345	abcesos	1
29346	abatiendo	1
29347	abatidísimo	1
29348	abatida	1
29349	abarcado	1
29350	abarcaban	1
29351	abarca	1
29352	abanicón	1
29353	abanicarse	1
29354	abandonaros	1
29355	abandonaron	1
29356	abandonarlo	1
29357	abandonaría	1
29358	abandonaremos	1
29359	abandonalo	1
29360	abandonados	1
29361	abandonadas	1
29362	abandonaba	1
29363	abalorio	1
29364	abalanzándose	1
29365	abalanzado	1
29366	abajito	1
29367	abadesa	1

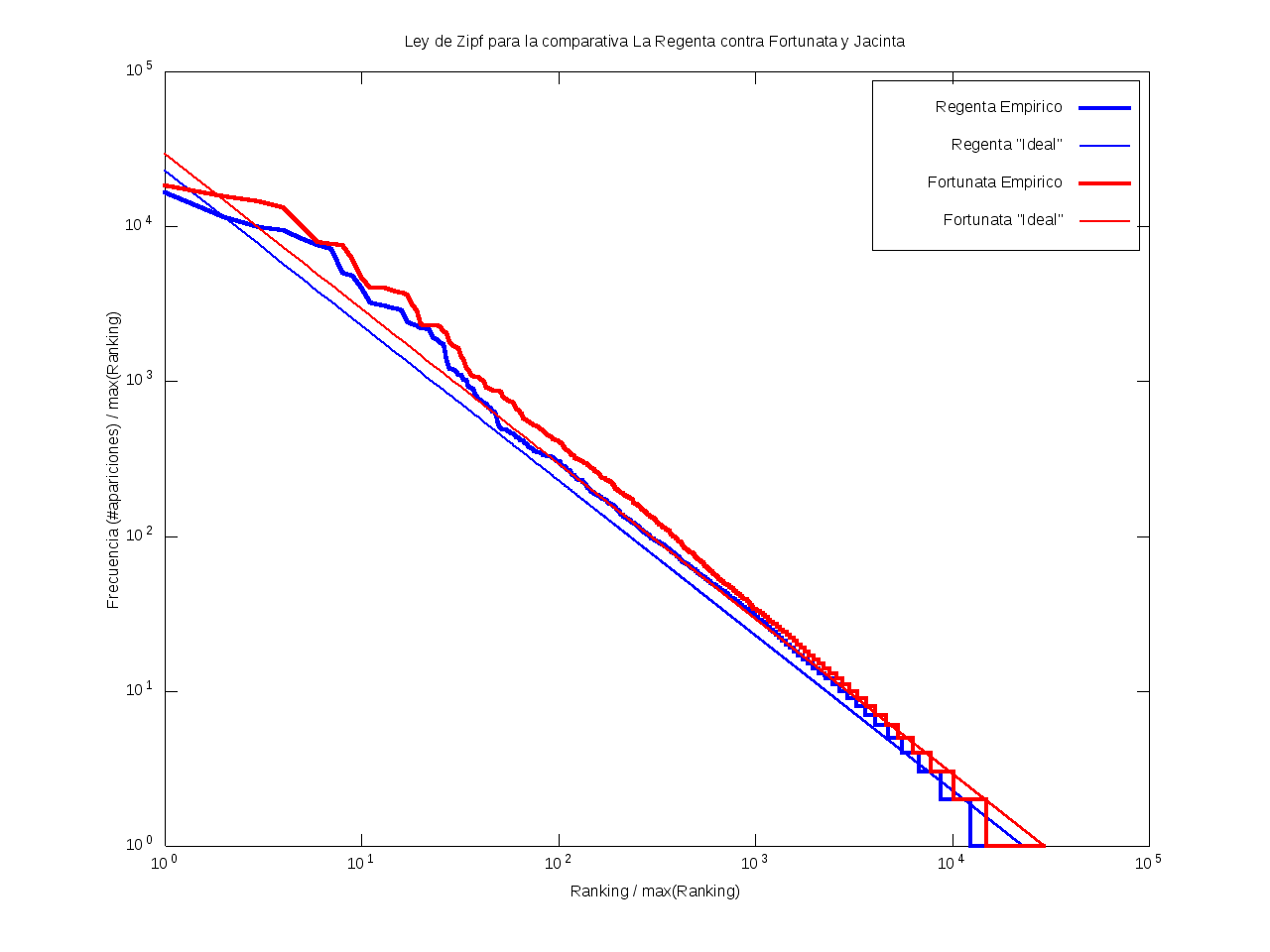
Mostrar todo

Test de Dunning

El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.

Fórmula:

- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde L(p,k,n) = p^k * (1-p)^(n-k)
con

ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
ni = número total de palabras del conjunto i.
pi = probabilidad de la palabra en el conjunto i = ki/ni.

Para encontrar las palabras distintivas se enfrentará un conjunto (Regenta) (conjunto 1) contra el otro (Fortunata) (conjunto 2) y viceversa.

A continuación se muestra una lista de todas las palabras presentes en los textos, ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas. Haga click en la palabra para ver su definición según el diccionario de la RAE.

Palabra	Regenta (308254)	Fortunata (394672)	Dunning -2log(lambda)
don	1798	79	2405.817
ana	898	0	1481.963
me	638	3140	1251.532
magistral	769	2	1243.386
fortunata	0	869	1004.008
víctor	490	0	808.279
álvaro	490	0	808.279
regenta	478	0	788.474
vetusta	471	0	776.921
te	225	1430	707.305
jacinta	0	571	659.521
mesía	373	0	615.202
lupe	0	521	601.741
fermín	350	0	577.253
quintanar	306	0	504.659
había	2212	1393	447.315
petra	241	2	376.556
guillermina	0	320	369.520
rubín	0	314	362.589
del	3016	2310	352.145
maxi	0	304	351.038
el	8268	7919	348.389
frígilis	211	0	347.947
maximiliano	0	295	340.643
era	2301	1656	327.130
obdulia	195	0	321.557
anita	190	0	313.310
paula	173	0	285.272
pas	171	0	281.973
que	9901	15616	277.122
tía	13	315	275.758
dijo	326	1073	257.558
provisor	155	0	255.585
pues	249	903	250.655
paco	171	4	248.453
d	51	404	231.303
marquesa	159	4	229.237
tan	328	1028	227.483
mauricia	0	192	221.684
yo	712	1722	220.245
barbarita	0	190	219.375
vegallana	132	0	217.654
ronzal	130	0	214.356
de	16580	18253	207.782
pompeyo	125	0	206.110
ozores	124	0	204.461
porque	401	1094	185.744
casino	118	1	184.171
tú	141	572	183.828
mí	120	499	165.198
él	1208	883	163.373
catedral	121	5	163.217
ripamilán	97	0	159.937
santos	131	9	159.583
izquierdo	1	145	157.098
he	135	519	155.828
ballester	0	134	154.709
foja	93	0	153.341
obispo	128	10	150.848
los	4033	3930	149.772
glocester	90	0	148.394
moreno	5	158	145.975
juan	53	310	143.495
estupiñá	0	123	142.007
además	206	52	140.388
mi	291	801	138.502
feijoo	0	119	137.389
baldomero	0	119	137.389
orgaz	83	0	136.851
lo	2335	4028	135.650
guimarán	82	0	135.202
visitación	102	5	133.556
papitos	0	114	131.615
vaya	27	223	130.826
nicolás	0	113	130.461
vivero	77	0	126.957
pablo	6	145	126.835
bien	355	894	126.454
en	7137	7609	125.696
es	1193	2263	125.593
señor	460	254	122.195
bermúdez	74	0	122.010
calle	115	425	121.014
esta	351	872	119.270
chico	18	182	118.788
evaristo	0	102	117.760
plácido	0	101	116.605
muy	555	1215	116.281
sin	1097	863	116.009
digo	49	261	111.528
vetustenses	67	0	110.468
santa	107	392	110.274
petronila	66	0	108.819
usted	822	1626	107.979
delfín	0	93	107.368
aquí	178	530	106.934
luego	40	232	106.642
según	194	63	106.343
vetustense	64	0	105.521
replicó	7	129	105.306
cuando	494	1085	104.903
le	2436	4034	103.358
cara	84	329	101.152
arcipreste	61	0	100.575
no	4999	7657	100.068
canónigo	83	6	99.827
ah	25	182	98.798
placer	87	8	97.782
espolón	59	0	97.277
sobrino	1	92	96.808
barinaga	57	0	93.979
has	33	197	92.683
cruz	66	275	91.224
creía	200	77	91.222
teresina	55	0	90.682
frutos	54	0	89.033
aquello	266	129	88.441
jáuregui	0	76	87.740
rato	22	161	87.693
edelmira	53	0	87.384
teresa	52	0	85.735
tengo	86	309	84.569
villalonga	0	73	84.277
severiana	0	73	84.277
tu	77	289	84.019
samaniego	0	72	83.122
ha	343	778	83.013
mira	20	150	82.998
madre	267	135	82.949
somoza	50	0	82.437
voy	52	231	82.428
parque	59	2	81.981
caserón	59	2	81.981
custodio	49	0	80.788
arcediano	48	0	79.140
nos	102	333	78.788
josé	3	86	77.993
juanito	6	98	77.153
arnaiz	0	66	76.195
salón	97	20	75.994
páez	46	0	75.842
carraspique	46	0	75.842
ganas	5	92	75.065
ay	36	182	74.104
llamaba	117	33	72.930
estás	22	144	72.650
benítez	44	0	72.544
visita	159	62	71.419
fue	237	569	71.217
versos	52	2	70.935
saturnino	43	0	70.896
hablaba	161	64	70.641
si	1173	2032	69.906
anuncia	51	2	69.363
marqués	123	39	68.995
habían	302	180	68.756
familia	36	175	68.593
está	230	551	68.564
pituso	0	59	68.113
quizás	4	81	67.847
crespo	41	0	67.598
ti	36	173	67.036
trabuco	40	0	65.949
mente	4	79	65.733
obscuro	39	0	64.300
obscuridad	39	0	64.300
amor	268	156	64.114
marquesito	44	1	64.108
cosas	159	414	63.318
saturno	38	0	62.652
camila	38	0	62.652
aurora	4	76	62.572
tienes	39	174	62.378
bosque	37	0	61.003
idea	104	305	59.787
anselmo	36	0	59.354
para	1377	2285	59.187
ridículo	64	10	58.451
pasión	101	31	58.413
aldea	44	2	58.399
confesonario	55	6	58.388
dije	4	72	58.375
hay	245	553	58.121
quieres	19	119	58.105
encimada	35	0	57.705
fin	162	408	57.669
vi	7	82	57.174
robustiano	34	0	56.056
palomares	34	0	56.056
persona	47	183	55.827
recordaba	68	13	55.763
clero	48	4	55.553
verás	7	80	55.197
piedad	90	26	54.956
va	85	259	54.475
sabía	279	178	54.463
señores	112	41	54.134
templo	47	4	54.066
tiene	182	435	53.783
tentación	41	2	53.729
parece	105	296	53.706
confesión	54	7	53.639
estuvo	33	148	53.357
indicó	1	53	52.875
aquella	764	666	52.827
fermo	32	0	52.759
sr	2	58	52.718
mas	13	96	52.591
quería	328	226	52.574
reales	7	77	52.246
micaelas	0	45	51.950
hace	77	239	51.935
gritaba	57	9	51.791
cayetano	48	5	51.790
mona	1	52	51.758
botica	1	52	51.758
empezó	20	114	51.644
este	314	650	51.320
tenorio	31	0	51.110
sotana	45	4	51.102
carlos	62	12	50.475
da	41	162	50.352
cual	108	295	50.141
duelo	35	1	49.720
aparisi	0	43	49.641
pensaba	203	117	49.549
veces	307	211	49.545
marqueses	30	0	49.461
fortunato	30	0	49.461
gente	29	133	49.110
conmigo	10	83	48.822
y	9457	13277	48.692
despacho	73	19	48.578
habría	29	132	48.352
señoritas	34	1	48.129
segunda	19	107	47.983
coro	54	9	47.746
ido	49	175	47.473
fundadora	1	48	47.299
teatro	89	30	46.988
pies	113	47	46.813
veo	18	103	46.812
oh	130	60	46.612
águeda	28	0	46.164
tías	44	5	46.020
volvía	101	39	45.897
lejos	117	51	45.521
juventud	54	10	45.100
tío	1	46	45.074
enteramente	0	39	45.023
suave	32	1	44.951
mourelo	27	0	44.515
loreto	27	0	44.515
lábaro	27	0	44.515
aya	27	0	44.515
presidente	35	2	44.453
echó	11	81	44.291
allí	450	361	44.184
di	2	50	44.065
figuraba	47	7	43.917
doncella	47	7	43.917
mamá	19	102	43.881
marido	120	304	43.576
dos	334	658	42.886
primavera	26	0	42.866
prados	26	0	42.866
celedonio	26	0	42.866
carretera	26	0	42.866
cármenes	26	0	42.866
amores	56	12	42.805
podía	369	283	42.600
general	83	29	42.209
vamos	61	191	42.134
mirando	23	109	41.642
ruiz	0	36	41.560
ratito	0	36	41.560
juanín	0	36	41.560
joaquín	55	12	41.548
absurdo	43	6	41.387
bedoya	25	0	41.218
infeliz	16	91	41.148
confesar	49	9	41.114
seguro	89	34	40.959
reír	8	68	40.544
capilla	66	19	40.422
iglesia	134	69	40.351
baile	40	5	40.326
manteo	29	1	40.198
recuerdos	35	3	40.178
luna	52	11	40.080
virtud	88	34	39.961
ex	50	10	39.913
ii	6	61	39.912
mejillas	44	7	39.829
torquemada	2	46	39.774
aquellos	232	156	39.696
obscuras	24	0	39.569
comenzó	24	0	39.569
anoche	5	57	39.284
qué	1097	1782	39.276
ji	0	34	39.251
ninguna	27	115	39.131
gusta	11	75	38.948
carcajadas	39	5	38.915
ver	280	560	38.785
prefería	34	3	38.696
silencio	112	53	38.674
romántico	28	1	38.618
otra	324	629	38.541
decía	414	337	38.417
olmedo	0	33	38.096
delfina	0	33	38.096
tienda	22	102	38.095
devota	23	0	37.920
bonita	4	52	37.806
gritó	94	40	37.785
al	2168	2312	37.512
personas	44	149	37.341
muñoz	1	39	37.319
gana	11	73	37.193
chica	20	96	37.152
palacio	44	8	37.129
antojaba	27	1	37.041
señora	229	473	37.032
benigna	0	32	36.942
casa	487	874	36.734
ateo	35	4	36.529
bonito	3	47	36.508
estamos	11	72	36.321
trifón	22	0	36.271
fandiño	22	0	36.271
encogió	22	0	36.271
casta	10	69	36.129
culto	43	8	35.818
mañana	106	263	35.815
confesor	41	7	35.798
superiora	0	31	35.787
cava	0	31	35.787
barón	26	1	35.466
jamás	90	39	35.299
rufina	29	2	35.290
dulce	79	31	35.210
torre	34	4	35.100
necesario	34	4	35.100
honrada	9	65	35.095
rostro	100	47	34.890
viene	32	120	34.837
mala	65	186	34.762
jesús	67	23	34.711
quedose	0	30	34.633
beneficiado	21	0	34.623
pálido	42	8	34.514
peligro	59	18	34.310
etc	49	12	34.149
alto	82	34	34.106
barca	25	1	33.895
adentros	25	1	33.895
lecho	79	32	33.854
pobrecito	0	29	33.478
feliciana	0	29	33.478
bárbara	3	44	33.428
basilio	5	51	33.421
tontería	2	40	33.393
criados	37	6	33.174
perales	20	0	32.974
obscura	20	0	32.974
canónigos	20	0	32.974
escándalo	53	15	32.937
estoy	94	235	32.609
segismundo	3	43	32.406
dando	43	139	32.349
ciudad	44	10	32.337
farmacia	0	28	32.324
farmacéutico	0	28	32.324
conque	0	28	32.324
compras	0	28	32.324
diferentes	6	53	32.280
vano	27	2	32.268
añadía	27	2	32.268
calumnia	32	4	32.260
casi	192	130	32.254
demás	150	92	32.067
quiero	96	237	31.869
esa	126	289	31.835
invierno	38	7	31.831
cómoda	1	34	31.817
digno	47	12	31.744
oía	90	42	31.740
pocas	74	30	31.677
religión	86	39	31.638
miserable	58	19	31.513
materia	45	11	31.404
ilusión	3	42	31.388
establecimiento	3	42	31.388
todo	917	903	31.367
remordimiento	29	3	31.363
delicia	29	3	31.363
voluptuosidad	19	0	31.325
nene	0	27	31.169
sor	10	63	30.896
sonrió	31	4	30.850
mística	23	1	30.761
uno	110	259	30.730
platón	1	33	30.722
han	68	184	30.644
viendo	19	85	30.558
contigo	5	48	30.535
pensar	126	73	30.425
día	272	522	30.414
otros	192	133	30.315
quevedo	2	37	30.234
ramo	0	26	30.015
prójima	0	26	30.015
hucha	0	26	30.015
aborrecía	28	3	29.915
mujer	286	542	29.841
obscurecer	18	0	29.676
fanatismo	18	0	29.676
instante	32	112	29.499
socios	30	4	29.448
ángel	15	74	29.424
diciendo	58	163	29.383
nubes	45	12	29.374
pereza	25	2	29.267
despreciaba	25	2	29.267
confesaba	25	2	29.267
con	3202	4637	29.254
galería	22	1	29.199
beata	22	1	29.199
iii	2	36	29.186
tomás	34	6	29.165
sabio	34	6	29.165
aquellas	190	133	29.131
echando	9	58	28.928
villuendas	0	25	28.861
nicanora	0	25	28.861
levantándose	0	25	28.861
dinero	48	143	28.861
cuanto	187	131	28.609
doña	414	733	28.579
elocuencia	27	3	28.473
enemigos	39	9	28.361
quieras	3	39	28.354
pieza	3	39	28.354
meter	3	39	28.354
madres	3	39	28.354
menos	328	272	28.236
procuraba	37	8	28.116
haciendo	42	130	28.106
lujuria	17	0	28.028
alas	35	7	27.938
atrevió	47	14	27.932
triunfo	33	6	27.846
vas	11	62	27.821
sentía	176	122	27.735
rafaela	0	24	27.706
patricia	0	24	27.706
pacheco	0	24	27.706
nones	0	24	27.706
paquito	21	1	27.641
luchar	21	1	27.641
sombra	67	28	27.582
preciso	33	111	27.527
influencia	45	13	27.476
ropa	37	119	27.463
cerca	115	67	27.452
chiquilla	3	38	27.350
presencia	64	26	27.324
tierra	86	43	27.208
poniendo	9	56	27.205
honra	38	9	27.133
afirmó	2	34	27.100
recordó	26	3	27.039
rayos	26	3	27.039
fantasía	26	3	27.039
borracho	26	3	27.039
vea	8	53	26.970
amo	58	22	26.915
supuesto	36	8	26.864
diciéndole	5	44	26.743
tomando	6	47	26.714
ambas	6	47	26.714
pedro	49	16	26.708
costa	28	4	26.668
libre	79	38	26.596
verte	0	23	26.552
olimpia	0	23	26.552
nena	0	23	26.552
marcela	0	23	26.552
chulita	0	23	26.552
roja	30	5	26.525
párroco	16	0	26.379
kempis	16	0	26.379
cenador	16	0	26.379
agustín	16	0	26.379
asilo	3	37	26.349
tocador	23	2	26.290
explicaba	23	2	26.290
sol	97	53	26.262
café	38	119	26.254
niño	50	142	26.142
germán	20	1	26.088
bismarck	20	1	26.088
sus	1018	1041	26.008
enemigo	57	22	25.914
embargo	57	22	25.914
sale	10	57	25.820
trataba	69	31	25.727
verano	45	14	25.697
importaba	45	14	25.697
traje	51	18	25.656
hoy	69	176	25.639
miserables	25	3	25.613
idiota	25	3	25.613
árboles	40	11	25.464
expresó	0	22	25.397
acá	13	64	25.396
aventura	27	4	25.291
ambición	27	4	25.291
quite	1	28	25.273
quitado	1	28	25.273
iv	1	28	25.273
ave	1	28	25.273
pesar	92	50	25.158
balcón	92	50	25.158
mientras	182	132	25.146
pedía	38	10	25.067
luz	147	99	25.044
conviene	7	48	25.025
sabes	49	138	24.982
hacer	187	371	24.870
estrecho	22	2	24.812
cabildo	22	2	24.812
beatas	22	2	24.812
aprensiones	22	2	24.812
verso	15	0	24.730
suspiró	15	0	24.730
rianzares	15	0	24.730
matalerejo	15	0	24.730
desaire	15	0	24.730
camoirán	15	0	24.730
tanto	166	337	24.727
triste	95	53	24.723
enamorado	44	14	24.595
diré	11	58	24.551
niebla	19	1	24.539
lloró	19	1	24.539
poner	37	114	24.449
joaquinito	34	8	24.390
fe	91	50	24.381
pero	1914	2097	24.353
sagrario	0	21	24.243
oscuridad	0	21	24.243
lodo	24	3	24.195
teniendo	1	27	24.190
encarnación	1	27	24.190
debía	152	105	24.182
clérigo	62	27	24.151
aún	42	123	24.039
quita	5	41	23.947
temía	55	22	23.942
eterna	26	4	23.923
llegaba	82	43	23.920
hojas	37	10	23.891
humedad	28	5	23.864
aquel	735	730	23.614
solemne	35	9	23.510
hermana	18	73	23.433
lógica	10	54	23.351
rubia	21	2	23.341
enamorada	21	2	23.341
cura	100	59	23.252
sintió	145	100	23.173
hostia	1	26	23.109
ginés	0	20	23.088
encargo	0	20	23.088
procurar	14	0	23.082
piadosas	14	0	23.082
juraba	14	0	23.082
jesuitas	14	0	23.082
infanzón	14	0	23.082
comenzaba	14	0	23.082
columpio	14	0	23.082
ta	18	1	22.995
liberal	41	13	22.995
irritaba	18	1	22.995
constantino	18	1	22.995
les	156	316	22.989
dogma	23	3	22.786
noble	51	20	22.747
huir	29	6	22.668
dan	12	58	22.600
especie	48	18	22.571
alegres	27	5	22.549
sé	147	300	22.453
duros	7	45	22.403
crees	7	45	22.403
caña	3	33	22.390
cantidad	3	33	22.390
pie	120	78	22.378
hablaban	52	21	22.367
sabían	34	9	22.324
estrépito	34	9	22.324
chicos	13	60	22.301
doy	5	39	22.109
sustancia	1	25	22.032
dado	52	138	22.024
frío	89	51	21.972
gozaba	32	8	21.961
caza	32	8	21.961
casar	2	29	21.944
zalamero	0	19	21.934
trujillo	0	19	21.934
suegra	0	19	21.934
revólver	0	19	21.934
pavos	0	19	21.934
oscuro	0	19	21.934
nuera	0	19	21.934
gumersindo	0	19	21.934
custodia	0	19	21.934
cordero	0	19	21.934
bribona	0	19	21.934
puso	85	196	21.922
fingía	20	2	21.879
diócesis	20	2	21.879
esas	50	134	21.854
vivo	12	57	21.825
cuales	10	52	21.733
fuego	67	33	21.722
poesía	30	7	21.648
hermano	37	109	21.542
puede	113	242	21.504
verja	17	1	21.458
magistrado	17	1	21.458
lejanos	17	1	21.458
acudía	17	1	21.458
poema	13	0	21.433
pernueces	13	0	21.433
padrinos	13	0	21.433
modista	13	0	21.433
encogía	13	0	21.433
egoísta	13	0	21.433
desafío	13	0	21.433
corfín	13	0	21.433
calleja	13	0	21.433
apagados	13	0	21.433
aldeana	13	0	21.433
sacando	3	32	21.412
detrás	94	56	21.412
cuidado	26	87	21.400
absolutamente	6	41	21.323
nadie	202	159	21.270
exigía	26	5	21.246
tendrá	5	38	21.199
manera	62	154	21.025
entendimiento	1	24	20.957
creerás	1	24	20.957
trae	2	28	20.925
crimen	42	15	20.859
ruido	92	55	20.801
simple	0	18	20.779
oscuras	0	18	20.779
improviso	0	18	20.779
fenelón	0	18	20.779
federico	0	18	20.779
duque	0	18	20.779
todos	427	398	20.776
leche	7	43	20.684
eran	333	297	20.568
sobre	508	488	20.542
toledo	3	31	20.439
poquito	3	31	20.439
leído	34	10	20.435
placeres	19	2	20.425
drama	19	2	20.425
aventuras	37	12	20.302
tema	4	34	20.271
murmuró	4	34	20.271
eres	43	118	20.248
ella	1021	1074	20.210
buscó	27	6	20.148
dé	10	50	20.140
seguía	83	48	20.114
vinagre	21	3	20.001
trueno	16	1	19.927
suertes	16	1	19.927
prosa	16	1	19.927
procuró	16	1	19.927
semblante	2	27	19.911
seguramente	2	27	19.911
barbaridad	2	27	19.911
novia	1	23	19.886
colonia	23	4	19.885
fuerza	132	93	19.865
dices	7	42	19.835
entrañas	41	15	19.827
ocho	61	30	19.824
ideal	35	11	19.796
literata	12	0	19.784
lascivia	12	0	19.784
hermandad	12	0	19.784
especialmente	12	0	19.784
devoraba	12	0	19.784
boulevard	12	0	19.784
padre	138	99	19.701
rata	0	17	19.625
ramón	0	17	19.625
manolo	0	17	19.625
fenómeno	0	17	19.625
extraordinariamente	0	17	19.625
cuerdo	0	17	19.625
billetes	0	17	19.625
libros	62	31	19.614
tras	23	78	19.589
nobles	30	8	19.582
horrible	6	39	19.574
puestos	3	30	19.473
quiere	100	215	19.356
llaman	10	49	19.354
joven	78	178	19.315
vez	392	365	19.185
veremos	7	41	18.992
prohibido	18	2	18.982
grosero	18	2	18.982
cómo	186	351	18.944
libro	51	23	18.912
púlpito	26	6	18.907
cenar	26	6	18.907
bestia	2	26	18.902
mozo	47	20	18.891
huerta	47	20	18.891
salud	66	35	18.872
retrato	1	22	18.819
quia	1	22	18.819
hubiera	186	148	18.819
buena	118	243	18.808
hizo	107	225	18.774
genio	6	38	18.709
campo	67	36	18.709
estrecha	24	5	18.678
sala	43	115	18.669
aun	35	100	18.630
tresillo	20	3	18.625
suficiente	20	3	18.625
esperaban	20	3	18.625
puedes	13	55	18.568
llegaban	22	4	18.564
cabeza	247	443	18.538
debajo	75	43	18.496
tocayo	0	16	18.471
tiró	0	16	18.471
sales	0	16	18.471
púsose	0	16	18.471
pontejos	0	16	18.471
pitusa	0	16	18.471
periodo	0	16	18.471
filomenas	0	16	18.471
casamiento	0	16	18.471
pase	4	32	18.420
servían	15	1	18.403
retórica	15	1	18.403
raíces	15	1	18.403
prestigio	15	1	18.403
chato	15	1	18.403
arqueólogo	15	1	18.403
tonta	11	50	18.286
leía	38	14	18.233
viera	15	59	18.230
vale	15	59	18.230
religioso	32	10	18.197
venganza	35	12	18.155
representa	11	0	18.135
profanación	11	0	18.135
otoño	11	0	18.135
oculto	11	0	18.135
necedades	11	0	18.135
murmurar	11	0	18.135
llenaban	11	0	18.135
latigazos	11	0	18.135
juró	11	0	18.135
imprudencia	11	0	18.135
eucaliptus	11	0	18.135
desfachatez	11	0	18.135
cubiertos	11	0	18.135
celosía	11	0	18.135
bosques	11	0	18.135
almunia	11	0	18.135
tomar	48	123	18.114
entró	90	195	18.009
tener	98	208	17.925
demasiado	66	36	17.925
sentándose	1	21	17.755
abur	1	21	17.755
ve	38	104	17.744
leyó	30	9	17.714
humilde	30	9	17.714
pongo	8	42	17.708
remordimientos	25	6	17.681
enfrente	47	21	17.662
criatura	5	34	17.623
ocurre	3	28	17.558
sonriente	17	2	17.550
ancho	17	2	17.550
nariz	11	49	17.533
alguna	74	167	17.529
santísima	4	31	17.505
número	4	31	17.505
cogía	4	31	17.505
dejaba	85	53	17.502
pronto	116	236	17.454
yerba	23	5	17.415
ponerse	17	62	17.322
vengas	0	15	17.316
tengas	0	15	17.316
señá	0	15	17.316
salita	0	15	17.316
pego	0	15	17.316
ochoa	0	15	17.316
levantose	0	15	17.316
ladrillos	0	15	17.316
ladrillo	0	15	17.316
insigne	0	15	17.316
expresarse	0	15	17.316
díjole	0	15	17.316
desdémona	0	15	17.316
chamberí	0	15	17.316
candelaria	0	15	17.316
cállate	0	15	17.316
bulla	0	15	17.316
armó	0	15	17.316
armar	0	15	17.316
mentira	12	51	17.308
piadosa	19	3	17.263
lucía	19	3	17.263
cita	19	3	17.263
calumnias	19	3	17.263
olvido	28	8	17.260
callaba	28	8	17.260
traición	21	4	17.256
saludó	21	4	17.256
aprensión	21	4	17.256
caso	93	198	17.245
amiga	71	161	17.144
entre	372	350	17.121
nobleza	31	10	17.099
monte	41	17	17.052
horas	126	92	17.052
mantón	6	36	17.001
disparates	14	55	16.968
solía	83	52	16.903
recogidas	2	24	16.901
quienes	2	24	16.901
cogiendo	2	24	16.901
sonrisas	14	1	16.888
seducción	14	1	16.888
incienso	14	1	16.888
huía	14	1	16.888
grosera	14	1	16.888
figuró	14	1	16.888
confesiones	14	1	16.888
cocinero	14	1	16.888
calderón	14	1	16.888
americano	14	1	16.888
sacristía	26	7	16.841
regente	38	15	16.813
veía	156	122	16.812
puerta	143	277	16.800
maldita	5	33	16.746
pelo	16	59	16.738
tratando	1	20	16.696
damas	56	29	16.696
almuerzo	1	20	16.696
secreto	51	25	16.662
serenidad	3	27	16.610
alcalde	29	9	16.598
riendo	4	30	16.597
movía	32	11	16.554
inútil	32	11	16.554
paseo	78	48	16.548
zorrilla	10	0	16.487
voluptuoso	10	0	16.487
voluptuosa	10	0	16.487
trébol	10	0	16.487
sujetaba	10	0	16.487
servanda	10	0	16.487
profanos	10	0	16.487
pisar	10	0	16.487
palomo	10	0	16.487
pálidos	10	0	16.487
obscuros	10	0	16.487
necedad	10	0	16.487
inés	10	0	16.487
gr	10	0	16.487
fulgosio	10	0	16.487
expedientes	10	0	16.487
delantero	10	0	16.487
clarín	10	0	16.487
cánticos	10	0	16.487
antigüedades	10	0	16.487
alerta	10	0	16.487
acendrada	10	0	16.487
verla	22	71	16.477
llevó	13	52	16.410
nueva	91	60	16.374
alegre	53	27	16.251
entonces	194	162	16.219
vulgares	22	5	16.168
sombras	22	5	16.168
cazador	22	5	16.168
vayas	0	14	16.162
valencia	0	14	16.162
tenéis	0	14	16.162
silvia	0	14	16.162
presunción	0	14	16.162
pobrecilla	0	14	16.162
meto	0	14	16.162
londres	0	14	16.162
liberación	0	14	16.162
jaquecas	0	14	16.162
hallábase	0	14	16.162
fíjate	0	14	16.162
existe	0	14	16.162
creeríase	0	14	16.162
comandanta	0	14	16.162
atroz	0	14	16.162
gesto	44	20	16.131
ensueños	16	2	16.130
hogar	33	12	16.067
carta	54	28	16.064
piel	30	10	16.018
protesta	20	4	15.964
interrumpió	20	4	15.964
clérigos	20	4	15.964
vejez	18	3	15.915
envidiaba	18	3	15.915
convidados	18	3	15.915
bóveda	18	3	15.915
audiencia	18	3	15.915
rápidamente	2	23	15.910
observando	2	23	15.910
isabel	2	23	15.910
ambos	19	64	15.906
estuvieron	5	32	15.878
hijos	23	72	15.873
solas	45	21	15.868
suspiro	4	29	15.697
saca	4	29	15.697
manifestó	4	29	15.697
cuento	7	37	15.696
tormento	25	7	15.677
vuelvo	3	26	15.670
cae	3	26	15.670
soltar	1	19	15.642
natividad	1	19	15.642
increíble	1	19	15.642
habiendo	1	19	15.642
domingos	1	19	15.642
arreglo	1	19	15.642
fondo	63	36	15.640
parecían	80	51	15.638
tales	94	64	15.555
energía	42	19	15.505
fama	31	11	15.504
mundo	303	280	15.484
rumores	13	1	15.382
remediarlo	13	1	15.382
pavimento	13	1	15.382
hermosísima	13	1	15.382
carretela	13	1	15.382
cantaban	13	1	15.382
apoyaba	13	1	15.382
boca	93	193	15.363
mil	70	155	15.347
francamente	6	34	15.325
pañuelo	22	69	15.262
provincia	35	14	15.235
cuestión	48	24	15.184
buscar	54	29	15.092
o	635	989	15.071
dar	121	237	15.066
demonios	5	31	15.018
i	13	50	15.009
pondré	0	13	15.007
pedernero	0	13	15.007
mosca	0	13	15.007
mesías	0	13	15.007
marras	0	13	15.007
manolita	0	13	15.007
indulgencia	0	13	15.007
hebra	0	13	15.007
facunda	0	13	15.007
expresiones	0	13	15.007
echaron	0	13	15.007
discurriendo	0	13	15.007
desea	0	13	15.007
decirte	0	13	15.007
créetelo	0	13	15.007
chuletas	0	13	15.007
admirablemente	0	13	15.007
junta	26	8	15.000
dulces	26	8	15.000
digna	26	8	15.000
acaso	44	21	14.993
tanta	36	95	14.970
criadas	21	5	14.938
cobarde	21	5	14.938
verdaderamente	2	22	14.926
manuel	2	22	14.926
llevo	2	22	14.926
almorzar	2	22	14.926
querido	70	43	14.910
haces	7	36	14.892
locura	36	15	14.877
violento	9	0	14.838
trascoro	9	0	14.838
romería	9	0	14.838
rebelión	9	0	14.838
peláez	9	0	14.838
muralla	9	0	14.838
morado	9	0	14.838
místicos	9	0	14.838
mezclaban	9	0	14.838
loma	9	0	14.838
glorieta	9	0	14.838
froilán	9	0	14.838
estrechos	9	0	14.838
estrado	9	0	14.838
dinástico	9	0	14.838
cuervo	9	0	14.838
conserje	9	0	14.838
chateaubriand	9	0	14.838
ceñida	9	0	14.838
católicos	9	0	14.838
catalejo	9	0	14.838
brisa	9	0	14.838
antojaban	9	0	14.838
admirado	9	0	14.838
expresar	4	28	14.805
botas	10	43	14.790
ponen	3	25	14.738
piezas	3	25	14.738
cojo	3	25	14.738
boda	3	25	14.738
admirable	3	25	14.738
imitar	15	2	14.724
diputado	15	2	14.724
celestina	15	2	14.724
mano	172	315	14.702
tenemos	17	58	14.701
quinta	19	4	14.689
distraído	19	4	14.689
ves	23	70	14.687
cuerpo	174	145	14.672
tarasca	1	18	14.593
pañuelos	1	18	14.593
juicios	1	18	14.593
cuenta	61	138	14.592
paraguas	17	3	14.582
misticismo	17	3	14.582
lluvia	17	3	14.582
formidable	17	3	14.582
elemento	17	3	14.582
chispas	24	7	14.531
posible	30	83	14.486
arte	76	49	14.457
cuarto	69	151	14.404
gabinete	78	51	14.333
esto	468	747	14.221
llegado	61	36	14.174
espiritual	54	30	14.166
toma	15	53	14.153
partido	43	21	14.132
ojos	347	333	14.118
tarde	208	182	14.108
ridícula	22	6	14.101
alguien	10	42	14.059
pueblo	106	78	14.003
expresaba	2	21	13.950
esposos	2	21	13.950
conoces	2	21	13.950
coja	2	21	13.950
antonio	2	21	13.950
trajo	4	27	13.922
hice	4	27	13.922
decían	56	32	13.902
siglos	25	8	13.898
moría	25	8	13.898
salesas	12	1	13.888
poético	12	1	13.888
marismas	12	1	13.888
lontananza	12	1	13.888
escopeta	12	1	13.888
dominó	12	1	13.888
desesperado	12	1	13.888
consiguió	12	1	13.888
codicia	12	1	13.888
capitán	12	1	13.888
aragonés	12	1	13.888
vuelvas	0	12	13.853
toquilla	0	12	13.853
república	0	12	13.853
presteza	0	12	13.853
manila	0	12	13.853
jerónima	0	12	13.853
gobernación	0	12	13.853
estremecer	0	12	13.853
entré	0	12	13.853
diabla	0	12	13.853
desazón	0	12	13.853
concluida	0	12	13.853
charla	0	12	13.853
repitió	12	46	13.748
propósito	40	19	13.730
lucha	20	5	13.725
habilidad	20	5	13.725
fortaleza	20	5	13.725
tonterías	6	32	13.685
actitud	6	32	13.685
comprendió	36	16	13.630
morenos	1	17	13.549
mirándola	1	17	13.549
individuos	1	17	13.549
dígame	1	17	13.549
das	1	17	13.549
curiosidad	23	68	13.529
propio	36	92	13.461
dice	87	178	13.446
tus	17	56	13.436
sonaban	18	4	13.432
sabría	18	4	13.432
romanticismo	18	4	13.432
prudencia	18	4	13.432
orilla	18	4	13.432
naturales	18	4	13.432
bravo	18	4	13.432
antiguas	18	4	13.432
solían	23	7	13.404
caballo	37	17	13.353
voz	235	213	13.349
volviendo	10	41	13.336
terminar	14	2	13.334
pensaban	14	2	13.334
espinas	14	2	13.334
escribió	14	2	13.334
elocuente	14	2	13.334
castidad	14	2	13.334
belén	5	29	13.326
deber	33	14	13.317
chocolate	7	34	13.313
quejaba	16	3	13.268
íntimos	16	3	13.268
cómico	16	3	13.268
colorado	16	3	13.268
cantando	16	3	13.268
venerables	8	0	13.189
trasaltar	8	0	13.189
tordo	8	0	13.189
teoría	8	0	13.189
sendas	8	0	13.189
secular	8	0	13.189
roquete	8	0	13.189
robles	8	0	13.189
reaccionario	8	0	13.189
prosaica	8	0	13.189
preferían	8	0	13.189
platónico	8	0	13.189
parches	8	0	13.189
pantorrilla	8	0	13.189
oratorio	8	0	13.189
oleaje	8	0	13.189
obispado	8	0	13.189
incapaces	8	0	13.189
halagaba	8	0	13.189
godino	8	0	13.189
figuraban	8	0	13.189
fantasma	8	0	13.189
exigir	8	0	13.189
esbelta	8	0	13.189
entregada	8	0	13.189
dulcísima	8	0	13.189
disimulados	8	0	13.189
desafiar	8	0	13.189
contracayes	8	0	13.189
contentó	8	0	13.189
cómicos	8	0	13.189
champaña	8	0	13.189
cabaña	8	0	13.189
brigadiera	8	0	13.189
barquilla	8	0	13.189
atribuía	8	0	13.189
atenerse	8	0	13.189
aridez	8	0	13.189
anhelos	8	0	13.189
aludía	8	0	13.189
adornaban	8	0	13.189
alegría	90	64	13.184
esperanza	38	18	13.100
dónde	79	164	13.070
corredor	12	45	13.062
vecindad	4	26	13.049
verme	2	20	12.982
ponga	2	20	12.982
pido	2	20	12.982
mete	2	20	12.982
jueves	2	20	12.982
fui	2	20	12.982
estuve	2	20	12.982
digas	2	20	12.982
creas	2	20	12.982
cafés	2	20	12.982
agregó	2	20	12.982
ratos	13	47	12.971
anchas	21	6	12.944
amaba	21	6	12.944
admiraba	21	6	12.944
tonto	14	49	12.905
sonreía	39	19	12.867
hora	162	137	12.830
tinieblas	24	8	12.814
seguida	45	24	12.736
servía	35	16	12.725
paseos	35	16	12.725
cosa	231	396	12.720
preguntaba	31	13	12.703
veas	0	11	12.698
tuno	0	11	12.698
trastorno	0	11	12.698
paréceme	0	11	12.698
obrador	0	11	12.698
hazte	0	11	12.698
hablamos	0	11	12.698
furia	0	11	12.698
filipinas	0	11	12.698
figurarte	0	11	12.698
determinó	0	11	12.698
daré	0	11	12.698
bonifacio	0	11	12.698
acostar	0	11	12.698
nada	434	690	12.694
necesitaba	52	30	12.663
entrar	70	148	12.584
acciones	7	33	12.538
satisfacer	19	5	12.533
salir	93	185	12.530
tuyo	1	16	12.513
turbación	1	16	12.513
profesor	1	16	12.513
llevándose	1	16	12.513
llevan	1	16	12.513
lío	1	16	12.513
hubieras	1	16	12.513
estaré	1	16	12.513
contarle	1	16	12.513
castelar	1	16	12.513
arroz	1	16	12.513
poder	95	70	12.497
hará	5	28	12.495
acento	5	28	12.495
colores	36	17	12.469
pobre	127	238	12.430
dio	97	191	12.411
tirano	11	1	12.406
serios	11	1	12.406
preocupado	11	1	12.406
p	11	1	12.406
maíz	11	1	12.406
jurado	11	1	12.406
italiana	11	1	12.406
higiene	11	1	12.406
flamenco	11	1	12.406
exposición	11	1	12.406
diccionario	11	1	12.406
desaparecía	11	1	12.406
cubría	11	1	12.406
contigua	11	1	12.406
colocaba	11	1	12.406
canciones	11	1	12.406
aldeas	11	1	12.406
sacó	12	44	12.385
cristales	32	14	12.385
comprendía	32	14	12.385
presentó	25	9	12.308
filósofo	25	9	12.308
venga	20	60	12.264
leer	56	34	12.242
órgano	17	4	12.195
in	17	4	12.195
hipocresía	17	4	12.195
gris	17	4	12.195
contemplaba	17	4	12.195
timidez	4	25	12.186
diera	4	25	12.186
entero	43	23	12.106
hubiese	33	15	12.098
vengan	2	19	12.022
indecente	2	19	12.022
hagas	3	22	11.997
habrían	3	22	11.997
caras	3	22	11.997
volar	15	3	11.973
viejos	15	3	11.973
ruidos	15	3	11.973
pudor	15	3	11.973
pistola	15	3	11.973
intenso	15	3	11.973
espeso	15	3	11.973
adelantado	15	3	11.973
vocación	13	2	11.961
teología	13	2	11.961
suspiraba	13	2	11.961
seminario	13	2	11.961
sacerdotes	13	2	11.961
novena	13	2	11.961
estimaba	13	2	11.961
escenario	13	2	11.961
encantos	13	2	11.961
adulterio	13	2	11.961
ponía	50	113	11.911
médico	73	50	11.886
espíritu	118	94	11.886
esos	39	94	11.877
maneras	26	10	11.869
ambiente	26	10	11.869
nervios	34	16	11.838
subía	39	20	11.824
vive	11	41	11.803
dura	11	41	11.803
risa	22	63	11.789
decente	7	32	11.774
negros	30	13	11.765
calló	23	8	11.751
caballeros	23	8	11.751
bueno	97	189	11.751
pez	5	27	11.675
madera	35	17	11.603
hermoso	35	17	11.603
sofá	17	53	11.602
sobrina	15	49	11.599
están	44	102	11.581
turrón	0	10	11.544
trastornada	0	10	11.544
toque	0	10	11.544
tenderos	0	10	11.544
sobrinito	0	10	11.544
sentose	0	10	11.544
ramsés	0	10	11.544
peines	0	10	11.544
pascual	0	10	11.544
paquetes	0	10	11.544
papeletas	0	10	11.544
padilla	0	10	11.544
oyose	0	10	11.544
nacional	0	10	11.544
mismamente	0	10	11.544
mañas	0	10	11.544
manicomio	0	10	11.544
juárez	0	10	11.544
josefinas	0	10	11.544
harás	0	10	11.544
extravagancias	0	10	11.544
eulalia	0	10	11.544
endivido	0	10	11.544
eché	0	10	11.544
duermo	0	10	11.544
diversos	0	10	11.544
disco	0	10	11.544
descompuesta	0	10	11.544
deogracias	0	10	11.544
dábale	0	10	11.544
corrida	0	10	11.544
arreglará	0	10	11.544
antonia	0	10	11.544
andrés	0	10	11.544
alumnos	0	10	11.544
yacían	7	0	11.541
voltaire	7	0	11.541
semillas	7	0	11.541
rizos	7	0	11.541
reluciente	7	0	11.541
regencia	7	0	11.541
recordaban	7	0	11.541
pulcro	7	0	11.541
protestaba	7	0	11.541
procurado	7	0	11.541
prelado	7	0	11.541
prefirió	7	0	11.541
poderosos	7	0	11.541
plebeyos	7	0	11.541
perfumado	7	0	11.541
paulinas	7	0	11.541
paraguay	7	0	11.541
ocultando	7	0	11.541
necia	7	0	11.541
nata	7	0	11.541
murmuraciones	7	0	11.541
monótono	7	0	11.541
mezclaba	7	0	11.541
mecedora	7	0	11.541
maliciosos	7	0	11.541
maledicencia	7	0	11.541
lasciva	7	0	11.541
irritatio	7	0	11.541
inmortal	7	0	11.541
impíos	7	0	11.541
impío	7	0	11.541
imitaban	7	0	11.541
humillaba	7	0	11.541
gozado	7	0	11.541
fingían	7	0	11.541
est	7	0	11.541
distraídos	7	0	11.541
distinción	7	0	11.541
diestro	7	0	11.541
desafiando	7	0	11.541
cuadrado	7	0	11.541
contestaban	7	0	11.541
conservador	7	0	11.541
comenzaron	7	0	11.541
comenzado	7	0	11.541
cofradías	7	0	11.541
cirios	7	0	11.541
cereza	7	0	11.541
castaños	7	0	11.541
cascabeles	7	0	11.541
carnal	7	0	11.541
cánones	7	0	11.541
calumniado	7	0	11.541
buscado	7	0	11.541
brecha	7	0	11.541
artillero	7	0	11.541
arrojarse	7	0	11.541
armarios	7	0	11.541
aristócratas	7	0	11.541
aras	7	0	11.541
alvarito	7	0	11.541
álamos	7	0	11.541
airoso	7	0	11.541
abdicación	7	0	11.541
chiquillos	8	34	11.539
madrid	73	150	11.513
re	1	15	11.483
razonable	1	15	11.483
pensé	1	15	11.483
huevo	1	15	11.483
fiebre	31	14	11.472
haber	122	99	11.451
nuevo	91	68	11.447
curas	48	28	11.427
acababa	48	28	11.427
aire	109	86	11.376
sexo	18	5	11.363
sermones	18	5	11.363
notado	18	5	11.363
creían	18	5	11.363
bastaba	18	5	11.363
mandó	9	36	11.360
manto	4	24	11.334
gozo	4	24	11.334
pocos	49	29	11.318
encontraba	59	38	11.251
rival	21	7	11.212
material	21	7	11.212
gozar	21	7	11.212
malicia	28	12	11.147
furioso	28	12	11.147
entrado	11	40	11.130
estos	104	198	11.124
tira	3	21	11.104
tendré	3	21	11.104
quitó	3	21	11.104
coge	3	21	11.104
aseguro	3	21	11.104
tremendo	2	18	11.073
rencor	2	18	11.073
fea	2	18	11.073
facha	2	18	11.073
gusto	53	116	11.069
juro	7	31	11.021
sentimientos	13	44	11.016
golpe	13	44	11.016
sabe	123	227	11.009
preocupaciones	16	4	10.980
personajes	16	4	10.980
moralidad	16	4	10.980
fieles	16	4	10.980
especial	16	4	10.980
engañaba	16	4	10.980
alcohol	16	4	10.980
lágrimas	64	43	10.969
volaba	10	1	10.939
tersa	10	1	10.939
s	10	1	10.939
pupilas	10	1	10.939
perfumes	10	1	10.939
murmuración	10	1	10.939
moribundo	10	1	10.939
mordía	10	1	10.939
hierba	10	1	10.939
fingió	10	1	10.939
entendían	10	1	10.939
curia	10	1	10.939
conversión	10	1	10.939
capillas	10	1	10.939
baronesa	10	1	10.939
amorosa	10	1	10.939
adivinar	10	1	10.939
verde	45	26	10.925
ciencia	45	26	10.925
total	5	26	10.866
almas	29	13	10.846
tal	249	414	10.829
disparate	8	33	10.812
amistad	46	27	10.811
repetía	34	17	10.755
cien	34	17	10.755
muchos	133	112	10.727
contacto	22	8	10.711
afición	22	8	10.711
símbolo	14	3	10.701
paseaban	14	3	10.701
faroles	14	3	10.701
desnudos	14	3	10.701
corrían	14	3	10.701
contemplación	14	3	10.701
palco	19	6	10.697
fonda	19	6	10.697
eclesiástico	19	6	10.697
asustado	19	6	10.697
espalda	40	22	10.695
rum	12	2	10.610
religiosidad	12	2	10.610
reflejos	12	2	10.610
necios	12	2	10.610
merienda	12	2	10.610
materias	12	2	10.610
liga	12	2	10.610
fuentes	12	2	10.610
estrechas	12	2	10.610
columnas	12	2	10.610
brillantes	12	2	10.610
berlina	12	2	10.610
humor	48	29	10.606
jefe	30	14	10.579
retirarse	4	23	10.494
malo	35	84	10.494
duro	11	39	10.466
vuelves	1	14	10.462
píldoras	1	14	10.462
ocurren	1	14	10.462
merezco	1	14	10.462
creerlo	1	14	10.462
conocí	1	14	10.462
bocas	1	14	10.462
bastón	1	14	10.462
aplicación	1	14	10.462
situación	25	66	10.409
particular	16	49	10.396
observó	16	49	10.396
zancuda	0	9	10.390
zalamerías	0	9	10.390
vivamente	0	9	10.390
vidas	0	9	10.390
verlas	0	9	10.390
verdugo	0	9	10.390
veis	0	9	10.390
ved	0	9	10.390
vallejo	0	9	10.390
tontín	0	9	10.390
tom	0	9	10.390
tenedor	0	9	10.390
súbito	0	9	10.390
sosegada	0	9	10.390
setiembre	0	9	10.390
recién	0	9	10.390
quitándose	0	9	10.390
puedas	0	9	10.390
propiamente	0	9	10.390
prim	0	9	10.390
portamonedas	0	9	10.390
ponce	0	9	10.390
pitusín	0	9	10.390
pillín	0	9	10.390
pi	0	9	10.390
pater	0	9	10.390
párpado	0	9	10.390
pareciole	0	9	10.390
papás	0	9	10.390
merluza	0	9	10.390
mereces	0	9	10.390
materna	0	9	10.390
mantones	0	9	10.390
jarabe	0	9	10.390
jacinto	0	9	10.390
jabón	0	9	10.390
inclusa	0	9	10.390
imperial	0	9	10.390
hule	0	9	10.390
horacio	0	9	10.390
fuensanta	0	9	10.390
fresa	0	9	10.390
fiereza	0	9	10.390
extravagantes	0	9	10.390
expresándose	0	9	10.390
especialidad	0	9	10.390
entrole	0	9	10.390
engracia	0	9	10.390
donaire	0	9	10.390
dialéctica	0	9	10.390
desventurado	0	9	10.390
demente	0	9	10.390
demencia	0	9	10.390
créelo	0	9	10.390
cogiéndola	0	9	10.390
cesaba	0	9	10.390
calamidad	0	9	10.390
cádiz	0	9	10.390
beneficencia	0	9	10.390
bastantes	0	9	10.390
banca	0	9	10.390
balbució	0	9	10.390
atentamente	0	9	10.390
arreglando	0	9	10.390
apostamos	0	9	10.390
anteayer	0	9	10.390
alzaba	0	9	10.390
almirez	0	9	10.390
afuera	0	9	10.390
afligida	0	9	10.390
acordose	0	9	10.390
pensó	98	77	10.384
juicio	14	45	10.373
poeta	23	9	10.285
escrito	23	9	10.285
honradez	7	30	10.280
blanco	52	33	10.274
tocan	3	20	10.222
socorro	3	20	10.222
sentar	3	20	10.222
pelos	3	20	10.222
naturalmente	3	20	10.222
envidia	37	20	10.218
rincones	17	5	10.217
farol	17	5	10.217
grandeza	20	7	10.151
aristocracia	20	7	10.151
vii	2	17	10.135
tropa	2	17	10.135
muchísimo	2	17	10.135
dime	2	17	10.135
concluir	2	17	10.135
bruscamente	2	17	10.135
detuvo	32	16	10.123
abierto	32	16	10.123
rabia	8	32	10.098
os	8	32	10.098
cuál	8	32	10.098
compra	5	25	10.070
diez	45	100	10.012
carne	76	56	9.997
devoción	28	13	9.949
abría	28	13	9.949
sido	214	201	9.946
partes	39	22	9.932
pasa	30	74	9.926
vieja	24	10	9.918
zorros	6	0	9.892
volaban	6	0	9.892
vinculete	6	0	9.892
valladolid	6	0	9.892
urraca	6	0	9.892
ubi	6	0	9.892
truenos	6	0	9.892
traslacerca	6	0	9.892
tordos	6	0	9.892
tendía	6	0	9.892
suplicaba	6	0	9.892
sucedía	6	0	9.892
subterráneos	6	0	9.892
solteronas	6	0	9.892
solícita	6	0	9.892
silencioso	6	0	9.892
separando	6	0	9.892
sapo	6	0	9.892
restituto	6	0	9.892
relámpagos	6	0	9.892
reflejaban	6	0	9.892
recitaba	6	0	9.892
ps	6	0	9.892
prosaico	6	0	9.892
probaban	6	0	9.892
pretendían	6	0	9.892
plataforma	6	0	9.892
pinche	6	0	9.892
pimienta	6	0	9.892
pilares	6	0	9.892
perspectiva	6	0	9.892
perfumada	6	0	9.892
pécora	6	0	9.892
opina	6	0	9.892
oeste	6	0	9.892
ocurrencia	6	0	9.892
ocultos	6	0	9.892
notario	6	0	9.892
montañés	6	0	9.892
monótona	6	0	9.892
millonario	6	0	9.892
metáforas	6	0	9.892
mentía	6	0	9.892
mediquillo	6	0	9.892
mantel	6	0	9.892
luchaba	6	0	9.892
lúbrica	6	0	9.892
lope	6	0	9.892
llamaría	6	0	9.892
ligas	6	0	9.892
ladridos	6	0	9.892
indiferentes	6	0	9.892
indianos	6	0	9.892
importuno	6	0	9.892
ilustrísima	6	0	9.892
idealidad	6	0	9.892
húmedas	6	0	9.892
horrorizaba	6	0	9.892
horrísono	6	0	9.892
hiciesen	6	0	9.892
halagado	6	0	9.892
h	6	0	9.892
exponerse	6	0	9.892
espiar	6	0	9.892
escalofrío	6	0	9.892
engordar	6	0	9.892
dote	6	0	9.892
dominios	6	0	9.892
devotas	6	0	9.892
desiertos	6	0	9.892
derrotado	6	0	9.892
dejasen	6	0	9.892
culta	6	0	9.892
crucificado	6	0	9.892
comprendían	6	0	9.892
colondres	6	0	9.892
colgaduras	6	0	9.892
cogote	6	0	9.892
cognac	6	0	9.892
ceremonias	6	0	9.892
ceñido	6	0	9.892
catequistas	6	0	9.892
canónico	6	0	9.892
bóvedas	6	0	9.892
bautista	6	0	9.892
barquero	6	0	9.892
barandilla	6	0	9.892
avena	6	0	9.892
avanzados	6	0	9.892
auténticos	6	0	9.892
atrevidos	6	0	9.892
atrevería	6	0	9.892
asalto	6	0	9.892
arrugado	6	0	9.892
araña	6	0	9.892
apearse	6	0	9.892
anticuario	6	0	9.892
amorosos	6	0	9.892
alzacuello	6	0	9.892
sentimiento	17	50	9.850
soy	110	203	9.842
temer	15	4	9.791
nave	15	4	9.791
místico	15	4	9.791
matarla	15	4	9.791
vuelve	12	40	9.779
echado	12	40	9.779
años	186	171	9.779
pintado	6	27	9.768
llamaban	34	18	9.751
buscaba	34	18	9.751
contestaba	29	14	9.707
recordar	21	8	9.695
civil	21	8	9.695
ocasión	64	45	9.686
pena	22	59	9.635
hombros	51	33	9.616
rosa	18	6	9.610
novelas	25	11	9.599
cuadro	25	11	9.599
continuó	25	11	9.599
sería	111	92	9.571
estas	155	270	9.567
conforme	7	29	9.551
vencedor	9	1	9.491
suplicó	9	1	9.491
separado	9	1	9.491
saltaban	9	1	9.491
saboreaba	9	1	9.491
respetaba	9	1	9.491
raíz	9	1	9.491
polka	9	1	9.491
orillas	9	1	9.491
naves	9	1	9.491
jesuita	9	1	9.491
infalibilidad	9	1	9.491
ilustrada	9	1	9.491
idealismo	9	1	9.491
grandezas	9	1	9.491
disimulada	9	1	9.491
deprisa	9	1	9.491
delicias	9	1	9.491
deán	9	1	9.491
convertía	9	1	9.491
contentaba	9	1	9.491
conferencias	9	1	9.491
cantó	9	1	9.491
b	9	1	9.491
venían	30	15	9.490
trabajo	44	97	9.471
tejados	13	3	9.453
teatros	13	3	9.453
sacrificios	13	3	9.453
rinconada	13	3	9.453
recinto	13	3	9.453
místicas	13	3	9.453
locuras	13	3	9.453
devoto	13	3	9.453
comulgar	13	3	9.453
amado	13	3	9.453
sosiego	1	13	9.451
signo	1	13	9.451
referente	1	13	9.451
ministerio	1	13	9.451
lanzó	1	13	9.451
horriblemente	1	13	9.451
alzando	1	13	9.451
vanidad	36	20	9.443
siquiera	80	61	9.413
vinieron	3	19	9.354
perdone	3	19	9.354
escaleras	3	19	9.354
cogió	18	51	9.344
creído	26	12	9.320
sacrificio	22	9	9.309
redondo	22	9	9.309
familiar	22	9	9.309
cena	22	9	9.309
cantaba	22	9	9.309
notó	31	16	9.295
gordo	9	33	9.289
consigo	9	33	9.289
adoración	5	24	9.287
perseguía	11	2	9.282
perezosa	11	2	9.282
mezclado	11	2	9.282
libertino	11	2	9.282
leyenda	11	2	9.282
explicó	11	2	9.282
evidente	11	2	9.282
calidad	11	2	9.282
punto	67	134	9.272
tenga	16	47	9.237
pone	16	47	9.237
zapatería	0	8	9.235
trujillos	0	8	9.235
traspaso	0	8	9.235
timo	0	8	9.235
tilín	0	8	9.235
teta	0	8	9.235
suelos	0	8	9.235
sinvergüenza	0	8	9.235
siéntese	0	8	9.235
sentíase	0	8	9.235
secar	0	8	9.235
samaniegas	0	8	9.235
salmerón	0	8	9.235
relimpio	0	8	9.235
rectitud	0	8	9.235
protege	0	8	9.235
pretextos	0	8	9.235
portarse	0	8	9.235
pongas	0	8	9.235
plenitud	0	8	9.235
perra	0	8	9.235
pequeñuelo	0	8	9.235
peine	0	8	9.235
pañolería	0	8	9.235
oscura	0	8	9.235
obligaciones	0	8	9.235
movida	0	8	9.235
mayormente	0	8	9.235
matrimonial	0	8	9.235
matarme	0	8	9.235
lelo	0	8	9.235
lela	0	8	9.235
juicioso	0	8	9.235
hízole	0	8	9.235
hazme	0	8	9.235
harías	0	8	9.235
glacial	0	8	9.235
fugaz	0	8	9.235
finísimo	0	8	9.235
felisa	0	8	9.235
exactamente	0	8	9.235
estabas	0	8	9.235
espectro	0	8	9.235
entereza	0	8	9.235
enterando	0	8	9.235
enfadar	0	8	9.235
echose	0	8	9.235
echamos	0	8	9.235
dudo	0	8	9.235
doscientos	0	8	9.235
desconcertó	0	8	9.235
dátiles	0	8	9.235
criar	0	8	9.235
cordura	0	8	9.235
contrabando	0	8	9.235
considerablemente	0	8	9.235
comiéndose	0	8	9.235
cirila	0	8	9.235
cerrojo	0	8	9.235
casorio	0	8	9.235
cabos	0	8	9.235
burro	0	8	9.235
apures	0	8	9.235
anarquista	0	8	9.235
alborotada	0	8	9.235
aguanta	0	8	9.235
agitación	0	8	9.235
administrador	0	8	9.235
acercose	0	8	9.235
esperaba	59	41	9.230
vienes	2	16	9.210
pegar	2	16	9.210
lotería	2	16	9.210
hallaba	2	16	9.210
hábitos	2	16	9.210
encontré	2	16	9.210
domicilio	2	16	9.210
sentir	61	43	9.165
traer	12	39	9.155
cargo	12	39	9.155
hacia	94	176	9.152
duda	61	124	9.140
íntimo	19	7	9.116
guante	19	7	9.116
decir	259	420	9.103
tablas	16	5	9.098
saltar	16	5	9.098
intereses	16	5	9.098
emociones	16	5	9.098
desierto	16	5	9.098
deleite	16	5	9.098
siguiente	41	91	9.076
podido	39	23	9.075
olvidado	27	13	9.075
enfermedad	39	23	9.075
dejaban	27	13	9.075
son	145	253	9.054
adelante	66	48	9.040
paciencia	21	56	9.032
vendrá	6	26	9.022
meterse	6	26	9.022
isla	6	26	9.022
van	30	72	8.995
volvían	23	10	8.978
vencer	23	10	8.978
temblaba	23	10	8.978
oídos	23	10	8.978
elegantes	23	10	8.978
hambre	40	24	8.972
ataque	33	18	8.962
hermosa	51	34	8.920
hablado	51	34	8.920
fuese	76	58	8.916
niños	25	63	8.912
noche	230	377	8.880
señorita	29	70	8.878
costumbres	28	14	8.857
problema	4	21	8.854
atrevía	34	19	8.819
puedo	56	115	8.807
quisiera	28	68	8.764
hacen	28	68	8.764
entendía	43	27	8.711
quedaba	56	39	8.708
poniéndose	8	30	8.708
victoria	20	8	8.705
locos	20	8	8.705
espada	20	8	8.705
cera	24	11	8.692
valía	35	20	8.688
cayó	16	46	8.674
desprecio	29	15	8.663
muchas	127	111	8.658
refería	14	4	8.630
discretamente	14	4	8.630
contraste	14	4	8.630
baños	14	4	8.630
auditorio	14	4	8.630
alfombra	14	4	8.630
amigas	15	44	8.625
ni	672	736	8.554
repugnante	17	6	8.551
escrúpulos	17	6	8.551
salida	12	38	8.543
crea	12	38	8.543
buen	205	196	8.538
verdad	162	276	8.519
sinceridad	5	23	8.518
local	5	23	8.518
morir	46	30	8.506
revelaba	3	18	8.500
modales	3	18	8.500
campanilla	3	18	8.500
elegante	37	22	8.462
acercó	37	22	8.462
villa	1	12	8.451
tomarlo	1	12	8.451
recibimiento	1	12	8.451
préstamos	1	12	8.451
paquete	1	12	8.451
oírla	1	12	8.451
nieto	1	12	8.451
morirme	1	12	8.451
miguel	1	12	8.451
ix	1	12	8.451
inexplicable	1	12	8.451
indecible	1	12	8.451
escalones	1	12	8.451
añadiendo	1	12	8.451
alhajas	1	12	8.451
hermosura	47	31	8.448
estilo	47	31	8.448
suyos	25	12	8.443
cuadros	25	12	8.443
verdadero	25	62	8.430
mirar	36	81	8.424
tres	130	228	8.410
sea	86	161	8.367
pasaban	38	23	8.363
llevaban	21	9	8.360
trastos	2	15	8.298
simón	2	15	8.298
mías	2	15	8.298
llevarle	2	15	8.298
fisonomía	2	15	8.298
extensión	2	15	8.298
encargado	2	15	8.298
alzar	2	15	8.298
escalera	35	79	8.295
escena	39	24	8.273
zapico	5	0	8.243
zaguán	5	0	8.243
vegetar	5	0	8.243
truchas	5	0	8.243
tricot	5	0	8.243
torcía	5	0	8.243
tísica	5	0	8.243
tenerse	5	0	8.243
soto	5	0	8.243
sofisma	5	0	8.243
sesgo	5	0	8.243
señorona	5	0	8.243
sendos	5	0	8.243
semi	5	0	8.243
santianes	5	0	8.243
sanar	5	0	8.243
sacrificarse	5	0	8.243
rúa	5	0	8.243
rozagante	5	0	8.243
rindió	5	0	8.243
rigodón	5	0	8.243
reputaba	5	0	8.243
remordía	5	0	8.243
relucientes	5	0	8.243
redacción	5	0	8.243
rectoral	5	0	8.243
rector	5	0	8.243
puertos	5	0	8.243
provocativa	5	0	8.243
protectrices	5	0	8.243
propasaba	5	0	8.243
prebendado	5	0	8.243
postigo	5	0	8.243
patenas	5	0	8.243
pareciera	5	0	8.243
parajes	5	0	8.243
panera	5	0	8.243
ostensible	5	0	8.243
osado	5	0	8.243
organista	5	0	8.243
olías	5	0	8.243
ocultaban	5	0	8.243
ocaso	5	0	8.243
obsesión	5	0	8.243
obdulita	5	0	8.243
noroeste	5	0	8.243
nauplia	5	0	8.243
murmuraban	5	0	8.243
murciélago	5	0	8.243
muceta	5	0	8.243
mostraban	5	0	8.243
mojarse	5	0	8.243
meliflua	5	0	8.243
martillazos	5	0	8.243
marquetería	5	0	8.243
mariposas	5	0	8.243
manantial	5	0	8.243
maldecir	5	0	8.243
magistrados	5	0	8.243
lugareño	5	0	8.243
librea	5	0	8.243
lectores	5	0	8.243
látigo	5	0	8.243
languidez	5	0	8.243
jilgueros	5	0	8.243
inveterada	5	0	8.243
interesantes	5	0	8.243
insinuante	5	0	8.243
inmundicias	5	0	8.243
inmaculada	5	0	8.243
injusta	5	0	8.243
indiscreta	5	0	8.243
inconsciente	5	0	8.243
iconoclasta	5	0	8.243
ibi	5	0	8.243
huido	5	0	8.243
huertas	5	0	8.243
horrorosa	5	0	8.243
heno	5	0	8.243
hechizos	5	0	8.243
grillos	5	0	8.243
fuí	5	0	8.243
fluxus	5	0	8.243
fingirse	5	0	8.243
favorito	5	0	8.243
fatuos	5	0	8.243
excesiva	5	0	8.243
et	5	0	8.243
estuco	5	0	8.243
estantes	5	0	8.243
estante	5	0	8.243
estallaban	5	0	8.243
espontánea	5	0	8.243
esperaría	5	0	8.243
espectadores	5	0	8.243
escribano	5	0	8.243
erudito	5	0	8.243
envidiaban	5	0	8.243
emma	5	0	8.243
elegía	5	0	8.243
disimulos	5	0	8.243
destrozar	5	0	8.243
despertador	5	0	8.243
describir	5	0	8.243
desabrida	5	0	8.243
cuclillas	5	0	8.243
cruzado	5	0	8.243
cristianismo	5	0	8.243
contiguo	5	0	8.243
conquistador	5	0	8.243
complot	5	0	8.243
cómplices	5	0	8.243
colás	5	0	8.243
clerigalla	5	0	8.243
chin	5	0	8.243
chalequeras	5	0	8.243
cenceño	5	0	8.243
cedido	5	0	8.243
cazadora	5	0	8.243
capellanías	5	0	8.243
cantares	5	0	8.243
campiña	5	0	8.243
campestres	5	0	8.243
cachet	5	0	8.243
blasfemias	5	0	8.243
blanquecino	5	0	8.243
barcaza	5	0	8.243
balmes	5	0	8.243
bailarinas	5	0	8.243
bailarina	5	0	8.243
azotar	5	0	8.243
ávila	5	0	8.243
ausentes	5	0	8.243
asís	5	0	8.243
arqueológico	5	0	8.243
armónica	5	0	8.243
anunciación	5	0	8.243
ampuloso	5	0	8.243
amarillento	5	0	8.243
amarillenta	5	0	8.243
amaban	5	0	8.243
alusiones	5	0	8.243
almíbar	5	0	8.243
alababa	5	0	8.243
adversario	5	0	8.243
adornos	5	0	8.243
adoraban	5	0	8.243
acercado	5	0	8.243
aceras	5	0	8.243
abominable	5	0	8.243
tila	12	3	8.235
orador	12	3	8.235
mísero	12	3	8.235
meditaba	12	3	8.235
húmeda	12	3	8.235
fervor	12	3	8.235
despreciar	12	3	8.235
contemplar	12	3	8.235
cargados	12	3	8.235
biblioteca	12	3	8.235
bailes	12	3	8.235
altos	12	3	8.235
vulgar	26	13	8.224
asuntos	26	13	8.224
algunos	123	108	8.202
menudo	32	18	8.195
diga	17	47	8.190
difícil	17	47	8.190
podían	53	37	8.185
contestó	53	37	8.185
venir	37	82	8.140
soltó	7	27	8.135
hijas	41	26	8.115
negaba	18	7	8.109
hastío	18	7	8.109
dentro	170	159	8.101
vulgaris	0	7	8.081
vivísima	0	7	8.081
vistiendo	0	7	8.081
verídico	0	7	8.081
venden	0	7	8.081
vástagos	0	7	8.081
variar	0	7	8.081
tropiezo	0	7	8.081
tremendas	0	7	8.081
trastornado	0	7	8.081
traes	0	7	8.081
tomara	0	7	8.081
tirria	0	7	8.081
tiologías	0	7	8.081
tiesas	0	7	8.081
tie	0	7	8.081
ternera	0	7	8.081
teniente	0	7	8.081
tantísima	0	7	8.081
talmente	0	7	8.081
sobrinos	0	7	8.081
sintieron	0	7	8.081
semos	0	7	8.081
samaritana	0	7	8.081
rubinius	0	7	8.081
ricamente	0	7	8.081
retratos	0	7	8.081
réspice	0	7	8.081
resoplidos	0	7	8.081
resmas	0	7	8.081
referentes	0	7	8.081
reconocimiento	0	7	8.081
recíprocamente	0	7	8.081
quítate	0	7	8.081
prontamente	0	7	8.081
profundísimo	0	7	8.081
primerito	0	7	8.081
portera	0	7	8.081
pobrecillo	0	7	8.081
placeras	0	7	8.081
piojín	0	7	8.081
periodos	0	7	8.081
perfecciones	0	7	8.081
pensión	0	7	8.081
penetró	0	7	8.081
peinetas	0	7	8.081
pechos	0	7	8.081
pae	0	7	8.081
oíase	0	7	8.081
muleta	0	7	8.081
montado	0	7	8.081
milicia	0	7	8.081
metiose	0	7	8.081
metí	0	7	8.081
marca	0	7	8.081
malvina	0	7	8.081
maldades	0	7	8.081
magín	0	7	8.081
llegué	0	7	8.081
leo	0	7	8.081
lastimoso	0	7	8.081
lances	0	7	8.081
judía	0	7	8.081
inscripción	0	7	8.081
inmensidad	0	7	8.081
increíbles	0	7	8.081
hijito	0	7	8.081
hembras	0	7	8.081
guano	0	7	8.081
friolera	0	7	8.081
faldones	0	7	8.081
exclamaciones	0	7	8.081
estampas	0	7	8.081
espérate	0	7	8.081
escritura	0	7	8.081
escarola	0	7	8.081
eras	0	7	8.081
érale	0	7	8.081
enracimaban	0	7	8.081
engañas	0	7	8.081
energías	0	7	8.081
encuentre	0	7	8.081
encontrara	0	7	8.081
eche	0	7	8.081
dígale	0	7	8.081
desbordaba	0	7	8.081
deme	0	7	8.081
crudo	0	7	8.081
cosiendo	0	7	8.081
cortedad	0	7	8.081
convulsiva	0	7	8.081
comunidad	0	7	8.081
compraré	0	7	8.081
compinche	0	7	8.081
cogí	0	7	8.081
cobrador	0	7	8.081
chiquitín	0	7	8.081
chilló	0	7	8.081
cascote	0	7	8.081
cartilla	0	7	8.081
cariñosas	0	7	8.081
cargando	0	7	8.081
característico	0	7	8.081
cantón	0	7	8.081
cambiaría	0	7	8.081
bromuro	0	7	8.081
baza	0	7	8.081
barullo	0	7	8.081
barriga	0	7	8.081
atónita	0	7	8.081
atocha	0	7	8.081
aterrada	0	7	8.081
asentimiento	0	7	8.081
arrastrada	0	7	8.081
armada	0	7	8.081
armaba	0	7	8.081
aptitud	0	7	8.081
apreciación	0	7	8.081
alburquerque	0	7	8.081
agudo	0	7	8.081
acometida	0	7	8.081
acentuando	0	7	8.081
acentuada	0	7	8.081
satisfecho	33	19	8.069
vigilia	8	1	8.065
verdura	8	1	8.065
tristes	22	10	8.065
trasnochadores	8	1	8.065
temible	8	1	8.065
tajada	8	1	8.065
suprema	8	1	8.065
seducir	8	1	8.065
ridículas	8	1	8.065
resumen	8	1	8.065
reconciliar	8	1	8.065
presentaba	22	10	8.065
predicador	8	1	8.065
pinos	8	1	8.065
perdices	8	1	8.065
obstáculos	8	1	8.065
niego	8	1	8.065
minas	8	1	8.065
mentir	8	1	8.065
majestuoso	8	1	8.065
licenciado	8	1	8.065
jugadores	8	1	8.065
hojarasca	8	1	8.065
gobernadora	8	1	8.065
fingida	8	1	8.065
fantasmas	8	1	8.065
experiencia	22	10	8.065
exigían	8	1	8.065
espiaba	8	1	8.065
despreciado	8	1	8.065
comedias	22	10	8.065
colchón	8	1	8.065
charcos	8	1	8.065
castilla	8	1	8.065
carnaval	8	1	8.065
buscaban	8	1	8.065
brasas	8	1	8.065
saco	4	20	8.056
pecadora	4	20	8.056
mando	4	20	8.056
inquietud	4	20	8.056
entender	42	27	8.046
vieron	8	29	8.033
dieron	8	29	8.033
comprar	14	41	8.012
vergüenza	60	44	8.011
suaves	15	5	8.009
solitario	15	5	8.009
infinito	15	5	8.009
entera	15	5	8.009
batalla	15	5	8.009
aseguraba	15	5	8.009
solo	88	72	7.995
teja	10	2	7.982
supremo	10	2	7.982
supersticioso	10	2	7.982
solemnemente	10	2	7.982
rodeado	10	2	7.982
pechera	10	2	7.982
importantes	10	2	7.982
gritaron	10	2	7.982
expansiva	10	2	7.982
escandaloso	10	2	7.982
dorada	10	2	7.982
delgada	10	2	7.982
crucero	10	2	7.982
convidado	10	2	7.982
convalecencia	10	2	7.982
castaño	10	2	7.982
aprovechaba	10	2	7.982
afortunadamente	10	2	7.982
casarse	13	39	7.972
pueda	9	31	7.971
oro	64	48	7.955
honor	65	49	7.945
haga	12	37	7.944
cuartos	11	35	7.933
palabra	87	161	7.913
durante	32	73	7.911
caer	74	58	7.910
llegó	106	91	7.853
semejante	28	66	7.852
minutos	35	21	7.851
estado	66	128	7.801
sino	131	227	7.792
gritos	47	32	7.776
salen	5	22	7.765
temprano	36	22	7.757
político	19	8	7.744
valen	3	17	7.662
taller	3	17	7.662
sean	3	17	7.662
resulta	3	17	7.662
pusiera	3	17	7.662
mental	3	17	7.662
inmenso	3	17	7.662
cuatro	74	140	7.642
viuda	36	79	7.602
llenos	24	12	7.592
humana	16	44	7.583
pusieron	6	24	7.574
pedazo	6	24	7.574
medios	6	24	7.574
haré	6	24	7.574
voluntad	54	39	7.554
prometido	16	6	7.523
obligaba	16	6	7.523
escalofríos	16	6	7.523
asomaba	16	6	7.523
tentaciones	13	4	7.500
poética	13	4	7.500
pendiente	13	4	7.500
conocía	59	44	7.469
tontas	1	11	7.463
tomándole	1	11	7.463
tengamos	1	11	7.463
temerosa	1	11	7.463
supe	1	11	7.463
soltaba	1	11	7.463
siga	1	11	7.463
sepas	1	11	7.463
sacristán	1	11	7.463
poseía	1	11	7.463
poniéndole	1	11	7.463
peores	1	11	7.463
peldaños	1	11	7.463
obtener	1	11	7.463
maternidad	1	11	7.463
leal	1	11	7.463
incredulidad	1	11	7.463
hallándose	1	11	7.463
gasto	1	11	7.463
entran	1	11	7.463
ejemplos	1	11	7.463
den	1	11	7.463
comercial	1	11	7.463
bonitos	1	11	7.463
bendición	1	11	7.463
barcelona	1	11	7.463
algodón	1	11	7.463
abre	1	11	7.463
orgullo	40	26	7.458
cabo	40	26	7.458
resultado	7	26	7.449
ocultar	20	9	7.439
asustada	20	9	7.439
acercarse	20	9	7.439
volví	2	14	7.402
tunante	2	14	7.402
trasto	2	14	7.402
soltando	2	14	7.402
revés	2	14	7.402
faltado	2	14	7.402
dependientes	2	14	7.402
cállese	2	14	7.402
bonitas	2	14	7.402
billete	2	14	7.402
angelical	2	14	7.402
amas	2	14	7.402
piedras	25	13	7.400
diablo	25	13	7.400
juntos	41	27	7.399
quitaba	8	28	7.374
cariño	31	70	7.359
prosiguió	12	36	7.358
habitación	12	36	7.358
levita	32	19	7.341
serlo	9	30	7.334
nueve	10	32	7.322
metió	10	32	7.322
toda	221	356	7.311
quitar	4	19	7.275
protección	4	19	7.275
confusión	4	19	7.275
casó	4	19	7.275
debe	42	88	7.248
trata	26	14	7.231
sueños	26	14	7.231
hemos	30	68	7.231
oreja	21	10	7.180
hola	21	10	7.180
dolores	21	10	7.180
polvo	46	32	7.175
tenido	44	91	7.153
personaje	17	7	7.134
paseaba	17	7	7.134
medias	17	7	7.134
hipócrita	17	7	7.134
diablos	17	7	7.134
delito	17	7	7.134
pecado	48	34	7.112
quedaban	27	15	7.082
jóvenes	27	15	7.082
comprender	27	15	7.082
miedo	133	122	7.079
fría	35	22	7.073
quién	183	177	7.069
sacaba	16	43	7.055
mes	16	43	7.055
universo	11	3	7.050
secas	11	3	7.050
robusto	11	3	7.050
robusta	11	3	7.050
oraciones	11	3	7.050
museo	11	3	7.050
montaña	11	3	7.050
injusticia	11	3	7.050
extremos	11	3	7.050
estridente	11	3	7.050
desnuda	11	3	7.050
caprichos	11	3	7.050
butacas	11	3	7.050
asustaba	11	3	7.050
ven	25	59	7.042
deseando	5	21	7.029
habrá	28	64	6.976
lenguaje	15	41	6.975
salvación	22	11	6.959
respetable	22	11	6.959
pormenores	22	11	6.959
vicario	14	5	6.953
triunfante	14	5	6.953
tapia	14	5	6.953
suponía	14	5	6.953
sincera	14	5	6.953
picante	14	5	6.953
oración	14	5	6.953
oportuno	14	5	6.953
olvidó	14	5	6.953
modos	14	5	6.953
dejarle	14	5	6.953
decírselo	14	5	6.953
confidencias	14	5	6.953
ancha	14	5	6.953
agradable	14	5	6.953
sentidos	28	16	6.951
zaragata	0	6	6.926
vusté	0	6	6.926
vuestra	0	6	6.926
volverlo	0	6	6.926
ulmus	0	6	6.926
tumulto	0	6	6.926
trastada	0	6	6.926
tranvía	0	6	6.926
tintoreros	0	6	6.926
tellería	0	6	6.926
tardanza	0	6	6.926
talentos	0	6	6.926
sylvestris	0	6	6.926
sumamente	0	6	6.926
súbitamente	0	6	6.926
sosona	0	6	6.926
sopetón	0	6	6.926
soñé	0	6	6.926
solutamente	0	6	6.926
sílaba	0	6	6.926
sentiré	0	6	6.926
saladero	0	6	6.926
sacara	0	6	6.926
rudeza	0	6	6.926
rosquillas	0	6	6.926
rompiera	0	6	6.926
rías	0	6	6.926
revolucionario	0	6	6.926
revienta	0	6	6.926
reproducción	0	6	6.926
repóblica	0	6	6.926
renegando	0	6	6.926
reírme	0	6	6.926
regreso	0	6	6.926
regalos	0	6	6.926
rebajo	0	6	6.926
raimundo	0	6	6.926
rabiando	0	6	6.926
quitárselo	0	6	6.926
querré	0	6	6.926
provenía	0	6	6.926
pronunciando	0	6	6.926
poquitín	0	6	6.926
pongamos	0	6	6.926
pondremos	0	6	6.926
pito	0	6	6.926
pianito	0	6	6.926
pianista	0	6	6.926
perversidad	0	6	6.926
peregrino	0	6	6.926
paterna	0	6	6.926
pasito	0	6	6.926
pasé	0	6	6.926
paréntesis	0	6	6.926
palotada	0	6	6.926
paice	0	6	6.926
pagaré	0	6	6.926
olvide	0	6	6.926
oficiosidad	0	6	6.926
observadora	0	6	6.926
noria	0	6	6.926
muelas	0	6	6.926
muchísima	0	6	6.926
motor	0	6	6.926
moderaos	0	6	6.926
metieron	0	6	6.926
meterme	0	6	6.926
medicamento	0	6	6.926
mazapán	0	6	6.926
mango	0	6	6.926
malditas	0	6	6.926
maja	0	6	6.926
lulio	0	6	6.926
lógico	0	6	6.926
llego	0	6	6.926
llegándose	0	6	6.926
leganés	0	6	6.926
lámina	0	6	6.926
ju	0	6	6.926
jeta	0	6	6.926
jerez	0	6	6.926
hechura	0	6	6.926
haciéndola	0	6	6.926
gravelinas	0	6	6.926
gilimón	0	6	6.926
gatitos	0	6	6.926
finuras	0	6	6.926
finalmente	0	6	6.926
ferrocarriles	0	6	6.926
ferocidad	0	6	6.926
fárrago	0	6	6.926
extracto	0	6	6.926
expresado	0	6	6.926
examinó	0	6	6.926
entretener	0	6	6.926
encargos	0	6	6.926
empiezan	0	6	6.926
empezando	0	6	6.926
droguería	0	6	6.926
dolorida	0	6	6.926
divorcio	0	6	6.926
diole	0	6	6.926
dímelo	0	6	6.926
determinar	0	6	6.926
despidiose	0	6	6.926
desenvolverse	0	6	6.926
desempeñar	0	6	6.926
desdichado	0	6	6.926
descollaba	0	6	6.926
dándote	0	6	6.926
dadas	0	6	6.926
cuentes	0	6	6.926
cuchara	0	6	6.926
cuartito	0	6	6.926
créete	0	6	6.926
credencial	0	6	6.926
cosillas	0	6	6.926
consternada	0	6	6.926
conservaban	0	6	6.926
compré	0	6	6.926
comadrón	0	6	6.926
cohibida	0	6	6.926
cogiéndole	0	6	6.926
coco	0	6	6.926
chucherías	0	6	6.926
cesante	0	6	6.926
catarro	0	6	6.926
casaron	0	6	6.926
cartagena	0	6	6.926
cargue	0	6	6.926
canuto	0	6	6.926
cantidades	0	6	6.926
cajita	0	6	6.926
caí	0	6	6.926
bronca	0	6	6.926
brío	0	6	6.926
bordes	0	6	6.926
bonilla	0	6	6.926
bayona	0	6	6.926
bautizo	0	6	6.926
barricadas	0	6	6.926
azucenas	0	6	6.926
ayún	0	6	6.926
arsénico	0	6	6.926
arreglarse	0	6	6.926
apuntes	0	6	6.926
apretándole	0	6	6.926
apreciando	0	6	6.926
aposento	0	6	6.926
apelar	0	6	6.926
anteojos	0	6	6.926
amarillos	0	6	6.926
amalia	0	6	6.926
alternativas	0	6	6.926
albert	0	6	6.926
aflicción	0	6	6.926
achuchón	0	6	6.926
acechando	0	6	6.926
abatimiento	0	6	6.926
soledad	38	25	6.875
amante	38	25	6.875
casas	27	62	6.849
habías	3	16	6.842
decirme	3	16	6.842
debemos	3	16	6.842
creen	3	16	6.842
chasco	3	16	6.842
botella	3	16	6.842
ardor	3	16	6.842
próxima	13	37	6.840
periódicos	29	17	6.834
fingiendo	18	8	6.815
egoísmo	18	8	6.815
cristal	18	8	6.815
amarillo	18	8	6.815
camino	91	78	6.789
hermanos	7	25	6.780
herencia	7	25	6.780
pasando	18	46	6.730
maldito	8	27	6.730
dirección	8	27	6.730
déjame	8	27	6.730
consuelo	30	18	6.729
estar	76	140	6.726
vueltas	26	60	6.724
tropezar	9	2	6.716
tenerla	9	2	6.716
soslayo	9	2	6.716
sonreían	9	2	6.716
sacudir	9	2	6.716
saborear	9	2	6.716
puñetazo	9	2	6.716
preferido	9	2	6.716
perezoso	9	2	6.716
páginas	9	2	6.716
ostentaba	9	2	6.716
naturalismo	9	2	6.716
invisibles	9	2	6.716
imprudente	9	2	6.716
huérfana	9	2	6.716
granada	9	2	6.716
fríos	9	2	6.716
frac	9	2	6.716
encantaba	9	2	6.716
dormían	9	2	6.716
contentarse	9	2	6.716
calvario	9	2	6.716
burlaba	9	2	6.716
atrevían	9	2	6.716
atormentaba	9	2	6.716
aristócrata	9	2	6.716
apagado	9	2	6.716
acólito	9	2	6.716
respuesta	9	29	6.712
disposición	9	29	6.712
dándole	9	29	6.712
blanca	42	29	6.688
yacía	7	1	6.667
venas	7	1	6.667
velaba	7	1	6.667
urgente	7	1	6.667
umbral	7	1	6.667
tranquilamente	7	1	6.667
tibia	7	1	6.667
teólogo	7	1	6.667
sustos	7	1	6.667
sublevaba	7	1	6.667
sastre	7	1	6.667
saciar	7	1	6.667
sabor	7	1	6.667
rita	7	1	6.667
retumbaban	7	1	6.667
repentina	7	1	6.667
repasaba	7	1	6.667
repartía	7	1	6.667
protestas	7	1	6.667
prohibía	7	1	6.667
positivas	7	1	6.667
podredumbre	7	1	6.667
peligrosos	7	1	6.667
palcos	7	1	6.667
nerviosas	7	1	6.667
necio	7	1	6.667
manteos	7	1	6.667
limpias	7	1	6.667
irritado	7	1	6.667
intensa	7	1	6.667
insultos	7	1	6.667
inclusive	7	1	6.667
hubiesen	7	1	6.667
globo	7	1	6.667
galerías	7	1	6.667
fanático	7	1	6.667
exageraciones	7	1	6.667
esbelto	7	1	6.667
entrega	7	1	6.667
discutió	7	1	6.667
disculpa	7	1	6.667
describía	7	1	6.667
delicioso	7	1	6.667
cuaresma	7	1	6.667
confesarlo	7	1	6.667
complacía	7	1	6.667
comparar	7	1	6.667
comenzar	7	1	6.667
caería	7	1	6.667
bulliciosa	7	1	6.667
borbotones	7	1	6.667
blandura	7	1	6.667
ausente	7	1	6.667
atraía	7	1	6.667
acordado	7	1	6.667
acontecimientos	7	1	6.667
falta	71	132	6.635
resolución	24	13	6.603
asco	24	13	6.603
tiempos	25	58	6.600
zarzas	4	0	6.595
wals	4	0	6.595
volverían	4	0	6.595
viudedad	4	0	6.595
villano	4	0	6.595
vigorosa	4	0	6.595
verosimilitud	4	0	6.595
vengar	4	0	6.595
veleidades	4	0	6.595
valla	4	0	6.595
vacilante	4	0	6.595
trotaconventos	4	0	6.595
tributaba	4	0	6.595
traviata	4	0	6.595
tratase	4	0	6.595
tornasoles	4	0	6.595
tomillo	4	0	6.595
toga	4	0	6.595
tocarla	4	0	6.595
tibieza	4	0	6.595
tertulín	4	0	6.595
territorial	4	0	6.595
terremoto	4	0	6.595
tenor	4	0	6.595
tempore	4	0	6.595
técnicos	4	0	6.595
tarsila	4	0	6.595
tardaría	4	0	6.595
tapices	4	0	6.595
tácito	4	0	6.595
tablado	4	0	6.595
sustituto	4	0	6.595
súplicas	4	0	6.595
supina	4	0	6.595
sumido	4	0	6.595
sótanos	4	0	6.595
sorpresas	4	0	6.595
sórdido	4	0	6.595
soplar	4	0	6.595
sonreído	4	0	6.595
socarrón	4	0	6.595
sobado	4	0	6.595
simonía	4	0	6.595
simbólico	4	0	6.595
seto	4	0	6.595
sentimentalismo	4	0	6.595
sebo	4	0	6.595
sangrando	4	0	6.595
sagradas	4	0	6.595
saboreado	4	0	6.595
sables	4	0	6.595
sabiamente	4	0	6.595
ruso	4	0	6.595
retablo	4	0	6.595
respetaban	4	0	6.595
respectivo	4	0	6.595
resonancias	4	0	6.595
reparto	4	0	6.595
renunciaba	4	0	6.595
relieves	4	0	6.595
rejuvenecido	4	0	6.595
refresco	4	0	6.595
reclamaban	4	0	6.595
recitar	4	0	6.595
recitando	4	0	6.595
recargado	4	0	6.595
rasgaba	4	0	6.595
rapavelas	4	0	6.595
quiá	4	0	6.595
q	4	0	6.595
púrpura	4	0	6.595
punzante	4	0	6.595
pulvisés	4	0	6.595
pulquérrimo	4	0	6.595
pulla	4	0	6.595
pudiesen	4	0	6.595
psicología	4	0	6.595
protestó	4	0	6.595
protesto	4	0	6.595
prosaicas	4	0	6.595
prohibidos	4	0	6.595
prohibida	4	0	6.595
procuraban	4	0	6.595
pretendiendo	4	0	6.595
presentaron	4	0	6.595
preocupaban	4	0	6.595
pontífice	4	0	6.595
platea	4	0	6.595
plásticas	4	0	6.595
pistolas	4	0	6.595
pipa	4	0	6.595
pinchaban	4	0	6.595
pillastre	4	0	6.595
pesadillas	4	0	6.595
pensadores	4	0	6.595
peguetas	4	0	6.595
paseó	4	0	6.595
partidarios	4	0	6.595
parroquial	4	0	6.595
parecerle	4	0	6.595
parcerisa	4	0	6.595
pajarillo	4	0	6.595
pacto	4	0	6.595
pábulo	4	0	6.595
osaba	4	0	6.595
olvidé	4	0	6.595
obscurantista	4	0	6.595
obispos	4	0	6.595
nubecillas	4	0	6.595
novicia	4	0	6.595
náufragos	4	0	6.595
naturalista	4	0	6.595
nacían	4	0	6.595
nácar	4	0	6.595
murmuradores	4	0	6.595
mundanas	4	0	6.595
montaraz	4	0	6.595
misioneros	4	0	6.595
mísera	4	0	6.595
meretrices	4	0	6.595
margen	4	0	6.595
marasmo	4	0	6.595
maquiavelismo	4	0	6.595
mansos	4	0	6.595
mandilón	4	0	6.595
malvados	4	0	6.595
mainate	4	0	6.595
madrugaba	4	0	6.595
lugareña	4	0	6.595
luchó	4	0	6.595
lícito	4	0	6.595
liberalismo	4	0	6.595
legos	4	0	6.595
lechuguino	4	0	6.595
laureles	4	0	6.595
laterales	4	0	6.595
larvas	4	0	6.595
laico	4	0	6.595
ladraba	4	0	6.595
lacayos	4	0	6.595
jubilado	4	0	6.595
je	4	0	6.595
iriarte	4	0	6.595
insultaba	4	0	6.595
inodoro	4	0	6.595
inminente	4	0	6.595
injusticias	4	0	6.595
injertaba	4	0	6.595
indumentaria	4	0	6.595
improvisó	4	0	6.595
iluminar	4	0	6.595
illo	4	0	6.595
il	4	0	6.595
humillados	4	0	6.595
huerto	4	0	6.595
horno	4	0	6.595
heroica	4	0	6.595
herejes	4	0	6.595
hachas	4	0	6.595
grotesca	4	0	6.595
gregorio	4	0	6.595
granate	4	0	6.595
grabado	4	0	6.595
gorriones	4	0	6.595
fuere	4	0	6.595
frotaba	4	0	6.595
folletines	4	0	6.595
flotaban	4	0	6.595
floridos	4	0	6.595
florida	4	0	6.595
flora	4	0	6.595
filial	4	0	6.595
factor	4	0	6.595
extraviado	4	0	6.595
excomulgar	4	0	6.595
eufemismos	4	0	6.595
estufa	4	0	6.595
estribo	4	0	6.595
estameña	4	0	6.595
estallaba	4	0	6.595
espiando	4	0	6.595
escuchaban	4	0	6.595
escandalosos	4	0	6.595
esbeltos	4	0	6.595
eróticas	4	0	6.595
epigramas	4	0	6.595
envidió	4	0	6.595
envidias	4	0	6.595
envidiable	4	0	6.595
enterrar	4	0	6.595
enternecido	4	0	6.595
enternecida	4	0	6.595
enternecía	4	0	6.595
empleaban	4	0	6.595
efímero	4	0	6.595
duran	4	0	6.595
dominicales	4	0	6.595
documentos	4	0	6.595
distingo	4	0	6.595
disparatada	4	0	6.595
disimuló	4	0	6.595
disculpaba	4	0	6.595
diabólica	4	0	6.595
devotos	4	0	6.595
devocionario	4	0	6.595
despreciaban	4	0	6.595
desmoronaba	4	0	6.595
deslumbrar	4	0	6.595
desdeñar	4	0	6.595
descendiente	4	0	6.595
desahogaba	4	0	6.595
desafía	4	0	6.595
demasías	4	0	6.595
decirla	4	0	6.595
dandy	4	0	6.595
cumbre	4	0	6.595
crónica	4	0	6.595
corujedo	4	0	6.595
corteses	4	0	6.595
correcto	4	0	6.595
copia	4	0	6.595
convertidos	4	0	6.595
convenían	4	0	6.595
convencidos	4	0	6.595
contrarrestar	4	0	6.595
contradicción	4	0	6.595
consolarle	4	0	6.595
confidencial	4	0	6.595
confesárselo	4	0	6.595
confesando	4	0	6.595
condenaba	4	0	6.595
cónclave	4	0	6.595
conciudadanos	4	0	6.595
conciertos	4	0	6.595
complicados	4	0	6.595
comenzaban	4	0	6.595
comendador	4	0	6.595
colocada	4	0	6.595
coincidiendo	4	0	6.595
coincidía	4	0	6.595
cohetes	4	0	6.595
clava	4	0	6.595
clásicos	4	0	6.595
clásica	4	0	6.595
churrigueresco	4	0	6.595
chorizos	4	0	6.595
charadas	4	0	6.595
césped	4	0	6.595
cerero	4	0	6.595
cavilosa	4	0	6.595
casto	4	0	6.595
caseros	4	0	6.595
cascada	4	0	6.595
cardenal	4	0	6.595
cansó	4	0	6.595
campanero	4	0	6.595
caminar	4	0	6.595
calentaba	4	0	6.595
calada	4	0	6.595
botánico	4	0	6.595
borla	4	0	6.595
boquirroto	4	0	6.595
bonachón	4	0	6.595
boj	4	0	6.595
besarle	4	0	6.595
beltrand	4	0	6.595
barítono	4	0	6.595
barbero	4	0	6.595
bandos	4	0	6.595
bancarrota	4	0	6.595
balde	4	0	6.595
bailado	4	0	6.595
bacantes	4	0	6.595
azar	4	0	6.595
azafrán	4	0	6.595
aventurado	4	0	6.595
audaz	4	0	6.595
atribuían	4	0	6.595
atrevieron	4	0	6.595
atleta	4	0	6.595
asquerosas	4	0	6.595
arrodillada	4	0	6.595
arraigadas	4	0	6.595
ardua	4	0	6.595
arcángel	4	0	6.595
apuraban	4	0	6.595
aprovechase	4	0	6.595
apostólico	4	0	6.595
aplastaba	4	0	6.595
apiñados	4	0	6.595
apetecible	4	0	6.595
antiquísima	4	0	6.595
antero	4	0	6.595
animaban	4	0	6.595
análisis	4	0	6.595
anales	4	0	6.595
amapola	4	0	6.595
amaneradas	4	0	6.595
altivo	4	0	6.595
alpaca	4	0	6.595
alemanes	4	0	6.595
aldeano	4	0	6.595
alabanza	4	0	6.595
adolescente	4	0	6.595
adolescencia	4	0	6.595
admiraban	4	0	6.595
acusaba	4	0	6.595
acusa	4	0	6.595
aburren	4	0	6.595
abrumaba	4	0	6.595
aborrece	4	0	6.595
abalorios	4	0	6.595
momento	137	128	6.568
hijo	138	232	6.553
impaciencia	19	9	6.550
habido	19	9	6.550
monjas	16	42	6.539
universal	15	6	6.529
pensador	15	6	6.529
muchachas	15	6	6.529
dudaba	15	6	6.529
arrogante	15	6	6.529
tuvieran	2	13	6.524
matado	2	13	6.524
encender	2	13	6.524
echo	2	13	6.524
echándose	2	13	6.524
dale	2	13	6.524
grande	87	156	6.516
quieran	4	18	6.512
llevaron	4	18	6.512
francia	4	18	6.512
figúrate	4	18	6.512
alegro	4	18	6.512
todas	284	294	6.510
verbo	1	10	6.491
quizá	1	10	6.491
puse	1	10	6.491
pulgas	1	10	6.491
ponte	1	10	6.491
pareces	1	10	6.491
paloma	1	10	6.491
palillo	1	10	6.491
mantas	1	10	6.491
lleve	1	10	6.491
línea	1	10	6.491
habrías	1	10	6.491
haberla	1	10	6.491
gozosa	1	10	6.491
fuertemente	1	10	6.491
facultad	1	10	6.491
estate	1	10	6.491
efecto	71	58	6.491
disposiciones	1	10	6.491
discurrió	1	10	6.491
dirás	1	10	6.491
desvaríos	1	10	6.491
casarme	1	10	6.491
bota	1	10	6.491
bebida	1	10	6.491
alargando	1	10	6.491
venía	95	83	6.488
manos	128	217	6.484
sí	677	758	6.425
tratándose	12	4	6.407
temperamento	12	4	6.407
sospechas	12	4	6.407
romántica	12	4	6.407
pollos	12	4	6.407
poderosa	12	4	6.407
latín	12	4	6.407
hablemos	12	4	6.407
exige	12	4	6.407
enérgico	12	4	6.407
empleaba	12	4	6.407
discutía	12	4	6.407
chimenea	12	4	6.407
catecismo	12	4	6.407
casero	12	4	6.407
ataques	12	4	6.407
aburría	12	4	6.407
ideas	90	160	6.375
fijo	35	23	6.350
vestía	20	10	6.326
echarle	5	20	6.311
remedio	43	87	6.298
llevar	32	69	6.270
rincón	37	25	6.248
poca	18	45	6.242
parte	139	232	6.233
apetito	12	34	6.229
vagamente	16	7	6.192
tirar	6	22	6.192
práctica	6	22	6.192
palo	6	22	6.192
murmuraba	16	7	6.192
español	6	22	6.192
diferencia	6	22	6.192
carnes	6	22	6.192
arena	16	7	6.192
adentro	6	22	6.192
real	17	43	6.138
levantaba	21	11	6.137
igual	10	30	6.132
creí	10	30	6.132
tuve	7	24	6.128
severidad	7	24	6.128
chiquillo	7	24	6.128
supiera	28	17	6.121
ocurría	8	26	6.103
convicción	8	26	6.103
abrir	8	26	6.103
hombre	318	486	6.098
fuerte	106	96	6.045
tremenda	3	15	6.042
toros	3	15	6.042
paca	3	15	6.042
monstruo	3	15	6.042
haciéndole	3	15	6.042
durmió	3	15	6.042
desagradable	3	15	6.042
consecuencia	3	15	6.042
conceptos	3	15	6.042
chillidos	3	15	6.042
viaje	29	18	6.033
formas	29	18	6.033
hierro	44	32	6.026
motivo	45	33	6.008
caridad	45	33	6.008
sacar	20	48	5.996
un	3121	3767	5.990
saberlo	22	12	5.975
veían	30	19	5.956
banco	50	38	5.948
grandes	102	92	5.943
mío	68	125	5.942
hacerle	15	39	5.941
vaga	13	5	5.934
tocado	13	5	5.934
mártir	13	5	5.934
lugares	13	5	5.934
descalza	13	5	5.934
bajos	13	5	5.934
suelo	50	97	5.919
gestos	17	8	5.919
brillaban	17	8	5.919
zas	10	3	5.905
vigor	10	3	5.905
varas	10	3	5.905
sorprendido	10	3	5.905
sofismas	10	3	5.905
roce	10	3	5.905
muro	10	3	5.905
jugaba	10	3	5.905
flaca	10	3	5.905
finos	10	3	5.905
fiestas	10	3	5.905
espesa	10	3	5.905
escandalosa	10	3	5.905
entregaba	10	3	5.905
columna	10	3	5.905
campos	10	3	5.905
aviso	10	3	5.905
aparente	10	3	5.905
amargura	10	3	5.905
amanecer	10	3	5.905
ajedrez	10	3	5.905
verá	19	46	5.880
corría	32	21	5.826
volverás	0	5	5.772
visajes	0	5	5.772
violentamente	0	5	5.772
villaamil	0	5	5.772
vigas	0	5	5.772
viéndote	0	5	5.772
vibración	0	5	5.772
verificado	0	5	5.772
veleta	0	5	5.772
variedades	0	5	5.772
vacilación	0	5	5.772
unirse	0	5	5.772
turquesas	0	5	5.772
trompetilla	0	5	5.772
triquiñuelas	0	5	5.772
trayecto	0	5	5.772
travesura	0	5	5.772
trajera	0	5	5.772
traigas	0	5	5.772
traerme	0	5	5.772
trabajan	0	5	5.772
tornó	0	5	5.772
tomarme	0	5	5.772
tomaré	0	5	5.772
todito	0	5	5.772
tiras	0	5	5.772
tiita	0	5	5.772
tenías	0	5	5.772
tartera	0	5	5.772
tarda	0	5	5.772
tapujos	0	5	5.772
tabernillas	0	5	5.772
suficiencia	0	5	5.772
sucedieron	0	5	5.772
socorrerla	0	5	5.772
sobrevino	0	5	5.772
sobreponerse	0	5	5.772
situaciones	0	5	5.772
simplezas	0	5	5.772
servidora	0	5	5.772
senquá	0	5	5.772
sedación	0	5	5.772
secta	0	5	5.772
sayo	0	5	5.772
salgas	0	5	5.772
salamanca	0	5	5.772
sacrificar	0	5	5.772
sacaría	0	5	5.772
ruda	0	5	5.772
revuelto	0	5	5.772
reviento	0	5	5.772
reventando	0	5	5.772
retirose	0	5	5.772
resultando	0	5	5.772
resplandecía	0	5	5.772
reinado	0	5	5.772
regalitos	0	5	5.772
refunfuñando	0	5	5.772
recibo	0	5	5.772
recadito	0	5	5.772
razonamiento	0	5	5.772
quitose	0	5	5.772
quintos	0	5	5.772
quinientos	0	5	5.772
quicio	0	5	5.772
quédate	0	5	5.772
quedarme	0	5	5.772
quedábase	0	5	5.772
prontito	0	5	5.772
pretendo	0	5	5.772
presuroso	0	5	5.772
presunciones	0	5	5.772
presumida	0	5	5.772
presentose	0	5	5.772
presentan	0	5	5.772
preciosidad	0	5	5.772
prácticos	0	5	5.772
postre	0	5	5.772
poseen	0	5	5.772
portillo	0	5	5.772
porté	0	5	5.772
portales	0	5	5.772
poquillo	0	5	5.772
pongan	0	5	5.772
ponerte	0	5	5.772
poderlo	0	5	5.772
plancha	0	5	5.772
plaf	0	5	5.772
placera	0	5	5.772
pintados	0	5	5.772
pillete	0	5	5.772
pillería	0	5	5.772
pierdes	0	5	5.772
picor	0	5	5.772
pesquis	0	5	5.772
pescado	0	5	5.772
perteneciente	0	5	5.772
peldaño	0	5	5.772
pelagatos	0	5	5.772
pegarte	0	5	5.772
patrocinio	0	5	5.772
pastelera	0	5	5.772
pasmaron	0	5	5.772
parroquiana	0	5	5.772
parido	0	5	5.772
papelito	0	5	5.772
panadería	0	5	5.772
panacea	0	5	5.772
palabritas	0	5	5.772
palabrita	0	5	5.772
paices	0	5	5.772
olían	0	5	5.772
odoripherus	0	5	5.772
numancia	0	5	5.772
notaron	0	5	5.772
napoleónica	0	5	5.772
muestrario	0	5	5.772
mota	0	5	5.772
morros	0	5	5.772
monarquía	0	5	5.772
mismito	0	5	5.772
mírame	0	5	5.772
miquis	0	5	5.772
miiii	0	5	5.772
menudillos	0	5	5.772
melitona	0	5	5.772
melenas	0	5	5.772
mediano	0	5	5.772
marchas	0	5	5.772
marcado	0	5	5.772
mantillo	0	5	5.772
manifiesto	0	5	5.772
mandaré	0	5	5.772
mama	0	5	5.772
madura	0	5	5.772
machacar	0	5	5.772
lucida	0	5	5.772
lozanía	0	5	5.772
loba	0	5	5.772
llevarme	0	5	5.772
llevaran	0	5	5.772
llamándola	0	5	5.772
lindos	0	5	5.772
limpiado	0	5	5.772
lienzos	0	5	5.772
libra	0	5	5.772
liado	0	5	5.772
legal	0	5	5.772
lanzado	0	5	5.772
laboratorio	0	5	5.772
labia	0	5	5.772
interna	0	5	5.772
intensísimo	0	5	5.772
insensible	0	5	5.772
infiernos	0	5	5.772
infalibles	0	5	5.772
indeciso	0	5	5.772
incomodarse	0	5	5.772
incomodado	0	5	5.772
impresionó	0	5	5.772
impertinentes	0	5	5.772
ibas	0	5	5.772
huérfanos	0	5	5.772
hospicio	0	5	5.772
hocicos	0	5	5.772
hízolo	0	5	5.772
hipotecas	0	5	5.772
higos	0	5	5.772
heredó	0	5	5.772
hala	0	5	5.772
hágalo	0	5	5.772
haciéndolo	0	5	5.772
gradualmente	0	5	5.772
gemido	0	5	5.772
gatillos	0	5	5.772
ganga	0	5	5.772
furibunda	0	5	5.772
fotografías	0	5	5.772
flin	0	5	5.772
fascinación	0	5	5.772
extrañeza	0	5	5.772
extranjeros	0	5	5.772
examinando	0	5	5.772
exámenes	0	5	5.772
esforzándose	0	5	5.772
escorial	0	5	5.772
entretuvo	0	5	5.772
entretenida	0	5	5.772
enderezar	0	5	5.772
endeble	0	5	5.772
empeñadas	0	5	5.772
elementales	0	5	5.772
efectivo	0	5	5.772
económicas	0	5	5.772
dormitorios	0	5	5.772
diversas	0	5	5.772
disponiéndose	0	5	5.772
dirigirse	0	5	5.772
dimpués	0	5	5.772
dijiste	0	5	5.772
diamante	0	5	5.772
detúvose	0	5	5.772
determinaciones	0	5	5.772
desplegar	0	5	5.772
deslizándose	0	5	5.772
deseosa	0	5	5.772
descubre	0	5	5.772
desarrollarse	0	5	5.772
derramar	0	5	5.772
dejarte	0	5	5.772
dejarme	0	5	5.772
dejándola	0	5	5.772
deis	0	5	5.772
dedillo	0	5	5.772
décimo	0	5	5.772
decías	0	5	5.772
curiosear	0	5	5.772
cuña	0	5	5.772
cubil	0	5	5.772
cuadra	0	5	5.772
creyeron	0	5	5.772
creeré	0	5	5.772
créeme	0	5	5.772
coscorrones	0	5	5.772
correos	0	5	5.772
corredora	0	5	5.772
coraje	0	5	5.772
convencimiento	0	5	5.772
consternación	0	5	5.772
conmovía	0	5	5.772
congreso	0	5	5.772
cojita	0	5	5.772
cogieron	0	5	5.772
cogerle	0	5	5.772
clareaba	0	5	5.772
circunstantes	0	5	5.772
cigarrillo	0	5	5.772
chillando	0	5	5.772
chillaba	0	5	5.772
chí	0	5	5.772
chapa	0	5	5.772
chalán	0	5	5.772
celosa	0	5	5.772
cebada	0	5	5.772
cavidad	0	5	5.772
carteras	0	5	5.772
carnicería	0	5	5.772
cariñosamente	0	5	5.772
cánovas	0	5	5.772
calmó	0	5	5.772
calmarle	0	5	5.772
callo	0	5	5.772
caletre	0	5	5.772
calderilla	0	5	5.772
caballería	0	5	5.772
burgos	0	5	5.772
botín	0	5	5.772
bilboquet	0	5	5.772
bicerra	0	5	5.772
bastones	0	5	5.772
bastero	0	5	5.772
barbaridades	0	5	5.772
bajón	0	5	5.772
bajan	0	5	5.772
ayunas	0	5	5.772
atendiendo	0	5	5.772
asno	0	5	5.772
artesa	0	5	5.772
arreglaré	0	5	5.772
arreglada	0	5	5.772
arenas	0	5	5.772
apurar	0	5	5.772
aprisa	0	5	5.772
aprenden	0	5	5.772
apreciable	0	5	5.772
apartando	0	5	5.772
aparentaba	0	5	5.772
antiespasmódica	0	5	5.772
alumnas	0	5	5.772
alejándose	0	5	5.772
alcanzar	0	5	5.772
alcalá	0	5	5.772
agudísimo	0	5	5.772
agonías	0	5	5.772
afirmativamente	0	5	5.772
adquiriendo	0	5	5.772
adoptiva	0	5	5.772
acerté	0	5	5.772
acepta	0	5	5.772
acentuado	0	5	5.772
abuelito	0	5	5.772
sacerdote	33	22	5.771
seas	4	17	5.769
retiro	4	17	5.769
remediar	4	17	5.769
compañera	4	17	5.769
pico	13	35	5.764
pasillo	13	35	5.764
hija	144	237	5.754
pálida	24	14	5.713
después	418	622	5.709
pagaba	18	9	5.694
hecha	12	33	5.687
entraron	12	33	5.687
viii	2	12	5.667
traeré	2	12	5.667
tercero	2	12	5.667
tendremos	2	12	5.667
síntoma	2	12	5.667
serás	2	12	5.667
sazón	2	12	5.667
santísimo	2	12	5.667
registro	2	12	5.667
realmente	2	12	5.667
pronunciar	2	12	5.667
ponerme	2	12	5.667
piensas	2	12	5.667
personalidad	2	12	5.667
pelota	2	12	5.667
pasas	2	12	5.667
oí	2	12	5.667
obstante	2	12	5.667
jugando	2	12	5.667
inglaterra	2	12	5.667
individuo	2	12	5.667
horribles	2	12	5.667
grosería	2	12	5.667
forzoso	2	12	5.667
cuarta	2	12	5.667
cría	2	12	5.667
costura	2	12	5.667
cerebral	2	12	5.667
arrojando	2	12	5.667
repente	72	61	5.656
mostraba	11	31	5.618
sesos	5	19	5.613
rompió	5	19	5.613
responder	5	19	5.613
hacienda	5	19	5.613
correspondencia	5	19	5.613
cólera	25	15	5.608
desgracia	38	27	5.579
vulgo	14	6	5.573
tigre	14	6	5.573
saludaba	14	6	5.573
olía	14	6	5.573
jardín	14	6	5.573
inefable	14	6	5.573
encanto	14	6	5.573
constante	14	6	5.573
apoyó	14	6	5.573
yema	1	9	5.537
viático	1	9	5.537
traiga	1	9	5.537
suplicio	1	9	5.537
renglón	1	9	5.537
purísima	1	9	5.537
portería	1	9	5.537
plantón	1	9	5.537
mu	1	9	5.537
irá	1	9	5.537
indecentes	1	9	5.537
gastaba	1	9	5.537
finca	1	9	5.537
figurábase	1	9	5.537
febrero	1	9	5.537
fatigado	1	9	5.537
excelentes	1	9	5.537
examinaba	1	9	5.537
escalón	1	9	5.537
entrase	1	9	5.537
durmiendo	1	9	5.537
dosis	1	9	5.537
determinación	1	9	5.537
detalles	1	9	5.537
delincuente	1	9	5.537
culpa	64	53	5.537
casados	1	9	5.537
cálculo	1	9	5.537
atendía	1	9	5.537
aseo	1	9	5.537
apartaba	1	9	5.537
alargó	1	9	5.537
acuerda	1	9	5.537
enferma	40	29	5.531
mesas	6	21	5.530
limpio	6	21	5.530
enterarse	6	21	5.530
averiguar	6	21	5.530
anciano	6	21	5.530
plato	9	27	5.519
fuerzas	26	16	5.515
cansado	26	16	5.515
visiones	19	10	5.506
soñaba	19	10	5.506
cesar	19	10	5.506
sigue	8	25	5.495
retiró	7	23	5.495
ponían	7	23	5.495
vicente	8	2	5.490
utilidad	8	2	5.490
tendió	8	2	5.490
sucedido	8	2	5.490
siesta	8	2	5.490
saludable	8	2	5.490
salones	8	2	5.490
roble	8	2	5.490
racional	8	2	5.490
prometía	8	2	5.490
podrida	8	2	5.490
perseguir	8	2	5.490
palacios	8	2	5.490
paisano	8	2	5.490
nazareno	8	2	5.490
mitología	8	2	5.490
melancólico	8	2	5.490
manejaba	8	2	5.490
macho	8	2	5.490
indigna	8	2	5.490
hundida	8	2	5.490
gentes	8	2	5.490
galantería	8	2	5.490
flotante	8	2	5.490
estupidez	8	2	5.490
dignas	8	2	5.490
confuso	8	2	5.490
concluía	8	2	5.490
callaban	8	2	5.490
cabellos	8	2	5.490
billar	8	2	5.490
américa	8	2	5.490
alumbraba	8	2	5.490
alejaba	8	2	5.490
agosto	8	2	5.490
admirar	8	2	5.490
segura	43	32	5.480
piedra	46	35	5.451
cuyo	15	38	5.444
par	19	45	5.424
infierno	28	18	5.364
cristiano	28	18	5.364
será	55	103	5.360
testigo	11	4	5.355
rezaba	11	4	5.355
palidez	11	4	5.355
náuseas	11	4	5.355
murmullo	11	4	5.355
movían	11	4	5.355
infames	11	4	5.355
flaqueza	11	4	5.355
fijos	11	4	5.355
creerse	11	4	5.355
coquetería	11	4	5.355
chistes	11	4	5.355
arrastraba	11	4	5.355
apóstol	11	4	5.355
antiguos	11	4	5.355
aceptó	11	4	5.355
sonreír	20	11	5.347
luces	20	11	5.347
daño	20	11	5.347
órdenes	14	36	5.344
vírgenes	6	1	5.305
vehemente	6	1	5.305
vapores	6	1	5.305
usía	6	1	5.305
tresillistas	6	1	5.305
tormentos	6	1	5.305
tentador	6	1	5.305
talar	6	1	5.305
silbidos	6	1	5.305
servirle	6	1	5.305
señalaba	6	1	5.305
seglar	6	1	5.305
satisfechos	6	1	5.305
salas	6	1	5.305
ruegos	6	1	5.305
rubor	6	1	5.305
rocío	6	1	5.305
rizada	6	1	5.305
rítmico	6	1	5.305
restaurant	6	1	5.305
rencores	6	1	5.305
regalado	6	1	5.305
ramona	6	1	5.305
preparándose	6	1	5.305
preferir	6	1	5.305
positivo	6	1	5.305
pegajosa	6	1	5.305
orgía	6	1	5.305
olores	6	1	5.305
ofrecían	6	1	5.305
océano	6	1	5.305
novenas	6	1	5.305
montañas	6	1	5.305
monotonía	6	1	5.305
modernos	6	1	5.305
mina	6	1	5.305
mataba	6	1	5.305
marinero	6	1	5.305
manga	6	1	5.305
llueve	6	1	5.305
leían	6	1	5.305
lámparas	6	1	5.305
interlocutor	6	1	5.305
intensidad	6	1	5.305
insultar	6	1	5.305
insistir	6	1	5.305
inercia	6	1	5.305
inclinarse	6	1	5.305
impiedad	6	1	5.305
ilustres	6	1	5.305
ídem	6	1	5.305
guardaban	6	1	5.305
gallardo	6	1	5.305
fiaba	6	1	5.305
expansión	6	1	5.305
eternamente	6	1	5.305
estalló	6	1	5.305
escéptico	6	1	5.305
enamora	6	1	5.305
emprendía	6	1	5.305
disputando	6	1	5.305
disparar	6	1	5.305
decidor	6	1	5.305
débiles	6	1	5.305
cruzaban	6	1	5.305
corral	6	1	5.305
convertirse	6	1	5.305
contenida	6	1	5.305
confesaban	6	1	5.305
comparaba	6	1	5.305
colecciones	6	1	5.305
ceguera	6	1	5.305
casullas	6	1	5.305
campanas	6	1	5.305
cadenas	6	1	5.305
burlado	6	1	5.305
batirse	6	1	5.305
basílica	6	1	5.305
balandrán	6	1	5.305
ateísmo	6	1	5.305
asqueroso	6	1	5.305
arrimado	6	1	5.305
antepecho	6	1	5.305
antaño	6	1	5.305
amoríos	6	1	5.305
aludiendo	6	1	5.305
alabar	6	1	5.305
alabanzas	6	1	5.305
adelantar	6	1	5.305
abonados	6	1	5.305
paredes	29	19	5.301
pasó	61	112	5.293
revolución	15	7	5.289
cubierta	15	7	5.289
verdades	3	14	5.264
pones	3	14	5.264
pidiendo	3	14	5.264
manta	3	14	5.264
habrás	3	14	5.264
gorda	3	14	5.264
delantal	3	14	5.264
dándose	3	14	5.264
conveniente	3	14	5.264
baúl	3	14	5.264
apartar	3	14	5.264
aguantar	3	14	5.264
media	101	93	5.263
modelo	13	34	5.250
corriente	30	20	5.247
mucho	342	513	5.200
darle	35	71	5.191
hechos	17	41	5.188
caído	17	41	5.188
ellos	137	133	5.162
ocurrió	12	32	5.161
muchacho	12	32	5.161
demonio	12	32	5.161
acuerdo	12	32	5.161
negro	82	73	5.109
lectura	22	13	5.098
negocio	11	30	5.080
jaqueca	11	30	5.080
entra	11	30	5.080
bajó	11	30	5.080
malas	16	39	5.074
ternura	16	8	5.061
melancolía	16	8	5.061
juegos	16	8	5.061
cuidados	16	8	5.061
bolsa	16	8	5.061
perro	35	25	5.060
tuya	4	16	5.049
sostenía	4	16	5.049
extranjero	4	16	5.049
empezaban	4	16	5.049
desconsuelo	4	16	5.049
cajas	4	16	5.049
amiguita	4	16	5.049
ante	78	69	5.015
esfuerzo	23	14	4.999
desde	251	264	4.962
plomo	12	5	4.959
original	12	5	4.959
intimidad	12	5	4.959
indigno	12	5	4.959
gritar	12	5	4.959
excepción	12	5	4.959
exaltada	12	5	4.959
conquista	12	5	4.959
ayuntamiento	12	5	4.959
alimento	12	5	4.959
lástima	43	83	4.955
vengo	9	26	4.949
última	43	33	4.949
limpia	9	26	4.949
capellán	9	26	4.949
perder	48	38	4.947
zurriágame	3	0	4.946
zumbaron	3	0	4.946
vocinglero	3	0	4.946
viudez	3	0	4.946
virtuoso	3	0	4.946
vibraban	3	0	4.946
verdugos	3	0	4.946
verdores	3	0	4.946
vencerle	3	0	4.946
vencerla	3	0	4.946
vejete	3	0	4.946
vanidades	3	0	4.946
valles	3	0	4.946
utilizar	3	0	4.946
unidad	3	0	4.946
turgente	3	0	4.946
turgencias	3	0	4.946
tupido	3	0	4.946
trompa	3	0	4.946
tristón	3	0	4.946
trasladarse	3	0	4.946
trasladar	3	0	4.946
transtiberina	3	0	4.946
transformada	3	0	4.946
tralla	3	0	4.946
toses	3	0	4.946
tosco	3	0	4.946
tortura	3	0	4.946
tórtolas	3	0	4.946
torrentes	3	0	4.946
torneado	3	0	4.946
todd	3	0	4.946
tirso	3	0	4.946
tires	3	0	4.946
tirada	3	0	4.946
tibio	3	0	4.946
termasaltas	3	0	4.946
terco	3	0	4.946
terciando	3	0	4.946
teológico	3	0	4.946
teñía	3	0	4.946
tensión	3	0	4.946
teneatis	3	0	4.946
temblona	3	0	4.946
telar	3	0	4.946
tapabocas	3	0	4.946
tambaleaba	3	0	4.946
tacos	3	0	4.946
taburetes	3	0	4.946
taberneros	3	0	4.946
suspiraban	3	0	4.946
suspira	3	0	4.946
suspendieron	3	0	4.946
supuestos	3	0	4.946
supremos	3	0	4.946
supersticiosamente	3	0	4.946
sugerido	3	0	4.946
suficientes	3	0	4.946
sudaban	3	0	4.946
sucumbir	3	0	4.946
subrepticia	3	0	4.946
stabat	3	0	4.946
spirto	3	0	4.946
sospeche	3	0	4.946
sospechase	3	0	4.946
sospecharlo	3	0	4.946
sospechaban	3	0	4.946
sonrieron	3	0	4.946
sonado	3	0	4.946
soledades	3	0	4.946
sojuzgada	3	0	4.946
sinodal	3	0	4.946
sine	3	0	4.946
silueta	3	0	4.946
sidra	3	0	4.946
sentiría	3	0	4.946
sensual	3	0	4.946
sencillas	3	0	4.946
seminarista	3	0	4.946
seducirle	3	0	4.946
secularizar	3	0	4.946
sectario	3	0	4.946
santiguarse	3	0	4.946
sandio	3	0	4.946
salpicaba	3	0	4.946
salacia	3	0	4.946
sacrificado	3	0	4.946
rurales	3	0	4.946
ruiseñor	3	0	4.946
ruines	3	0	4.946
ruborizó	3	0	4.946
rubios	3	0	4.946
rosina	3	0	4.946
rosetones	3	0	4.946
románticos	3	0	4.946
rocín	3	0	4.946
risum	3	0	4.946
ribeteadoras	3	0	4.946
reuniones	3	0	4.946
retrocedía	3	0	4.946
retoños	3	0	4.946
resquicios	3	0	4.946
respetada	3	0	4.946
reseco	3	0	4.946
reputó	3	0	4.946
reprensible	3	0	4.946
repetidos	3	0	4.946
repentinas	3	0	4.946
reparte	3	0	4.946
reparado	3	0	4.946
renegaba	3	0	4.946
rendición	3	0	4.946
renan	3	0	4.946
remolinos	3	0	4.946
relucía	3	0	4.946
relativas	3	0	4.946
regañadientes	3	0	4.946
regalista	3	0	4.946
reflejando	3	0	4.946
refleja	3	0	4.946
refinado	3	0	4.946
redomado	3	0	4.946
rediós	3	0	4.946
recurría	3	0	4.946
recordándole	3	0	4.946
recogerla	3	0	4.946
recluta	3	0	4.946
reasumiendo	3	0	4.946
rasgó	3	0	4.946
rasgaban	3	0	4.946
rasero	3	0	4.946
quintana	3	0	4.946
quebrantada	3	0	4.946
puñadas	3	0	4.946
punzadas	3	0	4.946
pullas	3	0	4.946
puf	3	0	4.946
públicas	3	0	4.946
provinciano	3	0	4.946
providencial	3	0	4.946
propasarse	3	0	4.946
prólogo	3	0	4.946
prohibir	3	0	4.946
profanado	3	0	4.946
procurase	3	0	4.946
procurador	3	0	4.946
privilegio	3	0	4.946
presidía	3	0	4.946
prepararle	3	0	4.946
preocupados	3	0	4.946
prematura	3	0	4.946
predominaba	3	0	4.946
predilección	3	0	4.946
praxíteles	3	0	4.946
postres	3	0	4.946
postergado	3	0	4.946
positivismo	3	0	4.946
pos	3	0	4.946
porteros	3	0	4.946
poniente	3	0	4.946
pomaradas	3	0	4.946
pollastres	3	0	4.946
poetisa	3	0	4.946
poderío	3	0	4.946
poblados	3	0	4.946
pluviales	3	0	4.946
plumero	3	0	4.946
plazuelas	3	0	4.946
plateresco	3	0	4.946
plateas	3	0	4.946
petit	3	0	4.946
petimetre	3	0	4.946
pestillo	3	0	4.946
pese	3	0	4.946
perrero	3	0	4.946
perpendicular	3	0	4.946
perniciosa	3	0	4.946
perífrasis	3	0	4.946
perezosos	3	0	4.946
pequeñeces	3	0	4.946
pellizcaba	3	0	4.946
pelado	3	0	4.946
pegajoso	3	0	4.946
peculiar	3	0	4.946
pecaminosa	3	0	4.946
patos	3	0	4.946
patéticos	3	0	4.946
pasatiempo	3	0	4.946
pasadizo	3	0	4.946
parterres	3	0	4.946
paralelas	3	0	4.946
panurgo	3	0	4.946
panteón	3	0	4.946
panteísmo	3	0	4.946
palmaditas	3	0	4.946
pagaría	3	0	4.946
pagana	3	0	4.946
pabellón	3	0	4.946
otorgó	3	0	4.946
ostentoso	3	0	4.946
ostentosa	3	0	4.946
ostentar	3	0	4.946
órganos	3	0	4.946
ordalías	3	0	4.946
oprimió	3	0	4.946
opinaban	3	0	4.946
ondulantes	3	0	4.946
ondulante	3	0	4.946
olvidito	3	0	4.946
olfatear	3	0	4.946
olfateaba	3	0	4.946
oidor	3	0	4.946
ocultándose	3	0	4.946
ocio	3	0	4.946
obscurecía	3	0	4.946
obligados	3	0	4.946
obligaban	3	0	4.946
objeciones	3	0	4.946
numerosos	3	0	4.946
núcleo	3	0	4.946
notarlo	3	0	4.946
nono	3	0	4.946
neutral	3	0	4.946
negaban	3	0	4.946
narrativa	3	0	4.946
narraba	3	0	4.946
mundanal	3	0	4.946
mordido	3	0	4.946
monumentos	3	0	4.946
monumentales	3	0	4.946
montico	3	0	4.946
montaraces	3	0	4.946
monstruos	3	0	4.946
monótonas	3	0	4.946
monopolio	3	0	4.946
móndame	3	0	4.946
monaguillos	3	0	4.946
molinero	3	0	4.946
mojada	3	0	4.946
mitrado	3	0	4.946
misteriosamente	3	0	4.946
mirase	3	0	4.946
mineros	3	0	4.946
millares	3	0	4.946
milagrosa	3	0	4.946
miga	3	0	4.946
midió	3	0	4.946
miasmas	3	0	4.946
mercader	3	0	4.946
mensuales	3	0	4.946
melunga	3	0	4.946
melancólicos	3	0	4.946
melancólicas	3	0	4.946
mejía	3	0	4.946
mediocritas	3	0	4.946
medían	3	0	4.946
mediaba	3	0	4.946
máxima	3	0	4.946
mater	3	0	4.946
mari	3	0	4.946
mantenían	3	0	4.946
manoseadas	3	0	4.946
manolillo	3	0	4.946
maniquí	3	0	4.946
malvado	3	0	4.946
malhaya	3	0	4.946
majaderos	3	0	4.946
magnate	3	0	4.946
maduro	3	0	4.946
madreselva	3	0	4.946
lumbrera	3	0	4.946
ludibrio	3	0	4.946
lozana	3	0	4.946
lomas	3	0	4.946
lodazal	3	0	4.946
lluvias	3	0	4.946
lid	3	0	4.946
libaciones	3	0	4.946
leyera	3	0	4.946
lascivo	3	0	4.946
lasciami	3	0	4.946
lapsus	3	0	4.946
lanas	3	0	4.946
laderas	3	0	4.946
l	3	0	4.946
justos	3	0	4.946
jurisconsulto	3	0	4.946
jorge	3	0	4.946
jipijapa	3	0	4.946
jactarse	3	0	4.946
irracional	3	0	4.946
iris	3	0	4.946
intratable	3	0	4.946
intersticio	3	0	4.946
insisto	3	0	4.946
inquisidor	3	0	4.946
inquietos	3	0	4.946
inquebrantable	3	0	4.946
innominada	3	0	4.946
ingeniero	3	0	4.946
inexorable	3	0	4.946
inepto	3	0	4.946
indignidad	3	0	4.946
incurable	3	0	4.946
incómoda	3	0	4.946
improper	3	0	4.946
importunos	3	0	4.946
importuna	3	0	4.946
ímpetu	3	0	4.946
imperdonable	3	0	4.946
imaginaria	3	0	4.946
ilustraciones	3	0	4.946
ilustración	3	0	4.946
ilegítimos	3	0	4.946
ídolos	3	0	4.946
huraña	3	0	4.946
huracanes	3	0	4.946
hundir	3	0	4.946
humores	3	0	4.946
hondonada	3	0	4.946
holocausto	3	0	4.946
hipógrifo	3	0	4.946
higiénicas	3	0	4.946
híbrido	3	0	4.946
heroínas	3	0	4.946
halagos	3	0	4.946
hablarla	3	0	4.946
habituales	3	0	4.946
gótica	3	0	4.946
goteras	3	0	4.946
góndola	3	0	4.946
goberna	3	0	4.946
globulus	3	0	4.946
generalizada	3	0	4.946
gaudeamus	3	0	4.946
gangosa	3	0	4.946
gacetillero	3	0	4.946
fulgencia	3	0	4.946
frívolo	3	0	4.946
franjas	3	0	4.946
forzosa	3	0	4.946
folletín	3	0	4.946
fogoso	3	0	4.946
flotando	3	0	4.946
florido	3	0	4.946
flojedad	3	0	4.946
flato	3	0	4.946
fisiológico	3	0	4.946
firmes	3	0	4.946
firmar	3	0	4.946
filosofar	3	0	4.946
figurín	3	0	4.946
fidias	3	0	4.946
fiambres	3	0	4.946
feuillet	3	0	4.946
favorecer	3	0	4.946
fauna	3	0	4.946
fanatizado	3	0	4.946
fabricaba	3	0	4.946
extremosa	3	0	4.946
extensos	3	0	4.946
experto	3	0	4.946
exigido	3	0	4.946
excomunión	3	0	4.946
europeo	3	0	4.946
estrepitosos	3	0	4.946
estrepitosas	3	0	4.946
estío	3	0	4.946
estercolero	3	0	4.946
estanquillo	3	0	4.946
espontáneo	3	0	4.946
esponjas	3	0	4.946
esplendoroso	3	0	4.946
esplendores	3	0	4.946
espiga	3	0	4.946
esperma	3	0	4.946
esparcidas	3	0	4.946
espaldar	3	0	4.946
esgrima	3	0	4.946
escarlata	3	0	4.946
escarabajos	3	0	4.946
esbeltez	3	0	4.946
envidiosos	3	0	4.946
entremeses	3	0	4.946
entregaban	3	0	4.946
entiendan	3	0	4.946
enterrado	3	0	4.946
enternecimientos	3	0	4.946
entenderlo	3	0	4.946
enrique	3	0	4.946
enredaba	3	0	4.946
enguantada	3	0	4.946
engañarle	3	0	4.946
enfriaba	3	0	4.946
encerronas	3	0	4.946
encaramarse	3	0	4.946
encaramado	3	0	4.946
enamoró	3	0	4.946
empuñaba	3	0	4.946
empeñaban	3	0	4.946
empecatada	3	0	4.946
embalsamado	3	0	4.946
ejércitos	3	0	4.946
efímeras	3	0	4.946
educada	3	0	4.946
eclipsado	3	0	4.946
durado	3	0	4.946
duradera	3	0	4.946
dogmas	3	0	4.946
dividían	3	0	4.946
dividía	3	0	4.946
divertir	3	0	4.946
diva	3	0	4.946
dispersaron	3	0	4.946
disparatados	3	0	4.946
disolvente	3	0	4.946
disimulaban	3	0	4.946
discordia	3	0	4.946
directiva	3	0	4.946
diamantes	3	0	4.946
diálogos	3	0	4.946
diagonales	3	0	4.946
desvencijada	3	0	4.946
destellos	3	0	4.946
despidieron	3	0	4.946
desnudas	3	0	4.946
deslumbrante	3	0	4.946
deshonrado	3	0	4.946
deseó	3	0	4.946
desencajado	3	0	4.946
descripción	3	0	4.946
desconfiar	3	0	4.946
desconfiada	3	0	4.946
desaparecían	3	0	4.946
desafiaba	3	0	4.946
deletérea	3	0	4.946
dejadme	3	0	4.946
declamando	3	0	4.946
decisivo	3	0	4.946
curación	3	0	4.946
cumbres	3	0	4.946
cultivo	3	0	4.946
culinario	3	0	4.946
cuaderno	3	0	4.946
crujientes	3	0	4.946
creyese	3	0	4.946
creyentes	3	0	4.946
creyéndome	3	0	4.946
crear	3	0	4.946
costureras	3	0	4.946
cortinaje	3	0	4.946
cortejo	3	0	4.946
corrosiva	3	0	4.946
corresponsal	3	0	4.946
corregía	3	0	4.946
correctas	3	0	4.946
corralada	3	0	4.946
coronados	3	0	4.946
convirtiendo	3	0	4.946
convertirlos	3	0	4.946
conversar	3	0	4.946
contorno	3	0	4.946
contera	3	0	4.946
contemporáneos	3	0	4.946
construía	3	0	4.946
conspirador	3	0	4.946
consolas	3	0	4.946
conociese	3	0	4.946
confusos	3	0	4.946
confesonarios	3	0	4.946
condicionales	3	0	4.946
condenaban	3	0	4.946
concluían	3	0	4.946
concentrada	3	0	4.946
compungido	3	0	4.946
compromete	3	0	4.946
comprimidos	3	0	4.946
compatible	3	0	4.946
comité	3	0	4.946
comidilla	3	0	4.946
cómicas	3	0	4.946
comarca	3	0	4.946
colonos	3	0	4.946
coincidido	3	0	4.946
codiciada	3	0	4.946
clementina	3	0	4.946
ciriales	3	0	4.946
cilicios	3	0	4.946
científicas	3	0	4.946
cid	3	0	4.946
churrigueresca	3	0	4.946
chaparrón	3	0	4.946
cerrazón	3	0	4.946
ceñir	3	0	4.946
censurar	3	0	4.946
censura	3	0	4.946
cenicienta	3	0	4.946
cenaba	3	0	4.946
celosías	3	0	4.946
cebolletas	3	0	4.946
cauce	3	0	4.946
castor	3	0	4.946
cascaciruelas	3	0	4.946
casaderas	3	0	4.946
carrillos	3	0	4.946
carreteras	3	0	4.946
carneros	3	0	4.946
caprichosas	3	0	4.946
cañada	3	0	4.946
canastillo	3	0	4.946
campillo	3	0	4.946
campaneros	3	0	4.946
caminaba	3	0	4.946
calumniar	3	0	4.946
cálices	3	0	4.946
cajero	3	0	4.946
cadete	3	0	4.946
cachipote	3	0	4.946
cábalas	3	0	4.946
burbujas	3	0	4.946
bucólico	3	0	4.946
brutalidad	3	0	4.946
brindando	3	0	4.946
brasa	3	0	4.946
bostezó	3	0	4.946
borrico	3	0	4.946
bordada	3	0	4.946
bonachona	3	0	4.946
bom	3	0	4.946
bofetón	3	0	4.946
bobalicones	3	0	4.946
blusa	3	0	4.946
beneficiados	3	0	4.946
belisario	3	0	4.946
bebían	3	0	4.946
be	3	0	4.946
batín	3	0	4.946
batiendo	3	0	4.946
barragana	3	0	4.946
baroncito	3	0	4.946
bañaba	3	0	4.946
baladí	3	0	4.946
badajo	3	0	4.946
bactriana	3	0	4.946
bacante	3	0	4.946
azulada	3	0	4.946
azotó	3	0	4.946
ayudara	3	0	4.946
audaces	3	0	4.946
aturdían	3	0	4.946
aturde	3	0	4.946
atravesando	3	0	4.946
asustarle	3	0	4.946
asustados	3	0	4.946
áspero	3	0	4.946
asientos	3	0	4.946
ascender	3	0	4.946
artísticos	3	0	4.946
artesones	3	0	4.946
artefacto	3	0	4.946
arrugada	3	0	4.946
arrugaba	3	0	4.946
arrodillarse	3	0	4.946
arriesgar	3	0	4.946
arrastraban	3	0	4.946
arrancaban	3	0	4.946
aromas	3	0	4.946
armeros	3	0	4.946
armazón	3	0	4.946
aquelarre	3	0	4.946
aplazar	3	0	4.946
apasionados	3	0	4.946
antiquísimas	3	0	4.946
antesala	3	0	4.946
anguloso	3	0	4.946
angelina	3	0	4.946
anemia	3	0	4.946
ancas	3	0	4.946
anaqueles	3	0	4.946
análogas	3	0	4.946
anacronismos	3	0	4.946
amontonados	3	0	4.946
amontonada	3	0	4.946
ambicioso	3	0	4.946
amarle	3	0	4.946
alrededores	3	0	4.946
almohadones	3	0	4.946
almíbares	3	0	4.946
aleteo	3	0	4.946
alemana	3	0	4.946
alegorías	3	0	4.946
alcaravanes	3	0	4.946
agregada	3	0	4.946
agolpaban	3	0	4.946
agapita	3	0	4.946
afeminado	3	0	4.946
adulaba	3	0	4.946
adoradores	3	0	4.946
adorador	3	0	4.946
admitido	3	0	4.946
acólitos	3	0	4.946
acendrado	3	0	4.946
abundantes	3	0	4.946
abstracto	3	0	4.946
abstracta	3	0	4.946
absorbente	3	0	4.946
ábside	3	0	4.946
abrochó	3	0	4.946
abolengo	3	0	4.946
aberraciones	3	0	4.946
abandonarle	3	0	4.946
abandonaban	3	0	4.946
puro	44	34	4.945
veinticinco	5	18	4.938
suelto	5	18	4.938
quedar	5	18	4.938
patas	5	18	4.938
echarse	5	18	4.938
dichoso	5	18	4.938
orden	38	75	4.919
imaginar	8	24	4.905
humanas	8	24	4.905
criado	8	24	4.905
pasan	6	20	4.889
decoro	6	20	4.889
preparaba	17	9	4.875
largos	17	9	4.875
íntima	17	9	4.875
indignación	17	9	4.875
contenerse	17	9	4.875
capricho	17	9	4.875
ayer	30	62	4.860
viveza	2	11	4.833
viciosa	2	11	4.833
saque	2	11	4.833
recelo	2	11	4.833
quieto	2	11	4.833
querías	2	11	4.833
pega	2	11	4.833
parroquianos	2	11	4.833
miro	2	11	4.833
harto	2	11	4.833
gustaban	2	11	4.833
guitarra	2	11	4.833
formando	2	11	4.833
enseñar	2	11	4.833
ejército	2	11	4.833
distinguir	2	11	4.833
dispuso	2	11	4.833
dichas	2	11	4.833
decencia	2	11	4.833
dato	2	11	4.833
charlando	2	11	4.833
admirables	2	11	4.833
útil	9	3	4.805
tocaban	9	3	4.805
sienes	9	3	4.805
rodeaban	9	3	4.805
respiró	9	3	4.805
respiraba	9	3	4.805
reflexiones	9	3	4.805
recursos	9	3	4.805
pulcritud	9	3	4.805
paseando	9	3	4.805
oprimía	9	3	4.805
obligó	9	3	4.805
negó	9	3	4.805
frecuentes	9	3	4.805
flaco	9	3	4.805
encerraba	9	3	4.805
embozo	9	3	4.805
doradas	9	3	4.805
damasco	9	3	4.805
consentía	9	3	4.805
conquistar	9	3	4.805
comparación	9	3	4.805
blanda	9	3	4.805
audacia	9	3	4.805
asistir	9	3	4.805
activa	9	3	4.805
quiera	44	84	4.777
queda	13	33	4.751
lleva	17	40	4.735
coger	17	40	4.735
busca	17	40	4.735
milagro	18	10	4.722
echar	29	60	4.722
amable	18	10	4.722
ahí	71	125	4.713
atrás	62	53	4.681
sagrado	13	6	4.660
obreros	13	6	4.660
liberales	13	6	4.660
indispensable	13	6	4.660
escribía	13	6	4.660
escondido	13	6	4.660
azules	13	6	4.660
arrojaba	13	6	4.660
amabilidad	13	6	4.660
pareja	12	31	4.652
yerta	0	4	4.618
yeciones	0	4	4.618
yeción	0	4	4.618
vus	0	4	4.618
volcán	0	4	4.618
vocablo	0	4	4.618
vínole	0	4	4.618
vinieran	0	4	4.618
vimos	0	4	4.618
viajar	0	4	4.618
viajante	0	4	4.618
verbi	0	4	4.618
vente	0	4	4.618
vengaré	0	4	4.618
veneración	0	4	4.618
vendida	0	4	4.618
veíase	0	4	4.618
vagar	0	4	4.618
vaciado	0	4	4.618
uvas	0	4	4.618
ultramar	0	4	4.618
tuvieras	0	4	4.618
turco	0	4	4.618
tun	0	4	4.618
tufo	0	4	4.618
trozo	0	4	4.618
tropezaron	0	4	4.618
tropas	0	4	4.618
trombón	0	4	4.618
trocaba	0	4	4.618
triunfar	0	4	4.618
tristísima	0	4	4.618
trinqué	0	4	4.618
travieso	0	4	4.618
tratarte	0	4	4.618
trataré	0	4	4.618
tratan	0	4	4.618
trastornos	0	4	4.618
trastornaba	0	4	4.618
trastamara	0	4	4.618
trapitos	0	4	4.618
trapisondas	0	4	4.618
tranquilizarla	0	4	4.618
tragaderas	0	4	4.618
tráete	0	4	4.618
trabaje	0	4	4.618
tomes	0	4	4.618
tocaya	0	4	4.618
tocata	0	4	4.618
tocara	0	4	4.618
tiernas	0	4	4.618
tétrica	0	4	4.618
terrorífica	0	4	4.618
tempranito	0	4	4.618
tararí	0	4	4.618
tantísimos	0	4	4.618
talonario	0	4	4.618
sustancias	0	4	4.618
suspicaz	0	4	4.618
suspendiendo	0	4	4.618
suizo	0	4	4.618
suegros	0	4	4.618
sudorosa	0	4	4.618
sosteniendo	0	4	4.618
sosiégate	0	4	4.618
sortijillas	0	4	4.618
someter	0	4	4.618
solfa	0	4	4.618
sofía	0	4	4.618
sodio	0	4	4.618
sobrante	0	4	4.618
sirviera	0	4	4.618
sintiéndose	0	4	4.618
sillita	0	4	4.618
significan	0	4	4.618
significación	0	4	4.618
severamente	0	4	4.618
serrano	0	4	4.618
serrana	0	4	4.618
serías	0	4	4.618
seríamos	0	4	4.618
seductora	0	4	4.618
secándose	0	4	4.618
satanás	0	4	4.618
sáqueme	0	4	4.618
samaniegos	0	4	4.618
saltara	0	4	4.618
sablazo	0	4	4.618
rótulos	0	4	4.618
ropita	0	4	4.618
ridiculez	0	4	4.618
revolviéndose	0	4	4.618
revolcándose	0	4	4.618
reventar	0	4	4.618
reveló	0	4	4.618
retiraron	0	4	4.618
retirándose	0	4	4.618
reticencia	0	4	4.618
resistiéndose	0	4	4.618
resiste	0	4	4.618
repartió	0	4	4.618
renegar	0	4	4.618
remojo	0	4	4.618
religiosamente	0	4	4.618
relacionadas	0	4	4.618
reías	0	4	4.618
rehízo	0	4	4.618
regularidad	0	4	4.618
refrescaba	0	4	4.618
refiero	0	4	4.618
rédito	0	4	4.618
redacciones	0	4	4.618
recomiendo	0	4	4.618
recomendándole	0	4	4.618
recoge	0	4	4.618
recocho	0	4	4.618
reclusa	0	4	4.618
rechazo	0	4	4.618
quitarán	0	4	4.618
quitara	0	4	4.618
quercus	0	4	4.618
quédese	0	4	4.618
purificación	0	4	4.618
purifica	0	4	4.618
puntual	0	4	4.618
publicaciones	0	4	4.618
pronunciamiento	0	4	4.618
pronunciación	0	4	4.618
prontitud	0	4	4.618
prolongar	0	4	4.618
produzca	0	4	4.618
produciéndole	0	4	4.618
prodigios	0	4	4.618
pretenden	0	4	4.618
presurosa	0	4	4.618
prestó	0	4	4.618
preguntándole	0	4	4.618
pregúntale	0	4	4.618
preciosísima	0	4	4.618
prácticamente	0	4	4.618
poseedor	0	4	4.618
pondrán	0	4	4.618
pondrá	0	4	4.618
pollas	0	4	4.618
podías	0	4	4.618
plencia	0	4	4.618
platerías	0	4	4.618
placidez	0	4	4.618
plácemes	0	4	4.618
pinto	0	4	4.618
pierda	0	4	4.618
piénselo	0	4	4.618
picoteando	0	4	4.618
picarona	0	4	4.618
pesó	0	4	4.618
pescadores	0	4	4.618
perverso	0	4	4.618
perplejidad	0	4	4.618
peripecia	0	4	4.618
perdónala	0	4	4.618
perdis	0	4	4.618
pepito	0	4	4.618
pelea	0	4	4.618
peinarse	0	4	4.618
pegarme	0	4	4.618
pegándose	0	4	4.618
pedernal	0	4	4.618
patillas	0	4	4.618
patético	0	4	4.618
parrafito	0	4	4.618
parola	0	4	4.618
parentescos	0	4	4.618
pararon	0	4	4.618
paquetito	0	4	4.618
papelera	0	4	4.618
pandereta	0	4	4.618
pagarés	0	4	4.618
pachorra	0	4	4.618
oscuros	0	4	4.618
organización	0	4	4.618
orgánica	0	4	4.618
ofrecimientos	0	4	4.618
ocurriole	0	4	4.618
obtenido	0	4	4.618
obrera	0	4	4.618
nuevamente	0	4	4.618
noté	0	4	4.618
notando	0	4	4.618
nodriza	0	4	4.618
niñita	0	4	4.618
niegues	0	4	4.618
neófita	0	4	4.618
negarás	0	4	4.618
narcissus	0	4	4.618
nacidos	0	4	4.618
nacen	0	4	4.618
mus	0	4	4.618
muriera	0	4	4.618
mujeronas	0	4	4.618
mugidos	0	4	4.618
mugido	0	4	4.618
mudanzas	0	4	4.618
mostrábase	0	4	4.618
moñas	0	4	4.618
monas	0	4	4.618
molido	0	4	4.618
molestaban	0	4	4.618
modistas	0	4	4.618
misericordia	0	4	4.618
mírela	0	4	4.618
miré	0	4	4.618
mírala	0	4	4.618
mirábale	0	4	4.618
mico	0	4	4.618
metro	0	4	4.618
metidos	0	4	4.618
mercurio	0	4	4.618
mentar	0	4	4.618
memo	0	4	4.618
mejoró	0	4	4.618
matute	0	4	4.618
matarte	0	4	4.618
marquesas	0	4	4.618
marimorena	0	4	4.618
mañanita	0	4	4.618
manifestarse	0	4	4.618
manguito	0	4	4.618
malito	0	4	4.618
maldecido	0	4	4.618
maduras	0	4	4.618
madrecita	0	4	4.618
machacárselo	0	4	4.618
machacando	0	4	4.618
llorente	0	4	4.618
llevaremos	0	4	4.618
llevara	0	4	4.618
llevándole	0	4	4.618
llamados	0	4	4.618
llamábase	0	4	4.618
lívida	0	4	4.618
linda	0	4	4.618
leona	0	4	4.618
lavapiés	0	4	4.618
láudano	0	4	4.618
lápida	0	4	4.618
lagrimita	0	4	4.618
juntamente	0	4	4.618
juiciosa	0	4	4.618
irías	0	4	4.618
interlocutora	0	4	4.618
interiormente	0	4	4.618
intereso	0	4	4.618
intentaba	0	4	4.618
instruirse	0	4	4.618
inseguro	0	4	4.618
inmuebles	0	4	4.618
ingeniosa	0	4	4.618
individual	0	4	4.618
indicación	0	4	4.618
incorporose	0	4	4.618
inclinose	0	4	4.618
inclinaciones	0	4	4.618
inciso	0	4	4.618
inauguración	0	4	4.618
impulsaba	0	4	4.618
importe	0	4	4.618
imparcialidad	0	4	4.618
igualmente	0	4	4.618
ignominias	0	4	4.618
humedecieron	0	4	4.618
huerfanito	0	4	4.618
huchas	0	4	4.618
hortaleza	0	4	4.618
homicidio	0	4	4.618
hilaridad	0	4	4.618
herrero	0	4	4.618
heces	0	4	4.618
hartarse	0	4	4.618
hartaba	0	4	4.618
harta	0	4	4.618
hambres	0	4	4.618
hallarse	0	4	4.618
gusanillo	0	4	4.618
guisado	0	4	4.618
guerras	0	4	4.618
guardarropa	0	4	4.618
guardan	0	4	4.618
gruñidos	0	4	4.618
gresca	0	4	4.618
greñas	0	4	4.618
granuja	0	4	4.618
grandiosa	0	4	4.618
gozosos	0	4	4.618
gori	0	4	4.618
gobierna	0	4	4.618
gigantea	0	4	4.618
generala	0	4	4.618
gemidos	0	4	4.618
ganitas	0	4	4.618
fulgor	0	4	4.618
frunció	0	4	4.618
frunciendo	0	4	4.618
fraude	0	4	4.618
francos	0	4	4.618
forro	0	4	4.618
formarse	0	4	4.618
flandes	0	4	4.618
fingiéndose	0	4	4.618
fíjese	0	4	4.618
fijando	0	4	4.618
figurando	0	4	4.618
fideos	0	4	4.618
fiar	0	4	4.618
ferrolana	0	4	4.618
fatuidad	0	4	4.618
farsante	0	4	4.618
fardo	0	4	4.618
faltara	0	4	4.618
faetón	0	4	4.618
extravagancia	0	4	4.618
expresivo	0	4	4.618
expresiva	0	4	4.618
existir	0	4	4.618
existiera	0	4	4.618
exhaló	0	4	4.618
exhalación	0	4	4.618
excusas	0	4	4.618
etiquetas	0	4	4.618
estruendo	0	4	4.618
estirón	0	4	4.618
estipendio	0	4	4.618
estampía	0	4	4.618
establecimientos	0	4	4.618
esquelita	0	4	4.618
espontaneidad	0	4	4.618
espiritistas	0	4	4.618
escurría	0	4	4.618
escondrijo	0	4	4.618
escobas	0	4	4.618
escalerilla	0	4	4.618
equivocaba	0	4	4.618
epiléptica	0	4	4.618
envidio	0	4	4.618
entusiasmos	0	4	4.618
entregas	0	4	4.618
entidad	0	4	4.618
entenderá	0	4	4.618
enredo	0	4	4.618
enojada	0	4	4.618
engañé	0	4	4.618
engañarme	0	4	4.618
encerrarme	0	4	4.618
encerrarle	0	4	4.618
empujándole	0	4	4.618
emplearía	0	4	4.618
empeñan	0	4	4.618
elogió	0	4	4.618
eches	0	4	4.618
echarme	0	4	4.618
durara	0	4	4.618
duquesa	0	4	4.618
duérmete	0	4	4.618
drogas	0	4	4.618
dorotea	0	4	4.618
donnell	0	4	4.618
donativos	0	4	4.618
dispongo	0	4	4.618
dispone	0	4	4.618
disminuir	0	4	4.618
discurro	0	4	4.618
directora	0	4	4.618
dineros	0	4	4.618
dilo	0	4	4.618
diligencias	0	4	4.618
dilema	0	4	4.618
díjome	0	4	4.618
diciéndolo	0	4	4.618
devuelve	0	4	4.618
deudor	0	4	4.618
detenerla	0	4	4.618
detalle	0	4	4.618
desusado	0	4	4.618
desusada	0	4	4.618
desplegaban	0	4	4.618
desplegaba	0	4	4.618
despierte	0	4	4.618
despachó	0	4	4.618
despabilado	0	4	4.618
desmejorada	0	4	4.618
desmedido	0	4	4.618
desgraciadamente	0	4	4.618
deseamos	0	4	4.618
desdichada	0	4	4.618
desconsolado	0	4	4.618
desconsolada	0	4	4.618
desconcertado	0	4	4.618
descomponerse	0	4	4.618
derivativo	0	4	4.618
demostraciones	0	4	4.618
debieran	0	4	4.618
dañada	0	4	4.618
danzante	0	4	4.618
dámaso	0	4	4.618
cultivaba	0	4	4.618
cuchilleros	0	4	4.618
cuchichearon	0	4	4.618
cuantito	0	4	4.618
crío	0	4	4.618
crines	0	4	4.618
criando	0	4	4.618
criaba	0	4	4.618
cretonas	0	4	4.618
crespón	0	4	4.618
costra	0	4	4.618
correcciones	0	4	4.618
corpus	0	4	4.618
coñac	0	4	4.618
convido	0	4	4.618
convéncete	0	4	4.618
convencerás	0	4	4.618
contrarias	0	4	4.618
contante	0	4	4.618
contándole	0	4	4.618
contados	0	4	4.618
constituye	0	4	4.618
consolidado	0	4	4.618
consiento	0	4	4.618
consejera	0	4	4.618
confesora	0	4	4.618
condenadas	0	4	4.618
concerniente	0	4	4.618
comunicarle	0	4	4.618
comunica	0	4	4.618
comprarle	0	4	4.618
comprada	0	4	4.618
componían	0	4	4.618
completar	0	4	4.618
completaban	0	4	4.618
compasiva	0	4	4.618
compararse	0	4	4.618
comieron	0	4	4.618
combinados	0	4	4.618
combinado	0	4	4.618
coleta	0	4	4.618
col	0	4	4.618
cogerte	0	4	4.618
cogeré	0	4	4.618
cobranza	0	4	4.618
cobra	0	4	4.618
cifras	0	4	4.618
chuletita	0	4	4.618
chiquito	0	4	4.618
chiquillas	0	4	4.618
chiflada	0	4	4.618
chaveta	0	4	4.618
champagne	0	4	4.618
chacota	0	4	4.618
casita	0	4	4.618
casarredonda	0	4	4.618
carretillas	0	4	4.618
carnero	0	4	4.618
cargaba	0	4	4.618
carcelera	0	4	4.618
caramelos	0	4	4.618
carambita	0	4	4.618
cañizares	0	4	4.618
cantinela	0	4	4.618
cantería	0	4	4.618
canso	0	4	4.618
canalla	0	4	4.618
camorra	0	4	4.618
calzones	0	4	4.618
callose	0	4	4.618
callados	0	4	4.618
calladita	0	4	4.618
calixta	0	4	4.618
calcula	0	4	4.618
calaverada	0	4	4.618
cacharro	0	4	4.618
buscas	0	4	4.618
bulle	0	4	4.618
bromazo	0	4	4.618
bringas	0	4	4.618
borrado	0	4	4.618
boquita	0	4	4.618
bonaparte	0	4	4.618
bolsín	0	4	4.618
biberón	0	4	4.618
biarritz	0	4	4.618
besándola	0	4	4.618
benévola	0	4	4.618
bautismo	0	4	4.618
barreño	0	4	4.618
barrenderos	0	4	4.618
baratijas	0	4	4.618
bandera	0	4	4.618
bálsamo	0	4	4.618
bajaré	0	4	4.618
babero	0	4	4.618
babas	0	4	4.618
azorado	0	4	4.618
aversión	0	4	4.618
auxiliar	0	4	4.618
austria	0	4	4.618
atrozmente	0	4	4.618
atrevida	0	4	4.618
atractivos	0	4	4.618
atizó	0	4	4.618
atavío	0	4	4.618
asustarse	0	4	4.618
aspirando	0	4	4.618
asista	0	4	4.618
asimilación	0	4	4.618
ascendiente	0	4	4.618
articular	0	4	4.618
arrepentidas	0	4	4.618
arman	0	4	4.618
arguyó	0	4	4.618
argumentación	0	4	4.618
apunta	0	4	4.618
aptitudes	0	4	4.618
aprenda	0	4	4.618
apostolado	0	4	4.618
apetecer	0	4	4.618
añadidura	0	4	4.618
anteanoche	0	4	4.618
animalito	0	4	4.618
anécdotas	0	4	4.618
anaquelería	0	4	4.618
alfonsismo	0	4	4.618
alegrías	0	4	4.618
alegraría	0	4	4.618
alborotados	0	4	4.618
alabardero	0	4	4.618
ajetreo	0	4	4.618
aguárdese	0	4	4.618
agradecidísimo	0	4	4.618
agitó	0	4	4.618
afirmativo	0	4	4.618
adúuultera	0	4	4.618
adrede	0	4	4.618
adoro	0	4	4.618
administrativa	0	4	4.618
adefesio	0	4	4.618
acuesto	0	4	4.618
actriz	0	4	4.618
acreedor	0	4	4.618
acostumbrando	0	4	4.618
acordé	0	4	4.618
acordar	0	4	4.618
acordábase	0	4	4.618
acometido	0	4	4.618
acometer	0	4	4.618
acariciándole	0	4	4.618
acabadita	0	4	4.618
abundaba	0	4	4.618
abuelita	0	4	4.618
abrazándola	0	4	4.618
veréis	1	8	4.605
trago	1	8	4.605
sujetos	1	8	4.605
sienten	1	8	4.605
siéntate	1	8	4.605
salado	1	8	4.605
sacaron	1	8	4.605
reñir	1	8	4.605
redentor	1	8	4.605
rabiar	1	8	4.605
próximas	1	8	4.605
problemas	1	8	4.605
poníase	1	8	4.605
perdí	1	8	4.605
pasmada	1	8	4.605
panderetas	1	8	4.605
onda	1	8	4.605
ofendida	1	8	4.605
novios	1	8	4.605
mostró	1	8	4.605
misántropo	1	8	4.605
menuda	1	8	4.605
lustre	1	8	4.605
jota	1	8	4.605
irás	1	8	4.605
inquieta	1	8	4.605
horteras	1	8	4.605
haberme	1	8	4.605
guardando	1	8	4.605
gordos	1	8	4.605
generoso	1	8	4.605
fraternal	1	8	4.605
estarás	1	8	4.605
económica	1	8	4.605
dueña	1	8	4.605
dichosos	1	8	4.605
desasosiego	1	8	4.605
dentadura	1	8	4.605
comentario	1	8	4.605
clarito	1	8	4.605
castiga	1	8	4.605
cabra	1	8	4.605
boticario	1	8	4.605
basilisco	1	8	4.605
bajito	1	8	4.605
bacalao	1	8	4.605
aproximaba	1	8	4.605
aprende	1	8	4.605
apartado	1	8	4.605
alzó	1	8	4.605
abandonó	1	8	4.605
poco	459	512	4.591
niña	87	80	4.568
impresión	11	29	4.559
cogido	11	29	4.559
cuánto	25	53	4.548
mar	52	43	4.526
loca	52	43	4.526
trabajando	3	13	4.511
tocante	3	13	4.511
tirando	3	13	4.511
temores	3	13	4.511
quitarle	3	13	4.511
práctico	3	13	4.511
pondría	3	13	4.511
madrugada	3	13	4.511
guardar	3	13	4.511
faltas	3	13	4.511
compañeras	3	13	4.511
benevolencia	3	13	4.511
abra	3	13	4.511
principal	50	41	4.502
cuentas	15	36	4.497
tristezas	20	12	4.486
secretos	20	12	4.486
movimientos	20	12	4.486
faldas	20	12	4.486
padres	10	27	4.474
cincuenta	10	27	4.474
ustedes	83	76	4.461
señorito	45	36	4.460
debo	38	29	4.458
imaginación	39	30	4.453
vago	14	7	4.428
raso	14	7	4.428
planes	14	7	4.428
acudir	14	7	4.428
ley	24	51	4.412
otro	303	453	4.409
mismos	21	13	4.395
extraño	21	13	4.395
decirle	29	59	4.362
traigo	4	15	4.354
ponerle	4	15	4.354
pescuezo	4	15	4.354
nació	4	15	4.354
lista	4	15	4.354
herida	4	15	4.354
formaban	4	15	4.354
comprendo	4	15	4.354
trazas	10	4	4.353
tabla	10	4	4.353
senderos	10	4	4.353
ruina	10	4	4.353
recreo	10	4	4.353
preparar	10	4	4.353
plantas	10	4	4.353
percal	10	4	4.353
llovía	10	4	4.353
invencible	10	4	4.353
ignoraba	10	4	4.353
dormirse	10	4	4.353
dignos	10	4	4.353
conservar	10	4	4.353
conseguía	10	4	4.353
borrachos	10	4	4.353
aficionado	10	4	4.353
adoraba	10	4	4.353
tiendas	8	23	4.337
pillo	8	23	4.337
mucha	64	113	4.331
mandaba	22	14	4.318
vergonzoso	7	2	4.315
tormenta	7	2	4.315
torcida	7	2	4.315
toldo	7	2	4.315
sigilo	7	2	4.315
resuelta	7	2	4.315
respetables	7	2	4.315
resolver	7	2	4.315
reflexionar	7	2	4.315
rápidas	7	2	4.315
puerto	7	2	4.315
posturas	7	2	4.315
pardas	7	2	4.315
parda	7	2	4.315
oposición	7	2	4.315
negarse	7	2	4.315
memorias	7	2	4.315
maravillas	7	2	4.315
íntimas	7	2	4.315
intelectual	7	2	4.315
insustancial	7	2	4.315
idolatría	7	2	4.315
gloriosa	7	2	4.315
evidencia	7	2	4.315
estragos	7	2	4.315
entregarse	7	2	4.315
dirigía	7	2	4.315
cordel	7	2	4.315
consagrada	7	2	4.315
confesado	7	2	4.315
cazar	7	2	4.315
campanario	7	2	4.315
caldo	7	2	4.315
bultos	7	2	4.315
batallas	7	2	4.315
avergonzada	7	2	4.315
arruinado	7	2	4.315
aplicaba	7	2	4.315
animó	7	2	4.315
americanos	7	2	4.315
alborotar	7	2	4.315
aguda	7	2	4.315
aficionados	7	2	4.315
admite	7	2	4.315
acompañaban	7	2	4.315
acercaban	7	2	4.315
abismos	7	2	4.315
sostener	7	21	4.292
edificio	7	21	4.292
andando	7	21	4.292
tontos	5	17	4.286
reja	5	17	4.286
pa	5	17	4.286
oyeron	5	17	4.286
bola	5	17	4.286
vara	6	19	4.272
reserva	6	19	4.272
pudiendo	6	19	4.272
caminos	6	19	4.272
ello	87	81	4.257
acordaba	23	15	4.253
singular	15	8	4.245
inmóvil	15	8	4.245
ilusiones	15	8	4.245
conversaciones	15	8	4.245
consistía	15	8	4.245
altas	15	8	4.245
mujeres	73	126	4.221
sereno	24	16	4.197
ningún	42	79	4.197
palabras	117	190	4.162
punta	12	30	4.161
valor	55	47	4.159
sublime	25	17	4.150
tuviera	22	47	4.140
terrible	26	18	4.110
ramas	26	18	4.110
virtuosa	16	9	4.097
semejantes	16	9	4.097
merecía	16	9	4.097
estudiante	16	9	4.097
escenas	16	9	4.097
abiertos	16	9	4.097
alma	285	309	4.089
a	7535	9945	4.063
hacían	49	41	4.060
pensando	67	60	4.051
balcones	28	20	4.048
figura	47	39	4.033
vientre	11	5	4.032
tierna	11	5	4.032
sierra	11	5	4.032
seductor	11	5	4.032
santas	11	5	4.032
prójimo	11	5	4.032
ganar	11	5	4.032
filas	11	5	4.032
extendía	11	5	4.032
excursiones	11	5	4.032
escasa	11	5	4.032
disciplina	11	5	4.032
convencido	11	5	4.032
continuar	11	5	4.032
católico	11	5	4.032
católica	11	5	4.032
ansias	11	5	4.032
agradecía	11	5	4.032
trayendo	2	10	4.028
tipos	2	10	4.028
telas	2	10	4.028
suelen	2	10	4.028
prestaba	2	10	4.028
pata	2	10	4.028
mirándole	2	10	4.028
menudencias	2	10	4.028
llamaron	2	10	4.028
inmediato	2	10	4.028
hayas	2	10	4.028
guardo	2	10	4.028
entro	2	10	4.028
entretenía	2	10	4.028
efusión	2	10	4.028
cuba	2	10	4.028
condenado	2	10	4.028
borde	2	10	4.028
almacén	2	10	4.028
letras	29	21	4.024
fortuna	29	21	4.024
eso	400	446	4.024
dios	311	461	4.023
cinco	45	83	4.012
mayores	30	22	4.005
interior	21	45	4.005
andaba	18	40	4.004
encontró	44	36	3.997
gracias	36	69	3.994
zapateros	5	1	3.991
xv	5	1	3.991
victorias	5	1	3.991
vericuetos	5	1	3.991
vendido	5	1	3.991
vencía	5	1	3.991
traidores	5	1	3.991
tradición	5	1	3.991
tocarle	5	1	3.991
tarima	5	1	3.991
taciturno	5	1	3.991
superstición	5	1	3.991
sosa	5	1	3.991
sorprender	5	1	3.991
solicitar	5	1	3.991
solemnidades	5	1	3.991
sobresaltos	5	1	3.991
serviría	5	1	3.991
señoril	5	1	3.991
santuario	5	1	3.991
saltos	5	1	3.991
sable	5	1	3.991
rugió	5	1	3.991
respetado	5	1	3.991
resortes	5	1	3.991
resorte	5	1	3.991
resistió	5	1	3.991
representando	5	1	3.991
representan	5	1	3.991
quo	5	1	3.991
punzantes	5	1	3.991
pulcra	5	1	3.991
provincial	5	1	3.991
progresos	5	1	3.991
presta	5	1	3.991
preparaban	5	1	3.991
prefiere	5	1	3.991
predicaba	5	1	3.991
pisaba	5	1	3.991
perderse	5	1	3.991
perderla	5	1	3.991
pendían	5	1	3.991
peligrosas	5	1	3.991
parroquias	5	1	3.991
parecidos	5	1	3.991
pagaban	5	1	3.991
oso	5	1	3.991
oprimían	5	1	3.991
olla	5	1	3.991
obedecían	5	1	3.991
notaban	5	1	3.991
non	5	1	3.991
mujercita	5	1	3.991
morían	5	1	3.991
mordió	5	1	3.991
misteriosos	5	1	3.991
mismísimo	5	1	3.991
miércoles	5	1	3.991
metros	5	1	3.991
matices	5	1	3.991
mareo	5	1	3.991
luciendo	5	1	3.991
levantaban	5	1	3.991
leñador	5	1	3.991
interesado	5	1	3.991
insolencia	5	1	3.991
insinuaciones	5	1	3.991
inexpugnable	5	1	3.991
incidente	5	1	3.991
inagotable	5	1	3.991
importaban	5	1	3.991
ilustrísimo	5	1	3.991
horroroso	5	1	3.991
gutural	5	1	3.991
griego	5	1	3.991
grabados	5	1	3.991
gentil	5	1	3.991
gallos	5	1	3.991
fumaba	5	1	3.991
fogón	5	1	3.991
faltan	5	1	3.991
exijo	5	1	3.991
excesos	5	1	3.991
exagerada	5	1	3.991
esplendor	5	1	3.991
esparcidos	5	1	3.991
escandalosas	5	1	3.991
encerró	5	1	3.991
edificante	5	1	3.991
echarlo	5	1	3.991
dulzuras	5	1	3.991
dominado	5	1	3.991
doctora	5	1	3.991
dobló	5	1	3.991
disimuladamente	5	1	3.991
dirían	5	1	3.991
difuntos	5	1	3.991
dictador	5	1	3.991
devorar	5	1	3.991
desnudez	5	1	3.991
desesperada	5	1	3.991
desengaño	5	1	3.991
descargó	5	1	3.991
descansaba	5	1	3.991
curaba	5	1	3.991
cuevas	5	1	3.991
convite	5	1	3.991
convirtió	5	1	3.991
convertían	5	1	3.991
contornos	5	1	3.991
consideraban	5	1	3.991
conocerlo	5	1	3.991
cerezas	5	1	3.991
ceñía	5	1	3.991
cenas	5	1	3.991
caserones	5	1	3.991
cartuchos	5	1	3.991
carmesí	5	1	3.991
callejas	5	1	3.991
bello	5	1	3.991
bastó	5	1	3.991
ayudarle	5	1	3.991
astros	5	1	3.991
armiño	5	1	3.991
arañas	5	1	3.991
apuntando	5	1	3.991
aprobación	5	1	3.991
aplausos	5	1	3.991
antigüedad	5	1	3.991
anteojo	5	1	3.991
anís	5	1	3.991
alababan	5	1	3.991
admitió	5	1	3.991
acacias	5	1	3.991
absolución	5	1	3.991
gato	31	23	3.989
lloraba	17	10	3.977
fuesen	17	10	3.977
esperar	32	24	3.977
ejemplo	41	33	3.971
puesto	69	119	3.967
niñas	35	27	3.957
andar	26	53	3.948
trabajar	14	33	3.926
ministro	18	11	3.878
cerrado	18	11	3.878
blancos	18	11	3.878
vela	9	24	3.871
sorpresa	9	24	3.871
pide	9	24	3.871
decirse	9	24	3.871
bendito	9	24	3.871
asombro	9	24	3.871
cielo	102	99	3.848
viejo	57	50	3.818
iría	19	12	3.797
instinto	19	12	3.797
sospechar	12	6	3.796
saltaba	12	6	3.796
religiosos	12	6	3.796
parecida	12	6	3.796
muda	12	6	3.796
leguas	12	6	3.796
incapaz	12	6	3.796
espíritus	12	6	3.796
acababan	12	6	3.796
casado	8	22	3.791
repito	3	12	3.787
escritorio	3	12	3.787
distinta	3	12	3.787
dieran	3	12	3.787
dejara	3	12	3.787
compromiso	3	12	3.787
colegio	3	12	3.787
cesta	3	12	3.787
andan	3	12	3.787
ajeno	3	12	3.787
zarzuela	8	3	3.762
tenue	8	3	3.762
tembló	8	3	3.762
sorda	8	3	3.762
seña	8	3	3.762
sacramentos	8	3	3.762
románticas	8	3	3.762
revelaciones	8	3	3.762
pudiese	8	3	3.762
precauciones	8	3	3.762
positiva	8	3	3.762
piadoso	8	3	3.762
perdiz	8	3	3.762
palmo	8	3	3.762
mueble	8	3	3.762
mediante	8	3	3.762
máquinas	8	3	3.762
literatura	8	3	3.762
juramento	8	3	3.762
jugaban	8	3	3.762
jinete	8	3	3.762
interrumpía	8	3	3.762
infinita	8	3	3.762
hilos	8	3	3.762
fraile	8	3	3.762
favores	8	3	3.762
escocesa	8	3	3.762
enaguas	8	3	3.762
diferente	8	3	3.762
desconfianza	8	3	3.762
delgado	8	3	3.762
continente	8	3	3.762
cómplice	8	3	3.762
claustro	8	3	3.762
cadena	8	3	3.762
baño	8	3	3.762
aspiraba	8	3	3.762
aprovechar	8	3	3.762
antojó	8	3	3.762
anduvo	8	3	3.762
andadas	8	3	3.762
actual	8	3	3.762
parecido	16	36	3.744
único	68	62	3.740
doce	27	54	3.736
servir	20	13	3.729
principios	7	20	3.725
maestra	7	20	3.725
mis	63	109	3.706
vuestro	1	7	3.701
vosotros	1	7	3.701
vocablos	1	7	3.701
vigilar	1	7	3.701
váyase	1	7	3.701
tratos	1	7	3.701
tocada	1	7	3.701
tendrían	1	7	3.701
tendrán	1	7	3.701
teatral	1	7	3.701
simplemente	1	7	3.701
serle	1	7	3.701
serie	1	7	3.701
sagunto	1	7	3.701
ropas	1	7	3.701
reputación	1	7	3.701
repitiendo	1	7	3.701
reparar	1	7	3.701
reírse	1	7	3.701
redención	1	7	3.701
reconociendo	1	7	3.701
puñalada	1	7	3.701
puñados	1	7	3.701
protestante	1	7	3.701
probarlo	1	7	3.701
pon	1	7	3.701
perrerías	1	7	3.701
permanecía	1	7	3.701
pegarle	1	7	3.701
paseíto	1	7	3.701
parta	1	7	3.701
pantalla	1	7	3.701
padece	1	7	3.701
ocuparse	1	7	3.701
nieves	1	7	3.701
moño	1	7	3.701
merino	1	7	3.701
lozoya	1	7	3.701
llevada	1	7	3.701
introducir	1	7	3.701
iluminado	1	7	3.701
hágame	1	7	3.701
hacerte	1	7	3.701
hablándole	1	7	3.701
guardias	1	7	3.701
grata	1	7	3.701
gonzález	1	7	3.701
generosidad	1	7	3.701
feroz	1	7	3.701
faltando	1	7	3.701
examinar	1	7	3.701
espantosa	1	7	3.701
entrara	1	7	3.701
enmienda	1	7	3.701
enfado	1	7	3.701
encuentras	1	7	3.701
empuje	1	7	3.701
echándole	1	7	3.701
dómine	1	7	3.701
des	1	7	3.701
departamento	1	7	3.701
delantera	1	7	3.701
decíale	1	7	3.701
cumplimiento	1	7	3.701
cumple	1	7	3.701
cuentan	1	7	3.701
contrariedad	1	7	3.701
conteniendo	1	7	3.701
construcción	1	7	3.701
comunicación	1	7	3.701
cláusulas	1	7	3.701
cifra	1	7	3.701
celoso	1	7	3.701
cavilar	1	7	3.701
caramba	1	7	3.701
canela	1	7	3.701
aumentar	1	7	3.701
alhaja	1	7	3.701
alarmada	1	7	3.701
pensamiento	57	100	3.694
cerebro	66	60	3.688
sabiendo	4	14	3.687
planta	4	14	3.687
marzo	4	14	3.687
llegando	4	14	3.687
iremos	4	14	3.687
haberse	4	14	3.687
febril	4	14	3.687
extraordinario	4	14	3.687
digan	4	14	3.687
déjate	4	14	3.687
clavado	4	14	3.687
encima	36	68	3.684
vecinas	6	18	3.679
impresiones	6	18	3.679
llegaron	21	14	3.673
cerró	21	14	3.673
cantar	21	14	3.673
actividad	21	14	3.673
trató	5	16	3.661
refugio	5	16	3.661
quedándose	5	16	3.661
pago	5	16	3.661
mostrando	5	16	3.661
misas	5	16	3.661
inspiración	5	16	3.661
infantil	5	16	3.661
echa	5	16	3.661
concluido	5	16	3.661
pecho	38	71	3.655
música	48	41	3.637
cocina	40	74	3.631
susto	22	15	3.626
viernes	13	7	3.616
temblorosa	13	7	3.616
reconocía	13	7	3.616
mismas	13	7	3.616
lejano	13	7	3.616
ironía	13	7	3.616
inclinaba	13	7	3.616
ignorancia	13	7	3.616
gustos	13	7	3.616
dejaron	13	7	3.616
corro	13	7	3.616
caliente	13	7	3.616
altura	13	7	3.616
acompañaba	13	7	3.616
estómago	15	34	3.615
hago	18	39	3.601
resistir	23	16	3.587
temor	11	27	3.576
humano	11	27	3.576
esté	11	27	3.576
natural	61	55	3.561
notar	24	17	3.556
carácter	23	47	3.533
emoción	25	18	3.530
dolor	59	53	3.511
esposo	39	32	3.503
francisco	27	20	3.492
sentido	58	52	3.486
prueba	28	21	3.480
seguían	14	8	3.475
sed	14	8	3.475
reina	14	8	3.475
recordando	14	8	3.475
pliegues	14	8	3.475
peligros	14	8	3.475
llenas	14	8	3.475
leyendo	14	8	3.475
hábito	14	8	3.475
discreta	14	8	3.475
desnudo	14	8	3.475
condiciones	14	8	3.475
acero	14	8	3.475
siglo	29	22	3.471
necesito	29	22	3.471
terreno	35	28	3.469
recuerdo	35	28	3.469
parecen	10	25	3.468
lección	10	25	3.468
iré	10	25	3.468
solos	34	27	3.464
zapatones	0	3	3.463
zancas	0	3	3.463
vueltos	0	3	3.463
vuelca	0	3	3.463
votar	0	3	3.463
vómitos	0	3	3.463
volumen	0	3	3.463
vizcaína	0	3	3.463
vivísimo	0	3	3.463
vitoria	0	3	3.463
violentísimo	0	3	3.463
viajeros	0	3	3.463
vestirle	0	3	3.463
vestiré	0	3	3.463
versó	0	3	3.463
verificose	0	3	3.463
verificó	0	3	3.463
verídicamente	0	3	3.463
veredas	0	3	3.463
venturoso	0	3	3.463
ventas	0	3	3.463
vendedores	0	3	3.463
vendedor	0	3	3.463
veíanse	0	3	3.463
varoniles	0	3	3.463
variaron	0	3	3.463
variando	0	3	3.463
variado	0	3	3.463
varía	0	3	3.463
valerosa	0	3	3.463
valeriano	0	3	3.463
vagón	0	3	3.463
vagabundo	0	3	3.463
vagabunda	0	3	3.463
uy	0	3	3.463
usuales	0	3	3.463
usaron	0	3	3.463
usadas	0	3	3.463
ultrajar	0	3	3.463
trocó	0	3	3.463
triviales	0	3	3.463
tristísimo	0	3	3.463
triquitraque	0	3	3.463
trinidad	0	3	3.463
trifulca	0	3	3.463
tribulación	0	3	3.463
trémulo	0	3	3.463
trazar	0	3	3.463
tratante	0	3	3.463
trastorna	0	3	3.463
trapisondista	0	3	3.463
tranquilízate	0	3	3.463
trajín	0	3	3.463
trajeran	0	3	3.463
trajecito	0	3	3.463
tráiganme	0	3	3.463
tragado	0	3	3.463
trabajadora	0	3	3.463
toser	0	3	3.463
toquillas	0	3	3.463
tontaina	0	3	3.463
tomándose	0	3	3.463
toditos	0	3	3.463
tirita	0	3	3.463
tirarlos	0	3	3.463
tirarle	0	3	3.463
tirándole	0	3	3.463
tiorras	0	3	3.463
tiñe	0	3	3.463
tifus	0	3	3.463
tetuán	0	3	3.463
tenerlos	0	3	3.463
tenducho	0	3	3.463
tasa	0	3	3.463
tartán	0	3	3.463
tarambana	0	3	3.463
tapando	0	3	3.463
tantísimo	0	3	3.463
tantísimas	0	3	3.463
talentazo	0	3	3.463
talco	0	3	3.463
tagarotes	0	3	3.463
tácita	0	3	3.463
tabiques	0	3	3.463
t	0	3	3.463
suscriciones	0	3	3.463
suiza	0	3	3.463
suéltame	0	3	3.463
sucesivos	0	3	3.463
subsecretario	0	3	3.463
subordinación	0	3	3.463
súbita	0	3	3.463
subiéndose	0	3	3.463
subí	0	3	3.463
sótano	0	3	3.463
sostiene	0	3	3.463
sopas	0	3	3.463
sonaran	0	3	3.463
sombrerito	0	3	3.463
soltado	0	3	3.463
solomillo	0	3	3.463
solita	0	3	3.463
soliloquios	0	3	3.463
sofoques	0	3	3.463
sofocadísima	0	3	3.463
soeces	0	3	3.463
sirviente	0	3	3.463
siniestra	0	3	3.463
singapore	0	3	3.463
simpleza	0	3	3.463
sillar	0	3	3.463
sigüenza	0	3	3.463
serenos	0	3	3.463
serenó	0	3	3.463
serafines	0	3	3.463
separados	0	3	3.463
sentase	0	3	3.463
sentara	0	3	3.463
sensata	0	3	3.463
senos	0	3	3.463
seguimos	0	3	3.463
secreteo	0	3	3.463
secreteándose	0	3	3.463
satánica	0	3	3.463
sartén	0	3	3.463
sarampión	0	3	3.463
saques	0	3	3.463
saña	0	3	3.463
sándalo	0	3	3.463
sánchez	0	3	3.463
samaniega	0	3	3.463
saliste	0	3	3.463
salirse	0	3	3.463
salidita	0	3	3.463
saldo	0	3	3.463
sahumar	0	3	3.463
sagaces	0	3	3.463
sacuden	0	3	3.463
sacas	0	3	3.463
sabidurías	0	3	3.463
sabéis	0	3	3.463
sabedor	0	3	3.463
ruidosa	0	3	3.463
rondas	0	3	3.463
rompería	0	3	3.463
romanos	0	3	3.463
rogó	0	3	3.463
roe	0	3	3.463
rivalidad	0	3	3.463
riquísimos	0	3	3.463
riquísimo	0	3	3.463
riñendo	0	3	3.463
ríete	0	3	3.463
revolvían	0	3	3.463
reventones	0	3	3.463
revancha	0	3	3.463
reuma	0	3	3.463
retuvo	0	3	3.463
retiráronse	0	3	3.463
resueltamente	0	3	3.463
resquicio	0	3	3.463
responderle	0	3	3.463
respetos	0	3	3.463
respetabilísima	0	3	3.463
resentimientos	0	3	3.463
resabio	0	3	3.463
reproducía	0	3	3.463
reprimenda	0	3	3.463
reprender	0	3	3.463
reponerse	0	3	3.463
repitiera	0	3	3.463
repaso	0	3	3.463
repartiendo	0	3	3.463
reparador	0	3	3.463
reoyos	0	3	3.463
relamía	0	3	3.463
rejilla	0	3	3.463
regaliz	0	3	3.463
refrescó	0	3	3.463
reformas	0	3	3.463
refajo	0	3	3.463
recorrió	0	3	3.463
recomendara	0	3	3.463
recogieron	0	3	3.463
reclusas	0	3	3.463
recibiría	0	3	3.463
rebotica	0	3	3.463
rayado	0	3	3.463
rasguñar	0	3	3.463
rasgueadas	0	3	3.463
randa	0	3	3.463
ramoncita	0	3	3.463
ramaje	0	3	3.463
ralo	0	3	3.463
rabioso	0	3	3.463
rabiosa	0	3	3.463
quiten	0	3	3.463
quitándole	0	3	3.463
quietecito	0	3	3.463
quererse	0	3	3.463
querencia	0	3	3.463
quelo	0	3	3.463
quedas	0	3	3.463
quedábanse	0	3	3.463
pusiéronle	0	3	3.463
punzada	0	3	3.463
puntualmente	0	3	3.463
puntualidad	0	3	3.463
puff	0	3	3.463
puerca	0	3	3.463
púa	0	3	3.463
prusianos	0	3	3.463
protegida	0	3	3.463
protegía	0	3	3.463
propiedades	0	3	3.463
pronunciada	0	3	3.463
prométeme	0	3	3.463
productos	0	3	3.463
producíale	0	3	3.463
probaré	0	3	3.463
privado	0	3	3.463
privaciones	0	3	3.463
prisas	0	3	3.463
principia	0	3	3.463
primorosas	0	3	3.463
primitivos	0	3	3.463
primas	0	3	3.463
previsión	0	3	3.463
preverlo	0	3	3.463
prevengo	0	3	3.463
pretextando	0	3	3.463
prestan	0	3	3.463
presos	0	3	3.463
presintió	0	3	3.463
presento	0	3	3.463
presentará	0	3	3.463
presentara	0	3	3.463
preparémonos	0	3	3.463
preocupada	0	3	3.463
preguntita	0	3	3.463
pregones	0	3	3.463
precursores	0	3	3.463
precedieron	0	3	3.463
practicante	0	3	3.463
practicaba	0	3	3.463
potásico	0	3	3.463
postración	0	3	3.463
portarme	0	3	3.463
porta	0	3	3.463
porrazos	0	3	3.463
poros	0	3	3.463
poquitito	0	3	3.463
ponme	0	3	3.463
ponlo	0	3	3.463
ponérselo	0	3	3.463
pondrás	0	3	3.463
ponderar	0	3	3.463
polla	0	3	3.463
polkas	0	3	3.463
polisón	0	3	3.463
podéis	0	3	3.463
planto	0	3	3.463
plantan	0	3	3.463
pintarte	0	3	3.463
pingajos	0	3	3.463
pim	0	3	3.463
píldora	0	3	3.463
pilas	0	3	3.463
pida	0	3	3.463
picotazos	0	3	3.463
picando	0	3	3.463
piar	0	3	3.463
pianitos	0	3	3.463
petitorios	0	3	3.463
pesadito	0	3	3.463
perversos	0	3	3.463
perrito	0	3	3.463
perrera	0	3	3.463
peripecias	0	3	3.463
pérfido	0	3	3.463
pérdidas	0	3	3.463
percibió	0	3	3.463
pentecostés	0	3	3.463
penitenciario	0	3	3.463
penita	0	3	3.463
penando	0	3	3.463
penales	0	3	3.463
peludo	0	3	3.463
peloteras	0	3	3.463
pegaría	0	3	3.463
pegadizo	0	3	3.463
pedidos	0	3	3.463
peco	0	3	3.463
pavía	0	3	3.463
pavero	0	3	3.463
patrona	0	3	3.463
patraña	0	3	3.463
patochada	0	3	3.463
patita	0	3	3.463
pateo	0	3	3.463
pateada	0	3	3.463
pasmará	0	3	3.463
pasen	0	3	3.463
pasándole	0	3	3.463
partos	0	3	3.463
partieron	0	3	3.463
particularidades	0	3	3.463
participación	0	3	3.463
partición	0	3	3.463
parose	0	3	3.463
parentela	0	3	3.463
parecerme	0	3	3.463
parecerlo	0	3	3.463
paralela	0	3	3.463
parados	0	3	3.463
parado	0	3	3.463
papamoscas	0	3	3.463
palomos	0	3	3.463
paliza	0	3	3.463
palideciendo	0	3	3.463
palanca	0	3	3.463
pajarito	0	3	3.463
pagos	0	3	3.463
ovejas	0	3	3.463
ostentación	0	3	3.463
oscurísimo	0	3	3.463
orificios	0	3	3.463
ordinarias	0	3	3.463
ordenada	0	3	3.463
órdago	0	3	3.463
oposiciones	0	3	3.463
omitir	0	3	3.463
olvidaré	0	3	3.463
olvidara	0	3	3.463
olorcillo	0	3	3.463
óleo	0	3	3.463
ojerosa	0	3	3.463
ojeras	0	3	3.463
oída	0	3	3.463
oferta	0	3	3.463
ofensas	0	3	3.463
ofendería	0	3	3.463
ocurriósele	0	3	3.463
ocurriera	0	3	3.463
ocuparon	0	3	3.463
obvio	0	3	3.463
obstrucciones	0	3	3.463
obispa	0	3	3.463
obedezca	0	3	3.463
obedeció	0	3	3.463
nudillos	0	3	3.463
nublaron	0	3	3.463
novelda	0	3	3.463
nombro	0	3	3.463
niñito	0	3	3.463
niñería	0	3	3.463
nicolasa	0	3	3.463
neurosis	0	3	3.463
nenito	0	3	3.463
nenín	0	3	3.463
negrito	0	3	3.463
negociante	0	3	3.463
negativo	0	3	3.463
nativo	0	3	3.463
murrias	0	3	3.463
murria	0	3	3.463
murieron	0	3	3.463
mugrienta	0	3	3.463
mueras	0	3	3.463
mudanza	0	3	3.463
móvil	0	3	3.463
movidas	0	3	3.463
morrión	0	3	3.463
morisquetas	0	3	3.463
moriré	0	3	3.463
moriones	0	3	3.463
morejón	0	3	3.463
moraba	0	3	3.463
monstruosidad	0	3	3.463
monserga	0	3	3.463
monísimo	0	3	3.463
molinillos	0	3	3.463
modesta	0	3	3.463
mocedad	0	3	3.463
mitones	0	3	3.463
mires	0	3	3.463
mírenlo	0	3	3.463
miremos	0	3	3.463
miraré	0	3	3.463
mirara	0	3	3.463
mirándome	0	3	3.463
míralos	0	3	3.463
miradores	0	3	3.463
mirad	0	3	3.463
ministración	0	3	3.463
mimosos	0	3	3.463
meterla	0	3	3.463
merecen	0	3	3.463
merecemos	0	3	3.463
mercados	0	3	3.463
menudeaban	0	3	3.463
mendigos	0	3	3.463
mendigo	0	3	3.463
mendicidad	0	3	3.463
melindres	0	3	3.463
melchor	0	3	3.463
medicamentos	0	3	3.463
mechón	0	3	3.463
maternales	0	3	3.463
mataré	0	3	3.463
masticando	0	3	3.463
mascando	0	3	3.463
marrullerías	0	3	3.463
marianas	0	3	3.463
mareas	0	3	3.463
marean	0	3	3.463
marchara	0	3	3.463
maravillosas	0	3	3.463
manzanares	0	3	3.463
manubrio	0	3	3.463
mantiene	0	3	3.463
manoteando	0	3	3.463
manotada	0	3	3.463
maniquís	0	3	3.463
manifiestan	0	3	3.463
manifestábase	0	3	3.463
mangonear	0	3	3.463
manden	0	3	3.463
mandara	0	3	3.463
manceba	0	3	3.463
mamarrachos	0	3	3.463
malísimo	0	3	3.463
maleza	0	3	3.463
magras	0	3	3.463
magníficas	0	3	3.463
madriz	0	3	3.463
lobo	0	3	3.463
lléveselo	0	3	3.463
llévate	0	3	3.463
llevarte	0	3	3.463
llamole	0	3	3.463
llamarme	0	3	3.463
lisonja	0	3	3.463
lindo	0	3	3.463
lindísimo	0	3	3.463
lindas	0	3	3.463
linajes	0	3	3.463
librarle	0	3	3.463
levanta	0	3	3.463
letreros	0	3	3.463
leopardi	0	3	3.463
lengüetazos	0	3	3.463
legalidad	0	3	3.463
lectoral	0	3	3.463
lavo	0	3	3.463
laven	0	3	3.463
lava	0	3	3.463
latas	0	3	3.463
lata	0	3	3.463
lárgate	0	3	3.463
lanzar	0	3	3.463
lanzada	0	3	3.463
lanilla	0	3	3.463
lago	0	3	3.463
ladronas	0	3	3.463
lacio	0	3	3.463
jurisdicción	0	3	3.463
juraría	0	3	3.463
jui	0	3	3.463
judas	0	3	3.463
jotas	0	3	3.463
japonesa	0	3	3.463
jamases	0	3	3.463
jacintilla	0	3	3.463
isabelita	0	3	3.463
irregular	0	3	3.463
irán	0	3	3.463
ioduro	0	3	3.463
inundada	0	3	3.463
intranquilidad	0	3	3.463
íntimamente	0	3	3.463
interrogó	0	3	3.463
interrogaba	0	3	3.463
interponía	0	3	3.463
intensísima	0	3	3.463
institutriz	0	3	3.463
institutos	0	3	3.463
instintivamente	0	3	3.463
insensata	0	3	3.463
insano	0	3	3.463
inquisidora	0	3	3.463
inquilina	0	3	3.463
inocentona	0	3	3.463
inmiscuirse	0	3	3.463
inglesas	0	3	3.463
ingeniosas	0	3	3.463
infunde	0	3	3.463
inferioridad	0	3	3.463
inevitable	0	3	3.463
inesperadamente	0	3	3.463
industrial	0	3	3.463
indulgentes	0	3	3.463
indolencia	0	3	3.463
individua	0	3	3.463
indirecta	0	3	3.463
indicio	0	3	3.463
indefinible	0	3	3.463
incrédulo	0	3	3.463
incorporado	0	3	3.463
inconstante	0	3	3.463
importaría	0	3	3.463
impetuosa	0	3	3.463
imperdible	0	3	3.463
imaginó	0	3	3.463
ildefonso	0	3	3.463
idolatraba	0	3	3.463
íbase	0	3	3.463
huye	0	3	3.463
hundido	0	3	3.463
humareda	0	3	3.463
huevera	0	3	3.463
huelen	0	3	3.463
huele	0	3	3.463
hubieron	0	3	3.463
horizontal	0	3	3.463
hondísimo	0	3	3.463
hervía	0	3	3.463
herramientas	0	3	3.463
herméticamente	0	3	3.463
hato	0	3	3.463
hallando	0	3	3.463
halla	0	3	3.463
habríamos	0	3	3.463
hablose	0	3	3.463
hablarles	0	3	3.463
habladurías	0	3	3.463
habitante	0	3	3.463
habíalo	0	3	3.463
gustó	0	3	3.463
guste	0	3	3.463
gustavito	0	3	3.463
gustará	0	3	3.463
guita	0	3	3.463
guisantes	0	3	3.463
guindillas	0	3	3.463
guardaron	0	3	3.463
guapote	0	3	3.463
gruesas	0	3	3.463
gritería	0	3	3.463
granito	0	3	3.463
gozaban	0	3	3.463
golpeando	0	3	3.463
golosos	0	3	3.463
gases	0	3	3.463
garrotillo	0	3	3.463
gargarismos	0	3	3.463
garfios	0	3	3.463
garatusas	0	3	3.463
ganaban	0	3	3.463
gallegos	0	3	3.463
gabinetito	0	3	3.463
gabanes	0	3	3.463
funesta	0	3	3.463
fundaba	0	3	3.463
frugal	0	3	3.463
fritangas	0	3	3.463
friegas	0	3	3.463
fregar	0	3	3.463
frascos	0	3	3.463
fraga	0	3	3.463
fosfato	0	3	3.463
for	0	3	3.463
fleco	0	3	3.463
físicamente	0	3	3.463
financieras	0	3	3.463
figueras	0	3	3.463
fecundo	0	3	3.463
febriles	0	3	3.463
favorece	0	3	3.463
favorcito	0	3	3.463
fatigadísima	0	3	3.463
fatigadas	0	3	3.463
fastidio	0	3	3.463
farmacéuticos	0	3	3.463
farmacéutica	0	3	3.463
fardos	0	3	3.463
famélico	0	3	3.463
falte	0	3	3.463
faltábale	0	3	3.463
falsete	0	3	3.463
falleció	0	3	3.463
facundia	0	3	3.463
facturas	0	3	3.463
fabricando	0	3	3.463
extranjeras	0	3	3.463
externa	0	3	3.463
expresan	0	3	3.463
explanada	0	3	3.463
expectativa	0	3	3.463
expectante	0	3	3.463
existido	0	3	3.463
exhalando	0	3	3.463
examinarse	0	3	3.463
examinándole	0	3	3.463
exaltándose	0	3	3.463
evolución	0	3	3.463
evocando	0	3	3.463
evasivamente	0	3	3.463
evasión	0	3	3.463
estrujón	0	3	3.463
estricnina	0	3	3.463
estrechamente	0	3	3.463
estrafalario	0	3	3.463
estéis	0	3	3.463
estaremos	0	3	3.463
establecerse	0	3	3.463
esplín	0	3	3.463
espléndido	0	3	3.463
esperpento	0	3	3.463
esperaremos	0	3	3.463
específico	0	3	3.463
esfinge	0	3	3.463
esenciales	0	3	3.463
esconden	0	3	3.463
escobillón	0	3	3.463
escayolas	0	3	3.463
escandalizar	0	3	3.463
escabeche	0	3	3.463
éranle	0	3	3.463
éralo	0	3	3.463
equivale	0	3	3.463
epigastrio	0	3	3.463
envolverse	0	3	3.463
envido	0	3	3.463
envenenar	0	3	3.463
envenenamiento	0	3	3.463
envalentonó	0	3	3.463
entrometida	0	3	3.463
entretenimientos	0	3	3.463
entres	0	3	3.463
entren	0	3	3.463
entrecano	0	3	3.463
entráronle	0	3	3.463
entrañablemente	0	3	3.463
entrambos	0	3	3.463
entrábale	0	3	3.463
enterose	0	3	3.463
enteraron	0	3	3.463
enterándose	0	3	3.463
enseñaré	0	3	3.463
enojosa	0	3	3.463
ennoblece	0	3	3.463
enfadó	0	3	3.463
enfadarse	0	3	3.463
eneas	0	3	3.463
encendiendo	0	3	3.463
encargar	0	3	3.463
encarga	0	3	3.463
encandilados	0	3	3.463
encaminó	0	3	3.463
enana	0	3	3.463
emplasto	0	3	3.463
empiezo	0	3	3.463
empezaría	0	3	3.463
empaque	0	3	3.463
empalagosas	0	3	3.463
emblema	0	3	3.463
embargaba	0	3	3.463
embarazo	0	3	3.463
elevando	0	3	3.463
elegir	0	3	3.463
electrizaba	0	3	3.463
ejercitarse	0	3	3.463
eje	0	3	3.463
edificación	0	3	3.463
echárselas	0	3	3.463
echaré	0	3	3.463
echándoselas	0	3	3.463
durmiose	0	3	3.463
durmieron	0	3	3.463
durmiera	0	3	3.463
dulcísimos	0	3	3.463
duela	0	3	3.463
ducha	0	3	3.463
dragón	0	3	3.463
domiciliaria	0	3	3.463
distantes	0	3	3.463
dispensa	0	3	3.463
disparada	0	3	3.463
disgustada	0	3	3.463
dirigiose	0	3	3.463
dirigían	0	3	3.463
dinidá	0	3	3.463
dígole	0	3	3.463
digerir	0	3	3.463
dificilillo	0	3	3.463
dializado	0	3	3.463
deteniendo	0	3	3.463
desvelado	0	3	3.463
destrozaba	0	3	3.463
despropósitos	0	3	3.463
desproporción	0	3	3.463
desplegó	0	3	3.463
desplegando	0	3	3.463
despacito	0	3	3.463
desórdenes	0	3	3.463
desordenada	0	3	3.463
desolada	0	3	3.463
desnudarse	0	3	3.463
desmedrada	0	3	3.463
deshilachada	0	3	3.463
desesperados	0	3	3.463
desempeñó	0	3	3.463
descubrían	0	3	3.463
descrito	0	3	3.463
descontento	0	3	3.463
desconoce	0	3	3.463
desbarajuste	0	3	3.463
desarrolló	0	3	3.463
desagradaba	0	3	3.463
derroche	0	3	3.463
derechita	0	3	3.463
deplorable	0	3	3.463
denunciaba	0	3	3.463
dejemos	0	3	3.463
dejémonos	0	3	3.463
dedicado	0	3	3.463
decírmelo	0	3	3.463
decirles	0	3	3.463
decido	0	3	3.463
debidos	0	3	3.463
dársele	0	3	3.463
daremos	0	3	3.463
darás	0	3	3.463
dándome	0	3	3.463
curiosidades	0	3	3.463
curarle	0	3	3.463
cumplidas	0	3	3.463
cumpla	0	3	3.463
cuitas	0	3	3.463
cuidadito	0	3	3.463
cueros	0	3	3.463
cuéntame	0	3	3.463
cuchitril	0	3	3.463
cucharas	0	3	3.463
cuatrocientos	0	3	3.463
cuajada	0	3	3.463
cristiandad	0	3	3.463
crié	0	3	3.463
críe	0	3	3.463
crezca	0	3	3.463
creerte	0	3	3.463
creeréis	0	3	3.463
créanmelo	0	3	3.463
costados	0	3	3.463
corros	0	3	3.463
corrigen	0	3	3.463
corrí	0	3	3.463
corretaje	0	3	3.463
corresponden	0	3	3.463
corista	0	3	3.463
corinto	0	3	3.463
convidó	0	3	3.463
convenga	0	3	3.463
contratas	0	3	3.463
contracción	0	3	3.463
continuidad	0	3	3.463
contingencia	0	3	3.463
contentísima	0	3	3.463
contentará	0	3	3.463
contenían	0	3	3.463
contemporizar	0	3	3.463
contemporánea	0	3	3.463
contaste	0	3	3.463
consumado	0	3	3.463
consultarle	0	3	3.463
consuele	0	3	3.463
considerables	0	3	3.463
conservarse	0	3	3.463
consecuente	0	3	3.463
conocimos	0	3	3.463
conocedor	0	3	3.463
conmovido	0	3	3.463
conmovida	0	3	3.463
conjunción	0	3	3.463
confiando	0	3	3.463
conducen	0	3	3.463
concurrir	0	3	3.463
concurrencia	0	3	3.463
comunicativo	0	3	3.463
comunicaciones	0	3	3.463
comprometido	0	3	3.463
comprendieron	0	3	3.463
comportamiento	0	3	3.463
comparaciones	0	3	3.463
compaginar	0	3	3.463
comérselo	0	3	3.463
comerciales	0	3	3.463
comas	0	3	3.463
coloradita	0	3	3.463
coloque	0	3	3.463
cojín	0	3	3.463
cogidas	0	3	3.463
cogería	0	3	3.463
cochinada	0	3	3.463
claritas	0	3	3.463
claques	0	3	3.463
citada	0	3	3.463
cimiento	0	3	3.463
cicatero	0	3	3.463
chupaba	0	3	3.463
chuleta	0	3	3.463
chisme	0	3	3.463
chinita	0	3	3.463
chillar	0	3	3.463
chilla	0	3	3.463
charló	0	3	3.463
charlaron	0	3	3.463
cese	0	3	3.463
cerebrales	0	3	3.463
cerciorarse	0	3	3.463
cencerro	0	3	3.463
cavilo	0	3	3.463
cavilación	0	3	3.463
cavernosa	0	3	3.463
cautivaba	0	3	3.463
cautelosamente	0	3	3.463
catado	0	3	3.463
castrense	0	3	3.463
castita	0	3	3.463
casamos	0	3	3.463
casaca	0	3	3.463
carúnculas	0	3	3.463
carnicero	0	3	3.463
carecer	0	3	3.463
carbones	0	3	3.463
carbonería	0	3	3.463
cápsulas	0	3	3.463
cáñamo	0	3	3.463
cantoras	0	3	3.463
canastillas	0	3	3.463
camps	0	3	3.463
cambiazo	0	3	3.463
cambian	0	3	3.463
camastro	0	3	3.463
camaraíta	0	3	3.463
callejuelas	0	3	3.463
callandito	0	3	3.463
calladito	0	3	3.463
calentando	0	3	3.463
caimán	0	3	3.463
caerá	0	3	3.463
caca	0	3	3.463
busqué	0	3	3.463
buscarse	0	3	3.463
burros	0	3	3.463
burras	0	3	3.463
burrada	0	3	3.463
burlar	0	3	3.463
buenazo	0	3	3.463
brocha	0	3	3.463
brisas	0	3	3.463
bríos	0	3	3.463
bravas	0	3	3.463
botines	0	3	3.463
botijos	0	3	3.463
botijo	0	3	3.463
borrachona	0	3	3.463
bofes	0	3	3.463
bobos	0	3	3.463
berroqueña	0	3	3.463
berrinchín	0	3	3.463
berridos	0	3	3.463
berrido	0	3	3.463
benditos	0	3	3.463
belga	0	3	3.463
belenes	0	3	3.463
bebiéndose	0	3	3.463
bayetas	0	3	3.463
bases	0	3	3.463
barros	0	3	3.463
barriles	0	3	3.463
barricada	0	3	3.463
barbián	0	3	3.463
baratura	0	3	3.463
barandal	0	3	3.463
baqueta	0	3	3.463
baldosines	0	3	3.463
baldomerito	0	3	3.463
bájate	0	3	3.463
babosos	0	3	3.463
azoramiento	0	3	3.463
azorada	0	3	3.463
ayúdame	0	3	3.463
avivó	0	3	3.463
aviado	0	3	3.463
averigüe	0	3	3.463
avanzaron	0	3	3.463
autoritario	0	3	3.463
autoritaria	0	3	3.463
autócrata	0	3	3.463
aumentan	0	3	3.463
aula	0	3	3.463
atropellarse	0	3	3.463
atropellado	0	3	3.463
atropelladamente	0	3	3.463
atroces	0	3	3.463
atrayéndola	0	3	3.463
atrasadas	0	3	3.463
atontado	0	3	3.463
atontada	0	3	3.463
atolladero	0	3	3.463
atiza	0	3	3.463
atienda	0	3	3.463
aterradora	0	3	3.463
atando	0	3	3.463
asunción	0	3	3.463
asomáronse	0	3	3.463
asomándose	0	3	3.463
asistencia	0	3	3.463
asimismo	0	3	3.463
asimilarse	0	3	3.463
aseveración	0	3	3.463
asado	0	3	3.463
artesón	0	3	3.463
arsenal	0	3	3.463
arrugando	0	3	3.463
arrojan	0	3	3.463
arrodillándose	0	3	3.463
arrepiéntete	0	3	3.463
arrepentirse	0	3	3.463
arreglaremos	0	3	3.463
arreglaban	0	3	3.463
arrechucho	0	3	3.463
arrebatada	0	3	3.463
armaban	0	3	3.463
aritmético	0	3	3.463
aritmética	0	3	3.463
ardientemente	0	3	3.463
apuró	0	3	3.463
apure	0	3	3.463
apunte	0	3	3.463
apuestas	0	3	3.463
aprueba	0	3	3.463
aprisita	0	3	3.463
apresurándose	0	3	3.463
aprendería	0	3	3.463
aplacado	0	3	3.463
apetecía	0	3	3.463
apático	0	3	3.463
anulación	0	3	3.463
antoje	0	3	3.463
antemano	0	3	3.463
ansiosa	0	3	3.463
anochecido	0	3	3.463
angustiosa	0	3	3.463
angelitos	0	3	3.463
ándate	0	3	3.463
amenazándole	0	3	3.463
ambulantes	0	3	3.463
amasando	0	3	3.463
almorzado	0	3	3.463
almendra	0	3	3.463
alijo	0	3	3.463
algarrobos	0	3	3.463
aletargaba	0	3	3.463
alcantarilla	0	3	3.463
alarmadísima	0	3	3.463
alambique	0	3	3.463
ajustarle	0	3	3.463
ahorro	0	3	3.463
agujereada	0	3	3.463
aguardó	0	3	3.463
aguarda	0	3	3.463
aguantando	0	3	3.463
aguador	0	3	3.463
agrandaba	0	3	3.463
agradeciendo	0	3	3.463
agraciados	0	3	3.463
agraciada	0	3	3.463
agotado	0	3	3.463
agachó	0	3	3.463
afectó	0	3	3.463
adusta	0	3	3.463
adquiridos	0	3	3.463
adoquines	0	3	3.463
adarme	0	3	3.463
acusón	0	3	3.463
acostose	0	3	3.463
acostarle	0	3	3.463
acostaré	0	3	3.463
acordara	0	3	3.463
acomodaba	0	3	3.463
ácido	0	3	3.463
aciago	0	3	3.463
acertando	0	3	3.463
acercar	0	3	3.463
acercábase	0	3	3.463
acepto	0	3	3.463
acentuaba	0	3	3.463
accionando	0	3	3.463
accesible	0	3	3.463
acantonamos	0	3	3.463
acabados	0	3	3.463
abstraído	0	3	3.463
absorbedero	0	3	3.463
absolutismo	0	3	3.463
abriose	0	3	3.463
abriese	0	3	3.463
abriéndose	0	3	3.463
abrazando	0	3	3.463
abatido	0	3	3.463
abandonará	0	3	3.463
volviera	9	4	3.407
vistió	9	4	3.407
violín	9	4	3.407
torpe	9	4	3.407
taza	9	4	3.407
sudaba	9	4	3.407
salvarse	9	4	3.407
roma	9	4	3.407
población	9	4	3.407
pesimismo	9	4	3.407
perfume	9	4	3.407
materialista	9	4	3.407
leve	9	4	3.407
ingrata	9	4	3.407
inclinada	9	4	3.407
etiqueta	9	4	3.407
esclavo	9	4	3.407
emprender	9	4	3.407
conventos	9	4	3.407
continuo	9	4	3.407
consultar	9	4	3.407
celebraba	9	4	3.407
cadáver	9	4	3.407
autores	9	4	3.407
aureola	9	4	3.407
amenazaba	9	4	3.407
agradecimiento	9	4	3.407
algunas	83	137	3.397
sillón	9	23	3.365
seré	9	23	3.365
romper	9	23	3.365
acción	9	23	3.365
volviéndose	15	9	3.364
inclinó	15	9	3.364
fiesta	15	9	3.364
espaldas	15	9	3.364
cerrar	15	9	3.364
destino	13	30	3.362
comer	64	109	3.356
llorar	24	48	3.321
zumbaba	2	0	3.297
zig	2	0	3.297
zarzamora	2	0	3.297
zagal	2	0	3.297
yugo	2	0	3.297
york	2	0	3.297
vulgarísima	2	0	3.297
vos	2	0	3.297
voluptuosamente	2	0	3.297
voluntariamente	2	0	3.297
voluntades	2	0	3.297
volaría	2	0	3.297
vociferó	2	0	3.297
vistalegre	2	0	3.297
viscoso	2	0	3.297
viscosa	2	0	3.297
virtuosísima	2	0	3.297
virginal	2	0	3.297
violeta	2	0	3.297
violentar	2	0	3.297
viniesen	2	0	3.297
vinajeras	2	0	3.297
villegas	2	0	3.297
vigorosas	2	0	3.297
vigilias	2	0	3.297
viga	2	0	3.297
viejecillo	2	0	3.297
vibrantes	2	0	3.297
vestiduras	2	0	3.297
vespucios	2	0	3.297
vespucio	2	0	3.297
vertiginosas	2	0	3.297
verticales	2	0	3.297
verjas	2	0	3.297
veritas	2	0	3.297
veranillo	2	0	3.297
ventorrillos	2	0	3.297
veniales	2	0	3.297
vengábase	2	0	3.297
vendemos	2	0	3.297
venciste	2	0	3.297
vencieron	2	0	3.297
vencían	2	0	3.297
vencerían	2	0	3.297
vencerás	2	0	3.297
vence	2	0	3.297
vanamente	2	0	3.297
vanagloria	2	0	3.297
valdés	2	0	3.297
vade	2	0	3.297
vacilantes	2	0	3.297
úrsula	2	0	3.297
ultramontanos	2	0	3.297
ultrajes	2	0	3.297
ultrajados	2	0	3.297
ultra	2	0	3.297
uf	2	0	3.297
turcos	2	0	3.297
turbas	2	0	3.297
turba	2	0	3.297
tuo	2	0	3.297
tubinga	2	0	3.297
truquage	2	0	3.297
trovadores	2	0	3.297
tropezaban	2	0	3.297
triunfó	2	0	3.297
triunfador	2	0	3.297
tributando	2	0	3.297
trepaban	2	0	3.297
travesaño	2	0	3.297
transformarse	2	0	3.297
tranquilícese	2	0	3.297
trama	2	0	3.297
tragarse	2	0	3.297
traducir	2	0	3.297
tradicionales	2	0	3.297
tostados	2	0	3.297
tortuosas	2	0	3.297
torso	2	0	3.297
torneada	2	0	3.297
topó	2	0	3.297
topo	2	0	3.297
toos	2	0	3.297
tontiloco	2	0	3.297
tonsurado	2	0	3.297
tomillares	2	0	3.297
tolerarlas	2	0	3.297
tocadas	2	0	3.297
to	2	0	3.297
titulaba	2	0	3.297
tirarse	2	0	3.297
timorato	2	0	3.297
times	2	0	3.297
tiemblan	2	0	3.297
tié	2	0	3.297
thorum	2	0	3.297
the	2	0	3.297
testarudo	2	0	3.297
tesorera	2	0	3.297
terminaba	2	0	3.297
teóricos	2	0	3.297
teológica	2	0	3.297
teologías	2	0	3.297
teñían	2	0	3.297
tentada	2	0	3.297
tenorios	2	0	3.297
temibles	2	0	3.297
temerarias	2	0	3.297
temen	2	0	3.297
temblores	2	0	3.297
temblonas	2	0	3.297
técnicas	2	0	3.297
tarsa	2	0	3.297
tardía	2	0	3.297
tapicero	2	0	3.297
tapadillo	2	0	3.297
tañidos	2	0	3.297
tamaza	2	0	3.297
tamañas	2	0	3.297
tamaña	2	0	3.297
talía	2	0	3.297
taco	2	0	3.297
tacaño	2	0	3.297
tac	2	0	3.297
sutilmente	2	0	3.297
sustituir	2	0	3.297
suplicado	2	0	3.297
superlativos	2	0	3.297
sumidos	2	0	3.297
sumidas	2	0	3.297
sumía	2	0	3.297
sufrido	2	0	3.297
sufre	2	0	3.297
sudeste	2	0	3.297
sucumbiría	2	0	3.297
suculentos	2	0	3.297
sucedáneos	2	0	3.297
subterráneas	2	0	3.297
subterránea	2	0	3.297
subrepticio	2	0	3.297
submarina	2	0	3.297
suavizar	2	0	3.297
suavizaba	2	0	3.297
sospechado	2	0	3.297
soplos	2	0	3.297
soñada	2	0	3.297
sonrisita	2	0	3.297
sonaron	2	0	3.297
sonámbulo	2	0	3.297
sonajas	2	0	3.297
sombrillas	2	0	3.297
solícito	2	0	3.297
solicitantes	2	0	3.297
solicitante	2	0	3.297
solicitadas	2	0	3.297
soldada	2	0	3.297
solariegas	2	0	3.297
solapada	2	0	3.297
socorrido	2	0	3.297
sobrinilla	2	0	3.297
sobrenaturales	2	0	3.297
sistemático	2	0	3.297
sistemáticamente	2	0	3.297
sinuosas	2	0	3.297
síntesis	2	0	3.297
simoníaco	2	0	3.297
simoniaco	2	0	3.297
similor	2	0	3.297
simétricos	2	0	3.297
simétrico	2	0	3.297
silbantes	2	0	3.297
silbaban	2	0	3.297
signum	2	0	3.297
significar	2	0	3.297
sierva	2	0	3.297
sicilia	2	0	3.297
setentón	2	0	3.297
sesudos	2	0	3.297
serre	2	0	3.297
serrar	2	0	3.297
seráfico	2	0	3.297
sepultados	2	0	3.297
seor	2	0	3.297
señuelo	2	0	3.297
señorial	2	0	3.297
sentimentales	2	0	3.297
sentarme	2	0	3.297
sensuales	2	0	3.297
sensibilidad	2	0	3.297
sendero	2	0	3.297
senda	2	0	3.297
seminaristas	2	0	3.297
seglares	2	0	3.297
segada	2	0	3.297
secaba	2	0	3.297
scortum	2	0	3.297
satisface	2	0	3.297
satín	2	0	3.297
sarcasmos	2	0	3.297
santiguó	2	0	3.297
sans	2	0	3.297
sancionado	2	0	3.297
salvarle	2	0	3.297
salvarla	2	0	3.297
salvaría	2	0	3.297
sálvamelo	2	0	3.297
salvaban	2	0	3.297
saltaría	2	0	3.297
salsa	2	0	3.297
saldremos	2	0	3.297
sajón	2	0	3.297
sacro	2	0	3.297
sacrílegas	2	0	3.297
sacrificarme	2	0	3.297
sacrificaban	2	0	3.297
sabrían	2	0	3.297
saborearle	2	0	3.297
saborea	2	0	3.297
saborcillo	2	0	3.297
rumiar	2	0	3.297
ruega	2	0	3.297
ruborosa	2	0	3.297
rubí	2	0	3.297
rousseau	2	0	3.297
rosal	2	0	3.297
rosadas	2	0	3.297
roncos	2	0	3.297
románico	2	0	3.297
rolliza	2	0	3.297
rojizos	2	0	3.297
roedores	2	0	3.297
rodrigón	2	0	3.297
rodeando	2	0	3.297
rodamos	2	0	3.297
roces	2	0	3.297
risueñas	2	0	3.297
riñe	2	0	3.297
rigoroso	2	0	3.297
rigorosa	2	0	3.297
rige	2	0	3.297
riesgos	2	0	3.297
rezan	2	0	3.297
revoltosos	2	0	3.297
revistas	2	0	3.297
retrocedido	2	0	3.297
retro	2	0	3.297
retraso	2	0	3.297
retraía	2	0	3.297
retozonas	2	0	3.297
retorcían	2	0	3.297
retoño	2	0	3.297
restituyó	2	0	3.297
restituiría	2	0	3.297
restituido	2	0	3.297
respetuoso	2	0	3.297
respectiva	2	0	3.297
resonancia	2	0	3.297
resolverán	2	0	3.297
resignaban	2	0	3.297
reservado	2	0	3.297
resbaladizo	2	0	3.297
resaltando	2	0	3.297
rerum	2	0	3.297
requisitos	2	0	3.297
requiescat	2	0	3.297
reps	2	0	3.297
representada	2	0	3.297
reprendió	2	0	3.297
repitieron	2	0	3.297
repentinos	2	0	3.297
repatriación	2	0	3.297
renunciara	2	0	3.297
renglones	2	0	3.297
renegado	2	0	3.297
renegaban	2	0	3.297
rendijas	2	0	3.297
renacer	2	0	3.297
remontándose	2	0	3.297
rejuvenecía	2	0	3.297
regueros	2	0	3.297
regordeta	2	0	3.297
registró	2	0	3.297
regía	2	0	3.297
regatas	2	0	3.297
regalaban	2	0	3.297
referirlos	2	0	3.297
reemplazar	2	0	3.297
redil	2	0	3.297
rededor	2	0	3.297
redactores	2	0	3.297
recurrido	2	0	3.297
rectificaba	2	0	3.297
recrearse	2	0	3.297
recrear	2	0	3.297
recordarle	2	0	3.297
recordado	2	0	3.297
reconocido	2	0	3.297
recónditos	2	0	3.297
recoletas	2	0	3.297
recolección	2	0	3.297
recodo	2	0	3.297
reclutas	2	0	3.297
recitó	2	0	3.297
recita	2	0	3.297
recipiente	2	0	3.297
recibiendo	2	0	3.297
recatadas	2	0	3.297
recargada	2	0	3.297
rebeldía	2	0	3.297
rebaños	2	0	3.297
reata	2	0	3.297
realismo	2	0	3.297
rayitas	2	0	3.297
rasguño	2	0	3.297
raquíticas	2	0	3.297
ramitos	2	0	3.297
raído	2	0	3.297
rabió	2	0	3.297
quiebra	2	0	3.297
querrían	2	0	3.297
quebraban	2	0	3.297
puntiagudo	2	0	3.297
pundonoroso	2	0	3.297
pun	2	0	3.297
púlpitos	2	0	3.297
pulmón	2	0	3.297
pulgadas	2	0	3.297
pulcras	2	0	3.297
puerco	2	0	3.297
pueblecillo	2	0	3.297
publicado	2	0	3.297
psicológicos	2	0	3.297
prudentísimo	2	0	3.297
provocativos	2	0	3.297
provocase	2	0	3.297
provocaciones	2	0	3.297
provocaba	2	0	3.297
provisorato	2	0	3.297
provincialismo	2	0	3.297
provinciales	2	0	3.297
protestado	2	0	3.297
protestaban	2	0	3.297
protagonista	2	0	3.297
prostituida	2	0	3.297
prosaicos	2	0	3.297
propusieron	2	0	3.297
propone	2	0	3.297
prolongó	2	0	3.297
prohibidas	2	0	3.297
profusión	2	0	3.297
profesa	2	0	3.297
profanas	2	0	3.297
profanaba	2	0	3.297
prodigarse	2	0	3.297
prodigado	2	0	3.297
procuraría	2	0	3.297
procul	2	0	3.297
procesiones	2	0	3.297
proceden	2	0	3.297
probarle	2	0	3.297
probabilidad	2	0	3.297
privilegios	2	0	3.297
primaveras	2	0	3.297
pretendida	2	0	3.297
prestados	2	0	3.297
presidenta	2	0	3.297
presenciaban	2	0	3.297
prescripciones	2	0	3.297
prescindía	2	0	3.297
preparan	2	0	3.297
preparados	2	0	3.297
preocupa	2	0	3.297
premiar	2	0	3.297
pregonando	2	0	3.297
preferencias	2	0	3.297
predicando	2	0	3.297
predicadores	2	0	3.297
predica	2	0	3.297
preclaros	2	0	3.297
precipitar	2	0	3.297
precipitados	2	0	3.297
preces	2	0	3.297
prebendados	2	0	3.297
pp	2	0	3.297
postrada	2	0	3.297
postiza	2	0	3.297
postigos	2	0	3.297
pórticos	2	0	3.297
portátil	2	0	3.297
porqué	2	0	3.297
populacho	2	0	3.297
pontificia	2	0	3.297
pontifical	2	0	3.297
pomares	2	0	3.297
politiquilla	2	0	3.297
poéticos	2	0	3.297
podaba	2	0	3.297
poblaba	2	0	3.297
plomizo	2	0	3.297
plegarias	2	0	3.297
platónicamente	2	0	3.297
platerescos	2	0	3.297
plastón	2	0	3.297
plástica	2	0	3.297
plantones	2	0	3.297
plano	2	0	3.297
placas	2	0	3.297
pisotón	2	0	3.297
pisarle	2	0	3.297
pisaban	2	0	3.297
piruetas	2	0	3.297
piropo	2	0	3.297
pintarle	2	0	3.297
pilón	2	0	3.297
pílades	2	0	3.297
picarescas	2	0	3.297
pías	2	0	3.297
petrica	2	0	3.297
pésima	2	0	3.297
pescaron	2	0	3.297
pésame	2	0	3.297
persuadir	2	0	3.297
personilla	2	0	3.297
persigue	2	0	3.297
perseguidas	2	0	3.297
perseguida	2	0	3.297
permitirse	2	0	3.297
permítame	2	0	3.297
perjudica	2	0	3.297
períodos	2	0	3.297
pergamino	2	0	3.297
perdían	2	0	3.297
peñón	2	0	3.297
penetrantes	2	0	3.297
penetra	2	0	3.297
pendón	2	0	3.297
pendía	2	0	3.297
pegaban	2	0	3.297
pedirla	2	0	3.297
pedestre	2	0	3.297
pedante	2	0	3.297
pedagógico	2	0	3.297
pecaminoso	2	0	3.297
pecaminosas	2	0	3.297
pausadas	2	0	3.297
patrimonio	2	0	3.297
pastoril	2	0	3.297
pasmos	2	0	3.297
pasioncilla	2	0	3.297
pasiegos	2	0	3.297
pasatiempos	2	0	3.297
pasadizos	2	0	3.297
partículas	2	0	3.297
participó	2	0	3.297
parsimonia	2	0	3.297
párrocos	2	0	3.297
parques	2	0	3.297
paroxismo	2	0	3.297
parodias	2	0	3.297
pardiez	2	0	3.297
parcería	2	0	3.297
parase	2	0	3.297
páramo	2	0	3.297
paraje	2	0	3.297
papando	2	0	3.297
papanatas	2	0	3.297
pañales	2	0	3.297
panzudas	2	0	3.297
pantorrillas	2	0	3.297
pantoja	2	0	3.297
paniaguados	2	0	3.297
palpable	2	0	3.297
palmera	2	0	3.297
palidece	2	0	3.297
palaciegas	2	0	3.297
paje	2	0	3.297
pajas	2	0	3.297
paisanos	2	0	3.297
pagó	2	0	3.297
pagada	2	0	3.297
pace	2	0	3.297
osa	2	0	3.297
ortodoxos	2	0	3.297
ortigas	2	0	3.297
ornitólogo	2	0	3.297
ornamento	2	0	3.297
orlada	2	0	3.297
originado	2	0	3.297
or	2	0	3.297
optimista	2	0	3.297
oprime	2	0	3.297
oponían	2	0	3.297
opacas	2	0	3.297
ondulaciones	2	0	3.297
olvidaría	2	0	3.297
olfateado	2	0	3.297
ojillos	2	0	3.297
ojeroso	2	0	3.297
oidium	2	0	3.297
ofrenda	2	0	3.297
oda	2	0	3.297
ocupase	2	0	3.297
ocupados	2	0	3.297
ocultarlo	2	0	3.297
ociosos	2	0	3.297
ocasionadas	2	0	3.297
obstinó	2	0	3.297
obstinado	2	0	3.297
obsequiándote	2	0	3.297
obscenidades	2	0	3.297
obligo	2	0	3.297
obedecido	2	0	3.297
nubecilla	2	0	3.297
novelesca	2	0	3.297
nobis	2	0	3.297
neuralgia	2	0	3.297
nerviosilla	2	0	3.297
negruzco	2	0	3.297
negruzca	2	0	3.297
negarme	2	0	3.297
negando	2	0	3.297
negaciones	2	0	3.297
necesitado	2	0	3.297
neblina	2	0	3.297
nazarena	2	0	3.297
navegar	2	0	3.297
natura	2	0	3.297
natillas	2	0	3.297
nado	2	0	3.297
mutuas	2	0	3.297
murmura	2	0	3.297
mozalbete	2	0	3.297
movile	2	0	3.297
mostrencos	2	0	3.297
mortifica	2	0	3.297
morirás	2	0	3.297
moreto	2	0	3.297
morderla	2	0	3.297
moratín	2	0	3.297
montañesa	2	0	3.297
monótonos	2	0	3.297
molière	2	0	3.297
molicie	2	0	3.297
molestarla	2	0	3.297
molestado	2	0	3.297
mojigata	2	0	3.297
mojadura	2	0	3.297
modificar	2	0	3.297
moderada	2	0	3.297
modelada	2	0	3.297
mirarles	2	0	3.297
minoría	2	0	3.297
mínguez	2	0	3.297
minerva	2	0	3.297
minarle	2	0	3.297
minar	2	0	3.297
minando	2	0	3.297
mimosas	2	0	3.297
millonaria	2	0	3.297
migajas	2	0	3.297
miedosos	2	0	3.297
midas	2	0	3.297
microscopio	2	0	3.297
mezquina	2	0	3.297
mezclar	2	0	3.297
meticulosa	2	0	3.297
mesándose	2	0	3.297
meretriz	2	0	3.297
mercancía	2	0	3.297
mentecato	2	0	3.297
melosa	2	0	3.297
melódica	2	0	3.297
meléndez	2	0	3.297
mefistófeles	2	0	3.297
medrando	2	0	3.297
meditaría	2	0	3.297
medido	2	0	3.297
mediar	2	0	3.297
medallón	2	0	3.297
mecedoras	2	0	3.297
mazorca	2	0	3.297
matutinas	2	0	3.297
matarlos	2	0	3.297
matanzas	2	0	3.297
mástil	2	0	3.297
masculino	2	0	3.297
mascaba	2	0	3.297
marrullero	2	0	3.297
marrón	2	0	3.297
maroto	2	0	3.297
margarita	2	0	3.297
marejada	2	0	3.297
marearle	2	0	3.297
mareaban	2	0	3.297
maquiavelo	2	0	3.297
maquiavélico	2	0	3.297
manzanos	2	0	3.297
manrique	2	0	3.297
manolé	2	0	3.297
maniqueos	2	0	3.297
maníaco	2	0	3.297
manejando	2	0	3.297
mandatos	2	0	3.297
mancebos	2	0	3.297
maltratados	2	0	3.297
malsano	2	0	3.297
malorum	2	0	3.297
maldiciente	2	0	3.297
maldecían	2	0	3.297
maldecía	2	0	3.297
majestuosamente	2	0	3.297
magullaba	2	0	3.297
magnetismo	2	0	3.297
madrugón	2	0	3.297
macizos	2	0	3.297
lutero	2	0	3.297
lune	2	0	3.297
lujosas	2	0	3.297
lugarteniente	2	0	3.297
lugareños	2	0	3.297
lucientes	2	0	3.297
luciente	2	0	3.297
lucecillas	2	0	3.297
lucas	2	0	3.297
lona	2	0	3.297
lomos	2	0	3.297
locuacidad	2	0	3.297
locales	2	0	3.297
llueva	2	0	3.297
llovería	2	0	3.297
lloras	2	0	3.297
llegará	2	0	3.297
llantos	2	0	3.297
llames	2	0	3.297
llamémoslo	2	0	3.297
literatas	2	0	3.297
listas	2	0	3.297
lisonjas	2	0	3.297
lírico	2	0	3.297
lira	2	0	3.297
linajudos	2	0	3.297
linajudo	2	0	3.297
ligorio	2	0	3.297
ligerezas	2	0	3.297
liebres	2	0	3.297
lides	2	0	3.297
lícitos	2	0	3.297
librase	2	0	3.297
librarla	2	0	3.297
libraba	2	0	3.297
liberalotes	2	0	3.297
liberalote	2	0	3.297
li	2	0	3.297
levítico	2	0	3.297
levantándolo	2	0	3.297
letrina	2	0	3.297
lengüeta	2	0	3.297
legitimidad	2	0	3.297
leerlo	2	0	3.297
leerlas	2	0	3.297
lear	2	0	3.297
leandro	2	0	3.297
laurel	2	0	3.297
latón	2	0	3.297
latino	2	0	3.297
latamente	2	0	3.297
lascivas	2	0	3.297
lanzas	2	0	3.297
lánguida	2	0	3.297
lamían	2	0	3.297
lamentó	2	0	3.297
lacónicamente	2	0	3.297
kilómetros	2	0	3.297
jubón	2	0	3.297
jubiló	2	0	3.297
jesuitismo	2	0	3.297
jaspe	2	0	3.297
jarrones	2	0	3.297
jaquet	2	0	3.297
japoneses	2	0	3.297
jamonas	2	0	3.297
jactaba	2	0	3.297
irrupción	2	0	3.297
irritarse	2	0	3.297
irritara	2	0	3.297
irritante	2	0	3.297
irrisoria	2	0	3.297
irrevocables	2	0	3.297
irrespetuoso	2	0	3.297
irreprochables	2	0	3.297
irreflexiva	2	0	3.297
irnos	2	0	3.297
irguió	2	0	3.297
invulnerable	2	0	3.297
involuntario	2	0	3.297
inventores	2	0	3.297
invencibles	2	0	3.297
inundó	2	0	3.297
intransigencia	2	0	3.297
intolerancia	2	0	3.297
intervención	2	0	3.297
interrumpir	2	0	3.297
interrumpiendo	2	0	3.297
interrumpían	2	0	3.297
interpretado	2	0	3.297
interpretaba	2	0	3.297
intermedio	2	0	3.297
interina	2	0	3.297
interesados	2	0	3.297
inter	2	0	3.297
intempestiva	2	0	3.297
integridad	2	0	3.297
insustanciales	2	0	3.297
insultante	2	0	3.297
insultaban	2	0	3.297
insulta	2	0	3.297
insuficiente	2	0	3.297
instintiva	2	0	3.297
insistían	2	0	3.297
insípidos	2	0	3.297
insípida	2	0	3.297
insinuarle	2	0	3.297
insinuación	2	0	3.297
insinuaba	2	0	3.297
insignes	2	0	3.297
inopinada	2	0	3.297
inofensiva	2	0	3.297
injertar	2	0	3.297
iniquidad	2	0	3.297
inimitable	2	0	3.297
inhabitable	2	0	3.297
infundir	2	0	3.297
influyentes	2	0	3.297
influyente	2	0	3.297
influía	2	0	3.297
inflo	2	0	3.297
infiltraba	2	0	3.297
infanzones	2	0	3.297
inesperado	2	0	3.297
indescriptible	2	0	3.297
indefectiblemente	2	0	3.297
incrustaba	2	0	3.297
incompleta	2	0	3.297
incompatibles	2	0	3.297
incólume	2	0	3.297
incógnito	2	0	3.297
inclinaron	2	0	3.297
incitante	2	0	3.297
incalificable	2	0	3.297
inaugural	2	0	3.297
impunemente	2	0	3.297
impuestas	2	0	3.297
impúdica	2	0	3.297
imprudencias	2	0	3.297
improvisadas	2	0	3.297
improvisaba	2	0	3.297
importunas	2	0	3.297
impondría	2	0	3.297
implícitamente	2	0	3.297
impía	2	0	3.297
imitaré	2	0	3.297
imitador	2	0	3.297
imaginado	2	0	3.297
ilumine	2	0	3.297
iluminando	2	0	3.297
iluminaban	2	0	3.297
ignorarlo	2	0	3.297
idolillo	2	0	3.297
huyo	2	0	3.297
hurto	2	0	3.297
hundiendo	2	0	3.297
huiré	2	0	3.297
huida	2	0	3.297
huí	2	0	3.297
huesuda	2	0	3.297
horrorosos	2	0	3.297
hornos	2	0	3.297
hornilla	2	0	3.297
hornacinas	2	0	3.297
homo	2	0	3.297
hojeó	2	0	3.297
hojalata	2	0	3.297
hisopos	2	0	3.297
hiponax	2	0	3.297
higienista	2	0	3.297
hierático	2	0	3.297
hierática	2	0	3.297
hieran	2	0	3.297
heroicas	2	0	3.297
herodes	2	0	3.297
hermoseado	2	0	3.297
herederas	2	0	3.297
heredera	2	0	3.297
heredara	2	0	3.297
hércules	2	0	3.297
herbario	2	0	3.297
helados	2	0	3.297
hechizado	2	0	3.297
hebdomadario	2	0	3.297
hastiado	2	0	3.297
hartazgo	2	0	3.297
halagaría	2	0	3.297
hacinados	2	0	3.297
haciendas	2	0	3.297
hachazos	2	0	3.297
hablarme	2	0	3.297
habitaban	2	0	3.297
habano	2	0	3.297
gusano	2	0	3.297
gula	2	0	3.297
guiarla	2	0	3.297
guiada	2	0	3.297
guarnición	2	0	3.297
gruta	2	0	3.297
grotescos	2	0	3.297
gritase	2	0	3.297
gritado	2	0	3.297
griegas	2	0	3.297
griega	2	0	3.297
grava	2	0	3.297
gratuitos	2	0	3.297
granizo	2	0	3.297
graciosísimo	2	0	3.297
gozó	2	0	3.297
götinga	2	0	3.297
goda	2	0	3.297
gigante	2	0	3.297
gesticulaban	2	0	3.297
gertrudis	2	0	3.297
genui	2	0	3.297
genuflexiones	2	0	3.297
geniales	2	0	3.297
generalizaba	2	0	3.297
generalife	2	0	3.297
generalidades	2	0	3.297
gazmoñería	2	0	3.297
gavilanes	2	0	3.297
gastrónomo	2	0	3.297
gasa	2	0	3.297
garza	2	0	3.297
gárrulos	2	0	3.297
gárrulas	2	0	3.297
garra	2	0	3.297
gañán	2	0	3.297
ganosas	2	0	3.297
ganchos	2	0	3.297
ganaderos	2	0	3.297
ganadero	2	0	3.297
galanterías	2	0	3.297
galanteo	2	0	3.297
galanes	2	0	3.297
gaitas	2	0	3.297
gacetilleros	2	0	3.297
futuros	2	0	3.297
fundadores	2	0	3.297
fumaban	2	0	3.297
fragilidad	2	0	3.297
fortificar	2	0	3.297
forraba	2	0	3.297
forminge	2	0	3.297
formadas	2	0	3.297
forcejeaba	2	0	3.297
foncé	2	0	3.297
flotaba	2	0	3.297
floricultura	2	0	3.297
florete	2	0	3.297
florecillas	2	0	3.297
floreciente	2	0	3.297
flautas	2	0	3.297
flauta	2	0	3.297
flanqueada	2	0	3.297
flammarion	2	0	3.297
flamenca	2	0	3.297
fingimiento	2	0	3.297
filtraba	2	0	3.297
filosóficamente	2	0	3.297
filosofando	2	0	3.297
filius	2	0	3.297
fígaro	2	0	3.297
fiambre	2	0	3.297
fía	2	0	3.297
fervorosamente	2	0	3.297
ferviente	2	0	3.297
ferreruelo	2	0	3.297
fermento	2	0	3.297
féretro	2	0	3.297
felonía	2	0	3.297
felicitaba	2	0	3.297
fé	2	0	3.297
favorita	2	0	3.297
faut	2	0	3.297
fatigaban	2	0	3.297
fascinado	2	0	3.297
farolero	2	0	3.297
fangosos	2	0	3.297
fanatizados	2	0	3.297
faltarían	2	0	3.297
faldero	2	0	3.297
facilitó	2	0	3.297
facilitaban	2	0	3.297
exuberantes	2	0	3.297
extremis	2	0	3.297
expuestas	2	0	3.297
exponemos	2	0	3.297
explicaron	2	0	3.297
explicaría	2	0	3.297
explicando	2	0	3.297
explicaban	2	0	3.297
excitaciones	2	0	3.297
excita	2	0	3.297
excesivos	2	0	3.297
excelencias	2	0	3.297
exageradamente	2	0	3.297
exagera	2	0	3.297
evocaba	2	0	3.297
eunuco	2	0	3.297
eudoro	2	0	3.297
ética	2	0	3.297
eternidades	2	0	3.297
etelvina	2	0	3.297
estupefacto	2	0	3.297
estudiarla	2	0	3.297
estrellada	2	0	3.297
estrechado	2	0	3.297
estrada	2	0	3.297
estorbaré	2	0	3.297
estaño	2	0	3.297
estanquillos	2	0	3.297
estallidos	2	0	3.297
esquivando	2	0	3.297
esputo	2	0	3.297
espiritualismo	2	0	3.297
espina	2	0	3.297
espín	2	0	3.297
espía	2	0	3.297
especulaciones	2	0	3.297
espantados	2	0	3.297
espadachín	2	0	3.297
esencias	2	0	3.297
escupirle	2	0	3.297
escribían	2	0	3.297
escribanos	2	0	3.297
escote	2	0	3.297
escotada	2	0	3.297
escasez	2	0	3.297
escarnio	2	0	3.297
escarcha	2	0	3.297
escarceos	2	0	3.297
escaparía	2	0	3.297
escandalosamente	2	0	3.297
escandalizó	2	0	3.297
escandalizarse	2	0	3.297
escalinata	2	0	3.297
escajos	2	0	3.297
erre	2	0	3.297
eróticos	2	0	3.297
erótico	2	0	3.297
erótica	2	0	3.297
eriza	2	0	3.297
erard	2	0	3.297
envidiar	2	0	3.297
envidiables	2	0	3.297
envalentonado	2	0	3.297
entusiástico	2	0	3.297
entregase	2	0	3.297
entregarla	2	0	3.297
entregadas	2	0	3.297
entreacto	2	0	3.297
entreabiertas	2	0	3.297
enterrador	2	0	3.297
enterar	2	0	3.297
entendidos	2	0	3.297
entenderle	2	0	3.297
entenderla	2	0	3.297
entallado	2	0	3.297
entablaron	2	0	3.297
ensueño	2	0	3.297
enseñorearse	2	0	3.297
ensayos	2	0	3.297
ensayar	2	0	3.297
ensayado	2	0	3.297
ensanchaba	2	0	3.297
enroscaban	2	0	3.297
enramadas	2	0	3.297
enormísima	2	0	3.297
ennoblecía	2	0	3.297
ennegrecida	2	0	3.297
enlutadas	2	0	3.297
enlutada	2	0	3.297
enjugaba	2	0	3.297
enjambres	2	0	3.297
engordarla	2	0	3.297
engendrado	2	0	3.297
engaños	2	0	3.297
enfrascado	2	0	3.297
encogiendo	2	0	3.297
enamoraban	2	0	3.297
emprendiese	2	0	3.297
emporio	2	0	3.297
empirismo	2	0	3.297
empeñados	2	0	3.297
empanadas	2	0	3.297
empalagaba	2	0	3.297
empadronamiento	2	0	3.297
eminentes	2	0	3.297
embutidos	2	0	3.297
embutido	2	0	3.297
embozadamente	2	0	3.297
emborracharse	2	0	3.297
emborracharon	2	0	3.297
embocadura	2	0	3.297
embarazosa	2	0	3.297
elegías	2	0	3.297
electorales	2	0	3.297
égida	2	0	3.297
eficaces	2	0	3.297
educandas	2	0	3.297
edificantes	2	0	3.297
edificada	2	0	3.297
edifica	2	0	3.297
economías	2	0	3.297
eclesiásticos	2	0	3.297
echara	2	0	3.297
ecbátana	2	0	3.297
ebrio	2	0	3.297
dumas	2	0	3.297
dulcísimas	2	0	3.297
dufour	2	0	3.297
donna	2	0	3.297
dones	2	0	3.297
dominus	2	0	3.297
domador	2	0	3.297
dolió	2	0	3.297
doblando	2	0	3.297
divisa	2	0	3.297
distender	2	0	3.297
dispensas	2	0	3.297
disimuladas	2	0	3.297
disfruto	2	0	3.297
disfrazar	2	0	3.297
disfrazaba	2	0	3.297
disecado	2	0	3.297
discutido	2	0	3.297
disculpó	2	0	3.297
disculpas	2	0	3.297
discrecional	2	0	3.297
discordantes	2	0	3.297
disciplinadas	2	0	3.297
diminutivos	2	0	3.297
digestiones	2	0	3.297
dibujada	2	0	3.297
desvergüenzas	2	0	3.297
desvanes	2	0	3.297
desvanecer	2	0	3.297
despreciará	2	0	3.297
despojó	2	0	3.297
despiertos	2	0	3.297
desperdiciar	2	0	3.297
despellejar	2	0	3.297
despedazada	2	0	3.297
despedazaba	2	0	3.297
desocupada	2	0	3.297
deslumbrantes	2	0	3.297
deslumbran	2	0	3.297
deslumbrador	2	0	3.297
deslucían	2	0	3.297
deslizaban	2	0	3.297
deslenguado	2	0	3.297
desinteresado	2	0	3.297
designios	2	0	3.297
deshacerle	2	0	3.297
desfigurada	2	0	3.297
desfallecer	2	0	3.297
desfachatada	2	0	3.297
desengañarse	2	0	3.297
desenganchar	2	0	3.297
desenfrenada	2	0	3.297
desechaba	2	0	3.297
desdeñando	2	0	3.297
desdeñaba	2	0	3.297
descuidados	2	0	3.297
descuento	2	0	3.297
descubiertos	2	0	3.297
descriptiva	2	0	3.297
descreídos	2	0	3.297
desconfiando	2	0	3.297
descarnado	2	0	3.297
descalzas	2	0	3.297
descabellada	2	0	3.297
desarrollada	2	0	3.297
desanimado	2	0	3.297
desagravios	2	0	3.297
desafinado	2	0	3.297
desafiase	2	0	3.297
desafiado	2	0	3.297
desacreditado	2	0	3.297
desabridos	2	0	3.297
derretía	2	0	3.297
depositados	2	0	3.297
deploraba	2	0	3.297
demostrarle	2	0	3.297
demostrado	2	0	3.297
demócrata	2	0	3.297
deliquio	2	0	3.297
delgados	2	0	3.297
deleznable	2	0	3.297
delata	2	0	3.297
dejarlos	2	0	3.297
degenerar	2	0	3.297
definido	2	0	3.297
definida	2	0	3.297
defensores	2	0	3.297
dedican	2	0	3.297
decorosamente	2	0	3.297
declararon	2	0	3.297
declararme	2	0	3.297
debieron	2	0	3.297
darwinismo	2	0	3.297
cundió	2	0	3.297
culpaba	2	0	3.297
cuerpecito	2	0	3.297
cucuruchos	2	0	3.297
cuchicheaba	2	0	3.297
cuarteto	2	0	3.297
cuantía	2	0	3.297
crucifícale	2	0	3.297
cronicones	2	0	3.297
crispaba	2	0	3.297
crisóstomo	2	0	3.297
cripta	2	0	3.297
crestas	2	0	3.297
cresta	2	0	3.297
creerme	2	0	3.297
creaba	2	0	3.297
crasitud	2	0	3.297
costaban	2	0	3.297
corujedos	2	0	3.297
cortesano	2	0	3.297
cortaplumas	2	0	3.297
corroborar	2	0	3.297
corriste	2	0	3.297
correligionario	2	0	3.297
correligionarias	2	0	3.297
corpulento	2	0	3.297
corporales	2	0	3.297
corporaciones	2	0	3.297
cornucopias	2	0	3.297
coristas	2	0	3.297
coquetona	2	0	3.297
coquetear	2	0	3.297
coqueta	2	0	3.297
copias	2	0	3.297
copiado	2	0	3.297
convirtieron	2	0	3.297
converso	2	0	3.297
conversaban	2	0	3.297
convencionales	2	0	3.297
contribuía	2	0	3.297
contraventanas	2	0	3.297
contraído	2	0	3.297
contrahecha	2	0	3.297
contradictorio	2	0	3.297
contingente	2	0	3.297
contertulios	2	0	3.297
contentándose	2	0	3.297
contendiente	2	0	3.297
consuma	2	0	3.297
consultas	2	0	3.297
consultando	2	0	3.297
conspiraba	2	0	3.297
consonantes	2	0	3.297
consistir	2	0	3.297
consistente	2	0	3.297
consistencia	2	0	3.297
consiguieron	2	0	3.297
conservadores	2	0	3.297
consentirá	2	0	3.297
consentimiento	2	0	3.297
consejero	2	0	3.297
conseguían	2	0	3.297
conjurados	2	0	3.297
conjurado	2	0	3.297
conjuración	2	0	3.297
congresos	2	0	3.297
congéneres	2	0	3.297
confundirse	2	0	3.297
confunde	2	0	3.297
confortable	2	0	3.297
confort	2	0	3.297
confirmábase	2	0	3.297
confidentes	2	0	3.297
confiaban	2	0	3.297
confesores	2	0	3.297
confesata	2	0	3.297
conducían	2	0	3.297
condes	2	0	3.297
concurrían	2	0	3.297
concubina	2	0	3.297
concretas	2	0	3.297
conciliábulos	2	0	3.297
conciliábulo	2	0	3.297
concedían	2	0	3.297
concebía	2	0	3.297
comunicativa	2	0	3.297
comulgaría	2	0	3.297
comte	2	0	3.297
compromisario	2	0	3.297
comprometerla	2	0	3.297
comprimida	2	0	3.297
comprenda	2	0	3.297
compareció	2	0	3.297
comparada	2	0	3.297
comparable	2	0	3.297
compadecían	2	0	3.297
cómodos	2	0	3.297
cómodamente	2	0	3.297
comm	2	0	3.297
comienza	2	0	3.297
comenzada	2	0	3.297
comentar	2	0	3.297
comentaban	2	0	3.297
comentaba	2	0	3.297
comadronas	2	0	3.297
coloso	2	0	3.297
coloca	2	0	3.297
colmar	2	0	3.297
colmada	2	0	3.297
colgó	2	0	3.297
colectivo	2	0	3.297
coleccionador	2	0	3.297
coincide	2	0	3.297
cohechos	2	0	3.297
codorniz	2	0	3.297
codeándose	2	0	3.297
codazos	2	0	3.297
cocineros	2	0	3.297
cocineras	2	0	3.297
cocheras	2	0	3.297
cloaca	2	0	3.297
clavarse	2	0	3.297
claudicante	2	0	3.297
clarisas	2	0	3.297
clarinetes	2	0	3.297
clandestino	2	0	3.297
claire	2	0	3.297
clac	2	0	3.297
cito	2	0	3.297
citando	2	0	3.297
citaban	2	0	3.297
cirino	2	0	3.297
circulante	2	0	3.297
circos	2	0	3.297
cinto	2	0	3.297
cínicos	2	0	3.297
cínico	2	0	3.297
cigarras	2	0	3.297
cientos	2	0	3.297
chocaban	2	0	3.297
chitón	2	0	3.297
chito	2	0	3.297
chirridos	2	0	3.297
chiripa	2	0	3.297
chinto	2	0	3.297
chascarrillos	2	0	3.297
chas	2	0	3.297
chartreuse	2	0	3.297
chaparrones	2	0	3.297
chantre	2	0	3.297
chalet	2	0	3.297
chalecos	2	0	3.297
cestas	2	0	3.297
cercos	2	0	3.297
cercanos	2	0	3.297
cerbatana	2	0	3.297
cepillar	2	0	3.297
censuras	2	0	3.297
cenaron	2	0	3.297
celucos	2	0	3.297
celestes	2	0	3.297
cejijunto	2	0	3.297
cebo	2	0	3.297
cauterio	2	0	3.297
categórica	2	0	3.297
cataratas	2	0	3.297
casuchas	2	0	3.297
casual	2	0	3.297
casarían	2	0	3.297
carvajal	2	0	3.297
carnaza	2	0	3.297
carnales	2	0	3.297
cárdeno	2	0	3.297
carboneras	2	0	3.297
carámbano	2	0	3.297
carabina	2	0	3.297
capullos	2	0	3.297
capitoné	2	0	3.297
cañonazos	2	0	3.297
canturia	2	0	3.297
cántico	2	0	3.297
cante	2	0	3.297
cantaron	2	0	3.297
canónicas	2	0	3.297
cancel	2	0	3.297
camareros	2	0	3.297
calzar	2	0	3.297
calvicie	2	0	3.297
calumniaba	2	0	3.297
callarán	2	0	3.297
caliza	2	0	3.297
calificaba	2	0	3.297
califas	2	0	3.297
caldos	2	0	3.297
calderonianas	2	0	3.297
calatayud	2	0	3.297
cacique	2	0	3.297
cacho	2	0	3.297
caballeritos	2	0	3.297
caballeresco	2	0	3.297
caballerescas	2	0	3.297
c	2	0	3.297
búsquela	2	0	3.297
buscasen	2	0	3.297
burlador	2	0	3.297
burgueses	2	0	3.297
bum	2	0	3.297
bullicioso	2	0	3.297
bullanguera	2	0	3.297
bujía	2	0	3.297
bucólicos	2	0	3.297
brillar	2	0	3.297
brilla	2	0	3.297
brigadier	2	0	3.297
breñas	2	0	3.297
borradas	2	0	3.297
boquiabierta	2	0	3.297
bonete	2	0	3.297
blindado	2	0	3.297
blasfemar	2	0	3.297
blanquísimo	2	0	3.297
bizarro	2	0	3.297
bis	2	0	3.297
billares	2	0	3.297
bijou	2	0	3.297
bigotillo	2	0	3.297
bernesga	2	0	3.297
benito	2	0	3.297
beneméritos	2	0	3.297
beneficiao	2	0	3.297
benavides	2	0	3.297
belvedere	2	0	3.297
bebés	2	0	3.297
beatífica	2	0	3.297
beatería	2	0	3.297
baterías	2	0	3.297
bastidores	2	0	3.297
bastaron	2	0	3.297
barroco	2	0	3.297
barriada	2	0	3.297
baronesas	2	0	3.297
barbilindo	2	0	3.297
barata	2	0	3.297
bañan	2	0	3.297
bañaban	2	0	3.297
banquetes	2	0	3.297
balduque	2	0	3.297
balbucear	2	0	3.297
balaustrada	2	0	3.297
balanceo	2	0	3.297
bajera	2	0	3.297
bailé	2	0	3.297
báculo	2	0	3.297
baco	2	0	3.297
babuchas	2	0	3.297
azote	2	0	3.297
azor	2	0	3.297
azafranada	2	0	3.297
ayunos	2	0	3.297
ayuno	2	0	3.297
ayudo	2	0	3.297
ayudarme	2	0	3.297
axioma	2	0	3.297
avizor	2	0	3.297
avisan	2	0	3.297
averiguó	2	0	3.297
avergonzaban	2	0	3.297
aventurilla	2	0	3.297
avenido	2	0	3.297
avellanas	2	0	3.297
avanzar	2	0	3.297
autonomía	2	0	3.297
automático	2	0	3.297
auricular	2	0	3.297
aurea	2	0	3.297
auras	2	0	3.297
aturdirse	2	0	3.297
aturdía	2	0	3.297
atronaba	2	0	3.297
atrición	2	0	3.297
atribulado	2	0	3.297
atribuir	2	0	3.297
atrévete	2	0	3.297
atrever	2	0	3.297
atravesaban	2	0	3.297
atragantó	2	0	3.297
atrae	2	0	3.297
atormenten	2	0	3.297
atormentarse	2	0	3.297
atolondramiento	2	0	3.297
atañe	2	0	3.297
atadas	2	0	3.297
asustara	2	0	3.297
asustadiza	2	0	3.297
asomados	2	0	3.297
asistió	2	0	3.297
asistieron	2	0	3.297
asistiera	2	0	3.297
asisten	2	0	3.297
asfixiaba	2	0	3.297
asesinar	2	0	3.297
aserto	2	0	3.297
aseguraban	2	0	3.297
asedio	2	0	3.297
asedian	2	0	3.297
asceta	2	0	3.297
artífice	2	0	3.297
articulista	2	0	3.297
artesonado	2	0	3.297
artesanos	2	0	3.297
arrullos	2	0	3.297
arruina	2	0	3.297
arrojara	2	0	3.297
arrojada	2	0	3.297
arrinconado	2	0	3.297
arrinconada	2	0	3.297
arrimada	2	0	3.297
arrepentía	2	0	3.297
arrastrase	2	0	3.297
arrastrara	2	0	3.297
arrastradas	2	0	3.297
areo	2	0	3.297
arenga	2	0	3.297
área	2	0	3.297
arduos	2	0	3.297
arduo	2	0	3.297
arceas	2	0	3.297
arcadia	2	0	3.297
arboricultura	2	0	3.297
arbolillos	2	0	3.297
arboleda	2	0	3.297
arbolado	2	0	3.297
arabescos	2	0	3.297
aquiles	2	0	3.297
aquéllos	2	0	3.297
apuesta	2	0	3.297
aprovecha	2	0	3.297
apretarla	2	0	3.297
apoyados	2	0	3.297
apóstata	2	0	3.297
apostasía	2	0	3.297
apostar	2	0	3.297
apoderado	2	0	3.297
aplaudió	2	0	3.297
aplastar	2	0	3.297
aplastadas	2	0	3.297
apiñadas	2	0	3.297
apetitosos	2	0	3.297
apetitosa	2	0	3.297
apencar	2	0	3.297
aparentes	2	0	3.297
apagadas	2	0	3.297
anuncian	2	0	3.297
antonomasia	2	0	3.297
antitéticos	2	0	3.297
antinomia	2	0	3.297
antífrasis	2	0	3.297
anticipo	2	0	3.297
anónimos	2	0	3.297
anónimo	2	0	3.297
annatas	2	0	3.297
animadora	2	0	3.297
anima	2	0	3.297
anhelante	2	0	3.297
angelillo	2	0	3.297
anfiteatro	2	0	3.297
anegado	2	0	3.297
andrajosos	2	0	3.297
andén	2	0	3.297
andará	2	0	3.297
anafrodita	2	0	3.297
amontonaban	2	0	3.297
ambrosio	2	0	3.297
ámbitos	2	0	3.297
amarlas	2	0	3.297
amaré	2	0	3.297
amanerada	2	0	3.297
amador	2	0	3.297
alvarín	2	0	3.297
alusivos	2	0	3.297
alusivo	2	0	3.297
aludió	2	0	3.297
aludido	2	0	3.297
alude	2	0	3.297
altruista	2	0	3.297
altiva	2	0	3.297
alteración	2	0	3.297
altanera	2	0	3.297
almohadillas	2	0	3.297
almo	2	0	3.297
almidonada	2	0	3.297
alimentado	2	0	3.297
alejandría	2	0	3.297
aleación	2	0	3.297
aldeanas	2	0	3.297
aldabón	2	0	3.297
alcanzaron	2	0	3.297
alborotadores	2	0	3.297
alambicado	2	0	3.297
alambicada	2	0	3.297
alaba	2	0	3.297
airecillo	2	0	3.297
ahorrarme	2	0	3.297
ahondaba	2	0	3.297
aguantaba	2	0	3.297
aguaceros	2	0	3.297
agridulce	2	0	3.297
agravó	2	0	3.297
agradarla	2	0	3.297
afirman	2	0	3.297
afeminamiento	2	0	3.297
afeitados	2	0	3.297
afectado	2	0	3.297
adusto	2	0	3.297
adornado	2	0	3.297
adoratrices	2	0	3.297
adocenados	2	0	3.297
admiten	2	0	3.297
admita	2	0	3.297
admiraciones	2	0	3.297
adelantada	2	0	3.297
adaptación	2	0	3.297
acusación	2	0	3.297
acumulado	2	0	3.297
actualidad	2	0	3.297
actuales	2	0	3.297
acreditados	2	0	3.297
acostumbró	2	0	3.297
acostumbraban	2	0	3.297
aconsejado	2	0	3.297
acompasados	2	0	3.297
acompañarle	2	0	3.297
acoger	2	0	3.297
achaque	2	0	3.297
achacoso	2	0	3.297
acequia	2	0	3.297
aceituna	2	0	3.297
accediendo	2	0	3.297
acaloró	2	0	3.297
acabarse	2	0	3.297
abusado	2	0	3.297
abusaba	2	0	3.297
abusa	2	0	3.297
abundaban	2	0	3.297
abultadas	2	0	3.297
abstengo	2	0	3.297
absolvía	2	0	3.297
abrumados	2	0	3.297
abroño	2	0	3.297
abrochaba	2	0	3.297
abrazado	2	0	3.297
abrasarse	2	0	3.297
abrasados	2	0	3.297
abordar	2	0	3.297
abonadas	2	0	3.297
abismarse	2	0	3.297
abecedario	2	0	3.297
abdomen	2	0	3.297
abandonase	2	0	3.297
abandonarse	2	0	3.297
subían	16	10	3.276
permiso	16	10	3.276
eterno	16	10	3.276
aparecía	16	10	3.276
plazuela	8	21	3.269
mandar	8	21	3.269
dudas	8	21	3.269
ja	21	43	3.257
siguientes	2	9	3.256
salí	2	9	3.256
regocijo	2	9	3.256
quedé	2	9	3.256
picos	2	9	3.256
patatas	2	9	3.256
pájara	2	9	3.256
nación	2	9	3.256
mostrarse	2	9	3.256
molina	2	9	3.256
meditaciones	2	9	3.256
matrimonios	2	9	3.256
magdalena	2	9	3.256
letrero	2	9	3.256
ladrona	2	9	3.256
judías	2	9	3.256
intentó	2	9	3.256
huéspedes	2	9	3.256
huecos	2	9	3.256
heredero	2	9	3.256
goces	2	9	3.256
gasta	2	9	3.256
freno	2	9	3.256
estarse	2	9	3.256
entere	2	9	3.256
diciembre	2	9	3.256
descuida	2	9	3.256
déjese	2	9	3.256
cinta	2	9	3.256
carros	2	9	3.256
bolsillos	2	9	3.256
ascuas	2	9	3.256
entrando	12	28	3.238
dejar	61	56	3.232
deseaba	18	38	3.214
caricias	17	11	3.205
yerbas	6	2	3.203
visitaban	6	2	3.203
vagos	6	2	3.203
tranquilos	6	2	3.203
torbellino	6	2	3.203
tolerar	6	2	3.203
tinte	6	2	3.203
terminó	6	2	3.203
soñador	6	2	3.203
sofocaba	6	2	3.203
silbaba	6	2	3.203
roca	6	2	3.203
repugnantes	6	2	3.203
rejas	6	2	3.203
régimen	6	2	3.203
recuerda	6	2	3.203
queridas	6	2	3.203
pretendiente	6	2	3.203
pilar	6	2	3.203
perversión	6	2	3.203
pavor	6	2	3.203
pataditas	6	2	3.203
oyeran	6	2	3.203
oportunidad	6	2	3.203
olvidada	6	2	3.203
monaguillo	6	2	3.203
miedos	6	2	3.203
médica	6	2	3.203
mecánico	6	2	3.203
materiales	6	2	3.203
marina	6	2	3.203
malicioso	6	2	3.203
llover	6	2	3.203
límites	6	2	3.203
lenta	6	2	3.203
jardines	6	2	3.203
impuso	6	2	3.203
igualdad	6	2	3.203
hipócritas	6	2	3.203
héroe	6	2	3.203
gritaban	6	2	3.203
fray	6	2	3.203
flacas	6	2	3.203
filósofos	6	2	3.203
familiares	6	2	3.203
extravíos	6	2	3.203
enamorar	6	2	3.203
eficacia	6	2	3.203
doncellas	6	2	3.203
distinguidas	6	2	3.203
disputaba	6	2	3.203
digámoslo	6	2	3.203
descalzos	6	2	3.203
cutis	6	2	3.203
crujir	6	2	3.203
creencias	6	2	3.203
cordial	6	2	3.203
conyugal	6	2	3.203
convicciones	6	2	3.203
conveniencia	6	2	3.203
convaleciente	6	2	3.203
contestado	6	2	3.203
confidente	6	2	3.203
complicada	6	2	3.203
compadecía	6	2	3.203
citaba	6	2	3.203
chusco	6	2	3.203
capítulo	6	2	3.203
beneficio	6	2	3.203
bebió	6	2	3.203
bando	6	2	3.203
asperezas	6	2	3.203
aristocrático	6	2	3.203
ardían	6	2	3.203
aprobaba	6	2	3.203
apretados	6	2	3.203
anchos	6	2	3.203
afirmaba	6	2	3.203
manía	15	33	3.201
obligación	7	19	3.185
inspiraba	7	19	3.185
hilo	7	19	3.185
corta	7	19	3.185
venido	30	57	3.172
vuelven	10	5	3.163
sobrenatural	10	5	3.163
serena	10	5	3.163
reconoció	10	5	3.163
milagros	10	5	3.163
luis	10	5	3.163
haberlo	10	5	3.163
explicar	10	5	3.163
doloroso	10	5	3.163
declarar	10	5	3.163
cursis	10	5	3.163
convertido	10	5	3.163
constancia	10	5	3.163
consiguiente	10	5	3.163
bienes	10	5	3.163
bancos	10	5	3.163
arco	10	5	3.163
pudiera	58	53	3.152
señas	18	12	3.148
exaltación	18	12	3.148
espectáculo	18	12	3.148
advirtió	18	12	3.148
contar	25	49	3.123
queriendo	11	26	3.116
inglés	11	26	3.116
feo	11	26	3.116
dicha	11	26	3.116
suceso	6	17	3.114
simpatía	6	17	3.114
próximo	6	17	3.114
doctrina	6	17	3.114
rigor	19	13	3.102
humildad	19	13	3.102
frialdad	19	13	3.102
calor	56	51	3.099
volveré	3	11	3.096
viéndole	3	11	3.096
trajeron	3	11	3.096
tiraba	3	11	3.096
tiestos	3	11	3.096
sociedades	3	11	3.096
sobra	3	11	3.096
simpática	3	11	3.096
sacan	3	11	3.096
rossini	3	11	3.096
relativa	3	11	3.096
rastro	3	11	3.096
portero	3	11	3.096
pertenecía	3	11	3.096
permitió	3	11	3.096
mande	3	11	3.096
lavar	3	11	3.096
independencia	3	11	3.096
hiciese	3	11	3.096
favorable	3	11	3.096
extraordinaria	3	11	3.096
encendió	3	11	3.096
déjeme	3	11	3.096
dará	3	11	3.096
cuente	3	11	3.096
consideración	3	11	3.096
civilización	3	11	3.096
botones	3	11	3.096
barrios	3	11	3.096
afecto	3	11	3.096
frase	39	33	3.080
llevado	14	31	3.069
lentamente	5	15	3.066
empezaron	5	15	3.066
vestidos	20	14	3.065
vean	4	13	3.052
suponer	4	13	3.052
sofocada	4	13	3.052
parezca	4	13	3.052
parecíale	4	13	3.052
mostrador	4	13	3.052
llamada	4	13	3.052
judío	4	13	3.052
huevos	4	13	3.052
final	4	13	3.052
fecha	4	13	3.052
éxito	4	13	3.052
apoyando	4	13	3.052
bajo	75	72	3.042
rumor	21	15	3.036
perdía	22	16	3.013
entierro	22	16	3.013
acercaba	22	16	3.013
rodillas	34	28	3.009
voces	33	27	2.998
tuvieron	10	24	2.998
fiera	10	24	2.998
dejado	33	27	2.998
abrigo	10	24	2.998
sonaba	23	17	2.996
profunda	23	17	2.996
débil	23	17	2.996
celos	32	26	2.988
servidumbre	11	6	2.987
párpados	11	6	2.987
libres	11	6	2.987
gozando	11	6	2.987
fuente	11	6	2.987
espirituales	11	6	2.987
encontraban	11	6	2.987
decidió	11	6	2.987
pájaros	24	18	2.983
estaba	731	858	2.982
noticia	19	39	2.981
darse	31	25	2.980
antiguo	25	19	2.974
anterior	30	24	2.973
religiosa	29	23	2.969
pecados	28	22	2.966
altar	28	22	2.966
país	16	34	2.941
pregunta	13	29	2.938
muerto	49	44	2.921
política	21	42	2.906
mitad	21	42	2.906
haya	21	42	2.906
ciertos	21	42	2.906
iba	333	375	2.899
señal	9	22	2.883
paso	109	111	2.875
solemnidad	12	7	2.857
regiones	12	7	2.857
ocupaciones	12	7	2.857
estatua	12	7	2.857
distraída	12	7	2.857
matrimonio	18	37	2.843
oído	77	75	2.836
xi	1	6	2.833
votación	1	6	2.833
voló	1	6	2.833
viéndola	1	6	2.833
vendiendo	1	6	2.833
vender	1	6	2.833
vais	1	6	2.833
vacilando	1	6	2.833
urbanidad	1	6	2.833
tunantes	1	6	2.833
transformación	1	6	2.833
traerle	1	6	2.833
tonillo	1	6	2.833
tocas	1	6	2.833
tintero	1	6	2.833
tengan	1	6	2.833
techos	1	6	2.833
solar	1	6	2.833
sofocado	1	6	2.833
sientes	1	6	2.833
salimos	1	6	2.833
rutinas	1	6	2.833
rudo	1	6	2.833
rótulo	1	6	2.833
rondaba	1	6	2.833
revolvió	1	6	2.833
revoluciones	1	6	2.833
reventaba	1	6	2.833
recta	1	6	2.833
recados	1	6	2.833
quererme	1	6	2.833
queréis	1	6	2.833
pum	1	6	2.833
propongo	1	6	2.833
procedimientos	1	6	2.833
porrazo	1	6	2.833
porquerías	1	6	2.833
ponerlo	1	6	2.833
podrás	1	6	2.833
plantó	1	6	2.833
picador	1	6	2.833
pertenece	1	6	2.833
pegó	1	6	2.833
pegando	1	6	2.833
oírte	1	6	2.833
ofreciéndole	1	6	2.833
obtuvo	1	6	2.833
narciso	1	6	2.833
mugre	1	6	2.833
misteriosas	1	6	2.833
metamorfosis	1	6	2.833
médicis	1	6	2.833
magnífica	1	6	2.833
llora	1	6	2.833
limpios	1	6	2.833
letargo	1	6	2.833
lavarse	1	6	2.833
jarana	1	6	2.833
invitó	1	6	2.833
insensato	1	6	2.833
ingenuidad	1	6	2.833
infundía	1	6	2.833
impedir	1	6	2.833
hongo	1	6	2.833
hierros	1	6	2.833
hiciste	1	6	2.833
gustaría	1	6	2.833
grato	1	6	2.833
garbanzo	1	6	2.833
fusiles	1	6	2.833
frotándose	1	6	2.833
fincas	1	6	2.833
faz	1	6	2.833
facilidad	1	6	2.833
expresando	1	6	2.833
existían	1	6	2.833
existencias	1	6	2.833
estés	1	6	2.833
espinazo	1	6	2.833
espantoso	1	6	2.833
entresuelo	1	6	2.833
entornada	1	6	2.833
enteraba	1	6	2.833
enseñó	1	6	2.833
ejecución	1	6	2.833
efectiva	1	6	2.833
dormitorio	1	6	2.833
distribución	1	6	2.833
dile	1	6	2.833
descarada	1	6	2.833
dependiente	1	6	2.833
depende	1	6	2.833
dejose	1	6	2.833
dárselo	1	6	2.833
cuñada	1	6	2.833
creías	1	6	2.833
coyuntura	1	6	2.833
contaré	1	6	2.833
conocidas	1	6	2.833
componía	1	6	2.833
combinación	1	6	2.833
casco	1	6	2.833
cargan	1	6	2.833
camisas	1	6	2.833
calentura	1	6	2.833
brutos	1	6	2.833
brusca	1	6	2.833
bondadoso	1	6	2.833
banqueta	1	6	2.833
arranco	1	6	2.833
apellido	1	6	2.833
angelito	1	6	2.833
altercado	1	6	2.833
alivio	1	6	2.833
alboroto	1	6	2.833
ágil	1	6	2.833
agente	1	6	2.833
afrenta	1	6	2.833
afectando	1	6	2.833
acertaba	1	6	2.833
acceso	1	6	2.833
acabo	1	6	2.833
hacerlo	15	32	2.805
víctimas	7	3	2.787
tertulios	7	3	2.787
soplo	7	3	2.787
socio	7	3	2.787
septiembre	7	3	2.787
separarse	7	3	2.787
señalado	7	3	2.787
secreta	7	3	2.787
resignación	7	3	2.787
poderoso	7	3	2.787
pesadas	7	3	2.787
pensaría	7	3	2.787
penitentes	7	3	2.787
pellizco	7	3	2.787
náufrago	7	3	2.787
mudo	7	3	2.787
molestar	7	3	2.787
mareaba	7	3	2.787
intrigas	7	3	2.787
inclinación	7	3	2.787
imitaba	7	3	2.787
idas	7	3	2.787
frecuente	7	3	2.787
estirar	7	3	2.787
encendidas	7	3	2.787
elogios	7	3	2.787
divino	7	3	2.787
descubrimiento	7	3	2.787
corazonada	7	3	2.787
contaban	7	3	2.787
consentido	7	3	2.787
confiesa	7	3	2.787
confesarse	7	3	2.787
cesaron	7	3	2.787
cargadas	7	3	2.787
campana	7	3	2.787
ayudar	7	3	2.787
avergonzado	7	3	2.787
atractivo	7	3	2.787
arroja	7	3	2.787
arranques	7	3	2.787
aparecían	7	3	2.787
amenazó	7	3	2.787
absurdos	7	3	2.787
breve	8	20	2.774
apreciar	8	20	2.774
dejando	20	40	2.767
temblar	13	8	2.758
sudor	13	8	2.758
sabiduría	13	8	2.758
probable	13	8	2.758
piano	13	8	2.758
molestaba	13	8	2.758
cerraba	13	8	2.758
tantas	55	51	2.754
algún	79	128	2.754
wamba	4	1	2.745
víspera	4	1	2.745
violines	4	1	2.745
vigilaba	4	1	2.745
vestían	4	1	2.745
verosímil	4	1	2.745
verían	4	1	2.745
vacaciones	4	1	2.745
turbaba	4	1	2.745
túnica	4	1	2.745
tropezado	4	1	2.745
trasladó	4	1	2.745
trágico	4	1	2.745
tolerable	4	1	2.745
títulos	4	1	2.745
tímida	4	1	2.745
tibias	4	1	2.745
terminada	4	1	2.745
tendidos	4	1	2.745
temporal	4	1	2.745
talleres	4	1	2.745
suculento	4	1	2.745
sonoras	4	1	2.745
sollozando	4	1	2.745
sólidos	4	1	2.745
soberbios	4	1	2.745
silenciosos	4	1	2.745
señalada	4	1	2.745
secretas	4	1	2.745
salvador	4	1	2.745
saltado	4	1	2.745
sacrílego	4	1	2.745
ronco	4	1	2.745
retorcidos	4	1	2.745
respeta	4	1	2.745
reprensión	4	1	2.745
reparaba	4	1	2.745
regaló	4	1	2.745
reflejaba	4	1	2.745
refinada	4	1	2.745
radical	4	1	2.745
rabillo	4	1	2.745
quintillas	4	1	2.745
publicaba	4	1	2.745
propinas	4	1	2.745
propina	4	1	2.745
prometer	4	1	2.745
prohíbe	4	1	2.745
progresistas	4	1	2.745
profano	4	1	2.745
producto	4	1	2.745
prodigaba	4	1	2.745
prisiones	4	1	2.745
pretensión	4	1	2.745
prescindir	4	1	2.745
preocupación	4	1	2.745
pómulos	4	1	2.745
piadosos	4	1	2.745
perseguían	4	1	2.745
perdidas	4	1	2.745
perdería	4	1	2.745
peligrosa	4	1	2.745
pátina	4	1	2.745
pajarera	4	1	2.745
ostentaban	4	1	2.745
oficios	4	1	2.745
oficiales	4	1	2.745
nublado	4	1	2.745
nostalgia	4	1	2.745
nogal	4	1	2.745
niñerías	4	1	2.745
nimiedades	4	1	2.745
nerviosos	4	1	2.745
mustio	4	1	2.745
muriese	4	1	2.745
murallas	4	1	2.745
municipio	4	1	2.745
mozas	4	1	2.745
molestarle	4	1	2.745
mitra	4	1	2.745
meditó	4	1	2.745
mataría	4	1	2.745
mantenía	4	1	2.745
malva	4	1	2.745
madrugador	4	1	2.745
locas	4	1	2.745
llamaradas	4	1	2.745
llagas	4	1	2.745
juzgaba	4	1	2.745
justa	4	1	2.745
jurar	4	1	2.745
juntaban	4	1	2.745
jerarquía	4	1	2.745
irritada	4	1	2.745
irreverente	4	1	2.745
invocaba	4	1	2.745
intensos	4	1	2.745
instaló	4	1	2.745
inmundo	4	1	2.745
influjo	4	1	2.745
indirectas	4	1	2.745
india	4	1	2.745
incentivo	4	1	2.745
idealista	4	1	2.745
hortalizas	4	1	2.745
hondas	4	1	2.745
homenaje	4	1	2.745
hipótesis	4	1	2.745
herejía	4	1	2.745
hazañas	4	1	2.745
gozan	4	1	2.745
gemelos	4	1	2.745
gatillo	4	1	2.745
gacetilla	4	1	2.745
francisca	4	1	2.745
fragmentos	4	1	2.745
formada	4	1	2.745
fibras	4	1	2.745
falsedad	4	1	2.745
exuberante	4	1	2.745
extendían	4	1	2.745
excepcional	4	1	2.745
evangélica	4	1	2.745
estudia	4	1	2.745
estrechar	4	1	2.745
estirado	4	1	2.745
estimaban	4	1	2.745
estatuas	4	1	2.745
esquivaba	4	1	2.745
escuchó	4	1	2.745
erguía	4	1	2.745
entendámonos	4	1	2.745
engañarse	4	1	2.745
endiablado	4	1	2.745
embriagado	4	1	2.745
emanaciones	4	1	2.745
egipcios	4	1	2.745
dorados	4	1	2.745
dominarse	4	1	2.745
dineral	4	1	2.745
dignísimo	4	1	2.745
desvanecerse	4	1	2.745
destacándose	4	1	2.745
desinteresada	4	1	2.745
deshecho	4	1	2.745
deshacía	4	1	2.745
desesperaba	4	1	2.745
depositar	4	1	2.745
cultos	4	1	2.745
creación	4	1	2.745
corrillos	4	1	2.745
corporal	4	1	2.745
cordón	4	1	2.745
convirtiera	4	1	2.745
consunción	4	1	2.745
consumía	4	1	2.745
consuela	4	1	2.745
congojas	4	1	2.745
congoja	4	1	2.745
concilio	4	1	2.745
concejales	4	1	2.745
complicaciones	4	1	2.745
comparando	4	1	2.745
cómodo	4	1	2.745
colinas	4	1	2.745
clavaban	4	1	2.745
clásico	4	1	2.745
civiles	4	1	2.745
cieno	4	1	2.745
chillona	4	1	2.745
cazadores	4	1	2.745
catarata	4	1	2.745
carca	4	1	2.745
característica	4	1	2.745
canarios	4	1	2.745
calzaba	4	1	2.745
calvo	4	1	2.745
calorcillo	4	1	2.745
calificar	4	1	2.745
calientes	4	1	2.745
calculaba	4	1	2.745
calabazas	4	1	2.745
burlándose	4	1	2.745
burlaban	4	1	2.745
besaba	4	1	2.745
barría	4	1	2.745
barniz	4	1	2.745
babilonia	4	1	2.745
atacaba	4	1	2.745
asomo	4	1	2.745
asistido	4	1	2.745
asistían	4	1	2.745
artillería	4	1	2.745
arqueología	4	1	2.745
aprovechan	4	1	2.745
apresuraba	4	1	2.745
aprensiva	4	1	2.745
aplaudía	4	1	2.745
apasionada	4	1	2.745
apagó	4	1	2.745
ansiedades	4	1	2.745
aludir	4	1	2.745
aldeanos	4	1	2.745
airado	4	1	2.745
águilas	4	1	2.745
agudos	4	1	2.745
acompañaron	4	1	2.745
acarició	4	1	2.745
aburrida	4	1	2.745
aborrecido	4	1	2.745
abandonaba	4	1	2.745
silla	31	57	2.713
más	1733	2337	2.701
resuelto	14	9	2.682
misteriosa	14	9	2.682
horizonte	14	9	2.682
gobernador	14	9	2.682
bailar	14	9	2.682
términos	11	25	2.679
seriedad	11	25	2.679
recibir	11	25	2.679
prendas	11	25	2.679
frente	80	79	2.676
providencia	7	18	2.672
negocios	7	18	2.672
siete	24	46	2.662
cuya	24	46	2.662
corazón	111	173	2.649
alcoba	58	97	2.642
cuello	36	31	2.630
satisfecha	15	10	2.623
periódico	15	10	2.623
hablo	15	10	2.623
elegancia	15	10	2.623
ausencia	15	10	2.623
infame	34	29	2.593
llevando	6	16	2.580
guapo	6	16	2.580
difunto	6	16	2.580
contó	6	16	2.580
completa	6	16	2.580
artículo	6	16	2.580
derechos	16	11	2.578
ardiente	16	11	2.578
pensamientos	33	28	2.575
primeros	16	33	2.568
larga	32	27	2.559
valiente	10	23	2.553
probar	10	23	2.553
nosotras	10	23	2.553
metía	10	23	2.553
limosna	10	23	2.553
hiciera	10	23	2.553
creer	36	64	2.549
tienen	40	70	2.548
prima	17	12	2.544
pretexto	17	12	2.544
descubierto	17	12	2.544
muebles	13	28	2.535
ir	103	161	2.535
esperando	13	28	2.535
conocer	13	28	2.535
trémula	8	4	2.531
timbre	8	4	2.531
testigos	8	4	2.531
tendida	8	4	2.531
temblor	8	4	2.531
sutiles	8	4	2.531
sacudió	8	4	2.531
relámpago	8	4	2.531
preparativos	8	4	2.531
prefiero	8	4	2.531
prado	8	4	2.531
poéticas	8	4	2.531
pequeños	8	4	2.531
movió	8	4	2.531
melancólica	8	4	2.531
humildes	8	4	2.531
grano	8	4	2.531
forastero	8	4	2.531
flaquezas	8	4	2.531
escapar	8	4	2.531
disponía	8	4	2.531
disimulado	8	4	2.531
carbón	8	4	2.531
campanadas	8	4	2.531
arrancar	8	4	2.531
amos	8	4	2.531
abrían	8	4	2.531
comía	30	25	2.529
ojo	23	44	2.525
x	2	8	2.524
volviose	2	8	2.524
vistazo	2	8	2.524
veré	2	8	2.524
véase	2	8	2.524
vámonos	2	8	2.524
tirón	2	8	2.524
tino	2	8	2.524
subida	2	8	2.524
sienta	2	8	2.524
seso	2	8	2.524
sentí	2	8	2.524
saldrá	2	8	2.524
rompe	2	8	2.524
reconciliación	2	8	2.524
pusieran	2	8	2.524
préstamo	2	8	2.524
preso	2	8	2.524
preguntando	2	8	2.524
podríamos	2	8	2.524
personales	2	8	2.524
percha	2	8	2.524
pasaría	2	8	2.524
partía	2	8	2.524
pardos	2	8	2.524
naranja	2	8	2.524
muestra	2	8	2.524
meta	2	8	2.524
llevas	2	8	2.524
llevarse	2	8	2.524
llamo	2	8	2.524
legítima	2	8	2.524
latines	2	8	2.524
inspira	2	8	2.524
insana	2	8	2.524
honradas	2	8	2.524
hiel	2	8	2.524
guardado	2	8	2.524
estimación	2	8	2.524
enseña	2	8	2.524
enormes	2	8	2.524
discurrir	2	8	2.524
cuidadosamente	2	8	2.524
cortinas	2	8	2.524
corrillo	2	8	2.524
carita	2	8	2.524
asusta	2	8	2.524
asomaban	2	8	2.524
ascos	2	8	2.524
ánimos	2	8	2.524
acabe	2	8	2.524
presentes	18	13	2.518
novela	18	13	2.518
muchacha	18	13	2.518
disimulo	18	13	2.518
deshonra	18	13	2.518
acordó	18	13	2.518
servicio	29	24	2.515
olor	29	24	2.515
delante	89	141	2.512
pura	46	42	2.511
vuelva	5	14	2.504
tratado	5	14	2.504
sonó	5	14	2.504
seres	5	14	2.504
perdona	5	14	2.504
hacerme	5	14	2.504
finas	5	14	2.504
enfermos	5	14	2.504
domingo	5	14	2.504
notaba	19	14	2.499
cristiana	19	14	2.499
haría	27	22	2.493
social	18	36	2.491
garganta	20	15	2.486
necesita	25	20	2.478
marcha	25	20	2.478
rojo	21	16	2.477
copa	21	16	2.477
belleza	22	17	2.473
ilustre	23	18	2.471
evitar	23	18	2.471
únicamente	4	12	2.453
temeroso	4	12	2.453
sucesión	4	12	2.453
sencillez	4	12	2.453
seamos	4	12	2.453
rasgos	4	12	2.453
quedan	4	12	2.453
militares	4	12	2.453
medicinas	4	12	2.453
aguja	4	12	2.453
velar	3	10	2.445
tomaron	3	10	2.445
sentados	3	10	2.445
relucir	3	10	2.445
quise	3	10	2.445
produjo	3	10	2.445
primogénito	3	10	2.445
operación	3	10	2.445
nota	3	10	2.445
municipal	3	10	2.445
miren	3	10	2.445
miras	3	10	2.445
menester	3	10	2.445
maderas	3	10	2.445
inquieto	3	10	2.445
inmediata	3	10	2.445
imposibles	3	10	2.445
frenesí	3	10	2.445
estallido	3	10	2.445
disputa	3	10	2.445
despierta	3	10	2.445
dejase	3	10	2.445
darte	3	10	2.445
darme	3	10	2.445
dame	3	10	2.445
crédito	3	10	2.445
comunicaba	3	10	2.445
coma	3	10	2.445
ceremonia	3	10	2.445
caballerito	3	10	2.445
barbas	3	10	2.445
amada	3	10	2.445
advertir	3	10	2.445
adquirir	3	10	2.445
bromas	20	39	2.432
salieron	15	31	2.430
seguridad	9	21	2.428
inteligencia	9	21	2.428
dispuesta	9	21	2.428
vista	41	71	2.427
último	41	71	2.427
fueron	41	71	2.427
importa	39	68	2.422
meses	37	65	2.420
gran	216	317	2.414
san	107	111	2.406
puesta	12	26	2.400
visitaba	9	5	2.361
vaciló	9	5	2.361
trecho	9	5	2.361
reacción	9	5	2.361
promesas	9	5	2.361
partidario	9	5	2.361
opinaba	9	5	2.361
ocultaba	9	5	2.361
jesucristo	9	5	2.361
hielo	9	5	2.361
esperó	9	5	2.361
eficaz	9	5	2.361
dorado	9	5	2.361
choque	9	5	2.361
cargada	9	5	2.361
caída	9	5	2.361
atento	9	5	2.361
asomó	9	5	2.361
armario	9	5	2.361
rico	17	34	2.352
ninguno	17	34	2.352
zurrón	0	2	2.309
zurita	0	2	2.309
zurcir	0	2	2.309
zorro	0	2	2.309
zócalo	0	2	2.309
zipizape	0	2	2.309
zarandearte	0	2	2.309
zagalona	0	2	2.309
yoduro	0	2	2.309
yio	0	2	2.309
yia	0	2	2.309
yéndose	0	2	2.309
yemas	0	2	2.309
yacente	0	2	2.309
wagner	0	2	2.309
vuestras	0	2	2.309
voraz	0	2	2.309
voracidad	0	2	2.309
vomitar	0	2	2.309
volviste	0	2	2.309
volviéndolo	0	2	2.309
volviéndole	0	2	2.309
volvías	0	2	2.309
volveríamos	0	2	2.309
volteretas	0	2	2.309
volcados	0	2	2.309
volarse	0	2	2.309
volaron	0	2	2.309
vocerrón	0	2	2.309
vivísimos	0	2	2.309
viviremos	0	2	2.309
viviré	0	2	2.309
viveros	0	2	2.309
víveres	0	2	2.309
vivacidad	0	2	2.309
vivaaaa	0	2	2.309
viudas	0	2	2.309
vistiéndose	0	2	2.309
vistiéndome	0	2	2.309
visitarte	0	2	2.309
vira	0	2	2.309
viose	0	2	2.309
violentísima	0	2	2.309
viole	0	2	2.309
violado	0	2	2.309
vine	0	2	2.309
vínculos	0	2	2.309
vigorosos	0	2	2.309
vigilarla	0	2	2.309
vigilaban	0	2	2.309
viéronle	0	2	2.309
vidrioso	0	2	2.309
viciosos	0	2	2.309
viajantes	0	2	2.309
viaducto	0	2	2.309
verídicos	0	2	2.309
verídica	0	2	2.309
ventorro	0	2	2.309
ventilación	0	2	2.309
venderlo	0	2	2.309
venda	0	2	2.309
vellón	0	2	2.309
velarla	0	2	2.309
veíais	0	2	2.309
vegetales	0	2	2.309
vascular	0	2	2.309
variadísima	0	2	2.309
vanidosa	0	2	2.309
valiosas	0	2	2.309
válgame	0	2	2.309
vales	0	2	2.309
valenciana	0	2	2.309
vacilado	0	2	2.309
uste	0	2	2.309
unir	0	2	2.309
uniéndose	0	2	2.309
uniendo	0	2	2.309
undécimo	0	2	2.309
unánimemente	0	2	2.309
tuyas	0	2	2.309
tuvimos	0	2	2.309
tutelar	0	2	2.309
tuteaban	0	2	2.309
tupé	0	2	2.309
tumor	0	2	2.309
trun	0	2	2.309
trousseaux	0	2	2.309
tropical	0	2	2.309
trompicones	0	2	2.309
trofeo	0	2	2.309
trocándose	0	2	2.309
trocado	0	2	2.309
trivial	0	2	2.309
triunfales	0	2	2.309
trinquetada	0	2	2.309
trinos	0	2	2.309
trincó	0	2	2.309
trincando	0	2	2.309
trinando	0	2	2.309
trinaba	0	2	2.309
triangular	0	2	2.309
tremolina	0	2	2.309
trazada	0	2	2.309
travesuras	0	2	2.309
traten	0	2	2.309
trate	0	2	2.309
tratarme	0	2	2.309
tratarles	0	2	2.309
tratarían	0	2	2.309
trataría	0	2	2.309
trastorné	0	2	2.309
trastornase	0	2	2.309
trastornar	0	2	2.309
trastornan	0	2	2.309
trasteando	0	2	2.309
trastadas	0	2	2.309
traspasado	0	2	2.309
trasluz	0	2	2.309
traseros	0	2	2.309
transporte	0	2	2.309
transparencias	0	2	2.309
transmitido	0	2	2.309
transfigurado	0	2	2.309
transfigurada	0	2	2.309
transferencia	0	2	2.309
trangullones	0	2	2.309
trancos	0	2	2.309
tramposa	0	2	2.309
trámite	0	2	2.309
trajecitos	0	2	2.309
trajeado	0	2	2.309
tráigame	0	2	2.309
traicionero	0	2	2.309
traicionera	0	2	2.309
traías	0	2	2.309
tragaldabas	0	2	2.309
tráfago	0	2	2.309
traerlo	0	2	2.309
traemos	0	2	2.309
tradicionalista	0	2	2.309
trabar	0	2	2.309
trabajillo	0	2	2.309
trabajen	0	2	2.309
trabajaron	0	2	2.309
trabajaré	0	2	2.309
trabajara	0	2	2.309
totalidad	0	2	2.309
toscamente	0	2	2.309
tosa	0	2	2.309
torva	0	2	2.309
tortuosa	0	2	2.309
tortas	0	2	2.309
tornaron	0	2	2.309
topete	0	2	2.309
tontuela	0	2	2.309
tontito	0	2	2.309
tontamente	0	2	2.309
tontainas	0	2	2.309
tonadilla	0	2	2.309
tomen	0	2	2.309
tómelo	0	2	2.309
tomarlos	0	2	2.309
tómalo	0	2	2.309
tomad	0	2	2.309
toledana	0	2	2.309
toíto	0	2	2.309
todita	0	2	2.309
tocino	0	2	2.309
tocaron	0	2	2.309
tocará	0	2	2.309
tocándose	0	2	2.309
tizne	0	2	2.309
tiznada	0	2	2.309
titulada	0	2	2.309
tisú	0	2	2.309
tirito	0	2	2.309
tiré	0	2	2.309
tire	0	2	2.309
tirarte	0	2	2.309
tirarlo	0	2	2.309
tiraré	0	2	2.309
tirana	0	2	2.309
tiraban	0	2	2.309
tiqui	0	2	2.309
tinturas	0	2	2.309
tinglado	0	2	2.309
tin	0	2	2.309
timideces	0	2	2.309
tijeretas	0	2	2.309
tiito	0	2	2.309
tienta	0	2	2.309
teruel	0	2	2.309
terrenal	0	2	2.309
terno	0	2	2.309
ternero	0	2	2.309
terminantes	0	2	2.309
terminados	0	2	2.309
tercia	0	2	2.309
teñir	0	2	2.309
tenuemente	0	2	2.309
tenlo	0	2	2.309
teníase	0	2	2.309
teníale	0	2	2.309
teníala	0	2	2.309
tenerte	0	2	2.309
tenerme	0	2	2.309
tendrías	0	2	2.309
tendencia	0	2	2.309
tempestuoso	0	2	2.309
temiera	0	2	2.309
tejidos	0	2	2.309
tejares	0	2	2.309
tecla	0	2	2.309
techumbre	0	2	2.309
tate	0	2	2.309
tarumba	0	2	2.309
tarro	0	2	2.309
tardando	0	2	2.309
tarascas	0	2	2.309
tapaban	0	2	2.309
tantismo	0	2	2.309
tantismas	0	2	2.309
tanda	0	2	2.309
tamañita	0	2	2.309
tallada	0	2	2.309
tableado	0	2	2.309
tabacos	0	2	2.309
susurró	0	2	2.309
sustraerse	0	2	2.309
sustitución	0	2	2.309
sustentada	0	2	2.309
suspensa	0	2	2.309
suspendía	0	2	2.309
suscrición	0	2	2.309
susceptible	0	2	2.309
susana	0	2	2.309
surtían	0	2	2.309
surgió	0	2	2.309
surgían	0	2	2.309
surge	0	2	2.309
surcos	0	2	2.309
suprimir	0	2	2.309
suponerse	0	2	2.309
supón	0	2	2.309
supieras	0	2	2.309
superchería	0	2	2.309
suministrarle	0	2	2.309
sumergirse	0	2	2.309
sumergía	0	2	2.309
sulfato	0	2	2.309
sujetas	0	2	2.309
sujetarle	0	2	2.309
sujetarla	0	2	2.309
sujeción	0	2	2.309
sui	0	2	2.309
sugestivo	0	2	2.309
suez	0	2	2.309
suéltela	0	2	2.309
sueltan	0	2	2.309
sucesivo	0	2	2.309
sublimemente	0	2	2.309
subastas	0	2	2.309
suavizando	0	2	2.309
sostienen	0	2	2.309
sostendrá	0	2	2.309
sospechará	0	2	2.309
sosón	0	2	2.309
sortija	0	2	2.309
sorprendente	0	2	2.309
sorprende	0	2	2.309
sordera	0	2	2.309
sopicaldo	0	2	2.309
sopera	0	2	2.309
sonatas	0	2	2.309
sonando	0	2	2.309
sombrilla	0	2	2.309
sombrías	0	2	2.309
solteros	0	2	2.309
soltarle	0	2	2.309
sollozaba	0	2	2.309
soliloquio	0	2	2.309
solemnísimo	0	2	2.309
solares	0	2	2.309
solapa	0	2	2.309
sofocó	0	2	2.309
sofocante	0	2	2.309
socorrida	0	2	2.309
socorrer	0	2	2.309
sobrinitos	0	2	2.309
sobrinillo	0	2	2.309
sobresaltado	0	2	2.309
sobresalían	0	2	2.309
sobres	0	2	2.309
sobraba	0	2	2.309
sobones	0	2	2.309
sobón	0	2	2.309
soberanamente	0	2	2.309
soba	0	2	2.309
sito	0	2	2.309
sirvan	0	2	2.309
sintiose	0	2	2.309
sintéticas	0	2	2.309
singularísimas	0	2	2.309
sinceros	0	2	2.309
simpatizaba	0	2	2.309
simpáticas	0	2	2.309
simbolizaba	0	2	2.309
sillero	0	2	2.309
silenciosamente	0	2	2.309
siguiese	0	2	2.309
significara	0	2	2.309
sigamos	0	2	2.309
sesuda	0	2	2.309
sesada	0	2	2.309
servidos	0	2	2.309
serpentón	0	2	2.309
seretas	0	2	2.309
serafín	0	2	2.309
sepulcral	0	2	2.309
separas	0	2	2.309
separan	0	2	2.309
sepamos	0	2	2.309
sépalo	0	2	2.309
señoritingo	0	2	2.309
sentida	0	2	2.309
sentándola	0	2	2.309
sentando	0	2	2.309
sensatez	0	2	2.309
semíramis	0	2	2.309
sellada	0	2	2.309
selectas	0	2	2.309
segundas	0	2	2.309
seguimiento	0	2	2.309
seguidita	0	2	2.309
segovia	0	2	2.309
sedas	0	2	2.309
seáis	0	2	2.309
saraos	0	2	2.309
santito	0	2	2.309
santificación	0	2	2.309
santiago	0	2	2.309
santamente	0	2	2.309
sanidad	0	2	2.309
samaritanas	0	2	2.309
salvarnos	0	2	2.309
salvan	0	2	2.309
salvajismo	0	2	2.309
salude	0	2	2.309
salteados	0	2	2.309
salte	0	2	2.309
salitas	0	2	2.309
saliéndole	0	2	2.309
salíamos	0	2	2.309
salgan	0	2	2.309
saldrás	0	2	2.309
saint	0	2	2.309
sahumaremos	0	2	2.309
sagasta	0	2	2.309
saeta	0	2	2.309
sacudiéndose	0	2	2.309
sacudían	0	2	2.309
sacrifica	0	2	2.309
sacramentado	0	2	2.309
sacola	0	2	2.309
sacase	0	2	2.309
sacarme	0	2	2.309
sacarlos	0	2	2.309
sacarían	0	2	2.309
sacaré	0	2	2.309
sacándola	0	2	2.309
sácalo	0	2	2.309
sacábale	0	2	2.309
sabrosísimo	0	2	2.309
rutinarias	0	2	2.309
ruptura	0	2	2.309
rugido	0	2	2.309
rudos	0	2	2.309
rudas	0	2	2.309
rúbricas	0	2	2.309
royan	0	2	2.309
rosarios	0	2	2.309
rorró	0	2	2.309
roñoso	0	2	2.309
rondón	0	2	2.309
rondando	0	2	2.309
rompían	0	2	2.309
rompa	0	2	2.309
rodilleras	0	2	2.309
robándome	0	2	2.309
ro	0	2	2.309
rivero	0	2	2.309
risita	0	2	2.309
risilla	0	2	2.309
riquísimas	0	2	2.309
riñones	0	2	2.309
riñonadas	0	2	2.309
rigurosa	0	2	2.309
rígido	0	2	2.309
rifa	0	2	2.309
ridiculizar	0	2	2.309
riales	0	2	2.309
rezongando	0	2	2.309
rezonas	0	2	2.309
rezaré	0	2	2.309
revoltijo	0	2	2.309
revoco	0	2	2.309
revivir	0	2	2.309
revivió	0	2	2.309
revisó	0	2	2.309
revisando	0	2	2.309
reviente	0	2	2.309
revestía	0	2	2.309
reventara	0	2	2.309
reventado	0	2	2.309
reunirse	0	2	2.309
retrospectivos	0	2	2.309
retratado	0	2	2.309
retozar	0	2	2.309
retóricas	0	2	2.309
retorciéndose	0	2	2.309
retírate	0	2	2.309
retirarme	0	2	2.309
retiraría	0	2	2.309
retiraré	0	2	2.309
retirara	0	2	2.309
retener	0	2	2.309
retahíla	0	2	2.309
resulte	0	2	2.309
resultaría	0	2	2.309
resultaban	0	2	2.309
restregándose	0	2	2.309
restallido	0	2	2.309
respondiéndose	0	2	2.309
respondiendo	0	2	2.309
respondido	0	2	2.309
respondí	0	2	2.309
responderme	0	2	2.309
respóndeme	0	2	2.309
respiros	0	2	2.309
resolviose	0	2	2.309
resolvieron	0	2	2.309
resignarse	0	2	2.309
residentes	0	2	2.309
resguardándose	0	2	2.309
reservar	0	2	2.309
reservándose	0	2	2.309
requetefinos	0	2	2.309
requemada	0	2	2.309
requemaba	0	2	2.309
reputado	0	2	2.309
reprodujo	0	2	2.309
reproducían	0	2	2.309
representó	0	2	2.309
representándose	0	2	2.309
reposadas	0	2	2.309
repoblicanos	0	2	2.309
réplica	0	2	2.309
repicar	0	2	2.309
repetida	0	2	2.309
repelones	0	2	2.309
reparan	0	2	2.309
reparadora	0	2	2.309
reos	0	2	2.309
reñiría	0	2	2.309
reñida	0	2	2.309
renqueando	0	2	2.309
renovando	0	2	2.309
renovados	0	2	2.309
renovado	0	2	2.309
reniegue	0	2	2.309
remesas	0	2	2.309
remedándole	0	2	2.309
rematado	0	2	2.309
relumbraban	0	2	2.309
relatores	0	2	2.309
relacionarse	0	2	2.309
relacionados	0	2	2.309
reírnos	0	2	2.309
reirá	0	2	2.309
reintegro	0	2	2.309
reinaban	0	2	2.309
rehusó	0	2	2.309
regurgitación	0	2	2.309
reguapo	0	2	2.309
regresaría	0	2	2.309
regresaban	0	2	2.309
regocijaba	0	2	2.309
registra	0	2	2.309
regimiento	0	2	2.309
regañón	0	2	2.309
regalito	0	2	2.309
refunfuñó	0	2	2.309
refugiose	0	2	2.309
refrescarle	0	2	2.309
refregándose	0	2	2.309
reflexionó	0	2	2.309
reflexiona	0	2	2.309
refistolera	0	2	2.309
refiriéndole	0	2	2.309
referidos	0	2	2.309
refajos	0	2	2.309
reducirla	0	2	2.309
reduciendo	0	2	2.309
reduce	0	2	2.309
redentora	0	2	2.309
recuerdan	0	2	2.309
rectifica	0	2	2.309
recortarlo	0	2	2.309
recortados	0	2	2.309
reconocerse	0	2	2.309
recónditas	0	2	2.309
reconcentrar	0	2	2.309
recogiéndose	0	2	2.309
recogí	0	2	2.309
recógete	0	2	2.309
reclusión	0	2	2.309
reclinar	0	2	2.309
reclamación	0	2	2.309
recientemente	0	2	2.309
recibirlos	0	2	2.309
recibirla	0	2	2.309
recibes	0	2	2.309
reciben	0	2	2.309
reciba	0	2	2.309
receptividad	0	2	2.309
recepción	0	2	2.309
receloso	0	2	2.309
recela	0	2	2.309
recataba	0	2	2.309
recaer	0	2	2.309
rebosar	0	2	2.309
rebajarme	0	2	2.309
realizó	0	2	2.309
realizarse	0	2	2.309
realizarlo	0	2	2.309
realidades	0	2	2.309
razonar	0	2	2.309
rayaban	0	2	2.309
ratero	0	2	2.309
ratas	0	2	2.309
rastras	0	2	2.309
rasguños	0	2	2.309
rascó	0	2	2.309
rasa	0	2	2.309
rarísima	0	2	2.309
rareza	0	2	2.309
raquítico	0	2	2.309
rapaza	0	2	2.309
rapaz	0	2	2.309
rancio	0	2	2.309
rameado	0	2	2.309
raigones	0	2	2.309
rabietina	0	2	2.309
rabie	0	2	2.309
rabadilla	0	2	2.309
ra	0	2	2.309
quitaste	0	2	2.309
quitarvos	0	2	2.309
quitarte	0	2	2.309
quitársela	0	2	2.309
quitarles	0	2	2.309
quincena	0	2	2.309
quiéreme	0	2	2.309
quiebro	0	2	2.309
quevedos	0	2	2.309
quesos	0	2	2.309
querindango	0	2	2.309
queráis	0	2	2.309
quemo	0	2	2.309
quemas	0	2	2.309
quemarse	0	2	2.309
quejarte	0	2	2.309
quedito	0	2	2.309
quedes	0	2	2.309
queden	0	2	2.309
quedáronse	0	2	2.309
quedamente	0	2	2.309
quebrantan	0	2	2.309
pusieras	0	2	2.309
purificarse	0	2	2.309
pur	0	2	2.309
puntera	0	2	2.309
puntadita	0	2	2.309
pulpitillo	0	2	2.309
pulga	0	2	2.309
puéstose	0	2	2.309
pue	0	2	2.309
pudiente	0	2	2.309
pruritos	0	2	2.309
pruebes	0	2	2.309
prueben	0	2	2.309
proyectil	0	2	2.309
provista	0	2	2.309
provisión	0	2	2.309
proveerse	0	2	2.309
protestanta	0	2	2.309
protegían	0	2	2.309
prospectos	0	2	2.309
prorrumpiendo	0	2	2.309
propietaria	0	2	2.309
prometí	0	2	2.309
prométame	0	2	2.309
prolongación	0	2	2.309
prohibirle	0	2	2.309
prohibiendo	0	2	2.309
profetizando	0	2	2.309
profético	0	2	2.309
profecías	0	2	2.309
profecía	0	2	2.309
producirse	0	2	2.309
procures	0	2	2.309
procedían	0	2	2.309
procederes	0	2	2.309
probara	0	2	2.309
probada	0	2	2.309
privados	0	2	2.309
principian	0	2	2.309
principiaba	0	2	2.309
previsor	0	2	2.309
prevenir	0	2	2.309
prevaleció	0	2	2.309
pretender	0	2	2.309
presumiendo	0	2	2.309
prestase	0	2	2.309
presentando	0	2	2.309
presentábase	0	2	2.309
presagio	0	2	2.309
prepárese	0	2	2.309
prepare	0	2	2.309
prepárate	0	2	2.309
prendida	0	2	2.309
prendado	0	2	2.309
premeditación	0	2	2.309
prehistórica	0	2	2.309
preguntole	0	2	2.309
preguntarles	0	2	2.309
pregón	0	2	2.309
prefieres	0	2	2.309
preferiré	0	2	2.309
predominio	0	2	2.309
precisado	0	2	2.309
precisa	0	2	2.309
precipitemos	0	2	2.309
precipitaste	0	2	2.309
precipitación	0	2	2.309
preciosidades	0	2	2.309
preciados	0	2	2.309
precedidas	0	2	2.309
precedida	0	2	2.309
praga	0	2	2.309
practicar	0	2	2.309
potro	0	2	2.309
potaje	0	2	2.309
positivos	0	2	2.309
posesionarse	0	2	2.309
poseedores	0	2	2.309
posados	0	2	2.309
posado	0	2	2.309
portaré	0	2	2.309
portar	0	2	2.309
portante	0	2	2.309
portando	0	2	2.309
poniéndome	0	2	2.309
poniéndolos	0	2	2.309
poniéndoles	0	2	2.309
poníale	0	2	2.309
ponferrada	0	2	2.309
ponérsele	0	2	2.309
ponemos	0	2	2.309
polvoriento	0	2	2.309
polluelo	0	2	2.309
pollería	0	2	2.309
polisones	0	2	2.309
podrías	0	2	2.309
poderlas	0	2	2.309
poderla	0	2	2.309
pobretín	0	2	2.309
plumaje	0	2	2.309
plum	0	2	2.309
plin	0	2	2.309
plieguecitos	0	2	2.309
pleno	0	2	2.309
plegando	0	2	2.309
plazoleta	0	2	2.309
platito	0	2	2.309
plasencia	0	2	2.309
plañidero	0	2	2.309
plantose	0	2	2.309
planteando	0	2	2.309
planté	0	2	2.309
plantarse	0	2	2.309
plantarle	0	2	2.309
plancheta	0	2	2.309
planchando	0	2	2.309
planas	0	2	2.309
plam	0	2	2.309
placentera	0	2	2.309
pla	0	2	2.309
pivote	0	2	2.309
pisotones	0	2	2.309
pisoteando	0	2	2.309
pirran	0	2	2.309
pirraba	0	2	2.309
pirámides	0	2	2.309
piores	0	2	2.309
piñón	0	2	2.309
pinturera	0	2	2.309
pinté	0	2	2.309
pintándole	0	2	2.309
pintando	0	2	2.309
pingo	0	2	2.309
pindongona	0	2	2.309
pinchas	0	2	2.309
pincha	0	2	2.309
pildoritas	0	2	2.309
pif	0	2	2.309
piececita	0	2	2.309
pidiole	0	2	2.309
pezón	0	2	2.309
petrolero	0	2	2.309
pesimistas	0	2	2.309
pescó	0	2	2.309
pescados	0	2	2.309
pescadero	0	2	2.309
pesares	0	2	2.309
pesadamente	0	2	2.309
perversa	0	2	2.309
pertinentes	0	2	2.309
pertenecido	0	2	2.309
persuasiva	0	2	2.309
personalmente	0	2	2.309
persignándose	0	2	2.309
persignaba	0	2	2.309
persa	0	2	2.309
perrillo	0	2	2.309
perradas	0	2	2.309
perorata	0	2	2.309
permaneciendo	0	2	2.309
periodismo	0	2	2.309
periódicamente	0	2	2.309
peri	0	2	2.309
perfectos	0	2	2.309
perdurable	0	2	2.309
perdularios	0	2	2.309
perdonará	0	2	2.309
perdiste	0	2	2.309
percibía	0	2	2.309
pequeñito	0	2	2.309
pepitas	0	2	2.309
pepes	0	2	2.309
peorcito	0	2	2.309
pensaron	0	2	2.309
pensada	0	2	2.309
peniques	0	2	2.309
península	0	2	2.309
penetraron	0	2	2.309
peneque	0	2	2.309
pelotera	0	2	2.309
pelotazo	0	2	2.309
pelmazos	0	2	2.309
pella	0	2	2.309
pelitos	0	2	2.309
pelito	0	2	2.309
peletería	0	2	2.309
pelaban	0	2	2.309
peineta	0	2	2.309
peinándose	0	2	2.309
peinadoras	0	2	2.309
peinadora	0	2	2.309
peinada	0	2	2.309
pegué	0	2	2.309
pegotes	0	2	2.309
pegaron	0	2	2.309
pegadas	0	2	2.309
pedirte	0	2	2.309
pedirme	0	2	2.309
pedirles	0	2	2.309
pediremos	0	2	2.309
pedí	0	2	2.309
pecas	0	2	2.309
payo	0	2	2.309
pavorosa	0	2	2.309
paveros	0	2	2.309
pava	0	2	2.309
patriarcal	0	2	2.309
pateando	0	2	2.309
patatín	0	2	2.309
patatán	0	2	2.309
pataleta	0	2	2.309
pataleos	0	2	2.309
pataleando	0	2	2.309
patá	0	2	2.309
pastilla	0	2	2.309
pastelería	0	2	2.309
pasteleras	0	2	2.309
pasmosas	0	2	2.309
pasmó	0	2	2.309
pásmense	0	2	2.309
pasmarote	0	2	2.309
pases	0	2	2.309
pasee	0	2	2.309
paseamos	0	2	2.309
pasasen	0	2	2.309
pasarlo	0	2	2.309
pasarle	0	2	2.309
pasarían	0	2	2.309
pasaré	0	2	2.309
pasándose	0	2	2.309
pasamos	0	2	2.309
pasamanos	0	2	2.309
pasajeros	0	2	2.309
partiendo	0	2	2.309
particularidad	0	2	2.309
participando	0	2	2.309
partían	0	2	2.309
parson	0	2	2.309
parroquianas	0	2	2.309
parlamento	0	2	2.309
parisiense	0	2	2.309
parezco	0	2	2.309
párese	0	2	2.309
pareciéndose	0	2	2.309
parecíame	0	2	2.309
paré	0	2	2.309
paradójico	0	2	2.309
paradero	0	2	2.309
paradas	0	2	2.309
parabienes	0	2	2.309
papelista	0	2	2.309
paparrucha	0	2	2.309
pañosa	0	2	2.309
pañolón	0	2	2.309
pañolito	0	2	2.309
pañería	0	2	2.309
panfilona	0	2	2.309
panderetazos	0	2	2.309
pamema	0	2	2.309
palpitación	0	2	2.309
palmotear	0	2	2.309
palmitas	0	2	2.309
palmetazos	0	2	2.309
palmetazo	0	2	2.309
palitos	0	2	2.309
palillos	0	2	2.309
paletos	0	2	2.309
paletada	0	2	2.309
paleta	0	2	2.309
paladar	0	2	2.309
palabrería	0	2	2.309
pajeles	0	2	2.309
pajarillos	0	2	2.309
pajarete	0	2	2.309
paicía	0	2	2.309
pagarla	0	2	2.309
pagan	0	2	2.309
padillita	0	2	2.309
paciente	0	2	2.309
oyéronse	0	2	2.309
ostras	0	2	2.309
oscurece	0	2	2.309
oriundo	0	2	2.309
orgullosas	0	2	2.309
orgías	0	2	2.309
orfila	0	2	2.309
ordenar	0	2	2.309
ordenanzas	0	2	2.309
ordenan	0	2	2.309
ordenado	0	2	2.309
oratorias	0	2	2.309
orán	0	2	2.309
opulentos	0	2	2.309
optimistas	0	2	2.309
olvidará	0	2	2.309
olorosas	0	2	2.309
olivos	0	2	2.309
olivares	0	2	2.309
olfatorios	0	2	2.309
ojal	0	2	2.309
oíanse	0	2	2.309
oíale	0	2	2.309
ofuscado	0	2	2.309
ofrecí	0	2	2.309
oficiosa	0	2	2.309
oficiar	0	2	2.309
oficialas	0	2	2.309
oficiala	0	2	2.309
oficiaba	0	2	2.309
ofende	0	2	2.309
ocurrírseme	0	2	2.309
ocurrirá	0	2	2.309
ocupemos	0	2	2.309
ocuparme	0	2	2.309
ocupan	0	2	2.309
oculte	0	2	2.309
obtenerla	0	2	2.309
obstrucción	0	2	2.309
observaron	0	2	2.309
observándole	0	2	2.309
observándola	0	2	2.309
observancia	0	2	2.309
obsequiar	0	2	2.309
obedeces	0	2	2.309
núñez	0	2	2.309
numeradas	0	2	2.309
numen	0	2	2.309
novillos	0	2	2.309
noviazgo	0	2	2.309
noventa	0	2	2.309
novelería	0	2	2.309
novelera	0	2	2.309
novar	0	2	2.309
noto	0	2	2.309
notarse	0	2	2.309
normalmente	0	2	2.309
nombrar	0	2	2.309
nómbrame	0	2	2.309
niñera	0	2	2.309
nietos	0	2	2.309
nicarona	0	2	2.309
netos	0	2	2.309
neta	0	2	2.309
neri	0	2	2.309
nenes	0	2	2.309
neísmo	0	2	2.309
negose	0	2	2.309
nea	0	2	2.309
nazca	0	2	2.309
nasal	0	2	2.309
narrando	0	2	2.309
nardos	0	2	2.309
nardo	0	2	2.309
nápoles	0	2	2.309
nalgas	0	2	2.309
naciste	0	2	2.309
nacieron	0	2	2.309
nabucodonosor	0	2	2.309
músicas	0	2	2.309
musicales	0	2	2.309
muove	0	2	2.309
municipales	0	2	2.309
muletillas	0	2	2.309
muletilla	0	2	2.309
muladar	0	2	2.309
mujerona	0	2	2.309
muge	0	2	2.309
muevo	0	2	2.309
muertecito	0	2	2.309
muérete	0	2	2.309
muerdo	0	2	2.309
mueran	0	2	2.309
muele	0	2	2.309
mudéjares	0	2	2.309
movilidad	0	2	2.309
móviles	0	2	2.309
moverme	0	2	2.309
motivada	0	2	2.309
motas	0	2	2.309
mostráronse	0	2	2.309
morriña	0	2	2.309
morrazo	0	2	2.309
mormón	0	2	2.309
morenito	0	2	2.309
morboso	0	2	2.309
moralista	0	2	2.309
moraleja	0	2	2.309
moñuca	0	2	2.309
monjil	0	2	2.309
monerías	0	2	2.309
mondongo	0	2	2.309
momia	0	2	2.309
momentito	0	2	2.309
molinete	0	2	2.309
molestarme	0	2	2.309
molestaran	0	2	2.309
modosa	0	2	2.309
modestita	0	2	2.309
modelado	0	2	2.309
moco	0	2	2.309
mitón	0	2	2.309
misita	0	2	2.309
misionero	0	2	2.309
misantropía	0	2	2.309
mirosté	0	2	2.309
mirolo	0	2	2.309
míreme	0	2	2.309
mírelos	0	2	2.309
miráronla	0	2	2.309
miraría	0	2	2.309
mirará	0	2	2.309
mirador	0	2	2.309
mirábalas	0	2	2.309
minio	0	2	2.309
mineral	0	2	2.309
mimir	0	2	2.309
mímica	0	2	2.309
mimbres	0	2	2.309
mimar	0	2	2.309
mimando	0	2	2.309
mima	0	2	2.309
miajita	0	2	2.309
mezquinos	0	2	2.309
mezclábase	0	2	2.309
metódica	0	2	2.309
metieran	0	2	2.309
metiéndolo	0	2	2.309
merinos	0	2	2.309
merecidos	0	2	2.309
mercachifle	0	2	2.309
meñique	0	2	2.309
mensajeros	0	2	2.309
mensaje	0	2	2.309
menosprecio	0	2	2.309
menestrala	0	2	2.309
menestra	0	2	2.309
menesterosos	0	2	2.309
meneos	0	2	2.309
menéese	0	2	2.309
meneando	0	2	2.309
mendizábal	0	2	2.309
mención	0	2	2.309
mena	0	2	2.309
melodrama	0	2	2.309
melancolías	0	2	2.309
mediterránea	0	2	2.309
meditemos	0	2	2.309
medianamente	0	2	2.309
mediación	0	2	2.309
meca	0	2	2.309
mausoleos	0	2	2.309
matritenses	0	2	2.309
matinal	0	2	2.309
materno	0	2	2.309
mataron	0	2	2.309
matarles	0	2	2.309
mataran	0	2	2.309
mastín	0	2	2.309
masticación	0	2	2.309
masónica	0	2	2.309
martos	0	2	2.309
martirizaba	0	2	2.309
marrasquino	0	2	2.309
marmotona	0	2	2.309
mariposita	0	2	2.309
maridillo	0	2	2.309
mareos	0	2	2.309
marees	0	2	2.309
mareados	0	2	2.309
márchese	0	2	2.309
marché	0	2	2.309
marchase	0	2	2.309
marcharon	0	2	2.309
marcharme	0	2	2.309
marcharé	0	2	2.309
marcar	0	2	2.309
marcados	0	2	2.309
marcada	0	2	2.309
marcaban	0	2	2.309
marcaba	0	2	2.309
maravillosamente	0	2	2.309
maravillada	0	2	2.309
maquinaria	0	2	2.309
mañosa	0	2	2.309
manteniendo	0	2	2.309
mantenerle	0	2	2.309
mantelería	0	2	2.309
mantecadas	0	2	2.309
manotazos	0	2	2.309
manjavacas	0	2	2.309
manifestaron	0	2	2.309
manifestarlo	0	2	2.309
maniáticas	0	2	2.309
manguitos	0	2	2.309
mandes	0	2	2.309
mándeme	0	2	2.309
mandarte	0	2	2.309
mandarines	0	2	2.309
mandará	0	2	2.309
máncharras	0	2	2.309
manazas	0	2	2.309
mamón	0	2	2.309
mamando	0	2	2.309
maltrató	0	2	2.309
maltratar	0	2	2.309
maltratado	0	2	2.309
malsanos	0	2	2.309
malograse	0	2	2.309
malita	0	2	2.309
maleante	0	2	2.309
majadería	0	2	2.309
magníficos	0	2	2.309
mágico	0	2	2.309
maestras	0	2	2.309
madrina	0	2	2.309
madrileña	0	2	2.309
madriguera	0	2	2.309
madejas	0	2	2.309
madapolanes	0	2	2.309
máculas	0	2	2.309
macana	0	2	2.309
luteranos	0	2	2.309
lutera	0	2	2.309
lustrosa	0	2	2.309
lunática	0	2	2.309
lujos	0	2	2.309
lúgubremente	0	2	2.309
lucimiento	0	2	2.309
lotes	0	2	2.309
loterías	0	2	2.309
losa	0	2	2.309
lord	0	2	2.309
loquinaria	0	2	2.309
lópez	0	2	2.309
logra	0	2	2.309
locomotoras	0	2	2.309
llore	0	2	2.309
lloraste	0	2	2.309
llévese	0	2	2.309
llevéis	0	2	2.309
llevé	0	2	2.309
llevarían	0	2	2.309
llevándolo	0	2	2.309
llevadera	0	2	2.309
llenara	0	2	2.309
llamarte	0	2	2.309
llamador	0	2	2.309
llamábanla	0	2	2.309
liviano	0	2	2.309
lipendi	0	2	2.309
líos	0	2	2.309
lindísimos	0	2	2.309
lindísimas	0	2	2.309
lince	0	2	2.309
limpión	0	2	2.309
limitado	0	2	2.309
lié	0	2	2.309
libritos	0	2	2.309
liberaremos	0	2	2.309
liberar	0	2	2.309
liada	0	2	2.309
liaba	0	2	2.309
lía	0	2	2.309
levantan	0	2	2.309
leoneses	0	2	2.309
lentes	0	2	2.309
lente	0	2	2.309
legítimos	0	2	2.309
leerás	0	2	2.309
lebrel	0	2	2.309
lea	0	2	2.309
lavada	0	2	2.309
latitud	0	2	2.309
lastimeros	0	2	2.309
largó	0	2	2.309
largaba	0	2	2.309
laredo	0	2	2.309
lanzaron	0	2	2.309
lanzarme	0	2	2.309
lanzarla	0	2	2.309
lanzando	0	2	2.309
lanillas	0	2	2.309
láminas	0	2	2.309
lamentar	0	2	2.309
laissez	0	2	2.309
lagrimones	0	2	2.309
lagarta	0	2	2.309
ladrando	0	2	2.309
ladino	0	2	2.309
labrada	0	2	2.309
laberinto	0	2	2.309
laberíntico	0	2	2.309
king	0	2	2.309
juzgue	0	2	2.309
juzgó	0	2	2.309
jures	0	2	2.309
juramentos	0	2	2.309
junde	0	2	2.309
junda	0	2	2.309
junco	0	2	2.309
juimos	0	2	2.309
judaísmo	0	2	2.309
jubilar	0	2	2.309
jorobar	0	2	2.309
jicarazo	0	2	2.309
javiera	0	2	2.309
jarabes	0	2	2.309
japonés	0	2	2.309
jaleo	0	2	2.309
jactándose	0	2	2.309
jactábase	0	2	2.309
jaciendo	0	2	2.309
irún	0	2	2.309
írsele	0	2	2.309
irresistibles	0	2	2.309
irregularidad	0	2	2.309
irradiación	0	2	2.309
irguiéndose	0	2	2.309
involucrar	0	2	2.309
invitados	0	2	2.309
invitación	0	2	2.309
invento	0	2	2.309
inventé	0	2	2.309
invente	0	2	2.309
inventas	0	2	2.309
inventan	0	2	2.309
inválida	0	2	2.309
invadiendo	0	2	2.309
inundaron	0	2	2.309
intervengo	0	2	2.309
interrupción	0	2	2.309
intermitente	0	2	2.309
intermediario	0	2	2.309
interesara	0	2	2.309
interesantísima	0	2	2.309
intentara	0	2	2.309
intentando	0	2	2.309
intellectus	0	2	2.309
intelectualmente	0	2	2.309
intelectuales	0	2	2.309
intacto	0	2	2.309
insultado	0	2	2.309
insubordinaba	0	2	2.309
instructivo	0	2	2.309
instintivo	0	2	2.309
instantáneamente	0	2	2.309
instaláronse	0	2	2.309
instalada	0	2	2.309
instalación	0	2	2.309
inspirábale	0	2	2.309
inspector	0	2	2.309
insignias	0	2	2.309
inservibles	0	2	2.309
insensatos	0	2	2.309
inseguridad	0	2	2.309
inquilinas	0	2	2.309
inquietó	0	2	2.309
inquietísima	0	2	2.309
inquietarse	0	2	2.309
inmortales	0	2	2.309
inmensos	0	2	2.309
inmediatos	0	2	2.309
ininteligibles	0	2	2.309
iniciativas	0	2	2.309
iniciada	0	2	2.309
inicia	0	2	2.309
ingredientes	0	2	2.309
infundió	0	2	2.309
infortunado	0	2	2.309
inflado	0	2	2.309
infausto	0	2	2.309
infamante	0	2	2.309
inexplicables	0	2	2.309
inexperta	0	2	2.309
inestimable	0	2	2.309
ineficacia	0	2	2.309
indisciplina	0	2	2.309
indilugencias	0	2	2.309
indignó	0	2	2.309
indicándole	0	2	2.309
indicada	0	2	2.309
indicaciones	0	2	2.309
independientes	0	2	2.309
indemnización	0	2	2.309
indagar	0	2	2.309
incumbencias	0	2	2.309
inculta	0	2	2.309
incrédula	0	2	2.309
inconstantes	0	2	2.309
inconscientemente	0	2	2.309
incomprensibles	0	2	2.309
incomodó	0	2	2.309
incendios	0	2	2.309
inapetencia	0	2	2.309
inacabables	0	2	2.309
impulsada	0	2	2.309
imprimiendo	0	2	2.309
impresionaron	0	2	2.309
impresionado	0	2	2.309
impresa	0	2	2.309
impotentes	0	2	2.309
imposibilitaban	0	2	2.309
impedirme	0	2	2.309
impedía	0	2	2.309
impavidez	0	2	2.309
imaginándose	0	2	2.309
iluminen	0	2	2.309
iluminaron	0	2	2.309
iluminadas	0	2	2.309
ignorando	0	2	2.309
íes	0	2	2.309
idumeo	0	2	2.309
idolatraré	0	2	2.309
idolatrando	0	2	2.309
ideación	0	2	2.309
íbanse	0	2	2.309
huraño	0	2	2.309
hunda	0	2	2.309
húmera	0	2	2.309
humaredas	0	2	2.309
huéspeda	0	2	2.309
huerfanitos	0	2	2.309
hubiérase	0	2	2.309
hostilidad	0	2	2.309
hostil	0	2	2.309
hosanna	0	2	2.309
horripilaba	0	2	2.309
horrendo	0	2	2.309
hornillo	0	2	2.309
honroso	0	2	2.309
honras	0	2	2.309
hondura	0	2	2.309
hondísima	0	2	2.309
homicida	0	2	2.309
holgura	0	2	2.309
hocicuda	0	2	2.309
hízose	0	2	2.309
hinchado	0	2	2.309
hincapié	0	2	2.309
hilada	0	2	2.309
hijitos	0	2	2.309
hidalguía	0	2	2.309
hidalgo	0	2	2.309
hicieras	0	2	2.309
heterogeneidad	0	2	2.309
hervidero	0	2	2.309
hernán	0	2	2.309
hermosuras	0	2	2.309
hermosota	0	2	2.309
hazlo	0	2	2.309
hayamos	0	2	2.309
hatchisschina	0	2	2.309
hastiaba	0	2	2.309
harte	0	2	2.309
hartas	0	2	2.309
harmonium	0	2	2.309
haraganes	0	2	2.309
hamos	0	2	2.309
hambrienta	0	2	2.309
hallábanse	0	2	2.309
hagáis	0	2	2.309
haciéndote	0	2	2.309
hacías	0	2	2.309
hacíamos	0	2	2.309
hacíalo	0	2	2.309
hacíala	0	2	2.309
hablándoles	0	2	2.309
habilidoso	0	2	2.309
habiéndose	0	2	2.309
habiéndole	0	2	2.309
haberte	0	2	2.309
habaneras	0	2	2.309
gustase	0	2	2.309
gustarme	0	2	2.309
gustarle	0	2	2.309
gustando	0	2	2.309
gustábale	0	2	2.309
guitarreo	0	2	2.309
guillati	0	2	2.309
guasoncita	0	2	2.309
guasitas	0	2	2.309
guasas	0	2	2.309
guardarlos	0	2	2.309
guardadito	0	2	2.309
guapetonas	0	2	2.309
gro	0	2	2.309
greda	0	2	2.309
gratas	0	2	2.309
granujería	0	2	2.309
grandón	0	2	2.309
grandísimas	0	2	2.309
gradual	0	2	2.309
gotitas	0	2	2.309
gorras	0	2	2.309
gobernaor	0	2	2.309
gobernadores	0	2	2.309
globos	0	2	2.309
gitanesca	0	2	2.309
gibraltar	0	2	2.309
getafe	0	2	2.309
geniazo	0	2	2.309
generosa	0	2	2.309
generis	0	2	2.309
gelatinosas	0	2	2.309
gaveta	0	2	2.309
gatuperio	0	2	2.309
gatesca	0	2	2.309
gateras	0	2	2.309
gastarla	0	2	2.309
garrafales	0	2	2.309
garabato	0	2	2.309
ganita	0	2	2.309
gangas	0	2	2.309
gandulones	0	2	2.309
gande	0	2	2.309
gama	0	2	2.309
galón	0	2	2.309
galeras	0	2	2.309
galapaguito	0	2	2.309
fusilen	0	2	2.309
furibundo	0	2	2.309
fuoco	0	2	2.309
fundándose	0	2	2.309
fundan	0	2	2.309
fundamental	0	2	2.309
fundadoras	0	2	2.309
fuguilla	0	2	2.309
fugó	0	2	2.309
fuertecillo	0	2	2.309
fruncimiento	0	2	2.309
fruncidas	0	2	2.309
frotado	0	2	2.309
frota	0	2	2.309
frita	0	2	2.309
fresas	0	2	2.309
frenético	0	2	2.309
fregado	0	2	2.309
fraternales	0	2	2.309
franquearon	0	2	2.309
franqueaban	0	2	2.309
francesota	0	2	2.309
fracasos	0	2	2.309
fracaso	0	2	2.309
forzosamente	0	2	2.309
forraje	0	2	2.309
formara	0	2	2.309
fogosa	0	2	2.309
fluxión	0	2	2.309
fluctuando	0	2	2.309
florín	0	2	2.309
floreados	0	2	2.309
flojos	0	2	2.309
flojilla	0	2	2.309
flequillo	0	2	2.309
flechas	0	2	2.309
flauteados	0	2	2.309
flácida	0	2	2.309
fisiológica	0	2	2.309
fisgona	0	2	2.309
fiscalizadora	0	2	2.309
fiscales	0	2	2.309
firmas	0	2	2.309
finísimas	0	2	2.309
finezas	0	2	2.309
finales	0	2	2.309
filtrándose	0	2	2.309
filomena	0	2	2.309
fijose	0	2	2.309
fijaremos	0	2	2.309
fijándose	0	2	2.309
figurada	0	2	2.309
figuración	0	2	2.309
fiero	0	2	2.309
fierecita	0	2	2.309
fiebres	0	2	2.309
fichú	0	2	2.309
fétida	0	2	2.309
festín	0	2	2.309
fernández	0	2	2.309
fenelona	0	2	2.309
felicitar	0	2	2.309
felicitaciones	0	2	2.309
felicitaban	0	2	2.309
felicísima	0	2	2.309
federal	0	2	2.309
fecundidad	0	2	2.309
favorezca	0	2	2.309
favoreció	0	2	2.309
fatigoso	0	2	2.309
fases	0	2	2.309
fase	0	2	2.309
fantasmona	0	2	2.309
fanfarronadas	0	2	2.309
faltarme	0	2	2.309
fallido	0	2	2.309
fallecimiento	0	2	2.309
fallar	0	2	2.309
falansterio	0	2	2.309
faenas	0	2	2.309
factible	0	2	2.309
facilitado	0	2	2.309
facilillo	0	2	2.309
facetas	0	2	2.309
facción	0	2	2.309
fabulista	0	2	2.309
fábula	0	2	2.309
fabricación	0	2	2.309
extremado	0	2	2.309
extinguida	0	2	2.309
extinguían	0	2	2.309
extienden	0	2	2.309
externos	0	2	2.309
extenso	0	2	2.309
expulsión	0	2	2.309
expulsado	0	2	2.309
expuesta	0	2	2.309
exprisiones	0	2	2.309
expresivos	0	2	2.309
expresada	0	2	2.309
exponga	0	2	2.309
explotan	0	2	2.309
expliquemos	0	2	2.309
explícame	0	2	2.309
expirando	0	2	2.309
experimentaron	0	2	2.309
expeditivo	0	2	2.309
expedir	0	2	2.309
éxitos	0	2	2.309
existió	0	2	2.309
exhortación	0	2	2.309
excitadísima	0	2	2.309
excelsa	0	2	2.309
excelencia	0	2	2.309
examinarle	0	2	2.309
examinan	0	2	2.309
examinado	0	2	2.309
evitarle	0	2	2.309
evita	0	2	2.309
evidentes	0	2	2.309
evasivas	0	2	2.309
eucaristía	0	2	2.309
etapas	0	2	2.309
etapa	0	2	2.309
estúpidas	0	2	2.309
estúpidamente	0	2	2.309
estudió	0	2	2.309
estudiadas	0	2	2.309
estudiada	0	2	2.309
estucadas	0	2	2.309
estrofa	0	2	2.309
estribillos	0	2	2.309
estrenar	0	2	2.309
estrenada	0	2	2.309
estremecimiento	0	2	2.309
estrelló	0	2	2.309
estrello	0	2	2.309
estrellarse	0	2	2.309
estrecheces	0	2	2.309
estrechándole	0	2	2.309
estirones	0	2	2.309
estirándose	0	2	2.309
estimulaba	0	2	2.309
estimula	0	2	2.309
estimo	0	2	2.309
estilos	0	2	2.309
estiércol	0	2	2.309
estese	0	2	2.309
esterilidad	0	2	2.309
estarla	0	2	2.309
estaríamos	0	2	2.309
estafa	0	2	2.309
estacazo	0	2	2.309
estaca	0	2	2.309
estableció	0	2	2.309
establece	0	2	2.309
espumarajos	0	2	2.309
espléndidos	0	2	2.309
espiritui	0	2	2.309
espiritualmente	0	2	2.309
espiral	0	2	2.309
espinal	0	2	2.309
esperaré	0	2	2.309
esperándote	0	2	2.309
espectros	0	2	2.309
espasmódico	0	2	2.309
espasmódica	0	2	2.309
esparteros	0	2	2.309
esparcimiento	0	2	2.309
esparcieron	0	2	2.309
esparciendo	0	2	2.309
esparcía	0	2	2.309
esparce	0	2	2.309
espantables	0	2	2.309
esmerose	0	2	2.309
eslabón	0	2	2.309
esférica	0	2	2.309
esencialmente	0	2	2.309
escupo	0	2	2.309
escueza	0	2	2.309
escuece	0	2	2.309
escritor	0	2	2.309
escribieran	0	2	2.309
escondiendo	0	2	2.309
escogiese	0	2	2.309
escocia	0	2	2.309
escéptica	0	2	2.309
escarnecerle	0	2	2.309
escapaban	0	2	2.309
escandalera	0	2	2.309
escanciar	0	2	2.309
escalonados	0	2	2.309
escabulló	0	2	2.309
erizo	0	2	2.309
ergotina	0	2	2.309
er	0	2	2.309
equivocadamente	0	2	2.309
equidad	0	2	2.309
episodio	0	2	2.309
epiléptico	0	2	2.309
epidermis	0	2	2.309
enzarzando	0	2	2.309
envolviéndose	0	2	2.309
envolviendo	0	2	2.309
enviudar	0	2	2.309
envidiosona	0	2	2.309
enviaba	0	2	2.309
envalentonándose	0	2	2.309
entusiasta	0	2	2.309
entristeció	0	2	2.309
entrevió	0	2	2.309
entreveía	0	2	2.309
entretienes	0	2	2.309
entreteniéndose	0	2	2.309
entretenidas	0	2	2.309
entremezclaban	0	2	2.309
entremedio	0	2	2.309
entregarás	0	2	2.309
entregaran	0	2	2.309
entraste	0	2	2.309
entraran	0	2	2.309
entrará	0	2	2.309
entrañaban	0	2	2.309
entrábamos	0	2	2.309
entonación	0	2	2.309
entona	0	2	2.309
entiéndete	0	2	2.309
entiéndelo	0	2	2.309
enternecían	0	2	2.309
enterara	0	2	2.309
entendimientos	0	2	2.309
entenderemos	0	2	2.309
enséñemela	0	2	2.309
enseñarla	0	2	2.309
enseñaría	0	2	2.309
enseñan	0	2	2.309
ensayándose	0	2	2.309
ensalmo	0	2	2.309
ensaladera	0	2	2.309
enredando	0	2	2.309
enredan	0	2	2.309
enorgullecía	0	2	2.309
enojoso	0	2	2.309
enojarse	0	2	2.309
enmendó	0	2	2.309
enmendado	0	2	2.309
enmedio	0	2	2.309
enlaces	0	2	2.309
enlace	0	2	2.309
enjuta	0	2	2.309
enhoramala	0	2	2.309
enhebrada	0	2	2.309
engrudo	0	2	2.309
engranados	0	2	2.309
engrana	0	2	2.309
engolosinar	0	2	2.309
engatusarás	0	2	2.309
engañes	0	2	2.309
engañarte	0	2	2.309
engañados	0	2	2.309
enfurruñaba	0	2	2.309
enfrenar	0	2	2.309
enfermiza	0	2	2.309
enfática	0	2	2.309
enfadas	0	2	2.309
endilgó	0	2	2.309
enderezando	0	2	2.309
encuentres	0	2	2.309
encorvado	0	2	2.309
encontrose	0	2	2.309
encontronazo	0	2	2.309
encontreme	0	2	2.309
encontradizo	0	2	2.309
encontrábamos	0	2	2.309
encerrose	0	2	2.309
encerradita	0	2	2.309
encerradas	0	2	2.309
encefalitis	0	2	2.309
encargándole	0	2	2.309
encargando	0	2	2.309
encarar	0	2	2.309
encaramándose	0	2	2.309
encantaban	0	2	2.309
encaminado	0	2	2.309
encalabrinado	0	2	2.309
encajado	0	2	2.309
encadenamiento	0	2	2.309
empujaron	0	2	2.309
empujar	0	2	2.309
empujándola	0	2	2.309
empujan	0	2	2.309
empréstito	0	2	2.309
empleomanía	0	2	2.309
emplee	0	2	2.309
emplearon	0	2	2.309
emplean	0	2	2.309
empiezas	0	2	2.309
empiece	0	2	2.309
empeñe	0	2	2.309
empeñar	0	2	2.309
empaquetado	0	2	2.309
empañados	0	2	2.309
eminencia	0	2	2.309
embustes	0	2	2.309
embocó	0	2	2.309
embistió	0	2	2.309
embebecía	0	2	2.309
embarazada	0	2	2.309
emanación	0	2	2.309
emanaba	0	2	2.309
emana	0	2	2.309
elegantísima	0	2	2.309
ejes	0	2	2.309
ejercitar	0	2	2.309
ejercen	0	2	2.309
ejemplaridad	0	2	2.309
egoistón	0	2	2.309
egipto	0	2	2.309
egipcia	0	2	2.309
efigie	0	2	2.309
eficacísimo	0	2	2.309
educatriz	0	2	2.309
educativas	0	2	2.309
educarla	0	2	2.309
edredón	0	2	2.309
económicos	0	2	2.309
eclipsaba	0	2	2.309
échate	0	2	2.309
echaremos	0	2	2.309
echándosela	0	2	2.309
echábaselas	0	2	2.309
durmientes	0	2	2.309
durmiente	0	2	2.309
durito	0	2	2.309
duraron	0	2	2.309
duramente	0	2	2.309
duquesas	0	2	2.309
dulzona	0	2	2.309
duermen	0	2	2.309
dueñas	0	2	2.309
duelen	0	2	2.309
dudes	0	2	2.309
dudarse	0	2	2.309
dudarlo	0	2	2.309
droga	0	2	2.309
doscientas	0	2	2.309
dorregaray	0	2	2.309
dormirme	0	2	2.309
dormidito	0	2	2.309
dormí	0	2	2.309
donaires	0	2	2.309
domingueras	0	2	2.309
dominaron	0	2	2.309
dominarle	0	2	2.309
domada	0	2	2.309
doler	0	2	2.309
docto	0	2	2.309
docilidad	0	2	2.309
dobleces	0	2	2.309
divirtiéndote	0	2	2.309
divierte	0	2	2.309
dividieron	0	2	2.309
divide	0	2	2.309
divertidas	0	2	2.309
distribuir	0	2	2.309
distraerme	0	2	2.309
distinguiendo	0	2	2.309
distinguen	0	2	2.309
disponga	0	2	2.309
dispensar	0	2	2.309
disparidad	0	2	2.309
disparatadas	0	2	2.309
disparadero	0	2	2.309
disolviendo	0	2	2.309
disipado	0	2	2.309
disimularla	0	2	2.309
disfrutan	0	2	2.309
disfavor	0	2	2.309
dirigirlo	0	2	2.309
dirigida	0	2	2.309
dirigen	0	2	2.309
diríale	0	2	2.309
dinerales	0	2	2.309
diminutivo	0	2	2.309
dilatado	0	2	2.309
dijimos	0	2	2.309
diéronle	0	2	2.309
dictadas	0	2	2.309
dicta	0	2	2.309
diciéndoles	0	2	2.309
diabólico	0	2	2.309
devoró	0	2	2.309
devolución	0	2	2.309
devane	0	2	2.309
devanaba	0	2	2.309
deudos	0	2	2.309
deudores	0	2	2.309
detuviéronse	0	2	2.309
detuvieran	0	2	2.309
determinose	0	2	2.309
desvarío	0	2	2.309
destruyendo	0	2	2.309
destruyen	0	2	2.309
destruir	0	2	2.309
destrozados	0	2	2.309
destinillo	0	2	2.309
desterrar	0	2	2.309
desprende	0	2	2.309
despreciarle	0	2	2.309
desposada	0	2	2.309
desplomó	0	2	2.309
despintadas	0	2	2.309
despidiéronse	0	2	2.309
despejo	0	2	2.309
despejar	0	2	2.309
despeinada	0	2	2.309
despega	0	2	2.309
despachaderas	0	2	2.309
despabiló	0	2	2.309
despabilo	0	2	2.309
despabilarse	0	2	2.309
despabilándose	0	2	2.309
despabilada	0	2	2.309
desmentirse	0	2	2.309
desmentiría	0	2	2.309
desmentir	0	2	2.309
desmedrado	0	2	2.309
desmayar	0	2	2.309
desmandarse	0	2	2.309
deslomo	0	2	2.309
deslizaba	0	2	2.309
desleían	0	2	2.309
desilusionó	0	2	2.309
deshonroso	0	2	2.309
deshonre	0	2	2.309
deshonor	0	2	2.309
deshilachados	0	2	2.309
deshilachado	0	2	2.309
deshago	0	2	2.309
desgarraba	0	2	2.309
desgarbado	0	2	2.309
desgana	0	2	2.309
desgajaba	0	2	2.309
desgaire	0	2	2.309
desflorando	0	2	2.309
desfilando	0	2	2.309
desfilaban	0	2	2.309
desenvueltas	0	2	2.309
desempeñara	0	2	2.309
desembuchaba	0	2	2.309
desembozándose	0	2	2.309
desechos	0	2	2.309
deseas	0	2	2.309
desdigo	0	2	2.309
descubro	0	2	2.309
descubriese	0	2	2.309
descubriéndose	0	2	2.309
descubra	0	2	2.309
descosido	0	2	2.309
descortés	0	2	2.309
desconsoladas	0	2	2.309
desconocía	0	2	2.309
desconfiaba	0	2	2.309
desconcertada	0	2	2.309
descompuso	0	2	2.309
descolgar	0	2	2.309
descifrar	0	2	2.309
descendientes	0	2	2.309
descendencia	0	2	2.309
descendemos	0	2	2.309
descarriada	0	2	2.309
descaradamente	0	2	2.309
descansos	0	2	2.309
descabezar	0	2	2.309
desavenencias	0	2	2.309
desatinar	0	2	2.309
desatinado	0	2	2.309
desastroso	0	2	2.309
desarrollar	0	2	2.309
desarrollando	0	2	2.309
desarmada	0	2	2.309
desalquilado	0	2	2.309
desaguisado	0	2	2.309
desagradables	0	2	2.309
desacato	0	2	2.309
derrumbaba	0	2	2.309
derribados	0	2	2.309
derivan	0	2	2.309
derechito	0	2	2.309
depresiones	0	2	2.309
depreciación	0	2	2.309
depravación	0	2	2.309
depósitos	0	2	2.309
depositaría	0	2	2.309
deplorando	0	2	2.309
denuncias	0	2	2.309
dengoso	0	2	2.309
demostración	0	2	2.309
democrático	0	2	2.309
demagogia	0	2	2.309
delirando	0	2	2.309
delineantes	0	2	2.309
dele	0	2	2.309
dejosas	0	2	2.309
dejándoles	0	2	2.309
dejábase	0	2	2.309
definir	0	2	2.309
defenderme	0	2	2.309
defenderé	0	2	2.309
dedito	0	2	2.309
dedicarme	0	2	2.309
decírsela	0	2	2.309
decidirá	0	2	2.309
dechado	0	2	2.309
debíamos	0	2	2.309
deambulación	0	2	2.309
databa	0	2	2.309
dándoles	0	2	2.309
dándolas	0	2	2.309
dámele	0	2	2.309
dais	0	2	2.309
dádivas	0	2	2.309
dábase	0	2	2.309
curtis	0	2	2.309
cure	0	2	2.309
curan	0	2	2.309
cundía	0	2	2.309
cúmulo	0	2	2.309
cumplo	0	2	2.309
cultivado	0	2	2.309
cultivada	0	2	2.309
cuidó	0	2	2.309
cuidaban	0	2	2.309
cuerdos	0	2	2.309
cuentecita	0	2	2.309
cucurucho	0	2	2.309
cucharadas	0	2	2.309
cubrirla	0	2	2.309
cubrir	0	2	2.309
cúbico	0	2	2.309
cubas	0	2	2.309
cuartillo	0	2	2.309
cuarterón	0	2	2.309
cuarentena	0	2	2.309
cualsiquiera	0	2	2.309
cuajarones	0	2	2.309
cuadrote	0	2	2.309
cuadritos	0	2	2.309
cuadrito	0	2	2.309
cuadrilátero	0	2	2.309
cuadernillos	0	2	2.309
cruzaron	0	2	2.309
críticas	0	2	2.309
cristina	0	2	2.309
crió	0	2	2.309
criaturita	0	2	2.309
crías	0	2	2.309
criarle	0	2	2.309
criamos	0	2	2.309
criadita	0	2	2.309
cretona	0	2	2.309
creída	0	2	2.309
créemelo	0	2	2.309
crean	0	2	2.309
créamelo	0	2	2.309
creados	0	2	2.309
crasa	0	2	2.309
cotorrearon	0	2	2.309
costeó	0	2	2.309
cosita	0	2	2.309
cose	0	2	2.309
coruñas	0	2	2.309
cortesías	0	2	2.309
corté	0	2	2.309
cortarse	0	2	2.309
cortaron	0	2	2.309
cortaran	0	2	2.309
cortándole	0	2	2.309
cortadillo	0	2	2.309
cortaban	0	2	2.309
corruptor	0	2	2.309
corrompida	0	2	2.309
corroborando	0	2	2.309
corresponder	0	2	2.309
corregida	0	2	2.309
correccional	0	2	2.309
corpacho	0	2	2.309
cornezuelo	0	2	2.309
cornetas	0	2	2.309
corizas	0	2	2.309
coriza	0	2	2.309
cordera	0	2	2.309
corcho	0	2	2.309
copita	0	2	2.309
copiaba	0	2	2.309
cónyuges	0	2	2.309
convulsiones	0	2	2.309
convirtiose	0	2	2.309
convidaron	0	2	2.309
convidando	0	2	2.309
convertirla	0	2	2.309
convertimos	0	2	2.309
conveníale	0	2	2.309
convengo	0	2	2.309
convenciera	0	2	2.309
convencerla	0	2	2.309
contusiones	0	2	2.309
contusión	0	2	2.309
contundentes	0	2	2.309
contundente	0	2	2.309
contribuir	0	2	2.309
contrato	0	2	2.309
contrata	0	2	2.309
contrastes	0	2	2.309
contrasentido	0	2	2.309
contrariarle	0	2	2.309
contrariaba	0	2	2.309
contole	0	2	2.309
continuas	0	2	2.309
contestole	0	2	2.309
contesté	0	2	2.309
contestara	0	2	2.309
contestando	0	2	2.309
contestaciones	0	2	2.309
contenerla	0	2	2.309
contemplativa	0	2	2.309
contaron	0	2	2.309
contarlas	0	2	2.309
contador	0	2	2.309
contabilidad	0	2	2.309
consumos	0	2	2.309
consumir	0	2	2.309
consume	0	2	2.309
consumar	0	2	2.309
consumada	0	2	2.309
consultara	0	2	2.309
constituyéndose	0	2	2.309
constituía	0	2	2.309
constipar	0	2	2.309
constar	0	2	2.309
constantes	0	2	2.309
consortes	0	2	2.309
consoló	0	2	2.309
consolara	0	2	2.309
consolábase	0	2	2.309
consienta	0	2	2.309
considero	0	2	2.309
considere	0	2	2.309
considerándose	0	2	2.309
considerándole	0	2	2.309
consideran	0	2	2.309
conservatorio	0	2	2.309
consagrados	0	2	2.309
conozcan	0	2	2.309
conmoción	0	2	2.309
conllevar	0	2	2.309
confió	0	2	2.309
confines	0	2	2.309
configuración	0	2	2.309
confiar	0	2	2.309
confianzudo	0	2	2.309
confianzuda	0	2	2.309
confecciones	0	2	2.309
conejo	0	2	2.309
conducir	0	2	2.309
condensaba	0	2	2.309
condenes	0	2	2.309
concurría	0	2	2.309
concubinato	0	2	2.309
conciliadora	0	2	2.309
conciliador	0	2	2.309
conciliación	0	2	2.309
concertada	0	2	2.309
conceptuaba	0	2	2.309
concedido	0	2	2.309
concavidad	0	2	2.309
comunicarse	0	2	2.309
comunicaron	0	2	2.309
comunicando	0	2	2.309
comunicaban	0	2	2.309
comulgan	0	2	2.309
compungida	0	2	2.309
comprometas	0	2	2.309
compres	0	2	2.309
compradora	0	2	2.309
compradas	0	2	2.309
compota	0	2	2.309
composturas	0	2	2.309
componendas	0	2	2.309
compone	0	2	2.309
completaba	0	2	2.309
compararme	0	2	2.309
compadezco	0	2	2.309
compadecer	0	2	2.309
cometían	0	2	2.309
comerías	0	2	2.309
comedero	0	2	2.309
combinando	0	2	2.309
combatirle	0	2	2.309
colorista	0	2	2.309
colonias	0	2	2.309
colocase	0	2	2.309
colocaron	0	2	2.309
colocara	0	2	2.309
colocados	0	2	2.309
colocadas	0	2	2.309
colgándose	0	2	2.309
coleto	0	2	2.309
cogiéndose	0	2	2.309
coges	0	2	2.309
cogerlos	0	2	2.309
cogen	0	2	2.309
cocinilla	0	2	2.309
cocinerita	0	2	2.309
cociendo	0	2	2.309
cocía	0	2	2.309
cochina	0	2	2.309
clorótica	0	2	2.309
clorhidrato	0	2	2.309
clínicas	0	2	2.309
cleriguito	0	2	2.309
claveteado	0	2	2.309
clavelero	0	2	2.309
claustral	0	2	2.309
clarita	0	2	2.309
clarear	0	2	2.309
claraboyas	0	2	2.309
claque	0	2	2.309
citunas	0	2	2.309
cisco	0	2	2.309
cierran	0	2	2.309
chuscadas	0	2	2.309
churumbé	0	2	2.309
chumbos	0	2	2.309
chulas	0	2	2.309
chufas	0	2	2.309
chuchería	0	2	2.309
chubasca	0	2	2.309
choza	0	2	2.309
chocolatito	0	2	2.309
chocolates	0	2	2.309
chocolatera	0	2	2.309
chocheces	0	2	2.309
chitito	0	2	2.309
chistó	0	2	2.309
chisté	0	2	2.309
chistaba	0	2	2.309
chispita	0	2	2.309
chispeantes	0	2	2.309
chirris	0	2	2.309
chiquititas	0	2	2.309
chiquilladas	0	2	2.309
chiquillada	0	2	2.309
chínchirri	0	2	2.309
chinche	0	2	2.309
chillería	0	2	2.309
chifle	0	2	2.309
chiflarse	0	2	2.309
chifladura	0	2	2.309
chiflados	0	2	2.309
chifla	0	2	2.309
chi	0	2	2.309
cheong	0	2	2.309
chavales	0	2	2.309
chavala	0	2	2.309
chascos	0	2	2.309
charlatánicas	0	2	2.309
charlaban	0	2	2.309
charlaba	0	2	2.309
charca	0	2	2.309
chaquetas	0	2	2.309
chaqué	0	2	2.309
chanchullos	0	2	2.309
chamusquina	0	2	2.309
chambras	0	2	2.309
chales	0	2	2.309
chalana	0	2	2.309
chafalditas	0	2	2.309
chafado	0	2	2.309
chafada	0	2	2.309
cevil	0	2	2.309
ceuta	0	2	2.309
cesantes	0	2	2.309
cesaban	0	2	2.309
certidumbre	0	2	2.309
certeza	0	2	2.309
cerrojos	0	2	2.309
cerrase	0	2	2.309
cerciorose	0	2	2.309
ceñidos	0	2	2.309
centrales	0	2	2.309
centigramo	0	2	2.309
centeno	0	2	2.309
cencerrada	0	2	2.309
cenando	0	2	2.309
celador	0	2	2.309
cejijunta	0	2	2.309
cedo	0	2	2.309
ceca	0	2	2.309
cebollino	0	2	2.309
cayese	0	2	2.309
caviloso	0	2	2.309
cavilaba	0	2	2.309
cavernas	0	2	2.309
cautivar	0	2	2.309
cautivaban	0	2	2.309
cautelosa	0	2	2.309
causante	0	2	2.309
caudaloso	0	2	2.309
cato	0	2	2.309
caten	0	2	2.309
categóricas	0	2	2.309
categóricamente	0	2	2.309
catarroso	0	2	2.309
catarlo	0	2	2.309
catálogos	0	2	2.309
castañetazos	0	2	2.309
castaña	0	2	2.309
casillero	0	2	2.309
cásese	0	2	2.309
cases	0	2	2.309
cáscaras	0	2	2.309
cásate	0	2	2.309
carunculosa	0	2	2.309
cartones	0	2	2.309
cartea	0	2	2.309
carromato	0	2	2.309
carromatero	0	2	2.309
carretas	0	2	2.309
carlismo	0	2	2.309
cariz	0	2	2.309
caritativo	0	2	2.309
caritativas	0	2	2.309
caritativa	0	2	2.309
caridades	0	2	2.309
cargó	0	2	2.309
cargaban	0	2	2.309
carece	0	2	2.309
carátula	0	2	2.309
carantoñas	0	2	2.309
capotes	0	2	2.309
capitana	0	2	2.309
capitalito	0	2	2.309
capirote	0	2	2.309
capciosas	0	2	2.309
caoba	0	2	2.309
cañamón	0	2	2.309
cantos	0	2	2.309
cantonales	0	2	2.309
cantaría	0	2	2.309
candorosamente	0	2	2.309
canciller	0	2	2.309
canaleja	0	2	2.309
campechana	0	2	2.309
campar	0	2	2.309
campante	0	2	2.309
campanillazo	0	2	2.309
camisería	0	2	2.309
camello	0	2	2.309
cambrí	0	2	2.309
cambiazos	0	2	2.309
cambiaron	0	2	2.309
cambiara	0	2	2.309
cambiante	0	2	2.309
calzada	0	2	2.309
calvas	0	2	2.309
calurosos	0	2	2.309
calumnió	0	2	2.309
cálmese	0	2	2.309
callosa	0	2	2.309
caldeado	0	2	2.309
caldeada	0	2	2.309
calcule	0	2	2.309
calculan	0	2	2.309
calaveradas	0	2	2.309
calambres	0	2	2.309
calabaza	0	2	2.309
cajitas	0	2	2.309
cafetero	0	2	2.309
caerle	0	2	2.309
caerás	0	2	2.309
cachemira	0	2	2.309
caballete	0	2	2.309
caballerosidad	0	2	2.309
caballera	0	2	2.309
cab	0	2	2.309
buscándole	0	2	2.309
burradas	0	2	2.309
burda	0	2	2.309
buenavista	0	2	2.309
búcaros	0	2	2.309
brutalidades	0	2	2.309
brujería	0	2	2.309
bromear	0	2	2.309
brochar	0	2	2.309
brochado	0	2	2.309
brocal	0	2	2.309
brindose	0	2	2.309
brindó	0	2	2.309
bribonaza	0	2	2.309
bribonas	0	2	2.309
breva	0	2	2.309
bregó	0	2	2.309
bregar	0	2	2.309
bregando	0	2	2.309
brecolera	0	2	2.309
bravura	0	2	2.309
bozo	0	2	2.309
botonaduras	0	2	2.309
botitas	0	2	2.309
boticas	0	2	2.309
boteros	0	2	2.309
botellita	0	2	2.309
borroso	0	2	2.309
borrando	0	2	2.309
borlas	0	2	2.309
borceguíes	0	2	2.309
boquete	0	2	2.309
bonos	0	2	2.309
bonitísimos	0	2	2.309
bonitísimo	0	2	2.309
bónibus	0	2	2.309
bondades	0	2	2.309
bomberos	0	2	2.309
bojío	0	2	2.309
bodegones	0	2	2.309
bodas	0	2	2.309
bocaza	0	2	2.309
bobito	0	2	2.309
bóbilis	0	2	2.309
bobas	0	2	2.309
bistec	0	2	2.309
bierzo	0	2	2.309
bienaventurados	0	2	2.309
besuqueos	0	2	2.309
besarme	0	2	2.309
berzas	0	2	2.309
berrinche	0	2	2.309
berreaba	0	2	2.309
bernardino	0	2	2.309
bermellón	0	2	2.309
bermejos	0	2	2.309
benigno	0	2	2.309
benéficas	0	2	2.309
benditas	0	2	2.309
bendecirán	0	2	2.309
bellísima	0	2	2.309
béjar	0	2	2.309
beethoven	0	2	2.309
bedmar	0	2	2.309
beberemos	0	2	2.309
bebe	0	2	2.309
beatriz	0	2	2.309
bazares	0	2	2.309
batistas	0	2	2.309
batidor	0	2	2.309
basurero	0	2	2.309
bastidor	0	2	2.309
bastas	0	2	2.309
bastara	0	2	2.309
bastábale	0	2	2.309
barruntaba	0	2	2.309
barrionuevo	0	2	2.309
barrabás	0	2	2.309
barbarie	0	2	2.309
bárbaras	0	2	2.309
barajar	0	2	2.309
banderillas	0	2	2.309
banderas	0	2	2.309
baldosín	0	2	2.309
baldosa	0	2	2.309
balanza	0	2	2.309
balances	0	2	2.309
bajen	0	2	2.309
bajé	0	2	2.309
bajarlo	0	2	2.309
bailad	0	2	2.309
badulaques	0	2	2.309
babilla	0	2	2.309
babia	0	2	2.309
baberos	0	2	2.309
azuzaba	0	2	2.309
azuleaba	0	2	2.309
azucarillos	0	2	2.309
azoten	0	2	2.309
azahares	0	2	2.309
ayudarás	0	2	2.309
ayudante	0	2	2.309
ayudadas	0	2	2.309
avivando	0	2	2.309
avivaba	0	2	2.309
avisas	0	2	2.309
avisadas	0	2	2.309
avío	0	2	2.309
avino	0	2	2.309
ávida	0	2	2.309
aviada	0	2	2.309
averiguo	0	2	2.309
averiguando	0	2	2.309
aventurera	0	2	2.309
avanzara	0	2	2.309
avanza	0	2	2.309
ausentarse	0	2	2.309
aumentaban	0	2	2.309
aulas	0	2	2.309
aujeritos	0	2	2.309
augusta	0	2	2.309
atufado	0	2	2.309
atufa	0	2	2.309
atropina	0	2	2.309
atreviose	0	2	2.309
atrevíase	0	2	2.309
atreveré	0	2	2.309
atracones	0	2	2.309
atontadas	0	2	2.309
atónito	0	2	2.309
atiendo	0	2	2.309
aterrador	0	2	2.309
aterra	0	2	2.309
atenuar	0	2	2.309
atenuado	0	2	2.309
atemperar	0	2	2.309
ataúdes	0	2	2.309
atarlas	0	2	2.309
atajarla	0	2	2.309
atadero	0	2	2.309
asusto	0	2	2.309
asustadísimo	0	2	2.309
asomose	0	2	2.309
asomé	0	2	2.309
asombres	0	2	2.309
asombrarse	0	2	2.309
asombra	0	2	2.309
asomarse	0	2	2.309
asociar	0	2	2.309
asociaciones	0	2	2.309
asociaba	0	2	2.309
asintió	0	2	2.309
asiáticos	0	2	2.309
asiático	0	2	2.309
asesinarme	0	2	2.309
asesinaban	0	2	2.309
asentadores	0	2	2.309
asegurártelo	0	2	2.309
asegurarte	0	2	2.309
asegurándose	0	2	2.309
aseguran	0	2	2.309
ascenso	0	2	2.309
asaltado	0	2	2.309
arrulló	0	2	2.309
arrullándole	0	2	2.309
arrugó	0	2	2.309
arropó	0	2	2.309
arrope	0	2	2.309
arrojé	0	2	2.309
arrojándose	0	2	2.309
arrogantísima	0	2	2.309
arroba	0	2	2.309
arrimados	0	2	2.309
arrimaba	0	2	2.309
arriendo	0	2	2.309
arribita	0	2	2.309
arrepiente	0	2	2.309
arreglara	0	2	2.309
arreglador	0	2	2.309
arregladito	0	2	2.309
arreció	0	2	2.309
arrastren	0	2	2.309
arrancose	0	2	2.309
arrancada	0	2	2.309
arrabal	0	2	2.309
arqueando	0	2	2.309
arpegios	0	2	2.309
armara	0	2	2.309
armados	0	2	2.309
argumentaba	0	2	2.309
arganzuela	0	2	2.309
arcón	0	2	2.309
arcano	0	2	2.309
ara	0	2	2.309
aquiescencia	0	2	2.309
apuradas	0	2	2.309
apuntaron	0	2	2.309
apuntalada	0	2	2.309
aproximaciones	0	2	2.309
aproximación	0	2	2.309
apropiarse	0	2	2.309
apretándosela	0	2	2.309
aprendas	0	2	2.309
aprendamos	0	2	2.309
apreciaban	0	2	2.309
apoderose	0	2	2.309
aplicara	0	2	2.309
aplaudo	0	2	2.309
aplacarle	0	2	2.309
aplacara	0	2	2.309
apilados	0	2	2.309
apesta	0	2	2.309
apenada	0	2	2.309
apegada	0	2	2.309
apee	0	2	2.309
apechugar	0	2	2.309
apartarse	0	2	2.309
apartaron	0	2	2.309
apartara	0	2	2.309
apartados	0	2	2.309
aparentó	0	2	2.309
aparecen	0	2	2.309
aparadores	0	2	2.309
apañaditas	0	2	2.309
añejos	0	2	2.309
anunciándole	0	2	2.309
antojaron	0	2	2.309
antipatías	0	2	2.309
antagonismo	0	2	2.309
ansiosas	0	2	2.309
anonadada	0	2	2.309
anonada	0	2	2.309
anises	0	2	2.309
animar	0	2	2.309
anhelantes	0	2	2.309
angelote	0	2	2.309
angelón	0	2	2.309
angélica	0	2	2.309
aneurisma	0	2	2.309
andróminas	0	2	2.309
andrea	0	2	2.309
ándese	0	2	2.309
ande	0	2	2.309
andante	0	2	2.309
andanada	0	2	2.309
andana	0	2	2.309
anatemas	0	2	2.309
anatema	0	2	2.309
anacoreta	0	2	2.309
ampliación	0	2	2.309
amoscándose	0	2	2.309
amonestando	0	2	2.309
amonestación	0	2	2.309
amiguitos	0	2	2.309
amigote	0	2	2.309
ambiciosa	0	2	2.309
amasado	0	2	2.309
amarra	0	2	2.309
amarguras	0	2	2.309
amargas	0	2	2.309
amará	0	2	2.309
amanece	0	2	2.309
amancebamiento	0	2	2.309
alzaban	0	2	2.309
álvarez	0	2	2.309
alumna	0	2	2.309
alucinar	0	2	2.309
altísimo	0	2	2.309
alternar	0	2	2.309
altere	0	2	2.309
alteraba	0	2	2.309
altarito	0	2	2.309
alquiló	0	2	2.309
alquileres	0	2	2.309
alpargatas	0	2	2.309
almuerzos	0	2	2.309
almorzando	0	2	2.309
almendras	0	2	2.309
almejas	0	2	2.309
almacenistas	0	2	2.309
allegados	0	2	2.309
alimaña	0	2	2.309
algas	0	2	2.309
alfonsino	0	2	2.309
alevoso	0	2	2.309
aletargado	0	2	2.309
aleros	0	2	2.309
alejose	0	2	2.309
alegrose	0	2	2.309
alegrará	0	2	2.309
alcoy	0	2	2.309
alcanzan	0	2	2.309
alcanzado	0	2	2.309
álbumes	0	2	2.309
albricias	0	2	2.309
alborozo	0	2	2.309
alborotase	0	2	2.309
alborotaría	0	2	2.309
albo	0	2	2.309
albardero	0	2	2.309
alarmaba	0	2	2.309
alargándole	0	2	2.309
ajuste	0	2	2.309
ajumao	0	2	2.309
ajadas	0	2	2.309
airosos	0	2	2.309
airados	0	2	2.309
ahumadas	0	2	2.309
ahogue	0	2	2.309
ahogo	0	2	2.309
ahogas	0	2	2.309
ahilada	0	2	2.309
aguzando	0	2	2.309
aguárdate	0	2	2.309
aguántate	0	2	2.309
agresora	0	2	2.309
agresión	0	2	2.309
agrado	0	2	2.309
agradecen	0	2	2.309
agotó	0	2	2.309
agonizante	0	2	2.309
agitándose	0	2	2.309
agitaban	0	2	2.309
agasajado	0	2	2.309
agasajaditos	0	2	2.309
agasajaba	0	2	2.309
agarrando	0	2	2.309
afrontar	0	2	2.309
aflojó	0	2	2.309
afloja	0	2	2.309
afloencias	0	2	2.309
afligidas	0	2	2.309
afligía	0	2	2.309
afirmo	0	2	2.309
afirmativas	0	2	2.309
afinidad	0	2	2.309
afinar	0	2	2.309
afilado	0	2	2.309
aficionada	0	2	2.309
afeitarse	0	2	2.309
afeitaba	0	2	2.309
afectan	0	2	2.309
afeaba	0	2	2.309
adormeció	0	2	2.309
adoptivo	0	2	2.309
admitirla	0	2	2.309
admiro	0	2	2.309
administraron	0	2	2.309
administradora	0	2	2.309
adecuado	0	2	2.309
adecuada	0	2	2.309
acusador	0	2	2.309
acumular	0	2	2.309
acuéstese	0	2	2.309
acuerde	0	2	2.309
actividades	0	2	2.309
acostumbran	0	2	2.309
acostase	0	2	2.309
acostarte	0	2	2.309
acostáronse	0	2	2.309
acostados	0	2	2.309
acorralada	0	2	2.309
acordeón	0	2	2.309
acordando	0	2	2.309
acoquinar	0	2	2.309
acongojadísima	0	2	2.309
acompaño	0	2	2.309
acompañaría	0	2	2.309
acomode	0	2	2.309
acometió	0	2	2.309
acometiese	0	2	2.309
acometiendo	0	2	2.309
acogoto	0	2	2.309
acobardó	0	2	2.309
aclarar	0	2	2.309
aceptarlo	0	2	2.309
aceptaría	0	2	2.309
aceptada	0	2	2.309
aceptable	0	2	2.309
acentuó	0	2	2.309
aceitosas	0	2	2.309
accidental	0	2	2.309
accedió	0	2	2.309
acaricia	0	2	2.309
acallarle	0	2	2.309
acabes	0	2	2.309
acabé	0	2	2.309
acabamiento	0	2	2.309
aburrirás	0	2	2.309
abundamiento	0	2	2.309
abultaba	0	2	2.309
absorbiendo	0	2	2.309
absolutas	0	2	2.309
abrígate	0	2	2.309
abrigadito	0	2	2.309
abrieron	0	2	2.309
abres	0	2	2.309
abrazaron	0	2	2.309
abrazarle	0	2	2.309
abrazarla	0	2	2.309
aborrecerte	0	2	2.309
aborrecerla	0	2	2.309
aborreceré	0	2	2.309
abordó	0	2	2.309
abollada	0	2	2.309
aboliciones	0	2	2.309
abatir	0	2	2.309
abatieron	0	2	2.309
abandone	0	2	2.309
abandonarla	0	2	2.309
abandonando	0	2	2.309
abalanzó	0	2	2.309
levantó	38	34	2.308
sucesos	8	19	2.307
cárcel	8	19	2.307
botón	8	19	2.307
acabar	8	19	2.307
brazos	90	92	2.300
favor	19	37	2.294
tristeza	49	46	2.283
señoras	82	83	2.272
habla	36	32	2.260
entusiasmo	36	32	2.260
perdón	21	40	2.251
ventajas	10	6	2.243
tribunal	10	6	2.243
tambor	10	6	2.243
sentimental	10	6	2.243
saludar	10	6	2.243
repetir	10	6	2.243
propaganda	10	6	2.243
pesaba	10	6	2.243
perdonaba	10	6	2.243
majadero	10	6	2.243
hembra	10	6	2.243
frías	10	6	2.243
entregado	10	6	2.243
dispense	10	6	2.243
despedía	10	6	2.243
cursi	10	6	2.243
cerrados	10	6	2.243
brillaba	10	6	2.243
atender	10	6	2.243
atado	10	6	2.243
arroyo	10	6	2.243
piso	35	31	2.236
deseo	46	43	2.198
vendría	7	17	2.191
sacado	7	17	2.191
río	33	29	2.191
aguas	7	17	2.191
llamar	27	49	2.181
vulgaridades	5	2	2.176
vaguedad	5	2	2.176
turbado	5	2	2.176
tropezones	5	2	2.176
tropezaba	5	2	2.176
tranquilas	5	2	2.176
tomate	5	2	2.176
tiranía	5	2	2.176
tijeras	5	2	2.176
tesoros	5	2	2.176
temían	5	2	2.176
telarañas	5	2	2.176
sudores	5	2	2.176
subterráneo	5	2	2.176
sorprendía	5	2	2.176
sacaban	5	2	2.176
ritmo	5	2	2.176
regazo	5	2	2.176
quejó	5	2	2.176
quejidos	5	2	2.176
próximamente	5	2	2.176
prostitución	5	2	2.176
proporción	5	2	2.176
presentaban	5	2	2.176
preocupaba	5	2	2.176
plantar	5	2	2.176
pilletes	5	2	2.176
pequeñez	5	2	2.176
pastores	5	2	2.176
panza	5	2	2.176
palmatoria	5	2	2.176
pálidas	5	2	2.176
países	5	2	2.176
oyese	5	2	2.176
orgulloso	5	2	2.176
ordinariamente	5	2	2.176
óperas	5	2	2.176
nuca	5	2	2.176
naranjas	5	2	2.176
murmurando	5	2	2.176
muelle	5	2	2.176
moriría	5	2	2.176
mezclada	5	2	2.176
metafísica	5	2	2.176
merecer	5	2	2.176
llenando	5	2	2.176
literaria	5	2	2.176
levemente	5	2	2.176
jugador	5	2	2.176
jergón	5	2	2.176
inventar	5	2	2.176
interrumpido	5	2	2.176
insufrible	5	2	2.176
indignado	5	2	2.176
incierto	5	2	2.176
impuesto	5	2	2.176
hablaría	5	2	2.176
groseramente	5	2	2.176
granos	5	2	2.176
gastadas	5	2	2.176
gaita	5	2	2.176
fusil	5	2	2.176
fúnebres	5	2	2.176
fornido	5	2	2.176
firmemente	5	2	2.176
fachada	5	2	2.176
extendiendo	5	2	2.176
exquisita	5	2	2.176
exponía	5	2	2.176
exacto	5	2	2.176
estéril	5	2	2.176
escribo	5	2	2.176
escondió	5	2	2.176
entendió	5	2	2.176
elogio	5	2	2.176
elementos	5	2	2.176
durar	5	2	2.176
dócil	5	2	2.176
disputar	5	2	2.176
discursos	5	2	2.176
desierta	5	2	2.176
demostraba	5	2	2.176
cuervos	5	2	2.176
consintió	5	2	2.176
consagró	5	2	2.176
colgada	5	2	2.176
colegas	5	2	2.176
cháchara	5	2	2.176
cerraban	5	2	2.176
carruaje	5	2	2.176
capaces	5	2	2.176
brinco	5	2	2.176
brillo	5	2	2.176
bordadas	5	2	2.176
bocados	5	2	2.176
bellas	5	2	2.176
bajas	5	2	2.176
asomar	5	2	2.176
artística	5	2	2.176
apoyarse	5	2	2.176
alias	5	2	2.176
alardes	5	2	2.176
afirmación	5	2	2.176
admitía	5	2	2.176
admiró	5	2	2.176
accesos	5	2	2.176
acariciando	5	2	2.176
abusos	5	2	2.176
memoria	35	61	2.167
temblando	11	7	2.159
suavidad	11	7	2.159
señoritos	11	7	2.159
rosas	11	7	2.159
rodeada	11	7	2.159
perfección	11	7	2.159
olas	11	7	2.159
morada	11	7	2.159
mate	11	7	2.159
irresistible	11	7	2.159
instrumento	11	7	2.159
faltaban	11	7	2.159
esperanzas	11	7	2.159
empeño	11	7	2.159
dirigió	11	7	2.159
puertas	18	35	2.157
sepa	13	27	2.155
sentado	13	27	2.155
plata	31	27	2.148
hicieron	10	22	2.134
figuras	10	22	2.134
siento	20	38	2.115
nuevas	29	25	2.108
propósitos	12	8	2.099
promesa	12	8	2.099
probablemente	12	8	2.099
oriente	12	8	2.099
instintos	12	8	2.099
entendido	12	8	2.099
dominaba	12	8	2.099
discreción	12	8	2.099
despertaba	12	8	2.099
abnegación	12	8	2.099
rosario	6	15	2.081
respiración	6	15	2.081
observar	6	15	2.081
faltó	6	15	2.081
claras	6	15	2.081
cejas	6	15	2.081
cabezas	6	15	2.081
bata	6	15	2.081
llega	15	30	2.075
hubieran	27	23	2.071
llevaba	53	87	2.070
vivían	13	9	2.055
tronco	13	9	2.055
repugnancia	13	9	2.055
defendía	13	9	2.055
conseguido	13	9	2.055
atmósfera	13	9	2.055
algazara	13	9	2.055
mejores	26	22	2.053
ronca	14	10	2.024
puños	14	10	2.024
mármol	14	10	2.024
fatiga	14	10	2.024
agujero	14	10	2.024
bah	24	20	2.023
estuviera	17	33	2.019
pienso	12	25	2.017
parís	12	25	2.017
zozobra	1	5	2.014
zona	1	5	2.014
zarpa	1	5	2.014
vosotras	1	5	2.014
volada	1	5	2.014
viudo	1	5	2.014
verles	1	5	2.014
veamos	1	5	2.014
valiéndose	1	5	2.014
tubos	1	5	2.014
tránsito	1	5	2.014
transición	1	5	2.014
tranquilizaba	1	5	2.014
tomase	1	5	2.014
tomándolo	1	5	2.014
tocándole	1	5	2.014
tiembla	1	5	2.014
temporadas	1	5	2.014
tambores	1	5	2.014
suba	1	5	2.014
sonrisilla	1	5	2.014
solteras	1	5	2.014
rufinita	1	5	2.014
ronquidos	1	5	2.014
ríes	1	5	2.014
recomendó	1	5	2.014
recomendación	1	5	2.014
recobrando	1	5	2.014
quitando	1	5	2.014
quinto	1	5	2.014
quijada	1	5	2.014
quietud	1	5	2.014
quedase	1	5	2.014
prosperidad	1	5	2.014
prometo	1	5	2.014
procedencia	1	5	2.014
prestar	1	5	2.014
prestamista	1	5	2.014
pozos	1	5	2.014
populares	1	5	2.014
plazo	1	5	2.014
platillo	1	5	2.014
pisto	1	5	2.014
pintoresco	1	5	2.014
pendientes	1	5	2.014
peces	1	5	2.014
peca	1	5	2.014
patios	1	5	2.014
patíbulo	1	5	2.014
particularmente	1	5	2.014
pareciendo	1	5	2.014
palmito	1	5	2.014
oyéndola	1	5	2.014
olfato	1	5	2.014
ocurrieron	1	5	2.014
nociones	1	5	2.014
muñeco	1	5	2.014
mulas	1	5	2.014
muelles	1	5	2.014
movido	1	5	2.014
mote	1	5	2.014
mostrándose	1	5	2.014
mostrándole	1	5	2.014
metiéndose	1	5	2.014
mecanismo	1	5	2.014
maten	1	5	2.014
mamar	1	5	2.014
llevaré	1	5	2.014
llegaré	1	5	2.014
libras	1	5	2.014
largamente	1	5	2.014
inquilinos	1	5	2.014
inaudita	1	5	2.014
imparcial	1	5	2.014
iluminaba	1	5	2.014
humorado	1	5	2.014
hormigas	1	5	2.014
hondos	1	5	2.014
hocico	1	5	2.014
hígado	1	5	2.014
hágase	1	5	2.014
guasa	1	5	2.014
guapetona	1	5	2.014
gravemente	1	5	2.014
gratis	1	5	2.014
giro	1	5	2.014
gentío	1	5	2.014
gallardamente	1	5	2.014
fundada	1	5	2.014
forzada	1	5	2.014
flan	1	5	2.014
fijamente	1	5	2.014
figurines	1	5	2.014
feas	1	5	2.014
extranjera	1	5	2.014
expectación	1	5	2.014
estúpidos	1	5	2.014
estupenda	1	5	2.014
estupefacción	1	5	2.014
estáis	1	5	2.014
establecer	1	5	2.014
escaparates	1	5	2.014
escapa	1	5	2.014
erudición	1	5	2.014
envoltorio	1	5	2.014
enredadera	1	5	2.014
encontrase	1	5	2.014
encontramos	1	5	2.014
encogimiento	1	5	2.014
duermes	1	5	2.014
dudoso	1	5	2.014
duchas	1	5	2.014
documento	1	5	2.014
digamos	1	5	2.014
determinaba	1	5	2.014
detenidamente	1	5	2.014
despidiendo	1	5	2.014
deseara	1	5	2.014
descuidada	1	5	2.014
descanse	1	5	2.014
desayuno	1	5	2.014
desatino	1	5	2.014
desairada	1	5	2.014
dejaré	1	5	2.014
decidir	1	5	2.014
cuñado	1	5	2.014
cuide	1	5	2.014
cristóbal	1	5	2.014
cotorra	1	5	2.014
corsé	1	5	2.014
contrabandista	1	5	2.014
contadas	1	5	2.014
consulta	1	5	2.014
conservando	1	5	2.014
conformarse	1	5	2.014
conformaba	1	5	2.014
comprenderá	1	5	2.014
cofre	1	5	2.014
chistar	1	5	2.014
charlar	1	5	2.014
cascarón	1	5	2.014
cartera	1	5	2.014
cariños	1	5	2.014
cándido	1	5	2.014
calva	1	5	2.014
bloque	1	5	2.014
betún	1	5	2.014
avanzaba	1	5	2.014
atracción	1	5	2.014
alquilar	1	5	2.014
almacenes	1	5	2.014
airada	1	5	2.014
agudeza	1	5	2.014
adorada	1	5	2.014
acusaciones	1	5	2.014
acostada	1	5	2.014
acompañe	1	5	2.014
abro	1	5	2.014
podría	47	78	2.012
santo	66	66	2.011
quien	229	331	2.006
rayo	15	11	2.002
partida	9	20	2.002
inocencia	15	11	2.002
huesos	15	11	2.002
costaba	15	11	2.002
serían	22	18	1.998
loco	49	47	1.998
camisa	21	17	1.989
multitud	16	12	1.988
falso	16	12	1.988
cuesta	16	12	1.988
fiel	20	16	1.982
querer	54	88	1.981
vestirse	5	13	1.980
uñas	5	13	1.980
regalo	5	13	1.980
pude	5	13	1.980
miraron	5	13	1.980
majestad	5	13	1.980
justo	17	13	1.980
hablaremos	5	13	1.980
fórmula	5	13	1.980
dejan	5	13	1.980
concepción	5	13	1.980
comprendiendo	5	13	1.980
verdes	18	14	1.977
muere	18	14	1.977
gorro	18	14	1.977
fábrica	18	14	1.977
casualidad	18	14	1.977
unas	75	118	1.974
antes	223	251	1.956
lleno	37	34	1.950
esposa	50	82	1.938
piensa	14	28	1.937
dedo	14	28	1.937
vil	6	3	1.898
venció	6	3	1.898
tropezando	6	3	1.898
tesis	6	3	1.898
sesión	6	3	1.898
separar	6	3	1.898
señaló	6	3	1.898
sentían	6	3	1.898
segundos	6	3	1.898
salve	6	3	1.898
saludando	6	3	1.898
sacudiendo	6	3	1.898
rompo	6	3	1.898
respirando	6	3	1.898
rentas	6	3	1.898
recobraba	6	3	1.898
recibieron	6	3	1.898
quisieron	6	3	1.898
prestado	6	3	1.898
penetraba	6	3	1.898
oyes	6	3	1.898
morena	6	3	1.898
manifestación	6	3	1.898
maliciosa	6	3	1.898
luchas	6	3	1.898
llamarla	6	3	1.898
juana	6	3	1.898
interiores	6	3	1.898
insistía	6	3	1.898
indecoroso	6	3	1.898
impone	6	3	1.898
hallazgo	6	3	1.898
ganancia	6	3	1.898
gabán	6	3	1.898
fantástico	6	3	1.898
expuso	6	3	1.898
espectáculos	6	3	1.898
esencia	6	3	1.898
escuchar	6	3	1.898
esclava	6	3	1.898
escala	6	3	1.898
elecciones	6	3	1.898
disimulando	6	3	1.898
disgustaba	6	3	1.898
diplomacia	6	3	1.898
despotismo	6	3	1.898
delicadas	6	3	1.898
crepúsculo	6	3	1.898
convidaba	6	3	1.898
contentos	6	3	1.898
confesó	6	3	1.898
cierta	46	76	1.898
chiste	6	3	1.898
charco	6	3	1.898
celebrar	6	3	1.898
cansarse	6	3	1.898
blancura	6	3	1.898
bebido	6	3	1.898
barco	6	3	1.898
asistía	6	3	1.898
arrastrar	6	3	1.898
apuntaba	6	3	1.898
apretada	6	3	1.898
amenaza	6	3	1.898
águila	6	3	1.898
acudían	6	3	1.898
verán	4	11	1.896
unidos	4	11	1.896
sueltas	4	11	1.896
reconozco	4	11	1.896
raya	4	11	1.896
merecido	4	11	1.896
imposible	35	32	1.896
haciéndose	4	11	1.896
hablador	4	11	1.896
gorra	4	11	1.896
excitación	4	11	1.896
enojo	4	11	1.896
disponer	4	11	1.896
despecho	4	11	1.896
desear	4	11	1.896
cuyas	4	11	1.896
consiste	4	11	1.896
condenada	4	11	1.896
breves	4	11	1.896
arrepentimiento	4	11	1.896
apuntó	4	11	1.896
animación	4	11	1.896
primera	62	99	1.888
monja	11	23	1.880
guapa	11	23	1.880
acerca	11	23	1.880
velas	8	18	1.872
sirve	8	18	1.872
recibido	8	18	1.872
gustan	8	18	1.872
funciones	8	18	1.872
contado	8	18	1.872
bruto	8	18	1.872
azúcar	8	18	1.872
daban	44	42	1.851
piernas	33	30	1.844
volverá	2	7	1.843
verdaderas	2	7	1.843
valientes	2	7	1.843
vacilar	2	7	1.843
tratamiento	2	7	1.843
tendrás	2	7	1.843
temple	2	7	1.843
sueltos	2	7	1.843
sueldo	2	7	1.843
sonido	2	7	1.843
seremos	2	7	1.843
revolviendo	2	7	1.843
recogida	2	7	1.843
recibían	2	7	1.843
rabo	2	7	1.843
quieta	2	7	1.843
quererle	2	7	1.843
pregunto	2	7	1.843
postas	2	7	1.843
polvos	2	7	1.843
pleito	2	7	1.843
picar	2	7	1.843
permanecer	2	7	1.843
perla	2	7	1.843
parándose	2	7	1.843
oyen	2	7	1.843
llamamos	2	7	1.843
jarro	2	7	1.843
historias	2	7	1.843
fiscal	2	7	1.843
firma	2	7	1.843
finísima	2	7	1.843
equivocación	2	7	1.843
enterada	2	7	1.843
enhorabuena	2	7	1.843
dureza	2	7	1.843
divinas	2	7	1.843
distintos	2	7	1.843
dijeran	2	7	1.843
demostrando	2	7	1.843
creció	2	7	1.843
créalo	2	7	1.843
cortas	2	7	1.843
concejal	2	7	1.843
causaban	2	7	1.843
callarse	2	7	1.843
bruja	2	7	1.843
bajado	2	7	1.843
aterraba	2	7	1.843
apoyar	2	7	1.843
noticias	18	34	1.842
vendía	3	9	1.839
u	3	9	1.839
tragaba	3	9	1.839
traen	3	9	1.839
soldados	3	9	1.839
salvajes	3	9	1.839
salta	3	9	1.839
saliva	3	9	1.839
pulmones	3	9	1.839
primitivo	3	9	1.839
pólvora	3	9	1.839
pensativo	3	9	1.839
números	3	9	1.839
necesitas	3	9	1.839
necesidades	3	9	1.839
modas	3	9	1.839
miran	3	9	1.839
llamando	3	9	1.839
inspirado	3	9	1.839
indulgente	3	9	1.839
hagan	3	9	1.839
goce	3	9	1.839
gobernar	3	9	1.839
faena	3	9	1.839
exclusivamente	3	9	1.839
encendida	3	9	1.839
dijese	3	9	1.839
delirante	3	9	1.839
corredores	3	9	1.839
colocación	3	9	1.839
boba	3	9	1.839
antipático	3	9	1.839
alfonso	3	9	1.839
afectos	3	9	1.839
gracia	65	103	1.838
mal	252	287	1.835
matar	20	37	1.815
medicina	13	26	1.799
juego	31	28	1.793
capaz	31	28	1.793
tertulia	28	49	1.784
todavía	92	97	1.776
varias	30	27	1.768
presente	30	27	1.768
iban	59	94	1.759
trampa	7	16	1.744
duró	7	16	1.744
consejo	7	16	1.744
ansiedad	7	16	1.744
sano	10	21	1.743
hoja	10	21	1.743
españa	15	29	1.743
cintura	10	21	1.743
arma	10	21	1.743
vicios	7	4	1.738
vengarse	7	4	1.738
valle	7	4	1.738
unción	7	4	1.738
sotanas	7	4	1.738
separaba	7	4	1.738
resolvió	7	4	1.738
parejas	7	4	1.738
ondas	7	4	1.738
octubre	7	4	1.738
merced	7	4	1.738
matarle	7	4	1.738
limosnas	7	4	1.738
imitación	7	4	1.738
herido	7	4	1.738
distinguía	7	4	1.738
crueldad	7	4	1.738
cristianos	7	4	1.738
callaron	7	4	1.738
cal	7	4	1.738
brutal	7	4	1.738
bala	7	4	1.738
avaricia	7	4	1.738
alarde	7	4	1.738
ajena	7	4	1.738
agradar	7	4	1.738
abril	7	4	1.738
abanico	7	4	1.738
confianza	49	48	1.735
siendo	40	38	1.734
suya	56	56	1.706
completamente	17	32	1.706
como	1866	2294	1.706
cama	67	105	1.694
conozco	19	35	1.681
necesidad	38	36	1.676
basta	38	36	1.676
techo	26	23	1.672
casos	21	38	1.666
sentarse	12	24	1.660
desgraciado	12	24	1.660
interés	27	47	1.658
sitio	25	44	1.656
zurriagazo	1	0	1.649
zurcidos	1	0	1.649
zurbarán	1	0	1.649
zumbaban	1	0	1.649
zumarri	1	0	1.649
zuecos	1	0	1.649
zueco	1	0	1.649
zuavo	1	0	1.649
zoológica	1	0	1.649
zodiaco	1	0	1.649
zarzaparrilla	1	0	1.649
zarza	1	0	1.649
zarandeando	1	0	1.649
zarandeaban	1	0	1.649
zaquizamí	1	0	1.649
zamarra	1	0	1.649
zamacois	1	0	1.649
zalamea	1	0	1.649
zag	1	0	1.649
zafio	1	0	1.649
yodo	1	0	1.649
xxx	1	0	1.649
xxviii	1	0	1.649
xxvii	1	0	1.649
xxvi	1	0	1.649
xxv	1	0	1.649
xxix	1	0	1.649
xxiv	1	0	1.649
xxiii	1	0	1.649
xxii	1	0	1.649
xxi	1	0	1.649
xx	1	0	1.649
xviii	1	0	1.649
xvii	1	0	1.649
wisseman	1	0	1.649
wieland	1	0	1.649
washingtonia	1	0	1.649
w	1	0	1.649
voyageur	1	0	1.649
vox	1	0	1.649
votaron	1	0	1.649
votaciones	1	0	1.649
volviolos	1	0	1.649
volvimos	1	0	1.649
volviéramos	1	0	1.649
volvernos	1	0	1.649
volutas	1	0	1.649
voluptuosas	1	0	1.649
voluntario	1	0	1.649
volteriano	1	0	1.649
volatilizándolo	1	0	1.649
volaré	1	0	1.649
volara	1	0	1.649
vogt	1	0	1.649
vocis	1	0	1.649
vocinglera	1	0	1.649
vociferando	1	0	1.649
vociferaban	1	0	1.649
vociferaba	1	0	1.649
vocifera	1	0	1.649
vocaciones	1	0	1.649
vobis	1	0	1.649
vizconde	1	0	1.649
vivirlas	1	0	1.649
vividos	1	0	1.649
vividor	1	0	1.649
viví	1	0	1.649
vivendi	1	0	1.649
vivarachos	1	0	1.649
vituperar	1	0	1.649
vitriolo	1	0	1.649
vitandos	1	0	1.649
vitalidad	1	0	1.649
vitalicia	1	0	1.649
vita	1	0	1.649
vístose	1	0	1.649
vistosas	1	0	1.649
vistieron	1	0	1.649
vistiera	1	0	1.649
vislumbres	1	0	1.649
vislumbrar	1	0	1.649
visitara	1	0	1.649
visitamos	1	0	1.649
visitaciones	1	0	1.649
viseo	1	0	1.649
viscosos	1	0	1.649
vis	1	0	1.649
virtutis	1	0	1.649
virilidad	1	0	1.649
viriles	1	0	1.649
virchov	1	0	1.649
vir	1	0	1.649
violentando	1	0	1.649
violas	1	0	1.649
viña	1	0	1.649
viniere	1	0	1.649
vinci	1	0	1.649
vinader	1	0	1.649
villavieja	1	0	1.649
villanas	1	0	1.649
villafranca	1	0	1.649
vigorizar	1	0	1.649
vigilaré	1	0	1.649
vigilara	1	0	1.649
vigentes	1	0	1.649
vieses	1	0	1.649
viéramos	1	0	1.649
vientecillo	1	0	1.649
viéndolas	1	0	1.649
vien	1	0	1.649
viejecito	1	0	1.649
vidriosa	1	0	1.649
videor	1	0	1.649
vidente	1	0	1.649
victis	1	0	1.649
vicia	1	0	1.649
vicepresidente	1	0	1.649
vicarios	1	0	1.649
vibrando	1	0	1.649
viborezno	1	0	1.649
viajaba	1	0	1.649
viable	1	0	1.649
vetustente	1	0	1.649
vetustas	1	0	1.649
veteranos	1	0	1.649
vestusta	1	0	1.649
vestiglos	1	0	1.649
vertió	1	0	1.649
vertieron	1	0	1.649
vertederos	1	0	1.649
versículo	1	0	1.649
versate	1	0	1.649
versalles	1	0	1.649
veros	1	0	1.649
vermis	1	0	1.649
veremundo	1	0	1.649
verdosas	1	0	1.649
verdinegro	1	0	1.649
verbum	1	0	1.649
verbosidad	1	0	1.649
veraniega	1	0	1.649
veraneo	1	0	1.649
veraneado	1	0	1.649
veraneaban	1	0	1.649
veraneaba	1	0	1.649
venzo	1	0	1.649
ventrílocuo	1	0	1.649
ventilen	1	0	1.649
ventilar	1	0	1.649
ventilaba	1	0	1.649
venteros	1	0	1.649
venirle	1	0	1.649
venideras	1	0	1.649
venias	1	0	1.649
vengándose	1	0	1.649
vengando	1	0	1.649
vengaban	1	0	1.649
venero	1	0	1.649
venerando	1	0	1.649
veneciana	1	0	1.649
vendiese	1	0	1.649
vencí	1	0	1.649
vencerlos	1	0	1.649
vencerlas	1	0	1.649
venales	1	0	1.649
velludo	1	0	1.649
velluda	1	0	1.649
vellones	1	0	1.649
velis	1	0	1.649
veleidoso	1	0	1.649
velarle	1	0	1.649
velando	1	0	1.649
velados	1	0	1.649
velado	1	0	1.649
vejetes	1	0	1.649
vejamen	1	0	1.649
veíalo	1	0	1.649
veíalas	1	0	1.649
veguellinas	1	0	1.649
vegetando	1	0	1.649
vegetaba	1	0	1.649
vegallanas	1	0	1.649
vedado	1	0	1.649
veáis	1	0	1.649
vauban	1	0	1.649
vate	1	0	1.649
vastos	1	0	1.649
vastísimos	1	0	1.649
vasares	1	0	1.649
variadas	1	0	1.649
vaqueros	1	0	1.649
vaquero	1	0	1.649
vaporosos	1	0	1.649
vaporoso	1	0	1.649
vaporosa	1	0	1.649
vanidosos	1	0	1.649
vanidoso	1	0	1.649
vanagloriaba	1	0	1.649
vampiro	1	0	1.649
valió	1	0	1.649
válgate	1	0	1.649
valetudinario	1	0	1.649
valerosos	1	0	1.649
valentísimo	1	0	1.649
valentía	1	0	1.649
valdrían	1	0	1.649
valdiñón	1	0	1.649
vaina	1	0	1.649
vae	1	0	1.649
uva	1	0	1.649
utrecht	1	0	1.649
utilizado	1	0	1.649
utilizaba	1	0	1.649
utilitario	1	0	1.649
utilidades	1	0	1.649
utile	1	0	1.649
utero	1	0	1.649
utensilios	1	0	1.649
usurpador	1	0	1.649
usual	1	0	1.649
usen	1	0	1.649
usase	1	0	1.649
usarse	1	0	1.649
usarlo	1	0	1.649
usados	1	0	1.649
us	1	0	1.649
urgentísimo	1	0	1.649
urdido	1	0	1.649
urbicesorbi	1	0	1.649
urbano	1	0	1.649
urbana	1	0	1.649
unto	1	0	1.649
untados	1	0	1.649
untaba	1	0	1.649
universidades	1	0	1.649
universi	1	0	1.649
unísono	1	0	1.649
uní	1	0	1.649
une	1	0	1.649
ultratelúrica	1	0	1.649
ultramontano	1	0	1.649
ultramontanismo	1	0	1.649
ultramontanas	1	0	1.649
ultrajando	1	0	1.649
ultrajada	1	0	1.649
ulloa	1	0	1.649
ujier	1	0	1.649
ue	1	0	1.649
tuy	1	0	1.649
tuviéramos	1	0	1.649
turres	1	0	1.649
turquía	1	0	1.649
turpia	1	0	1.649
turnaban	1	0	1.649
turgencia	1	0	1.649
turbias	1	0	1.649
turbándose	1	0	1.649
turbamulta	1	0	1.649
turbaciones	1	0	1.649
tupida	1	0	1.649
túnicas	1	0	1.649
tumbados	1	0	1.649
tuesta	1	0	1.649
tuerces	1	0	1.649
tuerca	1	0	1.649
tuae	1	0	1.649
truqueurs	1	0	1.649
truncado	1	0	1.649
truenan	1	0	1.649
troya	1	0	1.649
tropo	1	0	1.649
tropiece	1	0	1.649
tropezasen	1	0	1.649
tronaba	1	0	1.649
trompeteada	1	0	1.649
trompas	1	0	1.649
trocitos	1	0	1.649
trochas	1	0	1.649
trocha	1	0	1.649
trocarse	1	0	1.649
trocados	1	0	1.649
triunfe	1	0	1.649
triunfantes	1	0	1.649
triunfando	1	0	1.649
triunfa	1	0	1.649
tripulando	1	0	1.649
tripulaban	1	0	1.649
trincheras	1	0	1.649
trinchante	1	0	1.649
trifoncito	1	0	1.649
trifoncillo	1	0	1.649
trifona	1	0	1.649
tridentino	1	0	1.649
tributó	1	0	1.649
tributaban	1	0	1.649
tribus	1	0	1.649
triángulo	1	0	1.649
trepando	1	0	1.649
trepaba	1	0	1.649
trepa	1	0	1.649
trenzados	1	0	1.649
trena	1	0	1.649
trémolo	1	0	1.649
treguas	1	0	1.649
travesaños	1	0	1.649
tratable	1	0	1.649
trasvolado	1	0	1.649
trasplantada	1	0	1.649
trasplantaba	1	0	1.649
trasnochado	1	0	1.649
trasnochaban	1	0	1.649
traslucir	1	0	1.649
trasladaron	1	0	1.649
trasladarle	1	0	1.649
trasladándonos	1	0	1.649
trasladan	1	0	1.649
trasladaba	1	0	1.649
trascender	1	0	1.649
trapicheo	1	0	1.649
trapacero	1	0	1.649
transportada	1	0	1.649
transparentando	1	0	1.649
transmitían	1	0	1.649
transigió	1	0	1.649
transigía	1	0	1.649
transfusiones	1	0	1.649
transfusión	1	0	1.649
trances	1	0	1.649
tramposo	1	0	1.649
tramaban	1	0	1.649
tragas	1	0	1.649
tragármela	1	0	1.649
tragaría	1	0	1.649
tragaban	1	0	1.649
traerlos	1	0	1.649
traductora	1	0	1.649
traducidos	1	0	1.649
tradicionalmente	1	0	1.649
trabucos	1	0	1.649
trabajase	1	0	1.649
tostasen	1	0	1.649
tostado	1	0	1.649
tostadas	1	0	1.649
tosiendo	1	0	1.649
tosido	1	0	1.649
toscas	1	0	1.649
torvo	1	0	1.649
torrente	1	0	1.649
tornillos	1	0	1.649
tornadiza	1	0	1.649
tormentas	1	0	1.649
torcuato	1	0	1.649
torcieron	1	0	1.649
torciéndose	1	0	1.649
torciendo	1	0	1.649
torcedor	1	0	1.649
toral	1	0	1.649
toraces	1	0	1.649
tópicos	1	0	1.649
too	1	0	1.649
tontunas	1	0	1.649
tontina	1	0	1.649
tontear	1	0	1.649
ton	1	0	1.649
tomos	1	0	1.649
tomarán	1	0	1.649
tomadas	1	0	1.649
toleres	1	0	1.649
toleraron	1	0	1.649
tolerarlo	1	0	1.649
toleran	1	0	1.649
toleradas	1	0	1.649
toleraban	1	0	1.649
tocarás	1	0	1.649
tocándola	1	0	1.649
tobillo	1	0	1.649
tiznes	1	0	1.649
tiznándole	1	0	1.649
tiznado	1	0	1.649
titulados	1	0	1.649
titulado	1	0	1.649
tito	1	0	1.649
titilar	1	0	1.649
títeres	1	0	1.649
titanes	1	0	1.649
titán	1	0	1.649
tirsos	1	0	1.649
tiritando	1	0	1.649
tirilla	1	0	1.649
tiránico	1	0	1.649
tiple	1	0	1.649
tiñéndolo	1	0	1.649
tinteros	1	0	1.649
timoratos	1	0	1.649
timorata	1	0	1.649
tímidas	1	0	1.649
timarse	1	0	1.649
timaban	1	0	1.649
tiende	1	0	1.649
tiemblas	1	0	1.649
tiburón	1	0	1.649
thackeray	1	0	1.649
tetrarca	1	0	1.649
tessitura	1	0	1.649
terrorista	1	0	1.649
terrores	1	0	1.649
terrenas	1	0	1.649
terrados	1	0	1.649
terrado	1	0	1.649
terpsícore	1	0	1.649
termómetro	1	0	1.649
termine	1	0	1.649
terminasen	1	0	1.649
terminaciones	1	0	1.649
terminaban	1	0	1.649
tergiversemos	1	0	1.649
tercos	1	0	1.649
terciar	1	0	1.649
terciado	1	0	1.649
terciaba	1	0	1.649
tercetos	1	0	1.649
terapéutica	1	0	1.649
teórica	1	0	1.649
teológicos	1	0	1.649
teócrito	1	0	1.649
teocrático	1	0	1.649
tentarse	1	0	1.649
tentadores	1	0	1.649
tentadora	1	0	1.649
tentáculos	1	0	1.649
tenientes	1	0	1.649
tenida	1	0	1.649
tenias	1	0	1.649
tenia	1	0	1.649
tenerles	1	0	1.649
tenebrosa	1	0	1.649
tendieron	1	0	1.649
tempranos	1	0	1.649
temporis	1	0	1.649
tempora	1	0	1.649
templete	1	0	1.649
templanza	1	0	1.649
tempestades	1	0	1.649
tempé	1	0	1.649
temiéndolo	1	0	1.649
temías	1	0	1.649
temes	1	0	1.649
temerones	1	0	1.649
temeridades	1	0	1.649
temeridad	1	0	1.649
temblorcico	1	0	1.649
temblase	1	0	1.649
temblaron	1	0	1.649
temblábale	1	0	1.649
telones	1	0	1.649
telescopio	1	0	1.649
telegramas	1	0	1.649
tejadillos	1	0	1.649
tecum	1	0	1.649
técnico	1	0	1.649
tecnicismo	1	0	1.649
técnica	1	0	1.649
taurina	1	0	1.649
tatiste	1	0	1.649
tasso	1	0	1.649
tascaba	1	0	1.649
tarso	1	0	1.649
tarsilita	1	0	1.649
tardaban	1	0	1.649
tapiceros	1	0	1.649
tape	1	0	1.649
taparse	1	0	1.649
taparelli	1	0	1.649
tapadillos	1	0	1.649
tañida	1	0	1.649
tañía	1	0	1.649
tañedor	1	0	1.649
tantico	1	0	1.649
tambaleándose	1	0	1.649
tamaños	1	0	1.649
talismán	1	0	1.649
talares	1	0	1.649
tajos	1	0	1.649
taimado	1	0	1.649
taigeto	1	0	1.649
tahúr	1	0	1.649
tagarnina	1	0	1.649
tafurería	1	0	1.649
tafetán	1	0	1.649
taconeo	1	0	1.649
taciturnos	1	0	1.649
taciturnas	1	0	1.649
tácitos	1	0	1.649
tachó	1	0	1.649
tachado	1	0	1.649
tacha	1	0	1.649
taburete	1	0	1.649
tablillas	1	0	1.649
tableros	1	0	1.649
tabernáculo	1	0	1.649
suum	1	0	1.649
sutilísimas	1	0	1.649
susurros	1	0	1.649
sustraérsele	1	0	1.649
sustentase	1	0	1.649
sustentadas	1	0	1.649
sustanciales	1	0	1.649
suspirado	1	0	1.649
suspicacias	1	0	1.649
suspendo	1	0	1.649
suspendiesen	1	0	1.649
suspende	1	0	1.649
susodicho	1	0	1.649
suscitar	1	0	1.649
suscitaba	1	0	1.649
surgiendo	1	0	1.649
surcadas	1	0	1.649
surbicesorbi	1	0	1.649
suprimiendo	1	0	1.649
suprimida	1	0	1.649
suprimían	1	0	1.649
supra	1	0	1.649
suponiéndole	1	0	1.649
suponíalo	1	0	1.649
suponérseles	1	0	1.649
suponerlo	1	0	1.649
suplir	1	0	1.649
suplicaron	1	0	1.649
suplicarle	1	0	1.649
suplicar	1	0	1.649
suplica	1	0	1.649
suplían	1	0	1.649
suplía	1	0	1.649
suple	1	0	1.649
superfino	1	0	1.649
superficialidades	1	0	1.649
superficialidad	1	0	1.649
superan	1	0	1.649
supeditado	1	0	1.649
supeditada	1	0	1.649
suñera	1	0	1.649
suntuosa	1	0	1.649
sunt	1	0	1.649
sumirlo	1	0	1.649
suministraba	1	0	1.649
sumas	1	0	1.649
sumando	1	0	1.649
sum	1	0	1.649
sulfure	1	0	1.649
sujetando	1	0	1.649
sujétale	1	0	1.649
suizas	1	0	1.649
suicidarnos	1	0	1.649
sugiriese	1	0	1.649
sugiriéndole	1	0	1.649
sugieran	1	0	1.649
sugeridas	1	0	1.649
sufrirlos	1	0	1.649
sufrirle	1	0	1.649
sufrirlas	1	0	1.649
sufragio	1	0	1.649
sufra	1	0	1.649
suenan	1	0	1.649
sueldos	1	0	1.649
suecos	1	0	1.649
sueco	1	0	1.649
suecia	1	0	1.649
sucursal	1	0	1.649
sucumbían	1	0	1.649
sucesores	1	0	1.649
sucesivas	1	0	1.649
sucesiva	1	0	1.649
sucedieran	1	0	1.649
sucediéndose	1	0	1.649
sucederse	1	0	1.649
sucedáneo	1	0	1.649
sucedan	1	0	1.649
subversivo	1	0	1.649
subversiva	1	0	1.649
subvenciones	1	0	1.649
suburbios	1	0	1.649
subsuelo	1	0	1.649
substituía	1	0	1.649
subsistir	1	0	1.649
subsiguiente	1	0	1.649
subrepticios	1	0	1.649
subrayó	1	0	1.649
subrayando	1	0	1.649
subrayadas	1	0	1.649
subrayaba	1	0	1.649
sublimizado	1	0	1.649
sublimiza	1	0	1.649
sublevarse	1	0	1.649
sublevaron	1	0	1.649
sublevado	1	0	1.649
sublevadas	1	0	1.649
subjetivo	1	0	1.649
subirla	1	0	1.649
subidos	1	0	1.649
subidas	1	0	1.649
súbditos	1	0	1.649
suavice	1	0	1.649
stulta	1	0	1.649
stream	1	0	1.649
strauss	1	0	1.649
stoa	1	0	1.649
sprit	1	0	1.649
sposa	1	0	1.649
splendorum	1	0	1.649
spiritu	1	0	1.649
spínolas	1	0	1.649
sousa	1	0	1.649
sospecharse	1	0	1.649
sosiéguese	1	0	1.649
sorteaba	1	0	1.649
sorprendiera	1	0	1.649
sorprendiéndola	1	0	1.649
sorprendían	1	0	1.649
sorprenderle	1	0	1.649
sorprenda	1	0	1.649
sordomudos	1	0	1.649
sórdidos	1	0	1.649
sórdidas	1	0	1.649
sórdida	1	0	1.649
sorbos	1	0	1.649
sorbete	1	0	1.649
soportable	1	0	1.649
soporíferos	1	0	1.649
sopló	1	0	1.649
soplarse	1	0	1.649
soñolientos	1	0	1.649
soñarlo	1	0	1.649
soñaré	1	0	1.649
soñadores	1	0	1.649
sonsoniche	1	0	1.649
sonrojaba	1	0	1.649
sonriéndoles	1	0	1.649
sonreírse	1	0	1.649
sonorosos	1	0	1.649
sonetos	1	0	1.649
sondearle	1	0	1.649
sondeado	1	0	1.649
sonasen	1	0	1.649
sonase	1	0	1.649
sonarían	1	0	1.649
sonantes	1	0	1.649
sonante	1	0	1.649
sonámbulos	1	0	1.649
sonados	1	0	1.649
somieda	1	0	1.649
sometieron	1	0	1.649
sometidos	1	0	1.649
somete	1	0	1.649
someros	1	0	1.649
somera	1	0	1.649
solterona	1	0	1.649
sollozo	1	0	1.649
soliviantados	1	0	1.649
solideo	1	0	1.649
sólidas	1	0	1.649
solidaria	1	0	1.649
solícitos	1	0	1.649
solicitaron	1	0	1.649
solicitan	1	0	1.649
solicitado	1	0	1.649
solicitada	1	0	1.649
solicitación	1	0	1.649
solicita	1	0	1.649
solfeó	1	0	1.649
solazarse	1	0	1.649
soit	1	0	1.649
sofocaciones	1	0	1.649
sofiones	1	0	1.649
sociable	1	0	1.649
socia	1	0	1.649
sochantre	1	0	1.649
sobrón	1	0	1.649
sobrios	1	0	1.649
sobrinitas	1	0	1.649
sobrevivirían	1	0	1.649
sobrevivirá	1	0	1.649
sobrevenía	1	0	1.649
sobresaltadas	1	0	1.649
sobrenadó	1	0	1.649
sobrehumano	1	0	1.649
sobrecogió	1	0	1.649
sobrecogían	1	0	1.649
sobrecogería	1	0	1.649
sobramos	1	0	1.649
sobradamente	1	0	1.649
sobrada	1	0	1.649
soberanos	1	0	1.649
soberanía	1	0	1.649
sixto	1	0	1.649
sitial	1	0	1.649
sitiada	1	0	1.649
sitiaba	1	0	1.649
sistemática	1	0	1.649
sisas	1	0	1.649
sisar	1	0	1.649
siria	1	0	1.649
sirenas	1	0	1.649
sirena	1	0	1.649
sinuoso	1	0	1.649
sinuosidades	1	0	1.649
sinuosa	1	0	1.649
sintiéndolo	1	0	1.649
sintetizan	1	0	1.649
sinónimo	1	0	1.649
síncopes	1	0	1.649
sinapismos	1	0	1.649
simultáneo	1	0	1.649
simulacros	1	0	1.649
simulaba	1	0	1.649
simplicidad	1	0	1.649
simonías	1	0	1.649
simétricas	1	0	1.649
simeón	1	0	1.649
simbolismos	1	0	1.649
simbólica	1	0	1.649
simancas	1	0	1.649
sima	1	0	1.649
silva	1	0	1.649
silenciosas	1	0	1.649
silencios	1	0	1.649
silbar	1	0	1.649
silbándoles	1	0	1.649
silbado	1	0	1.649
siguiesen	1	0	1.649
sígueme	1	0	1.649
significativo	1	0	1.649
significativas	1	0	1.649
significada	1	0	1.649
sigiloso	1	0	1.649
sigas	1	0	1.649
sietemesinos	1	0	1.649
sierpes	1	0	1.649
siemprevivas	1	0	1.649
sic	1	0	1.649
sevillano	1	0	1.649
severísima	1	0	1.649
sesgaba	1	0	1.649
sesentona	1	0	1.649
servilmente	1	0	1.649
servilletero	1	0	1.649
servilletas	1	0	1.649
servicial	1	0	1.649
serviam	1	0	1.649
serrallo	1	0	1.649
serpentones	1	0	1.649
serpeando	1	0	1.649
serpeaba	1	0	1.649
serpea	1	0	1.649
serenísimo	1	0	1.649
serenatas	1	0	1.649
serenata	1	0	1.649
sequedades	1	0	1.649
sepultadas	1	0	1.649
sepárese	1	0	1.649
separarme	1	0	1.649
separarlo	1	0	1.649
separarlas	1	0	1.649
separarla	1	0	1.649
señoriles	1	0	1.649
señoa	1	0	1.649
señalo	1	0	1.649
señaladas	1	0	1.649
señalaban	1	0	1.649
sentirlos	1	0	1.649
sentirle	1	0	1.649
sentirlas	1	0	1.649
sentarte	1	0	1.649
sentarnos	1	0	1.649
sentao	1	0	1.649
sensualista	1	0	1.649
sensualismo	1	0	1.649
sensualidad	1	0	1.649
sensiblería	1	0	1.649
sensatos	1	0	1.649
sensatamente	1	0	1.649
sencillísimo	1	0	1.649
sempiternas	1	0	1.649
semillero	1	0	1.649
semicírculo	1	0	1.649
semicientífico	1	0	1.649
sementales	1	0	1.649
semejanzas	1	0	1.649
sembrados	1	0	1.649
sembraba	1	0	1.649
selvática	1	0	1.649
selva	1	0	1.649
seguirán	1	0	1.649
seguí	1	0	1.649
segadora	1	0	1.649
segaban	1	0	1.649
sedúzcanmela	1	0	1.649
sedujeron	1	0	1.649
seducírselo	1	0	1.649
sedoso	1	0	1.649
sediento	1	0	1.649
sedentarismo	1	0	1.649
sedentario	1	0	1.649
sedentaria	1	0	1.649
secundum	1	0	1.649
secundario	1	0	1.649
secundarias	1	0	1.649
secundaria	1	0	1.649
secundar	1	0	1.649
secundaba	1	0	1.649
secularizándose	1	0	1.649
secularización	1	0	1.649
secuestrarlo	1	0	1.649
secuestramos	1	0	1.649
secuentia	1	0	1.649
secretamente	1	0	1.649
secchi	1	0	1.649
secarse	1	0	1.649
sebastopol	1	0	1.649
sauces	1	0	1.649
sauce	1	0	1.649
saturnillo	1	0	1.649
saturación	1	0	1.649
satisfagan	1	0	1.649
satisfacerles	1	0	1.649
satisfacerle	1	0	1.649
sátira	1	0	1.649
satinado	1	0	1.649
satán	1	0	1.649
sastrerías	1	0	1.649
sarraceno	1	0	1.649
sardou	1	0	1.649
sardónica	1	0	1.649
santurrón	1	0	1.649
santina	1	0	1.649
santiguado	1	0	1.649
santiguaba	1	0	1.649
santificante	1	0	1.649
sansón	1	0	1.649
sansimoniano	1	0	1.649
sanitario	1	0	1.649
sanguis	1	0	1.649
sanguinolenta	1	0	1.649
sanguinario	1	0	1.649
sanguijuelas	1	0	1.649
sangrientamente	1	0	1.649
sangrar	1	0	1.649
sangraban	1	0	1.649
sandunga	1	0	1.649
sandalias	1	0	1.649
sanctos	1	0	1.649
sanctorum	1	0	1.649
sancti	1	0	1.649
sancionaría	1	0	1.649
sanción	1	0	1.649
sanase	1	0	1.649
sanaría	1	0	1.649
sanaba	1	0	1.649
sálvense	1	0	1.649
salvaremos	1	0	1.649
salvara	1	0	1.649
salvada	1	0	1.649
salvaba	1	0	1.649
salus	1	0	1.649
salúdele	1	0	1.649
saludarse	1	0	1.649
saludarme	1	0	1.649
saludaran	1	0	1.649
saludado	1	0	1.649
salté	1	0	1.649
saltarlo	1	0	1.649
saltarines	1	0	1.649
saltará	1	0	1.649
salpimentar	1	0	1.649
salpicar	1	0	1.649
salomónicas	1	0	1.649
salmones	1	0	1.649
salmistas	1	0	1.649
salirle	1	0	1.649
salientes	1	0	1.649
salidas	1	0	1.649
salid	1	0	1.649
saldaba	1	0	1.649
salchichón	1	0	1.649
sahumados	1	0	1.649
sagrarios	1	0	1.649
sacudirles	1	0	1.649
sacrosanto	1	0	1.649
sacris	1	0	1.649
sacrifico	1	0	1.649
sacrificase	1	0	1.649
sacrificaría	1	0	1.649
sacrificándose	1	0	1.649
sacrifican	1	0	1.649
sacramentales	1	0	1.649
sacramental	1	0	1.649
sacias	1	0	1.649
sacerdotisa	1	0	1.649
sacatrapos	1	0	1.649
sacarte	1	0	1.649
sacarlo	1	0	1.649
sacao	1	0	1.649
sabores	1	0	1.649
saboreó	1	0	1.649
sabihondo	1	0	1.649
saberle	1	0	1.649
sábelo	1	0	1.649
sabandija	1	0	1.649
sabanas	1	0	1.649
rústico	1	0	1.649
rural	1	0	1.649
rumorosa	1	0	1.649
rumiase	1	0	1.649
rumiara	1	0	1.649
rumbosa	1	0	1.649
ruleta	1	0	1.649
ruinosas	1	0	1.649
ruinosa	1	0	1.649
rugir	1	0	1.649
ruedo	1	0	1.649
rudesinda	1	0	1.649
rucutucua	1	0	1.649
ruborizándose	1	0	1.649
ruborizadas	1	0	1.649
rubores	1	0	1.649
rubita	1	0	1.649
rozase	1	0	1.649
rozarse	1	0	1.649
rozando	1	0	1.649
rozagantes	1	0	1.649
rozado	1	0	1.649
rozaba	1	0	1.649
royéndolo	1	0	1.649
rotundo	1	0	1.649
rotin	1	0	1.649
rosendo	1	0	1.649
rorro	1	0	1.649
roquetes	1	0	1.649
roquero	1	0	1.649
ropón	1	0	1.649
ronzalillo	1	0	1.649
ronzalesco	1	0	1.649
ronzalesca	1	0	1.649
rompiéndome	1	0	1.649
rompecabezas	1	0	1.649
romea	1	0	1.649
romas	1	0	1.649
romanus	1	0	1.649
romantismo	1	0	1.649
románica	1	0	1.649
romancero	1	0	1.649
romanas	1	0	1.649
rollizos	1	0	1.649
rollizo	1	0	1.649
roían	1	0	1.649
rogativas	1	0	1.649
rogaba	1	0	1.649
rodearte	1	0	1.649
rodear	1	0	1.649
rodaron	1	0	1.649
rococó	1	0	1.649
roció	1	0	1.649
rociaba	1	0	1.649
robustas	1	0	1.649
robledales	1	0	1.649
robas	1	0	1.649
robándole	1	0	1.649
robando	1	0	1.649
rivalizar	1	0	1.649
rivales	1	0	1.649
rítmicos	1	0	1.649
ristre	1	0	1.649
rire	1	0	1.649
rio	1	0	1.649
riño	1	0	1.649
riñeran	1	0	1.649
ríñeme	1	0	1.649
rima	1	0	1.649
riguroso	1	0	1.649
rigolade	1	0	1.649
rigodones	1	0	1.649
rigidez	1	0	1.649
rifas	1	0	1.649
riendas	1	0	1.649
riegan	1	0	1.649
ridente	1	0	1.649
rezumaba	1	0	1.649
rezarle	1	0	1.649
rezagados	1	0	1.649
rewólver	1	0	1.649
revue	1	0	1.649
revoltoso	1	0	1.649
revoltosas	1	0	1.649
revolando	1	0	1.649
reverso	1	0	1.649
reverbero	1	0	1.649
reverberada	1	0	1.649
revele	1	0	1.649
revelase	1	0	1.649
reúna	1	0	1.649
retumbante	1	0	1.649
retumba	1	0	1.649
retrospectivo	1	0	1.649
retrospectiva	1	0	1.649
retrocediendo	1	0	1.649
retrataba	1	0	1.649
retrasó	1	0	1.649
retrasen	1	0	1.649
retrae	1	0	1.649
retractase	1	0	1.649
retractarse	1	0	1.649
retractación	1	0	1.649
retour	1	0	1.649
retórico	1	0	1.649
retorció	1	0	1.649
retorcida	1	0	1.649
retorcerse	1	0	1.649
retocados	1	0	1.649
retirasen	1	0	1.649
retirarlo	1	0	1.649
retebién	1	0	1.649
retarde	1	0	1.649
retado	1	0	1.649
resumía	1	0	1.649
resucitaba	1	0	1.649
resucita	1	0	1.649
restriñimientos	1	0	1.649
restringido	1	0	1.649
restreñimientos	1	0	1.649
restituya	1	0	1.649
restituirse	1	0	1.649
restituirlo	1	0	1.649
restituir	1	0	1.649
restituida	1	0	1.649
restituía	1	0	1.649
restaurando	1	0	1.649
restaurado	1	0	1.649
restañar	1	0	1.649
responsos	1	0	1.649
respondieron	1	0	1.649
responda	1	0	1.649
respiraban	1	0	1.649
respetuosa	1	0	1.649
respetaron	1	0	1.649
respetadas	1	0	1.649
respetabilísimos	1	0	1.649
respectivamente	1	0	1.649
respecta	1	0	1.649
respaldos	1	0	1.649
resonaron	1	0	1.649
resonante	1	0	1.649
resolvérsele	1	0	1.649
resolvería	1	0	1.649
resolvamos	1	0	1.649
resistiría	1	0	1.649
resistían	1	0	1.649
resignó	1	0	1.649
resignaron	1	0	1.649
resignarnos	1	0	1.649
resignan	1	0	1.649
residir	1	0	1.649
reservarían	1	0	1.649
reservaban	1	0	1.649
reseñada	1	0	1.649
resentido	1	0	1.649
rescatar	1	0	1.649
resbaló	1	0	1.649
resbalas	1	0	1.649
resbalaba	1	0	1.649
requirió	1	0	1.649
requerida	1	0	1.649
requebrarla	1	0	1.649
reputaciones	1	0	1.649
reputábala	1	0	1.649
repugnándole	1	0	1.649
repugnancias	1	0	1.649
repugnan	1	0	1.649
republicanitos	1	0	1.649
republicana	1	0	1.649
reproducen	1	0	1.649
reprimió	1	0	1.649
represiva	1	0	1.649
representativo	1	0	1.649
representársela	1	0	1.649
representarse	1	0	1.649
representado	1	0	1.649
representadas	1	0	1.649
reprendo	1	0	1.649
reprendiese	1	0	1.649
reprendido	1	0	1.649
reposaba	1	0	1.649
reportase	1	0	1.649
reportarse	1	0	1.649
repone	1	0	1.649
repliegues	1	0	1.649
replicar	1	0	1.649
replicado	1	0	1.649
repletos	1	0	1.649
repleta	1	0	1.649
repiqueteo	1	0	1.649
repiquen	1	0	1.649
repetiría	1	0	1.649
repertorio	1	0	1.649
repercutiendo	1	0	1.649
repentista	1	0	1.649
repartiros	1	0	1.649
repartidos	1	0	1.649
repartida	1	0	1.649
repartan	1	0	1.649
repararon	1	0	1.649
reo	1	0	1.649
renuncio	1	0	1.649
renunciarla	1	0	1.649
renunciando	1	0	1.649
renunciado	1	0	1.649
renueva	1	0	1.649
rentístico	1	0	1.649
renovar	1	0	1.649
renovada	1	0	1.649
reniega	1	0	1.649
rendondilla	1	0	1.649
rendimiento	1	0	1.649
rendían	1	0	1.649
rencorosas	1	0	1.649
renaciera	1	0	1.649
renacían	1	0	1.649
removiendo	1	0	1.649
removida	1	0	1.649
removían	1	0	1.649
remover	1	0	1.649
remordiera	1	0	1.649
remontar	1	0	1.649
remonísima	1	0	1.649
remolones	1	0	1.649
remolacha	1	0	1.649
remito	1	0	1.649
remitido	1	0	1.649
remiso	1	0	1.649
remendón	1	0	1.649
remendando	1	0	1.649
remendados	1	0	1.649
remendado	1	0	1.649
remedia	1	0	1.649
remedaban	1	0	1.649
remanso	1	0	1.649
relojes	1	0	1.649
rellenas	1	0	1.649
reliquia	1	0	1.649
relevaban	1	0	1.649
relator	1	0	1.649
relativos	1	0	1.649
relajar	1	0	1.649
relajamiento	1	0	1.649
relajado	1	0	1.649
rejuveneciendo	1	0	1.649
reivindicar	1	0	1.649
reivindicación	1	0	1.649
reintegrado	1	0	1.649
reinase	1	0	1.649
reinas	1	0	1.649
reinar	1	0	1.649
rehusar	1	0	1.649
rehabilitarse	1	0	1.649
regumque	1	0	1.649
regulam	1	0	1.649
regocijó	1	0	1.649
reglamentarios	1	0	1.649
registrándole	1	0	1.649
rege	1	0	1.649
regazados	1	0	1.649
regateo	1	0	1.649
regatear	1	0	1.649
regatean	1	0	1.649
regalen	1	0	1.649
regalarle	1	0	1.649
regalan	1	0	1.649
regalados	1	0	1.649
regaladas	1	0	1.649
regada	1	0	1.649
refutaría	1	0	1.649
refugiadas	1	0	1.649
refugiábanse	1	0	1.649
refugiaba	1	0	1.649
refuerzos	1	0	1.649
refrigerado	1	0	1.649
refriega	1	0	1.649
refrenada	1	0	1.649
refractaban	1	0	1.649
reforzada	1	0	1.649
reformistas	1	0	1.649
reformista	1	0	1.649
reflexionando	1	0	1.649
reflejados	1	0	1.649
reflejado	1	0	1.649
reflejadas	1	0	1.649
refinamiento	1	0	1.649
refinados	1	0	1.649
refieren	1	0	1.649
referírselas	1	0	1.649
referiré	1	0	1.649
reencarnación	1	0	1.649
reemplazarlas	1	0	1.649
reedificaba	1	0	1.649
reduplicado	1	0	1.649
redundantes	1	0	1.649
redundancia	1	0	1.649
redujo	1	0	1.649
reducto	1	0	1.649
reducirle	1	0	1.649
redondos	1	0	1.649
redondillas	1	0	1.649
redondeaban	1	0	1.649
redoma	1	0	1.649
redoble	1	0	1.649
redivivo	1	0	1.649
rediviva	1	0	1.649
redimirse	1	0	1.649
redimirle	1	0	1.649
redimir	1	0	1.649
redimidas	1	0	1.649
redactor	1	0	1.649
redactaré	1	0	1.649
recurrió	1	0	1.649
reculó	1	0	1.649
recuerden	1	0	1.649
rectificando	1	0	1.649
rectángulos	1	0	1.649
rectángulo	1	0	1.649
rectangular	1	0	1.649
rectae	1	0	1.649
recreos	1	0	1.649
recrearme	1	0	1.649
recreándonos	1	0	1.649
recostole	1	0	1.649
recostó	1	0	1.649
recortes	1	0	1.649
recortado	1	0	1.649
recorriese	1	0	1.649
recorrían	1	0	1.649
recordasen	1	0	1.649
recordarla	1	0	1.649
recordará	1	0	1.649
recordara	1	0	1.649
recordadas	1	0	1.649
recopilación	1	0	1.649
reconvención	1	0	1.649
recontaba	1	0	1.649
reconquista	1	0	1.649
reconociera	1	0	1.649
reconocí	1	0	1.649
recóndita	1	0	1.649
reconcilió	1	0	1.649
reconciliarme	1	0	1.649
reconciliaría	1	0	1.649
reconciliarás	1	0	1.649
reconcentradas	1	0	1.649
reconcentrada	1	0	1.649
recompensar	1	0	1.649
recomendarle	1	0	1.649
recogidos	1	0	1.649
recogemos	1	0	1.649
recobraste	1	0	1.649
recobrará	1	0	1.649
recitados	1	0	1.649
recíproca	1	0	1.649
recintos	1	0	1.649
recibirá	1	0	1.649
recibimos	1	0	1.649
recibiéndolas	1	0	1.649
recias	1	0	1.649
rechinasen	1	0	1.649
rechinaran	1	0	1.649
rechinaban	1	0	1.649
rechazar	1	0	1.649
rechazando	1	0	1.649
rechazadas	1	0	1.649
recentales	1	0	1.649
recelosas	1	0	1.649
recaudado	1	0	1.649
recatados	1	0	1.649
recatadamente	1	0	1.649
recatada	1	0	1.649
recalcitrantes	1	0	1.649
rebuscar	1	0	1.649
rebuscaban	1	0	1.649
rebrinquen	1	0	1.649
rebozo	1	0	1.649
rebozado	1	0	1.649
rebozada	1	0	1.649
rebotaron	1	0	1.649
rebosaba	1	0	1.649
reblandecer	1	0	1.649
rebeliones	1	0	1.649
rebela	1	0	1.649
rebasaría	1	0	1.649
rebasara	1	0	1.649
rebajó	1	0	1.649
rebajando	1	0	1.649
reaparecía	1	0	1.649
reanudados	1	0	1.649
reanuda	1	0	1.649
reanimó	1	0	1.649
realizados	1	0	1.649
realizaban	1	0	1.649
reacias	1	0	1.649
reaccionarios	1	0	1.649
rayó	1	0	1.649
rayar	1	0	1.649
ratificó	1	0	1.649
rastrero	1	0	1.649
rastrera	1	0	1.649
raspaba	1	0	1.649
rasgarse	1	0	1.649
rasgara	1	0	1.649
rasgando	1	0	1.649
rasgadas	1	0	1.649
rarísimas	1	0	1.649
rapto	1	0	1.649
rapsodias	1	0	1.649
rapidísima	1	0	1.649
rapado	1	0	1.649
rapa	1	0	1.649
ramillete	1	0	1.649
ramificaciones	1	0	1.649
ramerilla	1	0	1.649
ramayana	1	0	1.649
raídas	1	0	1.649
racionalmente	1	0	1.649
racionalismo	1	0	1.649
rabiosos	1	0	1.649
rabian	1	0	1.649
quum	1	0	1.649
quod	1	0	1.649
quisque	1	0	1.649
quisiste	1	0	1.649
quisicosa	1	0	1.649
quis	1	0	1.649
quinti	1	0	1.649
quijotescos	1	0	1.649
quijotada	1	0	1.649
quietismo	1	0	1.649
quiés	1	0	1.649
qui	1	0	1.649
question	1	0	1.649
querríamos	1	0	1.649
queridísima	1	0	1.649
queríala	1	0	1.649
quererlos	1	0	1.649
quererlo	1	0	1.649
querella	1	0	1.649
quemarlo	1	0	1.649
quemadura	1	0	1.649
quejumbrosos	1	0	1.649
queje	1	0	1.649
quejaron	1	0	1.649
quejabas	1	0	1.649
quejaban	1	0	1.649
quedarte	1	0	1.649
quedarían	1	0	1.649
quebrantarse	1	0	1.649
quebrándose	1	0	1.649
quebrada	1	0	1.649
quebraba	1	0	1.649
quanti	1	0	1.649
quando	1	0	1.649
quam	1	0	1.649
pústulas	1	0	1.649
pusilánime	1	0	1.649
purulentas	1	0	1.649
purpurinos	1	0	1.649
puridad	1	0	1.649
pupilo	1	0	1.649
puñada	1	0	1.649
puntuación	1	0	1.649
puntillo	1	0	1.649
puntiagudas	1	0	1.649
puntiaguda	1	0	1.649
puntales	1	0	1.649
pundonor	1	0	1.649
pumaradas	1	0	1.649
pumarada	1	0	1.649
pulvis	1	0	1.649
pulverizarse	1	0	1.649
pulverizar	1	0	1.649
pululan	1	0	1.649
pululáis	1	0	1.649
pulsa	1	0	1.649
pulidas	1	0	1.649
pugnaban	1	0	1.649
pugnaba	1	0	1.649
pugna	1	0	1.649
puéstole	1	0	1.649
pués	1	0	1.649
puerros	1	0	1.649
puerro	1	0	1.649
puerperio	1	0	1.649
puerperales	1	0	1.649
puerilidades	1	0	1.649
pudrirse	1	0	1.649
pudriría	1	0	1.649
pudrirá	1	0	1.649
pudrían	1	0	1.649
pudren	1	0	1.649
pudra	1	0	1.649
pudorosa	1	0	1.649
pudiéramos	1	0	1.649
pudientes	1	0	1.649
pudibundo	1	0	1.649
publicarlas	1	0	1.649
publicaría	1	0	1.649
publicar	1	0	1.649
públicamente	1	0	1.649
publicación	1	0	1.649
psíquico	1	0	1.649
psicológico	1	0	1.649
psicológicas	1	0	1.649
psicológicamente	1	0	1.649
psicologías	1	0	1.649
pseudoclásico	1	0	1.649
prudentemente	1	0	1.649
proyectaba	1	0	1.649
provocativo	1	0	1.649
provocarlas	1	0	1.649
provocan	1	0	1.649
provocados	1	0	1.649
provocador	1	0	1.649
provoca	1	0	1.649
provisores	1	0	1.649
provisionalmente	1	0	1.649
provinciana	1	0	1.649
proviene	1	0	1.649
proverbial	1	0	1.649
proveer	1	0	1.649
provechosa	1	0	1.649
protoplasma	1	0	1.649
protestase	1	0	1.649
protestara	1	0	1.649
protestan	1	0	1.649
protegió	1	0	1.649
prostituta	1	0	1.649
prosternaban	1	0	1.649
próspero	1	0	1.649
prosperaría	1	0	1.649
prosperaba	1	0	1.649
prosopopeya	1	0	1.649
prosigue	1	0	1.649
prosigas	1	0	1.649
prosélito	1	0	1.649
proseguir	1	0	1.649
prorrumpir	1	0	1.649
prorrumpiéramos	1	0	1.649
propter	1	0	1.649
proponemos	1	0	1.649
propietarios	1	0	1.649
prophani	1	0	1.649
propedéutica	1	0	1.649
propasó	1	0	1.649
propasase	1	0	1.649
propasado	1	0	1.649
propasa	1	0	1.649
propalando	1	0	1.649
propalaba	1	0	1.649
propala	1	0	1.649
propagandistas	1	0	1.649
propagaban	1	0	1.649
pronosticado	1	0	1.649
promulgó	1	0	1.649
prominencias	1	0	1.649
prometían	1	0	1.649
prometerse	1	0	1.649
prometerla	1	0	1.649
prometería	1	0	1.649
prolongándose	1	0	1.649
prolongadas	1	0	1.649
prolongaban	1	0	1.649
prolija	1	0	1.649
proletarios	1	0	1.649
proletarias	1	0	1.649
prole	1	0	1.649
prohibiría	1	0	1.649
prohibiera	1	0	1.649
prohibían	1	0	1.649
prohíban	1	0	1.649
progresa	1	0	1.649
profiriese	1	0	1.649
profesaron	1	0	1.649
profesar	1	0	1.649
profesadas	1	0	1.649
profanó	1	0	1.649
profanarlo	1	0	1.649
profanaran	1	0	1.649
profanaban	1	0	1.649
produciendo	1	0	1.649
prodromos	1	0	1.649
prodigiosamente	1	0	1.649
prodigara	1	0	1.649
prodigalidad	1	0	1.649
pródiga	1	0	1.649
procurose	1	0	1.649
procurarla	1	0	1.649
procurándolo	1	0	1.649
procuradores	1	0	1.649
proclamarse	1	0	1.649
proclamamos	1	0	1.649
proclama	1	0	1.649
procedente	1	0	1.649
proboscidio	1	0	1.649
probidad	1	0	1.649
probecicos	1	0	1.649
probasen	1	0	1.649
proba	1	0	1.649
privilegiado	1	0	1.649
privilegiadas	1	0	1.649
privilegiada	1	0	1.649
privarse	1	0	1.649
privarle	1	0	1.649
priva	1	0	1.649
prístina	1	0	1.649
prismáticos	1	0	1.649
principium	1	0	1.649
principado	1	0	1.649
princesas	1	0	1.649
primorosa	1	0	1.649
primordiales	1	0	1.649
primicias	1	0	1.649
primerizos	1	0	1.649
primerizo	1	0	1.649
primeriza	1	0	1.649
previamente	1	0	1.649
preveo	1	0	1.649
prevenirnos	1	0	1.649
prevenirle	1	0	1.649
prevenía	1	0	1.649
prevaricaciones	1	0	1.649
prevaliéndose	1	0	1.649
prevaleciese	1	0	1.649
pretil	1	0	1.649
pretexta	1	0	1.649
pretéritos	1	0	1.649
pretericiones	1	0	1.649
pretendí	1	0	1.649
pretenda	1	0	1.649
presurosos	1	0	1.649
presuntuoso	1	0	1.649
presuntuosa	1	0	1.649
presumiese	1	0	1.649
presumidillas	1	0	1.649
presumían	1	0	1.649
prestaríamos	1	0	1.649
prestaría	1	0	1.649
presillas	1	0	1.649
presiento	1	0	1.649
presidió	1	0	1.649
presidiera	1	0	1.649
presididos	1	0	1.649
presidido	1	0	1.649
presentían	1	0	1.649
presentía	1	0	1.649
presenten	1	0	1.649
presentase	1	0	1.649
presentarlo	1	0	1.649
presentaría	1	0	1.649
presentada	1	0	1.649
presenciaba	1	0	1.649
preseas	1	0	1.649
presea	1	0	1.649
prescribe	1	0	1.649
prescindirían	1	0	1.649
prescindiendo	1	0	1.649
prescindido	1	0	1.649
prescindamos	1	0	1.649
presas	1	0	1.649
prerrogativa	1	0	1.649
prepararme	1	0	1.649
prepararían	1	0	1.649
prepararía	1	0	1.649
preparándolos	1	0	1.649
preparadas	1	0	1.649
preocupó	1	0	1.649
preocupándole	1	0	1.649
preocupan	1	0	1.649
preñadas	1	0	1.649
prensas	1	0	1.649
prensados	1	0	1.649
prendieran	1	0	1.649
prendido	1	0	1.649
prendían	1	0	1.649
prenderle	1	0	1.649
premioso	1	0	1.649
premiosas	1	0	1.649
premiarle	1	0	1.649
premiaba	1	0	1.649
premeditada	1	0	1.649
preguntase	1	0	1.649
preguntarte	1	0	1.649
preguntaré	1	0	1.649
pregonero	1	0	1.649
pregonaban	1	0	1.649
prefirieron	1	0	1.649
prefieren	1	0	1.649
prefiera	1	0	1.649
preferiría	1	0	1.649
prefación	1	0	1.649
preeminentes	1	0	1.649
predominar	1	0	1.649
predominaban	1	0	1.649
predomina	1	0	1.649
predique	1	0	1.649
predios	1	0	1.649
predio	1	0	1.649
predilectos	1	0	1.649
predilecciones	1	0	1.649
predicas	1	0	1.649
predicado	1	0	1.649
predicaban	1	0	1.649
preclara	1	0	1.649
precisas	1	0	1.649
precipitarse	1	0	1.649
precipitaban	1	0	1.649
precipita	1	0	1.649
precipicios	1	0	1.649
preciosos	1	0	1.649
precian	1	0	1.649
preciaban	1	0	1.649
precia	1	0	1.649
precedía	1	0	1.649
preceden	1	0	1.649
precavido	1	0	1.649
prebendas	1	0	1.649
practicaron	1	0	1.649
practican	1	0	1.649
practicada	1	0	1.649
poussin	1	0	1.649
pour	1	0	1.649
potros	1	0	1.649
potentado	1	0	1.649
potencias	1	0	1.649
postró	1	0	1.649
postizos	1	0	1.649
posteriores	1	0	1.649
postdata	1	0	1.649
post	1	0	1.649
possumus	1	0	1.649
posponerle	1	0	1.649
posesiones	1	0	1.649
poseerla	1	0	1.649
poseerás	1	0	1.649
posaban	1	0	1.649
posaba	1	0	1.649
portuguesa	1	0	1.649
portugués	1	0	1.649
portocarrero	1	0	1.649
portier	1	0	1.649
portentosa	1	0	1.649
portento	1	0	1.649
portátiles	1	0	1.649
portador	1	0	1.649
portaban	1	0	1.649
porfía	1	0	1.649
porches	1	0	1.649
poquísimo	1	0	1.649
populoso	1	0	1.649
populi	1	0	1.649
pontificii	1	0	1.649
pontificado	1	0	1.649
ponío	1	0	1.649
poniéndosele	1	0	1.649
ponérselas	1	0	1.649
ponernos	1	0	1.649
pomposo	1	0	1.649
pompa	1	0	1.649
pomarada	1	0	1.649
polvorosas	1	0	1.649
polvorín	1	0	1.649
polvorientas	1	0	1.649
polvareda	1	0	1.649
polo	1	0	1.649
pollastre	1	0	1.649
polizontes	1	0	1.649
pólizas	1	0	1.649
poliuto	1	0	1.649
pólipo	1	0	1.649
polilla	1	0	1.649
poleas	1	0	1.649
polainas	1	0	1.649
polaco	1	0	1.649
poetizados	1	0	1.649
poetillas	1	0	1.649
poetilla	1	0	1.649
poe	1	0	1.649
podredumbres	1	0	1.649
pocula	1	0	1.649
pocilgas	1	0	1.649
pobretes	1	0	1.649
pobladas	1	0	1.649
poblada	1	0	1.649
poblachones	1	0	1.649
poblachón	1	0	1.649
plun	1	0	1.649
plomiza	1	0	1.649
plenos	1	0	1.649
plenamente	1	0	1.649
plegadera	1	0	1.649
plegaba	1	0	1.649
plebeyas	1	0	1.649
plebeya	1	0	1.649
platónicos	1	0	1.649
plateresca	1	0	1.649
plásticos	1	0	1.649
plástico	1	0	1.649
plasticidad	1	0	1.649
plantando	1	0	1.649
plantados	1	0	1.649
planicies	1	0	1.649
planetas	1	0	1.649
planchadoras	1	0	1.649
pizpiretas	1	0	1.649
pizpireta	1	0	1.649
pizarro	1	0	1.649
pittore	1	0	1.649
pitonisa	1	0	1.649
pitisa	1	0	1.649
pitillos	1	0	1.649
pistilos	1	0	1.649
pista	1	0	1.649
pisoteadas	1	0	1.649
pisoteada	1	0	1.649
piscis	1	0	1.649
pisarlas	1	0	1.649
pisara	1	0	1.649
pisado	1	0	1.649
pirueta	1	0	1.649
piquillo	1	0	1.649
piquemos	1	0	1.649
piqué	1	0	1.649
pionono	1	0	1.649
piña	1	0	1.649
pinzones	1	0	1.649
pintorescas	1	0	1.649
pintarse	1	0	1.649
pintaría	1	0	1.649
pintao	1	0	1.649
pinón	1	0	1.649
pinchó	1	0	1.649
pincharle	1	0	1.649
pincharlas	1	0	1.649
pinchándole	1	0	1.649
pinchado	1	0	1.649
pinchaba	1	0	1.649
pimpollo	1	0	1.649
pigault	1	0	1.649
pietista	1	0	1.649
picoteaba	1	0	1.649
picota	1	0	1.649
picona	1	0	1.649
pichones	1	0	1.649
picarísima	1	0	1.649
picarilla	1	0	1.649
picachos	1	0	1.649
piara	1	0	1.649
piafar	1	0	1.649
phorminx	1	0	1.649
petirrojos	1	0	1.649
petatur	1	0	1.649
petardos	1	0	1.649
pétalos	1	0	1.649
pespunteados	1	0	1.649
peseteros	1	0	1.649
pescaremos	1	0	1.649
pescante	1	0	1.649
pesaría	1	0	1.649
pesándole	1	0	1.649
pesadísimo	1	0	1.649
pervertido	1	0	1.649
pervertidas	1	0	1.649
pervertía	1	0	1.649
perú	1	0	1.649
perturbadora	1	0	1.649
pertinente	1	0	1.649
pertinaz	1	0	1.649
perteneció	1	0	1.649
perteneciera	1	0	1.649
perteneces	1	0	1.649
pertenecerle	1	0	1.649
persuadidos	1	0	1.649
persuadido	1	0	1.649
persuadida	1	0	1.649
personificar	1	0	1.649
personifican	1	0	1.649
personificaciones	1	0	1.649
personalidades	1	0	1.649
persistente	1	0	1.649
persiguiéndose	1	0	1.649
persignarse	1	0	1.649
pérsica	1	0	1.649
perseguirla	1	0	1.649
perseguidor	1	0	1.649
perpetuos	1	0	1.649
perorando	1	0	1.649
perol	1	0	1.649
permitiese	1	0	1.649
permita	1	0	1.649
permanezca	1	0	1.649
permanecido	1	0	1.649
perladas	1	0	1.649
perjuicios	1	0	1.649
perjudicaría	1	0	1.649
perjudicar	1	0	1.649
peritonitis	1	0	1.649
perito	1	0	1.649
peripatético	1	0	1.649
periféricos	1	0	1.649
pergeño	1	0	1.649
pergeñadas	1	0	1.649
perfumería	1	0	1.649
perfidia	1	0	1.649
perfeccionarse	1	0	1.649
perfeccionando	1	0	1.649
perezosamente	1	0	1.649
perezas	1	0	1.649
perentoria	1	0	1.649
peregrinación	1	0	1.649
pereda	1	0	1.649
perecedero	1	0	1.649
perdonóselos	1	0	1.649
perdonase	1	0	1.649
perdonarlo	1	0	1.649
perdonarle	1	0	1.649
perdonándoselo	1	0	1.649
perdonando	1	0	1.649
perdonadle	1	0	1.649
perdonaban	1	0	1.649
perdigones	1	0	1.649
perdigonada	1	0	1.649
perdigón	1	0	1.649
perceptivas	1	0	1.649
percalina	1	0	1.649
peraltados	1	0	1.649
per	1	0	1.649
pequeñísimo	1	0	1.649
pequeñísima	1	0	1.649
pepinillos	1	0	1.649
peonza	1	0	1.649
peones	1	0	1.649
peoncillo	1	0	1.649
peñasco	1	0	1.649
penuria	1	0	1.649
penúltimo	1	0	1.649
penúltima	1	0	1.649
pense	1	0	1.649
pensadorzuelo	1	0	1.649
pensadas	1	0	1.649
penitenciarias	1	0	1.649
péndulos	1	0	1.649
pendones	1	0	1.649
pender	1	0	1.649
pendencias	1	0	1.649
pendebat	1	0	1.649
penachos	1	0	1.649
penacho	1	0	1.649
peluconas	1	0	1.649
pelotas	1	0	1.649
peligró	1	0	1.649
peligra	1	0	1.649
peleo	1	0	1.649
peleé	1	0	1.649
pelada	1	0	1.649
peino	1	0	1.649
peinamos	1	0	1.649
peinador	1	0	1.649
pegarnos	1	0	1.649
pegajosos	1	0	1.649
pegajosas	1	0	1.649
pedigüeño	1	0	1.649
pedestal	1	0	1.649
pedantón	1	0	1.649
pedantesca	1	0	1.649
pedantes	1	0	1.649
pedagógicas	1	0	1.649
pecuniarios	1	0	1.649
peculiares	1	0	1.649
pechinas	1	0	1.649
peccata	1	0	1.649
pecará	1	0	1.649
pecadillo	1	0	1.649
pebetero	1	0	1.649
pche	1	0	1.649
pavorosos	1	0	1.649
pavés	1	0	1.649
pausado	1	0	1.649
pauperum	1	0	1.649
paulo	1	0	1.649
paulatinos	1	0	1.649
paulatinamente	1	0	1.649
patronato	1	0	1.649
patrocinado	1	0	1.649
patris	1	0	1.649
patriótica	1	0	1.649
patriotas	1	0	1.649
patearle	1	0	1.649
patarata	1	0	1.649
pastoreo	1	0	1.649
pasteur	1	0	1.649
pasmasen	1	0	1.649
pasivos	1	0	1.649
paseándola	1	0	1.649
pasea	1	0	1.649
pascal	1	0	1.649
pasarlas	1	0	1.649
pasarla	1	0	1.649
pasao	1	0	1.649
pasándolos	1	0	1.649
pasamano	1	0	1.649
pasabas	1	0	1.649
parves	1	0	1.649
parvedad	1	0	1.649
partiquino	1	0	1.649
partió	1	0	1.649
partícula	1	0	1.649
parterre	1	0	1.649
parteras	1	0	1.649
parroquiales	1	0	1.649
paroxismos	1	0	1.649
parodiar	1	0	1.649
parodiaba	1	0	1.649
parodia	1	0	1.649
parnaso	1	0	1.649
parisién	1	0	1.649
parezcan	1	0	1.649
parejita	1	0	1.649
paredones	1	0	1.649
parecérselo	1	0	1.649
parecernos	1	0	1.649
parecerla	1	0	1.649
parduzco	1	0	1.649
pardeaba	1	0	1.649
pardales	1	0	1.649
parciales	1	0	1.649
parangón	1	0	1.649
paran	1	0	1.649
paralelos	1	0	1.649
paralelo	1	0	1.649
parábanse	1	0	1.649
papista	1	0	1.649
papisa	1	0	1.649
papelucho	1	0	1.649
panzuda	1	0	1.649
pantorriiiilla	1	0	1.649
panteísticos	1	0	1.649
panteística	1	0	1.649
panteísta	1	0	1.649
panteísmos	1	0	1.649
panoplia	1	0	1.649
paniaguado	1	0	1.649
panegíricos	1	0	1.649
palúdicas	1	0	1.649
palparles	1	0	1.649
palmario	1	0	1.649
pallavicini	1	0	1.649
palisandro	1	0	1.649
palinodia	1	0	1.649
palillero	1	0	1.649
paliducha	1	0	1.649
palido	1	0	1.649
palafrén	1	0	1.649
pajarracos	1	0	1.649
pajarita	1	0	1.649
pajar	1	0	1.649
paix	1	0	1.649
pagina	1	0	1.649
pagase	1	0	1.649
pagárselo	1	0	1.649
pagaron	1	0	1.649
pagarías	1	0	1.649
pagaríamos	1	0	1.649
paganos	1	0	1.649
pagamos	1	0	1.649
pagados	1	0	1.649
pagaderos	1	0	1.649
pagaderas	1	0	1.649
paece	1	0	1.649
padrazo	1	0	1.649
padezcas	1	0	1.649
padecieron	1	0	1.649
padeces	1	0	1.649
padecerla	1	0	1.649
padecerá	1	0	1.649
pacientes	1	0	1.649
pábilos	1	0	1.649
oyesen	1	0	1.649
oxígeno	1	0	1.649
oxidadas	1	0	1.649
ovaladas	1	0	1.649
oval	1	0	1.649
ovación	1	0	1.649
otrosí	1	0	1.649
otorgaría	1	0	1.649
otorgar	1	0	1.649
otorgaba	1	0	1.649
otoños	1	0	1.649
otoñada	1	0	1.649
ostracismo	1	0	1.649
ostentosos	1	0	1.649
ostentosas	1	0	1.649
ostensiblemente	1	0	1.649
osó	1	0	1.649
osaron	1	0	1.649
osadas	1	0	1.649
ortodoxas	1	0	1.649
ortodoxa	1	0	1.649
orto	1	0	1.649
orsini	1	0	1.649
oró	1	0	1.649
orladas	1	0	1.649
orlaban	1	0	1.649
originó	1	0	1.649
originarse	1	0	1.649
origina	1	0	1.649
orientarse	1	0	1.649
orientalista	1	0	1.649
orgullos	1	0	1.649
orgullito	1	0	1.649
orgasmo	1	0	1.649
organizado	1	0	1.649
organizaba	1	0	1.649
organdí	1	0	1.649
orejeras	1	0	1.649
ordo	1	0	1.649
ordine	1	0	1.649
ordenase	1	0	1.649
órbita	1	0	1.649
oradoras	1	0	1.649
orado	1	0	1.649
opusieron	1	0	1.649
opusiera	1	0	1.649
óptima	1	0	1.649
óptico	1	0	1.649
oprimiéndose	1	0	1.649
opresor	1	0	1.649
oppert	1	0	1.649
opositor	1	0	1.649
oportunísimo	1	0	1.649
oportunamente	1	0	1.649
opino	1	0	1.649
opinar	1	0	1.649
opinan	1	0	1.649
opaco	1	0	1.649
ondeado	1	0	1.649
ondeadas	1	0	1.649
ondeada	1	0	1.649
omnilateral	1	0	1.649
ominosos	1	0	1.649
ominoso	1	0	1.649
olvidastes	1	0	1.649
olvidase	1	0	1.649
olvidas	1	0	1.649
olvidarlo	1	0	1.649
olvidarlas	1	0	1.649
olvidadas	1	0	1.649
olimpo	1	0	1.649
olfateo	1	0	1.649
ojivales	1	0	1.649
oirían	1	0	1.649
oirás	1	0	1.649
oigámoslo	1	0	1.649
óigalo	1	0	1.649
oi	1	0	1.649
ogaño	1	0	1.649
ofrecida	1	0	1.649
ofidiana	1	0	1.649
ofensivas	1	0	1.649
ofendidos	1	0	1.649
ofendían	1	0	1.649
ofenderle	1	0	1.649
odias	1	0	1.649
odiarme	1	0	1.649
odiar	1	0	1.649
odas	1	0	1.649
ocurrieran	1	0	1.649
ocuparé	1	0	1.649
ocupábase	1	0	1.649
ocultéis	1	0	1.649
ocultase	1	0	1.649
ocultaron	1	0	1.649
ocultarlos	1	0	1.649
ocultarlas	1	0	1.649
ochentón	1	0	1.649
obstinada	1	0	1.649
obseso	1	0	1.649
observatorios	1	0	1.649
observatorio	1	0	1.649
observarle	1	0	1.649
observamos	1	0	1.649
observadores	1	0	1.649
observaban	1	0	1.649
obsequiarle	1	0	1.649
obsequiaban	1	0	1.649
obsequiaba	1	0	1.649
obscurezca	1	0	1.649
obscurecida	1	0	1.649
obscurantismo	1	0	1.649
obraban	1	0	1.649
oblonga	1	0	1.649
obligatorio	1	0	1.649
obligase	1	0	1.649
obligarle	1	0	1.649
obligarla	1	0	1.649
obligaríanles	1	0	1.649
obligara	1	0	1.649
obligando	1	0	1.649
oblicuos	1	0	1.649
oblicuo	1	0	1.649
objetó	1	0	1.649
objetivo	1	0	1.649
objetado	1	0	1.649
objetaba	1	0	1.649
objeción	1	0	1.649
obispillo	1	0	1.649
obediente	1	0	1.649
obedecí	1	0	1.649
obedecerle	1	0	1.649
obdulias	1	0	1.649
obcecado	1	0	1.649
nutrir	1	0	1.649
numeroso	1	0	1.649
nulo	1	0	1.649
nulas	1	0	1.649
nudos	1	0	1.649
nublada	1	0	1.649
nubarrones	1	0	1.649
noviazgos	1	0	1.649
novenario	1	0	1.649
noveladores	1	0	1.649
notorio	1	0	1.649
noticierismo	1	0	1.649
noten	1	0	1.649
notasen	1	0	1.649
notadas	1	0	1.649
notabilidad	1	0	1.649
not	1	0	1.649
noruega	1	0	1.649
normandos	1	0	1.649
nordeste	1	0	1.649
nomine	1	0	1.649
nombrando	1	0	1.649
nolis	1	0	1.649
nogales	1	0	1.649
nodrizas	1	0	1.649
nocivas	1	0	1.649
nocedal	1	0	1.649
noblemente	1	0	1.649
nobilísimo	1	0	1.649
nivelaba	1	0	1.649
nisi	1	0	1.649
ninon	1	0	1.649
nínive	1	0	1.649
ninfa	1	0	1.649
nimbo	1	0	1.649
nihil	1	0	1.649
nevatilla	1	0	1.649
nevase	1	0	1.649
nevado	1	0	1.649
nevaba	1	0	1.649
neutra	1	0	1.649
nemrod	1	0	1.649
nemorosos	1	0	1.649
negruzcas	1	0	1.649
negruras	1	0	1.649
negrillo	1	0	1.649
negligencia	1	0	1.649
negarte	1	0	1.649
negarla	1	0	1.649
negándoles	1	0	1.649
negado	1	0	1.649
nefastos	1	0	1.649
nefasta	1	0	1.649
nefas	1	0	1.649
necesiten	1	0	1.649
necesitarlos	1	0	1.649
necesitarlas	1	0	1.649
necesitáis	1	0	1.649
necesitábamos	1	0	1.649
nebuloso	1	0	1.649
nay	1	0	1.649
navegados	1	0	1.649
navegación	1	0	1.649
naval	1	0	1.649
náutica	1	0	1.649
naturans	1	0	1.649
naturalísimo	1	0	1.649
natalicio	1	0	1.649
natalia	1	0	1.649
natal	1	0	1.649
narrar	1	0	1.649
narigudo	1	0	1.649
naipes	1	0	1.649
naipe	1	0	1.649
naciera	1	0	1.649
mutua	1	0	1.649
mustios	1	0	1.649
mustias	1	0	1.649
mustia	1	0	1.649
muslos	1	0	1.649
musgosas	1	0	1.649
musculosa	1	0	1.649
musa	1	0	1.649
murmuren	1	0	1.649
murmurase	1	0	1.649
murmuraría	1	0	1.649
murmuran	1	0	1.649
murmurador	1	0	1.649
murmurado	1	0	1.649
muriéndonos	1	0	1.649
muñeira	1	0	1.649
mundanales	1	0	1.649
munda	1	0	1.649
multiplicándose	1	0	1.649
multiplicadas	1	0	1.649
mullido	1	0	1.649
mulata	1	0	1.649
mujerota	1	0	1.649
muévete	1	0	1.649
muerdes	1	0	1.649
mueblista	1	0	1.649
mueblaje	1	0	1.649
múdese	1	0	1.649
mucetas	1	0	1.649
mr	1	0	1.649
moviesen	1	0	1.649
movieron	1	0	1.649
moverlos	1	0	1.649
moverla	1	0	1.649
movediza	1	0	1.649
mostradas	1	0	1.649
mosco	1	0	1.649
mortificarme	1	0	1.649
mortificar	1	0	1.649
mortificado	1	0	1.649
mortífero	1	0	1.649
mortífera	1	0	1.649
morosos	1	0	1.649
morigerado	1	0	1.649
morigerada	1	0	1.649
morería	1	0	1.649
morenas	1	0	1.649
mordieron	1	0	1.649
mordían	1	0	1.649
morderse	1	0	1.649
mordería	1	0	1.649
mordedura	1	0	1.649
morcillas	1	0	1.649
morbosa	1	0	1.649
mórbido	1	0	1.649
morbidez	1	0	1.649
mórbida	1	0	1.649
moran	1	0	1.649
moralizarla	1	0	1.649
mora	1	0	1.649
monterilla	1	0	1.649
montecristo	1	0	1.649
montase	1	0	1.649
montados	1	0	1.649
montadas	1	0	1.649
monstruoso	1	0	1.649
monstruosas	1	0	1.649
monolito	1	0	1.649
monocromos	1	0	1.649
monjitas	1	0	1.649
monjío	1	0	1.649
monje	1	0	1.649
mónica	1	0	1.649
monescillo	1	0	1.649
monederos	1	0	1.649
monedero	1	0	1.649
mondes	1	0	1.649
mondar	1	0	1.649
monda	1	0	1.649
monástica	1	0	1.649
monagos	1	0	1.649
momentánea	1	0	1.649
molinos	1	0	1.649
molineros	1	0	1.649
moliera	1	0	1.649
molestos	1	0	1.649
molestarse	1	0	1.649
molestándolos	1	0	1.649
molestándoles	1	0	1.649
molestándole	1	0	1.649
moleslo	1	0	1.649
moleschott	1	0	1.649
moléculas	1	0	1.649
molécula	1	0	1.649
molduras	1	0	1.649
mojigatos	1	0	1.649
mojigangas	1	0	1.649
mojando	1	0	1.649
mojados	1	0	1.649
mojadas	1	0	1.649
mohicanos	1	0	1.649
modus	1	0	1.649
modificaciones	1	0	1.649
modificaba	1	0	1.649
moderados	1	0	1.649
mochuelos	1	0	1.649
mobiliario	1	0	1.649
mo	1	0	1.649
mixto	1	0	1.649
mixtificación	1	0	1.649
mitológicos	1	0	1.649
mitologías	1	0	1.649
mitigado	1	0	1.649
mitigada	1	0	1.649
místicamente	1	0	1.649
misiva	1	0	1.649
misérrimo	1	0	1.649
míseros	1	0	1.649
miserablemente	1	0	1.649
mirones	1	0	1.649
mirlaba	1	0	1.649
mirarás	1	0	1.649
mirándoos	1	0	1.649
mírale	1	0	1.649
minuta	1	0	1.649
minué	1	0	1.649
minuciosa	1	0	1.649
miniatura	1	0	1.649
minero	1	0	1.649
mineralógicas	1	0	1.649
minerales	1	0	1.649
mímicos	1	0	1.649
milo	1	0	1.649
milito	1	0	1.649
militantes	1	0	1.649
militaba	1	0	1.649
miliarias	1	0	1.649
milano	1	0	1.649
milagrosamente	1	0	1.649
mienta	1	0	1.649
midiéramos	1	0	1.649
mide	1	0	1.649
mica	1	0	1.649
mezclase	1	0	1.649
mezclarse	1	0	1.649
mezclándose	1	0	1.649
mezclados	1	0	1.649
meus	1	0	1.649
meum	1	0	1.649
metropolitano	1	0	1.649
metralla	1	0	1.649
metodista	1	0	1.649
metiditos	1	0	1.649
metidito	1	0	1.649
metidas	1	0	1.649
meteorológicos	1	0	1.649
meteorología	1	0	1.649
metalizado	1	0	1.649
metálicos	1	0	1.649
metafóricamente	1	0	1.649
mesetas	1	0	1.649
mescolanzas	1	0	1.649
mesaba	1	0	1.649
mermas	1	0	1.649
meritorio	1	0	1.649
meritoria	1	0	1.649
meriendo	1	0	1.649
meridionales	1	0	1.649
merendado	1	0	1.649
merendaba	1	0	1.649
merecimiento	1	0	1.649
merecidísimo	1	0	1.649
merecerles	1	0	1.649
mera	1	0	1.649
menudeando	1	0	1.649
menudean	1	0	1.649
mentor	1	0	1.649
mentón	1	0	1.649
mentido	1	0	1.649
mentida	1	0	1.649
mentían	1	0	1.649
mentarla	1	0	1.649
menjurjes	1	0	1.649
menguada	1	0	1.649
menguaba	1	0	1.649
mengua	1	0	1.649
meneses	1	0	1.649
meneaban	1	0	1.649
mendrugos	1	0	1.649
mendrugo	1	0	1.649
mencionaré	1	0	1.649
memento	1	0	1.649
membibres	1	0	1.649
meloso	1	0	1.649
melosas	1	0	1.649
melodiosa	1	0	1.649
melodías	1	0	1.649
melocotón	1	0	1.649
meliora	1	0	1.649
melindrán	1	0	1.649
melifluo	1	0	1.649
mejorase	1	0	1.649
mejorarán	1	0	1.649
méjico	1	0	1.649
mefistofélicos	1	0	1.649
medró	1	0	1.649
medro	1	0	1.649
medrar	1	0	1.649
medran	1	0	1.649
medrados	1	0	1.649
medite	1	0	1.649
meditan	1	0	1.649
medianoche	1	0	1.649
medianeras	1	0	1.649
medalla	1	0	1.649
mecida	1	0	1.649
mecía	1	0	1.649
mecánicamente	1	0	1.649
mazas	1	0	1.649
mayúscula	1	0	1.649
mayorazguetes	1	0	1.649
mayorazguete	1	0	1.649
mayorazgo	1	0	1.649
mayoral	1	0	1.649
mayaba	1	0	1.649
máximo	1	0	1.649
máximas	1	0	1.649
maudsley	1	0	1.649
matutinos	1	0	1.649
matutino	1	0	1.649
matutina	1	0	1.649
matriculados	1	0	1.649
matriculadas	1	0	1.649
matrícula	1	0	1.649
matinée	1	0	1.649
matiella	1	0	1.649
matemáticos	1	0	1.649
matemáticamente	1	0	1.649
maté	1	0	1.649
matarse	1	0	1.649
mátale	1	0	1.649
masini	1	0	1.649
masculinos	1	0	1.649
masculinas	1	0	1.649
marsilla	1	0	1.649
marquesitas	1	0	1.649
marquesina	1	0	1.649
mármoles	1	0	1.649
marmitón	1	0	1.649
maritornes	1	0	1.649
marimacho	1	0	1.649
marearlos	1	0	1.649
mareantes	1	0	1.649
mare	1	0	1.649
marchitos	1	0	1.649
marchitaban	1	0	1.649
maravillado	1	0	1.649
maragato	1	0	1.649
maquinillas	1	0	1.649
maquinación	1	0	1.649
mapa	1	0	1.649
manuscrito	1	0	1.649
manu	1	0	1.649
mantuvieron	1	0	1.649
manterola	1	0	1.649
mantengo	1	0	1.649
mantengas	1	0	1.649
mantenerlo	1	0	1.649
mantendría	1	0	1.649
manriques	1	0	1.649
manoseando	1	0	1.649
manolesco	1	0	1.649
manola	1	0	1.649
manirrota	1	0	1.649
maniqueo	1	0	1.649
maniobras	1	0	1.649
manifestase	1	0	1.649
manifestándose	1	0	1.649
manifestamos	1	0	1.649
mandobles	1	0	1.649
mandilona	1	0	1.649
mandarse	1	0	1.649
mandarlo	1	0	1.649
mandamos	1	0	1.649
manchara	1	0	1.649
manchar	1	0	1.649
manchándolos	1	0	1.649
manchan	1	0	1.649
manar	1	0	1.649
mampostería	1	0	1.649
maltratadas	1	0	1.649
malquistarle	1	0	1.649
maliciado	1	0	1.649
maliciaban	1	0	1.649
malhumor	1	0	1.649
malhechor	1	0	1.649
malgré	1	0	1.649
malgastado	1	0	1.649
malgastada	1	0	1.649
malévolas	1	0	1.649
maldiciendo	1	0	1.649
maldecirá	1	0	1.649
malbaratado	1	0	1.649
malamente	1	0	1.649
malabares	1	0	1.649
majestuosos	1	0	1.649
majas	1	0	1.649
majaderías	1	0	1.649
maizales	1	0	1.649
maitines	1	0	1.649
mainates	1	0	1.649
mahoma	1	0	1.649
magyares	1	0	1.649
magullar	1	0	1.649
magno	1	0	1.649
magnético	1	0	1.649
magnéticas	1	0	1.649
magnates	1	0	1.649
magnanimidad	1	0	1.649
magistrales	1	0	1.649
maduros	1	0	1.649
madrugue	1	0	1.649
madrugo	1	0	1.649
madrugaría	1	0	1.649
madrugado	1	0	1.649
madrileñitos	1	0	1.649
madrejón	1	0	1.649
madrastra	1	0	1.649
madona	1	0	1.649
maderita	1	0	1.649
macizo	1	0	1.649
maciza	1	0	1.649
macilento	1	0	1.649
machacan	1	0	1.649
macedónico	1	0	1.649
macabra	1	0	1.649
macabeos	1	0	1.649
luzbel	1	0	1.649
luys	1	0	1.649
lusitana	1	0	1.649
lupus	1	0	1.649
lunares	1	0	1.649
lujosos	1	0	1.649
luján	1	0	1.649
lugareñas	1	0	1.649
lugarejo	1	0	1.649
lucubraciones	1	0	1.649
lucro	1	0	1.649
lucrecio	1	0	1.649
lucrar	1	0	1.649
luciferum	1	0	1.649
lucifer	1	0	1.649
luciéramos	1	0	1.649
lucí	1	0	1.649
lucho	1	0	1.649
luché	1	0	1.649
lucharía	1	0	1.649
luchador	1	0	1.649
lucerna	1	0	1.649
lucaaam	1	0	1.649
lúbricos	1	0	1.649
lubricidad	1	0	1.649
lúbricas	1	0	1.649
lozanías	1	0	1.649
lovelace	1	0	1.649
lote	1	0	1.649
lot	1	0	1.649
losas	1	0	1.649
loriga	1	0	1.649
loquitur	1	0	1.649
loquillo	1	0	1.649
loquillas	1	0	1.649
longevidad	1	0	1.649
longanizas	1	0	1.649
logomaquias	1	0	1.649
lodazales	1	0	1.649
locus	1	0	1.649
localidad	1	0	1.649
lobezno	1	0	1.649
loable	1	0	1.649
llovió	1	0	1.649
lloviera	1	0	1.649
llorón	1	0	1.649
lloréis	1	0	1.649
lloraría	1	0	1.649
lloraré	1	0	1.649
llorará	1	0	1.649
llevarnos	1	0	1.649
llevármela	1	0	1.649
llevarles	1	0	1.649
llevarás	1	0	1.649
llevarán	1	0	1.649
llevándoselo	1	0	1.649
llévame	1	0	1.649
llevadas	1	0	1.649
llenen	1	0	1.649
llenaría	1	0	1.649
llenará	1	0	1.649
llenándole	1	0	1.649
llegasen	1	0	1.649
llanuras	1	0	1.649
llanura	1	0	1.649
llámelo	1	0	1.649
llamativos	1	0	1.649
llamativa	1	0	1.649
llamárselo	1	0	1.649
llamarnos	1	0	1.649
llamarlo	1	0	1.649
llamarlas	1	0	1.649
llamaremos	1	0	1.649
llamándolos	1	0	1.649
litigantes	1	0	1.649
literato	1	0	1.649
listillas	1	0	1.649
listado	1	0	1.649
lisonjeado	1	0	1.649
lisonjea	1	0	1.649
lisa	1	0	1.649
líricamente	1	0	1.649
lírica	1	0	1.649
líquida	1	0	1.649
liquen	1	0	1.649
liquefacta	1	0	1.649
lionense	1	0	1.649
linfas	1	0	1.649
lindoro	1	0	1.649
linajudas	1	0	1.649
límpido	1	0	1.649
límpida	1	0	1.649
limones	1	0	1.649
limítrofe	1	0	1.649
limitarse	1	0	1.649
ligamen	1	0	1.649
ligados	1	0	1.649
life	1	0	1.649
lidiaba	1	0	1.649
licenciarse	1	0	1.649
librepensamiento	1	0	1.649
librepensador	1	0	1.649
librasen	1	0	1.649
libraco	1	0	1.649
libelo	1	0	1.649
libellus	1	0	1.649
leyeron	1	0	1.649
levítica	1	0	1.649
levantisca	1	0	1.649
levantados	1	0	1.649
leva	1	0	1.649
letanía	1	0	1.649
lesiones	1	0	1.649
lesión	1	0	1.649
lesbos	1	0	1.649
leproso	1	0	1.649
leonor	1	0	1.649
leones	1	0	1.649
leonardo	1	0	1.649
lentos	1	0	1.649
lenidad	1	0	1.649
lengüetería	1	0	1.649
lenclós	1	0	1.649
lego	1	0	1.649
legislación	1	0	1.649
legendarios	1	0	1.649
lege	1	0	1.649
legalmente	1	0	1.649
leerse	1	0	1.649
leerme	1	0	1.649
léela	1	0	1.649
lectora	1	0	1.649
lechuguinos	1	0	1.649
lechoso	1	0	1.649
lechosa	1	0	1.649
leccioncita	1	0	1.649
lebrun	1	0	1.649
léanla	1	0	1.649
laxitud	1	0	1.649
lavaron	1	0	1.649
laurent	1	0	1.649
laudes	1	0	1.649
laudatores	1	0	1.649
latorre	1	0	1.649
latitudinario	1	0	1.649
latió	1	0	1.649
latieron	1	0	1.649
lateral	1	0	1.649
late	1	0	1.649
lastimarla	1	0	1.649
lastimara	1	0	1.649
lastimaban	1	0	1.649
lastima	1	0	1.649
lascivos	1	0	1.649
lanzándose	1	0	1.649
lante	1	0	1.649
lánguidos	1	0	1.649
lánguido	1	0	1.649
languidecer	1	0	1.649
lánguidas	1	0	1.649
lánguidamente	1	0	1.649
lanchas	1	0	1.649
lancha	1	0	1.649
láncese	1	0	1.649
lampiño	1	0	1.649
laminada	1	0	1.649
lamiéndose	1	0	1.649
lamiendo	1	0	1.649
lamidas	1	0	1.649
lamería	1	0	1.649
lamentaron	1	0	1.649
lamentando	1	0	1.649
lamentamos	1	0	1.649
lamenta	1	0	1.649
lamego	1	0	1.649
lamartine	1	0	1.649
laicos	1	0	1.649
lagar	1	0	1.649
ladre	1	0	1.649
lacrimosa	1	0	1.649
lacrimae	1	0	1.649
lacónico	1	0	1.649
lacónicas	1	0	1.649
lacónica	1	0	1.649
lacería	1	0	1.649
labriegos	1	0	1.649
labranza	1	0	1.649
labraba	1	0	1.649
laberintos	1	0	1.649
labe	1	0	1.649
kirschen	1	0	1.649
kilómetro	1	0	1.649
juzgarse	1	0	1.649
juzgada	1	0	1.649
juzgaban	1	0	1.649
justillo	1	0	1.649
justificables	1	0	1.649
justas	1	0	1.649
jurisconsultos	1	0	1.649
juris	1	0	1.649
jurídico	1	0	1.649
juremos	1	0	1.649
juraste	1	0	1.649
jurarse	1	0	1.649
jurarle	1	0	1.649
jurándose	1	0	1.649
jurada	1	0	1.649
juraban	1	0	1.649
junturas	1	0	1.649
juntaran	1	0	1.649
juntado	1	0	1.649
juguetona	1	0	1.649
jugueteando	1	0	1.649
jugueteaban	1	0	1.649
jugándose	1	0	1.649
jugáis	1	0	1.649
jugábamos	1	0	1.649
judit	1	0	1.649
jubileos	1	0	1.649
jubilé	1	0	1.649
joyero	1	0	1.649
jorobado	1	0	1.649
jornaleros	1	0	1.649
jónico	1	0	1.649
jocoso	1	0	1.649
jocoserio	1	0	1.649
jirones	1	0	1.649
jirón	1	0	1.649
jinojo	1	0	1.649
jesuítica	1	0	1.649
jerusalén	1	0	1.649
jerusalem	1	0	1.649
jeroma	1	0	1.649
jerga	1	0	1.649
jeremías	1	0	1.649
jerárquicos	1	0	1.649
jehová	1	0	1.649
jazmín	1	0	1.649
jaropes	1	0	1.649
jardineros	1	0	1.649
jardinero	1	0	1.649
japón	1	0	1.649
jamones	1	0	1.649
jaleadores	1	0	1.649
jactancioso	1	0	1.649
jactanciosa	1	0	1.649
jaco	1	0	1.649
jaccoud	1	0	1.649
jacas	1	0	1.649
jabalíes	1	0	1.649
j	1	0	1.649
ítem	1	0	1.649
israelitas	1	0	1.649
israel	1	0	1.649
islote	1	0	1.649
isis	1	0	1.649
is	1	0	1.649
irrupciones	1	0	1.649
irritarla	1	0	1.649
irritar	1	0	1.649
irritados	1	0	1.649
irrita	1	0	1.649
irrisión	1	0	1.649
irreverentes	1	0	1.649
irresponsabilidad	1	0	1.649
irreprochable	1	0	1.649
irremisiblemente	1	0	1.649
irremediable	1	0	1.649
irreflexivas	1	0	1.649
irreflexivamente	1	0	1.649
irradiaba	1	0	1.649
irracionales	1	0	1.649
irónicos	1	0	1.649
irónico	1	0	1.649
iria	1	0	1.649
ipsa	1	0	1.649
io	1	0	1.649
invitarle	1	0	1.649
invitarla	1	0	1.649
invitándole	1	0	1.649
invita	1	0	1.649
invirtieron	1	0	1.649
inveterado	1	0	1.649
inveteradas	1	0	1.649
investigar	1	0	1.649
invernante	1	0	1.649
invernadero	1	0	1.649
invernáculo	1	0	1.649
inventaron	1	0	1.649
inventados	1	0	1.649
inventaban	1	0	1.649
invenciones	1	0	1.649
invasores	1	0	1.649
invasor	1	0	1.649
invasiones	1	0	1.649
inválidas	1	0	1.649
invadieron	1	0	1.649
invadida	1	0	1.649
inusitadas	1	0	1.649
inundarle	1	0	1.649
inundara	1	0	1.649
inundar	1	0	1.649
intuiciones	1	0	1.649
intuición	1	0	1.649
intrusos	1	0	1.649
introduzcan	1	0	1.649
intrincados	1	0	1.649
intrigantes	1	0	1.649
intrigado	1	0	1.649
intrépidas	1	0	1.649
intransigentes	1	0	1.649
intimo	1	0	1.649
intimarle	1	0	1.649
intimaba	1	0	1.649
intestinal	1	0	1.649
intervinieran	1	0	1.649
intervenido	1	0	1.649
intersticios	1	0	1.649
interrumpirla	1	0	1.649
interrumpieron	1	0	1.649
interrumpen	1	0	1.649
interrogatorios	1	0	1.649
interrogatorio	1	0	1.649
interrogarle	1	0	1.649
interrogante	1	0	1.649
interpretó	1	0	1.649
interponiendo	1	0	1.649
interioridades	1	0	1.649
interinos	1	0	1.649
interinas	1	0	1.649
interinamente	1	0	1.649
interesarla	1	0	1.649
intercolumnios	1	0	1.649
intercolumnio	1	0	1.649
interceptado	1	0	1.649
intentona	1	0	1.649
intentaré	1	0	1.649
intenta	1	0	1.649
intensas	1	0	1.649
intensamente	1	0	1.649
intende	1	0	1.649
intencionados	1	0	1.649
intempestivo	1	0	1.649
intellectu	1	0	1.649
íntegro	1	0	1.649
integrar	1	0	1.649
integrante	1	0	1.649
integral	1	0	1.649
intacta	1	0	1.649
insurrectos	1	0	1.649
insultó	1	0	1.649
insultara	1	0	1.649
insultando	1	0	1.649
insulsos	1	0	1.649
insulsez	1	0	1.649
insulsas	1	0	1.649
insulsa	1	0	1.649
instrumentista	1	0	1.649
instruidas	1	0	1.649
instituto	1	0	1.649
instigara	1	0	1.649
instalar	1	0	1.649
inspire	1	0	1.649
inspirará	1	0	1.649
inspirados	1	0	1.649
inspiraciones	1	0	1.649
insomnios	1	0	1.649
insólito	1	0	1.649
insolenta	1	0	1.649
insistimos	1	0	1.649
insistieron	1	0	1.649
insinuar	1	0	1.649
insinuado	1	0	1.649
insignificancia	1	0	1.649
insidiosos	1	0	1.649
inservible	1	0	1.649
insertar	1	0	1.649
inseparables	1	0	1.649
inquisidores	1	0	1.649
inquirió	1	0	1.649
inquietarle	1	0	1.649
inoportunos	1	0	1.649
inoportunamente	1	0	1.649
inoportuna	1	0	1.649
inopinado	1	0	1.649
innovación	1	0	1.649
inmaculados	1	0	1.649
inmaculado	1	0	1.649
injustísima	1	0	1.649
injertos	1	0	1.649
injerto	1	0	1.649
injerencias	1	0	1.649
iniciales	1	0	1.649
iniciado	1	0	1.649
iniciadas	1	0	1.649
inhibirse	1	0	1.649
inhibía	1	0	1.649
ingresos	1	0	1.649
ingresamos	1	0	1.649
ingenuos	1	0	1.649
ingenuo	1	0	1.649
ingenuas	1	0	1.649
ingénitos	1	0	1.649
ingénita	1	0	1.649
ingeniara	1	0	1.649
infusorios	1	0	1.649
infundan	1	0	1.649
infructuosa	1	0	1.649
infringir	1	0	1.649
infraganti	1	0	1.649
influyó	1	0	1.649
influido	1	0	1.649
influencias	1	0	1.649
inflexibles	1	0	1.649
inflamable	1	0	1.649
inflados	1	0	1.649
inflaba	1	0	1.649
infestarse	1	0	1.649
infestado	1	0	1.649
infecundos	1	0	1.649
infausta	1	0	1.649
infamatorio	1	0	1.649
infalibidad	1	0	1.649
infali	1	0	1.649
inextinguible	1	0	1.649
inexpertos	1	0	1.649
inesperados	1	0	1.649
inescrutables	1	0	1.649
inertes	1	0	1.649
ineludible	1	0	1.649
indumentario	1	0	1.649
indómitos	1	0	1.649
indomable	1	0	1.649
indiscutibles	1	0	1.649
indiscretos	1	0	1.649
indiscretas	1	0	1.649
indisciplinado	1	0	1.649
indiqué	1	0	1.649
indique	1	0	1.649
indios	1	0	1.649
indignos	1	0	1.649
indignas	1	0	1.649
indignaría	1	0	1.649
indignamente	1	0	1.649
indígena	1	0	1.649
indicarse	1	0	1.649
indicarán	1	0	1.649
indicando	1	0	1.649
indescifrable	1	0	1.649
indemnizaciones	1	0	1.649
indefinidos	1	0	1.649
indefenso	1	0	1.649
indecorosas	1	0	1.649
indecencia	1	0	1.649
indagadas	1	0	1.649
incuria	1	0	1.649
incurables	1	0	1.649
inculcará	1	0	1.649
incrustadas	1	0	1.649
incrusta	1	0	1.649
incruentos	1	0	1.649
incruentas	1	0	1.649
incorregible	1	0	1.649
incorrecto	1	0	1.649
incorrectas	1	0	1.649
incorporaban	1	0	1.649
inconveniencia	1	0	1.649
incontrastable	1	0	1.649
inconscientes	1	0	1.649
inconfesables	1	0	1.649
inconexos	1	0	1.649
incompatibilidades	1	0	1.649
incomparables	1	0	1.649
incomparablemente	1	0	1.649
incomodo	1	0	1.649
incomodidades	1	0	1.649
incombustible	1	0	1.649
incoherentes	1	0	1.649
incoherencia	1	0	1.649
inclinan	1	0	1.649
inclinados	1	0	1.649
inclinaban	1	0	1.649
incisos	1	0	1.649
inciertos	1	0	1.649
incentivos	1	0	1.649
incendiada	1	0	1.649
incauto	1	0	1.649
incasables	1	0	1.649
incalificables	1	0	1.649
incalculable	1	0	1.649
inauguren	1	0	1.649
inaugurar	1	0	1.649
inauguraban	1	0	1.649
inaudito	1	0	1.649
inarticulada	1	0	1.649
inarco	1	0	1.649
inapetencias	1	0	1.649
inanimados	1	0	1.649
inalienables	1	0	1.649
inadvertencia	1	0	1.649
inacabable	1	0	1.649
imputaban	1	0	1.649
impusiese	1	0	1.649
impusieron	1	0	1.649
impusiera	1	0	1.649
impuse	1	0	1.649
impureza	1	0	1.649
impura	1	0	1.649
impune	1	0	1.649
impúdicas	1	0	1.649
improvisaron	1	0	1.649
improvisados	1	0	1.649
improvisaban	1	0	1.649
improvisa	1	0	1.649
impropiamente	1	0	1.649
improperios	1	0	1.649
ímprobo	1	0	1.649
impresionaban	1	0	1.649
impresiona	1	0	1.649
imprescindible	1	0	1.649
impregnado	1	0	1.649
imprecaciones	1	0	1.649
imprecaba	1	0	1.649
impotencia	1	0	1.649
impostura	1	0	1.649
imposición	1	0	1.649
importunase	1	0	1.649
importó	1	0	1.649
importasen	1	0	1.649
importarle	1	0	1.649
importantísimo	1	0	1.649
importadores	1	0	1.649
importado	1	0	1.649
impongan	1	0	1.649
imponerme	1	0	1.649
imponerle	1	0	1.649
imponentes	1	0	1.649
imploro	1	0	1.649
implícito	1	0	1.649
implícitas	1	0	1.649
implacables	1	0	1.649
impidiesen	1	0	1.649
impide	1	0	1.649
impías	1	0	1.649
impermeable	1	0	1.649
imperiosas	1	0	1.649
impericia	1	0	1.649
imperiales	1	0	1.649
imperando	1	0	1.649
impedirlos	1	0	1.649
impedido	1	0	1.649
impecable	1	0	1.649
imitarse	1	0	1.649
imitara	1	0	1.649
imbuirlas	1	0	1.649
imantada	1	0	1.649
imanes	1	0	1.649
imán	1	0	1.649
imagínole	1	0	1.649
imaginarlo	1	0	1.649
imaginarios	1	0	1.649
imaginada	1	0	1.649
imaginaciones	1	0	1.649
ilustrarse	1	0	1.649
ilusos	1	0	1.649
ilmo	1	0	1.649
iliteratas	1	0	1.649
ilíada	1	0	1.649
ilegítima	1	0	1.649
ilegibles	1	0	1.649
igualdades	1	0	1.649
ignoraría	1	0	1.649
ignora	1	0	1.649
idénticos	1	0	1.649
idealizar	1	0	1.649
id	1	0	1.649
ictericia	1	0	1.649
íberos	1	0	1.649
huyes	1	0	1.649
huyen	1	0	1.649
hurtos	1	0	1.649
hurtado	1	0	1.649
hurgaba	1	0	1.649
hundió	1	0	1.649
hundimos	1	0	1.649
hundidas	1	0	1.649
hundíamos	1	0	1.649
humour	1	0	1.649
humilló	1	0	1.649
humíllate	1	0	1.649
humillaría	1	0	1.649
humedecerse	1	0	1.649
humedecer	1	0	1.649
humanizada	1	0	1.649
humanizaban	1	0	1.649
humanitarias	1	0	1.649
humanidades	1	0	1.649
humani	1	0	1.649
huiría	1	0	1.649
hugonotes	1	0	1.649
hugo	1	0	1.649
huevecillo	1	0	1.649
huestes	1	0	1.649
huesca	1	0	1.649
huertos	1	0	1.649
huérfanas	1	0	1.649
huelo	1	0	1.649
hueles	1	0	1.649
huela	1	0	1.649
hostilidades	1	0	1.649
hospitalidad	1	0	1.649
hospicios	1	0	1.649
hospiciano	1	0	1.649
horticultura	1	0	1.649
hortelano	1	0	1.649
hormiga	1	0	1.649
horchaterías	1	0	1.649
honrosa	1	0	1.649
honraba	1	0	1.649
honni	1	0	1.649
hongos	1	0	1.649
honestamente	1	0	1.649
honduras	1	0	1.649
hondonadas	1	0	1.649
homini	1	0	1.649
homero	1	0	1.649
hombreándose	1	0	1.649
holgada	1	0	1.649
hojaldres	1	0	1.649
hodie	1	0	1.649
hita	1	0	1.649
histerismo	1	0	1.649
histérica	1	0	1.649
hiriese	1	0	1.649
hipotéticos	1	0	1.649
hipotérmico	1	0	1.649
hipotecada	1	0	1.649
hipopótamos	1	0	1.649
hipódromos	1	0	1.649
hiperbólicas	1	0	1.649
hiperbólica	1	0	1.649
hinojos	1	0	1.649
hinchó	1	0	1.649
hilaba	1	0	1.649
hijuelos	1	0	1.649
higuera	1	0	1.649
high	1	0	1.649
hierocrático	1	0	1.649
hierbas	1	0	1.649
hielos	1	0	1.649
hidalga	1	0	1.649
hic	1	0	1.649
heterogéneos	1	0	1.649
heterogénea	1	0	1.649
hervir	1	0	1.649
herradura	1	0	1.649
herpéticos	1	0	1.649
heroicidad	1	0	1.649
herodías	1	0	1.649
hermanitos	1	0	1.649
herirle	1	0	1.649
herían	1	0	1.649
heréticas	1	0	1.649
herética	1	0	1.649
heresiarcas	1	0	1.649
heresiarca	1	0	1.649
heredan	1	0	1.649
heredad	1	0	1.649
herborizando	1	0	1.649
hepatitis	1	0	1.649
henao	1	0	1.649
hemostática	1	0	1.649
helándole	1	0	1.649
hegemonía	1	0	1.649
hedores	1	0	1.649
hediondas	1	0	1.649
hechuras	1	0	1.649
hechizo	1	0	1.649
hastía	1	0	1.649
harinas	1	0	1.649
haríamos	1	0	1.649
haraposa	1	0	1.649
harapos	1	0	1.649
harapo	1	0	1.649
harán	1	0	1.649
hame	1	0	1.649
hambrientos	1	0	1.649
hamaca	1	0	1.649
hallé	1	0	1.649
hallarás	1	0	1.649
hallará	1	0	1.649
halladas	1	0	1.649
halagüeños	1	0	1.649
halagasen	1	0	1.649
halagaron	1	0	1.649
halagada	1	0	1.649
halagaban	1	0	1.649
halaga	1	0	1.649
hagámosela	1	0	1.649
haec	1	0	1.649
hachones	1	0	1.649
hacérsenos	1	0	1.649
hacérsela	1	0	1.649
hablasteis	1	0	1.649
hablasen	1	0	1.649
hablaríamos	1	0	1.649
habláramos	1	0	1.649
hablándose	1	0	1.649
hablábamos	1	0	1.649
habitaron	1	0	1.649
habitar	1	0	1.649
habitan	1	0	1.649
habitado	1	0	1.649
habitable	1	0	1.649
hábilmente	1	0	1.649
hábiles	1	0	1.649
habet	1	0	1.649
haberlas	1	0	1.649
gutierre	1	0	1.649
gustazo	1	0	1.649
gulf	1	0	1.649
guisar	1	0	1.649
guisaban	1	0	1.649
guíe	1	0	1.649
guías	1	0	1.649
guerrero	1	0	1.649
guarecidos	1	0	1.649
guardolo	1	0	1.649
guardillas	1	0	1.649
guardé	1	0	1.649
guardándose	1	0	1.649
guardándonos	1	0	1.649
guardador	1	0	1.649
guadalquivir	1	0	1.649
gruyer	1	0	1.649
grupa	1	0	1.649
gruesecillo	1	0	1.649
grotescas	1	0	1.649
grites	1	0	1.649
grillo	1	0	1.649
grilletes	1	0	1.649
grilleras	1	0	1.649
grijalte	1	0	1.649
griegos	1	0	1.649
graznar	1	0	1.649
graznado	1	0	1.649
gravísimo	1	0	1.649
grasientas	1	0	1.649
granizada	1	0	1.649
graneado	1	0	1.649
grandísimos	1	0	1.649
grandiosas	1	0	1.649
grandilocuentes	1	0	1.649
gráficas	1	0	1.649
gradas	1	0	1.649
graciosamente	1	0	1.649
gozquecillo	1	0	1.649
gozose	1	0	1.649
gozase	1	0	1.649
gozarlo	1	0	1.649
gozará	1	0	1.649
gozamos	1	0	1.649
goza	1	0	1.649
goteaban	1	0	1.649
gorros	1	0	1.649
gorrona	1	0	1.649
gorrión	1	0	1.649
gorjeos	1	0	1.649
gorjeaban	1	0	1.649
gongorino	1	0	1.649
góngora	1	0	1.649
gomogga	1	0	1.649
golpeó	1	0	1.649
golpeaban	1	0	1.649
golondrinas	1	0	1.649
gollería	1	0	1.649
golfos	1	0	1.649
gobiernan	1	0	1.649
gloriosamente	1	0	1.649
giros	1	0	1.649
giras	1	0	1.649
giraldi	1	0	1.649
ginebrino	1	0	1.649
gimnásticos	1	0	1.649
gimnasio	1	0	1.649
gil	1	0	1.649
gigantona	1	0	1.649
gigantón	1	0	1.649
gigantesca	1	0	1.649
gigantes	1	0	1.649
gesticularíamos	1	0	1.649
gerundio	1	0	1.649
geométricos	1	0	1.649
geométricas	1	0	1.649
geométrica	1	0	1.649
geológicos	1	0	1.649
geográficos	1	0	1.649
genuinamente	1	0	1.649
gentleman	1	0	1.649
gentiles	1	0	1.649
genios	1	0	1.649
genil	1	0	1.649
gazmoña	1	0	1.649
gayarre	1	0	1.649
gaya	1	0	1.649
gauthier	1	0	1.649
gatazo	1	0	1.649
gastronómicos	1	0	1.649
gastronómico	1	0	1.649
gastroenteritis	1	0	1.649
gástrico	1	0	1.649
gastó	1	0	1.649
gasten	1	0	1.649
gastase	1	0	1.649
gastada	1	0	1.649
gastaban	1	0	1.649
gaseosos	1	0	1.649
garzos	1	0	1.649
garden	1	0	1.649
garcilaso	1	0	1.649
garante	1	0	1.649
ganosos	1	0	1.649
ganoso	1	0	1.649
ganosa	1	0	1.649
ganarnos	1	0	1.649
ganaría	1	0	1.649
gananciales	1	0	1.649
ganados	1	0	1.649
ganadera	1	0	1.649
gamo	1	0	1.649
galope	1	0	1.649
gallineros	1	0	1.649
gallardísima	1	0	1.649
gallardete	1	0	1.649
galicismos	1	0	1.649
galerna	1	0	1.649
galardonaron	1	0	1.649
galantear	1	0	1.649
gaitero	1	0	1.649
gacha	1	0	1.649
gacetillas	1	0	1.649
futraque	1	0	1.649
fútiles	1	0	1.649
fustis	1	0	1.649
fusilémosle	1	0	1.649
furtivos	1	0	1.649
furtivo	1	0	1.649
fungosa	1	0	1.649
funesto	1	0	1.649
fundido	1	0	1.649
fundidas	1	0	1.649
fundición	1	0	1.649
funde	1	0	1.649
fundarse	1	0	1.649
fundamentos	1	0	1.649
fundaciones	1	0	1.649
funámbula	1	0	1.649
fuman	1	0	1.649
fumador	1	0	1.649
fumado	1	0	1.649
fulanito	1	0	1.649
fulanita	1	0	1.649
fuguillas	1	0	1.649
fueses	1	0	1.649
frutales	1	0	1.649
frustó	1	0	1.649
fruela	1	0	1.649
frotar	1	0	1.649
frontones	1	0	1.649
frontispicio	1	0	1.649
frondosos	1	0	1.649
frívolos	1	0	1.649
frisar	1	0	1.649
frisaban	1	0	1.649
frigorífico	1	0	1.649
frenéticas	1	0	1.649
frecuentase	1	0	1.649
frecuentan	1	0	1.649
frecuentado	1	0	1.649
fraternizar	1	0	1.649
frascueeeelo	1	0	1.649
francklin	1	0	1.649
franciscos	1	0	1.649
franciscas	1	0	1.649
fraigerundio	1	0	1.649
fr	1	0	1.649
fosforeras	1	0	1.649
fosco	1	0	1.649
fortuitos	1	0	1.649
fortísima	1	0	1.649
fortificaba	1	0	1.649
fortalezas	1	0	1.649
fortalecían	1	0	1.649
forró	1	0	1.649
forradas	1	0	1.649
foros	1	0	1.649
fornidos	1	0	1.649
formulismo	1	0	1.649
formemos	1	0	1.649
forjado	1	0	1.649
forcejeaban	1	0	1.649
forajidos	1	0	1.649
fontanero	1	0	1.649
follis	1	0	1.649
follajes	1	0	1.649
fogonazo	1	0	1.649
fluir	1	0	1.649
flota	1	0	1.649
floricultor	1	0	1.649
flórez	1	0	1.649
floreros	1	0	1.649
flojas	1	0	1.649
flegmasías	1	0	1.649
flegmasía	1	0	1.649
flatus	1	0	1.649
flanqueándola	1	0	1.649
flanes	1	0	1.649
flammarión	1	0	1.649
flamígeros	1	0	1.649
flamencas	1	0	1.649
flagrantes	1	0	1.649
fisiólogo	1	0	1.649
fisiológicos	1	0	1.649
fisiológicas	1	0	1.649
fisiológicamente	1	0	1.649
fiscalías	1	0	1.649
firmó	1	0	1.649
fingiera	1	0	1.649
fingidas	1	0	1.649
fingen	1	0	1.649
finado	1	0	1.649
filtro	1	0	1.649
filtrando	1	0	1.649
filtrado	1	0	1.649
filtración	1	0	1.649
filosofastros	1	0	1.649
filosofaba	1	0	1.649
filón	1	0	1.649
filis	1	0	1.649
filigrana	1	0	1.649
filarmónico	1	0	1.649
fijara	1	0	1.649
fijaban	1	0	1.649
figuronas	1	0	1.649
figurillas	1	0	1.649
figúreselo	1	0	1.649
figures	1	0	1.649
figurársele	1	0	1.649
figuraríamos	1	0	1.649
figurándoselo	1	0	1.649
figurándosela	1	0	1.649
figaro	1	0	1.649
fierabrás	1	0	1.649
fielding	1	0	1.649
fidelísimo	1	0	1.649
fidei	1	0	1.649
fiarse	1	0	1.649
fían	1	0	1.649
fiada	1	0	1.649
feudalismo	1	0	1.649
feudales	1	0	1.649
fertilidad	1	0	1.649
fértiles	1	0	1.649
fementida	1	0	1.649
femeniles	1	0	1.649
felinos	1	0	1.649
felinas	1	0	1.649
felicitó	1	0	1.649
felice	1	0	1.649
feísima	1	0	1.649
feijóo	1	0	1.649
federación	1	0	1.649
fecit	1	0	1.649
fealdades	1	0	1.649
favorecida	1	0	1.649
favorecerle	1	0	1.649
fatigosas	1	0	1.649
fatalista	1	0	1.649
fastuosidad	1	0	1.649
fastos	1	0	1.649
fastidiosos	1	0	1.649
fastidiarle	1	0	1.649
fascinada	1	0	1.649
fas	1	0	1.649
farnesios	1	0	1.649
fariseas	1	0	1.649
faringe	1	0	1.649
faraones	1	0	1.649
fantasías	1	0	1.649
fantaseaba	1	0	1.649
fangoso	1	0	1.649
fanfarrones	1	0	1.649
fanatizada	1	0	1.649
fanáticas	1	0	1.649
fanal	1	0	1.649
famosísimo	1	0	1.649
faltriquera	1	0	1.649
falten	1	0	1.649
faltemos	1	0	1.649
faltarle	1	0	1.649
faltaré	1	0	1.649
falsísima	1	0	1.649
falsificó	1	0	1.649
falsificado	1	0	1.649
falló	1	0	1.649
fallo	1	0	1.649
fallidas	1	0	1.649
falange	1	0	1.649
faisán	1	0	1.649
facultativos	1	0	1.649
facultativa	1	0	1.649
factum	1	0	1.649
factorías	1	0	1.649
factores	1	0	1.649
façon	1	0	1.649
facistol	1	0	1.649
facimus	1	0	1.649
facilitaba	1	0	1.649
facial	1	0	1.649
fachenda	1	0	1.649
fabuloso	1	0	1.649
fabulosas	1	0	1.649
fabricado	1	0	1.649
fabricada	1	0	1.649
fabrica	1	0	1.649
fabiolita	1	0	1.649
fabiola	1	0	1.649
extrememos	1	0	1.649
extremas	1	0	1.649
extravió	1	0	1.649
extraviaba	1	0	1.649
extrañar	1	0	1.649
extrañado	1	0	1.649
extinguir	1	0	1.649
extinguiera	1	0	1.649
extenuado	1	0	1.649
extendiera	1	0	1.649
extendiéndome	1	0	1.649
extendida	1	0	1.649
extenderse	1	0	1.649
extática	1	0	1.649
extasiado	1	0	1.649
extasiada	1	0	1.649
expropiación	1	0	1.649
exprofeso	1	0	1.649
exprimían	1	0	1.649
exprese	1	0	1.649
expositio	1	0	1.649
exportado	1	0	1.649
exponiendo	1	0	1.649
expones	1	0	1.649
exponerte	1	0	1.649
exponerla	1	0	1.649
expone	1	0	1.649
expondría	1	0	1.649
explotarlos	1	0	1.649
explotarlo	1	0	1.649
explotaré	1	0	1.649
exploremos	1	0	1.649
exploraciones	1	0	1.649
explíquemelo	1	0	1.649
explicárselo	1	0	1.649
explicárselas	1	0	1.649
explicársela	1	0	1.649
explicará	1	0	1.649
explican	1	0	1.649
explicados	1	0	1.649
expiraba	1	0	1.649
experimentar	1	0	1.649
experiencias	1	0	1.649
expedita	1	0	1.649
expediciones	1	0	1.649
expedicionario	1	0	1.649
expansivas	1	0	1.649
exótica	1	0	1.649
exorbitantes	1	0	1.649
exorbitante	1	0	1.649
existiese	1	0	1.649
existente	1	0	1.649
exíjase	1	0	1.649
exigua	1	0	1.649
exigiría	1	0	1.649
exigió	1	0	1.649
exigieron	1	0	1.649
exigiendo	1	0	1.649
exhaustas	1	0	1.649
exhalaban	1	0	1.649
exegéticas	1	0	1.649
execración	1	0	1.649
excusar	1	0	1.649
excusadas	1	0	1.649
excusa	1	0	1.649
excomulgado	1	0	1.649
excluye	1	0	1.649
exclaustrar	1	0	1.649
exclamado	1	0	1.649
excitarlo	1	0	1.649
excitadota	1	0	1.649
excitados	1	0	1.649
excitadilla	1	0	1.649
excitadas	1	0	1.649
exceptuaba	1	0	1.649
excelentísima	1	0	1.649
excedía	1	0	1.649
excavaciones	1	0	1.649
examino	1	0	1.649
examinarme	1	0	1.649
exaltó	1	0	1.649
exaltas	1	0	1.649
exaltaciones	1	0	1.649
exalta	1	0	1.649
exagerarlos	1	0	1.649
exagerado	1	0	1.649
exageradísima	1	0	1.649
exactos	1	0	1.649
evocarla	1	0	1.649
evocar	1	0	1.649
evocados	1	0	1.649
evite	1	0	1.649
evitarse	1	0	1.649
evitarlos	1	0	1.649
evitara	1	0	1.649
evidentemente	1	0	1.649
evaporaban	1	0	1.649
evaporaba	1	0	1.649
evangelii	1	0	1.649
eureka	1	0	1.649
eufemismo	1	0	1.649
eucologio	1	0	1.649
eucaliptos	1	0	1.649
etruscos	1	0	1.649
etnógrafo	1	0	1.649
eternizaba	1	0	1.649
était	1	0	1.649
estuvieras	1	0	1.649
estupro	1	0	1.649
estupefactos	1	0	1.649
estudioso	1	0	1.649
estudiarse	1	0	1.649
estudiaría	1	0	1.649
estudiaban	1	0	1.649
estucado	1	0	1.649
estrujarse	1	0	1.649
estrujándose	1	0	1.649
estrujado	1	0	1.649
estridentes	1	0	1.649
estribor	1	0	1.649
estremeciéndose	1	0	1.649
estrechaban	1	0	1.649
estrangulada	1	0	1.649
estrangulación	1	0	1.649
estrados	1	0	1.649
estote	1	0	1.649
estorninos	1	0	1.649
estorbos	1	0	1.649
estorbase	1	0	1.649
estorbarse	1	0	1.649
estoraque	1	0	1.649
estoposa	1	0	1.649
estola	1	0	1.649
estimule	1	0	1.649
estimando	1	0	1.649
estimado	1	0	1.649
estilita	1	0	1.649
estilista	1	0	1.649
estériles	1	0	1.649
estereotipada	1	0	1.649
ester	1	0	1.649
estepas	1	0	1.649
estemos	1	0	1.649
estatutos	1	0	1.649
estáte	1	0	1.649
estanquero	1	0	1.649
estandartes	1	0	1.649
estandarte	1	0	1.649
estancamiento	1	0	1.649
estancadas	1	0	1.649
estampilla	1	0	1.649
estambres	1	0	1.649
estambre	1	0	1.649
estallaron	1	0	1.649
estallarme	1	0	1.649
estacada	1	0	1.649
establos	1	0	1.649
establo	1	0	1.649
establecidas	1	0	1.649
esquivar	1	0	1.649
esquilas	1	0	1.649
esquilache	1	0	1.649
esquela	1	0	1.649
espumar	1	0	1.649
espuela	1	0	1.649
espontáneos	1	0	1.649
esponjosa	1	0	1.649
esponjan	1	0	1.649
espolios	1	0	1.649
esplendorosa	1	0	1.649
espirituosos	1	0	1.649
espiritualísima	1	0	1.649
espirar	1	0	1.649
espirando	1	0	1.649
espío	1	0	1.649
espinosas	1	0	1.649
espinosa	1	0	1.649
espinos	1	0	1.649
espifor	1	0	1.649
espiarlos	1	0	1.649
espesura	1	0	1.649
espesísima	1	0	1.649
esperemos	1	0	1.649
esperarse	1	0	1.649
esperarla	1	0	1.649
esperará	1	0	1.649
espejismo	1	0	1.649
espectación	1	0	1.649
especificado	1	0	1.649
especialistas	1	0	1.649
especialista	1	0	1.649
especialísima	1	0	1.649
especiales	1	0	1.649
esparcida	1	0	1.649
espantosas	1	0	1.649
espantó	1	0	1.649
espantes	1	0	1.649
espantando	1	0	1.649
espantadiza	1	0	1.649
espaldera	1	0	1.649
espaciosos	1	0	1.649
espacioso	1	0	1.649
espaciada	1	0	1.649
esotéricos	1	0	1.649
esmerado	1	0	1.649
esforzó	1	0	1.649
esforzarse	1	0	1.649
esenciada	1	0	1.649
escupirá	1	0	1.649
esculturales	1	0	1.649
escultural	1	0	1.649
escultóricos	1	0	1.649
escuetas	1	0	1.649
escudriñó	1	0	1.649
escudriñado	1	0	1.649
escuchase	1	0	1.649
escucharle	1	0	1.649
escuchando	1	0	1.649
escuchad	1	0	1.649
escuálido	1	0	1.649
escuadra	1	0	1.649
escrupulosos	1	0	1.649
escrupulosidad	1	0	1.649
escrupulosamente	1	0	1.649
escrituras	1	0	1.649
escribiría	1	0	1.649
escribieron	1	0	1.649
escribas	1	0	1.649
escríbame	1	0	1.649
escozor	1	0	1.649
escotillón	1	0	1.649
escosura	1	0	1.649
escorias	1	0	1.649
escopetas	1	0	1.649
escondrijos	1	0	1.649
escondieron	1	0	1.649
escondiéndose	1	0	1.649
esconderla	1	0	1.649
escolios	1	0	1.649
escolasticismo	1	0	1.649
escolástica	1	0	1.649
escoja	1	0	1.649
escogitar	1	0	1.649
escogieron	1	0	1.649
escogidísimos	1	0	1.649
escogidísimo	1	0	1.649
escogen	1	0	1.649
escocés	1	0	1.649
escobazos	1	0	1.649
escobazo	1	0	1.649
esclavas	1	0	1.649
esclarecidos	1	0	1.649
escayola	1	0	1.649
escatimados	1	0	1.649
escasos	1	0	1.649
escasearían	1	0	1.649
escaseando	1	0	1.649
escarchas	1	0	1.649
escarabajo	1	0	1.649
escapularios	1	0	1.649
escapatoria	1	0	1.649
escaparían	1	0	1.649
escandalizarte	1	0	1.649
escandalizando	1	0	1.649
escandalizado	1	0	1.649
escandalizaba	1	0	1.649
escame	1	0	1.649
escamandro	1	0	1.649
escalpelo	1	0	1.649
escalasen	1	0	1.649
escalar	1	0	1.649
escabrosas	1	0	1.649
esbirros	1	0	1.649
esbirro	1	0	1.649
ésas	1	0	1.649
eruptos	1	0	1.649
eruditamente	1	0	1.649
erudita	1	0	1.649
eructaba	1	0	1.649
errónea	1	0	1.649
erradamente	1	0	1.649
erotismo	1	0	1.649
ermitaño	1	0	1.649
erizó	1	0	1.649
erizaron	1	0	1.649
erizándose	1	0	1.649
erizando	1	0	1.649
erizados	1	0	1.649
erizada	1	0	1.649
erizaban	1	0	1.649
erguido	1	0	1.649
ergo	1	0	1.649
erba	1	0	1.649
erat	1	0	1.649
erario	1	0	1.649
equivocar	1	0	1.649
equivocando	1	0	1.649
equivocados	1	0	1.649
equitativo	1	0	1.649
equinoccio	1	0	1.649
equilibrios	1	0	1.649
epopeya	1	0	1.649
epílogo	1	0	1.649
epigramático	1	0	1.649
epidemia	1	0	1.649
epicuro	1	0	1.649
epicurista	1	0	1.649
epicureísmo	1	0	1.649
épico	1	0	1.649
epiceno	1	0	1.649
epicena	1	0	1.649
épica	1	0	1.649
epanadiplosis	1	0	1.649
envolviole	1	0	1.649
envolverla	1	0	1.649
envidiando	1	0	1.649
envidiados	1	0	1.649
enviados	1	0	1.649
envenenando	1	0	1.649
envenenaban	1	0	1.649
envejeciendo	1	0	1.649
envejecía	1	0	1.649
envanecían	1	0	1.649
enumerar	1	0	1.649
enumeraciones	1	0	1.649
enumeración	1	0	1.649
enturbiar	1	0	1.649
entumecimiento	1	0	1.649
entumecidos	1	0	1.649
entumecida	1	0	1.649
entumecían	1	0	1.649
entumecía	1	0	1.649
entrometido	1	0	1.649
entreverados	1	0	1.649
entretienen	1	0	1.649
entretengan	1	0	1.649
entremetidos	1	0	1.649
entremetido	1	0	1.649
entregárselo	1	0	1.649
entregarlo	1	0	1.649
entregara	1	0	1.649
entregándose	1	0	1.649
entregándolas	1	0	1.649
entreabrió	1	0	1.649
entreabiertos	1	0	1.649
entrasen	1	0	1.649
entrarle	1	0	1.649
entraras	1	0	1.649
entraña	1	0	1.649
entradas	1	0	1.649
entorpecimientos	1	0	1.649
entornó	1	0	1.649
entornándolos	1	0	1.649
entornado	1	0	1.649
entonadas	1	0	1.649
entomólogo	1	0	1.649
entomológicas	1	0	1.649
entierren	1	0	1.649
entierre	1	0	1.649
entibiaba	1	0	1.649
enterrarán	1	0	1.649
enterramientos	1	0	1.649
enterraba	1	0	1.649
enternezco	1	0	1.649
enternecerse	1	0	1.649
enternecer	1	0	1.649
enteren	1	0	1.649
enterarle	1	0	1.649
enterados	1	0	1.649
entendiendo	1	0	1.649
entendidas	1	0	1.649
entenderían	1	0	1.649
ente	1	0	1.649
entallada	1	0	1.649
ensuciar	1	0	1.649
ensortijado	1	0	1.649
ensoñadora	1	0	1.649
ensoñación	1	0	1.649
enseñorease	1	0	1.649
enseñoreados	1	0	1.649
enseñes	1	0	1.649
ensayó	1	0	1.649
ensanche	1	0	1.649
ensancharse	1	0	1.649
ensanchándose	1	0	1.649
ensalzarás	1	0	1.649
enroscarse	1	0	1.649
enroscándose	1	0	1.649
enrevesados	1	0	1.649
enredó	1	0	1.649
enredaderas	1	0	1.649
enojosísimos	1	0	1.649
ennoblecemos	1	0	1.649
ennegrecidos	1	0	1.649
ennegrecidas	1	0	1.649
ennegrecían	1	0	1.649
enmudece	1	0	1.649
enmascarado	1	0	1.649
enloquecidas	1	0	1.649
enlazaba	1	0	1.649
enjutos	1	0	1.649
enjugó	1	0	1.649
enjugar	1	0	1.649
enjaulado	1	0	1.649
enjaulada	1	0	1.649
enhiesto	1	0	1.649
engrandecía	1	0	1.649
engrandecer	1	0	1.649
engordase	1	0	1.649
engordando	1	0	1.649
engomada	1	0	1.649
engolfarse	1	0	1.649
englobado	1	0	1.649
engendraban	1	0	1.649
engañaste	1	0	1.649
engañarlos	1	0	1.649
engañándose	1	0	1.649
enganchó	1	0	1.649
enganchados	1	0	1.649
enganchado	1	0	1.649
enganchaba	1	0	1.649
engalanadas	1	0	1.649
enfundadas	1	0	1.649
enfriaban	1	0	1.649
enfrenados	1	0	1.649
enfrascarse	1	0	1.649
enfrascados	1	0	1.649
enfilándose	1	0	1.649
enfermucho	1	0	1.649
enfermero	1	0	1.649
enfermemos	1	0	1.649
enfermaste	1	0	1.649
enfermar	1	0	1.649
enfant	1	0	1.649
enfadarle	1	0	1.649
enerve	1	0	1.649
energúmenos	1	0	1.649
energúmeno	1	0	1.649
endiosas	1	0	1.649
endiosarse	1	0	1.649
enderezarle	1	0	1.649
endémicos	1	0	1.649
encubridoras	1	0	1.649
encorvadas	1	0	1.649
encontremos	1	0	1.649
encontrársela	1	0	1.649
encontrarán	1	0	1.649
encontraran	1	0	1.649
encontrados	1	0	1.649
encomendó	1	0	1.649
encomendaron	1	0	1.649
encogiéndose	1	0	1.649
encogerse	1	0	1.649
encoge	1	0	1.649
enclenques	1	0	1.649
encina	1	0	1.649
encierros	1	0	1.649
encierras	1	0	1.649
encierra	1	0	1.649
enchufaban	1	0	1.649
encharcados	1	0	1.649
encerraron	1	0	1.649
encerado	1	0	1.649
encendiese	1	0	1.649
encenderla	1	0	1.649
encenagó	1	0	1.649
encenagados	1	0	1.649
encenagaba	1	0	1.649
encauzada	1	0	1.649
encarnizada	1	0	1.649
encarnaba	1	0	1.649
encareciendo	1	0	1.649
encarcelado	1	0	1.649
encaraman	1	0	1.649
encaramaban	1	0	1.649
encaprichara	1	0	1.649
encaprichadas	1	0	1.649
encapotado	1	0	1.649
encantar	1	0	1.649
encajarte	1	0	1.649
enanos	1	0	1.649
enamoro	1	0	1.649
enamoren	1	0	1.649
enamorarla	1	0	1.649
enamorándome	1	0	1.649
enamoran	1	0	1.649
enamoraba	1	0	1.649
enaltecerla	1	0	1.649
empuño	1	0	1.649
empuñar	1	0	1.649
empujasen	1	0	1.649
empujado	1	0	1.649
empujaban	1	0	1.649
emprendían	1	0	1.649
emprendemos	1	0	1.649
empotrados	1	0	1.649
empotrado	1	0	1.649
empolvada	1	0	1.649
empleará	1	0	1.649
emplea	1	0	1.649
emplazamiento	1	0	1.649
emplastos	1	0	1.649
empingorotados	1	0	1.649
empingorotado	1	0	1.649
empinados	1	0	1.649
empezara	1	0	1.649
empero	1	0	1.649
emperifolladas	1	0	1.649
empeorar	1	0	1.649
empedradas	1	0	1.649
empedrada	1	0	1.649
empecía	1	0	1.649
empecatado	1	0	1.649
empecatadas	1	0	1.649
emparejó	1	0	1.649
emparejarse	1	0	1.649
emparejaron	1	0	1.649
emparejaba	1	0	1.649
emparedados	1	0	1.649
emparedada	1	0	1.649
empapelado	1	0	1.649
empapando	1	0	1.649
empalmándose	1	0	1.649
empadronar	1	0	1.649
emisarios	1	0	1.649
emisario	1	0	1.649
emigró	1	0	1.649
emigrada	1	0	1.649
embutiendo	1	0	1.649
embutida	1	0	1.649
embute	1	0	1.649
embrutecían	1	0	1.649
embrollo	1	0	1.649
embrollado	1	0	1.649
embrollaba	1	0	1.649
embrión	1	0	1.649
embozarse	1	0	1.649
embozando	1	0	1.649
embozan	1	0	1.649
embozadas	1	0	1.649
embozada	1	0	1.649
embozaban	1	0	1.649
embozaba	1	0	1.649
embotar	1	0	1.649
emboscadas	1	0	1.649
emborracharle	1	0	1.649
emborrachan	1	0	1.649
embelleció	1	0	1.649
embargó	1	0	1.649
embarcarte	1	0	1.649
embarazosos	1	0	1.649
embarazosas	1	0	1.649
emancipado	1	0	1.649
emancipación	1	0	1.649
eludiendo	1	0	1.649
eloïm	1	0	1.649
élite	1	0	1.649
eligiesen	1	0	1.649
elevados	1	0	1.649
elevada	1	0	1.649
elegido	1	0	1.649
elegíaca	1	0	1.649
elegantón	1	0	1.649
elegantemente	1	0	1.649
elegancias	1	0	1.649
elefante	1	0	1.649
eléctricos	1	0	1.649
electores	1	0	1.649
elector	1	0	1.649
ejercitaba	1	0	1.649
ejerció	1	0	1.649
ejerciendo	1	0	1.649
ejercido	1	0	1.649
ejecutor	1	0	1.649
ego	1	0	1.649
églogas	1	0	1.649
égloga	1	0	1.649
egipcias	1	0	1.649
egida	1	0	1.649
egeria	1	0	1.649
efusivo	1	0	1.649
efluvios	1	0	1.649
efímeros	1	0	1.649
efímera	1	0	1.649
educó	1	0	1.649
eduardo	1	0	1.649
editor	1	0	1.649
edificando	1	0	1.649
edifican	1	0	1.649
edicto	1	0	1.649
edgar	1	0	1.649
edemíaca	1	0	1.649
ecuestre	1	0	1.649
economizarlo	1	0	1.649
economato	1	0	1.649
eclipsar	1	0	1.649
eciomo	1	0	1.649
échele	1	0	1.649
echasen	1	0	1.649
ecco	1	0	1.649
ebria	1	0	1.649
ébano	1	0	1.649
ebanista	1	0	1.649
è	1	0	1.649
é	1	0	1.649
durará	1	0	1.649
duraderos	1	0	1.649
dupanloup	1	0	1.649
dúo	1	0	1.649
dumio	1	0	1.649
dum	1	0	1.649
dulzones	1	0	1.649
dudosas	1	0	1.649
dudemos	1	0	1.649
dudase	1	0	1.649
dudaban	1	0	1.649
dúctil	1	0	1.649
dualista	1	0	1.649
dramaturgo	1	0	1.649
dramáticas	1	0	1.649
dovelas	1	0	1.649
dotó	1	0	1.649
dotar	1	0	1.649
dosimétrico	1	0	1.649
doseletes	1	0	1.649
dorso	1	0	1.649
dormitan	1	0	1.649
dormidas	1	0	1.649
dórico	1	0	1.649
donosura	1	0	1.649
donosa	1	0	1.649
dominase	1	0	1.649
dominarnos	1	0	1.649
dominarla	1	0	1.649
dominándolos	1	0	1.649
dominándola	1	0	1.649
dominados	1	0	1.649
dominada	1	0	1.649
domiciliada	1	0	1.649
domesticado	1	0	1.649
domaba	1	0	1.649
dolorosos	1	0	1.649
döllinger	1	0	1.649
dolido	1	0	1.649
dolería	1	0	1.649
dogmáticos	1	0	1.649
dogmático	1	0	1.649
dogmáticas	1	0	1.649
doctrino	1	0	1.649
docente	1	0	1.649
doceañista	1	0	1.649
dixit	1	0	1.649
divulgar	1	0	1.649
divulgado	1	0	1.649
divisó	1	0	1.649
divisibles	1	0	1.649
divisas	1	0	1.649
divirtiendo	1	0	1.649
divinos	1	0	1.649
divinam	1	0	1.649
divido	1	0	1.649
dividido	1	0	1.649
divertiría	1	0	1.649
divertidísima	1	0	1.649
disuelven	1	0	1.649
disuelve	1	0	1.649
disueltas	1	0	1.649
disuelta	1	0	1.649
disuadía	1	0	1.649
distributiva	1	0	1.649
distrajeran	1	0	1.649
distraídas	1	0	1.649
distraían	1	0	1.649
distraerte	1	0	1.649
distraerla	1	0	1.649
distraerían	1	0	1.649
distraer	1	0	1.649
distintamente	1	0	1.649
distinguirse	1	0	1.649
distinguirlos	1	0	1.649
distinguirlo	1	0	1.649
distinguidísimo	1	0	1.649
distinciones	1	0	1.649
disputándose	1	0	1.649
dispusiera	1	0	1.649
disponían	1	0	1.649
disponerse	1	0	1.649
dispersos	1	0	1.649
dispersar	1	0	1.649
dispersándose	1	0	1.649
dispersa	1	0	1.649
dispensase	1	0	1.649
dispensado	1	0	1.649
disparo	1	0	1.649
disparitas	1	0	1.649
disparatando	1	0	1.649
disparataba	1	0	1.649
disolvió	1	0	1.649
disolviera	1	0	1.649
disolvía	1	0	1.649
disolverse	1	0	1.649
disminuyó	1	0	1.649
disminuyendo	1	0	1.649
disminuían	1	0	1.649
dislate	1	0	1.649
disimulase	1	0	1.649
disimularon	1	0	1.649
disimularlos	1	0	1.649
disgustillo	1	0	1.649
disgustarse	1	0	1.649
disgustaron	1	0	1.649
disgustarle	1	0	1.649
disgustan	1	0	1.649
disfrazasen	1	0	1.649
disfrazase	1	0	1.649
disfrazadas	1	0	1.649
disertaciones	1	0	1.649
disertaba	1	0	1.649
discutirla	1	0	1.649
discutiría	1	0	1.649
discursito	1	0	1.649
disculparlo	1	0	1.649
disculpables	1	0	1.649
discretísimas	1	0	1.649
discreteo	1	0	1.649
disciplentes	1	0	1.649
dirigiese	1	0	1.649
dirigieron	1	0	1.649
directores	1	0	1.649
dionisíacas	1	0	1.649
dinidad	1	0	1.649
dinásticos	1	0	1.649
dimisionario	1	0	1.649
dilucidar	1	0	1.649
dilatación	1	0	1.649
dilacerar	1	0	1.649
díjolo	1	0	1.649
dijes	1	0	1.649
dignificar	1	0	1.649
dignidades	1	0	1.649
dignatario	1	0	1.649
dignase	1	0	1.649
dignarse	1	0	1.649
dignaba	1	0	1.649
digestivas	1	0	1.649
díganme	1	0	1.649
difuntas	1	0	1.649
difundirse	1	0	1.649
difundían	1	0	1.649
dificultaban	1	0	1.649
dificilísima	1	0	1.649
diezmos	1	0	1.649
dieta	1	0	1.649
diestra	1	0	1.649
dies	1	0	1.649
diecisiete	1	0	1.649
die	1	0	1.649
dictatorial	1	0	1.649
dictaría	1	0	1.649
dictadura	1	0	1.649
dico	1	0	1.649
dickens	1	0	1.649
diciéndoselo	1	0	1.649
dichosas	1	0	1.649
dicharacheros	1	0	1.649
dibujó	1	0	1.649
dibujar	1	0	1.649
dibujándose	1	0	1.649
dibujaban	1	0	1.649
dibujaba	1	0	1.649
diana	1	0	1.649
diaforético	1	0	1.649
diáfano	1	0	1.649
diácono	1	0	1.649
diablesas	1	0	1.649
diablejo	1	0	1.649
devuelto	1	0	1.649
devoran	1	0	1.649
devora	1	0	1.649
devolvieran	1	0	1.649
devolviéndole	1	0	1.649
devolviendo	1	0	1.649
devolvían	1	0	1.649
devastación	1	0	1.649
devanadera	1	0	1.649
deux	1	0	1.649
deus	1	0	1.649
deudo	1	0	1.649
detractores	1	0	1.649
detonación	1	0	1.649
determinaban	1	0	1.649
deteriorando	1	0	1.649
detenemos	1	0	1.649
desvivo	1	0	1.649
desviadas	1	0	1.649
desvergonzarse	1	0	1.649
desvergonzados	1	0	1.649
desvergonzado	1	0	1.649
desvencijado	1	0	1.649
desvencijadas	1	0	1.649
desvaneció	1	0	1.649
desvaneciendo	1	0	1.649
desvanecidos	1	0	1.649
desvanecíase	1	0	1.649
desvalijado	1	0	1.649
desuso	1	0	1.649
destruyó	1	0	1.649
destruyeron	1	0	1.649
destrucción	1	0	1.649
destrozarme	1	0	1.649
destrozáis	1	0	1.649
destocándose	1	0	1.649
destocado	1	0	1.649
desterrada	1	0	1.649
desteñía	1	0	1.649
destemplado	1	0	1.649
destartalado	1	0	1.649
desquitaba	1	0	1.649
desprovistos	1	0	1.649
desproporcionadas	1	0	1.649
desprestigio	1	0	1.649
despreocupada	1	0	1.649
despreciase	1	0	1.649
despreciarse	1	0	1.649
despreciaros	1	0	1.649
despreciara	1	0	1.649
despreciándolos	1	0	1.649
despreciándole	1	0	1.649
despreciándolas	1	0	1.649
despojo	1	0	1.649
despojaban	1	0	1.649
despojaba	1	0	1.649
despoblado	1	0	1.649
desplumarle	1	0	1.649
desplomaba	1	0	1.649
desplieguen	1	0	1.649
despídame	1	0	1.649
despertarnos	1	0	1.649
despertarle	1	0	1.649
despertadora	1	0	1.649
desperezarse	1	0	1.649
desperdiciado	1	0	1.649
despeñada	1	0	1.649
despeluznado	1	0	1.649
despellejarse	1	0	1.649
despellejaban	1	0	1.649
despellejaba	1	0	1.649
despejarse	1	0	1.649
despejados	1	0	1.649
despejadas	1	0	1.649
despeinarse	1	0	1.649
despedirlos	1	0	1.649
despedazara	1	0	1.649
despedazar	1	0	1.649
despedazado	1	0	1.649
despearse	1	0	1.649
despeada	1	0	1.649
desparramándose	1	0	1.649
desparramaban	1	0	1.649
despabilaban	1	0	1.649
desorientada	1	0	1.649
desollar	1	0	1.649
desocupados	1	0	1.649
desocupadas	1	0	1.649
desnudó	1	0	1.649
desnudeces	1	0	1.649
desnudar	1	0	1.649
desmoronarse	1	0	1.649
desmoronar	1	0	1.649
desmorona	1	0	1.649
desmesurada	1	0	1.649
desmayos	1	0	1.649
desmayé	1	0	1.649
desmayaron	1	0	1.649
desmayadas	1	0	1.649
desmantelada	1	0	1.649
desmanes	1	0	1.649
desmadejado	1	0	1.649
desmadejadas	1	0	1.649
deslumbro	1	0	1.649
deslumbradora	1	0	1.649
deslumbrada	1	0	1.649
deslumbraban	1	0	1.649
desliz	1	0	1.649
deslices	1	0	1.649
desleído	1	0	1.649
desistieron	1	0	1.649
desistido	1	0	1.649
desiertas	1	0	1.649
desidia	1	0	1.649
deshonran	1	0	1.649
deshonesto	1	0	1.649
deshojadas	1	0	1.649
deshilachaban	1	0	1.649
desheredados	1	0	1.649
desharía	1	0	1.649
deshaciéndola	1	0	1.649
desgarrarse	1	0	1.649
desgarrando	1	0	1.649
desgarrador	1	0	1.649
desgarradas	1	0	1.649
desgarraban	1	0	1.649
desgajarse	1	0	1.649
desfiladero	1	0	1.649
desfallecimiento	1	0	1.649
desfallecidos	1	0	1.649
desfallecía	1	0	1.649
desestero	1	0	1.649
desespera	1	0	1.649
desenvoltura	1	0	1.649
desentonar	1	0	1.649
desentona	1	0	1.649
desenterrado	1	0	1.649
desentendido	1	0	1.649
desengañados	1	0	1.649
desenfreno	1	0	1.649
desencanto	1	0	1.649
desencadenado	1	0	1.649
desempeña	1	0	1.649
desembolsos	1	0	1.649
desembarco	1	0	1.649
desechado	1	0	1.649
desechaban	1	0	1.649
dese	1	0	1.649
desdiga	1	0	1.649
desdentada	1	0	1.649
descuidillo	1	0	1.649
descuidarse	1	0	1.649
descuidaba	1	0	1.649
descubrirlos	1	0	1.649
descubrirlo	1	0	1.649
descubrieron	1	0	1.649
descubriéndole	1	0	1.649
descubridor	1	0	1.649
descuartizaba	1	0	1.649
descriptivas	1	0	1.649
descripciones	1	0	1.649
descreimiento	1	0	1.649
descreídas	1	0	1.649
descotada	1	0	1.649
descoser	1	0	1.649
desconsoladoras	1	0	1.649
desconsolador	1	0	1.649
desconocíamos	1	0	1.649
desconocen	1	0	1.649
descomponerla	1	0	1.649
descompasado	1	0	1.649
descollando	1	0	1.649
descollaban	1	0	1.649
descolgarse	1	0	1.649
descolgarla	1	0	1.649
descolgaba	1	0	1.649
descoco	1	0	1.649
desciñó	1	0	1.649
descifró	1	0	1.649
descifrarlas	1	0	1.649
desceñida	1	0	1.649
descenso	1	0	1.649
descendimiento	1	0	1.649
descarnadas	1	0	1.649
descarnaba	1	0	1.649
descargaría	1	0	1.649
descansan	1	0	1.649
descansaban	1	0	1.649
descaminos	1	0	1.649
descaminada	1	0	1.649
descalzaba	1	0	1.649
descabellado	1	0	1.649
desbordar	1	0	1.649
desbordado	1	0	1.649
desbanque	1	0	1.649
desbancado	1	0	1.649
desataron	1	0	1.649
desata	1	0	1.649
desarróllase	1	0	1.649
desarrolla	1	0	1.649
desarreglos	1	0	1.649
desaprobación	1	0	1.649
desapasionado	1	0	1.649
desapartarse	1	0	1.649
desapareciera	1	0	1.649
desaparecíamos	1	0	1.649
desanimar	1	0	1.649
desanduvo	1	0	1.649
desandando	1	0	1.649
desaliño	1	0	1.649
desalientos	1	0	1.649
desairarlos	1	0	1.649
desairarle	1	0	1.649
desairarla	1	0	1.649
desairados	1	0	1.649
desairadas	1	0	1.649
desahuciarlo	1	0	1.649
desahuciado	1	0	1.649
desahogue	1	0	1.649
desahogaban	1	0	1.649
desagravio	1	0	1.649
desagradecida	1	0	1.649
desafió	1	0	1.649
desafíe	1	0	1.649
desafiarle	1	0	1.649
desafiaría	1	0	1.649
desacreditó	1	0	1.649
desacreditarse	1	0	1.649
desacreditándote	1	0	1.649
desacreditan	1	0	1.649
desacredita	1	0	1.649
desaciertos	1	0	1.649
desabrochándose	1	0	1.649
derrumbara	1	0	1.649
derrumbar	1	0	1.649
derrotada	1	0	1.649
derrochaban	1	0	1.649
derritiéndose	1	0	1.649
derríbela	1	0	1.649
derribarme	1	0	1.649
derribado	1	0	1.649
derribaba	1	0	1.649
derretirá	1	0	1.649
derretían	1	0	1.649
derivados	1	0	1.649
derivación	1	0	1.649
depresivo	1	0	1.649
deprecaba	1	0	1.649
depositario	1	0	1.649
depositando	1	0	1.649
depositado	1	0	1.649
depositadas	1	0	1.649
depositaba	1	0	1.649
dependiese	1	0	1.649
depender	1	0	1.649
departamentos	1	0	1.649
dentera	1	0	1.649
densidad	1	0	1.649
demostré	1	0	1.649
demostraban	1	0	1.649
demontres	1	0	1.649
demoler	1	0	1.649
demodoco	1	0	1.649
demasía	1	0	1.649
demagoga	1	0	1.649
deliró	1	0	1.649
delirado	1	0	1.649
delincuentes	1	0	1.649
delicadísima	1	0	1.649
deliberó	1	0	1.649
deliberemos	1	0	1.649
deliberase	1	0	1.649
deliberaron	1	0	1.649
deliberar	1	0	1.649
deliberado	1	0	1.649
delgadilla	1	0	1.649
deletéreos	1	0	1.649
deleitasen	1	0	1.649
deleitábale	1	0	1.649
delegado	1	0	1.649
delegación	1	0	1.649
delatores	1	0	1.649
delator	1	0	1.649
delató	1	0	1.649
delatase	1	0	1.649
delatarse	1	0	1.649
delataron	1	0	1.649
delatar	1	0	1.649
delataban	1	0	1.649
delataba	1	0	1.649
delanteros	1	0	1.649
dejaste	1	0	1.649
dejarían	1	0	1.649
dejaras	1	0	1.649
déjà	1	0	1.649
deísmo	1	0	1.649
degradarse	1	0	1.649
degradarla	1	0	1.649
degradan	1	0	1.649
degradado	1	0	1.649
degollarla	1	0	1.649
degollar	1	0	1.649
degollado	1	0	1.649
degli	1	0	1.649
degeneraba	1	0	1.649
defraudaba	1	0	1.649
definirse	1	0	1.649
definía	1	0	1.649
defienden	1	0	1.649
defensiva	1	0	1.649
defensas	1	0	1.649
defenderla	1	0	1.649
defectillo	1	0	1.649
dedique	1	0	1.649
dedicándonos	1	0	1.649
decurión	1	0	1.649
decretos	1	0	1.649
declarada	1	0	1.649
declamador	1	0	1.649
declamado	1	0	1.649
declamaba	1	0	1.649
decisiva	1	0	1.649
decírsele	1	0	1.649
decirlos	1	0	1.649
decimales	1	0	1.649
décima	1	0	1.649
decidores	1	0	1.649
decidiendo	1	0	1.649
decida	1	0	1.649
decentemente	1	0	1.649
decantado	1	0	1.649
decaimientos	1	0	1.649
decaído	1	0	1.649
decadencias	1	0	1.649
debilucho	1	0	1.649
debiéramos	1	0	1.649
debiéndolo	1	0	1.649
debíase	1	0	1.649
debérsela	1	0	1.649
davídicas	1	0	1.649
dativo	1	0	1.649
dárselos	1	0	1.649
darro	1	0	1.649
dardos	1	0	1.649
dañaría	1	0	1.649
dañaba	1	0	1.649
dándola	1	0	1.649
damiselas	1	0	1.649
dami	1	0	1.649
dalila	1	0	1.649
daga	1	0	1.649
dadme	1	0	1.649
custodire	1	0	1.649
cúspide	1	0	1.649
cursilona	1	0	1.649
currente	1	0	1.649
curiosón	1	0	1.649
curiales	1	0	1.649
curando	1	0	1.649
cunero	1	0	1.649
cundiese	1	0	1.649
cúmulus	1	0	1.649
cumulus	1	0	1.649
cumplirlas	1	0	1.649
cumplirá	1	0	1.649
cumplimientos	1	0	1.649
cumplieron	1	0	1.649
cumplieran	1	0	1.649
cumplen	1	0	1.649
cumpleaños	1	0	1.649
cumín	1	0	1.649
cum	1	0	1.649
cultus	1	0	1.649
cultivara	1	0	1.649
cultivan	1	0	1.649
cultas	1	0	1.649
culparle	1	0	1.649
culpar	1	0	1.649
culotte	1	0	1.649
culinarias	1	0	1.649
culata	1	0	1.649
cuique	1	0	1.649
cuidase	1	0	1.649
cuidara	1	0	1.649
cuidada	1	0	1.649
cueto	1	0	1.649
cuestores	1	0	1.649
cuerdamente	1	0	1.649
cuelgue	1	0	1.649
cuelgan	1	0	1.649
cubriera	1	0	1.649
cubriéndolos	1	0	1.649
cubriéndola	1	0	1.649
cubríale	1	0	1.649
cubren	1	0	1.649
cuartucho	1	0	1.649
cuartilla	1	0	1.649
cuartas	1	0	1.649
cuadriculado	1	0	1.649
cuadras	1	0	1.649
cuadradillos	1	0	1.649
cuadradas	1	0	1.649
cuadraban	1	0	1.649
cruzarse	1	0	1.649
cruzada	1	0	1.649
cruza	1	0	1.649
crusología	1	0	1.649
cruelísimo	1	0	1.649
crucifixión	1	0	1.649
crucificó	1	0	1.649
cronométrica	1	0	1.649
cromáticas	1	0	1.649
croiset	1	0	1.649
criticaron	1	0	1.649
cristos	1	0	1.649
cristinos	1	0	1.649
cristalino	1	0	1.649
cristalinas	1	0	1.649
cristalina	1	0	1.649
cristalerías	1	0	1.649
crispan	1	0	1.649
crispados	1	0	1.649
crispadas	1	0	1.649
crisol	1	0	1.649
crisálida	1	0	1.649
crin	1	0	1.649
criminalmente	1	0	1.649
criaos	1	0	1.649
criao	1	0	1.649
creyesen	1	0	1.649
creó	1	0	1.649
crema	1	0	1.649
creíale	1	0	1.649
creíala	1	0	1.649
creernos	1	0	1.649
creerlos	1	0	1.649
creerían	1	0	1.649
crédulas	1	0	1.649
crédula	1	0	1.649
creciese	1	0	1.649
crecían	1	0	1.649
crecería	1	0	1.649
crece	1	0	1.649
créanme	1	0	1.649
covent	1	0	1.649
covadonga	1	0	1.649
covachuelismo	1	0	1.649
cotorrón	1	0	1.649
coto	1	0	1.649
cotización	1	0	1.649
cotidianas	1	0	1.649
cota	1	0	1.649
costurero	1	0	1.649
costoso	1	0	1.649
costase	1	0	1.649
costas	1	0	1.649
costara	1	0	1.649
cosquilleo	1	0	1.649
cosméticos	1	0	1.649
cosechero	1	0	1.649
cosechas	1	0	1.649
corzos	1	0	1.649
corvetas	1	0	1.649
cortito	1	0	1.649
cortinillas	1	0	1.649
corruptela	1	0	1.649
corrupciones	1	0	1.649
corrosivo	1	0	1.649
corrompidas	1	0	1.649
corrompía	1	0	1.649
corromperla	1	0	1.649
corromper	1	0	1.649
corroboraba	1	0	1.649
corrijan	1	0	1.649
corridos	1	0	1.649
correveidile	1	0	1.649
correspondió	1	0	1.649
correspondiera	1	0	1.649
corresponderle	1	0	1.649
correligionarios	1	0	1.649
correctos	1	0	1.649
correccionalista	1	0	1.649
corran	1	0	1.649
corralón	1	0	1.649
corrales	1	0	1.649
corpulentas	1	0	1.649
corpiño	1	0	1.649
coronas	1	0	1.649
coronarse	1	0	1.649
coronarlo	1	0	1.649
coronar	1	0	1.649
coronando	1	0	1.649
coronaba	1	0	1.649
corolario	1	0	1.649
cornamenta	1	0	1.649
corintio	1	0	1.649
cordilleras	1	0	1.649
cordillera	1	0	1.649
cordialmente	1	0	1.649
corderos	1	0	1.649
corcovados	1	0	1.649
coram	1	0	1.649
coraceros	1	0	1.649
coquetismo	1	0	1.649
coqueteaban	1	0	1.649
copones	1	0	1.649
copla	1	0	1.649
copiaremos	1	0	1.649
copiar	1	0	1.649
copiando	1	0	1.649
copiados	1	0	1.649
copiada	1	0	1.649
coordinar	1	0	1.649
coooosa	1	0	1.649
convulso	1	0	1.649
convocándole	1	0	1.649
convocados	1	0	1.649
convivencia	1	0	1.649
conviniesen	1	0	1.649
conviniese	1	0	1.649
convierten	1	0	1.649
convídesele	1	0	1.649
convidase	1	0	1.649
convidarles	1	0	1.649
convidándoles	1	0	1.649
conversiones	1	0	1.649
convergencia	1	0	1.649
conventual	1	0	1.649
convenirle	1	0	1.649
convenir	1	0	1.649
convenida	1	0	1.649
convencernos	1	0	1.649
convencerme	1	0	1.649
convenceré	1	0	1.649
contumaz	1	0	1.649
controversias	1	0	1.649
contribuyo	1	0	1.649
contribuyente	1	0	1.649
contribuye	1	0	1.649
contribuirá	1	0	1.649
contribuido	1	0	1.649
contribuían	1	0	1.649
contribución	1	0	1.649
contratado	1	0	1.649
contrastaban	1	0	1.649
contrasentidos	1	0	1.649
contrariar	1	0	1.649
contrajudías	1	0	1.649
contradiciéndose	1	0	1.649
contradiciendo	1	0	1.649
contradecirse	1	0	1.649
contradanza	1	0	1.649
contoneo	1	0	1.649
continuos	1	0	1.649
continúo	1	0	1.649
continuasen	1	0	1.649
continuado	1	0	1.649
continentes	1	0	1.649
contestaras	1	0	1.649
contentón	1	0	1.649
contentaron	1	0	1.649
contentar	1	0	1.649
contentándonos	1	0	1.649
contentadiza	1	0	1.649
conteniéndose	1	0	1.649
contenerte	1	0	1.649
contenerlos	1	0	1.649
contemporáneas	1	0	1.649
contemplativo	1	0	1.649
contemplarían	1	0	1.649
contarla	1	0	1.649
contarían	1	0	1.649
contándoselo	1	0	1.649
contándome	1	0	1.649
contándoles	1	0	1.649
contagió	1	0	1.649
contagiar	1	0	1.649
contagiado	1	0	1.649
contactos	1	0	1.649
consumidores	1	0	1.649
consumes	1	0	1.649
consultaron	1	0	1.649
consultaría	1	0	1.649
consules	1	0	1.649
construyó	1	0	1.649
construyendo	1	0	1.649
construyan	1	0	1.649
constipada	1	0	1.649
constipaba	1	0	1.649
constelaciones	1	0	1.649
constelación	1	0	1.649
constantinopla	1	0	1.649
constaban	1	0	1.649
conspiraciones	1	0	1.649
consolidó	1	0	1.649
consolémonos	1	0	1.649
consolase	1	0	1.649
consolaría	1	0	1.649
consolará	1	0	1.649
consolador	1	0	1.649
consistorios	1	0	1.649
consiguiera	1	0	1.649
consiguientes	1	0	1.649
conservo	1	0	1.649
conservaduría	1	0	1.649
conservadoras	1	0	1.649
conserjería	1	0	1.649
consentiría	1	0	1.649
consentidas	1	0	1.649
consejeros	1	0	1.649
consejas	1	0	1.649
consagrarse	1	0	1.649
consagrarlos	1	0	1.649
consagrarle	1	0	1.649
consagrándose	1	0	1.649
consabido	1	0	1.649
conquistaron	1	0	1.649
conquistarla	1	0	1.649
conquistaba	1	0	1.649
cono	1	0	1.649
conmutó	1	0	1.649
conmoverse	1	0	1.649
conmemoraban	1	0	1.649
conmemora	1	0	1.649
conjuro	1	0	1.649
conjurar	1	0	1.649
conjuraba	1	0	1.649
conjetura	1	0	1.649
cónicos	1	0	1.649
congruas	1	0	1.649
congregarla	1	0	1.649
congraciándose	1	0	1.649
congojosa	1	0	1.649
congeniaban	1	0	1.649
confundiéndose	1	0	1.649
confundiendo	1	0	1.649
confunda	1	0	1.649
confortante	1	0	1.649
confitero	1	0	1.649
confiterías	1	0	1.649
confirmación	1	0	1.649
confirma	1	0	1.649
confiéseme	1	0	1.649
confiaría	1	0	1.649
confiadote	1	0	1.649
confiada	1	0	1.649
confesarle	1	0	1.649
confesarla	1	0	1.649
confesaré	1	0	1.649
confesados	1	0	1.649
conferenciaban	1	0	1.649
confectu	1	0	1.649
condiscípulo	1	0	1.649
condescendiente	1	0	1.649
condensadas	1	0	1.649
condenó	1	0	1.649
condene	1	0	1.649
condenase	1	0	1.649
condenarlo	1	0	1.649
condenaría	1	0	1.649
condecoraciones	1	0	1.649
concurridas	1	0	1.649
concupiscente	1	0	1.649
concupiscencias	1	0	1.649
concreten	1	0	1.649
concretar	1	0	1.649
concordato	1	0	1.649
conciso	1	0	1.649
concilios	1	0	1.649
concilió	1	0	1.649
concilia	1	0	1.649
concesiones	1	0	1.649
concertar	1	0	1.649
conceptuosos	1	0	1.649
concepta	1	0	1.649
concederle	1	0	1.649
cóncava	1	0	1.649
concausas	1	0	1.649
comunicárselo	1	0	1.649
comunicará	1	0	1.649
comunican	1	0	1.649
comunicados	1	0	1.649
comulgó	1	0	1.649
comulgando	1	0	1.649
comulgaba	1	0	1.649
comulga	1	0	1.649
compuso	1	0	1.649
compunción	1	0	1.649
comprometida	1	0	1.649
comprometían	1	0	1.649
comprometernos	1	0	1.649
comprobar	1	0	1.649
comprobados	1	0	1.649
comprime	1	0	1.649
comprenderle	1	0	1.649
comprenderlas	1	0	1.649
comprarlos	1	0	1.649
comprarla	1	0	1.649
composiciones	1	0	1.649
composicioncilla	1	0	1.649
componenda	1	0	1.649
completan	1	0	1.649
complejas	1	0	1.649
complazco	1	0	1.649
complacíase	1	0	1.649
complaces	1	0	1.649
complaceros	1	0	1.649
competente	1	0	1.649
compensara	1	0	1.649
compenetran	1	0	1.649
compartía	1	0	1.649
comparten	1	0	1.649
compares	1	0	1.649
comparen	1	0	1.649
comparanza	1	0	1.649
comparados	1	0	1.649
comparaban	1	0	1.649
compadres	1	0	1.649
compadeciéndose	1	0	1.649
compadecidos	1	0	1.649
commis	1	0	1.649
comistrajos	1	0	1.649
comiste	1	0	1.649
comisionista	1	0	1.649
comisario	1	0	1.649
comineros	1	0	1.649
comiesen	1	0	1.649
comienzan	1	0	1.649
comías	1	0	1.649
cometiese	1	0	1.649
cómetela	1	0	1.649
comercios	1	0	1.649
comerciando	1	0	1.649
comerciaban	1	0	1.649
comercia	1	0	1.649
comentarlas	1	0	1.649
comentado	1	0	1.649
comentada	1	0	1.649
comensalía	1	0	1.649
comehostias	1	0	1.649
comedimiento	1	0	1.649
comedidos	1	0	1.649
comedidas	1	0	1.649
comediantes	1	0	1.649
combinaban	1	0	1.649
combatirla	1	0	1.649
combatiré	1	0	1.649
combatió	1	0	1.649
combatiendo	1	0	1.649
combatido	1	0	1.649
combatida	1	0	1.649
comarcanos	1	0	1.649
columpiaron	1	0	1.649
columpiar	1	0	1.649
columbraba	1	0	1.649
coloradilla	1	0	1.649
colono	1	0	1.649
colonial	1	0	1.649
colones	1	0	1.649
colocaran	1	0	1.649
colocando	1	0	1.649
colmó	1	0	1.649
colmaba	1	0	1.649
collis	1	0	1.649
collares	1	0	1.649
collados	1	0	1.649
colgaron	1	0	1.649
colgarlo	1	0	1.649
colgadizos	1	0	1.649
colerilla	1	0	1.649
colegiala	1	0	1.649
colectividades	1	0	1.649
colectivamente	1	0	1.649
colasa	1	0	1.649
colas	1	0	1.649
colaboraba	1	0	1.649
cójala	1	0	1.649
coincidiese	1	0	1.649
coincidencias	1	0	1.649
coimbra	1	0	1.649
cogerás	1	0	1.649
coeteris	1	0	1.649
coetáneos	1	0	1.649
coetáneo	1	0	1.649
coercitivo	1	0	1.649
codillos	1	0	1.649
codiciosa	1	0	1.649
codiciar	1	0	1.649
codeaban	1	0	1.649
codeaba	1	0	1.649
codazo	1	0	1.649
cocotte	1	0	1.649
cocinaba	1	0	1.649
cochera	1	0	1.649
cobrárselo	1	0	1.649
cobrarlos	1	0	1.649
cobrarla	1	0	1.649
cobrarían	1	0	1.649
cobrándole	1	0	1.649
cobos	1	0	1.649
cobijados	1	0	1.649
cobijaba	1	0	1.649
cobija	1	0	1.649
cobertizo	1	0	1.649
coadjutor	1	0	1.649
cloacas	1	0	1.649
climatológica	1	0	1.649
clientes	1	0	1.649
cliente	1	0	1.649
clerófobo	1	0	1.649
clerófoba	1	0	1.649
clavijas	1	0	1.649
claveteada	1	0	1.649
clavaron	1	0	1.649
clavarlos	1	0	1.649
clavarás	1	0	1.649
clasificarla	1	0	1.649
claraboya	1	0	1.649
clandestinamente	1	0	1.649
clamar	1	0	1.649
clama	1	0	1.649
civis	1	0	1.649
ciutti	1	0	1.649
ciudadano	1	0	1.649
ciudadanas	1	0	1.649
citarse	1	0	1.649
citar	1	0	1.649
citan	1	0	1.649
ciruelo	1	0	1.649
cirrus	1	0	1.649
circunstanciales	1	0	1.649
circulo	1	0	1.649
circulillos	1	0	1.649
circulando	1	0	1.649
ciñó	1	0	1.649
ciñendo	1	0	1.649
ciñen	1	0	1.649
cínicamente	1	0	1.649
cínica	1	0	1.649
cinegético	1	0	1.649
cinegéticas	1	0	1.649
cincel	1	0	1.649
cimodocea	1	0	1.649
cimas	1	0	1.649
cilíndricos	1	0	1.649
cigarreras	1	0	1.649
cierzo	1	0	1.649
ciervo	1	0	1.649
ciernes	1	0	1.649
científico	1	0	1.649
científica	1	0	1.649
ciel	1	0	1.649
ciegas	1	0	1.649
cicuta	1	0	1.649
ciclopios	1	0	1.649
ciclópea	1	0	1.649
cíclope	1	0	1.649
ciclones	1	0	1.649
ciclo	1	0	1.649
cíclades	1	0	1.649
chusquin	1	0	1.649
churriguerescos	1	0	1.649
chupó	1	0	1.649
chupándose	1	0	1.649
chulo	1	0	1.649
chubascos	1	0	1.649
chorritos	1	0	1.649
chorretadas	1	0	1.649
choques	1	0	1.649
chomel	1	0	1.649
chochas	1	0	1.649
chocasen	1	0	1.649
chocarían	1	0	1.649
chisporroteos	1	0	1.649
chisporroteo	1	0	1.649
chisporroteaba	1	0	1.649
chipre	1	0	1.649
chiflao	1	0	1.649
chiaror	1	0	1.649
chevrière	1	0	1.649
che	1	0	1.649
chasquidos	1	0	1.649
charanga	1	0	1.649
chaquetón	1	0	1.649
chaquet	1	0	1.649
chapas	1	0	1.649
chantal	1	0	1.649
chance	1	0	1.649
chambones	1	0	1.649
chambergo	1	0	1.649
chalets	1	0	1.649
cesantías	1	0	1.649
cesado	1	0	1.649
cerviz	1	0	1.649
cervantesca	1	0	1.649
certámenes	1	0	1.649
cerro	1	0	1.649
cerriles	1	0	1.649
cerrarlos	1	0	1.649
cerraduras	1	0	1.649
cernida	1	0	1.649
cernía	1	0	1.649
ceremoniosos	1	0	1.649
ceremonioso	1	0	1.649
ceremonial	1	0	1.649
cereales	1	0	1.649
cerdas	1	0	1.649
cercioraba	1	0	1.649
cercenando	1	0	1.649
cepo	1	0	1.649
cepilla	1	0	1.649
ceños	1	0	1.649
centuria	1	0	1.649
centros	1	0	1.649
centímetro	1	0	1.649
centésima	1	0	1.649
centelleaba	1	0	1.649
censuró	1	0	1.649
censuren	1	0	1.649
censores	1	0	1.649
censor	1	0	1.649
ceno	1	0	1.649
cenit	1	0	1.649
ceniciento	1	0	1.649
cenicientas	1	0	1.649
cenarás	1	0	1.649
cenaban	1	0	1.649
celtíberos	1	0	1.649
celtas	1	0	1.649
celosos	1	0	1.649
celonio	1	0	1.649
celestinas	1	0	1.649
celesta	1	0	1.649
celeres	1	0	1.649
celenio	1	0	1.649
celebrarlos	1	0	1.649
celebrarla	1	0	1.649
celebraría	1	0	1.649
celebrara	1	0	1.649
celebrando	1	0	1.649
celaba	1	0	1.649
cejijuntos	1	0	1.649
cejase	1	0	1.649
cejaría	1	0	1.649
ceguedad	1	0	1.649
cegaba	1	0	1.649
cefiso	1	0	1.649
céfiro	1	0	1.649
cedros	1	0	1.649
cedí	1	0	1.649
cederá	1	0	1.649
cebollas	1	0	1.649
ce	1	0	1.649
cazurro	1	0	1.649
cazuela	1	0	1.649
cazas	1	0	1.649
cazaron	1	0	1.649
cazara	1	0	1.649
cazan	1	0	1.649
cazado	1	0	1.649
cazaderos	1	0	1.649
caveant	1	0	1.649
cavar	1	0	1.649
cavando	1	0	1.649
cavadores	1	0	1.649
cavada	1	0	1.649
cauto	1	0	1.649
cautivó	1	0	1.649
causaron	1	0	1.649
causan	1	0	1.649
causada	1	0	1.649
caulis	1	0	1.649
cathedra	1	0	1.649
catedráticos	1	0	1.649
cátate	1	0	1.649
catalunga	1	0	1.649
catálogo	1	0	1.649
catafalcos	1	0	1.649
catacumbas	1	0	1.649
casulla	1	0	1.649
casuismo	1	0	1.649
castigue	1	0	1.649
castigó	1	0	1.649
castigarlos	1	0	1.649
castigaran	1	0	1.649
castigaban	1	0	1.649
castigaba	1	0	1.649
castañedos	1	0	1.649
castañares	1	0	1.649
casquivano	1	0	1.649
caseta	1	0	1.649
caserías	1	0	1.649
casería	1	0	1.649
caseosa	1	0	1.649
casará	1	0	1.649
casándose	1	0	1.649
casamatas	1	0	1.649
casadera	1	0	1.649
cartulina	1	0	1.649
cartujo	1	0	1.649
cartelas	1	0	1.649
cartapacio	1	0	1.649
carrick	1	0	1.649
carraspiques	1	0	1.649
carracas	1	0	1.649
carolo	1	0	1.649
carolina	1	0	1.649
carnoso	1	0	1.649
carnosa	1	0	1.649
carnavalesco	1	0	1.649
caritativos	1	0	1.649
cargantes	1	0	1.649
carestía	1	0	1.649
cardona	1	0	1.649
cardiopatía	1	0	1.649
cardíacos	1	0	1.649
cárdenos	1	0	1.649
cárdena	1	0	1.649
cardan	1	0	1.649
carcamal	1	0	1.649
carbonizaban	1	0	1.649
carbayeda	1	0	1.649
carátulas	1	0	1.649
carambolas	1	0	1.649
caracolear	1	0	1.649
capullo	1	0	1.649
capua	1	0	1.649
capotón	1	0	1.649
capitulares	1	0	1.649
capitular	1	0	1.649
capiteles	1	0	1.649
capitaneaban	1	0	1.649
capisco	1	0	1.649
capelo	1	0	1.649
capalleja	1	0	1.649
caótico	1	0	1.649
caos	1	0	1.649
cañedo	1	0	1.649
cañamones	1	0	1.649
cantatrices	1	0	1.649
cantarse	1	0	1.649
cantaran	1	0	1.649
cantándole	1	0	1.649
cantados	1	0	1.649
cansase	1	0	1.649
canonistas	1	0	1.649
canónigas	1	0	1.649
canónicos	1	0	1.649
candidaturas	1	0	1.649
cándida	1	0	1.649
candentes	1	0	1.649
candelillas	1	0	1.649
candelabro	1	0	1.649
candado	1	0	1.649
cancerbero	1	0	1.649
canariera	1	0	1.649
canales	1	0	1.649
cana	1	0	1.649
campesinas	1	0	1.649
campbell	1	0	1.649
campanillazos	1	0	1.649
campamento	1	0	1.649
camisolín	1	0	1.649
camisola	1	0	1.649
caminaban	1	0	1.649
cambie	1	0	1.649
cambiaban	1	0	1.649
cambia	1	0	1.649
camarote	1	0	1.649
camaradas	1	0	1.649
calzo	1	0	1.649
calzadas	1	0	1.649
calzaban	1	0	1.649
calvicies	1	0	1.649
calumniosas	1	0	1.649
calumniosa	1	0	1.649
calumnian	1	0	1.649
calumniadores	1	0	1.649
calumniaban	1	0	1.649
calorosa	1	0	1.649
calomarde	1	0	1.649
callos	1	0	1.649
callis	1	0	1.649
callejuela	1	0	1.649
callejones	1	0	1.649
callase	1	0	1.649
caliginosas	1	0	1.649
calificada	1	0	1.649
cálidas	1	0	1.649
calepino	1	0	1.649
calentar	1	0	1.649
calentándose	1	0	1.649
calentaban	1	0	1.649
calefacción	1	0	1.649
calculador	1	0	1.649
calcetines	1	0	1.649
calaverilla	1	0	1.649
calamo	1	0	1.649
cajonería	1	0	1.649
cajistas	1	0	1.649
caídas	1	0	1.649
cafetera	1	0	1.649
cadenillas	1	0	1.649
cadenciosas	1	0	1.649
cadenaaa	1	0	1.649
cacofónico	1	0	1.649
caciquil	1	0	1.649
cachos	1	0	1.649
cachazudas	1	0	1.649
cachazuda	1	0	1.649
cachaza	1	0	1.649
cacería	1	0	1.649
cabremos	1	0	1.649
cabotaje	1	0	1.649
cables	1	0	1.649
cabezota	1	0	1.649
cabalmente	1	0	1.649
caballerosos	1	0	1.649
caballeroso	1	0	1.649
caballeriza	1	0	1.649
caballeretes	1	0	1.649
cabalística	1	0	1.649
byroniano	1	0	1.649
byron	1	0	1.649
búsquenle	1	0	1.649
búsquelo	1	0	1.649
busilis	1	0	1.649
busco	1	0	1.649
buscárselos	1	0	1.649
buscarlas	1	0	1.649
buscándote	1	0	1.649
buscadas	1	0	1.649
burlonas	1	0	1.649
burlescos	1	0	1.649
burlesco	1	0	1.649
burlarían	1	0	1.649
burdos	1	0	1.649
bulló	1	0	1.649
bullían	1	0	1.649
bullen	1	0	1.649
bullanguero	1	0	1.649
buitre	1	0	1.649
buhoneros	1	0	1.649
bufos	1	0	1.649
bucólicas	1	0	1.649
buchner	1	0	1.649
bruyère	1	0	1.649
brusquer	1	0	1.649
brujas	1	0	1.649
brota	1	0	1.649
brooke	1	0	1.649
bronces	1	0	1.649
brochada	1	0	1.649
briscada	1	0	1.649
briosos	1	0	1.649
brindar	1	0	1.649
brindaba	1	0	1.649
brincar	1	0	1.649
brincan	1	0	1.649
brincaban	1	0	1.649
brincaba	1	0	1.649
brilló	1	0	1.649
brillaron	1	0	1.649
brillará	1	0	1.649
brillando	1	0	1.649
brevísima	1	0	1.649
bretón	1	0	1.649
brechas	1	0	1.649
brava	1	0	1.649
bramidos	1	0	1.649
bramar	1	0	1.649
brama	1	0	1.649
braga	1	0	1.649
braceando	1	0	1.649
boutade	1	0	1.649
bouquet	1	0	1.649
botonazos	1	0	1.649
botarga	1	0	1.649
botánicas	1	0	1.649
botando	1	0	1.649
bostezara	1	0	1.649
bostezado	1	0	1.649
bostezaban	1	0	1.649
bostezaba	1	0	1.649
borrosos	1	0	1.649
borrón	1	0	1.649
borrasca	1	0	1.649
borrador	1	0	1.649
borrada	1	0	1.649
borrachón	1	0	1.649
borracheras	1	0	1.649
borona	1	0	1.649
bordó	1	0	1.649
bordeando	1	0	1.649
borda	1	0	1.649
boquirris	1	0	1.649
bonus	1	0	1.649
bombardeo	1	0	1.649
bolsón	1	0	1.649
bolera	1	0	1.649
bogando	1	0	1.649
bofetá	1	0	1.649
bodegas	1	0	1.649
bodega	1	0	1.649
bock	1	0	1.649
bochornosos	1	0	1.649
bochornosa	1	0	1.649
bocacalle	1	0	1.649
bobalicona	1	0	1.649
bloqueo	1	0	1.649
bloqueadas	1	0	1.649
blindaje	1	0	1.649
blasfemos	1	0	1.649
blasfemia	1	0	1.649
blasfeme	1	0	1.649
blasfemaba	1	0	1.649
blanquísima	1	0	1.649
blanquecinas	1	0	1.649
blandones	1	0	1.649
blandiéndolo	1	0	1.649
blandía	1	0	1.649
bizarra	1	0	1.649
bizantina	1	0	1.649
birrete	1	0	1.649
bípedo	1	0	1.649
bion	1	0	1.649
biografías	1	0	1.649
bilioso	1	0	1.649
bílbilis	1	0	1.649
bilateral	1	0	1.649
bienquisto	1	0	1.649
bienquista	1	0	1.649
bibliófilo	1	0	1.649
bibelot	1	0	1.649
bi	1	0	1.649
bethlehem	1	0	1.649
bestialidad	1	0	1.649
bestial	1	0	1.649
besas	1	0	1.649
besara	1	0	1.649
besada	1	0	1.649
besaban	1	0	1.649
berruguete	1	0	1.649
berroqueño	1	0	1.649
bernardo	1	0	1.649
bernard	1	0	1.649
bermudo	1	0	1.649
berlín	1	0	1.649
bengala	1	0	1.649
beneplácito	1	0	1.649
benemérito	1	0	1.649
beneficioso	1	0	1.649
benedicto	1	0	1.649
bendiga	1	0	1.649
bendecir	1	0	1.649
bendecían	1	0	1.649
bendecía	1	0	1.649
belo	1	0	1.649
bellos	1	0	1.649
belloritas	1	0	1.649
bellaquerías	1	0	1.649
bellacas	1	0	1.649
belem	1	0	1.649
begonia	1	0	1.649
becerro	1	0	1.649
bebedores	1	0	1.649
beatuela	1	0	1.649
bayonetazos	1	0	1.649
bautizar	1	0	1.649
battistini	1	0	1.649
batrania	1	0	1.649
bato	1	0	1.649
batiría	1	0	1.649
batieran	1	0	1.649
batía	1	0	1.649
baten	1	0	1.649
batas	1	0	1.649
batallones	1	0	1.649
batallón	1	0	1.649
bastos	1	0	1.649
bastonazos	1	0	1.649
basteado	1	0	1.649
basteada	1	0	1.649
bastase	1	0	1.649
bastarle	1	0	1.649
bastará	1	0	1.649
bastan	1	0	1.649
bastamos	1	0	1.649
basquiña	1	0	1.649
barullón	1	0	1.649
barullero	1	0	1.649
barrió	1	0	1.649
barriera	1	0	1.649
barriadas	1	0	1.649
barreras	1	0	1.649
barreno	1	0	1.649
barrenaba	1	0	1.649
barnizados	1	0	1.649
barnizada	1	0	1.649
báquico	1	0	1.649
bañarse	1	0	1.649
bañarme	1	0	1.649
bañando	1	0	1.649
bañados	1	0	1.649
baña	1	0	1.649
banqueros	1	0	1.649
bandolero	1	0	1.649
bandidos	1	0	1.649
bamboleaban	1	0	1.649
bambalinas	1	0	1.649
balzac	1	0	1.649
baltasar	1	0	1.649
baldo	1	0	1.649
balbuceó	1	0	1.649
balaustres	1	0	1.649
bájese	1	0	1.649
bajarte	1	0	1.649
bajarme	1	0	1.649
bailasen	1	0	1.649
bailaron	1	0	1.649
bailarín	1	0	1.649
bailan	1	0	1.649
bailábamos	1	0	1.649
baglivio	1	0	1.649
badulaque	1	0	1.649
bachillera	1	0	1.649
babor	1	0	1.649
babilónicos	1	0	1.649
babilónico	1	0	1.649
azuzarlas	1	0	1.649
azulados	1	0	1.649
azucarera	1	0	1.649
azotarla	1	0	1.649
azotada	1	0	1.649
azotacalles	1	0	1.649
azogue	1	0	1.649
ayunaría	1	0	1.649
ayudó	1	0	1.649
ayuden	1	0	1.649
ayudémonos	1	0	1.649
ayudas	1	0	1.649
ayudaron	1	0	1.649
ayudarlos	1	0	1.649
ayudaremos	1	0	1.649
ayudantes	1	0	1.649
ayudábala	1	0	1.649
axis	1	0	1.649
avisaría	1	0	1.649
avisarán	1	0	1.649
avisaba	1	0	1.649
avisa	1	0	1.649
avinagrados	1	0	1.649
avinagrado	1	0	1.649
averigüé	1	0	1.649
averiados	1	0	1.649
averiada	1	0	1.649
avergüence	1	0	1.649
avergonzarme	1	0	1.649
avergonzarla	1	0	1.649
avergonzando	1	0	1.649
avergonzadas	1	0	1.649
aventurero	1	0	1.649
aventurarse	1	0	1.649
aventuradas	1	0	1.649
aventuraba	1	0	1.649
aventado	1	0	1.649
avenirse	1	0	1.649
avenidos	1	0	1.649
avellanos	1	0	1.649
avellanado	1	0	1.649
avasallan	1	0	1.649
avasalladores	1	0	1.649
avaros	1	0	1.649
avalora	1	0	1.649
autos	1	0	1.649
autorizar	1	0	1.649
autorizaba	1	0	1.649
autómatas	1	0	1.649
autolatría	1	0	1.649
ausenta	1	0	1.649
aura	1	0	1.649
aúpa	1	0	1.649
aunarme	1	0	1.649
aúnan	1	0	1.649
aumentado	1	0	1.649
aulló	1	0	1.649
augustas	1	0	1.649
audiencias	1	0	1.649
atusando	1	0	1.649
atusaba	1	0	1.649
aturdiendo	1	0	1.649
aturdidos	1	0	1.649
atropellaban	1	0	1.649
atronando	1	0	1.649
atronador	1	0	1.649
atriles	1	0	1.649
atribuyendo	1	0	1.649
atribuye	1	0	1.649
atribulada	1	0	1.649
atribuciones	1	0	1.649
atrevidísima	1	0	1.649
atreverme	1	0	1.649
atravesasen	1	0	1.649
atravesadas	1	0	1.649
atraerle	1	0	1.649
atraería	1	0	1.649
atraen	1	0	1.649
átomos	1	0	1.649
átomo	1	0	1.649
atizaron	1	0	1.649
atestadas	1	0	1.649
atesoraba	1	0	1.649
atesora	1	0	1.649
aterrado	1	0	1.649
aterida	1	0	1.649
atenía	1	0	1.649
atenea	1	0	1.649
atemorizado	1	0	1.649
atea	1	0	1.649
atávicas	1	0	1.649
atarse	1	0	1.649
atalaya	1	0	1.649
atajo	1	0	1.649
atajado	1	0	1.649
ataco	1	0	1.649
atacarte	1	0	1.649
atacarle	1	0	1.649
ataban	1	0	1.649
asustemos	1	0	1.649
asustarte	1	0	1.649
asustaría	1	0	1.649
asueto	1	0	1.649
astri	1	0	1.649
astillas	1	0	1.649
assistentiam	1	0	1.649
aspirado	1	0	1.649
aspiradas	1	0	1.649
ásperos	1	0	1.649
aspa	1	0	1.649
asombrosamente	1	0	1.649
asombraban	1	0	1.649
asomasen	1	0	1.649
asomaran	1	0	1.649
asolado	1	0	1.649
asociarla	1	0	1.649
asistirlos	1	0	1.649
asirle	1	0	1.649
asimilaba	1	0	1.649
asignatura	1	0	1.649
asfixiarse	1	0	1.649
asfixiado	1	0	1.649
aseveraba	1	0	1.649
asestaban	1	0	1.649
asesorado	1	0	1.649
asesinarla	1	0	1.649
asentaba	1	0	1.649
asegurarle	1	0	1.649
asegurada	1	0	1.649
asediaban	1	0	1.649
asediaba	1	0	1.649
asedia	1	0	1.649
ascética	1	0	1.649
ascendiendo	1	0	1.649
asafétida	1	0	1.649
asada	1	0	1.649
as	1	0	1.649
arúspice	1	0	1.649
articulillo	1	0	1.649
articulejo	1	0	1.649
artela	1	0	1.649
artefactos	1	0	1.649
arruine	1	0	1.649
arruinarle	1	0	1.649
arruinados	1	0	1.649
arrugase	1	0	1.649
arrugar	1	0	1.649
arrugados	1	0	1.649
arrugaditos	1	0	1.649
arrugadas	1	0	1.649
arropada	1	0	1.649
arrojasen	1	0	1.649
arrojárselo	1	0	1.649
arrojarme	1	0	1.649
arrojarlo	1	0	1.649
arrojarles	1	0	1.649
arrobado	1	0	1.649
arrinconadas	1	0	1.649
arrimaron	1	0	1.649
arriesgándose	1	0	1.649
arriesgado	1	0	1.649
arriesgada	1	0	1.649
arresto	1	0	1.649
arrepintió	1	0	1.649
arrendamientos	1	0	1.649
arremolinó	1	0	1.649
arremolinaban	1	0	1.649
arremetida	1	0	1.649
arrellanados	1	0	1.649
arrellanado	1	0	1.649
arreglarás	1	0	1.649
arrebatando	1	0	1.649
arrebataba	1	0	1.649
arrasados	1	0	1.649
arras	1	0	1.649
arrancasen	1	0	1.649
arrancas	1	0	1.649
arrancarlo	1	0	1.649
arrancaría	1	0	1.649
arrancándoles	1	0	1.649
arrancándola	1	0	1.649
arrancados	1	0	1.649
arraigo	1	0	1.649
arraigaba	1	0	1.649
arqueológicos	1	0	1.649
arouet	1	0	1.649
aromático	1	0	1.649
aromáticas	1	0	1.649
armonioso	1	0	1.649
armonías	1	0	1.649
armisticios	1	0	1.649
armisticio	1	0	1.649
armiños	1	0	1.649
aristocráticos	1	0	1.649
arisco	1	0	1.649
ariscas	1	0	1.649
áridos	1	0	1.649
argumosa	1	0	1.649
argos	1	0	1.649
arengas	1	0	1.649
arduas	1	0	1.649
ardilla	1	0	1.649
ardiera	1	0	1.649
arde	1	0	1.649
arcones	1	0	1.649
arciprestazgo	1	0	1.649
arcilla	1	0	1.649
archimonástica	1	0	1.649
arcadias	1	0	1.649
arboricultor	1	0	1.649
arbitrista	1	0	1.649
arbitrar	1	0	1.649
arañazo	1	0	1.649
aragonesa	1	0	1.649
árabes	1	0	1.649
aquilata	1	0	1.649
aquéllas	1	0	1.649
apurasen	1	0	1.649
apuntara	1	0	1.649
apuntado	1	0	1.649
aproximando	1	0	1.649
aproximadamente	1	0	1.649
aprovechemos	1	0	1.649
aprovecharon	1	0	1.649
aprovecharlo	1	0	1.649
aprovecharlas	1	0	1.649
aprovechándose	1	0	1.649
aprovechado	1	0	1.649
apropósito	1	0	1.649
aprobando	1	0	1.649
aprobado	1	0	1.649
aprisionaba	1	0	1.649
aprietos	1	0	1.649
apretarse	1	0	1.649
apretándose	1	0	1.649
apresure	1	0	1.649
aprendices	1	0	1.649
aprendí	1	0	1.649
apreciarlos	1	0	1.649
aprecia	1	0	1.649
approbante	1	0	1.649
apoyos	1	0	1.649
apoyadas	1	0	1.649
apostatar	1	0	1.649
apostados	1	0	1.649
aportaría	1	0	1.649
apoplético	1	0	1.649
apoplejía	1	0	1.649
apólogos	1	0	1.649
apologías	1	0	1.649
apodos	1	0	1.649
apodere	1	0	1.649
apoderando	1	0	1.649
apocalípticas	1	0	1.649
apocados	1	0	1.649
aplico	1	0	1.649
aplicable	1	0	1.649
aplazando	1	0	1.649
aplazado	1	0	1.649
aplazaba	1	0	1.649
aplauso	1	0	1.649
aplaudiese	1	0	1.649
aplaudidos	1	0	1.649
aplaudido	1	0	1.649
aplaudían	1	0	1.649
aplastemos	1	0	1.649
aplastarla	1	0	1.649
aplastarían	1	0	1.649
aplacaban	1	0	1.649
apiñada	1	0	1.649
apiñábase	1	0	1.649
ápice	1	0	1.649
apiadarse	1	0	1.649
apiadaba	1	0	1.649
apetecida	1	0	1.649
apetecibles	1	0	1.649
apesto	1	0	1.649
apestas	1	0	1.649
aperitivos	1	0	1.649
apeó	1	0	1.649
apelmazada	1	0	1.649
apellidaban	1	0	1.649
apellidaba	1	0	1.649
apego	1	0	1.649
apearon	1	0	1.649
apeado	1	0	1.649
apeaba	1	0	1.649
apasionamiento	1	0	1.649
apartaría	1	0	1.649
aparta	1	0	1.649
aparentan	1	0	1.649
aparecérsele	1	0	1.649
aparatoso	1	0	1.649
aparador	1	0	1.649
apañaré	1	0	1.649
apagase	1	0	1.649
añosos	1	0	1.649
añicos	1	0	1.649
añado	1	0	1.649
añadiría	1	0	1.649
añadían	1	0	1.649
anuncita	1	0	1.649
anuncias	1	0	1.649
anunciándoles	1	0	1.649
anulo	1	0	1.649
anual	1	0	1.649
antro	1	0	1.649
antonelli	1	0	1.649
antolínez	1	0	1.649
antojos	1	0	1.649
antojase	1	0	1.649
antojársele	1	0	1.649
antojara	1	0	1.649
antojado	1	0	1.649
antojadiza	1	0	1.649
antojábasele	1	0	1.649
antítesis	1	0	1.649
antiespasmódicos	1	0	1.649
anticuarios	1	0	1.649
anticuada	1	0	1.649
anticipándose	1	0	1.649
anticipando	1	0	1.649
antepasados	1	0	1.649
ansiando	1	0	1.649
ansiaban	1	0	1.649
anónimas	1	0	1.649
anónima	1	0	1.649
aniquilarme	1	0	1.649
aniquilarle	1	0	1.649
aniquilados	1	0	1.649
animen	1	0	1.649
animaron	1	0	1.649
animando	1	0	1.649
animan	1	0	1.649
animalucho	1	0	1.649
animalejo	1	0	1.649
aniceto	1	0	1.649
anhelaban	1	0	1.649
angustiado	1	0	1.649
angustiaba	1	0	1.649
anguilas	1	0	1.649
angola	1	0	1.649
angélico	1	0	1.649
angarillas	1	0	1.649
anfibológico	1	0	1.649
anfibios	1	0	1.649
anfibio	1	0	1.649
anegó	1	0	1.649
anegarse	1	0	1.649
anegamos	1	0	1.649
anegaban	1	0	1.649
anduviese	1	0	1.649
anduvieran	1	0	1.649
andrómaca	1	0	1.649
andrina	1	0	1.649
anday	1	0	1.649
andarín	1	0	1.649
andaluces	1	0	1.649
andábamos	1	0	1.649
ancor	1	0	1.649
anchuras	1	0	1.649
anchísima	1	0	1.649
anch	1	0	1.649
análogo	1	0	1.649
analogías	1	0	1.649
analogía	1	0	1.649
análoga	1	0	1.649
analizarla	1	0	1.649
analítica	1	0	1.649
anagnórisis	1	0	1.649
anafrodíticos	1	0	1.649
anafrodítico	1	0	1.649
anafroditas	1	0	1.649
anacreóntica	1	0	1.649
amueblada	1	0	1.649
amplios	1	0	1.649
amplias	1	0	1.649
ampliar	1	0	1.649
amparando	1	0	1.649
amotinados	1	0	1.649
amostazado	1	0	1.649
amortajada	1	0	1.649
amorcillo	1	0	1.649
amoratado	1	0	1.649
amontonado	1	0	1.649
amontonaba	1	0	1.649
amoldarse	1	0	1.649
amó	1	0	1.649
amnistía	1	0	1.649
amistosas	1	0	1.649
américo	1	0	1.649
américas	1	0	1.649
americanilla	1	0	1.649
amenizaba	1	0	1.649
amenidad	1	0	1.649
amengua	1	0	1.649
amenazarla	1	0	1.649
amenazándome	1	0	1.649
amen	1	0	1.649
ambiciones	1	0	1.649
ambicionaba	1	0	1.649
amazacotada	1	0	1.649
amasijo	1	0	1.649
amasados	1	0	1.649
amarrado	1	0	1.649
amarla	1	0	1.649
amarillez	1	0	1.649
amarillentos	1	0	1.649
amarilleaba	1	0	1.649
amarilis	1	0	1.649
amaños	1	0	1.649
amansando	1	0	1.649
amanecido	1	0	1.649
amagos	1	0	1.649
amagó	1	0	1.649
amaga	1	0	1.649
amadas	1	0	1.649
alzasen	1	0	1.649
alzase	1	0	1.649
alvarico	1	0	1.649
aluvión	1	0	1.649
alusiva	1	0	1.649
alumbramiento	1	0	1.649
alumbraban	1	0	1.649
aludían	1	0	1.649
alucinas	1	0	1.649
altruistas	1	0	1.649
altozano	1	0	1.649
altisonante	1	0	1.649
altísimos	1	0	1.649
alterarse	1	0	1.649
alteraciones	1	0	1.649
altaneros	1	0	1.649
altanero	1	0	1.649
alondras	1	0	1.649
almohadillado	1	0	1.649
almohadillada	1	0	1.649
almidonadas	1	0	1.649
almibarados	1	0	1.649
almibarado	1	0	1.649
almenas	1	0	1.649
almacenó	1	0	1.649
alleluia	1	0	1.649
allanarlo	1	0	1.649
aliviada	1	0	1.649
aliviaban	1	0	1.649
alineado	1	0	1.649
alimentan	1	0	1.649
alimentación	1	0	1.649
alimañas	1	0	1.649
alientan	1	0	1.649
alicientes	1	0	1.649
alharaca	1	0	1.649
algodones	1	0	1.649
algaradas	1	0	1.649
alforjas	1	0	1.649
alfonsos	1	0	1.649
alfiletero	1	0	1.649
alfayate	1	0	1.649
aletean	1	0	1.649
alero	1	0	1.649
alemania	1	0	1.649
alejaran	1	0	1.649
alegué	1	0	1.649
alegrarle	1	0	1.649
alegaba	1	0	1.649
aleccionado	1	0	1.649
aleatorio	1	0	1.649
aldebarán	1	0	1.649
aldabonazos	1	0	1.649
aldabonazo	1	0	1.649
aldabonada	1	0	1.649
alcurnia	1	0	1.649
alcubilla	1	0	1.649
alcornoque	1	0	1.649
alcohólicos	1	0	1.649
alcides	1	0	1.649
alcanzase	1	0	1.649
alcanzara	1	0	1.649
alcanzados	1	0	1.649
alcaldito	1	0	1.649
alcaldesa	1	0	1.649
alcaide	1	0	1.649
alcacer	1	0	1.649
álbum	1	0	1.649
alboroque	1	0	1.649
alborada	1	0	1.649
albión	1	0	1.649
albergaba	1	0	1.649
alberca	1	0	1.649
albéitar	1	0	1.649
albas	1	0	1.649
albañal	1	0	1.649
alarmasen	1	0	1.649
alarmará	1	0	1.649
alargarse	1	0	1.649
alarcón	1	0	1.649
alancardan	1	0	1.649
alambicadas	1	0	1.649
alacenas	1	0	1.649
alacena	1	0	1.649
alabarle	1	0	1.649
alabarla	1	0	1.649
alabados	1	0	1.649
alabada	1	0	1.649
ajutorium	1	0	1.649
ajustadas	1	0	1.649
ajustábase	1	0	1.649
ajenjo	1	0	1.649
ajado	1	0	1.649
aislarla	1	0	1.649
aislador	1	0	1.649
aislada	1	0	1.649
ahuyentaba	1	0	1.649
ahumados	1	0	1.649
ahorró	1	0	1.649
ahorrada	1	0	1.649
ahorcarse	1	0	1.649
ahorcar	1	0	1.649
ahogó	1	0	1.649
ahogaron	1	0	1.649
ahogarlo	1	0	1.649
ahogarla	1	0	1.649
ahogados	1	0	1.649
ahogaban	1	0	1.649
ahítas	1	0	1.649
ahíta	1	0	1.649
aguzaba	1	0	1.649
agustinito	1	0	1.649
aguijones	1	0	1.649
aguijonearle	1	0	1.649
aguerrido	1	0	1.649
aguantado	1	0	1.649
agrónomo	1	0	1.649
agrietadas	1	0	1.649
agrietada	1	0	1.649
agreste	1	0	1.649
agregadas	1	0	1.649
agravante	1	0	1.649
agravaba	1	0	1.649
agradézcaselo	1	0	1.649
agradezcamos	1	0	1.649
agradecerlo	1	0	1.649
agradecería	1	0	1.649
agrade	1	0	1.649
agradado	1	0	1.649
agotando	1	0	1.649
agostado	1	0	1.649
agostada	1	0	1.649
agoreras	1	0	1.649
agonizaba	1	0	1.649
agonía	1	0	1.649
agolpándose	1	0	1.649
agolpaba	1	0	1.649
agobiados	1	0	1.649
aglomeraron	1	0	1.649
aglomeración	1	0	1.649
agitada	1	0	1.649
agentes	1	0	1.649
agencias	1	0	1.649
agencia	1	0	1.649
agazapado	1	0	1.649
agasajos	1	0	1.649
agarran	1	0	1.649
agachar	1	0	1.649
agachándose	1	0	1.649
agachado	1	0	1.649
afrodisíaco	1	0	1.649
afortunados	1	0	1.649
aforismo	1	0	1.649
aflojara	1	0	1.649
aflojando	1	0	1.649
aflojaban	1	0	1.649
aflojaba	1	0	1.649
aflija	1	0	1.649
afligió	1	0	1.649
afirma	1	0	1.649
afinaban	1	0	1.649
afilador	1	0	1.649
aficionara	1	0	1.649
afianzaría	1	0	1.649
affma	1	0	1.649
afeminados	1	0	1.649
afeitar	1	0	1.649
afectuosa	1	0	1.649
afectivo	1	0	1.649
afectísimo	1	0	1.649
afectar	1	0	1.649
afearlo	1	0	1.649
afablemente	1	0	1.649
aeroterapia	1	0	1.649
aéreo	1	0	1.649
aereación	1	0	1.649
advertirse	1	0	1.649
adversa	1	0	1.649
advenediza	1	0	1.649
adustos	1	0	1.649
adúlteras	1	0	1.649
aduladores	1	0	1.649
aducía	1	0	1.649
adquirieron	1	0	1.649
adquirían	1	0	1.649
adquirí	1	0	1.649
adornadas	1	0	1.649
adormecerla	1	0	1.649
adorarle	1	0	1.649
adorarla	1	0	1.649
adorados	1	0	1.649
adolescentes	1	0	1.649
adocenado	1	0	1.649
adocenada	1	0	1.649
adobes	1	0	1.649
admitirlos	1	0	1.649
admitieron	1	0	1.649
admitían	1	0	1.649
admiré	1	0	1.649
admirándole	1	0	1.649
admirándolas	1	0	1.649
admirados	1	0	1.649
admiradora	1	0	1.649
admirador	1	0	1.649
administrar	1	0	1.649
adjuntos	1	0	1.649
adjetivos	1	0	1.649
adiosito	1	0	1.649
adhesión	1	0	1.649
adherirme	1	0	1.649
aderezos	1	0	1.649
adelantarlo	1	0	1.649
adelantarle	1	0	1.649
adelantándose	1	0	1.649
adelantados	1	0	1.649
adecuados	1	0	1.649
adecuadas	1	0	1.649
adaptarse	1	0	1.649
adamascado	1	0	1.649
acústico	1	0	1.649
acusó	1	0	1.649
acuso	1	0	1.649
acusemos	1	0	1.649
acusara	1	0	1.649
acusada	1	0	1.649
acudiesen	1	0	1.649
acudiese	1	0	1.649
acuda	1	0	1.649
acti	1	0	1.649
acróbata	1	0	1.649
acribillada	1	0	1.649
acreditadas	1	0	1.649
acreditaban	1	0	1.649
acostumbre	1	0	1.649
acostarla	1	0	1.649
acostabas	1	0	1.649
acosarla	1	0	1.649
acortaban	1	0	1.649
acontecimiento	1	0	1.649
acontecemos	1	0	1.649
aconsejó	1	0	1.649
aconsejes	1	0	1.649
aconsejaron	1	0	1.649
aconsejan	1	0	1.649
aconsejada	1	0	1.649
aconsejaban	1	0	1.649
acongojaba	1	0	1.649
acompasado	1	0	1.649
acompáñenos	1	0	1.649
acompáñeme	1	0	1.649
acompañarse	1	0	1.649
acompañarlos	1	0	1.649
acomodaron	1	0	1.649
acomodamiento	1	0	1.649
acogido	1	0	1.649
acogidas	1	0	1.649
acogíase	1	0	1.649
acogerse	1	0	1.649
aclimató	1	0	1.649
aclimataba	1	0	1.649
aclararlo	1	0	1.649
aclamación	1	0	1.649
aciertos	1	0	1.649
achico	1	0	1.649
achicaba	1	0	1.649
achaparrado	1	0	1.649
achaparrada	1	0	1.649
achantarse	1	0	1.649
achacó	1	0	1.649
acervo	1	0	1.649
acertaría	1	0	1.649
acerquen	1	0	1.649
acerque	1	0	1.649
aceros	1	0	1.649
acércate	1	0	1.649
acercará	1	0	1.649
acercamos	1	0	1.649
aceptaré	1	0	1.649
aceptámosla	1	0	1.649
aceptables	1	0	1.649
acendrados	1	0	1.649
acelerar	1	0	1.649
aceleraba	1	0	1.649
acecharse	1	0	1.649
accionaba	1	0	1.649
accesorios	1	0	1.649
accèsit	1	0	1.649
accedido	1	0	1.649
accedería	1	0	1.649
acceder	1	0	1.649
acatarrada	1	0	1.649
acartonada	1	0	1.649
acarreaba	1	0	1.649
acaricie	1	0	1.649
acariciarte	1	0	1.649
acariciadores	1	0	1.649
acariciado	1	0	1.649
acariciaban	1	0	1.649
acaparó	1	0	1.649
acaparadores	1	0	1.649
acantos	1	0	1.649
acantilados	1	0	1.649
acamparon	1	0	1.649
acalorado	1	0	1.649
acalló	1	0	1.649
acaben	1	0	1.649
acabemos	1	0	1.649
acabasen	1	0	1.649
acabársele	1	0	1.649
acabará	1	0	1.649
acabamos	1	0	1.649
abuse	1	0	1.649
abusarse	1	0	1.649
aburro	1	0	1.649
aburrieran	1	0	1.649
aburriendo	1	0	1.649
abundasen	1	0	1.649
abundantemente	1	0	1.649
abundando	1	0	1.649
abultada	1	0	1.649
abuelo	1	0	1.649
absueltos	1	0	1.649
absuelto	1	0	1.649
abstuviese	1	0	1.649
abstuviera	1	0	1.649
abstraída	1	0	1.649
abstractos	1	0	1.649
abstiene	1	0	1.649
abstenerse	1	0	1.649
abstenerme	1	0	1.649
abstendría	1	0	1.649
abstención	1	0	1.649
absortos	1	0	1.649
absorben	1	0	1.649
absolvería	1	0	1.649
absolutos	1	0	1.649
abrumándole	1	0	1.649
abrumando	1	0	1.649
abrumadores	1	0	1.649
abroquelado	1	0	1.649
abrochar	1	0	1.649
abrochando	1	0	1.649
abrochado	1	0	1.649
abrochada	1	0	1.649
abriles	1	0	1.649
abrigan	1	0	1.649
abrigábala	1	0	1.649
abrigaba	1	0	1.649
abrieran	1	0	1.649
abreviada	1	0	1.649
ábreme	1	0	1.649
abrazase	1	0	1.649
abrazada	1	0	1.649
ábrase	1	0	1.649
abrasarme	1	0	1.649
abrasadores	1	0	1.649
aborrecían	1	0	1.649
aborrecerá	1	0	1.649
abordase	1	0	1.649
abomino	1	0	1.649
abominación	1	0	1.649
abominaba	1	0	1.649
abogadote	1	0	1.649
abogado	1	0	1.649
abogadillos	1	0	1.649
abogadetes	1	0	1.649
abofetear	1	0	1.649
abluciones	1	0	1.649
ablativo	1	0	1.649
ablandado	1	0	1.649
abismado	1	0	1.649
abismada	1	0	1.649
abertura	1	0	1.649
abelardo	1	0	1.649
abeja	1	0	1.649
abarcándola	1	0	1.649
abarcaba	1	0	1.649
abanicándose	1	0	1.649
abanicaba	1	0	1.649
abandonarme	1	0	1.649
venerable	8	5	1.638
sutil	8	5	1.638
serias	8	5	1.638
reyes	8	5	1.638
rama	8	5	1.638
pureza	8	5	1.638
plumas	8	5	1.638
pepa	8	5	1.638
ora	8	5	1.638
necesitó	8	5	1.638
llegaría	8	5	1.638
inverosímil	8	5	1.638
ingrato	8	5	1.638
estudiaba	8	5	1.638
espere	8	5	1.638
esmero	8	5	1.638
enseñanza	8	5	1.638
disimulaba	8	5	1.638
despertado	8	5	1.638
curvas	8	5	1.638
cualidades	8	5	1.638
cortés	8	5	1.638
convertir	8	5	1.638
contuvo	8	5	1.638
catástrofe	8	5	1.638
adivinaba	8	5	1.638
claro	93	99	1.629
admiración	24	21	1.627
sal	6	14	1.619
risueña	6	14	1.619
profundamente	6	14	1.619
preparado	6	14	1.619
pegado	6	14	1.619
pasará	6	14	1.619
moviendo	6	14	1.619
marcharse	6	14	1.619
lados	6	14	1.619
duele	6	14	1.619
abriendo	6	14	1.619
vete	9	19	1.607
mañanas	9	19	1.607
franqueza	9	19	1.607
salvaje	14	27	1.606
plan	14	27	1.606
xiv	3	1	1.602
vuelos	3	1	1.602
votó	3	1	1.602
villanía	3	1	1.602
vicisitudes	3	1	1.602
vibrante	3	1	1.602
vejiga	3	1	1.602
varillas	3	1	1.602
vanos	3	1	1.602
vanas	3	1	1.602
vana	3	1	1.602
vacas	3	1	1.602
unanimidad	3	1	1.602
unánime	3	1	1.602
turgentes	3	1	1.602
tronado	3	1	1.602
tronada	3	1	1.602
trigo	3	1	1.602
traza	3	1	1.602
trasladado	3	1	1.602
tosía	3	1	1.602
tortuga	3	1	1.602
tiara	3	1	1.602
testero	3	1	1.602
terminado	3	1	1.602
tejas	3	1	1.602
tapada	3	1	1.602
tajadas	3	1	1.602
taciturna	3	1	1.602
supersticiosa	3	1	1.602
sumida	3	1	1.602
sospechara	3	1	1.602
sosos	3	1	1.602
soporífero	3	1	1.602
soplando	3	1	1.602
sonrosado	3	1	1.602
sombría	3	1	1.602
solidez	3	1	1.602
soles	3	1	1.602
socialista	3	1	1.602
siluetas	3	1	1.602
silbido	3	1	1.602
separarnos	3	1	1.602
separándose	3	1	1.602
separada	3	1	1.602
semilla	3	1	1.602
saya	3	1	1.602
satisfechas	3	1	1.602
satisfacía	3	1	1.602
sagrados	3	1	1.602
sagacidad	3	1	1.602
sacrílegos	3	1	1.602
sabrosos	3	1	1.602
rústica	3	1	1.602
ruin	3	1	1.602
ruborizarse	3	1	1.602
rosada	3	1	1.602
roque	3	1	1.602
rodean	3	1	1.602
ríos	3	1	1.602
ríase	3	1	1.602
reunir	3	1	1.602
reunido	3	1	1.602
retorcía	3	1	1.602
reticencias	3	1	1.602
resucitar	3	1	1.602
resplandores	3	1	1.602
resonantes	3	1	1.602
resignado	3	1	1.602
reservas	3	1	1.602
resbalar	3	1	1.602
repasando	3	1	1.602
rendía	3	1	1.602
renacía	3	1	1.602
remontaba	3	1	1.602
reliquias	3	1	1.602
refuerzo	3	1	1.602
referían	3	1	1.602
reconocían	3	1	1.602
reconocerlo	3	1	1.602
recompensa	3	1	1.602
reclamaba	3	1	1.602
recios	3	1	1.602
realizado	3	1	1.602
rasgar	3	1	1.602
quincalla	3	1	1.602
purga	3	1	1.602
puntapiés	3	1	1.602
publicó	3	1	1.602
prudentes	3	1	1.602
provocada	3	1	1.602
proscenio	3	1	1.602
prolongaba	3	1	1.602
prohibición	3	1	1.602
profanar	3	1	1.602
profana	3	1	1.602
pródigo	3	1	1.602
prodigar	3	1	1.602
presidir	3	1	1.602
presidiendo	3	1	1.602
presidida	3	1	1.602
prender	3	1	1.602
preliminares	3	1	1.602
preguntaron	3	1	1.602
praderas	3	1	1.602
positivamente	3	1	1.602
portentos	3	1	1.602
pordiosero	3	1	1.602
poesías	3	1	1.602
poemas	3	1	1.602
pocilga	3	1	1.602
pliego	3	1	1.602
pitillo	3	1	1.602
pinta	3	1	1.602
pesebre	3	1	1.602
perlas	3	1	1.602
perezosas	3	1	1.602
perenne	3	1	1.602
perdonó	3	1	1.602
perderme	3	1	1.602
pepita	3	1	1.602
penetraban	3	1	1.602
pellejos	3	1	1.602
pecaba	3	1	1.602
paúl	3	1	1.602
pasmosa	3	1	1.602
pasmados	3	1	1.602
paseado	3	1	1.602
participaban	3	1	1.602
parábolas	3	1	1.602
palmas	3	1	1.602
palmadita	3	1	1.602
palidecía	3	1	1.602
palabreja	3	1	1.602
pagano	3	1	1.602
orla	3	1	1.602
oratoria	3	1	1.602
oradores	3	1	1.602
oponía	3	1	1.602
opio	3	1	1.602
olvidados	3	1	1.602
olvidaban	3	1	1.602
ojeriza	3	1	1.602
odiosos	3	1	1.602
obstina	3	1	1.602
obligar	3	1	1.602
obedezco	3	1	1.602
nombraba	3	1	1.602
nocturnos	3	1	1.602
nilo	3	1	1.602
necesitar	3	1	1.602
navajas	3	1	1.602
narración	3	1	1.602
mutuamente	3	1	1.602
mula	3	1	1.602
mueva	3	1	1.602
monumento	3	1	1.602
mojaba	3	1	1.602
milagroso	3	1	1.602
miembro	3	1	1.602
metrópoli	3	1	1.602
meseta	3	1	1.602
merecían	3	1	1.602
menudos	3	1	1.602
marineros	3	1	1.602
manzanas	3	1	1.602
mantenerse	3	1	1.602
manosear	3	1	1.602
manjares	3	1	1.602
mandaría	3	1	1.602
manchaba	3	1	1.602
malagueñas	3	1	1.602
majestuosa	3	1	1.602
maestros	3	1	1.602
maestría	3	1	1.602
m	3	1	1.602
lucir	3	1	1.602
lola	3	1	1.602
llamasen	3	1	1.602
liviandad	3	1	1.602
lejanas	3	1	1.602
lavándose	3	1	1.602
lavabo	3	1	1.602
latina	3	1	1.602
juzga	3	1	1.602
justamente	3	1	1.602
juntarse	3	1	1.602
jubilación	3	1	1.602
job	3	1	1.602
jamona	3	1	1.602
irritaban	3	1	1.602
irreverencia	3	1	1.602
inventos	3	1	1.602
intervalos	3	1	1.602
interminables	3	1	1.602
intemperie	3	1	1.602
instalado	3	1	1.602
insolentes	3	1	1.602
inoportuno	3	1	1.602
inmoral	3	1	1.602
injuria	3	1	1.602
indias	3	1	1.602
incipiente	3	1	1.602
incidentes	3	1	1.602
impuro	3	1	1.602
imprudentes	3	1	1.602
imposiciones	3	1	1.602
impasible	3	1	1.602
imitaciones	3	1	1.602
ignominioso	3	1	1.602
húmedo	3	1	1.602
hojuelas	3	1	1.602
hipócrates	3	1	1.602
helechos	3	1	1.602
guiaba	3	1	1.602
genuflexión	3	1	1.602
generación	3	1	1.602
gárrulo	3	1	1.602
garantía	3	1	1.602
gabinetes	3	1	1.602
funda	3	1	1.602
frecuentar	3	1	1.602
franja	3	1	1.602
franela	3	1	1.602
frágil	3	1	1.602
formalmente	3	1	1.602
forasteros	3	1	1.602
flotar	3	1	1.602
fíes	3	1	1.602
femenil	3	1	1.602
fanáticos	3	1	1.602
explíquese	3	1	1.602
expediente	3	1	1.602
expansivo	3	1	1.602
exhibición	3	1	1.602
excitaban	3	1	1.602
excepciones	3	1	1.602
exaltaba	3	1	1.602
exagerar	3	1	1.602
estrechaba	3	1	1.602
estímulos	3	1	1.602
establecía	3	1	1.602
esposas	3	1	1.602
espontáneamente	3	1	1.602
espiritualidad	3	1	1.602
espiritista	3	1	1.602
espesas	3	1	1.602
esperado	3	1	1.602
esfera	3	1	1.602
esconderse	3	1	1.602
escogido	3	1	1.602
escasas	3	1	1.602
ésa	3	1	1.602
envidiada	3	1	1.602
enseñaban	3	1	1.602
enramada	3	1	1.602
encogido	3	1	1.602
elevación	3	1	1.602
elevaba	3	1	1.602
echase	3	1	1.602
diversiones	3	1	1.602
distante	3	1	1.602
disparó	3	1	1.602
disparatar	3	1	1.602
disparaba	3	1	1.602
disimularlo	3	1	1.602
disimulan	3	1	1.602
discutían	3	1	1.602
diputados	3	1	1.602
dinamita	3	1	1.602
digestión	3	1	1.602
diabólicos	3	1	1.602
diablura	3	1	1.602
destierro	3	1	1.602
desplomado	3	1	1.602
desfallecimientos	3	1	1.602
desengañado	3	1	1.602
desechar	3	1	1.602
desafíos	3	1	1.602
derribar	3	1	1.602
demasiada	3	1	1.602
delgadas	3	1	1.602
déjela	3	1	1.602
decoroso	3	1	1.602
decoraciones	3	1	1.602
crónicas	3	1	1.602
crochet	3	1	1.602
creyente	3	1	1.602
creyéndose	3	1	1.602
cortesana	3	1	1.602
cortadas	3	1	1.602
coraza	3	1	1.602
convertirle	3	1	1.602
conversando	3	1	1.602
contratiempo	3	1	1.602
contrariedades	3	1	1.602
consolarla	3	1	1.602
consola	3	1	1.602
consienten	3	1	1.602
conquistado	3	1	1.602
conjeturas	3	1	1.602
confusas	3	1	1.602
conformes	3	1	1.602
confitería	3	1	1.602
conatos	3	1	1.602
complicado	3	1	1.602
complicadas	3	1	1.602
complacer	3	1	1.602
comodidades	3	1	1.602
colectiva	3	1	1.602
cofradía	3	1	1.602
código	3	1	1.602
codiciado	3	1	1.602
cobardía	3	1	1.602
cobardes	3	1	1.602
circunspecto	3	1	1.602
circunloquios	3	1	1.602
circo	3	1	1.602
chuzo	3	1	1.602
chispa	3	1	1.602
chiflado	3	1	1.602
cepillo	3	1	1.602
celebraban	3	1	1.602
cazaba	3	1	1.602
cayeron	3	1	1.602
causarle	3	1	1.602
casillas	3	1	1.602
carreras	3	1	1.602
cargos	3	1	1.602
caprichosa	3	1	1.602
capítulos	3	1	1.602
candidato	3	1	1.602
candeleros	3	1	1.602
candelas	3	1	1.602
campanarios	3	1	1.602
buscase	3	1	1.602
buscarte	3	1	1.602
bulliciosos	3	1	1.602
bucólica	3	1	1.602
bruscos	3	1	1.602
brusco	3	1	1.602
brotaban	3	1	1.602
bolsas	3	1	1.602
bolos	3	1	1.602
blanquecina	3	1	1.602
bíblico	3	1	1.602
bandadas	3	1	1.602
bailaba	3	1	1.602
ayudarla	3	1	1.602
avisado	3	1	1.602
avergonzó	3	1	1.602
aventurar	3	1	1.602
atacar	3	1	1.602
astucia	3	1	1.602
aspiración	3	1	1.602
asomos	3	1	1.602
asistiendo	3	1	1.602
ascensión	3	1	1.602
arreos	3	1	1.602
armonizar	3	1	1.602
armoniosa	3	1	1.602
apagaban	3	1	1.602
apaga	3	1	1.602
anunciado	3	1	1.602
análogos	3	1	1.602
anacleto	3	1	1.602
amigotes	3	1	1.602
ambicionar	3	1	1.602
amables	3	1	1.602
alentar	3	1	1.602
alcantarillas	3	1	1.602
alarmarse	3	1	1.602
alaridos	3	1	1.602
ajustar	3	1	1.602
aguardaba	3	1	1.602
afilados	3	1	1.602
advertido	3	1	1.602
adúltero	3	1	1.602
adonde	3	1	1.602
adivinado	3	1	1.602
acompañara	3	1	1.602
acogió	3	1	1.602
aclimatación	3	1	1.602
achacaba	3	1	1.602
acechaba	3	1	1.602
acataba	3	1	1.602
abuso	3	1	1.602
abono	3	1	1.602
primero	71	110	1.588
rodar	9	6	1.574
pierde	9	6	1.574
ocupaba	9	6	1.574
nieve	9	6	1.574
militar	9	6	1.574
invisible	9	6	1.574
huyendo	9	6	1.574
frescas	9	6	1.574
dominio	9	6	1.574
culpas	9	6	1.574
clavados	9	6	1.574
ceniza	9	6	1.574
celo	9	6	1.574
caro	9	6	1.574
aturdido	9	6	1.574
arquitectura	9	6	1.574
tomado	16	30	1.570
asiento	16	30	1.570
fuertes	21	18	1.566
esfuerzos	21	18	1.566
convenía	21	18	1.566
comedia	21	18	1.566
animal	21	18	1.566
sonrisa	34	32	1.560
cualquiera	34	32	1.560
exclamó	50	80	1.552
segundo	30	51	1.551
profundo	20	17	1.548
sarcasmo	10	7	1.533
ministra	10	7	1.533
hondo	10	7	1.533
francés	10	7	1.533
figurarse	10	7	1.533
fidelidad	10	7	1.533
echaban	10	7	1.533
cortar	10	7	1.533
apoyada	10	7	1.533
almohadas	10	7	1.533
abismo	10	7	1.533
reloj	33	31	1.532
diría	33	31	1.532
pueden	22	39	1.529
vaso	11	22	1.522
tratar	11	22	1.522
preguntas	11	22	1.522
formalidad	11	22	1.522
muerte	77	81	1.519
pueblos	18	15	1.517
llamado	18	15	1.517
estrellas	18	15	1.517
proponía	11	8	1.506
presa	11	8	1.506
inmediatamente	11	8	1.506
enfermedades	11	8	1.506
discreto	11	8	1.506
comisión	11	8	1.506
cargado	11	8	1.506
gas	17	14	1.504
visitas	32	30	1.503
lugar	32	30	1.503
premio	5	12	1.499
peseta	5	12	1.499
pedirle	5	12	1.499
parentesco	5	12	1.499
mirarla	5	12	1.499
leopoldo	5	12	1.499
extrañas	5	12	1.499
descompuesto	5	12	1.499
caracteres	5	12	1.499
arreglar	5	12	1.499
aceite	5	12	1.499
sermón	16	13	1.494
llorando	16	13	1.494
ejercicio	16	13	1.494
tarea	12	9	1.491
sana	12	9	1.491
penitencia	12	9	1.491
lámpara	12	9	1.491
ladrones	12	9	1.491
indiferencia	12	9	1.491
dulzura	12	9	1.491
cubierto	12	9	1.491
consideraba	12	9	1.491
ciega	12	9	1.491
acercándose	12	9	1.491
ventanas	15	12	1.487
pluma	15	12	1.487
moverse	15	12	1.487
cumplido	15	12	1.487
comían	15	12	1.487
cementerio	15	12	1.487
alrededor	15	12	1.487
vuelo	13	10	1.484
taberna	13	10	1.484
sencilla	13	10	1.484
negar	13	10	1.484
millones	13	10	1.484
mangas	13	10	1.484
conoció	13	10	1.484
castigo	13	10	1.484
terciopelo	14	11	1.483
robado	14	11	1.483
despedirse	14	11	1.483
descanso	14	11	1.483
aliento	14	11	1.483
ser	437	517	1.477
trance	8	17	1.471
trabajaba	8	17	1.471
regular	8	17	1.471
novedades	8	17	1.471
desgraciada	8	17	1.471
defensa	8	17	1.471
conocimiento	8	17	1.471
ciento	8	17	1.471
toca	13	25	1.468
cumplir	13	25	1.468
ánimo	48	48	1.462
alta	48	48	1.462
agua	104	113	1.455
viento	30	28	1.447
adiós	30	28	1.447
talento	29	49	1.431
mesa	94	141	1.428
viva	21	37	1.401
algo	321	448	1.398
tiros	4	10	1.387
temas	4	10	1.387
sirven	4	10	1.387
sabios	4	10	1.387
ratón	4	10	1.387
presenta	4	10	1.387
preguntarle	4	10	1.387
navidad	4	10	1.387
molestia	4	10	1.387
listo	4	10	1.387
grandísima	4	10	1.387
física	4	10	1.387
espero	4	10	1.387
escapó	4	10	1.387
encontrando	4	10	1.387
cobre	4	10	1.387
chaleco	4	10	1.387
acecho	4	10	1.387
dejo	10	20	1.384
máquina	27	25	1.363
imagen	27	25	1.363
veras	32	53	1.347
pobres	36	35	1.343
hacerse	26	24	1.336
viven	7	15	1.335
velo	7	15	1.335
tocando	7	15	1.335
té	7	15	1.335
suspiros	7	15	1.335
paño	7	15	1.335
modestia	7	15	1.335
facciones	7	15	1.335
desorden	7	15	1.335
ángeles	7	15	1.335
hecho	178	255	1.332
daría	12	23	1.331
cuentos	12	23	1.331
volver	73	111	1.316
seis	26	44	1.299
pasado	76	115	1.291
usan	3	8	1.290
unión	3	8	1.290
tos	3	8	1.290
tomaría	3	8	1.290
superiores	3	8	1.290
rompiendo	3	8	1.290
riéndose	3	8	1.290
rayas	3	8	1.290
permaneció	3	8	1.290
pasados	3	8	1.290
parroquiano	3	8	1.290
ojalá	3	8	1.290
observaciones	3	8	1.290
muestras	3	8	1.290
medir	3	8	1.290
maña	3	8	1.290
lúgubre	3	8	1.290
ignominia	3	8	1.290
hagamos	3	8	1.290
garbanzos	3	8	1.290
formar	3	8	1.290
extraños	3	8	1.290
estudiantes	3	8	1.290
empleo	3	8	1.290
edades	3	8	1.290
dejé	3	8	1.290
costado	3	8	1.290
corazones	3	8	1.290
conste	3	8	1.290
conformidad	3	8	1.290
competencia	3	8	1.290
clavos	3	8	1.290
cesto	3	8	1.290
centinela	3	8	1.290
buscarle	3	8	1.290
bomba	3	8	1.290
bárbaro	3	8	1.290
aragón	3	8	1.290
apartó	3	8	1.290
añadir	3	8	1.290
antipatía	3	8	1.290
americana	3	8	1.290
altares	3	8	1.290
lado	129	144	1.276
zapato	4	2	1.265
viudita	4	2	1.265
vidrios	4	2	1.265
vacante	4	2	1.265
trovador	4	2	1.265
trote	4	2	1.265
troncos	4	2	1.265
trechos	4	2	1.265
tórtola	4	2	1.265
terrenos	4	2	1.265
tenacidad	4	2	1.265
telégrafo	4	2	1.265
tabaco	4	2	1.265
subo	4	2	1.265
solitarias	4	2	1.265
solicitud	4	2	1.265
sobrinita	4	2	1.265
siniestro	4	2	1.265
sepultura	4	2	1.265
señalar	4	2	1.265
sentirlo	4	2	1.265
seculares	4	2	1.265
saludaban	4	2	1.265
salmón	4	2	1.265
saldré	4	2	1.265
sacerdocio	4	2	1.265
rizado	4	2	1.265
rigores	4	2	1.265
rienda	4	2	1.265
ríen	4	2	1.265
reyertas	4	2	1.265
revela	4	2	1.265
responde	4	2	1.265
reconoce	4	2	1.265
quemaba	4	2	1.265
quema	4	2	1.265
quejido	4	2	1.265
quebraderos	4	2	1.265
puñaladas	4	2	1.265
probables	4	2	1.265
princesa	4	2	1.265
preparación	4	2	1.265
pórtico	4	2	1.265
plebeyo	4	2	1.265
plebe	4	2	1.265
plática	4	2	1.265
perpetua	4	2	1.265
perilla	4	2	1.265
panorama	4	2	1.265
optimismo	4	2	1.265
ochavo	4	2	1.265
occidente	4	2	1.265
obliga	4	2	1.265
noé	4	2	1.265
necesarias	4	2	1.265
mortales	4	2	1.265
moradas	4	2	1.265
miramientos	4	2	1.265
mimado	4	2	1.265
metálica	4	2	1.265
masas	4	2	1.265
madrileño	4	2	1.265
lucirse	4	2	1.265
llame	4	2	1.265
linterna	4	2	1.265
latidos	4	2	1.265
juntando	4	2	1.265
invitado	4	2	1.265
inventado	4	2	1.265
intachable	4	2	1.265
indiscreción	4	2	1.265
inclinado	4	2	1.265
iluminada	4	2	1.265
ignorante	4	2	1.265
humillado	4	2	1.265
honestas	4	2	1.265
heroína	4	2	1.265
heroico	4	2	1.265
helado	4	2	1.265
hablillas	4	2	1.265
hablé	4	2	1.265
guisa	4	2	1.265
guiñaba	4	2	1.265
gruesos	4	2	1.265
grados	4	2	1.265
gastado	4	2	1.265
fumar	4	2	1.265
fuegos	4	2	1.265
fruta	4	2	1.265
fausto	4	2	1.265
fantásticos	4	2	1.265
explicarlo	4	2	1.265
expedición	4	2	1.265
expansiones	4	2	1.265
exclamar	4	2	1.265
estribos	4	2	1.265
estreno	4	2	1.265
estallar	4	2	1.265
eses	4	2	1.265
escondidas	4	2	1.265
escaso	4	2	1.265
enteros	4	2	1.265
entendemos	4	2	1.265
encendían	4	2	1.265
enamorados	4	2	1.265
empleó	4	2	1.265
elevarse	4	2	1.265
elevar	4	2	1.265
divertían	4	2	1.265
distinguido	4	2	1.265
disgustado	4	2	1.265
discusiones	4	2	1.265
disciplinas	4	2	1.265
directa	4	2	1.265
dimisión	4	2	1.265
diluvio	4	2	1.265
descrédito	4	2	1.265
descender	4	2	1.265
dejará	4	2	1.265
dejamos	4	2	1.265
degradación	4	2	1.265
defendían	4	2	1.265
decorosa	4	2	1.265
cubiertas	4	2	1.265
convidar	4	2	1.265
convenció	4	2	1.265
considerable	4	2	1.265
conservado	4	2	1.265
consagraba	4	2	1.265
confundían	4	2	1.265
condena	4	2	1.265
compuesto	4	2	1.265
complacencia	4	2	1.265
cometer	4	2	1.265
colección	4	2	1.265
cocinas	4	2	1.265
chusma	4	2	1.265
chaqueta	4	2	1.265
causado	4	2	1.265
catalán	4	2	1.265
castellano	4	2	1.265
casaban	4	2	1.265
casaba	4	2	1.265
cartón	4	2	1.265
caracol	4	2	1.265
cantan	4	2	1.265
brutales	4	2	1.265
brotar	4	2	1.265
borrachera	4	2	1.265
atormentaban	4	2	1.265
aprovechó	4	2	1.265
apoyándose	4	2	1.265
ancianos	4	2	1.265
alejaban	4	2	1.265
agrada	4	2	1.265
afectación	4	2	1.265
admirada	4	2	1.265
adivinó	4	2	1.265
acusado	4	2	1.265
acostaba	4	2	1.265
absurdas	4	2	1.265
xii	1	4	1.262
vulgaridad	1	4	1.262
volverla	1	4	1.262
vivirá	1	4	1.262
vísperas	1	4	1.262
viruelas	1	4	1.262
viñas	1	4	1.262
viniendo	1	4	1.262
víbora	1	4	1.262
ventanillo	1	4	1.262
vena	1	4	1.262
velocidad	1	4	1.262
vastísimo	1	4	1.262
vástago	1	4	1.262
valían	1	4	1.262
usté	1	4	1.262
tute	1	4	1.262
túnel	1	4	1.262
trono	1	4	1.262
tronar	1	4	1.262
tristemente	1	4	1.262
transijo	1	4	1.262
transacción	1	4	1.262
traída	1	4	1.262
toro	1	4	1.262
tomé	1	4	1.262
tomarla	1	4	1.262
terminantemente	1	4	1.262
teorías	1	4	1.262
tenaz	1	4	1.262
tareas	1	4	1.262
tapó	1	4	1.262
tapias	1	4	1.262
tapándose	1	4	1.262
tacón	1	4	1.262
sudar	1	4	1.262
sosegado	1	4	1.262
soltero	1	4	1.262
socorros	1	4	1.262
sobremesa	1	4	1.262
sobras	1	4	1.262
sirves	1	4	1.262
simpatías	1	4	1.262
símbolos	1	4	1.262
sillares	1	4	1.262
siguiera	1	4	1.262
secretario	1	4	1.262
sebastián	1	4	1.262
sabroso	1	4	1.262
sabrosas	1	4	1.262
rotos	1	4	1.262
riñas	1	4	1.262
rezos	1	4	1.262
retroceso	1	4	1.262
retintín	1	4	1.262
res	1	4	1.262
reposado	1	4	1.262
remate	1	4	1.262
relajación	1	4	1.262
refiere	1	4	1.262
reducida	1	4	1.262
recreándose	1	4	1.262
reclama	1	4	1.262
recibiera	1	4	1.262
recibí	1	4	1.262
recetas	1	4	1.262
receta	1	4	1.262
recelosa	1	4	1.262
quisieras	1	4	1.262
quid	1	4	1.262
quejumbrosa	1	4	1.262
quejándose	1	4	1.262
quedó	54	84	1.262
pusiese	1	4	1.262
profundísima	1	4	1.262
prevención	1	4	1.262
portó	1	4	1.262
permitiera	1	4	1.262
perdulario	1	4	1.262
penoso	1	4	1.262
penetrante	1	4	1.262
pellejo	1	4	1.262
pegan	1	4	1.262
pegados	1	4	1.262
pecadoras	1	4	1.262
pasmaba	1	4	1.262
pasajes	1	4	1.262
pagado	1	4	1.262
orillo	1	4	1.262
orígenes	1	4	1.262
ordenaba	1	4	1.262
olvides	1	4	1.262
olvida	1	4	1.262
olé	1	4	1.262
oírlo	1	4	1.262
ofrecieron	1	4	1.262
nombró	1	4	1.262
nidos	1	4	1.262
nacimientos	1	4	1.262
mueren	1	4	1.262
moviéndose	1	4	1.262
moralmente	1	4	1.262
mocosos	1	4	1.262
mimo	1	4	1.262
mequetrefe	1	4	1.262
mentalmente	1	4	1.262
mensual	1	4	1.262
menesteres	1	4	1.262
meditabunda	1	4	1.262
maravillosa	1	4	1.262
maquinalmente	1	4	1.262
manifestaciones	1	4	1.262
maniática	1	4	1.262
mandarla	1	4	1.262
mandando	1	4	1.262
maná	1	4	1.262
majo	1	4	1.262
lúgubres	1	4	1.262
loza	1	4	1.262
lograba	1	4	1.262
limpiándose	1	4	1.262
limón	1	4	1.262
labrado	1	4	1.262
juncos	1	4	1.262
jovialidad	1	4	1.262
jamón	1	4	1.262
islas	1	4	1.262
intranquilo	1	4	1.262
intranquila	1	4	1.262
instantánea	1	4	1.262
insinuó	1	4	1.262
ingenua	1	4	1.262
inflexiones	1	4	1.262
inferiores	1	4	1.262
incomodada	1	4	1.262
impedirlo	1	4	1.262
imaginarse	1	4	1.262
iluminados	1	4	1.262
humorístico	1	4	1.262
honradamente	1	4	1.262
habré	1	4	1.262
guiñando	1	4	1.262
guarde	1	4	1.262
guardas	1	4	1.262
guardaré	1	4	1.262
grecia	1	4	1.262
grandioso	1	4	1.262
graciosas	1	4	1.262
galera	1	4	1.262
fundó	1	4	1.262
fuéramos	1	4	1.262
fragancia	1	4	1.262
firmado	1	4	1.262
figuro	1	4	1.262
fechas	1	4	1.262
fealdad	1	4	1.262
favorables	1	4	1.262
familiaridad	1	4	1.262
extrañaba	1	4	1.262
extiende	1	4	1.262
explosión	1	4	1.262
explico	1	4	1.262
existen	1	4	1.262
exclamación	1	4	1.262
estuviste	1	4	1.262
estanque	1	4	1.262
espartero	1	4	1.262
españolas	1	4	1.262
espaciosa	1	4	1.262
equivocada	1	4	1.262
entendida	1	4	1.262
engañando	1	4	1.262
enfadada	1	4	1.262
enfada	1	4	1.262
encaró	1	4	1.262
empleos	1	4	1.262
empleando	1	4	1.262
emperador	1	4	1.262
echas	1	4	1.262
displicencia	1	4	1.262
diciéndome	1	4	1.262
dichos	1	4	1.262
desvelada	1	4	1.262
desprenderse	1	4	1.262
despidiéndose	1	4	1.262
despejada	1	4	1.262
despachaba	1	4	1.262
deshora	1	4	1.262
deshonrada	1	4	1.262
descubría	1	4	1.262
desconcierto	1	4	1.262
descomponiéndose	1	4	1.262
desatinos	1	4	1.262
desaparecieron	1	4	1.262
defiende	1	4	1.262
decoración	1	4	1.262
declaro	1	4	1.262
darlos	1	4	1.262
damos	1	4	1.262
curita	1	4	1.262
cuchufletas	1	4	1.262
cucharilla	1	4	1.262
cucharada	1	4	1.262
crudos	1	4	1.262
creerán	1	4	1.262
correspondían	1	4	1.262
corra	1	4	1.262
coplas	1	4	1.262
convenientes	1	4	1.262
contrarios	1	4	1.262
contestarle	1	4	1.262
consorte	1	4	1.262
conocieron	1	4	1.262
conociera	1	4	1.262
comprometo	1	4	1.262
compostura	1	4	1.262
combinadas	1	4	1.262
colgados	1	4	1.262
circunstancia	1	4	1.262
chillonas	1	4	1.262
céntimos	1	4	1.262
celebraron	1	4	1.262
caserío	1	4	1.262
capirotes	1	4	1.262
cantero	1	4	1.262
cantera	1	4	1.262
cansaba	1	4	1.262
camelias	1	4	1.262
caes	1	4	1.262
cadáveres	1	4	1.262
bicho	1	4	1.262
averiguarlo	1	4	1.262
avariento	1	4	1.262
avanzando	1	4	1.262
ausencias	1	4	1.262
ató	1	4	1.262
aspereza	1	4	1.262
áspera	1	4	1.262
arreglos	1	4	1.262
arrancarse	1	4	1.262
aprenderá	1	4	1.262
apatía	1	4	1.262
antón	1	4	1.262
antipáticos	1	4	1.262
angosta	1	4	1.262
amplitud	1	4	1.262
alfileres	1	4	1.262
alcanzaba	1	4	1.262
alborotado	1	4	1.262
ala	1	4	1.262
airosa	1	4	1.262
agujerito	1	4	1.262
afligido	1	4	1.262
afectuoso	1	4	1.262
adúlteros	1	4	1.262
aduana	1	4	1.262
acompañaré	1	4	1.262
acompañadas	1	4	1.262
acertar	1	4	1.262
acentos	1	4	1.262
acecha	1	4	1.262
acalorada	1	4	1.262
acabaría	1	4	1.262
abren	1	4	1.262
estaría	23	21	1.255
debilidad	23	21	1.255
callar	23	21	1.255
suavemente	9	18	1.245
soberbia	9	18	1.245
observación	9	18	1.245
bajar	9	18	1.245
acuerdas	9	18	1.245
abajo	73	78	1.230
vieras	2	6	1.226
viéndose	2	6	1.226
verlos	2	6	1.226
vayan	2	6	1.226
tranquilizó	2	6	1.226
tomas	2	6	1.226
tomarle	2	6	1.226
tez	2	6	1.226
tablero	2	6	1.226
sospechando	2	6	1.226
sentadas	2	6	1.226
saqué	2	6	1.226
rezo	2	6	1.226
revolvía	2	6	1.226
respaldo	2	6	1.226
repartir	2	6	1.226
reparó	2	6	1.226
relativamente	2	6	1.226
reglas	2	6	1.226
recomendado	2	6	1.226
recobró	2	6	1.226
recibe	2	6	1.226
realizar	2	6	1.226
quitarse	2	6	1.226
quede	2	6	1.226
quedará	2	6	1.226
quedando	2	6	1.226
puestas	2	6	1.226
prepararse	2	6	1.226
papas	2	6	1.226
oyéndole	2	6	1.226
obedeciendo	2	6	1.226
niegue	2	6	1.226
narrador	2	6	1.226
mirándose	2	6	1.226
mimos	2	6	1.226
mamarracho	2	6	1.226
llavín	2	6	1.226
legítimo	2	6	1.226
jugado	2	6	1.226
instrucción	2	6	1.226
infaliblemente	2	6	1.226
humanos	2	6	1.226
hables	2	6	1.226
hablarte	2	6	1.226
gustar	2	6	1.226
golosa	2	6	1.226
fórmulas	2	6	1.226
fijas	2	6	1.226
felipe	2	6	1.226
fatigada	2	6	1.226
ésta	2	6	1.226
enteró	2	6	1.226
enero	2	6	1.226
encendidos	2	6	1.226
eléctrico	2	6	1.226
culebra	2	6	1.226
cuerdas	2	6	1.226
creería	2	6	1.226
créame	2	6	1.226
cortó	2	6	1.226
cortes	2	6	1.226
constantemente	2	6	1.226
compuesta	2	6	1.226
comes	2	6	1.226
coloquio	2	6	1.226
cocido	2	6	1.226
célebres	2	6	1.226
causas	2	6	1.226
caudal	2	6	1.226
canonjía	2	6	1.226
caen	2	6	1.226
cabellera	2	6	1.226
bullicio	2	6	1.226
base	2	6	1.226
aparentar	2	6	1.226
anunció	2	6	1.226
anunciando	2	6	1.226
alargaba	2	6	1.226
alambre	2	6	1.226
agradezco	2	6	1.226
agradecer	2	6	1.226
abuela	2	6	1.226
amigos	75	113	1.207
intención	21	19	1.204
fresca	21	19	1.204
antigua	21	19	1.204
traían	6	13	1.200
talle	6	13	1.200
subiendo	6	13	1.200
pícara	6	13	1.200
metal	6	13	1.200
estuvieran	6	13	1.200
enorme	6	13	1.200
conservaba	6	13	1.200
arranque	6	13	1.200
convento	27	45	1.196
noches	53	55	1.188
correr	39	39	1.188
despertar	20	18	1.178
sola	73	110	1.176
hacía	234	272	1.173
vivir	63	96	1.166
narices	13	24	1.165
guerra	13	24	1.165
expresión	41	65	1.165
movimiento	21	36	1.155
zurcidor	0	1	1.154
zumo	0	1	1.154
zumbón	0	1	1.154
zumban	0	1	1.154
zozobras	0	1	1.154
zote	0	1	1.154
zoquetes	0	1	1.154
zoquete	0	1	1.154
zopencos	0	1	1.154
zarzal	0	1	1.154
zarandearse	0	1	1.154
zarandean	0	1	1.154
zaragüelles	0	1	1.154
zapatito	0	1	1.154
zapatetas	0	1	1.154
zapateado	0	1	1.154
zapatas	0	1	1.154
zanahorias	0	1	1.154
zampo	0	1	1.154
zampado	0	1	1.154
zampa	0	1	1.154
zamoranos	0	1	1.154
zambullida	0	1	1.154
zambombazos	0	1	1.154
zamarras	0	1	1.154
zaleas	0	1	1.154
zalea	0	1	1.154
zalamera	0	1	1.154
zahúrdas	0	1	1.154
zahorí	0	1	1.154
zagalote	0	1	1.154
zagalón	0	1	1.154
zafiote	0	1	1.154
zafias	0	1	1.154
zafia	0	1	1.154
zafarme	0	1	1.154
zacarías	0	1	1.154
yesos	0	1	1.154
yeserías	0	1	1.154
yerra	0	1	1.154
yernos	0	1	1.154
yermo	0	1	1.154
yéndome	0	1	1.154
yacen	0	1	1.154
wellington	0	1	1.154
walses	0	1	1.154
vulgarote	0	1	1.154
vueltecita	0	1	1.154
vuelco	0	1	1.154
vuelan	0	1	1.154
vu	0	1	1.154
votantes	0	1	1.154
votando	0	1	1.154
vómito	0	1	1.154
vomitivos	0	1	1.154
volviole	0	1	1.154
volvime	0	1	1.154
volviesen	0	1	1.154
volviéronle	0	1	1.154
volviéndolos	0	1	1.154
volviéndoles	0	1	1.154
volvíale	0	1	1.154
volverte	0	1	1.154
volverle	0	1	1.154
volvámonos	0	1	1.154
voluntariosa	0	1	1.154
voluntarios	0	1	1.154
voluntaria	0	1	1.154
voluminosa	0	1	1.154
voluble	0	1	1.154
volteo	0	1	1.154
volteando	0	1	1.154
volé	0	1	1.154
volcó	0	1	1.154
volcara	0	1	1.154
volcar	0	1	1.154
volcado	0	1	1.154
volatines	0	1	1.154
volátil	0	1	1.154
volandas	0	1	1.154
voladora	0	1	1.154
vocerío	0	1	1.154
vocecilla	0	1	1.154
vocear	0	1	1.154
vivito	0	1	1.154
vivísimas	0	1	1.154
vivís	0	1	1.154
vivirías	0	1	1.154
vivirían	0	1	1.154
viviría	0	1	1.154
vivieras	0	1	1.154
vivieran	0	1	1.154
vivíamos	0	1	1.154
vivaaa	0	1	1.154
viudos	0	1	1.154
vitalicio	0	1	1.154
vistiose	0	1	1.154
vistillas	0	1	1.154
vistiese	0	1	1.154
vistiéndolo	0	1	1.154
vistiéndola	0	1	1.154
vistes	0	1	1.154
visten	0	1	1.154
vislumbran	0	1	1.154
visito	0	1	1.154
visítela	0	1	1.154
visitase	0	1	1.154
visitaron	0	1	1.154
visitarme	0	1	1.154
visitante	0	1	1.154
visitándola	0	1	1.154
visitando	0	1	1.154
visitada	0	1	1.154
visionario	0	1	1.154
visillos	0	1	1.154
visibles	0	1	1.154
virutas	0	1	1.154
virus	0	1	1.154
viruela	0	1	1.154
virosos	0	1	1.154
viró	0	1	1.154
vírgulas	0	1	1.154
violo	0	1	1.154
violentó	0	1	1.154
violentísimas	0	1	1.154
violentarse	0	1	1.154
violados	0	1	1.154
violadas	0	1	1.154
vinosas	0	1	1.154
viniéronle	0	1	1.154
vinieras	0	1	1.154
vindicta	0	1	1.154
vínculo	0	1	1.154
vinazo	0	1	1.154
vinateros	0	1	1.154
villaviciosa	0	1	1.154
villas	0	1	1.154
villarreal	0	1	1.154
villahermosa	0	1	1.154
vigorizó	0	1	1.154
vigorizan	0	1	1.154
vigorización	0	1	1.154
vigorizaba	0	1	1.154
vigilase	0	1	1.154
vigilarlas	0	1	1.154
vigilantes	0	1	1.154
vigilante	0	1	1.154
vigilando	0	1	1.154
vigilado	0	1	1.154
vigilada	0	1	1.154
vigía	0	1	1.154
vigente	0	1	1.154
vierte	0	1	1.154
viéronse	0	1	1.154
vierais	0	1	1.154
viente	0	1	1.154
viéndoselo	0	1	1.154
viéndome	0	1	1.154
viéndolo	0	1	1.154
viéndoles	0	1	1.154
viejona	0	1	1.154
viejecillos	0	1	1.154
vidita	0	1	1.154
victorioso	0	1	1.154
viciosote	0	1	1.154
viciosonas	0	1	1.154
viciosas	0	1	1.154
viciado	0	1	1.154
vicaría	0	1	1.154
vibró	0	1	1.154
vibratorio	0	1	1.154
víboras	0	1	1.154
viana	0	1	1.154
viajecito	0	1	1.154
viabilidad	0	1	1.154
via	0	1	1.154
vetustos	0	1	1.154
veto	0	1	1.154
vestiglo	0	1	1.154
vestigio	0	1	1.154
vestidito	0	1	1.154
vestidita	0	1	1.154
vertidas	0	1	1.154
vértice	0	1	1.154
verter	0	1	1.154
versiones	0	1	1.154
verruguita	0	1	1.154
vernet	0	1	1.154
verificaría	0	1	1.154
verifican	0	1	1.154
verificada	0	1	1.154
verificábase	0	1	1.154
verídicas	0	1	1.154
verías	0	1	1.154
veríais	0	1	1.154
verduras	0	1	1.154
verdulera	0	1	1.154
verdoso	0	1	1.154
verdosa	0	1	1.154
verdor	0	1	1.154
verbales	0	1	1.154
verba	0	1	1.154
veraz	0	1	1.154
veranear	0	1	1.154
veracidad	0	1	1.154
vera	0	1	1.154
venturosa	0	1	1.154
ventosa	0	1	1.154
ventorrillo	0	1	1.154
ventilara	0	1	1.154
ventilados	0	1	1.154
ventanuchos	0	1	1.154
ventanucha	0	1	1.154
ventajoso	0	1	1.154
venís	0	1	1.154
venirte	0	1	1.154
venirme	0	1	1.154
venideros	0	1	1.154
venialmente	0	1	1.154
vengativos	0	1	1.154
véngase	0	1	1.154
venerandas	0	1	1.154
venerado	0	1	1.154
veneradas	0	1	1.154
venera	0	1	1.154
venenosas	0	1	1.154
venenosa	0	1	1.154
vendiéndolos	0	1	1.154
vendidos	0	1	1.154
vendíalos	0	1	1.154
vendí	0	1	1.154
vendes	0	1	1.154
venderle	0	1	1.154
venderla	0	1	1.154
venderían	0	1	1.154
vendehumos	0	1	1.154
vencimiento	0	1	1.154
vencerlo	0	1	1.154
vencerá	0	1	1.154
velito	0	1	1.154
velitas	0	1	1.154
veletas	0	1	1.154
velaría	0	1	1.154
velaremos	0	1	1.154
velándosele	0	1	1.154
veladores	0	1	1.154
velaban	0	1	1.154
vejeces	0	1	1.154
veintiuno	0	1	1.154
veintiocho	0	1	1.154
veíalos	0	1	1.154
vegetativa	0	1	1.154
veee	0	1	1.154
vedlo	0	1	1.154
vedlas	0	1	1.154
vedan	0	1	1.154
vecindades	0	1	1.154
veámoslo	0	1	1.154
véalo	0	1	1.154
váyanse	0	1	1.154
vaticinó	0	1	1.154
vaticinios	0	1	1.154
vaticinar	0	1	1.154
vaticinan	0	1	1.154
vaticinaba	0	1	1.154
vasto	0	1	1.154
vasta	0	1	1.154
vasito	0	1	1.154
vasijas	0	1	1.154
vascongadas	0	1	1.154
vasco	0	1	1.154
varoncitos	0	1	1.154
varitas	0	1	1.154
varita	0	1	1.154
varisis	0	1	1.154
varió	0	1	1.154
variarle	0	1	1.154
variaran	0	1	1.154
vargueño	0	1	1.154
vareo	0	1	1.154
vareando	0	1	1.154
vaqueta	0	1	1.154
vapulean	0	1	1.154
vaporcito	0	1	1.154
vanaglorió	0	1	1.154
vampiros	0	1	1.154
valores	0	1	1.154
valoraciones	0	1	1.154
vallehermoso	0	1	1.154
valledor	0	1	1.154
vallecas	0	1	1.154
valioso	0	1	1.154
valimiento	0	1	1.154
válida	0	1	1.154
valgo	0	1	1.154
válganos	0	1	1.154
valgamos	0	1	1.154
valerte	0	1	1.154
valeriana	0	1	1.154
valenciennes	0	1	1.154
vaho	0	1	1.154
vagones	0	1	1.154
vagancia	0	1	1.154
vagabundos	0	1	1.154
vagaba	0	1	1.154
vadita	0	1	1.154
vacuna	0	1	1.154
vació	0	1	1.154
vacilo	0	1	1.154
vacilaron	0	1	1.154
vacilará	0	1	1.154
vaciaba	0	1	1.154
utilísimas	0	1	1.154
usurparle	0	1	1.154
usurpan	0	1	1.154
usurpación	0	1	1.154
usureros	0	1	1.154
usurera	0	1	1.154
usurarias	0	1	1.154
usuraria	0	1	1.154
usufructuaria	0	1	1.154
usufructo	0	1	1.154
ustés	0	1	1.154
usó	0	1	1.154
usaré	0	1	1.154
uribe	0	1	1.154
urgía	0	1	1.154
urgentes	0	1	1.154
urgencia	0	1	1.154
urdimbres	0	1	1.154
urdidas	0	1	1.154
urbanas	0	1	1.154
untado	0	1	1.154
untada	0	1	1.154
universitario	0	1	1.154
uniste	0	1	1.154
unirte	0	1	1.154
unirles	0	1	1.154
uniones	0	1	1.154
uniformidad	0	1	1.154
uniformes	0	1	1.154
uniformados	0	1	1.154
unicornio	0	1	1.154
únicas	0	1	1.154
uníanse	0	1	1.154
unían	0	1	1.154
ungüento	0	1	1.154
ungidas	0	1	1.154
unen	0	1	1.154
ultratumba	0	1	1.154
ultramarinos	0	1	1.154
úlceras	0	1	1.154
ujeros	0	1	1.154
ujeritos	0	1	1.154
úes	0	1	1.154
ubre	0	1	1.154
tuyos	0	1	1.154
tuviéronle	0	1	1.154
tuviéronla	0	1	1.154
tutora	0	1	1.154
tutearle	0	1	1.154
tuteándose	0	1	1.154
tuteándola	0	1	1.154
tutea	0	1	1.154
tururú	0	1	1.154
turulatos	0	1	1.154
turulato	0	1	1.154
turrones	0	1	1.154
turquí	0	1	1.154
turégano	0	1	1.154
turca	0	1	1.154
turbulenta	0	1	1.154
turbose	0	1	1.154
turbo	0	1	1.154
turbia	0	1	1.154
turbadísima	0	1	1.154
turbaban	0	1	1.154
turbábala	0	1	1.154
tundiéndole	0	1	1.154
tunanterías	0	1	1.154
tunantas	0	1	1.154
tuna	0	1	1.154
tumultuoso	0	1	1.154
tumbaba	0	1	1.154
tullerías	0	1	1.154
tuétano	0	1	1.154
tubería	0	1	1.154
truncadas	0	1	1.154
truncada	0	1	1.154
trujillesca	0	1	1.154
trujillas	0	1	1.154
truhán	0	1	1.154
trufas	0	1	1.154
trueque	0	1	1.154
truena	0	1	1.154
truchimán	0	1	1.154
tropiezos	0	1	1.154
tronó	0	1	1.154
tronchos	0	1	1.154
tronaron	0	1	1.154
trompo	0	1	1.154
trompetitas	0	1	1.154
trompetillas	0	1	1.154
trompazos	0	1	1.154
trompadas	0	1	1.154
trofeos	0	1	1.154
trocase	0	1	1.154
trocaran	0	1	1.154
trocara	0	1	1.154
trocar	0	1	1.154
trocábase	0	1	1.154
trocaban	0	1	1.154
trizas	0	1	1.154
triunfase	0	1	1.154
triunfara	0	1	1.154
trituro	0	1	1.154
triturada	0	1	1.154
tristísimos	0	1	1.154
tris	0	1	1.154
triquiñuela	0	1	1.154
tripudas	0	1	1.154
trípode	0	1	1.154
tripicallero	0	1	1.154
trinquis	0	1	1.154
trinquen	0	1	1.154
trinco	0	1	1.154
trincaron	0	1	1.154
trincan	0	1	1.154
trinca	0	1	1.154
trinan	0	1	1.154
trimestres	0	1	1.154
trigos	0	1	1.154
trifulcas	0	1	1.154
tribuna	0	1	1.154
triana	0	1	1.154
treta	0	1	1.154
trescientos	0	1	1.154
trescientas	0	1	1.154
trepadora	0	1	1.154
trenes	0	1	1.154
trencilla	0	1	1.154
tremens	0	1	1.154
trebejos	0	1	1.154
trazo	0	1	1.154
trazáronla	0	1	1.154
trazarle	0	1	1.154
trazando	0	1	1.154
trazados	0	1	1.154
trazadas	0	1	1.154
trayéndole	0	1	1.154
trayéndola	0	1	1.154
traviesos	0	1	1.154
traviatta	0	1	1.154
traviatonas	0	1	1.154
travesía	0	1	1.154
tratose	0	1	1.154
trátele	0	1	1.154
tratas	0	1	1.154
tratáronse	0	1	1.154
tratarnos	0	1	1.154
tratarlos	0	1	1.154
trataremos	0	1	1.154
tratándoles	0	1	1.154
tratándola	0	1	1.154
tratamientos	0	1	1.154
trátame	0	1	1.154
tratadistas	0	1	1.154
tratadas	0	1	1.154
tratábase	0	1	1.154
tratábame	0	1	1.154
tratábala	0	1	1.154
trastornarle	0	1	1.154
trastornadas	0	1	1.154
trastornaban	0	1	1.154
trastocar	0	1	1.154
trastea	0	1	1.154
trastazos	0	1	1.154
trasquilase	0	1	1.154
traspiés	0	1	1.154
traspié	0	1	1.154
traspasó	0	1	1.154
traspasándole	0	1	1.154
traspasando	0	1	1.154
traspasan	0	1	1.154
traspasaban	0	1	1.154
trasmitiendo	0	1	1.154
traslucirse	0	1	1.154
trasladándola	0	1	1.154
trasladando	0	1	1.154
trasladada	0	1	1.154
traslación	0	1	1.154
trasegarlo	0	1	1.154
trascienden	0	1	1.154
trap	0	1	1.154
transparentado	0	1	1.154
transparencia	0	1	1.154
transmitirlo	0	1	1.154
transmitir	0	1	1.154
transmitió	0	1	1.154
transmitiendo	0	1	1.154
transmitía	0	1	1.154
transmiten	0	1	1.154
transmite	0	1	1.154
transmigrar	0	1	1.154
transmigraban	0	1	1.154
tránsitos	0	1	1.154
transigiendo	0	1	1.154
transigido	0	1	1.154
transigían	0	1	1.154
transiciones	0	1	1.154
transforme	0	1	1.154
transformar	0	1	1.154
transformándose	0	1	1.154
transformaban	0	1	1.154
transforma	0	1	1.154
transfiguraciones	0	1	1.154
transfiguraba	0	1	1.154
transcurso	0	1	1.154
transcurrió	0	1	1.154
transcurrían	0	1	1.154
tranquilizarle	0	1	1.154
tranquilizaré	0	1	1.154
tranquilizándose	0	1	1.154
tranquilizándola	0	1	1.154
tranquilizando	0	1	1.154
tranquilizadora	0	1	1.154
tranquilizador	0	1	1.154
tranquilices	0	1	1.154
trancazo	0	1	1.154
tranca	0	1	1.154
tramposos	0	1	1.154
trámites	0	1	1.154
trajiste	0	1	1.154
trajines	0	1	1.154
trajineros	0	1	1.154
trajesen	0	1	1.154
trajéronle	0	1	1.154
trajerais	0	1	1.154
tráiganos	0	1	1.154
tráigamela	0	1	1.154
tráigala	0	1	1.154
traicioneros	0	1	1.154
traíanla	0	1	1.154
trague	0	1	1.154
tragón	0	1	1.154
tragicómicos	0	1	1.154
tragándose	0	1	1.154
tragándole	0	1	1.154
tragan	0	1	1.154
tragaluz	0	1	1.154
tragadero	0	1	1.154
tragacanto	0	1	1.154
tragábamos	0	1	1.154
traga	0	1	1.154
traficante	0	1	1.154
trafalgar	0	1	1.154
tráetelo	0	1	1.154
traerte	0	1	1.154
traerse	0	1	1.154
traérnosle	0	1	1.154
traerlas	0	1	1.154
traerán	0	1	1.154
tráele	0	1	1.154
tradújose	0	1	1.154
traducirse	0	1	1.154
traducirla	0	1	1.154
traducía	0	1	1.154
trabucazos	0	1	1.154
trabucan	0	1	1.154
trabó	0	1	1.154
trabase	0	1	1.154
trabándose	0	1	1.154
trabajosamente	0	1	1.154
trabajillos	0	1	1.154
trabajes	0	1	1.154
trabajarla	0	1	1.154
trabajaría	0	1	1.154
trabájalo	0	1	1.154
trabajadoras	0	1	1.154
trabado	0	1	1.154
trababa	0	1	1.154
tóxicos	0	1	1.154
toxicación	0	1	1.154
totalmente	0	1	1.154
tostadita	0	1	1.154
tostaba	0	1	1.154
tosquedad	0	1	1.154
toso	0	1	1.154
tose	0	1	1.154
toscos	0	1	1.154
torzales	0	1	1.154
torvamente	0	1	1.154
tortuoso	0	1	1.154
tórtolos	0	1	1.154
tortolitos	0	1	1.154
tortoleo	0	1	1.154
tortillita	0	1	1.154
torrero	0	1	1.154
torreón	0	1	1.154
torrellas	0	1	1.154
torniquete	0	1	1.154
tornillándola	0	1	1.154
torneo	0	1	1.154
torneando	0	1	1.154
torneadita	0	1	1.154
tornasol	0	1	1.154
tornas	0	1	1.154
torna	0	1	1.154
toril	0	1	1.154
toreado	0	1	1.154
toreaba	0	1	1.154
torcerse	0	1	1.154
torceduras	0	1	1.154
tórax	0	1	1.154
torácica	0	1	1.154
toquen	0	1	1.154
toquéis	0	1	1.154
toquecito	0	1	1.154
topar	0	1	1.154
topacio	0	1	1.154
tontuna	0	1	1.154
tontita	0	1	1.154
tontees	0	1	1.154
tonteando	0	1	1.154
tontadas	0	1	1.154
tonsurados	0	1	1.154
tonito	0	1	1.154
tónicos	0	1	1.154
tónica	0	1	1.154
tomole	0	1	1.154
tomola	0	1	1.154
tomemos	0	1	1.154
toméis	0	1	1.154
tómbola	0	1	1.154
tomazo	0	1	1.154
tomates	0	1	1.154
tomarnos	0	1	1.154
tomarlas	0	1	1.154
tomarían	0	1	1.154
tomaríale	0	1	1.154
tomaremos	0	1	1.154
tomáramos	0	1	1.154
tomamos	0	1	1.154
tomáis	0	1	1.154
tomador	0	1	1.154
tomábase	0	1	1.154
tomábala	0	1	1.154
tolú	0	1	1.154
tolosa	0	1	1.154
tolondrón	0	1	1.154
tollina	0	1	1.154
tolerancias	0	1	1.154
toledano	0	1	1.154
toilette	0	1	1.154
toco	0	1	1.154
tocati	0	1	1.154
tocarme	0	1	1.154
tocarlo	0	1	1.154
tocarían	0	1	1.154
tocaría	0	1	1.154
tocaré	0	1	1.154
tocaran	0	1	1.154
tocándoles	0	1	1.154
tocados	0	1	1.154
tocábamos	0	1	1.154
toallas	0	1	1.154
tizona	0	1	1.154
tiznando	0	1	1.154
títulas	0	1	1.154
titubeando	0	1	1.154
titubeaba	0	1	1.154
tirotearse	0	1	1.154
tiritos	0	1	1.154
tiritar	0	1	1.154
tiritaba	0	1	1.154
tiren	0	1	1.154
tirase	0	1	1.154
tirársela	0	1	1.154
tiraron	0	1	1.154
tirarás	0	1	1.154
tiranístico	0	1	1.154
tiránica	0	1	1.154
tirándose	0	1	1.154
tiranas	0	1	1.154
tiradores	0	1	1.154
tirádola	0	1	1.154
tirabuzones	0	1	1.154
tirabas	0	1	1.154
tirábalo	0	1	1.154
tiquitique	0	1	1.154
tiote	0	1	1.154
tiotas	0	1	1.154
tiota	0	1	1.154
tiorra	0	1	1.154
tiona	0	1	1.154
tiólogos	0	1	1.154
tiñoso	0	1	1.154
tiñosa	0	1	1.154
tiñéndosela	0	1	1.154
tintura	0	1	1.154
tintes	0	1	1.154
tiniente	0	1	1.154
tinajas	0	1	1.154
tina	0	1	1.154
timos	0	1	1.154
timonear	0	1	1.154
tímidos	0	1	1.154
timbrado	0	1	1.154
timbales	0	1	1.154
timarte	0	1	1.154
timan	0	1	1.154
timadora	0	1	1.154
tílburi	0	1	1.154
tijeretazo	0	1	1.154
tijera	0	1	1.154
tiesto	0	1	1.154
tiernísimos	0	1	1.154
tiento	0	1	1.154
tientes	0	1	1.154
tienden	0	1	1.154
tien	0	1	1.154
tiburones	0	1	1.154
tiburonas	0	1	1.154
tibidabo	0	1	1.154
thinville	0	1	1.154
textualmente	0	1	1.154
tetita	0	1	1.154
tetera	0	1	1.154
tetánica	0	1	1.154
testuz	0	1	1.154
testeros	0	1	1.154
testera	0	1	1.154
testar	0	1	1.154
tesorería	0	1	1.154
tertuliantes	0	1	1.154
tersos	0	1	1.154
tersas	0	1	1.154
terrestre	0	1	1.154
terraza	0	1	1.154
terráqueo	0	1	1.154
terra	0	1	1.154
ternos	0	1	1.154
terneza	0	1	1.154
ternerito	0	1	1.154
terne	0	1	1.154
terminase	0	1	1.154
terminarse	0	1	1.154
terciopelos	0	1	1.154
terció	0	1	1.154
tercio	0	1	1.154
terciándose	0	1	1.154
terapéutico	0	1	1.154
terapéuticas	0	1	1.154
teóricas	0	1	1.154
teológicas	0	1	1.154
teogonías	0	1	1.154
teogonía	0	1	1.154
teñirse	0	1	1.154
teñidos	0	1	1.154
teñida	0	1	1.154
tenuidad	0	1	1.154
tentó	0	1	1.154
tentarte	0	1	1.154
tentarían	0	1	1.154
tentaba	0	1	1.154
tenla	0	1	1.154
teniéndose	0	1	1.154
teniéndole	0	1	1.154
teniéndola	0	1	1.154
tenidas	0	1	1.154
teníanle	0	1	1.154
teníalas	0	1	1.154
téngalo	0	1	1.154
tenedores	0	1	1.154
tened	0	1	1.154
tenebrosos	0	1	1.154
tenebroso	0	1	1.154
tendréis	0	1	1.154
tendralos	0	1	1.154
tendones	0	1	1.154
tendiera	0	1	1.154
tendíanse	0	1	1.154
tenderse	0	1	1.154
tenderil	0	1	1.154
tenderete	0	1	1.154
tenacillas	0	1	1.154
tenacidades	0	1	1.154
temporadillas	0	1	1.154
temporadilla	0	1	1.154
templadita	0	1	1.154
tempestuosos	0	1	1.154
temerás	0	1	1.154
teméis	0	1	1.154
tembláronle	0	1	1.154
temblara	0	1	1.154
tembladores	0	1	1.154
temamos	0	1	1.154
telegráficos	0	1	1.154
telegráfico	0	1	1.154
telegrafías	0	1	1.154
telegrafiarse	0	1	1.154
telegrafía	0	1	1.154
telares	0	1	1.154
tejavana	0	1	1.154
tejar	0	1	1.154
tegel	0	1	1.154
tediosas	0	1	1.154
tediosa	0	1	1.154
tecleando	0	1	1.154
tecleaban	0	1	1.154
tecleaba	0	1	1.154
tea	0	1	1.154
tazón	0	1	1.154
tauromaquia	0	1	1.154
taurómacas	0	1	1.154
tasado	0	1	1.154
tasada	0	1	1.154
tasaba	0	1	1.154
tartamudeó	0	1	1.154
tartamudeando	0	1	1.154
tardecillo	0	1	1.154
tardas	0	1	1.154
tardaré	0	1	1.154
tardara	0	1	1.154
tardan	0	1	1.154
tardamos	0	1	1.154
tarancón	0	1	1.154
tarabilla	0	1	1.154
tapujo	0	1	1.154
tapujito	0	1	1.154
tapón	0	1	1.154
tapase	0	1	1.154
tapas	0	1	1.154
tapándoselo	0	1	1.154
tapan	0	1	1.154
tapadita	0	1	1.154
tapadera	0	1	1.154
tañido	0	1	1.154
tañer	0	1	1.154
tantooo	0	1	1.154
tantismos	0	1	1.154
tantearemos	0	1	1.154
tantear	0	1	1.154
tanteado	0	1	1.154
tangente	0	1	1.154
tamente	0	1	1.154
tamborazos	0	1	1.154
tamañitas	0	1	1.154
taludes	0	1	1.154
talluditos	0	1	1.154
talludito	0	1	1.154
tallo	0	1	1.154
talles	0	1	1.154
tallas	0	1	1.154
tallarla	0	1	1.154
tallando	0	1	1.154
talcualita	0	1	1.154
talavera	0	1	1.154
taladraban	0	1	1.154
tala	0	1	1.154
tahona	0	1	1.154
tagarote	0	1	1.154
tafetanes	0	1	1.154
táctico	0	1	1.154
tácticas	0	1	1.154
táctica	0	1	1.154
tachuelas	0	1	1.154
tacaña	0	1	1.154
tablitas	0	1	1.154
tablajero	0	1	1.154
tablajera	0	1	1.154
tabernero	0	1	1.154
tabacazo	0	1	1.154
sutilizaron	0	1	1.154
sutilizado	0	1	1.154
sutilísimo	0	1	1.154
susurraron	0	1	1.154
sustraernos	0	1	1.154
sustraer	0	1	1.154
sustituyeron	0	1	1.154
sustituye	0	1	1.154
sustituirla	0	1	1.154
sustancioso	0	1	1.154
sustanciosa	0	1	1.154
suspirona	0	1	1.154
suspire	0	1	1.154
suspiras	0	1	1.154
suspirante	0	1	1.154
suspicacia	0	1	1.154
suspenso	0	1	1.154
suspendido	0	1	1.154
suspenderlo	0	1	1.154
susodichos	0	1	1.154
suscritoras	0	1	1.154
suscritor	0	1	1.154
suscripciones	0	1	1.154
suscricioncita	0	1	1.154
suscribió	0	1	1.154
suscitara	0	1	1.154
suscepciones	0	1	1.154
surtidos	0	1	1.154
surtido	0	1	1.154
surtía	0	1	1.154
surgir	0	1	1.154
surgieran	0	1	1.154
surgía	0	1	1.154
surco	0	1	1.154
supuesta	0	1	1.154
suprimo	0	1	1.154
suprimirse	0	1	1.154
suprimirlo	0	1	1.154
suprimido	0	1	1.154
súpose	0	1	1.154
suponiéndolo	0	1	1.154
suponiéndoles	0	1	1.154
suponían	0	1	1.154
suponíales	0	1	1.154
suponga	0	1	1.154
suponérsela	0	1	1.154
suponeres	0	1	1.154
suponemos	0	1	1.154
suplió	0	1	1.154
suplicándole	0	1	1.154
suplementos	0	1	1.154
suplementario	0	1	1.154
súpitas	0	1	1.154
supiste	0	1	1.154
supersticiones	0	1	1.154
superfirolíticos	0	1	1.154
superfirolíticas	0	1	1.154
superficiales	0	1	1.154
superciliar	0	1	1.154
superávit	0	1	1.154
superarla	0	1	1.154
superaban	0	1	1.154
supera	0	1	1.154
sumisa	0	1	1.154
suministrado	0	1	1.154
sumergirla	0	1	1.154
sumergiendo	0	1	1.154
sulfurándose	0	1	1.154
sujetose	0	1	1.154
sujetarse	0	1	1.154
sujetaron	0	1	1.154
sujetarles	0	1	1.154
sujetaran	0	1	1.154
sujetan	0	1	1.154
sujetada	0	1	1.154
suicido	0	1	1.154
suicide	0	1	1.154
sugiriera	0	1	1.154
sugestionada	0	1	1.154
sugeríanle	0	1	1.154
sugeríale	0	1	1.154
sufrirte	0	1	1.154
sufriría	0	1	1.154
sufrieron	0	1	1.154
sufriendo	0	1	1.154
sufragios	0	1	1.154
sueñecito	0	1	1.154
sueñecillo	0	1	1.154
sueñan	0	1	1.154
sueno	0	1	1.154
suenen	0	1	1.154
suéltese	0	1	1.154
sueltecito	0	1	1.154
sudadas	0	1	1.154
suda	0	1	1.154
sucumbió	0	1	1.154
sucediera	0	1	1.154
sucedidos	0	1	1.154
sucedían	0	1	1.154
sucederme	0	1	1.154
sucederá	0	1	1.154
subyugando	0	1	1.154
subyugada	0	1	1.154
subsistiendo	0	1	1.154
subsistía	0	1	1.154
subsistencia	0	1	1.154
subsiste	0	1	1.154
subsidio	0	1	1.154
subsecretarios	0	1	1.154
sublimidades	0	1	1.154
sublimaban	0	1	1.154
sublevo	0	1	1.154
subirlas	0	1	1.154
subiré	0	1	1.154
subiese	0	1	1.154
subiéronle	0	1	1.154
subiéndosele	0	1	1.154
subiéndome	0	1	1.154
súbdito	0	1	1.154
subalterno	0	1	1.154
subalterna	0	1	1.154
suárez	0	1	1.154
sotabanco	0	1	1.154
sostienes	0	1	1.154
sostenimiento	0	1	1.154
sosteniéndose	0	1	1.154
sosteniéndola	0	1	1.154
sostenías	0	1	1.154
sostenerse	0	1	1.154
sostén	0	1	1.154
sospechen	0	1	1.154
sosería	0	1	1.154
sosegó	0	1	1.154
sosegarle	0	1	1.154
sosegando	0	1	1.154
sosegadamente	0	1	1.154
sosas	0	1	1.154
sosamente	0	1	1.154
sortilegio	0	1	1.154
sortearlo	0	1	1.154
sortearle	0	1	1.154
sortear	0	1	1.154
sorteando	0	1	1.154
sorpresita	0	1	1.154
sorprendo	0	1	1.154
sorprendiese	0	1	1.154
sorprendidos	0	1	1.154
sorprendí	0	1	1.154
sorprenderá	0	1	1.154
sorna	0	1	1.154
sordamente	0	1	1.154
sorbo	0	1	1.154
sorbió	0	1	1.154
sorbieran	0	1	1.154
sorber	0	1	1.154
sorbe	0	1	1.154
soportan	0	1	1.154
soportado	0	1	1.154
soplaron	0	1	1.154
soplao	0	1	1.154
sopesarlos	0	1	1.154
soñaron	0	1	1.154
soñadas	0	1	1.154
sonsaques	0	1	1.154
sonsacado	0	1	1.154
sonrosados	0	1	1.154
sonrojos	0	1	1.154
sonrojo	0	1	1.154
sonríes	0	1	1.154
sonriéndose	0	1	1.154
sonoridad	0	1	1.154
sondéela	0	1	1.154
sondeaba	0	1	1.154
sondaje	0	1	1.154
sonarme	0	1	1.154
sonándose	0	1	1.154
sonándola	0	1	1.154
sonambulismo	0	1	1.154
somnolencias	0	1	1.154
sometiera	0	1	1.154
sometiéndose	0	1	1.154
sometían	0	1	1.154
someterlas	0	1	1.154
someta	0	1	1.154
someras	0	1	1.154
sombrillazo	0	1	1.154
sombreritos	0	1	1.154
sombrerero	0	1	1.154
sombreo	0	1	1.154
sombrajos	0	1	1.154
soluciones	0	1	1.154
soltole	0	1	1.154
solterones	0	1	1.154
soltería	0	1	1.154
soltaste	0	1	1.154
soltarla	0	1	1.154
soltarían	0	1	1.154
soltara	0	1	1.154
soltaban	0	1	1.154
sollozar	0	1	1.154
soliviantada	0	1	1.154
solitos	0	1	1.154
solito	0	1	1.154
solidificación	0	1	1.154
solidificaba	0	1	1.154
solidifica	0	1	1.154
solicito	0	1	1.154
solicitara	0	1	1.154
solicitados	0	1	1.154
solfeo	0	1	1.154
soleta	0	1	1.154
soldevilla	0	1	1.154
soldarla	0	1	1.154
soldadura	0	1	1.154
soldaditos	0	1	1.154
solaz	0	1	1.154
solana	0	1	1.154
sojuzgado	0	1	1.154
sogas	0	1	1.154
soforas	0	1	1.154
sofocones	0	1	1.154
sofoco	0	1	1.154
sofocase	0	1	1.154
sofocarse	0	1	1.154
sofocaban	0	1	1.154
sofisterías	0	1	1.154
soez	0	1	1.154
socorriome	0	1	1.154
socorrió	0	1	1.154
socorriese	0	1	1.154
socorridas	0	1	1.154
socorrías	0	1	1.154
socorría	0	1	1.154
socorrerme	0	1	1.154
socorreremos	0	1	1.154
socorrerá	0	1	1.154
socorre	0	1	1.154
socórrale	0	1	1.154
socavaban	0	1	1.154
socarronas	0	1	1.154
sobrevive	0	1	1.154
sobreviniese	0	1	1.154
sobreviene	0	1	1.154
sobrevenirle	0	1	1.154
sobrevenido	0	1	1.154
sobrestante	0	1	1.154
sobresaltó	0	1	1.154
sobresalientes	0	1	1.154
sobrepujó	0	1	1.154
sobreponiéndose	0	1	1.154
sobreponían	0	1	1.154
sobreponía	0	1	1.154
sobreparto	0	1	1.154
sobredorada	0	1	1.154
sobrecoge	0	1	1.154
sobraron	0	1	1.154
sobrantes	0	1	1.154
sobrando	0	1	1.154
sobraban	0	1	1.154
soberbias	0	1	1.154
sobar	0	1	1.154
situó	0	1	1.154
situados	0	1	1.154
sita	0	1	1.154
sístole	0	1	1.154
sistematizar	0	1	1.154
sirvientes	0	1	1.154
sirviéndole	0	1	1.154
sirvas	0	1	1.154
siquera	0	1	1.154
sinvergüenzones	0	1	1.154
sinvergüenzonas	0	1	1.154
sintiole	0	1	1.154
sintieses	0	1	1.154
sintieran	0	1	1.154
sintético	0	1	1.154
sinrazón	0	1	1.154
sinónimos	0	1	1.154
sinodales	0	1	1.154
sinificancia	0	1	1.154
siniestros	0	1	1.154
singularidad	0	1	1.154
singer	0	1	1.154
sinfonías	0	1	1.154
sinfonía	0	1	1.154
síncopas	0	1	1.154
sinceridades	0	1	1.154
simultáneamente	0	1	1.154
simulado	0	1	1.154
simpson	0	1	1.154
simplona	0	1	1.154
simplín	0	1	1.154
simplicitas	0	1	1.154
simples	0	1	1.154
simpatizase	0	1	1.154
simpatizado	0	1	1.154
simpáticos	0	1	1.154
simones	0	1	1.154
similares	0	1	1.154
simbolismo	0	1	1.154
silogismos	0	1	1.154
silleta	0	1	1.154
silfidones	0	1	1.154
silfidona	0	1	1.154
sílfide	0	1	1.154
silbe	0	1	1.154
silbándole	0	1	1.154
silbando	0	1	1.154
silabeo	0	1	1.154
sigunda	0	1	1.154
siguiole	0	1	1.154
siguiéndoles	0	1	1.154
sigues	0	1	1.154
sietes	0	1	1.154
siervas	0	1	1.154
sientan	0	1	1.154
siéndolo	0	1	1.154
siéndole	0	1	1.154
siego	0	1	1.154
sicilianas	0	1	1.154
sicario	0	1	1.154
sibarita	0	1	1.154
shangai	0	1	1.154
sevicia	0	1	1.154
severísimos	0	1	1.154
severísimamente	0	1	1.154
severidades	0	1	1.154
severiano	0	1	1.154
sétimo	0	1	1.154
setecientas	0	1	1.154
sesudo	0	1	1.154
sesudas	0	1	1.154
sesera	0	1	1.154
servirte	0	1	1.154
servirles	0	1	1.154
servirá	0	1	1.154
servilón	0	1	1.154
servidores	0	1	1.154
serte	0	1	1.154
sert	0	1	1.154
serpentine	0	1	1.154
serosa	0	1	1.154
sermoneo	0	1	1.154
sermonearle	0	1	1.154
sermonearé	0	1	1.154
sermoneaba	0	1	1.154
sermoncito	0	1	1.154
sermonazo	0	1	1.154
sermonarias	0	1	1.154
seríale	0	1	1.154
sereta	0	1	1.154
serénese	0	1	1.154
serene	0	1	1.154
serénate	0	1	1.154
serenase	0	1	1.154
serenaron	0	1	1.154
serenarás	0	1	1.154
serenado	0	1	1.154
séquito	0	1	1.154
seque	0	1	1.154
sepulturas	0	1	1.154
sepultarse	0	1	1.154
sepultado	0	1	1.154
séptimo	0	1	1.154
separes	0	1	1.154
separáronse	0	1	1.154
separaremos	0	1	1.154
separábanse	0	1	1.154
seo	0	1	1.154
señoriticas	0	1	1.154
señorete	0	1	1.154
señó	0	1	1.154
señale	0	1	1.154
señalarse	0	1	1.154
señalándote	0	1	1.154
sentirme	0	1	1.154
sentirás	0	1	1.154
sentirá	0	1	1.154
sentinas	0	1	1.154
sentías	0	1	1.154
sentíala	0	1	1.154
sentenciador	0	1	1.154
senté	0	1	1.154
sentáronse	0	1	1.154
sentaré	0	1	1.154
sentándosele	0	1	1.154
sentadita	0	1	1.154
sentábase	0	1	1.154
sensibles	0	1	1.154
sensiblemente	0	1	1.154
sensato	0	1	1.154
sencillísima	0	1	1.154
senador	0	1	1.154
semioscura	0	1	1.154
semestres	0	1	1.154
semestre	0	1	1.154
semeja	0	1	1.154
sembrando	0	1	1.154
selló	0	1	1.154
sellaíto	0	1	1.154
seiscientos	0	1	1.154
seguirlos	0	1	1.154
seguirían	0	1	1.154
seguiríamos	0	1	1.154
seguirás	0	1	1.154
seguío	0	1	1.154
seguimientos	0	1	1.154
seguíales	0	1	1.154
seguíala	0	1	1.154
segovianos	0	1	1.154
segar	0	1	1.154
segándole	0	1	1.154
seducidas	0	1	1.154
sedimentado	0	1	1.154
sedientos	0	1	1.154
sedienta	0	1	1.154
sedeño	0	1	1.154
sede	0	1	1.154
sedante	0	1	1.154
sedanes	0	1	1.154
sedán	0	1	1.154
secuestradoras	0	1	1.154
secuestrado	0	1	1.154
secretito	0	1	1.154
secreteos	0	1	1.154
secreteó	0	1	1.154
secretearse	0	1	1.154
secreteara	0	1	1.154
secó	0	1	1.154
secaron	0	1	1.154
secarle	0	1	1.154
secara	0	1	1.154
secamente	0	1	1.154
secaderos	0	1	1.154
secadero	0	1	1.154
sebosa	0	1	1.154
scott	0	1	1.154
scirroso	0	1	1.154
schiller	0	1	1.154
sc	0	1	1.154
sazonarla	0	1	1.154
sazonado	0	1	1.154
sayos	0	1	1.154
saturada	0	1	1.154
satisfactoria	0	1	1.154
satisfacían	0	1	1.154
satisfacerse	0	1	1.154
satisfacerlos	0	1	1.154
satisfacerlo	0	1	1.154
satisfacerla	0	1	1.154
satisfacciones	0	1	1.154
satenes	0	1	1.154
sastrería	0	1	1.154
sastra	0	1	1.154
sartas	0	1	1.154
sarta	0	1	1.154
sarna	0	1	1.154
sargentos	0	1	1.154
sargento	0	1	1.154
sardina	0	1	1.154
sarcástico	0	1	1.154
sarao	0	1	1.154
saquitos	0	1	1.154
saquito	0	1	1.154
sapientísimas	0	1	1.154
sañudamente	0	1	1.154
sañuda	0	1	1.154
santona	0	1	1.154
santisma	0	1	1.154
santifiquísimas	0	1	1.154
santificarnos	0	1	1.154
santander	0	1	1.154
sanitarismo	0	1	1.154
sanguinolento	0	1	1.154
sanguínea	0	1	1.154
sanguinaria	0	1	1.154
sangrientos	0	1	1.154
sangraran	0	1	1.154
sandía	0	1	1.154
sandez	0	1	1.154
sancta	0	1	1.154
sancionadora	0	1	1.154
sanas	0	1	1.154
sanarte	0	1	1.154
sanara	0	1	1.154
sanan	0	1	1.154
sanado	0	1	1.154
salvarías	0	1	1.154
salvaré	0	1	1.154
salvará	0	1	1.154
salvando	0	1	1.154
salvamento	0	1	1.154
salvajito	0	1	1.154
salvajita	0	1	1.154
salvajadas	0	1	1.154
salvadoras	0	1	1.154
salvadera	0	1	1.154
saludes	0	1	1.154
saludarte	0	1	1.154
saludáronse	0	1	1.154
saludarles	0	1	1.154
saludadores	0	1	1.154
saltimbanquis	0	1	1.154
saltarla	0	1	1.154
saltaran	0	1	1.154
saltándosele	0	1	1.154
saltándola	0	1	1.154
saltamontes	0	1	1.154
salsas	0	1	1.154
salpicaron	0	1	1.154
salpicado	0	1	1.154
salpicada	0	1	1.154
salobre	0	1	1.154
salmuera	0	1	1.154
salivita	0	1	1.154
salivazos	0	1	1.154
salivazo	0	1	1.154
salís	0	1	1.154
salieran	0	1	1.154
saliditas	0	1	1.154
saldrían	0	1	1.154
saldrán	0	1	1.154
saldar	0	1	1.154
saldan	0	1	1.154
salaremos	0	1	1.154
saladísimo	0	1	1.154
saladas	0	1	1.154
sajonas	0	1	1.154
sahumerio	0	1	1.154
sagra	0	1	1.154
saetazos	0	1	1.154
saetas	0	1	1.154
sacudo	0	1	1.154
sacudirme	0	1	1.154
sacudirlas	0	1	1.154
sacudiré	0	1	1.154
sacudimiento	0	1	1.154
sacudieran	0	1	1.154
sacudiéndoles	0	1	1.154
sacudiéndole	0	1	1.154
sacude	0	1	1.154
sacrilegios	0	1	1.154
sacrifíquese	0	1	1.154
sacrifique	0	1	1.154
saciedad	0	1	1.154
saciaba	0	1	1.154
sacerdotales	0	1	1.154
sacáronla	0	1	1.154
sacarles	0	1	1.154
sacarlas	0	1	1.154
sacarán	0	1	1.154
sácanos	0	1	1.154
sacándose	0	1	1.154
sacándome	0	1	1.154
sacándolos	0	1	1.154
sacamos	0	1	1.154
sácalos	0	1	1.154
sacados	0	1	1.154
sacadas	0	1	1.154
sacábala	0	1	1.154
sabusté	0	1	1.154
sabríais	0	1	1.154
sabremos	0	1	1.154
sabrán	0	1	1.154
saboréate	0	1	1.154
sabiéndolas	0	1	1.154
sabiendas	0	1	1.154
sabíamos	0	1	1.154
sabeees	0	1	1.154
sabedoras	0	1	1.154
sabañones	0	1	1.154
sábados	0	1	1.154
rústicos	0	1	1.154
rústicas	0	1	1.154
rusticación	0	1	1.154
rusos	0	1	1.154
rupertito	0	1	1.154
rumiarlas	0	1	1.154
rumiaba	0	1	1.154
rumbos	0	1	1.154
rumbeles	0	1	1.154
ruinoso	0	1	1.154
ruidito	0	1	1.154
ruedita	0	1	1.154
ruede	0	1	1.154
rudimentarios	0	1	1.154
ruborizada	0	1	1.154
rubines	0	1	1.154
rubias	0	1	1.154
rubén	0	1	1.154
rropa	0	1	1.154
rozó	0	1	1.154
rozamiento	0	1	1.154
rozadura	0	1	1.154
royendo	0	1	1.154
rotura	0	1	1.154
rothschild	0	1	1.154
roten	0	1	1.154
rostchild	0	1	1.154
rossiniano	0	1	1.154
rosicler	0	1	1.154
rosca	0	1	1.154
rosados	0	1	1.154
ros	0	1	1.154
rorrooó	0	1	1.154
ropillas	0	1	1.154
ropaje	0	1	1.154
roñosas	0	1	1.154
roña	0	1	1.154
ronde	0	1	1.154
rondara	0	1	1.154
roncaban	0	1	1.154
roncaba	0	1	1.154
rompí	0	1	1.154
romperte	0	1	1.154
romperle	0	1	1.154
rompemos	0	1	1.154
rómpeme	0	1	1.154
rompelanzas	0	1	1.154
romos	0	1	1.154
rombo	0	1	1.154
romanzas	0	1	1.154
románicos	0	1	1.154
romancesco	0	1	1.154
romancesca	0	1	1.154
romadizo	0	1	1.154
rollos	0	1	1.154
rojizas	0	1	1.154
roído	0	1	1.154
roger	0	1	1.154
rogaron	0	1	1.154
rogarle	0	1	1.154
roer	0	1	1.154
roedor	0	1	1.154
rodil	0	1	1.154
rodearse	0	1	1.154
rodadas	0	1	1.154
rociada	0	1	1.154
rocas	0	1	1.154
robustecer	0	1	1.154
robos	0	1	1.154
robó	0	1	1.154
roben	0	1	1.154
robe	0	1	1.154
robaste	0	1	1.154
robaron	0	1	1.154
robármelo	0	1	1.154
robaré	0	1	1.154
robaran	0	1	1.154
robará	0	1	1.154
robara	0	1	1.154
robándoselo	0	1	1.154
roban	0	1	1.154
robaban	0	1	1.154
road	0	1	1.154
rizosa	0	1	1.154
rizarse	0	1	1.154
rivalidades	0	1	1.154
ritual	0	1	1.154
ritornellos	0	1	1.154
ritmos	0	1	1.154
risitas	0	1	1.154
risibles	0	1	1.154
risible	0	1	1.154
ripio	0	1	1.154
riose	0	1	1.154
rioja	0	1	1.154
riñan	0	1	1.154
ringorrangos	0	1	1.154
rindiera	0	1	1.154
rinde	0	1	1.154
rimpuesta	0	1	1.154
rimero	0	1	1.154
rimados	0	1	1.154
rija	0	1	1.154
rigurosas	0	1	1.154
rigoristas	0	1	1.154
rígidamente	0	1	1.154
rifle	0	1	1.154
rifarla	0	1	1.154
rieras	0	1	1.154
rieran	0	1	1.154
riéndole	0	1	1.154
ridiculizando	0	1	1.154
ridículamente	0	1	1.154
ricardo	0	1	1.154
ricacha	0	1	1.154
ribeteada	0	1	1.154
ribete	0	1	1.154
rezumos	0	1	1.154
rezumía	0	1	1.154
rezumados	0	1	1.154
rezongó	0	1	1.154
rezongar	0	1	1.154
rezongaba	0	1	1.154
rezarían	0	1	1.154
rezándole	0	1	1.154
rézale	0	1	1.154
rezagada	0	1	1.154
rezado	0	1	1.154
rezaban	0	1	1.154
revuelve	0	1	1.154
revuelcos	0	1	1.154
revuelco	0	1	1.154
revolviese	0	1	1.154
revolvieron	0	1	1.154
revolviéndola	0	1	1.154
revolverlas	0	1	1.154
revoloteó	0	1	1.154
revolotear	0	1	1.154
revoloteaban	0	1	1.154
revolcose	0	1	1.154
revolcarse	0	1	1.154
reviviendo	0	1	1.154
revistió	0	1	1.154
revistiéndolas	0	1	1.154
revisten	0	1	1.154
revisión	0	1	1.154
revisaré	0	1	1.154
reviradas	0	1	1.154
revientan	0	1	1.154
revestirse	0	1	1.154
revestir	0	1	1.154
revestimiento	0	1	1.154
reveses	0	1	1.154
revertida	0	1	1.154
reversión	0	1	1.154
reverente	0	1	1.154
reverencia	0	1	1.154
reverdeció	0	1	1.154
reverdeciendo	0	1	1.154
reverdecidas	0	1	1.154
reverdecer	0	1	1.154
reverdece	0	1	1.154
reverberos	0	1	1.154
reverberar	0	1	1.154
reventas	0	1	1.154
reventaban	0	1	1.154
revenidos	0	1	1.154
revelarte	0	1	1.154
revelara	0	1	1.154
revelada	0	1	1.154
reunió	0	1	1.154
reunieran	0	1	1.154
reuniendo	0	1	1.154
reunía	0	1	1.154
reúne	0	1	1.154
reumáticos	0	1	1.154
retuvieron	0	1	1.154
retumbantes	0	1	1.154
retumban	0	1	1.154
retumbado	0	1	1.154
retrogradaba	0	1	1.154
retratarse	0	1	1.154
retratar	0	1	1.154
retratada	0	1	1.154
retrataaar	0	1	1.154
retrasados	0	1	1.154
retrasada	0	1	1.154
retraimiento	0	1	1.154
retraerse	0	1	1.154
retozos	0	1	1.154
retortijado	0	1	1.154
retortero	0	1	1.154
retóricos	0	1	1.154
retorciendo	0	1	1.154
retorcidas	0	1	1.154
retorcedura	0	1	1.154
retor	0	1	1.154
retoñado	0	1	1.154
retocando	0	1	1.154
reto	0	1	1.154
retires	0	1	1.154
retire	0	1	1.154
retirase	0	1	1.154
retirarlos	0	1	1.154
retirarle	0	1	1.154
retiraran	0	1	1.154
retirándolo	0	1	1.154
retirando	0	1	1.154
retiradamente	0	1	1.154
retirábase	0	1	1.154
retiraban	0	1	1.154
reteniéndole	0	1	1.154
reteniéndola	0	1	1.154
retenido	0	1	1.154
retenían	0	1	1.154
retenerlo	0	1	1.154
retenerle	0	1	1.154
retención	0	1	1.154
retemblar	0	1	1.154
retazos	0	1	1.154
resurgía	0	1	1.154
resultole	0	1	1.154
resultasen	0	1	1.154
resultase	0	1	1.154
resultarle	0	1	1.154
resultará	0	1	1.154
resultara	0	1	1.154
resultar	0	1	1.154
resuella	0	1	1.154
resucitara	0	1	1.154
resucitan	0	1	1.154
restregón	0	1	1.154
restregó	0	1	1.154
restregáronle	0	1	1.154
restregado	0	1	1.154
restregaba	0	1	1.154
restauradas	0	1	1.154
restauraba	0	1	1.154
restañaba	0	1	1.154
restantes	0	1	1.154
restallaban	0	1	1.154
restablecimiento	0	1	1.154
restablecer	0	1	1.154
restaba	0	1	1.154
resta	0	1	1.154
resquebrajaba	0	1	1.154
responso	0	1	1.154
responsabilidades	0	1	1.154
respondona	0	1	1.154
respondiome	0	1	1.154
respondieran	0	1	1.154
respondiera	0	1	1.154
respondiéndome	0	1	1.154
respondiéndole	0	1	1.154
respondería	0	1	1.154
respóndame	0	1	1.154
resplandeció	0	1	1.154
resplandecientes	0	1	1.154
resplandeciendo	0	1	1.154
resplandecían	0	1	1.154
respirase	0	1	1.154
respirado	0	1	1.154
respiraderos	0	1	1.154
respirable	0	1	1.154
respingar	0	1	1.154
respingados	0	1	1.154
respingadas	0	1	1.154
réspices	0	1	1.154
respetuosamente	0	1	1.154
respetosa	0	1	1.154
respéteme	0	1	1.154
respetad	0	1	1.154
respetabilísimo	0	1	1.154
respetabilísimas	0	1	1.154
resoplido	0	1	1.154
resonarán	0	1	1.154
resolvimos	0	1	1.154
resolviéndose	0	1	1.154
resolviendo	0	1	1.154
resolvíase	0	1	1.154
resolverlos	0	1	1.154
resolverlo	0	1	1.154
resolverá	0	1	1.154
resobándose	0	1	1.154
resobado	0	1	1.154
resobaba	0	1	1.154
resma	0	1	1.154
resisto	0	1	1.154
resistirlo	0	1	1.154
resistiese	0	1	1.154
resistieras	0	1	1.154
resistiera	0	1	1.154
resistiendo	0	1	1.154
resistes	0	1	1.154
resistente	0	1	1.154
resistencias	0	1	1.154
resisten	0	1	1.154
resinas	0	1	1.154
resigne	0	1	1.154
resignadas	0	1	1.154
resido	0	1	1.154
residían	0	1	1.154
residía	0	1	1.154
reside	0	1	1.154
resguardo	0	1	1.154
resguardar	0	1	1.154
reservo	0	1	1.154
reservarse	0	1	1.154
reservando	0	1	1.154
reservadísimo	0	1	1.154
resentirse	0	1	1.154
resentimiento	0	1	1.154
reselles	0	1	1.154
resecaban	0	1	1.154
rescoldo	0	1	1.154
resbalón	0	1	1.154
resaltar	0	1	1.154
resalao	0	1	1.154
requisito	0	1	1.154
requetefinas	0	1	1.154
requesón	0	1	1.154
requería	0	1	1.154
requemo	0	1	1.154
requemado	0	1	1.154
requejo	0	1	1.154
reputados	0	1	1.154
reputaban	0	1	1.154
repuntaba	0	1	1.154
repulsión	0	1	1.154
repulgos	0	1	1.154
repulgo	0	1	1.154
repugnaría	0	1	1.154
repúblicas	0	1	1.154
reprodujeron	0	1	1.154
reprodujera	0	1	1.154
reproducir	0	1	1.154
reproduciéndose	0	1	1.154
reproduciéndolo	0	1	1.154
reproduciendo	0	1	1.154
reproducídose	0	1	1.154
reproducidas	0	1	1.154
reprobación	0	1	1.154
reprobables	0	1	1.154
reprimir	0	1	1.154
represente	0	1	1.154
representaron	0	1	1.154
representaciones	0	1	1.154
reprendieran	0	1	1.154
reprenderla	0	1	1.154
repreciosa	0	1	1.154
repostero	0	1	1.154
reposada	0	1	1.154
reponiéndose	0	1	1.154
reponiendo	0	1	1.154
reponerte	0	1	1.154
repoblicanas	0	1	1.154
repliegue	0	1	1.154
repliégate	0	1	1.154
repitiese	0	1	1.154
repitiéndose	0	1	1.154
repitiéndole	0	1	1.154
repítelas	0	1	1.154
repiques	0	1	1.154
repicando	0	1	1.154
repetírselo	0	1	1.154
repasó	0	1	1.154
repartiría	0	1	1.154
reparta	0	1	1.154
reparona	0	1	1.154
repares	0	1	1.154
reparatrices	0	1	1.154
repararía	0	1	1.154
repara	0	1	1.154
repantigado	0	1	1.154
rentita	0	1	1.154
renovó	0	1	1.154
renovase	0	1	1.154
renovará	0	1	1.154
renovaciones	0	1	1.154
renovaba	0	1	1.154
rengloncito	0	1	1.154
renegó	0	1	1.154
rendidísimo	0	1	1.154
rendidísima	0	1	1.154
rencorcillo	0	1	1.154
remuerde	0	1	1.154
removió	0	1	1.154
removieran	0	1	1.154
remotísimo	0	1	1.154
remotamente	0	1	1.154
remos	0	1	1.154
remontó	0	1	1.154
remontarme	0	1	1.154
remontabas	0	1	1.154
remonona	0	1	1.154
remolcándola	0	1	1.154
remitiese	0	1	1.154
remitidas	0	1	1.154
remitía	0	1	1.154
remite	0	1	1.154
reminiscencias	0	1	1.154
remilgadas	0	1	1.154
remilgada	0	1	1.154
remiendo	0	1	1.154
remesa	0	1	1.154
remendarla	0	1	1.154
remendada	0	1	1.154
remedos	0	1	1.154
remedo	0	1	1.154
remedie	0	1	1.154
remediaban	0	1	1.154
remedando	0	1	1.154
remeda	0	1	1.154
remataron	0	1	1.154
rematar	0	1	1.154
rematadas	0	1	1.154
remataban	0	1	1.154
remala	0	1	1.154
remadera	0	1	1.154
remachando	0	1	1.154
relumbrones	0	1	1.154
relumbrón	0	1	1.154
relumbrantes	0	1	1.154
relumbrante	0	1	1.154
relojería	0	1	1.154
relevase	0	1	1.154
relevado	0	1	1.154
relatos	0	1	1.154
relatando	0	1	1.154
relataba	0	1	1.154
relampagueaban	0	1	1.154
relamiendo	0	1	1.154
relámete	0	1	1.154
relamerse	0	1	1.154
relajadas	0	1	1.154
relacionase	0	1	1.154
relacionara	0	1	1.154
relacionado	0	1	1.154
relacionaban	0	1	1.154
relaciona	0	1	1.154
rejuvenece	0	1	1.154
reiterándole	0	1	1.154
reiterando	0	1	1.154
reíros	0	1	1.154
reirías	0	1	1.154
reirían	0	1	1.154
reiré	0	1	1.154
reirás	0	1	1.154
reintegraría	0	1	1.154
reinos	0	1	1.154
reinó	0	1	1.154
reincidir	0	1	1.154
reincidente	0	1	1.154
reinara	0	1	1.154
reímos	0	1	1.154
reíase	0	1	1.154
reíamos	0	1	1.154
reí	0	1	1.154
rehusaron	0	1	1.154
rehuido	0	1	1.154
rehecho	0	1	1.154
rehacerse	0	1	1.154
rehacer	0	1	1.154
reguapa	0	1	1.154
regresar	0	1	1.154
regresaba	0	1	1.154
regresa	0	1	1.154
regrande	0	1	1.154
regordete	0	1	1.154
regocijar	0	1	1.154
regocijándose	0	1	1.154
regocijadas	0	1	1.154
regocijada	0	1	1.154
reglamentario	0	1	1.154
registraremos	0	1	1.154
registrado	0	1	1.154
regimientos	0	1	1.154
regenerarte	0	1	1.154
regenerarlas	0	1	1.154
regenerada	0	1	1.154
regeneraciones	0	1	1.154
regeneraba	0	1	1.154
regateando	0	1	1.154
regateaba	0	1	1.154
regaños	0	1	1.154
regañona	0	1	1.154
regañó	0	1	1.154
regaño	0	1	1.154
regañar	0	1	1.154
regando	0	1	1.154
regalona	0	1	1.154
regalé	0	1	1.154
regalarte	0	1	1.154
regaláronle	0	1	1.154
regaláramos	0	1	1.154
regalaba	0	1	1.154
regaderas	0	1	1.154
regaba	0	1	1.154
refutara	0	1	1.154
refunfuños	0	1	1.154
refunfuñas	0	1	1.154
refunfuñan	0	1	1.154
refundiéndose	0	1	1.154
refundida	0	1	1.154
refulgentes	0	1	1.154
refrescan	0	1	1.154
refrénate	0	1	1.154
refrenase	0	1	1.154
refrenarse	0	1	1.154
refrenar	0	1	1.154
refregones	0	1	1.154
refregarte	0	1	1.154
refregar	0	1	1.154
refractario	0	1	1.154
reforme	0	1	1.154
reformase	0	1	1.154
reformar	0	1	1.154
reformada	0	1	1.154
reflexiva	0	1	1.154
reflexiono	0	1	1.154
reflexionaba	0	1	1.154
reflejándose	0	1	1.154
reflejábase	0	1	1.154
refirencias	0	1	1.154
refinarlos	0	1	1.154
refinar	0	1	1.154
refinamientos	0	1	1.154
refiérome	0	1	1.154
refiera	0	1	1.154
referirle	0	1	1.154
referirían	0	1	1.154
referencias	0	1	1.154
referencia	0	1	1.154
refeos	0	1	1.154
refectorio	0	1	1.154
reductos	0	1	1.154
reducirlo	0	1	1.154
reduciéndose	0	1	1.154
reducidos	0	1	1.154
reducidas	0	1	1.154
reducen	0	1	1.154
redondel	0	1	1.154
redondear	0	1	1.154
redondeado	0	1	1.154
redentorista	0	1	1.154
redenciones	0	1	1.154
redaño	0	1	1.154
redactar	0	1	1.154
redactada	0	1	1.154
rectilíneas	0	1	1.154
recrudecimiento	0	1	1.154
recreábase	0	1	1.154
recrea	0	1	1.154
recostase	0	1	1.154
recortaran	0	1	1.154
recortándolo	0	1	1.154
recorta	0	1	1.154
recorrieron	0	1	1.154
recordase	0	1	1.154
recordarme	0	1	1.154
recordarás	0	1	1.154
reconstruí	0	1	1.154
reconstituyentes	0	1	1.154
reconozca	0	1	1.154
reconoces	0	1	1.154
reconocerlas	0	1	1.154
reconoceremos	0	1	1.154
reconocerá	0	1	1.154
reconocen	0	1	1.154
recondenada	0	1	1.154
reconciliémonos	0	1	1.154
reconciliaron	0	1	1.154
reconciliado	0	1	1.154
reconciliábamos	0	1	1.154
reconcilia	0	1	1.154
reconcentrado	0	1	1.154
recomponía	0	1	1.154
recompensaba	0	1	1.154
recomiendan	0	1	1.154
recomendé	0	1	1.154
recomendando	0	1	1.154
recomendadas	0	1	1.154
recomendada	0	1	1.154
recomendables	0	1	1.154
recogiéndolo	0	1	1.154
recogiéndole	0	1	1.154
recogían	0	1	1.154
recogerlos	0	1	1.154
recogerlas	0	1	1.154
recogeremos	0	1	1.154
recogeré	0	1	1.154
recogerá	0	1	1.154
recobrada	0	1	1.154
recoba	0	1	1.154
reclinó	0	1	1.154
reclinatorios	0	1	1.154
reclinado	0	1	1.154
reclamarlo	0	1	1.154
reclamará	0	1	1.154
reclamado	0	1	1.154
recio	0	1	1.154
recibirme	0	1	1.154
recibirle	0	1	1.154
recibirás	0	1	1.154
recibiome	0	1	1.154
recibías	0	1	1.154
recíbele	0	1	1.154
rechupidos	0	1	1.154
rechupete	0	1	1.154
rechupando	0	1	1.154
rechupado	0	1	1.154
rechinando	0	1	1.154
rechina	0	1	1.154
rechazó	0	1	1.154
rechazara	0	1	1.154
rechazándola	0	1	1.154
rechazada	0	1	1.154
rechacemos	0	1	1.154
recetaría	0	1	1.154
recetábale	0	1	1.154
recayese	0	1	1.154
recayera	0	1	1.154
recaudados	0	1	1.154
recaudador	0	1	1.154
recaudación	0	1	1.154
recatándose	0	1	1.154
recatado	0	1	1.154
recargaba	0	1	1.154
recapacitando	0	1	1.154
recalentaban	0	1	1.154
recalcar	0	1	1.154
recaen	0	1	1.154
recae	0	1	1.154
recaditos	0	1	1.154
rebuznó	0	1	1.154
rebuznar	0	1	1.154
rebusque	0	1	1.154
rebuscó	0	1	1.154
rebuscada	0	1	1.154
rebuscaba	0	1	1.154
rebullicio	0	1	1.154
rebulle	0	1	1.154
rebosaban	0	1	1.154
reblandeció	0	1	1.154
reblandecimiento	0	1	1.154
rebeló	0	1	1.154
rebelarse	0	1	1.154
rebasaron	0	1	1.154
rebasados	0	1	1.154
rebañaba	0	1	1.154
rebaña	0	1	1.154
rebanada	0	1	1.154
rebajes	0	1	1.154
rebajase	0	1	1.154
rebajaremos	0	1	1.154
rebajado	0	1	1.154
rebajada	0	1	1.154
reapertura	0	1	1.154
reaparecieron	0	1	1.154
reaparecer	0	1	1.154
reaparecen	0	1	1.154
reanudar	0	1	1.154
reanimaba	0	1	1.154
realizarlos	0	1	1.154
realizarla	0	1	1.154
realizaría	0	1	1.154
realizara	0	1	1.154
realizadas	0	1	1.154
realizada	0	1	1.154
realización	0	1	1.154
realito	0	1	1.154
realista	0	1	1.154
realice	0	1	1.154
realetes	0	1	1.154
reacciones	0	1	1.154
razonando	0	1	1.154
razonamientos	0	1	1.154
razonador	0	1	1.154
razona	0	1	1.154
rayuela	0	1	1.154
rayana	0	1	1.154
rayaditas	0	1	1.154
raudo	0	1	1.154
ratifico	0	1	1.154
ratera	0	1	1.154
rastros	0	1	1.154
rastrear	0	1	1.154
rásquese	0	1	1.154
rasque	0	1	1.154
raspe	0	1	1.154
raspándolo	0	1	1.154
rasos	0	1	1.154
rasguñaban	0	1	1.154
rasgueo	0	1	1.154
rasguear	0	1	1.154
rasgueando	0	1	1.154
rascarse	0	1	1.154
rascan	0	1	1.154
ráscame	0	1	1.154
rarificaciones	0	1	1.154
rarezas	0	1	1.154
raquitismo	0	1	1.154
raquíticos	0	1	1.154
rapazuelo	0	1	1.154
raparte	0	1	1.154
rapadas	0	1	1.154
rapada	0	1	1.154
rapacidad	0	1	1.154
ranero	0	1	1.154
randas	0	1	1.154
rancias	0	1	1.154
ramplona	0	1	1.154
rampas	0	1	1.154
rampa	0	1	1.154
ramojo	0	1	1.154
rameados	0	1	1.154
rameaditas	0	1	1.154
ramalazo	0	1	1.154
rallando	0	1	1.154
rajada	0	1	1.154
radio	0	1	1.154
radicaba	0	1	1.154
racionó	0	1	1.154
racionarse	0	1	1.154
racionarnos	0	1	1.154
racionalistas	0	1	1.154
rabos	0	1	1.154
rabito	0	1	1.154
rabiosito	0	1	1.154
rabiosilla	0	1	1.154
rabietinas	0	1	1.154
rabiará	0	1	1.154
rabeles	0	1	1.154
rabel	0	1	1.154
quitósele	0	1	1.154
quitole	0	1	1.154
quites	0	1	1.154
quíteme	0	1	1.154
quité	0	1	1.154
quitas	0	1	1.154
quitárselas	0	1	1.154
quitáronle	0	1	1.154
quitármelo	0	1	1.154
quitármela	0	1	1.154
quitarlos	0	1	1.154
quitarlo	0	1	1.154
quitaría	0	1	1.154
quitaré	0	1	1.154
quitaran	0	1	1.154
quitaos	0	1	1.154
quitándome	0	1	1.154
quitamos	0	1	1.154
quítale	0	1	1.154
quitádmelo	0	1	1.154
quisto	0	1	1.154
quisieren	0	1	1.154
quisierais	0	1	1.154
quirúrgicamente	0	1	1.154
quiquiriquí	0	1	1.154
quintín	0	1	1.154
quintero	0	1	1.154
quintal	0	1	1.154
quinina	0	1	1.154
quina	0	1	1.154
quilo	0	1	1.154
quijotesco	0	1	1.154
quijadas	0	1	1.154
quietos	0	1	1.154
quieles	0	1	1.154
quiebros	0	1	1.154
quiebras	0	1	1.154
quiebran	0	1	1.154
quesitos	0	1	1.154
quesada	0	1	1.154
queriéndome	0	1	1.154
queriéndole	0	1	1.154
queriéndola	0	1	1.154
queridos	0	1	1.154
queridísimos	0	1	1.154
querenciosa	0	1	1.154
querencias	0	1	1.154
queramos	0	1	1.154
querámonos	0	1	1.154
quepan	0	1	1.154
queme	0	1	1.154
quemazón	0	1	1.154
quemasteis	0	1	1.154
quemaron	0	1	1.154
quemándose	0	1	1.154
quejáronse	0	1	1.154
quejarás	0	1	1.154
quejar	0	1	1.154
quejando	0	1	1.154
quejamos	0	1	1.154
quedeme	0	1	1.154
quedaste	0	1	1.154
quedasen	0	1	1.154
quedarías	0	1	1.154
quedarás	0	1	1.154
quebrantar	0	1	1.154
quebrantado	0	1	1.154
quebrantadas	0	1	1.154
qartos	0	1	1.154
putrefacción	0	1	1.154
putona	0	1	1.154
putativa	0	1	1.154
púsolos	0	1	1.154
púsole	0	1	1.154
pusimos	0	1	1.154
pusiéronla	0	1	1.154
púseme	0	1	1.154
purito	0	1	1.154
purificarla	0	1	1.154
purificará	0	1	1.154
purificado	0	1	1.154
purés	0	1	1.154
puñales	0	1	1.154
punzón	0	1	1.154
punzadora	0	1	1.154
puntualísimo	0	1	1.154
puntualidades	0	1	1.154
puntillosa	0	1	1.154
puntilla	0	1	1.154
puntear	0	1	1.154
punteados	0	1	1.154
puntada	0	1	1.154
pundonorosas	0	1	1.154
pulverizo	0	1	1.154
pulverizado	0	1	1.154
pulverizadas	0	1	1.154
pulsera	0	1	1.154
pulsaciones	0	1	1.154
pulsación	0	1	1.154
pulpejo	0	1	1.154
pulpa	0	1	1.154
pulmonías	0	1	1.154
pulirse	0	1	1.154
pulimentado	0	1	1.154
puliéndola	0	1	1.154
puliendo	0	1	1.154
pulgares	0	1	1.154
pujante	0	1	1.154
puertecilla	0	1	1.154
puerquísima	0	1	1.154
puercas	0	1	1.154
puercachones	0	1	1.154
pueblecitos	0	1	1.154
pudiste	0	1	1.154
pudimos	0	1	1.154
pucheta	0	1	1.154
pucheritos	0	1	1.154
pucherito	0	1	1.154
públicos	0	1	1.154
publicista	0	1	1.154
publicarlos	0	1	1.154
publicantones	0	1	1.154
publicanos	0	1	1.154
publica	0	1	1.154
psch	0	1	1.154
pruuun	0	1	1.154
prum	0	1	1.154
prueban	0	1	1.154
prudhonianas	0	1	1.154
prudencial	0	1	1.154
proyectando	0	1	1.154
proyectan	0	1	1.154
proyección	0	1	1.154
provino	0	1	1.154
provenirle	0	1	1.154
provenir	0	1	1.154
provenido	0	1	1.154
provenían	0	1	1.154
provendrá	0	1	1.154
proveía	0	1	1.154
protoioduro	0	1	1.154
protestamos	0	1	1.154
protegiéndole	0	1	1.154
protegidos	0	1	1.154
protegerte	0	1	1.154
protegerle	0	1	1.154
protegería	0	1	1.154
protegeré	0	1	1.154
protegerá	0	1	1.154
protegen	0	1	1.154
protectoras	0	1	1.154
proteccionistas	0	1	1.154
protecciones	0	1	1.154
prostituyese	0	1	1.154
prosterne	0	1	1.154
prospera	0	1	1.154
prosiguieron	0	1	1.154
prosiguiendo	0	1	1.154
prosélitos	0	1	1.154
prorrumpió	0	1	1.154
prorrumpieron	0	1	1.154
prórrogas	0	1	1.154
propuso	19	17	1.154
propusimos	0	1	1.154
propusieran	0	1	1.154
propuse	0	1	1.154
proporcionó	0	1	1.154
proporcionase	0	1	1.154
proporcionales	0	1	1.154
proporcionadamente	0	1	1.154
proporcionábale	0	1	1.154
proporcionaba	0	1	1.154
proporciona	0	1	1.154
proponiéndose	0	1	1.154
proponiendo	0	1	1.154
propongámosla	0	1	1.154
propongamos	0	1	1.154
propones	0	1	1.154
proponerte	0	1	1.154
proponérselo	0	1	1.154
proponerse	0	1	1.154
proponerles	0	1	1.154
propónense	0	1	1.154
propinó	0	1	1.154
propinilla	0	1	1.154
propicios	0	1	1.154
propenso	0	1	1.154
propensa	0	1	1.154
propendían	0	1	1.154
propague	0	1	1.154
pronunciarlo	0	1	1.154
pronunciara	0	1	1.154
pronunciándolas	0	1	1.154
pronunciadas	0	1	1.154
pronunciaban	0	1	1.154
prontos	0	1	1.154
prontísimo	0	1	1.154
pronosticando	0	1	1.154
promulgando	0	1	1.154
promulga	0	1	1.154
promontorio	0	1	1.154
prominentes	0	1	1.154
prometiste	0	1	1.154
prometiéndole	0	1	1.154
prometíaselas	0	1	1.154
prolongarse	0	1	1.154
prolongando	0	1	1.154
prolongado	0	1	1.154
prolijidad	0	1	1.154
prolijamente	0	1	1.154
prolífica	0	1	1.154
prójimas	0	1	1.154
proive	0	1	1.154
prohijar	0	1	1.154
prohibiciones	0	1	1.154
prohibí	0	1	1.154
prohíben	0	1	1.154
progresivo	0	1	1.154
progresistón	0	1	1.154
progresado	0	1	1.154
progenie	0	1	1.154
profundísimamente	0	1	1.154
profundidad	0	1	1.154
profetizaron	0	1	1.154
profeta	0	1	1.154
profesora	0	1	1.154
profesionales	0	1	1.154
profesando	0	1	1.154
profanidad	0	1	1.154
prodújose	0	1	1.154
produjeron	0	1	1.154
produjera	0	1	1.154
productores	0	1	1.154
producirlos	0	1	1.154
producirán	0	1	1.154
produciéndose	0	1	1.154
producidos	0	1	1.154
producíase	0	1	1.154
prodrómico	0	1	1.154
prodigole	0	1	1.154
prodigándole	0	1	1.154
prodigaban	0	1	1.154
procuremos	0	1	1.154
procure	0	1	1.154
procurarle	0	1	1.154
procuraré	0	1	1.154
proclamas	0	1	1.154
proclamar	0	1	1.154
prócida	0	1	1.154
procesionalmente	0	1	1.154
proceroso	0	1	1.154
procediera	0	1	1.154
procedamos	0	1	1.154
procacidad	0	1	1.154
probrecilla	0	1	1.154
probeza	0	1	1.154
probes	0	1	1.154
probe	0	1	1.154
probártelo	0	1	1.154
probarla	0	1	1.154
probaría	0	1	1.154
probaran	0	1	1.154
probará	0	1	1.154
probadas	0	1	1.154
privar	0	1	1.154
privándose	0	1	1.154
privándole	0	1	1.154
privadas	0	1	1.154
prismática	0	1	1.154
prisma	0	1	1.154
pringado	0	1	1.154
pringadas	0	1	1.154
príncipes	0	1	1.154
primordial	0	1	1.154
primito	0	1	1.154
primarias	0	1	1.154
primaria	0	1	1.154
price	0	1	1.154
previstos	0	1	1.154
previsora	0	1	1.154
previas	0	1	1.154
previa	0	1	1.154
preventivo	0	1	1.154
prevenirlo	0	1	1.154
prevenidos	0	1	1.154
prevenciones	0	1	1.154
preveía	0	1	1.154
prevaricaban	0	1	1.154
prevalecido	0	1	1.154
prevalecer	0	1	1.154
prevalece	0	1	1.154
pretendiera	0	1	1.154
pretenderás	0	1	1.154
presunta	0	1	1.154
presumiera	0	1	1.154
presumes	0	1	1.154
prestidigitaciones	0	1	1.154
prestaros	0	1	1.154
prestarle	0	1	1.154
prestara	0	1	1.154
prestándole	0	1	1.154
prestamistas	0	1	1.154
prestaban	0	1	1.154
presona	0	1	1.154
presientes	0	1	1.154
presienten	0	1	1.154
presidios	0	1	1.154
presidieran	0	1	1.154
presidiarios	0	1	1.154
presidencial	0	1	1.154
preservativo	0	1	1.154
presentido	0	1	1.154
preséntate	0	1	1.154
presentársele	0	1	1.154
presentáronse	0	1	1.154
presentándose	0	1	1.154
presentándole	0	1	1.154
presentándola	0	1	1.154
presencié	0	1	1.154
presenciaron	0	1	1.154
presencian	0	1	1.154
prescrito	0	1	1.154
presbíteros	0	1	1.154
presagiar	0	1	1.154
preparo	0	1	1.154
preparen	0	1	1.154
preparé	0	1	1.154
preparatorias	0	1	1.154
prepararon	0	1	1.154
prepararla	0	1	1.154
prepararemos	0	1	1.154
preparándole	0	1	1.154
preparábase	0	1	1.154
prendió	0	1	1.154
prendiendo	0	1	1.154
prendidas	0	1	1.154
prendarse	0	1	1.154
prendara	0	1	1.154
prendaba	0	1	1.154
premiten	0	1	1.154
premite	0	1	1.154
premiso	0	1	1.154
premiados	0	1	1.154
prejuicios	0	1	1.154
preguntonas	0	1	1.154
preguntome	0	1	1.154
preguntitas	0	1	1.154
pregúnteselo	0	1	1.154
pregúntenle	0	1	1.154
pregunten	0	1	1.154
preguntársela	0	1	1.154
preguntarlo	0	1	1.154
preguntaría	0	1	1.154
preguntará	0	1	1.154
preguntábamos	0	1	1.154
pregone	0	1	1.154
prefieras	0	1	1.154
preferiremos	0	1	1.154
predico	0	1	1.154
predicara	0	1	1.154
predestinados	0	1	1.154
predecesores	0	1	1.154
predecesoras	0	1	1.154
precursoras	0	1	1.154
precozmente	0	1	1.154
precisos	0	1	1.154
precipites	0	1	1.154
precipitada	0	1	1.154
precipicio	0	1	1.154
preciosísimos	0	1	1.154
preciosas	0	1	1.154
preciábase	0	1	1.154
preceder	0	1	1.154
precedente	0	1	1.154
precede	0	1	1.154
práxedes	0	1	1.154
pragmáticas	0	1	1.154
pradoluengo	0	1	1.154
practico	0	1	1.154
practicarla	0	1	1.154
practicantes	0	1	1.154
practicando	0	1	1.154
practicado	0	1	1.154
practicadas	0	1	1.154
practicable	0	1	1.154
practica	0	1	1.154
potingues	0	1	1.154
potingue	0	1	1.154
potestad	0	1	1.154
potes	0	1	1.154
potentadas	0	1	1.154
potentada	0	1	1.154
potasio	0	1	1.154
postrimerías	0	1	1.154
postrado	0	1	1.154
postizas	0	1	1.154
poste	0	1	1.154
postal	0	1	1.154
posesionarían	0	1	1.154
poseído	0	1	1.154
poseída	0	1	1.154
poseerlo	0	1	1.154
poseedora	0	1	1.154
posea	0	1	1.154
posarle	0	1	1.154
posadas	0	1	1.154
portugal	0	1	1.154
portear	0	1	1.154
portazos	0	1	1.154
portazo	0	1	1.154
portas	0	1	1.154
portarte	0	1	1.154
portarnos	0	1	1.154
portan	0	1	1.154
portamos	0	1	1.154
portabas	0	1	1.154
porfiaba	0	1	1.154
pordioseaba	0	1	1.154
porcelanescas	0	1	1.154
poquitos	0	1	1.154
poquita	0	1	1.154
poquísimos	0	1	1.154
poquísimas	0	1	1.154
ponzoñoso	0	1	1.154
pontevedra	0	1	1.154
ponle	0	1	1.154
poniéndoselos	0	1	1.154
poniéndola	0	1	1.154
poníasele	0	1	1.154
ponías	0	1	1.154
poníala	0	1	1.154
pongámosle	0	1	1.154
pongámonos	0	1	1.154
póngalo	0	1	1.154
ponérteme	0	1	1.154
ponérmela	0	1	1.154
ponerles	0	1	1.154
ponéis	0	1	1.154
ponedla	0	1	1.154
pondrías	0	1	1.154
pondrían	0	1	1.154
pondríamos	0	1	1.154
ponderarle	0	1	1.154
ponderando	0	1	1.154
ponderaciones	0	1	1.154
ponderaban	0	1	1.154
ponderaba	0	1	1.154
poncio	0	1	1.154
ponchera	0	1	1.154
pompones	0	1	1.154
pómez	0	1	1.154
pomada	0	1	1.154
polvorosos	0	1	1.154
polvorosa	0	1	1.154
polvillo	0	1	1.154
polluela	0	1	1.154
pollita	0	1	1.154
pollino	0	1	1.154
polleros	0	1	1.154
pollerías	0	1	1.154
pollera	0	1	1.154
polizonte	0	1	1.154
politicastros	0	1	1.154
polinesia	0	1	1.154
policiacos	0	1	1.154
policíaca	0	1	1.154
polemista	0	1	1.154
podridas	0	1	1.154
podíamos	0	1	1.154
poderse	0	1	1.154
poderme	0	1	1.154
poderle	0	1	1.154
podamos	0	1	1.154
poción	0	1	1.154
pócima	0	1	1.154
pocillo	0	1	1.154
pobrísima	0	1	1.154
pobrete	0	1	1.154
pobrecitas	0	1	1.154
pobrecillas	0	1	1.154
poblaciones	0	1	1.154
poblaban	0	1	1.154
plumonía	0	1	1.154
plumear	0	1	1.154
plumacho	0	1	1.154
plim	0	1	1.154
pléyade	0	1	1.154
pleticó	0	1	1.154
pleticar	0	1	1.154
plenipotenciario	0	1	1.154
pléiticas	0	1	1.154
pleitazo	0	1	1.154
platónicas	0	1	1.154
platicando	0	1	1.154
platica	0	1	1.154
platero	0	1	1.154
platería	0	1	1.154
plateado	0	1	1.154
plateada	0	1	1.154
plataformas	0	1	1.154
plasta	0	1	1.154
plañidera	0	1	1.154
plantilla	0	1	1.154
plantifiquen	0	1	1.154
planteo	0	1	1.154
plantear	0	1	1.154
planteándole	0	1	1.154
planteado	0	1	1.154
planteaba	0	1	1.154
plantea	0	1	1.154
plantársele	0	1	1.154
plantaron	0	1	1.154
plantarme	0	1	1.154
plantaremos	0	1	1.154
plantándose	0	1	1.154
plantada	0	1	1.154
planos	0	1	1.154
planicie	0	1	1.154
planeta	0	1	1.154
planche	0	1	1.154
planchándole	0	1	1.154
planchaba	0	1	1.154
plaga	0	1	1.154
placita	0	1	1.154
placidito	0	1	1.154
placeros	0	1	1.154
placenteros	0	1	1.154
placentero	0	1	1.154
place	0	1	1.154
pizarras	0	1	1.154
pizarra	0	1	1.154
pitusiana	0	1	1.154
pituitaria	0	1	1.154
pitos	0	1	1.154
pitón	0	1	1.154
pitoja	0	1	1.154
pitofufito	0	1	1.154
pitita	0	1	1.154
pítima	0	1	1.154
pitidos	0	1	1.154
pitarás	0	1	1.154
pita	0	1	1.154
pistos	0	1	1.154
pisotearla	0	1	1.154
pisotea	0	1	1.154
piscicultura	0	1	1.154
pisas	0	1	1.154
pisárselas	0	1	1.154
pisándoles	0	1	1.154
piruétano	0	1	1.154
pirra	0	1	1.154
pirineo	0	1	1.154
piratería	0	1	1.154
pira	0	1	1.154
piquito	0	1	1.154
piques	0	1	1.154
pique	0	1	1.154
pior	0	1	1.154
piojosa	0	1	1.154
piñones	0	1	1.154
pintiparada	0	1	1.154
pintarlas	0	1	1.154
pintándose	0	1	1.154
pintaban	0	1	1.154
pinitos	0	1	1.154
pingajo	0	1	1.154
pindonga	0	1	1.154
pinchase	0	1	1.154
pinchamos	0	1	1.154
pinchacitos	0	1	1.154
pinceles	0	1	1.154
pincelada	0	1	1.154
pincel	0	1	1.154
pináculo	0	1	1.154
pimpollos	0	1	1.154
piltrafas	0	1	1.154
piltrafa	0	1	1.154
pilosa	0	1	1.154
pillines	0	1	1.154
pillincito	0	1	1.154
pillinadas	0	1	1.154
pille	0	1	1.154
pilatos	0	1	1.154
pilastrones	0	1	1.154
pignoró	0	1	1.154
pignorado	0	1	1.154
pifias	0	1	1.154
pifia	0	1	1.154
piernazas	0	1	1.154
pierdas	0	1	1.154
pierdan	0	1	1.154
piensen	0	1	1.154
piensasté	0	1	1.154
piedrecita	0	1	1.154
piececitas	0	1	1.154
pidiéronle	0	1	1.154
pidieras	0	1	1.154
pidieran	0	1	1.154
pídeselo	0	1	1.154
pídele	0	1	1.154
pidas	0	1	1.154
pidan	0	1	1.154
pidámosle	0	1	1.154
picorcillo	0	1	1.154
picó	0	1	1.154
pichoncitos	0	1	1.154
pichona	0	1	1.154
picas	0	1	1.154
picaronaza	0	1	1.154
picaporte	0	1	1.154
picapedreros	0	1	1.154
picadura	0	1	1.154
picadilly	0	1	1.154
picadillo	0	1	1.154
piazo	0	1	1.154
pianino	0	1	1.154
pianillo	0	1	1.154
pian	0	1	1.154
piache	0	1	1.154
pía	0	1	1.154
petrarca	0	1	1.154
petimetres	0	1	1.154
petaba	0	1	1.154
pestilencia	0	1	1.154
pestífera	0	1	1.154
pesquisas	0	1	1.154
pespuntar	0	1	1.154
pésemelo	0	1	1.154
pescuezos	0	1	1.154
pesco	0	1	1.154
pescadilla	0	1	1.154
pescaban	0	1	1.154
pesase	0	1	1.154
pesadumbres	0	1	1.154
pesadita	0	1	1.154
pesadísima	0	1	1.154
pervertírsele	0	1	1.154
pervertir	0	1	1.154
pervertimos	0	1	1.154
perturbe	0	1	1.154
perturbase	0	1	1.154
perturbar	0	1	1.154
perturbadas	0	1	1.154
perturbaciones	0	1	1.154
perturbaba	0	1	1.154
pertinencia	0	1	1.154
pertenezco	0	1	1.154
pertenecí	0	1	1.154
pertenecer	0	1	1.154
persuasivas	0	1	1.154
persuadí	0	1	1.154
personó	0	1	1.154
personificado	0	1	1.154
personificaba	0	1	1.154
personarse	0	1	1.154
personaron	0	1	1.154
personalizar	0	1	1.154
personalizando	0	1	1.154
personalidá	0	1	1.154
persistió	0	1	1.154
persistieron	0	1	1.154
persistían	0	1	1.154
persistentes	0	1	1.154
persiste	0	1	1.154
persiguiéndole	0	1	1.154
persignó	0	1	1.154
persiga	0	1	1.154
perseverando	0	1	1.154
persépolis	0	1	1.154
perseguirte	0	1	1.154
perseguidora	0	1	1.154
persecutorio	0	1	1.154
perruna	0	1	1.154
perrería	0	1	1.154
perrazo	0	1	1.154
perras	0	1	1.154
perpleja	0	1	1.154
perpiñá	0	1	1.154
perpetuidad	0	1	1.154
perpetuase	0	1	1.154
perpetuarse	0	1	1.154
pernoctar	0	1	1.154
perniquiebres	0	1	1.154
pernetas	0	1	1.154
permuta	0	1	1.154
permitírselo	0	1	1.154
permitirlos	0	1	1.154
permitirles	0	1	1.154
permitiría	0	1	1.154
permitirá	0	1	1.154
permitiole	0	1	1.154
permitieran	0	1	1.154
permitiéndole	0	1	1.154
permitiendo	0	1	1.154
permitíale	0	1	1.154
permiten	0	1	1.154
permitas	0	1	1.154
permanentes	0	1	1.154
permanecieron	0	1	1.154
permanecían	0	1	1.154
perjudicial	0	1	1.154
periquito	0	1	1.154
periquillo	0	1	1.154
período	0	1	1.154
periodistas	0	1	1.154
periodiqueros	0	1	1.154
periódicas	0	1	1.154
periespíritu	0	1	1.154
pericos	0	1	1.154
pericial	0	1	1.154
pergeñada	0	1	1.154
pergenio	0	1	1.154
perfumadas	0	1	1.154
perfilados	0	1	1.154
perfeccionado	0	1	1.154
perfec	0	1	1.154
perezca	0	1	1.154
perendengues	0	1	1.154
perejil	0	1	1.154
peregrinas	0	1	1.154
peregrina	0	1	1.154
pereciendo	0	1	1.154
perecemos	0	1	1.154
perece	0	1	1.154
perdoné	0	1	1.154
perdonas	0	1	1.154
perdonarte	0	1	1.154
perdonárselos	0	1	1.154
perdonarnos	0	1	1.154
perdonaré	0	1	1.154
perdonándosela	0	1	1.154
perdonan	0	1	1.154
perdonamos	0	1	1.154
perdonadas	0	1	1.154
perdiose	0	1	1.154
perdío	0	1	1.154
perdidamente	0	1	1.154
perderte	0	1	1.154
perderles	0	1	1.154
perderé	0	1	1.154
perdemos	0	1	1.154
percusión	0	1	1.154
percloruro	0	1	1.154
percibir	0	1	1.154
percibida	0	1	1.154
percheros	0	1	1.154
perchero	0	1	1.154
perchel	0	1	1.154
peques	0	1	1.154
pequeñuelas	0	1	1.154
pequeñitas	0	1	1.154
pequeñita	0	1	1.154
pequemos	0	1	1.154
peque	0	1	1.154
peptona	0	1	1.154
peñuelas	0	1	1.154
peñascales	0	1	1.154
peñas	0	1	1.154
pensiono	0	1	1.154
pensaste	0	1	1.154
pensasen	0	1	1.154
pensaré	0	1	1.154
pensarás	0	1	1.154
pensarán	0	1	1.154
pensad	0	1	1.154
pensabas	0	1	1.154
penosísimos	0	1	1.154
penosas	0	1	1.154
penosamente	0	1	1.154
penitas	0	1	1.154
penetres	0	1	1.154
penetré	0	1	1.154
penetrase	0	1	1.154
penetrarse	0	1	1.154
penetraras	0	1	1.154
penetrándose	0	1	1.154
penetrada	0	1	1.154
penetración	0	1	1.154
pene	0	1	1.154
péndulo	0	1	1.154
pendoncillo	0	1	1.154
pendolista	0	1	1.154
pendencia	0	1	1.154
pencas	0	1	1.154
penates	0	1	1.154
penar	0	1	1.154
penalidad	0	1	1.154
penal	0	1	1.154
penado	0	1	1.154
pelusa	0	1	1.154
peluda	0	1	1.154
peluche	0	1	1.154
pelotones	0	1	1.154
pelotilla	0	1	1.154
pelotada	0	1	1.154
pelmazo	0	1	1.154
pellizcándole	0	1	1.154
pellizcando	0	1	1.154
pelliza	0	1	1.154
pelleja	0	1	1.154
pelinegra	0	1	1.154
peleando	0	1	1.154
pelando	0	1	1.154
pelaje	0	1	1.154
pelafustán	0	1	1.154
peladilla	0	1	1.154
peinose	0	1	1.154
peinarte	0	1	1.154
peinando	0	1	1.154
peinados	0	1	1.154
peina	0	1	1.154
pégueme	0	1	1.154
pegue	0	1	1.154
pegote	0	1	1.154
pegasteis	0	1	1.154
pegase	0	1	1.154
pegárselo	0	1	1.154
pegársela	0	1	1.154
pegármela	0	1	1.154
pegaré	0	1	1.154
pegaras	0	1	1.154
pegándomela	0	1	1.154
pégame	0	1	1.154
pedrisco	0	1	1.154
pedrada	0	1	1.154
pedís	0	1	1.154
pedirás	0	1	1.154
pedigüeñas	0	1	1.154
pedías	0	1	1.154
pedernales	0	1	1.154
pedal	0	1	1.154
pedacito	0	1	1.154
pecosa	0	1	1.154
pecó	0	1	1.154
pechugón	0	1	1.154
pechona	0	1	1.154
pececillos	0	1	1.154
pecase	0	1	1.154
pecara	0	1	1.154
pecando	0	1	1.154
pe	0	1	1.154
payasa	0	1	1.154
pavonadas	0	1	1.154
pavisosa	0	1	1.154
patulea	0	1	1.154
patrióticos	0	1	1.154
patrimonial	0	1	1.154
patriarcalismo	0	1	1.154
patoso	0	1	1.154
patológicos	0	1	1.154
patológico	0	1	1.154
patito	0	1	1.154
patinar	0	1	1.154
patinadores	0	1	1.154
patinación	0	1	1.154
pateta	0	1	1.154
paterno	0	1	1.154
paternidad	0	1	1.154
paternalmente	0	1	1.154
patencures	0	1	1.154
patee	0	1	1.154
pateándole	0	1	1.154
patatitas	0	1	1.154
pataplum	0	1	1.154
patalea	0	1	1.154
patadillas	0	1	1.154
pastoreaba	0	1	1.154
pastorales	0	1	1.154
pastelón	0	1	1.154
pastel	0	1	1.154
passer	0	1	1.154
pasola	0	1	1.154
pasmoso	0	1	1.154
pasmose	0	1	1.154
pasmarte	0	1	1.154
pasmarotes	0	1	1.154
pasmarías	0	1	1.154
pasmaré	0	1	1.154
pasmaran	0	1	1.154
pasman	0	1	1.154
pasivo	0	1	1.154
pasividad	0	1	1.154
pasivas	0	1	1.154
pasitos	0	1	1.154
pasita	0	1	1.154
pasillos	19	17	1.154
pasiega	0	1	1.154
paseítos	0	1	1.154
paséese	0	1	1.154
paséate	0	1	1.154
pasearnos	0	1	1.154
paseante	0	1	1.154
paseábanse	0	1	1.154
pasáronle	0	1	1.154
pasarme	0	1	1.154
pasaríamos	0	1	1.154
pasaras	0	1	1.154
pasaporte	0	1	1.154
pasamanería	0	1	1.154
pasadita	0	1	1.154
pasábanse	0	1	1.154
párvulos	0	1	1.154
partirse	0	1	1.154
partirle	0	1	1.154
partiese	0	1	1.154
partieran	0	1	1.154
partiéndole	0	1	1.154
partidita	0	1	1.154
partícipes	0	1	1.154
partícipe	0	1	1.154
participaste	0	1	1.154
participaciones	0	1	1.154
parten	0	1	1.154
partan	0	1	1.154
parriba	0	1	1.154
parrales	0	1	1.154
parral	0	1	1.154
parra	0	1	1.154
parlanchín	0	1	1.154
parlamentarismo	0	1	1.154
parlamentarios	0	1	1.154
parlamentario	0	1	1.154
parlamentaria	0	1	1.154
parlamentando	0	1	1.154
park	0	1	1.154
parir	0	1	1.154
pariera	0	1	1.154
parienta	0	1	1.154
pariendo	0	1	1.154
paridas	0	1	1.154
parida	0	1	1.154
parias	0	1	1.154
parían	0	1	1.154
paría	0	1	1.154
parezcas	0	1	1.154
pareciome	0	1	1.154
pareciesen	0	1	1.154
pareciéronle	0	1	1.154
pareciéralo	0	1	1.154
pareciéndole	0	1	1.154
parecérsele	0	1	1.154
pare	0	1	1.154
pardillo	0	1	1.154
pardessus	0	1	1.154
párate	0	1	1.154
parásito	0	1	1.154
parasitario	0	1	1.154
paráronse	0	1	1.154
parará	0	1	1.154
parara	0	1	1.154
paramento	0	1	1.154
paralizado	0	1	1.154
paralizadas	0	1	1.154
paralítico	0	1	1.154
paralítica	0	1	1.154
parálisis	0	1	1.154
paralelamente	0	1	1.154
paraguazo	0	1	1.154
paradójica	0	1	1.154
parábase	0	1	1.154
paquetitos	0	1	1.154
papos	0	1	1.154
pápiros	0	1	1.154
papelitos	0	1	1.154
papelistas	0	1	1.154
papelillo	0	1	1.154
papeletitas	0	1	1.154
papelejos	0	1	1.154
papelejo	0	1	1.154
papé	0	1	1.154
papal	0	1	1.154
papaíto	0	1	1.154
papagayo	0	1	1.154
pañero	0	1	1.154
panzudo	0	1	1.154
pantuflas	0	1	1.154
panteístas	0	1	1.154
pantaloncitos	0	1	1.154
pantallas	0	1	1.154
pantaleón	0	1	1.154
panoli	0	1	1.154
panificación	0	1	1.154
pánfila	0	1	1.154
pandillas	0	1	1.154
pancorvo	0	1	1.154
panadero	0	1	1.154
panaceas	0	1	1.154
pámpano	0	1	1.154
paludismo	0	1	1.154
palpó	0	1	1.154
palpitar	0	1	1.154
palpitante	0	1	1.154
palpitando	0	1	1.154
palpe	0	1	1.154
palpaban	0	1	1.154
palotes	0	1	1.154
palote	0	1	1.154
palosanto	0	1	1.154
palmoteándole	0	1	1.154
palmos	0	1	1.154
palmarios	0	1	1.154
palmaria	0	1	1.154
palito	0	1	1.154
palideces	0	1	1.154
paliativos	0	1	1.154
paleto	0	1	1.154
paletilla	0	1	1.154
palatino	0	1	1.154
palastro	0	1	1.154
palante	0	1	1.154
paladares	0	1	1.154
palabrillas	0	1	1.154
palabrilla	0	1	1.154
palabrero	0	1	1.154
pala	0	1	1.154
pal	0	1	1.154
pajita	0	1	1.154
pajes	0	1	1.154
pajarraco	0	1	1.154
pajaritos	0	1	1.154
paisajista	0	1	1.154
paicían	0	1	1.154
paicerse	0	1	1.154
paicen	0	1	1.154
paguen	0	1	1.154
pagué	0	1	1.154
paginitas	0	1	1.154
pagarme	0	1	1.154
pagara	0	1	1.154
pagándole	0	1	1.154
pagando	0	1	1.154
paella	0	1	1.154
padezcamos	0	1	1.154
padecían	0	1	1.154
padecí	0	1	1.154
padecerías	0	1	1.154
padecería	0	1	1.154
padecen	0	1	1.154
pacificar	0	1	1.154
pacificadoras	0	1	1.154
pábilo	0	1	1.154
pabellones	0	1	1.154
oyoles	0	1	1.154
oyola	0	1	1.154
oyeras	0	1	1.154
óyense	0	1	1.154
oyéndose	0	1	1.154
oyéndolo	0	1	1.154
óyeme	0	1	1.154
óvalo	0	1	1.154
otorgase	0	1	1.154
otorgarle	0	1	1.154
otorgándose	0	1	1.154
otero	0	1	1.154
otelo	0	1	1.154
ostra	0	1	1.154
oscurecen	0	1	1.154
oscilaba	0	1	1.154
osara	0	1	1.154
ortógrafo	0	1	1.154
ornitológicas	0	1	1.154
oriundos	0	1	1.154
orinó	0	1	1.154
orihuela	0	1	1.154
originalísimo	0	1	1.154
orientándose	0	1	1.154
orgullosamente	0	1	1.154
organizó	0	1	1.154
organizarse	0	1	1.154
organizador	0	1	1.154
organizadas	0	1	1.154
organizada	0	1	1.154
organillo	0	1	1.154
orejitas	0	1	1.154
orejita	0	1	1.154
orearan	0	1	1.154
orea	0	1	1.154
ordinariotes	0	1	1.154
ordinariota	0	1	1.154
ordinarieces	0	1	1.154
ordenador	0	1	1.154
ordenadas	0	1	1.154
ordenación	0	1	1.154
ordenaban	0	1	1.154
orbe	0	1	1.154
oratorios	0	1	1.154
orates	0	1	1.154
oraba	0	1	1.154
opusiéronse	0	1	1.154
opulento	0	1	1.154
opuestos	0	1	1.154
optimismos	0	1	1.154
opta	0	1	1.154
oprimidas	0	1	1.154
oportunista	0	1	1.154
oponiendo	0	1	1.154
opongo	0	1	1.154
opóngase	0	1	1.154
oponga	0	1	1.154
oponen	0	1	1.154
opinado	0	1	1.154
opiáceo	0	1	1.154
ópalo	0	1	1.154
opacos	0	1	1.154
opacidad	0	1	1.154
opaca	0	1	1.154
ooooh	0	1	1.154
onza	0	1	1.154
onofre	0	1	1.154
onduladas	0	1	1.154
ondeando	0	1	1.154
onde	0	1	1.154
omoplato	0	1	1.154
omnipotente	0	1	1.154
omnímodo	0	1	1.154
ómnibus	0	1	1.154
omitida	0	1	1.154
omisiones	0	1	1.154
ombligo	0	1	1.154
olviden	0	1	1.154
olvídate	0	1	1.154
olvidarte	0	1	1.154
olvidárseles	0	1	1.154
olvidaron	0	1	1.154
olvidáramos	0	1	1.154
olvidándose	0	1	1.154
olvidadizos	0	1	1.154
olózaga	0	1	1.154
olorosísimas	0	1	1.154
olmos	0	1	1.154
oliva	0	1	1.154
olió	0	1	1.154
olimpa	0	1	1.154
olfatorias	0	1	1.154
olfatea	0	1	1.154
óleos	0	1	1.154
oleeé	0	1	1.154
oleadas	0	1	1.154
ojeador	0	1	1.154
ojeadas	0	1	1.154
ojales	0	1	1.154
ojalateros	0	1	1.154
oírnos	0	1	1.154
oírles	0	1	1.154
oiría	0	1	1.154
oiré	0	1	1.154
oímos	0	1	1.154
oigas	0	1	1.154
oídas	0	1	1.154
oíanle	0	1	1.154
oíamos	0	1	1.154
oíales	0	1	1.154
ofuscaras	0	1	1.154
ofuscándose	0	1	1.154
ofrecimiento	0	1	1.154
ofreciéndoseles	0	1	1.154
ofreciéndose	0	1	1.154
ofreciéndolo	0	1	1.154
ofreciéndoles	0	1	1.154
ofrecíase	0	1	1.154
ofrecérselo	0	1	1.154
ofrecerse	0	1	1.154
ofrecerme	0	1	1.154
ofrecerles	0	1	1.154
ofrecerla	0	1	1.154
ofrecerá	0	1	1.154
ofrécele	0	1	1.154
oficiosos	0	1	1.154
oficinalis	0	1	1.154
ofícialas	0	1	1.154
ofensor	0	1	1.154
ofensiva	0	1	1.154
ofendió	0	1	1.154
ofendiera	0	1	1.154
ofendiendo	0	1	1.154
odisea	0	1	1.154
odié	0	1	1.154
ocurrirle	0	1	1.154
ocurrirían	0	1	1.154
ocurriome	0	1	1.154
ocurriendo	0	1	1.154
ocurridos	0	1	1.154
ocurrente	0	1	1.154
ocurran	0	1	1.154
ocupes	0	1	1.154
ocuparte	0	1	1.154
ocuparían	0	1	1.154
ocuparía	0	1	1.154
ocupándola	0	1	1.154
ocupando	0	1	1.154
ocupador	0	1	1.154
ocultis	0	1	1.154
ocultarte	0	1	1.154
ocultarse	0	1	1.154
ocultáronse	0	1	1.154
ocultarían	0	1	1.154
ocultara	0	1	1.154
ocultamente	0	1	1.154
ocular	0	1	1.154
ocre	0	1	1.154
ochentines	0	1	1.154
ochavito	0	1	1.154
ocasionó	0	1	1.154
ocasionan	0	1	1.154
ocasionado	0	1	1.154
ocasionaban	0	1	1.154
ocasiona	0	1	1.154
obtienen	0	1	1.154
obteniendo	0	1	1.154
obtenidas	0	1	1.154
obstruían	0	1	1.154
obstino	0	1	1.154
obstinas	0	1	1.154
obstinación	0	1	1.154
obstetricia	0	1	1.154
observole	0	1	1.154
observaste	0	1	1.154
observas	0	1	1.154
observarse	0	1	1.154
observarla	0	1	1.154
obsérvale	0	1	1.154
observados	0	1	1.154
observada	0	1	1.154
observábale	0	1	1.154
observábala	0	1	1.154
obsequiosissimus	0	1	1.154
obre	0	1	1.154
obrase	0	1	1.154
obrando	0	1	1.154
obran	0	1	1.154
obrado	0	1	1.154
obraba	0	1	1.154
obligas	0	1	1.154
obligaran	0	1	1.154
oblicuidad	0	1	1.154
objetivos	0	1	1.154
objetiva	0	1	1.154
obeso	0	1	1.154
obesidad	0	1	1.154
obedecen	0	1	1.154
ñoños	0	1	1.154
nutría	0	1	1.154
numismático	0	1	1.154
numérico	0	1	1.154
nulidad	0	1	1.154
nula	0	1	1.154
nuevecitas	0	1	1.154
nudoso	0	1	1.154
nubló	0	1	1.154
nublaba	0	1	1.154
novísimo	0	1	1.154
noviciado	0	1	1.154
novias	0	1	1.154
noveno	0	1	1.154
novelista	0	1	1.154
novelesco	0	1	1.154
novelador	0	1	1.154
novel	0	1	1.154
novecientos	0	1	1.154
noticiero	0	1	1.154
notarios	0	1	1.154
notándose	0	1	1.154
notabilísima	0	1	1.154
notabilidades	0	1	1.154
notábase	0	1	1.154
nostri	0	1	1.154
normalizar	0	1	1.154
normales	0	1	1.154
norma	0	1	1.154
noramala	0	1	1.154
nominativas	0	1	1.154
nominal	0	1	1.154
nómina	0	1	1.154
nomenclaturas	0	1	1.154
nomenclátor	0	1	1.154
nombrarla	0	1	1.154
nombrara	0	1	1.154
nombran	0	1	1.154
nombrados	0	1	1.154
nombrado	0	1	1.154
nombrábase	0	1	1.154
nombraban	0	1	1.154
nociva	0	1	1.154
nochecita	0	1	1.154
nobilísimos	0	1	1.154
nobilísima	0	1	1.154
nobiliarias	0	1	1.154
nizán	0	1	1.154
nitro	0	1	1.154
níquel	0	1	1.154
nipis	0	1	1.154
niñeras	0	1	1.154
nieva	0	1	1.154
nietecito	0	1	1.154
newton	0	1	1.154
neutralizado	0	1	1.154
neto	0	1	1.154
nerviosísima	0	1	1.154
neptuno	0	1	1.154
nenita	0	1	1.154
negrazo	0	1	1.154
negociara	0	1	1.154
negociar	0	1	1.154
negligente	0	1	1.154
negativos	0	1	1.154
negativas	0	1	1.154
negaran	0	1	1.154
negándose	0	1	1.154
negábase	0	1	1.154
nefandos	0	1	1.154
nefandas	0	1	1.154
necesitaré	0	1	1.154
necesitando	0	1	1.154
neas	0	1	1.154
navidades	0	1	1.154
navas	0	1	1.154
navarra	0	1	1.154
navaja	0	1	1.154
naufragios	0	1	1.154
naufragio	0	1	1.154
náufraga	0	1	1.154
náu	0	1	1.154
nato	0	1	1.154
nasales	0	1	1.154
narradora	0	1	1.154
narra	0	1	1.154
narina	0	1	1.154
narigudos	0	1	1.154
naricillas	0	1	1.154
narcótico	0	1	1.154
narcisus	0	1	1.154
naranjo	0	1	1.154
naranjeros	0	1	1.154
naranjado	0	1	1.154
napoleónicas	0	1	1.154
nansouk	0	1	1.154
najo	0	1	1.154
najabao	0	1	1.154
nadasen	0	1	1.154
nadase	0	1	1.154
nadamos	0	1	1.154
nadaban	0	1	1.154
naciones	0	1	1.154
nacerá	0	1	1.154
mutuo	0	1	1.154
mutismo	0	1	1.154
mutaciones	0	1	1.154
musotros	0	1	1.154
muslito	0	1	1.154
músicos	0	1	1.154
murmurantes	0	1	1.154
murieras	0	1	1.154
muriéndome	0	1	1.154
murgas	0	1	1.154
murcia	0	1	1.154
multitudes	0	1	1.154
multiplica	0	1	1.154
mulo	0	1	1.154
muladares	0	1	1.154
mujeriego	0	1	1.154
mujeraza	0	1	1.154
mugrientas	0	1	1.154
mugir	0	1	1.154
muestrarios	0	1	1.154
muerde	0	1	1.154
muerdas	0	1	1.154
muerda	0	1	1.154
muellemente	0	1	1.154
mudemos	0	1	1.154
mudas	0	1	1.154
mudaron	0	1	1.154
mudara	0	1	1.154
mudan	0	1	1.154
mucosa	0	1	1.154
mucílago	0	1	1.154
muchísimas	0	1	1.154
muchachones	0	1	1.154
mozuela	0	1	1.154
mozart	0	1	1.154
mozárabe	0	1	1.154
moyano	0	1	1.154
moviéndola	0	1	1.154
movible	0	1	1.154
movíase	0	1	1.154
movías	0	1	1.154
motivaran	0	1	1.154
motivados	0	1	1.154
motivado	0	1	1.154
motejaban	0	1	1.154
moteja	0	1	1.154
mostrose	0	1	1.154
mostraron	0	1	1.154
mostrarla	0	1	1.154
mostrándoselos	0	1	1.154
mostrándoselo	0	1	1.154
mostrándolos	0	1	1.154
mostrándolo	0	1	1.154
mostrándola	0	1	1.154
mostrado	0	1	1.154
mosquitero	0	1	1.154
mosquita	0	1	1.154
moscones	0	1	1.154
mortuorio	0	1	1.154
mortifique	0	1	1.154
mortificó	0	1	1.154
mortificara	0	1	1.154
mortificando	0	1	1.154
mortificaciones	0	1	1.154
mortero	0	1	1.154
mortecina	0	1	1.154
mortalmente	0	1	1.154
mortaja	0	1	1.154
morrones	0	1	1.154
morritos	0	1	1.154
morris	0	1	1.154
morralla	0	1	1.154
morral	0	1	1.154
morrada	0	1	1.154
morosidades	0	1	1.154
moró	0	1	1.154
morisco	0	1	1.154
morisca	0	1	1.154
morírseme	0	1	1.154
morirían	0	1	1.154
moriríamos	0	1	1.154
moriremos	0	1	1.154
morí	0	1	1.154
mordiscos	0	1	1.154
mordiscar	0	1	1.154
mordida	0	1	1.154
mordentes	0	1	1.154
moras	0	1	1.154
morar	0	1	1.154
moquito	0	1	1.154
moquillo	0	1	1.154
moños	0	1	1.154
monumentalidad	0	1	1.154
montpensier	0	1	1.154
montose	0	1	1.154
montoncitos	0	1	1.154
montesinos	0	1	1.154
montesa	0	1	1.154
montés	0	1	1.154
montemuru	0	1	1.154
monteleón	0	1	1.154
montarse	0	1	1.154
montarlo	0	1	1.154
monstruosos	0	1	1.154
monstrua	0	1	1.154
monopolizaron	0	1	1.154
monopolizando	0	1	1.154
monopolizaban	0	1	1.154
monomaniacos	0	1	1.154
monomaniaca	0	1	1.154
monísimos	0	1	1.154
monísimas	0	1	1.154
monises	0	1	1.154
monín	0	1	1.154
monilla	0	1	1.154
monigote	0	1	1.154
mongólico	0	1	1.154
monetaria	0	1	1.154
monea	0	1	1.154
monde	0	1	1.154
moncloa	0	1	1.154
monasterio	0	1	1.154
monarquías	0	1	1.154
monamente	0	1	1.154
mon	0	1	1.154
momias	0	1	1.154
momentitos	0	1	1.154
momentico	0	1	1.154
momentáneamente	0	1	1.154
molusco	0	1	1.154
molto	0	1	1.154
molleja	0	1	1.154
molinillo	0	1	1.154
molida	0	1	1.154
molía	0	1	1.154
molestó	0	1	1.154
molestísimas	0	1	1.154
molestísima	0	1	1.154
molestase	0	1	1.154
molestarte	0	1	1.154
molestaré	0	1	1.154
molestará	0	1	1.154
molestan	0	1	1.154
molestábale	0	1	1.154
moler	0	1	1.154
moldearla	0	1	1.154
mojó	0	1	1.154
mojicón	0	1	1.154
mojaría	0	1	1.154
mojándole	0	1	1.154
mojamos	0	1	1.154
mojama	0	1	1.154
mohosos	0	1	1.154
mohosas	0	1	1.154
modulaciones	0	1	1.154
modosita	0	1	1.154
modorra	0	1	1.154
moditos	0	1	1.154
modistos	0	1	1.154
modistillas	0	1	1.154
modificó	0	1	1.154
modificación	0	1	1.154
modestísimo	0	1	1.154
modestamente	0	1	1.154
modere	0	1	1.154
moderarse	0	1	1.154
moderantismo	0	1	1.154
moderando	0	1	1.154
moderaísmo	0	1	1.154
moderación	0	1	1.154
modelito	0	1	1.154
modele	0	1	1.154
modelaban	0	1	1.154
mochila	0	1	1.154
mocetón	0	1	1.154
mixtura	0	1	1.154
mitras	0	1	1.154
mitos	0	1	1.154
mitológico	0	1	1.154
mitchell	0	1	1.154
mistress	0	1	1.154
mistos	0	1	1.154
mistiquerías	0	1	1.154
misté	0	1	1.154
misitas	0	1	1.154
misericordias	0	1	1.154
míseras	0	1	1.154
míseramente	0	1	1.154
misales	0	1	1.154
mironas	0	1	1.154
mirola	0	1	1.154
mirlo	0	1	1.154
miriñaque	0	1	1.154
mírelo	0	1	1.154
mirarlos	0	1	1.154
mirarlas	0	1	1.154
miraran	0	1	1.154
míranse	0	1	1.154
miranda	0	1	1.154
miramos	0	1	1.154
míralo	0	1	1.154
mirados	0	1	1.154
mirábase	0	1	1.154
mirábanse	0	1	1.154
mirábanla	0	1	1.154
mirábamos	0	1	1.154
mirábales	0	1	1.154
minueto	0	1	1.154
minuciosas	0	1	1.154
ministerialismo	0	1	1.154
minino	0	1	1.154
miniaturita	0	1	1.154
mimosidad	0	1	1.154
mimitos	0	1	1.154
mimarle	0	1	1.154
mimadito	0	1	1.154
mimadita	0	1	1.154
mimada	0	1	1.154
millonarios	0	1	1.154
millas	0	1	1.154
milicianos	0	1	1.154
milaneses	0	1	1.154
miiiii	0	1	1.154
mies	0	1	1.154
mielero	0	1	1.154
midiera	0	1	1.154
miden	0	1	1.154
micos	0	1	1.154
micho	0	1	1.154
miajitas	0	1	1.154
miaja	0	1	1.154
métome	0	1	1.154
metodizando	0	1	1.154
metódicas	0	1	1.154
metiole	0	1	1.154
metiese	0	1	1.154
metiéndola	0	1	1.154
metidita	0	1	1.154
metíase	0	1	1.154
métete	0	1	1.154
metes	0	1	1.154
meterte	0	1	1.154
meterlos	0	1	1.154
meteré	0	1	1.154
meterá	0	1	1.154
metempsícosis	0	1	1.154
metemos	0	1	1.154
mételo	0	1	1.154
mételes	0	1	1.154
metas	0	1	1.154
metan	0	1	1.154
metamos	0	1	1.154
metálicamente	0	1	1.154
metales	0	1	1.154
metáis	0	1	1.154
metá	0	1	1.154
mesonero	0	1	1.154
mesón	0	1	1.154
mesocrático	0	1	1.154
mesita	0	1	1.154
mesianitis	0	1	1.154
mescolanza	0	1	1.154
mermó	0	1	1.154
mermar	0	1	1.154
mermados	0	1	1.154
meriendan	0	1	1.154
merezcas	0	1	1.154
merengue	0	1	1.154
merengada	0	1	1.154
merenderos	0	1	1.154
mereció	0	1	1.154
merecimientos	0	1	1.154
mereciesen	0	1	1.154
merecerlo	0	1	1.154
merecería	0	1	1.154
merecéis	0	1	1.154
merecedor	0	1	1.154
mercuriales	0	1	1.154
mercurial	0	1	1.154
mercenarias	0	1	1.154
mercancías	0	1	1.154
mercachifles	0	1	1.154
menudillo	0	1	1.154
mentó	0	1	1.154
mentiroso	0	1	1.154
mentirosas	0	1	1.154
mentirosa	0	1	1.154
mentirilla	0	1	1.154
mentirijillas	0	1	1.154
mentirijilla	0	1	1.154
mentarlo	0	1	1.154
mensajes	0	1	1.154
menospreciar	0	1	1.154
menjurje	0	1	1.154
menistro	0	1	1.154
meningo	0	1	1.154
menina	0	1	1.154
mengue	0	1	1.154
menguaban	0	1	1.154
menease	0	1	1.154
menearse	0	1	1.154
meneallo	0	1	1.154
meneada	0	1	1.154
menea	0	1	1.154
mendiry	0	1	1.154
mendigas	0	1	1.154
mendicante	0	1	1.154
mencionar	0	1	1.154
mencionados	0	1	1.154
mencionada	0	1	1.154
menaje	0	1	1.154
memos	0	1	1.154
memoriales	0	1	1.154
memorial	0	1	1.154
membrillo	0	1	1.154
melón	0	1	1.154
melómanos	0	1	1.154
melómano	0	1	1.154
melodramáticos	0	1	1.154
melodramática	0	1	1.154
melicianos	0	1	1.154
melenudos	0	1	1.154
melenuda	0	1	1.154
melena	0	1	1.154
melaera	0	1	1.154
mela	0	1	1.154
mejoras	0	1	1.154
mejoraré	0	1	1.154
meetings	0	1	1.154
medroso	0	1	1.154
medrosica	0	1	1.154
medrosa	0	1	1.154
medió	0	1	1.154
medidor	0	1	1.154
medicinales	0	1	1.154
mediasen	0	1	1.154
mediascañas	0	1	1.154
mediaron	0	1	1.154
medianero	0	1	1.154
mediando	0	1	1.154
medíalas	0	1	1.154
mediaban	0	1	1.154
meciéndose	0	1	1.154
mechas	0	1	1.154
meces	0	1	1.154
mécele	0	1	1.154
mecánicos	0	1	1.154
mazmorra	0	1	1.154
maximiliana	0	1	1.154
mauro	0	1	1.154
maulas	0	1	1.154
matuteros	0	1	1.154
matriz	0	1	1.154
matritense	0	1	1.154
matrimoñesca	0	1	1.154
matricularse	0	1	1.154
matrices	0	1	1.154
matorrales	0	1	1.154
matitas	0	1	1.154
materialmente	0	1	1.154
materialidades	0	1	1.154
materialidad	0	1	1.154
matemos	0	1	1.154
matemática	0	1	1.154
mátate	0	1	1.154
matarnos	0	1	1.154
mataremos	0	1	1.154
matanza	0	1	1.154
mátameles	0	1	1.154
matadores	0	1	1.154
matachines	0	1	1.154
masticarlos	0	1	1.154
massarnau	0	1	1.154
massanielo	0	1	1.154
masque	0	1	1.154
masónico	0	1	1.154
masones	0	1	1.154
mascullones	0	1	1.154
mascullando	0	1	1.154
mascota	0	1	1.154
mascase	0	1	1.154
masarnau	0	1	1.154
martirios	0	1	1.154
martillos	0	1	1.154
martillase	0	1	1.154
martes	0	1	1.154
marsella	0	1	1.154
marrullería	0	1	1.154
marranos	0	1	1.154
marrano	0	1	1.154
marranadas	0	1	1.154
marranada	0	1	1.154
marítimos	0	1	1.154
marisabidilla	0	1	1.154
mariquita	0	1	1.154
marinas	0	1	1.154
marica	0	1	1.154
mariana	0	1	1.154
margaritas	0	1	1.154
marearse	0	1	1.154
marearla	0	1	1.154
marearán	0	1	1.154
mareante	0	1	1.154
mareando	0	1	1.154
marcó	0	1	1.154
marchose	0	1	1.154
marchito	0	1	1.154
marchitas	0	1	1.154
marchitarse	0	1	1.154
marche	0	1	1.154
márchate	0	1	1.154
marchasen	0	1	1.154
marcharan	0	1	1.154
marchante	0	1	1.154
marchándose	0	1	1.154
marchan	0	1	1.154
marchádose	0	1	1.154
marchaban	0	1	1.154
marcas	0	1	1.154
marcarles	0	1	1.154
marcándolos	0	1	1.154
marcan	0	1	1.154
marcador	0	1	1.154
marcadas	0	1	1.154
marcadamente	0	1	1.154
maravilloso	0	1	1.154
maravillase	0	1	1.154
maravillarse	0	1	1.154
maravillaron	0	1	1.154
maravillábase	0	1	1.154
maravillaban	0	1	1.154
maravillaba	0	1	1.154
marañas	0	1	1.154
maraña	0	1	1.154
maragatos	0	1	1.154
maragatería	0	1	1.154
maquinales	0	1	1.154
maquina	0	1	1.154
mañoso	0	1	1.154
mañosito	0	1	1.154
mañosas	0	1	1.154
manzanilla	0	1	1.154
manueles	0	1	1.154
mantuviera	0	1	1.154
mantenga	0	1	1.154
mantenerla	0	1	1.154
mansas	0	1	1.154
manoteaba	0	1	1.154
manotazo	0	1	1.154
manoseándole	0	1	1.154
manolos	0	1	1.154
manolitos	0	1	1.154
manjar	0	1	1.154
maniobrar	0	1	1.154
manifiesten	0	1	1.154
manifieste	0	1	1.154
manifestose	0	1	1.154
manifestárselo	0	1	1.154
manifestarle	0	1	1.154
mangueros	0	1	1.154
mangonee	0	1	1.154
mangoneando	0	1	1.154
mangonean	0	1	1.154
mangoneado	0	1	1.154
manglares	0	1	1.154
manetizan	0	1	1.154
manejos	0	1	1.154
manejes	0	1	1.154
manejarte	0	1	1.154
manejándole	0	1	1.154
manejada	0	1	1.154
manecita	0	1	1.154
mane	0	1	1.154
mandole	0	1	1.154
mandola	0	1	1.154
mandingas	0	1	1.154
mandíbulas	0	1	1.154
mándelas	0	1	1.154
mandéis	0	1	1.154
mandaste	0	1	1.154
mandas	0	1	1.154
mandarme	0	1	1.154
mandarles	0	1	1.154
mandarín	0	1	1.154
mandare	0	1	1.154
mandaran	0	1	1.154
mandándole	0	1	1.154
mándale	0	1	1.154
mandados	0	1	1.154
mandábala	0	1	1.154
mancilla	0	1	1.154
manchurrones	0	1	1.154
manchego	0	1	1.154
manchega	0	1	1.154
mancháis	0	1	1.154
manaza	0	1	1.154
manadas	0	1	1.154
manada	0	1	1.154
mamotretos	0	1	1.154
mamotreto	0	1	1.154
mamen	0	1	1.154
mameluco	0	1	1.154
mamándose	0	1	1.154
mamaíta	0	1	1.154
mamaba	0	1	1.154
maltrate	0	1	1.154
maltrajeao	0	1	1.154
malsonante	0	1	1.154
malquerencia	0	1	1.154
malogró	0	1	1.154
maligno	0	1	1.154
maleta	0	1	1.154
maleficiar	0	1	1.154
maledicencias	0	1	1.154
maleada	0	1	1.154
maldonadas	0	1	1.154
malditamente	0	1	1.154
maldecidos	0	1	1.154
maldecida	0	1	1.154
malchara	0	1	1.154
malayas	0	1	1.154
malaventurado	0	1	1.154
malakoff	0	1	1.154
málaga	0	1	1.154
majestuosas	0	1	1.154
majagranzas	0	1	1.154
majadera	0	1	1.154
mahones	0	1	1.154
magullada	0	1	1.154
magnánimos	0	1	1.154
magisterio	0	1	1.154
maestrita	0	1	1.154
madurez	0	1	1.154
madure	0	1	1.154
maduran	0	1	1.154
madrugues	0	1	1.154
madrugadores	0	1	1.154
madruga	0	1	1.154
madroños	0	1	1.154
madroñaje	0	1	1.154
madrastras	0	1	1.154
madrás	0	1	1.154
madoz	0	1	1.154
macuquinas	0	1	1.154
macilenta	0	1	1.154
machos	0	1	1.154
machito	0	1	1.154
machete	0	1	1.154
machetazos	0	1	1.154
machaqué	0	1	1.154
machamartillo	0	1	1.154
machacones	0	1	1.154
machacarla	0	1	1.154
machacante	0	1	1.154
machacado	0	1	1.154
luteras	0	1	1.154
luterano	0	1	1.154
lustros	0	1	1.154
lugo	0	1	1.154
luengos	0	1	1.154
lucrativo	0	1	1.154
lucirme	0	1	1.154
lucio	0	1	1.154
lúcidos	0	1	1.154
lucidez	0	1	1.154
lucharían	0	1	1.154
luchana	0	1	1.154
luchan	0	1	1.154
lucecita	0	1	1.154
lozanas	0	1	1.154
lourdes	0	1	1.154
lotero	0	1	1.154
lotérica	0	1	1.154
lorito	0	1	1.154
lores	0	1	1.154
lorenzo	0	1	1.154
lorenzana	0	1	1.154
loquito	0	1	1.154
lontananzas	0	1	1.154
lonja	0	1	1.154
longaniza	0	1	1.154
londonenses	0	1	1.154
lombardas	0	1	1.154
lombarda	0	1	1.154
logras	0	1	1.154
lograrlo	0	1	1.154
lograría	0	1	1.154
logradas	0	1	1.154
lógicos	0	1	1.154
lógicamente	0	1	1.154
logia	0	1	1.154
lodos	0	1	1.154
locurilla	0	1	1.154
locuaces	0	1	1.154
locamente	0	1	1.154
lóbulos	0	1	1.154
lóbrego	0	1	1.154
lóbregas	0	1	1.154
lobos	0	1	1.154
lobas	0	1	1.154
lluvioso	0	1	1.154
llueven	0	1	1.154
lloverá	0	1	1.154
llorosa	0	1	1.154
lloros	0	1	1.154
llorones	0	1	1.154
llorona	0	1	1.154
lloriqueo	0	1	1.154
lloriquear	0	1	1.154
llores	0	1	1.154
llorase	0	1	1.154
llorarle	0	1	1.154
llorándome	0	1	1.154
lloradas	0	1	1.154
llevose	0	1	1.154
llevola	0	1	1.154
lleves	0	1	1.154
llevárselos	0	1	1.154
llevársele	0	1	1.154
lleváronle	0	1	1.154
llevárnoslo	0	1	1.154
llevárnosle	0	1	1.154
llevármelo	0	1	1.154
llevármele	0	1	1.154
llevarlas	0	1	1.154
llevándoselas	0	1	1.154
llevándolos	0	1	1.154
llévalos	0	1	1.154
llévalo	0	1	1.154
llevábase	0	1	1.154
llevabas	0	1	1.154
llenola	0	1	1.154
llénese	0	1	1.154
llenéis	0	1	1.154
llenarles	0	1	1.154
llenarla	0	1	1.154
llenaran	0	1	1.154
llenándose	0	1	1.154
llenábase	0	1	1.154
llegues	0	1	1.154
lleguen	0	1	1.154
llegose	0	1	1.154
llégate	0	1	1.154
llegarse	0	1	1.154
llegarás	0	1	1.154
llegándole	0	1	1.154
llegados	0	1	1.154
llegadas	0	1	1.154
llamola	0	1	1.154
llamársela	0	1	1.154
llamáronle	0	1	1.154
llamaríamos	0	1	1.154
llamarás	0	1	1.154
llamarada	0	1	1.154
llámanse	0	1	1.154
llamándome	0	1	1.154
llámame	0	1	1.154
llámalos	0	1	1.154
llámalo	0	1	1.154
llamabas	0	1	1.154
llamábamos	0	1	1.154
lla	0	1	1.154
livianos	0	1	1.154
liviandades	0	1	1.154
liverpool	0	1	1.154
litros	0	1	1.154
litro	0	1	1.154
listones	0	1	1.154
lisonjeros	0	1	1.154
lisonjero	0	1	1.154
lisonjear	0	1	1.154
liso	0	1	1.154
lisiados	0	1	1.154
lirón	0	1	1.154
liquidar	0	1	1.154
liquidada	0	1	1.154
líquenes	0	1	1.154
lió	0	1	1.154
linneo	0	1	1.154
linfática	0	1	1.154
lindísima	0	1	1.154
lindezas	0	1	1.154
linderos	0	1	1.154
lindaba	0	1	1.154
limpié	0	1	1.154
limpiasen	0	1	1.154
limpiarte	0	1	1.154
limpiarse	0	1	1.154
limpiarlos	0	1	1.154
limpiarlo	0	1	1.154
limpiara	0	1	1.154
limpiados	0	1	1.154
limpiaban	0	1	1.154
limosnita	0	1	1.154
limítrofes	0	1	1.154
limitose	0	1	1.154
limitó	0	1	1.154
limitados	0	1	1.154
lija	0	1	1.154
ligar	0	1	1.154
ligaba	0	1	1.154
lidiar	0	1	1.154
lición	0	1	1.154
licencioso	0	1	1.154
licenciatura	0	1	1.154
licenciarla	0	1	1.154
librote	0	1	1.154
librillos	0	1	1.154
libreta	0	1	1.154
librecambista	0	1	1.154
libré	0	1	1.154
librarlas	0	1	1.154
líbrame	0	1	1.154
librado	0	1	1.154
liberticidas	0	1	1.154
liberó	0	1	1.154
liberalescos	0	1	1.154
liarte	0	1	1.154
liar	0	1	1.154
liándose	0	1	1.154
liados	0	1	1.154
leyeras	0	1	1.154
leyeran	0	1	1.154
leyéndolas	0	1	1.154
leyendas	0	1	1.154
levitín	0	1	1.154
levantes	0	1	1.154
levanten	0	1	1.154
levanté	0	1	1.154
levantase	0	1	1.154
levantarme	0	1	1.154
levantarles	0	1	1.154
levantarle	0	1	1.154
levantarlas	0	1	1.154
levantaré	0	1	1.154
levantará	0	1	1.154
levantándola	0	1	1.154
levantamiento	0	1	1.154
levantadas	0	1	1.154
levantábase	0	1	1.154
levadura	0	1	1.154
letargos	0	1	1.154
lérida	0	1	1.154
lepanto	0	1	1.154
leopardo	0	1	1.154
leoncillo	0	1	1.154
leñera	0	1	1.154
lentejuelas	0	1	1.154
lentas	0	1	1.154
lengüetazo	0	1	1.154
lengüetas	0	1	1.154
lengüecita	0	1	1.154
lenguaza	0	1	1.154
lenguaraces	0	1	1.154
lenguados	0	1	1.154
leitoral	0	1	1.154
leí	0	1	1.154
legitimidades	0	1	1.154
legía	0	1	1.154
legalizado	0	1	1.154
legación	0	1	1.154
leerte	0	1	1.154
leerle	0	1	1.154
leemos	0	1	1.154
lechuzos	0	1	1.154
lechuzas	0	1	1.154
lean	0	1	1.154
leales	0	1	1.154
lazaretos	0	1	1.154
lazareto	0	1	1.154
lazadas	0	1	1.154
lazada	0	1	1.154
lavose	0	1	1.154
lavemos	0	1	1.154
lave	0	1	1.154
lavatorio	0	1	1.154
lavas	0	1	1.154
lavarle	0	1	1.154
lavaría	0	1	1.154
lavaré	0	1	1.154
lavando	0	1	1.154
lavaduras	0	1	1.154
lavadero	0	1	1.154
laura	0	1	1.154
laudatorio	0	1	1.154
laudable	0	1	1.154
latro	0	1	1.154
latonero	0	1	1.154
latitudes	0	1	1.154
latinos	0	1	1.154
latinas	0	1	1.154
latente	0	1	1.154
lastre	0	1	1.154
lastraba	0	1	1.154
lastimosísimo	0	1	1.154
lastimosísima	0	1	1.154
lastimó	0	1	1.154
lastimera	0	1	1.154
lástimas	0	1	1.154
lastimándose	0	1	1.154
lastimado	0	1	1.154
laringe	0	1	1.154
larguísimas	0	1	1.154
larguilucho	0	1	1.154
largue	0	1	1.154
largaran	0	1	1.154
largara	0	1	1.154
largar	0	1	1.154
largamos	0	1	1.154
largado	0	1	1.154
lara	0	1	1.154
lapso	0	1	1.154
lápidas	0	1	1.154
lápices	0	1	1.154
lañador	0	1	1.154
lanzará	0	1	1.154
lanzara	0	1	1.154
lanzaban	0	1	1.154
lanuza	0	1	1.154
lantigua	0	1	1.154
langostino	0	1	1.154
langosta	0	1	1.154
lanceta	0	1	1.154
laminotas	0	1	1.154
laminitas	0	1	1.154
lamido	0	1	1.154
lamentarse	0	1	1.154
lamentaciones	0	1	1.154
lamentábase	0	1	1.154
lamentaban	0	1	1.154
lamen	0	1	1.154
laica	0	1	1.154
lagrimitas	0	1	1.154
lagos	0	1	1.154
lagartijo	0	1	1.154
laganitos	0	1	1.154
ladronicio	0	1	1.154
ladrillazo	0	1	1.154
ladrándole	0	1	1.154
ladra	0	1	1.154
ladinamente	0	1	1.154
ladeando	0	1	1.154
lacto	0	1	1.154
lactancia	0	1	1.154
lacrimoso	0	1	1.154
lacerias	0	1	1.154
lacerante	0	1	1.154
labrando	0	1	1.154
labrados	0	1	1.154
labradas	0	1	1.154
laborioso	0	1	1.154
labiano	0	1	1.154
juzgues	0	1	1.154
juzguéis	0	1	1.154
juzgo	0	1	1.154
juzgándose	0	1	1.154
juzgan	0	1	1.154
juzgábase	0	1	1.154
juveniles	0	1	1.154
justificadas	0	1	1.154
justificación	0	1	1.154
justicieras	0	1	1.154
justiciera	0	1	1.154
justiciada	0	1	1.154
juros	0	1	1.154
jurídica	0	1	1.154
juras	0	1	1.154
jurarme	0	1	1.154
jurarlo	0	1	1.154
juntose	0	1	1.154
juntó	0	1	1.154
juntitos	0	1	1.154
juntillas	0	1	1.154
juntáronse	0	1	1.154
juntábanse	0	1	1.154
jumeras	0	1	1.154
jum	0	1	1.154
juliana	0	1	1.154
juiciosos	0	1	1.154
juiciosísimo	0	1	1.154
juiciosillo	0	1	1.154
juiciosas	0	1	1.154
jugué	0	1	1.154
jugosos	0	1	1.154
jugó	0	1	1.154
jugasen	0	1	1.154
jugase	0	1	1.154
jugarreta	0	1	1.154
jugaron	0	1	1.154
jugarle	0	1	1.154
juergas	0	1	1.154
juegas	0	1	1.154
jueces	0	1	1.154
júcar	0	1	1.154
jubileo	0	1	1.154
jubilarte	0	1	1.154
jubilarse	0	1	1.154
jovenzuelas	0	1	1.154
jovenzuela	0	1	1.154
jovencito	0	1	1.154
jovellar	0	1	1.154
josés	0	1	1.154
josef	0	1	1.154
jorobándonos	0	1	1.154
jorobados	0	1	1.154
jorobadita	0	1	1.154
jorobada	0	1	1.154
jormiguita	0	1	1.154
jordán	0	1	1.154
jonjabaron	0	1	1.154
joloanas	0	1	1.154
jollines	0	1	1.154
joaquina	0	1	1.154
jipíos	0	1	1.154
jiménez	0	1	1.154
jierros	0	1	1.154
jierro	0	1	1.154
jesuítico	0	1	1.154
jesuíticamente	0	1	1.154
jeroglíficos	0	1	1.154
jeroglífico	0	1	1.154
jergones	0	1	1.154
jerarquías	0	1	1.154
jena	0	1	1.154
jayanes	0	1	1.154
jayán	0	1	1.154
javanesas	0	1	1.154
jaulones	0	1	1.154
játiva	0	1	1.154
jarrito	0	1	1.154
jarretiera	0	1	1.154
jardinillo	0	1	1.154
jardinería	0	1	1.154
jáquima	0	1	1.154
jaquecoso	0	1	1.154
james	0	1	1.154
jaleos	0	1	1.154
jalapa	0	1	1.154
jaez	0	1	1.154
jacquard	0	1	1.154
jacometrenzo	0	1	1.154
jacintillo	0	1	1.154
jabonadura	0	1	1.154
itinerario	0	1	1.154
istmo	0	1	1.154
israelita	0	1	1.154
isprisiones	0	1	1.154
iscariote	0	1	1.154
irujo	0	1	1.154
irte	0	1	1.154
irrites	0	1	1.154
irritarle	0	1	1.154
irritadas	0	1	1.154
irritábase	0	1	1.154
irreverentemente	0	1	1.154
irreparables	0	1	1.154
irlos	0	1	1.154
irlas	0	1	1.154
irlandas	0	1	1.154
irla	0	1	1.154
irascibilidad	0	1	1.154
iracundo	0	1	1.154
iracunda	0	1	1.154
ipso	0	1	1.154
inza	0	1	1.154
inyectados	0	1	1.154
inyectaban	0	1	1.154
invóqueles	0	1	1.154
involuntarios	0	1	1.154
involucre	0	1	1.154
involución	0	1	1.154
invocó	0	1	1.154
invocaciones	0	1	1.154
invocación	0	1	1.154
invoca	0	1	1.154
invitole	0	1	1.154
inviten	0	1	1.154
invite	0	1	1.154
invitase	0	1	1.154
invitaron	0	1	1.154
invitará	0	1	1.154
invitaciones	0	1	1.154
investigó	0	1	1.154
investigador	0	1	1.154
investigación	0	1	1.154
inverosímiles	0	1	1.154
inventiva	0	1	1.154
inventéis	0	1	1.154
inventase	0	1	1.154
inventarlo	0	1	1.154
inventariar	0	1	1.154
inventará	0	1	1.154
inventadas	0	1	1.154
invadió	0	1	1.154
invaden	0	1	1.154
inusitada	0	1	1.154
inundose	0	1	1.154
inundándola	0	1	1.154
inundación	0	1	1.154
intuitiva	0	1	1.154
introdujo	0	1	1.154
introductora	0	1	1.154
introducirse	0	1	1.154
introducirlo	0	1	1.154
introducen	0	1	1.154
intríngulis	0	1	1.154
intrigüelas	0	1	1.154
intrigante	0	1	1.154
intrigantas	0	1	1.154
intransitable	0	1	1.154
intranquilizó	0	1	1.154
intolerante	0	1	1.154
intimando	0	1	1.154
intervinieron	0	1	1.154
intervenían	0	1	1.154
interrumpan	0	1	1.154
interrogar	0	1	1.154
interrogándose	0	1	1.154
interrogándola	0	1	1.154
interrogando	0	1	1.154
interrogador	0	1	1.154
interrogada	0	1	1.154
interrogaciones	0	1	1.154
interrogación	0	1	1.154
interprete	0	1	1.154
interpretándolos	0	1	1.154
interpretándola	0	1	1.154
interpretabas	0	1	1.154
interponiéndose	0	1	1.154
internos	0	1	1.154
internaron	0	1	1.154
intermedia	0	1	1.154
interioridad	0	1	1.154
interesantísimo	0	1	1.154
interesan	0	1	1.154
interesaban	0	1	1.154
interceptaron	0	1	1.154
intercedí	0	1	1.154
intercede	0	1	1.154
interceda	0	1	1.154
intentos	0	1	1.154
intentase	0	1	1.154
intentaron	0	1	1.154
intentarlo	0	1	1.154
intentaría	0	1	1.154
intensísimas	0	1	1.154
intencionada	0	1	1.154
intempestivas	0	1	1.154
intactas	0	1	1.154
insurreccionó	0	1	1.154
insurrección	0	1	1.154
insurgentes	0	1	1.154
insurgente	0	1	1.154
insulté	0	1	1.154
insultase	0	1	1.154
insultarle	0	1	1.154
ínsulas	0	1	1.154
ínsula	0	1	1.154
insuficientes	0	1	1.154
insubordina	0	1	1.154
instruye	0	1	1.154
instrumentos	0	1	1.154
instruirte	0	1	1.154
instructiva	0	1	1.154
instancias	0	1	1.154
instalose	0	1	1.154
instalarse	0	1	1.154
instalándose	0	1	1.154
instalaban	0	1	1.154
instalaba	0	1	1.154
instado	0	1	1.154
instaban	0	1	1.154
instaba	0	1	1.154
inspirole	0	1	1.154
inspiraron	0	1	1.154
inspirarle	0	1	1.154
inspirar	0	1	1.154
inspirándome	0	1	1.154
inspirabas	0	1	1.154
inspeccionando	0	1	1.154
inspecciona	0	1	1.154
insolvente	0	1	1.154
insolvencias	0	1	1.154
insolvencia	0	1	1.154
insoluble	0	1	1.154
insistiré	0	1	1.154
insistiese	0	1	1.154
insiste	0	1	1.154
insípido	0	1	1.154
insinuarse	0	1	1.154
insinuantes	0	1	1.154
insinuándose	0	1	1.154
insignia	0	1	1.154
insepulto	0	1	1.154
insensatez	0	1	1.154
inseguros	0	1	1.154
inseguras	0	1	1.154
inquirir	0	1	1.154
inquiriendo	0	1	1.154
inquilino	0	1	1.154
inquietamente	0	1	1.154
inquietaba	0	1	1.154
inopinadamente	0	1	1.154
inocentada	0	1	1.154
innegable	0	1	1.154
innatas	0	1	1.154
inmutó	0	1	1.154
inmutarse	0	1	1.154
inmutada	0	1	1.154
inmutables	0	1	1.154
inmunidad	0	1	1.154
inmunda	0	1	1.154
inmueble	0	1	1.154
inmorales	0	1	1.154
inmensas	0	1	1.154
inmensamente	0	1	1.154
injustos	0	1	1.154
injertado	0	1	1.154
ininteligible	0	1	1.154
iniciose	0	1	1.154
iniciarlo	0	1	1.154
iniciar	0	1	1.154
iniciándole	0	1	1.154
inician	0	1	1.154
iniciadoras	0	1	1.154
iniciadora	0	1	1.154
iniciábasele	0	1	1.154
iniciábase	0	1	1.154
iniciaba	0	1	1.154
inhumanas	0	1	1.154
inhabitables	0	1	1.154
inhábiles	0	1	1.154
inhábil	0	1	1.154
ingreso	0	1	1.154
ingresara	0	1	1.154
ingresar	0	1	1.154
ingratuelo	0	1	1.154
inglesotes	0	1	1.154
inglesote	0	1	1.154
inglesones	0	1	1.154
inglesona	0	1	1.154
ingestión	0	1	1.154
ingente	0	1	1.154
ingénito	0	1	1.154
ingeniosos	0	1	1.154
ingeniosísimos	0	1	1.154
infundirte	0	1	1.154
infundirse	0	1	1.154
infundiéndole	0	1	1.154
infundíanle	0	1	1.154
infundían	0	1	1.154
infundíale	0	1	1.154
infundes	0	1	1.154
infunden	0	1	1.154
infructuoso	0	1	1.154
infranqueables	0	1	1.154
infortunada	0	1	1.154
informarse	0	1	1.154
informarlo	0	1	1.154
informándose	0	1	1.154
informadora	0	1	1.154
informado	0	1	1.154
informada	0	1	1.154
informaba	0	1	1.154
informa	0	1	1.154
influyese	0	1	1.154
influyendo	0	1	1.154
influir	0	1	1.154
infló	0	1	1.154
infligir	0	1	1.154
inflexibilidad	0	1	1.154
inflándose	0	1	1.154
inflamado	0	1	1.154
inflamación	0	1	1.154
inflamaba	0	1	1.154
inflaban	0	1	1.154
infinitivos	0	1	1.154
infestada	0	1	1.154
infelizote	0	1	1.154
infamar	0	1	1.154
inexpresiva	0	1	1.154
inexpertas	0	1	1.154
inervación	0	1	1.154
inequívoca	0	1	1.154
ineptas	0	1	1.154
inepta	0	1	1.154
ineficaz	0	1	1.154
ineducado	0	1	1.154
ineducada	0	1	1.154
industriosa	0	1	1.154
indultos	0	1	1.154
indulto	0	1	1.154
indújole	0	1	1.154
indujo	0	1	1.154
indujeran	0	1	1.154
indudables	0	1	1.154
induce	0	1	1.154
indolente	0	1	1.154
indivudua	0	1	1.154
individualizar	0	1	1.154
individualidades	0	1	1.154
individuales	0	1	1.154
indispuesta	0	1	1.154
indisoluble	0	1	1.154
indirecto	0	1	1.154
indirectamente	0	1	1.154
indinos	0	1	1.154
indina	0	1	1.154
indilugencia	0	1	1.154
indignarse	0	1	1.154
indignarían	0	1	1.154
indigestos	0	1	1.154
indigéstate	0	1	1.154
indigestan	0	1	1.154
indigestada	0	1	1.154
indigestaba	0	1	1.154
indigente	0	1	1.154
índices	0	1	1.154
indicáronle	0	1	1.154
indicarle	0	1	1.154
indicara	0	1	1.154
indiana	0	1	1.154
indeterminado	0	1	1.154
indestructibles	0	1	1.154
indemnizarse	0	1	1.154
indemnizaba	0	1	1.154
indefinido	0	1	1.154
indefensos	0	1	1.154
indecorosa	0	1	1.154
indecibles	0	1	1.154
indecentonas	0	1	1.154
indecentísimos	0	1	1.154
indagatorias	0	1	1.154
indagando	0	1	1.154
indagador	0	1	1.154
indagación	0	1	1.154
indagaba	0	1	1.154
incumbía	0	1	1.154
incultura	0	1	1.154
incultivados	0	1	1.154
inculpabilidad	0	1	1.154
incrustando	0	1	1.154
increpar	0	1	1.154
increpaba	0	1	1.154
incorrección	0	1	1.154
incorporan	0	1	1.154
incorporábase	0	1	1.154
incontrastables	0	1	1.154
inconsolables	0	1	1.154
inconsecuencia	0	1	1.154
inconmensurables	0	1	1.154
inconmensurable	0	1	1.154
inconcuso	0	1	1.154
incomprensible	0	1	1.154
incompletos	0	1	1.154
incompletas	0	1	1.154
incómodo	0	1	1.154
incomodé	0	1	1.154
incomodase	0	1	1.154
incomodara	0	1	1.154
incomodar	0	1	1.154
incomodándose	0	1	1.154
incomodan	0	1	1.154
incomodadísima	0	1	1.154
incomodadas	0	1	1.154
incoloras	0	1	1.154
incluyeran	0	1	1.154
inclusero	0	1	1.154
incluido	0	1	1.154
inclino	0	1	1.154
inclinábase	0	1	1.154
incitó	0	1	1.154
incitar	0	1	1.154
incitantes	0	1	1.154
incitada	0	1	1.154
incidencia	0	1	1.154
incertidumbres	0	1	1.154
incautas	0	1	1.154
incautado	0	1	1.154
incautación	0	1	1.154
incautaba	0	1	1.154
incapacidad	0	1	1.154
inarmónica	0	1	1.154
inapetente	0	1	1.154
inamovible	0	1	1.154
inalterada	0	1	1.154
inalterable	0	1	1.154
inactivo	0	1	1.154
inactividad	0	1	1.154
inaccesible	0	1	1.154
imputado	0	1	1.154
impulsión	0	1	1.154
impulsado	0	1	1.154
impulsábala	0	1	1.154
impulsa	0	1	1.154
impúber	0	1	1.154
improvisador	0	1	1.154
impropios	0	1	1.154
improbable	0	1	1.154
imprimir	0	1	1.154
imprimía	0	1	1.154
imprimen	0	1	1.154
impresos	0	1	1.154
impresionar	0	1	1.154
impresionaba	0	1	1.154
impregnadas	0	1	1.154
imprecación	0	1	1.154
imposibilitándola	0	1	1.154
importunarla	0	1	1.154
importarán	0	1	1.154
importadoras	0	1	1.154
importador	0	1	1.154
imponiendo	0	1	1.154
imponíale	0	1	1.154
imponérsele	0	1	1.154
implorar	0	1	1.154
implorando	0	1	1.154
implantado	0	1	1.154
impido	0	1	1.154
impidiéndose	0	1	1.154
impíamente	0	1	1.154
impetrando	0	1	1.154
impersonal	0	1	1.154
imperfecciones	0	1	1.154
imperaba	0	1	1.154
impenetrabilidad	0	1	1.154
impedirla	0	1	1.154
impediré	0	1	1.154
impávida	0	1	1.154
impares	0	1	1.154
impalpable	0	1	1.154
impacienta	0	1	1.154
imítela	0	1	1.154
imitativa	0	1	1.154
imitarlo	0	1	1.154
imitarla	0	1	1.154
imitado	0	1	1.154
imbuyen	0	1	1.154
imbecilidad	0	1	1.154
imbéciles	0	1	1.154
imagínese	0	1	1.154
imagínate	0	1	1.154
imaginársela	0	1	1.154
imaginario	0	1	1.154
imaginan	0	1	1.154
imaginamos	0	1	1.154
imaginacioncilla	0	1	1.154
ilustrando	0	1	1.154
ilustran	0	1	1.154
ilusorio	0	1	1.154
ilusionó	0	1	1.154
ilusioncita	0	1	1.154
ilusionarse	0	1	1.154
ilusionándose	0	1	1.154
ilusionan	0	1	1.154
ilusionado	0	1	1.154
ilusionaba	0	1	1.154
iluminará	0	1	1.154
iluminación	0	1	1.154
ilimitado	0	1	1.154
iiii	0	1	1.154
igualarían	0	1	1.154
igualara	0	1	1.154
igualada	0	1	1.154
igualaban	0	1	1.154
ignoras	0	1	1.154
ignorar	0	1	1.154
ignoran	0	1	1.154
ignominiosamente	0	1	1.154
iglesita	0	1	1.154
idos	0	1	1.154
idolatrías	0	1	1.154
idolatrar	0	1	1.154
idolatra	0	1	1.154
ideó	0	1	1.154
idéntico	0	1	1.154
ideítas	0	1	1.154
idease	0	1	1.154
idear	0	1	1.154
ideada	0	1	1.154
iconografía	0	1	1.154
huyas	0	1	1.154
hurón	0	1	1.154
hurgado	0	1	1.154
hundirse	0	1	1.154
hundiose	0	1	1.154
hundiéronse	0	1	1.154
hundidos	0	1	1.154
hundían	0	1	1.154
hundía	0	1	1.154
húndete	0	1	1.154
hunden	0	1	1.154
humos	0	1	1.154
humorada	0	1	1.154
humo	19	17	1.154
humillen	0	1	1.154
humillarles	0	1	1.154
humildísimo	0	1	1.154
humanitario	0	1	1.154
humanamente	0	1	1.154
hules	0	1	1.154
huevitos	0	1	1.154
hueverito	0	1	1.154
huevería	0	1	1.154
hueveras	0	1	1.154
huérfano	0	1	1.154
huelva	0	1	1.154
huelgas	0	1	1.154
huelga	0	1	1.154
huecas	0	1	1.154
hubiérales	0	1	1.154
hostigó	0	1	1.154
hostigándole	0	1	1.154
horrorizadas	0	1	1.154
horrorice	0	1	1.154
horripilé	0	1	1.154
horripiladas	0	1	1.154
horripila	0	1	1.154
horrenda	0	1	1.154
horquillas	0	1	1.154
hornito	0	1	1.154
hormiguilla	0	1	1.154
hormiguero	0	1	1.154
horita	0	1	1.154
hordas	0	1	1.154
horcas	0	1	1.154
honrarle	0	1	1.154
honradote	0	1	1.154
honradito	0	1	1.154
honradísimo	0	1	1.154
honradeces	0	1	1.154
honorarios	0	1	1.154
honorabilidad	0	1	1.154
honguito	0	1	1.154
honestos	0	1	1.154
hondísimos	0	1	1.154
hondísimas	0	1	1.154
hondero	0	1	1.154
hombrón	0	1	1.154
hombría	0	1	1.154
hombrada	0	1	1.154
hombrachón	0	1	1.154
hollín	0	1	1.154
holgazanote	0	1	1.154
holgazana	0	1	1.154
holgados	0	1	1.154
holgadísimas	0	1	1.154
holandas	0	1	1.154
hojitas	0	1	1.154
hociquitos	0	1	1.154
hociquearemos	0	1	1.154
hocicadas	0	1	1.154
hocicada	0	1	1.154
hízome	0	1	1.154
hízola	0	1	1.154
histrionismo	0	1	1.154
histriónica	0	1	1.154
historiador	0	1	1.154
hispanófilo	0	1	1.154
hispana	0	1	1.154
hirviendo	0	1	1.154
hirió	0	1	1.154
hirieran	0	1	1.154
hiriera	0	1	1.154
hiriendo	0	1	1.154
hipotéticamente	0	1	1.154
hipotecan	0	1	1.154
hipotecado	0	1	1.154
hipoquitropíticas	0	1	1.154
hipódromo	0	1	1.154
hipocritón	0	1	1.154
hipocráticos	0	1	1.154
hipocráticas	0	1	1.154
hipo	0	1	1.154
hiperquinesia	0	1	1.154
hiperbólicos	0	1	1.154
hiperbólico	0	1	1.154
hipérbole	0	1	1.154
hindostán	0	1	1.154
hincósele	0	1	1.154
hinchar	0	1	1.154
hinchándose	0	1	1.154
hinchada	0	1	1.154
hinchaba	0	1	1.154
hincar	0	1	1.154
hilvanarlos	0	1	1.154
hilito	0	1	1.154
hilillos	0	1	1.154
hileras	0	1	1.154
hildebrando	0	1	1.154
hilar	0	1	1.154
hiladito	0	1	1.154
hilaban	0	1	1.154
hijastra	0	1	1.154
higuí	0	1	1.154
higo	0	1	1.154
higa	0	1	1.154
hierven	0	1	1.154
hiero	0	1	1.154
hiere	0	1	1.154
hidropesía	0	1	1.154
hidrógeno	0	1	1.154
hide	0	1	1.154
hicimos	0	1	1.154
hiciéronle	0	1	1.154
híceme	0	1	1.154
heterogéneo	0	1	1.154
heterodoxa	0	1	1.154
hervores	0	1	1.154
herrería	0	1	1.154
herraje	0	1	1.154
heroísmos	0	1	1.154
hermosotes	0	1	1.154
hermosismo	0	1	1.154
hermosísimas	0	1	1.154
hermosamente	0	1	1.154
hermanillo	0	1	1.154
herejotes	0	1	1.154
herejote	0	1	1.154
hereditario	0	1	1.154
herede	0	1	1.154
heredáis	0	1	1.154
heredadas	0	1	1.154
hereda	0	1	1.154
hepáticas	0	1	1.154
hendiduras	0	1	1.154
henchido	0	1	1.154
hemorragia	0	1	1.154
hemoptisis	0	1	1.154
hemicráneo	0	1	1.154
heliotropo	0	1	1.154
heliogábalo	0	1	1.154
helénica	0	1	1.154
helena	0	1	1.154
helas	0	1	1.154
helaron	0	1	1.154
heine	0	1	1.154
hediondo	0	1	1.154
hechicero	0	1	1.154
hebillas	0	1	1.154
haymarket	0	1	1.154
hatchiss	0	1	1.154
hartaran	0	1	1.154
hartándose	0	1	1.154
hartan	0	1	1.154
harpías	0	1	1.154
harpía	0	1	1.154
haragán	0	1	1.154
hamburgo	0	1	1.154
hallole	0	1	1.154
hallo	0	1	1.154
hallazgos	0	1	1.154
hállase	0	1	1.154
halláronse	0	1	1.154
hallaron	0	1	1.154
hallar	0	1	1.154
hallamos	0	1	1.154
hallado	0	1	1.154
hálito	0	1	1.154
halcón	0	1	1.154
halagarle	0	1	1.154
hágote	0	1	1.154
hágolo	0	1	1.154
háganme	0	1	1.154
haeckel	0	1	1.154
hacinadas	0	1	1.154
haciéndosele	0	1	1.154
haciéndomelo	0	1	1.154
hacíanla	0	1	1.154
haches	0	1	1.154
hacérselos	0	1	1.154
hacendosa	0	1	1.154
hacendista	0	1	1.154
haced	0	1	1.154
habríase	0	1	1.154
habríale	0	1	1.154
habremos	0	1	1.154
habrase	0	1	1.154
háblele	0	1	1.154
hablarás	0	1	1.154
hablaras	0	1	1.154
hablarán	0	1	1.154
habladoras	0	1	1.154
hablabas	0	1	1.154
habilísimas	0	1	1.154
habiéndote	0	1	1.154
habiéndome	0	1	1.154
habiéndolo	0	1	1.154
habíales	0	1	1.154
habíalas	0	1	1.154
habíala	0	1	1.154
habia	0	1	1.154
habértelo	0	1	1.154
guttenberg	0	1	1.154
gustosos	0	1	1.154
gustosamente	0	1	1.154
gustosa	0	1	1.154
gustes	0	1	1.154
gustara	0	1	1.154
gustable	0	1	1.154
guras	0	1	1.154
gurapas	0	1	1.154
guitarrista	0	1	1.154
guisotes	0	1	1.154
guiso	0	1	1.154
guisas	0	1	1.154
guisadas	0	1	1.154
guisaba	0	1	1.154
guirigay	0	1	1.154
guiños	0	1	1.154
guiño	0	1	1.154
guiñar	0	1	1.154
guiñados	0	1	1.154
guiñada	0	1	1.154
guindilla	0	1	1.154
guindalera	0	1	1.154
guillotinadas	0	1	1.154
guillermo	0	1	1.154
guillado	0	1	1.154
guijarro	0	1	1.154
guiase	0	1	1.154
guiarte	0	1	1.154
guiarse	0	1	1.154
guiándolas	0	1	1.154
guiando	0	1	1.154
guiado	0	1	1.154
guetaria	0	1	1.154
guerrillero	0	1	1.154
guerrera	0	1	1.154
güeno	0	1	1.154
güelvo	0	1	1.154
güélvete	0	1	1.154
guelbenzu	0	1	1.154
guealés	0	1	1.154
gubernativo	0	1	1.154
gubernamentales	0	1	1.154
gubernamental	0	1	1.154
gubernación	0	1	1.154
guasón	0	1	1.154
guasee	0	1	1.154
guarismo	0	1	1.154
guaridas	0	1	1.154
guarida	0	1	1.154
guardesas	0	1	1.154
guardes	0	1	1.154
guárdelo	0	1	1.154
guárdate	0	1	1.154
guardárselo	0	1	1.154
guardarlo	0	1	1.154
guardarle	0	1	1.154
guardarla	0	1	1.154
guardarían	0	1	1.154
guardándolo	0	1	1.154
guardamos	0	1	1.154
guárdalo	0	1	1.154
guárdala	0	1	1.154
guardadora	0	1	1.154
guardadas	0	1	1.154
guardacantón	0	1	1.154
guardabrisas	0	1	1.154
guardábalo	0	1	1.154
guapito	0	1	1.154
guapines	0	1	1.154
guapín	0	1	1.154
guapillas	0	1	1.154
guapezas	0	1	1.154
guapeza	0	1	1.154
guapetones	0	1	1.154
guapamente	0	1	1.154
guadalupe	0	1	1.154
grupito	0	1	1.154
gruesísima	0	1	1.154
grúas	0	1	1.154
gros	0	1	1.154
grite	0	1	1.154
grita	0	1	1.154
grifos	0	1	1.154
greña	0	1	1.154
gremios	0	1	1.154
gremio	0	1	1.154
gravitó	0	1	1.154
gravitativo	0	1	1.154
gravísimas	0	1	1.154
granuloso	0	1	1.154
granulosa	0	1	1.154
granulaciones	0	1	1.154
granujita	0	1	1.154
grandullón	0	1	1.154
grandones	0	1	1.154
grandemente	0	1	1.154
grandecitos	0	1	1.154
grandecitas	0	1	1.154
grandecita	0	1	1.154
granadinas	0	1	1.154
gramos	0	1	1.154
gramo	0	1	1.154
gramaticales	0	1	1.154
grajeas	0	1	1.154
gráficamente	0	1	1.154
graduación	0	1	1.154
graduaba	0	1	1.154
gradaciones	0	1	1.154
graciosísima	0	1	1.154
grabadas	0	1	1.154
grababan	0	1	1.154
gozosas	0	1	1.154
gozón	0	1	1.154
goznes	0	1	1.154
gozaremos	0	1	1.154
gozaré	0	1	1.154
gotita	0	1	1.154
goterones	0	1	1.154
gotear	0	1	1.154
gorritas	0	1	1.154
gorrita	0	1	1.154
gorrinos	0	1	1.154
gorrina	0	1	1.154
gorjeo	0	1	1.154
gordura	0	1	1.154
gordito	0	1	1.154
gordita	0	1	1.154
gordísimo	0	1	1.154
golviésemos	0	1	1.154
golver	0	1	1.154
golpeaba	0	1	1.154
golpazos	0	1	1.154
goloso	0	1	1.154
golondrina	0	1	1.154
gollerías	0	1	1.154
goled	0	1	1.154
gola	0	1	1.154
goiri	0	1	1.154
goëthe	0	1	1.154
gocen	0	1	1.154
gocemos	0	1	1.154
gobernarte	0	1	1.154
gobernarlo	0	1	1.154
gobernara	0	1	1.154
gobernando	0	1	1.154
gobernable	0	1	1.154
gobernábala	0	1	1.154
gluten	0	1	1.154
glotona	0	1	1.154
gloriosas	0	1	1.154
glóbulos	0	1	1.154
glóbulo	0	1	1.154
gitano	0	1	1.154
gitani	0	1	1.154
gitanas	0	1	1.154
girones	0	1	1.154
girasoles	0	1	1.154
girase	0	1	1.154
girar	0	1	1.154
giraba	0	1	1.154
gimnástica	0	1	1.154
gimnasias	0	1	1.154
gimiendo	0	1	1.154
gilís	0	1	1.154
gigantones	0	1	1.154
gestión	0	1	1.154
germen	0	1	1.154
genuino	0	1	1.154
gentualla	0	1	1.154
generosos	0	1	1.154
generalización	0	1	1.154
generadora	0	1	1.154
genealógico	0	1	1.154
gendarme	0	1	1.154
gelsemina	0	1	1.154
gaznate	0	1	1.154
gaznápiro	0	1	1.154
gazmoño	0	1	1.154
gayola	0	1	1.154
gatuno	0	1	1.154
gaterías	0	1	1.154
gatería	0	1	1.154
gatera	0	1	1.154
gasté	0	1	1.154
gaste	0	1	1.154
gastas	0	1	1.154
gastarse	0	1	1.154
gastarlo	0	1	1.154
gastarían	0	1	1.154
gastaré	0	1	1.154
gastarás	0	1	1.154
gastará	0	1	1.154
gastándolo	0	1	1.154
gaseosa	0	1	1.154
gasas	0	1	1.154
garrulería	0	1	1.154
garrotazo	0	1	1.154
garró	0	1	1.154
garrapatos	0	1	1.154
garrafas	0	1	1.154
garlochín	0	1	1.154
garita	0	1	1.154
garfio	0	1	1.154
garfiñé	0	1	1.154
garfiñaran	0	1	1.154
garbosa	0	1	1.154
garantíceme	0	1	1.154
garabito	0	1	1.154
ganso	0	1	1.154
gangrenada	0	1	1.154
gane	0	1	1.154
gandía	0	1	1.154
ganarle	0	1	1.154
ganaremos	0	1	1.154
ganarás	0	1	1.154
ganará	0	1	1.154
ganapán	0	1	1.154
ganándose	0	1	1.154
ganábalo	0	1	1.154
galonado	0	1	1.154
gallinejera	0	1	1.154
gallineja	0	1	1.154
gallináceas	0	1	1.154
galletas	0	1	1.154
gallegas	0	1	1.154
gallega	0	1	1.154
gallardísimo	0	1	1.154
gallardeaba	0	1	1.154
galindo	0	1	1.154
galimatías	0	1	1.154
gaeta	0	1	1.154
gachas	0	1	1.154
gabachos	0	1	1.154
gabachas	0	1	1.154
fustes	0	1	1.154
fusileros	0	1	1.154
fusilaron	0	1	1.154
fusilar	0	1	1.154
fusilaba	0	1	1.154
furtivas	0	1	1.154
furiosamente	0	1	1.154
furibundas	0	1	1.154
funestos	0	1	1.154
funestas	0	1	1.154
funerales	0	1	1.154
funeral	0	1	1.154
fundirnos	0	1	1.154
fundiéndose	0	1	1.154
fundarme	0	1	1.154
fundándonos	0	1	1.154
fundándome	0	1	1.154
fundando	0	1	1.154
fundamentales	0	1	1.154
fundamenta	0	1	1.154
fundados	0	1	1.154
fundábase	0	1	1.154
fundabas	0	1	1.154
funcionara	0	1	1.154
funcionar	0	1	1.154
funcionante	0	1	1.154
funcionando	0	1	1.154
funcionaban	0	1	1.154
fumarse	0	1	1.154
fumándose	0	1	1.154
fumada	0	1	1.154
fuma	0	1	1.154
fulastre	0	1	1.154
fuisteis	0	1	1.154
fugitivos	0	1	1.154
fugitiva	0	1	1.154
fugaces	0	1	1.154
fuertecilla	0	1	1.154
fueren	0	1	1.154
fuentecillas	0	1	1.154
fuencarral	0	1	1.154
fu	0	1	1.154
frustrar	0	1	1.154
fruslerías	0	1	1.154
fruncir	0	1	1.154
fruncidos	0	1	1.154
fruncida	0	1	1.154
fruición	0	1	1.154
frugalidad	0	1	1.154
froten	0	1	1.154
frote	0	1	1.154
frotasen	0	1	1.154
frotándole	0	1	1.154
frotándola	0	1	1.154
frotábase	0	1	1.154
frotaban	0	1	1.154
frontiles	0	1	1.154
frontil	0	1	1.154
frontero	0	1	1.154
fronteras	0	1	1.154
frontales	0	1	1.154
frondoso	0	1	1.154
frívola	0	1	1.154
fritas	0	1	1.154
fritanga	0	1	1.154
frigidísimo	0	1	1.154
fríes	0	1	1.154
frieron	0	1	1.154
fresquecito	0	1	1.154
fresquecita	0	1	1.154
fresno	0	1	1.154
frescuras	0	1	1.154
frescachona	0	1	1.154
frescachón	0	1	1.154
frenopático	0	1	1.154
freír	0	1	1.154
freidera	0	1	1.154
fregoteo	0	1	1.154
fregotee	0	1	1.154
fregaré	0	1	1.154
fregando	0	1	1.154
fregaban	0	1	1.154
fregaba	0	1	1.154
freeeesero	0	1	1.154
frecuentemente	0	1	1.154
frecuentando	0	1	1.154
freatas	0	1	1.154
frasecilla	0	1	1.154
frasear	0	1	1.154
frascuelo	0	1	1.154
franquezas	0	1	1.154
francesillas	0	1	1.154
francesilla	0	1	1.154
francachelas	0	1	1.154
fragatonas	0	1	1.154
fouquier	0	1	1.154
fotográfico	0	1	1.154
fortunatita	0	1	1.154
fortunatas	0	1	1.154
fortunaaá	0	1	1.154
fortalecimiento	0	1	1.154
fortalecídose	0	1	1.154
fortalecido	0	1	1.154
fortalecen	0	1	1.154
fortalece	0	1	1.154
forros	0	1	1.154
forraría	0	1	1.154
foro	0	1	1.154
formuló	0	1	1.154
formularlo	0	1	1.154
formular	0	1	1.154
formose	0	1	1.154
fórmico	0	1	1.154
forme	0	1	1.154
formarte	0	1	1.154
formarle	0	1	1.154
formarlas	0	1	1.154
formaría	0	1	1.154
formalito	0	1	1.154
formalita	0	1	1.154
formación	0	1	1.154
forjarse	0	1	1.154
forjar	0	1	1.154
forcejear	0	1	1.154
forcejeando	0	1	1.154
forasteras	0	1	1.154
forajido	0	1	1.154
fontainebleau	0	1	1.154
fomentas	0	1	1.154
folletos	0	1	1.154
folletito	0	1	1.154
fogosas	0	1	1.154
fluidos	0	1	1.154
fluido	0	1	1.154
flote	0	1	1.154
florilogios	0	1	1.154
floridas	0	1	1.154
floreos	0	1	1.154
florecer	0	1	1.154
flojita	0	1	1.154
flexiones	0	1	1.154
flexibilidad	0	1	1.154
flechazo	0	1	1.154
flecharla	0	1	1.154
flechadas	0	1	1.154
flechaba	0	1	1.154
flecha	0	1	1.154
flatulento	0	1	1.154
flatulenta	0	1	1.154
flaquear	0	1	1.154
flaqueaban	0	1	1.154
flaqueaba	0	1	1.154
flanco	0	1	1.154
flameando	0	1	1.154
fláccidas	0	1	1.154
fisonómico	0	1	1.154
fiscalizar	0	1	1.154
firmísima	0	1	1.154
firmando	0	1	1.154
firmamento	0	1	1.154
finiquito	0	1	1.154
fingidamente	0	1	1.154
financiero	0	1	1.154
financiera	0	1	1.154
finamente	0	1	1.154
finalizar	0	1	1.154
filtrar	0	1	1.154
filipina	0	1	1.154
filibustero	0	1	1.154
filiación	0	1	1.154
filantrópicas	0	1	1.154
filantrópica	0	1	1.154
fije	0	1	1.154
fijáronse	0	1	1.154
fijarlas	0	1	1.154
fijaría	0	1	1.154
fijados	0	1	1.154
figurose	0	1	1.154
figurones	0	1	1.154
figuritas	0	1	1.154
figurita	0	1	1.154
figúrenselo	0	1	1.154
figúrense	0	1	1.154
figuremos	0	1	1.154
figuré	0	1	1.154
figure	0	1	1.154
figurarme	0	1	1.154
figuraran	0	1	1.154
figuraciones	0	1	1.154
figuerola	0	1	1.154
fíese	0	1	1.154
fierro	0	1	1.154
fieros	0	1	1.154
fierezas	0	1	1.154
fierecilla	0	1	1.154
fielmente	0	1	1.154
fidelidades	0	1	1.154
fidedignas	0	1	1.154
fíate	0	1	1.154
fiasco	0	1	1.154
fiara	0	1	1.154
fiambrera	0	1	1.154
feúcha	0	1	1.154
fétidas	0	1	1.154
fetiches	0	1	1.154
festoneados	0	1	1.154
festiva	0	1	1.154
fértil	0	1	1.154
ferruje	0	1	1.154
ferretero	0	1	1.154
ferretería	0	1	1.154
ferretera	0	1	1.154
ferocidades	0	1	1.154
feroces	0	1	1.154
fernán	0	1	1.154
fermentaron	0	1	1.154
fermentando	0	1	1.154
fermentados	0	1	1.154
fermenta	0	1	1.154
feotes	0	1	1.154
feona	0	1	1.154
feón	0	1	1.154
fénico	0	1	1.154
fenicias	0	1	1.154
femeninas	0	1	1.154
felpudos	0	1	1.154
felpilla	0	1	1.154
felpa	0	1	1.154
felicito	0	1	1.154
felicíteme	0	1	1.154
felicitándose	0	1	1.154
felicidades	0	1	1.154
feíto	0	1	1.154
feísimo	0	1	1.154
fedro	0	1	1.154
fecundísimo	0	1	1.154
feculentos	0	1	1.154
fechadura	0	1	1.154
featón	0	1	1.154
favoreciéndoles	0	1	1.154
favoreciendo	0	1	1.154
favorecidos	0	1	1.154
favorecen	0	1	1.154
favorablemente	0	1	1.154
fatigándose	0	1	1.154
fatigando	0	1	1.154
fatigadísimo	0	1	1.154
fatídicas	0	1	1.154
fatídica	0	1	1.154
fastidioso	0	1	1.154
fastidiosa	0	1	1.154
fastídiese	0	1	1.154
fastidien	0	1	1.154
fastidie	0	1	1.154
fastidiar	0	1	1.154
fascinador	0	1	1.154
fascinaban	0	1	1.154
farsantuelo	0	1	1.154
farolona	0	1	1.154
farfantonas	0	1	1.154
farfantona	0	1	1.154
fare	0	1	1.154
fantasmonas	0	1	1.154
fantasmón	0	1	1.154
fantasmagórica	0	1	1.154
fantasmagorías	0	1	1.154
fantasiar	0	1	1.154
fanfarronería	0	1	1.154
fanegas	0	1	1.154
fandangos	0	1	1.154
fandango	0	1	1.154
familiona	0	1	1.154
familión	0	1	1.154
familiarizarse	0	1	1.154
familiarizaran	0	1	1.154
familiarizara	0	1	1.154
familiarizado	0	1	1.154
familiarizadas	0	1	1.154
familiaridades	0	1	1.154
famélicas	0	1	1.154
faltoncito	0	1	1.154
faltón	0	1	1.154
faltes	0	1	1.154
faltarnos	0	1	1.154
faltarás	0	1	1.154
falsísimo	0	1	1.154
falsificadas	0	1	1.154
falsificación	0	1	1.154
falseamiento	0	1	1.154
falsarias	0	1	1.154
falle	0	1	1.154
falla	0	1	1.154
faldón	0	1	1.154
fajita	0	1	1.154
fajas	0	1	1.154
fajarlo	0	1	1.154
fajado	0	1	1.154
facto	0	1	1.154
facilitaran	0	1	1.154
facilitan	0	1	1.154
fachas	0	1	1.154
faccioso	0	1	1.154
fabulosos	0	1	1.154
fabrican	0	1	1.154
ezquerdo	0	1	1.154
eylau	0	1	1.154
extremando	0	1	1.154
extremaba	0	1	1.154
extrema	0	1	1.154
extrayendo	0	1	1.154
extraviarse	0	1	1.154
extraviadas	0	1	1.154
extraordinarias	0	1	1.154
extrañísima	0	1	1.154
extrañe	0	1	1.154
extrañase	0	1	1.154
extrañará	0	1	1.154
extrañando	0	1	1.154
extranjis	0	1	1.154
extranjerote	0	1	1.154
extranjerizado	0	1	1.154
extranjerismo	0	1	1.154
extraía	0	1	1.154
extraerle	0	1	1.154
extraer	0	1	1.154
extractor	0	1	1.154
extracción	0	1	1.154
extra	0	1	1.154
extirpación	0	1	1.154
extinguieran	0	1	1.154
extinguía	0	1	1.154
exterminios	0	1	1.154
exterminio	0	1	1.154
exteriorizarse	0	1	1.154
extenuación	0	1	1.154
extensiones	0	1	1.154
extendiéndose	0	1	1.154
extenderlas	0	1	1.154
extáticos	0	1	1.154
expusiera	0	1	1.154
expurgación	0	1	1.154
expulsarla	0	1	1.154
expulsados	0	1	1.154
expulsadas	0	1	1.154
expugnador	0	1	1.154
exprimidas	0	1	1.154
express	0	1	1.154
expresase	0	1	1.154
expresarlo	0	1	1.154
expresarle	0	1	1.154
expresarlas	0	1	1.154
expresándole	0	1	1.154
expresábase	0	1	1.154
expositor	0	1	1.154
exposiciones	0	1	1.154
exponían	0	1	1.154
expondré	0	1	1.154
explotarse	0	1	1.154
explotados	0	1	1.154
exploró	0	1	1.154
explore	0	1	1.154
exploraba	0	1	1.154
explícitamente	0	1	1.154
explicas	0	1	1.154
explicártelo	0	1	1.154
explicaran	0	1	1.154
explaye	0	1	1.154
explayándose	0	1	1.154
explanó	0	1	1.154
expiró	0	1	1.154
expiraron	0	1	1.154
expirar	0	1	1.154
expirantes	0	1	1.154
expiraban	0	1	1.154
expiar	0	1	1.154
expiad	0	1	1.154
expertísimo	0	1	1.154
experimentó	0	1	1.154
experimentando	0	1	1.154
experimentales	0	1	1.154
experimentada	0	1	1.154
expensas	0	1	1.154
expenden	0	1	1.154
exitazo	0	1	1.154
existirá	0	1	1.154
existan	0	1	1.154
exista	0	1	1.154
eximios	0	1	1.154
eximio	0	1	1.154
exigüidad	0	1	1.154
exigirle	0	1	1.154
exigí	0	1	1.154
exiges	0	1	1.154
exigente	0	1	1.154
exhortaba	0	1	1.154
exhibir	0	1	1.154
exhibe	0	1	1.154
exhausta	0	1	1.154
exhalar	0	1	1.154
exhalaba	0	1	1.154
excluyó	0	1	1.154
exclusivo	0	1	1.154
exclusión	0	1	1.154
excluían	0	1	1.154
exclaustrados	0	1	1.154
exclaustrado	0	1	1.154
excite	0	1	1.154
excitase	0	1	1.154
excitadísimo	0	1	1.154
excentricidades	0	1	1.154
excéntricas	0	1	1.154
excelsos	0	1	1.154
excelso	0	1	1.154
exasperaba	0	1	1.154
examinemos	0	1	1.154
examine	0	1	1.154
examinase	0	1	1.154
examinarlas	0	1	1.154
examinarla	0	1	1.154
examínalo	0	1	1.154
examínale	0	1	1.154
examinadas	0	1	1.154
exaltarse	0	1	1.154
exaltando	0	1	1.154
exabrupto	0	1	1.154
evocó	0	1	1.154
evocadas	0	1	1.154
evocación	0	1	1.154
eviten	0	1	1.154
evitarlas	0	1	1.154
evitaban	0	1	1.154
eventuales	0	1	1.154
evasivos	0	1	1.154
evasiva	0	1	1.154
evaporado	0	1	1.154
evangelísticos	0	1	1.154
evangelistas	0	1	1.154
evangelios	0	1	1.154
evangélicos	0	1	1.154
evangélico	0	1	1.154
europeos	0	1	1.154
europeas	0	1	1.154
eugenio	0	1	1.154
éufrates	0	1	1.154
eton	0	1	1.154
etnográfico	0	1	1.154
eternos	0	1	1.154
etéreo	0	1	1.154
etéreas	0	1	1.154
etalaje	0	1	1.154
estuvimos	0	1	1.154
estuviesen	0	1	1.154
estupores	0	1	1.154
estupideces	0	1	1.154
estupendos	0	1	1.154
estupendo	0	1	1.154
estudiosos	0	1	1.154
estudias	0	1	1.154
estudiarle	0	1	1.154
estudiaré	0	1	1.154
estudiantillo	0	1	1.154
estudiantiles	0	1	1.154
estudiándole	0	1	1.154
estuchitos	0	1	1.154
estrujaron	0	1	1.154
estrujarla	0	1	1.154
estropearon	0	1	1.154
estropear	0	1	1.154
estropeándose	0	1	1.154
estropeado	0	1	1.154
estropeadísima	0	1	1.154
estropeada	0	1	1.154
estropea	0	1	1.154
estropajosas	0	1	1.154
estropajosa	0	1	1.154
estropajo	0	1	1.154
estrofas	0	1	1.154
estro	0	1	1.154
estrictamente	0	1	1.154
estribación	0	1	1.154
estrenó	0	1	1.154
estrenaríamos	0	1	1.154
estrenaré	0	1	1.154
estrenara	0	1	1.154
estrenado	0	1	1.154
estrenaba	0	1	1.154
estrena	0	1	1.154
estremece	0	1	1.154
estrellarla	0	1	1.154
estrellándolas	0	1	1.154
estrecharle	0	1	1.154
estrechándola	0	1	1.154
estrechando	0	1	1.154
estraza	0	1	1.154
estratégico	0	1	1.154
estrangulándola	0	1	1.154
estrambóticas	0	1	1.154
estrambótica	0	1	1.154
estragado	0	1	1.154
estrafalarios	0	1	1.154
estrabismo	0	1	1.154
estotra	0	1	1.154
estornudos	0	1	1.154
estornudo	0	1	1.154
estorbe	0	1	1.154
estorbaban	0	1	1.154
estómagos	0	1	1.154
estólidos	0	1	1.154
estolidez	0	1	1.154
estoico	0	1	1.154
estoicismo	0	1	1.154
estoica	0	1	1.154
estofados	0	1	1.154
estofadas	0	1	1.154
estocada	0	1	1.154
estirpes	0	1	1.154
estirase	0	1	1.154
estirarse	0	1	1.154
estirarlo	0	1	1.154
estiraran	0	1	1.154
estirados	0	1	1.154
estiradas	0	1	1.154
estimuló	0	1	1.154
estimulante	0	1	1.154
estimulándole	0	1	1.154
estimulando	0	1	1.154
estimulada	0	1	1.154
estimó	0	1	1.154
estimaran	0	1	1.154
estimados	0	1	1.154
estimada	0	1	1.154
estilan	0	1	1.154
estila	0	1	1.154
estigma	0	1	1.154
estéticas	0	1	1.154
esternón	0	1	1.154
esterlinas	0	1	1.154
esteritas	0	1	1.154
esterita	0	1	1.154
esteras	0	1	1.154
esteparios	0	1	1.154
estepa	0	1	1.154
estentórea	0	1	1.154
estaturas	0	1	1.154
estatuario	0	1	1.154
estático	0	1	1.154
estática	0	1	1.154
estarte	0	1	1.154
estaribel	0	1	1.154
estarcidos	0	1	1.154
estarcido	0	1	1.154
estantigua	0	1	1.154
estantería	0	1	1.154
estancias	0	1	1.154
estampó	0	1	1.154
estampitas	0	1	1.154
estampido	0	1	1.154
estámpelo	0	1	1.154
estampar	0	1	1.154
estampado	0	1	1.154
estampadas	0	1	1.154
estampaba	0	1	1.154
estallo	0	1	1.154
estallase	0	1	1.154
estafetas	0	1	1.154
estafase	0	1	1.154
estafarles	0	1	1.154
estafar	0	1	1.154
estafamos	0	1	1.154
establezcamos	0	1	1.154
estableciendo	0	1	1.154
establecidos	0	1	1.154
establecerme	0	1	1.154
estábase	0	1	1.154
estábanlo	0	1	1.154
esquinazo	0	1	1.154
esquelitas	0	1	1.154
esquelas	0	1	1.154
espumas	0	1	1.154
espuerta	0	1	1.154
espuelas	0	1	1.154
espotrique	0	1	1.154
espotricarás	0	1	1.154
espotrica	0	1	1.154
espontáneas	0	1	1.154
espontanearse	0	1	1.154
espolvoreada	0	1	1.154
esplines	0	1	1.154
esplinado	0	1	1.154
esplendidez	0	1	1.154
espléndidas	0	1	1.154
espléndidamente	0	1	1.154
espirituosa	0	1	1.154
espiritualizar	0	1	1.154
espigadita	0	1	1.154
espichamos	0	1	1.154
espichaba	0	1	1.154
espich	0	1	1.154
espetó	0	1	1.154
espetarle	0	1	1.154
espetaría	0	1	1.154
espetando	0	1	1.154
espetaba	0	1	1.154
espeta	0	1	1.154
espérese	0	1	1.154
esperes	0	1	1.154
esperarme	0	1	1.154
esperarían	0	1	1.154
esperamos	0	1	1.154
esperabas	0	1	1.154
espeluznante	0	1	1.154
espejuelos	0	1	1.154
especulativas	0	1	1.154
especulación	0	1	1.154
específicos	0	1	1.154
espátula	0	1	1.154
espatarrados	0	1	1.154
espasmos	0	1	1.154
espasmo	0	1	1.154
espárragos	0	1	1.154
esparcimientos	0	1	1.154
españolizada	0	1	1.154
españita	0	1	1.154
espante	0	1	1.154
espantas	0	1	1.154
espantarlo	0	1	1.154
espantara	0	1	1.154
espantar	0	1	1.154
espantan	0	1	1.154
espantajos	0	1	1.154
espantadas	0	1	1.154
espaldilla	0	1	1.154
espaldarazo	0	1	1.154
espaciosísima	0	1	1.154
espació	0	1	1.154
espachurrar	0	1	1.154
esmeró	0	1	1.154
esmerándose	0	1	1.154
esmeradísimos	0	1	1.154
esmeraba	0	1	1.154
esmaltadas	0	1	1.154
eslabonaba	0	1	1.154
esgrimió	0	1	1.154
esgrimiéndola	0	1	1.154
esforzarte	0	1	1.154
esforzábase	0	1	1.154
eserina	0	1	1.154
esencialísimo	0	1	1.154
escurro	0	1	1.154
escurriendo	0	1	1.154
escurridiza	0	1	1.154
escurrían	0	1	1.154
escurrí	0	1	1.154
escurren	0	1	1.154
escupiera	0	1	1.154
escupidera	0	1	1.154
escupe	0	1	1.154
esculapio	0	1	1.154
escuezan	0	1	1.154
escuetos	0	1	1.154
escuerzo	0	1	1.154
escuecen	0	1	1.154
escudriñadoras	0	1	1.154
escudriñaba	0	1	1.154
escudito	0	1	1.154
escudilla	0	1	1.154
escudero	0	1	1.154
escuchara	0	1	1.154
escualidez	0	1	1.154
escuadrones	0	1	1.154
escrutinios	0	1	1.154
escrutinio	0	1	1.154
escrutadora	0	1	1.154
escrutador	0	1	1.154
escritas	0	1	1.154
escribirse	0	1	1.154
escribirás	0	1	1.154
escribiente	0	1	1.154
escribiéndole	0	1	1.154
escribidores	0	1	1.154
escribida	0	1	1.154
escríbele	0	1	1.154
escozorcillo	0	1	1.154
escorzos	0	1	1.154
escoplos	0	1	1.154
escopetilla	0	1	1.154
escondo	0	1	1.154
escondidísimo	0	1	1.154
escondí	0	1	1.154
esconderme	0	1	1.154
esconderé	0	1	1.154
escóndelo	0	1	1.154
escomienzo	0	1	1.154
escoltaron	0	1	1.154
escoltando	0	1	1.154
escoltado	0	1	1.154
escoltadas	0	1	1.154
escoltada	0	1	1.154
escollos	0	1	1.154
escolásticos	0	1	1.154
escolar	0	1	1.154
escocía	0	1	1.154
escocer	0	1	1.154
escobones	0	1	1.154
esclavizarles	0	1	1.154
esclavizar	0	1	1.154
esclavitudes	0	1	1.154
esclarecerla	0	1	1.154
escenita	0	1	1.154
escaseces	0	1	1.154
escasean	0	1	1.154
escaseaban	0	1	1.154
escarnecida	0	1	1.154
escarmientos	0	1	1.154
escarmiente	0	1	1.154
escarmentar	0	1	1.154
escarmentada	0	1	1.154
escarlatina	0	1	1.154
escarbando	0	1	1.154
escarbaba	0	1	1.154
escaray	0	1	1.154
escapose	0	1	1.154
escapo	0	1	1.154
escapes	0	1	1.154
escapé	0	1	1.154
escaparte	0	1	1.154
escapárseme	0	1	1.154
escaparse	0	1	1.154
escapada	0	1	1.154
escaños	0	1	1.154
escanciaba	0	1	1.154
escamoteos	0	1	1.154
escamotees	0	1	1.154
escamoteadas	0	1	1.154
escamosa	0	1	1.154
escamonea	0	1	1.154
escamón	0	1	1.154
escamo	0	1	1.154
escamas	0	1	1.154
escamarse	0	1	1.154
escamaba	0	1	1.154
escaldado	0	1	1.154
escalas	0	1	1.154
escalafón	0	1	1.154
escabullo	0	1	1.154
escabullirse	0	1	1.154
escabecharnos	0	1	1.154
escabecharla	0	1	1.154
escabechadas	0	1	1.154
esbozarse	0	1	1.154
esbeltísimo	0	1	1.154
erres	0	1	1.154
eroísma	0	1	1.154
erizado	0	1	1.154
erizaba	0	1	1.154
erigido	0	1	1.154
erección	0	1	1.154
érase	0	1	1.154
érales	0	1	1.154
equivoqué	0	1	1.154
equivoque	0	1	1.154
equívocos	0	1	1.154
equivocas	0	1	1.154
equivocarme	0	1	1.154
equivocaría	0	1	1.154
equivocan	0	1	1.154
equivocamos	0	1	1.154
equipos	0	1	1.154
equipo	0	1	1.154
equipajes	0	1	1.154
equilibrarás	0	1	1.154
equilibradas	0	1	1.154
equilibraban	0	1	1.154
equi	0	1	1.154
epopeyas	0	1	1.154
epitafios	0	1	1.154
epilépticos	0	1	1.154
epilépticas	0	1	1.154
epígrafe	0	1	1.154
epidérmicas	0	1	1.154
epaminondas	0	1	1.154
enzarzó	0	1	1.154
enzarzaran	0	1	1.154
enzarzados	0	1	1.154
enzarzado	0	1	1.154
enzarzaban	0	1	1.154
envuelvas	0	1	1.154
envueltitos	0	1	1.154
envolvíase	0	1	1.154
envolverlos	0	1	1.154
enviudé	0	1	1.154
enviudaste	0	1	1.154
enviole	0	1	1.154
envilecen	0	1	1.154
envidiarían	0	1	1.154
enviciados	0	1	1.154
enviciadas	0	1	1.154
enviaré	0	1	1.154
enviar	0	1	1.154
enviado	0	1	1.154
envenene	0	1	1.154
envenenas	0	1	1.154
envenenarse	0	1	1.154
envenenara	0	1	1.154
envenena	0	1	1.154
envejecidas	0	1	1.154
envejecida	0	1	1.154
envejecer	0	1	1.154
envejece	0	1	1.154
envalentonaban	0	1	1.154
envainó	0	1	1.154
entusiasmes	0	1	1.154
entusiasmas	0	1	1.154
entusiasmándose	0	1	1.154
entusiasman	0	1	1.154
entusiasmaban	0	1	1.154
enturbiando	0	1	1.154
entrometimiento	0	1	1.154
entrometerse	0	1	1.154
entristeciendo	0	1	1.154
entristecía	0	1	1.154
entreviendo	0	1	1.154
entrevía	0	1	1.154
entreverando	0	1	1.154
entrevé	0	1	1.154
entretenle	0	1	1.154
entretenidos	0	1	1.154
entretenga	0	1	1.154
entretendría	0	1	1.154
entresacando	0	1	1.154
entremezcladas	0	1	1.154
entremezclada	0	1	1.154
entregues	0	1	1.154
entregue	0	1	1.154
entregárselos	0	1	1.154
entregándoselo	0	1	1.154
entregando	0	1	1.154
entregábase	0	1	1.154
entregábalos	0	1	1.154
entrecortadas	0	1	1.154
entrecortaba	0	1	1.154
entrecanos	0	1	1.154
entreabriendo	0	1	1.154
entreabierta	0	1	1.154
entrarme	0	1	1.154
entrarían	0	1	1.154
entrañaba	0	1	1.154
éntranle	0	1	1.154
entrambas	0	1	1.154
entramado	0	1	1.154
entortolarse	0	1	1.154
entorpecimiento	0	1	1.154
entorpecían	0	1	1.154
entorpecerle	0	1	1.154
entorpecería	0	1	1.154
entornadas	0	1	1.154
entonan	0	1	1.154
entonaban	0	1	1.154
entiesaba	0	1	1.154
entienda	0	1	1.154
enterrasen	0	1	1.154
enterneciéndose	0	1	1.154
enternecerían	0	1	1.154
enterita	0	1	1.154
entérese	0	1	1.154
enteres	0	1	1.154
enteremos	0	1	1.154
enteraste	0	1	1.154
enteraría	0	1	1.154
enteraré	0	1	1.154
entenebrecidos	0	1	1.154
entendiesen	0	1	1.154
entendí	0	1	1.154
entenderías	0	1	1.154
entendederas	0	1	1.154
entendedera	0	1	1.154
entendamos	0	1	1.154
entenada	0	1	1.154
entarimado	0	1	1.154
entablose	0	1	1.154
ensuciarlo	0	1	1.154
ensuciaré	0	1	1.154
ensucian	0	1	1.154
ensuciados	0	1	1.154
ensuciaba	0	1	1.154
ensordecían	0	1	1.154
ensordecedor	0	1	1.154
ensordece	0	1	1.154
ensoberbecido	0	1	1.154
ensoberbecía	0	1	1.154
ensimisme	0	1	1.154
enseñoreando	0	1	1.154
enseñen	0	1	1.154
enséñemelo	0	1	1.154
enseñé	0	1	1.154
enseñe	0	1	1.154
enseñas	0	1	1.154
enseñárselo	0	1	1.154
enseñarme	0	1	1.154
enseñarles	0	1	1.154
enseñará	0	1	1.154
enseñándosela	0	1	1.154
enseñándome	0	1	1.154
enseñándola	0	1	1.154
enséñame	0	1	1.154
enséñale	0	1	1.154
enseñabas	0	1	1.154
ensarriá	0	1	1.154
ensañas	0	1	1.154
ensangrentados	0	1	1.154
ensalzaron	0	1	1.154
ensalza	0	1	1.154
enroscada	0	1	1.154
enroscaba	0	1	1.154
enronquecido	0	1	1.154
enrojecidos	0	1	1.154
enrojecidas	0	1	1.154
enriquecido	0	1	1.154
enriquecer	0	1	1.154
enrevesado	0	1	1.154
enrevesadas	0	1	1.154
enrevesada	0	1	1.154
enrejados	0	1	1.154
enrejado	0	1	1.154
enrejadas	0	1	1.154
enrejada	0	1	1.154
enredarse	0	1	1.154
enredarme	0	1	1.154
enredadora	0	1	1.154
enranciaran	0	1	1.154
enramaban	0	1	1.154
enojó	0	1	1.154
enojado	0	1	1.154
enojábanla	0	1	1.154
ennobleciendo	0	1	1.154
ennoblecerse	0	1	1.154
ennegrecido	0	1	1.154
enmudecía	0	1	1.154
enmudecer	0	1	1.154
enmohecidas	0	1	1.154
enmiendes	0	1	1.154
enmendarse	0	1	1.154
enmendar	0	1	1.154
enmendada	0	1	1.154
enmascarando	0	1	1.154
enluto	0	1	1.154
enlutados	0	1	1.154
enloquecía	0	1	1.154
enloquecerme	0	1	1.154
enloquecer	0	1	1.154
enlazan	0	1	1.154
enlazadas	0	1	1.154
enjuto	0	1	1.154
enjutísimas	0	1	1.154
enjaretarle	0	1	1.154
enjabonáronle	0	1	1.154
enigmas	0	1	1.154
engullir	0	1	1.154
engrosando	0	1	1.154
engrosaba	0	1	1.154
engrasado	0	1	1.154
engrandecerte	0	1	1.154
engranaje	0	1	1.154
engorden	0	1	1.154
engordas	0	1	1.154
engolosinaron	0	1	1.154
engolosina	0	1	1.154
engolfó	0	1	1.154
engolfada	0	1	1.154
engendros	0	1	1.154
engendra	0	1	1.154
engatusas	0	1	1.154
engatusar	0	1	1.154
engatusando	0	1	1.154
engatusa	0	1	1.154
engastado	0	1	1.154
engarzada	0	1	1.154
engarza	0	1	1.154
engarnos	0	1	1.154
engarfiñaron	0	1	1.154
engañosa	0	1	1.154
engañen	0	1	1.154
engañe	0	1	1.154
engañase	0	1	1.154
engañarás	0	1	1.154
engañara	0	1	1.154
engañamos	0	1	1.154
engañadores	0	1	1.154
engañábase	0	1	1.154
engancha	0	1	1.154
engalanó	0	1	1.154
engalanarse	0	1	1.154
enfurruñas	0	1	1.154
enfurruñados	0	1	1.154
enfurruñado	0	1	1.154
enfureció	0	1	1.154
enfureciendo	0	1	1.154
enfriase	0	1	1.154
enfriarás	0	1	1.154
enfriaran	0	1	1.154
enfriar	0	1	1.154
enfrenada	0	1	1.154
enfrenaba	0	1	1.154
enfrascaron	0	1	1.154
enflaquecido	0	1	1.154
enfermó	0	1	1.154
enfermera	0	1	1.154
enfermara	0	1	1.154
enfáticos	0	1	1.154
enfáticas	0	1	1.154
enfadosas	0	1	1.154
enfadé	0	1	1.154
enfade	0	1	1.154
enfadarías	0	1	1.154
enfadaré	0	1	1.154
enfadará	0	1	1.154
enfadan	0	1	1.154
enfadadito	0	1	1.154
enérgicas	0	1	1.154
endurecimiento	0	1	1.154
endurecidos	0	1	1.154
endurecida	0	1	1.154
endurecía	0	1	1.154
endulzó	0	1	1.154
endulzara	0	1	1.154
endividos	0	1	1.154
endiñarles	0	1	1.154
endilgarle	0	1	1.154
endiablo	0	1	1.154
endiablados	0	1	1.154
enderezó	0	1	1.154
enderezarse	0	1	1.154
enderezarán	0	1	1.154
enderezaran	0	1	1.154
enderezado	0	1	1.154
enderezaba	0	1	1.154
endemoniados	0	1	1.154
encuentros	0	1	1.154
encubra	0	1	1.154
encorvarse	0	1	1.154
encopetada	0	1	1.154
encontronazos	0	1	1.154
encontrolo	0	1	1.154
encontrole	0	1	1.154
encontrola	0	1	1.154
encontrémela	0	1	1.154
encontrarte	0	1	1.154
encontrársele	0	1	1.154
encontrarme	0	1	1.154
encontrarlos	0	1	1.154
encontrarlo	0	1	1.154
encontrarían	0	1	1.154
encontraré	0	1	1.154
enconos	0	1	1.154
encomiástico	0	1	1.154
encomiando	0	1	1.154
encomendole	0	1	1.154
encomendaba	0	1	1.154
encolerizado	0	1	1.154
encogimientos	0	1	1.154
encogerlo	0	1	1.154
enclenque	0	1	1.154
encintado	0	1	1.154
encierran	0	1	1.154
enciclopédica	0	1	1.154
encía	0	1	1.154
encharcadas	0	1	1.154
encharcada	0	1	1.154
encharcad	0	1	1.154
encerrarán	0	1	1.154
encerrando	0	1	1.154
encenegándose	0	1	1.154
encendiera	0	1	1.154
encendiéndolas	0	1	1.154
encenderlas	0	1	1.154
encendería	0	1	1.154
encenágate	0	1	1.154
encefálico	0	1	1.154
encauzarlo	0	1	1.154
encastilló	0	1	1.154
encasquetarme	0	1	1.154
encasquetan	0	1	1.154
encasquetado	0	1	1.154
encasquetada	0	1	1.154
encasquetaba	0	1	1.154
encarose	0	1	1.154
encarnarse	0	1	1.154
encarnándose	0	1	1.154
encarna	0	1	1.154
encariñarte	0	1	1.154
encariñan	0	1	1.154
encariñada	0	1	1.154
encariñaba	0	1	1.154
encargue	0	1	1.154
encárgate	0	1	1.154
encargase	0	1	1.154
encargarte	0	1	1.154
encargarle	0	1	1.154
encargaremos	0	1	1.154
encargaras	0	1	1.154
encargara	0	1	1.154
encargados	0	1	1.154
encargábase	0	1	1.154
encareció	0	1	1.154
encarecimientos	0	1	1.154
encarecer	0	1	1.154
encarcelada	0	1	1.154
encaramando	0	1	1.154
encaprichó	0	1	1.154
encapricharte	0	1	1.154
encantando	0	1	1.154
encantan	0	1	1.154
encantados	0	1	1.154
encantador	0	1	1.154
encanta	0	1	1.154
encanijado	0	1	1.154
encanijada	0	1	1.154
encanecido	0	1	1.154
encanallan	0	1	1.154
encanallamiento	0	1	1.154
encanallado	0	1	1.154
encaminaron	0	1	1.154
encaminarla	0	1	1.154
encamarme	0	1	1.154
encamada	0	1	1.154
encalabrinada	0	1	1.154
encajó	0	1	1.154
encajería	0	1	1.154
encajera	0	1	1.154
encajaba	0	1	1.154
encadenando	0	1	1.154
enardecía	0	1	1.154
enanita	0	1	1.154
enamorisca	0	1	1.154
enamoraran	0	1	1.154
enamoradito	0	1	1.154
enaltecido	0	1	1.154
enaltecerlo	0	1	1.154
enaltecer	0	1	1.154
emulsión	0	1	1.154
empujones	0	1	1.154
empujole	0	1	1.154
empujola	0	1	1.154
empujaran	0	1	1.154
empujará	0	1	1.154
empujándose	0	1	1.154
empuja	0	1	1.154
empuerca	0	1	1.154
emprendiera	0	1	1.154
empozado	0	1	1.154
empolvadas	0	1	1.154
empolva	0	1	1.154
empollar	0	1	1.154
empollándola	0	1	1.154
empobreciesen	0	1	1.154
empobrecida	0	1	1.154
emplomadas	0	1	1.154
empleolo	0	1	1.154
empleíto	0	1	1.154
empleitas	0	1	1.154
empleasen	0	1	1.154
emplearla	0	1	1.154
empleábale	0	1	1.154
empingorotó	0	1	1.154
empingorotadas	0	1	1.154
empingorotada	0	1	1.154
empinándose	0	1	1.154
empina	0	1	1.154
empieces	0	1	1.154
empezase	0	1	1.154
empezaremos	0	1	1.154
empezaré	0	1	1.154
empezarás	0	1	1.154
empezarán	0	1	1.154
emperifollada	0	1	1.154
emperejilarse	0	1	1.154
emperejilado	0	1	1.154
empeoró	0	1	1.154
empeoraba	0	1	1.154
empeñemos	0	1	1.154
empeñáronse	0	1	1.154
empeñarme	0	1	1.154
empeñarás	0	1	1.154
empeñará	0	1	1.154
empeñando	0	1	1.154
empeñadamente	0	1	1.154
empeñábase	0	1	1.154
empenachados	0	1	1.154
empedrados	0	1	1.154
empedernidas	0	1	1.154
emparrados	0	1	1.154
emparentada	0	1	1.154
emparejan	0	1	1.154
empaquetados	0	1	1.154
empañado	0	1	1.154
empalme	0	1	1.154
empalmaste	0	1	1.154
empalmaba	0	1	1.154
empalagosos	0	1	1.154
empalagoso	0	1	1.154
emolumentos	0	1	1.154
emoliente	0	1	1.154
emitir	0	1	1.154
emitía	0	1	1.154
emisión	0	1	1.154
eminencias	0	1	1.154
emilion	0	1	1.154
emilio	0	1	1.154
eméticos	0	1	1.154
emético	0	1	1.154
emersión	0	1	1.154
embusteros	0	1	1.154
embusteras	0	1	1.154
embudo	0	1	1.154
embruteció	0	1	1.154
embrutecido	0	1	1.154
embrutecida	0	1	1.154
embrutecerse	0	1	1.154
embrionario	0	1	1.154
embriagó	0	1	1.154
embriago	0	1	1.154
embriagarle	0	1	1.154
embriagaba	0	1	1.154
embozadito	0	1	1.154
embotarse	0	1	1.154
emboscada	0	1	1.154
emborrachen	0	1	1.154
emboce	0	1	1.154
embobar	0	1	1.154
embiste	0	1	1.154
embetunadas	0	1	1.154
embestirla	0	1	1.154
embestidas	0	1	1.154
embestida	0	1	1.154
embelleciéndose	0	1	1.154
embellecían	0	1	1.154
embellecer	0	1	1.154
embelesarse	0	1	1.154
embelesan	0	1	1.154
embelesado	0	1	1.154
embelesadas	0	1	1.154
embelesada	0	1	1.154
embebecimiento	0	1	1.154
embebecida	0	1	1.154
embebe	0	1	1.154
embaulará	0	1	1.154
embaucara	0	1	1.154
embaucar	0	1	1.154
embaucando	0	1	1.154
embarulló	0	1	1.154
embarullarse	0	1	1.154
embarullar	0	1	1.154
embarullaba	0	1	1.154
embargué	0	1	1.154
embargaron	0	1	1.154
embargaría	0	1	1.154
embarcase	0	1	1.154
embarcaciones	0	1	1.154
embarcación	0	1	1.154
embaldosados	0	1	1.154
embalajes	0	1	1.154
embajador	0	1	1.154
embadurnadas	0	1	1.154
embadurnada	0	1	1.154
emancipaste	0	1	1.154
emanciparía	0	1	1.154
emanada	0	1	1.154
emanaban	0	1	1.154
eludir	0	1	1.154
elogiaron	0	1	1.154
elogiarle	0	1	1.154
elogian	0	1	1.154
elle	0	1	1.154
elimine	0	1	1.154
eliminar	0	1	1.154
eliminación	0	1	1.154
eliminaba	0	1	1.154
eligió	0	1	1.154
elige	0	1	1.154
elevado	0	1	1.154
elevaban	0	1	1.154
elegirte	0	1	1.154
elegantona	0	1	1.154
elegantísimo	0	1	1.154
electriza	0	1	1.154
elduayen	0	1	1.154
elasticidad	0	1	1.154
elástica	0	1	1.154
elaboradas	0	1	1.154
elaboraba	0	1	1.154
ejido	0	1	1.154
ejerzo	0	1	1.154
ejercitando	0	1	1.154
ejercitaban	0	1	1.154
ejercían	0	1	1.154
ejerce	0	1	1.154
ejecutarla	0	1	1.154
ejecuta	0	1	1.154
efusiones	0	1	1.154
efeméride	0	1	1.154
efectuó	0	1	1.154
efectuase	0	1	1.154
efectuarse	0	1	1.154
efectivos	0	1	1.154
efectividad	0	1	1.154
eduqué	0	1	1.154
educatrices	0	1	1.154
educativa	0	1	1.154
educarse	0	1	1.154
educarle	0	1	1.154
educarlas	0	1	1.154
educaré	0	1	1.154
educaran	0	1	1.154
educan	0	1	1.154
educados	0	1	1.154
educadito	0	1	1.154
educa	0	1	1.154
edificó	0	1	1.154
edificársenos	0	1	1.154
edificarse	0	1	1.154
edificara	0	1	1.154
edificadas	0	1	1.154
edecán	0	1	1.154
ecuménico	0	1	1.154
ecónomo	0	1	1.154
economizar	0	1	1.154
economistas	0	1	1.154
eclipsó	0	1	1.154
eclipse	0	1	1.154
eclipsaban	0	1	1.154
echole	0	1	1.154
échenme	0	1	1.154
échenle	0	1	1.154
echen	0	1	1.154
echemos	0	1	1.154
echaste	0	1	1.154
echártela	0	1	1.154
echárnosla	0	1	1.154
echarnos	0	1	1.154
echarles	0	1	1.154
echarían	0	1	1.154
echaría	0	1	1.154
echarás	0	1	1.154
echará	0	1	1.154
echándotelas	0	1	1.154
echándotela	0	1	1.154
échame	0	1	1.154
echadito	0	1	1.154
echabas	0	1	1.154
echábamos	0	1	1.154
echábalo	0	1	1.154
echábalas	0	1	1.154
duritos	0	1	1.154
durísima	0	1	1.154
duretes	0	1	1.154
durete	0	1	1.154
durábale	0	1	1.154
duques	0	1	1.154
duodécimo	0	1	1.154
dulcificó	0	1	1.154
dulcificarla	0	1	1.154
dulcificando	0	1	1.154
duerman	0	1	1.154
duelitos	0	1	1.154
duden	0	1	1.154
dude	0	1	1.154
dudara	0	1	1.154
dudan	0	1	1.154
dubitativo	0	1	1.154
dubarry	0	1	1.154
dualismos	0	1	1.154
dromedario	0	1	1.154
droguista	0	1	1.154
drástico	0	1	1.154
dramón	0	1	1.154
dramita	0	1	1.154
dover	0	1	1.154
dotrina	0	1	1.154
dotarle	0	1	1.154
dormiste	0	1	1.154
dormirte	0	1	1.154
dormirnos	0	1	1.154
dormirlas	0	1	1.154
dormiría	0	1	1.154
dormiré	0	1	1.154
dormilones	0	1	1.154
dormilón	0	1	1.154
dormías	0	1	1.154
dorando	0	1	1.154
doraba	0	1	1.154
donativo	0	1	1.154
domingueros	0	1	1.154
domine	0	1	1.154
dominantes	0	1	1.154
dominan	0	1	1.154
domicilios	0	1	1.154
domiciliarios	0	1	1.154
domestiquen	0	1	1.154
domesticidad	0	1	1.154
domesticaremos	0	1	1.154
domesticar	0	1	1.154
domarle	0	1	1.154
domaríamos	0	1	1.154
domar	0	1	1.154
domado	0	1	1.154
dolorido	0	1	1.154
doloridas	0	1	1.154
doliesen	0	1	1.154
doliese	0	1	1.154
dolieron	0	1	1.154
doliente	0	1	1.154
dolerle	0	1	1.154
dolencia	0	1	1.154
dogal	0	1	1.154
doctrinarios	0	1	1.154
doctrinario	0	1	1.154
doctoral	0	1	1.154
docilota	0	1	1.154
doblones	0	1	1.154
dobloncito	0	1	1.154
doblemos	0	1	1.154
doblegarse	0	1	1.154
doblase	0	1	1.154
doblarlos	0	1	1.154
doblarlo	0	1	1.154
doblados	0	1	1.154
dobladitos	0	1	1.154
dobladillar	0	1	1.154
dobladas	0	1	1.154
do	0	1	1.154
divulgasen	0	1	1.154
divisoria	0	1	1.154
divisara	0	1	1.154
divisado	0	1	1.154
divirtió	0	1	1.154
divirtiera	0	1	1.154
divierto	0	1	1.154
diviertan	0	1	1.154
divididas	0	1	1.154
dividíanse	0	1	1.154
dividendos	0	1	1.154
dividendo	0	1	1.154
dividen	0	1	1.154
divertirte	0	1	1.154
divertimientos	0	1	1.154
divertidos	0	1	1.154
divertíanla	0	1	1.154
divertí	0	1	1.154
diverso	0	1	1.154
diversidad	0	1	1.154
diversa	0	1	1.154
diurna	0	1	1.154
diuréticos	0	1	1.154
disuélvase	0	1	1.154
disuelto	0	1	1.154
disuadirle	0	1	1.154
distritos	0	1	1.154
distribuyendo	0	1	1.154
distribuirse	0	1	1.154
distribuidos	0	1	1.154
distribuido	0	1	1.154
distrayendo	0	1	1.154
distrajeron	0	1	1.154
distraigo	0	1	1.154
distráiganme	0	1	1.154
distraidita	0	1	1.154
distráete	0	1	1.154
distraería	0	1	1.154
distraedme	0	1	1.154
disto	0	1	1.154
distinguirle	0	1	1.154
distinguirla	0	1	1.154
distinguieron	0	1	1.154
distinguiéndose	0	1	1.154
distinguí	0	1	1.154
diste	0	1	1.154
distaba	0	1	1.154
disputase	0	1	1.154
disputara	0	1	1.154
disputábanse	0	1	1.154
dispuestilla	0	1	1.154
disponibles	0	1	1.154
dispersas	0	1	1.154
dispersaban	0	1	1.154
dispepsias	0	1	1.154
dispepsia	0	1	1.154
dispensó	0	1	1.154
dispensarme	0	1	1.154
dispensará	0	1	1.154
dispensadora	0	1	1.154
disparos	0	1	1.154
disparatadamente	0	1	1.154
dispararlos	0	1	1.154
disparándole	0	1	1.154
disparan	0	1	1.154
disolutos	0	1	1.154
disoluto	0	1	1.154
disolución	0	1	1.154
disminuye	0	1	1.154
disloquemos	0	1	1.154
dislocará	0	1	1.154
disiparan	0	1	1.154
disipará	0	1	1.154
disipación	0	1	1.154
disipaban	0	1	1.154
disinificantes	0	1	1.154
disimulas	0	1	1.154
disimularse	0	1	1.154
disimilo	0	1	1.154
disgustarla	0	1	1.154
disgustar	0	1	1.154
disgustaban	0	1	1.154
disfrute	0	1	1.154
disfruta	0	1	1.154
disfrazaron	0	1	1.154
disfrazan	0	1	1.154
disfrazados	0	1	1.154
disertaron	0	1	1.154
diseño	0	1	1.154
disentimiento	0	1	1.154
disensiones	0	1	1.154
diseminaban	0	1	1.154
disección	0	1	1.154
discutiremos	0	1	1.154
discutiré	0	1	1.154
discutirá	0	1	1.154
discutiose	0	1	1.154
discutíamos	0	1	1.154
discute	0	1	1.154
discursazo	0	1	1.154
discurriera	0	1	1.154
discurres	0	1	1.154
discurre	0	1	1.154
discurras	0	1	1.154
disculpose	0	1	1.154
disculparse	0	1	1.154
disculpar	0	1	1.154
disculpan	0	1	1.154
discrepando	0	1	1.154
discrepaban	0	1	1.154
discípula	0	1	1.154
disciplinaria	0	1	1.154
discernimiento	0	1	1.154
dirigirá	0	1	1.154
dirigieran	0	1	1.154
dirigiera	0	1	1.154
dirías	0	1	1.154
diranle	0	1	1.154
diquiá	0	1	1.154
dipósito	0	1	1.154
diplomáticas	0	1	1.154
diplomacias	0	1	1.154
diploma	0	1	1.154
diósela	0	1	1.154
diosecito	0	1	1.154
diose	0	1	1.154
díos	0	1	1.154
diome	0	1	1.154
dinos	0	1	1.154
dimetria	0	1	1.154
dímelas	0	1	1.154
dímela	0	1	1.154
diluviaba	0	1	1.154
dilucidemos	0	1	1.154
diligentísima	0	1	1.154
dilatadas	0	1	1.154
dilatada	0	1	1.154
díjoles	0	1	1.154
dijesen	0	1	1.154
digresiones	0	1	1.154
dígolo	0	1	1.154
dignado	0	1	1.154
digitalina	0	1	1.154
digital	0	1	1.154
digiere	0	1	1.154
digestivo	0	1	1.154
digerido	0	1	1.154
dígamelo	0	1	1.154
difundido	0	1	1.154
dificultara	0	1	1.154
diferir	0	1	1.154
diferiencia	0	1	1.154
diferencian	0	1	1.154
diferenciaban	0	1	1.154
difamatorios	0	1	1.154
diestros	0	1	1.154
diéronse	0	1	1.154
diéranle	0	1	1.154
dierais	0	1	1.154
dientecillos	0	1	1.154
dido	0	1	1.154
dictó	0	1	1.154
dictar	0	1	1.154
dictaba	0	1	1.154
diciéndote	0	1	1.154
diciéndolas	0	1	1.154
dicharachera	0	1	1.154
dibujan	0	1	1.154
díaz	0	1	1.154
diátesis	0	1	1.154
diarias	0	1	1.154
diaria	0	1	1.154
diaquilón	0	1	1.154
diantres	0	1	1.154
dianches	0	1	1.154
diamantinos	0	1	1.154
dialécticas	0	1	1.154
diagnóstico	0	1	1.154
diafanidad	0	1	1.154
diáfana	0	1	1.154
diablesca	0	1	1.154
dextrina	0	1	1.154
devuelves	0	1	1.154
devorarle	0	1	1.154
devorarla	0	1	1.154
devorado	0	1	1.154
devoraban	0	1	1.154
devolviéndoselo	0	1	1.154
devolvérselos	0	1	1.154
devolverle	0	1	1.154
devolverlas	0	1	1.154
devolvería	0	1	1.154
devoluciones	0	1	1.154
devastadores	0	1	1.154
devastaba	0	1	1.154
devano	0	1	1.154
devanarse	0	1	1.154
devanar	0	1	1.154
devanamos	0	1	1.154
devanábamos	0	1	1.154
deudora	0	1	1.154
detiénese	0	1	1.154
detestable	0	1	1.154
determino	0	1	1.154
determiné	0	1	1.154
determinas	0	1	1.154
determináronse	0	1	1.154
determinaremos	0	1	1.154
determinando	0	1	1.154
determinan	0	1	1.154
determinados	0	1	1.154
determina	0	1	1.154
deteriorado	0	1	1.154
deteniéndola	0	1	1.154
deteníase	0	1	1.154
detenían	0	1	1.154
detengas	0	1	1.154
detenga	0	1	1.154
detenernos	0	1	1.154
detallistas	0	1	1.154
desviven	0	1	1.154
desvió	0	1	1.154
desviar	0	1	1.154
desviado	0	1	1.154
desvergonzó	0	1	1.154
desventurados	0	1	1.154
desventura	0	1	1.154
desventajosa	0	1	1.154
desventajas	0	1	1.154
desventaja	0	1	1.154
desvelo	0	1	1.154
desvelados	0	1	1.154
desvela	0	1	1.154
desvariar	0	1	1.154
desvariando	0	1	1.154
desvanecieron	0	1	1.154
desvalidos	0	1	1.154
desvalido	0	1	1.154
destruyo	0	1	1.154
destruyese	0	1	1.154
destruirlos	0	1	1.154
destruirlo	0	1	1.154
destruido	0	1	1.154
destructoras	0	1	1.154
destrución	0	1	1.154
destrozará	0	1	1.154
destinósele	0	1	1.154
destinatario	0	1	1.154
destilando	0	1	1.154
destiladera	0	1	1.154
destilaba	0	1	1.154
desterrarlo	0	1	1.154
desterrando	0	1	1.154
desterrados	0	1	1.154
desternillaba	0	1	1.154
destape	0	1	1.154
destapas	0	1	1.154
destapar	0	1	1.154
destapaba	0	1	1.154
destacose	0	1	1.154
destacó	0	1	1.154
desquicien	0	1	1.154
desquiciaron	0	1	1.154
desquiciamiento	0	1	1.154
despuntaban	0	1	1.154
desprovista	0	1	1.154
desproporcionadamente	0	1	1.154
desprevenida	0	1	1.154
desprestigiaría	0	1	1.154
desprestigiar	0	1	1.154
desprendió	0	1	1.154
desprendiese	0	1	1.154
desprendiendo	0	1	1.154
desprendía	0	1	1.154
desprenderme	0	1	1.154
despreciadas	0	1	1.154
despotricar	0	1	1.154
despótico	0	1	1.154
despóticamente	0	1	1.154
despótica	0	1	1.154
despojaron	0	1	1.154
desplumó	0	1	1.154
desplumar	0	1	1.154
desplumados	0	1	1.154
desplumadoras	0	1	1.154
desplomose	0	1	1.154
desplomada	0	1	1.154
desplomaban	0	1	1.154
desplegadas	0	1	1.154
desplantes	0	1	1.154
despinta	0	1	1.154
despiertísima	0	1	1.154
despido	0	1	1.154
despidiéronla	0	1	1.154
despidiera	0	1	1.154
despiden	0	1	1.154
despídase	0	1	1.154
despiadado	0	1	1.154
desperté	0	1	1.154
despertase	0	1	1.154
despertáronse	0	1	1.154
despertaré	0	1	1.154
despertándose	0	1	1.154
desperna	0	1	1.154
desperezos	0	1	1.154
desperezo	0	1	1.154
desperezara	0	1	1.154
desperdicio	0	1	1.154
despercudir	0	1	1.154
despercudida	0	1	1.154
despepita	0	1	1.154
despeñó	0	1	1.154
despeñaperros	0	1	1.154
despejaría	0	1	1.154
despejará	0	1	1.154
despejándole	0	1	1.154
despejadísimo	0	1	1.154
despejaban	0	1	1.154
despedirles	0	1	1.154
despedirlas	0	1	1.154
despedazaría	0	1	1.154
despedazados	0	1	1.154
despechada	0	1	1.154
despavorido	0	1	1.154
despavoridas	0	1	1.154
desparramados	0	1	1.154
despachos	0	1	1.154
despácheme	0	1	1.154
despaché	0	1	1.154
despachase	0	1	1.154
despachara	0	1	1.154
despachando	0	1	1.154
despachados	0	1	1.154
despacha	0	1	1.154
despabile	0	1	1.154
despabilarme	0	1	1.154
desorientados	0	1	1.154
desorientaba	0	1	1.154
desorganización	0	1	1.154
desordenadas	0	1	1.154
desollaron	0	1	1.154
desojaban	0	1	1.154
desocuparme	0	1	1.154
desocupado	0	1	1.154
desobedientes	0	1	1.154
desobediencia	0	1	1.154
desobedecería	0	1	1.154
desnudabas	0	1	1.154
desmoralizados	0	1	1.154
desmontó	0	1	1.154
desmintieran	0	1	1.154
desmintiendo	0	1	1.154
desmiente	0	1	1.154
desmerecía	0	1	1.154
desmerecer	0	1	1.154
desmerece	0	1	1.154
desmenuzadas	0	1	1.154
desmenuzaba	0	1	1.154
desmentirá	0	1	1.154
desmentidas	0	1	1.154
desmemoriado	0	1	1.154
desmejorarse	0	1	1.154
desmejoramiento	0	1	1.154
desmejoradillo	0	1	1.154
desmedidamente	0	1	1.154
desmayó	0	1	1.154
desmayan	0	1	1.154
desmandase	0	1	1.154
desmanda	0	1	1.154
desmadejada	0	1	1.154
deslucida	0	1	1.154
deslomar	0	1	1.154
deslizose	0	1	1.154
deslizar	0	1	1.154
deslizando	0	1	1.154
deslizado	0	1	1.154
desligado	0	1	1.154
desligada	0	1	1.154
deslicen	0	1	1.154
desliando	0	1	1.154
desliaba	0	1	1.154
deslealtades	0	1	1.154
deslealtad	0	1	1.154
desistió	0	1	1.154
desinteresados	0	1	1.154
desilusiones	0	1	1.154
desilusionada	0	1	1.154
desilusión	0	1	1.154
designaré	0	1	1.154
designará	0	1	1.154
designado	0	1	1.154
designada	0	1	1.154
desiderátum	0	1	1.154
deshonró	0	1	1.154
deshonras	0	1	1.154
deshonrarme	0	1	1.154
deshonrarán	0	1	1.154
deshojar	0	1	1.154
deshelaba	0	1	1.154
deshaciéndose	0	1	1.154
deshaciendo	0	1	1.154
deshabitada	0	1	1.154
desgranadas	0	1	1.154
desgraciadas	0	1	1.154
desgobernando	0	1	1.154
desgaste	0	1	1.154
desgastase	0	1	1.154
desgastará	0	1	1.154
desgarran	0	1	1.154
desgarrado	0	1	1.154
desgañitarse	0	1	1.154
desganada	0	1	1.154
desflorar	0	1	1.154
desfile	0	1	1.154
desfilaron	0	1	1.154
desfilar	0	1	1.154
desfigurarla	0	1	1.154
desfigurados	0	1	1.154
desfiguraba	0	1	1.154
desfavorecido	0	1	1.154
desfavorables	0	1	1.154
desfavorablemente	0	1	1.154
desesperarse	0	1	1.154
desesperaría	0	1	1.154
desesperante	0	1	1.154
desesperadamente	0	1	1.154
desertar	0	1	1.154
deserción	0	1	1.154
desequilibrio	0	1	1.154
desequilibraba	0	1	1.154
deseosas	0	1	1.154
desenvuelve	0	1	1.154
desenvuelta	0	1	1.154
desenvolvía	0	1	1.154
desenvolveros	0	1	1.154
desenvolverme	0	1	1.154
desenvolver	0	1	1.154
desentumecían	0	1	1.154
desentumecía	0	1	1.154
desentrañar	0	1	1.154
desentono	0	1	1.154
desentonada	0	1	1.154
desenroscarse	0	1	1.154
desenrosca	0	1	1.154
desenojaría	0	1	1.154
desenojar	0	1	1.154
desengonzado	0	1	1.154
desengáñese	0	1	1.154
desengañarle	0	1	1.154
desengañaos	0	1	1.154
desenfundan	0	1	1.154
desenfadada	0	1	1.154
desencuadernarse	0	1	1.154
desencarna	0	1	1.154
desencajados	0	1	1.154
desempeñes	0	1	1.154
desempeñarlo	0	1	1.154
desempeñarla	0	1	1.154
desempeñan	0	1	1.154
desembuchas	0	1	1.154
desembuchando	0	1	1.154
desembocar	0	1	1.154
desembarcos	0	1	1.154
desembarcar	0	1	1.154
desellando	0	1	1.154
deseé	0	1	1.154
deseché	0	1	1.154
desecharon	0	1	1.154
desecharla	0	1	1.154
desechando	0	1	1.154
desechados	0	1	1.154
desechadas	0	1	1.154
desearan	0	1	1.154
deseándolo	0	1	1.154
deseándole	0	1	1.154
desean	0	1	1.154
desdoblado	0	1	1.154
desdoblaba	0	1	1.154
desdijera	0	1	1.154
desdiciéndose	0	1	1.154
desdicha	0	1	1.154
desdice	0	1	1.154
desdeñosas	0	1	1.154
desdeñosa	0	1	1.154
desdeñado	0	1	1.154
desdentado	0	1	1.154
desdecirme	0	1	1.154
descuidillos	0	1	1.154
descuidero	0	1	1.154
descuidera	0	1	1.154
descuidar	0	1	1.154
descuidaban	0	1	1.154
descuentos	0	1	1.154
descuelgue	0	1	1.154
descuelgas	0	1	1.154
descuelga	0	1	1.154
descubriremos	0	1	1.154
descubriolo	0	1	1.154
descubrimos	0	1	1.154
descubriera	0	1	1.154
descubrí	0	1	1.154
descubren	0	1	1.154
descubras	0	1	1.154
descuartizarla	0	1	1.154
descuartizar	0	1	1.154
descuartizada	0	1	1.154
descuartice	0	1	1.154
descrita	0	1	1.154
descrismándose	0	1	1.154
descriptivo	0	1	1.154
describirse	0	1	1.154
descorrían	0	1	1.154
descorrer	0	1	1.154
descorazonó	0	1	1.154
descorazonamiento	0	1	1.154
descorazonado	0	1	1.154
descontentos	0	1	1.154
descontándole	0	1	1.154
descontadas	0	1	1.154
desconsuelos	0	1	1.154
desconsoladora	0	1	1.154
desconsoladísima	0	1	1.154
desconsolaba	0	1	1.154
desconsideradamente	0	1	1.154
desconozco	0	1	1.154
desconociendo	0	1	1.154
desconfías	0	1	1.154
desconfianzas	0	1	1.154
desconcertados	0	1	1.154
desconcertaba	0	1	1.154
descompusiera	0	1	1.154
descompostura	0	1	1.154
descomposición	0	1	1.154
descomponiéndole	0	1	1.154
descomponían	0	1	1.154
descomedida	0	1	1.154
descolorido	0	1	1.154
descoloridas	0	1	1.154
descollaría	0	1	1.154
descollar	0	1	1.154
descolgarte	0	1	1.154
descolgarlos	0	1	1.154
descolgándose	0	1	1.154
desclavar	0	1	1.154
descifraba	0	1	1.154
descendido	0	1	1.154
descendían	0	1	1.154
descascaraba	0	1	1.154
descartaba	0	1	1.154
descarriado	0	1	1.154
descarriadas	0	1	1.154
descargos	0	1	1.154
descargo	0	1	1.154
descargasen	0	1	1.154
descargase	0	1	1.154
descargándosela	0	1	1.154
descargando	0	1	1.154
descargados	0	1	1.154
descansó	0	1	1.154
descanses	0	1	1.154
descansen	0	1	1.154
descansaron	0	1	1.154
descansado	0	1	1.154
descansada	0	1	1.154
descamisado	0	1	1.154
descalzarle	0	1	1.154
descalcitos	0	1	1.154
descalabré	0	1	1.154
descalabrado	0	1	1.154
descalabra	0	1	1.154
descaecimiento	0	1	1.154
descabezando	0	1	1.154
descabezado	0	1	1.154
descabezaban	0	1	1.154
descabaladas	0	1	1.154
desbravase	0	1	1.154
desbordarse	0	1	1.154
desbordamientos	0	1	1.154
desbordamiento	0	1	1.154
desbordaban	0	1	1.154
desbastaron	0	1	1.154
desbastar	0	1	1.154
desbastándola	0	1	1.154
desbarro	0	1	1.154
desbarraba	0	1	1.154
desbaratarse	0	1	1.154
desbaratar	0	1	1.154
desbaratando	0	1	1.154
desbarataba	0	1	1.154
desbarata	0	1	1.154
desbandó	0	1	1.154
desbandan	0	1	1.154
desbandada	0	1	1.154
desazonaba	0	1	1.154
desayunarse	0	1	1.154
desavío	0	1	1.154
desavenidos	0	1	1.154
desatinadas	0	1	1.154
desate	0	1	1.154
desatar	0	1	1.154
desatado	0	1	1.154
desatada	0	1	1.154
desastres	0	1	1.154
desastre	0	1	1.154
desasosegado	0	1	1.154
desasosegada	0	1	1.154
desasosegaba	0	1	1.154
desaseo	0	1	1.154
desaseado	0	1	1.154
desarrollaron	0	1	1.154
desarrollándosele	0	1	1.154
desarrolladas	0	1	1.154
desarrollaban	0	1	1.154
desarregladas	0	1	1.154
desarreglada	0	1	1.154
desarraigar	0	1	1.154
desarmarle	0	1	1.154
desarmar	0	1	1.154
desaprobar	0	1	1.154
desapartaísos	0	1	1.154
desapartada	0	1	1.154
desapariciones	0	1	1.154
desaparezca	0	1	1.154
desapareciendo	0	1	1.154
desaparecida	0	1	1.154
desanimarte	0	1	1.154
desanimándose	0	1	1.154
desanimados	0	1	1.154
desamparadas	0	1	1.154
desamparada	0	1	1.154
desamortización	0	1	1.154
desamor	0	1	1.154
desalmado	0	1	1.154
desalentaban	0	1	1.154
desalada	0	1	1.154
desairaban	0	1	1.154
desahucios	0	1	1.154
desahogos	0	1	1.154
desahogó	0	1	1.154
desahógate	0	1	1.154
desahogaran	0	1	1.154
desahogándola	0	1	1.154
desahogadamente	0	1	1.154
desahogada	0	1	1.154
desagrado	0	1	1.154
desagradaron	0	1	1.154
desagradablemente	0	1	1.154
desafueros	0	1	1.154
desaforadamente	0	1	1.154
desafinar	0	1	1.154
desafinamos	0	1	1.154
desafiaban	0	1	1.154
desacredito	0	1	1.154
desacordes	0	1	1.154
desacierto	0	1	1.154
desabrocharon	0	1	1.154
desabrigues	0	1	1.154
desabrigo	0	1	1.154
desabrigara	0	1	1.154
desabrigado	0	1	1.154
desabridísimo	0	1	1.154
desabotonar	0	1	1.154
desaborida	0	1	1.154
derroteros	0	1	1.154
derrotar	0	1	1.154
derrotados	0	1	1.154
derrochador	0	1	1.154
derritieran	0	1	1.154
derritiendo	0	1	1.154
derribando	0	1	1.154
derribada	0	1	1.154
derramo	0	1	1.154
derrames	0	1	1.154
derramaba	0	1	1.154
derrama	0	1	1.154
derogando	0	1	1.154
derogada	0	1	1.154
derivado	0	1	1.154
derivadas	0	1	1.154
derivaciones	0	1	1.154
derivaba	0	1	1.154
deriva	0	1	1.154
derechitos	0	1	1.154
derechas	0	1	1.154
derechamente	0	1	1.154
depurar	0	1	1.154
depravados	0	1	1.154
depravado	0	1	1.154
depravaciones	0	1	1.154
deplorar	0	1	1.154
dependiera	0	1	1.154
departió	0	1	1.154
deparó	0	1	1.154
depare	0	1	1.154
deparándote	0	1	1.154
denuncies	0	1	1.154
denunciado	0	1	1.154
denunciaban	0	1	1.154
denuestos	0	1	1.154
dentición	0	1	1.154
dentelladas	0	1	1.154
denso	0	1	1.154
densísimo	0	1	1.154
denotaban	0	1	1.154
denominó	0	1	1.154
denominaciones	0	1	1.154
denominación	0	1	1.154
denme	0	1	1.154
denle	0	1	1.154
dengues	0	1	1.154
dengosas	0	1	1.154
dengosa	0	1	1.154
denegaciones	0	1	1.154
demuestras	0	1	1.154
demudó	0	1	1.154
demudado	0	1	1.154
demostrarlo	0	1	1.154
demostraré	0	1	1.154
demostrándolo	0	1	1.154
demolieron	0	1	1.154
demolición	0	1	1.154
democráticas	0	1	1.154
democrática	0	1	1.154
demi	0	1	1.154
demetria	0	1	1.154
demencias	0	1	1.154
demasiadas	0	1	1.154
demagógica	0	1	1.154
delta	0	1	1.154
delos	0	1	1.154
delirium	0	1	1.154
delirios	0	1	1.154
delirara	0	1	1.154
delirar	0	1	1.154
delira	0	1	1.154
delicadito	0	1	1.154
deliberadamente	0	1	1.154
deliberada	0	1	1.154
delfinito	0	1	1.154
delfines	0	1	1.154
deleznables	0	1	1.154
delegando	0	1	1.154
delatarla	0	1	1.154
delantito	0	1	1.154
delación	0	1	1.154
dejoso	0	1	1.154
dejolo	0	1	1.154
dejoles	0	1	1.154
dejola	0	1	1.154
déjemelo	0	1	1.154
déjase	0	1	1.154
dejártela	0	1	1.154
dejárselos	0	1	1.154
dejarnos	0	1	1.154
dejarles	0	1	1.154
dejaremos	0	1	1.154
dejarás	0	1	1.154
déjanos	0	1	1.154
dejándotela	0	1	1.154
dejándonos	0	1	1.154
dejándome	0	1	1.154
dejándolo	0	1	1.154
déjamele	0	1	1.154
déjalo	0	1	1.154
déjales	0	1	1.154
dejáis	0	1	1.154
dejadez	0	1	1.154
dejadas	0	1	1.154
dejábalos	0	1	1.154
deicidas	0	1	1.154
dehesa	0	1	1.154
degüello	0	1	1.154
degüellan	0	1	1.154
degrada	0	1	1.154
degollina	0	1	1.154
degollada	0	1	1.154
deglutaba	0	1	1.154
degeneración	0	1	1.154
defraudaciones	0	1	1.154
definiendo	0	1	1.154
defiéndete	0	1	1.154
déficit	0	1	1.154
defensivo	0	1	1.154
defendiéndose	0	1	1.154
defendidos	0	1	1.154
defendida	0	1	1.154
defenderlo	0	1	1.154
defenderlas	0	1	1.154
defendemos	0	1	1.154
defectuosísima	0	1	1.154
deducirse	0	1	1.154
deduciendo	0	1	1.154
deduce	0	1	1.154
deditos	0	1	1.154
dedico	0	1	1.154
dedicas	0	1	1.154
dedicaría	0	1	1.154
dédalos	0	1	1.154
dedal	0	1	1.154
decorosas	0	1	1.154
decoró	0	1	1.154
decorativas	0	1	1.154
decorativamente	0	1	1.154
decorar	0	1	1.154
decoran	0	1	1.154
decoraban	0	1	1.154
decoraba	0	1	1.154
decomisura	0	1	1.154
declinación	0	1	1.154
declarase	0	1	1.154
declaras	0	1	1.154
declararlo	0	1	1.154
declararía	0	1	1.154
declarando	0	1	1.154
declaran	0	1	1.154
declamatorio	0	1	1.154
decisivas	0	1	1.154
decírselas	0	1	1.154
deciros	0	1	1.154
decirnos	0	1	1.154
décimos	0	1	1.154
decimos	0	1	1.154
decidirían	0	1	1.154
decidiría	0	1	1.154
decidiose	0	1	1.154
decidieron	0	1	1.154
decídete	0	1	1.154
deciden	0	1	1.154
decidáis	0	1	1.154
decible	0	1	1.154
decíase	0	1	1.154
decíanle	0	1	1.154
decíame	0	1	1.154
decíalas	0	1	1.154
decentísimo	0	1	1.154
decayendo	0	1	1.154
decaída	0	1	1.154
decaía	0	1	1.154
débitos	0	1	1.154
debilitarse	0	1	1.154
debilitada	0	1	1.154
debieras	0	1	1.154
debiendo	0	1	1.154
deberíamos	0	1	1.154
deberá	0	1	1.154
deba	0	1	1.154
davidson	0	1	1.154
david	0	1	1.154
dátil	0	1	1.154
dáselo	0	1	1.154
dártelo	0	1	1.154
daros	0	1	1.154
dármelo	0	1	1.154
dármelas	0	1	1.154
darlo	0	1	1.154
darías	0	1	1.154
darán	0	1	1.154
dañino	0	1	1.154
dañan	0	1	1.154
dañados	0	1	1.154
dañado	0	1	1.154
danzando	0	1	1.154
danme	0	1	1.154
daniel	0	1	1.154
dandys	0	1	1.154
dándosela	0	1	1.154
dándolo	0	1	1.154
dámelo	0	1	1.154
damasquería	0	1	1.154
daganzo	0	1	1.154
dádselo	0	1	1.154
dados	0	1	1.154
dadivosos	0	1	1.154
daca	0	1	1.154
dabas	0	1	1.154
dábanse	0	1	1.154
dábalo	0	1	1.154
cutíes	0	1	1.154
custodiarla	0	1	1.154
custodiaba	0	1	1.154
cursilerías	0	1	1.154
cursilería	0	1	1.154
cursaban	0	1	1.154
curó	0	1	1.154
curo	0	1	1.154
curiosona	0	1	1.154
curiosísimo	0	1	1.154
curioseo	0	1	1.154
curiosas	0	1	1.154
curdela	0	1	1.154
curda	0	1	1.154
curárselas	0	1	1.154
curara	0	1	1.154
curánganos	0	1	1.154
curadas	0	1	1.154
cúpulas	0	1	1.154
cupiesen	0	1	1.154
cuotas	0	1	1.154
cuñas	0	1	1.154
cuñados	0	1	1.154
cuñadita	0	1	1.154
cunitas	0	1	1.154
cunita	0	1	1.154
cundiendo	0	1	1.154
cunas	0	1	1.154
cumplirlo	0	1	1.154
cumplirla	0	1	1.154
cumpliré	0	1	1.154
cumplidísima	0	1	1.154
cumplían	0	1	1.154
cumples	0	1	1.154
cúmplase	0	1	1.154
cumplamos	0	1	1.154
cultivarlo	0	1	1.154
culpabilidad	0	1	1.154
culito	0	1	1.154
cuitado	0	1	1.154
cuiste	0	1	1.154
cuides	0	1	1.154
cuidarme	0	1	1.154
cuidarlos	0	1	1.154
cuidarla	0	1	1.154
cuidaré	0	1	1.154
cuidará	0	1	1.154
cuidándole	0	1	1.154
cuidándolas	0	1	1.154
cuidadoso	0	1	1.154
cueza	0	1	1.154
cuestionar	0	1	1.154
cuestionando	0	1	1.154
cuestionaban	0	1	1.154
cuentera	0	1	1.154
cuéntenme	0	1	1.154
cuéntanos	0	1	1.154
cuéntale	0	1	1.154
cuéntala	0	1	1.154
cuelguen	0	1	1.154
cuélgueme	0	1	1.154
cuelgo	0	1	1.154
cuela	0	1	1.154
cuco	0	1	1.154
cuchillote	0	1	1.154
cuchillito	0	1	1.154
cuchilladas	0	1	1.154
cuchicheó	0	1	1.154
cucharillas	0	1	1.154
cucharetazos	0	1	1.154
cucaracha	0	1	1.154
cucamonas	0	1	1.154
cubriole	0	1	1.154
cubriéronle	0	1	1.154
cubrieron	0	1	1.154
cubriendo	0	1	1.154
cúbrete	0	1	1.154
cubres	0	1	1.154
cúbrele	0	1	1.154
cubilete	0	1	1.154
cúbicas	0	1	1.154
cúbica	0	1	1.154
cuatros	0	1	1.154
cuatrillones	0	1	1.154
cuartillas	0	1	1.154
cuarterones	0	1	1.154
cuartelesco	0	1	1.154
cuantiosas	0	1	1.154
cuanti	0	1	1.154
cuanta	0	1	1.154
cualisquiera	0	1	1.154
cuajo	0	1	1.154
cuaje	0	1	1.154
cuajarse	0	1	1.154
cuadrumana	0	1	1.154
cuadró	0	1	1.154
cuadrilongo	0	1	1.154
cuadrilla	0	1	1.154
cuadril	0	1	1.154
cuadratura	0	1	1.154
cuadrase	0	1	1.154
cuadrángano	0	1	1.154
cuadraba	0	1	1.154
cuadernos	0	1	1.154
cruzáronse	0	1	1.154
cruzarnos	0	1	1.154
cruzándose	0	1	1.154
cruzamiento	0	1	1.154
crujidos	0	1	1.154
crujida	0	1	1.154
crujías	0	1	1.154
cruelísimas	0	1	1.154
cruelísima	0	1	1.154
crudísimo	0	1	1.154
crudillo	0	1	1.154
crucis	0	1	1.154
crucifique	0	1	1.154
crucificando	0	1	1.154
crucificados	0	1	1.154
crucifica	0	1	1.154
cruceta	0	1	1.154
croto	0	1	1.154
croquetita	0	1	1.154
cromwell	0	1	1.154
criticó	0	1	1.154
criticando	0	1	1.154
cristianamente	0	1	1.154
cristalitos	0	1	1.154
crispamientos	0	1	1.154
crinolinas	0	1	1.154
criminala	0	1	1.154
criáronle	0	1	1.154
criaron	0	1	1.154
criarlos	0	1	1.154
criarlo	0	1	1.154
criaré	0	1	1.154
creyolo	0	1	1.154
creyérase	0	1	1.154
creyeran	0	1	1.154
crespones	0	1	1.154
crenchas	0	1	1.154
creímos	0	1	1.154
creíamos	0	1	1.154
creételo	0	1	1.154
creérmelo	0	1	1.154
creerlas	0	1	1.154
credo	0	1	1.154
credencialeja	0	1	1.154
crecieron	0	1	1.154
crecidos	0	1	1.154
crecidito	0	1	1.154
creciditas	0	1	1.154
crecidita	0	1	1.154
creánmelo	0	1	1.154
creamos	0	1	1.154
créamela	0	1	1.154
creadoras	0	1	1.154
creaciones	0	1	1.154
coyunturas	0	1	1.154
covacha	0	1	1.154
courtray	0	1	1.154
cotta	0	1	1.154
cotorrear	0	1	1.154
cotorreaban	0	1	1.154
cotorras	0	1	1.154
cotizaciones	0	1	1.154
cotiza	0	1	1.154
cotidiano	0	1	1.154
costurones	0	1	1.154
costuras	0	1	1.154
costras	0	1	1.154
costeo	0	1	1.154
costear	0	1	1.154
costeando	0	1	1.154
costaría	0	1	1.154
costanilla	0	1	1.154
cósmico	0	1	1.154
cosidos	0	1	1.154
cosidas	0	1	1.154
cosida	0	1	1.154
cosedoras	0	1	1.154
cosecheros	0	1	1.154
cortísimo	0	1	1.154
cortinones	0	1	1.154
cortinón	0	1	1.154
cortinilla	0	1	1.154
cortesanas	0	1	1.154
corten	0	1	1.154
cortase	0	1	1.154
cortarte	0	1	1.154
cortarme	0	1	1.154
cortarían	0	1	1.154
cortaría	0	1	1.154
cortará	0	1	1.154
cortante	0	1	1.154
cortándose	0	1	1.154
cortadito	0	1	1.154
cortadísima	0	1	1.154
corsés	0	1	1.154
corsario	0	1	1.154
corruptora	0	1	1.154
corrompe	0	1	1.154
corriole	0	1	1.154
corrígete	0	1	1.154
corrige	0	1	1.154
corriéndola	0	1	1.154
corriendito	0	1	1.154
corridas	0	1	1.154
corríase	0	1	1.154
corríale	0	1	1.154
corretear	0	1	1.154
correteando	0	1	1.154
correspondencias	0	1	1.154
correrse	0	1	1.154
correrla	0	1	1.154
correría	0	1	1.154
corregirte	0	1	1.154
corregirla	0	1	1.154
corregían	0	1	1.154
correderas	0	1	1.154
corredera	0	1	1.154
correctivos	0	1	1.154
correctísima	0	1	1.154
corras	0	1	1.154
corpulenta	0	1	1.154
corpulencia	0	1	1.154
corpórea	0	1	1.154
coronen	0	1	1.154
cornuda	0	1	1.154
corito	0	1	1.154
corifeos	0	1	1.154
coria	0	1	1.154
cordones	0	1	1.154
cordilla	0	1	1.154
cordiales	0	1	1.154
cordelero	0	1	1.154
cordelería	0	1	1.154
corambres	0	1	1.154
coral	0	1	1.154
coqueteaba	0	1	1.154
coquera	0	1	1.154
copulativas	0	1	1.154
copudo	0	1	1.154
copo	0	1	1.154
coplitas	0	1	1.154
copio	0	1	1.154
copiadores	0	1	1.154
copete	0	1	1.154
convulsivo	0	1	1.154
convirtieran	0	1	1.154
convirtiéndose	0	1	1.154
convierto	0	1	1.154
convierta	0	1	1.154
convienen	0	1	1.154
convide	0	1	1.154
convidara	0	1	1.154
convidadas	0	1	1.154
convidaban	0	1	1.154
convidábale	0	1	1.154
convida	0	1	1.154
convexidad	0	1	1.154
convertirlo	0	1	1.154
convertirlas	0	1	1.154
convertiría	0	1	1.154
convertiré	0	1	1.154
conversos	0	1	1.154
convénzase	0	1	1.154
convenimos	0	1	1.154
convencionalismo	0	1	1.154
convencían	0	1	1.154
convences	0	1	1.154
convencerías	0	1	1.154
convencerá	0	1	1.154
convéncele	0	1	1.154
contuso	0	1	1.154
contrista	0	1	1.154
contrincante	0	1	1.154
contribuciones	0	1	1.154
contreras	0	1	1.154
contraviniendo	0	1	1.154
contraventores	0	1	1.154
contratos	0	1	1.154
contratista	0	1	1.154
contratar	0	1	1.154
contratación	0	1	1.154
contrastar	0	1	1.154
contrastando	0	1	1.154
contrariaron	0	1	1.154
contrariada	0	1	1.154
contrariábala	0	1	1.154
contraída	0	1	1.154
contraía	0	1	1.154
contrafalda	0	1	1.154
contraer	0	1	1.154
contraen	0	1	1.154
contrae	0	1	1.154
contradijo	0	1	1.154
contradiciéndole	0	1	1.154
contradice	0	1	1.154
contradecirla	0	1	1.154
contradanzas	0	1	1.154
contracciones	0	1	1.154
contrabandistas	0	1	1.154
contonean	0	1	1.154
contome	0	1	1.154
continuaremos	0	1	1.154
continuara	0	1	1.154
continúan	0	1	1.154
continuadamente	0	1	1.154
continuación	0	1	1.154
continencia	0	1	1.154
contesto	0	1	1.154
contestarse	0	1	1.154
contestarles	0	1	1.154
contéstame	0	1	1.154
contestábale	0	1	1.154
conteras	0	1	1.154
contentísimo	0	1	1.154
conténtate	0	1	1.154
contentarás	0	1	1.154
contentábase	0	1	1.154
contenidas	0	1	1.154
contengo	0	1	1.154
contenga	0	1	1.154
contenerme	0	1	1.154
contendientes	0	1	1.154
contemporizador	0	1	1.154
contemplándole	0	1	1.154
contemplándola	0	1	1.154
contase	0	1	1.154
contártelo	0	1	1.154
contarte	0	1	1.154
contármelo	0	1	1.154
contarme	0	1	1.154
contarlos	0	1	1.154
contaría	0	1	1.154
contaremos	0	1	1.154
contará	0	1	1.154
contándote	0	1	1.154
contamos	0	1	1.154
contagiosas	0	1	1.154
contagiada	0	1	1.154
contaduría	0	1	1.154
contábale	0	1	1.154
consumirte	0	1	1.154
consumidor	0	1	1.154
consumido	0	1	1.154
consumen	0	1	1.154
consultarme	0	1	1.154
consultarlo	0	1	1.154
consultaré	0	1	1.154
consultándose	0	1	1.154
consúltalo	0	1	1.154
consultada	0	1	1.154
cónsul	0	1	1.154
construiré	0	1	1.154
construidos	0	1	1.154
constructivo	0	1	1.154
constructiva	0	1	1.154
construcciones	0	1	1.154
constituyo	0	1	1.154
constituyesen	0	1	1.154
constitutivo	0	1	1.154
constitutiva	0	1	1.154
constituirse	0	1	1.154
constituciones	0	1	1.154
constipase	0	1	1.154
consternados	0	1	1.154
constara	0	1	1.154
conspiran	0	1	1.154
conspicuo	0	1	1.154
conspicuas	0	1	1.154
consonante	0	1	1.154
consonancia	0	1	1.154
consolemos	0	1	1.154
consolé	0	1	1.154
consolarte	0	1	1.154
consolarnos	0	1	1.154
consolaré	0	1	1.154
consoladoras	0	1	1.154
consolado	0	1	1.154
consistió	0	1	1.154
consistentes	0	1	1.154
consista	0	1	1.154
consignar	0	1	1.154
consignada	0	1	1.154
consideré	0	1	1.154
considerarte	0	1	1.154
considerarse	0	1	1.154
considerara	0	1	1.154
considéralo	0	1	1.154
considerábanla	0	1	1.154
conservarla	0	1	1.154
conservaré	0	1	1.154
conservadas	0	1	1.154
consentirse	0	1	1.154
consentimos	0	1	1.154
consentían	0	1	1.154
consecutivos	0	1	1.154
consecuentes	0	1	1.154
consciente	0	1	1.154
consagraría	0	1	1.154
consagraremos	0	1	1.154
consagra	0	1	1.154
conquistó	0	1	1.154
conquistara	0	1	1.154
conozcas	0	1	1.154
conociole	0	1	1.154
conociéndola	0	1	1.154
conocías	0	1	1.154
conocerían	0	1	1.154
conoceremos	0	1	1.154
conoceré	0	1	1.154
conocerás	0	1	1.154
conocedores	0	1	1.154
conocedoras	0	1	1.154
conocedora	0	1	1.154
connivencia	0	1	1.154
conmovió	0	1	1.154
conmovidísima	0	1	1.154
conmovedora	0	1	1.154
conmovedor	0	1	1.154
conminación	0	1	1.154
conllevando	0	1	1.154
conjunciones	0	1	1.154
congrio	0	1	1.154
congregarse	0	1	1.154
congratularse	0	1	1.154
congestionaba	0	1	1.154
congenialidad	0	1	1.154
confundo	0	1	1.154
confundirme	0	1	1.154
confundieran	0	1	1.154
confundiera	0	1	1.154
confundida	0	1	1.154
confunden	0	1	1.154
confrontar	0	1	1.154
confrontándolas	0	1	1.154
confortaron	0	1	1.154
confortado	0	1	1.154
conformó	0	1	1.154
confórmese	0	1	1.154
conformaron	0	1	1.154
conformarnos	0	1	1.154
conformará	0	1	1.154
conformándose	0	1	1.154
conformado	0	1	1.154
conflictos	0	1	1.154
confitó	0	1	1.154
confirmo	0	1	1.154
confirmase	0	1	1.154
confirmaron	0	1	1.154
confirmarlo	0	1	1.154
confirmándose	0	1	1.154
confín	0	1	1.154
confiéselo	0	1	1.154
confiesas	0	1	1.154
confiesan	0	1	1.154
confiésame	0	1	1.154
confíe	0	1	1.154
confíate	0	1	1.154
confiase	0	1	1.154
confiarme	0	1	1.154
confiadas	0	1	1.154
confía	0	1	1.154
confesionario	0	1	1.154
confesaste	0	1	1.154
confesarte	0	1	1.154
confesarían	0	1	1.154
confesándose	0	1	1.154
confesada	0	1	1.154
confeccionados	0	1	1.154
confeccionada	0	1	1.154
confeccionaba	0	1	1.154
confabulado	0	1	1.154
confabulada	0	1	1.154
confabulación	0	1	1.154
confabulaban	0	1	1.154
condújola	0	1	1.154
conductos	0	1	1.154
conductores	0	1	1.154
conductor	0	1	1.154
conducirse	0	1	1.154
conducidos	0	1	1.154
conducido	0	1	1.154
conducidas	0	1	1.154
conducida	0	1	1.154
condoliéndose	0	1	1.154
condiscípulos	0	1	1.154
condimentado	0	1	1.154
condensarse	0	1	1.154
condensándose	0	1	1.154
condensaban	0	1	1.154
condenarás	0	1	1.154
condenación	0	1	1.154
concurriendo	0	1	1.154
concurrentes	0	1	1.154
concurre	0	1	1.154
conculcar	0	1	1.154
concretándose	0	1	1.154
concretan	0	1	1.154
concordaban	0	1	1.154
concordaba	0	1	1.154
concluyese	0	1	1.154
concluyeron	0	1	1.154
concluyera	0	1	1.154
concluyentes	0	1	1.154
concluye	0	1	1.154
conclusiones	0	1	1.154
concluirla	0	1	1.154
concluiría	0	1	1.154
concluimos	0	1	1.154
concluidas	0	1	1.154
concisión	0	1	1.154
conciliasen	0	1	1.154
conciliarse	0	1	1.154
conciliaba	0	1	1.154
concierne	0	1	1.154
concibiendo	0	1	1.154
concibe	0	1	1.154
concesión	0	1	1.154
concertados	0	1	1.154
concernientes	0	1	1.154
conceptuándola	0	1	1.154
concentrándose	0	1	1.154
concentrado	0	1	1.154
concentración	0	1	1.154
concediendo	0	1	1.154
concedía	0	1	1.154
concede	0	1	1.154
concebiría	0	1	1.154
concebir	0	1	1.154
concebido	0	1	1.154
concebí	0	1	1.154
cóncavos	0	1	1.154
cóncavo	0	1	1.154
concatenación	0	1	1.154
comunícase	0	1	1.154
comunicase	0	1	1.154
comunicándose	0	1	1.154
comunicadas	0	1	1.154
comunicada	0	1	1.154
comulgas	0	1	1.154
comulgaron	0	1	1.154
compusiera	0	1	1.154
compuestos	0	1	1.154
comprometió	0	1	1.154
comprometerle	0	1	1.154
comprometen	0	1	1.154
comprobarse	0	1	1.154
comprobación	0	1	1.154
compro	0	1	1.154
comprimiéndose	0	1	1.154
compresión	0	1	1.154
comprensible	0	1	1.154
comprendiolo	0	1	1.154
comprenderlo	0	1	1.154
comprenderías	0	1	1.154
comprenderían	0	1	1.154
comprenderás	0	1	1.154
comprenden	0	1	1.154
comprendemos	0	1	1.154
compremos	0	1	1.154
cómpreme	0	1	1.154
compraste	0	1	1.154
comprasen	0	1	1.154
comprase	0	1	1.154
comprárselo	0	1	1.154
compraron	0	1	1.154
comprarme	0	1	1.154
comprarlo	0	1	1.154
compraría	0	1	1.154
compraremos	0	1	1.154
compráramos	0	1	1.154
comprara	0	1	1.154
comprando	0	1	1.154
compran	0	1	1.154
compramos	0	1	1.154
comprados	0	1	1.154
compraban	0	1	1.154
compotas	0	1	1.154
compositores	0	1	1.154
composicioncita	0	1	1.154
componiéndose	0	1	1.154
componíase	0	1	1.154
compones	0	1	1.154
compondremos	0	1	1.154
complicar	0	1	1.154
completó	0	1	1.154
completas	0	1	1.154
completado	0	1	1.154
complacido	0	1	1.154
complacidísima	0	1	1.154
complacida	0	1	1.154
complacerla	0	1	1.154
competir	0	1	1.154
competidores	0	1	1.154
competía	0	1	1.154
compensó	0	1	1.154
compenetraron	0	1	1.154
compenetrando	0	1	1.154
compatibilidad	0	1	1.154
compasivos	0	1	1.154
compases	0	1	1.154
comparsas	0	1	1.154
comparsa	0	1	1.154
comparativos	0	1	1.154
comparativo	0	1	1.154
compararlo	0	1	1.154
comparan	0	1	1.154
compañerismo	0	1	1.154
compaña	0	1	1.154
compagina	0	1	1.154
compadecida	0	1	1.154
compadécete	0	1	1.154
compadecerte	0	1	1.154
cómodas	0	1	1.154
comitentes	0	1	1.154
comiteles	0	1	1.154
comistrajo	0	1	1.154
comistraje	0	1	1.154
comiquito	0	1	1.154
cominos	0	1	1.154
comiéndoselo	0	1	1.154
comiéndosele	0	1	1.154
comiéndolo	0	1	1.154
cómicamente	0	1	1.154
comí	0	1	1.154
cometió	0	1	1.154
cometieron	0	1	1.154
cometerlas	0	1	1.154
cometas	0	1	1.154
cometa	0	1	1.154
comérsele	0	1	1.154
comérselas	0	1	1.154
comérsela	0	1	1.154
comerlos	0	1	1.154
comerla	0	1	1.154
comeré	0	1	1.154
comercian	0	1	1.154
comerás	0	1	1.154
comerán	0	1	1.154
comenzando	0	1	1.154
comentos	0	1	1.154
comentase	0	1	1.154
comenencias	0	1	1.154
comenencia	0	1	1.154
cómeme	0	1	1.154
comediante	0	1	1.154
comedianta	0	1	1.154
combustible	0	1	1.154
combinada	0	1	1.154
combina	0	1	1.154
combatiente	0	1	1.154
combatían	0	1	1.154
comático	0	1	1.154
comanditaria	0	1	1.154
comadre	0	1	1.154
columnarias	0	1	1.154
columbró	0	1	1.154
colose	0	1	1.154
colosales	0	1	1.154
colorao	0	1	1.154
coloquios	0	1	1.154
colóqueme	0	1	1.154
coloqué	0	1	1.154
colocártelos	0	1	1.154
colocarme	0	1	1.154
colocarlo	0	1	1.154
colocarle	0	1	1.154
colocarlas	0	1	1.154
colocao	0	1	1.154
colocándose	0	1	1.154
colocan	0	1	1.154
colocaciones	0	1	1.154
colocaban	0	1	1.154
coló	0	1	1.154
colmado	0	1	1.154
collarines	0	1	1.154
colisión	0	1	1.154
coligió	0	1	1.154
coligieron	0	1	1.154
coliflor	0	1	1.154
colguemos	0	1	1.154
colgarle	0	1	1.154
colgaría	0	1	1.154
colgara	0	1	1.154
colgándosele	0	1	1.154
colgándome	0	1	1.154
colgajo	0	1	1.154
coletazos	0	1	1.154
coléricas	0	1	1.154
colegiata	0	1	1.154
colectas	0	1	1.154
coleccionistas	0	1	1.154
coleccionista	0	1	1.154
coleccionarlos	0	1	1.154
colé	0	1	1.154
colarse	0	1	1.154
colaríamos	0	1	1.154
colaría	0	1	1.154
colado	0	1	1.154
colada	0	1	1.154
colaban	0	1	1.154
colaba	0	1	1.154
cojines	0	1	1.154
cojera	0	1	1.154
cojearás	0	1	1.154
cojeaban	0	1	1.154
cohonestar	0	1	1.154
cohibido	0	1	1.154
cohibían	0	1	1.154
cohibía	0	1	1.154
cogiste	0	1	1.154
cogiola	0	1	1.154
cogiéronse	0	1	1.154
cogieran	0	1	1.154
cogiéndolo	0	1	1.154
cogiéndolas	0	1	1.154
cogiditos	0	1	1.154
cogerme	0	1	1.154
cogerá	0	1	1.154
cógelo	0	1	1.154
cogéis	0	1	1.154
cofrades	0	1	1.154
codificación	0	1	1.154
codiciosas	0	1	1.154
coclearia	0	1	1.154
cocidas	0	1	1.154
cochino	0	1	1.154
cochinamente	0	1	1.154
cochinadas	0	1	1.154
cochecillo	0	1	1.154
coca	0	1	1.154
cobró	0	1	1.154
cobrase	0	1	1.154
cobraron	0	1	1.154
cobraría	0	1	1.154
cobradores	0	1	1.154
cobrado	0	1	1.154
cobrábale	0	1	1.154
cobraba	0	1	1.154
cobalto	0	1	1.154
co	0	1	1.154
clubs	0	1	1.154
cloral	0	1	1.154
clima	0	1	1.154
clientela	0	1	1.154
clerofobia	0	1	1.154
clericales	0	1	1.154
clavetee	0	1	1.154
claveteara	0	1	1.154
claveteando	0	1	1.154
claveteados	0	1	1.154
claves	0	1	1.154
clavazón	0	1	1.154
clavase	0	1	1.154
clavársele	0	1	1.154
clavarles	0	1	1.154
clavarla	0	1	1.154
clavamos	0	1	1.154
clarísima	0	1	1.154
clarines	0	1	1.154
clarificado	0	1	1.154
claréate	0	1	1.154
clareando	0	1	1.154
clarea	0	1	1.154
clandestinos	0	1	1.154
clamas	0	1	1.154
clamaron	0	1	1.154
clabos	0	1	1.154
clabar	0	1	1.154
civilizo	0	1	1.154
civilizados	0	1	1.154
civilizaciones	0	1	1.154
citutina	0	1	1.154
citita	0	1	1.154
cite	0	1	1.154
cisne	0	1	1.154
ciscos	0	1	1.154
cirugía	0	1	1.154
ciruelas	0	1	1.154
cirineo	0	1	1.154
cirilo	0	1	1.154
circunscrita	0	1	1.154
circunferencias	0	1	1.154
circundan	0	1	1.154
circulito	0	1	1.154
circulaban	0	1	1.154
cinturas	0	1	1.154
cincuentona	0	1	1.154
cimbros	0	1	1.154
cimarra	0	1	1.154
cilindro	0	1	1.154
cigarrillos	0	1	1.154
cierras	0	1	1.154
cienfuegos	0	1	1.154
cielito	0	1	1.154
cicutina	0	1	1.154
ciclón	0	1	1.154
cicerone	0	1	1.154
cicerón	0	1	1.154
cicatriz	0	1	1.154
cicateros	0	1	1.154
cibeles	0	1	1.154
cianuro	0	1	1.154
chuscada	0	1	1.154
chusca	0	1	1.154
churruca	0	1	1.154
chupe	0	1	1.154
chupase	0	1	1.154
chupas	0	1	1.154
chuparse	0	1	1.154
chuparla	0	1	1.154
chupado	0	1	1.154
chupada	0	1	1.154
chulito	0	1	1.154
chulesca	0	1	1.154
chula	0	1	1.154
chu	0	1	1.154
christophorus	0	1	1.154
chovelar	0	1	1.154
chorreras	0	1	1.154
chorrear	0	1	1.154
choquezuela	0	1	1.154
chopos	0	1	1.154
chocolatero	0	1	1.154
chochos	0	1	1.154
chocheemos	0	1	1.154
chocarrera	0	1	1.154
chocaron	0	1	1.154
chocantes	0	1	1.154
chocante	0	1	1.154
choca	0	1	1.154
chistosísima	0	1	1.154
chisto	0	1	1.154
chisteras	0	1	1.154
chistasen	0	1	1.154
chistaré	0	1	1.154
chistara	0	1	1.154
chispos	0	1	1.154
chispazos	0	1	1.154
chismosos	0	1	1.154
chismorreo	0	1	1.154
chismorreando	0	1	1.154
chismográfico	0	1	1.154
chismajos	0	1	1.154
chisgarabís	0	1	1.154
chis	0	1	1.154
chirlata	0	1	1.154
chiripón	0	1	1.154
chirimbolos	0	1	1.154
chirigotas	0	1	1.154
chiquitos	0	1	1.154
chiquitito	0	1	1.154
chiquitita	0	1	1.154
chiquirrininas	0	1	1.154
chiquillín	0	1	1.154
chiquillería	0	1	1.154
chinos	0	1	1.154
chinescos	0	1	1.154
chinesca	0	1	1.154
chinchoso	0	1	1.154
chinchón	0	1	1.154
chinchillas	0	1	1.154
chinas	0	1	1.154
chille	0	1	1.154
chifló	0	1	1.154
chiflaba	0	1	1.154
chicooo	0	1	1.154
chichones	0	1	1.154
chicha	0	1	1.154
chavo	0	1	1.154
chauvinisme	0	1	1.154
chasqueado	0	1	1.154
chasqueada	0	1	1.154
charrán	0	1	1.154
charoles	0	1	1.154
charlatana	0	1	1.154
charlaría	0	1	1.154
charlaremos	0	1	1.154
chaquetillas	0	1	1.154
chapuzón	0	1	1.154
chapuzarse	0	1	1.154
chapuzaba	0	1	1.154
chapurraba	0	1	1.154
chapoteo	0	1	1.154
chapoteaban	0	1	1.154
chapapote	0	1	1.154
chanfaina	0	1	1.154
chancleta	0	1	1.154
champignons	0	1	1.154
chambritas	0	1	1.154
chambelán	0	1	1.154
chalanescas	0	1	1.154
chafé	0	1	1.154
chafarrinones	0	1	1.154
chafarle	0	1	1.154
chachito	0	1	1.154
chabacana	0	1	1.154
cetrería	0	1	1.154
céspedes	0	1	1.154
cesaran	0	1	1.154
cerrarse	0	1	1.154
cerrarle	0	1	1.154
cerraré	0	1	1.154
cerrándose	0	1	1.154
cerrándolos	0	1	1.154
cerrándoles	0	1	1.154
ceros	0	1	1.154
cero	0	1	1.154
ceremoniosas	0	1	1.154
ceremoniosamente	0	1	1.154
cerebros	0	1	1.154
cerdea	0	1	1.154
cerda	0	1	1.154
cercioró	0	1	1.154
cerámica	0	1	1.154
cepillos	0	1	1.154
cepa	0	1	1.154
centuplicado	0	1	1.154
centrípeto	0	1	1.154
centrífuga	0	1	1.154
centinelas	0	1	1.154
centímetros	0	1	1.154
centenes	0	1	1.154
centenares	0	1	1.154
centén	0	1	1.154
centelleo	0	1	1.154
cenizas	0	1	1.154
cenital	0	1	1.154
cenefas	0	1	1.154
cenagosa	0	1	1.154
celitos	0	1	1.154
célibe	0	1	1.154
celibatarios	0	1	1.154
celeridad	0	1	1.154
celemín	0	1	1.154
celebridades	0	1	1.154
celebridad	0	1	1.154
celebrarse	0	1	1.154
celebrarlo	0	1	1.154
celebrándose	0	1	1.154
celebrada	0	1	1.154
celaje	0	1	1.154
celadas	0	1	1.154
cejar	0	1	1.154
ceguezuelo	0	1	1.154
cegué	0	1	1.154
cegarse	0	1	1.154
cegarla	0	1	1.154
cefalálgicos	0	1	1.154
cedazo	0	1	1.154
ceceoso	0	1	1.154
ceceo	0	1	1.154
cebón	0	1	1.154
cebáronse	0	1	1.154
cebados	0	1	1.154
cebaba	0	1	1.154
cazuelas	0	1	1.154
cazó	0	1	1.154
cazo	0	1	1.154
cazarlo	0	1	1.154
cazadas	0	1	1.154
cazable	0	1	1.154
cayose	0	1	1.154
cavour	0	1	1.154
caviles	0	1	1.154
cavilando	0	1	1.154
cavidades	0	1	1.154
cavernoso	0	1	1.154
cautivan	0	1	1.154
cautivábale	0	1	1.154
cauteloso	0	1	1.154
causo	0	1	1.154
causaría	0	1	1.154
causara	0	1	1.154
causados	0	1	1.154
causábale	0	1	1.154
caudalito	0	1	1.154
catre	0	1	1.154
catoliquísima	0	1	1.154
católicamente	0	1	1.154
cató	0	1	1.154
catilinario	0	1	1.154
caterva	0	1	1.154
catequizas	0	1	1.154
catequizador	0	1	1.154
categóricarnente	0	1	1.154
categorías	0	1	1.154
catedrática	0	1	1.154
cátedras	0	1	1.154
catecúmenos	0	1	1.154
catecúmeno	0	1	1.154
catecúmena	0	1	1.154
caté	0	1	1.154
catástrofes	0	1	1.154
catarral	0	1	1.154
catarían	0	1	1.154
cataplasma	0	1	1.154
cátalas	0	1	1.154
catalanas	0	1	1.154
cataduras	0	1	1.154
catadura	0	1	1.154
catador	0	1	1.154
cataba	0	1	1.154
casucha	0	1	1.154
casualmente	0	1	1.154
castro	0	1	1.154
castrametación	0	1	1.154
castiza	0	1	1.154
castigase	0	1	1.154
castigas	0	1	1.154
castigarles	0	1	1.154
castigarle	0	1	1.154
castigara	0	1	1.154
castigando	0	1	1.154
castigada	0	1	1.154
castas	0	1	1.154
castañetazo	0	1	1.154
castamente	0	1	1.154
casquillo	0	1	1.154
casquería	0	1	1.154
caspitina	0	1	1.154
caspa	0	1	1.154
casose	0	1	1.154
casitas	0	1	1.154
casetas	0	1	1.154
caseras	0	1	1.154
cascarones	0	1	1.154
cascarla	0	1	1.154
cascajo	0	1	1.154
cascado	0	1	1.154
cascadas	0	1	1.154
casarle	0	1	1.154
casarlas	0	1	1.154
casarías	0	1	1.154
casaré	0	1	1.154
casaras	0	1	1.154
casan	0	1	1.154
casamientos	0	1	1.154
cásale	0	1	1.154
casaditas	0	1	1.154
casadita	0	1	1.154
cartuja	0	1	1.154
cartita	0	1	1.154
carteros	0	1	1.154
cartero	0	1	1.154
cartelón	0	1	1.154
cartel	0	1	1.154
carteaba	0	1	1.154
carrozas	0	1	1.154
carrilleras	0	1	1.154
carrillera	0	1	1.154
carrilladas	0	1	1.154
carretes	0	1	1.154
carraspeo	0	1	1.154
carrascales	0	1	1.154
carrasca	0	1	1.154
carpetazo	0	1	1.154
carpetas	0	1	1.154
carpeta	0	1	1.154
carnicerías	0	1	1.154
carnecitas	0	1	1.154
carnavalesca	0	1	1.154
carnavales	0	1	1.154
carminoso	0	1	1.154
cariñitos	0	1	1.154
caribes	0	1	1.154
caribe	0	1	1.154
cariacontecido	0	1	1.154
cargas	0	1	1.154
cargarlo	0	1	1.154
cargarás	0	1	1.154
cargara	0	1	1.154
cargábanle	0	1	1.154
careciese	0	1	1.154
careciendo	0	1	1.154
cardo	0	1	1.154
cardiaca	0	1	1.154
cardarle	0	1	1.154
carcundas	0	1	1.154
cárceles	0	1	1.154
carceleros	0	1	1.154
carcelero	0	1	1.154
carcajadita	0	1	1.154
caraiter	0	1	1.154
caracterizar	0	1	1.154
caracterizan	0	1	1.154
caracolitos	0	1	1.154
carabanchel	0	1	1.154
capuchoncitos	0	1	1.154
captura	0	1	1.154
caprichoso	0	1	1.154
capote	0	1	1.154
capotas	0	1	1.154
capitaneadas	0	1	1.154
capitalizaba	0	1	1.154
capitalazo	0	1	1.154
capitación	0	1	1.154
capita	0	1	1.154
capearlo	0	1	1.154
capcioso	0	1	1.154
caño	0	1	1.154
cañí	0	1	1.154
cañamoncito	0	1	1.154
cañamazo	0	1	1.154
canturriaba	0	1	1.154
cantorrios	0	1	1.154
cantor	0	1	1.154
cantones	0	1	1.154
cantonalismo	0	1	1.154
cantina	0	1	1.154
canterac	0	1	1.154
cantazo	0	1	1.154
cantase	0	1	1.154
cantarle	0	1	1.154
cantaré	0	1	1.154
cantará	0	1	1.154
cantantes	0	1	1.154
cántale	0	1	1.154
cantadas	0	1	1.154
cantabile	0	1	1.154
canses	0	1	1.154
cansemos	0	1	1.154
cansarme	0	1	1.154
cansarás	0	1	1.154
cansará	0	1	1.154
cansamos	0	1	1.154
cansadita	0	1	1.154
cansábase	0	1	1.154
canonjías	0	1	1.154
canonizarlas	0	1	1.154
canonizaremos	0	1	1.154
canonizar	0	1	1.154
canonizada	0	1	1.154
canonizable	0	1	1.154
canonizaban	0	1	1.154
canina	0	1	1.154
canillas	0	1	1.154
canijo	0	1	1.154
caníbales	0	1	1.154
candilones	0	1	1.154
candidez	0	1	1.154
candideces	0	1	1.154
candidatura	0	1	1.154
cándidas	0	1	1.154
candelero	0	1	1.154
candados	0	1	1.154
cancillerías	0	1	1.154
cancelación	0	1	1.154
cancamurria	0	1	1.154
canastos	0	1	1.154
canasto	0	1	1.154
canastas	0	1	1.154
canarias	0	1	1.154
canapé	0	1	1.154
canallas	0	1	1.154
canallada	0	1	1.154
canalejas	0	1	1.154
camús	0	1	1.154
camuesa	0	1	1.154
campaneo	0	1	1.154
camita	0	1	1.154
camisolas	0	1	1.154
camiones	0	1	1.154
caminatas	0	1	1.154
camellos	0	1	1.154
cambias	0	1	1.154
cambiarte	0	1	1.154
cambiaran	0	1	1.154
cambiándolos	0	1	1.154
cambiándolo	0	1	1.154
cambiada	0	1	1.154
camarilla	0	1	1.154
camarero	0	1	1.154
camarera	0	1	1.154
camará	0	1	1.154
camaleones	0	1	1.154
calzoncillos	0	1	1.154
calzarse	0	1	1.154
calzará	0	1	1.154
calzan	0	1	1.154
calvinista	0	1	1.154
calumniaste	0	1	1.154
calumniadora	0	1	1.154
calumniador	0	1	1.154
calo	0	1	1.154
calme	0	1	1.154
cálmate	0	1	1.154
calmando	0	1	1.154
calman	0	1	1.154
callémonos	0	1	1.154
callejeras	0	1	1.154
callé	0	1	1.154
cállatela	0	1	1.154
callas	0	1	1.154
callarte	0	1	1.154
callaré	0	1	1.154
callara	0	1	1.154
callao	0	1	1.154
callaíto	0	1	1.154
calladitos	0	1	1.154
cáliz	0	1	1.154
caligráficos	0	1	1.154
caligrafía	0	1	1.154
calificó	0	1	1.154
calificado	0	1	1.154
calienta	0	1	1.154
calidá	0	1	1.154
calenturas	0	1	1.154
calentito	0	1	1.154
calentitas	0	1	1.154
calentita	0	1	1.154
calenté	0	1	1.154
calentaste	0	1	1.154
calentarte	0	1	1.154
calentármela	0	1	1.154
calentarlo	0	1	1.154
calentarle	0	1	1.154
calentándome	0	1	1.154
calentándolo	0	1	1.154
caldito	0	1	1.154
calderería	0	1	1.154
caldeos	0	1	1.154
caldeando	0	1	1.154
calculó	0	1	1.154
calculé	0	1	1.154
calculas	0	1	1.154
calculada	0	1	1.154
calco	0	1	1.154
calcetín	0	1	1.154
calcárea	0	1	1.154
calatrava	0	1	1.154
calandrias	0	1	1.154
calandria	0	1	1.154
calándoselos	0	1	1.154
calándose	0	1	1.154
calaínos	0	1	1.154
calainos	0	1	1.154
calábase	0	1	1.154
calaba	0	1	1.154
cajista	0	1	1.154
cajetilla	0	1	1.154
caíste	0	1	1.154
caímos	0	1	1.154
caíme	0	1	1.154
caídos	0	1	1.154
cafres	0	1	1.154
cafre	0	1	1.154
cafeteros	0	1	1.154
caerán	0	1	1.154
caenas	0	1	1.154
caemos	0	1	1.154
caduca	0	1	1.154
cadmio	0	1	1.154
cadencioso	0	1	1.154
cadencias	0	1	1.154
cadavérica	0	1	1.154
cadávere	0	1	1.154
cacumen	0	1	1.154
caciquismo	0	1	1.154
cachucha	0	1	1.154
cachorros	0	1	1.154
cachorro	0	1	1.154
cacharrería	0	1	1.154
cacerola	0	1	1.154
cacareo	0	1	1.154
cacarearlo	0	1	1.154
cacao	0	1	1.154
cacahuetes	0	1	1.154
cabrón	0	1	1.154
cabritos	0	1	1.154
cabriolas	0	1	1.154
cable	0	1	1.154
cabestrillo	0	1	1.154
caben	0	1	1.154
cabellerías	0	1	1.154
cabecilla	0	1	1.154
caballista	0	1	1.154
caballerizas	0	1	1.154
caballerete	0	1	1.154
cabalitos	0	1	1.154
buscona	0	1	1.154
buscón	0	1	1.154
buscaste	0	1	1.154
buscármelo	0	1	1.154
buscaríamos	0	1	1.154
buscaremos	0	1	1.154
buscaran	0	1	1.154
burris	0	1	1.154
burra	0	1	1.154
burocracia	0	1	1.154
burlones	0	1	1.154
burlón	0	1	1.154
burlen	0	1	1.154
búrlate	0	1	1.154
burladores	0	1	1.154
burguesía	0	1	1.154
burgués	0	1	1.154
burbujeaba	0	1	1.154
buñuelo	0	1	1.154
bullangas	0	1	1.154
bullanga	0	1	1.154
buleros	0	1	1.154
bufón	0	1	1.154
bufidos	0	1	1.154
bufandas	0	1	1.154
bufaban	0	1	1.154
bufaba	0	1	1.154
budistas	0	1	1.154
budista	0	1	1.154
bruta	0	1	1.154
bruños	0	1	1.154
bruñido	0	1	1.154
bruñida	0	1	1.154
brujerías	0	1	1.154
brrrr	0	1	1.154
brrr	0	1	1.154
brr	0	1	1.154
broza	0	1	1.154
brotes	0	1	1.154
brotaran	0	1	1.154
brotan	0	1	1.154
brotado	0	1	1.154
broncíneos	0	1	1.154
broncas	0	1	1.154
bromee	0	1	1.154
bromeas	0	1	1.154
bromeando	0	1	1.154
brochazos	0	1	1.154
brochase	0	1	1.154
brocados	0	1	1.154
brisca	0	1	1.154
brindarles	0	1	1.154
brincando	0	1	1.154
brillantísima	0	1	1.154
brillantez	0	1	1.154
brihuega	0	1	1.154
bribones	0	1	1.154
bribonada	0	1	1.154
breviarios	0	1	1.154
brevas	0	1	1.154
bregué	0	1	1.154
bregaron	0	1	1.154
brega	0	1	1.154
brebajes	0	1	1.154
brazadas	0	1	1.154
braveza	0	1	1.154
braserón	0	1	1.154
branco	0	1	1.154
bracmánica	0	1	1.154
bracitos	0	1	1.154
bracete	0	1	1.154
bracero	0	1	1.154
braceaban	0	1	1.154
boya	0	1	1.154
boxear	0	1	1.154
box	0	1	1.154
botoneras	0	1	1.154
botita	0	1	1.154
boticarito	0	1	1.154
boticarios	0	1	1.154
boticarín	0	1	1.154
botes	0	1	1.154
botellazo	0	1	1.154
botaratadas	0	1	1.154
botaratada	0	1	1.154
bostezando	0	1	1.154
bosquejada	0	1	1.154
borrosas	0	1	1.154
borriqueros	0	1	1.154
borricales	0	1	1.154
borricada	0	1	1.154
borre	0	1	1.154
borrascosos	0	1	1.154
borrarlas	0	1	1.154
borrara	0	1	1.154
borrachas	0	1	1.154
borlita	0	1	1.154
borleo	0	1	1.154
borgias	0	1	1.154
bordo	0	1	1.154
bordaron	0	1	1.154
bordar	0	1	1.154
bordan	0	1	1.154
bordadores	0	1	1.154
bordador	0	1	1.154
bordaban	0	1	1.154
borbones	0	1	1.154
boqueás	0	1	1.154
boqueadas	0	1	1.154
boquea	0	1	1.154
bonitísima	0	1	1.154
bonitamente	0	1	1.154
bonísimo	0	1	1.154
bonísima	0	1	1.154
bonillas	0	1	1.154
bonibus	0	1	1.154
bondadosamente	0	1	1.154
bonancibles	0	1	1.154
bollos	0	1	1.154
bollo	0	1	1.154
bollero	0	1	1.154
bollería	0	1	1.154
bólido	0	1	1.154
boletín	0	1	1.154
bohardillón	0	1	1.154
bohardillas	0	1	1.154
bocona	0	1	1.154
bocanadas	0	1	1.154
bobones	0	1	1.154
bobona	0	1	1.154
bobón	0	1	1.154
boberías	0	1	1.154
bobería	0	1	1.154
bloques	0	1	1.154
blondas	0	1	1.154
blinco	0	1	1.154
blasonados	0	1	1.154
blanqueará	0	1	1.154
blanquean	0	1	1.154
blanqueado	0	1	1.154
bizmas	0	1	1.154
bizma	0	1	1.154
bizcochitos	0	1	1.154
bizcochito	0	1	1.154
bizcas	0	1	1.154
bizcando	0	1	1.154
bizca	0	1	1.154
bizantinas	0	1	1.154
bisteques	0	1	1.154
bisoño	0	1	1.154
bismark	0	1	1.154
birmingham	0	1	1.154
birló	0	1	1.154
birlado	0	1	1.154
birla	0	1	1.154
biricornio	0	1	1.154
biombo	0	1	1.154
billetito	0	1	1.154
bigotito	0	1	1.154
bigotes	0	1	1.154
bigotera	0	1	1.154
bifurcación	0	1	1.154
biftec	0	1	1.154
bienaventuranza	0	1	1.154
bienaventurado	0	1	1.154
bienandanzas	0	1	1.154
bienandanza	0	1	1.154
bicoca	0	1	1.154
bichos	0	1	1.154
bichito	0	1	1.154
betsabée	0	1	1.154
besuqueó	0	1	1.154
besuqueo	0	1	1.154
besuqueándose	0	1	1.154
besugos	0	1	1.154
besárselos	0	1	1.154
besándose	0	1	1.154
besan	0	1	1.154
besamanos	0	1	1.154
besadlas	0	1	1.154
besadera	0	1	1.154
berza	0	1	1.154
berrugones	0	1	1.154
berroqueñas	0	1	1.154
berro	0	1	1.154
berreando	0	1	1.154
bermingán	0	1	1.154
bergantes	0	1	1.154
bergante	0	1	1.154
bergantas	0	1	1.154
berganta	0	1	1.154
berdan	0	1	1.154
benignita	0	1	1.154
benignidad	0	1	1.154
benévolo	0	1	1.154
benevolencias	0	1	1.154
benévolamente	0	1	1.154
benéficos	0	1	1.154
beneficios	0	1	1.154
bendijo	0	1	1.154
bendigo	0	1	1.154
bendiciendo	0	1	1.154
bendicen	0	1	1.154
bendecirá	0	1	1.154
bendecidas	0	1	1.154
bemol	0	1	1.154
bellotes	0	1	1.154
bellotas	0	1	1.154
bellota	0	1	1.154
belladona	0	1	1.154
belicosas	0	1	1.154
belfort	0	1	1.154
belencita	0	1	1.154
beldad	0	1	1.154
begonias	0	1	1.154
befa	0	1	1.154
becerradas	0	1	1.154
bebimos	0	1	1.154
bebieron	0	1	1.154
bebiéndola	0	1	1.154
bebí	0	1	1.154
beberse	0	1	1.154
beberías	0	1	1.154
beberé	0	1	1.154
beben	0	1	1.154
bebedor	0	1	1.154
bebé	0	1	1.154
beba	0	1	1.154
beato	0	1	1.154
baztán	0	1	1.154
bazofias	0	1	1.154
bazofia	0	1	1.154
bautizos	0	1	1.154
bautizaré	0	1	1.154
bautizan	0	1	1.154
batuta	0	1	1.154
batón	0	1	1.154
batlló	0	1	1.154
batita	0	1	1.154
batiéndola	0	1	1.154
batidas	0	1	1.154
bate	0	1	1.154
batallitas	0	1	1.154
batahola	0	1	1.154
bastiones	0	1	1.154
bastimentos	0	1	1.154
baste	0	1	1.154
bastaría	0	1	1.154
bastardos	0	1	1.154
bastar	0	1	1.154
bastándoles	0	1	1.154
bastándole	0	1	1.154
basilea	0	1	1.154
báscula	0	1	1.154
bascas	0	1	1.154
basamento	0	1	1.154
basadas	0	1	1.154
bártulos	0	1	1.154
barruntó	0	1	1.154
barrilitos	0	1	1.154
barrigón	0	1	1.154
barrieran	0	1	1.154
barrido	0	1	1.154
barrida	0	1	1.154
barrerme	0	1	1.154
barrerle	0	1	1.154
barreremos	0	1	1.154
barrenos	0	1	1.154
barrendero	0	1	1.154
barreduras	0	1	1.154
barre	0	1	1.154
barranco	0	1	1.154
barrancas	0	1	1.154
barrabasadas	0	1	1.154
barrabasada	0	1	1.154
barquitos	0	1	1.154
barquito	0	1	1.154
barquinazo	0	1	1.154
barnices	0	1	1.154
bargueño	0	1	1.154
bardales	0	1	1.154
barcia	0	1	1.154
barbilla	0	1	1.154
barbianas	0	1	1.154
barbería	0	1	1.154
baratillos	0	1	1.154
barástolis	0	1	1.154
barajaban	0	1	1.154
bar	0	1	1.154
baqueteados	0	1	1.154
banquetas	0	1	1.154
bandoleros	0	1	1.154
banderita	0	1	1.154
banderillero	0	1	1.154
bandejas	0	1	1.154
banastas	0	1	1.154
banasta	0	1	1.154
baluarte	0	1	1.154
balsain	0	1	1.154
balsa	0	1	1.154
ballesta	0	1	1.154
baldón	0	1	1.154
baldío	0	1	1.154
baldada	0	1	1.154
balconcillo	0	1	1.154
balbucir	0	1	1.154
balbucientes	0	1	1.154
balbuciendo	0	1	1.154
balbucía	0	1	1.154
balandranes	0	1	1.154
balancines	0	1	1.154
balancín	0	1	1.154
balanceos	0	1	1.154
balanceó	0	1	1.154
balancearse	0	1	1.154
balanceara	0	1	1.154
balanceándose	0	1	1.154
balance	0	1	1.154
baladronada	0	1	1.154
bajoncito	0	1	1.154
bajita	0	1	1.154
bajísimos	0	1	1.154
bajezas	0	1	1.154
bajase	0	1	1.154
bajarla	0	1	1.154
bajarían	0	1	1.154
bajaría	0	1	1.154
bajándola	0	1	1.154
bajáis	0	1	1.154
bajábala	0	1	1.154
bailoteando	0	1	1.154
bailo	0	1	1.154
bailly	0	1	1.154
baillière	0	1	1.154
bailara	0	1	1.154
bailadas	0	1	1.154
baguetilla	0	1	1.154
bagaje	0	1	1.154
badila	0	1	1.154
bachillería	0	1	1.154
baches	0	1	1.154
babieca	0	1	1.154
babel	0	1	1.154
azuzándole	0	1	1.154
azuzan	0	1	1.154
azuzáis	0	1	1.154
azuzado	0	1	1.154
azulejos	0	1	1.154
azulado	0	1	1.154
azucarillo	0	1	1.154
azotaina	0	1	1.154
azalea	0	1	1.154
azada	0	1	1.154
aza	0	1	1.154
ayunar	0	1	1.154
ayunaba	0	1	1.154
ayuna	0	1	1.154
ayudemos	0	1	1.154
ayudéis	0	1	1.154
ayudarte	0	1	1.154
ayudáronla	0	1	1.154
ayudarles	0	1	1.154
ayudaré	0	1	1.154
avivar	0	1	1.154
avispados	0	1	1.154
avispado	0	1	1.154
avispada	0	1	1.154
avisasteis	0	1	1.154
avisaste	0	1	1.154
avisaron	0	1	1.154
avisaremos	0	1	1.154
avisarás	0	1	1.154
avisando	0	1	1.154
avisada	0	1	1.154
avíos	0	1	1.154
avine	0	1	1.154
aviesa	0	1	1.154
avidez	0	1	1.154
ávidas	0	1	1.154
aviarme	0	1	1.154
aviarla	0	1	1.154
aviar	0	1	1.154
averígüelo	0	1	1.154
averiguase	0	1	1.154
averiguarle	0	1	1.154
averiguaría	0	1	1.154
averiguaré	0	1	1.154
averiguadores	0	1	1.154
averiguador	0	1	1.154
averiguación	0	1	1.154
avergüenzo	0	1	1.154
avergonzose	0	1	1.154
avergonzados	0	1	1.154
aventuremos	0	1	1.154
aventurábase	0	1	1.154
aventajada	0	1	1.154
aventaja	0	1	1.154
avenencia	0	1	1.154
avasallador	0	1	1.154
avariciosa	0	1	1.154
avanzadas	0	1	1.154
auxiliase	0	1	1.154
auxiliarse	0	1	1.154
auxiliarla	0	1	1.154
auxiliado	0	1	1.154
autorizarme	0	1	1.154
autorizan	0	1	1.154
autorizada	0	1	1.154
autoritarios	0	1	1.154
autoritarias	0	1	1.154
autoritariamente	0	1	1.154
autorice	0	1	1.154
autocrático	0	1	1.154
autocrática	0	1	1.154
autenticidad	0	1	1.154
austerlitz	0	1	1.154
austeridad	0	1	1.154
auspicios	0	1	1.154
ausento	0	1	1.154
ausentarme	0	1	1.154
ausentándose	0	1	1.154
ausculte	0	1	1.154
auscultarle	0	1	1.154
aurorita	0	1	1.154
auroras	0	1	1.154
aumentos	0	1	1.154
aumente	0	1	1.154
aumentase	0	1	1.154
aumentaron	0	1	1.154
aumentarlas	0	1	1.154
aumentando	0	1	1.154
auméntame	0	1	1.154
aumentada	0	1	1.154
augurios	0	1	1.154
audición	0	1	1.154
audacias	0	1	1.154
atusó	0	1	1.154
atusarte	0	1	1.154
atusada	0	1	1.154
aturullo	0	1	1.154
aturullada	0	1	1.154
aturdió	0	1	1.154
aturdidísima	0	1	1.154
atufo	0	1	1.154
atropelló	0	1	1.154
atropellando	0	1	1.154
atropellada	0	1	1.154
atronaban	0	1	1.154
atril	0	1	1.154
atribuyéndole	0	1	1.154
atrevidilla	0	1	1.154
atravesósele	0	1	1.154
atravesole	0	1	1.154
atravesase	0	1	1.154
atravesándolo	0	1	1.154
atravesándole	0	1	1.154
atravesados	0	1	1.154
atraso	0	1	1.154
atrasados	0	1	1.154
atrasaditos	0	1	1.154
atrasa	0	1	1.154
atrapo	0	1	1.154
atrapado	0	1	1.154
atraídos	0	1	1.154
atraída	0	1	1.154
atracciones	0	1	1.154
atrácate	0	1	1.154
atracaba	0	1	1.154
atosigaba	0	1	1.154
atormentó	0	1	1.154
atormentarme	0	1	1.154
atormentándole	0	1	1.154
atormentada	0	1	1.154
atormenta	0	1	1.154
atontarse	0	1	1.154
atmosférico	0	1	1.154
atletas	0	1	1.154
atlas	0	1	1.154
atizé	0	1	1.154
atizándose	0	1	1.154
atizado	0	1	1.154
atisbos	0	1	1.154
atisbando	0	1	1.154
atisbadora	0	1	1.154
atinado	0	1	1.154
atinadas	0	1	1.154
atildado	0	1	1.154
atildada	0	1	1.154
atestiguó	0	1	1.154
atestiguaban	0	1	1.154
aterrorizarla	0	1	1.154
aterrorizada	0	1	1.154
aterró	0	1	1.154
aterradoras	0	1	1.154
atenuase	0	1	1.154
atenuada	0	1	1.154
atenuaciones	0	1	1.154
atenuación	0	1	1.154
atenúa	0	1	1.154
atentísimamente	0	1	1.154
atentar	0	1	1.154
atendido	0	1	1.154
atendidas	0	1	1.154
atenazó	0	1	1.154
atenazado	0	1	1.154
atenazaba	0	1	1.154
ateas	0	1	1.154
atavismo	0	1	1.154
atavíen	0	1	1.154
ataviarse	0	1	1.154
atascó	0	1	1.154
atascaban	0	1	1.154
atarugándolo	0	1	1.154
atarugaba	0	1	1.154
ataros	0	1	1.154
ataron	0	1	1.154
atarme	0	1	1.154
atarles	0	1	1.154
atarés	0	1	1.154
atareado	0	1	1.154
atañen	0	1	1.154
atajarle	0	1	1.154
atajar	0	1	1.154
atajan	0	1	1.154
atáis	0	1	1.154
atadijo	0	1	1.154
atacó	0	1	1.154
atacados	0	1	1.154
atacada	0	1	1.154
asustose	0	1	1.154
asustas	0	1	1.154
asustarme	0	1	1.154
asustaré	0	1	1.154
asustaran	0	1	1.154
asustando	0	1	1.154
asustadísima	0	1	1.154
asustadas	0	1	1.154
asustábase	0	1	1.154
asustaban	0	1	1.154
astucias	0	1	1.154
astilla	0	1	1.154
asté	0	1	1.154
asquerosísimas	0	1	1.154
asquerosidades	0	1	1.154
aspires	0	1	1.154
aspiradores	0	1	1.154
aspaviento	0	1	1.154
aspasia	0	1	1.154
asomes	0	1	1.154
asombrosa	0	1	1.154
asombró	0	1	1.154
asómbrese	0	1	1.154
asombréis	0	1	1.154
asombre	0	1	1.154
asombráronse	0	1	1.154
asombrarías	0	1	1.154
asombrarás	0	1	1.154
asombrándose	0	1	1.154
asombraba	0	1	1.154
asomase	0	1	1.154
asoma	0	1	1.154
asoleado	0	1	1.154
asociándolos	0	1	1.154
asociadas	0	1	1.154
asociada	0	1	1.154
asmático	0	1	1.154
asistirla	0	1	1.154
asistiría	0	1	1.154
asistente	0	1	1.154
asín	0	1	1.154
asimilan	0	1	1.154
asimiladas	0	1	1.154
asilados	0	1	1.154
asignarle	0	1	1.154
asignara	0	1	1.154
asienta	0	1	1.154
asida	0	1	1.154
asiática	0	1	1.154
aseveró	0	1	1.154
asesinó	0	1	1.154
asesinatos	0	1	1.154
asesinando	0	1	1.154
asesina	0	1	1.154
aserrar	0	1	1.154
aseñorado	0	1	1.154
asentir	0	1	1.154
asentía	0	1	1.154
asensio	0	1	1.154
asemejaban	0	1	1.154
asemeja	0	1	1.154
aseguremos	0	1	1.154
asegure	0	1	1.154
aseguraron	0	1	1.154
asegurarla	0	1	1.154
aseguraría	0	1	1.154
aseguraran	0	1	1.154
asegurándole	0	1	1.154
asegúrame	0	1	1.154
aseguradas	0	1	1.154
aseadísima	0	1	1.154
aseada	0	1	1.154
ascua	0	1	1.154
ascendió	0	1	1.154
asaltó	0	1	1.154
asaltáronle	0	1	1.154
asalta	0	1	1.154
asadura	0	1	1.154
asador	0	1	1.154
asacristanado	0	1	1.154
asaban	0	1	1.154
asa	0	1	1.154
artimañas	0	1	1.154
artilleros	0	1	1.154
artificioso	0	1	1.154
articuló	0	1	1.154
articulazo	0	1	1.154
articularse	0	1	1.154
articulando	0	1	1.154
articulaciones	0	1	1.154
articulación	0	1	1.154
artesianos	0	1	1.154
artesas	0	1	1.154
arsenioso	0	1	1.154
arrumacos	0	1	1.154
arrullas	0	1	1.154
arrullándose	0	1	1.154
arrullando	0	1	1.154
arrullan	0	1	1.154
arrulla	0	1	1.154
arruinen	0	1	1.154
arruinaron	0	1	1.154
arruinar	0	1	1.154
arrugarse	0	1	1.154
arrolla	0	1	1.154
arroje	0	1	1.154
arrojas	0	1	1.154
arrojándole	0	1	1.154
arrojadas	0	1	1.154
arrogantillo	0	1	1.154
arrodillose	0	1	1.154
arrodillaste	0	1	1.154
arrobo	0	1	1.154
arrobamientos	0	1	1.154
arrobamiento	0	1	1.154
arrimo	0	1	1.154
arrimarse	0	1	1.154
arrimándose	0	1	1.154
arrimaban	0	1	1.154
arriesgáronse	0	1	1.154
arriero	0	1	1.154
arrepintiose	0	1	1.154
arrepintiera	0	1	1.154
arrepintiendo	0	1	1.154
arrepiento	0	1	1.154
arrepientes	0	1	1.154
arrepienten	0	1	1.154
arrepentirte	0	1	1.154
arrepentimientos	0	1	1.154
arrendaba	0	1	1.154
arremangó	0	1	1.154
arremangados	0	1	1.154
arreglole	0	1	1.154
arreglito	0	1	1.154
arreglen	0	1	1.154
arregléis	0	1	1.154
arréglatelas	0	1	1.154
arreglase	0	1	1.154
arreglándose	0	1	1.154
arréglame	0	1	1.154
arreglados	0	1	1.154
arregladitas	0	1	1.154
arregladita	0	1	1.154
arredraba	0	1	1.154
arrecogidas	0	1	1.154
arreciar	0	1	1.154
arrechuchos	0	1	1.154
arrebolada	0	1	1.154
arrebatándole	0	1	1.154
arreaba	0	1	1.154
arrastrarse	0	1	1.154
arrastraron	0	1	1.154
arrastrarán	0	1	1.154
arrastrándote	0	1	1.154
arrastrándose	0	1	1.154
arrastran	0	1	1.154
arrastra	0	1	1.154
arrasado	0	1	1.154
arranqué	0	1	1.154
arrancarles	0	1	1.154
arrancándose	0	1	1.154
arrancándolos	0	1	1.154
arrancan	0	1	1.154
arramblaron	0	1	1.154
arramblaban	0	1	1.154
arraigados	0	1	1.154
arquitectónico	0	1	1.154
arquitectónica	0	1	1.154
arqueos	0	1	1.154
arqueo	0	1	1.154
arqueadas	0	1	1.154
aros	0	1	1.154
arneses	0	1	1.154
armose	0	1	1.154
armonizando	0	1	1.154
armonizadas	0	1	1.154
armonizaba	0	1	1.154
armole	0	1	1.154
armo	0	1	1.154
armejas	0	1	1.154
armasen	0	1	1.154
armase	0	1	1.154
armaron	0	1	1.154
armarme	0	1	1.154
armarías	0	1	1.154
armándose	0	1	1.154
armándole	0	1	1.154
armadores	0	1	1.154
armadas	0	1	1.154
aritméticos	0	1	1.154
aritméticas	0	1	1.154
aristarco	0	1	1.154
arias	0	1	1.154
arguyéndose	0	1	1.154
argumentar	0	1	1.154
argumentando	0	1	1.154
argüía	0	1	1.154
argollitas	0	1	1.154
argollas	0	1	1.154
argentino	0	1	1.154
arganda	0	1	1.154
argamasillesca	0	1	1.154
arengando	0	1	1.154
arenales	0	1	1.154
ardorosos	0	1	1.154
ardides	0	1	1.154
ardid	0	1	1.154
ardería	0	1	1.154
arden	0	1	1.154
arda	0	1	1.154
arcola	0	1	1.154
archipámpano	0	1	1.154
arcanos	0	1	1.154
arcadas	0	1	1.154
arbusto	0	1	1.154
arboledas	0	1	1.154
arbitrios	0	1	1.154
arbitrio	0	1	1.154
arbitrando	0	1	1.154
árbitra	0	1	1.154
aravaca	0	1	1.154
arañó	0	1	1.154
arañé	0	1	1.154
arañarle	0	1	1.154
arañar	0	1	1.154
arañando	0	1	1.154
arañada	0	1	1.154
arañaban	0	1	1.154
arango	0	1	1.154
aranceles	0	1	1.154
arancelarios	0	1	1.154
arancelarias	0	1	1.154
arancelaria	0	1	1.154
arancel	0	1	1.154
arábiga	0	1	1.154
arabesco	0	1	1.154
apurillos	0	1	1.154
apuradísima	0	1	1.154
apura	0	1	1.154
apuntárselas	0	1	1.154
apuntarle	0	1	1.154
apuntaré	0	1	1.154
apuntándole	0	1	1.154
apuntadas	0	1	1.154
apuntaban	0	1	1.154
apuestan	0	1	1.154
aproximaría	0	1	1.154
aproximar	0	1	1.154
aproximada	0	1	1.154
aproximaban	0	1	1.154
aproxima	0	1	1.154
aprovecharnos	0	1	1.154
aprovechará	0	1	1.154
aprovechara	0	1	1.154
aprovechamiento	0	1	1.154
aprovecháis	0	1	1.154
aprovechadas	0	1	1.154
aprovechaban	0	1	1.154
apropiado	0	1	1.154
apropiada	0	1	1.154
apropiación	0	1	1.154
aprobase	0	1	1.154
aprobada	0	1	1.154
aprobaban	0	1	1.154
aprisionar	0	1	1.154
aprietes	0	1	1.154
aprietas	0	1	1.154
apretura	0	1	1.154
apretársele	0	1	1.154
apretándoselo	0	1	1.154
apretándola	0	1	1.154
apresuré	0	1	1.154
apresúrate	0	1	1.154
apresurase	0	1	1.154
apresuraron	0	1	1.154
apresurar	0	1	1.154
apresuradamente	0	1	1.154
apresurada	0	1	1.154
aprendo	0	1	1.154
aprendizaje	0	1	1.154
aprendieron	0	1	1.154
apréndetelo	0	1	1.154
apréndete	0	1	1.154
aprendes	0	1	1.154
aprenderán	0	1	1.154
aprendemos	0	1	1.154
aprended	0	1	1.154
aprendan	0	1	1.154
apremiaron	0	1	1.154
apremiarla	0	1	1.154
apremiantes	0	1	1.154
apremiado	0	1	1.154
apremiaban	0	1	1.154
apremiaba	0	1	1.154
apreciarlas	0	1	1.154
apreciarán	0	1	1.154
apreciados	0	1	1.154
apreciado	0	1	1.154
apreciadas	0	1	1.154
apreciables	0	1	1.154
apreciabilísimo	0	1	1.154
apreciabilísima	0	1	1.154
apoye	0	1	1.154
apoyaturas	0	1	1.154
apóyate	0	1	1.154
apoyaban	0	1	1.154
apoya	0	1	1.154
apóstrofe	0	1	1.154
apostólicos	0	1	1.154
aposentados	0	1	1.154
aportaste	0	1	1.154
aportar	0	1	1.154
aportaban	0	1	1.154
aportaba	0	1	1.154
aporreo	0	1	1.154
aporreando	0	1	1.154
aporrean	0	1	1.154
aporreada	0	1	1.154
aporrea	0	1	1.154
apología	0	1	1.154
apoderaron	0	1	1.154
apoderada	0	1	1.154
apoderaban	0	1	1.154
apócrifo	0	1	1.154
apocamiento	0	1	1.154
apocado	0	1	1.154
apliquen	0	1	1.154
aplícate	0	1	1.154
aplicarlo	0	1	1.154
aplicados	0	1	1.154
aplicado	0	1	1.154
aplicaditos	0	1	1.154
aplicadísimo	0	1	1.154
aplicadísima	0	1	1.154
aplazó	0	1	1.154
aplazarlo	0	1	1.154
aplaudirse	0	1	1.154
aplaudir	0	1	1.154
aplaudiesen	0	1	1.154
aplaudieron	0	1	1.154
aplaudiéndose	0	1	1.154
aplastando	0	1	1.154
aplanado	0	1	1.154
aplanada	0	1	1.154
aplacó	0	1	1.154
aplacaría	0	1	1.154
aplacará	0	1	1.154
aplacando	0	1	1.154
aplacada	0	1	1.154
aplacaba	0	1	1.154
aplaca	0	1	1.154
apio	0	1	1.154
apilaba	0	1	1.154
apetezca	0	1	1.154
apeteciendo	0	1	1.154
apetecido	0	1	1.154
apetecían	0	1	1.154
apestando	0	1	1.154
aperreada	0	1	1.154
apergaminaba	0	1	1.154
apercibiendo	0	1	1.154
apeose	0	1	1.154
apencó	0	1	1.154
apenado	0	1	1.154
apelo	0	1	1.154
apelmazándose	0	1	1.154
apelmazaban	0	1	1.154
apechuguemos	0	1	1.154
apechugue	0	1	1.154
apechugó	0	1	1.154
apáticamente	0	1	1.154
apartola	0	1	1.154
aparté	0	1	1.154
apartase	0	1	1.154
apartas	0	1	1.154
apartarte	0	1	1.154
apartarlo	0	1	1.154
apartarla	0	1	1.154
apartándolas	0	1	1.154
apartan	0	1	1.154
apartamientos	0	1	1.154
apártame	0	1	1.154
aparezco	0	1	1.154
aparezca	0	1	1.154
aparentase	0	1	1.154
aparejos	0	1	1.154
aparejo	0	1	1.154
aparejados	0	1	1.154
apareciese	0	1	1.154
apareciera	0	1	1.154
aparecerán	0	1	1.154
aparecerá	0	1	1.154
apañados	0	1	1.154
apañado	0	1	1.154
apañaditos	0	1	1.154
apañadita	0	1	1.154
apaña	0	1	1.154
apandando	0	1	1.154
apalearle	0	1	1.154
apalean	0	1	1.154
apalabrado	0	1	1.154
apalabradas	0	1	1.154
apaisada	0	1	1.154
apagolo	0	1	1.154
apagaste	0	1	1.154
apagarse	0	1	1.154
apagarlas	0	1	1.154
apagaría	0	1	1.154
apagaran	0	1	1.154
apagábase	0	1	1.154
apabullar	0	1	1.154
aorta	0	1	1.154
añadirse	0	1	1.154
añadiéndole	0	1	1.154
añada	0	1	1.154
anuncié	0	1	1.154
anunciarte	0	1	1.154
anunciarme	0	1	1.154
anunciará	0	1	1.154
anunciara	0	1	1.154
anunciándose	0	1	1.154
anunciaban	0	1	1.154
anularse	0	1	1.154
anular	0	1	1.154
anulando	0	1	1.154
anula	0	1	1.154
anudado	0	1	1.154
anualmente	0	1	1.154
antorchas	0	1	1.154
antoñita	0	1	1.154
antonieta	0	1	1.154
antojitos	0	1	1.154
antojito	0	1	1.154
antojaría	0	1	1.154
antiquísimos	0	1	1.154
antípodas	0	1	1.154
antipatriótico	0	1	1.154
antipáticas	0	1	1.154
antioquía	0	1	1.154
antigualla	0	1	1.154
antiespasmódico	0	1	1.154
antieconómico	0	1	1.154
antidinásticas	0	1	1.154
anticuados	0	1	1.154
anticonstitucional	0	1	1.154
anticipó	0	1	1.154
anticiparse	0	1	1.154
anticipándome	0	1	1.154
anticipaban	0	1	1.154
antequera	0	1	1.154
anteponen	0	1	1.154
antepechos	0	1	1.154
anteojazo	0	1	1.154
antediluvianos	0	1	1.154
antediluviana	0	1	1.154
antagonista	0	1	1.154
antagonismos	0	1	1.154
ansiosos	0	1	1.154
ansiados	0	1	1.154
anotaciones	0	1	1.154
anormal	0	1	1.154
anonadar	0	1	1.154
anonadando	0	1	1.154
anonadado	0	1	1.154
anonadaba	0	1	1.154
anomalías	0	1	1.154
anómala	0	1	1.154
aniquilar	0	1	1.154
aniquilan	0	1	1.154
animose	0	1	1.154
anímese	0	1	1.154
animarse	0	1	1.154
animarle	0	1	1.154
animarla	0	1	1.154
animándole	0	1	1.154
animadísimo	0	1	1.154
animadas	0	1	1.154
animábale	0	1	1.154
anillos	0	1	1.154
anillo	0	1	1.154
anillas	0	1	1.154
anidara	0	1	1.154
anida	0	1	1.154
anhela	0	1	1.154
angustiada	0	1	1.154
angulosas	0	1	1.154
angulema	0	1	1.154
anguila	0	1	1.154
angosturas	0	1	1.154
anglómano	0	1	1.154
anglicanizados	0	1	1.154
angelita	0	1	1.154
angelicales	0	1	1.154
anfitriones	0	1	1.154
anestésico	0	1	1.154
anegándose	0	1	1.154
anega	0	1	1.154
anduve	0	1	1.154
andurriales	0	1	1.154
andrajosas	0	1	1.154
ando	0	1	1.154
andarse	0	1	1.154
andarían	0	1	1.154
andarás	0	1	1.154
andamio	0	1	1.154
andamiajes	0	1	1.154
andaluza	0	1	1.154
andábanle	0	1	1.154
ancladas	0	1	1.154
ancianas	0	1	1.154
anchoas	0	1	1.154
anatomías	0	1	1.154
anascotes	0	1	1.154
analizó	0	1	1.154
analizara	0	1	1.154
anafres	0	1	1.154
anacletus	0	1	1.154
anabaptista	0	1	1.154
amueblados	0	1	1.154
amuebladas	0	1	1.154
amputación	0	1	1.154
ampolla	0	1	1.154
amplísima	0	1	1.154
ampare	0	1	1.154
ampararles	0	1	1.154
ampararán	0	1	1.154
amparaba	0	1	1.154
ampara	0	1	1.154
amotinó	0	1	1.154
amoscose	0	1	1.154
amortajó	0	1	1.154
amortajaron	0	1	1.154
amorraba	0	1	1.154
amorcito	0	1	1.154
amontones	0	1	1.154
amontone	0	1	1.154
amontonaron	0	1	1.154
amoniaco	0	1	1.154
amonestó	0	1	1.154
amoldarlas	0	1	1.154
amoldara	0	1	1.154
amoldada	0	1	1.154
amodorrado	0	1	1.154
amito	0	1	1.154
amistoso	0	1	1.154
amistosamente	0	1	1.154
amilanarse	0	1	1.154
amilana	0	1	1.154
amigota	0	1	1.154
amigablemente	0	1	1.154
amenizó	0	1	1.154
ameniza	0	1	1.154
amenguársele	0	1	1.154
amenguar	0	1	1.154
amenazándolos	0	1	1.154
amenazadores	0	1	1.154
amenazada	0	1	1.154
ame	0	1	1.154
ámbar	0	1	1.154
amazónica	0	1	1.154
amazonas	0	1	1.154
amasara	0	1	1.154
amasábanlo	0	1	1.154
amasábalo	0	1	1.154
amartelamiento	0	1	1.154
amarre	0	1	1.154
amarrara	0	1	1.154
amarrar	0	1	1.154
amarrada	0	1	1.154
amargarán	0	1	1.154
amargan	0	1	1.154
amargaban	0	1	1.154
amargaba	0	1	1.154
amaremos	0	1	1.154
amara	0	1	1.154
amañada	0	1	1.154
amantísima	0	1	1.154
amanse	0	1	1.154
amansarla	0	1	1.154
amansará	0	1	1.154
amansaban	0	1	1.154
amansa	0	1	1.154
amanezco	0	1	1.154
amanezca	0	1	1.154
amaneramientos	0	1	1.154
amándola	0	1	1.154
amancebada	0	1	1.154
amalgama	0	1	1.154
amagado	0	1	1.154
amaestrados	0	1	1.154
amábale	0	1	1.154
alzarse	0	1	1.154
alzándolos	0	1	1.154
alzándole	0	1	1.154
alzamiento	0	1	1.154
alzada	0	1	1.154
alumbré	0	1	1.154
alumbrándose	0	1	1.154
alumbrando	0	1	1.154
alumbramientos	0	1	1.154
alumbrado	0	1	1.154
aluego	0	1	1.154
aludidos	0	1	1.154
alucinado	0	1	1.154
alucinada	0	1	1.154
alucinaciones	0	1	1.154
altona	0	1	1.154
altísima	0	1	1.154
alteza	0	1	1.154
alternativa	0	1	1.154
alternadamente	0	1	1.154
alterna	0	1	1.154
alterando	0	1	1.154
alterada	0	1	1.154
altarucho	0	1	1.154
altaneramente	0	1	1.154
alsacia	0	1	1.154
alquilan	0	1	1.154
alquilado	0	1	1.154
alquila	0	1	1.154
alpargatitas	0	1	1.154
alones	0	1	1.154
alojamiento	0	1	1.154
alojaba	0	1	1.154
almuerzas	0	1	1.154
almuerza	0	1	1.154
almorzó	0	1	1.154
almorzaron	0	1	1.154
almorzaría	0	1	1.154
almorzaré	0	1	1.154
almorzarás	0	1	1.154
almorzaran	0	1	1.154
almorzará	0	1	1.154
almorzaban	0	1	1.154
almorcemos	0	1	1.154
almonedas	0	1	1.154
almireces	0	1	1.154
almería	0	1	1.154
almendrita	0	1	1.154
almendrado	0	1	1.154
almansa	0	1	1.154
almanaques	0	1	1.154
almagre	0	1	1.154
almacenista	0	1	1.154
aller	0	1	1.154
allegro	0	1	1.154
allego	0	1	1.154
allegadizo	0	1	1.154
allanamiento	0	1	1.154
alivió	0	1	1.154
aliviarle	0	1	1.154
alivian	0	1	1.154
aliviado	0	1	1.154
aliviaba	0	1	1.154
alivia	0	1	1.154
aliñada	0	1	1.154
alinearon	0	1	1.154
alimentarlo	0	1	1.154
alimentados	0	1	1.154
alilao	0	1	1.154
aligerándole	0	1	1.154
aligeraba	0	1	1.154
aligera	0	1	1.154
alifonso	0	1	1.154
alicante	0	1	1.154
aliar	0	1	1.154
alhajita	0	1	1.154
álgido	0	1	1.154
algeciras	0	1	1.154
algarroba	0	1	1.154
alfonsina	0	1	1.154
alfombrita	0	1	1.154
alfombrado	0	1	1.154
alfombrada	0	1	1.154
alfilerazo	0	1	1.154
alfargías	0	1	1.154
alevosa	0	1	1.154
aletargarse	0	1	1.154
alentó	0	1	1.154
alentarme	0	1	1.154
alentara	0	1	1.154
alentado	0	1	1.154
alentada	0	1	1.154
alelí	0	1	1.154
alejaron	0	1	1.154
alejándole	0	1	1.154
alegrones	0	1	1.154
alegras	0	1	1.154
alegrarte	0	1	1.154
alegrarla	0	1	1.154
alegraríamos	0	1	1.154
alegraran	0	1	1.154
alegrado	0	1	1.154
alegrábanse	0	1	1.154
alegar	0	1	1.154
aldeota	0	1	1.154
alcorcón	0	1	1.154
alcohólico	0	1	1.154
alcohólicas	0	1	1.154
alcoholatos	0	1	1.154
alcira	0	1	1.154
alcé	0	1	1.154
alcarria	0	1	1.154
alcarreño	0	1	1.154
alcaraz	0	1	1.154
alcanzas	0	1	1.154
alcanzarla	0	1	1.154
alcanzaría	0	1	1.154
alcanfor	0	1	1.154
alcánceme	0	1	1.154
alcaloide	0	1	1.154
alcaldía	0	1	1.154
alcahuetas	0	1	1.154
alcachofas	0	1	1.154
alborozada	0	1	1.154
alborotos	0	1	1.154
alborotes	0	1	1.154
alborotemos	0	1	1.154
alboroté	0	1	1.154
alborotaron	0	1	1.154
alborotadamente	0	1	1.154
albis	0	1	1.154
albillo	0	1	1.154
albergarse	0	1	1.154
albergar	0	1	1.154
albergaban	0	1	1.154
albaricoque	0	1	1.154
albardería	0	1	1.154
albahaca	0	1	1.154
alarmas	0	1	1.154
alarmaron	0	1	1.154
alarmándose	0	1	1.154
alarmando	0	1	1.154
alarmados	0	1	1.154
alarido	0	1	1.154
alargué	0	1	1.154
alargaron	0	1	1.154
alargarle	0	1	1.154
alargar	0	1	1.154
alargándosela	0	1	1.154
alargamiento	0	1	1.154
alargábalo	0	1	1.154
alardeando	0	1	1.154
alardeaba	0	1	1.154
alardea	0	1	1.154
alamedas	0	1	1.154
alados	0	1	1.154
alabarderos	0	1	1.154
akos	0	1	1.154
ajusticiar	0	1	1.154
ajusticiados	0	1	1.154
ajustaré	0	1	1.154
ajustarán	0	1	1.154
ajustándolos	0	1	1.154
ajustados	0	1	1.154
ajustaba	0	1	1.154
ajuntaron	0	1	1.154
ajumarse	0	1	1.154
ajumaíto	0	1	1.154
ajuares	0	1	1.154
ajos	0	1	1.154
ajito	0	1	1.154
ajenjos	0	1	1.154
ajardinados	0	1	1.154
ajan	0	1	1.154
airote	0	1	1.154
airear	0	1	1.154
airadas	0	1	1.154
ahuyentase	0	1	1.154
ahuyentar	0	1	1.154
ahuyentan	0	1	1.154
ahuma	0	1	1.154
ahuecar	0	1	1.154
ahuecados	0	1	1.154
ahuecadas	0	1	1.154
ahueca	0	1	1.154
ahorrarse	0	1	1.154
ahorcarme	0	1	1.154
ahondando	0	1	1.154
ahola	0	1	1.154
ahoguillo	0	1	1.154
ahogos	0	1	1.154
ahogarte	0	1	1.154
ahogaría	0	1	1.154
ahogaran	0	1	1.154
ahogándola	0	1	1.154
ahogado	0	1	1.154
ahogadas	0	1	1.154
ahíto	0	1	1.154
ahilado	0	1	1.154
ahijado	0	1	1.154
ahijada	0	1	1.154
aguzadores	0	1	1.154
aguzaban	0	1	1.154
agujeritos	0	1	1.154
agujereados	0	1	1.154
aguirre	0	1	1.154
aguinaldo	0	1	1.154
aguileña	0	1	1.154
agudísimos	0	1	1.154
agudísima	0	1	1.154
aguaron	0	1	1.154
aguardo	0	1	1.154
aguardientito	0	1	1.154
aguardientazo	0	1	1.154
aguárdense	0	1	1.154
aguardaron	0	1	1.154
aguantó	0	1	1.154
aguanten	0	1	1.154
aguánteme	0	1	1.154
aguante	0	1	1.154
aguantas	0	1	1.154
aguantarme	0	1	1.154
aguantarle	0	1	1.154
aguantaría	0	1	1.154
aguantamos	0	1	1.154
aguadores	0	1	1.154
agrupar	0	1	1.154
agricultura	0	1	1.154
agriaba	0	1	1.154
agresor	0	1	1.154
agregando	0	1	1.154
agregábansele	0	1	1.154
agregaba	0	1	1.154
agredida	0	1	1.154
agraviadas	0	1	1.154
agravación	0	1	1.154
agrandando	0	1	1.154
agrandado	0	1	1.154
agrandada	0	1	1.154
agradó	0	1	1.154
agradezcáis	0	1	1.154
agradecimientos	0	1	1.154
agradecerían	0	1	1.154
agradeceremos	0	1	1.154
agradéceme	0	1	1.154
agradaron	0	1	1.154
agradan	0	1	1.154
agradabilísimo	0	1	1.154
agradábanle	0	1	1.154
agració	0	1	1.154
agraciadas	0	1	1.154
agotarse	0	1	1.154
agostaba	0	1	1.154
agonizada	0	1	1.154
agobia	0	1	1.154
agitato	0	1	1.154
agitara	0	1	1.154
agitante	0	1	1.154
agitanada	0	1	1.154
agitadas	0	1	1.154
ágiles	0	1	1.154
agenciado	0	1	1.154
agasajarle	0	1	1.154
agasajar	0	1	1.154
agasajando	0	1	1.154
agasajan	0	1	1.154
agarrotes	0	1	1.154
agarrose	0	1	1.154
agarré	0	1	1.154
agarre	0	1	1.154
agarrase	0	1	1.154
agarras	0	1	1.154
agarraron	0	1	1.154
agarrarlo	0	1	1.154
agarrándole	0	1	1.154
agarrados	0	1	1.154
agarradas	0	1	1.154
agarra	0	1	1.154
agallas	0	1	1.154
agachaban	0	1	1.154
agacha	0	1	1.154
afrontando	0	1	1.154
afrentas	0	1	1.154
afrentar	0	1	1.154
afluía	0	1	1.154
aflojé	0	1	1.154
afloje	0	1	1.154
aflojarse	0	1	1.154
aflojarle	0	1	1.154
aflojar	0	1	1.154
aflijas	0	1	1.154
afligidísimo	0	1	1.154
aflige	0	1	1.154
aflictivo	0	1	1.154
aflictiva	0	1	1.154
aflicciones	0	1	1.154
aflamencado	0	1	1.154
afirme	0	1	1.154
afirmativos	0	1	1.154
afirmase	0	1	1.154
afinó	0	1	1.154
afinidades	0	1	1.154
afines	0	1	1.154
afinado	0	1	1.154
afinadas	0	1	1.154
afinaba	0	1	1.154
afiliarse	0	1	1.154
afilándolas	0	1	1.154
afiladas	0	1	1.154
afilaban	0	1	1.154
afianzando	0	1	1.154
afianzaba	0	1	1.154
aferrada	0	1	1.154
aferraba	0	1	1.154
afeiten	0	1	1.154
afeite	0	1	1.154
afeitadito	0	1	1.154
afeitada	0	1	1.154
afectuosos	0	1	1.154
afectase	0	1	1.154
afectarte	0	1	1.154
afectaron	0	1	1.154
afectadísimo	0	1	1.154
afección	0	1	1.154
afeaban	0	1	1.154
afanándose	0	1	1.154
afanados	0	1	1.154
afanadora	0	1	1.154
afanada	0	1	1.154
advirtiera	0	1	1.154
advirtiéndole	0	1	1.154
adviniese	0	1	1.154
adviértele	0	1	1.154
advierte	0	1	1.154
adviertas	0	1	1.154
adviértale	0	1	1.154
advertían	0	1	1.154
adversidad	0	1	1.154
adventicia	0	1	1.154
adustez	0	1	1.154
adustas	0	1	1.154
adultero	0	1	1.154
adulterios	0	1	1.154
adulteraba	0	1	1.154
adulona	0	1	1.154
adulando	0	1	1.154
adquiriría	0	1	1.154
adquiriré	0	1	1.154
adquieren	0	1	1.154
adquieran	0	1	1.154
adornarse	0	1	1.154
adornados	0	1	1.154
adormilado	0	1	1.154
adormidera	0	1	1.154
adormeciera	0	1	1.154
adormecido	0	1	1.154
adormecía	0	1	1.154
adormecerse	0	1	1.154
adoren	0	1	1.154
adore	0	1	1.154
adorarte	0	1	1.154
adorarse	0	1	1.154
adoraron	0	1	1.154
adorarme	0	1	1.154
adoraría	0	1	1.154
adoraré	0	1	1.154
adoraran	0	1	1.154
adorara	0	1	1.154
adoramos	0	1	1.154
adorabas	0	1	1.154
adoquinando	0	1	1.154
adoquinadas	0	1	1.154
adoptó	0	1	1.154
adopte	0	1	1.154
adoptarlo	0	1	1.154
adoptarla	0	1	1.154
adoptaría	0	1	1.154
adonis	0	1	1.154
adolecieran	0	1	1.154
adobado	0	1	1.154
admitirlo	0	1	1.154
admitirle	0	1	1.154
admitiesen	0	1	1.154
admitiendo	0	1	1.154
admitidas	0	1	1.154
admitamos	0	1	1.154
admisión	0	1	1.154
admirose	0	1	1.154
admirase	0	1	1.154
admiras	0	1	1.154
admiraron	0	1	1.154
admiran	0	1	1.154
admiramos	0	1	1.154
admiradas	0	1	1.154
admirábala	0	1	1.154
administre	0	1	1.154
administrativo	0	1	1.154
administrativas	0	1	1.154
administraba	0	1	1.154
administra	0	1	1.154
adjudicó	0	1	1.154
adjudicado	0	1	1.154
adjetivo	0	1	1.154
adiviné	0	1	1.154
adivinarlo	0	1	1.154
adivinanza	0	1	1.154
adivinándole	0	1	1.154
adivinabas	0	1	1.154
adicto	0	1	1.154
adhiriéndose	0	1	1.154
adhiere	0	1	1.154
adheridos	0	1	1.154
adeudaba	0	1	1.154
aderezo	0	1	1.154
aderezado	0	1	1.154
aderezada	0	1	1.154
adepto	0	1	1.154
adelgazadas	0	1	1.154
adelgazada	0	1	1.154
adelanto	0	1	1.154
adelantarían	0	1	1.154
adelantan	0	1	1.154
adelantamos	0	1	1.154
adela	0	1	1.154
adecentase	0	1	1.154
adecentarse	0	1	1.154
adecentaras	0	1	1.154
adecentar	0	1	1.154
adecentado	0	1	1.154
adaptando	0	1	1.154
adaptada	0	1	1.154
adaptaban	0	1	1.154
adagio	0	1	1.154
acuse	0	1	1.154
acusaré	0	1	1.154
acusándose	0	1	1.154
acusándoles	0	1	1.154
acusádose	0	1	1.154
acurrucó	0	1	1.154
acurrucada	0	1	1.154
acuñar	0	1	1.154
acueste	0	1	1.154
acuerdos	0	1	1.154
acuerden	0	1	1.154
acueducto	0	1	1.154
acudo	0	1	1.154
acudiremos	0	1	1.154
acudiré	0	1	1.154
acudimos	0	1	1.154
acudiera	0	1	1.154
acudas	0	1	1.154
acubilla	0	1	1.154
actuar	0	1	1.154
actuando	0	1	1.154
activamente	0	1	1.154
activaba	0	1	1.154
acrisolada	0	1	1.154
acribilló	0	1	1.154
acribillarlas	0	1	1.154
acredite	0	1	1.154
acreditadísimo	0	1	1.154
acreditada	0	1	1.154
acrecía	0	1	1.154
acostumbres	0	1	1.154
acostumbré	0	1	1.154
acostumbrarse	0	1	1.154
acostumbraran	0	1	1.154
acostumbradas	0	1	1.154
acosté	0	1	1.154
acostáronle	0	1	1.154
acostarme	0	1	1.154
acostaría	0	1	1.154
acostaremos	0	1	1.154
acostando	0	1	1.154
acosen	0	1	1.154
acosándoles	0	1	1.154
acosando	0	1	1.154
acosados	0	1	1.154
acorte	0	1	1.154
acortarse	0	1	1.154
acortar	0	1	1.154
acortando	0	1	1.154
acortaba	0	1	1.154
acorralan	0	1	1.154
acorde	0	1	1.154
acordarme	0	1	1.154
acordaré	0	1	1.154
acordará	0	1	1.154
acordándome	0	1	1.154
acordada	0	1	1.154
acordabas	0	1	1.154
acorazó	0	1	1.154
acopio	0	1	1.154
acopiando	0	1	1.154
acopiada	0	1	1.154
aconteciendo	0	1	1.154
acontece	0	1	1.154
aconsejo	0	1	1.154
aconséjele	0	1	1.154
aconséjate	0	1	1.154
aconsejas	0	1	1.154
aconsejármelas	0	1	1.154
acónito	0	1	1.154
acompañolas	0	1	1.154
acompañes	0	1	1.154
acompañantes	0	1	1.154
acompañante	0	1	1.154
acompañándola	0	1	1.154
acompañan	0	1	1.154
acompañamos	0	1	1.154
acompañábanle	0	1	1.154
acompañábanla	0	1	1.154
acomodó	0	1	1.154
acomodaticios	0	1	1.154
acomodarse	0	1	1.154
acomodar	0	1	1.154
acomodándose	0	1	1.154
acomodando	0	1	1.154
acomodado	0	1	1.154
acomodada	0	1	1.154
acometía	0	1	1.154
acometerla	0	1	1.154
acometería	0	1	1.154
acoja	0	1	1.154
acobardes	0	1	1.154
acobardarse	0	1	1.154
acobardaron	0	1	1.154
acobardarme	0	1	1.154
acobardará	0	1	1.154
acobardado	0	1	1.154
aclaró	0	1	1.154
aclare	0	1	1.154
aclaran	0	1	1.154
aclaración	0	1	1.154
aclara	0	1	1.154
aclamaciones	0	1	1.154
aciertan	0	1	1.154
acídula	0	1	1.154
acidez	0	1	1.154
acicaló	0	1	1.154
aciaga	0	1	1.154
achuchones	0	1	1.154
achicharrados	0	1	1.154
achicarte	0	1	1.154
achantado	0	1	1.154
achantada	0	1	1.154
acetato	0	1	1.154
acertijos	0	1	1.154
acertaré	0	1	1.154
acertados	0	1	1.154
acertadas	0	1	1.154
acertaban	0	1	1.154
acerqueme	0	1	1.154
acercósele	0	1	1.154
acercara	0	1	1.154
acercan	0	1	1.154
acerbísimo	0	1	1.154
acerbísimas	0	1	1.154
acéptelo	0	1	1.154
acepté	0	1	1.154
acéptalo	0	1	1.154
aceptación	0	1	1.154
acentuole	0	1	1.154
acentuar	0	1	1.154
acentúan	0	1	1.154
acentuación	0	1	1.154
acémilas	0	1	1.154
aceleró	0	1	1.154
aceleradas	0	1	1.154
aceitosa	0	1	1.154
acechas	0	1	1.154
acecharlas	0	1	1.154
acecharan	0	1	1.154
acechándola	0	1	1.154
acechador	0	1	1.154
acechaban	0	1	1.154
acebuche	0	1	1.154
accidentados	0	1	1.154
accidentada	0	1	1.154
accedieron	0	1	1.154
acaudalada	0	1	1.154
acatemos	0	1	1.154
acatarrado	0	1	1.154
acatar	0	1	1.154
acariciarlo	0	1	1.154
acariciándoselo	0	1	1.154
acariciándolas	0	1	1.154
acaparamientos	0	1	1.154
acantonar	0	1	1.154
acampan	0	1	1.154
acalores	0	1	1.154
acalorándose	0	1	1.154
acalorándole	0	1	1.154
acaloran	0	1	1.154
acaloradamente	0	1	1.154
acallaban	0	1	1.154
acaeció	0	1	1.154
acabas	0	1	1.154
acabarán	0	1	1.154
acabáramos	0	1	1.154
aburriste	0	1	1.154
aburrir	0	1	1.154
aburrió	0	1	1.154
aburriera	0	1	1.154
aburridísima	0	1	1.154
aburríale	0	1	1.154
aburres	0	1	1.154
aburra	0	1	1.154
abundan	0	1	1.154
abulte	0	1	1.154
abstrusas	0	1	1.154
abstraerse	0	1	1.154
absteniéndose	0	1	1.154
absorción	0	1	1.154
absorbió	0	1	1.154
absorbederos	0	1	1.154
absolverás	0	1	1.154
absolutista	0	1	1.154
abrumara	0	1	1.154
abrumadoras	0	1	1.154
abruma	0	1	1.154
abroñigal	0	1	1.154
abrocharte	0	1	1.154
abrirlos	0	1	1.154
abrirla	0	1	1.154
abriremos	0	1	1.154
abriolo	0	1	1.154
abriole	0	1	1.154
abrigase	0	1	1.154
abrigas	0	1	1.154
abrigarte	0	1	1.154
abrigarse	0	1	1.154
abrigar	0	1	1.154
abrigándose	0	1	1.154
abrigándole	0	1	1.154
abrigados	0	1	1.154
abrigaditos	0	1	1.154
abrigaditas	0	1	1.154
abrigábamos	0	1	1.154
abriéndolos	0	1	1.154
abriéndole	0	1	1.154
abriéndolas	0	1	1.154
abriéndola	0	1	1.154
abrí	0	1	1.154
abreviemos	0	1	1.154
abrevie	0	1	1.154
abreviarlos	0	1	1.154
abreviarlo	0	1	1.154
ábrete	0	1	1.154
abrazola	0	1	1.154
abrazara	0	1	1.154
abrazándose	0	1	1.154
abrazándole	0	1	1.154
abrazados	0	1	1.154
abrasado	0	1	1.154
abras	0	1	1.154
abran	0	1	1.154
abracitos	0	1	1.154
abovedada	0	1	1.154
abotonándose	0	1	1.154
aborregado	0	1	1.154
aborrecimiento	0	1	1.154
aborreciera	0	1	1.154
aborrecidas	0	1	1.154
aborrecida	0	1	1.154
aborrecerlo	0	1	1.154
aborrecerle	0	1	1.154
aboque	0	1	1.154
abonos	0	1	1.154
abona	0	1	1.154
abominando	0	1	1.154
abolladuras	0	1	1.154
abollados	0	1	1.154
abolieron	0	1	1.154
abolida	0	1	1.154
abogaba	0	1	1.154
abocose	0	1	1.154
aboco	0	1	1.154
abochornada	0	1	1.154
aboca	0	1	1.154
abnegaciones	0	1	1.154
ablande	0	1	1.154
ablandaría	0	1	1.154
ablanda	0	1	1.154
abigarrado	0	1	1.154
abigarradas	0	1	1.154
abiertamente	0	1	1.154
abejorro	0	1	1.154
abejón	0	1	1.154
abejas	0	1	1.154
abcesos	0	1	1.154
abatiendo	0	1	1.154
abatidísimo	0	1	1.154
abatida	0	1	1.154
abarcado	0	1	1.154
abarcaban	0	1	1.154
abarca	0	1	1.154
abanicón	0	1	1.154
abanicarse	0	1	1.154
abandonaros	0	1	1.154
abandonaron	0	1	1.154
abandonaría	0	1	1.154
abandonaremos	0	1	1.154
abandonalo	0	1	1.154
abalorio	0	1	1.154
abalanzándose	0	1	1.154
abalanzado	0	1	1.154
abajito	0	1	1.154
abadesa	0	1	1.154
ocurrido	15	27	1.151
barrio	15	27	1.151
somos	19	33	1.148
manda	19	33	1.148
conversación	61	93	1.135
pidió	18	16	1.130
novio	18	16	1.130
barba	18	16	1.130
vibraciones	5	3	1.121
turbó	5	3	1.121
turbar	5	3	1.121
tabique	5	3	1.121
solitarios	5	3	1.121
sois	5	3	1.121
sastres	5	3	1.121
ruinas	5	3	1.121
robaba	5	3	1.121
ría	5	3	1.121
retirada	5	3	1.121
recorría	5	3	1.121
recomendaciones	5	3	1.121
preguntaban	5	3	1.121
porción	5	3	1.121
perjuicio	5	3	1.121
palma	5	3	1.121
orquesta	5	3	1.121
opuso	5	3	1.121
oportuna	5	3	1.121
ola	5	3	1.121
ofendido	5	3	1.121
negativa	5	3	1.121
nacía	5	3	1.121
mojado	5	3	1.121
medidas	5	3	1.121
mares	5	3	1.121
manzana	5	3	1.121
mandil	5	3	1.121
mandaban	5	3	1.121
madrugar	5	3	1.121
llevase	5	3	1.121
llenado	5	3	1.121
lazos	5	3	1.121
infiel	5	3	1.121
imaginaba	5	3	1.121
heladas	5	3	1.121
habrán	5	3	1.121
fragua	5	3	1.121
flexible	5	3	1.121
figurándose	5	3	1.121
fieras	5	3	1.121
ferias	5	3	1.121
exageración	5	3	1.121
envueltos	5	3	1.121
entusiasmado	5	3	1.121
encinas	5	3	1.121
encerrarse	5	3	1.121
eléctrica	5	3	1.121
dramática	5	3	1.121
disfrazado	5	3	1.121
diplomático	5	3	1.121
danza	5	3	1.121
cuestas	5	3	1.121
cuchicheos	5	3	1.121
crujía	5	3	1.121
cortada	5	3	1.121
contarse	5	3	1.121
concurso	5	3	1.121
burdeos	5	3	1.121
bruces	5	3	1.121
atrocidad	5	3	1.121
aseguró	5	3	1.121
ardía	5	3	1.121
apuro	5	3	1.121
alcanza	5	3	1.121
alba	5	3	1.121
adónde	5	3	1.121
aceptaba	5	3	1.121
aburrirse	5	3	1.121
pozo	17	15	1.107
orejas	8	16	1.107
levantar	17	15	1.107
letra	17	15	1.107
horror	17	15	1.107
estudiar	8	16	1.107
bajaba	17	15	1.107
extremo	28	27	1.103
cada	175	201	1.101
comedor	43	44	1.089
recibía	16	14	1.085
pulso	16	14	1.085
penas	16	14	1.085
beber	16	14	1.085
perfectamente	27	26	1.073
cuándo	27	26	1.073
vecina	5	11	1.067
suele	5	11	1.067
restauración	5	11	1.067
relato	5	11	1.067
relación	5	11	1.067
policía	5	11	1.067
podré	5	11	1.067
pesetas	5	11	1.067
pavo	5	11	1.067
dichosa	5	11	1.067
debiera	5	11	1.067
cortado	5	11	1.067
comiendo	5	11	1.067
amistades	5	11	1.067
vestida	15	13	1.064
puramente	15	13	1.064
sombrero	33	53	1.061
tercera	10	19	1.057
cabello	10	19	1.057
unos	94	138	1.055
volviese	6	4	1.049
vientos	6	4	1.049
tropezó	6	4	1.049
tendido	6	4	1.049
telón	6	4	1.049
tardar	6	4	1.049
tacto	6	4	1.049
soñar	6	4	1.049
seductores	6	4	1.049
respectivos	6	4	1.049
representar	6	4	1.049
ras	6	4	1.049
pequeñas	6	4	1.049
obedecía	6	4	1.049
muros	6	4	1.049
llevarla	6	4	1.049
llamarle	6	4	1.049
lector	6	4	1.049
instituciones	6	4	1.049
inerte	6	4	1.049
excursión	6	4	1.049
excitada	6	4	1.049
estremeció	6	4	1.049
engañó	6	4	1.049
encarnado	6	4	1.049
empeñado	6	4	1.049
educado	6	4	1.049
duraba	6	4	1.049
cuna	6	4	1.049
conducía	6	4	1.049
chocar	6	4	1.049
cátedra	6	4	1.049
carlistas	6	4	1.049
aturdimiento	6	4	1.049
arrancaba	6	4	1.049
animaba	6	4	1.049
amargo	6	4	1.049
aficiones	6	4	1.049
acordarse	6	4	1.049
accidentes	6	4	1.049
abrazó	6	4	1.049
objetos	14	12	1.044
divertirse	14	12	1.044
atrevido	14	12	1.044
reía	20	34	1.034
razones	12	22	1.032
importancia	12	22	1.032
encuentro	12	22	1.032
dijera	12	22	1.032
declaró	12	22	1.032
vencido	13	11	1.027
sopa	13	11	1.027
corre	13	11	1.027
autor	13	11	1.027
otras	162	186	1.026
fino	18	31	1.024
conoce	16	28	1.019
falda	25	24	1.014
vestido	29	47	1.013
gustaba	29	47	1.013
violencia	7	5	1.012
venidas	7	5	1.012
usurero	7	5	1.012
somnolencia	7	5	1.012
silenciosa	7	5	1.012
severa	7	5	1.012
ruedas	7	5	1.012
región	7	5	1.012
quejas	7	5	1.012
pedían	7	5	1.012
pánico	7	5	1.012
palomas	7	5	1.012
pacífico	7	5	1.012
oculta	7	5	1.012
ideales	7	5	1.012
fúnebre	7	5	1.012
frecuencia	7	5	1.012
formado	7	5	1.012
espuma	7	5	1.012
encerrado	7	5	1.012
detenerse	7	5	1.012
colgado	7	5	1.012
castigar	7	5	1.012
salvo	12	10	1.011
pobrecita	12	10	1.011
músculos	12	10	1.011
morales	12	10	1.011
miel	12	10	1.011
inconveniente	12	10	1.011
hacerla	12	10	1.011
dejarse	12	10	1.011
criminal	12	10	1.011
cigarro	12	10	1.011
atreverse	12	10	1.011
armonía	12	10	1.011
abandono	12	10	1.011
color	53	56	1.001
puntillas	11	9	0.999
paraíso	11	9	0.999
gracioso	11	9	0.999
diálogo	11	9	0.999
cuyos	11	9	0.999
zapatillas	8	6	0.994
superioridad	8	6	0.994
solitaria	8	6	0.994
servicios	8	6	0.994
proyectos	8	6	0.994
pasear	8	6	0.994
ordinario	8	6	0.994
ocupaban	8	6	0.994
mortal	8	6	0.994
médicos	8	6	0.994
junto	61	92	0.994
hábil	8	6	0.994
groseras	8	6	0.994
galán	8	6	0.994
exigencias	8	6	0.994
exclamaba	8	6	0.994
engaña	8	6	0.994
duerme	8	6	0.994
dolorosa	8	6	0.994
distracciones	8	6	0.994
creo	97	108	0.994
comió	8	6	0.994
atravesó	8	6	0.994
asustó	8	6	0.994
abandonada	8	6	0.994
salvar	10	8	0.991
olvidaba	10	8	0.991
molino	10	8	0.991
mato	10	8	0.991
marchaba	10	8	0.991
llamarse	10	8	0.991
decidido	10	8	0.991
colorada	10	8	0.991
sequedad	9	7	0.989
sencillo	9	7	0.989
propuesto	9	7	0.989
programa	9	7	0.989
prensa	9	7	0.989
necesaria	9	7	0.989
efectos	9	7	0.989
contraria	9	7	0.989
codos	9	7	0.989
citas	9	7	0.989
abandonado	9	7	0.989
año	56	85	0.988
filosofía	24	23	0.984
primer	58	62	0.973
vía	7	14	0.969
trabajos	7	14	0.969
progreso	7	14	0.969
podrían	7	14	0.969
pequeño	7	14	0.969
notas	7	14	0.969
moscas	7	14	0.969
fácil	25	41	0.969
despacio	7	14	0.969
descubrir	7	14	0.969
cortesía	7	14	0.969
vino	54	82	0.958
sangre	63	68	0.951
público	51	54	0.944
fuera	185	260	0.944
serio	38	39	0.939
salva	4	9	0.936
sacarle	4	9	0.936
rasgo	4	9	0.936
piden	4	9	0.936
permitían	4	9	0.936
perfecto	4	9	0.936
napoleón	4	9	0.936
mostrar	4	9	0.936
meterle	4	9	0.936
máscara	4	9	0.936
incluso	4	9	0.936
implacable	4	9	0.936
gruesa	4	9	0.936
gala	4	9	0.936
fijó	4	9	0.936
extendió	4	9	0.936
estábamos	4	9	0.936
dotes	4	9	0.936
docena	4	9	0.936
distracción	4	9	0.936
distinto	4	9	0.936
diario	4	9	0.936
depósito	4	9	0.936
contestación	4	9	0.936
consentir	4	9	0.936
carmen	4	9	0.936
bendita	4	9	0.936
arrepentida	4	9	0.936
acabó	22	21	0.925
vecino	9	17	0.921
tamaño	9	17	0.921
nacimiento	9	17	0.921
merece	9	17	0.921
lance	9	17	0.921
espacio	9	17	0.921
divina	9	17	0.921
crecía	9	17	0.921
ademán	9	17	0.921
ama	56	60	0.916
suyo	35	55	0.910
juntas	11	20	0.899
bondad	11	20	0.899
amantes	11	20	0.899
nerviosa	21	20	0.896
vienen	15	26	0.894
pasaron	15	26	0.894
dormía	29	29	0.883
opinión	36	37	0.878
tocaba	20	19	0.867
nosotros	42	44	0.862
mire	31	49	0.855
contento	28	28	0.853
ese	165	232	0.851
precisamente	19	18	0.838
montes	19	18	0.838
sesenta	6	12	0.830
saltó	6	12	0.830
saliera	6	12	0.830
príncipe	6	12	0.830
leña	6	12	0.830
error	6	12	0.830
concluyó	6	12	0.830
celestial	6	12	0.830
cavilaciones	6	12	0.830
acompañado	6	12	0.830
brazo	67	99	0.828
escribir	27	27	0.822
bastante	54	81	0.820
respecto	20	33	0.816
dignidad	20	33	0.816
hablar	133	153	0.813
volvieron	18	17	0.809
trabaja	3	7	0.809
torno	3	7	0.809
tieso	3	7	0.809
sostenían	3	7	0.809
sitios	3	7	0.809
sigo	3	7	0.809
resultó	3	7	0.809
repuso	3	7	0.809
raras	3	7	0.809
quisiese	3	7	0.809
quedaría	3	7	0.809
progresista	3	7	0.809
políticos	3	7	0.809
piense	3	7	0.809
picardía	3	7	0.809
penosa	3	7	0.809
parada	3	7	0.809
ocurrían	3	7	0.809
ocupado	3	7	0.809
obediencia	3	7	0.809
mortificaba	3	7	0.809
migas	3	7	0.809
mercantil	3	7	0.809
lucido	3	7	0.809
lealtad	3	7	0.809
infamia	3	7	0.809
indudable	3	7	0.809
índole	3	7	0.809
impropio	3	7	0.809
halló	3	7	0.809
guapísima	3	7	0.809
ganando	3	7	0.809
gafas	3	7	0.809
esforzaba	3	7	0.809
distintas	3	7	0.809
diese	3	7	0.809
desgracias	3	7	0.809
descuide	3	7	0.809
decidirse	3	7	0.809
cortos	3	7	0.809
clavó	3	7	0.809
china	3	7	0.809
busto	3	7	0.809
burlesca	3	7	0.809
bobo	3	7	0.809
atrevo	3	7	0.809
arriba	74	82	0.809
apretando	3	7	0.809
aprendiendo	3	7	0.809
anarquía	3	7	0.809
mía	81	118	0.807
ventana	33	34	0.788
sentó	33	34	0.788
nuestra	33	34	0.788
sagrada	8	15	0.785
niñez	8	15	0.785
habitaciones	8	15	0.785
guardia	8	15	0.785
bulto	8	15	0.785
donde	186	218	0.782
apareció	16	27	0.782
reían	17	16	0.780
personal	17	16	0.780
pagar	17	16	0.780
montón	17	16	0.780
hable	17	16	0.780
afán	17	16	0.780
miradas	42	64	0.777
víctima	25	40	0.776
vuelta	62	68	0.774
uso	14	24	0.770
podrá	14	24	0.770
debían	14	24	0.770
ayuda	14	24	0.770
furor	10	18	0.767
familias	10	18	0.767
come	10	18	0.767
excelente	12	21	0.764
decirlo	12	21	0.764
actos	12	21	0.764
gloria	32	33	0.758
caía	32	33	0.758
ladrón	16	15	0.752
enfermo	40	61	0.747
entraba	53	79	0.740
raza	15	14	0.723
procesión	15	14	0.723
escape	15	14	0.723
coche	49	53	0.722
clase	49	53	0.722
felicidad	23	23	0.701
conocido	23	23	0.701
nunca	165	230	0.698
suma	14	13	0.695
sucia	14	13	0.695
falsa	14	13	0.695
apretaba	14	13	0.695
acostarse	14	13	0.695
viviendo	2	5	0.694
vendré	2	5	0.694
vapor	2	5	0.694
valer	2	5	0.694
vaca	2	5	0.694
usado	2	5	0.694
tramo	2	5	0.694
trágica	2	5	0.694
tragando	2	5	0.694
toques	2	5	0.694
tirado	2	5	0.694
terquedad	2	5	0.694
sostengo	2	5	0.694
sorprendida	2	5	0.694
robustez	2	5	0.694
reza	2	5	0.694
reunión	2	5	0.694
repetición	2	5	0.694
rascaba	2	5	0.694
radiante	2	5	0.694
quitan	2	5	0.694
pucheros	2	5	0.694
puchero	2	5	0.694
protector	2	5	0.694
producían	2	5	0.694
produce	2	5	0.694
poseer	2	5	0.694
pintaba	2	5	0.694
pierdo	2	5	0.694
pieles	2	5	0.694
pides	2	5	0.694
picada	2	5	0.694
pertenecían	2	5	0.694
permitiéndose	2	5	0.694
perdones	2	5	0.694
pensativa	2	5	0.694
patética	2	5	0.694
patada	2	5	0.694
párrafo	2	5	0.694
ordenó	2	5	0.694
operaciones	2	5	0.694
observa	2	5	0.694
nido	2	5	0.694
muñeca	2	5	0.694
mudarse	2	5	0.694
molde	2	5	0.694
mimoso	2	5	0.694
menudas	2	5	0.694
menores	2	5	0.694
mejorado	2	5	0.694
maldición	2	5	0.694
madrileños	2	5	0.694
lunes	2	5	0.694
llevándola	2	5	0.694
llamaré	2	5	0.694
levantaron	2	5	0.694
lee	2	5	0.694
labores	2	5	0.694
joyas	2	5	0.694
inventaba	2	5	0.694
inspección	2	5	0.694
insistencia	2	5	0.694
ínfulas	2	5	0.694
gordas	2	5	0.694
gatas	2	5	0.694
gastar	2	5	0.694
garras	2	5	0.694
festivo	2	5	0.694
estén	2	5	0.694
esconde	2	5	0.694
equivocarse	2	5	0.694
entrevista	2	5	0.694
entrever	2	5	0.694
entraría	2	5	0.694
enseñarle	2	5	0.694
enemiga	2	5	0.694
encuentran	2	5	0.694
encontraría	2	5	0.694
ejercicios	2	5	0.694
dominante	2	5	0.694
dirigir	2	5	0.694
dijéramos	2	5	0.694
diferencias	2	5	0.694
desvanecía	2	5	0.694
despertaban	2	5	0.694
descansa	2	5	0.694
desarrollo	2	5	0.694
desabrido	2	5	0.694
dejas	2	5	0.694
date	2	5	0.694
curva	2	5	0.694
curado	2	5	0.694
cumplidos	2	5	0.694
cortaba	2	5	0.694
correspondiente	2	5	0.694
contara	2	5	0.694
conozca	2	5	0.694
confidencia	2	5	0.694
condenados	2	5	0.694
concordia	2	5	0.694
comunicó	2	5	0.694
comerse	2	5	0.694
cesó	2	5	0.694
castillos	2	5	0.694
cabezadas	2	5	0.694
bandeja	2	5	0.694
avanzó	2	5	0.694
atenta	2	5	0.694
atada	2	5	0.694
apreciaba	2	5	0.694
apoyo	2	5	0.694
alturas	2	5	0.694
albañiles	2	5	0.694
acertó	2	5	0.694
acercando	2	5	0.694
acabara	2	5	0.694
reposo	5	10	0.692
puñal	5	10	0.692
paga	5	10	0.692
padrino	5	10	0.692
moneda	5	10	0.692
existía	5	10	0.692
exaltado	5	10	0.692
estrella	5	10	0.692
estando	5	10	0.692
efectivamente	5	10	0.692
echan	5	10	0.692
cuestiones	5	10	0.692
ceño	5	10	0.692
anunciaba	5	10	0.692
angustia	5	10	0.692
almohada	5	10	0.692
adquirido	5	10	0.692
acostumbrada	5	10	0.692
siguió	41	62	0.691
costumbre	42	45	0.687
permitía	17	28	0.683
miraban	17	28	0.683
creyendo	17	28	0.683
besos	17	28	0.683
la	11489	14563	0.672
tardes	13	12	0.668
sospechaba	13	12	0.668
sentaba	13	12	0.668
parroquia	13	12	0.668
comprendido	13	12	0.668
aparte	13	12	0.668
traído	15	25	0.665
simpático	15	25	0.665
satisfacción	15	25	0.665
papeles	15	25	0.665
bolsillo	15	25	0.665
así	347	419	0.651
tome	7	13	0.650
tocó	7	13	0.650
síntomas	7	13	0.650
ricas	7	13	0.650
perdonar	7	13	0.650
paja	7	13	0.650
misterios	7	13	0.650
dormida	7	13	0.650
días	179	248	0.650
delicada	7	13	0.650
artículos	7	13	0.650
tranquilidad	13	22	0.649
acera	13	22	0.649
visitar	12	11	0.641
sucio	12	11	0.641
odio	12	11	0.641
observaba	12	11	0.641
llanto	12	11	0.641
engaño	12	11	0.641
comido	12	11	0.641
primeras	21	21	0.640
momentos	21	21	0.640
volverse	11	19	0.639
recado	11	19	0.639
once	11	19	0.639
llamó	28	29	0.639
sujeto	9	16	0.637
prenda	9	16	0.637
negras	9	16	0.637
estudio	9	16	0.637
delicado	9	16	0.637
parecía	267	320	0.634
zurriago	2	1	0.633
zánganos	2	1	0.633
werther	2	1	0.633
vuelvan	2	1	0.633
volado	2	1	0.633
vocabulario	2	1	0.633
vivieron	2	1	0.633
vivaracho	2	1	0.633
visual	2	1	0.633
viso	2	1	0.633
vislumbraba	2	1	0.633
viril	2	1	0.633
viles	2	1	0.633
viesen	2	1	0.633
vergonzante	2	1	0.633
venirse	2	1	0.633
vendió	2	1	0.633
vencidas	2	1	0.633
valerse	2	1	0.633
vacilaciones	2	1	0.633
utilitaria	2	1	0.633
tutti	2	1	0.633
tuteaba	2	1	0.633
tumba	2	1	0.633
trompetas	2	1	0.633
triunfaba	2	1	0.633
trepar	2	1	0.633
traviesa	2	1	0.633
tratamos	2	1	0.633
trapillo	2	1	0.633
transacciones	2	1	0.633
tranquilizar	2	1	0.633
traducción	2	1	0.633
trabajadores	2	1	0.633
tosió	2	1	0.633
torrecilla	2	1	0.633
torpezas	2	1	0.633
tonel	2	1	0.633
tomándola	2	1	0.633
tirantez	2	1	0.633
tirador	2	1	0.633
tinto	2	1	0.633
tiemblo	2	1	0.633
tic	2	1	0.633
tente	2	1	0.633
templos	2	1	0.633
temperatura	2	1	0.633
tardase	2	1	0.633
tapete	2	1	0.633
tangible	2	1	0.633
talones	2	1	0.633
talón	2	1	0.633
tacones	2	1	0.633
suspendida	2	1	0.633
surtidores	2	1	0.633
suplicando	2	1	0.633
supiese	2	1	0.633
sujetaban	2	1	0.633
sugestiones	2	1	0.633
sugería	2	1	0.633
subrepticiamente	2	1	0.633
subiera	2	1	0.633
subasta	2	1	0.633
subamos	2	1	0.633
sospechosa	2	1	0.633
sortijas	2	1	0.633
sorprendidas	2	1	0.633
sordidez	2	1	0.633
soñolienta	2	1	0.633
socialistas	2	1	0.633
sobro	2	1	0.633
soberana	2	1	0.633
situado	2	1	0.633
sirviendo	2	1	0.633
simulacro	2	1	0.633
sillones	2	1	0.633
significativa	2	1	0.633
significado	2	1	0.633
sexto	2	1	0.633
setos	2	1	0.633
sentirla	2	1	0.633
seguras	2	1	0.633
segundón	2	1	0.633
seducido	2	1	0.633
sapos	2	1	0.633
sangría	2	1	0.633
salvedades	2	1	0.633
sacristanes	2	1	0.633
sacos	2	1	0.633
sacándole	2	1	0.633
rutinario	2	1	0.633
rozaban	2	1	0.633
rondar	2	1	0.633
romana	2	1	0.633
rollo	2	1	0.633
rogado	2	1	0.633
rodeo	2	1	0.633
rodeados	2	1	0.633
rizoso	2	1	0.633
riquísima	2	1	0.633
rinden	2	1	0.633
riesgo	2	1	0.633
retumbó	2	1	0.633
retumbaba	2	1	0.633
retrasar	2	1	0.633
resuelva	2	1	0.633
resucitado	2	1	0.633
respete	2	1	0.633
resonar	2	1	0.633
reses	2	1	0.633
resbaladiza	2	1	0.633
republicanismo	2	1	0.633
repetido	2	1	0.633
reñían	2	1	0.633
rendir	2	1	0.633
regulares	2	1	0.633
referido	2	1	0.633
redondas	2	1	0.633
rectificó	2	1	0.633
recorren	2	1	0.633
recetó	2	1	0.633
recaída	2	1	0.633
rebelaba	2	1	0.633
razonables	2	1	0.633
rayaba	2	1	0.633
rapé	2	1	0.633
ranas	2	1	0.633
raída	2	1	0.633
radicalmente	2	1	0.633
racionales	2	1	0.633
rabiaba	2	1	0.633
quintas	2	1	0.633
quietas	2	1	0.633
queso	2	1	0.633
queridísimo	2	1	0.633
quejado	2	1	0.633
purísimo	2	1	0.633
puñetazos	2	1	0.633
puntiagudos	2	1	0.633
pulgar	2	1	0.633
protegido	2	1	0.633
proporcionada	2	1	0.633
proponerle	2	1	0.633
propicia	2	1	0.633
pronuncian	2	1	0.633
procaz	2	1	0.633
prisioneros	2	1	0.633
presentados	2	1	0.633
preparase	2	1	0.633
preguntárselo	2	1	0.633
predilecta	2	1	0.633
precocidad	2	1	0.633
precisar	2	1	0.633
pormenor	2	1	0.633
popularidad	2	1	0.633
polichinela	2	1	0.633
polémicas	2	1	0.633
podrido	2	1	0.633
pliegue	2	1	0.633
pleitos	2	1	0.633
pimientos	2	1	0.633
pilluelos	2	1	0.633
pila	2	1	0.633
pican	2	1	0.633
petitorio	2	1	0.633
pesimista	2	1	0.633
perpetuo	2	1	0.633
pérdida	2	1	0.633
pensase	2	1	0.633
pediré	2	1	0.633
pecadores	2	1	0.633
pecaban	2	1	0.633
pausas	2	1	0.633
pausada	2	1	0.633
patrón	2	1	0.633
pato	2	1	0.633
pataleo	2	1	0.633
pastoral	2	1	0.633
pásmese	2	1	0.633
pasiva	2	1	0.633
pasajero	2	1	0.633
pasajeras	2	1	0.633
parecerían	2	1	0.633
parecerá	2	1	0.633
paquita	2	1	0.633
palomar	2	1	0.633
padrenuestros	2	1	0.633
osos	2	1	0.633
osaría	2	1	0.633
orientales	2	1	0.633
orfandad	2	1	0.633
ordenanza	2	1	0.633
ordenados	2	1	0.633
olorosa	2	1	0.633
oigan	2	1	0.633
ofrecen	2	1	0.633
oficialmente	2	1	0.633
ofendía	2	1	0.633
ocurrencias	2	1	0.633
ocultárselo	2	1	0.633
obsequios	2	1	0.633
obsequio	2	1	0.633
obrero	2	1	0.633
obligándole	2	1	0.633
obligan	2	1	0.633
nueces	2	1	0.633
nocturnas	2	1	0.633
negrura	2	1	0.633
negación	2	1	0.633
necias	2	1	0.633
necesitará	2	1	0.633
nauseabundo	2	1	0.633
mundanos	2	1	0.633
mundana	2	1	0.633
mueca	2	1	0.633
muchedumbres	2	1	0.633
motín	2	1	0.633
mordiéndose	2	1	0.633
mordiendo	2	1	0.633
morados	2	1	0.633
moqueta	2	1	0.633
molestas	2	1	0.633
mister	2	1	0.633
misiones	2	1	0.633
miliciano	2	1	0.633
miente	2	1	0.633
midiendo	2	1	0.633
meten	2	1	0.633
metálicas	2	1	0.633
meriendas	2	1	0.633
menoscabo	2	1	0.633
medía	2	1	0.633
medallas	2	1	0.633
matrona	2	1	0.633
matiz	2	1	0.633
marcho	2	1	0.633
mansión	2	1	0.633
manolito	2	1	0.633
maniático	2	1	0.633
maneja	2	1	0.633
mandato	2	1	0.633
mancharse	2	1	0.633
maltratada	2	1	0.633
malsana	2	1	0.633
malicias	2	1	0.633
malhumorado	2	1	0.633
maldicientes	2	1	0.633
maldice	2	1	0.633
mágica	2	1	0.633
lunar	2	1	0.633
luciría	2	1	0.633
luce	2	1	0.633
lograr	2	1	0.633
llegas	2	1	0.633
llana	2	1	0.633
llamadas	2	1	0.633
liturgia	2	1	0.633
literarios	2	1	0.633
listos	2	1	0.633
limpió	2	1	0.633
licores	2	1	0.633
librotes	2	1	0.633
librepensadores	2	1	0.633
librándose	2	1	0.633
libertinos	2	1	0.633
lesa	2	1	0.633
leerla	2	1	0.633
lavandera	2	1	0.633
lavan	2	1	0.633
lamentándose	2	1	0.633
ladró	2	1	0.633
juvenil	2	1	0.633
jurando	2	1	0.633
jura	2	1	0.633
júpiter	2	1	0.633
juntan	2	1	0.633
jornada	2	1	0.633
joco	2	1	0.633
jinetes	2	1	0.633
jilguero	2	1	0.633
jefes	2	1	0.633
jactancia	2	1	0.633
irrevocable	2	1	0.633
irrespetuosas	2	1	0.633
irreparable	2	1	0.633
invitaba	2	1	0.633
inventando	2	1	0.633
inventada	2	1	0.633
inventa	2	1	0.633
invadido	2	1	0.633
inundaban	2	1	0.633
intolerable	2	1	0.633
intervino	2	1	0.633
intervalo	2	1	0.633
interrupciones	2	1	0.633
interesar	2	1	0.633
inteligible	2	1	0.633
insufribles	2	1	0.633
instruido	2	1	0.633
insistente	2	1	0.633
inquietas	2	1	0.633
inmóviles	2	1	0.633
injusto	2	1	0.633
ingenios	2	1	0.633
influye	2	1	0.633
inflamados	2	1	0.633
infieles	2	1	0.633
inesperada	2	1	0.633
industrias	2	1	0.633
incomoda	2	1	0.633
impurezas	2	1	0.633
improvisar	2	1	0.633
improvisado	2	1	0.633
impresionable	2	1	0.633
importación	2	1	0.633
imparcialmente	2	1	0.633
impacientarse	2	1	0.633
imaginando	2	1	0.633
idólatra	2	1	0.633
huracán	2	1	0.633
hunde	2	1	0.633
humillaciones	2	1	0.633
horroriza	2	1	0.633
horizontales	2	1	0.633
hinchando	2	1	0.633
hinchados	2	1	0.633
herejías	2	1	0.633
herederos	2	1	0.633
hablarse	2	1	0.633
habitaba	2	1	0.633
guirnaldas	2	1	0.633
guiñó	2	1	0.633
gótico	2	1	0.633
gitana	2	1	0.633
gesticulaba	2	1	0.633
gastados	2	1	0.633
gárrula	2	1	0.633
garantías	2	1	0.633
ganadas	2	1	0.633
gallego	2	1	0.633
furores	2	1	0.633
furiosos	2	1	0.633
frecuenta	2	1	0.633
fomento	2	1	0.633
fofa	2	1	0.633
flojo	2	1	0.633
finito	2	1	0.633
figurémonos	2	1	0.633
férula	2	1	0.633
ferrocarril	2	1	0.633
femenina	2	1	0.633
fecunda	2	1	0.633
fauces	2	1	0.633
fatuo	2	1	0.633
fatigas	2	1	0.633
fatigaba	2	1	0.633
fariseos	2	1	0.633
fantástica	2	1	0.633
fanática	2	1	0.633
faltaron	2	1	0.633
faltaría	2	1	0.633
fabricar	2	1	0.633
extrañó	2	1	0.633
exteriores	2	1	0.633
exquisitas	2	1	0.633
expresaban	2	1	0.633
explícito	2	1	0.633
explicado	2	1	0.633
exordio	2	1	0.633
exigen	2	1	0.633
excusó	2	1	0.633
exclusiva	2	1	0.633
estucada	2	1	0.633
estrepitosa	2	1	0.633
estrellitas	2	1	0.633
estrangulado	2	1	0.633
estirando	2	1	0.633
estiman	2	1	0.633
estela	2	1	0.633
estanco	2	1	0.633
estadística	2	1	0.633
espinoso	2	1	0.633
espías	2	1	0.633
espesos	2	1	0.633
esperándole	2	1	0.633
espectador	2	1	0.633
especies	2	1	0.633
esferas	2	1	0.633
escudriñar	2	1	0.633
escudriñando	2	1	0.633
escuálida	2	1	0.633
escriben	2	1	0.633
escriba	2	1	0.633
escondites	2	1	0.633
escondían	2	1	0.633
escoge	2	1	0.633
esclavos	2	1	0.633
escépticos	2	1	0.633
escalo	2	1	0.633
esbeltas	2	1	0.633
episodios	2	1	0.633
envuelve	2	1	0.633
envueltas	2	1	0.633
envidioso	2	1	0.633
envenenado	2	1	0.633
envenenada	2	1	0.633
entristecían	2	1	0.633
entrañable	2	1	0.633
entornados	2	1	0.633
enterrarle	2	1	0.633
enterneció	2	1	0.633
enternecimiento	2	1	0.633
enterasen	2	1	0.633
engomado	2	1	0.633
enfermizo	2	1	0.633
enérgicamente	2	1	0.633
encomendarse	2	1	0.633
enciende	2	1	0.633
enamoradas	2	1	0.633
empresario	2	1	0.633
emprendido	2	1	0.633
empapelar	2	1	0.633
embozos	2	1	0.633
emborrachado	2	1	0.633
embargado	2	1	0.633
educadas	2	1	0.633
educaba	2	1	0.633
edificado	2	1	0.633
duraban	2	1	0.633
dolían	2	1	0.633
doctores	2	1	0.633
divididos	2	1	0.633
distingos	2	1	0.633
disputan	2	1	0.633
dispuestas	2	1	0.633
dispénseme	2	1	0.633
disimula	2	1	0.633
disfrutar	2	1	0.633
diosa	2	1	0.633
dimensiones	2	1	0.633
dignamente	2	1	0.633
dígalo	2	1	0.633
diecinueve	2	1	0.633
dicharachos	2	1	0.633
diariamente	2	1	0.633
diabólicas	2	1	0.633
diablillos	2	1	0.633
devorando	2	1	0.633
determinada	2	1	0.633
detenimiento	2	1	0.633
desvergonzada	2	1	0.633
desquite	2	1	0.633
despreocupación	2	1	0.633
desprecian	2	1	0.633
despojado	2	1	0.633
despilfarros	2	1	0.633
despertarla	2	1	0.633
despedir	2	1	0.633
desmenuzar	2	1	0.633
desmayado	2	1	0.633
deslumbrado	2	1	0.633
deslumbraba	2	1	0.633
desengaños	2	1	0.633
descuidadas	2	1	0.633
desconfía	2	1	0.633
descarado	2	1	0.633
descansando	2	1	0.633
depositó	2	1	0.633
dependía	2	1	0.633
deleitaba	2	1	0.633
dejarlo	2	1	0.633
dejarán	2	1	0.633
defiendo	2	1	0.633
dedicaban	2	1	0.633
decreto	2	1	0.633
declare	2	1	0.633
declararse	2	1	0.633
decirlas	2	1	0.633
décimas	2	1	0.633
decaer	2	1	0.633
decadente	2	1	0.633
curarme	2	1	0.633
cultivar	2	1	0.633
culminante	2	1	0.633
culinaria	2	1	0.633
cueva	2	1	0.633
cuchicheaban	2	1	0.633
cubrían	2	1	0.633
crujió	2	1	0.633
cruelmente	2	1	0.633
cromos	2	1	0.633
credulidad	2	1	0.633
créditos	2	1	0.633
creado	2	1	0.633
costar	2	1	0.633
cortésmente	2	1	0.633
cortan	2	1	0.633
corrompido	2	1	0.633
coros	2	1	0.633
coronada	2	1	0.633
cordialidad	2	1	0.633
coqueterías	2	1	0.633
copos	2	1	0.633
copón	2	1	0.633
convertidas	2	1	0.633
convenio	2	1	0.633
contradictorias	2	1	0.633
construían	2	1	0.633
consta	2	1	0.633
conspirar	2	1	0.633
consolaban	2	1	0.633
consigue	2	1	0.633
consagrado	2	1	0.633
conocerla	2	1	0.633
confundido	2	1	0.633
conduce	2	1	0.633
condicional	2	1	0.633
condeno	2	1	0.633
concurridos	2	1	0.633
conceder	2	1	0.633
conato	2	1	0.633
comunicar	2	1	0.633
comprendiera	2	1	0.633
comprendí	2	1	0.633
compleja	2	1	0.633
complaciéndose	2	1	0.633
complacerle	2	1	0.633
compensar	2	1	0.633
compara	2	1	0.633
compadecerse	2	1	0.633
comedido	2	1	0.633
combate	2	1	0.633
columbrar	2	1	0.633
coliseo	2	1	0.633
colina	2	1	0.633
colgadura	2	1	0.633
colapso	2	1	0.633
clavel	2	1	0.633
clavarle	2	1	0.633
citó	2	1	0.633
citados	2	1	0.633
cima	2	1	0.633
cilicio	2	1	0.633
cierre	2	1	0.633
chupan	2	1	0.633
chorreaba	2	1	0.633
chiquita	2	1	0.633
chinescas	2	1	0.633
chasquido	2	1	0.633
césar	2	1	0.633
ceremoniosa	2	1	0.633
cenó	2	1	0.633
cenado	2	1	0.633
celibato	2	1	0.633
celestiales	2	1	0.633
celdas	2	1	0.633
cegado	2	1	0.633
cédula	2	1	0.633
cede	2	1	0.633
cayeran	2	1	0.633
catolicismo	2	1	0.633
casualidades	2	1	0.633
castañuelas	2	1	0.633
castañas	2	1	0.633
cartucho	2	1	0.633
carpintero	2	1	0.633
cardos	2	1	0.633
caprichosos	2	1	0.633
cantado	2	1	0.633
cansando	2	1	0.633
calidades	2	1	0.633
calenturienta	2	1	0.633
buscaron	2	1	0.633
buque	2	1	0.633
brotó	2	1	0.633
brevedad	2	1	0.633
bramaba	2	1	0.633
bote	2	1	0.633
bostezo	2	1	0.633
borrosa	2	1	0.633
borracha	2	1	0.633
bochorno	2	1	0.633
bobadas	2	1	0.633
blasfemando	2	1	0.633
besa	2	1	0.633
benéfica	2	1	0.633
bebiendo	2	1	0.633
beatos	2	1	0.633
batista	2	1	0.633
batiéndose	2	1	0.633
batacazo	2	1	0.633
bañándose	2	1	0.633
banquero	2	1	0.633
balas	2	1	0.633
bajeza	2	1	0.633
bailaban	2	1	0.633
azotando	2	1	0.633
azota	2	1	0.633
ayúdeme	2	1	0.633
ayude	2	1	0.633
avellana	2	1	0.633
avanzada	2	1	0.633
autoriza	2	1	0.633
auténtica	2	1	0.633
atraviesa	2	1	0.633
atravesado	2	1	0.633
atónitos	2	1	0.633
ateos	2	1	0.633
atendió	2	1	0.633
ásperas	2	1	0.633
asombrado	2	1	0.633
asomaron	2	1	0.633
asomara	2	1	0.633
asiduo	2	1	0.633
asesinado	2	1	0.633
artificios	2	1	0.633
artificiales	2	1	0.633
arrullo	2	1	0.633
arruinando	2	1	0.633
arrojo	2	1	0.633
arrojaron	2	1	0.633
arrojarle	2	1	0.633
arraigado	2	1	0.633
arqueológica	2	1	0.633
armoniosas	2	1	0.633
armería	2	1	0.633
arisca	2	1	0.633
argentina	2	1	0.633
árbitro	2	1	0.633
apoteosis	2	1	0.633
apoderó	2	1	0.633
aplicaciones	2	1	0.633
aplica	2	1	0.633
aplaude	2	1	0.633
aplasto	2	1	0.633
aplastado	2	1	0.633
aparentemente	2	1	0.633
aparatosa	2	1	0.633
aparatos	2	1	0.633
añadido	2	1	0.633
anunciarse	2	1	0.633
anticuado	2	1	0.633
aniversario	2	1	0.633
aniquilamiento	2	1	0.633
angulosa	2	1	0.633
angostas	2	1	0.633
anden	2	1	0.633
andamiaje	2	1	0.633
anatomía	2	1	0.633
analizar	2	1	0.633
amorosamente	2	1	0.633
amazona	2	1	0.633
amargos	2	1	0.633
amargor	2	1	0.633
amanerado	2	1	0.633
amando	2	1	0.633
aman	2	1	0.633
alumbrar	2	1	0.633
altozanos	2	1	0.633
alternativamente	2	1	0.633
alternaban	2	1	0.633
alimentarse	2	1	0.633
alimentaba	2	1	0.633
alhambra	2	1	0.633
aleluya	2	1	0.633
alegra	2	1	0.633
alcoholismo	2	1	0.633
alarmar	2	1	0.633
alarmado	2	1	0.633
alambicados	2	1	0.633
ahogarle	2	1	0.633
ahogándose	2	1	0.633
ahoga	2	1	0.633
agarrado	2	1	0.633
afortunado	2	1	0.633
afligidos	2	1	0.633
advertirle	2	1	0.633
advertida	2	1	0.633
advertencia	2	1	0.633
adquirida	2	1	0.633
adelantarse	2	1	0.633
adán	2	1	0.633
acusarse	2	1	0.633
acuesta	2	1	0.633
acuerdan	2	1	0.633
actualmente	2	1	0.633
acostumbrados	2	1	0.633
acordes	2	1	0.633
acordaban	2	1	0.633
aconseja	2	1	0.633
acomodo	2	1	0.633
aclaraba	2	1	0.633
acercase	2	1	0.633
acariciaba	2	1	0.633
académico	2	1	0.633
académica	2	1	0.633
abusar	2	1	0.633
aburrían	2	1	0.633
abuelos	2	1	0.633
abstracciones	2	1	0.633
abstinencia	2	1	0.633
abriría	2	1	0.633
abriera	2	1	0.633
aberración	2	1	0.633
abdicar	2	1	0.633
llena	40	43	0.631
sólo	172	203	0.616
so	11	10	0.615
semanas	11	10	0.615
proyecto	11	10	0.615
platos	11	10	0.615
orgullosa	11	10	0.615
mayo	11	10	0.615
magnífico	11	10	0.615
iglesias	11	10	0.615
dudar	11	10	0.615
conocían	11	10	0.615
amparo	11	10	0.615
viviendas	1	3	0.613
vivan	1	3	0.613
vistoso	1	3	0.613
visionaria	1	3	0.613
visiblemente	1	3	0.613
vidrio	1	3	0.613
veterano	1	3	0.613
vergonzosas	1	3	0.613
venta	1	3	0.613
vendrás	1	3	0.613
vencedora	1	3	0.613
velón	1	3	0.613
veintitrés	1	3	0.613
vehículo	1	3	0.613
vehemencia	1	3	0.613
variaba	1	3	0.613
valdría	1	3	0.613
vagaban	1	3	0.613
uníase	1	3	0.613
tunanta	1	3	0.613
tufillo	1	3	0.613
tribunales	1	3	0.613
trepidación	1	3	0.613
traté	1	3	0.613
tratarse	1	3	0.613
tratarla	1	3	0.613
transcurrido	1	3	0.613
tramando	1	3	0.613
tragué	1	3	0.613
traerla	1	3	0.613
traería	1	3	0.613
trabajó	1	3	0.613
tomada	1	3	0.613
tiesos	1	3	0.613
tiernísimo	1	3	0.613
ternezas	1	3	0.613
terminando	1	3	0.613
tendiendo	1	3	0.613
temido	1	3	0.613
temerario	1	3	0.613
telégrafos	1	3	0.613
teclas	1	3	0.613
teatrales	1	3	0.613
tardaron	1	3	0.613
tardado	1	3	0.613
surgido	1	3	0.613
suposición	1	3	0.613
suplico	1	3	0.613
sujetándole	1	3	0.613
sufrimientos	1	3	0.613
sostenido	1	3	0.613
sospechó	1	3	0.613
soportar	1	3	0.613
sonda	1	3	0.613
sonada	1	3	0.613
solterón	1	3	0.613
soltaron	1	3	0.613
sólido	1	3	0.613
solidaridad	1	3	0.613
solamente	1	3	0.613
sobresalto	1	3	0.613
sobresaltada	1	3	0.613
soberano	1	3	0.613
sirva	1	3	0.613
sien	1	3	0.613
serpiente	1	3	0.613
serenarse	1	3	0.613
separaban	1	3	0.613
sello	1	3	0.613
seguirá	1	3	0.613
secciones	1	3	0.613
salvó	1	3	0.613
saluda	1	3	0.613
sacudirse	1	3	0.613
sacada	1	3	0.613
rúbrica	1	3	0.613
ron	1	3	0.613
revolucionarios	1	3	0.613
reunidos	1	3	0.613
resurrección	1	3	0.613
resuello	1	3	0.613
respuestas	1	3	0.613
reprendía	1	3	0.613
replicaba	1	3	0.613
renovación	1	3	0.613
remoto	1	3	0.613
regularmente	1	3	0.613
regresó	1	3	0.613
reglamento	1	3	0.613
registrar	1	3	0.613
refrán	1	3	0.613
réditos	1	3	0.613
reconocieron	1	3	0.613
reconocerle	1	3	0.613
recibida	1	3	0.613
rebosando	1	3	0.613
raudal	1	3	0.613
ración	1	3	0.613
racha	1	3	0.613
quito	1	3	0.613
quítese	1	3	0.613
quitaron	1	3	0.613
querrías	1	3	0.613
quepa	1	3	0.613
quedaré	1	3	0.613
pueriles	1	3	0.613
proposiciones	1	3	0.613
propagandista	1	3	0.613
prodigiosa	1	3	0.613
presentimientos	1	3	0.613
presenciado	1	3	0.613
pregúntaselo	1	3	0.613
pregonar	1	3	0.613
prefiriendo	1	3	0.613
precipitó	1	3	0.613
precipitadamente	1	3	0.613
precios	1	3	0.613
posee	1	3	0.613
portezuela	1	3	0.613
porquería	1	3	0.613
póngase	1	3	0.613
platillos	1	3	0.613
planchar	1	3	0.613
piensan	1	3	0.613
picaresco	1	3	0.613
pesara	1	3	0.613
persuasión	1	3	0.613
peros	1	3	0.613
permito	1	3	0.613
permitir	1	3	0.613
permitieron	1	3	0.613
perdonaría	1	3	0.613
perdiéndose	1	3	0.613
peras	1	3	0.613
pequeñuelos	1	3	0.613
pensamos	1	3	0.613
peluquería	1	3	0.613
peinar	1	3	0.613
peinadas	1	3	0.613
pegarse	1	3	0.613
patriota	1	3	0.613
pastillas	1	3	0.613
pasmadas	1	3	0.613
participaba	1	3	0.613
panecillo	1	3	0.613
pamplinas	1	3	0.613
padezco	1	3	0.613
ovillo	1	3	0.613
oprimiendo	1	3	0.613
oprimida	1	3	0.613
opresión	1	3	0.613
olivo	1	3	0.613
oliente	1	3	0.613
ojitos	1	3	0.613
ojazos	1	3	0.613
oficiando	1	3	0.613
ocurrir	1	3	0.613
ocupe	1	3	0.613
obedece	1	3	0.613
nuez	1	3	0.613
notoria	1	3	0.613
normal	1	3	0.613
nefando	1	3	0.613
naturalistas	1	3	0.613
musgo	1	3	0.613
músculo	1	3	0.613
muecas	1	3	0.613
mostrarle	1	3	0.613
morfina	1	3	0.613
monosílabo	1	3	0.613
monólogo	1	3	0.613
moleste	1	3	0.613
minuciosamente	1	3	0.613
mimaba	1	3	0.613
método	1	3	0.613
metiera	1	3	0.613
mequetrefes	1	3	0.613
mejorar	1	3	0.613
medita	1	3	0.613
mecheros	1	3	0.613
matas	1	3	0.613
matara	1	3	0.613
matadero	1	3	0.613
máscaras	1	3	0.613
marcharte	1	3	0.613
marcando	1	3	0.613
maquinal	1	3	0.613
manchada	1	3	0.613
luminosos	1	3	0.613
lucidos	1	3	0.613
llamaran	1	3	0.613
llamará	1	3	0.613
ligereza	1	3	0.613
levantara	1	3	0.613
lento	1	3	0.613
lanzaba	1	3	0.613
jaime	1	3	0.613
irritación	1	3	0.613
inventó	1	3	0.613
intermitentes	1	3	0.613
interesarse	1	3	0.613
intentaban	1	3	0.613
inspiran	1	3	0.613
insomnio	1	3	0.613
iniciarse	1	3	0.613
ingenieros	1	3	0.613
infracción	1	3	0.613
indispensables	1	3	0.613
incorporó	1	3	0.613
inconsolable	1	3	0.613
incierta	1	3	0.613
incendio	1	3	0.613
inapreciable	1	3	0.613
imposibilidad	1	3	0.613
importará	1	3	0.613
importan	1	3	0.613
imbécil	1	3	0.613
iluminó	1	3	0.613
ilumina	1	3	0.613
hinchazón	1	3	0.613
haremos	1	3	0.613
haciéndoles	1	3	0.613
hablaran	1	3	0.613
habíase	1	3	0.613
guedejas	1	3	0.613
gruñó	1	3	0.613
grillete	1	3	0.613
gesticulando	1	3	0.613
gemir	1	3	0.613
garabatos	1	3	0.613
futuras	1	3	0.613
fuiste	1	3	0.613
fuga	1	3	0.613
fuero	1	3	0.613
frutas	1	3	0.613
fruncido	1	3	0.613
frontera	1	3	0.613
fritos	1	3	0.613
frecuentaba	1	3	0.613
fraganti	1	3	0.613
fósforos	1	3	0.613
formaron	1	3	0.613
físicas	1	3	0.613
firmeza	1	3	0.613
fineza	1	3	0.613
filosofías	1	3	0.613
fijado	1	3	0.613
figurar	1	3	0.613
ficción	1	3	0.613
fibra	1	3	0.613
felpudo	1	3	0.613
favorecido	1	3	0.613
fabricante	1	3	0.613
extremidades	1	3	0.613
extraviada	1	3	0.613
exquisitos	1	3	0.613
explosiva	1	3	0.613
explicase	1	3	0.613
explicaré	1	3	0.613
explicara	1	3	0.613
excitó	1	3	0.613
estuviéramos	1	3	0.613
estudiando	1	3	0.613
estudiado	1	3	0.613
estrepitoso	1	3	0.613
esperaron	1	3	0.613
esparció	1	3	0.613
escupiendo	1	3	0.613
escepticismo	1	3	0.613
escarmiento	1	3	0.613
errante	1	3	0.613
equivoco	1	3	0.613
equivalía	1	3	0.613
envolvían	1	3	0.613
entusiastas	1	3	0.613
entusiasmarse	1	3	0.613
entusiasmaba	1	3	0.613
entretiene	1	3	0.613
entras	1	3	0.613
entienden	1	3	0.613
enseñaron	1	3	0.613
enseñanzas	1	3	0.613
enigma	1	3	0.613
encontrarla	1	3	0.613
encarnados	1	3	0.613
emulación	1	3	0.613
empeñas	1	3	0.613
empedrado	1	3	0.613
embuste	1	3	0.613
elegida	1	3	0.613
durase	1	3	0.613
duerma	1	3	0.613
domina	1	3	0.613
doblado	1	3	0.613
distrajo	1	3	0.613
distinguió	1	3	0.613
disminuía	1	3	0.613
discurrido	1	3	0.613
discretas	1	3	0.613
diligentes	1	3	0.613
dictando	1	3	0.613
dictamen	1	3	0.613
determinaron	1	3	0.613
detener	1	3	0.613
desvanecimiento	1	3	0.613
destrozado	1	3	0.613
destempladas	1	3	0.613
despachar	1	3	0.613
desigualdades	1	3	0.613
deshacer	1	3	0.613
deshace	1	3	0.613
desenfado	1	3	0.613
descubrirse	1	3	0.613
descendiendo	1	3	0.613
descendía	1	3	0.613
descalzo	1	3	0.613
desasirse	1	3	0.613
desabrimiento	1	3	0.613
dengue	1	3	0.613
déjele	1	3	0.613
definitivo	1	3	0.613
defenderle	1	3	0.613
declaraban	1	3	0.613
decisión	1	3	0.613
debiste	1	3	0.613
dársela	1	3	0.613
curarse	1	3	0.613
cumpliría	1	3	0.613
cuelga	1	3	0.613
cuajados	1	3	0.613
crueles	1	3	0.613
creyéndolo	1	3	0.613
corriéndose	1	3	0.613
coronilla	1	3	0.613
convenza	1	3	0.613
continua	1	3	0.613
contesta	1	3	0.613
contemplaban	1	3	0.613
contarles	1	3	0.613
construir	1	3	0.613
constituían	1	3	0.613
conspiradores	1	3	0.613
considerado	1	3	0.613
conserve	1	3	0.613
consabida	1	3	0.613
conocería	1	3	0.613
confundidos	1	3	0.613
concedo	1	3	0.613
comúnmente	1	3	0.613
compre	1	3	0.613
compasivo	1	3	0.613
comerá	1	3	0.613
combinar	1	3	0.613
coman	1	3	0.613
colosal	1	3	0.613
colorines	1	3	0.613
colocarse	1	3	0.613
colgadas	1	3	0.613
colgaban	1	3	0.613
cogiera	1	3	0.613
cogerlo	1	3	0.613
coces	1	3	0.613
clavándole	1	3	0.613
clavan	1	3	0.613
clamó	1	3	0.613
cipreses	1	3	0.613
chupa	1	3	0.613
chulos	1	3	0.613
chistera	1	3	0.613
chinitas	1	3	0.613
chanza	1	3	0.613
cerilla	1	3	0.613
céntimo	1	3	0.613
cementerios	1	3	0.613
cedía	1	3	0.613
cebolla	1	3	0.613
cautiverio	1	3	0.613
case	1	3	0.613
cáscara	1	3	0.613
casarte	1	3	0.613
casara	1	3	0.613
carmín	1	3	0.613
caricia	1	3	0.613
carcas	1	3	0.613
caracoles	1	3	0.613
capota	1	3	0.613
cansados	1	3	0.613
cansa	1	3	0.613
canario	1	3	0.613
campanillas	1	3	0.613
calculo	1	3	0.613
calado	1	3	0.613
cachivaches	1	3	0.613
cabras	1	3	0.613
brea	1	3	0.613
bramido	1	3	0.613
bostezos	1	3	0.613
borró	1	3	0.613
borrascas	1	3	0.613
bodegón	1	3	0.613
baúles	1	3	0.613
bastaban	1	3	0.613
barcos	1	3	0.613
ayudará	1	3	0.613
aumento	1	3	0.613
aullidos	1	3	0.613
atrayendo	1	3	0.613
atormentando	1	3	0.613
atados	1	3	0.613
asustes	1	3	0.613
asomando	1	3	0.613
asesinato	1	3	0.613
asegura	1	3	0.613
ascendía	1	3	0.613
asaltaron	1	3	0.613
artificial	1	3	0.613
arreglaría	1	3	0.613
arreglan	1	3	0.613
arreglaba	1	3	0.613
arrebató	1	3	0.613
arcos	1	3	0.613
aprobar	1	3	0.613
aprieta	1	3	0.613
aprendía	1	3	0.613
apreció	1	3	0.613
aposentos	1	3	0.613
apoderarse	1	3	0.613
apoderaba	1	3	0.613
aplastada	1	3	0.613
aplacar	1	3	0.613
anticipar	1	3	0.613
anticipaba	1	3	0.613
antecedentes	1	3	0.613
ánimas	1	3	0.613
animados	1	3	0.613
animada	1	3	0.613
andrajos	1	3	0.613
andas	1	3	0.613
andalucía	1	3	0.613
amaneramiento	1	3	0.613
alpiste	1	3	0.613
almorzaba	1	3	0.613
alientos	1	3	0.613
alfiler	1	3	0.613
alegrar	1	3	0.613
alegraban	1	3	0.613
alcanzó	1	3	0.613
alcances	1	3	0.613
alborote	1	3	0.613
alborotando	1	3	0.613
alborotaban	1	3	0.613
ahogar	1	3	0.613
aguarde	1	3	0.613
aguanto	1	3	0.613
agradaban	1	3	0.613
agitaba	1	3	0.613
agilidad	1	3	0.613
agarró	1	3	0.613
agarrándose	1	3	0.613
afueras	1	3	0.613
afirmar	1	3	0.613
afanaba	1	3	0.613
advierto	1	3	0.613
adquisición	1	3	0.613
adquirió	1	3	0.613
adornada	1	3	0.613
adoptar	1	3	0.613
admito	1	3	0.613
admirando	1	3	0.613
adivina	1	3	0.613
adefesios	1	3	0.613
acumulando	1	3	0.613
acuestes	1	3	0.613
acuéstate	1	3	0.613
acudiendo	1	3	0.613
acritud	1	3	0.613
acreedores	1	3	0.613
acontecía	1	3	0.613
acontecer	1	3	0.613
acompaña	1	3	0.613
acierta	1	3	0.613
aceitunas	1	3	0.613
acariciar	1	3	0.613
acaloraba	1	3	0.613
acabose	1	3	0.613
acabando	1	3	0.613
abrumador	1	3	0.613
abreviar	1	3	0.613
abrasa	1	3	0.613
aborrecen	1	3	0.613
visto	163	192	0.612
dejó	71	80	0.612
nuevos	20	20	0.609
ira	39	42	0.603
cree	30	46	0.597
vería	10	9	0.589
varón	10	9	0.589
propiedad	10	9	0.589
pícaro	10	9	0.589
minuto	10	9	0.589
llenaba	10	9	0.589
insistió	10	9	0.589
indudablemente	10	9	0.589
ídolo	10	9	0.589
costó	10	9	0.589
comentarios	10	9	0.589
caballos	10	9	0.589
bronce	10	9	0.589
absoluto	10	9	0.589
por	2879	3617	0.579
moda	19	19	0.579
flor	19	19	0.579
espera	19	19	0.579
entraban	19	19	0.579
encontrado	19	19	0.579
disgusto	19	19	0.579
común	19	19	0.579
oyó	49	54	0.576
compañía	32	34	0.572
oye	28	43	0.567
rompía	9	8	0.565
rápida	9	8	0.565
pastor	9	8	0.565
ópera	9	8	0.565
misterioso	9	8	0.565
ingleses	9	8	0.565
impaciente	9	8	0.565
enseñaba	9	8	0.565
dominar	9	8	0.565
doméstica	9	8	0.565
declaración	9	8	0.565
cuánta	9	8	0.565
aspavientos	9	8	0.565
ahogaba	9	8	0.565
vivienda	4	8	0.553
vivas	4	8	0.553
viniese	4	8	0.553
usar	4	8	0.553
semejanza	4	8	0.553
rojos	4	8	0.553
rodando	4	8	0.553
rezando	4	8	0.553
resplandor	4	8	0.553
rápido	4	8	0.553
quitaban	4	8	0.553
queremos	4	8	0.553
pulmonía	4	8	0.553
picaba	4	8	0.553
paños	4	8	0.553
ofrecido	4	8	0.553
meditación	4	8	0.553
maravilla	4	8	0.553
manifestaba	4	8	0.553
ligera	4	8	0.553
levanto	4	8	0.553
labor	4	8	0.553
injurias	4	8	0.553
infernal	4	8	0.553
fondos	4	8	0.553
esencial	4	8	0.553
determinado	4	8	0.553
dejes	4	8	0.553
decidida	4	8	0.553
cuerpos	4	8	0.553
cráneo	4	8	0.553
conflicto	4	8	0.553
castillo	4	8	0.553
cálculos	4	8	0.553
aumentaba	4	8	0.553
apuros	4	8	0.553
anochecer	4	8	0.553
acompañar	4	8	0.553
se	4779	6206	0.550
salió	103	145	0.545
salían	31	33	0.543
vencida	8	7	0.542
torcido	8	7	0.542
saludo	8	7	0.542
palique	8	7	0.542
pájaro	8	7	0.542
mozos	8	7	0.542
lazo	8	7	0.542
hubo	63	71	0.542
gotas	8	7	0.542
escándalos	8	7	0.542
economía	8	7	0.542
correo	8	7	0.542
compañeros	8	7	0.542
campaña	8	7	0.542
cambiar	8	7	0.542
besó	8	7	0.542
animales	8	7	0.542
alegraba	8	7	0.542
fueran	26	40	0.538
volvería	12	20	0.532
nuestros	12	20	0.532
distancia	12	20	0.532
propia	39	58	0.528
visitarla	3	2	0.525
viceversa	3	2	0.525
vestigios	3	2	0.525
veríamos	3	2	0.525
venimos	3	2	0.525
vacíos	3	2	0.525
turbarse	3	2	0.525
transformó	3	2	0.525
transformaba	3	2	0.525
traiciones	3	2	0.525
tragó	3	2	0.525
trágicas	3	2	0.525
tiernos	3	2	0.525
temperamentos	3	2	0.525
tálamo	3	2	0.525
suspirar	3	2	0.525
suspendió	3	2	0.525
suspender	3	2	0.525
sucedió	3	2	0.525
sospechosas	3	2	0.525
sordos	3	2	0.525
sonora	3	2	0.525
separaron	3	2	0.525
separa	3	2	0.525
sentencias	3	2	0.525
sentencia	3	2	0.525
sentaron	3	2	0.525
seguidas	3	2	0.525
saludos	3	2	0.525
sacrílega	3	2	0.525
romano	3	2	0.525
rodrigo	3	2	0.525
rezó	3	2	0.525
reyerta	3	2	0.525
retumbar	3	2	0.525
resuelve	3	2	0.525
respiro	3	2	0.525
reservaba	3	2	0.525
resbalando	3	2	0.525
republicano	3	2	0.525
repleto	3	2	0.525
repite	3	2	0.525
registros	3	2	0.525
regalar	3	2	0.525
reflejo	3	2	0.525
recorrido	3	2	0.525
reclamar	3	2	0.525
ratones	3	2	0.525
quemar	3	2	0.525
purgatorio	3	2	0.525
puntería	3	2	0.525
protestar	3	2	0.525
profundas	3	2	0.525
profanaciones	3	2	0.525
probaba	3	2	0.525
presenciar	3	2	0.525
pompadour	3	2	0.525
poderosas	3	2	0.525
playa	3	2	0.525
pláticas	3	2	0.525
pintó	3	2	0.525
perseverancia	3	2	0.525
permitirle	3	2	0.525
pecadillos	3	2	0.525
pasajera	3	2	0.525
partidos	3	2	0.525
partidas	3	2	0.525
parecidas	3	2	0.525
palpitaba	3	2	0.525
ortografía	3	2	0.525
originalidad	3	2	0.525
opone	3	2	0.525
olvidando	3	2	0.525
nocturna	3	2	0.525
necesitamos	3	2	0.525
necesariamente	3	2	0.525
musical	3	2	0.525
multiplicaba	3	2	0.525
mortificaban	3	2	0.525
moderno	3	2	0.525
miserere	3	2	0.525
ministros	3	2	0.525
mereciera	3	2	0.525
matorral	3	2	0.525
matemáticas	3	2	0.525
masón	3	2	0.525
martínez	3	2	0.525
maligna	3	2	0.525
madero	3	2	0.525
lucían	3	2	0.525
lloraban	3	2	0.525
llenarse	3	2	0.525
literario	3	2	0.525
lisonjeras	3	2	0.525
líquidos	3	2	0.525
lamentos	3	2	0.525
jadeante	3	2	0.525
irónica	3	2	0.525
intriga	3	2	0.525
intermitencias	3	2	0.525
interminable	3	2	0.525
inmortalidad	3	2	0.525
indiscreto	3	2	0.525
indicar	3	2	0.525
indiano	3	2	0.525
incorporarse	3	2	0.525
incansable	3	2	0.525
impacientaba	3	2	0.525
humillarse	3	2	0.525
humildemente	3	2	0.525
huellas	3	2	0.525
horrorizado	3	2	0.525
horca	3	2	0.525
honrados	3	2	0.525
honesta	3	2	0.525
hipocritona	3	2	0.525
higiénico	3	2	0.525
heredada	3	2	0.525
hebilla	3	2	0.525
hacerles	3	2	0.525
habilidades	3	2	0.525
gusanos	3	2	0.525
guijarros	3	2	0.525
gruñir	3	2	0.525
gruñía	3	2	0.525
grotesco	3	2	0.525
grietas	3	2	0.525
gramática	3	2	0.525
goma	3	2	0.525
golpecitos	3	2	0.525
garbo	3	2	0.525
floja	3	2	0.525
feudal	3	2	0.525
feria	3	2	0.525
falsas	3	2	0.525
extravagante	3	2	0.525
expuesto	3	2	0.525
explique	3	2	0.525
excelentísimo	3	2	0.525
estampa	3	2	0.525
esparcido	3	2	0.525
espantaba	3	2	0.525
escupió	3	2	0.525
escupía	3	2	0.525
escritores	3	2	0.525
escribirle	3	2	0.525
esclavina	3	2	0.525
epístola	3	2	0.525
entendiese	3	2	0.525
engañaban	3	2	0.525
encantado	3	2	0.525
encantada	3	2	0.525
empapado	3	2	0.525
embozado	3	2	0.525
electricidad	3	2	0.525
electoral	3	2	0.525
dudó	3	2	0.525
distrito	3	2	0.525
disputas	3	2	0.525
dispuestos	3	2	0.525
dirigido	3	2	0.525
déspota	3	2	0.525
despertando	3	2	0.525
despedirme	3	2	0.525
despedirla	3	2	0.525
desnudaba	3	2	0.525
desigualdad	3	2	0.525
deseaban	3	2	0.525
derribo	3	2	0.525
déjale	3	2	0.525
declarado	3	2	0.525
cumplió	3	2	0.525
cubrió	3	2	0.525
cubo	3	2	0.525
cruzaba	3	2	0.525
cristianas	3	2	0.525
creador	3	2	0.525
corrupción	3	2	0.525
convence	3	2	0.525
controversia	3	2	0.525
contagio	3	2	0.525
conquistas	3	2	0.525
conocerse	3	2	0.525
confundía	3	2	0.525
conejos	3	2	0.525
comprometía	3	2	0.525
comprometer	3	2	0.525
compañías	3	2	0.525
colocó	3	2	0.525
cobrando	3	2	0.525
club	3	2	0.525
clavadas	3	2	0.525
circular	3	2	0.525
cintas	3	2	0.525
chubasco	3	2	0.525
chorro	3	2	0.525
chismes	3	2	0.525
chic	3	2	0.525
charol	3	2	0.525
cerdos	3	2	0.525
cedió	3	2	0.525
caudillo	3	2	0.525
catedrático	3	2	0.525
canteros	3	2	0.525
calzados	3	2	0.525
caigo	3	2	0.525
cabizbajo	3	2	0.525
cabían	3	2	0.525
buscarlos	3	2	0.525
buscan	3	2	0.525
bienestar	3	2	0.525
bellezas	3	2	0.525
basto	3	2	0.525
azahar	3	2	0.525
ayudaban	3	2	0.525
atrio	3	2	0.525
asustan	3	2	0.525
asegurarse	3	2	0.525
asechanzas	3	2	0.525
arrojase	3	2	0.525
arregló	3	2	0.525
arreglado	3	2	0.525
arrebatos	3	2	0.525
arrebato	3	2	0.525
arrancando	3	2	0.525
aristocrática	3	2	0.525
arbustos	3	2	0.525
apodo	3	2	0.525
apagar	3	2	0.525
antojo	3	2	0.525
anti	3	2	0.525
ansiaba	3	2	0.525
anémico	3	2	0.525
andaría	3	2	0.525
amonestaciones	3	2	0.525
amenazado	3	2	0.525
alegró	3	2	0.525
alcázar	3	2	0.525
albergue	3	2	0.525
agria	3	2	0.525
advertía	3	2	0.525
adora	3	2	0.525
admitir	3	2	0.525
adelantaba	3	2	0.525
acudido	3	2	0.525
actores	3	2	0.525
acierto	3	2	0.525
tapaba	7	6	0.522
sabré	7	6	0.522
religiosas	7	6	0.522
preparada	7	6	0.522
poetas	7	6	0.522
pisando	7	6	0.522
persecución	7	6	0.522
pedido	7	6	0.522
na	7	6	0.522
mayoría	7	6	0.522
luto	7	6	0.522
junio	7	6	0.522
estarían	7	6	0.522
equilibrio	7	6	0.522
deudas	7	6	0.522
creerá	7	6	0.522
clavaba	7	6	0.522
cajones	7	6	0.522
butaca	7	6	0.522
apretado	7	6	0.522
apariencia	7	6	0.522
aparición	7	6	0.522
maestro	24	25	0.520
vivos	17	17	0.518
única	19	30	0.518
quince	17	17	0.518
empezado	17	17	0.518
tardó	10	17	0.517
seguido	10	17	0.517
sábanas	10	17	0.517
célebre	10	17	0.517
quisieran	6	11	0.516
puntos	6	11	0.516
perdición	6	11	0.516
males	6	11	0.516
infidelidad	6	11	0.516
haz	6	11	0.516
cuartel	6	11	0.516
considerar	6	11	0.516
capas	6	11	0.516
callado	6	11	0.516
relaciones	30	32	0.515
miraba	78	111	0.515
flores	30	32	0.515
solución	8	14	0.510
querrá	8	14	0.510
monedas	8	14	0.510
irse	8	14	0.510
empezaba	41	45	0.507
vistas	6	5	0.506
vidrieras	6	5	0.506
verlo	6	5	0.506
vende	6	5	0.506
vecindario	6	5	0.506
torpes	6	5	0.506
tinta	6	5	0.506
tientas	6	5	0.506
tejado	6	5	0.506
sopor	6	5	0.506
sinceramente	6	5	0.506
seriamente	6	5	0.506
sábana	6	5	0.506
resistía	6	5	0.506
quejarse	6	5	0.506
pudieron	6	5	0.506
procurando	6	5	0.506
pretendía	6	5	0.506
pinturas	6	5	0.506
pino	6	5	0.506
picaresca	6	5	0.506
pasaje	6	5	0.506
ocupada	6	5	0.506
muchedumbre	6	5	0.506
mia	6	5	0.506
metían	6	5	0.506
lomo	6	5	0.506
llegase	6	5	0.506
jaula	6	5	0.506
heredado	6	5	0.506
grises	6	5	0.506
franco	6	5	0.506
follaje	6	5	0.506
fango	6	5	0.506
escondida	6	5	0.506
escoger	6	5	0.506
empresas	6	5	0.506
despensa	6	5	0.506
desaparecer	6	5	0.506
dejándose	6	5	0.506
corrieron	6	5	0.506
conserva	6	5	0.506
conocimientos	6	5	0.506
compás	6	5	0.506
combinaciones	6	5	0.506
clerical	6	5	0.506
cañón	6	5	0.506
cansada	6	5	0.506
agradeció	6	5	0.506
votos	4	3	0.497
vemos	4	3	0.497
veintisiete	4	3	0.497
vehementes	4	3	0.497
vasos	4	3	0.497
usando	4	3	0.497
universidad	4	3	0.497
tributo	4	3	0.497
tisis	4	3	0.497
tedio	4	3	0.497
suela	4	3	0.497
sudando	4	3	0.497
soportales	4	3	0.497
solicitaba	4	3	0.497
singularmente	4	3	0.497
severo	4	3	0.497
secos	4	3	0.497
salvarme	4	3	0.497
sacudía	4	3	0.497
sabia	4	3	0.497
rodeos	4	3	0.497
ridículos	4	3	0.497
representaban	4	3	0.497
puente	4	3	0.497
prometiendo	4	3	0.497
producir	4	3	0.497
presentado	4	3	0.497
presbítero	4	3	0.497
premios	4	3	0.497
pío	4	3	0.497
picardías	4	3	0.497
permanente	4	3	0.497
pausadamente	4	3	0.497
palmada	4	3	0.497
ordinarios	4	3	0.497
obstáculo	4	3	0.497
noviembre	4	3	0.497
nieblas	4	3	0.497
muertes	4	3	0.497
morirá	4	3	0.497
mató	4	3	0.497
matan	4	3	0.497
marea	4	3	0.497
marcial	4	3	0.497
mancebo	4	3	0.497
mamás	4	3	0.497
lamentaba	4	3	0.497
juntar	4	3	0.497
irían	4	3	0.497
incertidumbre	4	3	0.497
huyó	4	3	0.497
hermanitas	4	3	0.497
hayan	4	3	0.497
habana	4	3	0.497
graciosos	4	3	0.497
gimnasia	4	3	0.497
generales	4	3	0.497
filosófico	4	3	0.497
exquisito	4	3	0.497
excesivo	4	3	0.497
esperase	4	3	0.497
espacios	4	3	0.497
escuelas	4	3	0.497
enterase	4	3	0.497
entenderse	4	3	0.497
engañada	4	3	0.497
encarnada	4	3	0.497
emprendió	4	3	0.497
elocuentes	4	3	0.497
ejemplar	4	3	0.497
duras	4	3	0.497
discretos	4	3	0.497
dirigiéndose	4	3	0.497
desmayada	4	3	0.497
descargaba	4	3	0.497
desaires	4	3	0.497
delicados	4	3	0.497
dejen	4	3	0.497
dejaría	4	3	0.497
declara	4	3	0.497
continuaban	4	3	0.497
consiente	4	3	0.497
consagrar	4	3	0.497
comunión	4	3	0.497
comparado	4	3	0.497
chimeneas	4	3	0.497
cayera	4	3	0.497
burlas	4	3	0.497
besar	4	3	0.497
autoridades	4	3	0.497
atrasado	4	3	0.497
asfixia	4	3	0.497
arrojaban	4	3	0.497
arcas	4	3	0.497
aprobó	4	3	0.497
apretadas	4	3	0.497
apasionado	4	3	0.497
apagaba	4	3	0.497
alusión	4	3	0.497
alimentos	4	3	0.497
ajustado	4	3	0.497
ajustada	4	3	0.497
ahumado	4	3	0.497
ad	4	3	0.497
acompañarla	4	3	0.497
acompañamiento	4	3	0.497
aceptado	4	3	0.497
acabase	4	3	0.497
abrigado	4	3	0.497
aborrecer	4	3	0.497
vivió	5	4	0.496
vestíbulo	5	4	0.496
vagas	5	4	0.496
triunfos	5	4	0.496
tierras	5	4	0.496
tardaba	5	4	0.496
tapar	5	4	0.496
suponiendo	5	4	0.496
superficie	5	4	0.496
sumo	5	4	0.496
sujetó	5	4	0.496
sujeta	5	4	0.496
sufría	5	4	0.496
sucede	5	4	0.496
soso	5	4	0.496
sombrío	5	4	0.496
soltera	5	4	0.496
servilleta	5	4	0.496
rutina	5	4	0.496
rió	5	4	0.496
repetidas	5	4	0.496
refirió	5	4	0.496
recorriendo	5	4	0.496
producido	5	4	0.496
perseguido	5	4	0.496
permite	5	4	0.496
peor	61	69	0.496
pegada	5	4	0.496
pasmado	5	4	0.496
ofender	5	4	0.496
ocupación	5	4	0.496
observado	5	4	0.496
obedecer	5	4	0.496
molesta	5	4	0.496
modesto	5	4	0.496
llano	5	4	0.496
literarias	5	4	0.496
lienzo	5	4	0.496
libremente	5	4	0.496
lápiz	5	4	0.496
inundaba	5	4	0.496
ingratitud	5	4	0.496
horrorizada	5	4	0.496
himno	5	4	0.496
golosinas	5	4	0.496
ganarse	5	4	0.496
famosa	5	4	0.496
explica	5	4	0.496
eternas	5	4	0.496
estrechez	5	4	0.496
estiró	5	4	0.496
espantada	5	4	0.496
embustero	5	4	0.496
eco	5	4	0.496
dueños	5	4	0.496
domésticos	5	4	0.496
disfrutaba	5	4	0.496
cumplía	5	4	0.496
cruzó	5	4	0.496
cruzando	5	4	0.496
cruzados	5	4	0.496
creyera	5	4	0.496
considerando	5	4	0.496
confianzas	5	4	0.496
comezón	5	4	0.496
colgando	5	4	0.496
canción	5	4	0.496
bilis	5	4	0.496
biblia	5	4	0.496
besugo	5	4	0.496
bayeta	5	4	0.496
ayudado	5	4	0.496
artístico	5	4	0.496
ademanes	5	4	0.496
acordándose	5	4	0.496
usaba	23	24	0.490
seria	23	24	0.490
mata	16	16	0.487
corrió	29	31	0.486
virgen	40	59	0.482
verle	40	59	0.482
treinta	22	34	0.479
justicia	27	41	0.479
alguno	27	41	0.479
oír	68	97	0.470
sillas	15	24	0.466
humanidad	15	24	0.466
contenta	15	24	0.466
firme	22	23	0.460
seco	15	15	0.457
e	46	67	0.457
despidió	15	15	0.457
beso	15	15	0.457
cristo	30	45	0.456
tocar	13	21	0.441
entrada	13	21	0.441
misa	33	49	0.437
seno	21	22	0.431
hablarle	14	14	0.426
entiendo	14	14	0.426
coronel	14	14	0.426
pruebas	11	18	0.418
fija	11	18	0.418
espanto	11	18	0.418
compañero	11	18	0.418
ciertas	47	68	0.418
cayendo	11	18	0.418
obra	67	77	0.417
volverme	3	6	0.415
viviera	3	6	0.415
vidriera	3	6	0.415
ventanilla	3	6	0.415
vacilaba	3	6	0.415
turbada	3	6	0.415
trabajado	3	6	0.415
tomarse	3	6	0.415
tenerlo	3	6	0.415
tendero	3	6	0.415
tapa	3	6	0.415
sucesor	3	6	0.415
subieron	3	6	0.415
sonrosada	3	6	0.415
sietemesino	3	6	0.415
sexos	3	6	0.415
sevilla	3	6	0.415
separación	3	6	0.415
sábado	3	6	0.415
risueño	3	6	0.415
retiraba	3	6	0.415
reparación	3	6	0.415
reído	3	6	0.415
protectora	3	6	0.415
prodigio	3	6	0.415
preguntado	3	6	0.415
posibles	3	6	0.415
plácida	3	6	0.415
pisos	3	6	0.415
pegaba	3	6	0.415
pedacitos	3	6	0.415
pagarle	3	6	0.415
notables	3	6	0.415
nace	3	6	0.415
montones	3	6	0.415
mirarse	3	6	0.415
memorable	3	6	0.415
luchando	3	6	0.415
llorado	3	6	0.415
llamándole	3	6	0.415
julio	3	6	0.415
juega	3	6	0.415
jovial	3	6	0.415
irme	3	6	0.415
intervenir	3	6	0.415
indiferente	3	6	0.415
indicaba	3	6	0.415
gozoso	3	6	0.415
frasco	3	6	0.415
filosófica	3	6	0.415
engañan	3	6	0.415
encierro	3	6	0.415
encerrada	3	6	0.415
emigración	3	6	0.415
diván	3	6	0.415
diciéndose	3	6	0.415
deteniéndose	3	6	0.415
cuidando	3	6	0.415
conocida	3	6	0.415
comandante	3	6	0.415
círculos	3	6	0.415
brincos	3	6	0.415
atravesar	3	6	0.415
aprecio	3	6	0.415
agradecida	3	6	0.415
acabaron	3	6	0.415
querida	31	46	0.407
superior	26	28	0.402
pensado	20	21	0.402
quedaron	9	15	0.399
debió	9	15	0.399
codo	9	15	0.399
rubio	13	13	0.396
ofreció	13	13	0.396
inteligente	13	13	0.396
infancia	13	13	0.396
guardaba	13	13	0.396
grupos	13	13	0.396
discurso	13	13	0.396
ricos	16	25	0.392
rara	16	25	0.392
entiende	16	25	0.392
completo	16	25	0.392
buscando	16	25	0.392
quieren	21	32	0.388
papá	21	32	0.388
querían	31	34	0.387
significaba	7	12	0.385
pollo	7	12	0.385
padecer	7	12	0.385
oyera	7	12	0.385
mecánica	7	12	0.385
gatos	7	12	0.385
deseado	7	12	0.385
crítico	7	12	0.385
comprado	7	12	0.385
colcha	7	12	0.385
casadas	7	12	0.385
agujeros	7	12	0.385
saldría	5	9	0.384
ríe	5	9	0.384
mover	5	9	0.384
mono	5	9	0.384
mentiras	5	9	0.384
guarda	5	9	0.384
gota	5	9	0.384
estatura	5	9	0.384
españoles	5	9	0.384
entrecejo	5	9	0.384
colocar	5	9	0.384
cobrar	5	9	0.384
ciertamente	5	9	0.384
aprender	5	9	0.384
anhelo	5	9	0.384
asunto	41	46	0.377
tranquila	25	27	0.375
varios	19	20	0.372
desdén	19	20	0.372
últimas	12	12	0.366
sociales	12	12	0.366
roto	12	12	0.366
motivos	12	12	0.366
impulsos	12	12	0.366
frescura	12	12	0.366
asesino	12	12	0.366
una	2206	2873	0.365
peso	14	22	0.364
rey	19	29	0.358
primo	19	29	0.358
levantarse	19	29	0.358
calles	35	39	0.355
abrió	35	39	0.355
pasaba	81	113	0.349
muerta	24	26	0.347
pública	18	19	0.343
capital	18	19	0.343
nervioso	12	19	0.337
limpieza	12	19	0.337
claramente	12	19	0.337
pared	29	32	0.335
nube	11	11	0.335
insignificante	11	11	0.335
farsa	11	11	0.335
doctor	11	11	0.335
deberes	11	11	0.335
blancas	11	11	0.335
aburrimiento	11	11	0.335
encontrar	22	33	0.334
tantos	44	50	0.332
criada	39	44	0.330
respondió	17	26	0.328
inocente	17	26	0.328
fina	17	26	0.328
salía	67	78	0.325
maría	33	48	0.321
anda	33	48	0.321
quedado	23	25	0.320
compasión	23	25	0.320
circunstancias	23	25	0.320
dicho	175	237	0.318
llave	25	37	0.316
sistema	17	18	0.315
tuvo	113	155	0.311
feliz	36	52	0.311
vestir	10	16	0.310
masa	10	16	0.310
llama	43	49	0.310
hueco	10	16	0.310
estuviese	10	16	0.310
crisis	10	16	0.310
ayudaba	10	16	0.310
zapatos	10	10	0.305
sospecha	10	10	0.305
resistencia	10	10	0.305
prometió	10	10	0.305
materialismo	10	10	0.305
maldad	10	10	0.305
inocentes	10	10	0.305
inglesa	10	10	0.305
desconocida	10	10	0.305
cerrando	10	10	0.305
burla	10	10	0.305
razón	86	119	0.302
también	378	466	0.299
saliendo	15	23	0.299
su	3084	4000	0.295
leyes	22	24	0.293
atención	48	68	0.290
quedarse	16	17	0.286
parar	16	17	0.286
oigo	8	13	0.286
muero	8	13	0.286
lumbre	8	13	0.286
encuentra	8	13	0.286
dijeron	8	13	0.286
copas	8	13	0.286
colmo	8	13	0.286
canto	8	13	0.286
calzado	8	13	0.286
bajando	8	13	0.286
cierto	96	132	0.284
yendo	2	4	0.277
viviese	2	4	0.277
viviente	2	4	0.277
visitado	2	4	0.277
violentas	2	4	0.277
violenta	2	4	0.277
violencias	2	4	0.277
vendrán	2	4	0.277
uña	2	4	0.277
trompeta	2	4	0.277
trenzas	2	4	0.277
trataron	2	4	0.277
tragedia	2	4	0.277
tráeme	2	4	0.277
tradiciones	2	4	0.277
toalla	2	4	0.277
templado	2	4	0.277
teje	2	4	0.277
tarjeta	2	4	0.277
talante	2	4	0.277
susurro	2	4	0.277
supongamos	2	4	0.277
supieron	2	4	0.277
sostuvo	2	4	0.277
soltura	2	4	0.277
signos	2	4	0.277
significa	2	4	0.277
separó	2	4	0.277
secretaría	2	4	0.277
santidades	2	4	0.277
sabias	2	4	0.277
rotas	2	4	0.277
rogar	2	4	0.277
revuelta	2	4	0.277
revolucionaria	2	4	0.277
revelado	2	4	0.277
resultados	2	4	0.277
respetabilidad	2	4	0.277
remota	2	4	0.277
remilgos	2	4	0.277
remedios	2	4	0.277
reforma	2	4	0.277
reflexión	2	4	0.277
rebelde	2	4	0.277
raros	2	4	0.277
quitará	2	4	0.277
quedara	2	4	0.277
púas	2	4	0.277
proteger	2	4	0.277
proponer	2	4	0.277
propietario	2	4	0.277
profundos	2	4	0.277
profesión	2	4	0.277
privada	2	4	0.277
previsto	2	4	0.277
podrán	2	4	0.277
plena	2	4	0.277
pintadas	2	4	0.277
pienses	2	4	0.277
picado	2	4	0.277
pestañear	2	4	0.277
perspicaz	2	4	0.277
perfiles	2	4	0.277
pediría	2	4	0.277
patata	2	4	0.277
pasearse	2	4	0.277
partir	2	4	0.277
pararse	2	4	0.277
padeciendo	2	4	0.277
opuesto	2	4	0.277
onzas	2	4	0.277
olvidarse	2	4	0.277
oírlas	2	4	0.277
odios	2	4	0.277
odiaba	2	4	0.277
naturalezas	2	4	0.277
muslo	2	4	0.277
músico	2	4	0.277
muscular	2	4	0.277
moro	2	4	0.277
mohín	2	4	0.277
miles	2	4	0.277
mechones	2	4	0.277
manotadas	2	4	0.277
mampara	2	4	0.277
maldiciones	2	4	0.277
llevaría	2	4	0.277
llenar	2	4	0.277
levitas	2	4	0.277
jaulas	2	4	0.277
instantes	2	4	0.277
inscripciones	2	4	0.277
ingenioso	2	4	0.277
indignada	2	4	0.277
imperturbable	2	4	0.277
ida	2	4	0.277
hortera	2	4	0.277
holanda	2	4	0.277
históricos	2	4	0.277
hicieran	2	4	0.277
hermosísimo	2	4	0.277
habladores	2	4	0.277
grasa	2	4	0.277
gobernaba	2	4	0.277
gastan	2	4	0.277
formaba	2	4	0.277
fernando	2	4	0.277
faja	2	4	0.277
esqueleto	2	4	0.277
escultura	2	4	0.277
escribiendo	2	4	0.277
equivocó	2	4	0.277
equipaje	2	4	0.277
ensimismada	2	4	0.277
ensayo	2	4	0.277
enredos	2	4	0.277
encubridora	2	4	0.277
ejercer	2	4	0.277
echarla	2	4	0.277
discípulo	2	4	0.277
dibujos	2	4	0.277
desprendimiento	2	4	0.277
despejado	2	4	0.277
despedidas	2	4	0.277
desempeñaba	2	4	0.277
desdichas	2	4	0.277
desdeñoso	2	4	0.277
describiendo	2	4	0.277
desconocidas	2	4	0.277
descarga	2	4	0.277
derramado	2	4	0.277
cuidarle	2	4	0.277
cuida	2	4	0.277
cuáles	2	4	0.277
crónico	2	4	0.277
cristianar	2	4	0.277
criminales	2	4	0.277
contemplarla	2	4	0.277
consuelos	2	4	0.277
constitución	2	4	0.277
conocen	2	4	0.277
confiaba	2	4	0.277
condenar	2	4	0.277
concierto	2	4	0.277
complexión	2	4	0.277
comensales	2	4	0.277
colocado	2	4	0.277
cogidos	2	4	0.277
cogían	2	4	0.277
clavada	2	4	0.277
cierra	2	4	0.277
chino	2	4	0.277
cerdo	2	4	0.277
central	2	4	0.277
cediendo	2	4	0.277
categoría	2	4	0.277
casé	2	4	0.277
bufanda	2	4	0.277
asquerosa	2	4	0.277
armando	2	4	0.277
aproximarse	2	4	0.277
aprovechando	2	4	0.277
aplomo	2	4	0.277
aparecieron	2	4	0.277
anhelaba	2	4	0.277
alcobas	2	4	0.277
áfrica	2	4	0.277
afabilidad	2	4	0.277
acostado	2	4	0.277
acaban	2	4	0.277
tolerancia	9	9	0.274
resultaba	9	9	0.274
respetar	9	9	0.274
insignificantes	9	9	0.274
examen	9	9	0.274
empieza	9	9	0.274
dificultad	9	9	0.274
artes	9	9	0.274
arrojó	9	9	0.274
v	18	27	0.273
dicen	40	57	0.271
plaza	55	64	0.270
largas	13	20	0.269
impulso	13	20	0.269
casada	21	23	0.267
variedad	6	10	0.266
salga	6	10	0.266
sacramento	6	10	0.266
pizca	6	10	0.266
perdono	6	10	0.266
misión	6	10	0.266
mesilla	6	10	0.266
infelices	6	10	0.266
imponía	6	10	0.266
envuelto	6	10	0.266
director	6	10	0.266
corrección	6	10	0.266
cometido	6	10	0.266
catorce	6	10	0.266
auxilio	6	10	0.266
administración	6	10	0.266
terror	31	35	0.259
pariente	15	16	0.257
ofrecía	15	16	0.257
coches	15	16	0.257
clases	15	16	0.257
dormido	21	31	0.256
voto	4	7	0.255
viniera	4	7	0.255
venus	4	7	0.255
traigan	4	7	0.255
sublimes	4	7	0.255
serán	4	7	0.255
sacudida	4	7	0.255
respectivas	4	7	0.255
renta	4	7	0.255
recorrer	4	7	0.255
protestantes	4	7	0.255
preciosa	4	7	0.255
paró	4	7	0.255
obligado	4	7	0.255
llegara	4	7	0.255
ligeramente	4	7	0.255
labio	4	7	0.255
habíamos	4	7	0.255
finura	4	7	0.255
éste	4	7	0.255
escribe	4	7	0.255
enseñando	4	7	0.255
difunta	4	7	0.255
despedían	4	7	0.255
descansar	4	7	0.255
derecha	32	46	0.255
culpable	4	7	0.255
chicas	4	7	0.255
cañas	4	7	0.255
caiga	4	7	0.255
basura	4	7	0.255
aplicó	4	7	0.255
ansia	4	7	0.255
acompañada	4	7	0.255
mirada	54	63	0.251
viese	8	8	0.244
veneno	8	8	0.244
sordo	8	8	0.244
retirado	8	8	0.244
reconocer	8	8	0.244
pintada	8	8	0.244
industria	8	8	0.244
fruto	8	8	0.244
escapaba	8	8	0.244
divinidad	8	8	0.244
diligencia	8	8	0.244
cuántos	8	8	0.244
crianza	8	8	0.244
calla	8	8	0.244
bigote	8	8	0.244
atrevimiento	8	8	0.244
acostó	8	8	0.244
acabado	8	8	0.244
ocasiones	16	24	0.243
malos	24	35	0.243
izquierda	16	24	0.243
empezar	16	24	0.243
frases	20	22	0.241
hablando	41	58	0.240
propias	11	17	0.239
pedazos	11	17	0.239
medida	11	17	0.239
golpes	11	17	0.239
contener	11	17	0.239
pasos	56	78	0.232
nombre	59	82	0.232
cualquier	59	82	0.232
representaba	14	15	0.229
extraña	14	15	0.229
dueño	19	28	0.226
suerte	33	47	0.221
dormir	33	47	0.221
nuestro	34	39	0.219
pasiones	19	21	0.215
seguir	29	33	0.214
educación	22	32	0.214
últimos	14	21	0.213
trampas	7	7	0.213
torpeza	7	7	0.213
tonos	7	7	0.213
salto	14	21	0.213
rosita	7	7	0.213
restos	7	7	0.213
pesado	7	7	0.213
pantalón	7	7	0.213
ofrecer	7	7	0.213
moderna	7	7	0.213
intentar	7	7	0.213
futura	7	7	0.213
explicarse	7	7	0.213
errores	7	7	0.213
dramas	7	7	0.213
disimular	14	21	0.213
contenía	7	7	0.213
callada	7	7	0.213
cabecera	7	7	0.213
brillante	7	7	0.213
bebía	7	7	0.213
arrastrando	7	7	0.213
seda	24	27	0.212
oficio	24	27	0.212
dispuesto	24	27	0.212
medio	122	165	0.211
trapo	9	14	0.210
muera	9	14	0.210
mejor	231	284	0.210
explicaciones	9	14	0.210
divertido	9	14	0.210
cerrada	9	14	0.210
cariñosa	9	14	0.210
aprendido	9	14	0.210
sueño	57	79	0.209
allá	167	224	0.208
contrario	25	36	0.205
porvenir	13	14	0.201
llaves	13	14	0.201
pedir	33	38	0.198
espejo	17	25	0.196
vicio	28	32	0.192
deje	18	20	0.190
corte	18	20	0.190
carrera	20	29	0.185
virtudes	6	6	0.183
turno	6	6	0.183
terribles	6	6	0.183
seguirle	6	6	0.183
saliese	6	6	0.183
puros	6	6	0.183
proporciones	6	6	0.183
petróleo	6	6	0.183
pecar	6	6	0.183
morirse	6	6	0.183
iniciativa	6	6	0.183
hito	6	6	0.183
golosina	6	6	0.183
gallinas	6	6	0.183
fijaba	6	6	0.183
estorbaba	6	6	0.183
encontrarse	6	6	0.183
defecto	6	6	0.183
debido	6	6	0.183
cautela	6	6	0.183
blando	6	6	0.183
baba	6	6	0.183
aturdida	6	6	0.183
arrancarle	6	6	0.183
apetitos	6	6	0.183
animado	6	6	0.183
abundante	6	6	0.183
suceder	7	11	0.182
pintura	7	11	0.182
murió	12	18	0.182
muchachos	7	11	0.182
marchar	7	11	0.182
hablan	7	11	0.182
graciosa	12	18	0.182
ganaba	7	11	0.182
éxtasis	7	11	0.182
delirio	12	18	0.182
dejarla	7	11	0.182
defender	7	11	0.182
cola	7	11	0.182
bofetada	7	11	0.182
ahora	364	480	0.181
dedos	50	59	0.180
pretensiones	12	13	0.174
paraba	12	13	0.174
mirado	12	13	0.174
engañar	12	13	0.174
apretó	12	13	0.174
aparecer	12	13	0.174
aguardiente	12	13	0.174
subir	36	42	0.167
metido	22	25	0.166
eh	15	22	0.166
vida	326	405	0.164
lengua	35	49	0.164
modo	147	180	0.161
estará	18	26	0.156
transeúntes	5	8	0.155
tertulias	5	8	0.155
sumisión	5	8	0.155
recogiendo	5	8	0.155
pueril	5	8	0.155
presupuesto	5	8	0.155
penetrar	5	8	0.155
oficina	5	8	0.155
mediodía	5	8	0.155
insoportable	5	8	0.155
hospital	5	8	0.155
guardó	5	8	0.155
escondite	5	8	0.155
envuelta	5	8	0.155
doméstico	5	8	0.155
desaparecido	5	8	0.155
curso	5	8	0.155
confusa	5	8	0.155
cabe	5	8	0.155
aparato	5	8	0.155
volando	5	5	0.152
transigir	5	5	0.152
tomo	10	15	0.152
título	5	5	0.152
soplaba	5	5	0.152
sobrinas	5	5	0.152
rojas	5	5	0.152
repugnaba	5	5	0.152
recoger	10	15	0.152
reciente	5	5	0.152
ráfaga	5	5	0.152
puras	5	5	0.152
probado	5	5	0.152
presidio	5	5	0.152
preparó	5	5	0.152
perfecta	10	15	0.152
párrafos	5	5	0.152
opinó	5	5	0.152
oficinas	5	5	0.152
notable	5	5	0.152
niega	5	5	0.152
muertas	5	5	0.152
moros	5	5	0.152
mientes	5	5	0.152
maternal	5	5	0.152
manías	5	5	0.152
librar	5	5	0.152
levantando	5	5	0.152
lenguas	5	5	0.152
invención	5	5	0.152
índice	5	5	0.152
hechas	5	5	0.152
hablaré	5	5	0.152
groseros	5	5	0.152
fundamento	5	5	0.152
fijarse	5	5	0.152
famoso	5	5	0.152
escudo	5	5	0.152
escuchaba	5	5	0.152
echada	5	5	0.152
doblar	5	5	0.152
displicente	5	5	0.152
directamente	5	5	0.152
darles	5	5	0.152
curar	5	5	0.152
criaturas	5	5	0.152
convencer	5	5	0.152
conferencia	10	15	0.152
conciencias	5	5	0.152
combatir	5	5	0.152
cigarros	5	5	0.152
chocho	5	5	0.152
careta	5	5	0.152
callejón	5	5	0.152
avisar	5	5	0.152
atreve	5	5	0.152
aspirar	5	5	0.152
arrojado	5	5	0.152
argumentos	10	15	0.152
apretar	5	5	0.152
antipática	5	5	0.152
anteriores	5	5	0.152
amorosas	5	5	0.152
alejó	5	5	0.152
alcance	5	5	0.152
ajenas	5	5	0.152
activo	5	5	0.152
ya	906	1180	0.150
prisa	21	30	0.149
sufrir	11	12	0.147
soñado	11	12	0.147
regla	11	12	0.147
nombres	11	12	0.147
naturaleza	48	57	0.147
creyó	48	57	0.147
verdadera	24	34	0.145
echaba	24	34	0.145
capa	24	34	0.145
oyendo	21	24	0.144
buenas	51	70	0.143
obras	27	38	0.142
prudente	16	18	0.141
zascandil	1	2	0.138
zarzuelas	1	2	0.138
zapatilla	1	2	0.138
zángano	1	2	0.138
zambulló	1	2	0.138
xvi	1	2	0.138
vuélvete	1	2	0.138
visos	1	2	0.138
visera	1	2	0.138
vilo	1	2	0.138
viena	1	2	0.138
vicioso	1	2	0.138
vibraba	1	2	0.138
vértigo	1	2	0.138
vernos	1	2	0.138
verbigracia	1	2	0.138
venida	1	2	0.138
venid	1	2	0.138
venenos	1	2	0.138
venecia	1	2	0.138
vendrían	1	2	0.138
valeroso	1	2	0.138
valentías	1	2	0.138
valemos	1	2	0.138
vaguedades	1	2	0.138
útiles	1	2	0.138
usura	1	2	0.138
únicos	1	2	0.138
unía	1	2	0.138
tuerce	1	2	0.138
trozos	1	2	0.138
tropel	1	2	0.138
trimestre	1	2	0.138
trazaba	1	2	0.138
tratarlo	1	2	0.138
trasunto	1	2	0.138
traqueteo	1	2	0.138
trajese	1	2	0.138
traerá	1	2	0.138
tortilla	1	2	0.138
torpemente	1	2	0.138
tornaba	1	2	0.138
toreros	1	2	0.138
toleraría	1	2	0.138
tole	1	2	0.138
tocase	1	2	0.138
tiraría	1	2	0.138
tímido	1	2	0.138
terso	1	2	0.138
ternuras	1	2	0.138
teñidas	1	2	0.138
tentativa	1	2	0.138
tentando	1	2	0.138
tendríamos	1	2	0.138
tenaces	1	2	0.138
temprana	1	2	0.138
templar	1	2	0.138
temerarios	1	2	0.138
tejido	1	2	0.138
tapizada	1	2	0.138
tamañitos	1	2	0.138
tallado	1	2	0.138
taimada	1	2	0.138
tácitamente	1	2	0.138
suspensión	1	2	0.138
suspendidos	1	2	0.138
supremacía	1	2	0.138
supersticiosas	1	2	0.138
suicida	1	2	0.138
sugirió	1	2	0.138
sufrirá	1	2	0.138
sufrió	1	2	0.138
suene	1	2	0.138
sucesivamente	1	2	0.138
suceda	1	2	0.138
subterfugios	1	2	0.138
sublevaban	1	2	0.138
suben	1	2	0.138
sostenga	1	2	0.138
sospechoso	1	2	0.138
sonidos	1	2	0.138
sometido	1	2	0.138
solemnes	1	2	0.138
soga	1	2	0.138
sofocar	1	2	0.138
socialismo	1	2	0.138
singularísima	1	2	0.138
simetría	1	2	0.138
sillería	1	2	0.138
sientas	1	2	0.138
shakespeare	1	2	0.138
sépase	1	2	0.138
sepan	1	2	0.138
sensatas	1	2	0.138
seguiré	1	2	0.138
seductoras	1	2	0.138
seduce	1	2	0.138
seducciones	1	2	0.138
secuestrador	1	2	0.138
secando	1	2	0.138
satisfizo	1	2	0.138
satánico	1	2	0.138
sarcástica	1	2	0.138
saquen	1	2	0.138
santurrona	1	2	0.138
sanó	1	2	0.138
salada	1	2	0.138
sacrificada	1	2	0.138
sacaste	1	2	0.138
sacaran	1	2	0.138
sabrás	1	2	0.138
saboreando	1	2	0.138
rumorcillo	1	2	0.138
ruidosas	1	2	0.138
rompen	1	2	0.138
robarle	1	2	0.138
rígida	1	2	0.138
revuelven	1	2	0.138
revolverse	1	2	0.138
revelando	1	2	0.138
retozaba	1	2	0.138
retiran	1	2	0.138
retira	1	2	0.138
resultas	1	2	0.138
resplandeciente	1	2	0.138
respira	1	2	0.138
respeten	1	2	0.138
residencia	1	2	0.138
reservados	1	2	0.138
repugna	1	2	0.138
repuesto	1	2	0.138
representante	1	2	0.138
repetirlo	1	2	0.138
repecho	1	2	0.138
reparten	1	2	0.138
reparos	1	2	0.138
reparaciones	1	2	0.138
reñirle	1	2	0.138
reñía	1	2	0.138
rendirse	1	2	0.138
rendidas	1	2	0.138
rehuía	1	2	0.138
registrando	1	2	0.138
regio	1	2	0.138
regeneración	1	2	0.138
redobló	1	2	0.138
redimido	1	2	0.138
redimía	1	2	0.138
rectas	1	2	0.138
recorre	1	2	0.138
recordarlo	1	2	0.138
reconocerla	1	2	0.138
reconocería	1	2	0.138
recóndito	1	2	0.138
recogen	1	2	0.138
recetaba	1	2	0.138
rebeldes	1	2	0.138
reanudó	1	2	0.138
realizando	1	2	0.138
razonaba	1	2	0.138
raquítica	1	2	0.138
racimos	1	2	0.138
rabien	1	2	0.138
rábano	1	2	0.138
quítame	1	2	0.138
quintales	1	2	0.138
quemó	1	2	0.138
quemado	1	2	0.138
quedaremos	1	2	0.138
pusiste	1	2	0.138
pupila	1	2	0.138
puntapié	1	2	0.138
puntal	1	2	0.138
pué	1	2	0.138
publicidad	1	2	0.138
pruebe	1	2	0.138
proyectada	1	2	0.138
provocado	1	2	0.138
protegiendo	1	2	0.138
propuesta	1	2	0.138
proponían	1	2	0.138
proponga	1	2	0.138
profesores	1	2	0.138
profeso	1	2	0.138
producida	1	2	0.138
procurarse	1	2	0.138
procedimiento	1	2	0.138
probarme	1	2	0.138
privación	1	2	0.138
primitivas	1	2	0.138
previo	1	2	0.138
pretendientes	1	2	0.138
preste	1	2	0.138
prestada	1	2	0.138
presión	1	2	0.138
presentable	1	2	0.138
prepara	1	2	0.138
preguntes	1	2	0.138
pregunte	1	2	0.138
preguntara	1	2	0.138
precursor	1	2	0.138
precedido	1	2	0.138
precaución	1	2	0.138
postizo	1	2	0.138
posterior	1	2	0.138
posarse	1	2	0.138
portaba	1	2	0.138
ponerlos	1	2	0.138
pompas	1	2	0.138
policías	1	2	0.138
polémica	1	2	0.138
pobretería	1	2	0.138
pluralidad	1	2	0.138
plazos	1	2	0.138
platicar	1	2	0.138
pitando	1	2	0.138
pintoresca	1	2	0.138
pingos	1	2	0.138
picarescos	1	2	0.138
pescas	1	2	0.138
pescador	1	2	0.138
pesas	1	2	0.138
pesadez	1	2	0.138
persiguiendo	1	2	0.138
persecuciones	1	2	0.138
peroles	1	2	0.138
periodista	1	2	0.138
perdóname	1	2	0.138
percales	1	2	0.138
penumbra	1	2	0.138
penosos	1	2	0.138
penetrando	1	2	0.138
pelear	1	2	0.138
pelayo	1	2	0.138
pela	1	2	0.138
pedimos	1	2	0.138
pedantería	1	2	0.138
paul	1	2	0.138
patrones	1	2	0.138
patitas	1	2	0.138
paternales	1	2	0.138
pastora	1	2	0.138
pasto	1	2	0.138
pasteles	1	2	0.138
pastelero	1	2	0.138
pastas	1	2	0.138
pasmaban	1	2	0.138
pasemos	1	2	0.138
pasearon	1	2	0.138
pasean	1	2	0.138
parto	1	2	0.138
parrilla	1	2	0.138
parió	1	2	0.138
pararrayos	1	2	0.138
paradojas	1	2	0.138
palpitaciones	1	2	0.138
palio	1	2	0.138
pajaritas	1	2	0.138
pagarás	1	2	0.138
pacíficos	1	2	0.138
oveja	1	2	0.138
osuna	1	2	0.138
osadía	1	2	0.138
ortiz	1	2	0.138
organismo	1	2	0.138
opulenta	1	2	0.138
oportunas	1	2	0.138
olvidos	1	2	0.138
olvidan	1	2	0.138
oírme	1	2	0.138
oirá	1	2	0.138
óigame	1	2	0.138
ofenda	1	2	0.138
ocurriría	1	2	0.138
ocurra	1	2	0.138
ocupa	1	2	0.138
ocultado	1	2	0.138
ociosa	1	2	0.138
occidental	1	2	0.138
observo	1	2	0.138
novelescos	1	2	0.138
notada	1	2	0.138
nenas	1	2	0.138
negarán	1	2	0.138
necesite	1	2	0.138
necesitara	1	2	0.138
nebulosa	1	2	0.138
nazcan	1	2	0.138
navegando	1	2	0.138
naranjos	1	2	0.138
nadar	1	2	0.138
nadando	1	2	0.138
naciente	1	2	0.138
naciendo	1	2	0.138
mutuos	1	2	0.138
muñecos	1	2	0.138
mujerzuela	1	2	0.138
mujeril	1	2	0.138
mueres	1	2	0.138
mostrase	1	2	0.138
mostrarlo	1	2	0.138
mostaza	1	2	0.138
morimos	1	2	0.138
morcilla	1	2	0.138
montada	1	2	0.138
monta	1	2	0.138
moldes	1	2	0.138
moderado	1	2	0.138
miss	1	2	0.138
mismísima	1	2	0.138
minucioso	1	2	0.138
ministerios	1	2	0.138
miento	1	2	0.138
metiéndole	1	2	0.138
mentarle	1	2	0.138
meneó	1	2	0.138
médula	1	2	0.138
medianería	1	2	0.138
matemático	1	2	0.138
marmolillo	1	2	0.138
marcharía	1	2	0.138
mantuvo	1	2	0.138
mantillas	1	2	0.138
manojo	1	2	0.138
mandé	1	2	0.138
maltrecho	1	2	0.138
malla	1	2	0.138
malestar	1	2	0.138
malditos	1	2	0.138
madrugones	1	2	0.138
maderos	1	2	0.138
machacaba	1	2	0.138
lustroso	1	2	0.138
lucidas	1	2	0.138
lucero	1	2	0.138
lóbrega	1	2	0.138
lloriqueando	1	2	0.138
llegarían	1	2	0.138
llegaremos	1	2	0.138
llamémosle	1	2	0.138
liebre	1	2	0.138
levantaría	1	2	0.138
lema	1	2	0.138
lavó	1	2	0.138
lavadas	1	2	0.138
lastimada	1	2	0.138
largarse	1	2	0.138
lanza	1	2	0.138
lamentable	1	2	0.138
lagarto	1	2	0.138
ladrar	1	2	0.138
kock	1	2	0.138
juzgando	1	2	0.138
jure	1	2	0.138
juegan	1	2	0.138
judíos	1	2	0.138
jornal	1	2	0.138
inventario	1	2	0.138
invariablemente	1	2	0.138
invadía	1	2	0.138
intimidades	1	2	0.138
intervenía	1	2	0.138
interpretación	1	2	0.138
instrucciones	1	2	0.138
inquisición	1	2	0.138
innata	1	2	0.138
inició	1	2	0.138
inicial	1	2	0.138
ingratos	1	2	0.138
ingenuamente	1	2	0.138
informes	1	2	0.138
informe	1	2	0.138
infinitas	1	2	0.138
infatigable	1	2	0.138
inequívocas	1	2	0.138
indiscutible	1	2	0.138
indignaba	1	2	0.138
indica	1	2	0.138
indecisa	1	2	0.138
indecencias	1	2	0.138
incurría	1	2	0.138
incorporada	1	2	0.138
incomodidad	1	2	0.138
incomodaba	1	2	0.138
incoherente	1	2	0.138
impreso	1	2	0.138
impresionables	1	2	0.138
imponían	1	2	0.138
imponerse	1	2	0.138
impidiera	1	2	0.138
impertinencias	1	2	0.138
imperioso	1	2	0.138
imperceptible	1	2	0.138
imita	1	2	0.138
ilustradas	1	2	0.138
ignorantes	1	2	0.138
idilio	1	2	0.138
huyeron	1	2	0.138
humillación	1	2	0.138
horrorosas	1	2	0.138
hormigueo	1	2	0.138
horchata	1	2	0.138
hondamente	1	2	0.138
hombruna	1	2	0.138
heroísmo	1	2	0.138
heredar	1	2	0.138
hazle	1	2	0.138
hacha	1	2	0.138
habitados	1	2	0.138
habíanle	1	2	0.138
habérselas	1	2	0.138
guárdese	1	2	0.138
guardada	1	2	0.138
gruñendo	1	2	0.138
grillera	1	2	0.138
grifo	1	2	0.138
granujas	1	2	0.138
grada	1	2	0.138
gobiernos	1	2	0.138
genial	1	2	0.138
gatito	1	2	0.138
gastando	1	2	0.138
gancho	1	2	0.138
ganara	1	2	0.138
ganada	1	2	0.138
gaceta	1	2	0.138
fundador	1	2	0.138
fundación	1	2	0.138
fuer	1	2	0.138
frenéticos	1	2	0.138
fortísimo	1	2	0.138
forrados	1	2	0.138
fornos	1	2	0.138
formulando	1	2	0.138
formó	1	2	0.138
foco	1	2	0.138
flamantes	1	2	0.138
filigranas	1	2	0.138
figuran	1	2	0.138
fichas	1	2	0.138
farolón	1	2	0.138
faltará	1	2	0.138
fábulas	1	2	0.138
extremeño	1	2	0.138
extravío	1	2	0.138
extendidos	1	2	0.138
extendidas	1	2	0.138
expresa	1	2	0.138
exponer	1	2	0.138
explotación	1	2	0.138
expliques	1	2	0.138
explícate	1	2	0.138
exigencia	1	2	0.138
excluía	1	2	0.138
excitantes	1	2	0.138
excitante	1	2	0.138
evitado	1	2	0.138
evitaba	1	2	0.138
europea	1	2	0.138
estupor	1	2	0.138
estupefacta	1	2	0.138
estudian	1	2	0.138
estuche	1	2	0.138
estremecimientos	1	2	0.138
estremecía	1	2	0.138
estirada	1	2	0.138
estiraba	1	2	0.138
estético	1	2	0.138
estampada	1	2	0.138
establecido	1	2	0.138
espliego	1	2	0.138
esperé	1	2	0.138
esparcir	1	2	0.138
espantajo	1	2	0.138
espanta	1	2	0.138
esgrimía	1	2	0.138
esforzaban	1	2	0.138
escribirlas	1	2	0.138
escombros	1	2	0.138
escolta	1	2	0.138
escapas	1	2	0.138
escapan	1	2	0.138
equívoca	1	2	0.138
equilibrado	1	2	0.138
episcopal	1	2	0.138
envolvió	1	2	0.138
envolver	1	2	0.138
entretenían	1	2	0.138
entregándole	1	2	0.138
entregan	1	2	0.138
entonado	1	2	0.138
entendernos	1	2	0.138
ensimismado	1	2	0.138
enroscadas	1	2	0.138
enjambre	1	2	0.138
engordado	1	2	0.138
enfriado	1	2	0.138
enfadado	1	2	0.138
enérgicos	1	2	0.138
endemoniada	1	2	0.138
encontrará	1	2	0.138
encienden	1	2	0.138
encerrar	1	2	0.138
encerrados	1	2	0.138
empuñando	1	2	0.138
empujón	1	2	0.138
emprendieron	1	2	0.138
emprendedor	1	2	0.138
empolvado	1	2	0.138
empinada	1	2	0.138
empezamos	1	2	0.138
empeñada	1	2	0.138
empecé	1	2	0.138
embustera	1	2	0.138
embrutecimiento	1	2	0.138
embrujado	1	2	0.138
emborrachaba	1	2	0.138
embeleso	1	2	0.138
embebecido	1	2	0.138
embajada	1	2	0.138
ejecutivo	1	2	0.138
egoístas	1	2	0.138
educar	1	2	0.138
editores	1	2	0.138
ecos	1	2	0.138
echados	1	2	0.138
dure	1	2	0.138
dudando	1	2	0.138
domésticas	1	2	0.138
doblaron	1	2	0.138
doblándose	1	2	0.138
distintivo	1	2	0.138
disponiendo	1	2	0.138
disparatado	1	2	0.138
discutiendo	1	2	0.138
disculpando	1	2	0.138
discípulos	1	2	0.138
diretes	1	2	0.138
directo	1	2	0.138
dimes	1	2	0.138
diapasón	1	2	0.138
devolvió	1	2	0.138
devaneo	1	2	0.138
detuvieron	1	2	0.138
desvergüenza	1	2	0.138
desventurada	1	2	0.138
desvelos	1	2	0.138
destreza	1	2	0.138
destinados	1	2	0.138
desplomarse	1	2	0.138
desperdicios	1	2	0.138
despego	1	2	0.138
despavorida	1	2	0.138
desolación	1	2	0.138
desmentía	1	2	0.138
desmayo	1	2	0.138
desmaya	1	2	0.138
desmañado	1	2	0.138
desiguales	1	2	0.138
desgarrada	1	2	0.138
desfavorable	1	2	0.138
descubiertas	1	2	0.138
descompone	1	2	0.138
descargado	1	2	0.138
desazones	1	2	0.138
desatinada	1	2	0.138
desaparición	1	2	0.138
desapacible	1	2	0.138
desanimaba	1	2	0.138
desalentada	1	2	0.138
desalado	1	2	0.138
derrota	1	2	0.138
deliraba	1	2	0.138
delicadísimo	1	2	0.138
delicadezas	1	2	0.138
deleites	1	2	0.138
dejarlas	1	2	0.138
deforme	1	2	0.138
definitivamente	1	2	0.138
defendió	1	2	0.138
decidía	1	2	0.138
decálogo	1	2	0.138
debida	1	2	0.138
debías	1	2	0.138
darla	1	2	0.138
dardo	1	2	0.138
daña	1	2	0.138
curiosa	1	2	0.138
curial	1	2	0.138
curaría	1	2	0.138
curada	1	2	0.138
cúpula	1	2	0.138
cumpliendo	1	2	0.138
cuellos	1	2	0.138
cuchillos	1	2	0.138
cruzan	1	2	0.138
cromo	1	2	0.138
creerle	1	2	0.138
creciendo	1	2	0.138
cotarro	1	2	0.138
cositas	1	2	0.138
cosecha	1	2	0.138
cortarle	1	2	0.138
cortados	1	2	0.138
corrigió	1	2	0.138
corriese	1	2	0.138
corren	1	2	0.138
corregir	1	2	0.138
correctamente	1	2	0.138
corporación	1	2	0.138
córdoba	1	2	0.138
corbatas	1	2	0.138
corales	1	2	0.138
conyugales	1	2	0.138
convenciendo	1	2	0.138
convencerle	1	2	0.138
contrición	1	2	0.138
contratiempos	1	2	0.138
contradecían	1	2	0.138
contienda	1	2	0.138
conteste	1	2	0.138
contentas	1	2	0.138
contenerle	1	2	0.138
contemplado	1	2	0.138
contada	1	2	0.138
consuelan	1	2	0.138
consternado	1	2	0.138
conspiración	1	2	0.138
consolando	1	2	0.138
conocieran	1	2	0.138
conmiseración	1	2	0.138
confundidas	1	2	0.138
confiado	1	2	0.138
confesarme	1	2	0.138
concreto	1	2	0.138
concluyen	1	2	0.138
concha	1	2	0.138
concertando	1	2	0.138
comprendida	1	2	0.138
complicidad	1	2	0.138
complaciente	1	2	0.138
comparó	1	2	0.138
comparo	1	2	0.138
compadece	1	2	0.138
comisiones	1	2	0.138
comienzos	1	2	0.138
cometiera	1	2	0.138
combatientes	1	2	0.138
colérica	1	2	0.138
coincidir	1	2	0.138
cobro	1	2	0.138
cisterna	1	2	0.138
cirio	1	2	0.138
cimientos	1	2	0.138
chocando	1	2	0.138
chicuela	1	2	0.138
chata	1	2	0.138
cervantes	1	2	0.138
cerradas	1	2	0.138
ceñudo	1	2	0.138
celeste	1	2	0.138
cegó	1	2	0.138
cazando	1	2	0.138
caverna	1	2	0.138
cavador	1	2	0.138
causar	1	2	0.138
catedrales	1	2	0.138
catar	1	2	0.138
cataclismo	1	2	0.138
castos	1	2	0.138
caseríos	1	2	0.138
casaría	1	2	0.138
cartitas	1	2	0.138
carteles	1	2	0.138
carreteros	1	2	0.138
carpanta	1	2	0.138
cargante	1	2	0.138
cardenales	1	2	0.138
capitalista	1	2	0.138
capellanes	1	2	0.138
capacidad	1	2	0.138
cansadas	1	2	0.138
candelabros	1	2	0.138
canal	1	2	0.138
camas	1	2	0.138
calzonazos	1	2	0.138
calza	1	2	0.138
calores	1	2	0.138
calmarse	1	2	0.138
calmaba	1	2	0.138
callejera	1	2	0.138
calladas	1	2	0.138
calibre	1	2	0.138
calados	1	2	0.138
calabozo	1	2	0.138
caín	1	2	0.138
cachetes	1	2	0.138
cabezada	1	2	0.138
buscaré	1	2	0.138
buscara	1	2	0.138
burocráticas	1	2	0.138
bujías	1	2	0.138
buey	1	2	0.138
buche	1	2	0.138
brígida	1	2	0.138
bribón	1	2	0.138
brevemente	1	2	0.138
bravos	1	2	0.138
botarate	1	2	0.138
bordado	1	2	0.138
bolsistas	1	2	0.138
bobalicón	1	2	0.138
blandos	1	2	0.138
biografía	1	2	0.138
besado	1	2	0.138
benéfico	1	2	0.138
bebo	1	2	0.138
batería	1	2	0.138
bastado	1	2	0.138
baratas	1	2	0.138
balbuciente	1	2	0.138
baje	1	2	0.138
azucarada	1	2	0.138
ayudada	1	2	0.138
avise	1	2	0.138
avisaré	1	2	0.138
autora	1	2	0.138
auténtico	1	2	0.138
atrevidas	1	2	0.138
atravesada	1	2	0.138
atraían	1	2	0.138
atraer	1	2	0.138
atengo	1	2	0.138
ataúd	1	2	0.138
atareada	1	2	0.138
atar	1	2	0.138
ataca	1	2	0.138
ataba	1	2	0.138
asturiana	1	2	0.138
asquerosos	1	2	0.138
aspectos	1	2	0.138
aspas	1	2	0.138
asiste	1	2	0.138
asesinos	1	2	0.138
asegurarlo	1	2	0.138
asegurando	1	2	0.138
asaltaba	1	2	0.138
arrogantes	1	2	0.138
arrepintiéndose	1	2	0.138
arreglarlo	1	2	0.138
arrebatado	1	2	0.138
aro	1	2	0.138
armadura	1	2	0.138
arder	1	2	0.138
apuras	1	2	0.138
apurarse	1	2	0.138
apreciaciones	1	2	0.138
apóstrofes	1	2	0.138
apostaba	1	2	0.138
aplicando	1	2	0.138
aplacarla	1	2	0.138
apestaba	1	2	0.138
apasionadas	1	2	0.138
apartadas	1	2	0.138
apartada	1	2	0.138
apariciones	1	2	0.138
angustioso	1	2	0.138
andamos	1	2	0.138
amoratada	1	2	0.138
ameno	1	2	0.138
amenazas	1	2	0.138
amaneció	1	2	0.138
alza	1	2	0.138
alteró	1	2	0.138
altercados	1	2	0.138
alterar	1	2	0.138
alimenta	1	2	0.138
algos	1	2	0.138
aletargada	1	2	0.138
alborotó	1	2	0.138
alarmó	1	2	0.138
alarmantes	1	2	0.138
alambres	1	2	0.138
alabando	1	2	0.138
ajajá	1	2	0.138
airosas	1	2	0.138
ahorraba	1	2	0.138
ahorita	1	2	0.138
agüero	1	2	0.138
aguardando	1	2	0.138
agrícola	1	2	0.138
agradeceré	1	2	0.138
agradábale	1	2	0.138
agarrarse	1	2	0.138
agarraban	1	2	0.138
afeitado	1	2	0.138
afanes	1	2	0.138
afables	1	2	0.138
advertencias	1	2	0.138
adulterado	1	2	0.138
adúltera	1	2	0.138
adorar	1	2	0.138
admirarla	1	2	0.138
adelantos	1	2	0.138
acuestas	1	2	0.138
acude	1	2	0.138
acuarelas	1	2	0.138
acreditado	1	2	0.138
acordarte	1	2	0.138
acordaron	1	2	0.138
acompañó	1	2	0.138
acompañase	1	2	0.138
acompañados	1	2	0.138
acíbar	1	2	0.138
abyección	1	2	0.138
abultado	1	2	0.138
absorto	1	2	0.138
absorta	1	2	0.138
abrumada	1	2	0.138
abrirse	1	2	0.138
perros	13	19	0.136
clara	13	19	0.136
mismo	320	421	0.135
visión	3	5	0.133
visible	3	5	0.133
vieran	3	5	0.133
verdaderos	3	5	0.133
torres	3	5	0.133
toman	3	5	0.133
teme	3	5	0.133
suicidio	3	5	0.133
suelas	3	5	0.133
sostenida	3	5	0.133
soñadora	3	5	0.133
sincero	3	5	0.133
sílabas	3	5	0.133
seguros	3	5	0.133
sacarla	3	5	0.133
rompimiento	3	5	0.133
revelar	3	5	0.133
resumidas	3	5	0.133
respondo	3	5	0.133
red	3	5	0.133
recobrado	3	5	0.133
quedamos	3	5	0.133
primores	3	5	0.133
posesión	3	5	0.133
pliegos	3	5	0.133
pierden	3	5	0.133
pesca	3	5	0.133
pasta	3	5	0.133
pasase	3	5	0.133
pague	3	5	0.133
paces	3	5	0.133
obrar	3	5	0.133
obligada	3	5	0.133
muñecas	3	5	0.133
mortuoria	3	5	0.133
montera	3	5	0.133
méritos	3	5	0.133
marcos	3	5	0.133
marchó	3	5	0.133
lleven	3	5	0.133
llegada	3	5	0.133
ligeras	3	5	0.133
lavado	3	5	0.133
intento	3	5	0.133
hotel	3	5	0.133
hijita	3	5	0.133
herir	3	5	0.133
gata	3	5	0.133
gastos	3	5	0.133
franceses	3	5	0.133
figúrese	3	5	0.133
feos	3	5	0.133
estaciones	3	5	0.133
ensalada	3	5	0.133
encajes	3	5	0.133
ejercía	3	5	0.133
discurría	3	5	0.133
diabluras	3	5	0.133
dedicó	3	5	0.133
debate	3	5	0.133
darían	3	5	0.133
curioso	3	5	0.133
cuero	3	5	0.133
correspondía	3	5	0.133
contempló	3	5	0.133
consumados	3	5	0.133
conocidos	3	5	0.133
concluyendo	3	5	0.133
comprendes	3	5	0.133
compraba	3	5	0.133
comería	3	5	0.133
cogerla	3	5	0.133
bestias	3	5	0.133
bella	3	5	0.133
aumentó	3	5	0.133
atributos	3	5	0.133
apuntar	3	5	0.133
aparecido	3	5	0.133
andado	3	5	0.133
alejado	3	5	0.133
afectaba	3	5	0.133
adorno	3	5	0.133
acudieron	3	5	0.133
ventura	4	4	0.122
varones	4	4	0.122
ultrajado	4	4	0.122
terminante	4	4	0.122
tempestad	4	4	0.122
supongo	4	4	0.122
sucias	4	4	0.122
sócrates	4	4	0.122
sagaz	4	4	0.122
robo	4	4	0.122
revista	4	4	0.122
referir	4	4	0.122
recto	4	4	0.122
recomendaba	4	4	0.122
recogido	4	4	0.122
recobrar	4	4	0.122
rebaño	4	4	0.122
querría	4	4	0.122
quehaceres	4	4	0.122
provincias	4	4	0.122
pintor	4	4	0.122
pintar	4	4	0.122
pica	4	4	0.122
peligroso	4	4	0.122
pares	4	4	0.122
página	4	4	0.122
monos	4	4	0.122
manifestar	4	4	0.122
licor	4	4	0.122
librarse	4	4	0.122
lavaba	4	4	0.122
lágrima	4	4	0.122
institución	4	4	0.122
inofensivo	4	4	0.122
inefables	4	4	0.122
inconvenientes	4	4	0.122
hoguera	4	4	0.122
histórica	4	4	0.122
historia	63	76	0.122
hablas	4	4	0.122
grana	4	4	0.122
frescos	4	4	0.122
franca	4	4	0.122
fatalidad	4	4	0.122
externo	4	4	0.122
espejos	4	4	0.122
escrúpulo	4	4	0.122
escondía	4	4	0.122
escaparate	4	4	0.122
épocas	4	4	0.122
empeñaba	4	4	0.122
embriaguez	4	4	0.122
elección	4	4	0.122
dramático	4	4	0.122
docenas	4	4	0.122
disputaban	4	4	0.122
demostrar	4	4	0.122
cuerno	4	4	0.122
cuchicheo	4	4	0.122
cuán	4	4	0.122
crecer	4	4	0.122
contorsiones	4	4	0.122
comodidad	4	4	0.122
comerciantes	4	4	0.122
colgar	4	4	0.122
colchones	4	4	0.122
chorreando	4	4	0.122
casera	4	4	0.122
canta	4	4	0.122
callando	4	4	0.122
caerse	4	4	0.122
barrer	4	4	0.122
atrocidades	4	4	0.122
apagada	4	4	0.122
ajenos	4	4	0.122
ahínco	4	4	0.122
abusando	4	4	0.122
absurda	4	4	0.122
abrazos	4	4	0.122
trapos	8	12	0.121
sonriendo	29	34	0.121
siguieron	8	12	0.121
pantalones	8	12	0.121
lecturas	8	12	0.121
impertinente	8	12	0.121
guantes	8	12	0.121
furiosa	8	12	0.121
emplear	8	12	0.121
despierto	8	12	0.121
broma	29	34	0.121
arrojar	8	12	0.121
suyas	10	11	0.120
subido	10	11	0.120
posición	10	11	0.120
oírle	10	11	0.120
mandado	10	11	0.120
criterio	10	11	0.120
pierna	15	17	0.118
oían	15	17	0.118
imágenes	15	17	0.118
estación	15	17	0.118
cartas	15	17	0.118
caían	15	17	0.118
saber	123	164	0.116
baja	34	47	0.116
azul	28	39	0.116
tiempo	284	354	0.113
verse	24	28	0.111
tenía	610	767	0.111
tono	66	80	0.108
estúpido	11	16	0.107
contemplando	11	16	0.107
absoluta	11	16	0.107
siempre	332	415	0.106
miró	69	93	0.105
lujo	19	22	0.103
dama	47	64	0.103
añadió	45	54	0.103
consejos	14	20	0.099
supo	32	38	0.098
negra	32	38	0.098
tomaba	35	48	0.096
recibió	14	16	0.096
oiga	14	16	0.096
hermanas	14	16	0.096
graves	14	16	0.096
despertó	14	16	0.096
árbol	14	16	0.096
apariencias	14	16	0.096
través	9	10	0.095
tomaban	9	10	0.095
término	9	10	0.095
sur	9	10	0.095
sabrá	9	10	0.095
responsabilidad	9	10	0.095
redonda	9	10	0.095
proposición	9	10	0.095
producía	9	10	0.095
precio	9	10	0.095
isidro	9	10	0.095
dirán	9	10	0.095
desesperación	9	10	0.095
descuido	9	10	0.095
claridad	20	28	0.094
tren	23	27	0.093
subió	23	32	0.093
hasta	352	441	0.092
vivimos	3	3	0.091
viajes	6	9	0.091
vergonzosos	3	3	0.091
vergonzosa	3	3	0.091
velos	3	3	0.091
velador	3	3	0.091
varonil	6	9	0.091
vacía	6	9	0.091
unida	3	3	0.091
trece	3	3	0.091
tratara	6	9	0.091
transparentes	3	3	0.091
trajes	6	9	0.091
tráfico	3	3	0.091
tomó	40	48	0.091
toleraba	3	3	0.091
tentativas	3	3	0.091
suplicante	3	3	0.091
sucios	3	3	0.091
soñó	3	3	0.091
sonríe	3	3	0.091
sobriedad	3	3	0.091
semejaba	3	3	0.091
savia	3	3	0.091
sardinas	3	3	0.091
sandeces	3	3	0.091
sabrosa	3	3	0.091
rusia	3	3	0.091
ronda	6	9	0.091
romero	3	3	0.091
rodearon	3	3	0.091
rodea	3	3	0.091
roba	3	3	0.091
riñón	3	3	0.091
revelaban	3	3	0.091
respetando	3	3	0.091
resignada	3	3	0.091
repentino	3	3	0.091
reparo	3	3	0.091
relieve	3	3	0.091
reino	6	9	0.091
redes	3	3	0.091
rechazaba	3	3	0.091
recato	3	3	0.091
raro	6	9	0.091
racimo	3	3	0.091
quererla	3	3	0.091
pupitre	3	3	0.091
pudieran	6	9	0.091
presumir	3	3	0.091
presumía	3	3	0.091
predilecto	3	3	0.091
predicar	3	3	0.091
popular	6	9	0.091
podremos	3	3	0.091
picantes	3	3	0.091
peste	3	3	0.091
pescar	3	3	0.091
pesa	3	3	0.091
perspicacia	3	3	0.091
perfil	6	9	0.091
pensará	3	3	0.091
pellizcos	3	3	0.091
paseándose	3	3	0.091
pasara	6	9	0.091
pasadas	3	3	0.091
oponer	3	3	0.091
oliendo	3	3	0.091
odioso	3	3	0.091
odiosa	3	3	0.091
ocultó	3	3	0.091
ociosas	3	3	0.091
nacionales	3	3	0.091
mundano	6	9	0.091
mueve	3	3	0.091
mudos	3	3	0.091
moribunda	3	3	0.091
morder	3	3	0.091
monosílabos	3	3	0.091
molesto	3	3	0.091
míos	6	9	0.091
miembros	3	3	0.091
mezquino	3	3	0.091
mezclando	3	3	0.091
mezcladas	3	3	0.091
martín	3	3	0.091
marear	3	3	0.091
mantilla	6	9	0.091
manejar	3	3	0.091
mandarle	3	3	0.091
lujosa	3	3	0.091
locuaz	3	3	0.091
lloro	3	3	0.091
llenan	3	3	0.091
llegue	6	9	0.091
lívido	3	3	0.091
límite	3	3	0.091
licencias	3	3	0.091
lana	6	9	0.091
juguetes	3	3	0.091
inmundicia	3	3	0.091
infinitamente	3	3	0.091
imperiosa	3	3	0.091
ilustrado	3	3	0.091
idioma	3	3	0.091
humorismo	3	3	0.091
hablará	3	3	0.091
habitantes	3	3	0.091
glorioso	3	3	0.091
ganan	3	3	0.091
gallina	3	3	0.091
gallarda	3	3	0.091
fundado	3	3	0.091
función	6	9	0.091
formidables	3	3	0.091
finge	3	3	0.091
fila	6	9	0.091
fijaron	3	3	0.091
femenino	3	3	0.091
falsos	3	3	0.091
fáciles	3	3	0.091
europa	3	3	0.091
estribillo	3	3	0.091
estrechó	3	3	0.091
estima	3	3	0.091
estarán	3	3	0.091
esquinas	3	3	0.091
espionaje	3	3	0.091
espadas	3	3	0.091
escogía	3	3	0.091
enérgica	3	3	0.091
encarnadas	3	3	0.091
empujaba	3	3	0.091
duraría	3	3	0.091
distraerse	3	3	0.091
distinguían	3	3	0.091
dignó	3	3	0.091
dígase	3	3	0.091
destacaba	3	3	0.091
desprecia	3	3	0.091
despojos	3	3	0.091
desparpajo	3	3	0.091
deshonrar	3	3	0.091
descargar	3	3	0.091
dejaran	3	3	0.091
creencia	3	3	0.091
crecido	3	3	0.091
correcta	3	3	0.091
convencida	3	3	0.091
constaba	3	3	0.091
consolar	3	3	0.091
conservación	3	3	0.091
confirmó	3	3	0.091
confieso	3	3	0.091
comunes	6	9	0.091
compromisos	3	3	0.091
comitiva	3	3	0.091
cometía	3	3	0.091
colmena	3	3	0.091
cielos	3	3	0.091
chorros	3	3	0.091
chillones	3	3	0.091
chillido	3	3	0.091
chal	3	3	0.091
cerco	3	3	0.091
celda	6	9	0.091
caros	3	3	0.091
cargar	3	3	0.091
cantara	3	3	0.091
candoroso	3	3	0.091
calavera	3	3	0.091
buscarlo	3	3	0.091
burlona	3	3	0.091
bromitas	3	3	0.091
borrar	3	3	0.091
bocado	6	9	0.091
banquete	3	3	0.091
bailando	3	3	0.091
baila	3	3	0.091
avergonzaba	3	3	0.091
atreviéndose	3	3	0.091
astuta	3	3	0.091
astorga	3	3	0.091
artistas	3	3	0.091
apretones	3	3	0.091
amén	3	3	0.091
alegrarse	3	3	0.091
alarmante	3	3	0.091
alarma	3	3	0.091
agarrada	3	3	0.091
afirmaciones	3	3	0.091
adorado	3	3	0.091
acuérdate	3	3	0.091
acompañando	3	3	0.091
acercaron	3	3	0.091
aceptar	6	9	0.091
aburrido	6	9	0.091
abundancia	3	3	0.091
abrasaba	3	3	0.091
pasar	96	118	0.088
deja	27	32	0.087
volvió	154	191	0.086
las	2939	3736	0.086
cuerda	18	21	0.084
conducta	18	21	0.084
papel	58	78	0.081
tesoro	9	13	0.078
señales	9	13	0.078
sentirse	9	13	0.078
recogió	9	13	0.078
principalmente	9	13	0.078
perdió	9	13	0.078
mirarle	9	13	0.078
juez	9	13	0.078
gratitud	9	13	0.078
felices	9	13	0.078
facultades	9	13	0.078
debes	9	13	0.078
causaba	9	13	0.078
vio	157	207	0.077
contaba	22	26	0.076
caballero	33	45	0.076
puño	13	15	0.075
pausa	13	15	0.075
nuestras	13	15	0.075
corriendo	13	15	0.075
carga	13	15	0.075
cajón	13	15	0.075
amar	13	15	0.075
pan	30	41	0.074
tendría	26	31	0.072
pequeña	12	17	0.072
sirvió	8	9	0.071
señalando	8	9	0.071
perdiendo	8	9	0.071
parecer	24	33	0.071
misterio	8	9	0.071
mercado	8	9	0.071
martirio	8	9	0.071
llamas	8	9	0.071
levantado	8	9	0.071
exterior	8	9	0.071
estúpida	8	9	0.071
entiendes	8	9	0.071
encendido	8	9	0.071
empleados	8	9	0.071
barro	8	9	0.071
pepe	34	41	0.067
santidad	17	20	0.066
menor	17	20	0.066
abierta	17	20	0.066
derecho	46	56	0.064
zumbido	2	2	0.061
volveremos	2	2	0.061
volverán	2	2	0.061
vives	2	2	0.061
vivaracha	2	2	0.061
vinos	2	2	0.061
veranos	2	2	0.061
venganzas	2	2	0.061
veintiséis	2	2	0.061
vega	2	2	0.061
valdrá	2	2	0.061
vajilla	2	2	0.061
vagando	2	2	0.061
usaban	2	2	0.061
usa	2	2	0.061
ultraje	2	2	0.061
últimamente	4	6	0.061
tul	2	2	0.061
triunfado	2	2	0.061
tripas	4	6	0.061
tregua	2	2	0.061
traspasaba	2	2	0.061
trapicheos	2	2	0.061
transformaciones	2	2	0.061
transeúnte	2	2	0.061
traidora	2	2	0.061
traídas	2	2	0.061
trabajador	2	2	0.061
trabajaban	2	2	0.061
tornillo	2	2	0.061
torneados	2	2	0.061
tirantes	2	2	0.061
tintas	2	2	0.061
testimonio	4	6	0.061
tertulio	2	2	0.061
terca	2	2	0.061
tendencias	2	2	0.061
temporales	2	2	0.061
templada	2	2	0.061
temblorosas	2	2	0.061
tapiz	2	2	0.061
susceptibilidad	2	2	0.061
supone	2	2	0.061
sumergido	2	2	0.061
suficientemente	2	2	0.061
suciedad	2	2	0.061
sonsonete	2	2	0.061
sofocados	2	2	0.061
socarrona	2	2	0.061
sobrado	2	2	0.061
sistemas	2	2	0.061
sintiera	4	6	0.061
servidor	2	2	0.061
señoronas	2	2	0.061
sembrado	2	2	0.061
seguirla	2	2	0.061
seducía	2	2	0.061
salvado	4	6	0.061
saludaron	2	2	0.061
saludarla	2	2	0.061
salero	2	2	0.061
sacudidas	2	2	0.061
sabías	2	2	0.061
saberse	2	2	0.061
run	4	6	0.061
rostros	2	2	0.061
rompieron	2	2	0.061
rodeadas	2	2	0.061
rodaba	2	2	0.061
robustos	2	2	0.061
risueños	2	2	0.061
retroceder	2	2	0.061
retozona	2	2	0.061
retorcer	2	2	0.061
resonó	2	2	0.061
resabios	2	2	0.061
repugnaban	2	2	0.061
representación	4	6	0.061
reñido	2	2	0.061
renunció	2	2	0.061
remontarse	2	2	0.061
refiriendo	2	2	0.061
reducía	2	2	0.061
rectificar	2	2	0.061
reconciliarse	2	2	0.061
recomendar	2	2	0.061
recogía	2	2	0.061
rechinar	2	2	0.061
quisiéramos	2	2	0.061
quinqué	4	6	0.061
química	2	2	0.061
quimeras	2	2	0.061
quiénes	2	2	0.061
quererte	2	2	0.061
prurito	4	6	0.061
provocar	2	2	0.061
provisiones	4	6	0.061
provisional	2	2	0.061
prórroga	2	2	0.061
pronunciado	2	2	0.061
profesado	2	2	0.061
profesaba	2	2	0.061
pringue	2	2	0.061
pretende	2	2	0.061
presto	2	2	0.061
presentar	4	6	0.061
precoces	2	2	0.061
prácticas	4	6	0.061
potencia	2	2	0.061
porcelana	2	2	0.061
ponerla	4	6	0.061
políticas	2	2	0.061
podridos	2	2	0.061
poderes	2	2	0.061
plazas	2	2	0.061
pistoletazo	2	2	0.061
pirámide	2	2	0.061
pintas	2	2	0.061
pinchazos	2	2	0.061
petaca	2	2	0.061
pesos	2	2	0.061
pesando	2	2	0.061
pesados	4	6	0.061
pesada	4	6	0.061
perdonarla	2	2	0.061
perdidos	4	6	0.061
perderlo	2	2	0.061
perderle	2	2	0.061
peón	2	2	0.061
pensándolo	2	2	0.061
penitencias	2	2	0.061
peinaba	2	2	0.061
patente	2	2	0.061
panes	2	2	0.061
oyentes	2	2	0.061
ordena	2	2	0.061
oprimido	2	2	0.061
ojival	2	2	0.061
ofrezca	2	2	0.061
ofreciera	2	2	0.061
ofrecerle	2	2	0.061
ocioso	2	2	0.061
ochocientos	2	2	0.061
nupcial	2	2	0.061
nudo	4	6	0.061
notase	2	2	0.061
nichos	2	2	0.061
nevada	2	2	0.061
negarle	2	2	0.061
murmullos	2	2	0.061
muevas	2	2	0.061
mudéjar	2	2	0.061
mudaba	2	2	0.061
mole	2	2	0.061
misericordioso	2	2	0.061
mírele	2	2	0.061
mirarlo	2	2	0.061
mínimo	2	2	0.061
mieles	2	2	0.061
metálico	4	6	0.061
metafísico	2	2	0.061
mercaderes	2	2	0.061
menear	2	2	0.061
mejorcito	2	2	0.061
meditabundo	2	2	0.061
mediados	2	2	0.061
maza	4	6	0.061
matilde	2	2	0.061
mascar	2	2	0.061
mártires	2	2	0.061
mareada	2	2	0.061
manirroto	2	2	0.061
manejo	2	2	0.061
maneje	2	2	0.061
mandan	2	2	0.061
manchado	2	2	0.061
maliciosas	2	2	0.061
magia	2	2	0.061
luminoso	2	2	0.061
logrado	2	2	0.061
llovido	2	2	0.061
llevárselo	2	2	0.061
llevamos	2	2	0.061
llegaran	2	2	0.061
llegamos	2	2	0.061
limpiando	4	6	0.061
licencia	2	2	0.061
librería	2	2	0.061
lentitud	2	2	0.061
leída	2	2	0.061
labrar	2	2	0.061
labrador	2	2	0.061
judicial	2	2	0.061
joya	4	6	0.061
italiano	2	2	0.061
italia	2	2	0.061
irresponsable	2	2	0.061
invasión	2	2	0.061
invariable	2	2	0.061
inútilmente	2	2	0.061
inutilidad	2	2	0.061
intimar	2	2	0.061
interno	2	2	0.061
interesada	2	2	0.061
intenciones	4	6	0.061
inquina	2	2	0.061
inquietudes	2	2	0.061
infantiles	2	2	0.061
indicios	2	2	0.061
independiente	2	2	0.061
indefinidamente	2	2	0.061
incorporándose	2	2	0.061
inclinar	2	2	0.061
imponente	2	2	0.061
impertinencia	2	2	0.061
impedían	2	2	0.061
idiotas	2	2	0.061
hurtadillas	2	2	0.061
humillar	2	2	0.061
huella	2	2	0.061
hueca	2	2	0.061
hoyo	2	2	0.061
horrores	4	6	0.061
honores	2	2	0.061
honesto	2	2	0.061
honda	2	2	0.061
hermanita	2	2	0.061
hacerlos	2	2	0.061
hablarían	2	2	0.061
hablara	4	6	0.061
habladora	2	2	0.061
habéis	4	6	0.061
gustado	4	6	0.061
guillotina	2	2	0.061
guía	2	2	0.061
guardaría	2	2	0.061
grandísimo	4	6	0.061
gozándose	2	2	0.061
giró	2	2	0.061
generaciones	2	2	0.061
gemía	2	2	0.061
garrote	2	2	0.061
ganancias	4	6	0.061
galones	2	2	0.061
gallardía	2	2	0.061
galápago	2	2	0.061
fundar	4	6	0.061
fumando	2	2	0.061
fugitivo	2	2	0.061
fueros	2	2	0.061
fuelle	2	2	0.061
frotó	2	2	0.061
francesa	4	6	0.061
frailes	2	2	0.061
forrado	2	2	0.061
forrada	2	2	0.061
flacos	2	2	0.061
físicos	2	2	0.061
firmaba	2	2	0.061
fío	4	6	0.061
fingido	2	2	0.061
filosóficos	2	2	0.061
fijeza	2	2	0.061
fieltro	2	2	0.061
fatigosa	2	2	0.061
fatigados	2	2	0.061
faro	2	2	0.061
famosos	2	2	0.061
familiarmente	2	2	0.061
f	2	2	0.061
extender	2	2	0.061
expuestos	2	2	0.061
explicarme	2	2	0.061
explicarle	2	2	0.061
exceso	2	2	0.061
exageradas	2	2	0.061
evitarlo	2	2	0.061
etcétera	2	2	0.061
estorbo	2	2	0.061
estorba	2	2	0.061
estética	2	2	0.061
estertor	2	2	0.061
esponja	2	2	0.061
espléndida	4	6	0.061
esperarle	2	2	0.061
especias	2	2	0.061
escogió	2	2	0.061
escandalizada	2	2	0.061
erizadas	2	2	0.061
éramos	2	2	0.061
equivocaciones	2	2	0.061
envejecido	2	2	0.061
entusiasmada	2	2	0.061
entremos	2	2	0.061
entregar	4	6	0.061
entierros	2	2	0.061
enteras	2	2	0.061
entendieron	2	2	0.061
entendiera	2	2	0.061
enfático	2	2	0.061
enfadaba	2	2	0.061
endiablada	2	2	0.061
encontrarle	2	2	0.061
encogidos	2	2	0.061
encendía	4	6	0.061
encargaba	2	2	0.061
encarándose	2	2	0.061
encaje	2	2	0.061
empuñó	2	2	0.061
empleada	2	2	0.061
embozó	2	2	0.061
elogiaba	2	2	0.061
elevadas	2	2	0.061
eclesiásticas	2	2	0.061
dramáticos	2	2	0.061
dominando	2	2	0.061
doblaba	2	2	0.061
divierten	2	2	0.061
divierta	2	2	0.061
divertida	2	2	0.061
distinguidos	2	2	0.061
distinguida	2	2	0.061
distancias	2	2	0.061
dirige	2	2	0.061
difusa	2	2	0.061
diego	2	2	0.061
dieciséis	2	2	0.061
dibujo	2	2	0.061
devolvía	2	2	0.061
detiene	2	2	0.061
detenerme	2	2	0.061
desvanecida	2	2	0.061
destinos	2	2	0.061
destinado	2	2	0.061
destinadas	2	2	0.061
destinada	2	2	0.061
desterrado	2	2	0.061
despreciable	2	2	0.061
despide	2	2	0.061
despertara	2	2	0.061
deshacerse	2	2	0.061
desdenes	2	2	0.061
descuidado	2	2	0.061
descubriendo	2	2	0.061
descomunal	2	2	0.061
descomponía	2	2	0.061
descendió	2	2	0.061
desató	2	2	0.061
desahogar	2	2	0.061
derredor	2	2	0.061
demuestra	2	2	0.061
demos	2	2	0.061
demonches	2	2	0.061
dejos	2	2	0.061
dejándote	2	2	0.061
definición	2	2	0.061
defendido	2	2	0.061
decide	4	6	0.061
decaimiento	2	2	0.061
decadencia	2	2	0.061
darnos	2	2	0.061
cumplida	2	2	0.061
cultura	2	2	0.061
cruces	4	6	0.061
críticos	2	2	0.061
creíase	2	2	0.061
creemos	2	2	0.061
creciente	2	2	0.061
costurera	2	2	0.061
corva	2	2	0.061
cortando	2	2	0.061
corazonadas	2	2	0.061
copioso	2	2	0.061
convertida	2	2	0.061
convencerse	2	2	0.061
contradecir	2	2	0.061
contiene	2	2	0.061
contestaron	2	2	0.061
consumo	2	2	0.061
consultaba	2	2	0.061
construida	2	2	0.061
consoladora	2	2	0.061
consintiera	2	2	0.061
consideró	2	2	0.061
considera	2	2	0.061
conseguirlo	4	6	0.061
consagración	2	2	0.061
confusiones	2	2	0.061
condescendencia	2	2	0.061
complicación	2	2	0.061
compensaba	2	2	0.061
comiera	2	2	0.061
cómica	4	6	0.061
colgaba	2	2	0.061
codearse	2	2	0.061
cocinera	4	6	0.061
ciudades	2	2	0.061
citado	2	2	0.061
cinismo	2	2	0.061
ciencias	2	2	0.061
ciegamente	2	2	0.061
chorreaban	2	2	0.061
cesantía	2	2	0.061
cerradura	2	2	0.061
celebró	2	2	0.061
ceder	4	6	0.061
causó	2	2	0.061
cascabel	2	2	0.061
carlista	4	6	0.061
cariñosos	2	2	0.061
caricaturas	2	2	0.061
cargamento	2	2	0.061
carbonera	2	2	0.061
capones	2	2	0.061
cántaro	2	2	0.061
campanada	2	2	0.061
cambiando	2	2	0.061
camarada	2	2	0.061
caderas	2	2	0.061
cabecita	2	2	0.061
cabal	2	2	0.061
buscarme	4	6	0.061
brindis	2	2	0.061
botellas	2	2	0.061
bostezar	2	2	0.061
borrego	2	2	0.061
bordados	2	2	0.061
bombo	2	2	0.061
bolas	4	6	0.061
blanquísimos	2	2	0.061
blanduras	2	2	0.061
besándole	2	2	0.061
bendiciones	2	2	0.061
barra	2	2	0.061
bárbaros	2	2	0.061
bandido	2	2	0.061
azotes	2	2	0.061
azotaba	2	2	0.061
ayes	4	6	0.061
avisos	2	2	0.061
auxilios	2	2	0.061
augusto	2	2	0.061
atrevimientos	2	2	0.061
atreva	2	2	0.061
atrasada	2	2	0.061
atormentado	2	2	0.061
atentado	2	2	0.061
atenciones	2	2	0.061
asomado	2	2	0.061
asomada	2	2	0.061
artísticas	2	2	0.061
arrullaba	2	2	0.061
arrugas	2	2	0.061
arregla	4	6	0.061
arrancado	2	2	0.061
armatoste	2	2	0.061
ardores	2	2	0.061
ardiendo	2	2	0.061
ardentísima	2	2	0.061
aquélla	2	2	0.061
aprendió	2	2	0.061
anzuelo	2	2	0.061
anunciar	4	6	0.061
animándose	2	2	0.061
angosto	2	2	0.061
amiguitas	2	2	0.061
amenazando	2	2	0.061
alumbrada	2	2	0.061
alborota	2	2	0.061
aislamiento	2	2	0.061
ahorros	4	6	0.061
aguardar	2	2	0.061
agitado	2	2	0.061
adulación	2	2	0.061
adquiridas	2	2	0.061
adquiría	2	2	0.061
adivinación	2	2	0.061
adelantó	2	2	0.061
adelanta	2	2	0.061
actor	2	2	0.061
acosado	2	2	0.061
aconsejarle	2	2	0.061
aclaraban	2	2	0.061
acertado	2	2	0.061
academia	2	2	0.061
aburre	2	2	0.061
abrazar	2	2	0.061
aborreciendo	2	2	0.061
abogados	2	2	0.061
abanicos	4	6	0.061
abandona	2	2	0.061
esquina	21	25	0.060
pudo	108	134	0.059
pobreza	12	14	0.056
muertos	12	14	0.056
vuelto	37	45	0.054
sociedad	41	55	0.051
miseria	22	30	0.051
zaragoza	7	10	0.050
queja	7	10	0.050
postura	7	10	0.050
palmadas	7	10	0.050
ofrece	7	10	0.050
llenó	7	10	0.050
insolente	7	10	0.050
infalible	7	10	0.050
imperio	7	10	0.050
haberle	7	10	0.050
formal	7	10	0.050
dolía	7	10	0.050
datos	7	10	0.050
contando	7	10	0.050
carro	7	10	0.050
canas	7	10	0.050
blas	7	10	0.050
apresuró	7	10	0.050
agradaba	7	10	0.050
abrazo	7	10	0.050
existencia	19	26	0.049
ciego	19	26	0.049
yeso	7	8	0.048
temporada	7	8	0.048
revelación	7	8	0.048
proceder	7	8	0.048
paz	38	51	0.048
paternal	7	8	0.048
patadas	7	8	0.048
paisaje	7	8	0.048
manchas	7	8	0.048
legua	7	8	0.048
hermosas	7	8	0.048
equivocado	7	8	0.048
doble	7	8	0.048
discutir	7	8	0.048
discusión	7	8	0.048
despedida	7	8	0.048
delicadeza	7	8	0.048
cuidaba	7	8	0.048
cariñoso	7	8	0.048
cambiado	7	8	0.048
suelta	10	14	0.047
rezar	10	14	0.047
ordinaria	10	14	0.047
norte	16	22	0.047
mérito	16	22	0.047
hueso	10	14	0.047
ganado	10	14	0.047
estancia	10	14	0.047
cuarenta	13	18	0.046
centro	13	18	0.046
labios	56	69	0.045
fresco	24	29	0.044
vivía	40	49	0.043
gobierno	28	34	0.043
tampoco	67	83	0.040
forma	29	39	0.040
vivido	11	13	0.038
pensarlo	11	13	0.038
interesante	11	13	0.038
diente	11	13	0.038
mayor	127	159	0.035
respeto	39	48	0.034
principio	39	48	0.034
hablaron	15	18	0.034
león	19	23	0.033
veinte	27	33	0.032
libertad	31	38	0.032
edad	33	44	0.031
zurcido	1	1	0.030
zarandajas	1	1	0.030
zapatero	2	3	0.030
zancadilla	1	1	0.030
xix	1	1	0.030
xiii	1	1	0.030
vulgarmente	2	3	0.030
vulgarísimo	1	1	0.030
vuestros	1	1	0.030
vuela	1	1	0.030
vuecencia	1	1	0.030
votaba	1	1	0.030
volvíase	1	1	0.030
volvemos	2	3	0.030
voluminoso	1	1	0.030
vocales	1	1	0.030
vitrina	1	1	0.030
vistosos	1	1	0.030
vistos	1	1	0.030
visitó	2	3	0.030
visitarle	1	1	0.030
virtuosas	1	1	0.030
villancicos	1	1	0.030
vigoroso	1	1	0.030
viéndolos	1	1	0.030
vías	1	1	0.030
viajado	1	1	0.030
vestuario	1	1	0.030
vestimos	1	1	0.030
vestimenta	1	1	0.030
vertiente	1	1	0.030
vertido	1	1	0.030
vertical	1	1	0.030
versión	1	1	0.030
verificar	1	1	0.030
vergüenzas	1	1	0.030
verduleras	1	1	0.030
ventanillas	1	1	0.030
venia	1	1	0.030
vengarme	1	1	0.030
vengado	1	1	0.030
vengaba	2	3	0.030
vendo	1	1	0.030
vendían	2	3	0.030
venderse	1	1	0.030
venderlos	1	1	0.030
venciendo	1	1	0.030
vencerme	1	1	0.030
vello	2	3	0.030
veíala	1	1	0.030
vegetación	1	1	0.030
vayamos	2	3	0.030
variantes	1	1	0.030
variados	1	1	0.030
variada	1	1	0.030
variación	1	1	0.030
vanagloriarse	1	1	0.030
valieran	1	1	0.030
valido	2	3	0.030
valera	1	1	0.030
vaivenes	1	1	0.030
vacías	1	1	0.030
vacantes	1	1	0.030
usos	1	1	0.030
usara	1	1	0.030
usada	1	1	0.030
unió	1	1	0.030
unido	2	3	0.030
unidas	1	1	0.030
tuviste	1	1	0.030
tuviesen	2	3	0.030
tutor	1	1	0.030
tutela	1	1	0.030
turris	1	1	0.030
turcas	1	1	0.030
turbio	1	1	0.030
turbarle	1	1	0.030
turbante	1	1	0.030
tumban	1	1	0.030
tugurios	1	1	0.030
tuberculosis	1	1	0.030
trotes	1	1	0.030
tronados	1	1	0.030
triunfal	1	1	0.030
triunfaban	1	1	0.030
triple	1	1	0.030
tripa	1	1	0.030
tributar	1	1	0.030
tremendos	2	3	0.030
trazó	1	1	0.030
tratarle	1	1	0.030
tratándole	2	3	0.030
tratados	1	1	0.030
trastienda	2	3	0.030
traspasar	1	1	0.030
trasnochar	1	1	0.030
trasladándose	1	1	0.030
trascendencia	1	1	0.030
tranvías	1	1	0.030
transparente	1	1	0.030
transparentarse	1	1	0.030
transformismo	1	1	0.030
transformase	1	1	0.030
transformado	1	1	0.030
tranquilizado	1	1	0.030
traídos	1	1	0.030
traidoras	1	1	0.030
tragos	2	3	0.030
trágicos	1	1	0.030
tragedias	1	1	0.030
tragaluces	1	1	0.030
trabillas	1	1	0.030
tosca	2	3	0.030
tortuosos	1	1	0.030
tortillas	1	1	0.030
torero	2	3	0.030
torcidos	1	1	0.030
torcidas	2	3	0.030
tópico	1	1	0.030
topetazo	1	1	0.030
tomará	1	1	0.030
tolera	1	1	0.030
tocarlos	1	1	0.030
titubear	1	1	0.030
tísico	1	1	0.030
tiroteo	1	1	0.030
tiro	17	23	0.030
tíos	2	3	0.030
tímpano	1	1	0.030
timaba	1	1	0.030
tigres	1	1	0.030
tiesa	2	3	0.030
tiernísima	1	1	0.030
tibios	1	1	0.030
textos	2	3	0.030
tétrico	1	1	0.030
terruño	1	1	0.030
terrón	1	1	0.030
territorio	1	1	0.030
terranova	1	1	0.030
terminadas	1	1	0.030
tercas	1	1	0.030
teólogos	1	1	0.030
tenues	1	1	0.030
tentar	1	1	0.030
teníamos	2	3	0.030
tenerlas	1	1	0.030
tendían	1	1	0.030
tender	1	1	0.030
temió	2	3	0.030
temida	1	1	0.030
temeraria	1	1	0.030
temblorosos	1	1	0.030
tembloroso	1	1	0.030
tejiendo	1	1	0.030
tazas	1	1	0.030
tartana	1	1	0.030
tardo	1	1	0.030
tardío	1	1	0.030
tardé	1	1	0.030
taparle	1	1	0.030
tapado	1	1	0.030
tamizada	1	1	0.030
tamiz	1	1	0.030
tamboril	1	1	0.030
tallos	1	1	0.030
talla	2	3	0.030
talegas	1	1	0.030
tacita	1	1	0.030
tabernas	2	3	0.030
sutilezas	1	1	0.030
sutileza	1	1	0.030
sustancial	1	1	0.030
suspirando	2	3	0.030
suscripción	1	1	0.030
surgieron	1	1	0.030
surcaban	1	1	0.030
súplica	1	1	0.030
superficial	1	1	0.030
superaba	1	1	0.030
sumergida	1	1	0.030
sujetar	2	3	0.030
sugirieron	1	1	0.030
sugestión	1	1	0.030
sugerían	1	1	0.030
sufrimiento	1	1	0.030
sufridos	1	1	0.030
sueña	2	3	0.030
suegro	1	1	0.030
sudario	1	1	0.030
suculenta	1	1	0.030
subteniente	1	1	0.030
subsiguientes	1	1	0.030
sublevó	1	1	0.030
subleva	1	1	0.030
súbitas	1	1	0.030
subiría	1	1	0.030
subes	1	1	0.030
subalternos	1	1	0.030
sport	1	1	0.030
sostendré	1	1	0.030
sospecho	1	1	0.030
sospechabas	1	1	0.030
sorprendieron	1	1	0.030
sordina	1	1	0.030
sordas	1	1	0.030
soporífera	1	1	0.030
soplándose	1	1	0.030
soñoliento	1	1	0.030
soñolientas	1	1	0.030
sonrosadas	1	1	0.030
sonoro	1	1	0.030
sondear	1	1	0.030
sonara	1	1	0.030
sonámbula	1	1	0.030
sometida	1	1	0.030
sometía	1	1	0.030
sombríos	1	1	0.030
soltarse	1	1	0.030
soltarlo	1	1	0.030
sólidamente	1	1	0.030
solemos	1	1	0.030
solecismos	1	1	0.030
solapas	1	1	0.030
socarronería	2	3	0.030
sobrio	1	1	0.030
sobrecogía	1	1	0.030
sobran	1	1	0.030
sobadas	1	1	0.030
sobaco	1	1	0.030
situada	1	1	0.030
sirvieron	1	1	0.030
sinrazones	1	1	0.030
singulares	1	1	0.030
síncope	1	1	0.030
sinceras	1	1	0.030
simultáneos	1	1	0.030
símil	1	1	0.030
simiente	1	1	0.030
silbante	1	1	0.030
siguen	2	3	0.030
significaban	2	3	0.030
sigan	1	1	0.030
sibila	1	1	0.030
sexta	1	1	0.030
severos	1	1	0.030
severas	1	1	0.030
sesiones	1	1	0.030
serviles	1	1	0.030
servida	1	1	0.030
servíale	1	1	0.030
serones	1	1	0.030
sernos	1	1	0.030
serme	1	1	0.030
seráfica	1	1	0.030
separose	1	1	0.030
separadas	1	1	0.030
señalados	1	1	0.030
señala	1	1	0.030
sentimos	1	1	0.030
sentíalo	1	1	0.030
senil	1	1	0.030
sencillos	1	1	0.030
semejaban	2	3	0.030
sembrara	1	1	0.030
sembrar	1	1	0.030
sellos	1	1	0.030
selecto	1	1	0.030
seguridades	1	1	0.030
seguirlas	1	1	0.030
seguiría	2	3	0.030
seguiremos	1	1	0.030
seducida	1	1	0.030
secretillo	1	1	0.030
secado	1	1	0.030
secaban	1	1	0.030
sazonada	1	1	0.030
sayones	1	1	0.030
satíricos	1	1	0.030
satén	1	1	0.030
saqueaban	1	1	0.030
sanos	1	1	0.030
sangrienta	1	1	0.030
sancho	1	1	0.030
salvadora	1	1	0.030
saludarle	1	1	0.030
saludarlas	1	1	0.030
saludándola	1	1	0.030
saludables	1	1	0.030
saltase	1	1	0.030
saltaron	2	3	0.030
saltan	1	1	0.030
salomón	1	1	0.030
sacudimientos	1	1	0.030
sacudiéndola	1	1	0.030
sacudido	1	1	0.030
sacrilegio	1	1	0.030
sacrificaba	1	1	0.030
sacerdotal	1	1	0.030
sacará	1	1	0.030
sablazos	1	1	0.030
saberlas	1	1	0.030
rutinarios	1	1	0.030
rutinaria	1	1	0.030
rumboso	1	1	0.030
ruinosos	1	1	0.030
ruidosos	1	1	0.030
rugidos	1	1	0.030
rugía	1	1	0.030
ruego	1	1	0.030
ruedos	1	1	0.030
roncas	1	1	0.030
roncando	1	1	0.030
rompiéndose	1	1	0.030
romperse	1	1	0.030
romperla	1	1	0.030
romerías	1	1	0.030
rojizo	1	1	0.030
roía	1	1	0.030
rogando	1	1	0.030
rodríguez	1	1	0.030
rodó	1	1	0.030
rodeó	1	1	0.030
robledo	1	1	0.030
robar	2	3	0.030
ritos	1	1	0.030
rito	2	3	0.030
riquezas	2	3	0.030
riñó	1	1	0.030
riña	1	1	0.030
rinconadas	1	1	0.030
rieron	2	3	0.030
riego	2	3	0.030
ricacho	1	1	0.030
ribetes	2	3	0.030
ribera	1	1	0.030
ríanse	1	1	0.030
rían	1	1	0.030
rezaría	1	1	0.030
rezagadas	1	1	0.030
revueltos	2	3	0.030
revueltas	2	3	0.030
revoltosa	1	1	0.030
revestido	1	1	0.030
revestían	1	1	0.030
reverencias	1	1	0.030
reventó	1	1	0.030
revelaron	1	1	0.030
revelarle	1	1	0.030
reveladas	1	1	0.030
reunidas	1	1	0.030
reunían	2	3	0.030
retuerce	1	1	0.030
retrocedió	2	3	0.030
retrasaba	1	1	0.030
retorta	1	1	0.030
retiré	1	1	0.030
retirar	2	3	0.030
retina	1	1	0.030
retardaba	1	1	0.030
retaba	1	1	0.030
resultan	1	1	0.030
resuelven	1	1	0.030
resueltos	1	1	0.030
restaurar	1	1	0.030
restablecido	1	1	0.030
respiraron	1	1	0.030
respetuosos	1	1	0.030
respetaran	1	1	0.030
resonaban	1	1	0.030
resonaba	1	1	0.030
resolvía	1	1	0.030
resolverse	1	1	0.030
resoluciones	1	1	0.030
resistido	1	1	0.030
reservarle	1	1	0.030
reservada	2	3	0.030
resbalan	1	1	0.030
resbalaban	1	1	0.030
requerido	1	1	0.030
reprenden	1	1	0.030
repique	1	1	0.030
repasar	2	3	0.030
repartirse	1	1	0.030
repartido	1	1	0.030
repartidas	1	1	0.030
repartían	1	1	0.030
reparando	1	1	0.030
renuncia	1	1	0.030
renovaban	1	1	0.030
rendirle	1	1	0.030
rencoroso	1	1	0.030
rencorosa	1	1	0.030
renacimiento	1	1	0.030
removía	1	1	0.030
remotos	2	3	0.030
remotas	2	3	0.030
remolque	1	1	0.030
rematados	1	1	0.030
relucían	1	1	0.030
relojero	1	1	0.030
relativo	2	3	0.030
relamida	1	1	0.030
relacionaba	1	1	0.030
reiteradas	1	1	0.030
reiría	2	3	0.030
reíanse	1	1	0.030
rehuir	1	1	0.030
regar	1	1	0.030
refugió	1	1	0.030
refugiarse	1	1	0.030
refrescar	1	1	0.030
reflexivo	1	1	0.030
refiriéndose	1	1	0.030
referirse	2	3	0.030
redoblar	1	1	0.030
recuento	1	1	0.030
rectos	1	1	0.030
recreaban	1	1	0.030
recreaba	2	3	0.030
recostaba	1	1	0.030
recortar	2	3	0.030
recortadas	1	1	0.030
recortaba	1	1	0.030
reconocidos	1	1	0.030
reconocida	1	1	0.030
reconciliaciones	1	1	0.030
recomienda	2	3	0.030
recomendados	1	1	0.030
recoletos	1	1	0.030
recojo	1	1	0.030
recoja	1	1	0.030
recogimiento	2	3	0.030
recogerlo	1	1	0.030
reclinada	1	1	0.030
reclamando	1	1	0.030
recientes	1	1	0.030
recibidas	1	1	0.030
rechinaba	1	1	0.030
recelos	1	1	0.030
rece	1	1	0.030
recayó	1	1	0.030
recatarse	1	1	0.030
recaía	1	1	0.030
rebullir	1	1	0.030
rebosa	1	1	0.030
rebeca	1	1	0.030
rebajarse	1	1	0.030
rebajar	1	1	0.030
rebaja	1	1	0.030
reapareció	1	1	0.030
raudales	1	1	0.030
ratoncillo	1	1	0.030
rascándose	1	1	0.030
rápidos	1	1	0.030
rancios	1	1	0.030
rana	1	1	0.030
ramilletes	1	1	0.030
ralea	1	1	0.030
raja	1	1	0.030
raciocinios	1	1	0.030
raciocinio	2	3	0.030
r	1	1	0.030
quitarme	1	1	0.030
quisquilloso	1	1	0.030
quinientas	1	1	0.030
químicos	1	1	0.030
químico	1	1	0.030
quijote	2	3	0.030
querrás	1	1	0.030
querrán	1	1	0.030
quemando	1	1	0.030
quejumbroso	1	1	0.030
quejo	1	1	0.030
quedaran	1	1	0.030
quedaos	1	1	0.030
quedábamos	1	1	0.030
purísimas	1	1	0.030
purificada	1	1	0.030
purezas	1	1	0.030
puñado	1	1	0.030
puntadas	1	1	0.030
pulgada	1	1	0.030
pujanza	1	1	0.030
pugilato	1	1	0.030
puerilidad	1	1	0.030
puercos	1	1	0.030
pudre	1	1	0.030
pudieras	1	1	0.030
publicaban	1	1	0.030
pruebo	1	1	0.030
proyectiles	1	1	0.030
proyectado	1	1	0.030
próximos	2	3	0.030
provocó	1	1	0.030
provisto	1	1	0.030
provincianos	1	1	0.030
provechosos	1	1	0.030
provechosas	1	1	0.030
protestaron	1	1	0.030
protejo	1	1	0.030
proteja	1	1	0.030
proporcionado	1	1	0.030
propalar	1	1	0.030
propagar	1	1	0.030
pronunció	1	1	0.030
pronunciaron	1	1	0.030
pronunciaba	2	3	0.030
pronuncia	1	1	0.030
pronta	2	3	0.030
pronósticos	1	1	0.030
prometida	1	1	0.030
promete	1	1	0.030
prolonga	1	1	0.030
prohibió	1	1	0.030
profesaban	1	1	0.030
proezas	1	1	0.030
producidas	1	1	0.030
producen	2	3	0.030
prodigioso	1	1	0.030
prodigando	1	1	0.030
procuro	1	1	0.030
procurará	1	1	0.030
procura	1	1	0.030
proceso	2	3	0.030
procedentes	1	1	0.030
procede	1	1	0.030
probando	2	3	0.030
probabilidades	2	3	0.030
pro	1	1	0.030
prisionero	1	1	0.030
prisionera	2	3	0.030
principiar	1	1	0.030
primos	1	1	0.030
primitiva	2	3	0.030
primita	1	1	0.030
primeramente	1	1	0.030
prevenida	1	1	0.030
pretérita	1	1	0.030
prestidigitador	1	1	0.030
presidiario	1	1	0.030
presidencia	1	1	0.030
presentarles	1	1	0.030
presentación	1	1	0.030
presenció	1	1	0.030
presenciara	1	1	0.030
presbiterio	1	1	0.030
preocuparse	1	1	0.030
prematuro	1	1	0.030
pregunté	2	3	0.030
preguntarme	1	1	0.030
preguntándose	1	1	0.030
pregonaba	1	1	0.030
preferible	1	1	0.030
preferencia	2	3	0.030
predisposición	1	1	0.030
predicó	1	1	0.030
precisión	1	1	0.030
precipitaba	1	1	0.030
preciaba	2	3	0.030
precepto	1	1	0.030
pragmática	1	1	0.030
potente	1	1	0.030
póstuma	1	1	0.030
posta	1	1	0.030
posiciones	1	1	0.030
posibilidad	2	3	0.030
poseo	1	1	0.030
poseerte	1	1	0.030
posada	2	3	0.030
porte	1	1	0.030
porra	1	1	0.030
porfiado	1	1	0.030
ponérsela	1	1	0.030
polvorienta	1	1	0.030
plomizas	1	1	0.030
platónica	1	1	0.030
plateadas	1	1	0.030
plantaba	1	1	0.030
planchas	1	1	0.030
planchado	1	1	0.030
placa	1	1	0.030
pitanza	1	1	0.030
pitágoras	1	1	0.030
pisoteado	1	1	0.030
pisándose	1	1	0.030
piratas	1	1	0.030
pintorescos	1	1	0.030
pintón	2	3	0.030
pingües	1	1	0.030
pinares	1	1	0.030
pin	1	1	0.030
pillastres	1	1	0.030
pidieron	1	1	0.030
pidiera	2	3	0.030
pidiéndole	1	1	0.030
picazón	1	1	0.030
pícaros	1	1	0.030
picará	1	1	0.030
petrificada	1	1	0.030
pestañas	2	3	0.030
pescaba	1	1	0.030
pesaban	1	1	0.030
perversas	1	1	0.030
perturbado	1	1	0.030
pertenecen	1	1	0.030
persuadirle	1	1	0.030
perspectivas	1	1	0.030
persistía	1	1	0.030
persiguió	1	1	0.030
persiguen	1	1	0.030
permitirme	1	1	0.030
periódica	1	1	0.030
perifollo	1	1	0.030
pergaminos	1	1	0.030
pérez	1	1	0.030
perdóneme	2	3	0.030
perdonara	1	1	0.030
perdiese	1	1	0.030
perdieron	1	1	0.030
perdiera	1	1	0.030
peña	2	3	0.030
pentagrama	1	1	0.030
pensarse	1	1	0.030
peluca	2	3	0.030
pellizcaban	1	1	0.030
peinó	1	1	0.030
pedradas	2	3	0.030
pechuga	2	3	0.030
pecaminosos	1	1	0.030
pecador	2	3	0.030
patrióticas	1	1	0.030
patriarca	1	1	0.030
patrañas	1	1	0.030
patena	1	1	0.030
pasmo	2	3	0.030
pasmábase	1	1	0.030
pasma	1	1	0.030
pascuas	2	3	0.030
pasaremos	1	1	0.030
pasaran	1	1	0.030
participar	2	3	0.030
parisienses	1	1	0.030
pareciese	2	3	0.030
parecíanle	1	1	0.030
parecería	2	3	0.030
pareceres	1	1	0.030
parche	1	1	0.030
parca	1	1	0.030
pararía	1	1	0.030
parábola	1	1	0.030
paraban	2	3	0.030
panegírico	1	1	0.030
palpar	1	1	0.030
palpando	1	1	0.030
palpables	1	1	0.030
palpaba	1	1	0.030
palmeras	1	1	0.030
palideció	1	1	0.030
palidecer	1	1	0.030
palas	1	1	0.030
palación	1	1	0.030
palabrotas	1	1	0.030
pagarlo	1	1	0.030
pagarán	1	1	0.030
pagará	2	3	0.030
paganismo	1	1	0.030
padrenuestro	1	1	0.030
padezca	1	1	0.030
padeció	2	3	0.030
padecimientos	1	1	0.030
pactos	1	1	0.030
pacos	1	1	0.030
pacíficamente	1	1	0.030
pacífica	2	3	0.030
otorgado	1	1	0.030
ostentando	1	1	0.030
ostentan	1	1	0.030
oscilando	1	1	0.030
osar	1	1	0.030
osados	1	1	0.030
orza	1	1	0.030
oropel	1	1	0.030
ornato	1	1	0.030
originales	1	1	0.030
oriental	1	1	0.030
orgullosos	1	1	0.030
ordenarse	1	1	0.030
orangutanes	1	1	0.030
oráculo	1	1	0.030
opulencia	1	1	0.030
opuestas	1	1	0.030
opuesta	1	1	0.030
oprimidos	1	1	0.030
opresiones	1	1	0.030
oportunos	1	1	0.030
omnipotencia	1	1	0.030
olvidarla	1	1	0.030
olido	1	1	0.030
olfateando	1	1	0.030
ojivas	1	1	0.030
oírlos	1	1	0.030
ofensa	2	3	0.030
ofenderse	1	1	0.030
ocurrírsele	1	1	0.030
ocupándose	1	1	0.030
ocupadas	1	1	0.030
ocultes	1	1	0.030
ocultas	1	1	0.030
ocultarle	1	1	0.030
octavo	1	1	0.030
octava	1	1	0.030
ociosidad	2	3	0.030
ochavos	1	1	0.030
ocasional	1	1	0.030
obstinaba	1	1	0.030
observe	1	1	0.030
obsequiadas	1	1	0.030
obligaron	1	1	0.030
oblicuas	1	1	0.030
obedientes	1	1	0.030
nuncio	1	1	0.030
numerosa	1	1	0.030
novísima	1	1	0.030
novelistas	1	1	0.030
nombramientos	1	1	0.030
nombramiento	1	1	0.030
nombra	1	1	0.030
niegas	1	1	0.030
neos	1	1	0.030
neo	1	1	0.030
negase	1	1	0.030
negaron	1	1	0.030
necesitados	1	1	0.030
necesitaban	2	3	0.030
navío	1	1	0.030
nacida	1	1	0.030
nací	1	1	0.030
musas	1	1	0.030
murillo	2	3	0.030
muriéndose	1	1	0.030
muñón	1	1	0.030
munificencia	1	1	0.030
múltiples	1	1	0.030
multas	1	1	0.030
mueven	1	1	0.030
mudó	2	3	0.030
mudar	2	3	0.030
mudando	1	1	0.030
muchísimos	1	1	0.030
muchachuelas	1	1	0.030
mozalbetes	1	1	0.030
moviese	1	1	0.030
moviera	1	1	0.030
movibles	1	1	0.030
motes	1	1	0.030
mosquitos	2	3	0.030
mosquito	2	3	0.030
mortificarla	1	1	0.030
mortificación	2	3	0.030
morro	1	1	0.030
moralizar	1	1	0.030
moña	1	1	0.030
monumental	1	1	0.030
montar	1	1	0.030
montaba	1	1	0.030
monstruosa	1	1	0.030
monjes	1	1	0.030
monísima	2	3	0.030
mollera	1	1	0.030
molestias	2	3	0.030
mojar	1	1	0.030
modismos	1	1	0.030
modificado	1	1	0.030
modernas	2	3	0.030
mochuelo	1	1	0.030
mirarme	1	1	0.030
mirarían	1	1	0.030
miramiento	1	1	0.030
mirábala	1	1	0.030
miope	1	1	0.030
mimosa	1	1	0.030
mímicas	1	1	0.030
mimaban	1	1	0.030
millón	1	1	0.030
militante	1	1	0.030
miedosa	1	1	0.030
mezquita	1	1	0.030
mezcló	1	1	0.030
metz	1	1	0.030
metérselo	1	1	0.030
mero	1	1	0.030
mereciese	1	1	0.030
mentís	1	1	0.030
mentales	1	1	0.030
menestrales	1	1	0.030
meneo	1	1	0.030
méndez	1	1	0.030
melancólicamente	1	1	0.030
mejoraba	1	1	0.030
meditado	1	1	0.030
medirse	1	1	0.030
medianas	1	1	0.030
mediana	2	3	0.030
mecha	1	1	0.030
matronas	1	1	0.030
matías	1	1	0.030
materialistas	1	1	0.030
mateo	1	1	0.030
matase	1	1	0.030
masca	1	1	0.030
martirizarle	1	1	0.030
martillazo	1	1	0.030
marte	1	1	0.030
marquilla	1	1	0.030
mariscos	1	1	0.030
mariposa	1	1	0.030
marinos	1	1	0.030
marino	1	1	0.030
marimachos	1	1	0.030
mareado	1	1	0.030
marchando	1	1	0.030
maquinaciones	1	1	0.030
mantenido	1	1	0.030
manteleta	1	1	0.030
manteles	1	1	0.030
manteca	2	3	0.030
mansedumbre	2	3	0.030
mansa	1	1	0.030
manifestara	1	1	0.030
manifestado	1	1	0.030
manifestaban	1	1	0.030
manejaban	1	1	0.030
mandria	1	1	0.030
mandasen	1	1	0.030
mandase	1	1	0.030
mandaron	1	1	0.030
mandaremos	1	1	0.030
mandamientos	1	1	0.030
mandamiento	1	1	0.030
manchadas	1	1	0.030
maltrataba	1	1	0.030
mago	1	1	0.030
magnitud	1	1	0.030
magnética	1	1	0.030
magistratura	1	1	0.030
madurando	1	1	0.030
madrileñas	1	1	0.030
madrigueras	1	1	0.030
madrigales	1	1	0.030
madeja	1	1	0.030
machacona	1	1	0.030
macetas	1	1	0.030
luminosas	1	1	0.030
lugarón	1	1	0.030
luenga	1	1	0.030
lucrativa	1	1	0.030
lució	1	1	0.030
luciera	1	1	0.030
luchaban	1	1	0.030
loquilla	1	1	0.030
lonjas	1	1	0.030
logrando	1	1	0.030
lloviendo	1	1	0.030
llevarlo	1	1	0.030
llevará	2	3	0.030
llevados	1	1	0.030
llenaron	2	3	0.030
lleguemos	1	1	0.030
llaneza	1	1	0.030
llamen	1	1	0.030
llamé	1	1	0.030
llamarán	1	1	0.030
llamara	1	1	0.030
llaga	1	1	0.030
liviana	1	1	0.030
lisonjera	1	1	0.030
liquidación	2	3	0.030
linaje	2	3	0.030
limpiaron	1	1	0.030
limpiarle	1	1	0.030
limpiaba	2	3	0.030
limitada	1	1	0.030
limitaban	1	1	0.030
limbo	1	1	0.030
ligeros	1	1	0.030
ligaduras	1	1	0.030
licenciados	1	1	0.030
librerías	1	1	0.030
librara	1	1	0.030
liberté	1	1	0.030
libertades	2	3	0.030
leves	2	3	0.030
levante	2	3	0.030
levántate	1	1	0.030
levantada	2	3	0.030
lentejas	1	1	0.030
lees	1	1	0.030
leen	1	1	0.030
lechuga	1	1	0.030
lavaban	1	1	0.030
latigazo	1	1	0.030
latía	1	1	0.030
lastimosa	1	1	0.030
lastimero	1	1	0.030
lastimar	1	1	0.030
lastimaba	1	1	0.030
larguísima	1	1	0.030
landó	1	1	0.030
lamparilla	1	1	0.030
lamía	1	1	0.030
lamento	1	1	0.030
lacayo	2	3	0.030
laboriosa	1	1	0.030
justificar	1	1	0.030
júramelo	1	1	0.030
jurados	1	1	0.030
juntaba	1	1	0.030
jugo	1	1	0.030
jovellanos	1	1	0.030
jofaina	1	1	0.030
jícara	1	1	0.030
jericó	1	1	0.030
jarras	2	3	0.030
jardineras	1	1	0.030
jadeantes	1	1	0.030
irritó	1	1	0.030
irritabilidad	1	1	0.030
irremediables	1	1	0.030
irregularidades	1	1	0.030
ironías	1	1	0.030
irisados	1	1	0.030
involucremos	1	1	0.030
invocando	2	3	0.030
invitar	1	1	0.030
invitando	1	1	0.030
inventor	1	1	0.030
inválido	1	1	0.030
invadían	1	1	0.030
intrusa	1	1	0.030
introdujese	1	1	0.030
introduciendo	1	1	0.030
introducido	1	1	0.030
intimó	1	1	0.030
interrumpiera	1	1	0.030
interrumpiéndole	1	1	0.030
interrumpida	1	1	0.030
interrumpas	1	1	0.030
intérprete	1	1	0.030
interpretar	1	1	0.030
interlocutores	1	1	0.030
interjecciones	1	1	0.030
interino	1	1	0.030
interceptaban	1	1	0.030
intenté	1	1	0.030
intentado	1	1	0.030
intendente	1	1	0.030
inteligentes	1	1	0.030
intachables	1	1	0.030
instó	1	1	0.030
instantáneo	1	1	0.030
instancia	1	1	0.030
inspirarse	1	1	0.030
inspiraban	2	3	0.030
insoportables	1	1	0.030
insolencias	1	1	0.030
insistiendo	1	1	0.030
insistido	1	1	0.030
insisten	1	1	0.030
inseparable	1	1	0.030
insensiblemente	2	3	0.030
insectos	1	1	0.030
insecto	1	1	0.030
inquietaban	1	1	0.030
inocentadas	1	1	0.030
innumerables	1	1	0.030
innovador	1	1	0.030
innobles	1	1	0.030
inmundas	1	1	0.030
inmovilidad	1	1	0.030
inmoralidad	1	1	0.030
inmodestia	1	1	0.030
inmemorial	2	3	0.030
inmediaciones	1	1	0.030
injuriosas	1	1	0.030
iniciación	1	1	0.030
inflexible	2	3	0.030
infinitos	2	3	0.030
infernales	2	3	0.030
infantería	1	1	0.030
infante	1	1	0.030
infamias	1	1	0.030
inexperto	1	1	0.030
inesperadas	1	1	0.030
industriales	2	3	0.030
indino	1	1	0.030
indignaban	1	1	0.030
indicaron	1	1	0.030
indicado	1	1	0.030
incurrir	1	1	0.030
incumbencia	1	1	0.030
incorruptible	1	1	0.030
incorrecta	1	1	0.030
inconstancia	1	1	0.030
incompatible	1	1	0.030
incomparable	2	3	0.030
incomodarme	1	1	0.030
incensario	1	1	0.030
incautos	1	1	0.030
inauguró	1	1	0.030
inanición	1	1	0.030
inaguantable	1	1	0.030
impulsan	1	1	0.030
impuesta	1	1	0.030
improvisada	1	1	0.030
improvisación	1	1	0.030
impropias	1	1	0.030
impropia	2	3	0.030
imprimían	1	1	0.030
impresas	1	1	0.030
impotente	1	1	0.030
imponer	1	1	0.030
imponen	1	1	0.030
impidió	1	1	0.030
ímpetus	1	1	0.030
imperiosos	1	1	0.030
imperativo	1	1	0.030
impedirle	1	1	0.030
impacientes	1	1	0.030
imaginativos	1	1	0.030
imaginarla	1	1	0.030
ilusorios	1	1	0.030
iluminarme	1	1	0.030
ilegal	1	1	0.030
iguale	1	1	0.030
ignore	1	1	0.030
ignorada	1	1	0.030
idéntica	1	1	0.030
ibérica	1	1	0.030
íbamos	2	3	0.030
humorísticas	1	1	0.030
humorística	1	1	0.030
humillante	1	1	0.030
humeante	1	1	0.030
huían	1	1	0.030
huésped	1	1	0.030
hubiéramos	2	3	0.030
hoz	1	1	0.030
hoteles	1	1	0.030
hostias	2	3	0.030
hortaliza	1	1	0.030
horizontes	2	3	0.030
horada	1	1	0.030
honrar	1	1	0.030
honrando	1	1	0.030
honorario	1	1	0.030
honestidad	1	1	0.030
hombrunas	1	1	0.030
holgazanes	1	1	0.030
holgazanería	1	1	0.030
holgadamente	1	1	0.030
hogares	1	1	0.030
hoc	2	3	0.030
históricas	2	3	0.030
hiperbólicamente	1	1	0.030
hincaba	1	1	0.030
himnos	1	1	0.030
higiénicos	1	1	0.030
hidra	1	1	0.030
herreros	1	1	0.030
herrar	1	1	0.030
heridos	1	1	0.030
heridas	2	3	0.030
hería	1	1	0.030
heráldica	1	1	0.030
heló	1	1	0.030
helar	1	1	0.030
hazaña	1	1	0.030
harina	1	1	0.030
hamlet	1	1	0.030
hambriento	2	3	0.030
hagámonos	1	1	0.030
haciéndome	1	1	0.030
hacíale	1	1	0.030
hache	1	1	0.030
hacérsele	1	1	0.030
hacernos	2	3	0.030
hacerlas	1	1	0.030
hablen	1	1	0.030
háblame	1	1	0.030
habita	1	1	0.030
haberlos	1	1	0.030
habas	1	1	0.030
guturales	1	1	0.030
gutapercha	1	1	0.030
gustoso	1	1	0.030
gustas	1	1	0.030
gusanera	1	1	0.030
guiar	1	1	0.030
guarden	1	1	0.030
guardase	1	1	0.030
guardarlas	1	1	0.030
guardamalletas	1	1	0.030
guardados	1	1	0.030
guapos	1	1	0.030
groserías	1	1	0.030
grasiento	1	1	0.030
gracejo	2	3	0.030
golpecito	1	1	0.030
gobernarse	1	1	0.030
gloriosos	1	1	0.030
girando	1	1	0.030
gimió	1	1	0.030
gigantescas	1	1	0.030
gestación	1	1	0.030
geografía	2	3	0.030
gentuza	2	3	0.030
gentileza	1	1	0.030
generalmente	2	3	0.030
garcía	2	3	0.030
ganzúa	1	1	0.030
ganamos	1	1	0.030
galleta	1	1	0.030
galileo	1	1	0.030
galgo	1	1	0.030
galdós	1	1	0.030
galas	1	1	0.030
galantes	1	1	0.030
galante	2	3	0.030
furiosas	1	1	0.030
furibundos	1	1	0.030
funcionario	1	1	0.030
funcionaba	1	1	0.030
fulminó	1	1	0.030
fulminantes	1	1	0.030
fulgores	1	1	0.030
fulano	2	3	0.030
fuimos	1	1	0.030
frustrado	1	1	0.030
frotando	1	1	0.030
frontal	1	1	0.030
frivolidad	1	1	0.030
frisaba	1	1	0.030
fríamente	1	1	0.030
frenética	1	1	0.030
frecuentaban	1	1	0.030
francesas	1	1	0.030
fragmento	1	1	0.030
frágiles	2	3	0.030
fragancias	1	1	0.030
fósforo	2	3	0.030
fortunas	1	1	0.030
fortifica	1	1	0.030
forman	1	1	0.030
formales	2	3	0.030
flema	1	1	0.030
flecos	1	1	0.030
flamencos	1	1	0.030
flamante	1	1	0.030
fisonomías	1	1	0.030
finitas	1	1	0.030
fingir	2	3	0.030
fingimientos	1	1	0.030
fingidos	1	1	0.030
filípica	2	3	0.030
filete	1	1	0.030
filantrópicos	1	1	0.030
filantrópico	1	1	0.030
filantropía	1	1	0.030
fijar	2	3	0.030
fijan	1	1	0.030
ficciones	1	1	0.030
fiado	1	1	0.030
fétido	1	1	0.030
fervorosa	1	1	0.030
fervientes	1	1	0.030
fenómenos	2	3	0.030
felizmente	2	3	0.030
felicitaron	1	1	0.030
favorecían	1	1	0.030
favorecía	2	3	0.030
fatua	1	1	0.030
fatales	1	1	0.030
fascinaba	1	1	0.030
farsas	1	1	0.030
fantásticas	1	1	0.030
fantásticamente	1	1	0.030
famosas	1	1	0.030
faltase	1	1	0.030
falsificada	1	1	0.030
fallecido	1	1	0.030
facilita	1	1	0.030
fachadas	1	1	0.030
fábricas	2	3	0.030
fa	1	1	0.030
extremada	2	3	0.030
extravían	1	1	0.030
extraviados	2	3	0.030
extraordinarios	1	1	0.030
extraído	1	1	0.030
extinguirse	1	1	0.030
extinguido	1	1	0.030
extendido	2	3	0.030
expreso	1	1	0.030
expresivas	1	1	0.030
explotar	2	3	0.030
expliquen	1	1	0.030
expertos	1	1	0.030
expertas	1	1	0.030
experimentos	1	1	0.030
experimento	1	1	0.030
experimentaba	2	3	0.030
exóticas	1	1	0.030
existieran	1	1	0.030
exenta	1	1	0.030
execrables	1	1	0.030
execrable	1	1	0.030
excusaba	1	1	0.030
excesivamente	1	1	0.030
excepcionales	1	1	0.030
examina	1	1	0.030
exaltados	1	1	0.030
exaltadas	1	1	0.030
exagerando	1	1	0.030
exageraba	2	3	0.030
exacta	2	3	0.030
eternidad	2	3	0.030
estuches	1	1	0.030
estrujar	1	1	0.030
estrujaba	1	1	0.030
estropicio	1	1	0.030
estricta	1	1	0.030
estremecerse	1	1	0.030
estragados	1	1	0.030
estorbarle	1	1	0.030
estorbar	1	1	0.030
estofa	1	1	0.030
estocadas	1	1	0.030
estirpe	1	1	0.030
estímulo	1	1	0.030
estera	1	1	0.030
estarlo	2	3	0.030
estalle	1	1	0.030
establecen	1	1	0.030
estable	1	1	0.030
esquilón	1	1	0.030
esqueletos	1	1	0.030
esprit	1	1	0.030
espiritualista	1	1	0.030
esperándola	1	1	0.030
esperan	2	3	0.030
esparto	2	3	0.030
espantado	2	3	0.030
esmerada	1	1	0.030
escupiría	1	1	0.030
escultor	1	1	0.030
escueta	1	1	0.030
escuchado	1	1	0.030
escucha	2	3	0.030
escrupuloso	2	3	0.030
escrupulosa	1	1	0.030
escribiré	1	1	0.030
escribiera	1	1	0.030
escondidos	2	3	0.030
escondería	1	1	0.030
esconder	2	3	0.030
escogidos	1	1	0.030
escogidas	1	1	0.030
escogida	1	1	0.030
escocias	1	1	0.030
escénico	1	1	0.030
escarnecía	1	1	0.030
escapatorias	2	3	0.030
escapase	1	1	0.030
escaparon	1	1	0.030
escapadas	1	1	0.030
escandalizan	1	1	0.030
escalonada	1	1	0.030
eruditos	1	1	0.030
equivoca	1	1	0.030
envuelven	1	1	0.030
envidiosa	2	3	0.030
envidiado	1	1	0.030
enviarle	1	1	0.030
entusiasmó	1	1	0.030
entrometidos	1	1	0.030
entrometidas	1	1	0.030
entretenimiento	1	1	0.030
entretenido	2	3	0.030
entrego	2	3	0.030
entregarme	1	1	0.030
entregarle	1	1	0.030
entregaría	1	1	0.030
entregados	1	1	0.030
entraremos	1	1	0.030
entraré	2	3	0.030
entramos	1	1	0.030
entornaba	1	1	0.030
entidades	1	1	0.030
entendieran	1	1	0.030
entenderé	1	1	0.030
entendedor	1	1	0.030
entablaba	1	1	0.030
enseñarte	1	1	0.030
enseñándole	1	1	0.030
ensartadas	1	1	0.030
enroscado	1	1	0.030
enredar	2	3	0.030
enredado	1	1	0.030
enredada	1	1	0.030
enredaban	1	1	0.030
enreda	1	1	0.030
enojaba	1	1	0.030
enlazados	1	1	0.030
enjugando	1	1	0.030
engendrar	1	1	0.030
enganchadas	1	1	0.030
enfurecía	1	1	0.030
enfriara	1	1	0.030
enemistad	1	1	0.030
encopetadas	1	1	0.030
encontraremos	1	1	0.030
encontrábase	1	1	0.030
encomienda	1	1	0.030
encogida	1	1	0.030
encinta	1	1	0.030
encienda	1	1	0.030
encerrona	1	1	0.030
encerrarla	1	1	0.030
encerrándose	1	1	0.030
encerraban	1	1	0.030
encendieron	2	3	0.030
encenderse	1	1	0.030
encargarse	1	1	0.030
encargaría	1	1	0.030
encargadas	1	1	0.030
encargada	1	1	0.030
encargaban	1	1	0.030
encantadora	1	1	0.030
encajan	1	1	0.030
enano	1	1	0.030
enamoramiento	1	1	0.030
enajenación	1	1	0.030
empujó	2	3	0.030
empujando	1	1	0.030
emprenderla	1	1	0.030
emplearse	1	1	0.030
empleara	1	1	0.030
empequeñecido	1	1	0.030
empeñarse	2	3	0.030
empeñaron	1	1	0.030
empedernido	1	1	0.030
empecemos	1	1	0.030
empapada	1	1	0.030
empalagosa	1	1	0.030
eminentemente	1	1	0.030
eminente	1	1	0.030
emigrar	1	1	0.030
embrutecía	1	1	0.030
embriagada	1	1	0.030
embozándose	1	1	0.030
emborrachaban	1	1	0.030
embobado	1	1	0.030
emanciparse	1	1	0.030
elogiando	1	1	0.030
elemental	2	3	0.030
elástico	1	1	0.030
elaboración	1	1	0.030
ejemplares	2	3	0.030
edificaba	1	1	0.030
economista	1	1	0.030
eclipses	1	1	0.030
echarlos	1	1	0.030
ebro	1	1	0.030
durmiese	1	1	0.030
durmiéndola	1	1	0.030
duración	1	1	0.030
dulzón	1	1	0.030
dulcísimo	1	1	0.030
duelos	1	1	0.030
dudosa	1	1	0.030
dotada	1	1	0.030
dormitar	1	1	0.030
dormitaban	1	1	0.030
dormitaba	1	1	0.030
dormiremos	1	1	0.030
domini	1	1	0.030
doctrinas	2	3	0.030
dobla	1	1	0.030
divisar	1	1	0.030
divinidades	2	3	0.030
dividió	1	1	0.030
divertirme	1	1	0.030
diversión	2	3	0.030
disuadir	1	1	0.030
distrajera	1	1	0.030
distraía	2	3	0.030
distraerle	1	1	0.030
distrae	1	1	0.030
distingue	1	1	0.030
disputó	1	1	0.030
disputárselo	1	1	0.030
disputaron	1	1	0.030
dispersión	1	1	0.030
dispersado	1	1	0.030
disolvían	1	1	0.030
disolventes	2	3	0.030
disoluta	1	1	0.030
dislocado	1	1	0.030
dislocada	1	1	0.030
disipar	1	1	0.030
disgustó	2	3	0.030
disfrazada	1	1	0.030
disertación	1	1	0.030
disciplinarias	1	1	0.030
discernir	1	1	0.030
dirigiendo	2	3	0.030
diríase	1	1	0.030
diremos	1	1	0.030
direcciones	1	1	0.030
diputación	1	1	0.030
diplomática	1	1	0.030
dintel	1	1	0.030
dinastía	1	1	0.030
diminuto	1	1	0.030
diligente	1	1	0.030
digería	1	1	0.030
dificultaba	1	1	0.030
difícilmente	2	3	0.030
diesen	1	1	0.030
diéramos	1	1	0.030
dieciocho	2	3	0.030
dictan	1	1	0.030
dibujando	1	1	0.030
dibujado	1	1	0.030
devorándola	1	1	0.030
devocionarios	1	1	0.030
detuviera	1	1	0.030
determinarse	1	1	0.030
determinadas	1	1	0.030
detenido	1	1	0.030
detenida	1	1	0.030
detenerlo	1	1	0.030
detenerle	1	1	0.030
desvaneciéndose	1	1	0.030
desvanecido	2	3	0.030
desvanecidas	1	1	0.030
desvanecen	1	1	0.030
desván	1	1	0.030
destruía	1	1	0.030
destinaba	1	1	0.030
destajo	1	1	0.030
destacaban	1	1	0.030
despuntaba	1	1	0.030
despropósito	1	1	0.030
desprendido	1	1	0.030
despreció	1	1	0.030
desplumaban	1	1	0.030
despilfarro	1	1	0.030
despídete	1	1	0.030
despertaron	2	3	0.030
despedido	1	1	0.030
despache	1	1	0.030
desmedida	1	1	0.030
desmayados	1	1	0.030
desmayaba	1	1	0.030
deslizó	1	1	0.030
deslizarse	1	1	0.030
deshizo	2	3	0.030
deshechas	1	1	0.030
deshacían	1	1	0.030
deshacen	1	1	0.030
desgraciados	2	3	0.030
deseoso	1	1	0.030
desenlace	1	1	0.030
desengañadas	1	1	0.030
desempeñado	1	1	0.030
desecho	1	1	0.030
desdoro	1	1	0.030
descuidos	1	1	0.030
descubrieran	1	1	0.030
describe	1	1	0.030
descontenta	1	1	0.030
desconocidos	1	1	0.030
descastada	1	1	0.030
descaro	2	3	0.030
descarnada	1	1	0.030
descargada	1	1	0.030
desataban	1	1	0.030
desamparado	1	1	0.030
desairar	2	3	0.030
desahogan	1	1	0.030
desacreditar	1	1	0.030
derribarle	1	1	0.030
derrengado	1	1	0.030
derramó	1	1	0.030
derrame	1	1	0.030
derramarse	1	1	0.030
derramamiento	1	1	0.030
depositaban	1	1	0.030
densa	1	1	0.030
demuestran	1	1	0.030
demonche	1	1	0.030
demócratas	1	1	0.030
demanda	1	1	0.030
demagogo	1	1	0.030
delitos	2	3	0.030
deliciosos	1	1	0.030
dejémoslo	1	1	0.030
dejándole	2	3	0.030
déjala	1	1	0.030
definitiva	2	3	0.030
deficiencias	1	1	0.030
defensor	1	1	0.030
defendiera	1	1	0.030
defendiendo	1	1	0.030
deducía	1	1	0.030
dedicarse	2	3	0.030
dedicar	1	1	0.030
decretó	1	1	0.030
decretado	1	1	0.030
declive	1	1	0.030
declarados	1	1	0.030
declaraciones	1	1	0.030
declamaciones	1	1	0.030
decírtelo	1	1	0.030
decidiera	1	1	0.030
decididamente	1	1	0.030
decidí	1	1	0.030
débilmente	1	1	0.030
debilitado	1	1	0.030
deberían	1	1	0.030
debería	1	1	0.030
darwinista	1	1	0.030
darwin	1	1	0.030
dárselas	1	1	0.030
daños	1	1	0.030
dante	1	1	0.030
curtidos	1	1	0.030
curtido	1	1	0.030
curiosos	1	1	0.030
cuota	1	1	0.030
cuneta	1	1	0.030
cumplirse	1	1	0.030
cumplidamente	1	1	0.030
cumplas	1	1	0.030
cultivando	1	1	0.030
culpables	1	1	0.030
culebras	2	3	0.030
cuestan	1	1	0.030
cuernos	1	1	0.030
cuchicheando	1	1	0.030
cubrirse	1	1	0.030
cubiletes	1	1	0.030
cúbicos	1	1	0.030
cuartetos	1	1	0.030
cruzar	1	1	0.030
crujieron	1	1	0.030
crudezas	1	1	0.030
crudas	1	1	0.030
cruda	2	3	0.030
crucifijo	2	3	0.030
criticar	1	1	0.030
criterios	1	1	0.030
criaban	1	1	0.030
creerla	1	1	0.030
crecimiento	2	3	0.030
creces	1	1	0.030
crearía	1	1	0.030
créanlo	1	1	0.030
crac	1	1	0.030
costera	1	1	0.030
costará	1	1	0.030
cosido	1	1	0.030
cosía	1	1	0.030
coscorrón	1	1	0.030
corroboró	1	1	0.030
corrigiendo	1	1	0.030
correspondientes	2	3	0.030
correrías	1	1	0.030
correa	1	1	0.030
corpachón	1	1	0.030
coronado	1	1	0.030
coronadas	1	1	0.030
cornisas	1	1	0.030
cornisa	1	1	0.030
corneta	1	1	0.030
corchetes	1	1	0.030
corbatín	1	1	0.030
corazoncito	1	1	0.030
copiosamente	1	1	0.030
convocando	1	1	0.030
conviniera	1	1	0.030
conveniencias	1	1	0.030
convendría	2	3	0.030
convencional	2	3	0.030
convencía	2	3	0.030
contrincantes	1	1	0.030
contratantes	1	1	0.030
contrastaba	1	1	0.030
contrahechas	1	1	0.030
contradicciones	1	1	0.030
contradecía	2	3	0.030
continuase	1	1	0.030
contenti	1	1	0.030
contentaría	1	1	0.030
contentado	1	1	0.030
contentaban	1	1	0.030
contemplo	1	1	0.030
contemplarse	1	1	0.030
contemplaciones	1	1	0.030
conté	1	1	0.030
contárselo	1	1	0.030
contarás	1	1	0.030
contándose	1	1	0.030
consumían	1	1	0.030
consumaría	1	1	0.030
consultó	1	1	0.030
consultado	2	3	0.030
consuetudinaria	1	1	0.030
construido	1	1	0.030
construidas	1	1	0.030
constituyen	1	1	0.030
constituida	1	1	0.030
constipado	1	1	0.030
conspirando	1	1	0.030
consolarse	1	1	0.030
consolarme	1	1	0.030
consiguiendo	1	1	0.030
consiguen	1	1	0.030
consigna	1	1	0.030
considerarle	1	1	0.030
considerada	1	1	0.030
considerábase	1	1	0.030
conservas	1	1	0.030
conservadora	1	1	0.030
conservada	1	1	0.030
conquistando	1	1	0.030
conquistada	1	1	0.030
conozcamos	1	1	0.030
conociendo	2	3	0.030
conocerle	2	3	0.030
conocerá	1	1	0.030
conjuraban	1	1	0.030
congregados	1	1	0.030
congestión	1	1	0.030
confusamente	1	1	0.030
confundamos	1	1	0.030
confirmar	1	1	0.030
confirmaba	1	1	0.030
confesaron	1	1	0.030
confeccionar	1	1	0.030
condujo	1	1	0.030
condimento	1	1	0.030
condenarse	1	1	0.030
condenando	1	1	0.030
conde	2	3	0.030
concurrida	1	1	0.030
concretamente	1	1	0.030
conclusión	2	3	0.030
concibió	1	1	0.030
conchas	1	1	0.030
concertado	1	1	0.030
comunidades	1	1	0.030
comunicado	1	1	0.030
compuertas	1	1	0.030
comprimió	1	1	0.030
comprimidas	1	1	0.030
comprendan	1	1	0.030
compraran	1	1	0.030
compradores	1	1	0.030
componer	2	3	0.030
componen	1	1	0.030
compondría	1	1	0.030
completos	1	1	0.030
complemento	1	1	0.030
complacencias	1	1	0.030
complace	1	1	0.030
compatibles	1	1	0.030
compare	1	1	0.030
compadre	1	1	0.030
compadeció	1	1	0.030
compadecerle	1	1	0.030
compactas	1	1	0.030
comisuras	1	1	0.030
comisionados	1	1	0.030
comino	1	1	0.030
comilonas	1	1	0.030
comidas	2	3	0.030
comezones	1	1	0.030
cometiendo	1	1	0.030
cometidos	1	1	0.030
cometí	1	1	0.030
comentando	1	1	0.030
comemos	1	1	0.030
combustión	1	1	0.030
combinaba	1	1	0.030
colorete	1	1	0.030
colorados	2	3	0.030
coloradas	1	1	0.030
colón	1	1	0.030
colmillo	1	1	0.030
colegios	1	1	0.030
colegiales	2	3	0.030
colega	2	3	0.030
colación	2	3	0.030
coincidencia	1	1	0.030
cohonestarse	1	1	0.030
cohete	1	1	0.030
cogiese	1	1	0.030
codornices	1	1	0.030
codillo	1	1	0.030
cobras	1	1	0.030
cobran	1	1	0.030
clave	1	1	0.030
clavándose	1	1	0.030
claudio	1	1	0.030
clasificar	1	1	0.030
claridades	1	1	0.030
clamor	1	1	0.030
clamaba	1	1	0.030
civilizado	1	1	0.030
civilizada	1	1	0.030
ciudadanos	2	3	0.030
circunspección	1	1	0.030
circulación	2	3	0.030
cinturón	1	1	0.030
cintajos	1	1	0.030
cigüeña	1	1	0.030
cierro	1	1	0.030
cicatrices	1	1	0.030
chupar	1	1	0.030
chupando	2	3	0.030
chorrea	1	1	0.030
chocaba	1	1	0.030
chirrido	1	1	0.030
chillón	1	1	0.030
charlatán	1	1	0.030
charlado	1	1	0.030
chambra	1	1	0.030
cetro	1	1	0.030
cesando	1	1	0.030
cesa	1	1	0.030
cerril	1	1	0.030
cerillas	2	3	0.030
cercano	2	3	0.030
cercana	1	1	0.030
ceñuda	1	1	0.030
ceñidas	1	1	0.030
cenarían	1	1	0.030
celebro	1	1	0.030
celebrado	1	1	0.030
celajes	1	1	0.030
cefalalgia	1	1	0.030
católicas	2	3	0.030
categórico	1	1	0.030
catarros	1	1	0.030
catalanes	1	1	0.030
catafalco	1	1	0.030
cataclismos	1	1	0.030
castigos	2	3	0.030
castellana	1	1	0.030
castañeteo	1	1	0.030
casinos	1	1	0.030
casilla	1	1	0.030
casase	1	1	0.030
carruajes	1	1	0.030
carretero	1	1	0.030
carpinteros	1	1	0.030
caricatura	1	1	0.030
cargarse	1	1	0.030
caretas	1	1	0.030
carecía	2	3	0.030
cárdenas	2	3	0.030
carcunda	1	1	0.030
carcomida	1	1	0.030
característicos	1	1	0.030
capitanes	1	1	0.030
capciosa	1	1	0.030
cañones	2	3	0.030
canten	1	1	0.030
cántaros	1	1	0.030
cantante	1	1	0.030
cantábrico	1	1	0.030
cansaron	1	1	0.030
cansar	2	3	0.030
canon	1	1	0.030
candorosa	1	1	0.030
candil	1	1	0.030
canceles	1	1	0.030
camposanto	1	1	0.030
campestre	1	1	0.030
campesinos	1	1	0.030
campechano	2	3	0.030
caminando	1	1	0.030
camilla	1	1	0.030
cambios	2	3	0.030
cambió	2	3	0.030
cambiaba	2	3	0.030
camarín	1	1	0.030
cámara	2	3	0.030
calzón	2	3	0.030
calmar	2	3	0.030
calmándose	1	1	0.030
calmado	1	1	0.030
callejero	1	1	0.030
callaría	1	1	0.030
callan	1	1	0.030
calentarse	2	3	0.030
calendario	1	1	0.030
caldeaba	1	1	0.030
calcular	1	1	0.030
calceta	1	1	0.030
calaveras	1	1	0.030
calatravas	1	1	0.030
cadera	1	1	0.030
cachete	1	1	0.030
cacharros	2	3	0.030
cacerolas	1	1	0.030
cabizbaja	1	1	0.030
cabida	1	1	0.030
cabañas	1	1	0.030
caballerías	1	1	0.030
caballeresca	1	1	0.030
ca	1	1	0.030
bustos	1	1	0.030
buscarla	2	3	0.030
buscaría	2	3	0.030
buscándola	1	1	0.030
buscada	1	1	0.030
burlasen	1	1	0.030
burlando	1	1	0.030
burlan	1	1	0.030
bulas	1	1	0.030
bula	1	1	0.030
bufando	1	1	0.030
bruscas	1	1	0.030
brotando	1	1	0.030
bromista	1	1	0.030
brocado	1	1	0.030
bramante	1	1	0.030
bozal	1	1	0.030
botánica	1	1	0.030
borro	1	1	0.030
borran	1	1	0.030
borraban	1	1	0.030
borraba	1	1	0.030
blasfemo	1	1	0.030
blanquear	1	1	0.030
blandamente	1	1	0.030
bizcocho	2	3	0.030
bizco	1	1	0.030
bilbao	1	1	0.030
bienhechora	1	1	0.030
besaron	1	1	0.030
besarla	1	1	0.030
besando	1	1	0.030
benévolos	1	1	0.030
bebiese	1	1	0.030
bebiera	1	1	0.030
bebería	1	1	0.030
bazar	2	3	0.030
batirme	1	1	0.030
batido	1	1	0.030
bastiat	1	1	0.030
barroquismo	1	1	0.030
barriendo	1	1	0.030
baratos	2	3	0.030
baraja	1	1	0.030
bañado	1	1	0.030
bandas	1	1	0.030
bandada	1	1	0.030
banda	2	3	0.030
balda	1	1	0.030
balanceaban	1	1	0.030
bajarán	1	1	0.030
bajada	1	1	0.030
bachiller	1	1	0.030
babosa	1	1	0.030
azufre	1	1	0.030
azotaban	1	1	0.030
azares	1	1	0.030
ayudase	1	1	0.030
ayudarnos	1	1	0.030
ayudaría	1	1	0.030
ayudando	2	3	0.030
ayudan	2	3	0.030
ayudados	1	1	0.030
avisó	1	1	0.030
aviene	1	1	0.030
averiguado	2	3	0.030
averiguaciones	1	1	0.030
aventurillas	1	1	0.030
aventurándose	1	1	0.030
avenida	1	1	0.030
avenía	1	1	0.030
avaro	1	1	0.030
autorizado	1	1	0.030
aunque	219	276	0.030
atropellos	1	1	0.030
atropello	1	1	0.030
atribuyeron	1	1	0.030
atreviera	2	3	0.030
atreví	1	1	0.030
atreverías	1	1	0.030
atravesaron	1	1	0.030
atrajo	1	1	0.030
atraído	1	1	0.030
atragantaban	1	1	0.030
atracón	1	1	0.030
atormentarle	1	1	0.030
atormentarla	1	1	0.030
atonía	1	1	0.030
atiende	1	1	0.030
atice	1	1	0.030
atestados	1	1	0.030
aterrados	1	1	0.030
atenuaba	1	1	0.030
ateneo	1	1	0.030
atarla	1	1	0.030
atan	1	1	0.030
ata	1	1	0.030
asuste	2	3	0.030
asusté	1	1	0.030
asustar	2	3	0.030
asturias	1	1	0.030
astronomía	1	1	0.030
astro	1	1	0.030
aspiraciones	2	3	0.030
aspiraban	1	1	0.030
aspira	1	1	0.030
asombrada	2	3	0.030
asociación	1	1	0.030
asistirle	1	1	0.030
asiduos	1	1	0.030
asia	1	1	0.030
asegurado	1	1	0.030
ascetismo	1	1	0.030
ascendido	1	1	0.030
asar	1	1	0.030
asamblea	1	1	0.030
asaltar	1	1	0.030
artesano	1	1	0.030
arrullado	1	1	0.030
arrullaban	1	1	0.030
arrollado	1	1	0.030
arrojarla	1	1	0.030
arrogancia	2	3	0.030
arrodilladas	1	1	0.030
arrobas	2	3	0.030
arrimó	1	1	0.030
arriesgados	1	1	0.030
arrieros	1	1	0.030
arrepentido	2	3	0.030
arreo	1	1	0.030
arrastró	1	1	0.030
arrancó	2	3	0.030
arrancaron	1	1	0.030
arrancarla	1	1	0.030
arraigada	1	1	0.030
arrabales	1	1	0.030
arquitecto	1	1	0.030
aroma	1	1	0.030
árnica	2	3	0.030
armónico	1	1	0.030
armado	2	3	0.030
aristocráticas	1	1	0.030
argucias	1	1	0.030
arenilla	1	1	0.030
arengaba	1	1	0.030
arenal	2	3	0.030
ardió	1	1	0.030
ardentísimo	1	1	0.030
archivo	1	1	0.030
arañazos	1	1	0.030
apuren	1	1	0.030
apuran	1	1	0.030
aproximó	2	3	0.030
aprobadas	1	1	0.030
aprisionados	1	1	0.030
aprietan	1	1	0.030
aprensivo	1	1	0.030
aprendiz	1	1	0.030
aprendiera	1	1	0.030
aprendidas	1	1	0.030
aprendían	1	1	0.030
apremiante	1	1	0.030
apoyado	2	3	0.030
apóstoles	2	3	0.030
apostaría	1	1	0.030
apostado	1	1	0.030
aplicarse	1	1	0.030
aplicándose	1	1	0.030
apetitoso	1	1	0.030
apéndice	1	1	0.030
apearme	1	1	0.030
aparto	1	1	0.030
apartarle	1	1	0.030
apartamiento	1	1	0.030
apartaban	1	1	0.030
aparentarla	1	1	0.030
aparentando	2	3	0.030
apareciendo	2	3	0.030
aparece	2	3	0.030
apaleaban	1	1	0.030
apagarla	1	1	0.030
apacentaba	1	1	0.030
anuncios	1	1	0.030
anuncio	2	3	0.030
anunciarle	1	1	0.030
anunciadas	1	1	0.030
antoja	2	3	0.030
antiguamente	1	1	0.030
anticipos	1	1	0.030
anticipado	1	1	0.030
anticipada	1	1	0.030
antecesores	1	1	0.030
antecesor	1	1	0.030
anochecía	1	1	0.030
animalitos	1	1	0.030
ángulos	1	1	0.030
anegar	1	1	0.030
anduvieron	1	1	0.030
anduviera	1	1	0.030
andrajosa	1	1	0.030
andrajo	1	1	0.030
andaríamos	1	1	0.030
anchura	1	1	0.030
anacronismo	1	1	0.030
amplia	1	1	0.030
ampararse	1	1	0.030
amoratados	1	1	0.030
amiguito	1	1	0.030
amenazar	1	1	0.030
amenazándola	1	1	0.030
amenazador	1	1	0.030
amenazaban	1	1	0.030
amenas	1	1	0.030
ambulante	1	1	0.030
amarillentas	1	1	0.030
amarillas	2	3	0.030
amaranto	1	1	0.030
amanecía	1	1	0.030
amago	1	1	0.030
alumbra	1	1	0.030
alucinación	2	3	0.030
altivez	1	1	0.030
alternando	1	1	0.030
alteres	1	1	0.030
altanería	1	1	0.030
alquiler	2	3	0.030
almohadón	1	1	0.030
almidón	1	1	0.030
alineadas	1	1	0.030
alimentada	1	1	0.030
alianza	1	1	0.030
alfombras	1	1	0.030
alentaba	1	1	0.030
alejar	2	3	0.030
alejandro	2	3	0.030
alegremente	1	1	0.030
alegrase	1	1	0.030
alegórica	1	1	0.030
alegoría	1	1	0.030
alegando	1	1	0.030
alcanzamos	1	1	0.030
alcanzaban	1	1	0.030
alborotan	1	1	0.030
albedrío	1	1	0.030
albañil	2	3	0.030
albaicín	1	1	0.030
alabó	1	1	0.030
alaban	1	1	0.030
alabado	2	3	0.030
aislados	1	1	0.030
aislado	1	1	0.030
ahorrar	1	1	0.030
ahorcado	1	1	0.030
ahogarse	1	1	0.030
ahogando	1	1	0.030
aguzado	1	1	0.030
agudezas	1	1	0.030
aguacero	1	1	0.030
agrias	1	1	0.030
agriado	1	1	0.030
agregarse	1	1	0.030
agravios	2	3	0.030
agravio	1	1	0.030
agradeces	1	1	0.030
agradecerle	1	1	0.030
agradece	1	1	0.030
agradarle	1	1	0.030
agradables	2	3	0.030
agradablemente	1	1	0.030
agasajada	1	1	0.030
agarraba	1	1	0.030
africana	1	1	0.030
afrento	1	1	0.030
aforismos	1	1	0.030
afirmativa	1	1	0.030
afirmarse	1	1	0.030
afiló	1	1	0.030
aferradas	1	1	0.030
advirtieron	1	1	0.030
adulaban	1	1	0.030
adquiera	1	1	0.030
adornó	1	1	0.030
adornar	1	1	0.030
adormecida	1	1	0.030
adorando	1	1	0.030
adoptado	1	1	0.030
admitiera	1	1	0.030
admitida	1	1	0.030
admiraría	1	1	0.030
admira	1	1	0.030
administrado	1	1	0.030
adivinarle	1	1	0.030
adivinando	1	1	0.030
adivinaciones	1	1	0.030
adiciones	1	1	0.030
adamado	1	1	0.030
acusadora	1	1	0.030
acusaban	1	1	0.030
acuérdese	1	1	0.030
acuden	1	1	0.030
actrices	1	1	0.030
actitudes	1	1	0.030
acta	1	1	0.030
acostumbra	1	1	0.030
acostaron	1	1	0.030
acostara	1	1	0.030
acordase	1	1	0.030
acordaría	1	1	0.030
acordarás	2	3	0.030
aconsejarte	1	1	0.030
aconsejaría	1	1	0.030
aconsejar	2	3	0.030
aconsejaba	2	3	0.030
acomoda	1	1	0.030
acogida	1	1	0.030
aciertas	1	1	0.030
achacaban	1	1	0.030
acertada	1	1	0.030
acerico	1	1	0.030
acerados	1	1	0.030
acechar	1	1	0.030
accionistas	1	1	0.030
acariciarle	1	1	0.030
acallar	1	1	0.030
académicos	1	1	0.030
acabarás	1	1	0.030
abusas	1	1	0.030
aburrirle	1	1	0.030
aburriéndose	1	1	0.030
aburridos	1	1	0.030
aburridas	1	1	0.030
abunda	1	1	0.030
absuelta	1	1	0.030
absorbía	1	1	0.030
abrumadora	1	1	0.030
abrochándose	1	1	0.030
abrirá	1	1	0.030
abrigos	1	1	0.030
abrigara	1	1	0.030
abreviaturas	1	1	0.030
abrazaba	1	1	0.030
aborrezco	2	3	0.030
abonado	1	1	0.030
abandonarlo	1	1	0.030
abandonados	1	1	0.030
abandonadas	1	1	0.030
traía	30	40	0.028
tenerle	6	7	0.028
temiendo	6	7	0.028
rodeaba	6	7	0.028
rendida	6	7	0.028
proximidad	6	7	0.028
preparando	6	7	0.028
pasada	6	7	0.028
metida	6	7	0.028
meditando	6	7	0.028
lejana	6	7	0.028
inútiles	6	7	0.028
héroes	6	7	0.028
hereje	6	7	0.028
futuro	6	7	0.028
estados	6	7	0.028
envolvía	6	7	0.028
enamorarse	6	7	0.028
divertía	6	7	0.028
disgustos	6	7	0.028
cruzadas	6	7	0.028
abiertas	6	7	0.028
condición	14	19	0.027
aspecto	14	19	0.027
tuviese	11	15	0.025
salido	27	36	0.025
eclesiástica	11	15	0.025
sabemos	8	11	0.024
principales	8	11	0.024
papa	8	11	0.024
mejilla	8	11	0.024
marfil	8	11	0.024
mantener	8	11	0.024
largo	47	62	0.024
encontraron	8	11	0.024
decentes	8	11	0.024
cuidar	8	11	0.024
cosquillas	8	11	0.024
comprende	8	11	0.024
ceja	8	11	0.024
vigilancia	5	7	0.023
ventaja	5	7	0.023
valga	5	7	0.023
uniforme	5	7	0.023
testamento	5	7	0.023
temblaban	5	7	0.023
sollozos	5	7	0.023
saltando	5	7	0.023
salgo	5	7	0.023
rueda	5	7	0.023
rodilla	5	7	0.023
pillos	5	7	0.023
permitido	5	7	0.023
perdonado	5	7	0.023
parientes	10	12	0.023
padecía	10	12	0.023
oírse	5	7	0.023
ocupar	5	7	0.023
necesitan	5	7	0.023
nacer	5	7	0.023
muriendo	5	7	0.023
mundos	5	7	0.023
miserias	5	7	0.023
marchado	5	7	0.023
limpiar	5	7	0.023
júbilo	5	7	0.023
inclinando	5	7	0.023
hacemos	5	7	0.023
físico	10	12	0.023
fines	5	7	0.023
explicación	5	7	0.023
excitado	5	7	0.023
esclavitud	5	7	0.023
encargó	5	7	0.023
empresa	5	7	0.023
edificios	5	7	0.023
económico	5	7	0.023
deliciosa	5	7	0.023
cruel	10	12	0.023
crímenes	5	7	0.023
corona	5	7	0.023
consideraciones	5	7	0.023
consecuencias	5	7	0.023
arranca	5	7	0.023
aplicar	5	7	0.023
agradecido	5	7	0.023
afable	5	7	0.023
acaba	10	12	0.023
seca	14	17	0.022
preguntar	14	17	0.022
perdida	14	17	0.022
grupo	14	17	0.022
cuantos	14	17	0.022
concepto	14	17	0.022
caja	14	17	0.022
cabía	14	17	0.022
sentada	18	22	0.021
ea	18	22	0.021
habló	45	56	0.020
patio	31	41	0.019
hombres	68	89	0.019
deseos	31	41	0.019
daba	175	221	0.018
propios	18	24	0.017
realidad	38	50	0.016
comercio	28	37	0.016
hombro	25	31	0.014
cambio	25	31	0.014
semana	17	21	0.012
quiso	59	77	0.012
escuela	17	21	0.012
viste	5	6	0.011
vestidas	5	6	0.011
tierno	5	6	0.011
suena	5	6	0.011
sirvo	5	6	0.011
siguiendo	5	6	0.011
servido	9	11	0.011
sensaciones	5	6	0.011
saben	22	29	0.011
risas	9	11	0.011
responsable	5	6	0.011
renunciar	5	6	0.011
provecho	9	11	0.011
prisión	5	6	0.011
presentimiento	5	6	0.011
portado	5	6	0.011
podemos	9	11	0.011
peinado	5	6	0.011
pascua	5	6	0.011
pareció	32	42	0.011
palos	9	11	0.011
oponerse	5	6	0.011
olvidar	12	16	0.011
moza	9	11	0.011
meditar	5	6	0.011
matando	5	6	0.011
martillo	5	6	0.011
mancha	5	6	0.011
ligero	9	11	0.011
lecciones	12	16	0.011
histórico	5	6	0.011
hermosos	5	6	0.011
género	32	42	0.011
fatal	5	6	0.011
exactitud	5	6	0.011
enseñado	5	6	0.011
énfasis	5	6	0.011
dulcemente	5	6	0.011
dificultades	12	16	0.011
difíciles	5	6	0.011
descubrió	5	6	0.011
desconocido	13	16	0.011
corto	9	11	0.011
corrientes	5	6	0.011
convenido	5	6	0.011
contestar	12	16	0.011
consolaba	5	6	0.011
compró	5	6	0.011
claros	5	6	0.011
bofetadas	9	11	0.011
bajaban	5	6	0.011
aves	5	6	0.011
autoridad	22	29	0.011
artista	12	16	0.011
armas	9	11	0.011
apretón	5	6	0.011
andaban	5	6	0.011
amoroso	5	6	0.011
amarilla	5	6	0.011
amarga	5	6	0.011
ajo	5	6	0.011
agujas	5	6	0.011
acostumbrado	9	11	0.011
abandonar	5	6	0.011
buenos	39	51	0.010
preguntó	70	91	0.009
portal	29	38	0.009
riqueza	9	12	0.008
presentarse	9	12	0.008
líneas	9	12	0.008
inferior	9	12	0.008
inclinándose	9	12	0.008
gravedad	9	12	0.008
corrido	9	12	0.008
cochero	9	12	0.008
tranquilo	26	34	0.007
dientes	26	34	0.007
viejas	6	8	0.006
trataban	6	8	0.006
tercer	6	8	0.006
tela	16	21	0.006
señorío	6	8	0.006
rapidez	6	8	0.006
ramos	6	8	0.006
penitente	6	8	0.006
patria	16	21	0.006
padecido	6	8	0.006
origen	6	8	0.006
misma	137	177	0.006
mezcla	6	8	0.006
llegar	68	86	0.006
interesaba	6	8	0.006
guapas	6	8	0.006
faltar	6	8	0.006
escoba	6	8	0.006
defectos	6	8	0.006
coser	6	8	0.006
comida	20	25	0.006
clavo	6	8	0.006
ángulo	6	8	0.006
acudió	6	8	0.006
dirá	16	20	0.005
círculo	16	20	0.005
apenas	54	70	0.005
respirar	12	15	0.004
estaban	117	151	0.004
contra	104	132	0.004
conseguir	12	15	0.004
causa	37	48	0.004
calma	23	30	0.004
acto	23	30	0.004
veinticuatro	3	4	0.003
urna	3	4	0.003
tubo	3	4	0.003
tranquilizarse	3	4	0.003
traidor	3	4	0.003
tradicional	3	4	0.003
torcer	3	4	0.003
tiran	3	4	0.003
texto	3	4	0.003
tesón	3	4	0.003
terrones	3	4	0.003
supieran	3	4	0.003
soldado	3	4	0.003
setenta	3	4	0.003
sepulcro	3	4	0.003
sensible	3	4	0.003
sensación	8	10	0.003
rumbo	3	4	0.003
rota	3	4	0.003
rica	13	17	0.003
revolver	3	4	0.003
respondía	20	26	0.003
remiendos	3	4	0.003
reinaba	8	10	0.003
recurso	3	4	0.003
recurrir	3	4	0.003
ráfagas	3	4	0.003
puedan	3	4	0.003
procedía	3	4	0.003
probó	3	4	0.003
precoz	3	4	0.003
pobrecitos	3	4	0.003
plantado	3	4	0.003
planchadora	3	4	0.003
pisadas	3	4	0.003
pestes	3	4	0.003
pesadumbre	3	4	0.003
pesadilla	8	10	0.003
pensara	3	4	0.003
patriotismo	3	4	0.003
pasarse	3	4	0.003
oler	3	4	0.003
ojuelos	3	4	0.003
ofreciendo	3	4	0.003
ocupó	3	4	0.003
necesarios	3	4	0.003
mejoría	3	4	0.003
luminosa	3	4	0.003
logró	3	4	0.003
llevársela	3	4	0.003
juguete	3	4	0.003
jugar	13	17	0.003
interesa	3	4	0.003
imprenta	3	4	0.003
imitando	3	4	0.003
húmedos	3	4	0.003
helada	3	4	0.003
harían	3	4	0.003
habitual	3	4	0.003
habíale	3	4	0.003
grueso	3	4	0.003
géneros	3	4	0.003
ganó	3	4	0.003
fueras	3	4	0.003
fraternidad	3	4	0.003
filosóficas	3	4	0.003
filo	3	4	0.003
excitar	3	4	0.003
estudios	8	10	0.003
escritos	3	4	0.003
escrita	3	4	0.003
época	20	26	0.003
entretenerse	3	4	0.003
entretanto	3	4	0.003
entregó	3	4	0.003
entablar	3	4	0.003
engañado	13	17	0.003
ellas	78	99	0.003
edificar	3	4	0.003
dioses	3	4	0.003
devolver	3	4	0.003
devaneos	3	4	0.003
desmejorado	3	4	0.003
desaliento	3	4	0.003
desairado	3	4	0.003
desahogo	3	4	0.003
demostró	3	4	0.003
defenderse	3	4	0.003
dedicaba	3	4	0.003
declaraba	8	10	0.003
dada	3	4	0.003
cuidarse	3	4	0.003
corteza	3	4	0.003
corresponde	3	4	0.003
convinieron	3	4	0.003
continuando	3	4	0.003
conocemos	3	4	0.003
conjunto	8	10	0.003
confundir	3	4	0.003
confiese	3	4	0.003
conducto	3	4	0.003
composición	3	4	0.003
comestibles	3	4	0.003
comerciante	8	10	0.003
cogida	3	4	0.003
clavar	3	4	0.003
clavando	3	4	0.003
carbonero	3	4	0.003
caramelo	3	4	0.003
capitales	3	4	0.003
burlarse	3	4	0.003
brotaba	3	4	0.003
bondadosa	3	4	0.003
barras	3	4	0.003
bajaron	3	4	0.003
aventuró	3	4	0.003
asegurar	8	10	0.003
arca	3	4	0.003
apurado	3	4	0.003
apuesto	3	4	0.003
anegada	3	4	0.003
andaluz	3	4	0.003
amigo	147	187	0.003
amena	3	4	0.003
amadeo	3	4	0.003
alborotaba	3	4	0.003
ajuar	3	4	0.003
afectada	3	4	0.003
acostumbraba	3	4	0.003
achaques	3	4	0.003
accidente	3	4	0.003
sintiendo	19	24	0.002
sabido	19	24	0.002
grado	19	24	0.002
vecinos	10	13	0.001
trato	26	33	0.001
tragar	4	5	0.001
tostada	4	5	0.001
tipo	10	13	0.001
tímidamente	4	5	0.001
tenazas	4	5	0.001
temo	10	13	0.001
sube	10	13	0.001
sorprendió	4	5	0.001
soñando	4	5	0.001
sonar	4	5	0.001
sombreros	4	5	0.001
sólida	4	5	0.001
soberbio	4	5	0.001
sentaban	4	5	0.001
seguidos	4	5	0.001
resto	10	13	0.001
repetían	4	5	0.001
rendido	4	5	0.001
religiones	4	5	0.001
reducido	4	5	0.001
reclamo	4	5	0.001
pseudo	4	5	0.001
pintores	4	5	0.001
particulares	4	5	0.001
parecieron	4	5	0.001
parecerse	4	5	0.001
pana	4	5	0.001
opiniones	4	5	0.001
oficial	4	5	0.001
observador	4	5	0.001
objeto	26	33	0.001
negarlo	4	5	0.001
naturalidad	4	5	0.001
metiendo	4	5	0.001
marco	4	5	0.001
llegan	4	5	0.001
llamase	4	5	0.001
líquido	4	5	0.001
juzgar	4	5	0.001
importante	15	19	0.001
iguales	10	13	0.001
hablase	4	5	0.001
gruñido	4	5	0.001
glorias	4	5	0.001
gallo	10	13	0.001
excitaba	4	5	0.001
escapado	4	5	0.001
empeñó	4	5	0.001
empeña	4	5	0.001
disparado	4	5	0.001
devociones	4	5	0.001
detenía	4	5	0.001
desigual	4	5	0.001
descubierta	4	5	0.001
debilidades	4	5	0.001
debí	4	5	0.001
cuchillo	10	13	0.001
cuántas	10	13	0.001
crítica	10	13	0.001
cortina	4	5	0.001
convino	4	5	0.001
convierte	4	5	0.001
contenido	4	5	0.001
ciegos	4	5	0.001
cerveza	4	5	0.001
cascos	4	5	0.001
carcajada	10	13	0.001
busque	4	5	0.001
brasero	4	5	0.001
barato	4	5	0.001
atravesaba	4	5	0.001
arrastrado	4	5	0.001
ardientes	4	5	0.001
aquél	4	5	0.001
apurada	4	5	0.001
apacible	4	5	0.001
angustias	4	5	0.001
aires	15	19	0.001
abstracción	4	5	0.001
abrirle	4	5	0.001
vacío	7	9	0.000
tenían	89	114	0.000
ten	14	18	0.000
siente	11	14	0.000
quedo	11	14	0.000
puntas	7	9	0.000
precioso	7	9	0.000
perdido	43	55	0.000
pardo	7	9	0.000
novedad	11	14	0.000
nacido	18	23	0.000
moral	50	64	0.000
maridos	11	14	0.000
inmensa	11	14	0.000
ingenio	7	9	0.000
honrado	14	18	0.000
grito	11	14	0.000
gritando	7	9	0.000
grave	29	37	0.000
figurado	7	9	0.000
faltaba	40	51	0.000
fácilmente	11	14	0.000
evangelio	7	9	0.000
española	14	18	0.000
enterado	11	14	0.000
empleado	11	14	0.000
deuda	7	9	0.000
desapareció	7	9	0.000
deben	14	18	0.000
cuantas	11	14	0.000
corbata	7	9	0.000
continuaba	18	23	0.000
conciencia	81	104	0.000
comen	7	9	0.000
cansancio	7	9	0.000
argumento	11	14	0.000

Mostrar todo