Comparativa: El Libro del Buen Amor contra La Celestina
Índice
Información General
| Título: | El Libro del Buen Amor |
|---|
| Autor: | El Arcipreste de Hita |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 60948 |
|---|
| #Palabras distintas: | 11479 |
|---|
| Type-Token ratio: | 18.83% |
|---|
|
| Título: | La Celestina |
|---|
| Autor: | Fernando de Rojas |
|---|
| Idioma: | Castellano |
|---|
| #Palabras total: | 68450 |
|---|
| #Palabras distintas: | 9189 |
|---|
| Type-Token ratio: | 13.42% |
|---|
|
Ley de Heaps - Saturación léxica
La Ley de Heaps es una ley empírica que predice el tamaño del vocabulario dado un texto.
Esto es, nos da una estimación del número de palabras distintas (v) dado el número total de palabras (n) de que consta el texto,
según la fórmula
v = K*n^b
donde b está entre 0 y 1 (habitualmente entre 0.4 y 0.6)
y K es una cierta constante, habitualmente entre 10 y 100.
En particular, mayores valores de b se corresponden con vocabularios más grandes,
en el sentido de que aumentan rápidamente;
mientras que se tienen valores menores de b cuando casi todo el vocabulario aparece al principio
y luego se van añadiendo muy pocos términos nuevos (el vocabulario se satura rápidamente).
| Buen_Amor | Celestina |
|---|
| #Palabras: | #Palabras distintas: |
|---|
| 1218 | 550 |
| 2436 | 936 |
| 3654 | 1237 |
| 4872 | 1588 |
| 6090 | 1972 |
| 7308 | 2232 |
| 8526 | 2561 |
| 9744 | 2861 |
| 10962 | 3171 |
| 12180 | 3414 |
| 13398 | 3693 |
| 14616 | 3996 |
| 15834 | 4260 |
| 17052 | 4509 |
| 18270 | 4741 |
| 19488 | 5031 |
| 20706 | 5249 |
| 21924 | 5515 |
| 23142 | 5755 |
| 24360 | 5959 |
| 25578 | 6175 |
| 26796 | 6374 |
| 28014 | 6543 |
| 29232 | 6727 |
| 30450 | 6897 |
| 31668 | 7131 |
| 32886 | 7321 |
| 34104 | 7470 |
| 35322 | 7636 |
| 36540 | 7838 |
| 37758 | 8036 |
| 38976 | 8268 |
| 40194 | 8475 |
| 41412 | 8680 |
| 42630 | 8912 |
| 43848 | 9092 |
| 45066 | 9299 |
| 46284 | 9558 |
| 47502 | 9749 |
| 48720 | 9936 |
| 49938 | 10118 |
| 51156 | 10260 |
| 52374 | 10411 |
| 53592 | 10560 |
| 54810 | 10698 |
| 56028 | 10872 |
| 57246 | 11032 |
| 58464 | 11160 |
| 59682 | 11301 |
| 60900 | 11475 |
| 60948 | 11479 |
|
| #Palabras: | #Palabras distintas: |
|---|
| 1369 | 637 |
| 2738 | 1043 |
| 4107 | 1479 |
| 5476 | 1845 |
| 6845 | 2185 |
| 8214 | 2499 |
| 9583 | 2876 |
| 10952 | 3126 |
| 12321 | 3356 |
| 13690 | 3549 |
| 15059 | 3822 |
| 16428 | 4070 |
| 17797 | 4318 |
| 19166 | 4483 |
| 20535 | 4663 |
| 21904 | 4827 |
| 23273 | 4980 |
| 24642 | 5115 |
| 26011 | 5299 |
| 27380 | 5451 |
| 28749 | 5615 |
| 30118 | 5744 |
| 31487 | 5870 |
| 32856 | 5996 |
| 34225 | 6120 |
| 35594 | 6257 |
| 36963 | 6410 |
| 38332 | 6538 |
| 39701 | 6733 |
| 41070 | 6851 |
| 42439 | 6953 |
| 43808 | 7063 |
| 45177 | 7173 |
| 46546 | 7268 |
| 47915 | 7407 |
| 49284 | 7521 |
| 50653 | 7644 |
| 52022 | 7760 |
| 53391 | 7872 |
| 54760 | 8014 |
| 56129 | 8121 |
| 57498 | 8229 |
| 58867 | 8338 |
| 60236 | 8423 |
| 61605 | 8546 |
| 62974 | 8654 |
| 64343 | 8755 |
| 65712 | 8880 |
| 67081 | 9015 |
| 68450 | 9189 |
|
|
Ajuste por mínimos cuadrados de los datos a K*n^b: |
| Buen_Amor |
|
Celestina |
| K = 2.203 |
|
K = 7.093 |
| b = 0.779 |
|
b = 0.647 |

|
Ley de Zipf
La ley de Zipf es una ley empírica que se basa en el principio de mínimos esfuerzo.
Esto es, supone que existe un pequeño número de palabras, las más "conocidas", que son utilizadas con mucha frecuencia,
mientras que hay un gran número de palabras son poco empleadas.
Matemáticamente esto quiere decir que la frecuencia (número de apariciones) de una palabra cualquiera
es inversamente proporcional a su ranking,
entendido como su posición en una lista de las palabras presentes en el texto ordenada descendentemente en función de su frecuencia.
Así, la palabra más frecuente aparecerá aproximadamente dos veces más que la segunda palabra más frecuente,
unas tres veces más que la tercera palabra más frecuente, etc.
Gráficamente, cuando una curva se encuentra por encima de la recta "ideal"
quiere decir que el texto emplea recurrentemente un número de palabras muy reducido,
habiendo muy pocas que aparezcan con poca frecuencia.
Por el contrario, cuando la curva se encuentra por debajo de la "ideal",
el texto contiene un vocabulario más amplio, con muchas palabras que aparecen relativamente pocas veces.
| Buen_Amor | Celestina |
Ilustración del principio de mínimo esfuerzo: |
| Rank | Palabra | Frec |
|---|
| 1 | de | 2043 |
| 2 | que | 1886 |
| 3 | la | 1751 |
| 4 | é | 1663 |
| 5 | el | 1473 |
| 6 | non | 1228 |
| 7 | en | 1167 |
| 8 | á | 863 |
| 9 | por | 820 |
| 10 | con | 752 |
| 11 | los | 611 |
| 12 | las | 546 |
| 13 | lo | 497 |
| 14 | es | 480 |
| 15 | su | 474 |
| 16 | del | 426 |
| 17 | al | 395 |
| 18 | se | 325 |
| 19 | más | 325 |
| 20 | me | 304 |
| 21 | y | 298 |
| 22 | vos | 293 |
| 23 | a | 282 |
| 24 | yo | 274 |
| 25 | mi | 272 |
| 26 | como | 253 |
| 27 | tu | 249 |
| 28 | nin | 247 |
| 29 | un | 238 |
| 30 | e | 233 |
| 31 | te | 225 |
| 32 | grand | 214 |
| 33 | le | 212 |
| 34 | muy | 207 |
| 35 | bien | 202 |
| 36 | dios | 201 |
| 37 | mucho | 199 |
| 38 | sus | 178 |
| 39 | amor | 177 |
| 40 | todo | 175 |
| 41 | mal | 169 |
| 42 | fué | 167 |
| 43 | ome | 164 |
| 44 | él | 160 |
| 45 | sy | 155 |
| 46 | todos | 150 |
| 47 | l | 149 |
| 48 | una | 145 |
| 49 | para | 144 |
| 50 | dueña | 144 |
| 51 | diz | 140 |
| 52 | son | 139 |
| 53 | buen | 138 |
| 54 | byen | 134 |
| 55 | tan | 128 |
| 56 | si | 124 |
| 57 | quando | 121 |
| 58 | tal | 118 |
| 59 | quien | 117 |
| 60 | muchos | 115 |
| 61 | ella | 112 |
| 62 | tú | 111 |
| 63 | toda | 111 |
| 64 | esto | 110 |
| 65 | no | 109 |
| 66 | mí | 107 |
| 67 | dixo | 107 |
| 68 | era | 104 |
| 69 | luego | 103 |
| 70 | syn | 102 |
| 71 | do | 102 |
| 72 | buena | 102 |
| 73 | ya | 101 |
| 74 | nunca | 100 |
| 75 | esta | 100 |
| 76 | nos | 98 |
| 77 | mundo | 97 |
| 78 | don | 96 |
| 79 | qué | 94 |
| 80 | qu | 94 |
| 81 | ca | 94 |
| 82 | desque | 93 |
| 83 | mas | 92 |
| 84 | señor | 91 |
| 85 | porque | 91 |
| 86 | d | 90 |
| 87 | quanto | 88 |
| 88 | ó | 88 |
| 89 | día | 88 |
| 90 | vieja | 86 |
| 91 | puede | 85 |
| 92 | muger | 85 |
| 93 | ser | 84 |
| 94 | cosa | 81 |
| 95 | este | 80 |
| 96 | muchas | 78 |
| 97 | poco | 77 |
| 98 | todas | 75 |
| 99 | pues | 75 |
| 100 | señora | 74 |
| 101 | coraçón | 74 |
| 102 | ante | 73 |
| 103 | otro | 72 |
| 104 | ay | 72 |
| 105 | vino | 70 |
| 106 | fabla | 69 |
| 107 | pero | 66 |
| 108 | aquí | 64 |
| 109 | dize | 63 |
| 110 | cómo | 61 |
| 111 | sea | 60 |
| 112 | muerte | 60 |
| 113 | ty | 59 |
| 114 | vida | 57 |
| 115 | mucha | 56 |
| 116 | libro | 56 |
| 117 | tanto | 55 |
| 118 | miedo | 55 |
| 119 | dar | 55 |
| 120 | ha | 53 |
| 121 | uno | 52 |
| 122 | tus | 52 |
| 123 | santa | 52 |
| 124 | amigo | 52 |
| 125 | fazer | 50 |
| 126 | cada | 50 |
| 127 | sienpre | 47 |
| 128 | lobo | 47 |
| 129 | grandes | 47 |
| 130 | casa | 47 |
| 131 | arcipreste | 47 |
| 132 | vy | 46 |
| 133 | otros | 46 |
| 134 | mala | 46 |
| 135 | dos | 46 |
| 136 | primero | 45 |
| 137 | león | 45 |
| 138 | otra | 44 |
| 139 | mis | 44 |
| 140 | faze | 44 |
| 141 | cosas | 44 |
| 142 | há | 43 |
| 143 | pecado | 42 |
| 144 | hé | 42 |
| 145 | faz | 42 |
| 146 | ende | 42 |
| 147 | carnal | 42 |
| 148 | tiene | 41 |
| 149 | omes | 41 |
| 150 | contra | 41 |
| 151 | algo | 41 |
| 152 | sin | 40 |
| 153 | dueñas | 40 |
| 154 | ally | 40 |
| 155 | vuestra | 39 |
| 156 | está | 39 |
| 157 | oy | 38 |
| 158 | mano | 38 |
| 159 | les | 38 |
| 160 | he | 38 |
| 161 | doña | 38 |
| 162 | aver | 38 |
| 163 | agora | 38 |
| 164 | diablo | 37 |
| 165 | alma | 37 |
| 166 | sé | 36 |
| 167 | estava | 36 |
| 168 | mayor | 35 |
| 169 | fecho | 35 |
| 170 | estas | 35 |
| 171 | s | 34 |
| 172 | quál | 34 |
| 173 | ora | 34 |
| 174 | grande | 34 |
| 175 | fuese | 34 |
| 176 | fablar | 34 |
| 177 | eres | 34 |
| 178 | ellos | 34 |
| 179 | tres | 33 |
| 180 | maría | 33 |
| 181 | manos | 33 |
| 182 | madre | 33 |
| 183 | lugar | 33 |
| 184 | grant | 33 |
| 185 | della | 33 |
| 186 | cuerpo | 33 |
| 187 | anda | 33 |
| 188 | syenpre | 32 |
| 189 | seso | 32 |
| 190 | manera | 32 |
| 191 | m | 32 |
| 192 | después | 32 |
| 193 | da | 32 |
| 194 | atal | 32 |
| 195 | aquel | 32 |
| 196 | tienpo | 31 |
| 197 | ti | 31 |
| 198 | nada | 31 |
| 199 | muncho | 31 |
| 200 | fuego | 31 |
| 201 | clérigos | 31 |
| 202 | viene | 30 |
| 203 | só | 30 |
| 204 | so | 30 |
| 205 | quiero | 30 |
| 206 | perder | 30 |
| 207 | mijor | 30 |
| 208 | fueron | 30 |
| 209 | estar | 30 |
| 210 | entre | 30 |
| 211 | aquesta | 30 |
| 212 | santo | 29 |
| 213 | quiere | 29 |
| 214 | quier | 29 |
| 215 | otras | 29 |
| 216 | ojos | 29 |
| 217 | obra | 29 |
| 218 | ni | 29 |
| 219 | fuerte | 29 |
| 220 | fijo | 29 |
| 221 | dió | 29 |
| 222 | dezir | 29 |
| 223 | dél | 29 |
| 224 | chica | 29 |
| 225 | bueno | 29 |
| 226 | arçipreste | 29 |
| 227 | vuestro | 28 |
| 228 | sobre | 28 |
| 229 | segund | 28 |
| 230 | mejor | 28 |
| 231 | gran | 28 |
| 232 | ayna | 28 |
| 233 | verdat | 27 |
| 234 | tenía | 27 |
| 235 | qual | 27 |
| 236 | o | 27 |
| 237 | noble | 27 |
| 238 | fija | 27 |
| 239 | fasta | 27 |
| 240 | dolor | 27 |
| 241 | dixe | 27 |
| 242 | ál | 27 |
| 243 | virgen | 26 |
| 244 | va | 26 |
| 245 | tyene | 26 |
| 246 | quieres | 26 |
| 247 | pena | 26 |
| 248 | fizo | 26 |
| 249 | estos | 26 |
| 250 | dinero | 26 |
| 251 | días | 26 |
| 252 | dan | 26 |
| 253 | creo | 26 |
| 254 | así | 26 |
| 255 | amiga | 26 |
| 256 | saber | 25 |
| 257 | sabe | 25 |
| 258 | quién | 25 |
| 259 | poder | 25 |
| 260 | pierde | 25 |
| 261 | nuestro | 25 |
| 262 | noche | 25 |
| 263 | mesura | 25 |
| 264 | han | 25 |
| 265 | fermosa | 25 |
| 266 | digo | 25 |
| 267 | amigos | 25 |
| 268 | tierra | 24 |
| 269 | serviçio | 24 |
| 270 | seas | 24 |
| 271 | pan | 24 |
| 272 | loco | 24 |
| 273 | dicho | 24 |
| 274 | deve | 24 |
| 275 | cras | 24 |
| 276 | buenas | 24 |
| 277 | ver | 23 |
| 278 | ventura | 23 |
| 279 | sola | 23 |
| 280 | ovo | 23 |
| 281 | obras | 23 |
| 282 | munchos | 23 |
| 283 | mandado | 23 |
| 284 | eran | 23 |
| 285 | desta | 23 |
| 286 | desir | 23 |
| 287 | avía | 23 |
| 288 | arte | 23 |
| 289 | aqueste | 23 |
| 290 | alegría | 23 |
| 291 | yr | 22 |
| 292 | vezes | 22 |
| 293 | quiera | 22 |
| 294 | puedo | 22 |
| 295 | parte | 22 |
| 296 | nuestra | 22 |
| 297 | mugeres | 22 |
| 298 | menos | 22 |
| 299 | malas | 22 |
| 300 | fiz | 22 |
| 301 | faré | 22 |
| 302 | derecho | 22 |
| 303 | carrera | 22 |
| 304 | cantar | 22 |
| 305 | asno | 22 |
| 306 | tales | 21 |
| 307 | t | 21 |
| 308 | querría | 21 |
| 309 | punto | 21 |
| 310 | palabras | 21 |
| 311 | otrosí | 21 |
| 312 | mur | 21 |
| 313 | medio | 21 |
| 314 | dineros | 21 |
| 315 | desto | 21 |
| 316 | conssejo | 21 |
| 317 | cabo | 21 |
| 318 | almas | 21 |
| 319 | algunos | 21 |
| 320 | viejo | 20 |
| 321 | tener | 20 |
| 322 | synon | 20 |
| 323 | sí | 20 |
| 324 | quieren | 20 |
| 325 | quantas | 20 |
| 326 | poeta | 20 |
| 327 | penitençia | 20 |
| 328 | malo | 20 |
| 329 | ladrón | 20 |
| 330 | grado | 20 |
| 331 | graçia | 20 |
| 332 | ffué | 20 |
| 333 | enxienplo | 20 |
| 334 | endrina | 20 |
| 335 | dé | 20 |
| 336 | color | 20 |
| 337 | c | 20 |
| 338 | aquesto | 20 |
| 339 | año | 20 |
| 340 | andan | 20 |
| 341 | alcalle | 20 |
| 342 | val | 19 |
| 343 | sotil | 19 |
| 344 | solo | 19 |
| 345 | será | 19 |
| 346 | quiso | 19 |
| 347 | pueden | 19 |
| 348 | pobres | 19 |
| 349 | pobre | 19 |
| 350 | locura | 19 |
| 351 | faser | 19 |
| 352 | fallo | 19 |
| 353 | ello | 19 |
| 354 | dende | 19 |
| 355 | dame | 19 |
| 356 | chico | 19 |
| 357 | ayuda | 19 |
| 358 | as | 19 |
| 359 | vyno | 18 |
| 360 | triste | 18 |
| 361 | saña | 18 |
| 362 | pecados | 18 |
| 363 | padre | 18 |
| 364 | natura | 18 |
| 365 | mill | 18 |
| 366 | memoria | 18 |
| 367 | mar | 18 |
| 368 | juego | 18 |
| 369 | fazen | 18 |
| 370 | çielo | 18 |
| 371 | cavallo | 18 |
| 372 | carta | 18 |
| 373 | boca | 18 |
| 374 | asy | 18 |
| 375 | ama | 18 |
| 376 | vido | 17 |
| 377 | van | 17 |
| 378 | trotaconventos | 17 |
| 379 | trabajo | 17 |
| 380 | sentençia | 17 |
| 381 | salud | 17 |
| 382 | pudo | 17 |
| 383 | mora | 17 |
| 384 | fuerça | 17 |
| 385 | fe | 17 |
| 386 | están | 17 |
| 387 | esa | 17 |
| 388 | començó | 17 |
| 389 | çerca | 17 |
| 390 | ansy | 17 |
| 391 | agua | 17 |
| 392 | vegadas | 16 |
| 393 | tomar | 16 |
| 394 | ssy | 16 |
| 395 | siglo | 16 |
| 396 | segundo | 16 |
| 397 | rey | 16 |
| 398 | quantos | 16 |
| 399 | puso | 16 |
| 400 | podía | 16 |
| 401 | poca | 16 |
| 402 | pies | 16 |
| 403 | pesar | 16 |
| 404 | pecador | 16 |
| 405 | ojo | 16 |
| 406 | muerto | 16 |
| 407 | matar | 16 |
| 408 | mañana | 16 |
| 409 | fazes | 16 |
| 410 | fama | 16 |
| 411 | estando | 16 |
| 412 | entendimiento | 16 |
| 413 | dizen | 16 |
| 414 | diga | 16 |
| 415 | dientes | 16 |
| 416 | conpaña | 16 |
| 417 | comer | 16 |
| 418 | carne | 16 |
| 419 | aun | 16 |
| 420 | veo | 15 |
| 421 | uso | 15 |
| 422 | toma | 15 |
| 423 | tengo | 15 |
| 424 | tarde | 15 |
| 425 | señores | 15 |
| 426 | salvo | 15 |
| 427 | rrey | 15 |
| 428 | quaresma | 15 |
| 429 | primera | 15 |
| 430 | pequeña | 15 |
| 431 | palabra | 15 |
| 432 | orejas | 15 |
| 433 | onrra | 15 |
| 434 | nuevas | 15 |
| 435 | menudo | 15 |
| 436 | mata | 15 |
| 437 | mandó | 15 |
| 438 | guarda | 15 |
| 439 | fallé | 15 |
| 440 | esperança | 15 |
| 441 | cabeça | 15 |
| 442 | años | 15 |
| 443 | andava | 15 |
| 444 | andar | 15 |
| 445 | amar | 15 |
| 446 | yra | 14 |
| 447 | vienen | 14 |
| 448 | verguença | 14 |
| 449 | verdadero | 14 |
| 450 | sobervia | 14 |
| 451 | sabes | 14 |
| 452 | puesto | 14 |
| 453 | posada | 14 |
| 454 | poridat | 14 |
| 455 | pelea | 14 |
| 456 | merçed | 14 |
| 457 | males | 14 |
| 458 | loçana | 14 |
| 459 | literatura | 14 |
| 460 | fuera | 14 |
| 461 | fermoso | 14 |
| 462 | faga | 14 |
| 463 | entender | 14 |
| 464 | dura | 14 |
| 465 | contigo | 14 |
| 466 | contesçió | 14 |
| 467 | comienço | 14 |
| 468 | comía | 14 |
| 469 | cobdiçia | 14 |
| 470 | çierto | 14 |
| 471 | cantares | 14 |
| 472 | buenos | 14 |
| 473 | ayuno | 14 |
| 474 | armas | 14 |
| 475 | aquella | 14 |
| 476 | an | 14 |
| 477 | vil | 13 |
| 478 | viejas | 13 |
| 479 | vete | 13 |
| 480 | veses | 13 |
| 481 | versos | 13 |
| 482 | venus | 13 |
| 483 | vano | 13 |
| 484 | tristesa | 13 |
| 485 | traye | 13 |
| 486 | suyo | 13 |
| 487 | sería | 13 |
| 488 | sabio | 13 |
| 489 | rrespuesta | 13 |
| 490 | rrazón | 13 |
| 491 | pocos | 13 |
| 492 | plaser | 13 |
| 493 | peor | 13 |
| 494 | partes | 13 |
| 495 | papa | 13 |
| 496 | maneras | 13 |
| 497 | lengua | 13 |
| 498 | leal | 13 |
| 499 | juan | 13 |
| 500 | joyas | 13 |
| 501 | gelo | 13 |
| 502 | fiso | 13 |
| 503 | fiesta | 13 |
| 504 | estás | 13 |
| 505 | ésta | 13 |
| 506 | ese | 13 |
| 507 | ellas | 13 |
| 508 | dó | 13 |
| 509 | díxome | 13 |
| 510 | demanda | 13 |
| 511 | cuyta | 13 |
| 512 | coyta | 13 |
| 513 | avrás | 13 |
| 514 | aunque | 13 |
| 515 | aquestos | 13 |
| 516 | aquestas | 13 |
| 517 | alto | 13 |
| 518 | alegre | 13 |
| 519 | ado | 13 |
| 520 | vuestros | 12 |
| 521 | vuestras | 12 |
| 522 | venir | 12 |
| 523 | traya | 12 |
| 524 | todavía | 12 |
| 525 | servir | 12 |
| 526 | salvaçión | 12 |
| 527 | rrico | 12 |
| 528 | quieras | 12 |
| 529 | puerto | 12 |
| 530 | puerta | 12 |
| 531 | puedes | 12 |
| 532 | pueda | 12 |
| 533 | perdido | 12 |
| 534 | parayso | 12 |
| 535 | oyr | 12 |
| 536 | ninguno | 12 |
| 537 | n | 12 |
| 538 | monjas | 12 |
| 539 | monja | 12 |
| 540 | mester | 12 |
| 541 | mesquino | 12 |
| 542 | mayores | 12 |
| 543 | manda | 12 |
| 544 | malos | 12 |
| 545 | loxuria | 12 |
| 546 | libros | 12 |
| 547 | hita | 12 |
| 548 | gloria | 12 |
| 549 | gentes | 12 |
| 550 | fuy | 12 |
| 551 | fer | 12 |
| 552 | fase | 12 |
| 553 | fará | 12 |
| 554 | eso | 12 |
| 555 | enemigo | 12 |
| 556 | enamorado | 12 |
| 557 | doñ | 12 |
| 558 | dise | 12 |
| 559 | dichos | 12 |
| 560 | deste | 12 |
| 561 | dellos | 12 |
| 562 | cuydado | 12 |
| 563 | cuyda | 12 |
| 564 | cuerdo | 12 |
| 565 | com | 12 |
| 566 | cartas | 12 |
| 567 | abogado | 12 |
| 568 | yva | 11 |
| 569 | yaze | 11 |
| 570 | villa | 11 |
| 571 | vez | 11 |
| 572 | verso | 11 |
| 573 | venieron | 11 |
| 574 | venido | 11 |
| 575 | venga | 11 |
| 576 | vençer | 11 |
| 577 | tod | 11 |
| 578 | tanta | 11 |
| 579 | sierra | 11 |
| 580 | sant | 11 |
| 581 | quería | 11 |
| 582 | queda | 11 |
| 583 | provecho | 11 |
| 584 | preso | 11 |
| 585 | preçio | 11 |
| 586 | porqué | 11 |
| 587 | plazer | 11 |
| 588 | peroque | 11 |
| 589 | oro | 11 |
| 590 | misa | 11 |
| 591 | mengua | 11 |
| 592 | marido | 11 |
| 593 | maguer | 11 |
| 594 | loca | 11 |
| 595 | ley | 11 |
| 596 | hombre | 11 |
| 597 | guisa | 11 |
| 598 | gente | 11 |
| 599 | estoria | 11 |
| 600 | éste | 11 |
| 601 | dulçe | 11 |
| 602 | dióme | 11 |
| 603 | dellas | 11 |
| 604 | das | 11 |
| 605 | cruz | 11 |
| 606 | çierta | 11 |
| 607 | camino | 11 |
| 608 | blanca | 11 |
| 609 | avíe | 11 |
| 610 | aves | 11 |
| 611 | ave | 11 |
| 612 | atan | 11 |
| 613 | ansí | 11 |
| 614 | alguna | 11 |
| 615 | vista | 10 |
| 616 | vale | 10 |
| 617 | temor | 10 |
| 618 | talla | 10 |
| 619 | sserrana | 10 |
| 620 | sol | 10 |
| 621 | siete | 10 |
| 622 | sean | 10 |
| 623 | seades | 10 |
| 624 | sátira | 10 |
| 625 | sañudo | 10 |
| 626 | salvar | 10 |
| 627 | saca | 10 |
| 628 | rraçón | 10 |
| 629 | queredes | 10 |
| 630 | presto | 10 |
| 631 | pone | 10 |
| 632 | podría | 10 |
| 633 | oviste | 10 |
| 634 | oso | 10 |
| 635 | oraçión | 10 |
| 636 | nonbre | 10 |
| 637 | neçio | 10 |
| 638 | muncha | 10 |
| 639 | muda | 10 |
| 640 | moça | 10 |
| 641 | mismo | 10 |
| 642 | mío | 10 |
| 643 | mientes | 10 |
| 644 | mía | 10 |
| 645 | mesmo | 10 |
| 646 | maestrías | 10 |
| 647 | llama | 10 |
| 648 | gozos | 10 |
| 649 | gallo | 10 |
| 650 | fuertes | 10 |
| 651 | fuero | 10 |
| 652 | frío | 10 |
| 653 | fecha | 10 |
| 654 | far | 10 |
| 655 | falso | 10 |
| 656 | falsa | 10 |
| 657 | esfuerço | 10 |
| 658 | engaña | 10 |
| 659 | dulçes | 10 |
| 660 | disen | 10 |
| 661 | digas | 10 |
| 662 | dava | 10 |
| 663 | daño | 10 |
| 664 | cunple | 10 |
| 665 | culpa | 10 |
| 666 | cuerpos | 10 |
| 667 | coplas | 10 |
| 668 | convusco | 10 |
| 669 | conplido | 10 |
| 670 | cobro | 10 |
| 671 | clérigo | 10 |
| 672 | çiençia | 10 |
| 673 | cara | 10 |
| 674 | avedes | 10 |
| 675 | alta | 10 |
| 676 | ageno | 10 |
| 677 | açipreste | 10 |
| 678 | yantar | 9 |
| 679 | vyda | 9 |
| 680 | voluntad | 9 |
| 681 | viste | 9 |
| 682 | viento | 9 |
| 683 | vaya | 9 |
| 684 | tyenen | 9 |
| 685 | tyenda | 9 |
| 686 | trebejo | 9 |
| 687 | trayo | 9 |
| 688 | traer | 9 |
| 689 | torpe | 9 |
| 690 | somos | 9 |
| 691 | sólo | 9 |
| 692 | sey | 9 |
| 693 | sano | 9 |
| 694 | rroydo | 9 |
| 695 | quisiese | 9 |
| 696 | qualquier | 9 |
| 697 | pueblo | 9 |
| 698 | prueva | 9 |
| 699 | presta | 9 |
| 700 | porfía | 9 |
| 701 | plaça | 9 |
| 702 | persona | 9 |
| 703 | peresa | 9 |
| 704 | peña | 9 |
| 705 | penas | 9 |
| 706 | paz | 9 |
| 707 | paso | 9 |
| 708 | pasado | 9 |
| 709 | par | 9 |
| 710 | ove | 9 |
| 711 | oras | 9 |
| 712 | ofiçio | 9 |
| 713 | nuevo | 9 |
| 714 | nueva | 9 |
| 715 | negro | 9 |
| 716 | nasçe | 9 |
| 717 | muerta | 9 |
| 718 | morada | 9 |
| 719 | mes | 9 |
| 720 | lydiar | 9 |
| 721 | loores | 9 |
| 722 | llaga | 9 |
| 723 | levantóse | 9 |
| 724 | in | 9 |
| 725 | iglesia | 9 |
| 726 | galgo | 9 |
| 727 | firme | 9 |
| 728 | fijos | 9 |
| 729 | falla | 9 |
| 730 | envidia | 9 |
| 731 | entrar | 9 |
| 732 | entramos | 9 |
| 733 | entonces | 9 |
| 734 | dizes | 9 |
| 735 | diré | 9 |
| 736 | dexa | 9 |
| 737 | desides | 9 |
| 738 | dentro | 9 |
| 739 | dando | 9 |
| 740 | cuervo | 9 |
| 741 | cuello | 9 |
| 742 | cual | 9 |
| 743 | creer | 9 |
| 744 | creçe | 9 |
| 745 | conviene | 9 |
| 746 | consejo | 9 |
| 747 | conpañas | 9 |
| 748 | comadre | 9 |
| 749 | çiegos | 9 |
| 750 | cavalleros | 9 |
| 751 | cantica | 9 |
| 752 | cadaque | 9 |
| 753 | caçador | 9 |
| 754 | bestias | 9 |
| 755 | bendiçión | 9 |
| 756 | asi | 9 |
| 757 | aquellos | 9 |
| 758 | aquél | 9 |
| 759 | antes | 9 |
| 760 | andando | 9 |
| 761 | amidos | 9 |
| 762 | allá | 9 |
| 763 | algún | 9 |
| 764 | abogados | 9 |
| 765 | yase | 8 |
| 766 | vien | 8 |
| 767 | verdad | 8 |
| 768 | venida | 8 |
| 769 | vegada | 8 |
| 770 | vagar | 8 |
| 771 | vacas | 8 |
| 772 | unas | 8 |
| 773 | tyenpo | 8 |
| 774 | trigo | 8 |
| 775 | topo | 8 |
| 776 | tomó | 8 |
| 777 | tomé | 8 |
| 778 | tien | 8 |
| 779 | tí | 8 |
| 780 | terçero | 8 |
| 781 | tenga | 8 |
| 782 | talavera | 8 |
| 783 | sociedad | 8 |
| 784 | sinon | 8 |
| 785 | sílabas | 8 |
| 786 | signo | 8 |
| 787 | seya | 8 |
| 788 | sepa | 8 |
| 789 | seer | 8 |
| 790 | sangre | 8 |
| 791 | salen | 8 |
| 792 | sale | 8 |
| 793 | saben | 8 |
| 794 | querer | 8 |
| 795 | quántos | 8 |
| 796 | quales | 8 |
| 797 | provar | 8 |
| 798 | poquillo | 8 |
| 799 | poner | 8 |
| 800 | pocas | 8 |
| 801 | pie | 8 |
| 802 | perdón | 8 |
| 803 | pequeño | 8 |
| 804 | pavón | 8 |
| 805 | parientes | 8 |
| 806 | pajas | 8 |
| 807 | ovieron | 8 |
| 808 | orden | 8 |
| 809 | miente | 8 |
| 810 | menssajero | 8 |
| 811 | mató | 8 |
| 812 | matas | 8 |
| 813 | manjar | 8 |
| 814 | mançebo | 8 |
| 815 | lymosna | 8 |
| 816 | locos | 8 |
| 817 | jugar | 8 |
| 818 | garçón | 8 |
| 819 | fechos | 8 |
| 820 | fazía | 8 |
| 821 | faría | 8 |
| 822 | fablas | 8 |
| 823 | exençión | 8 |
| 824 | et | 8 |
| 825 | españa | 8 |
| 826 | engaño | 8 |
| 827 | duena | 8 |
| 828 | dubda | 8 |
| 829 | doliente | 8 |
| 830 | dixieron | 8 |
| 831 | díxel | 8 |
| 832 | dexar | 8 |
| 833 | desonrra | 8 |
| 834 | deseo | 8 |
| 835 | demás | 8 |
| 836 | david | 8 |
| 837 | cuerda | 8 |
| 838 | cuenta | 8 |
| 839 | conmigo | 8 |
| 840 | comigo | 8 |
| 841 | comiença | 8 |
| 842 | chicas | 8 |
| 843 | cata | 8 |
| 844 | canta | 8 |
| 845 | busca | 8 |
| 846 | bever | 8 |
| 847 | aya | 8 |
| 848 | aventura | 8 |
| 849 | arçobispo | 8 |
| 850 | aquello | 8 |
| 851 | anssy | 8 |
| 852 | amos | 8 |
| 853 | amores | 8 |
| 854 | amador | 8 |
| 855 | abutarda | 8 |
| 856 | yerra | 7 |
| 857 | yd | 7 |
| 858 | xristianos | 7 |
| 859 | vydo | 7 |
| 860 | visto | 7 |
| 861 | viçio | 7 |
| 862 | vianda | 7 |
| 863 | verná | 7 |
| 864 | verdadera | 7 |
| 865 | vençe | 7 |
| 866 | vea | 7 |
| 867 | vana | 7 |
| 868 | valor | 7 |
| 869 | valiente | 7 |
| 870 | usar | 7 |
| 871 | usan | 7 |
| 872 | tyenes | 7 |
| 873 | tyen | 7 |
| 874 | tuerto | 7 |
| 875 | tristeza | 7 |
| 876 | traes | 7 |
| 877 | trae | 7 |
| 878 | toledo | 7 |
| 879 | tienen | 7 |
| 880 | tiempo | 7 |
| 881 | thesoros | 7 |
| 882 | spíritu | 7 |
| 883 | sonbra | 7 |
| 884 | solás | 7 |
| 885 | sodes | 7 |
| 886 | sino | 7 |
| 887 | serrana | 7 |
| 888 | seríe | 7 |
| 889 | santos | 7 |
| 890 | sana | 7 |
| 891 | san | 7 |
| 892 | rruego | 7 |
| 893 | rranas | 7 |
| 894 | razón | 7 |
| 895 | rasón | 7 |
| 896 | quexa | 7 |
| 897 | queso | 7 |
| 898 | prestar | 7 |
| 899 | presos | 7 |
| 900 | presión | 7 |
| 901 | pos | 7 |
| 902 | poderoso | 7 |
| 903 | pitas | 7 |
| 904 | pieça | 7 |
| 905 | piadat | 7 |
| 906 | pessar | 7 |
| 907 | perro | 7 |
| 908 | pensamientos | 7 |
| 909 | penada | 7 |
| 910 | pedro | 7 |
| 911 | pecho | 7 |
| 912 | paresçe | 7 |
| 913 | paños | 7 |
| 914 | pagar | 7 |
| 915 | pagado | 7 |
| 916 | paga | 7 |
| 917 | ovidio | 7 |
| 918 | nobles | 7 |
| 919 | nesçio | 7 |
| 920 | natural | 7 |
| 921 | morir | 7 |
| 922 | mintroso | 7 |
| 923 | mesnada | 7 |
| 924 | mejores | 7 |
| 925 | media | 7 |
| 926 | marfusa | 7 |
| 927 | maña | 7 |
| 928 | mandar | 7 |
| 929 | lygero | 7 |
| 930 | lyd | 7 |
| 931 | loçano | 7 |
| 932 | leyes | 7 |
| 933 | lágrimas | 7 |
| 934 | juyzio | 7 |
| 935 | júpiter | 7 |
| 936 | jamás | 7 |
| 937 | hay | 7 |
| 938 | gula | 7 |
| 939 | guardar | 7 |
| 940 | guardan | 7 |
| 941 | guardada | 7 |
| 942 | griegos | 7 |
| 943 | griego | 7 |
| 944 | grave | 7 |
| 945 | goloso | 7 |
| 946 | golondrina | 7 |
| 947 | gana | 7 |
| 948 | furto | 7 |
| 949 | folgura | 7 |
| 950 | flor | 7 |
| 951 | fermosura | 7 |
| 952 | fermosos | 7 |
| 953 | etc | 7 |
| 954 | estudo | 7 |
| 955 | estavan | 7 |
| 956 | esos | 7 |
| 957 | escripto | 7 |
| 958 | entró | 7 |
| 959 | entiende | 7 |
| 960 | enemigos | 7 |
| 961 | enemiga | 7 |
| 962 | end | 7 |
| 963 | duelo | 7 |
| 964 | dieron | 7 |
| 965 | dicha | 7 |
| 966 | dice | 7 |
| 967 | deziendo | 7 |
| 968 | deyuso | 7 |
| 969 | dexó | 7 |
| 970 | desea | 7 |
| 971 | dello | 7 |
| 972 | dedes | 7 |
| 973 | decir | 7 |
| 974 | dados | 7 |
| 975 | dada | 7 |
| 976 | cura | 7 |
| 977 | cuando | 7 |
| 978 | cree | 7 |
| 979 | coydando | 7 |
| 980 | cordura | 7 |
| 981 | cordero | 7 |
| 982 | conçejo | 7 |
| 983 | conbrás | 7 |
| 984 | comiese | 7 |
| 985 | clara | 7 |
| 986 | çiento | 7 |
| 987 | çerrada | 7 |
| 988 | çelo | 7 |
| 989 | castellana | 7 |
| 990 | casar | 7 |
| 991 | casamiento | 7 |
| 992 | cántigas | 7 |
| 993 | callar | 7 |
| 994 | caer | 7 |
| 995 | caça | 7 |
| 996 | burla | 7 |
| 997 | boz | 7 |
| 998 | blanco | 7 |
| 999 | bestia | 7 |
| 1000 | ayas | 7 |
| 1001 | atanto | 7 |
| 1002 | amada | 7 |
| 1003 | alguno | 7 |
| 1004 | algunas | 7 |
| 1005 | águila | 7 |
| 1006 | xristos | 6 |
| 1007 | xiv | 6 |
| 1008 | ximio | 6 |
| 1009 | vertud | 6 |
| 1010 | venían | 6 |
| 1011 | venía | 6 |
| 1012 | veer | 6 |
| 1013 | vedes | 6 |
| 1014 | varón | 6 |
| 1015 | vanagloria | 6 |
| 1016 | trobar | 6 |
| 1017 | tira | 6 |
| 1018 | tienes | 6 |
| 1019 | tenemos | 6 |
| 1020 | tardança | 6 |
| 1021 | tantos | 6 |
| 1022 | taniendo | 6 |
| 1023 | talente | 6 |
| 1024 | talante | 6 |
| 1025 | solaz | 6 |
| 1026 | señas | 6 |
| 1027 | segunt | 6 |
| 1028 | sañuda | 6 |
| 1029 | salve | 6 |
| 1030 | salvador | 6 |
| 1031 | salva | 6 |
| 1032 | sacó | 6 |
| 1033 | ruiz | 6 |
| 1034 | rrica | 6 |
| 1035 | quexura | 6 |
| 1036 | quered | 6 |
| 1037 | quatro | 6 |
| 1038 | quáles | 6 |
| 1039 | puertas | 6 |
| 1040 | pud | 6 |
| 1041 | provada | 6 |
| 1042 | presente | 6 |
| 1043 | popular | 6 |
| 1044 | ponen | 6 |
| 1045 | pon | 6 |
| 1046 | poetas | 6 |
| 1047 | poesía | 6 |
| 1048 | podieres | 6 |
| 1049 | podedes | 6 |
| 1050 | poble | 6 |
| 1051 | pleito | 6 |
| 1052 | pierden | 6 |
| 1053 | piensa | 6 |
| 1054 | piedra | 6 |
| 1055 | pido | 6 |
| 1056 | pide | 6 |
| 1057 | pesa | 6 |
| 1058 | personas | 6 |
| 1059 | pelleja | 6 |
| 1060 | pelayo | 6 |
| 1061 | pecar | 6 |
| 1062 | pariente | 6 |
| 1063 | pagada | 6 |
| 1064 | oya | 6 |
| 1065 | otrosy | 6 |
| 1066 | omíllome | 6 |
| 1067 | ocho | 6 |
| 1068 | nuestros | 6 |
| 1069 | nuestras | 6 |
| 1070 | nota | 6 |
| 1071 | nasçen | 6 |
| 1072 | murió | 6 |
| 1073 | muere | 6 |
| 1074 | muela | 6 |
| 1075 | mortal | 6 |
| 1076 | moros | 6 |
| 1077 | monte | 6 |
| 1078 | moço | 6 |
| 1079 | misma | 6 |
| 1080 | miel | 6 |
| 1081 | mesa | 6 |
| 1082 | mensajera | 6 |
| 1083 | menéndez | 6 |
| 1084 | melón | 6 |
| 1085 | melesina | 6 |
| 1086 | medida | 6 |
| 1087 | maravilla | 6 |
| 1088 | mansilla | 6 |
| 1089 | maldat | 6 |
| 1090 | maestro | 6 |
| 1091 | luxuria | 6 |
| 1092 | lucha | 6 |
| 1093 | lleno | 6 |
| 1094 | llena | 6 |
| 1095 | lírica | 6 |
| 1096 | liebres | 6 |
| 1097 | juez | 6 |
| 1098 | judíos | 6 |
| 1099 | jhesuxristo | 6 |
| 1100 | ingenio | 6 |
| 1101 | huerta | 6 |
| 1102 | hasta | 6 |
| 1103 | guía | 6 |
| 1104 | guarde | 6 |
| 1105 | guardatvos | 6 |
| 1106 | graçias | 6 |
| 1107 | gestos | 6 |
| 1108 | ganar | 6 |
| 1109 | fues | 6 |
| 1110 | frías | 6 |
| 1111 | frayres | 6 |
| 1112 | forca | 6 |
| 1113 | forado | 6 |
| 1114 | flaca | 6 |
| 1115 | ffiz | 6 |
| 1116 | ffaze | 6 |
| 1117 | fermosas | 6 |
| 1118 | ferido | 6 |
| 1119 | feo | 6 |
| 1120 | fazían | 6 |
| 1121 | fasen | 6 |
| 1122 | falló | 6 |
| 1123 | fallarás | 6 |
| 1124 | fallar | 6 |
| 1125 | fados | 6 |
| 1126 | facer | 6 |
| 1127 | extraordinario | 6 |
| 1128 | estrado | 6 |
| 1129 | estonçe | 6 |
| 1130 | éstas | 6 |
| 1131 | estades | 6 |
| 1132 | espera | 6 |
| 1133 | espanto | 6 |
| 1134 | espanta | 6 |
| 1135 | escritores | 6 |
| 1136 | escrito | 6 |
| 1137 | escarnio | 6 |
| 1138 | escarnida | 6 |
| 1139 | enbía | 6 |
| 1140 | elada | 6 |
| 1141 | edad | 6 |
| 1142 | echar | 6 |
| 1143 | echa | 6 |
| 1144 | duro | 6 |
| 1145 | donde | 6 |
| 1146 | diste | 6 |
| 1147 | dióle | 6 |
| 1148 | digades | 6 |
| 1149 | dexes | 6 |
| 1150 | destas | 6 |
| 1151 | desirvos | 6 |
| 1152 | desde | 6 |
| 1153 | derecha | 6 |
| 1154 | dedos | 6 |
| 1155 | decreto | 6 |
| 1156 | dart | 6 |
| 1157 | cuydados | 6 |
| 1158 | crió | 6 |
| 1159 | costumbres | 6 |
| 1160 | costados | 6 |
| 1161 | cossa | 6 |
| 1162 | corrida | 6 |
| 1163 | copla | 6 |
| 1164 | convento | 6 |
| 1165 | contesçe | 6 |
| 1166 | conplida | 6 |
| 1167 | conpañía | 6 |
| 1168 | conorte | 6 |
| 1169 | comen | 6 |
| 1170 | come | 6 |
| 1171 | cóm | 6 |
| 1172 | chata | 6 |
| 1173 | castigo | 6 |
| 1174 | cassar | 6 |
| 1175 | casos | 6 |
| 1176 | casado | 6 |
| 1177 | canto | 6 |
| 1178 | cabritos | 6 |
| 1179 | cabellos | 6 |
| 1180 | cabdal | 6 |
| 1181 | bravo | 6 |
| 1182 | bienes | 6 |
| 1183 | ayudar | 6 |
| 1184 | avrá | 6 |
| 1185 | aved | 6 |
| 1186 | ardit | 6 |
| 1187 | apuesta | 6 |
| 1188 | apólogos | 6 |
| 1189 | ant | 6 |
| 1190 | animalias | 6 |
| 1191 | andavan | 6 |
| 1192 | andas | 6 |
| 1193 | amas | 6 |
| 1194 | algund | 6 |
| 1195 | aldea | 6 |
| 1196 | acaso | 6 |
| 1197 | acaesçe | 6 |
| 1198 | ynfierno | 5 |
| 1199 | vyeres | 5 |
| 1200 | vyanda | 5 |
| 1201 | vinieron | 5 |
| 1202 | viere | 5 |
| 1203 | vienes | 5 |
| 1204 | veyen | 5 |
| 1205 | veya | 5 |
| 1206 | vesina | 5 |
| 1207 | verás | 5 |
| 1208 | verano | 5 |
| 1209 | vellaco | 5 |
| 1210 | vees | 5 |
| 1211 | varones | 5 |
| 1212 | usado | 5 |
| 1213 | usa | 5 |
| 1214 | urraca | 5 |
| 1215 | unos | 5 |
| 1216 | trotera | 5 |
| 1217 | trayan | 5 |
| 1218 | tras | 5 |
| 1219 | tetrástrofo | 5 |
| 1220 | tenías | 5 |
| 1221 | tenedes | 5 |
| 1222 | teme | 5 |
| 1223 | temas | 5 |
| 1224 | tarda | 5 |
| 1225 | tacha | 5 |
| 1226 | suelo | 5 |
| 1227 | suele | 5 |
| 1228 | soy | 5 |
| 1229 | sospirando | 5 |
| 1230 | sofrir | 5 |
| 1231 | sobervio | 5 |
| 1232 | sobejo | 5 |
| 1233 | sinalefa | 5 |
| 1234 | sigue | 5 |
| 1235 | siente | 5 |
| 1236 | siempre | 5 |
| 1237 | serviendo | 5 |
| 1238 | servidor | 5 |
| 1239 | señero | 5 |
| 1240 | semeja | 5 |
| 1241 | seguro | 5 |
| 1242 | seguida | 5 |
| 1243 | sed | 5 |
| 1244 | saya | 5 |
| 1245 | sardinas | 5 |
| 1246 | salyó | 5 |
| 1247 | sacramento | 5 |
| 1248 | saçón | 5 |
| 1249 | sabidoría | 5 |
| 1250 | sabía | 5 |
| 1251 | rrudo | 5 |
| 1252 | rromanos | 5 |
| 1253 | rrío | 5 |
| 1254 | rrespondióle | 5 |
| 1255 | rrasones | 5 |
| 1256 | rrana | 5 |
| 1257 | riqueza | 5 |
| 1258 | reyna | 5 |
| 1259 | reyes | 5 |
| 1260 | respuesta | 5 |
| 1261 | quito | 5 |
| 1262 | quisieres | 5 |
| 1263 | quisiere | 5 |
| 1264 | quinto | 5 |
| 1265 | qui | 5 |
| 1266 | quesieres | 5 |
| 1267 | querrá | 5 |
| 1268 | quán | 5 |
| 1269 | pusieron | 5 |
| 1270 | pura | 5 |
| 1271 | puerca | 5 |
| 1272 | profeta | 5 |
| 1273 | pro | 5 |
| 1274 | priso | 5 |
| 1275 | primitivo | 5 |
| 1276 | primer | 5 |
| 1277 | prado | 5 |
| 1278 | pongo | 5 |
| 1279 | podrían | 5 |
| 1280 | podremos | 5 |
| 1281 | podiese | 5 |
| 1282 | podemos | 5 |
| 1283 | plazo | 5 |
| 1284 | piernas | 5 |
| 1285 | perdida | 5 |
| 1286 | penado | 5 |
| 1287 | pella | 5 |
| 1288 | pechos | 5 |
| 1289 | pecadores | 5 |
| 1290 | pavor | 5 |
| 1291 | paredes | 5 |
| 1292 | oyó | 5 |
| 1293 | oyere | 5 |
| 1294 | otea | 5 |
| 1295 | oreja | 5 |
| 1296 | olvido | 5 |
| 1297 | olvides | 5 |
| 1298 | olvidar | 5 |
| 1299 | olvida | 5 |
| 1300 | nona | 5 |
| 1301 | negra | 5 |
| 1302 | naturales | 5 |
| 1303 | nasçió | 5 |
| 1304 | munchas | 5 |
| 1305 | mueren | 5 |
| 1306 | mudo | 5 |
| 1307 | mostró | 5 |
| 1308 | mostrar | 5 |
| 1309 | moryr | 5 |
| 1310 | mortales | 5 |
| 1311 | missa | 5 |
| 1312 | mías | 5 |
| 1313 | mesquina | 5 |
| 1314 | menor | 5 |
| 1315 | mejoría | 5 |
| 1316 | manjares | 5 |
| 1317 | mando | 5 |
| 1318 | mançebillo | 5 |
| 1319 | maestría | 5 |
| 1320 | lynaje | 5 |
| 1321 | luenga | 5 |
| 1322 | limpio | 5 |
| 1323 | ligero | 5 |
| 1324 | liebre | 5 |
| 1325 | lid | 5 |
| 1326 | levar | 5 |
| 1327 | levantar | 5 |
| 1328 | leña | 5 |
| 1329 | lazeria | 5 |
| 1330 | laseria | 5 |
| 1331 | juyzios | 5 |
| 1332 | infierno | 5 |
| 1333 | infante | 5 |
| 1334 | huésped | 5 |
| 1335 | hoy | 5 |
| 1336 | hermano | 5 |
| 1337 | hemistiquios | 5 |
| 1338 | hedat | 5 |
| 1339 | grano | 5 |
| 1340 | golpe | 5 |
| 1341 | gil | 5 |
| 1342 | gelas | 5 |
| 1343 | garoça | 5 |
| 1344 | fynca | 5 |
| 1345 | fuyme | 5 |
| 1346 | francesa | 5 |
| 1347 | fiel | 5 |
| 1348 | ffueron | 5 |
| 1349 | ffabló | 5 |
| 1350 | fenbras | 5 |
| 1351 | fea | 5 |
| 1352 | fasiendo | 5 |
| 1353 | fases | 5 |
| 1354 | fas | 5 |
| 1355 | farás | 5 |
| 1356 | fagas | 5 |
| 1357 | fado | 5 |
| 1358 | fablo | 5 |
| 1359 | fablando | 5 |
| 1360 | estrumentos | 5 |
| 1361 | estrelleros | 5 |
| 1362 | estrañas | 5 |
| 1363 | estraña | 5 |
| 1364 | escriptura | 5 |
| 1365 | entr | 5 |
| 1366 | entendiendo | 5 |
| 1367 | enojo | 5 |
| 1368 | engañar | 5 |
| 1369 | enbió | 5 |
| 1370 | dyz | 5 |
| 1371 | dotor | 5 |
| 1372 | doquier | 5 |
| 1373 | dona | 5 |
| 1374 | domingo | 5 |
| 1375 | dízelo | 5 |
| 1376 | díxole | 5 |
| 1377 | dirá | 5 |
| 1378 | diól | 5 |
| 1379 | dies | 5 |
| 1380 | dezía | 5 |
| 1381 | deven | 5 |
| 1382 | devemos | 5 |
| 1383 | demandar | 5 |
| 1384 | dedo | 5 |
| 1385 | darvos | 5 |
| 1386 | daría | 5 |
| 1387 | dapño | 5 |
| 1388 | dado | 5 |
| 1389 | culuebra | 5 |
| 1390 | cuestas | 5 |
| 1391 | cuero | 5 |
| 1392 | cuentas | 5 |
| 1393 | cuanto | 5 |
| 1394 | cruel | 5 |
| 1395 | crey | 5 |
| 1396 | coytas | 5 |
| 1397 | coyda | 5 |
| 1398 | coxo | 5 |
| 1399 | cortés | 5 |
| 1400 | corredor | 5 |
| 1401 | corre | 5 |
| 1402 | consolaçión | 5 |
| 1403 | conplir | 5 |
| 1404 | conejo | 5 |
| 1405 | comió | 5 |
| 1406 | claramente | 5 |
| 1407 | çinta | 5 |
| 1408 | çinco | 5 |
| 1409 | çima | 5 |
| 1410 | cierto | 5 |
| 1411 | cerca | 5 |
| 1412 | çena | 5 |
| 1413 | cayada | 5 |
| 1414 | catar | 5 |
| 1415 | castigos | 5 |
| 1416 | caridat | 5 |
| 1417 | canpo | 5 |
| 1418 | can | 5 |
| 1419 | cama | 5 |
| 1420 | callejas | 5 |
| 1421 | calla | 5 |
| 1422 | cabrón | 5 |
| 1423 | cabras | 5 |
| 1424 | buscar | 5 |
| 1425 | bondad | 5 |
| 1426 | bodas | 5 |
| 1427 | bevir | 5 |
| 1428 | bermejas | 5 |
| 1429 | avya | 5 |
| 1430 | avremos | 5 |
| 1431 | avían | 5 |
| 1432 | artes | 5 |
| 1433 | aprovecha | 5 |
| 1434 | ángeles | 5 |
| 1435 | angel | 5 |
| 1436 | amo | 5 |
| 1437 | amargura | 5 |
| 1438 | allí | 5 |
| 1439 | allega | 5 |
| 1440 | algos | 5 |
| 1441 | agudo | 5 |
| 1442 | açúcar | 5 |
| 1443 | acabada | 5 |
| 1444 | yuy | 4 |
| 1445 | yervas | 4 |
| 1446 | yerro | 4 |
| 1447 | vyl | 4 |
| 1448 | vyene | 4 |
| 1449 | voz | 4 |
| 1450 | vó | 4 |
| 1451 | villano | 4 |
| 1452 | vieron | 4 |
| 1453 | vieres | 4 |
| 1454 | vía | 4 |
| 1455 | vi | 4 |
| 1456 | vestir | 4 |
| 1457 | vesindat | 4 |
| 1458 | venino | 4 |
| 1459 | veníe | 4 |
| 1460 | venid | 4 |
| 1461 | vengo | 4 |
| 1462 | vee | 4 |
| 1463 | veades | 4 |
| 1464 | vas | 4 |
| 1465 | vanidat | 4 |
| 1466 | valyentes | 4 |
| 1467 | valya | 4 |
| 1468 | vallejo | 4 |
| 1469 | valía | 4 |
| 1470 | valen | 4 |
| 1471 | uñas | 4 |
| 1472 | umanal | 4 |
| 1473 | tuyo | 4 |
| 1474 | tristura | 4 |
| 1475 | traydor | 4 |
| 1476 | trabaja | 4 |
| 1477 | torre | 4 |
| 1478 | toro | 4 |
| 1479 | toman | 4 |
| 1480 | tomad | 4 |
| 1481 | toçino | 4 |
| 1482 | testigos | 4 |
| 1483 | terçia | 4 |
| 1484 | tened | 4 |
| 1485 | temen | 4 |
| 1486 | tañe | 4 |
| 1487 | tantas | 4 |
| 1488 | tablero | 4 |
| 1489 | syervo | 4 |
| 1490 | suyos | 4 |
| 1491 | suso | 4 |
| 1492 | suerte | 4 |
| 1493 | ssyenpre | 4 |
| 1494 | sson | 4 |
| 1495 | sse | 4 |
| 1496 | sobrar | 4 |
| 1497 | sobra | 4 |
| 1498 | seyendo | 4 |
| 1499 | sesso | 4 |
| 1500 | serví | 4 |
| 1501 | señalada | 4 |
| 1502 | señal | 4 |
| 1503 | seno | 4 |
| 1504 | segunda | 4 |
| 1505 | santiago | 4 |
| 1506 | salyr | 4 |
| 1507 | salya | 4 |
| 1508 | salutaçión | 4 |
| 1509 | salto | 4 |
| 1510 | salterio | 4 |
| 1511 | salió | 4 |
| 1512 | salieron | 4 |
| 1513 | saetas | 4 |
| 1514 | sacaste | 4 |
| 1515 | sacar | 4 |
| 1516 | sabios | 4 |
| 1517 | rrostro | 4 |
| 1518 | rroma | 4 |
| 1519 | rriquesa | 4 |
| 1520 | rribera | 4 |
| 1521 | rrespondió | 4 |
| 1522 | rresçebir | 4 |
| 1523 | rredes | 4 |
| 1524 | rravia | 4 |
| 1525 | rraçones | 4 |
| 1526 | roydo | 4 |
| 1527 | roma | 4 |
| 1528 | rico | 4 |
| 1529 | respondió | 4 |
| 1530 | realismo | 4 |
| 1531 | real | 4 |
| 1532 | raposa | 4 |
| 1533 | quita | 4 |
| 1534 | quise | 4 |
| 1535 | quexar | 4 |
| 1536 | querades | 4 |
| 1537 | quema | 4 |
| 1538 | quedo | 4 |
| 1539 | quebranta | 4 |
| 1540 | puymaigre | 4 |
| 1541 | pulgar | 4 |
| 1542 | puedan | 4 |
| 1543 | prosa | 4 |
| 1544 | privado | 4 |
| 1545 | prieto | 4 |
| 1546 | priessa | 4 |
| 1547 | prez | 4 |
| 1548 | presona | 4 |
| 1549 | preçiado | 4 |
| 1550 | podrá | 4 |
| 1551 | podiere | 4 |
| 1552 | pleitos | 4 |
| 1553 | plazía | 4 |
| 1554 | plazentera | 4 |
| 1555 | pico | 4 |
| 1556 | piadosa | 4 |
| 1557 | petiçión | 4 |
| 1558 | pereza | 4 |
| 1559 | peresoso | 4 |
| 1560 | perentoria | 4 |
| 1561 | perdió | 4 |
| 1562 | perdieron | 4 |
| 1563 | perdidos | 4 |
| 1564 | perdí | 4 |
| 1565 | perderé | 4 |
| 1566 | pensando | 4 |
| 1567 | pellote | 4 |
| 1568 | peligros | 4 |
| 1569 | peligro | 4 |
| 1570 | peçes | 4 |
| 1571 | patriarcas | 4 |
| 1572 | pater | 4 |
| 1573 | pastores | 4 |
| 1574 | passava | 4 |
| 1575 | passada | 4 |
| 1576 | pasión | 4 |
| 1577 | pascua | 4 |
| 1578 | pasada | 4 |
| 1579 | parta | 4 |
| 1580 | paño | 4 |
| 1581 | palos | 4 |
| 1582 | palaçio | 4 |
| 1583 | pagas | 4 |
| 1584 | pagan | 4 |
| 1585 | oyen | 4 |
| 1586 | oydo | 4 |
| 1587 | ovejas | 4 |
| 1588 | oveja | 4 |
| 1589 | otrosi | 4 |
| 1590 | onrrada | 4 |
| 1591 | ondas | 4 |
| 1592 | onbre | 4 |
| 1593 | olvidado | 4 |
| 1594 | obrar | 4 |
| 1595 | nombre | 4 |
| 1596 | nobleza | 4 |
| 1597 | nieve | 4 |
| 1598 | neçios | 4 |
| 1599 | naturalmente | 4 |
| 1600 | morió | 4 |
| 1601 | montañas | 4 |
| 1602 | monges | 4 |
| 1603 | monge | 4 |
| 1604 | molyno | 4 |
| 1605 | mienta | 4 |
| 1606 | mesturero | 4 |
| 1607 | mercado | 4 |
| 1608 | mentiras | 4 |
| 1609 | menores | 4 |
| 1610 | mastyn | 4 |
| 1611 | manteles | 4 |
| 1612 | mançebía | 4 |
| 1613 | maestras | 4 |
| 1614 | lysonjas | 4 |
| 1615 | lyeve | 4 |
| 1616 | luz | 4 |
| 1617 | lunes | 4 |
| 1618 | loor | 4 |
| 1619 | loçanas | 4 |
| 1620 | loava | 4 |
| 1621 | loada | 4 |
| 1622 | llorando | 4 |
| 1623 | llenas | 4 |
| 1624 | llamó | 4 |
| 1625 | llagas | 4 |
| 1626 | lieva | 4 |
| 1627 | levanta | 4 |
| 1628 | latino | 4 |
| 1629 | justiçia | 4 |
| 1630 | juguetes | 4 |
| 1631 | juegos | 4 |
| 1632 | intellectum | 4 |
| 1633 | iglesias | 4 |
| 1634 | hubiera | 4 |
| 1635 | hombres | 4 |
| 1636 | hermitano | 4 |
| 1637 | hemos | 4 |
| 1638 | harto | 4 |
| 1639 | hadeduro | 4 |
| 1640 | haber | 4 |
| 1641 | gulhara | 4 |
| 1642 | guárdeme | 4 |
| 1643 | guárdate | 4 |
| 1644 | guadalhajara | 4 |
| 1645 | graja | 4 |
| 1646 | gordos | 4 |
| 1647 | gordo | 4 |
| 1648 | goço | 4 |
| 1649 | gloriosa | 4 |
| 1650 | gesto | 4 |
| 1651 | género | 4 |
| 1652 | gato | 4 |
| 1653 | gallos | 4 |
| 1654 | galardón | 4 |
| 1655 | fyn | 4 |
| 1656 | fúxo | 4 |
| 1657 | furtar | 4 |
| 1658 | fueste | 4 |
| 1659 | fuesen | 4 |
| 1660 | fuése | 4 |
| 1661 | fuerza | 4 |
| 1662 | fuere | 4 |
| 1663 | fuente | 4 |
| 1664 | fruto | 4 |
| 1665 | fruente | 4 |
| 1666 | freno | 4 |
| 1667 | frayre | 4 |
| 1668 | frayle | 4 |
| 1669 | franco | 4 |
| 1670 | foyr | 4 |
| 1671 | flaco | 4 |
| 1672 | fize | 4 |
| 1673 | figura | 4 |
| 1674 | figo | 4 |
| 1675 | fieres | 4 |
| 1676 | fidalgo | 4 |
| 1677 | ffizo | 4 |
| 1678 | feziese | 4 |
| 1679 | feziera | 4 |
| 1680 | ferió | 4 |
| 1681 | faziendo | 4 |
| 1682 | fazedes | 4 |
| 1683 | fast | 4 |
| 1684 | fasía | 4 |
| 1685 | fasedes | 4 |
| 1686 | farina | 4 |
| 1687 | fallado | 4 |
| 1688 | falaguera | 4 |
| 1689 | fago | 4 |
| 1690 | fagamos | 4 |
| 1691 | fagades | 4 |
| 1692 | fable | 4 |
| 1693 | fablado | 4 |
| 1694 | fablad | 4 |
| 1695 | estorçer | 4 |
| 1696 | estido | 4 |
| 1697 | estaba | 4 |
| 1698 | esquiva | 4 |
| 1699 | espritu | 4 |
| 1700 | español | 4 |
| 1701 | espaldas | 4 |
| 1702 | escusar | 4 |
| 1703 | escritor | 4 |
| 1704 | escolar | 4 |
| 1705 | escaso | 4 |
| 1706 | escanto | 4 |
| 1707 | ero | 4 |
| 1708 | entyendo | 4 |
| 1709 | entrada | 4 |
| 1710 | entonçe | 4 |
| 1711 | entienda | 4 |
| 1712 | entendedor | 4 |
| 1713 | ensienplo | 4 |
| 1714 | engaños | 4 |
| 1715 | ençima | 4 |
| 1716 | ençerrada | 4 |
| 1717 | enbydia | 4 |
| 1718 | enbidia | 4 |
| 1719 | enbiada | 4 |
| 1720 | dyneros | 4 |
| 1721 | dya | 4 |
| 1722 | dy | 4 |
| 1723 | dulçor | 4 |
| 1724 | dulce | 4 |
| 1725 | duda | 4 |
| 1726 | dubdando | 4 |
| 1727 | dramático | 4 |
| 1728 | donayre | 4 |
| 1729 | dolençia | 4 |
| 1730 | díxele | 4 |
| 1731 | dixel | 4 |
| 1732 | ditado | 4 |
| 1733 | dina | 4 |
| 1734 | dile | 4 |
| 1735 | diese | 4 |
| 1736 | diablos | 4 |
| 1737 | devo | 4 |
| 1738 | devía | 4 |
| 1739 | deves | 4 |
| 1740 | desseo | 4 |
| 1741 | despecho | 4 |
| 1742 | desiendo | 4 |
| 1743 | desía | 4 |
| 1744 | deseos | 4 |
| 1745 | descobrir | 4 |
| 1746 | deredor | 4 |
| 1747 | denostar | 4 |
| 1748 | delante | 4 |
| 1749 | dávale | 4 |
| 1750 | darte | 4 |
| 1751 | daré | 4 |
| 1752 | darán | 4 |
| 1753 | dará | 4 |
| 1754 | dança | 4 |
| 1755 | dal | 4 |
| 1756 | cuytas | 4 |
| 1757 | cuytado | 4 |
| 1758 | cuydan | 4 |
| 1759 | cuydades | 4 |
| 1760 | cunplido | 4 |
| 1761 | cueva | 4 |
| 1762 | cuest | 4 |
| 1763 | cuerdas | 4 |
| 1764 | criminal | 4 |
| 1765 | criatura | 4 |
| 1766 | criados | 4 |
| 1767 | criado | 4 |
| 1768 | creençia | 4 |
| 1769 | creed | 4 |
| 1770 | creas | 4 |
| 1771 | coytado | 4 |
| 1772 | costunbres | 4 |
| 1773 | costunbre | 4 |
| 1774 | cortesía | 4 |
| 1775 | corneja | 4 |
| 1776 | corazón | 4 |
| 1777 | coraçones | 4 |
| 1778 | contyenda | 4 |
| 1779 | contienda | 4 |
| 1780 | conssejas | 4 |
| 1781 | consigo | 4 |
| 1782 | conplyr | 4 |
| 1783 | conpañero | 4 |
| 1784 | conocido | 4 |
| 1785 | conçebiste | 4 |
| 1786 | comunal | 4 |
| 1787 | comisión | 4 |
| 1788 | comienças | 4 |
| 1789 | coma | 4 |
| 1790 | clerecia | 4 |
| 1791 | çiertas | 4 |
| 1792 | çiertamente | 4 |
| 1793 | cierta | 4 |
| 1794 | çibdat | 4 |
| 1795 | cayó | 4 |
| 1796 | catad | 4 |
| 1797 | castigar | 4 |
| 1798 | cassado | 4 |
| 1799 | casada | 4 |
| 1800 | carneros | 4 |
| 1801 | caras | 4 |
| 1802 | çapatas | 4 |
| 1803 | cantando | 4 |
| 1804 | canpana | 4 |
| 1805 | canal | 4 |
| 1806 | cabeza | 4 |
| 1807 | cabe | 4 |
| 1808 | busqué | 4 |
| 1809 | burro | 4 |
| 1810 | buey | 4 |
| 1811 | brava | 4 |
| 1812 | blanchete | 4 |
| 1813 | biva | 4 |
| 1814 | besa | 4 |
| 1815 | bermejos | 4 |
| 1816 | bella | 4 |
| 1817 | beldat | 4 |
| 1818 | barrio | 4 |
| 1819 | ayuso | 4 |
| 1820 | ayer | 4 |
| 1821 | averes | 4 |
| 1822 | astrología | 4 |
| 1823 | arzobispo | 4 |
| 1824 | artistas | 4 |
| 1825 | arde | 4 |
| 1826 | apuesto | 4 |
| 1827 | aprovechar | 4 |
| 1828 | apóstol | 4 |
| 1829 | aperçebido | 4 |
| 1830 | apenas | 4 |
| 1831 | antiguos | 4 |
| 1832 | ando | 4 |
| 1833 | aman | 4 |
| 1834 | amades | 4 |
| 1835 | amad | 4 |
| 1836 | altas | 4 |
| 1837 | alcalde | 4 |
| 1838 | alano | 4 |
| 1839 | alahé | 4 |
| 1840 | aguda | 4 |
| 1841 | aguas | 4 |
| 1842 | acorrer | 4 |
| 1843 | açidia | 4 |
| 1844 | abenençia | 4 |
| 1845 | yt | 3 |
| 1846 | yremos | 3 |
| 1847 | yrás | 3 |
| 1848 | yaz | 3 |
| 1849 | xristiano | 3 |
| 1850 | vyeron | 3 |
| 1851 | vozes | 3 |
| 1852 | voluntat | 3 |
| 1853 | voluntades | 3 |
| 1854 | voces | 3 |
| 1855 | vo | 3 |
| 1856 | vió | 3 |
| 1857 | vilesa | 3 |
| 1858 | viga | 3 |
| 1859 | viernes | 3 |
| 1860 | vientre | 3 |
| 1861 | viejos | 3 |
| 1862 | viçioso | 3 |
| 1863 | via | 3 |
| 1864 | veyendo | 3 |
| 1865 | veye | 3 |
| 1866 | vestidos | 3 |
| 1867 | vestido | 3 |
| 1868 | vestida | 3 |
| 1869 | vesino | 3 |
| 1870 | ves | 3 |
| 1871 | veredes | 3 |
| 1872 | veré | 3 |
| 1873 | verdades | 3 |
| 1874 | verdaderos | 3 |
| 1875 | véovos | 3 |
| 1876 | vente | 3 |
| 1877 | venit | 3 |
| 1878 | veníen | 3 |
| 1879 | vengan | 3 |
| 1880 | vendiendo | 3 |
| 1881 | vençen | 3 |
| 1882 | vemos | 3 |
| 1883 | veçino | 3 |
| 1884 | veces | 3 |
| 1885 | veas | 3 |
| 1886 | ve | 3 |
| 1887 | vayan | 3 |
| 1888 | vayades | 3 |
| 1889 | vanidades | 3 |
| 1890 | valer | 3 |
| 1891 | vaca | 3 |
| 1892 | uvas | 3 |
| 1893 | usó | 3 |
| 1894 | usava | 3 |
| 1895 | usando | 3 |
| 1896 | usada | 3 |
| 1897 | truchas | 3 |
| 1898 | trucha | 3 |
| 1899 | trobas | 3 |
| 1900 | trobador | 3 |
| 1901 | troba | 3 |
| 1902 | tristes | 3 |
| 1903 | traynel | 3 |
| 1904 | trayes | 3 |
| 1905 | trayen | 3 |
| 1906 | trayçión | 3 |
| 1907 | tovo | 3 |
| 1908 | torpedat | 3 |
| 1909 | torné | 3 |
| 1910 | tornado | 3 |
| 1911 | tornada | 3 |
| 1912 | torna | 3 |
| 1913 | tomes | 3 |
| 1914 | tomemos | 3 |
| 1915 | tomedes | 3 |
| 1916 | tomas | 3 |
| 1917 | tomado | 3 |
| 1918 | tocar | 3 |
| 1919 | toca | 3 |
| 1920 | tienda | 3 |
| 1921 | tiempos | 3 |
| 1922 | tibi | 3 |
| 1923 | thesoro | 3 |
| 1924 | testo | 3 |
| 1925 | terrenal | 3 |
| 1926 | tenprano | 3 |
| 1927 | tenían | 3 |
| 1928 | tengan | 3 |
| 1929 | temió | 3 |
| 1930 | tema | 3 |
| 1931 | tampoco | 3 |
| 1932 | tamaña | 3 |
| 1933 | tabernario | 3 |
| 1934 | synple | 3 |
| 1935 | sygue | 3 |
| 1936 | suya | 3 |
| 1937 | susio | 3 |
| 1938 | superior | 3 |
| 1939 | sunt | 3 |
| 1940 | suma | 3 |
| 1941 | suelta | 3 |
| 1942 | ssyn | 3 |
| 1943 | ssu | 3 |
| 1944 | ssobre | 3 |
| 1945 | ssé | 3 |
| 1946 | ssanta | 3 |
| 1947 | ssabe | 3 |
| 1948 | spritu | 3 |
| 1949 | sospiros | 3 |
| 1950 | sosegada | 3 |
| 1951 | sortija | 3 |
| 1952 | sonajas | 3 |
| 1953 | solteras | 3 |
| 1954 | solía | 3 |
| 1955 | soldada | 3 |
| 1956 | soláz | 3 |
| 1957 | solamente | 3 |
| 1958 | sobredicho | 3 |
| 1959 | sirve | 3 |
| 1960 | siguen | 3 |
| 1961 | signos | 3 |
| 1962 | siesta | 3 |
| 1963 | siendo | 3 |
| 1964 | sido | 3 |
| 1965 | sicut | 3 |
| 1966 | seys | 3 |
| 1967 | sesto | 3 |
| 1968 | sesta | 3 |
| 1969 | servido | 3 |
| 1970 | servicio | 3 |
| 1971 | serranillas | 3 |
| 1972 | serás | 3 |
| 1973 | seña | 3 |
| 1974 | sentióse | 3 |
| 1975 | sendero | 3 |
| 1976 | semiente | 3 |
| 1977 | seguramente | 3 |
| 1978 | segura | 3 |
| 1979 | seguir | 3 |
| 1980 | seca | 3 |
| 1981 | sanudo | 3 |
| 1982 | santidat | 3 |
| 1983 | sandío | 3 |
| 1984 | sanas | 3 |
| 1985 | saly | 3 |
| 1986 | salvaje | 3 |
| 1987 | salmón | 3 |
| 1988 | salmista | 3 |
| 1989 | salido | 3 |
| 1990 | salida | 3 |
| 1991 | sal | 3 |
| 1992 | sabydor | 3 |
| 1993 | sabrás | 3 |
| 1994 | sabidor | 3 |
| 1995 | sabido | 3 |
| 1996 | sabida | 3 |
| 1997 | sabedes | 3 |
| 1998 | ruego | 3 |
| 1999 | rrosa | 3 |
| 2000 | rromano | 3 |
| 2001 | rromançe | 3 |
| 2002 | rriso | 3 |
| 2003 | rricos | 3 |
| 2004 | rreyr | 3 |
| 2005 | rresplandor | 3 |
| 2006 | rresçíbenle | 3 |
| 2007 | rres | 3 |
| 2008 | rreguardan | 3 |
| 2009 | rrayz | 3 |
| 2010 | rrato | 3 |
| 2011 | rrasón | 3 |
| 2012 | rrapossa | 3 |
| 2013 | rraposa | 3 |
| 2014 | rosa | 3 |
| 2015 | ríos | 3 |
| 2016 | río | 3 |
| 2017 | respondióle | 3 |
| 2018 | requiere | 3 |
| 2019 | realidad | 3 |
| 2020 | rato | 3 |
| 2021 | ranas | 3 |
| 2022 | rana | 3 |
| 2023 | rama | 3 |
| 2024 | raçón | 3 |
| 2025 | quod | 3 |
| 2026 | quisto | 3 |
| 2027 | quiérome | 3 |
| 2028 | quexoso | 3 |
| 2029 | queríen | 3 |
| 2030 | querían | 3 |
| 2031 | querençia | 3 |
| 2032 | querella | 3 |
| 2033 | quebrar | 3 |
| 2034 | quebranto | 3 |
| 2035 | quarto | 3 |
| 2036 | quarta | 3 |
| 2037 | quánto | 3 |
| 2038 | quam | 3 |
| 2039 | pyntor | 3 |
| 2040 | puntos | 3 |
| 2041 | pujar | 3 |
| 2042 | puerco | 3 |
| 2043 | pued | 3 |
| 2044 | pudiera | 3 |
| 2045 | pude | 3 |
| 2046 | proverbio | 3 |
| 2047 | provados | 3 |
| 2048 | prometen | 3 |
| 2049 | promete | 3 |
| 2050 | promesas | 3 |
| 2051 | profecta | 3 |
| 2052 | probablemente | 3 |
| 2053 | prisión | 3 |
| 2054 | principalmente | 3 |
| 2055 | primeros | 3 |
| 2056 | prima | 3 |
| 2057 | prietas | 3 |
| 2058 | prestos | 3 |
| 2059 | preste | 3 |
| 2060 | prendes | 3 |
| 2061 | prender | 3 |
| 2062 | prenda | 3 |
| 2063 | pregunta | 3 |
| 2064 | preçiosas | 3 |
| 2065 | preçian | 3 |
| 2066 | preçia | 3 |
| 2067 | portal | 3 |
| 2068 | poquilla | 3 |
| 2069 | poderío | 3 |
| 2070 | pobresa | 3 |
| 2071 | pobredat | 3 |
| 2072 | plega | 3 |
| 2073 | plaz | 3 |
| 2074 | plasentero | 3 |
| 2075 | plasentería | 3 |
| 2076 | plasentera | 3 |
| 2077 | plase | 3 |
| 2078 | plan | 3 |
| 2079 | plaçer | 3 |
| 2080 | plaças | 3 |
| 2081 | pintura | 3 |
| 2082 | pintada | 3 |
| 2083 | pierda | 3 |
| 2084 | pienssa | 3 |
| 2085 | piedat | 3 |
| 2086 | pidieron | 3 |
| 2087 | piden | 3 |
| 2088 | pescueço | 3 |
| 2089 | pesares | 3 |
| 2090 | personal | 3 |
| 2091 | personaje | 3 |
| 2092 | peresçen | 3 |
| 2093 | perdy | 3 |
| 2094 | perdizes | 3 |
| 2095 | pequeno | 3 |
| 2096 | penssando | 3 |
| 2097 | pensó | 3 |
| 2098 | pensat | 3 |
| 2099 | pensar | 3 |
| 2100 | péndolas | 3 |
| 2101 | pelos | 3 |
| 2102 | pediere | 3 |
| 2103 | pastor | 3 |
| 2104 | passar | 3 |
| 2105 | pasó | 3 |
| 2106 | pasar | 3 |
| 2107 | pasados | 3 |
| 2108 | pasa | 3 |
| 2109 | parlero | 3 |
| 2110 | pariste | 3 |
| 2111 | parienta | 3 |
| 2112 | paresçía | 3 |
| 2113 | parece | 3 |
| 2114 | pánfilo | 3 |
| 2115 | panes | 3 |
| 2116 | pandero | 3 |
| 2117 | pamphilus | 3 |
| 2118 | padres | 3 |
| 2119 | oye | 3 |
| 2120 | oydos | 3 |
| 2121 | oyas | 3 |
| 2122 | oviese | 3 |
| 2123 | otrossy | 3 |
| 2124 | otorgar | 3 |
| 2125 | otorgan | 3 |
| 2126 | orgulloso | 3 |
| 2127 | ordenados | 3 |
| 2128 | oraçiones | 3 |
| 2129 | omildat | 3 |
| 2130 | ofresco | 3 |
| 2131 | obispos | 3 |
| 2132 | nyn | 3 |
| 2133 | nuez | 3 |
| 2134 | nueve | 3 |
| 2135 | nueses | 3 |
| 2136 | notas | 3 |
| 2137 | nonbrada | 3 |
| 2138 | nonbles | 3 |
| 2139 | nido | 3 |
| 2140 | nesçios | 3 |
| 2141 | negras | 3 |
| 2142 | naturaleza | 3 |
| 2143 | nasçer | 3 |
| 2144 | my | 3 |
| 2145 | muro | 3 |
| 2146 | mures | 3 |
| 2147 | mula | 3 |
| 2148 | mujeres | 3 |
| 2149 | mujer | 3 |
| 2150 | mueve | 3 |
| 2151 | mueva | 3 |
| 2152 | muestra | 3 |
| 2153 | mueran | 3 |
| 2154 | mudar | 3 |
| 2155 | movió | 3 |
| 2156 | mostraré | 3 |
| 2157 | morría | 3 |
| 2158 | moradas | 3 |
| 2159 | monferrado | 3 |
| 2160 | molino | 3 |
| 2161 | modo | 3 |
| 2162 | moças | 3 |
| 2163 | mismos | 3 |
| 2164 | misas | 3 |
| 2165 | mintrosa | 3 |
| 2166 | miércoles | 3 |
| 2167 | miento | 3 |
| 2168 | mienbros | 3 |
| 2169 | meter | 3 |
| 2170 | mesurado | 3 |
| 2171 | mesurada | 3 |
| 2172 | messa | 3 |
| 2173 | mesma | 3 |
| 2174 | merienda | 3 |
| 2175 | merchandía | 3 |
| 2176 | meos | 3 |
| 2177 | mensajero | 3 |
| 2178 | mensajería | 3 |
| 2179 | menester | 3 |
| 2180 | mençión | 3 |
| 2181 | meaja | 3 |
| 2182 | mea | 3 |
| 2183 | materiales | 3 |
| 2184 | mastines | 3 |
| 2185 | martes | 3 |
| 2186 | março | 3 |
| 2187 | maravillosa | 3 |
| 2188 | mañas | 3 |
| 2189 | manuel | 3 |
| 2190 | mantenençia | 3 |
| 2191 | mandava | 3 |
| 2192 | mandan | 3 |
| 2193 | mançebos | 3 |
| 2194 | mançana | 3 |
| 2195 | maldad | 3 |
| 2196 | malandança | 3 |
| 2197 | mager | 3 |
| 2198 | maestros | 3 |
| 2199 | maestra | 3 |
| 2200 | madalena | 3 |
| 2201 | maça | 3 |
| 2202 | lygera | 3 |
| 2203 | lyévate | 3 |
| 2204 | lyeva | 3 |
| 2205 | lydian | 3 |
| 2206 | luengos | 3 |
| 2207 | luengas | 3 |
| 2208 | logrero | 3 |
| 2209 | logar | 3 |
| 2210 | lodo | 3 |
| 2211 | loçanos | 3 |
| 2212 | loçanía | 3 |
| 2213 | loado | 3 |
| 2214 | llegado | 3 |
| 2215 | llano | 3 |
| 2216 | llamado | 3 |
| 2217 | lírico | 3 |
| 2218 | linaje | 3 |
| 2219 | liçión | 3 |
| 2220 | libreste | 3 |
| 2221 | libertino | 3 |
| 2222 | leyó | 3 |
| 2223 | leyda | 3 |
| 2224 | levó | 3 |
| 2225 | levava | 3 |
| 2226 | levase | 3 |
| 2227 | letuarios | 3 |
| 2228 | letras | 3 |
| 2229 | letrados | 3 |
| 2230 | letrado | 3 |
| 2231 | lea | 3 |
| 2232 | lança | 3 |
| 2233 | lana | 3 |
| 2234 | laguna | 3 |
| 2235 | lago | 3 |
| 2236 | labros | 3 |
| 2237 | labrada | 3 |
| 2238 | juzgar | 3 |
| 2239 | juglares | 3 |
| 2240 | juglar | 3 |
| 2241 | jugando | 3 |
| 2242 | jueves | 3 |
| 2243 | judgar | 3 |
| 2244 | judas | 3 |
| 2245 | jornada | 3 |
| 2246 | intençión | 3 |
| 2247 | instrumentos | 3 |
| 2248 | henares | 3 |
| 2249 | hemistiquio | 3 |
| 2250 | hechos | 3 |
| 2251 | hecho | 3 |
| 2252 | hán | 3 |
| 2253 | hace | 3 |
| 2254 | gulpeja | 3 |
| 2255 | guitarra | 3 |
| 2256 | guardo | 3 |
| 2257 | guardat | 3 |
| 2258 | guardas | 3 |
| 2259 | guardares | 3 |
| 2260 | gualardón | 3 |
| 2261 | grulla | 3 |
| 2262 | greçia | 3 |
| 2263 | graves | 3 |
| 2264 | graçiosa | 3 |
| 2265 | grabiel | 3 |
| 2266 | gozo | 3 |
| 2267 | gosos | 3 |
| 2268 | glosa | 3 |
| 2269 | general | 3 |
| 2270 | garçía | 3 |
| 2271 | garça | 3 |
| 2272 | garavatos | 3 |
| 2273 | garavato | 3 |
| 2274 | ganado | 3 |
| 2275 | gallynas | 3 |
| 2276 | gallyna | 3 |
| 2277 | gallinas | 3 |
| 2278 | fynqué | 3 |
| 2279 | fynque | 3 |
| 2280 | fyncó | 3 |
| 2281 | fuya | 3 |
| 2282 | fulana | 3 |
| 2283 | fuemos | 3 |
| 2284 | fruta | 3 |
| 2285 | frontera | 3 |
| 2286 | fresco | 3 |
| 2287 | francia | 3 |
| 2288 | forniçio | 3 |
| 2289 | fonda | 3 |
| 2290 | flores | 3 |
| 2291 | flacas | 3 |
| 2292 | fízole | 3 |
| 2293 | físose | 3 |
| 2294 | fino | 3 |
| 2295 | final | 3 |
| 2296 | fijas | 3 |
| 2297 | fierro | 3 |
| 2298 | fiere | 3 |
| 2299 | ffazes | 3 |
| 2300 | ffasta | 3 |
| 2301 | ffablar | 3 |
| 2302 | ferir | 3 |
| 2303 | feriendo | 3 |
| 2304 | ferida | 3 |
| 2305 | fegura | 3 |
| 2306 | fechura | 3 |
| 2307 | fartar | 3 |
| 2308 | faredes | 3 |
| 2309 | fanbre | 3 |
| 2310 | falsos | 3 |
| 2311 | falle | 3 |
| 2312 | fallava | 3 |
| 2313 | falagos | 3 |
| 2314 | falagera | 3 |
| 2315 | falagava | 3 |
| 2316 | falagar | 3 |
| 2317 | façia | 3 |
| 2318 | fábulas | 3 |
| 2319 | fabló | 3 |
| 2320 | fables | 3 |
| 2321 | estrumentes | 3 |
| 2322 | estrofas | 3 |
| 2323 | estrena | 3 |
| 2324 | estrella | 3 |
| 2325 | estraños | 3 |
| 2326 | estraño | 3 |
| 2327 | éstos | 3 |
| 2328 | estorva | 3 |
| 2329 | estó | 3 |
| 2330 | estilo | 3 |
| 2331 | esquivo | 3 |
| 2332 | espuelas | 3 |
| 2333 | escusas | 3 |
| 2334 | escuderos | 3 |
| 2335 | escriptas | 3 |
| 2336 | escribir | 3 |
| 2337 | escrevir | 3 |
| 2338 | escondida | 3 |
| 2339 | escogida | 3 |
| 2340 | escoge | 3 |
| 2341 | escarnido | 3 |
| 2342 | escalera | 3 |
| 2343 | errado | 3 |
| 2344 | entrava | 3 |
| 2345 | entrado | 3 |
| 2346 | entendida | 3 |
| 2347 | entendederas | 3 |
| 2348 | entendedera | 3 |
| 2349 | enssienplo | 3 |
| 2350 | enperador | 3 |
| 2351 | enmendar | 3 |
| 2352 | enim | 3 |
| 2353 | enigma | 3 |
| 2354 | engañoso | 3 |
| 2355 | engañador | 3 |
| 2356 | engañada | 3 |
| 2357 | encubre | 3 |
| 2358 | encubiertas | 3 |
| 2359 | ençiende | 3 |
| 2360 | enbya | 3 |
| 2361 | enamorada | 3 |
| 2362 | emienda | 3 |
| 2363 | embargo | 3 |
| 2364 | eclesiástica | 3 |
| 2365 | echóle | 3 |
| 2366 | echó | 3 |
| 2367 | ea | 3 |
| 2368 | dyxo | 3 |
| 2369 | dyos | 3 |
| 2370 | dyó | 3 |
| 2371 | duz | 3 |
| 2372 | duros | 3 |
| 2373 | dotores | 3 |
| 2374 | dormir | 3 |
| 2375 | doñeos | 3 |
| 2376 | doñear | 3 |
| 2377 | doñeador | 3 |
| 2378 | donas | 3 |
| 2379 | dominum | 3 |
| 2380 | domine | 3 |
| 2381 | doma | 3 |
| 2382 | díxol | 3 |
| 2383 | dixol | 3 |
| 2384 | dixiéronle | 3 |
| 2385 | dix | 3 |
| 2386 | ditados | 3 |
| 2387 | dises | 3 |
| 2388 | diser | 3 |
| 2389 | díselo | 3 |
| 2390 | diríe | 3 |
| 2391 | diría | 3 |
| 2392 | dirévos | 3 |
| 2393 | direvos | 3 |
| 2394 | dime | 3 |
| 2395 | dijo | 3 |
| 2396 | diesen | 3 |
| 2397 | diéronle | 3 |
| 2398 | dieres | 3 |
| 2399 | diéredes | 3 |
| 2400 | diere | 3 |
| 2401 | diente | 3 |
| 2402 | dexóme | 3 |
| 2403 | dexieron | 3 |
| 2404 | dexat | 3 |
| 2405 | dexas | 3 |
| 2406 | devoçión | 3 |
| 2407 | devezes | 3 |
| 2408 | deus | 3 |
| 2409 | déstos | 3 |
| 2410 | destos | 3 |
| 2411 | desputar | 3 |
| 2412 | desputaçión | 3 |
| 2413 | desirte | 3 |
| 2414 | desires | 3 |
| 2415 | desid | 3 |
| 2416 | desechar | 3 |
| 2417 | desaguisado | 3 |
| 2418 | desa | 3 |
| 2419 | derrama | 3 |
| 2420 | departe | 3 |
| 2421 | demandó | 3 |
| 2422 | déles | 3 |
| 2423 | delantera | 3 |
| 2424 | defiende | 3 |
| 2425 | defender | 3 |
| 2426 | decretales | 3 |
| 2427 | debió | 3 |
| 2428 | debemos | 3 |
| 2429 | debdo | 3 |
| 2430 | davan | 3 |
| 2431 | dat | 3 |
| 2432 | darl | 3 |
| 2433 | dañoso | 3 |
| 2434 | dale | 3 |
| 2435 | dabo | 3 |
| 2436 | cuydós | 3 |
| 2437 | cuydé | 3 |
| 2438 | cuydar | 3 |
| 2439 | curso | 3 |
| 2440 | curas | 3 |
| 2441 | cunplir | 3 |
| 2442 | cunplen | 3 |
| 2443 | cuerdos | 3 |
| 2444 | cubas | 3 |
| 2445 | cuatro | 3 |
| 2446 | cuaresma | 3 |
| 2447 | cualidades | 3 |
| 2448 | crían | 3 |
| 2449 | creades | 3 |
| 2450 | cossas | 3 |
| 2451 | corriendo | 3 |
| 2452 | correr | 3 |
| 2453 | corona | 3 |
| 2454 | cornejo | 3 |
| 2455 | corder | 3 |
| 2456 | contreçión | 3 |
| 2457 | contr | 3 |
| 2458 | contender | 3 |
| 2459 | constituçión | 3 |
| 2460 | consseja | 3 |
| 2461 | consiguiente | 3 |
| 2462 | consienta | 3 |
| 2463 | conpaño | 3 |
| 2464 | conosçía | 3 |
| 2465 | confonda | 3 |
| 2466 | confesión | 3 |
| 2467 | conejos | 3 |
| 2468 | conbid | 3 |
| 2469 | comido | 3 |
| 2470 | cómico | 3 |
| 2471 | començé | 3 |
| 2472 | comamos | 3 |
| 2473 | colores | 3 |
| 2474 | cojo | 3 |
| 2475 | cobre | 3 |
| 2476 | cobrar | 3 |
| 2477 | cobertera | 3 |
| 2478 | cobdiçian | 3 |
| 2479 | clavo | 3 |
| 2480 | clases | 3 |
| 2481 | claro | 3 |
| 2482 | claridat | 3 |
| 2483 | cita | 3 |
| 2484 | cima | 3 |
| 2485 | çiertos | 3 |
| 2486 | çient | 3 |
| 2487 | çibdad | 3 |
| 2488 | choça | 3 |
| 2489 | chançonetas | 3 |
| 2490 | çevo | 3 |
| 2491 | cervantes | 3 |
| 2492 | çercado | 3 |
| 2493 | çenteno | 3 |
| 2494 | çeniza | 3 |
| 2495 | çeçina | 3 |
| 2496 | cay | 3 |
| 2497 | causas | 3 |
| 2498 | caudal | 3 |
| 2499 | catón | 3 |
| 2500 | católica | 3 |
| 2501 | cató | 3 |
| 2502 | cathólica | 3 |
| 2503 | catat | 3 |
| 2504 | catando | 3 |
| 2505 | castro | 3 |
| 2506 | castiga | 3 |
| 2507 | castellanos | 3 |
| 2508 | castellano | 3 |
| 2509 | casas | 3 |
| 2510 | carnero | 3 |
| 2511 | caridad | 3 |
| 2512 | capones | 3 |
| 2513 | capa | 3 |
| 2514 | cantan | 3 |
| 2515 | cantadera | 3 |
| 2516 | candela | 3 |
| 2517 | campo | 3 |
| 2518 | camisa | 3 |
| 2519 | camineros | 3 |
| 2520 | calle | 3 |
| 2521 | cal | 3 |
| 2522 | caderas | 3 |
| 2523 | cadenas | 3 |
| 2524 | cadena | 3 |
| 2525 | cadaldía | 3 |
| 2526 | caçar | 3 |
| 2527 | cabrones | 3 |
| 2528 | cabestro | 3 |
| 2529 | cabaña | 3 |
| 2530 | byenes | 3 |
| 2531 | buscas | 3 |
| 2532 | burlas | 3 |
| 2533 | buhona | 3 |
| 2534 | bugía | 3 |
| 2535 | buenandança | 3 |
| 2536 | breve | 3 |
| 2537 | brasa | 3 |
| 2538 | braços | 3 |
| 2539 | bozes | 3 |
| 2540 | boses | 3 |
| 2541 | bondat | 3 |
| 2542 | bona | 3 |
| 2543 | bolver | 3 |
| 2544 | bodigos | 3 |
| 2545 | blanda | 3 |
| 2546 | biuda | 3 |
| 2547 | bevíe | 3 |
| 2548 | bermejo | 3 |
| 2549 | bermeja | 3 |
| 2550 | bendito | 3 |
| 2551 | bendicha | 3 |
| 2552 | bendeçión | 3 |
| 2553 | baylando | 3 |
| 2554 | bavieca | 3 |
| 2555 | baratas | 3 |
| 2556 | baraja | 3 |
| 2557 | ballena | 3 |
| 2558 | baldío | 3 |
| 2559 | balde | 3 |
| 2560 | azeyte | 3 |
| 2561 | ayudado | 3 |
| 2562 | ayades | 3 |
| 2563 | avydo | 3 |
| 2564 | avino | 3 |
| 2565 | avia | 3 |
| 2566 | aventurar | 3 |
| 2567 | avemos | 3 |
| 2568 | avarizia | 3 |
| 2569 | avariçia | 3 |
| 2570 | atierra | 3 |
| 2571 | assentóse | 3 |
| 2572 | ascondido | 3 |
| 2573 | ardid | 3 |
| 2574 | arçobispos | 3 |
| 2575 | árboles | 3 |
| 2576 | arávigo | 3 |
| 2577 | apostado | 3 |
| 2578 | apoderado | 3 |
| 2579 | aparejada | 3 |
| 2580 | ansuelo | 3 |
| 2581 | angosto | 3 |
| 2582 | ande | 3 |
| 2583 | anchas | 3 |
| 2584 | anbos | 3 |
| 2585 | amatar | 3 |
| 2586 | amarillo | 3 |
| 2587 | amarga | 3 |
| 2588 | amado | 3 |
| 2589 | alva | 3 |
| 2590 | alunbrar | 3 |
| 2591 | alguien | 3 |
| 2592 | alfonso | 3 |
| 2593 | alegrías | 3 |
| 2594 | alegrar | 3 |
| 2595 | aldeano | 3 |
| 2596 | alcança | 3 |
| 2597 | alcalá | 3 |
| 2598 | alaba | 3 |
| 2599 | ajeno | 3 |
| 2600 | ajena | 3 |
| 2601 | aguisado | 3 |
| 2602 | agraz | 3 |
| 2603 | afruenta | 3 |
| 2604 | afogar | 3 |
| 2605 | afán | 3 |
| 2606 | además | 3 |
| 2607 | acusaçión | 3 |
| 2608 | acuerdo | 3 |
| 2609 | acuçioso | 3 |
| 2610 | acorre | 3 |
| 2611 | achaque | 3 |
| 2612 | acaesçió | 3 |
| 2613 | acabado | 3 |
| 2614 | acaba | 3 |
| 2615 | acá | 3 |
| 2616 | aborrida | 3 |
| 2617 | ablanda | 3 |
| 2618 | abbad | 3 |
| 2619 | abades | 3 |
| 2620 | yvan | 2 |
| 2621 | yuso | 2 |
| 2622 | yredes | 2 |
| 2623 | yrado | 2 |
| 2624 | ymágenes | 2 |
| 2625 | yjadas | 2 |
| 2626 | ygual | 2 |
| 2627 | yerva | 2 |
| 2628 | yerran | 2 |
| 2629 | yermo | 2 |
| 2630 | yegua | 2 |
| 2631 | ydvos | 2 |
| 2632 | yazía | 2 |
| 2633 | yaser | 2 |
| 2634 | yantava | 2 |
| 2635 | yantares | 2 |
| 2636 | yaga | 2 |
| 2637 | xaquima | 2 |
| 2638 | vyñas | 2 |
| 2639 | vynome | 2 |
| 2640 | vyn | 2 |
| 2641 | vyeja | 2 |
| 2642 | vya | 2 |
| 2643 | vult | 2 |
| 2644 | vuelve | 2 |
| 2645 | vosotros | 2 |
| 2646 | volo | 2 |
| 2647 | vivos | 2 |
| 2648 | vivían | 2 |
| 2649 | vivet | 2 |
| 2650 | vistos | 2 |
| 2651 | vistas | 2 |
| 2652 | vísperas | 2 |
| 2653 | visión | 2 |
| 2654 | virginidad | 2 |
| 2655 | virgillio | 2 |
| 2656 | viñas | 2 |
| 2657 | vinos | 2 |
| 2658 | villas | 2 |
| 2659 | villana | 2 |
| 2660 | viles | 2 |
| 2661 | vigas | 2 |
| 2662 | viese | 2 |
| 2663 | vies | 2 |
| 2664 | viera | 2 |
| 2665 | víctima | 2 |
| 2666 | viandas | 2 |
| 2667 | viaje | 2 |
| 2668 | veynte | 2 |
| 2669 | veyalo | 2 |
| 2670 | vey | 2 |
| 2671 | vestiglo | 2 |
| 2672 | vesinas | 2 |
| 2673 | vernía | 2 |
| 2674 | vergueña | 2 |
| 2675 | vergüença | 2 |
| 2676 | vergilio | 2 |
| 2677 | vereda | 2 |
| 2678 | verdaderamente | 2 |
| 2679 | verças | 2 |
| 2680 | venta | 2 |
| 2681 | vénme | 2 |
| 2682 | veniste | 2 |
| 2683 | veniera | 2 |
| 2684 | venie | 2 |
| 2685 | vengue | 2 |
| 2686 | vengas | 2 |
| 2687 | vendido | 2 |
| 2688 | venden | 2 |
| 2689 | vendemos | 2 |
| 2690 | vendedor | 2 |
| 2691 | vende | 2 |
| 2692 | vençido | 2 |
| 2693 | vencido | 2 |
| 2694 | vencedor | 2 |
| 2695 | vençamos | 2 |
| 2696 | ven | 2 |
| 2697 | velo | 2 |
| 2698 | velloso | 2 |
| 2699 | velado | 2 |
| 2700 | vela | 2 |
| 2701 | vegilia | 2 |
| 2702 | vegedat | 2 |
| 2703 | vega | 2 |
| 2704 | veçina | 2 |
| 2705 | veçes | 2 |
| 2706 | véase | 2 |
| 2707 | váyase | 2 |
| 2708 | vayas | 2 |
| 2709 | vayamos | 2 |
| 2710 | vate | 2 |
| 2711 | vassallo | 2 |
| 2712 | varruntan | 2 |
| 2713 | vaqueros | 2 |
| 2714 | vaquera | 2 |
| 2715 | vánse | 2 |
| 2716 | vanas | 2 |
| 2717 | valyente | 2 |
| 2718 | valme | 2 |
| 2719 | valentía | 2 |
| 2720 | valençia | 2 |
| 2721 | valdría | 2 |
| 2722 | valdíos | 2 |
| 2723 | vagaroso | 2 |
| 2724 | vado | 2 |
| 2725 | uvias | 2 |
| 2726 | urías | 2 |
| 2727 | universo | 2 |
| 2728 | ungento | 2 |
| 2729 | últimos | 2 |
| 2730 | uéspet | 2 |
| 2731 | ueso | 2 |
| 2732 | tyrat | 2 |
| 2733 | tyra | 2 |
| 2734 | tynta | 2 |
| 2735 | tyento | 2 |
| 2736 | tuyos | 2 |
| 2737 | trueno | 2 |
| 2738 | troyas | 2 |
| 2739 | troya | 2 |
| 2740 | troxo | 2 |
| 2741 | troxieron | 2 |
| 2742 | troteras | 2 |
| 2743 | trota | 2 |
| 2744 | troco | 2 |
| 2745 | trist | 2 |
| 2746 | trinidad | 2 |
| 2747 | tribulança | 2 |
| 2748 | treynta | 2 |
| 2749 | tremer | 2 |
| 2750 | trefudo | 2 |
| 2751 | trechón | 2 |
| 2752 | trayle | 2 |
| 2753 | traydo | 2 |
| 2754 | traxo | 2 |
| 2755 | trax | 2 |
| 2756 | travas | 2 |
| 2757 | travando | 2 |
| 2758 | tratado | 2 |
| 2759 | trastorne | 2 |
| 2760 | traspaso | 2 |
| 2761 | trahedes | 2 |
| 2762 | trágico | 2 |
| 2763 | tragar | 2 |
| 2764 | traen | 2 |
| 2765 | trabajan | 2 |
| 2766 | tozino | 2 |
| 2767 | tovyeres | 2 |
| 2768 | toviese | 2 |
| 2769 | toviere | 2 |
| 2770 | tortolilla | 2 |
| 2771 | torres | 2 |
| 2772 | toros | 2 |
| 2773 | tornó | 2 |
| 2774 | torno | 2 |
| 2775 | tornéme | 2 |
| 2776 | torne | 2 |
| 2777 | tordos | 2 |
| 2778 | torcaças | 2 |
| 2779 | tono | 2 |
| 2780 | tomen | 2 |
| 2781 | tomaron | 2 |
| 2782 | tomaré | 2 |
| 2783 | tómala | 2 |
| 2784 | tiras | 2 |
| 2785 | tinajas | 2 |
| 2786 | tienpos | 2 |
| 2787 | testigo | 2 |
| 2788 | testamento | 2 |
| 2789 | terné | 2 |
| 2790 | terceronas | 2 |
| 2791 | terçera | 2 |
| 2792 | terçer | 2 |
| 2793 | tente | 2 |
| 2794 | teniendo | 2 |
| 2795 | teníe | 2 |
| 2796 | tenidos | 2 |
| 2797 | tenida | 2 |
| 2798 | tenia | 2 |
| 2799 | tengas | 2 |
| 2800 | tengades | 2 |
| 2801 | tenerse | 2 |
| 2802 | tendió | 2 |
| 2803 | tenblar | 2 |
| 2804 | tén | 2 |
| 2805 | temple | 2 |
| 2806 | temo | 2 |
| 2807 | temida | 2 |
| 2808 | temeroso | 2 |
| 2809 | temer | 2 |
| 2810 | tardinero | 2 |
| 2811 | tardar | 2 |
| 2812 | tañía | 2 |
| 2813 | tañer | 2 |
| 2814 | tánto | 2 |
| 2815 | tanida | 2 |
| 2816 | tanbién | 2 |
| 2817 | tamaño | 2 |
| 2818 | talle | 2 |
| 2819 | talega | 2 |
| 2820 | tajador | 2 |
| 2821 | tahur | 2 |
| 2822 | tachas | 2 |
| 2823 | taças | 2 |
| 2824 | tablada | 2 |
| 2825 | tabla | 2 |
| 2826 | tabernas | 2 |
| 2827 | tabardo | 2 |
| 2828 | syrvo | 2 |
| 2829 | syrve | 2 |
| 2830 | synples | 2 |
| 2831 | suyas | 2 |
| 2832 | supo | 2 |
| 2833 | super | 2 |
| 2834 | sum | 2 |
| 2835 | sueras | 2 |
| 2836 | sueno | 2 |
| 2837 | suena | 2 |
| 2838 | suelto | 2 |
| 2839 | suelen | 2 |
| 2840 | sueldos | 2 |
| 2841 | sucede | 2 |
| 2842 | sube | 2 |
| 2843 | suave | 2 |
| 2844 | ssus | 2 |
| 2845 | ssierra | 2 |
| 2846 | ssienpre | 2 |
| 2847 | ssi | 2 |
| 2848 | sser | 2 |
| 2849 | sseñora | 2 |
| 2850 | ssea | 2 |
| 2851 | ssaña | 2 |
| 2852 | ssanto | 2 |
| 2853 | sperança | 2 |
| 2854 | sotileza | 2 |
| 2855 | sotiles | 2 |
| 2856 | sotar | 2 |
| 2857 | sospiro | 2 |
| 2858 | sospechas | 2 |
| 2859 | sosiego | 2 |
| 2860 | sosegado | 2 |
| 2861 | sortijas | 2 |
| 2862 | sordo | 2 |
| 2863 | sopieres | 2 |
| 2864 | soñado | 2 |
| 2865 | sonetes | 2 |
| 2866 | sonante | 2 |
| 2867 | soltar | 2 |
| 2868 | solos | 2 |
| 2869 | sobir | 2 |
| 2870 | sobió | 2 |
| 2871 | sobía | 2 |
| 2872 | sirven | 2 |
| 2873 | sirva | 2 |
| 2874 | siquiera | 2 |
| 2875 | silva | 2 |
| 2876 | sílaba | 2 |
| 2877 | siguientes | 2 |
| 2878 | sigua | 2 |
| 2879 | sierpe | 2 |
| 2880 | siento | 2 |
| 2881 | sienta | 2 |
| 2882 | sienbra | 2 |
| 2883 | siella | 2 |
| 2884 | seyle | 2 |
| 2885 | severo | 2 |
| 2886 | seteno | 2 |
| 2887 | sesos | 2 |
| 2888 | servirla | 2 |
| 2889 | servila | 2 |
| 2890 | servienta | 2 |
| 2891 | servida | 2 |
| 2892 | serlo | 2 |
| 2893 | serías | 2 |
| 2894 | serían | 2 |
| 2895 | seré | 2 |
| 2896 | serán | 2 |
| 2897 | señoras | 2 |
| 2898 | señales | 2 |
| 2899 | señalado | 2 |
| 2900 | sentyr | 2 |
| 2901 | sentir | 2 |
| 2902 | sentido | 2 |
| 2903 | senda | 2 |
| 2904 | senales | 2 |
| 2905 | semejante | 2 |
| 2906 | semanas | 2 |
| 2907 | sello | 2 |
| 2908 | segurança | 2 |
| 2909 | segurado | 2 |
| 2910 | segurada | 2 |
| 2911 | seguiendo | 2 |
| 2912 | seguido | 2 |
| 2913 | seglares | 2 |
| 2914 | seda | 2 |
| 2915 | séate | 2 |
| 2916 | sayones | 2 |
| 2917 | satirizar | 2 |
| 2918 | satírico | 2 |
| 2919 | sartenes | 2 |
| 2920 | sarna | 2 |
| 2921 | sardina | 2 |
| 2922 | santidad | 2 |
| 2923 | santas | 2 |
| 2924 | sanos | 2 |
| 2925 | sanará | 2 |
| 2926 | salvado | 2 |
| 2927 | salut | 2 |
| 2928 | saltó | 2 |
| 2929 | salta | 2 |
| 2930 | saliera | 2 |
| 2931 | saldrás | 2 |
| 2932 | saladas | 2 |
| 2933 | salada | 2 |
| 2934 | sacrifiçio | 2 |
| 2935 | sacól | 2 |
| 2936 | sacas | 2 |
| 2937 | sácalo | 2 |
| 2938 | sabyo | 2 |
| 2939 | sabya | 2 |
| 2940 | sabrosas | 2 |
| 2941 | sabor | 2 |
| 2942 | sabiendo | 2 |
| 2943 | sabemos | 2 |
| 2944 | sabed | 2 |
| 2945 | sábado | 2 |
| 2946 | ryo | 2 |
| 2947 | ruegovos | 2 |
| 2948 | ruégote | 2 |
| 2949 | rudo | 2 |
| 2950 | rruys | 2 |
| 2951 | rruega | 2 |
| 2952 | rroyn | 2 |
| 2953 | rrosado | 2 |
| 2954 | rropa | 2 |
| 2955 | rromeros | 2 |
| 2956 | rrogué | 2 |
| 2957 | rrogar | 2 |
| 2958 | rrogando | 2 |
| 2959 | rrodiella | 2 |
| 2960 | rrocío | 2 |
| 2961 | rroçín | 2 |
| 2962 | rrobar | 2 |
| 2963 | rriqueza | 2 |
| 2964 | rrimas | 2 |
| 2965 | rrimar | 2 |
| 2966 | rriendo | 2 |
| 2967 | rríe | 2 |
| 2968 | rribal | 2 |
| 2969 | rreyes | 2 |
| 2970 | rretrayas | 2 |
| 2971 | rretraheres | 2 |
| 2972 | rretoçar | 2 |
| 2973 | rresuçitado | 2 |
| 2974 | rrespuso | 2 |
| 2975 | rresponder | 2 |
| 2976 | rrespondas | 2 |
| 2977 | rresplandeçiente | 2 |
| 2978 | rreservados | 2 |
| 2979 | rresçibiera | 2 |
| 2980 | rresçiben | 2 |
| 2981 | rresçebiste | 2 |
| 2982 | rrequieres | 2 |
| 2983 | rrencura | 2 |
| 2984 | rrelusiente | 2 |
| 2985 | rreligiosos | 2 |
| 2986 | rrehierta | 2 |
| 2987 | rrehez | 2 |
| 2988 | rreheses | 2 |
| 2989 | rrefertero | 2 |
| 2990 | rred | 2 |
| 2991 | rreçio | 2 |
| 2992 | rreçelo | 2 |
| 2993 | rrecabda | 2 |
| 2994 | rramos | 2 |
| 2995 | rrama | 2 |
| 2996 | rraçión | 2 |
| 2997 | rrabé | 2 |
| 2998 | rogar | 2 |
| 2999 | rodo | 2 |
| 3000 | ricos | 2 |
| 3001 | rica | 2 |
| 3002 | rezio | 2 |
| 3003 | rezas | 2 |
| 3004 | reys | 2 |
| 3005 | respondióme | 2 |
| 3006 | resia | 2 |
| 3007 | rencura | 2 |
| 3008 | reçio | 2 |
| 3009 | reçelo | 2 |
| 3010 | reçar | 2 |
| 3011 | recabdo | 2 |
| 3012 | recabdat | 2 |
| 3013 | recabdarás | 2 |
| 3014 | rebtedes | 2 |
| 3015 | radío | 2 |
| 3016 | raçones | 2 |
| 3017 | rabí | 2 |
| 3018 | quitar | 2 |
| 3019 | quista | 2 |
| 3020 | quisiste | 2 |
| 3021 | quisiera | 2 |
| 3022 | quis | 2 |
| 3023 | quinçe | 2 |
| 3024 | quieran | 2 |
| 3025 | quiebra | 2 |
| 3026 | quicumque | 2 |
| 3027 | quiçá | 2 |
| 3028 | quexo | 2 |
| 3029 | quesiere | 2 |
| 3030 | querellas | 2 |
| 3031 | querellando | 2 |
| 3032 | queramos | 2 |
| 3033 | quequier | 2 |
| 3034 | quantía | 2 |
| 3035 | quand | 2 |
| 3036 | qua | 2 |
| 3037 | pytas | 2 |
| 3038 | pyntados | 2 |
| 3039 | pyntado | 2 |
| 3040 | pyntadas | 2 |
| 3041 | pynta | 2 |
| 3042 | pyerde | 2 |
| 3043 | pyden | 2 |
| 3044 | pyco | 2 |
| 3045 | pycaça | 2 |
| 3046 | puyol | 2 |
| 3047 | puse | 2 |
| 3048 | puro | 2 |
| 3049 | puntadas | 2 |
| 3050 | puestos | 2 |
| 3051 | puestas | 2 |
| 3052 | puesta | 2 |
| 3053 | puercos | 2 |
| 3054 | puente | 2 |
| 3055 | puédelos | 2 |
| 3056 | puedas | 2 |
| 3057 | pueblas | 2 |
| 3058 | pudieron | 2 |
| 3059 | público | 2 |
| 3060 | pública | 2 |
| 3061 | prueba | 2 |
| 3062 | provó | 2 |
| 3063 | provechoso | 2 |
| 3064 | provaron | 2 |
| 3065 | provado | 2 |
| 3066 | propuso | 2 |
| 3067 | propio | 2 |
| 3068 | prometistes | 2 |
| 3069 | prometemos | 2 |
| 3070 | proçesión | 2 |
| 3071 | procesión | 2 |
| 3072 | probable | 2 |
| 3073 | priores | 2 |
| 3074 | prinçipales | 2 |
| 3075 | principales | 2 |
| 3076 | primo | 2 |
| 3077 | primitivos | 2 |
| 3078 | primeramente | 2 |
| 3079 | presiones | 2 |
| 3080 | presentaron | 2 |
| 3081 | presas | 2 |
| 3082 | premia | 2 |
| 3083 | preguntaron | 2 |
| 3084 | preguntan | 2 |
| 3085 | preçiosa | 2 |
| 3086 | preçiados | 2 |
| 3087 | preçiada | 2 |
| 3088 | prancha | 2 |
| 3089 | postigo | 2 |
| 3090 | pospone | 2 |
| 3091 | posadas | 2 |
| 3092 | posa | 2 |
| 3093 | portiello | 2 |
| 3094 | porné | 2 |
| 3095 | porfiaron | 2 |
| 3096 | porfiado | 2 |
| 3097 | porfia | 2 |
| 3098 | poquillejo | 2 |
| 3099 | pontifical | 2 |
| 3100 | pones | 2 |
| 3101 | ponert | 2 |
| 3102 | poemas | 2 |
| 3103 | poema | 2 |
| 3104 | podrida | 2 |
| 3105 | podrás | 2 |
| 3106 | podrán | 2 |
| 3107 | podies | 2 |
| 3108 | podían | 2 |
| 3109 | podert | 2 |
| 3110 | poderosos | 2 |
| 3111 | poço | 2 |
| 3112 | poc | 2 |
| 3113 | pobreza | 2 |
| 3114 | pleyto | 2 |
| 3115 | pleytesía | 2 |
| 3116 | plazeres | 2 |
| 3117 | plaseres | 2 |
| 3118 | plasenteras | 2 |
| 3119 | planeta | 2 |
| 3120 | plaço | 2 |
| 3121 | plaçentero | 2 |
| 3122 | pisa | 2 |
| 3123 | piñones | 2 |
| 3124 | piñas | 2 |
| 3125 | pintó | 2 |
| 3126 | pinta | 2 |
| 3127 | pino | 2 |
| 3128 | piérdese | 2 |
| 3129 | pierdas | 2 |
| 3130 | pierdan | 2 |
| 3131 | pienso | 2 |
| 3132 | piel | 2 |
| 3133 | piedras | 2 |
| 3134 | pides | 2 |
| 3135 | pid | 2 |
| 3136 | picaña | 2 |
| 3137 | piadoso | 2 |
| 3138 | pez | 2 |
| 3139 | petafio | 2 |
| 3140 | pesos | 2 |
| 3141 | pesó | 2 |
| 3142 | peso | 2 |
| 3143 | pescados | 2 |
| 3144 | pescador | 2 |
| 3145 | pésales | 2 |
| 3146 | pesada | 2 |
| 3147 | perros | 2 |
| 3148 | periglo | 2 |
| 3149 | peresosso | 2 |
| 3150 | peresçe | 2 |
| 3151 | perenal | 2 |
| 3152 | pereçoso | 2 |
| 3153 | pereçe | 2 |
| 3154 | perdones | 2 |
| 3155 | perdone | 2 |
| 3156 | perdonado | 2 |
| 3157 | perdimiento | 2 |
| 3158 | perdiese | 2 |
| 3159 | perdiçes | 2 |
| 3160 | perdet | 2 |
| 3161 | perdería | 2 |
| 3162 | peral | 2 |
| 3163 | pera | 2 |
| 3164 | pequeños | 2 |
| 3165 | pequeñas | 2 |
| 3166 | pequena | 2 |
| 3167 | pepita | 2 |
| 3168 | pepión | 2 |
| 3169 | peoría | 2 |
| 3170 | peores | 2 |
| 3171 | peón | 2 |
| 3172 | penssé | 2 |
| 3173 | penssaré | 2 |
| 3174 | pensavan | 2 |
| 3175 | penitencia | 2 |
| 3176 | penaredes | 2 |
| 3177 | penar | 2 |
| 3178 | pellejo | 2 |
| 3179 | peligrosas | 2 |
| 3180 | peligrosa | 2 |
| 3181 | pelear | 2 |
| 3182 | peleador | 2 |
| 3183 | pedricar | 2 |
| 3184 | pedir | 2 |
| 3185 | pedides | 2 |
| 3186 | pedaço | 2 |
| 3187 | pecó | 2 |
| 3188 | pechar | 2 |
| 3189 | pecha | 2 |
| 3190 | payas | 2 |
| 3191 | pavones | 2 |
| 3192 | pastrañas | 2 |
| 3193 | pasqua | 2 |
| 3194 | pasé | 2 |
| 3195 | pasava | 2 |
| 3196 | pasaron | 2 |
| 3197 | pasarero | 2 |
| 3198 | pasarás | 2 |
| 3199 | pasando | 2 |
| 3200 | pasaje | 2 |
| 3201 | pas | 2 |
| 3202 | parvas | 2 |
| 3203 | party | 2 |
| 3204 | parto | 2 |
| 3205 | partirse | 2 |
| 3206 | partir | 2 |
| 3207 | partíme | 2 |
| 3208 | partida | 2 |
| 3209 | paró | 2 |
| 3210 | parlera | 2 |
| 3211 | parir | 2 |
| 3212 | parió | 2 |
| 3213 | paresçer | 2 |
| 3214 | paresçen | 2 |
| 3215 | pares | 2 |
| 3216 | parejo | 2 |
| 3217 | pared | 2 |
| 3218 | paras | 2 |
| 3219 | paranças | 2 |
| 3220 | paran | 2 |
| 3221 | papel | 2 |
| 3222 | papagayo | 2 |
| 3223 | panderos | 2 |
| 3224 | palmas | 2 |
| 3225 | palma | 2 |
| 3226 | palabrillas | 2 |
| 3227 | paja | 2 |
| 3228 | pago | 2 |
| 3229 | página | 2 |
| 3230 | págase | 2 |
| 3231 | págam | 2 |
| 3232 | pagadas | 2 |
| 3233 | paçiençia | 2 |
| 3234 | pablo | 2 |
| 3235 | oyredes | 2 |
| 3236 | oyeron | 2 |
| 3237 | oyeres | 2 |
| 3238 | oydme | 2 |
| 3239 | oyd | 2 |
| 3240 | óvose | 2 |
| 3241 | oviesen | 2 |
| 3242 | ovies | 2 |
| 3243 | oviera | 2 |
| 3244 | ov | 2 |
| 3245 | otramente | 2 |
| 3246 | otorgóle | 2 |
| 3247 | otorgo | 2 |
| 3248 | oteros | 2 |
| 3249 | otero | 2 |
| 3250 | oteo | 2 |
| 3251 | oteas | 2 |
| 3252 | osado | 2 |
| 3253 | osadas | 2 |
| 3254 | osa | 2 |
| 3255 | ortolano | 2 |
| 3256 | ortelano | 2 |
| 3257 | origine | 2 |
| 3258 | orientales | 2 |
| 3259 | oriental | 2 |
| 3260 | orgullya | 2 |
| 3261 | orgullo | 2 |
| 3262 | orejudo | 2 |
| 3263 | ordinario | 2 |
| 3264 | ordinaria | 2 |
| 3265 | orça | 2 |
| 3266 | oración | 2 |
| 3267 | orabuena | 2 |
| 3268 | opiniones | 2 |
| 3269 | opera | 2 |
| 3270 | onrrar | 2 |
| 3271 | onrrados | 2 |
| 3272 | onrrado | 2 |
| 3273 | onda | 2 |
| 3274 | omnium | 2 |
| 3275 | olvidares | 2 |
| 3276 | olor | 2 |
| 3277 | ollas | 2 |
| 3278 | oler | 2 |
| 3279 | ofrenda | 2 |
| 3280 | ofrecerse | 2 |
| 3281 | ofiçios | 2 |
| 3282 | odreçillo | 2 |
| 3283 | oculos | 2 |
| 3284 | nuevos | 2 |
| 3285 | nuevamente | 2 |
| 3286 | novios | 2 |
| 3287 | novillo | 2 |
| 3288 | novela | 2 |
| 3289 | noticias | 2 |
| 3290 | nostri | 2 |
| 3291 | noster | 2 |
| 3292 | nosotros | 2 |
| 3293 | noria | 2 |
| 3294 | nonbrado | 2 |
| 3295 | nonble | 2 |
| 3296 | noches | 2 |
| 3297 | nocharniegos | 2 |
| 3298 | noblezas | 2 |
| 3299 | noblesas | 2 |
| 3300 | noblesa | 2 |
| 3301 | niño | 2 |
| 3302 | ninguna | 2 |
| 3303 | ningún | 2 |
| 3304 | nietos | 2 |
| 3305 | nief | 2 |
| 3306 | nemiga | 2 |
| 3307 | negros | 2 |
| 3308 | neçesidat | 2 |
| 3309 | navancos | 2 |
| 3310 | natas | 2 |
| 3311 | nasón | 2 |
| 3312 | nasçieron | 2 |
| 3313 | nasçido | 2 |
| 3314 | nasçida | 2 |
| 3315 | nasca | 2 |
| 3316 | narizes | 2 |
| 3317 | nadie | 2 |
| 3318 | nadar | 2 |
| 3319 | nació | 2 |
| 3320 | naçe | 2 |
| 3321 | musa | 2 |
| 3322 | muradal | 2 |
| 3323 | mundano | 2 |
| 3324 | muestran | 2 |
| 3325 | muertes | 2 |
| 3326 | muertas | 2 |
| 3327 | mots | 2 |
| 3328 | mostrase | 2 |
| 3329 | mostrado | 2 |
| 3330 | morredes | 2 |
| 3331 | morieron | 2 |
| 3332 | moreno | 2 |
| 3333 | monje | 2 |
| 3334 | mongas | 2 |
| 3335 | moneda | 2 |
| 3336 | mollera | 2 |
| 3337 | moçuelo | 2 |
| 3338 | misericordia | 2 |
| 3339 | mirra | 2 |
| 3340 | mintrosos | 2 |
| 3341 | mil | 2 |
| 3342 | miembros | 2 |
| 3343 | miedos | 2 |
| 3344 | miaja | 2 |
| 3345 | mexía | 2 |
| 3346 | metrificar | 2 |
| 3347 | meto | 2 |
| 3348 | mete | 2 |
| 3349 | mesmos | 2 |
| 3350 | mesiellas | 2 |
| 3351 | meses | 2 |
| 3352 | mesajera | 2 |
| 3353 | meryenda | 2 |
| 3354 | merino | 2 |
| 3355 | meresçimiento | 2 |
| 3356 | meresçíen | 2 |
| 3357 | meresçían | 2 |
| 3358 | meresçes | 2 |
| 3359 | meresçer | 2 |
| 3360 | meresçen | 2 |
| 3361 | mercadero | 2 |
| 3362 | mentyra | 2 |
| 3363 | mensaje | 2 |
| 3364 | menguará | 2 |
| 3365 | menguados | 2 |
| 3366 | menguado | 2 |
| 3367 | menguada | 2 |
| 3368 | menga | 2 |
| 3369 | meis | 2 |
| 3370 | medroso | 2 |
| 3371 | medioeval | 2 |
| 3372 | medelín | 2 |
| 3373 | meajas | 2 |
| 3374 | mates | 2 |
| 3375 | matava | 2 |
| 3376 | mátanse | 2 |
| 3377 | matando | 2 |
| 3378 | matan | 2 |
| 3379 | maste | 2 |
| 3380 | masillero | 2 |
| 3381 | marina | 2 |
| 3382 | maridos | 2 |
| 3383 | marcos | 2 |
| 3384 | marco | 2 |
| 3385 | mansyllas | 2 |
| 3386 | manssa | 2 |
| 3387 | manso | 2 |
| 3388 | mansa | 2 |
| 3389 | manifiesto | 2 |
| 3390 | manga | 2 |
| 3391 | mandamientos | 2 |
| 3392 | mançebya | 2 |
| 3393 | mançanas | 2 |
| 3394 | maltrecho | 2 |
| 3395 | malsabyda | 2 |
| 3396 | malquerençia | 2 |
| 3397 | malfetría | 2 |
| 3398 | malapresas | 2 |
| 3399 | malandante | 2 |
| 3400 | maguera | 2 |
| 3401 | magra | 2 |
| 3402 | magestat | 2 |
| 3403 | magera | 2 |
| 3404 | madrina | 2 |
| 3405 | madona | 2 |
| 3406 | madero | 2 |
| 3407 | madera | 2 |
| 3408 | maços | 2 |
| 3409 | maço | 2 |
| 3410 | maçada | 2 |
| 3411 | lyviano | 2 |
| 3412 | lysa | 2 |
| 3413 | lynage | 2 |
| 3414 | lyebre | 2 |
| 3415 | lybro | 2 |
| 3416 | lus | 2 |
| 3417 | lunbre | 2 |
| 3418 | luengo | 2 |
| 3419 | lot | 2 |
| 3420 | loriga | 2 |
| 3421 | logares | 2 |
| 3422 | locuras | 2 |
| 3423 | loçoya | 2 |
| 3424 | loba | 2 |
| 3425 | loa | 2 |
| 3426 | lloró | 2 |
| 3427 | llora | 2 |
| 3428 | llevó | 2 |
| 3429 | llevar | 2 |
| 3430 | llevan | 2 |
| 3431 | llevado | 2 |
| 3432 | llenos | 2 |
| 3433 | llenero | 2 |
| 3434 | llegues | 2 |
| 3435 | llegava | 2 |
| 3436 | llegar | 2 |
| 3437 | llegados | 2 |
| 3438 | llegadas | 2 |
| 3439 | llegada | 2 |
| 3440 | llana | 2 |
| 3441 | llamar | 2 |
| 3442 | llamaban | 2 |
| 3443 | llagado | 2 |
| 3444 | lisión | 2 |
| 3445 | linpio | 2 |
| 3446 | lino | 2 |
| 3447 | ligeros | 2 |
| 3448 | liévastelo | 2 |
| 3449 | lienzo | 2 |
| 3450 | lidiar | 2 |
| 3451 | librete | 2 |
| 3452 | libre | 2 |
| 3453 | librar | 2 |
| 3454 | leyendo | 2 |
| 3455 | leydas | 2 |
| 3456 | lexos | 2 |
| 3457 | levóme | 2 |
| 3458 | levólos | 2 |
| 3459 | levóla | 2 |
| 3460 | levantan | 2 |
| 3461 | levantado | 2 |
| 3462 | letuario | 2 |
| 3463 | lenguaje | 2 |
| 3464 | leídos | 2 |
| 3465 | leer | 2 |
| 3466 | leen | 2 |
| 3467 | ledo | 2 |
| 3468 | ledanía | 2 |
| 3469 | lector | 2 |
| 3470 | lechos | 2 |
| 3471 | leche | 2 |
| 3472 | lealtat | 2 |
| 3473 | lealtad | 2 |
| 3474 | leales | 2 |
| 3475 | lazos | 2 |
| 3476 | lazerio | 2 |
| 3477 | lasrados | 2 |
| 3478 | laso | 2 |
| 3479 | lasa | 2 |
| 3480 | largos | 2 |
| 3481 | lardo | 2 |
| 3482 | lançó | 2 |
| 3483 | lagar | 2 |
| 3484 | ladrar | 2 |
| 3485 | laços | 2 |
| 3486 | laço | 2 |
| 3487 | labrador | 2 |
| 3488 | juzga | 2 |
| 3489 | juventud | 2 |
| 3490 | jusga | 2 |
| 3491 | juro | 2 |
| 3492 | juran | 2 |
| 3493 | jura | 2 |
| 3494 | juntado | 2 |
| 3495 | juntadas | 2 |
| 3496 | juglaria | 2 |
| 3497 | jugaremos | 2 |
| 3498 | juega | 2 |
| 3499 | judiós | 2 |
| 3500 | judío | 2 |
| 3501 | judgaron | 2 |
| 3502 | judgando | 2 |
| 3503 | jograría | 2 |
| 3504 | joglares | 2 |
| 3505 | jodíos | 2 |
| 3506 | job | 2 |
| 3507 | jhesúxristo | 2 |
| 3508 | jhesú | 2 |
| 3509 | jhesu | 2 |
| 3510 | jacob | 2 |
| 3511 | ironía | 2 |
| 3512 | iré | 2 |
| 3513 | ira | 2 |
| 3514 | invierno | 2 |
| 3515 | introducción | 2 |
| 3516 | intento | 2 |
| 3517 | intellectus | 2 |
| 3518 | instruam | 2 |
| 3519 | ingenios | 2 |
| 3520 | iii | 2 |
| 3521 | ii | 2 |
| 3522 | ihesuxristo | 2 |
| 3523 | idea | 2 |
| 3524 | hunda | 2 |
| 3525 | humanidad | 2 |
| 3526 | humana | 2 |
| 3527 | huesos | 2 |
| 3528 | huérfana | 2 |
| 3529 | huerco | 2 |
| 3530 | hominis | 2 |
| 3531 | historia | 2 |
| 3532 | hevos | 2 |
| 3533 | hermana | 2 |
| 3534 | hemanuel | 2 |
| 3535 | heda | 2 |
| 3536 | haya | 2 |
| 3537 | hava | 2 |
| 3538 | hato | 2 |
| 3539 | has | 2 |
| 3540 | harta | 2 |
| 3541 | harnero | 2 |
| 3542 | halo | 2 |
| 3543 | halla | 2 |
| 3544 | hacía | 2 |
| 3545 | hacer | 2 |
| 3546 | hac | 2 |
| 3547 | habla | 2 |
| 3548 | había | 2 |
| 3549 | guisas | 2 |
| 3550 | guisado | 2 |
| 3551 | guíe | 2 |
| 3552 | guiar | 2 |
| 3553 | guiador | 2 |
| 3554 | guardó | 2 |
| 3555 | guárdevos | 2 |
| 3556 | guardes | 2 |
| 3557 | guardé | 2 |
| 3558 | guardase | 2 |
| 3559 | guardarvos | 2 |
| 3560 | guardará | 2 |
| 3561 | guárdame | 2 |
| 3562 | guárdalo | 2 |
| 3563 | guadalajara | 2 |
| 3564 | gritador | 2 |
| 3565 | grey | 2 |
| 3566 | gradieris | 2 |
| 3567 | gracias | 2 |
| 3568 | gracia | 2 |
| 3569 | gotera | 2 |
| 3570 | gota | 2 |
| 3571 | gostar | 2 |
| 3572 | goso | 2 |
| 3573 | golpes | 2 |
| 3574 | golpeja | 2 |
| 3575 | golossyna | 2 |
| 3576 | golosinas | 2 |
| 3577 | golhin | 2 |
| 3578 | golfines | 2 |
| 3579 | glosó | 2 |
| 3580 | gigante | 2 |
| 3581 | gentil | 2 |
| 3582 | gela | 2 |
| 3583 | gatos | 2 |
| 3584 | gatas | 2 |
| 3585 | garrida | 2 |
| 3586 | garnacho | 2 |
| 3587 | garçones | 2 |
| 3588 | ganaron | 2 |
| 3589 | gamos | 2 |
| 3590 | gaha | 2 |
| 3591 | gadea | 2 |
| 3592 | fyna | 2 |
| 3593 | fuyó | 2 |
| 3594 | fuyendo | 2 |
| 3595 | fuyen | 2 |
| 3596 | fuyan | 2 |
| 3597 | fuxieron | 2 |
| 3598 | fuste | 2 |
| 3599 | furtos | 2 |
| 3600 | furtas | 2 |
| 3601 | fundamento | 2 |
| 3602 | fueros | 2 |
| 3603 | fuéles | 2 |
| 3604 | fue | 2 |
| 3605 | frutas | 2 |
| 3606 | fría | 2 |
| 3607 | franqueza | 2 |
| 3608 | frandes | 2 |
| 3609 | françisco | 2 |
| 3610 | fraco | 2 |
| 3611 | foyas | 2 |
| 3612 | forno | 2 |
| 3613 | formó | 2 |
| 3614 | formada | 2 |
| 3615 | forçó | 2 |
| 3616 | forçar | 2 |
| 3617 | fondos | 2 |
| 3618 | folía | 2 |
| 3619 | folgar | 2 |
| 3620 | flaqueza | 2 |
| 3621 | flaqueça | 2 |
| 3622 | fízol | 2 |
| 3623 | fita | 2 |
| 3624 | físico | 2 |
| 3625 | firmabo | 2 |
| 3626 | finca | 2 |
| 3627 | fin | 2 |
| 3628 | filósofo | 2 |
| 3629 | fijuelos | 2 |
| 3630 | figuras | 2 |
| 3631 | fieren | 2 |
| 3632 | fiança | 2 |
| 3633 | fía | 2 |
| 3634 | ffuese | 2 |
| 3635 | ffuego | 2 |
| 3636 | ffize | 2 |
| 3637 | ffija | 2 |
| 3638 | ffeciste | 2 |
| 3639 | ffazíe | 2 |
| 3640 | ffazen | 2 |
| 3641 | ffallo | 2 |
| 3642 | fesistes | 2 |
| 3643 | ferreros | 2 |
| 3644 | ferrand | 2 |
| 3645 | ferirla | 2 |
| 3646 | feriólo | 2 |
| 3647 | fería | 2 |
| 3648 | feria | 2 |
| 3649 | fenbra | 2 |
| 3650 | femençia | 2 |
| 3651 | feçiese | 2 |
| 3652 | feas | 2 |
| 3653 | fealdat | 2 |
| 3654 | fé | 2 |
| 3655 | fazie | 2 |
| 3656 | faysanes | 2 |
| 3657 | faya | 2 |
| 3658 | fasienda | 2 |
| 3659 | fasia | 2 |
| 3660 | fasaña | 2 |
| 3661 | fartes | 2 |
| 3662 | fantasía | 2 |
| 3663 | falsedat | 2 |
| 3664 | falsas | 2 |
| 3665 | fallyr | 2 |
| 3666 | fallesçidas | 2 |
| 3667 | fallesçen | 2 |
| 3668 | fallesçe | 2 |
| 3669 | falléme | 2 |
| 3670 | fallaredes | 2 |
| 3671 | fallarán | 2 |
| 3672 | fallan | 2 |
| 3673 | fallamos | 2 |
| 3674 | faldas | 2 |
| 3675 | fagan | 2 |
| 3676 | fadaron | 2 |
| 3677 | fablévos | 2 |
| 3678 | fablavan | 2 |
| 3679 | fablava | 2 |
| 3680 | fablat | 2 |
| 3681 | fablares | 2 |
| 3682 | fablare | 2 |
| 3683 | fablamos | 2 |
| 3684 | exultemus | 2 |
| 3685 | extraño | 2 |
| 3686 | expiatoria | 2 |
| 3687 | eva | 2 |
| 3688 | europa | 2 |
| 3689 | étrangère | 2 |
| 3690 | estudiantes | 2 |
| 3691 | estordido | 2 |
| 3692 | estemos | 2 |
| 3693 | estavas | 2 |
| 3694 | estaría | 2 |
| 3695 | estaño | 2 |
| 3696 | estança | 2 |
| 3697 | estameña | 2 |
| 3698 | estado | 2 |
| 3699 | estacas | 2 |
| 3700 | esse | 2 |
| 3701 | esposas | 2 |
| 3702 | espíritu | 2 |
| 3703 | espinazo | 2 |
| 3704 | espinas | 2 |
| 3705 | espina | 2 |
| 3706 | espetos | 2 |
| 3707 | espero | 2 |
| 3708 | esperar | 2 |
| 3709 | espantos | 2 |
| 3710 | espantes | 2 |
| 3711 | espante | 2 |
| 3712 | espantar | 2 |
| 3713 | espada | 2 |
| 3714 | esmerado | 2 |
| 3715 | esme | 2 |
| 3716 | esforçado | 2 |
| 3717 | escusa | 2 |
| 3718 | escuro | 2 |
| 3719 | escuela | 2 |
| 3720 | escudero | 2 |
| 3721 | escuchar | 2 |
| 3722 | escuchado | 2 |
| 3723 | escucha | 2 |
| 3724 | escrupulosos | 2 |
| 3725 | escritura | 2 |
| 3726 | escripta | 2 |
| 3727 | escribió | 2 |
| 3728 | escreví | 2 |
| 3729 | escotar | 2 |
| 3730 | escota | 2 |
| 3731 | escolares | 2 |
| 3732 | escoja | 2 |
| 3733 | escogido | 2 |
| 3734 | escarva | 2 |
| 3735 | escarda | 2 |
| 3736 | escaparedes | 2 |
| 3737 | esas | 2 |
| 3738 | erudita | 2 |
| 3739 | erudición | 2 |
| 3740 | error | 2 |
| 3741 | erró | 2 |
| 3742 | errar | 2 |
| 3743 | errada | 2 |
| 3744 | erías | 2 |
| 3745 | eriales | 2 |
| 3746 | eras | 2 |
| 3747 | épica | 2 |
| 3748 | enxerir | 2 |
| 3749 | entyende | 2 |
| 3750 | entyenda | 2 |
| 3751 | entristeçer | 2 |
| 3752 | entrara | 2 |
| 3753 | entrad | 2 |
| 3754 | entra | 2 |
| 3755 | entiendo | 2 |
| 3756 | entiendes | 2 |
| 3757 | entero | 2 |
| 3758 | entera | 2 |
| 3759 | entendiere | 2 |
| 3760 | entendiera | 2 |
| 3761 | entendet | 2 |
| 3762 | entenderlo | 2 |
| 3763 | entendemiento | 2 |
| 3764 | entençión | 2 |
| 3765 | enperadores | 2 |
| 3766 | enojes | 2 |
| 3767 | enmienda | 2 |
| 3768 | enlaças | 2 |
| 3769 | engorres | 2 |
| 3770 | engañosas | 2 |
| 3771 | engañosa | 2 |
| 3772 | engañas | 2 |
| 3773 | engañadas | 2 |
| 3774 | enganado | 2 |
| 3775 | enfraquesçes | 2 |
| 3776 | enforcaron | 2 |
| 3777 | enforcado | 2 |
| 3778 | enfiesta | 2 |
| 3779 | endiablada | 2 |
| 3780 | encontradas | 2 |
| 3781 | encomiendo | 2 |
| 3782 | encomienda | 2 |
| 3783 | encogidos | 2 |
| 3784 | encobyerto | 2 |
| 3785 | encobrir | 2 |
| 3786 | encobierto | 2 |
| 3787 | encobiertas | 2 |
| 3788 | ençienso | 2 |
| 3789 | ençerrado | 2 |
| 3790 | ençendemiento | 2 |
| 3791 | encantador | 2 |
| 3792 | enbuelvas | 2 |
| 3793 | enbióme | 2 |
| 3794 | enbióles | 2 |
| 3795 | enbiava | 2 |
| 3796 | enbiar | 2 |
| 3797 | enbargue | 2 |
| 3798 | enatío | 2 |
| 3799 | enarta | 2 |
| 3800 | enano | 2 |
| 3801 | elemento | 2 |
| 3802 | ejemplo | 2 |
| 3803 | egualdad | 2 |
| 3804 | echóme | 2 |
| 3805 | echasen | 2 |
| 3806 | echaron | 2 |
| 3807 | echan | 2 |
| 3808 | è | 2 |
| 3809 | dyme | 2 |
| 3810 | dyeres | 2 |
| 3811 | dyablo | 2 |
| 3812 | duras | 2 |
| 3813 | dulçemente | 2 |
| 3814 | duenas | 2 |
| 3815 | dubdar | 2 |
| 3816 | dubdança | 2 |
| 3817 | dramática | 2 |
| 3818 | dormiendo | 2 |
| 3819 | doñeguil | 2 |
| 3820 | doñea | 2 |
| 3821 | donosas | 2 |
| 3822 | donosa | 2 |
| 3823 | dono | 2 |
| 3824 | donçella | 2 |
| 3825 | dolores | 2 |
| 3826 | dolientes | 2 |
| 3827 | doler | 2 |
| 3828 | dolençias | 2 |
| 3829 | doctos | 2 |
| 3830 | dobladas | 2 |
| 3831 | doblada | 2 |
| 3832 | díxoles | 2 |
| 3833 | dixiste | 2 |
| 3834 | distes | 2 |
| 3835 | discípulos | 2 |
| 3836 | discípulo | 2 |
| 3837 | díos | 2 |
| 3838 | dióm | 2 |
| 3839 | dino | 2 |
| 3840 | dilitoria | 2 |
| 3841 | dilexi | 2 |
| 3842 | dil | 2 |
| 3843 | digan | 2 |
| 3844 | diezmo | 2 |
| 3845 | diés | 2 |
| 3846 | diera | 2 |
| 3847 | dichas | 2 |
| 3848 | dicen | 2 |
| 3849 | dezirt | 2 |
| 3850 | dexistes | 2 |
| 3851 | dexiere | 2 |
| 3852 | dexe | 2 |
| 3853 | dexaron | 2 |
| 3854 | dexan | 2 |
| 3855 | déxame | 2 |
| 3856 | déxalo | 2 |
| 3857 | dexallo | 2 |
| 3858 | dexades | 2 |
| 3859 | dexad | 2 |
| 3860 | devoto | 2 |
| 3861 | deviersas | 2 |
| 3862 | deviera | 2 |
| 3863 | devíe | 2 |
| 3864 | deveses | 2 |
| 3865 | devedes | 2 |
| 3866 | devaneo | 2 |
| 3867 | detyen | 2 |
| 3868 | detener | 2 |
| 3869 | desyr | 2 |
| 3870 | destruye | 2 |
| 3871 | désta | 2 |
| 3872 | desseos | 2 |
| 3873 | desposado | 2 |
| 3874 | deso | 2 |
| 3875 | desirme | 2 |
| 3876 | desimos | 2 |
| 3877 | desildo | 2 |
| 3878 | desilde | 2 |
| 3879 | desíe | 2 |
| 3880 | desidme | 2 |
| 3881 | desídesme | 2 |
| 3882 | deseoso | 2 |
| 3883 | desecharán | 2 |
| 3884 | desecha | 2 |
| 3885 | dese | 2 |
| 3886 | desdeñarse | 2 |
| 3887 | descumunión | 2 |
| 3888 | descúbrese | 2 |
| 3889 | desafiedes | 2 |
| 3890 | derribóle | 2 |
| 3891 | derredor | 2 |
| 3892 | departyr | 2 |
| 3893 | departir | 2 |
| 3894 | dentera | 2 |
| 3895 | denodado | 2 |
| 3896 | demudar | 2 |
| 3897 | demudada | 2 |
| 3898 | demandes | 2 |
| 3899 | demandas | 2 |
| 3900 | demandare | 2 |
| 3901 | demandan | 2 |
| 3902 | delgados | 2 |
| 3903 | delgada | 2 |
| 3904 | deleytava | 2 |
| 3905 | delaciones | 2 |
| 3906 | dejado | 2 |
| 3907 | defienden | 2 |
| 3908 | deffiende | 2 |
| 3909 | deffendimiento | 2 |
| 3910 | defensiones | 2 |
| 3911 | debe | 2 |
| 3912 | dávanle | 2 |
| 3913 | dávales | 2 |
| 3914 | datme | 2 |
| 3915 | dasle | 2 |
| 3916 | darme | 2 |
| 3917 | dardo | 2 |
| 3918 | dapno | 2 |
| 3919 | dañosas | 2 |
| 3920 | daños | 2 |
| 3921 | dañados | 2 |
| 3922 | dante | 2 |
| 3923 | danos | 2 |
| 3924 | danle | 2 |
| 3925 | daniel | 2 |
| 3926 | dándole | 2 |
| 3927 | dam | 2 |
| 3928 | dadnos | 2 |
| 3929 | dadme | 2 |
| 3930 | dad | 2 |
| 3931 | cyerto | 2 |
| 3932 | cuytar | 2 |
| 3933 | cuydéme | 2 |
| 3934 | cuyas | 2 |
| 3935 | custunbre | 2 |
| 3936 | cunplidas | 2 |
| 3937 | cultura | 2 |
| 3938 | culpado | 2 |
| 3939 | cuervos | 2 |
| 3940 | cuento | 2 |
| 3941 | cuentan | 2 |
| 3942 | cucaña | 2 |
| 3943 | cubre | 2 |
| 3944 | cualquiera | 2 |
| 3945 | cualquier | 2 |
| 3946 | cuales | 2 |
| 3947 | cruzada | 2 |
| 3948 | cristiano | 2 |
| 3949 | cristiana | 2 |
| 3950 | criador | 2 |
| 3951 | cría | 2 |
| 3952 | creyó | 2 |
| 3953 | creyeron | 2 |
| 3954 | cresçe | 2 |
| 3955 | creet | 2 |
| 3956 | creen | 2 |
| 3957 | creemos | 2 |
| 3958 | creedes | 2 |
| 3959 | creçen | 2 |
| 3960 | coytoso | 2 |
| 3961 | coytados | 2 |
| 3962 | coydó | 2 |
| 3963 | coydas | 2 |
| 3964 | coydado | 2 |
| 3965 | covil | 2 |
| 3966 | covarde | 2 |
| 3967 | costumbre | 2 |
| 3968 | costas | 2 |
| 3969 | costado | 2 |
| 3970 | corvillo | 2 |
| 3971 | corrió | 2 |
| 3972 | corriente | 2 |
| 3973 | corrienda | 2 |
| 3974 | corres | 2 |
| 3975 | corren | 2 |
| 3976 | corredera | 2 |
| 3977 | corderos | 2 |
| 3978 | cordel | 2 |
| 3979 | copa | 2 |
| 3980 | convirtió | 2 |
| 3981 | convienen | 2 |
| 3982 | contrito | 2 |
| 3983 | contriçión | 2 |
| 3984 | contrarios | 2 |
| 3985 | contrario | 2 |
| 3986 | contraria | 2 |
| 3987 | contiendas | 2 |
| 3988 | contesció | 2 |
| 3989 | contesca | 2 |
| 3990 | contemporáneos | 2 |
| 3991 | conteçe | 2 |
| 3992 | contar | 2 |
| 3993 | consygo | 2 |
| 3994 | constunbres | 2 |
| 3995 | conssolaçión | 2 |
| 3996 | conssejó | 2 |
| 3997 | conssejado | 2 |
| 3998 | consentyr | 2 |
| 3999 | consejos | 2 |
| 4000 | conquista | 2 |
| 4001 | conpusiçión | 2 |
| 4002 | conpuesta | 2 |
| 4003 | conpradme | 2 |
| 4004 | conplidamente | 2 |
| 4005 | conpletas | 2 |
| 4006 | conplado | 2 |
| 4007 | conpañon | 2 |
| 4008 | conpanía | 2 |
| 4009 | conozco | 2 |
| 4010 | conosco | 2 |
| 4011 | conosçí | 2 |
| 4012 | conosçen | 2 |
| 4013 | conortan | 2 |
| 4014 | conorta | 2 |
| 4015 | conocía | 2 |
| 4016 | conocer | 2 |
| 4017 | conocemos | 2 |
| 4018 | connusco | 2 |
| 4019 | confuerto | 2 |
| 4020 | confesor | 2 |
| 4021 | confadre | 2 |
| 4022 | condes | 2 |
| 4023 | conde | 2 |
| 4024 | conclusyón | 2 |
| 4025 | conçiençia | 2 |
| 4026 | conçiença | 2 |
| 4027 | concha | 2 |
| 4028 | conbides | 2 |
| 4029 | comyençan | 2 |
| 4030 | comunales | 2 |
| 4031 | común | 2 |
| 4032 | compuso | 2 |
| 4033 | comíe | 2 |
| 4034 | començóle | 2 |
| 4035 | començól | 2 |
| 4036 | començaron | 2 |
| 4037 | comedyr | 2 |
| 4038 | combinaciones | 2 |
| 4039 | colosal | 2 |
| 4040 | colorido | 2 |
| 4041 | colmillo | 2 |
| 4042 | collaços | 2 |
| 4043 | colgó | 2 |
| 4044 | colgar | 2 |
| 4045 | colgado | 2 |
| 4046 | colgadas | 2 |
| 4047 | cola | 2 |
| 4048 | cogido | 2 |
| 4049 | codiçioso | 2 |
| 4050 | coçina | 2 |
| 4051 | cochino | 2 |
| 4052 | coçes | 2 |
| 4053 | cobros | 2 |
| 4054 | cobra | 2 |
| 4055 | cobierto | 2 |
| 4056 | cobertor | 2 |
| 4057 | cobdiçiar | 2 |
| 4058 | clerical | 2 |
| 4059 | clásico | 2 |
| 4060 | claridad | 2 |
| 4061 | claras | 2 |
| 4062 | çivera | 2 |
| 4063 | ciudad | 2 |
| 4064 | çítola | 2 |
| 4065 | çinquenta | 2 |
| 4066 | çinfonía | 2 |
| 4067 | çiervo | 2 |
| 4068 | cient | 2 |
| 4069 | çiencia | 2 |
| 4070 | çien | 2 |
| 4071 | çielos | 2 |
| 4072 | ciegos | 2 |
| 4073 | çiego | 2 |
| 4074 | çiegan | 2 |
| 4075 | çiega | 2 |
| 4076 | çibdades | 2 |
| 4077 | chicos | 2 |
| 4078 | çertero | 2 |
| 4079 | çertera | 2 |
| 4080 | çerrar | 2 |
| 4081 | çerrado | 2 |
| 4082 | çentella | 2 |
| 4083 | çeloso | 2 |
| 4084 | çelos | 2 |
| 4085 | çelada | 2 |
| 4086 | çejas | 2 |
| 4087 | çeja | 2 |
| 4088 | çeguedat | 2 |
| 4089 | caya | 2 |
| 4090 | cavallero | 2 |
| 4091 | catorce | 2 |
| 4092 | cativo | 2 |
| 4093 | çatico | 2 |
| 4094 | catase | 2 |
| 4095 | cataron | 2 |
| 4096 | catan | 2 |
| 4097 | catadura | 2 |
| 4098 | castigó | 2 |
| 4099 | castiella | 2 |
| 4100 | castañas | 2 |
| 4101 | casta | 2 |
| 4102 | cassas | 2 |
| 4103 | cassarse | 2 |
| 4104 | cassamientos | 2 |
| 4105 | cassamiento | 2 |
| 4106 | cassa | 2 |
| 4107 | casó | 2 |
| 4108 | casase | 2 |
| 4109 | casarse | 2 |
| 4110 | casaría | 2 |
| 4111 | casados | 2 |
| 4112 | casadas | 2 |
| 4113 | carro | 2 |
| 4114 | carreras | 2 |
| 4115 | carniçero | 2 |
| 4116 | carniçerías | 2 |
| 4117 | carnes | 2 |
| 4118 | carga | 2 |
| 4119 | cardenal | 2 |
| 4120 | caramiello | 2 |
| 4121 | çapatos | 2 |
| 4122 | capas | 2 |
| 4123 | caño | 2 |
| 4124 | cañavera | 2 |
| 4125 | cantores | 2 |
| 4126 | cantigas | 2 |
| 4127 | cantas | 2 |
| 4128 | cantador | 2 |
| 4129 | cantado | 2 |
| 4130 | çanpoña | 2 |
| 4131 | canpanas | 2 |
| 4132 | canciller | 2 |
| 4133 | camarones | 2 |
| 4134 | calor | 2 |
| 4135 | calleja | 2 |
| 4136 | callando | 2 |
| 4137 | callad | 2 |
| 4138 | calderas | 2 |
| 4139 | calatrava | 2 |
| 4140 | calandria | 2 |
| 4141 | calaba | 2 |
| 4142 | çafir | 2 |
| 4143 | caçurros | 2 |
| 4144 | caçones | 2 |
| 4145 | cabría | 2 |
| 4146 | cabra | 2 |
| 4147 | cabello | 2 |
| 4148 | cabeças | 2 |
| 4149 | caballeros | 2 |
| 4150 | byvrás | 2 |
| 4151 | buscad | 2 |
| 4152 | bullen | 2 |
| 4153 | buhonas | 2 |
| 4154 | buexes | 2 |
| 4155 | buenora | 2 |
| 4156 | buelta | 2 |
| 4157 | breves | 2 |
| 4158 | bramuras | 2 |
| 4159 | bramava | 2 |
| 4160 | braço | 2 |
| 4161 | boquilla | 2 |
| 4162 | bondades | 2 |
| 4163 | boda | 2 |
| 4164 | blancos | 2 |
| 4165 | blancas | 2 |
| 4166 | bivo | 2 |
| 4167 | biven | 2 |
| 4168 | bivda | 2 |
| 4169 | bienobrar | 2 |
| 4170 | biblioteca | 2 |
| 4171 | bevido | 2 |
| 4172 | beve | 2 |
| 4173 | benedictus | 2 |
| 4174 | baxo | 2 |
| 4175 | bavoquía | 2 |
| 4176 | barvas | 2 |
| 4177 | barrunta | 2 |
| 4178 | barriles | 2 |
| 4179 | barata | 2 |
| 4180 | barajas | 2 |
| 4181 | baldón | 2 |
| 4182 | ayuntan | 2 |
| 4183 | ayunav | 2 |
| 4184 | ayres | 2 |
| 4185 | ayrado | 2 |
| 4186 | ayrada | 2 |
| 4187 | ayamos | 2 |
| 4188 | avríe | 2 |
| 4189 | avredes | 2 |
| 4190 | aviñón | 2 |
| 4191 | aviendo | 2 |
| 4192 | avena | 2 |
| 4193 | avancuerda | 2 |
| 4194 | autores | 2 |
| 4195 | autor | 2 |
| 4196 | aún | 2 |
| 4197 | atyende | 2 |
| 4198 | atura | 2 |
| 4199 | atrevudo | 2 |
| 4200 | atrevo | 2 |
| 4201 | atrevido | 2 |
| 4202 | atrever | 2 |
| 4203 | atiende | 2 |
| 4204 | atender | 2 |
| 4205 | atanta | 2 |
| 4206 | atanbor | 2 |
| 4207 | atales | 2 |
| 4208 | atalaya | 2 |
| 4209 | atahonas | 2 |
| 4210 | atados | 2 |
| 4211 | atado | 2 |
| 4212 | ata | 2 |
| 4213 | asunto | 2 |
| 4214 | asuelven | 2 |
| 4215 | astraga | 2 |
| 4216 | assy | 2 |
| 4217 | assentar | 2 |
| 4218 | assentado | 2 |
| 4219 | assecha | 2 |
| 4220 | asombradizos | 2 |
| 4221 | asoma | 2 |
| 4222 | asentada | 2 |
| 4223 | ascona | 2 |
| 4224 | asañes | 2 |
| 4225 | arvejas | 2 |
| 4226 | artista | 2 |
| 4227 | artero | 2 |
| 4228 | artera | 2 |
| 4229 | arrepiente | 2 |
| 4230 | arrepentyr | 2 |
| 4231 | arredrado | 2 |
| 4232 | arrancada | 2 |
| 4233 | arranca | 2 |
| 4234 | armar | 2 |
| 4235 | armados | 2 |
| 4236 | armado | 2 |
| 4237 | arma | 2 |
| 4238 | arena | 2 |
| 4239 | ardores | 2 |
| 4240 | arden | 2 |
| 4241 | arco | 2 |
| 4242 | arcas | 2 |
| 4243 | árbol | 2 |
| 4244 | aquellas | 2 |
| 4245 | apuestos | 2 |
| 4246 | apropiada | 2 |
| 4247 | apriesa | 2 |
| 4248 | aprendí | 2 |
| 4249 | apodo | 2 |
| 4250 | aperçebudo | 2 |
| 4251 | aperçebidos | 2 |
| 4252 | aperçebida | 2 |
| 4253 | apellido | 2 |
| 4254 | apartó | 2 |
| 4255 | apartar | 2 |
| 4256 | apartadas | 2 |
| 4257 | aparta | 2 |
| 4258 | añal | 2 |
| 4259 | antón | 2 |
| 4260 | antología | 2 |
| 4261 | antojos | 2 |
| 4262 | antojo | 2 |
| 4263 | anos | 2 |
| 4264 | ánima | 2 |
| 4265 | anima | 2 |
| 4266 | ángel | 2 |
| 4267 | andarían | 2 |
| 4268 | andaré | 2 |
| 4269 | anchos | 2 |
| 4270 | ancheta | 2 |
| 4271 | amxy | 2 |
| 4272 | amorosos | 2 |
| 4273 | amorosa | 2 |
| 4274 | amigotes | 2 |
| 4275 | ameste | 2 |
| 4276 | amenaças | 2 |
| 4277 | amén | 2 |
| 4278 | amen | 2 |
| 4279 | amavan | 2 |
| 4280 | amava | 2 |
| 4281 | amase | 2 |
| 4282 | amariella | 2 |
| 4283 | amará | 2 |
| 4284 | amando | 2 |
| 4285 | alvos | 2 |
| 4286 | alvarda | 2 |
| 4287 | altura | 2 |
| 4288 | altísimos | 2 |
| 4289 | alteza | 2 |
| 4290 | almuerço | 2 |
| 4291 | algúnd | 2 |
| 4292 | alguaçil | 2 |
| 4293 | alexandre | 2 |
| 4294 | alejandrino | 2 |
| 4295 | alégrome | 2 |
| 4296 | alcántara | 2 |
| 4297 | alçando | 2 |
| 4298 | alcançarían | 2 |
| 4299 | albornoz | 2 |
| 4300 | albogues | 2 |
| 4301 | alas | 2 |
| 4302 | alardo | 2 |
| 4303 | alana | 2 |
| 4304 | alabo | 2 |
| 4305 | alabes | 2 |
| 4306 | ajenos | 2 |
| 4307 | ahora | 2 |
| 4308 | aguijón | 2 |
| 4309 | aguija | 2 |
| 4310 | agüero | 2 |
| 4311 | agraviado | 2 |
| 4312 | agosto | 2 |
| 4313 | agenas | 2 |
| 4314 | afeytes | 2 |
| 4315 | aduxo | 2 |
| 4316 | adulterio | 2 |
| 4317 | adoraron | 2 |
| 4318 | adoquier | 2 |
| 4319 | admite | 2 |
| 4320 | adiestra | 2 |
| 4321 | adevino | 2 |
| 4322 | adelante | 2 |
| 4323 | adán | 2 |
| 4324 | acusa | 2 |
| 4325 | acuerde | 2 |
| 4326 | acorro | 2 |
| 4327 | acorres | 2 |
| 4328 | acordados | 2 |
| 4329 | acomiendo | 2 |
| 4330 | acoje | 2 |
| 4331 | acoger | 2 |
| 4332 | açiprestes | 2 |
| 4333 | acabó | 2 |
| 4334 | acabar | 2 |
| 4335 | abyerta | 2 |
| 4336 | abta | 2 |
| 4337 | abstinençia | 2 |
| 4338 | aborresçer | 2 |
| 4339 | abogada | 2 |
| 4340 | abierto | 2 |
| 4341 | abierta | 2 |
| 4342 | abeytar | 2 |
| 4343 | abdiençia | 2 |
| 4344 | abaxóse | 2 |
| 4345 | abaxar | 2 |
| 4346 | abarcas | 2 |
| 4347 | aba | 2 |
| 4348 | zanjó | 1 |
| 4349 | yz | 1 |
| 4350 | yverniso | 1 |
| 4351 | yvase | 1 |
| 4352 | yvas | 1 |
| 4353 | yvalo | 1 |
| 4354 | yvagela | 1 |
| 4355 | yuntar | 1 |
| 4356 | yúgo | 1 |
| 4357 | yugo | 1 |
| 4358 | yugero | 1 |
| 4359 | ysrael | 1 |
| 4360 | ysopete | 1 |
| 4361 | ysayas | 1 |
| 4362 | ysac | 1 |
| 4363 | yrvos | 1 |
| 4364 | yrm | 1 |
| 4365 | yrgyendo | 1 |
| 4366 | yrés | 1 |
| 4367 | yrán | 1 |
| 4368 | yrados | 1 |
| 4369 | yradas | 1 |
| 4370 | yrada | 1 |
| 4371 | ypocresía | 1 |
| 4372 | ypocrás | 1 |
| 4373 | ynojos | 1 |
| 4374 | ynojo | 1 |
| 4375 | ynoçente | 1 |
| 4376 | ynfernal | 1 |
| 4377 | yncan | 1 |
| 4378 | ymos | 1 |
| 4379 | ymajen | 1 |
| 4380 | ymagen | 1 |
| 4381 | yjares | 1 |
| 4382 | ygualas | 1 |
| 4383 | ygualadera | 1 |
| 4384 | yerta | 1 |
| 4385 | yerros | 1 |
| 4386 | yerre | 1 |
| 4387 | yérralo | 1 |
| 4388 | yernos | 1 |
| 4389 | yermas | 1 |
| 4390 | yerguen | 1 |
| 4391 | yergos | 1 |
| 4392 | yendo | 1 |
| 4393 | yen | 1 |
| 4394 | yela | 1 |
| 4395 | yeguerisa | 1 |
| 4396 | ydos | 1 |
| 4397 | ydo | 1 |
| 4398 | yda | 1 |
| 4399 | yazíe | 1 |
| 4400 | yazes | 1 |
| 4401 | yasía | 1 |
| 4402 | yases | 1 |
| 4403 | yas | 1 |
| 4404 | yantes | 1 |
| 4405 | yantado | 1 |
| 4406 | yago | 1 |
| 4407 | yaçiendo | 1 |
| 4408 | yaçe | 1 |
| 4409 | xymio | 1 |
| 4410 | xristo | 1 |
| 4411 | xriste | 1 |
| 4412 | xiii | 1 |
| 4413 | xi | 1 |
| 4414 | xergas | 1 |
| 4415 | xarope | 1 |
| 4416 | vyyuela | 1 |
| 4417 | vyudas | 1 |
| 4418 | vysta | 1 |
| 4419 | vyó | 1 |
| 4420 | vyña | 1 |
| 4421 | vynose | 1 |
| 4422 | vynóme | 1 |
| 4423 | vynieron | 1 |
| 4424 | vyllenchón | 1 |
| 4425 | vyllanos | 1 |
| 4426 | vyllanía | 1 |
| 4427 | vyllanchón | 1 |
| 4428 | vylezas | 1 |
| 4429 | vylesa | 1 |
| 4430 | vyga | 1 |
| 4431 | vyese | 1 |
| 4432 | vyento | 1 |
| 4433 | vyenen | 1 |
| 4434 | vydose | 1 |
| 4435 | vydol | 1 |
| 4436 | vyd | 1 |
| 4437 | vyçyos | 1 |
| 4438 | vyçyo | 1 |
| 4439 | vyçios | 1 |
| 4440 | vyçio | 1 |
| 4441 | vyandas | 1 |
| 4442 | vulgar | 1 |
| 4443 | vuestr | 1 |
| 4444 | vueltas | 1 |
| 4445 | vuelos | 1 |
| 4446 | vuelo | 1 |
| 4447 | vostra | 1 |
| 4448 | voses | 1 |
| 4449 | vóme | 1 |
| 4450 | volubilidad | 1 |
| 4451 | vollaz | 1 |
| 4452 | volk | 1 |
| 4453 | volando | 1 |
| 4454 | volado | 1 |
| 4455 | vocales | 1 |
| 4456 | vocal | 1 |
| 4457 | vobis | 1 |
| 4458 | vizina | 1 |
| 4459 | vivo | 1 |
| 4460 | vivit | 1 |
| 4461 | vivió | 1 |
| 4462 | vivificó | 1 |
| 4463 | vivía | 1 |
| 4464 | viveza | 1 |
| 4465 | vive | 1 |
| 4466 | viuela | 1 |
| 4467 | viuda | 1 |
| 4468 | vistió | 1 |
| 4469 | vistía | 1 |
| 4470 | vistes | 1 |
| 4471 | visten | 1 |
| 4472 | vístelo | 1 |
| 4473 | visité | 1 |
| 4474 | visitas | 1 |
| 4475 | visitando | 1 |
| 4476 | visita | 1 |
| 4477 | visible | 1 |
| 4478 | visagra | 1 |
| 4479 | virtutis | 1 |
| 4480 | virtuosa | 1 |
| 4481 | virtudes | 1 |
| 4482 | virtud | 1 |
| 4483 | virgo | 1 |
| 4484 | vírgenes | 1 |
| 4485 | virgam | 1 |
| 4486 | viras | 1 |
| 4487 | violado | 1 |
| 4488 | vio | 1 |
| 4489 | viñadero | 1 |
| 4490 | vínome | 1 |
| 4491 | vínole | 1 |
| 4492 | viniésedes | 1 |
| 4493 | vinieronlos | 1 |
| 4494 | vinier | 1 |
| 4495 | víneme | 1 |
| 4496 | vine | 1 |
| 4497 | vinas | 1 |
| 4498 | vinagre | 1 |
| 4499 | vin | 1 |
| 4500 | vime | 1 |
| 4501 | villeza | 1 |
| 4502 | villena | 1 |
| 4503 | villanía | 1 |
| 4504 | villanescas | 1 |
| 4505 | villanas | 1 |
| 4506 | vileza | 1 |
| 4507 | vihuela | 1 |
| 4508 | vigisuela | 1 |
| 4509 | vieux | 1 |
| 4510 | viés | 1 |
| 4511 | vientos | 1 |
| 4512 | viénesme | 1 |
| 4513 | vídote | 1 |
| 4514 | vídolo | 1 |
| 4515 | vidente | 1 |
| 4516 | videare | 1 |
| 4517 | vid | 1 |
| 4518 | viçiosos | 1 |
| 4519 | viciosa | 1 |
| 4520 | vicario | 1 |
| 4521 | vibdas | 1 |
| 4522 | vías | 1 |
| 4523 | viam | 1 |
| 4524 | vezino | 1 |
| 4525 | vezindat | 1 |
| 4526 | vezindades | 1 |
| 4527 | vezina | 1 |
| 4528 | vezada | 1 |
| 4529 | veza | 1 |
| 4530 | veyo | 1 |
| 4531 | veyla | 1 |
| 4532 | veyes | 1 |
| 4533 | veyan | 1 |
| 4534 | veyalos | 1 |
| 4535 | veyades | 1 |
| 4536 | vevir | 1 |
| 4537 | vevido | 1 |
| 4538 | vevía | 1 |
| 4539 | vesugos | 1 |
| 4540 | vestuario | 1 |
| 4541 | vestros | 1 |
| 4542 | vestra | 1 |
| 4543 | vestió | 1 |
| 4544 | vestiéronle | 1 |
| 4545 | vestíe | 1 |
| 4546 | vestiduras | 1 |
| 4547 | vestidura | 1 |
| 4548 | vestidla | 1 |
| 4549 | vestidas | 1 |
| 4550 | vesinos | 1 |
| 4551 | vervos | 1 |
| 4552 | vertyendo | 1 |
| 4553 | vertu | 1 |
| 4554 | verter | 1 |
| 4555 | verte | 1 |
| 4556 | verssos | 1 |
| 4557 | versificación | 1 |
| 4558 | verné | 1 |
| 4559 | verme | 1 |
| 4560 | veritatis | 1 |
| 4561 | verificaron | 1 |
| 4562 | veríedes | 1 |
| 4563 | verguenças | 1 |
| 4564 | vergoñosa | 1 |
| 4565 | vergoña | 1 |
| 4566 | vergonçoso | 1 |
| 4567 | veremos | 1 |
| 4568 | verdura | 1 |
| 4569 | verdeles | 1 |
| 4570 | verçuelas | 1 |
| 4571 | verbum | 1 |
| 4572 | verbos | 1 |
| 4573 | veras | 1 |
| 4574 | verán | 1 |
| 4575 | veracidad | 1 |
| 4576 | ventris | 1 |
| 4577 | venternía | 1 |
| 4578 | venternero | 1 |
| 4579 | venternera | 1 |
| 4580 | ventaja | 1 |
| 4581 | veno | 1 |
| 4582 | venite | 1 |
| 4583 | venistes | 1 |
| 4584 | veniésedes | 1 |
| 4585 | veniéronse | 1 |
| 4586 | veniere | 1 |
| 4587 | venienl | 1 |
| 4588 | venien | 1 |
| 4589 | venides | 1 |
| 4590 | venidas | 1 |
| 4591 | veniales | 1 |
| 4592 | vengó | 1 |
| 4593 | véngase | 1 |
| 4594 | vengar | 1 |
| 4595 | vengades | 1 |
| 4596 | vengada | 1 |
| 4597 | vendió | 1 |
| 4598 | vendimiar | 1 |
| 4599 | vendíe | 1 |
| 4600 | vendidas | 1 |
| 4601 | vender | 1 |
| 4602 | vendemiento | 1 |
| 4603 | vençimiento | 1 |
| 4604 | venciendo | 1 |
| 4605 | vençida | 1 |
| 4606 | vençerse | 1 |
| 4607 | vençeremos | 1 |
| 4608 | venceremos | 1 |
| 4609 | vençerás | 1 |
| 4610 | vençemos | 1 |
| 4611 | vençedor | 1 |
| 4612 | vence | 1 |
| 4613 | vença | 1 |
| 4614 | venados | 1 |
| 4615 | venado | 1 |
| 4616 | vena | 1 |
| 4617 | vellosas | 1 |
| 4618 | vellosa | 1 |
| 4619 | vellacos | 1 |
| 4620 | vellaca | 1 |
| 4621 | vele | 1 |
| 4622 | veldat | 1 |
| 4623 | velaron | 1 |
| 4624 | velada | 1 |
| 4625 | vejezuela | 1 |
| 4626 | vejéz | 1 |
| 4627 | vejez | 1 |
| 4628 | vejedat | 1 |
| 4629 | veen | 1 |
| 4630 | veemos | 1 |
| 4631 | veedes | 1 |
| 4632 | vedeganbre | 1 |
| 4633 | vedado | 1 |
| 4634 | ved | 1 |
| 4635 | veçindades | 1 |
| 4636 | véanse | 1 |
| 4637 | vean | 1 |
| 4638 | veádeslas | 1 |
| 4639 | vé | 1 |
| 4640 | vayo | 1 |
| 4641 | vayle | 1 |
| 4642 | vayladas | 1 |
| 4643 | vayase | 1 |
| 4644 | vassalo | 1 |
| 4645 | vassallos | 1 |
| 4646 | vasos | 1 |
| 4647 | vasío | 1 |
| 4648 | vasías | 1 |
| 4649 | vasía | 1 |
| 4650 | vase | 1 |
| 4651 | vasallos | 1 |
| 4652 | vasallo | 1 |
| 4653 | varruntólo | 1 |
| 4654 | varraganes | 1 |
| 4655 | varonil | 1 |
| 4656 | varona | 1 |
| 4657 | varias | 1 |
| 4658 | variar | 1 |
| 4659 | variado | 1 |
| 4660 | variadísimas | 1 |
| 4661 | variadas | 1 |
| 4662 | varga | 1 |
| 4663 | varas | 1 |
| 4664 | varajas | 1 |
| 4665 | vara | 1 |
| 4666 | vaqueriso | 1 |
| 4667 | vaquerisa | 1 |
| 4668 | vaqueriços | 1 |
| 4669 | vanse | 1 |
| 4670 | vanos | 1 |
| 4671 | vandurria | 1 |
| 4672 | vandero | 1 |
| 4673 | vanæ | 1 |
| 4674 | valyere | 1 |
| 4675 | valyan | 1 |
| 4676 | valy | 1 |
| 4677 | valsavin | 1 |
| 4678 | valo | 1 |
| 4679 | válme | 1 |
| 4680 | vallesteros | 1 |
| 4681 | vallestero | 1 |
| 4682 | valles | 1 |
| 4683 | vallena | 1 |
| 4684 | vallejos | 1 |
| 4685 | valladares | 1 |
| 4686 | valientes | 1 |
| 4687 | valiéndose | 1 |
| 4688 | valíe | 1 |
| 4689 | valie | 1 |
| 4690 | vales | 1 |
| 4691 | valentya | 1 |
| 4692 | valedes | 1 |
| 4693 | valdrí | 1 |
| 4694 | valdrán | 1 |
| 4695 | valdía | 1 |
| 4696 | valdevacas | 1 |
| 4697 | valdemoriello | 1 |
| 4698 | valde | 1 |
| 4699 | valas | 1 |
| 4700 | valan | 1 |
| 4701 | valadí | 1 |
| 4702 | vala | 1 |
| 4703 | vagidos | 1 |
| 4704 | uvia | 1 |
| 4705 | uter | 1 |
| 4706 | ut | 1 |
| 4707 | uses | 1 |
| 4708 | usé | 1 |
| 4709 | usare | 1 |
| 4710 | usaje | 1 |
| 4711 | usados | 1 |
| 4712 | urruca | 1 |
| 4713 | urdiendo | 1 |
| 4714 | urdiales | 1 |
| 4715 | universidades | 1 |
| 4716 | universal | 1 |
| 4717 | unido | 1 |
| 4718 | unidad | 1 |
| 4719 | unicuique | 1 |
| 4720 | único | 1 |
| 4721 | única | 1 |
| 4722 | ungente | 1 |
| 4723 | unçión | 1 |
| 4724 | unción | 1 |
| 4725 | umiçidio | 1 |
| 4726 | umano | 1 |
| 4727 | umanidad | 1 |
| 4728 | umana | 1 |
| 4729 | última | 1 |
| 4730 | ufanas | 1 |
| 4731 | ufana | 1 |
| 4732 | uertas | 1 |
| 4733 | uerco | 1 |
| 4734 | tyzones | 1 |
| 4735 | tyzonadores | 1 |
| 4736 | tyznado | 1 |
| 4737 | tysones | 1 |
| 4738 | tyról | 1 |
| 4739 | tyró | 1 |
| 4740 | tyrava | 1 |
| 4741 | tyras | 1 |
| 4742 | tyrarías | 1 |
| 4743 | tyrares | 1 |
| 4744 | tyña | 1 |
| 4745 | tyntos | 1 |
| 4746 | tynto | 1 |
| 4747 | tyntas | 1 |
| 4748 | tyesta | 1 |
| 4749 | tyerra | 1 |
| 4750 | tyénese | 1 |
| 4751 | tyénenle | 1 |
| 4752 | tyénelas | 1 |
| 4753 | tyenden | 1 |
| 4754 | tyenbla | 1 |
| 4755 | tyempo | 1 |
| 4756 | tya | 1 |
| 4757 | tuya | 1 |
| 4758 | tuvieran | 1 |
| 4759 | tuum | 1 |
| 4760 | tuo | 1 |
| 4761 | tunbal | 1 |
| 4762 | tumba | 1 |
| 4763 | tuis | 1 |
| 4764 | tui | 1 |
| 4765 | tuero | 1 |
| 4766 | tuelte | 1 |
| 4767 | tuelle | 1 |
| 4768 | tuelga | 1 |
| 4769 | tuæ | 1 |
| 4770 | tuae | 1 |
| 4771 | truhanes | 1 |
| 4772 | truhanería | 1 |
| 4773 | tróxovos | 1 |
| 4774 | tróxote | 1 |
| 4775 | tróxolo | 1 |
| 4776 | tróxole | 1 |
| 4777 | tróxo | 1 |
| 4778 | troxistes | 1 |
| 4779 | troxies | 1 |
| 4780 | troxiéronlos | 1 |
| 4781 | troxiéronlo | 1 |
| 4782 | troxiello | 1 |
| 4783 | trotero | 1 |
| 4784 | trotas | 1 |
| 4785 | trotalla | 1 |
| 4786 | tropel | 1 |
| 4787 | tronpas | 1 |
| 4788 | troca | 1 |
| 4789 | trobo | 1 |
| 4790 | trobase | 1 |
| 4791 | trobaríades | 1 |
| 4792 | trobadores | 1 |
| 4793 | triunfalmente | 1 |
| 4794 | triunfal | 1 |
| 4795 | tristísimamente | 1 |
| 4796 | tristis | 1 |
| 4797 | tristençia | 1 |
| 4798 | tristán | 1 |
| 4799 | trisca | 1 |
| 4800 | triperas | 1 |
| 4801 | trillar | 1 |
| 4802 | trillando | 1 |
| 4803 | trillan | 1 |
| 4804 | trilla | 1 |
| 4805 | triçesimo | 1 |
| 4806 | tribulaçión | 1 |
| 4807 | triasandalos | 1 |
| 4808 | trexnada | 1 |
| 4809 | trexna | 1 |
| 4810 | trevo | 1 |
| 4811 | tresientos | 1 |
| 4812 | treseño | 1 |
| 4813 | treperas | 1 |
| 4814 | trentanario | 1 |
| 4815 | trenidat | 1 |
| 4816 | trença | 1 |
| 4817 | tremor | 1 |
| 4818 | tregua | 1 |
| 4819 | trefuda | 1 |
| 4820 | treçientos | 1 |
| 4821 | treçientas | 1 |
| 4822 | trechadas | 1 |
| 4823 | trebejos | 1 |
| 4824 | tráyoles | 1 |
| 4825 | traylla | 1 |
| 4826 | traygo | 1 |
| 4827 | trayendo | 1 |
| 4828 | trayeme | 1 |
| 4829 | trayedes | 1 |
| 4830 | traydores | 1 |
| 4831 | trayas | 1 |
| 4832 | tray | 1 |
| 4833 | travó | 1 |
| 4834 | traviessa | 1 |
| 4835 | traviesos | 1 |
| 4836 | travesuras | 1 |
| 4837 | travesura | 1 |
| 4838 | traveseros | 1 |
| 4839 | travé | 1 |
| 4840 | travava | 1 |
| 4841 | travaron | 1 |
| 4842 | travar | 1 |
| 4843 | trával | 1 |
| 4844 | travadas | 1 |
| 4845 | trava | 1 |
| 4846 | trastorna | 1 |
| 4847 | traspuso | 1 |
| 4848 | traspassa | 1 |
| 4849 | trasnochadas | 1 |
| 4850 | trasnochada | 1 |
| 4851 | traslado | 1 |
| 4852 | trasfagos | 1 |
| 4853 | trascendental | 1 |
| 4854 | trascala | 1 |
| 4855 | transformaba | 1 |
| 4856 | transforma | 1 |
| 4857 | trançe | 1 |
| 4858 | trança | 1 |
| 4859 | tranca | 1 |
| 4860 | tramoyas | 1 |
| 4861 | tramasen | 1 |
| 4862 | trama | 1 |
| 4863 | trajo | 1 |
| 4864 | traía | 1 |
| 4865 | trahes | 1 |
| 4866 | traheré | 1 |
| 4867 | trahe | 1 |
| 4868 | tragonía | 1 |
| 4869 | tragas | 1 |
| 4870 | tragallos | 1 |
| 4871 | tragallo | 1 |
| 4872 | traéslos | 1 |
| 4873 | traeré | 1 |
| 4874 | traella | 1 |
| 4875 | traduce | 1 |
| 4876 | tradición | 1 |
| 4877 | trabazones | 1 |
| 4878 | trabar | 1 |
| 4879 | trabajedes | 1 |
| 4880 | trabajé | 1 |
| 4881 | trabajava | 1 |
| 4882 | trabajat | 1 |
| 4883 | trabajar | 1 |
| 4884 | trabajamos | 1 |
| 4885 | tóvose | 1 |
| 4886 | tóvos | 1 |
| 4887 | tovistes | 1 |
| 4888 | tovillos | 1 |
| 4889 | tovieses | 1 |
| 4890 | tovies | 1 |
| 4891 | tovieron | 1 |
| 4892 | tovieres | 1 |
| 4893 | toviera | 1 |
| 4894 | tóvel | 1 |
| 4895 | tove | 1 |
| 4896 | total | 1 |
| 4897 | tosino | 1 |
| 4898 | tos | 1 |
| 4899 | tórtolas | 1 |
| 4900 | torresno | 1 |
| 4901 | toronja | 1 |
| 4902 | tornóse | 1 |
| 4903 | tornóle | 1 |
| 4904 | torneses | 1 |
| 4905 | tórnese | 1 |
| 4906 | torneo | 1 |
| 4907 | tornedes | 1 |
| 4908 | tornear | 1 |
| 4909 | tornava | 1 |
| 4910 | tórnate | 1 |
| 4911 | tornas | 1 |
| 4912 | tornaríe | 1 |
| 4913 | tornares | 1 |
| 4914 | tornarán | 1 |
| 4915 | tornar | 1 |
| 4916 | tórnanse | 1 |
| 4917 | tornad | 1 |
| 4918 | torméntasle | 1 |
| 4919 | tormenta | 1 |
| 4920 | tordo | 1 |
| 4921 | tora | 1 |
| 4922 | tope | 1 |
| 4923 | tonadillas | 1 |
| 4924 | tonadas | 1 |
| 4925 | tomóme | 1 |
| 4926 | tomóm | 1 |
| 4927 | tomóla | 1 |
| 4928 | tomeste | 1 |
| 4929 | tómeme | 1 |
| 4930 | tómelo | 1 |
| 4931 | tome | 1 |
| 4932 | tomavan | 1 |
| 4933 | tomava | 1 |
| 4934 | tomatlo | 1 |
| 4935 | tomat | 1 |
| 4936 | tomaste | 1 |
| 4937 | tomasen | 1 |
| 4938 | tomarse | 1 |
| 4939 | tomáronlo | 1 |
| 4940 | tomará | 1 |
| 4941 | tómanse | 1 |
| 4942 | tomando | 1 |
| 4943 | tómalo | 1 |
| 4944 | tomados | 1 |
| 4945 | tolomeo | 1 |
| 4946 | tollidos | 1 |
| 4947 | toledos | 1 |
| 4948 | toledana | 1 |
| 4949 | tocón | 1 |
| 4950 | toco | 1 |
| 4951 | tocantes | 1 |
| 4952 | tocados | 1 |
| 4953 | tob | 1 |
| 4954 | tiróse | 1 |
| 4955 | tiró | 1 |
| 4956 | tirava | 1 |
| 4957 | tiraste | 1 |
| 4958 | tiraron | 1 |
| 4959 | tirare | 1 |
| 4960 | tirarán | 1 |
| 4961 | tirará | 1 |
| 4962 | tirar | 1 |
| 4963 | tirando | 1 |
| 4964 | tiran | 1 |
| 4965 | tiradvos | 1 |
| 4966 | tiñó | 1 |
| 4967 | tintas | 1 |
| 4968 | timor | 1 |
| 4969 | timet | 1 |
| 4970 | tiesta | 1 |
| 4971 | tiento | 1 |
| 4972 | tiénenlo | 1 |
| 4973 | tienenle | 1 |
| 4974 | tienblan | 1 |
| 4975 | tíen | 1 |
| 4976 | tíbi | 1 |
| 4977 | tiberio | 1 |
| 4978 | tholomeo | 1 |
| 4979 | thessoreros | 1 |
| 4980 | thesorero | 1 |
| 4981 | texto | 1 |
| 4982 | texido | 1 |
| 4983 | texedor | 1 |
| 4984 | tetástrofo | 1 |
| 4985 | tetas | 1 |
| 4986 | testos | 1 |
| 4987 | testimonio | 1 |
| 4988 | terrón | 1 |
| 4989 | terníe | 1 |
| 4990 | ternía | 1 |
| 4991 | terneras | 1 |
| 4992 | terná | 1 |
| 4993 | teresa | 1 |
| 4994 | terciar | 1 |
| 4995 | tercerones | 1 |
| 4996 | tercera | 1 |
| 4997 | teología | 1 |
| 4998 | teócrito | 1 |
| 4999 | tentaçión | 1 |
| 5000 | tenptaçiones | 1 |
| 5001 | tenpro | 1 |
| 5002 | tenpradas | 1 |
| 5003 | tenprad | 1 |
| 5004 | tenporal | 1 |
| 5005 | tenporadas | 1 |
| 5006 | tenporada | 1 |
| 5007 | tenplano | 1 |
| 5008 | tenplamiento | 1 |
| 5009 | tenlo | 1 |
| 5010 | teníen | 1 |
| 5011 | teníanse | 1 |
| 5012 | teníal | 1 |
| 5013 | teníades | 1 |
| 5014 | tení | 1 |
| 5015 | teni | 1 |
| 5016 | tengámoslo | 1 |
| 5017 | téngala | 1 |
| 5018 | tenert | 1 |
| 5019 | tenerlo | 1 |
| 5020 | tenerle | 1 |
| 5021 | tendióse | 1 |
| 5022 | tendiendo | 1 |
| 5023 | tendidos | 1 |
| 5024 | tender | 1 |
| 5025 | tendejones | 1 |
| 5026 | tenblores | 1 |
| 5027 | tenasas | 1 |
| 5028 | tenaças | 1 |
| 5029 | ten | 1 |
| 5030 | temiste | 1 |
| 5031 | temióte | 1 |
| 5032 | temiendo | 1 |
| 5033 | temí | 1 |
| 5034 | temerosas | 1 |
| 5035 | temerosa | 1 |
| 5036 | temeríe | 1 |
| 5037 | témense | 1 |
| 5038 | temedes | 1 |
| 5039 | temed | 1 |
| 5040 | temades | 1 |
| 5041 | telo | 1 |
| 5042 | telar | 1 |
| 5043 | tecum | 1 |
| 5044 | techo | 1 |
| 5045 | taverna | 1 |
| 5046 | távano | 1 |
| 5047 | tardó | 1 |
| 5048 | tardo | 1 |
| 5049 | tardineros | 1 |
| 5050 | tardía | 1 |
| 5051 | tardes | 1 |
| 5052 | tardamiento | 1 |
| 5053 | taravilla | 1 |
| 5054 | tapujos | 1 |
| 5055 | tapete | 1 |
| 5056 | tañen | 1 |
| 5057 | tant | 1 |
| 5058 | tanía | 1 |
| 5059 | tangan | 1 |
| 5060 | tanga | 1 |
| 5061 | taner | 1 |
| 5062 | tanbyén | 1 |
| 5063 | tanbyen | 1 |
| 5064 | también | 1 |
| 5065 | tamaños | 1 |
| 5066 | tamañas | 1 |
| 5067 | talyón | 1 |
| 5068 | talentos | 1 |
| 5069 | talento | 1 |
| 5070 | talaveranos | 1 |
| 5071 | tajones | 1 |
| 5072 | tajava | 1 |
| 5073 | tajadores | 1 |
| 5074 | tajadero | 1 |
| 5075 | tajada | 1 |
| 5076 | tahures | 1 |
| 5077 | tafurerias | 1 |
| 5078 | tachar | 1 |
| 5079 | tacendo | 1 |
| 5080 | taça | 1 |
| 5081 | taborete | 1 |
| 5082 | tabor | 1 |
| 5083 | tabletas | 1 |
| 5084 | tableros | 1 |
| 5085 | tablax | 1 |
| 5086 | tablas | 1 |
| 5087 | tablajeros | 1 |
| 5088 | tablajero | 1 |
| 5089 | tablagero | 1 |
| 5090 | syrviendo | 1 |
| 5091 | syrvela | 1 |
| 5092 | synventura | 1 |
| 5093 | synrazón | 1 |
| 5094 | synpleza | 1 |
| 5095 | sylvar | 1 |
| 5096 | sylva | 1 |
| 5097 | syllo | 1 |
| 5098 | syllas | 1 |
| 5099 | syguirán | 1 |
| 5100 | sygnos | 1 |
| 5101 | syete | 1 |
| 5102 | syesta | 1 |
| 5103 | syerva | 1 |
| 5104 | syerra | 1 |
| 5105 | syente | 1 |
| 5106 | syendo | 1 |
| 5107 | syenbra | 1 |
| 5108 | syempre | 1 |
| 5109 | suzidad | 1 |
| 5110 | suviste | 1 |
| 5111 | sustracción | 1 |
| 5112 | suscipe | 1 |
| 5113 | susaña | 1 |
| 5114 | surugiano | 1 |
| 5115 | suprimían | 1 |
| 5116 | supone | 1 |
| 5117 | suplido | 1 |
| 5118 | sufro | 1 |
| 5119 | sufría | 1 |
| 5120 | sufraja | 1 |
| 5121 | suficientes | 1 |
| 5122 | sueño | 1 |
| 5123 | sueña | 1 |
| 5124 | suenan | 1 |
| 5125 | sueles | 1 |
| 5126 | suélense | 1 |
| 5127 | suelas | 1 |
| 5128 | suegros | 1 |
| 5129 | suegras | 1 |
| 5130 | sudava | 1 |
| 5131 | sucedió | 1 |
| 5132 | suceder | 1 |
| 5133 | substituyéndole | 1 |
| 5134 | sublimemente | 1 |
| 5135 | sublime | 1 |
| 5136 | subjetivo | 1 |
| 5137 | subió | 1 |
| 5138 | subida | 1 |
| 5139 | suben | 1 |
| 5140 | súbditos | 1 |
| 5141 | súbante | 1 |
| 5142 | suavicen | 1 |
| 5143 | sua | 1 |
| 5144 | ssyl | 1 |
| 5145 | ssyga | 1 |
| 5146 | ssusiedad | 1 |
| 5147 | ssuerte | 1 |
| 5148 | ssoto | 1 |
| 5149 | ssotileza | 1 |
| 5150 | ssotierra | 1 |
| 5151 | ssospiros | 1 |
| 5152 | ssospecha | 1 |
| 5153 | ssoria | 1 |
| 5154 | ssopo | 1 |
| 5155 | ssonar | 1 |
| 5156 | ssoltura | 1 |
| 5157 | ssolás | 1 |
| 5158 | ssogas | 1 |
| 5159 | ssodes | 1 |
| 5160 | ssobervia | 1 |
| 5161 | ssiete | 1 |
| 5162 | ssevilla | 1 |
| 5163 | ssesos | 1 |
| 5164 | sseso | 1 |
| 5165 | sseñor | 1 |
| 5166 | ssenty | 1 |
| 5167 | ssenda | 1 |
| 5168 | ssenbré | 1 |
| 5169 | ssenbrar | 1 |
| 5170 | ssemejava | 1 |
| 5171 | sseméjasme | 1 |
| 5172 | ssellada | 1 |
| 5173 | sseguro | 1 |
| 5174 | ssegura | 1 |
| 5175 | ssegovia | 1 |
| 5176 | sseda | 1 |
| 5177 | ssecarás | 1 |
| 5178 | sseas | 1 |
| 5179 | ssávalos | 1 |
| 5180 | ssant | 1 |
| 5181 | ssangre | 1 |
| 5182 | ssangrar | 1 |
| 5183 | ssan | 1 |
| 5184 | ssalyó | 1 |
| 5185 | ssalvo | 1 |
| 5186 | ssalve | 1 |
| 5187 | ssalvar | 1 |
| 5188 | ssalió | 1 |
| 5189 | ssalga | 1 |
| 5190 | ssalen | 1 |
| 5191 | ssacóme | 1 |
| 5192 | ssácasla | 1 |
| 5193 | ssabuesos | 1 |
| 5194 | ssabría | 1 |
| 5195 | ssabores | 1 |
| 5196 | ssabios | 1 |
| 5197 | ssabido | 1 |
| 5198 | ssabedes | 1 |
| 5199 | ssabed | 1 |
| 5200 | spirital | 1 |
| 5201 | sovart | 1 |
| 5202 | sotylesa | 1 |
| 5203 | sotyl | 1 |
| 5204 | sotove | 1 |
| 5205 | sotos | 1 |
| 5206 | sotilezas | 1 |
| 5207 | sotilesa | 1 |
| 5208 | sotiéranlo | 1 |
| 5209 | soterremos | 1 |
| 5210 | soterrar | 1 |
| 5211 | soterraña | 1 |
| 5212 | soterné | 1 |
| 5213 | sotecho | 1 |
| 5214 | sota | 1 |
| 5215 | sostienta | 1 |
| 5216 | sossegar | 1 |
| 5217 | sossegado | 1 |
| 5218 | sossegada | 1 |
| 5219 | sospiré | 1 |
| 5220 | sospiravas | 1 |
| 5221 | sospira | 1 |
| 5222 | sospesas | 1 |
| 5223 | sospechosas | 1 |
| 5224 | sospeche | 1 |
| 5225 | sospechan | 1 |
| 5226 | sospecha | 1 |
| 5227 | sosegar | 1 |
| 5228 | sosegadvos | 1 |
| 5229 | sosegadas | 1 |
| 5230 | sosaños | 1 |
| 5231 | sosaño | 1 |
| 5232 | sosañar | 1 |
| 5233 | sosañada | 1 |
| 5234 | sos | 1 |
| 5235 | sortyja | 1 |
| 5236 | soria | 1 |
| 5237 | sordos | 1 |
| 5238 | sorda | 1 |
| 5239 | soprepujando | 1 |
| 5240 | sópom | 1 |
| 5241 | sopo | 1 |
| 5242 | sopitaña | 1 |
| 5243 | sopiesen | 1 |
| 5244 | sopiésedes | 1 |
| 5245 | sopiese | 1 |
| 5246 | sopiere | 1 |
| 5247 | sopessa | 1 |
| 5248 | sopesa | 1 |
| 5249 | soñava | 1 |
| 5250 | sonreyendo | 1 |
| 5251 | sonó | 1 |
| 5252 | sonete | 1 |
| 5253 | sonbriella | 1 |
| 5254 | sonbrero | 1 |
| 5255 | sonará | 1 |
| 5256 | somovióla | 1 |
| 5257 | somovimientos | 1 |
| 5258 | somosierra | 1 |
| 5259 | somo | 1 |
| 5260 | somióse | 1 |
| 5261 | somidas | 1 |
| 5262 | someten | 1 |
| 5263 | someros | 1 |
| 5264 | soma | 1 |
| 5265 | solyan | 1 |
| 5266 | soltura | 1 |
| 5267 | soltó | 1 |
| 5268 | soltera | 1 |
| 5269 | soltalde | 1 |
| 5270 | soltado | 1 |
| 5271 | sollo | 1 |
| 5272 | solitario | 1 |
| 5273 | solenidat | 1 |
| 5274 | soldadas | 1 |
| 5275 | solasar | 1 |
| 5276 | solar | 1 |
| 5277 | solapadas | 1 |
| 5278 | solapadamente | 1 |
| 5279 | solamiente | 1 |
| 5280 | sojorno | 1 |
| 5281 | soguilla | 1 |
| 5282 | soga | 1 |
| 5283 | sofrirte | 1 |
| 5284 | social | 1 |
| 5285 | socavados | 1 |
| 5286 | socarrón | 1 |
| 5287 | sobyr | 1 |
| 5288 | sobrino | 1 |
| 5289 | sobrina | 1 |
| 5290 | sobrevienta | 1 |
| 5291 | sobresolados | 1 |
| 5292 | sobresalieron | 1 |
| 5293 | sobresalientes | 1 |
| 5294 | sobresaliendo | 1 |
| 5295 | sobresalen | 1 |
| 5296 | sobrepuso | 1 |
| 5297 | sobreçejas | 1 |
| 5298 | sobrado | 1 |
| 5299 | sobr | 1 |
| 5300 | sobiese | 1 |
| 5301 | sobieron | 1 |
| 5302 | sobido | 1 |
| 5303 | sobida | 1 |
| 5304 | soberviosa | 1 |
| 5305 | sobervios | 1 |
| 5306 | sobervientas | 1 |
| 5307 | sobervi | 1 |
| 5308 | sobejos | 1 |
| 5309 | sobejas | 1 |
| 5310 | sobacos | 1 |
| 5311 | sobaco | 1 |
| 5312 | sirvo | 1 |
| 5313 | sirviríe | 1 |
| 5314 | sirviendo | 1 |
| 5315 | sinpre | 1 |
| 5316 | sinples | 1 |
| 5317 | sinple | 1 |
| 5318 | siniestra | 1 |
| 5319 | sine | 1 |
| 5320 | sinceridad | 1 |
| 5321 | silvó | 1 |
| 5322 | silos | 1 |
| 5323 | sillas | 1 |
| 5324 | sillares | 1 |
| 5325 | silla | 1 |
| 5326 | silinçio | 1 |
| 5327 | silere | 1 |
| 5328 | silencio | 1 |
| 5329 | siguió | 1 |
| 5330 | siguiese | 1 |
| 5331 | siguieron | 1 |
| 5332 | sigues | 1 |
| 5333 | sigo | 1 |
| 5334 | significado | 1 |
| 5335 | siga | 1 |
| 5336 | siervos | 1 |
| 5337 | siervo | 1 |
| 5338 | sientes | 1 |
| 5339 | sienpr | 1 |
| 5340 | sibias | 1 |
| 5341 | sevilla | 1 |
| 5342 | severas | 1 |
| 5343 | set | 1 |
| 5344 | sesudo | 1 |
| 5345 | servos | 1 |
| 5346 | servivos | 1 |
| 5347 | servirte | 1 |
| 5348 | servirt | 1 |
| 5349 | servió | 1 |
| 5350 | servímosle | 1 |
| 5351 | servimos | 1 |
| 5352 | serviera | 1 |
| 5353 | servientes | 1 |
| 5354 | servíe | 1 |
| 5355 | servidos | 1 |
| 5356 | servidores | 1 |
| 5357 | serviçios | 1 |
| 5358 | servian | 1 |
| 5359 | serven | 1 |
| 5360 | serrano | 1 |
| 5361 | serranilla | 1 |
| 5362 | serranía | 1 |
| 5363 | serpiente | 1 |
| 5364 | sermones | 1 |
| 5365 | sermón | 1 |
| 5366 | serios | 1 |
| 5367 | seria | 1 |
| 5368 | serena | 1 |
| 5369 | seremos | 1 |
| 5370 | sequuntur | 1 |
| 5371 | sepulcro | 1 |
| 5372 | septeno | 1 |
| 5373 | separado | 1 |
| 5374 | sepan | 1 |
| 5375 | sepades | 1 |
| 5376 | seo | 1 |
| 5377 | señuelo | 1 |
| 5378 | señorío | 1 |
| 5379 | señoreándole | 1 |
| 5380 | señeros | 1 |
| 5381 | señeras | 1 |
| 5382 | señera | 1 |
| 5383 | señalados | 1 |
| 5384 | señaladamente | 1 |
| 5385 | señala | 1 |
| 5386 | senuelo | 1 |
| 5387 | sentiría | 1 |
| 5388 | sentimientos | 1 |
| 5389 | sentimiento | 1 |
| 5390 | sentía | 1 |
| 5391 | sentenciosos | 1 |
| 5392 | sentencioso | 1 |
| 5393 | sentenciosa | 1 |
| 5394 | sentencias | 1 |
| 5395 | sentencia | 1 |
| 5396 | sensyllas | 1 |
| 5397 | sensaciones | 1 |
| 5398 | senores | 1 |
| 5399 | senor | 1 |
| 5400 | senderos | 1 |
| 5401 | sendebar | 1 |
| 5402 | sencillas | 1 |
| 5403 | senbrar | 1 |
| 5404 | senbrada | 1 |
| 5405 | semine | 1 |
| 5406 | semejava | 1 |
| 5407 | semejas | 1 |
| 5408 | semejará | 1 |
| 5409 | semejar | 1 |
| 5410 | semejança | 1 |
| 5411 | semejan | 1 |
| 5412 | semana | 1 |
| 5413 | selmana | 1 |
| 5414 | sellos | 1 |
| 5415 | sellados | 1 |
| 5416 | seguros | 1 |
| 5417 | seguramiente | 1 |
| 5418 | segur | 1 |
| 5419 | segundos | 1 |
| 5420 | según | 1 |
| 5421 | segun | 1 |
| 5422 | seguirla | 1 |
| 5423 | seguiré | 1 |
| 5424 | seguiéremos | 1 |
| 5425 | seguiente | 1 |
| 5426 | seguiendol | 1 |
| 5427 | seguidores | 1 |
| 5428 | seguidla | 1 |
| 5429 | seguían | 1 |
| 5430 | seguía | 1 |
| 5431 | segovia | 1 |
| 5432 | segidor | 1 |
| 5433 | segida | 1 |
| 5434 | segava | 1 |
| 5435 | sediento | 1 |
| 5436 | sede | 1 |
| 5437 | secundum | 1 |
| 5438 | sécanse | 1 |
| 5439 | séavos | 1 |
| 5440 | scolares | 1 |
| 5441 | sayón | 1 |
| 5442 | sayas | 1 |
| 5443 | savia | 1 |
| 5444 | sauses | 1 |
| 5445 | saúl | 1 |
| 5446 | satysfaçión | 1 |
| 5447 | satisfaçión | 1 |
| 5448 | satírica | 1 |
| 5449 | satán | 1 |
| 5450 | sasón | 1 |
| 5451 | sas | 1 |
| 5452 | sartas | 1 |
| 5453 | sartal | 1 |
| 5454 | sarta | 1 |
| 5455 | sarnosa | 1 |
| 5456 | sarmientos | 1 |
| 5457 | saqué | 1 |
| 5458 | saque | 1 |
| 5459 | sapientiæ | 1 |
| 5460 | sapiençia | 1 |
| 5461 | sañoso | 1 |
| 5462 | sañosa | 1 |
| 5463 | santolalla | 1 |
| 5464 | santillana | 1 |
| 5465 | santillán | 1 |
| 5466 | santiguávame | 1 |
| 5467 | santiguar | 1 |
| 5468 | santiga | 1 |
| 5469 | sanssón | 1 |
| 5470 | sanidat | 1 |
| 5471 | sangrientos | 1 |
| 5472 | sangrienta | 1 |
| 5473 | sangrías | 1 |
| 5474 | sangría | 1 |
| 5475 | sangr | 1 |
| 5476 | sanes | 1 |
| 5477 | sane | 1 |
| 5478 | sandía | 1 |
| 5479 | sancristán | 1 |
| 5480 | sancho | 1 |
| 5481 | sánchez | 1 |
| 5482 | sanar | 1 |
| 5483 | sanan | 1 |
| 5484 | salyrá | 1 |
| 5485 | salyda | 1 |
| 5486 | salvos | 1 |
| 5487 | salvó | 1 |
| 5488 | salves | 1 |
| 5489 | salvava | 1 |
| 5490 | sálvaslo | 1 |
| 5491 | salvarnos | 1 |
| 5492 | salvaría | 1 |
| 5493 | salvarás | 1 |
| 5494 | salvamiento | 1 |
| 5495 | salvajina | 1 |
| 5496 | saludó | 1 |
| 5497 | saludes | 1 |
| 5498 | salúdavos | 1 |
| 5499 | saludava | 1 |
| 5500 | saluda | 1 |
| 5501 | saltos | 1 |
| 5502 | salterios | 1 |
| 5503 | salteóm | 1 |
| 5504 | saltar | 1 |
| 5505 | saltando | 1 |
| 5506 | saltan | 1 |
| 5507 | salpreso | 1 |
| 5508 | salpresas | 1 |
| 5509 | salpresa | 1 |
| 5510 | salomón | 1 |
| 5511 | salmos | 1 |
| 5512 | salmo | 1 |
| 5513 | salirá | 1 |
| 5514 | salir | 1 |
| 5515 | saliéredes | 1 |
| 5516 | saliendo | 1 |
| 5517 | salie | 1 |
| 5518 | salidos | 1 |
| 5519 | salidas | 1 |
| 5520 | salgo | 1 |
| 5521 | salga | 1 |
| 5522 | saldrá | 1 |
| 5523 | salas | 1 |
| 5524 | salamo | 1 |
| 5525 | sagude | 1 |
| 5526 | saguda | 1 |
| 5527 | sagrados | 1 |
| 5528 | sagrado | 1 |
| 5529 | sagrada | 1 |
| 5530 | saeta | 1 |
| 5531 | saet | 1 |
| 5532 | sacudiendo | 1 |
| 5533 | sacrefiçios | 1 |
| 5534 | sacramentos | 1 |
| 5535 | sacol | 1 |
| 5536 | sacógelo | 1 |
| 5537 | saçerdotal | 1 |
| 5538 | sacástelo | 1 |
| 5539 | sacase | 1 |
| 5540 | sacarte | 1 |
| 5541 | sacaron | 1 |
| 5542 | sacarle | 1 |
| 5543 | sacaren | 1 |
| 5544 | sacaredes | 1 |
| 5545 | sacaré | 1 |
| 5546 | sacan | 1 |
| 5547 | sácame | 1 |
| 5548 | sácala | 1 |
| 5549 | sacado | 1 |
| 5550 | sacada | 1 |
| 5551 | sabyendas | 1 |
| 5552 | sabyençia | 1 |
| 5553 | sabyduría | 1 |
| 5554 | sabydores | 1 |
| 5555 | sabrosos | 1 |
| 5556 | sabrosa | 1 |
| 5557 | sabré | 1 |
| 5558 | saborado | 1 |
| 5559 | sabogas | 1 |
| 5560 | sabiente | 1 |
| 5561 | sabiençia | 1 |
| 5562 | sabíen | 1 |
| 5563 | sabíe | 1 |
| 5564 | sabie | 1 |
| 5565 | sabidos | 1 |
| 5566 | sabiamente | 1 |
| 5567 | sabeslas | 1 |
| 5568 | sabernos | 1 |
| 5569 | saberlos | 1 |
| 5570 | saberlo | 1 |
| 5571 | sabençia | 1 |
| 5572 | sábelo | 1 |
| 5573 | sábelas | 1 |
| 5574 | sabçe | 1 |
| 5575 | sabado | 1 |
| 5576 | sa | 1 |
| 5577 | ryos | 1 |
| 5578 | ryome | 1 |
| 5579 | ryncón | 1 |
| 5580 | ryma | 1 |
| 5581 | rye | 1 |
| 5582 | ryco | 1 |
| 5583 | ryca | 1 |
| 5584 | ruyz | 1 |
| 5585 | ruyseñores | 1 |
| 5586 | rumiar | 1 |
| 5587 | rugiente | 1 |
| 5588 | ruegas | 1 |
| 5589 | ruegal | 1 |
| 5590 | ruega | 1 |
| 5591 | rueda | 1 |
| 5592 | rrysueña | 1 |
| 5593 | rruysynor | 1 |
| 5594 | rruydo | 1 |
| 5595 | rruybarvo | 1 |
| 5596 | rrumiar | 1 |
| 5597 | rruégovos | 1 |
| 5598 | rruegos | 1 |
| 5599 | rruéganle | 1 |
| 5600 | rruegan | 1 |
| 5601 | rruegal | 1 |
| 5602 | rrudos | 1 |
| 5603 | rrudeza | 1 |
| 5604 | rruçío | 1 |
| 5605 | rrúçio | 1 |
| 5606 | rruby | 1 |
| 5607 | rroysyñor | 1 |
| 5608 | rroydos | 1 |
| 5609 | rroto | 1 |
| 5610 | rrotas | 1 |
| 5611 | rrota | 1 |
| 5612 | rrostros | 1 |
| 5613 | rrosata | 1 |
| 5614 | rrosario | 1 |
| 5615 | rrondón | 1 |
| 5616 | rronda | 1 |
| 5617 | rronçesvalles | 1 |
| 5618 | rromero | 1 |
| 5619 | rromerías | 1 |
| 5620 | rromería | 1 |
| 5621 | rromanze | 1 |
| 5622 | rroldán | 1 |
| 5623 | rrogueste | 1 |
| 5624 | rrogó | 1 |
| 5625 | rrogele | 1 |
| 5626 | rrogela | 1 |
| 5627 | rrogarle | 1 |
| 5628 | rrogándote | 1 |
| 5629 | rrogamos | 1 |
| 5630 | rroer | 1 |
| 5631 | rroe | 1 |
| 5632 | rrodillas | 1 |
| 5633 | rrodilla | 1 |
| 5634 | rrodesno | 1 |
| 5635 | rrodas | 1 |
| 5636 | rrodando | 1 |
| 5637 | rroby | 1 |
| 5638 | rroble | 1 |
| 5639 | rrobas | 1 |
| 5640 | rroban | 1 |
| 5641 | rrixo | 1 |
| 5642 | rrisetes | 1 |
| 5643 | rriquesas | 1 |
| 5644 | rriplicaçiones | 1 |
| 5645 | rriofrío | 1 |
| 5646 | rrientes | 1 |
| 5647 | rríen | 1 |
| 5648 | rriega | 1 |
| 5649 | rricamente | 1 |
| 5650 | rribaldo | 1 |
| 5651 | rreyres | 1 |
| 5652 | rreyerien | 1 |
| 5653 | rreyendo | 1 |
| 5654 | rreye | 1 |
| 5655 | rrevolviendo | 1 |
| 5656 | rrevierta | 1 |
| 5657 | rreveses | 1 |
| 5658 | rrevatado | 1 |
| 5659 | rretuvo | 1 |
| 5660 | rretrayda | 1 |
| 5661 | rretraya | 1 |
| 5662 | rretraes | 1 |
| 5663 | rretraer | 1 |
| 5664 | rretorno | 1 |
| 5665 | rretoçando | 1 |
| 5666 | rretientas | 1 |
| 5667 | rreteñir | 1 |
| 5668 | rretentóle | 1 |
| 5669 | rretentar | 1 |
| 5670 | rretenientes | 1 |
| 5671 | rretaço | 1 |
| 5672 | rrestrojos | 1 |
| 5673 | rresses | 1 |
| 5674 | rrespuestas | 1 |
| 5675 | rrespondióme | 1 |
| 5676 | rrespondile | 1 |
| 5677 | rrespondieron | 1 |
| 5678 | rrespondiera | 1 |
| 5679 | rresponderán | 1 |
| 5680 | rresponden | 1 |
| 5681 | rresponde | 1 |
| 5682 | rrespondades | 1 |
| 5683 | rresplandesçería | 1 |
| 5684 | rresplandesçer | 1 |
| 5685 | rresio | 1 |
| 5686 | rreses | 1 |
| 5687 | rresellosa | 1 |
| 5688 | rresçibo | 1 |
| 5689 | rresçibióme | 1 |
| 5690 | rresçibiéronle | 1 |
| 5691 | rresçibieron | 1 |
| 5692 | rresçibidas | 1 |
| 5693 | rresçibida | 1 |
| 5694 | rresçibían | 1 |
| 5695 | rresçibe | 1 |
| 5696 | rresçélome | 1 |
| 5697 | rresçelades | 1 |
| 5698 | rresçebyr | 1 |
| 5699 | rresçebirlos | 1 |
| 5700 | rresçebirle | 1 |
| 5701 | rresçebiól | 1 |
| 5702 | rresçebidas | 1 |
| 5703 | rresaron | 1 |
| 5704 | rresaré | 1 |
| 5705 | rrequerida | 1 |
| 5706 | rrequena | 1 |
| 5707 | rrepuntan | 1 |
| 5708 | rrepunta | 1 |
| 5709 | rrepuesto | 1 |
| 5710 | rrepuesta | 1 |
| 5711 | rrepto | 1 |
| 5712 | rreportorio | 1 |
| 5713 | rrepiso | 1 |
| 5714 | rrepiente | 1 |
| 5715 | rrepetido | 1 |
| 5716 | rrepeso | 1 |
| 5717 | rrepara | 1 |
| 5718 | rreñidor | 1 |
| 5719 | rreñid | 1 |
| 5720 | rrenuevo | 1 |
| 5721 | rrenta | 1 |
| 5722 | rrensyllas | 1 |
| 5723 | rrensilla | 1 |
| 5724 | rrensellosa | 1 |
| 5725 | rrenir | 1 |
| 5726 | rrencor | 1 |
| 5727 | rrençilla | 1 |
| 5728 | rremira | 1 |
| 5729 | rremesçe | 1 |
| 5730 | rremendar | 1 |
| 5731 | rremenbrança | 1 |
| 5732 | rrematar | 1 |
| 5733 | rrematan | 1 |
| 5734 | rremaneçiste | 1 |
| 5735 | rrelusíe | 1 |
| 5736 | rrelijosas | 1 |
| 5737 | rreligioso | 1 |
| 5738 | rreligiosas | 1 |
| 5739 | rreligiosa | 1 |
| 5740 | rrehiertas | 1 |
| 5741 | rrehertero | 1 |
| 5742 | rrehertado | 1 |
| 5743 | rrehazer | 1 |
| 5744 | rrehallas | 1 |
| 5745 | rreguardava | 1 |
| 5746 | rreguarda | 1 |
| 5747 | rregno | 1 |
| 5748 | rregnando | 1 |
| 5749 | rregistro | 1 |
| 5750 | rregava | 1 |
| 5751 | rregateras | 1 |
| 5752 | rregañada | 1 |
| 5753 | rregaço | 1 |
| 5754 | rrefusando | 1 |
| 5755 | rrefitorios | 1 |
| 5756 | rrefitor | 1 |
| 5757 | rrefierto | 1 |
| 5758 | rrefezes | 1 |
| 5759 | rrefés | 1 |
| 5760 | rreferteras | 1 |
| 5761 | rrefaze | 1 |
| 5762 | rrefases | 1 |
| 5763 | rredréme | 1 |
| 5764 | rredrado | 1 |
| 5765 | rredrada | 1 |
| 5766 | rredondos | 1 |
| 5767 | rredondo | 1 |
| 5768 | rredero | 1 |
| 5769 | rrecudyr | 1 |
| 5770 | rrecudas | 1 |
| 5771 | rrecuda | 1 |
| 5772 | rrecreçer | 1 |
| 5773 | rreconvençión | 1 |
| 5774 | rrecíbenle | 1 |
| 5775 | rrecelose | 1 |
| 5776 | rreçeledes | 1 |
| 5777 | rreçelan | 1 |
| 5778 | rrecaudo | 1 |
| 5779 | rreçando | 1 |
| 5780 | rrecado | 1 |
| 5781 | rrecabo | 1 |
| 5782 | rrecabdos | 1 |
| 5783 | rrecabdo | 1 |
| 5784 | rrecabdeste | 1 |
| 5785 | rrecabdava | 1 |
| 5786 | rrecabdan | 1 |
| 5787 | rrecabdamos | 1 |
| 5788 | rrecabado | 1 |
| 5789 | rrecaba | 1 |
| 5790 | rrebuznar | 1 |
| 5791 | rrebuélveslo | 1 |
| 5792 | rrebtedes | 1 |
| 5793 | rrebtado | 1 |
| 5794 | rrebolvedor | 1 |
| 5795 | rrebevió | 1 |
| 5796 | rrebató | 1 |
| 5797 | rrebatado | 1 |
| 5798 | rrebatadas | 1 |
| 5799 | rreales | 1 |
| 5800 | rreal | 1 |
| 5801 | rrazones | 1 |
| 5802 | rrays | 1 |
| 5803 | rrayo | 1 |
| 5804 | rraviosa | 1 |
| 5805 | rraviará | 1 |
| 5806 | rratiello | 1 |
| 5807 | rrastrojo | 1 |
| 5808 | rrastro | 1 |
| 5809 | rrasonaron | 1 |
| 5810 | rrasonar | 1 |
| 5811 | rrason | 1 |
| 5812 | rrasgaredes | 1 |
| 5813 | rrascan | 1 |
| 5814 | rrasa | 1 |
| 5815 | rraposya | 1 |
| 5816 | rraposo | 1 |
| 5817 | rraposilla | 1 |
| 5818 | rrapáz | 1 |
| 5819 | rrapás | 1 |
| 5820 | rrando | 1 |
| 5821 | rralas | 1 |
| 5822 | rrahez | 1 |
| 5823 | rrafezes | 1 |
| 5824 | rradío | 1 |
| 5825 | rradía | 1 |
| 5826 | rraçiones | 1 |
| 5827 | rraça | 1 |
| 5828 | rraby | 1 |
| 5829 | rrabíes | 1 |
| 5830 | rrabí | 1 |
| 5831 | rotos | 1 |
| 5832 | rostro | 1 |
| 5833 | rose | 1 |
| 5834 | rosas | 1 |
| 5835 | ronco | 1 |
| 5836 | ronca | 1 |
| 5837 | rompió | 1 |
| 5838 | romeros | 1 |
| 5839 | romanos | 1 |
| 5840 | romano | 1 |
| 5841 | romançe | 1 |
| 5842 | romance | 1 |
| 5843 | roman | 1 |
| 5844 | rojas | 1 |
| 5845 | rogué | 1 |
| 5846 | rogóme | 1 |
| 5847 | rogavan | 1 |
| 5848 | rogava | 1 |
| 5849 | rogaron | 1 |
| 5850 | rodré | 1 |
| 5851 | rodeóme | 1 |
| 5852 | rodar | 1 |
| 5853 | roçapoco | 1 |
| 5854 | roça | 1 |
| 5855 | robré | 1 |
| 5856 | robo | 1 |
| 5857 | rixo | 1 |
| 5858 | ritmos | 1 |
| 5859 | risueña | 1 |
| 5860 | risuena | 1 |
| 5861 | riso | 1 |
| 5862 | risete | 1 |
| 5863 | risco | 1 |
| 5864 | riquesa | 1 |
| 5865 | riñosas | 1 |
| 5866 | rimar | 1 |
| 5867 | ricome | 1 |
| 5868 | ribera | 1 |
| 5869 | ribalde | 1 |
| 5870 | rezó | 1 |
| 5871 | rezo | 1 |
| 5872 | rezar | 1 |
| 5873 | reyr | 1 |
| 5874 | reynos | 1 |
| 5875 | reynas | 1 |
| 5876 | reyentes | 1 |
| 5877 | rex | 1 |
| 5878 | revolucionario | 1 |
| 5879 | revolucionaria | 1 |
| 5880 | revés | 1 |
| 5881 | reventazón | 1 |
| 5882 | revatamiento | 1 |
| 5883 | retraer | 1 |
| 5884 | retorcido | 1 |
| 5885 | retiñendo | 1 |
| 5886 | retiente | 1 |
| 5887 | retentar | 1 |
| 5888 | retaçar | 1 |
| 5889 | resume | 1 |
| 5890 | responsión | 1 |
| 5891 | respondiolos | 1 |
| 5892 | respondióles | 1 |
| 5893 | respondieron | 1 |
| 5894 | respondí | 1 |
| 5895 | respondería | 1 |
| 5896 | responden | 1 |
| 5897 | responde | 1 |
| 5898 | responda | 1 |
| 5899 | resplandeçiente | 1 |
| 5900 | respeto | 1 |
| 5901 | respectivamente | 1 |
| 5902 | resonando | 1 |
| 5903 | resolló | 1 |
| 5904 | resio | 1 |
| 5905 | resçibida | 1 |
| 5906 | resçelé | 1 |
| 5907 | resçebido | 1 |
| 5908 | reptar | 1 |
| 5909 | representaciones | 1 |
| 5910 | representación | 1 |
| 5911 | repito | 1 |
| 5912 | repican | 1 |
| 5913 | repetirvos | 1 |
| 5914 | repega | 1 |
| 5915 | reparar | 1 |
| 5916 | repara | 1 |
| 5917 | reñir | 1 |
| 5918 | reñiendo | 1 |
| 5919 | renunçiaría | 1 |
| 5920 | renta | 1 |
| 5921 | rensilla | 1 |
| 5922 | renda | 1 |
| 5923 | rencores | 1 |
| 5924 | rencor | 1 |
| 5925 | renacimiento | 1 |
| 5926 | remota | 1 |
| 5927 | remos | 1 |
| 5928 | remírase | 1 |
| 5929 | remeçe | 1 |
| 5930 | remanga | 1 |
| 5931 | reluze | 1 |
| 5932 | relusiente | 1 |
| 5933 | reluçientes | 1 |
| 5934 | religioso | 1 |
| 5935 | religiosa | 1 |
| 5936 | religión | 1 |
| 5937 | reina | 1 |
| 5938 | regocijos | 1 |
| 5939 | regocijado | 1 |
| 5940 | regno | 1 |
| 5941 | regla | 1 |
| 5942 | región | 1 |
| 5943 | regina | 1 |
| 5944 | refrenar | 1 |
| 5945 | refleja | 1 |
| 5946 | refertyr | 1 |
| 5947 | reduçir | 1 |
| 5948 | reduce | 1 |
| 5949 | redruejas | 1 |
| 5950 | redrar | 1 |
| 5951 | redes | 1 |
| 5952 | reddes | 1 |
| 5953 | recudieron | 1 |
| 5954 | recte | 1 |
| 5955 | recordar | 1 |
| 5956 | reconvenyr | 1 |
| 5957 | reconvençión | 1 |
| 5958 | reciura | 1 |
| 5959 | reçios | 1 |
| 5960 | reçiamente | 1 |
| 5961 | reçevirlo | 1 |
| 5962 | reçebir | 1 |
| 5963 | recata | 1 |
| 5964 | reçando | 1 |
| 5965 | recabo | 1 |
| 5966 | recabé | 1 |
| 5967 | recabdó | 1 |
| 5968 | recabdares | 1 |
| 5969 | recabdar | 1 |
| 5970 | recabdado | 1 |
| 5971 | rebusnar | 1 |
| 5972 | rebusnando | 1 |
| 5973 | rebatada | 1 |
| 5974 | rebata | 1 |
| 5975 | realista | 1 |
| 5976 | realidades | 1 |
| 5977 | razones | 1 |
| 5978 | razonar | 1 |
| 5979 | raza | 1 |
| 5980 | rayzes | 1 |
| 5981 | rayz | 1 |
| 5982 | raynela | 1 |
| 5983 | rayado | 1 |
| 5984 | ravia | 1 |
| 5985 | rastrojo | 1 |
| 5986 | rasión | 1 |
| 5987 | rascaña | 1 |
| 5988 | rascador | 1 |
| 5989 | rapossa | 1 |
| 5990 | rapaça | 1 |
| 5991 | ramos | 1 |
| 5992 | ramo | 1 |
| 5993 | ralo | 1 |
| 5994 | raheses | 1 |
| 5995 | ración | 1 |
| 5996 | raças | 1 |
| 5997 | rabygalga | 1 |
| 5998 | rabiosa | 1 |
| 5999 | rabadán | 1 |
| 6000 | quomodo | 1 |
| 6001 | quixotes | 1 |
| 6002 | quiteria | 1 |
| 6003 | quítate | 1 |
| 6004 | quitat | 1 |
| 6005 | quisyese | 1 |
| 6006 | quisyeres | 1 |
| 6007 | quisome | 1 |
| 6008 | quísole | 1 |
| 6009 | quisistes | 1 |
| 6010 | quisiesse | 1 |
| 6011 | quisieren | 1 |
| 6012 | quisicosa | 1 |
| 6013 | quisá | 1 |
| 6014 | quintero | 1 |
| 6015 | quinta | 1 |
| 6016 | quima | 1 |
| 6017 | quijote | 1 |
| 6018 | quigéredes | 1 |
| 6019 | quiérovos | 1 |
| 6020 | quierovos | 1 |
| 6021 | quiérom | 1 |
| 6022 | quiérolas | 1 |
| 6023 | quiérente | 1 |
| 6024 | quiérem | 1 |
| 6025 | quiérasme | 1 |
| 6026 | quiérala | 1 |
| 6027 | quiebre | 1 |
| 6028 | quibus | 1 |
| 6029 | quexóse | 1 |
| 6030 | quexan | 1 |
| 6031 | quexades | 1 |
| 6032 | quevedesca | 1 |
| 6033 | quesyste | 1 |
| 6034 | quesuelos | 1 |
| 6035 | questiones | 1 |
| 6036 | quessiese | 1 |
| 6037 | quésome | 1 |
| 6038 | quesistes | 1 |
| 6039 | quesieron | 1 |
| 6040 | quese | 1 |
| 6041 | querríes | 1 |
| 6042 | querríedes | 1 |
| 6043 | querrías | 1 |
| 6044 | querríades | 1 |
| 6045 | querrello | 1 |
| 6046 | querrán | 1 |
| 6047 | queriéndolos | 1 |
| 6048 | queriéndol | 1 |
| 6049 | queríe | 1 |
| 6050 | queridos | 1 |
| 6051 | querido | 1 |
| 6052 | querida | 1 |
| 6053 | queríamos | 1 |
| 6054 | queríalos | 1 |
| 6055 | queríalo | 1 |
| 6056 | querí | 1 |
| 6057 | queretnos | 1 |
| 6058 | queretmos | 1 |
| 6059 | queret | 1 |
| 6060 | queremos | 1 |
| 6061 | querellarse | 1 |
| 6062 | queréllanse | 1 |
| 6063 | querellándos | 1 |
| 6064 | quereldo | 1 |
| 6065 | queredla | 1 |
| 6066 | quequiera | 1 |
| 6067 | quepa | 1 |
| 6068 | quémasle | 1 |
| 6069 | quemado | 1 |
| 6070 | quemadas | 1 |
| 6071 | quem | 1 |
| 6072 | quedos | 1 |
| 6073 | quedó | 1 |
| 6074 | quedillo | 1 |
| 6075 | quedava | 1 |
| 6076 | quedas | 1 |
| 6077 | quedar | 1 |
| 6078 | quedan | 1 |
| 6079 | quedado | 1 |
| 6080 | queças | 1 |
| 6081 | queça | 1 |
| 6082 | quebredes | 1 |
| 6083 | quebraría | 1 |
| 6084 | quebraria | 1 |
| 6085 | quebrará | 1 |
| 6086 | quebrantos | 1 |
| 6087 | quebrantó | 1 |
| 6088 | quebrantan | 1 |
| 6089 | quebrantado | 1 |
| 6090 | quebrantada | 1 |
| 6091 | queblantedes | 1 |
| 6092 | queblantada | 1 |
| 6093 | quatorçe | 1 |
| 6094 | quasi | 1 |
| 6095 | quartero | 1 |
| 6096 | quaresm | 1 |
| 6097 | quarenta | 1 |
| 6098 | quánta | 1 |
| 6099 | quanta | 1 |
| 6100 | quant | 1 |
| 6101 | quándo | 1 |
| 6102 | qualsequier | 1 |
| 6103 | quærite | 1 |
| 6104 | quæ | 1 |
| 6105 | quadrupea | 1 |
| 6106 | quadrillos | 1 |
| 6107 | quadrilla | 1 |
| 6108 | quadriles | 1 |
| 6109 | quadriella | 1 |
| 6110 | quadrado | 1 |
| 6111 | quadernos | 1 |
| 6112 | quaderna | 1 |
| 6113 | pytofleras | 1 |
| 6114 | pyñones | 1 |
| 6115 | pyntóle | 1 |
| 6116 | pyntol | 1 |
| 6117 | pynté | 1 |
| 6118 | pyntase | 1 |
| 6119 | pyntalla | 1 |
| 6120 | pyntada | 1 |
| 6121 | pyno | 1 |
| 6122 | pynar | 1 |
| 6123 | pydote | 1 |
| 6124 | pússome | 1 |
| 6125 | pusso | 1 |
| 6126 | púsonos | 1 |
| 6127 | púsome | 1 |
| 6128 | púsole | 1 |
| 6129 | púsola | 1 |
| 6130 | pusle | 1 |
| 6131 | pusiste | 1 |
| 6132 | pusiese | 1 |
| 6133 | pus | 1 |
| 6134 | purgatorio | 1 |
| 6135 | purgando | 1 |
| 6136 | puras | 1 |
| 6137 | puño | 1 |
| 6138 | puñé | 1 |
| 6139 | puñados | 1 |
| 6140 | puñada | 1 |
| 6141 | puña | 1 |
| 6142 | puntarme | 1 |
| 6143 | puntares | 1 |
| 6144 | punta | 1 |
| 6145 | puno | 1 |
| 6146 | punir | 1 |
| 6147 | puné | 1 |
| 6148 | punase | 1 |
| 6149 | punan | 1 |
| 6150 | puna | 1 |
| 6151 | pulsa | 1 |
| 6152 | pulpo | 1 |
| 6153 | pulió | 1 |
| 6154 | pujaste | 1 |
| 6155 | pujada | 1 |
| 6156 | puja | 1 |
| 6157 | puez | 1 |
| 6158 | puerte | 1 |
| 6159 | puerro | 1 |
| 6160 | puédevos | 1 |
| 6161 | puédense | 1 |
| 6162 | puédelo | 1 |
| 6163 | puédel | 1 |
| 6164 | pueblos | 1 |
| 6165 | pueble | 1 |
| 6166 | puebla | 1 |
| 6167 | pudren | 1 |
| 6168 | pudiesen | 1 |
| 6169 | pudiese | 1 |
| 6170 | pudieres | 1 |
| 6171 | pudía | 1 |
| 6172 | publicado | 1 |
| 6173 | psicológico | 1 |
| 6174 | psalmo | 1 |
| 6175 | prymera | 1 |
| 6176 | pruévolo | 1 |
| 6177 | pruevo | 1 |
| 6178 | pruévalo | 1 |
| 6179 | prudencia | 1 |
| 6180 | proyecho | 1 |
| 6181 | provorás | 1 |
| 6182 | provólo | 1 |
| 6183 | provincia | 1 |
| 6184 | proveste | 1 |
| 6185 | proverbyo | 1 |
| 6186 | proverbios | 1 |
| 6187 | provéme | 1 |
| 6188 | provélo | 1 |
| 6189 | provechossa | 1 |
| 6190 | provechosas | 1 |
| 6191 | provechos | 1 |
| 6192 | provea | 1 |
| 6193 | prové | 1 |
| 6194 | provarse | 1 |
| 6195 | provares | 1 |
| 6196 | provaredes | 1 |
| 6197 | provare | 1 |
| 6198 | provadlo | 1 |
| 6199 | protagonista | 1 |
| 6200 | prosas | 1 |
| 6201 | prosaico | 1 |
| 6202 | propusso | 1 |
| 6203 | propósito | 1 |
| 6204 | propongo | 1 |
| 6205 | propingos | 1 |
| 6206 | propiedat | 1 |
| 6207 | propiedades | 1 |
| 6208 | propiamente | 1 |
| 6209 | propiadat | 1 |
| 6210 | propia | 1 |
| 6211 | pronunçio | 1 |
| 6212 | pronunçie | 1 |
| 6213 | pronunciando | 1 |
| 6214 | pronunçiaçión | 1 |
| 6215 | promisiones | 1 |
| 6216 | promisión | 1 |
| 6217 | promety | 1 |
| 6218 | prometióles | 1 |
| 6219 | prometióle | 1 |
| 6220 | prometiól | 1 |
| 6221 | prometió | 1 |
| 6222 | prometil | 1 |
| 6223 | prometieres | 1 |
| 6224 | prometíe | 1 |
| 6225 | prometes | 1 |
| 6226 | prométeme | 1 |
| 6227 | prometem | 1 |
| 6228 | prometedes | 1 |
| 6229 | prometas | 1 |
| 6230 | prometades | 1 |
| 6231 | prometa | 1 |
| 6232 | prólogo | 1 |
| 6233 | profundo | 1 |
| 6234 | profunda | 1 |
| 6235 | proficias | 1 |
| 6236 | proffeçía | 1 |
| 6237 | profetizado | 1 |
| 6238 | profetas | 1 |
| 6239 | profesas | 1 |
| 6240 | profectas | 1 |
| 6241 | profeçías | 1 |
| 6242 | profeçía | 1 |
| 6243 | producciones | 1 |
| 6244 | prodigalidad | 1 |
| 6245 | procuraçiones | 1 |
| 6246 | proclama | 1 |
| 6247 | proçesso | 1 |
| 6248 | proçeso | 1 |
| 6249 | proceso | 1 |
| 6250 | proçesiones | 1 |
| 6251 | probedat | 1 |
| 6252 | pró | 1 |
| 6253 | prizes | 1 |
| 6254 | privados | 1 |
| 6255 | prisso | 1 |
| 6256 | prisionado | 1 |
| 6257 | prisco | 1 |
| 6258 | prisa | 1 |
| 6259 | principio | 1 |
| 6260 | principal | 1 |
| 6261 | primos | 1 |
| 6262 | primeras | 1 |
| 6263 | prietos | 1 |
| 6264 | prieta | 1 |
| 6265 | priesas | 1 |
| 6266 | priesa | 1 |
| 6267 | priegos | 1 |
| 6268 | priado | 1 |
| 6269 | previsión | 1 |
| 6270 | pretendió | 1 |
| 6271 | presuras | 1 |
| 6272 | prestóle | 1 |
| 6273 | prestará | 1 |
| 6274 | prestado | 1 |
| 6275 | presno | 1 |
| 6276 | presiste | 1 |
| 6277 | presiese | 1 |
| 6278 | presentól | 1 |
| 6279 | presentes | 1 |
| 6280 | presentava | 1 |
| 6281 | presenta | 1 |
| 6282 | presençia | 1 |
| 6283 | prescindir | 1 |
| 6284 | preñada | 1 |
| 6285 | prendiól | 1 |
| 6286 | prendió | 1 |
| 6287 | prendieron | 1 |
| 6288 | prendiendo | 1 |
| 6289 | prendíe | 1 |
| 6290 | prendedero | 1 |
| 6291 | prendas | 1 |
| 6292 | prenada | 1 |
| 6293 | prejuro | 1 |
| 6294 | preguntóme | 1 |
| 6295 | preguntóle | 1 |
| 6296 | preguntéle | 1 |
| 6297 | pregunté | 1 |
| 6298 | preguntarle | 1 |
| 6299 | preguntara | 1 |
| 6300 | preguntar | 1 |
| 6301 | pregones | 1 |
| 6302 | pregonero | 1 |
| 6303 | pregonedes | 1 |
| 6304 | pregón | 1 |
| 6305 | preferible | 1 |
| 6306 | predístesle | 1 |
| 6307 | predicaçiones | 1 |
| 6308 | predicación | 1 |
| 6309 | preçioso | 1 |
| 6310 | preçiedes | 1 |
| 6311 | preçiava | 1 |
| 6312 | preçiará | 1 |
| 6313 | preciará | 1 |
| 6314 | préçiala | 1 |
| 6315 | preçiadas | 1 |
| 6316 | preciada | 1 |
| 6317 | precia | 1 |
| 6318 | preçes | 1 |
| 6319 | preces | 1 |
| 6320 | precedió | 1 |
| 6321 | prebenda | 1 |
| 6322 | prea | 1 |
| 6323 | praser | 1 |
| 6324 | prados | 1 |
| 6325 | practico | 1 |
| 6326 | pozos | 1 |
| 6327 | poyo | 1 |
| 6328 | potrillo | 1 |
| 6329 | potestades | 1 |
| 6330 | potest | 1 |
| 6331 | postura | 1 |
| 6332 | postiza | 1 |
| 6333 | postilla | 1 |
| 6334 | postema | 1 |
| 6335 | postas | 1 |
| 6336 | post | 1 |
| 6337 | possaríe | 1 |
| 6338 | possada | 1 |
| 6339 | posó | 1 |
| 6340 | posístete | 1 |
| 6341 | posistes | 1 |
| 6342 | posiste | 1 |
| 6343 | posiéronle | 1 |
| 6344 | posee | 1 |
| 6345 | posar | 1 |
| 6346 | posadería | 1 |
| 6347 | porydat | 1 |
| 6348 | portillo | 1 |
| 6349 | portiellos | 1 |
| 6350 | portaré | 1 |
| 6351 | portadgo | 1 |
| 6352 | porra | 1 |
| 6353 | porquerizo | 1 |
| 6354 | poridades | 1 |
| 6355 | poridad | 1 |
| 6356 | porfya | 1 |
| 6357 | porfiosos | 1 |
| 6358 | porfioso | 1 |
| 6359 | porfiedes | 1 |
| 6360 | porfías | 1 |
| 6361 | porfias | 1 |
| 6362 | porfiar | 1 |
| 6363 | porfiando | 1 |
| 6364 | porfían | 1 |
| 6365 | porfaçaría | 1 |
| 6366 | porfaçaba | 1 |
| 6367 | pór | 1 |
| 6368 | poquyllo | 1 |
| 6369 | poquillas | 1 |
| 6370 | poquiello | 1 |
| 6371 | populares | 1 |
| 6372 | popa | 1 |
| 6373 | poniéndose | 1 |
| 6374 | poníe | 1 |
| 6375 | ponía | 1 |
| 6376 | póngolo | 1 |
| 6377 | pongelo | 1 |
| 6378 | ponga | 1 |
| 6379 | póneslos | 1 |
| 6380 | pónelo | 1 |
| 6381 | ponçoñar | 1 |
| 6382 | ponçoña | 1 |
| 6383 | pompa | 1 |
| 6384 | polvos | 1 |
| 6385 | polvo | 1 |
| 6386 | polso | 1 |
| 6387 | polo | 1 |
| 6388 | pollo | 1 |
| 6389 | políticas | 1 |
| 6390 | polifemo | 1 |
| 6391 | poetillas | 1 |
| 6392 | podríe | 1 |
| 6393 | podridos | 1 |
| 6394 | podrias | 1 |
| 6395 | podrian | 1 |
| 6396 | podri | 1 |
| 6397 | podredes | 1 |
| 6398 | podré | 1 |
| 6399 | podiste | 1 |
| 6400 | podiesse | 1 |
| 6401 | podíese | 1 |
| 6402 | podieren | 1 |
| 6403 | podierdes | 1 |
| 6404 | podíen | 1 |
| 6405 | podi | 1 |
| 6406 | podervos | 1 |
| 6407 | poderosso | 1 |
| 6408 | poderosa | 1 |
| 6409 | poderíos | 1 |
| 6410 | poderes | 1 |
| 6411 | podencos | 1 |
| 6412 | podémoslos | 1 |
| 6413 | pode | 1 |
| 6414 | podar | 1 |
| 6415 | podamos | 1 |
| 6416 | podades | 1 |
| 6417 | pobló | 1 |
| 6418 | pobleza | 1 |
| 6419 | pobles | 1 |
| 6420 | pobledat | 1 |
| 6421 | poblarla | 1 |
| 6422 | poblados | 1 |
| 6423 | poblada | 1 |
| 6424 | población | 1 |
| 6425 | pluma | 1 |
| 6426 | plúgo | 1 |
| 6427 | plugo | 1 |
| 6428 | plomados | 1 |
| 6429 | plógo | 1 |
| 6430 | pliegos | 1 |
| 6431 | pleytés | 1 |
| 6432 | pleyteamiento | 1 |
| 6433 | pletisía | 1 |
| 6434 | pletesía | 1 |
| 6435 | pletea | 1 |
| 6436 | plena | 1 |
| 6437 | plebis | 1 |
| 6438 | plázete | 1 |
| 6439 | plazes | 1 |
| 6440 | plázeme | 1 |
| 6441 | plaze | 1 |
| 6442 | platón | 1 |
| 6443 | plata | 1 |
| 6444 | plasíe | 1 |
| 6445 | plases | 1 |
| 6446 | plasenteros | 1 |
| 6447 | plasençia | 1 |
| 6448 | planto | 1 |
| 6449 | plantas | 1 |
| 6450 | planetas | 1 |
| 6451 | plana | 1 |
| 6452 | plaga | 1 |
| 6453 | plado | 1 |
| 6454 | plaços | 1 |
| 6455 | plaçenteros | 1 |
| 6456 | plaçenterías | 1 |
| 6457 | plaçentera | 1 |
| 6458 | plaçe | 1 |
| 6459 | pixota | 1 |
| 6460 | pitoflero | 1 |
| 6461 | pissa | 1 |
| 6462 | pisada | 1 |
| 6463 | pior | 1 |
| 6464 | pintoresca | 1 |
| 6465 | pintor | 1 |
| 6466 | pintase | 1 |
| 6467 | pintarla | 1 |
| 6468 | pintar | 1 |
| 6469 | pintados | 1 |
| 6470 | pintado | 1 |
| 6471 | pintadas | 1 |
| 6472 | pindárico | 1 |
| 6473 | pincel | 1 |
| 6474 | pimienta | 1 |
| 6475 | pilatos | 1 |
| 6476 | pihuelas | 1 |
| 6477 | piérdense | 1 |
| 6478 | piensso | 1 |
| 6479 | pienssas | 1 |
| 6480 | piensas | 1 |
| 6481 | piélagos | 1 |
| 6482 | piélago | 1 |
| 6483 | piedad | 1 |
| 6484 | pié | 1 |
| 6485 | pidyeron | 1 |
| 6486 | pidré | 1 |
| 6487 | pidistes | 1 |
| 6488 | pidió | 1 |
| 6489 | pidieres | 1 |
| 6490 | pidiéndotelo | 1 |
| 6491 | pidiendo | 1 |
| 6492 | pidías | 1 |
| 6493 | pidas | 1 |
| 6494 | pida | 1 |
| 6495 | picaresca | 1 |
| 6496 | picardías | 1 |
| 6497 | picañas | 1 |
| 6498 | picaças | 1 |
| 6499 | picaça | 1 |
| 6500 | piadosas | 1 |
| 6501 | piadad | 1 |
| 6502 | philósophos | 1 |
| 6503 | philosofía | 1 |
| 6504 | peynde | 1 |
| 6505 | petulante | 1 |
| 6506 | petid | 1 |
| 6507 | petiçiones | 1 |
| 6508 | petición | 1 |
| 6509 | pestorejo | 1 |
| 6510 | pestilençia | 1 |
| 6511 | pestañas | 1 |
| 6512 | pessas | 1 |
| 6513 | pessa | 1 |
| 6514 | péselo | 1 |
| 6515 | pesebres | 1 |
| 6516 | pescuçudo | 1 |
| 6517 | pescado | 1 |
| 6518 | pesas | 1 |
| 6519 | pesará | 1 |
| 6520 | pesado | 1 |
| 6521 | pertenesçen | 1 |
| 6522 | pertenesçe | 1 |
| 6523 | pertenençia | 1 |
| 6524 | pertenecer | 1 |
| 6525 | pertenecen | 1 |
| 6526 | pertenece | 1 |
| 6527 | persygues | 1 |
| 6528 | personifica | 1 |
| 6529 | perrochianos | 1 |
| 6530 | perrochano | 1 |
| 6531 | perrillo | 1 |
| 6532 | peroqu | 1 |
| 6533 | perlados | 1 |
| 6534 | perlado | 1 |
| 6535 | perjuros | 1 |
| 6536 | perjuro | 1 |
| 6537 | perjureste | 1 |
| 6538 | perhenales | 1 |
| 6539 | perfecto | 1 |
| 6540 | perezosos | 1 |
| 6541 | perezoso | 1 |
| 6542 | peresosos | 1 |
| 6543 | peresosas | 1 |
| 6544 | peresas | 1 |
| 6545 | pereçer | 1 |
| 6546 | pereça | 1 |
| 6547 | perdurables | 1 |
| 6548 | perdurable | 1 |
| 6549 | perdudo | 1 |
| 6550 | perdredes | 1 |
| 6551 | perdonóla | 1 |
| 6552 | perdonó | 1 |
| 6553 | perdonastes | 1 |
| 6554 | perdonados | 1 |
| 6555 | perdona | 1 |
| 6556 | perdises | 1 |
| 6557 | perdióla | 1 |
| 6558 | perdiera | 1 |
| 6559 | perdiendo | 1 |
| 6560 | perdidas | 1 |
| 6561 | perdiçión | 1 |
| 6562 | perdición | 1 |
| 6563 | perdíame | 1 |
| 6564 | perdía | 1 |
| 6565 | perderla | 1 |
| 6566 | perderedes | 1 |
| 6567 | perderás | 1 |
| 6568 | perderán | 1 |
| 6569 | perderá | 1 |
| 6570 | perdédesvos | 1 |
| 6571 | perçebydvos | 1 |
| 6572 | peratiñen | 1 |
| 6573 | peras | 1 |
| 6574 | pequeñuelas | 1 |
| 6575 | pequenos | 1 |
| 6576 | pequé | 1 |
| 6577 | pepiones | 1 |
| 6578 | peones | 1 |
| 6579 | peñolas | 1 |
| 6580 | péñola | 1 |
| 6581 | peñavera | 1 |
| 6582 | peñascos | 1 |
| 6583 | peñas | 1 |
| 6584 | penssó | 1 |
| 6585 | penssemos | 1 |
| 6586 | penssavan | 1 |
| 6587 | penssar | 1 |
| 6588 | penssamiento | 1 |
| 6589 | pensedes | 1 |
| 6590 | pensé | 1 |
| 6591 | pensastes | 1 |
| 6592 | pensaron | 1 |
| 6593 | pensaré | 1 |
| 6594 | pensamiento | 1 |
| 6595 | pensador | 1 |
| 6596 | pensadas | 1 |
| 6597 | penintençia | 1 |
| 6598 | península | 1 |
| 6599 | peneste | 1 |
| 6600 | pendones | 1 |
| 6601 | pendón | 1 |
| 6602 | pendon | 1 |
| 6603 | péndola | 1 |
| 6604 | penaste | 1 |
| 6605 | penarás | 1 |
| 6606 | penarán | 1 |
| 6607 | penades | 1 |
| 6608 | pelygros | 1 |
| 6609 | pelól | 1 |
| 6610 | peló | 1 |
| 6611 | pelmaços | 1 |
| 6612 | pellota | 1 |
| 6613 | pellico | 1 |
| 6614 | pellejos | 1 |
| 6615 | pellejas | 1 |
| 6616 | pelleas | 1 |
| 6617 | peligrar | 1 |
| 6618 | peleo | 1 |
| 6619 | pelarvos | 1 |
| 6620 | peláronle | 1 |
| 6621 | pelaça | 1 |
| 6622 | pegujares | 1 |
| 6623 | pegatas | 1 |
| 6624 | pegan | 1 |
| 6625 | pedricas | 1 |
| 6626 | pedricadores | 1 |
| 6627 | pedricaderas | 1 |
| 6628 | pedrero | 1 |
| 6629 | pedradas | 1 |
| 6630 | pedió | 1 |
| 6631 | pediese | 1 |
| 6632 | pedieres | 1 |
| 6633 | pediendo | 1 |
| 6634 | pedidor | 1 |
| 6635 | pedibus | 1 |
| 6636 | pedaços | 1 |
| 6637 | pecheros | 1 |
| 6638 | peçados | 1 |
| 6639 | pecadesno | 1 |
| 6640 | pecada | 1 |
| 6641 | peca | 1 |
| 6642 | paviotes | 1 |
| 6643 | paviotas | 1 |
| 6644 | paveznos | 1 |
| 6645 | pavesnos | 1 |
| 6646 | paula | 1 |
| 6647 | pastrija | 1 |
| 6648 | pastraña | 1 |
| 6649 | pastora | 1 |
| 6650 | pastija | 1 |
| 6651 | passos | 1 |
| 6652 | passó | 1 |
| 6653 | passo | 1 |
| 6654 | passe | 1 |
| 6655 | passando | 1 |
| 6656 | passan | 1 |
| 6657 | passa | 1 |
| 6658 | pasose | 1 |
| 6659 | pasillo | 1 |
| 6660 | pases | 1 |
| 6661 | páselo | 1 |
| 6662 | pase | 1 |
| 6663 | pasçía | 1 |
| 6664 | pasas | 1 |
| 6665 | pasaremos | 1 |
| 6666 | pasan | 1 |
| 6667 | pasádesvos | 1 |
| 6668 | pasaderas | 1 |
| 6669 | pasaban | 1 |
| 6670 | paryentes | 1 |
| 6671 | partyrle | 1 |
| 6672 | partyr | 1 |
| 6673 | partyóse | 1 |
| 6674 | partyme | 1 |
| 6675 | partirnos | 1 |
| 6676 | partirías | 1 |
| 6677 | partióse | 1 |
| 6678 | partió | 1 |
| 6679 | partiere | 1 |
| 6680 | partidor | 1 |
| 6681 | particularizar | 1 |
| 6682 | participa | 1 |
| 6683 | partí | 1 |
| 6684 | párteslo | 1 |
| 6685 | pártese | 1 |
| 6686 | parteras | 1 |
| 6687 | parten | 1 |
| 6688 | parteçión | 1 |
| 6689 | parrales | 1 |
| 6690 | parósem | 1 |
| 6691 | paro | 1 |
| 6692 | parlylla | 1 |
| 6693 | parlinas | 1 |
| 6694 | parlava | 1 |
| 6695 | parlatorio | 1 |
| 6696 | parlas | 1 |
| 6697 | parlares | 1 |
| 6698 | parlando | 1 |
| 6699 | parlador | 1 |
| 6700 | parladera | 1 |
| 6701 | parís | 1 |
| 6702 | paris | 1 |
| 6703 | pariría | 1 |
| 6704 | parientas | 1 |
| 6705 | paridas | 1 |
| 6706 | parezcan | 1 |
| 6707 | paresçiente | 1 |
| 6708 | paresçían | 1 |
| 6709 | paresçes | 1 |
| 6710 | paresçerá | 1 |
| 6711 | parescas | 1 |
| 6712 | paresca | 1 |
| 6713 | parentesco | 1 |
| 6714 | paren | 1 |
| 6715 | parejos | 1 |
| 6716 | parejas | 1 |
| 6717 | parecido | 1 |
| 6718 | pare | 1 |
| 6719 | pardo | 1 |
| 6720 | pardiós | 1 |
| 6721 | pardales | 1 |
| 6722 | pardal | 1 |
| 6723 | parçioneros | 1 |
| 6724 | parava | 1 |
| 6725 | parasti | 1 |
| 6726 | parase | 1 |
| 6727 | pararvos | 1 |
| 6728 | parança | 1 |
| 6729 | paral | 1 |
| 6730 | paráfrasis | 1 |
| 6731 | parados | 1 |
| 6732 | papo | 1 |
| 6733 | papas | 1 |
| 6734 | papagayos | 1 |
| 6735 | pano | 1 |
| 6736 | panderete | 1 |
| 6737 | panares | 1 |
| 6738 | panar | 1 |
| 6739 | panadera | 1 |
| 6740 | paloma | 1 |
| 6741 | palo | 1 |
| 6742 | palmada | 1 |
| 6743 | palio | 1 |
| 6744 | palas | 1 |
| 6745 | palançiana | 1 |
| 6746 | palanca | 1 |
| 6747 | paladina | 1 |
| 6748 | palacio | 1 |
| 6749 | pala | 1 |
| 6750 | pajés | 1 |
| 6751 | pajatamo | 1 |
| 6752 | pajares | 1 |
| 6753 | pagós | 1 |
| 6754 | pagó | 1 |
| 6755 | pagé | 1 |
| 6756 | pagávas | 1 |
| 6757 | pagavan | 1 |
| 6758 | pagarse | 1 |
| 6759 | pagaron | 1 |
| 6760 | pagares | 1 |
| 6761 | pagarás | 1 |
| 6762 | pagados | 1 |
| 6763 | pagad | 1 |
| 6764 | pág | 1 |
| 6765 | padrastro | 1 |
| 6766 | padan | 1 |
| 6767 | paçiendo | 1 |
| 6768 | paciençia | 1 |
| 6769 | pacem | 1 |
| 6770 | oytme | 1 |
| 6771 | oystes | 1 |
| 6772 | oyremos | 1 |
| 6773 | oyrá | 1 |
| 6774 | oyólo | 1 |
| 6775 | oyolo | 1 |
| 6776 | óyle | 1 |
| 6777 | oylda | 1 |
| 6778 | oyeren | 1 |
| 6779 | oyeredes | 1 |
| 6780 | oyera | 1 |
| 6781 | oyéndolas | 1 |
| 6782 | oyendo | 1 |
| 6783 | óyeme | 1 |
| 6784 | oydores | 1 |
| 6785 | oydor | 1 |
| 6786 | oydes | 1 |
| 6787 | oydas | 1 |
| 6788 | oyda | 1 |
| 6789 | oyan | 1 |
| 6790 | oxte | 1 |
| 6791 | ovyste | 1 |
| 6792 | ovydyo | 1 |
| 6793 | ovydio | 1 |
| 6794 | óvosele | 1 |
| 6795 | ovóse | 1 |
| 6796 | óvomelo | 1 |
| 6797 | óvolas | 1 |
| 6798 | ovieses | 1 |
| 6799 | ovieralos | 1 |
| 6800 | oviérades | 1 |
| 6801 | ovier | 1 |
| 6802 | ovejero | 1 |
| 6803 | otr | 1 |
| 6804 | otorgó | 1 |
| 6805 | otórgeselo | 1 |
| 6806 | otorgatme | 1 |
| 6807 | otorgáronlo | 1 |
| 6808 | otorgaría | 1 |
| 6809 | otorgado | 1 |
| 6810 | otonio | 1 |
| 6811 | oteóme | 1 |
| 6812 | otear | 1 |
| 6813 | otéame | 1 |
| 6814 | ostyas | 1 |
| 6815 | ostiense | 1 |
| 6816 | ostalaje | 1 |
| 6817 | ospital | 1 |
| 6818 | ospedado | 1 |
| 6819 | osol | 1 |
| 6820 | osarvos | 1 |
| 6821 | osaría | 1 |
| 6822 | osada | 1 |
| 6823 | os | 1 |
| 6824 | oruela | 1 |
| 6825 | ortiz | 1 |
| 6826 | oropesa | 1 |
| 6827 | orior | 1 |
| 6828 | originalísima | 1 |
| 6829 | original | 1 |
| 6830 | origen | 1 |
| 6831 | oriella | 1 |
| 6832 | orgullosa | 1 |
| 6833 | órganos | 1 |
| 6834 | ordenó | 1 |
| 6835 | órdenes | 1 |
| 6836 | ordenes | 1 |
| 6837 | ordenada | 1 |
| 6838 | ordena | 1 |
| 6839 | ordeales | 1 |
| 6840 | opulencia | 1 |
| 6841 | opuestas | 1 |
| 6842 | opinión | 1 |
| 6843 | opinar | 1 |
| 6844 | onrren | 1 |
| 6845 | onrrava | 1 |
| 6846 | onrraría | 1 |
| 6847 | onrradas | 1 |
| 6848 | onrr | 1 |
| 6849 | onesto | 1 |
| 6850 | onestad | 1 |
| 6851 | onde | 1 |
| 6852 | onbros | 1 |
| 6853 | onbligo | 1 |
| 6854 | omyl | 1 |
| 6855 | omnibus | 1 |
| 6856 | omite | 1 |
| 6857 | omisión | 1 |
| 6858 | omilmente | 1 |
| 6859 | omillava | 1 |
| 6860 | omillan | 1 |
| 6861 | omilla | 1 |
| 6862 | omilidat | 1 |
| 6863 | omildes | 1 |
| 6864 | omil | 1 |
| 6865 | omenaje | 1 |
| 6866 | omeçida | 1 |
| 6867 | omanidat | 1 |
| 6868 | olvyda | 1 |
| 6869 | olvidóse | 1 |
| 6870 | olvidés | 1 |
| 6871 | olvidas | 1 |
| 6872 | olvidará | 1 |
| 6873 | olvidada | 1 |
| 6874 | olla | 1 |
| 6875 | oiste | 1 |
| 6876 | oírse | 1 |
| 6877 | ogaño | 1 |
| 6878 | ofrescas | 1 |
| 6879 | ofreçiol | 1 |
| 6880 | ofreçió | 1 |
| 6881 | ofrecil | 1 |
| 6882 | ofrecieron | 1 |
| 6883 | ofreçervos | 1 |
| 6884 | ofreçeremos | 1 |
| 6885 | ofreçémostelo | 1 |
| 6886 | ofrece | 1 |
| 6887 | oficio | 1 |
| 6888 | offreçió | 1 |
| 6889 | offiçia | 1 |
| 6890 | ofenderé | 1 |
| 6891 | odresillo | 1 |
| 6892 | odite | 1 |
| 6893 | oderunt | 1 |
| 6894 | octosílabos | 1 |
| 6895 | ochenta | 1 |
| 6896 | ochavado | 1 |
| 6897 | occidental | 1 |
| 6898 | ocasyón | 1 |
| 6899 | ocasión | 1 |
| 6900 | obre | 1 |
| 6901 | obrarlo | 1 |
| 6902 | obrare | 1 |
| 6903 | obrando | 1 |
| 6904 | obladas | 1 |
| 6905 | oblaçiones | 1 |
| 6906 | oblaçión | 1 |
| 6907 | obla | 1 |
| 6908 | objetivo | 1 |
| 6909 | obispo | 1 |
| 6910 | obediençia | 1 |
| 6911 | obedesçer | 1 |
| 6912 | obedesçen | 1 |
| 6913 | ñoñeces | 1 |
| 6914 | ny | 1 |
| 6915 | nuzía | 1 |
| 6916 | nuezes | 1 |
| 6917 | nuestr | 1 |
| 6918 | nués | 1 |
| 6919 | nues | 1 |
| 6920 | nueras | 1 |
| 6921 | nudo | 1 |
| 6922 | nublos | 1 |
| 6923 | nublo | 1 |
| 6924 | novo | 1 |
| 6925 | novilla | 1 |
| 6926 | noviçios | 1 |
| 6927 | novelesco | 1 |
| 6928 | novedades | 1 |
| 6929 | notario | 1 |
| 6930 | notador | 1 |
| 6931 | nostres | 1 |
| 6932 | nostras | 1 |
| 6933 | nostra | 1 |
| 6934 | nonbrar | 1 |
| 6935 | nomine | 1 |
| 6936 | nombrada | 1 |
| 6937 | nolite | 1 |
| 6938 | noli | 1 |
| 6939 | nol | 1 |
| 6940 | nogera | 1 |
| 6941 | nogales | 1 |
| 6942 | noctibus | 1 |
| 6943 | nocherniegos | 1 |
| 6944 | nocherniego | 1 |
| 6945 | nobiscum | 1 |
| 6946 | niños | 1 |
| 6947 | niña | 1 |
| 6948 | ningunos | 1 |
| 6949 | ningund | 1 |
| 6950 | ningunas | 1 |
| 6951 | nimia | 1 |
| 6952 | nieva | 1 |
| 6953 | niev | 1 |
| 6954 | niegue | 1 |
| 6955 | niego | 1 |
| 6956 | niega | 1 |
| 6957 | niebla | 1 |
| 6958 | nevada | 1 |
| 6959 | nesçia | 1 |
| 6960 | nesçesidat | 1 |
| 6961 | nesçedat | 1 |
| 6962 | nenbrar | 1 |
| 6963 | nemo | 1 |
| 6964 | negó | 1 |
| 6965 | negedes | 1 |
| 6966 | negar | 1 |
| 6967 | negado | 1 |
| 6968 | neçuelo | 1 |
| 6969 | neçias | 1 |
| 6970 | neçiacha | 1 |
| 6971 | necesitaba | 1 |
| 6972 | neçedat | 1 |
| 6973 | ne | 1 |
| 6974 | nazaret | 1 |
| 6975 | nazarenus | 1 |
| 6976 | nave | 1 |
| 6977 | navajas | 1 |
| 6978 | natus | 1 |
| 6979 | naturas | 1 |
| 6980 | naturaleça | 1 |
| 6981 | nason | 1 |
| 6982 | nasçistes | 1 |
| 6983 | nasçióle | 1 |
| 6984 | nasçiera | 1 |
| 6985 | nasciera | 1 |
| 6986 | nasçía | 1 |
| 6987 | nasçí | 1 |
| 6988 | nascí | 1 |
| 6989 | nasçemiento | 1 |
| 6990 | naryz | 1 |
| 6991 | nariz | 1 |
| 6992 | nariçes | 1 |
| 6993 | narices | 1 |
| 6994 | nados | 1 |
| 6995 | nado | 1 |
| 6996 | nadando | 1 |
| 6997 | nacisteis | 1 |
| 6998 | naçiste | 1 |
| 6999 | naciese | 1 |
| 7000 | nacieron | 1 |
| 7001 | nacientes | 1 |
| 7002 | naciendo | 1 |
| 7003 | naçido | 1 |
| 7004 | naçençia | 1 |
| 7005 | nabucodonossor | 1 |
| 7006 | mys | 1 |
| 7007 | myo | 1 |
| 7008 | myll | 1 |
| 7009 | myércoles | 1 |
| 7010 | muyta | 1 |
| 7011 | muymaigre | 1 |
| 7012 | muvió | 1 |
| 7013 | músculos | 1 |
| 7014 | musas | 1 |
| 7015 | muros | 1 |
| 7016 | murmullo | 1 |
| 7017 | murisillo | 1 |
| 7018 | murieron | 1 |
| 7019 | muñós | 1 |
| 7020 | muñecas | 1 |
| 7021 | muñeca | 1 |
| 7022 | mundum | 1 |
| 7023 | mund | 1 |
| 7024 | mulus | 1 |
| 7025 | mulieribus | 1 |
| 7026 | muliere | 1 |
| 7027 | muladar | 1 |
| 7028 | mujerzuelas | 1 |
| 7029 | mugrones | 1 |
| 7030 | muevo | 1 |
| 7031 | muestre | 1 |
| 7032 | muéstrale | 1 |
| 7033 | muertos | 1 |
| 7034 | muera | 1 |
| 7035 | muele | 1 |
| 7036 | muedo | 1 |
| 7037 | muebles | 1 |
| 7038 | múdaste | 1 |
| 7039 | mudáronse | 1 |
| 7040 | mudan | 1 |
| 7041 | mudamos | 1 |
| 7042 | mudada | 1 |
| 7043 | muchedumbre | 1 |
| 7044 | moysén | 1 |
| 7045 | moya | 1 |
| 7046 | movilidad | 1 |
| 7047 | moverse | 1 |
| 7048 | mover | 1 |
| 7049 | motete | 1 |
| 7050 | motes | 1 |
| 7051 | mota | 1 |
| 7052 | mostrava | 1 |
| 7053 | mostratme | 1 |
| 7054 | mostrart | 1 |
| 7055 | mostrares | 1 |
| 7056 | mostradme | 1 |
| 7057 | mostradas | 1 |
| 7058 | mosca | 1 |
| 7059 | mortui | 1 |
| 7060 | morteçino | 1 |
| 7061 | morrás | 1 |
| 7062 | morrá | 1 |
| 7063 | moró | 1 |
| 7064 | moriuntur | 1 |
| 7065 | morisco | 1 |
| 7066 | morisca | 1 |
| 7067 | moriere | 1 |
| 7068 | moriendo | 1 |
| 7069 | morides | 1 |
| 7070 | moresillo | 1 |
| 7071 | mores | 1 |
| 7072 | moré | 1 |
| 7073 | mordedora | 1 |
| 7074 | mordaças | 1 |
| 7075 | moras | 1 |
| 7076 | morarme | 1 |
| 7077 | moraré | 1 |
| 7078 | moralizadora | 1 |
| 7079 | moralista | 1 |
| 7080 | moral | 1 |
| 7081 | morador | 1 |
| 7082 | morado | 1 |
| 7083 | montón | 1 |
| 7084 | montesyna | 1 |
| 7085 | montessas | 1 |
| 7086 | montés | 1 |
| 7087 | montes | 1 |
| 7088 | monteros | 1 |
| 7089 | montaraz | 1 |
| 7090 | montaña | 1 |
| 7091 | monsseñer | 1 |
| 7092 | monssener | 1 |
| 7093 | monseñer | 1 |
| 7094 | monsener | 1 |
| 7095 | monpeller | 1 |
| 7096 | monopolizar | 1 |
| 7097 | monjes | 1 |
| 7098 | mongibel | 1 |
| 7099 | mongía | 1 |
| 7100 | monesterios | 1 |
| 7101 | monesterio | 1 |
| 7102 | monedero | 1 |
| 7103 | moneca | 1 |
| 7104 | moldes | 1 |
| 7105 | mojigatos | 1 |
| 7106 | moje | 1 |
| 7107 | mojados | 1 |
| 7108 | moisén | 1 |
| 7109 | mohalinar | 1 |
| 7110 | modorría | 1 |
| 7111 | modelo | 1 |
| 7112 | moçuela | 1 |
| 7113 | moços | 1 |
| 7114 | moçetas | 1 |
| 7115 | moçedat | 1 |
| 7116 | mixía | 1 |
| 7117 | mitroso | 1 |
| 7118 | mitra | 1 |
| 7119 | mitológica | 1 |
| 7120 | mitas | 1 |
| 7121 | missericordia | 1 |
| 7122 | mismas | 1 |
| 7123 | miserere | 1 |
| 7124 | mires | 1 |
| 7125 | mirava | 1 |
| 7126 | miras | 1 |
| 7127 | mirar | 1 |
| 7128 | miraglos | 1 |
| 7129 | mirabilia | 1 |
| 7130 | mio | 1 |
| 7131 | mintyendo | 1 |
| 7132 | mintrosas | 1 |
| 7133 | mintira | 1 |
| 7134 | ministros | 1 |
| 7135 | ministerio | 1 |
| 7136 | milano | 1 |
| 7137 | mijoría | 1 |
| 7138 | mijores | 1 |
| 7139 | mijo | 1 |
| 7140 | miguel | 1 |
| 7141 | migel | 1 |
| 7142 | mies | 1 |
| 7143 | mierca | 1 |
| 7144 | mientras | 1 |
| 7145 | mientas | 1 |
| 7146 | miénbresevos | 1 |
| 7147 | mienbre | 1 |
| 7148 | mienbran | 1 |
| 7149 | mielgas | 1 |
| 7150 | mied | 1 |
| 7151 | midas | 1 |
| 7152 | michi | 1 |
| 7153 | mia | 1 |
| 7154 | mezquino | 1 |
| 7155 | mexilla | 1 |
| 7156 | mexías | 1 |
| 7157 | metydo | 1 |
| 7158 | métricas | 1 |
| 7159 | métricamente | 1 |
| 7160 | métrica | 1 |
| 7161 | metió | 1 |
| 7162 | metido | 1 |
| 7163 | meterte | 1 |
| 7164 | meten | 1 |
| 7165 | mételos | 1 |
| 7166 | metal | 1 |
| 7167 | mesturárardes | 1 |
| 7168 | mesturado | 1 |
| 7169 | mesturada | 1 |
| 7170 | messurada | 1 |
| 7171 | messonero | 1 |
| 7172 | messes | 1 |
| 7173 | mesquita | 1 |
| 7174 | mesquindat | 1 |
| 7175 | mesquinas | 1 |
| 7176 | mesón | 1 |
| 7177 | mesnadas | 1 |
| 7178 | mesmas | 1 |
| 7179 | meseta | 1 |
| 7180 | mesericordia | 1 |
| 7181 | mescláronme | 1 |
| 7182 | mescladores | 1 |
| 7183 | mesas | 1 |
| 7184 | mesajero | 1 |
| 7185 | meryno | 1 |
| 7186 | merjelina | 1 |
| 7187 | merinos | 1 |
| 7188 | meriendas | 1 |
| 7189 | meresçiente | 1 |
| 7190 | meresçería | 1 |
| 7191 | meresçeré | 1 |
| 7192 | meresçedes | 1 |
| 7193 | meresçe | 1 |
| 7194 | merescas | 1 |
| 7195 | meresca | 1 |
| 7196 | mereçiste | 1 |
| 7197 | mereçedes | 1 |
| 7198 | merçet | 1 |
| 7199 | merçedes | 1 |
| 7200 | mercar | 1 |
| 7201 | mercados | 1 |
| 7202 | mercadores | 1 |
| 7203 | mercader | 1 |
| 7204 | meramente | 1 |
| 7205 | menudillos | 1 |
| 7206 | menudillo | 1 |
| 7207 | mentyras | 1 |
| 7208 | mentyr | 1 |
| 7209 | menty | 1 |
| 7210 | mentira | 1 |
| 7211 | mentir | 1 |
| 7212 | mente | 1 |
| 7213 | menssajera | 1 |
| 7214 | mensaj | 1 |
| 7215 | mens | 1 |
| 7216 | menospreçiada | 1 |
| 7217 | menospreçia | 1 |
| 7218 | menoscabo | 1 |
| 7219 | menoretas | 1 |
| 7220 | menguas | 1 |
| 7221 | menguare | 1 |
| 7222 | menguan | 1 |
| 7223 | menguamos | 1 |
| 7224 | mengías | 1 |
| 7225 | mengía | 1 |
| 7226 | menge | 1 |
| 7227 | meneos | 1 |
| 7228 | menéalas | 1 |
| 7229 | menea | 1 |
| 7230 | mendigos | 1 |
| 7231 | mendigo | 1 |
| 7232 | menciona | 1 |
| 7233 | mençebillo | 1 |
| 7234 | menbratvos | 1 |
| 7235 | menando | 1 |
| 7236 | mena | 1 |
| 7237 | melinas | 1 |
| 7238 | melezina | 1 |
| 7239 | melesinas | 1 |
| 7240 | mêle | 1 |
| 7241 | melchior | 1 |
| 7242 | mejorar | 1 |
| 7243 | mei | 1 |
| 7244 | medrosos | 1 |
| 7245 | medre | 1 |
| 7246 | meditabuntur | 1 |
| 7247 | meditabor | 1 |
| 7248 | medias | 1 |
| 7249 | mediante | 1 |
| 7250 | medianera | 1 |
| 7251 | medianamente | 1 |
| 7252 | meder | 1 |
| 7253 | maytines | 1 |
| 7254 | máys | 1 |
| 7255 | mayoría | 1 |
| 7256 | mayordoma | 1 |
| 7257 | maxmordos | 1 |
| 7258 | matynes | 1 |
| 7259 | matrimonio | 1 |
| 7260 | matóse | 1 |
| 7261 | matólo | 1 |
| 7262 | matóla | 1 |
| 7263 | mato | 1 |
| 7264 | matina | 1 |
| 7265 | matices | 1 |
| 7266 | mateste | 1 |
| 7267 | matásteme | 1 |
| 7268 | matástel | 1 |
| 7269 | mataste | 1 |
| 7270 | matasses | 1 |
| 7271 | matases | 1 |
| 7272 | matarya | 1 |
| 7273 | matáronlo | 1 |
| 7274 | mataron | 1 |
| 7275 | matarm | 1 |
| 7276 | matarás | 1 |
| 7277 | matará | 1 |
| 7278 | matándol | 1 |
| 7279 | matamigos | 1 |
| 7280 | matador | 1 |
| 7281 | matad | 1 |
| 7282 | matacanes | 1 |
| 7283 | mastuerço | 1 |
| 7284 | mastina | 1 |
| 7285 | mástel | 1 |
| 7286 | massa | 1 |
| 7287 | masnada | 1 |
| 7288 | masiella | 1 |
| 7289 | maselleras | 1 |
| 7290 | marynero | 1 |
| 7291 | maryna | 1 |
| 7292 | marydo | 1 |
| 7293 | marya | 1 |
| 7294 | martyriada | 1 |
| 7295 | martínez | 1 |
| 7296 | martillazo | 1 |
| 7297 | márteres | 1 |
| 7298 | marta | 1 |
| 7299 | marroquia | 1 |
| 7300 | marqués | 1 |
| 7301 | marinero | 1 |
| 7302 | marías | 1 |
| 7303 | marfyl | 1 |
| 7304 | marfúz | 1 |
| 7305 | mares | 1 |
| 7306 | maravilloso | 1 |
| 7307 | maravillose | 1 |
| 7308 | maravillosas | 1 |
| 7309 | maravillós | 1 |
| 7310 | maravíllome | 1 |
| 7311 | maravilléme | 1 |
| 7312 | maravillas | 1 |
| 7313 | maravillado | 1 |
| 7314 | maravedy | 1 |
| 7315 | maño | 1 |
| 7316 | mañanas | 1 |
| 7317 | manuales | 1 |
| 7318 | mantyene | 1 |
| 7319 | mantoviste | 1 |
| 7320 | manto | 1 |
| 7321 | mantienen | 1 |
| 7322 | mantiene | 1 |
| 7323 | mantién | 1 |
| 7324 | mantenga | 1 |
| 7325 | mantener | 1 |
| 7326 | manteca | 1 |
| 7327 | mansillera | 1 |
| 7328 | mansellero | 1 |
| 7329 | mansamente | 1 |
| 7330 | manparado | 1 |
| 7331 | mane | 1 |
| 7332 | mándote | 1 |
| 7333 | mandóme | 1 |
| 7334 | mandólos | 1 |
| 7335 | mandóles | 1 |
| 7336 | mandóle | 1 |
| 7337 | mandéle | 1 |
| 7338 | mandel | 1 |
| 7339 | mandé | 1 |
| 7340 | mande | 1 |
| 7341 | mandávale | 1 |
| 7342 | mandato | 1 |
| 7343 | mandatle | 1 |
| 7344 | mandatis | 1 |
| 7345 | mandase | 1 |
| 7346 | mandas | 1 |
| 7347 | mandaron | 1 |
| 7348 | mandamos | 1 |
| 7349 | mandamiento | 1 |
| 7350 | mándalos | 1 |
| 7351 | mandados | 1 |
| 7352 | mandadero | 1 |
| 7353 | mandada | 1 |
| 7354 | mandad | 1 |
| 7355 | mançilla | 1 |
| 7356 | mançebillos | 1 |
| 7357 | mançebilla | 1 |
| 7358 | mançebiello | 1 |
| 7359 | mançebéz | 1 |
| 7360 | mançebez | 1 |
| 7361 | mancebas | 1 |
| 7362 | mançeba | 1 |
| 7363 | mançeb | 1 |
| 7364 | manca | 1 |
| 7365 | manadilla | 1 |
| 7366 | manadiellas | 1 |
| 7367 | malva | 1 |
| 7368 | malum | 1 |
| 7369 | maltraher | 1 |
| 7370 | malsañudo | 1 |
| 7371 | malsabydas | 1 |
| 7372 | malsaber | 1 |
| 7373 | malqueriente | 1 |
| 7374 | malquerido | 1 |
| 7375 | malquebrantó | 1 |
| 7376 | malquebrantado | 1 |
| 7377 | malpagar | 1 |
| 7378 | malmordiendo | 1 |
| 7379 | maliçiosa | 1 |
| 7380 | malferido | 1 |
| 7381 | malfecho | 1 |
| 7382 | malfado | 1 |
| 7383 | malface | 1 |
| 7384 | malestorvar | 1 |
| 7385 | malespantados | 1 |
| 7386 | malesculcada | 1 |
| 7387 | malengañada | 1 |
| 7388 | malefiçios | 1 |
| 7389 | malefiçio | 1 |
| 7390 | maldolyente | 1 |
| 7391 | maldiziendo | 1 |
| 7392 | maldíxole | 1 |
| 7393 | maldito | 1 |
| 7394 | maldita | 1 |
| 7395 | maldigan | 1 |
| 7396 | maldicha | 1 |
| 7397 | maldezir | 1 |
| 7398 | maldesir | 1 |
| 7399 | maldesiente | 1 |
| 7400 | maldenostada | 1 |
| 7401 | maldades | 1 |
| 7402 | malchufados | 1 |
| 7403 | malcasar | 1 |
| 7404 | malcasa | 1 |
| 7405 | malapresso | 1 |
| 7406 | malapreso | 1 |
| 7407 | malapresa | 1 |
| 7408 | malangosto | 1 |
| 7409 | malandar | 1 |
| 7410 | majestat | 1 |
| 7411 | majar | 1 |
| 7412 | magrillo | 1 |
| 7413 | magrilla | 1 |
| 7414 | mágica | 1 |
| 7415 | magestad | 1 |
| 7416 | magadaña | 1 |
| 7417 | magadana | 1 |
| 7418 | magada | 1 |
| 7419 | maestrya | 1 |
| 7420 | maduros | 1 |
| 7421 | maduro | 1 |
| 7422 | maduras | 1 |
| 7423 | madura | 1 |
| 7424 | madrugeste | 1 |
| 7425 | madrugava | 1 |
| 7426 | madrugador | 1 |
| 7427 | madrugadas | 1 |
| 7428 | madrugada | 1 |
| 7429 | madres | 1 |
| 7430 | madexa | 1 |
| 7431 | macizo | 1 |
| 7432 | macizas | 1 |
| 7433 | maçar | 1 |
| 7434 | lyxa | 1 |
| 7435 | lyviandat | 1 |
| 7436 | lystada | 1 |
| 7437 | lysongia | 1 |
| 7438 | lynpio | 1 |
| 7439 | lynpiesa | 1 |
| 7440 | lynpieça | 1 |
| 7441 | lynpiar | 1 |
| 7442 | lynpia | 1 |
| 7443 | lyndero | 1 |
| 7444 | lynaj | 1 |
| 7445 | lymosma | 1 |
| 7446 | lygerezas | 1 |
| 7447 | lyévela | 1 |
| 7448 | lyevas | 1 |
| 7449 | lyevan | 1 |
| 7450 | lyévalos | 1 |
| 7451 | lyendo | 1 |
| 7452 | lydié | 1 |
| 7453 | lydiando | 1 |
| 7454 | lydia | 1 |
| 7455 | lyçión | 1 |
| 7456 | lyçion | 1 |
| 7457 | lyçençia | 1 |
| 7458 | lyçencia | 1 |
| 7459 | lybrados | 1 |
| 7460 | lybertat | 1 |
| 7461 | lxii | 1 |
| 7462 | luzero | 1 |
| 7463 | luvias | 1 |
| 7464 | lutos | 1 |
| 7465 | luto | 1 |
| 7466 | lusiente | 1 |
| 7467 | lupanares | 1 |
| 7468 | luna | 1 |
| 7469 | lujuriosas | 1 |
| 7470 | lueñe | 1 |
| 7471 | lucura | 1 |
| 7472 | lucis | 1 |
| 7473 | lucifer | 1 |
| 7474 | luchemos | 1 |
| 7475 | luchase | 1 |
| 7476 | lucerna | 1 |
| 7477 | lucanor | 1 |
| 7478 | losas | 1 |
| 7479 | losa | 1 |
| 7480 | loros | 1 |
| 7481 | lorigas | 1 |
| 7482 | lorda | 1 |
| 7483 | lópez | 1 |
| 7484 | lonja | 1 |
| 7485 | longe | 1 |
| 7486 | lomos | 1 |
| 7487 | loemos | 1 |
| 7488 | loe | 1 |
| 7489 | loçan | 1 |
| 7490 | locamente | 1 |
| 7491 | lobuno | 1 |
| 7492 | lobos | 1 |
| 7493 | loaré | 1 |
| 7494 | loan | 1 |
| 7495 | loador | 1 |
| 7496 | loades | 1 |
| 7497 | load | 1 |
| 7498 | llovía | 1 |
| 7499 | llorosos | 1 |
| 7500 | lloroso | 1 |
| 7501 | lloro | 1 |
| 7502 | llorente | 1 |
| 7503 | llorava | 1 |
| 7504 | lloraríedes | 1 |
| 7505 | llevava | 1 |
| 7506 | llévate | 1 |
| 7507 | llevarse | 1 |
| 7508 | llevadas | 1 |
| 7509 | llevada | 1 |
| 7510 | llevaban | 1 |
| 7511 | lleva | 1 |
| 7512 | lleña | 1 |
| 7513 | llegué | 1 |
| 7514 | llegue | 1 |
| 7515 | llegóme | 1 |
| 7516 | llegaron | 1 |
| 7517 | lléganse | 1 |
| 7518 | llegaban | 1 |
| 7519 | llegaba | 1 |
| 7520 | llega | 1 |
| 7521 | llamóse | 1 |
| 7522 | llamen | 1 |
| 7523 | llamedes | 1 |
| 7524 | llamavan | 1 |
| 7525 | llamatme | 1 |
| 7526 | llamasen | 1 |
| 7527 | llamase | 1 |
| 7528 | llamas | 1 |
| 7529 | llamaría | 1 |
| 7530 | llámanse | 1 |
| 7531 | llaman | 1 |
| 7532 | llamadas | 1 |
| 7533 | llagaron | 1 |
| 7534 | lixo | 1 |
| 7535 | livianos | 1 |
| 7536 | liviana | 1 |
| 7537 | literario | 1 |
| 7538 | literarias | 1 |
| 7539 | literal | 1 |
| 7540 | lisyón | 1 |
| 7541 | listada | 1 |
| 7542 | lisonja | 1 |
| 7543 | lisongero | 1 |
| 7544 | lisonga | 1 |
| 7545 | linpiarme | 1 |
| 7546 | linpia | 1 |
| 7547 | lingua | 1 |
| 7548 | limosnas | 1 |
| 7549 | limosna | 1 |
| 7550 | límites | 1 |
| 7551 | ligongero | 1 |
| 7552 | ligítima | 1 |
| 7553 | ligión | 1 |
| 7554 | ligeras | 1 |
| 7555 | ligeramente | 1 |
| 7556 | ligera | 1 |
| 7557 | ligado | 1 |
| 7558 | lieves | 1 |
| 7559 | lieve | 1 |
| 7560 | liévastela | 1 |
| 7561 | lievas | 1 |
| 7562 | liévanle | 1 |
| 7563 | lievanle | 1 |
| 7564 | liévagelos | 1 |
| 7565 | lienda | 1 |
| 7566 | lidiase | 1 |
| 7567 | lidiando | 1 |
| 7568 | lidian | 1 |
| 7569 | lidiaban | 1 |
| 7570 | liçionario | 1 |
| 7571 | lichiga | 1 |
| 7572 | liçençia | 1 |
| 7573 | liçencia | 1 |
| 7574 | librillo | 1 |
| 7575 | libres | 1 |
| 7576 | libras | 1 |
| 7577 | líbrame | 1 |
| 7578 | librador | 1 |
| 7579 | libra | 1 |
| 7580 | libertades | 1 |
| 7581 | liber | 1 |
| 7582 | leyva | 1 |
| 7583 | leys | 1 |
| 7584 | leyeres | 1 |
| 7585 | leyere | 1 |
| 7586 | leyéndolas | 1 |
| 7587 | leyendas | 1 |
| 7588 | leye | 1 |
| 7589 | léxico | 1 |
| 7590 | levómelo | 1 |
| 7591 | levome | 1 |
| 7592 | levólo | 1 |
| 7593 | levol | 1 |
| 7594 | levógelos | 1 |
| 7595 | levaryas | 1 |
| 7596 | levarla | 1 |
| 7597 | levaremos | 1 |
| 7598 | levaré | 1 |
| 7599 | levará | 1 |
| 7600 | levantós | 1 |
| 7601 | levantóle | 1 |
| 7602 | levanten | 1 |
| 7603 | levantéme | 1 |
| 7604 | levántasles | 1 |
| 7605 | levántasle | 1 |
| 7606 | levántase | 1 |
| 7607 | levantáronse | 1 |
| 7608 | levantados | 1 |
| 7609 | levándol | 1 |
| 7610 | levando | 1 |
| 7611 | levado | 1 |
| 7612 | levadlo | 1 |
| 7613 | levadas | 1 |
| 7614 | levad | 1 |
| 7615 | letura | 1 |
| 7616 | letrada | 1 |
| 7617 | letra | 1 |
| 7618 | lesnedri | 1 |
| 7619 | lepra | 1 |
| 7620 | leo | 1 |
| 7621 | lenguas | 1 |
| 7622 | lejos | 1 |
| 7623 | leída | 1 |
| 7624 | leguas | 1 |
| 7625 | legualá | 1 |
| 7626 | legos | 1 |
| 7627 | legislación | 1 |
| 7628 | legar | 1 |
| 7629 | legado | 1 |
| 7630 | leerlo | 1 |
| 7631 | leemos | 1 |
| 7632 | leda | 1 |
| 7633 | lectores | 1 |
| 7634 | leçión | 1 |
| 7635 | leçion | 1 |
| 7636 | lechones | 1 |
| 7637 | lechón | 1 |
| 7638 | leçençia | 1 |
| 7639 | lebrero | 1 |
| 7640 | léase | 1 |
| 7641 | lealmente | 1 |
| 7642 | lazraron | 1 |
| 7643 | lazrado | 1 |
| 7644 | lazrada | 1 |
| 7645 | lazar | 1 |
| 7646 | lavor | 1 |
| 7647 | lavarse | 1 |
| 7648 | lavar | 1 |
| 7649 | lavanderas | 1 |
| 7650 | lava | 1 |
| 7651 | laus | 1 |
| 7652 | laudes | 1 |
| 7653 | laudaron | 1 |
| 7654 | laudamus | 1 |
| 7655 | laúd | 1 |
| 7656 | latón | 1 |
| 7657 | latina | 1 |
| 7658 | lastro | 1 |
| 7659 | lástima | 1 |
| 7660 | lastima | 1 |
| 7661 | lastarás | 1 |
| 7662 | lastan | 1 |
| 7663 | lasrada | 1 |
| 7664 | lasos | 1 |
| 7665 | laserios | 1 |
| 7666 | laserío | 1 |
| 7667 | lasaro | 1 |
| 7668 | largo | 1 |
| 7669 | largas | 1 |
| 7670 | largamente | 1 |
| 7671 | larga | 1 |
| 7672 | laredo | 1 |
| 7673 | lardero | 1 |
| 7674 | lantejas | 1 |
| 7675 | lanprea | 1 |
| 7676 | langue | 1 |
| 7677 | langostas | 1 |
| 7678 | lançe | 1 |
| 7679 | lanças | 1 |
| 7680 | laminero | 1 |
| 7681 | lame | 1 |
| 7682 | laga | 1 |
| 7683 | lætemur | 1 |
| 7684 | laetatus | 1 |
| 7685 | ladrones | 1 |
| 7686 | ladron | 1 |
| 7687 | ladrando | 1 |
| 7688 | ladra | 1 |
| 7689 | ladina | 1 |
| 7690 | laçio | 1 |
| 7691 | laçias | 1 |
| 7692 | laçerio | 1 |
| 7693 | labró | 1 |
| 7694 | labrança | 1 |
| 7695 | labradores | 1 |
| 7696 | labradas | 1 |
| 7697 | labia | 1 |
| 7698 | k | 1 |
| 7699 | juzgue | 1 |
| 7700 | juzgólo | 1 |
| 7701 | juzgat | 1 |
| 7702 | juzgarlo | 1 |
| 7703 | juzgarás | 1 |
| 7704 | juzgará | 1 |
| 7705 | juzgando | 1 |
| 7706 | juzgan | 1 |
| 7707 | juzgador | 1 |
| 7708 | juzgado | 1 |
| 7709 | juysio | 1 |
| 7710 | juxta | 1 |
| 7711 | justyçia | 1 |
| 7712 | justos | 1 |
| 7713 | justiçiado | 1 |
| 7714 | justavan | 1 |
| 7715 | justaré | 1 |
| 7716 | jusgar | 1 |
| 7717 | jusgador | 1 |
| 7718 | jurydiçión | 1 |
| 7719 | jurídicas | 1 |
| 7720 | jurasen | 1 |
| 7721 | jurando | 1 |
| 7722 | juntava | 1 |
| 7723 | juntáronse | 1 |
| 7724 | juntar | 1 |
| 7725 | juntan | 1 |
| 7726 | juntamiento | 1 |
| 7727 | juntados | 1 |
| 7728 | juntades | 1 |
| 7729 | junta | 1 |
| 7730 | julián | 1 |
| 7731 | juisio | 1 |
| 7732 | juguete | 1 |
| 7733 | juglarías | 1 |
| 7734 | juglara | 1 |
| 7735 | jugavan | 1 |
| 7736 | jugava | 1 |
| 7737 | jugásemos | 1 |
| 7738 | jugara | 1 |
| 7739 | jugadores | 1 |
| 7740 | jugaban | 1 |
| 7741 | juga | 1 |
| 7742 | juegas | 1 |
| 7743 | juegan | 1 |
| 7744 | jueces | 1 |
| 7745 | judías | 1 |
| 7746 | judgó | 1 |
| 7747 | judgan | 1 |
| 7748 | judgador | 1 |
| 7749 | judería | 1 |
| 7750 | judea | 1 |
| 7751 | judæorum | 1 |
| 7752 | jubileo | 1 |
| 7753 | juán | 1 |
| 7754 | joya | 1 |
| 7755 | joventud | 1 |
| 7756 | joven | 1 |
| 7757 | josé | 1 |
| 7758 | jornadas | 1 |
| 7759 | jonás | 1 |
| 7760 | johán | 1 |
| 7761 | joan | 1 |
| 7762 | joab | 1 |
| 7763 | jhesús | 1 |
| 7764 | jesuxristo | 1 |
| 7765 | jerusalén | 1 |
| 7766 | jeremías | 1 |
| 7767 | javalyn | 1 |
| 7768 | javali | 1 |
| 7769 | jamones | 1 |
| 7770 | jaldetas | 1 |
| 7771 | jafet | 1 |
| 7772 | jaez | 1 |
| 7773 | jabalyn | 1 |
| 7774 | j | 1 |
| 7775 | iustus | 1 |
| 7776 | ita | 1 |
| 7777 | iste | 1 |
| 7778 | isopete | 1 |
| 7779 | isaías | 1 |
| 7780 | irónico | 1 |
| 7781 | ir | 1 |
| 7782 | invidia | 1 |
| 7783 | invento | 1 |
| 7784 | inventar | 1 |
| 7785 | introdujo | 1 |
| 7786 | introd | 1 |
| 7787 | intrigantes | 1 |
| 7788 | intitula | 1 |
| 7789 | intérprete | 1 |
| 7790 | interés | 1 |
| 7791 | intenso | 1 |
| 7792 | intenciones | 1 |
| 7793 | intención | 1 |
| 7794 | instruyda | 1 |
| 7795 | instrumentes | 1 |
| 7796 | instrumente | 1 |
| 7797 | instruída | 1 |
| 7798 | instructa | 1 |
| 7799 | insociable | 1 |
| 7800 | insienplo | 1 |
| 7801 | inojos | 1 |
| 7802 | inogar | 1 |
| 7803 | inocente | 1 |
| 7804 | inoçençio | 1 |
| 7805 | inmundo | 1 |
| 7806 | injustamente | 1 |
| 7807 | injurias | 1 |
| 7808 | injuria | 1 |
| 7809 | injertándole | 1 |
| 7810 | initium | 1 |
| 7811 | inhonesta | 1 |
| 7812 | ingleses | 1 |
| 7813 | ingeniosa | 1 |
| 7814 | informada | 1 |
| 7815 | infiesto | 1 |
| 7816 | infernal | 1 |
| 7817 | infançones | 1 |
| 7818 | induzir | 1 |
| 7819 | indulgençias | 1 |
| 7820 | indoctos | 1 |
| 7821 | indino | 1 |
| 7822 | indico | 1 |
| 7823 | índice | 1 |
| 7824 | increíble | 1 |
| 7825 | incontrastable | 1 |
| 7826 | incomparable | 1 |
| 7827 | inclinada | 1 |
| 7828 | inchillas | 1 |
| 7829 | inche | 1 |
| 7830 | inchado | 1 |
| 7831 | importancia | 1 |
| 7832 | imitari | 1 |
| 7833 | imitador | 1 |
| 7834 | imitación | 1 |
| 7835 | imita | 1 |
| 7836 | illuc | 1 |
| 7837 | illos | 1 |
| 7838 | illorum | 1 |
| 7839 | illi | 1 |
| 7840 | il | 1 |
| 7841 | igualmente | 1 |
| 7842 | igualado | 1 |
| 7843 | igreja | 1 |
| 7844 | iesus | 1 |
| 7845 | ido | 1 |
| 7846 | idílico | 1 |
| 7847 | iba | 1 |
| 7848 | iaz | 1 |
| 7849 | i | 1 |
| 7850 | hy | 1 |
| 7851 | hurta | 1 |
| 7852 | hurón | 1 |
| 7853 | hundo | 1 |
| 7854 | humor | 1 |
| 7855 | humano | 1 |
| 7856 | huevo | 1 |
| 7857 | huéspedes | 1 |
| 7858 | hueso | 1 |
| 7859 | huérfanas | 1 |
| 7860 | huella | 1 |
| 7861 | huelgo | 1 |
| 7862 | huele | 1 |
| 7863 | hueca | 1 |
| 7864 | huço | 1 |
| 7865 | hubo | 1 |
| 7866 | hubiese | 1 |
| 7867 | hoz | 1 |
| 7868 | hostal | 1 |
| 7869 | hospedóm | 1 |
| 7870 | hoscos | 1 |
| 7871 | horaña | 1 |
| 7872 | honrrados | 1 |
| 7873 | honrrado | 1 |
| 7874 | honrado | 1 |
| 7875 | honor | 1 |
| 7876 | hondo | 1 |
| 7877 | hondamente | 1 |
| 7878 | honda | 1 |
| 7879 | homo | 1 |
| 7880 | hominum | 1 |
| 7881 | homero | 1 |
| 7882 | homeçida | 1 |
| 7883 | hogaças | 1 |
| 7884 | hizo | 1 |
| 7885 | hito | 1 |
| 7886 | his | 1 |
| 7887 | hipócritas | 1 |
| 7888 | hipócrates | 1 |
| 7889 | hijas | 1 |
| 7890 | hiebre | 1 |
| 7891 | hexasílabos | 1 |
| 7892 | hévoslo | 1 |
| 7893 | heviella | 1 |
| 7894 | hes | 1 |
| 7895 | herroso | 1 |
| 7896 | herror | 1 |
| 7897 | herren | 1 |
| 7898 | herré | 1 |
| 7899 | herrados | 1 |
| 7900 | herrada | 1 |
| 7901 | heroicos | 1 |
| 7902 | héroes | 1 |
| 7903 | hermita | 1 |
| 7904 | hermanos | 1 |
| 7905 | hermanas | 1 |
| 7906 | hermanados | 1 |
| 7907 | heridos | 1 |
| 7908 | herías | 1 |
| 7909 | herençia | 1 |
| 7910 | herege | 1 |
| 7911 | herederos | 1 |
| 7912 | heredarlo | 1 |
| 7913 | heredades | 1 |
| 7914 | heptasílabos | 1 |
| 7915 | hemençia | 1 |
| 7916 | helyçes | 1 |
| 7917 | helénicas | 1 |
| 7918 | héla | 1 |
| 7919 | hedifiçio | 1 |
| 7920 | hazalvaro | 1 |
| 7921 | hayar | 1 |
| 7922 | hayan | 1 |
| 7923 | havía | 1 |
| 7924 | havas | 1 |
| 7925 | hatos | 1 |
| 7926 | hascas | 1 |
| 7927 | hasalejas | 1 |
| 7928 | hás | 1 |
| 7929 | harte | 1 |
| 7930 | hartas | 1 |
| 7931 | harre | 1 |
| 7932 | harpa | 1 |
| 7933 | haría | 1 |
| 7934 | handora | 1 |
| 7935 | hallo | 1 |
| 7936 | hallar | 1 |
| 7937 | hállanse | 1 |
| 7938 | halía | 1 |
| 7939 | hado | 1 |
| 7940 | hadedur | 1 |
| 7941 | hadas | 1 |
| 7942 | hacinados | 1 |
| 7943 | haçina | 1 |
| 7944 | haciéndonos | 1 |
| 7945 | hacernos | 1 |
| 7946 | hacerles | 1 |
| 7947 | haçerio | 1 |
| 7948 | haça | 1 |
| 7949 | hablillas | 1 |
| 7950 | hablas | 1 |
| 7951 | hablaba | 1 |
| 7952 | habiendo | 1 |
| 7953 | habían | 1 |
| 7954 | haberse | 1 |
| 7955 | h | 1 |
| 7956 | guya | 1 |
| 7957 | gusta | 1 |
| 7958 | gusanos | 1 |
| 7959 | gulfara | 1 |
| 7960 | guió | 1 |
| 7961 | guiñó | 1 |
| 7962 | guiña | 1 |
| 7963 | guinando | 1 |
| 7964 | guillermo | 1 |
| 7965 | guido | 1 |
| 7966 | guerreros | 1 |
| 7967 | guerrera | 1 |
| 7968 | guerrea | 1 |
| 7969 | guère | 1 |
| 7970 | guárte | 1 |
| 7971 | guarnimientos | 1 |
| 7972 | guarnidos | 1 |
| 7973 | guarir | 1 |
| 7974 | guarida | 1 |
| 7975 | guaresçe | 1 |
| 7976 | guardiano | 1 |
| 7977 | guardeste | 1 |
| 7978 | guárdese | 1 |
| 7979 | guárdes | 1 |
| 7980 | guárdense | 1 |
| 7981 | guárdenos | 1 |
| 7982 | guárdelos | 1 |
| 7983 | guárdela | 1 |
| 7984 | guardava | 1 |
| 7985 | guardasen | 1 |
| 7986 | guardaron | 1 |
| 7987 | guardarlas | 1 |
| 7988 | guardaré | 1 |
| 7989 | guárdanlo | 1 |
| 7990 | guardando | 1 |
| 7991 | guardados | 1 |
| 7992 | guardador | 1 |
| 7993 | guardado | 1 |
| 7994 | guardadla | 1 |
| 7995 | guardades | 1 |
| 7996 | guardaderas | 1 |
| 7997 | guardadas | 1 |
| 7998 | guadalquivir | 1 |
| 7999 | grytadera | 1 |
| 8000 | grueso | 1 |
| 8001 | gruesa | 1 |
| 8002 | groya | 1 |
| 8003 | grojear | 1 |
| 8004 | gritos | 1 |
| 8005 | grito | 1 |
| 8006 | gritas | 1 |
| 8007 | gritando | 1 |
| 8008 | grillos | 1 |
| 8009 | griega | 1 |
| 8010 | gressus | 1 |
| 8011 | gregorio | 1 |
| 8012 | greco | 1 |
| 8013 | greales | 1 |
| 8014 | gravemente | 1 |
| 8015 | graniso | 1 |
| 8016 | granisava | 1 |
| 8017 | grandías | 1 |
| 8018 | grandeza | 1 |
| 8019 | granava | 1 |
| 8020 | granado | 1 |
| 8021 | granada | 1 |
| 8022 | grana | 1 |
| 8023 | gramatical | 1 |
| 8024 | grajos | 1 |
| 8025 | grajas | 1 |
| 8026 | gradesçido | 1 |
| 8027 | gradésçegelo | 1 |
| 8028 | gradan | 1 |
| 8029 | grad | 1 |
| 8030 | grabada | 1 |
| 8031 | goste | 1 |
| 8032 | gostarlas | 1 |
| 8033 | gosaste | 1 |
| 8034 | gorjeador | 1 |
| 8035 | gorgee | 1 |
| 8036 | gordilla | 1 |
| 8037 | gorda | 1 |
| 8038 | gonzalo | 1 |
| 8039 | goma | 1 |
| 8040 | golpado | 1 |
| 8041 | golpad | 1 |
| 8042 | golp | 1 |
| 8043 | golosyna | 1 |
| 8044 | golosos | 1 |
| 8045 | golosina | 1 |
| 8046 | golondryna | 1 |
| 8047 | golhines | 1 |
| 8048 | gobernad | 1 |
| 8049 | goárdame | 1 |
| 8050 | glosas | 1 |
| 8051 | gitarra | 1 |
| 8052 | gitar | 1 |
| 8053 | gisada | 1 |
| 8054 | girgonça | 1 |
| 8055 | gigantazo | 1 |
| 8056 | giar | 1 |
| 8057 | gestas | 1 |
| 8058 | gentiles | 1 |
| 8059 | genta | 1 |
| 8060 | gengibrante | 1 |
| 8061 | géneros | 1 |
| 8062 | gemidos | 1 |
| 8063 | gemido | 1 |
| 8064 | gayta | 1 |
| 8065 | gayos | 1 |
| 8066 | gayo | 1 |
| 8067 | gaviellas | 1 |
| 8068 | gaula | 1 |
| 8069 | gastar | 1 |
| 8070 | gaspar | 1 |
| 8071 | gasnar | 1 |
| 8072 | gasajo | 1 |
| 8073 | gasajados | 1 |
| 8074 | gasajado | 1 |
| 8075 | garvanços | 1 |
| 8076 | garnidos | 1 |
| 8077 | garnidas | 1 |
| 8078 | garniçiones | 1 |
| 8079 | garnacha | 1 |
| 8080 | gariofelata | 1 |
| 8081 | gargantero | 1 |
| 8082 | gardatla | 1 |
| 8083 | garçonía | 1 |
| 8084 | garças | 1 |
| 8085 | garbo | 1 |
| 8086 | garanón | 1 |
| 8087 | garabí | 1 |
| 8088 | gano | 1 |
| 8089 | gangosa | 1 |
| 8090 | ganarás | 1 |
| 8091 | ganançia | 1 |
| 8092 | gáname | 1 |
| 8093 | ganados | 1 |
| 8094 | ganades | 1 |
| 8095 | ganada | 1 |
| 8096 | gamellas | 1 |
| 8097 | galope | 1 |
| 8098 | gallofas | 1 |
| 8099 | gallina | 1 |
| 8100 | galleta | 1 |
| 8101 | gallegas | 1 |
| 8102 | gallega | 1 |
| 8103 | galilea | 1 |
| 8104 | galicia | 1 |
| 8105 | galga | 1 |
| 8106 | galeotes | 1 |
| 8107 | galardonado | 1 |
| 8108 | galardonada | 1 |
| 8109 | gaho | 1 |
| 8110 | g | 1 |
| 8111 | fyz | 1 |
| 8112 | fyta | 1 |
| 8113 | fyrmado | 1 |
| 8114 | fyno | 1 |
| 8115 | fynco | 1 |
| 8116 | fynchyr | 1 |
| 8117 | fynchadas | 1 |
| 8118 | fynchada | 1 |
| 8119 | fyncavades | 1 |
| 8120 | fyncava | 1 |
| 8121 | fyncase | 1 |
| 8122 | fyncaron | 1 |
| 8123 | fyncar | 1 |
| 8124 | fyncando | 1 |
| 8125 | fyncados | 1 |
| 8126 | fyncado | 1 |
| 8127 | fyncada | 1 |
| 8128 | fygura | 1 |
| 8129 | fygueras | 1 |
| 8130 | fygado | 1 |
| 8131 | fyesta | 1 |
| 8132 | fyere | 1 |
| 8133 | fyende | 1 |
| 8134 | fydalgo | 1 |
| 8135 | fyará | 1 |
| 8136 | fyar | 1 |
| 8137 | fyança | 1 |
| 8138 | fuyr | 1 |
| 8139 | fuylo | 1 |
| 8140 | fustes | 1 |
| 8141 | fusia | 1 |
| 8142 | furtó | 1 |
| 8143 | furtes | 1 |
| 8144 | furte | 1 |
| 8145 | fúrtasle | 1 |
| 8146 | furtase | 1 |
| 8147 | furtaron | 1 |
| 8148 | furtarías | 1 |
| 8149 | furtando | 1 |
| 8150 | furtallo | 1 |
| 8151 | furtados | 1 |
| 8152 | furtadas | 1 |
| 8153 | furniçio | 1 |
| 8154 | fumero | 1 |
| 8155 | fulano | 1 |
| 8156 | fuey | 1 |
| 8157 | fuésele | 1 |
| 8158 | fuesa | 1 |
| 8159 | fuertemente | 1 |
| 8160 | fuert | 1 |
| 8161 | fueronse | 1 |
| 8162 | fuéronlo | 1 |
| 8163 | fuéronles | 1 |
| 8164 | fuéronle | 1 |
| 8165 | fuerço | 1 |
| 8166 | fuerças | 1 |
| 8167 | fueran | 1 |
| 8168 | füera | 1 |
| 8169 | fuentfría | 1 |
| 8170 | fuentes | 1 |
| 8171 | fuémosnos | 1 |
| 8172 | fuémosle | 1 |
| 8173 | fuéme | 1 |
| 8174 | fuelo | 1 |
| 8175 | fuelga | 1 |
| 8176 | fructus | 1 |
| 8177 | fructa | 1 |
| 8178 | frores | 1 |
| 8179 | fror | 1 |
| 8180 | fronçidas | 1 |
| 8181 | friuras | 1 |
| 8182 | friura | 1 |
| 8183 | fritos | 1 |
| 8184 | fríos | 1 |
| 8185 | frida | 1 |
| 8186 | frey | 1 |
| 8187 | frema | 1 |
| 8188 | frecuentador | 1 |
| 8189 | fraze | 1 |
| 8190 | frayría | 1 |
| 8191 | fraylía | 1 |
| 8192 | frayla | 1 |
| 8193 | françia | 1 |
| 8194 | francas | 1 |
| 8195 | francamente | 1 |
| 8196 | franca | 1 |
| 8197 | fraguó | 1 |
| 8198 | foz | 1 |
| 8199 | foydor | 1 |
| 8200 | foydas | 1 |
| 8201 | foyd | 1 |
| 8202 | foya | 1 |
| 8203 | foxieron | 1 |
| 8204 | fostigarás | 1 |
| 8205 | fortuna | 1 |
| 8206 | fortaleza | 1 |
| 8207 | fornachos | 1 |
| 8208 | formeste | 1 |
| 8209 | forme | 1 |
| 8210 | formado | 1 |
| 8211 | forma | 1 |
| 8212 | forçaste | 1 |
| 8213 | forçados | 1 |
| 8214 | forçado | 1 |
| 8215 | forçada | 1 |
| 8216 | forados | 1 |
| 8217 | fonsarios | 1 |
| 8218 | fondo | 1 |
| 8219 | fomentada | 1 |
| 8220 | follya | 1 |
| 8221 | follón | 1 |
| 8222 | folguras | 1 |
| 8223 | folgavan | 1 |
| 8224 | folgaron | 1 |
| 8225 | folgaremos | 1 |
| 8226 | folgaredes | 1 |
| 8227 | folgad | 1 |
| 8228 | fojas | 1 |
| 8229 | foguera | 1 |
| 8230 | fogar | 1 |
| 8231 | floxa | 1 |
| 8232 | floresta | 1 |
| 8233 | flemosa | 1 |
| 8234 | flema | 1 |
| 8235 | flayres | 1 |
| 8236 | flayre | 1 |
| 8237 | flamencos | 1 |
| 8238 | flamenco | 1 |
| 8239 | fízose | 1 |
| 8240 | fízos | 1 |
| 8241 | fízome | 1 |
| 8242 | fizome | 1 |
| 8243 | fízom | 1 |
| 8244 | fízolos | 1 |
| 8245 | fízoles | 1 |
| 8246 | fizle | 1 |
| 8247 | fito | 1 |
| 8248 | físole | 1 |
| 8249 | fisle | 1 |
| 8250 | físicos | 1 |
| 8251 | física | 1 |
| 8252 | firmes | 1 |
| 8253 | firmemente | 1 |
| 8254 | firmado | 1 |
| 8255 | firma | 1 |
| 8256 | fio | 1 |
| 8257 | finos | 1 |
| 8258 | finojo | 1 |
| 8259 | finco | 1 |
| 8260 | finchida | 1 |
| 8261 | fincaste | 1 |
| 8262 | fincan | 1 |
| 8263 | fincada | 1 |
| 8264 | finas | 1 |
| 8265 | finados | 1 |
| 8266 | filius | 1 |
| 8267 | fijuelo | 1 |
| 8268 | fijosdalgo | 1 |
| 8269 | fijodalgo | 1 |
| 8270 | fijasdalgo | 1 |
| 8271 | fijadalgo | 1 |
| 8272 | figuran | 1 |
| 8273 | figos | 1 |
| 8274 | fígados | 1 |
| 8275 | fiestas | 1 |
| 8276 | fies | 1 |
| 8277 | fiero | 1 |
| 8278 | fieri | 1 |
| 8279 | fierbe | 1 |
| 8280 | fieles | 1 |
| 8281 | fiedes | 1 |
| 8282 | fiebre | 1 |
| 8283 | fidelísimo | 1 |
| 8284 | fidelidad | 1 |
| 8285 | fidei | 1 |
| 8286 | fidalguía | 1 |
| 8287 | ficarás | 1 |
| 8288 | fiancó | 1 |
| 8289 | fiadura | 1 |
| 8290 | ffyz | 1 |
| 8291 | ffyncó | 1 |
| 8292 | ffuy | 1 |
| 8293 | ffurtól | 1 |
| 8294 | ffurtava | 1 |
| 8295 | ffurtar | 1 |
| 8296 | ffurón | 1 |
| 8297 | ffuime | 1 |
| 8298 | ffuerte | 1 |
| 8299 | ffuéronse | 1 |
| 8300 | ffrançés | 1 |
| 8301 | fforadóse | 1 |
| 8302 | ffollya | 1 |
| 8303 | ffizvos | 1 |
| 8304 | ffízose | 1 |
| 8305 | ffiestas | 1 |
| 8306 | ffesieron | 1 |
| 8307 | ffecho | 1 |
| 8308 | ffazle | 1 |
| 8309 | ffázeslo | 1 |
| 8310 | ffázesles | 1 |
| 8311 | ffázele | 1 |
| 8312 | ffaz | 1 |
| 8313 | ffasíe | 1 |
| 8314 | ffases | 1 |
| 8315 | ffasaña | 1 |
| 8316 | ffaría | 1 |
| 8317 | ffallyr | 1 |
| 8318 | ffallarás | 1 |
| 8319 | ffaciendo | 1 |
| 8320 | ffabla | 1 |
| 8321 | feziste | 1 |
| 8322 | feziesen | 1 |
| 8323 | fezieron | 1 |
| 8324 | feziere | 1 |
| 8325 | fey | 1 |
| 8326 | fesyeron | 1 |
| 8327 | festino | 1 |
| 8328 | feste | 1 |
| 8329 | fesieron | 1 |
| 8330 | fesiere | 1 |
| 8331 | feses | 1 |
| 8332 | fervos | 1 |
| 8333 | ferrero | 1 |
| 8334 | ferrava | 1 |
| 8335 | ferrado | 1 |
| 8336 | fernández | 1 |
| 8337 | fernand | 1 |
| 8338 | fermosur | 1 |
| 8339 | fermosillos | 1 |
| 8340 | ferieron | 1 |
| 8341 | feríen | 1 |
| 8342 | feridos | 1 |
| 8343 | ferid | 1 |
| 8344 | feríanlo | 1 |
| 8345 | feno | 1 |
| 8346 | feniestras | 1 |
| 8347 | fenesçer | 1 |
| 8348 | féme | 1 |
| 8349 | feliz | 1 |
| 8350 | fegurada | 1 |
| 8351 | fediondo | 1 |
| 8352 | feçystelos | 1 |
| 8353 | feçyste | 1 |
| 8354 | feciste | 1 |
| 8355 | feçiesen | 1 |
| 8356 | feçieron | 1 |
| 8357 | feçiéredes | 1 |
| 8358 | febrero | 1 |
| 8359 | feblero | 1 |
| 8360 | fazte | 1 |
| 8361 | fazlo | 1 |
| 8362 | fazles | 1 |
| 8363 | fazíes | 1 |
| 8364 | faziente | 1 |
| 8365 | fazienda | 1 |
| 8366 | fazíen | 1 |
| 8367 | fazíe | 1 |
| 8368 | fazías | 1 |
| 8369 | fazíansele | 1 |
| 8370 | fazíanme | 1 |
| 8371 | fazianl | 1 |
| 8372 | fazet | 1 |
| 8373 | fázeste | 1 |
| 8374 | fázesme | 1 |
| 8375 | fázeslos | 1 |
| 8376 | fázeslo | 1 |
| 8377 | fázesle | 1 |
| 8378 | fazeslas | 1 |
| 8379 | fázesla | 1 |
| 8380 | fázes | 1 |
| 8381 | fazert | 1 |
| 8382 | fazerse | 1 |
| 8383 | fazerlo | 1 |
| 8384 | fazemos | 1 |
| 8385 | fázelo | 1 |
| 8386 | fázelas | 1 |
| 8387 | fazel | 1 |
| 8388 | fazedor | 1 |
| 8389 | fazañero | 1 |
| 8390 | fazañas | 1 |
| 8391 | fazaña | 1 |
| 8392 | faza | 1 |
| 8393 | fayle | 1 |
| 8394 | fay | 1 |
| 8395 | favas | 1 |
| 8396 | fasyendo | 1 |
| 8397 | faste | 1 |
| 8398 | fasle | 1 |
| 8399 | fasiéndola | 1 |
| 8400 | fasie | 1 |
| 8401 | faset | 1 |
| 8402 | fasert | 1 |
| 8403 | faserle | 1 |
| 8404 | fásenos | 1 |
| 8405 | fasemos | 1 |
| 8406 | fasedores | 1 |
| 8407 | fasedor | 1 |
| 8408 | fasedlo | 1 |
| 8409 | fascas | 1 |
| 8410 | fasañero | 1 |
| 8411 | fasañas | 1 |
| 8412 | faryna | 1 |
| 8413 | farte | 1 |
| 8414 | fartarás | 1 |
| 8415 | fartará | 1 |
| 8416 | farta | 1 |
| 8417 | faronía | 1 |
| 8418 | farón | 1 |
| 8419 | faríemos | 1 |
| 8420 | farías | 1 |
| 8421 | farias | 1 |
| 8422 | faremos | 1 |
| 8423 | fardida | 1 |
| 8424 | faraón | 1 |
| 8425 | farán | 1 |
| 8426 | fantasya | 1 |
| 8427 | fantástico | 1 |
| 8428 | fantasma | 1 |
| 8429 | fanbriento | 1 |
| 8430 | famoso | 1 |
| 8431 | famosísimo | 1 |
| 8432 | famosa | 1 |
| 8433 | faltado | 1 |
| 8434 | falssedat | 1 |
| 8435 | falssas | 1 |
| 8436 | falsó | 1 |
| 8437 | falsía | 1 |
| 8438 | falsamente | 1 |
| 8439 | fallós | 1 |
| 8440 | fallir | 1 |
| 8441 | fallías | 1 |
| 8442 | fallía | 1 |
| 8443 | fallese | 1 |
| 8444 | fallesçer | 1 |
| 8445 | falles | 1 |
| 8446 | fallençia | 1 |
| 8447 | fallen | 1 |
| 8448 | falleçedero | 1 |
| 8449 | falleçe | 1 |
| 8450 | fallase | 1 |
| 8451 | fallas | 1 |
| 8452 | fallaron | 1 |
| 8453 | fallares | 1 |
| 8454 | fallará | 1 |
| 8455 | fállanse | 1 |
| 8456 | falladas | 1 |
| 8457 | falimente | 1 |
| 8458 | faldragas | 1 |
| 8459 | falda | 1 |
| 8460 | falcón | 1 |
| 8461 | falanga | 1 |
| 8462 | falaguero | 1 |
| 8463 | falagaré | 1 |
| 8464 | falagada | 1 |
| 8465 | falagábale | 1 |
| 8466 | fágote | 1 |
| 8467 | fadrique | 1 |
| 8468 | fadiga | 1 |
| 8469 | fadas | 1 |
| 8470 | fadado | 1 |
| 8471 | factus | 1 |
| 8472 | factum | 1 |
| 8473 | façiet | 1 |
| 8474 | facientibus | 1 |
| 8475 | façienda | 1 |
| 8476 | façien | 1 |
| 8477 | façías | 1 |
| 8478 | façía | 1 |
| 8479 | fáçete | 1 |
| 8480 | façerte | 1 |
| 8481 | facere | 1 |
| 8482 | façer | 1 |
| 8483 | fáçenlo | 1 |
| 8484 | façen | 1 |
| 8485 | facen | 1 |
| 8486 | façemos | 1 |
| 8487 | façedes | 1 |
| 8488 | faced | 1 |
| 8489 | façe | 1 |
| 8490 | face | 1 |
| 8491 | façañas | 1 |
| 8492 | fabrilla | 1 |
| 8493 | fabrasen | 1 |
| 8494 | fabrar | 1 |
| 8495 | fablóme | 1 |
| 8496 | fablóle | 1 |
| 8497 | fablilla | 1 |
| 8498 | fabliella | 1 |
| 8499 | fabliau | 1 |
| 8500 | fableste | 1 |
| 8501 | fablen | 1 |
| 8502 | fablémoslo | 1 |
| 8503 | fabléla | 1 |
| 8504 | fablél | 1 |
| 8505 | fabledes | 1 |
| 8506 | fablé | 1 |
| 8507 | fablatle | 1 |
| 8508 | fablastes | 1 |
| 8509 | fáblasles | 1 |
| 8510 | fablarvos | 1 |
| 8511 | fablarnos | 1 |
| 8512 | fablarme | 1 |
| 8513 | fablaredes | 1 |
| 8514 | fablaré | 1 |
| 8515 | fablardes | 1 |
| 8516 | fablarás | 1 |
| 8517 | fablan | 1 |
| 8518 | fáblales | 1 |
| 8519 | fáblale | 1 |
| 8520 | fablador | 1 |
| 8521 | fabladme | 1 |
| 8522 | fabladla | 1 |
| 8523 | fabládesme | 1 |
| 8524 | fablaban | 1 |
| 8525 | f | 1 |
| 8526 | ezechías | 1 |
| 8527 | eyvernada | 1 |
| 8528 | ey | 1 |
| 8529 | extremo | 1 |
| 8530 | extollite | 1 |
| 8531 | explicit | 1 |
| 8532 | exido | 1 |
| 8533 | excumunión | 1 |
| 8534 | exclusivamente | 1 |
| 8535 | excelso | 1 |
| 8536 | excelsas | 1 |
| 8537 | exactitud | 1 |
| 8538 | evitar | 1 |
| 8539 | everniso | 1 |
| 8540 | evangelista | 1 |
| 8541 | eum | 1 |
| 8542 | estupendamente | 1 |
| 8543 | estudio | 1 |
| 8544 | estudie | 1 |
| 8545 | estudiarse | 1 |
| 8546 | estudiado | 1 |
| 8547 | estruendo | 1 |
| 8548 | estrólogos | 1 |
| 8549 | estricote | 1 |
| 8550 | estrenare | 1 |
| 8551 | estremo | 1 |
| 8552 | estremeçió | 1 |
| 8553 | estrellas | 1 |
| 8554 | estrecho | 1 |
| 8555 | estrecha | 1 |
| 8556 | estragaría | 1 |
| 8557 | estraga | 1 |
| 8558 | estorves | 1 |
| 8559 | estorvador | 1 |
| 8560 | estorvado | 1 |
| 8561 | estornudo | 1 |
| 8562 | estopa | 1 |
| 8563 | estonçes | 1 |
| 8564 | estomaticón | 1 |
| 8565 | estómago | 1 |
| 8566 | estodieron | 1 |
| 8567 | estodieres | 1 |
| 8568 | estivo | 1 |
| 8569 | estío | 1 |
| 8570 | estiércol | 1 |
| 8571 | estid | 1 |
| 8572 | estético | 1 |
| 8573 | estés | 1 |
| 8574 | estercuela | 1 |
| 8575 | ester | 1 |
| 8576 | estepa | 1 |
| 8577 | estedes | 1 |
| 8578 | estav | 1 |
| 8579 | estaré | 1 |
| 8580 | estarás | 1 |
| 8581 | estanbre | 1 |
| 8582 | estamos | 1 |
| 8583 | estadista | 1 |
| 8584 | estada | 1 |
| 8585 | estaçión | 1 |
| 8586 | estaca | 1 |
| 8587 | establyas | 1 |
| 8588 | establía | 1 |
| 8589 | estaban | 1 |
| 8590 | est | 1 |
| 8591 | essa | 1 |
| 8592 | esquivos | 1 |
| 8593 | esquivedes | 1 |
| 8594 | esquive | 1 |
| 8595 | esquivas | 1 |
| 8596 | esquilo | 1 |
| 8597 | esquilman | 1 |
| 8598 | espyciales | 1 |
| 8599 | espulgar | 1 |
| 8600 | espuela | 1 |
| 8601 | esposa | 1 |
| 8602 | esportilla | 1 |
| 8603 | espiritual | 1 |
| 8604 | espino | 1 |
| 8605 | espinaças | 1 |
| 8606 | espinacas | 1 |
| 8607 | espigas | 1 |
| 8608 | espienden | 1 |
| 8609 | espiçial | 1 |
| 8610 | espesura | 1 |
| 8611 | espessura | 1 |
| 8612 | espesas | 1 |
| 8613 | esperemos | 1 |
| 8614 | esperat | 1 |
| 8615 | esperando | 1 |
| 8616 | esperan | 1 |
| 8617 | esperades | 1 |
| 8618 | espendí | 1 |
| 8619 | espejo | 1 |
| 8620 | espéculo | 1 |
| 8621 | especulo | 1 |
| 8622 | espectadores | 1 |
| 8623 | especie | 1 |
| 8624 | especialísimo | 1 |
| 8625 | espeçia | 1 |
| 8626 | esparsido | 1 |
| 8627 | espárragos | 1 |
| 8628 | españoles | 1 |
| 8629 | española | 1 |
| 8630 | espantóse | 1 |
| 8631 | espantó | 1 |
| 8632 | espanten | 1 |
| 8633 | espantava | 1 |
| 8634 | espantaste | 1 |
| 8635 | espantase | 1 |
| 8636 | espantan | 1 |
| 8637 | espantados | 1 |
| 8638 | espantado | 1 |
| 8639 | espantadizos | 1 |
| 8640 | espantadas | 1 |
| 8641 | espantada | 1 |
| 8642 | espantable | 1 |
| 8643 | espagnol | 1 |
| 8644 | espaçio | 1 |
| 8645 | espacio | 1 |
| 8646 | espaçias | 1 |
| 8647 | esmeran | 1 |
| 8648 | esmera | 1 |
| 8649 | esgrima | 1 |
| 8650 | esfuerçe | 1 |
| 8651 | esfuerça | 1 |
| 8652 | esforçados | 1 |
| 8653 | esençiones | 1 |
| 8654 | ése | 1 |
| 8655 | escusóse | 1 |
| 8656 | escusóme | 1 |
| 8657 | escuses | 1 |
| 8658 | escuseras | 1 |
| 8659 | escusarvos | 1 |
| 8660 | escúsanos | 1 |
| 8661 | escusadas | 1 |
| 8662 | escusada | 1 |
| 8663 | escureçió | 1 |
| 8664 | escureçes | 1 |
| 8665 | escupir | 1 |
| 8666 | escúpenl | 1 |
| 8667 | esculares | 1 |
| 8668 | escuerço | 1 |
| 8669 | escudo | 1 |
| 8670 | escudiellas | 1 |
| 8671 | escudávanse | 1 |
| 8672 | escudados | 1 |
| 8673 | escucho | 1 |
| 8674 | escúcheme | 1 |
| 8675 | escúchame | 1 |
| 8676 | escrivir | 1 |
| 8677 | escriviese | 1 |
| 8678 | escriva | 1 |
| 8679 | escribirlo | 1 |
| 8680 | escribiéndose | 1 |
| 8681 | escrebiré | 1 |
| 8682 | escotes | 1 |
| 8683 | escoté | 1 |
| 8684 | escote | 1 |
| 8685 | escotan | 1 |
| 8686 | escotados | 1 |
| 8687 | escoplo | 1 |
| 8688 | escopieron | 1 |
| 8689 | esconderás | 1 |
| 8690 | esconder | 1 |
| 8691 | esconbra | 1 |
| 8692 | escomonión | 1 |
| 8693 | escoje | 1 |
| 8694 | escogiere | 1 |
| 8695 | escogiendo | 1 |
| 8696 | escogidos | 1 |
| 8697 | escogí | 1 |
| 8698 | escogerá | 1 |
| 8699 | escoger | 1 |
| 8700 | escogedes | 1 |
| 8701 | escofyna | 1 |
| 8702 | esclavina | 1 |
| 8703 | escenas | 1 |
| 8704 | escatima | 1 |
| 8705 | escasos | 1 |
| 8706 | escaseza | 1 |
| 8707 | escasa | 1 |
| 8708 | escarvas | 1 |
| 8709 | escarnios | 1 |
| 8710 | escarnidor | 1 |
| 8711 | escarneçerla | 1 |
| 8712 | escarcha | 1 |
| 8713 | escarbando | 1 |
| 8714 | escapó | 1 |
| 8715 | escapava | 1 |
| 8716 | escapasen | 1 |
| 8717 | escaparé | 1 |
| 8718 | escapar | 1 |
| 8719 | escapándose | 1 |
| 8720 | escapalla | 1 |
| 8721 | escantan | 1 |
| 8722 | escantamente | 1 |
| 8723 | escantaderas | 1 |
| 8724 | escantada | 1 |
| 8725 | escaminado | 1 |
| 8726 | escamas | 1 |
| 8727 | escalón | 1 |
| 8728 | esaú | 1 |
| 8729 | esaminados | 1 |
| 8730 | esaminado | 1 |
| 8731 | és | 1 |
| 8732 | erveras | 1 |
| 8733 | erudito | 1 |
| 8734 | erudiciones | 1 |
| 8735 | ersía | 1 |
| 8736 | errores | 1 |
| 8737 | errides | 1 |
| 8738 | erreste | 1 |
| 8739 | erremos | 1 |
| 8740 | errança | 1 |
| 8741 | ermada | 1 |
| 8742 | erizo | 1 |
| 8743 | eriso | 1 |
| 8744 | erencia | 1 |
| 8745 | eredades | 1 |
| 8746 | erçer | 1 |
| 8747 | érase | 1 |
| 8748 | equus | 1 |
| 8749 | epopeya | 1 |
| 8750 | épocas | 1 |
| 8751 | epinicio | 1 |
| 8752 | epifanía | 1 |
| 8753 | eñadió | 1 |
| 8754 | enxutos | 1 |
| 8755 | enxundias | 1 |
| 8756 | enxiridores | 1 |
| 8757 | enxienpro | 1 |
| 8758 | enxerida | 1 |
| 8759 | enxería | 1 |
| 8760 | enxanbre | 1 |
| 8761 | enxalvega | 1 |
| 8762 | enviso | 1 |
| 8763 | envileçes | 1 |
| 8764 | enviado | 1 |
| 8765 | envergonçada | 1 |
| 8766 | envelyñas | 1 |
| 8767 | enveleñó | 1 |
| 8768 | envejesçen | 1 |
| 8769 | envejeçedes | 1 |
| 8770 | envegeçí | 1 |
| 8771 | envade | 1 |
| 8772 | entyéndolos | 1 |
| 8773 | entyéndelo | 1 |
| 8774 | entyéndela | 1 |
| 8775 | entyendas | 1 |
| 8776 | enturbiada | 1 |
| 8777 | entróse | 1 |
| 8778 | entropeçar | 1 |
| 8779 | entristézese | 1 |
| 8780 | entristesco | 1 |
| 8781 | entristeçieron | 1 |
| 8782 | entristeçes | 1 |
| 8783 | entristeçe | 1 |
| 8784 | entreveró | 1 |
| 8785 | entrever | 1 |
| 8786 | entreponga | 1 |
| 8787 | entremos | 1 |
| 8788 | entremety | 1 |
| 8789 | entremetiesen | 1 |
| 8790 | entremeter | 1 |
| 8791 | entremeten | 1 |
| 8792 | entremete | 1 |
| 8793 | entredes | 1 |
| 8794 | entras | 1 |
| 8795 | entrañas | 1 |
| 8796 | entran | 1 |
| 8797 | entorreadas | 1 |
| 8798 | entorpecidos | 1 |
| 8799 | entienden | 1 |
| 8800 | entiéndela | 1 |
| 8801 | entiéndala | 1 |
| 8802 | enterró | 1 |
| 8803 | enteros | 1 |
| 8804 | enterizo | 1 |
| 8805 | enteramente | 1 |
| 8806 | entendy | 1 |
| 8807 | entendudo | 1 |
| 8808 | entendrían | 1 |
| 8809 | entendrian | 1 |
| 8810 | entendredes | 1 |
| 8811 | entendrán | 1 |
| 8812 | entendiese | 1 |
| 8813 | entendíen | 1 |
| 8814 | entendía | 1 |
| 8815 | entendí | 1 |
| 8816 | entendetlo | 1 |
| 8817 | entenderé | 1 |
| 8818 | entenderás | 1 |
| 8819 | entenderá | 1 |
| 8820 | entended | 1 |
| 8821 | entendades | 1 |
| 8822 | enteca | 1 |
| 8823 | ensyenpro | 1 |
| 8824 | ensyenplo | 1 |
| 8825 | ensueña | 1 |
| 8826 | enssienpro | 1 |
| 8827 | ensombrezcan | 1 |
| 8828 | ensina | 1 |
| 8829 | ensilla | 1 |
| 8830 | ensienpro | 1 |
| 8831 | ensías | 1 |
| 8832 | enseña | 1 |
| 8833 | ensayo | 1 |
| 8834 | ensaño | 1 |
| 8835 | ensañar | 1 |
| 8836 | ensalmaderas | 1 |
| 8837 | ensalçamientos | 1 |
| 8838 | ensalçada | 1 |
| 8839 | enriza | 1 |
| 8840 | enrique | 1 |
| 8841 | enrevesado | 1 |
| 8842 | enpuesta | 1 |
| 8843 | enprestadlo | 1 |
| 8844 | enpresta | 1 |
| 8845 | enprea | 1 |
| 8846 | enpós | 1 |
| 8847 | enpos | 1 |
| 8848 | enplea | 1 |
| 8849 | enplazóla | 1 |
| 8850 | enplasto | 1 |
| 8851 | enpiuelan | 1 |
| 8852 | enpieça | 1 |
| 8853 | enpesçer | 1 |
| 8854 | enpesçe | 1 |
| 8855 | enpero | 1 |
| 8856 | enperios | 1 |
| 8857 | enperesedes | 1 |
| 8858 | enpereçes | 1 |
| 8859 | enperante | 1 |
| 8860 | enpendolados | 1 |
| 8861 | enpeesçer | 1 |
| 8862 | enpeesçen | 1 |
| 8863 | enpecen | 1 |
| 8864 | enpeçe | 1 |
| 8865 | enpavonada | 1 |
| 8866 | enojoso | 1 |
| 8867 | enojóse | 1 |
| 8868 | enojosa | 1 |
| 8869 | enojedes | 1 |
| 8870 | enoje | 1 |
| 8871 | enójase | 1 |
| 8872 | enojados | 1 |
| 8873 | enmudeçes | 1 |
| 8874 | enmagresçen | 1 |
| 8875 | enloquesçes | 1 |
| 8876 | enloqueçidos | 1 |
| 8877 | enloqueçida | 1 |
| 8878 | enloquece | 1 |
| 8879 | enlaze | 1 |
| 8880 | enlase | 1 |
| 8881 | enlaçes | 1 |
| 8882 | enlabiadoras | 1 |
| 8883 | enjambre | 1 |
| 8884 | enimigo | 1 |
| 8885 | enhoto | 1 |
| 8886 | engrandecerla | 1 |
| 8887 | engraçio | 1 |
| 8888 | engraçias | 1 |
| 8889 | engeño | 1 |
| 8890 | engarzó | 1 |
| 8891 | engañosos | 1 |
| 8892 | engañólo | 1 |
| 8893 | engañedes | 1 |
| 8894 | engañaría | 1 |
| 8895 | engañare | 1 |
| 8896 | engañados | 1 |
| 8897 | engañado | 1 |
| 8898 | engañades | 1 |
| 8899 | enganan | 1 |
| 8900 | enfychisó | 1 |
| 8901 | enfriada | 1 |
| 8902 | enforma | 1 |
| 8903 | enforce | 1 |
| 8904 | enforcavan | 1 |
| 8905 | enforcar | 1 |
| 8906 | enforcados | 1 |
| 8907 | enforcada | 1 |
| 8908 | enflaquidas | 1 |
| 8909 | enflaquezes | 1 |
| 8910 | enflaquesçes | 1 |
| 8911 | enflaquesçen | 1 |
| 8912 | enflaqueçe | 1 |
| 8913 | enflama | 1 |
| 8914 | enfiestos | 1 |
| 8915 | enfernal | 1 |
| 8916 | enfermo | 1 |
| 8917 | enfaronea | 1 |
| 8918 | enfamedes | 1 |
| 8919 | enfamaron | 1 |
| 8920 | enfaman | 1 |
| 8921 | enfamamiento | 1 |
| 8922 | enfamado | 1 |
| 8923 | enfamada | 1 |
| 8924 | enervolas | 1 |
| 8925 | enero | 1 |
| 8926 | enerisan | 1 |
| 8927 | enduxo | 1 |
| 8928 | endurar | 1 |
| 8929 | endryna | 1 |
| 8930 | endrino | 1 |
| 8931 | endrinas | 1 |
| 8932 | endrin | 1 |
| 8933 | enderredor | 1 |
| 8934 | enderedor | 1 |
| 8935 | endechado | 1 |
| 8936 | endecha | 1 |
| 8937 | endecasílabos | 1 |
| 8938 | encumbrados | 1 |
| 8939 | encuentras | 1 |
| 8940 | encúbrese | 1 |
| 8941 | encuadrar | 1 |
| 8942 | encore | 1 |
| 8943 | encordado | 1 |
| 8944 | encontréme | 1 |
| 8945 | encontrém | 1 |
| 8946 | encontrada | 1 |
| 8947 | encone | 1 |
| 8948 | enconado | 1 |
| 8949 | enconada | 1 |
| 8950 | encomendados | 1 |
| 8951 | encoje | 1 |
| 8952 | encogidas | 1 |
| 8953 | encobyerta | 1 |
| 8954 | encobrid | 1 |
| 8955 | encobrí | 1 |
| 8956 | encobo | 1 |
| 8957 | encoba | 1 |
| 8958 | enclinando | 1 |
| 8959 | enclina | 1 |
| 8960 | enclavóme | 1 |
| 8961 | enclavaron | 1 |
| 8962 | enclaresçía | 1 |
| 8963 | encima | 1 |
| 8964 | encierra | 1 |
| 8965 | encías | 1 |
| 8966 | ençerraron | 1 |
| 8967 | ençendimiento | 1 |
| 8968 | ençendíen | 1 |
| 8969 | ençendíe | 1 |
| 8970 | ençendidos | 1 |
| 8971 | ençendidas | 1 |
| 8972 | ençendida | 1 |
| 8973 | ençendían | 1 |
| 8974 | ençender | 1 |
| 8975 | ençelado | 1 |
| 8976 | encasillado | 1 |
| 8977 | encargos | 1 |
| 8978 | encargó | 1 |
| 8979 | encargo | 1 |
| 8980 | encantóla | 1 |
| 8981 | encantó | 1 |
| 8982 | encantalla | 1 |
| 8983 | encantadora | 1 |
| 8984 | enbyote | 1 |
| 8985 | enbyo | 1 |
| 8986 | enbyamos | 1 |
| 8987 | enbuelto | 1 |
| 8988 | enbudo | 1 |
| 8989 | enbriagos | 1 |
| 8990 | enbota | 1 |
| 8991 | enbióte | 1 |
| 8992 | enbiéle | 1 |
| 8993 | enbiél | 1 |
| 8994 | enbié | 1 |
| 8995 | enbidiosos | 1 |
| 8996 | enbidioso | 1 |
| 8997 | enbíavos | 1 |
| 8998 | enbiátgelo | 1 |
| 8999 | enbiares | 1 |
| 9000 | enbían | 1 |
| 9001 | enbargo | 1 |
| 9002 | enbargan | 1 |
| 9003 | enbarga | 1 |
| 9004 | enbaçado | 1 |
| 9005 | enartar | 1 |
| 9006 | enartan | 1 |
| 9007 | enardece | 1 |
| 9008 | enarbolada | 1 |
| 9009 | enante | 1 |
| 9010 | enana | 1 |
| 9011 | enamoróme | 1 |
| 9012 | enamoréla | 1 |
| 9013 | enamorad | 1 |
| 9014 | enamora | 1 |
| 9015 | enamistad | 1 |
| 9016 | enajenas | 1 |
| 9017 | enajenado | 1 |
| 9018 | empuje | 1 |
| 9019 | empresa | 1 |
| 9020 | emprende | 1 |
| 9021 | empoçonas | 1 |
| 9022 | emplearse | 1 |
| 9023 | emplea | 1 |
| 9024 | emperador | 1 |
| 9025 | empelladas | 1 |
| 9026 | emparejar | 1 |
| 9027 | emendar | 1 |
| 9028 | emendaçión | 1 |
| 9029 | embargósele | 1 |
| 9030 | elevan | 1 |
| 9031 | elena | 1 |
| 9032 | elegía | 1 |
| 9033 | elegantísimo | 1 |
| 9034 | elegantes | 1 |
| 9035 | ejemplos | 1 |
| 9036 | ejemplar | 1 |
| 9037 | eguales | 1 |
| 9038 | egualar | 1 |
| 9039 | egualança | 1 |
| 9040 | egual | 1 |
| 9041 | eguado | 1 |
| 9042 | égloga | 1 |
| 9043 | egipto | 1 |
| 9044 | egipcios | 1 |
| 9045 | efectivamente | 1 |
| 9046 | edición | 1 |
| 9047 | eclesiásticos | 1 |
| 9048 | echólo | 1 |
| 9049 | echóla | 1 |
| 9050 | echól | 1 |
| 9051 | echat | 1 |
| 9052 | echáronm | 1 |
| 9053 | echara | 1 |
| 9054 | échanle | 1 |
| 9055 | echanla | 1 |
| 9056 | echalos | 1 |
| 9057 | échale | 1 |
| 9058 | ecequiel | 1 |
| 9059 | ecce | 1 |
| 9060 | dyzes | 1 |
| 9061 | dyspensa | 1 |
| 9062 | dyrévos | 1 |
| 9063 | dyóle | 1 |
| 9064 | dyna | 1 |
| 9065 | dyl | 1 |
| 9066 | dyez | 1 |
| 9067 | dyentes | 1 |
| 9068 | dus | 1 |
| 9069 | durmades | 1 |
| 9070 | duresa | 1 |
| 9071 | durasnos | 1 |
| 9072 | durar | 1 |
| 9073 | durador | 1 |
| 9074 | duques | 1 |
| 9075 | dulcia | 1 |
| 9076 | duero | 1 |
| 9077 | duermes | 1 |
| 9078 | dueño | 1 |
| 9079 | duele | 1 |
| 9080 | duela | 1 |
| 9081 | dudar | 1 |
| 9082 | dudança | 1 |
| 9083 | ducho | 1 |
| 9084 | ducha | 1 |
| 9085 | dubdosos | 1 |
| 9086 | drago | 1 |
| 9087 | dozy | 1 |
| 9088 | doy | 1 |
| 9089 | dotes | 1 |
| 9090 | dótelo | 1 |
| 9091 | dote | 1 |
| 9092 | doseno | 1 |
| 9093 | dormitorios | 1 |
| 9094 | dormitorio | 1 |
| 9095 | dormieron | 1 |
| 9096 | dormía | 1 |
| 9097 | doradas | 1 |
| 9098 | dorada | 1 |
| 9099 | doñosa | 1 |
| 9100 | doñeo | 1 |
| 9101 | doñegil | 1 |
| 9102 | doñas | 1 |
| 9103 | donsella | 1 |
| 9104 | donoso | 1 |
| 9105 | dones | 1 |
| 9106 | donear | 1 |
| 9107 | doneaderas | 1 |
| 9108 | doncella | 1 |
| 9109 | donceles | 1 |
| 9110 | donçel | 1 |
| 9111 | donable | 1 |
| 9112 | domó | 1 |
| 9113 | dóminus | 1 |
| 9114 | domino | 1 |
| 9115 | domini | 1 |
| 9116 | domar | 1 |
| 9117 | dolyente | 1 |
| 9118 | dolyéndome | 1 |
| 9119 | dolyendo | 1 |
| 9120 | doloridos | 1 |
| 9121 | dolioso | 1 |
| 9122 | dolióse | 1 |
| 9123 | dolíale | 1 |
| 9124 | dolía | 1 |
| 9125 | dolernos | 1 |
| 9126 | dolencia | 1 |
| 9127 | doledes | 1 |
| 9128 | dolçor | 1 |
| 9129 | dóla | 1 |
| 9130 | dola | 1 |
| 9131 | dodecasílabos | 1 |
| 9132 | doctrinas | 1 |
| 9133 | doctrina | 1 |
| 9134 | doctores | 1 |
| 9135 | doctas | 1 |
| 9136 | docena | 1 |
| 9137 | doçe | 1 |
| 9138 | dobler | 1 |
| 9139 | doble | 1 |
| 9140 | doblas | 1 |
| 9141 | doblarse | 1 |
| 9142 | dobla | 1 |
| 9143 | dízenlo | 1 |
| 9144 | dízenle | 1 |
| 9145 | dizeles | 1 |
| 9146 | díxote | 1 |
| 9147 | dixom | 1 |
| 9148 | dixistes | 1 |
| 9149 | dixiesen | 1 |
| 9150 | dixiese | 1 |
| 9151 | dixieronle | 1 |
| 9152 | dixieren | 1 |
| 9153 | dixiere | 1 |
| 9154 | dixiera | 1 |
| 9155 | díxiel | 1 |
| 9156 | dixeses | 1 |
| 9157 | dixere | 1 |
| 9158 | díxela | 1 |
| 9159 | díx | 1 |
| 9160 | divino | 1 |
| 9161 | divinidat | 1 |
| 9162 | diviesos | 1 |
| 9163 | dividirse | 1 |
| 9164 | divididos | 1 |
| 9165 | dividido | 1 |
| 9166 | diverssas | 1 |
| 9167 | diversas | 1 |
| 9168 | distinguen | 1 |
| 9169 | distingue | 1 |
| 9170 | disticha | 1 |
| 9171 | disputaçión | 1 |
| 9172 | dispenssar | 1 |
| 9173 | disolutos | 1 |
| 9174 | disiendo | 1 |
| 9175 | disíen | 1 |
| 9176 | dísenlo | 1 |
| 9177 | discretos | 1 |
| 9178 | disçípulo | 1 |
| 9179 | disciplina | 1 |
| 9180 | disanto | 1 |
| 9181 | disantero | 1 |
| 9182 | dis | 1 |
| 9183 | dirige | 1 |
| 9184 | dirías | 1 |
| 9185 | diretorio | 1 |
| 9186 | dirélas | 1 |
| 9187 | dirás | 1 |
| 9188 | dióte | 1 |
| 9189 | diosa | 1 |
| 9190 | diónos | 1 |
| 9191 | diómelo | 1 |
| 9192 | dióles | 1 |
| 9193 | dióla | 1 |
| 9194 | diógela | 1 |
| 9195 | diños | 1 |
| 9196 | dineradas | 1 |
| 9197 | dimittere | 1 |
| 9198 | diluído | 1 |
| 9199 | diligitis | 1 |
| 9200 | diles | 1 |
| 9201 | dilatoria | 1 |
| 9202 | dilas | 1 |
| 9203 | díjome | 1 |
| 9204 | digovos | 1 |
| 9205 | dígote | 1 |
| 9206 | digno | 1 |
| 9207 | dignidad | 1 |
| 9208 | digna | 1 |
| 9209 | dígante | 1 |
| 9210 | digamos | 1 |
| 9211 | dígal | 1 |
| 9212 | diestra | 1 |
| 9213 | dierum | 1 |
| 9214 | diéronlos | 1 |
| 9215 | dierdes | 1 |
| 9216 | diérale | 1 |
| 9217 | diéral | 1 |
| 9218 | dier | 1 |
| 9219 | dieciséis | 1 |
| 9220 | didáctico | 1 |
| 9221 | diçípulos | 1 |
| 9222 | diçió | 1 |
| 9223 | diçes | 1 |
| 9224 | diçen | 1 |
| 9225 | diçe | 1 |
| 9226 | dicat | 1 |
| 9227 | diasaturión | 1 |
| 9228 | diarrodon | 1 |
| 9229 | diantoso | 1 |
| 9230 | diamargaritón | 1 |
| 9231 | diagragante | 1 |
| 9232 | diaçymino | 1 |
| 9233 | diaçitrón | 1 |
| 9234 | diabro | 1 |
| 9235 | diabluras | 1 |
| 9236 | dia | 1 |
| 9237 | dezit | 1 |
| 9238 | dezirlo | 1 |
| 9239 | dezires | 1 |
| 9240 | dézir | 1 |
| 9241 | deziéndole | 1 |
| 9242 | dezíen | 1 |
| 9243 | dezidores | 1 |
| 9244 | dezidor | 1 |
| 9245 | dezidle | 1 |
| 9246 | dezid | 1 |
| 9247 | dezían | 1 |
| 9248 | dezeno | 1 |
| 9249 | deydat | 1 |
| 9250 | dexós | 1 |
| 9251 | dexólo | 1 |
| 9252 | dexóla | 1 |
| 9253 | dexo | 1 |
| 9254 | dexiste | 1 |
| 9255 | dexiese | 1 |
| 9256 | dexies | 1 |
| 9257 | dexieronle | 1 |
| 9258 | dexier | 1 |
| 9259 | déxevos | 1 |
| 9260 | dexen | 1 |
| 9261 | dexemos | 1 |
| 9262 | dexava | 1 |
| 9263 | déxatme | 1 |
| 9264 | déxasle | 1 |
| 9265 | dexarm | 1 |
| 9266 | dexarlo | 1 |
| 9267 | dexarla | 1 |
| 9268 | dexaríe | 1 |
| 9269 | dexaré | 1 |
| 9270 | dexarán | 1 |
| 9271 | dexaran | 1 |
| 9272 | dexara | 1 |
| 9273 | déxanl | 1 |
| 9274 | déxala | 1 |
| 9275 | devríen | 1 |
| 9276 | devotas | 1 |
| 9277 | devotamente | 1 |
| 9278 | devota | 1 |
| 9279 | devisa | 1 |
| 9280 | deviersos | 1 |
| 9281 | devier | 1 |
| 9282 | devie | 1 |
| 9283 | dévense | 1 |
| 9284 | dévenlo | 1 |
| 9285 | dévelo | 1 |
| 9286 | devegadas | 1 |
| 9287 | devédeslos | 1 |
| 9288 | devaneando | 1 |
| 9289 | devallen | 1 |
| 9290 | detóvome | 1 |
| 9291 | detove | 1 |
| 9292 | detiene | 1 |
| 9293 | determina | 1 |
| 9294 | detenía | 1 |
| 9295 | detenga | 1 |
| 9296 | detalle | 1 |
| 9297 | desyerra | 1 |
| 9298 | desyéndole | 1 |
| 9299 | desvió | 1 |
| 9300 | desvías | 1 |
| 9301 | desviada | 1 |
| 9302 | desvía | 1 |
| 9303 | desvergonçada | 1 |
| 9304 | desuso | 1 |
| 9305 | desusando | 1 |
| 9306 | destruymiento | 1 |
| 9307 | destrúyeslo | 1 |
| 9308 | destruyes | 1 |
| 9309 | destruydor | 1 |
| 9310 | destruydas | 1 |
| 9311 | destrues | 1 |
| 9312 | destroyr | 1 |
| 9313 | destris | 1 |
| 9314 | desterraremos | 1 |
| 9315 | déste | 1 |
| 9316 | dessollando | 1 |
| 9317 | dessolladas | 1 |
| 9318 | desseosos | 1 |
| 9319 | dessecha | 1 |
| 9320 | desseas | 1 |
| 9321 | dessean | 1 |
| 9322 | dessea | 1 |
| 9323 | desqu | 1 |
| 9324 | desputasen | 1 |
| 9325 | despueblas | 1 |
| 9326 | desprenden | 1 |
| 9327 | despreçias | 1 |
| 9328 | despreçiarán | 1 |
| 9329 | despreciado | 1 |
| 9330 | despreciaban | 1 |
| 9331 | desposa | 1 |
| 9332 | despojo | 1 |
| 9333 | despoje | 1 |
| 9334 | despójanse | 1 |
| 9335 | despoblaste | 1 |
| 9336 | despoblada | 1 |
| 9337 | despilfarrada | 1 |
| 9338 | despierto | 1 |
| 9339 | despertaron | 1 |
| 9340 | despertar | 1 |
| 9341 | despeñó | 1 |
| 9342 | despeñado | 1 |
| 9343 | despenseros | 1 |
| 9344 | despensadores | 1 |
| 9345 | despensa | 1 |
| 9346 | despechoso | 1 |
| 9347 | despechados | 1 |
| 9348 | despagar | 1 |
| 9349 | despaga | 1 |
| 9350 | despaçio | 1 |
| 9351 | desos | 1 |
| 9352 | desorejado | 1 |
| 9353 | desonrrada | 1 |
| 9354 | desollar | 1 |
| 9355 | desolladas | 1 |
| 9356 | desnudos | 1 |
| 9357 | desnudo | 1 |
| 9358 | desnuda | 1 |
| 9359 | desmuele | 1 |
| 9360 | desmesurados | 1 |
| 9361 | desmesurada | 1 |
| 9362 | desmentir | 1 |
| 9363 | desliza | 1 |
| 9364 | desleznadera | 1 |
| 9365 | desleída | 1 |
| 9366 | desitme | 1 |
| 9367 | desit | 1 |
| 9368 | desirse | 1 |
| 9369 | desirnos | 1 |
| 9370 | desírgelo | 1 |
| 9371 | desierto | 1 |
| 9372 | desíenme | 1 |
| 9373 | desían | 1 |
| 9374 | desí | 1 |
| 9375 | deshonrra | 1 |
| 9376 | desgradesçí | 1 |
| 9377 | desgarrándose | 1 |
| 9378 | desfízos | 1 |
| 9379 | desferrar | 1 |
| 9380 | desfegurado | 1 |
| 9381 | desfegurada | 1 |
| 9382 | desfecho | 1 |
| 9383 | desfeas | 1 |
| 9384 | desfazer | 1 |
| 9385 | desfases | 1 |
| 9386 | desfase | 1 |
| 9387 | desfaré | 1 |
| 9388 | desfanbrido | 1 |
| 9389 | desfallydo | 1 |
| 9390 | desfallesçen | 1 |
| 9391 | desface | 1 |
| 9392 | desesperars | 1 |
| 9393 | deserví | 1 |
| 9394 | deserrado | 1 |
| 9395 | deserradas | 1 |
| 9396 | deseosas | 1 |
| 9397 | desengaños | 1 |
| 9398 | desenfadado | 1 |
| 9399 | desenfadada | 1 |
| 9400 | desencantó | 1 |
| 9401 | deseche | 1 |
| 9402 | desecharle | 1 |
| 9403 | desechan | 1 |
| 9404 | deseavos | 1 |
| 9405 | deseas | 1 |
| 9406 | desean | 1 |
| 9407 | deseados | 1 |
| 9408 | deseado | 1 |
| 9409 | deseada | 1 |
| 9410 | desdonada | 1 |
| 9411 | desdiré | 1 |
| 9412 | desdicha | 1 |
| 9413 | desdezía | 1 |
| 9414 | desdesir | 1 |
| 9415 | desdeñoso | 1 |
| 9416 | desdeñosa | 1 |
| 9417 | desdeñedes | 1 |
| 9418 | desdeñamientos | 1 |
| 9419 | desdeñado | 1 |
| 9420 | desdeña | 1 |
| 9421 | desdén | 1 |
| 9422 | desd | 1 |
| 9423 | descumunales | 1 |
| 9424 | descumulgado | 1 |
| 9425 | descumulgada | 1 |
| 9426 | desculpada | 1 |
| 9427 | descubrió | 1 |
| 9428 | descubre | 1 |
| 9429 | describiendo | 1 |
| 9430 | describe | 1 |
| 9431 | descordia | 1 |
| 9432 | desconpón | 1 |
| 9433 | desconosçida | 1 |
| 9434 | desconocidas | 1 |
| 9435 | desconfuerta | 1 |
| 9436 | descomulgado | 1 |
| 9437 | descomonión | 1 |
| 9438 | descolgarlos | 1 |
| 9439 | descogerá | 1 |
| 9440 | descobyerta | 1 |
| 9441 | descobryr | 1 |
| 9442 | descobrimientos | 1 |
| 9443 | descobrilla | 1 |
| 9444 | descobrides | 1 |
| 9445 | descobrid | 1 |
| 9446 | descobrades | 1 |
| 9447 | descobierto | 1 |
| 9448 | descobierta | 1 |
| 9449 | desçiplina | 1 |
| 9450 | descifrar | 1 |
| 9451 | desçenir | 1 |
| 9452 | descendyó | 1 |
| 9453 | descendy | 1 |
| 9454 | desçendió | 1 |
| 9455 | desçendimiento | 1 |
| 9456 | desçendido | 1 |
| 9457 | descanssa | 1 |
| 9458 | descaminado | 1 |
| 9459 | descalabrados | 1 |
| 9460 | desbuélvete | 1 |
| 9461 | desbarato | 1 |
| 9462 | desayunar | 1 |
| 9463 | desayuda | 1 |
| 9464 | desaventuras | 1 |
| 9465 | desaventura | 1 |
| 9466 | desatyrisiendo | 1 |
| 9467 | desata | 1 |
| 9468 | désas | 1 |
| 9469 | desarrollo | 1 |
| 9470 | desaparece | 1 |
| 9471 | desamigos | 1 |
| 9472 | desamen | 1 |
| 9473 | desama | 1 |
| 9474 | desalyña | 1 |
| 9475 | desalmado | 1 |
| 9476 | desaguisada | 1 |
| 9477 | desagradescido | 1 |
| 9478 | desagradesçida | 1 |
| 9479 | desagradesçer | 1 |
| 9480 | desafiar | 1 |
| 9481 | desafiado | 1 |
| 9482 | desadonas | 1 |
| 9483 | desacuerdo | 1 |
| 9484 | desacordados | 1 |
| 9485 | desacordadas | 1 |
| 9486 | dés | 1 |
| 9487 | derrueca | 1 |
| 9488 | derrocóm | 1 |
| 9489 | derribóme | 1 |
| 9490 | derríbol | 1 |
| 9491 | derríbanse | 1 |
| 9492 | derriba | 1 |
| 9493 | derramó | 1 |
| 9494 | derramaron | 1 |
| 9495 | derramar | 1 |
| 9496 | derramado | 1 |
| 9497 | derechos | 1 |
| 9498 | derechero | 1 |
| 9499 | derechas | 1 |
| 9500 | derechamente | 1 |
| 9501 | deprender | 1 |
| 9502 | deprenden | 1 |
| 9503 | departidos | 1 |
| 9504 | departa | 1 |
| 9505 | deña | 1 |
| 9506 | denuestos | 1 |
| 9507 | denuesto | 1 |
| 9508 | denuestas | 1 |
| 9509 | denuestan | 1 |
| 9510 | denuedo | 1 |
| 9511 | denueda | 1 |
| 9512 | denteras | 1 |
| 9513 | denostemos | 1 |
| 9514 | denostava | 1 |
| 9515 | denostat | 1 |
| 9516 | denostando | 1 |
| 9517 | denostador | 1 |
| 9518 | denostada | 1 |
| 9519 | dénos | 1 |
| 9520 | denonado | 1 |
| 9521 | denodados | 1 |
| 9522 | denodada | 1 |
| 9523 | denidades | 1 |
| 9524 | den | 1 |
| 9525 | demuestra | 1 |
| 9526 | demudeste | 1 |
| 9527 | demuda | 1 |
| 9528 | demostrava | 1 |
| 9529 | demostrador | 1 |
| 9530 | demostrado | 1 |
| 9531 | demesuras | 1 |
| 9532 | demas | 1 |
| 9533 | demandudieres | 1 |
| 9534 | demándovos | 1 |
| 9535 | demandól | 1 |
| 9536 | demandéle | 1 |
| 9537 | demande | 1 |
| 9538 | demandavan | 1 |
| 9539 | demandava | 1 |
| 9540 | demandase | 1 |
| 9541 | demandaron | 1 |
| 9542 | demandado | 1 |
| 9543 | demandadas | 1 |
| 9544 | dellante | 1 |
| 9545 | delicados | 1 |
| 9546 | delicado | 1 |
| 9547 | delicadas | 1 |
| 9548 | delicada | 1 |
| 9549 | delgadas | 1 |
| 9550 | deléytase | 1 |
| 9551 | déle | 1 |
| 9552 | delanteros | 1 |
| 9553 | delantero | 1 |
| 9554 | delanteras | 1 |
| 9555 | delant | 1 |
| 9556 | dejóse | 1 |
| 9557 | dejos | 1 |
| 9558 | dejar | 1 |
| 9559 | degüella | 1 |
| 9560 | degollava | 1 |
| 9561 | degollando | 1 |
| 9562 | degenera | 1 |
| 9563 | defyendo | 1 |
| 9564 | defyendavos | 1 |
| 9565 | defiéndonos | 1 |
| 9566 | defiendo | 1 |
| 9567 | defiéndeme | 1 |
| 9568 | defienda | 1 |
| 9569 | deffenssiones | 1 |
| 9570 | deffendióse | 1 |
| 9571 | defesa | 1 |
| 9572 | defendrá | 1 |
| 9573 | defendiendo | 1 |
| 9574 | defendidos | 1 |
| 9575 | defendida | 1 |
| 9576 | defendernos | 1 |
| 9577 | defenderme | 1 |
| 9578 | defenderás | 1 |
| 9579 | deduzco | 1 |
| 9580 | decuere | 1 |
| 9581 | decretal | 1 |
| 9582 | decida | 1 |
| 9583 | debuxo | 1 |
| 9584 | debiera | 1 |
| 9585 | debido | 1 |
| 9586 | debatido | 1 |
| 9587 | debate | 1 |
| 9588 | debatas | 1 |
| 9589 | deán | 1 |
| 9590 | dávame | 1 |
| 9591 | dávades | 1 |
| 9592 | datnos | 1 |
| 9593 | datla | 1 |
| 9594 | dásme | 1 |
| 9595 | dásle | 1 |
| 9596 | dasla | 1 |
| 9597 | dártelo | 1 |
| 9598 | darse | 1 |
| 9599 | darle | 1 |
| 9600 | dário | 1 |
| 9601 | daríe | 1 |
| 9602 | darían | 1 |
| 9603 | dares | 1 |
| 9604 | daremos | 1 |
| 9605 | dardos | 1 |
| 9606 | darás | 1 |
| 9607 | dapñosa | 1 |
| 9608 | dapñas | 1 |
| 9609 | dapnos | 1 |
| 9610 | dañosa | 1 |
| 9611 | dañe | 1 |
| 9612 | dañar | 1 |
| 9613 | danse | 1 |
| 9614 | danoso | 1 |
| 9615 | dánle | 1 |
| 9616 | dándolo | 1 |
| 9617 | dándol | 1 |
| 9618 | dançar | 1 |
| 9619 | damos | 1 |
| 9620 | dáme | 1 |
| 9621 | damas | 1 |
| 9622 | dalyla | 1 |
| 9623 | dalgueva | 1 |
| 9624 | daldes | 1 |
| 9625 | dalda | 1 |
| 9626 | dades | 1 |
| 9627 | çynta | 1 |
| 9628 | çynió | 1 |
| 9629 | cx | 1 |
| 9630 | cuytoso | 1 |
| 9631 | cuytados | 1 |
| 9632 | cuytadas | 1 |
| 9633 | cuytada | 1 |
| 9634 | cuyo | 1 |
| 9635 | cuydóse | 1 |
| 9636 | cuydó | 1 |
| 9637 | cuydés | 1 |
| 9638 | cuydedes | 1 |
| 9639 | cuydavan | 1 |
| 9640 | cuydas | 1 |
| 9641 | cuydares | 1 |
| 9642 | cuydará | 1 |
| 9643 | cuydára | 1 |
| 9644 | cuydando | 1 |
| 9645 | cuya | 1 |
| 9646 | custodi | 1 |
| 9647 | custituçión | 1 |
| 9648 | cursso | 1 |
| 9649 | çurrón | 1 |
| 9650 | curioso | 1 |
| 9651 | curiales | 1 |
| 9652 | curanderas | 1 |
| 9653 | cuquero | 1 |
| 9654 | cuños | 1 |
| 9655 | cunplió | 1 |
| 9656 | cunplidos | 1 |
| 9657 | cunplida | 1 |
| 9658 | cunplan | 1 |
| 9659 | cunde | 1 |
| 9660 | cumunal | 1 |
| 9661 | cumbre | 1 |
| 9662 | cum | 1 |
| 9663 | culpar | 1 |
| 9664 | culpados | 1 |
| 9665 | culebra | 1 |
| 9666 | cuidados | 1 |
| 9667 | cueste | 1 |
| 9668 | cuestan | 1 |
| 9669 | cuestalada | 1 |
| 9670 | cuesta | 1 |
| 9671 | çuero | 1 |
| 9672 | cuernos | 1 |
| 9673 | cuerdamiente | 1 |
| 9674 | cuerdamente | 1 |
| 9675 | cuerbo | 1 |
| 9676 | cuentos | 1 |
| 9677 | cuelloalvo | 1 |
| 9678 | cuell | 1 |
| 9679 | cuélgente | 1 |
| 9680 | cuedo | 1 |
| 9681 | cuchillo | 1 |
| 9682 | cuáqueros | 1 |
| 9683 | cuantos | 1 |
| 9684 | cualquiere | 1 |
| 9685 | cuáles | 1 |
| 9686 | cuaderna | 1 |
| 9687 | cryador | 1 |
| 9688 | cruzniego | 1 |
| 9689 | cruza | 1 |
| 9690 | cruyziava | 1 |
| 9691 | crus | 1 |
| 9692 | cruelmente | 1 |
| 9693 | crueldat | 1 |
| 9694 | crueldad | 1 |
| 9695 | críticos | 1 |
| 9696 | crítico | 1 |
| 9697 | cristo | 1 |
| 9698 | cristianos | 1 |
| 9699 | cristal | 1 |
| 9700 | crío | 1 |
| 9701 | crimine | 1 |
| 9702 | criera | 1 |
| 9703 | crié | 1 |
| 9704 | criar | 1 |
| 9705 | criança | 1 |
| 9706 | criada | 1 |
| 9707 | creyese | 1 |
| 9708 | creyente | 1 |
| 9709 | creyendo | 1 |
| 9710 | creyen | 1 |
| 9711 | creyan | 1 |
| 9712 | cresciéndo | 1 |
| 9713 | cresçer | 1 |
| 9714 | creóselos | 1 |
| 9715 | creóselo | 1 |
| 9716 | creminales | 1 |
| 9717 | crementinas | 1 |
| 9718 | creído | 1 |
| 9719 | creetme | 1 |
| 9720 | creencia | 1 |
| 9721 | creedme | 1 |
| 9722 | creçió | 1 |
| 9723 | creció | 1 |
| 9724 | creçieron | 1 |
| 9725 | créçenme | 1 |
| 9726 | creadora | 1 |
| 9727 | coyunda | 1 |
| 9728 | coytral | 1 |
| 9729 | coytándome | 1 |
| 9730 | coytada | 1 |
| 9731 | coydo | 1 |
| 9732 | coydedes | 1 |
| 9733 | coydé | 1 |
| 9734 | coydavan | 1 |
| 9735 | coydares | 1 |
| 9736 | coydar | 1 |
| 9737 | coydan | 1 |
| 9738 | coydados | 1 |
| 9739 | coxqueas | 1 |
| 9740 | coxixo | 1 |
| 9741 | coxeades | 1 |
| 9742 | covardo | 1 |
| 9743 | cotas | 1 |
| 9744 | cota | 1 |
| 9745 | costumeros | 1 |
| 9746 | costumero | 1 |
| 9747 | costumera | 1 |
| 9748 | costribado | 1 |
| 9749 | costosas | 1 |
| 9750 | costillas | 1 |
| 9751 | costiellas | 1 |
| 9752 | costiella | 1 |
| 9753 | costellaçión | 1 |
| 9754 | costellación | 1 |
| 9755 | costase | 1 |
| 9756 | costanera | 1 |
| 9757 | cosseras | 1 |
| 9758 | coso | 1 |
| 9759 | cosineras | 1 |
| 9760 | cosina | 1 |
| 9761 | cosestorio | 1 |
| 9762 | cosejador | 1 |
| 9763 | cortólas | 1 |
| 9764 | cortóla | 1 |
| 9765 | cortó | 1 |
| 9766 | corto | 1 |
| 9767 | cortina | 1 |
| 9768 | cortiella | 1 |
| 9769 | corteses | 1 |
| 9770 | cortesanos | 1 |
| 9771 | cortes | 1 |
| 9772 | corteça | 1 |
| 9773 | cortar | 1 |
| 9774 | corta | 1 |
| 9775 | çorrón | 1 |
| 9776 | corrompida | 1 |
| 9777 | corríe | 1 |
| 9778 | corrido | 1 |
| 9779 | corría | 1 |
| 9780 | corrí | 1 |
| 9781 | correrse | 1 |
| 9782 | correrla | 1 |
| 9783 | correo | 1 |
| 9784 | corrella | 1 |
| 9785 | correderas | 1 |
| 9786 | corrección | 1 |
| 9787 | correa | 1 |
| 9788 | corrales | 1 |
| 9789 | corra | 1 |
| 9790 | corpudo | 1 |
| 9791 | coro | 1 |
| 9792 | cornudo | 1 |
| 9793 | cordojo | 1 |
| 9794 | corças | 1 |
| 9795 | corazones | 1 |
| 9796 | coral | 1 |
| 9797 | corages | 1 |
| 9798 | coraça | 1 |
| 9799 | copistas | 1 |
| 9800 | copia | 1 |
| 9801 | convyene | 1 |
| 9802 | convyén | 1 |
| 9803 | convien | 1 |
| 9804 | convertyr | 1 |
| 9805 | converte | 1 |
| 9806 | converso | 1 |
| 9807 | conveníe | 1 |
| 9808 | convencionales | 1 |
| 9809 | contyendas | 1 |
| 9810 | contuerçe | 1 |
| 9811 | contrecho | 1 |
| 9812 | contrallos | 1 |
| 9813 | contrallo | 1 |
| 9814 | contracciones | 1 |
| 9815 | continua | 1 |
| 9816 | contiende | 1 |
| 9817 | contestado | 1 |
| 9818 | contésçete | 1 |
| 9819 | contesçervos | 1 |
| 9820 | contésçel | 1 |
| 9821 | contésçal | 1 |
| 9822 | contentaba | 1 |
| 9823 | contenidos | 1 |
| 9824 | contendíendo | 1 |
| 9825 | contemporáneo | 1 |
| 9826 | contélas | 1 |
| 9827 | conteçióme | 1 |
| 9828 | conteciom | 1 |
| 9829 | conteçió | 1 |
| 9830 | contarse | 1 |
| 9831 | contados | 1 |
| 9832 | contado | 1 |
| 9833 | consyntyrá | 1 |
| 9834 | consuno | 1 |
| 9835 | consumado | 1 |
| 9836 | constelaçión | 1 |
| 9837 | conssentyd | 1 |
| 9838 | conssentir | 1 |
| 9839 | conssejavan | 1 |
| 9840 | consséjasme | 1 |
| 9841 | conssejar | 1 |
| 9842 | consonantes | 1 |
| 9843 | consintré | 1 |
| 9844 | conservó | 1 |
| 9845 | consentría | 1 |
| 9846 | conséjote | 1 |
| 9847 | consejóme | 1 |
| 9848 | consejó | 1 |
| 9849 | consejero | 1 |
| 9850 | consejas | 1 |
| 9851 | conséjame | 1 |
| 9852 | conquisto | 1 |
| 9853 | conquirense | 1 |
| 9854 | conpusso | 1 |
| 9855 | conpuso | 1 |
| 9856 | conpuse | 1 |
| 9857 | conpuesto | 1 |
| 9858 | conprarien | 1 |
| 9859 | conpraríe | 1 |
| 9860 | conpraría | 1 |
| 9861 | conprarás | 1 |
| 9862 | conprar | 1 |
| 9863 | conprador | 1 |
| 9864 | conpradas | 1 |
| 9865 | conprad | 1 |
| 9866 | conpósele | 1 |
| 9867 | conponer | 1 |
| 9868 | conpone | 1 |
| 9869 | conpón | 1 |
| 9870 | conplyda | 1 |
| 9871 | conplóla | 1 |
| 9872 | conplit | 1 |
| 9873 | conpliste | 1 |
| 9874 | conplisión | 1 |
| 9875 | conplieron | 1 |
| 9876 | conplidos | 1 |
| 9877 | conplid | 1 |
| 9878 | conpleta | 1 |
| 9879 | conplarás | 1 |
| 9880 | conpasión | 1 |
| 9881 | conparty | 1 |
| 9882 | conparaçión | 1 |
| 9883 | conparación | 1 |
| 9884 | conpañones | 1 |
| 9885 | conpañeras | 1 |
| 9886 | conpanón | 1 |
| 9887 | conpanero | 1 |
| 9888 | conpadre | 1 |
| 9889 | conozca | 1 |
| 9890 | conosço | 1 |
| 9891 | conosçiste | 1 |
| 9892 | conosçiere | 1 |
| 9893 | conosçienta | 1 |
| 9894 | conosçido | 1 |
| 9895 | conosçervos | 1 |
| 9896 | conoscer | 1 |
| 9897 | conosçemiento | 1 |
| 9898 | conoscan | 1 |
| 9899 | conortar | 1 |
| 9900 | conortadvos | 1 |
| 9901 | conortadme | 1 |
| 9902 | conoçieses | 1 |
| 9903 | conocidas | 1 |
| 9904 | conocían | 1 |
| 9905 | conoçer | 1 |
| 9906 | conocedor | 1 |
| 9907 | conoce | 1 |
| 9908 | conjuro | 1 |
| 9909 | conjetura | 1 |
| 9910 | congrio | 1 |
| 9911 | confunde | 1 |
| 9912 | confuerte | 1 |
| 9913 | conforme | 1 |
| 9914 | confites | 1 |
| 9915 | confisión | 1 |
| 9916 | confirmaçión | 1 |
| 9917 | confiesa | 1 |
| 9918 | confianza | 1 |
| 9919 | conffisión | 1 |
| 9920 | conffieso | 1 |
| 9921 | conffesor | 1 |
| 9922 | conffesión | 1 |
| 9923 | confessar | 1 |
| 9924 | confesar | 1 |
| 9925 | confesado | 1 |
| 9926 | conejero | 1 |
| 9927 | coneja | 1 |
| 9928 | condido | 1 |
| 9929 | condiciones | 1 |
| 9930 | condiçión | 1 |
| 9931 | condesados | 1 |
| 9932 | condesado | 1 |
| 9933 | condepñar | 1 |
| 9934 | condepnar | 1 |
| 9935 | condeñado | 1 |
| 9936 | condenedes | 1 |
| 9937 | condenado | 1 |
| 9938 | condenadas | 1 |
| 9939 | condedijos | 1 |
| 9940 | concuerda | 1 |
| 9941 | concordia | 1 |
| 9942 | concomen | 1 |
| 9943 | concluye | 1 |
| 9944 | conclusión | 1 |
| 9945 | conciencia | 1 |
| 9946 | conceptum | 1 |
| 9947 | concederé | 1 |
| 9948 | conbydes | 1 |
| 9949 | conbydar | 1 |
| 9950 | conbyd | 1 |
| 9951 | conbusco | 1 |
| 9952 | conbrían | 1 |
| 9953 | conbrí | 1 |
| 9954 | conbredes | 1 |
| 9955 | conblueça | 1 |
| 9956 | conbite | 1 |
| 9957 | conbidól | 1 |
| 9958 | conbidó | 1 |
| 9959 | conbidas | 1 |
| 9960 | conbidáronle | 1 |
| 9961 | conbidado | 1 |
| 9962 | comunidad | 1 |
| 9963 | comunicar | 1 |
| 9964 | comunes | 1 |
| 9965 | composiciones | 1 |
| 9966 | componer | 1 |
| 9967 | complimos | 1 |
| 9968 | compasión | 1 |
| 9969 | compañía | 1 |
| 9970 | comoquier | 1 |
| 9971 | comiólos | 1 |
| 9972 | comiólo | 1 |
| 9973 | cominad | 1 |
| 9974 | comienzos | 1 |
| 9975 | comiendo | 1 |
| 9976 | comiençe | 1 |
| 9977 | comiençan | 1 |
| 9978 | comíen | 1 |
| 9979 | comidir | 1 |
| 9980 | comides | 1 |
| 9981 | comidas | 1 |
| 9982 | comida | 1 |
| 9983 | cómica | 1 |
| 9984 | cometidos | 1 |
| 9985 | cometer | 1 |
| 9986 | comes | 1 |
| 9987 | comendón | 1 |
| 9988 | comendado | 1 |
| 9989 | començós | 1 |
| 9990 | començol | 1 |
| 9991 | començel | 1 |
| 9992 | començava | 1 |
| 9993 | començaríen | 1 |
| 9994 | començare | 1 |
| 9995 | començar | 1 |
| 9996 | començallo | 1 |
| 9997 | començada | 1 |
| 9998 | cómela | 1 |
| 9999 | comedir | 1 |
| 10000 | comedio | 1 |
| 10001 | comedieta | 1 |
| 10002 | comediendo | 1 |
| 10003 | comedidas | 1 |
| 10004 | comedid | 1 |
| 10005 | comedia | 1 |
| 10006 | comedí | 1 |
| 10007 | comedes | 1 |
| 10008 | comed | 1 |
| 10009 | combatientes | 1 |
| 10010 | combatidos | 1 |
| 10011 | combate | 1 |
| 10012 | comas | 1 |
| 10013 | comadreja | 1 |
| 10014 | coloreó | 1 |
| 10015 | coloran | 1 |
| 10016 | colorado | 1 |
| 10017 | colorada | 1 |
| 10018 | colmiellos | 1 |
| 10019 | collarada | 1 |
| 10020 | colgasen | 1 |
| 10021 | colgarien | 1 |
| 10022 | colgados | 1 |
| 10023 | colgada | 1 |
| 10024 | cohyta | 1 |
| 10025 | cohechadores | 1 |
| 10026 | cogitationes | 1 |
| 10027 | cogiéronle | 1 |
| 10028 | cogía | 1 |
| 10029 | cogí | 1 |
| 10030 | coger | 1 |
| 10031 | coge | 1 |
| 10032 | cofonda | 1 |
| 10033 | coffya | 1 |
| 10034 | coeda | 1 |
| 10035 | codyçyossos | 1 |
| 10036 | codorniz | 1 |
| 10037 | codorniçes | 1 |
| 10038 | codonate | 1 |
| 10039 | codiçiosa | 1 |
| 10040 | codiçio | 1 |
| 10041 | codiçies | 1 |
| 10042 | codiçiava | 1 |
| 10043 | codiçia | 1 |
| 10044 | codicia | 1 |
| 10045 | codeándose | 1 |
| 10046 | çoda | 1 |
| 10047 | çoçobra | 1 |
| 10048 | coçinas | 1 |
| 10049 | cocina | 1 |
| 10050 | cocho | 1 |
| 10051 | cochillo | 1 |
| 10052 | cochiello | 1 |
| 10053 | cobyerto | 1 |
| 10054 | cobró | 1 |
| 10055 | cobrimos | 1 |
| 10056 | cobré | 1 |
| 10057 | cobierta | 1 |
| 10058 | cobertura | 1 |
| 10059 | coberteras | 1 |
| 10060 | cobdyçia | 1 |
| 10061 | cobdiçiosso | 1 |
| 10062 | cobdiçiosos | 1 |
| 10063 | cobdiçióla | 1 |
| 10064 | cobdiçió | 1 |
| 10065 | cobdiçio | 1 |
| 10066 | cobdiçie | 1 |
| 10067 | cobdiçiava | 1 |
| 10068 | cobdiçiaron | 1 |
| 10069 | cobdiçi | 1 |
| 10070 | cobardía | 1 |
| 10071 | cobarden | 1 |
| 10072 | clero | 1 |
| 10073 | clerizones | 1 |
| 10074 | clerisones | 1 |
| 10075 | clerigo | 1 |
| 10076 | clerigalla | 1 |
| 10077 | clericalis | 1 |
| 10078 | clerezía | 1 |
| 10079 | clerezia | 1 |
| 10080 | cleresía | 1 |
| 10081 | clavos | 1 |
| 10082 | claustras | 1 |
| 10083 | claustra | 1 |
| 10084 | clásicos | 1 |
| 10085 | clásicas | 1 |
| 10086 | clarus | 1 |
| 10087 | clamores | 1 |
| 10088 | clamamos | 1 |
| 10089 | civil | 1 |
| 10090 | cítola | 1 |
| 10091 | çistel | 1 |
| 10092 | çisne | 1 |
| 10093 | çintas | 1 |
| 10094 | çinorias | 1 |
| 10095 | cinco | 1 |
| 10096 | çiminteryo | 1 |
| 10097 | çiminterios | 1 |
| 10098 | çiminterio | 1 |
| 10099 | çimiento | 1 |
| 10100 | cimas | 1 |
| 10101 | cimarrón | 1 |
| 10102 | çillero | 1 |
| 10103 | çigueña | 1 |
| 10104 | cigueña | 1 |
| 10105 | cigoñinos | 1 |
| 10106 | çierva | 1 |
| 10107 | cierva | 1 |
| 10108 | çierro | 1 |
| 10109 | çiérrate | 1 |
| 10110 | çierra | 1 |
| 10111 | çiençias | 1 |
| 10112 | ciençia | 1 |
| 10113 | ciencia | 1 |
| 10114 | cielo | 1 |
| 10115 | çiégaslos | 1 |
| 10116 | ciega | 1 |
| 10117 | cidras | 1 |
| 10118 | cid | 1 |
| 10119 | cíclope | 1 |
| 10120 | cibdat | 1 |
| 10121 | çibdadano | 1 |
| 10122 | chycos | 1 |
| 10123 | chycas | 1 |
| 10124 | chyca | 1 |
| 10125 | chufetas | 1 |
| 10126 | chufas | 1 |
| 10127 | chufa | 1 |
| 10128 | choto | 1 |
| 10129 | chorreando | 1 |
| 10130 | chocarrear | 1 |
| 10131 | chismografías | 1 |
| 10132 | chirriar | 1 |
| 10133 | chirlava | 1 |
| 10134 | chirlando | 1 |
| 10135 | chiquillos | 1 |
| 10136 | chiquillo | 1 |
| 10137 | chiquilla | 1 |
| 10138 | chiquiella | 1 |
| 10139 | cherevías | 1 |
| 10140 | chato | 1 |
| 10141 | chatas | 1 |
| 10142 | charcos | 1 |
| 10143 | chantre | 1 |
| 10144 | çevera | 1 |
| 10145 | çevadas | 1 |
| 10146 | cetera | 1 |
| 10147 | çesto | 1 |
| 10148 | çestilla | 1 |
| 10149 | çestil | 1 |
| 10150 | çesta | 1 |
| 10151 | çerviçes | 1 |
| 10152 | cerviçes | 1 |
| 10153 | certeza | 1 |
| 10154 | certera | 1 |
| 10155 | çertenidad | 1 |
| 10156 | çerteficado | 1 |
| 10157 | çerros | 1 |
| 10158 | çerro | 1 |
| 10159 | çerraron | 1 |
| 10160 | çerrarías | 1 |
| 10161 | çerraré | 1 |
| 10162 | cerrando | 1 |
| 10163 | çerraduras | 1 |
| 10164 | çerrados | 1 |
| 10165 | çermeña | 1 |
| 10166 | çereça | 1 |
| 10167 | çercól | 1 |
| 10168 | çercava | 1 |
| 10169 | çercanos | 1 |
| 10170 | çercanas | 1 |
| 10171 | çercana | 1 |
| 10172 | çercada | 1 |
| 10173 | çera | 1 |
| 10174 | çepos | 1 |
| 10175 | çepa | 1 |
| 10176 | cepa | 1 |
| 10177 | ceñirme | 1 |
| 10178 | çeñiglo | 1 |
| 10179 | çeñida | 1 |
| 10180 | centurio | 1 |
| 10181 | centro | 1 |
| 10182 | çentenos | 1 |
| 10183 | çenorias | 1 |
| 10184 | çenico | 1 |
| 10185 | çençerros | 1 |
| 10186 | çencerro | 1 |
| 10187 | cençeño | 1 |
| 10188 | çenava | 1 |
| 10189 | çenas | 1 |
| 10190 | çenaría | 1 |
| 10191 | çenarás | 1 |
| 10192 | çenar | 1 |
| 10193 | çemiento | 1 |
| 10194 | çementerio | 1 |
| 10195 | celosas | 1 |
| 10196 | celosa | 1 |
| 10197 | çeliçio | 1 |
| 10198 | celestinas | 1 |
| 10199 | celestina | 1 |
| 10200 | çeledes | 1 |
| 10201 | celebrados | 1 |
| 10202 | çelares | 1 |
| 10203 | celaré | 1 |
| 10204 | çelar | 1 |
| 10205 | çelan | 1 |
| 10206 | çelado | 1 |
| 10207 | çela | 1 |
| 10208 | çejo | 1 |
| 10209 | çegar | 1 |
| 10210 | cedieruédas | 1 |
| 10211 | çedaçuelo | 1 |
| 10212 | çeçinas | 1 |
| 10213 | ceçina | 1 |
| 10214 | çeçial | 1 |
| 10215 | cayósele | 1 |
| 10216 | cayn | 1 |
| 10217 | cayer | 1 |
| 10218 | cayen | 1 |
| 10219 | caye | 1 |
| 10220 | caydas | 1 |
| 10221 | cavas | 1 |
| 10222 | cavando | 1 |
| 10223 | cavan | 1 |
| 10224 | cavallunos | 1 |
| 10225 | cavallerías | 1 |
| 10226 | cavallar | 1 |
| 10227 | cavalgo | 1 |
| 10228 | cavalgar | 1 |
| 10229 | cavalgaduras | 1 |
| 10230 | cavalgadas | 1 |
| 10231 | cavalga | 1 |
| 10232 | cavadura | 1 |
| 10233 | cavadores | 1 |
| 10234 | cava | 1 |
| 10235 | cautiverio | 1 |
| 10236 | catyvos | 1 |
| 10237 | catyva | 1 |
| 10238 | catonis | 1 |
| 10239 | caton | 1 |
| 10240 | cato | 1 |
| 10241 | cathreda | 1 |
| 10242 | cathólico | 1 |
| 10243 | catholicæ | 1 |
| 10244 | cates | 1 |
| 10245 | categoría | 1 |
| 10246 | catedra | 1 |
| 10247 | catedes | 1 |
| 10248 | cataste | 1 |
| 10249 | catas | 1 |
| 10250 | cátaros | 1 |
| 10251 | cataré | 1 |
| 10252 | cátame | 1 |
| 10253 | catades | 1 |
| 10254 | castraron | 1 |
| 10255 | castos | 1 |
| 10256 | castiza | 1 |
| 10257 | castillos | 1 |
| 10258 | castillans | 1 |
| 10259 | castilla | 1 |
| 10260 | castigué | 1 |
| 10261 | castígate | 1 |
| 10262 | castigando | 1 |
| 10263 | castigadvos | 1 |
| 10264 | castigados | 1 |
| 10265 | castigado | 1 |
| 10266 | castigada | 1 |
| 10267 | castiello | 1 |
| 10268 | castidat | 1 |
| 10269 | castaños | 1 |
| 10270 | castanas | 1 |
| 10271 | casseras | 1 |
| 10272 | cassase | 1 |
| 10273 | cassarme | 1 |
| 10274 | cassadas | 1 |
| 10275 | cassada | 1 |
| 10276 | caso | 1 |
| 10277 | casimodo | 1 |
| 10278 | casilla | 1 |
| 10279 | casedes | 1 |
| 10280 | casco | 1 |
| 10281 | cascaveles | 1 |
| 10282 | casasen | 1 |
| 10283 | casarvos | 1 |
| 10284 | casarm | 1 |
| 10285 | casarlo | 1 |
| 10286 | casara | 1 |
| 10287 | casando | 1 |
| 10288 | casamentera | 1 |
| 10289 | cartajena | 1 |
| 10290 | carrizo | 1 |
| 10291 | carrión | 1 |
| 10292 | carrancas | 1 |
| 10293 | carrales | 1 |
| 10294 | caros | 1 |
| 10295 | caro | 1 |
| 10296 | carnosas | 1 |
| 10297 | carniçeros | 1 |
| 10298 | carniçería | 1 |
| 10299 | carner | 1 |
| 10300 | carnaval | 1 |
| 10301 | carnales | 1 |
| 10302 | carn | 1 |
| 10303 | carmen | 1 |
| 10304 | cargo | 1 |
| 10305 | cargado | 1 |
| 10306 | careta | 1 |
| 10307 | çarçillo | 1 |
| 10308 | çarçiellos | 1 |
| 10309 | carcelero | 1 |
| 10310 | cárçel | 1 |
| 10311 | çarça | 1 |
| 10312 | carboniento | 1 |
| 10313 | carbón | 1 |
| 10314 | çarapico | 1 |
| 10315 | caramillo | 1 |
| 10316 | caracteres | 1 |
| 10317 | carácter | 1 |
| 10318 | çaraças | 1 |
| 10319 | çaraça | 1 |
| 10320 | captiva | 1 |
| 10321 | capital | 1 |
| 10322 | capilla | 1 |
| 10323 | capellynas | 1 |
| 10324 | capellyna | 1 |
| 10325 | capelina | 1 |
| 10326 | capaz | 1 |
| 10327 | çapatero | 1 |
| 10328 | capada | 1 |
| 10329 | cañilleras | 1 |
| 10330 | cañamones | 1 |
| 10331 | cáñamo | 1 |
| 10332 | cantos | 1 |
| 10333 | cantón | 1 |
| 10334 | cántiga | 1 |
| 10335 | canticas | 1 |
| 10336 | cántic | 1 |
| 10337 | cantera | 1 |
| 10338 | canten | 1 |
| 10339 | cantavan | 1 |
| 10340 | cantávalo | 1 |
| 10341 | cantava | 1 |
| 10342 | cantate | 1 |
| 10343 | cantasses | 1 |
| 10344 | cantase | 1 |
| 10345 | cantarillo | 1 |
| 10346 | cantadores | 1 |
| 10347 | cantaderas | 1 |
| 10348 | cantad | 1 |
| 10349 | cantables | 1 |
| 10350 | cansses | 1 |
| 10351 | canssedes | 1 |
| 10352 | canssar | 1 |
| 10353 | canssada | 1 |
| 10354 | canssa | 1 |
| 10355 | cansé | 1 |
| 10356 | cansaría | 1 |
| 10357 | cansará | 1 |
| 10358 | cánsanme | 1 |
| 10359 | cansado | 1 |
| 10360 | cansada | 1 |
| 10361 | canonista | 1 |
| 10362 | canónigo | 1 |
| 10363 | canónico | 1 |
| 10364 | canónicas | 1 |
| 10365 | canistillo | 1 |
| 10366 | cangrejos | 1 |
| 10367 | canes | 1 |
| 10368 | candy | 1 |
| 10369 | candor | 1 |
| 10370 | candidez | 1 |
| 10371 | cancionero | 1 |
| 10372 | canción | 1 |
| 10373 | cánçeres | 1 |
| 10374 | çancadiella | 1 |
| 10375 | çanca | 1 |
| 10376 | canbio | 1 |
| 10377 | canastiello | 1 |
| 10378 | canasta | 1 |
| 10379 | canas | 1 |
| 10380 | cánamo | 1 |
| 10381 | canadas | 1 |
| 10382 | camuçia | 1 |
| 10383 | campar | 1 |
| 10384 | camissas | 1 |
| 10385 | caminos | 1 |
| 10386 | cambios | 1 |
| 10387 | cambio | 1 |
| 10388 | çamarras | 1 |
| 10389 | çamarón | 1 |
| 10390 | calyenta | 1 |
| 10391 | caloña | 1 |
| 10392 | calló | 1 |
| 10393 | callo | 1 |
| 10394 | calles | 1 |
| 10395 | callen | 1 |
| 10396 | callemos | 1 |
| 10397 | calledes | 1 |
| 10398 | cállate | 1 |
| 10399 | callará | 1 |
| 10400 | callades | 1 |
| 10401 | calientes | 1 |
| 10402 | caliéntat | 1 |
| 10403 | calibre | 1 |
| 10404 | calentura | 1 |
| 10405 | calentando | 1 |
| 10406 | calendas | 1 |
| 10407 | caldera | 1 |
| 10408 | calçar | 1 |
| 10409 | calcañares | 1 |
| 10410 | calbi | 1 |
| 10411 | calataút | 1 |
| 10412 | calandrias | 1 |
| 10413 | çalagarda | 1 |
| 10414 | calabaça | 1 |
| 10415 | cala | 1 |
| 10416 | çahorar | 1 |
| 10417 | cahen | 1 |
| 10418 | çafyr | 1 |
| 10419 | cáfila | 1 |
| 10420 | cáesete | 1 |
| 10421 | cadahalso | 1 |
| 10422 | caçurro | 1 |
| 10423 | caçurrías | 1 |
| 10424 | caçurra | 1 |
| 10425 | caçorría | 1 |
| 10426 | caço | 1 |
| 10427 | caças | 1 |
| 10428 | caçadores | 1 |
| 10429 | caç | 1 |
| 10430 | cabtivo | 1 |
| 10431 | cabrilla | 1 |
| 10432 | cabríe | 1 |
| 10433 | cabrían | 1 |
| 10434 | cabildo | 1 |
| 10435 | cabel | 1 |
| 10436 | cabeçudo | 1 |
| 10437 | cabeçeó | 1 |
| 10438 | cabçe | 1 |
| 10439 | cabañas | 1 |
| 10440 | caballería | 1 |
| 10441 | caballeresca | 1 |
| 10442 | cab | 1 |
| 10443 | byvos | 1 |
| 10444 | byvo | 1 |
| 10445 | byviredes | 1 |
| 10446 | byvió | 1 |
| 10447 | byvierdes | 1 |
| 10448 | byve | 1 |
| 10449 | byvas | 1 |
| 10450 | byvamos | 1 |
| 10451 | byva | 1 |
| 10452 | byuda | 1 |
| 10453 | byenfaser | 1 |
| 10454 | byenapreso | 1 |
| 10455 | byenandante | 1 |
| 10456 | buy | 1 |
| 10457 | buxyes | 1 |
| 10458 | buxía | 1 |
| 10459 | buxes | 1 |
| 10460 | busques | 1 |
| 10461 | busque | 1 |
| 10462 | buscólo | 1 |
| 10463 | buscava | 1 |
| 10464 | buscat | 1 |
| 10465 | buscaría | 1 |
| 10466 | buscando | 1 |
| 10467 | búsca | 1 |
| 10468 | burra | 1 |
| 10469 | burguesa | 1 |
| 10470 | burgos | 1 |
| 10471 | burgeses | 1 |
| 10472 | burgés | 1 |
| 10473 | burel | 1 |
| 10474 | bulrra | 1 |
| 10475 | bulliendo | 1 |
| 10476 | buhonería | 1 |
| 10477 | buhón | 1 |
| 10478 | buenaventura | 1 |
| 10479 | buenaval | 1 |
| 10480 | buenamiente | 1 |
| 10481 | buelve | 1 |
| 10482 | bryo | 1 |
| 10483 | bruto | 1 |
| 10484 | brusquedad | 1 |
| 10485 | brozna | 1 |
| 10486 | bronco | 1 |
| 10487 | broncha | 1 |
| 10488 | bronch | 1 |
| 10489 | brilla | 1 |
| 10490 | breviario | 1 |
| 10491 | brevemente | 1 |
| 10492 | brete | 1 |
| 10493 | bretañia | 1 |
| 10494 | bretaña | 1 |
| 10495 | bretador | 1 |
| 10496 | bravuras | 1 |
| 10497 | bravos | 1 |
| 10498 | bravas | 1 |
| 10499 | bramidos | 1 |
| 10500 | bramar | 1 |
| 10501 | braguero | 1 |
| 10502 | brafuneras | 1 |
| 10503 | bos | 1 |
| 10504 | borrico | 1 |
| 10505 | bordón | 1 |
| 10506 | boquirrubios | 1 |
| 10507 | bonus | 1 |
| 10508 | bonum | 1 |
| 10509 | bolviéndole | 1 |
| 10510 | bolverás | 1 |
| 10511 | bolsa | 1 |
| 10512 | boloña | 1 |
| 10513 | bollyçio | 1 |
| 10514 | bolliçio | 1 |
| 10515 | bolava | 1 |
| 10516 | bolar | 1 |
| 10517 | bolando | 1 |
| 10518 | bogar | 1 |
| 10519 | bodeguero | 1 |
| 10520 | bodegones | 1 |
| 10521 | bodega | 1 |
| 10522 | boço | 1 |
| 10523 | boceto | 1 |
| 10524 | boçes | 1 |
| 10525 | bocado | 1 |
| 10526 | bocabierto | 1 |
| 10527 | boba | 1 |
| 10528 | blav | 1 |
| 10529 | blando | 1 |
| 10530 | blancura | 1 |
| 10531 | blanchetes | 1 |
| 10532 | blago | 1 |
| 10533 | blaços | 1 |
| 10534 | blaço | 1 |
| 10535 | bive | 1 |
| 10536 | bisperada | 1 |
| 10537 | bienrrazonada | 1 |
| 10538 | bienquerençia | 1 |
| 10539 | bienparado | 1 |
| 10540 | bienfechores | 1 |
| 10541 | bienfecha | 1 |
| 10542 | bienfasyentes | 1 |
| 10543 | bienaventurado | 1 |
| 10544 | bienandante | 1 |
| 10545 | biblia | 1 |
| 10546 | bezes | 1 |
| 10547 | bevras | 1 |
| 10548 | bevió | 1 |
| 10549 | bevimos | 1 |
| 10550 | beviera | 1 |
| 10551 | beviendo | 1 |
| 10552 | beverría | 1 |
| 10553 | bevería | 1 |
| 10554 | beven | 1 |
| 10555 | bevedor | 1 |
| 10556 | bev | 1 |
| 10557 | beudos | 1 |
| 10558 | besos | 1 |
| 10559 | beso | 1 |
| 10560 | beserro | 1 |
| 10561 | beserrillo | 1 |
| 10562 | besava | 1 |
| 10563 | besáronle | 1 |
| 10564 | besar | 1 |
| 10565 | besan | 1 |
| 10566 | bervo | 1 |
| 10567 | berssabe | 1 |
| 10568 | berroqueña | 1 |
| 10569 | berracas | 1 |
| 10570 | bermeo | 1 |
| 10571 | berdones | 1 |
| 10572 | berceo | 1 |
| 10573 | bera | 1 |
| 10574 | beodo | 1 |
| 10575 | beo | 1 |
| 10576 | benito | 1 |
| 10577 | beneditos | 1 |
| 10578 | benedicta | 1 |
| 10579 | bendixo | 1 |
| 10580 | benditas | 1 |
| 10581 | benditamente | 1 |
| 10582 | bendita | 1 |
| 10583 | bendigo | 1 |
| 10584 | bendigamos | 1 |
| 10585 | bendichos | 1 |
| 10586 | bendicho | 1 |
| 10587 | bendiçen | 1 |
| 10588 | bendexiese | 1 |
| 10589 | belméz | 1 |
| 10590 | bellosa | 1 |
| 10591 | bello | 1 |
| 10592 | belén | 1 |
| 10593 | beldando | 1 |
| 10594 | beldad | 1 |
| 10595 | bel | 1 |
| 10596 | beçerros | 1 |
| 10597 | bebe | 1 |
| 10598 | beati | 1 |
| 10599 | beatas | 1 |
| 10600 | bé | 1 |
| 10601 | be | 1 |
| 10602 | bayona | 1 |
| 10603 | baxar | 1 |
| 10604 | baxa | 1 |
| 10605 | baviecas | 1 |
| 10606 | bautysta | 1 |
| 10607 | bautismo | 1 |
| 10608 | bautisat | 1 |
| 10609 | bausana | 1 |
| 10610 | batieron | 1 |
| 10611 | batallas | 1 |
| 10612 | batalla | 1 |
| 10613 | bastará | 1 |
| 10614 | barvos | 1 |
| 10615 | barvechos | 1 |
| 10616 | barvecho | 1 |
| 10617 | barva | 1 |
| 10618 | barrúntanos | 1 |
| 10619 | barruntan | 1 |
| 10620 | barril | 1 |
| 10621 | barragana | 1 |
| 10622 | barçilona | 1 |
| 10623 | barcas | 1 |
| 10624 | barbuda | 1 |
| 10625 | barbos | 1 |
| 10626 | bárbara | 1 |
| 10627 | barbados | 1 |
| 10628 | barato | 1 |
| 10629 | baratan | 1 |
| 10630 | barahunda | 1 |
| 10631 | baquerisa | 1 |
| 10632 | baño | 1 |
| 10633 | bañe | 1 |
| 10634 | baña | 1 |
| 10635 | bandurria | 1 |
| 10636 | bandera | 1 |
| 10637 | bambochadas | 1 |
| 10638 | baltasar | 1 |
| 10639 | balsamo | 1 |
| 10640 | ballesteros | 1 |
| 10641 | ballestas | 1 |
| 10642 | balidos | 1 |
| 10643 | balentía | 1 |
| 10644 | baldosa | 1 |
| 10645 | baldones | 1 |
| 10646 | baldonado | 1 |
| 10647 | baldonada | 1 |
| 10648 | baldíos | 1 |
| 10649 | balar | 1 |
| 10650 | balanzas | 1 |
| 10651 | balança | 1 |
| 10652 | bajo | 1 |
| 10653 | baja | 1 |
| 10654 | bahareros | 1 |
| 10655 | baena | 1 |
| 10656 | badil | 1 |
| 10657 | baço | 1 |
| 10658 | baçines | 1 |
| 10659 | baçín | 1 |
| 10660 | babylonia | 1 |
| 10661 | babilónico | 1 |
| 10662 | babilón | 1 |
| 10663 | ba | 1 |
| 10664 | b | 1 |
| 10665 | azar | 1 |
| 10666 | ayusso | 1 |
| 10667 | ayunten | 1 |
| 10668 | ayuntamos | 1 |
| 10669 | ayunta | 1 |
| 10670 | ayunos | 1 |
| 10671 | ayunava | 1 |
| 10672 | ayunar | 1 |
| 10673 | ayunador | 1 |
| 10674 | ayúdevos | 1 |
| 10675 | ayudéte | 1 |
| 10676 | ayudava | 1 |
| 10677 | ayudas | 1 |
| 10678 | ayudarte | 1 |
| 10679 | ayudares | 1 |
| 10680 | ayudaré | 1 |
| 10681 | ayudan | 1 |
| 10682 | ayúdame | 1 |
| 10683 | ayud | 1 |
| 10684 | ayras | 1 |
| 10685 | ayrados | 1 |
| 10686 | ayo | 1 |
| 10687 | ayala | 1 |
| 10688 | axuar | 1 |
| 10689 | axenúz | 1 |
| 10690 | axabeba | 1 |
| 10691 | avyva | 1 |
| 10692 | avyene | 1 |
| 10693 | avye | 1 |
| 10694 | avría | 1 |
| 10695 | avoleza | 1 |
| 10696 | avizores | 1 |
| 10697 | aviesos | 1 |
| 10698 | aviesa | 1 |
| 10699 | avienes | 1 |
| 10700 | aviene | 1 |
| 10701 | avién | 1 |
| 10702 | avíen | 1 |
| 10703 | avie | 1 |
| 10704 | avian | 1 |
| 10705 | avíala | 1 |
| 10706 | avet | 1 |
| 10707 | averte | 1 |
| 10708 | avérsevos | 1 |
| 10709 | averla | 1 |
| 10710 | avémoslo | 1 |
| 10711 | avellanas | 1 |
| 10712 | avarisia | 1 |
| 10713 | avariento | 1 |
| 10714 | autobiográfica | 1 |
| 10715 | autobiografía | 1 |
| 10716 | auteurs | 1 |
| 10717 | aurora | 1 |
| 10718 | aunqu | 1 |
| 10719 | aullar | 1 |
| 10720 | aueran | 1 |
| 10721 | auelo | 1 |
| 10722 | audiat | 1 |
| 10723 | atyncar | 1 |
| 10724 | atyenden | 1 |
| 10725 | atún | 1 |
| 10726 | atronar | 1 |
| 10727 | atribuyese | 1 |
| 10728 | atribuye | 1 |
| 10729 | atribulado | 1 |
| 10730 | atrevyme | 1 |
| 10731 | atrevuda | 1 |
| 10732 | atrevíme | 1 |
| 10733 | atraviesa | 1 |
| 10734 | atravesósel | 1 |
| 10735 | atravesós | 1 |
| 10736 | atravesó | 1 |
| 10737 | atormentar | 1 |
| 10738 | atormentado | 1 |
| 10739 | atordida | 1 |
| 10740 | atora | 1 |
| 10741 | atiza | 1 |
| 10742 | atildada | 1 |
| 10743 | atiene | 1 |
| 10744 | atiéndense | 1 |
| 10745 | atiéndele | 1 |
| 10746 | atenga | 1 |
| 10747 | atener | 1 |
| 10748 | atendiól | 1 |
| 10749 | atendiendo | 1 |
| 10750 | atas | 1 |
| 10751 | atar | 1 |
| 10752 | atantos | 1 |
| 10753 | atán | 1 |
| 10754 | atamaña | 1 |
| 10755 | atama | 1 |
| 10756 | atalvina | 1 |
| 10757 | atalayas | 1 |
| 10758 | ataja | 1 |
| 10759 | ataguylaco | 1 |
| 10760 | atabores | 1 |
| 10761 | atabor | 1 |
| 10762 | atabales | 1 |
| 10763 | asuntos | 1 |
| 10764 | asuero | 1 |
| 10765 | asuelvo | 1 |
| 10766 | asuelto | 1 |
| 10767 | asuelta | 1 |
| 10768 | astrosya | 1 |
| 10769 | astroso | 1 |
| 10770 | astrosa | 1 |
| 10771 | astrólogos | 1 |
| 10772 | astrológicas | 1 |
| 10773 | astralabio | 1 |
| 10774 | astragas | 1 |
| 10775 | astragarvos | 1 |
| 10776 | astragaríe | 1 |
| 10777 | astragando | 1 |
| 10778 | astragallo | 1 |
| 10779 | asta | 1 |
| 10780 | assonados | 1 |
| 10781 | assoma | 1 |
| 10782 | assi | 1 |
| 10783 | asseo | 1 |
| 10784 | assentó | 1 |
| 10785 | asseguro | 1 |
| 10786 | assegurando | 1 |
| 10787 | assaz | 1 |
| 10788 | assañóse | 1 |
| 10789 | assaño | 1 |
| 10790 | assaduras | 1 |
| 10791 | assadero | 1 |
| 10792 | assadas | 1 |
| 10793 | ásperos | 1 |
| 10794 | aspectos | 1 |
| 10795 | asosegadamente | 1 |
| 10796 | asonbra | 1 |
| 10797 | asomen | 1 |
| 10798 | asombrosa | 1 |
| 10799 | asombrarse | 1 |
| 10800 | asomada | 1 |
| 10801 | asolvióle | 1 |
| 10802 | asolvet | 1 |
| 10803 | asolverlos | 1 |
| 10804 | asolved | 1 |
| 10805 | asolvades | 1 |
| 10806 | asolución | 1 |
| 10807 | asnos | 1 |
| 10808 | asnería | 1 |
| 10809 | asmó | 1 |
| 10810 | asmar | 1 |
| 10811 | asinóles | 1 |
| 10812 | asinase | 1 |
| 10813 | asinado | 1 |
| 10814 | aseo | 1 |
| 10815 | asentados | 1 |
| 10816 | asentado | 1 |
| 10817 | asegurados | 1 |
| 10818 | asedos | 1 |
| 10819 | asedía | 1 |
| 10820 | ascut | 1 |
| 10821 | ascuso | 1 |
| 10822 | ascuchad | 1 |
| 10823 | ascucha | 1 |
| 10824 | asconder | 1 |
| 10825 | asconden | 1 |
| 10826 | ascenderunt | 1 |
| 10827 | asçendente | 1 |
| 10828 | asáz | 1 |
| 10829 | asaz | 1 |
| 10830 | asava | 1 |
| 10831 | asas | 1 |
| 10832 | asañe | 1 |
| 10833 | asañastes | 1 |
| 10834 | asadas | 1 |
| 10835 | asa | 1 |
| 10836 | arveja | 1 |
| 10837 | artístico | 1 |
| 10838 | artesas | 1 |
| 10839 | arterías | 1 |
| 10840 | artería | 1 |
| 10841 | arteras | 1 |
| 10842 | arrufastes | 1 |
| 10843 | arroz | 1 |
| 10844 | arroyos | 1 |
| 10845 | arrojóme | 1 |
| 10846 | arrojado | 1 |
| 10847 | arrimado | 1 |
| 10848 | arresido | 1 |
| 10849 | arrepintajas | 1 |
| 10850 | arrepintades | 1 |
| 10851 | arrepienta | 1 |
| 10852 | arrepenty | 1 |
| 10853 | arrepentudo | 1 |
| 10854 | arrepentiera | 1 |
| 10855 | arrepentido | 1 |
| 10856 | arrepentemiento | 1 |
| 10857 | arremetas | 1 |
| 10858 | arremangado | 1 |
| 10859 | arremanga | 1 |
| 10860 | arredróse | 1 |
| 10861 | arredrávanse | 1 |
| 10862 | arredrará | 1 |
| 10863 | arreçido | 1 |
| 10864 | arrebates | 1 |
| 10865 | arrebatamiento | 1 |
| 10866 | arraygar | 1 |
| 10867 | arraval | 1 |
| 10868 | arrastrados | 1 |
| 10869 | arras | 1 |
| 10870 | arrapa | 1 |
| 10871 | arranquemos | 1 |
| 10872 | arranque | 1 |
| 10873 | arrancase | 1 |
| 10874 | arrancar | 1 |
| 10875 | arrancando | 1 |
| 10876 | arrancados | 1 |
| 10877 | arrancado | 1 |
| 10878 | arpón | 1 |
| 10879 | armó | 1 |
| 10880 | armario | 1 |
| 10881 | ármanse | 1 |
| 10882 | arlotes | 1 |
| 10883 | arlotas | 1 |
| 10884 | aristótiles | 1 |
| 10885 | aristóteles | 1 |
| 10886 | aristofanesco | 1 |
| 10887 | arista | 1 |
| 10888 | arisca | 1 |
| 10889 | arigotes | 1 |
| 10890 | argumentos | 1 |
| 10891 | argamasa | 1 |
| 10892 | aresido | 1 |
| 10893 | arenques | 1 |
| 10894 | arenal | 1 |
| 10895 | ardura | 1 |
| 10896 | ardor | 1 |
| 10897 | ardiesse | 1 |
| 10898 | ardientes | 1 |
| 10899 | ardidamente | 1 |
| 10900 | arder | 1 |
| 10901 | ardedes | 1 |
| 10902 | arcos | 1 |
| 10903 | arçiprestes | 1 |
| 10904 | arciprestazgo | 1 |
| 10905 | arçidianos | 1 |
| 10906 | árbores | 1 |
| 10907 | arbil | 1 |
| 10908 | arar | 1 |
| 10909 | araña | 1 |
| 10910 | aranea | 1 |
| 10911 | aragonesismos | 1 |
| 10912 | aragonesas | 1 |
| 10913 | aragonés | 1 |
| 10914 | aradas | 1 |
| 10915 | arábigos | 1 |
| 10916 | arábiga | 1 |
| 10917 | aquexas | 1 |
| 10918 | aquexamiento | 1 |
| 10919 | aquexa | 1 |
| 10920 | aquest | 1 |
| 10921 | aquesse | 1 |
| 10922 | aqueso | 1 |
| 10923 | aquesa | 1 |
| 10924 | aques | 1 |
| 10925 | apuntado | 1 |
| 10926 | apuerte | 1 |
| 10927 | aprueva | 1 |
| 10928 | aprovechamiento | 1 |
| 10929 | aprovechado | 1 |
| 10930 | apropriados | 1 |
| 10931 | aprisca | 1 |
| 10932 | aprieto | 1 |
| 10933 | apriétame | 1 |
| 10934 | aprieta | 1 |
| 10935 | apretándolo | 1 |
| 10936 | apretadillos | 1 |
| 10937 | aprestos | 1 |
| 10938 | aprendieron | 1 |
| 10939 | aprender | 1 |
| 10940 | aprende | 1 |
| 10941 | apremidos | 1 |
| 10942 | aprémiame | 1 |
| 10943 | apremiado | 1 |
| 10944 | apreçia | 1 |
| 10945 | apreçebido | 1 |
| 10946 | aprecebido | 1 |
| 10947 | appellaron | 1 |
| 10948 | appellaciones | 1 |
| 10949 | apóstrofo | 1 |
| 10950 | apostoles | 1 |
| 10951 | apostizo | 1 |
| 10952 | apostisos | 1 |
| 10953 | apostados | 1 |
| 10954 | apost | 1 |
| 10955 | aponiendo | 1 |
| 10956 | aponía | 1 |
| 10957 | apongo | 1 |
| 10958 | apone | 1 |
| 10959 | apolonio | 1 |
| 10960 | apodas | 1 |
| 10961 | apocando | 1 |
| 10962 | apocalisi | 1 |
| 10963 | apocalipsi | 1 |
| 10964 | apilongados | 1 |
| 10965 | apesgado | 1 |
| 10966 | apesadumbrados | 1 |
| 10967 | apertar | 1 |
| 10968 | apertando | 1 |
| 10969 | aperos | 1 |
| 10970 | apero | 1 |
| 10971 | aperçibes | 1 |
| 10972 | aperçebydos | 1 |
| 10973 | aperçebydo | 1 |
| 10974 | apellydo | 1 |
| 10975 | apello | 1 |
| 10976 | apellidos | 1 |
| 10977 | apellidar | 1 |
| 10978 | apellásemos | 1 |
| 10979 | apelaron | 1 |
| 10980 | apega | 1 |
| 10981 | apedrear | 1 |
| 10982 | apedreado | 1 |
| 10983 | apeado | 1 |
| 10984 | apartes | 1 |
| 10985 | aparte | 1 |
| 10986 | apartan | 1 |
| 10987 | apartados | 1 |
| 10988 | aparesçió | 1 |
| 10989 | aparesçençia | 1 |
| 10990 | aparejan | 1 |
| 10991 | aparejamiento | 1 |
| 10992 | aparejados | 1 |
| 10993 | aparearse | 1 |
| 10994 | aparado | 1 |
| 10995 | aora | 1 |
| 10996 | aojadas | 1 |
| 10997 | añudar | 1 |
| 10998 | añejo | 1 |
| 10999 | añedir | 1 |
| 11000 | añafyl | 1 |
| 11001 | añafiles | 1 |
| 11002 | añado | 1 |
| 11003 | añadir | 1 |
| 11004 | añadió | 1 |
| 11005 | añadieres | 1 |
| 11006 | antygo | 1 |
| 11007 | antre | 1 |
| 11008 | antonio | 1 |
| 11009 | antojada | 1 |
| 11010 | antoja | 1 |
| 11011 | antipara | 1 |
| 11012 | antiguo | 1 |
| 11013 | antiguedat | 1 |
| 11014 | antigua | 1 |
| 11015 | anticanónica | 1 |
| 11016 | antaño | 1 |
| 11017 | anssarones | 1 |
| 11018 | ánssares | 1 |
| 11019 | ansarones | 1 |
| 11020 | ánsares | 1 |
| 11021 | anparança | 1 |
| 11022 | anoche | 1 |
| 11023 | ano | 1 |
| 11024 | anni | 1 |
| 11025 | ánimas | 1 |
| 11026 | animalyas | 1 |
| 11027 | aniellos | 1 |
| 11028 | angustura | 1 |
| 11029 | angustias | 1 |
| 11030 | angostillos | 1 |
| 11031 | angostas | 1 |
| 11032 | angosta | 1 |
| 11033 | angiellas | 1 |
| 11034 | anejo | 1 |
| 11035 | anega | 1 |
| 11036 | andut | 1 |
| 11037 | andudiese | 1 |
| 11038 | andudiere | 1 |
| 11039 | andude | 1 |
| 11040 | andit | 1 |
| 11041 | andés | 1 |
| 11042 | andes | 1 |
| 11043 | ander | 1 |
| 11044 | anden | 1 |
| 11045 | andémoslo | 1 |
| 11046 | andemos | 1 |
| 11047 | andávanse | 1 |
| 11048 | andariegos | 1 |
| 11049 | andariego | 1 |
| 11050 | andariegas | 1 |
| 11051 | andariega | 1 |
| 11052 | andares | 1 |
| 11053 | andaredes | 1 |
| 11054 | andança | 1 |
| 11055 | andamos | 1 |
| 11056 | ándame | 1 |
| 11057 | andalúz | 1 |
| 11058 | andalusía | 1 |
| 11059 | andador | 1 |
| 11060 | and | 1 |
| 11061 | ançiano | 1 |
| 11062 | ancho | 1 |
| 11063 | ancha | 1 |
| 11064 | anbiçia | 1 |
| 11065 | anbas | 1 |
| 11066 | analizado | 1 |
| 11067 | ánades | 1 |
| 11068 | án | 1 |
| 11069 | amugronadores | 1 |
| 11070 | amuerço | 1 |
| 11071 | amplios | 1 |
| 11072 | ámovos | 1 |
| 11073 | amortesçer | 1 |
| 11074 | amoríos | 1 |
| 11075 | amorem | 1 |
| 11076 | amolados | 1 |
| 11077 | amodorridos | 1 |
| 11078 | amodorrida | 1 |
| 11079 | amó | 1 |
| 11080 | amistat | 1 |
| 11081 | amistança | 1 |
| 11082 | amistad | 1 |
| 11083 | amisión | 1 |
| 11084 | amigas | 1 |
| 11085 | amenudo | 1 |
| 11086 | amenazar | 1 |
| 11087 | amenasava | 1 |
| 11088 | amenasas | 1 |
| 11089 | amenasar | 1 |
| 11090 | amenasan | 1 |
| 11091 | amenaçar | 1 |
| 11092 | amé | 1 |
| 11093 | ambas | 1 |
| 11094 | amatávase | 1 |
| 11095 | amatada | 1 |
| 11096 | amassadas | 1 |
| 11097 | amariellos | 1 |
| 11098 | amargos | 1 |
| 11099 | amargo | 1 |
| 11100 | amargan | 1 |
| 11101 | amares | 1 |
| 11102 | amanssar | 1 |
| 11103 | amanssa | 1 |
| 11104 | amalde | 1 |
| 11105 | amagotes | 1 |
| 11106 | amadas | 1 |
| 11107 | am | 1 |
| 11108 | alzó | 1 |
| 11109 | alza | 1 |
| 11110 | alynpiat | 1 |
| 11111 | aly | 1 |
| 11112 | alvillo | 1 |
| 11113 | alvardanes | 1 |
| 11114 | alvardana | 1 |
| 11115 | alvañares | 1 |
| 11116 | alvalá | 1 |
| 11117 | alunbrava | 1 |
| 11118 | alúnbrase | 1 |
| 11119 | alunbrando | 1 |
| 11120 | aluengan | 1 |
| 11121 | altybajo | 1 |
| 11122 | altra | 1 |
| 11123 | altos | 1 |
| 11124 | altesa | 1 |
| 11125 | altares | 1 |
| 11126 | altar | 1 |
| 11127 | altaba | 1 |
| 11128 | alquilado | 1 |
| 11129 | alonguemos | 1 |
| 11130 | alongado | 1 |
| 11131 | almuerças | 1 |
| 11132 | almuerça | 1 |
| 11133 | almueças | 1 |
| 11134 | almosar | 1 |
| 11135 | almorçava | 1 |
| 11136 | almohaça | 1 |
| 11137 | almofalla | 1 |
| 11138 | almibarados | 1 |
| 11139 | almajares | 1 |
| 11140 | almagra | 1 |
| 11141 | almadanas | 1 |
| 11142 | almadana | 1 |
| 11143 | allegar | 1 |
| 11144 | allegamiento | 1 |
| 11145 | allegado | 1 |
| 11146 | alla | 1 |
| 11147 | aljavas | 1 |
| 11148 | aljaba | 1 |
| 11149 | aliso | 1 |
| 11150 | alisandría | 1 |
| 11151 | alisandre | 1 |
| 11152 | alimentó | 1 |
| 11153 | aliento | 1 |
| 11154 | alhoz | 1 |
| 11155 | alhorre | 1 |
| 11156 | alholis | 1 |
| 11157 | alhiara | 1 |
| 11158 | alheña | 1 |
| 11159 | alheleles | 1 |
| 11160 | alhaonedes | 1 |
| 11161 | alhajas | 1 |
| 11162 | algarea | 1 |
| 11163 | alfierez | 1 |
| 11164 | alffonsus | 1 |
| 11165 | alferez | 1 |
| 11166 | alferes | 1 |
| 11167 | alfeñique | 1 |
| 11168 | alfenique | 1 |
| 11169 | alfayate | 1 |
| 11170 | alfamares | 1 |
| 11171 | alfajeme | 1 |
| 11172 | alfajas | 1 |
| 11173 | alfaja | 1 |
| 11174 | alexar | 1 |
| 11175 | alexandría | 1 |
| 11176 | alexa | 1 |
| 11177 | alevoso | 1 |
| 11178 | alevosas | 1 |
| 11179 | alemán | 1 |
| 11180 | aleluya | 1 |
| 11181 | alegres | 1 |
| 11182 | alegrava | 1 |
| 11183 | alégrate | 1 |
| 11184 | alégrase | 1 |
| 11185 | alegras | 1 |
| 11186 | alegráronse | 1 |
| 11187 | alégranse | 1 |
| 11188 | alegrança | 1 |
| 11189 | alegra | 1 |
| 11190 | alegada | 1 |
| 11191 | alega | 1 |
| 11192 | aldeanos | 1 |
| 11193 | alda | 1 |
| 11194 | alcudia | 1 |
| 11195 | alcoholeras | 1 |
| 11196 | alçó | 1 |
| 11197 | alcayueta | 1 |
| 11198 | alcarías | 1 |
| 11199 | alcarez | 1 |
| 11200 | alcaraz | 1 |
| 11201 | alçarás | 1 |
| 11202 | alçar | 1 |
| 11203 | alcanzan | 1 |
| 11204 | alcanzaban | 1 |
| 11205 | álçanse | 1 |
| 11206 | alcandora | 1 |
| 11207 | alcanço | 1 |
| 11208 | alcançe | 1 |
| 11209 | alcançara | 1 |
| 11210 | alcançar | 1 |
| 11211 | alcançan | 1 |
| 11212 | alçan | 1 |
| 11213 | alcalles | 1 |
| 11214 | alcahuetería | 1 |
| 11215 | alcahueta | 1 |
| 11216 | alça | 1 |
| 11217 | albures | 1 |
| 11218 | albuérbola | 1 |
| 11219 | alboroçó | 1 |
| 11220 | alboroçaron | 1 |
| 11221 | albogón | 1 |
| 11222 | alberche | 1 |
| 11223 | alaút | 1 |
| 11224 | alarde | 1 |
| 11225 | alarcos | 1 |
| 11226 | alanes | 1 |
| 11227 | alanas | 1 |
| 11228 | alabé | 1 |
| 11229 | alabar | 1 |
| 11230 | ajobo | 1 |
| 11231 | ajoba | 1 |
| 11232 | ajeños | 1 |
| 11233 | ajenas | 1 |
| 11234 | airada | 1 |
| 11235 | aiam | 1 |
| 11236 | ahevos | 1 |
| 11237 | ahembrados | 1 |
| 11238 | agusadera | 1 |
| 11239 | agusa | 1 |
| 11240 | agurero | 1 |
| 11241 | aguijones | 1 |
| 11242 | aguijó | 1 |
| 11243 | aguijo | 1 |
| 11244 | aguero | 1 |
| 11245 | agudos | 1 |
| 11246 | agudillos | 1 |
| 11247 | agudas | 1 |
| 11248 | aguardando | 1 |
| 11249 | aguaducho | 1 |
| 11250 | aguaçil | 1 |
| 11251 | agrillo | 1 |
| 11252 | agraviados | 1 |
| 11253 | agranizar | 1 |
| 11254 | agrada | 1 |
| 11255 | agra | 1 |
| 11256 | agostynes | 1 |
| 11257 | agena | 1 |
| 11258 | afynquela | 1 |
| 11259 | afyncovos | 1 |
| 11260 | afynco | 1 |
| 11261 | afyncava | 1 |
| 11262 | afyncáronle | 1 |
| 11263 | afyncándole | 1 |
| 11264 | afyncando | 1 |
| 11265 | afyncamiento | 1 |
| 11266 | afyncado | 1 |
| 11267 | afylada | 1 |
| 11268 | afusiavan | 1 |
| 11269 | afusiada | 1 |
| 11270 | afuera | 1 |
| 11271 | afrecho | 1 |
| 11272 | aforre | 1 |
| 11273 | aforrasen | 1 |
| 11274 | aforismos | 1 |
| 11275 | afogóse | 1 |
| 11276 | afogóla | 1 |
| 11277 | afógate | 1 |
| 11278 | afogarse | 1 |
| 11279 | afogaría | 1 |
| 11280 | afogado | 1 |
| 11281 | afiyncamiento | 1 |
| 11282 | afinques | 1 |
| 11283 | afines | 1 |
| 11284 | afincado | 1 |
| 11285 | afinca | 1 |
| 11286 | affyncada | 1 |
| 11287 | afeytadas | 1 |
| 11288 | afeminados | 1 |
| 11289 | afanan | 1 |
| 11290 | adyvas | 1 |
| 11291 | adúz | 1 |
| 11292 | adugo | 1 |
| 11293 | aducho | 1 |
| 11294 | aducha | 1 |
| 11295 | adragea | 1 |
| 11296 | adormiéronse | 1 |
| 11297 | adormiendo | 1 |
| 11298 | adormido | 1 |
| 11299 | adorava | 1 |
| 11300 | adorallo | 1 |
| 11301 | adora | 1 |
| 11302 | adonde | 1 |
| 11303 | adonada | 1 |
| 11304 | adona | 1 |
| 11305 | adolo | 1 |
| 11306 | adolesçer | 1 |
| 11307 | adoba | 1 |
| 11308 | admito | 1 |
| 11309 | admitía | 1 |
| 11310 | admirar | 1 |
| 11311 | adevinaron | 1 |
| 11312 | adevina | 1 |
| 11313 | adelyñas | 1 |
| 11314 | adeliñó | 1 |
| 11315 | adelantar | 1 |
| 11316 | adelantados | 1 |
| 11317 | adelantado | 1 |
| 11318 | adelanta | 1 |
| 11319 | adefinas | 1 |
| 11320 | adaragas | 1 |
| 11321 | adamares | 1 |
| 11322 | adamar | 1 |
| 11323 | adama | 1 |
| 11324 | adalid | 1 |
| 11325 | acussado | 1 |
| 11326 | acuso | 1 |
| 11327 | acusiossos | 1 |
| 11328 | acusava | 1 |
| 11329 | acusar | 1 |
| 11330 | açunbre | 1 |
| 11331 | acumulándolos | 1 |
| 11332 | acuesta | 1 |
| 11333 | acuerda | 1 |
| 11334 | acuda | 1 |
| 11335 | acre | 1 |
| 11336 | açotar | 1 |
| 11337 | acostunbrado | 1 |
| 11338 | acostunbrada | 1 |
| 11339 | acostumbrado | 1 |
| 11340 | acostar | 1 |
| 11341 | acórtase | 1 |
| 11342 | acortar | 1 |
| 11343 | acórrenos | 1 |
| 11344 | acorrednos | 1 |
| 11345 | acorredes | 1 |
| 11346 | acorra | 1 |
| 11347 | acordóse | 1 |
| 11348 | acordé | 1 |
| 11349 | acordavos | 1 |
| 11350 | acordatvos | 1 |
| 11351 | acordastes | 1 |
| 11352 | acordarse | 1 |
| 11353 | acordarán | 1 |
| 11354 | acordar | 1 |
| 11355 | acordado | 1 |
| 11356 | açor | 1 |
| 11357 | acontesçió | 1 |
| 11358 | acontecimientos | 1 |
| 11359 | acontecerles | 1 |
| 11360 | aconpañar | 1 |
| 11361 | aconpañados | 1 |
| 11362 | aconpañado | 1 |
| 11363 | aconpañada | 1 |
| 11364 | acompañaron | 1 |
| 11365 | acometiese | 1 |
| 11366 | acometidas | 1 |
| 11367 | acometerse | 1 |
| 11368 | acometerla | 1 |
| 11369 | acomete | 1 |
| 11370 | acometas | 1 |
| 11371 | acojer | 1 |
| 11372 | acogamonos | 1 |
| 11373 | açófar | 1 |
| 11374 | acobarda | 1 |
| 11375 | aclarado | 1 |
| 11376 | açiertas | 1 |
| 11377 | acierta | 1 |
| 11378 | açidya | 1 |
| 11379 | acidia | 1 |
| 11380 | açidente | 1 |
| 11381 | achaca | 1 |
| 11382 | açes | 1 |
| 11383 | açerté | 1 |
| 11384 | açertad | 1 |
| 11385 | aceros | 1 |
| 11386 | açércase | 1 |
| 11387 | açercándosse | 1 |
| 11388 | açerca | 1 |
| 11389 | acerca | 1 |
| 11390 | açeña | 1 |
| 11391 | açenia | 1 |
| 11392 | acecho | 1 |
| 11393 | açebyn | 1 |
| 11394 | acaya | 1 |
| 11395 | acaloñarnos | 1 |
| 11396 | açafrán | 1 |
| 11397 | acaesçimientos | 1 |
| 11398 | acaesçer | 1 |
| 11399 | académico | 1 |
| 11400 | acabesçí | 1 |
| 11401 | acabase | 1 |
| 11402 | acaban | 1 |
| 11403 | acabados | 1 |
| 11404 | acabad | 1 |
| 11405 | abyva | 1 |
| 11406 | abyertas | 1 |
| 11407 | aburra | 1 |
| 11408 | abundante | 1 |
| 11409 | abundancia | 1 |
| 11410 | abundaban | 1 |
| 11411 | abstracto | 1 |
| 11412 | absolver | 1 |
| 11413 | abryl | 1 |
| 11414 | abrit | 1 |
| 11415 | abrirle | 1 |
| 11416 | abriré | 1 |
| 11417 | abrir | 1 |
| 11418 | abriol | 1 |
| 11419 | abril | 1 |
| 11420 | abriendo | 1 |
| 11421 | abríela | 1 |
| 11422 | abrid | 1 |
| 11423 | abreviarvos | 1 |
| 11424 | abreviado | 1 |
| 11425 | abres | 1 |
| 11426 | abrebaron | 1 |
| 11427 | abré | 1 |
| 11428 | abras | 1 |
| 11429 | abrahán | 1 |
| 11430 | abraçóse | 1 |
| 11431 | abraçólo | 1 |
| 11432 | abraço | 1 |
| 11433 | abraçemos | 1 |
| 11434 | abraçar | 1 |
| 11435 | aborridos | 1 |
| 11436 | aborresçes | 1 |
| 11437 | aborresçerán | 1 |
| 11438 | aborrésçenle | 1 |
| 11439 | aborresçen | 1 |
| 11440 | aborresçe | 1 |
| 11441 | aborrescas | 1 |
| 11442 | aborrençia | 1 |
| 11443 | aborreçes | 1 |
| 11444 | abondo | 1 |
| 11445 | abondas | 1 |
| 11446 | abolengo | 1 |
| 11447 | abivo | 1 |
| 11448 | abive | 1 |
| 11449 | abivádvos | 1 |
| 11450 | ábitos | 1 |
| 11451 | ábito | 1 |
| 11452 | abismo | 1 |
| 11453 | abigarrado | 1 |
| 11454 | abeyte | 1 |
| 11455 | abertura | 1 |
| 11456 | aberné | 1 |
| 11457 | abentó | 1 |
| 11458 | abenidvos | 1 |
| 11459 | abengo | 1 |
| 11460 | abengas | 1 |
| 11461 | abenencia | 1 |
| 11462 | abel | 1 |
| 11463 | abejón | 1 |
| 11464 | abbatis | 1 |
| 11465 | abbades | 1 |
| 11466 | abaxo | 1 |
| 11467 | abaxé | 1 |
| 11468 | abaxarse | 1 |
| 11469 | abatyda | 1 |
| 11470 | abatióse | 1 |
| 11471 | abat | 1 |
| 11472 | abastar | 1 |
| 11473 | abastado | 1 |
| 11474 | abarredera | 1 |
| 11475 | abarcaron | 1 |
| 11476 | abarcar | 1 |
| 11477 | abarca | 1 |
| 11478 | aballar | 1 |
| 11479 | abad | 1 |
|
| Rank | Palabra | Frec |
|---|
| 1 | que | 3639 |
| 2 | de | 2604 |
| 3 | e | 2067 |
| 4 | la | 1474 |
| 5 | no | 1454 |
| 6 | a | 1336 |
| 7 | en | 1229 |
| 8 | el | 1075 |
| 9 | mi | 934 |
| 10 | por | 848 |
| 11 | me | 802 |
| 12 | con | 744 |
| 13 | tu | 723 |
| 14 | es | 680 |
| 15 | lo | 657 |
| 16 | los | 590 |
| 17 | mas | 579 |
| 18 | su | 562 |
| 19 | se | 543 |
| 20 | como | 508 |
| 21 | te | 504 |
| 22 | yo | 475 |
| 23 | si | 471 |
| 24 | o | 471 |
| 25 | las | 441 |
| 26 | para | 338 |
| 27 | pues | 313 |
| 28 | quien | 293 |
| 29 | cel | 280 |
| 30 | ni | 256 |
| 31 | esta | 256 |
| 32 | porque | 255 |
| 33 | le | 254 |
| 34 | del | 249 |
| 35 | dios | 233 |
| 36 | cal | 225 |
| 37 | semp | 212 |
| 38 | sus | 205 |
| 39 | tan | 196 |
| 40 | vn | 195 |
| 41 | bien | 195 |
| 42 | y | 192 |
| 43 | senora | 191 |
| 44 | sin | 190 |
| 45 | todo | 186 |
| 46 | al | 181 |
| 47 | ya | 177 |
| 48 | ha | 172 |
| 49 | assi | 169 |
| 50 | parm | 161 |
| 51 | casa | 160 |
| 52 | calisto | 160 |
| 53 | este | 156 |
| 54 | senor | 152 |
| 55 | ay | 152 |
| 56 | esto | 151 |
| 57 | melibea | 149 |
| 58 | vna | 144 |
| 59 | pero | 143 |
| 60 | ella | 143 |
| 61 | mal | 140 |
| 62 | mis | 139 |
| 63 | madre | 137 |
| 64 | sempronio | 135 |
| 65 | quando | 132 |
| 66 | agora | 125 |
| 67 | celestina | 122 |
| 68 | amor | 122 |
| 69 | tus | 120 |
| 70 | qual | 120 |
| 71 | melib | 117 |
| 72 | vida | 116 |
| 73 | tal | 116 |
| 74 | has | 116 |
| 75 | sino | 115 |
| 76 | ser | 114 |
| 77 | cosa | 113 |
| 78 | tiempo | 111 |
| 79 | avnque | 111 |
| 80 | todos | 110 |
| 81 | parmeno | 110 |
| 82 | he | 110 |
| 83 | vieja | 106 |
| 84 | ti | 104 |
| 85 | aquel | 104 |
| 86 | mucho | 103 |
| 87 | muy | 101 |
| 88 | quanto | 100 |
| 89 | tiene | 98 |
| 90 | poco | 98 |
| 91 | nos | 98 |
| 92 | quiero | 96 |
| 93 | otro | 96 |
| 94 | tengo | 95 |
| 95 | otra | 95 |
| 96 | son | 92 |
| 97 | mejor | 89 |
| 98 | donde | 87 |
| 99 | aquella | 87 |
| 100 | gran | 84 |
| 101 | aqui | 84 |
| 102 | pena | 82 |
| 103 | amo | 79 |
| 104 | buen | 77 |
| 105 | otros | 76 |
| 106 | hombre | 76 |
| 107 | nunca | 75 |
| 108 | era | 72 |
| 109 | dolor | 72 |
| 110 | dizes | 72 |
| 111 | dia | 72 |
| 112 | avn | 72 |
| 113 | parte | 71 |
| 114 | tanto | 70 |
| 115 | sea | 70 |
| 116 | fue | 70 |
| 117 | corazon | 69 |
| 118 | estas | 67 |
| 119 | entre | 66 |
| 120 | areu | 66 |
| 121 | plazer | 65 |
| 122 | puede | 64 |
| 123 | muerte | 64 |
| 124 | soy | 63 |
| 125 | razon | 62 |
| 126 | noche | 62 |
| 127 | buena | 62 |
| 128 | ver | 60 |
| 129 | elic | 60 |
| 130 | causa | 60 |
| 131 | todas | 58 |
| 132 | solo | 58 |
| 133 | mundo | 58 |
| 134 | manos | 58 |
| 135 | jamas | 58 |
| 136 | dos | 58 |
| 137 | cierto | 58 |
| 138 | hija | 57 |
| 139 | fin | 57 |
| 140 | triste | 56 |
| 141 | presto | 56 |
| 142 | muger | 56 |
| 143 | lucrecia | 54 |
| 144 | cosas | 54 |
| 145 | padre | 53 |
| 146 | esso | 53 |
| 147 | elicia | 53 |
| 148 | cada | 53 |
| 149 | mia | 52 |
| 150 | hazer | 52 |
| 151 | dezir | 52 |
| 152 | dar | 52 |
| 153 | estos | 50 |
| 154 | dizen | 50 |
| 155 | digo | 50 |
| 156 | segun | 49 |
| 157 | ojos | 49 |
| 158 | mira | 48 |
| 159 | tenia | 47 |
| 160 | lucr | 47 |
| 161 | hijo | 47 |
| 162 | alla | 47 |
| 163 | vno | 46 |
| 164 | verdad | 46 |
| 165 | mio | 46 |
| 166 | haze | 46 |
| 167 | despues | 46 |
| 168 | creo | 46 |
| 169 | toda | 45 |
| 170 | puerta | 45 |
| 171 | palabras | 44 |
| 172 | nuestro | 44 |
| 173 | hecho | 44 |
| 174 | esse | 44 |
| 175 | viene | 43 |
| 176 | tres | 43 |
| 177 | temor | 43 |
| 178 | prouecho | 43 |
| 179 | lengua | 43 |
| 180 | hasta | 43 |
| 181 | sabes | 42 |
| 182 | quieres | 42 |
| 183 | otras | 42 |
| 184 | han | 42 |
| 185 | da | 42 |
| 186 | aca | 42 |
| 187 | va | 41 |
| 188 | mayor | 41 |
| 189 | manera | 41 |
| 190 | habla | 41 |
| 191 | dize | 41 |
| 192 | areusa | 41 |
| 193 | vezes | 40 |
| 194 | venir | 40 |
| 195 | sera | 40 |
| 196 | ninguna | 40 |
| 197 | lugar | 40 |
| 198 | dicho | 40 |
| 199 | dias | 40 |
| 200 | calla | 40 |
| 201 | siempre | 39 |
| 202 | razones | 39 |
| 203 | os | 39 |
| 204 | muchas | 39 |
| 205 | desta | 39 |
| 206 | contigo | 39 |
| 207 | consejo | 39 |
| 208 | voluntad | 38 |
| 209 | quiere | 38 |
| 210 | parece | 38 |
| 211 | hombres | 38 |
| 212 | eres | 38 |
| 213 | alegre | 38 |
| 214 | tienes | 37 |
| 215 | poder | 37 |
| 216 | dulce | 37 |
| 217 | antes | 37 |
| 218 | yr | 36 |
| 219 | tener | 36 |
| 220 | sos | 36 |
| 221 | seso | 36 |
| 222 | oy | 36 |
| 223 | tanta | 35 |
| 224 | mozos | 35 |
| 225 | loco | 35 |
| 226 | fuera | 35 |
| 227 | comer | 35 |
| 228 | alto | 35 |
| 229 | venida | 34 |
| 230 | trabajo | 34 |
| 231 | sosia | 34 |
| 232 | sobre | 34 |
| 233 | nombre | 34 |
| 234 | mucha | 34 |
| 235 | les | 34 |
| 236 | cuerpo | 34 |
| 237 | boca | 34 |
| 238 | alli | 34 |
| 239 | algo | 34 |
| 240 | visto | 33 |
| 241 | vamos | 33 |
| 242 | saber | 33 |
| 243 | sabe | 33 |
| 244 | nuestra | 33 |
| 245 | mano | 33 |
| 246 | mala | 33 |
| 247 | hora | 33 |
| 248 | gloria | 33 |
| 249 | dime | 33 |
| 250 | alguna | 33 |
| 251 | veo | 32 |
| 252 | presente | 32 |
| 253 | muchos | 32 |
| 254 | mill | 32 |
| 255 | ellos | 32 |
| 256 | aya | 32 |
| 257 | tierra | 31 |
| 258 | seruicio | 31 |
| 259 | negocio | 31 |
| 260 | hablar | 31 |
| 261 | gozo | 31 |
| 262 | di | 31 |
| 263 | tales | 30 |
| 264 | sola | 30 |
| 265 | persona | 30 |
| 266 | necessidad | 30 |
| 267 | estoy | 30 |
| 268 | estan | 30 |
| 269 | desseo | 30 |
| 270 | calle | 30 |
| 271 | amores | 30 |
| 272 | veras | 29 |
| 273 | menos | 29 |
| 274 | menester | 29 |
| 275 | memoria | 29 |
| 276 | luego | 29 |
| 277 | honrra | 29 |
| 278 | gracias | 29 |
| 279 | essa | 29 |
| 280 | esperanza | 29 |
| 281 | comigo | 29 |
| 282 | cara | 29 |
| 283 | anda | 29 |
| 284 | amiga | 29 |
| 285 | salud | 28 |
| 286 | primera | 28 |
| 287 | obra | 28 |
| 288 | fuerza | 28 |
| 289 | deste | 28 |
| 290 | amigo | 28 |
| 291 | sangre | 27 |
| 292 | remedio | 27 |
| 293 | queda | 27 |
| 294 | pleberio | 27 |
| 295 | paresce | 27 |
| 296 | mientra | 27 |
| 297 | grande | 27 |
| 298 | fuego | 27 |
| 299 | fortuna | 27 |
| 300 | enojo | 27 |
| 301 | perdido | 26 |
| 302 | hauia | 26 |
| 303 | hauer | 26 |
| 304 | diablo | 26 |
| 305 | aquellos | 26 |
| 306 | anos | 26 |
| 307 | yerro | 25 |
| 308 | vosotros | 25 |
| 309 | sentido | 25 |
| 310 | secreto | 25 |
| 311 | oficio | 25 |
| 312 | fuesse | 25 |
| 313 | fazer | 25 |
| 314 | auto | 25 |
| 315 | vaya | 24 |
| 316 | palabra | 24 |
| 317 | nueuas | 24 |
| 318 | manto | 24 |
| 319 | gozar | 24 |
| 320 | contra | 24 |
| 321 | argumento | 24 |
| 322 | salir | 23 |
| 323 | querria | 23 |
| 324 | passo | 23 |
| 325 | ninguno | 23 |
| 326 | hermana | 23 |
| 327 | dano | 23 |
| 328 | dado | 23 |
| 329 | cordon | 23 |
| 330 | camino | 23 |
| 331 | vnos | 22 |
| 332 | virtud | 22 |
| 333 | vino | 22 |
| 334 | puedo | 22 |
| 335 | perdida | 22 |
| 336 | oydo | 22 |
| 337 | medio | 22 |
| 338 | hijos | 22 |
| 339 | do | 22 |
| 340 | deleyte | 22 |
| 341 | compania | 22 |
| 342 | auia | 22 |
| 343 | vista | 21 |
| 344 | viejo | 21 |
| 345 | vi | 21 |
| 346 | trist | 21 |
| 347 | tardanza | 21 |
| 348 | seria | 21 |
| 349 | primer | 21 |
| 350 | piensas | 21 |
| 351 | passado | 21 |
| 352 | oro | 21 |
| 353 | muerto | 21 |
| 354 | mozo | 21 |
| 355 | morir | 21 |
| 356 | llama | 21 |
| 357 | hazes | 21 |
| 358 | harto | 21 |
| 359 | grado | 21 |
| 360 | goze | 21 |
| 361 | fecho | 21 |
| 362 | fe | 21 |
| 363 | estaua | 21 |
| 364 | dio | 21 |
| 365 | dexa | 21 |
| 366 | della | 21 |
| 367 | creer | 21 |
| 368 | bueno | 21 |
| 369 | amigos | 21 |
| 370 | alma | 21 |
| 371 | algun | 21 |
| 372 | yra | 20 |
| 373 | tristeza | 20 |
| 374 | tras | 20 |
| 375 | tarde | 20 |
| 376 | suyo | 20 |
| 377 | siento | 20 |
| 378 | seas | 20 |
| 379 | quan | 20 |
| 380 | puesto | 20 |
| 381 | peor | 20 |
| 382 | passion | 20 |
| 383 | nada | 20 |
| 384 | justicia | 20 |
| 385 | huyr | 20 |
| 386 | hermano | 20 |
| 387 | gentil | 20 |
| 388 | estado | 20 |
| 389 | escucha | 20 |
| 390 | edad | 20 |
| 391 | dexar | 20 |
| 392 | descanso | 20 |
| 393 | cata | 20 |
| 394 | ali | 20 |
| 395 | voy | 19 |
| 396 | tambien | 19 |
| 397 | prima | 19 |
| 398 | padres | 19 |
| 399 | natura | 19 |
| 400 | hizo | 19 |
| 401 | haga | 19 |
| 402 | gente | 19 |
| 403 | eran | 19 |
| 404 | diziendo | 19 |
| 405 | caso | 19 |
| 406 | camara | 19 |
| 407 | andar | 19 |
| 408 | alegria | 19 |
| 409 | viuir | 18 |
| 410 | sofrir | 18 |
| 411 | querer | 18 |
| 412 | quantos | 18 |
| 413 | quales | 18 |
| 414 | primero | 18 |
| 415 | pies | 18 |
| 416 | pan | 18 |
| 417 | oyr | 18 |
| 418 | nosotros | 18 |
| 419 | muertos | 18 |
| 420 | huerto | 18 |
| 421 | hablando | 18 |
| 422 | falta | 18 |
| 423 | dinero | 18 |
| 424 | dexo | 18 |
| 425 | deue | 18 |
| 426 | demanda | 18 |
| 427 | dellas | 18 |
| 428 | cruel | 18 |
| 429 | conozco | 18 |
| 430 | complir | 18 |
| 431 | cauallero | 18 |
| 432 | basta | 18 |
| 433 | agua | 18 |
| 434 | adelante | 18 |
| 435 | ygual | 17 |
| 436 | vido | 17 |
| 437 | trae | 17 |
| 438 | toma | 17 |
| 439 | quatro | 17 |
| 440 | proposito | 17 |
| 441 | principio | 17 |
| 442 | peligro | 17 |
| 443 | oye | 17 |
| 444 | noble | 17 |
| 445 | mugeres | 17 |
| 446 | mayormente | 17 |
| 447 | llorar | 17 |
| 448 | llaga | 17 |
| 449 | hazen | 17 |
| 450 | hare | 17 |
| 451 | espada | 17 |
| 452 | esfuerzo | 17 |
| 453 | dormir | 17 |
| 454 | desto | 17 |
| 455 | delante | 17 |
| 456 | dando | 17 |
| 457 | cura | 17 |
| 458 | cargo | 17 |
| 459 | cabeza | 17 |
| 460 | asi | 17 |
| 461 | ante | 17 |
| 462 | vez | 16 |
| 463 | vejez | 16 |
| 464 | respuesta | 16 |
| 465 | pueda | 16 |
| 466 | presencia | 16 |
| 467 | podra | 16 |
| 468 | pleb | 16 |
| 469 | perder | 16 |
| 470 | muerta | 16 |
| 471 | merced | 16 |
| 472 | manana | 16 |
| 473 | honrrada | 16 |
| 474 | grandes | 16 |
| 475 | gracia | 16 |
| 476 | galardon | 16 |
| 477 | fuerte | 16 |
| 478 | fama | 16 |
| 479 | essas | 16 |
| 480 | entrar | 16 |
| 481 | dan | 16 |
| 482 | claro | 16 |
| 483 | cerca | 16 |
| 484 | cent | 16 |
| 485 | cabo | 16 |
| 486 | aquello | 16 |
| 487 | aquellas | 16 |
| 488 | amistad | 16 |
| 489 | vnas | 15 |
| 490 | tuyo | 15 |
| 491 | tristan | 15 |
| 492 | traygo | 15 |
| 493 | sospecha | 15 |
| 494 | siruientes | 15 |
| 495 | puertas | 15 |
| 496 | pone | 15 |
| 497 | pobre | 15 |
| 498 | piedras | 15 |
| 499 | pensar | 15 |
| 500 | osadia | 15 |
| 501 | nueuo | 15 |
| 502 | mesa | 15 |
| 503 | llaman | 15 |
| 504 | lagrimas | 15 |
| 505 | jesu | 15 |
| 506 | gana | 15 |
| 507 | estar | 15 |
| 508 | essos | 15 |
| 509 | espero | 15 |
| 510 | entra | 15 |
| 511 | digas | 15 |
| 512 | dexame | 15 |
| 513 | destos | 15 |
| 514 | desde | 15 |
| 515 | cibdad | 15 |
| 516 | ce | 15 |
| 517 | bienes | 15 |
| 518 | aues | 15 |
| 519 | armas | 15 |
| 520 | ano | 15 |
| 521 | ama | 15 |
| 522 | absencia | 15 |
| 523 | viendo | 14 |
| 524 | viejos | 14 |
| 525 | verguenza | 14 |
| 526 | vale | 14 |
| 527 | tomar | 14 |
| 528 | sube | 14 |
| 529 | so | 14 |
| 530 | siendo | 14 |
| 531 | sido | 14 |
| 532 | sano | 14 |
| 533 | rey | 14 |
| 534 | rato | 14 |
| 535 | quantas | 14 |
| 536 | puta | 14 |
| 537 | passados | 14 |
| 538 | oyes | 14 |
| 539 | necessario | 14 |
| 540 | natural | 14 |
| 541 | mismo | 14 |
| 542 | menor | 14 |
| 543 | loca | 14 |
| 544 | linaje | 14 |
| 545 | fiel | 14 |
| 546 | ellas | 14 |
| 547 | dire | 14 |
| 548 | diras | 14 |
| 549 | debaxo | 14 |
| 550 | dara | 14 |
| 551 | cuenta | 14 |
| 552 | criado | 14 |
| 553 | consigo | 14 |
| 554 | color | 14 |
| 555 | centurio | 14 |
| 556 | cama | 14 |
| 557 | breue | 14 |
| 558 | alisa | 14 |
| 559 | agradable | 14 |
| 560 | verte | 13 |
| 561 | verdadero | 13 |
| 562 | venido | 13 |
| 563 | venga | 13 |
| 564 | vea | 13 |
| 565 | van | 13 |
| 566 | traer | 13 |
| 567 | tormento | 13 |
| 568 | tienen | 13 |
| 569 | tia | 13 |
| 570 | tantas | 13 |
| 571 | sueno | 13 |
| 572 | somos | 13 |
| 573 | sentimiento | 13 |
| 574 | quiera | 13 |
| 575 | queria | 13 |
| 576 | quede | 13 |
| 577 | passos | 13 |
| 578 | partes | 13 |
| 579 | pago | 13 |
| 580 | oydos | 13 |
| 581 | ningun | 13 |
| 582 | hilado | 13 |
| 583 | hazia | 13 |
| 584 | don | 13 |
| 585 | dixo | 13 |
| 586 | diez | 13 |
| 587 | demas | 13 |
| 588 | dello | 13 |
| 589 | culpa | 13 |
| 590 | criada | 13 |
| 591 | buscar | 13 |
| 592 | anima | 13 |
| 593 | abre | 13 |
| 594 | viuo | 12 |
| 595 | vete | 12 |
| 596 | tristes | 12 |
| 597 | tha | 12 |
| 598 | suaue | 12 |
| 599 | sofrimiento | 12 |
| 600 | seras | 12 |
| 601 | secretos | 12 |
| 602 | quedo | 12 |
| 603 | qualquiera | 12 |
| 604 | pueden | 12 |
| 605 | propia | 12 |
| 606 | poca | 12 |
| 607 | pie | 12 |
| 608 | perdicion | 12 |
| 609 | pensamiento | 12 |
| 610 | pecado | 12 |
| 611 | passe | 12 |
| 612 | passada | 12 |
| 613 | paredes | 12 |
| 614 | nueua | 12 |
| 615 | muestra | 12 |
| 616 | moza | 12 |
| 617 | misma | 12 |
| 618 | mensaje | 12 |
| 619 | mate | 12 |
| 620 | maestra | 12 |
| 621 | locos | 12 |
| 622 | lloro | 12 |
| 623 | hy | 12 |
| 624 | horas | 12 |
| 625 | hermanos | 12 |
| 626 | gentileza | 12 |
| 627 | enfermo | 12 |
| 628 | dixe | 12 |
| 629 | destas | 12 |
| 630 | criados | 12 |
| 631 | consejos | 12 |
| 632 | cabellos | 12 |
| 633 | buenos | 12 |
| 634 | auer | 12 |
| 635 | verna | 11 |
| 636 | verme | 11 |
| 637 | vas | 11 |
| 638 | tuya | 11 |
| 639 | torna | 11 |
| 640 | seruir | 11 |
| 641 | sean | 11 |
| 642 | sabia | 11 |
| 643 | quieren | 11 |
| 644 | punto | 11 |
| 645 | podria | 11 |
| 646 | piensa | 11 |
| 647 | personas | 11 |
| 648 | pense | 11 |
| 649 | oyrte | 11 |
| 650 | obras | 11 |
| 651 | nuestras | 11 |
| 652 | matar | 11 |
| 653 | mar | 11 |
| 654 | llegar | 11 |
| 655 | juntas | 11 |
| 656 | gesto | 11 |
| 657 | estando | 11 |
| 658 | espacio | 11 |
| 659 | engano | 11 |
| 660 | enemigo | 11 |
| 661 | ello | 11 |
| 662 | duro | 11 |
| 663 | dixiste | 11 |
| 664 | dentro | 11 |
| 665 | cielo | 11 |
| 666 | cadena | 11 |
| 667 | ayer | 11 |
| 668 | as | 11 |
| 669 | ve | 10 |
| 670 | testigo | 10 |
| 671 | soledad | 10 |
| 672 | sepa | 10 |
| 673 | sentir | 10 |
| 674 | senal | 10 |
| 675 | seguro | 10 |
| 676 | saya | 10 |
| 677 | sanar | 10 |
| 678 | sacar | 10 |
| 679 | sabor | 10 |
| 680 | puedes | 10 |
| 681 | prosigue | 10 |
| 682 | poner | 10 |
| 683 | pocas | 10 |
| 684 | pensaua | 10 |
| 685 | paciencia | 10 |
| 686 | orden | 10 |
| 687 | oracion | 10 |
| 688 | nuestros | 10 |
| 689 | muertes | 10 |
| 690 | marido | 10 |
| 691 | mandas | 10 |
| 692 | llamar | 10 |
| 693 | juntos | 10 |
| 694 | huye | 10 |
| 695 | hermosura | 10 |
| 696 | hermosa | 10 |
| 697 | haziendo | 10 |
| 698 | hazienda | 10 |
| 699 | haz | 10 |
| 700 | hablas | 10 |
| 701 | graciosa | 10 |
| 702 | genero | 10 |
| 703 | ganado | 10 |
| 704 | fablar | 10 |
| 705 | escala | 10 |
| 706 | enfermedades | 10 |
| 707 | embidia | 10 |
| 708 | donzella | 10 |
| 709 | doliente | 10 |
| 710 | diligencia | 10 |
| 711 | digno | 10 |
| 712 | dientes | 10 |
| 713 | dicha | 10 |
| 714 | dezia | 10 |
| 715 | das | 10 |
| 716 | cuya | 10 |
| 717 | corazones | 10 |
| 718 | contrario | 10 |
| 719 | concierto | 10 |
| 720 | buenas | 10 |
| 721 | boz | 10 |
| 722 | autor | 10 |
| 723 | amada | 10 |
| 724 | alta | 10 |
| 725 | algunos | 10 |
| 726 | algunas | 10 |
| 727 | alcanzado | 10 |
| 728 | albricias | 10 |
| 729 | acto | 10 |
| 730 | yre | 9 |
| 731 | yras | 9 |
| 732 | vuestra | 9 |
| 733 | viua | 9 |
| 734 | vienes | 9 |
| 735 | ventura | 9 |
| 736 | ven | 9 |
| 737 | vees | 9 |
| 738 | veen | 9 |
| 739 | tuue | 9 |
| 740 | todavia | 9 |
| 741 | tenga | 9 |
| 742 | suelen | 9 |
| 743 | sotil | 9 |
| 744 | solicitud | 9 |
| 745 | silencio | 9 |
| 746 | sepas | 9 |
| 747 | sentidos | 9 |
| 748 | sana | 9 |
| 749 | sabido | 9 |
| 750 | rico | 9 |
| 751 | remediar | 9 |
| 752 | quiza | 9 |
| 753 | quiso | 9 |
| 754 | quisiere | 9 |
| 755 | puso | 9 |
| 756 | propio | 9 |
| 757 | pluma | 9 |
| 758 | paz | 9 |
| 759 | passar | 9 |
| 760 | passa | 9 |
| 761 | pagar | 9 |
| 762 | oportunidad | 9 |
| 763 | noches | 9 |
| 764 | mozas | 9 |
| 765 | mocedad | 9 |
| 766 | mayores | 9 |
| 767 | marauillo | 9 |
| 768 | mando | 9 |
| 769 | mancebos | 9 |
| 770 | locura | 9 |
| 771 | lleuo | 9 |
| 772 | llena | 9 |
| 773 | llegate | 9 |
| 774 | libre | 9 |
| 775 | juuentud | 9 |
| 776 | impossible | 9 |
| 777 | haura | 9 |
| 778 | hallo | 9 |
| 779 | hago | 9 |
| 780 | hablan | 9 |
| 781 | guardar | 9 |
| 782 | ganar | 9 |
| 783 | fuere | 9 |
| 784 | forma | 9 |
| 785 | fasta | 9 |
| 786 | falsa | 9 |
| 787 | fabla | 9 |
| 788 | entranas | 9 |
| 789 | entramos | 9 |
| 790 | entiendo | 9 |
| 791 | enemigos | 9 |
| 792 | dura | 9 |
| 793 | doze | 9 |
| 794 | deues | 9 |
| 795 | crueles | 9 |
| 796 | corre | 9 |
| 797 | contino | 9 |
| 798 | companeros | 9 |
| 799 | ciudad | 9 |
| 800 | cierta | 9 |
| 801 | cient | 9 |
| 802 | cauallos | 9 |
| 803 | catiuo | 9 |
| 804 | baxa | 9 |
| 805 | auias | 9 |
| 806 | asno | 9 |
| 807 | amantes | 9 |
| 808 | aliuio | 9 |
| 809 | alguno | 9 |
| 810 | adonde | 9 |
| 811 | abrir | 9 |
| 812 | yguales | 8 |
| 813 | yeruas | 8 |
| 814 | vuestro | 8 |
| 815 | visitar | 8 |
| 816 | ves | 8 |
| 817 | vellaco | 8 |
| 818 | vegez | 8 |
| 819 | tocas | 8 |
| 820 | tenemos | 8 |
| 821 | temo | 8 |
| 822 | suya | 8 |
| 823 | suele | 8 |
| 824 | sosiego | 8 |
| 825 | sientes | 8 |
| 826 | seys | 8 |
| 827 | sentencia | 8 |
| 828 | segura | 8 |
| 829 | saluo | 8 |
| 830 | ruydo | 8 |
| 831 | ropa | 8 |
| 832 | rio | 8 |
| 833 | relox | 8 |
| 834 | quel | 8 |
| 835 | quedan | 8 |
| 836 | quasi | 8 |
| 837 | priessa | 8 |
| 838 | plazeres | 8 |
| 839 | pides | 8 |
| 840 | pesar | 8 |
| 841 | perro | 8 |
| 842 | pensando | 8 |
| 843 | pensamientos | 8 |
| 844 | penado | 8 |
| 845 | passan | 8 |
| 846 | palos | 8 |
| 847 | oygo | 8 |
| 848 | oluido | 8 |
| 849 | odio | 8 |
| 850 | ninos | 8 |
| 851 | nascida | 8 |
| 852 | miedo | 8 |
| 853 | merece | 8 |
| 854 | mentiras | 8 |
| 855 | mengua | 8 |
| 856 | marauillas | 8 |
| 857 | malo | 8 |
| 858 | maldito | 8 |
| 859 | malas | 8 |
| 860 | lenguas | 8 |
| 861 | ingenio | 8 |
| 862 | houo | 8 |
| 863 | haras | 8 |
| 864 | halle | 8 |
| 865 | guerra | 8 |
| 866 | gracioso | 8 |
| 867 | gentes | 8 |
| 868 | fuy | 8 |
| 869 | fueron | 8 |
| 870 | flaca | 8 |
| 871 | fino | 8 |
| 872 | fijo | 8 |
| 873 | fatiga | 8 |
| 874 | falto | 8 |
| 875 | esperar | 8 |
| 876 | entrada | 8 |
| 877 | entender | 8 |
| 878 | ende | 8 |
| 879 | dubda | 8 |
| 880 | dexemos | 8 |
| 881 | desuariado | 8 |
| 882 | deseo | 8 |
| 883 | desdichada | 8 |
| 884 | descobrir | 8 |
| 885 | daua | 8 |
| 886 | dare | 8 |
| 887 | cuydado | 8 |
| 888 | cumple | 8 |
| 889 | costumbre | 8 |
| 890 | contraria | 8 |
| 891 | contienda | 8 |
| 892 | contenta | 8 |
| 893 | conoscida | 8 |
| 894 | conocer | 8 |
| 895 | confession | 8 |
| 896 | comedia | 8 |
| 897 | carga | 8 |
| 898 | capa | 8 |
| 899 | c | 8 |
| 900 | bullicio | 8 |
| 901 | buelue | 8 |
| 902 | bozes | 8 |
| 903 | boluer | 8 |
| 904 | atreuimiento | 8 |
| 905 | asaz | 8 |
| 906 | animales | 8 |
| 907 | amar | 8 |
| 908 | alcanzar | 8 |
| 909 | alcahueta | 8 |
| 910 | alas | 8 |
| 911 | ageno | 8 |
| 912 | vuestras | 7 |
| 913 | viue | 7 |
| 914 | viste | 7 |
| 915 | virtudes | 7 |
| 916 | virgos | 7 |
| 917 | viento | 7 |
| 918 | vicios | 7 |
| 919 | vengo | 7 |
| 920 | vender | 7 |
| 921 | vencido | 7 |
| 922 | vee | 7 |
| 923 | traes | 7 |
| 924 | traen | 7 |
| 925 | tiento | 7 |
| 926 | tenido | 7 |
| 927 | ten | 7 |
| 928 | tantos | 7 |
| 929 | suena | 7 |
| 930 | suba | 7 |
| 931 | siente | 7 |
| 932 | seruidores | 7 |
| 933 | sentia | 7 |
| 934 | senores | 7 |
| 935 | segundo | 7 |
| 936 | sanctos | 7 |
| 937 | saben | 7 |
| 938 | ruyn | 7 |
| 939 | ruego | 7 |
| 940 | rezio | 7 |
| 941 | quisieres | 7 |
| 942 | quieras | 7 |
| 943 | quanta | 7 |
| 944 | pudiera | 7 |
| 945 | procede | 7 |
| 946 | principal | 7 |
| 947 | presentes | 7 |
| 948 | ponga | 7 |
| 949 | podras | 7 |
| 950 | pocos | 7 |
| 951 | pobreza | 7 |
| 952 | plaza | 7 |
| 953 | piedad | 7 |
| 954 | peticion | 7 |
| 955 | pedir | 7 |
| 956 | pecho | 7 |
| 957 | parientes | 7 |
| 958 | ojo | 7 |
| 959 | negar | 7 |
| 960 | muera | 7 |
| 961 | mortal | 7 |
| 962 | monedas | 7 |
| 963 | momento | 7 |
| 964 | mochachas | 7 |
| 965 | miembros | 7 |
| 966 | mesma | 7 |
| 967 | mes | 7 |
| 968 | melezina | 7 |
| 969 | mato | 7 |
| 970 | mata | 7 |
| 971 | marauilla | 7 |
| 972 | llamado | 7 |
| 973 | limpio | 7 |
| 974 | licencia | 7 |
| 975 | ley | 7 |
| 976 | landre | 7 |
| 977 | juyzio | 7 |
| 978 | jarro | 7 |
| 979 | holgar | 7 |
| 980 | hizieron | 7 |
| 981 | herida | 7 |
| 982 | hechizera | 7 |
| 983 | hauias | 7 |
| 984 | haldas | 7 |
| 985 | hablo | 7 |
| 986 | goza | 7 |
| 987 | ganancia | 7 |
| 988 | frio | 7 |
| 989 | fresca | 7 |
| 990 | flaco | 7 |
| 991 | faze | 7 |
| 992 | estamos | 7 |
| 993 | esperiencia | 7 |
| 994 | espera | 7 |
| 995 | enojosa | 7 |
| 996 | enganos | 7 |
| 997 | enamorados | 7 |
| 998 | embalde | 7 |
| 999 | duda | 7 |
| 1000 | discretos | 7 |
| 1001 | discrecion | 7 |
| 1002 | diga | 7 |
| 1003 | dexes | 7 |
| 1004 | dexado | 7 |
| 1005 | deuemos | 7 |
| 1006 | des | 7 |
| 1007 | dellos | 7 |
| 1008 | deleytes | 7 |
| 1009 | danar | 7 |
| 1010 | dame | 7 |
| 1011 | cuesta | 7 |
| 1012 | crio | 7 |
| 1013 | crianza | 7 |
| 1014 | couardia | 7 |
| 1015 | contare | 7 |
| 1016 | contar | 7 |
| 1017 | conoscimiento | 7 |
| 1018 | comun | 7 |
| 1019 | comienzo | 7 |
| 1020 | claridad | 7 |
| 1021 | clara | 7 |
| 1022 | ceuo | 7 |
| 1023 | cargado | 7 |
| 1024 | canta | 7 |
| 1025 | callando | 7 |
| 1026 | cabe | 7 |
| 1027 | burlas | 7 |
| 1028 | buelta | 7 |
| 1029 | blanco | 7 |
| 1030 | ayre | 7 |
| 1031 | ayas | 7 |
| 1032 | ayan | 7 |
| 1033 | auiso | 7 |
| 1034 | arriba | 7 |
| 1035 | arrebatado | 7 |
| 1036 | animo | 7 |
| 1037 | ande | 7 |
| 1038 | amado | 7 |
| 1039 | alteracion | 7 |
| 1040 | alahe | 7 |
| 1041 | aguas | 7 |
| 1042 | yua | 6 |
| 1043 | yglesia | 6 |
| 1044 | ydo | 6 |
| 1045 | vso | 6 |
| 1046 | vozes | 6 |
| 1047 | voz | 6 |
| 1048 | vezina | 6 |
| 1049 | veynte | 6 |
| 1050 | verla | 6 |
| 1051 | verdadera | 6 |
| 1052 | ventanas | 6 |
| 1053 | venganza | 6 |
| 1054 | vayas | 6 |
| 1055 | varones | 6 |
| 1056 | vanos | 6 |
| 1057 | turbacion | 6 |
| 1058 | treynta | 6 |
| 1059 | traydora | 6 |
| 1060 | trato | 6 |
| 1061 | tenias | 6 |
| 1062 | tengas | 6 |
| 1063 | teneys | 6 |
| 1064 | temas | 6 |
| 1065 | tauerna | 6 |
| 1066 | suelo | 6 |
| 1067 | siquiera | 6 |
| 1068 | sienta | 6 |
| 1069 | sesos | 6 |
| 1070 | sentencias | 6 |
| 1071 | segunda | 6 |
| 1072 | sed | 6 |
| 1073 | sayo | 6 |
| 1074 | santa | 6 |
| 1075 | sant | 6 |
| 1076 | salen | 6 |
| 1077 | riquezas | 6 |
| 1078 | ricos | 6 |
| 1079 | recebido | 6 |
| 1080 | quita | 6 |
| 1081 | quisiera | 6 |
| 1082 | quexas | 6 |
| 1083 | querida | 6 |
| 1084 | quedar | 6 |
| 1085 | pudiesse | 6 |
| 1086 | posada | 6 |
| 1087 | podia | 6 |
| 1088 | pide | 6 |
| 1089 | perdona | 6 |
| 1090 | paga | 6 |
| 1091 | ogano | 6 |
| 1092 | officio | 6 |
| 1093 | nueuamente | 6 |
| 1094 | nombres | 6 |
| 1095 | necio | 6 |
| 1096 | necessidades | 6 |
| 1097 | muelas | 6 |
| 1098 | mostro | 6 |
| 1099 | mostrar | 6 |
| 1100 | missa | 6 |
| 1101 | mirar | 6 |
| 1102 | mirando | 6 |
| 1103 | mios | 6 |
| 1104 | mezquina | 6 |
| 1105 | mejores | 6 |
| 1106 | materia | 6 |
| 1107 | mande | 6 |
| 1108 | mandar | 6 |
| 1109 | mandado | 6 |
| 1110 | malos | 6 |
| 1111 | luz | 6 |
| 1112 | luto | 6 |
| 1113 | llorando | 6 |
| 1114 | llamas | 6 |
| 1115 | lisonjas | 6 |
| 1116 | libertad | 6 |
| 1117 | leal | 6 |
| 1118 | junto | 6 |
| 1119 | joya | 6 |
| 1120 | inconuenientes | 6 |
| 1121 | honestidad | 6 |
| 1122 | holgando | 6 |
| 1123 | hi | 6 |
| 1124 | hechos | 6 |
| 1125 | hecha | 6 |
| 1126 | hara | 6 |
| 1127 | hagas | 6 |
| 1128 | hablado | 6 |
| 1129 | gano | 6 |
| 1130 | fuerzas | 6 |
| 1131 | fuertes | 6 |
| 1132 | fuegos | 6 |
| 1133 | fruto | 6 |
| 1134 | franco | 6 |
| 1135 | fidelidad | 6 |
| 1136 | fazia | 6 |
| 1137 | fazen | 6 |
| 1138 | fauor | 6 |
| 1139 | fatigues | 6 |
| 1140 | falso | 6 |
| 1141 | estremos | 6 |
| 1142 | espaldas | 6 |
| 1143 | enfermedad | 6 |
| 1144 | enemiga | 6 |
| 1145 | encubrir | 6 |
| 1146 | encima | 6 |
| 1147 | dulces | 6 |
| 1148 | duerme | 6 |
| 1149 | duena | 6 |
| 1150 | duele | 6 |
| 1151 | doy | 6 |
| 1152 | discreto | 6 |
| 1153 | dira | 6 |
| 1154 | dilo | 6 |
| 1155 | dile | 6 |
| 1156 | dilacion | 6 |
| 1157 | dignos | 6 |
| 1158 | digna | 6 |
| 1159 | diferencia | 6 |
| 1160 | diesse | 6 |
| 1161 | dieron | 6 |
| 1162 | despedida | 6 |
| 1163 | desculpa | 6 |
| 1164 | dende | 6 |
| 1165 | daqui | 6 |
| 1166 | dale | 6 |
| 1167 | cuydados | 6 |
| 1168 | cupido | 6 |
| 1169 | cuerpos | 6 |
| 1170 | cuento | 6 |
| 1171 | cuentas | 6 |
| 1172 | conuiene | 6 |
| 1173 | conozcas | 6 |
| 1174 | conoscer | 6 |
| 1175 | conocida | 6 |
| 1176 | condicion | 6 |
| 1177 | comparacion | 6 |
| 1178 | companero | 6 |
| 1179 | comida | 6 |
| 1180 | claros | 6 |
| 1181 | cauallo | 6 |
| 1182 | carece | 6 |
| 1183 | canas | 6 |
| 1184 | caer | 6 |
| 1185 | cae | 6 |
| 1186 | bueltas | 6 |
| 1187 | broquel | 6 |
| 1188 | brazos | 6 |
| 1189 | boua | 6 |
| 1190 | blanca | 6 |
| 1191 | biuir | 6 |
| 1192 | atras | 6 |
| 1193 | aprouechar | 6 |
| 1194 | aprouecha | 6 |
| 1195 | aparte | 6 |
| 1196 | antigua | 6 |
| 1197 | angeles | 6 |
| 1198 | angel | 6 |
| 1199 | ando | 6 |
| 1200 | alegres | 6 |
| 1201 | alegra | 6 |
| 1202 | agenas | 6 |
| 1203 | agena | 6 |
| 1204 | acuestas | 6 |
| 1205 | acabar | 6 |
| 1206 | ymagen | 5 |
| 1207 | yendo | 5 |
| 1208 | visitacion | 5 |
| 1209 | virginidad | 5 |
| 1210 | vienen | 5 |
| 1211 | vezinas | 5 |
| 1212 | vestir | 5 |
| 1213 | verlo | 5 |
| 1214 | ventana | 5 |
| 1215 | ventaja | 5 |
| 1216 | venian | 5 |
| 1217 | vengar | 5 |
| 1218 | vemos | 5 |
| 1219 | vase | 5 |
| 1220 | traydo | 5 |
| 1221 | traya | 5 |
| 1222 | torre | 5 |
| 1223 | torpe | 5 |
| 1224 | tornar | 5 |
| 1225 | tome | 5 |
| 1226 | tomado | 5 |
| 1227 | tierras | 5 |
| 1228 | tierna | 5 |
| 1229 | tiempos | 5 |
| 1230 | temprano | 5 |
| 1231 | tablero | 5 |
| 1232 | suenos | 5 |
| 1233 | subamos | 5 |
| 1234 | sospechas | 5 |
| 1235 | sobra | 5 |
| 1236 | soberano | 5 |
| 1237 | singular | 5 |
| 1238 | simple | 5 |
| 1239 | serui | 5 |
| 1240 | sentida | 5 |
| 1241 | senoras | 5 |
| 1242 | senas | 5 |
| 1243 | segund | 5 |
| 1244 | seamos | 5 |
| 1245 | santos | 5 |
| 1246 | sale | 5 |
| 1247 | saco | 5 |
| 1248 | saca | 5 |
| 1249 | sabras | 5 |
| 1250 | ruega | 5 |
| 1251 | roma | 5 |
| 1252 | rogar | 5 |
| 1253 | rige | 5 |
| 1254 | reyna | 5 |
| 1255 | responder | 5 |
| 1256 | responde | 5 |
| 1257 | reposar | 5 |
| 1258 | reposa | 5 |
| 1259 | quise | 5 |
| 1260 | quesido | 5 |
| 1261 | querras | 5 |
| 1262 | pude | 5 |
| 1263 | prenada | 5 |
| 1264 | podre | 5 |
| 1265 | podemos | 5 |
| 1266 | plazeme | 5 |
| 1267 | pierdo | 5 |
| 1268 | pienses | 5 |
| 1269 | pido | 5 |
| 1270 | perdio | 5 |
| 1271 | perdi | 5 |
| 1272 | pequeno | 5 |
| 1273 | pensara | 5 |
| 1274 | pensado | 5 |
| 1275 | penas | 5 |
| 1276 | pelo | 5 |
| 1277 | pecadora | 5 |
| 1278 | passadas | 5 |
| 1279 | partir | 5 |
| 1280 | parayso | 5 |
| 1281 | parar | 5 |
| 1282 | par | 5 |
| 1283 | oyendo | 5 |
| 1284 | oyen | 5 |
| 1285 | orejas | 5 |
| 1286 | nouedad | 5 |
| 1287 | nino | 5 |
| 1288 | nascio | 5 |
| 1289 | muestran | 5 |
| 1290 | muero | 5 |
| 1291 | mudar | 5 |
| 1292 | morada | 5 |
| 1293 | modo | 5 |
| 1294 | meson | 5 |
| 1295 | mesmo | 5 |
| 1296 | merescimiento | 5 |
| 1297 | merecimiento | 5 |
| 1298 | mercedes | 5 |
| 1299 | medico | 5 |
| 1300 | media | 5 |
| 1301 | matas | 5 |
| 1302 | mataron | 5 |
| 1303 | marauilles | 5 |
| 1304 | manjar | 5 |
| 1305 | maluado | 5 |
| 1306 | maestro | 5 |
| 1307 | lugares | 5 |
| 1308 | lobo | 5 |
| 1309 | loable | 5 |
| 1310 | llore | 5 |
| 1311 | lleuar | 5 |
| 1312 | llanto | 5 |
| 1313 | llamada | 5 |
| 1314 | limpia | 5 |
| 1315 | liberalidad | 5 |
| 1316 | leydo | 5 |
| 1317 | lastimado | 5 |
| 1318 | lastima | 5 |
| 1319 | largo | 5 |
| 1320 | humana | 5 |
| 1321 | huessos | 5 |
| 1322 | huelgo | 5 |
| 1323 | houiesse | 5 |
| 1324 | honrrado | 5 |
| 1325 | hoja | 5 |
| 1326 | hiziera | 5 |
| 1327 | hize | 5 |
| 1328 | hauido | 5 |
| 1329 | haues | 5 |
| 1330 | harta | 5 |
| 1331 | haria | 5 |
| 1332 | grandeza | 5 |
| 1333 | grand | 5 |
| 1334 | gastado | 5 |
| 1335 | gallinas | 5 |
| 1336 | forzado | 5 |
| 1337 | flor | 5 |
| 1338 | flacos | 5 |
| 1339 | final | 5 |
| 1340 | fieles | 5 |
| 1341 | faltara | 5 |
| 1342 | falsas | 5 |
| 1343 | execucion | 5 |
| 1344 | estuue | 5 |
| 1345 | estilo | 5 |
| 1346 | esten | 5 |
| 1347 | esperan | 5 |
| 1348 | escuro | 5 |
| 1349 | escalera | 5 |
| 1350 | eras | 5 |
| 1351 | entremos | 5 |
| 1352 | entrauan | 5 |
| 1353 | entrambos | 5 |
| 1354 | entonce | 5 |
| 1355 | enganada | 5 |
| 1356 | enamorado | 5 |
| 1357 | empacho | 5 |
| 1358 | embia | 5 |
| 1359 | efeto | 5 |
| 1360 | dulzor | 5 |
| 1361 | dormido | 5 |
| 1362 | dolores | 5 |
| 1363 | diuersas | 5 |
| 1364 | diria | 5 |
| 1365 | dimelo | 5 |
| 1366 | diligente | 5 |
| 1367 | dichos | 5 |
| 1368 | dezirte | 5 |
| 1369 | dexe | 5 |
| 1370 | dexaua | 5 |
| 1371 | deuen | 5 |
| 1372 | determina | 5 |
| 1373 | desuios | 5 |
| 1374 | dessean | 5 |
| 1375 | desdichado | 5 |
| 1376 | descubre | 5 |
| 1377 | desconfianza | 5 |
| 1378 | desamor | 5 |
| 1379 | darte | 5 |
| 1380 | darle | 5 |
| 1381 | cuyo | 5 |
| 1382 | cruelmente | 5 |
| 1383 | crito | 5 |
| 1384 | creas | 5 |
| 1385 | couarde | 5 |
| 1386 | costumbres | 5 |
| 1387 | cortaron | 5 |
| 1388 | corazas | 5 |
| 1389 | conuersacion | 5 |
| 1390 | contento | 5 |
| 1391 | conseguir | 5 |
| 1392 | conosces | 5 |
| 1393 | conoces | 5 |
| 1394 | congoxa | 5 |
| 1395 | comido | 5 |
| 1396 | comen | 5 |
| 1397 | cobdicia | 5 |
| 1398 | ciento | 5 |
| 1399 | cayda | 5 |
| 1400 | catiua | 5 |
| 1401 | casas | 5 |
| 1402 | caro | 5 |
| 1403 | carnes | 5 |
| 1404 | carne | 5 |
| 1405 | capitan | 5 |
| 1406 | canto | 5 |
| 1407 | calor | 5 |
| 1408 | burla | 5 |
| 1409 | bouo | 5 |
| 1410 | biuos | 5 |
| 1411 | biuo | 5 |
| 1412 | biua | 5 |
| 1413 | beuer | 5 |
| 1414 | beneficio | 5 |
| 1415 | baxo | 5 |
| 1416 | balde | 5 |
| 1417 | azotes | 5 |
| 1418 | ayna | 5 |
| 1419 | auian | 5 |
| 1420 | astuta | 5 |
| 1421 | arte | 5 |
| 1422 | aquestos | 5 |
| 1423 | aparejos | 5 |
| 1424 | amas | 5 |
| 1425 | aman | 5 |
| 1426 | almazen | 5 |
| 1427 | aficion | 5 |
| 1428 | acuerdo | 5 |
| 1429 | acompanado | 5 |
| 1430 | achaque | 5 |
| 1431 | acarrea | 5 |
| 1432 | yuan | 4 |
| 1433 | yerran | 4 |
| 1434 | yerra | 4 |
| 1435 | yda | 4 |
| 1436 | vulgo | 4 |
| 1437 | vuestros | 4 |
| 1438 | vsar | 4 |
| 1439 | viuiendo | 4 |
| 1440 | viuas | 4 |
| 1441 | visita | 4 |
| 1442 | viniendo | 4 |
| 1443 | viejas | 4 |
| 1444 | vidas | 4 |
| 1445 | vicio | 4 |
| 1446 | via | 4 |
| 1447 | vezindad | 4 |
| 1448 | vestido | 4 |
| 1449 | vesle | 4 |
| 1450 | verdugo | 4 |
| 1451 | verdaderas | 4 |
| 1452 | verano | 4 |
| 1453 | venia | 4 |
| 1454 | vengas | 4 |
| 1455 | veas | 4 |
| 1456 | vean | 4 |
| 1457 | veamos | 4 |
| 1458 | varon | 4 |
| 1459 | vanas | 4 |
| 1460 | tuuo | 4 |
| 1461 | tuerto | 4 |
| 1462 | traydor | 4 |
| 1463 | tratado | 4 |
| 1464 | tragicomedia | 4 |
| 1465 | traemos | 4 |
| 1466 | trabajos | 4 |
| 1467 | touiesse | 4 |
| 1468 | toros | 4 |
| 1469 | tornate | 4 |
| 1470 | tormentos | 4 |
| 1471 | tomare | 4 |
| 1472 | toca | 4 |
| 1473 | titulo | 4 |
| 1474 | ternia | 4 |
| 1475 | ternas | 4 |
| 1476 | tercia | 4 |
| 1477 | tenerias | 4 |
| 1478 | tane | 4 |
| 1479 | suyos | 4 |
| 1480 | suplico | 4 |
| 1481 | supe | 4 |
| 1482 | sufrir | 4 |
| 1483 | suenan | 4 |
| 1484 | sueles | 4 |
| 1485 | sonido | 4 |
| 1486 | soliman | 4 |
| 1487 | solicita | 4 |
| 1488 | solamente | 4 |
| 1489 | sol | 4 |
| 1490 | soga | 4 |
| 1491 | sobresalto | 4 |
| 1492 | sobrado | 4 |
| 1493 | siruen | 4 |
| 1494 | siete | 4 |
| 1495 | sieruo | 4 |
| 1496 | seruida | 4 |
| 1497 | serpientes | 4 |
| 1498 | serian | 4 |
| 1499 | sere | 4 |
| 1500 | senti | 4 |
| 1501 | senales | 4 |
| 1502 | semejantes | 4 |
| 1503 | semejante | 4 |
| 1504 | seguridad | 4 |
| 1505 | seda | 4 |
| 1506 | secreta | 4 |
| 1507 | seays | 4 |
| 1508 | sancto | 4 |
| 1509 | sancta | 4 |
| 1510 | saludable | 4 |
| 1511 | salida | 4 |
| 1512 | salgo | 4 |
| 1513 | sabios | 4 |
| 1514 | sabiendo | 4 |
| 1515 | ruyndad | 4 |
| 1516 | rufian | 4 |
| 1517 | ruegote | 4 |
| 1518 | rota | 4 |
| 1519 | rostro | 4 |
| 1520 | ropas | 4 |
| 1521 | ronca | 4 |
| 1522 | rogado | 4 |
| 1523 | rodeos | 4 |
| 1524 | rodeado | 4 |
| 1525 | risa | 4 |
| 1526 | rigurosa | 4 |
| 1527 | ries | 4 |
| 1528 | riendas | 4 |
| 1529 | rezando | 4 |
| 1530 | reuerencia | 4 |
| 1531 | respondas | 4 |
| 1532 | reproches | 4 |
| 1533 | reciba | 4 |
| 1534 | recebir | 4 |
| 1535 | reboluer | 4 |
| 1536 | razonando | 4 |
| 1537 | razonable | 4 |
| 1538 | rayos | 4 |
| 1539 | quitar | 4 |
| 1540 | quexoso | 4 |
| 1541 | quexar | 4 |
| 1542 | questiones | 4 |
| 1543 | ques | 4 |
| 1544 | querrian | 4 |
| 1545 | quedaos | 4 |
| 1546 | quantidad | 4 |
| 1547 | qualquier | 4 |
| 1548 | punta | 4 |
| 1549 | puesta | 4 |
| 1550 | puedas | 4 |
| 1551 | publico | 4 |
| 1552 | publicar | 4 |
| 1553 | prudencia | 4 |
| 1554 | prouision | 4 |
| 1555 | prosperidad | 4 |
| 1556 | prometiste | 4 |
| 1557 | prometimientos | 4 |
| 1558 | prometido | 4 |
| 1559 | prometi | 4 |
| 1560 | promessa | 4 |
| 1561 | processo | 4 |
| 1562 | pro | 4 |
| 1563 | priuado | 4 |
| 1564 | priua | 4 |
| 1565 | principios | 4 |
| 1566 | presta | 4 |
| 1567 | presa | 4 |
| 1568 | prendieron | 4 |
| 1569 | pregunta | 4 |
| 1570 | precio | 4 |
| 1571 | possible | 4 |
| 1572 | possession | 4 |
| 1573 | porradas | 4 |
| 1574 | pongo | 4 |
| 1575 | pones | 4 |
| 1576 | ponen | 4 |
| 1577 | pollos | 4 |
| 1578 | podido | 4 |
| 1579 | pleyto | 4 |
| 1580 | pienso | 4 |
| 1581 | piedra | 4 |
| 1582 | perpetua | 4 |
| 1583 | perla | 4 |
| 1584 | perfeta | 4 |
| 1585 | perdon | 4 |
| 1586 | pequena | 4 |
| 1587 | pedi | 4 |
| 1588 | pedazos | 4 |
| 1589 | pecados | 4 |
| 1590 | pasos | 4 |
| 1591 | partida | 4 |
| 1592 | parescen | 4 |
| 1593 | pares | 4 |
| 1594 | parecia | 4 |
| 1595 | pano | 4 |
| 1596 | pagaras | 4 |
| 1597 | pagado | 4 |
| 1598 | oyo | 4 |
| 1599 | oyeme | 4 |
| 1600 | ouiesse | 4 |
| 1601 | oportuno | 4 |
| 1602 | onze | 4 |
| 1603 | olor | 4 |
| 1604 | ofrecimiento | 4 |
| 1605 | ocho | 4 |
| 1606 | negligente | 4 |
| 1607 | negligencia | 4 |
| 1608 | necia | 4 |
| 1609 | nasce | 4 |
| 1610 | narizes | 4 |
| 1611 | nadie | 4 |
| 1612 | murio | 4 |
| 1613 | murieron | 4 |
| 1614 | mundano | 4 |
| 1615 | muere | 4 |
| 1616 | mude | 4 |
| 1617 | motes | 4 |
| 1618 | moros | 4 |
| 1619 | moradas | 4 |
| 1620 | mora | 4 |
| 1621 | misericordia | 4 |
| 1622 | mias | 4 |
| 1623 | mezquino | 4 |
| 1624 | metal | 4 |
| 1625 | merecer | 4 |
| 1626 | melezinas | 4 |
| 1627 | matarme | 4 |
| 1628 | maria | 4 |
| 1629 | mantener | 4 |
| 1630 | mandaua | 4 |
| 1631 | luengas | 4 |
| 1632 | luenga | 4 |
| 1633 | locuras | 4 |
| 1634 | lloras | 4 |
| 1635 | lleue | 4 |
| 1636 | lleuan | 4 |
| 1637 | lleua | 4 |
| 1638 | llenos | 4 |
| 1639 | lleno | 4 |
| 1640 | llego | 4 |
| 1641 | llegada | 4 |
| 1642 | llame | 4 |
| 1643 | liuiano | 4 |
| 1644 | lisonja | 4 |
| 1645 | limpieza | 4 |
| 1646 | ligero | 4 |
| 1647 | lector | 4 |
| 1648 | lauor | 4 |
| 1649 | largas | 4 |
| 1650 | lanza | 4 |
| 1651 | juzgo | 4 |
| 1652 | juro | 4 |
| 1653 | junta | 4 |
| 1654 | judios | 4 |
| 1655 | juan | 4 |
| 1656 | interesse | 4 |
| 1657 | intercession | 4 |
| 1658 | innocencia | 4 |
| 1659 | indigno | 4 |
| 1660 | incomparable | 4 |
| 1661 | impide | 4 |
| 1662 | impetu | 4 |
| 1663 | hystoria | 4 |
| 1664 | humano | 4 |
| 1665 | houe | 4 |
| 1666 | honor | 4 |
| 1667 | honesta | 4 |
| 1668 | holguemos | 4 |
| 1669 | hiel | 4 |
| 1670 | hemos | 4 |
| 1671 | hembras | 4 |
| 1672 | hembra | 4 |
| 1673 | hauras | 4 |
| 1674 | hauian | 4 |
| 1675 | hauemos | 4 |
| 1676 | hallaras | 4 |
| 1677 | hallar | 4 |
| 1678 | halagos | 4 |
| 1679 | hables | 4 |
| 1680 | hable | 4 |
| 1681 | gusto | 4 |
| 1682 | guay | 4 |
| 1683 | guarte | 4 |
| 1684 | gorgueras | 4 |
| 1685 | gane | 4 |
| 1686 | fueste | 4 |
| 1687 | fuesses | 4 |
| 1688 | fueras | 4 |
| 1689 | fuente | 4 |
| 1690 | freno | 4 |
| 1691 | frayle | 4 |
| 1692 | forzoso | 4 |
| 1693 | flores | 4 |
| 1694 | flacas | 4 |
| 1695 | finalmente | 4 |
| 1696 | figura | 4 |
| 1697 | faltas | 4 |
| 1698 | faltar | 4 |
| 1699 | falsos | 4 |
| 1700 | estotro | 4 |
| 1701 | estenso | 4 |
| 1702 | estarias | 4 |
| 1703 | estare | 4 |
| 1704 | esperaua | 4 |
| 1705 | espejo | 4 |
| 1706 | especie | 4 |
| 1707 | especial | 4 |
| 1708 | espantado | 4 |
| 1709 | eso | 4 |
| 1710 | escura | 4 |
| 1711 | escuchando | 4 |
| 1712 | escalas | 4 |
| 1713 | errar | 4 |
| 1714 | entrare | 4 |
| 1715 | entonces | 4 |
| 1716 | entiendes | 4 |
| 1717 | entiende | 4 |
| 1718 | enojoso | 4 |
| 1719 | enojado | 4 |
| 1720 | engana | 4 |
| 1721 | encobrir | 4 |
| 1722 | encerrada | 4 |
| 1723 | enamorada | 4 |
| 1724 | empresa | 4 |
| 1725 | emperador | 4 |
| 1726 | embueltas | 4 |
| 1727 | echar | 4 |
| 1728 | echando | 4 |
| 1729 | echa | 4 |
| 1730 | ea | 4 |
| 1731 | donzellas | 4 |
| 1732 | donayres | 4 |
| 1733 | dixere | 4 |
| 1734 | diuina | 4 |
| 1735 | diuersos | 4 |
| 1736 | distancia | 4 |
| 1737 | disfauor | 4 |
| 1738 | diran | 4 |
| 1739 | dineros | 4 |
| 1740 | digan | 4 |
| 1741 | diessen | 4 |
| 1742 | dichoso | 4 |
| 1743 | dexaste | 4 |
| 1744 | dexando | 4 |
| 1745 | deuotos | 4 |
| 1746 | deuo | 4 |
| 1747 | detiene | 4 |
| 1748 | dessea | 4 |
| 1749 | despierto | 4 |
| 1750 | despierta | 4 |
| 1751 | desesperado | 4 |
| 1752 | desconsolada | 4 |
| 1753 | desastrado | 4 |
| 1754 | derecho | 4 |
| 1755 | den | 4 |
| 1756 | debdo | 4 |
| 1757 | dauid | 4 |
| 1758 | daria | 4 |
| 1759 | daras | 4 |
| 1760 | danos | 4 |
| 1761 | danado | 4 |
| 1762 | dadiua | 4 |
| 1763 | cuytada | 4 |
| 1764 | cuyos | 4 |
| 1765 | curar | 4 |
| 1766 | cuero | 4 |
| 1767 | crueldad | 4 |
| 1768 | cruda | 4 |
| 1769 | crees | 4 |
| 1770 | cree | 4 |
| 1771 | conueniente | 4 |
| 1772 | continuo | 4 |
| 1773 | continua | 4 |
| 1774 | contentar | 4 |
| 1775 | consiente | 4 |
| 1776 | conosciste | 4 |
| 1777 | conosce | 4 |
| 1778 | conoce | 4 |
| 1779 | congoxas | 4 |
| 1780 | confianza | 4 |
| 1781 | concordia | 4 |
| 1782 | concedido | 4 |
| 1783 | companera | 4 |
| 1784 | comiendo | 4 |
| 1785 | cobrar | 4 |
| 1786 | cierra | 4 |
| 1787 | ciego | 4 |
| 1788 | cerrar | 4 |
| 1789 | caydo | 4 |
| 1790 | causo | 4 |
| 1791 | casto | 4 |
| 1792 | canciones | 4 |
| 1793 | campo | 4 |
| 1794 | calzas | 4 |
| 1795 | callar | 4 |
| 1796 | calidad | 4 |
| 1797 | cabra | 4 |
| 1798 | buscando | 4 |
| 1799 | burlo | 4 |
| 1800 | brazo | 4 |
| 1801 | biuora | 4 |
| 1802 | bienauenturados | 4 |
| 1803 | bienauenturado | 4 |
| 1804 | besos | 4 |
| 1805 | batalla | 4 |
| 1806 | ayudame | 4 |
| 1807 | ayuda | 4 |
| 1808 | ayrada | 4 |
| 1809 | auria | 4 |
| 1810 | auisado | 4 |
| 1811 | auemos | 4 |
| 1812 | aue | 4 |
| 1813 | auarienta | 4 |
| 1814 | atormenta | 4 |
| 1815 | atento | 4 |
| 1816 | astucia | 4 |
| 1817 | ardiente | 4 |
| 1818 | arboles | 4 |
| 1819 | aquexa | 4 |
| 1820 | apetito | 4 |
| 1821 | apenas | 4 |
| 1822 | aparejo | 4 |
| 1823 | aparejadas | 4 |
| 1824 | antiguos | 4 |
| 1825 | animal | 4 |
| 1826 | angelica | 4 |
| 1827 | andan | 4 |
| 1828 | amenazas | 4 |
| 1829 | amarga | 4 |
| 1830 | amanesce | 4 |
| 1831 | altas | 4 |
| 1832 | allega | 4 |
| 1833 | alguazil | 4 |
| 1834 | alexandre | 4 |
| 1835 | alegro | 4 |
| 1836 | ahorcado | 4 |
| 1837 | agujas | 4 |
| 1838 | aguja | 4 |
| 1839 | agrada | 4 |
| 1840 | afuera | 4 |
| 1841 | aduersidades | 4 |
| 1842 | aduersa | 4 |
| 1843 | adoro | 4 |
| 1844 | admiracion | 4 |
| 1845 | aculla | 4 |
| 1846 | acuerdate | 4 |
| 1847 | acostumbrado | 4 |
| 1848 | acostar | 4 |
| 1849 | acorde | 4 |
| 1850 | acatamiento | 4 |
| 1851 | acabado | 4 |
| 1852 | abuelo | 4 |
| 1853 | zapatos | 3 |
| 1854 | yrme | 3 |
| 1855 | yran | 3 |
| 1856 | yguale | 3 |
| 1857 | yerua | 3 |
| 1858 | yerros | 3 |
| 1859 | yd | 3 |
| 1860 | vtilidad | 3 |
| 1861 | vosotras | 3 |
| 1862 | voluntades | 3 |
| 1863 | vnica | 3 |
| 1864 | viuos | 3 |
| 1865 | viniesse | 3 |
| 1866 | viniere | 3 |
| 1867 | vine | 3 |
| 1868 | vil | 3 |
| 1869 | vihuela | 3 |
| 1870 | vientos | 3 |
| 1871 | vezinos | 3 |
| 1872 | veya | 3 |
| 1873 | vestidos | 3 |
| 1874 | veslo | 3 |
| 1875 | verse | 3 |
| 1876 | verle | 3 |
| 1877 | venis | 3 |
| 1878 | venimos | 3 |
| 1879 | venidas | 3 |
| 1880 | veneno | 3 |
| 1881 | vence | 3 |
| 1882 | vellacos | 3 |
| 1883 | vanse | 3 |
| 1884 | vano | 3 |
| 1885 | vana | 3 |
| 1886 | vacaciones | 3 |
| 1887 | uer | 3 |
| 1888 | tristanico | 3 |
| 1889 | trayciones | 3 |
| 1890 | traycion | 3 |
| 1891 | trayan | 3 |
| 1892 | traxo | 3 |
| 1893 | traso | 3 |
| 1894 | tragar | 3 |
| 1895 | trabajar | 3 |
| 1896 | touiste | 3 |
| 1897 | toro | 3 |
| 1898 | tornen | 3 |
| 1899 | tornado | 3 |
| 1900 | tornada | 3 |
| 1901 | toque | 3 |
| 1902 | tocado | 3 |
| 1903 | tetas | 3 |
| 1904 | testigos | 3 |
| 1905 | terrible | 3 |
| 1906 | terne | 3 |
| 1907 | terna | 3 |
| 1908 | tente | 3 |
| 1909 | tenle | 3 |
| 1910 | teniades | 3 |
| 1911 | tenerte | 3 |
| 1912 | temporales | 3 |
| 1913 | temido | 3 |
| 1914 | temer | 3 |
| 1915 | tela | 3 |
| 1916 | taza | 3 |
| 1917 | tachas | 3 |
| 1918 | supo | 3 |
| 1919 | supiesse | 3 |
| 1920 | suelta | 3 |
| 1921 | sucessor | 3 |
| 1922 | subjeto | 3 |
| 1923 | soys | 3 |
| 1924 | sostiene | 3 |
| 1925 | sombra | 3 |
| 1926 | solia | 3 |
| 1927 | solazes | 3 |
| 1928 | soberuio | 3 |
| 1929 | siruiente | 3 |
| 1930 | sienten | 3 |
| 1931 | sientan | 3 |
| 1932 | seydo | 3 |
| 1933 | seruidor | 3 |
| 1934 | seruicios | 3 |
| 1935 | serlo | 3 |
| 1936 | serena | 3 |
| 1937 | sepultura | 3 |
| 1938 | sentiste | 3 |
| 1939 | sello | 3 |
| 1940 | seguros | 3 |
| 1941 | sciente | 3 |
| 1942 | sauanas | 3 |
| 1943 | sastre | 3 |
| 1944 | santo | 3 |
| 1945 | sanare | 3 |
| 1946 | saludables | 3 |
| 1947 | saltos | 3 |
| 1948 | salomon | 3 |
| 1949 | salio | 3 |
| 1950 | salido | 3 |
| 1951 | salga | 3 |
| 1952 | sales | 3 |
| 1953 | salario | 3 |
| 1954 | salamanca | 3 |
| 1955 | sala | 3 |
| 1956 | sacaua | 3 |
| 1957 | sacaras | 3 |
| 1958 | sabroso | 3 |
| 1959 | sabre | 3 |
| 1960 | sabio | 3 |
| 1961 | saberlo | 3 |
| 1962 | rufianes | 3 |
| 1963 | ruegan | 3 |
| 1964 | rueda | 3 |
| 1965 | rosas | 3 |
| 1966 | rompen | 3 |
| 1967 | rompe | 3 |
| 1968 | romano | 3 |
| 1969 | rogada | 3 |
| 1970 | roer | 3 |
| 1971 | rodillas | 3 |
| 1972 | rodear | 3 |
| 1973 | riqueza | 3 |
| 1974 | rincon | 3 |
| 1975 | rienda | 3 |
| 1976 | rica | 3 |
| 1977 | reyr | 3 |
| 1978 | reyno | 3 |
| 1979 | rescebido | 3 |
| 1980 | requiere | 3 |
| 1981 | representa | 3 |
| 1982 | reprehender | 3 |
| 1983 | reposo | 3 |
| 1984 | renta | 3 |
| 1985 | renir | 3 |
| 1986 | reliquias | 3 |
| 1987 | regir | 3 |
| 1988 | refran | 3 |
| 1989 | recreacion | 3 |
| 1990 | recibe | 3 |
| 1991 | recelo | 3 |
| 1992 | rayzes | 3 |
| 1993 | rayo | 3 |
| 1994 | rara | 3 |
| 1995 | rapina | 3 |
| 1996 | quisiesse | 3 |
| 1997 | quinze | 3 |
| 1998 | quierome | 3 |
| 1999 | quiebre | 3 |
| 2000 | quexosa | 3 |
| 2001 | quesiste | 3 |
| 2002 | querrias | 3 |
| 2003 | querra | 3 |
| 2004 | queridos | 3 |
| 2005 | querido | 3 |
| 2006 | querian | 3 |
| 2007 | quema | 3 |
| 2008 | quedese | 3 |
| 2009 | quedaua | 3 |
| 2010 | quedate | 3 |
| 2011 | quedaste | 3 |
| 2012 | quedasse | 3 |
| 2013 | quedas | 3 |
| 2014 | quedara | 3 |
| 2015 | quedando | 3 |
| 2016 | quebranto | 3 |
| 2017 | quebrando | 3 |
| 2018 | qualidad | 3 |
| 2019 | puse | 3 |
| 2020 | puntos | 3 |
| 2021 | pueblo | 3 |
| 2022 | pudo | 3 |
| 2023 | pudieron | 3 |
| 2024 | pudiere | 3 |
| 2025 | prouidencia | 3 |
| 2026 | proueer | 3 |
| 2027 | prouechoso | 3 |
| 2028 | prouechosa | 3 |
| 2029 | prospera | 3 |
| 2030 | propositos | 3 |
| 2031 | propiedades | 3 |
| 2032 | prometo | 3 |
| 2033 | prometimiento | 3 |
| 2034 | promete | 3 |
| 2035 | prolixidad | 3 |
| 2036 | premio | 3 |
| 2037 | preguntar | 3 |
| 2038 | potencia | 3 |
| 2039 | postremeria | 3 |
| 2040 | poquito | 3 |
| 2041 | ponzonoso | 3 |
| 2042 | ponzona | 3 |
| 2043 | poned | 3 |
| 2044 | pon | 3 |
| 2045 | poluos | 3 |
| 2046 | poluo | 3 |
| 2047 | poeta | 3 |
| 2048 | podran | 3 |
| 2049 | podian | 3 |
| 2050 | pobres | 3 |
| 2051 | plazido | 3 |
| 2052 | plaze | 3 |
| 2053 | plantas | 3 |
| 2054 | pisadas | 3 |
| 2055 | piernas | 3 |
| 2056 | pierden | 3 |
| 2057 | pierde | 3 |
| 2058 | pidas | 3 |
| 2059 | pesces | 3 |
| 2060 | perseuerancia | 3 |
| 2061 | perplexo | 3 |
| 2062 | perdono | 3 |
| 2063 | perdoname | 3 |
| 2064 | perdiz | 3 |
| 2065 | perdiste | 3 |
| 2066 | perdiera | 3 |
| 2067 | perdidas | 3 |
| 2068 | pensays | 3 |
| 2069 | penosa | 3 |
| 2070 | peno | 3 |
| 2071 | pende | 3 |
| 2072 | penar | 3 |
| 2073 | penan | 3 |
| 2074 | penada | 3 |
| 2075 | peligroso | 3 |
| 2076 | pedro | 3 |
| 2077 | pechos | 3 |
| 2078 | pece | 3 |
| 2079 | pecadores | 3 |
| 2080 | pecador | 3 |
| 2081 | patrimonio | 3 |
| 2082 | passiones | 3 |
| 2083 | passaua | 3 |
| 2084 | passamos | 3 |
| 2085 | pasado | 3 |
| 2086 | partezilla | 3 |
| 2087 | pario | 3 |
| 2088 | parescera | 3 |
| 2089 | pareces | 3 |
| 2090 | palacio | 3 |
| 2091 | pague | 3 |
| 2092 | pagare | 3 |
| 2093 | oyste | 3 |
| 2094 | oyras | 3 |
| 2095 | oyeres | 3 |
| 2096 | oyda | 3 |
| 2097 | ouo | 3 |
| 2098 | ouieron | 3 |
| 2099 | osadas | 3 |
| 2100 | ordenares | 3 |
| 2101 | ordenado | 3 |
| 2102 | opinion | 3 |
| 2103 | onde | 3 |
| 2104 | oluidar | 3 |
| 2105 | oluidados | 3 |
| 2106 | oluidado | 3 |
| 2107 | oluida | 3 |
| 2108 | ofrecido | 3 |
| 2109 | obrar | 3 |
| 2110 | obligado | 3 |
| 2111 | obligacion | 3 |
| 2112 | nuues | 3 |
| 2113 | nueue | 3 |
| 2114 | noticia | 3 |
| 2115 | norte | 3 |
| 2116 | nobleza | 3 |
| 2117 | nieue | 3 |
| 2118 | negro | 3 |
| 2119 | negocios | 3 |
| 2120 | naturales | 3 |
| 2121 | nascidas | 3 |
| 2122 | nasci | 3 |
| 2123 | nacido | 3 |
| 2124 | muro | 3 |
| 2125 | muestres | 3 |
| 2126 | mudanza | 3 |
| 2127 | mudado | 3 |
| 2128 | mouimientos | 3 |
| 2129 | motiuo | 3 |
| 2130 | mostre | 3 |
| 2131 | mortales | 3 |
| 2132 | monesterios | 3 |
| 2133 | moneda | 3 |
| 2134 | modos | 3 |
| 2135 | miras | 3 |
| 2136 | mirarias | 3 |
| 2137 | mirame | 3 |
| 2138 | ministros | 3 |
| 2139 | mil | 3 |
| 2140 | miel | 3 |
| 2141 | mezclada | 3 |
| 2142 | meytad | 3 |
| 2143 | meter | 3 |
| 2144 | mesura | 3 |
| 2145 | meses | 3 |
| 2146 | mercaduria | 3 |
| 2147 | mensajes | 3 |
| 2148 | mensajero | 3 |
| 2149 | mensajera | 3 |
| 2150 | meneo | 3 |
| 2151 | medre | 3 |
| 2152 | medrar | 3 |
| 2153 | medicos | 3 |
| 2154 | mediano | 3 |
| 2155 | medianera | 3 |
| 2156 | mataste | 3 |
| 2157 | marauillada | 3 |
| 2158 | mansa | 3 |
| 2159 | mandares | 3 |
| 2160 | mandame | 3 |
| 2161 | manda | 3 |
| 2162 | manas | 3 |
| 2163 | mana | 3 |
| 2164 | maltrates | 3 |
| 2165 | males | 3 |
| 2166 | magnifico | 3 |
| 2167 | magnificencia | 3 |
| 2168 | magdalena | 3 |
| 2169 | luziente | 3 |
| 2170 | luxuria | 3 |
| 2171 | luna | 3 |
| 2172 | luengo | 3 |
| 2173 | loquillo | 3 |
| 2174 | loores | 3 |
| 2175 | llores | 3 |
| 2176 | lloraras | 3 |
| 2177 | llegando | 3 |
| 2178 | llegado | 3 |
| 2179 | llega | 3 |
| 2180 | llamo | 3 |
| 2181 | llamauan | 3 |
| 2182 | llamaua | 3 |
| 2183 | llamados | 3 |
| 2184 | llagas | 3 |
| 2185 | lid | 3 |
| 2186 | libros | 3 |
| 2187 | liberal | 3 |
| 2188 | leyes | 3 |
| 2189 | leyendo | 3 |
| 2190 | leuantate | 3 |
| 2191 | leuantar | 3 |
| 2192 | leuantado | 3 |
| 2193 | letras | 3 |
| 2194 | letra | 3 |
| 2195 | legua | 3 |
| 2196 | lazo | 3 |
| 2197 | lastimeras | 3 |
| 2198 | ladron | 3 |
| 2199 | lado | 3 |
| 2200 | juzgues | 3 |
| 2201 | juzgue | 3 |
| 2202 | justa | 3 |
| 2203 | juez | 3 |
| 2204 | juego | 3 |
| 2205 | jubon | 3 |
| 2206 | jornada | 3 |
| 2207 | inuierno | 3 |
| 2208 | inuenciones | 3 |
| 2209 | instrumento | 3 |
| 2210 | injurias | 3 |
| 2211 | ingenios | 3 |
| 2212 | infierno | 3 |
| 2213 | infamia | 3 |
| 2214 | incurable | 3 |
| 2215 | importunidad | 3 |
| 2216 | imitar | 3 |
| 2217 | ignorancia | 3 |
| 2218 | huyda | 3 |
| 2219 | houieras | 3 |
| 2220 | houiera | 3 |
| 2221 | hiziesse | 3 |
| 2222 | hierro | 3 |
| 2223 | hermosas | 3 |
| 2224 | herido | 3 |
| 2225 | hechas | 3 |
| 2226 | hay | 3 |
| 2227 | hastio | 3 |
| 2228 | hasme | 3 |
| 2229 | hambre | 3 |
| 2230 | hallarte | 3 |
| 2231 | hallaron | 3 |
| 2232 | hallara | 3 |
| 2233 | hallan | 3 |
| 2234 | hachas | 3 |
| 2235 | hablaremos | 3 |
| 2236 | hablame | 3 |
| 2237 | habito | 3 |
| 2238 | grosseros | 3 |
| 2239 | gozara | 3 |
| 2240 | gozan | 3 |
| 2241 | gota | 3 |
| 2242 | gloriosa | 3 |
| 2243 | gemidos | 3 |
| 2244 | gato | 3 |
| 2245 | gastar | 3 |
| 2246 | ganan | 3 |
| 2247 | ganada | 3 |
| 2248 | gallina | 3 |
| 2249 | galanes | 3 |
| 2250 | fuiste | 3 |
| 2251 | fui | 3 |
| 2252 | fuese | 3 |
| 2253 | fueran | 3 |
| 2254 | frayles | 3 |
| 2255 | franqueza | 3 |
| 2256 | firmeza | 3 |
| 2257 | firmamento | 3 |
| 2258 | finge | 3 |
| 2259 | filosofos | 3 |
| 2260 | fiera | 3 |
| 2261 | fiar | 3 |
| 2262 | feria | 3 |
| 2263 | feo | 3 |
| 2264 | fecha | 3 |
| 2265 | febo | 3 |
| 2266 | faz | 3 |
| 2267 | fatigada | 3 |
| 2268 | fallaras | 3 |
| 2269 | faga | 3 |
| 2270 | faciones | 3 |
| 2271 | fablas | 3 |
| 2272 | euitar | 3 |
| 2273 | estuuiesse | 3 |
| 2274 | estudio | 3 |
| 2275 | estremadas | 3 |
| 2276 | estrellas | 3 |
| 2277 | estouiesse | 3 |
| 2278 | estoruar | 3 |
| 2279 | estima | 3 |
| 2280 | estes | 3 |
| 2281 | estaras | 3 |
| 2282 | estara | 3 |
| 2283 | estada | 3 |
| 2284 | espiritu | 3 |
| 2285 | espinas | 3 |
| 2286 | espere | 3 |
| 2287 | esperas | 3 |
| 2288 | esperando | 3 |
| 2289 | espanto | 3 |
| 2290 | espantados | 3 |
| 2291 | espadas | 3 |
| 2292 | espacioso | 3 |
| 2293 | esfuerza | 3 |
| 2294 | esforzados | 3 |
| 2295 | escuchar | 3 |
| 2296 | escriuir | 3 |
| 2297 | escote | 3 |
| 2298 | escoja | 3 |
| 2299 | enxemplo | 3 |
| 2300 | entretanto | 3 |
| 2301 | entrauas | 3 |
| 2302 | entrando | 3 |
| 2303 | entrambas | 3 |
| 2304 | entrad | 3 |
| 2305 | entienden | 3 |
| 2306 | entero | 3 |
| 2307 | entera | 3 |
| 2308 | enojos | 3 |
| 2309 | enganar | 3 |
| 2310 | enemistad | 3 |
| 2311 | endereza | 3 |
| 2312 | encuentro | 3 |
| 2313 | encomendo | 3 |
| 2314 | empecer | 3 |
| 2315 | embie | 3 |
| 2316 | embiar | 3 |
| 2317 | embarga | 3 |
| 2318 | echo | 3 |
| 2319 | echeneis | 3 |
| 2320 | duermes | 3 |
| 2321 | duelos | 3 |
| 2322 | dubdosa | 3 |
| 2323 | dozena | 3 |
| 2324 | doto | 3 |
| 2325 | dormiendo | 3 |
| 2326 | dixeron | 3 |
| 2327 | diste | 3 |
| 2328 | dissimular | 3 |
| 2329 | dissimulado | 3 |
| 2330 | discreta | 3 |
| 2331 | discipulo | 3 |
| 2332 | dificil | 3 |
| 2333 | diere | 3 |
| 2334 | diera | 3 |
| 2335 | dichosa | 3 |
| 2336 | diablos | 3 |
| 2337 | dezian | 3 |
| 2338 | dexaron | 3 |
| 2339 | dexare | 3 |
| 2340 | dexale | 3 |
| 2341 | dexala | 3 |
| 2342 | dexadas | 3 |
| 2343 | deuociones | 3 |
| 2344 | detente | 3 |
| 2345 | desuariar | 3 |
| 2346 | desso | 3 |
| 2347 | desseos | 3 |
| 2348 | desse | 3 |
| 2349 | despidese | 3 |
| 2350 | despide | 3 |
| 2351 | despenado | 3 |
| 2352 | despedir | 3 |
| 2353 | desonrra | 3 |
| 2354 | deso | 3 |
| 2355 | desesperacion | 3 |
| 2356 | desechan | 3 |
| 2357 | deseado | 3 |
| 2358 | descubra | 3 |
| 2359 | descubierto | 3 |
| 2360 | descansa | 3 |
| 2361 | dentera | 3 |
| 2362 | delinquente | 3 |
| 2363 | delicto | 3 |
| 2364 | delgado | 3 |
| 2365 | delgadas | 3 |
| 2366 | degollados | 3 |
| 2367 | declara | 3 |
| 2368 | dechado | 3 |
| 2369 | darme | 3 |
| 2370 | darias | 3 |
| 2371 | danada | 3 |
| 2372 | daca | 3 |
| 2373 | cumpliendo | 3 |
| 2374 | cumpla | 3 |
| 2375 | cuerdas | 3 |
| 2376 | cuchilladas | 3 |
| 2377 | crudo | 3 |
| 2378 | crea | 3 |
| 2379 | coxo | 3 |
| 2380 | cortesia | 3 |
| 2381 | correr | 3 |
| 2382 | corporal | 3 |
| 2383 | contaria | 3 |
| 2384 | consuelos | 3 |
| 2385 | consuelo | 3 |
| 2386 | consolar | 3 |
| 2387 | conoscido | 3 |
| 2388 | conoscia | 3 |
| 2389 | conocimiento | 3 |
| 2390 | conjuro | 3 |
| 2391 | conformes | 3 |
| 2392 | condiciones | 3 |
| 2393 | condenar | 3 |
| 2394 | conciertos | 3 |
| 2395 | concertado | 3 |
| 2396 | conceder | 3 |
| 2397 | compuso | 3 |
| 2398 | complido | 3 |
| 2399 | complida | 3 |
| 2400 | compassion | 3 |
| 2401 | come | 3 |
| 2402 | comamos | 3 |
| 2403 | coloradas | 3 |
| 2404 | colgado | 3 |
| 2405 | cobro | 3 |
| 2406 | cobdiciosa | 3 |
| 2407 | claras | 3 |
| 2408 | cielos | 3 |
| 2409 | cesse | 3 |
| 2410 | certifico | 3 |
| 2411 | cenir | 3 |
| 2412 | cena | 3 |
| 2413 | ceguedad | 3 |
| 2414 | cayo | 3 |
| 2415 | cayga | 3 |
| 2416 | causado | 3 |
| 2417 | castos | 3 |
| 2418 | castigos | 3 |
| 2419 | castigo | 3 |
| 2420 | castellana | 3 |
| 2421 | casos | 3 |
| 2422 | casar | 3 |
| 2423 | casados | 3 |
| 2424 | capital | 3 |
| 2425 | capaz | 3 |
| 2426 | cantares | 3 |
| 2427 | cansados | 3 |
| 2428 | cansada | 3 |
| 2429 | camisas | 3 |
| 2430 | calles | 3 |
| 2431 | callemos | 3 |
| 2432 | cadenilla | 3 |
| 2433 | busco | 3 |
| 2434 | busca | 3 |
| 2435 | burlador | 3 |
| 2436 | buelan | 3 |
| 2437 | brutos | 3 |
| 2438 | brocado | 3 |
| 2439 | breuemente | 3 |
| 2440 | braua | 3 |
| 2441 | bote | 3 |
| 2442 | bondad | 3 |
| 2443 | bolsa | 3 |
| 2444 | biuen | 3 |
| 2445 | bienauenturanza | 3 |
| 2446 | bienandante | 3 |
| 2447 | bestias | 3 |
| 2448 | besar | 3 |
| 2449 | baste | 3 |
| 2450 | bastante | 3 |
| 2451 | azeyte | 3 |
| 2452 | ayrado | 3 |
| 2453 | auras | 3 |
| 2454 | auisos | 3 |
| 2455 | auido | 3 |
| 2456 | atauios | 3 |
| 2457 | aspero | 3 |
| 2458 | asnos | 3 |
| 2459 | asco | 3 |
| 2460 | artificio | 3 |
| 2461 | armonia | 3 |
| 2462 | arguye | 3 |
| 2463 | arde | 3 |
| 2464 | arco | 3 |
| 2465 | aquexaua | 3 |
| 2466 | aproueche | 3 |
| 2467 | apetece | 3 |
| 2468 | apassionados | 3 |
| 2469 | aparejar | 3 |
| 2470 | anzuelo | 3 |
| 2471 | antiguedad | 3 |
| 2472 | animas | 3 |
| 2473 | angelico | 3 |
| 2474 | andas | 3 |
| 2475 | andad | 3 |
| 2476 | amonesta | 3 |
| 2477 | amigas | 3 |
| 2478 | ambos | 3 |
| 2479 | amargo | 3 |
| 2480 | amando | 3 |
| 2481 | amador | 3 |
| 2482 | almorzar | 3 |
| 2483 | allende | 3 |
| 2484 | allegue | 3 |
| 2485 | alcahuetas | 3 |
| 2486 | aguijones | 3 |
| 2487 | afrenta | 3 |
| 2488 | aduersidad | 3 |
| 2489 | adios | 3 |
| 2490 | aderezar | 3 |
| 2491 | adentro | 3 |
| 2492 | acuerdas | 3 |
| 2493 | acuerda | 3 |
| 2494 | actos | 3 |
| 2495 | acompanar | 3 |
| 2496 | acompana | 3 |
| 2497 | acelerados | 3 |
| 2498 | acelerado | 3 |
| 2499 | acaso | 3 |
| 2500 | absentes | 3 |
| 2501 | abrigo | 3 |
| 2502 | abreuia | 3 |
| 2503 | abrazos | 3 |
| 2504 | abeja | 3 |
| 2505 | abaxo | 3 |
| 2506 | abades | 3 |
| 2507 | zeloso | 2 |
| 2508 | zarazas | 2 |
| 2509 | yuas | 2 |
| 2510 | yremos | 2 |
| 2511 | ygualmente | 2 |
| 2512 | ygualara | 2 |
| 2513 | ydos | 2 |
| 2514 | yazeys | 2 |
| 2515 | vulgar | 2 |
| 2516 | voyme | 2 |
| 2517 | vo | 2 |
| 2518 | vnico | 2 |
| 2519 | vnguentos | 2 |
| 2520 | viuiria | 2 |
| 2521 | viuia | 2 |
| 2522 | viues | 2 |
| 2523 | vituperio | 2 |
| 2524 | vistelos | 2 |
| 2525 | visitasse | 2 |
| 2526 | visitando | 2 |
| 2527 | visitado | 2 |
| 2528 | visitada | 2 |
| 2529 | vision | 2 |
| 2530 | virtut | 2 |
| 2531 | virtuosa | 2 |
| 2532 | virgines | 2 |
| 2533 | virgilio | 2 |
| 2534 | virgen | 2 |
| 2535 | vio | 2 |
| 2536 | viniessedes | 2 |
| 2537 | vinieron | 2 |
| 2538 | vinagre | 2 |
| 2539 | viles | 2 |
| 2540 | viesses | 2 |
| 2541 | viessen | 2 |
| 2542 | vieres | 2 |
| 2543 | vieren | 2 |
| 2544 | viera | 2 |
| 2545 | viendote | 2 |
| 2546 | viendome | 2 |
| 2547 | viendola | 2 |
| 2548 | vide | 2 |
| 2549 | vfano | 2 |
| 2550 | vestiduras | 2 |
| 2551 | veslos | 2 |
| 2552 | vertieron | 2 |
| 2553 | vernos | 2 |
| 2554 | veria | 2 |
| 2555 | vergonzoso | 2 |
| 2556 | vereys | 2 |
| 2557 | veremos | 2 |
| 2558 | vere | 2 |
| 2559 | verdes | 2 |
| 2560 | venus | 2 |
| 2561 | vente | 2 |
| 2562 | vengador | 2 |
| 2563 | vendia | 2 |
| 2564 | venderme | 2 |
| 2565 | vencidos | 2 |
| 2566 | vencida | 2 |
| 2567 | venas | 2 |
| 2568 | velas | 2 |
| 2569 | veer | 2 |
| 2570 | veces | 2 |
| 2571 | veays | 2 |
| 2572 | vazios | 2 |
| 2573 | vazio | 2 |
| 2574 | variacion | 2 |
| 2575 | vandera | 2 |
| 2576 | valor | 2 |
| 2577 | valer | 2 |
| 2578 | valencia | 2 |
| 2579 | valen | 2 |
| 2580 | valala | 2 |
| 2581 | vagos | 2 |
| 2582 | un | 2 |
| 2583 | tuyos | 2 |
| 2584 | tuyas | 2 |
| 2585 | tusca | 2 |
| 2586 | turbe | 2 |
| 2587 | turbas | 2 |
| 2588 | turbado | 2 |
| 2589 | turbada | 2 |
| 2590 | turba | 2 |
| 2591 | truxiste | 2 |
| 2592 | troyanos | 2 |
| 2593 | troya | 2 |
| 2594 | tropezaras | 2 |
| 2595 | trobando | 2 |
| 2596 | trigo | 2 |
| 2597 | tribulacion | 2 |
| 2598 | treze | 2 |
| 2599 | tregua | 2 |
| 2600 | traydores | 2 |
| 2601 | traxeron | 2 |
| 2602 | traxe | 2 |
| 2603 | trauiesos | 2 |
| 2604 | trates | 2 |
| 2605 | tratas | 2 |
| 2606 | tratar | 2 |
| 2607 | tratan | 2 |
| 2608 | trasponer | 2 |
| 2609 | traspassa | 2 |
| 2610 | tragi | 2 |
| 2611 | trafagos | 2 |
| 2612 | traere | 2 |
| 2613 | trabajes | 2 |
| 2614 | trabaje | 2 |
| 2615 | touieron | 2 |
| 2616 | toue | 2 |
| 2617 | tortolas | 2 |
| 2618 | tornaste | 2 |
| 2619 | tornare | 2 |
| 2620 | tornara | 2 |
| 2621 | topado | 2 |
| 2622 | tomo | 2 |
| 2623 | tomes | 2 |
| 2624 | tomauas | 2 |
| 2625 | tomaras | 2 |
| 2626 | tomara | 2 |
| 2627 | toman | 2 |
| 2628 | tomada | 2 |
| 2629 | tomad | 2 |
| 2630 | tolomeo | 2 |
| 2631 | toledo | 2 |
| 2632 | tocino | 2 |
| 2633 | tocare | 2 |
| 2634 | tiros | 2 |
| 2635 | tiro | 2 |
| 2636 | tirando | 2 |
| 2637 | tiniebla | 2 |
| 2638 | tiernas | 2 |
| 2639 | tienda | 2 |
| 2640 | testimonio | 2 |
| 2641 | tesoros | 2 |
| 2642 | ternemos | 2 |
| 2643 | terminos | 2 |
| 2644 | tercero | 2 |
| 2645 | tercera | 2 |
| 2646 | tenla | 2 |
| 2647 | tenidas | 2 |
| 2648 | tenida | 2 |
| 2649 | tenian | 2 |
| 2650 | tengote | 2 |
| 2651 | tengan | 2 |
| 2652 | tenes | 2 |
| 2653 | tenazicas | 2 |
| 2654 | temporal | 2 |
| 2655 | templos | 2 |
| 2656 | templo | 2 |
| 2657 | temple | 2 |
| 2658 | temores | 2 |
| 2659 | temerosa | 2 |
| 2660 | teme | 2 |
| 2661 | teman | 2 |
| 2662 | techo | 2 |
| 2663 | tardasse | 2 |
| 2664 | tarda | 2 |
| 2665 | tacha | 2 |
| 2666 | tableros | 2 |
| 2667 | suspensa | 2 |
| 2668 | suplia | 2 |
| 2669 | suplan | 2 |
| 2670 | supito | 2 |
| 2671 | supiessen | 2 |
| 2672 | supieres | 2 |
| 2673 | supiera | 2 |
| 2674 | suma | 2 |
| 2675 | sufras | 2 |
| 2676 | suffrir | 2 |
| 2677 | subo | 2 |
| 2678 | subio | 2 |
| 2679 | subido | 2 |
| 2680 | sospiros | 2 |
| 2681 | sospechosa | 2 |
| 2682 | sospechar | 2 |
| 2683 | sordo | 2 |
| 2684 | sonaua | 2 |
| 2685 | sonar | 2 |
| 2686 | sometieron | 2 |
| 2687 | sombrosos | 2 |
| 2688 | sombras | 2 |
| 2689 | soldada | 2 |
| 2690 | sofrire | 2 |
| 2691 | sobreuiene | 2 |
| 2692 | sobrepuja | 2 |
| 2693 | sobraran | 2 |
| 2694 | sobrada | 2 |
| 2695 | sobire | 2 |
| 2696 | sobir | 2 |
| 2697 | sobido | 2 |
| 2698 | soberana | 2 |
| 2699 | sl | 2 |
| 2700 | siruiendo | 2 |
| 2701 | sirue | 2 |
| 2702 | siruan | 2 |
| 2703 | sintio | 2 |
| 2704 | sintieron | 2 |
| 2705 | sintiendo | 2 |
| 2706 | simpleza | 2 |
| 2707 | silla | 2 |
| 2708 | siguen | 2 |
| 2709 | sigue | 2 |
| 2710 | siglo | 2 |
| 2711 | sic | 2 |
| 2712 | seyle | 2 |
| 2713 | sesenta | 2 |
| 2714 | seruido | 2 |
| 2715 | serte | 2 |
| 2716 | serpiente | 2 |
| 2717 | serpentino | 2 |
| 2718 | seremos | 2 |
| 2719 | seran | 2 |
| 2720 | sepultados | 2 |
| 2721 | sepulcro | 2 |
| 2722 | sepan | 2 |
| 2723 | sepamos | 2 |
| 2724 | sentidas | 2 |
| 2725 | senorio | 2 |
| 2726 | senetud | 2 |
| 2727 | seneca | 2 |
| 2728 | semejanza | 2 |
| 2729 | semeja | 2 |
| 2730 | sembrar | 2 |
| 2731 | seguras | 2 |
| 2732 | seguir | 2 |
| 2733 | secretas | 2 |
| 2734 | secretaria | 2 |
| 2735 | secretamente | 2 |
| 2736 | sciencia | 2 |
| 2737 | sazon | 2 |
| 2738 | satisfazer | 2 |
| 2739 | saque | 2 |
| 2740 | santiguas | 2 |
| 2741 | santiguarme | 2 |
| 2742 | sanidad | 2 |
| 2743 | salue | 2 |
| 2744 | saltes | 2 |
| 2745 | salte | 2 |
| 2746 | saltaron | 2 |
| 2747 | saltar | 2 |
| 2748 | salgan | 2 |
| 2749 | sagaz | 2 |
| 2750 | sacasses | 2 |
| 2751 | sacarle | 2 |
| 2752 | sacando | 2 |
| 2753 | sacado | 2 |
| 2754 | sabria | 2 |
| 2755 | sabra | 2 |
| 2756 | sabias | 2 |
| 2757 | sabian | 2 |
| 2758 | ruydos | 2 |
| 2759 | ruda | 2 |
| 2760 | royendo | 2 |
| 2761 | roto | 2 |
| 2762 | romper | 2 |
| 2763 | romero | 2 |
| 2764 | rogare | 2 |
| 2765 | rodee | 2 |
| 2766 | rodea | 2 |
| 2767 | rigor | 2 |
| 2768 | riges | 2 |
| 2769 | rientes | 2 |
| 2770 | rien | 2 |
| 2771 | rezios | 2 |
| 2772 | rezia | 2 |
| 2773 | reuistas | 2 |
| 2774 | retraymiento | 2 |
| 2775 | retozar | 2 |
| 2776 | restaura | 2 |
| 2777 | resplandescientes | 2 |
| 2778 | resplandescen | 2 |
| 2779 | respeto | 2 |
| 2780 | rescibo | 2 |
| 2781 | resciben | 2 |
| 2782 | rescibe | 2 |
| 2783 | requerida | 2 |
| 2784 | reprehension | 2 |
| 2785 | reposado | 2 |
| 2786 | repartio | 2 |
| 2787 | renzilla | 2 |
| 2788 | reniremos | 2 |
| 2789 | renegar | 2 |
| 2790 | remos | 2 |
| 2791 | remirando | 2 |
| 2792 | remedies | 2 |
| 2793 | remediado | 2 |
| 2794 | reluze | 2 |
| 2795 | relieua | 2 |
| 2796 | regazo | 2 |
| 2797 | refrigerio | 2 |
| 2798 | redes | 2 |
| 2799 | red | 2 |
| 2800 | recuerda | 2 |
| 2801 | recordable | 2 |
| 2802 | recibiente | 2 |
| 2803 | reciben | 2 |
| 2804 | recibas | 2 |
| 2805 | recela | 2 |
| 2806 | recabdo | 2 |
| 2807 | recabdado | 2 |
| 2808 | razonamiento | 2 |
| 2809 | rastro | 2 |
| 2810 | raposa | 2 |
| 2811 | ramos | 2 |
| 2812 | ramera | 2 |
| 2813 | quite | 2 |
| 2814 | quitate | 2 |
| 2815 | quisiesses | 2 |
| 2816 | quierole | 2 |
| 2817 | quienquiera | 2 |
| 2818 | quiebra | 2 |
| 2819 | quexa | 2 |
| 2820 | querias | 2 |
| 2821 | queremos | 2 |
| 2822 | querellas | 2 |
| 2823 | quehazer | 2 |
| 2824 | quedos | 2 |
| 2825 | quedes | 2 |
| 2826 | queden | 2 |
| 2827 | quedarte | 2 |
| 2828 | quedaras | 2 |
| 2829 | quebrose | 2 |
| 2830 | quebrantamiento | 2 |
| 2831 | quebrados | 2 |
| 2832 | quarto | 2 |
| 2833 | puteria | 2 |
| 2834 | pusieron | 2 |
| 2835 | pusieran | 2 |
| 2836 | puestos | 2 |
| 2837 | puertos | 2 |
| 2838 | puedan | 2 |
| 2839 | publicos | 2 |
| 2840 | publicaua | 2 |
| 2841 | publica | 2 |
| 2842 | prueua | 2 |
| 2843 | prouisiones | 2 |
| 2844 | prouerbio | 2 |
| 2845 | prouar | 2 |
| 2846 | protestando | 2 |
| 2847 | proporcion | 2 |
| 2848 | propios | 2 |
| 2849 | prometio | 2 |
| 2850 | prometes | 2 |
| 2851 | proceden | 2 |
| 2852 | priuados | 2 |
| 2853 | primo | 2 |
| 2854 | presuncion | 2 |
| 2855 | prestas | 2 |
| 2856 | preso | 2 |
| 2857 | prender | 2 |
| 2858 | premios | 2 |
| 2859 | preguntando | 2 |
| 2860 | preguntale | 2 |
| 2861 | pregon | 2 |
| 2862 | preciosa | 2 |
| 2863 | prados | 2 |
| 2864 | prado | 2 |
| 2865 | potacion | 2 |
| 2866 | postrimeria | 2 |
| 2867 | possesion | 2 |
| 2868 | pospuesto | 2 |
| 2869 | posesion | 2 |
| 2870 | poseo | 2 |
| 2871 | posadas | 2 |
| 2872 | portaua | 2 |
| 2873 | pornan | 2 |
| 2874 | porna | 2 |
| 2875 | porfiado | 2 |
| 2876 | porfia | 2 |
| 2877 | poniendo | 2 |
| 2878 | ponia | 2 |
| 2879 | ponese | 2 |
| 2880 | ponerse | 2 |
| 2881 | ponense | 2 |
| 2882 | podiste | 2 |
| 2883 | poderoso | 2 |
| 2884 | poderio | 2 |
| 2885 | pluton | 2 |
| 2886 | plumas | 2 |
| 2887 | pluguiera | 2 |
| 2888 | plazera | 2 |
| 2889 | plata | 2 |
| 2890 | planta | 2 |
| 2891 | pintaua | 2 |
| 2892 | pintar | 2 |
| 2893 | pintado | 2 |
| 2894 | pildora | 2 |
| 2895 | pieza | 2 |
| 2896 | pierdes | 2 |
| 2897 | pierdas | 2 |
| 2898 | pierda | 2 |
| 2899 | piensen | 2 |
| 2900 | piense | 2 |
| 2901 | piensan | 2 |
| 2902 | piden | 2 |
| 2903 | pico | 2 |
| 2904 | pican | 2 |
| 2905 | piadosos | 2 |
| 2906 | pestilencia | 2 |
| 2907 | peso | 2 |
| 2908 | pesa | 2 |
| 2909 | perseueras | 2 |
| 2910 | perseuerar | 2 |
| 2911 | perros | 2 |
| 2912 | perplexidad | 2 |
| 2913 | perlas | 2 |
| 2914 | perezoso | 2 |
| 2915 | peregrinos | 2 |
| 2916 | perecio | 2 |
| 2917 | perdizes | 2 |
| 2918 | perdiere | 2 |
| 2919 | perdidos | 2 |
| 2920 | perderme | 2 |
| 2921 | perderas | 2 |
| 2922 | perdays | 2 |
| 2923 | pequenas | 2 |
| 2924 | penso | 2 |
| 2925 | pensauas | 2 |
| 2926 | pensadas | 2 |
| 2927 | penelope | 2 |
| 2928 | pene | 2 |
| 2929 | penaua | 2 |
| 2930 | penando | 2 |
| 2931 | penados | 2 |
| 2932 | penadas | 2 |
| 2933 | peligros | 2 |
| 2934 | pelea | 2 |
| 2935 | pega | 2 |
| 2936 | pedis | 2 |
| 2937 | pedirme | 2 |
| 2938 | pedirle | 2 |
| 2939 | pedido | 2 |
| 2940 | paxaros | 2 |
| 2941 | patria | 2 |
| 2942 | patadas | 2 |
| 2943 | pastor | 2 |
| 2944 | passaste | 2 |
| 2945 | passaren | 2 |
| 2946 | pasqua | 2 |
| 2947 | paso | 2 |
| 2948 | parto | 2 |
| 2949 | partio | 2 |
| 2950 | particularidades | 2 |
| 2951 | participacion | 2 |
| 2952 | participa | 2 |
| 2953 | parta | 2 |
| 2954 | paris | 2 |
| 2955 | parientas | 2 |
| 2956 | parezca | 2 |
| 2957 | paresciesse | 2 |
| 2958 | parescian | 2 |
| 2959 | parescia | 2 |
| 2960 | paresceme | 2 |
| 2961 | parentesco | 2 |
| 2962 | pared | 2 |
| 2963 | parecer | 2 |
| 2964 | pardios | 2 |
| 2965 | pararon | 2 |
| 2966 | paramento | 2 |
| 2967 | papeles | 2 |
| 2968 | papel | 2 |
| 2969 | papagayos | 2 |
| 2970 | palo | 2 |
| 2971 | paladar | 2 |
| 2972 | palacios | 2 |
| 2973 | pajas | 2 |
| 2974 | paja | 2 |
| 2975 | pagara | 2 |
| 2976 | padezco | 2 |
| 2977 | padezca | 2 |
| 2978 | padecer | 2 |
| 2979 | padece | 2 |
| 2980 | paciente | 2 |
| 2981 | oyrlo | 2 |
| 2982 | oyran | 2 |
| 2983 | oymos | 2 |
| 2984 | oya | 2 |
| 2985 | ouiere | 2 |
| 2986 | ouejas | 2 |
| 2987 | oue | 2 |
| 2988 | oso | 2 |
| 2989 | osar | 2 |
| 2990 | osan | 2 |
| 2991 | osados | 2 |
| 2992 | osadias | 2 |
| 2993 | osada | 2 |
| 2994 | ordenes | 2 |
| 2995 | ordenar | 2 |
| 2996 | ordena | 2 |
| 2997 | onestidad | 2 |
| 2998 | ondas | 2 |
| 2999 | omnia | 2 |
| 3000 | oluidaua | 2 |
| 3001 | olores | 2 |
| 3002 | ofrece | 2 |
| 3003 | oficios | 2 |
| 3004 | ocurre | 2 |
| 3005 | ocupado | 2 |
| 3006 | ocupada | 2 |
| 3007 | oculto | 2 |
| 3008 | ociosos | 2 |
| 3009 | ocasion | 2 |
| 3010 | obstara | 2 |
| 3011 | obrado | 2 |
| 3012 | obligados | 2 |
| 3013 | obligada | 2 |
| 3014 | obediencia | 2 |
| 3015 | numero | 2 |
| 3016 | nueuos | 2 |
| 3017 | nudos | 2 |
| 3018 | nublosas | 2 |
| 3019 | nouedades | 2 |
| 3020 | notable | 2 |
| 3021 | nombrar | 2 |
| 3022 | nocibles | 2 |
| 3023 | niegues | 2 |
| 3024 | niegan | 2 |
| 3025 | niega | 2 |
| 3026 | nido | 2 |
| 3027 | nescio | 2 |
| 3028 | nero | 2 |
| 3029 | nembrot | 2 |
| 3030 | negra | 2 |
| 3031 | negociar | 2 |
| 3032 | negociando | 2 |
| 3033 | negara | 2 |
| 3034 | necessarias | 2 |
| 3035 | necedad | 2 |
| 3036 | nauios | 2 |
| 3037 | nauio | 2 |
| 3038 | nasciendo | 2 |
| 3039 | nascido | 2 |
| 3040 | nascer | 2 |
| 3041 | nao | 2 |
| 3042 | musica | 2 |
| 3043 | murmuros | 2 |
| 3044 | murmurando | 2 |
| 3045 | mundanos | 2 |
| 3046 | muestras | 2 |
| 3047 | muestrame | 2 |
| 3048 | mueras | 2 |
| 3049 | mueran | 2 |
| 3050 | mudada | 2 |
| 3051 | mudable | 2 |
| 3052 | muda | 2 |
| 3053 | mouio | 2 |
| 3054 | mouimiento | 2 |
| 3055 | mouime | 2 |
| 3056 | mouer | 2 |
| 3057 | mostraste | 2 |
| 3058 | mostrare | 2 |
| 3059 | mostrado | 2 |
| 3060 | monuiedro | 2 |
| 3061 | montes | 2 |
| 3062 | monte | 2 |
| 3063 | molino | 2 |
| 3064 | mochacho | 2 |
| 3065 | missas | 2 |
| 3066 | miseros | 2 |
| 3067 | miserias | 2 |
| 3068 | miserable | 2 |
| 3069 | miro | 2 |
| 3070 | mire | 2 |
| 3071 | mirasse | 2 |
| 3072 | mirarte | 2 |
| 3073 | miramos | 2 |
| 3074 | ministro | 2 |
| 3075 | miguel | 2 |
| 3076 | metros | 2 |
| 3077 | metio | 2 |
| 3078 | metidos | 2 |
| 3079 | metida | 2 |
| 3080 | mete | 2 |
| 3081 | mesmos | 2 |
| 3082 | merecido | 2 |
| 3083 | merecen | 2 |
| 3084 | merecedor | 2 |
| 3085 | mercado | 2 |
| 3086 | mentiroso | 2 |
| 3087 | mentira | 2 |
| 3088 | mentar | 2 |
| 3089 | menosprecio | 2 |
| 3090 | menospreciado | 2 |
| 3091 | menores | 2 |
| 3092 | menjuy | 2 |
| 3093 | menguas | 2 |
| 3094 | menea | 2 |
| 3095 | mena | 2 |
| 3096 | medida | 2 |
| 3097 | mediana | 2 |
| 3098 | maten | 2 |
| 3099 | mataronle | 2 |
| 3100 | matara | 2 |
| 3101 | matame | 2 |
| 3102 | mataduras | 2 |
| 3103 | matadores | 2 |
| 3104 | mares | 2 |
| 3105 | marauillosa | 2 |
| 3106 | marauillar | 2 |
| 3107 | manzana | 2 |
| 3108 | manteniendo | 2 |
| 3109 | manteles | 2 |
| 3110 | manso | 2 |
| 3111 | mansedumbre | 2 |
| 3112 | manjares | 2 |
| 3113 | manilla | 2 |
| 3114 | manifiesto | 2 |
| 3115 | manifiestas | 2 |
| 3116 | manifiesta | 2 |
| 3117 | manifestauan | 2 |
| 3118 | maneras | 2 |
| 3119 | mandes | 2 |
| 3120 | manderecha | 2 |
| 3121 | mandaste | 2 |
| 3122 | manco | 2 |
| 3123 | mancebo | 2 |
| 3124 | maluada | 2 |
| 3125 | malla | 2 |
| 3126 | malicia | 2 |
| 3127 | malhechores | 2 |
| 3128 | maldizen | 2 |
| 3129 | maldicion | 2 |
| 3130 | maldad | 2 |
| 3131 | malauenturado | 2 |
| 3132 | maestras | 2 |
| 3133 | madura | 2 |
| 3134 | madrugaron | 2 |
| 3135 | madrugar | 2 |
| 3136 | madalena | 2 |
| 3137 | macias | 2 |
| 3138 | macedonia | 2 |
| 3139 | luzero | 2 |
| 3140 | lumbre | 2 |
| 3141 | loquito | 2 |
| 3142 | loor | 2 |
| 3143 | load | 2 |
| 3144 | lleuaua | 2 |
| 3145 | lleuaronla | 2 |
| 3146 | llegues | 2 |
| 3147 | llegamos | 2 |
| 3148 | llaues | 2 |
| 3149 | llamaron | 2 |
| 3150 | llamarme | 2 |
| 3151 | llamare | 2 |
| 3152 | llagado | 2 |
| 3153 | llagada | 2 |
| 3154 | lisonjeros | 2 |
| 3155 | ligeros | 2 |
| 3156 | ligeramente | 2 |
| 3157 | ligera | 2 |
| 3158 | lienzo | 2 |
| 3159 | libro | 2 |
| 3160 | libres | 2 |
| 3161 | librado | 2 |
| 3162 | lexias | 2 |
| 3163 | lexia | 2 |
| 3164 | leuanta | 2 |
| 3165 | leer | 2 |
| 3166 | leeldo | 2 |
| 3167 | leed | 2 |
| 3168 | lee | 2 |
| 3169 | lazos | 2 |
| 3170 | lazeria | 2 |
| 3171 | laud | 2 |
| 3172 | lata | 2 |
| 3173 | lastimada | 2 |
| 3174 | lasciuos | 2 |
| 3175 | largos | 2 |
| 3176 | largamente | 2 |
| 3177 | larga | 2 |
| 3178 | lana | 2 |
| 3179 | ladrona | 2 |
| 3180 | ladradores | 2 |
| 3181 | labrios | 2 |
| 3182 | labranzas | 2 |
| 3183 | labradas | 2 |
| 3184 | labor | 2 |
| 3185 | juzga | 2 |
| 3186 | justos | 2 |
| 3187 | justo | 2 |
| 3188 | juegos | 2 |
| 3189 | jactose | 2 |
| 3190 | inuidia | 2 |
| 3191 | inuentar | 2 |
| 3192 | inuencion | 2 |
| 3193 | interior | 2 |
| 3194 | intencion | 2 |
| 3195 | ingrato | 2 |
| 3196 | ingratitud | 2 |
| 3197 | infortunios | 2 |
| 3198 | infernales | 2 |
| 3199 | infernal | 2 |
| 3200 | induziendole | 2 |
| 3201 | indignidad | 2 |
| 3202 | indignes | 2 |
| 3203 | incogitado | 2 |
| 3204 | in | 2 |
| 3205 | imponiendo | 2 |
| 3206 | impida | 2 |
| 3207 | impedir | 2 |
| 3208 | impedimiento | 2 |
| 3209 | immerito | 2 |
| 3210 | huygamos | 2 |
| 3211 | huyes | 2 |
| 3212 | humo | 2 |
| 3213 | humilmente | 2 |
| 3214 | humilla | 2 |
| 3215 | humanidad | 2 |
| 3216 | huesped | 2 |
| 3217 | huerta | 2 |
| 3218 | huele | 2 |
| 3219 | hormiga | 2 |
| 3220 | honrras | 2 |
| 3221 | honestas | 2 |
| 3222 | holgue | 2 |
| 3223 | holgaua | 2 |
| 3224 | holgara | 2 |
| 3225 | hiziste | 2 |
| 3226 | hiziere | 2 |
| 3227 | hilos | 2 |
| 3228 | hijas | 2 |
| 3229 | hieres | 2 |
| 3230 | hideputa | 2 |
| 3231 | heziste | 2 |
| 3232 | hermoso | 2 |
| 3233 | heredera | 2 |
| 3234 | hechizos | 2 |
| 3235 | hazialo | 2 |
| 3236 | haurias | 2 |
| 3237 | haure | 2 |
| 3238 | hauiendo | 2 |
| 3239 | hauiamos | 2 |
| 3240 | hauerla | 2 |
| 3241 | harias | 2 |
| 3242 | harian | 2 |
| 3243 | harele | 2 |
| 3244 | hame | 2 |
| 3245 | hallaua | 2 |
| 3246 | halla | 2 |
| 3247 | hagote | 2 |
| 3248 | hagan | 2 |
| 3249 | hablemos | 2 |
| 3250 | hablauan | 2 |
| 3251 | hablaua | 2 |
| 3252 | hablaronte | 2 |
| 3253 | hablare | 2 |
| 3254 | guie | 2 |
| 3255 | guarecer | 2 |
| 3256 | guardado | 2 |
| 3257 | guarda | 2 |
| 3258 | gritos | 2 |
| 3259 | grauedad | 2 |
| 3260 | granos | 2 |
| 3261 | grandissimo | 2 |
| 3262 | gozoso | 2 |
| 3263 | gozosa | 2 |
| 3264 | gozarme | 2 |
| 3265 | gozaran | 2 |
| 3266 | gozando | 2 |
| 3267 | gotera | 2 |
| 3268 | gordo | 2 |
| 3269 | golpes | 2 |
| 3270 | golpe | 2 |
| 3271 | glorioso | 2 |
| 3272 | gentiles | 2 |
| 3273 | gasto | 2 |
| 3274 | gastaua | 2 |
| 3275 | garza | 2 |
| 3276 | garganta | 2 |
| 3277 | ganaria | 2 |
| 3278 | gamo | 2 |
| 3279 | gallo | 2 |
| 3280 | galan | 2 |
| 3281 | fuessemos | 2 |
| 3282 | fuertemente | 2 |
| 3283 | fueres | 2 |
| 3284 | fuercen | 2 |
| 3285 | fruta | 2 |
| 3286 | frescos | 2 |
| 3287 | frescas | 2 |
| 3288 | frente | 2 |
| 3289 | frecha | 2 |
| 3290 | franquezas | 2 |
| 3291 | forzada | 2 |
| 3292 | forro | 2 |
| 3293 | floxo | 2 |
| 3294 | florida | 2 |
| 3295 | fiziste | 2 |
| 3296 | fize | 2 |
| 3297 | firme | 2 |
| 3298 | firma | 2 |
| 3299 | finja | 2 |
| 3300 | fingido | 2 |
| 3301 | filosofo | 2 |
| 3302 | filosofia | 2 |
| 3303 | fijos | 2 |
| 3304 | fija | 2 |
| 3305 | fiero | 2 |
| 3306 | fieras | 2 |
| 3307 | fechos | 2 |
| 3308 | fechas | 2 |
| 3309 | faziendo | 2 |
| 3310 | fazerlos | 2 |
| 3311 | fauorecer | 2 |
| 3312 | fauorable | 2 |
| 3313 | fatigas | 2 |
| 3314 | fare | 2 |
| 3315 | familiar | 2 |
| 3316 | falte | 2 |
| 3317 | faltaua | 2 |
| 3318 | faltaria | 2 |
| 3319 | faltaran | 2 |
| 3320 | faltan | 2 |
| 3321 | falsedad | 2 |
| 3322 | falsarios | 2 |
| 3323 | fallo | 2 |
| 3324 | fallado | 2 |
| 3325 | fagas | 2 |
| 3326 | facultad | 2 |
| 3327 | fabrique | 2 |
| 3328 | fables | 2 |
| 3329 | fablaua | 2 |
| 3330 | fablasse | 2 |
| 3331 | fablando | 2 |
| 3332 | exemplo | 2 |
| 3333 | executar | 2 |
| 3334 | excelente | 2 |
| 3335 | euro | 2 |
| 3336 | eterna | 2 |
| 3337 | estuuiera | 2 |
| 3338 | estudia | 2 |
| 3339 | estruendo | 2 |
| 3340 | estremo | 2 |
| 3341 | estrano | 2 |
| 3342 | estrana | 2 |
| 3343 | estotra | 2 |
| 3344 | estomago | 2 |
| 3345 | estiercol | 2 |
| 3346 | estiende | 2 |
| 3347 | esterior | 2 |
| 3348 | estays | 2 |
| 3349 | estados | 2 |
| 3350 | estaciones | 2 |
| 3351 | essotro | 2 |
| 3352 | esquiuo | 2 |
| 3353 | esperimentado | 2 |
| 3354 | espantas | 2 |
| 3355 | espantar | 2 |
| 3356 | espantada | 2 |
| 3357 | espantables | 2 |
| 3358 | escusare | 2 |
| 3359 | escusar | 2 |
| 3360 | escusandose | 2 |
| 3361 | escuridad | 2 |
| 3362 | escuras | 2 |
| 3363 | escupieron | 2 |
| 3364 | escuderos | 2 |
| 3365 | escuda | 2 |
| 3366 | escucho | 2 |
| 3367 | escriuo | 2 |
| 3368 | escriuio | 2 |
| 3369 | escriuieron | 2 |
| 3370 | escritas | 2 |
| 3371 | escriptura | 2 |
| 3372 | escriptas | 2 |
| 3373 | escondidos | 2 |
| 3374 | escondida | 2 |
| 3375 | escogidos | 2 |
| 3376 | escarmiento | 2 |
| 3377 | escarmientan | 2 |
| 3378 | escape | 2 |
| 3379 | escapar | 2 |
| 3380 | escandalizes | 2 |
| 3381 | escalon | 2 |
| 3382 | error | 2 |
| 3383 | errados | 2 |
| 3384 | enzias | 2 |
| 3385 | entro | 2 |
| 3386 | entretalladura | 2 |
| 3387 | entraron | 2 |
| 3388 | entendido | 2 |
| 3389 | entendemos | 2 |
| 3390 | entendamos | 2 |
| 3391 | ensuziar | 2 |
| 3392 | ensano | 2 |
| 3393 | enojaste | 2 |
| 3394 | enojar | 2 |
| 3395 | engendro | 2 |
| 3396 | enganosa | 2 |
| 3397 | enganase | 2 |
| 3398 | enganado | 2 |
| 3399 | enferma | 2 |
| 3400 | enemistades | 2 |
| 3401 | eneas | 2 |
| 3402 | encubria | 2 |
| 3403 | encomiendas | 2 |
| 3404 | encomendado | 2 |
| 3405 | encomendadas | 2 |
| 3406 | encogimiento | 2 |
| 3407 | encerradas | 2 |
| 3408 | encendidas | 2 |
| 3409 | empos | 2 |
| 3410 | emplumada | 2 |
| 3411 | empleado | 2 |
| 3412 | empecible | 2 |
| 3413 | empece | 2 |
| 3414 | empachado | 2 |
| 3415 | embuelto | 2 |
| 3416 | embuelta | 2 |
| 3417 | embio | 2 |
| 3418 | embidioso | 2 |
| 3419 | embaxada | 2 |
| 3420 | eliso | 2 |
| 3421 | elena | 2 |
| 3422 | elementos | 2 |
| 3423 | egypto | 2 |
| 3424 | eficacia | 2 |
| 3425 | eche | 2 |
| 3426 | echaua | 2 |
| 3427 | echaron | 2 |
| 3428 | echan | 2 |
| 3429 | duros | 2 |
| 3430 | duras | 2 |
| 3431 | durable | 2 |
| 3432 | dulzura | 2 |
| 3433 | duermen | 2 |
| 3434 | dudoso | 2 |
| 3435 | dudo | 2 |
| 3436 | dubdas | 2 |
| 3437 | dozenas | 2 |
| 3438 | dorar | 2 |
| 3439 | dones | 2 |
| 3440 | dona | 2 |
| 3441 | domesticos | 2 |
| 3442 | doloroso | 2 |
| 3443 | dolorido | 2 |
| 3444 | dolia | 2 |
| 3445 | dolencia | 2 |
| 3446 | doble | 2 |
| 3447 | doblado | 2 |
| 3448 | dixeres | 2 |
| 3449 | dixele | 2 |
| 3450 | diuersidad | 2 |
| 3451 | dispuesto | 2 |
| 3452 | disfamar | 2 |
| 3453 | diselo | 2 |
| 3454 | discretas | 2 |
| 3455 | diosas | 2 |
| 3456 | dionos | 2 |
| 3457 | dilatar | 2 |
| 3458 | digolo | 2 |
| 3459 | dificile | 2 |
| 3460 | differencia | 2 |
| 3461 | diacitron | 2 |
| 3462 | dezidme | 2 |
| 3463 | dexenme | 2 |
| 3464 | dexen | 2 |
| 3465 | dexemplo | 2 |
| 3466 | dexas | 2 |
| 3467 | dexarle | 2 |
| 3468 | dexarasme | 2 |
| 3469 | dexalos | 2 |
| 3470 | dexada | 2 |
| 3471 | deuocion | 2 |
| 3472 | deuanea | 2 |
| 3473 | detrimento | 2 |
| 3474 | detractores | 2 |
| 3475 | destruyr | 2 |
| 3476 | destruyen | 2 |
| 3477 | destruya | 2 |
| 3478 | destemplado | 2 |
| 3479 | desseado | 2 |
| 3480 | dessas | 2 |
| 3481 | dessa | 2 |
| 3482 | despuelas | 2 |
| 3483 | despiden | 2 |
| 3484 | despereza | 2 |
| 3485 | despenseros | 2 |
| 3486 | despedido | 2 |
| 3487 | desmayos | 2 |
| 3488 | deshecho | 2 |
| 3489 | desechar | 2 |
| 3490 | desear | 2 |
| 3491 | deseada | 2 |
| 3492 | descubriesse | 2 |
| 3493 | descubres | 2 |
| 3494 | descubren | 2 |
| 3495 | descubierta | 2 |
| 3496 | descortes | 2 |
| 3497 | descontentos | 2 |
| 3498 | descontentamiento | 2 |
| 3499 | descontenta | 2 |
| 3500 | desconsolado | 2 |
| 3501 | desconfie | 2 |
| 3502 | descobriria | 2 |
| 3503 | descobria | 2 |
| 3504 | descargo | 2 |
| 3505 | descansar | 2 |
| 3506 | desatinado | 2 |
| 3507 | desata | 2 |
| 3508 | desastrada | 2 |
| 3509 | desarmado | 2 |
| 3510 | desafio | 2 |
| 3511 | desacompanada | 2 |
| 3512 | derrocar | 2 |
| 3513 | derredor | 2 |
| 3514 | derrames | 2 |
| 3515 | denuestos | 2 |
| 3516 | denuesto | 2 |
| 3517 | denostadas | 2 |
| 3518 | denostada | 2 |
| 3519 | demos | 2 |
| 3520 | demasiado | 2 |
| 3521 | demandan | 2 |
| 3522 | deliberar | 2 |
| 3523 | deliberacion | 2 |
| 3524 | delgada | 2 |
| 3525 | deleytoso | 2 |
| 3526 | deleytosas | 2 |
| 3527 | deleytosa | 2 |
| 3528 | delectable | 2 |
| 3529 | defendays | 2 |
| 3530 | dedalo | 2 |
| 3531 | debda | 2 |
| 3532 | dauan | 2 |
| 3533 | danza | 2 |
| 3534 | dante | 2 |
| 3535 | danosos | 2 |
| 3536 | danles | 2 |
| 3537 | dane | 2 |
| 3538 | dados | 2 |
| 3539 | dadiuas | 2 |
| 3540 | dada | 2 |
| 3541 | cuz | 2 |
| 3542 | cuyas | 2 |
| 3543 | cursos | 2 |
| 3544 | curso | 2 |
| 3545 | curo | 2 |
| 3546 | curas | 2 |
| 3547 | cumplir | 2 |
| 3548 | cumplio | 2 |
| 3549 | culpes | 2 |
| 3550 | culpas | 2 |
| 3551 | culpados | 2 |
| 3552 | culpado | 2 |
| 3553 | cuestan | 2 |
| 3554 | cueruo | 2 |
| 3555 | cuerdo | 2 |
| 3556 | cuerda | 2 |
| 3557 | cuentame | 2 |
| 3558 | cuentale | 2 |
| 3559 | cuelga | 2 |
| 3560 | cuchillada | 2 |
| 3561 | cubriesse | 2 |
| 3562 | cristiano | 2 |
| 3563 | crie | 2 |
| 3564 | crian | 2 |
| 3565 | criadas | 2 |
| 3566 | creyera | 2 |
| 3567 | crescer | 2 |
| 3568 | cresce | 2 |
| 3569 | creerse | 2 |
| 3570 | creerlo | 2 |
| 3571 | coxquillas | 2 |
| 3572 | cota | 2 |
| 3573 | costo | 2 |
| 3574 | costado | 2 |
| 3575 | cossario | 2 |
| 3576 | cortezas | 2 |
| 3577 | corte | 2 |
| 3578 | cortaste | 2 |
| 3579 | cortando | 2 |
| 3580 | corta | 2 |
| 3581 | corriendo | 2 |
| 3582 | corona | 2 |
| 3583 | coplas | 2 |
| 3584 | copia | 2 |
| 3585 | conuierte | 2 |
| 3586 | conuiertan | 2 |
| 3587 | contrarios | 2 |
| 3588 | contradezir | 2 |
| 3589 | contezca | 2 |
| 3590 | contentarle | 2 |
| 3591 | contentamiento | 2 |
| 3592 | contemplo | 2 |
| 3593 | consumen | 2 |
| 3594 | consuele | 2 |
| 3595 | consuela | 2 |
| 3596 | constancia | 2 |
| 3597 | consiste | 2 |
| 3598 | consientes | 2 |
| 3599 | considera | 2 |
| 3600 | conserue | 2 |
| 3601 | conserua | 2 |
| 3602 | consejaua | 2 |
| 3603 | conseja | 2 |
| 3604 | conosciendo | 2 |
| 3605 | conociste | 2 |
| 3606 | conociera | 2 |
| 3607 | conocido | 2 |
| 3608 | conmigo | 2 |
| 3609 | conjurote | 2 |
| 3610 | congoxoso | 2 |
| 3611 | congoxes | 2 |
| 3612 | conformidad | 2 |
| 3613 | conforme | 2 |
| 3614 | confiesso | 2 |
| 3615 | confiando | 2 |
| 3616 | confessar | 2 |
| 3617 | condenada | 2 |
| 3618 | concluye | 2 |
| 3619 | concluydo | 2 |
| 3620 | conclusiones | 2 |
| 3621 | conciertan | 2 |
| 3622 | concertada | 2 |
| 3623 | concedo | 2 |
| 3624 | concediste | 2 |
| 3625 | concediesse | 2 |
| 3626 | concebido | 2 |
| 3627 | comunicable | 2 |
| 3628 | comunes | 2 |
| 3629 | compuesta | 2 |
| 3630 | compra | 2 |
| 3631 | complidos | 2 |
| 3632 | complazer | 2 |
| 3633 | compara | 2 |
| 3634 | comiste | 2 |
| 3635 | comienzan | 2 |
| 3636 | comes | 2 |
| 3637 | comenzar | 2 |
| 3638 | combatido | 2 |
| 3639 | comadres | 2 |
| 3640 | comadre | 2 |
| 3641 | coma | 2 |
| 3642 | colores | 2 |
| 3643 | colgadas | 2 |
| 3644 | colacion | 2 |
| 3645 | col | 2 |
| 3646 | cogitaciones | 2 |
| 3647 | cobertura | 2 |
| 3648 | clauos | 2 |
| 3649 | clauo | 2 |
| 3650 | cirujanos | 2 |
| 3651 | cinta | 2 |
| 3652 | cincuenta | 2 |
| 3653 | cinco | 2 |
| 3654 | cimenterio | 2 |
| 3655 | cierre | 2 |
| 3656 | ciegos | 2 |
| 3657 | christianos | 2 |
| 3658 | cesto | 2 |
| 3659 | cesses | 2 |
| 3660 | cessa | 2 |
| 3661 | cerrad | 2 |
| 3662 | cerco | 2 |
| 3663 | cera | 2 |
| 3664 | cenidero | 2 |
| 3665 | celestial | 2 |
| 3666 | celar | 2 |
| 3667 | celada | 2 |
| 3668 | cejas | 2 |
| 3669 | cazar | 2 |
| 3670 | cazadas | 2 |
| 3671 | caydas | 2 |
| 3672 | cayan | 2 |
| 3673 | caxquete | 2 |
| 3674 | cautelas | 2 |
| 3675 | caualleros | 2 |
| 3676 | casamientos | 2 |
| 3677 | casamiento | 2 |
| 3678 | casada | 2 |
| 3679 | carpinteros | 2 |
| 3680 | caridad | 2 |
| 3681 | cargados | 2 |
| 3682 | cargada | 2 |
| 3683 | caresciendo | 2 |
| 3684 | caras | 2 |
| 3685 | capilla | 2 |
| 3686 | cantos | 2 |
| 3687 | cante | 2 |
| 3688 | cantando | 2 |
| 3689 | cantan | 2 |
| 3690 | cansancio | 2 |
| 3691 | cansado | 2 |
| 3692 | cancre | 2 |
| 3693 | cancion | 2 |
| 3694 | campanas | 2 |
| 3695 | caminante | 2 |
| 3696 | camas | 2 |
| 3697 | calzada | 2 |
| 3698 | callen | 2 |
| 3699 | callare | 2 |
| 3700 | callan | 2 |
| 3701 | callad | 2 |
| 3702 | calado | 2 |
| 3703 | caere | 2 |
| 3704 | cabezas | 2 |
| 3705 | caben | 2 |
| 3706 | cabecera | 2 |
| 3707 | buscasse | 2 |
| 3708 | buscad | 2 |
| 3709 | burlaste | 2 |
| 3710 | burlando | 2 |
| 3711 | burlado | 2 |
| 3712 | bulliendo | 2 |
| 3713 | buelues | 2 |
| 3714 | bueluas | 2 |
| 3715 | buelto | 2 |
| 3716 | buela | 2 |
| 3717 | bruto | 2 |
| 3718 | broqueles | 2 |
| 3719 | braueza | 2 |
| 3720 | bouos | 2 |
| 3721 | borrachos | 2 |
| 3722 | borracho | 2 |
| 3723 | boluerse | 2 |
| 3724 | boluera | 2 |
| 3725 | bolued | 2 |
| 3726 | boluamos | 2 |
| 3727 | bolar | 2 |
| 3728 | bocado | 2 |
| 3729 | blason | 2 |
| 3730 | blanda | 2 |
| 3731 | blancos | 2 |
| 3732 | blancas | 2 |
| 3733 | bisperas | 2 |
| 3734 | bienempleado | 2 |
| 3735 | beuo | 2 |
| 3736 | besando | 2 |
| 3737 | beneficios | 2 |
| 3738 | bendigate | 2 |
| 3739 | bastara | 2 |
| 3740 | baruuda | 2 |
| 3741 | baruas | 2 |
| 3742 | barrunto | 2 |
| 3743 | barro | 2 |
| 3744 | barriga | 2 |
| 3745 | barbuda | 2 |
| 3746 | baldonado | 2 |
| 3747 | baldon | 2 |
| 3748 | azumbre | 2 |
| 3749 | azeytes | 2 |
| 3750 | azero | 2 |
| 3751 | azemilero | 2 |
| 3752 | azahar | 2 |
| 3753 | ayamos | 2 |
| 3754 | auremos | 2 |
| 3755 | aure | 2 |
| 3756 | aueys | 2 |
| 3757 | auentaja | 2 |
| 3758 | auaricia | 2 |
| 3759 | atribulados | 2 |
| 3760 | atrae | 2 |
| 3761 | atormentes | 2 |
| 3762 | atencion | 2 |
| 3763 | atajes | 2 |
| 3764 | atajen | 2 |
| 3765 | atados | 2 |
| 3766 | atada | 2 |
| 3767 | assentar | 2 |
| 3768 | asperos | 2 |
| 3769 | aspereza | 2 |
| 3770 | aspera | 2 |
| 3771 | asientate | 2 |
| 3772 | asentada | 2 |
| 3773 | ascuras | 2 |
| 3774 | arrugada | 2 |
| 3775 | arrojan | 2 |
| 3776 | arrima | 2 |
| 3777 | arrepentirse | 2 |
| 3778 | arrebatada | 2 |
| 3779 | arrastren | 2 |
| 3780 | arnes | 2 |
| 3781 | armeros | 2 |
| 3782 | armar | 2 |
| 3783 | aristoteles | 2 |
| 3784 | arguyen | 2 |
| 3785 | arduo | 2 |
| 3786 | ardor | 2 |
| 3787 | arder | 2 |
| 3788 | arca | 2 |
| 3789 | aquexan | 2 |
| 3790 | aquesto | 2 |
| 3791 | aqueste | 2 |
| 3792 | aquestas | 2 |
| 3793 | aprende | 2 |
| 3794 | aposentamiento | 2 |
| 3795 | aplique | 2 |
| 3796 | aplazible | 2 |
| 3797 | aplaze | 2 |
| 3798 | apercibimiento | 2 |
| 3799 | apercibete | 2 |
| 3800 | apercebida | 2 |
| 3801 | apartate | 2 |
| 3802 | apartar | 2 |
| 3803 | apartan | 2 |
| 3804 | aparejados | 2 |
| 3805 | aparejada | 2 |
| 3806 | antojos | 2 |
| 3807 | antiguo | 2 |
| 3808 | antigo | 2 |
| 3809 | antepuerta | 2 |
| 3810 | anoche | 2 |
| 3811 | animosidad | 2 |
| 3812 | anillo | 2 |
| 3813 | anden | 2 |
| 3814 | andemos | 2 |
| 3815 | andaua | 2 |
| 3816 | andando | 2 |
| 3817 | andado | 2 |
| 3818 | amonestaciones | 2 |
| 3819 | amistades | 2 |
| 3820 | ames | 2 |
| 3821 | amays | 2 |
| 3822 | amaua | 2 |
| 3823 | amante | 2 |
| 3824 | amansar | 2 |
| 3825 | amansa | 2 |
| 3826 | amanecer | 2 |
| 3827 | amadores | 2 |
| 3828 | alzar | 2 |
| 3829 | alza | 2 |
| 3830 | aluorada | 2 |
| 3831 | aluayalde | 2 |
| 3832 | aluanares | 2 |
| 3833 | alua | 2 |
| 3834 | altos | 2 |
| 3835 | alterados | 2 |
| 3836 | alteraciones | 2 |
| 3837 | altera | 2 |
| 3838 | almohaza | 2 |
| 3839 | allegate | 2 |
| 3840 | aliuiado | 2 |
| 3841 | alhajas | 2 |
| 3842 | alcohol | 2 |
| 3843 | alcanzo | 2 |
| 3844 | alcanzara | 2 |
| 3845 | alcanza | 2 |
| 3846 | alaridos | 2 |
| 3847 | alarga | 2 |
| 3848 | alabo | 2 |
| 3849 | alabes | 2 |
| 3850 | alabanzas | 2 |
| 3851 | alabanza | 2 |
| 3852 | ajena | 2 |
| 3853 | agujeros | 2 |
| 3854 | aguijar | 2 |
| 3855 | agueros | 2 |
| 3856 | aguda | 2 |
| 3857 | agraz | 2 |
| 3858 | agras | 2 |
| 3859 | agradar | 2 |
| 3860 | agradan | 2 |
| 3861 | agenos | 2 |
| 3862 | afloxase | 2 |
| 3863 | afloxara | 2 |
| 3864 | afloxa | 2 |
| 3865 | afligidos | 2 |
| 3866 | afirmas | 2 |
| 3867 | afeto | 2 |
| 3868 | afanes | 2 |
| 3869 | afan | 2 |
| 3870 | adorar | 2 |
| 3871 | adereza | 2 |
| 3872 | aderece | 2 |
| 3873 | adam | 2 |
| 3874 | adalid | 2 |
| 3875 | acuse | 2 |
| 3876 | acuerde | 2 |
| 3877 | acostumbrados | 2 |
| 3878 | acostamos | 2 |
| 3879 | acostado | 2 |
| 3880 | acorro | 2 |
| 3881 | acordo | 2 |
| 3882 | acordar | 2 |
| 3883 | acordaos | 2 |
| 3884 | acompanemos | 2 |
| 3885 | acompanada | 2 |
| 3886 | aclarar | 2 |
| 3887 | acierto | 2 |
| 3888 | acidente | 2 |
| 3889 | acerca | 2 |
| 3890 | acarrean | 2 |
| 3891 | acarreado | 2 |
| 3892 | acaescido | 2 |
| 3893 | acaescer | 2 |
| 3894 | acabo | 2 |
| 3895 | acabasse | 2 |
| 3896 | acabarlo | 2 |
| 3897 | acabarla | 2 |
| 3898 | abuela | 2 |
| 3899 | absente | 2 |
| 3900 | abrojos | 2 |
| 3901 | abrenos | 2 |
| 3902 | abren | 2 |
| 3903 | abreme | 2 |
| 3904 | abrazo | 2 |
| 3905 | abrazarte | 2 |
| 3906 | abrazados | 2 |
| 3907 | abrase | 2 |
| 3908 | abrace | 2 |
| 3909 | ablande | 2 |
| 3910 | abiua | 2 |
| 3911 | abiertos | 2 |
| 3912 | abierto | 2 |
| 3913 | abiertamente | 2 |
| 3914 | abierta | 2 |
| 3915 | abastasse | 2 |
| 3916 | zurujanos | 1 |
| 3917 | zurujano | 1 |
| 3918 | zurrio | 1 |
| 3919 | zumos | 1 |
| 3920 | zufro | 1 |
| 3921 | zufre | 1 |
| 3922 | zozobras | 1 |
| 3923 | zozobra | 1 |
| 3924 | zofrirte | 1 |
| 3925 | zofrir | 1 |
| 3926 | zapatas | 1 |
| 3927 | zamora | 1 |
| 3928 | zaharenas | 1 |
| 3929 | yzquierdo | 1 |
| 3930 | yuamos | 1 |
| 3931 | ystorias | 1 |
| 3932 | ystoriales | 1 |
| 3933 | ysquierdo | 1 |
| 3934 | ysquierda | 1 |
| 3935 | yrse | 1 |
| 3936 | yrritados | 1 |
| 3937 | yrnos | 1 |
| 3938 | yrle | 1 |
| 3939 | yrian | 1 |
| 3940 | yrada | 1 |
| 3941 | ypocrita | 1 |
| 3942 | ypermestra | 1 |
| 3943 | ynocente | 1 |
| 3944 | ynes | 1 |
| 3945 | ymitauas | 1 |
| 3946 | ymaginamientos | 1 |
| 3947 | ymaginacion | 1 |
| 3948 | ymagina | 1 |
| 3949 | ylustrantes | 1 |
| 3950 | ylicito | 1 |
| 3951 | yjares | 1 |
| 3952 | ygualdad | 1 |
| 3953 | ygualar | 1 |
| 3954 | ygualada | 1 |
| 3955 | yglesias | 1 |
| 3956 | yerre | 1 |
| 3957 | yermos | 1 |
| 3958 | yedra | 1 |
| 3959 | ydras | 1 |
| 3960 | ydolo | 1 |
| 3961 | ydas | 1 |
| 3962 | xxi | 1 |
| 3963 | xo | 1 |
| 3964 | ximio | 1 |
| 3965 | xiij | 1 |
| 3966 | xiiij | 1 |
| 3967 | xergas | 1 |
| 3968 | xerga | 1 |
| 3969 | xenofon | 1 |
| 3970 | xarope | 1 |
| 3971 | xarcias | 1 |
| 3972 | xaques | 1 |
| 3973 | vulto | 1 |
| 3974 | vse | 1 |
| 3975 | vsaste | 1 |
| 3976 | vsaron | 1 |
| 3977 | vsan | 1 |
| 3978 | vsado | 1 |
| 3979 | vrdio | 1 |
| 3980 | voto | 1 |
| 3981 | vos | 1 |
| 3982 | volando | 1 |
| 3983 | voces | 1 |
| 3984 | vnturillas | 1 |
| 3985 | vnturas | 1 |
| 3986 | vntos | 1 |
| 3987 | vnto | 1 |
| 3988 | vntasnos | 1 |
| 3989 | vniversa | 1 |
| 3990 | vnicornio | 1 |
| 3991 | vltimas | 1 |
| 3992 | vltima | 1 |
| 3993 | viuiremos | 1 |
| 3994 | viuiras | 1 |
| 3995 | viuimos | 1 |
| 3996 | viuificar | 1 |
| 3997 | viuificacion | 1 |
| 3998 | viuiere | 1 |
| 3999 | viuido | 1 |
| 4000 | viuen | 1 |
| 4001 | vituperadores | 1 |
| 4002 | vitoria | 1 |
| 4003 | vistos | 1 |
| 4004 | vistiendo | 1 |
| 4005 | vistetele | 1 |
| 4006 | vistes | 1 |
| 4007 | vistas | 1 |
| 4008 | vistanse | 1 |
| 4009 | vispera | 1 |
| 4010 | viso | 1 |
| 4011 | visito | 1 |
| 4012 | visitenos | 1 |
| 4013 | visite | 1 |
| 4014 | visitaua | 1 |
| 4015 | visitare | 1 |
| 4016 | visitalla | 1 |
| 4017 | visitadas | 1 |
| 4018 | visitaciones | 1 |
| 4019 | virtuosas | 1 |
| 4020 | violetas | 1 |
| 4021 | violentos | 1 |
| 4022 | viniesses | 1 |
| 4023 | viniessen | 1 |
| 4024 | vinieren | 1 |
| 4025 | vinieras | 1 |
| 4026 | vinieran | 1 |
| 4027 | viniendola | 1 |
| 4028 | vinelo | 1 |
| 4029 | vinele | 1 |
| 4030 | vinas | 1 |
| 4031 | vina | 1 |
| 4032 | villadiego | 1 |
| 4033 | vigilancia | 1 |
| 4034 | vieses | 1 |
| 4035 | vies | 1 |
| 4036 | vierta | 1 |
| 4037 | vieronte | 1 |
| 4038 | viere | 1 |
| 4039 | vieras | 1 |
| 4040 | vientre | 1 |
| 4041 | vienesme | 1 |
| 4042 | viendoos | 1 |
| 4043 | vidrio | 1 |
| 4044 | victoria | 1 |
| 4045 | victo | 1 |
| 4046 | viciosos | 1 |
| 4047 | viciosas | 1 |
| 4048 | viciosa | 1 |
| 4049 | vicario | 1 |
| 4050 | viandas | 1 |
| 4051 | vianda | 1 |
| 4052 | vfana | 1 |
| 4053 | veys | 1 |
| 4054 | veynteno | 1 |
| 4055 | vestirlas | 1 |
| 4056 | vestidura | 1 |
| 4057 | vestida | 1 |
| 4058 | vesti | 1 |
| 4059 | vesme | 1 |
| 4060 | vesla | 1 |
| 4061 | vertida | 1 |
| 4062 | verti | 1 |
| 4063 | vernia | 1 |
| 4064 | vernemos | 1 |
| 4065 | verne | 1 |
| 4066 | vernas | 1 |
| 4067 | vernan | 1 |
| 4068 | vermejas | 1 |
| 4069 | verias | 1 |
| 4070 | vergonzosa | 1 |
| 4071 | vergilio | 1 |
| 4072 | vergel | 1 |
| 4073 | verduricas | 1 |
| 4074 | verdura | 1 |
| 4075 | verdugos | 1 |
| 4076 | verdades | 1 |
| 4077 | verdaderos | 1 |
| 4078 | verdaderamente | 1 |
| 4079 | vera | 1 |
| 4080 | veote | 1 |
| 4081 | veole | 1 |
| 4082 | venza | 1 |
| 4083 | ventores | 1 |
| 4084 | venti | 1 |
| 4085 | ventas | 1 |
| 4086 | ventanilla | 1 |
| 4087 | venidos | 1 |
| 4088 | venideras | 1 |
| 4089 | veniades | 1 |
| 4090 | vengues | 1 |
| 4091 | vengue | 1 |
| 4092 | vengara | 1 |
| 4093 | vengadas | 1 |
| 4094 | vengada | 1 |
| 4095 | venerable | 1 |
| 4096 | venenoso | 1 |
| 4097 | venenosa | 1 |
| 4098 | vendio | 1 |
| 4099 | vendible | 1 |
| 4100 | vendes | 1 |
| 4101 | venderlo | 1 |
| 4102 | venderia | 1 |
| 4103 | venden | 1 |
| 4104 | vende | 1 |
| 4105 | venciste | 1 |
| 4106 | vencimiento | 1 |
| 4107 | vencieron | 1 |
| 4108 | vencen | 1 |
| 4109 | velo | 1 |
| 4110 | vello | 1 |
| 4111 | vellaquillo | 1 |
| 4112 | vellaca | 1 |
| 4113 | vella | 1 |
| 4114 | velando | 1 |
| 4115 | velan | 1 |
| 4116 | vela | 1 |
| 4117 | vegetatiuo | 1 |
| 4118 | veela | 1 |
| 4119 | veedor | 1 |
| 4120 | veed | 1 |
| 4121 | vedado | 1 |
| 4122 | veate | 1 |
| 4123 | vazian | 1 |
| 4124 | vaziado | 1 |
| 4125 | vayo | 1 |
| 4126 | vasqueaua | 1 |
| 4127 | varonil | 1 |
| 4128 | varios | 1 |
| 4129 | variedades | 1 |
| 4130 | variable | 1 |
| 4131 | varde | 1 |
| 4132 | vardara | 1 |
| 4133 | vanidades | 1 |
| 4134 | vanidad | 1 |
| 4135 | vanamente | 1 |
| 4136 | vanagloria | 1 |
| 4137 | vallena | 1 |
| 4138 | valle | 1 |
| 4139 | valiera | 1 |
| 4140 | vales | 1 |
| 4141 | valerle | 1 |
| 4142 | valdria | 1 |
| 4143 | valasme | 1 |
| 4144 | valame | 1 |
| 4145 | vagado | 1 |
| 4146 | vado | 1 |
| 4147 | vacilando | 1 |
| 4148 | vaca | 1 |
| 4149 | uosotros | 1 |
| 4150 | uos | 1 |
| 4151 | unos | 1 |
| 4152 | una | 1 |
| 4153 | ultimo | 1 |
| 4154 | ulixes | 1 |
| 4155 | uerse | 1 |
| 4156 | uerme | 1 |
| 4157 | uenecia | 1 |
| 4158 | uale | 1 |
| 4159 | tuuiesse | 1 |
| 4160 | tuuiese | 1 |
| 4161 | tuuiera | 1 |
| 4162 | tutriz | 1 |
| 4163 | tutores | 1 |
| 4164 | turuino | 1 |
| 4165 | turuias | 1 |
| 4166 | turuada | 1 |
| 4167 | turco | 1 |
| 4168 | turbose | 1 |
| 4169 | turbias | 1 |
| 4170 | turbia | 1 |
| 4171 | turbaua | 1 |
| 4172 | turbasse | 1 |
| 4173 | turban | 1 |
| 4174 | turbame | 1 |
| 4175 | turbados | 1 |
| 4176 | tumbando | 1 |
| 4177 | tuetano | 1 |
| 4178 | trufas | 1 |
| 4179 | truenos | 1 |
| 4180 | trueco | 1 |
| 4181 | truchas | 1 |
| 4182 | troyana | 1 |
| 4183 | trotaconuentos | 1 |
| 4184 | tropiece | 1 |
| 4185 | tropezasse | 1 |
| 4186 | tropezado | 1 |
| 4187 | tropece | 1 |
| 4188 | tronco | 1 |
| 4189 | trocasse | 1 |
| 4190 | trocarlas | 1 |
| 4191 | trobara | 1 |
| 4192 | trobador | 1 |
| 4193 | troba | 1 |
| 4194 | tristezas | 1 |
| 4195 | tristemente | 1 |
| 4196 | tribunicia | 1 |
| 4197 | triaca | 1 |
| 4198 | tresquillar | 1 |
| 4199 | tresquilen | 1 |
| 4200 | tresquilanme | 1 |
| 4201 | tremunt | 1 |
| 4202 | tremo | 1 |
| 4203 | trementina | 1 |
| 4204 | tremen | 1 |
| 4205 | trebol | 1 |
| 4206 | traygays | 1 |
| 4207 | traygas | 1 |
| 4208 | traygan | 1 |
| 4209 | traydos | 1 |
| 4210 | trayas | 1 |
| 4211 | trayale | 1 |
| 4212 | traxeran | 1 |
| 4213 | trauiessa | 1 |
| 4214 | trauan | 1 |
| 4215 | trate | 1 |
| 4216 | tratays | 1 |
| 4217 | trataua | 1 |
| 4218 | tratarlo | 1 |
| 4219 | tratame | 1 |
| 4220 | tratables | 1 |
| 4221 | trata | 1 |
| 4222 | trastrocame | 1 |
| 4223 | traspuesta | 1 |
| 4224 | trasponga | 1 |
| 4225 | trasponen | 1 |
| 4226 | traspasso | 1 |
| 4227 | traspasse | 1 |
| 4228 | traspassaron | 1 |
| 4229 | traspasaron | 1 |
| 4230 | trances | 1 |
| 4231 | trance | 1 |
| 4232 | tramas | 1 |
| 4233 | trama | 1 |
| 4234 | trajes | 1 |
| 4235 | tragico | 1 |
| 4236 | tragedia | 1 |
| 4237 | tragado | 1 |
| 4238 | tragada | 1 |
| 4239 | traerte | 1 |
| 4240 | traergela | 1 |
| 4241 | traele | 1 |
| 4242 | tractaua | 1 |
| 4243 | trabajoso | 1 |
| 4244 | trabajosa | 1 |
| 4245 | trabajen | 1 |
| 4246 | trabajauas | 1 |
| 4247 | trabajara | 1 |
| 4248 | trabajadores | 1 |
| 4249 | trabajado | 1 |
| 4250 | trabaja | 1 |
| 4251 | touo | 1 |
| 4252 | touistes | 1 |
| 4253 | touiesses | 1 |
| 4254 | touiessen | 1 |
| 4255 | touieremos | 1 |
| 4256 | touieras | 1 |
| 4257 | touiera | 1 |
| 4258 | tostadas | 1 |
| 4259 | tostada | 1 |
| 4260 | toruellinos | 1 |
| 4261 | tortas | 1 |
| 4262 | tortarosa | 1 |
| 4263 | torrezno | 1 |
| 4264 | torres | 1 |
| 4265 | torpeza | 1 |
| 4266 | torpes | 1 |
| 4267 | torpemente | 1 |
| 4268 | torno | 1 |
| 4269 | tornese | 1 |
| 4270 | tornes | 1 |
| 4271 | tornemos | 1 |
| 4272 | tornays | 1 |
| 4273 | tornaua | 1 |
| 4274 | tornasse | 1 |
| 4275 | tornarte | 1 |
| 4276 | tornarme | 1 |
| 4277 | tornarlo | 1 |
| 4278 | tornarase | 1 |
| 4279 | tornaras | 1 |
| 4280 | tornanla | 1 |
| 4281 | tornandome | 1 |
| 4282 | tornan | 1 |
| 4283 | tornallo | 1 |
| 4284 | tornalle | 1 |
| 4285 | tornalas | 1 |
| 4286 | tornados | 1 |
| 4287 | tordo | 1 |
| 4288 | torcera | 1 |
| 4289 | torce | 1 |
| 4290 | torcato | 1 |
| 4291 | toquillas | 1 |
| 4292 | topome | 1 |
| 4293 | topauamos | 1 |
| 4294 | topasses | 1 |
| 4295 | topar | 1 |
| 4296 | tono | 1 |
| 4297 | tomen | 1 |
| 4298 | tomemosselo | 1 |
| 4299 | tomays | 1 |
| 4300 | tomaua | 1 |
| 4301 | tomaste | 1 |
| 4302 | tomaron | 1 |
| 4303 | tomarme | 1 |
| 4304 | tomarlo | 1 |
| 4305 | tomarias | 1 |
| 4306 | tomares | 1 |
| 4307 | tomalla | 1 |
| 4308 | tomados | 1 |
| 4309 | tollerar | 1 |
| 4310 | todopoderoso | 1 |
| 4311 | toco | 1 |
| 4312 | tocaua | 1 |
| 4313 | tocasse | 1 |
| 4314 | tocar | 1 |
| 4315 | tocame | 1 |
| 4316 | tocalla | 1 |
| 4317 | tocadas | 1 |
| 4318 | titulos | 1 |
| 4319 | tisbe | 1 |
| 4320 | tirauan | 1 |
| 4321 | tiras | 1 |
| 4322 | tirar | 1 |
| 4323 | tinta | 1 |
| 4324 | tinosa | 1 |
| 4325 | tinagica | 1 |
| 4326 | timidos | 1 |
| 4327 | tientan | 1 |
| 4328 | tienete | 1 |
| 4329 | tienente | 1 |
| 4330 | tieneme | 1 |
| 4331 | tienele | 1 |
| 4332 | tiende | 1 |
| 4333 | tiemplate | 1 |
| 4334 | tiemblo | 1 |
| 4335 | tiembla | 1 |
| 4336 | tibar | 1 |
| 4337 | thesoro | 1 |
| 4338 | thamar | 1 |
| 4339 | tez | 1 |
| 4340 | texon | 1 |
| 4341 | texo | 1 |
| 4342 | texido | 1 |
| 4343 | texedores | 1 |
| 4344 | teta | 1 |
| 4345 | testimoniar | 1 |
| 4346 | testantur | 1 |
| 4347 | tesifone | 1 |
| 4348 | terrones | 1 |
| 4349 | terron | 1 |
| 4350 | terrenales | 1 |
| 4351 | terremotos | 1 |
| 4352 | terrae | 1 |
| 4353 | ternias | 1 |
| 4354 | ternasme | 1 |
| 4355 | ternan | 1 |
| 4356 | termino | 1 |
| 4357 | terenciana | 1 |
| 4358 | tentare | 1 |
| 4359 | tentados | 1 |
| 4360 | tentador | 1 |
| 4361 | tentaciones | 1 |
| 4362 | tenme | 1 |
| 4363 | tenien | 1 |
| 4364 | teniamos | 1 |
| 4365 | tengotelo | 1 |
| 4366 | tengolo | 1 |
| 4367 | tenerlos | 1 |
| 4368 | tenerle | 1 |
| 4369 | tenerla | 1 |
| 4370 | tened | 1 |
| 4371 | tendido | 1 |
| 4372 | tendida | 1 |
| 4373 | tender | 1 |
| 4374 | tendente | 1 |
| 4375 | tenazuelas | 1 |
| 4376 | temporibus | 1 |
| 4377 | tempora | 1 |
| 4378 | templara | 1 |
| 4379 | templar | 1 |
| 4380 | templadico | 1 |
| 4381 | tempestad | 1 |
| 4382 | temperancia | 1 |
| 4383 | temio | 1 |
| 4384 | temia | 1 |
| 4385 | temes | 1 |
| 4386 | temerosos | 1 |
| 4387 | temeroso | 1 |
| 4388 | temere | 1 |
| 4389 | temen | 1 |
| 4390 | temblo | 1 |
| 4391 | temblando | 1 |
| 4392 | temamos | 1 |
| 4393 | tema | 1 |
| 4394 | telas | 1 |
| 4395 | telarana | 1 |
| 4396 | tassa | 1 |
| 4397 | tarpeya | 1 |
| 4398 | tardemos | 1 |
| 4399 | tardas | 1 |
| 4400 | tardar | 1 |
| 4401 | taraguntia | 1 |
| 4402 | tapan | 1 |
| 4403 | taniendo | 1 |
| 4404 | tania | 1 |
| 4405 | tanga | 1 |
| 4406 | taner | 1 |
| 4407 | tanen | 1 |
| 4408 | tanbien | 1 |
| 4409 | talega | 1 |
| 4410 | tajo | 1 |
| 4411 | tajada | 1 |
| 4412 | taja | 1 |
| 4413 | tahur | 1 |
| 4414 | tablilla | 1 |
| 4415 | tablas | 1 |
| 4416 | tablado | 1 |
| 4417 | tabladillo | 1 |
| 4418 | suziuelo | 1 |
| 4419 | suziedades | 1 |
| 4420 | suziedad | 1 |
| 4421 | suzias | 1 |
| 4422 | suzia | 1 |
| 4423 | suyas | 1 |
| 4424 | sutil | 1 |
| 4425 | susurrays | 1 |
| 4426 | susurrando | 1 |
| 4427 | sustentar | 1 |
| 4428 | suspensos | 1 |
| 4429 | suso | 1 |
| 4430 | supplico | 1 |
| 4431 | supitos | 1 |
| 4432 | supiesses | 1 |
| 4433 | supieses | 1 |
| 4434 | supieron | 1 |
| 4435 | supiere | 1 |
| 4436 | superflua | 1 |
| 4437 | sumarios | 1 |
| 4438 | sulfureos | 1 |
| 4439 | sujecion | 1 |
| 4440 | sufrio | 1 |
| 4441 | sufrimiento | 1 |
| 4442 | sufriera | 1 |
| 4443 | sufria | 1 |
| 4444 | sufrete | 1 |
| 4445 | sufres | 1 |
| 4446 | sufren | 1 |
| 4447 | sufrela | 1 |
| 4448 | sufre | 1 |
| 4449 | sufra | 1 |
| 4450 | suelto | 1 |
| 4451 | sueltes | 1 |
| 4452 | suelte | 1 |
| 4453 | sueldo | 1 |
| 4454 | sudar | 1 |
| 4455 | sucedieron | 1 |
| 4456 | suceder | 1 |
| 4457 | succedieron | 1 |
| 4458 | substancia | 1 |
| 4459 | subliman | 1 |
| 4460 | sublimado | 1 |
| 4461 | sublimada | 1 |
| 4462 | subjetos | 1 |
| 4463 | subjecto | 1 |
| 4464 | subjecion | 1 |
| 4465 | subito | 1 |
| 4466 | subir | 1 |
| 4467 | subidas | 1 |
| 4468 | subias | 1 |
| 4469 | subi | 1 |
| 4470 | suauissimo | 1 |
| 4471 | suauidad | 1 |
| 4472 | suaues | 1 |
| 4473 | studio | 1 |
| 4474 | stigie | 1 |
| 4475 | stellae | 1 |
| 4476 | sta | 1 |
| 4477 | spiritu | 1 |
| 4478 | speranza | 1 |
| 4479 | species | 1 |
| 4480 | spantalobos | 1 |
| 4481 | sostuuo | 1 |
| 4482 | sostienes | 1 |
| 4483 | sostengas | 1 |
| 4484 | sostenerse | 1 |
| 4485 | sostenemos | 1 |
| 4486 | sossiego | 1 |
| 4487 | sossegadas | 1 |
| 4488 | sossegada | 1 |
| 4489 | sospirar | 1 |
| 4490 | sospirando | 1 |
| 4491 | sospira | 1 |
| 4492 | sospechosos | 1 |
| 4493 | sospechoso | 1 |
| 4494 | sospeche | 1 |
| 4495 | sospechaste | 1 |
| 4496 | sospechan | 1 |
| 4497 | sosegado | 1 |
| 4498 | sosegadilla | 1 |
| 4499 | soruos | 1 |
| 4500 | sopa | 1 |
| 4501 | sono | 1 |
| 4502 | sones | 1 |
| 4503 | sonelo | 1 |
| 4504 | sonauas | 1 |
| 4505 | sometes | 1 |
| 4506 | someter | 1 |
| 4507 | soltura | 1 |
| 4508 | soltaste | 1 |
| 4509 | soltarme | 1 |
| 4510 | solos | 1 |
| 4511 | solicitos | 1 |
| 4512 | solicitar | 1 |
| 4513 | soleys | 1 |
| 4514 | soles | 1 |
| 4515 | soldase | 1 |
| 4516 | soldaremos | 1 |
| 4517 | soldara | 1 |
| 4518 | soldar | 1 |
| 4519 | solaz | 1 |
| 4520 | solana | 1 |
| 4521 | sojuzgaste | 1 |
| 4522 | sojuzgadas | 1 |
| 4523 | sojuzgada | 1 |
| 4524 | sofrite | 1 |
| 4525 | sofrirse | 1 |
| 4526 | sofrirle | 1 |
| 4527 | sofrillas | 1 |
| 4528 | sofrido | 1 |
| 4529 | sofisticos | 1 |
| 4530 | sofistica | 1 |
| 4531 | soffrir | 1 |
| 4532 | sodoma | 1 |
| 4533 | socrates | 1 |
| 4534 | socios | 1 |
| 4535 | sobreuino | 1 |
| 4536 | sobrenombre | 1 |
| 4537 | sobredicho | 1 |
| 4538 | sobrecargar | 1 |
| 4539 | sobraua | 1 |
| 4540 | sobraria | 1 |
| 4541 | sobran | 1 |
| 4542 | sobrados | 1 |
| 4543 | sobi | 1 |
| 4544 | soberuia | 1 |
| 4545 | soberuezcas | 1 |
| 4546 | sobaco | 1 |
| 4547 | siruienta | 1 |
| 4548 | siruas | 1 |
| 4549 | siruamos | 1 |
| 4550 | sintiesses | 1 |
| 4551 | sintiessen | 1 |
| 4552 | sintiessedes | 1 |
| 4553 | sintiesse | 1 |
| 4554 | sinrazon | 1 |
| 4555 | singulares | 1 |
| 4556 | singula | 1 |
| 4557 | sine | 1 |
| 4558 | sindicado | 1 |
| 4559 | simulado | 1 |
| 4560 | simplezico | 1 |
| 4561 | simples | 1 |
| 4562 | similitud | 1 |
| 4563 | siluo | 1 |
| 4564 | siguientes | 1 |
| 4565 | siguiente | 1 |
| 4566 | siguia | 1 |
| 4567 | siguese | 1 |
| 4568 | sigues | 1 |
| 4569 | signos | 1 |
| 4570 | signo | 1 |
| 4571 | sigas | 1 |
| 4572 | siganos | 1 |
| 4573 | sietecientas | 1 |
| 4574 | sieruas | 1 |
| 4575 | sierua | 1 |
| 4576 | sierra | 1 |
| 4577 | sidonio | 1 |
| 4578 | seyme | 1 |
| 4579 | sey | 1 |
| 4580 | sevilla | 1 |
| 4581 | seuilla | 1 |
| 4582 | seueridad | 1 |
| 4583 | setimo | 1 |
| 4584 | setenta | 1 |
| 4585 | sesto | 1 |
| 4586 | sesito | 1 |
| 4587 | seruis | 1 |
| 4588 | seruiremos | 1 |
| 4589 | seruientes | 1 |
| 4590 | seruidora | 1 |
| 4591 | seruias | 1 |
| 4592 | seruia | 1 |
| 4593 | sermon | 1 |
| 4594 | serle | 1 |
| 4595 | serias | 1 |
| 4596 | seriades | 1 |
| 4597 | sereys | 1 |
| 4598 | serenos | 1 |
| 4599 | serenissima | 1 |
| 4600 | sequen | 1 |
| 4601 | sepulturas | 1 |
| 4602 | sepultar | 1 |
| 4603 | senzilla | 1 |
| 4604 | senuelo | 1 |
| 4605 | sentirse | 1 |
| 4606 | sentiriades | 1 |
| 4607 | sentiria | 1 |
| 4608 | sentiran | 1 |
| 4609 | sentira | 1 |
| 4610 | sentimientos | 1 |
| 4611 | sentibles | 1 |
| 4612 | sentible | 1 |
| 4613 | sentenciar | 1 |
| 4614 | sensuales | 1 |
| 4615 | seno | 1 |
| 4616 | sendos | 1 |
| 4617 | sendas | 1 |
| 4618 | senaleja | 1 |
| 4619 | senalan | 1 |
| 4620 | semiramis | 1 |
| 4621 | semejassen | 1 |
| 4622 | semejar | 1 |
| 4623 | semejable | 1 |
| 4624 | seme | 1 |
| 4625 | sembrando | 1 |
| 4626 | semblante | 1 |
| 4627 | segurar | 1 |
| 4628 | seguirse | 1 |
| 4629 | seguirle | 1 |
| 4630 | seguira | 1 |
| 4631 | seguimiento | 1 |
| 4632 | seguille | 1 |
| 4633 | seguido | 1 |
| 4634 | seguia | 1 |
| 4635 | segadores | 1 |
| 4636 | segadas | 1 |
| 4637 | secundum | 1 |
| 4638 | secum | 1 |
| 4639 | sectas | 1 |
| 4640 | secretarios | 1 |
| 4641 | seco | 1 |
| 4642 | secas | 1 |
| 4643 | secarme | 1 |
| 4644 | scriptores | 1 |
| 4645 | screuir | 1 |
| 4646 | sauco | 1 |
| 4647 | satisfaze | 1 |
| 4648 | satisfare | 1 |
| 4649 | sarten | 1 |
| 4650 | sarmientos | 1 |
| 4651 | sardina | 1 |
| 4652 | saques | 1 |
| 4653 | saquen | 1 |
| 4654 | saquemos | 1 |
| 4655 | sapho | 1 |
| 4656 | santiguando | 1 |
| 4657 | santiguada | 1 |
| 4658 | santigua | 1 |
| 4659 | santidades | 1 |
| 4660 | sanson | 1 |
| 4661 | sanos | 1 |
| 4662 | sangustiado | 1 |
| 4663 | sanguino | 1 |
| 4664 | sanguijuela | 1 |
| 4665 | sane | 1 |
| 4666 | sanctas | 1 |
| 4667 | sanaua | 1 |
| 4668 | sanas | 1 |
| 4669 | sanarlo | 1 |
| 4670 | sanara | 1 |
| 4671 | salutacion | 1 |
| 4672 | saludan | 1 |
| 4673 | saludame | 1 |
| 4674 | saluar | 1 |
| 4675 | saluaje | 1 |
| 4676 | saluados | 1 |
| 4677 | salto | 1 |
| 4678 | salten | 1 |
| 4679 | saltemos | 1 |
| 4680 | salteadores | 1 |
| 4681 | salteada | 1 |
| 4682 | saltaparedes | 1 |
| 4683 | saltando | 1 |
| 4684 | saltan | 1 |
| 4685 | salta | 1 |
| 4686 | salsa | 1 |
| 4687 | salitre | 1 |
| 4688 | saliste | 1 |
| 4689 | salirse | 1 |
| 4690 | saliessen | 1 |
| 4691 | saliesse | 1 |
| 4692 | salieres | 1 |
| 4693 | saliera | 1 |
| 4694 | salidas | 1 |
| 4695 | salias | 1 |
| 4696 | salian | 1 |
| 4697 | saliamos | 1 |
| 4698 | salia | 1 |
| 4699 | sali | 1 |
| 4700 | salgome | 1 |
| 4701 | salgamos | 1 |
| 4702 | salenle | 1 |
| 4703 | saldra | 1 |
| 4704 | sal | 1 |
| 4705 | saetas | 1 |
| 4706 | sacude | 1 |
| 4707 | sacristanes | 1 |
| 4708 | sacristan | 1 |
| 4709 | sacrilega | 1 |
| 4710 | sacrificio | 1 |
| 4711 | sacasse | 1 |
| 4712 | sacasla | 1 |
| 4713 | sacarte | 1 |
| 4714 | sacaros | 1 |
| 4715 | sacaria | 1 |
| 4716 | sacaremos | 1 |
| 4717 | sacan | 1 |
| 4718 | sacamos | 1 |
| 4719 | sacadas | 1 |
| 4720 | sabuesos | 1 |
| 4721 | sabrosa | 1 |
| 4722 | sabran | 1 |
| 4723 | sabidora | 1 |
| 4724 | sabidor | 1 |
| 4725 | sabida | 1 |
| 4726 | sabialo | 1 |
| 4727 | sabete | 1 |
| 4728 | sabemos | 1 |
| 4729 | sabella | 1 |
| 4730 | sabedme | 1 |
| 4731 | ruysenores | 1 |
| 4732 | ruynmente | 1 |
| 4733 | ruynes | 1 |
| 4734 | ruyndades | 1 |
| 4735 | ruuios | 1 |
| 4736 | ruuia | 1 |
| 4737 | rueguen | 1 |
| 4738 | ruegue | 1 |
| 4739 | rueca | 1 |
| 4740 | rudentes | 1 |
| 4741 | rubricas | 1 |
| 4742 | rubies | 1 |
| 4743 | rubicundos | 1 |
| 4744 | roy | 1 |
| 4745 | rondemos | 1 |
| 4746 | ronces | 1 |
| 4747 | romulo | 1 |
| 4748 | rompimiento | 1 |
| 4749 | rompiera | 1 |
| 4750 | rompiendo | 1 |
| 4751 | rompenecios | 1 |
| 4752 | rompa | 1 |
| 4753 | romances | 1 |
| 4754 | romana | 1 |
| 4755 | romadizo | 1 |
| 4756 | rogue | 1 |
| 4757 | rogome | 1 |
| 4758 | rogo | 1 |
| 4759 | rogauan | 1 |
| 4760 | rogaste | 1 |
| 4761 | rogandome | 1 |
| 4762 | rogando | 1 |
| 4763 | rogadores | 1 |
| 4764 | rogad | 1 |
| 4765 | roen | 1 |
| 4766 | rodrigo | 1 |
| 4767 | rodearse | 1 |
| 4768 | rodeando | 1 |
| 4769 | rodara | 1 |
| 4770 | rociarias | 1 |
| 4771 | rocho | 1 |
| 4772 | rocadero | 1 |
| 4773 | robusta | 1 |
| 4774 | robo | 1 |
| 4775 | roble | 1 |
| 4776 | robaron | 1 |
| 4777 | robar | 1 |
| 4778 | roban | 1 |
| 4779 | robado | 1 |
| 4780 | ro | 1 |
| 4781 | riza | 1 |
| 4782 | rixoso | 1 |
| 4783 | risas | 1 |
| 4784 | rios | 1 |
| 4785 | riome | 1 |
| 4786 | rinieron | 1 |
| 4787 | rinen | 1 |
| 4788 | rine | 1 |
| 4789 | rimero | 1 |
| 4790 | rigurosos | 1 |
| 4791 | riguroso | 1 |
| 4792 | rigorosamente | 1 |
| 4793 | rigores | 1 |
| 4794 | rigera | 1 |
| 4795 | rieste | 1 |
| 4796 | riendo | 1 |
| 4797 | ricas | 1 |
| 4798 | ribera | 1 |
| 4799 | rezongadores | 1 |
| 4800 | reze | 1 |
| 4801 | rezare | 1 |
| 4802 | rezan | 1 |
| 4803 | rezado | 1 |
| 4804 | reza | 1 |
| 4805 | reys | 1 |
| 4806 | reyrme | 1 |
| 4807 | reynas | 1 |
| 4808 | reyes | 1 |
| 4809 | reya | 1 |
| 4810 | reuolucion | 1 |
| 4811 | reuisto | 1 |
| 4812 | reuista | 1 |
| 4813 | reui | 1 |
| 4814 | reuessar | 1 |
| 4815 | reuesar | 1 |
| 4816 | reues | 1 |
| 4817 | reuerenda | 1 |
| 4818 | reuerberar | 1 |
| 4819 | reuana | 1 |
| 4820 | retraydo | 1 |
| 4821 | retrayas | 1 |
| 4822 | retraimiento | 1 |
| 4823 | retraete | 1 |
| 4824 | retrae | 1 |
| 4825 | retozala | 1 |
| 4826 | retorciendo | 1 |
| 4827 | retinens | 1 |
| 4828 | resurrecion | 1 |
| 4829 | resultara | 1 |
| 4830 | resultan | 1 |
| 4831 | restuarar | 1 |
| 4832 | restituyo | 1 |
| 4833 | restitucion | 1 |
| 4834 | restaurara | 1 |
| 4835 | restaurar | 1 |
| 4836 | responso | 1 |
| 4837 | respondio | 1 |
| 4838 | respondiera | 1 |
| 4839 | respondido | 1 |
| 4840 | respondias | 1 |
| 4841 | respondes | 1 |
| 4842 | responderia | 1 |
| 4843 | respondera | 1 |
| 4844 | respondeme | 1 |
| 4845 | responda | 1 |
| 4846 | resplandesciente | 1 |
| 4847 | respecto | 1 |
| 4848 | resollos | 1 |
| 4849 | resistir | 1 |
| 4850 | resistencia | 1 |
| 4851 | resiste | 1 |
| 4852 | resfriado | 1 |
| 4853 | resciba | 1 |
| 4854 | rescebiste | 1 |
| 4855 | rescebir | 1 |
| 4856 | resabio | 1 |
| 4857 | requiero | 1 |
| 4858 | requieren | 1 |
| 4859 | requerir | 1 |
| 4860 | requerimientos | 1 |
| 4861 | requerimiento | 1 |
| 4862 | reputas | 1 |
| 4863 | reputaron | 1 |
| 4864 | republica | 1 |
| 4865 | reptilias | 1 |
| 4866 | reptilia | 1 |
| 4867 | reprueua | 1 |
| 4868 | reproche | 1 |
| 4869 | reprobas | 1 |
| 4870 | representas | 1 |
| 4871 | representada | 1 |
| 4872 | reprendiendolo | 1 |
| 4873 | reprende | 1 |
| 4874 | reprehensiones | 1 |
| 4875 | reprehendas | 1 |
| 4876 | repose | 1 |
| 4877 | reposan | 1 |
| 4878 | reportorio | 1 |
| 4879 | replicare | 1 |
| 4880 | replica | 1 |
| 4881 | repisar | 1 |
| 4882 | repiquete | 1 |
| 4883 | repica | 1 |
| 4884 | repetirla | 1 |
| 4885 | repartidos | 1 |
| 4886 | repartidas | 1 |
| 4887 | reparta | 1 |
| 4888 | reparo | 1 |
| 4889 | reo | 1 |
| 4890 | renzillas | 1 |
| 4891 | renteros | 1 |
| 4892 | renouaras | 1 |
| 4893 | renouar | 1 |
| 4894 | renouado | 1 |
| 4895 | reniego | 1 |
| 4896 | renia | 1 |
| 4897 | renglon | 1 |
| 4898 | rendirse | 1 |
| 4899 | rencor | 1 |
| 4900 | remudar | 1 |
| 4901 | remontado | 1 |
| 4902 | remojo | 1 |
| 4903 | remiro | 1 |
| 4904 | remira | 1 |
| 4905 | remetieron | 1 |
| 4906 | remediaua | 1 |
| 4907 | remediarse | 1 |
| 4908 | remediarlos | 1 |
| 4909 | remediara | 1 |
| 4910 | remedia | 1 |
| 4911 | remedasses | 1 |
| 4912 | remando | 1 |
| 4913 | relumbrays | 1 |
| 4914 | religiosa | 1 |
| 4915 | religion | 1 |
| 4916 | relieuan | 1 |
| 4917 | releerlo | 1 |
| 4918 | relatar | 1 |
| 4919 | relacion | 1 |
| 4920 | reja | 1 |
| 4921 | reintegracion | 1 |
| 4922 | rehuyria | 1 |
| 4923 | rehuyre | 1 |
| 4924 | rehuyr | 1 |
| 4925 | rehusaua | 1 |
| 4926 | rehusa | 1 |
| 4927 | rehinchays | 1 |
| 4928 | regla | 1 |
| 4929 | regisvos | 1 |
| 4930 | registro | 1 |
| 4931 | registrar | 1 |
| 4932 | region | 1 |
| 4933 | regidos | 1 |
| 4934 | regidor | 1 |
| 4935 | regia | 1 |
| 4936 | regeneracion | 1 |
| 4937 | regare | 1 |
| 4938 | regalos | 1 |
| 4939 | regalaua | 1 |
| 4940 | refranes | 1 |
| 4941 | refiero | 1 |
| 4942 | reduzido | 1 |
| 4943 | reduze | 1 |
| 4944 | reduxiste | 1 |
| 4945 | redunde | 1 |
| 4946 | redondo | 1 |
| 4947 | redondeza | 1 |
| 4948 | redomillas | 1 |
| 4949 | redomilla | 1 |
| 4950 | redencion | 1 |
| 4951 | recursos | 1 |
| 4952 | recuenta | 1 |
| 4953 | recordasedes | 1 |
| 4954 | recordando | 1 |
| 4955 | recontar | 1 |
| 4956 | reconoscimiento | 1 |
| 4957 | recogia | 1 |
| 4958 | recobran | 1 |
| 4959 | recibiria | 1 |
| 4960 | recibira | 1 |
| 4961 | recibir | 1 |
| 4962 | recibio | 1 |
| 4963 | recibiesse | 1 |
| 4964 | recibes | 1 |
| 4965 | recibeme | 1 |
| 4966 | rechazaua | 1 |
| 4967 | recelaua | 1 |
| 4968 | recebiran | 1 |
| 4969 | recebimiento | 1 |
| 4970 | recebidas | 1 |
| 4971 | recebid | 1 |
| 4972 | recebia | 1 |
| 4973 | recebi | 1 |
| 4974 | recaudo | 1 |
| 4975 | recaudado | 1 |
| 4976 | recabde | 1 |
| 4977 | recabdar | 1 |
| 4978 | rebuznando | 1 |
| 4979 | rebueluo | 1 |
| 4980 | rebueluas | 1 |
| 4981 | rebuelto | 1 |
| 4982 | rebozados | 1 |
| 4983 | rebozado | 1 |
| 4984 | reboluedores | 1 |
| 4985 | rebolcado | 1 |
| 4986 | rebentasse | 1 |
| 4987 | rebentarias | 1 |
| 4988 | rebentar | 1 |
| 4989 | real | 1 |
| 4990 | rayz | 1 |
| 4991 | raydo | 1 |
| 4992 | rayauan | 1 |
| 4993 | rayas | 1 |
| 4994 | raya | 1 |
| 4995 | rauio | 1 |
| 4996 | rauia | 1 |
| 4997 | ratos | 1 |
| 4998 | ratonado | 1 |
| 4999 | ratonada | 1 |
| 5000 | raton | 1 |
| 5001 | rasuras | 1 |
| 5002 | rasgues | 1 |
| 5003 | rasgases | 1 |
| 5004 | rasgare | 1 |
| 5005 | rasgados | 1 |
| 5006 | rascuno | 1 |
| 5007 | rascunes | 1 |
| 5008 | rascarle | 1 |
| 5009 | rascando | 1 |
| 5010 | rascacauallos | 1 |
| 5011 | raras | 1 |
| 5012 | rapido | 1 |
| 5013 | rapidas | 1 |
| 5014 | ranas | 1 |
| 5015 | ramo | 1 |
| 5016 | ramas | 1 |
| 5017 | rama | 1 |
| 5018 | raleza | 1 |
| 5019 | raciones | 1 |
| 5020 | racionero | 1 |
| 5021 | racion | 1 |
| 5022 | rabiosos | 1 |
| 5023 | rabiosa | 1 |
| 5024 | quixadas | 1 |
| 5025 | quito | 1 |
| 5026 | quitasteme | 1 |
| 5027 | quitasse | 1 |
| 5028 | quitarte | 1 |
| 5029 | quitarse | 1 |
| 5030 | quitaron | 1 |
| 5031 | quitarleslas | 1 |
| 5032 | quitarla | 1 |
| 5033 | quitare | 1 |
| 5034 | quitara | 1 |
| 5035 | quitanles | 1 |
| 5036 | quitamela | 1 |
| 5037 | quitame | 1 |
| 5038 | quitado | 1 |
| 5039 | quisto | 1 |
| 5040 | quisiste | 1 |
| 5041 | quisiessen | 1 |
| 5042 | quisieses | 1 |
| 5043 | quisierdes | 1 |
| 5044 | quisieras | 1 |
| 5045 | quiselo | 1 |
| 5046 | quinto | 1 |
| 5047 | quinientas | 1 |
| 5048 | quilates | 1 |
| 5049 | quietas | 1 |
| 5050 | quierote | 1 |
| 5051 | quierolo | 1 |
| 5052 | quierola | 1 |
| 5053 | quiereslo | 1 |
| 5054 | quiereseles | 1 |
| 5055 | quieran | 1 |
| 5056 | quier | 1 |
| 5057 | quiebren | 1 |
| 5058 | quiebrasnos | 1 |
| 5059 | quiebras | 1 |
| 5060 | quicios | 1 |
| 5061 | quexosos | 1 |
| 5062 | quexome | 1 |
| 5063 | quexo | 1 |
| 5064 | quexaua | 1 |
| 5065 | quexasseme | 1 |
| 5066 | quexase | 1 |
| 5067 | quexarme | 1 |
| 5068 | quexaran | 1 |
| 5069 | quexan | 1 |
| 5070 | questioncillas | 1 |
| 5071 | question | 1 |
| 5072 | querran | 1 |
| 5073 | queriendo | 1 |
| 5074 | quereys | 1 |
| 5075 | quereros | 1 |
| 5076 | quererlo | 1 |
| 5077 | querellan | 1 |
| 5078 | querella | 1 |
| 5079 | querays | 1 |
| 5080 | queramos | 1 |
| 5081 | quepa | 1 |
| 5082 | quemo | 1 |
| 5083 | queme | 1 |
| 5084 | quemaua | 1 |
| 5085 | quemaste | 1 |
| 5086 | quemas | 1 |
| 5087 | quemarnos | 1 |
| 5088 | quemar | 1 |
| 5089 | quemadas | 1 |
| 5090 | quemada | 1 |
| 5091 | quedito | 1 |
| 5092 | quedauanle | 1 |
| 5093 | quedauan | 1 |
| 5094 | quedarse | 1 |
| 5095 | quedaron | 1 |
| 5096 | quedaria | 1 |
| 5097 | quedare | 1 |
| 5098 | quedamos | 1 |
| 5099 | quedado | 1 |
| 5100 | quedada | 1 |
| 5101 | quebro | 1 |
| 5102 | quebreys | 1 |
| 5103 | quebre | 1 |
| 5104 | quebrasses | 1 |
| 5105 | quebrare | 1 |
| 5106 | quebraras | 1 |
| 5107 | quebrar | 1 |
| 5108 | quebrantar | 1 |
| 5109 | quebrantados | 1 |
| 5110 | quebranta | 1 |
| 5111 | quebradas | 1 |
| 5112 | quebrada | 1 |
| 5113 | quatorzeno | 1 |
| 5114 | quatitur | 1 |
| 5115 | quarta | 1 |
| 5116 | quarenta | 1 |
| 5117 | quantias | 1 |
| 5118 | qualidades | 1 |
| 5119 | putos | 1 |
| 5120 | putillos | 1 |
| 5121 | putillo | 1 |
| 5122 | putico | 1 |
| 5123 | putas | 1 |
| 5124 | pusose | 1 |
| 5125 | pusome | 1 |
| 5126 | pusiste | 1 |
| 5127 | pusilanimo | 1 |
| 5128 | pusiesse | 1 |
| 5129 | pusiera | 1 |
| 5130 | pusete | 1 |
| 5131 | puro | 1 |
| 5132 | purgo | 1 |
| 5133 | purgatorio | 1 |
| 5134 | purgara | 1 |
| 5135 | purgando | 1 |
| 5136 | puramente | 1 |
| 5137 | puppim | 1 |
| 5138 | punturas | 1 |
| 5139 | puntado | 1 |
| 5140 | puno | 1 |
| 5141 | punir | 1 |
| 5142 | punicion | 1 |
| 5143 | pungidos | 1 |
| 5144 | pungido | 1 |
| 5145 | punaladas | 1 |
| 5146 | punadas | 1 |
| 5147 | pulicena | 1 |
| 5148 | pulgares | 1 |
| 5149 | pugnes | 1 |
| 5150 | pugnado | 1 |
| 5151 | puestas | 1 |
| 5152 | puerto | 1 |
| 5153 | puercos | 1 |
| 5154 | puerca | 1 |
| 5155 | puente | 1 |
| 5156 | puedense | 1 |
| 5157 | puebla | 1 |
| 5158 | pudistes | 1 |
| 5159 | pudieses | 1 |
| 5160 | pudieres | 1 |
| 5161 | pudieremos | 1 |
| 5162 | publiquemos | 1 |
| 5163 | publicas | 1 |
| 5164 | publicando | 1 |
| 5165 | publicamente | 1 |
| 5166 | publicado | 1 |
| 5167 | prueuas | 1 |
| 5168 | prudentes | 1 |
| 5169 | prudente | 1 |
| 5170 | proximos | 1 |
| 5171 | prouoques | 1 |
| 5172 | prouocasme | 1 |
| 5173 | prouocas | 1 |
| 5174 | prouocara | 1 |
| 5175 | prouienen | 1 |
| 5176 | prouiene | 1 |
| 5177 | proueyste | 1 |
| 5178 | proueyesse | 1 |
| 5179 | proueydas | 1 |
| 5180 | prouey | 1 |
| 5181 | proueo | 1 |
| 5182 | proueamos | 1 |
| 5183 | prosperos | 1 |
| 5184 | prospero | 1 |
| 5185 | prosperete | 1 |
| 5186 | prosperamente | 1 |
| 5187 | prorogarle | 1 |
| 5188 | propusiera | 1 |
| 5189 | proprio | 1 |
| 5190 | propriedades | 1 |
| 5191 | propriedad | 1 |
| 5192 | proporna | 1 |
| 5193 | proponiendo | 1 |
| 5194 | proponia | 1 |
| 5195 | propheta | 1 |
| 5196 | propemodum | 1 |
| 5197 | pronuncian | 1 |
| 5198 | pronosticaste | 1 |
| 5199 | prompta | 1 |
| 5200 | promouera | 1 |
| 5201 | prometida | 1 |
| 5202 | prometia | 1 |
| 5203 | prometeslo | 1 |
| 5204 | prometen | 1 |
| 5205 | promessas | 1 |
| 5206 | promesas | 1 |
| 5207 | promesa | 1 |
| 5208 | prologo | 1 |
| 5209 | prolixos | 1 |
| 5210 | prolixo | 1 |
| 5211 | prolixas | 1 |
| 5212 | prolixa | 1 |
| 5213 | prohibiendo | 1 |
| 5214 | profundidad | 1 |
| 5215 | profetas | 1 |
| 5216 | profeta | 1 |
| 5217 | procures | 1 |
| 5218 | procuremos | 1 |
| 5219 | procure | 1 |
| 5220 | procuraste | 1 |
| 5221 | procuraron | 1 |
| 5222 | procurando | 1 |
| 5223 | procuran | 1 |
| 5224 | procurador | 1 |
| 5225 | procura | 1 |
| 5226 | procreen | 1 |
| 5227 | processiones | 1 |
| 5228 | proceder | 1 |
| 5229 | procedas | 1 |
| 5230 | proceda | 1 |
| 5231 | probatica | 1 |
| 5232 | proaza | 1 |
| 5233 | priuas | 1 |
| 5234 | priuaria | 1 |
| 5235 | priuar | 1 |
| 5236 | priuanza | 1 |
| 5237 | principiado | 1 |
| 5238 | principales | 1 |
| 5239 | primor | 1 |
| 5240 | primeros | 1 |
| 5241 | primeramente | 1 |
| 5242 | primas | 1 |
| 5243 | preuenir | 1 |
| 5244 | preuenidos | 1 |
| 5245 | preuaricadora | 1 |
| 5246 | presurosa | 1 |
| 5247 | presumptuosa | 1 |
| 5248 | presumes | 1 |
| 5249 | presumas | 1 |
| 5250 | prestar | 1 |
| 5251 | pressuroso | 1 |
| 5252 | pressura | 1 |
| 5253 | pressa | 1 |
| 5254 | presos | 1 |
| 5255 | presento | 1 |
| 5256 | preparas | 1 |
| 5257 | prenuncio | 1 |
| 5258 | prenderme | 1 |
| 5259 | prendelos | 1 |
| 5260 | prende | 1 |
| 5261 | prendas | 1 |
| 5262 | prenda | 1 |
| 5263 | premissas | 1 |
| 5264 | premias | 1 |
| 5265 | premia | 1 |
| 5266 | pregunto | 1 |
| 5267 | preguntes | 1 |
| 5268 | preguntarte | 1 |
| 5269 | preguntarme | 1 |
| 5270 | preguntarle | 1 |
| 5271 | preguntaras | 1 |
| 5272 | preguntandome | 1 |
| 5273 | preguntan | 1 |
| 5274 | preguntado | 1 |
| 5275 | preguntada | 1 |
| 5276 | pregones | 1 |
| 5277 | pregonas | 1 |
| 5278 | pregonan | 1 |
| 5279 | precie | 1 |
| 5280 | preciauan | 1 |
| 5281 | precias | 1 |
| 5282 | preciarte | 1 |
| 5283 | precia | 1 |
| 5284 | precepto | 1 |
| 5285 | precedente | 1 |
| 5286 | precede | 1 |
| 5287 | preambulos | 1 |
| 5288 | preambulo | 1 |
| 5289 | pozo | 1 |
| 5290 | poyo | 1 |
| 5291 | posturas | 1 |
| 5292 | postrero | 1 |
| 5293 | postigo | 1 |
| 5294 | postemas | 1 |
| 5295 | postema | 1 |
| 5296 | posseydos | 1 |
| 5297 | posseydo | 1 |
| 5298 | posseido | 1 |
| 5299 | posseerian | 1 |
| 5300 | posseen | 1 |
| 5301 | posiste | 1 |
| 5302 | poseydos | 1 |
| 5303 | posentado | 1 |
| 5304 | poseellas | 1 |
| 5305 | posee | 1 |
| 5306 | porne | 1 |
| 5307 | porfias | 1 |
| 5308 | porfiados | 1 |
| 5309 | poquitas | 1 |
| 5310 | poquillo | 1 |
| 5311 | ponte | 1 |
| 5312 | ponla | 1 |
| 5313 | pongas | 1 |
| 5314 | poneysme | 1 |
| 5315 | ponesme | 1 |
| 5316 | ponerte | 1 |
| 5317 | ponerlos | 1 |
| 5318 | ponerla | 1 |
| 5319 | poneos | 1 |
| 5320 | ponente | 1 |
| 5321 | poneldos | 1 |
| 5322 | pomo | 1 |
| 5323 | poluorizadas | 1 |
| 5324 | poluillos | 1 |
| 5325 | polonia | 1 |
| 5326 | pollitos | 1 |
| 5327 | poleo | 1 |
| 5328 | poetas | 1 |
| 5329 | poesias | 1 |
| 5330 | podrian | 1 |
| 5331 | podriala | 1 |
| 5332 | podiendolos | 1 |
| 5333 | podias | 1 |
| 5334 | poderte | 1 |
| 5335 | poderse | 1 |
| 5336 | poderosos | 1 |
| 5337 | poderosa | 1 |
| 5338 | podernos | 1 |
| 5339 | poderlo | 1 |
| 5340 | poderle | 1 |
| 5341 | podamos | 1 |
| 5342 | pobremente | 1 |
| 5343 | pluuias | 1 |
| 5344 | plomo | 1 |
| 5345 | plinio | 1 |
| 5346 | plega | 1 |
| 5347 | pleberico | 1 |
| 5348 | plazo | 1 |
| 5349 | plazia | 1 |
| 5350 | plazas | 1 |
| 5351 | plauto | 1 |
| 5352 | plato | 1 |
| 5353 | planto | 1 |
| 5354 | plante | 1 |
| 5355 | planetas | 1 |
| 5356 | planeta | 1 |
| 5357 | plaga | 1 |
| 5358 | piscina | 1 |
| 5359 | piramo | 1 |
| 5360 | pintor | 1 |
| 5361 | pinto | 1 |
| 5362 | pintemos | 1 |
| 5363 | pinte | 1 |
| 5364 | pintasse | 1 |
| 5365 | pintando | 1 |
| 5366 | pintan | 1 |
| 5367 | pintados | 1 |
| 5368 | pintada | 1 |
| 5369 | pinones | 1 |
| 5370 | pimpollo | 1 |
| 5371 | pierna | 1 |
| 5372 | pierdase | 1 |
| 5373 | pierdan | 1 |
| 5374 | pielago | 1 |
| 5375 | pidio | 1 |
| 5376 | pidieron | 1 |
| 5377 | pidiere | 1 |
| 5378 | pidiera | 1 |
| 5379 | pidiendome | 1 |
| 5380 | pidenles | 1 |
| 5381 | pidelo | 1 |
| 5382 | pidan | 1 |
| 5383 | pida | 1 |
| 5384 | picazas | 1 |
| 5385 | picar | 1 |
| 5386 | pias | 1 |
| 5387 | piadosas | 1 |
| 5388 | piadosa | 1 |
| 5389 | pia | 1 |
| 5390 | phrates | 1 |
| 5391 | philosophos | 1 |
| 5392 | philosomia | 1 |
| 5393 | philipo | 1 |
| 5394 | phebo | 1 |
| 5395 | phebeo | 1 |
| 5396 | peyne | 1 |
| 5397 | peynanla | 1 |
| 5398 | peynados | 1 |
| 5399 | peynadores | 1 |
| 5400 | petreras | 1 |
| 5401 | petrarcha | 1 |
| 5402 | peticiones | 1 |
| 5403 | pestiferos | 1 |
| 5404 | pestanas | 1 |
| 5405 | pesquisa | 1 |
| 5406 | pese | 1 |
| 5407 | pescas | 1 |
| 5408 | pescados | 1 |
| 5409 | pescadores | 1 |
| 5410 | pesassen | 1 |
| 5411 | pesame | 1 |
| 5412 | pesadumbre | 1 |
| 5413 | pesados | 1 |
| 5414 | pesadas | 1 |
| 5415 | peruertieras | 1 |
| 5416 | peruertido | 1 |
| 5417 | pertinacia | 1 |
| 5418 | pertenesce | 1 |
| 5419 | personaje | 1 |
| 5420 | persigues | 1 |
| 5421 | persigue | 1 |
| 5422 | perseuerando | 1 |
| 5423 | perseueran | 1 |
| 5424 | perseueracion | 1 |
| 5425 | perseuera | 1 |
| 5426 | perseguidor | 1 |
| 5427 | persecuciones | 1 |
| 5428 | persecucion | 1 |
| 5429 | perra | 1 |
| 5430 | perpetuo | 1 |
| 5431 | perpetuase | 1 |
| 5432 | perpetuas | 1 |
| 5433 | perniles | 1 |
| 5434 | pernil | 1 |
| 5435 | permites | 1 |
| 5436 | permite | 1 |
| 5437 | permission | 1 |
| 5438 | permanesce | 1 |
| 5439 | perlica | 1 |
| 5440 | pericles | 1 |
| 5441 | perfumes | 1 |
| 5442 | perfumera | 1 |
| 5443 | perfuma | 1 |
| 5444 | perficion | 1 |
| 5445 | perfetos | 1 |
| 5446 | perfecta | 1 |
| 5447 | perfecion | 1 |
| 5448 | perezcas | 1 |
| 5449 | peresciessen | 1 |
| 5450 | peresceria | 1 |
| 5451 | peregrinado | 1 |
| 5452 | perdurable | 1 |
| 5453 | perdonelos | 1 |
| 5454 | perdonele | 1 |
| 5455 | perdonar | 1 |
| 5456 | perdonada | 1 |
| 5457 | perdiendose | 1 |
| 5458 | perdian | 1 |
| 5459 | perdeys | 1 |
| 5460 | perderse | 1 |
| 5461 | perderle | 1 |
| 5462 | perderias | 1 |
| 5463 | perderiamos | 1 |
| 5464 | perdere | 1 |
| 5465 | perdera | 1 |
| 5466 | perdemos | 1 |
| 5467 | perdamos | 1 |
| 5468 | perbreue | 1 |
| 5469 | peque | 1 |
| 5470 | pepitas | 1 |
| 5471 | pepita | 1 |
| 5472 | pensemos | 1 |
| 5473 | pensatiuo | 1 |
| 5474 | pensaron | 1 |
| 5475 | pensarle | 1 |
| 5476 | pensarian | 1 |
| 5477 | pensaras | 1 |
| 5478 | pensallo | 1 |
| 5479 | penoso | 1 |
| 5480 | penetro | 1 |
| 5481 | penetre | 1 |
| 5482 | penetraron | 1 |
| 5483 | penes | 1 |
| 5484 | penen | 1 |
| 5485 | pendiere | 1 |
| 5486 | penauas | 1 |
| 5487 | penasse | 1 |
| 5488 | penase | 1 |
| 5489 | penaria | 1 |
| 5490 | penara | 1 |
| 5491 | pelon | 1 |
| 5492 | pellizcos | 1 |
| 5493 | pelligeros | 1 |
| 5494 | pelleja | 1 |
| 5495 | peligrosas | 1 |
| 5496 | peligre | 1 |
| 5497 | pelicano | 1 |
| 5498 | pelechar | 1 |
| 5499 | pelean | 1 |
| 5500 | pele | 1 |
| 5501 | pelan | 1 |
| 5502 | pelacejas | 1 |
| 5503 | pegones | 1 |
| 5504 | pegajosa | 1 |
| 5505 | pegado | 1 |
| 5506 | pedregoso | 1 |
| 5507 | pediste | 1 |
| 5508 | pedirte | 1 |
| 5509 | pedias | 1 |
| 5510 | pedazo | 1 |
| 5511 | peco | 1 |
| 5512 | pecco | 1 |
| 5513 | pecare | 1 |
| 5514 | pecadoras | 1 |
| 5515 | pe | 1 |
| 5516 | paxarera | 1 |
| 5517 | paxaras | 1 |
| 5518 | pauorosas | 1 |
| 5519 | pauor | 1 |
| 5520 | paulo | 1 |
| 5521 | patricidas | 1 |
| 5522 | paterno | 1 |
| 5523 | paterna | 1 |
| 5524 | pastores | 1 |
| 5525 | pastellera | 1 |
| 5526 | passionados | 1 |
| 5527 | passes | 1 |
| 5528 | passea | 1 |
| 5529 | passauan | 1 |
| 5530 | passatiempo | 1 |
| 5531 | passasse | 1 |
| 5532 | passarse | 1 |
| 5533 | passaremos | 1 |
| 5534 | passare | 1 |
| 5535 | passaran | 1 |
| 5536 | passando | 1 |
| 5537 | pasiphe | 1 |
| 5538 | pasiones | 1 |
| 5539 | pasion | 1 |
| 5540 | pasife | 1 |
| 5541 | pases | 1 |
| 5542 | pascia | 1 |
| 5543 | pasce | 1 |
| 5544 | pasaua | 1 |
| 5545 | pasatiempos | 1 |
| 5546 | pasasen | 1 |
| 5547 | pasar | 1 |
| 5548 | pasan | 1 |
| 5549 | pasados | 1 |
| 5550 | pasada | 1 |
| 5551 | partome | 1 |
| 5552 | partirme | 1 |
| 5553 | partiesses | 1 |
| 5554 | partiessen | 1 |
| 5555 | particular | 1 |
| 5556 | participe | 1 |
| 5557 | participan | 1 |
| 5558 | particion | 1 |
| 5559 | parti | 1 |
| 5560 | parthos | 1 |
| 5561 | partezica | 1 |
| 5562 | partera | 1 |
| 5563 | parten | 1 |
| 5564 | partas | 1 |
| 5565 | partamos | 1 |
| 5566 | paro | 1 |
| 5567 | parmenico | 1 |
| 5568 | parlero | 1 |
| 5569 | parleria | 1 |
| 5570 | parlar | 1 |
| 5571 | parlando | 1 |
| 5572 | parlan | 1 |
| 5573 | pariste | 1 |
| 5574 | parieres | 1 |
| 5575 | pariente | 1 |
| 5576 | parido | 1 |
| 5577 | paridad | 1 |
| 5578 | parezco | 1 |
| 5579 | parezcas | 1 |
| 5580 | paresciere | 1 |
| 5581 | parescido | 1 |
| 5582 | parescete | 1 |
| 5583 | paresces | 1 |
| 5584 | parens | 1 |
| 5585 | pareciendote | 1 |
| 5586 | parecen | 1 |
| 5587 | pareceme | 1 |
| 5588 | pare | 1 |
| 5589 | parate | 1 |
| 5590 | pararan | 1 |
| 5591 | paran | 1 |
| 5592 | parado | 1 |
| 5593 | paradillas | 1 |
| 5594 | papa | 1 |
| 5595 | panes | 1 |
| 5596 | pandero | 1 |
| 5597 | palmo | 1 |
| 5598 | palmada | 1 |
| 5599 | palma | 1 |
| 5600 | palanciano | 1 |
| 5601 | palabrilla | 1 |
| 5602 | pala | 1 |
| 5603 | pajezico | 1 |
| 5604 | pajes | 1 |
| 5605 | paje | 1 |
| 5606 | paguen | 1 |
| 5607 | pagos | 1 |
| 5608 | pagasse | 1 |
| 5609 | pagandole | 1 |
| 5610 | pagan | 1 |
| 5611 | pagalla | 1 |
| 5612 | pagados | 1 |
| 5613 | padrino | 1 |
| 5614 | padezcase | 1 |
| 5615 | padescido | 1 |
| 5616 | padescian | 1 |
| 5617 | padescer | 1 |
| 5618 | padescemos | 1 |
| 5619 | padecido | 1 |
| 5620 | pacificos | 1 |
| 5621 | pa | 1 |
| 5622 | oystes | 1 |
| 5623 | oyrle | 1 |
| 5624 | oyre | 1 |
| 5625 | oyra | 1 |
| 5626 | oylla | 1 |
| 5627 | oygas | 1 |
| 5628 | oyga | 1 |
| 5629 | oyessen | 1 |
| 5630 | oyentes | 1 |
| 5631 | oyendole | 1 |
| 5632 | oydme | 1 |
| 5633 | oydas | 1 |
| 5634 | oyas | 1 |
| 5635 | oyan | 1 |
| 5636 | oxear | 1 |
| 5637 | ouiessemos | 1 |
| 5638 | ouieres | 1 |
| 5639 | ouiera | 1 |
| 5640 | ouidio | 1 |
| 5641 | oueja | 1 |
| 5642 | otrie | 1 |
| 5643 | otri | 1 |
| 5644 | otorgado | 1 |
| 5645 | osso | 1 |
| 5646 | ose | 1 |
| 5647 | osauan | 1 |
| 5648 | osaua | 1 |
| 5649 | osaste | 1 |
| 5650 | osare | 1 |
| 5651 | osado | 1 |
| 5652 | osa | 1 |
| 5653 | ortolano | 1 |
| 5654 | ortelano | 1 |
| 5655 | ortelana | 1 |
| 5656 | ortaliza | 1 |
| 5657 | orpheo | 1 |
| 5658 | orode | 1 |
| 5659 | origen | 1 |
| 5660 | oriente | 1 |
| 5661 | orientales | 1 |
| 5662 | organo | 1 |
| 5663 | orfeo | 1 |
| 5664 | orestes | 1 |
| 5665 | oreja | 1 |
| 5666 | ordinario | 1 |
| 5667 | ordenola | 1 |
| 5668 | ordeno | 1 |
| 5669 | ordenemos | 1 |
| 5670 | ordene | 1 |
| 5671 | ordenaste | 1 |
| 5672 | ordenas | 1 |
| 5673 | ordenada | 1 |
| 5674 | orador | 1 |
| 5675 | ora | 1 |
| 5676 | opinando | 1 |
| 5677 | operaciones | 1 |
| 5678 | operacion | 1 |
| 5679 | onzeno | 1 |
| 5680 | onza | 1 |
| 5681 | onesto | 1 |
| 5682 | onestad | 1 |
| 5683 | onesta | 1 |
| 5684 | ondosos | 1 |
| 5685 | ondean | 1 |
| 5686 | oluides | 1 |
| 5687 | oluidemos | 1 |
| 5688 | oluidases | 1 |
| 5689 | oluidas | 1 |
| 5690 | oluidaron | 1 |
| 5691 | oluidaras | 1 |
| 5692 | oluidan | 1 |
| 5693 | oluidada | 1 |
| 5694 | olorosas | 1 |
| 5695 | oliendo | 1 |
| 5696 | olias | 1 |
| 5697 | oler | 1 |
| 5698 | ofrezco | 1 |
| 5699 | ofrescimientos | 1 |
| 5700 | ofrescimiento | 1 |
| 5701 | ofrescido | 1 |
| 5702 | ofrescia | 1 |
| 5703 | ofrescer | 1 |
| 5704 | ofrescele | 1 |
| 5705 | ofreciste | 1 |
| 5706 | ofrecian | 1 |
| 5707 | oficiales | 1 |
| 5708 | oficial | 1 |
| 5709 | offrezco | 1 |
| 5710 | offrescimientos | 1 |
| 5711 | offrescer | 1 |
| 5712 | offresce | 1 |
| 5713 | offrecimientos | 1 |
| 5714 | officios | 1 |
| 5715 | offertas | 1 |
| 5716 | offensione | 1 |
| 5717 | offension | 1 |
| 5718 | offendio | 1 |
| 5719 | offendido | 1 |
| 5720 | offendes | 1 |
| 5721 | offenderte | 1 |
| 5722 | offender | 1 |
| 5723 | offendedor | 1 |
| 5724 | ofensa | 1 |
| 5725 | ofendo | 1 |
| 5726 | ofender | 1 |
| 5727 | odioso | 1 |
| 5728 | odiosas | 1 |
| 5729 | odiosamente | 1 |
| 5730 | odiosa | 1 |
| 5731 | ocupes | 1 |
| 5732 | ocupan | 1 |
| 5733 | ocupados | 1 |
| 5734 | ocupa | 1 |
| 5735 | ocultamente | 1 |
| 5736 | octauo | 1 |
| 5737 | ociosa | 1 |
| 5738 | ochenta | 1 |
| 5739 | occupado | 1 |
| 5740 | obviant | 1 |
| 5741 | obsequias | 1 |
| 5742 | obro | 1 |
| 5743 | obren | 1 |
| 5744 | obrarse | 1 |
| 5745 | obraron | 1 |
| 5746 | obrara | 1 |
| 5747 | obliganseles | 1 |
| 5748 | obligan | 1 |
| 5749 | objecto | 1 |
| 5750 | obispos | 1 |
| 5751 | obispo | 1 |
| 5752 | obediente | 1 |
| 5753 | obedescian | 1 |
| 5754 | obedescerian | 1 |
| 5755 | obedescer | 1 |
| 5756 | obedecera | 1 |
| 5757 | obedecer | 1 |
| 5758 | obedecen | 1 |
| 5759 | obedece | 1 |
| 5760 | nutria | 1 |
| 5761 | nuezes | 1 |
| 5762 | nublados | 1 |
| 5763 | nublado | 1 |
| 5764 | nouicios | 1 |
| 5765 | noueno | 1 |
| 5766 | noturnos | 1 |
| 5767 | noturnas | 1 |
| 5768 | noturna | 1 |
| 5769 | notorio | 1 |
| 5770 | notad | 1 |
| 5771 | notables | 1 |
| 5772 | nosotras | 1 |
| 5773 | non | 1 |
| 5774 | nombrays | 1 |
| 5775 | nombras | 1 |
| 5776 | nombrarme | 1 |
| 5777 | nombraras | 1 |
| 5778 | nombrando | 1 |
| 5779 | nombrado | 1 |
| 5780 | nombrada | 1 |
| 5781 | nobles | 1 |
| 5782 | nobiscum | 1 |
| 5783 | nina | 1 |
| 5784 | nihil | 1 |
| 5785 | nigromantesa | 1 |
| 5786 | nietos | 1 |
| 5787 | nidada | 1 |
| 5788 | neuio | 1 |
| 5789 | nescios | 1 |
| 5790 | neguilla | 1 |
| 5791 | negras | 1 |
| 5792 | negociado | 1 |
| 5793 | negociacion | 1 |
| 5794 | negarles | 1 |
| 5795 | negare | 1 |
| 5796 | nefarios | 1 |
| 5797 | neciuelo | 1 |
| 5798 | necios | 1 |
| 5799 | necias | 1 |
| 5800 | necessitada | 1 |
| 5801 | necessarios | 1 |
| 5802 | necessaria | 1 |
| 5803 | necedades | 1 |
| 5804 | nebli | 1 |
| 5805 | nazca | 1 |
| 5806 | naypes | 1 |
| 5807 | navegantes | 1 |
| 5808 | nauidad | 1 |
| 5809 | naufragios | 1 |
| 5810 | nauegando | 1 |
| 5811 | nasciste | 1 |
| 5812 | nascimiento | 1 |
| 5813 | nascidos | 1 |
| 5814 | narrar | 1 |
| 5815 | narrando | 1 |
| 5816 | nariz | 1 |
| 5817 | narciso | 1 |
| 5818 | nadando | 1 |
| 5819 | nacion | 1 |
| 5820 | nacidos | 1 |
| 5821 | nacidas | 1 |
| 5822 | nace | 1 |
| 5823 | musicos | 1 |
| 5824 | musico | 1 |
| 5825 | musicas | 1 |
| 5826 | muros | 1 |
| 5827 | murmurio | 1 |
| 5828 | murmuras | 1 |
| 5829 | murmurar | 1 |
| 5830 | muriendo | 1 |
| 5831 | muramos | 1 |
| 5832 | mur | 1 |
| 5833 | multitud | 1 |
| 5834 | multiplicas | 1 |
| 5835 | mueues | 1 |
| 5836 | mueuen | 1 |
| 5837 | mueue | 1 |
| 5838 | muestro | 1 |
| 5839 | muestramela | 1 |
| 5840 | muertas | 1 |
| 5841 | mueres | 1 |
| 5842 | muerde | 1 |
| 5843 | muela | 1 |
| 5844 | mudo | 1 |
| 5845 | mudaua | 1 |
| 5846 | mudas | 1 |
| 5847 | mudaras | 1 |
| 5848 | mudanzas | 1 |
| 5849 | mudanse | 1 |
| 5850 | mudan | 1 |
| 5851 | mudables | 1 |
| 5852 | muchedumbre | 1 |
| 5853 | moxtrenco | 1 |
| 5854 | moxquete | 1 |
| 5855 | moxcas | 1 |
| 5856 | mouible | 1 |
| 5857 | mouia | 1 |
| 5858 | moueysme | 1 |
| 5859 | mouediza | 1 |
| 5860 | mote | 1 |
| 5861 | mostraua | 1 |
| 5862 | mostrarle | 1 |
| 5863 | mostrandoles | 1 |
| 5864 | mostrandole | 1 |
| 5865 | mostra | 1 |
| 5866 | mosto | 1 |
| 5867 | mostaza | 1 |
| 5868 | mosquetes | 1 |
| 5869 | mosquetas | 1 |
| 5870 | mortuorios | 1 |
| 5871 | morisca | 1 |
| 5872 | morirme | 1 |
| 5873 | morires | 1 |
| 5874 | morire | 1 |
| 5875 | moria | 1 |
| 5876 | mordio | 1 |
| 5877 | mordido | 1 |
| 5878 | mordian | 1 |
| 5879 | morder | 1 |
| 5880 | morciegalo | 1 |
| 5881 | morauas | 1 |
| 5882 | moraua | 1 |
| 5883 | moras | 1 |
| 5884 | morar | 1 |
| 5885 | morando | 1 |
| 5886 | moran | 1 |
| 5887 | monteses | 1 |
| 5888 | monjas | 1 |
| 5889 | momos | 1 |
| 5890 | momentaneos | 1 |
| 5891 | mollejar | 1 |
| 5892 | molinero | 1 |
| 5893 | molesto | 1 |
| 5894 | molestia | 1 |
| 5895 | molestas | 1 |
| 5896 | molde | 1 |
| 5897 | mojarte | 1 |
| 5898 | mojar | 1 |
| 5899 | moho | 1 |
| 5900 | mohino | 1 |
| 5901 | moderar | 1 |
| 5902 | mochachos | 1 |
| 5903 | mochacha | 1 |
| 5904 | mocedades | 1 |
| 5905 | mitigarlo | 1 |
| 5906 | mitigar | 1 |
| 5907 | mitad | 1 |
| 5908 | misto | 1 |
| 5909 | misterios | 1 |
| 5910 | mismas | 1 |
| 5911 | miserablemente | 1 |
| 5912 | misera | 1 |
| 5913 | mirra | 1 |
| 5914 | miraua | 1 |
| 5915 | mirate | 1 |
| 5916 | mirare | 1 |
| 5917 | miraras | 1 |
| 5918 | mirandome | 1 |
| 5919 | mirandole | 1 |
| 5920 | miralo | 1 |
| 5921 | miraglos | 1 |
| 5922 | mirad | 1 |
| 5923 | mintiome | 1 |
| 5924 | minos | 1 |
| 5925 | ministraron | 1 |
| 5926 | ministra | 1 |
| 5927 | minerua | 1 |
| 5928 | mimbre | 1 |
| 5929 | millifolia | 1 |
| 5930 | milanos | 1 |
| 5931 | milan | 1 |
| 5932 | milagrosamente | 1 |
| 5933 | milagros | 1 |
| 5934 | migajas | 1 |
| 5935 | migaja | 1 |
| 5936 | miento | 1 |
| 5937 | miente | 1 |
| 5938 | miembro | 1 |
| 5939 | miedos | 1 |
| 5940 | midiesse | 1 |
| 5941 | mezquinamente | 1 |
| 5942 | mezcles | 1 |
| 5943 | mezclando | 1 |
| 5944 | mezclado | 1 |
| 5945 | mezcla | 1 |
| 5946 | metro | 1 |
| 5947 | metrificadas | 1 |
| 5948 | metieron | 1 |
| 5949 | metido | 1 |
| 5950 | metete | 1 |
| 5951 | metes | 1 |
| 5952 | meterte | 1 |
| 5953 | metenla | 1 |
| 5954 | meten | 1 |
| 5955 | metelo | 1 |
| 5956 | metela | 1 |
| 5957 | metas | 1 |
| 5958 | messes | 1 |
| 5959 | messe | 1 |
| 5960 | mesonero | 1 |
| 5961 | mescer | 1 |
| 5962 | meritos | 1 |
| 5963 | merezco | 1 |
| 5964 | merezcan | 1 |
| 5965 | merezca | 1 |
| 5966 | merescieron | 1 |
| 5967 | merescias | 1 |
| 5968 | merescer | 1 |
| 5969 | merescen | 1 |
| 5970 | merendar | 1 |
| 5971 | merecio | 1 |
| 5972 | merecimientos | 1 |
| 5973 | mereciades | 1 |
| 5974 | mercadurias | 1 |
| 5975 | mercados | 1 |
| 5976 | menudos | 1 |
| 5977 | menudas | 1 |
| 5978 | mentos | 1 |
| 5979 | mentir | 1 |
| 5980 | mentarlo | 1 |
| 5981 | mentarla | 1 |
| 5982 | menstrua | 1 |
| 5983 | mensajeros | 1 |
| 5984 | menosprecios | 1 |
| 5985 | menospreciase | 1 |
| 5986 | menosprecia | 1 |
| 5987 | menguaua | 1 |
| 5988 | menguar | 1 |
| 5989 | menguan | 1 |
| 5990 | menesteres | 1 |
| 5991 | meneos | 1 |
| 5992 | menear | 1 |
| 5993 | mencion | 1 |
| 5994 | menandro | 1 |
| 5995 | memorias | 1 |
| 5996 | melon | 1 |
| 5997 | melodia | 1 |
| 5998 | melle | 1 |
| 5999 | mella | 1 |
| 6000 | melibeo | 1 |
| 6001 | melena | 1 |
| 6002 | mel | 1 |
| 6003 | mejoria | 1 |
| 6004 | mejora | 1 |
| 6005 | megera | 1 |
| 6006 | medremos | 1 |
| 6007 | medraua | 1 |
| 6008 | medrado | 1 |
| 6009 | medra | 1 |
| 6010 | medirse | 1 |
| 6011 | mediodia | 1 |
| 6012 | mediis | 1 |
| 6013 | medidos | 1 |
| 6014 | medido | 1 |
| 6015 | medicinas | 1 |
| 6016 | medicina | 1 |
| 6017 | mediante | 1 |
| 6018 | medianoche | 1 |
| 6019 | medianero | 1 |
| 6020 | medianamente | 1 |
| 6021 | medea | 1 |
| 6022 | mayordomo | 1 |
| 6023 | mayordoma | 1 |
| 6024 | mayo | 1 |
| 6025 | matronas | 1 |
| 6026 | matrimonio | 1 |
| 6027 | matizes | 1 |
| 6028 | mates | 1 |
| 6029 | materiales | 1 |
| 6030 | matele | 1 |
| 6031 | matauan | 1 |
| 6032 | matasse | 1 |
| 6033 | matase | 1 |
| 6034 | matarse | 1 |
| 6035 | matarian | 1 |
| 6036 | matare | 1 |
| 6037 | matanla | 1 |
| 6038 | matan | 1 |
| 6039 | matador | 1 |
| 6040 | massa | 1 |
| 6041 | mascara | 1 |
| 6042 | martirios | 1 |
| 6043 | martin | 1 |
| 6044 | martilogio | 1 |
| 6045 | martillos | 1 |
| 6046 | martillando | 1 |
| 6047 | marrubios | 1 |
| 6048 | maritales | 1 |
| 6049 | marital | 1 |
| 6050 | marineros | 1 |
| 6051 | marina | 1 |
| 6052 | margen | 1 |
| 6053 | marco | 1 |
| 6054 | marcada | 1 |
| 6055 | marauillome | 1 |
| 6056 | marauille | 1 |
| 6057 | marauillarme | 1 |
| 6058 | marauillarias | 1 |
| 6059 | marauedi | 1 |
| 6060 | manzilla | 1 |
| 6061 | manzanilla | 1 |
| 6062 | mantillo | 1 |
| 6063 | mantienes | 1 |
| 6064 | mantienen | 1 |
| 6065 | mantiene | 1 |
| 6066 | mantengas | 1 |
| 6067 | mantenga | 1 |
| 6068 | mantenedor | 1 |
| 6069 | mantecas | 1 |
| 6070 | manteandome | 1 |
| 6071 | mansos | 1 |
| 6072 | manoso | 1 |
| 6073 | manifiestase | 1 |
| 6074 | manifiestan | 1 |
| 6075 | manifestarte | 1 |
| 6076 | mangas | 1 |
| 6077 | manga | 1 |
| 6078 | mandote | 1 |
| 6079 | mandoles | 1 |
| 6080 | mandauas | 1 |
| 6081 | mandauan | 1 |
| 6082 | mandarlos | 1 |
| 6083 | mandarle | 1 |
| 6084 | mandaremos | 1 |
| 6085 | mandaras | 1 |
| 6086 | mandan | 1 |
| 6087 | mandamientos | 1 |
| 6088 | mandamiento | 1 |
| 6089 | mandalas | 1 |
| 6090 | mandadas | 1 |
| 6091 | mancebia | 1 |
| 6092 | manceba | 1 |
| 6093 | manan | 1 |
| 6094 | manada | 1 |
| 6095 | mama | 1 |
| 6096 | maluauiscos | 1 |
| 6097 | maltratas | 1 |
| 6098 | maltratarme | 1 |
| 6099 | maltratara | 1 |
| 6100 | maltratadas | 1 |
| 6101 | malsufrido | 1 |
| 6102 | malsofridas | 1 |
| 6103 | malproueyda | 1 |
| 6104 | malpintado | 1 |
| 6105 | malpegado | 1 |
| 6106 | malora | 1 |
| 6107 | mallogrado | 1 |
| 6108 | malicias | 1 |
| 6109 | malhizieron | 1 |
| 6110 | malhechora | 1 |
| 6111 | malganados | 1 |
| 6112 | maldoladas | 1 |
| 6113 | maldizientes | 1 |
| 6114 | maldiziente | 1 |
| 6115 | maldizes | 1 |
| 6116 | maldize | 1 |
| 6117 | malditas | 1 |
| 6118 | maldita | 1 |
| 6119 | maldigo | 1 |
| 6120 | maldiciones | 1 |
| 6121 | maldezientes | 1 |
| 6122 | maldades | 1 |
| 6123 | malauenturada | 1 |
| 6124 | majadero | 1 |
| 6125 | magullada | 1 |
| 6126 | maguera | 1 |
| 6127 | magros | 1 |
| 6128 | magno | 1 |
| 6129 | magnificencias | 1 |
| 6130 | magnificamente | 1 |
| 6131 | magnes | 1 |
| 6132 | maestros | 1 |
| 6133 | maduro | 1 |
| 6134 | madure | 1 |
| 6135 | madrugue | 1 |
| 6136 | madrugado | 1 |
| 6137 | madruga | 1 |
| 6138 | madrina | 1 |
| 6139 | madrigal | 1 |
| 6140 | madreselua | 1 |
| 6141 | madres | 1 |
| 6142 | madexitas | 1 |
| 6143 | madexas | 1 |
| 6144 | machos | 1 |
| 6145 | macho | 1 |
| 6146 | m | 1 |
| 6147 | luzentores | 1 |
| 6148 | lutosa | 1 |
| 6149 | lustrosa | 1 |
| 6150 | lustres | 1 |
| 6151 | luque | 1 |
| 6152 | luengos | 1 |
| 6153 | lucano | 1 |
| 6154 | loquillos | 1 |
| 6155 | loquillas | 1 |
| 6156 | loquilla | 1 |
| 6157 | loquear | 1 |
| 6158 | loo | 1 |
| 6159 | longura | 1 |
| 6160 | lomo | 1 |
| 6161 | lodo | 1 |
| 6162 | lobitos | 1 |
| 6163 | loba | 1 |
| 6164 | loar | 1 |
| 6165 | loandolos | 1 |
| 6166 | loado | 1 |
| 6167 | loadas | 1 |
| 6168 | llueue | 1 |
| 6169 | llouia | 1 |
| 6170 | lloros | 1 |
| 6171 | lloraua | 1 |
| 6172 | llorara | 1 |
| 6173 | llorandola | 1 |
| 6174 | lloran | 1 |
| 6175 | llorado | 1 |
| 6176 | lloradera | 1 |
| 6177 | llora | 1 |
| 6178 | lleva | 1 |
| 6179 | lleues | 1 |
| 6180 | lleuemos | 1 |
| 6181 | lleueme | 1 |
| 6182 | lleuauan | 1 |
| 6183 | lleuaste | 1 |
| 6184 | lleuassen | 1 |
| 6185 | lleuasse | 1 |
| 6186 | lleuas | 1 |
| 6187 | lleuarla | 1 |
| 6188 | lleuaria | 1 |
| 6189 | lleuaras | 1 |
| 6190 | lleuaran | 1 |
| 6191 | lleuara | 1 |
| 6192 | lleuamela | 1 |
| 6193 | lleuame | 1 |
| 6194 | lleuada | 1 |
| 6195 | lleuad | 1 |
| 6196 | llenas | 1 |
| 6197 | llegasse | 1 |
| 6198 | llegase | 1 |
| 6199 | llegas | 1 |
| 6200 | llegarse | 1 |
| 6201 | llegaron | 1 |
| 6202 | llegaria | 1 |
| 6203 | llegan | 1 |
| 6204 | llegados | 1 |
| 6205 | llaue | 1 |
| 6206 | llantos | 1 |
| 6207 | llano | 1 |
| 6208 | llanillas | 1 |
| 6209 | llanas | 1 |
| 6210 | llamola | 1 |
| 6211 | llameys | 1 |
| 6212 | llamela | 1 |
| 6213 | llamasse | 1 |
| 6214 | llamase | 1 |
| 6215 | llamaran | 1 |
| 6216 | llamara | 1 |
| 6217 | llamandome | 1 |
| 6218 | llamando | 1 |
| 6219 | llamame | 1 |
| 6220 | llamalda | 1 |
| 6221 | llagados | 1 |
| 6222 | lizos | 1 |
| 6223 | liuiandad | 1 |
| 6224 | liuianamente | 1 |
| 6225 | liuiana | 1 |
| 6226 | litigioso | 1 |
| 6227 | litigan | 1 |
| 6228 | litigado | 1 |
| 6229 | litem | 1 |
| 6230 | lite | 1 |
| 6231 | lisonjero | 1 |
| 6232 | lisonjera | 1 |
| 6233 | lision | 1 |
| 6234 | lisa | 1 |
| 6235 | lirios | 1 |
| 6236 | liquor | 1 |
| 6237 | liquescer | 1 |
| 6238 | lindos | 1 |
| 6239 | lindas | 1 |
| 6240 | linda | 1 |
| 6241 | limpienle | 1 |
| 6242 | limpiaste | 1 |
| 6243 | limpias | 1 |
| 6244 | limpiamente | 1 |
| 6245 | limpiado | 1 |
| 6246 | limpiad | 1 |
| 6247 | limosnas | 1 |
| 6248 | limones | 1 |
| 6249 | limon | 1 |
| 6250 | limites | 1 |
| 6251 | limite | 1 |
| 6252 | limitado | 1 |
| 6253 | limitada | 1 |
| 6254 | lima | 1 |
| 6255 | ligereza | 1 |
| 6256 | ligadura | 1 |
| 6257 | ligado | 1 |
| 6258 | liga | 1 |
| 6259 | liebres | 1 |
| 6260 | liebre | 1 |
| 6261 | lides | 1 |
| 6262 | licor | 1 |
| 6263 | licita | 1 |
| 6264 | licencias | 1 |
| 6265 | librarian | 1 |
| 6266 | librar | 1 |
| 6267 | libea | 1 |
| 6268 | liado | 1 |
| 6269 | leylo | 1 |
| 6270 | leyeren | 1 |
| 6271 | leyenda | 1 |
| 6272 | leya | 1 |
| 6273 | lexos | 1 |
| 6274 | levantate | 1 |
| 6275 | leues | 1 |
| 6276 | leuays | 1 |
| 6277 | leuauas | 1 |
| 6278 | leuaua | 1 |
| 6279 | leuaste | 1 |
| 6280 | leuaron | 1 |
| 6281 | leuante | 1 |
| 6282 | leuantasse | 1 |
| 6283 | leuantase | 1 |
| 6284 | leuantarse | 1 |
| 6285 | leuantaron | 1 |
| 6286 | leuantarme | 1 |
| 6287 | leuantanles | 1 |
| 6288 | leuantada | 1 |
| 6289 | leuamos | 1 |
| 6290 | leuado | 1 |
| 6291 | leuada | 1 |
| 6292 | letrado | 1 |
| 6293 | letania | 1 |
| 6294 | leon | 1 |
| 6295 | lena | 1 |
| 6296 | leguas | 1 |
| 6297 | legitima | 1 |
| 6298 | leda | 1 |
| 6299 | lectores | 1 |
| 6300 | lechuga | 1 |
| 6301 | lechones | 1 |
| 6302 | leandro | 1 |
| 6303 | lealtad | 1 |
| 6304 | leales | 1 |
| 6305 | lealdad | 1 |
| 6306 | laurel | 1 |
| 6307 | laureado | 1 |
| 6308 | lauadas | 1 |
| 6309 | lastimo | 1 |
| 6310 | lastimes | 1 |
| 6311 | lastimero | 1 |
| 6312 | lastime | 1 |
| 6313 | lastimasteme | 1 |
| 6314 | lastimas | 1 |
| 6315 | lastimandome | 1 |
| 6316 | lastiman | 1 |
| 6317 | lasciuo | 1 |
| 6318 | lapidaria | 1 |
| 6319 | laodice | 1 |
| 6320 | lanzo | 1 |
| 6321 | lanzan | 1 |
| 6322 | lanzada | 1 |
| 6323 | landrezilla | 1 |
| 6324 | lance | 1 |
| 6325 | lamentacion | 1 |
| 6326 | lamedor | 1 |
| 6327 | lambas | 1 |
| 6328 | laguna | 1 |
| 6329 | lagrimosos | 1 |
| 6330 | lagrimillas | 1 |
| 6331 | laganas | 1 |
| 6332 | ladrillados | 1 |
| 6333 | ladrido | 1 |
| 6334 | ladrado | 1 |
| 6335 | ladra | 1 |
| 6336 | lados | 1 |
| 6337 | lachrimarum | 1 |
| 6338 | labrarse | 1 |
| 6339 | labrar | 1 |
| 6340 | labrandera | 1 |
| 6341 | labradores | 1 |
| 6342 | labrado | 1 |
| 6343 | labores | 1 |
| 6344 | labios | 1 |
| 6345 | laberinto | 1 |
| 6346 | juzgaua | 1 |
| 6347 | juzgasses | 1 |
| 6348 | juzgaron | 1 |
| 6349 | juzgares | 1 |
| 6350 | juzgandome | 1 |
| 6351 | juzgando | 1 |
| 6352 | juzgan | 1 |
| 6353 | juyzios | 1 |
| 6354 | justiciar | 1 |
| 6355 | justemos | 1 |
| 6356 | justas | 1 |
| 6357 | justador | 1 |
| 6358 | jurista | 1 |
| 6359 | jurarias | 1 |
| 6360 | juramento | 1 |
| 6361 | jura | 1 |
| 6362 | juntemos | 1 |
| 6363 | junte | 1 |
| 6364 | juntassen | 1 |
| 6365 | juntarias | 1 |
| 6366 | juntaren | 1 |
| 6367 | juntan | 1 |
| 6368 | juntalos | 1 |
| 6369 | jugaste | 1 |
| 6370 | jugar | 1 |
| 6371 | jueues | 1 |
| 6372 | juegue | 1 |
| 6373 | judea | 1 |
| 6374 | juanes | 1 |
| 6375 | joyas | 1 |
| 6376 | joffre | 1 |
| 6377 | jesucristo | 1 |
| 6378 | jerusalem | 1 |
| 6379 | jazmin | 1 |
| 6380 | jasmin | 1 |
| 6381 | jarrillos | 1 |
| 6382 | jarrillo | 1 |
| 6383 | irrecuperables | 1 |
| 6384 | irrecuperable | 1 |
| 6385 | inuisible | 1 |
| 6386 | inuicem | 1 |
| 6387 | inuestigar | 1 |
| 6388 | inuernales | 1 |
| 6389 | inuentor | 1 |
| 6390 | intrinseco | 1 |
| 6391 | intollerable | 1 |
| 6392 | intolerable | 1 |
| 6393 | interrumper | 1 |
| 6394 | interrumpeles | 1 |
| 6395 | interrumpas | 1 |
| 6396 | interpretacion | 1 |
| 6397 | interposicion | 1 |
| 6398 | intercessor | 1 |
| 6399 | intento | 1 |
| 6400 | intellectuales | 1 |
| 6401 | insultan | 1 |
| 6402 | instrutos | 1 |
| 6403 | instrumentos | 1 |
| 6404 | instinto | 1 |
| 6405 | inspira | 1 |
| 6406 | insisto | 1 |
| 6407 | insipiente | 1 |
| 6408 | insigna | 1 |
| 6409 | insaciable | 1 |
| 6410 | inquirir | 1 |
| 6411 | inportunidad | 1 |
| 6412 | inopia | 1 |
| 6413 | inominiosos | 1 |
| 6414 | inocencia | 1 |
| 6415 | inobediente | 1 |
| 6416 | innocentes | 1 |
| 6417 | innocente | 1 |
| 6418 | inmerito | 1 |
| 6419 | injusto | 1 |
| 6420 | injusticia | 1 |
| 6421 | injuriosas | 1 |
| 6422 | injurian | 1 |
| 6423 | injuriado | 1 |
| 6424 | iniquo | 1 |
| 6425 | iniqua | 1 |
| 6426 | ingratos | 1 |
| 6427 | infundir | 1 |
| 6428 | infortunio | 1 |
| 6429 | infinjas | 1 |
| 6430 | infinitos | 1 |
| 6431 | indignos | 1 |
| 6432 | indigne | 1 |
| 6433 | indignamente | 1 |
| 6434 | indignacion | 1 |
| 6435 | indico | 1 |
| 6436 | indicio | 1 |
| 6437 | indeciso | 1 |
| 6438 | incuses | 1 |
| 6439 | incusarnos | 1 |
| 6440 | incusarla | 1 |
| 6441 | increyble | 1 |
| 6442 | increpandole | 1 |
| 6443 | inconueniente | 1 |
| 6444 | inconstancia | 1 |
| 6445 | incomportable | 1 |
| 6446 | incomparablemente | 1 |
| 6447 | incognito | 1 |
| 6448 | incogitada | 1 |
| 6449 | incluso | 1 |
| 6450 | incline | 1 |
| 6451 | inciertos | 1 |
| 6452 | incierta | 1 |
| 6453 | inchado | 1 |
| 6454 | incestuosos | 1 |
| 6455 | incertedumbre | 1 |
| 6456 | improuisos | 1 |
| 6457 | improuiso | 1 |
| 6458 | imprimio | 1 |
| 6459 | impressores | 1 |
| 6460 | impresso | 1 |
| 6461 | impression | 1 |
| 6462 | impotentes | 1 |
| 6463 | importunos | 1 |
| 6464 | importuno | 1 |
| 6465 | importunes | 1 |
| 6466 | importunado | 1 |
| 6467 | importancia | 1 |
| 6468 | impides | 1 |
| 6469 | impiden | 1 |
| 6470 | impidan | 1 |
| 6471 | impetus | 1 |
| 6472 | impetrado | 1 |
| 6473 | imperuio | 1 |
| 6474 | imperficion | 1 |
| 6475 | imperfeta | 1 |
| 6476 | imperfecion | 1 |
| 6477 | impedido | 1 |
| 6478 | impaciencia | 1 |
| 6479 | immortale | 1 |
| 6480 | imita | 1 |
| 6481 | im | 1 |
| 6482 | igual | 1 |
| 6483 | ignorar | 1 |
| 6484 | ignorante | 1 |
| 6485 | ignorando | 1 |
| 6486 | huyriales | 1 |
| 6487 | huyo | 1 |
| 6488 | huygas | 1 |
| 6489 | huyeron | 1 |
| 6490 | huyendo | 1 |
| 6491 | huyen | 1 |
| 6492 | huya | 1 |
| 6493 | huuieron | 1 |
| 6494 | huso | 1 |
| 6495 | hurto | 1 |
| 6496 | hurtar | 1 |
| 6497 | hurtando | 1 |
| 6498 | hurtados | 1 |
| 6499 | hundire | 1 |
| 6500 | hundimiento | 1 |
| 6501 | humillaos | 1 |
| 6502 | humilde | 1 |
| 6503 | humildad | 1 |
| 6504 | humanos | 1 |
| 6505 | humanas | 1 |
| 6506 | hueuos | 1 |
| 6507 | huestantigua | 1 |
| 6508 | huesso | 1 |
| 6509 | huesos | 1 |
| 6510 | huertas | 1 |
| 6511 | huerfanas | 1 |
| 6512 | huellas | 1 |
| 6513 | huelgue | 1 |
| 6514 | huelgas | 1 |
| 6515 | huelga | 1 |
| 6516 | huego | 1 |
| 6517 | huecos | 1 |
| 6518 | hoyo | 1 |
| 6519 | houiste | 1 |
| 6520 | houiesses | 1 |
| 6521 | houiessen | 1 |
| 6522 | houieremos | 1 |
| 6523 | houiere | 1 |
| 6524 | hospital | 1 |
| 6525 | horrible | 1 |
| 6526 | horado | 1 |
| 6527 | horaca | 1 |
| 6528 | honrrauan | 1 |
| 6529 | honrraua | 1 |
| 6530 | honrramos | 1 |
| 6531 | honesto | 1 |
| 6532 | honestad | 1 |
| 6533 | hondos | 1 |
| 6534 | holgo | 1 |
| 6535 | holgazan | 1 |
| 6536 | holgays | 1 |
| 6537 | holgastes | 1 |
| 6538 | holgasse | 1 |
| 6539 | holgase | 1 |
| 6540 | holgares | 1 |
| 6541 | holgaremos | 1 |
| 6542 | holgado | 1 |
| 6543 | hojas | 1 |
| 6544 | hojaplasma | 1 |
| 6545 | hizimos | 1 |
| 6546 | hinco | 1 |
| 6547 | hinches | 1 |
| 6548 | hinchen | 1 |
| 6549 | hinchar | 1 |
| 6550 | hinchada | 1 |
| 6551 | hincha | 1 |
| 6552 | hilo | 1 |
| 6553 | hilan | 1 |
| 6554 | higueruela | 1 |
| 6555 | higos | 1 |
| 6556 | higas | 1 |
| 6557 | higado | 1 |
| 6558 | hieruen | 1 |
| 6559 | hierue | 1 |
| 6560 | hieles | 1 |
| 6561 | hezimos | 1 |
| 6562 | hez | 1 |
| 6563 | hete | 1 |
| 6564 | heruolarios | 1 |
| 6565 | heruir | 1 |
| 6566 | heruientes | 1 |
| 6567 | heruia | 1 |
| 6568 | herreros | 1 |
| 6569 | herrerias | 1 |
| 6570 | herramienta | 1 |
| 6571 | herradores | 1 |
| 6572 | herodes | 1 |
| 6573 | hermandad | 1 |
| 6574 | hermanas | 1 |
| 6575 | herizo | 1 |
| 6576 | herire | 1 |
| 6577 | herencias | 1 |
| 6578 | herencia | 1 |
| 6579 | heregia | 1 |
| 6580 | heredo | 1 |
| 6581 | herede | 1 |
| 6582 | heredamientos | 1 |
| 6583 | henchir | 1 |
| 6584 | helo | 1 |
| 6585 | helias | 1 |
| 6586 | helecho | 1 |
| 6587 | helas | 1 |
| 6588 | hela | 1 |
| 6589 | hedor | 1 |
| 6590 | hedian | 1 |
| 6591 | hedia | 1 |
| 6592 | heder | 1 |
| 6593 | hedad | 1 |
| 6594 | hechizo | 1 |
| 6595 | hechizerias | 1 |
| 6596 | hechizeras | 1 |
| 6597 | hazme | 1 |
| 6598 | hazientes | 1 |
| 6599 | haziendose | 1 |
| 6600 | haziendola | 1 |
| 6601 | haziendas | 1 |
| 6602 | haziades | 1 |
| 6603 | hazese | 1 |
| 6604 | hazerte | 1 |
| 6605 | hazerme | 1 |
| 6606 | hazerlos | 1 |
| 6607 | hazerlo | 1 |
| 6608 | hazerla | 1 |
| 6609 | hazense | 1 |
| 6610 | hazemos | 1 |
| 6611 | hazelo | 1 |
| 6612 | hazelas | 1 |
| 6613 | hazedor | 1 |
| 6614 | hazed | 1 |
| 6615 | hazanas | 1 |
| 6616 | hayas | 1 |
| 6617 | hayan | 1 |
| 6618 | hauria | 1 |
| 6619 | hauran | 1 |
| 6620 | hauiale | 1 |
| 6621 | haueys | 1 |
| 6622 | hauerte | 1 |
| 6623 | hauerlo | 1 |
| 6624 | hauas | 1 |
| 6625 | hauada | 1 |
| 6626 | haua | 1 |
| 6627 | hasle | 1 |
| 6628 | hasla | 1 |
| 6629 | hartura | 1 |
| 6630 | harte | 1 |
| 6631 | harpias | 1 |
| 6632 | harpar | 1 |
| 6633 | harpadas | 1 |
| 6634 | harpada | 1 |
| 6635 | harpa | 1 |
| 6636 | harnero | 1 |
| 6637 | harina | 1 |
| 6638 | hariades | 1 |
| 6639 | haremos | 1 |
| 6640 | harda | 1 |
| 6641 | haran | 1 |
| 6642 | handrajoso | 1 |
| 6643 | hallastes | 1 |
| 6644 | hallase | 1 |
| 6645 | hallarme | 1 |
| 6646 | hallaria | 1 |
| 6647 | hallareys | 1 |
| 6648 | hallare | 1 |
| 6649 | hallaran | 1 |
| 6650 | hallanle | 1 |
| 6651 | hallada | 1 |
| 6652 | haldear | 1 |
| 6653 | haldeando | 1 |
| 6654 | halcones | 1 |
| 6655 | halaguero | 1 |
| 6656 | halagare | 1 |
| 6657 | halagar | 1 |
| 6658 | hagays | 1 |
| 6659 | hagamosle | 1 |
| 6660 | hadas | 1 |
| 6661 | hacer | 1 |
| 6662 | hac | 1 |
| 6663 | hablillas | 1 |
| 6664 | hablilla | 1 |
| 6665 | hablays | 1 |
| 6666 | hablarte | 1 |
| 6667 | hablarme | 1 |
| 6668 | hablarlo | 1 |
| 6669 | hablarla | 1 |
| 6670 | hablaria | 1 |
| 6671 | hablanse | 1 |
| 6672 | hablamos | 1 |
| 6673 | hablale | 1 |
| 6674 | guzques | 1 |
| 6675 | gustos | 1 |
| 6676 | guija | 1 |
| 6677 | guies | 1 |
| 6678 | guias | 1 |
| 6679 | guia | 1 |
| 6680 | guerras | 1 |
| 6681 | guarescer | 1 |
| 6682 | guardete | 1 |
| 6683 | guardese | 1 |
| 6684 | guardes | 1 |
| 6685 | guarden | 1 |
| 6686 | guardemos | 1 |
| 6687 | guarde | 1 |
| 6688 | guardaua | 1 |
| 6689 | guardas | 1 |
| 6690 | guardarle | 1 |
| 6691 | guardando | 1 |
| 6692 | guardan | 1 |
| 6693 | guardada | 1 |
| 6694 | guante | 1 |
| 6695 | guadalupe | 1 |
| 6696 | grossero | 1 |
| 6697 | grosezuelos | 1 |
| 6698 | grita | 1 |
| 6699 | grillos | 1 |
| 6700 | griegos | 1 |
| 6701 | griega | 1 |
| 6702 | graue | 1 |
| 6703 | granzones | 1 |
| 6704 | grano | 1 |
| 6705 | granillo | 1 |
| 6706 | granada | 1 |
| 6707 | grana | 1 |
| 6708 | gramonilla | 1 |
| 6709 | grados | 1 |
| 6710 | graciosos | 1 |
| 6711 | gozos | 1 |
| 6712 | gozome | 1 |
| 6713 | gozemos | 1 |
| 6714 | gozemonos | 1 |
| 6715 | gozasse | 1 |
| 6716 | gozas | 1 |
| 6717 | gozarlo | 1 |
| 6718 | gozarian | 1 |
| 6719 | gozariamos | 1 |
| 6720 | gozaremos | 1 |
| 6721 | gozamos | 1 |
| 6722 | gouernador | 1 |
| 6723 | gostaduras | 1 |
| 6724 | gorda | 1 |
| 6725 | golosina | 1 |
| 6726 | golosa | 1 |
| 6727 | golondrina | 1 |
| 6728 | gloriosos | 1 |
| 6729 | glorifico | 1 |
| 6730 | glorifican | 1 |
| 6731 | glorificado | 1 |
| 6732 | glorifica | 1 |
| 6733 | gloriado | 1 |
| 6734 | girifalte | 1 |
| 6735 | gimiendo | 1 |
| 6736 | gestos | 1 |
| 6737 | gestico | 1 |
| 6738 | gerunt | 1 |
| 6739 | george | 1 |
| 6740 | genuit | 1 |
| 6741 | gentilidad | 1 |
| 6742 | gentezilla | 1 |
| 6743 | generosa | 1 |
| 6744 | generos | 1 |
| 6745 | general | 1 |
| 6746 | gelo | 1 |
| 6747 | gela | 1 |
| 6748 | gayta | 1 |
| 6749 | gauilanes | 1 |
| 6750 | gastasse | 1 |
| 6751 | gastase | 1 |
| 6752 | gastas | 1 |
| 6753 | gastan | 1 |
| 6754 | gastala | 1 |
| 6755 | gasta | 1 |
| 6756 | garzones | 1 |
| 6757 | garuines | 1 |
| 6758 | garrido | 1 |
| 6759 | ganes | 1 |
| 6760 | ganen | 1 |
| 6761 | ganemos | 1 |
| 6762 | ganaste | 1 |
| 6763 | ganas | 1 |
| 6764 | ganare | 1 |
| 6765 | ganados | 1 |
| 6766 | gamones | 1 |
| 6767 | gallos | 1 |
| 6768 | gallillo | 1 |
| 6769 | gallego | 1 |
| 6770 | galgo | 1 |
| 6771 | galardones | 1 |
| 6772 | galardone | 1 |
| 6773 | galardonaste | 1 |
| 6774 | galardonas | 1 |
| 6775 | galardonare | 1 |
| 6776 | galardonados | 1 |
| 6777 | galardonada | 1 |
| 6778 | galanas | 1 |
| 6779 | fuya | 1 |
| 6780 | fuste | 1 |
| 6781 | fustas | 1 |
| 6782 | furto | 1 |
| 6783 | furtillos | 1 |
| 6784 | furtar | 1 |
| 6785 | furias | 1 |
| 6786 | fundamento | 1 |
| 6787 | fuistes | 1 |
| 6788 | fuisteme | 1 |
| 6789 | fuimos | 1 |
| 6790 | fuessen | 1 |
| 6791 | fueses | 1 |
| 6792 | fuesedes | 1 |
| 6793 | fuero | 1 |
| 6794 | frutuosas | 1 |
| 6795 | frutificando | 1 |
| 6796 | frontera | 1 |
| 6797 | froga | 1 |
| 6798 | frisado | 1 |
| 6799 | frios | 1 |
| 6800 | freyr | 1 |
| 6801 | frescor | 1 |
| 6802 | fregaste | 1 |
| 6803 | fregaron | 1 |
| 6804 | frechas | 1 |
| 6805 | fraude | 1 |
| 6806 | franjas | 1 |
| 6807 | francisco | 1 |
| 6808 | frances | 1 |
| 6809 | franca | 1 |
| 6810 | fragile | 1 |
| 6811 | forzosamente | 1 |
| 6812 | forzo | 1 |
| 6813 | forzaua | 1 |
| 6814 | forzaste | 1 |
| 6815 | forzar | 1 |
| 6816 | fortunas | 1 |
| 6817 | fortaleza | 1 |
| 6818 | formas | 1 |
| 6819 | formadas | 1 |
| 6820 | formada | 1 |
| 6821 | fontezicas | 1 |
| 6822 | fontezica | 1 |
| 6823 | folgura | 1 |
| 6824 | folgar | 1 |
| 6825 | flutuoso | 1 |
| 6826 | flutuosa | 1 |
| 6827 | fluctuant | 1 |
| 6828 | florido | 1 |
| 6829 | florezilla | 1 |
| 6830 | floresci | 1 |
| 6831 | florescen | 1 |
| 6832 | flaqueza | 1 |
| 6833 | flammae | 1 |
| 6834 | flamas | 1 |
| 6835 | fizo | 1 |
| 6836 | fizieran | 1 |
| 6837 | fiziera | 1 |
| 6838 | fiunt | 1 |
| 6839 | fisico | 1 |
| 6840 | fisica | 1 |
| 6841 | firmar | 1 |
| 6842 | fingiremos | 1 |
| 6843 | fingire | 1 |
| 6844 | fingiendote | 1 |
| 6845 | fingiendo | 1 |
| 6846 | fingidas | 1 |
| 6847 | fingidamente | 1 |
| 6848 | fingida | 1 |
| 6849 | fingendo | 1 |
| 6850 | fingen | 1 |
| 6851 | fines | 1 |
| 6852 | fincar | 1 |
| 6853 | finados | 1 |
| 6854 | finada | 1 |
| 6855 | fina | 1 |
| 6856 | filosomia | 1 |
| 6857 | filosofando | 1 |
| 6858 | filosofales | 1 |
| 6859 | filigres | 1 |
| 6860 | filar | 1 |
| 6861 | filado | 1 |
| 6862 | fijadalgo | 1 |
| 6863 | figuraseme | 1 |
| 6864 | figuras | 1 |
| 6865 | figurare | 1 |
| 6866 | figurar | 1 |
| 6867 | fiestas | 1 |
| 6868 | fies | 1 |
| 6869 | fierro | 1 |
| 6870 | fieldad | 1 |
| 6871 | fie | 1 |
| 6872 | fideputa | 1 |
| 6873 | fictas | 1 |
| 6874 | ficion | 1 |
| 6875 | fiauan | 1 |
| 6876 | fiara | 1 |
| 6877 | fiadora | 1 |
| 6878 | festiuidad | 1 |
| 6879 | festejando | 1 |
| 6880 | ferocidad | 1 |
| 6881 | fermosura | 1 |
| 6882 | fengir | 1 |
| 6883 | fengidos | 1 |
| 6884 | fenescieron | 1 |
| 6885 | fenescer | 1 |
| 6886 | femineo | 1 |
| 6887 | felicidad | 1 |
| 6888 | febre | 1 |
| 6889 | faziones | 1 |
| 6890 | fazienda | 1 |
| 6891 | faziase | 1 |
| 6892 | fazias | 1 |
| 6893 | fazes | 1 |
| 6894 | fazerte | 1 |
| 6895 | fazerme | 1 |
| 6896 | fazerle | 1 |
| 6897 | fazela | 1 |
| 6898 | fausto | 1 |
| 6899 | fauoreceme | 1 |
| 6900 | fauorables | 1 |
| 6901 | fatigar | 1 |
| 6902 | fatigan | 1 |
| 6903 | fatigados | 1 |
| 6904 | fastio | 1 |
| 6905 | farto | 1 |
| 6906 | farias | 1 |
| 6907 | faria | 1 |
| 6908 | fares | 1 |
| 6909 | fardeles | 1 |
| 6910 | faras | 1 |
| 6911 | fantastica | 1 |
| 6912 | fantasma | 1 |
| 6913 | fantasia | 1 |
| 6914 | fantaseado | 1 |
| 6915 | familiares | 1 |
| 6916 | fambre | 1 |
| 6917 | faltriquera | 1 |
| 6918 | falteme | 1 |
| 6919 | faltasse | 1 |
| 6920 | faltare | 1 |
| 6921 | faltandome | 1 |
| 6922 | faltandoles | 1 |
| 6923 | faltales | 1 |
| 6924 | faltado | 1 |
| 6925 | falsaua | 1 |
| 6926 | falsaste | 1 |
| 6927 | falsario | 1 |
| 6928 | fallesce | 1 |
| 6929 | fallecen | 1 |
| 6930 | fallaste | 1 |
| 6931 | fallare | 1 |
| 6932 | fallara | 1 |
| 6933 | faldetas | 1 |
| 6934 | falcon | 1 |
| 6935 | falacias | 1 |
| 6936 | fagase | 1 |
| 6937 | fagan | 1 |
| 6938 | facultades | 1 |
| 6939 | facile | 1 |
| 6940 | facil | 1 |
| 6941 | fabrican | 1 |
| 6942 | fabricadas | 1 |
| 6943 | fablemos | 1 |
| 6944 | fablassen | 1 |
| 6945 | fablares | 1 |
| 6946 | fablado | 1 |
| 6947 | exteriores | 1 |
| 6948 | explanara | 1 |
| 6949 | experiencia | 1 |
| 6950 | existencia | 1 |
| 6951 | exercicio | 1 |
| 6952 | exemplos | 1 |
| 6953 | executaste | 1 |
| 6954 | excesso | 1 |
| 6955 | excellencia | 1 |
| 6956 | excelentissimo | 1 |
| 6957 | excedio | 1 |
| 6958 | exceder | 1 |
| 6959 | eua | 1 |
| 6960 | etor | 1 |
| 6961 | etnicos | 1 |
| 6962 | et | 1 |
| 6963 | estuuieron | 1 |
| 6964 | estuuieren | 1 |
| 6965 | estudiantes | 1 |
| 6966 | estrumentos | 1 |
| 6967 | estriego | 1 |
| 6968 | estribo | 1 |
| 6969 | estrepito | 1 |
| 6970 | estrena | 1 |
| 6971 | estrelleras | 1 |
| 6972 | estrella | 1 |
| 6973 | estrecho | 1 |
| 6974 | estrecha | 1 |
| 6975 | estranos | 1 |
| 6976 | estranjero | 1 |
| 6977 | estranezas | 1 |
| 6978 | estragarlo | 1 |
| 6979 | estrado | 1 |
| 6980 | estouo | 1 |
| 6981 | estouimos | 1 |
| 6982 | estouiesedes | 1 |
| 6983 | estouiese | 1 |
| 6984 | estouiere | 1 |
| 6985 | estoruays | 1 |
| 6986 | estoruasse | 1 |
| 6987 | estoruarte | 1 |
| 6988 | estoruaras | 1 |
| 6989 | estoruan | 1 |
| 6990 | estoruales | 1 |
| 6991 | estorua | 1 |
| 6992 | estorcer | 1 |
| 6993 | estoraques | 1 |
| 6994 | estoraque | 1 |
| 6995 | estola | 1 |
| 6996 | estocadas | 1 |
| 6997 | estocada | 1 |
| 6998 | estimes | 1 |
| 6999 | estimas | 1 |
| 7000 | estimarse | 1 |
| 7001 | estimar | 1 |
| 7002 | esteriores | 1 |
| 7003 | estendieron | 1 |
| 7004 | estauas | 1 |
| 7005 | estarte | 1 |
| 7006 | estaria | 1 |
| 7007 | estaran | 1 |
| 7008 | estano | 1 |
| 7009 | estambre | 1 |
| 7010 | establo | 1 |
| 7011 | est | 1 |
| 7012 | essotra | 1 |
| 7013 | esquiuidad | 1 |
| 7014 | esquiuedad | 1 |
| 7015 | esquiuas | 1 |
| 7016 | esquiuandose | 1 |
| 7017 | esquiua | 1 |
| 7018 | espumajoso | 1 |
| 7019 | espulguen | 1 |
| 7020 | espuela | 1 |
| 7021 | espressare | 1 |
| 7022 | espresion | 1 |
| 7023 | espresaste | 1 |
| 7024 | esportillas | 1 |
| 7025 | espliego | 1 |
| 7026 | espiritual | 1 |
| 7027 | espina | 1 |
| 7028 | espessos | 1 |
| 7029 | esperta | 1 |
| 7030 | esperimiento | 1 |
| 7031 | esperimentados | 1 |
| 7032 | esperes | 1 |
| 7033 | esperen | 1 |
| 7034 | esperemos | 1 |
| 7035 | esperasses | 1 |
| 7036 | esperasse | 1 |
| 7037 | esperarte | 1 |
| 7038 | esperaramos | 1 |
| 7039 | esperarades | 1 |
| 7040 | esperandote | 1 |
| 7041 | esperamos | 1 |
| 7042 | esperame | 1 |
| 7043 | esperallas | 1 |
| 7044 | esperado | 1 |
| 7045 | esperadme | 1 |
| 7046 | esperad | 1 |
| 7047 | espele | 1 |
| 7048 | especulacion | 1 |
| 7049 | especificar | 1 |
| 7050 | especies | 1 |
| 7051 | especialmente | 1 |
| 7052 | espauorecian | 1 |
| 7053 | espantos | 1 |
| 7054 | espantemosla | 1 |
| 7055 | espante | 1 |
| 7056 | espantaras | 1 |
| 7057 | espantable | 1 |
| 7058 | espanta | 1 |
| 7059 | espaldarazos | 1 |
| 7060 | esotra | 1 |
| 7061 | esos | 1 |
| 7062 | eslauones | 1 |
| 7063 | esgarrochados | 1 |
| 7064 | esgamoches | 1 |
| 7065 | esfuerzate | 1 |
| 7066 | esforzaua | 1 |
| 7067 | esforzare | 1 |
| 7068 | esforzado | 1 |
| 7069 | esforzada | 1 |
| 7070 | esenta | 1 |
| 7071 | escusarte | 1 |
| 7072 | escusada | 1 |
| 7073 | escurre | 1 |
| 7074 | escuros | 1 |
| 7075 | escuresce | 1 |
| 7076 | escurecen | 1 |
| 7077 | escurece | 1 |
| 7078 | esculpidas | 1 |
| 7079 | escuelas | 1 |
| 7080 | escudrina | 1 |
| 7081 | escudo | 1 |
| 7082 | escudilla | 1 |
| 7083 | escudero | 1 |
| 7084 | escuchauas | 1 |
| 7085 | escuchatelo | 1 |
| 7086 | escuchas | 1 |
| 7087 | escucharte | 1 |
| 7088 | escuchandote | 1 |
| 7089 | escuchale | 1 |
| 7090 | escuchala | 1 |
| 7091 | escrupulosos | 1 |
| 7092 | escriuiendo | 1 |
| 7093 | escriue | 1 |
| 7094 | escritura | 1 |
| 7095 | escrito | 1 |
| 7096 | escoziote | 1 |
| 7097 | escondieron | 1 |
| 7098 | escondido | 1 |
| 7099 | escondidas | 1 |
| 7100 | escondete | 1 |
| 7101 | esconder | 1 |
| 7102 | esconda | 1 |
| 7103 | escogio | 1 |
| 7104 | escogian | 1 |
| 7105 | escoger | 1 |
| 7106 | escoge | 1 |
| 7107 | escobas | 1 |
| 7108 | escluya | 1 |
| 7109 | esclaua | 1 |
| 7110 | escarnios | 1 |
| 7111 | escardilla | 1 |
| 7112 | escapome | 1 |
| 7113 | escapara | 1 |
| 7114 | escapa | 1 |
| 7115 | escandalizar | 1 |
| 7116 | escanciar | 1 |
| 7117 | escallentar | 1 |
| 7118 | escallentador | 1 |
| 7119 | escalado | 1 |
| 7120 | esa | 1 |
| 7121 | errores | 1 |
| 7122 | erre | 1 |
| 7123 | erraran | 1 |
| 7124 | erradas | 1 |
| 7125 | errada | 1 |
| 7126 | erizo | 1 |
| 7127 | ereje | 1 |
| 7128 | eregias | 1 |
| 7129 | eregia | 1 |
| 7130 | ercules | 1 |
| 7131 | erades | 1 |
| 7132 | eraclito | 1 |
| 7133 | enxuto | 1 |
| 7134 | enuistiendolas | 1 |
| 7135 | enuiste | 1 |
| 7136 | enues | 1 |
| 7137 | enuergonzantes | 1 |
| 7138 | enuelesada | 1 |
| 7139 | enuejecida | 1 |
| 7140 | enuejeci | 1 |
| 7141 | enuejecer | 1 |
| 7142 | enuejece | 1 |
| 7143 | enuegescen | 1 |
| 7144 | enuegece | 1 |
| 7145 | enturuies | 1 |
| 7146 | entristecerme | 1 |
| 7147 | entristece | 1 |
| 7148 | entrexeridas | 1 |
| 7149 | entreueniendo | 1 |
| 7150 | entres | 1 |
| 7151 | entremetiesse | 1 |
| 7152 | entremetieren | 1 |
| 7153 | entremetas | 1 |
| 7154 | entremedias | 1 |
| 7155 | entredicho | 1 |
| 7156 | entrauamos | 1 |
| 7157 | entraua | 1 |
| 7158 | entrate | 1 |
| 7159 | entraste | 1 |
| 7160 | entrarnos | 1 |
| 7161 | entrara | 1 |
| 7162 | entranable | 1 |
| 7163 | entienda | 1 |
| 7164 | entibia | 1 |
| 7165 | enterramientos | 1 |
| 7166 | enternece | 1 |
| 7167 | entendimiento | 1 |
| 7168 | entendia | 1 |
| 7169 | entenderlas | 1 |
| 7170 | entendedor | 1 |
| 7171 | ensorde | 1 |
| 7172 | ensoberuecerse | 1 |
| 7173 | ensilla | 1 |
| 7174 | ensenoreado | 1 |
| 7175 | ensena | 1 |
| 7176 | ensangrentar | 1 |
| 7177 | ensanar | 1 |
| 7178 | ensananse | 1 |
| 7179 | ensanada | 1 |
| 7180 | enrubiar | 1 |
| 7181 | enredada | 1 |
| 7182 | enoramala | 1 |
| 7183 | enojote | 1 |
| 7184 | enojosas | 1 |
| 7185 | enojes | 1 |
| 7186 | enojarte | 1 |
| 7187 | enojan | 1 |
| 7188 | enojados | 1 |
| 7189 | enojada | 1 |
| 7190 | enmudescerias | 1 |
| 7191 | enmienda | 1 |
| 7192 | enlazastes | 1 |
| 7193 | enim | 1 |
| 7194 | engullir | 1 |
| 7195 | engordara | 1 |
| 7196 | engendre | 1 |
| 7197 | engendraua | 1 |
| 7198 | engendrara | 1 |
| 7199 | engendrar | 1 |
| 7200 | engendra | 1 |
| 7201 | enganoso | 1 |
| 7202 | enganosas | 1 |
| 7203 | enganando | 1 |
| 7204 | enganados | 1 |
| 7205 | enganador | 1 |
| 7206 | enfermos | 1 |
| 7207 | enemigas | 1 |
| 7208 | enefable | 1 |
| 7209 | endurecido | 1 |
| 7210 | enderezo | 1 |
| 7211 | enderezar | 1 |
| 7212 | enderezan | 1 |
| 7213 | encuentran | 1 |
| 7214 | encubro | 1 |
| 7215 | encubrio | 1 |
| 7216 | encubrimiento | 1 |
| 7217 | encubriendo | 1 |
| 7218 | encubrian | 1 |
| 7219 | encubresme | 1 |
| 7220 | encubiertos | 1 |
| 7221 | encubiertas | 1 |
| 7222 | encruzijada | 1 |
| 7223 | encorozada | 1 |
| 7224 | encontrasen | 1 |
| 7225 | encontrare | 1 |
| 7226 | encontraras | 1 |
| 7227 | enconan | 1 |
| 7228 | enconada | 1 |
| 7229 | encomparablemente | 1 |
| 7230 | encomiendo | 1 |
| 7231 | encomendauan | 1 |
| 7232 | encogido | 1 |
| 7233 | encogida | 1 |
| 7234 | encobrias | 1 |
| 7235 | encobria | 1 |
| 7236 | enclauijadas | 1 |
| 7237 | encienso | 1 |
| 7238 | enciendes | 1 |
| 7239 | encienden | 1 |
| 7240 | encerro | 1 |
| 7241 | encerramiento | 1 |
| 7242 | encerrados | 1 |
| 7243 | encerrado | 1 |
| 7244 | encerados | 1 |
| 7245 | encendios | 1 |
| 7246 | encendieron | 1 |
| 7247 | encendidos | 1 |
| 7248 | encendera | 1 |
| 7249 | encender | 1 |
| 7250 | encaxado | 1 |
| 7251 | encargo | 1 |
| 7252 | encarecen | 1 |
| 7253 | encantador | 1 |
| 7254 | encaneci | 1 |
| 7255 | encandelado | 1 |
| 7256 | enbalde | 1 |
| 7257 | enamoro | 1 |
| 7258 | emponzonado | 1 |
| 7259 | emplumenla | 1 |
| 7260 | empleadas | 1 |
| 7261 | empleada | 1 |
| 7262 | emplea | 1 |
| 7263 | empicotaron | 1 |
| 7264 | empezaron | 1 |
| 7265 | empezadas | 1 |
| 7266 | empenar | 1 |
| 7267 | empediria | 1 |
| 7268 | empache | 1 |
| 7269 | empachaua | 1 |
| 7270 | emilio | 1 |
| 7271 | emienda | 1 |
| 7272 | emendarse | 1 |
| 7273 | emendar | 1 |
| 7274 | emendada | 1 |
| 7275 | embueluas | 1 |
| 7276 | embueltos | 1 |
| 7277 | embotado | 1 |
| 7278 | embiude | 1 |
| 7279 | embiome | 1 |
| 7280 | embies | 1 |
| 7281 | embiemosle | 1 |
| 7282 | embidiosos | 1 |
| 7283 | embidiosas | 1 |
| 7284 | embidias | 1 |
| 7285 | embidiar | 1 |
| 7286 | embiauan | 1 |
| 7287 | embiarte | 1 |
| 7288 | embiarme | 1 |
| 7289 | embiara | 1 |
| 7290 | embiado | 1 |
| 7291 | embeuecimiento | 1 |
| 7292 | embaymientos | 1 |
| 7293 | embaxador | 1 |
| 7294 | embargado | 1 |
| 7295 | embarazo | 1 |
| 7296 | elisa | 1 |
| 7297 | elementa | 1 |
| 7298 | elegir | 1 |
| 7299 | elegante | 1 |
| 7300 | elefante | 1 |
| 7301 | elado | 1 |
| 7302 | elada | 1 |
| 7303 | egisto | 1 |
| 7304 | eficaz | 1 |
| 7305 | eficacemente | 1 |
| 7306 | effecto | 1 |
| 7307 | efetos | 1 |
| 7308 | efecto | 1 |
| 7309 | edifique | 1 |
| 7310 | edificios | 1 |
| 7311 | edades | 1 |
| 7312 | eclipse | 1 |
| 7313 | echemosle | 1 |
| 7314 | echaste | 1 |
| 7315 | echasse | 1 |
| 7316 | echasnos | 1 |
| 7317 | echase | 1 |
| 7318 | echare | 1 |
| 7319 | echanle | 1 |
| 7320 | echanlas | 1 |
| 7321 | echalla | 1 |
| 7322 | eburneo | 1 |
| 7323 | dureza | 1 |
| 7324 | dure | 1 |
| 7325 | durare | 1 |
| 7326 | durara | 1 |
| 7327 | durar | 1 |
| 7328 | duran | 1 |
| 7329 | duquesa | 1 |
| 7330 | duque | 1 |
| 7331 | dulzores | 1 |
| 7332 | duerma | 1 |
| 7333 | duela | 1 |
| 7334 | dudosa | 1 |
| 7335 | dudes | 1 |
| 7336 | dubdoso | 1 |
| 7337 | dragon | 1 |
| 7338 | drago | 1 |
| 7339 | dozeno | 1 |
| 7340 | dotasse | 1 |
| 7341 | dotados | 1 |
| 7342 | dotado | 1 |
| 7343 | dormiriemos | 1 |
| 7344 | dormilones | 1 |
| 7345 | dormieron | 1 |
| 7346 | dormias | 1 |
| 7347 | dormiamos | 1 |
| 7348 | dorados | 1 |
| 7349 | dorado | 1 |
| 7350 | doradas | 1 |
| 7351 | dorada | 1 |
| 7352 | donoso | 1 |
| 7353 | donosa | 1 |
| 7354 | dondyr | 1 |
| 7355 | donayre | 1 |
| 7356 | dominio | 1 |
| 7357 | doman | 1 |
| 7358 | dolorosas | 1 |
| 7359 | dolorosa | 1 |
| 7360 | doloriosas | 1 |
| 7361 | dolorida | 1 |
| 7362 | dolorcillos | 1 |
| 7363 | dolido | 1 |
| 7364 | doler | 1 |
| 7365 | doctrina | 1 |
| 7366 | doctos | 1 |
| 7367 | doctor | 1 |
| 7368 | dobles | 1 |
| 7369 | doblega | 1 |
| 7370 | doblas | 1 |
| 7371 | doblaron | 1 |
| 7372 | doblarnos | 1 |
| 7373 | doblar | 1 |
| 7374 | doblan | 1 |
| 7375 | doblada | 1 |
| 7376 | diziendole | 1 |
| 7377 | dixiesses | 1 |
| 7378 | dixiessen | 1 |
| 7379 | dixiere | 1 |
| 7380 | dixessen | 1 |
| 7381 | dixesse | 1 |
| 7382 | dixesen | 1 |
| 7383 | dixera | 1 |
| 7384 | diuision | 1 |
| 7385 | diuisible | 1 |
| 7386 | diuerso | 1 |
| 7387 | dite | 1 |
| 7388 | distraydo | 1 |
| 7389 | dissonos | 1 |
| 7390 | dissimulando | 1 |
| 7391 | dissimulaciones | 1 |
| 7392 | dissimula | 1 |
| 7393 | dissensiones | 1 |
| 7394 | dissension | 1 |
| 7395 | disputar | 1 |
| 7396 | dispuso | 1 |
| 7397 | dispusicion | 1 |
| 7398 | dispuestos | 1 |
| 7399 | disposicion | 1 |
| 7400 | dispongas | 1 |
| 7401 | disponer | 1 |
| 7402 | disponen | 1 |
| 7403 | disparze | 1 |
| 7404 | disminuyendo | 1 |
| 7405 | disminuyen | 1 |
| 7406 | discurrimos | 1 |
| 7407 | discricion | 1 |
| 7408 | discordias | 1 |
| 7409 | discordia | 1 |
| 7410 | discorde | 1 |
| 7411 | discorda | 1 |
| 7412 | discerneys | 1 |
| 7413 | direte | 1 |
| 7414 | dires | 1 |
| 7415 | diremos | 1 |
| 7416 | dirasle | 1 |
| 7417 | dirame | 1 |
| 7418 | diose | 1 |
| 7419 | diminuyessen | 1 |
| 7420 | diminuyelas | 1 |
| 7421 | diminuya | 1 |
| 7422 | diminutos | 1 |
| 7423 | diminuiendo | 1 |
| 7424 | diminucion | 1 |
| 7425 | dilato | 1 |
| 7426 | dilatas | 1 |
| 7427 | dilata | 1 |
| 7428 | digotelo | 1 |
| 7429 | digole | 1 |
| 7430 | dignidades | 1 |
| 7431 | dignidad | 1 |
| 7432 | dignas | 1 |
| 7433 | dignamente | 1 |
| 7434 | diganos | 1 |
| 7435 | digalo | 1 |
| 7436 | difieren | 1 |
| 7437 | dificultades | 1 |
| 7438 | dificultad | 1 |
| 7439 | difficultad | 1 |
| 7440 | differentes | 1 |
| 7441 | differencias | 1 |
| 7442 | diferirias | 1 |
| 7443 | diferentes | 1 |
| 7444 | diferente | 1 |
| 7445 | diezocho | 1 |
| 7446 | diezmos | 1 |
| 7447 | diestros | 1 |
| 7448 | diestro | 1 |
| 7449 | diesemos | 1 |
| 7450 | diese | 1 |
| 7451 | dieronle | 1 |
| 7452 | dierasme | 1 |
| 7453 | dido | 1 |
| 7454 | dichas | 1 |
| 7455 | diana | 1 |
| 7456 | dezis | 1 |
| 7457 | dezirtelo | 1 |
| 7458 | dezirme | 1 |
| 7459 | dezirles | 1 |
| 7460 | dezildes | 1 |
| 7461 | dezias | 1 |
| 7462 | deziades | 1 |
| 7463 | deydad | 1 |
| 7464 | dexemosle | 1 |
| 7465 | dexauas | 1 |
| 7466 | dexauan | 1 |
| 7467 | dexate | 1 |
| 7468 | dexastes | 1 |
| 7469 | dexase | 1 |
| 7470 | dexarse | 1 |
| 7471 | dexaras | 1 |
| 7472 | dexaos | 1 |
| 7473 | dexandola | 1 |
| 7474 | dexan | 1 |
| 7475 | dexamos | 1 |
| 7476 | dexamele | 1 |
| 7477 | dexalo | 1 |
| 7478 | deuria | 1 |
| 7479 | deuoto | 1 |
| 7480 | deuotas | 1 |
| 7481 | deuota | 1 |
| 7482 | deuido | 1 |
| 7483 | deuida | 1 |
| 7484 | deuia | 1 |
| 7485 | deueys | 1 |
| 7486 | deudos | 1 |
| 7487 | deudores | 1 |
| 7488 | deudor | 1 |
| 7489 | deudo | 1 |
| 7490 | deuaneen | 1 |
| 7491 | deuanear | 1 |
| 7492 | deuaneando | 1 |
| 7493 | detuuiesse | 1 |
| 7494 | detuue | 1 |
| 7495 | detras | 1 |
| 7496 | determinasse | 1 |
| 7497 | determinacion | 1 |
| 7498 | detenido | 1 |
| 7499 | detengas | 1 |
| 7500 | detengamos | 1 |
| 7501 | dete | 1 |
| 7502 | desuio | 1 |
| 7503 | desuiados | 1 |
| 7504 | desuia | 1 |
| 7505 | desuerguenza | 1 |
| 7506 | desuergonzado | 1 |
| 7507 | desuergonzadas | 1 |
| 7508 | desuergonzada | 1 |
| 7509 | desuentura | 1 |
| 7510 | desuellacaras | 1 |
| 7511 | desuarios | 1 |
| 7512 | desuariados | 1 |
| 7513 | destruyste | 1 |
| 7514 | destruyrlo | 1 |
| 7515 | destruyras | 1 |
| 7516 | destruycion | 1 |
| 7517 | destroza | 1 |
| 7518 | destroces | 1 |
| 7519 | destotra | 1 |
| 7520 | destorcieron | 1 |
| 7521 | destinadas | 1 |
| 7522 | destiladas | 1 |
| 7523 | destierro | 1 |
| 7524 | desterrar | 1 |
| 7525 | desterrado | 1 |
| 7526 | destemplose | 1 |
| 7527 | destar | 1 |
| 7528 | dessos | 1 |
| 7529 | desseoso | 1 |
| 7530 | dessee | 1 |
| 7531 | desseays | 1 |
| 7532 | desseauamos | 1 |
| 7533 | desseas | 1 |
| 7534 | dessearla | 1 |
| 7535 | dessear | 1 |
| 7536 | dessabrido | 1 |
| 7537 | desque | 1 |
| 7538 | despriuasse | 1 |
| 7539 | despreciando | 1 |
| 7540 | desposada | 1 |
| 7541 | despojes | 1 |
| 7542 | despoja | 1 |
| 7543 | despido | 1 |
| 7544 | despidiose | 1 |
| 7545 | despidio | 1 |
| 7546 | despidieron | 1 |
| 7547 | despidiente | 1 |
| 7548 | despidense | 1 |
| 7549 | despidays | 1 |
| 7550 | desperto | 1 |
| 7551 | despertays | 1 |
| 7552 | despertaron | 1 |
| 7553 | despertadora | 1 |
| 7554 | despertado | 1 |
| 7555 | desperezos | 1 |
| 7556 | despensa | 1 |
| 7557 | despenada | 1 |
| 7558 | despegarse | 1 |
| 7559 | despegado | 1 |
| 7560 | despega | 1 |
| 7561 | despedirse | 1 |
| 7562 | despedazaua | 1 |
| 7563 | despedazadas | 1 |
| 7564 | despedazada | 1 |
| 7565 | despedaces | 1 |
| 7566 | despartir | 1 |
| 7567 | despartidores | 1 |
| 7568 | desparte | 1 |
| 7569 | despacha | 1 |
| 7570 | desos | 1 |
| 7571 | desordenado | 1 |
| 7572 | desordenada | 1 |
| 7573 | desonrrado | 1 |
| 7574 | desocupada | 1 |
| 7575 | desnudaua | 1 |
| 7576 | desnudas | 1 |
| 7577 | desmesuradamente | 1 |
| 7578 | desmengue | 1 |
| 7579 | desmengua | 1 |
| 7580 | desmedido | 1 |
| 7581 | desmayo | 1 |
| 7582 | desmayes | 1 |
| 7583 | desmanda | 1 |
| 7584 | deslenguamiento | 1 |
| 7585 | desleales | 1 |
| 7586 | desierto | 1 |
| 7587 | deshonestos | 1 |
| 7588 | deshonestas | 1 |
| 7589 | deshonesta | 1 |
| 7590 | deshaziendo | 1 |
| 7591 | deshaze | 1 |
| 7592 | deshago | 1 |
| 7593 | desgrenado | 1 |
| 7594 | desgraciada | 1 |
| 7595 | desgozne | 1 |
| 7596 | desgoznarse | 1 |
| 7597 | desfuzia | 1 |
| 7598 | desflorar | 1 |
| 7599 | desfigurada | 1 |
| 7600 | desesperes | 1 |
| 7601 | desespere | 1 |
| 7602 | desesperas | 1 |
| 7603 | desesperanza | 1 |
| 7604 | desesperada | 1 |
| 7605 | deseos | 1 |
| 7606 | desentido | 1 |
| 7607 | desenterraua | 1 |
| 7608 | desenojaros | 1 |
| 7609 | desenconan | 1 |
| 7610 | desempenado | 1 |
| 7611 | desembuelta | 1 |
| 7612 | desemboltura | 1 |
| 7613 | desechas | 1 |
| 7614 | desechalla | 1 |
| 7615 | desechados | 1 |
| 7616 | desecha | 1 |
| 7617 | deseasse | 1 |
| 7618 | deseando | 1 |
| 7619 | desean | 1 |
| 7620 | desea | 1 |
| 7621 | desdore | 1 |
| 7622 | desdichados | 1 |
| 7623 | desdicha | 1 |
| 7624 | desdenes | 1 |
| 7625 | desden | 1 |
| 7626 | descuydar | 1 |
| 7627 | descuydados | 1 |
| 7628 | descuydado | 1 |
| 7629 | desculparte | 1 |
| 7630 | descuelga | 1 |
| 7631 | descuchar | 1 |
| 7632 | descubrirle | 1 |
| 7633 | descubrir | 1 |
| 7634 | descubrio | 1 |
| 7635 | descubrillo | 1 |
| 7636 | descubriendo | 1 |
| 7637 | descubresnos | 1 |
| 7638 | descubrele | 1 |
| 7639 | descubras | 1 |
| 7640 | descubiertos | 1 |
| 7641 | descriue | 1 |
| 7642 | descrece | 1 |
| 7643 | descontentamientos | 1 |
| 7644 | desconsuelo | 1 |
| 7645 | desconsuela | 1 |
| 7646 | desconoscido | 1 |
| 7647 | desconfies | 1 |
| 7648 | desconfiaua | 1 |
| 7649 | desconfiaron | 1 |
| 7650 | desconfiando | 1 |
| 7651 | desconciertos | 1 |
| 7652 | desconcierto | 1 |
| 7653 | desconciertan | 1 |
| 7654 | descolorido | 1 |
| 7655 | descobrire | 1 |
| 7656 | descienden | 1 |
| 7657 | descendientes | 1 |
| 7658 | descender | 1 |
| 7659 | descasaua | 1 |
| 7660 | descanses | 1 |
| 7661 | descansen | 1 |
| 7662 | descansara | 1 |
| 7663 | descansan | 1 |
| 7664 | descansados | 1 |
| 7665 | descalzos | 1 |
| 7666 | descalzarte | 1 |
| 7667 | descalzar | 1 |
| 7668 | descalce | 1 |
| 7669 | descalabrados | 1 |
| 7670 | descaezcas | 1 |
| 7671 | descaescimiento | 1 |
| 7672 | descabullir | 1 |
| 7673 | descabezados | 1 |
| 7674 | desbraue | 1 |
| 7675 | desbocado | 1 |
| 7676 | desbauando | 1 |
| 7677 | desayune | 1 |
| 7678 | desayudo | 1 |
| 7679 | desauenturado | 1 |
| 7680 | desauenturadas | 1 |
| 7681 | desauenturada | 1 |
| 7682 | desauentura | 1 |
| 7683 | desauenires | 1 |
| 7684 | desatino | 1 |
| 7685 | desatacados | 1 |
| 7686 | desastres | 1 |
| 7687 | desastre | 1 |
| 7688 | desasna | 1 |
| 7689 | desarmare | 1 |
| 7690 | desarman | 1 |
| 7691 | desapareciose | 1 |
| 7692 | desamparo | 1 |
| 7693 | desamparasse | 1 |
| 7694 | desamparan | 1 |
| 7695 | desamar | 1 |
| 7696 | desalinada | 1 |
| 7697 | desalabauas | 1 |
| 7698 | desalabas | 1 |
| 7699 | desagradescen | 1 |
| 7700 | desadormescieron | 1 |
| 7701 | desacordadas | 1 |
| 7702 | desacordada | 1 |
| 7703 | desacompanados | 1 |
| 7704 | desacompanado | 1 |
| 7705 | desabrido | 1 |
| 7706 | derribes | 1 |
| 7707 | derribar | 1 |
| 7708 | derribado | 1 |
| 7709 | derriba | 1 |
| 7710 | derramen | 1 |
| 7711 | derramaua | 1 |
| 7712 | derramar | 1 |
| 7713 | derramado | 1 |
| 7714 | derrama | 1 |
| 7715 | derechos | 1 |
| 7716 | derechas | 1 |
| 7717 | derecha | 1 |
| 7718 | depositado | 1 |
| 7719 | deponer | 1 |
| 7720 | departen | 1 |
| 7721 | denuestan | 1 |
| 7722 | dentrellas | 1 |
| 7723 | dentre | 1 |
| 7724 | denostado | 1 |
| 7725 | denominacion | 1 |
| 7726 | demuestran | 1 |
| 7727 | demude | 1 |
| 7728 | dempressa | 1 |
| 7729 | demosle | 1 |
| 7730 | demasias | 1 |
| 7731 | demasiada | 1 |
| 7732 | demando | 1 |
| 7733 | demande | 1 |
| 7734 | demandaua | 1 |
| 7735 | demandar | 1 |
| 7736 | demandado | 1 |
| 7737 | delitos | 1 |
| 7738 | delito | 1 |
| 7739 | delinquentes | 1 |
| 7740 | delictos | 1 |
| 7741 | delicados | 1 |
| 7742 | delicadas | 1 |
| 7743 | delibre | 1 |
| 7744 | deleytan | 1 |
| 7745 | deleytables | 1 |
| 7746 | dele | 1 |
| 7747 | degollaron | 1 |
| 7748 | degollado | 1 |
| 7749 | defeto | 1 |
| 7750 | deferimos | 1 |
| 7751 | defensiuas | 1 |
| 7752 | defension | 1 |
| 7753 | defendiole | 1 |
| 7754 | defendia | 1 |
| 7755 | defender | 1 |
| 7756 | deesas | 1 |
| 7757 | dedos | 1 |
| 7758 | dedo | 1 |
| 7759 | declinauan | 1 |
| 7760 | declina | 1 |
| 7761 | declaras | 1 |
| 7762 | declarame | 1 |
| 7763 | declarale | 1 |
| 7764 | declarado | 1 |
| 7765 | decir | 1 |
| 7766 | decimosesto | 1 |
| 7767 | decimoseptimo | 1 |
| 7768 | decimoquinto | 1 |
| 7769 | decimooctauo | 1 |
| 7770 | decimonono | 1 |
| 7771 | decimo | 1 |
| 7772 | deciende | 1 |
| 7773 | decender | 1 |
| 7774 | debuxo | 1 |
| 7775 | debilitado | 1 |
| 7776 | debdores | 1 |
| 7777 | debdas | 1 |
| 7778 | debate | 1 |
| 7779 | days | 1 |
| 7780 | daualo | 1 |
| 7781 | date | 1 |
| 7782 | dasme | 1 |
| 7783 | darnos | 1 |
| 7784 | daremos | 1 |
| 7785 | danosa | 1 |
| 7786 | danes | 1 |
| 7787 | dandoos | 1 |
| 7788 | danauan | 1 |
| 7789 | danara | 1 |
| 7790 | danan | 1 |
| 7791 | danados | 1 |
| 7792 | dana | 1 |
| 7793 | damos | 1 |
| 7794 | damas | 1 |
| 7795 | dalli | 1 |
| 7796 | dad | 1 |
| 7797 | d | 1 |
| 7798 | cuytas | 1 |
| 7799 | cuytado | 1 |
| 7800 | cuytadillas | 1 |
| 7801 | cuyta | 1 |
| 7802 | cuydosa | 1 |
| 7803 | cures | 1 |
| 7804 | curemos | 1 |
| 7805 | curays | 1 |
| 7806 | curauas | 1 |
| 7807 | curaua | 1 |
| 7808 | curaste | 1 |
| 7809 | curando | 1 |
| 7810 | curan | 1 |
| 7811 | curadas | 1 |
| 7812 | curada | 1 |
| 7813 | cupiesse | 1 |
| 7814 | cuna | 1 |
| 7815 | cumplo | 1 |
| 7816 | cumpliesse | 1 |
| 7817 | cumplia | 1 |
| 7818 | cumples | 1 |
| 7819 | cumbre | 1 |
| 7820 | culpeys | 1 |
| 7821 | culparas | 1 |
| 7822 | culpable | 1 |
| 7823 | culebras | 1 |
| 7824 | culebra | 1 |
| 7825 | culantrillo | 1 |
| 7826 | cueze | 1 |
| 7827 | cueros | 1 |
| 7828 | cuentos | 1 |
| 7829 | cuente | 1 |
| 7830 | cuentan | 1 |
| 7831 | cuentamelo | 1 |
| 7832 | cuentalo | 1 |
| 7833 | cuello | 1 |
| 7834 | cuchillo | 1 |
| 7835 | cubrio | 1 |
| 7836 | cubras | 1 |
| 7837 | cubranos | 1 |
| 7838 | cubra | 1 |
| 7839 | cubierto | 1 |
| 7840 | cruzes | 1 |
| 7841 | cruz | 1 |
| 7842 | crudos | 1 |
| 7843 | crudas | 1 |
| 7844 | cristianos | 1 |
| 7845 | cristiana | 1 |
| 7846 | crinados | 1 |
| 7847 | crimines | 1 |
| 7848 | crimen | 1 |
| 7849 | criaturas | 1 |
| 7850 | crias | 1 |
| 7851 | criar | 1 |
| 7852 | criamos | 1 |
| 7853 | cria | 1 |
| 7854 | creyeron | 1 |
| 7855 | creyeras | 1 |
| 7856 | creydo | 1 |
| 7857 | cresta | 1 |
| 7858 | crespos | 1 |
| 7859 | crescimientos | 1 |
| 7860 | cresciendo | 1 |
| 7861 | crescidos | 1 |
| 7862 | crescido | 1 |
| 7863 | crescidas | 1 |
| 7864 | crescen | 1 |
| 7865 | crepant | 1 |
| 7866 | creolo | 1 |
| 7867 | cremes | 1 |
| 7868 | creeslo | 1 |
| 7869 | creerte | 1 |
| 7870 | creeria | 1 |
| 7871 | creere | 1 |
| 7872 | creeras | 1 |
| 7873 | creemos | 1 |
| 7874 | creeme | 1 |
| 7875 | creciendo | 1 |
| 7876 | creci | 1 |
| 7877 | creceria | 1 |
| 7878 | crecer | 1 |
| 7879 | crece | 1 |
| 7880 | crato | 1 |
| 7881 | cratino | 1 |
| 7882 | cozina | 1 |
| 7883 | cozido | 1 |
| 7884 | cozes | 1 |
| 7885 | coxquillosicas | 1 |
| 7886 | coxqueays | 1 |
| 7887 | coxqueas | 1 |
| 7888 | coxquea | 1 |
| 7889 | coxa | 1 |
| 7890 | cotidiano | 1 |
| 7891 | cotidiana | 1 |
| 7892 | costasse | 1 |
| 7893 | costaria | 1 |
| 7894 | costa | 1 |
| 7895 | coso | 1 |
| 7896 | cosillas | 1 |
| 7897 | coseme | 1 |
| 7898 | corzo | 1 |
| 7899 | cortezon | 1 |
| 7900 | corteza | 1 |
| 7901 | cortesias | 1 |
| 7902 | cortes | 1 |
| 7903 | cortedad | 1 |
| 7904 | cortas | 1 |
| 7905 | cortaronle | 1 |
| 7906 | cortarla | 1 |
| 7907 | cortare | 1 |
| 7908 | cortar | 1 |
| 7909 | corrupta | 1 |
| 7910 | corrupcion | 1 |
| 7911 | corrumpas | 1 |
| 7912 | corrompio | 1 |
| 7913 | corrompiendo | 1 |
| 7914 | corromper | 1 |
| 7915 | corroborada | 1 |
| 7916 | corro | 1 |
| 7917 | corriesse | 1 |
| 7918 | corrientes | 1 |
| 7919 | corriente | 1 |
| 7920 | corridos | 1 |
| 7921 | corrido | 1 |
| 7922 | corres | 1 |
| 7923 | correria | 1 |
| 7924 | corren | 1 |
| 7925 | corremos | 1 |
| 7926 | correlarios | 1 |
| 7927 | corregieres | 1 |
| 7928 | corregido | 1 |
| 7929 | corregida | 1 |
| 7930 | corredora | 1 |
| 7931 | corrector | 1 |
| 7932 | correas | 1 |
| 7933 | corporalmente | 1 |
| 7934 | coronillas | 1 |
| 7935 | coronas | 1 |
| 7936 | cornudos | 1 |
| 7937 | cornudo | 1 |
| 7938 | cordero | 1 |
| 7939 | corderica | 1 |
| 7940 | cordelejos | 1 |
| 7941 | coral | 1 |
| 7942 | coraje | 1 |
| 7943 | copo | 1 |
| 7944 | conuiniente | 1 |
| 7945 | conuierta | 1 |
| 7946 | conuertir | 1 |
| 7947 | conuertio | 1 |
| 7948 | conuertido | 1 |
| 7949 | conuersar | 1 |
| 7950 | conuenibles | 1 |
| 7951 | conuencion | 1 |
| 7952 | conualesce | 1 |
| 7953 | contritos | 1 |
| 7954 | contray | 1 |
| 7955 | contrariedad | 1 |
| 7956 | contrariar | 1 |
| 7957 | contraminale | 1 |
| 7958 | contradize | 1 |
| 7959 | continuas | 1 |
| 7960 | contingibles | 1 |
| 7961 | contienen | 1 |
| 7962 | contiene | 1 |
| 7963 | contienden | 1 |
| 7964 | contescimientos | 1 |
| 7965 | contescimiento | 1 |
| 7966 | conterraneos | 1 |
| 7967 | contentos | 1 |
| 7968 | contentemonos | 1 |
| 7969 | contentate | 1 |
| 7970 | contentardes | 1 |
| 7971 | contentando | 1 |
| 7972 | contentan | 1 |
| 7973 | contenia | 1 |
| 7974 | contemplaua | 1 |
| 7975 | contemplasse | 1 |
| 7976 | contemplas | 1 |
| 7977 | contemplar | 1 |
| 7978 | contemplando | 1 |
| 7979 | contemplacion | 1 |
| 7980 | contecido | 1 |
| 7981 | contarte | 1 |
| 7982 | contara | 1 |
| 7983 | contado | 1 |
| 7984 | consumiosse | 1 |
| 7985 | consumidos | 1 |
| 7986 | consuma | 1 |
| 7987 | consuelate | 1 |
| 7988 | consuelala | 1 |
| 7989 | constituydas | 1 |
| 7990 | constitucion | 1 |
| 7991 | constelacion | 1 |
| 7992 | constantino | 1 |
| 7993 | constante | 1 |
| 7994 | consta | 1 |
| 7995 | consolatorias | 1 |
| 7996 | consolasse | 1 |
| 7997 | consolarle | 1 |
| 7998 | consoladora | 1 |
| 7999 | consolada | 1 |
| 8000 | consolacion | 1 |
| 8001 | consista | 1 |
| 8002 | consintio | 1 |
| 8003 | consintiesse | 1 |
| 8004 | consintientes | 1 |
| 8005 | consintiendo | 1 |
| 8006 | consiguiran | 1 |
| 8007 | consiguira | 1 |
| 8008 | consigas | 1 |
| 8009 | consiento | 1 |
| 8010 | consienten | 1 |
| 8011 | consientas | 1 |
| 8012 | consienta | 1 |
| 8013 | considerasse | 1 |
| 8014 | considerar | 1 |
| 8015 | considerando | 1 |
| 8016 | conseruar | 1 |
| 8017 | conseruado | 1 |
| 8018 | consequencia | 1 |
| 8019 | consentir | 1 |
| 8020 | consentimiento | 1 |
| 8021 | consejeros | 1 |
| 8022 | consejero | 1 |
| 8023 | consejera | 1 |
| 8024 | consejate | 1 |
| 8025 | conseguieron | 1 |
| 8026 | conseguida | 1 |
| 8027 | conquistas | 1 |
| 8028 | conquistador | 1 |
| 8029 | conquista | 1 |
| 8030 | conque | 1 |
| 8031 | conplir | 1 |
| 8032 | conplidamente | 1 |
| 8033 | conozcays | 1 |
| 8034 | conozca | 1 |
| 8035 | conoscio | 1 |
| 8036 | conosciesses | 1 |
| 8037 | conosciente | 1 |
| 8038 | conoscidos | 1 |
| 8039 | conoscidas | 1 |
| 8040 | conosciasme | 1 |
| 8041 | conoscias | 1 |
| 8042 | conoscerte | 1 |
| 8043 | conoscerlo | 1 |
| 8044 | conosceras | 1 |
| 8045 | conocio | 1 |
| 8046 | conociessen | 1 |
| 8047 | conociese | 1 |
| 8048 | conocidos | 1 |
| 8049 | conocia | 1 |
| 8050 | conocesme | 1 |
| 8051 | conocere | 1 |
| 8052 | conocen | 1 |
| 8053 | conjure | 1 |
| 8054 | conjugal | 1 |
| 8055 | conjecturar | 1 |
| 8056 | congrua | 1 |
| 8057 | congoxosa | 1 |
| 8058 | confuso | 1 |
| 8059 | confradias | 1 |
| 8060 | conforta | 1 |
| 8061 | confligunt | 1 |
| 8062 | confirmo | 1 |
| 8063 | confirmar | 1 |
| 8064 | confirma | 1 |
| 8065 | confiessas | 1 |
| 8066 | confiese | 1 |
| 8067 | confies | 1 |
| 8068 | confiemos | 1 |
| 8069 | conficionados | 1 |
| 8070 | confiar | 1 |
| 8071 | confia | 1 |
| 8072 | confessor | 1 |
| 8073 | confessado | 1 |
| 8074 | conferir | 1 |
| 8075 | confederacion | 1 |
| 8076 | confecionar | 1 |
| 8077 | confaciones | 1 |
| 8078 | conejo | 1 |
| 8079 | condenes | 1 |
| 8080 | condenados | 1 |
| 8081 | condena | 1 |
| 8082 | condemnada | 1 |
| 8083 | conde | 1 |
| 8084 | concurrieron | 1 |
| 8085 | concurren | 1 |
| 8086 | concordes | 1 |
| 8087 | concluyr | 1 |
| 8088 | concluydas | 1 |
| 8089 | concluya | 1 |
| 8090 | conciertame | 1 |
| 8091 | conciencia | 1 |
| 8092 | concibas | 1 |
| 8093 | concession | 1 |
| 8094 | concerto | 1 |
| 8095 | concerte | 1 |
| 8096 | concertauan | 1 |
| 8097 | concertant | 1 |
| 8098 | concepto | 1 |
| 8099 | concejo | 1 |
| 8100 | concedieran | 1 |
| 8101 | concebir | 1 |
| 8102 | concebida | 1 |
| 8103 | conbites | 1 |
| 8104 | comunmente | 1 |
| 8105 | comunicaua | 1 |
| 8106 | comunicarlas | 1 |
| 8107 | comunicar | 1 |
| 8108 | comunicandola | 1 |
| 8109 | comunican | 1 |
| 8110 | comunicados | 1 |
| 8111 | comunicado | 1 |
| 8112 | comunicables | 1 |
| 8113 | compuse | 1 |
| 8114 | compre | 1 |
| 8115 | compras | 1 |
| 8116 | comprarlo | 1 |
| 8117 | comprar | 1 |
| 8118 | comprado | 1 |
| 8119 | compradas | 1 |
| 8120 | comportable | 1 |
| 8121 | compliste | 1 |
| 8122 | compliras | 1 |
| 8123 | compliran | 1 |
| 8124 | complira | 1 |
| 8125 | complidas | 1 |
| 8126 | complesion | 1 |
| 8127 | complazerte | 1 |
| 8128 | complaze | 1 |
| 8129 | compensacion | 1 |
| 8130 | compelia | 1 |
| 8131 | compasion | 1 |
| 8132 | comparaste | 1 |
| 8133 | compararon | 1 |
| 8134 | compadre | 1 |
| 8135 | comio | 1 |
| 8136 | comiesses | 1 |
| 8137 | comiese | 1 |
| 8138 | comiere | 1 |
| 8139 | comienza | 1 |
| 8140 | comiendolo | 1 |
| 8141 | comience | 1 |
| 8142 | comica | 1 |
| 8143 | comiamos | 1 |
| 8144 | comia | 1 |
| 8145 | cometieron | 1 |
| 8146 | cometidos | 1 |
| 8147 | cometido | 1 |
| 8148 | cometidas | 1 |
| 8149 | cometemos | 1 |
| 8150 | cometa | 1 |
| 8151 | comerla | 1 |
| 8152 | comere | 1 |
| 8153 | comenzole | 1 |
| 8154 | comenzo | 1 |
| 8155 | comenzauas | 1 |
| 8156 | comenzaste | 1 |
| 8157 | comenzando | 1 |
| 8158 | comenzado | 1 |
| 8159 | comedor | 1 |
| 8160 | combide | 1 |
| 8161 | combidauan | 1 |
| 8162 | combidasses | 1 |
| 8163 | combidar | 1 |
| 8164 | combidan | 1 |
| 8165 | combidame | 1 |
| 8166 | combidada | 1 |
| 8167 | combida | 1 |
| 8168 | combatientes | 1 |
| 8169 | combate | 1 |
| 8170 | comas | 1 |
| 8171 | colorasse | 1 |
| 8172 | colorados | 1 |
| 8173 | collores | 1 |
| 8174 | collacion | 1 |
| 8175 | coligidas | 1 |
| 8176 | coligen | 1 |
| 8177 | colgara | 1 |
| 8178 | colchones | 1 |
| 8179 | colcha | 1 |
| 8180 | cola | 1 |
| 8181 | cogitacions | 1 |
| 8182 | cogiessen | 1 |
| 8183 | cogiendo | 1 |
| 8184 | coger | 1 |
| 8185 | coge | 1 |
| 8186 | codornizes | 1 |
| 8187 | cobrire | 1 |
| 8188 | cobrir | 1 |
| 8189 | cobri | 1 |
| 8190 | cobraste | 1 |
| 8191 | cobrallo | 1 |
| 8192 | cobra | 1 |
| 8193 | cobija | 1 |
| 8194 | cobdiciosos | 1 |
| 8195 | cobdicioso | 1 |
| 8196 | cobdicio | 1 |
| 8197 | cobdiciando | 1 |
| 8198 | clistenestra | 1 |
| 8199 | clientula | 1 |
| 8200 | clerigos | 1 |
| 8201 | clerezia | 1 |
| 8202 | clauellinas | 1 |
| 8203 | claudina | 1 |
| 8204 | claudiana | 1 |
| 8205 | claror | 1 |
| 8206 | clarimientes | 1 |
| 8207 | clamor | 1 |
| 8208 | citola | 1 |
| 8209 | cisne | 1 |
| 8210 | cipresses | 1 |
| 8211 | cintura | 1 |
| 8212 | cinen | 1 |
| 8213 | cincha | 1 |
| 8214 | cimera | 1 |
| 8215 | cimenterios | 1 |
| 8216 | cimentador | 1 |
| 8217 | ciguenas | 1 |
| 8218 | ciguena | 1 |
| 8219 | cieruo | 1 |
| 8220 | ciertos | 1 |
| 8221 | ciertas | 1 |
| 8222 | cierras | 1 |
| 8223 | cieno | 1 |
| 8224 | ciegue | 1 |
| 8225 | cicatrizar | 1 |
| 8226 | cibdades | 1 |
| 8227 | cibdadana | 1 |
| 8228 | christo | 1 |
| 8229 | christiano | 1 |
| 8230 | choza | 1 |
| 8231 | chiquito | 1 |
| 8232 | chica | 1 |
| 8233 | cherriadores | 1 |
| 8234 | charcos | 1 |
| 8235 | chapinazos | 1 |
| 8236 | chapin | 1 |
| 8237 | ceuasnos | 1 |
| 8238 | ceuara | 1 |
| 8239 | ceuan | 1 |
| 8240 | cesso | 1 |
| 8241 | cessen | 1 |
| 8242 | cessasse | 1 |
| 8243 | cessara | 1 |
| 8244 | cessar | 1 |
| 8245 | cesen | 1 |
| 8246 | ceruiz | 1 |
| 8247 | certificame | 1 |
| 8248 | certifica | 1 |
| 8249 | certidumbre | 1 |
| 8250 | certenidad | 1 |
| 8251 | cerrojos | 1 |
| 8252 | cerro | 1 |
| 8253 | cerrados | 1 |
| 8254 | cerrado | 1 |
| 8255 | cerradas | 1 |
| 8256 | cerrada | 1 |
| 8257 | cerillas | 1 |
| 8258 | cerdas | 1 |
| 8259 | cercana | 1 |
| 8260 | cercado | 1 |
| 8261 | cercadas | 1 |
| 8262 | cepacauallo | 1 |
| 8263 | centros | 1 |
| 8264 | centeno | 1 |
| 8265 | centellas | 1 |
| 8266 | cenido | 1 |
| 8267 | cencerrar | 1 |
| 8268 | cenaste | 1 |
| 8269 | cenar | 1 |
| 8270 | cenan | 1 |
| 8271 | celoso | 1 |
| 8272 | celosa | 1 |
| 8273 | celos | 1 |
| 8274 | celo | 1 |
| 8275 | celestiales | 1 |
| 8276 | celebros | 1 |
| 8277 | celadas | 1 |
| 8278 | cegaron | 1 |
| 8279 | cegaras | 1 |
| 8280 | cebolla | 1 |
| 8281 | caygo | 1 |
| 8282 | caygas | 1 |
| 8283 | caygan | 1 |
| 8284 | cayendo | 1 |
| 8285 | cayaras | 1 |
| 8286 | cayado | 1 |
| 8287 | caya | 1 |
| 8288 | cay | 1 |
| 8289 | caxuela | 1 |
| 8290 | caxquillo | 1 |
| 8291 | caxquetes | 1 |
| 8292 | caxco | 1 |
| 8293 | cautiuo | 1 |
| 8294 | cautiuaste | 1 |
| 8295 | cautelosa | 1 |
| 8296 | cautela | 1 |
| 8297 | causaste | 1 |
| 8298 | causas | 1 |
| 8299 | causaron | 1 |
| 8300 | causaran | 1 |
| 8301 | causara | 1 |
| 8302 | causar | 1 |
| 8303 | causadores | 1 |
| 8304 | causadora | 1 |
| 8305 | caualleria | 1 |
| 8306 | catorze | 1 |
| 8307 | catiuos | 1 |
| 8308 | catiuome | 1 |
| 8309 | catiuanse | 1 |
| 8310 | catiuan | 1 |
| 8311 | catiuadola | 1 |
| 8312 | catiuada | 1 |
| 8313 | catan | 1 |
| 8314 | catale | 1 |
| 8315 | castimonia | 1 |
| 8316 | castigues | 1 |
| 8317 | castigarias | 1 |
| 8318 | castigara | 1 |
| 8319 | castigar | 1 |
| 8320 | castigado | 1 |
| 8321 | castiga | 1 |
| 8322 | castidad | 1 |
| 8323 | castellanos | 1 |
| 8324 | castellano | 1 |
| 8325 | casi | 1 |
| 8326 | casan | 1 |
| 8327 | casallas | 1 |
| 8328 | casadas | 1 |
| 8329 | cartas | 1 |
| 8330 | carta | 1 |
| 8331 | carro | 1 |
| 8332 | carrasca | 1 |
| 8333 | carraca | 1 |
| 8334 | carnero | 1 |
| 8335 | carillas | 1 |
| 8336 | cargandola | 1 |
| 8337 | carescia | 1 |
| 8338 | caresceys | 1 |
| 8339 | caresce | 1 |
| 8340 | careciessen | 1 |
| 8341 | careceras | 1 |
| 8342 | carecer | 1 |
| 8343 | carceres | 1 |
| 8344 | caramillo | 1 |
| 8345 | captar | 1 |
| 8346 | capas | 1 |
| 8347 | capadocia | 1 |
| 8348 | capacetes | 1 |
| 8349 | capacete | 1 |
| 8350 | caos | 1 |
| 8351 | canten | 1 |
| 8352 | cantays | 1 |
| 8353 | cantare | 1 |
| 8354 | cantaras | 1 |
| 8355 | cantaran | 1 |
| 8356 | cantar | 1 |
| 8357 | cantanla | 1 |
| 8358 | cansando | 1 |
| 8359 | cansadas | 1 |
| 8360 | cansa | 1 |
| 8361 | canonigo | 1 |
| 8362 | canes | 1 |
| 8363 | candelillas | 1 |
| 8364 | candados | 1 |
| 8365 | canasce | 1 |
| 8366 | can | 1 |
| 8367 | campos | 1 |
| 8368 | camisa | 1 |
| 8369 | caminan | 1 |
| 8370 | camellos | 1 |
| 8371 | cambios | 1 |
| 8372 | camarilla | 1 |
| 8373 | calzo | 1 |
| 8374 | callo | 1 |
| 8375 | calleys | 1 |
| 8376 | callenta | 1 |
| 8377 | callejeras | 1 |
| 8378 | callaua | 1 |
| 8379 | callaras | 1 |
| 8380 | callamos | 1 |
| 8381 | callado | 1 |
| 8382 | calidades | 1 |
| 8383 | calderuela | 1 |
| 8384 | calderon | 1 |
| 8385 | caldereros | 1 |
| 8386 | calcanar | 1 |
| 8387 | calatayud | 1 |
| 8388 | calabazas | 1 |
| 8389 | caera | 1 |
| 8390 | caen | 1 |
| 8391 | caducan | 1 |
| 8392 | caducado | 1 |
| 8393 | caduca | 1 |
| 8394 | cadenas | 1 |
| 8395 | cacarear | 1 |
| 8396 | cabron | 1 |
| 8397 | cabritos | 1 |
| 8398 | cabrillas | 1 |
| 8399 | cabos | 1 |
| 8400 | cabello | 1 |
| 8401 | buytrera | 1 |
| 8402 | buscarnos | 1 |
| 8403 | buscaren | 1 |
| 8404 | buscanse | 1 |
| 8405 | buscan | 1 |
| 8406 | buscala | 1 |
| 8407 | buscado | 1 |
| 8408 | buscada | 1 |
| 8409 | bursia | 1 |
| 8410 | burlemos | 1 |
| 8411 | burleme | 1 |
| 8412 | burlar | 1 |
| 8413 | burdeles | 1 |
| 8414 | bulto | 1 |
| 8415 | bullendote | 1 |
| 8416 | bulle | 1 |
| 8417 | bulla | 1 |
| 8418 | bujelladas | 1 |
| 8419 | bueyes | 1 |
| 8420 | buey | 1 |
| 8421 | bueluen | 1 |
| 8422 | buelo | 1 |
| 8423 | buche | 1 |
| 8424 | bruxa | 1 |
| 8425 | breuissima | 1 |
| 8426 | breuedad | 1 |
| 8427 | brauos | 1 |
| 8428 | brauas | 1 |
| 8429 | brasas | 1 |
| 8430 | bramar | 1 |
| 8431 | bramando | 1 |
| 8432 | bragueta | 1 |
| 8433 | bragas | 1 |
| 8434 | bozeas | 1 |
| 8435 | bozear | 1 |
| 8436 | bozeando | 1 |
| 8437 | bozeador | 1 |
| 8438 | boyzuelo | 1 |
| 8439 | bouilla | 1 |
| 8440 | bouas | 1 |
| 8441 | botas | 1 |
| 8442 | bota | 1 |
| 8443 | borzeguies | 1 |
| 8444 | borra | 1 |
| 8445 | bordaduras | 1 |
| 8446 | borbollones | 1 |
| 8447 | bonita | 1 |
| 8448 | bonetes | 1 |
| 8449 | bonete | 1 |
| 8450 | bonanza | 1 |
| 8451 | boluieron | 1 |
| 8452 | boluia | 1 |
| 8453 | bollicio | 1 |
| 8454 | boleo | 1 |
| 8455 | bolaua | 1 |
| 8456 | bolantes | 1 |
| 8457 | bolando | 1 |
| 8458 | bohonero | 1 |
| 8459 | bofetada | 1 |
| 8460 | bodigo | 1 |
| 8461 | bodegones | 1 |
| 8462 | bodas | 1 |
| 8463 | boda | 1 |
| 8464 | bocas | 1 |
| 8465 | blasfemia | 1 |
| 8466 | blanquean | 1 |
| 8467 | blando | 1 |
| 8468 | blandas | 1 |
| 8469 | blancura | 1 |
| 8470 | biuoras | 1 |
| 8471 | biuimos | 1 |
| 8472 | biuiessen | 1 |
| 8473 | biuiesse | 1 |
| 8474 | biuieran | 1 |
| 8475 | biuiera | 1 |
| 8476 | biui | 1 |
| 8477 | biuas | 1 |
| 8478 | biuamos | 1 |
| 8479 | bitinia | 1 |
| 8480 | bienvenida | 1 |
| 8481 | bientratados | 1 |
| 8482 | bienempleada | 1 |
| 8483 | bienauenturadas | 1 |
| 8484 | bienauenturada | 1 |
| 8485 | bienandanzas | 1 |
| 8486 | bienamada | 1 |
| 8487 | bexiga | 1 |
| 8488 | beuiendo | 1 |
| 8489 | beuia | 1 |
| 8490 | beuen | 1 |
| 8491 | beuemos | 1 |
| 8492 | beua | 1 |
| 8493 | bestial | 1 |
| 8494 | bestia | 1 |
| 8495 | beso | 1 |
| 8496 | bese | 1 |
| 8497 | besaos | 1 |
| 8498 | bernardo | 1 |
| 8499 | bermellon | 1 |
| 8500 | benigno | 1 |
| 8501 | benditas | 1 |
| 8502 | bendita | 1 |
| 8503 | bendigaos | 1 |
| 8504 | bendiga | 1 |
| 8505 | beltran | 1 |
| 8506 | bellum | 1 |
| 8507 | belleza | 1 |
| 8508 | belen | 1 |
| 8509 | beldad | 1 |
| 8510 | baxes | 1 |
| 8511 | baxaua | 1 |
| 8512 | baxas | 1 |
| 8513 | baxarme | 1 |
| 8514 | baxame | 1 |
| 8515 | bastete | 1 |
| 8516 | bastaua | 1 |
| 8517 | bastasse | 1 |
| 8518 | bastare | 1 |
| 8519 | basilisco | 1 |
| 8520 | barua | 1 |
| 8521 | barruntas | 1 |
| 8522 | barruntan | 1 |
| 8523 | barruntado | 1 |
| 8524 | barrios | 1 |
| 8525 | barrio | 1 |
| 8526 | barriles | 1 |
| 8527 | barrilejos | 1 |
| 8528 | barrere | 1 |
| 8529 | barreras | 1 |
| 8530 | barrancos | 1 |
| 8531 | barra | 1 |
| 8532 | barcelona | 1 |
| 8533 | barbiponiente | 1 |
| 8534 | barbas | 1 |
| 8535 | barato | 1 |
| 8536 | baptista | 1 |
| 8537 | banos | 1 |
| 8538 | balsamo | 1 |
| 8539 | balanza | 1 |
| 8540 | balando | 1 |
| 8541 | badajo | 1 |
| 8542 | badajadas | 1 |
| 8543 | azumbres | 1 |
| 8544 | azucena | 1 |
| 8545 | azucarados | 1 |
| 8546 | azucarado | 1 |
| 8547 | azucaradas | 1 |
| 8548 | azotea | 1 |
| 8549 | azotandome | 1 |
| 8550 | azotado | 1 |
| 8551 | azogado | 1 |
| 8552 | azofeyfas | 1 |
| 8553 | aziago | 1 |
| 8554 | azemileros | 1 |
| 8555 | azafran | 1 |
| 8556 | azadonada | 1 |
| 8557 | azadon | 1 |
| 8558 | ayuso | 1 |
| 8559 | ayuntamientos | 1 |
| 8560 | ayuntamiento | 1 |
| 8561 | ayunas | 1 |
| 8562 | ayunara | 1 |
| 8563 | ayunar | 1 |
| 8564 | ayuna | 1 |
| 8565 | ayudo | 1 |
| 8566 | ayude | 1 |
| 8567 | ayudas | 1 |
| 8568 | ayudarte | 1 |
| 8569 | ayudaran | 1 |
| 8570 | ayudar | 1 |
| 8571 | ayudan | 1 |
| 8572 | ayres | 1 |
| 8573 | ayraste | 1 |
| 8574 | ayrados | 1 |
| 8575 | axuar | 1 |
| 8576 | axiensos | 1 |
| 8577 | aviniendo | 1 |
| 8578 | ave | 1 |
| 8579 | autos | 1 |
| 8580 | autorizantes | 1 |
| 8581 | autorizada | 1 |
| 8582 | aura | 1 |
| 8583 | aun | 1 |
| 8584 | aullido | 1 |
| 8585 | auiuas | 1 |
| 8586 | auiuadora | 1 |
| 8587 | auisote | 1 |
| 8588 | auise | 1 |
| 8589 | auisauate | 1 |
| 8590 | auisarte | 1 |
| 8591 | auisar | 1 |
| 8592 | auisale | 1 |
| 8593 | auisada | 1 |
| 8594 | auiendo | 1 |
| 8595 | auiaseme | 1 |
| 8596 | auiame | 1 |
| 8597 | auiades | 1 |
| 8598 | auerte | 1 |
| 8599 | auenture | 1 |
| 8600 | auenturauan | 1 |
| 8601 | auenturado | 1 |
| 8602 | auctoridad | 1 |
| 8603 | auctor | 1 |
| 8604 | aucto | 1 |
| 8605 | auariento | 1 |
| 8606 | auantaja | 1 |
| 8607 | atreuo | 1 |
| 8608 | atreuio | 1 |
| 8609 | atreuimientos | 1 |
| 8610 | atreuido | 1 |
| 8611 | atreues | 1 |
| 8612 | atreuer | 1 |
| 8613 | atreua | 1 |
| 8614 | atque | 1 |
| 8615 | atormente | 1 |
| 8616 | atormentadores | 1 |
| 8617 | atizan | 1 |
| 8618 | atiende | 1 |
| 8619 | athenienses | 1 |
| 8620 | athenas | 1 |
| 8621 | atestadas | 1 |
| 8622 | atesores | 1 |
| 8623 | atenta | 1 |
| 8624 | ateniense | 1 |
| 8625 | atenas | 1 |
| 8626 | atemorizados | 1 |
| 8627 | atauio | 1 |
| 8628 | ataras | 1 |
| 8629 | atan | 1 |
| 8630 | atamientos | 1 |
| 8631 | atajo | 1 |
| 8632 | atajasolazes | 1 |
| 8633 | atajas | 1 |
| 8634 | ataja | 1 |
| 8635 | asueta | 1 |
| 8636 | astuto | 1 |
| 8637 | astillas | 1 |
| 8638 | assimismo | 1 |
| 8639 | assimesmo | 1 |
| 8640 | assiento | 1 |
| 8641 | assienta | 1 |
| 8642 | assentemonos | 1 |
| 8643 | assente | 1 |
| 8644 | assentauan | 1 |
| 8645 | assentaua | 1 |
| 8646 | assentarnos | 1 |
| 8647 | assentaos | 1 |
| 8648 | assentadas | 1 |
| 8649 | assentada | 1 |
| 8650 | assegurando | 1 |
| 8651 | assaz | 1 |
| 8652 | assador | 1 |
| 8653 | asperece | 1 |
| 8654 | asperas | 1 |
| 8655 | aspado | 1 |
| 8656 | asombrar | 1 |
| 8657 | asombran | 1 |
| 8658 | asombra | 1 |
| 8659 | asolaste | 1 |
| 8660 | asnillo | 1 |
| 8661 | asna | 1 |
| 8662 | asiento | 1 |
| 8663 | asido | 1 |
| 8664 | asestara | 1 |
| 8665 | asento | 1 |
| 8666 | asechanzas | 1 |
| 8667 | ascanica | 1 |
| 8668 | asados | 1 |
| 8669 | asadores | 1 |
| 8670 | arufianada | 1 |
| 8671 | aruejas | 1 |
| 8672 | arto | 1 |
| 8673 | artificiales | 1 |
| 8674 | artifice | 1 |
| 8675 | artes | 1 |
| 8676 | arteros | 1 |
| 8677 | arrugar | 1 |
| 8678 | arrollada | 1 |
| 8679 | arrobas | 1 |
| 8680 | arrinconada | 1 |
| 8681 | arrime | 1 |
| 8682 | arrimarse | 1 |
| 8683 | arriendo | 1 |
| 8684 | arrezio | 1 |
| 8685 | arreziate | 1 |
| 8686 | arreziando | 1 |
| 8687 | arrepiente | 1 |
| 8688 | arrepentir | 1 |
| 8689 | arrepentido | 1 |
| 8690 | arrepentida | 1 |
| 8691 | arreo | 1 |
| 8692 | arrendar | 1 |
| 8693 | arrendado | 1 |
| 8694 | arremeter | 1 |
| 8695 | arremango | 1 |
| 8696 | arrean | 1 |
| 8697 | arreada | 1 |
| 8698 | arras | 1 |
| 8699 | arrancas | 1 |
| 8700 | arrabales | 1 |
| 8701 | aros | 1 |
| 8702 | aro | 1 |
| 8703 | arme | 1 |
| 8704 | armaos | 1 |
| 8705 | armale | 1 |
| 8706 | armados | 1 |
| 8707 | armado | 1 |
| 8708 | armada | 1 |
| 8709 | arma | 1 |
| 8710 | aristotiles | 1 |
| 8711 | ariadna | 1 |
| 8712 | argumentos | 1 |
| 8713 | argu | 1 |
| 8714 | argentadas | 1 |
| 8715 | arepiso | 1 |
| 8716 | are | 1 |
| 8717 | ardid | 1 |
| 8718 | ardia | 1 |
| 8719 | arcediano | 1 |
| 8720 | arcadores | 1 |
| 8721 | arbol | 1 |
| 8722 | arambre | 1 |
| 8723 | aradores | 1 |
| 8724 | arado | 1 |
| 8725 | aradas | 1 |
| 8726 | arabia | 1 |
| 8727 | aquis | 1 |
| 8728 | aquiriendo | 1 |
| 8729 | aquexes | 1 |
| 8730 | aquexe | 1 |
| 8731 | aquexarles | 1 |
| 8732 | aquexandole | 1 |
| 8733 | aquexale | 1 |
| 8734 | aquexada | 1 |
| 8735 | aquellotro | 1 |
| 8736 | apuntan | 1 |
| 8737 | apuneauamos | 1 |
| 8738 | apuleyo | 1 |
| 8739 | apto | 1 |
| 8740 | apta | 1 |
| 8741 | aprueuo | 1 |
| 8742 | aprueuelo | 1 |
| 8743 | aprueuas | 1 |
| 8744 | aprueua | 1 |
| 8745 | aprouechemos | 1 |
| 8746 | aprouechemonos | 1 |
| 8747 | aprouecharas | 1 |
| 8748 | aprouechara | 1 |
| 8749 | aprouechandose | 1 |
| 8750 | aprouechan | 1 |
| 8751 | aprouechado | 1 |
| 8752 | aprouarlo | 1 |
| 8753 | aprouados | 1 |
| 8754 | aprouado | 1 |
| 8755 | apriscos | 1 |
| 8756 | aprieten | 1 |
| 8757 | aprietale | 1 |
| 8758 | apriessa | 1 |
| 8759 | apriesa | 1 |
| 8760 | apretauas | 1 |
| 8761 | apretar | 1 |
| 8762 | apresures | 1 |
| 8763 | apresurate | 1 |
| 8764 | aprendi | 1 |
| 8765 | aprenden | 1 |
| 8766 | aprenda | 1 |
| 8767 | apremiaua | 1 |
| 8768 | apremiare | 1 |
| 8769 | apremiar | 1 |
| 8770 | aposentados | 1 |
| 8771 | aposentado | 1 |
| 8772 | aposentada | 1 |
| 8773 | apollo | 1 |
| 8774 | aplicando | 1 |
| 8775 | aplica | 1 |
| 8776 | aplacar | 1 |
| 8777 | apercibense | 1 |
| 8778 | apercebido | 1 |
| 8779 | apaziguado | 1 |
| 8780 | apartaua | 1 |
| 8781 | apartateme | 1 |
| 8782 | apartase | 1 |
| 8783 | apartas | 1 |
| 8784 | apartarme | 1 |
| 8785 | apartaran | 1 |
| 8786 | apartado | 1 |
| 8787 | apartada | 1 |
| 8788 | aparta | 1 |
| 8789 | aparrochada | 1 |
| 8790 | aparencia | 1 |
| 8791 | aparejate | 1 |
| 8792 | aparejastes | 1 |
| 8793 | aparejarnos | 1 |
| 8794 | aparejaos | 1 |
| 8795 | aparejando | 1 |
| 8796 | aparejado | 1 |
| 8797 | apareja | 1 |
| 8798 | apareceos | 1 |
| 8799 | apanes | 1 |
| 8800 | apaleados | 1 |
| 8801 | apaciguar | 1 |
| 8802 | apaciguanse | 1 |
| 8803 | apacentados | 1 |
| 8804 | aosadas | 1 |
| 8805 | aojando | 1 |
| 8806 | anuncian | 1 |
| 8807 | antojo | 1 |
| 8808 | antojare | 1 |
| 8809 | antojadizo | 1 |
| 8810 | antoja | 1 |
| 8811 | antipater | 1 |
| 8812 | antico | 1 |
| 8813 | antepone | 1 |
| 8814 | ansiosa | 1 |
| 8815 | ansia | 1 |
| 8816 | ansi | 1 |
| 8817 | ansarones | 1 |
| 8818 | animosos | 1 |
| 8819 | animos | 1 |
| 8820 | animes | 1 |
| 8821 | animalias | 1 |
| 8822 | angustiosa | 1 |
| 8823 | anelito | 1 |
| 8824 | anduuieren | 1 |
| 8825 | andrajo | 1 |
| 8826 | andouiera | 1 |
| 8827 | andes | 1 |
| 8828 | andauan | 1 |
| 8829 | andate | 1 |
| 8830 | andarte | 1 |
| 8831 | andares | 1 |
| 8832 | andaras | 1 |
| 8833 | andanza | 1 |
| 8834 | andamos | 1 |
| 8835 | andaca | 1 |
| 8836 | ancianos | 1 |
| 8837 | anciano | 1 |
| 8838 | anaxagoras | 1 |
| 8839 | anadones | 1 |
| 8840 | anaden | 1 |
| 8841 | ampare | 1 |
| 8842 | amos | 1 |
| 8843 | amortezcas | 1 |
| 8844 | amortescimientos | 1 |
| 8845 | amortescida | 1 |
| 8846 | amorosos | 1 |
| 8847 | amoroso | 1 |
| 8848 | amonestacion | 1 |
| 8849 | amengues | 1 |
| 8850 | amengue | 1 |
| 8851 | amenguas | 1 |
| 8852 | amenguado | 1 |
| 8853 | amenguadas | 1 |
| 8854 | amenguada | 1 |
| 8855 | amenaze | 1 |
| 8856 | amen | 1 |
| 8857 | amemos | 1 |
| 8858 | ame | 1 |
| 8859 | ambas | 1 |
| 8860 | ambar | 1 |
| 8861 | amasses | 1 |
| 8862 | amarte | 1 |
| 8863 | amarillo | 1 |
| 8864 | amarias | 1 |
| 8865 | amargura | 1 |
| 8866 | amargues | 1 |
| 8867 | amarguen | 1 |
| 8868 | amargos | 1 |
| 8869 | amargas | 1 |
| 8870 | amara | 1 |
| 8871 | amansaste | 1 |
| 8872 | amansaria | 1 |
| 8873 | amansado | 1 |
| 8874 | amanojada | 1 |
| 8875 | amanezcas | 1 |
| 8876 | amanescio | 1 |
| 8877 | amanesciesse | 1 |
| 8878 | amanesceria | 1 |
| 8879 | amanescer | 1 |
| 8880 | amaneciesse | 1 |
| 8881 | amamos | 1 |
| 8882 | amados | 1 |
| 8883 | amadas | 1 |
| 8884 | alzose | 1 |
| 8885 | alzauamos | 1 |
| 8886 | alzasse | 1 |
| 8887 | alzando | 1 |
| 8888 | alzadas | 1 |
| 8889 | alumbre | 1 |
| 8890 | alualinos | 1 |
| 8891 | altramuzes | 1 |
| 8892 | altiuo | 1 |
| 8893 | altitud | 1 |
| 8894 | altercar | 1 |
| 8895 | alteraua | 1 |
| 8896 | alterasete | 1 |
| 8897 | alteras | 1 |
| 8898 | altar | 1 |
| 8899 | alquile | 1 |
| 8900 | alonso | 1 |
| 8901 | almohadas | 1 |
| 8902 | almohada | 1 |
| 8903 | almizque | 1 |
| 8904 | almizcles | 1 |
| 8905 | almizcladas | 1 |
| 8906 | almazenes | 1 |
| 8907 | almas | 1 |
| 8908 | allego | 1 |
| 8909 | allegasse | 1 |
| 8910 | allegarse | 1 |
| 8911 | allegados | 1 |
| 8912 | allegado | 1 |
| 8913 | allegadas | 1 |
| 8914 | aljofar | 1 |
| 8915 | aliuiar | 1 |
| 8916 | aliuiadora | 1 |
| 8917 | aliuia | 1 |
| 8918 | alinde | 1 |
| 8919 | alimpiarla | 1 |
| 8920 | alguaziles | 1 |
| 8921 | algodones | 1 |
| 8922 | algalia | 1 |
| 8923 | alfocigos | 1 |
| 8924 | alfileres | 1 |
| 8925 | aleuosos | 1 |
| 8926 | aleto | 1 |
| 8927 | aleluyas | 1 |
| 8928 | alegraua | 1 |
| 8929 | alegrate | 1 |
| 8930 | alegras | 1 |
| 8931 | alegrarte | 1 |
| 8932 | alegraras | 1 |
| 8933 | alegrar | 1 |
| 8934 | alegramela | 1 |
| 8935 | alegrado | 1 |
| 8936 | aldea | 1 |
| 8937 | aldaua | 1 |
| 8938 | alcoholada | 1 |
| 8939 | alcibiades | 1 |
| 8940 | alcese | 1 |
| 8941 | alce | 1 |
| 8942 | alcarauan | 1 |
| 8943 | alcanzauamos | 1 |
| 8944 | alcanzasse | 1 |
| 8945 | alcanzaros | 1 |
| 8946 | alcanzare | 1 |
| 8947 | alcanzaran | 1 |
| 8948 | alcanzandola | 1 |
| 8949 | alcanzada | 1 |
| 8950 | alcandara | 1 |
| 8951 | alcalde | 1 |
| 8952 | alcahueteria | 1 |
| 8953 | alcahuete | 1 |
| 8954 | alcaduzes | 1 |
| 8955 | alboradas | 1 |
| 8956 | alberto | 1 |
| 8957 | albarrana | 1 |
| 8958 | albarda | 1 |
| 8959 | alarido | 1 |
| 8960 | alargues | 1 |
| 8961 | alarguemos | 1 |
| 8962 | alargasse | 1 |
| 8963 | alargarle | 1 |
| 8964 | alargar | 1 |
| 8965 | alarde | 1 |
| 8966 | alance | 1 |
| 8967 | alamo | 1 |
| 8968 | alambiques | 1 |
| 8969 | alacran | 1 |
| 8970 | alabe | 1 |
| 8971 | alabarme | 1 |
| 8972 | alabaran | 1 |
| 8973 | alabando | 1 |
| 8974 | alabame | 1 |
| 8975 | alabado | 1 |
| 8976 | alabadas | 1 |
| 8977 | alaba | 1 |
| 8978 | ala | 1 |
| 8979 | ahuyenta | 1 |
| 8980 | ahorco | 1 |
| 8981 | ahogaron | 1 |
| 8982 | ahito | 1 |
| 8983 | ahijados | 1 |
| 8984 | aguzase | 1 |
| 8985 | aguzan | 1 |
| 8986 | agujetas | 1 |
| 8987 | agujero | 1 |
| 8988 | aguilas | 1 |
| 8989 | aguila | 1 |
| 8990 | aguijon | 1 |
| 8991 | aguijas | 1 |
| 8992 | aguijando | 1 |
| 8993 | aguijado | 1 |
| 8994 | agues | 1 |
| 8995 | agudo | 1 |
| 8996 | agudas | 1 |
| 8997 | aguardaua | 1 |
| 8998 | aguardarte | 1 |
| 8999 | aguardando | 1 |
| 9000 | aguarda | 1 |
| 9001 | aguaduchos | 1 |
| 9002 | agripina | 1 |
| 9003 | agricultores | 1 |
| 9004 | agrauando | 1 |
| 9005 | agrado | 1 |
| 9006 | agradezco | 1 |
| 9007 | agradezcas | 1 |
| 9008 | agradezca | 1 |
| 9009 | agradesco | 1 |
| 9010 | agradescer | 1 |
| 9011 | agradescemos | 1 |
| 9012 | agradecido | 1 |
| 9013 | agradauan | 1 |
| 9014 | agradaua | 1 |
| 9015 | agradare | 1 |
| 9016 | agradado | 1 |
| 9017 | agradables | 1 |
| 9018 | agosto | 1 |
| 9019 | afrentas | 1 |
| 9020 | aforro | 1 |
| 9021 | afloxo | 1 |
| 9022 | afloxar | 1 |
| 9023 | aflijas | 1 |
| 9024 | aflige | 1 |
| 9025 | aflacar | 1 |
| 9026 | afistoles | 1 |
| 9027 | afirma | 1 |
| 9028 | affrenta | 1 |
| 9029 | affligida | 1 |
| 9030 | affirmaremos | 1 |
| 9031 | affirman | 1 |
| 9032 | affectos | 1 |
| 9033 | afeytes | 1 |
| 9034 | afeyte | 1 |
| 9035 | afecto | 1 |
| 9036 | aer | 1 |
| 9037 | adulterios | 1 |
| 9038 | aduersos | 1 |
| 9039 | aduersas | 1 |
| 9040 | aduersarios | 1 |
| 9041 | aduersario | 1 |
| 9042 | adriano | 1 |
| 9043 | adrezado | 1 |
| 9044 | adquiri | 1 |
| 9045 | adotiuo | 1 |
| 9046 | adormida | 1 |
| 9047 | adorando | 1 |
| 9048 | adobcion | 1 |
| 9049 | ado | 1 |
| 9050 | admite | 1 |
| 9051 | administrar | 1 |
| 9052 | administrador | 1 |
| 9053 | adicion | 1 |
| 9054 | adeuinos | 1 |
| 9055 | adeuinen | 1 |
| 9056 | adeuine | 1 |
| 9057 | adeuinas | 1 |
| 9058 | aderezan | 1 |
| 9059 | aderezado | 1 |
| 9060 | aderescen | 1 |
| 9061 | adelgazaua | 1 |
| 9062 | adeleta | 1 |
| 9063 | addicion | 1 |
| 9064 | adarga | 1 |
| 9065 | adan | 1 |
| 9066 | acusen | 1 |
| 9067 | acusaron | 1 |
| 9068 | acusare | 1 |
| 9069 | acusado | 1 |
| 9070 | acuesto | 1 |
| 9071 | acuestate | 1 |
| 9072 | acuesta | 1 |
| 9073 | acuerdaste | 1 |
| 9074 | acuden | 1 |
| 9075 | acuchillada | 1 |
| 9076 | actiuo | 1 |
| 9077 | acrescentaste | 1 |
| 9078 | acreciente | 1 |
| 9079 | acrecientas | 1 |
| 9080 | acrecientan | 1 |
| 9081 | acrecientame | 1 |
| 9082 | acrecentar | 1 |
| 9083 | acostumbre | 1 |
| 9084 | acostumbradas | 1 |
| 9085 | acostemonos | 1 |
| 9086 | acoste | 1 |
| 9087 | acostaua | 1 |
| 9088 | acostarte | 1 |
| 9089 | acostada | 1 |
| 9090 | acortaron | 1 |
| 9091 | acorrieron | 1 |
| 9092 | acorre | 1 |
| 9093 | acordele | 1 |
| 9094 | acordays | 1 |
| 9095 | acordarse | 1 |
| 9096 | acordara | 1 |
| 9097 | acordandome | 1 |
| 9098 | acordado | 1 |
| 9099 | acordada | 1 |
| 9100 | acontezca | 1 |
| 9101 | acontescimiento | 1 |
| 9102 | acontescido | 1 |
| 9103 | acontecio | 1 |
| 9104 | aconsejando | 1 |
| 9105 | aconsejan | 1 |
| 9106 | aconseja | 1 |
| 9107 | acompaneos | 1 |
| 9108 | acompanenos | 1 |
| 9109 | acompanen | 1 |
| 9110 | acompane | 1 |
| 9111 | acompanauala | 1 |
| 9112 | acompanassen | 1 |
| 9113 | acompanaron | 1 |
| 9114 | acompanara | 1 |
| 9115 | acompanan | 1 |
| 9116 | acompanadas | 1 |
| 9117 | acometido | 1 |
| 9118 | acometer | 1 |
| 9119 | acoge | 1 |
| 9120 | acoceando | 1 |
| 9121 | aclarate | 1 |
| 9122 | acion | 1 |
| 9123 | acierten | 1 |
| 9124 | achaques | 1 |
| 9125 | acertaran | 1 |
| 9126 | acertado | 1 |
| 9127 | acepto | 1 |
| 9128 | acelero | 1 |
| 9129 | aceleramientos | 1 |
| 9130 | aceleramiento | 1 |
| 9131 | acelerada | 1 |
| 9132 | acechaua | 1 |
| 9133 | acatando | 1 |
| 9134 | acatada | 1 |
| 9135 | acarreo | 1 |
| 9136 | acarree | 1 |
| 9137 | acarreara | 1 |
| 9138 | acarrear | 1 |
| 9139 | acaescieron | 1 |
| 9140 | acaescida | 1 |
| 9141 | acaece | 1 |
| 9142 | acabes | 1 |
| 9143 | acabaua | 1 |
| 9144 | acabaremos | 1 |
| 9145 | acabaran | 1 |
| 9146 | acaban | 1 |
| 9147 | acabala | 1 |
| 9148 | acabadas | 1 |
| 9149 | acabada | 1 |
| 9150 | acaba | 1 |
| 9151 | abundar | 1 |
| 9152 | abundantes | 1 |
| 9153 | abundancia | 1 |
| 9154 | abstener | 1 |
| 9155 | absentarse | 1 |
| 9156 | abrigasse | 1 |
| 9157 | abrie | 1 |
| 9158 | abri | 1 |
| 9159 | abrela | 1 |
| 9160 | abrazare | 1 |
| 9161 | abrazar | 1 |
| 9162 | abrazaos | 1 |
| 9163 | abrasadas | 1 |
| 9164 | abras | 1 |
| 9165 | aborrezcas | 1 |
| 9166 | aborrece | 1 |
| 9167 | abominable | 1 |
| 9168 | abollado | 1 |
| 9169 | ablandara | 1 |
| 9170 | ablandar | 1 |
| 9171 | ablanda | 1 |
| 9172 | abiuate | 1 |
| 9173 | abiuaron | 1 |
| 9174 | abiuan | 1 |
| 9175 | abito | 1 |
| 9176 | abiertas | 1 |
| 9177 | abezo | 1 |
| 9178 | abezar | 1 |
| 9179 | abezado | 1 |
| 9180 | abaxes | 1 |
| 9181 | abaxe | 1 |
| 9182 | abaxasse | 1 |
| 9183 | abaxada | 1 |
| 9184 | abatiose | 1 |
| 9185 | abatimiento | 1 |
| 9186 | abatido | 1 |
| 9187 | abastada | 1 |
| 9188 | abarca | 1 |
| 9189 | abad | 1 |
|
|
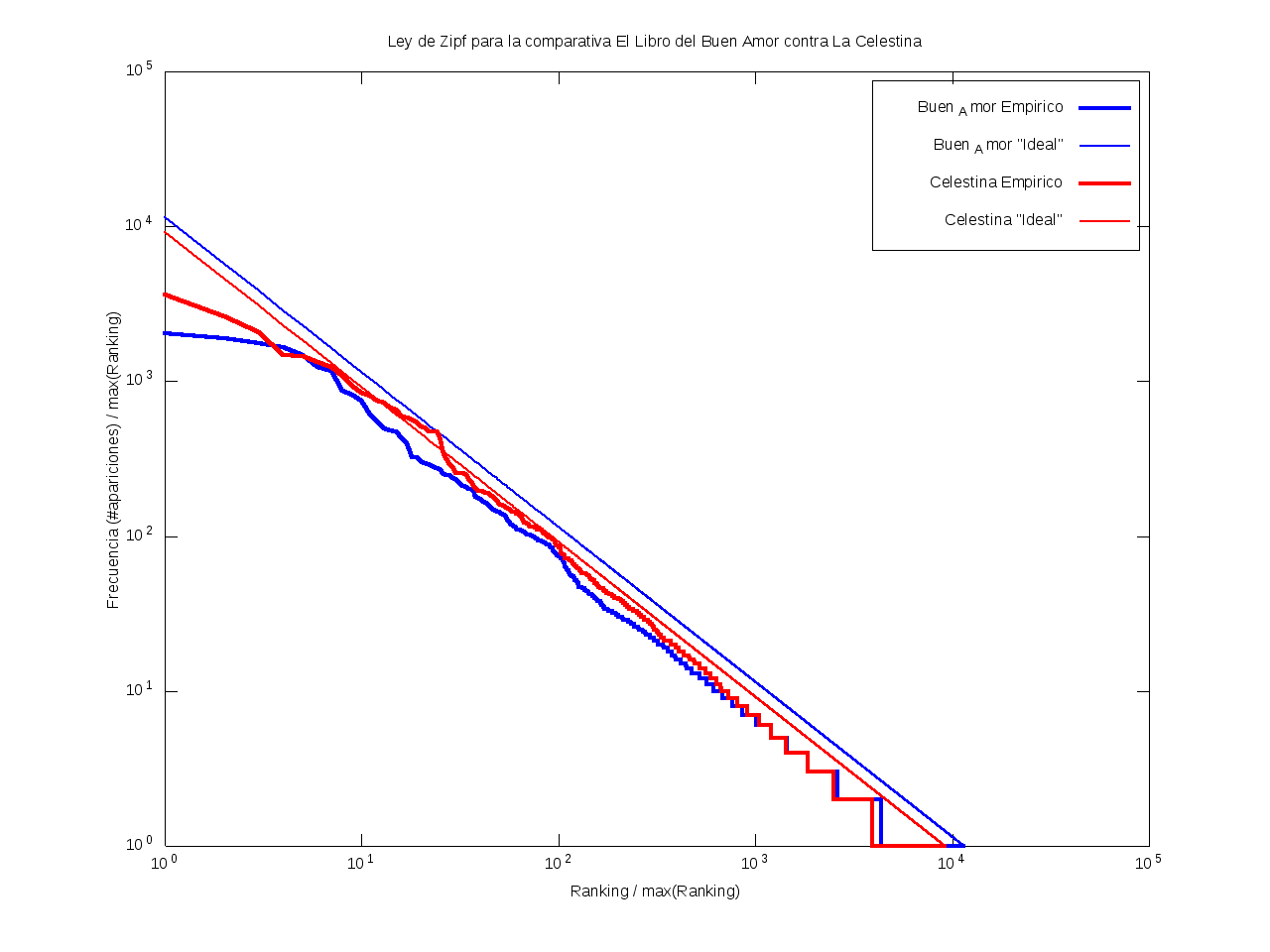
|
|
Mostrar todo
Recoger
|
Test de Dunning
El test de Dunning sirve para identificar las palabras distintivas de un texto.
En este caso lo utilizaremos para encontrar palabras distintivas de cada uno de los conjuntos que estamos comparando frente al otro.
Fórmula:
- 2 log(lambda) = 2 [ log L(p1,k1,n1)+log L(p2,k2,n2)-log L(p,k1,n1)-log L(p,k2,n2) ]
donde
L(p,k,n) = p^k * (1-p)^(n-k)
con
- ki = frecuencia (número de apariciones) de la palabra en el conjunto i.
- ni = número total de palabras del conjunto i.
- pi = probabilidad de la palabra en el conjunto i = ki/ni.
Para encontrar las palabras distintivas se enfrentará un conjunto (Buen_Amor) (conjunto 1)
contra el otro (Celestina) (conjunto 2) y viceversa.
A continuación se muestra una lista de todas las palabras presentes en los textos,
ordenadas por su puntuación en la razón de verosimilitud, indicando de cuál de ellos son distintivas.
Haga click en la palabra para ver su definición según el diccionario de la RAE.
Mostrar todo
Recoger


